Abstract
Let 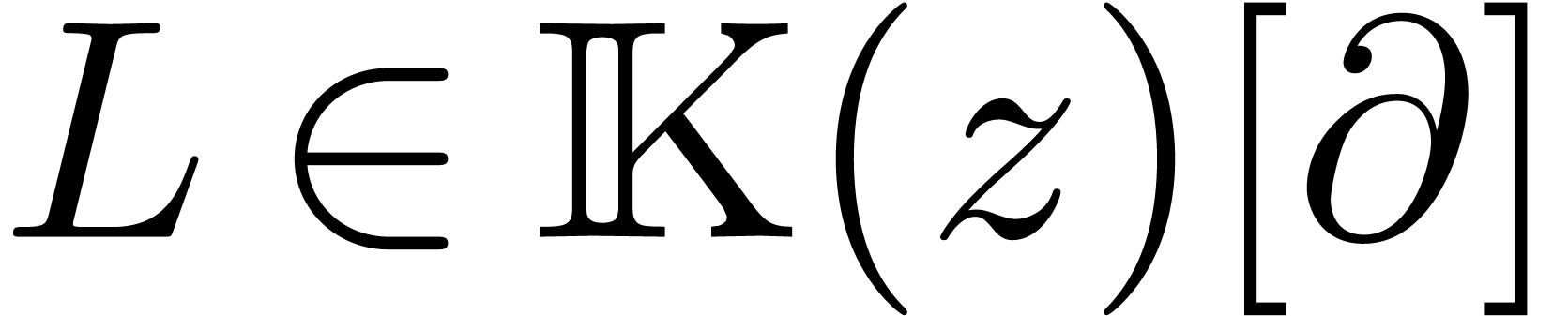 be a linear differential
operator, where
be a linear differential
operator, where  is an
effective algebraically closed subfield of
is an
effective algebraically closed subfield of  .
It can be shown that the differential Galois group of
.
It can be shown that the differential Galois group of 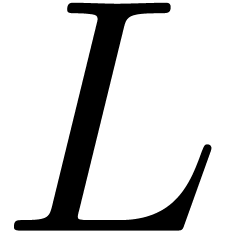 is generated (as a closed algebraic group) by
a finite number of monodromy matrices, Stokes matrices and matrices in
local exponential groups. Moreover, there exist fast algorithms for the
approximation of the entries of these matrices.
is generated (as a closed algebraic group) by
a finite number of monodromy matrices, Stokes matrices and matrices in
local exponential groups. Moreover, there exist fast algorithms for the
approximation of the entries of these matrices.
In this paper, we present a numeric-symbolic algorithm for the
computation of the closed algebraic subgroup generated by a finite
number of invertible matrices. Using the above results, this yields an
algorithm for the computation of differential Galois groups, when
computing with a sufficient precision.
Even though there is no straightforward way to find a “sufficient
precision” for guaranteeing the correctness of the end-result, it
is often possible to check a posteriori whether the end-result
is correct. In particular, we present a non-heuristic algorithm for the
factorization of linear differential operators.
Occasions: ANR Gecko meeting, Toulouse, 2006
Documents: slideshow, TeXmacs
source
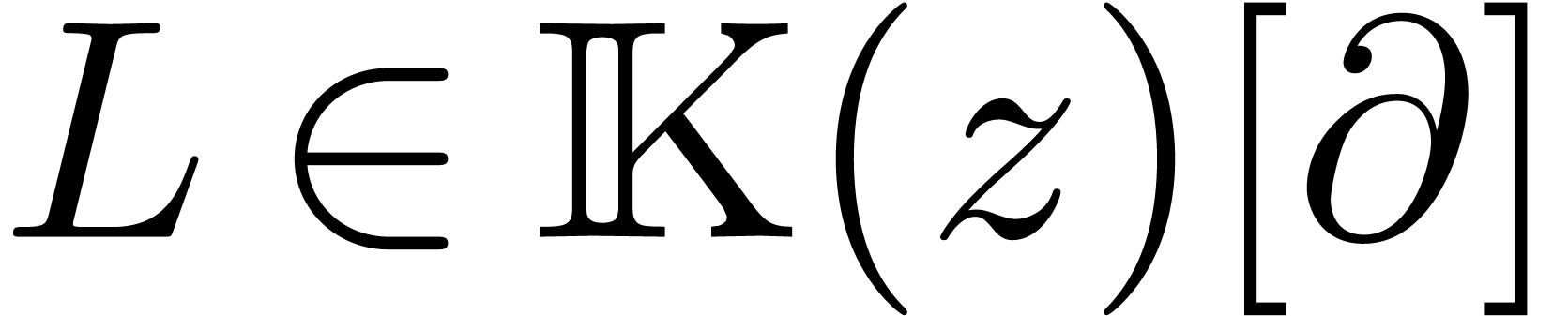 be a linear differential
operator, where
be a linear differential
operator, where  is an
effective algebraically closed subfield of
is an
effective algebraically closed subfield of  .
It can be shown that the differential Galois group of
.
It can be shown that the differential Galois group of 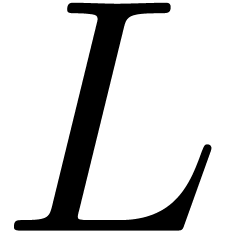 is generated (as a closed algebraic group) by
a finite number of monodromy matrices, Stokes matrices and matrices in
local exponential groups. Moreover, there exist fast algorithms for the
approximation of the entries of these matrices.
is generated (as a closed algebraic group) by
a finite number of monodromy matrices, Stokes matrices and matrices in
local exponential groups. Moreover, there exist fast algorithms for the
approximation of the entries of these matrices.