Abstract
One fundamental algorithmic problem is the efficient multiplication of
two 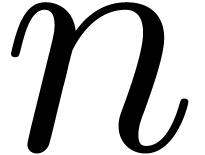 -bit integers. Let
-bit integers. Let 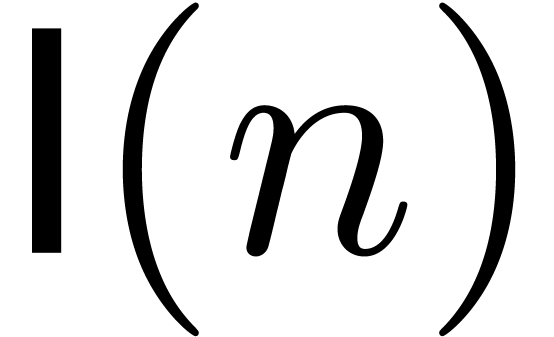 denote the time complexity for
this problem, in the Turing machine model with a finite number of tapes.
Until recently, the best asymptotical bound for
denote the time complexity for
this problem, in the Turing machine model with a finite number of tapes.
Until recently, the best asymptotical bound for 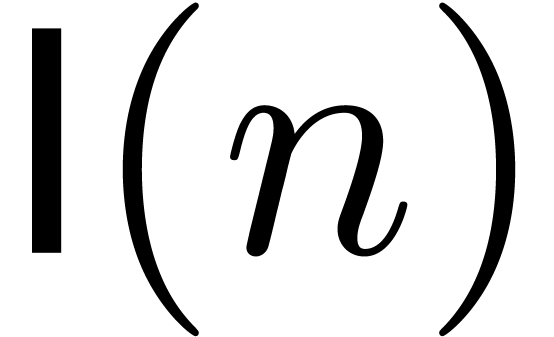 was due to Fürer. He proved that there exists
a constant
was due to Fürer. He proved that there exists
a constant 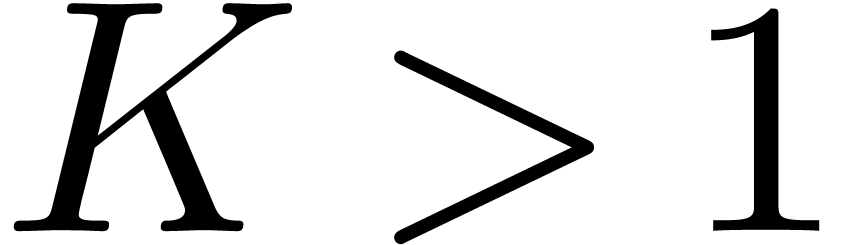 with
with
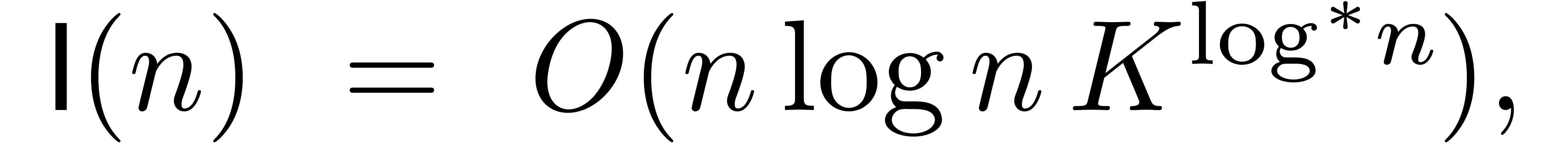
where  (for
(for 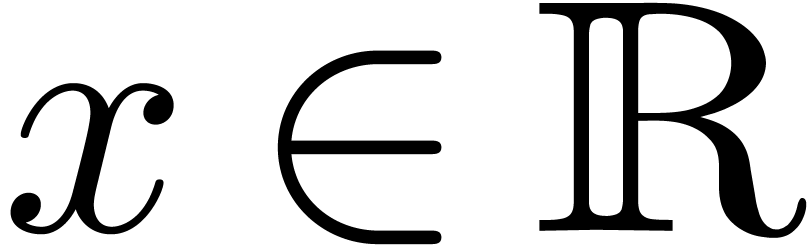 ) stands for the iterator of the logarithm.
That is,
) stands for the iterator of the logarithm.
That is,
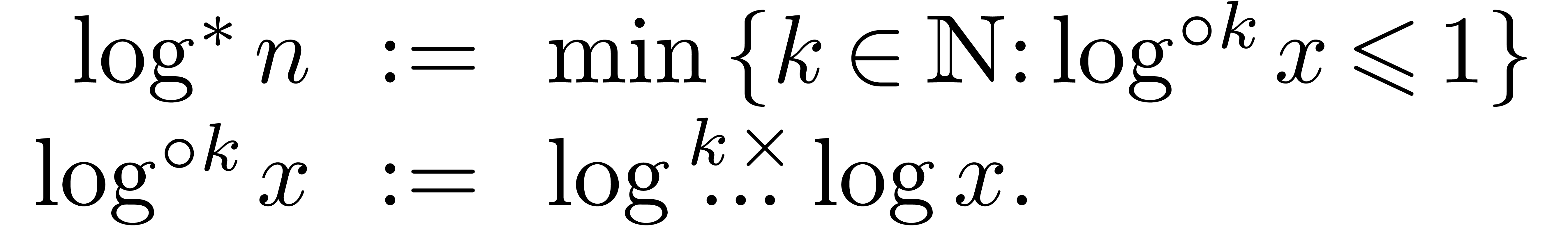
In our recent work, we managed to further improve this bound. Using a
new kind of algorithm, we proved that 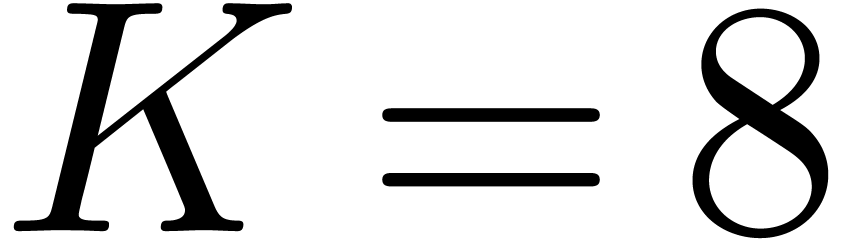 (and even
(and even 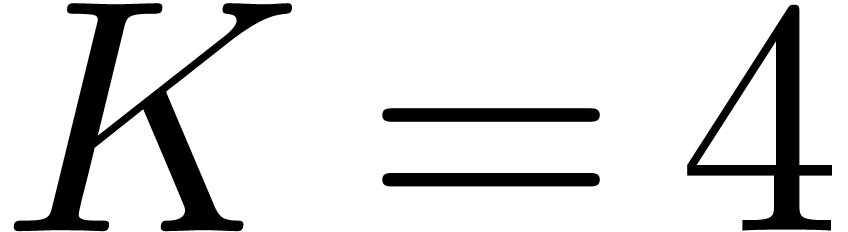 under the
condition that a certain number theoretic conjecture holds). We also
examined optimizations of Fürer's original approach, but it seems
that
under the
condition that a certain number theoretic conjecture holds). We also
examined optimizations of Fürer's original approach, but it seems
that 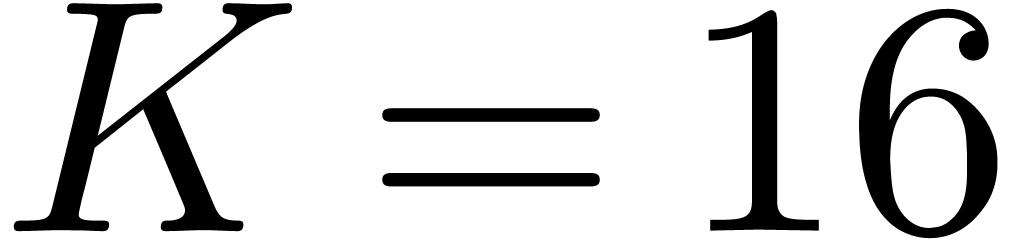 is the best bound that
can be obtained in this way.
is the best bound that
can be obtained in this way.
Occasion: Journées GDR-IM, Bordeaux, February 2,
2015
Coauthors: David Harvey,
Grégoire Lecerf
Documents: slideshow, TeXmacs
source
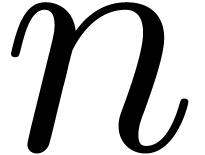 -bit integers. Let
-bit integers. Let 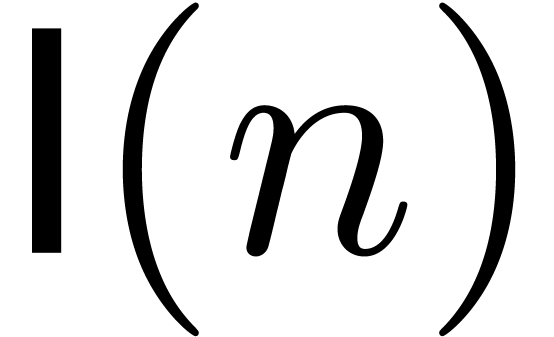 denote the time complexity for
this problem, in the Turing machine model with a finite number of tapes.
Until recently, the best asymptotical bound for
denote the time complexity for
this problem, in the Turing machine model with a finite number of tapes.
Until recently, the best asymptotical bound for 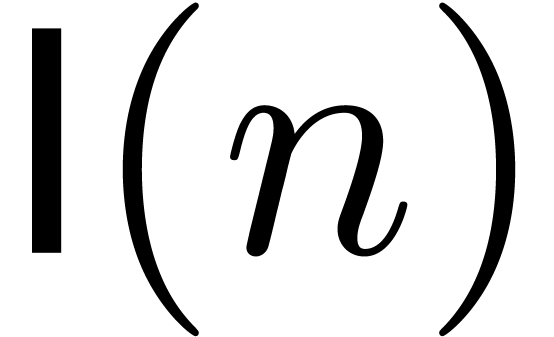 was due to Fürer. He proved that there exists
a constant
was due to Fürer. He proved that there exists
a constant 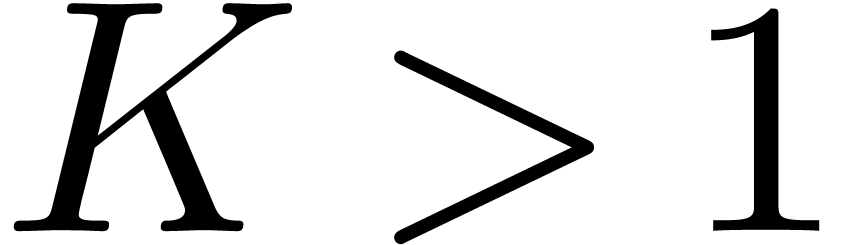 with
with
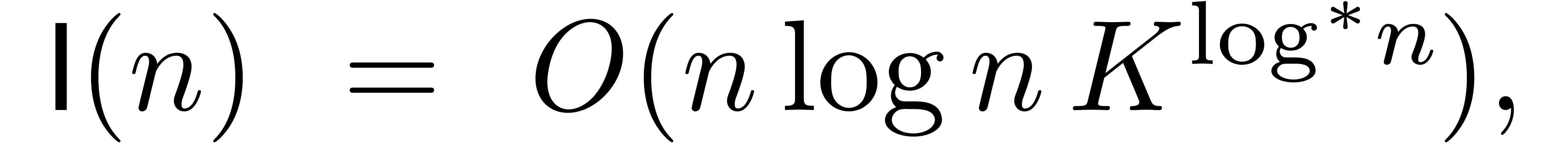
 (for
(for  ) stands for the iterator of the logarithm.
That is,
) stands for the iterator of the logarithm.
That is,
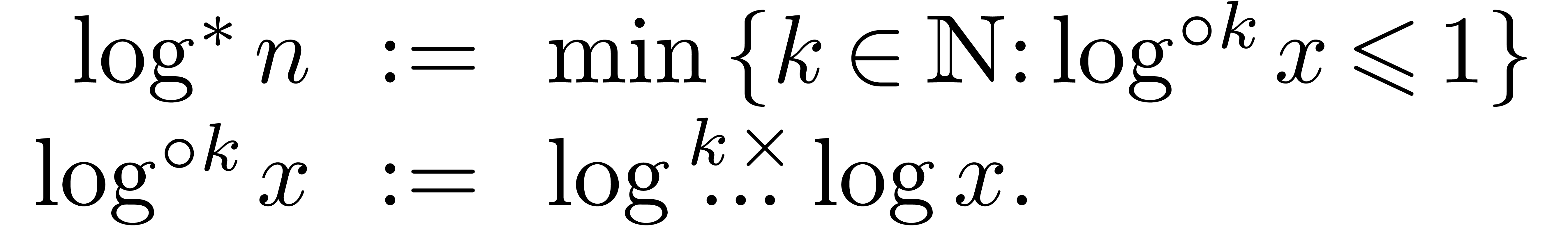
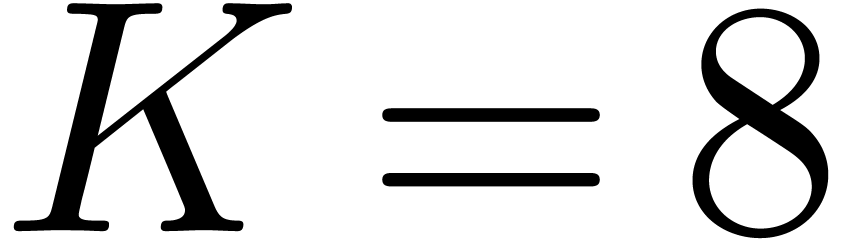 (and even
(and even 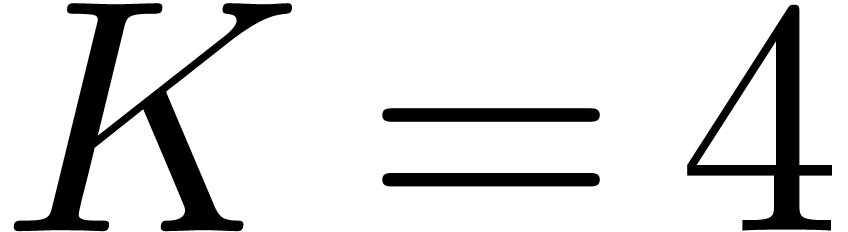 under the
condition that a certain number theoretic conjecture holds). We also
examined optimizations of Fürer's original approach, but it seems
that
under the
condition that a certain number theoretic conjecture holds). We also
examined optimizations of Fürer's original approach, but it seems
that 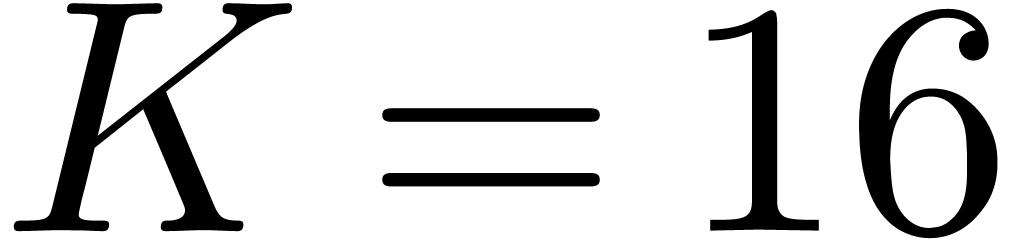 is the best bound that
can be obtained in this way.
is the best bound that
can be obtained in this way.