Abstract
Considérons une équation différentielle
linéaire 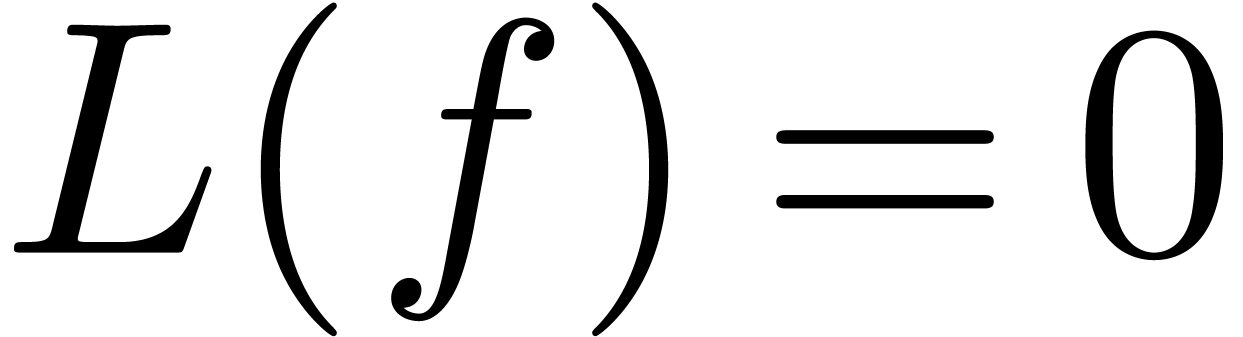 d'ordre
d'ordre
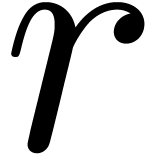 , dont les coefficients sont
des polynômes à coefficients rationnels. Si
l'équation n'admet que des singularités
régulières, un théorème classique de
Schlesinger dit que son groupe de Galois différentiel est
engendré en tant que sous groupe algébrique de
, dont les coefficients sont
des polynômes à coefficients rationnels. Si
l'équation n'admet que des singularités
régulières, un théorème classique de
Schlesinger dit que son groupe de Galois différentiel est
engendré en tant que sous groupe algébrique de 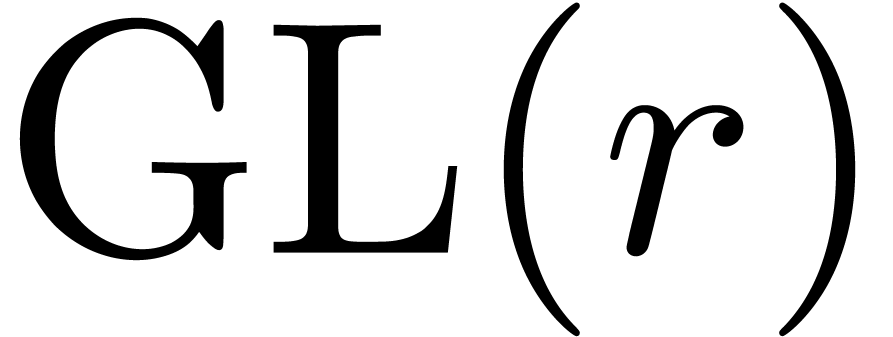 par les matrices de monodromie
autour des singularités de
par les matrices de monodromie
autour des singularités de 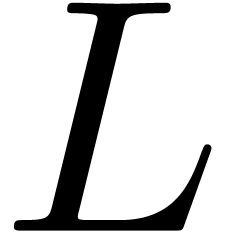 .
Ce « théorème de densité » se
généralise au cas non-Fuchsien en considérant
également des matrices de Stokes. Le but de cet exposé est
de montrer que ces théorèmes peuvent être rendus
effectifs dans une large mesure. Comme application, cela permet de
réduire certains problèmes a priori algébriques
concernant l'opérateur
.
Ce « théorème de densité » se
généralise au cas non-Fuchsien en considérant
également des matrices de Stokes. Le but de cet exposé est
de montrer que ces théorèmes peuvent être rendus
effectifs dans une large mesure. Comme application, cela permet de
réduire certains problèmes a priori algébriques
concernant l'opérateur 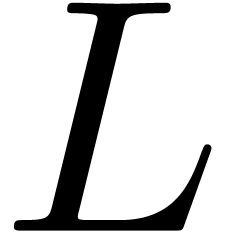 (comme la factorisation de
(comme la factorisation de 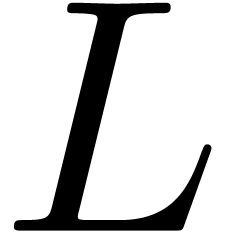 )
à des problèmes d'algèbre linéaire avec
comme coefficients des nombres complexes « holonômes
».
)
à des problèmes d'algèbre linéaire avec
comme coefficients des nombres complexes « holonômes
».
Occasion: séminaire différentiel,
Paris-Saclay, March 2, 2019
Documents: slideshow, TeXmacs
source
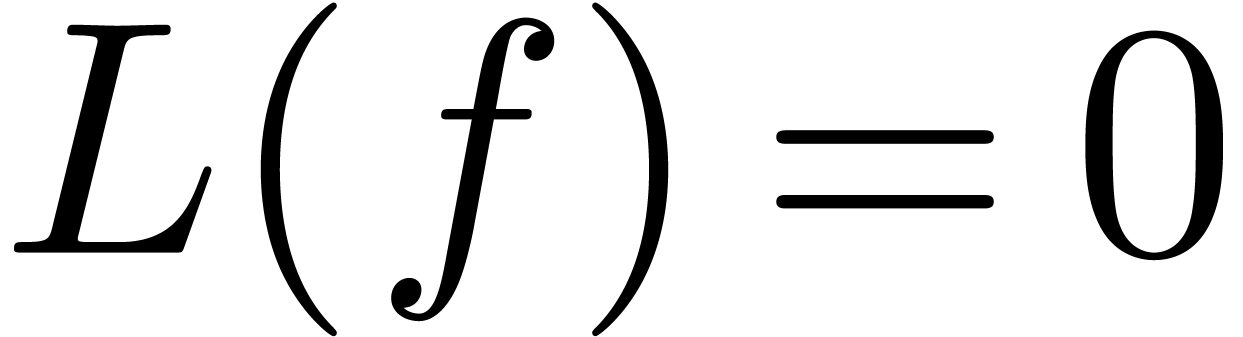 d'ordre
d'ordre
 , dont les coefficients sont
des polynômes à coefficients rationnels. Si
l'équation n'admet que des singularités
régulières, un théorème classique de
Schlesinger dit que son groupe de Galois différentiel est
engendré en tant que sous groupe algébrique de
, dont les coefficients sont
des polynômes à coefficients rationnels. Si
l'équation n'admet que des singularités
régulières, un théorème classique de
Schlesinger dit que son groupe de Galois différentiel est
engendré en tant que sous groupe algébrique de 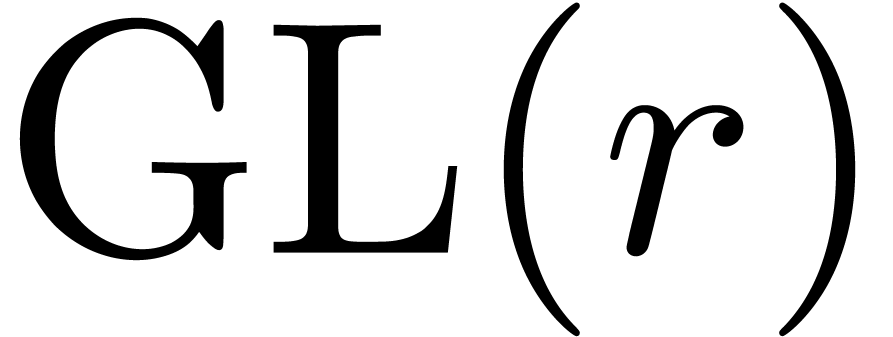 par les matrices de monodromie
autour des singularités de
par les matrices de monodromie
autour des singularités de 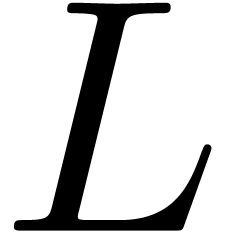 .
Ce « théorème de densité » se
généralise au cas non-Fuchsien en considérant
également des matrices de Stokes. Le but de cet exposé est
de montrer que ces théorèmes peuvent être rendus
effectifs dans une large mesure. Comme application, cela permet de
réduire certains problèmes a priori algébriques
concernant l'opérateur
.
Ce « théorème de densité » se
généralise au cas non-Fuchsien en considérant
également des matrices de Stokes. Le but de cet exposé est
de montrer que ces théorèmes peuvent être rendus
effectifs dans une large mesure. Comme application, cela permet de
réduire certains problèmes a priori algébriques
concernant l'opérateur 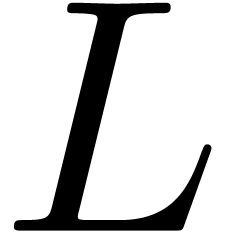 (comme la factorisation de
(comme la factorisation de 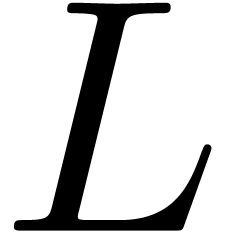 )
à des problèmes d'algèbre linéaire avec
comme coefficients des nombres complexes « holonômes
».
)
à des problèmes d'algèbre linéaire avec
comme coefficients des nombres complexes « holonômes
».