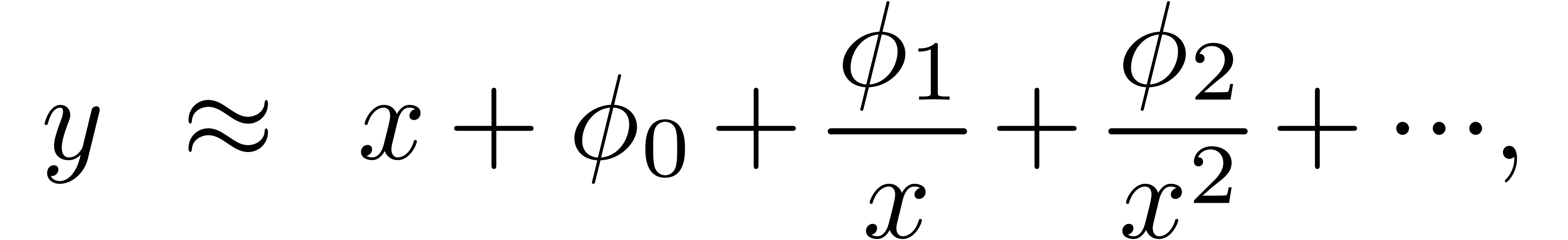 |
|
Abstract
It is known that an adaptation of Newton's method allows for the computation of functional inverses of formal power series. We show that it is possible to successfully use a similar algorithm in a fairly general analytical framework. This is well suited for functions that are highly tangent to identity and that can be expanded with respect to asymptotic scales of “exp-log functions”. We next apply our algorithm to various well-known functions coming from the world of quantitative finance. In particular, we deduce asymptotic expansions for the inverses of the Gaussian and the Black–Scholes pricing functions.
Keywords: Asymptotic expansion, algorithm, pricing, Hardy field, exp-log function, Black–Scholes formula
One notoriously complex problem in finance is the pricing of derivative products that are frequently traded on financial markets. Practitioners have proposed various sophisticated models for the dynamics of financial assets. In particular, it has been necessary to account for the existence of U-shaped “volatility smiles” which play a central role in the pricing of so-called vanilla options. Some models seem more reasonable than others because they explain not only the volatility smile, but also have properties that are directly exploitable in practice, notably the existence of easily implementable pricing formulas involving mathematical parameters that are easy to calibrate.
Subsequently, the volatility smile has been studied in a fairly general way, with a minimum of hypotheses on the probabilistic distribution of the assets [3, 4, 8, 16, 25]. This has made it possible to isolate intrinsic behaviours that are shared by a large number of models in the study of volatility smiles.
The next step has been to study the volatility smile in a model-free setting. This ultimately leads to focusing not on the Black–Scholes formula itself but on its inverse [10, 14, 30, 36]. A notable advantage of this approach is that it simplifies pricing problems. Indeed, in the case of vanilla options, such problems usually do not admit closed form solutions (except in the Black–Scholes model), so we need to resort to approximate solutions. Different techniques have been proposed to this purpose: perturbation methods with partial or stochastic differential equations, Lie symmetry theory, Watanabe theory, heat kernel expansion theory and Minakshisundaran–Pleijel's formula, large deviation theory, etc. [7, 12, 17, 20, 26, 27]. Most of these techniques give the asymptotics of price for large or small values of certain parameters involved in the computation of option prices. The study of the inverse function of the Black–Scholes formula then transforms vanilla option price asymptotics into implicit volatility asymptotics, which is the quantity of interest.
The problem of inverting Black–Scholes formula is challenging because of its non-analytic boundary behaviour. In fact, since the Black–Scholes model (as any other stochastic model) uses Brownian motion, it is not surprising that the asymptotics of the Black-Scholes formula involves logarithms. More precisely, after a suitable change of variables, the relation between vanilla option price and volatility can be expressed via an asymptotic expansion
where 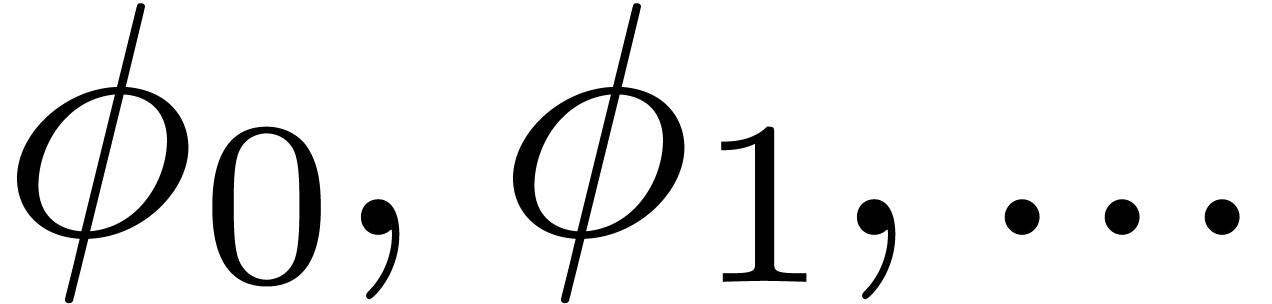 are polynomials in
are polynomials in  [10, 14]. In particular, this means that
[10, 14]. In particular, this means that
for every  . We are interested
in computing a similar expansion for
. We are interested
in computing a similar expansion for 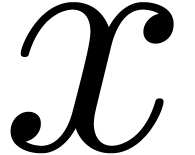 in terms of
in terms of
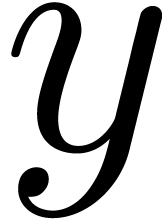 .
.
In computer algebra, various techniques have been developed for
asymptotic expansions in general asymptotic scales. For instance,
several algorithms exist for the asymptotic expansion of
“exp-log” functions [15, 22, 29, 34, 35]. Such functions are
built up from the rationals and an infinitely large variable  using the field operations, exponentiation and logarithm.
An example of an exp-log function is
using the field operations, exponentiation and logarithm.
An example of an exp-log function is 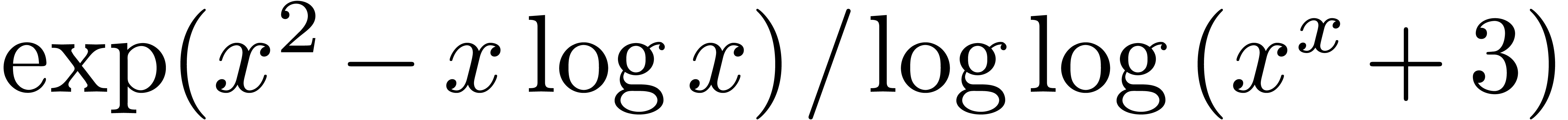 .
The theory of transseries [9, 21, 23]
makes it possible to cover asymptotic expansions of an even wider class
of functions comprising many formal solutions to non-linear differential
equations.
.
The theory of transseries [9, 21, 23]
makes it possible to cover asymptotic expansions of an even wider class
of functions comprising many formal solutions to non-linear differential
equations.
Several algorithms also exist for the functional inversion of exp-log
functions [32, 33]. However, the right-hand
side 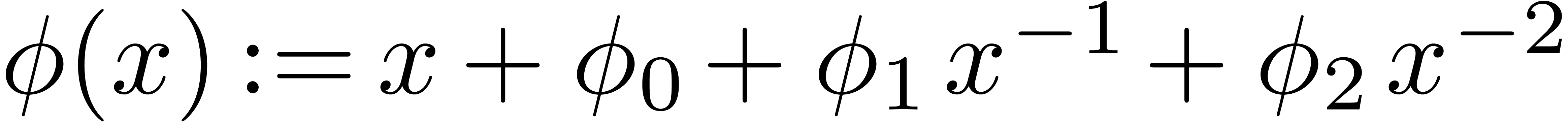 of (1) is usually not an
exp-log function, so these algorithms cannot be applied directly. When
considering
of (1) is usually not an
exp-log function, so these algorithms cannot be applied directly. When
considering 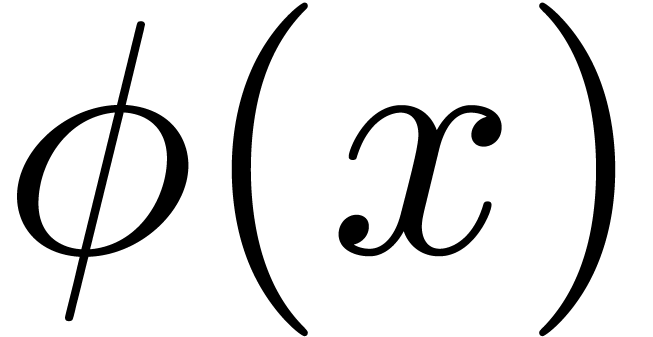 as a formal transseries, there are
also methods for computing the formal inverse
as a formal transseries, there are
also methods for computing the formal inverse 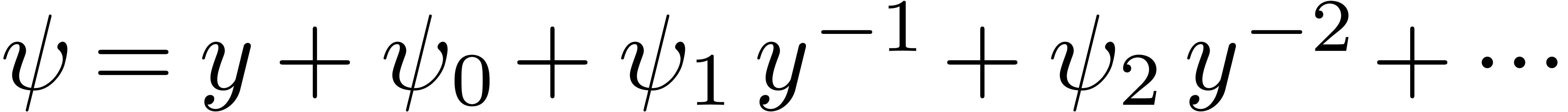 of
of
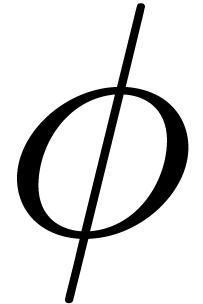 [21, 23]. However,
a priori, the analytic meaning (2) is lost during
such formal computations. In this paper, we will show how to invert
asymptotic expansions of the form (1) from the analytic
point of view.
[21, 23]. However,
a priori, the analytic meaning (2) is lost during
such formal computations. In this paper, we will show how to invert
asymptotic expansions of the form (1) from the analytic
point of view.
For each 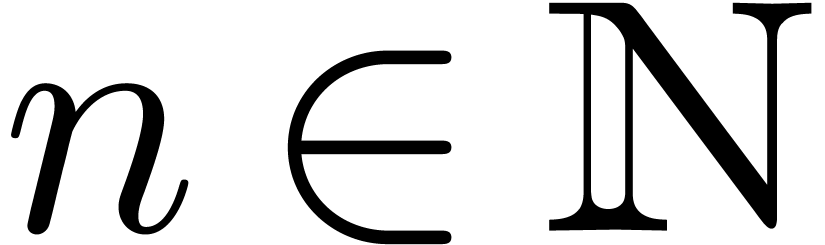 , let
, let  be the ring of
be the ring of  -fold
continuously differentiable functions at infinity (
-fold
continuously differentiable functions at infinity ( ). Then
). Then 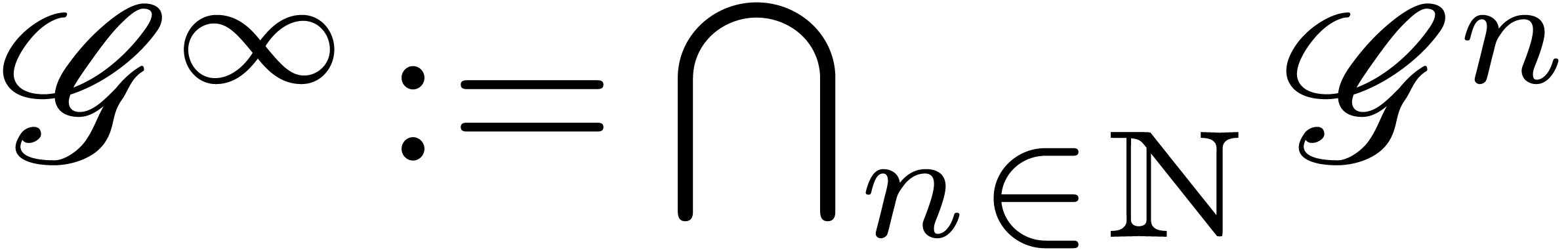 is a
differential ring. We recall that a Hardy field is a
differential subfield
is a
differential ring. We recall that a Hardy field is a
differential subfield  of
of  . It is well-known that Hardy fields [5,
18, 19] provide a suitable setting for
asymptotic analysis. In section 2, we will introduce the
abstract notion of an “effective Hardy field”, which
formalizes what we need in order to make this asymptotic calculus fully
effective. Typical examples of effective Hardy fields are generated by
exp-log functions. For instance, in Sections 2.3 and 2.4, we will show that
. It is well-known that Hardy fields [5,
18, 19] provide a suitable setting for
asymptotic analysis. In section 2, we will introduce the
abstract notion of an “effective Hardy field”, which
formalizes what we need in order to make this asymptotic calculus fully
effective. Typical examples of effective Hardy fields are generated by
exp-log functions. For instance, in Sections 2.3 and 2.4, we will show that 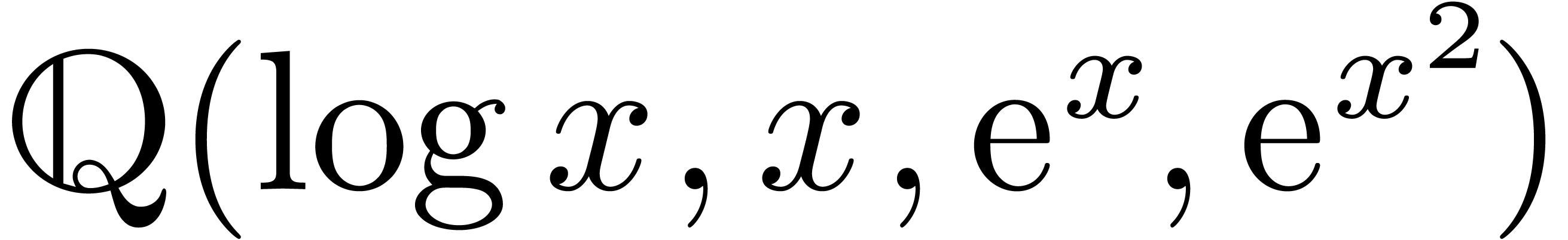 is effective
Hardy field. Using the aforementioned work on expansions of exp-log
functions, it is possible to construct various other effective Hardy
fields.
is effective
Hardy field. Using the aforementioned work on expansions of exp-log
functions, it is possible to construct various other effective Hardy
fields.
Let  be a Hardy field. We say that
be a Hardy field. We say that 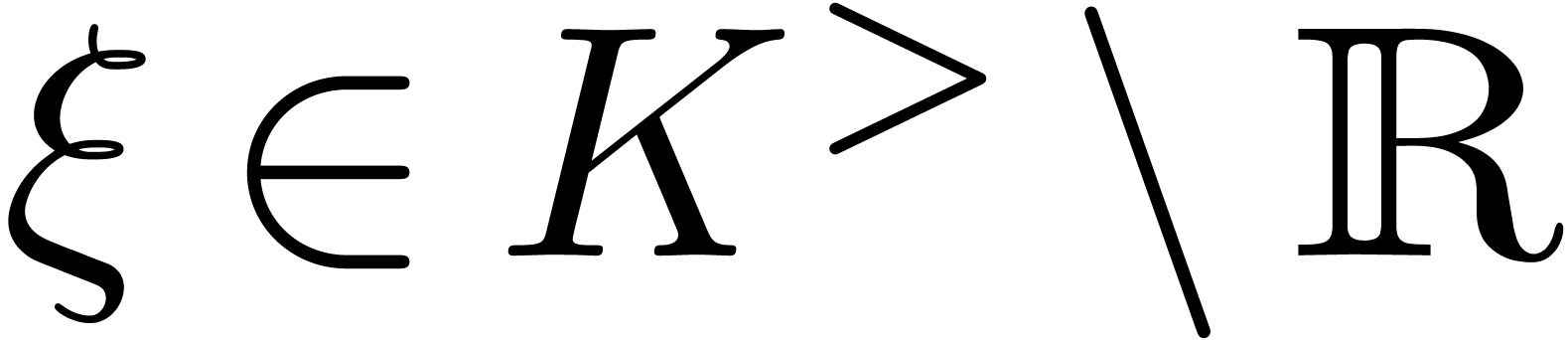 with
with 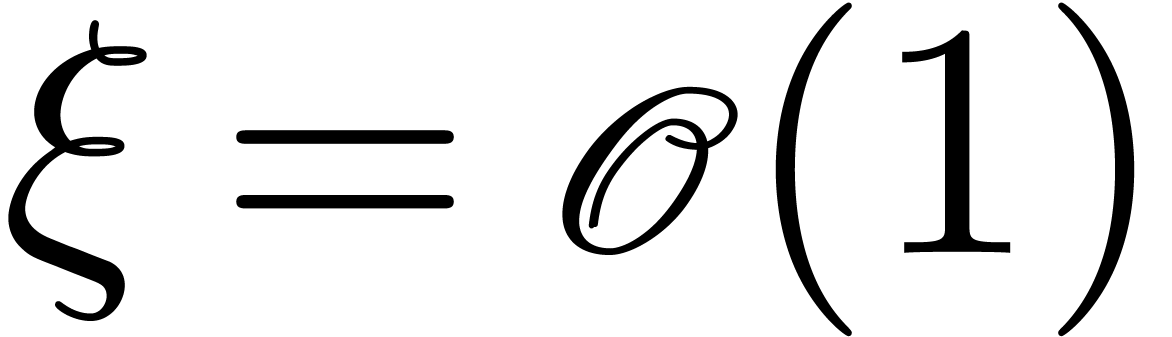 is steep if for any
is steep if for any
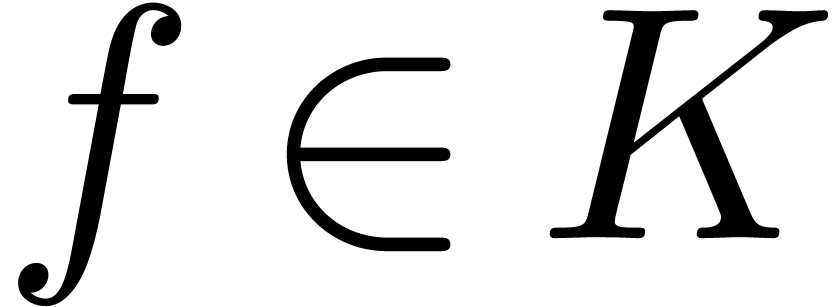 , there exists a
, there exists a 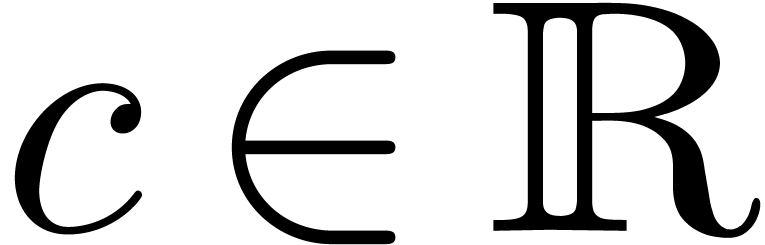 with
with  . An
element
. An
element 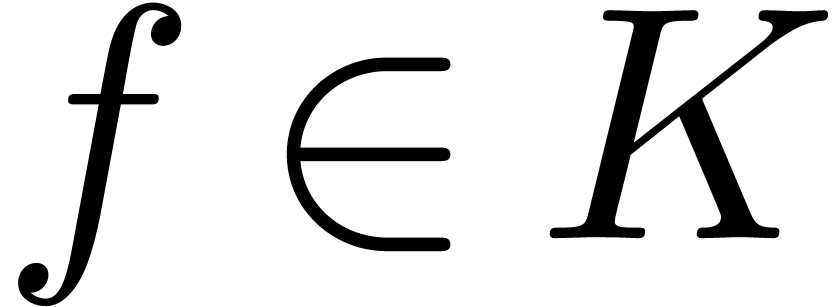 is said to be highly tangent to
identity if there exists a
is said to be highly tangent to
identity if there exists a  with
with 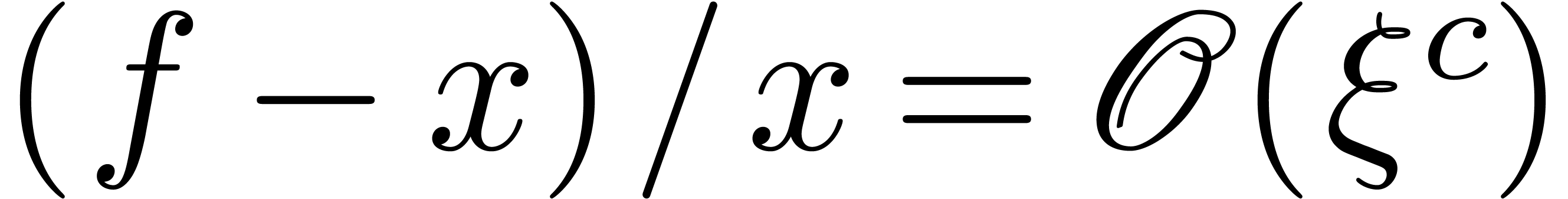 . For instance, if
. For instance, if 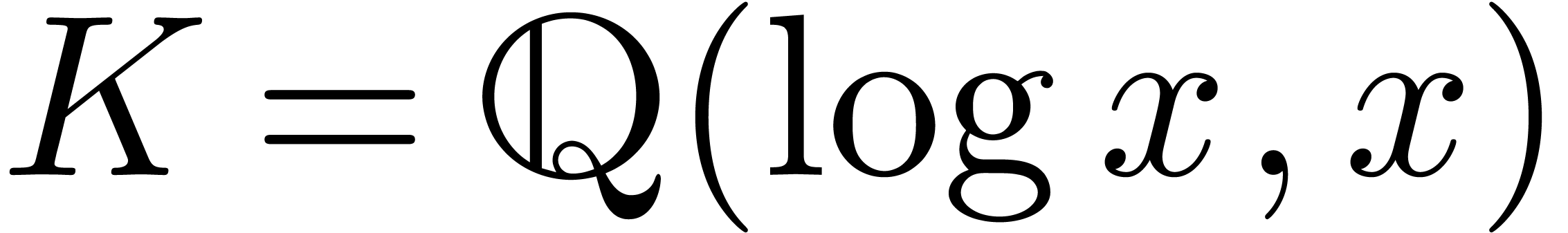 , then
, then 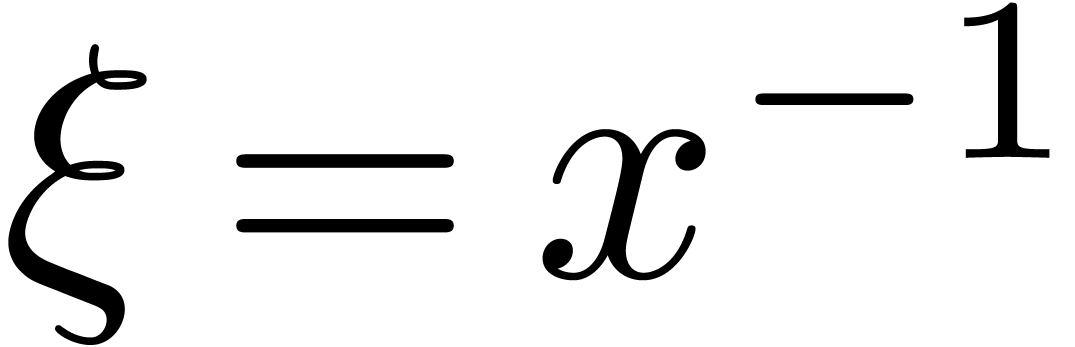 is steep and
is steep and
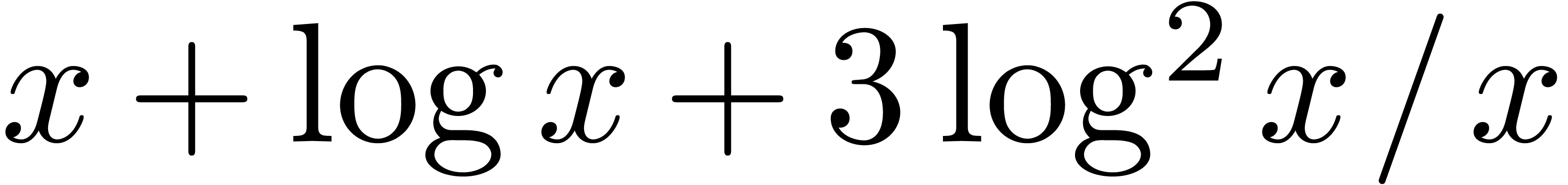 is highly tangent to identity, contrary to
is highly tangent to identity, contrary to 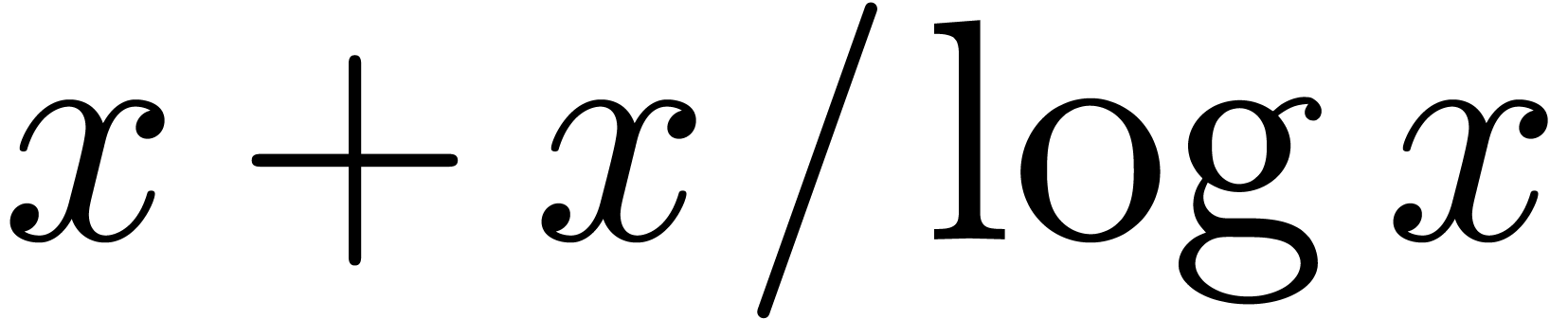 . Now assume that
. Now assume that  is an effective Hardy field. We say that a germ
is an effective Hardy field. We say that a germ 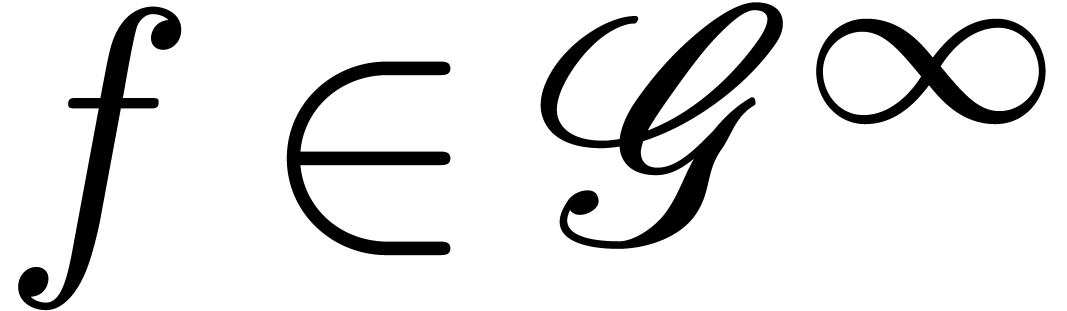 admits an effective asymptotic expansion over
admits an effective asymptotic expansion over  if
for every
if
for every 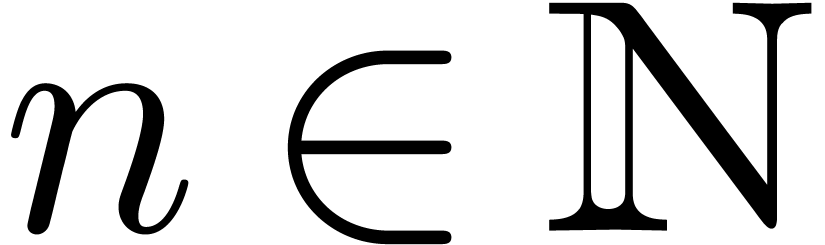 we can compute an element
we can compute an element 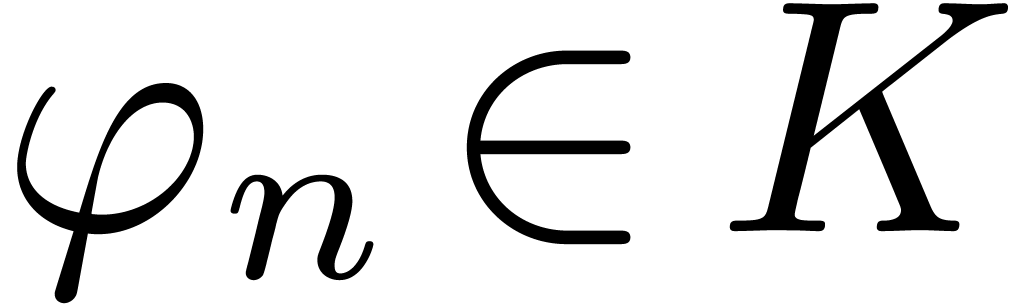 with
with 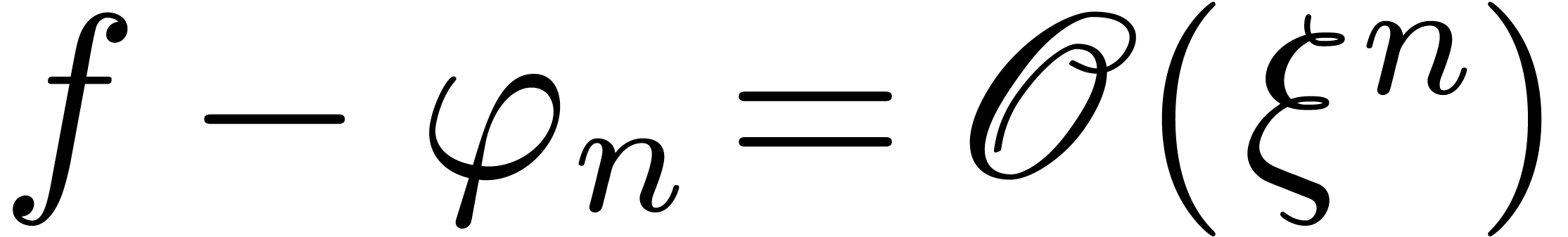 . If
. If 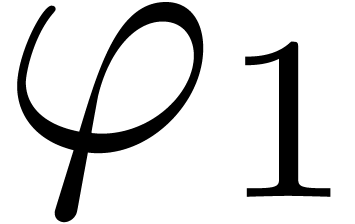 is highly tangent to identity and
is highly tangent to identity and  , then we will prove in Section 3
that
, then we will prove in Section 3
that 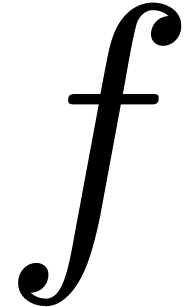 admits a functional inverse that also
admits an effective asymptotic expansion over
admits a functional inverse that also
admits an effective asymptotic expansion over  . Applied to the case when
. Applied to the case when 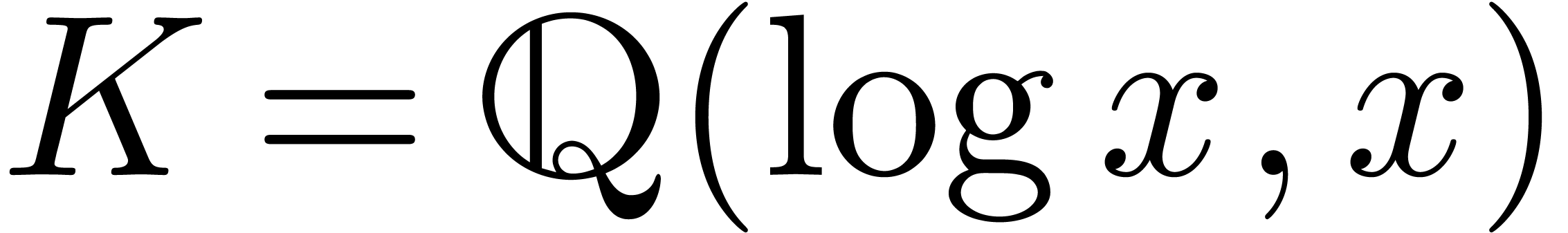 , this gives an algorithm for inverting asymptotic
expansions of the form (1). Our algorithm relies on two
main ingredients: Taylor's formula for right composition with functions
that are highly tangent to identity, and Newton's method for reducing
functional inversion to functional composition.
, this gives an algorithm for inverting asymptotic
expansions of the form (1). Our algorithm relies on two
main ingredients: Taylor's formula for right composition with functions
that are highly tangent to identity, and Newton's method for reducing
functional inversion to functional composition.
For our application to mathematical finance, it would have sufficed to
work with the particular effective Hardy field 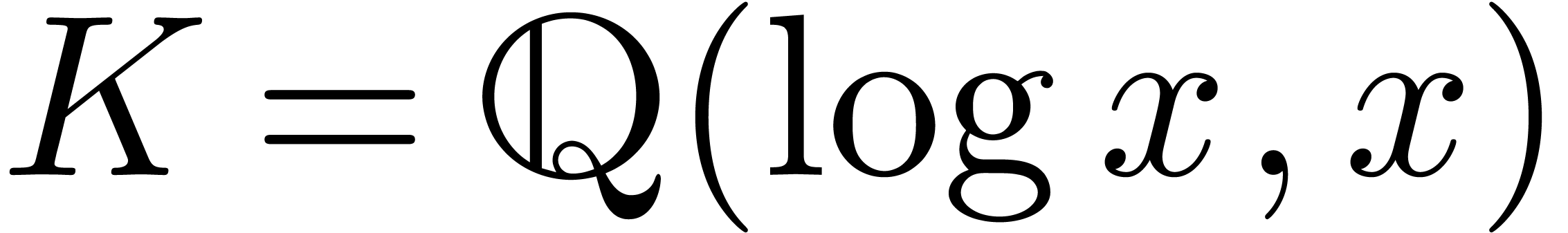 . There are several reasons why we have chosen to
prove our main result for general effective Hardy fields. First of all,
the more general result may be useful in other areas such as
combinatorics [31]. Indeed, functional inverses frequently
occur when analyzing asymptotic behavior using the saddle point method.
Secondly, our general setup only requires a moderate
“investment” in the terminology from Section 2.
Finally, it is natural to prove the results from Section 3
in this setup; the proofs would not become substantially shorter in the
special case when
. There are several reasons why we have chosen to
prove our main result for general effective Hardy fields. First of all,
the more general result may be useful in other areas such as
combinatorics [31]. Indeed, functional inverses frequently
occur when analyzing asymptotic behavior using the saddle point method.
Secondly, our general setup only requires a moderate
“investment” in the terminology from Section 2.
Finally, it is natural to prove the results from Section 3
in this setup; the proofs would not become substantially shorter in the
special case when 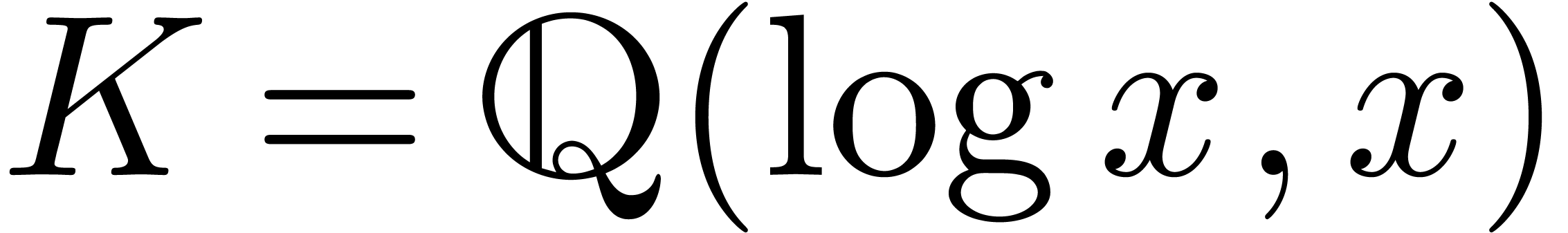 .
.
This paper contains three main contributions. As far as we are aware, the application of modern asymptotic expansion algorithms to mathematical finance is new. Secondly, we introduce the framework of effective Hardy fields which we believe to be of general interest for effective asymptotic analysis. One major advantage of this framework is that it separates the potentially difficult question of constructing a suitable effective Hardy field from its actual use. The existing literature on exp-log functions and transseries can be put to use for such constructions. But for various other problems, it suffices to assume the effective Hardy field to be given as a blackbox. The third contribution of this paper is to show that this is particularly the case for the inversion of asymptotic expansions that are “highly tangent to identity”.
Acknowledgment. We are very grateful to Martino Grasselli for his encouragement and for the careful reading of our work.
Consider the differential ring 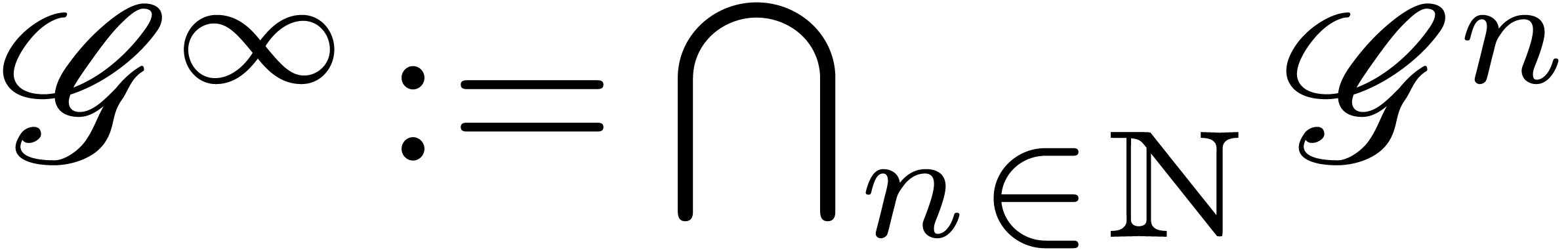 ,
where
,
where  denotes the ring of
denotes the ring of 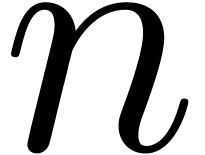 -fold continuously differentiable functions at
infinity (
-fold continuously differentiable functions at
infinity ( ) for each
) for each 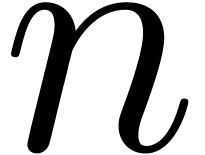 . We recall that a Hardy
field is a differential subfield
. We recall that a Hardy
field is a differential subfield  of
of  . Since any non zero element
. Since any non zero element  of Hardy fields is invertible, the sign of
of Hardy fields is invertible, the sign of 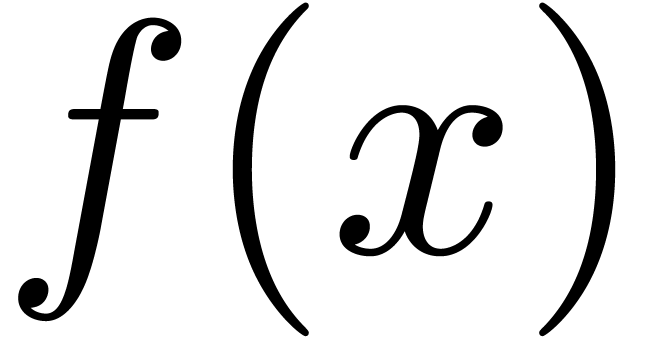 is ultimately constant for
is ultimately constant for  .
We define
.
We define  if
if 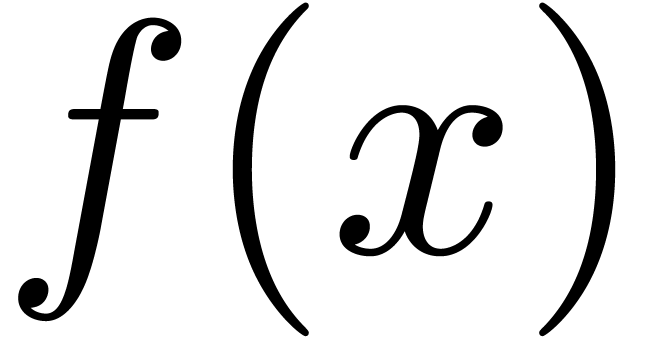 is
ultimately positive. It can be shown that this gives
is
ultimately positive. It can be shown that this gives  the structure of an ordered field.
the structure of an ordered field.
The well-known asymptotic relations  ,
,
 ,
,  and
and
 can be defined in terms of the ordering on
can be defined in terms of the ordering on  : given
: given 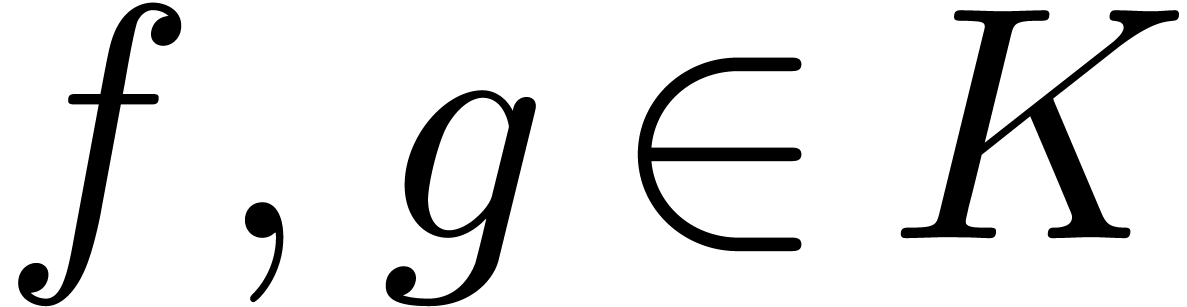 , we write
, we write

and
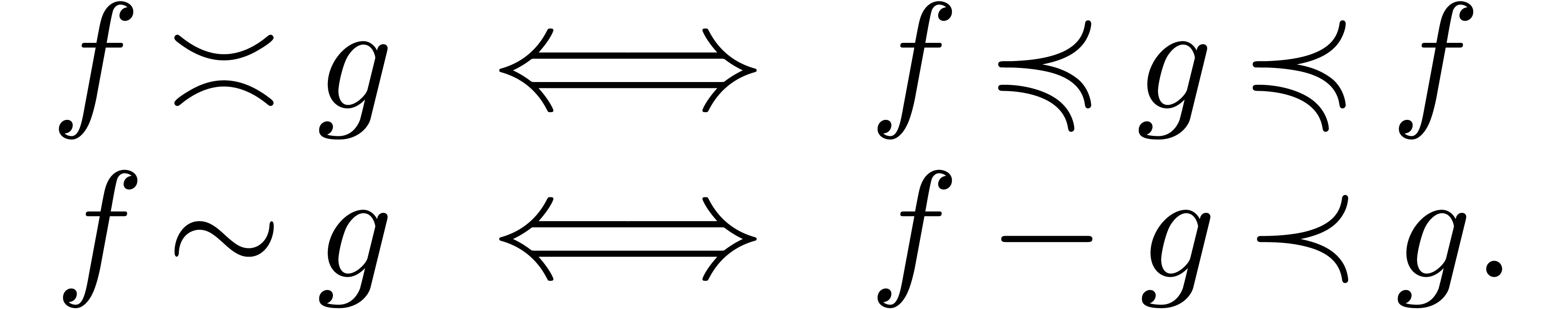
The quasi-ordering  is total on
is total on 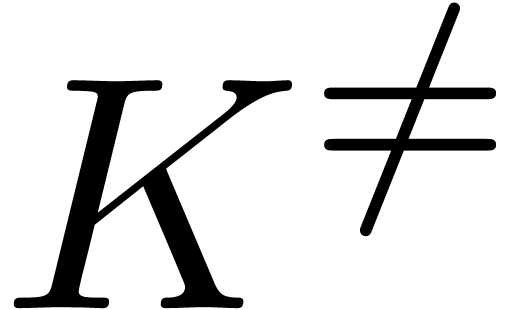 : given
: given 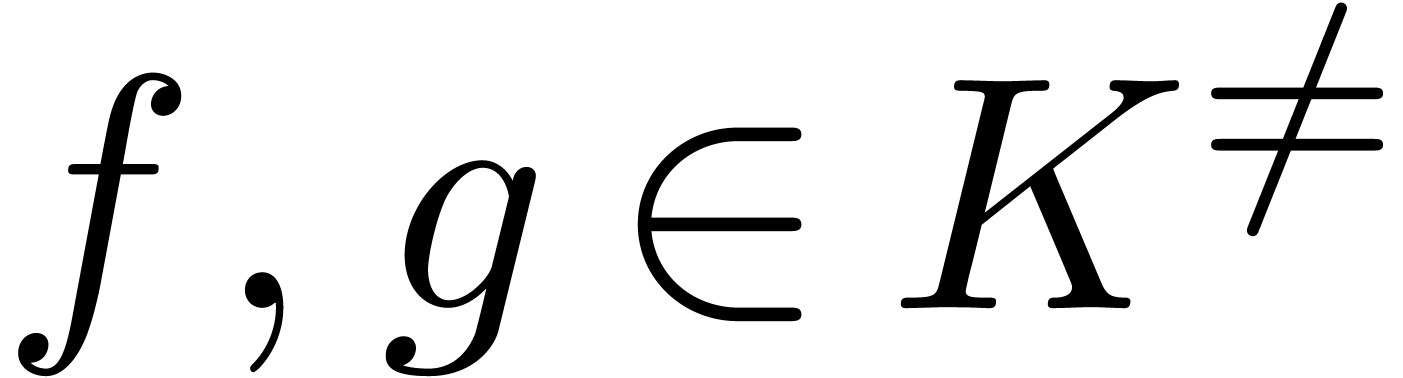 ,
we have
,
we have  .
.
Example  of exp-log germs at infinity is the smallest
subset of
of exp-log germs at infinity is the smallest
subset of  that contains
that contains  and the identity function, and which is closed under
and the identity function, and which is closed under  ,
,  ,
,
 ,
,  ,
,  and
and 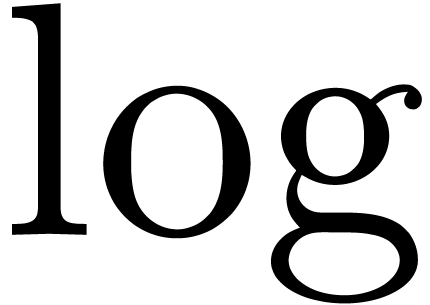 . For instance,
. For instance, 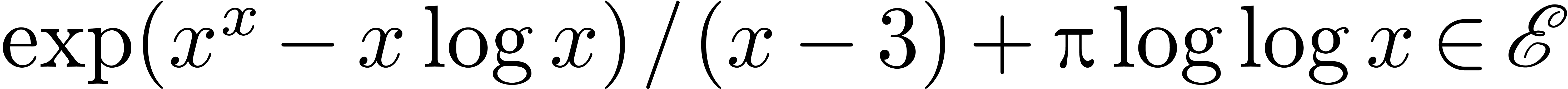 .
In his founding work [18, 19], Hardy showed
that
.
In his founding work [18, 19], Hardy showed
that  forms a Hardy field.
forms a Hardy field.
Example 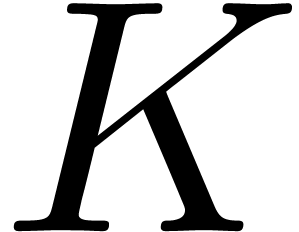 , its Liouville
closure
, its Liouville
closure 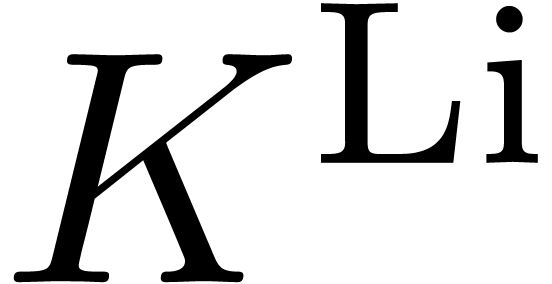 is the smallest subset of
is the smallest subset of  that contains
that contains  and that is stable
under
and that is stable
under  ,
,  ,
,  ,
,
 ,
, 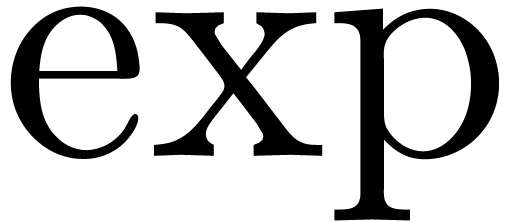 ,
, 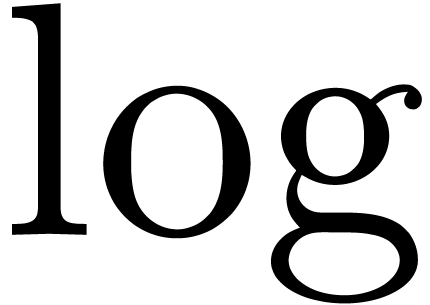 and integration. It is
well known that
and integration. It is
well known that 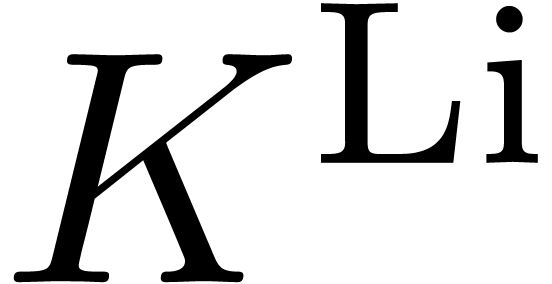 is again a Hardy field [5].
is again a Hardy field [5].
Let  be a Hardy field. Given
be a Hardy field. Given 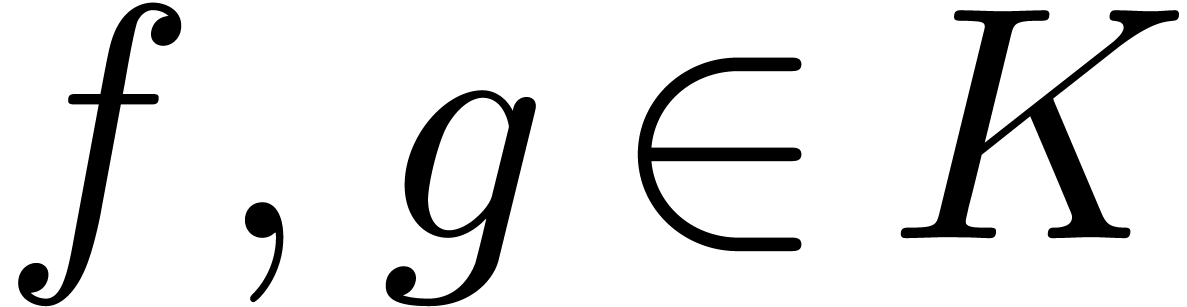 , let us show that
, let us show that
Let us first assume that  ,
whence
,
whence  , and let
, and let  and
and 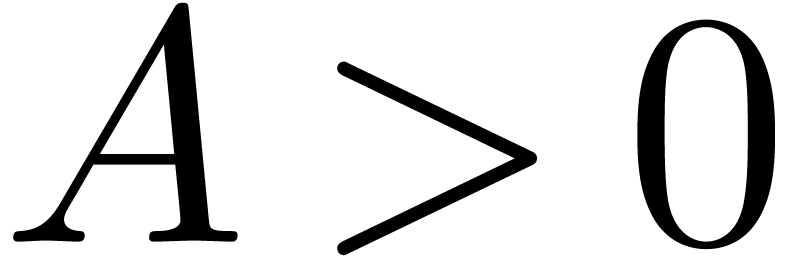 be such that
be such that 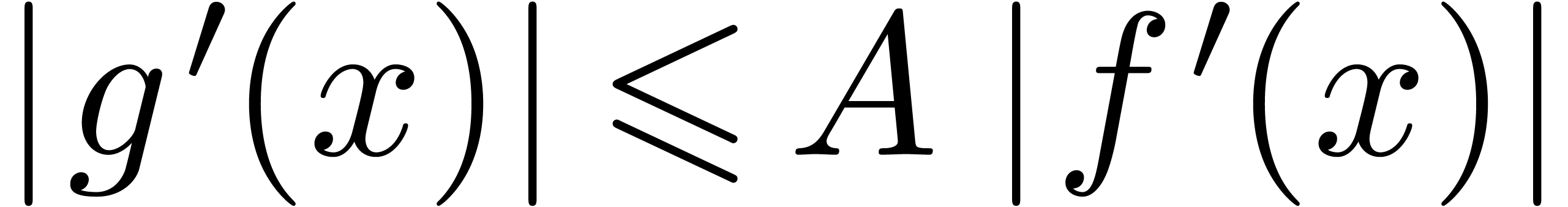 for all
for all 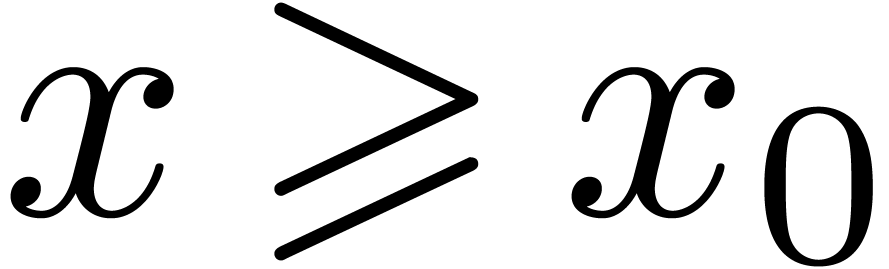 . Modulo a further
increase of
. Modulo a further
increase of 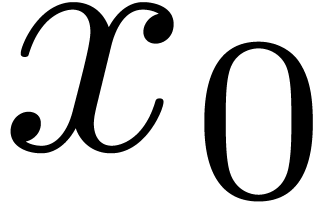 , we may assume
without loss of generality that the signs of
, we may assume
without loss of generality that the signs of 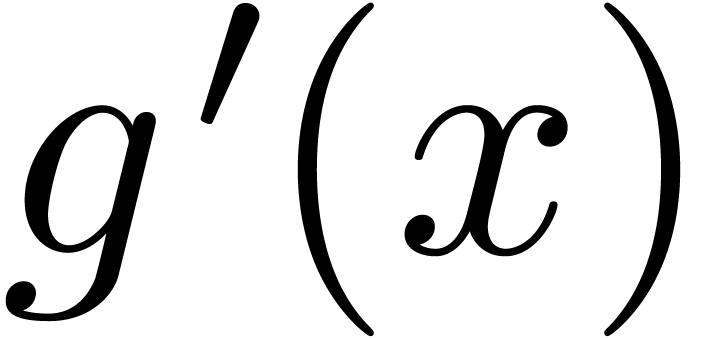 and
and
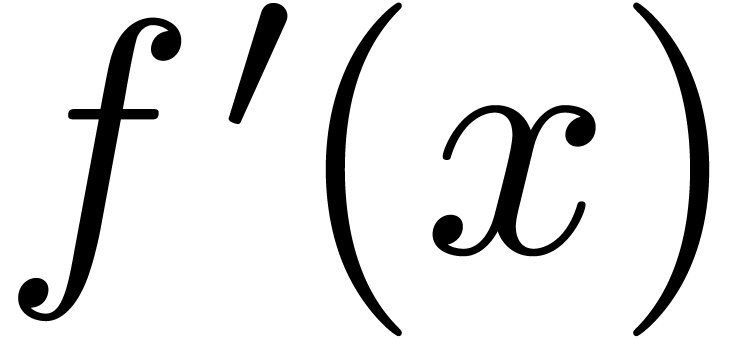 are constant for
are constant for  .
Then, for all
.
Then, for all 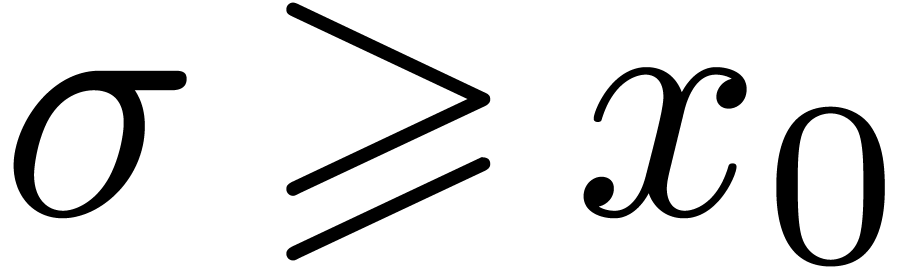 , we have
, we have
 |
(5) |
Consequently,  for suitable integration constants
for suitable integration constants
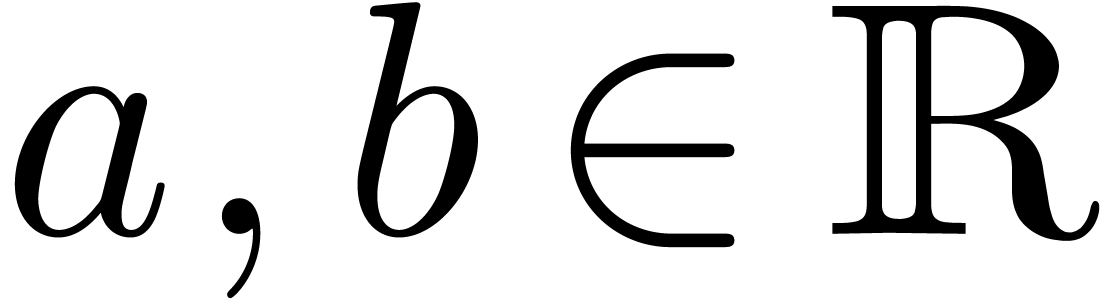 . If
. If  , then this yields
, then this yields  .
If
.
If  and
and  ,
then we may take
,
then we may take 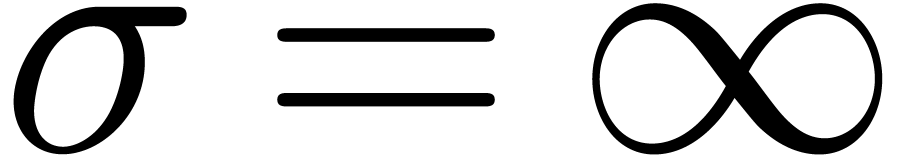 in (5), so that
in (5), so that
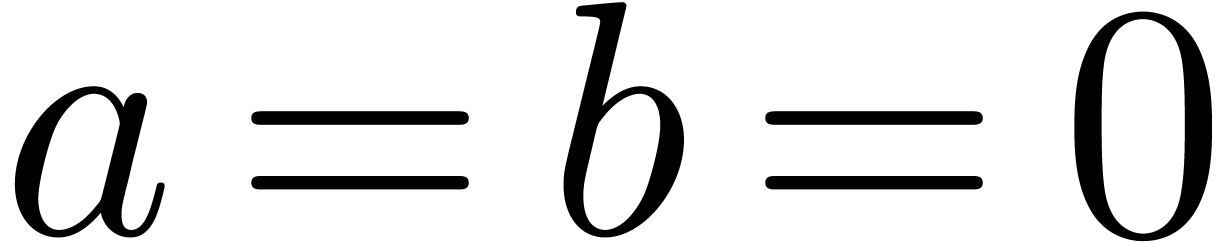 , and we again obtain
, and we again obtain  . If
. If  and
and
 , then we clearly have
, then we clearly have 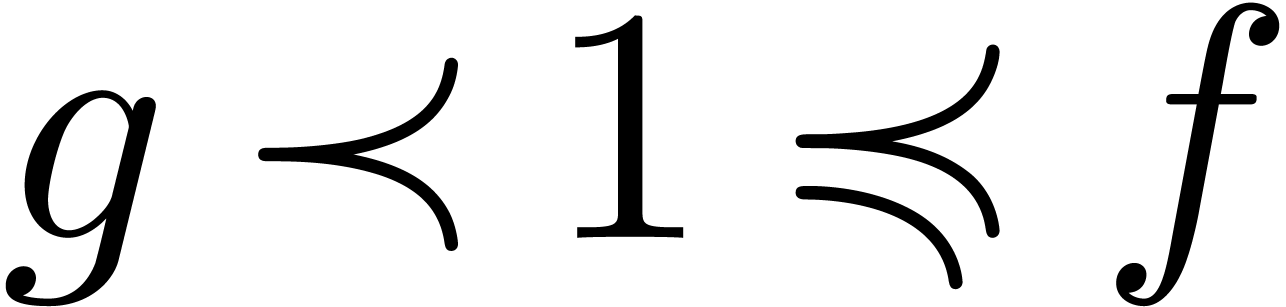 . This proves that
. This proves that 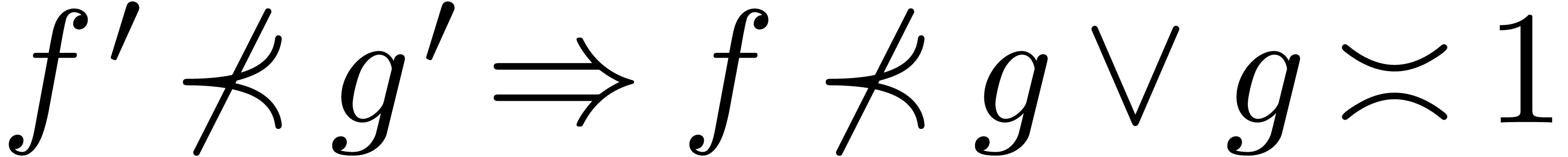 , which implies (4). One proves
, which implies (4). One proves
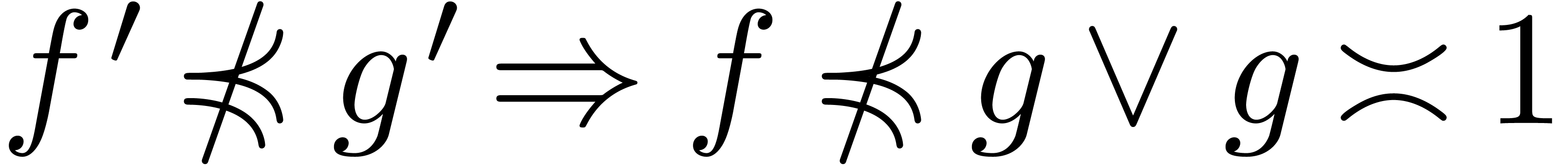 and (3) in a similar way.
and (3) in a similar way.
Let  be a Hardy field. We say that
be a Hardy field. We say that  is effective if its elements can be represented
by instances of a concrete data structure and if we have algorithms for
carrying out the basic operations
is effective if its elements can be represented
by instances of a concrete data structure and if we have algorithms for
carrying out the basic operations 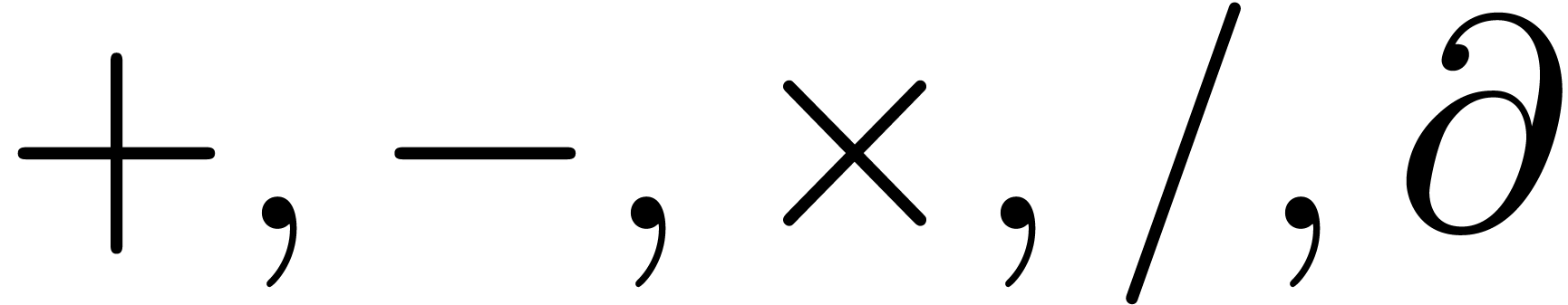 ,
as well as effective tests for the relations
,
as well as effective tests for the relations 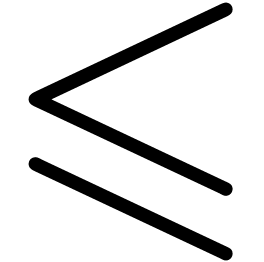 ,
,  ,
,  and
and  .
.
In particular, the effective inequality test for  yields an equality test. Inversely, if we have an algorithm to compute
signs of elements in
yields an equality test. Inversely, if we have an algorithm to compute
signs of elements in  , then
this yields effective inequality tests for both
, then
this yields effective inequality tests for both  and
and  . Similarly, if, given
. Similarly, if, given
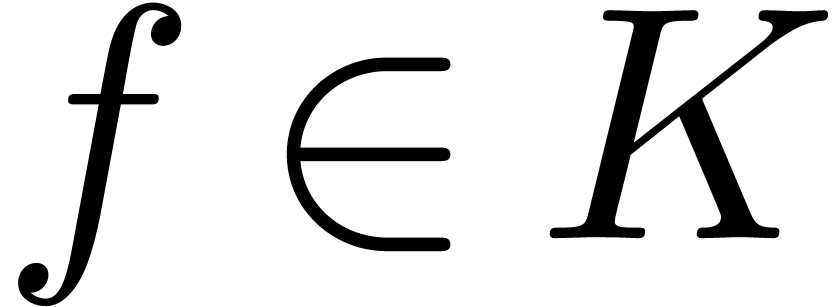 , we have a way to test
whether
, we have a way to test
whether  and
and  ,
then this yields effective tests for the relations
,
then this yields effective tests for the relations  and
and  . Indeed, given
. Indeed, given 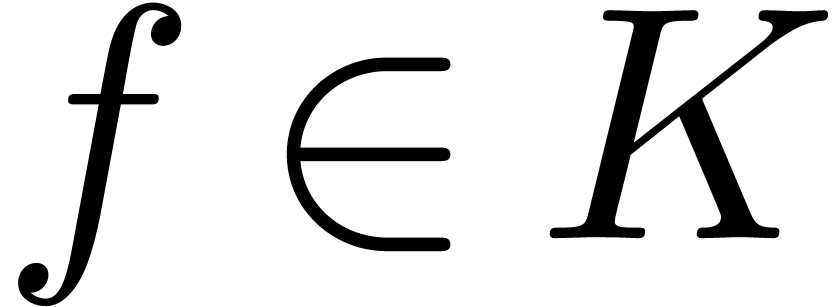 and
and 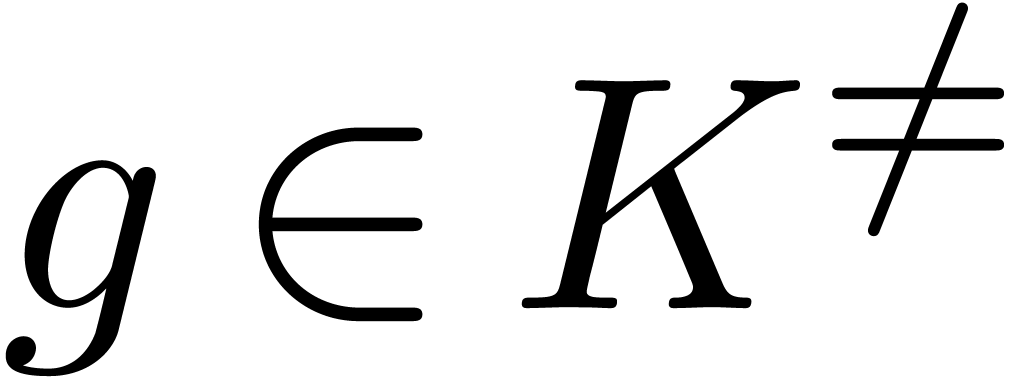 , we have
, we have
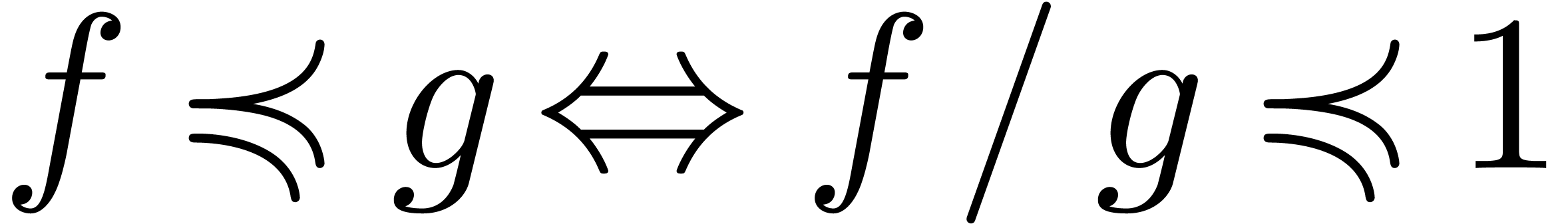 and
and 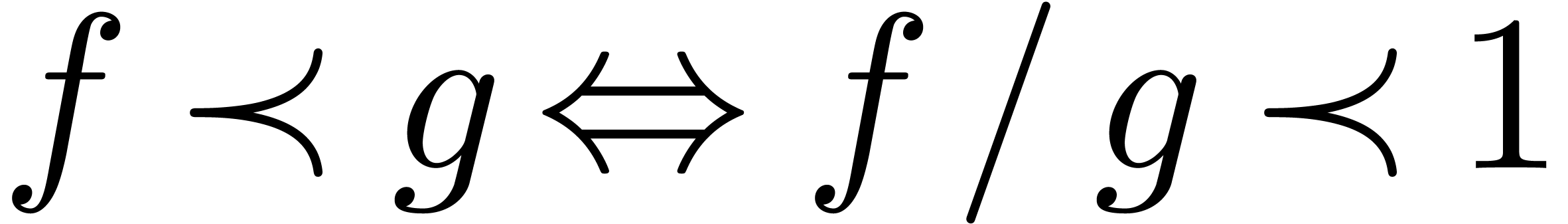 .
.
Example 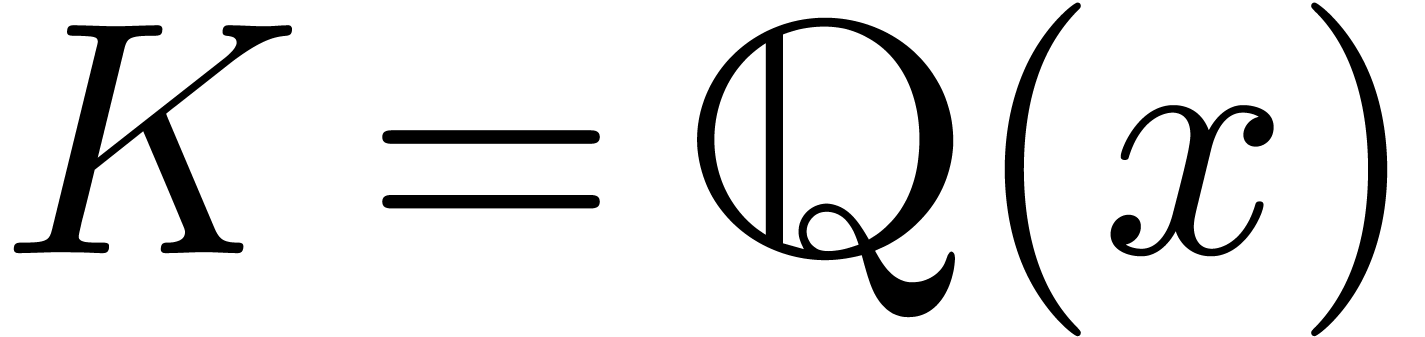 is an effective Hardy field. The basic
operations
is an effective Hardy field. The basic
operations  ,
,  ,
,  ,
,
 and
and  can clearly be
carried out by algorithm, and it is also clear how to do the equality
test. Now consider
can clearly be
carried out by algorithm, and it is also clear how to do the equality
test. Now consider 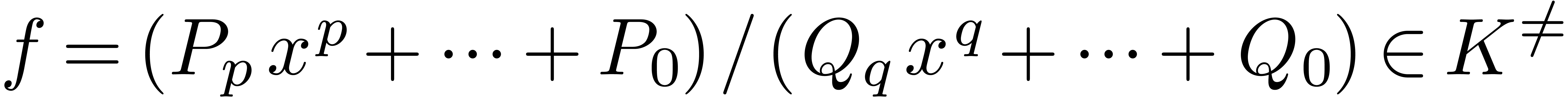 with
with 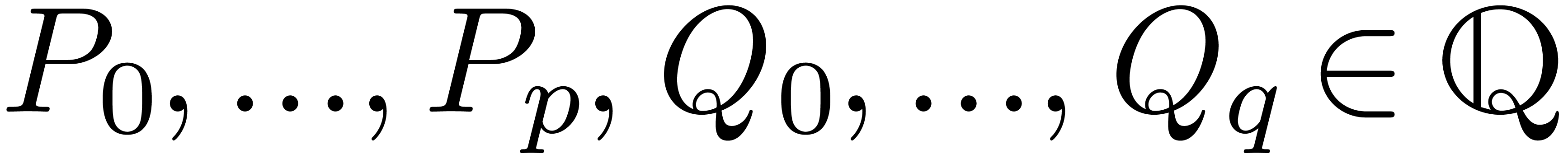 and
and 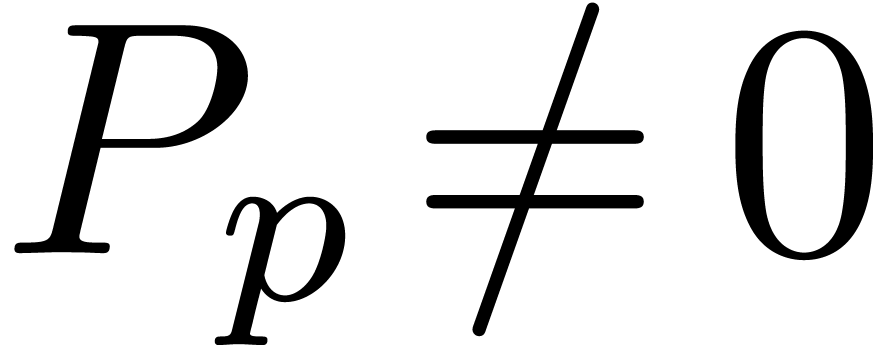 ,
, 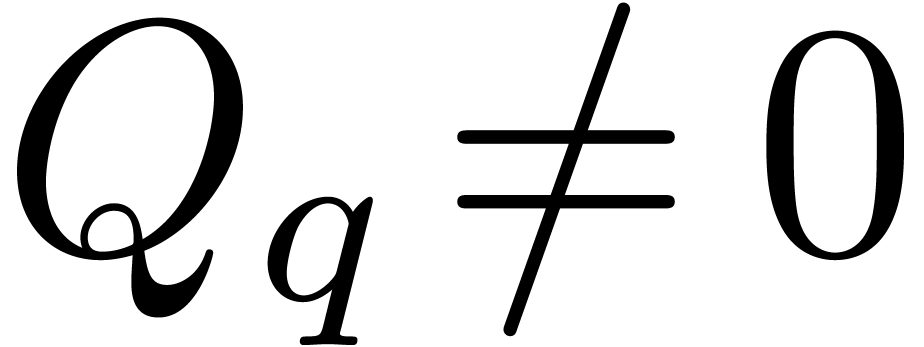 . Then
. Then 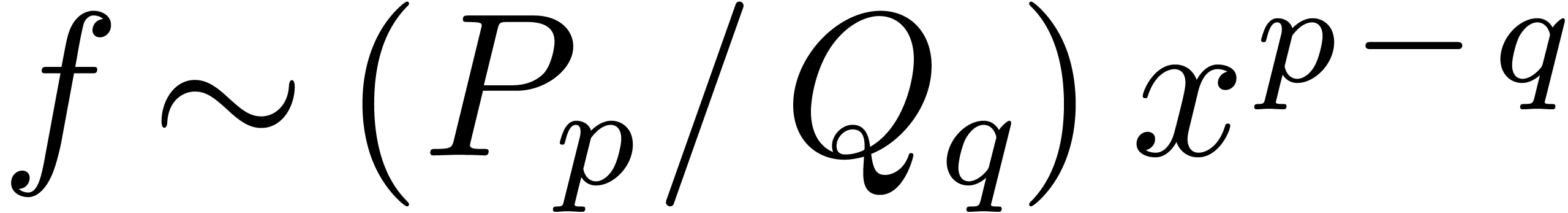 .
Consequently,
.
Consequently, 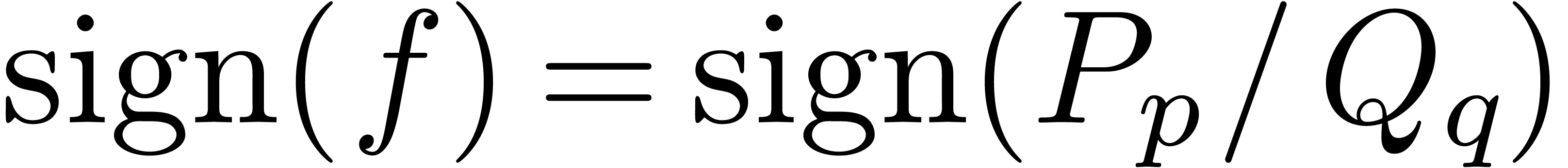 and
and  (resp.
(resp.  ).
).
Example 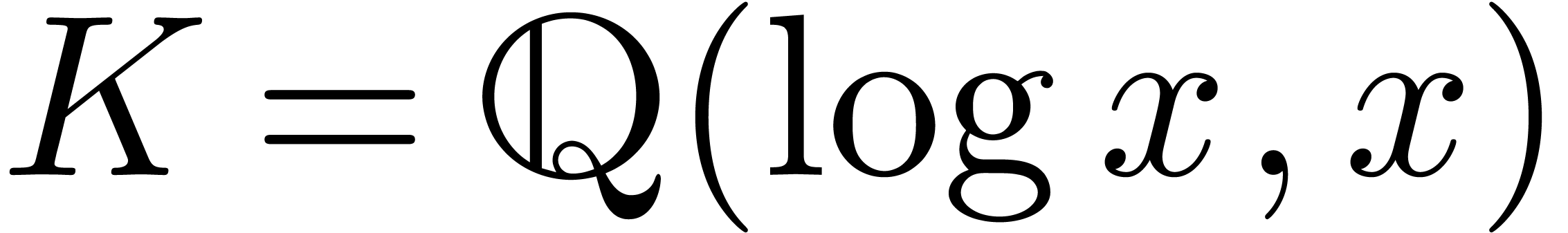 is an effective Hardy field. As above, the
basic operations
is an effective Hardy field. As above, the
basic operations  ,
,  ,
,  ,
,
 ,
,  and
the equality test are straightforward. Now any non zero element
and
the equality test are straightforward. Now any non zero element 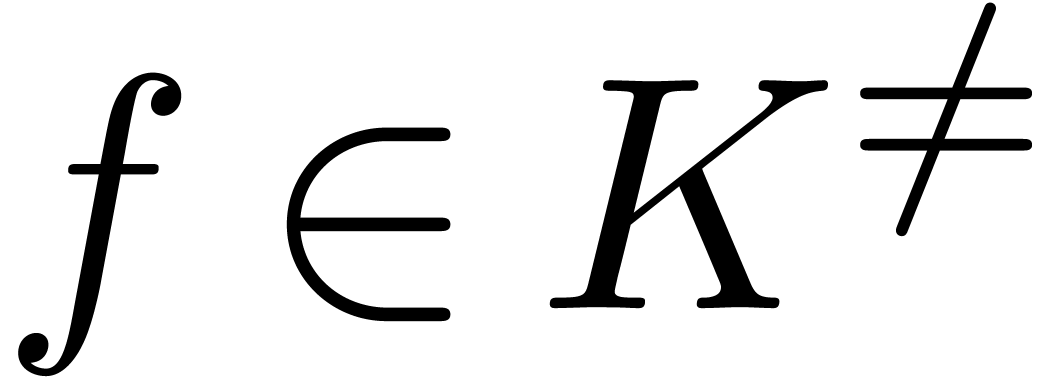 can be written as a fraction
can be written as a fraction 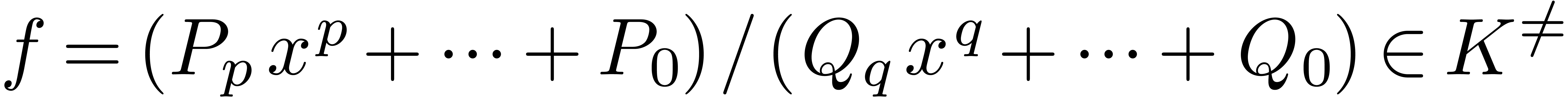 with
with  and
and 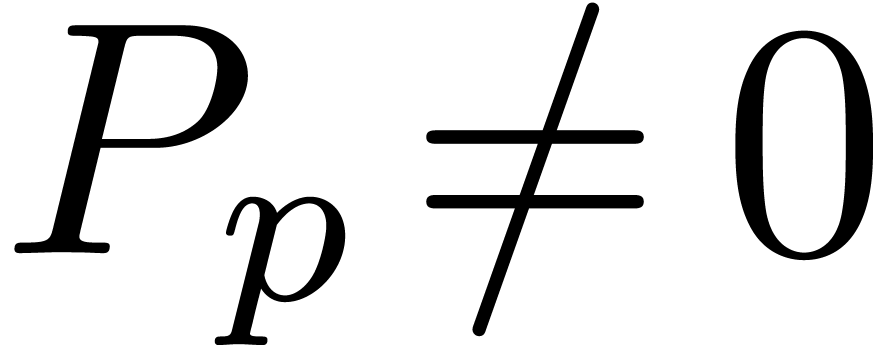 ,
,
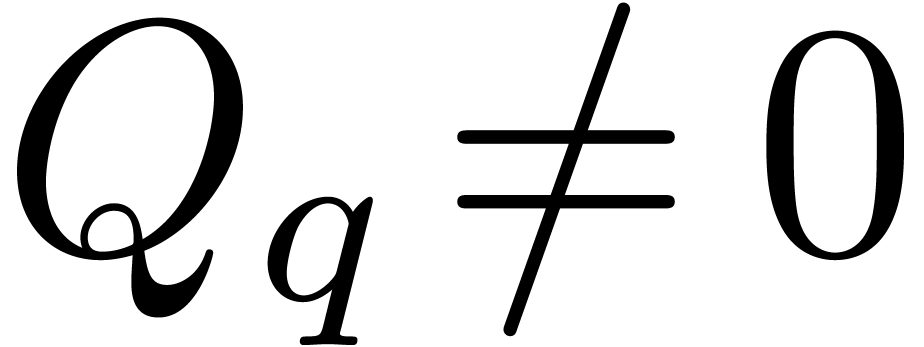 . Similarly, we may write
. Similarly, we may write
 with
with 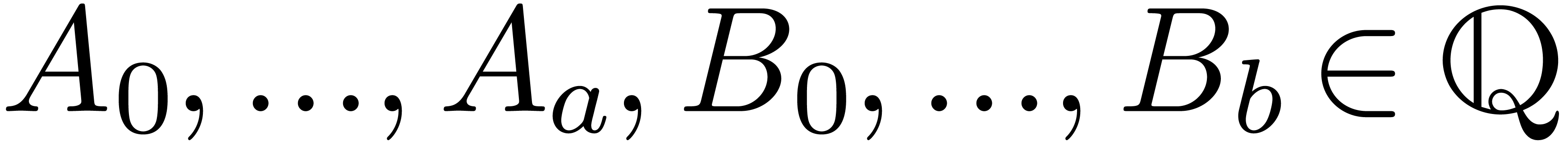 and
and 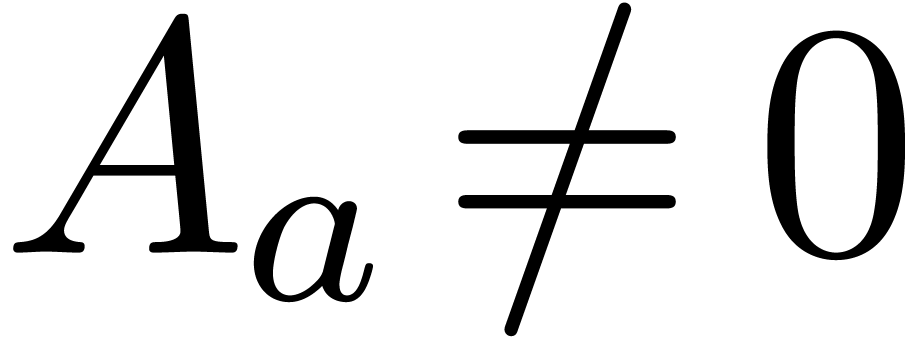 ,
, 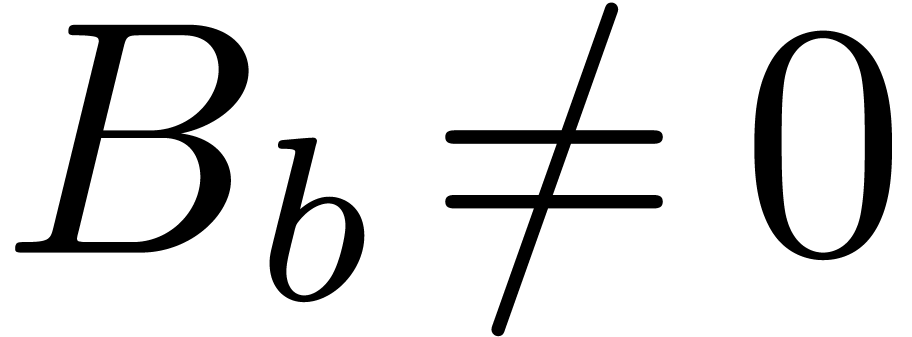 .
Then
.
Then 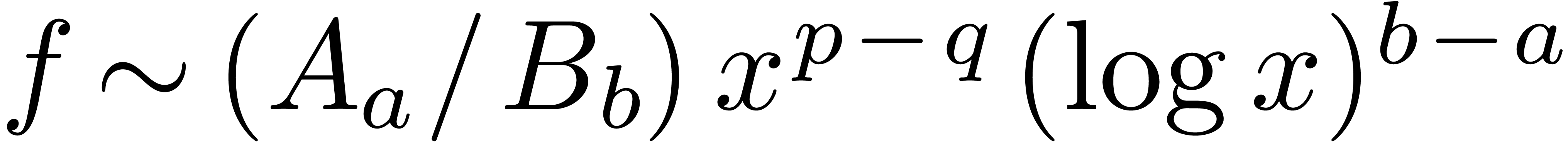 . Consequently,
. Consequently,  and
and 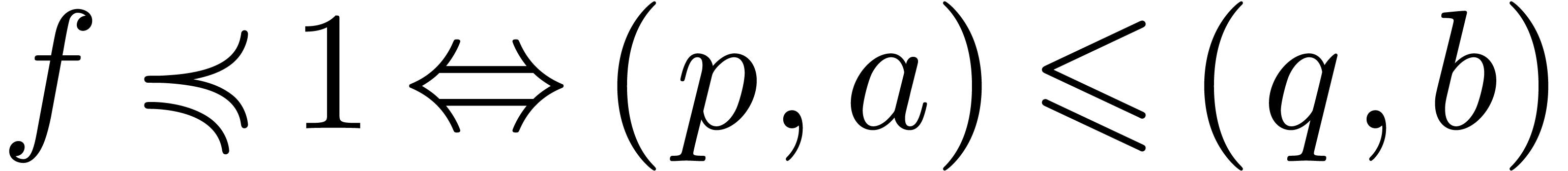 (resp.
(resp. 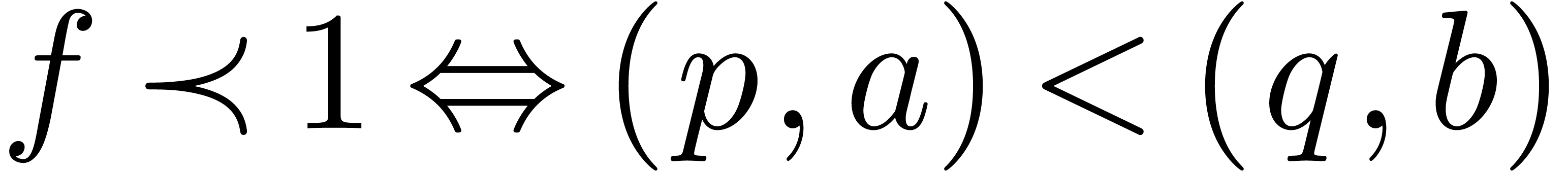 ). Here we used the lexicographical
ordering on pairs:
). Here we used the lexicographical
ordering on pairs:  if and only if
if and only if 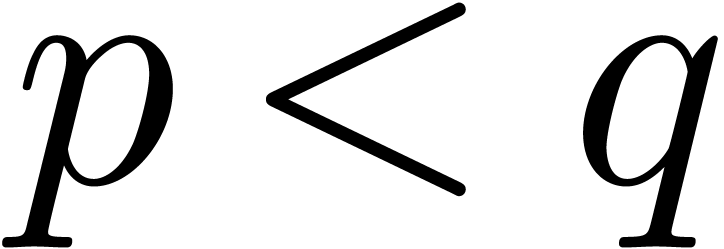 or
or 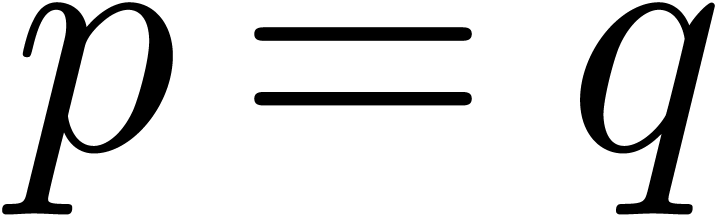 and
and 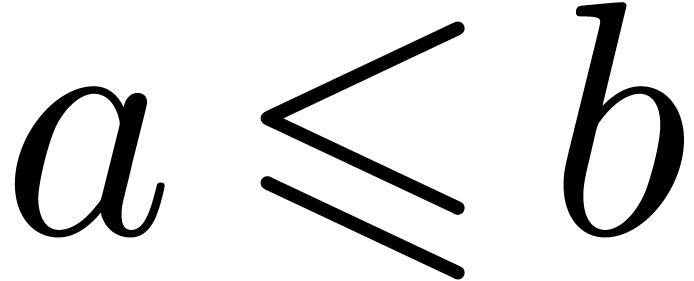 .
.
Example 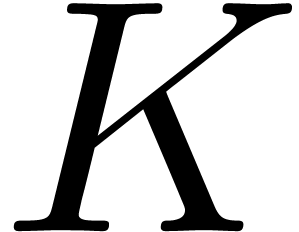 be an effective Hardy field and let
be an effective Hardy field and let 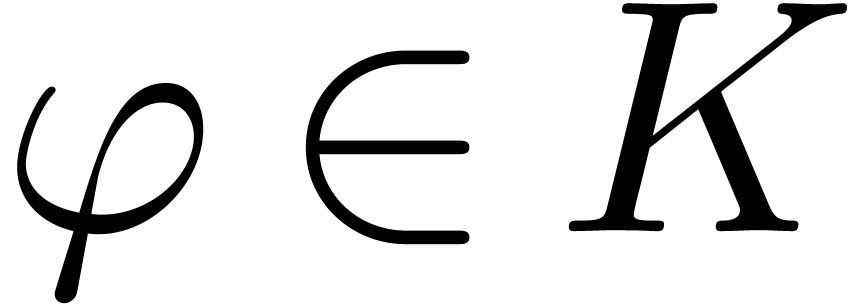 be such that
be such that 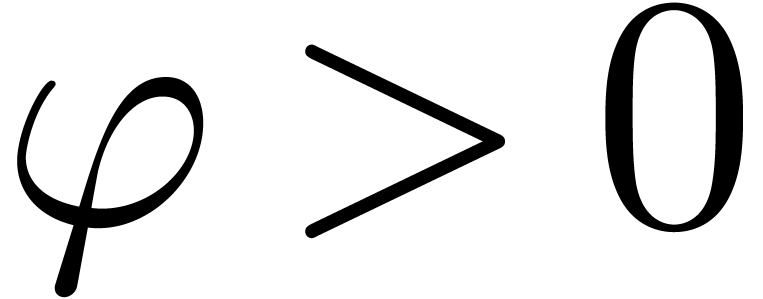 and
and  .
Then
.
Then 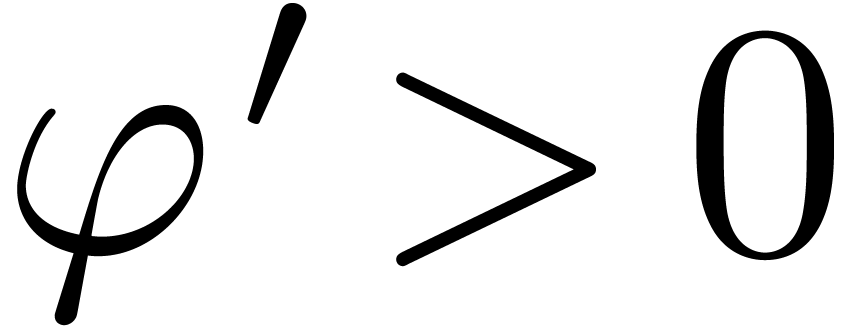 , whence
, whence  is ultimately strictly increasing and invertible for
composition. Let
is ultimately strictly increasing and invertible for
composition. Let 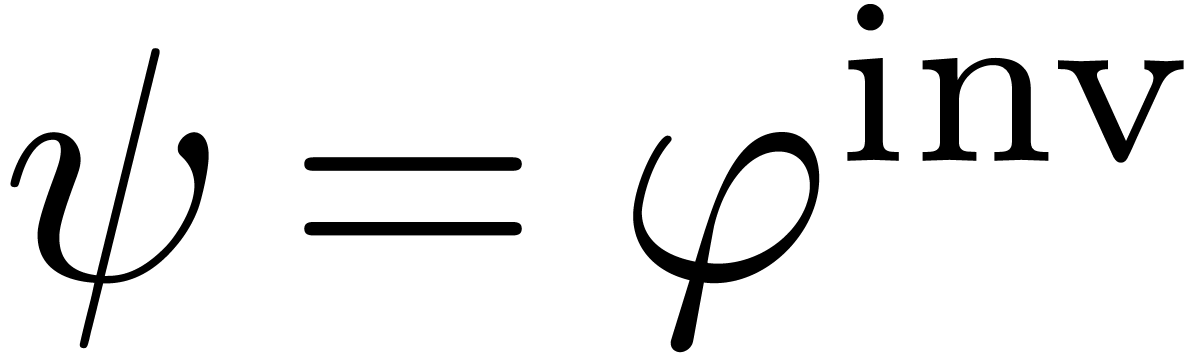 be the inverse of
be the inverse of  and assume that
and assume that  .
Then
.
Then  is again an effective Hardy field. Indeed,
since right composition preserves the field operations and the ordering,
is again an effective Hardy field. Indeed,
since right composition preserves the field operations and the ordering,
 is effectively isomorphic to
is effectively isomorphic to 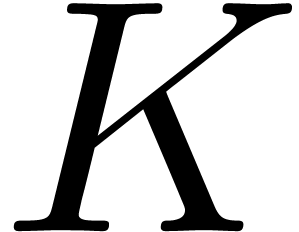 as an ordered field. The derivation on
as an ordered field. The derivation on  is given
by
is given
by 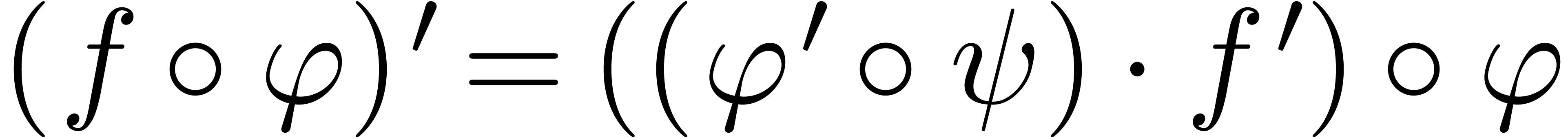 .
.
Let 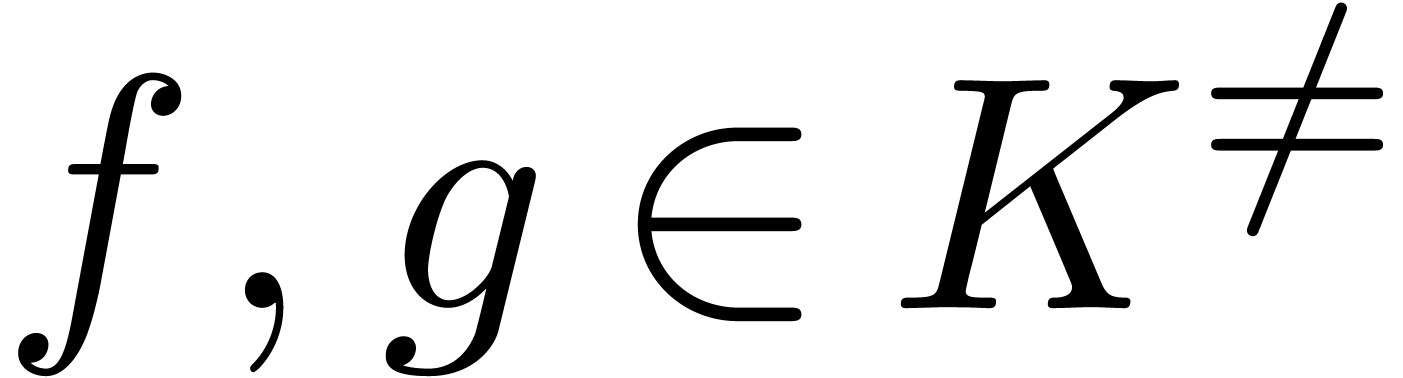 and let
and let  be such that
be such that
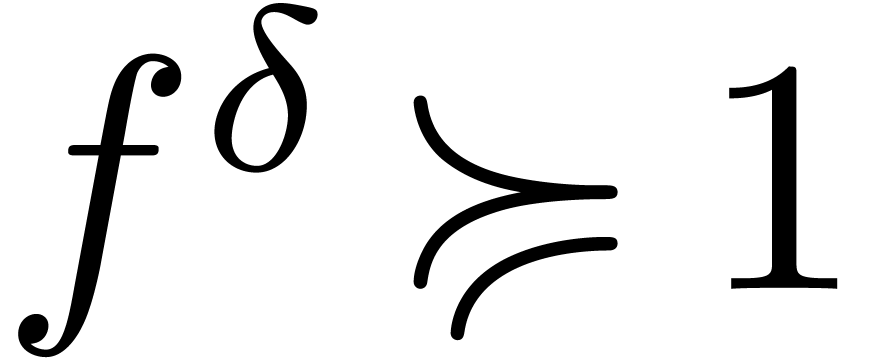 ,
, 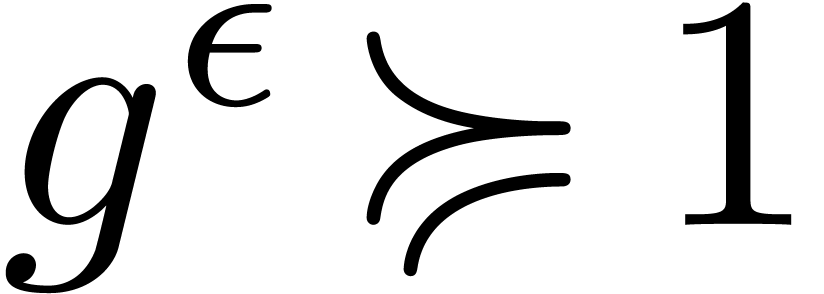 . We define the flatness relations
. We define the flatness relations  ,
,  and
and  by
by
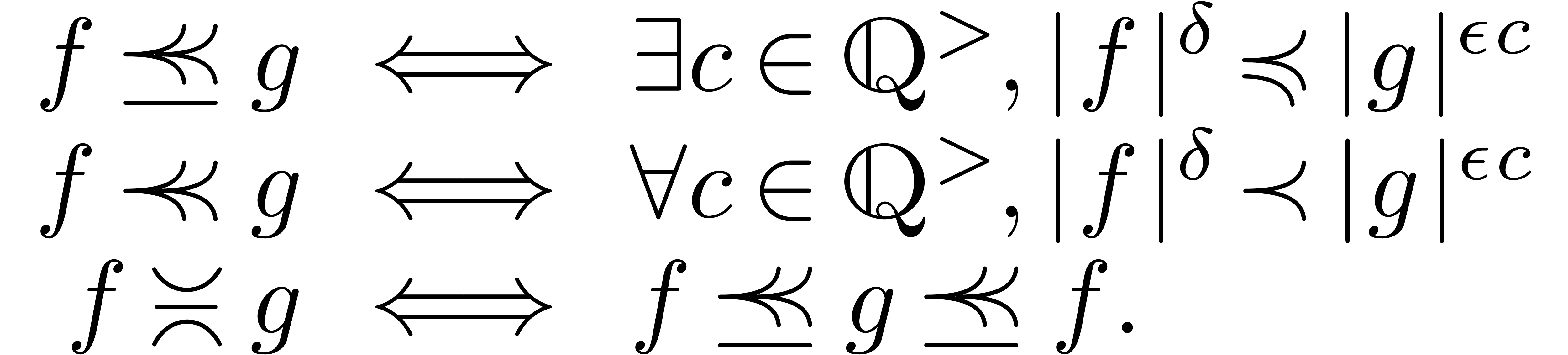
Let 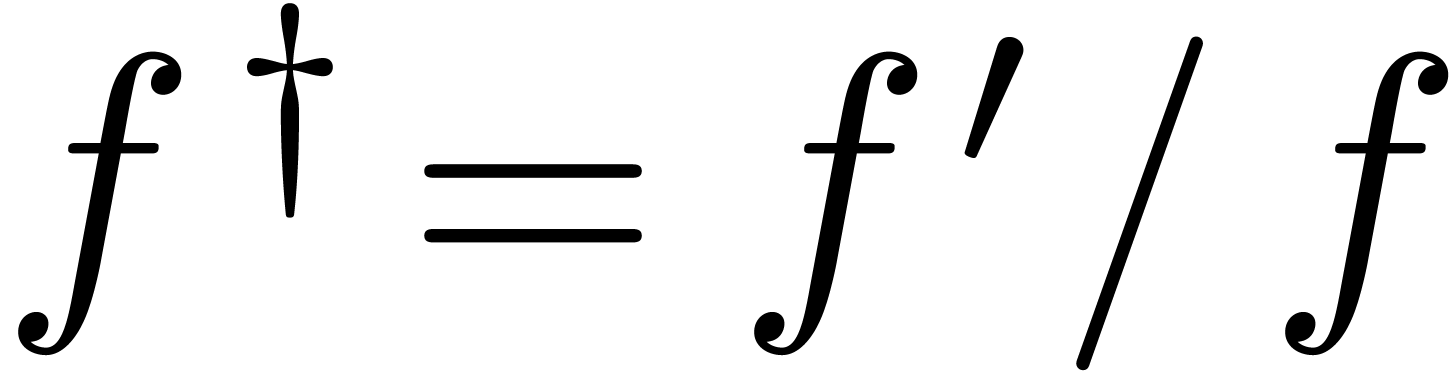 denote the logarithmic derivative of a
function
denote the logarithmic derivative of a
function 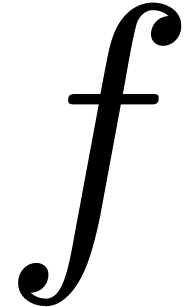 . Taking logarithms,
and using (3) and (4), we observe that
. Taking logarithms,
and using (3) and (4), we observe that
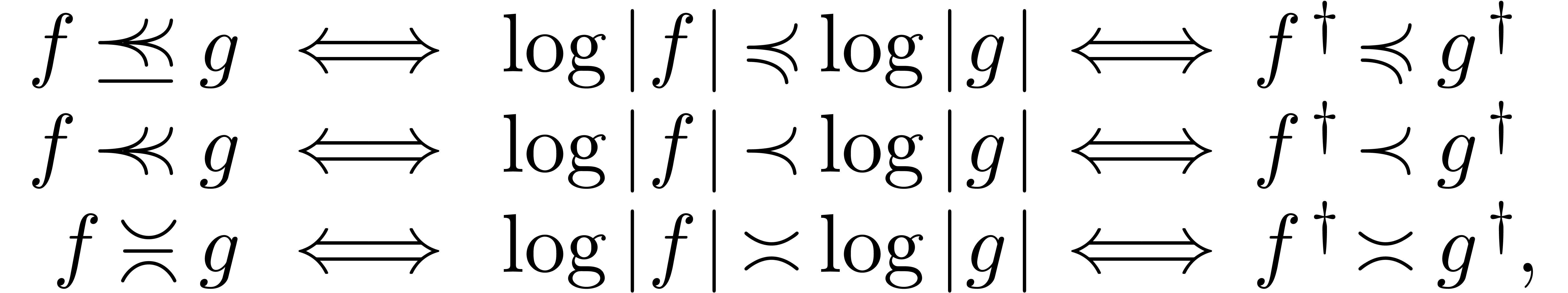
for all  and
and  .
.
An element 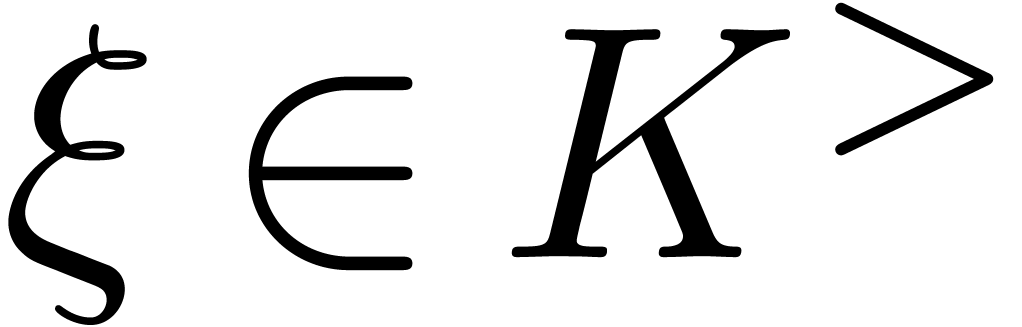 is said to be steep if
is said to be steep if  (whence
(whence  )
for all
)
for all 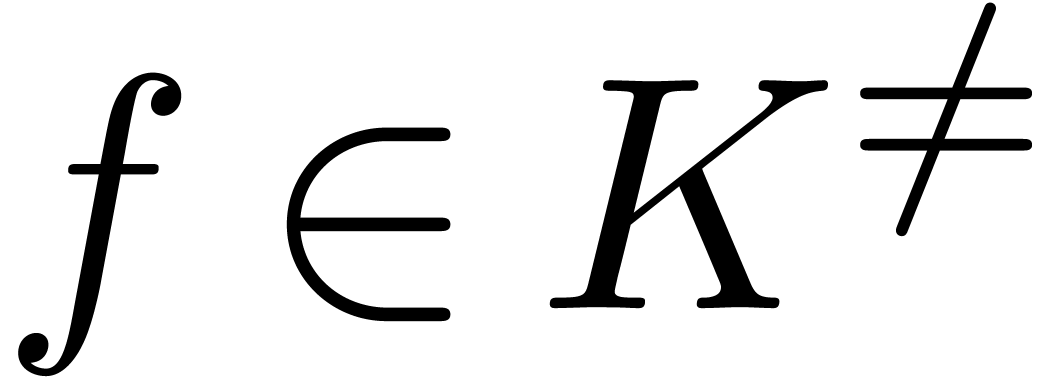 . If
. If  , then this allows us to define a valuation
with respect to
, then this allows us to define a valuation
with respect to  : we set
: we set 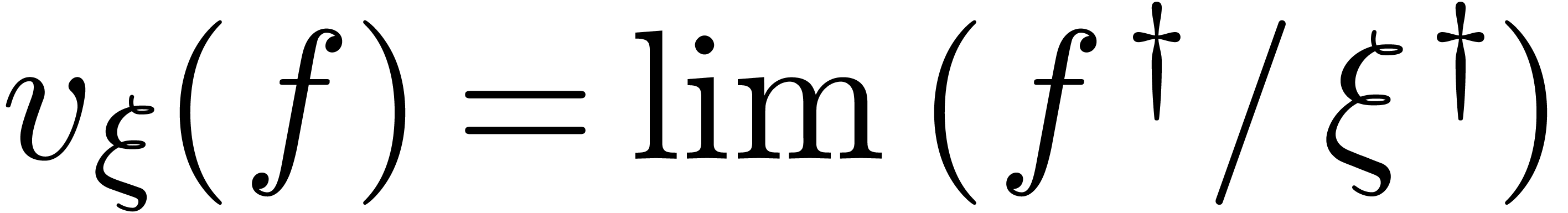 for
for 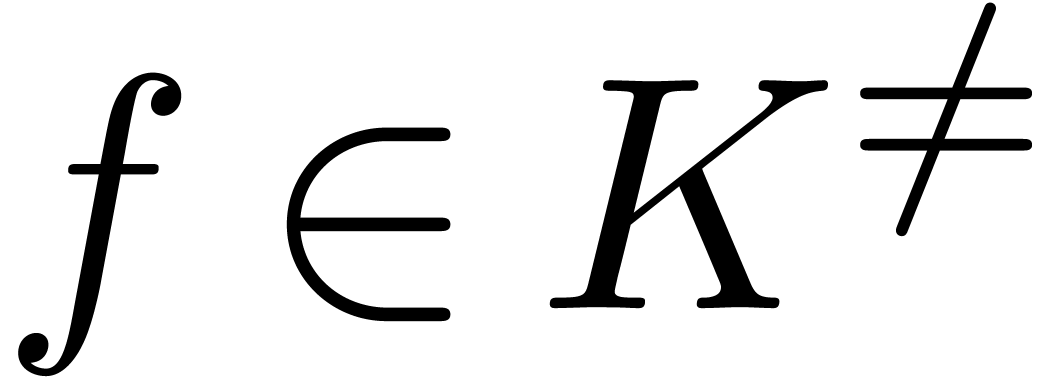 and
and 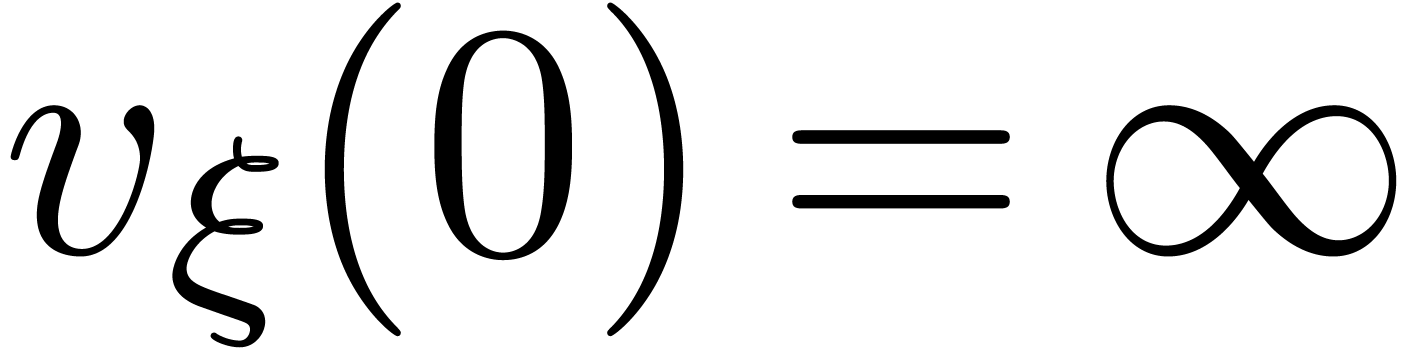 . Notice that the corresponding valuation group
. Notice that the corresponding valuation group
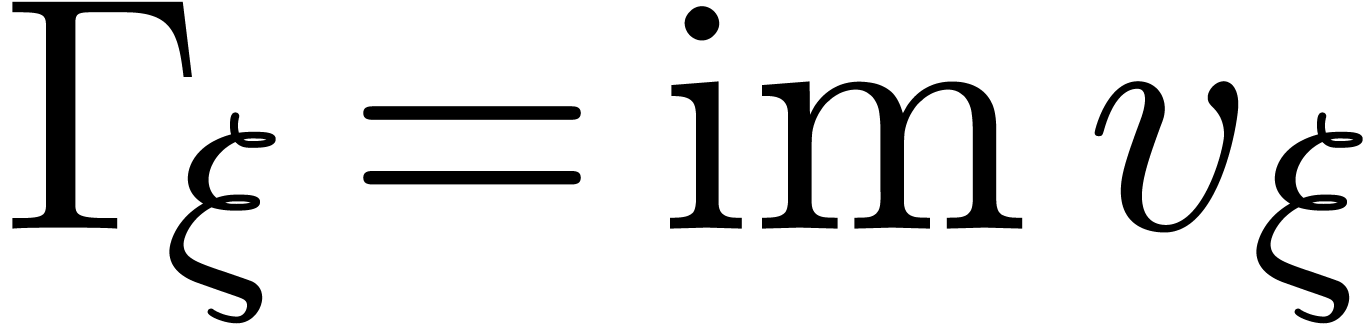 is a subgroup of
is a subgroup of  .
In particular,
.
In particular, 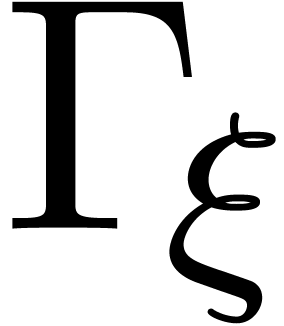 is Archimedean. For
is Archimedean. For 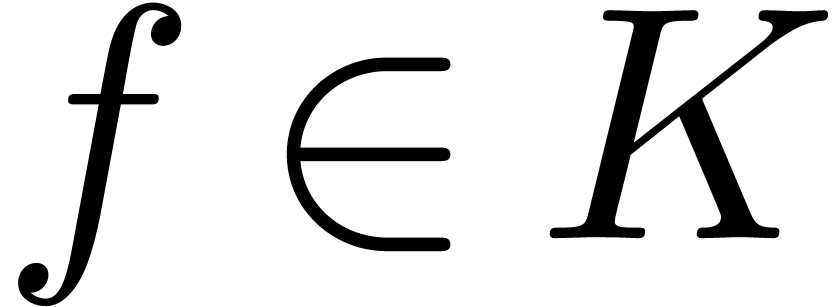 and
and 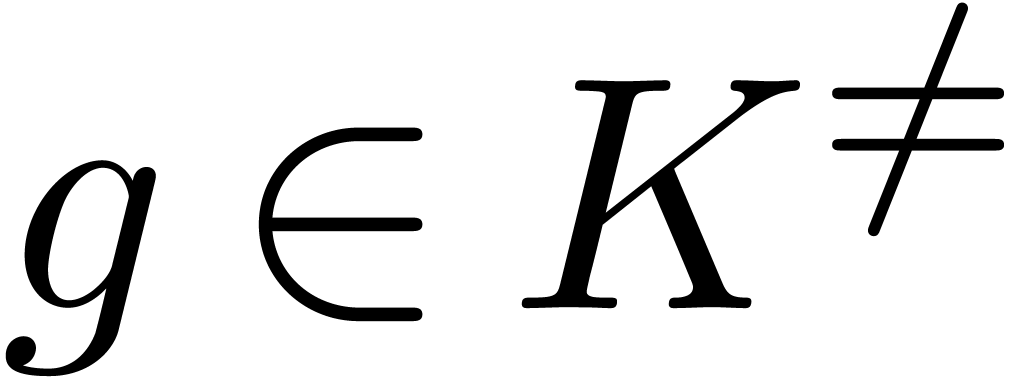 , we notice
that
, we notice
that
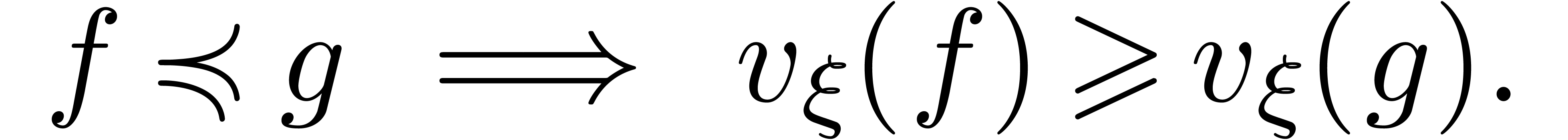
Indeed, since 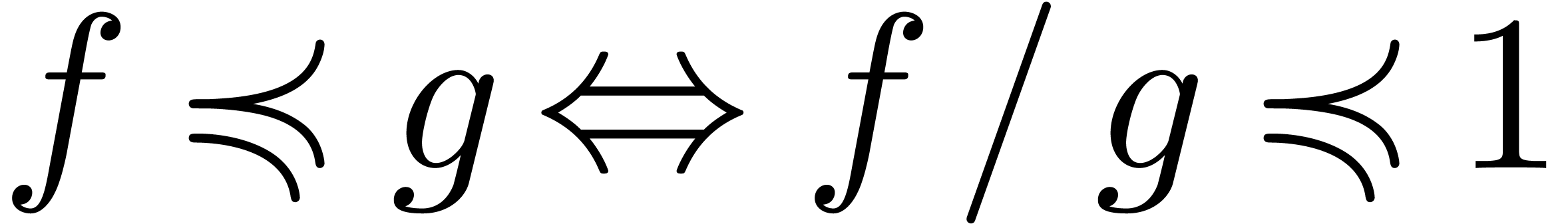 and
and 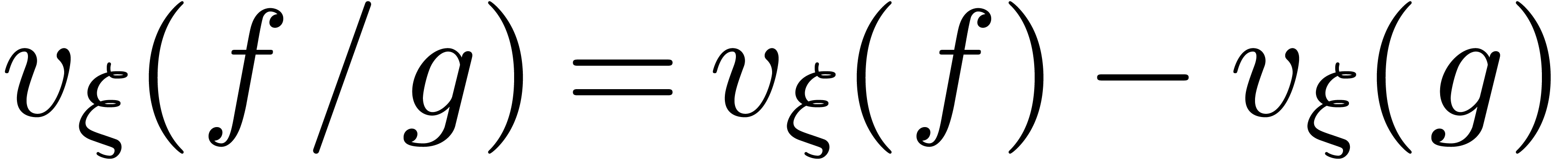 ,
it suffices to show this for
,
it suffices to show this for 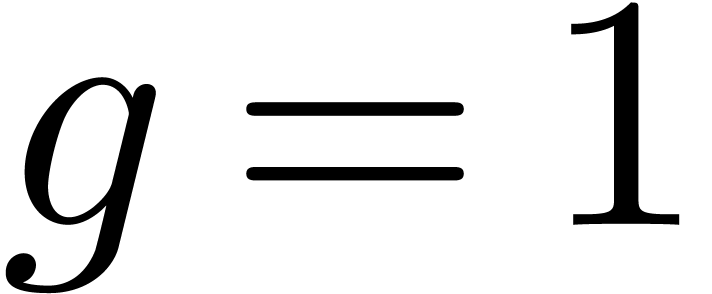 .
Now assume that
.
Now assume that 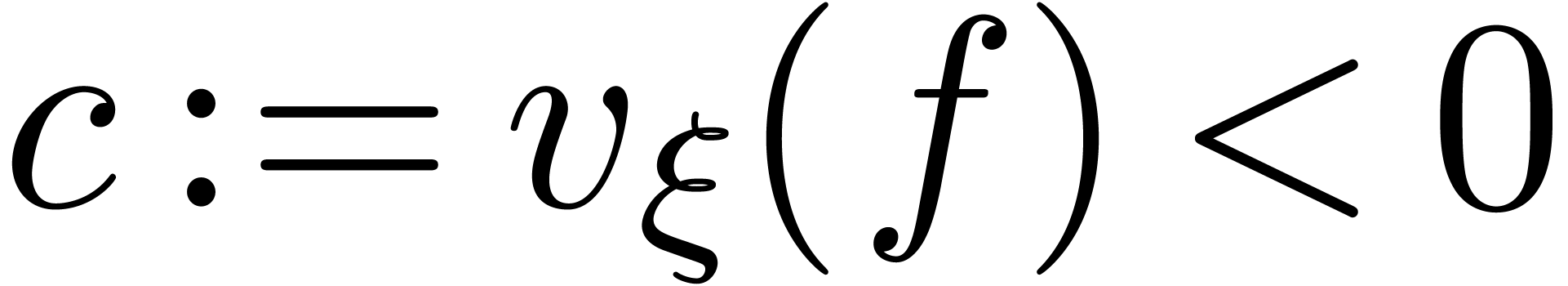 . Then
. Then 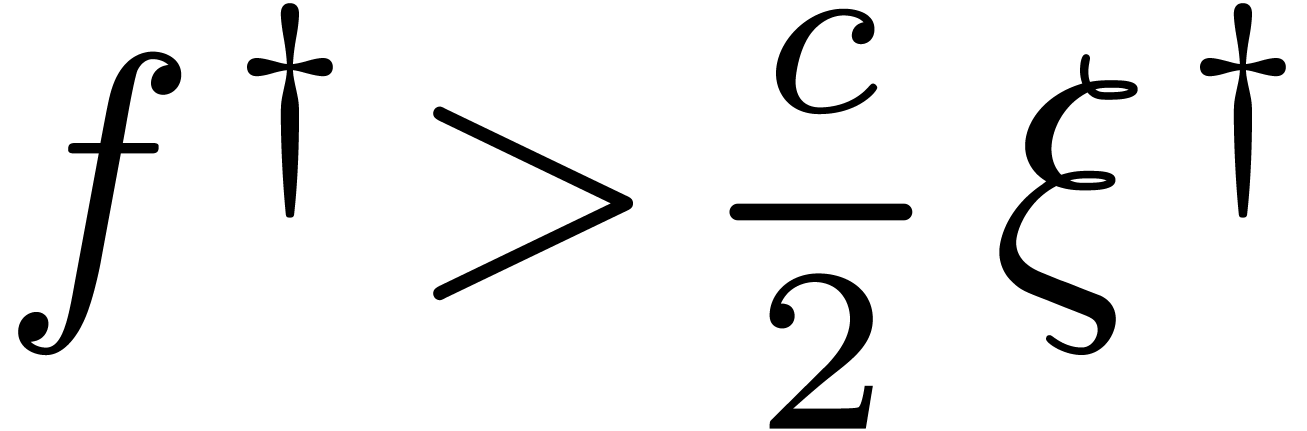 , whence
, whence 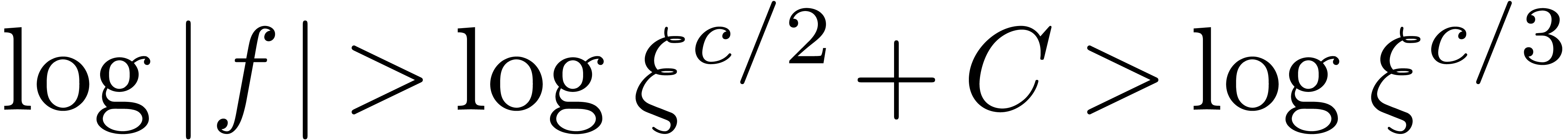 for some constant
for some constant 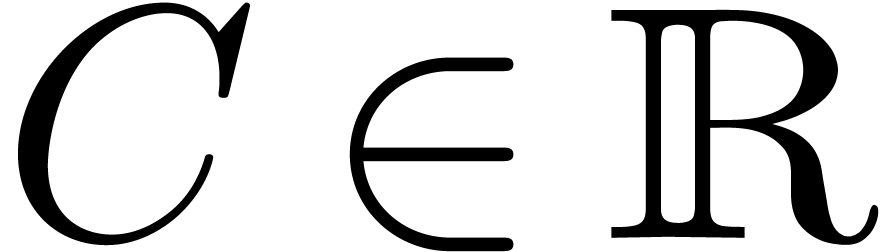 . It
follows that
. It
follows that 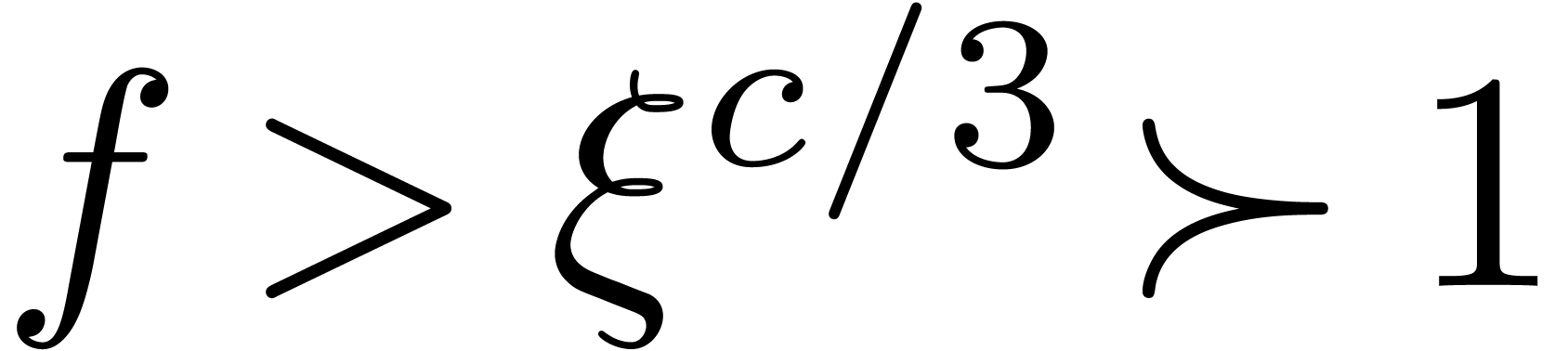 . If
. If  , then we also notice that
, then we also notice that 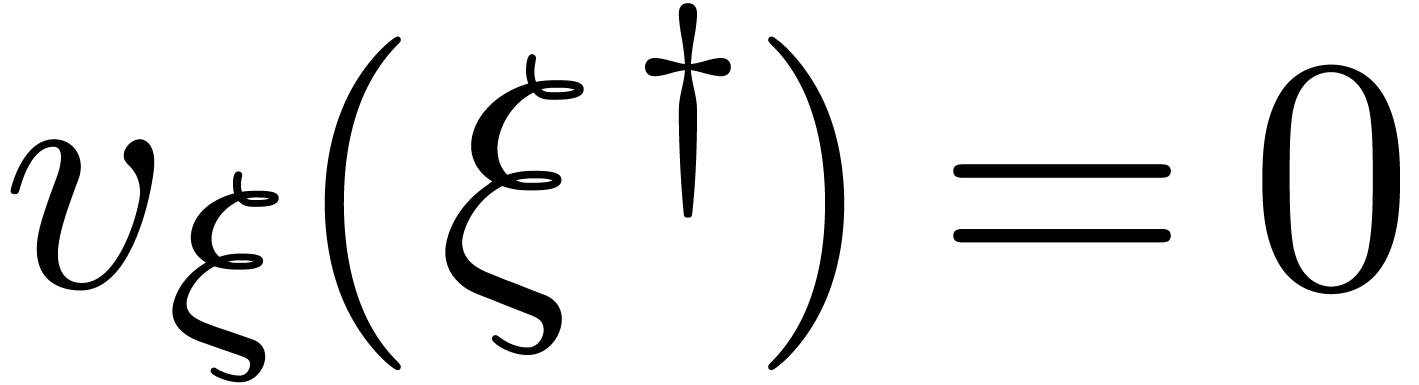 . Indeed,
. Indeed, 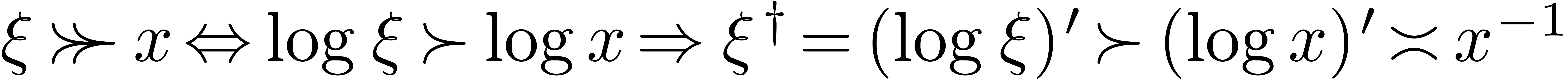 and
and 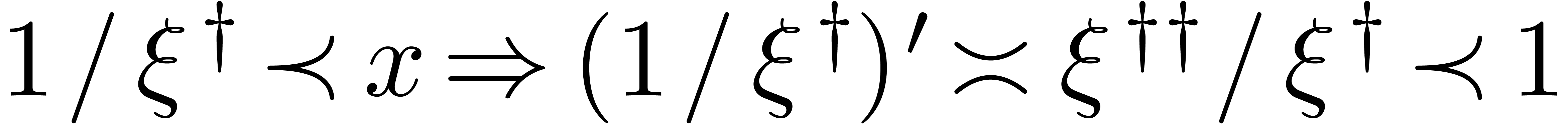 , whence
, whence 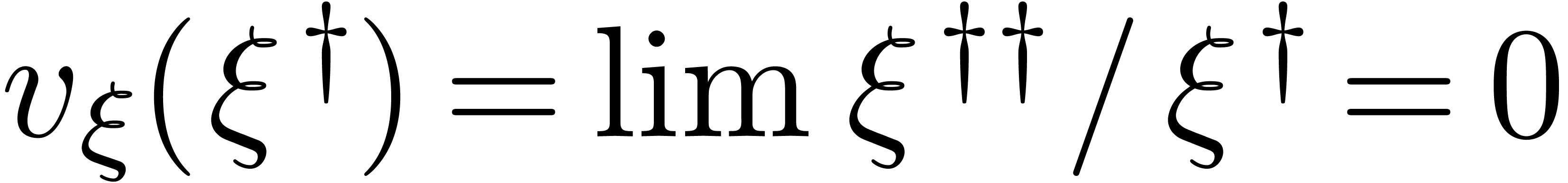 .
.
Two examples of steep elements are 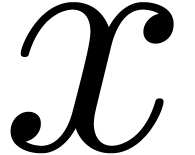 in
in  and
and 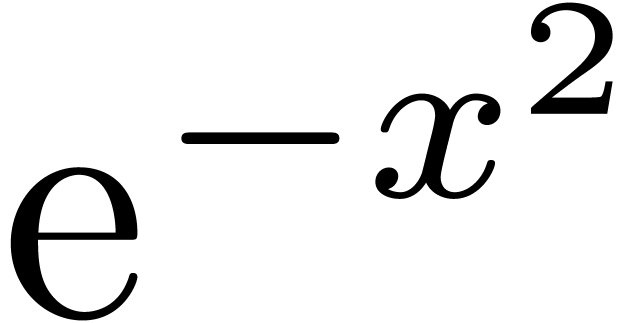 in
in 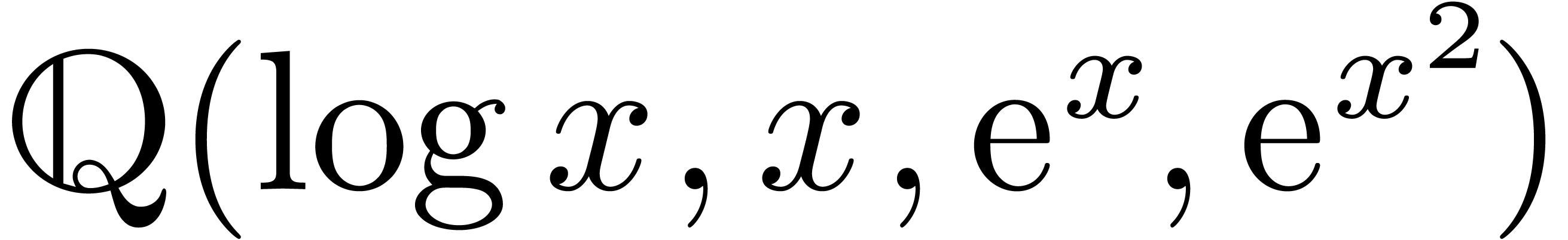 . The aim of the remainder of this section is to
generalize Example 4 and prove in particular that
. The aim of the remainder of this section is to
generalize Example 4 and prove in particular that 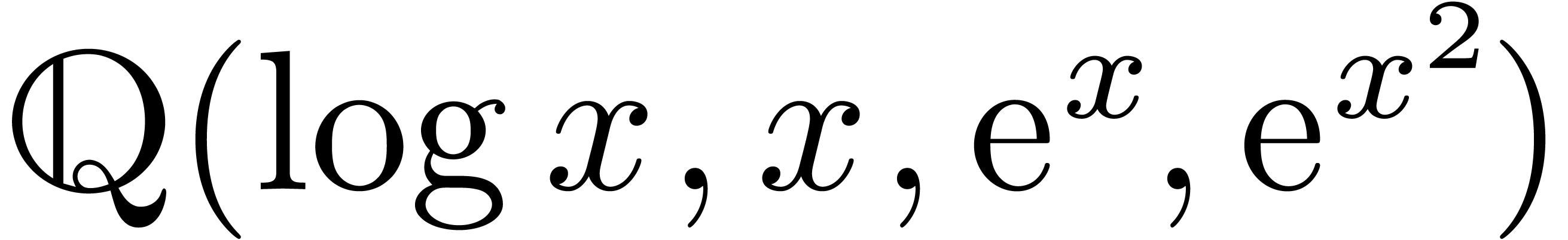 is indeed an effective Hardy field.
is indeed an effective Hardy field.
Let  be an effective Hardy field and let
be an effective Hardy field and let 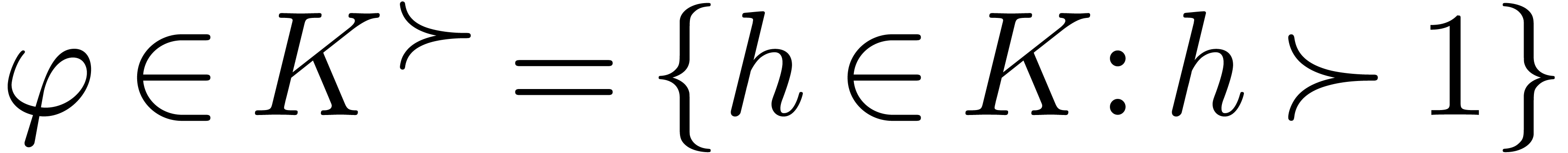 be such that
be such that  for all
for all 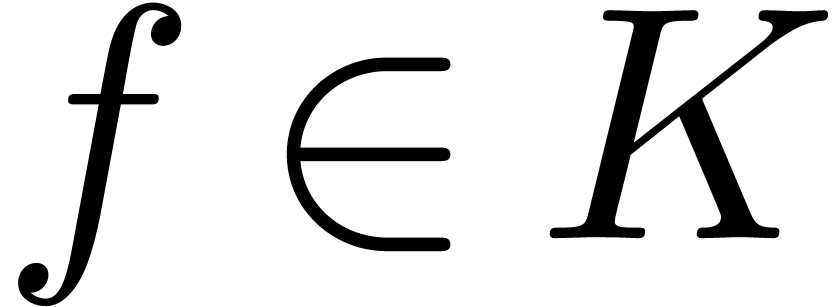 . By what precedes, this implies
that
. By what precedes, this implies
that 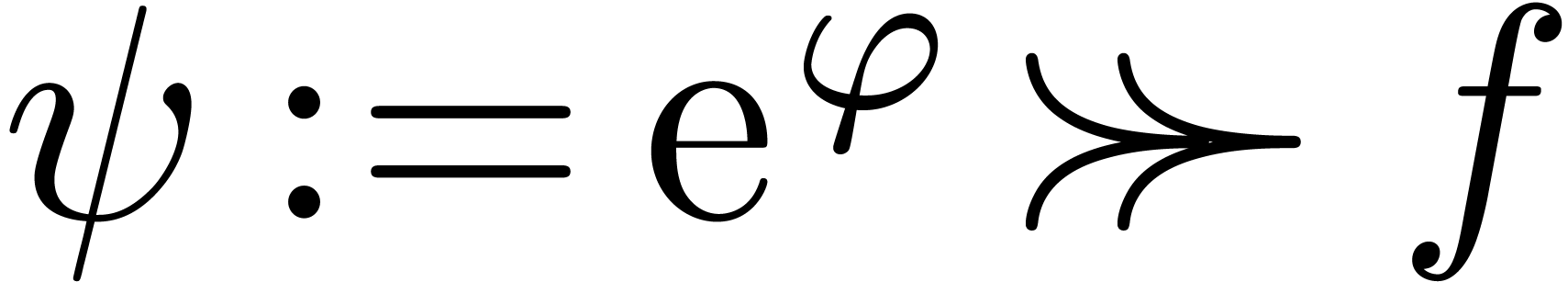 for all
for all 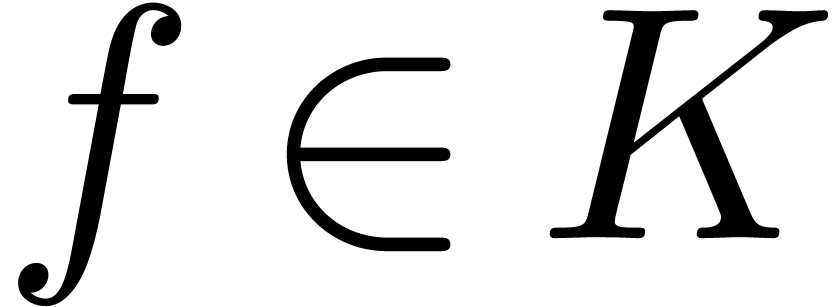 .
We claim that
.
We claim that 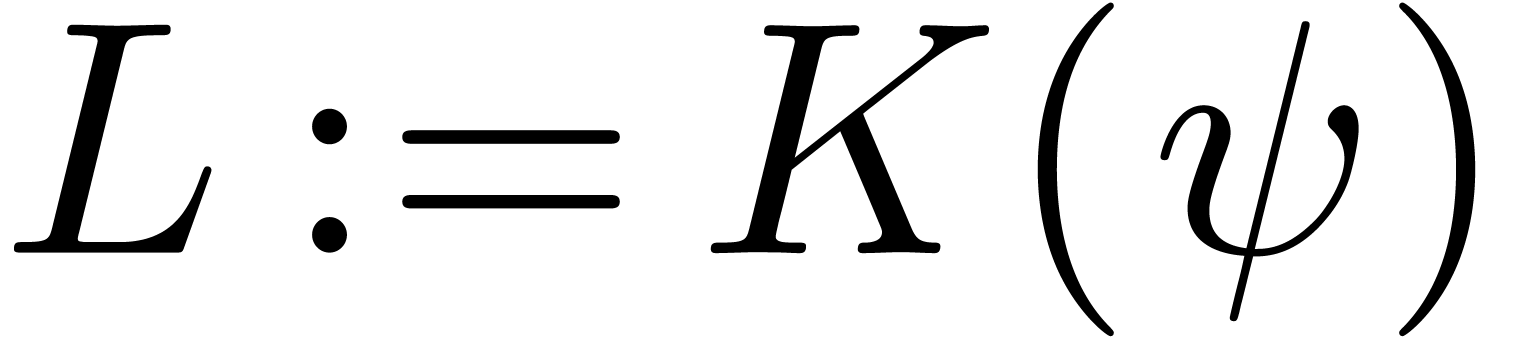 is again an effective Hardy field.
Modulo the replacement of
is again an effective Hardy field.
Modulo the replacement of 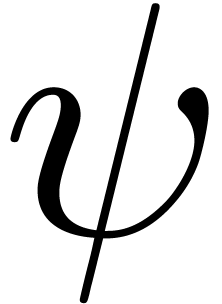 by
by 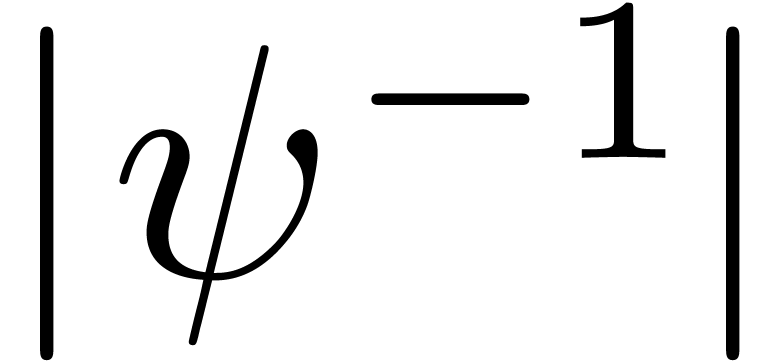 (and
(and  by
by  ),
we may assume without loss of generality that
),
we may assume without loss of generality that 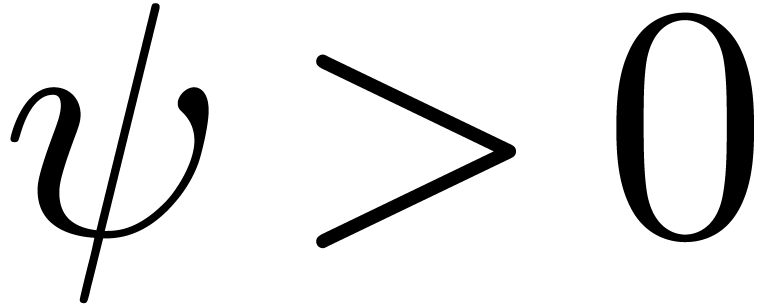 and
and  . We clearly have
algorithms for the field operations of
. We clearly have
algorithms for the field operations of  .
Using the rule
.
Using the rule 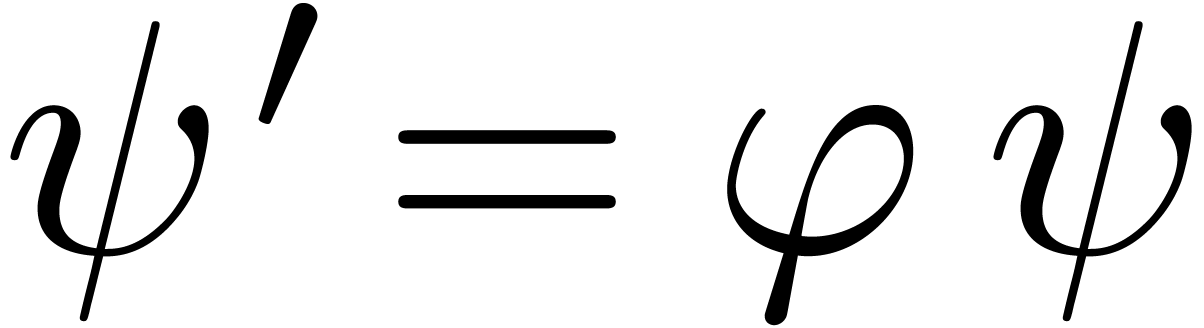 , it is also
straightforward to compute derivatives of elements of
, it is also
straightforward to compute derivatives of elements of  .
.
Now consider a polynomial 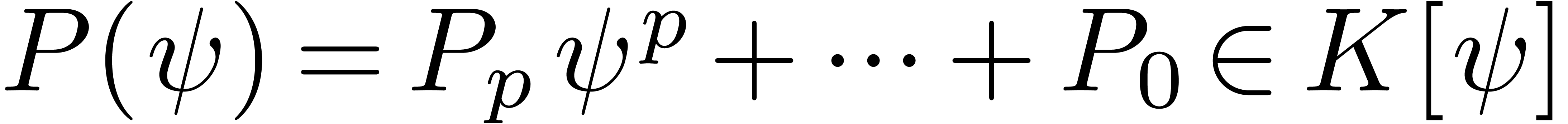 .
If
.
If 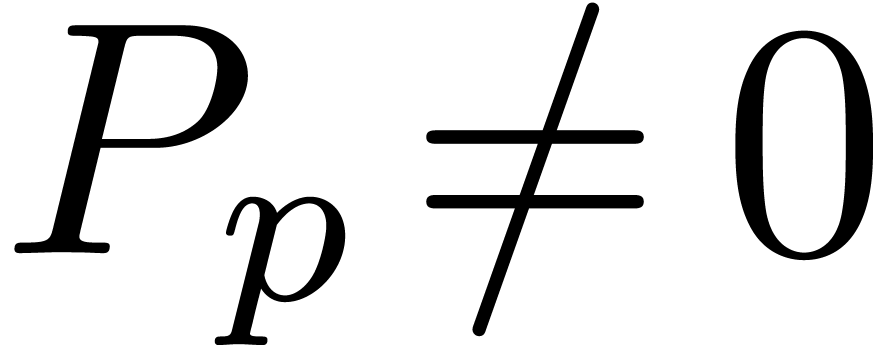 , then for each
, then for each  , we have
, we have  , so that
, so that  .
Hence
.
Hence 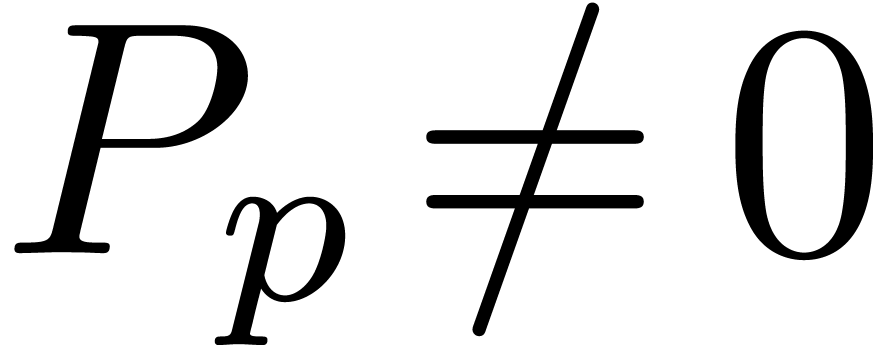 implies
implies  .
This also shows that
.
This also shows that 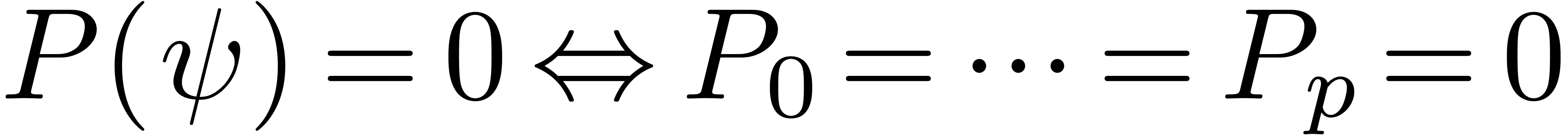 , which
provides us with an effective zero test for
, which
provides us with an effective zero test for 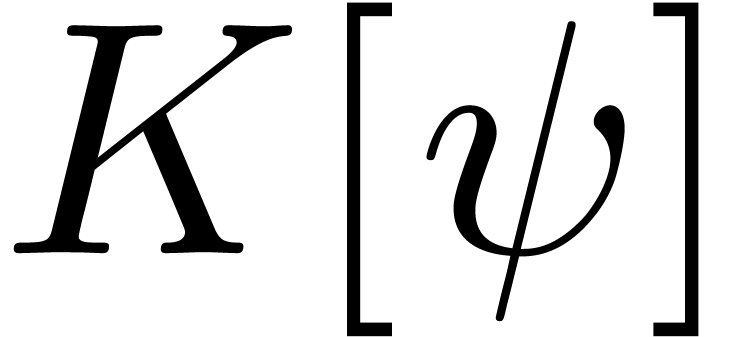 , as well as for
, as well as for  .
Given a rational function
.
Given a rational function 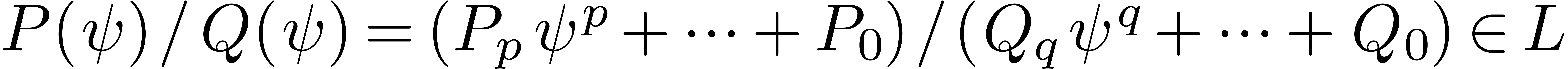 with
with 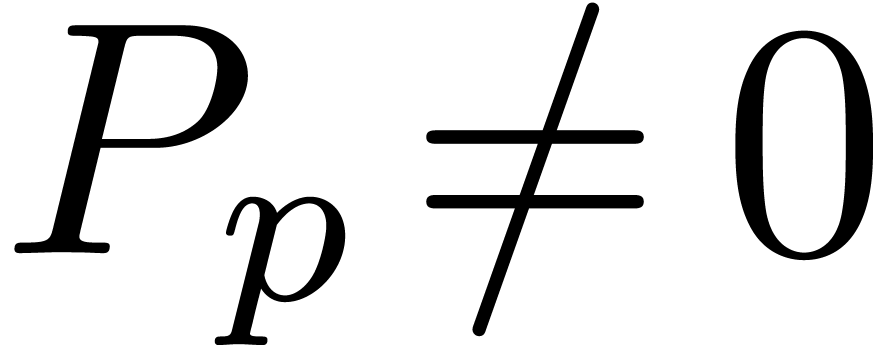 and
and 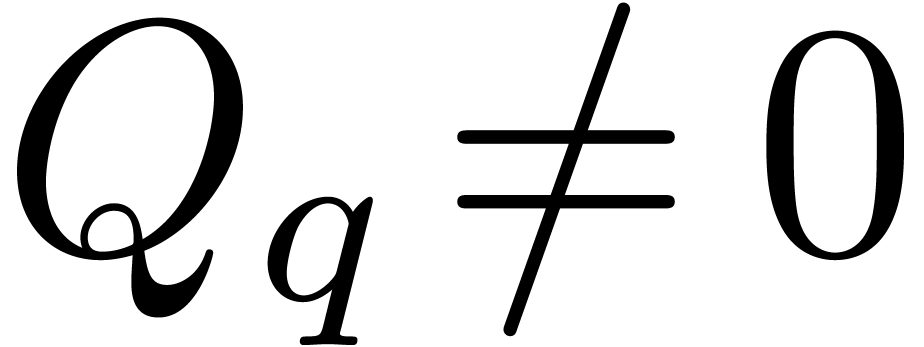 , we also have
, we also have 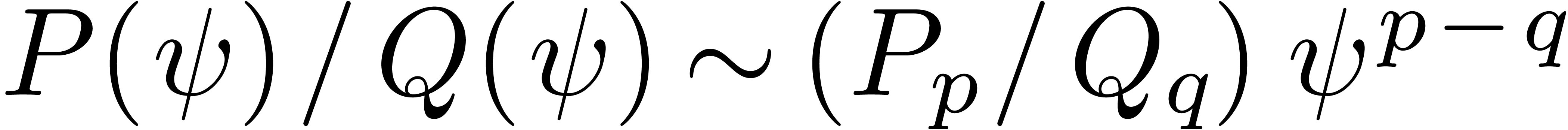 . Consequently,
. Consequently, 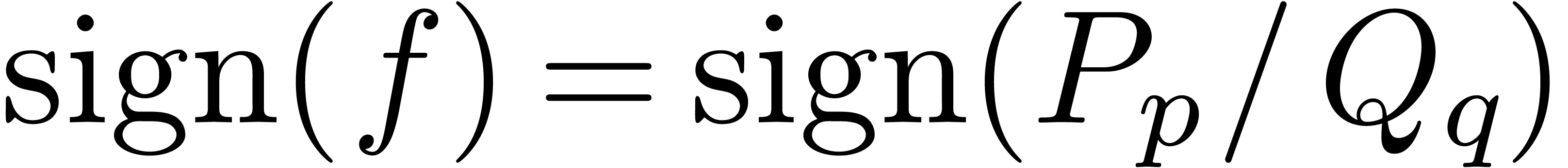 and
and  if and only if
if and only if 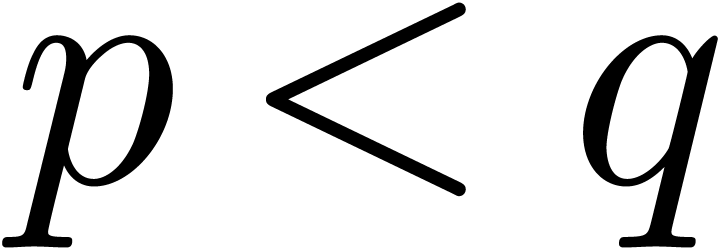 or
or
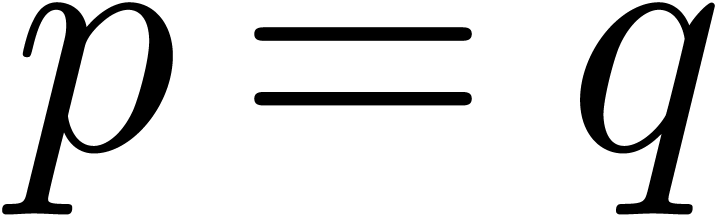 and
and  .
Similarly,
.
Similarly,  if and only if
if and only if  or
or 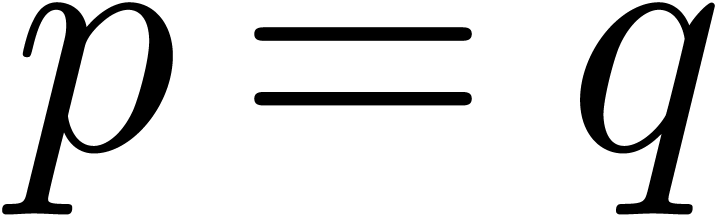 and
and  .
.
Example 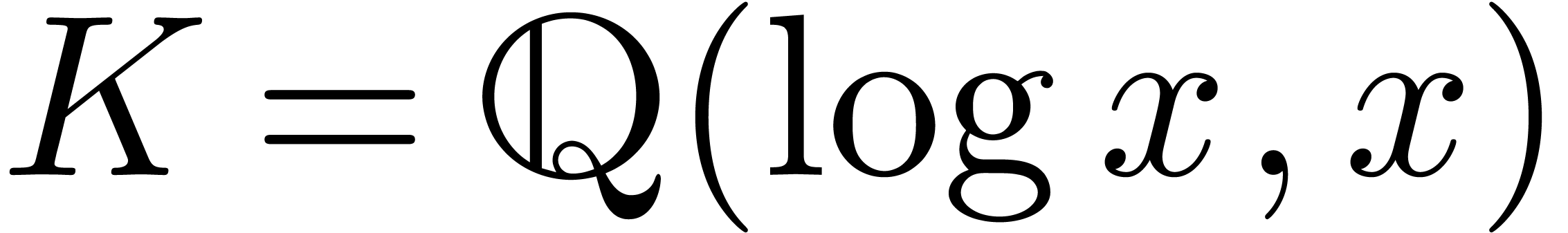 as in Example 4, applying the above
argument twice shows that both
as in Example 4, applying the above
argument twice shows that both 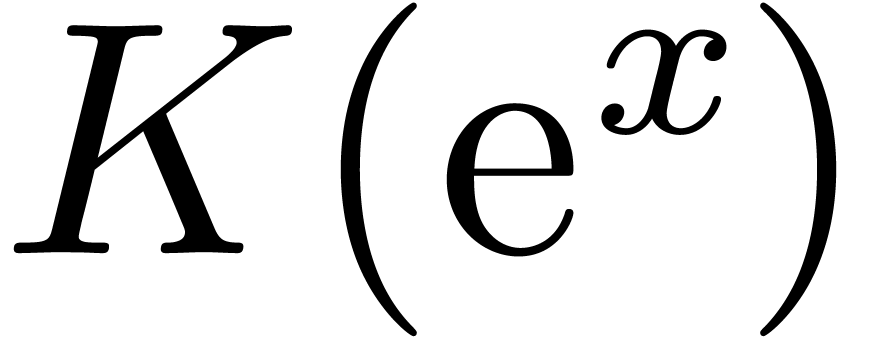 and
and 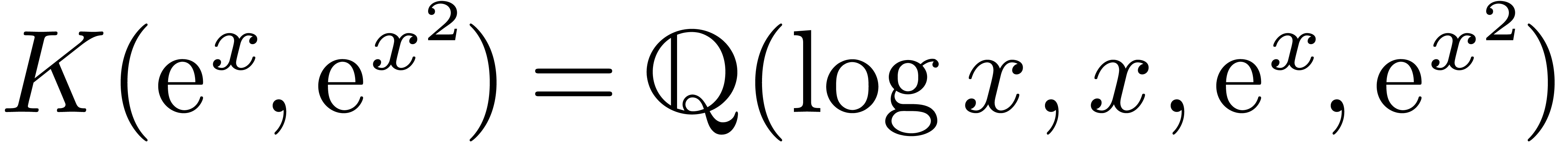 are effective Hardy fields. Applying Example 5
for
are effective Hardy fields. Applying Example 5
for 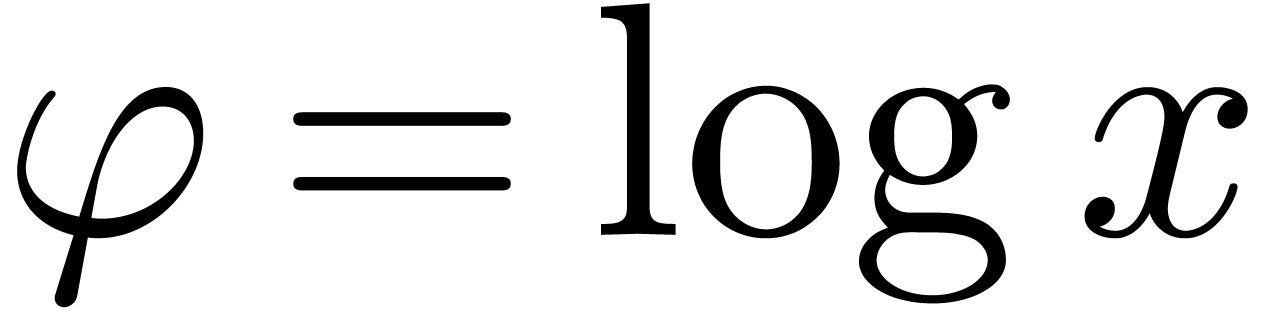 , we also obtain that
, we also obtain that
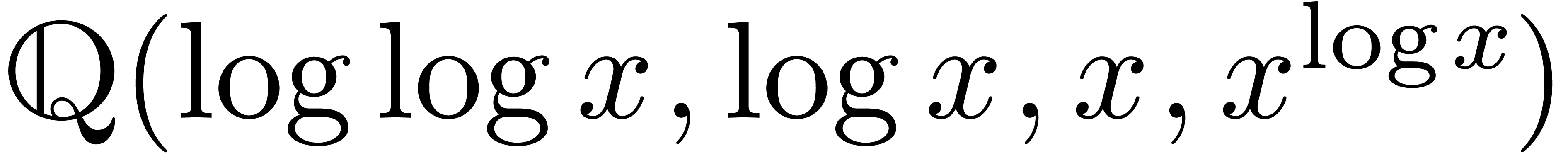 is an effective Hardy field.
is an effective Hardy field.
Remark  ,
one also needs to show that fields such as
,
one also needs to show that fields such as  form
effective Hardy fields. One even more difficult problem is to provide an
effective zero test for exp-log constants, i.e. constants
formed from the rationals, using
form
effective Hardy fields. One even more difficult problem is to provide an
effective zero test for exp-log constants, i.e. constants
formed from the rationals, using  ,
,
 ,
,  ,
,  ,
, 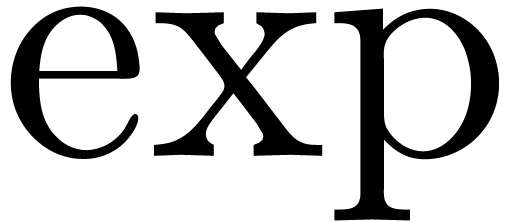 and
and 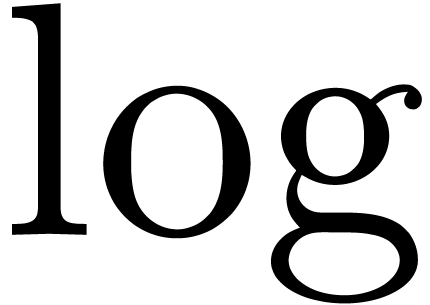 .
Provided that Schanuel's conjecture holds, such an algorithm was given
by Richardson [28]. His algorithm always returns correct
results, but might not terminate if one explicitly hits a counterexample
to the conjecture. Given a zero-test for exp-log constants, it can be
shown that
.
Provided that Schanuel's conjecture holds, such an algorithm was given
by Richardson [28]. His algorithm always returns correct
results, but might not terminate if one explicitly hits a counterexample
to the conjecture. Given a zero-test for exp-log constants, it can be
shown that  forms an effective Hardy field [22].
forms an effective Hardy field [22].
Let  be a Hardy field. Given
be a Hardy field. Given 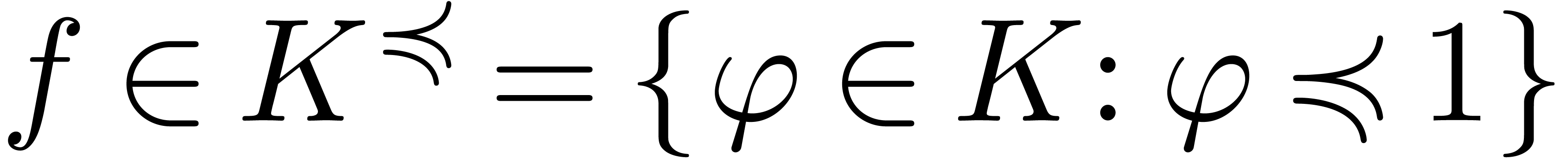 , there exists a unique
, there exists a unique 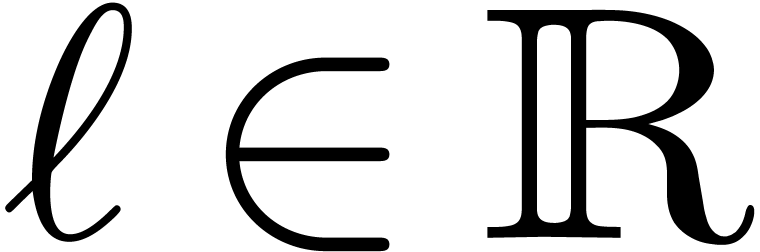 with
with 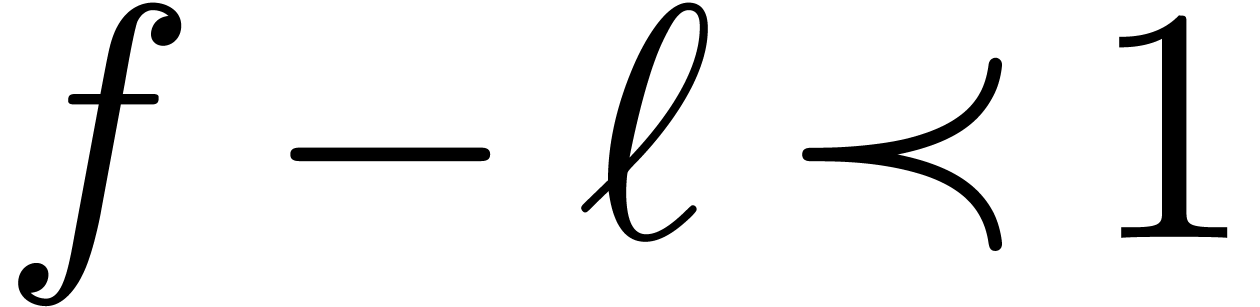 , which is called the
limit of
, which is called the
limit of 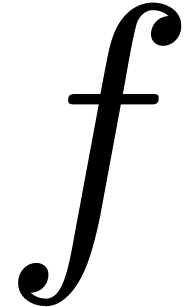 , and
denoted by
, and
denoted by 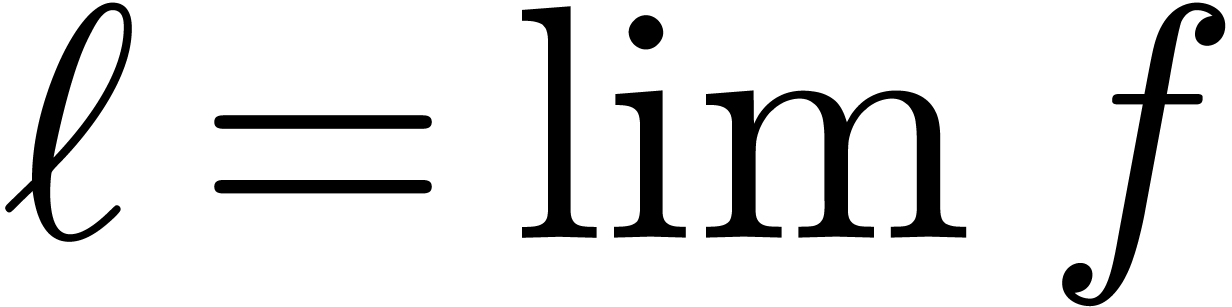 . We say that
. We say that  is closed under limits if
is closed under limits if 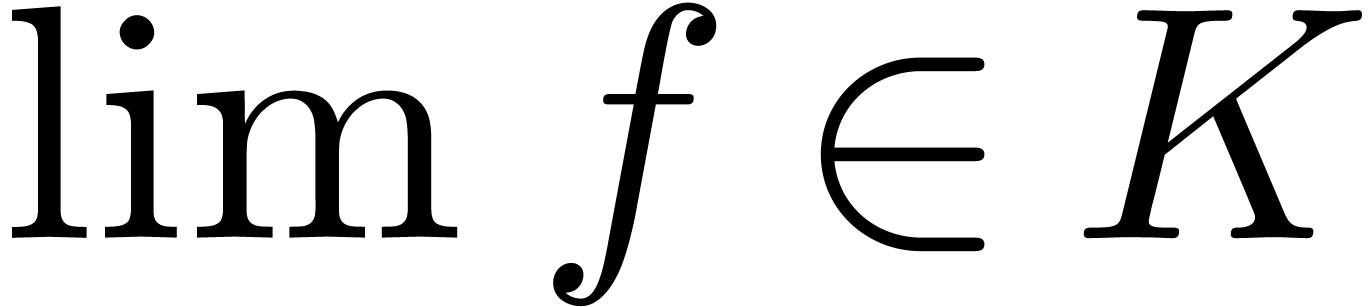 for all
for all 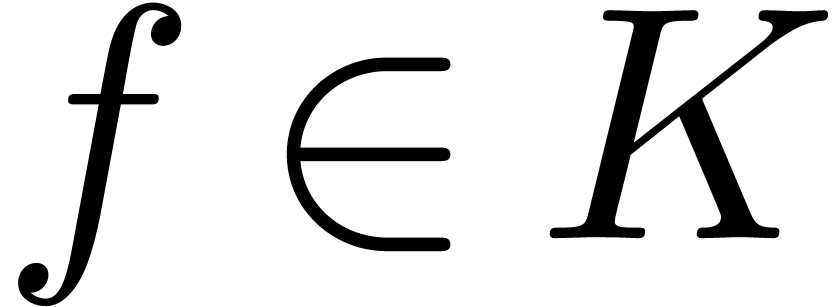 . If
. If  is effective and
is effective and  is computable, then we say that
is computable, then we say that
 admits an effective limit map.
admits an effective limit map.
An asymptotic scale for  is a
multiplicative subgroup
is a
multiplicative subgroup 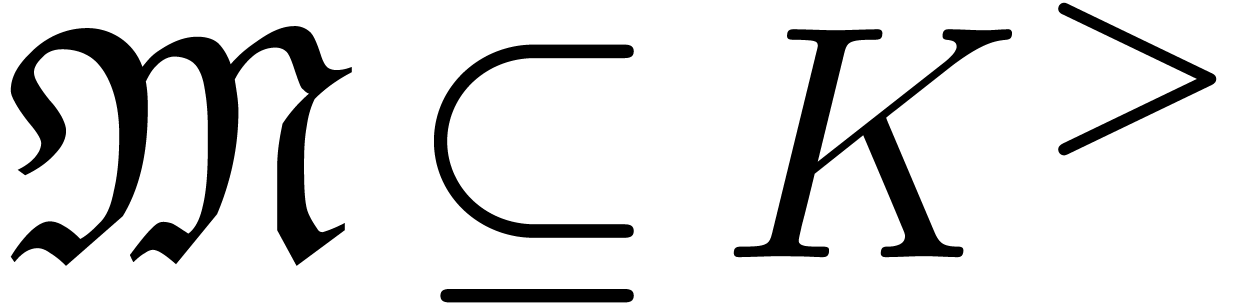 such that
such that  is totally ordered for
is totally ordered for  and such
that there exists a mapping
and such
that there exists a mapping 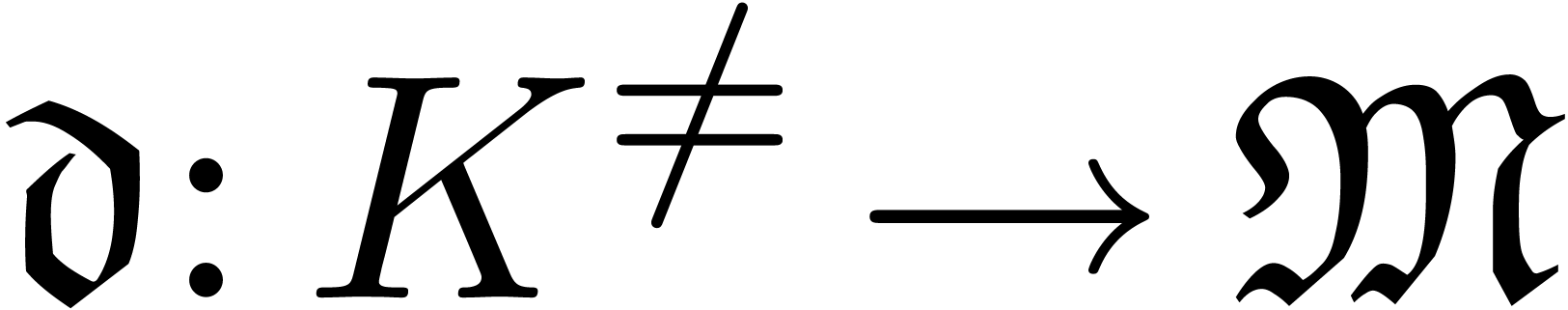 with
with 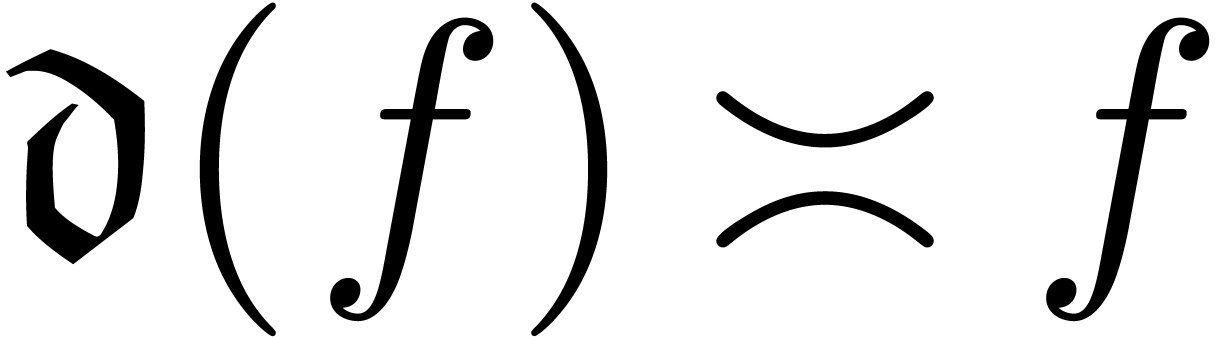 for all
for all  . We
call
. We
call 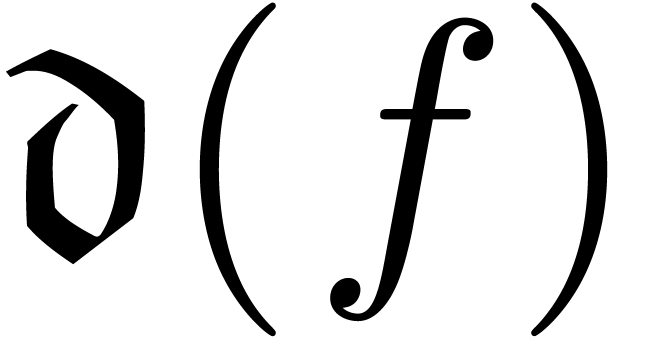 the dominant monomial of
the dominant monomial of  and notice that
and notice that  is necessarily a
group homomorphism. If
is necessarily a
group homomorphism. If  is effective and
is effective and  is computable, then we call
is computable, then we call  an effective asymptotic scale.
an effective asymptotic scale.
Assume that  is closed under limits and that
is closed under limits and that  also admits an asymptotic scale
also admits an asymptotic scale  . Given
. Given 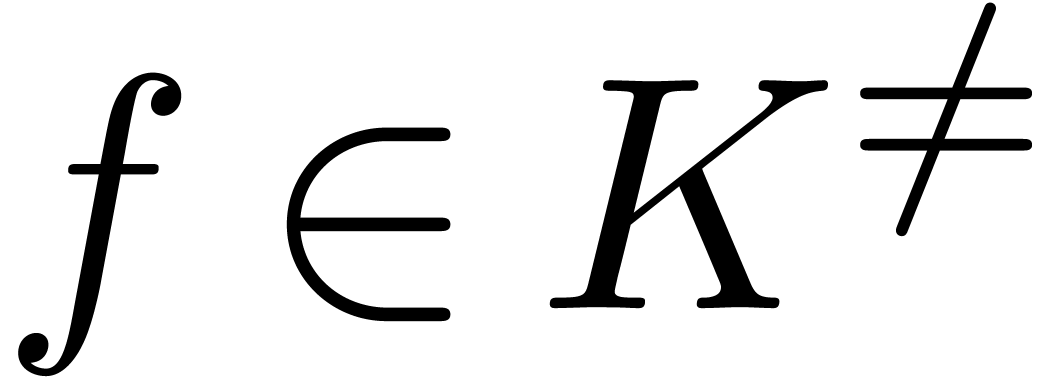 ,
we call
,
we call 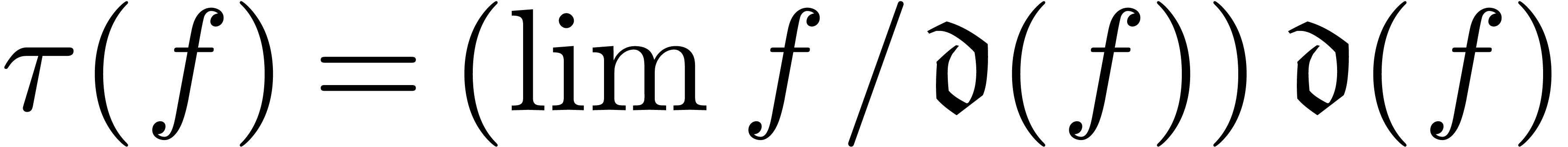 the dominant term of
the dominant term of  , and notice that
, and notice that 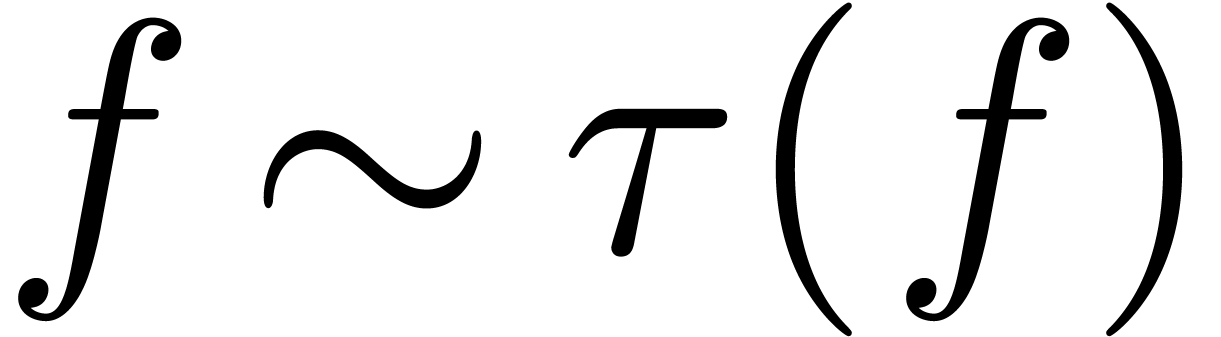 . If
. If  and
and  are both computable, then the same clearly holds for
are both computable, then the same clearly holds for  .
.
Example 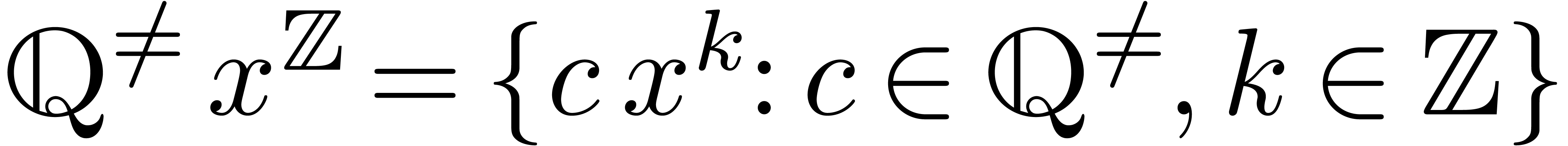 for any
for any 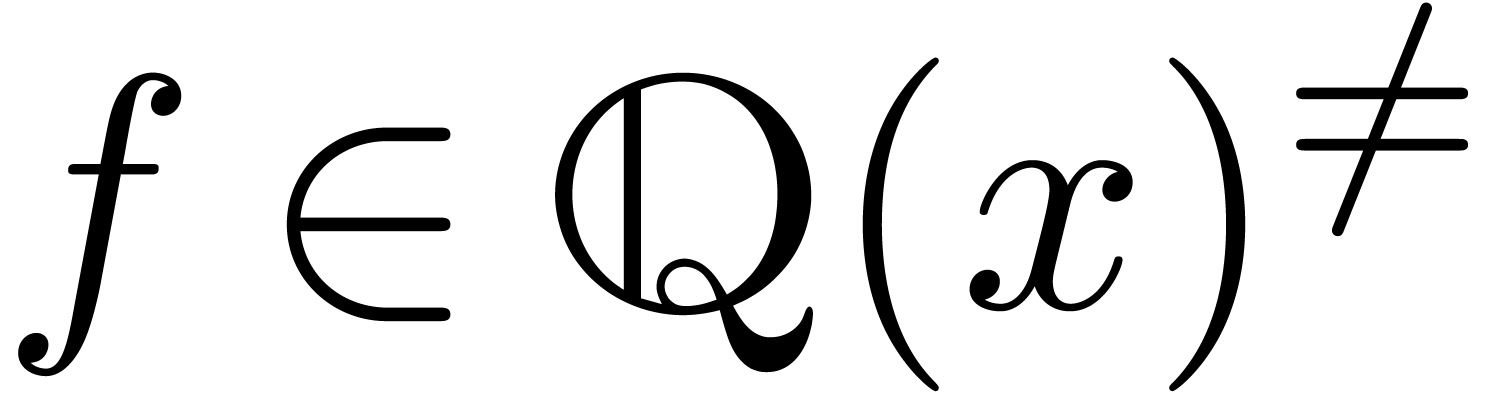 .
This both shows that
.
This both shows that 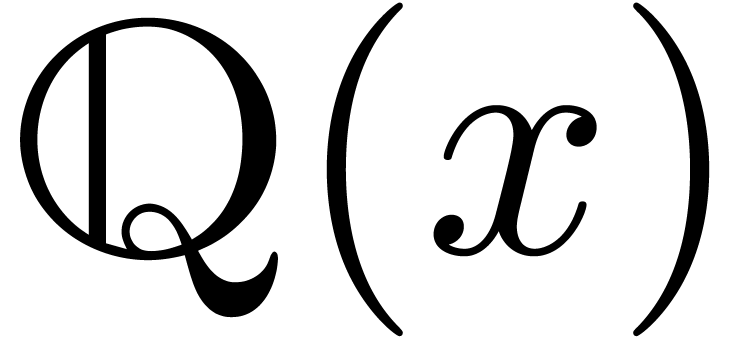 admits an effective limit
map and that it admits
admits an effective limit
map and that it admits 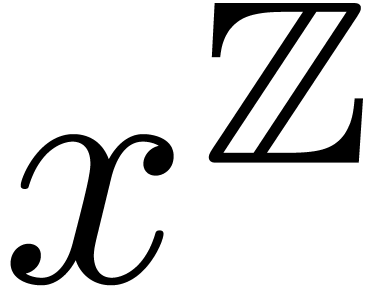 as an effective
asymptotic scale. Similarly, Example 4 shows that the same
holds for
as an effective
asymptotic scale. Similarly, Example 4 shows that the same
holds for 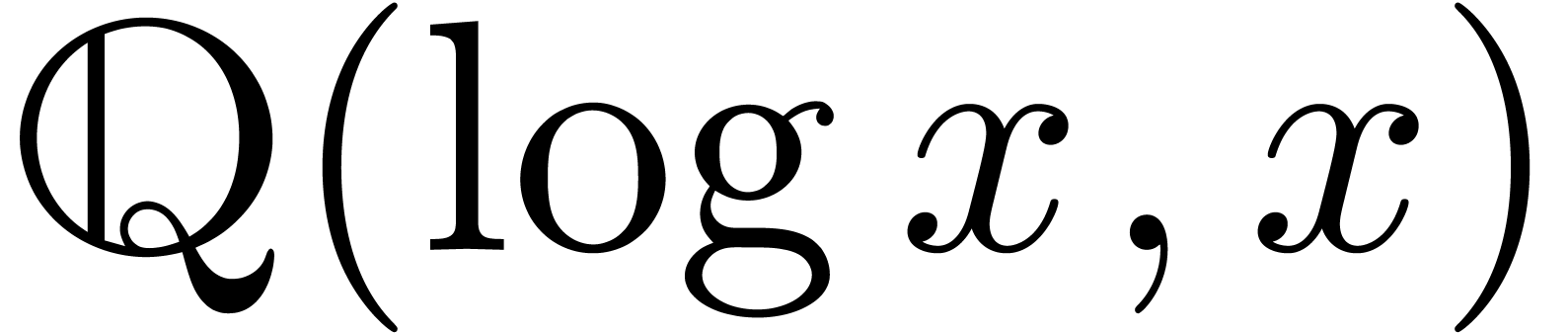 , in which case the
asymptotic scale becomes
, in which case the
asymptotic scale becomes 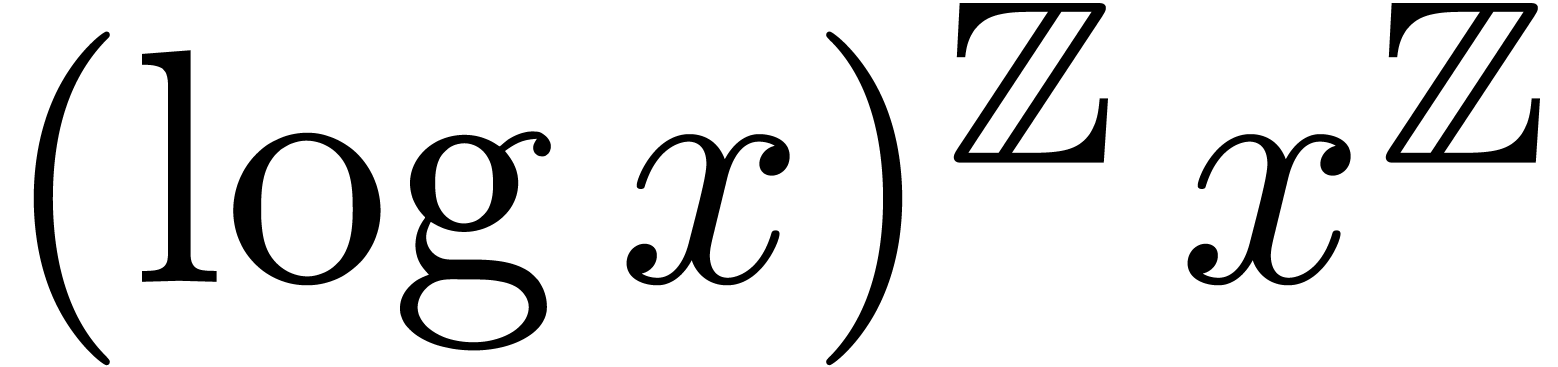 .
.
More generally, let 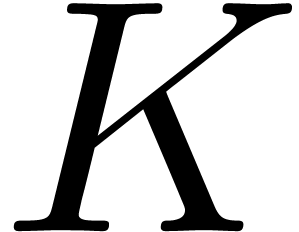 be an effective Hardy field
and let
be an effective Hardy field
and let  be as in Section 2.4.
Assume that
be as in Section 2.4.
Assume that 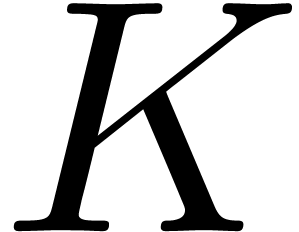 admits an effective limit map and
that
admits an effective limit map and
that  is an effective asymptotic scale. For each
is an effective asymptotic scale. For each
 , we have shown how to
compute an equivalent
, we have shown how to
compute an equivalent  with
with  and
and  . Since
. Since 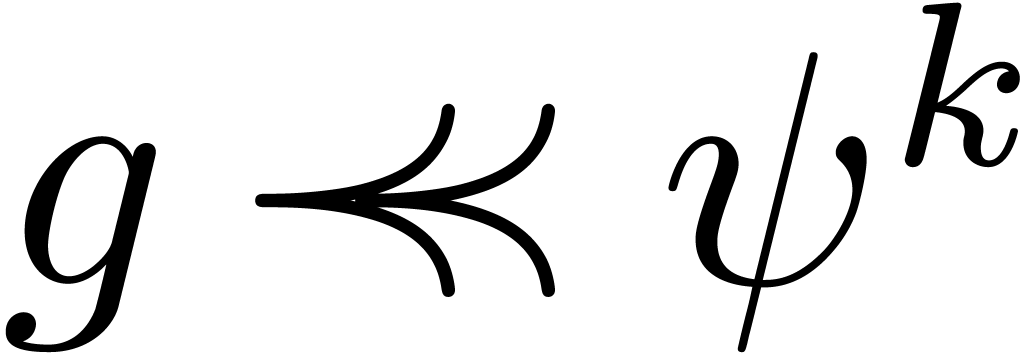 for any
for any 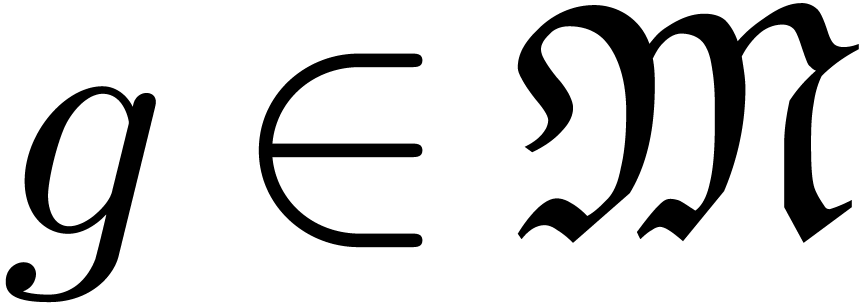 and
and 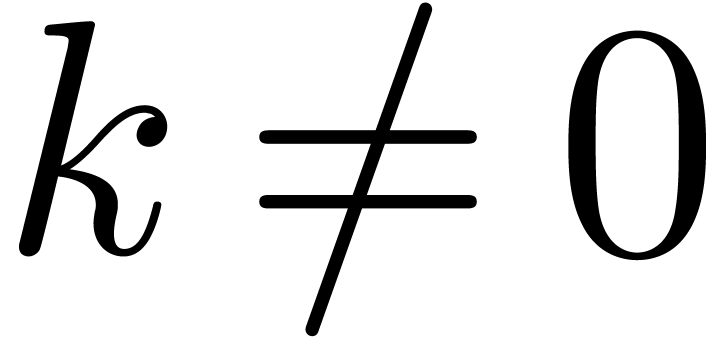 ,
the group
,
the group 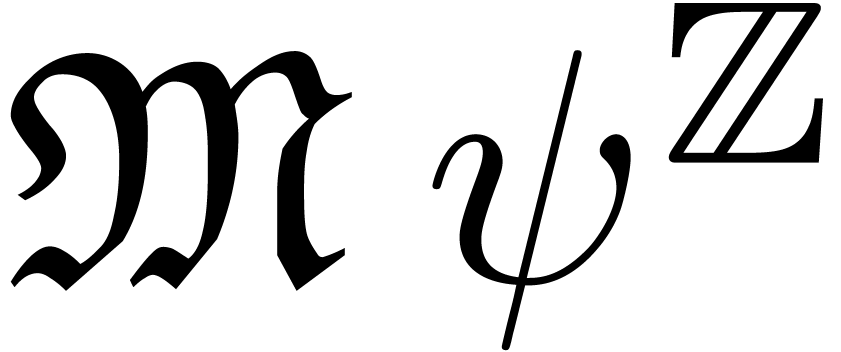 is totally ordered for
is totally ordered for  . This shows that
. This shows that 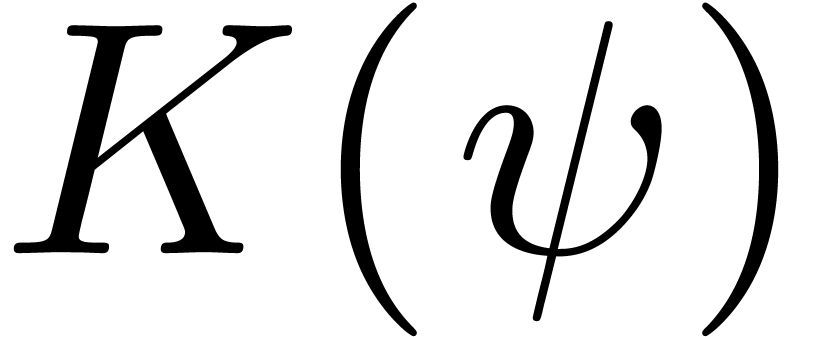 admits both an effective limit map and an effective asymptotic scale
admits both an effective limit map and an effective asymptotic scale
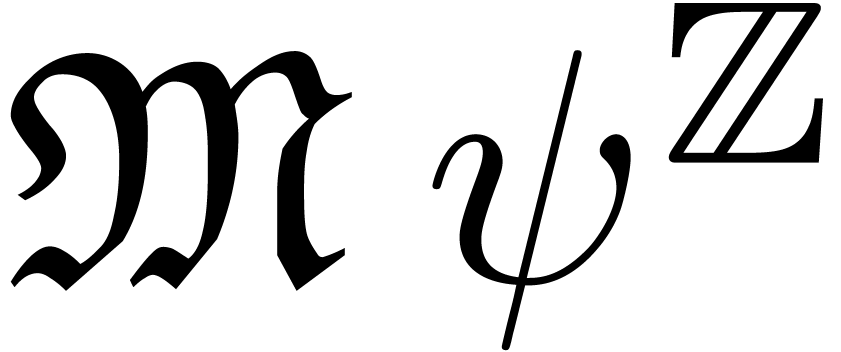 .
.
Example 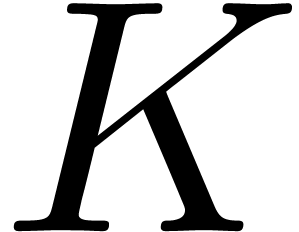 be an effective Hardy field and let
be an effective Hardy field and let  be as in
Example 5. If
be as in
Example 5. If 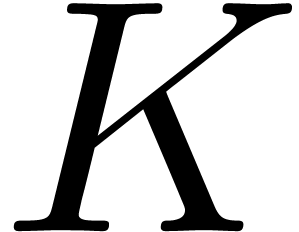 admits an effective
limit map, then so does
admits an effective
limit map, then so does  ,
since
,
since 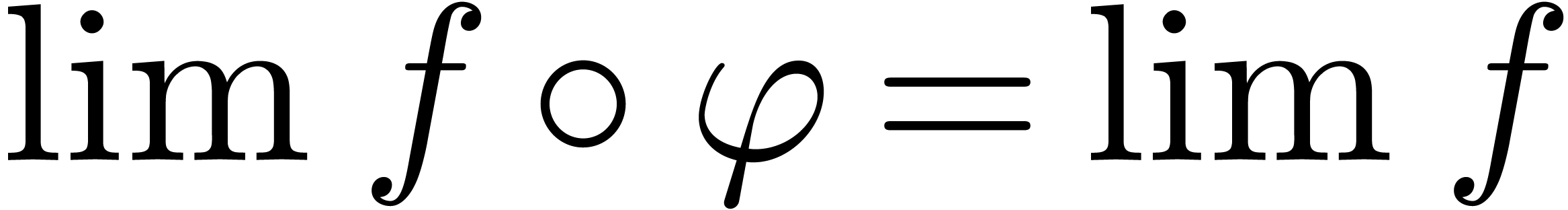 for all
for all  .
If
.
If  admits an effective asymptotic scale
admits an effective asymptotic scale  , then
, then  admits
admits  as an effective asymptotic scale, with
as an effective asymptotic scale, with
 for all
for all 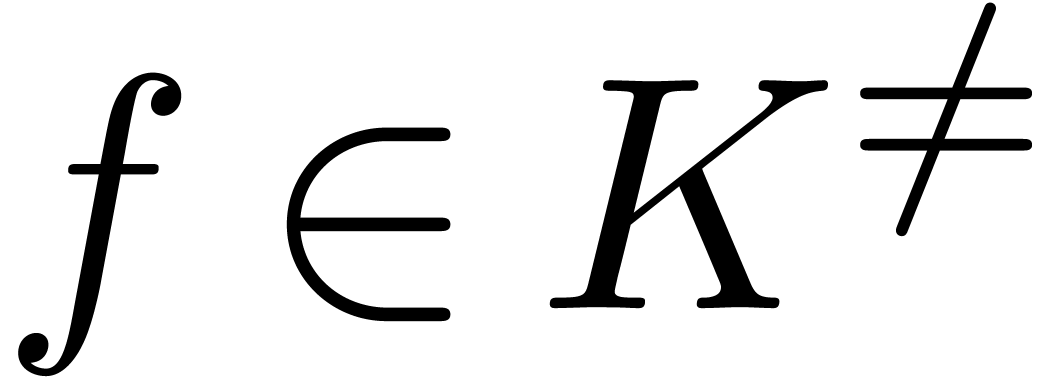 .
.
Let  be a Hardy field which contains the identity
function
be a Hardy field which contains the identity
function 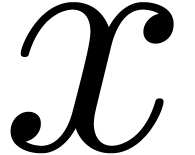 , as well as a steep
element
, as well as a steep
element 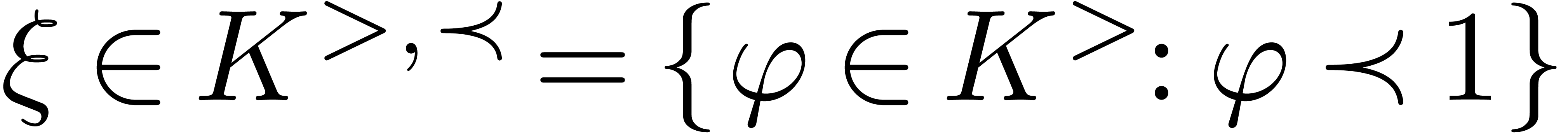 . If
. If  , then also assume that
, then also assume that 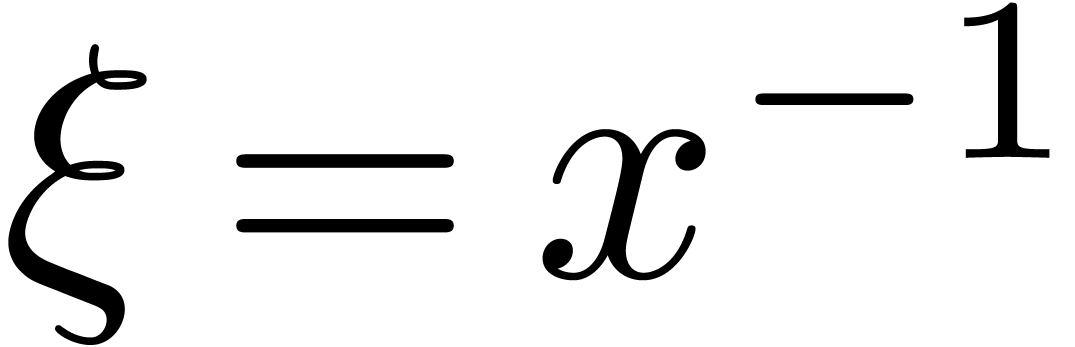 .
.
An element 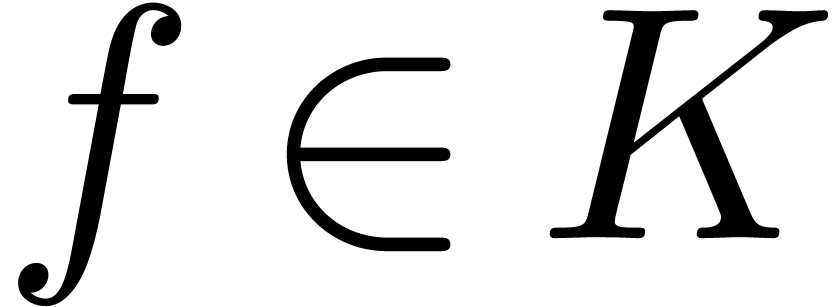 is said to be highly tangent to
identity if there exists a
is said to be highly tangent to
identity if there exists a  with
with 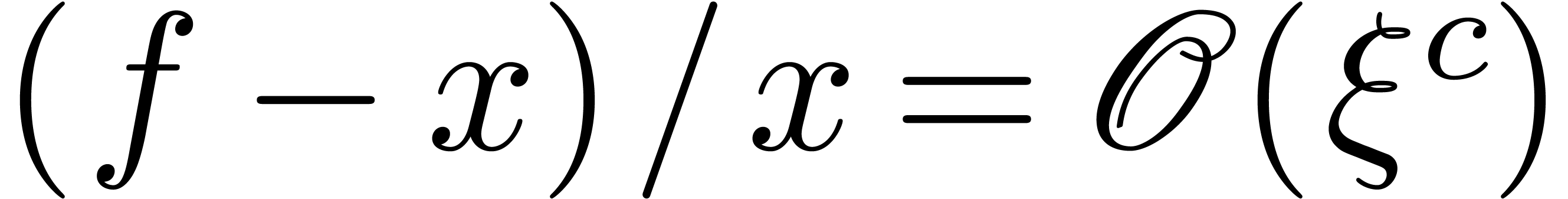 . Equivalently, this means that
. Equivalently, this means that
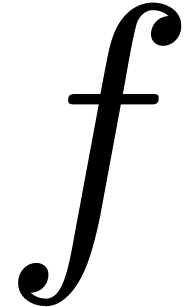 is of the form
is of the form 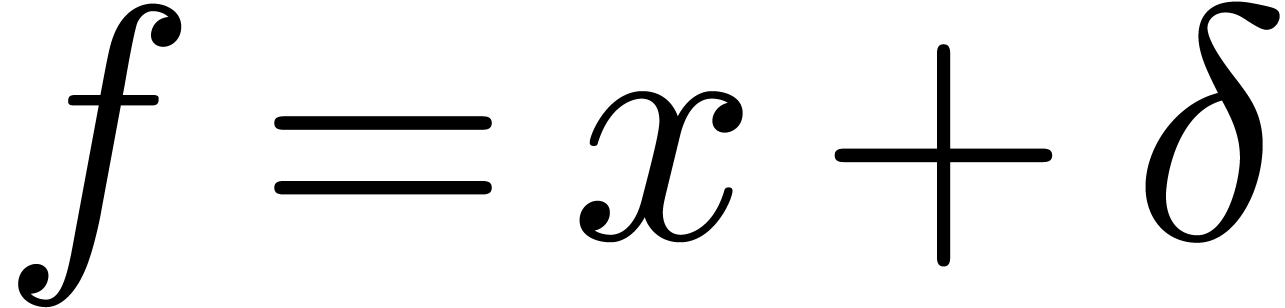 with
with
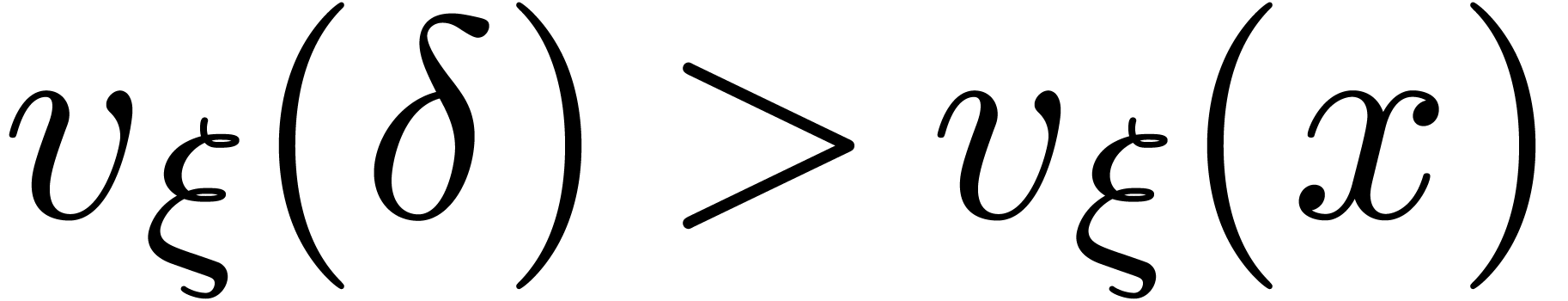 . If
. If 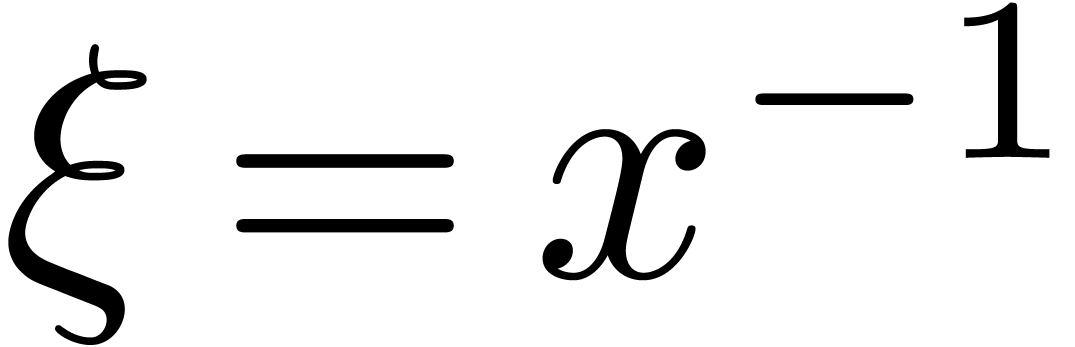 , then this is the case when
, then this is the case when 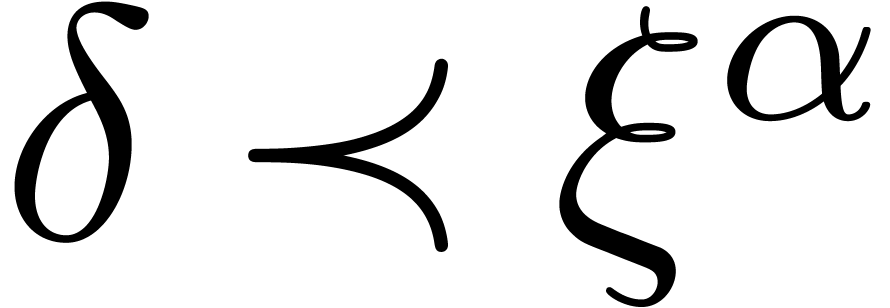 for some
for some 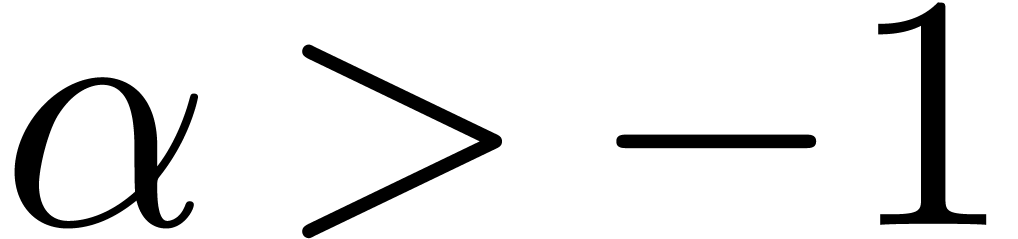 . If
. If  , then we rather should have
, then we rather should have 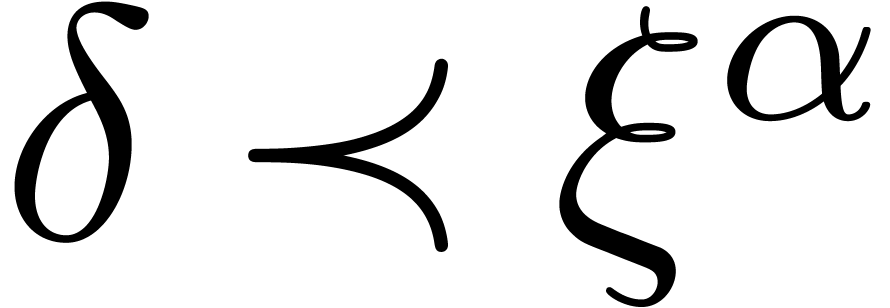 for some
for some 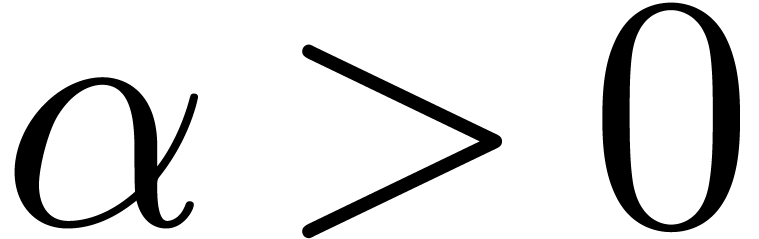 . In particular, in
both cases we have
. In particular, in
both cases we have  and even
and even 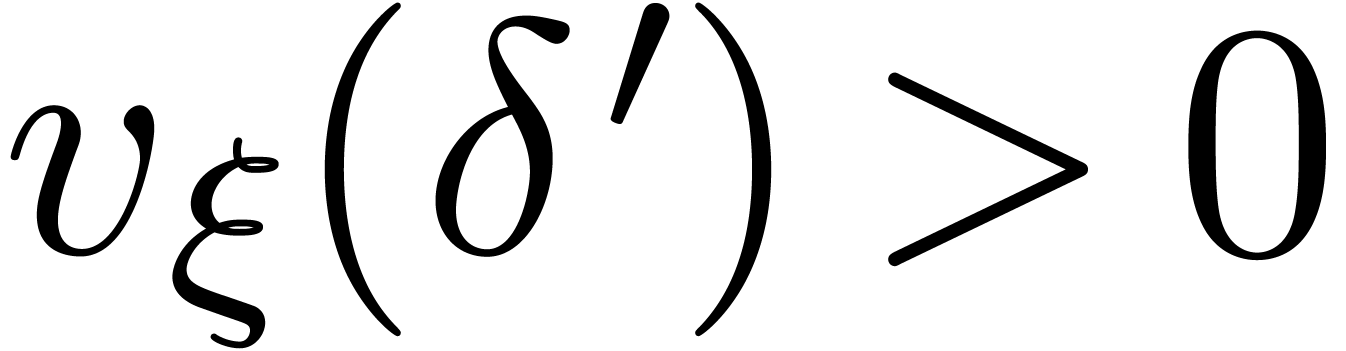 . We will denote by
. We will denote by  the
subset of
the
subset of  of all elements that are highly
tangent to identity.
of all elements that are highly
tangent to identity.
Since Hardy fields are not necessarily closed under composition and
functional inversion, the set  does not
necessarily form a group. The main aim of this section is to show that a
suitable completion of
does not
necessarily form a group. The main aim of this section is to show that a
suitable completion of  does form a group
(Theorem 20 below). Moreover, under suitable hypothesis,
there are algorithms for computing asymptotic expansions of compositions
and functional inverses.
does form a group
(Theorem 20 below). Moreover, under suitable hypothesis,
there are algorithms for computing asymptotic expansions of compositions
and functional inverses.
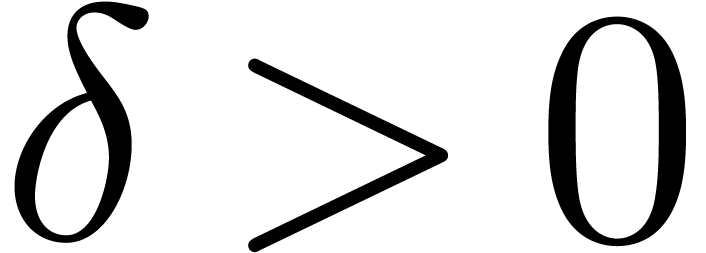
Lemma 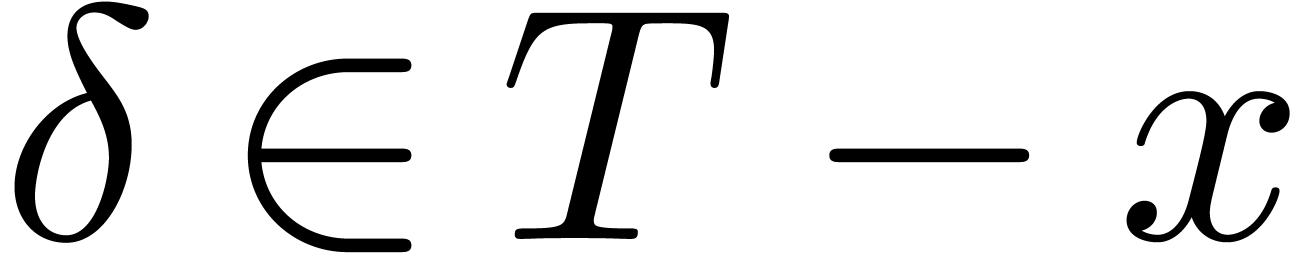 . Then for any germ
. Then for any germ 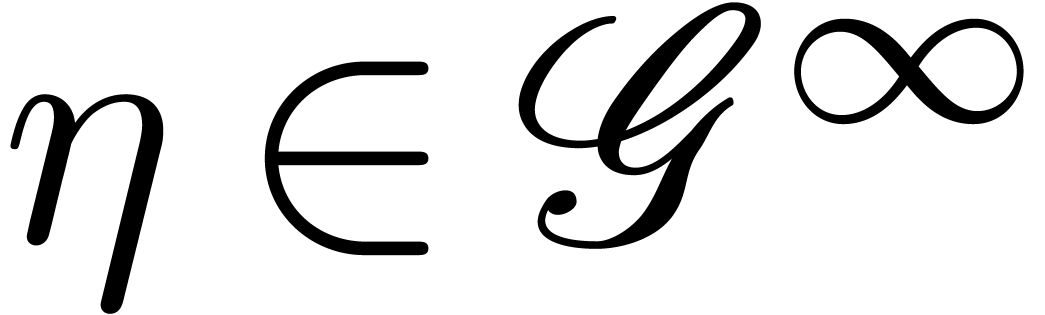 with
with  and
and 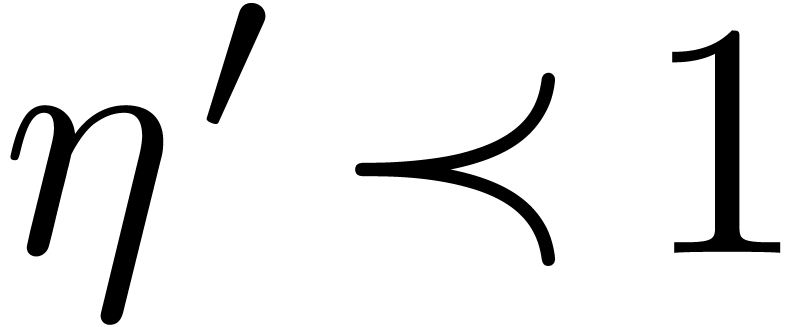 , we have
, we have
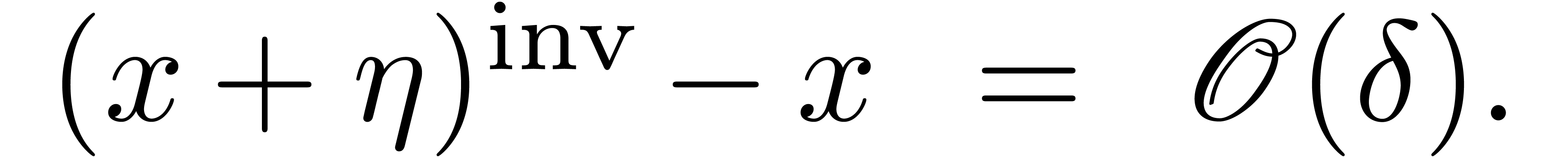
Proof. Without loss of generality, we may assume that
 . For any
. For any 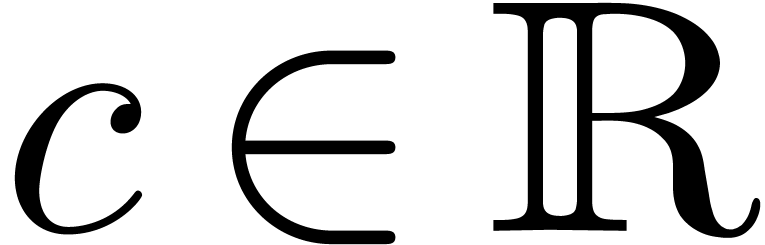 , we claim that
, we claim that 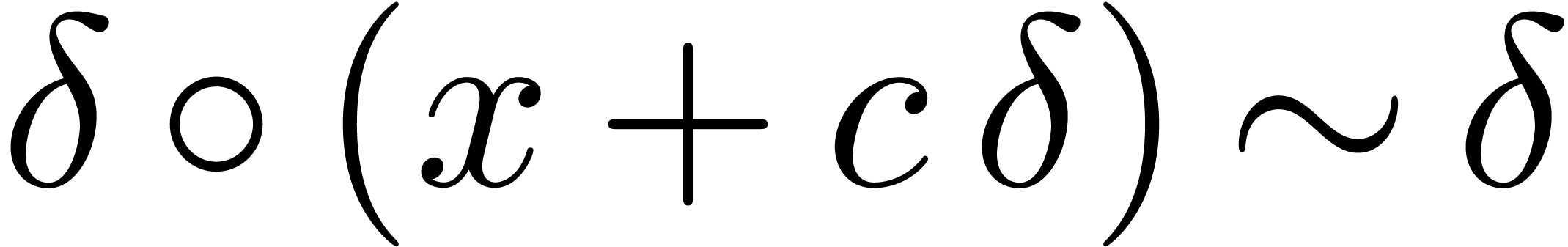 .
Indeed, given
.
Indeed, given  , let
, let 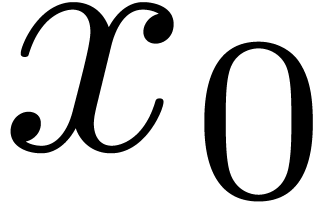 be such that
be such that 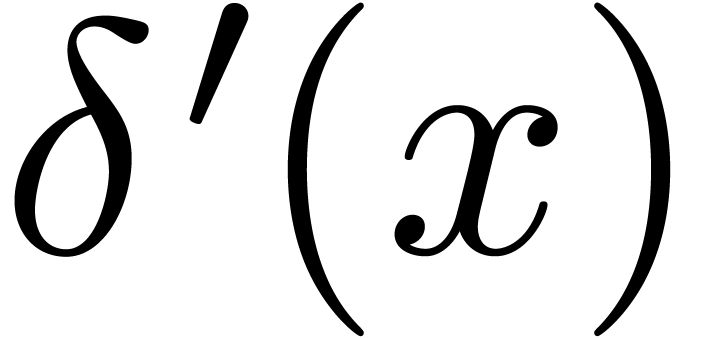 has constant sign and
has constant sign and
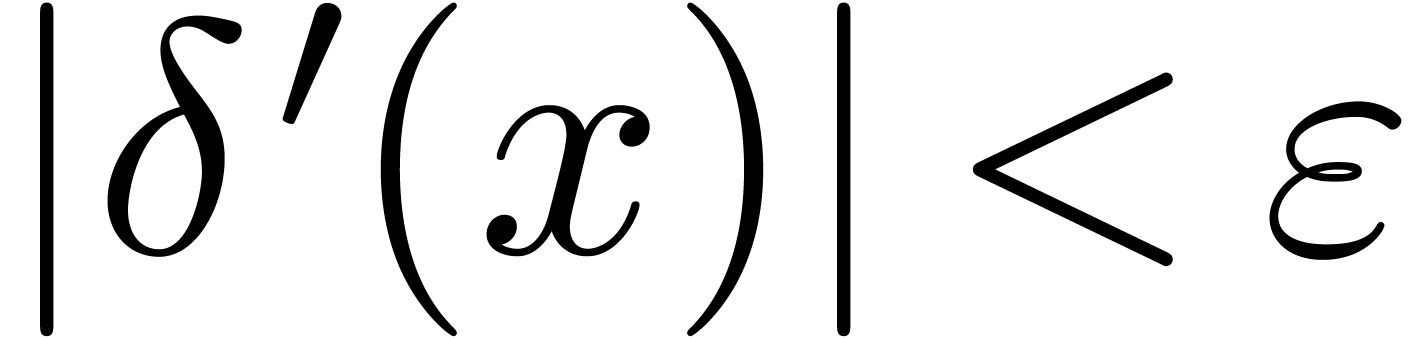 for
for  .
Assume also that
.
Assume also that 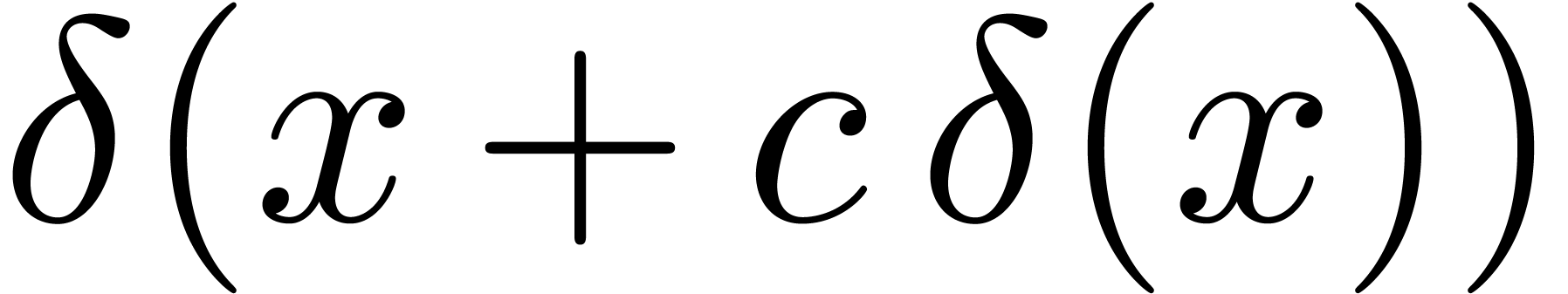 is defined for
is defined for  . Then
. Then
for all  . We conclude that
. We conclude that
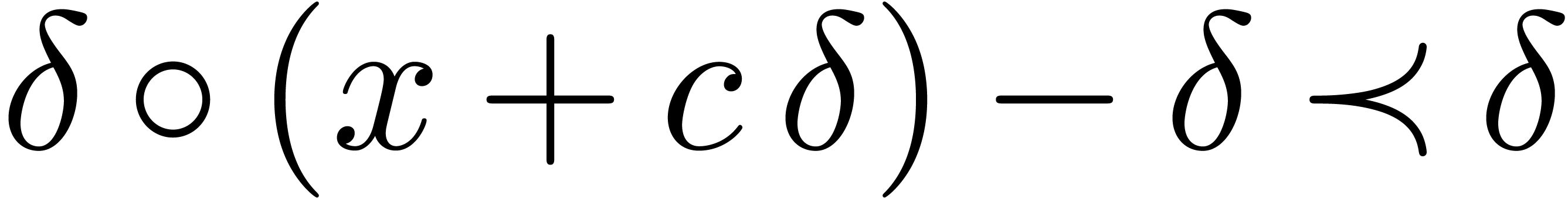 , by letting
, by letting  tend to zero.
tend to zero.
The assumption that 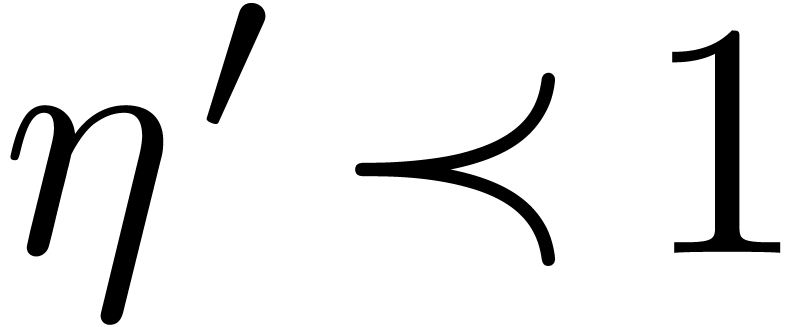 implies that
implies that 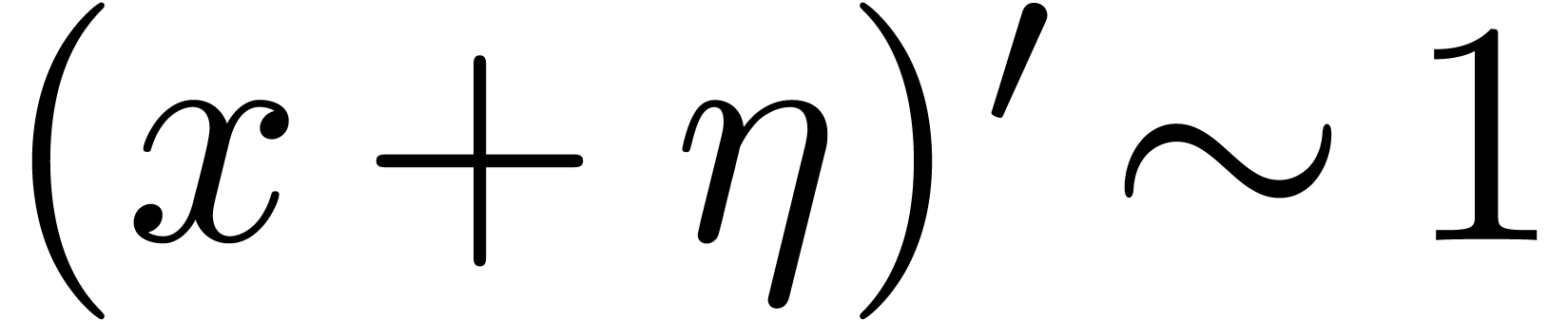 , whence
, whence 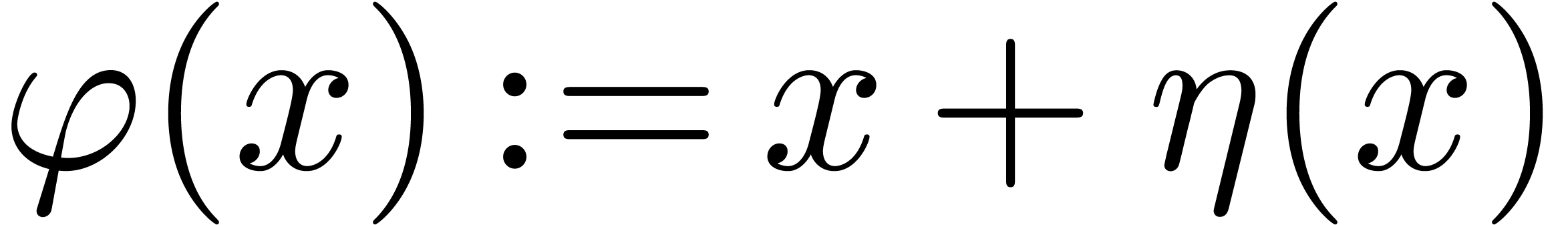 is strictly
increasing for sufficiently large
is strictly
increasing for sufficiently large 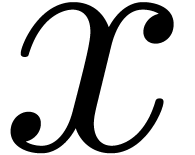 .
This shows that
.
This shows that  indeed admits an inverse
function
indeed admits an inverse
function  at infinity. Let
at infinity. Let 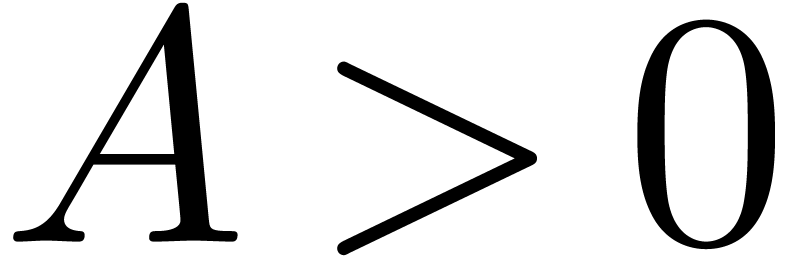 be such that
be such that 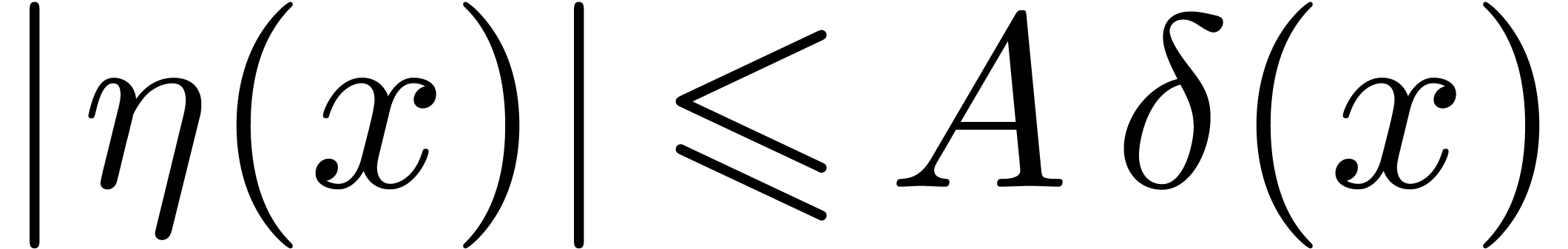 for sufficiently large
for sufficiently large 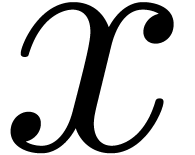 . Setting
. Setting 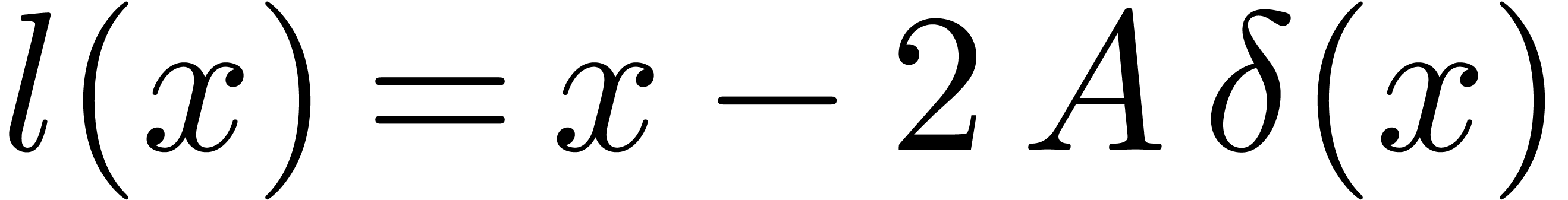 and
and  , our claim implies
, our claim implies
for sufficiently large  .
Since
.
Since  is strictly increasing, it follows that
is strictly increasing, it follows that
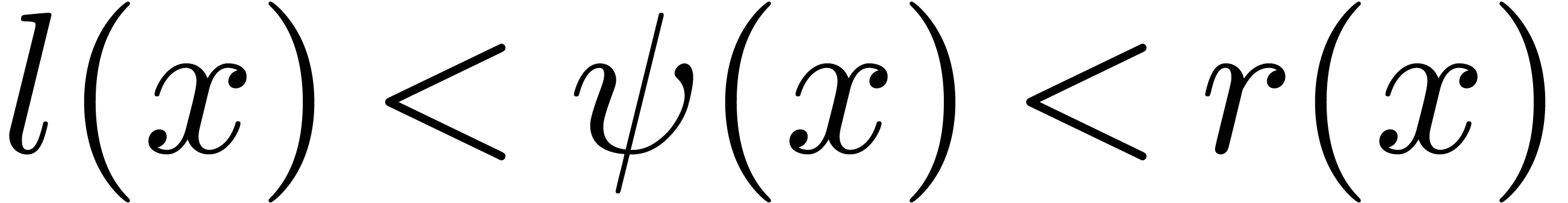 . In other words,
. In other words,  for sufficiently large
for sufficiently large 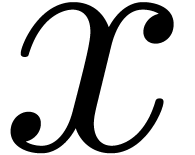 .
.
Lemma 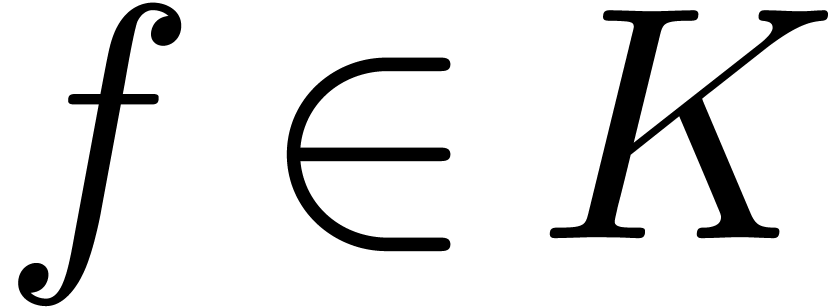 and
and  . Then
for any germs
. Then
for any germs  with
with  and
and
 , we have
, we have
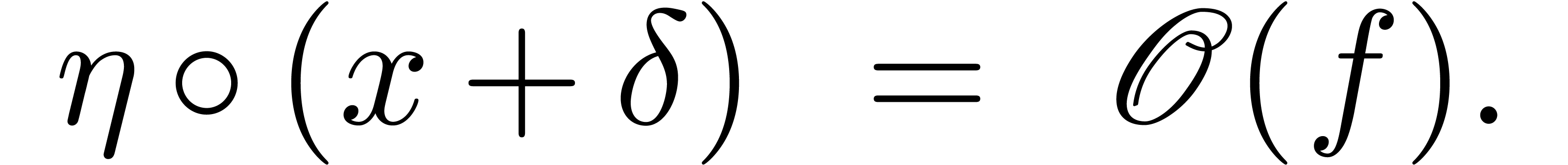
Proof. Since  is a steep
element, there exists a constant
is a steep
element, there exists a constant  with
with 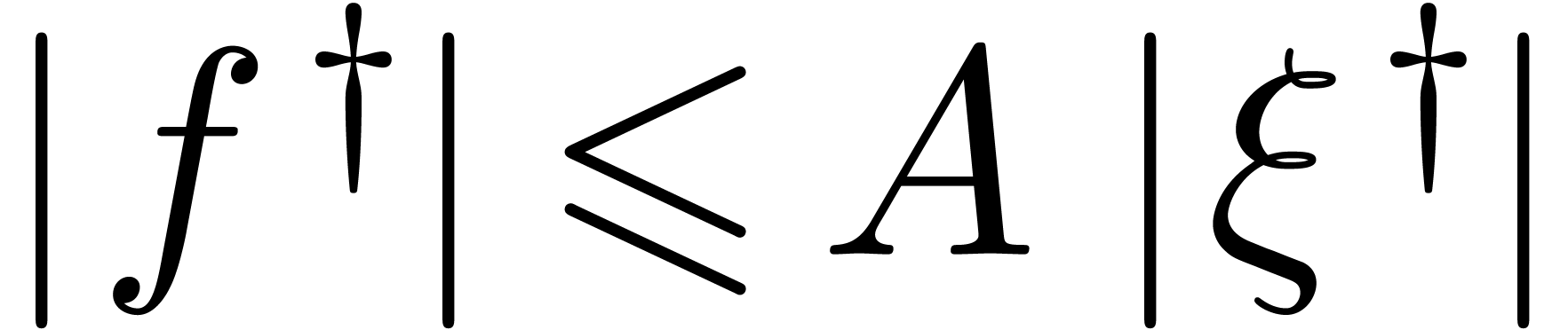 . We also notice that
. We also notice that 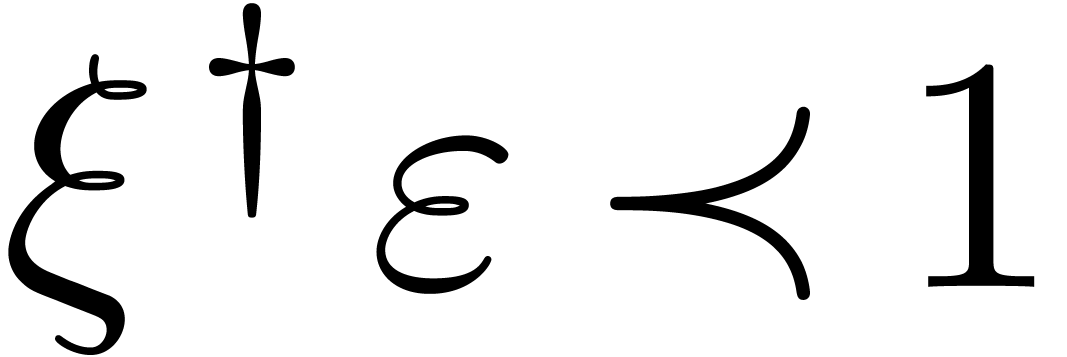 . Indeed, this is immediate if
. Indeed, this is immediate if 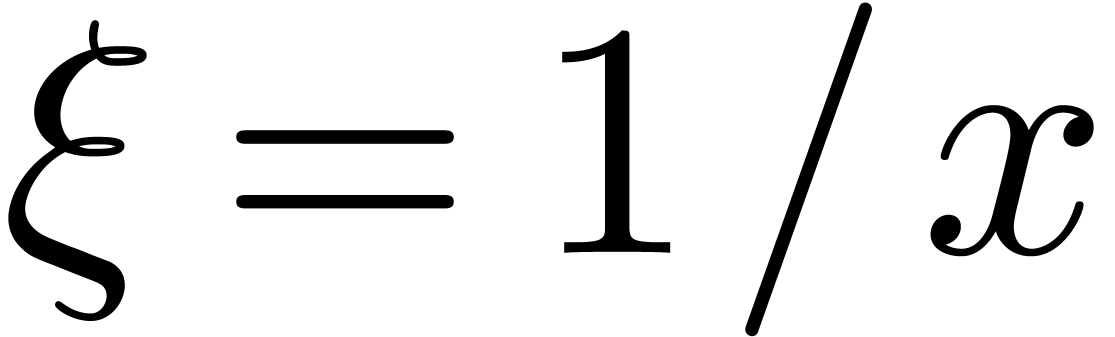 . If
. If  ,
then
,
then 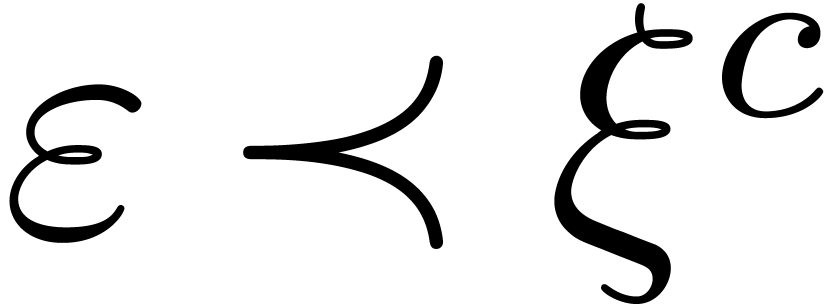 for some
for some  and
and 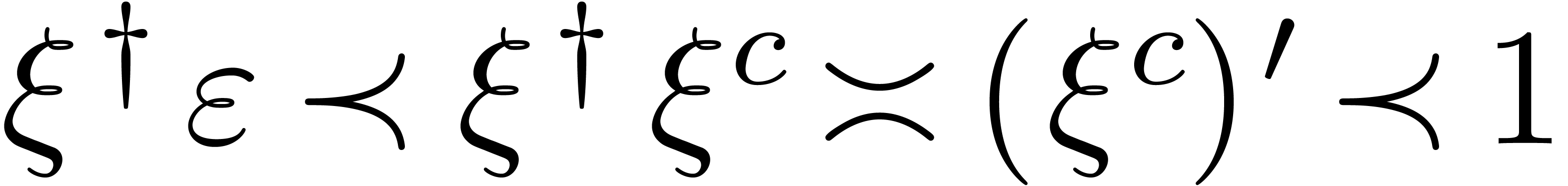 , since
, since 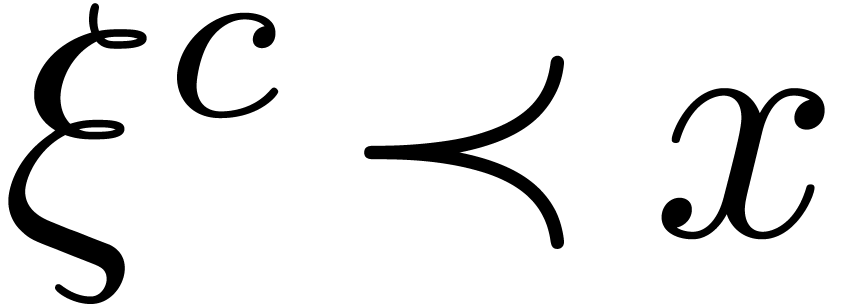 .
.
Let us first show that 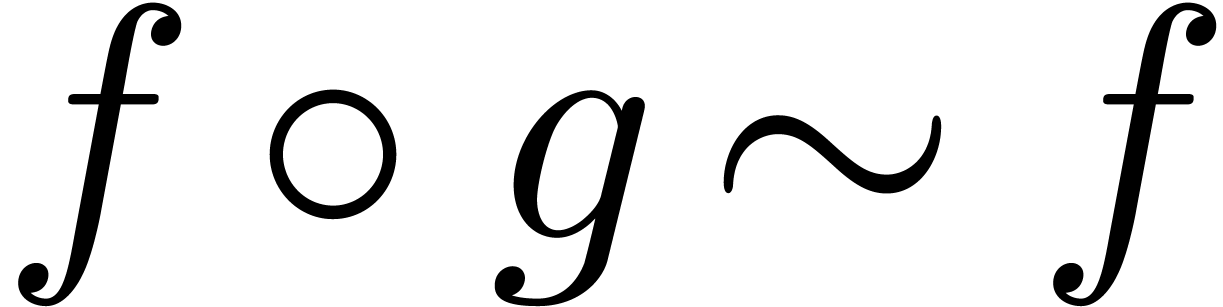 ,
whenever
,
whenever  and
and 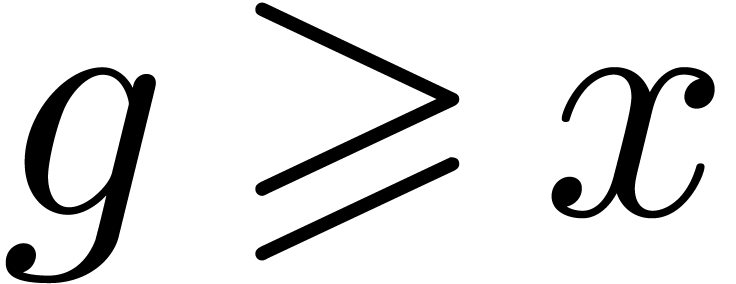 .
Since
.
Since  implies
implies 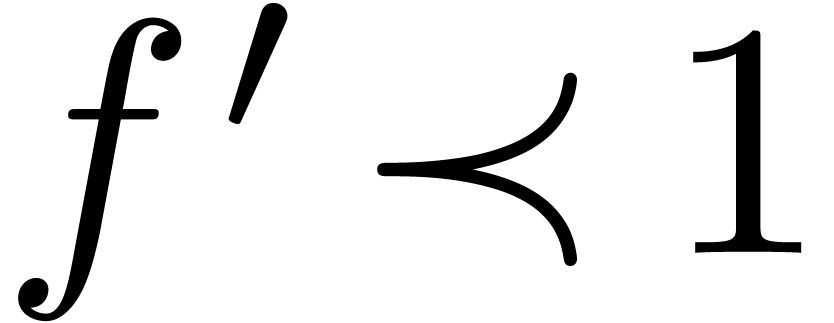 ,
the function
,
the function 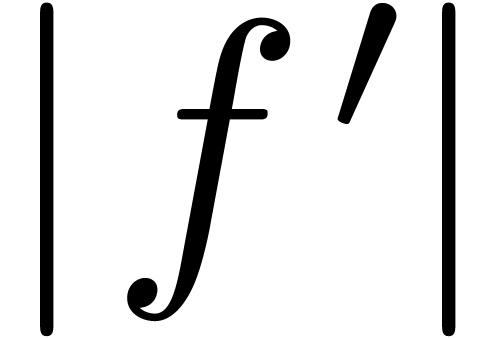 is ultimately decreasing. For
sufficiently large
is ultimately decreasing. For
sufficiently large  , it
follows that
, it
follows that  for
for  ,
whence
,
whence
Since 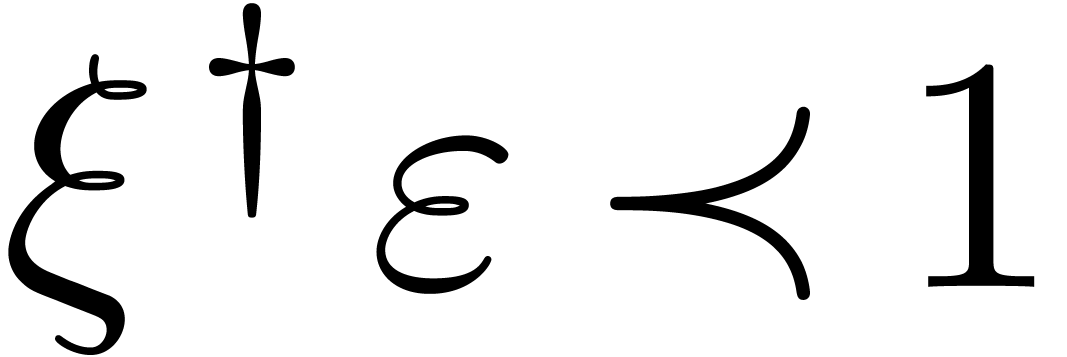 , this shows that
, this shows that 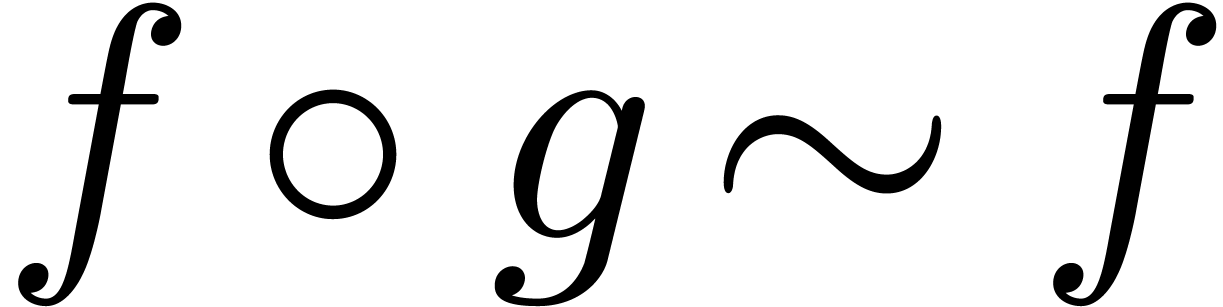 .
.
Let us next show that we also have 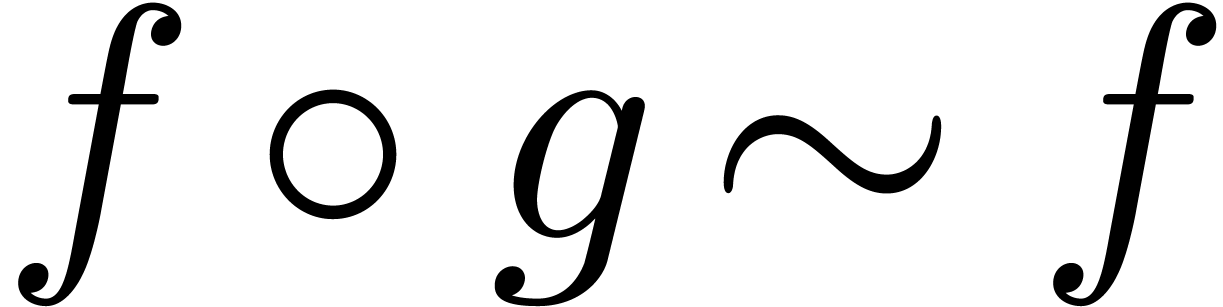 in the case
when
in the case
when  and
and  (so that
(so that 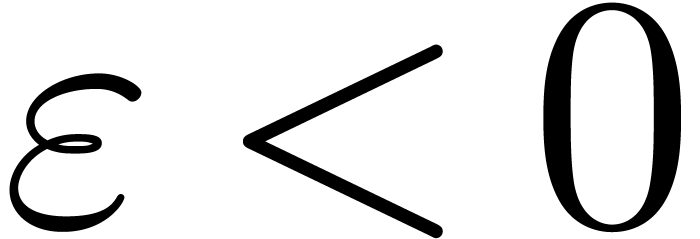 ). Then Lemma 10
implies
). Then Lemma 10
implies 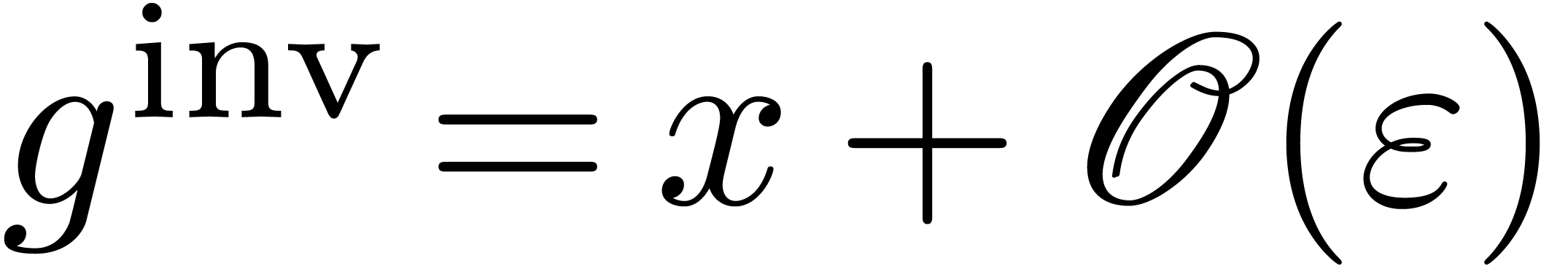 , whence
, whence 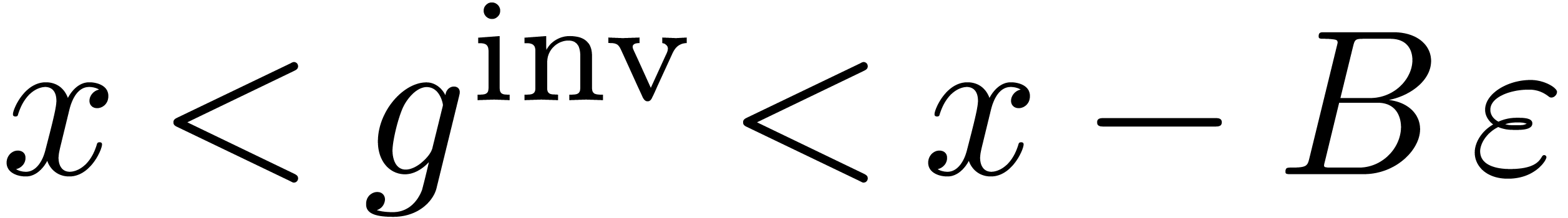 for some
for some 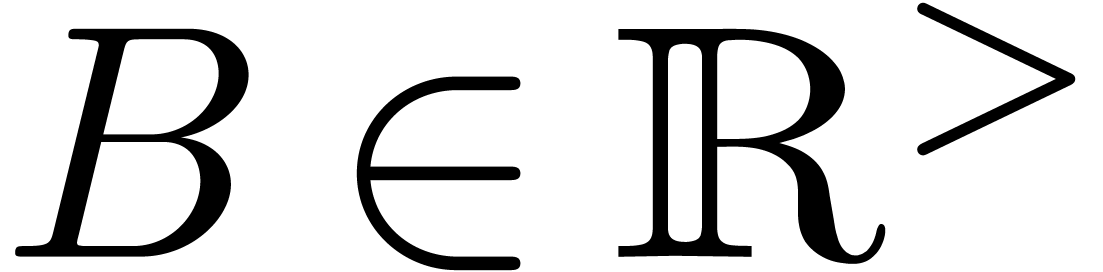 . Let
. Let
 . By what precedes, there
exists an
. By what precedes, there
exists an 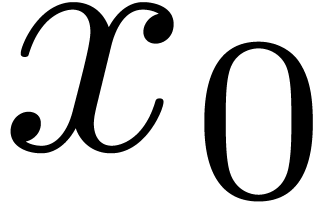 with
with 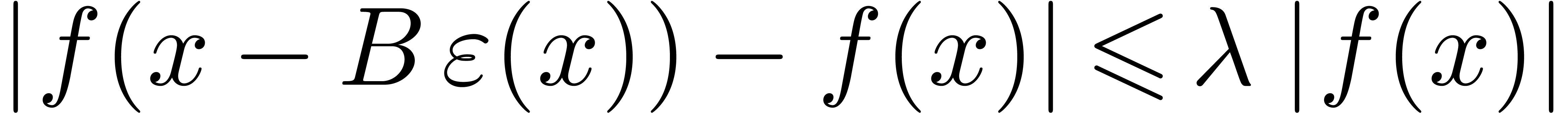 for all
for all
 . Modulo a further increase
of
. Modulo a further increase
of  , we may also arrange that
, we may also arrange that
 is monotonic for
is monotonic for  .
It follows that
.
It follows that 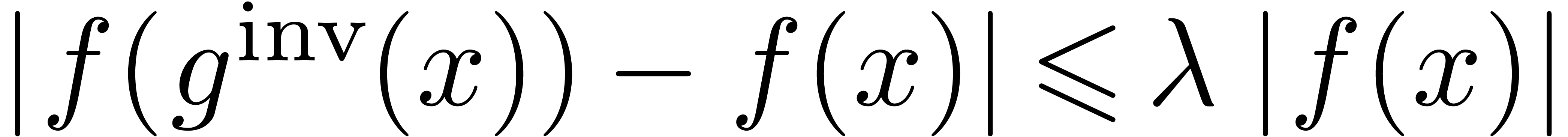 , whence
, whence
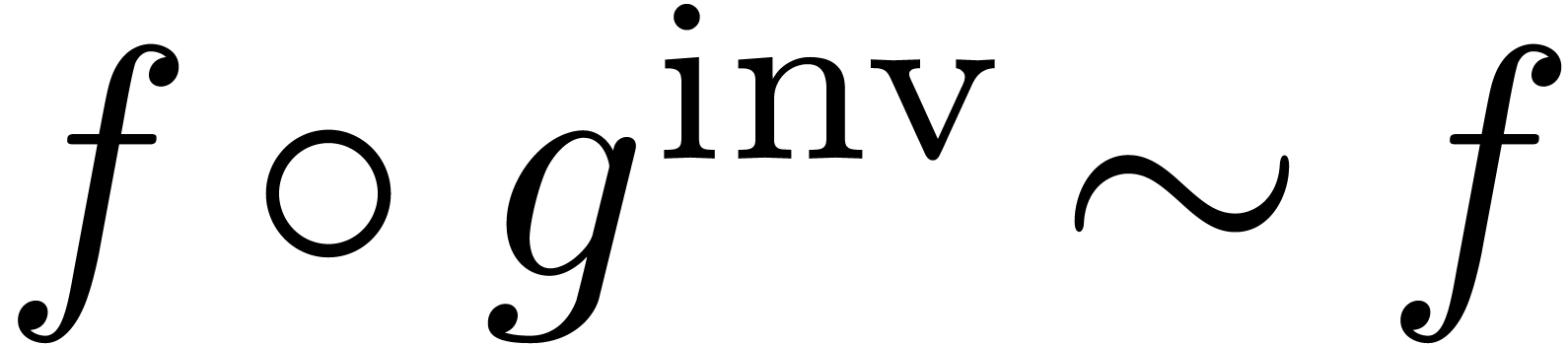 . Post-composing with
. Post-composing with  , we again obtain
, we again obtain 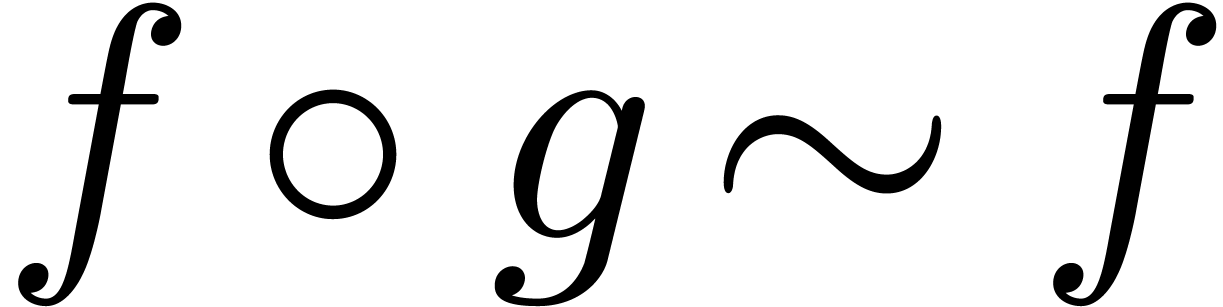 .
.
Let us finally assume that  .
Then the above arguments prove that
.
Then the above arguments prove that 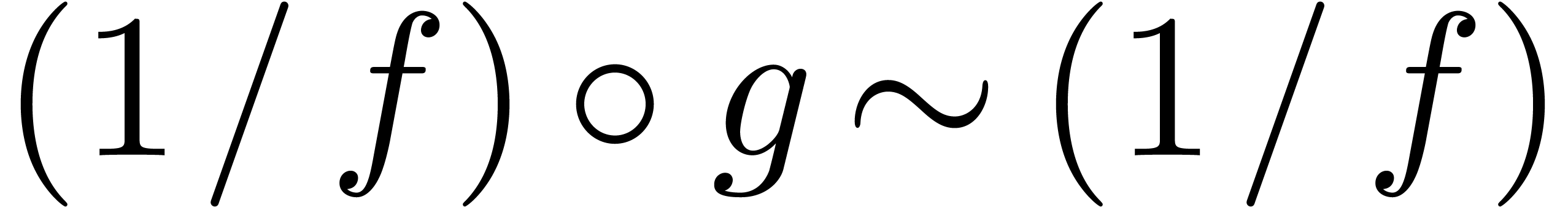 .
Consequently,
.
Consequently, 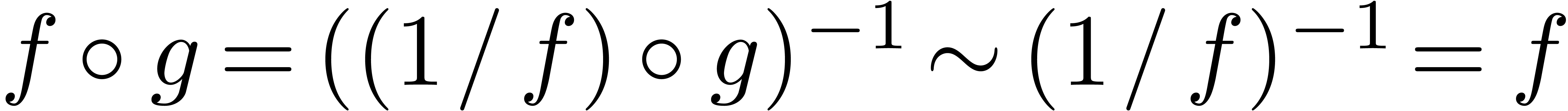 .
.
The above arguments conclude the proof in the case when 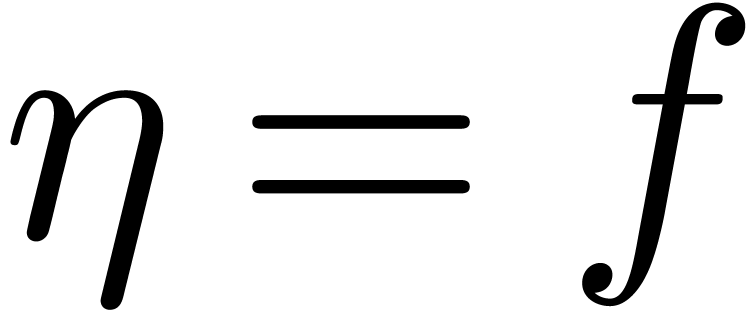 and
and 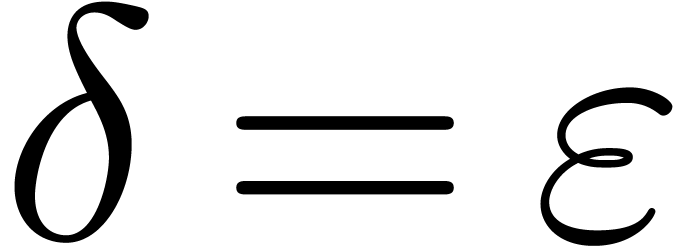 . Let us next consider
the case when we still have
. Let us next consider
the case when we still have 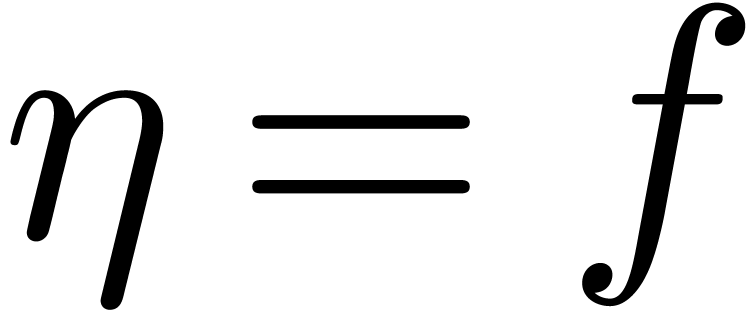 ,
but
,
but  is general. Let
is general. Let 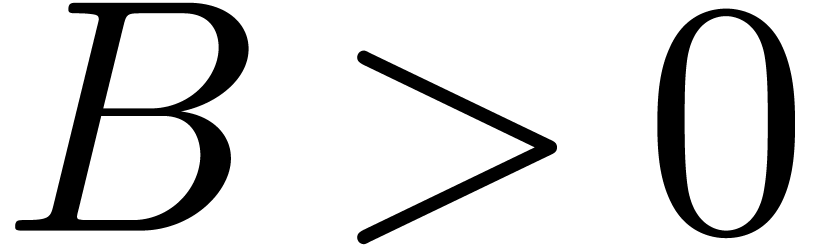 be
such that
be
such that 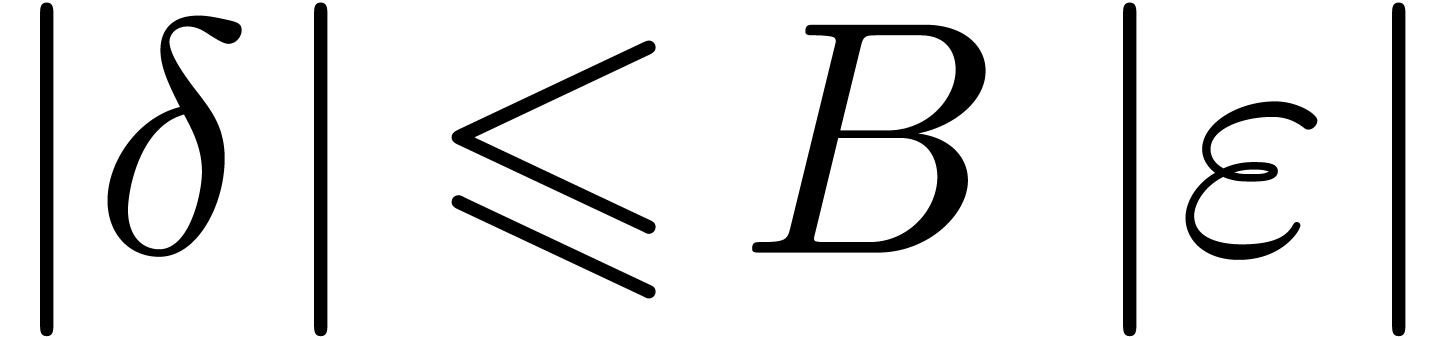 . For sufficiently
large
. For sufficiently
large 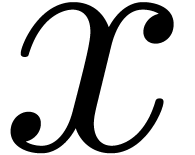 , it follows that
, it follows that 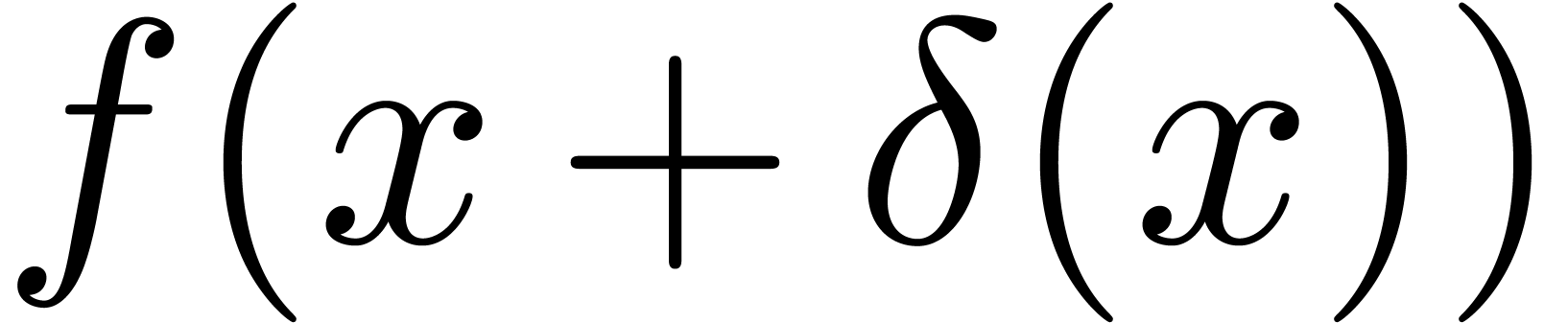 is comprised between
is comprised between 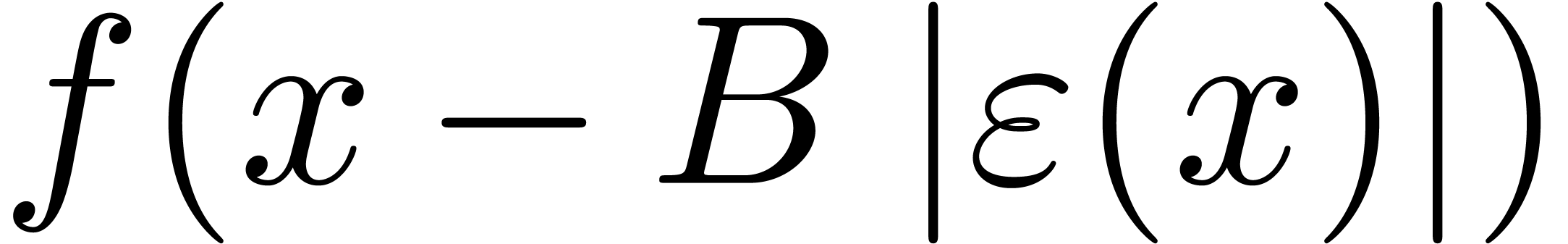 and
and
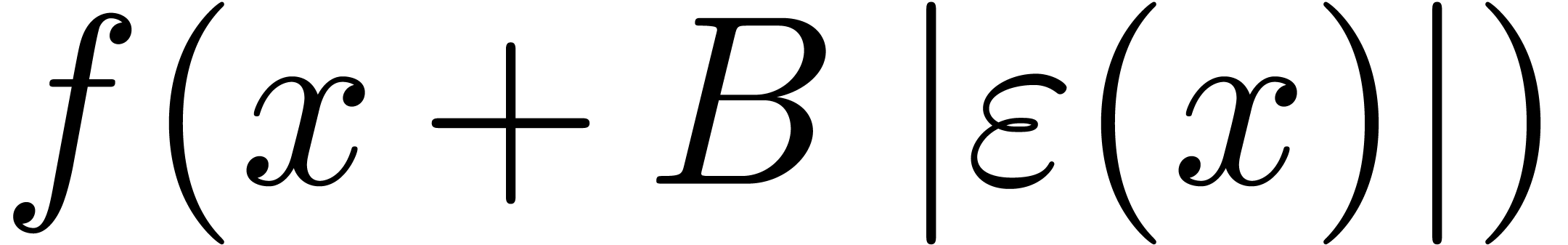 , which are both equivalent
to
, which are both equivalent
to 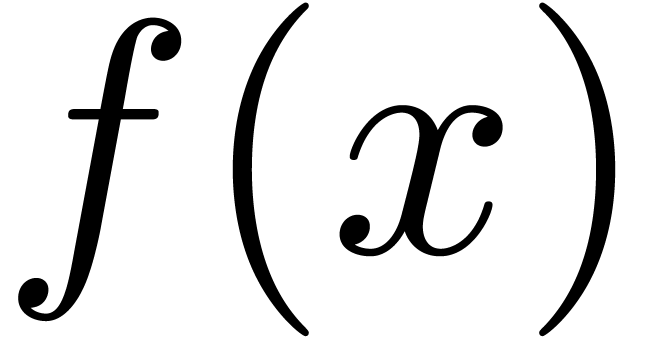 . This shows that
. This shows that 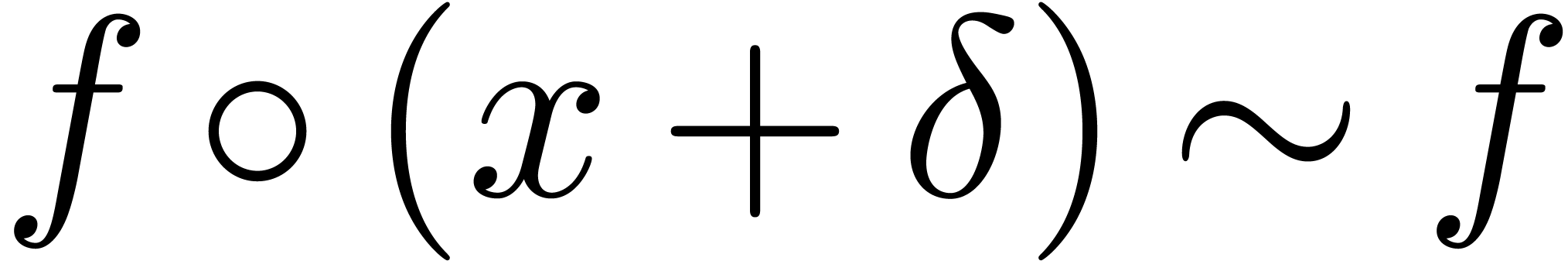 .
.
As to the general case, let  be such that
be such that 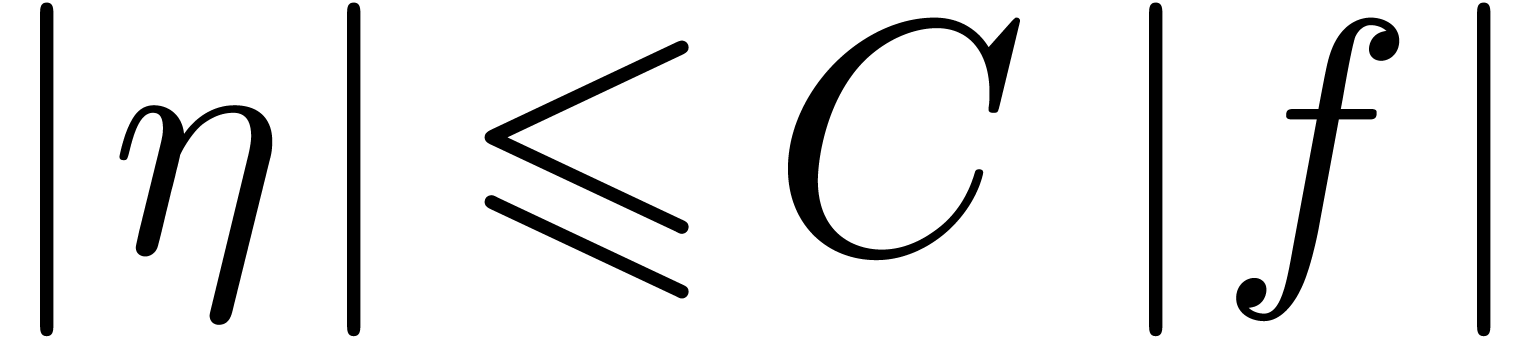 . By what precedes, we have
. By what precedes, we have 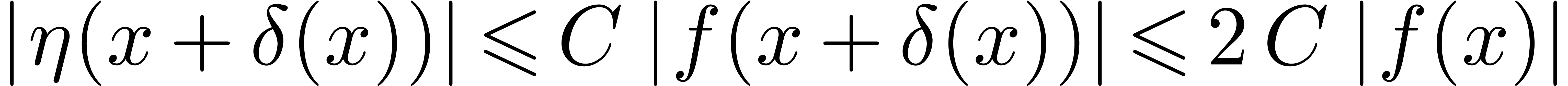 for all sufficiently large
for all sufficiently large 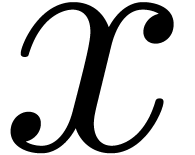 . This shows that
. This shows that 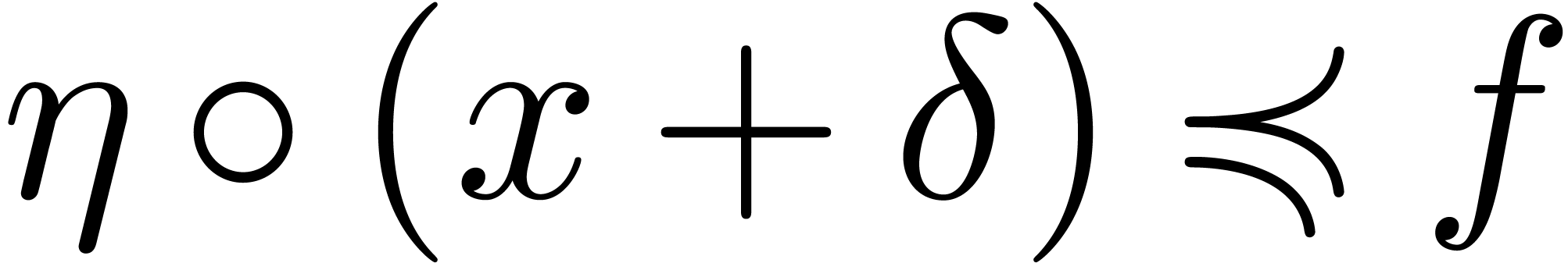 .
.
Lemma 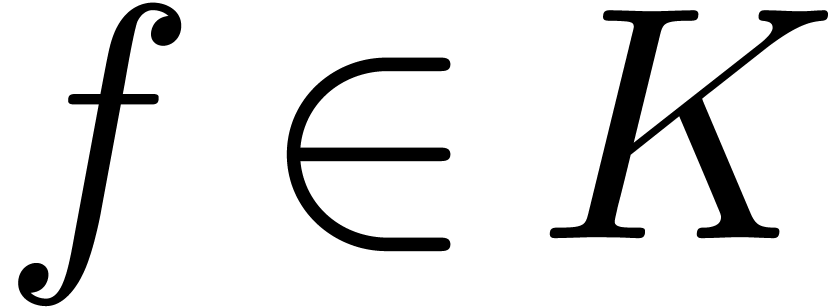 and
and 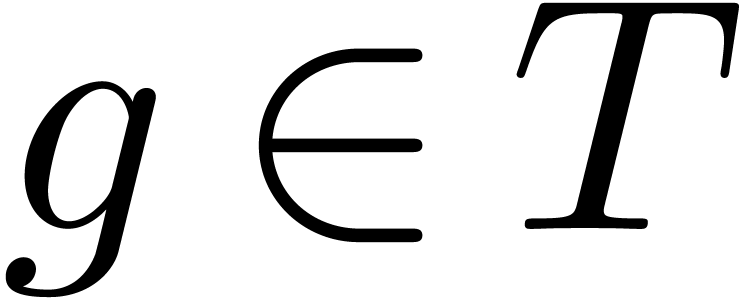 . Let
. Let
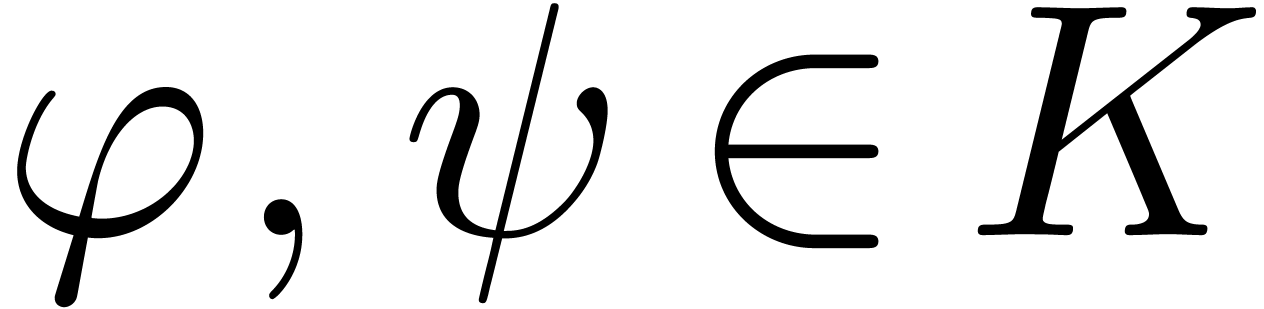 and
and 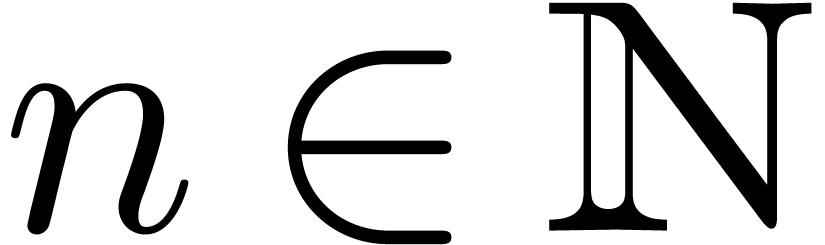 be such that
be such that 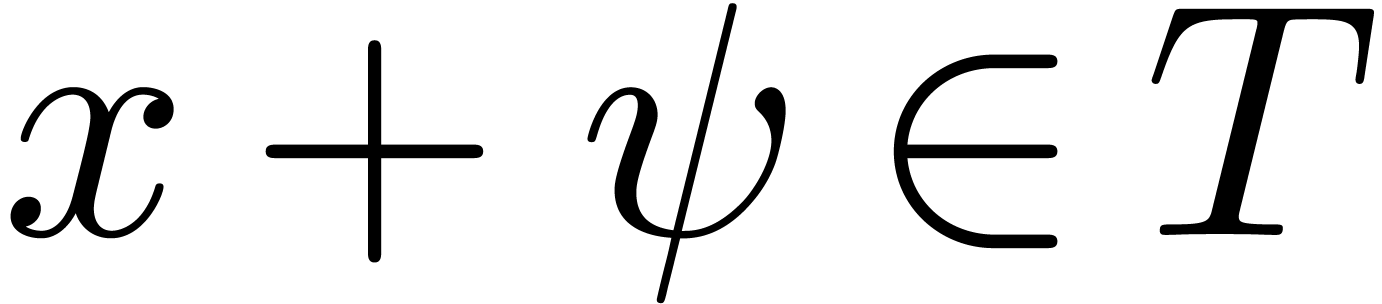 and
and 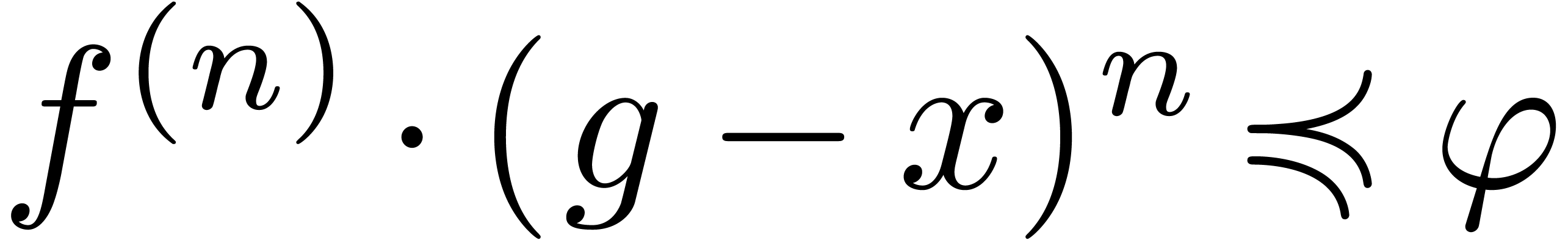 . Then
for any
. Then
for any 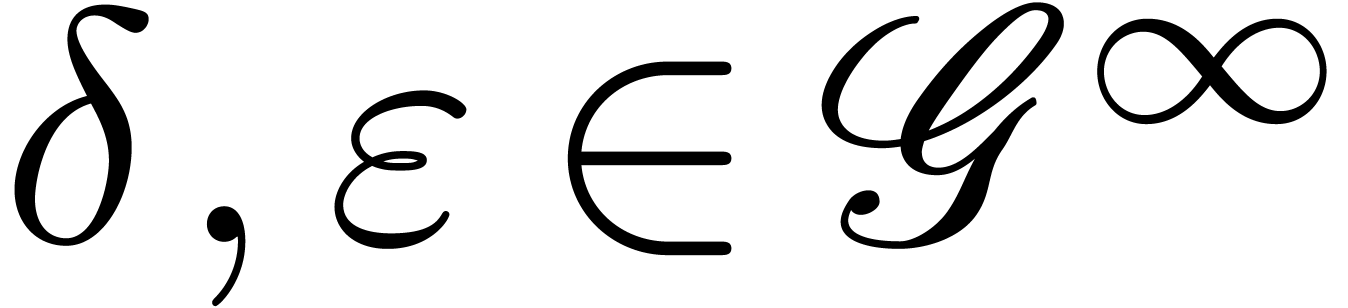 with
with  and
and  , we have
, we have
Proof. Let us first consider the case when  and consider
and consider
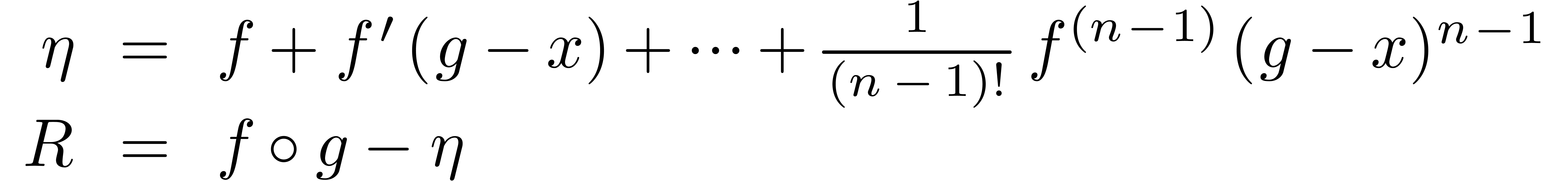
For sufficiently large 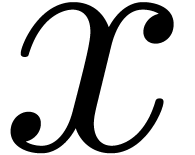 ,
Taylor's formula with integral remainder yields
,
Taylor's formula with integral remainder yields
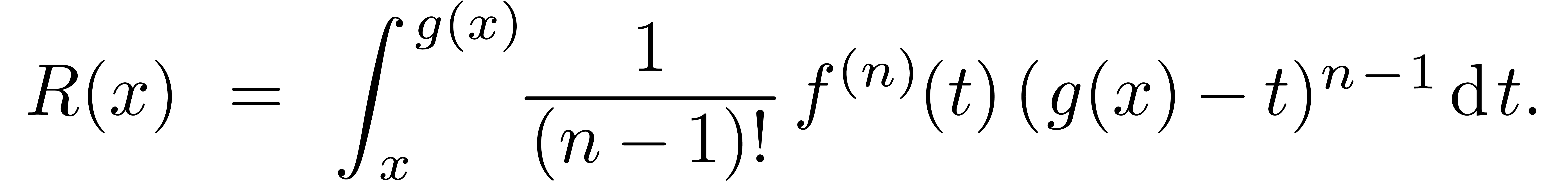
For sufficiently large 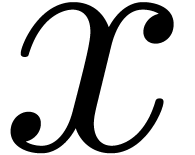 , the
function
, the
function 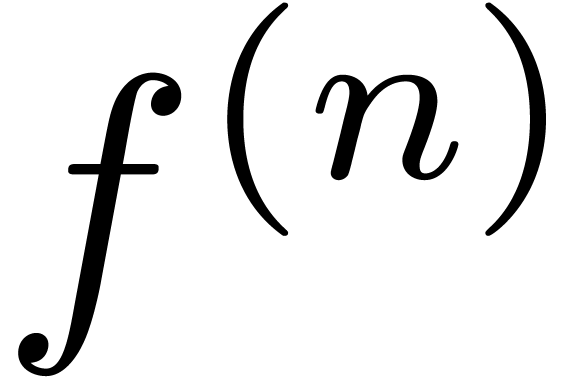 is also monotonic, whence
is also monotonic, whence
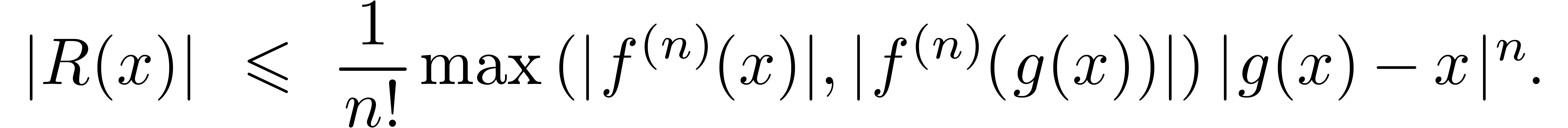
By Lemma 11, we have 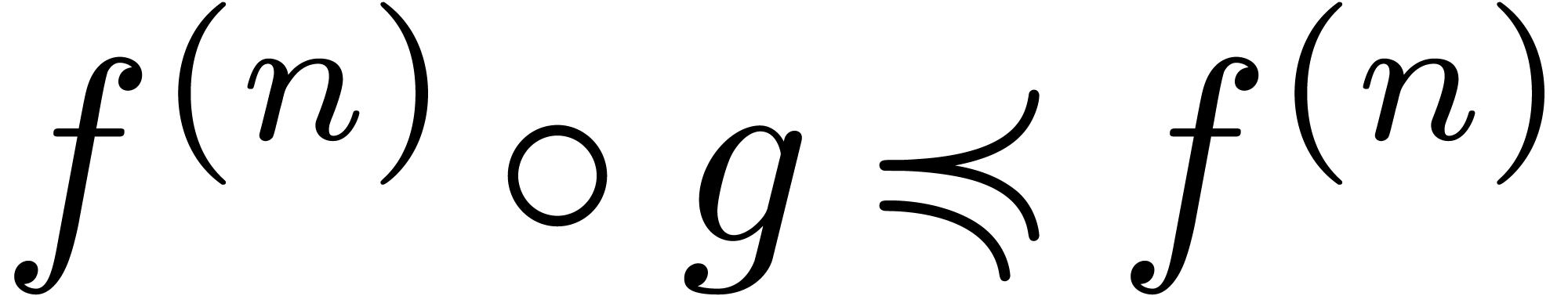 ,
whence
,
whence 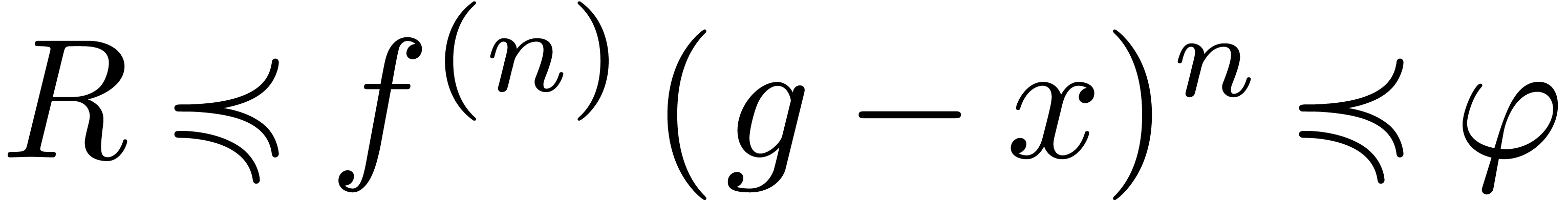 . This completes the
proof in the case when
. This completes the
proof in the case when  .
.
As to the general case, we have
for all sufficiently large 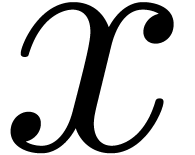 .
Now Lemmas 10 and 11 imply
.
Now Lemmas 10 and 11 imply 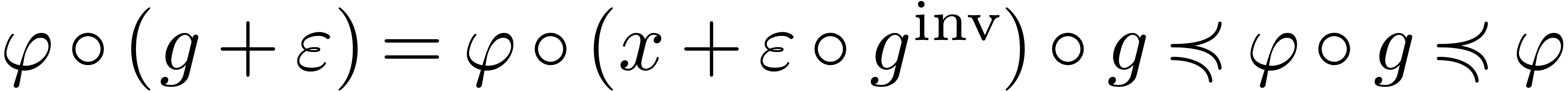 and similarly
and similarly 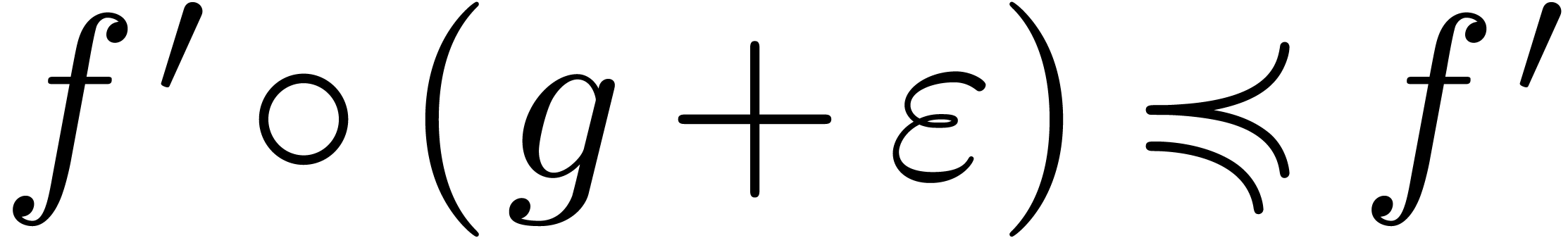 . Consequently,
. Consequently,
This concludes the proof in the general case.
Lemma 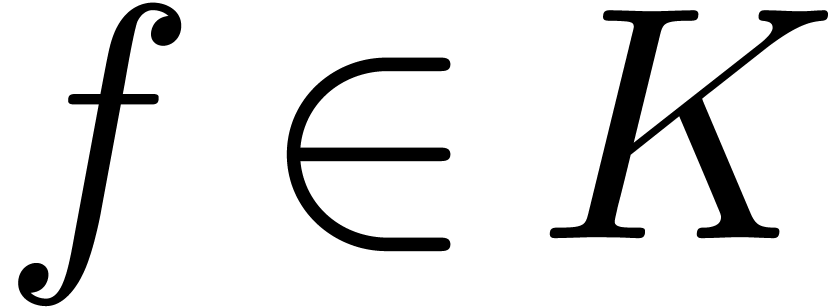 ,
, 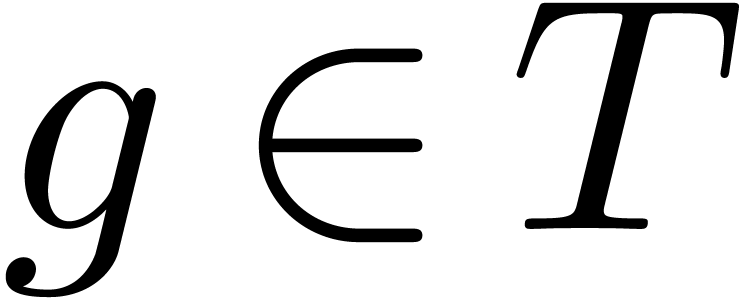 and
and
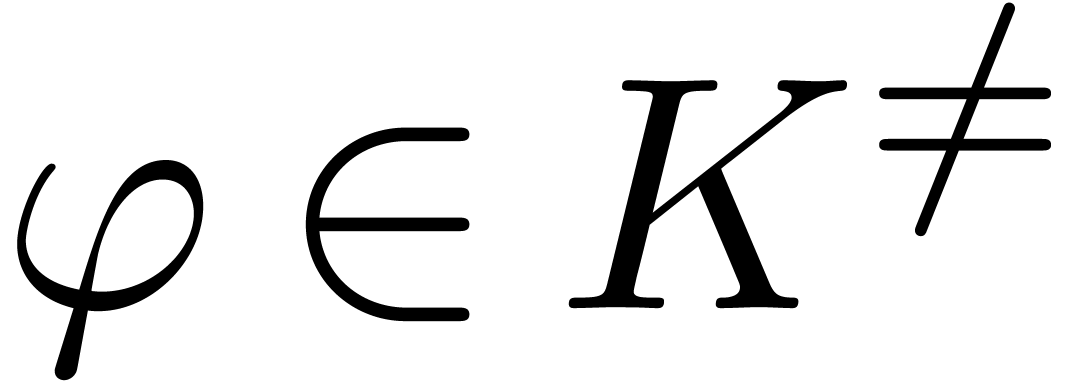 , there exists an
, there exists an 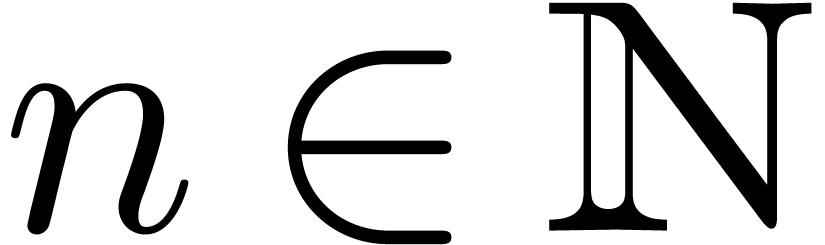 with
with 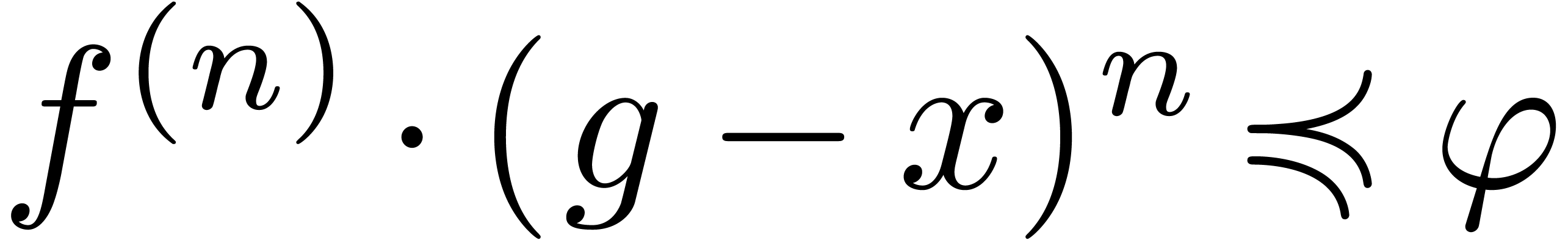 .
.
Proof. Let us first consider the case when 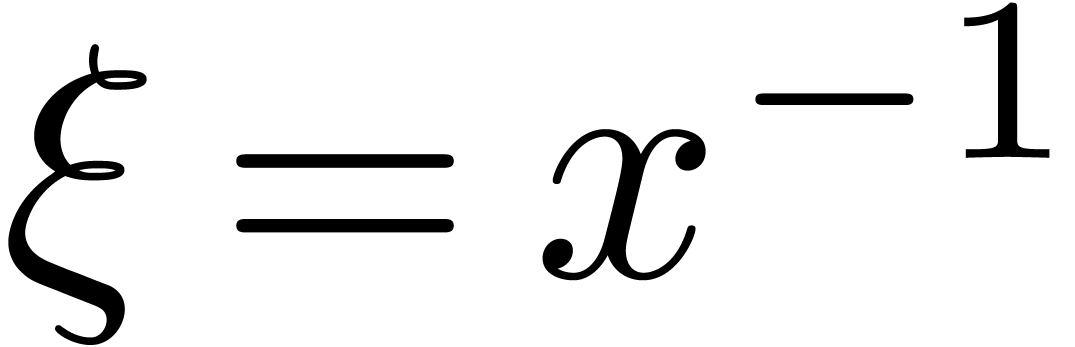 , so that
, so that 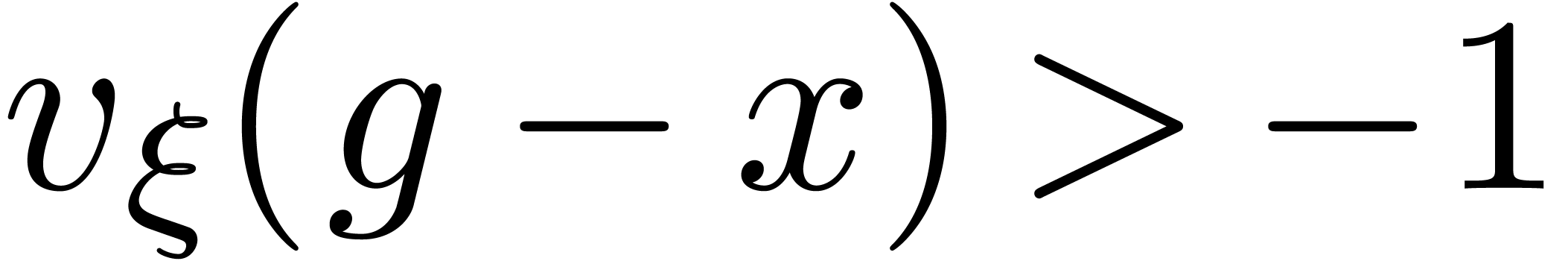 .
For any
.
For any 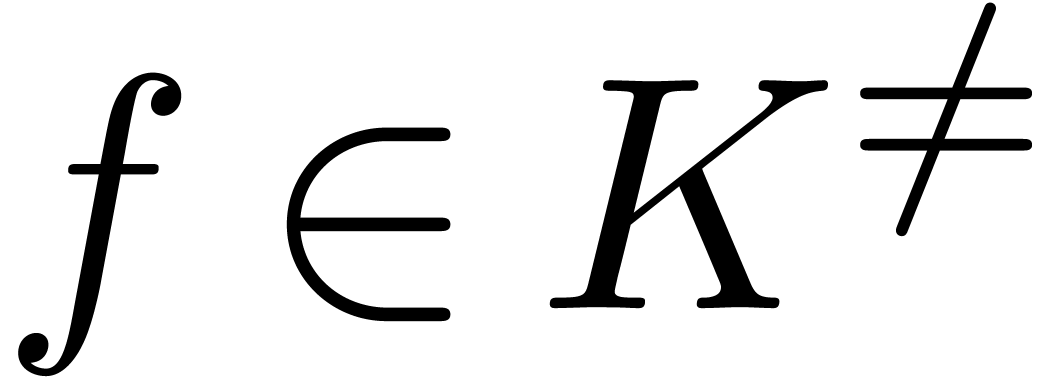 , we have
, we have 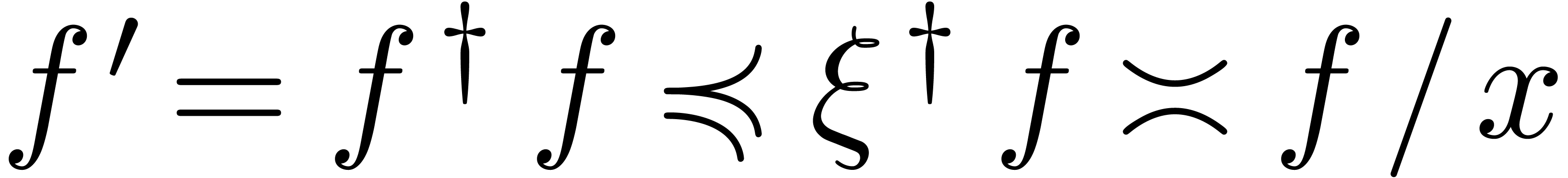 , whence
, whence 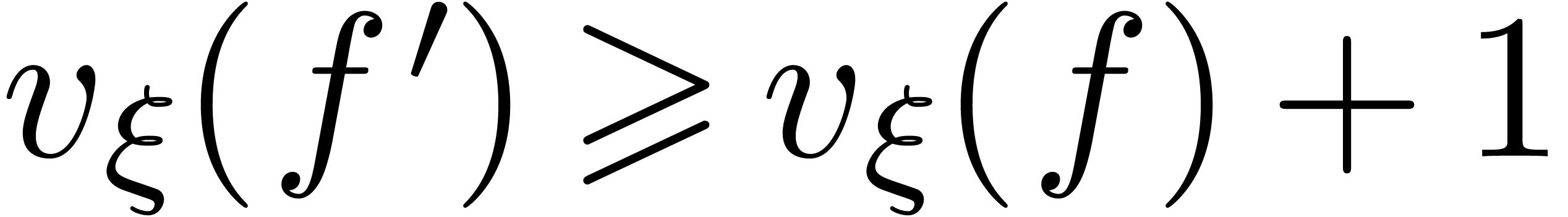 . Consequently,
. Consequently,
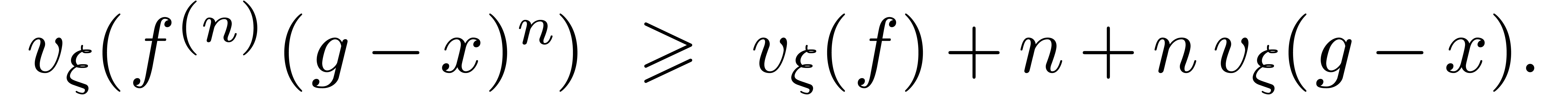
It thus suffices to take 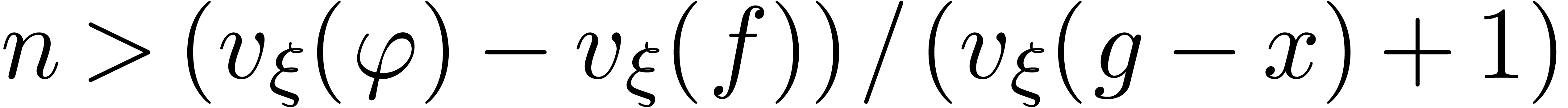 in order to ensure that
in order to ensure that
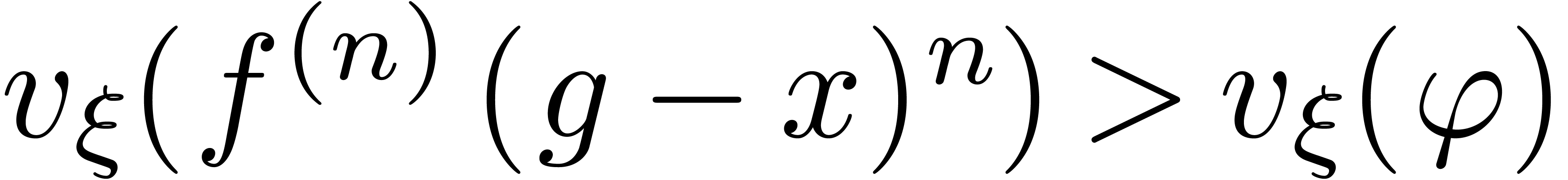 and therefore
and therefore 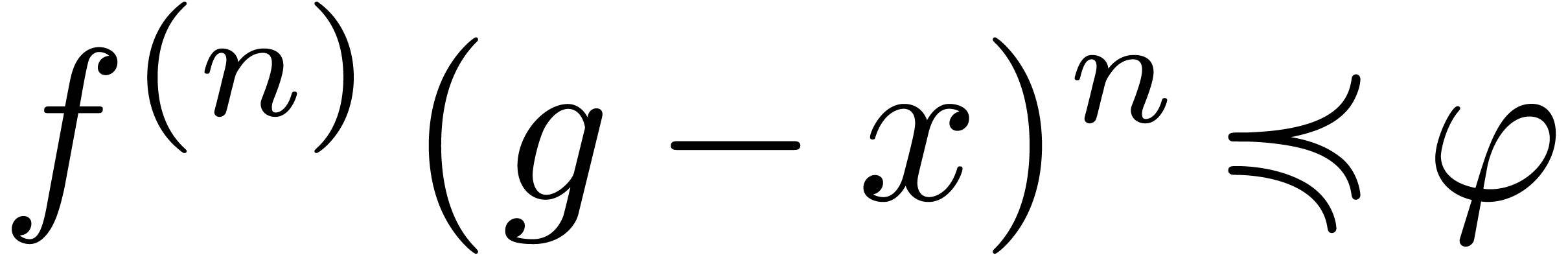 .
.
Assume next that  , so that
, so that
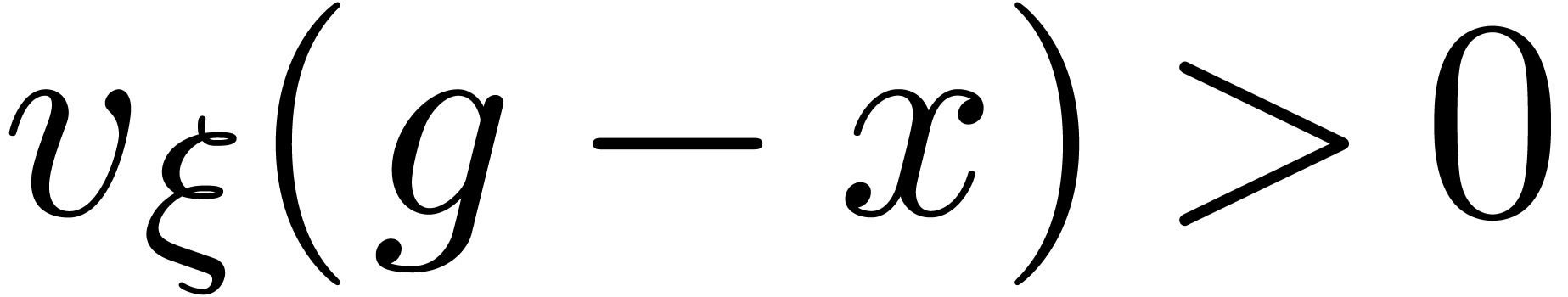 . We again have
. We again have 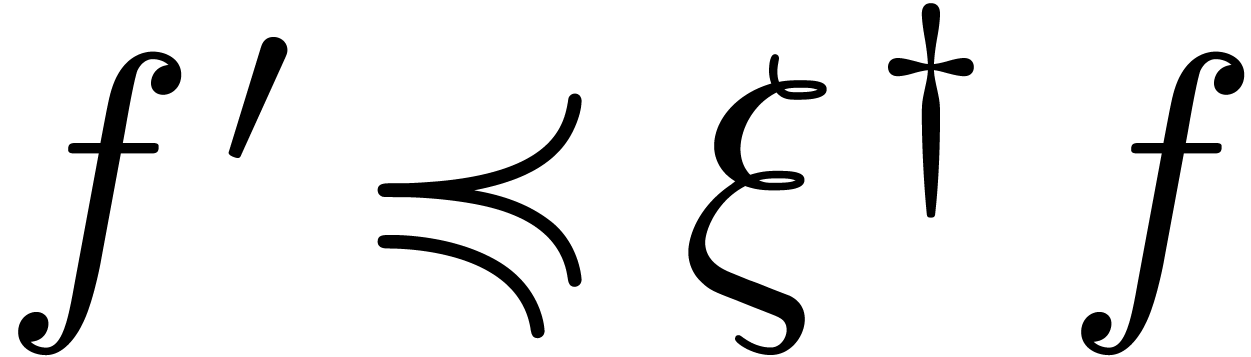 for all
for all 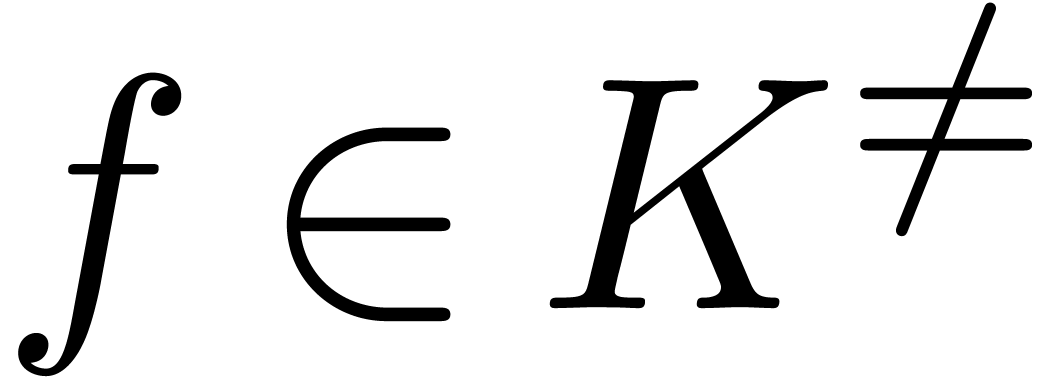 , but
this time, we rather obtain
, but
this time, we rather obtain 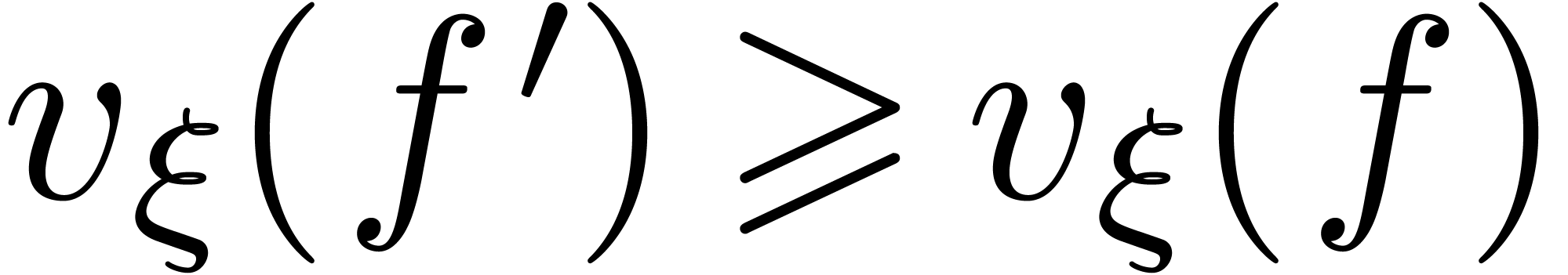 ,
since
,
since 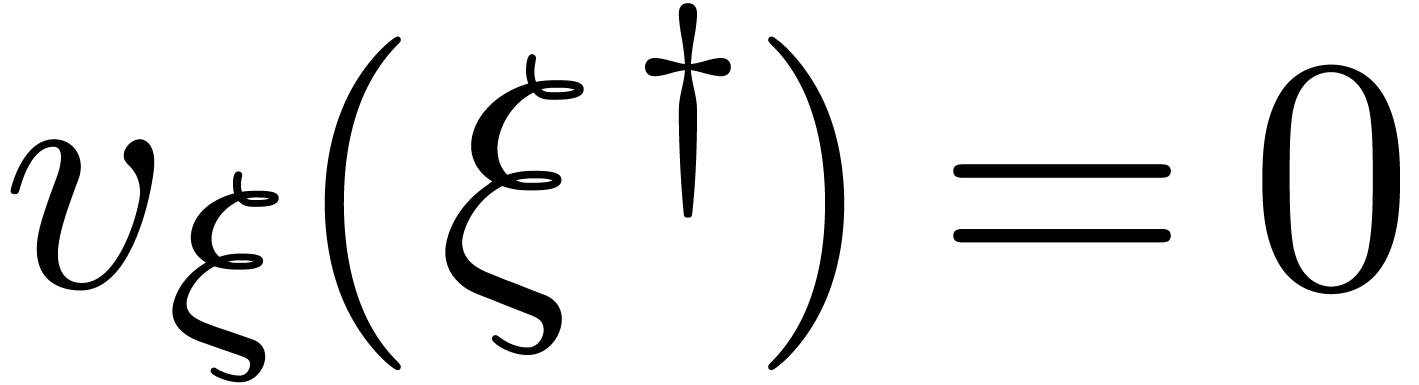 . Therefore,
. Therefore,
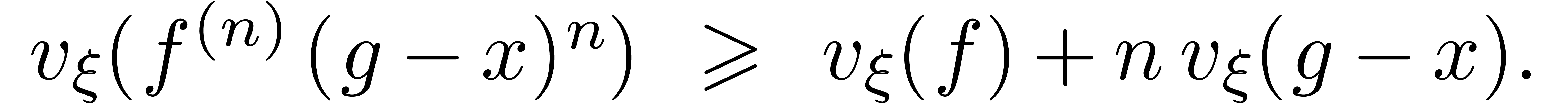
Taking 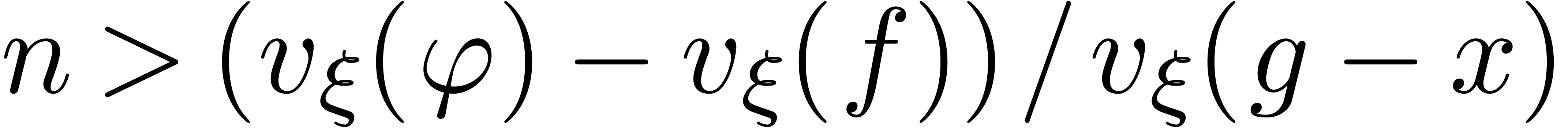 , we again obtain the
desired result.
, we again obtain the
desired result.
If  is an effective Hardy field, then the above
lemmas lead to the following algorithm for approximate composition:
is an effective Hardy field, then the above
lemmas lead to the following algorithm for approximate composition:
Algorithm compose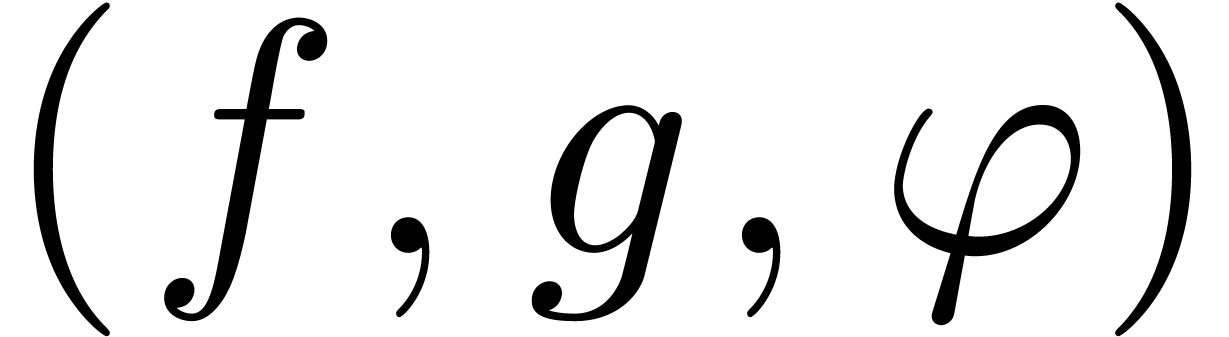
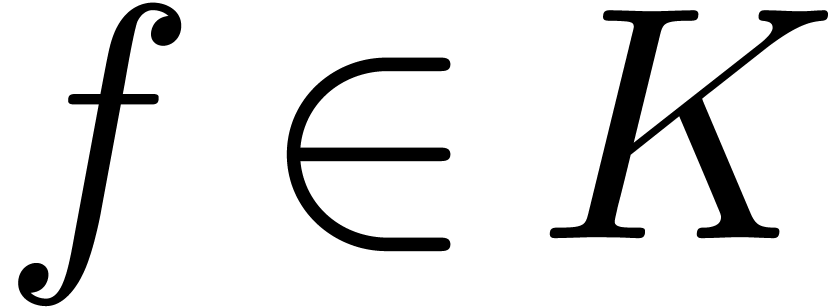 ,
,
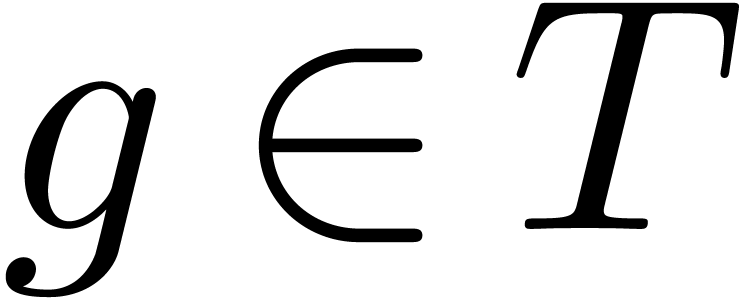 and
and 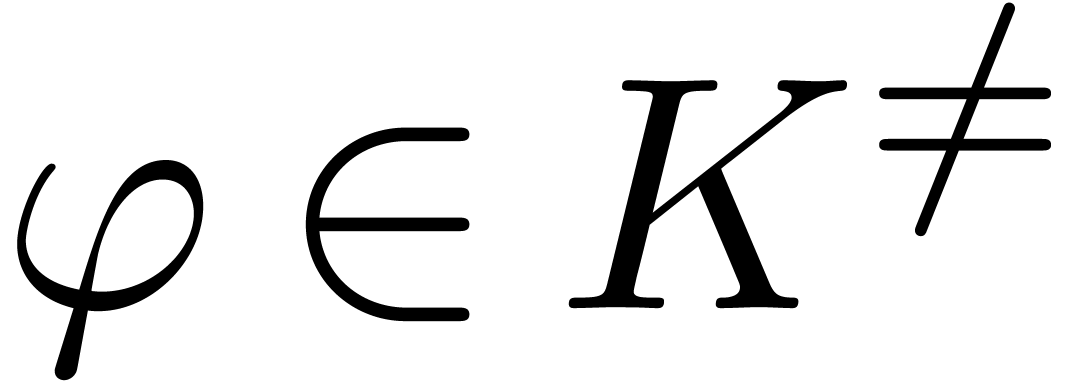 with
with 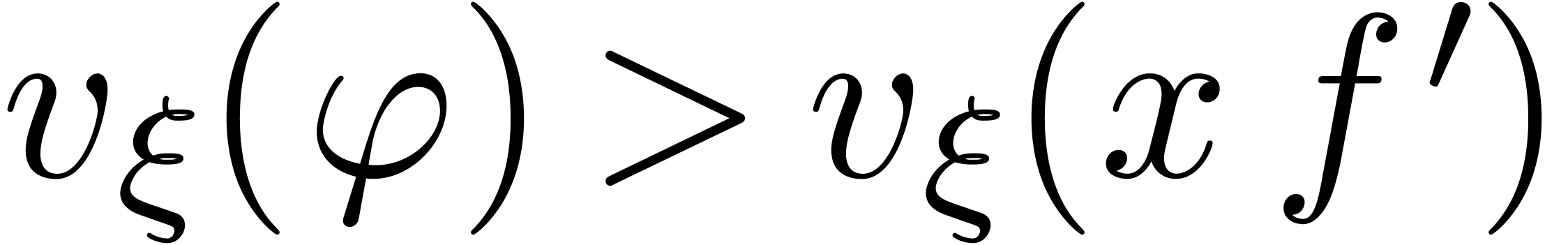
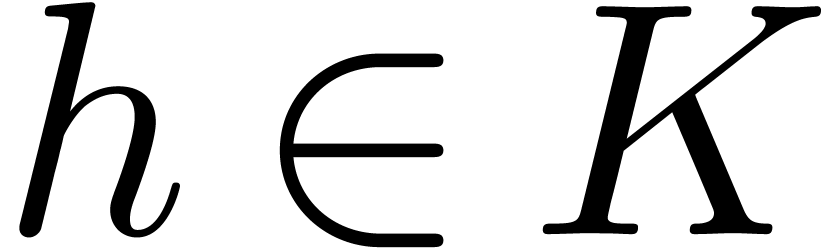 with
with 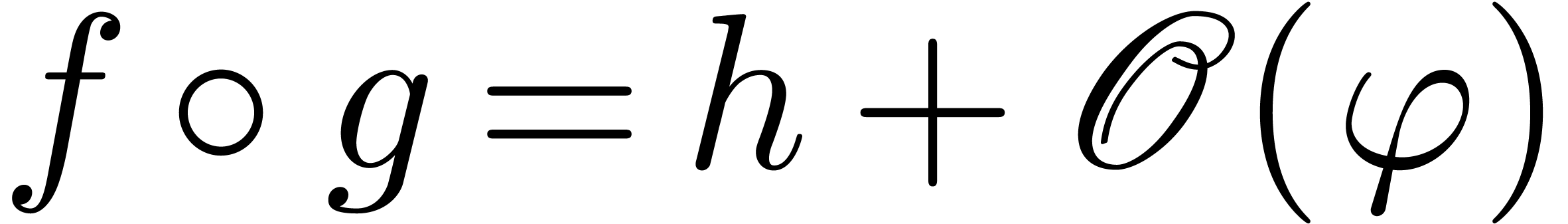
Moreover, for all 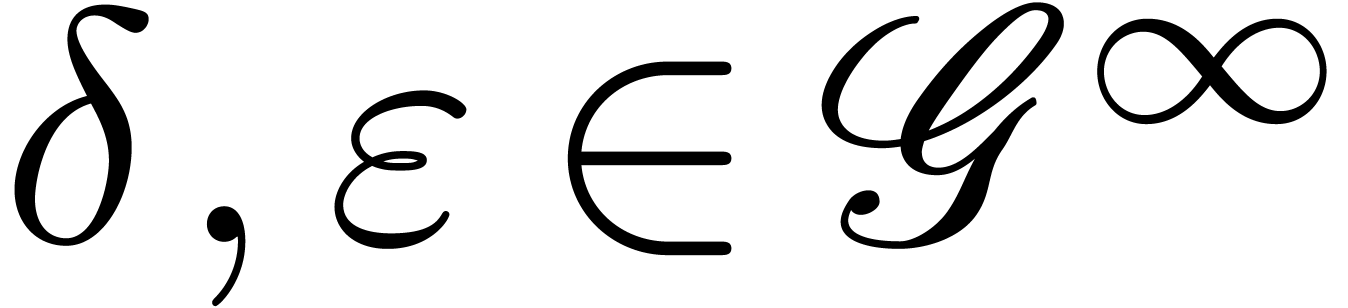 with
with  ,
, 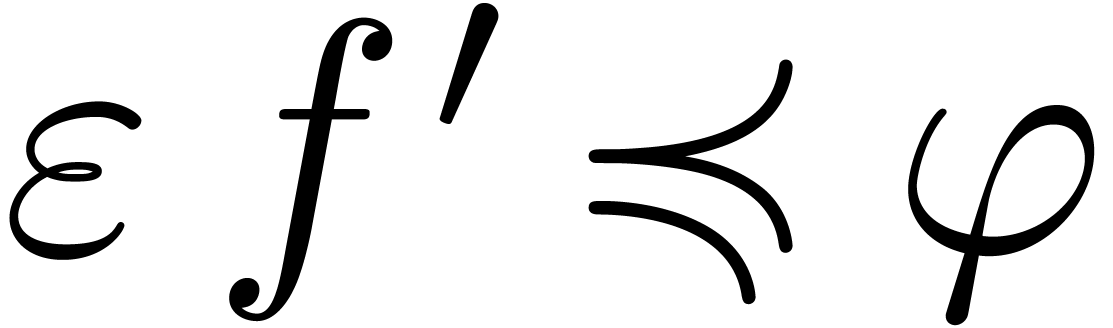 and
and 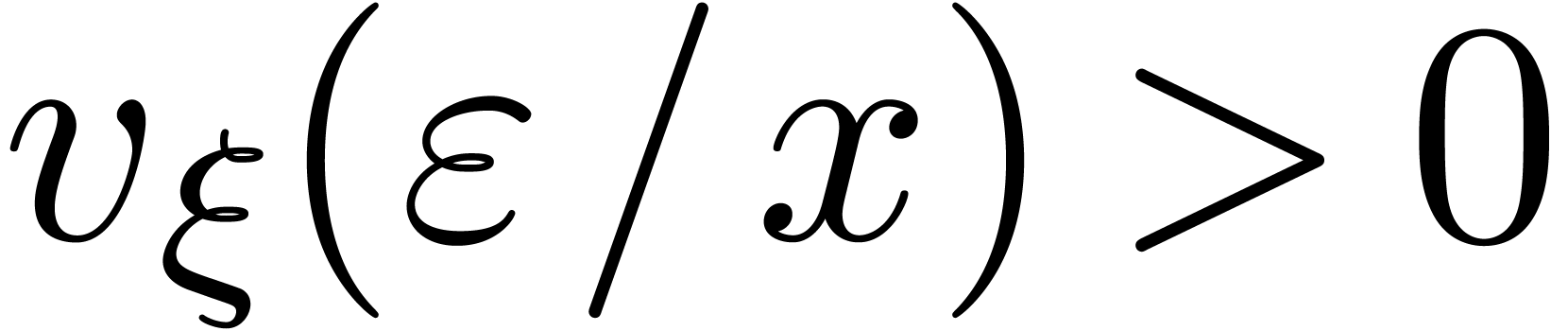 , we have
, we have 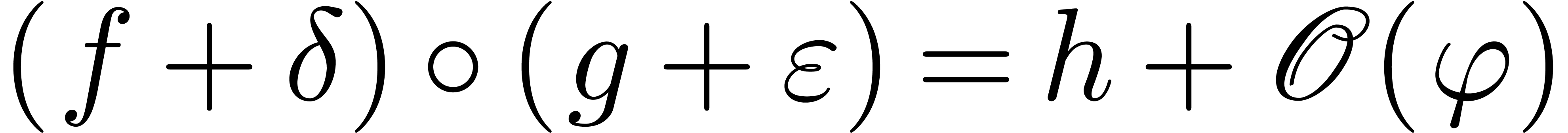
Let 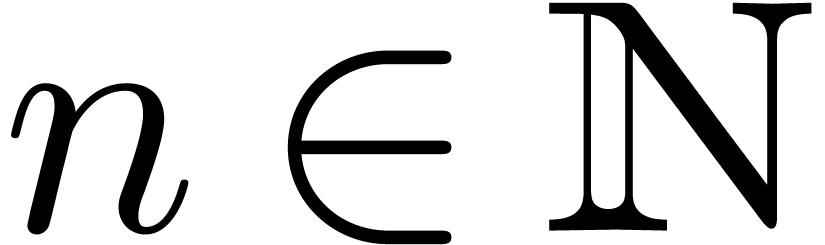 be minimal with
be minimal with 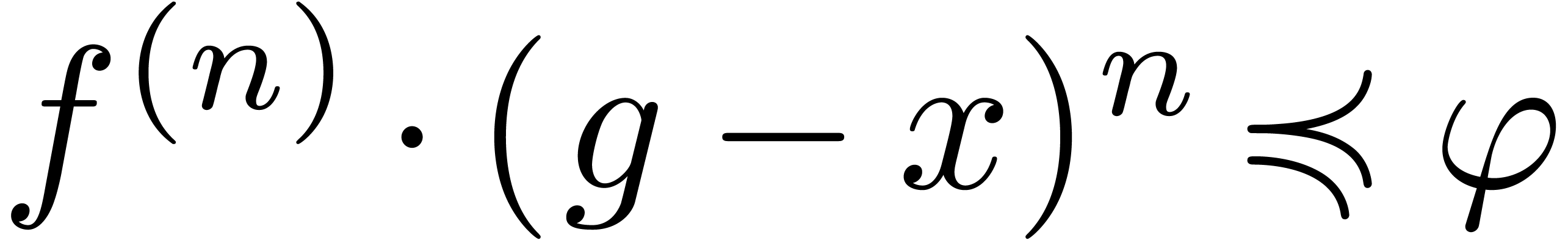
Return 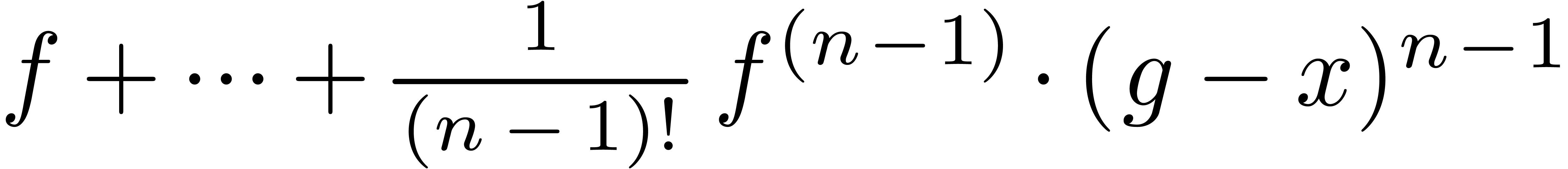
Theorem
Proof. The existence of 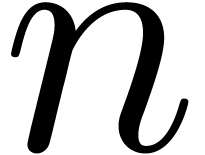 is
ensured by Lemma 13. Since
is
ensured by Lemma 13. Since  is
effective, we have an algorithm for doing the test
is
effective, we have an algorithm for doing the test  , which enables us to compute
, which enables us to compute 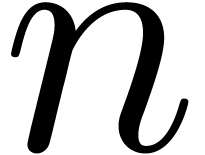 . Setting
. Setting 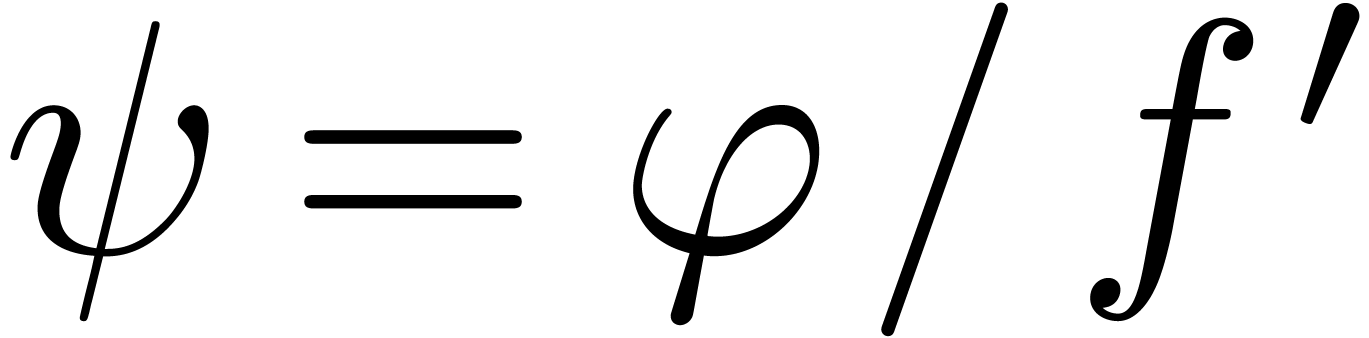 ,
our assumption that
,
our assumption that 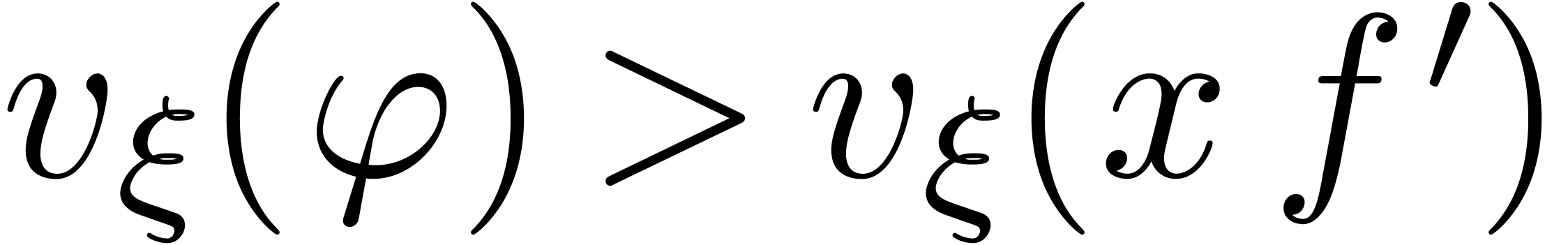 ensures that
ensures that  . The result now follows from Lemma 12.
. The result now follows from Lemma 12.
Remark  and
and  , it can be verified that
, it can be verified that 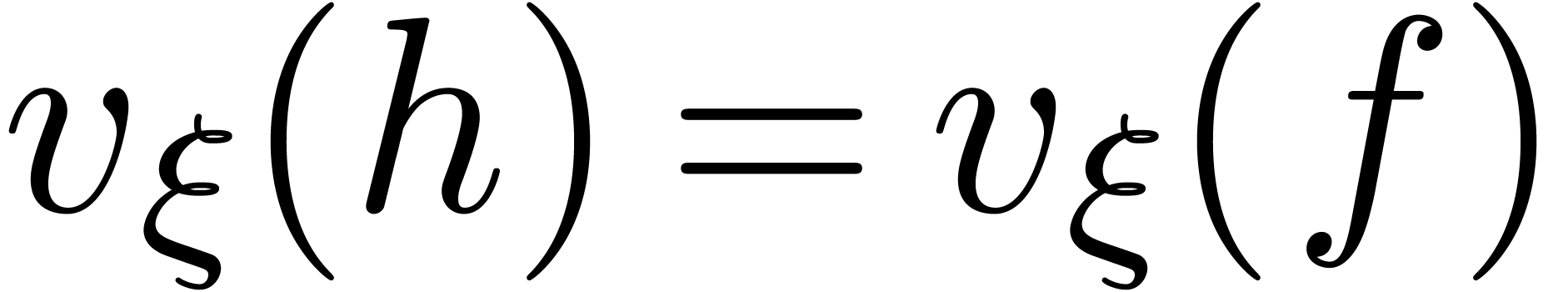 , that
, that  implies
implies 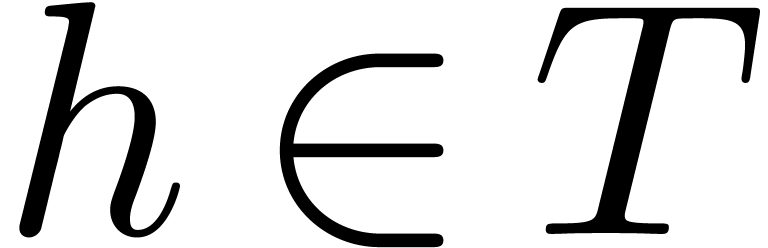 , and that
, and that 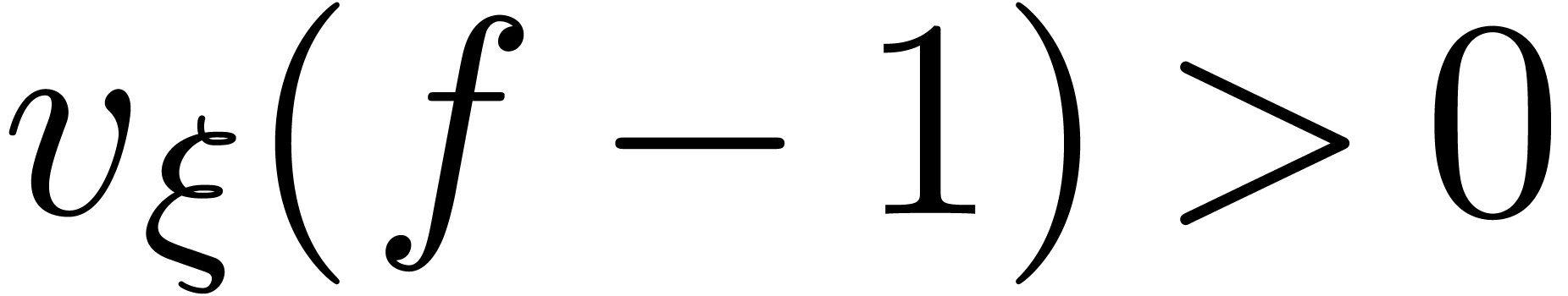 implies
implies 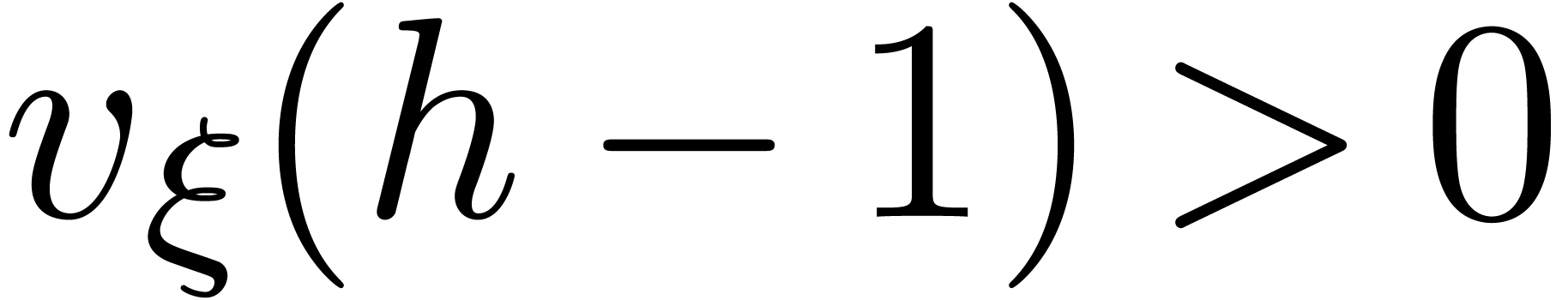 .
.
A well-known way to solve functional equations of the form 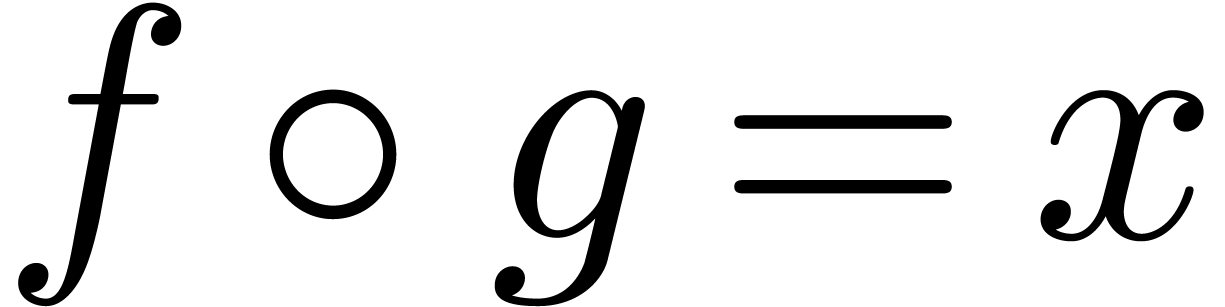 is Newton's method [6]. We will now show that
this method indeed yields a quadratic convergence in our setting.
is Newton's method [6]. We will now show that
this method indeed yields a quadratic convergence in our setting.
Lemma 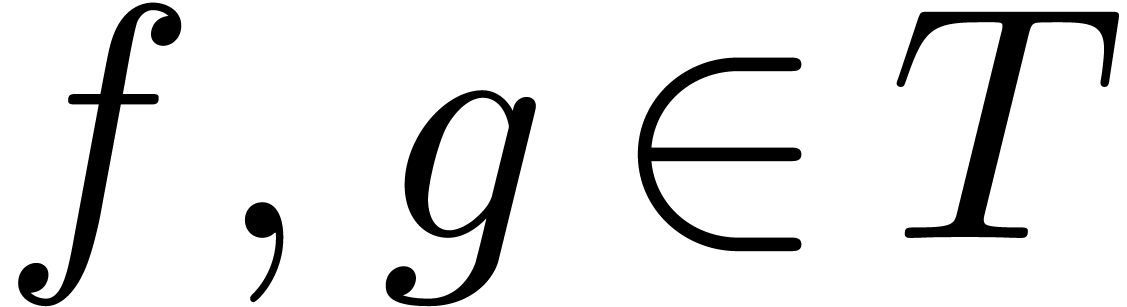 and
and  be such that
be such that 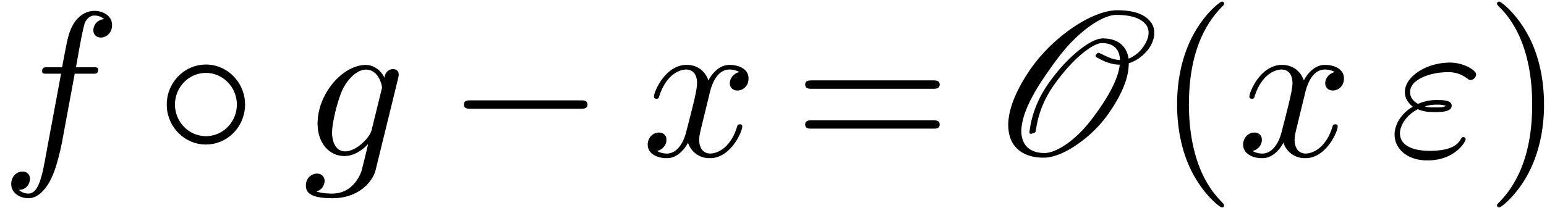 and
and 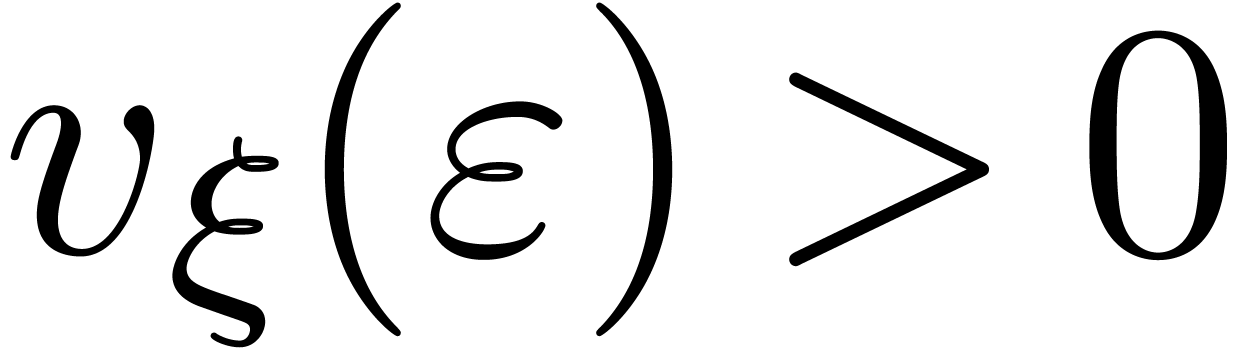 . Let
. Let  be such that
be such that
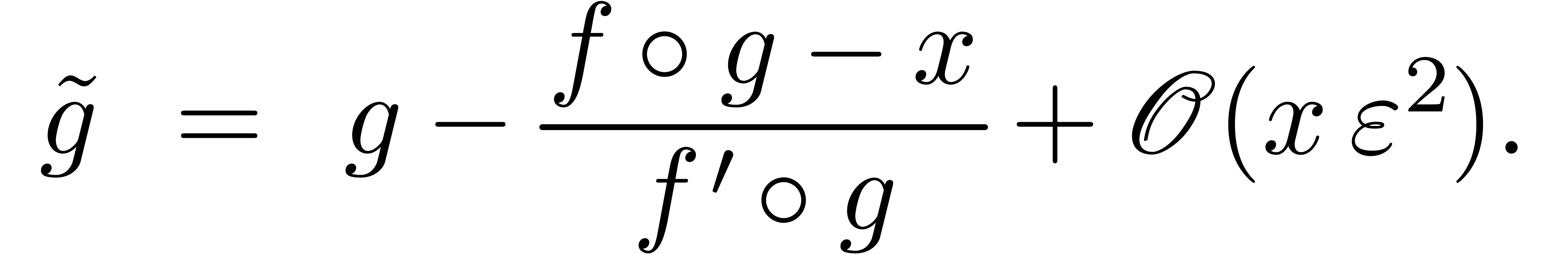
Then 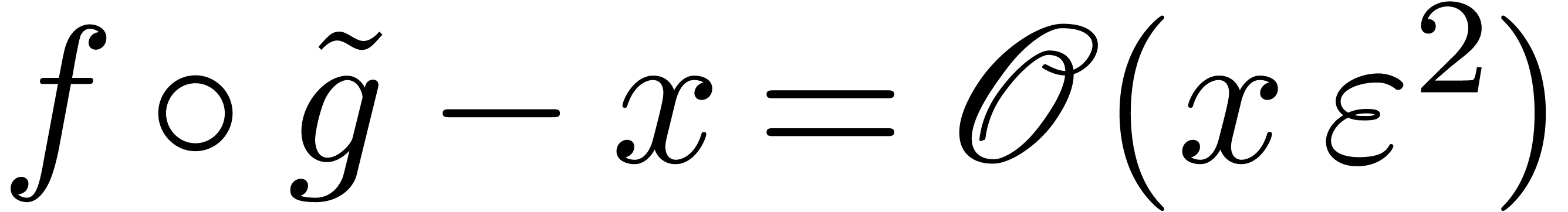 .
.
Proof. Since  ,
we notice that
,
we notice that 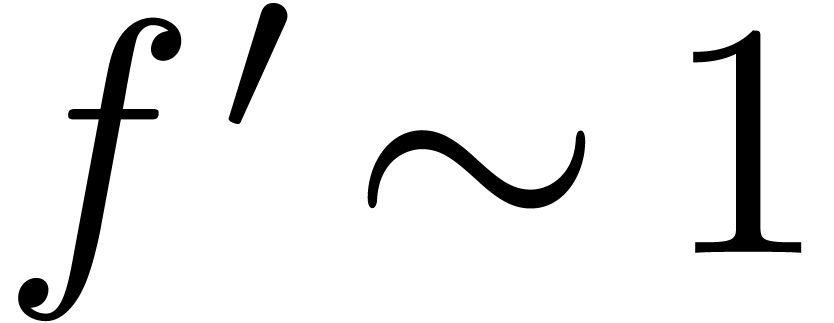 and
and 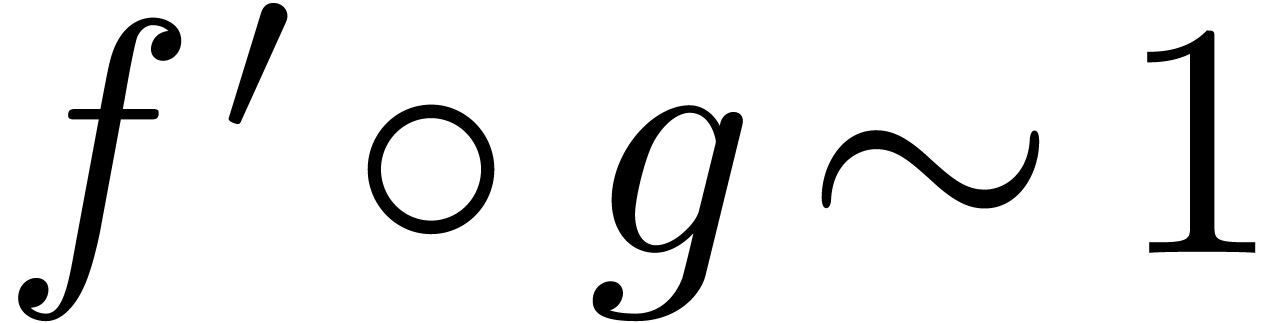 .
Let
.
Let 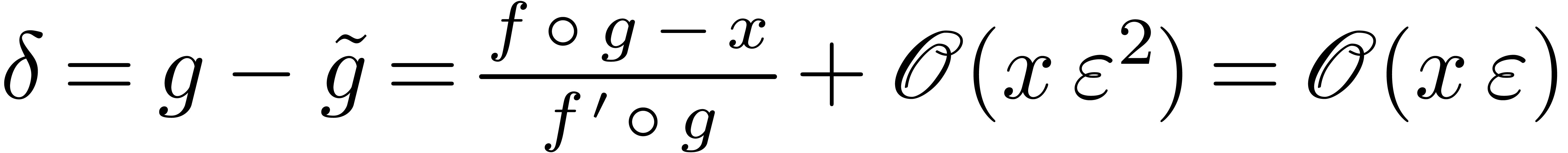 . For all sufficiently
large
. For all sufficiently
large 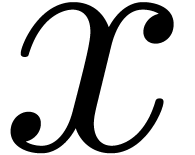 , we have
, we have
whence, using the ultimate monotonicity of 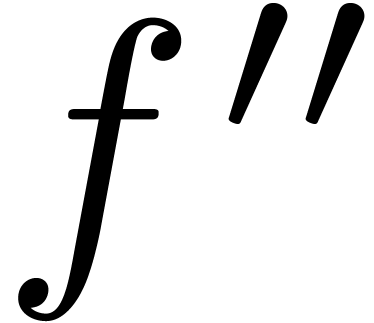 on
on
 ,
,
Using Lemma 11, we also have  and
and
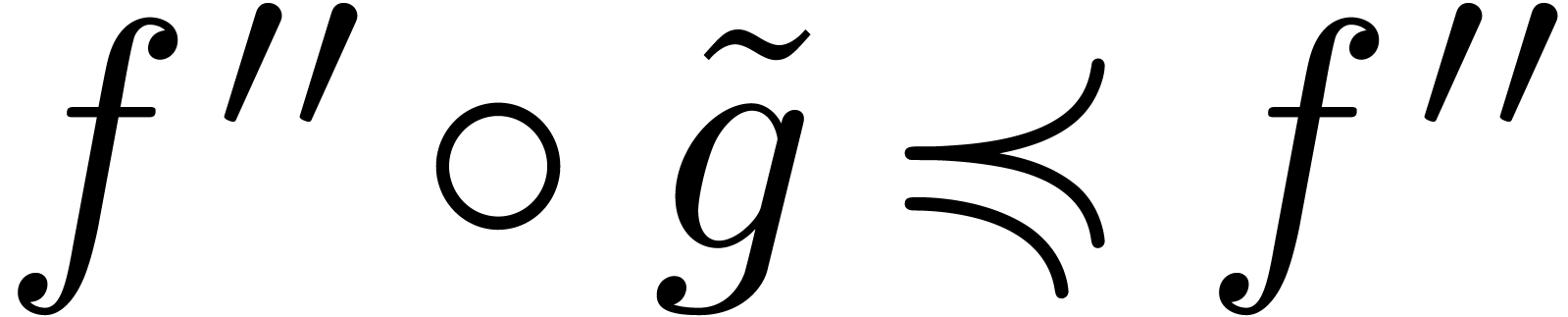 , whence
, whence
Consequently,
Now  implies
implies  and
and 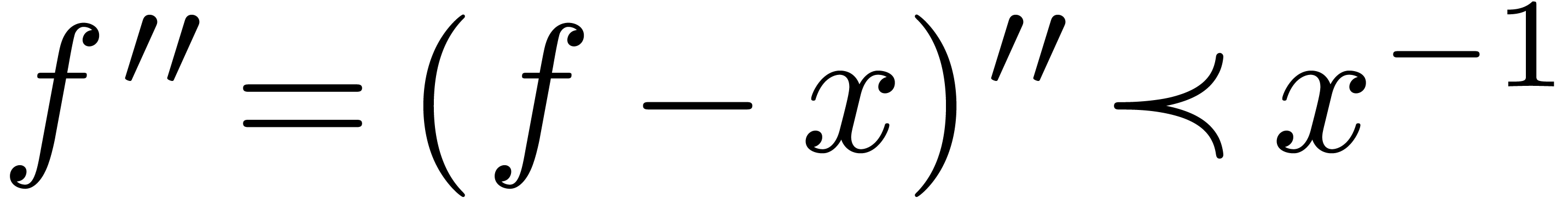 . Consequently,
. Consequently,
This completes the proof.
If  is an effective Hardy field, then this lemma
leads to the following algorithm for the computation of approximate
functional inverses:
is an effective Hardy field, then this lemma
leads to the following algorithm for the computation of approximate
functional inverses:
Algorithm invert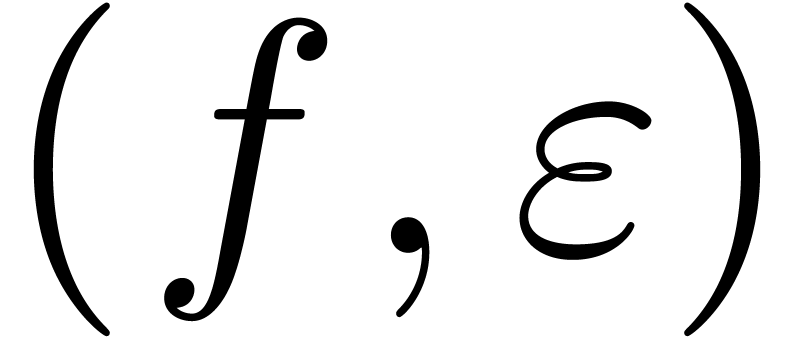
 and
and 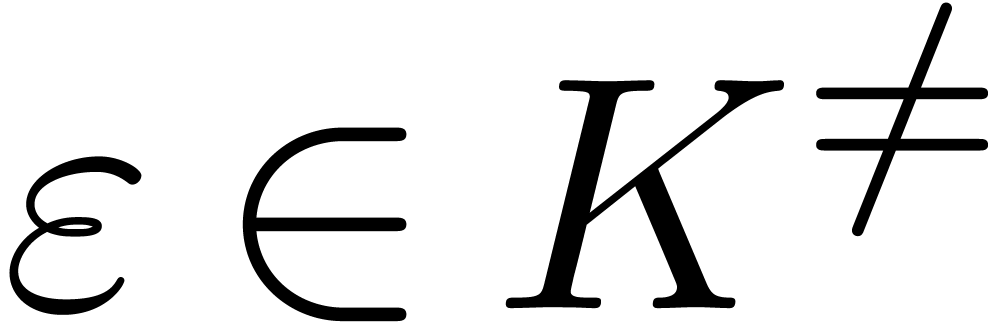 with
with 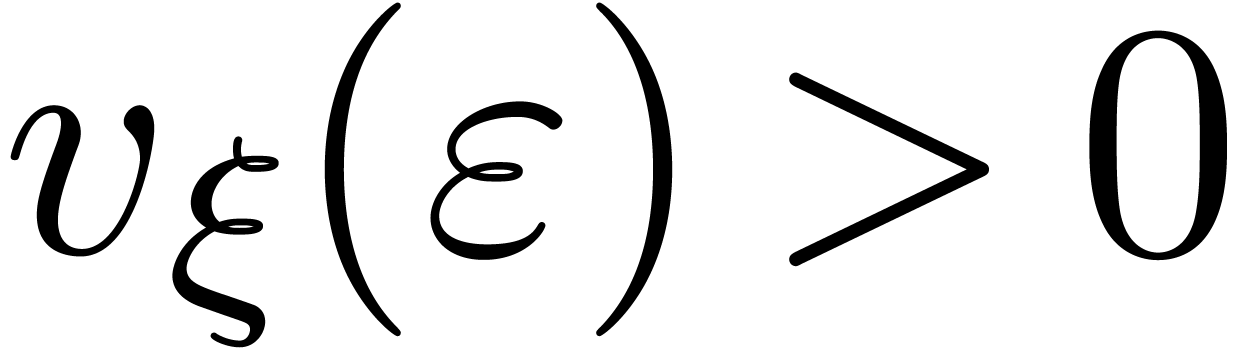
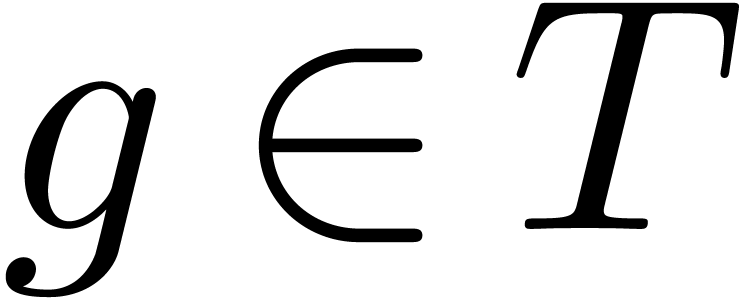 with
with 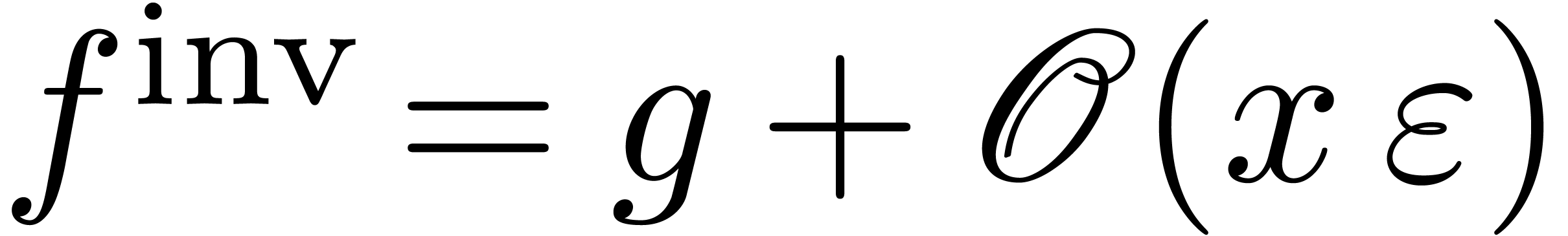
Moreover, for any  with
with 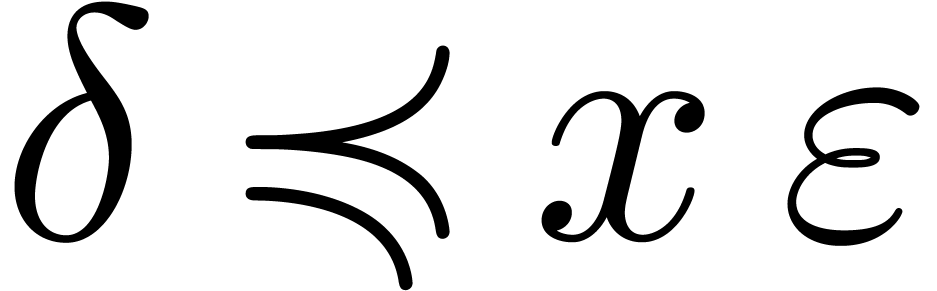 and
and  , we have
, we have 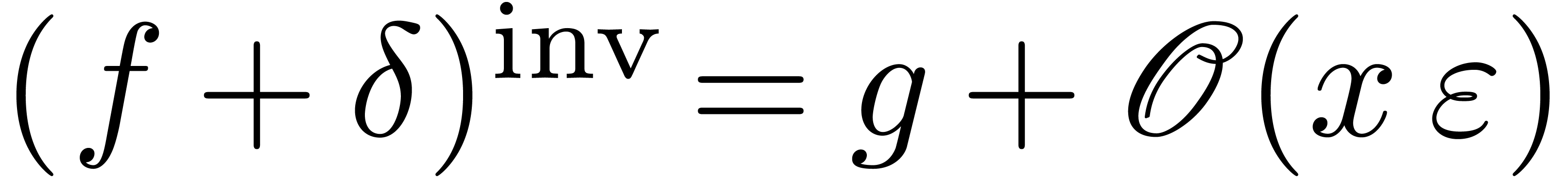
Let 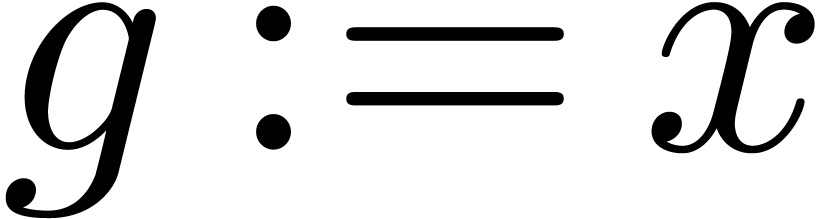
repeat
Let 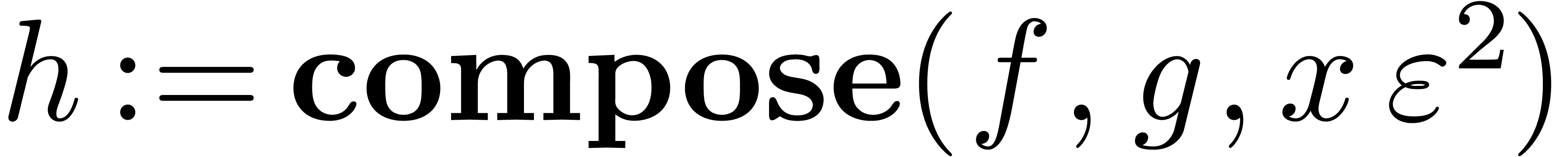
If 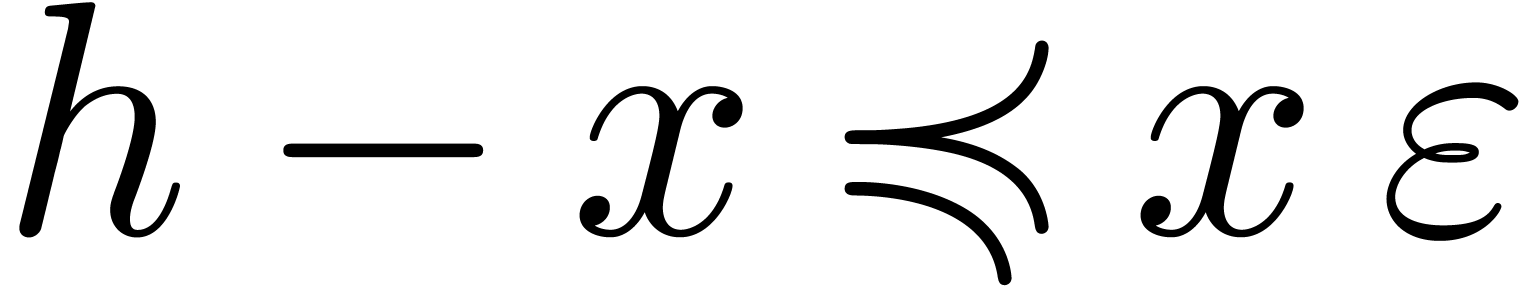 then return
then return 
Let 
Let 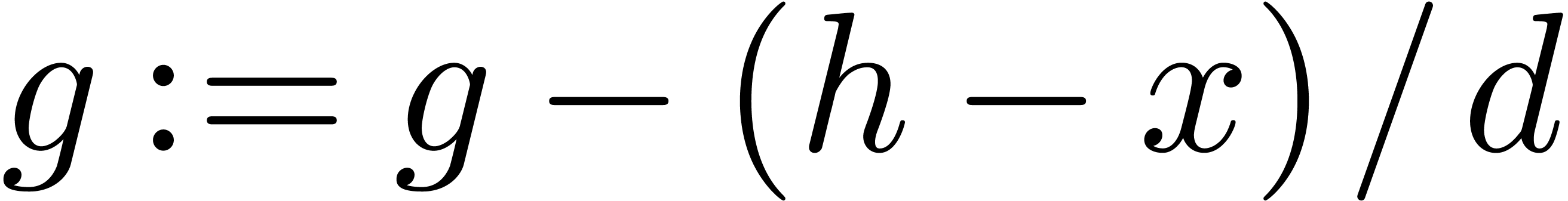
Theorem 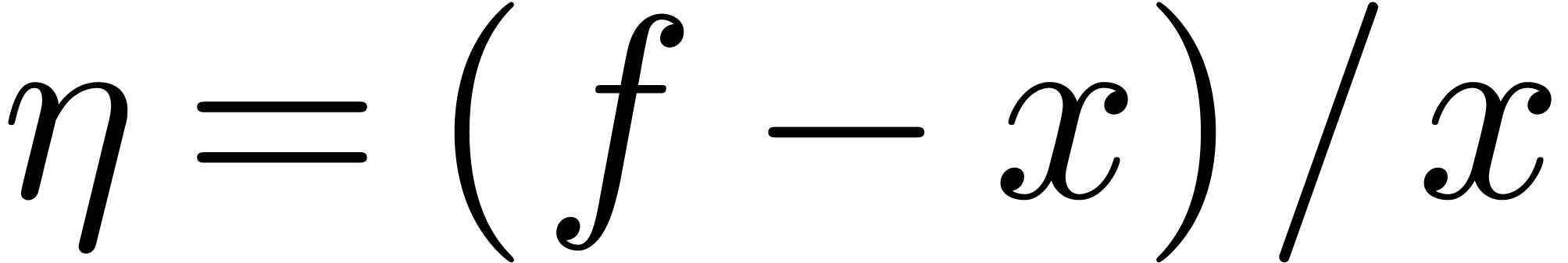 . The algorithm
. The algorithm 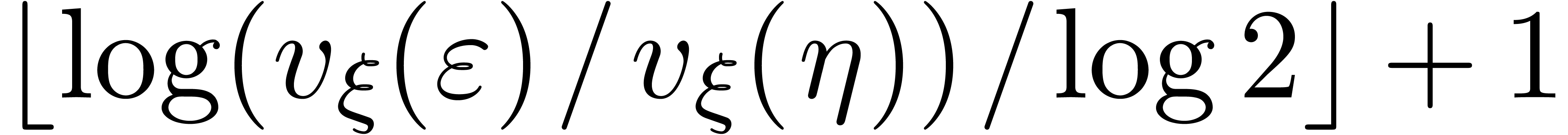 iterations of the main loop.
iterations of the main loop.
Proof. Let us first show that 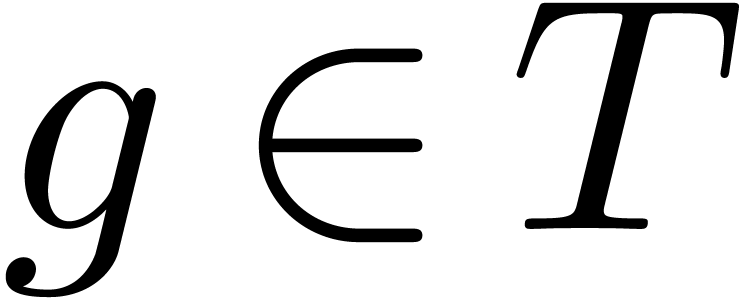 throughout the algorithm. This is clear at the start. At each iteration
throughout the algorithm. This is clear at the start. At each iteration
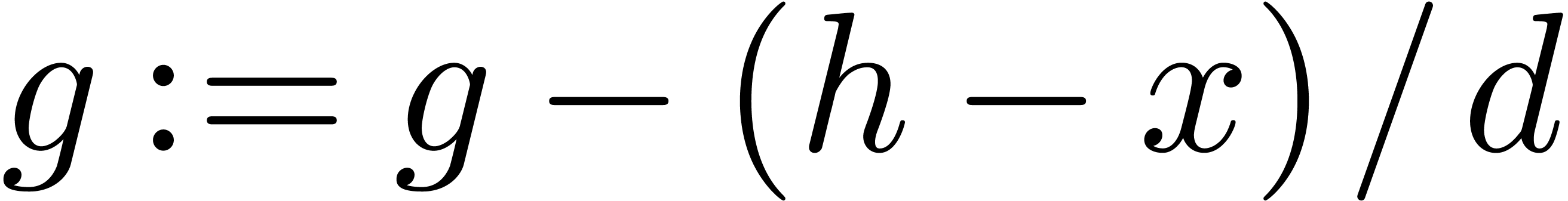 , Remark 15
implies
, Remark 15
implies 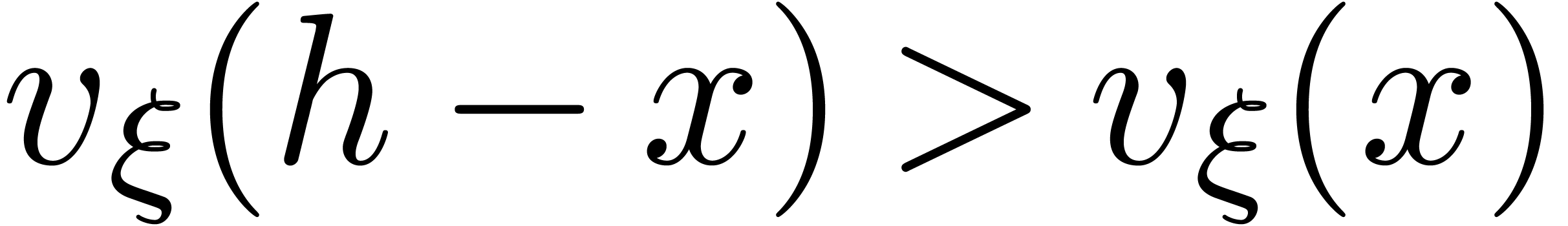 and
and 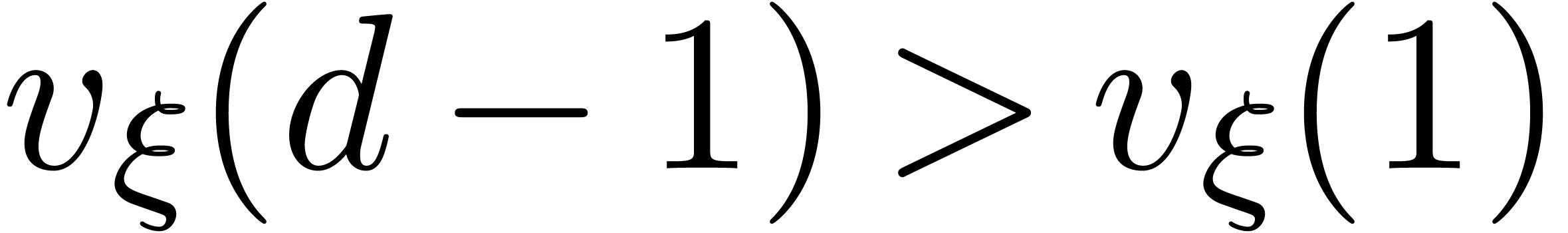 ,
whence
,
whence 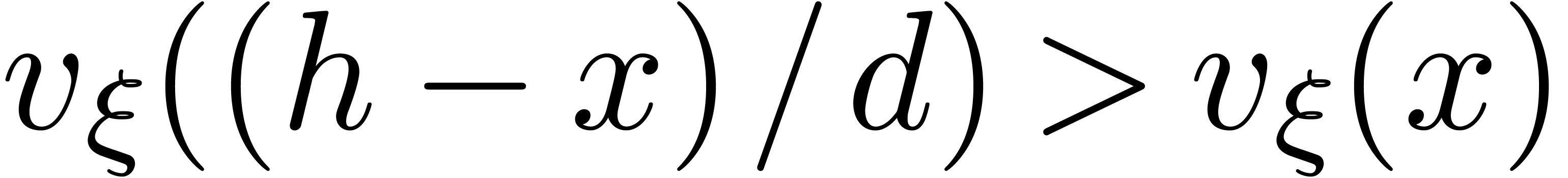 , so that
, so that 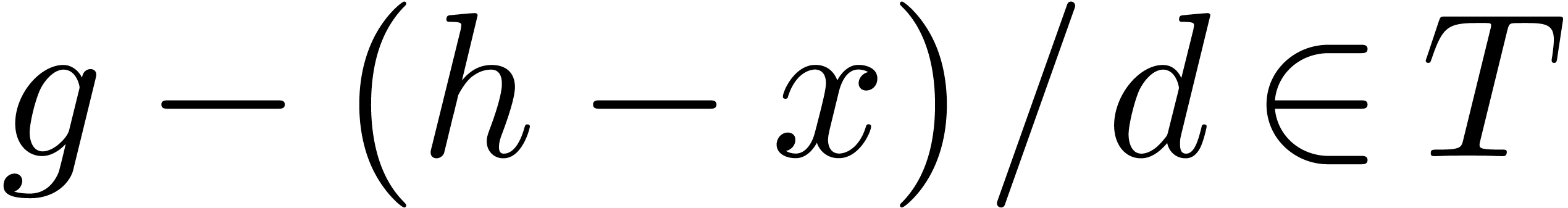 .
.
On termination, we have 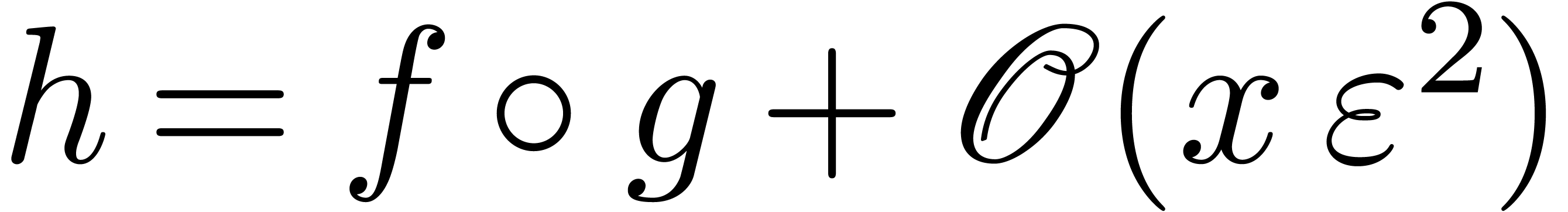 and
and 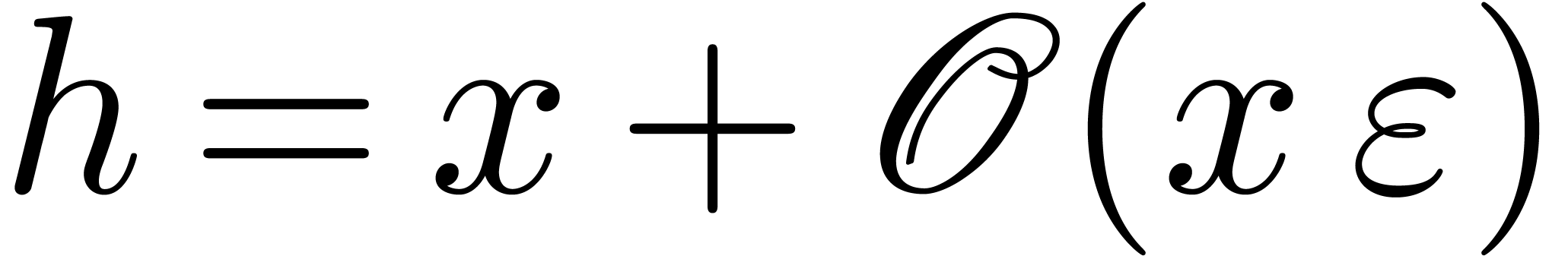 , whence
, whence 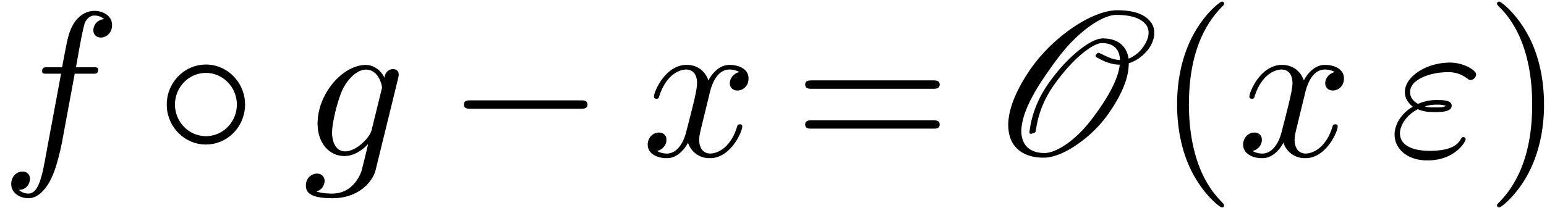 .
Applying Lemma 10 with
.
Applying Lemma 10 with  and
and 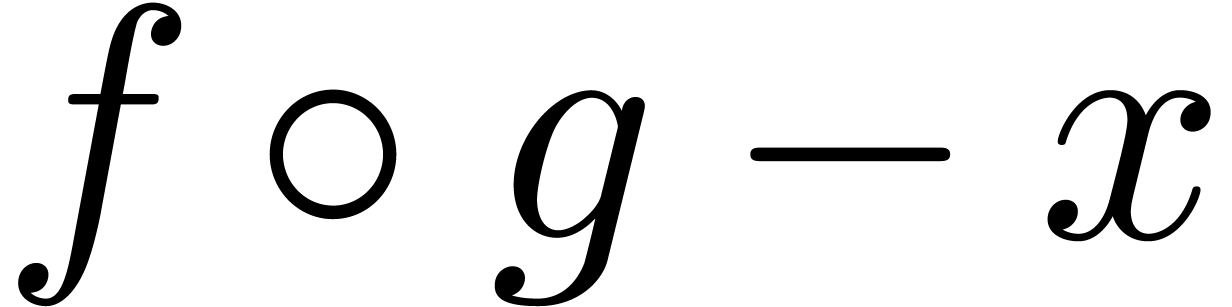 in the roles of
in the roles of  and
and  , we obtain
, we obtain  . Consequently,
. Consequently,  .
Furthermore,
.
Furthermore,  .
.
As to the termination, consider the quantity
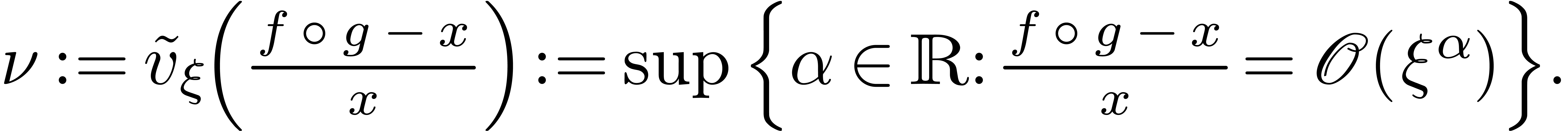
At the very start, we have 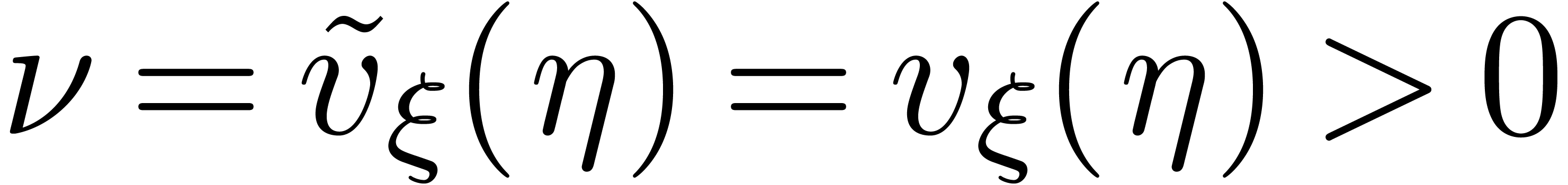 .
At every iteration
.
At every iteration 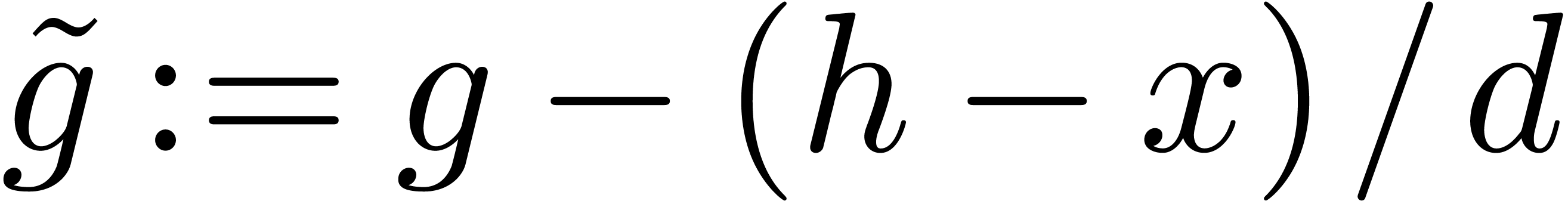 , we have
, we have
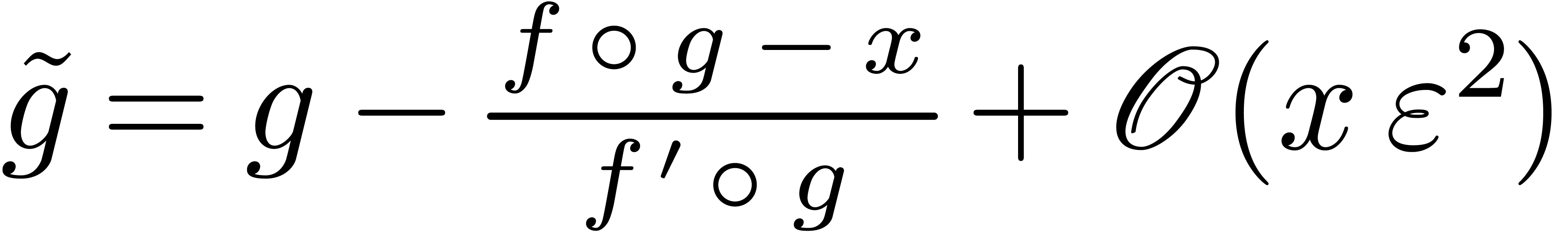 . Lemma 16
therefore ensures that
. Lemma 16
therefore ensures that  doubles at least, whereas
the algorithm terminates as soon as
doubles at least, whereas
the algorithm terminates as soon as 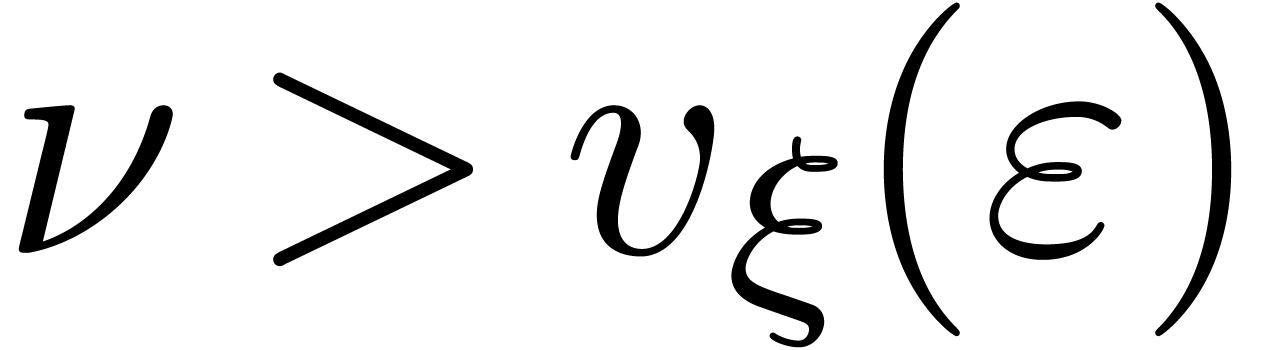 .
This happens after at most
.
This happens after at most 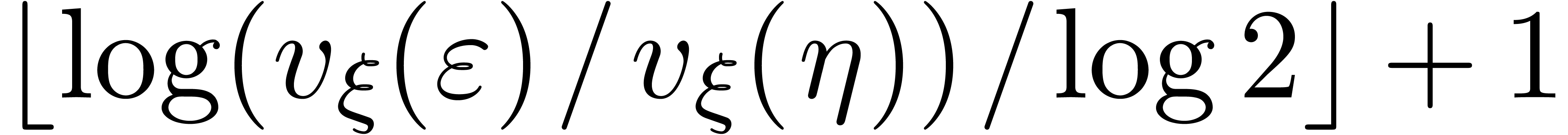 iterations.
iterations.
We now extend the definition of high tangency to identity to all germs.
We say that a germ 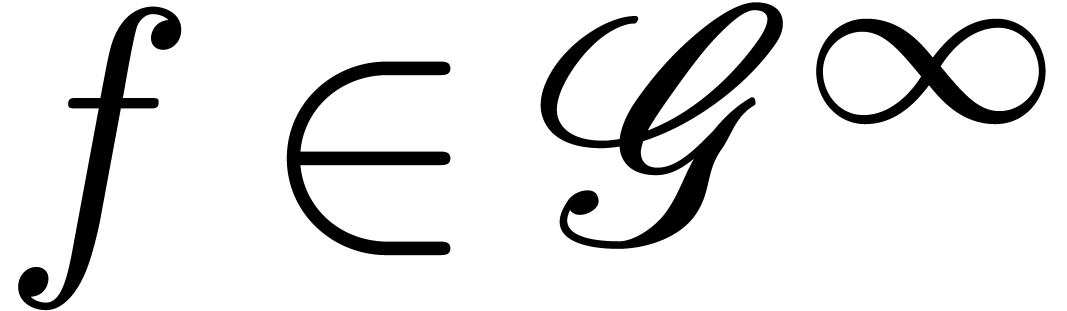 is highly tangent to
identity if there exists a
is highly tangent to
identity if there exists a  with
with 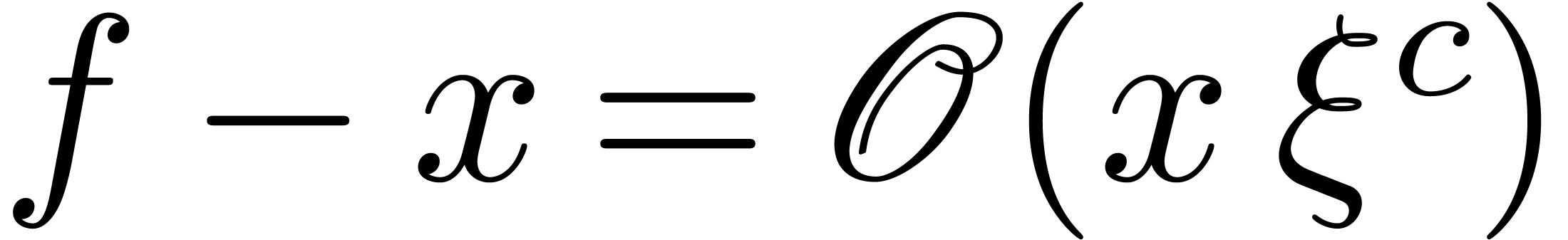 and
and 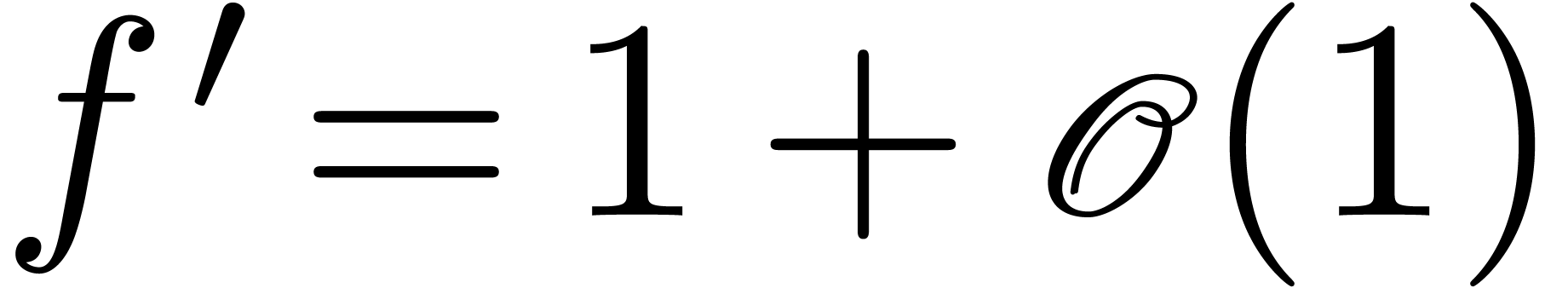 . We denote
by
. We denote
by  the set of such germs. We say that
the set of such germs. We say that 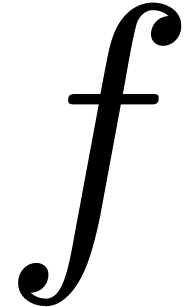 admits an asymptotic expansion over
admits an asymptotic expansion over  if for every
if for every 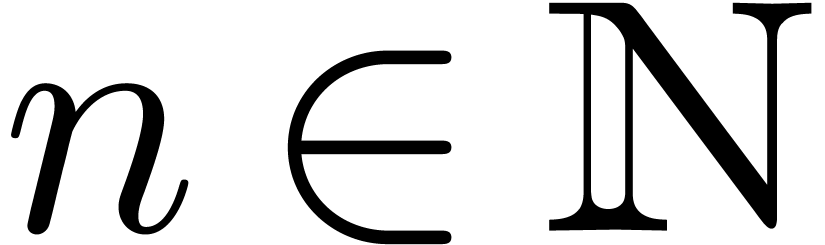 ,
there exists an element
,
there exists an element 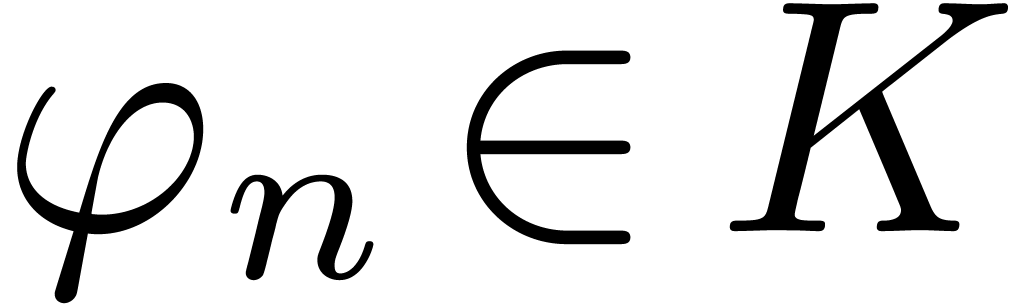 with
with 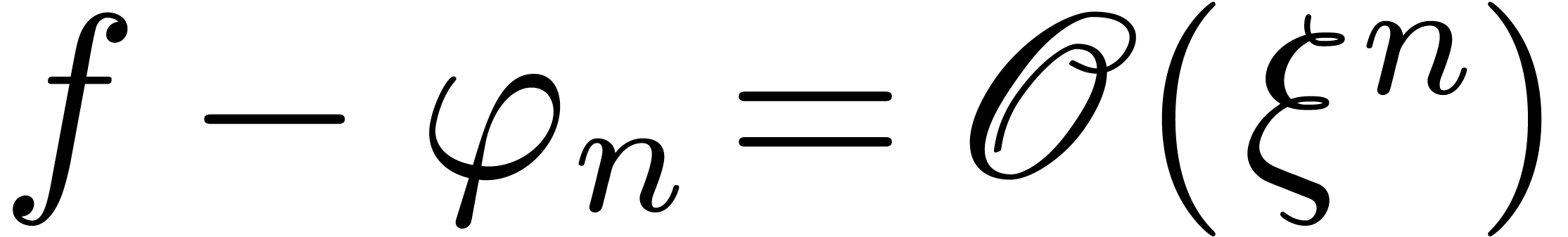 . If we have an algorithm for computing
. If we have an algorithm for computing  as a function of
as a function of 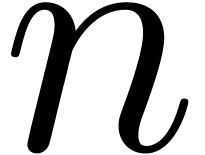 ,
then we say that
,
then we say that 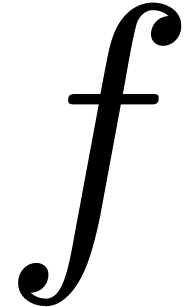 admits an effective
asymptotic expansion over
admits an effective
asymptotic expansion over  .
.
Proposition  and
and 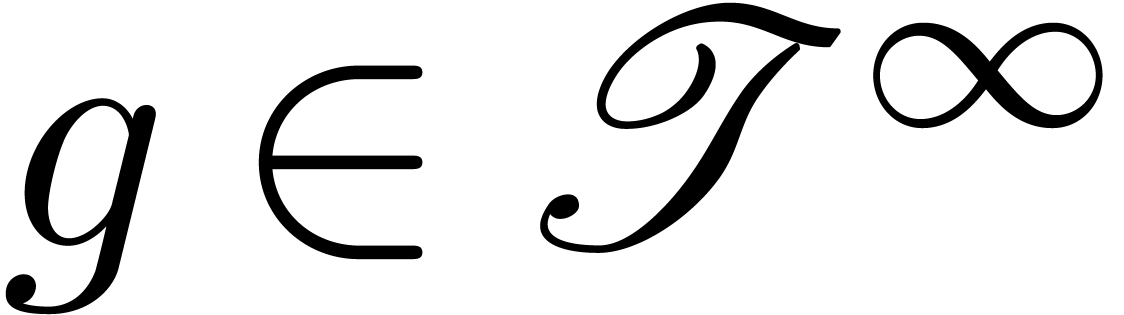 admit effective
asymptotic expansions over
admit effective
asymptotic expansions over  .
Then so does
.
Then so does  . If
. If 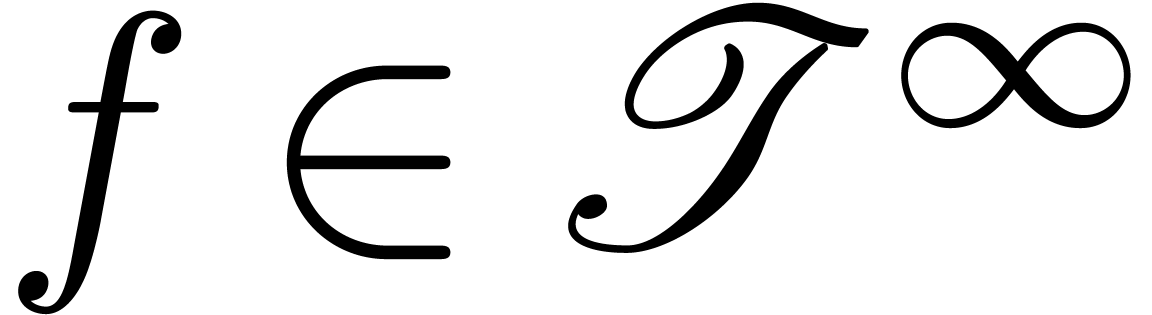 , then
, then  .
.
Proof. Given  ,
we may compute
,
we may compute 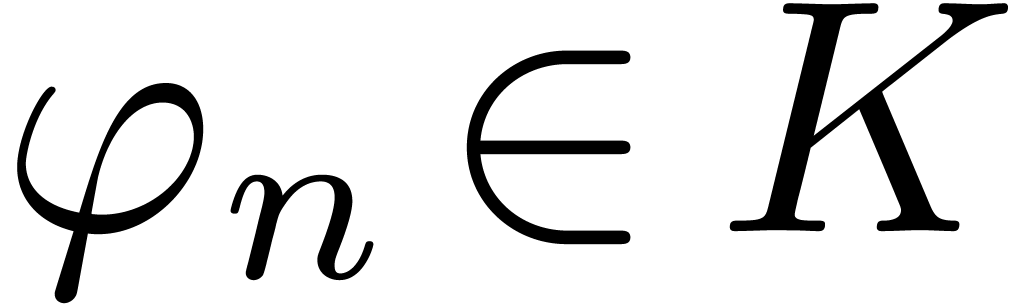 and
and 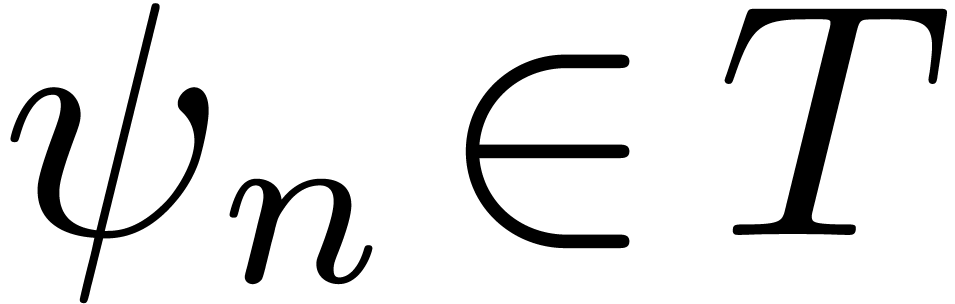 with
with
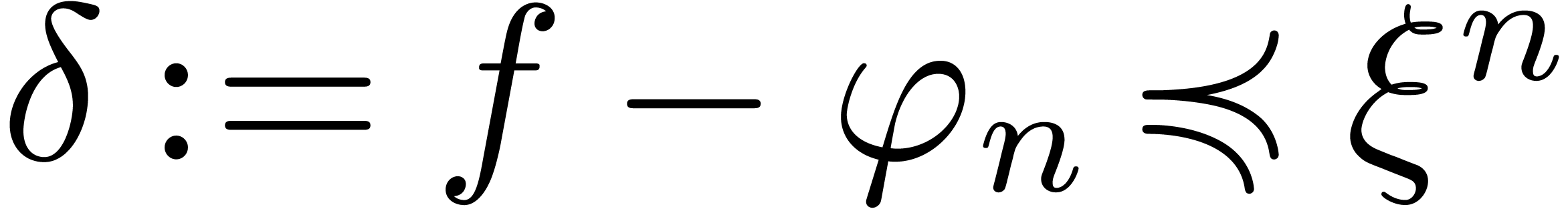 and
and 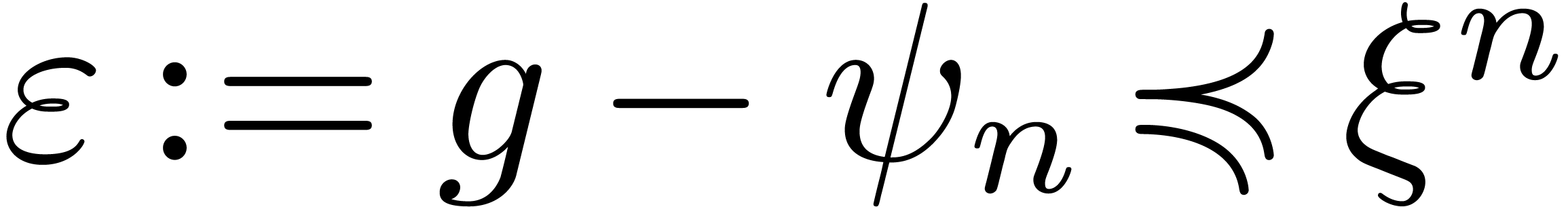 .
Assume that there exists an
.
Assume that there exists an  with
with 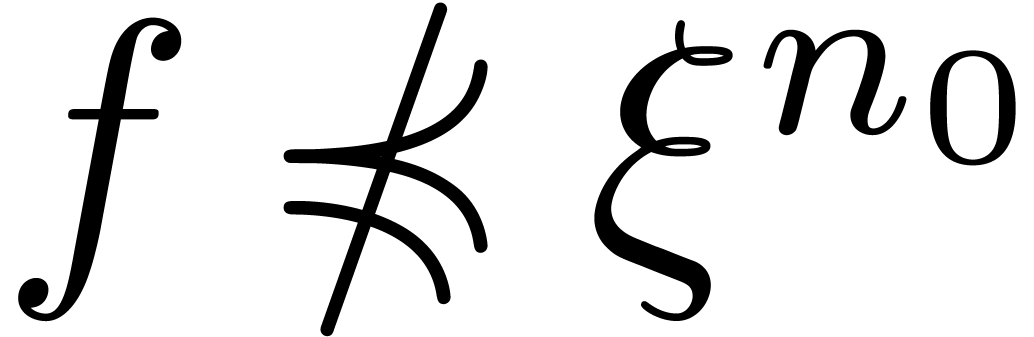 . Then for all
. Then for all 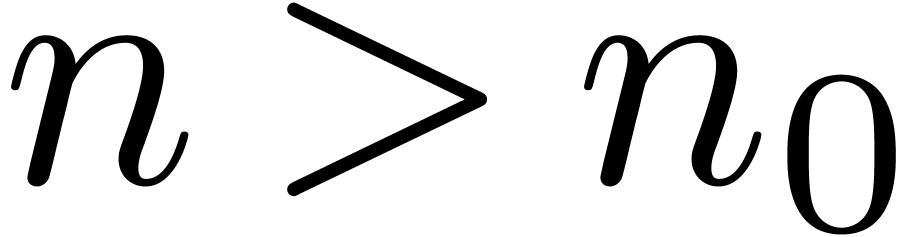 ,
we must have
,
we must have  and
and 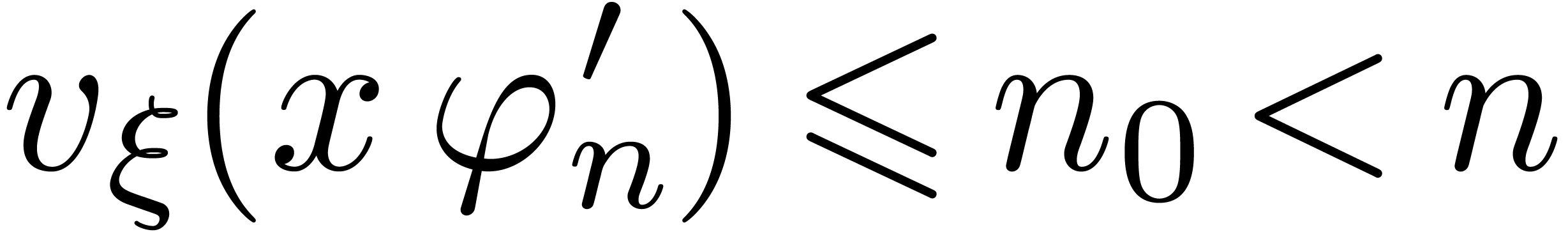 .
Consequently, we may compute
.
Consequently, we may compute  ,
and
,
and  . If
. If 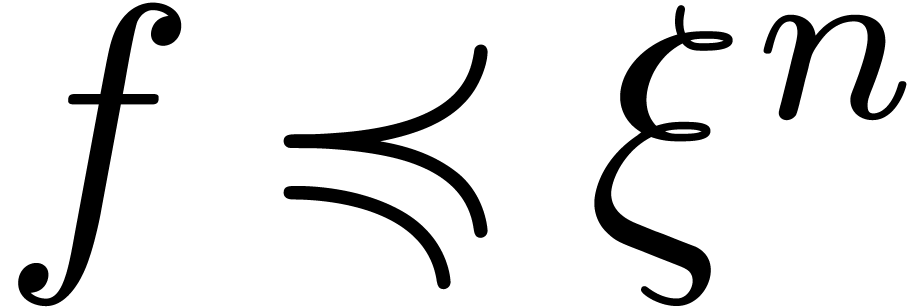 for all
for all 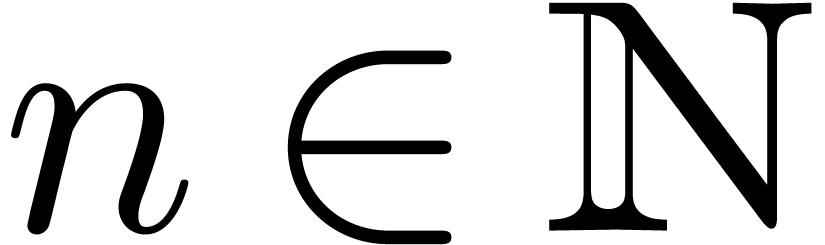 , then we also have
, then we also have
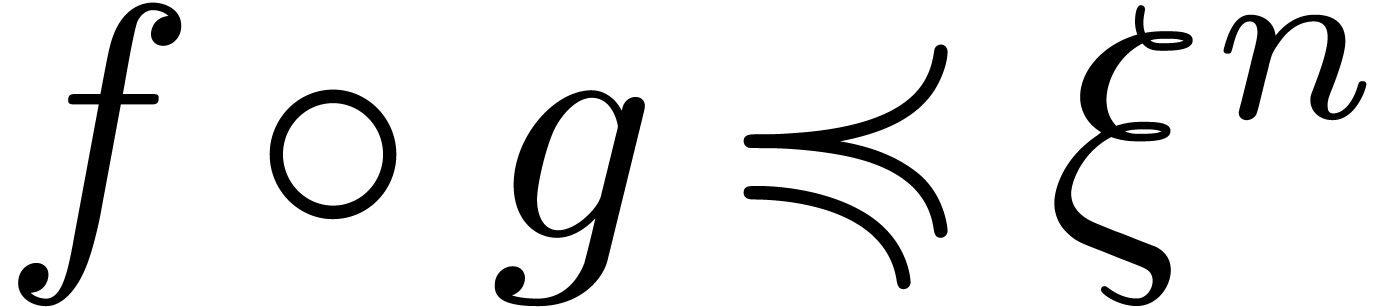 for all
for all 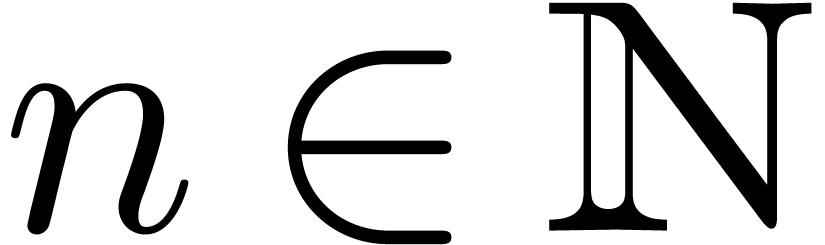 .
.
If 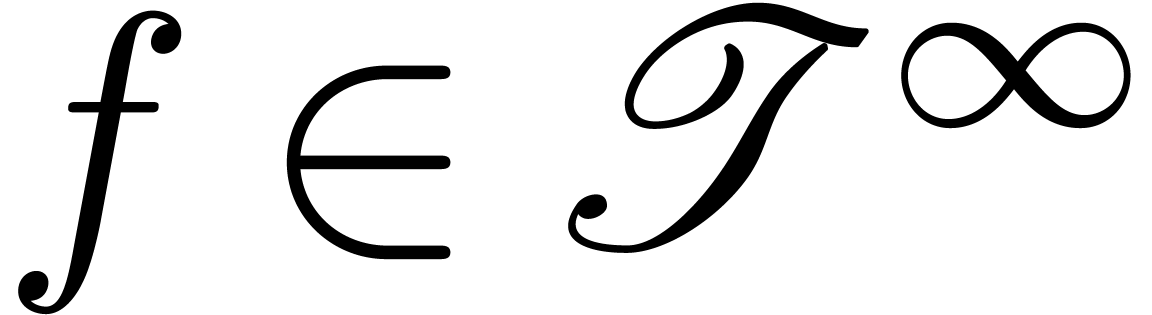 , then we also get
, then we also get 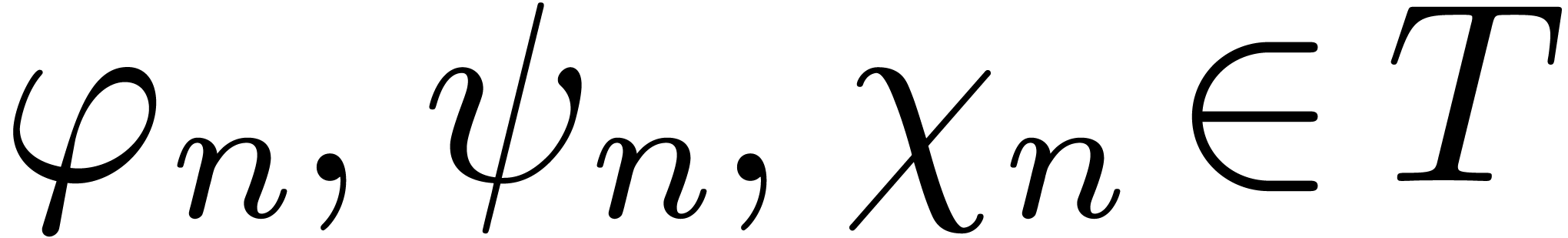 , whence
, whence  . Moreover,
. Moreover, 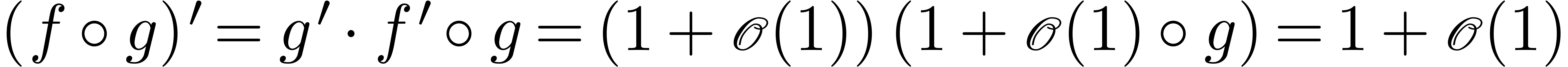 ,
whence
,
whence  .
.
Proposition 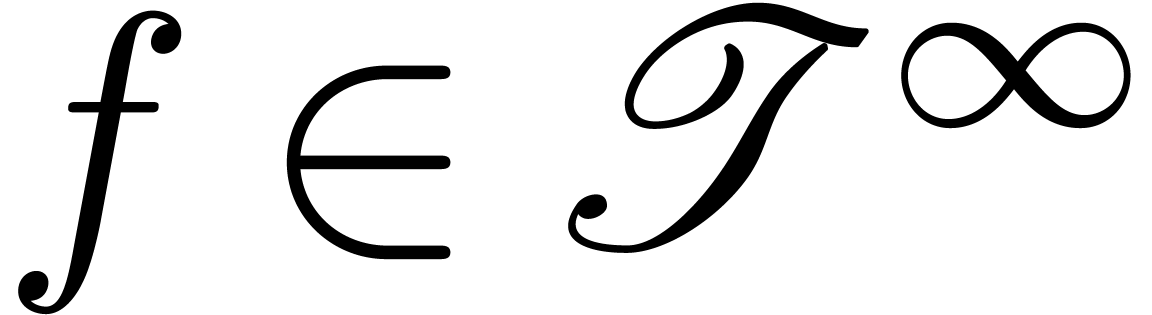 admits an effective asymptotic expansion over
admits an effective asymptotic expansion over
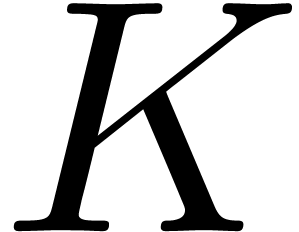 . Then so does
. Then so does 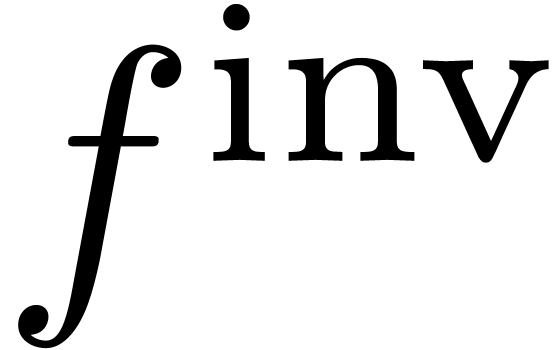 and
and 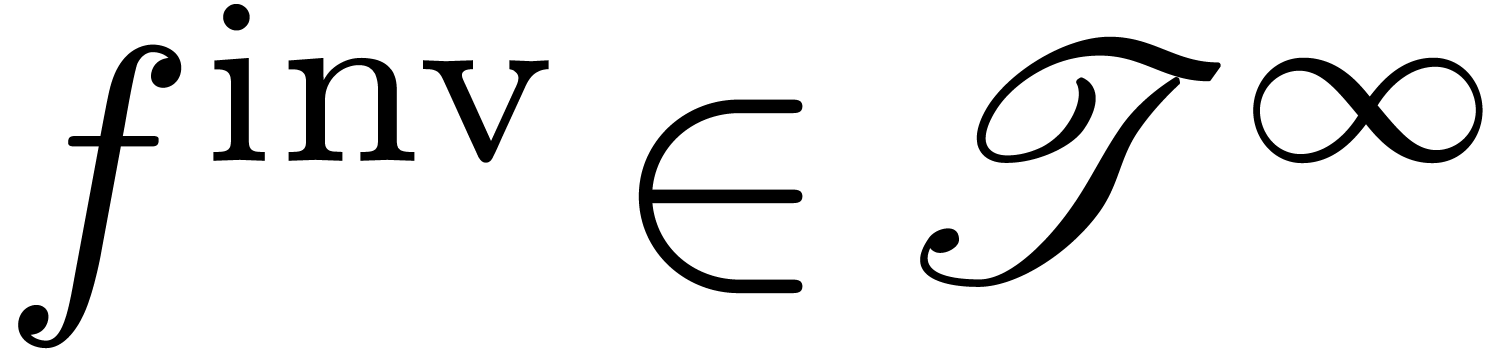 .
.
Proof. Given  ,
we may compute
,
we may compute 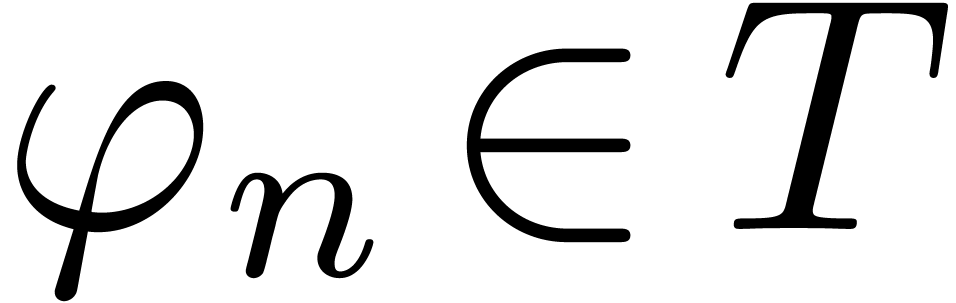 with
with 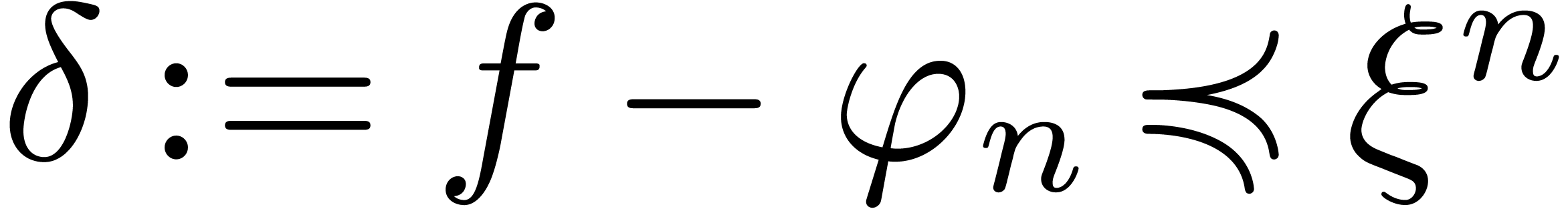 . Let
. Let 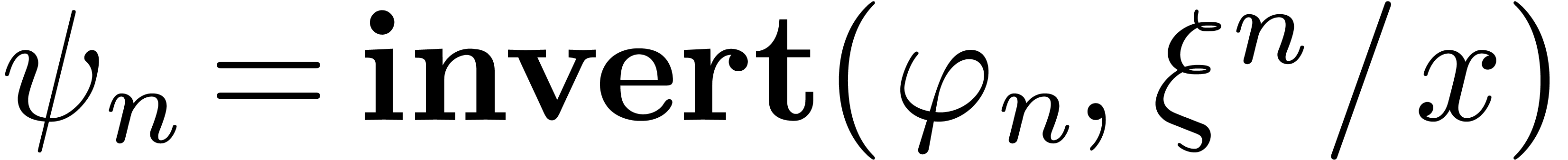 .
Then
.
Then  . Moreover,
. Moreover,  , whence
, whence 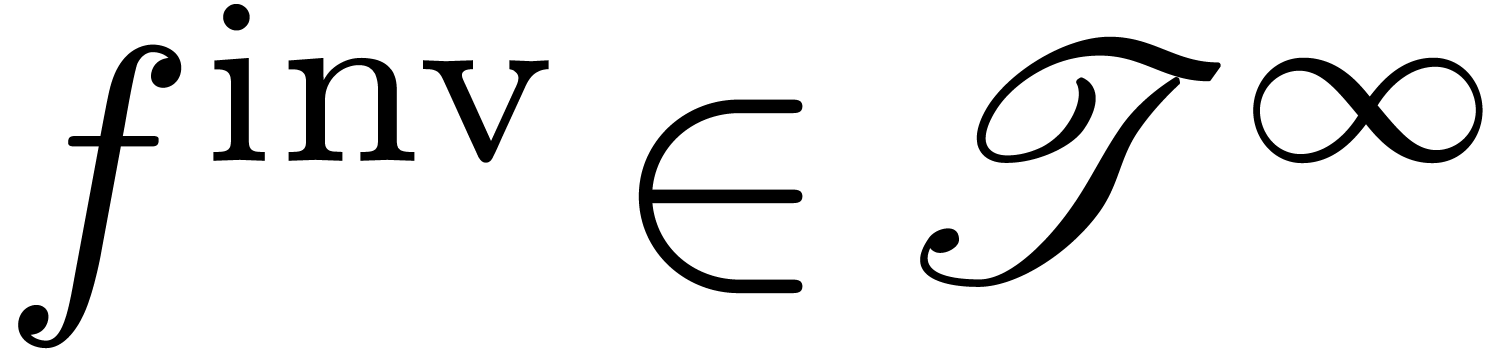 .
.
Combining these two propositions, we have shown the following:
Theorem
 that admit
effective asymptotic expansions over
that admit
effective asymptotic expansions over  forms a
group for functional composition.
forms a
group for functional composition.

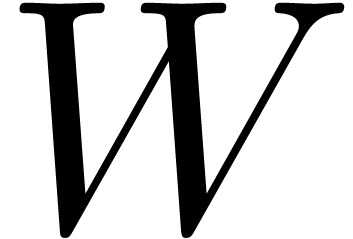 function
function
The Lambert 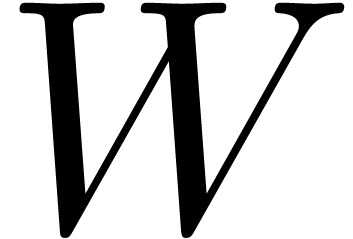 function is defined to be the
inverse function of
function is defined to be the
inverse function of 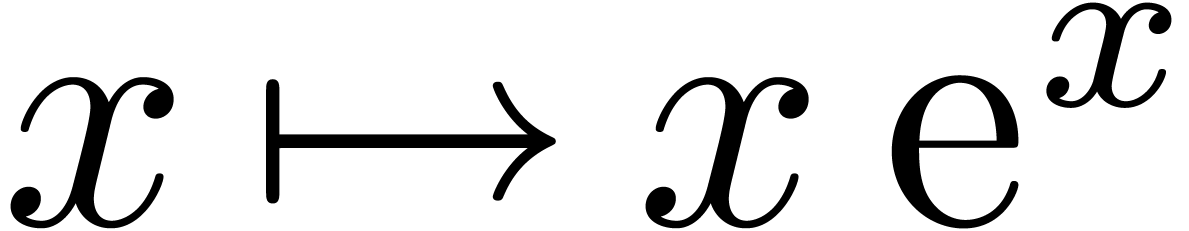 . Using
our algorithm, we can compute the asymptotic expansion of the inverse
function
. Using
our algorithm, we can compute the asymptotic expansion of the inverse
function 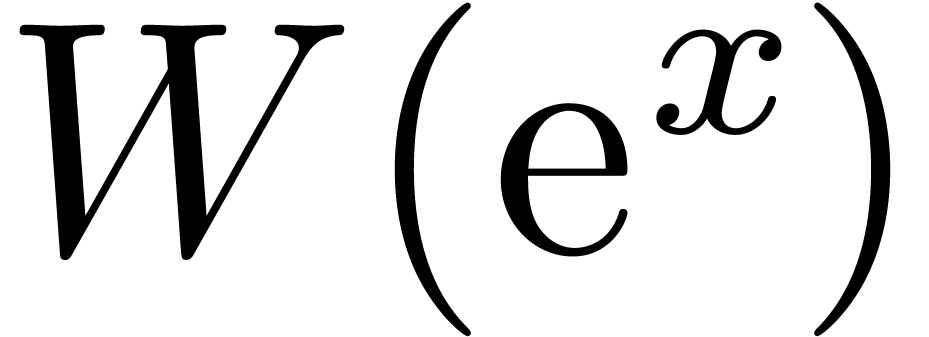 of
of  .
This also yields the asymptotic expansion of
.
This also yields the asymptotic expansion of 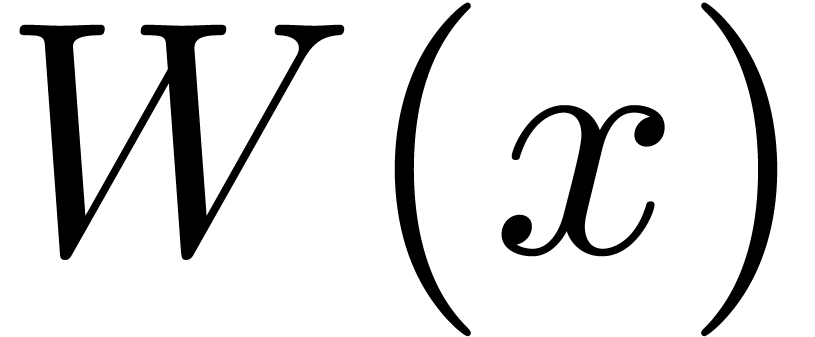 for
large
for
large 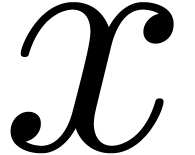 .
.
Let 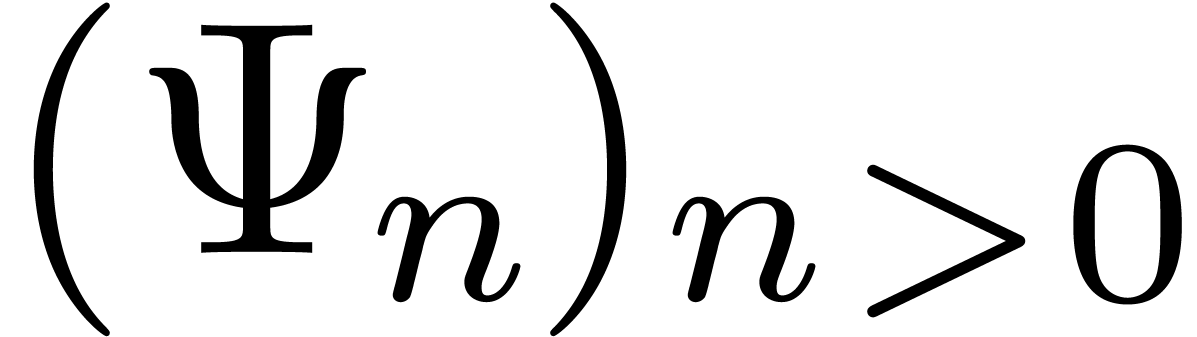 be defined formally by
be defined formally by
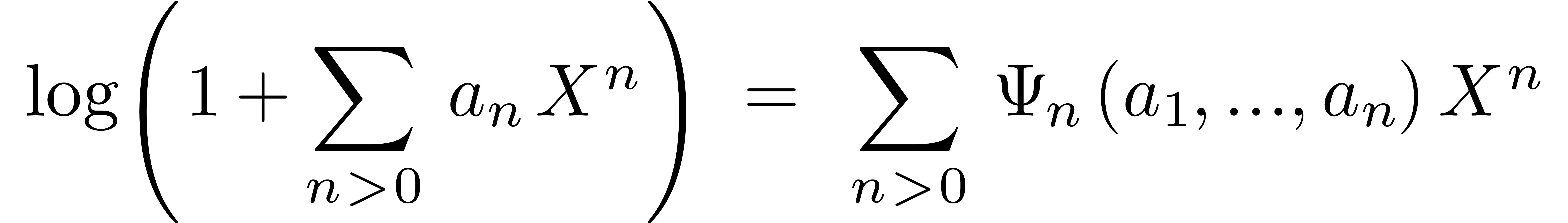
and let  be the Gaussian function:
be the Gaussian function:
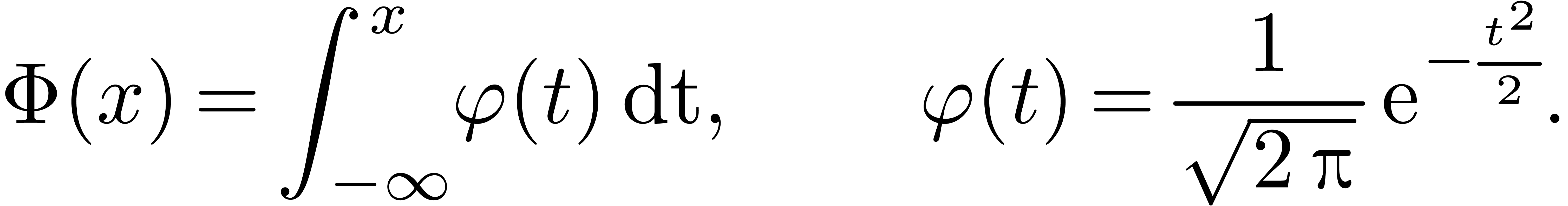
For any 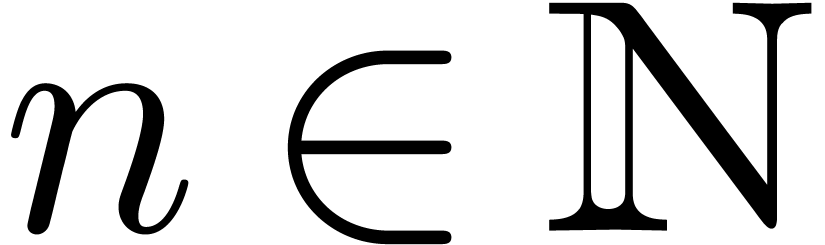 , we have the
well-known relation
, we have the
well-known relation
where we used the notation
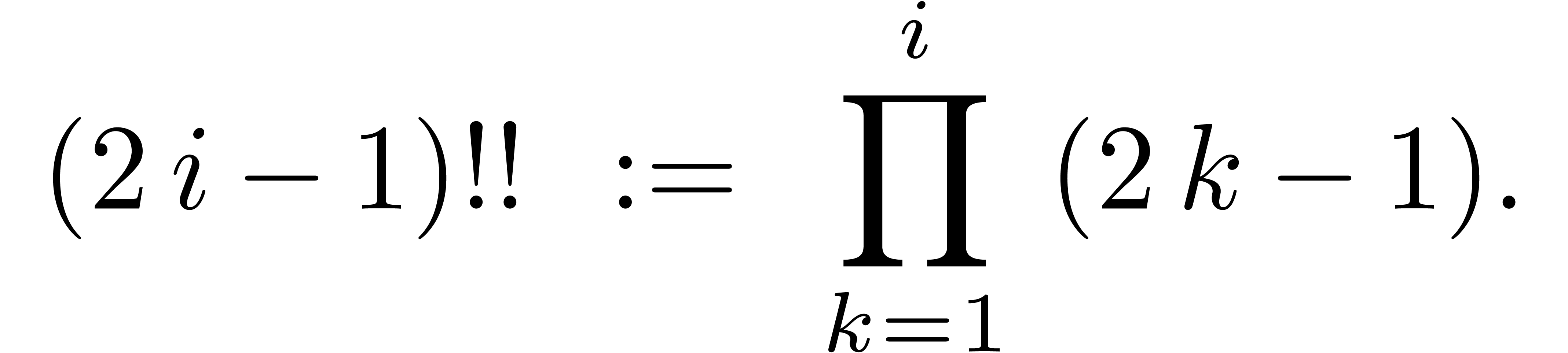
The relation (6) shows that
with 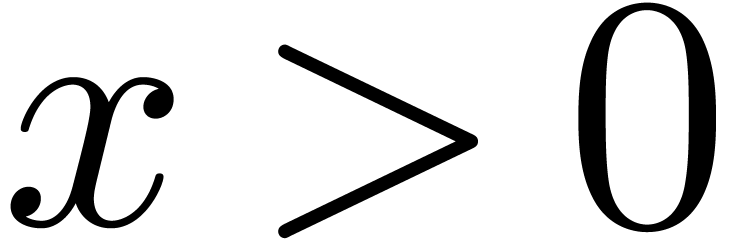 ,
,
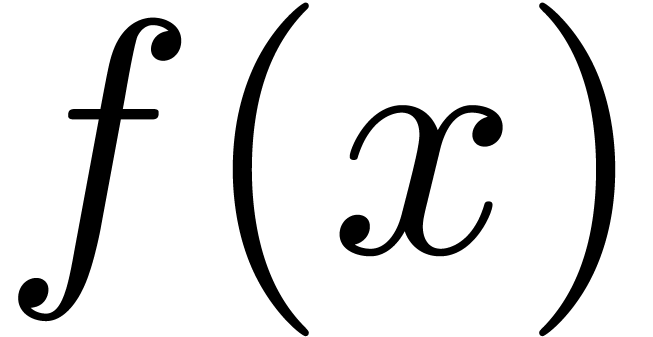 |
 |
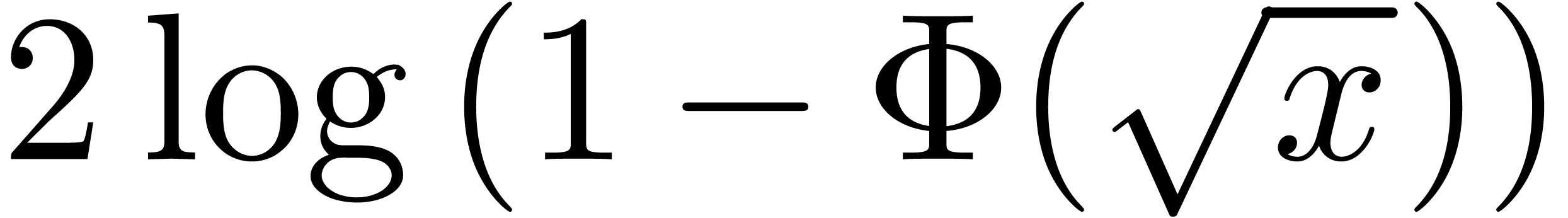 |
|
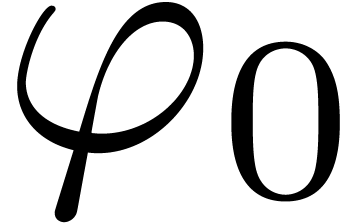 |
 |
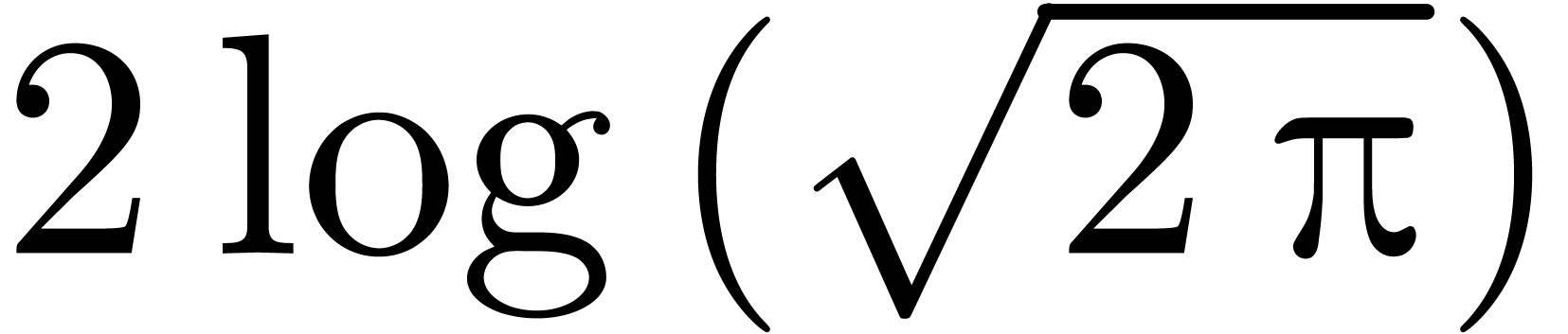 |
|
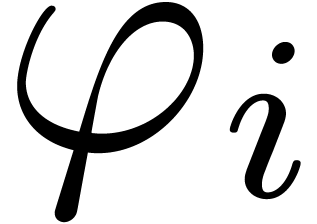 |
 |
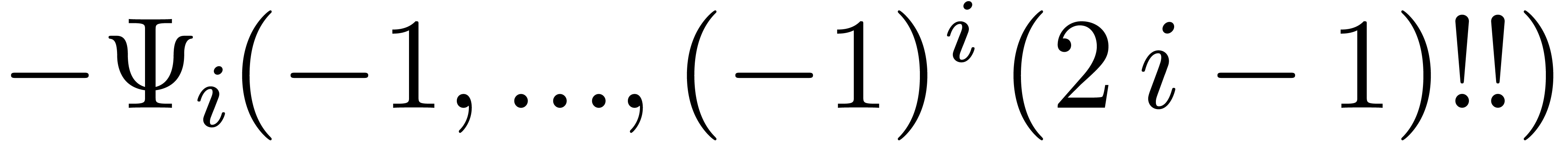 |
(i>0) |
Our algorithm now allows us to compute the asymptotic expansion of the
inverse function of Gaussian law at  .
This is potentially of great interest in finance when it comes to
calculate risk measures. The formula (7) gives itself an
asymptotic expansion of a Gaussian Value-at-Risk
.
This is potentially of great interest in finance when it comes to
calculate risk measures. The formula (7) gives itself an
asymptotic expansion of a Gaussian Value-at-Risk 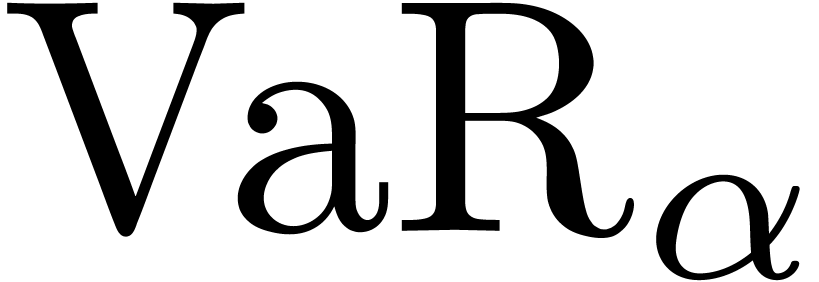 in terms of its confidence level
in terms of its confidence level  .
.
The expected shortfall of a portfolio with confidence level 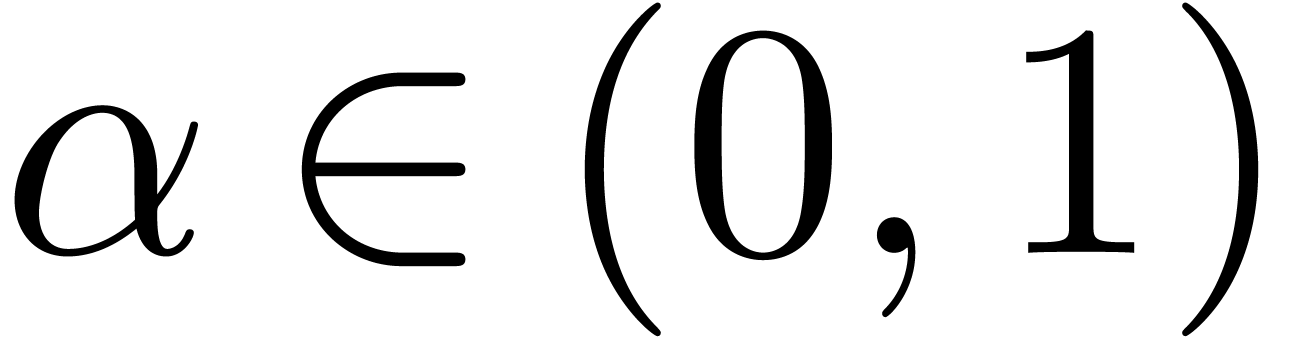 is the expected loss conditional that the loss is greater
than the
is the expected loss conditional that the loss is greater
than the  -th percentile of
the loss distribution. When the return of the portfolio is Gaussian with
mean
-th percentile of
the loss distribution. When the return of the portfolio is Gaussian with
mean 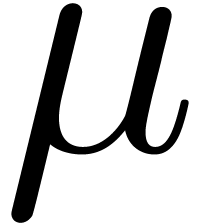 and volatility
and volatility  , the expected shortfall is
, the expected shortfall is
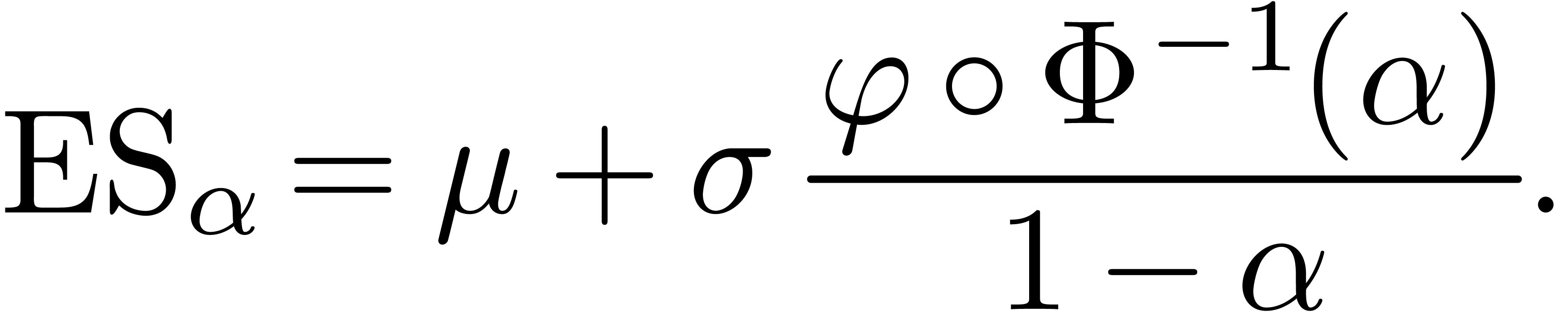
With 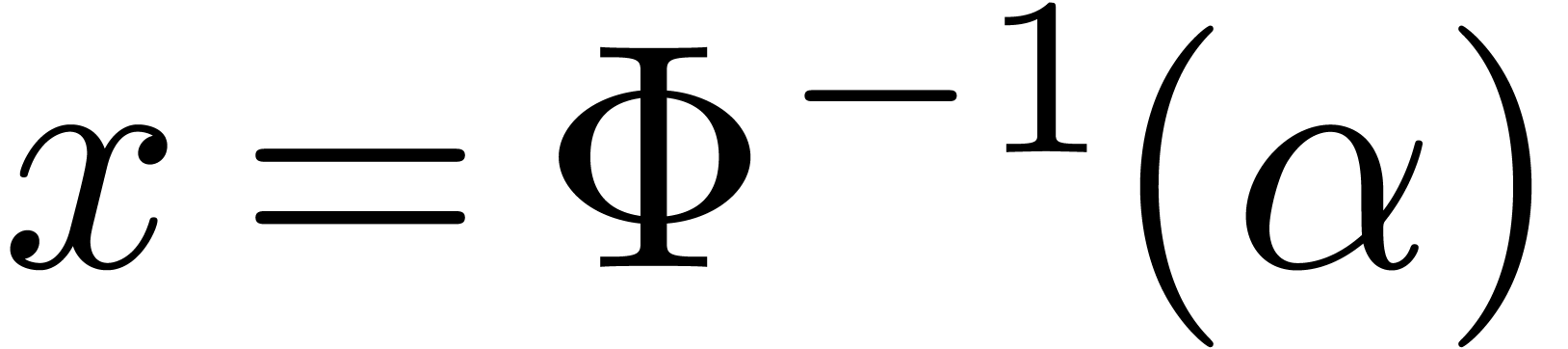 , the relation (6)
yields
, the relation (6)
yields
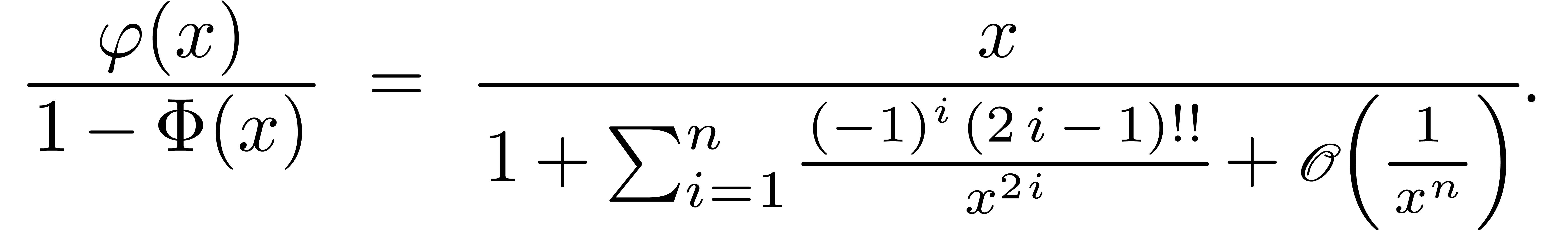
So, for some constants  , we
have
, we
have
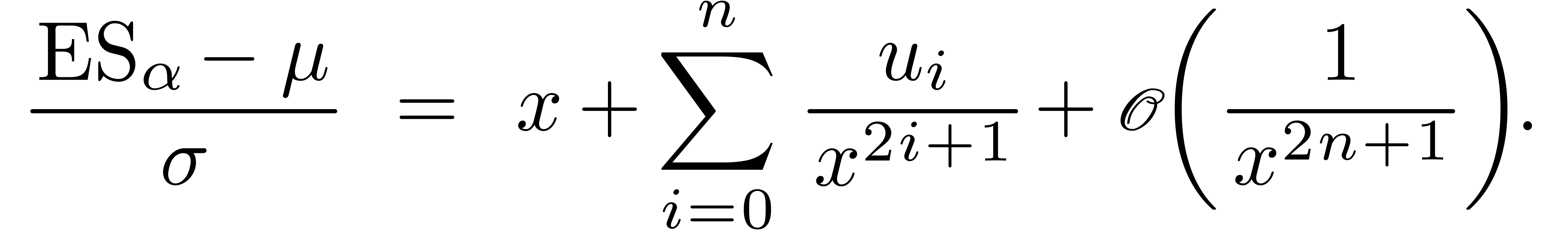
By inverting (7), we get an asymptotic expansion of 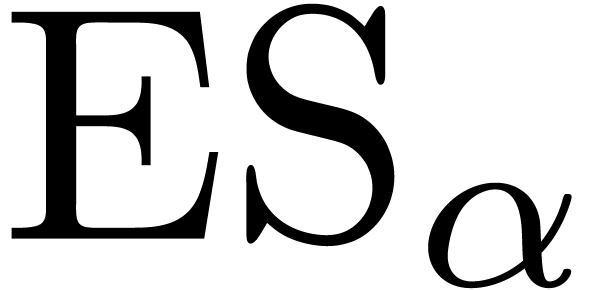 in terms of
in terms of 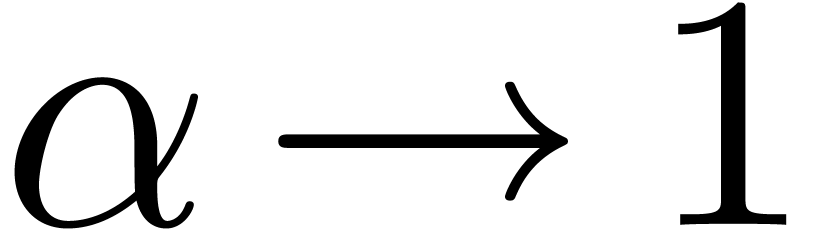 .
.
Let 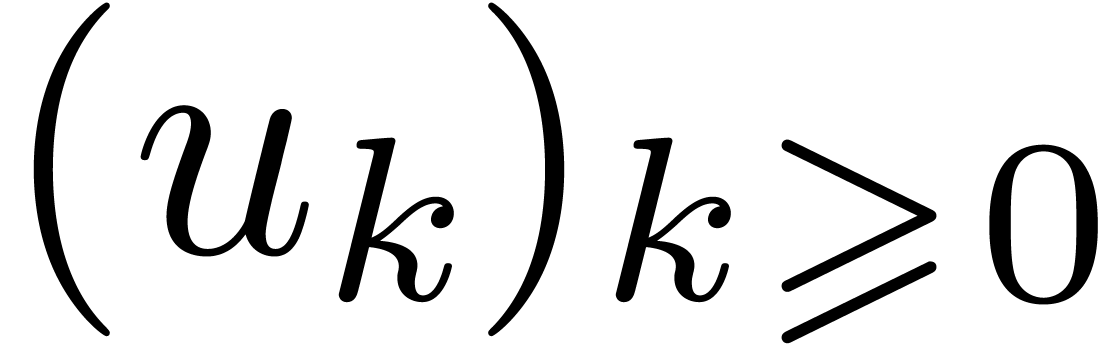 be defined by
be defined by 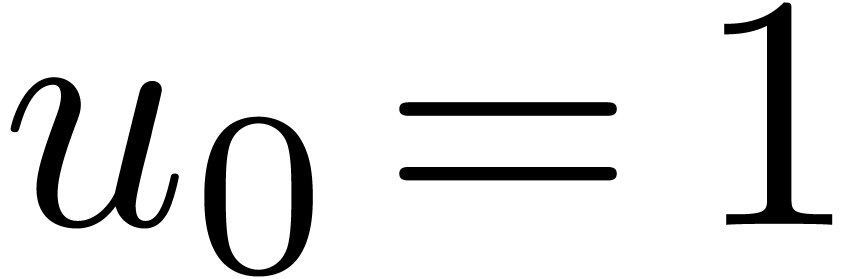 and,
for
and,
for  ,
, 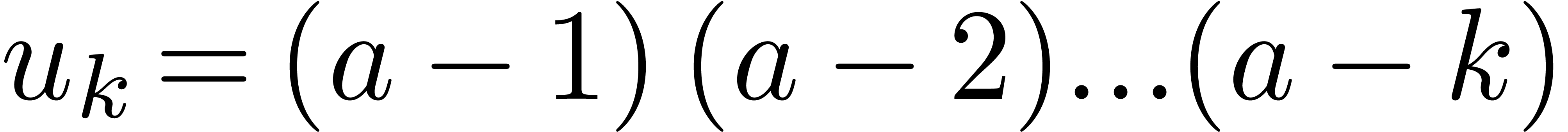 . A well-known relation for
. A well-known relation for 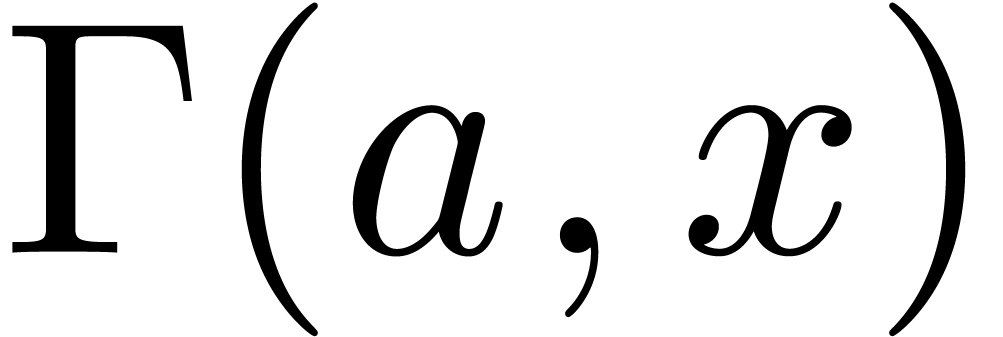 tells that for
tells that for 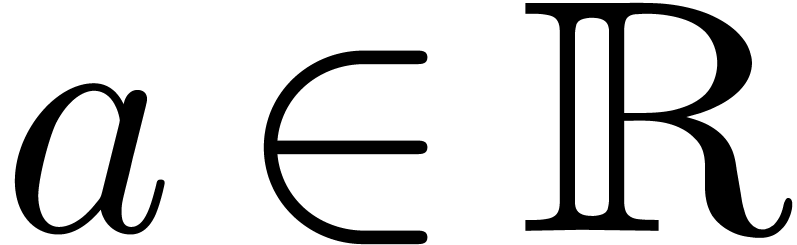 and
and  ,
,
Taking logarithms, we get
with 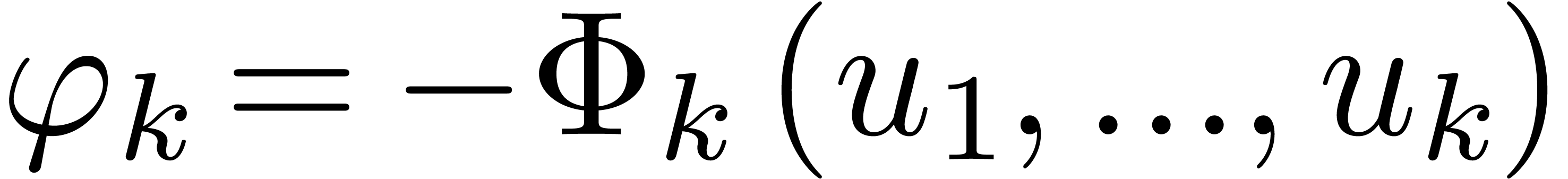 . Considering the CEV
process
. Considering the CEV
process
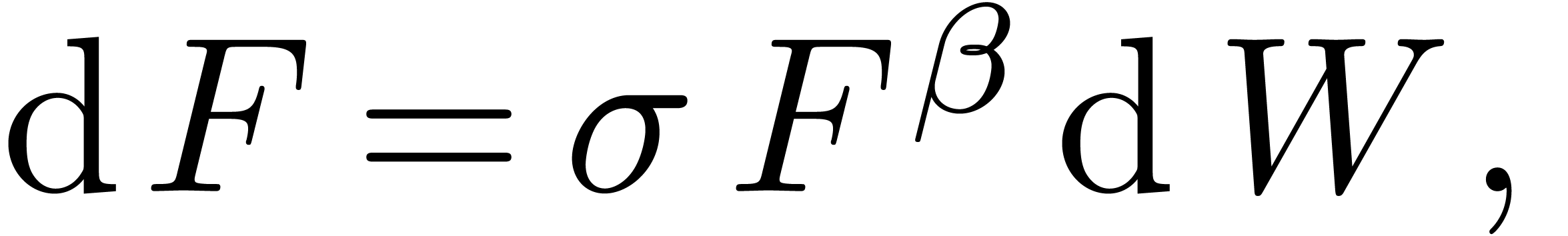
where 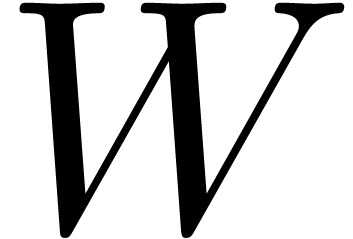 is a Brownian motion and
is a Brownian motion and  denotes for instance a forward rate, the probability of absorption at
zero before
denotes for instance a forward rate, the probability of absorption at
zero before 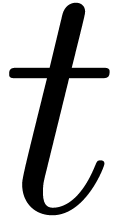 -time is given by
-time is given by
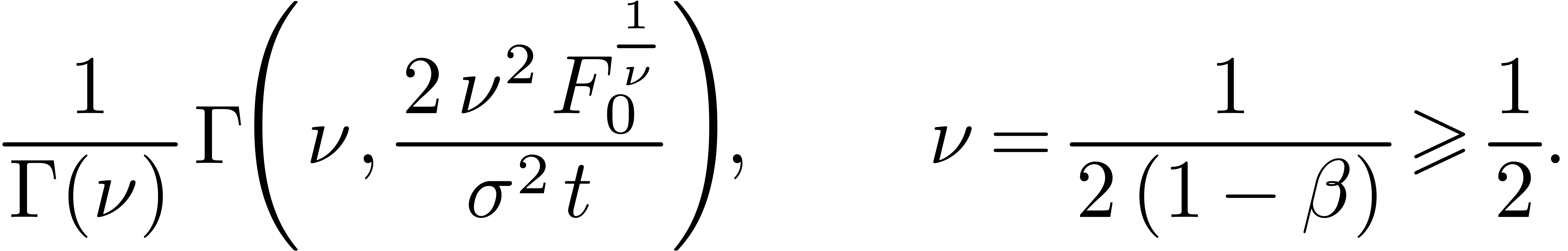
Inverting (9) gives a confidence interval where the
probability of absorption of  is lower than
is lower than  , asymptotically, for
, asymptotically, for 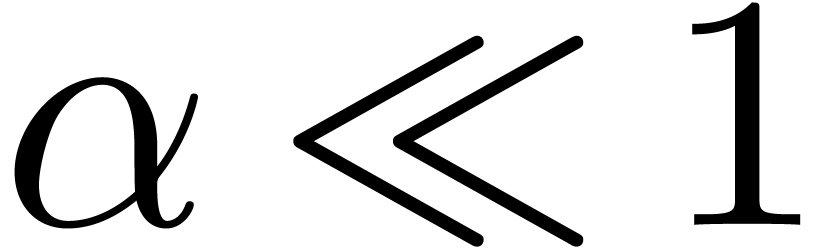 .
.
By definition, a call option is a contract which gives to the owner the
value 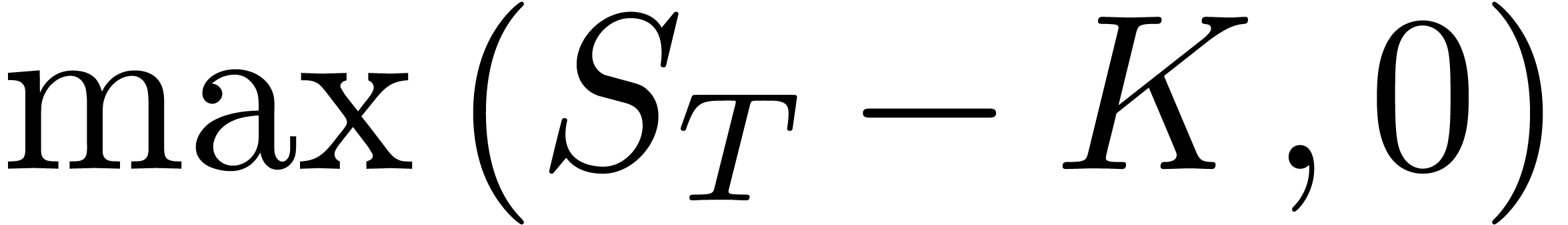 at a future
at a future  -date
(known today) called maturity of the contract, where
-date
(known today) called maturity of the contract, where 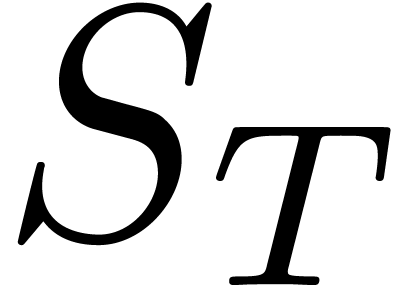 denotes the value at
denotes the value at  -date
(unknown today) of an asset (like a stock) whose initial value is
-date
(unknown today) of an asset (like a stock) whose initial value is 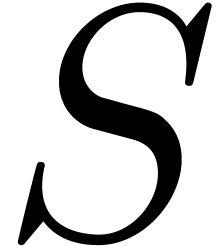 today, and
today, and  is a constant
called strike (known today). The initial price of this contract is
denoted by
is a constant
called strike (known today). The initial price of this contract is
denoted by 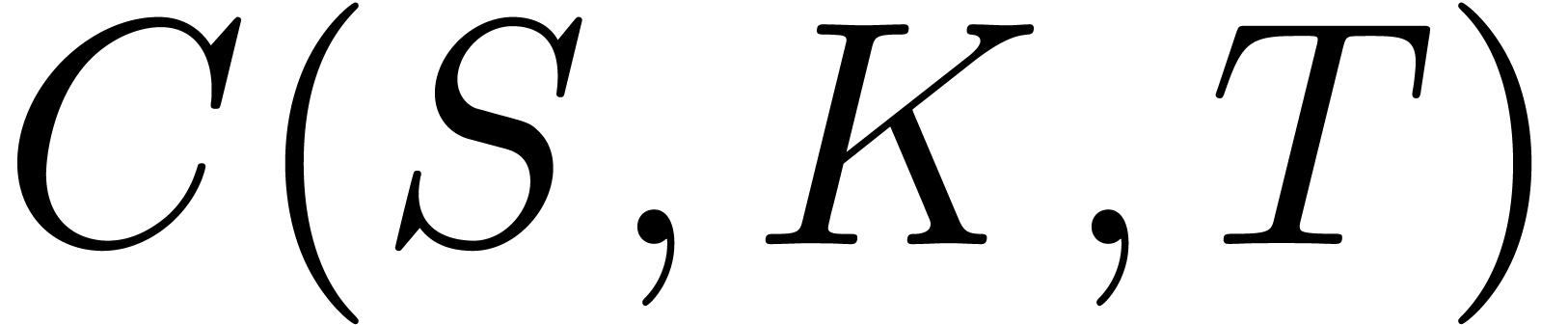 . In general, by
no-arbitrage arguments, the option price
. In general, by
no-arbitrage arguments, the option price 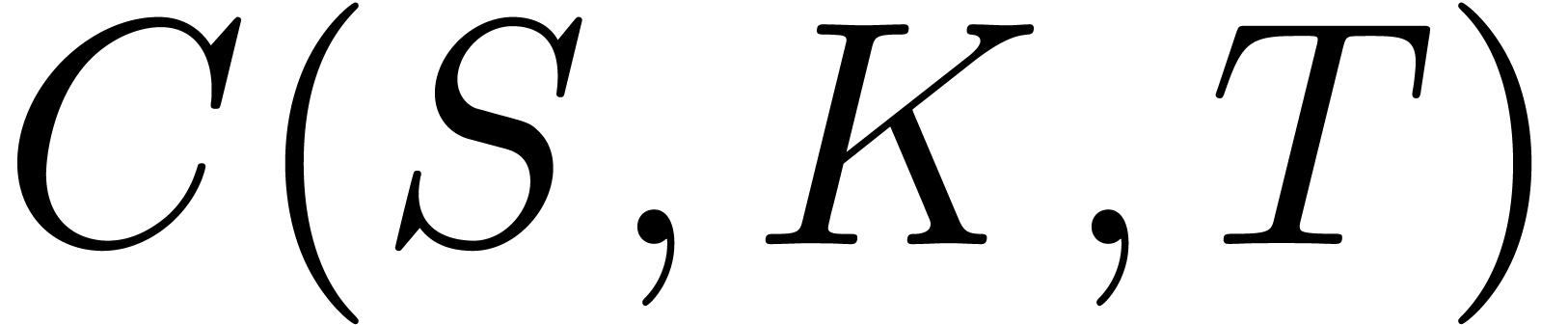 is
always greater than the “intrinsic value”
is
always greater than the “intrinsic value” 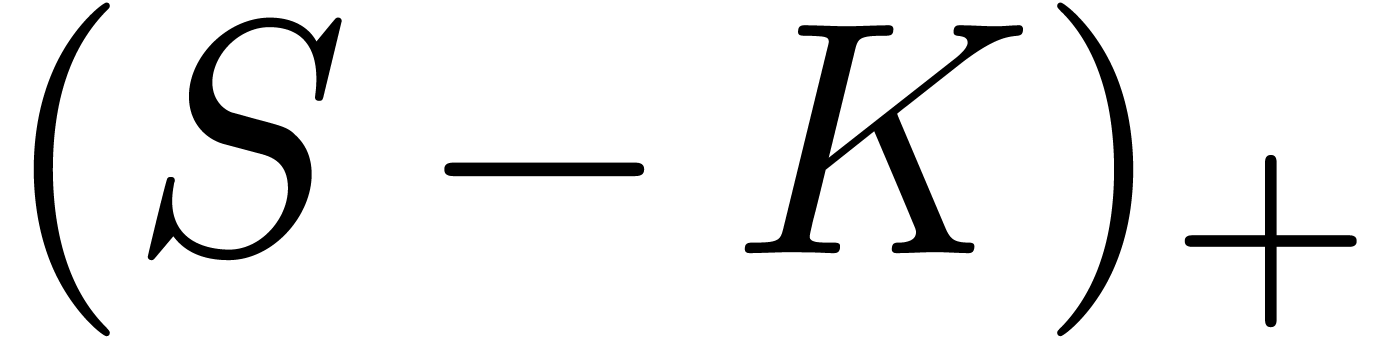 and lower than the spot value
and lower than the spot value  :
:
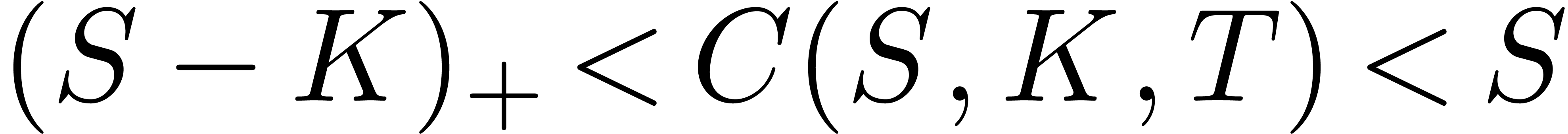
In the Black–Scholes model, the dynamics of 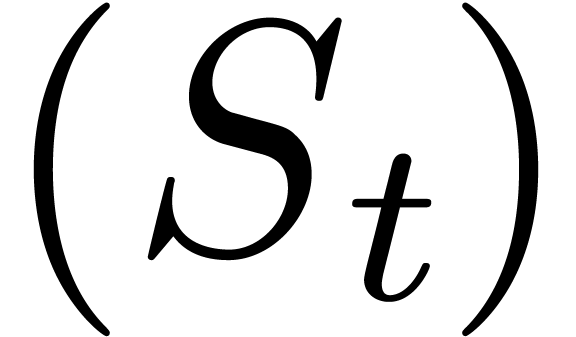 is assumed to be log-normal:
is assumed to be log-normal:

where 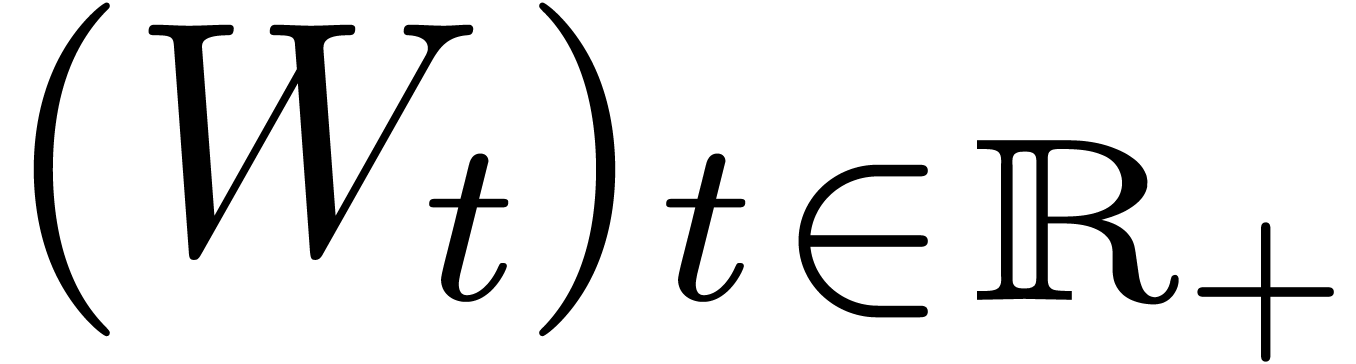 is a Brownian motion and
is a Brownian motion and  is a constant parameter called volatility. In this framework, the well
known Black–Scholes formula gives the price of any call option. It
can be shown that
is a constant parameter called volatility. In this framework, the well
known Black–Scholes formula gives the price of any call option. It
can be shown that
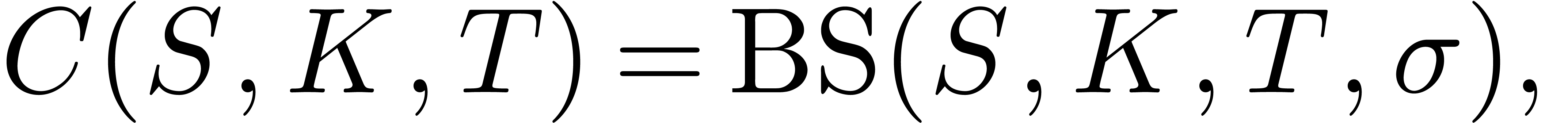
where
For simplicity, we have assumed that the interest rate is 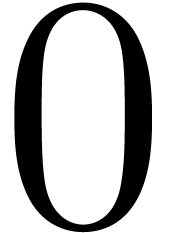 . If
. If 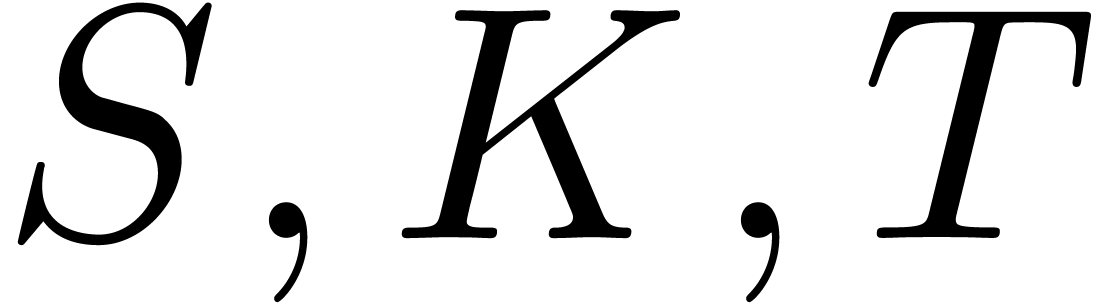 are fixed, then it
is easy to see that the function
are fixed, then it
is easy to see that the function
is non-decreasing and one to one from 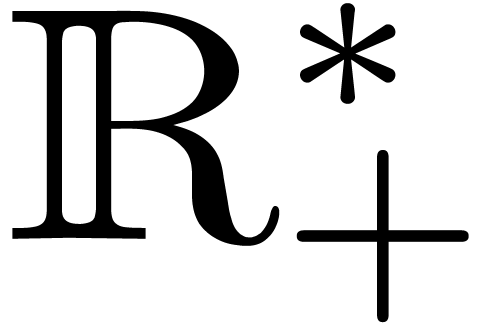 to
to 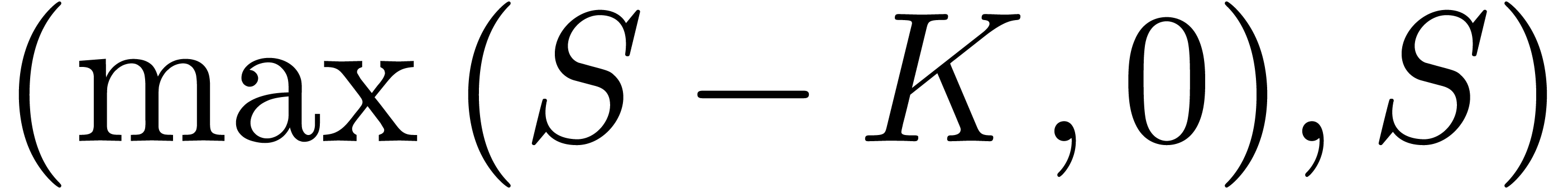 . Therefore, in an a
priori non Black–Scholes world and for a given call option
price
. Therefore, in an a
priori non Black–Scholes world and for a given call option
price 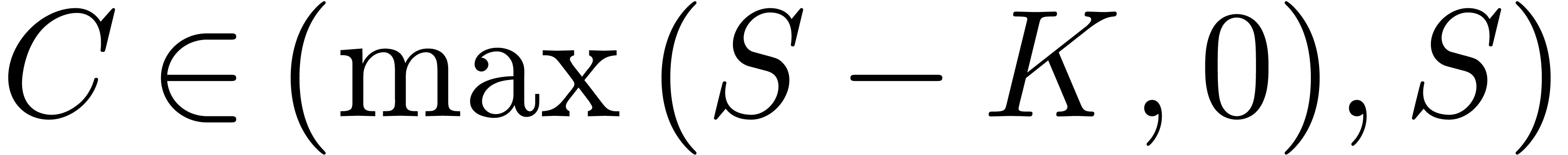 observed on the market, there is a unique
solution
observed on the market, there is a unique
solution 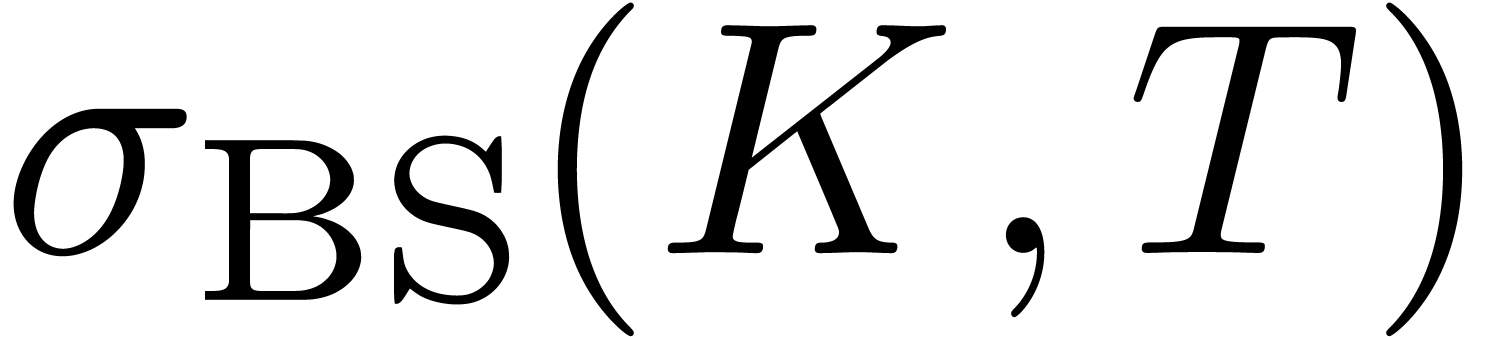 (or simply
(or simply 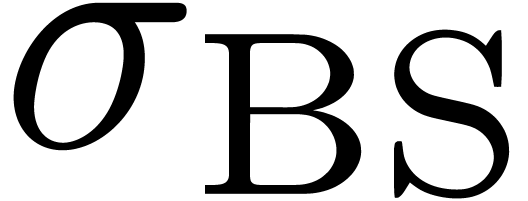 ) of the equation
) of the equation
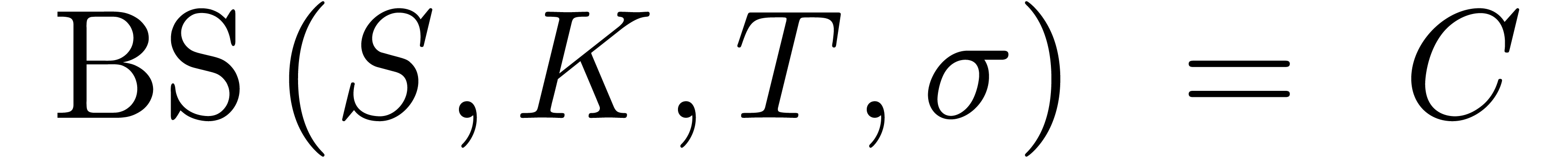
We call 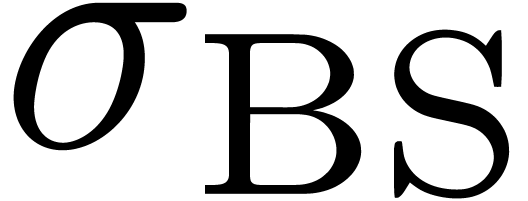 the Black–Scholes implied
volatility associated to
the Black–Scholes implied
volatility associated to  and
and  . For different reasons [10, 30], it is interesting to invert the
Black–Scholes function
. For different reasons [10, 30], it is interesting to invert the
Black–Scholes function 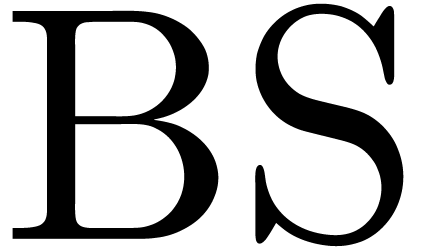 in (10).
For instance, using techniques from perturbation theory, sophisticated
stochastic models (in a non Black–Scholes world) give only
asymptotic expansions of an option price
in (10).
For instance, using techniques from perturbation theory, sophisticated
stochastic models (in a non Black–Scholes world) give only
asymptotic expansions of an option price  in
terms of the maturity
in
terms of the maturity  ,
whereas we really need a formula for the implied volatility [4,
20]. Indeed, call option prices are generally quoted in
term of implied volatilities (and not as prices). This can be achieved
in the following manner. In the Black–Scholes model and under the
conditions that
,
whereas we really need a formula for the implied volatility [4,
20]. Indeed, call option prices are generally quoted in
term of implied volatilities (and not as prices). This can be achieved
in the following manner. In the Black–Scholes model and under the
conditions that 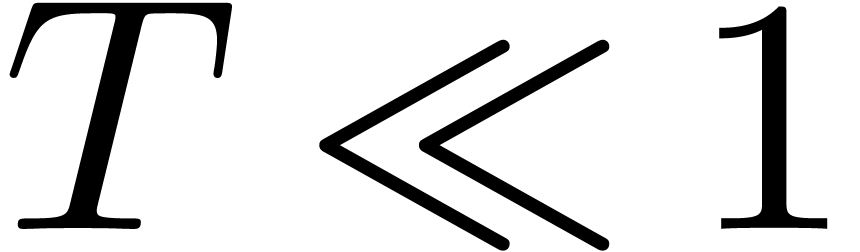 and
and 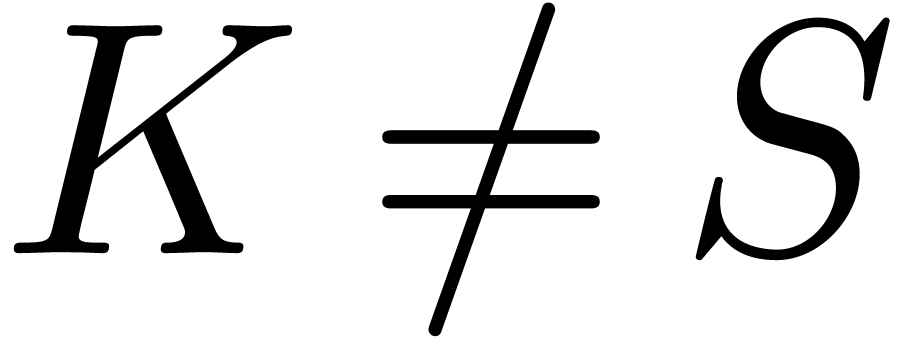 , it can be proved [14] that the
asymptotic expansion of the “time value”
, it can be proved [14] that the
asymptotic expansion of the “time value”  of the call price
of the call price 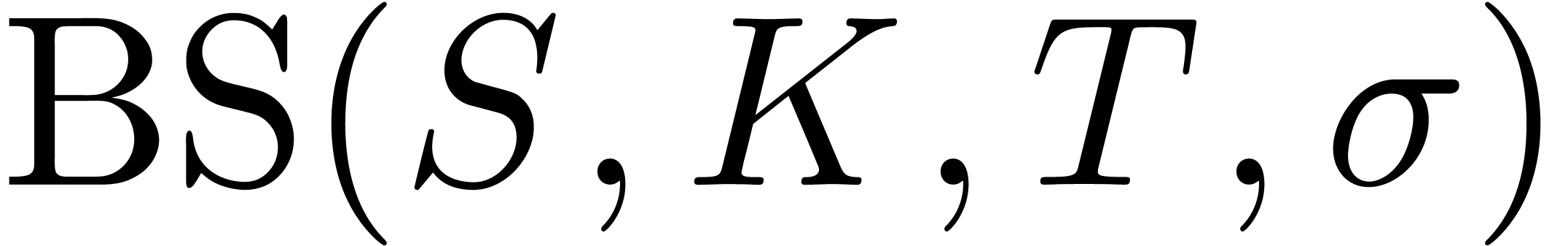 , defined
by
, defined
by
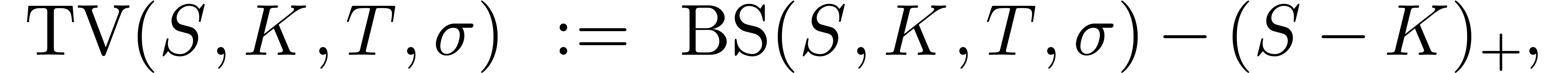
is given by
with 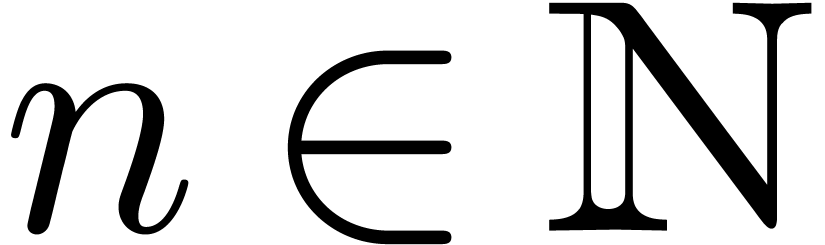 arbitrarily large,
arbitrarily large,
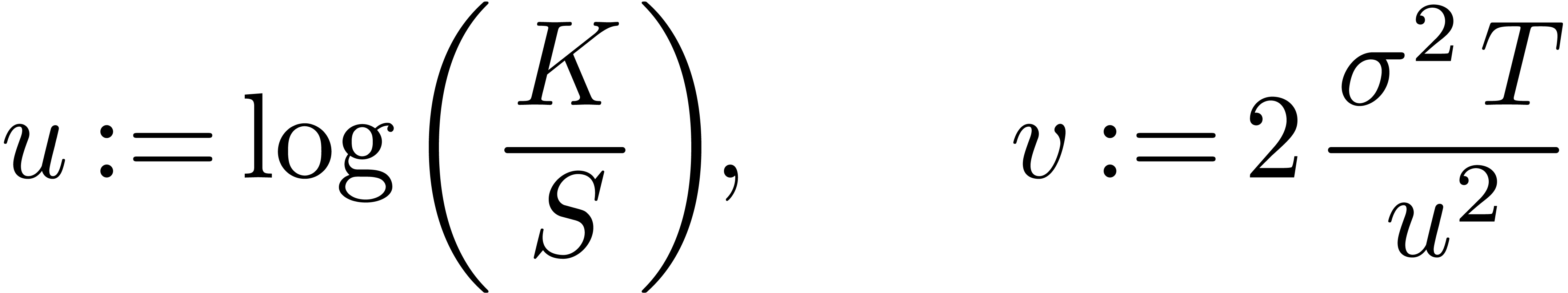
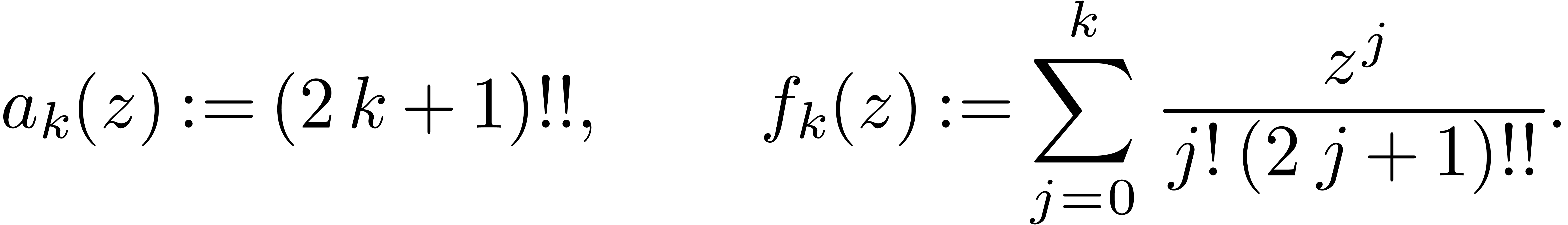
Therefore, setting
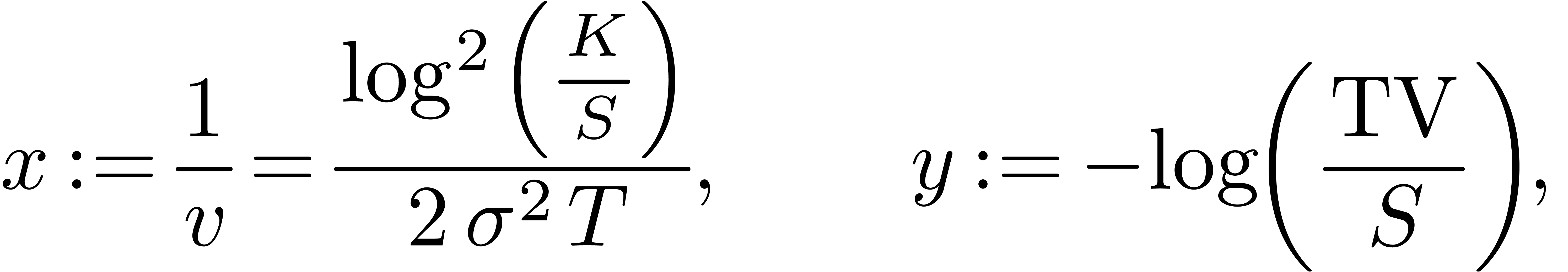
we have
for any integer 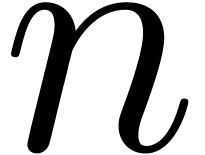 , where
, where
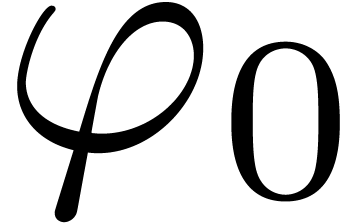 |
 |
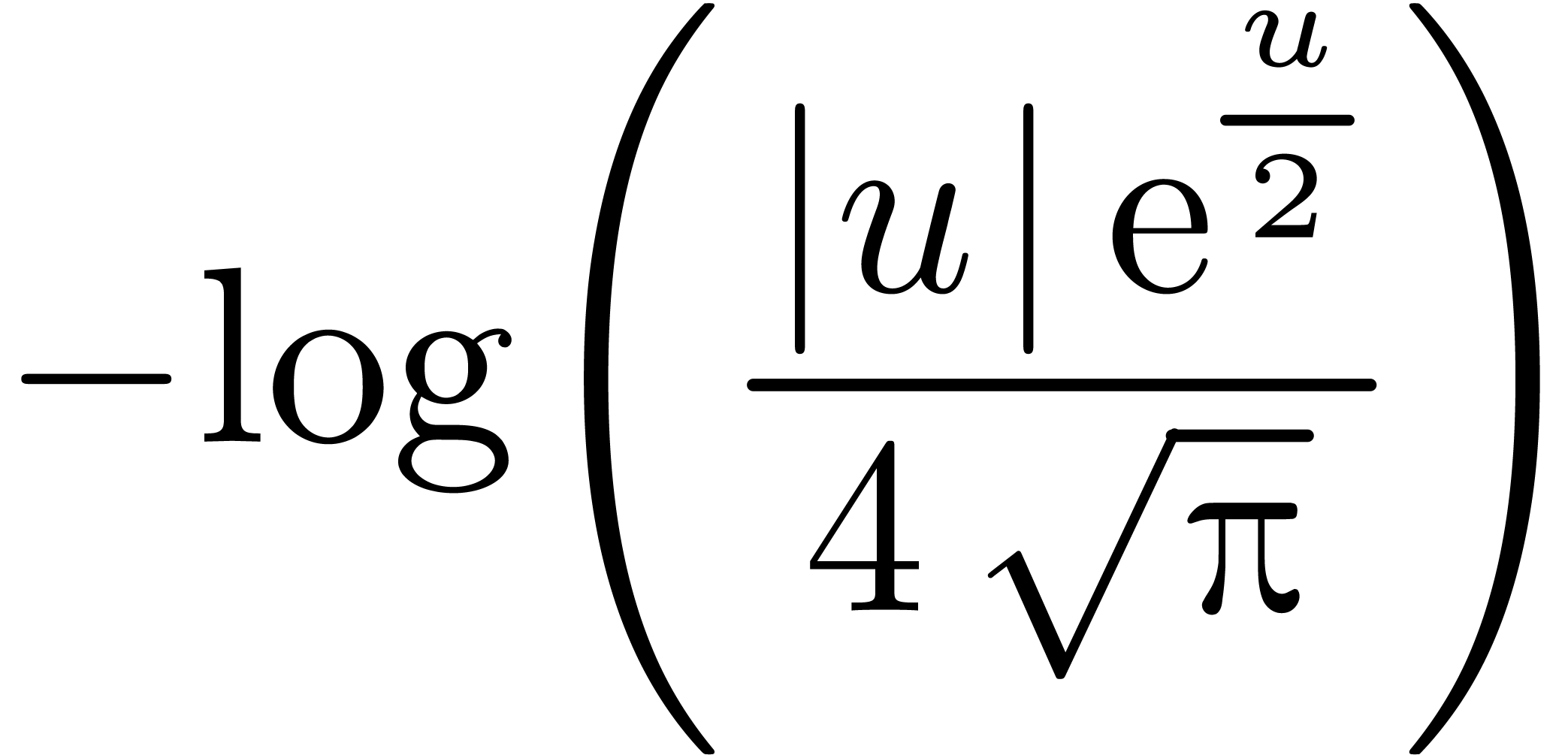 |
|
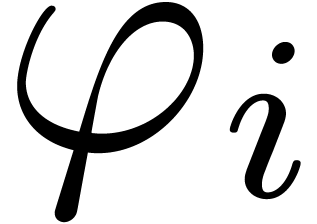 |
 |
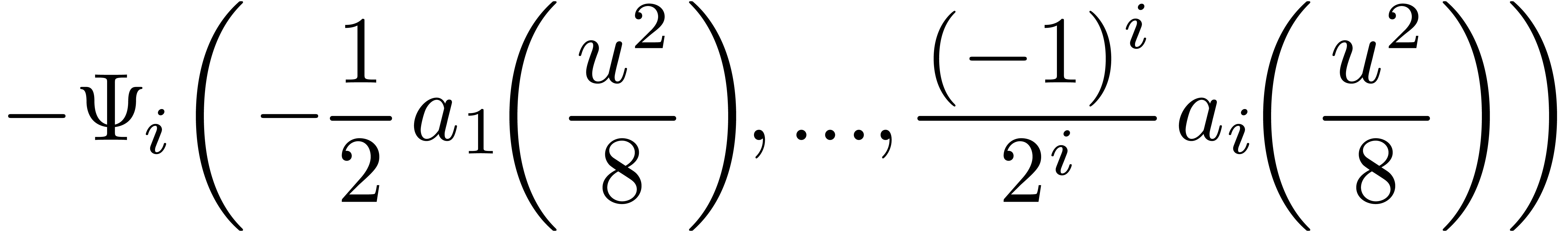 |
(i>0) |
Formula (12) is nothing but another expression for
Black-Scholes formula. Hence we get an asymptotic expansion for 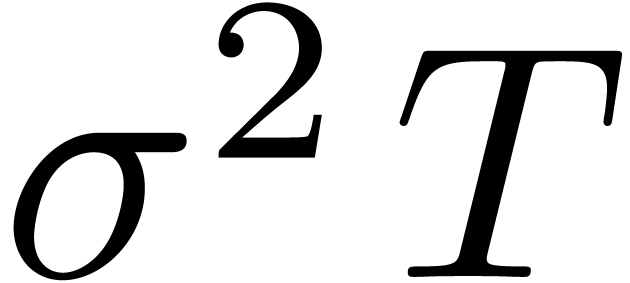 in terms of
in terms of 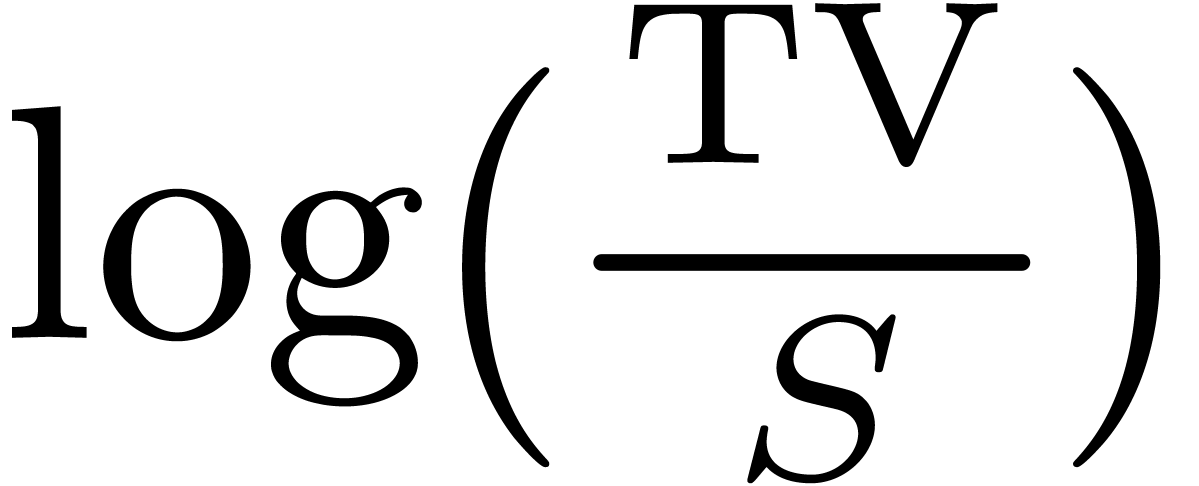 .
Note that (12) is an asymptotic expansion of a call price
in terms of
.
Note that (12) is an asymptotic expansion of a call price
in terms of 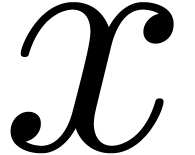 for large
for large 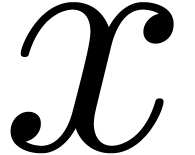 . So, it gives also an asymptotic expansion of a
call price when
. So, it gives also an asymptotic expansion of a
call price when 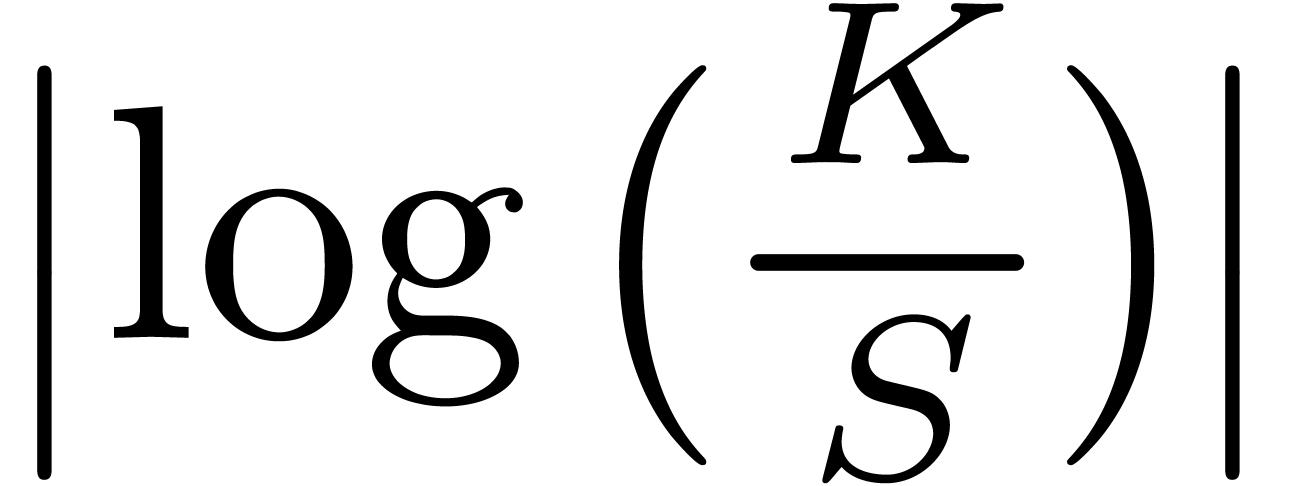 is large i.e. small strike or
large strike.
is large i.e. small strike or
large strike.
Notice also that there is another direct formula 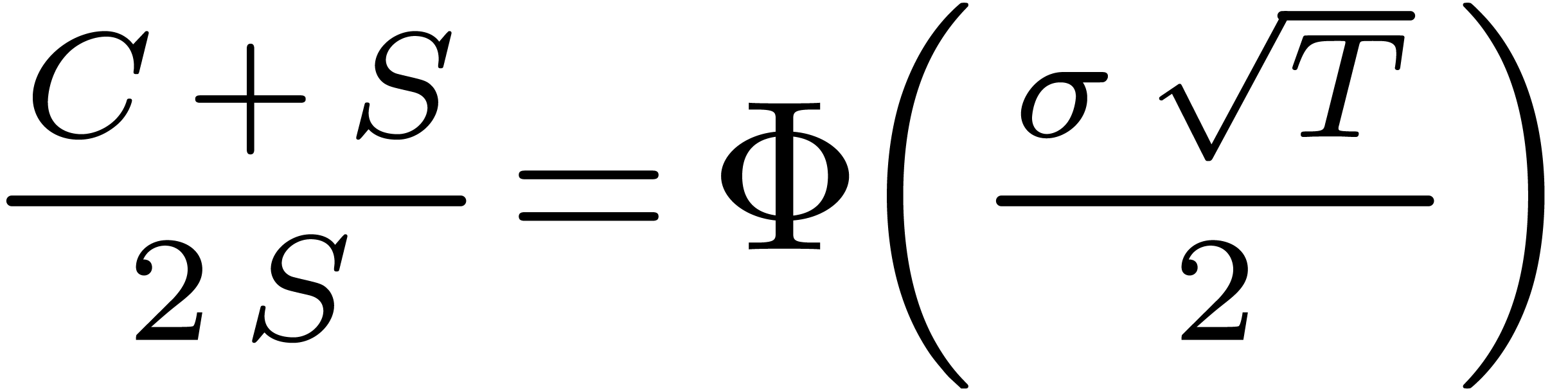 when
when 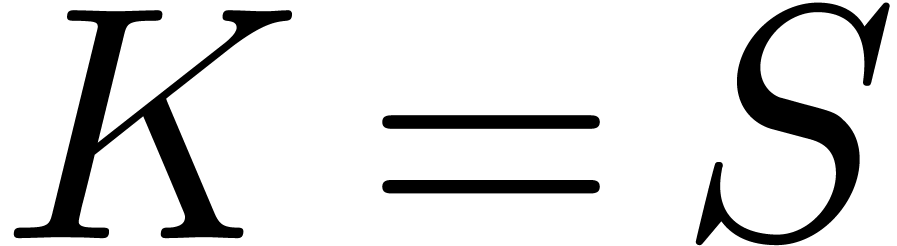 , which gives an
asymptotic expansion of
, which gives an
asymptotic expansion of  in terms of
in terms of 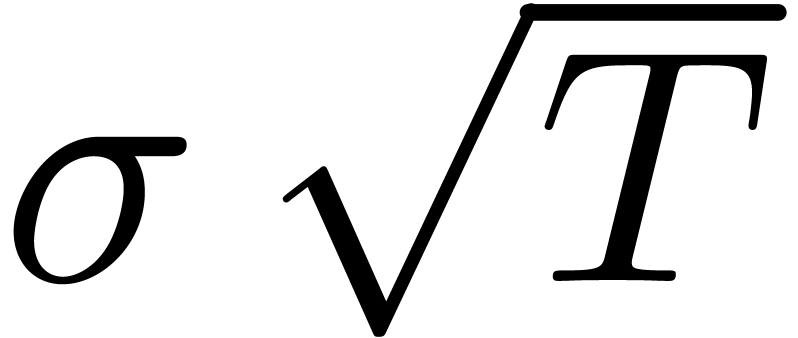 .
.
At the limit when 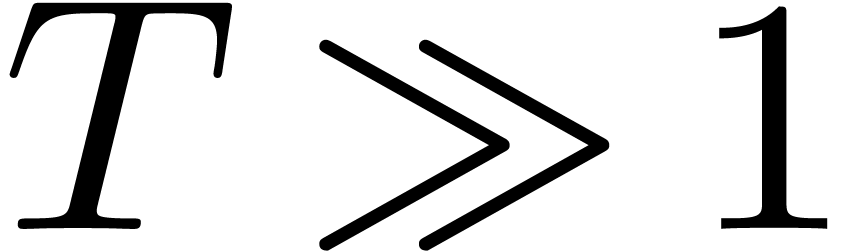 , the first
author previously obtained a similar result [14]. Setting
this time
, the first
author previously obtained a similar result [14]. Setting
this time
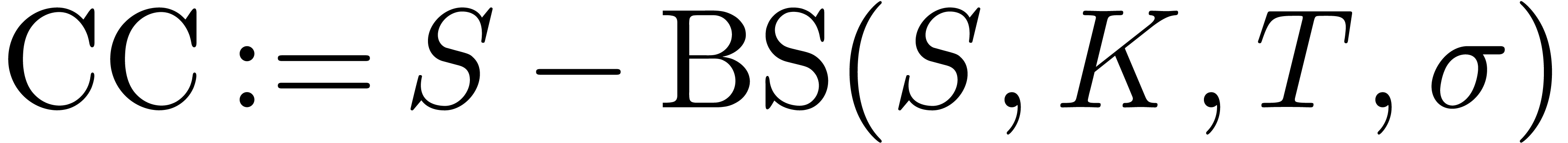
and
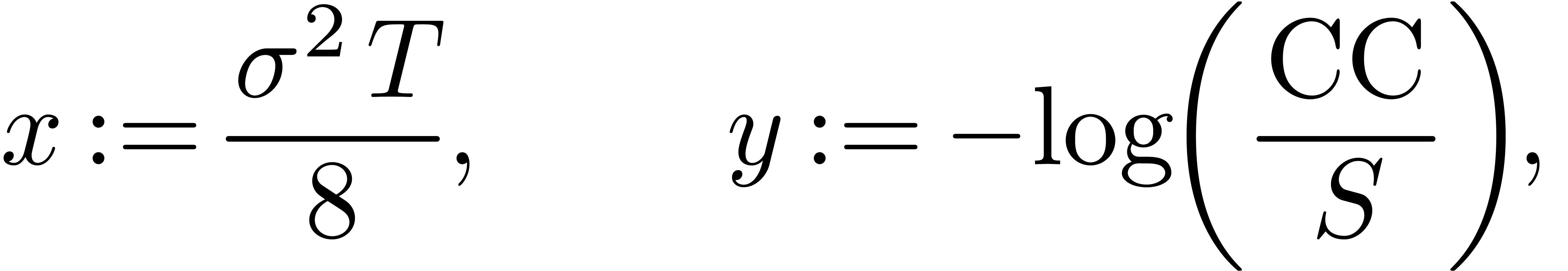
we have
where
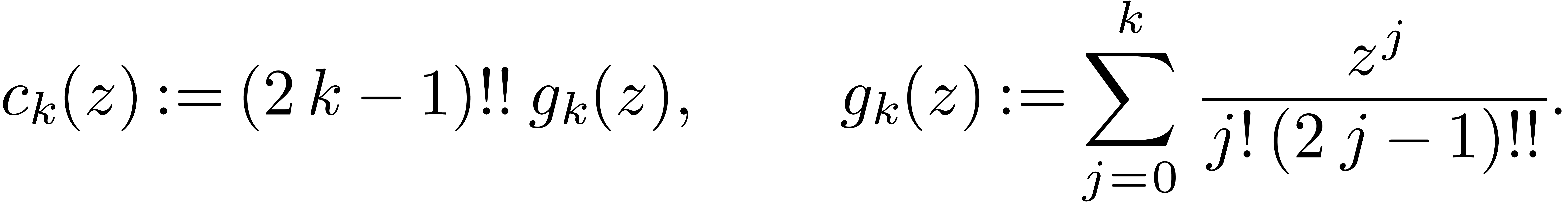
Therefore, we get
where
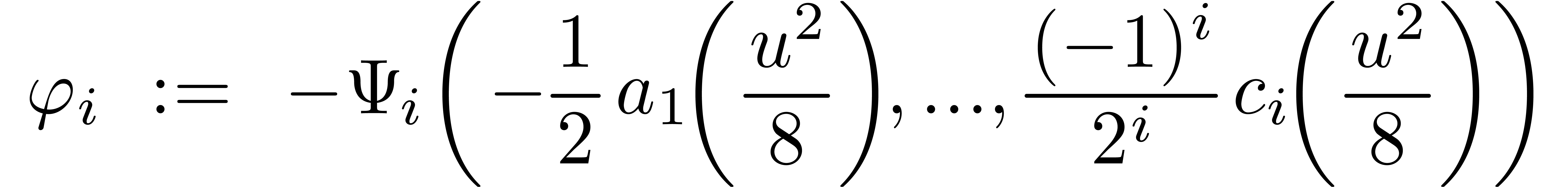 |
(i>0) |
In the Bachelier model, the dynamics of 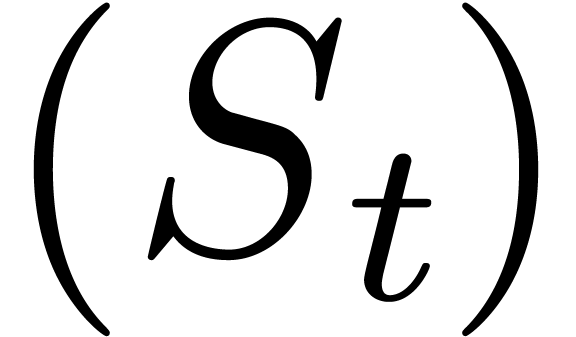 is
assumed to be normal:
is
assumed to be normal:
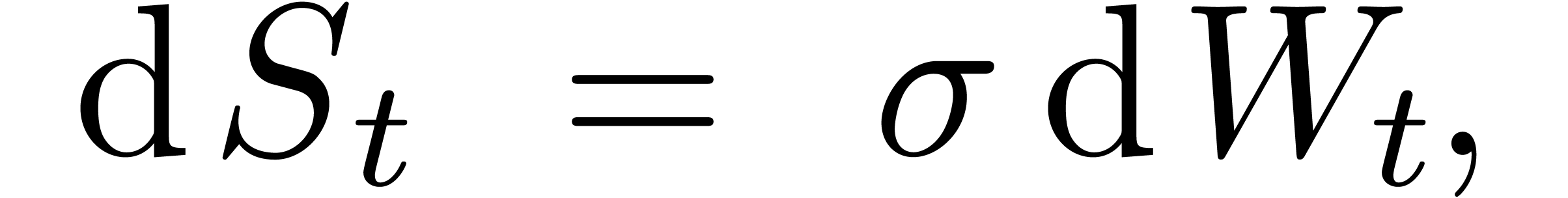
where 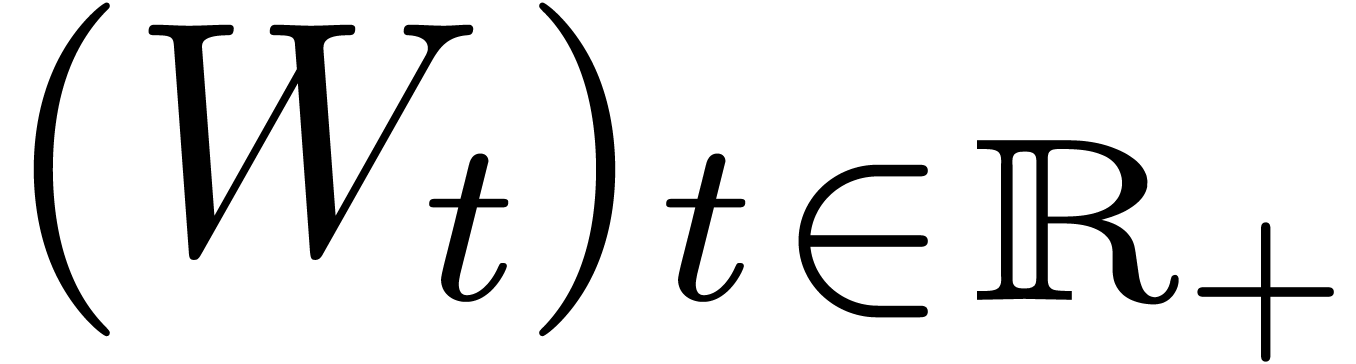 is a Brownian motion and
is a Brownian motion and  is a constant parameter called normal volatility. In this framework, the
price
is a constant parameter called normal volatility. In this framework, the
price  of a call option with strike
of a call option with strike  and expiry
and expiry  is given by Bachelier's
formula
is given by Bachelier's
formula
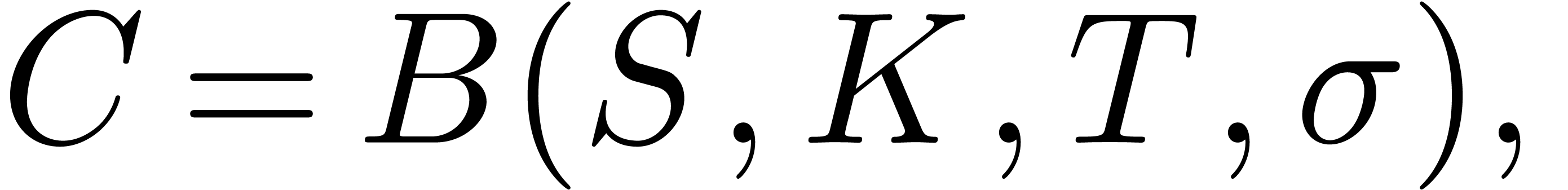
with
Denoting as before by
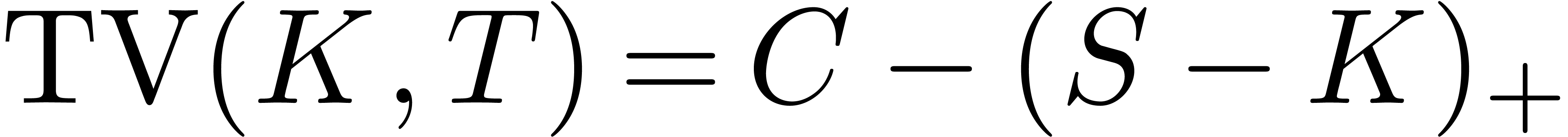
the time-value of the call option, we have
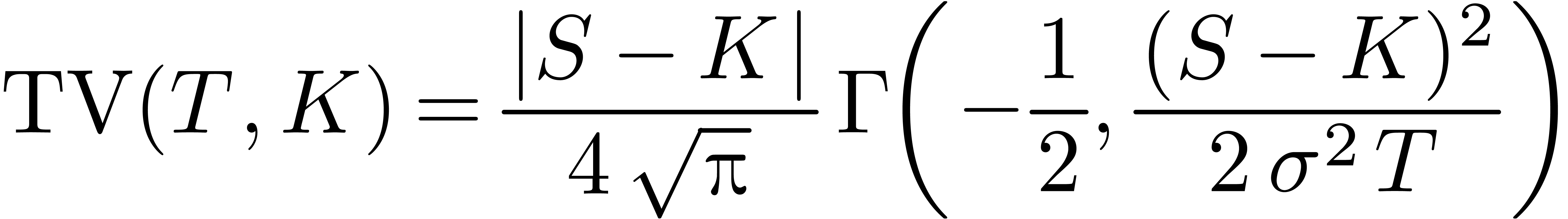
for 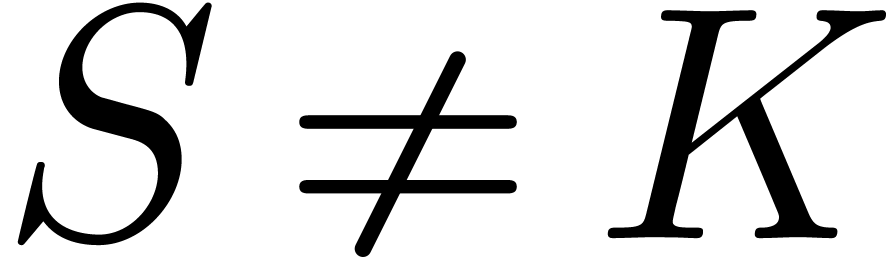 . So, using (8),
we deduce an asymptotic expansion of
. So, using (8),
we deduce an asymptotic expansion of 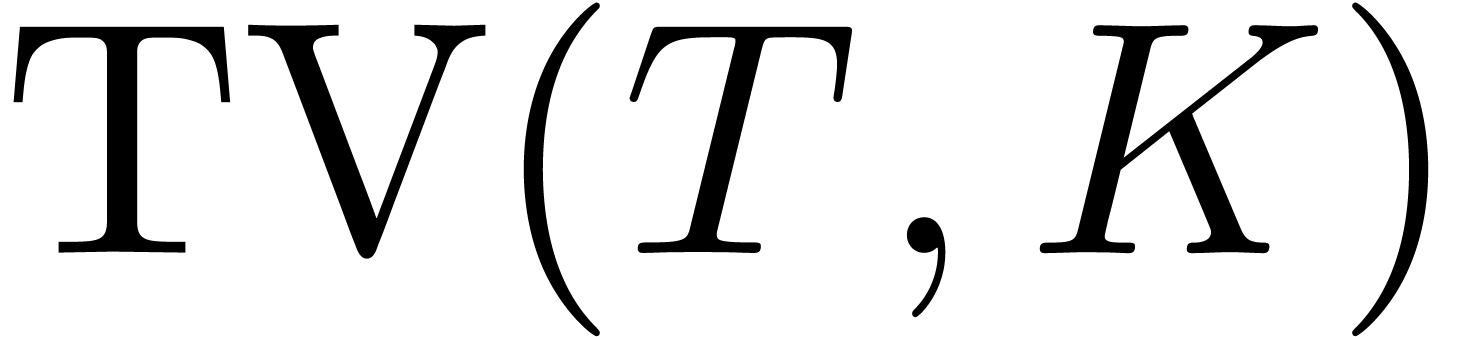 in terms of
in terms of
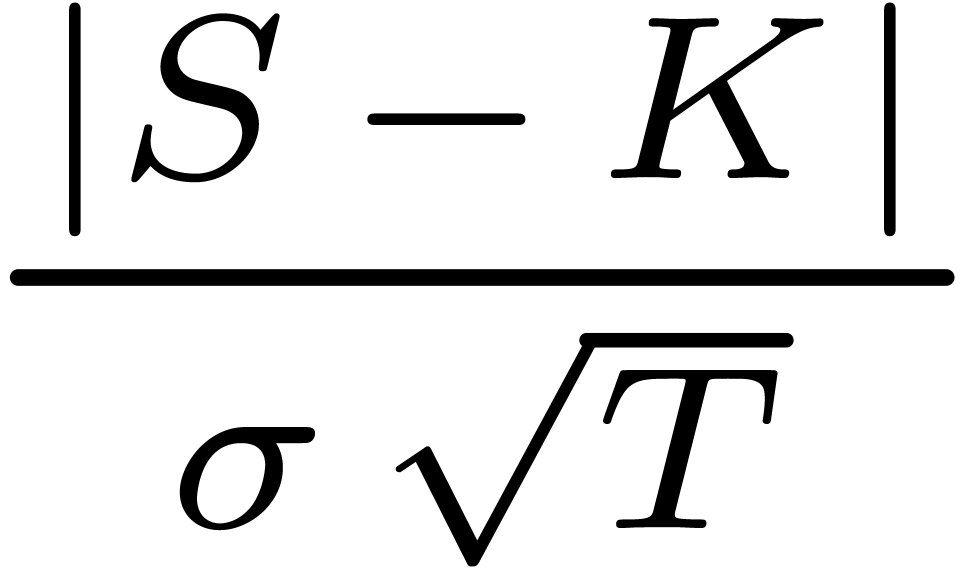 for large strike or small maturity in the
Bachelier model. By inverting the Gamma function as before, this gives
an asymptotic expansion of the normal volatility in terms of the
time-value
for large strike or small maturity in the
Bachelier model. By inverting the Gamma function as before, this gives
an asymptotic expansion of the normal volatility in terms of the
time-value  . Therefore, by
comparing with (11), we obtain an equivalence between
normal volatility and lognormal volatility in the cases when
. Therefore, by
comparing with (11), we obtain an equivalence between
normal volatility and lognormal volatility in the cases when  or
or  . For
example, when
. For
example, when  , the first
terms of the expansion are given by
, the first
terms of the expansion are given by
where 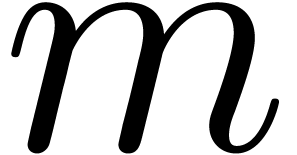 denotes the “moneyness”
denotes the “moneyness” 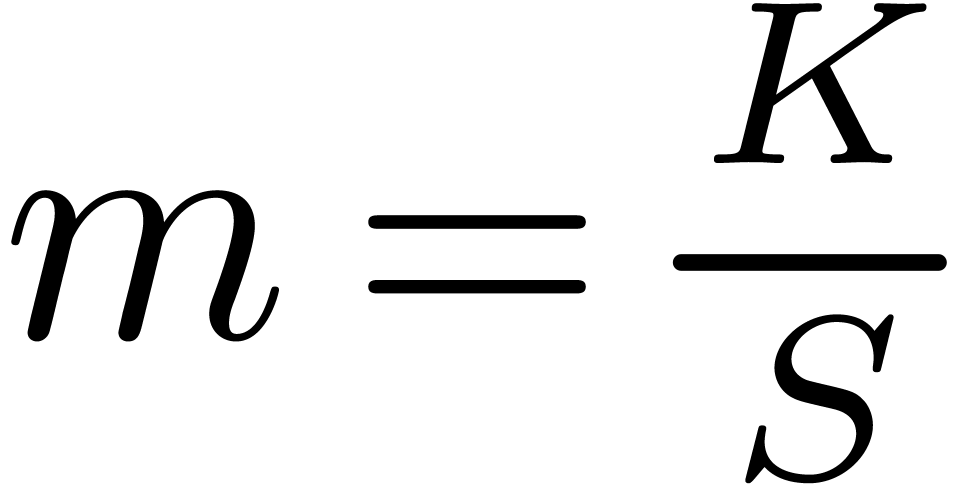 and
and 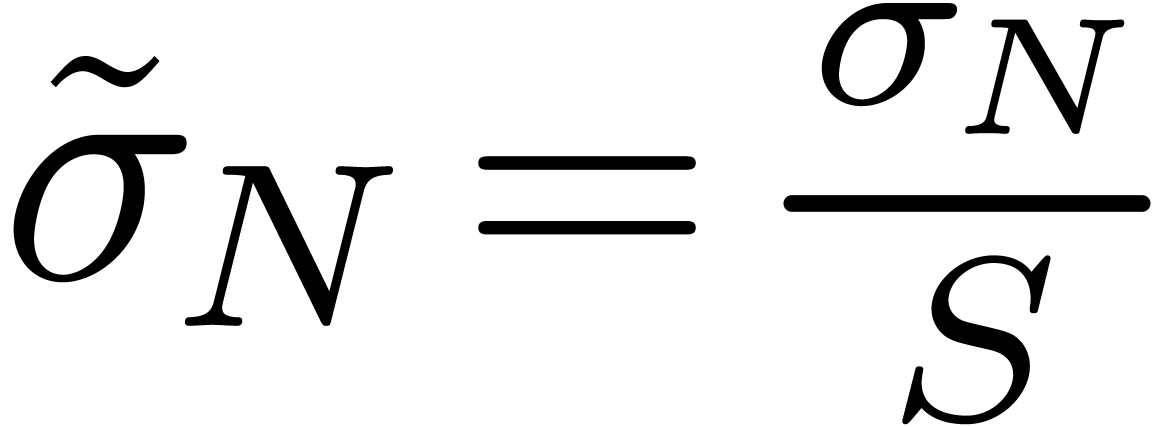 . Note
that at the money (
. Note
that at the money (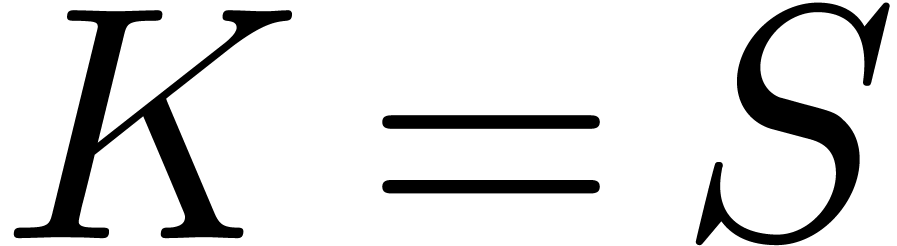 ), we have
a closed form formula [13]:
), we have
a closed form formula [13]:
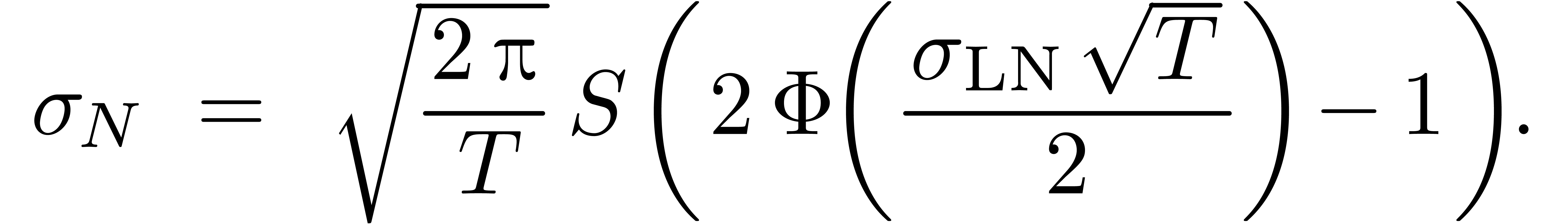
In particular, taking the derivative in (14) and then
letting 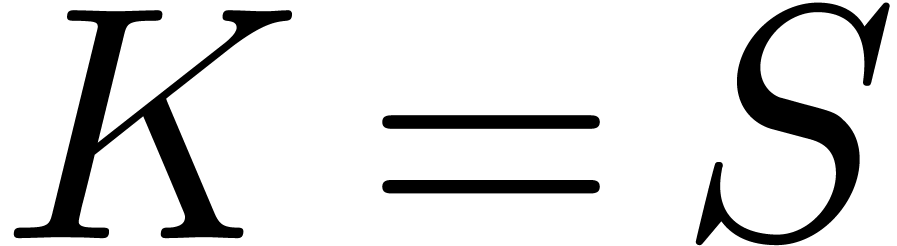 gives
gives
where  and
and 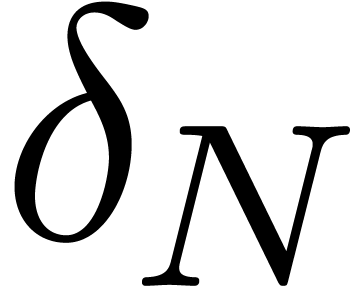 are the slopes
of the smiles of volatility at the money:
are the slopes
of the smiles of volatility at the money:
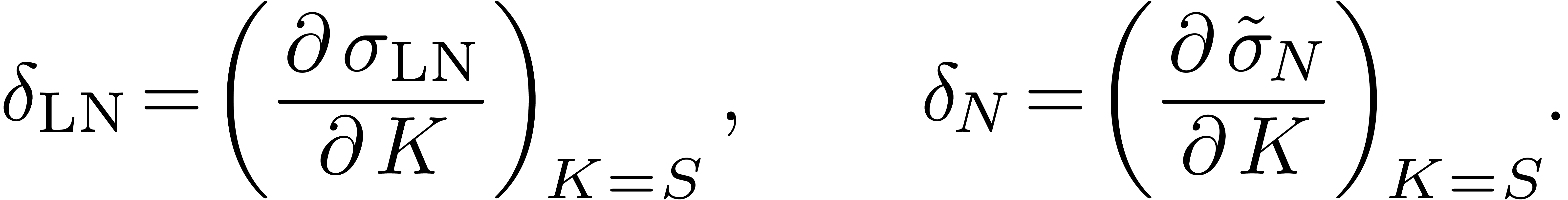
In particular when the volatility smile  is flat
at the money (
is flat
at the money ( ), we have:
), we have:
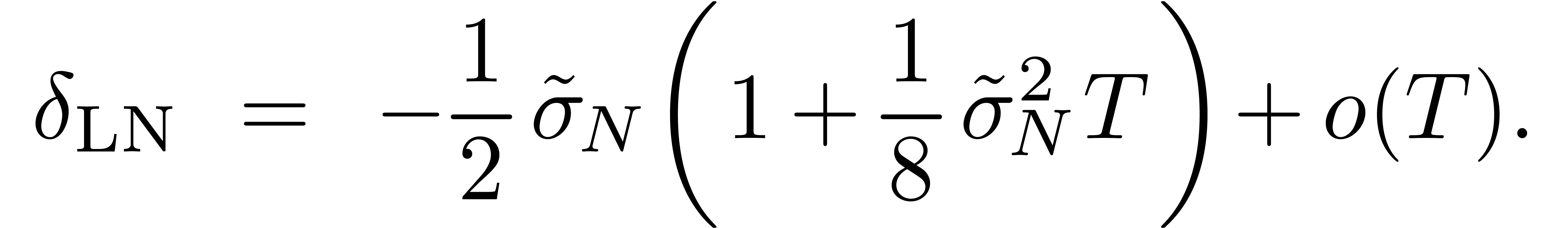
This is a refinement of a classical result 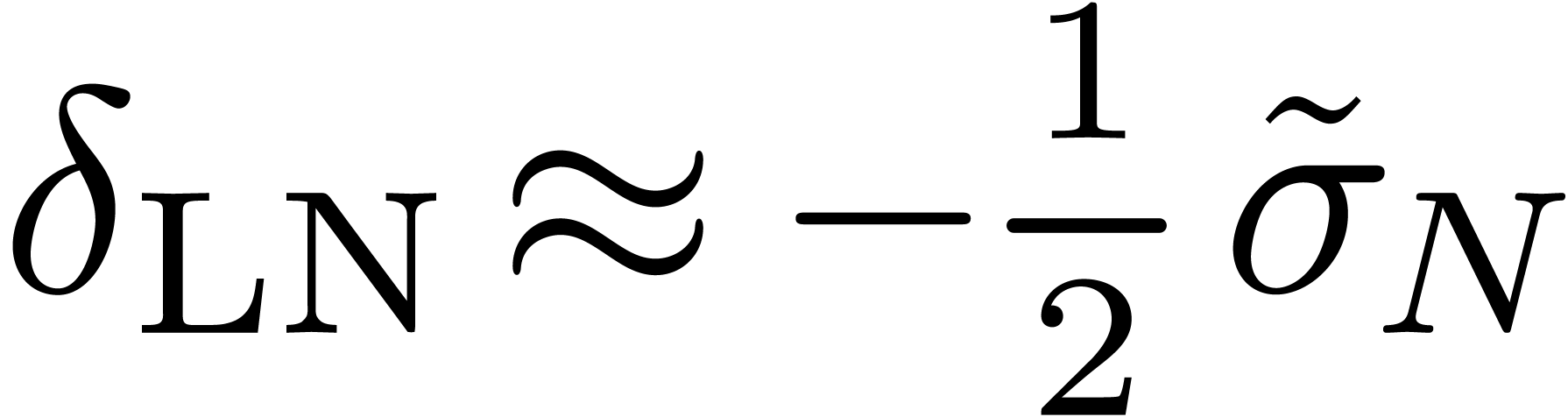 .
In general, (15) shows that if
.
In general, (15) shows that if 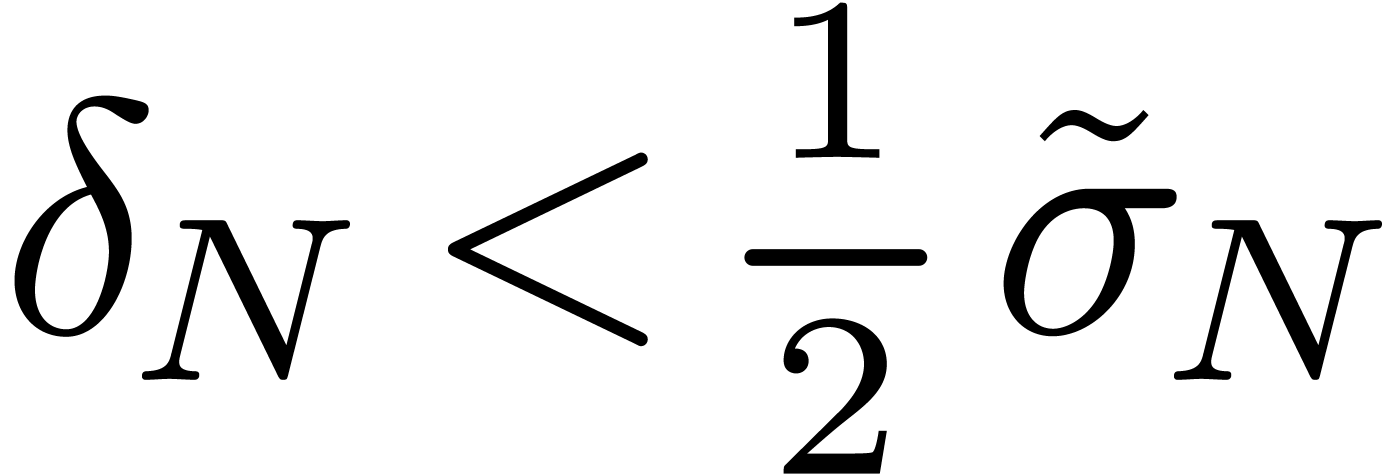 , then the slope of the volatility smile for the
lognormal volatility is negative and this condition holds up to order 1
in
, then the slope of the volatility smile for the
lognormal volatility is negative and this condition holds up to order 1
in  [13].
[13].
By inverting (12), we get the implied lognormal volatility
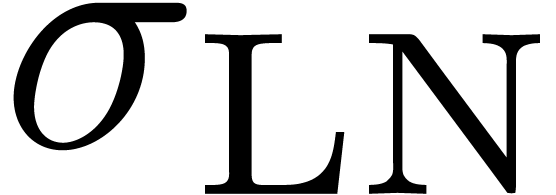 from the time-value
from the time-value  of
the call-option in a model-free setting. In general, thanks to Tanaka's
theorem, this time-value can be calculated by integrating the density
function of the stochastic process between
of
the call-option in a model-free setting. In general, thanks to Tanaka's
theorem, this time-value can be calculated by integrating the density
function of the stochastic process between  and
the maturity
and
the maturity  of the option. On the other hand,
this density function can be obtained using
Minakshisundaram–Pleijel expansion - modulo conditions of
regularity [2]. So, in general this allows to translate an
asymptotic expansion of
of the option. On the other hand,
this density function can be obtained using
Minakshisundaram–Pleijel expansion - modulo conditions of
regularity [2]. So, in general this allows to translate an
asymptotic expansion of 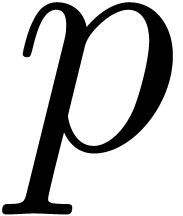 for
for  in an asymptotic expansion of
in an asymptotic expansion of 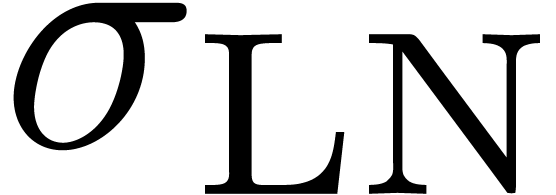 .
.
As an example, let us consider a local volatility model 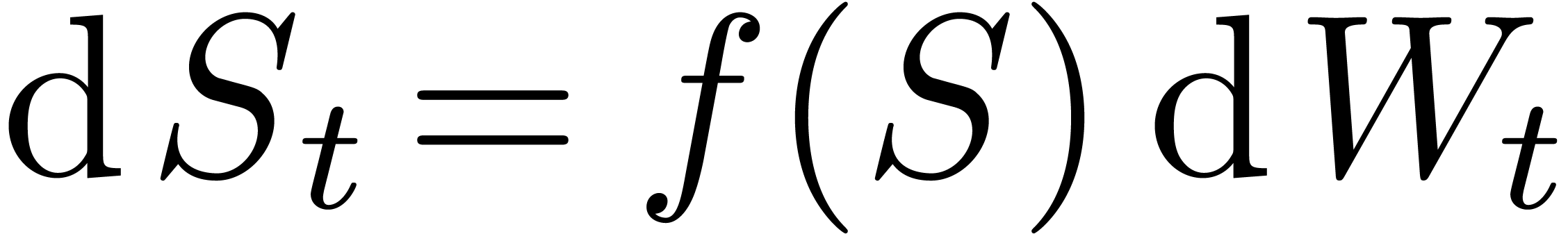 . Then Tanaka's formula reads:
. Then Tanaka's formula reads:
In this particular case, the Minakshisundaram–Pleijel expansion gives
with 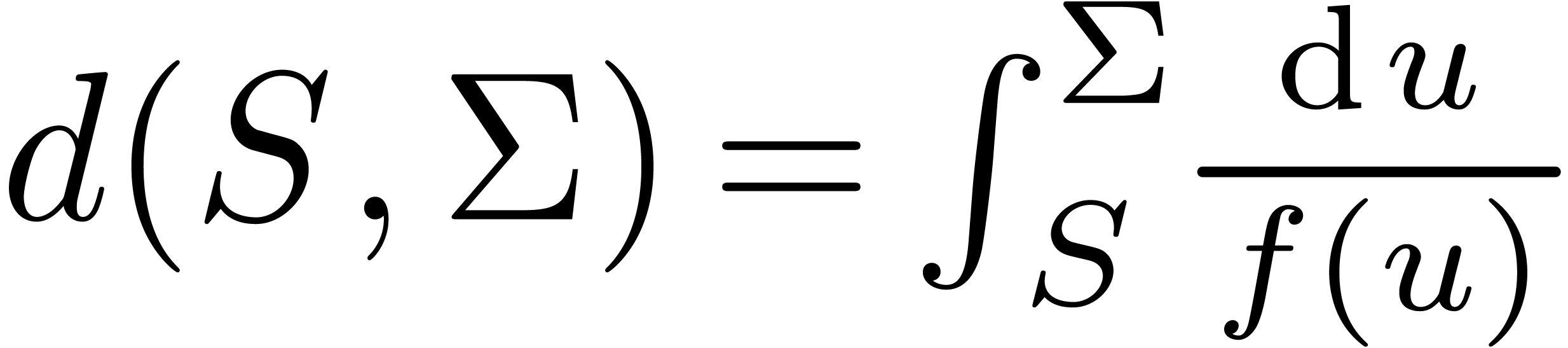 and
and 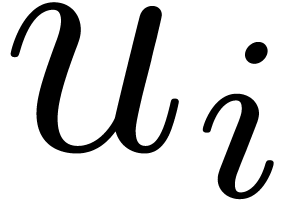 is explictly
given by induction [11, 37]. The asymptotic
expansion (17) can be integrated by part and thus give an
asymptotic expansion for
is explictly
given by induction [11, 37]. The asymptotic
expansion (17) can be integrated by part and thus give an
asymptotic expansion for 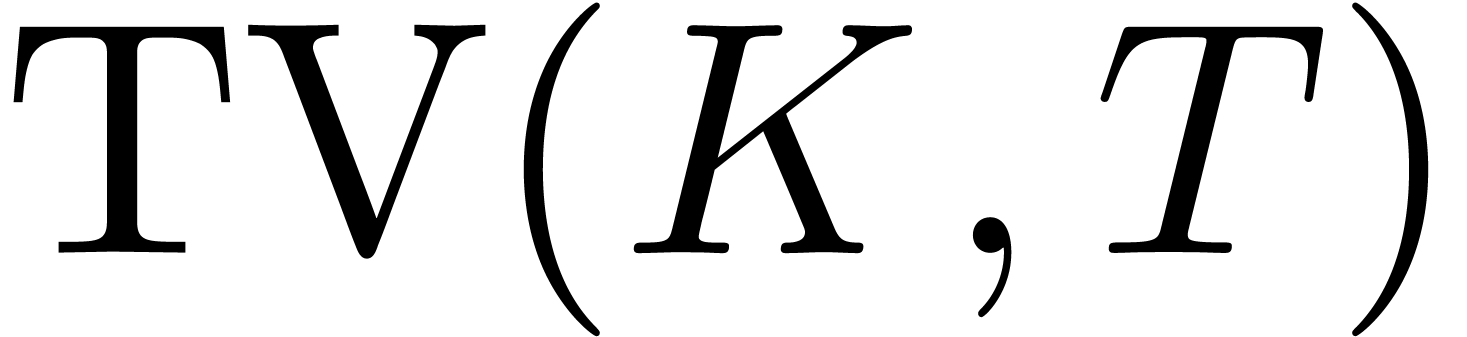 thanks to (16).
Finally, by inverting (12), we get asymptotic expansion of
the lognormal implied volatility.
thanks to (16).
Finally, by inverting (12), we get asymptotic expansion of
the lognormal implied volatility.
The stochastic differential equation for the CEV diffusion model is
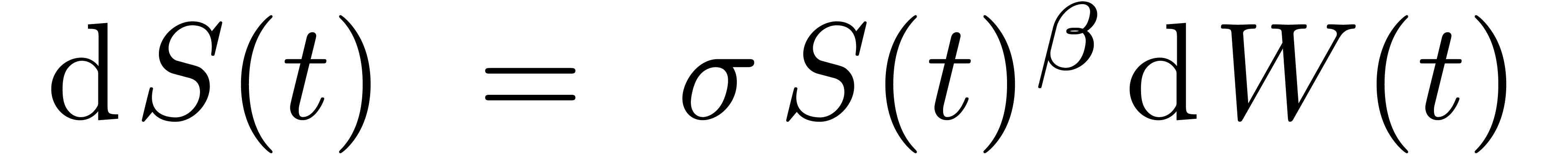
Let 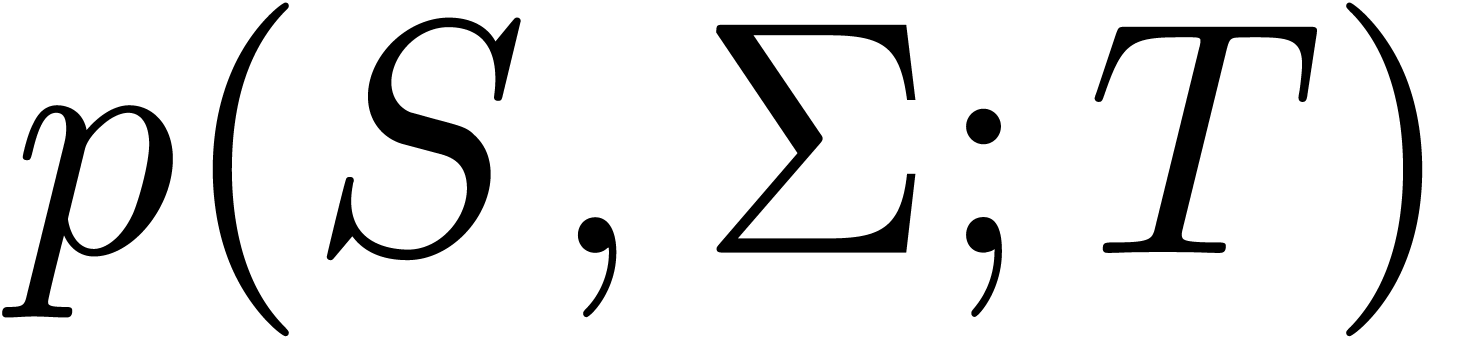 be the probability density function to get
state
be the probability density function to get
state 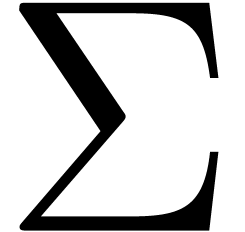 at
at  -time
starting from
-time
starting from 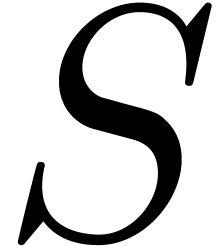 at time
at time 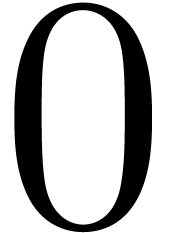 . There is a closed form formula for
. There is a closed form formula for 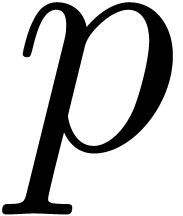 in terms of the modified Bessel function
in terms of the modified Bessel function  :
:
with 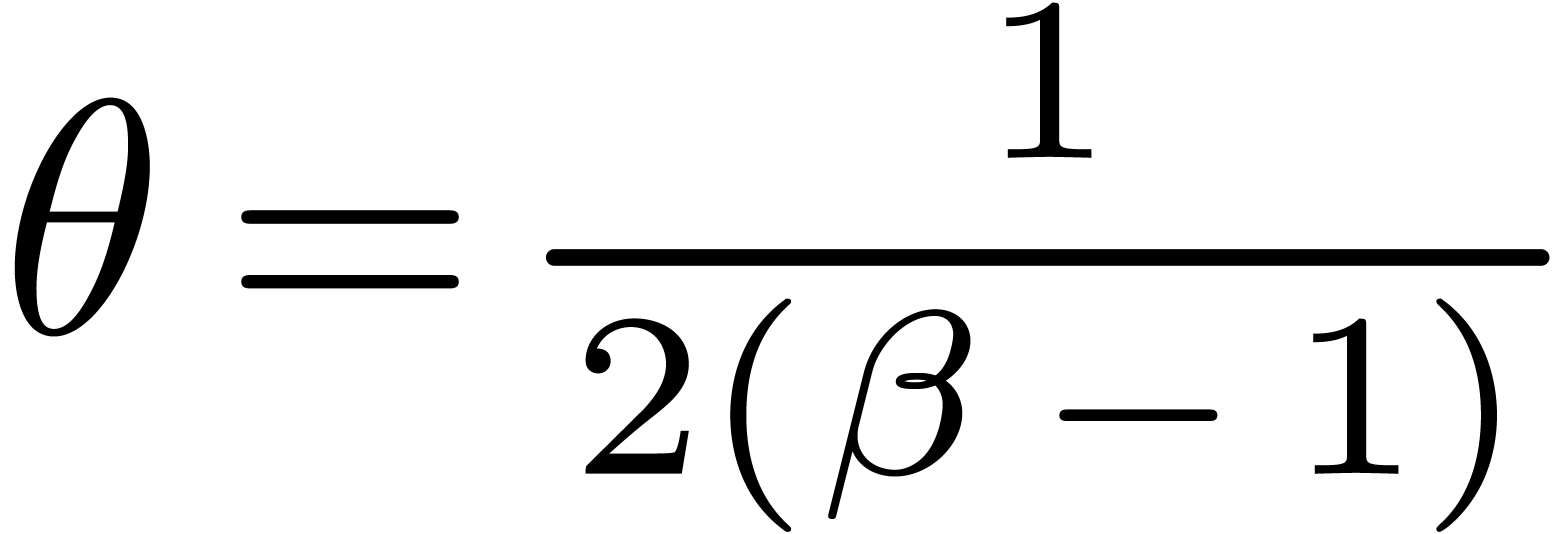 (in the most popular cases we have
(in the most popular cases we have 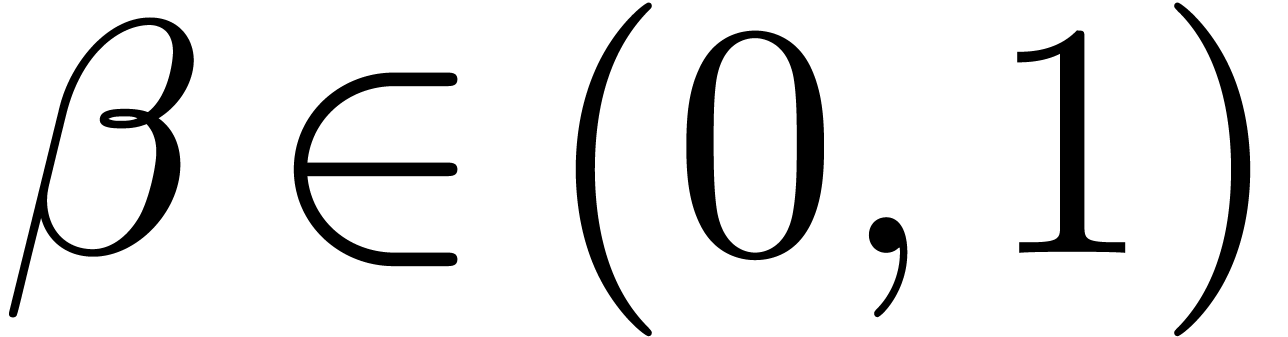 ) and
) and
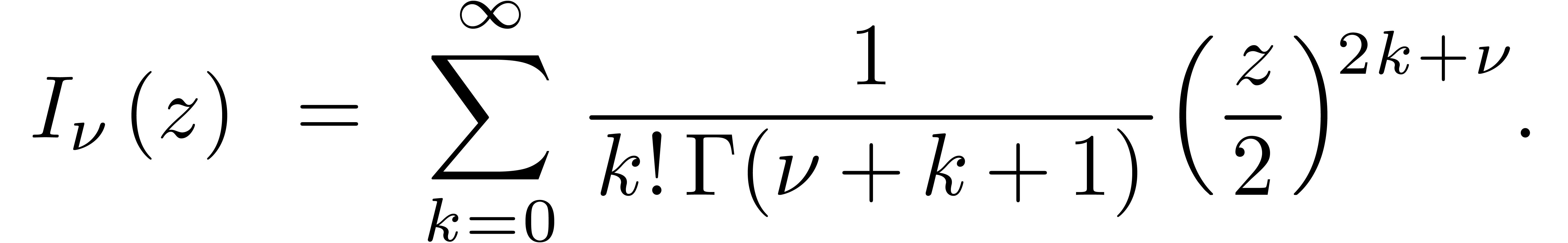 |
The following well known asymptotic expansion for  is due to Hankel:
is due to Hankel:
On the other hand, Tanaka's formula shows that the time-value
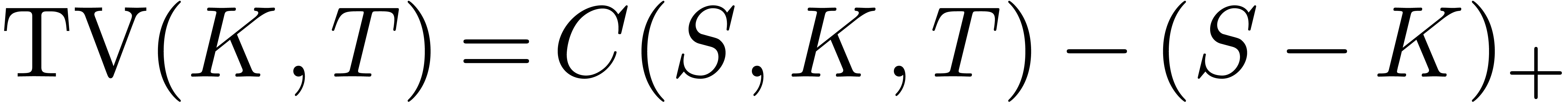
of the call-price 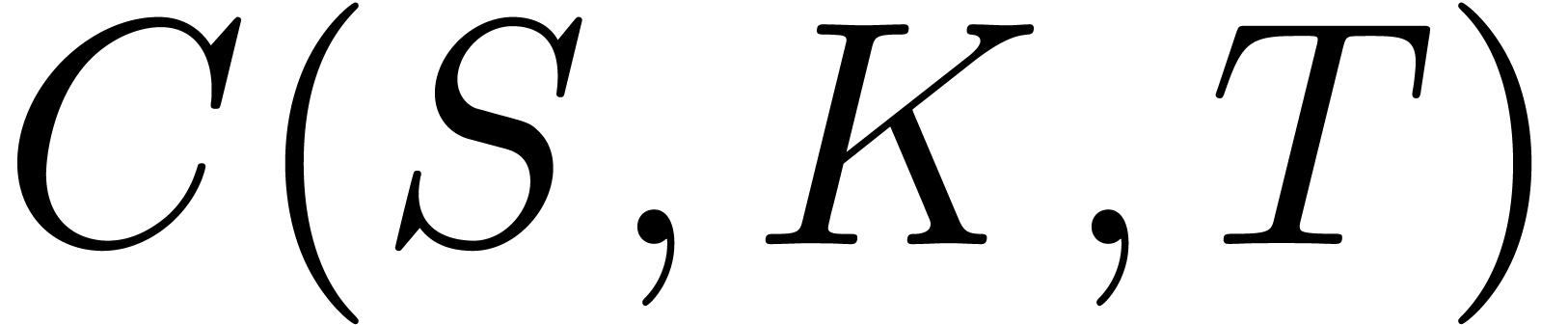 with strike
with strike  and maturity
and maturity  is given by
is given by
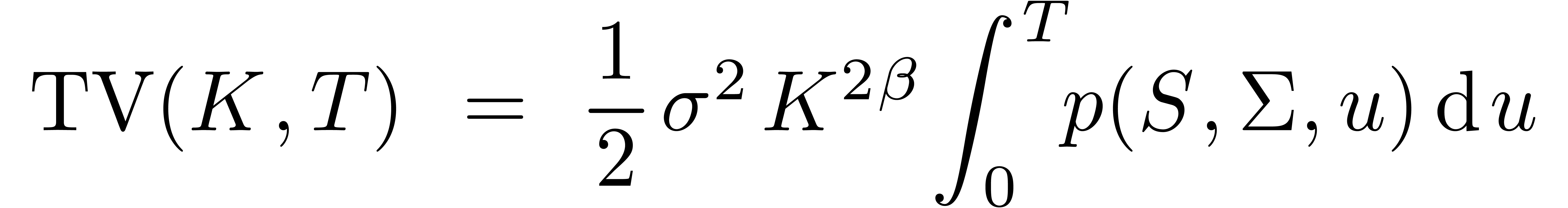 |
For short maturities  , the
combination of (18) and (20) yields an
asymptotic expansion of
, the
combination of (18) and (20) yields an
asymptotic expansion of 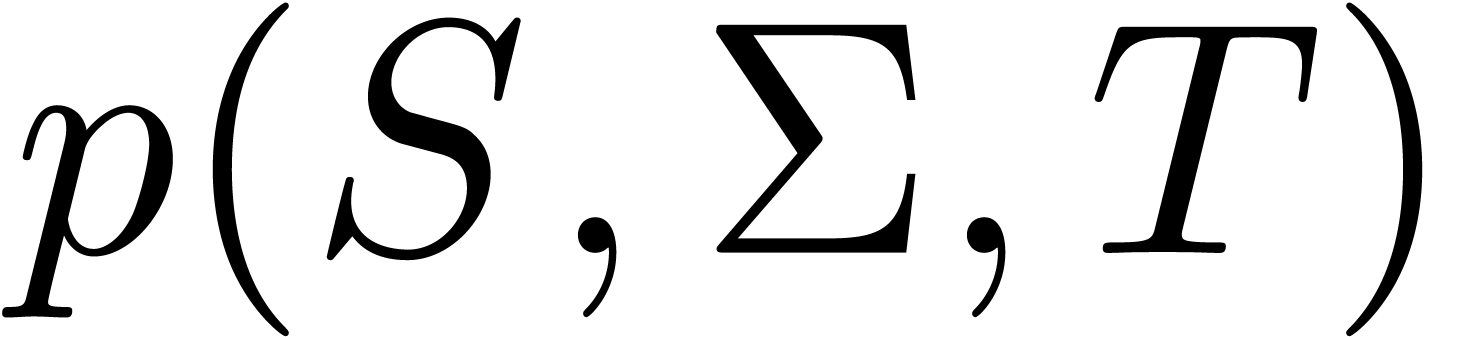 that can be integrated
by parts to any order with respect to
that can be integrated
by parts to any order with respect to  .
This leads to an asymptotic expansion of the time-value
.
This leads to an asymptotic expansion of the time-value 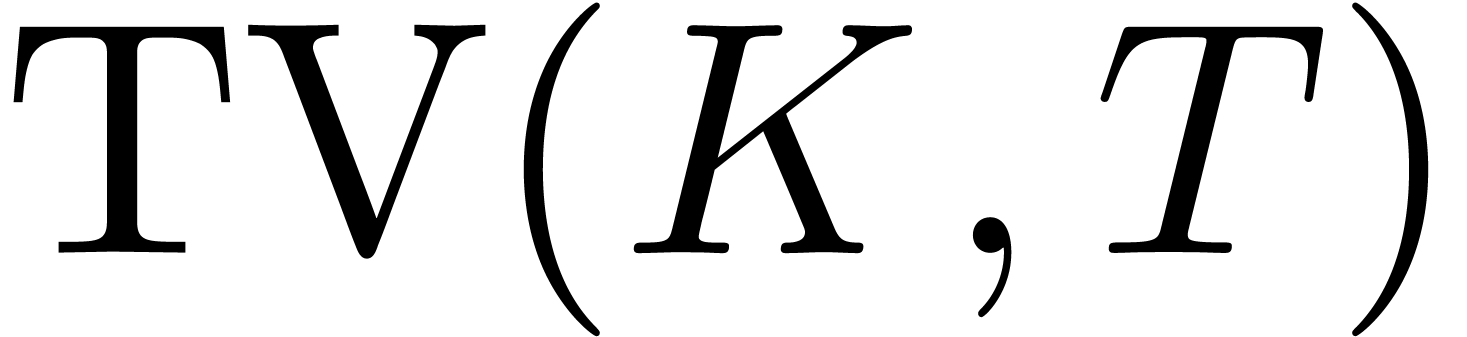 of a call price. Using an asymptotic expansion of the inverse function
of the Black-Scholes function seen in section 4.5, we
deduce an asymptotic expansion of the implied lognormal volatility of
the CEV model at any order in
of a call price. Using an asymptotic expansion of the inverse function
of the Black-Scholes function seen in section 4.5, we
deduce an asymptotic expansion of the implied lognormal volatility of
the CEV model at any order in  .
.
We did an experimental implementation of our algorithm in the 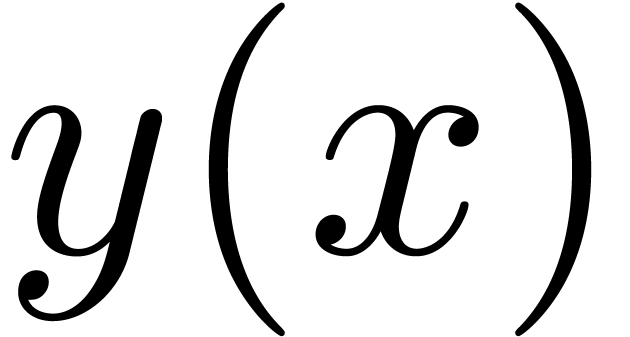 with an asymptotic expansion of the
form
with an asymptotic expansion of the
form
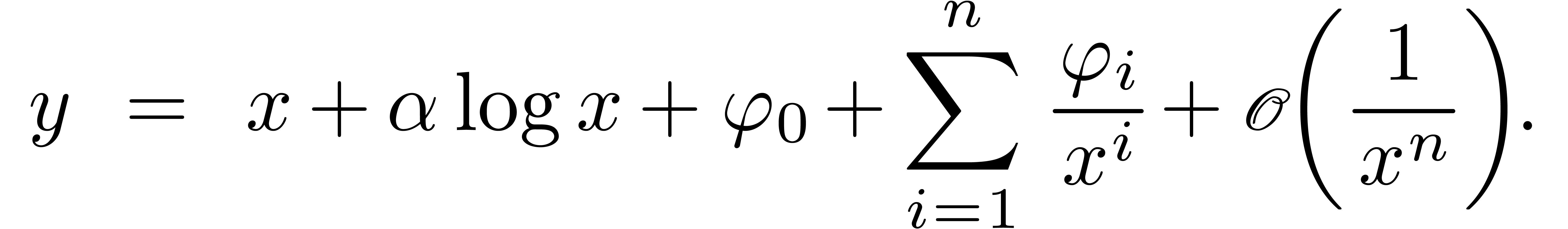
For 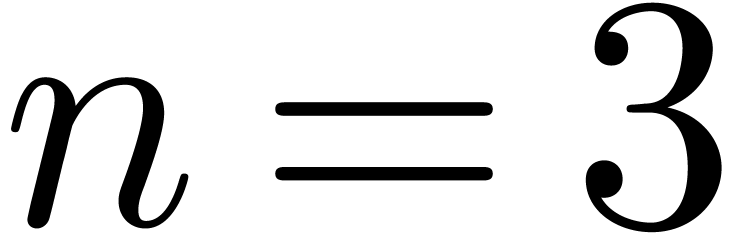 , our algorithm yields:
, our algorithm yields:

In this paper, we have presented an algorithm for calculating asymptotic expansions of functional inverses of functions that are highly tangent to identity. In particular, we obtained asymptotic expansions of the implied volatility of an option call price at any order in a model-free setting. hen, we have shown how this can be applied to the CEV model. It is envisaged to apply these techniques to more sophisticated models such as the SABR model [17]. More generally, it would be interesting to combine our approach with other algorithms for the calculation of heat kernel coefficients such as [1] to get automatic asymptotic expansion at any order of the implied volatility of option call prices for a large class of financial models [2].
I. G. Avramidi and R. Schimming. Algorithms for the Calculation of the Heat Kernel Coefficients, pages 150–162. Vieweg+Teubner Verlag, Wiesbaden, 1996.
I.G. Avramidi. Heat Kernel Method and its Applications. Birkhäuser, 2015.
S. Benaim and P. Friz. Smile asymptotics. ii. models with known moment generating functions. Journal of Applied Probability, 45(1):16–23, 2008.
H. Berestycki, I. Florent, and J. Busca. Asymptotics and calibration of local volatility models. Quantitative Finance, 2(1):61–69, 2002.
N. Bourbaki. Fonctions d'une variable réelle. Éléments de Mathématiques (Chap. 5). Hermann, 2-nd edition, 1961.
R. P. Brent and H. T. Kung. 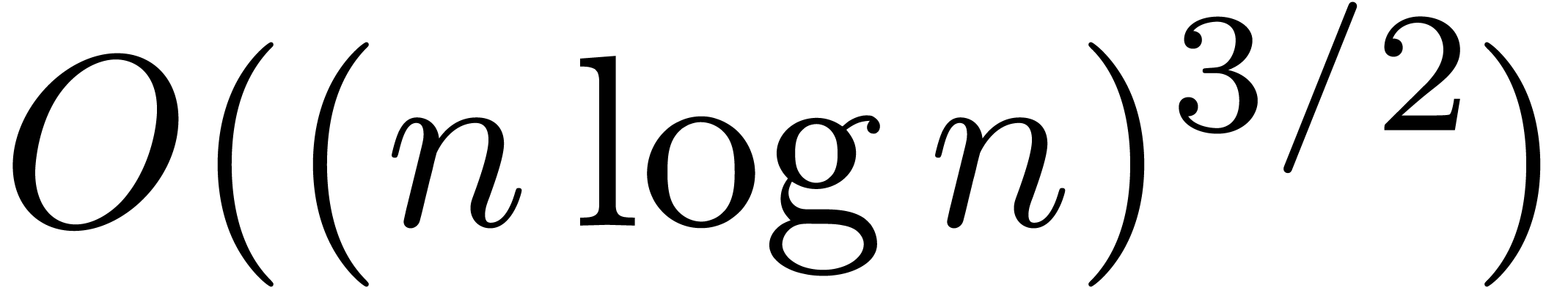 algorithms for composition and reversion of power series. In J.
F. Traub, editor, Analytic Computational Complexity.
Pittsburg, 1975. Proc. of a symposium on analytic computational
complexity held by Carnegie-Mellon University.
algorithms for composition and reversion of power series. In J.
F. Traub, editor, Analytic Computational Complexity.
Pittsburg, 1975. Proc. of a symposium on analytic computational
complexity held by Carnegie-Mellon University.
M. Craddock and M. Grasselli. Lie symmetry methods for local volatility models. Ssrn.com/abstract=2836817, 2016.
S. De Marco, C. Hillairet, and A. Jacquier. Shapes of implied volatility with positive mass at zero. SIAM J. Finan. Math., 8(1):709–737, 2017.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
K. Gao and R. Lee. Asymptotics of implied volatility to arbitrary order. Finance and Stochastics, 18(2):349–392, 2014.
J. Gatheral, E. P. Hsu, P. Laurence, C. Ouyang, and T.-H. Wang. Asymptotics of implied volatility in local volatility models. Mathematical Finance, 22(4):591–620, 2012.
P.K.F. Gatheral, A. Gulisashvili, A. Jacquier, and J. Teichmann. Large Deviations and Asymptotic Methods in Finance, volume 110 of Proceedings in Mathematics and Statistics. Springer-Verlag, 2015.
C. Grunspan. A note on the equivalence between the normal and the lognormal implied volatility : a model free approach. ArXiv:1112.1782, 2011.
C. Grunspan. Asymptotic expansions of the lognormal implied volatility: a model free approach. Technical Report 1112.1652, Arxiv, 2011.
D. Gruntz. On computing limits in a symbolic manipulation system. PhD thesis, E.T.H. Zürich, Switzerland, 1996.
A. Gulisashvili. Asymptotic formulas with error estimates for call pricing functions and the implied volatility at extreme strikes. SIAM J. Finan. Math., 1(1):609–641, 2010.
Kumar, D., Lesniewski, A. Hagan, P. and D. Woodward. Managing smile risk. Wilmott Magazine, pages 84–108, 2002.
G. H. Hardy. Orders of infinity. Cambridge Univ. Press, 1910.
G. H. Hardy. Properties of logarithmico-exponential functions. Proceedings of the London Mathematical Society, 10(2):54–90, 1911.
P. Henry-Labordère. A general asymptotic implied volatility for stochastic volatility models. Technical Report cond-mat/050431, Arxiv, 2005.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1997.
J. van der Hoeven. Generic asymptotic expansions. AAECC, 9(1):25–44, 1998.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
J. van der Hoeven, G. Lecerf, B. Mourrain et al. Mathemagix. 2002. http://www.mathemagix.org.
R. Lee. The moment formula for implied volatility at extreme strikes. Mathematical Finance, 14(3):469–480, 2004.
Forde M. and Jacquier A. Small-time asymptotics for an uncorrelated local-stochastic volatility model. Applied Mathematical Finance, 18(6):517–535, 2011.
O. Osajima. The asymptotic expansion formula of implied volatility for dynamic sabr model and fx hybrid model. Dx.doi.org/10.2139/ssrn.965265, 2007.
D. Richardson. Zero tests for constants in simple scientific computation. MCS, 1(1):21–37, 2007.
D. Richardson, B. Salvy, J. Shackell, and J. van der Hoeven. Expansions of exp-log functions. In Y. N. Lakhsman, editor, Proc. ISSAC '96, pages 309–313. Zürich, Switzerland, July 1996.
M. Roper and M. M. Rutkowski. On the relationship between the call price surface and the implied volatility surface close to expiry. International Journal of Theoretical and Applied Finance, 12(4):427–441, 2009.
B. Salvy. Asymptotique automatique et fonctions génératrices. PhD thesis, École Polytechnique, France, 1991.
B. Salvy and J. Shackell. Asymptotic expansions of functional inverses. In P. S. Wang, editor, Proc. ISSAC '92, pages 130–137. New York, 1992. ACM Press.
B. Salvy and J. Shackell. Symbolic asymptotics: multiseries of inverse functions. JSC, 27(6):543–563, 1999.
J. Shackell. Growth estimates for exp-log functions. JSC, 10:611–632, 1990.
J. Shackell. Symbolic asymptotics, volume 12 of Algorithms and computation in Mathematics. Springer-Verlag, 2004.
M.R. Tehranchi. Uniform bounds for black–scholes implied volatility. SIAM J. Finan. Math., 7(1):893–916, 2016.
K. Yoshida. On the fundamental solution of the parabolic equation in a Riemannian space. Osaka Mathematical Journal, 1(1), 1953.