On the complexity of multivariate
blockwise polynomial multiplication |
|
Joris van der Hoeven and
Grégoire Lecerf
|
|
Laboratoire d'Informatique, UMR 7161 CNRS
École polytechnique
91128 Palaiseau Cedex, France
|
|
{vdhoeven,
lecerf}@lix.polytechnique.fr
|
|
|
Abstract
In this article, we study the problem of multiplying two multivariate
polynomials which are somewhat but not too sparse, typically like
polynomials with convex supports. We design and analyze an algorithm
which is based on blockwise decomposition of the input polynomials, and
which performs the actual multiplication in an FFT model or some other
more general so called “evaluated model”. If the input
polynomials have total degrees at most 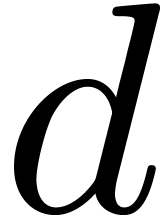 ,
then, under mild assumptions on the coefficient ring, we show that their
product can be computed with
,
then, under mild assumptions on the coefficient ring, we show that their
product can be computed with 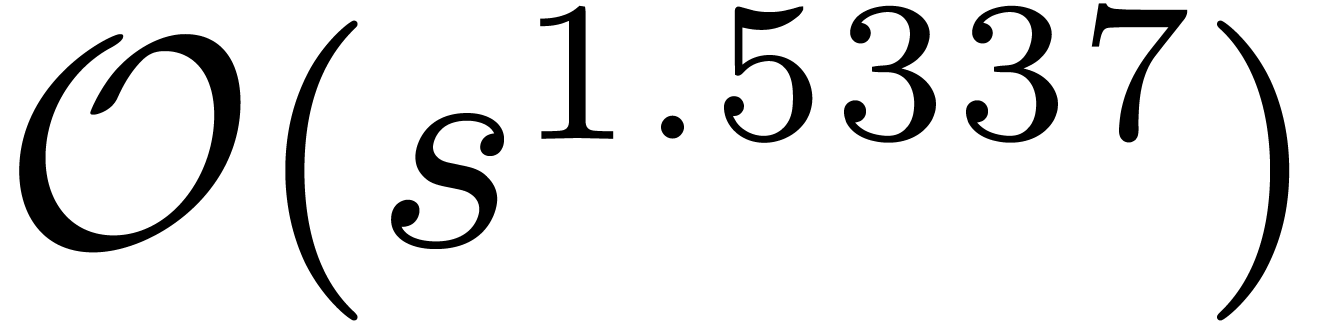 ring operations,
where
ring operations,
where  denotes the number of all the monomials of
total degree at most
denotes the number of all the monomials of
total degree at most 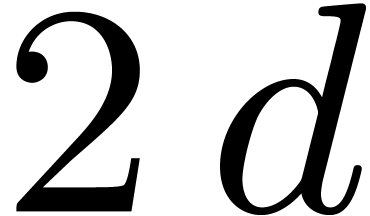 .
.
Keywords
sparse polynomial multiplication; multivariate power series;
evaluation-interpolation; algorithm
A.M.S. subject classification:
68W30
,
12-04
,
30B10
,
42-04
1.Introduction
Let  be an effective ring, which means
that we have a data structure for representing the elements of
be an effective ring, which means
that we have a data structure for representing the elements of  and algorithms for performing the ring operations in
and algorithms for performing the ring operations in  , including the equality test. The
complexity for multiplying two univariate polynomials with coefficients
in
, including the equality test. The
complexity for multiplying two univariate polynomials with coefficients
in  and of degree
and of degree 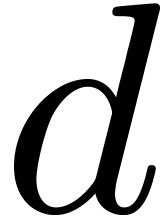 is
rather well understood [11, Chapter 8]. Let us recall that
for small
is
rather well understood [11, Chapter 8]. Let us recall that
for small 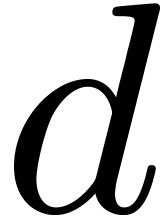 , one uses the
naive multiplication, as learned at high school, of complexity
, one uses the
naive multiplication, as learned at high school, of complexity 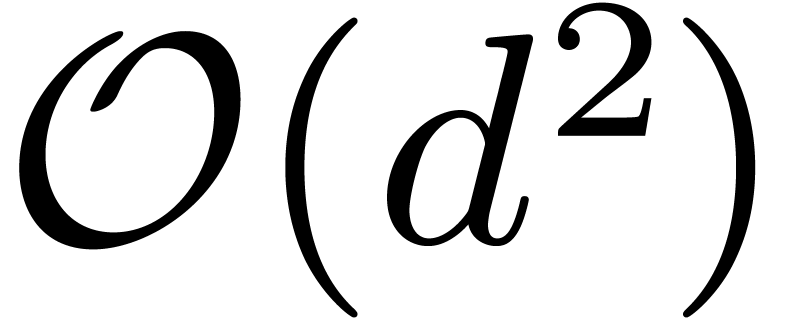 . For moderate
. For moderate 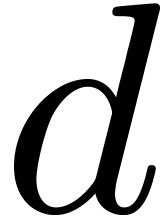 , one uses the Karatsuba multiplication [21], of complexity
, one uses the Karatsuba multiplication [21], of complexity 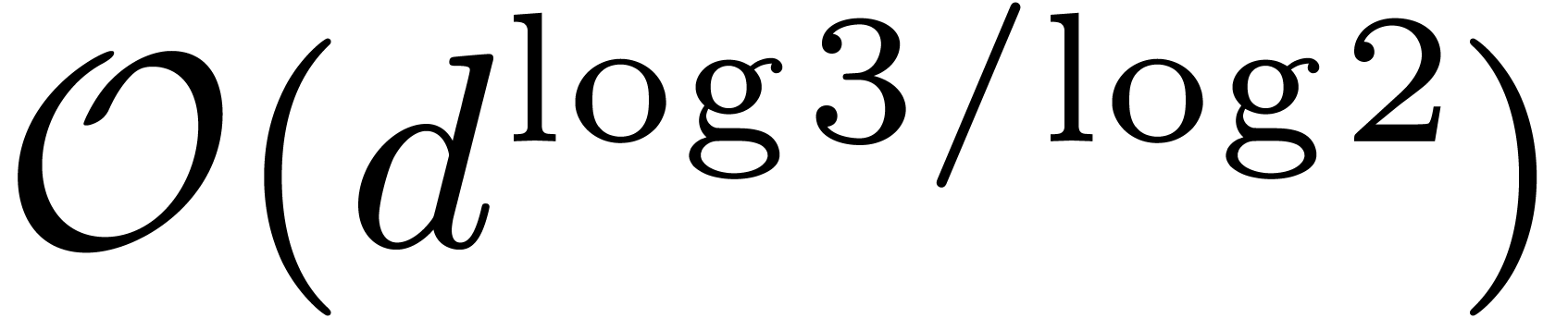 ,
or some higher order Toom-Cook scheme [4, 29],
of complexity
,
or some higher order Toom-Cook scheme [4, 29],
of complexity 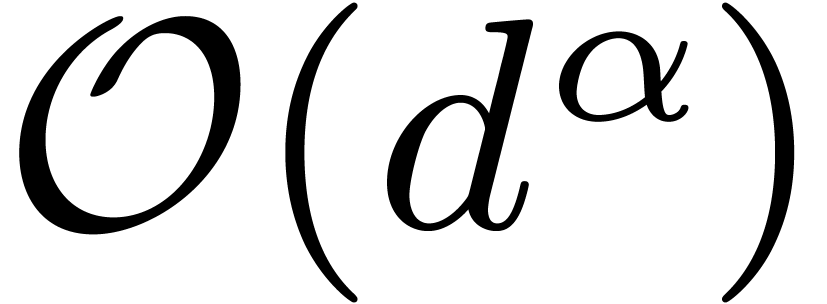 with
with 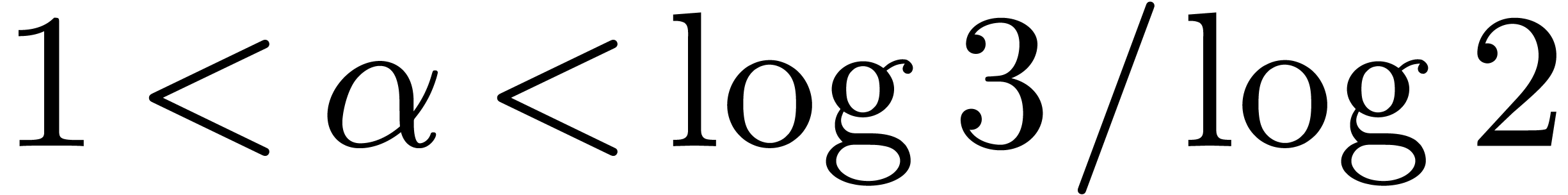 .
For large
.
For large 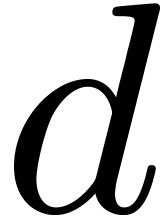 , one uses FFT [3, 5, 27] and TFT [14,
15] multiplications, both of complexity
, one uses FFT [3, 5, 27] and TFT [14,
15] multiplications, both of complexity 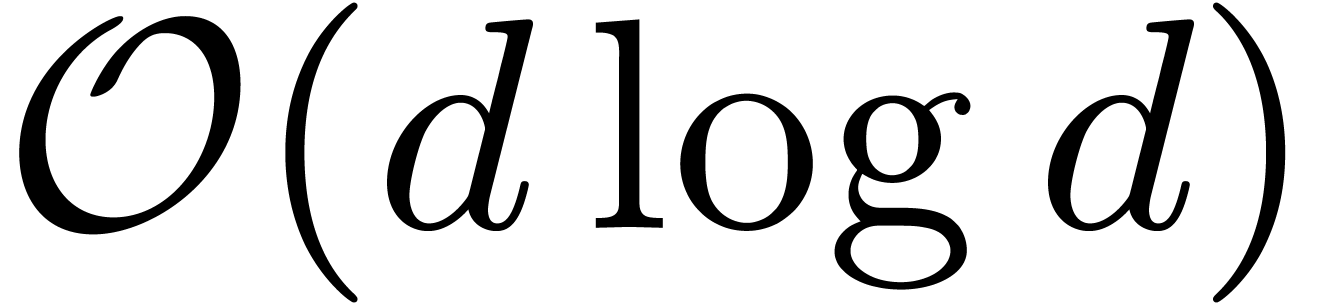 whenever
whenever  has sufficiently many
has sufficiently many 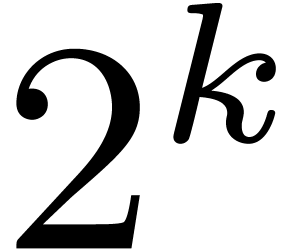 -th roots of unity, or the Cantor-Kaltofen
multiplication [3, 27] with complexity in
-th roots of unity, or the Cantor-Kaltofen
multiplication [3, 27] with complexity in 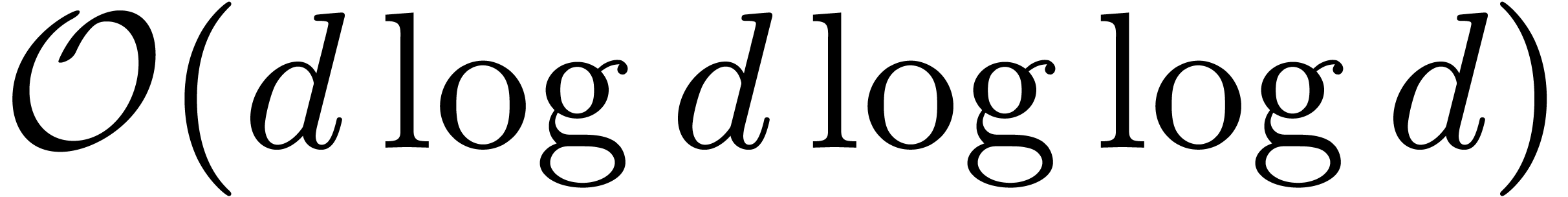 otherwise.
otherwise.
Unfortunately most of the techniques known in the univariate case do not
straightforwardly extend to several variables. Even for the known
extensions, the efficiency thresholds are different. For instance, the
naive product is generally softly optimal when sparse
representations are used, because the size of the output can grow
with the product of the sizes of the input. In fact, the nature of the
input supports plays a major role in the design of the algorithms and
the determination of their mutual thresholds. In this article, we focus
on and analyze an intermediate approach to several variables, which
roughly corresponds to an extension of the Karatsuba and Toom-Cook
strategies, and which turns out to be more efficient than the naive
multiplication for instance if the supports of the input polynomials are
rather dense in their respective convex hulls.
1.1Our contributions
The main idea in our blockwise polynomial multiplication is to cut the
supports in blocks of size  and to rewrite all
polynomials as “block polynomials” in
and to rewrite all
polynomials as “block polynomials” in  with “block coefficients” in
with “block coefficients” in
These block coefficients are then manipulated in a suitable
“evaluated model”, in which the multiplication is intended
to be faster than with the direct naive approach. The blockwise
polynomials are themselves multiplied in a naive manner. The precise
algorithm is described in Section 3.1, where we also
discuss the expected speedup compared to the naive product. A precise
complexity analysis is subtle because it depends too much on the nature
of the supports. Although the worse case bound turns out to be no better
than with the naive approach, we detail, in Section 3.2, a
way for quickly determining a good block size, that suits supports that
are not too small, not too thin, and rather dense in their convex hull.
Our Section 4 is devoted to implementation issues. We first
design a cache-friendly version of our blockwise product. Then we adapt
a blockwise product for multivariate power series truncated in total
degree. Finally, we discuss a technique to slightly improve the
blockwise approach for small and thin supports.
In Section 5 we analyze the complexity of the blockwise
product for two polynomials supported by monomials of degree at most
 : if
: if  contains
contains  in its center, then we show that their
product can be computed with
in its center, then we show that their
product can be computed with 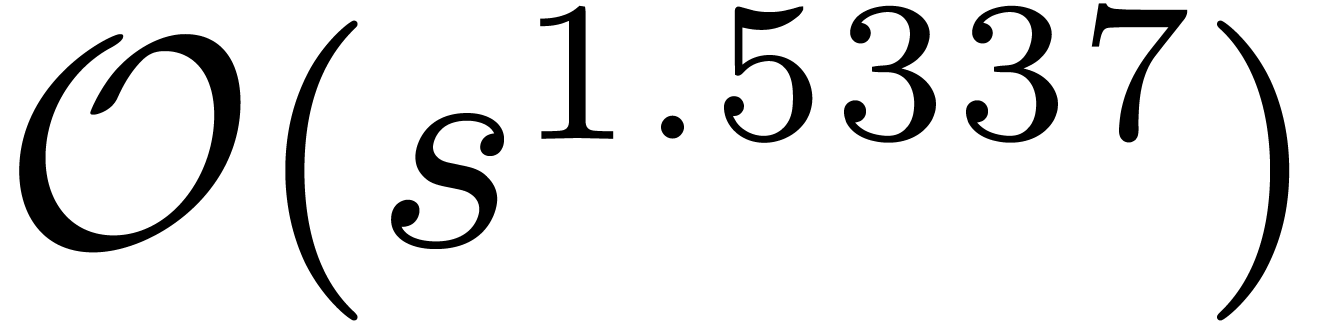 operations in
operations in  , where
, where  denotes the number of all the monomials of degree at most
denotes the number of all the monomials of degree at most 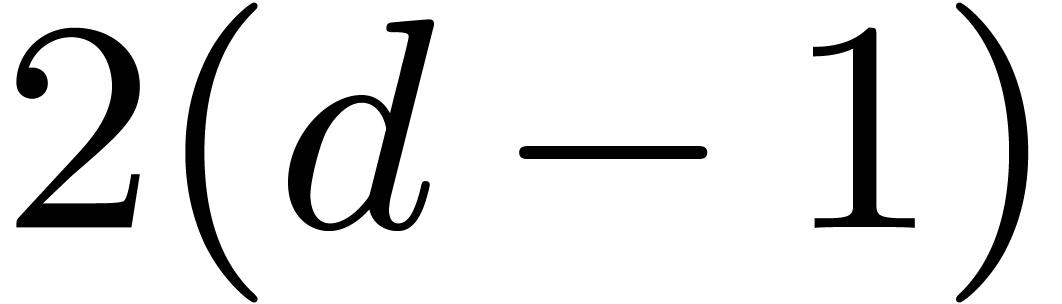 . Notice that the constant hidden behind the
latter
. Notice that the constant hidden behind the
latter  does not depend neither on
does not depend neither on 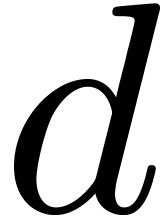 nor on the number of the variables. With no hypothesis on
nor on the number of the variables. With no hypothesis on
 , the complexity bound we
reach becomes in
, the complexity bound we
reach becomes in 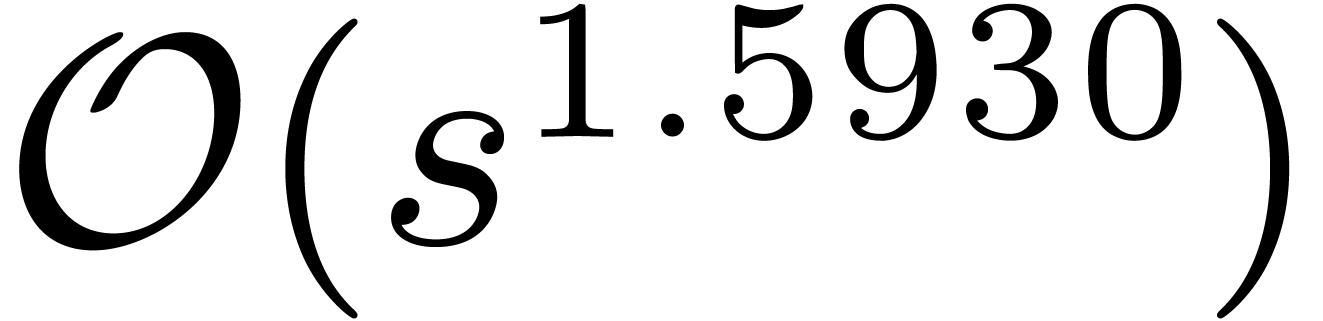 , by a
direct extension of the Karatsuba algorithm. Finally, we prove similar
complexity results for truncated power series
, by a
direct extension of the Karatsuba algorithm. Finally, we prove similar
complexity results for truncated power series
1.2Related works
Algorithms for multiplying multivariate polynomials and series have been
designed since the early ages of computer algebra [6, 7, 8, 20, 28]. Even
those based on the naive techniques are a matter of constant
improvements in terms of data structures, memory management,
vectorization and parallelization [10, 18, 23, 24, 25, 26, 30].
With a single variable  , the
usual way to multiply two polynomials
, the
usual way to multiply two polynomials  and
and  of degree
of degree  with the Karatsuba
algorithm begins with splitting
with the Karatsuba
algorithm begins with splitting  and
and  into
into 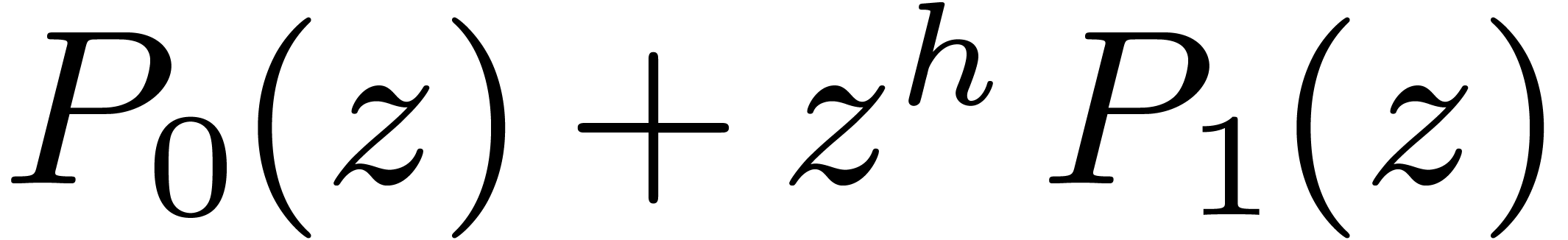 and
and 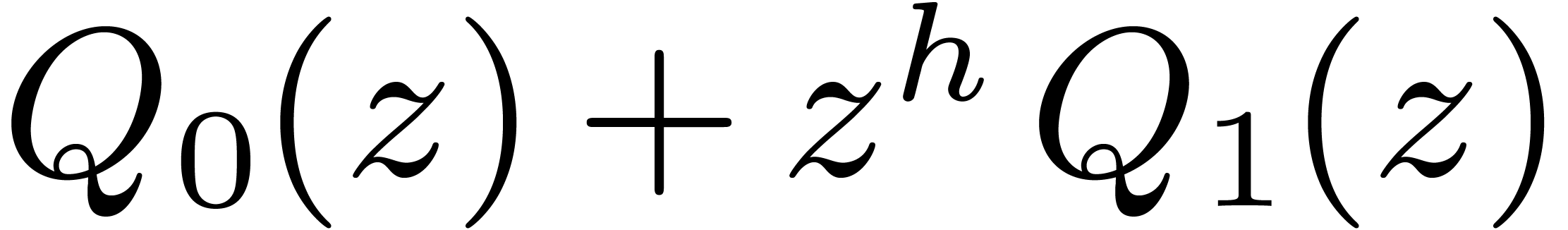 , where
, where 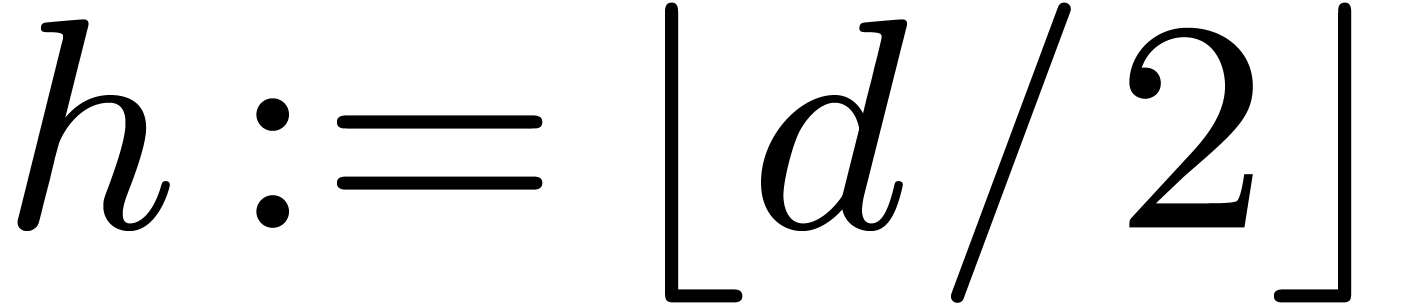 .
Then
.
Then 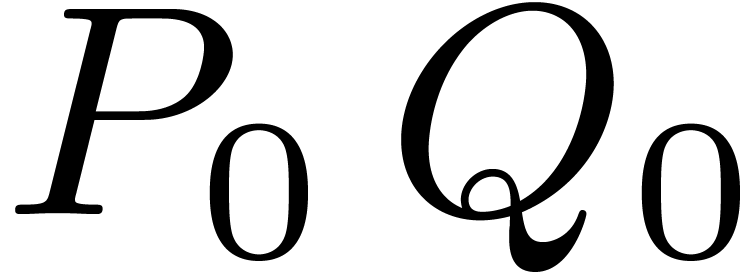 ,
, 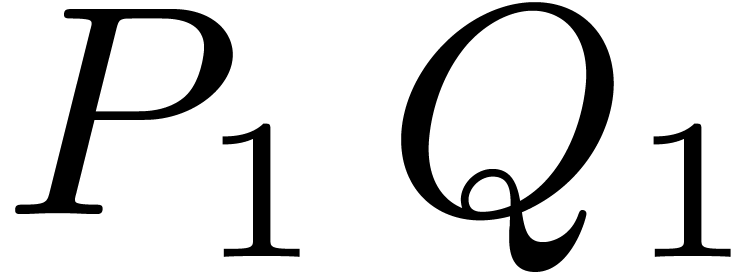 , and
, and 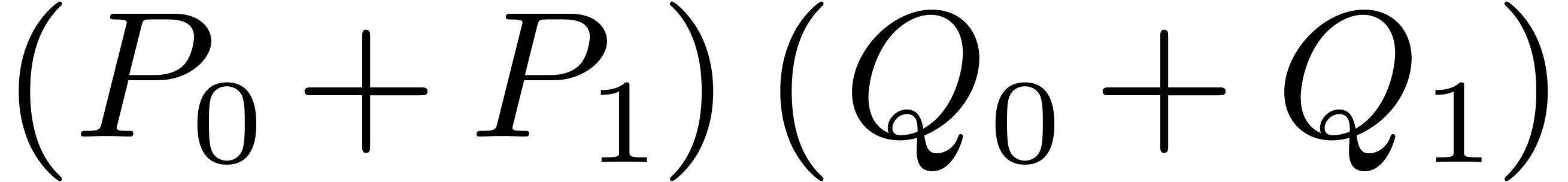 are computed
recursively. This approach has been studied for several variables [22], but it turns out to be efficient mainly for plain block
supports, as previously discussed in [8, Section 3].
are computed
recursively. This approach has been studied for several variables [22], but it turns out to be efficient mainly for plain block
supports, as previously discussed in [8, Section 3].
For any kind of support, there exist general purpose sparse
multiplication algorithms [2, 18]. They
feature quasi-linear complexity in terms of the sizes of the supports of
the input and of a given superset for the support of the product.
Nevertheless the logarithmic overhead of the latter algorithms is
important, and alternative approaches, directly based on the truncated
Fourier transform, have been designed in [14, 15,
19] for supports which are initial segments of  (i.e. sets of monomials which are
complementary to a monomial ideal), with the same order of efficiency as
the FFT multiplication for univariate polynomials.
(i.e. sets of monomials which are
complementary to a monomial ideal), with the same order of efficiency as
the FFT multiplication for univariate polynomials.
To the best of our knowledge, the blockwise technique was introduced, in
a somewhat sketchy manner, in [13, Section 6.3.3], and then
refined in [16, Section 6]. In the case of univariate
polynomials, its complexity has been analyzed in [12],
where important applications are also presented.
2.Conventions and notation
Throughout this article, we use the sparse representation for
the polynomials, and the computation tree model with the
total complexity point of view [1, Chapter 4] for
the complexity analysis of the algorithms. Informally speaking, this
means that complexity estimates charge a constant cost for each
arithmetic operation and the equality test in  , and that all the constants are thought to be
freely at our disposal.
, and that all the constants are thought to be
freely at our disposal.
2.1Block polynomials
Consider a multivariate polynomial 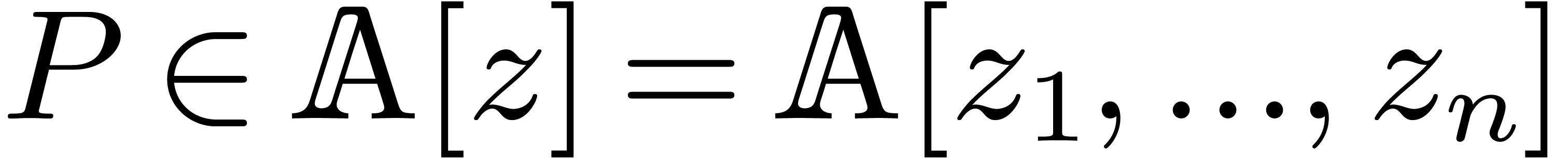 ,
also written as
,
also written as
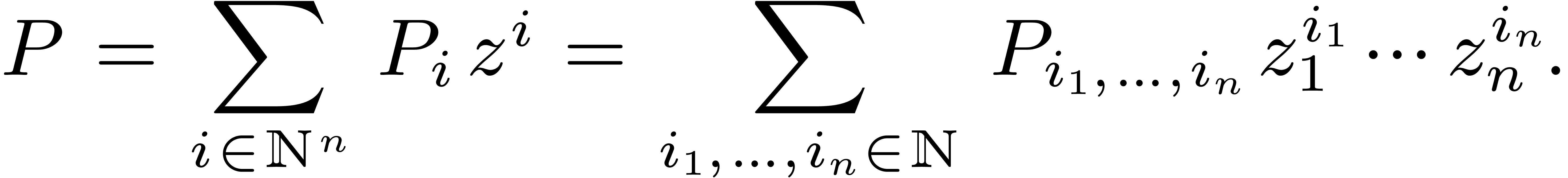
We define its support by  ,
and denote its cardinality
,
and denote its cardinality 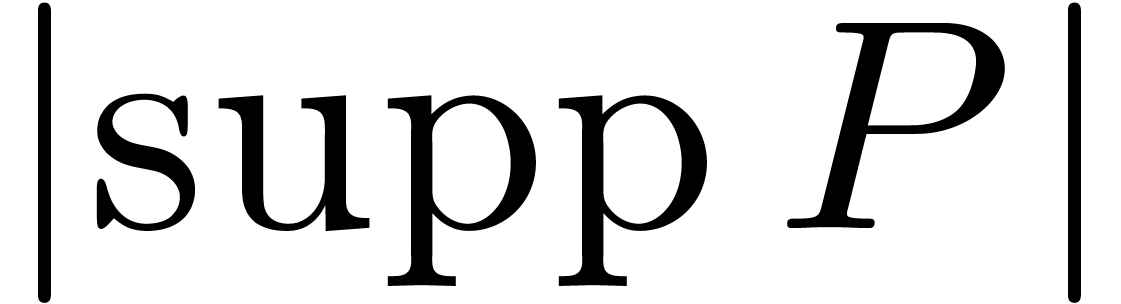 by
by 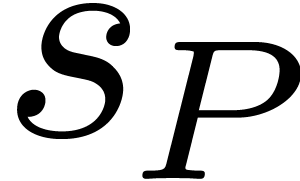 . We interpret
. We interpret 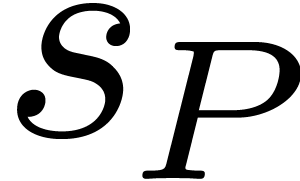 as the
sparse size of
as the
sparse size of 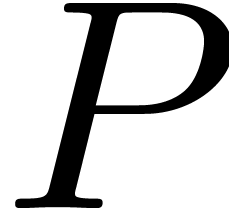 .
.
Given a vector 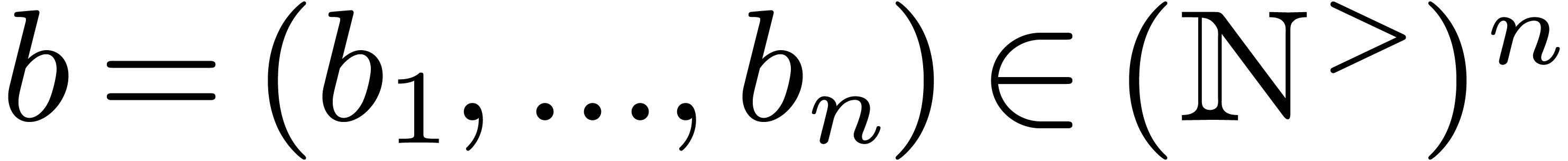 of positive integers, we define
the set of block coefficients at order
of positive integers, we define
the set of block coefficients at order 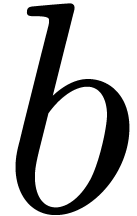 by
by
Any polynomial  can uniquely be rewritten as a
block polynomial
can uniquely be rewritten as a
block polynomial 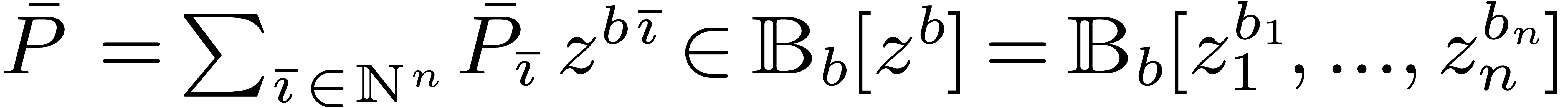 ,
where
,
where
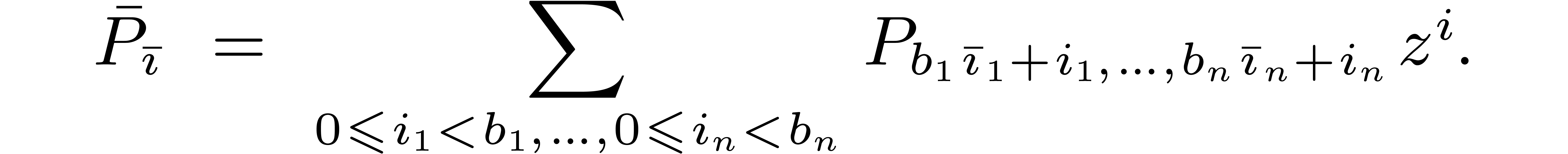
Given 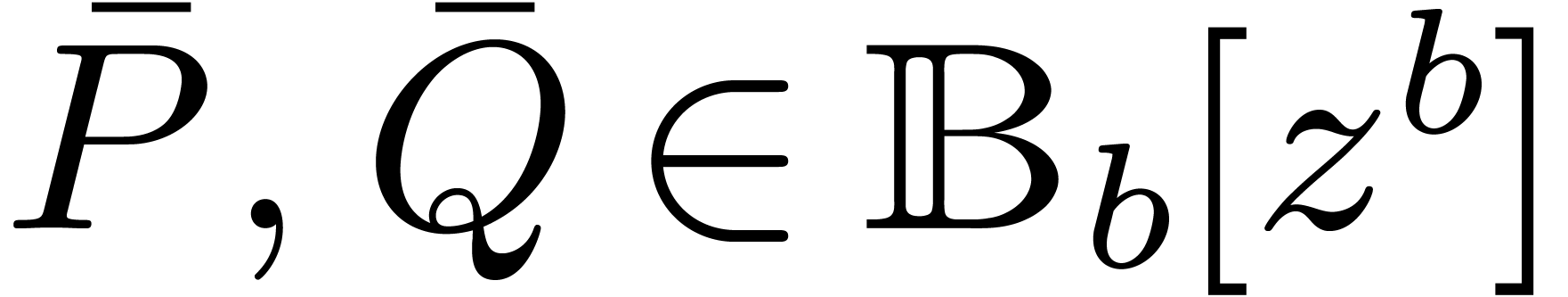 , we also notice that
, we also notice that
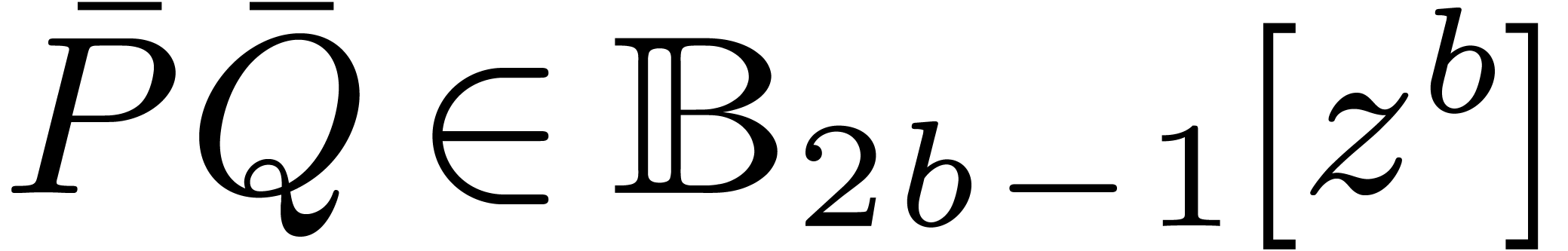 . We let
. We let  represent the size of the block
represent the size of the block  .
.
2.2Evaluation-interpolation schemes
A univariate evaluation-interpolation scheme in size  on
on  is the data of
is the data of
such that 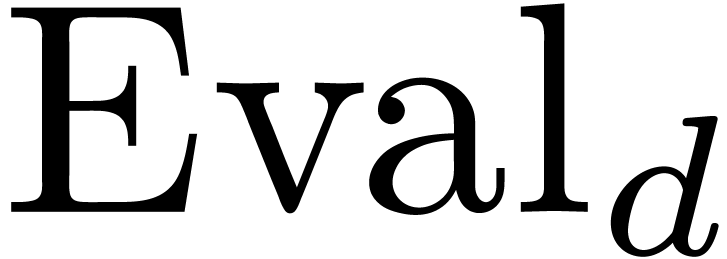 and
and 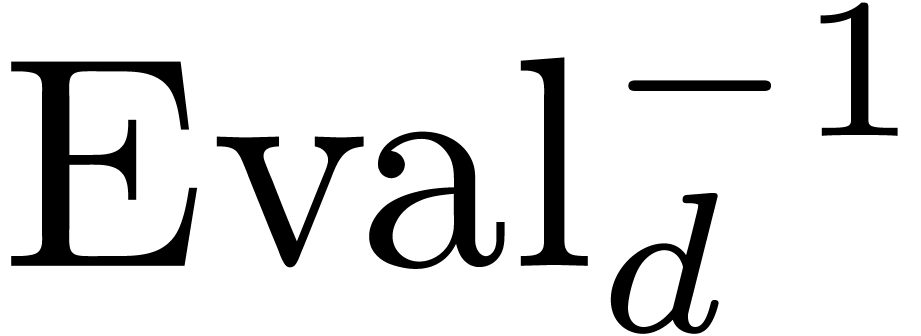 are linear
and
are linear
and

holds for all  and
and  in
in
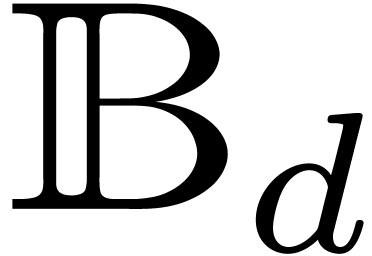 , where
, where  denotes the entry-wise product in
denotes the entry-wise product in 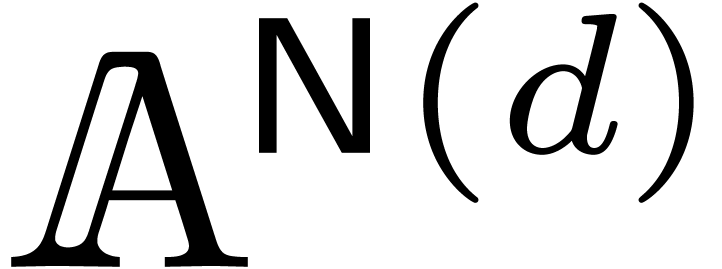 .
We write
.
We write 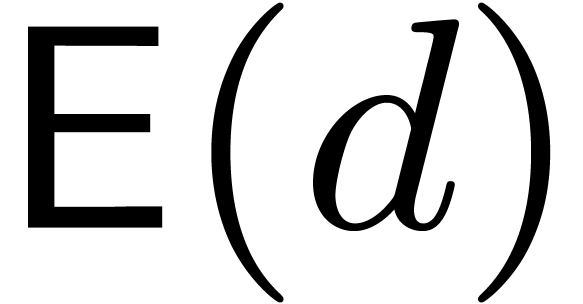 for a common bound on the complexity of
for a common bound on the complexity of
 and
and  ,
so that two polynomials in
,
so that two polynomials in 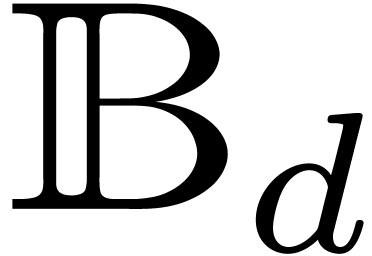 can be multiplied in
time
can be multiplied in
time 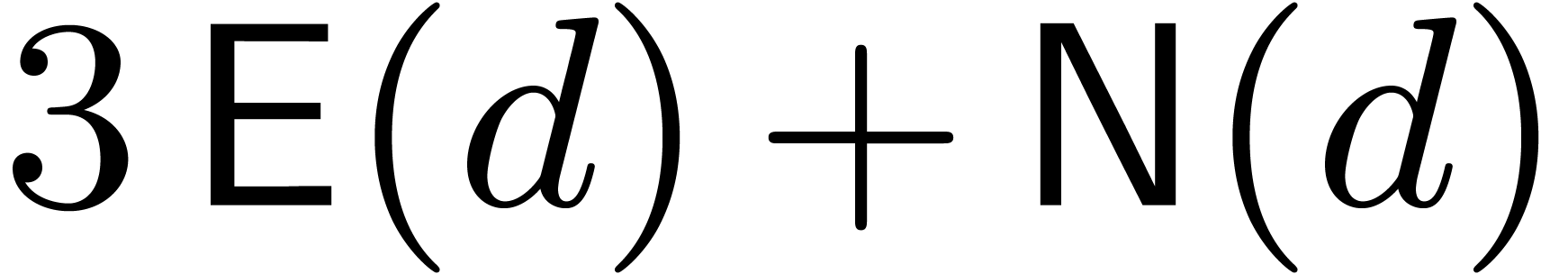 . For convenience we
still write
. For convenience we
still write 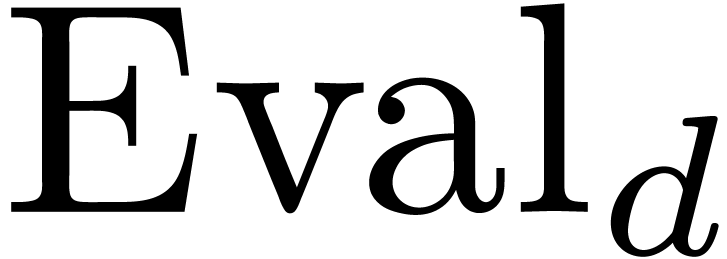 and
and 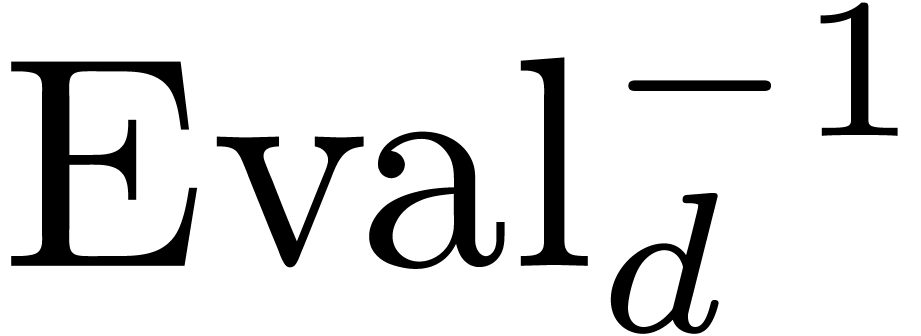 for
extensions to any
for
extensions to any  seen as a ring endowed with
the entry-wise product.
seen as a ring endowed with
the entry-wise product.
Example 1. The Karatsuba
algorithm for polynomials of degree  corresponds
to
corresponds
to  ,
,  ,
,
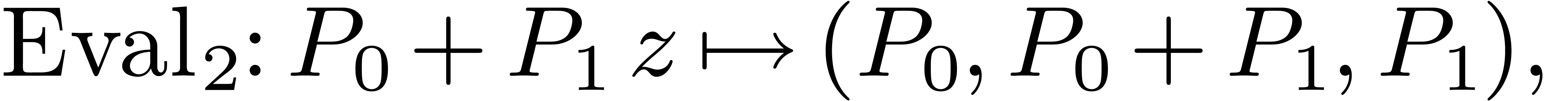
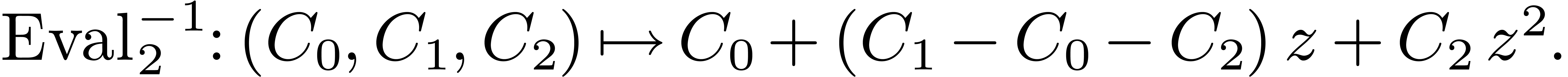
 can be interpreted as the evaluation of a
polynomial at the values
can be interpreted as the evaluation of a
polynomial at the values  ,
,
 , and
, and  . By induction, the Karatsuba algorithm for
polynomials of degree at most
. By induction, the Karatsuba algorithm for
polynomials of degree at most  corresponds to
corresponds to
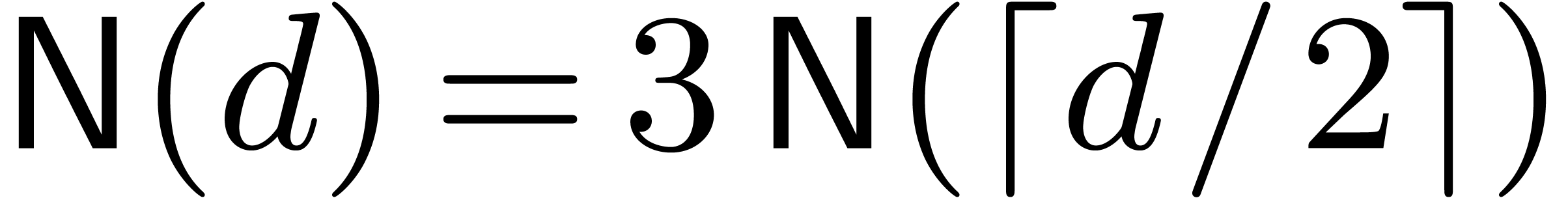 ,
,  , where
, where  is the block
polynomial of
is the block
polynomial of  with respect to
with respect to 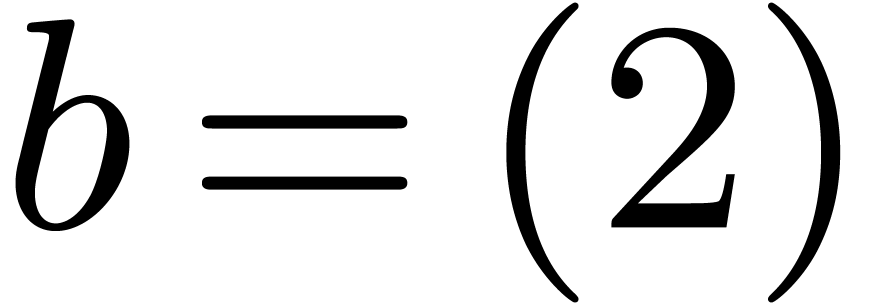 , and where
, and where 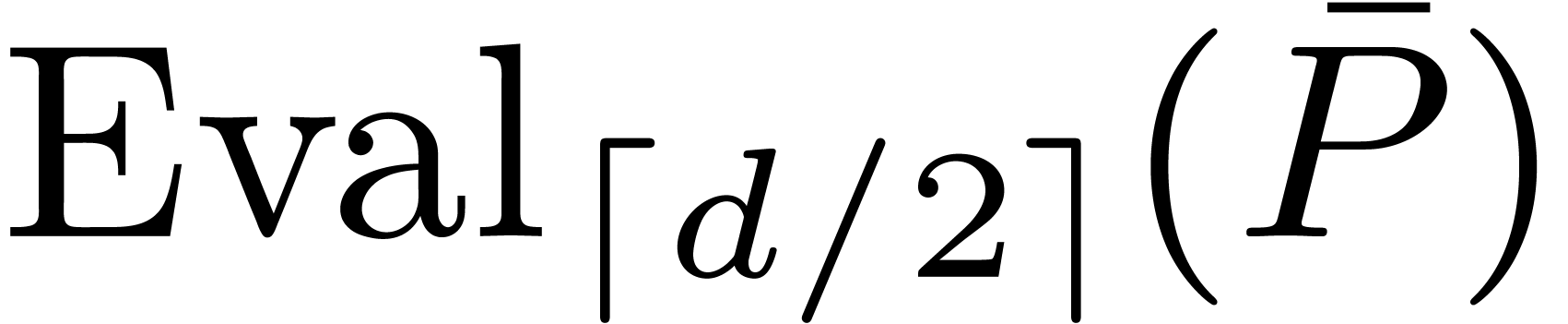 actually
corresponds to applying the extension of
actually
corresponds to applying the extension of 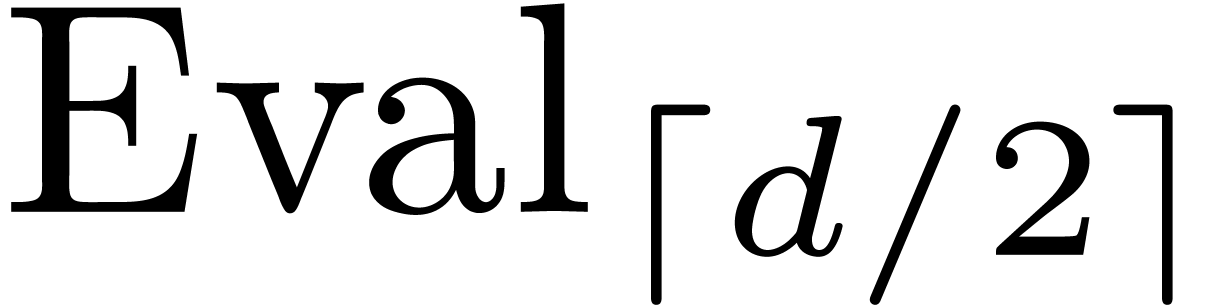 to
to
 . This yields
. This yields 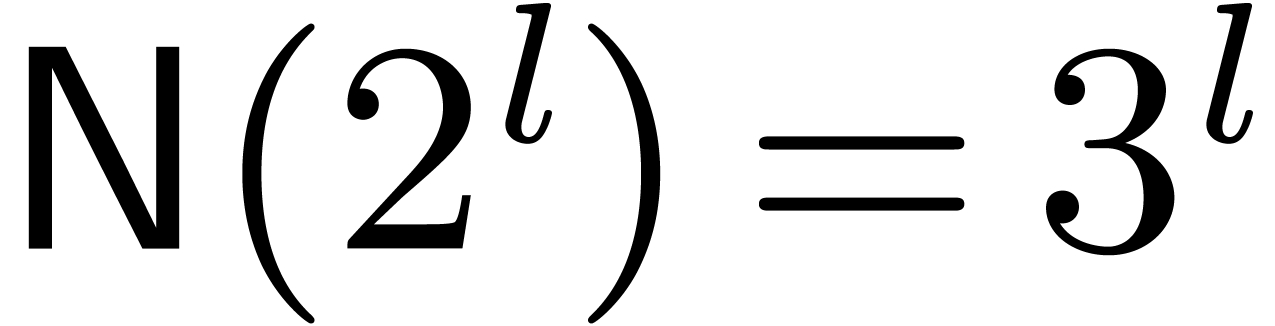 and
and 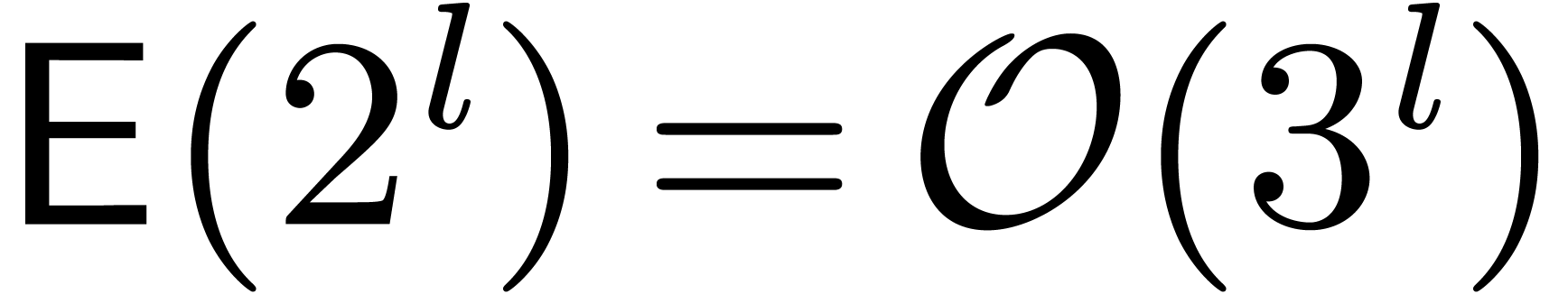 .
.
Univariate evaluation-interpolation schemes can be extended to several
variables as follows: if 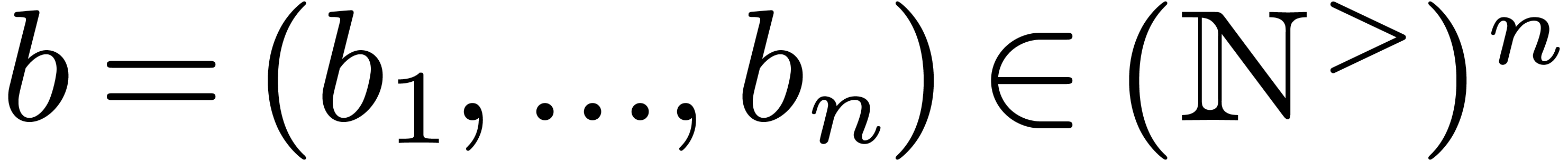 then we define
then we define 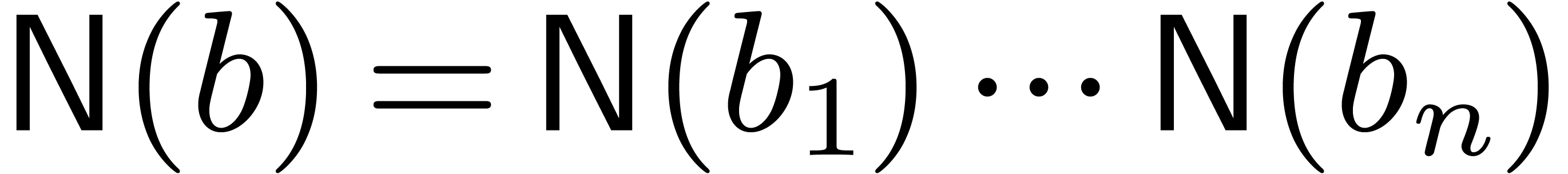 , define the maps
, define the maps
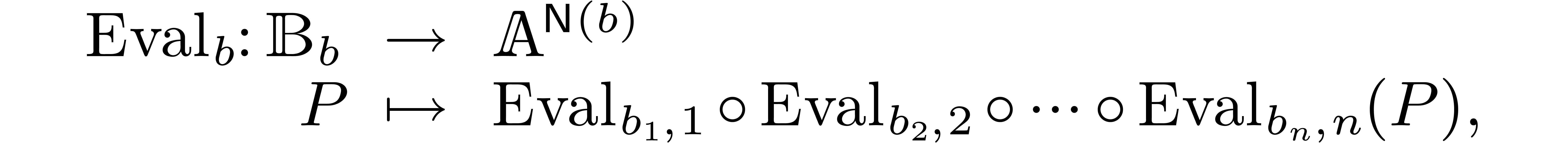
and take
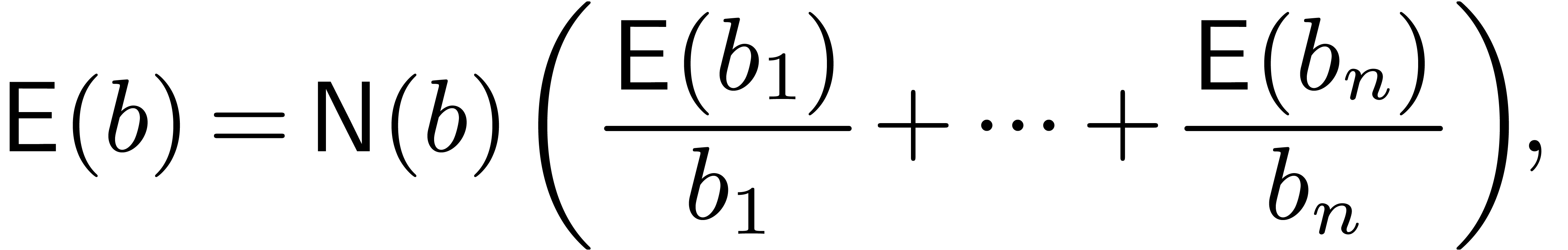 |
(1) |
where 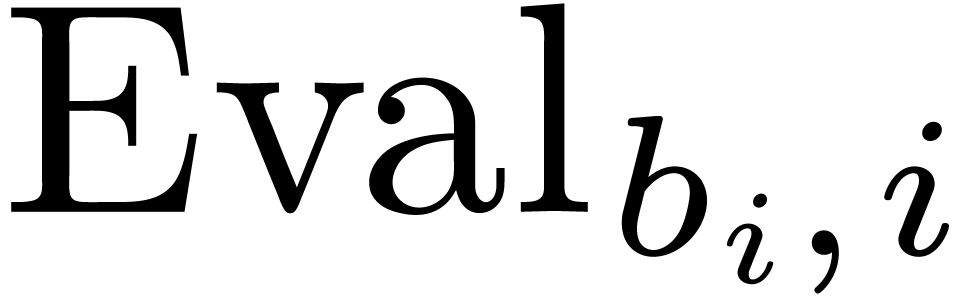 and
and 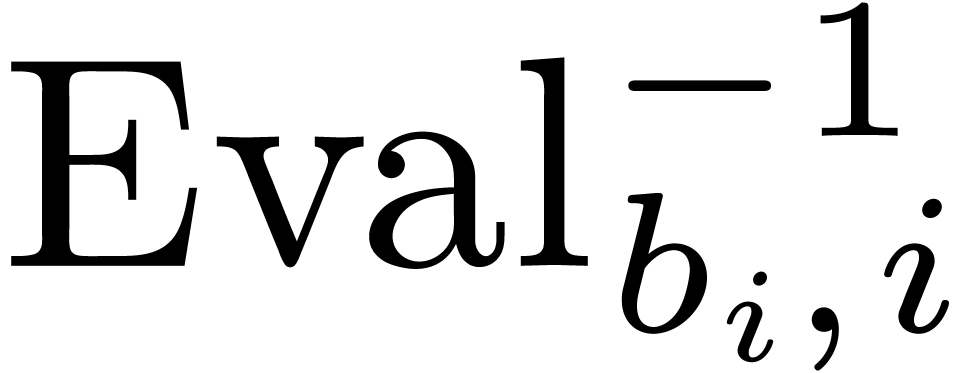 represent the
evaluation and interpolation with respect to the variable
represent the
evaluation and interpolation with respect to the variable 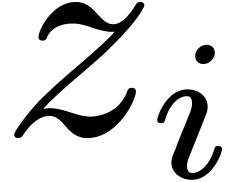 :
:
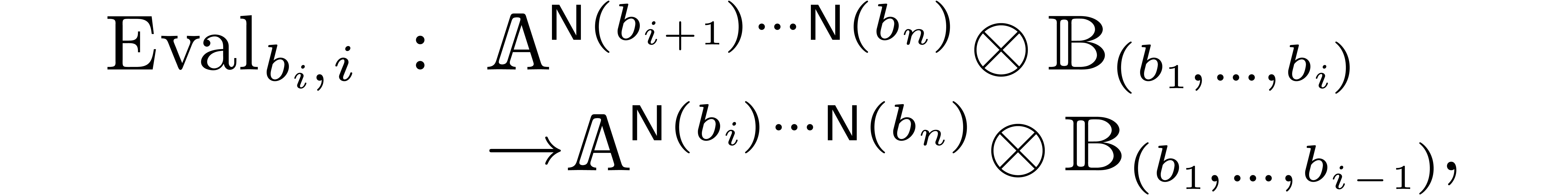
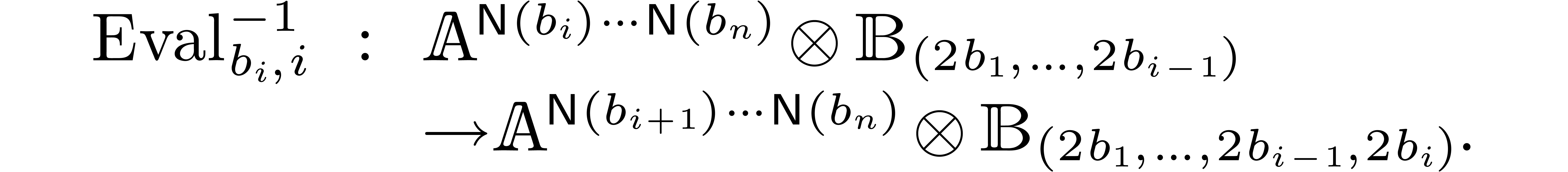
In the sequel we will only use multivariate evaluation-interpolation
schemes constructed in this way.
3.The basic algorithm
For what follows, we first assume that we have a strategy for picking a
suitable evaluation-interpolation scheme for any given block size 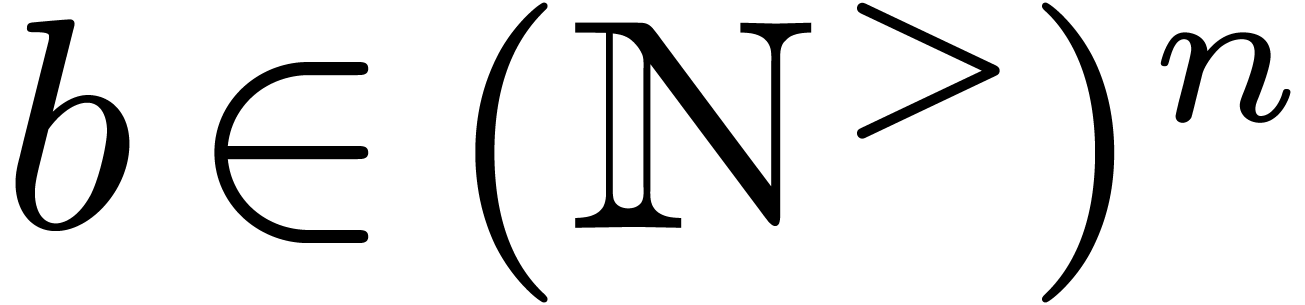 , and that we have a fast way to
compute the corresponding functions
, and that we have a fast way to
compute the corresponding functions 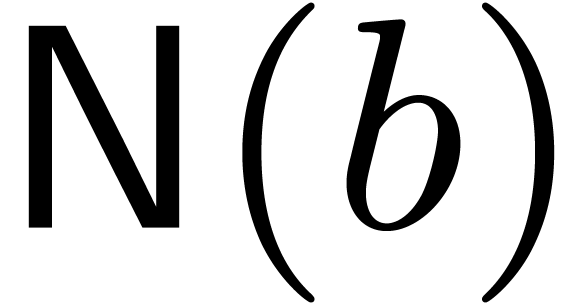 and
and 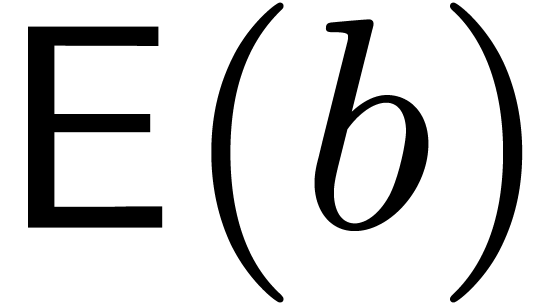 , at least approximately. We also
assume that
, at least approximately. We also
assume that 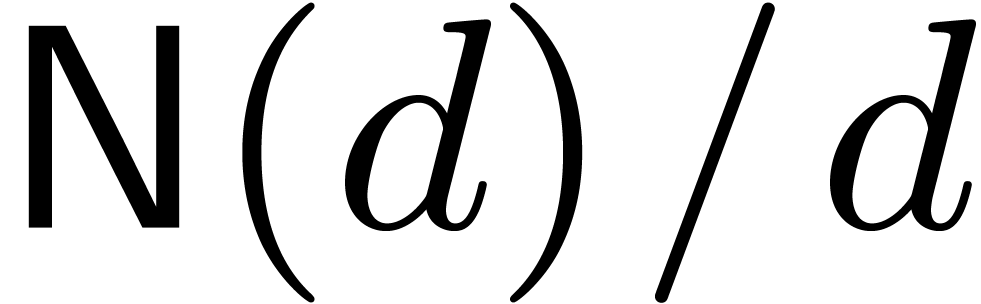 and
and 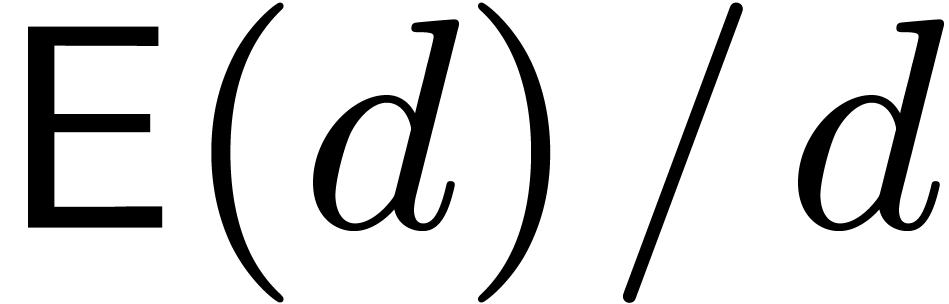 are
increasing functions.
are
increasing functions.
3.1Blockwise multiplication
Let us first assume that we have fixed a block size 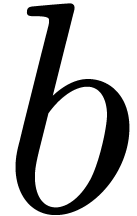 . The first version of our algorithm for
multiplying two multivariate polynomials
. The first version of our algorithm for
multiplying two multivariate polynomials 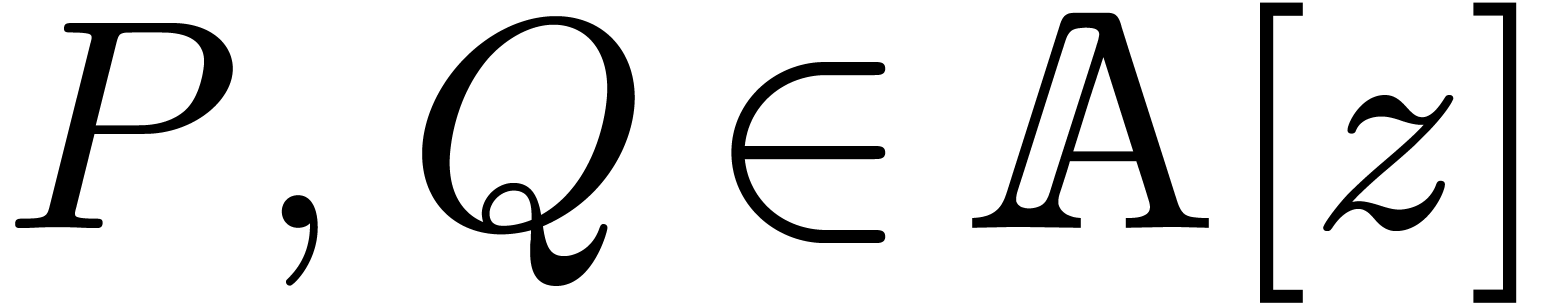 summarizes as follows:
summarizes as follows:
Algorithm block-multiply
Input: 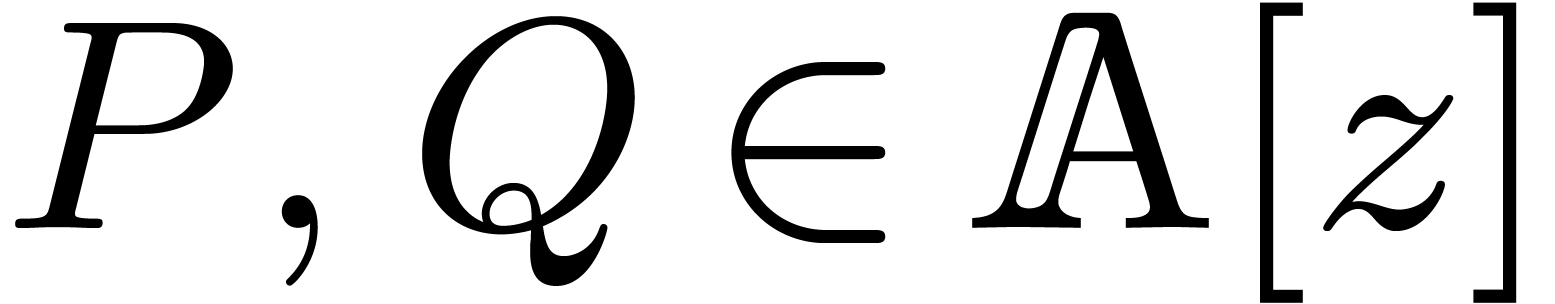 and
and 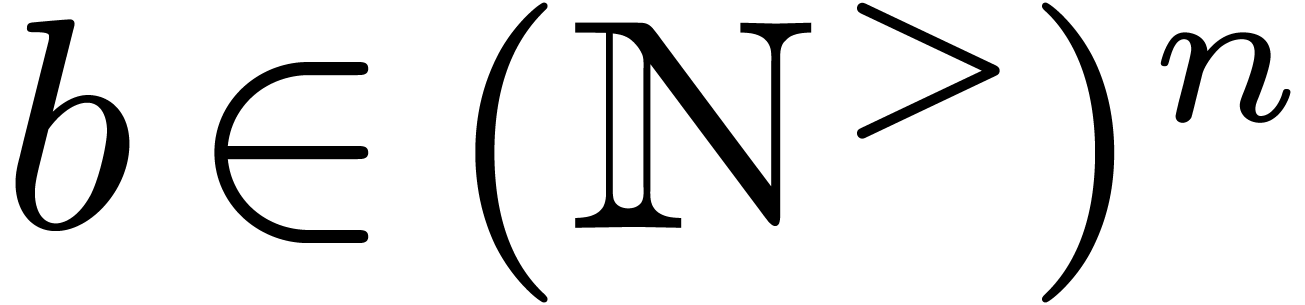 .
.
Output: 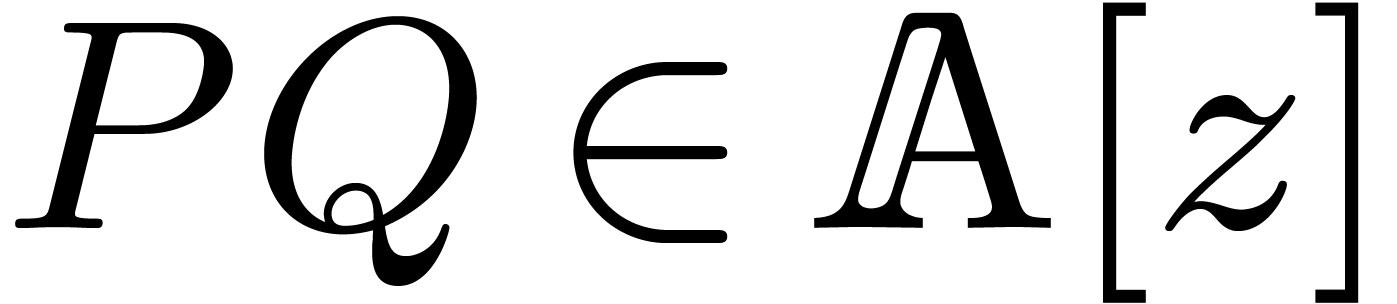 .
.
Let 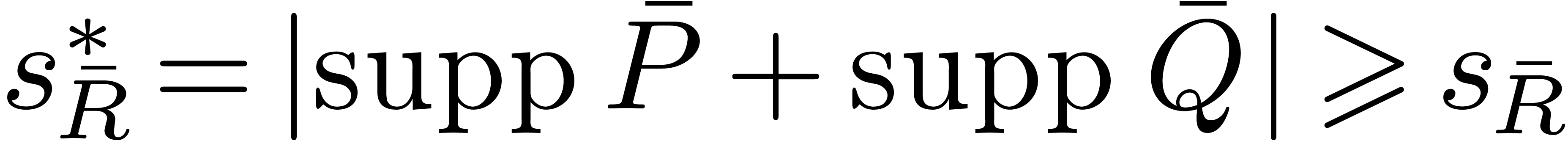 represent the size of
represent the size of  if there is no coefficient of
if there is no coefficient of  which accidentally
vanishes.
which accidentally
vanishes.
Proposition 2. The
algorithm block-multiply works
correctly as specified, and performs at most
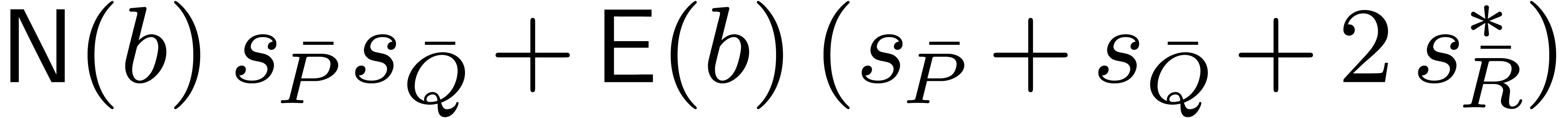
operations in  .
.
Proof. The correctness is clear from the
definitions. Step 1 performs no operation in  . Steps 2 and 4 require
. Steps 2 and 4 require 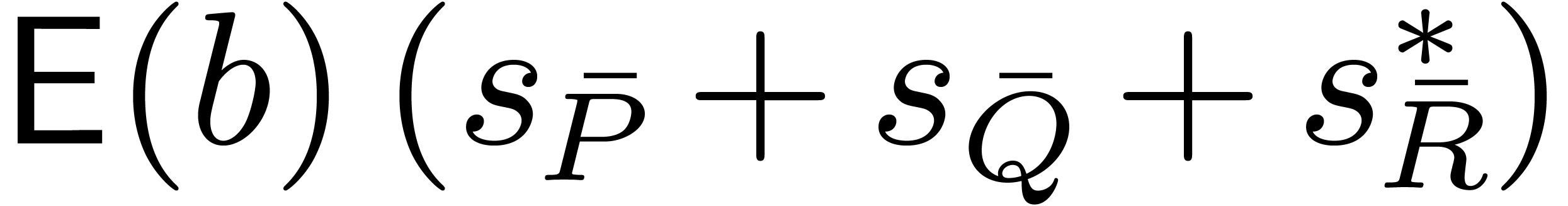 operations. Step 3 requires
operations. Step 3 requires 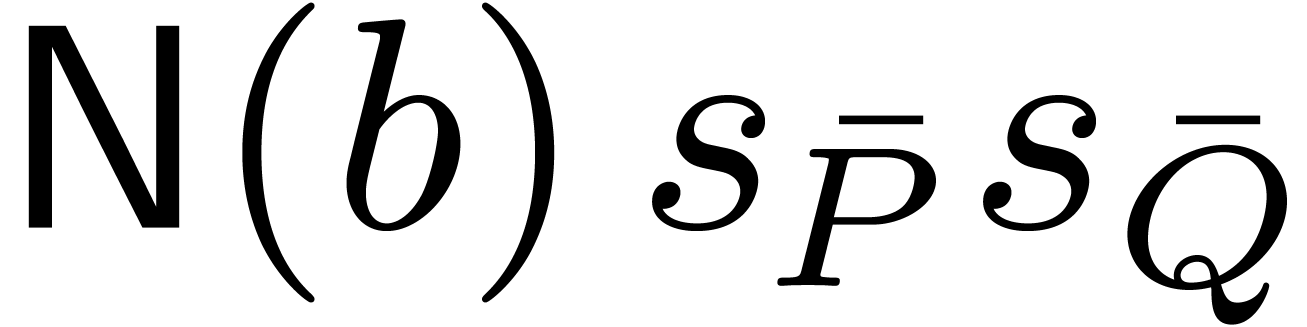 operations. Step 5
takes at most
operations. Step 5
takes at most  operations in order to add up
overlapping block coefficients, where
operations in order to add up
overlapping block coefficients, where  .
.
Unfortunately, without any structural knowledge about the supports of
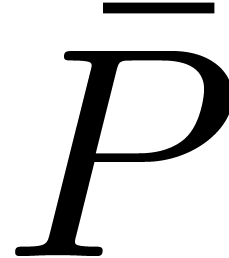 and
and  ,
the quantity
,
the quantity 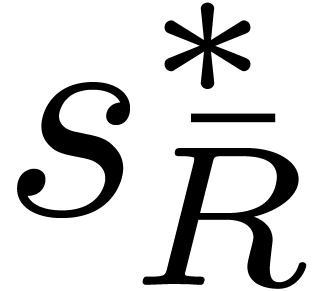 requires a time
requires a time 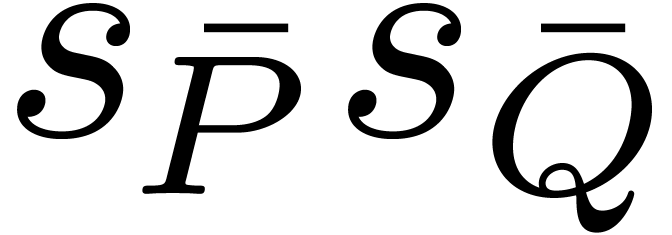 to be computed. In the next subsection we explain a heuristic approach
to find a good block size
to be computed. In the next subsection we explain a heuristic approach
to find a good block size 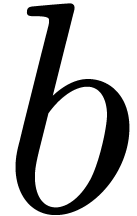 .
.
3.2Heuristic computation of the
block size
In order to complete our multiplication algorithm, we must explain how
to set the block size. Computing quickly the block size that minimizes
the number of operations in the product of two given polynomials 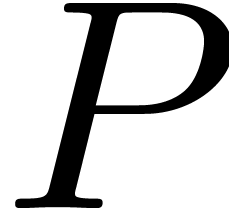 and
and  looks like a difficult
problem. In Section 5 we analyze it for asymptotically
large simplex supports, but, in this subsection, we describe a heuristic
for the general case.
looks like a difficult
problem. In Section 5 we analyze it for asymptotically
large simplex supports, but, in this subsection, we describe a heuristic
for the general case.
For approximating a good block size we first need to approximate the
complexity in Proposition 2 by a function, written 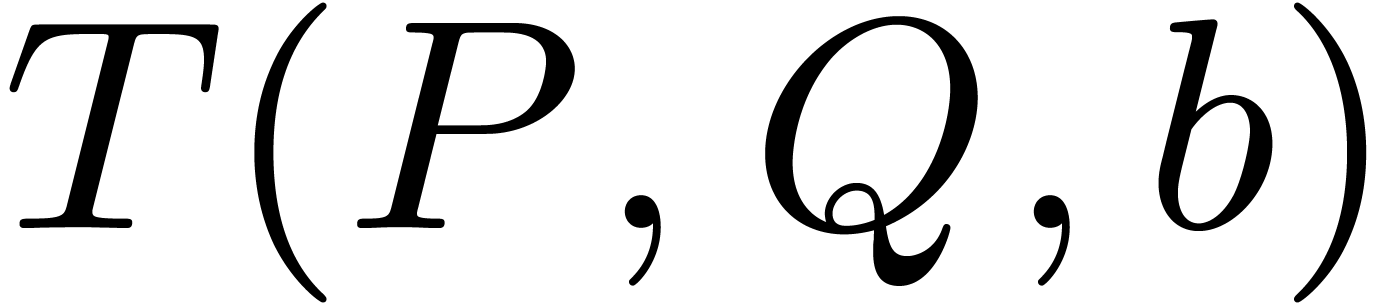 , which is intended to be easy to
compute in terms of
, which is intended to be easy to
compute in terms of 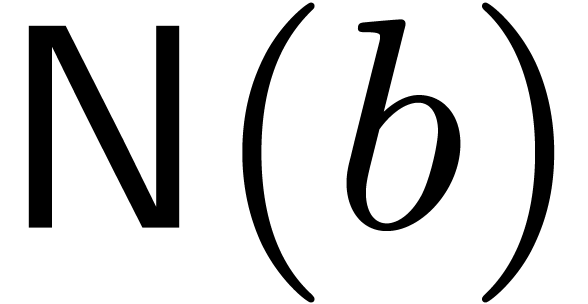 ,
, 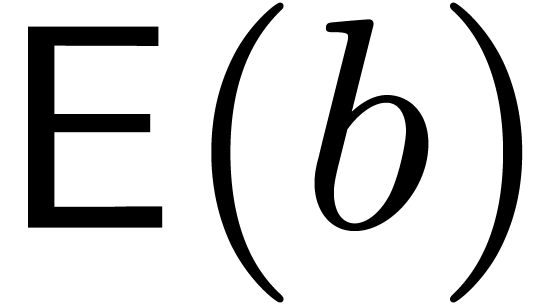 , and the input supports. For
instance one may opt for the formula
, and the input supports. For
instance one may opt for the formula
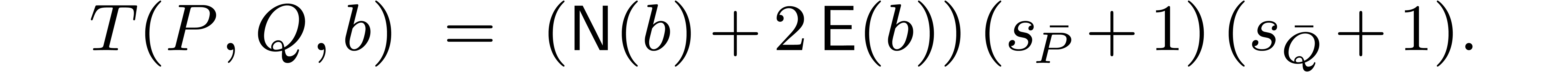
Nevertheless, if 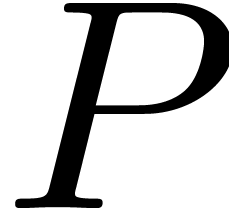 and
and  are
expected to be not too sparse, then one may assume
are
expected to be not too sparse, then one may assume 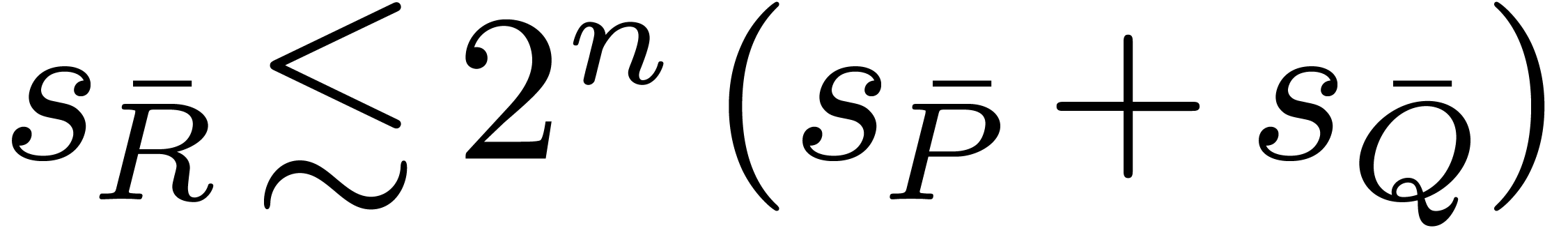 and use the formula
and use the formula
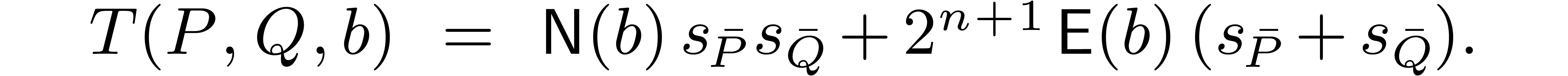
Then we begin the approximating process with 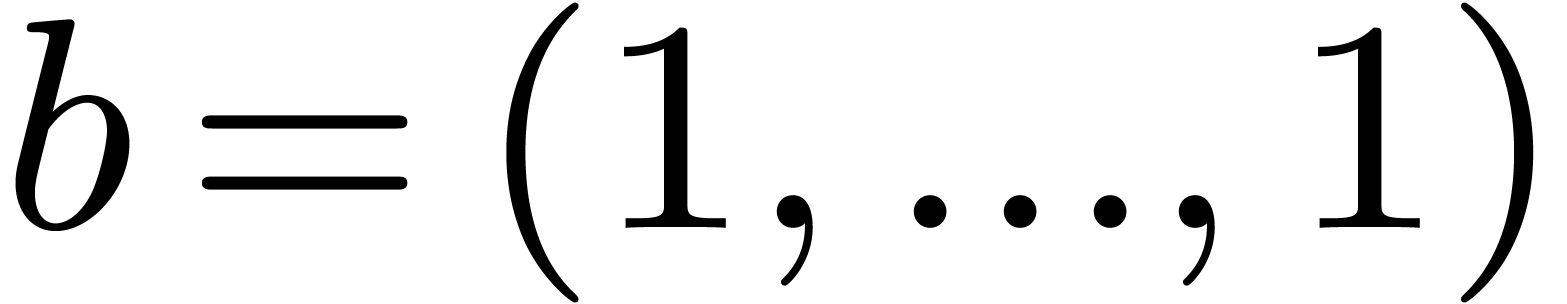 , and keep doubling the entry of
, and keep doubling the entry of 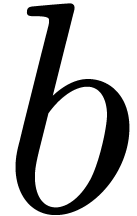 which reduces
which reduces 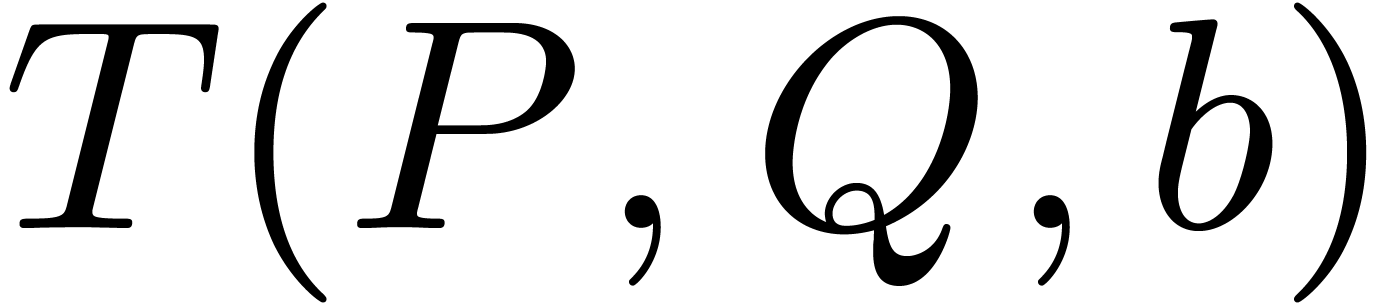 as much as possible. We stop as
soon as
as much as possible. We stop as
soon as 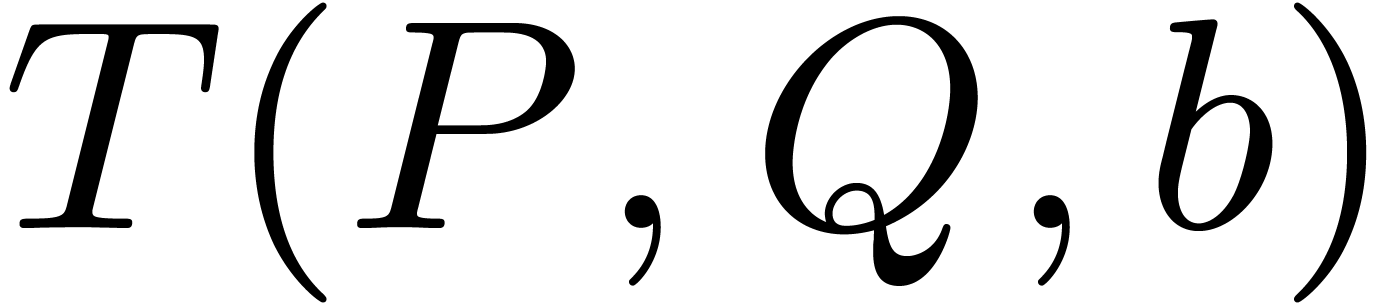 cannot be further reduced in this way.
Given
cannot be further reduced in this way.
Given 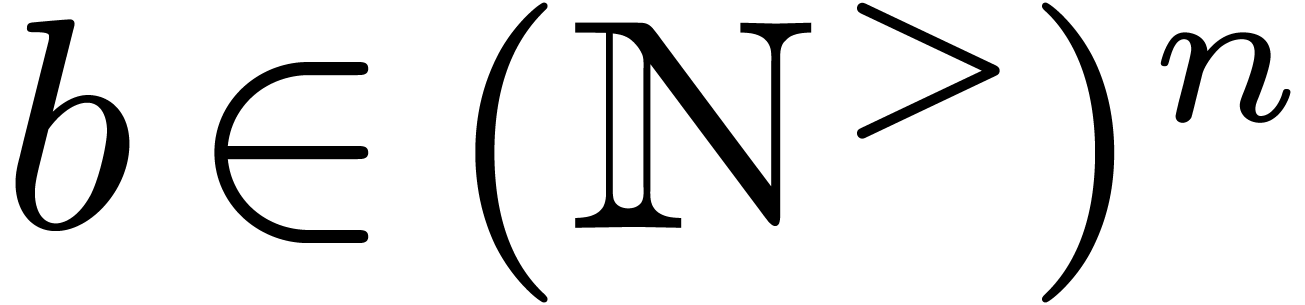 and
and 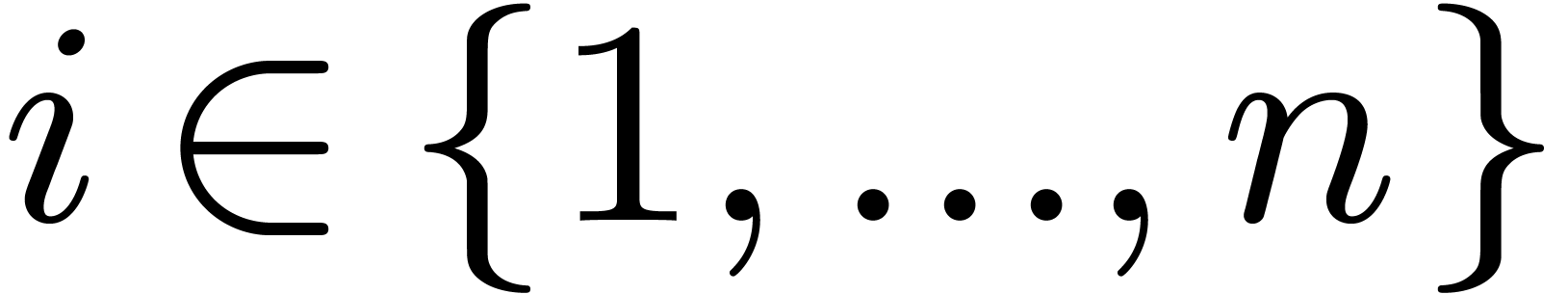 ,
we write
,
we write 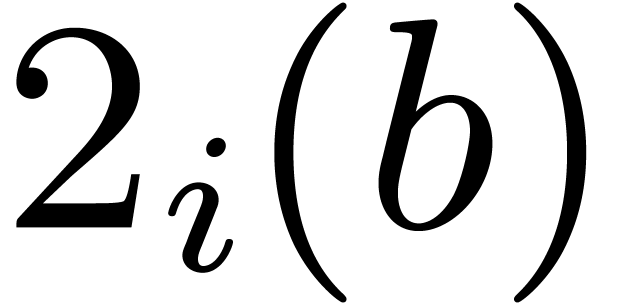 for
for 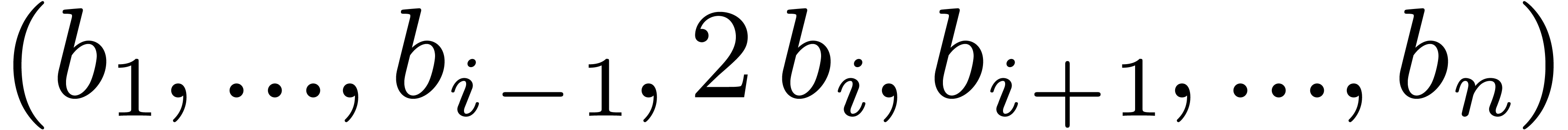 .
In order to make explicit the dependency in
.
In order to make explicit the dependency in 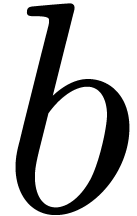 during the execution of the algorithm, we write
during the execution of the algorithm, we write 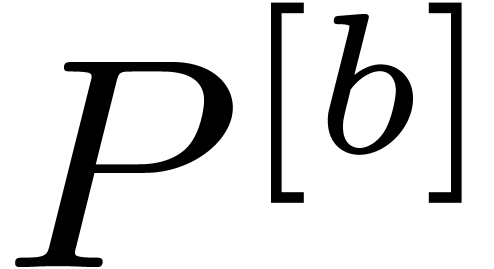 instead of
instead of  .
.
Algorithm block-size
Input:  .
.
Set 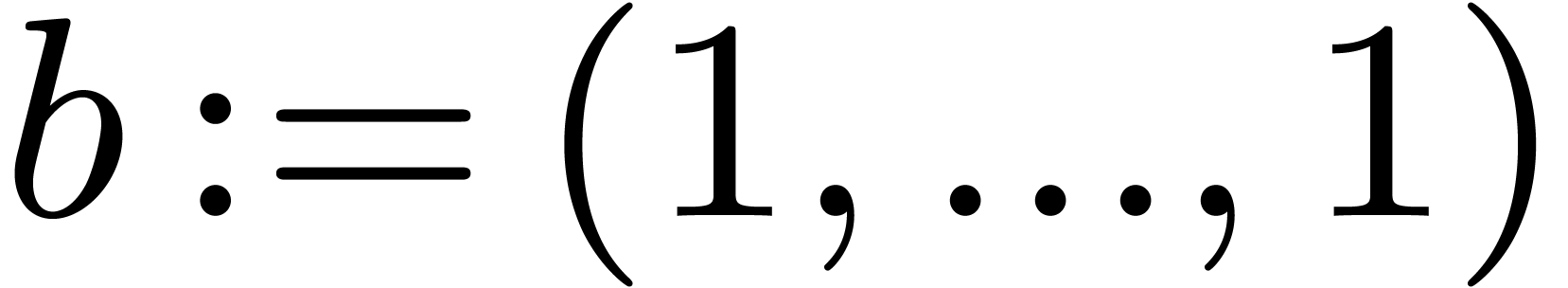 .
.
While 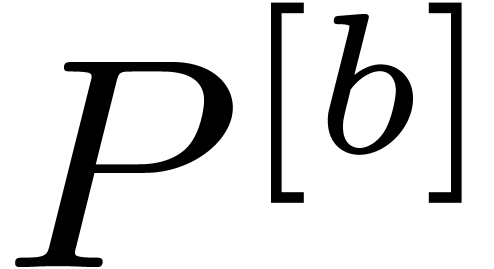 and
and 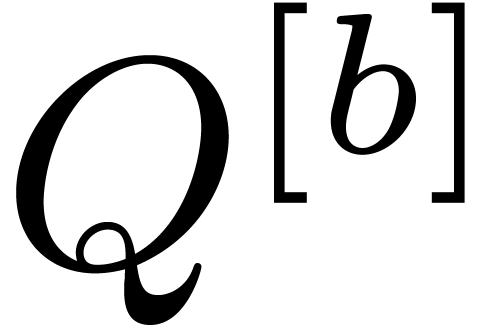 are
supported by at least two monomials repeat:
are
supported by at least two monomials repeat:
Let  be such that
be such that 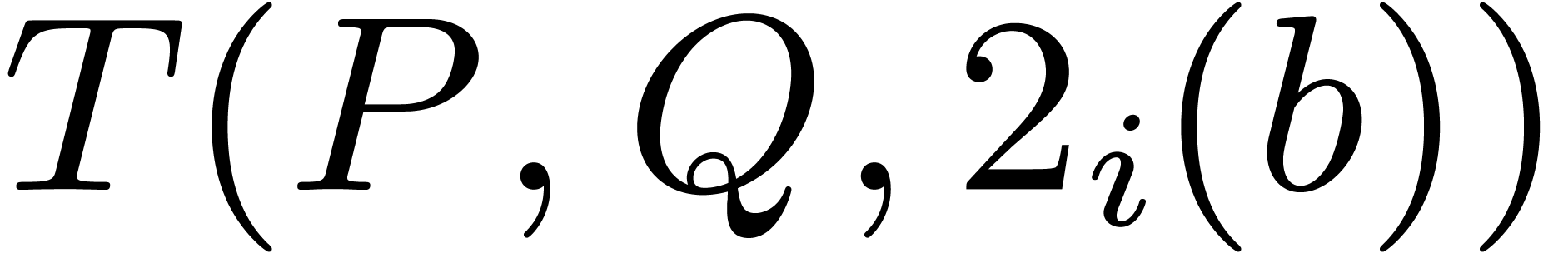 is
minimal.
is
minimal.
If 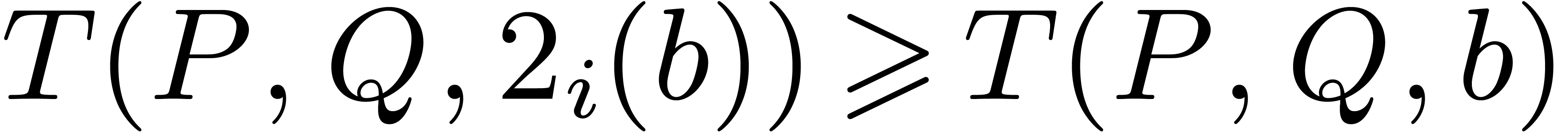 , then return
, then return 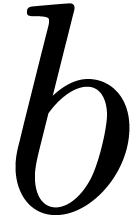 .
.
Set 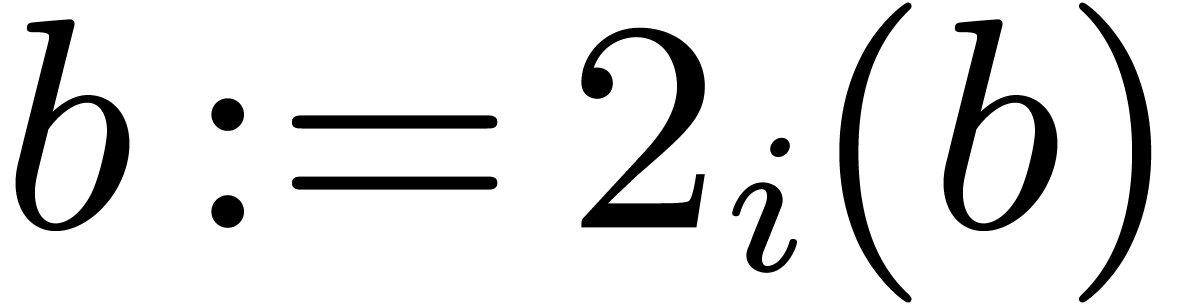 .
.
In the computation tree model over  ,
the block-size algorithm actually performs no operation in
,
the block-size algorithm actually performs no operation in
 . Its complexity must be
analyzed in terms of bit-operations, which means here
computation trees over
. Its complexity must be
analyzed in terms of bit-operations, which means here
computation trees over 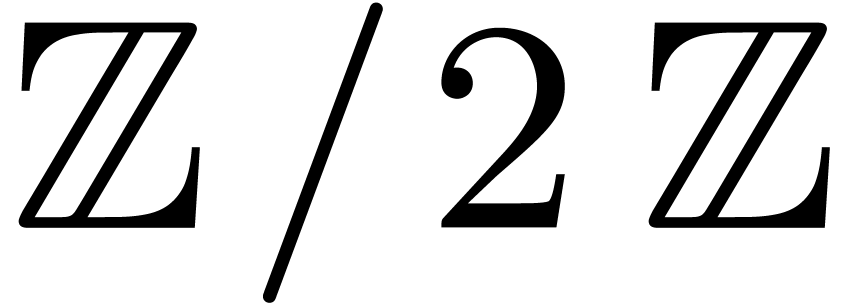 . For
this purpose we assume that the supports are represented by vectors of
monomials, with each monomial being stored as a vector of integers in
binary representation.
. For
this purpose we assume that the supports are represented by vectors of
monomials, with each monomial being stored as a vector of integers in
binary representation.
Proposition 3. If 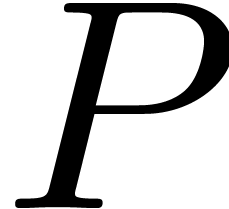 and
and  have total degrees at
most
have total degrees at
most 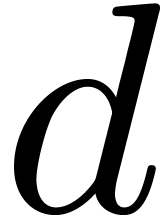 , then the algorithm
block-size performs
, then the algorithm
block-size performs 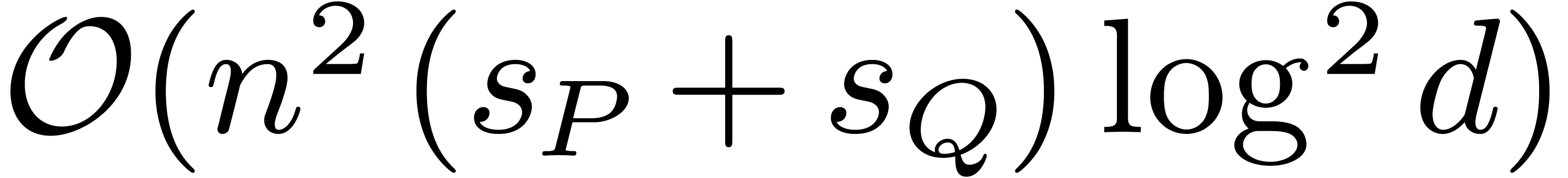 bit-operations, plus
bit-operations, plus 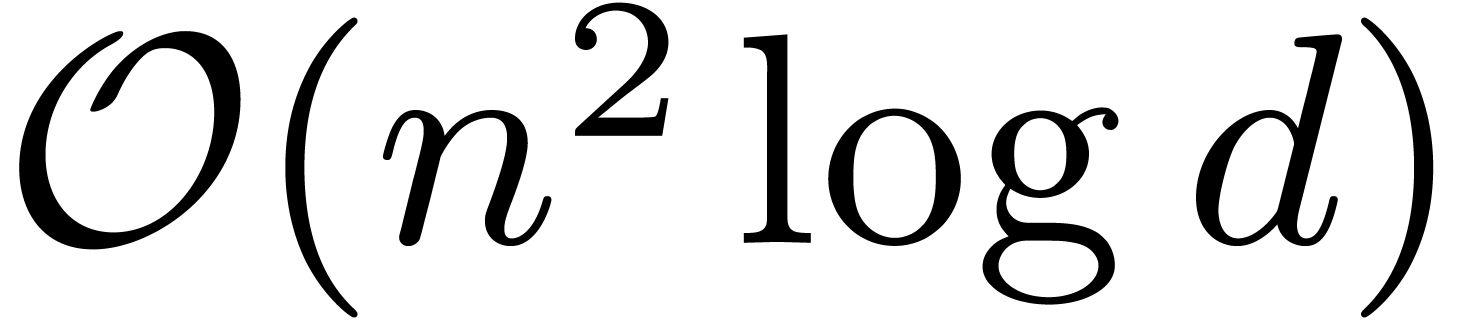 calls to the function
calls to the function  .
.
Proof. To run the algorithm block-size
efficiently, we maintain the sets 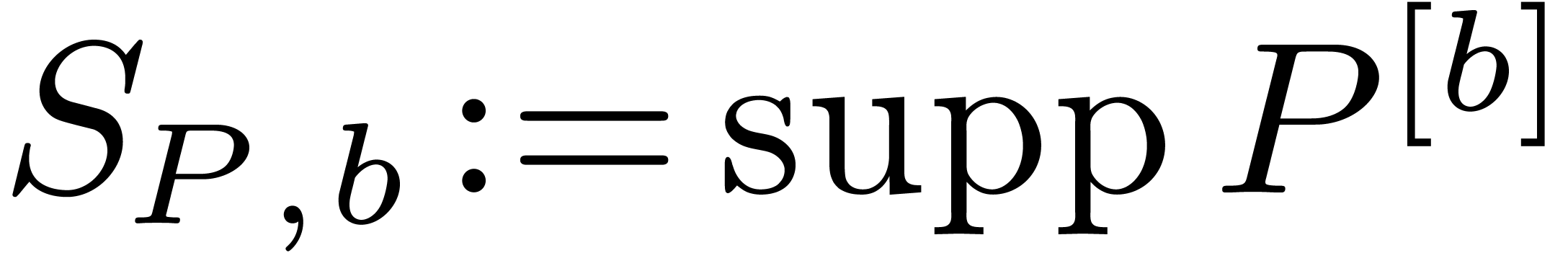 and
and 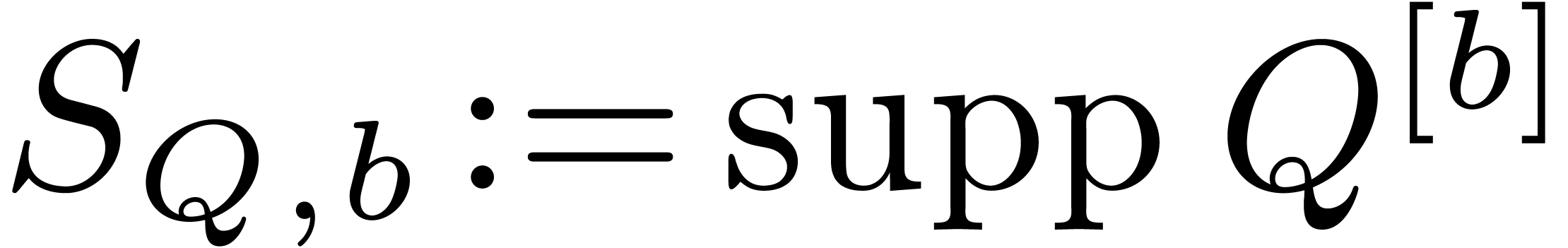 throughout the main loop. Since
throughout the main loop. Since 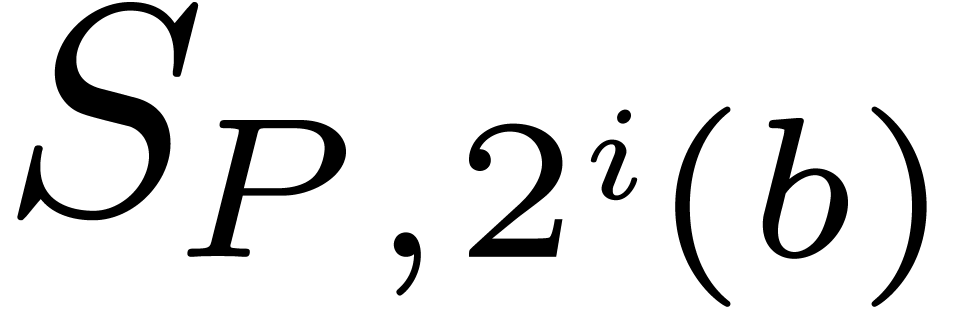 can be computed from
can be computed from 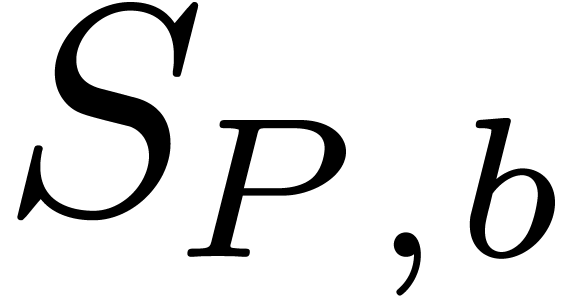 with
with 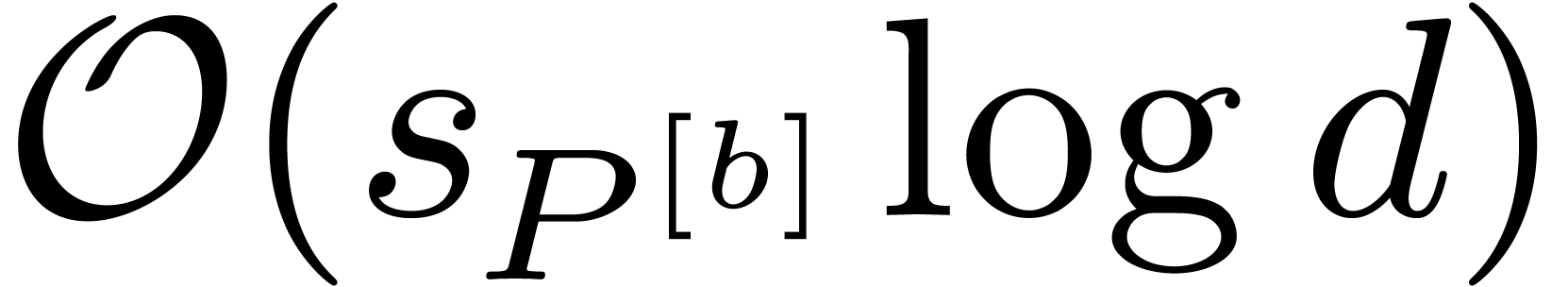 bit-operations, each iteration requires at most
bit-operations, each iteration requires at most 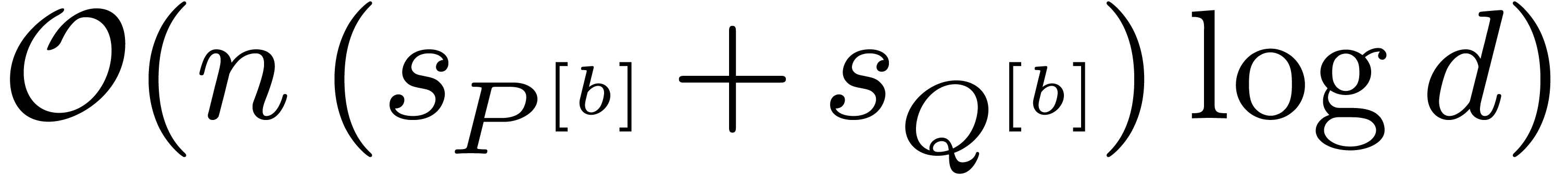 bit-operations. The number of iterations is bounded by
bit-operations. The number of iterations is bounded by 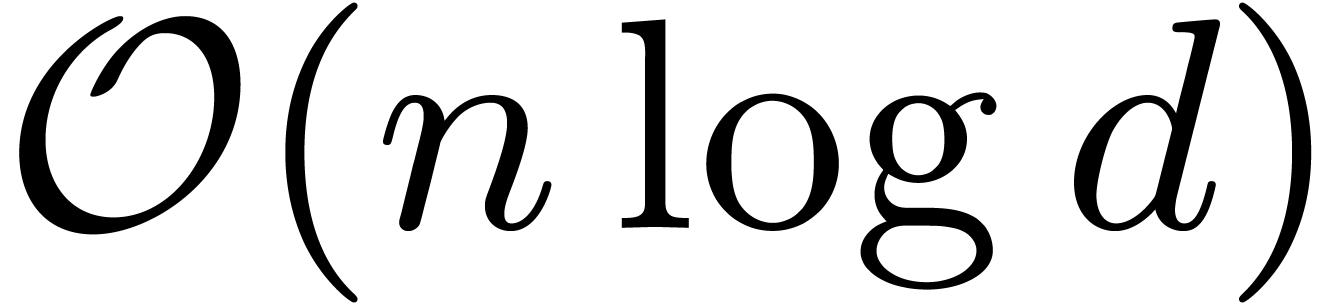 .
.
Remark that in favorable cases the first few iterations are expected to
approximately halve 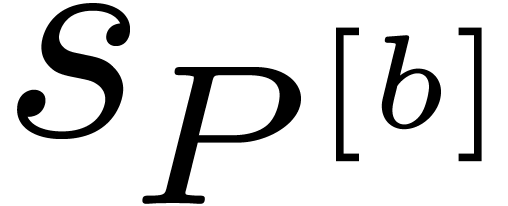 at each stage. The expected
total complexity thus becomes closer to
at each stage. The expected
total complexity thus becomes closer to 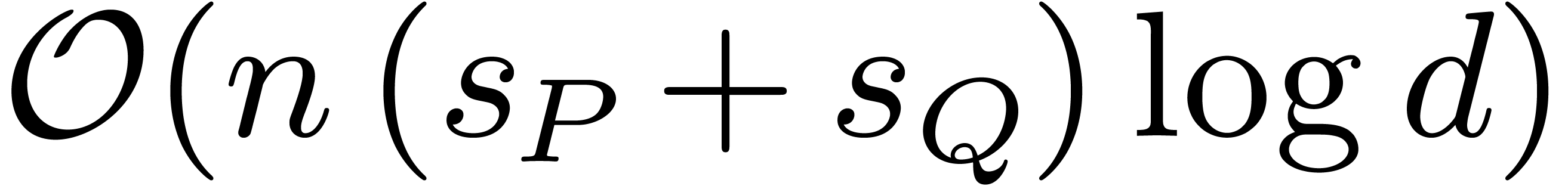 .
.
4.Variations
4.1Implementation issues
Several problems arise if one tries to implement the basic blockwise
multiplication algorithm from Section 3.1 without any
modification:
Both drawbacks can be removed by using a recursive multiplication
algorithm instead, where the evaluation-interpolation technique is
applied sequentially with respect to  for
suitable pairwise distinct
for
suitable pairwise distinct 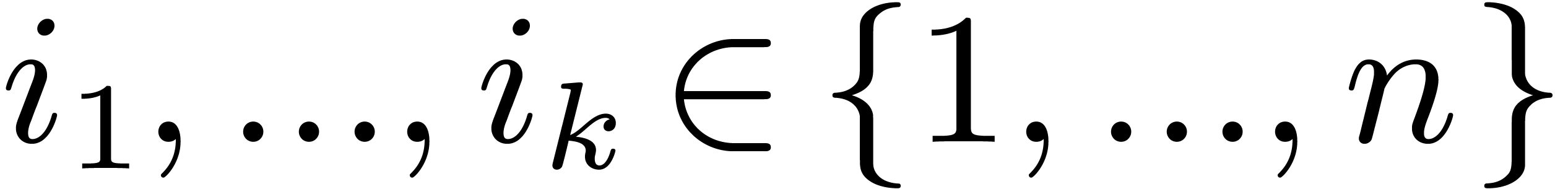 .
.
Algorithm improved-block-multiply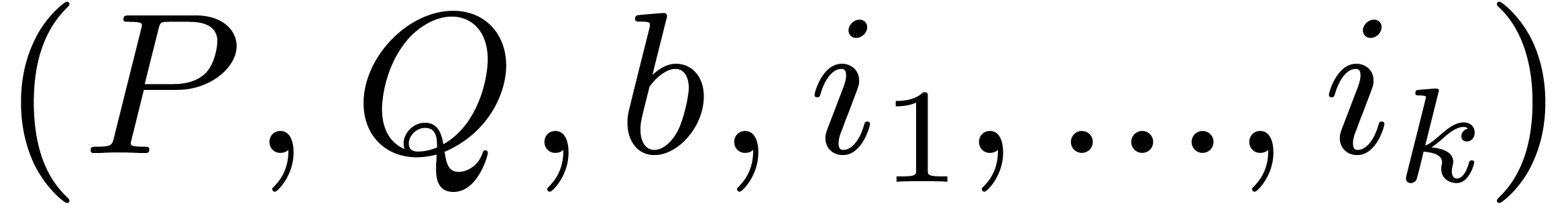
Output: 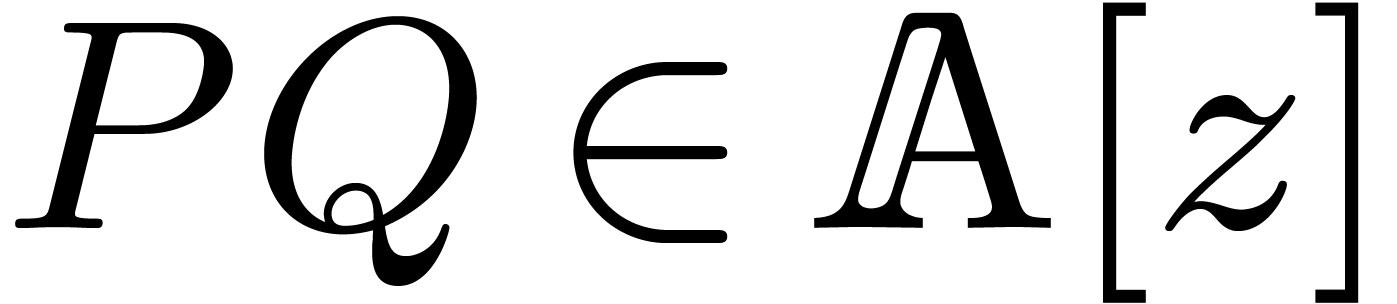 .
.
It is not hard to check that the improved algorithm has the same
complexity as the basic algorithm in terms of the number of operations
in  . Let us now examine how
to choose
. Let us now examine how
to choose  in order to increase the performance.
Setting
in order to increase the performance.
Setting 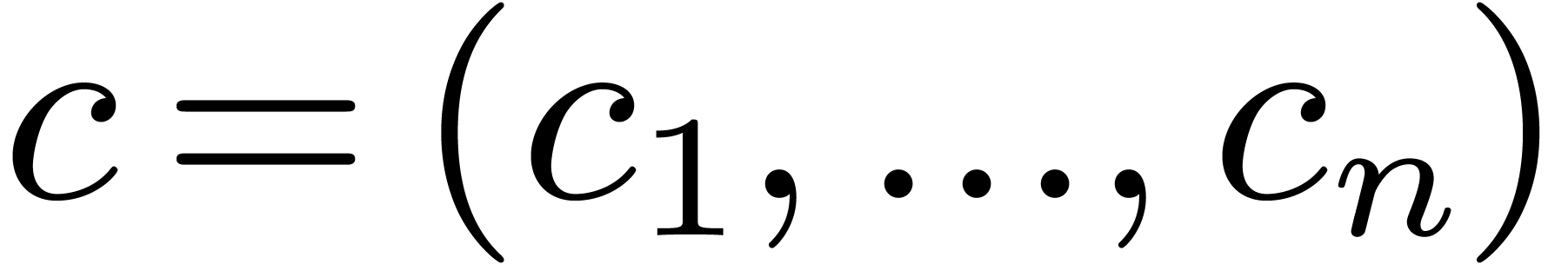 with
with
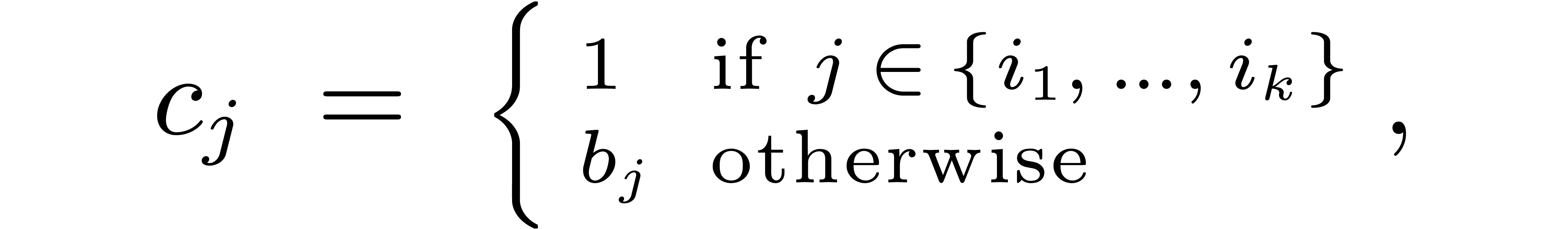
we first choose the set  in such a way that
in such a way that 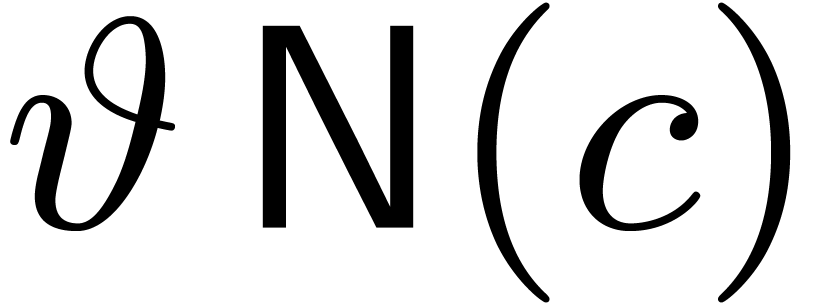 constants in
constants in  fit into cache
memory for a certain threshold
fit into cache
memory for a certain threshold 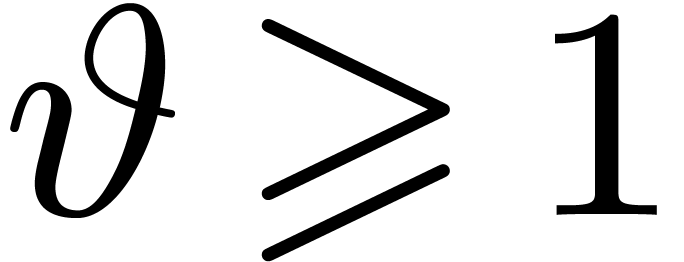 .
The idea is that the same coefficients should be reused as much as
possible in the inner multiplication, so
.
The idea is that the same coefficients should be reused as much as
possible in the inner multiplication, so 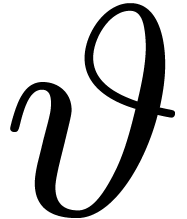 should
not be taken to small, e.g.
should
not be taken to small, e.g. 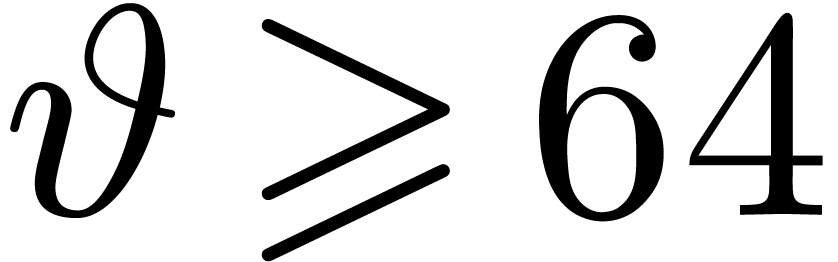 .
For a fixed set
.
For a fixed set  of indexes, we next take
of indexes, we next take  such that
such that  ,
thereby minimizing the memory consumption of the algorithm.
,
thereby minimizing the memory consumption of the algorithm.
4.2Truncated multiplication
Let  and
and 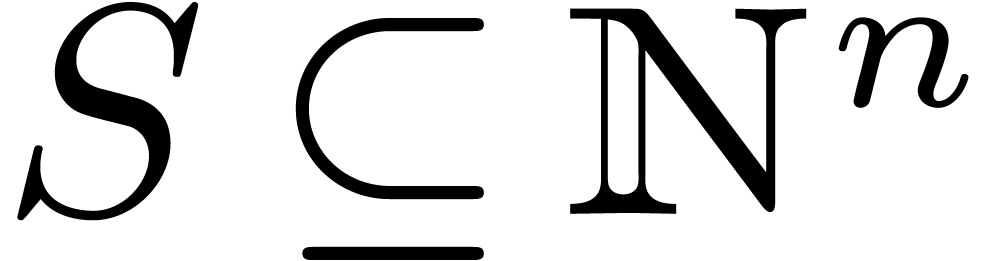 .
We define the truncation of
.
We define the truncation of  to
to  by
by 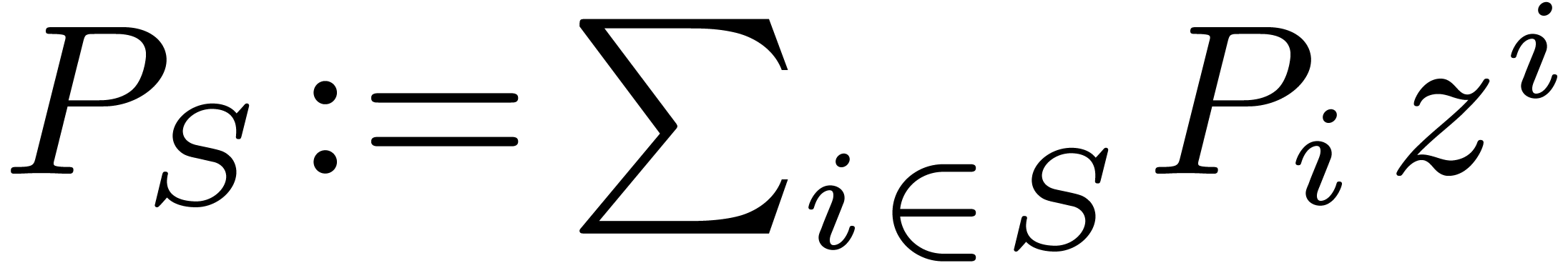 .
Notice that
.
Notice that 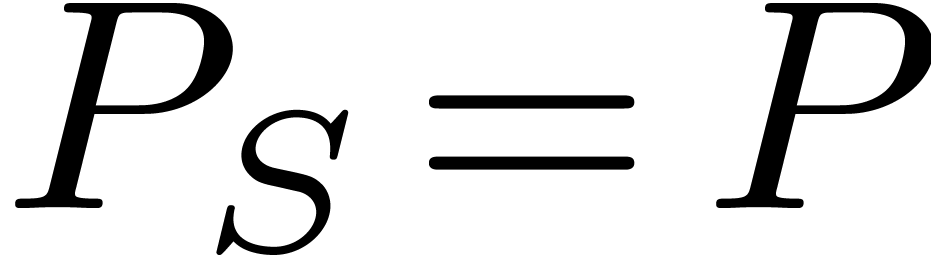 if, and only if,
if, and only if,  with
with 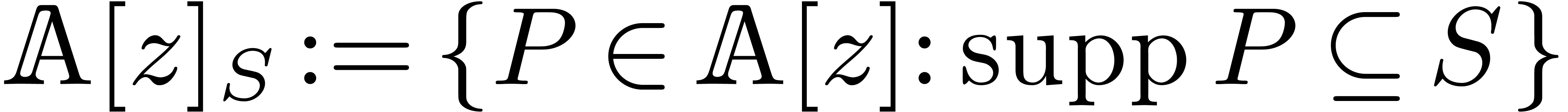 . It is sometimes
convenient to represent finite sets
. It is sometimes
convenient to represent finite sets 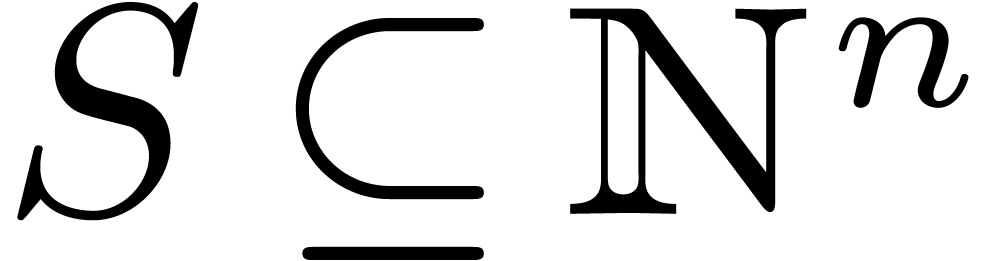 by
polynomials
by
polynomials  with
with 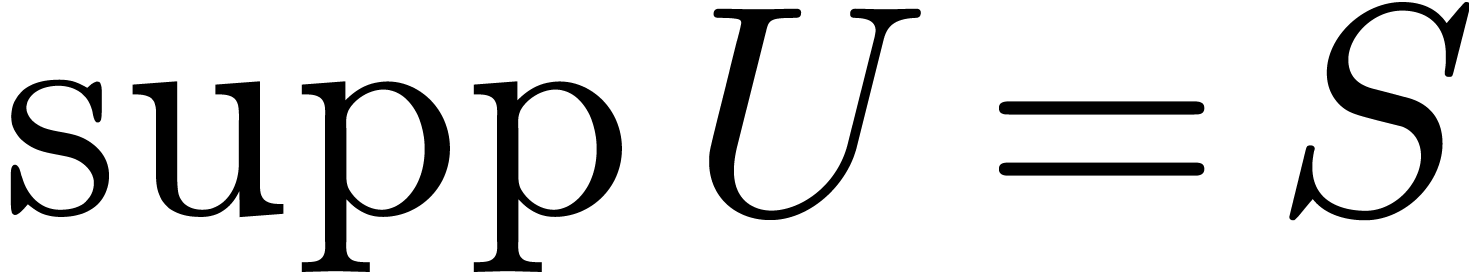 ,
for instance by taking
,
for instance by taking 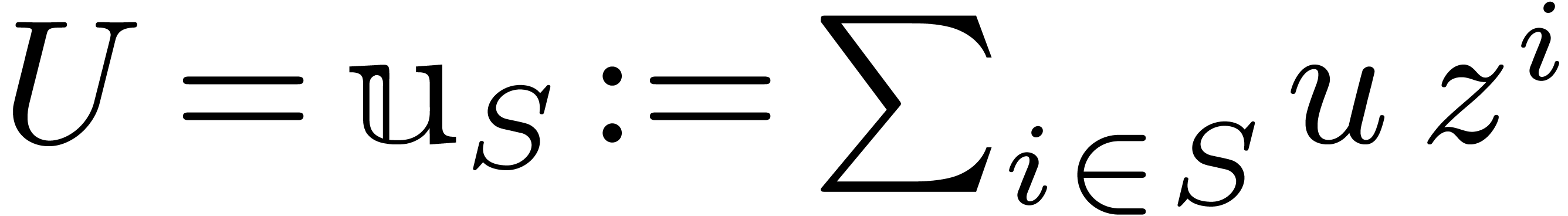 , for
a given
, for
a given 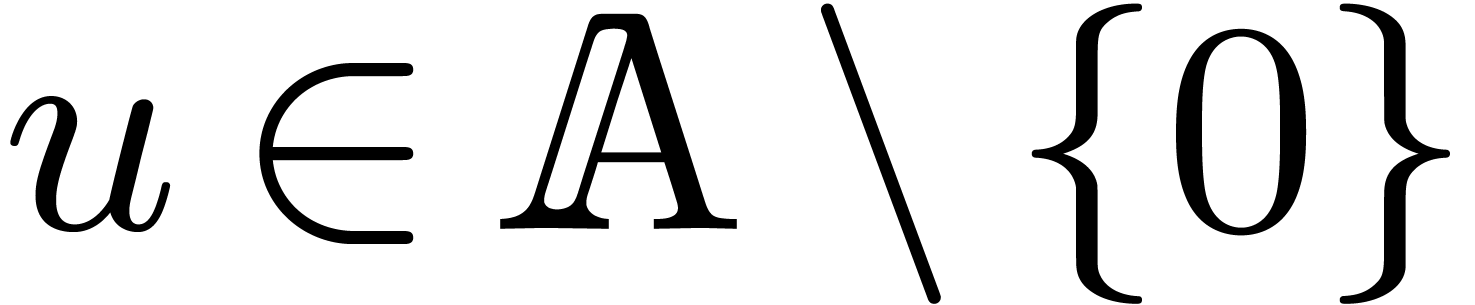 . Given
. Given 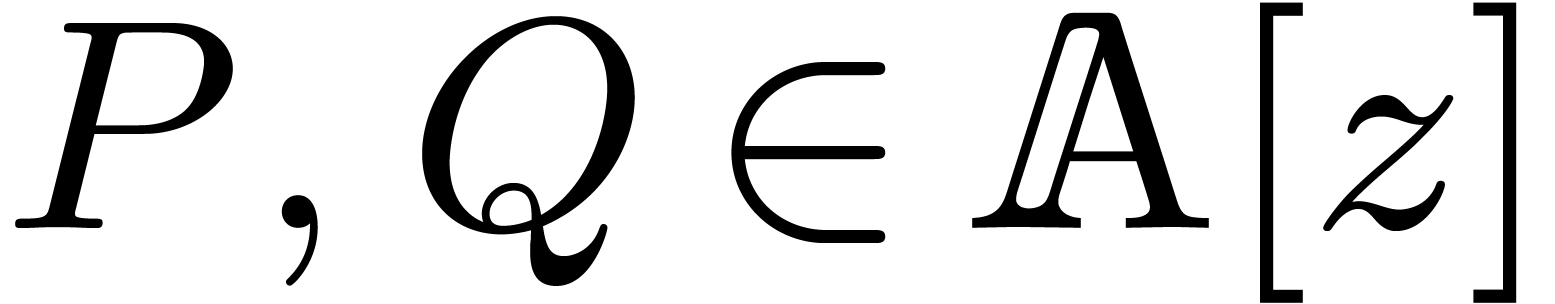 and a fixed support
and a fixed support 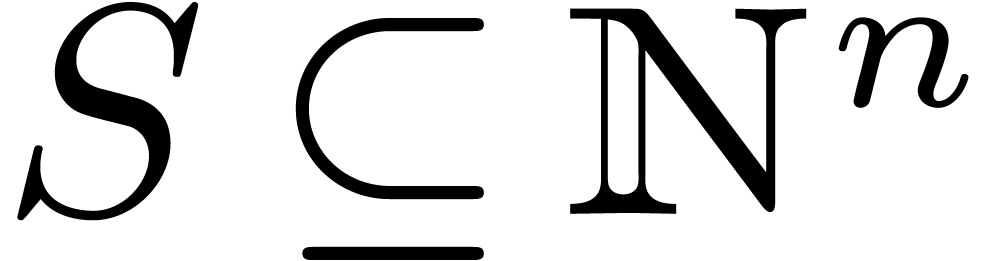 ,
the computation of
,
the computation of 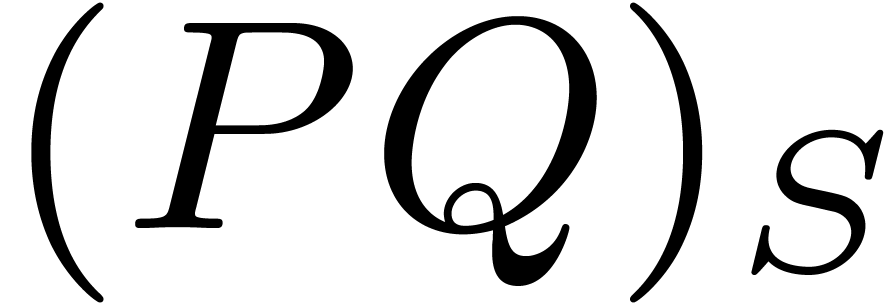 is called the truncated
multiplication. The basic blockwise multiplication algorithm is
adapted as follows:
is called the truncated
multiplication. The basic blockwise multiplication algorithm is
adapted as follows:
Algorithm truncated-block-multiply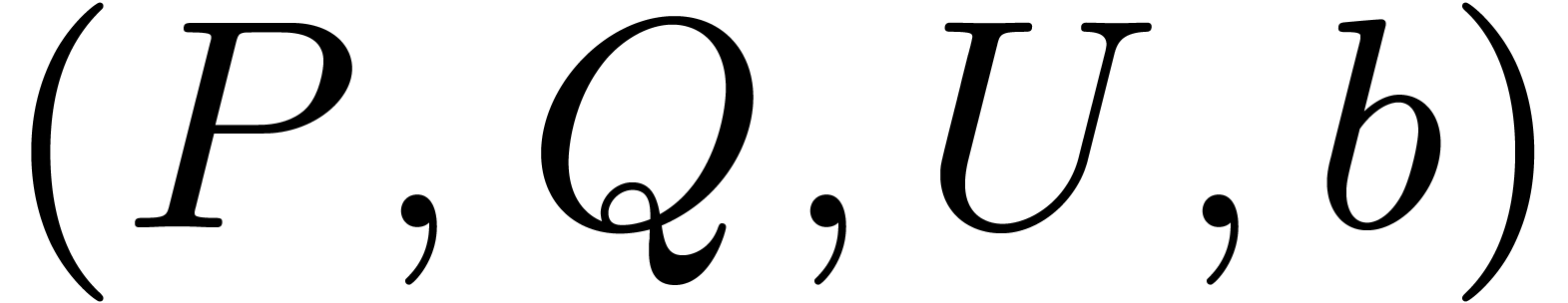
Input: 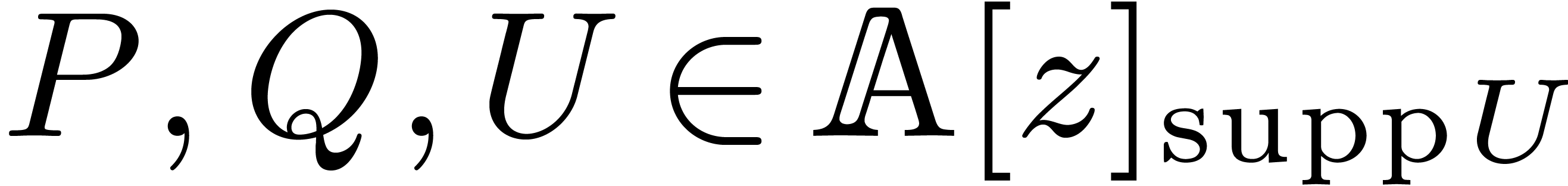 and
and 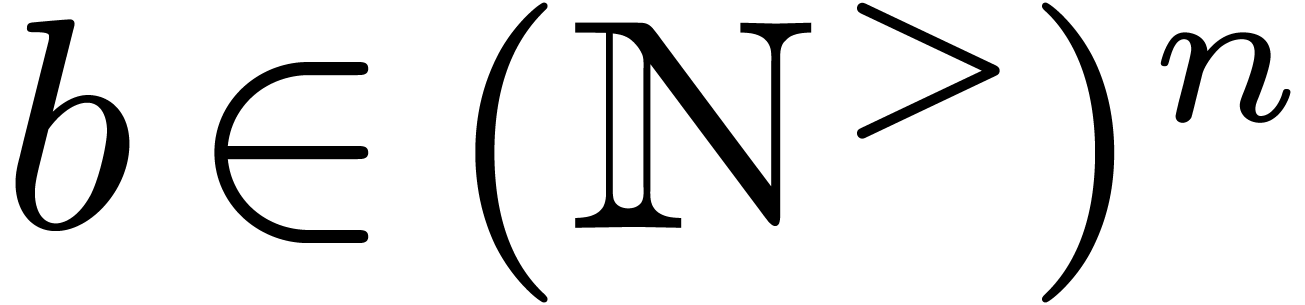 .
.
Output: 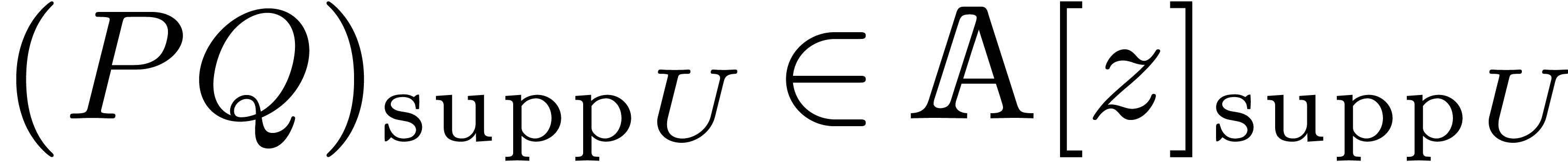 .
.
In a similar way as in Proposition 2, we can show that
truncated-block-multiply requires at
most
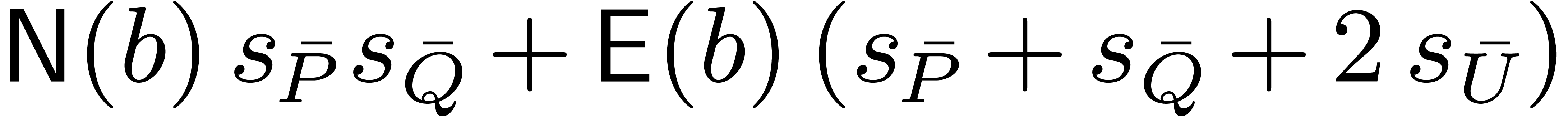 |
(2) |
operations in  . However, this
bound is very pessimistic since
. However, this
bound is very pessimistic since 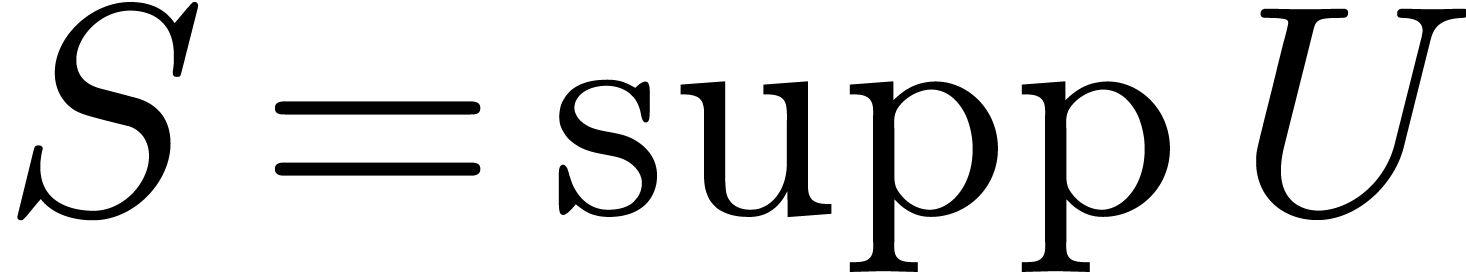 usually has a
special form which allows us to perform the naive truncated
multiplication in step 3 in much less than
usually has a
special form which allows us to perform the naive truncated
multiplication in step 3 in much less than 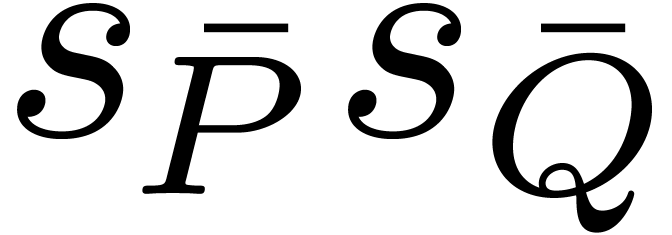 operations. For instance, in the special and important case of truncated
power series at order
operations. For instance, in the special and important case of truncated
power series at order 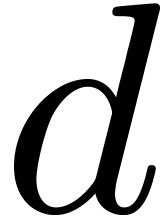 , we
have
, we
have
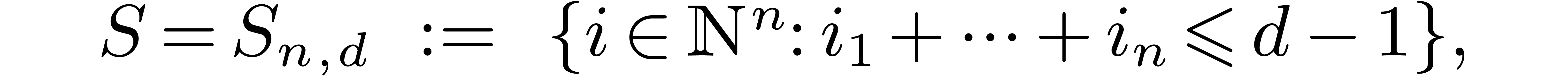
and, by [16, Section 6], 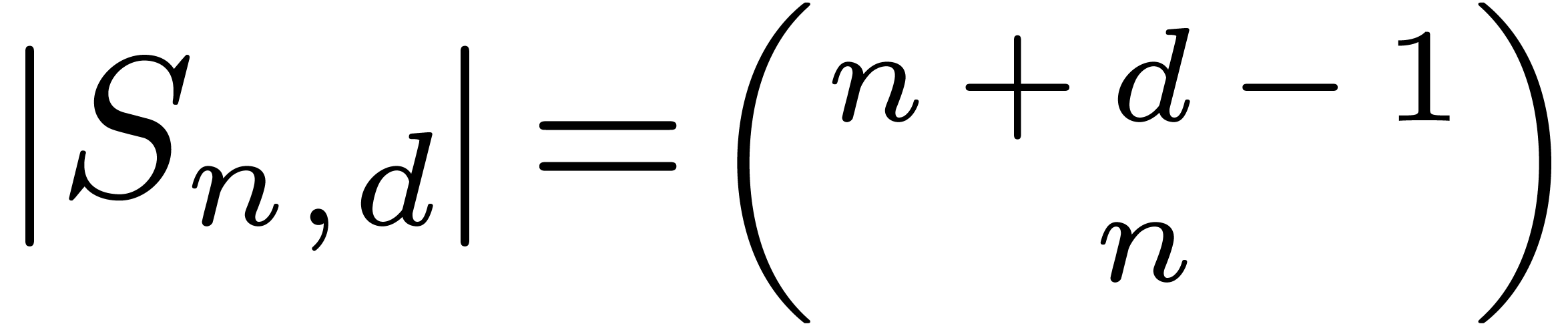 .
The naive truncated power series multiplication at order
.
The naive truncated power series multiplication at order 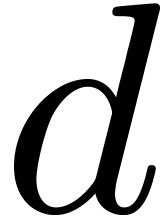 can be performed using only
can be performed using only
operations, as shown in [16, Section 6]. Hence, if  and
and 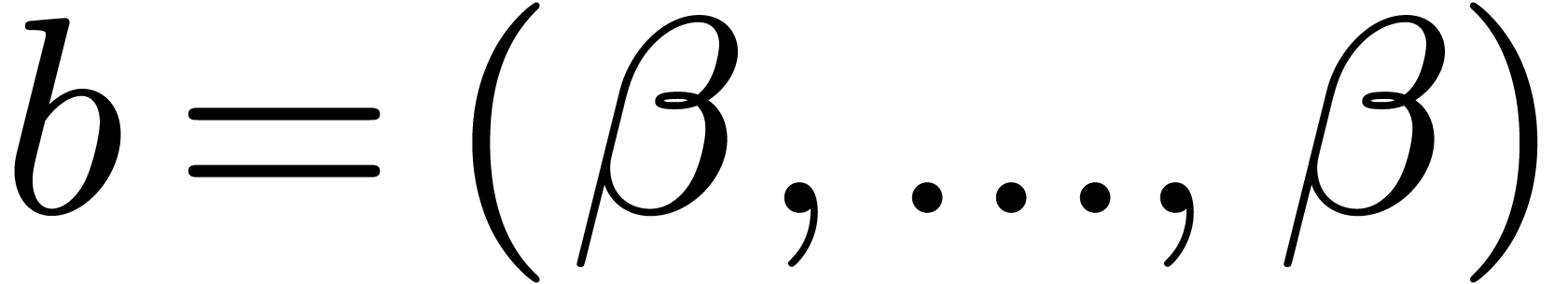 , so
that
, so
that 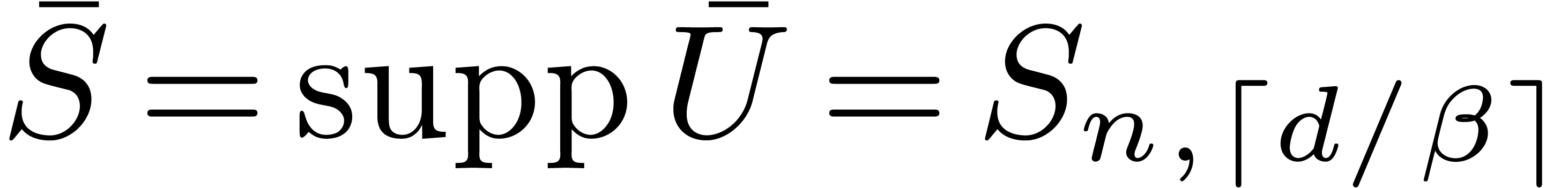 , then
, then 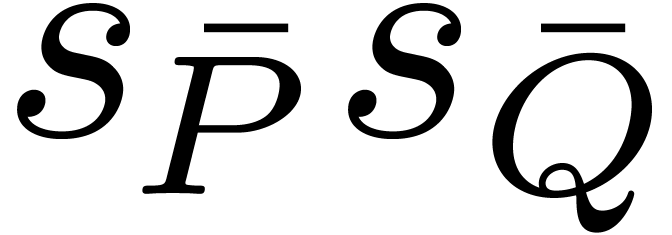 can be replaced by
can be replaced by 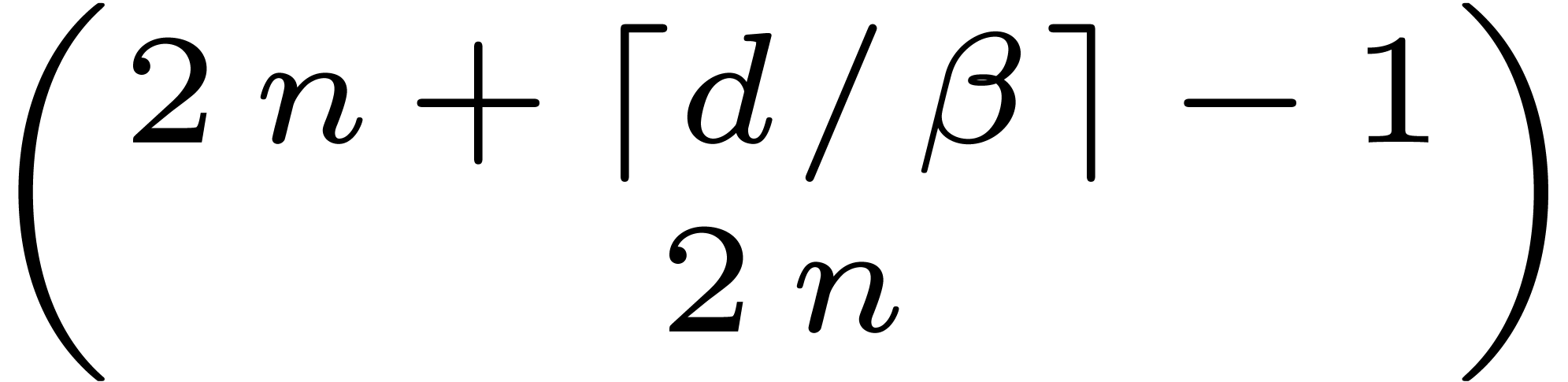 in our complexity bound (2).
in our complexity bound (2).
Assuming that we have a way to estimate the number of operations in 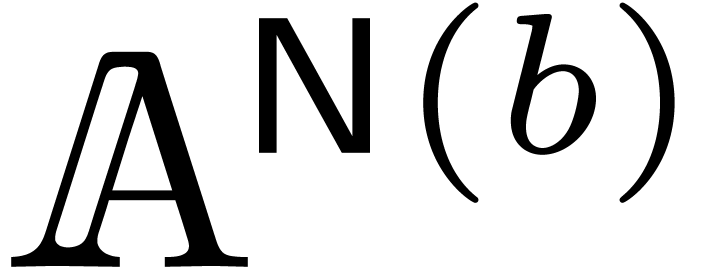 necessary to compute the truncated product
necessary to compute the truncated product  using the naive algorithm, we can adapt the heuristic of
Section 3.2 to determine a candidate block size. Finally
let us mention that the additional implementation tricks from Section 4.1 also extend to the truncated case in a straightforward
way.
using the naive algorithm, we can adapt the heuristic of
Section 3.2 to determine a candidate block size. Finally
let us mention that the additional implementation tricks from Section 4.1 also extend to the truncated case in a straightforward
way.
4.3Separate treatment of the border
If we increase the block size 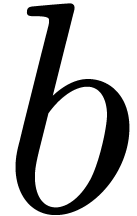 in
block-multiply, then the block coefficients
in
block-multiply, then the block coefficients  get sparser and sparser. At a certain point, this makes it
pointless to further increase
get sparser and sparser. At a certain point, this makes it
pointless to further increase 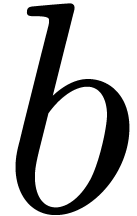 .
One final optimization which can often be applied is to decompose
.
One final optimization which can often be applied is to decompose 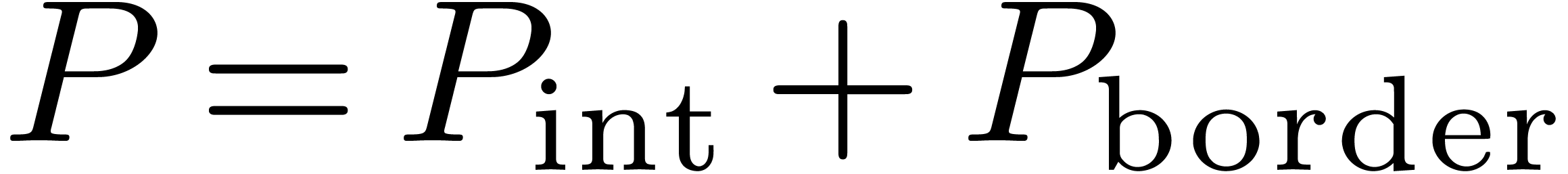 and
and 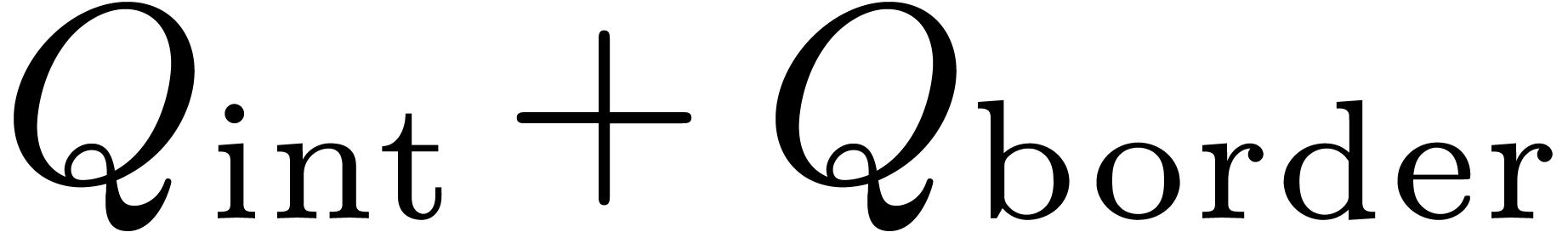 in a such a way that the
multiplication
in a such a way that the
multiplication 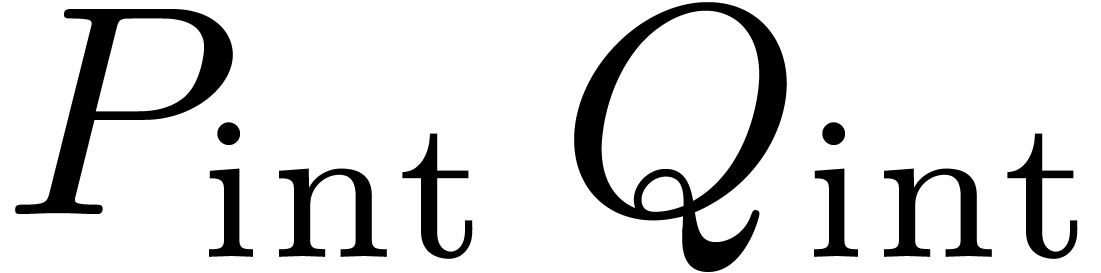 can be done using a larger block
size than the remaining part
can be done using a larger block
size than the remaining part 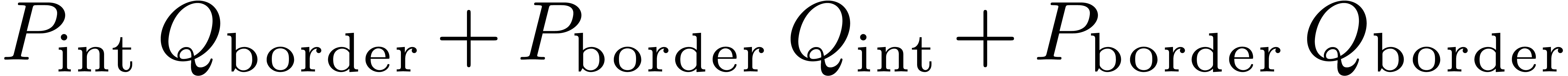 of the
multiplication
of the
multiplication  . Instead of
providing a full and rather technical algorithm, let us illustrate this
idea with the example
. Instead of
providing a full and rather technical algorithm, let us illustrate this
idea with the example
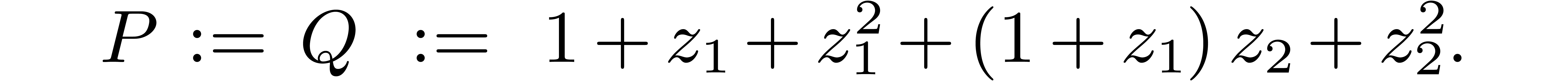
The naive multiplication performs  products in
products in
 The direct use of the Karatsuba algorithm with
The direct use of the Karatsuba algorithm with
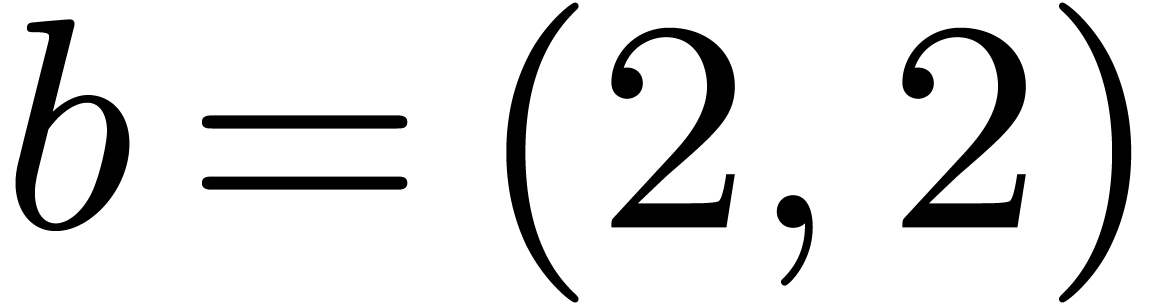 , reduces to the naive
product of two polynomials of
, reduces to the naive
product of two polynomials of  terms with
coefficients in
terms with
coefficients in  , which
amounts to
, which
amounts to 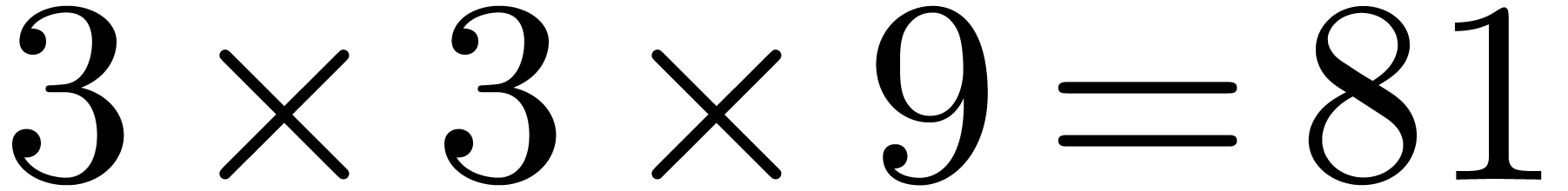 multiplications in
multiplications in  . If we decompose
. If we decompose  and
and
 into
into
then  takes
takes  products in
products in
 , and the naive
multiplication for
, and the naive
multiplication for 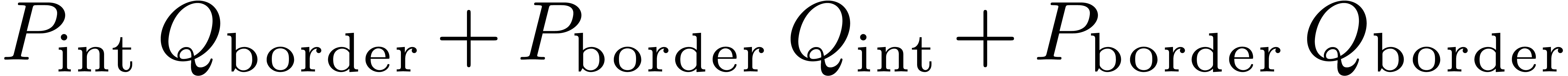 uses
uses  products in
products in  . In this
example, the separate treatment of the border saves 7 products in
. In this
example, the separate treatment of the border saves 7 products in  out of the 36 of the naive algorithm, and is faster
than the direct use of the blockwise algorithm.
out of the 36 of the naive algorithm, and is faster
than the direct use of the blockwise algorithm.
5.Uniform complexity analysis
In this section we focus on the specific and important problems of
multiplying polynomials 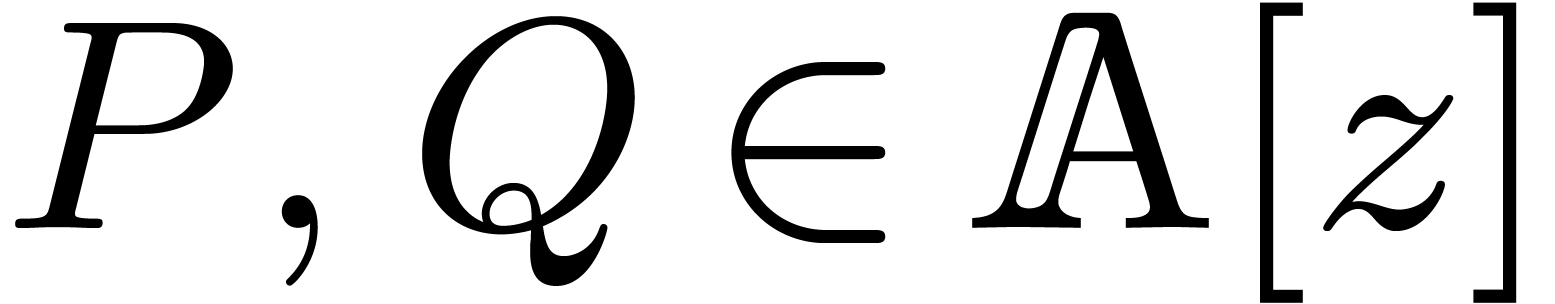 of total degree at most
of total degree at most
 , and truncated power series
at order
, and truncated power series
at order 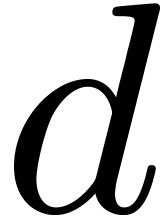 . Recall from
Section 4.2 that
. Recall from
Section 4.2 that 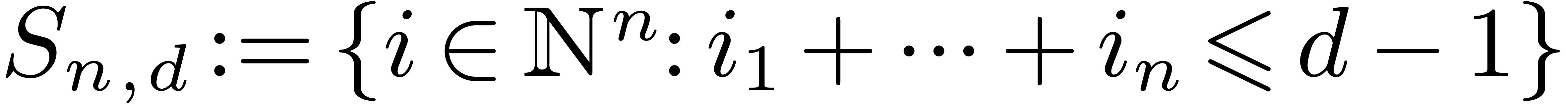 .
Let
.
Let
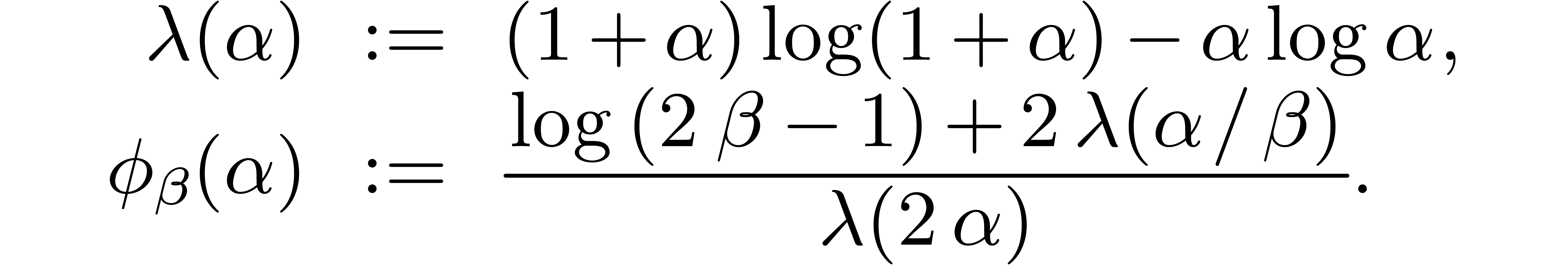
Let 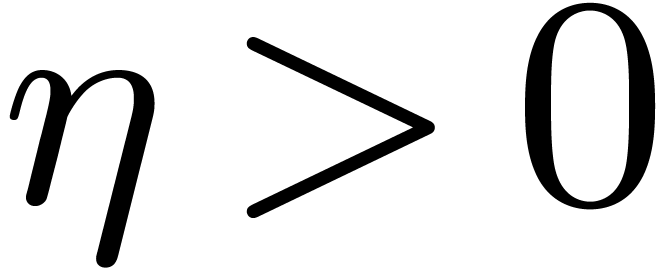 be the first value of
be the first value of  such that
such that 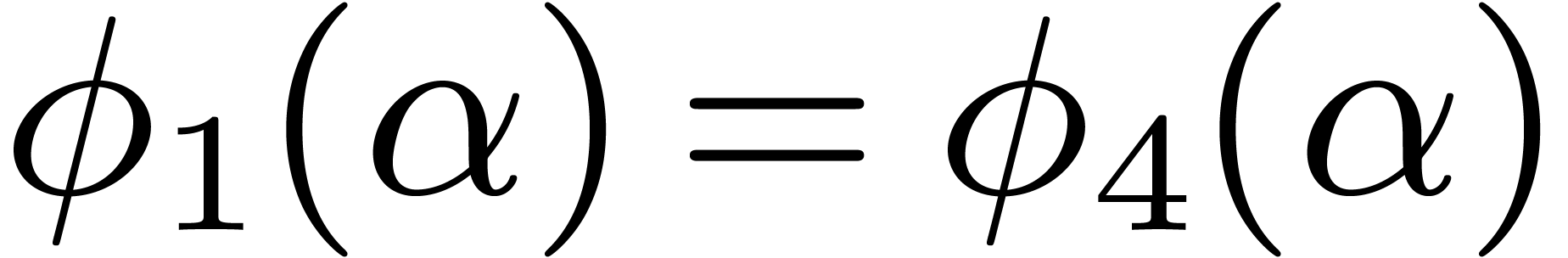 , and define
, and define 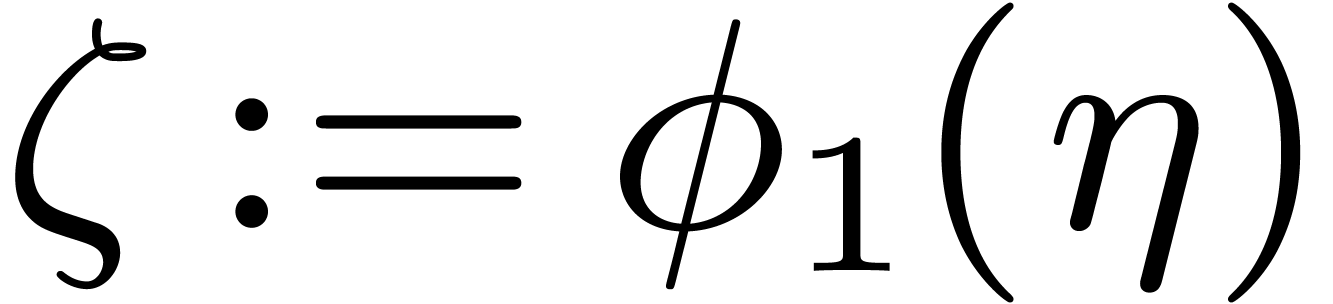 . Numeric computations yield
. Numeric computations yield 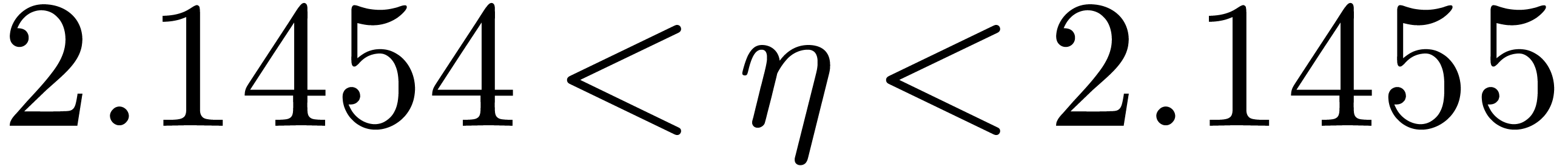 and
and  .
.
5.1Polynomial product
Theorem 4. Let
 , and assume that
, and assume that  admits evaluation-interpolation schemes with
admits evaluation-interpolation schemes with 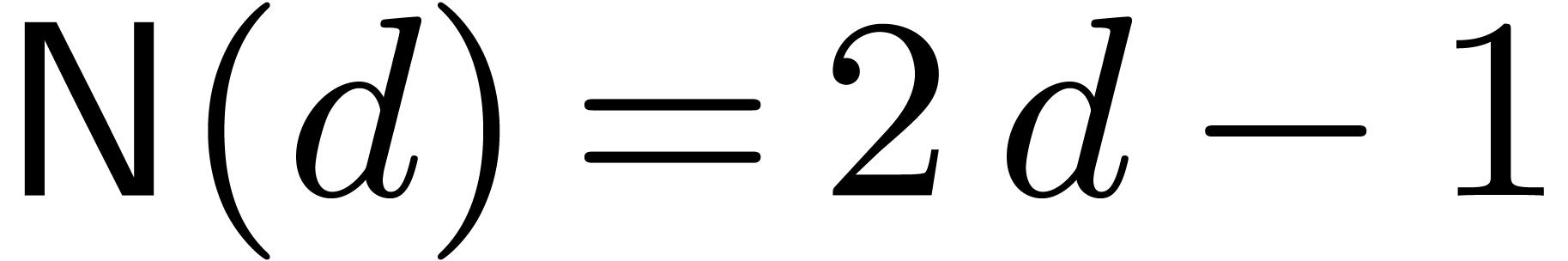 and
and 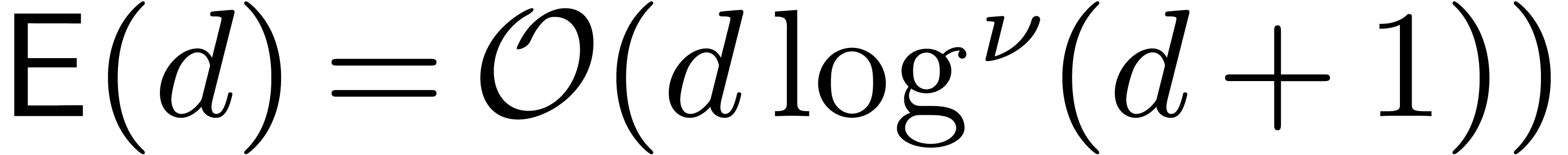 , for all
, for all
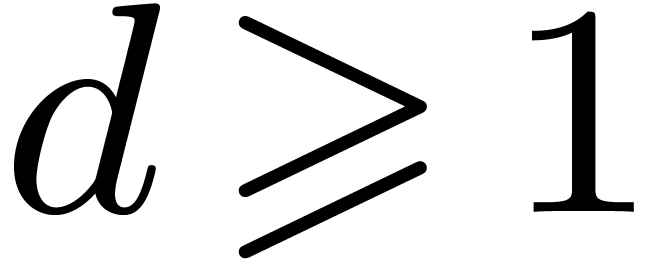 , and for some constant
, and for some constant 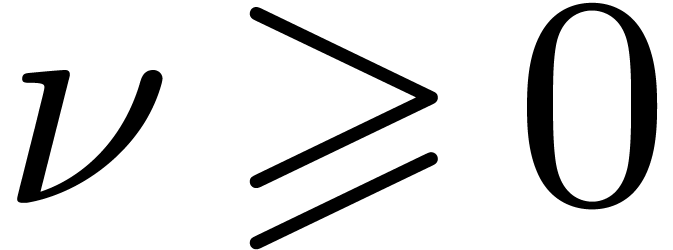 . Then two polynomials in
. Then two polynomials in 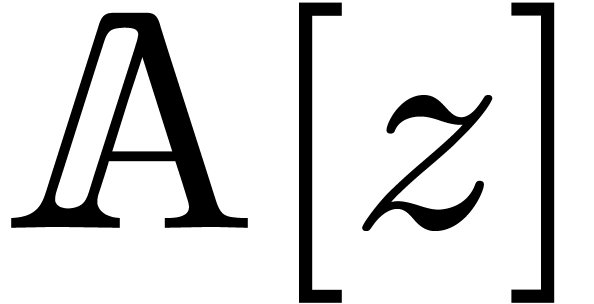 of degree at most
of degree at most  can be
multiplied with block-multiply using
at most
can be
multiplied with block-multiply using
at most 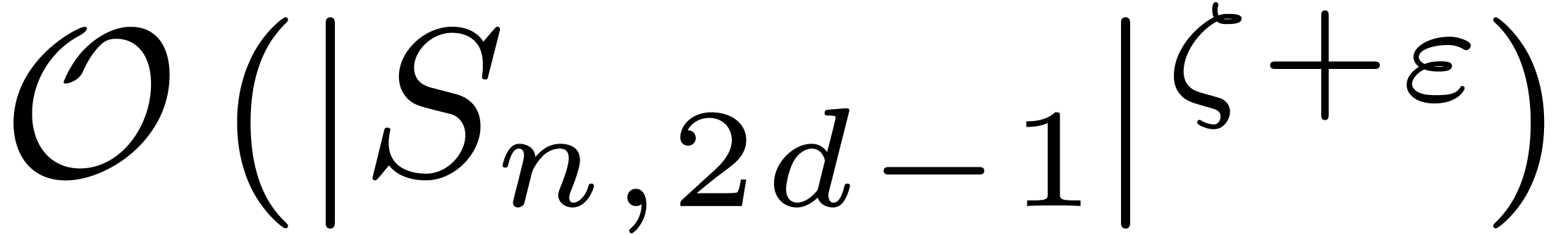 operations in
operations in  , if the sizes of the blocks
, if the sizes of the blocks 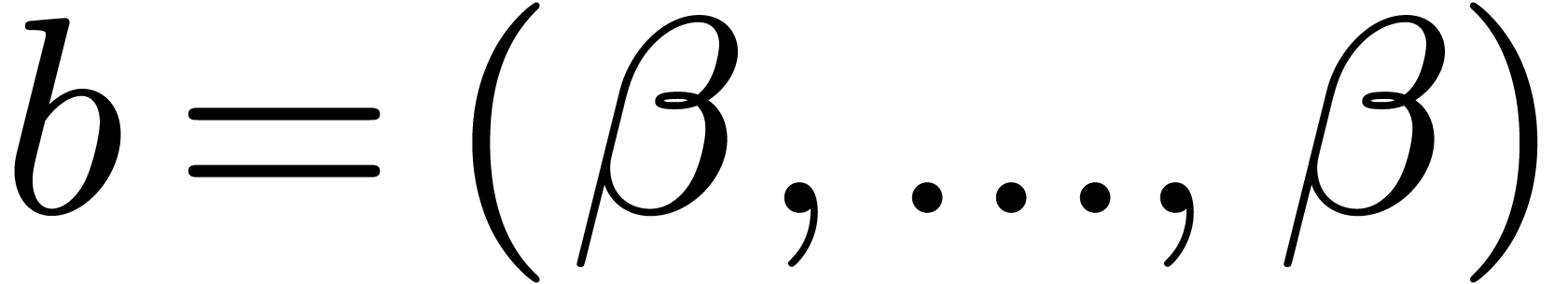 are chosen as follows:
are chosen as follows:
Proof. We introduce 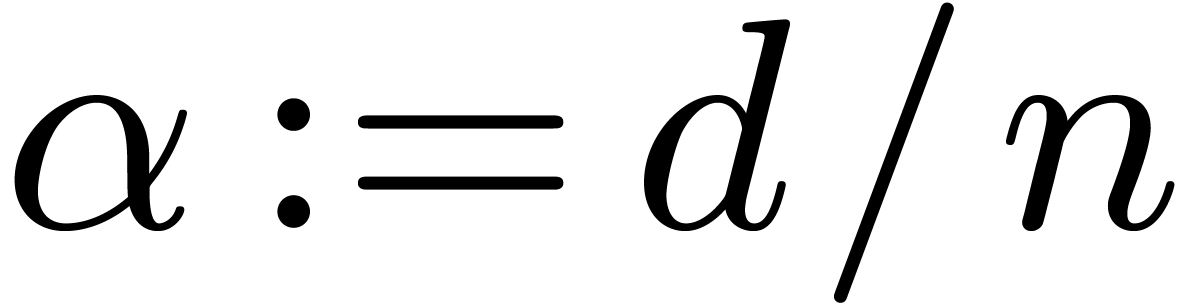 .
By Stirling's formula, there exists a constant
.
By Stirling's formula, there exists a constant 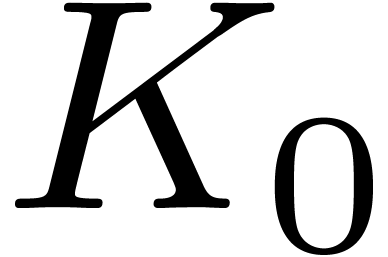 such that
such that

From 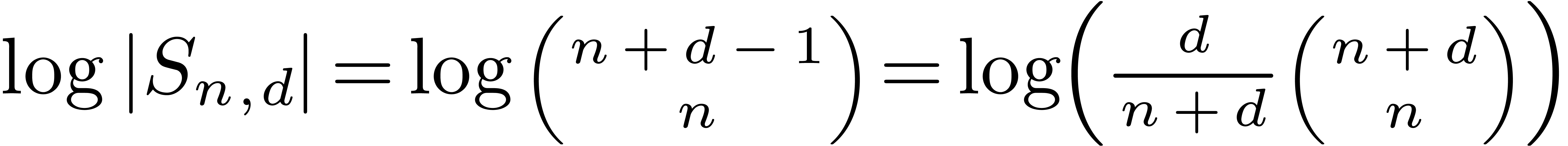 , we obtain the
existence of a constant
, we obtain the
existence of a constant 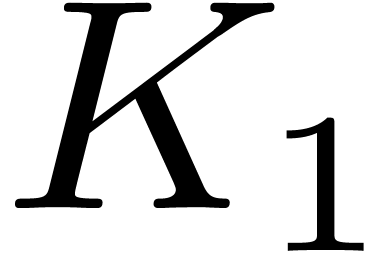 such that the following
inequality holds for all
such that the following
inequality holds for all 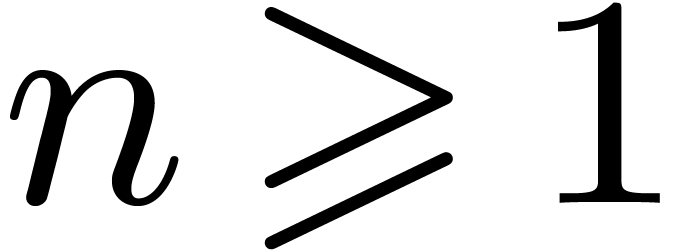 and
and 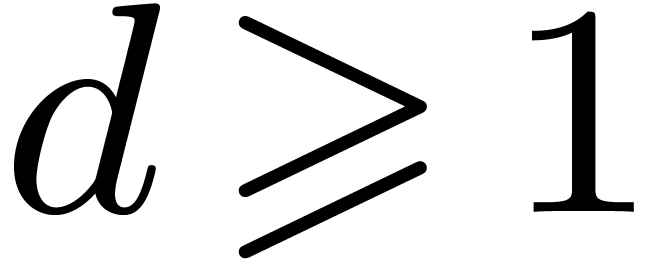 :
:
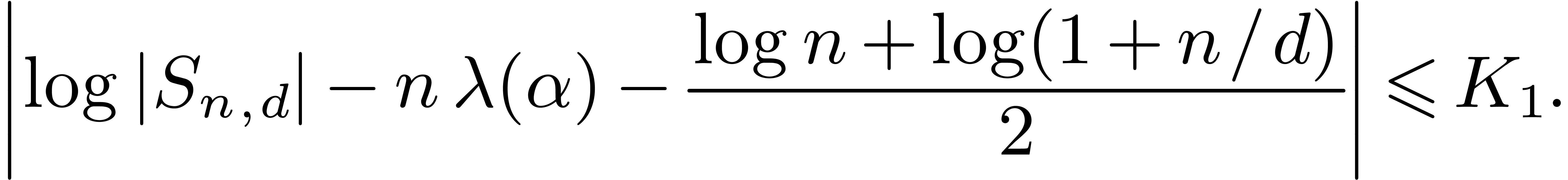
Therefore there exists a constant 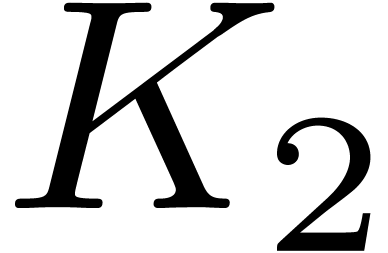 such that
such that
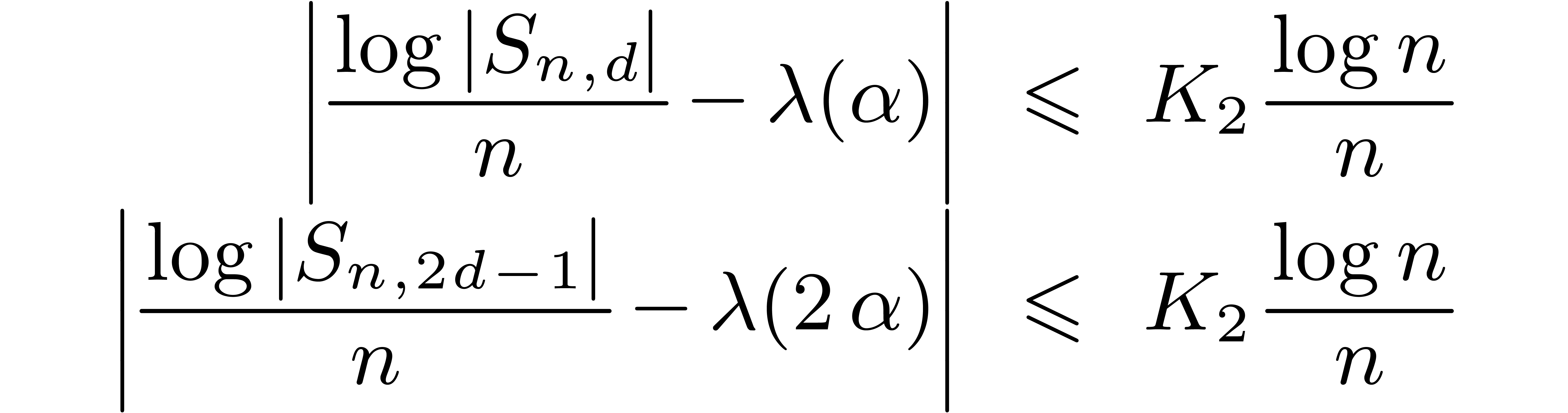
hold for all 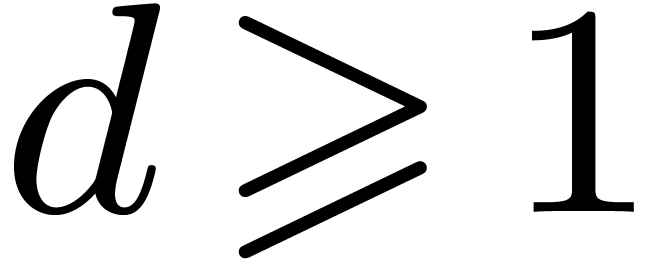 and
and  .
By Proposition 2, the cost of the multiplication is bounded
by
.
By Proposition 2, the cost of the multiplication is bounded
by 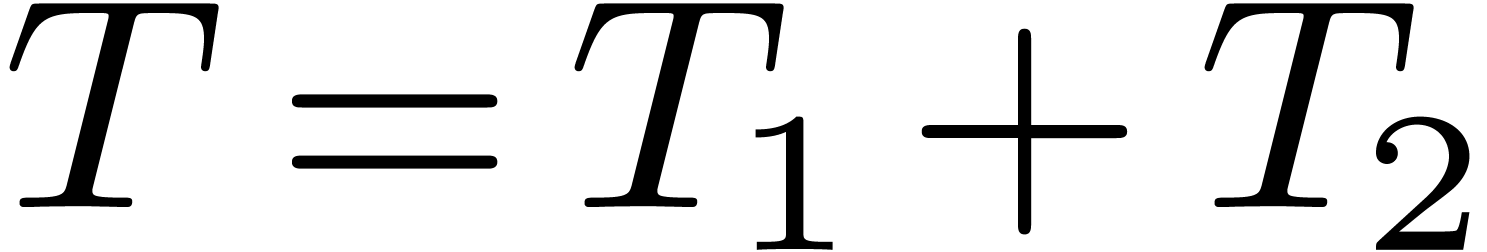 with
with
where 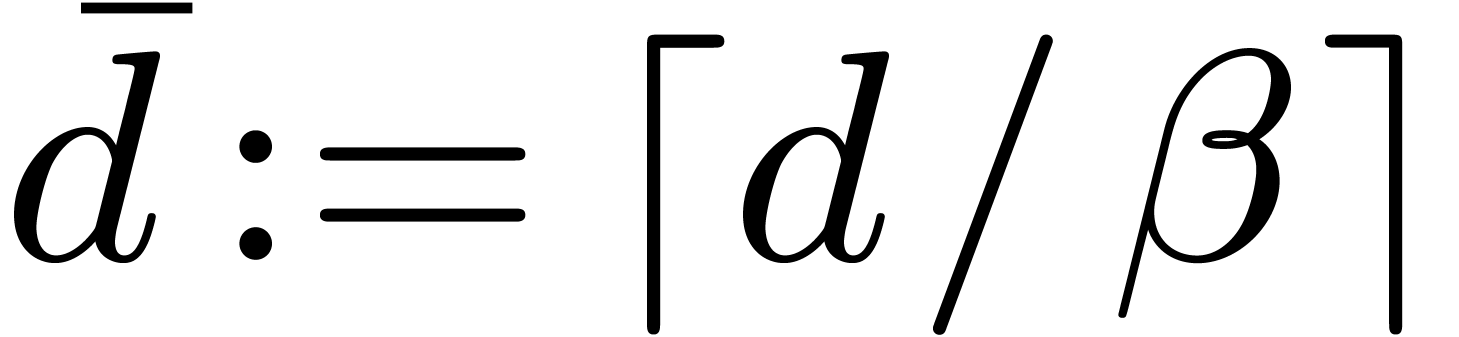 , since
, since  ,
,  ,
and
,
and 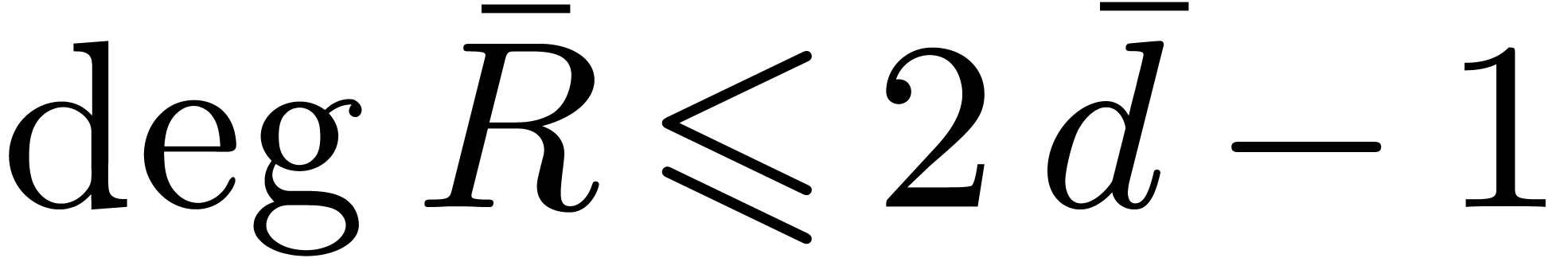 . With
. With 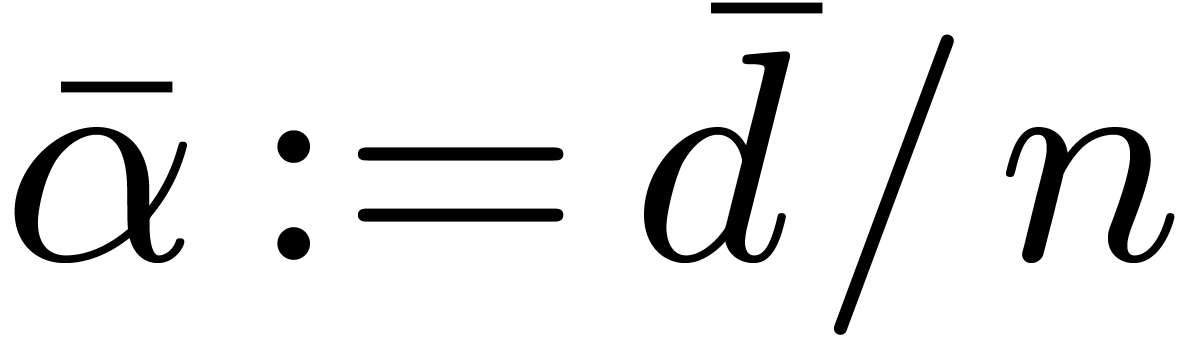 ,
, 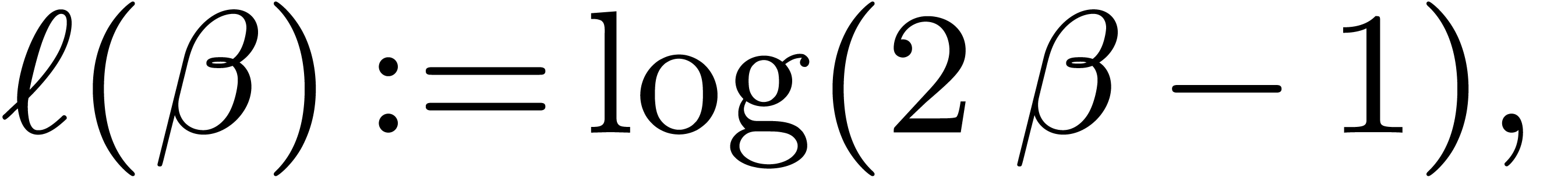 and
using (1), there exists a constant
and
using (1), there exists a constant
 such that:
such that:
Since 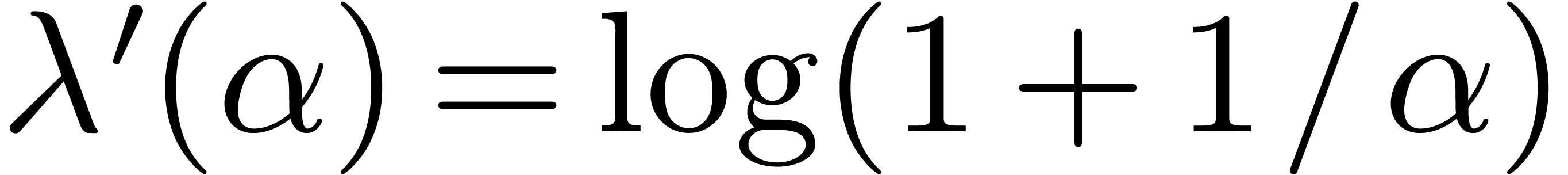 and since
and since 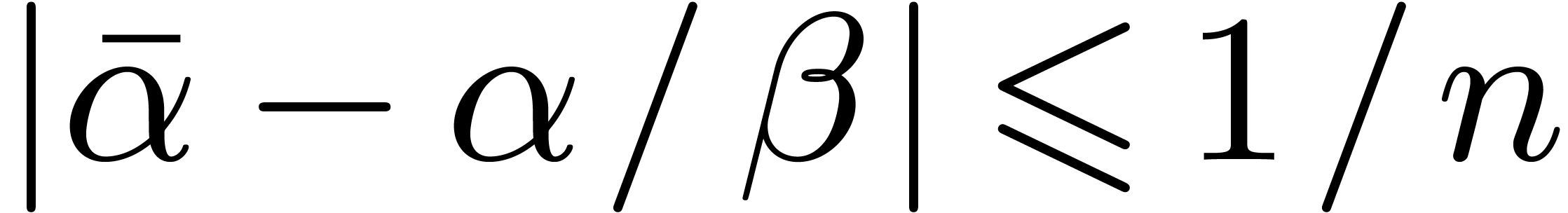 ,
we can bound
,
we can bound 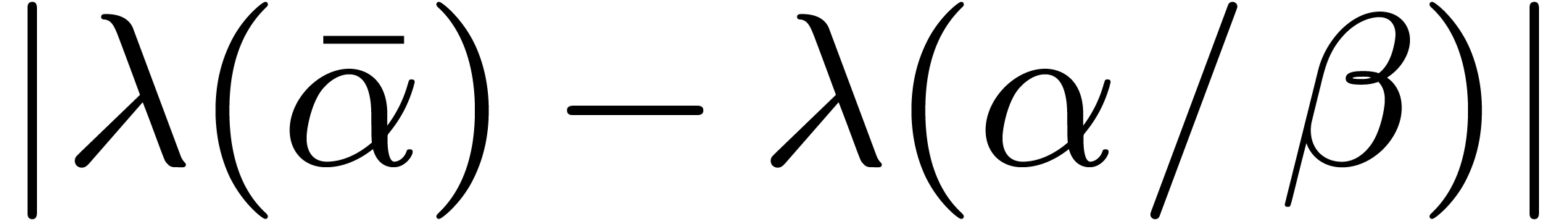 by
by 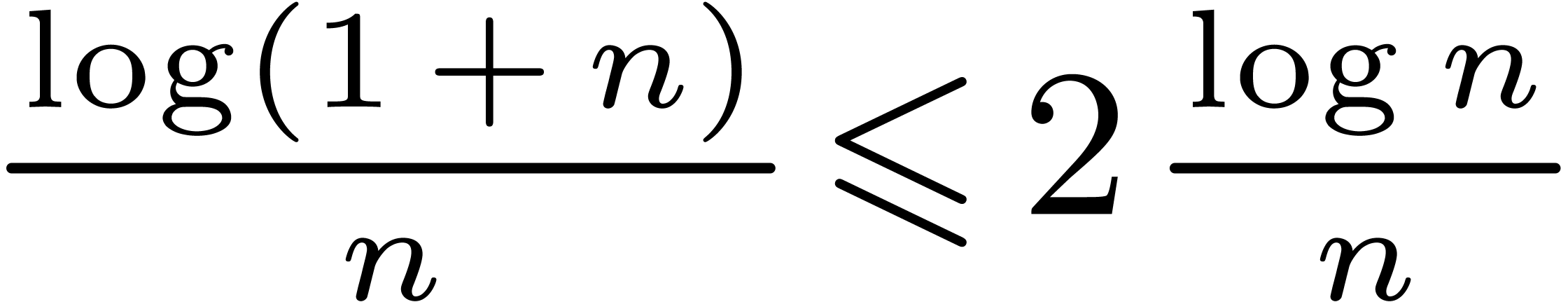 ,
and deduce the existence of an other constant
,
and deduce the existence of an other constant  such that
such that
From 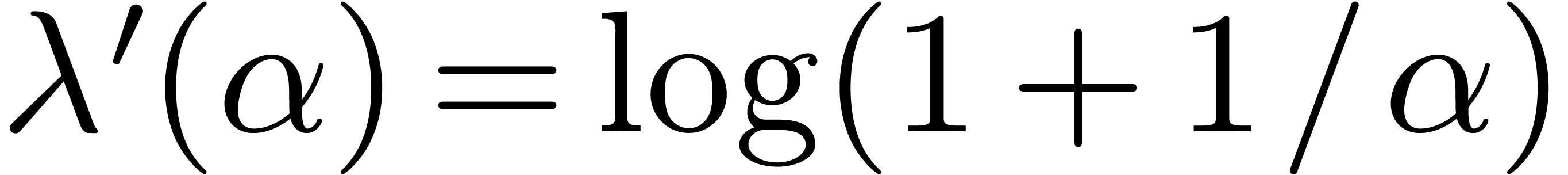 we have that
we have that 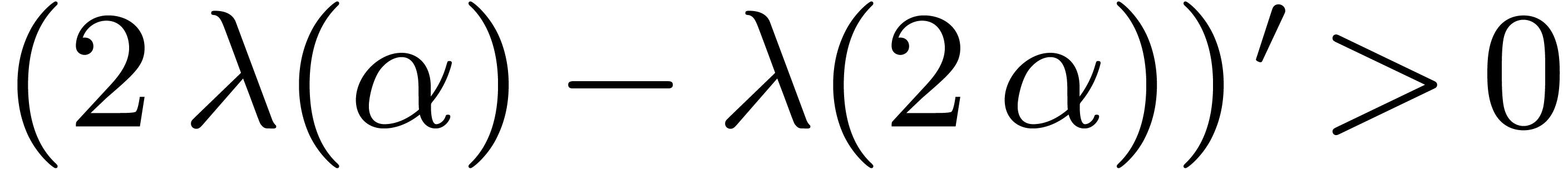 ,
and since
,
and since 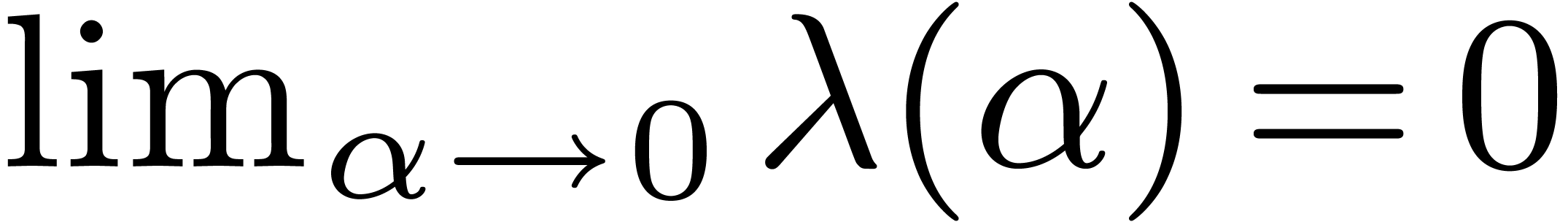 it follows that
it follows that 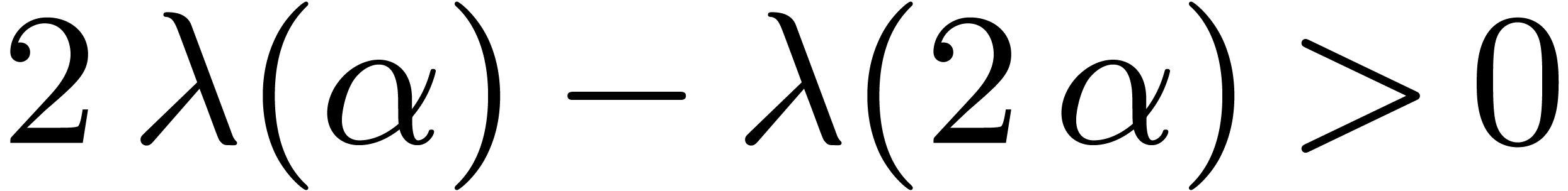 , and that there exists a constant
, and that there exists a constant 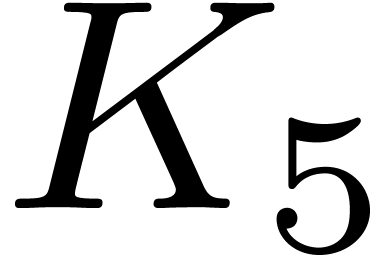 such that
such that
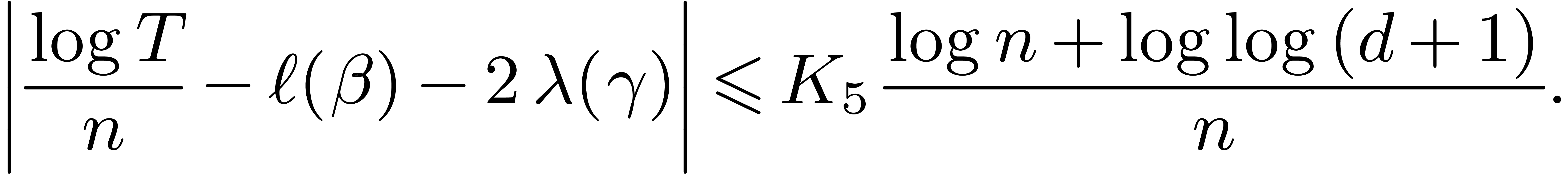 |
(3) |
In order to express the execution time in terms of the output size, we
thus have to study the function
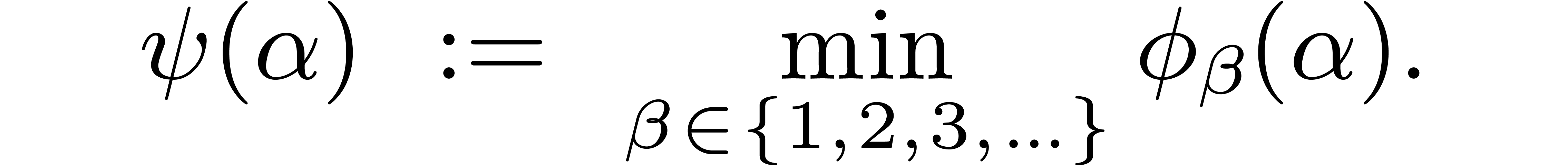
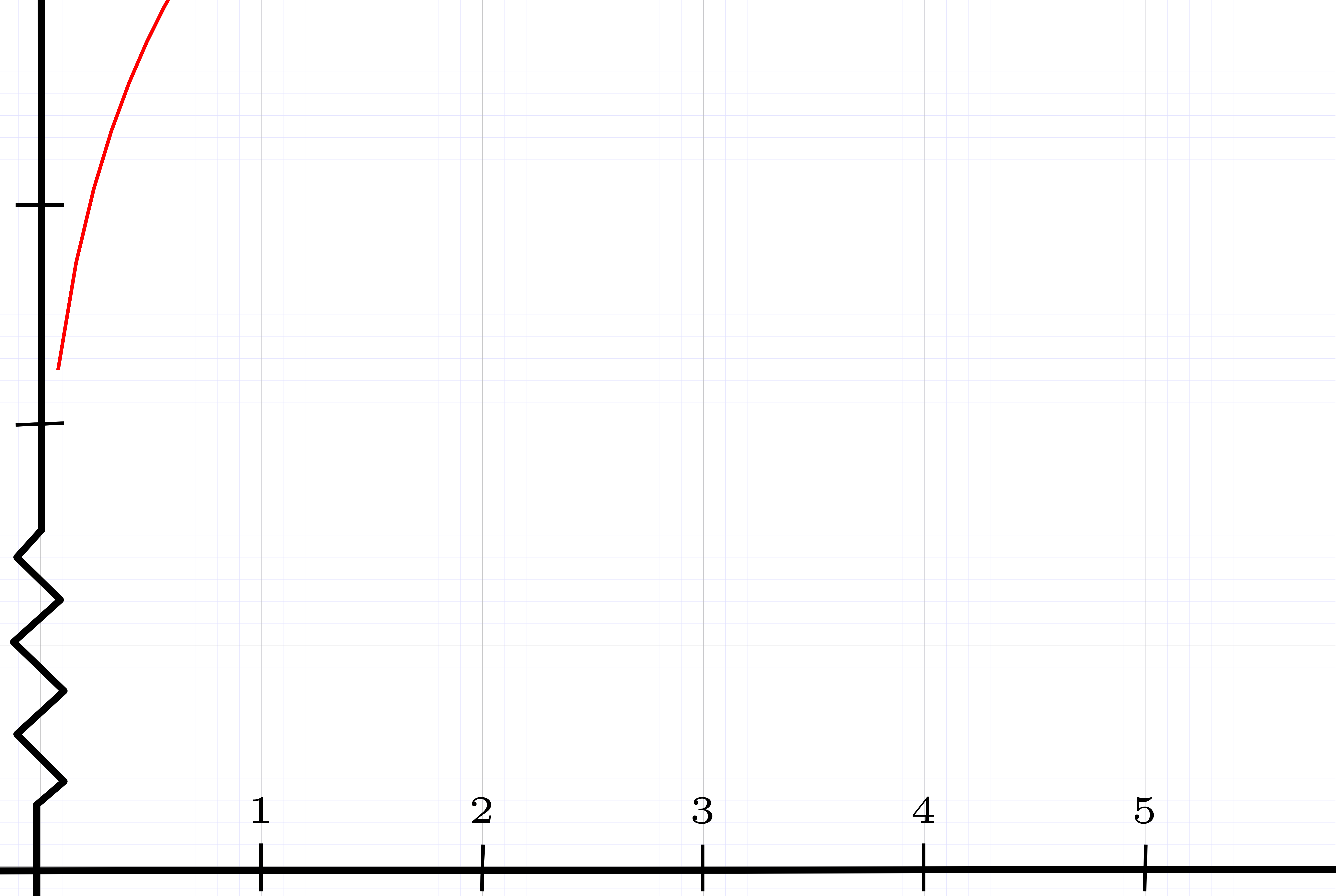
The first  are plotted in Figure 1.
The right limit of
are plotted in Figure 1.
The right limit of 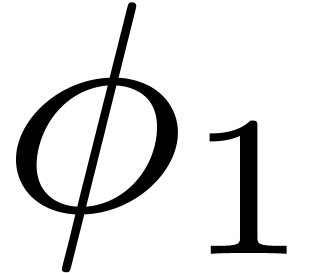 when
when  tends to
tends to 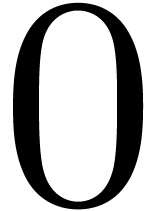 is 1, while the same limit for the
other
is 1, while the same limit for the
other  is
is  .
Since
.
Since 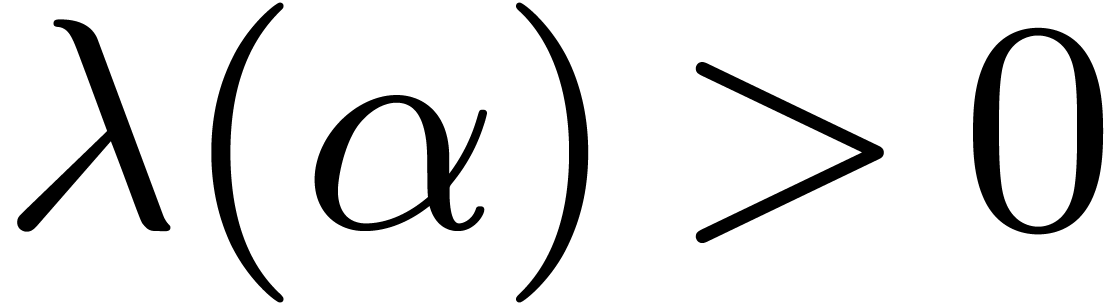 whenever
whenever 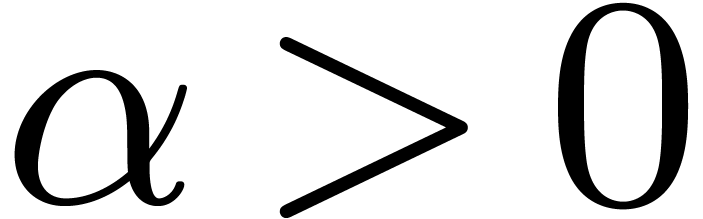 ,
the sign of
,
the sign of 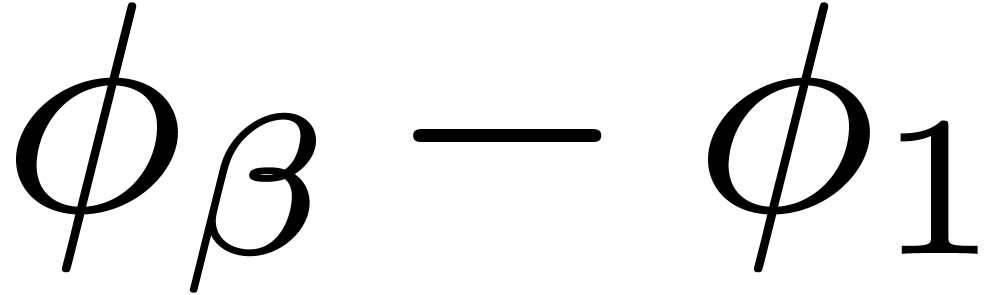 is the same as the one of
is the same as the one of
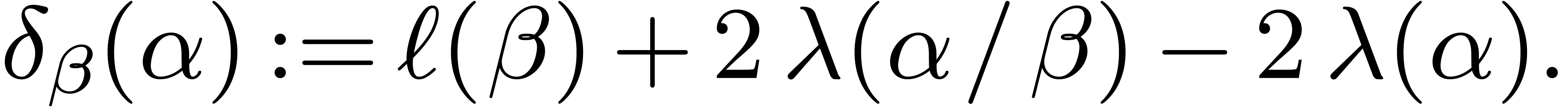
From 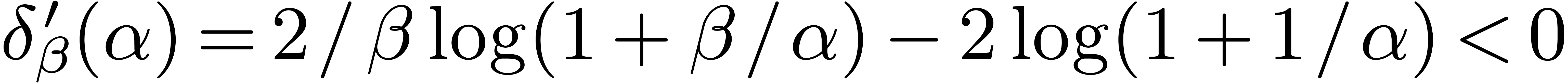 and
and 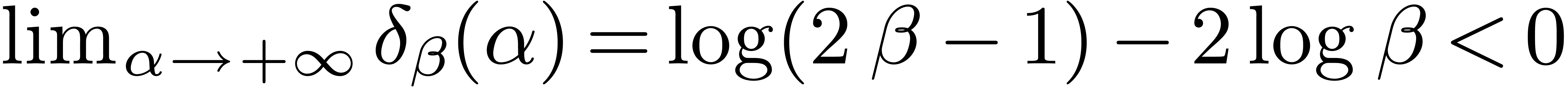 ,
it follows that there exists a unique zero, written
,
it follows that there exists a unique zero, written 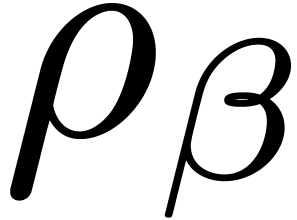 , of
, of 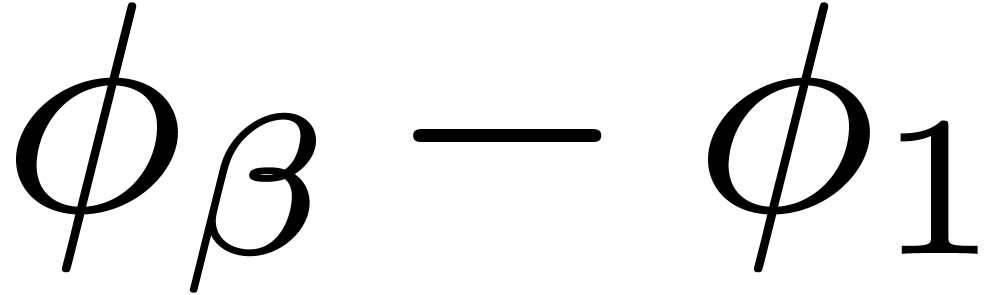 for each
for each 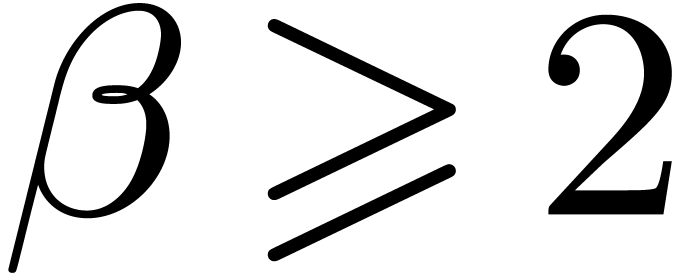 . These zeros can be approximated
by classical ball arithmetic techniques. We used the
numerix package (based on Mpfr [9]) of Mathemagix [17] to
obtain
. These zeros can be approximated
by classical ball arithmetic techniques. We used the
numerix package (based on Mpfr [9]) of Mathemagix [17] to
obtain 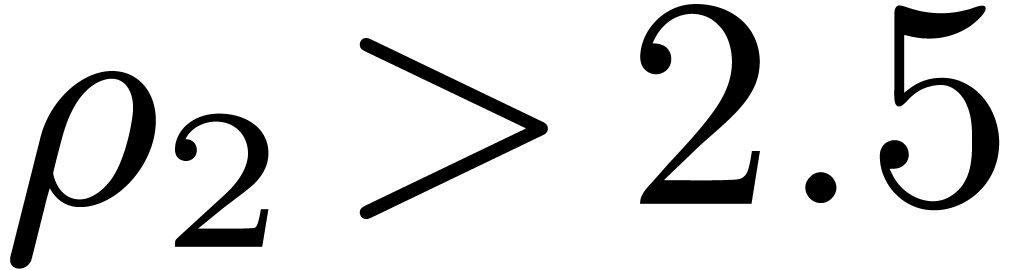 ,
, 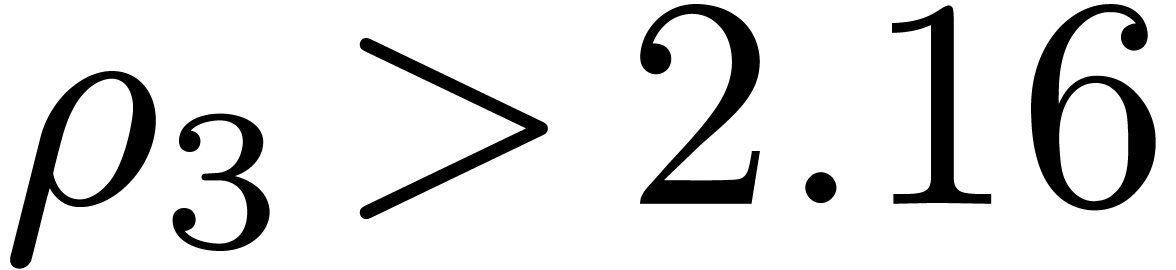 , and
, and 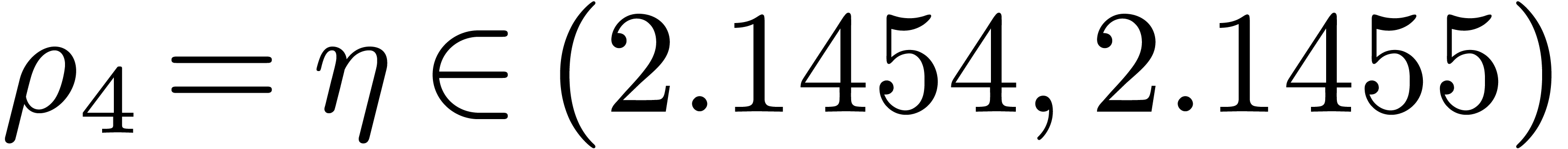 .
Still using ball arithmetic, one checks that
.
Still using ball arithmetic, one checks that  achieves its maximum for
achieves its maximum for 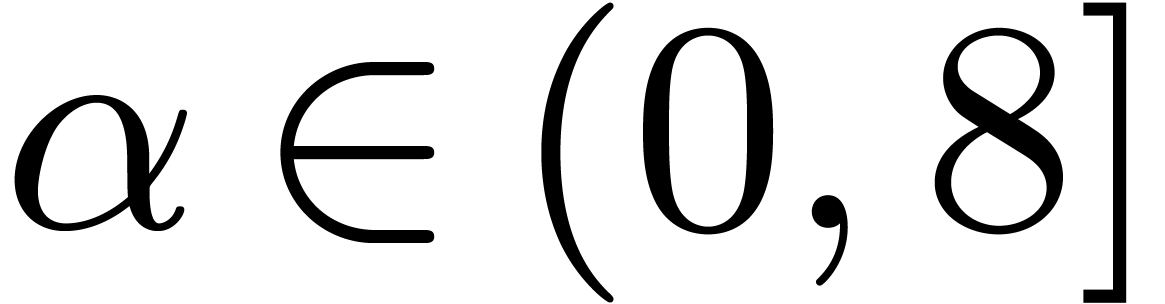 at
at 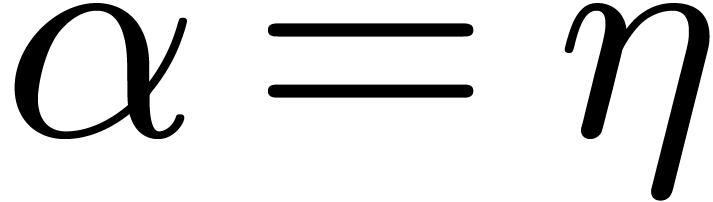 . Given
. Given 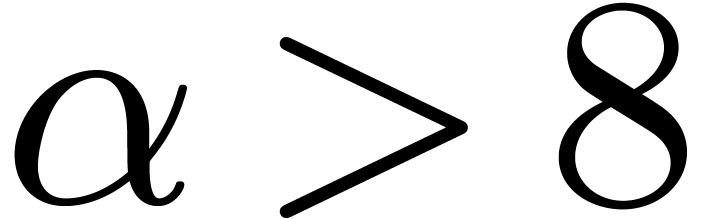 ,
Lemma 9 of the appendix shows that
,
Lemma 9 of the appendix shows that 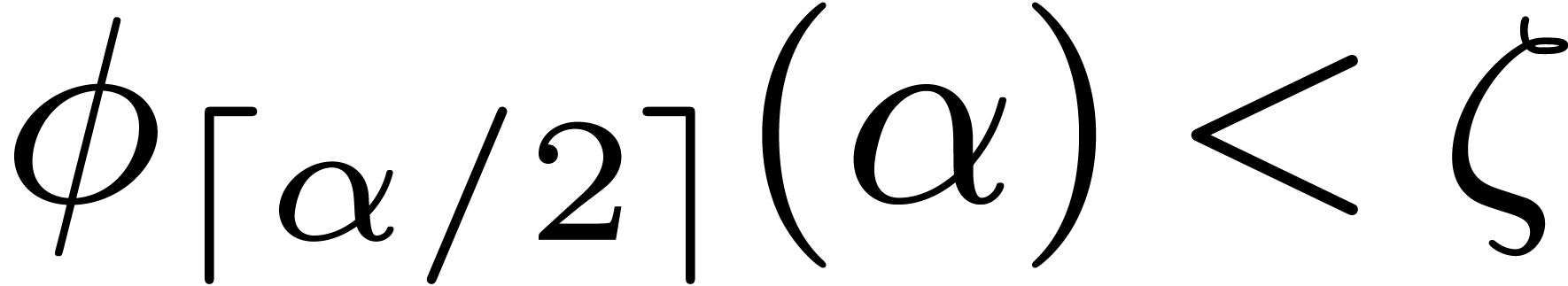 .
.
Finally, we have obtained so far that taking 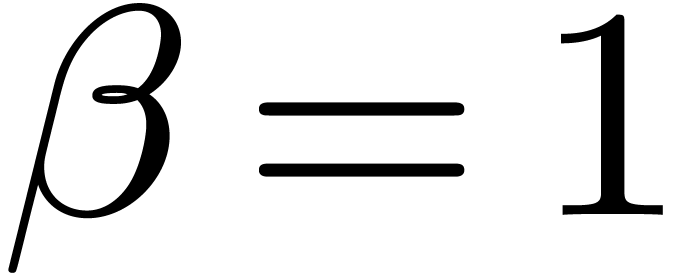 for
for
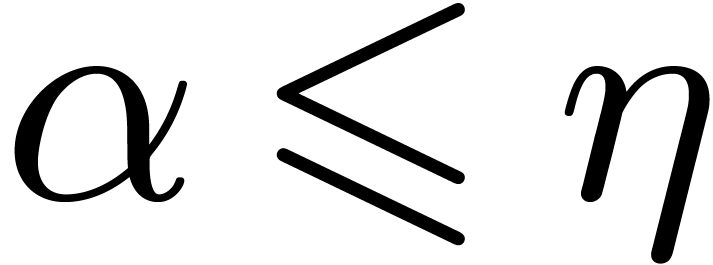 ,
, 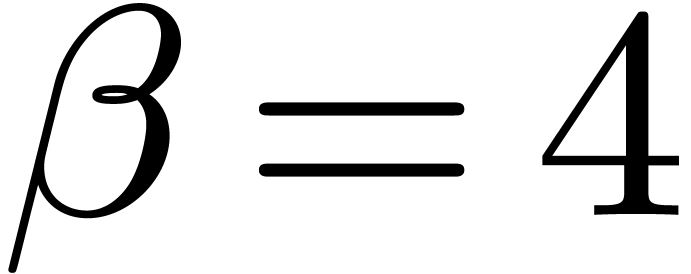 for
for
 and
and 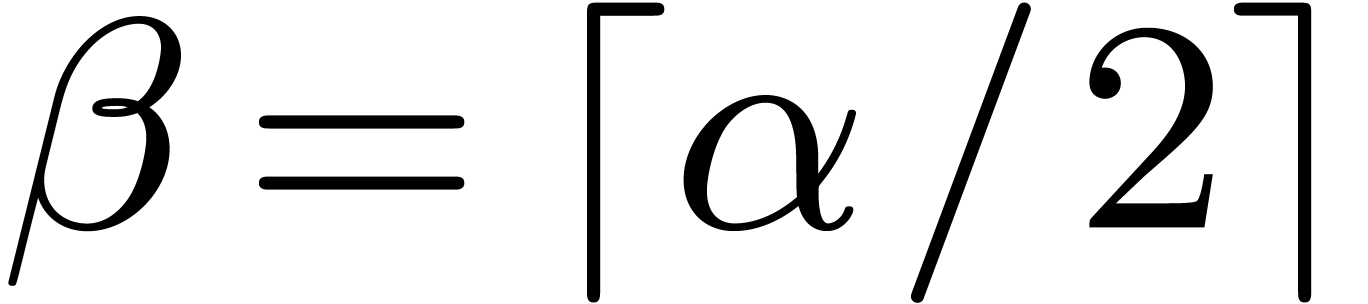 for larger
for larger  , the inequality
, the inequality 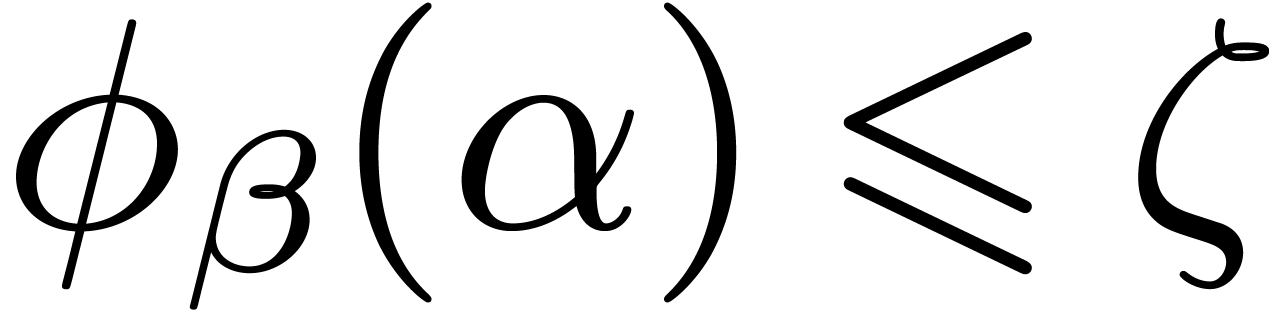 holds for all
holds for all 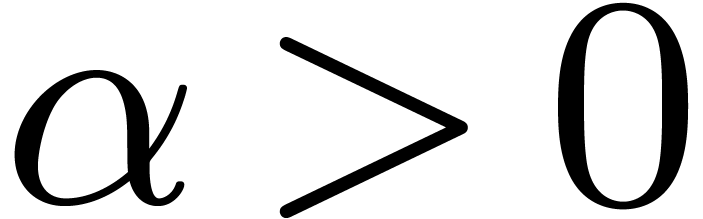 . Therefore
there exists a constant
. Therefore
there exists a constant  ,
such that
,
such that 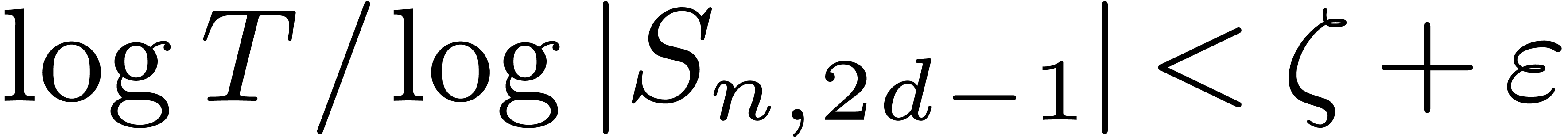 for all
for all 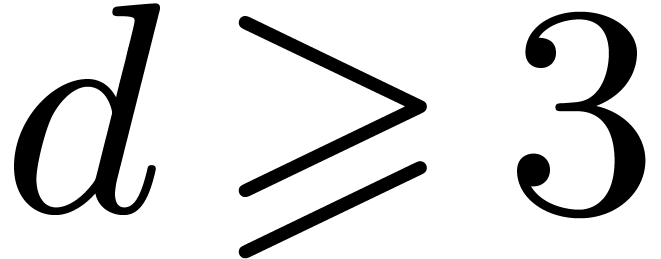 and
and
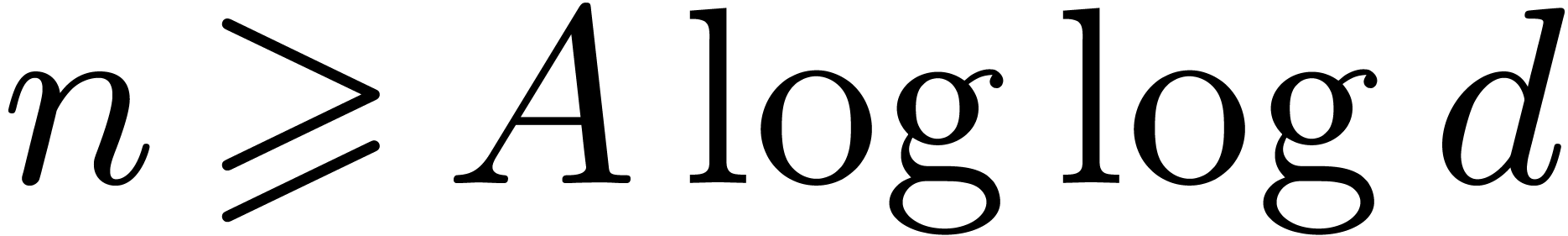 , or
, or 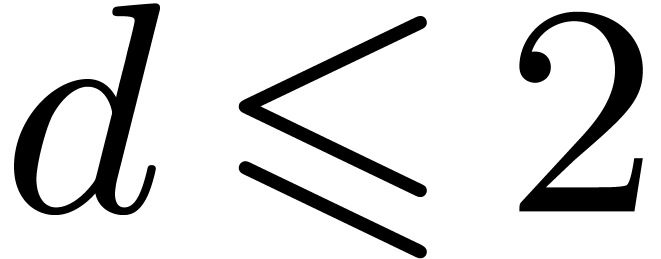 and
and 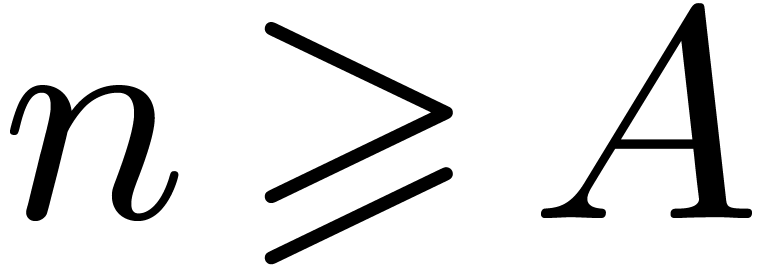 .
.
It remains to bound 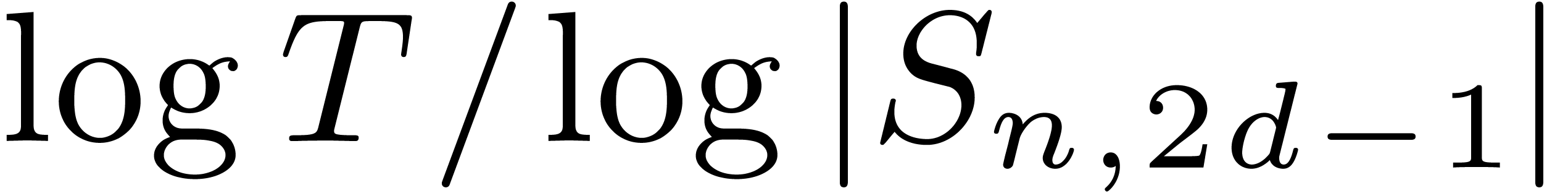 for
for 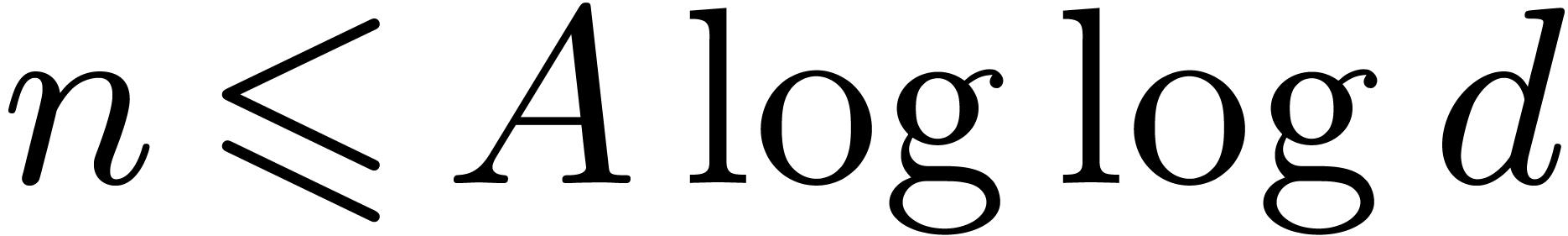 and
and 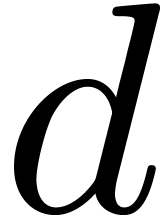 sufficiently large. There exists a constant
sufficiently large. There exists a constant
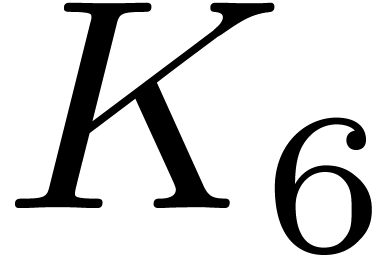 such that:
such that:
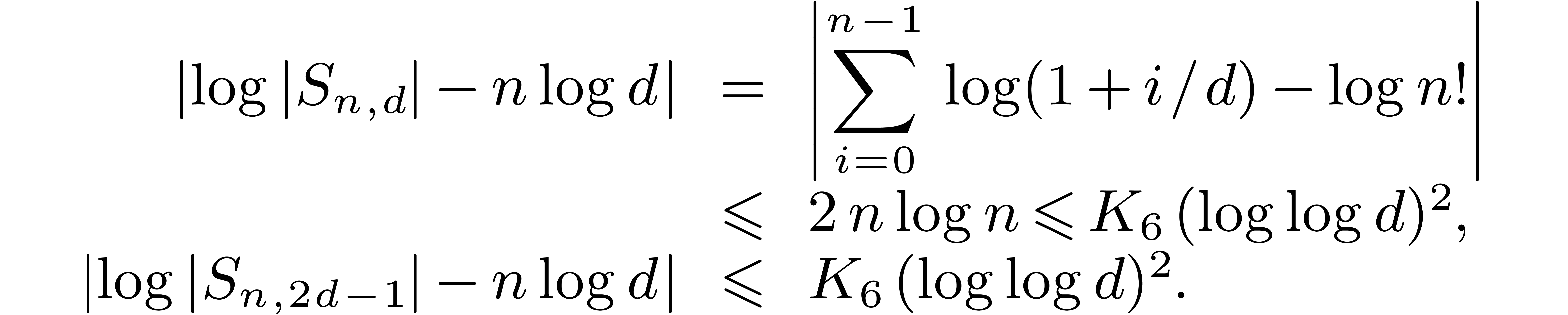
Therefore, taking 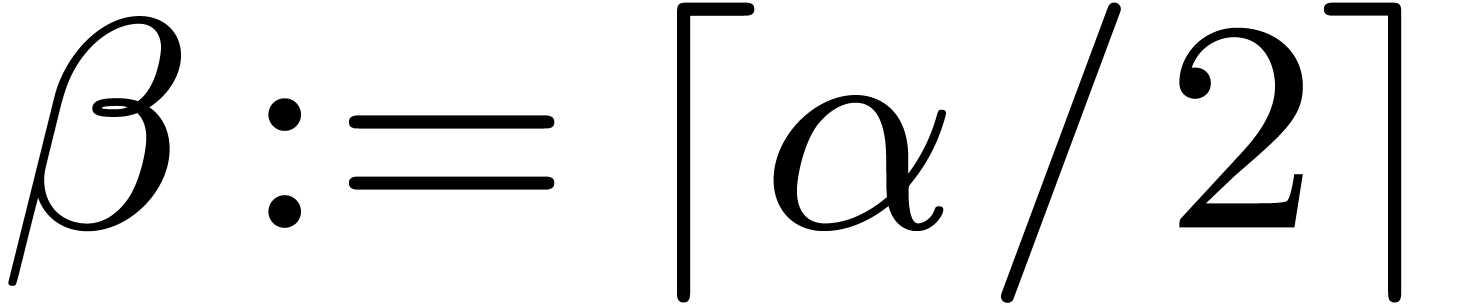 , there
exists a contant
, there
exists a contant 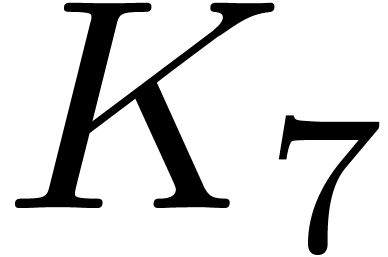 with
with
which implies that 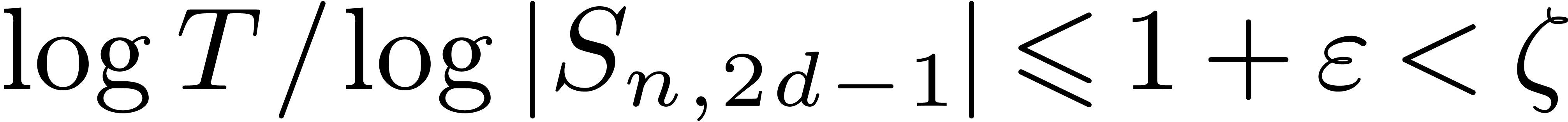 when
when 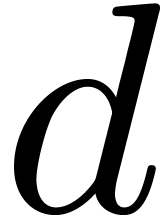 is sufficiently large.
is sufficiently large.
Remark 5. In the proof of Theorem 4,
it was convenient for computational purposes to explicitly chose  in terms of
in terms of  .
However our choice of
.
However our choice of  is suboptimal. For
instance, taking
is suboptimal. For
instance, taking 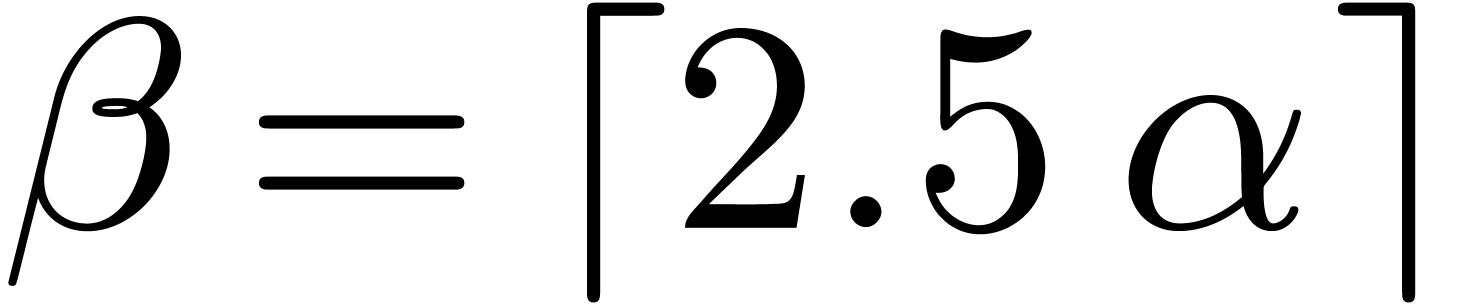 for
for 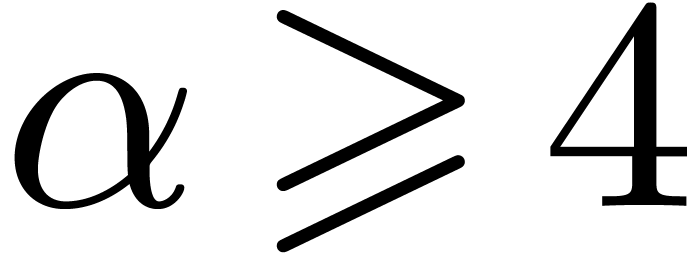 is
generally better whenever
is
generally better whenever 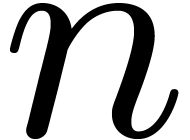 remains in
remains in 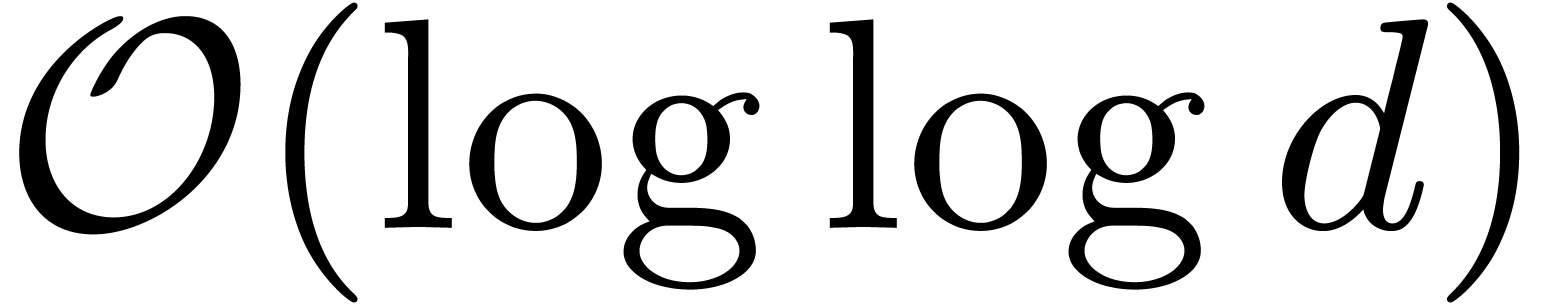 . In fact, we think that algorithm
block-size will do the choice of the block size just as
well and maybe even a little bit better from the latter bounds when
using a function
. In fact, we think that algorithm
block-size will do the choice of the block size just as
well and maybe even a little bit better from the latter bounds when
using a function  precise enough. A detailed
proof of this claim sounds quite technical, so we have not pursued this
direction any further in the present article. Nevertheless, the claim is
plausible for the following reasons:
precise enough. A detailed
proof of this claim sounds quite technical, so we have not pursued this
direction any further in the present article. Nevertheless, the claim is
plausible for the following reasons:
For rings which do not support large evaluation-interpolation schemes we
propose the following extension of Theorem 4.
Theorem 6. Let  , and assume that
, and assume that  admits a unit. Then two polynomials in
admits a unit. Then two polynomials in 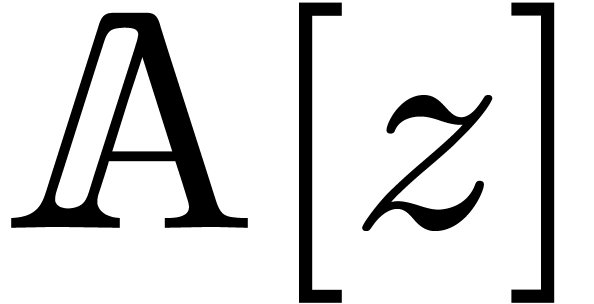 of degree
at most
of degree
at most  can be multiplied using at most
can be multiplied using at most 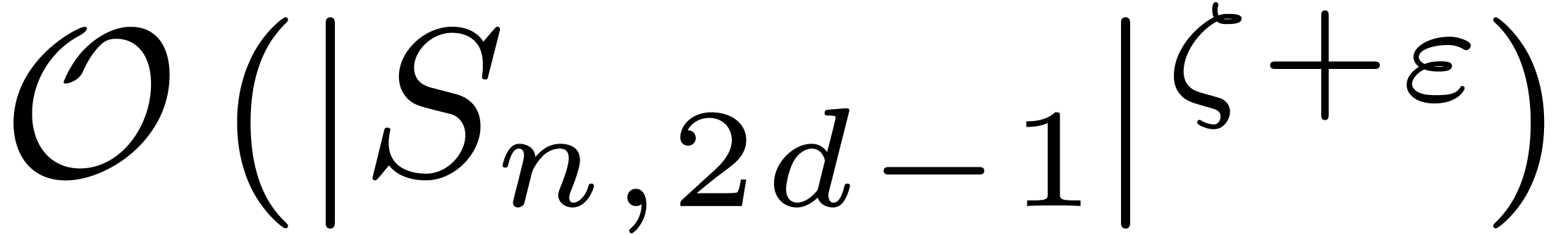 operations in
operations in  .
.
Proof. We use the Chinese remaindering technique
from [3]. It suffices to prove the theorem for 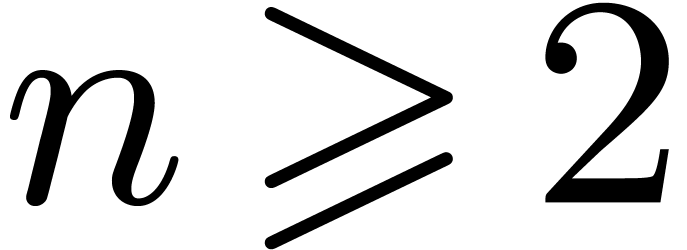 . The unit of
. The unit of  is
written
is
written 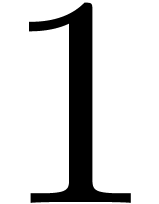 , and we introduce
, and we introduce
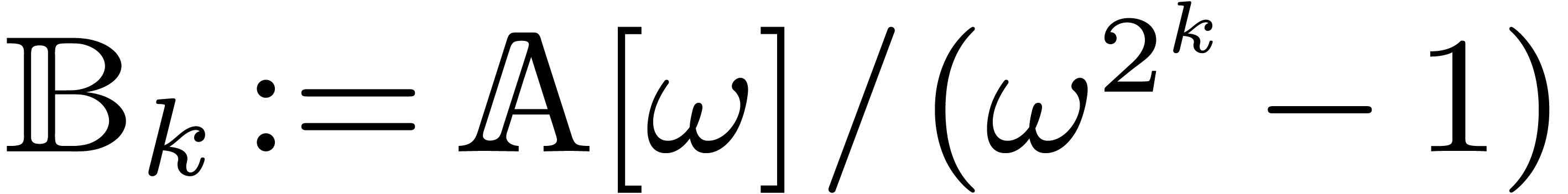 and
and 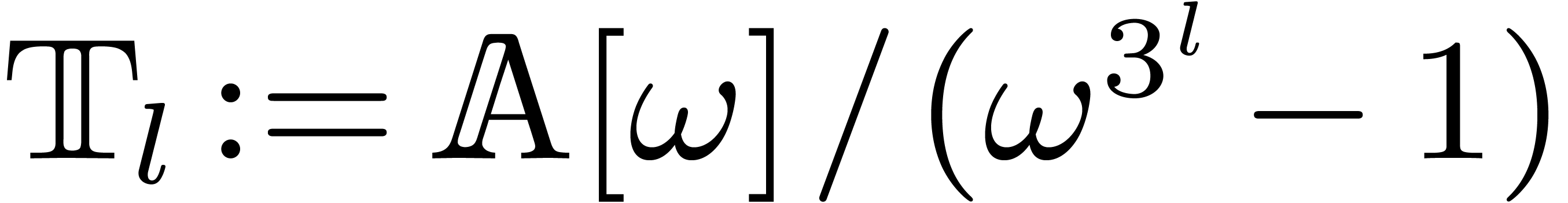 .
By using the aforementioned TFT algorithm, we can multiply
.
By using the aforementioned TFT algorithm, we can multiply 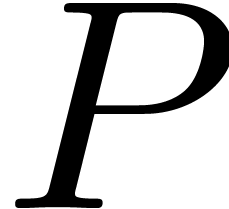 and
and  in
in 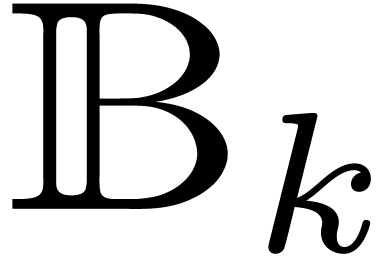 (resp. in
(resp. in  ) via Theorem 4, with
) via Theorem 4, with 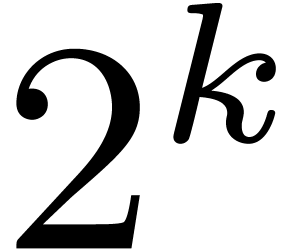 (resp. with
(resp. with 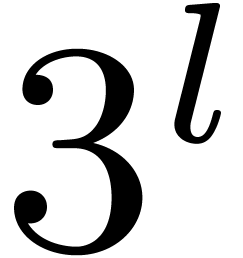 ) being the next power of
) being the next power of  (resp. of
(resp. of  ) of
) of  if we do not perform the divisions by
if we do not perform the divisions by  (resp. by
(resp. by  ). We thus obtain
). We thus obtain
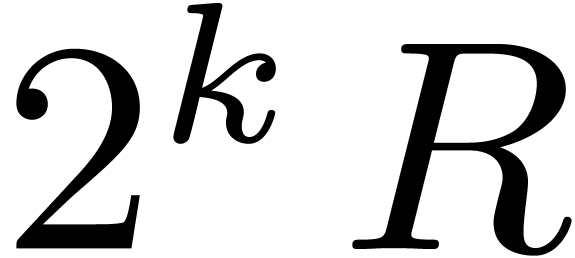 and
and 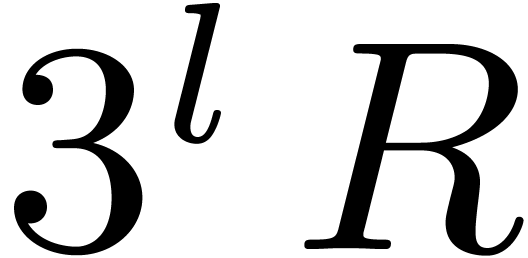 .
If
.
If 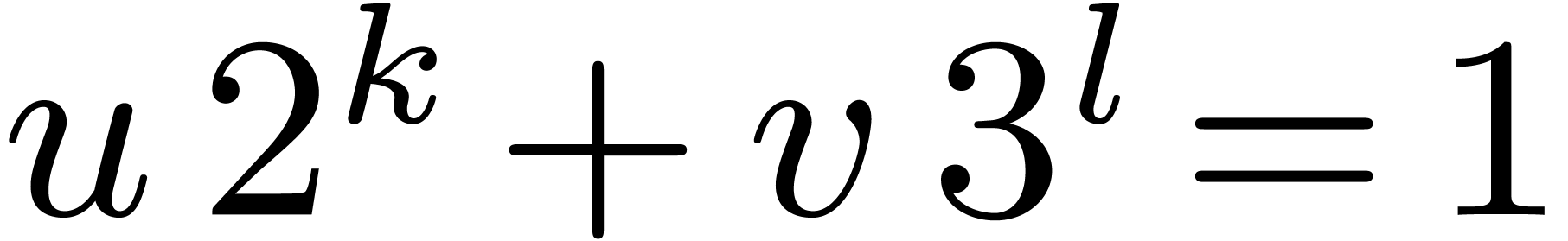 then we deduce
then we deduce 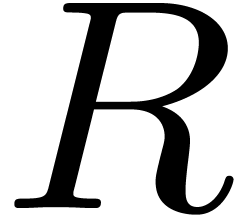 as
as
 .
.
Replacing all arithmetic operations in  by
arithmetic operations in
by
arithmetic operations in  gives rise to an
additional overhead of
gives rise to an
additional overhead of 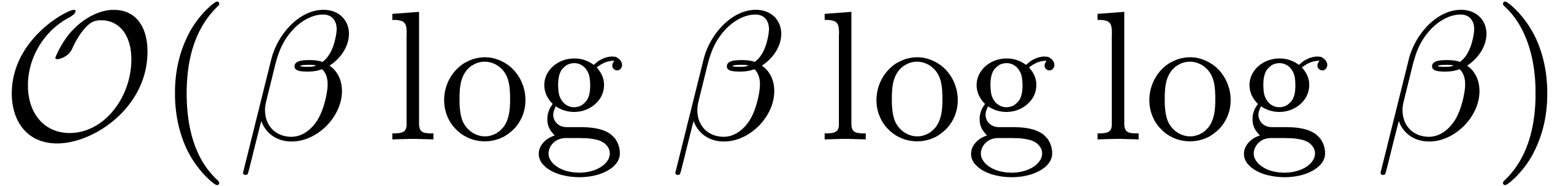 with respect to the
complexity analysis from the proof of Theorem 4. More
precisely, we have a new constant
with respect to the
complexity analysis from the proof of Theorem 4. More
precisely, we have a new constant 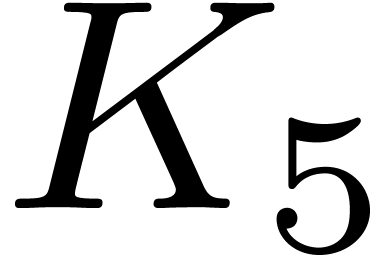 such that
such that
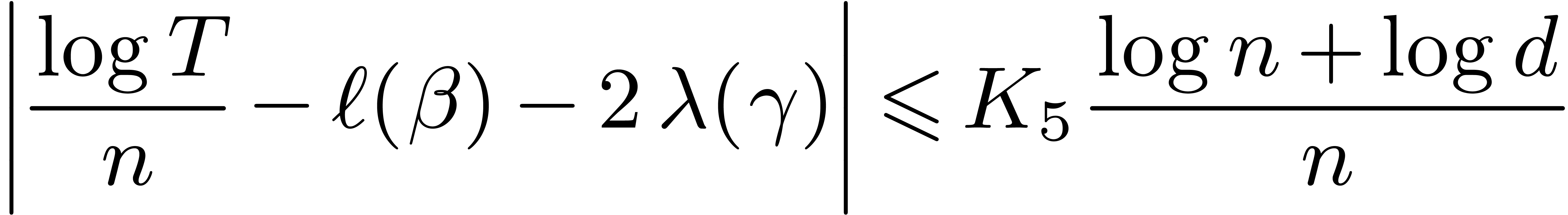
The result is thus proved for when 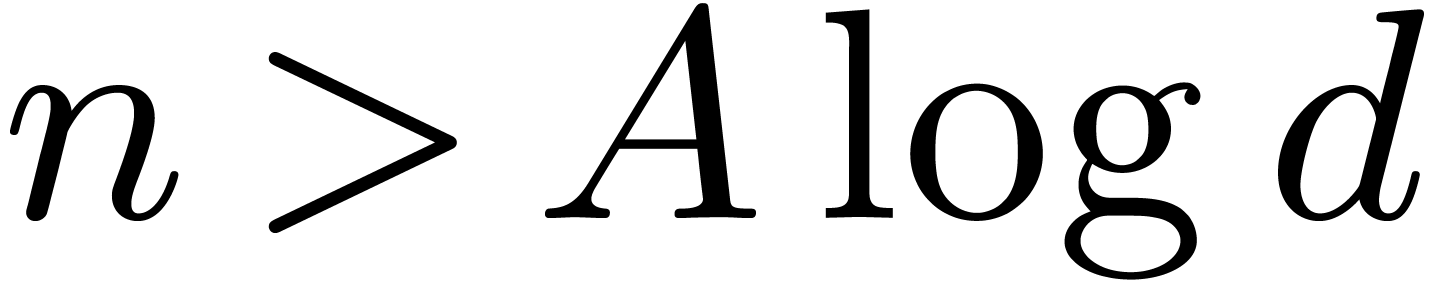 for a
sufficiently large constant
for a
sufficiently large constant  .
It remains to examine the case when
.
It remains to examine the case when 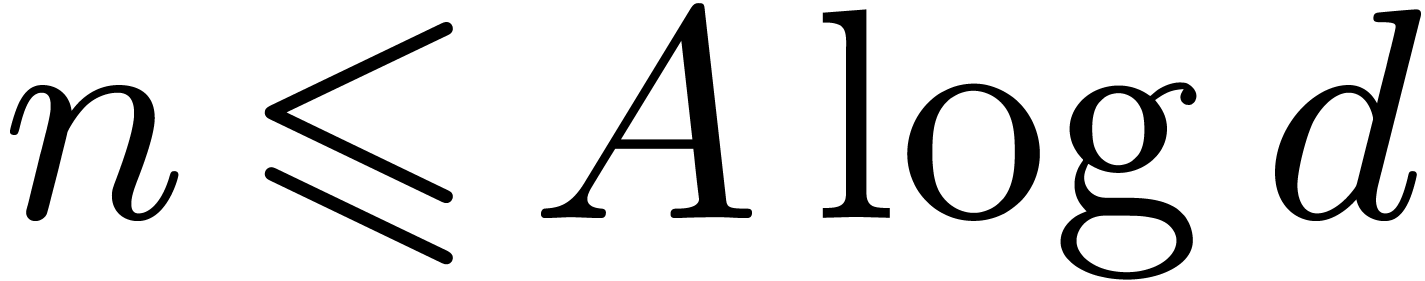 .
Again, we use a similar proof as at the end of Theorem 4,
with new constants
.
Again, we use a similar proof as at the end of Theorem 4,
with new constants 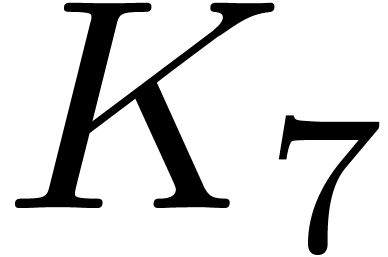 and
and 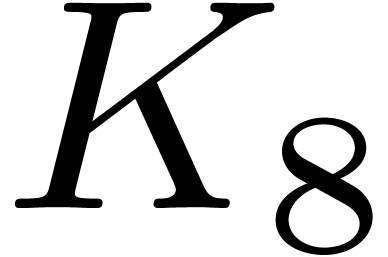 such that
such that
Hence 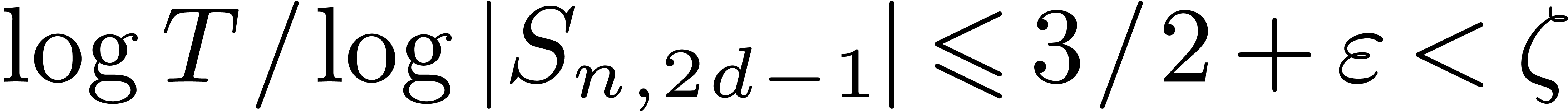 for
for 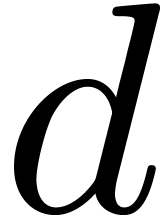 sufficiently
large.
sufficiently
large.
For rings which do not have a unit, we can use a Karatsuba
evaluation-interpolation scheme. For this purpose we introduce

Let  be the unique positive zero of
be the unique positive zero of  , and let
, and let 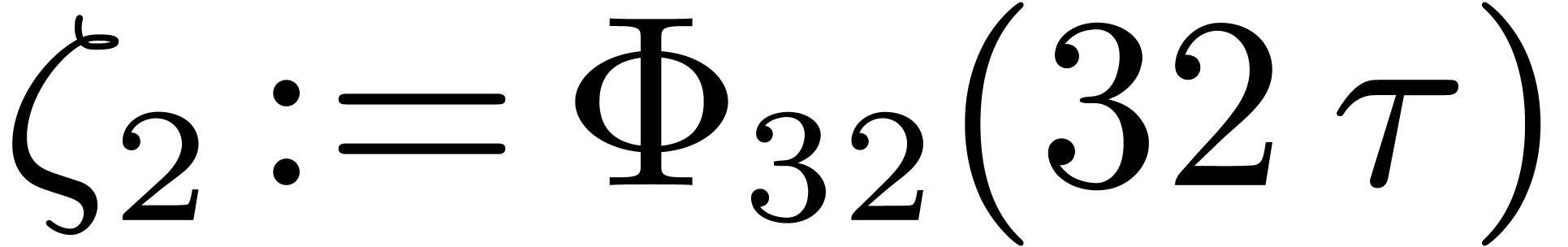 .
Numeric computations lead to
.
Numeric computations lead to  and
and  .
.
Theorem 7. Let
 , let
, let  be any ring. Then two polynomials in
be any ring. Then two polynomials in 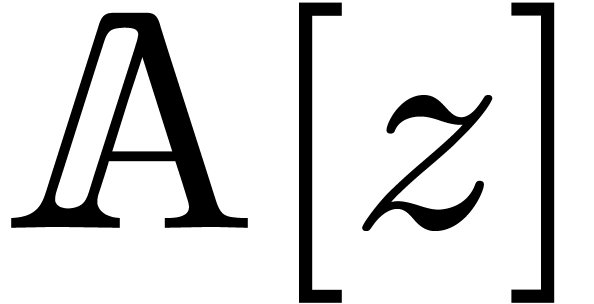 of degree
at most
of degree
at most  can be multiplied using at most
can be multiplied using at most 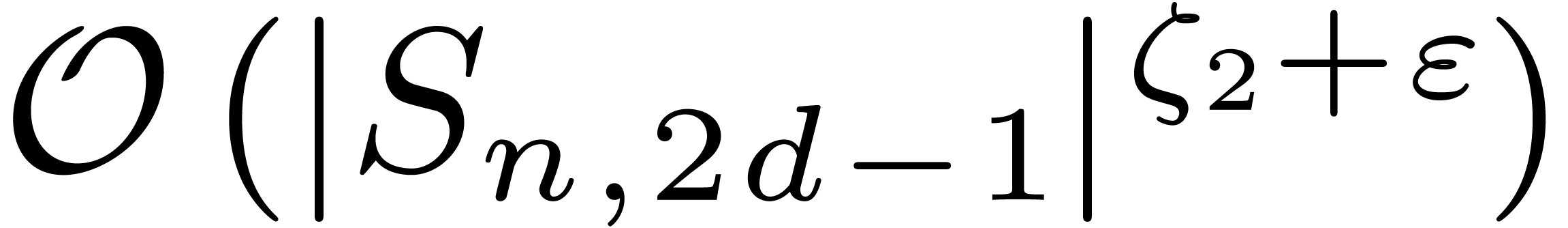 operations in
operations in  .
.
Proof. We use the Karatsuba scheme [16,
Section 2] with 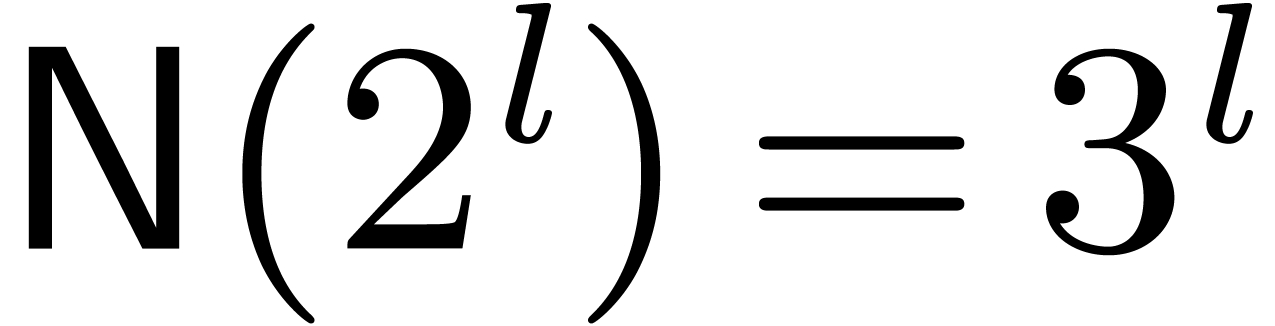 and
and 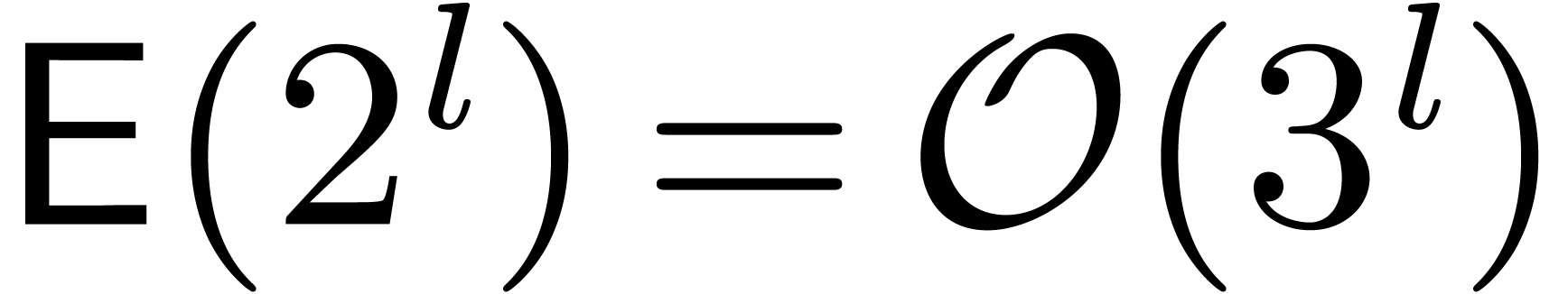 for
all
for
all 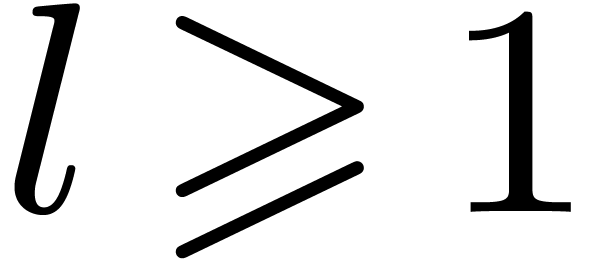 . We follow the proof of
Theorem 4 and begin with a new constant
. We follow the proof of
Theorem 4 and begin with a new constant 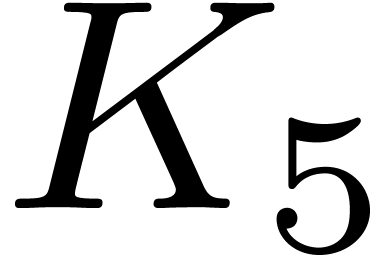 such that
such that
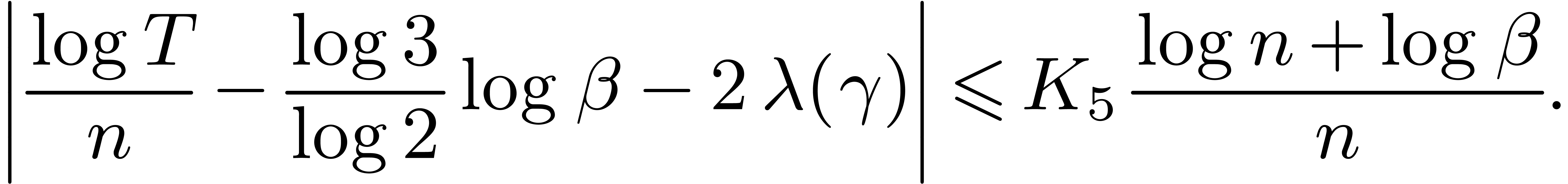
In order to express the execution time in terms of the output size, we
thus have to study the function
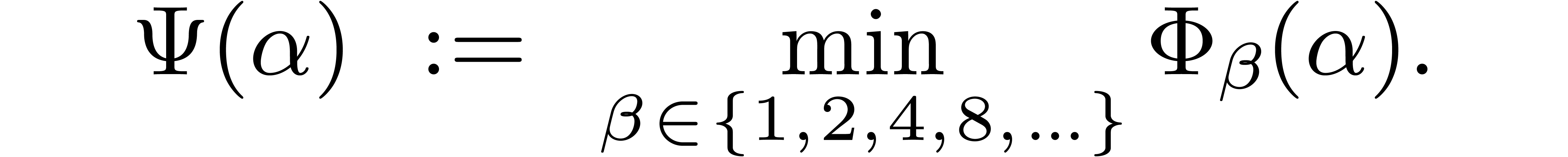
The right limit of 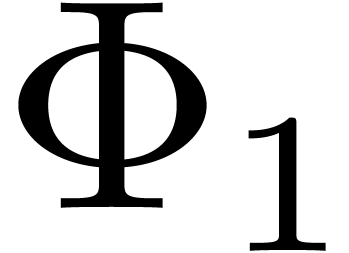 when
when  tends to
tends to 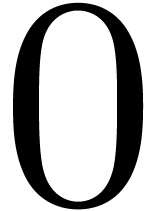 is 1, while the same limit for the
other
is 1, while the same limit for the
other 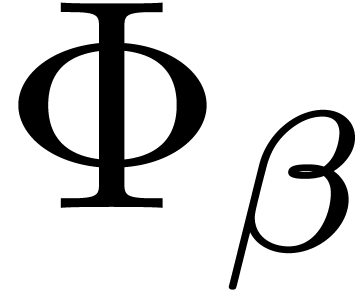 is
is  .
Since
.
Since 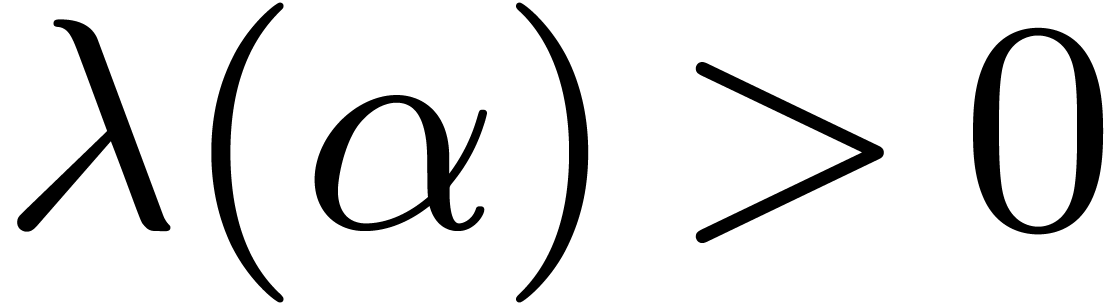 whenever
whenever 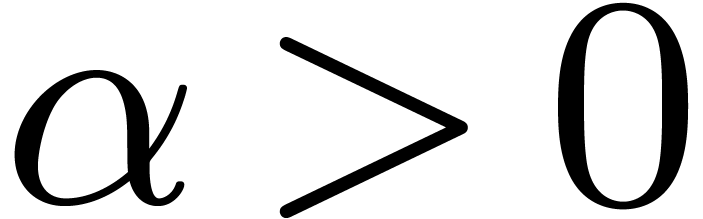 ,
the sign of
,
the sign of 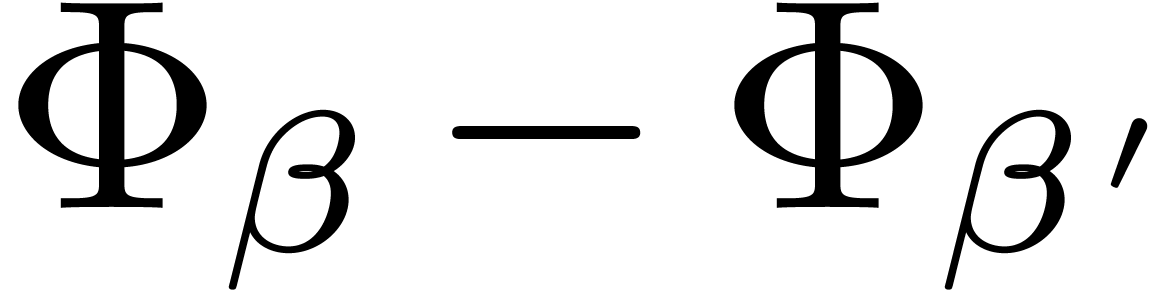 is the same as the one of
is the same as the one of
If 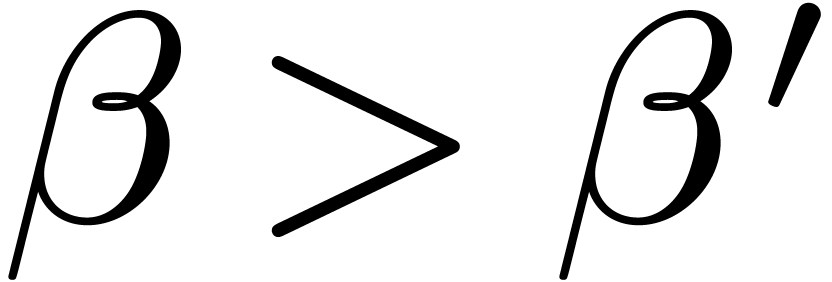 , then
, then 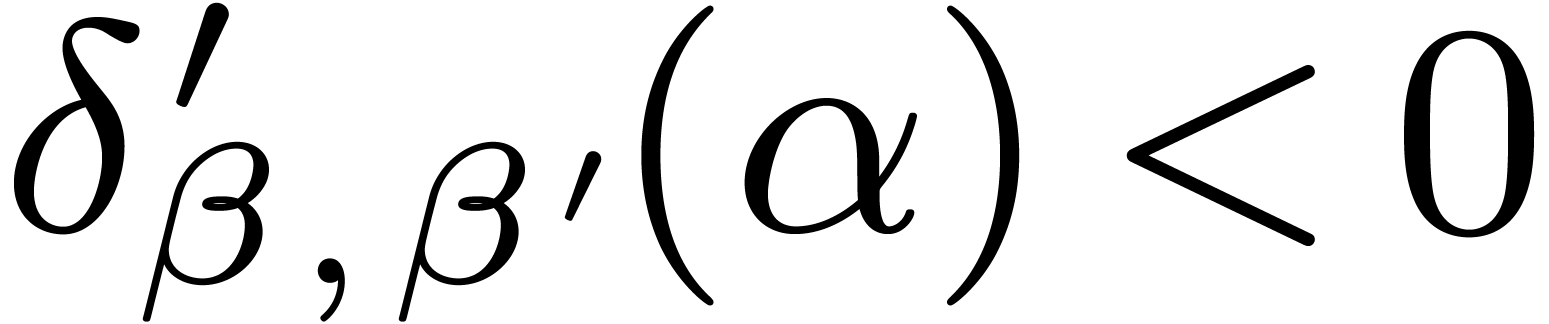 and
and 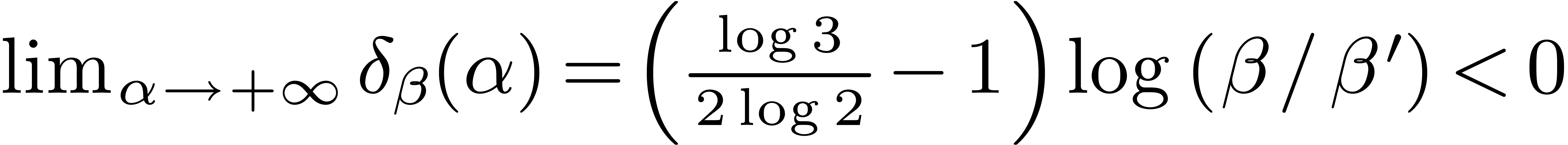 , which implies the
existence of a unique zero of
, which implies the
existence of a unique zero of  ,
written
,
written 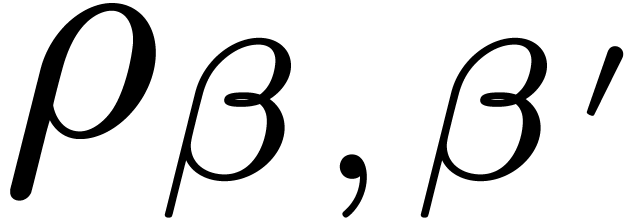 . In particular, with
. In particular, with
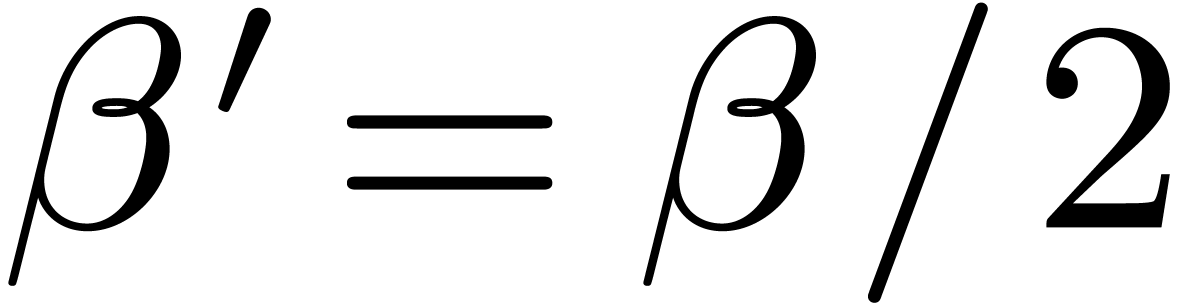 , we obtain
, we obtain 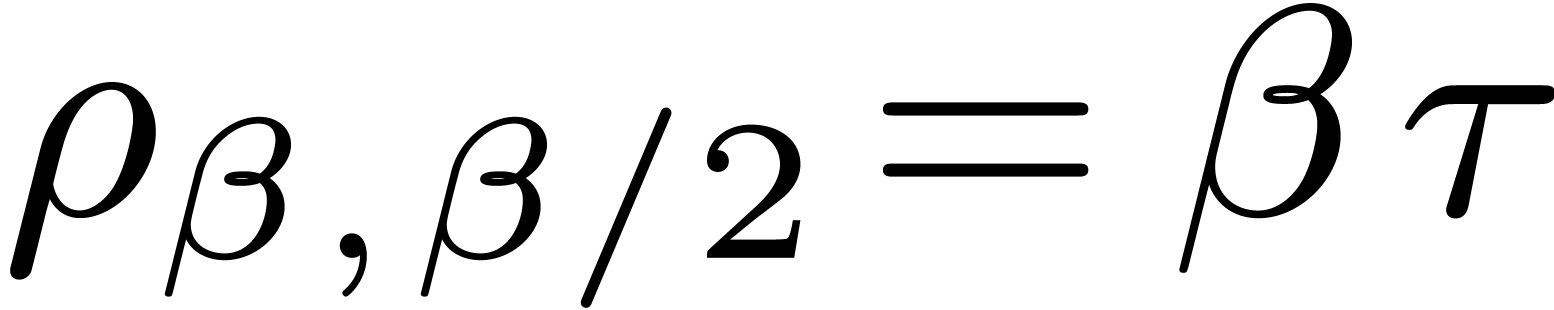 . For convenience we let
. For convenience we let  , and display the first few values:
, and display the first few values:

One can verify that  holds for all
holds for all 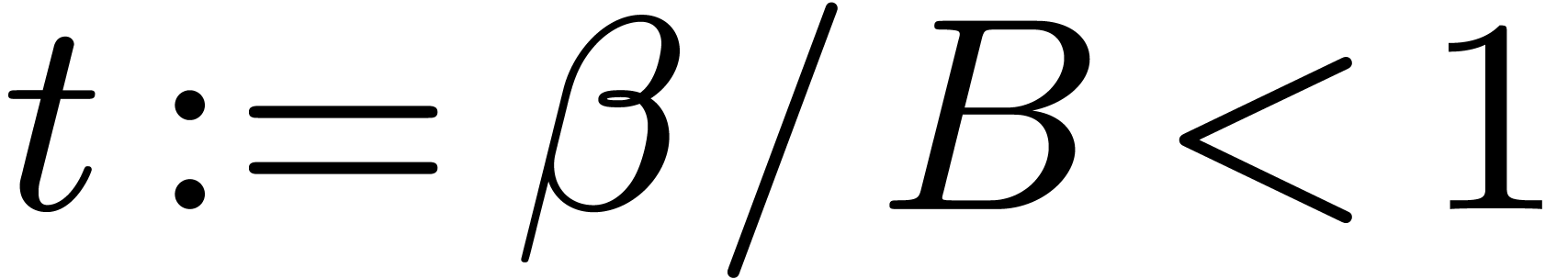 , which implies that
, which implies that  for all
for all 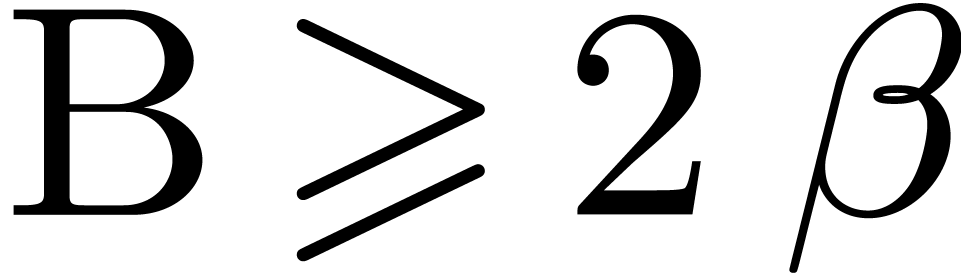 . Therefore
. Therefore 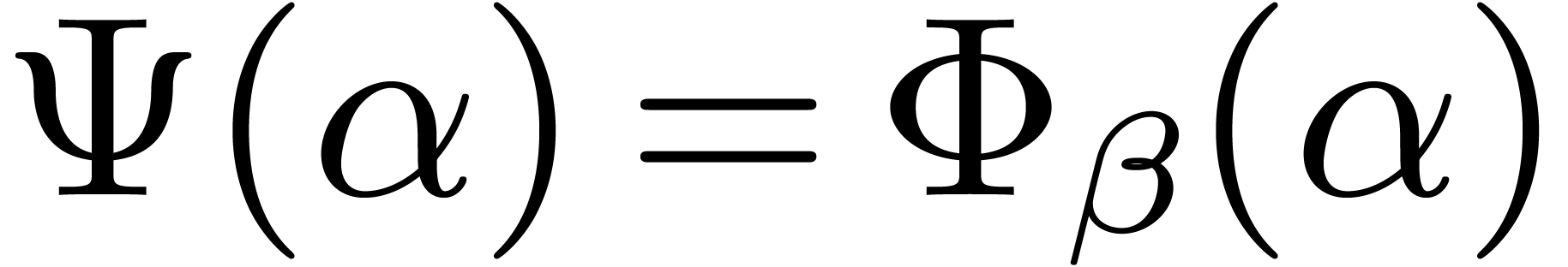 with
with 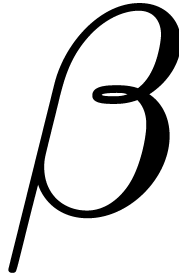 such that
such that  (with the convention that
(with the convention that 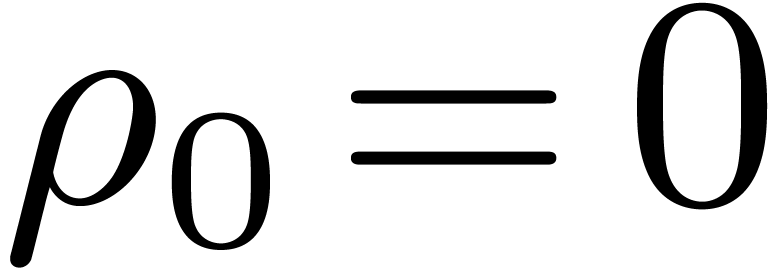 ).
Lemma 10 of the appendix provides us with
).
Lemma 10 of the appendix provides us with 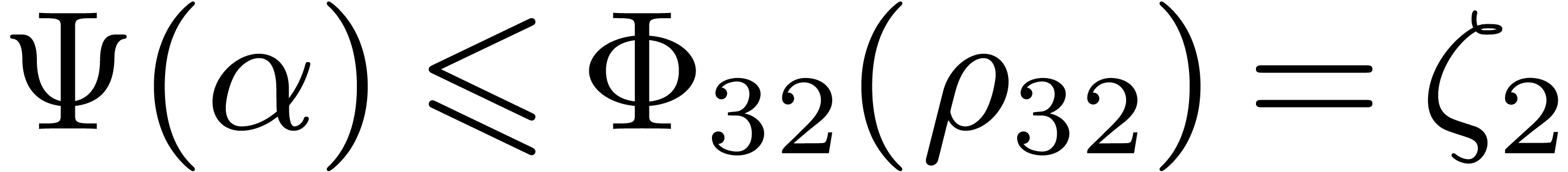 . Therefore there exists a constant
. Therefore there exists a constant  , such that
, such that 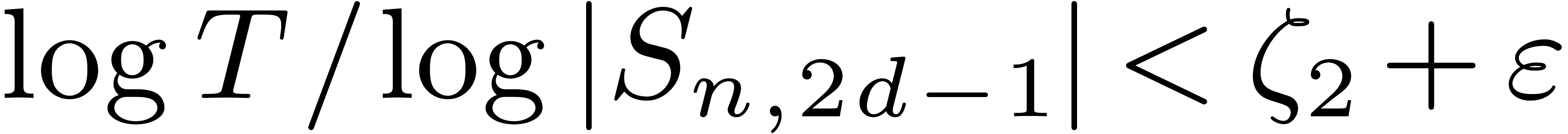 for all
for all 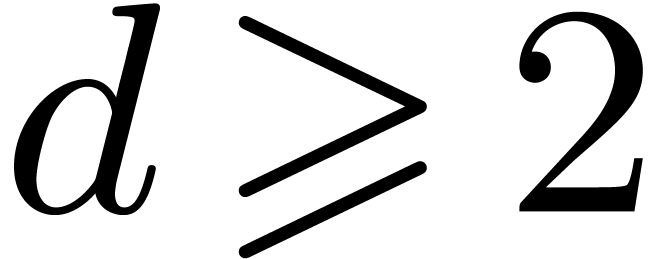 and
and 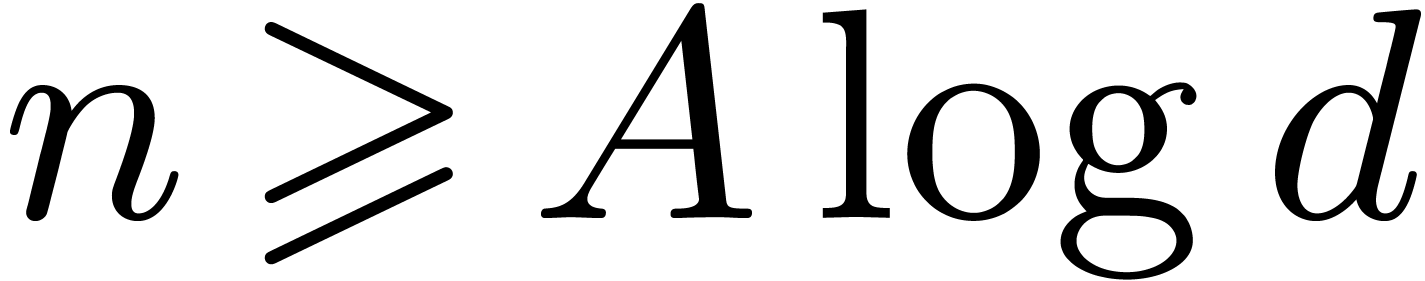 ,
or
,
or 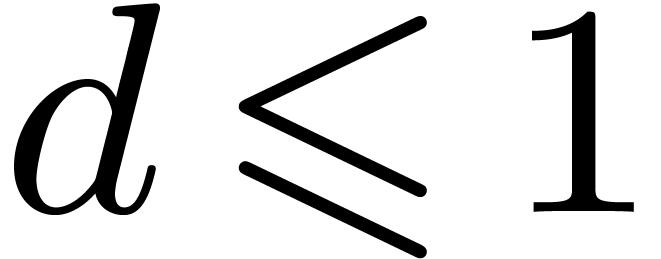 and
and 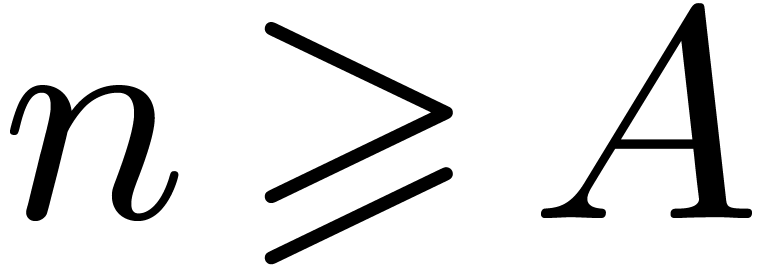 .
.
It remains to bound 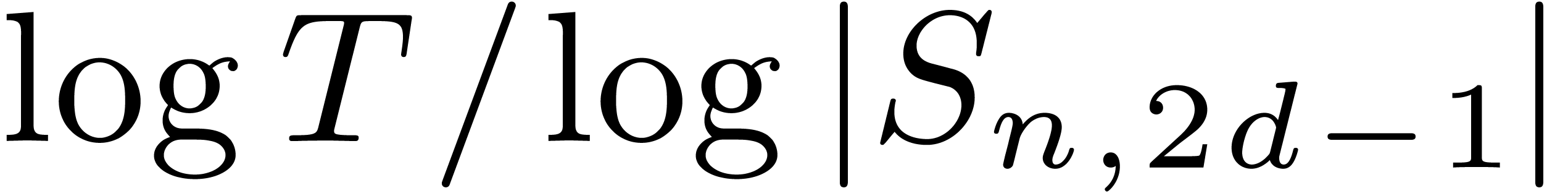 for
for 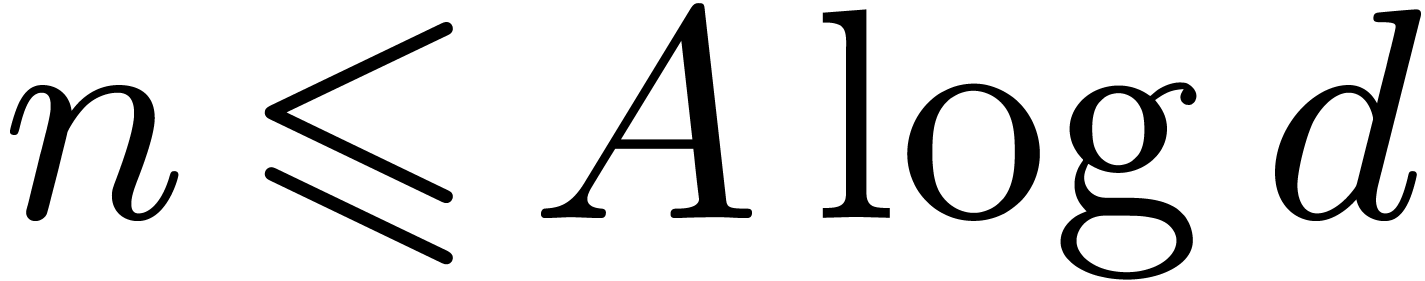 and
and 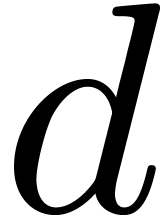 sufficiently large, as in the end of the
proof of Theorem 4. In this range we take
sufficiently large, as in the end of the
proof of Theorem 4. In this range we take 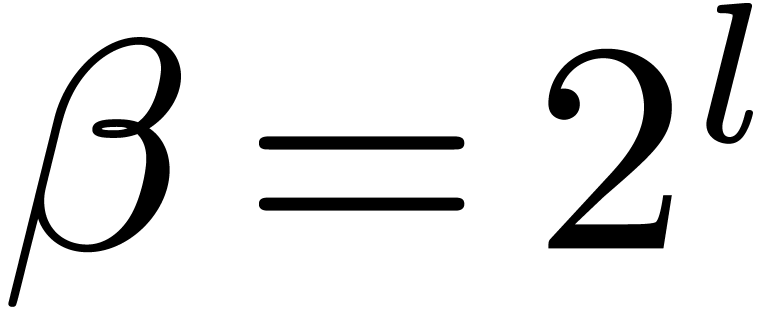 with
with 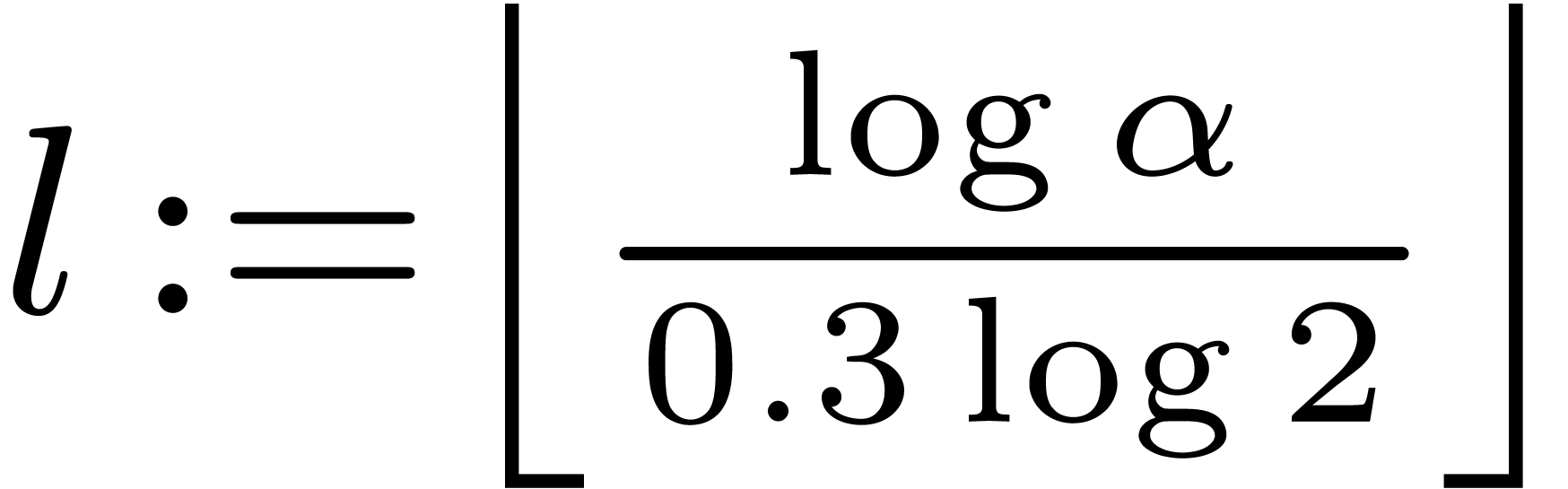 , so that
, so that 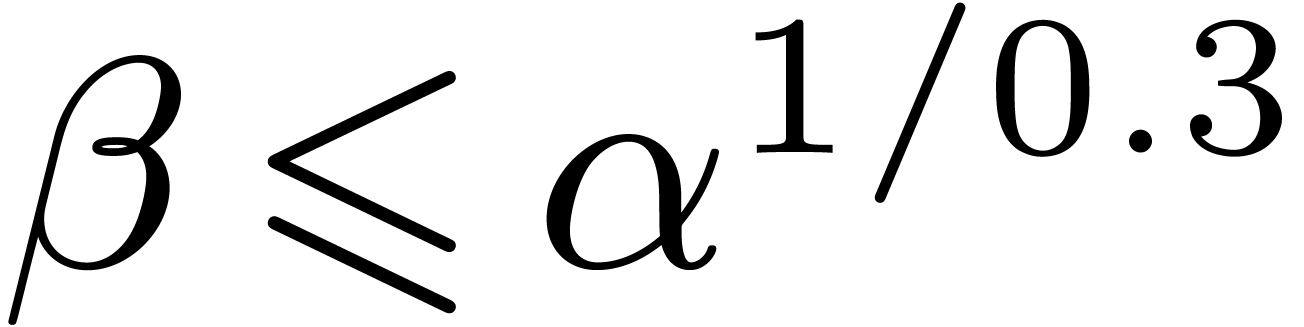 . There exist constants
. There exist constants 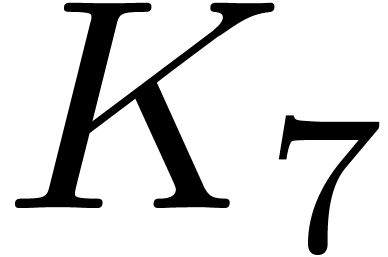 and
and 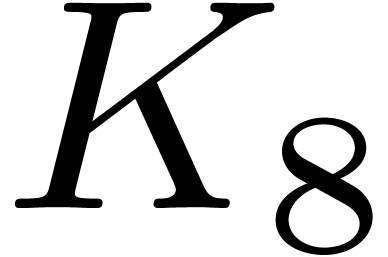 such that:
such that:
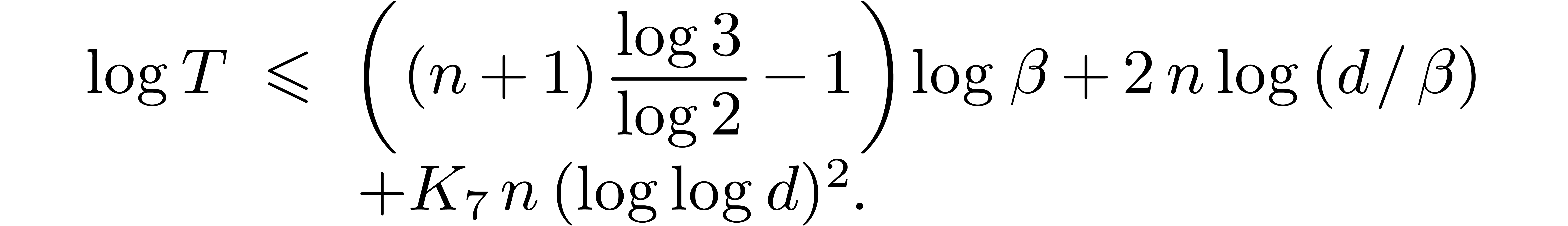
Therefore, using  , we have
, we have
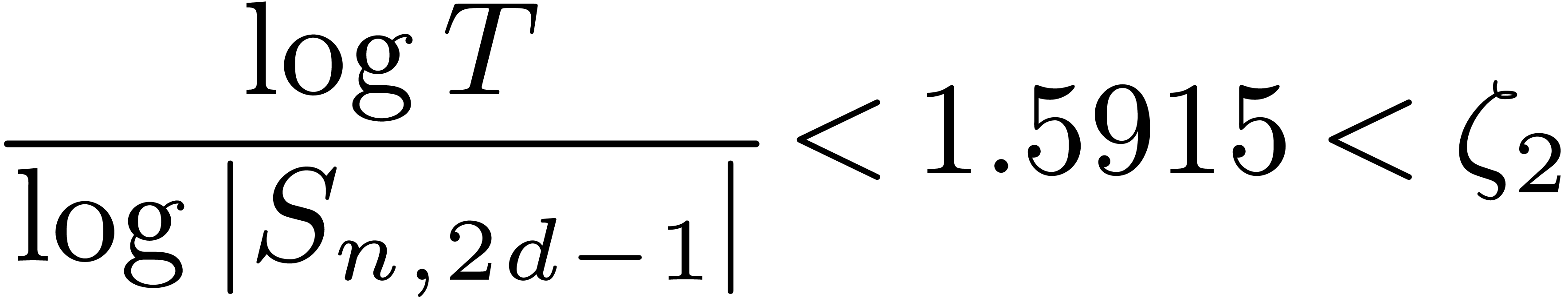
whenever 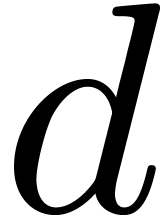 is sufficiently large.
is sufficiently large.
5.2Power series product
Theorem 8. Let
 , and assume that
, and assume that  admits evaluation-interpolation schemes with
admits evaluation-interpolation schemes with 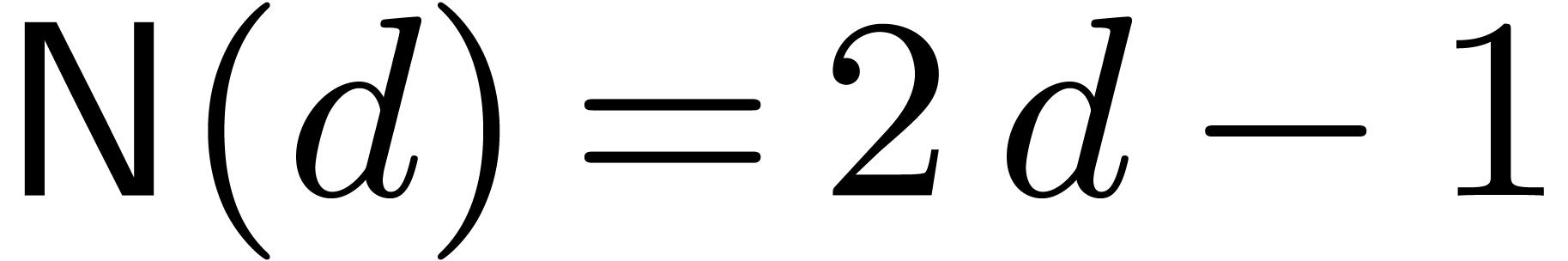 and
and 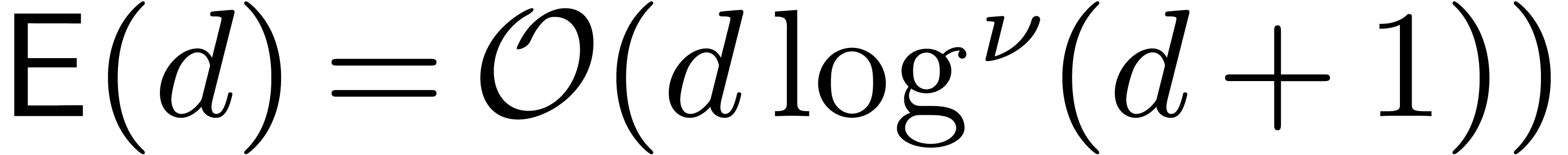 , for all
, for all
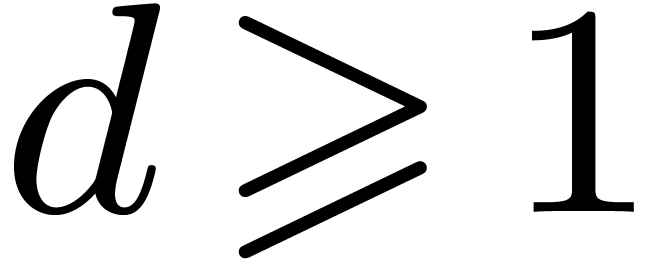 , and for some constant
, and for some constant  . Then two power series in
. Then two power series in 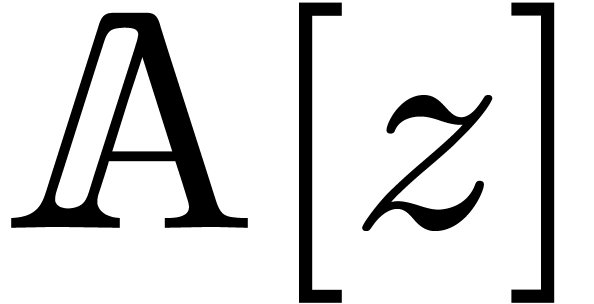 truncated at order
truncated at order 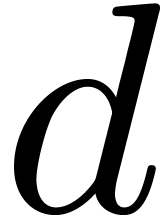 can be
multiplied with truncated-block-multiply
using at most
can be
multiplied with truncated-block-multiply
using at most 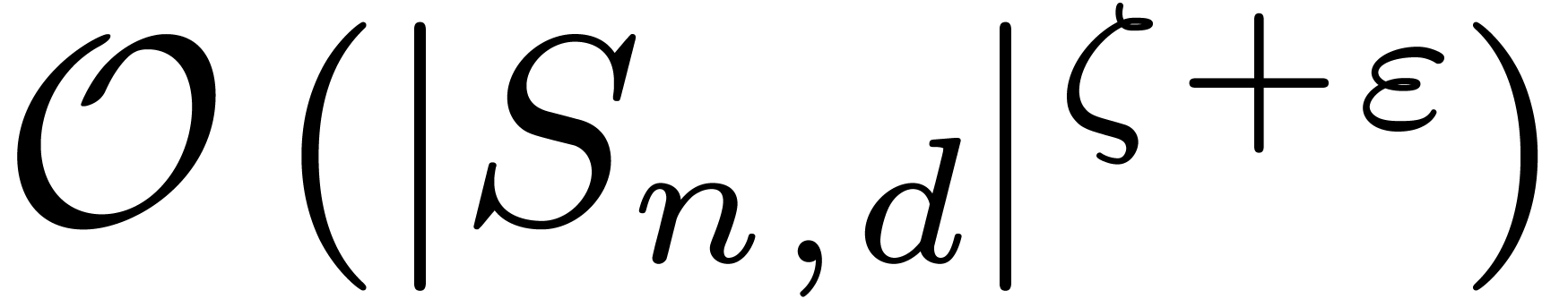 operations in
operations in  , if the sizes of the blocks
, if the sizes of the blocks 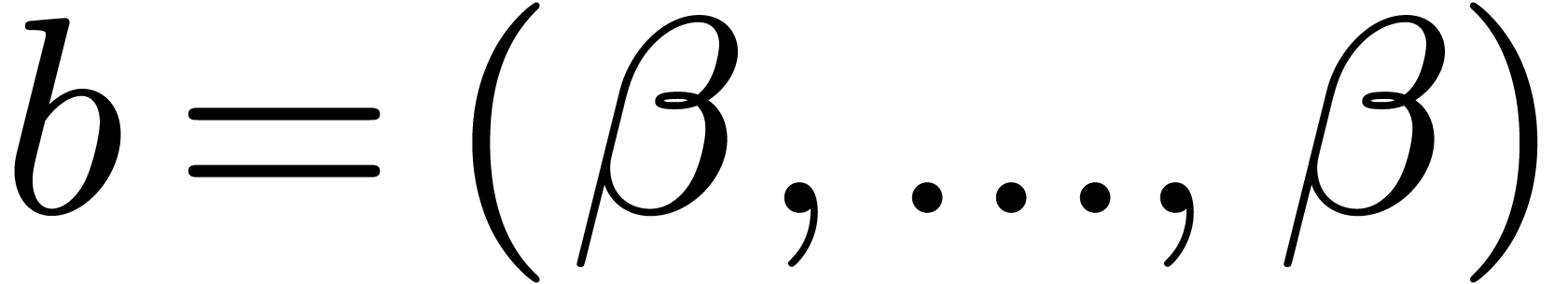 are chosen as follows:
are chosen as follows:
Proof. The proof is similar to the one of Theorem
4. In the present case, for a suitable new constant 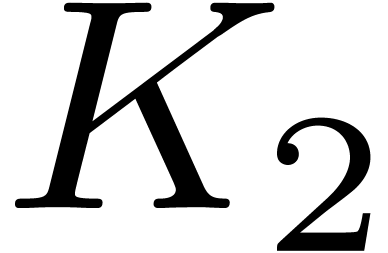 the following inequalities hold:
the following inequalities hold:
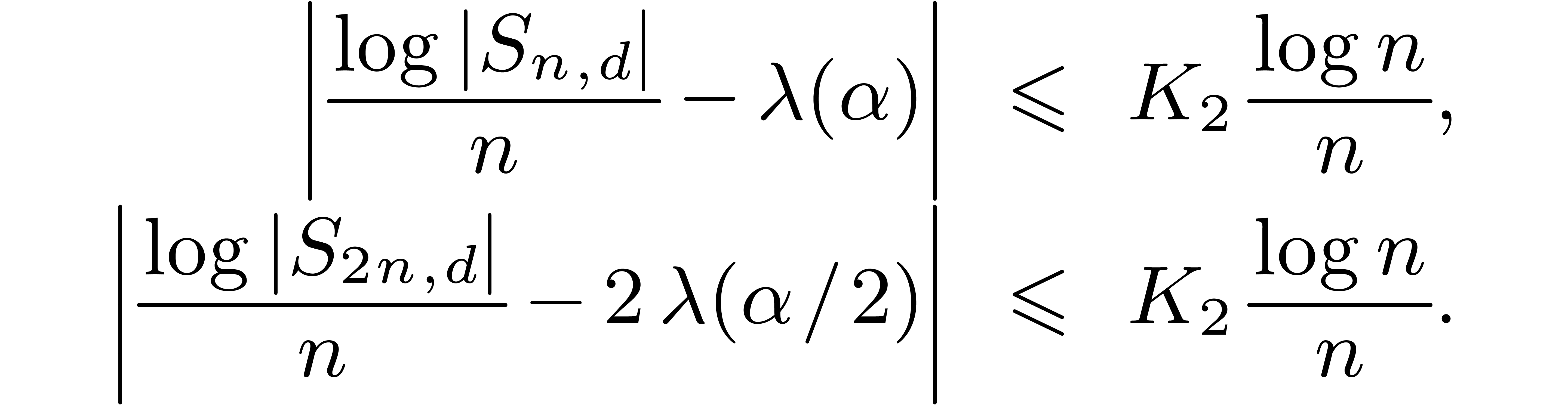
The cost of the multiplication is bounded by 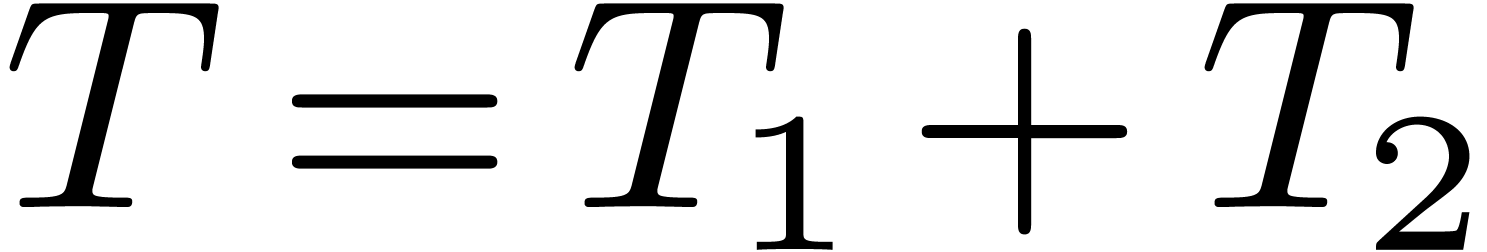 with
with 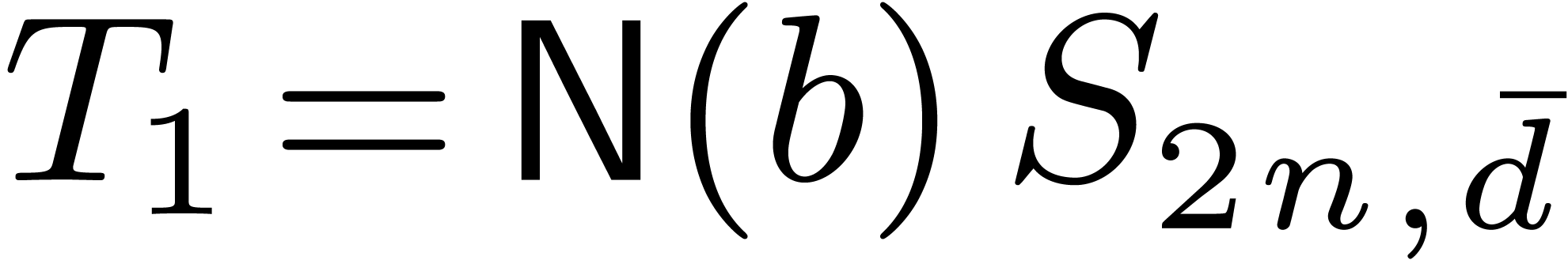 and
and 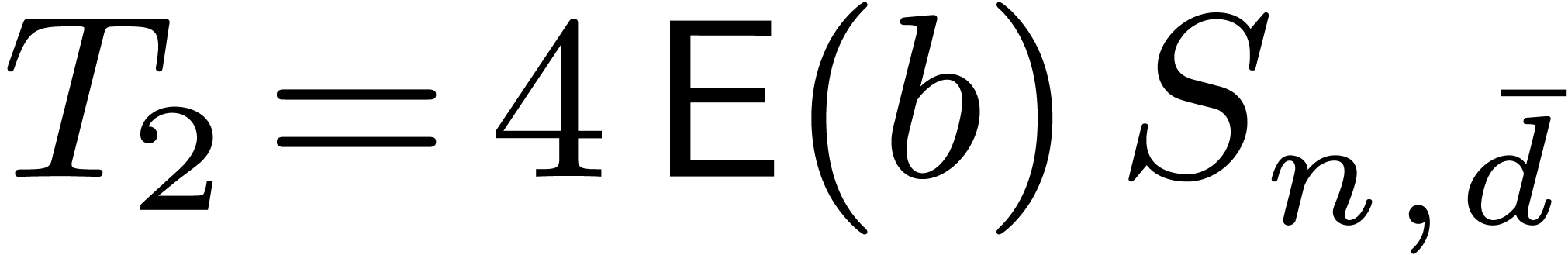 .
There exists a new constant
.
There exists a new constant  such that:
such that:
The present situation is similar to the one of the proof of Theorem 4, with 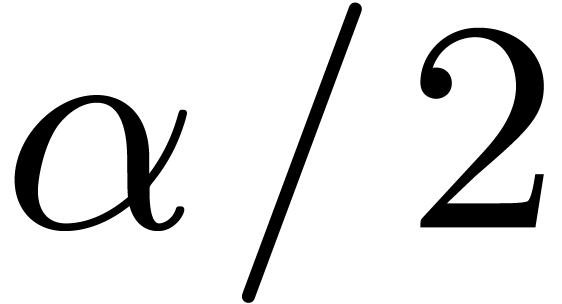 instead of
instead of  . Therefore by taking
. Therefore by taking 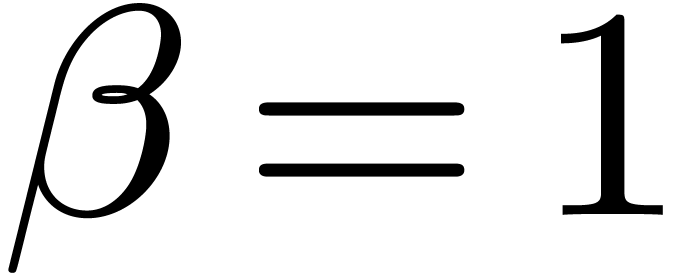 for
for 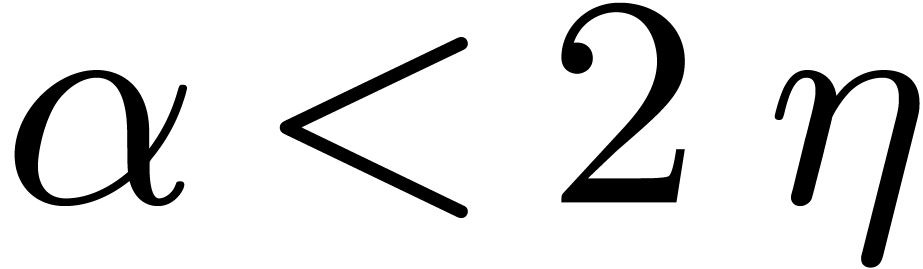 ,
, 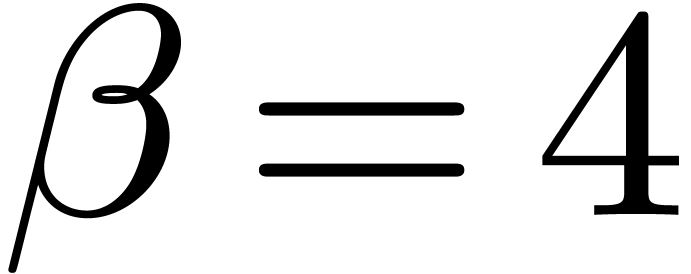 for
for  and
and 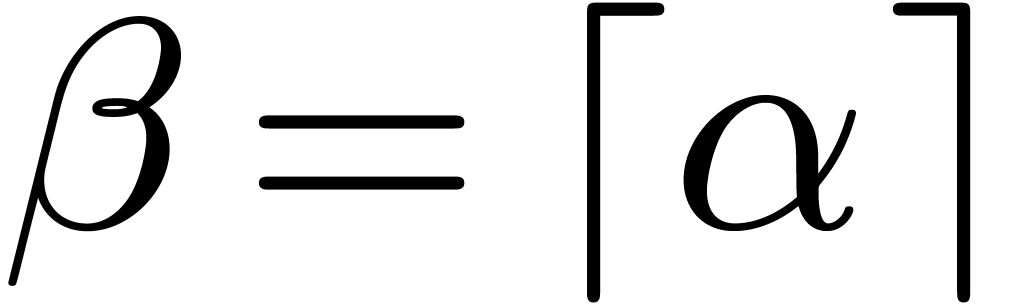 for larger
for larger  , there exists a constant
, there exists a constant  , such that
, such that 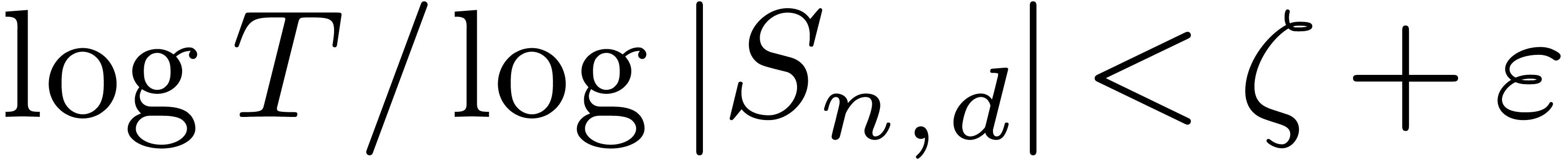 for all
for all 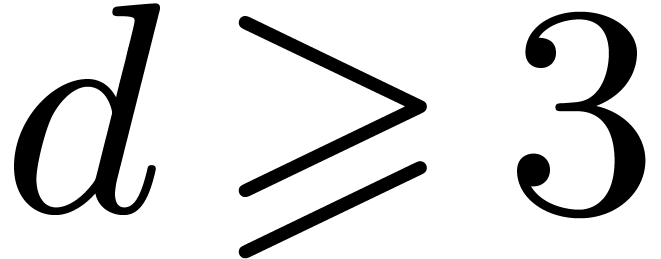 and
and 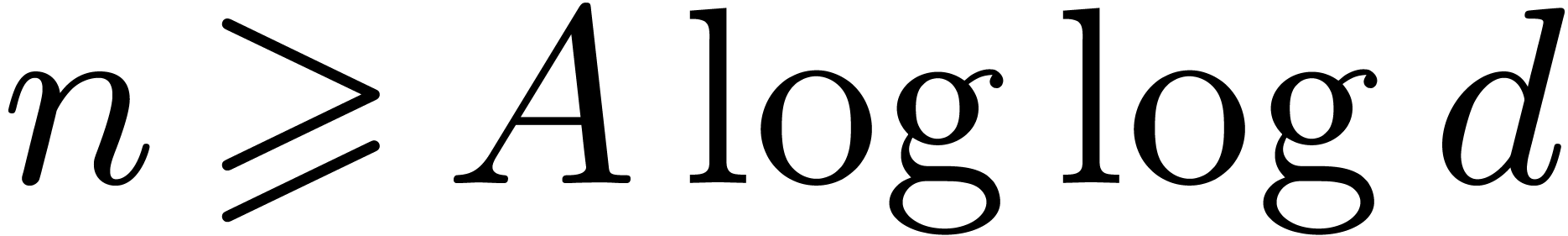 ,
or
,
or  and
and 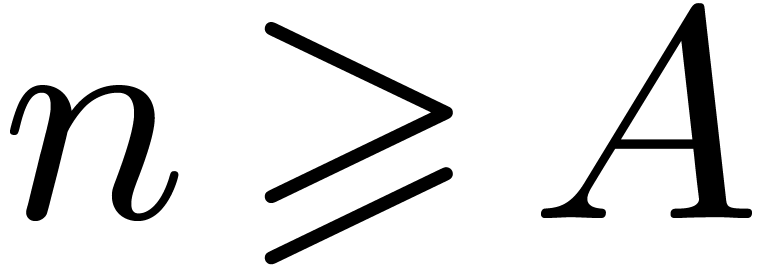 .
.
It remains to bound 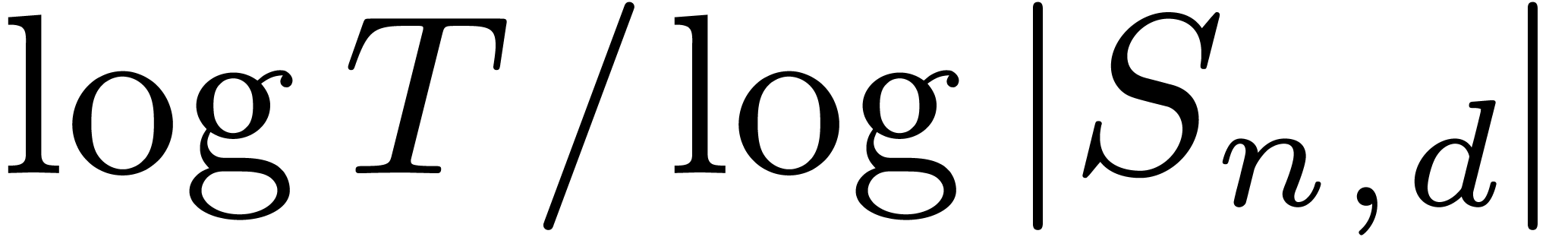 for
for 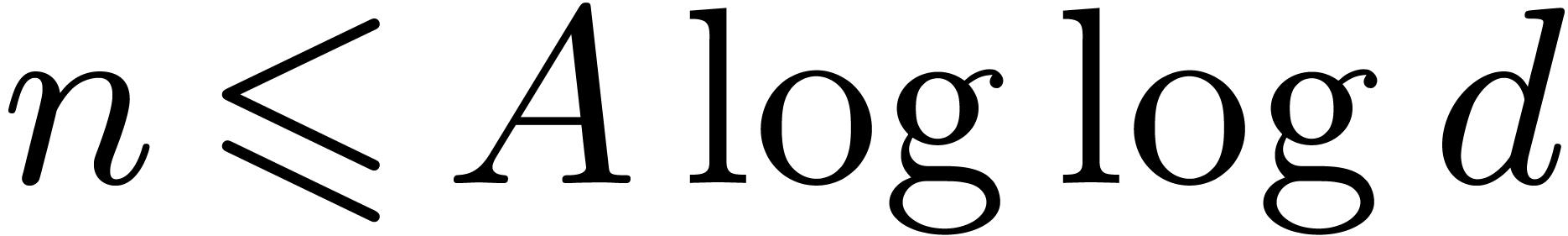 and
and 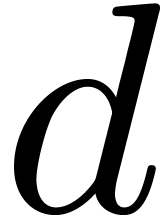 sufficiently large. There exists a new
constant
sufficiently large. There exists a new
constant 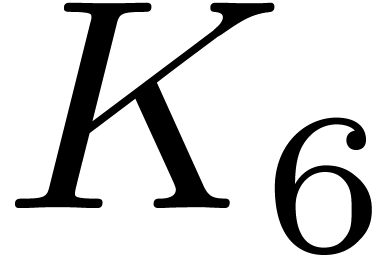 such that:
such that:
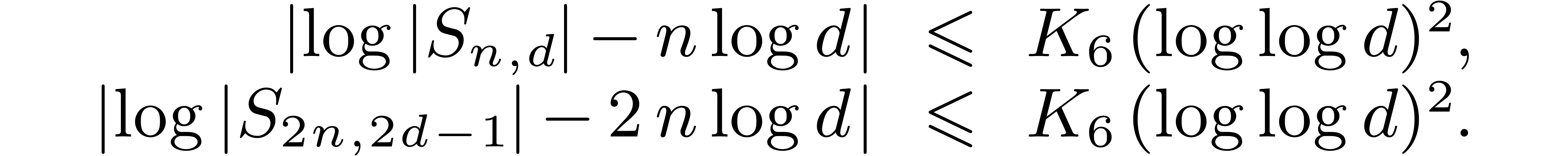
Taking 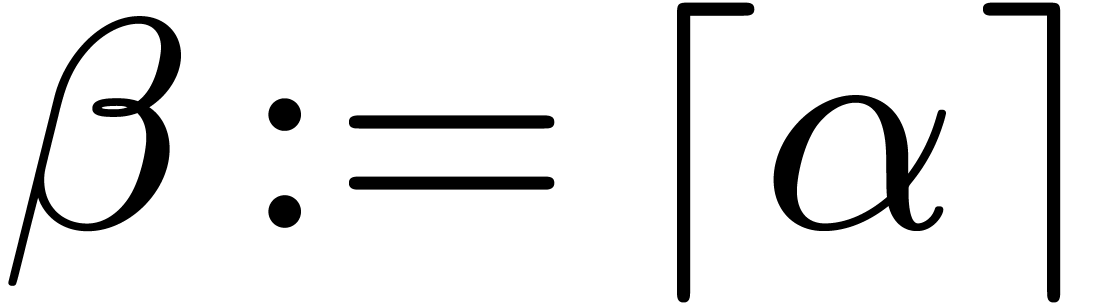 , we thus have a
contant
, we thus have a
contant  with
with
We conclude that 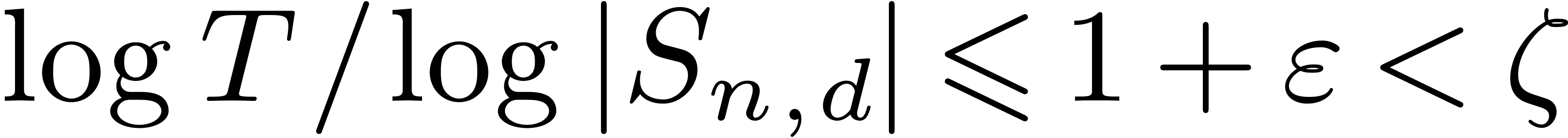 for
for 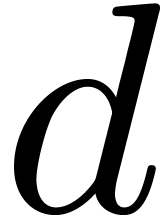 sufficiently large.
sufficiently large.
6.References
-
[1]
-
P. Bürgisser, M. Clausen, and M. A.
Shokrollahi. Algebraic complexity theory.
Springer-Verlag, 1997.
-
[2]
-
J. Canny, E. Kaltofen, and Y. Lakshman. Solving
systems of non-linear polynomial equations faster. In Proc.
ISSAC 1989, pages 121–128, Portland, Oregon, A.C.M.,
New York, 1989. ACM Press.
-
[3]
-
D. G. Cantor and E. Kaltofen. On fast
multiplication of polynomials over arbitrary algebras. Acta
Informatica, 28:693–701, 1991.
-
[4]
-
S. A. Cook. On the minimum computation time of
functions. PhD thesis, Harvard University, 1966.
-
[5]
-
J. W. Cooley and J. W. Tukey. An algorithm for the
machine calculation of complex Fourier series. Math.
Computat., 19:297–301, 1965.
-
[6]
-
S. Czapor, K. Geddes, and G. Labahn. Algorithms
for Computer Algebra. Kluwer Academic Publishers, 1992.
-
[7]
-
J. H. Davenport, Y. Siret, and É. Tournier.
Calcul formel : systèmes et algorithmes de
manipulations algébriques. Masson, Paris, France,
1987.
-
[8]
-
R. Fateman. Comparing the speed of programs for
sparse polynomial multiplication. SIGSAM Bull.,
37(1):4–15, 2003.
-
[9]
-
L. Fousse, G. Hanrot, V. Lefèvre, P.
Pélissier, and P. Zimmermann. MPFR: A
multiple-precision binary floating-point library with correct
rounding. ACM Transactions on Mathematical Software,
33(2), June 2007. Software available at http://www.mpfr.org.
-
[10]
-
M. Gastineau and J. Laskar. Development of TRIP:
Fast sparse multivariate polynomial multiplication using burst
tries. In Proceedings of ICCS 2006, LNCS 3992, pages
446–453. Springer, 2006.
-
[11]
-
J. von zur Gathen and J. Gerhard. Modern
Computer Algebra. Cambridge University Press, 2-nd
edition, 2003.
-
[12]
-
G. Hanrot and P. Zimmermann. A long note on
Mulders' short product. J. Symbolic Comput.,
37(3):391–401, 2004.
-
[13]
-
J. van der Hoeven. Relax, but don't be too lazy.
J. Symbolic Comput., 34(6):479–542, 2002.
-
[14]
-
J. van der Hoeven. The truncated Fourier transform
and applications. In J. Gutierrez, editor, Proc. ISSAC
2004, pages 290–296, Univ. of Cantabria, Santander,
Spain, July 4–7 2004.
-
[15]
-
J. van der Hoeven. Notes on the truncated Fourier
transform. Technical Report 2005-5, Université
Paris-Sud, Orsay, France, 2005.
-
[16]
-
J. van der Hoeven. Newton's method and FFT trading.
J. Symbolic Comput., 45(8), 2010.
-
[17]
-
J. van der Hoeven et al. Mathemagix. Available from
http://www.mathemagix.org, 2002.
-
[18]
-
J. van der Hoeven and G. Lecerf. On the
bit-complexity of sparse polynomial multiplication. Technical
Report http://hal.archives-ouvertes.fr/hal-00476223,
École polytechnique and CNRS, 2010.
-
[19]
-
J. van der Hoeven and É. Schost. Multi-point
evaluation in higher dimensions. Technical report, HAL, 2010.
http://hal.archives-ouvertes.fr/hal-00477658.
-
[20]
-
S. C. Johnson. Sparse polynomial arithmetic.
SIGSAM Bull., 8(3):63–71, 1974.
-
[21]
-
A. Karatsuba and J. Ofman. Multiplication of
multidigit numbers on automata. Soviet Physics Doklady,
7:595–596, 1963.
-
[22]
-
G. I. Malaschonok and E. S. Satina. Fast
multiplication and sparse structures. Programming and
Computer Software, 30(2):105–109, 2004.
-
[23]
-
M. Monagan and R. Pearce. Polynomial division using
dynamic arrays, heaps, and packed exponent vectors. In
Proc. of CASC 2007, pages 295–315. Springer,
2007.
-
[24]
-
M. Monagan and R. Pearce. Parallel sparse
polynomial multiplication using heaps. In Proc. ISSAC
2009, pages 263–270, New York, NY, USA, 2009. ACM.
-
[25]
-
M. Monagan and R. Pearce. Polynomial multiplication
and division in Maple 14. Communications in Computer
Algebra, 44(4):205–209, 2010.
-
[26]
-
M. Monagan and R. Pearce. Sparse polynomial pseudo
division using a heap. J. Symbolic Comput.,
46(7):807–822, 2011.
-
[27]
-
A. Schönhage and V. Strassen. Schnelle
Multiplikation grosser Zahlen. Computing,
7:281–292, 1971.
-
[28]
-
D. R. Stoutemyer. Which polynomial representation
is best? In Proceedings of the 1984 MACSYMA Users'
Conference: Schenectady, New York, July 23–25, 1984,
pages 221–243, 1984.
-
[29]
-
A. L. Toom. The complexity of a scheme of
functional elements realizing the multiplication of integers.
Soviet Mathematics, 4(2):714–716, 1963.
-
[30]
-
T. Yan. The geobucket data structure for
polynomials. J. Symbolic Comput., 25(3):285–293,
1998.
AppendixTechnical Lemmas
This appendix contains details on how one can bound the functions 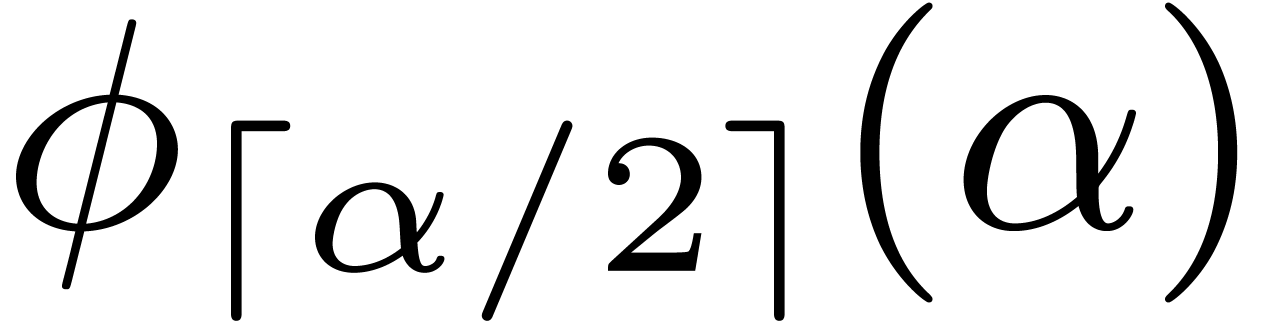 and
and  used in Section 5.
We first prove the bounds in an explicit neighbourhood of infinity and
then we rely on certified ball arithmetic for the remaining compact set.
used in Section 5.
We first prove the bounds in an explicit neighbourhood of infinity and
then we rely on certified ball arithmetic for the remaining compact set.
Lemma 9. For
all  we have
we have  .
.
Proof. Let  and
and  . We shall first show that
. We shall first show that 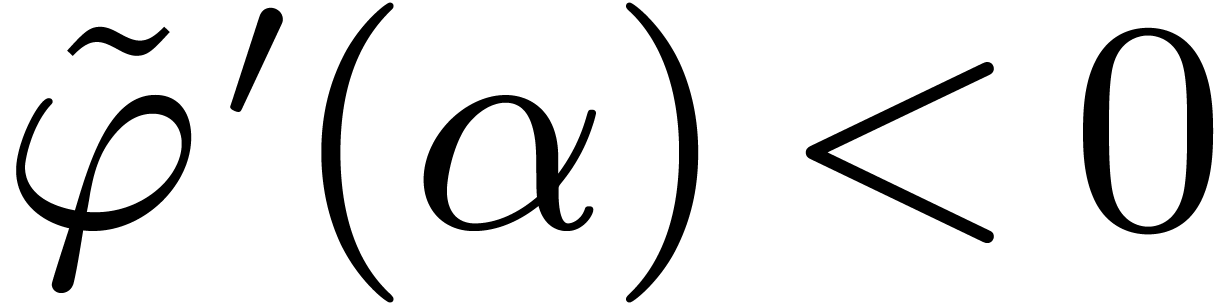 for all
for all 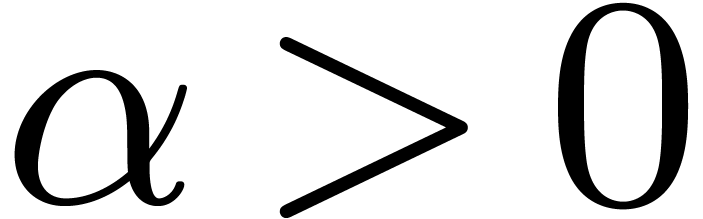 .
Let
.
Let  . Since
. Since 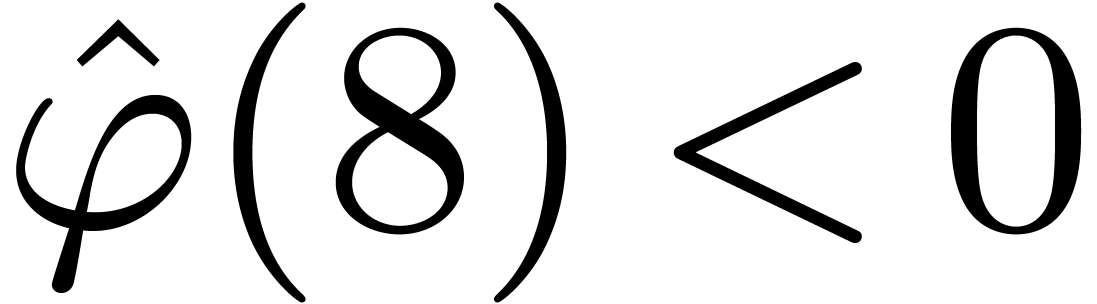 , it suffices to show that
, it suffices to show that 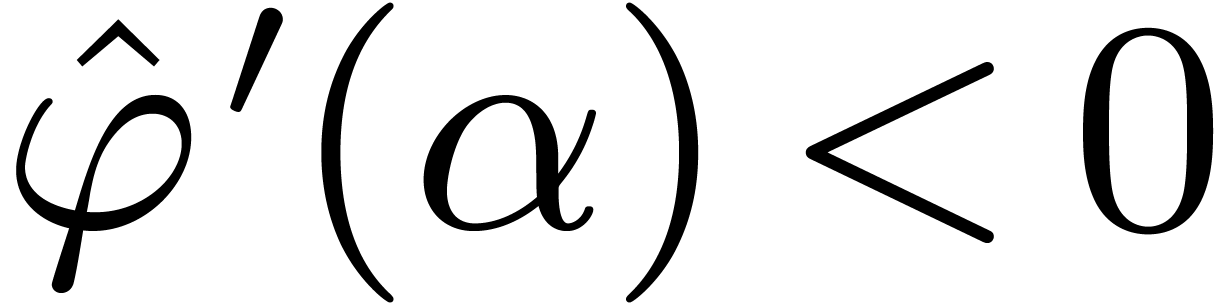 . Since
. Since  ,
we let
,
we let 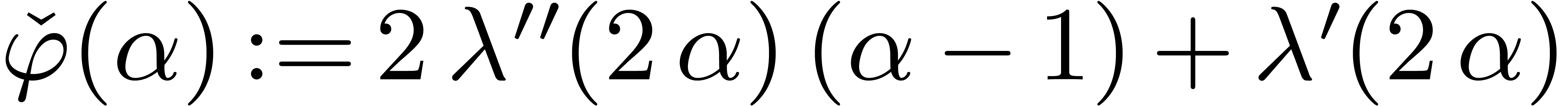 , and have to prove
that
, and have to prove
that 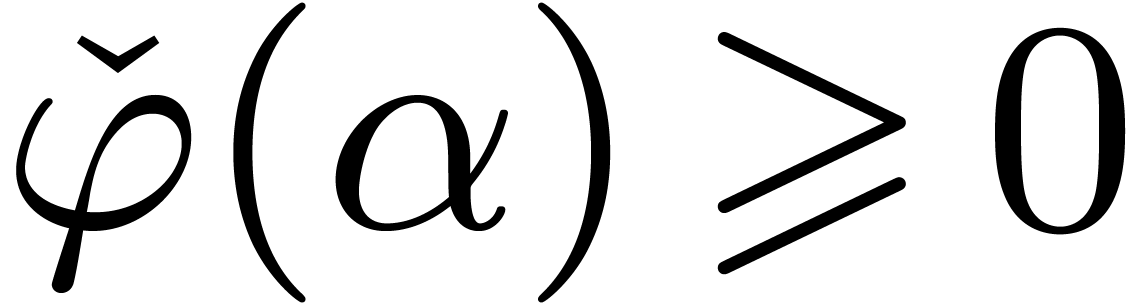 . The latter inequality
is correct since
. The latter inequality
is correct since 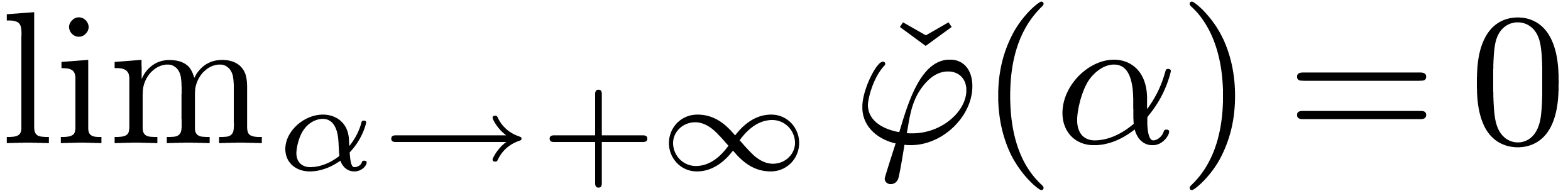 , and
, and 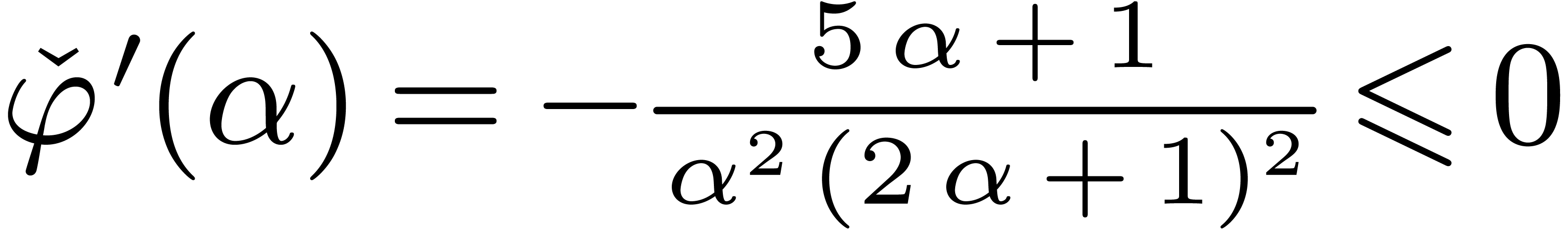 for
for 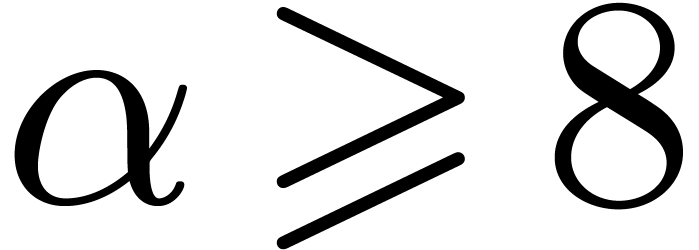 . On
the other hand, for
. On
the other hand, for 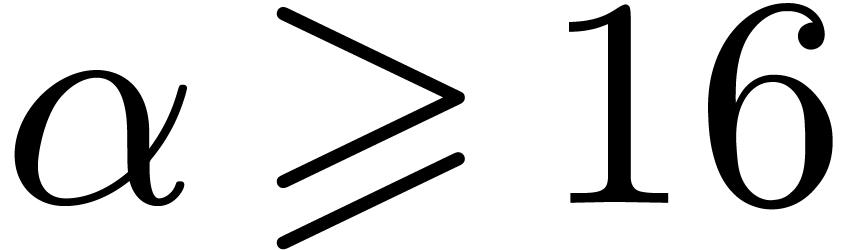 we have
we have
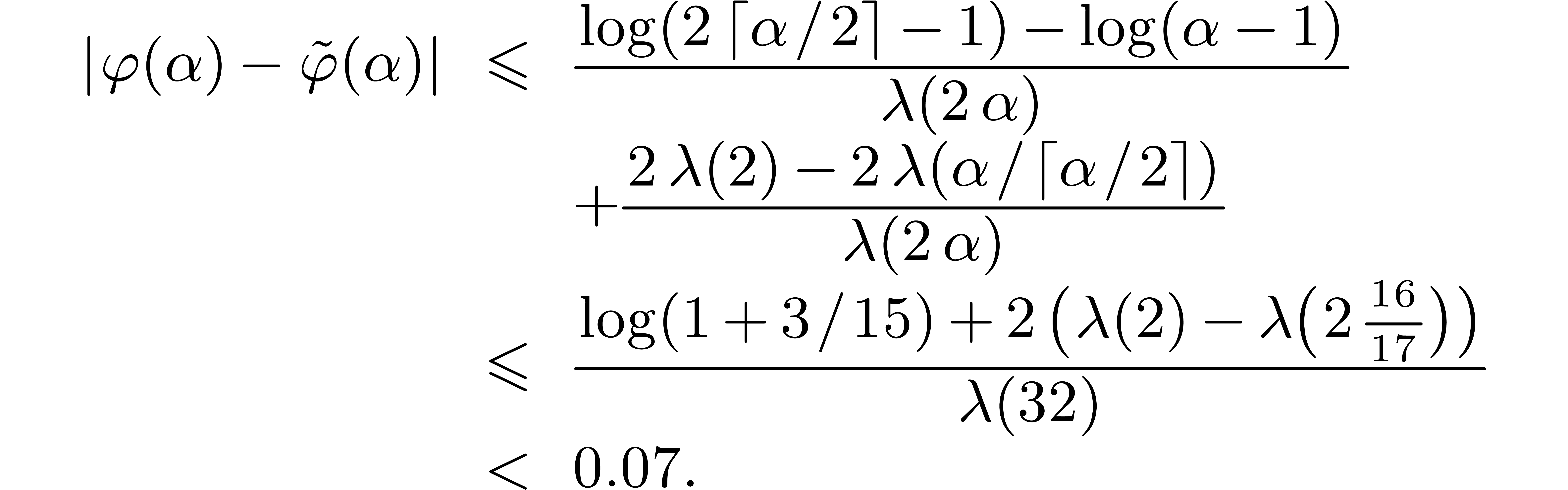
Since  , we have shown that
, we have shown that
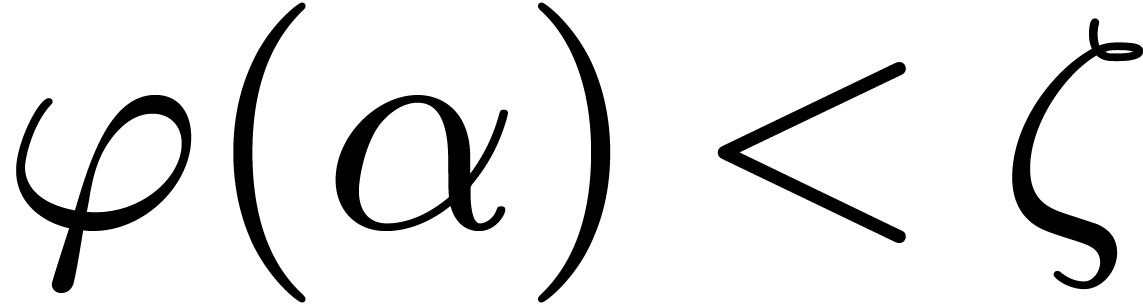 for
for  .
For
.
For  between
between  and
and  , we appeal to numeric computations
to verify that
, we appeal to numeric computations
to verify that 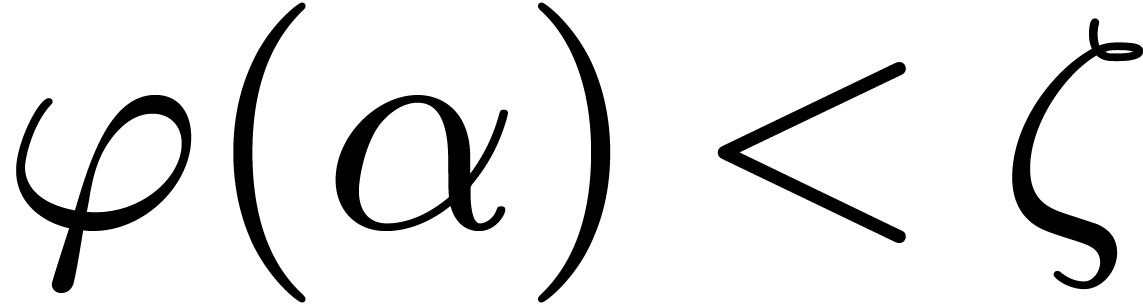 still holds.
still holds.
Lemma 10. For
all 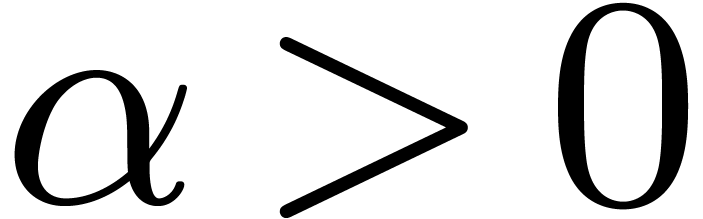 we have
we have 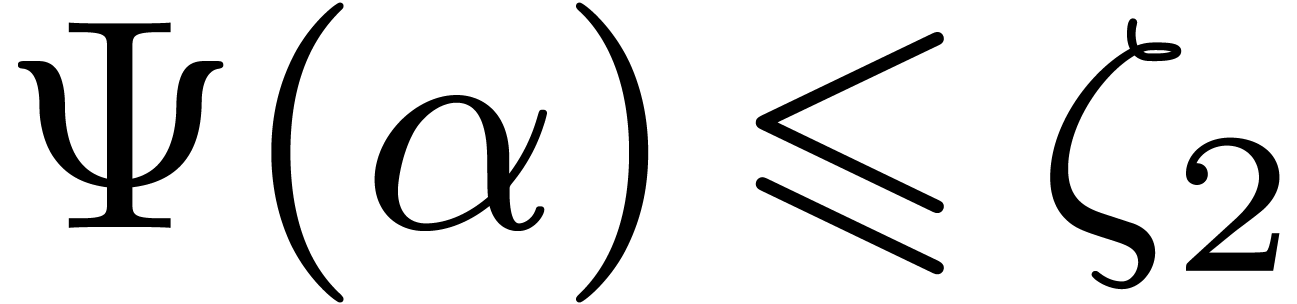 .
.
Proof. Let 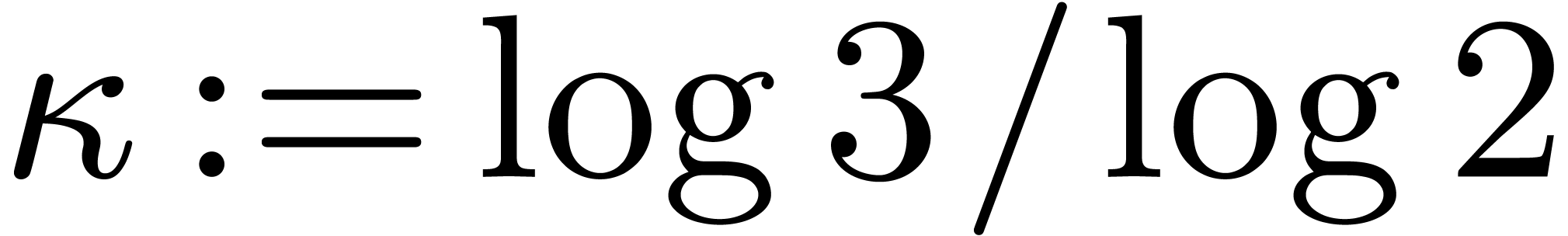 ,
and
,
and 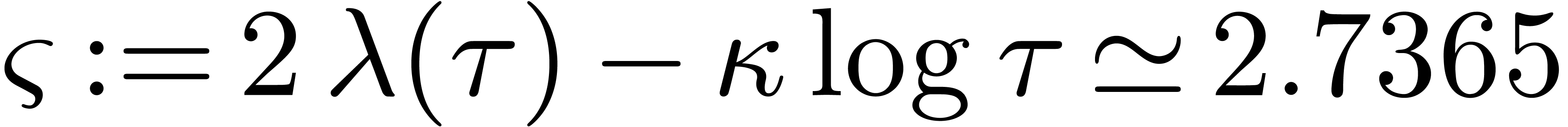 . Let
. Let 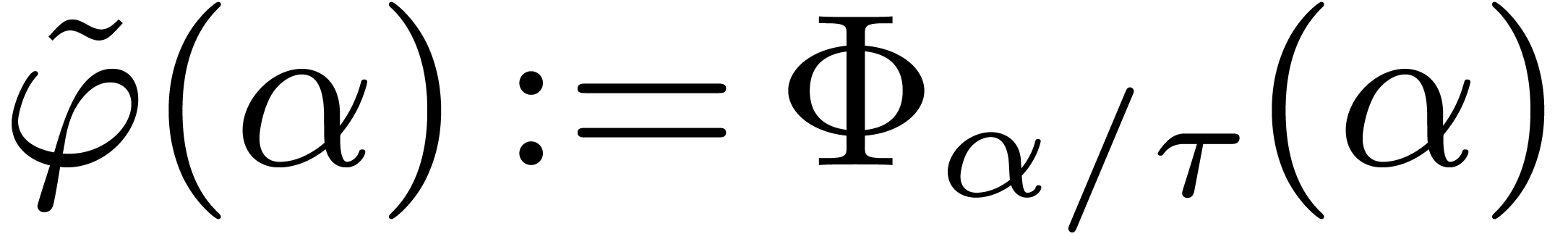 . We shall first show that
. We shall first show that 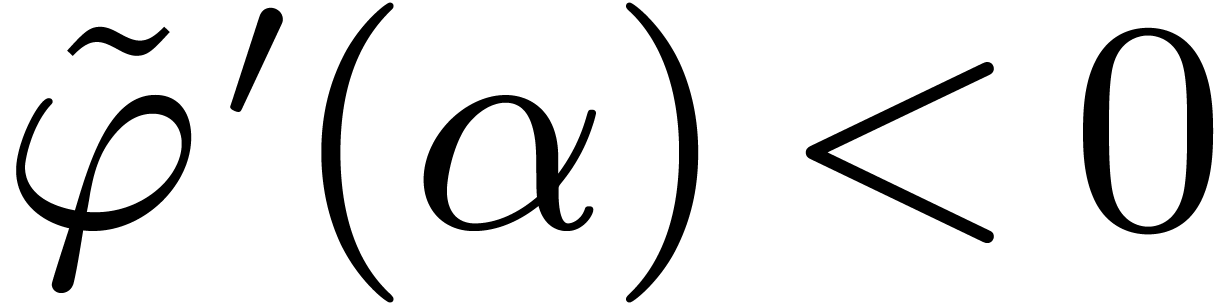 for all
for all 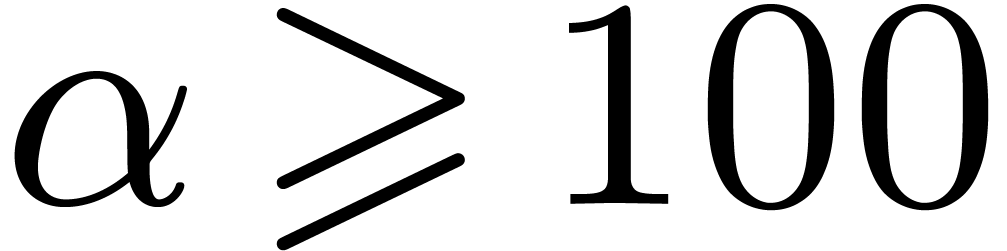 . Let
. Let 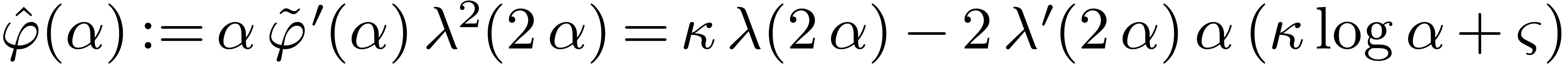 . Since
. Since 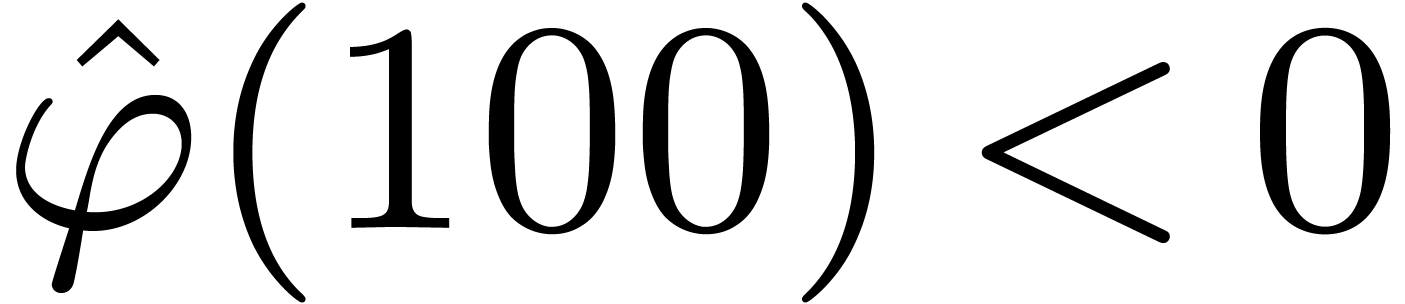 ,
it suffices to show that
,
it suffices to show that 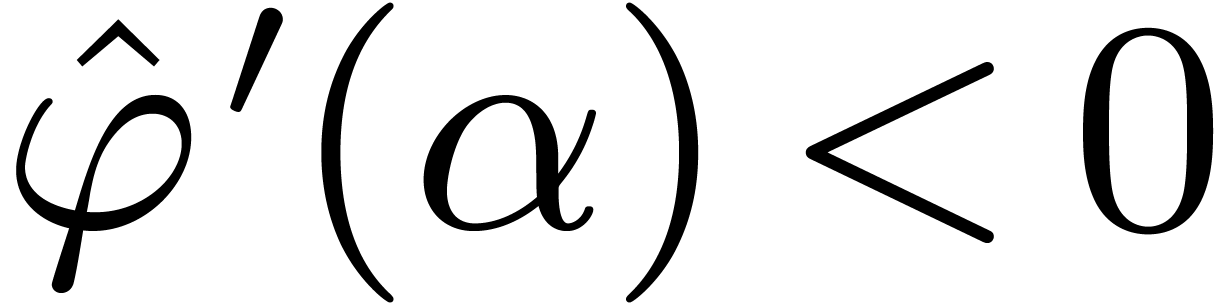 .
Since
.
Since 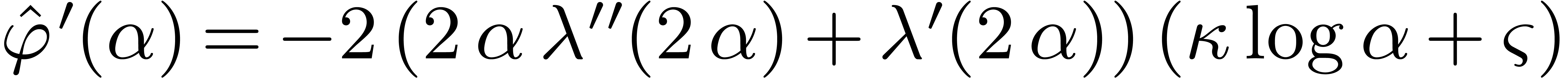 , we let
, we let 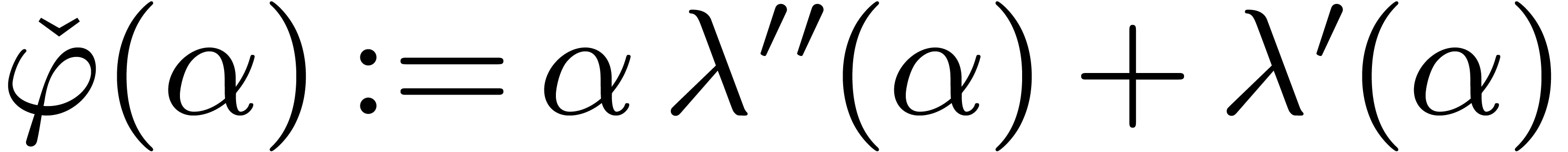 , and have to prove that
, and have to prove that 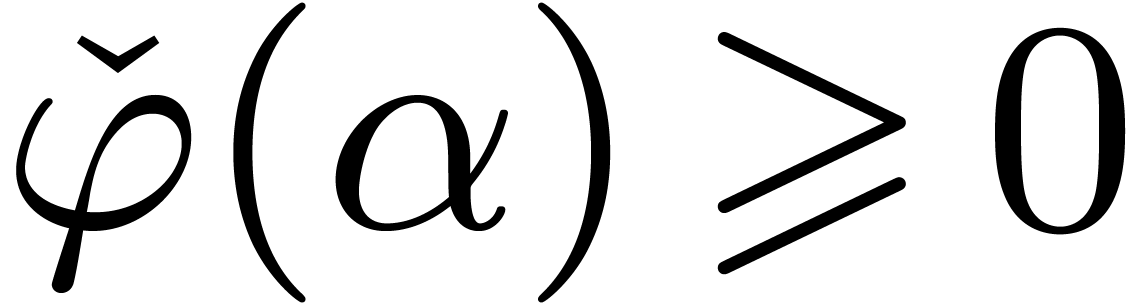 . The latter inequality is correct since
. The latter inequality is correct since 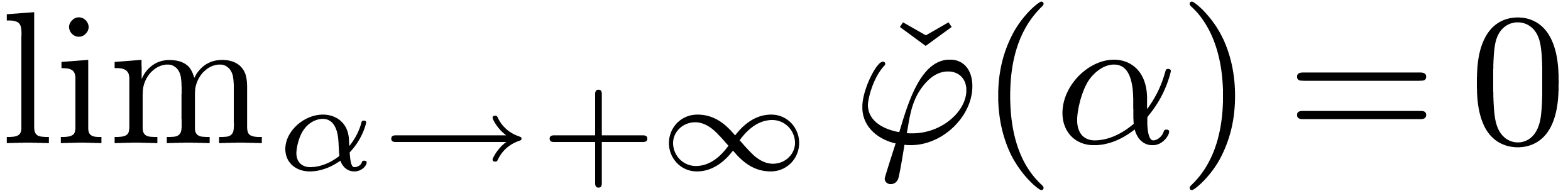 , and
, and 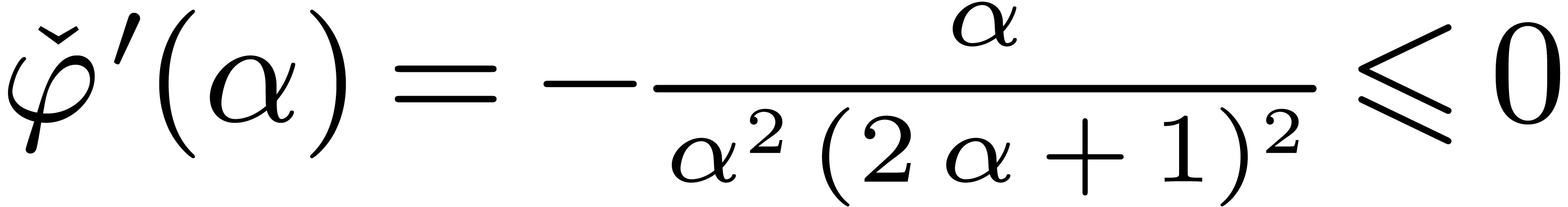 .
.
Let  and
and  .
We introduce
.
We introduce 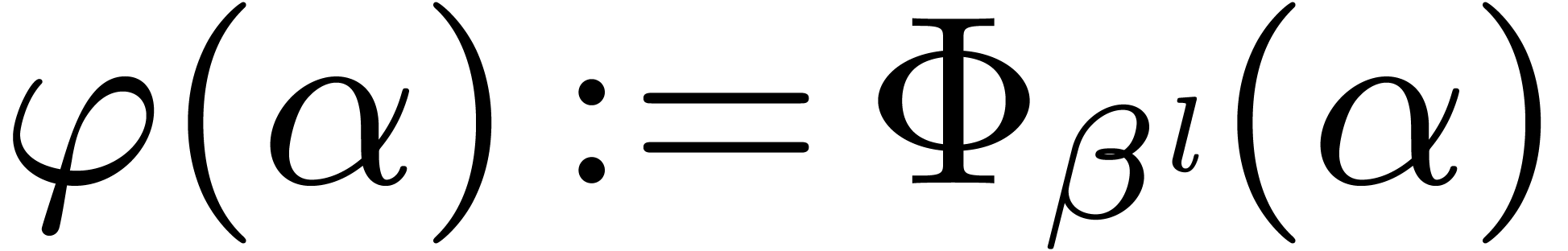 . Since
. Since 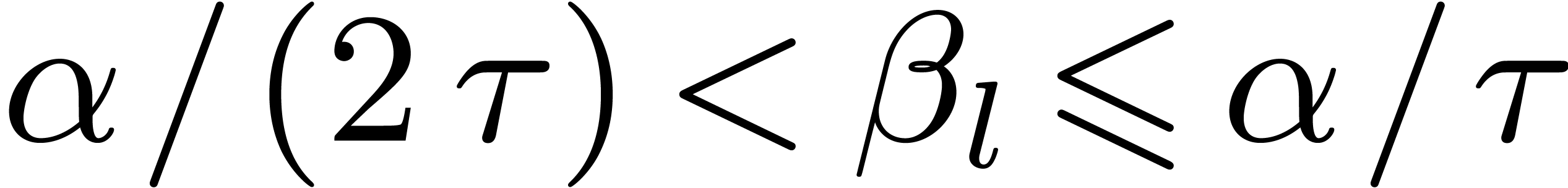 , for
, for 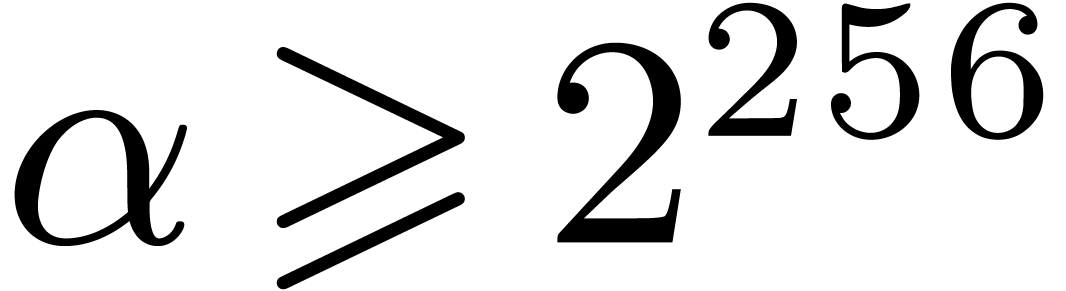 ,
we have
,
we have
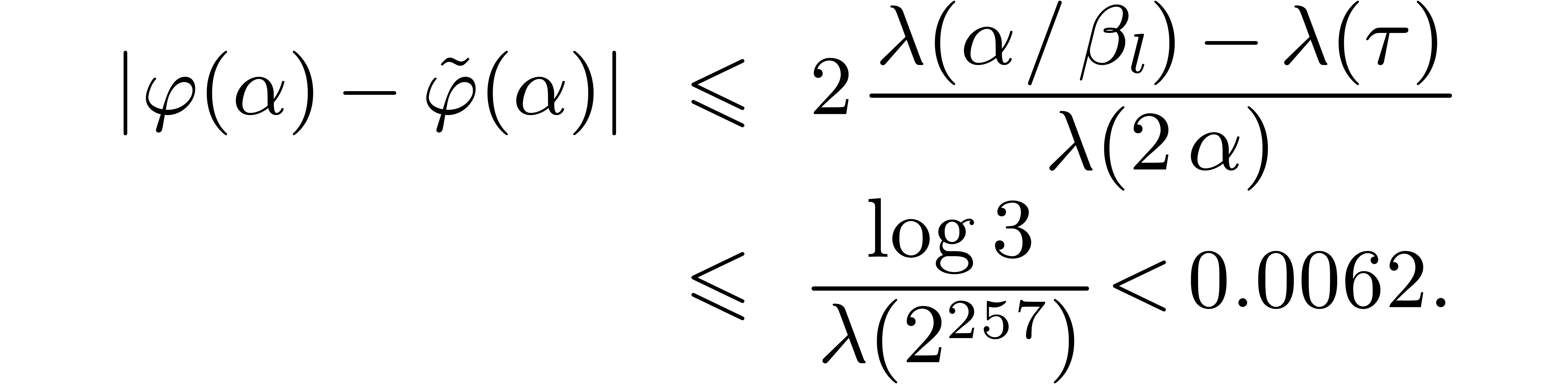
Since  , we have shown that
, we have shown that
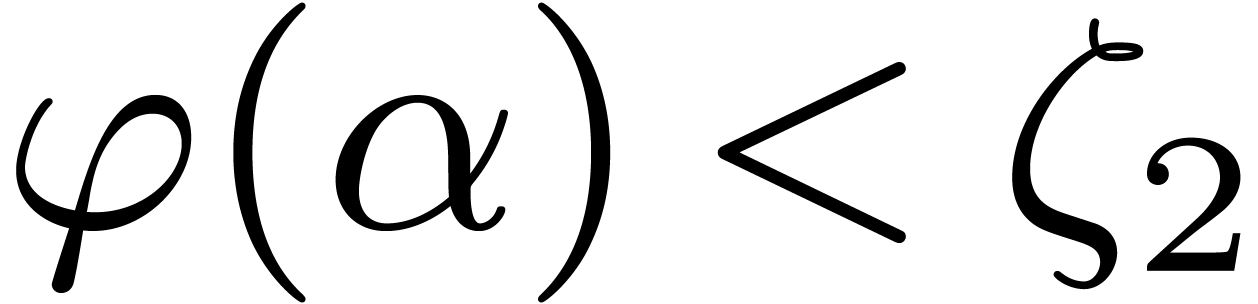 for
for 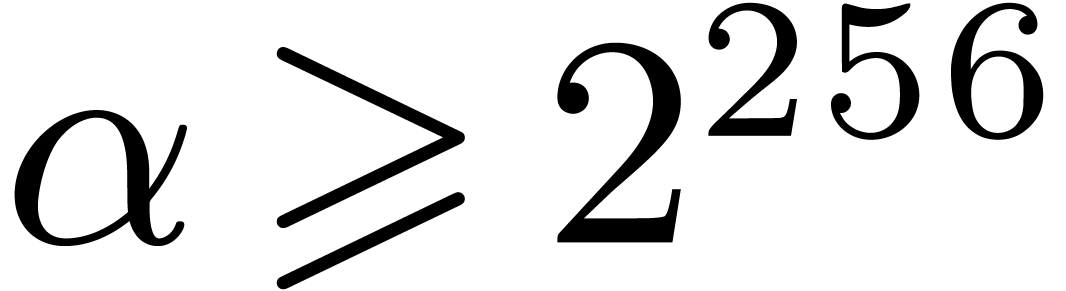 .
.
For 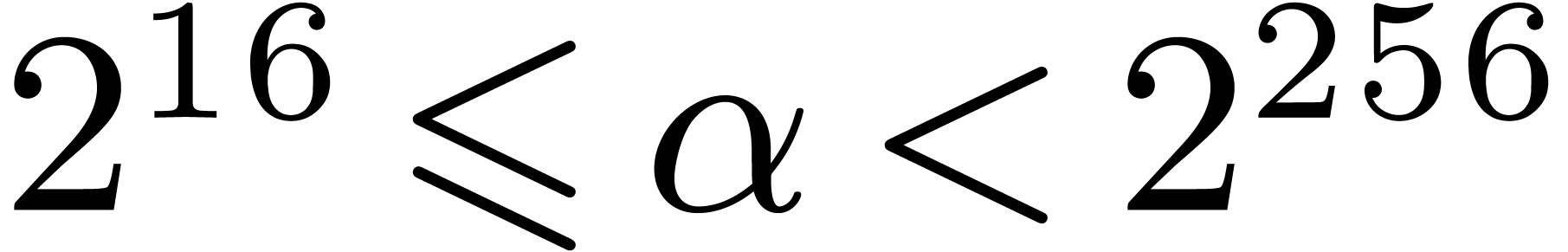 , we symbolically
computed
, we symbolically
computed 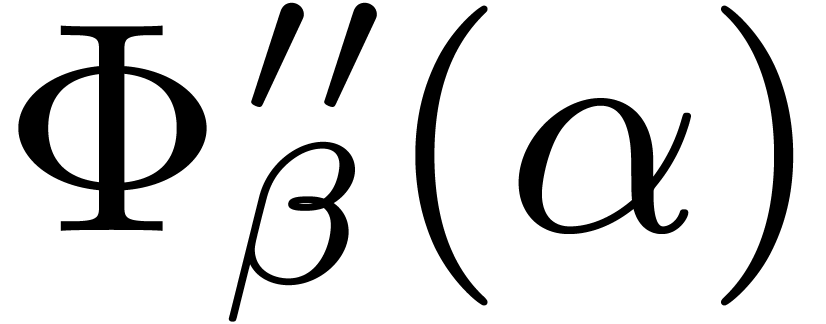 and straightforwardly lower bounded it
by a function
and straightforwardly lower bounded it
by a function 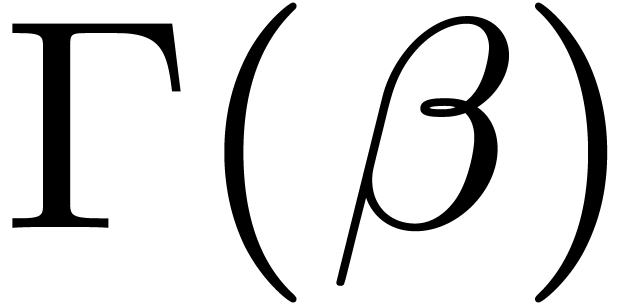 in the domain
in the domain 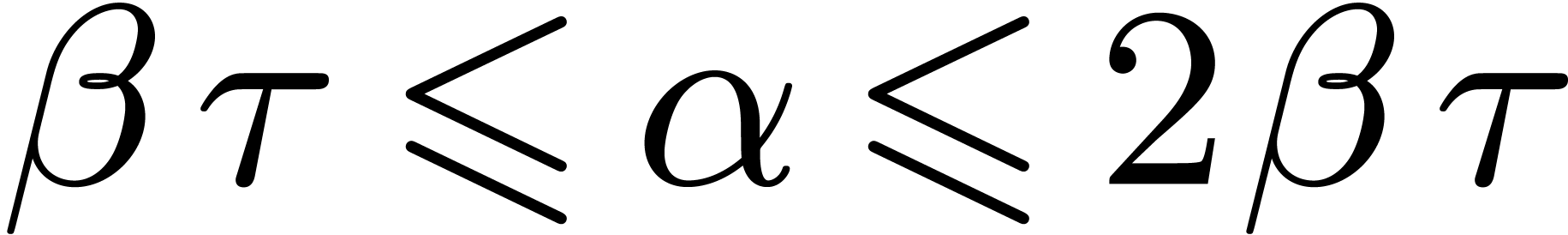 . For each value of
. For each value of 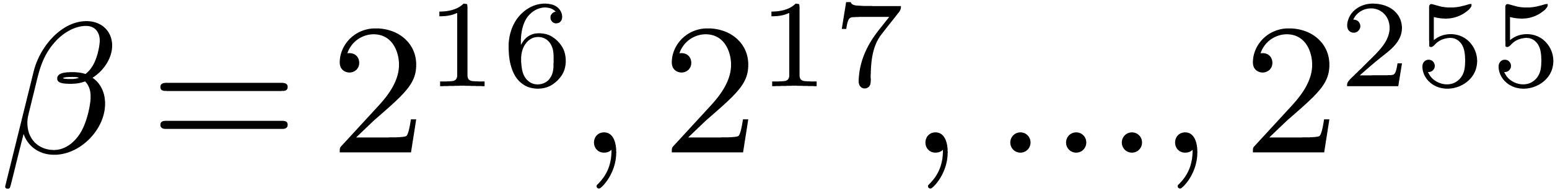 , we used ball arithmetic to show that
, we used ball arithmetic to show that 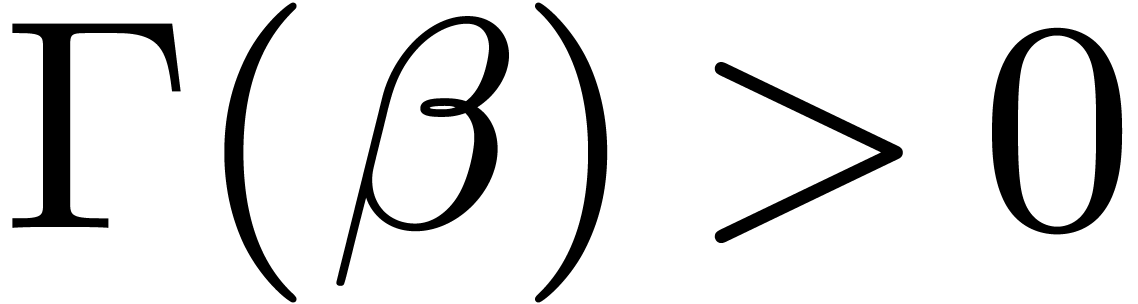 . For smaller values of
. For smaller values of  , we could directly compute that
, we could directly compute that 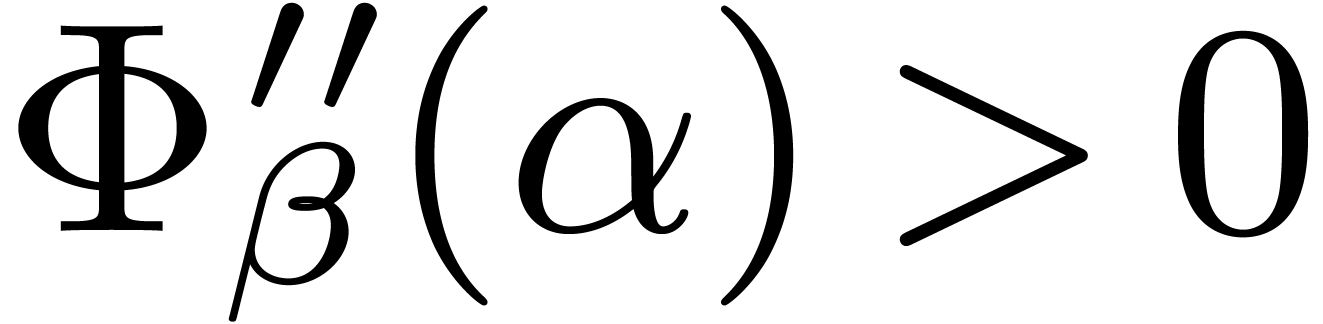 whenever
whenever 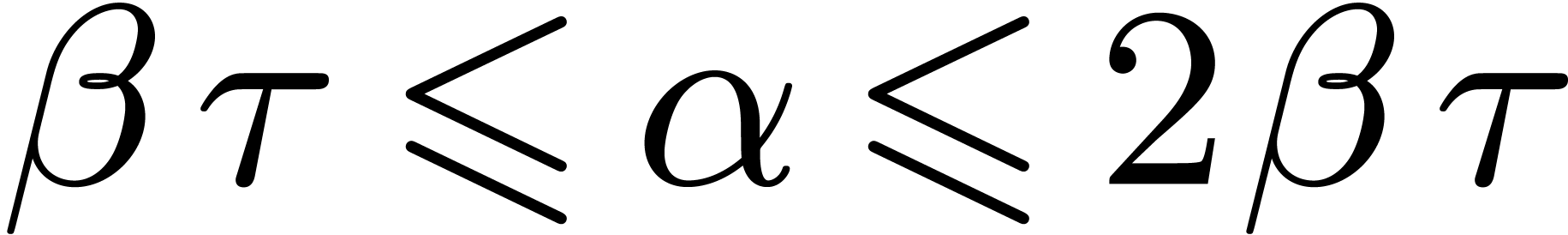 . Finally we
computed that
. Finally we
computed that 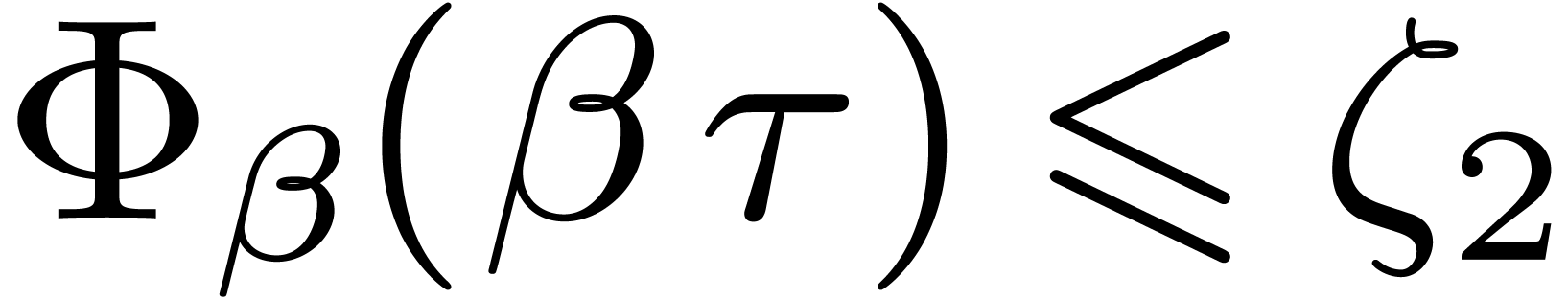 for all
for all  , which concludes the proof.
, which concludes the proof.

 . This work has
been partly supported by the French
. This work has
been partly supported by the French 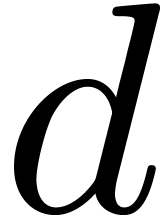 ,
,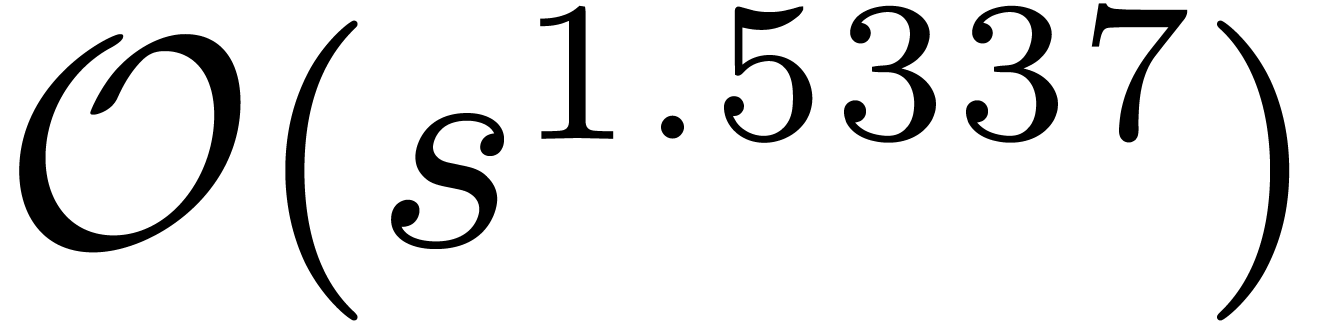 ring operations,
where
ring operations,
where  denotes the number of all the monomials of
total degree at most
denotes the number of all the monomials of
total degree at most 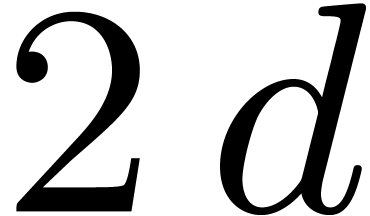 .
. be an effective ring, which means
that we have a data structure for representing the elements of
be an effective ring, which means
that we have a data structure for representing the elements of 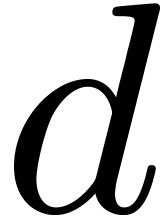 is
rather well understood [
is
rather well understood [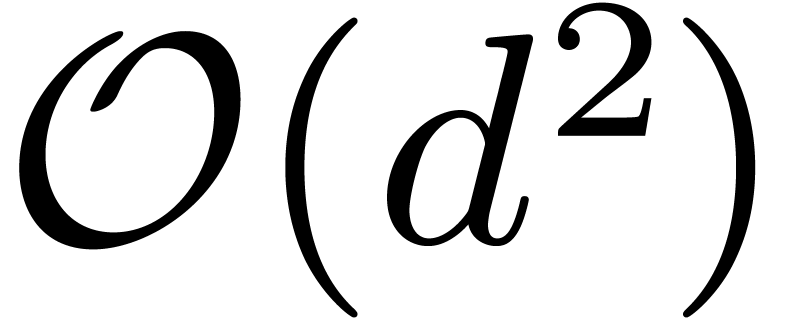 .
.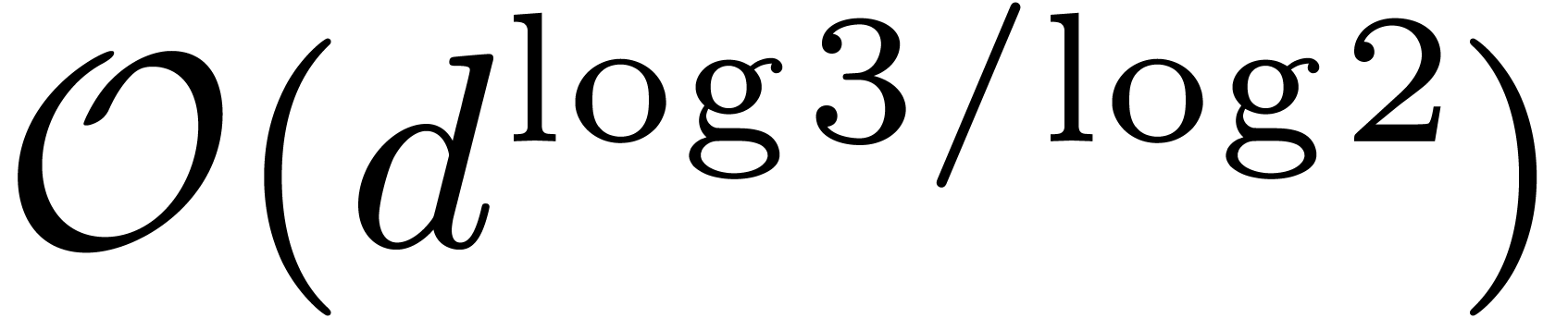 ,
,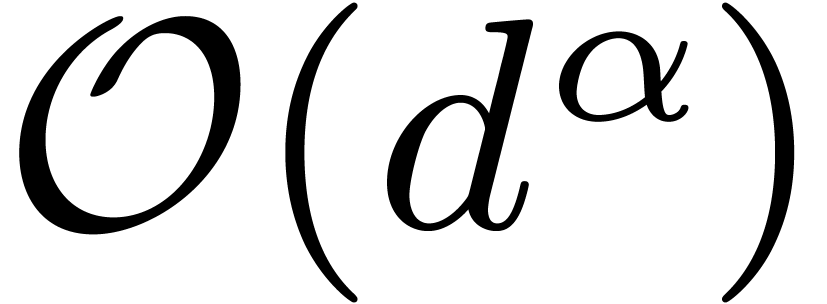 with
with 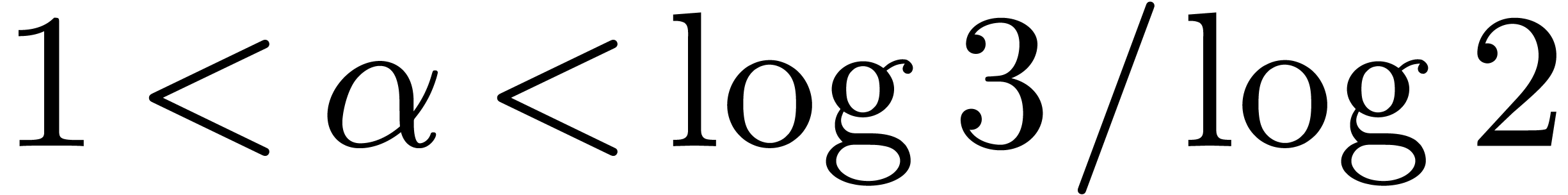 .
.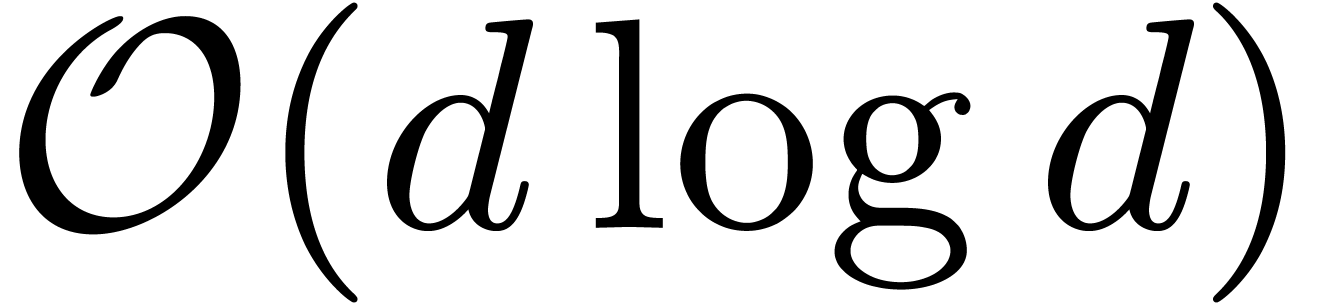 whenever
whenever  -th
-th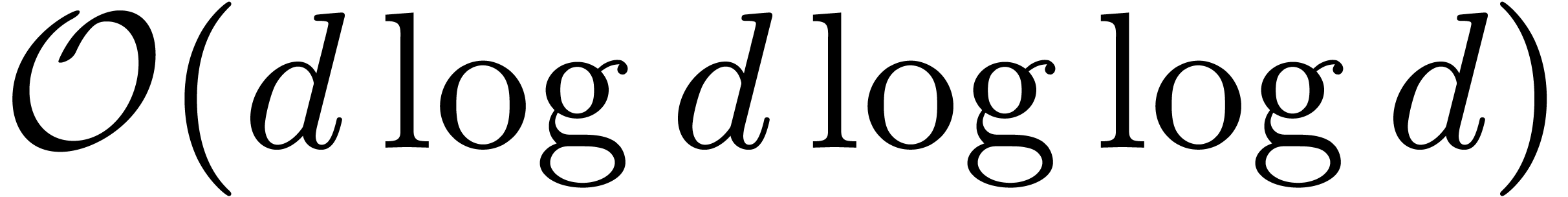 otherwise.
otherwise.
 and to rewrite all
polynomials as “block polynomials” in
and to rewrite all
polynomials as “block polynomials” in  with “block coefficients” in
with “block coefficients” in
 :
: in its center, then we show that their
product can be computed with
in its center, then we show that their
product can be computed with  denotes the number of all the monomials of degree at most
denotes the number of all the monomials of degree at most 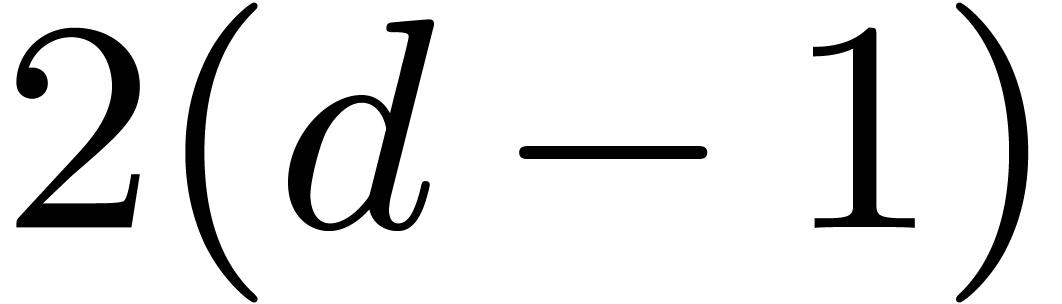 .
. does not depend neither on
does not depend neither on  ,
, ,
, and
and  of degree
of degree  and
and 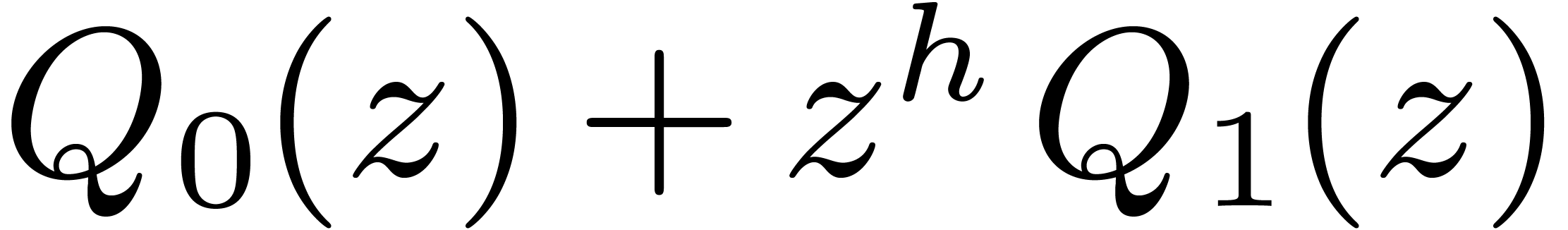 ,
,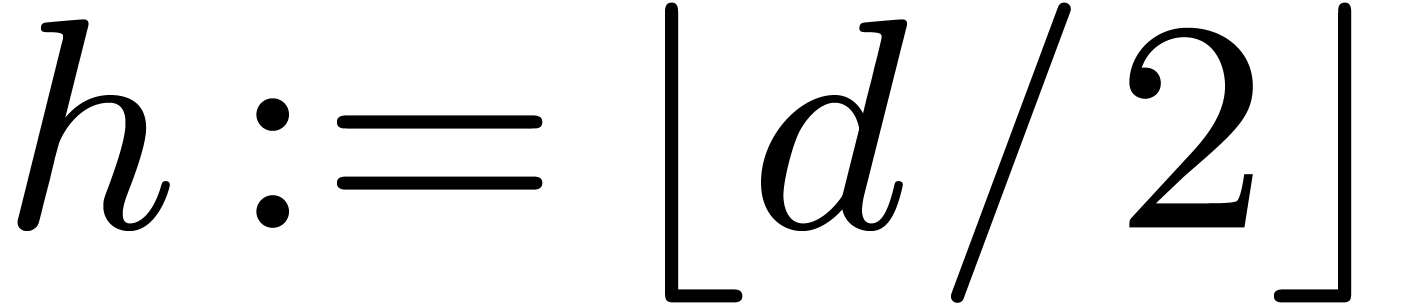 .
.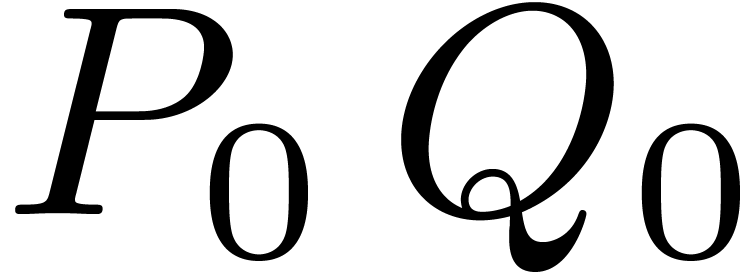 ,
,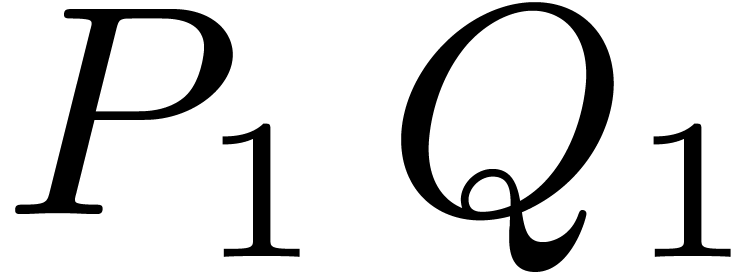 ,
,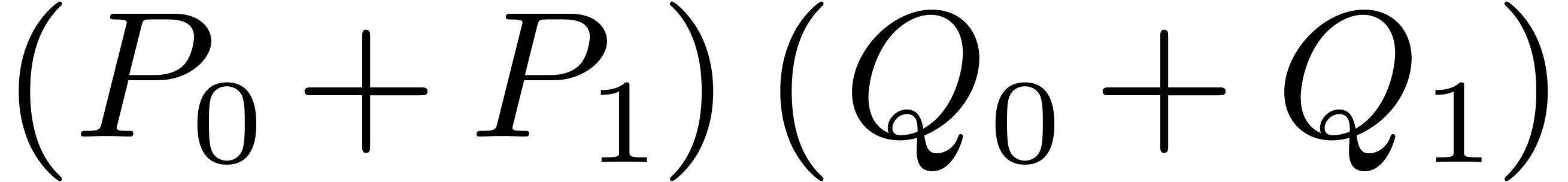 are computed
recursively. This approach has been studied for several variables [
are computed
recursively. This approach has been studied for several variables [ (i.e. sets of monomials which are
complementary to a monomial ideal), with the same order of efficiency as
the FFT multiplication for univariate polynomials.
(i.e. sets of monomials which are
complementary to a monomial ideal), with the same order of efficiency as
the FFT multiplication for univariate polynomials.
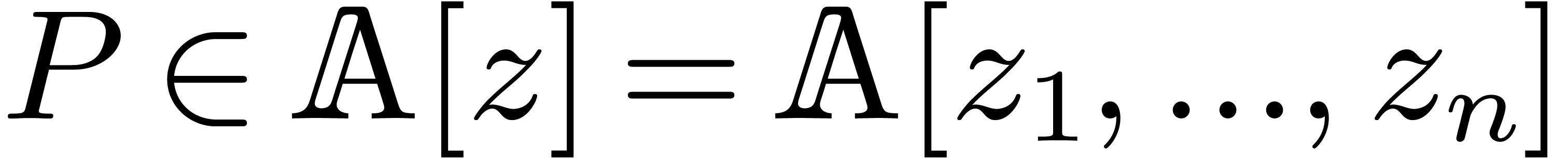 ,
,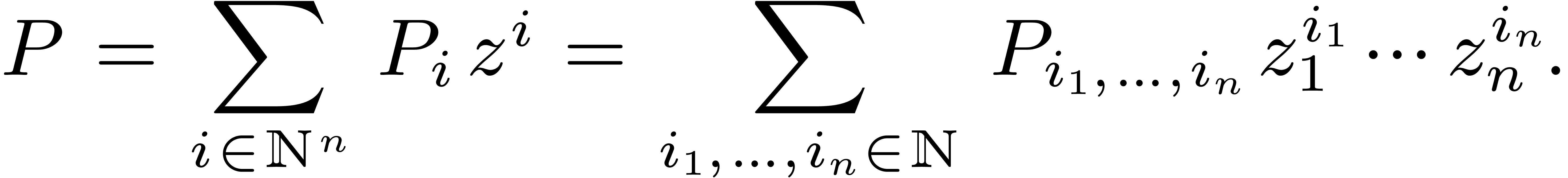
 ,
,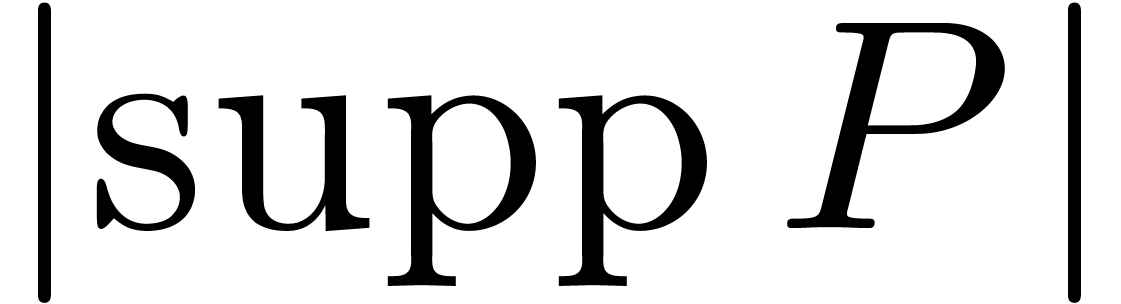 by
by  .
.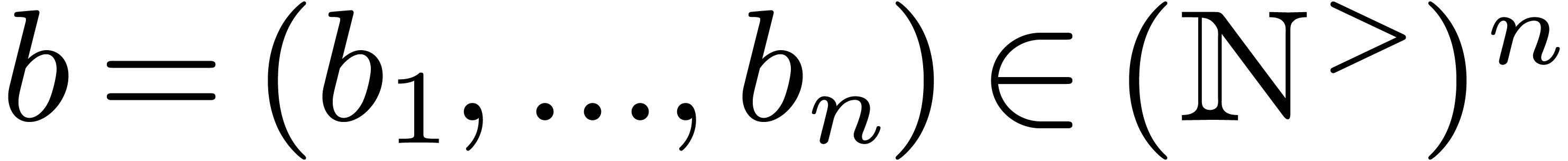 of positive integers, we define
the set of block coefficients at order
of positive integers, we define
the set of block coefficients at order  by
by
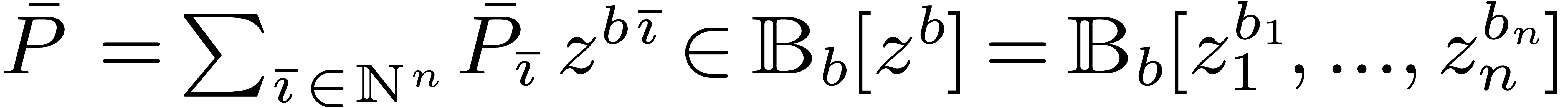 ,
,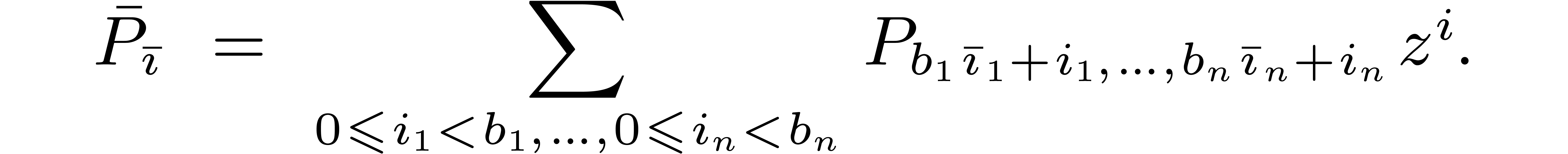
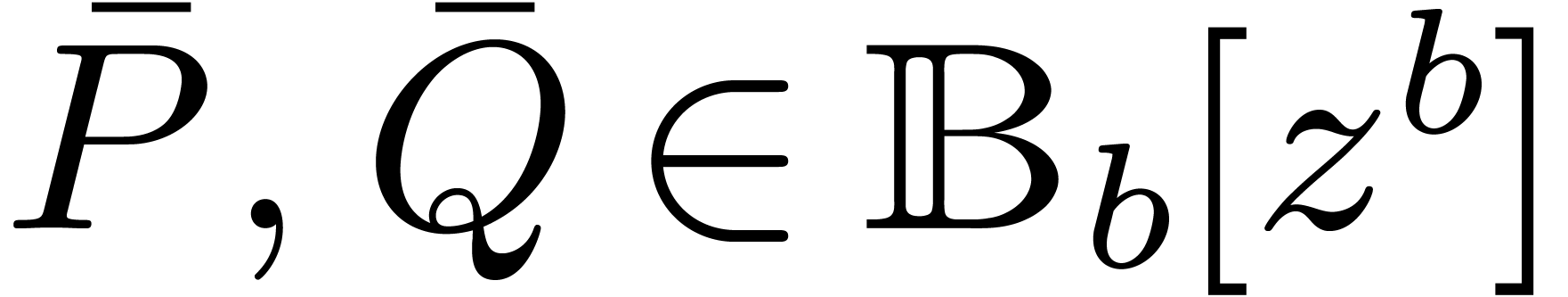 ,
,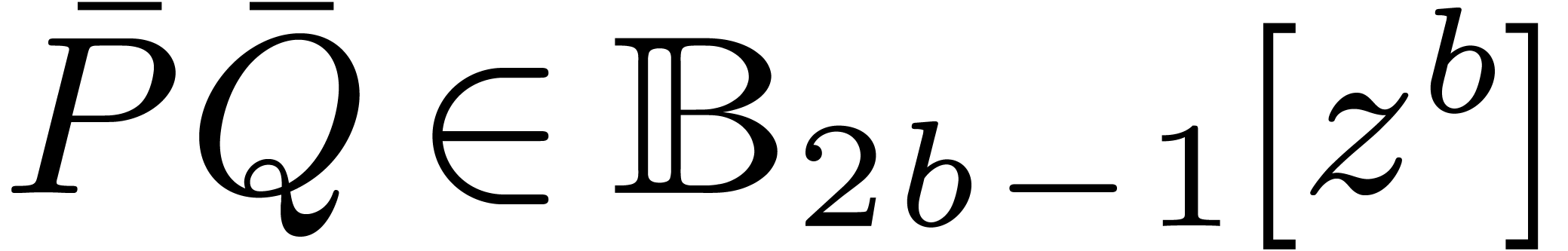 .
.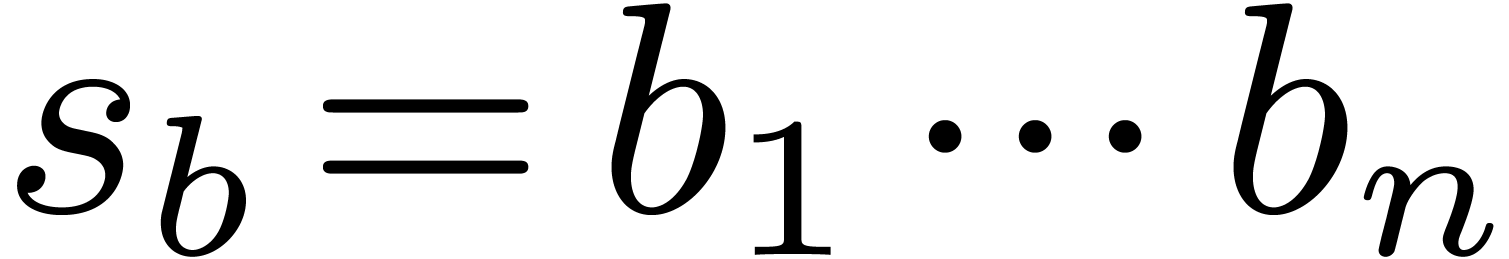 represent the size of the block
represent the size of the block 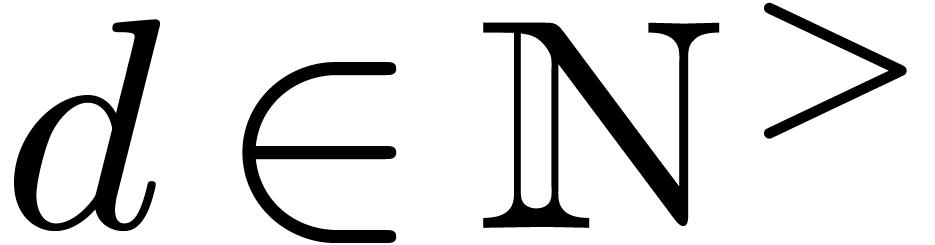 on
on 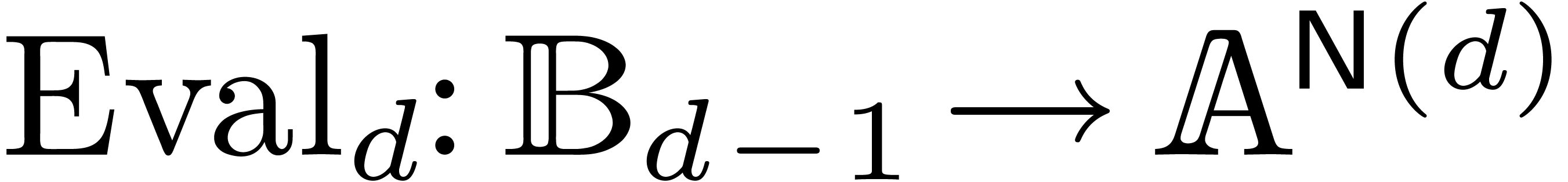 ,
,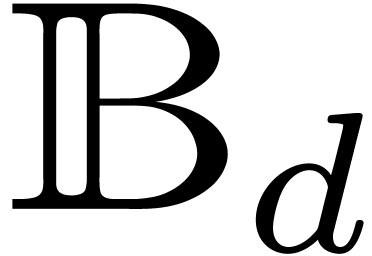 is the subset of polynomials in
is the subset of polynomials in 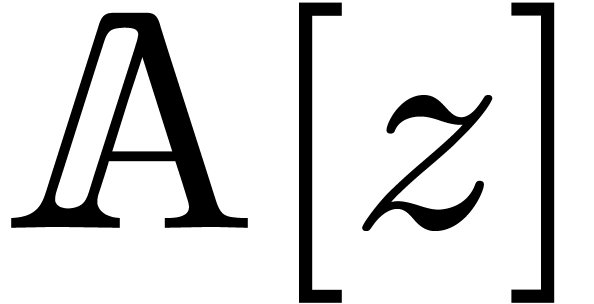 of degree at
most
of degree at
most 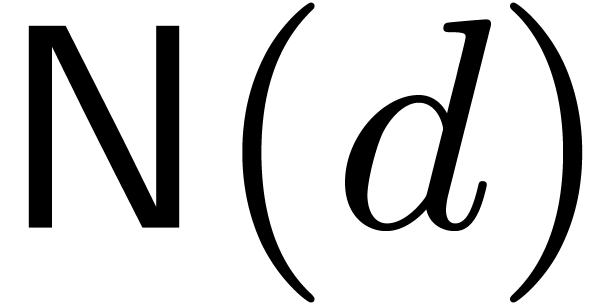 can be seen as the number of evaluation points,
and
can be seen as the number of evaluation points,
and
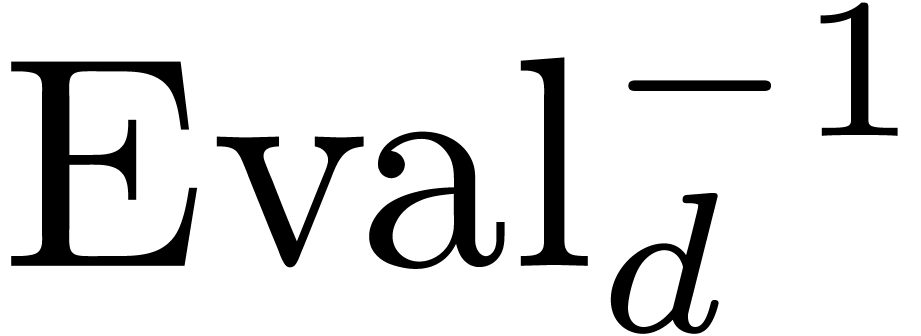 ,
,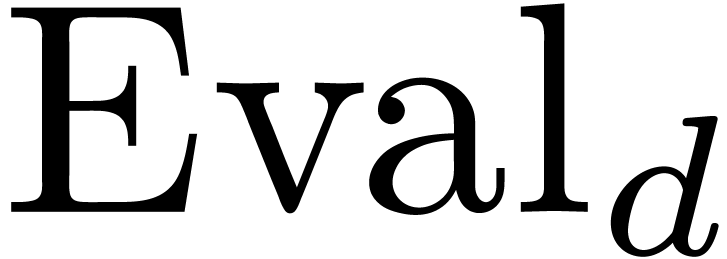 ,
,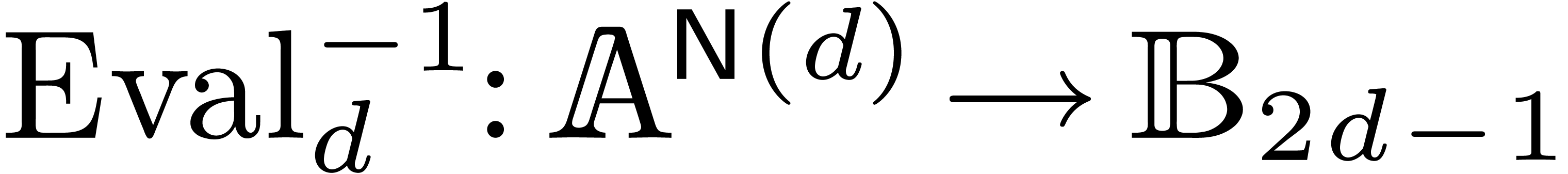 ,
,
 denotes the entry-wise product in
denotes the entry-wise product in 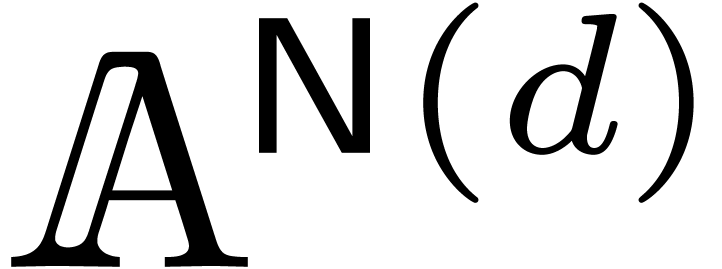 .
.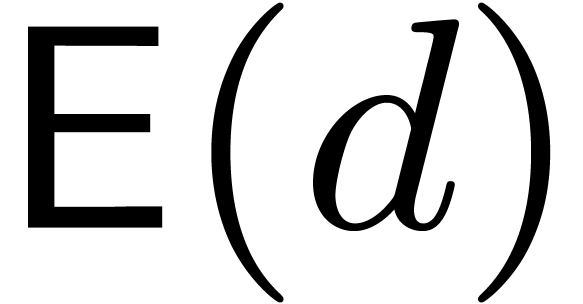 for a common bound on the complexity of
for a common bound on the complexity of
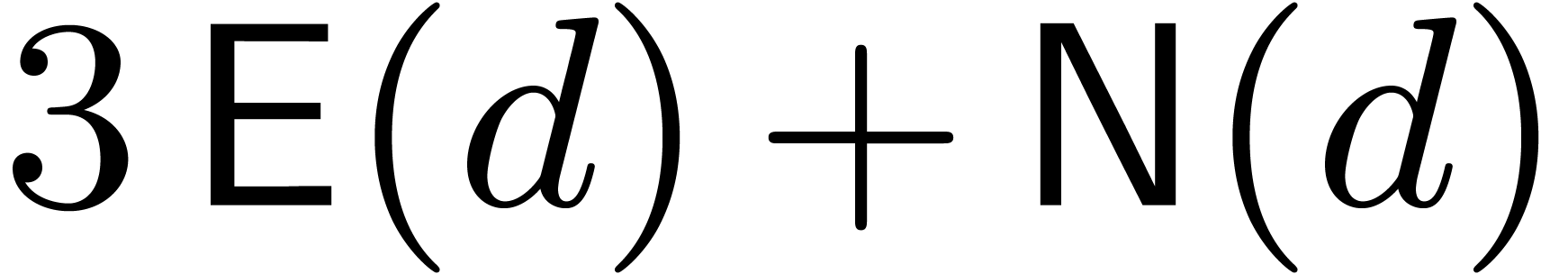 .
. seen as a ring endowed with
the entry-wise product.
seen as a ring endowed with
the entry-wise product.
 corresponds
to
corresponds
to  ,
, ,
,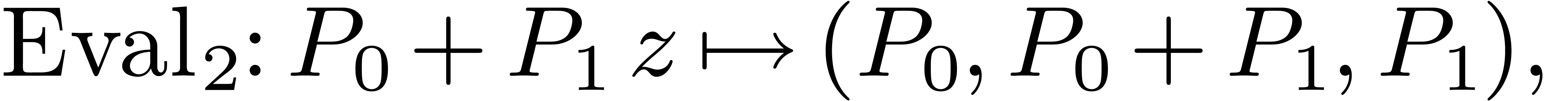
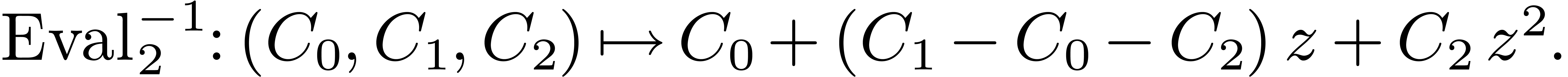
 can be interpreted as the evaluation of a
polynomial at the values
can be interpreted as the evaluation of a
polynomial at the values  ,
, .
. corresponds to
corresponds to
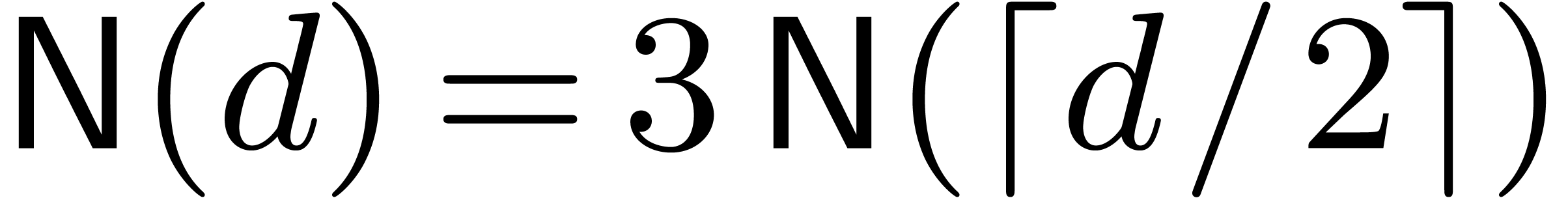 ,
, ,
, is the block
polynomial of
is the block
polynomial of  with respect to
with respect to 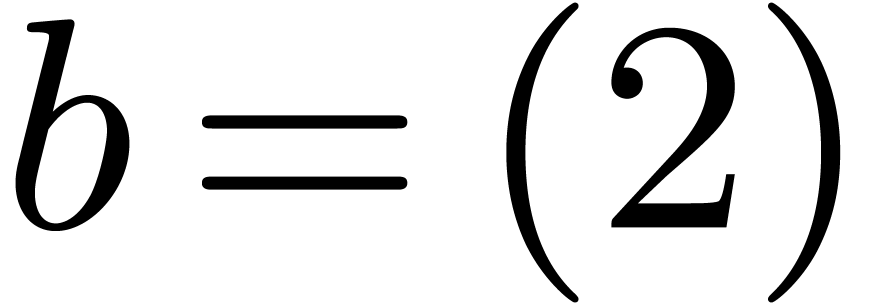 ,
,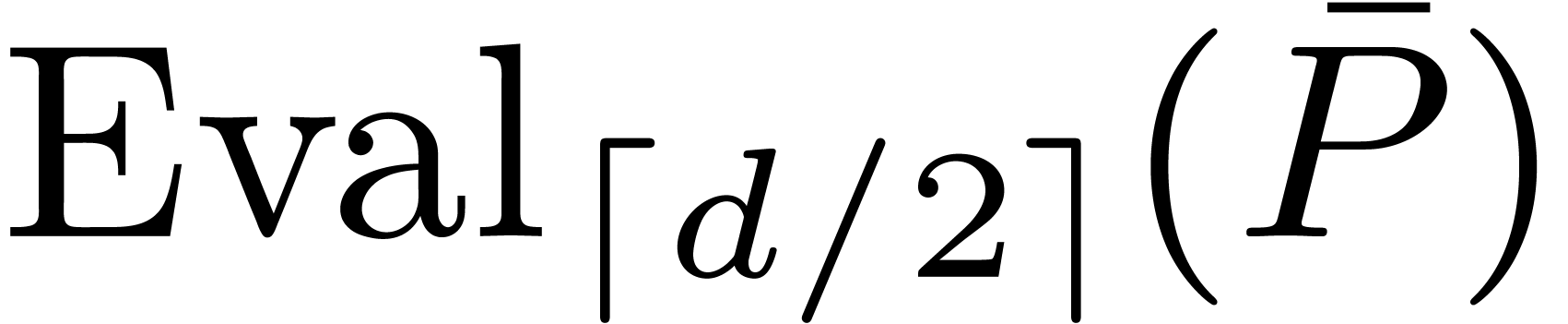 actually
corresponds to applying the extension of
actually
corresponds to applying the extension of 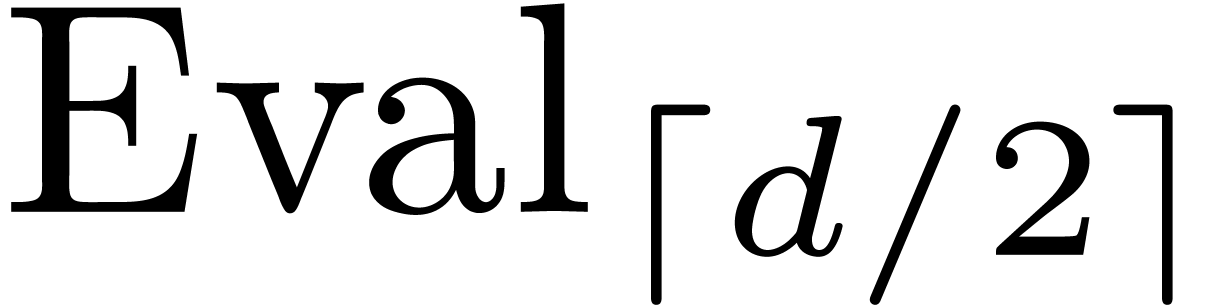 to
to
 .
.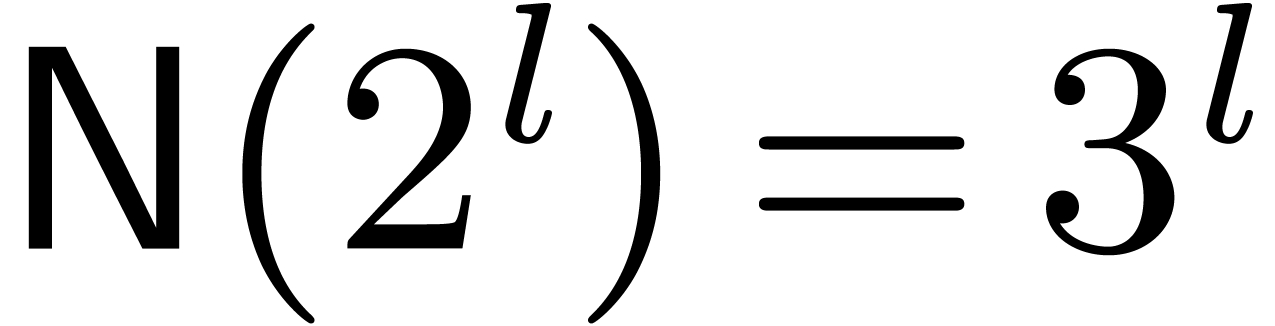 and
and 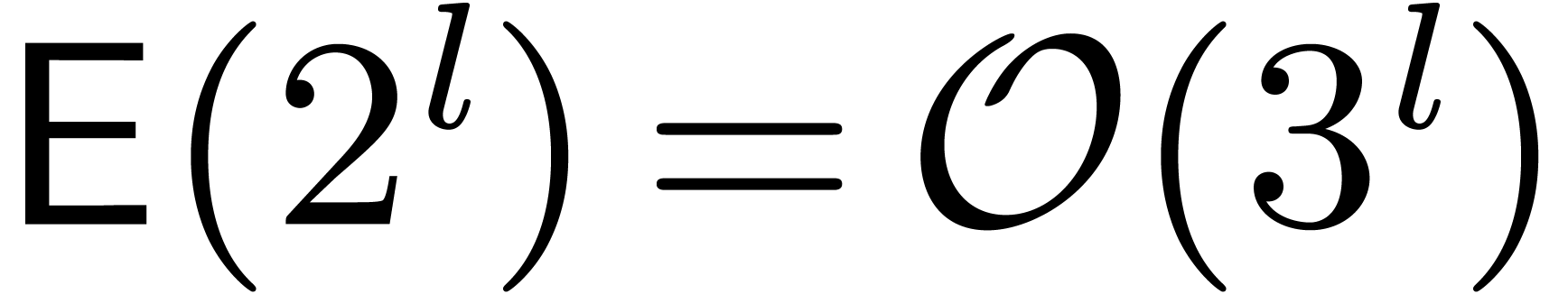 .
.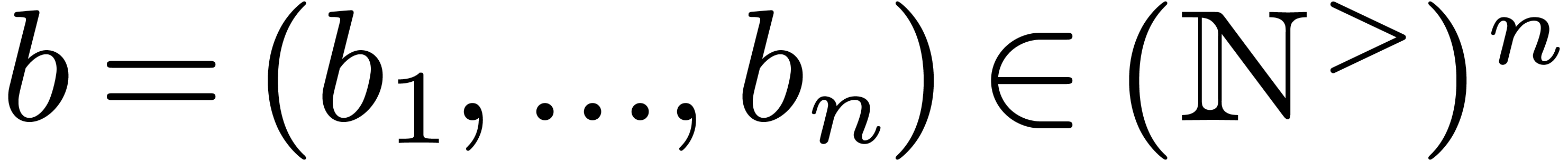 then we define
then we define 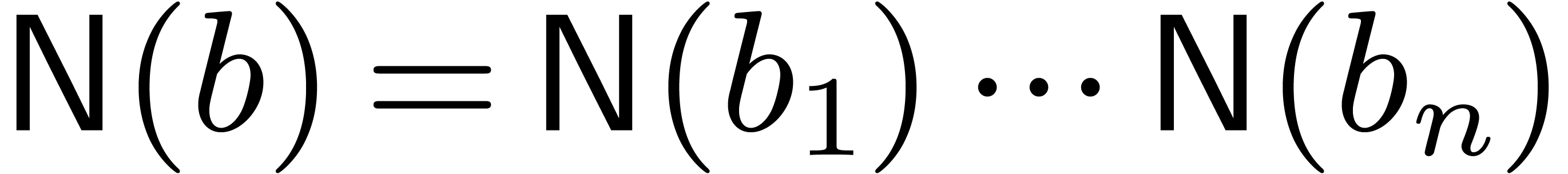 ,
,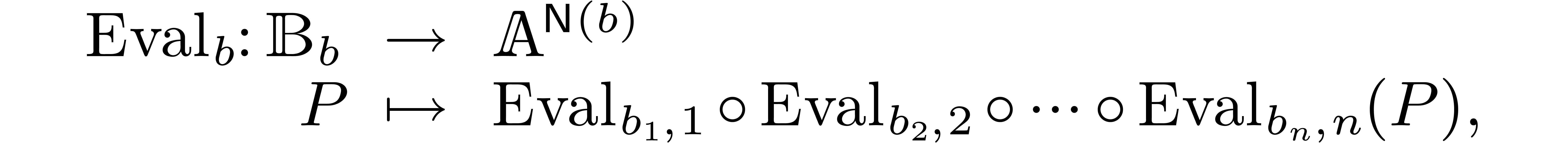
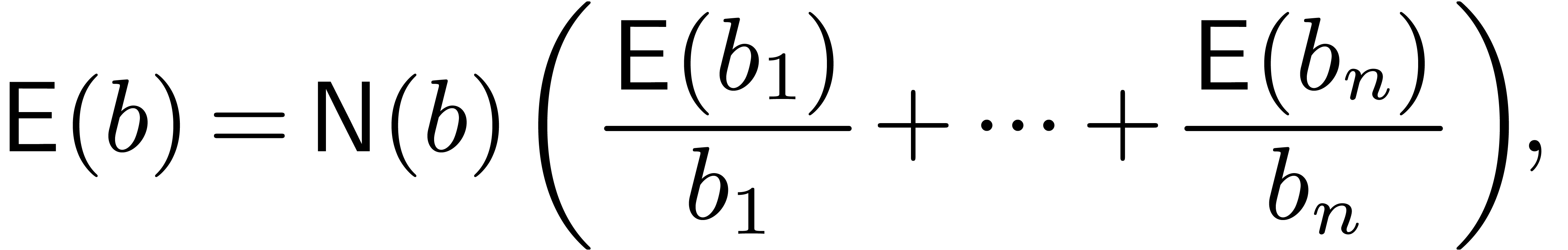
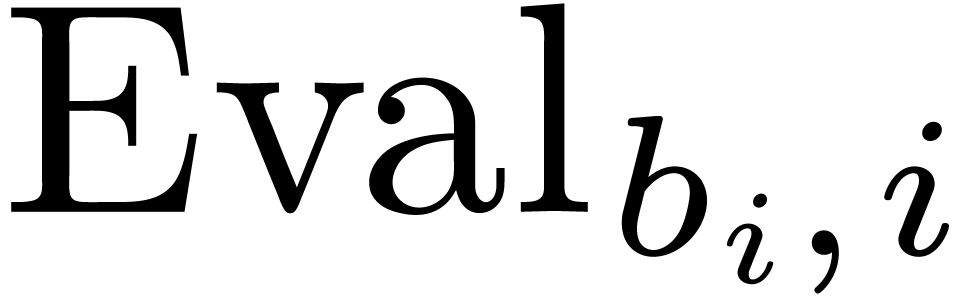 and
and 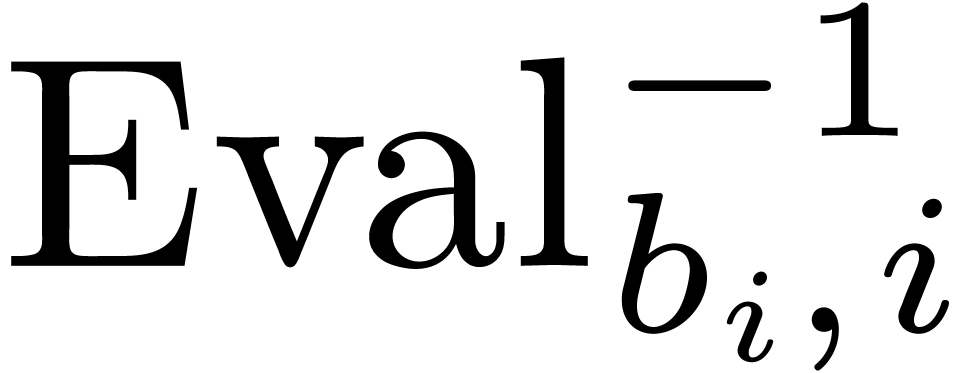 represent the
evaluation and interpolation with respect to the variable
represent the
evaluation and interpolation with respect to the variable 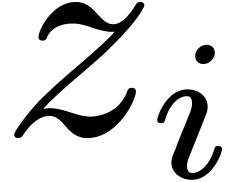 :
: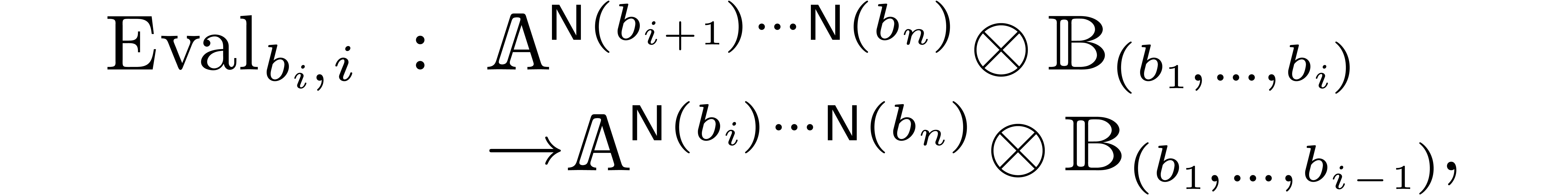
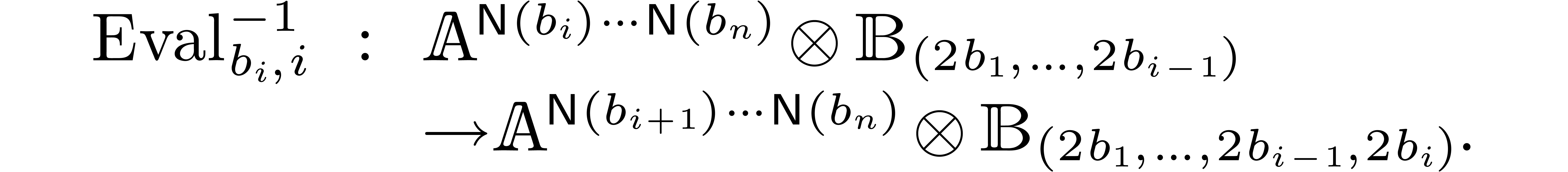
 ,
, and
and 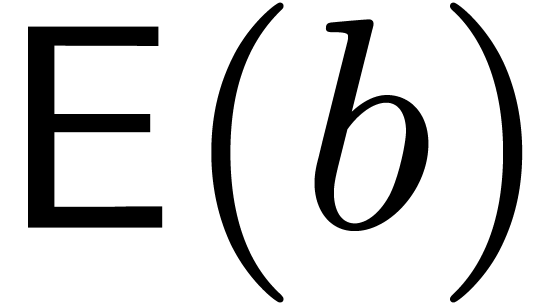 ,
,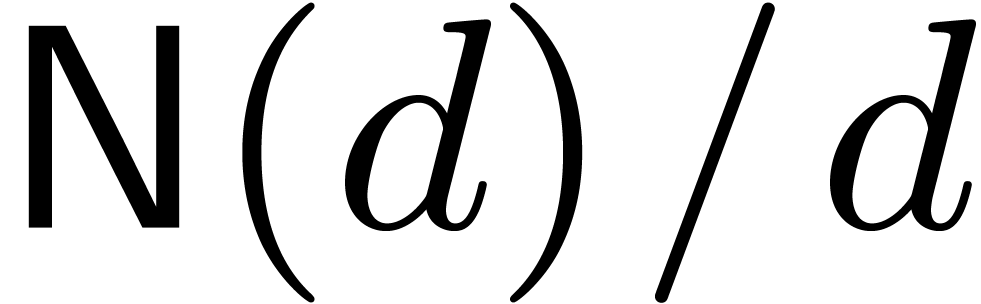 and
and 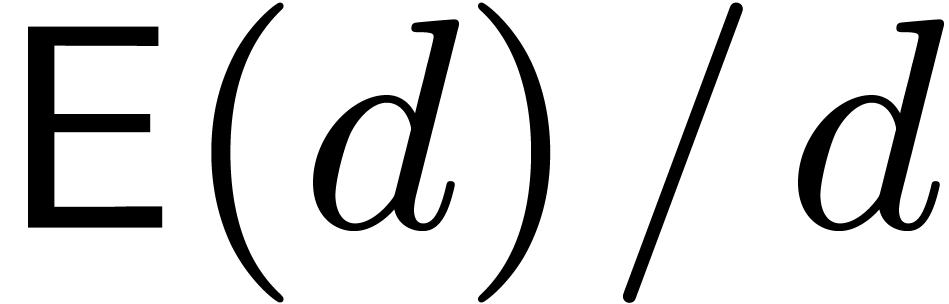 are
increasing functions.
are
increasing functions.
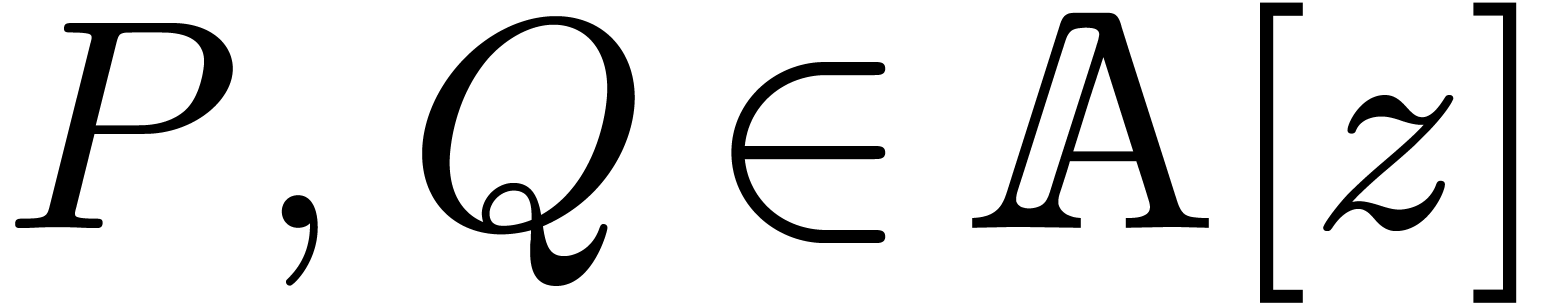 summarizes as follows:
summarizes as follows:

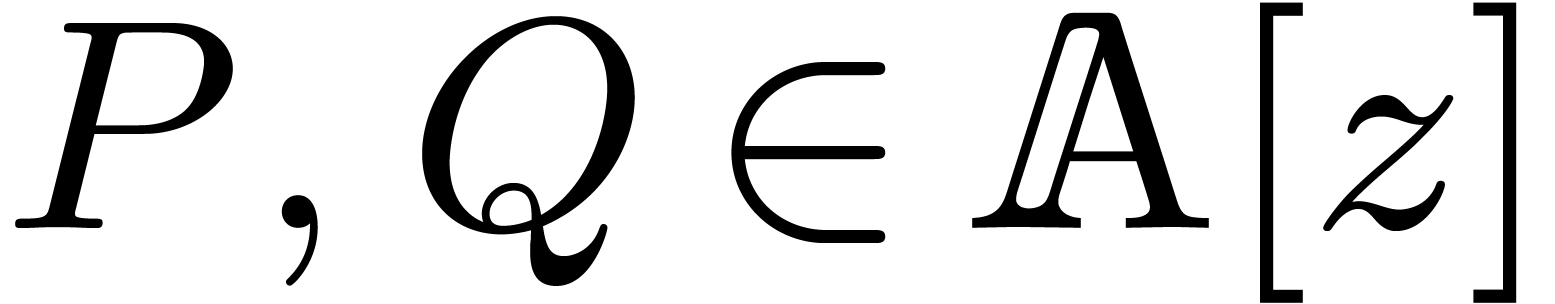 and
and 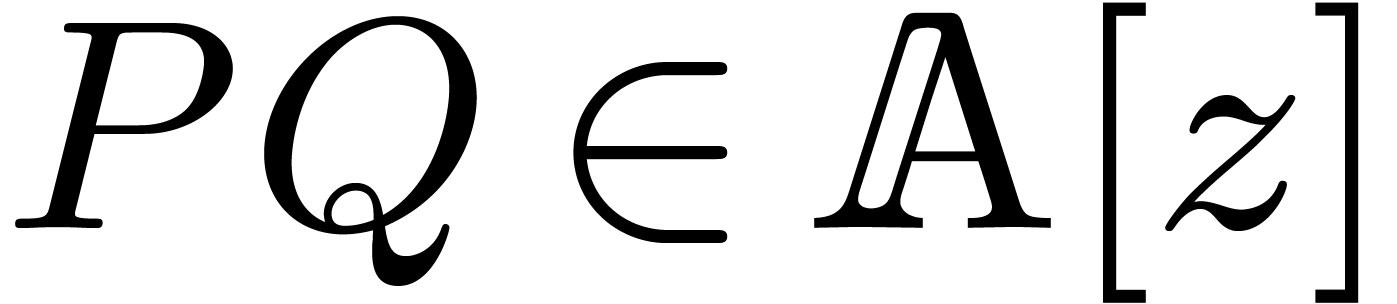 .
.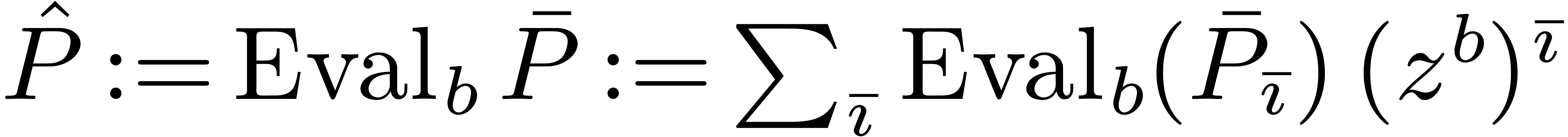 and
and  .
.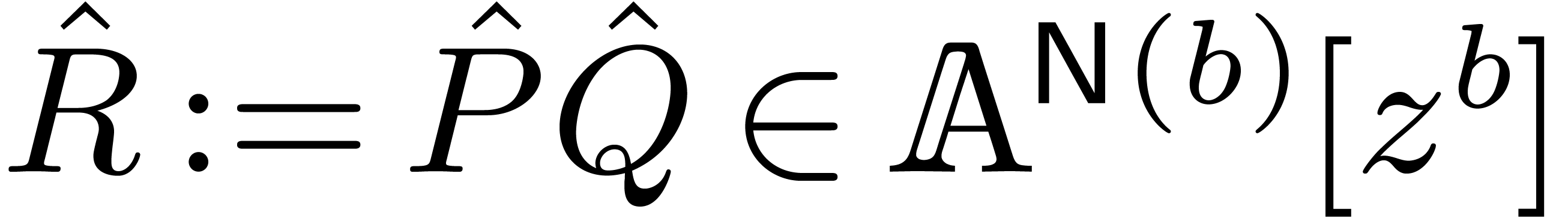 using the naive algorithm.
using the naive algorithm.
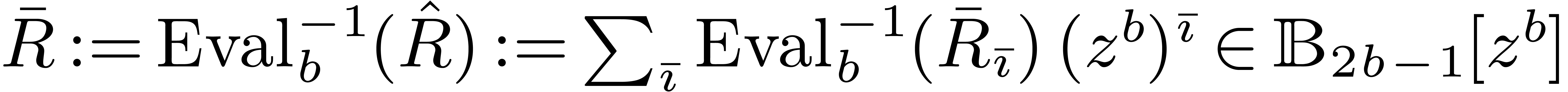 .
. as a polynomial
as a polynomial 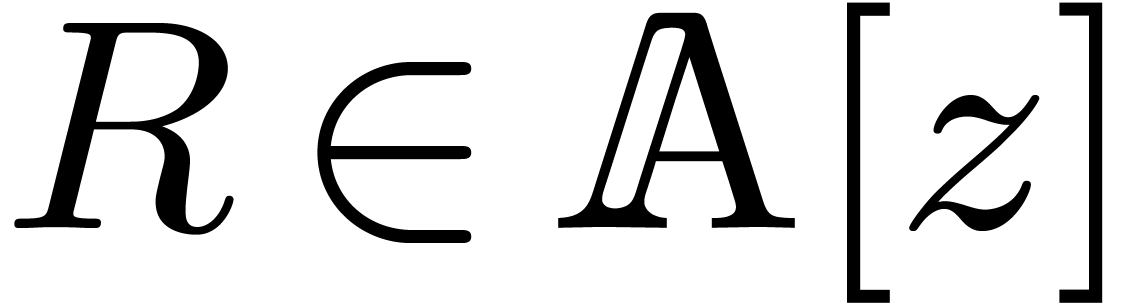 and return
and return  .
.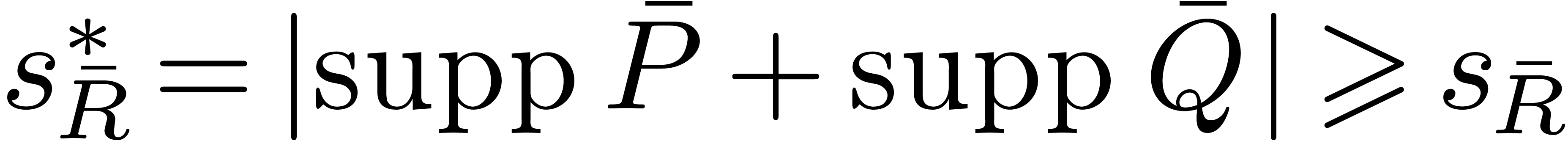 represent the size of
represent the size of 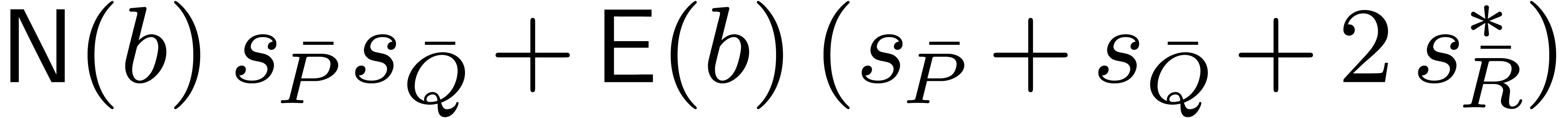
 .
.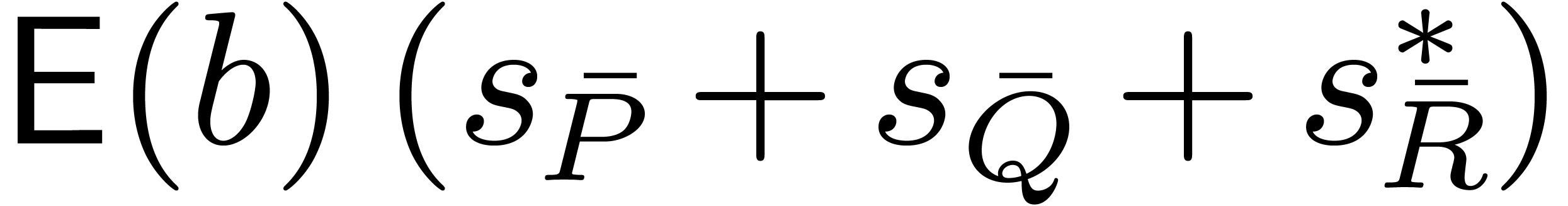 operations. Step 3 requires
operations. Step 3 requires 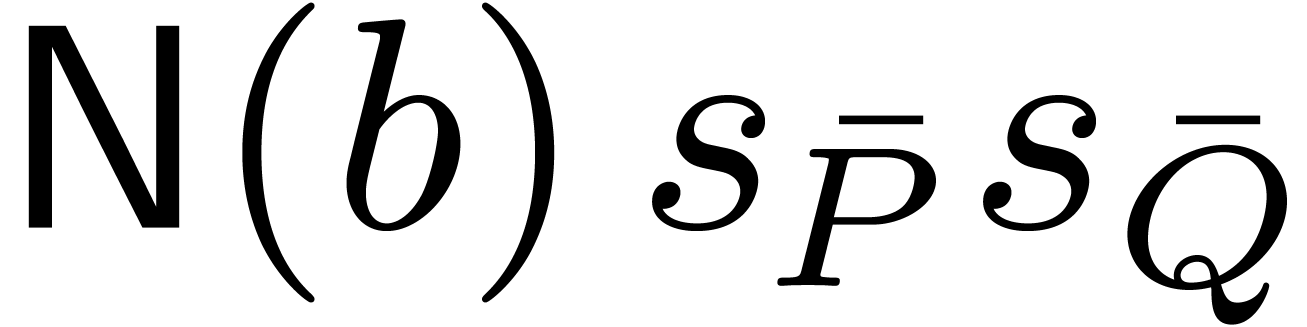 operations. Step 5
takes at most
operations. Step 5
takes at most  operations in order to add up
overlapping block coefficients, where
operations in order to add up
overlapping block coefficients, where  .
.
 and
and  ,
, requires a time
requires a time  to be computed. In the next subsection we explain a heuristic approach
to find a good block size
to be computed. In the next subsection we explain a heuristic approach
to find a good block size  ,
,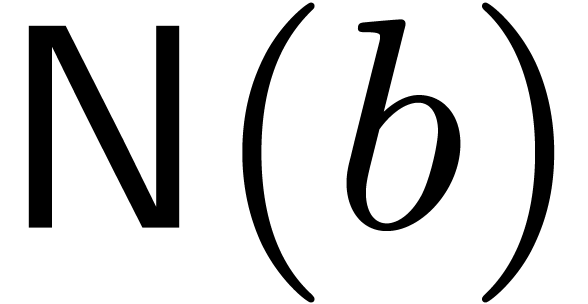 ,
,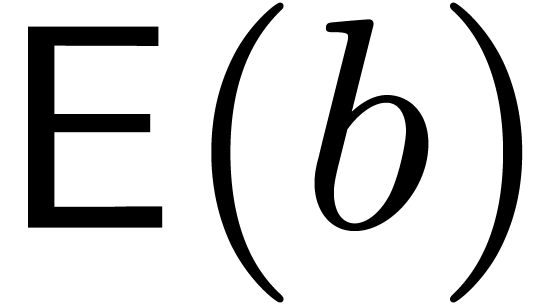 ,
,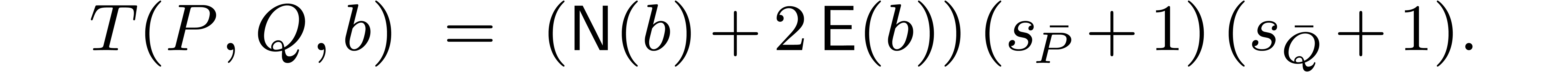
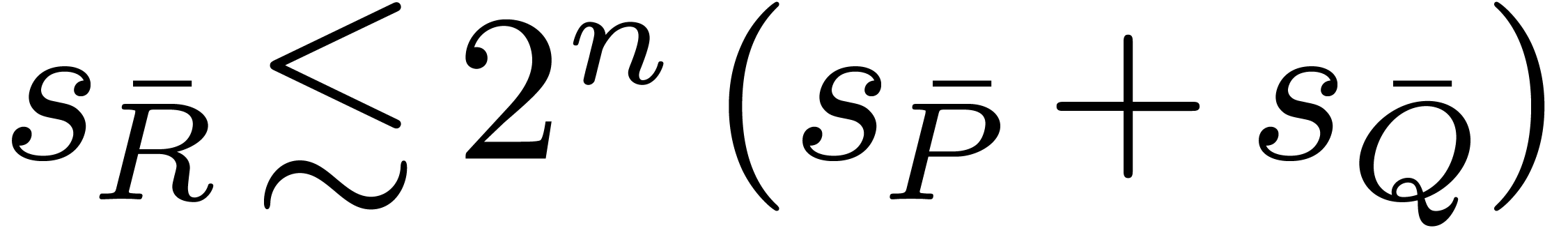 and use the formula
and use the formula
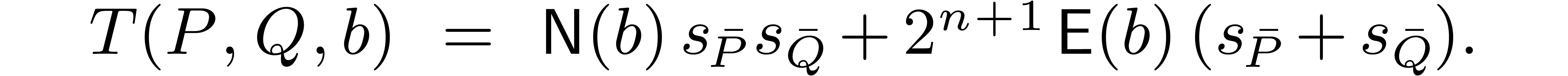
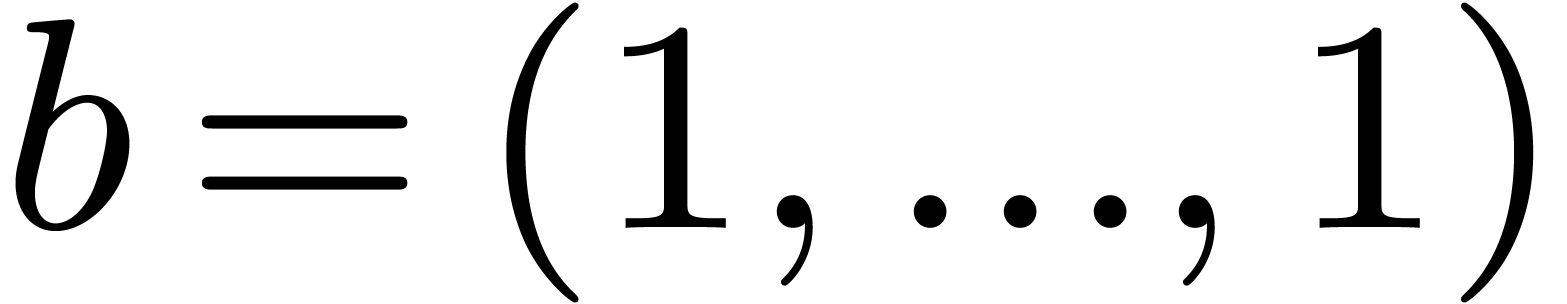 ,
,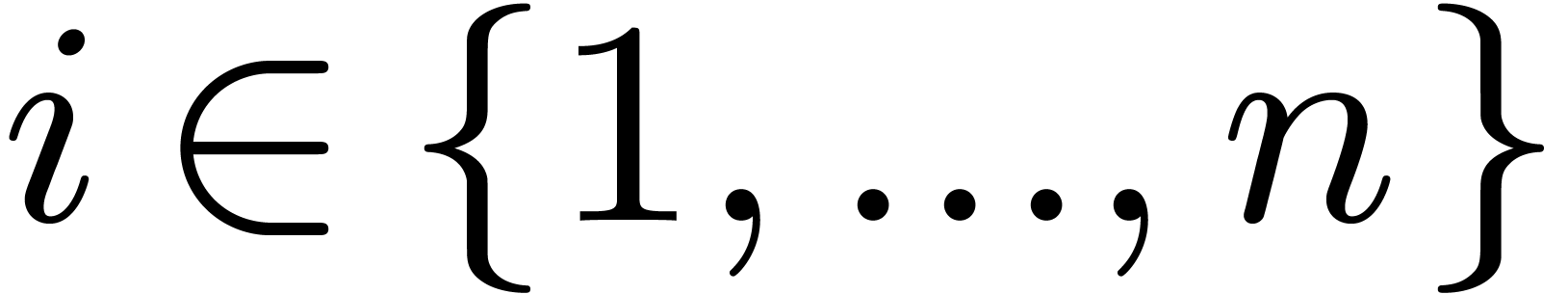 ,
,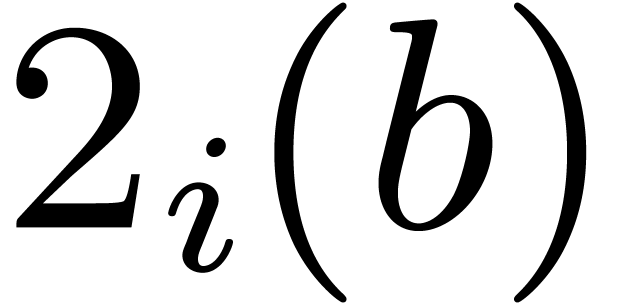 for
for 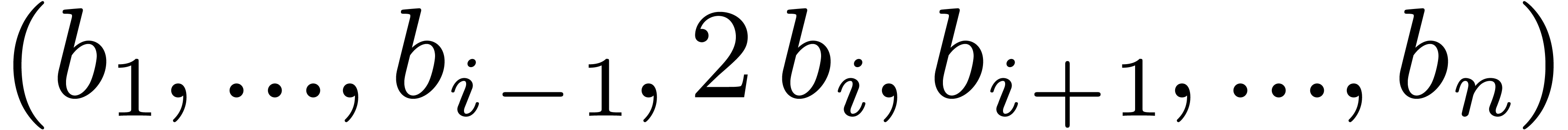 .
.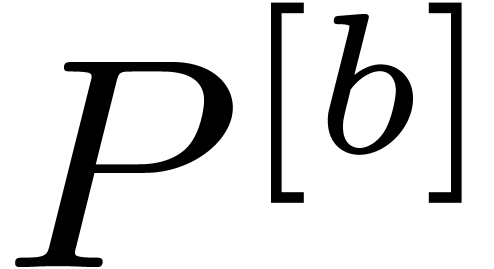 instead of
instead of 
 .
. .
. are
supported by at least two monomials repeat:
are
supported by at least two monomials repeat:
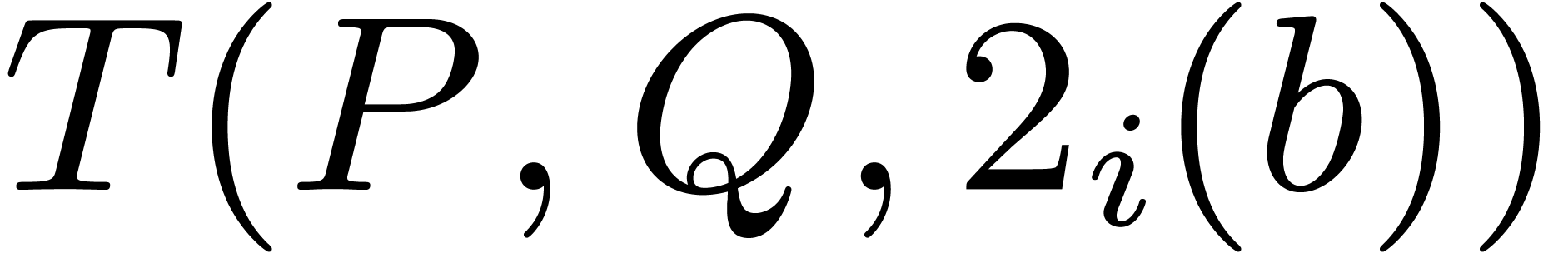 is
minimal.
is
minimal.
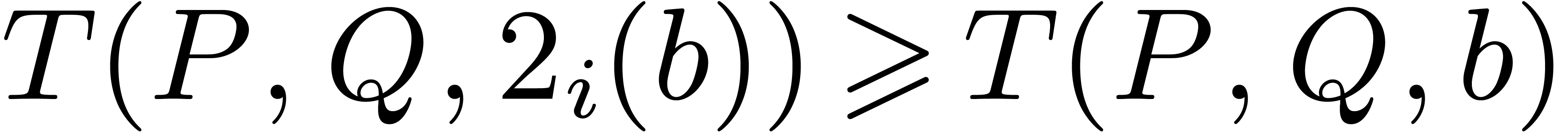 ,
, .
.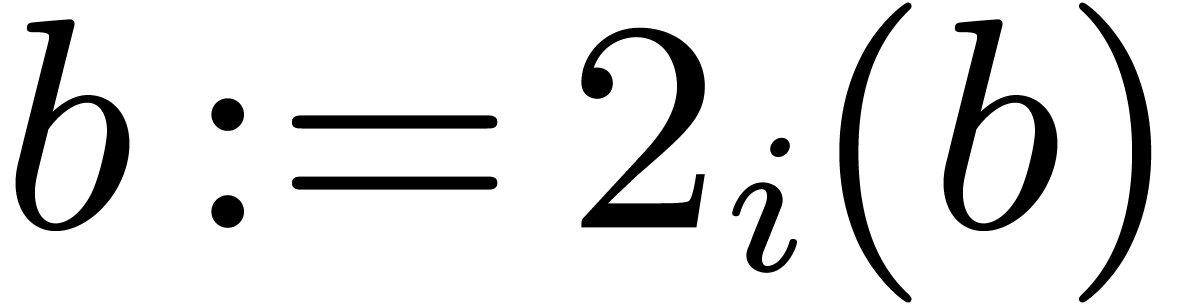 .
.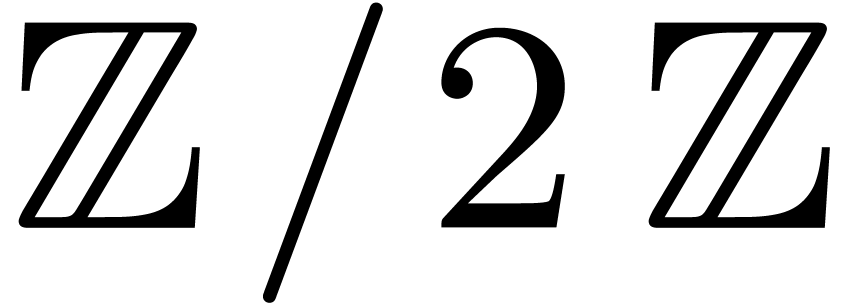 .
.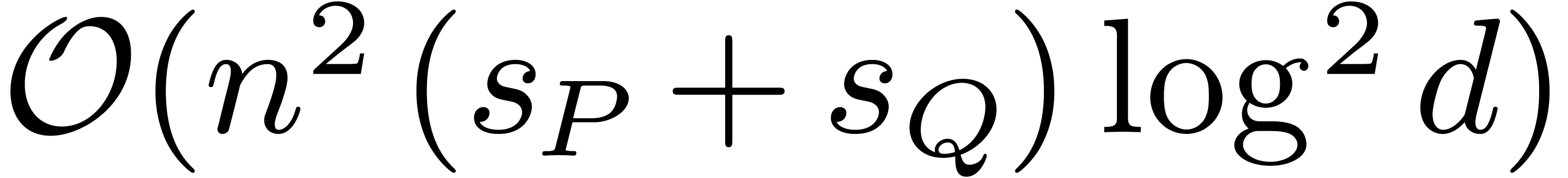 bit-operations, plus
bit-operations, plus 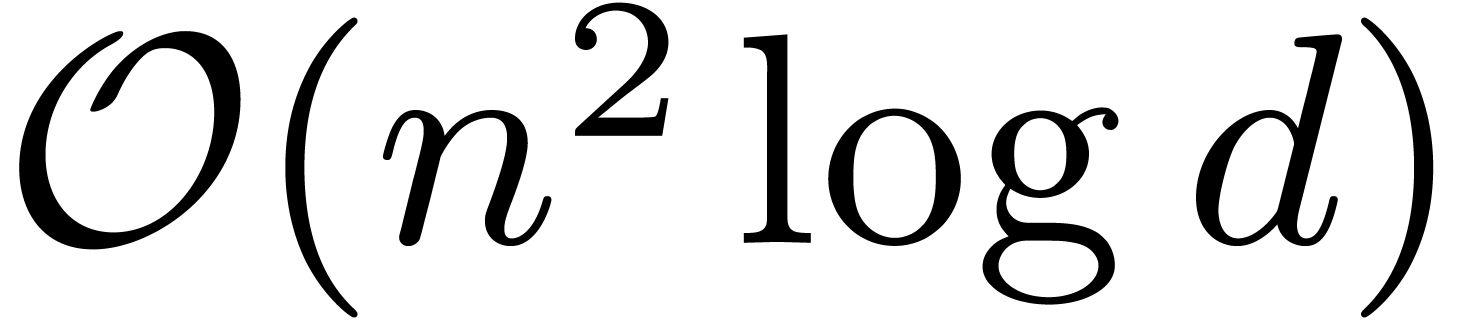 calls to the function
calls to the function  .
.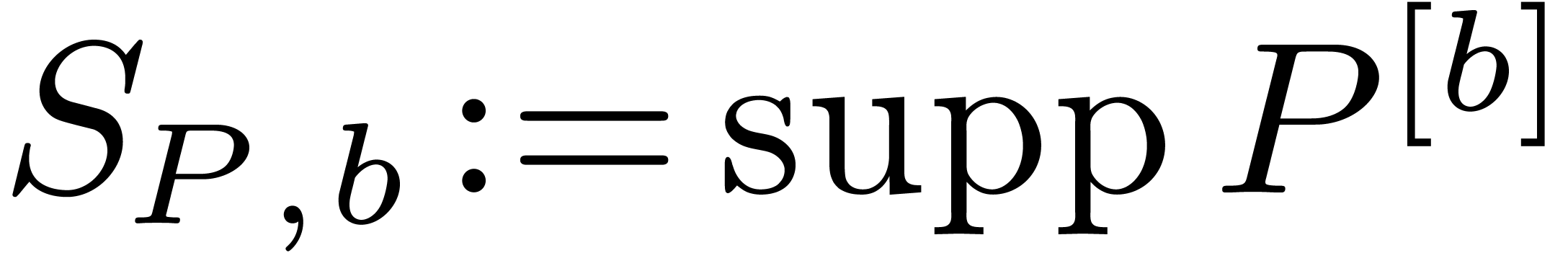 and
and 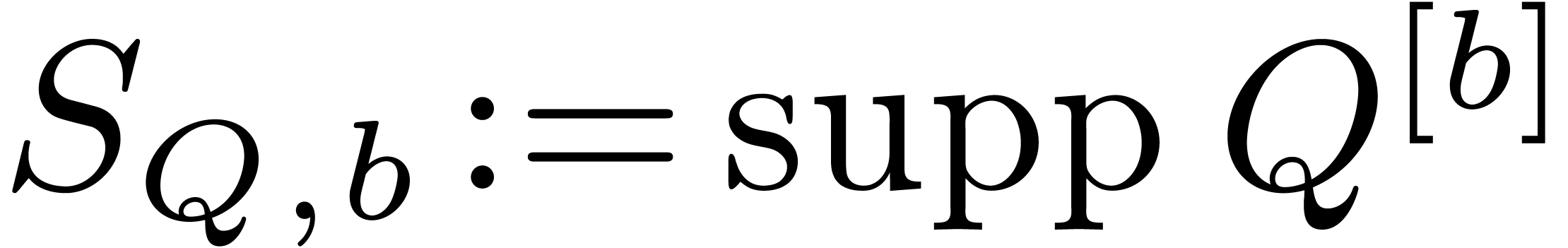 throughout the main loop. Since
throughout the main loop. Since 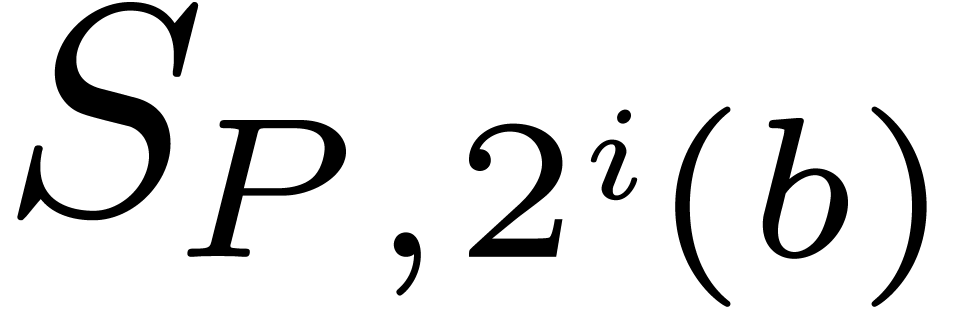 can be computed from
can be computed from 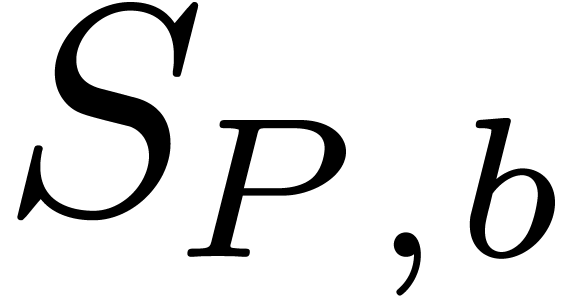 with
with 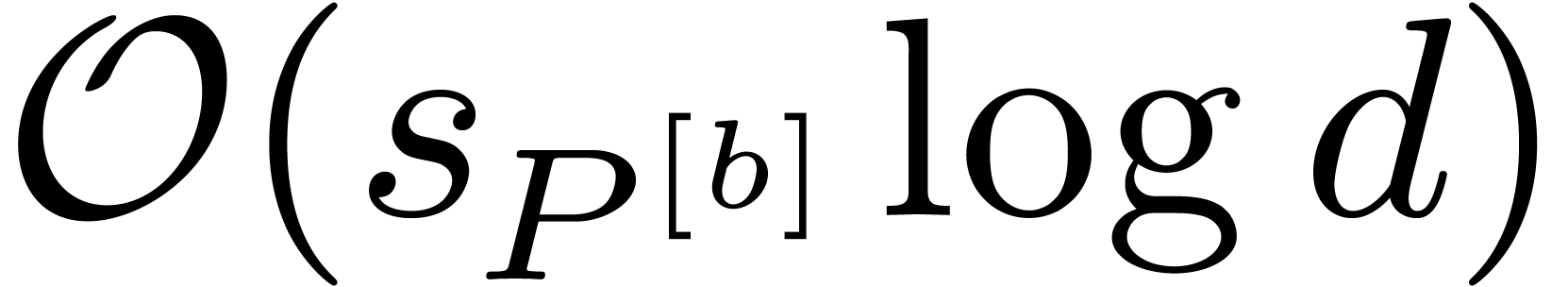 bit-operations, each iteration requires at most
bit-operations, each iteration requires at most 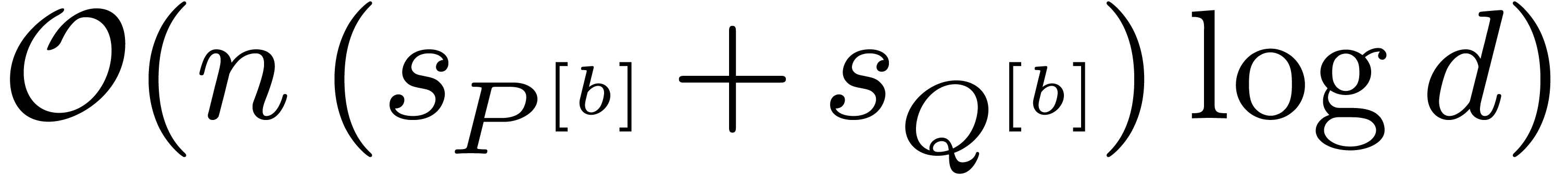 bit-operations. The number of iterations is bounded by
bit-operations. The number of iterations is bounded by 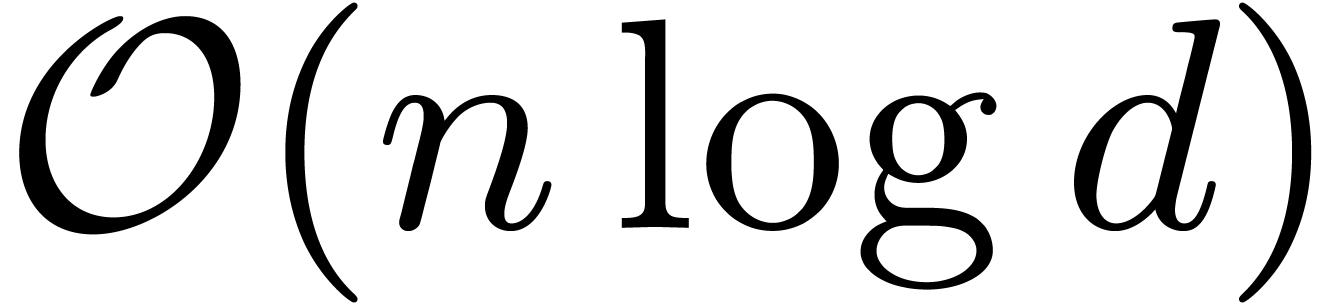 .
.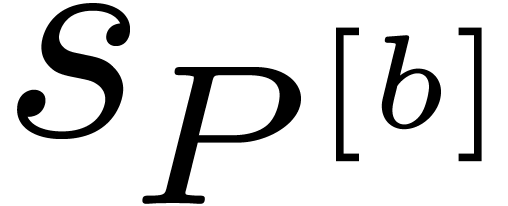 at each stage. The expected
total complexity thus becomes closer to
at each stage. The expected
total complexity thus becomes closer to 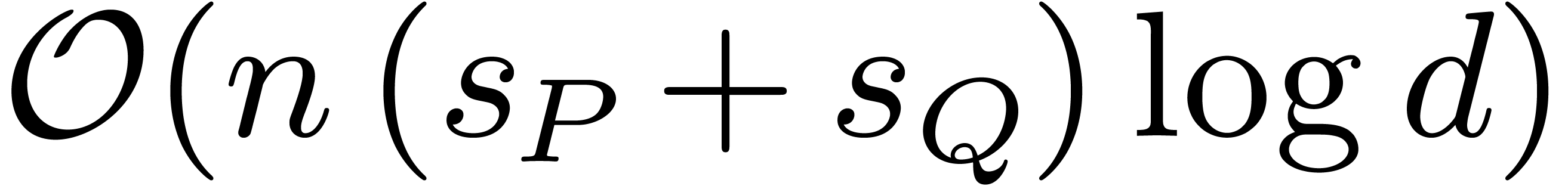 .
.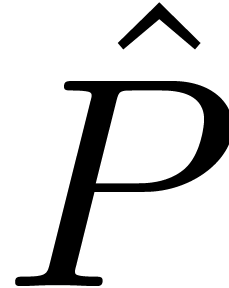 ,
, and
and 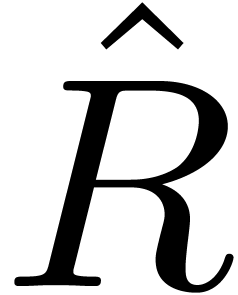 involves
involves 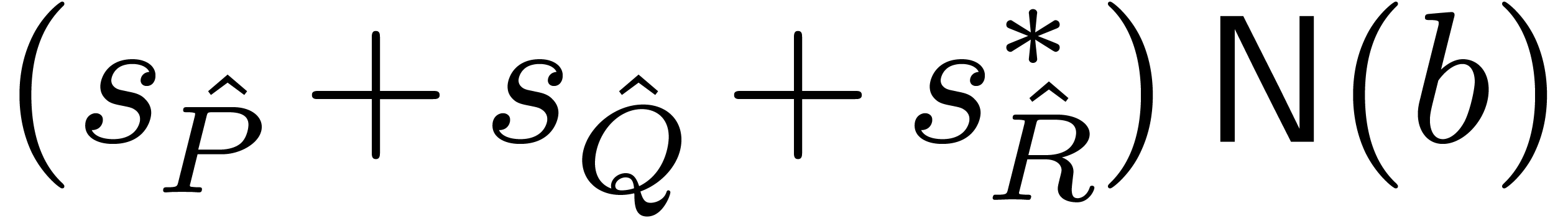 coefficients in
coefficients in 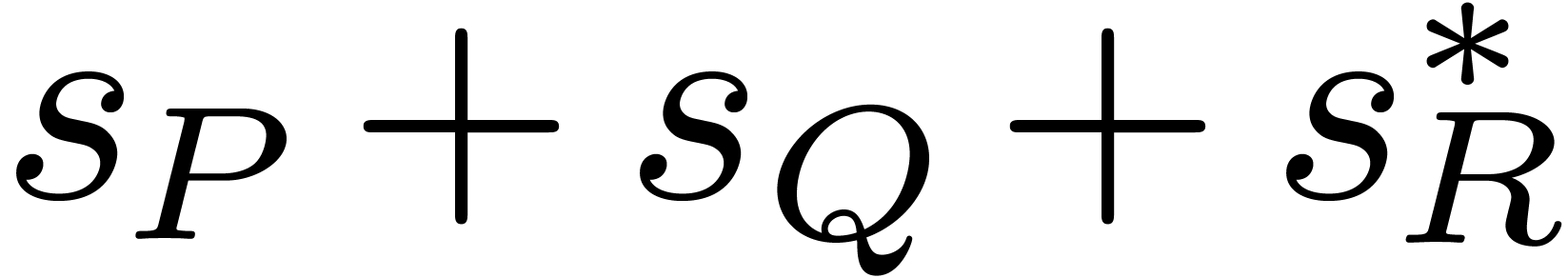 .
.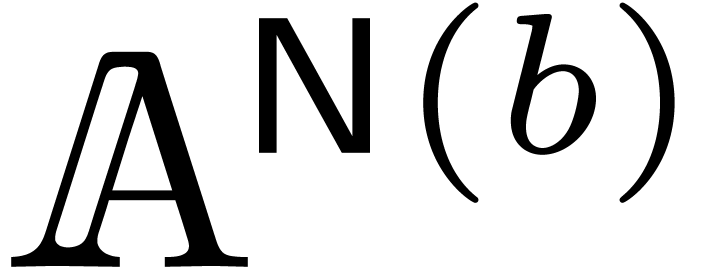 usually will not fit into
cache memory, which makes the algorithm highly cache inefficient.
usually will not fit into
cache memory, which makes the algorithm highly cache inefficient.
 for
suitable pairwise distinct
for
suitable pairwise distinct 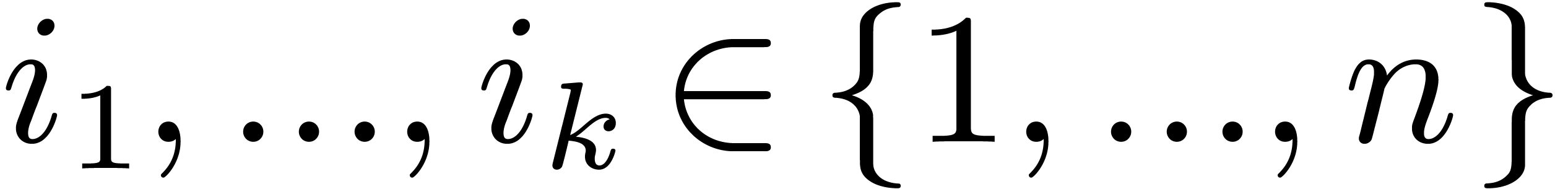 .
.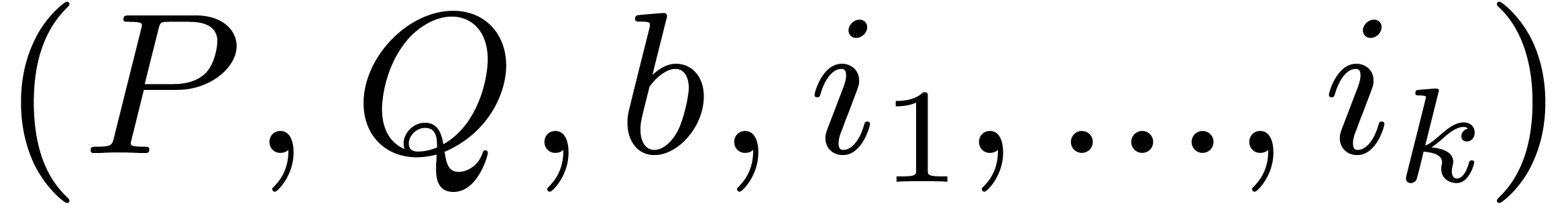
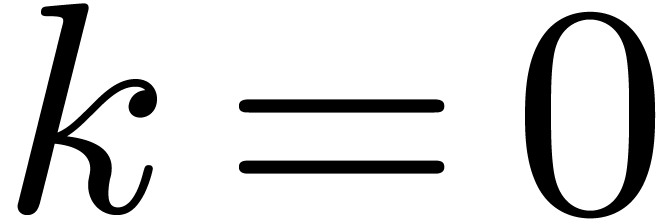 then return
block-multiply
then return
block-multiply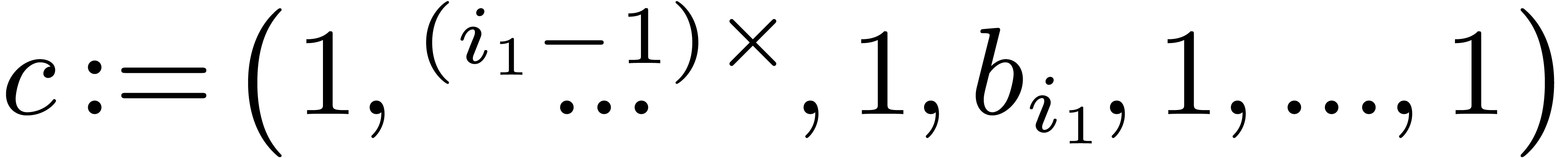 and
and
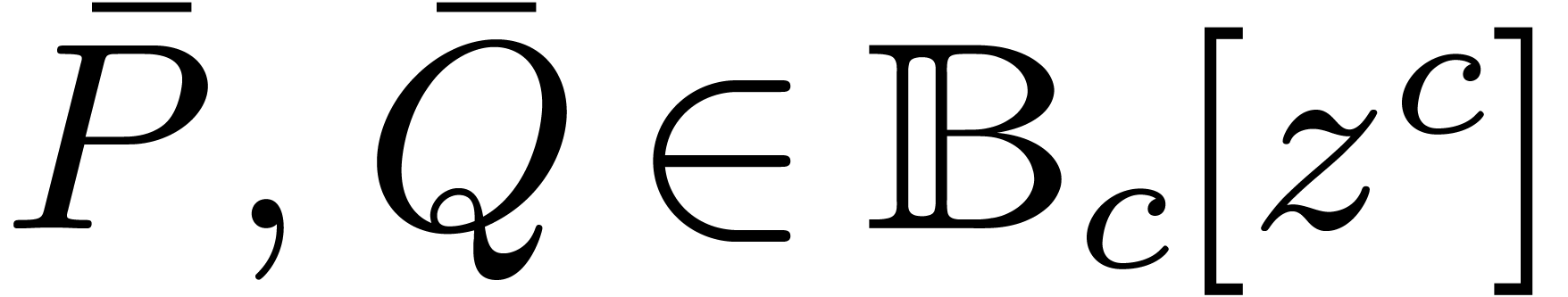 .
. and
and  .
. do
do
 ,
,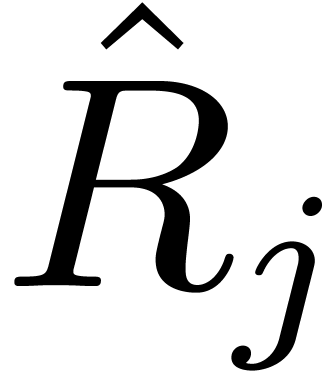 is identified to
is identified to 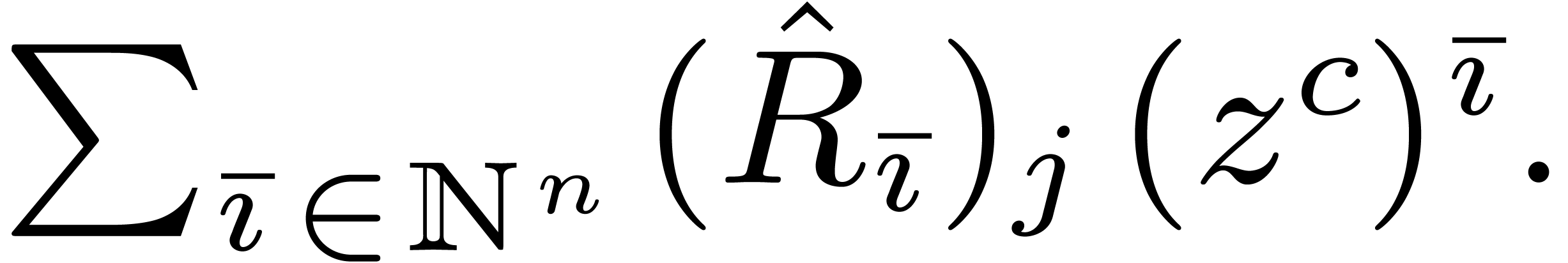
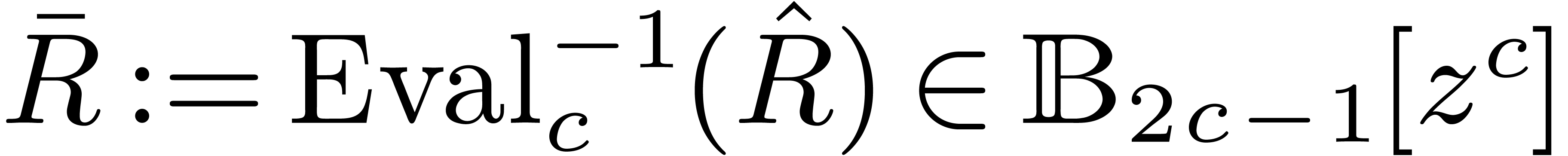 .
. in order to increase the performance.
Setting
in order to increase the performance.
Setting  with
with
 in such a way that
in such a way that  constants in
constants in  .
. should
not be taken to small, e.g.
should
not be taken to small, e.g.  .
. ,
, and
and 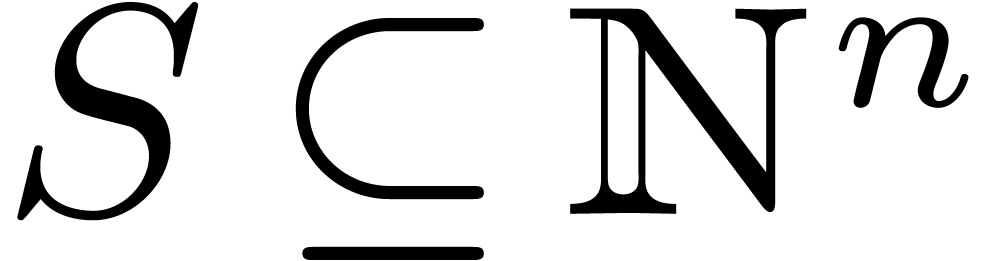 .
. to
to  by
by 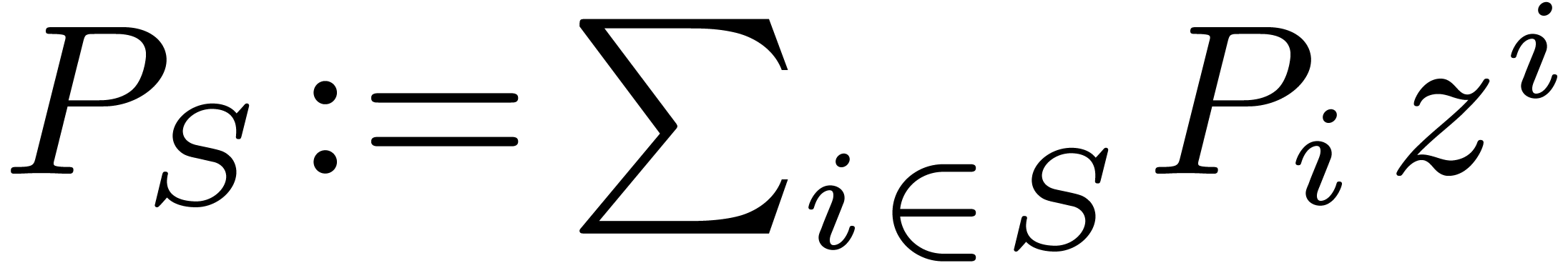 .
.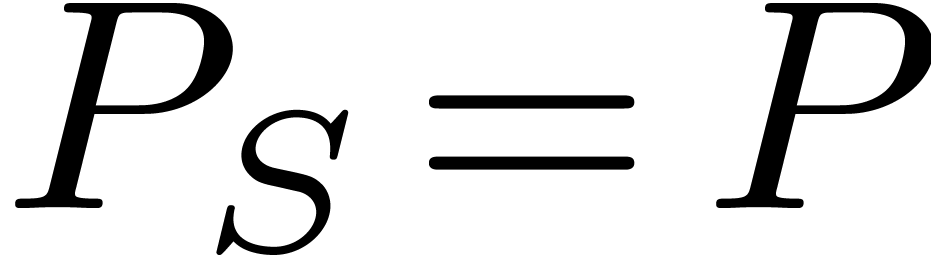 if, and only if,
if, and only if,  with
with 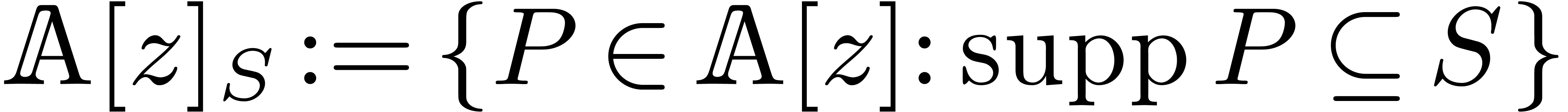 .
. with
with 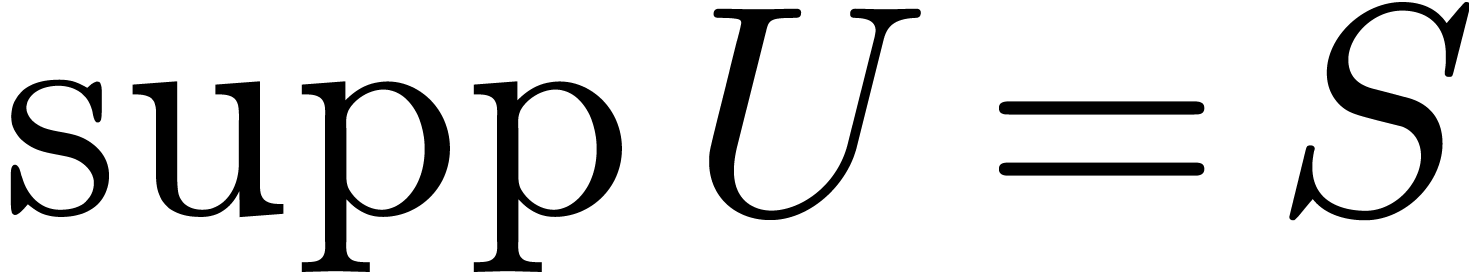 ,
,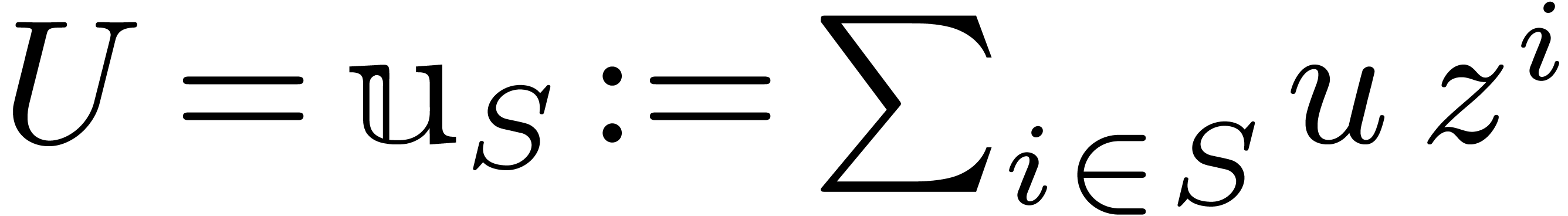 ,
,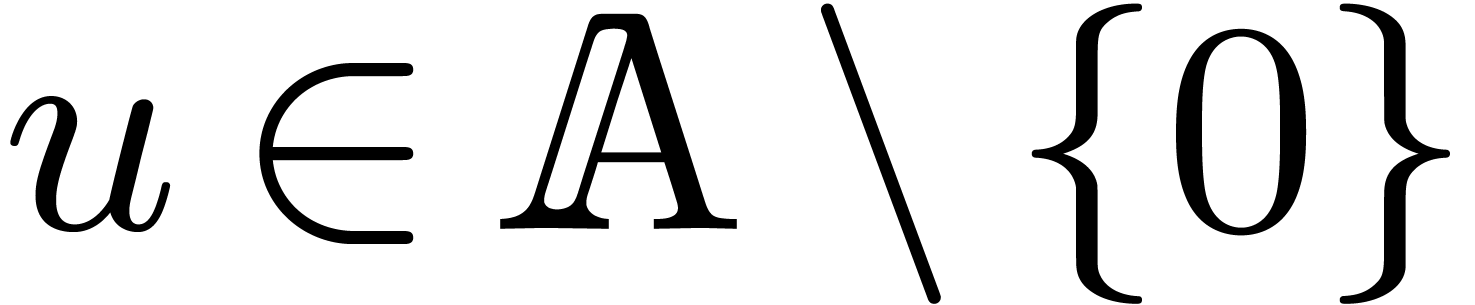 .
.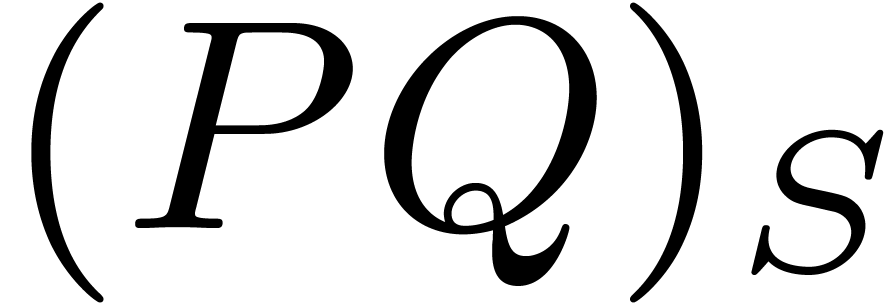 is called the truncated
multiplication. The basic blockwise multiplication algorithm is
adapted as follows:
is called the truncated
multiplication. The basic blockwise multiplication algorithm is
adapted as follows:
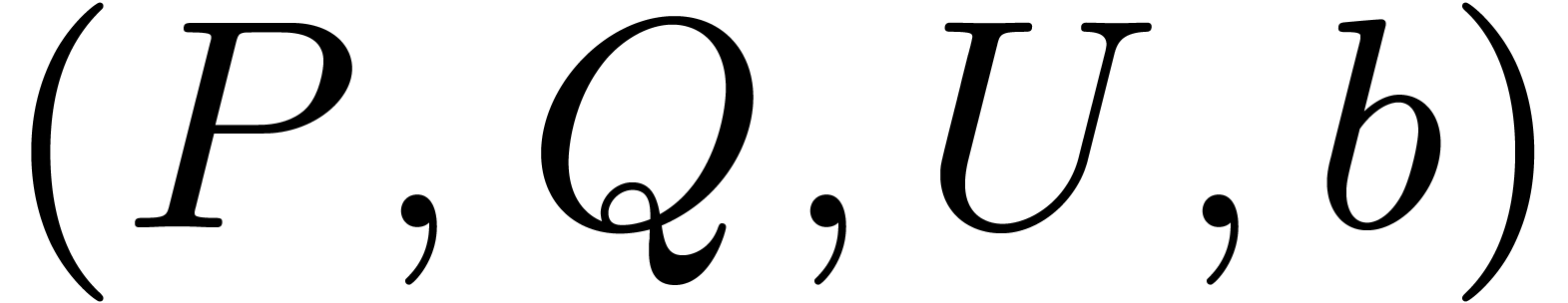
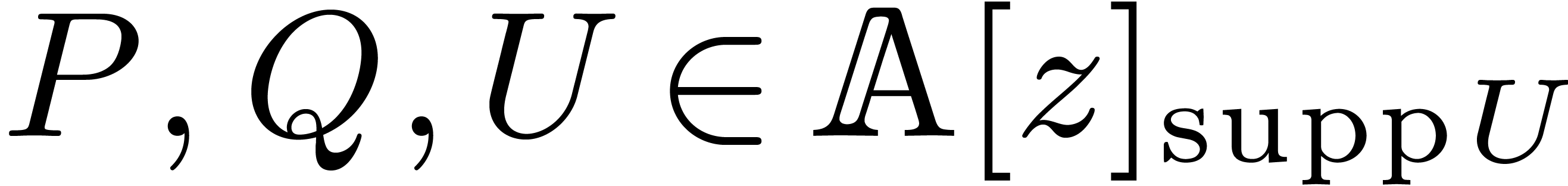 and
and 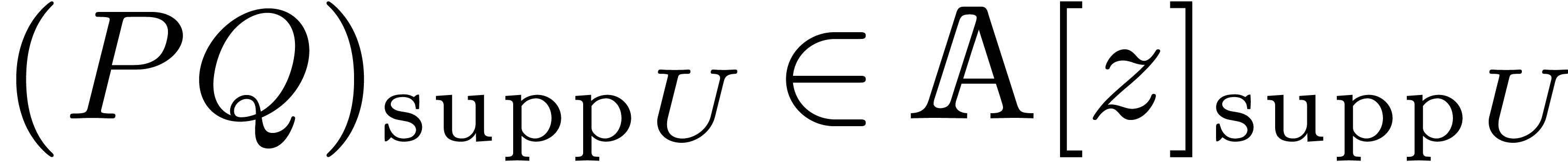 .
. as block polynomials
as block polynomials
 .
. and
and 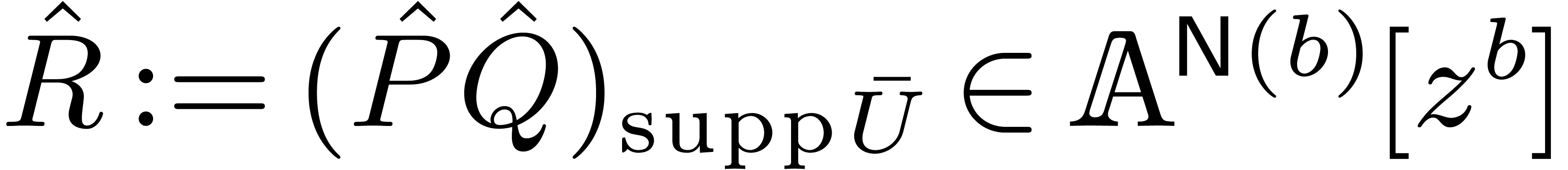 using a naive algorithm.
using a naive algorithm.
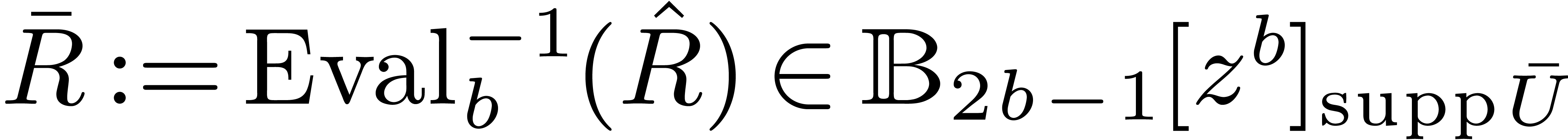 .
. .
.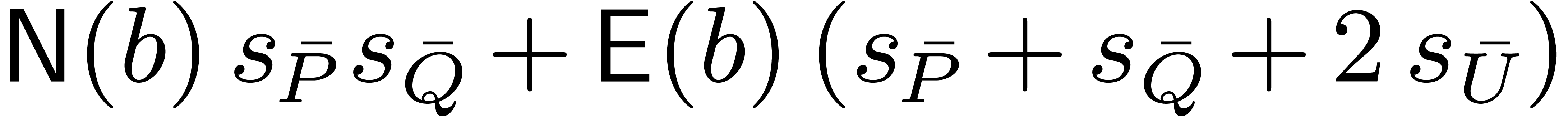
 usually has a
special form which allows us to perform the naive truncated
multiplication in step 3 in much less than
usually has a
special form which allows us to perform the naive truncated
multiplication in step 3 in much less than 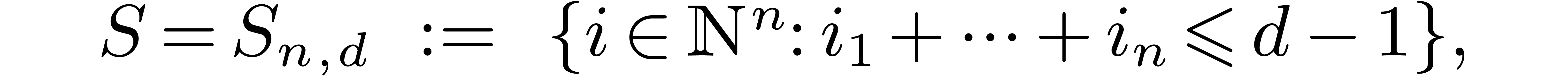
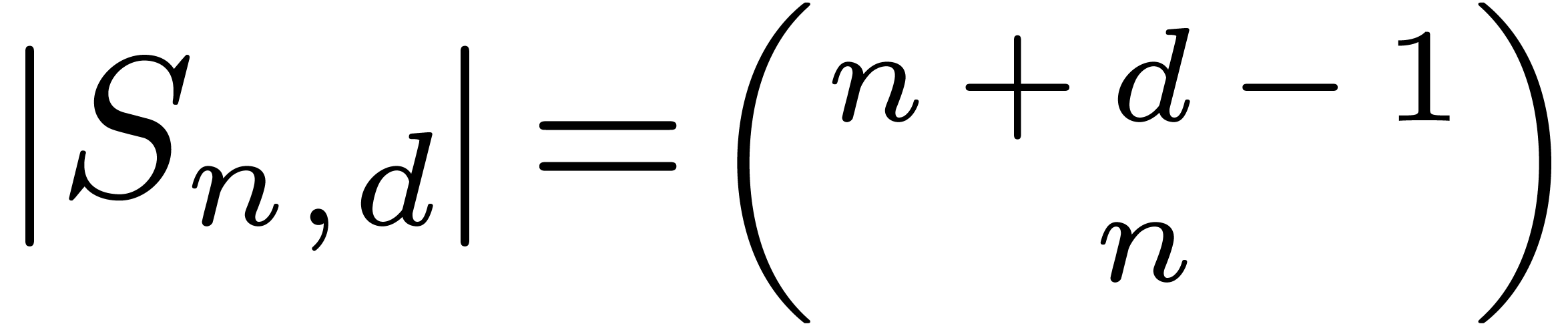 .
.
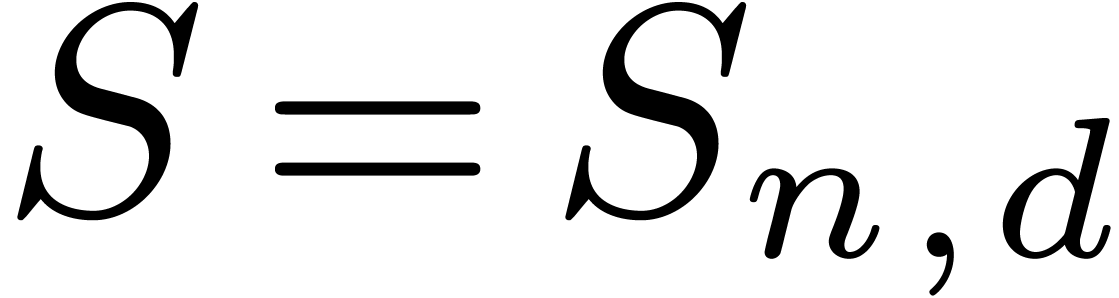 and
and 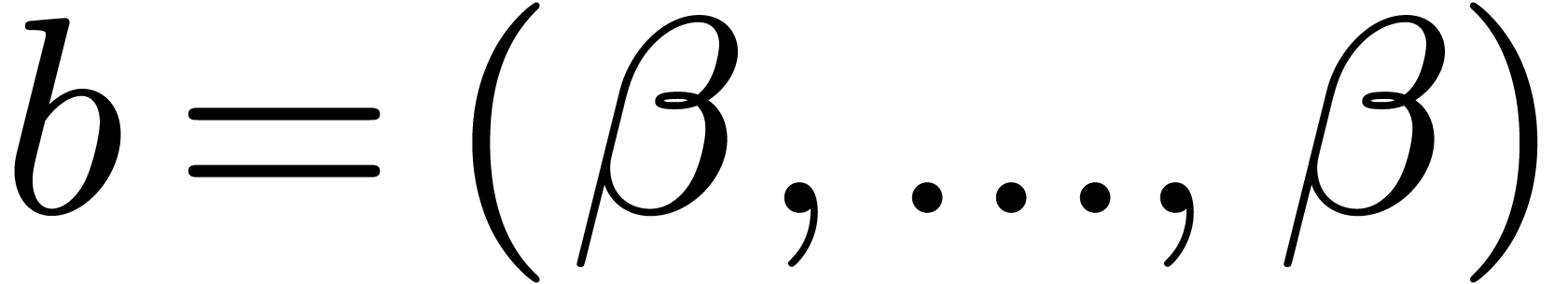 ,
,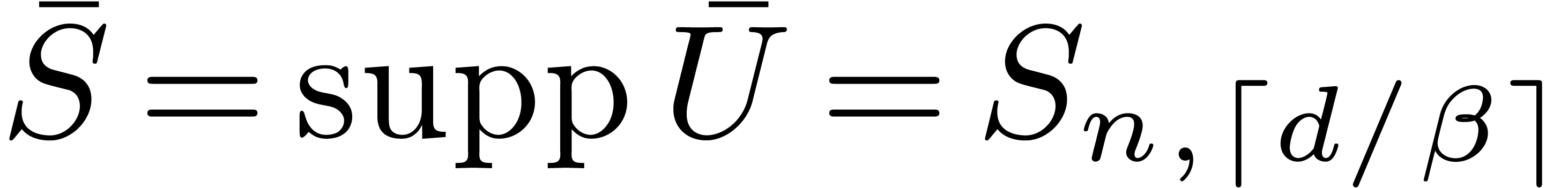 ,
,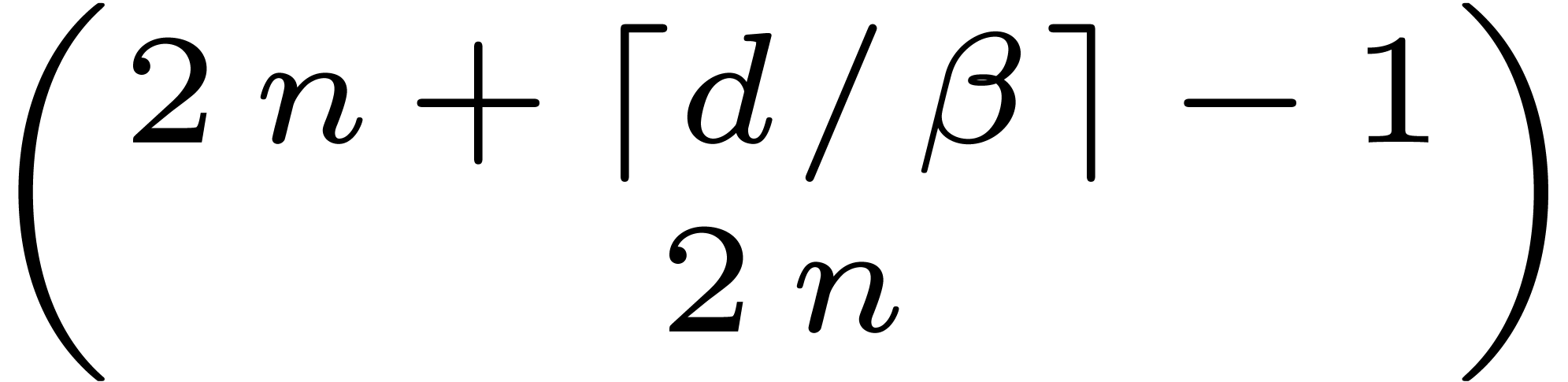 in our complexity bound (
in our complexity bound ( get sparser and sparser. At a certain point, this makes it
pointless to further increase
get sparser and sparser. At a certain point, this makes it
pointless to further increase 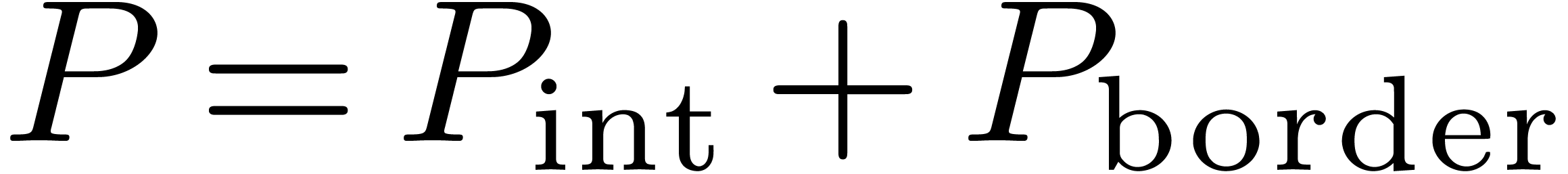 and
and 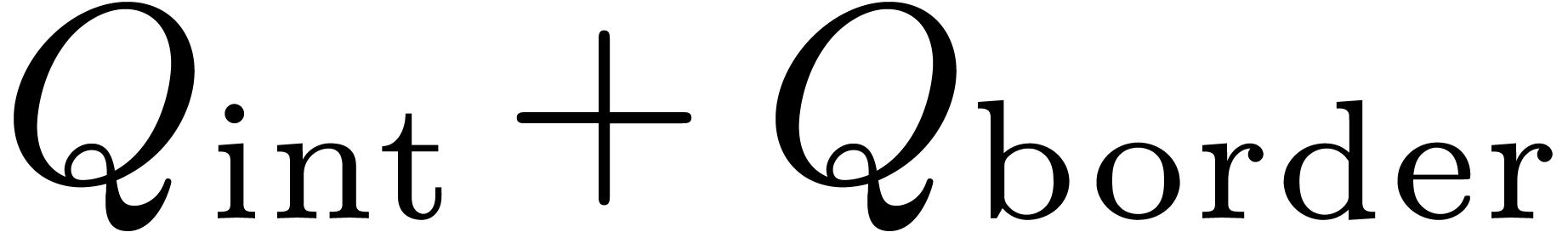 in a such a way that the
multiplication
in a such a way that the
multiplication 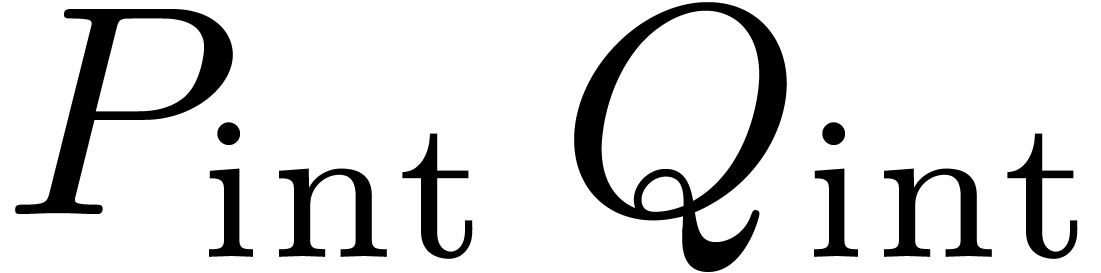 can be done using a larger block
size than the remaining part
can be done using a larger block
size than the remaining part 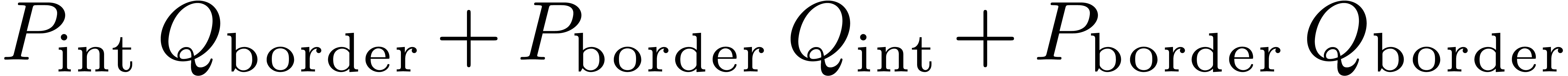 of the
multiplication
of the
multiplication  .
.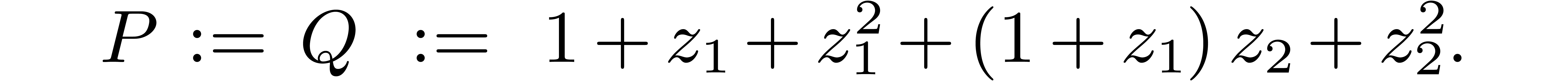
 products in
products in
 The direct use of the Karatsuba algorithm with
The direct use of the Karatsuba algorithm with
 ,
, terms with
coefficients in
terms with
coefficients in  ,
, multiplications in
multiplications in 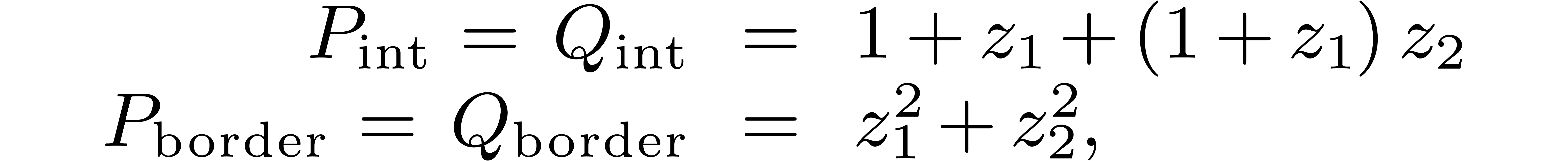
 products in
products in
 products in
products in 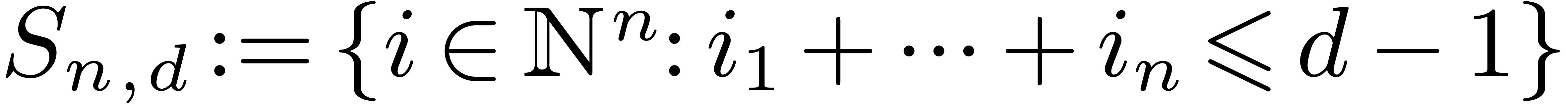 .
.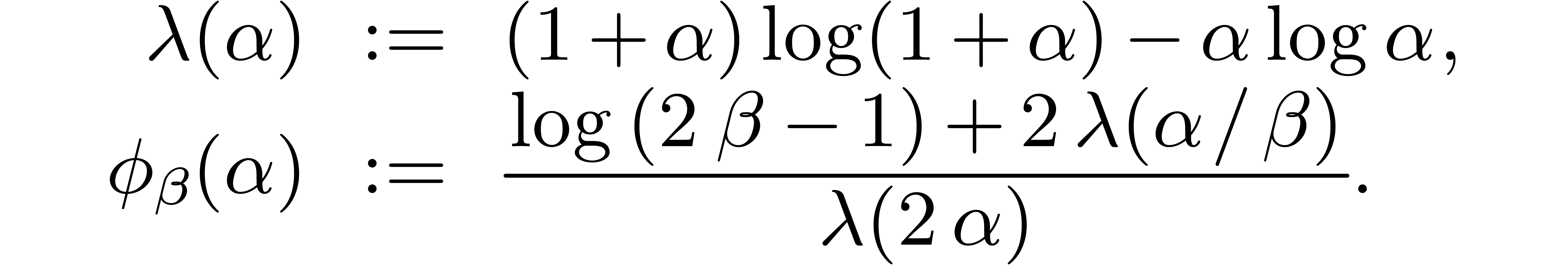
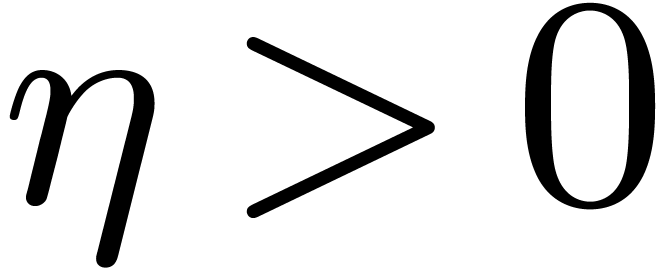 be the first value of
be the first value of  such that
such that 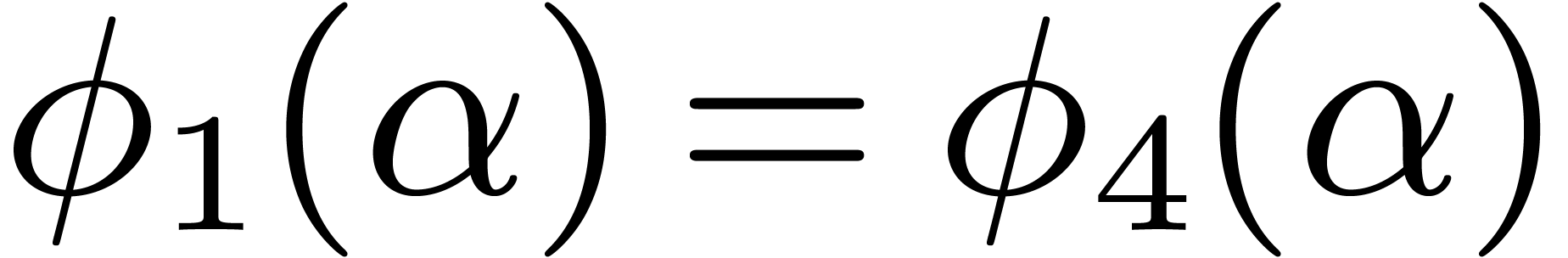 ,
,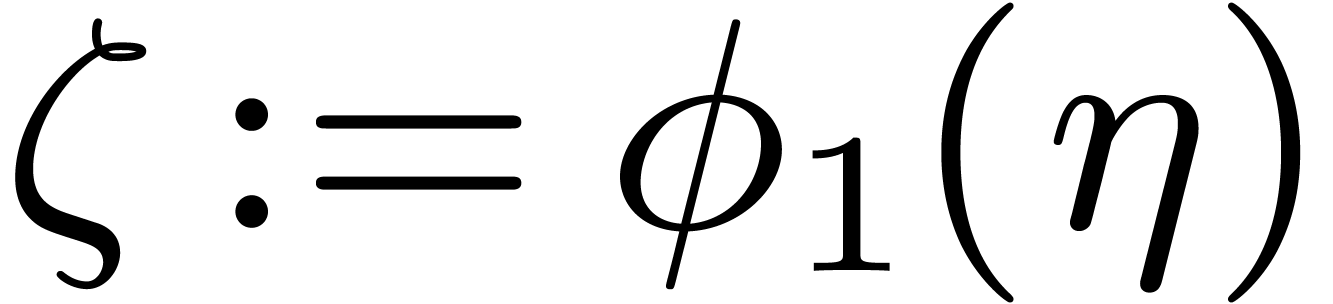 .
.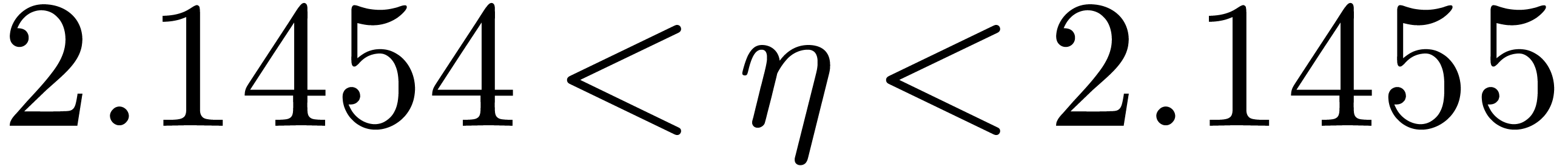 and
and  .
. ,
,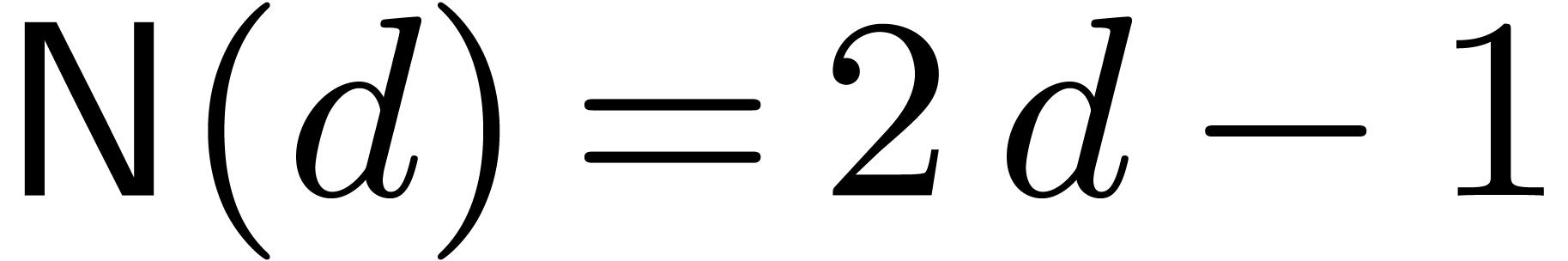 and
and 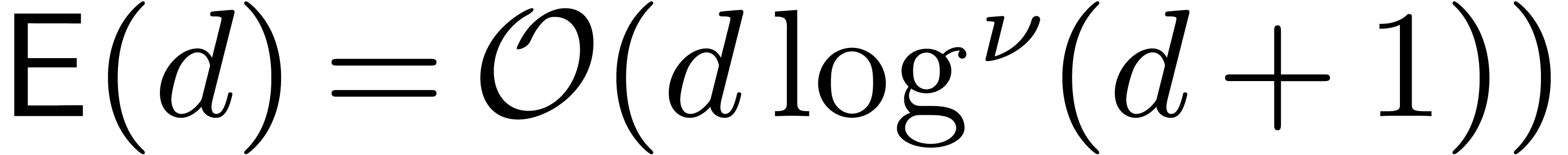 ,
,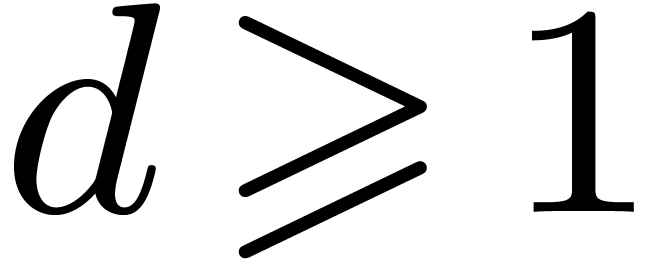 ,
, .
.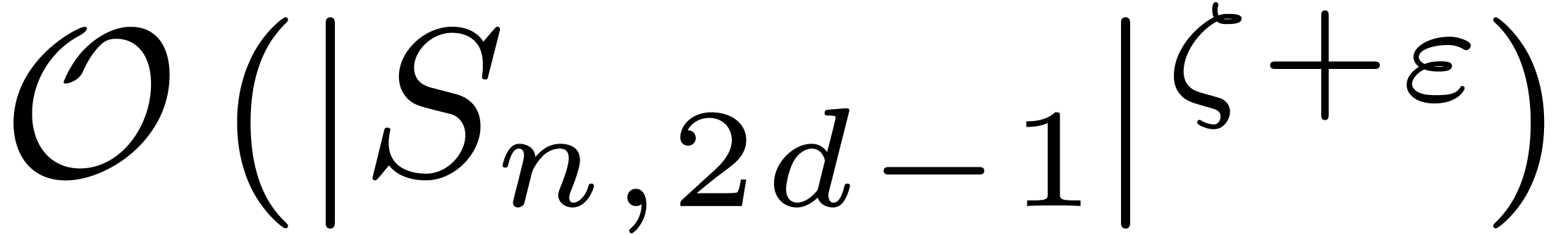 operations in
operations in 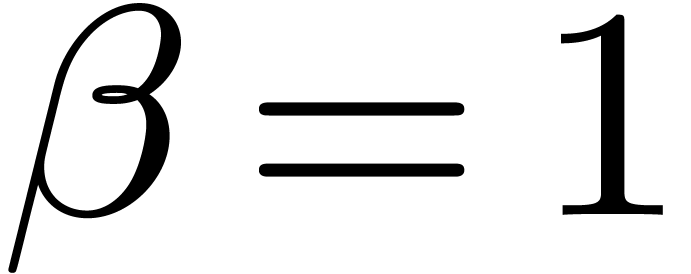 ,
,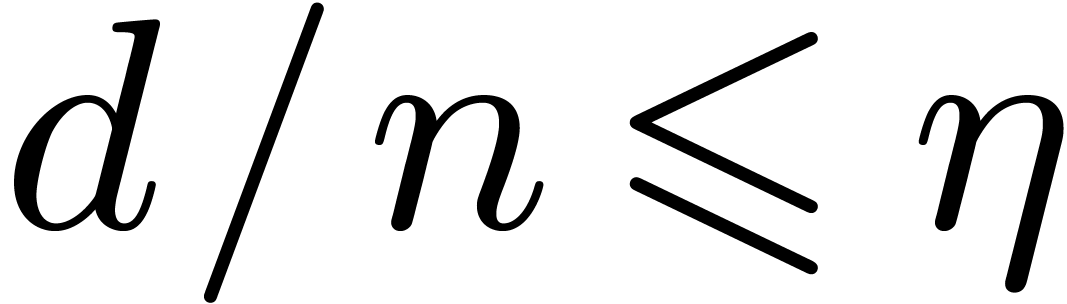 ,
,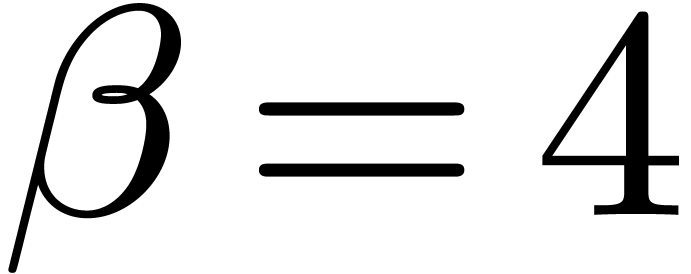 ,
,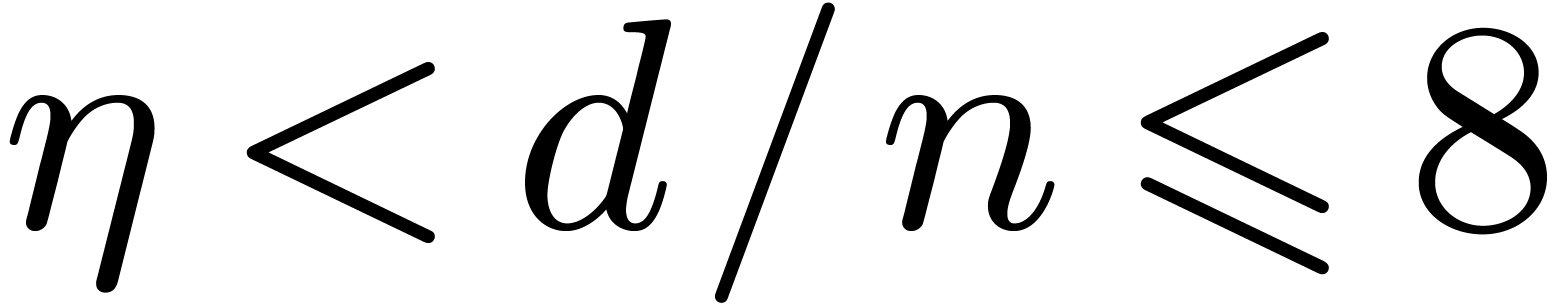 ,
,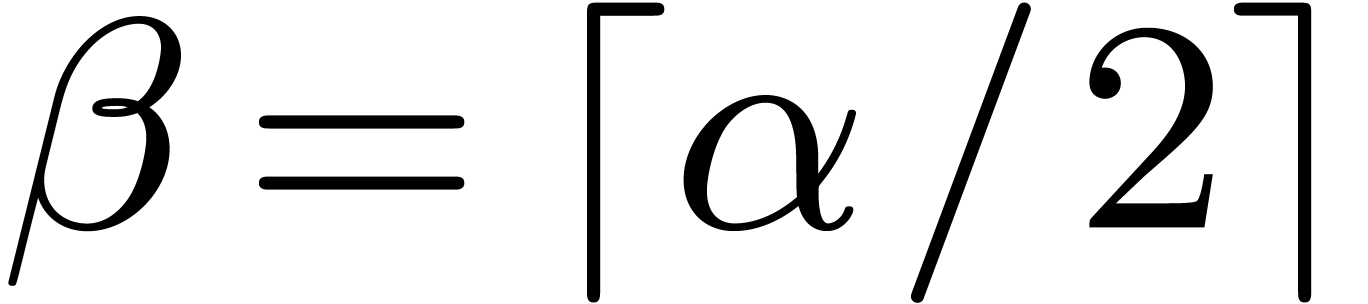 ,
,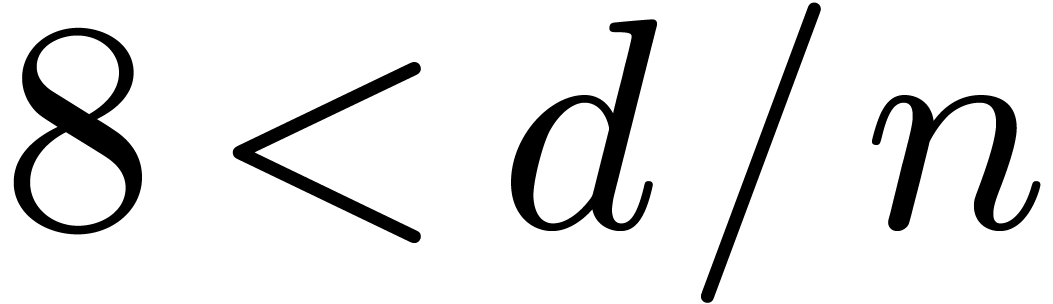 .
.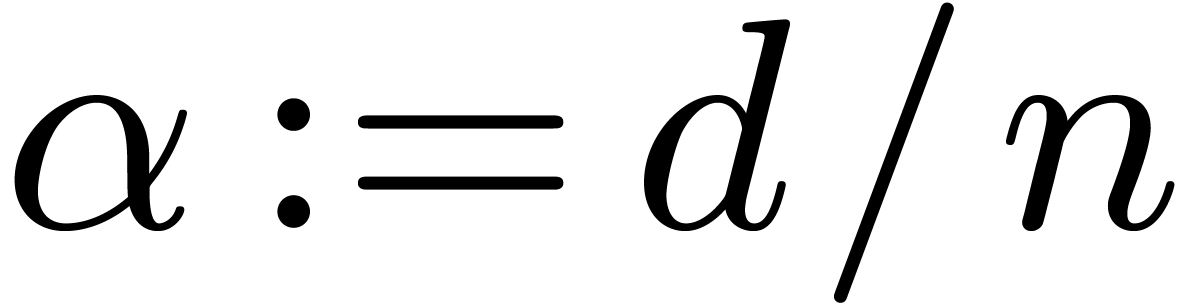 .
.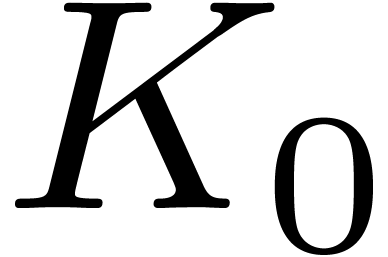 such that
such that

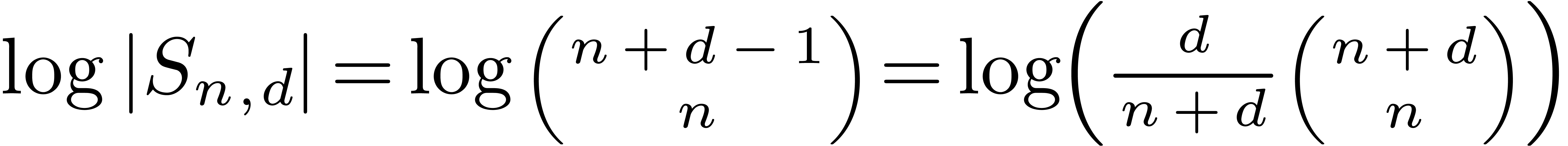 ,
,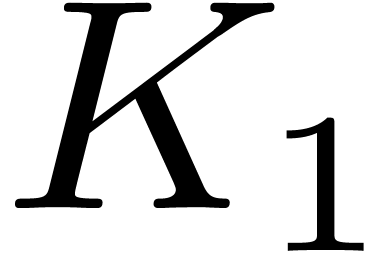 such that the following
inequality holds for all
such that the following
inequality holds for all  and
and 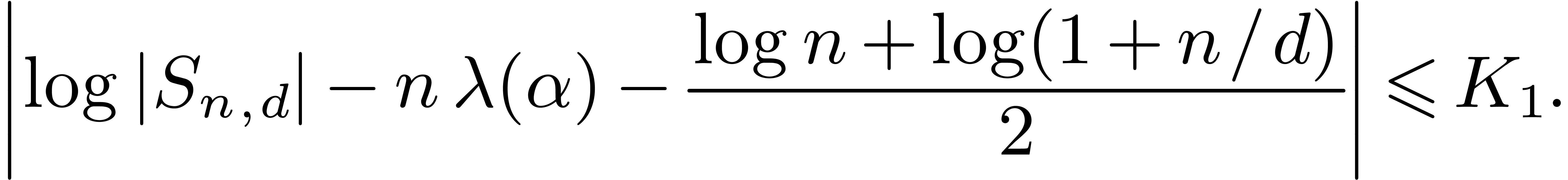
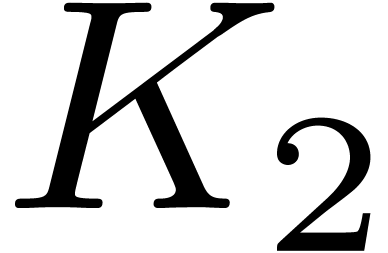 such that
such that
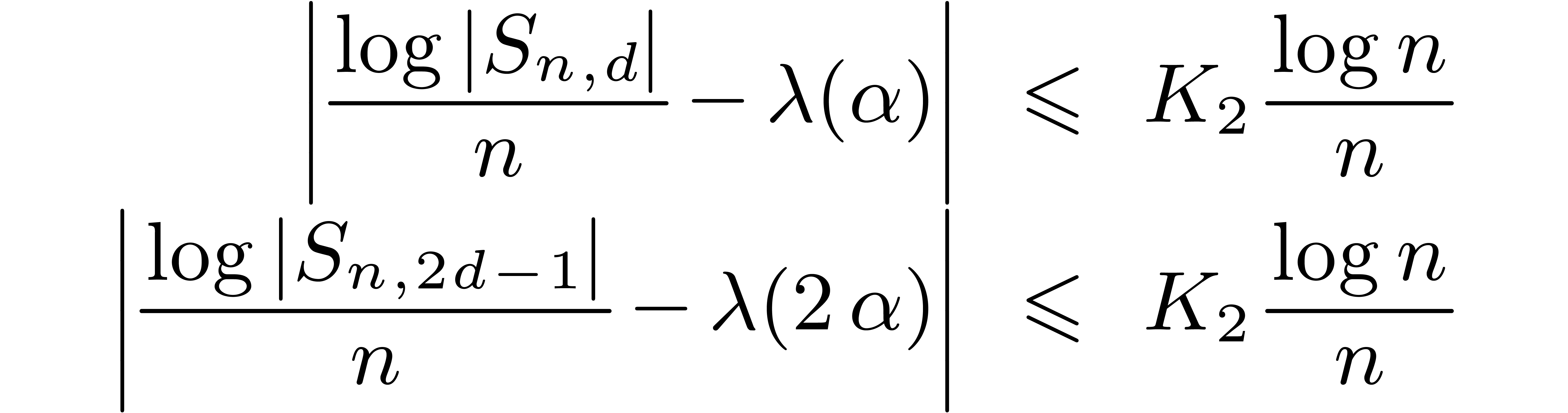
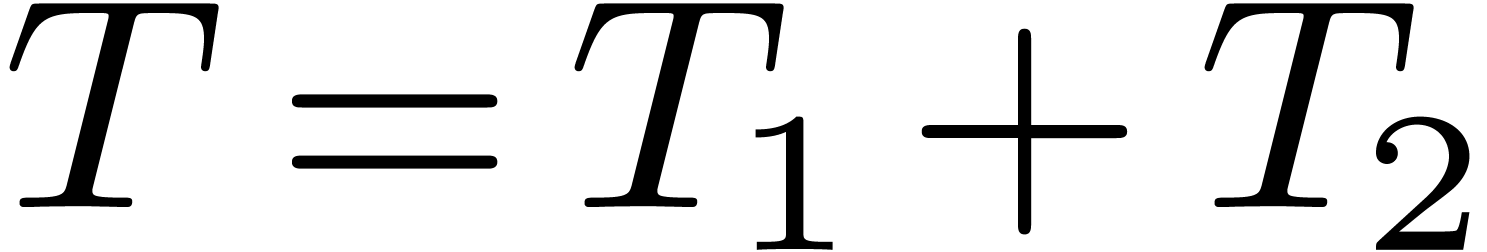 with
with
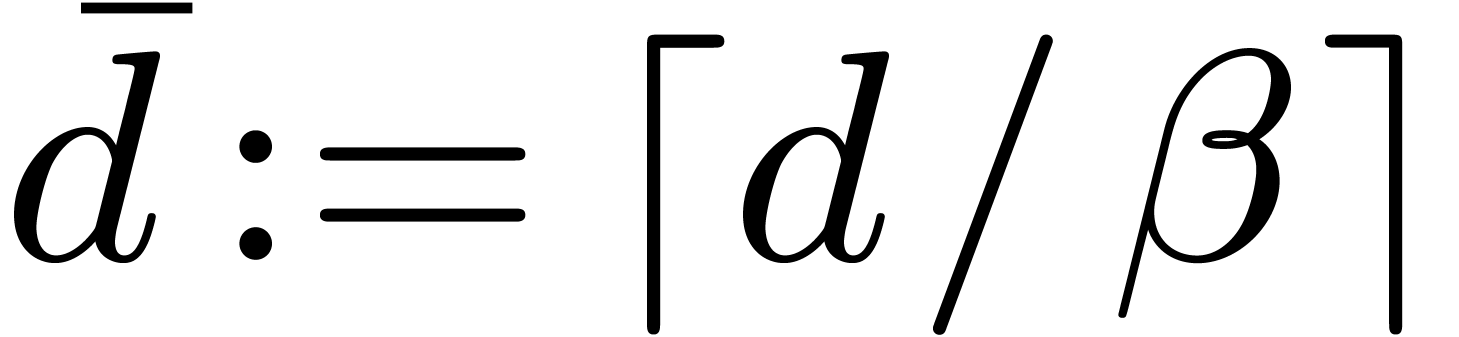 ,
, ,
, ,
,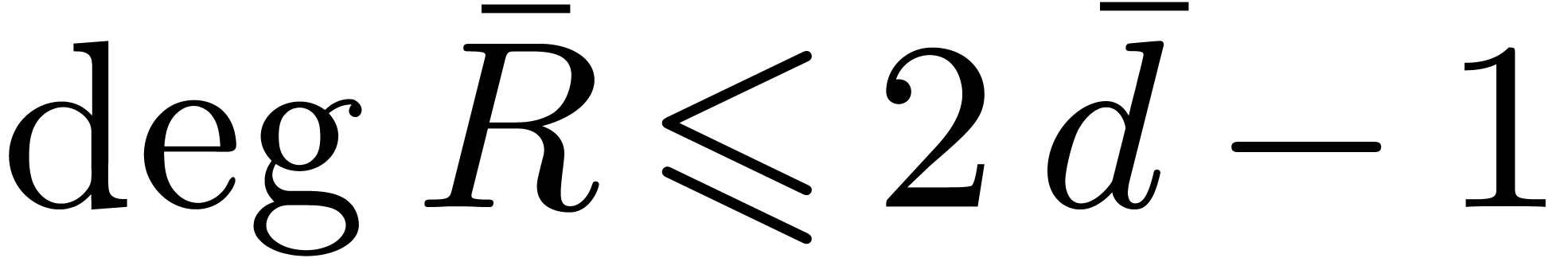 .
.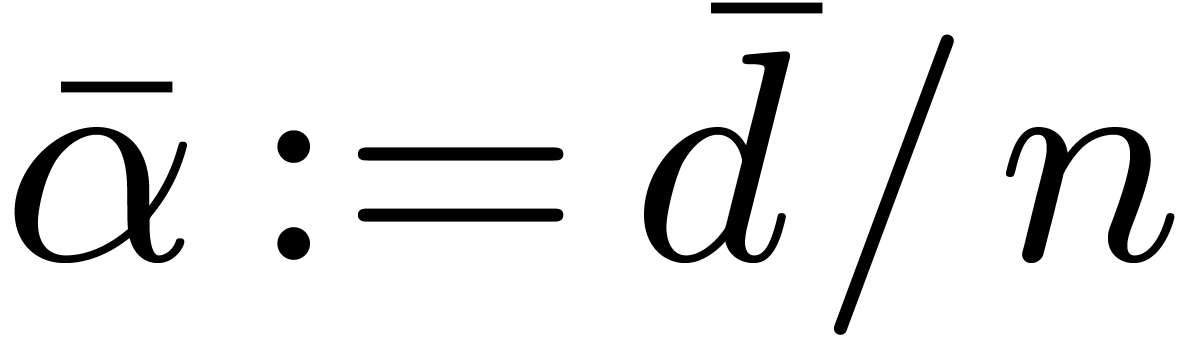 ,
,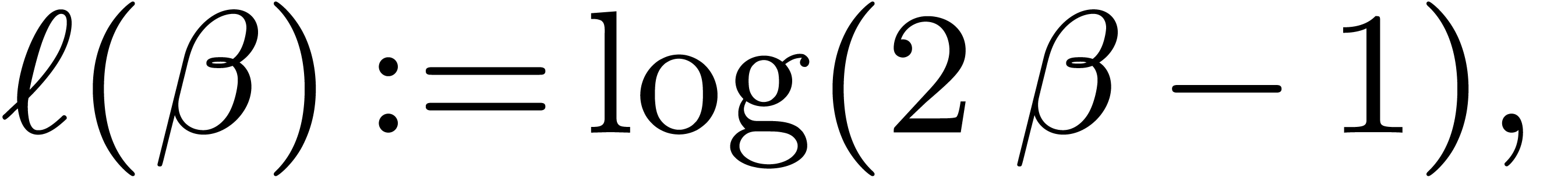 and
and such that:
such that:
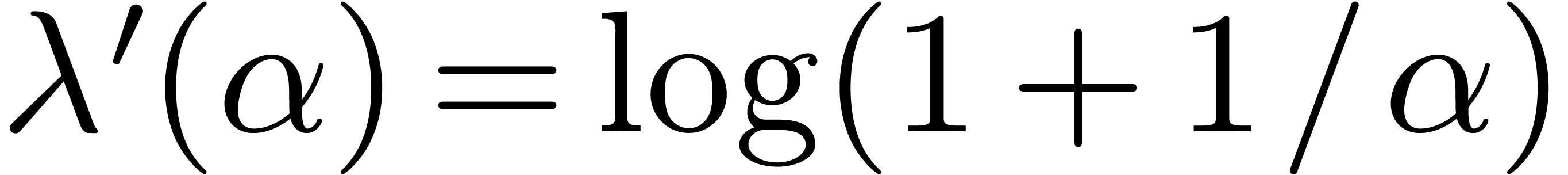 and since
and since 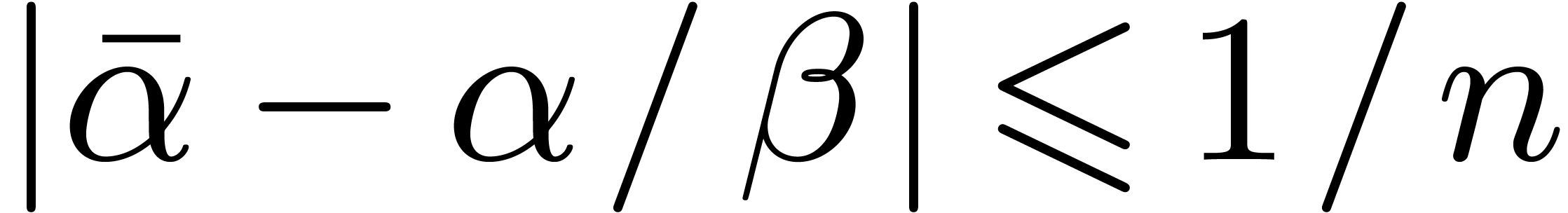 ,
,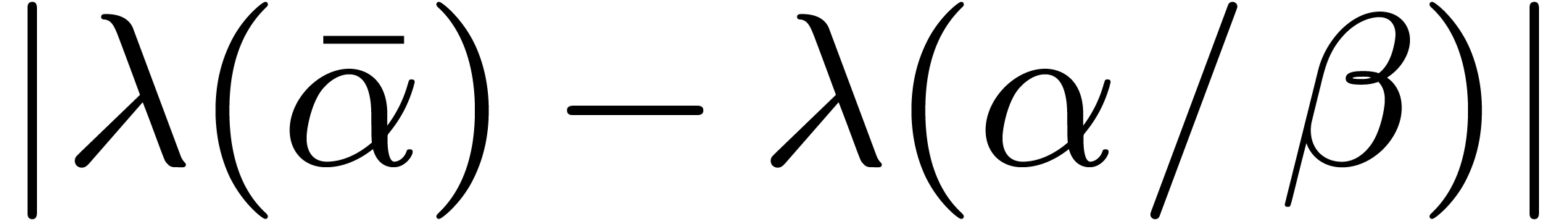 by
by 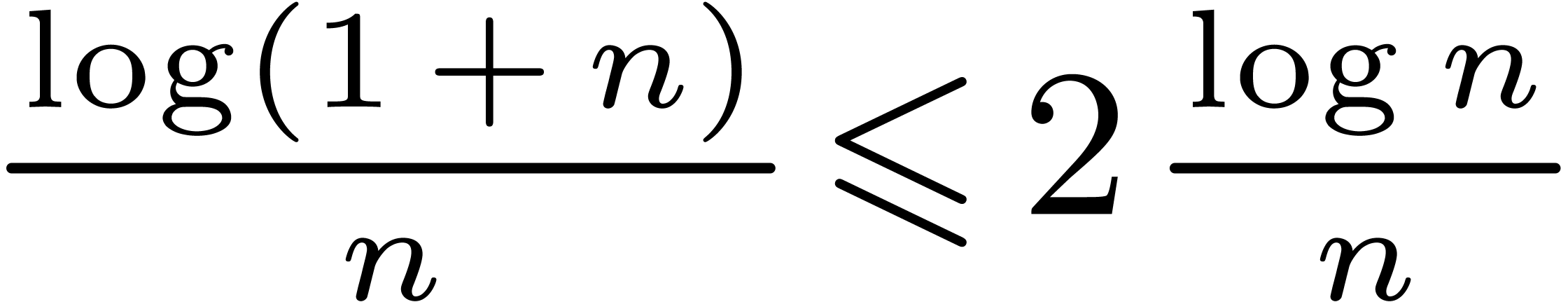 ,
, such that
such that
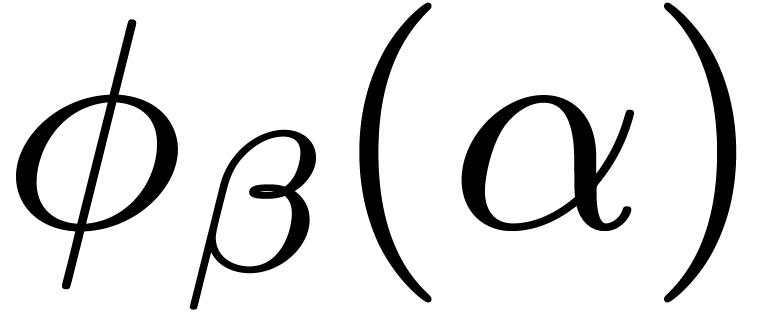 for various
for various 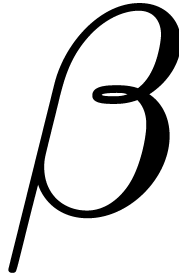 ,
,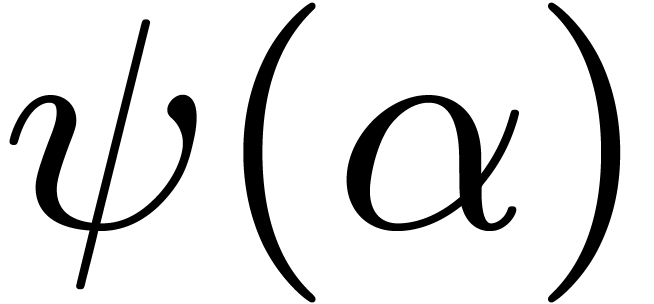 .
.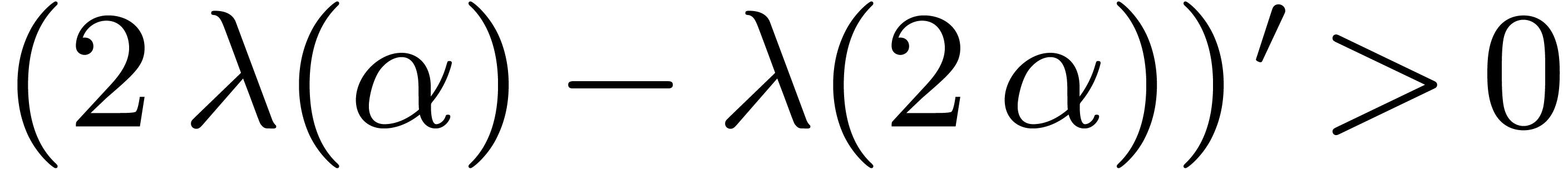 ,
,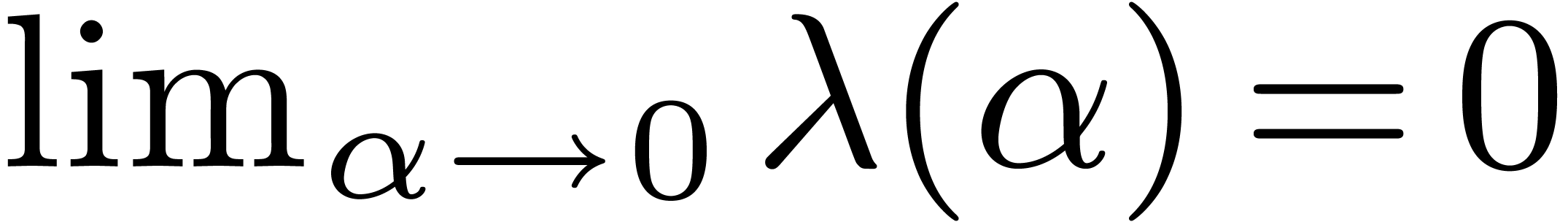 it follows that
it follows that 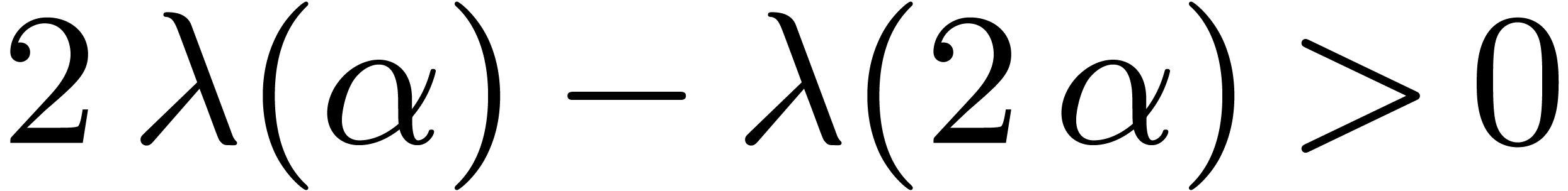 ,
, such that
such that
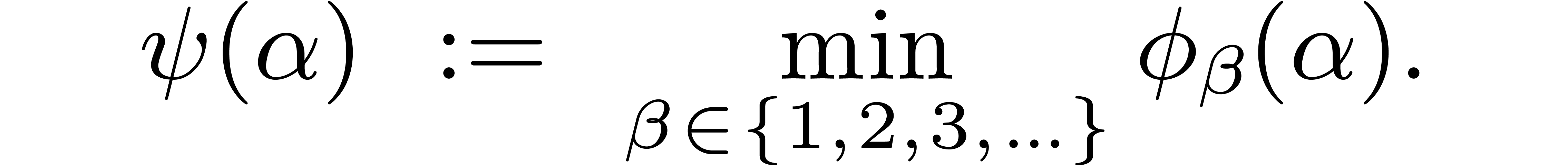
 are plotted in Figure
are plotted in Figure 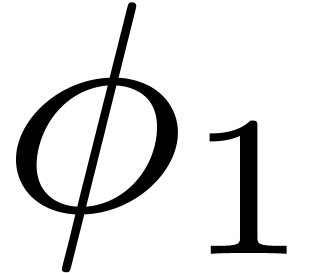 when
when  tends to
tends to 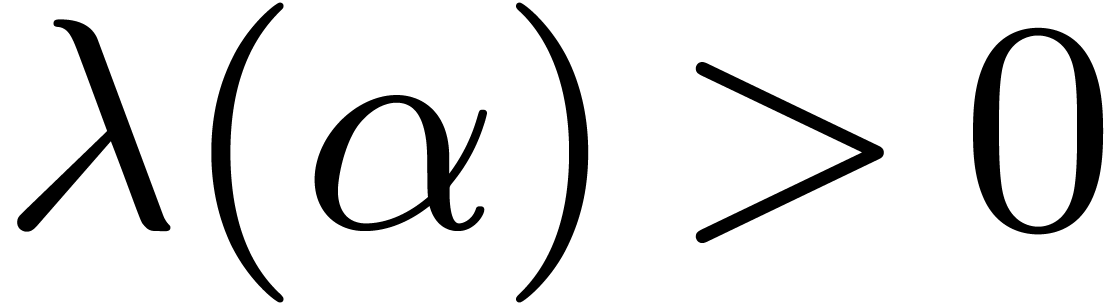 whenever
whenever  ,
,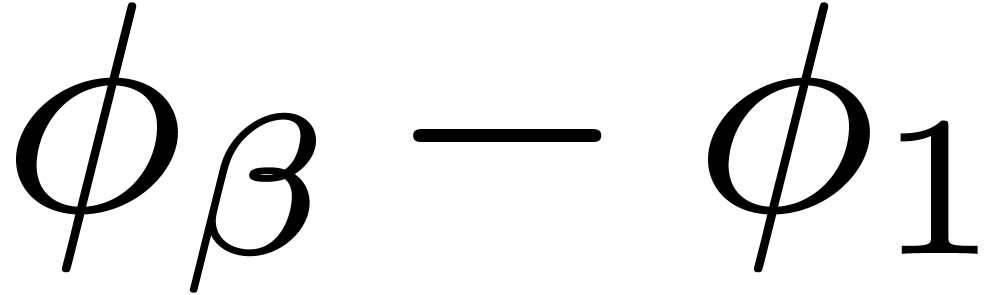 is the same as the one of
is the same as the one of
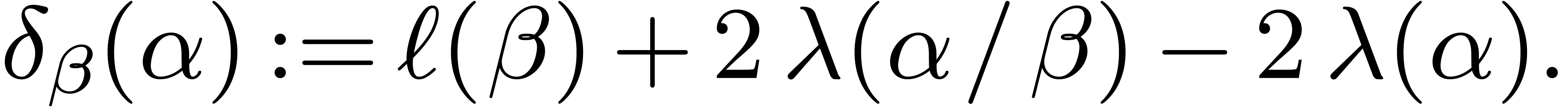
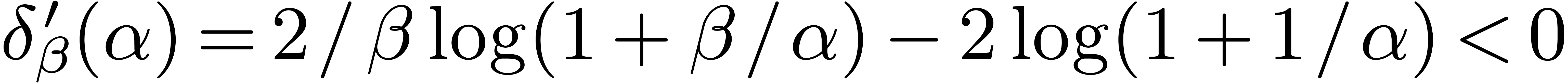 and
and 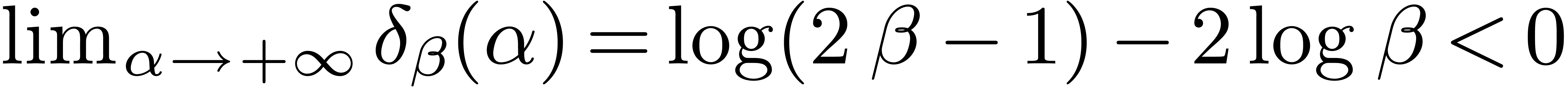 ,
, ,
, .
. ,
,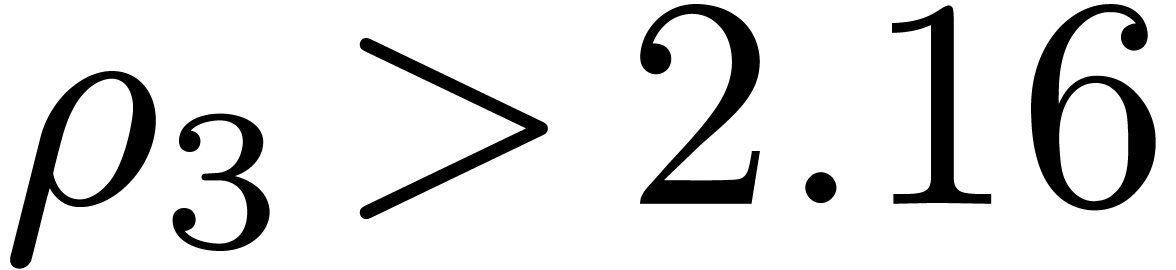 ,
,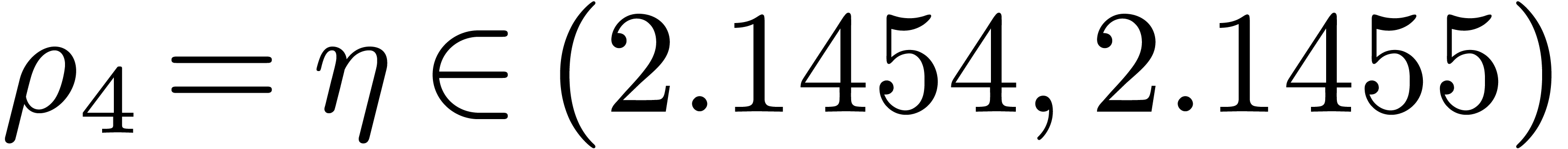 .
. achieves its maximum for
achieves its maximum for 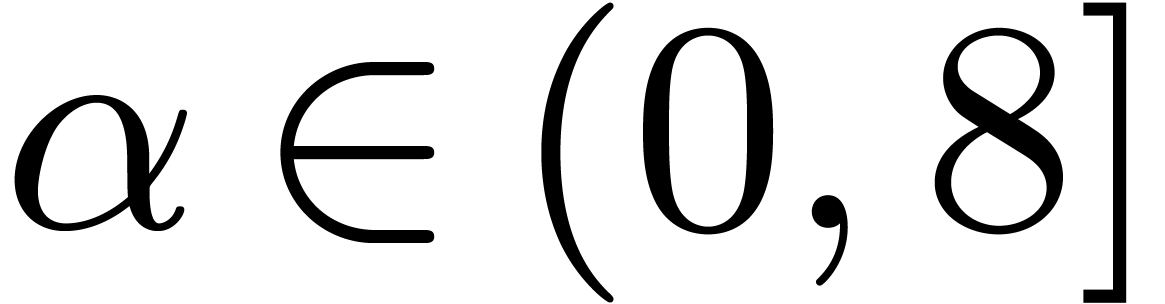 at
at 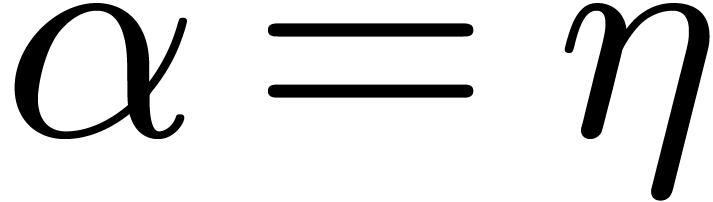 .
.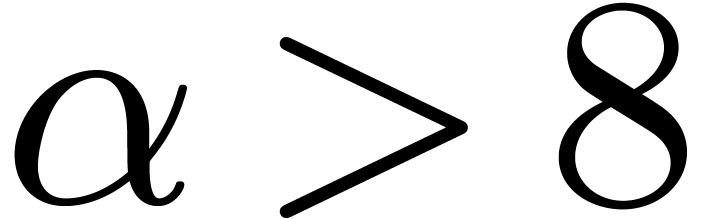 ,
,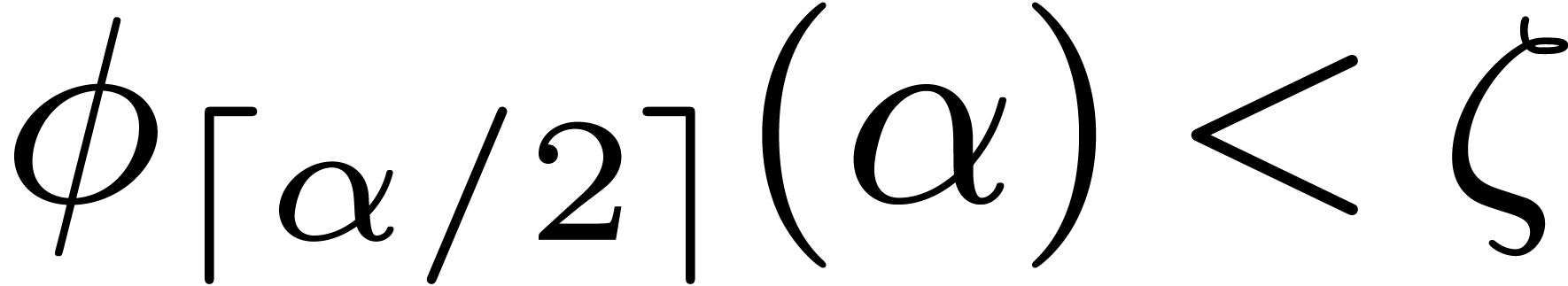 .
.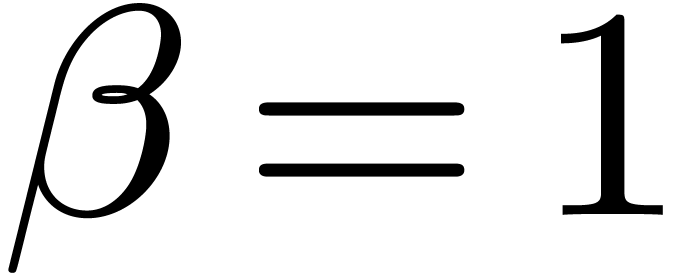 for
for
 ,
, for
for
 and
and  holds for all
holds for all  ,
, for all
for all  and
and
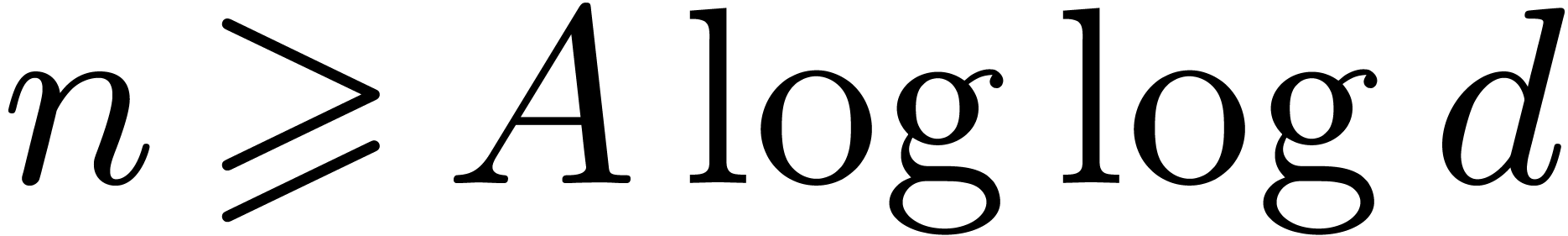 ,
, and
and 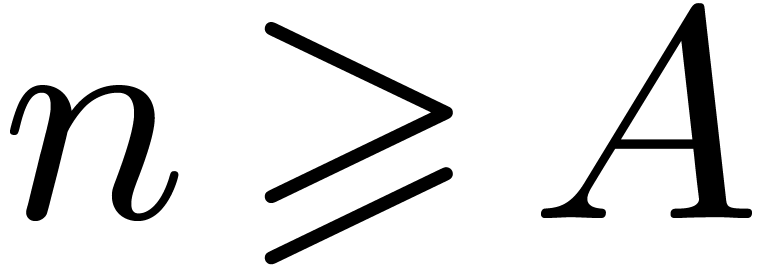 .
.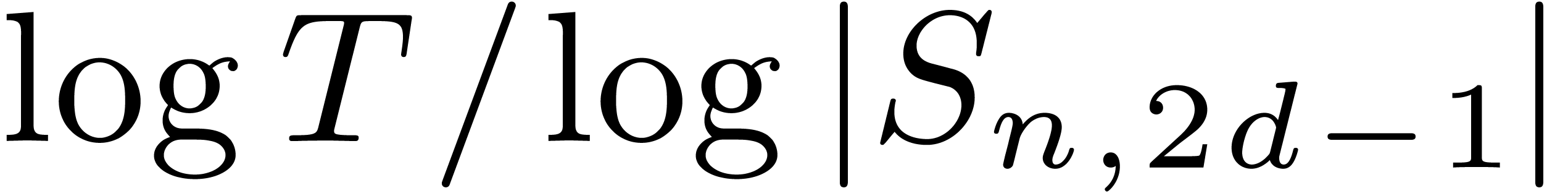 for
for 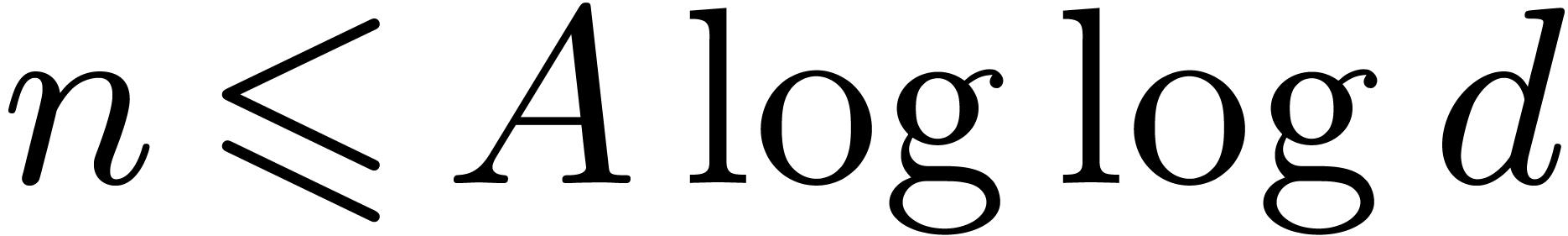 and
and 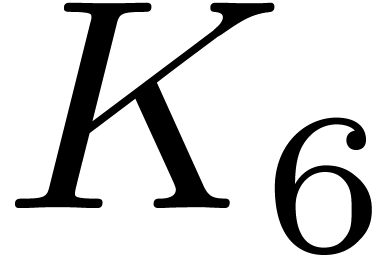 such that:
such that:
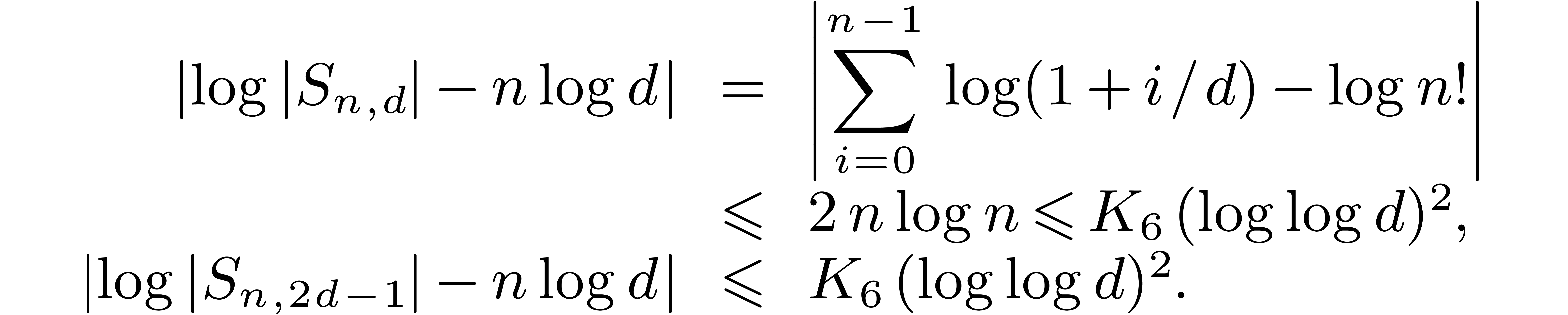
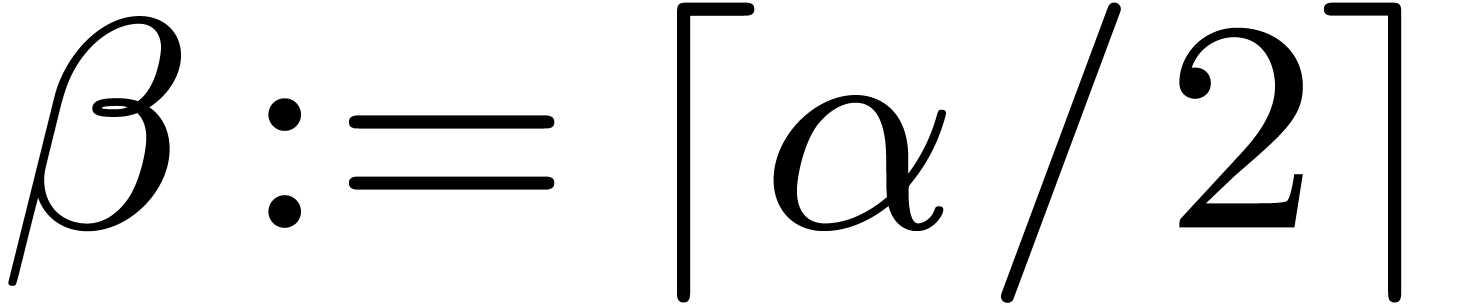 ,
,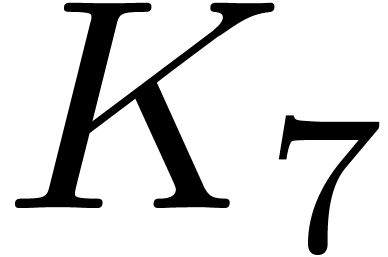 with
with
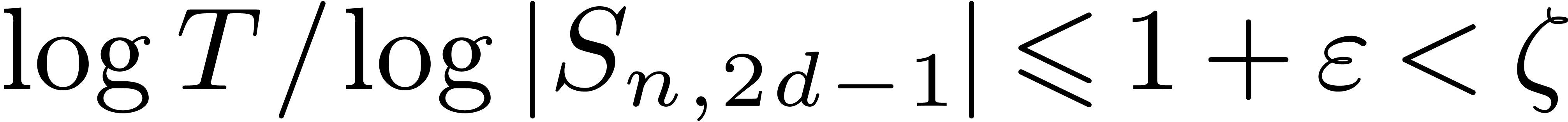 when
when 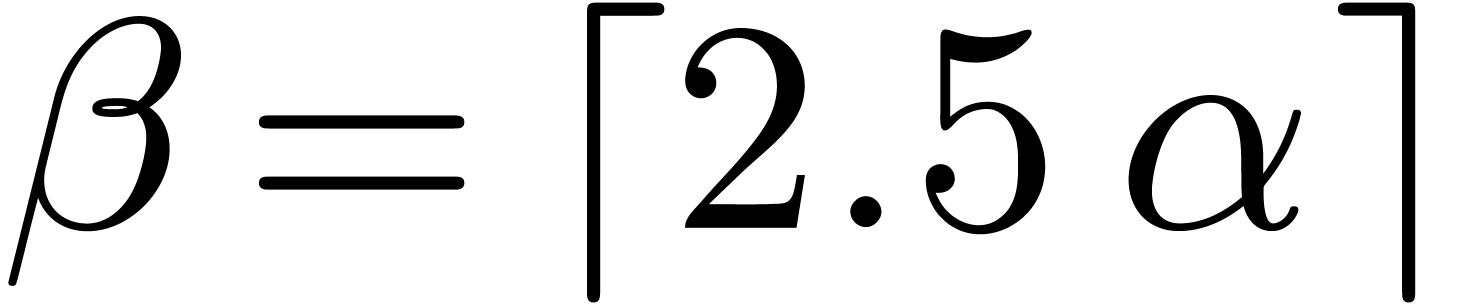 for
for  is
generally better whenever
is
generally better whenever  remains in
remains in 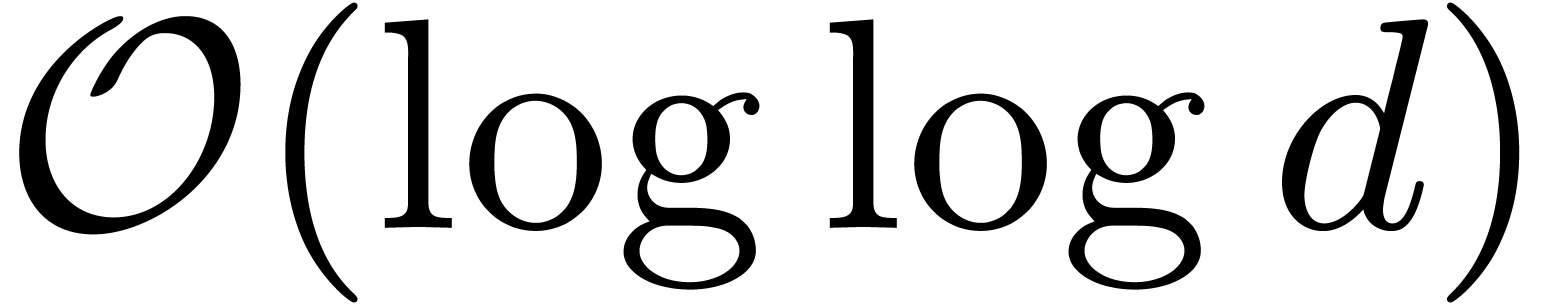 .
.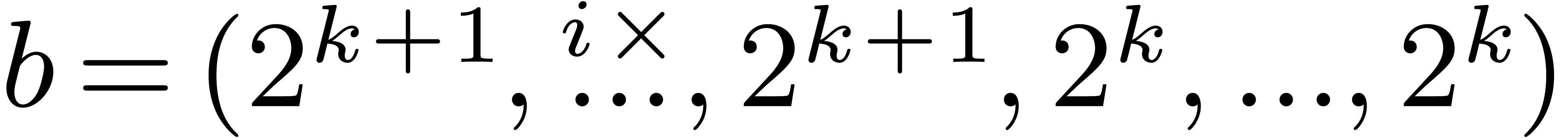 for some
for some  (and modulo
permutation of the indeterminates).
(and modulo
permutation of the indeterminates).
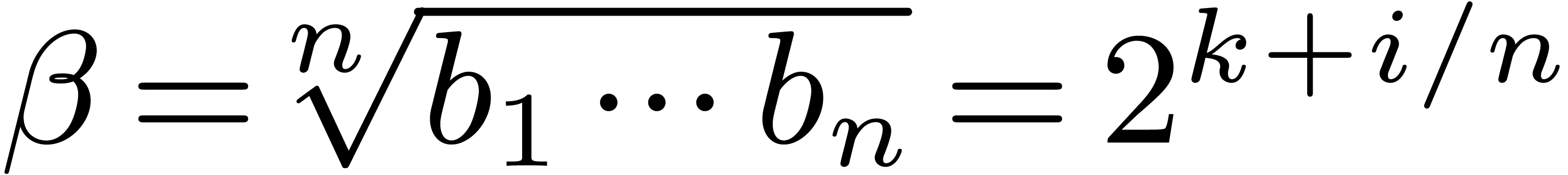 in the proof of
Theorem
in the proof of
Theorem  ,
,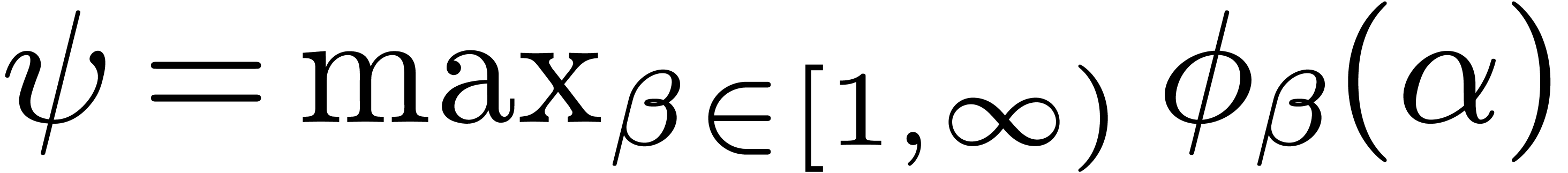 is
now reached at
is
now reached at 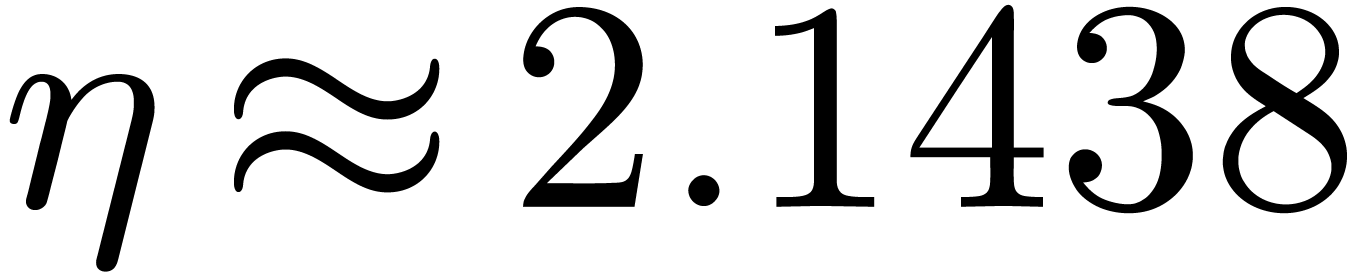 ,
,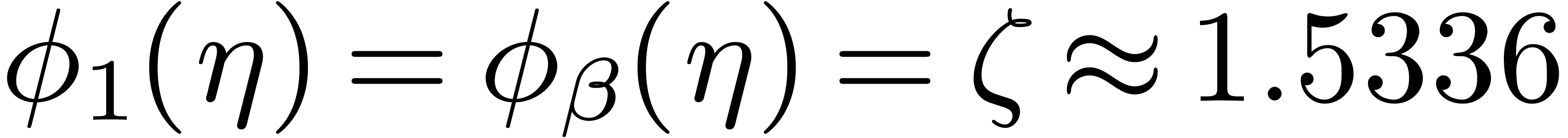 and
and 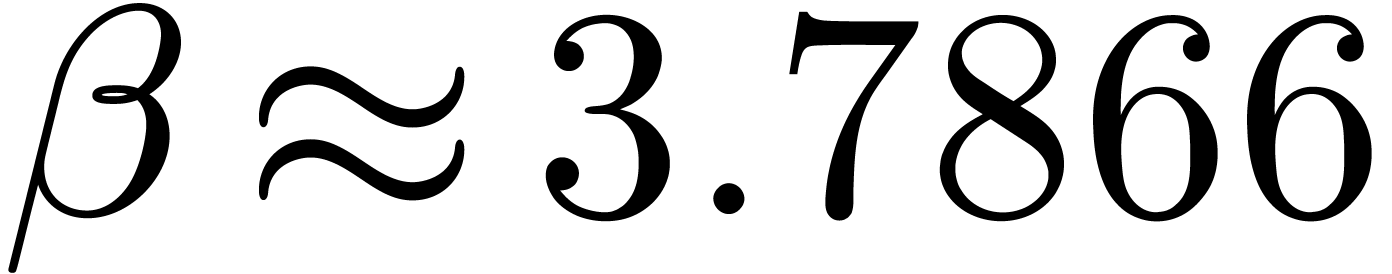 .
. .
.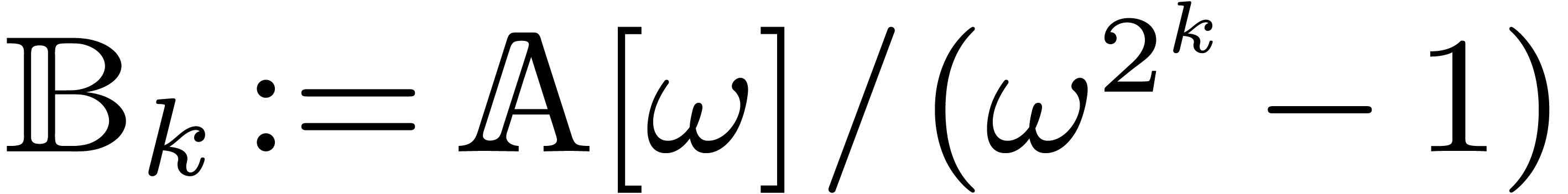 and
and  .
. (resp. in
(resp. in  )
)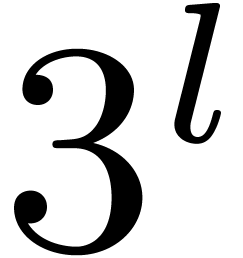 )
) (resp. of
(resp. of  )
)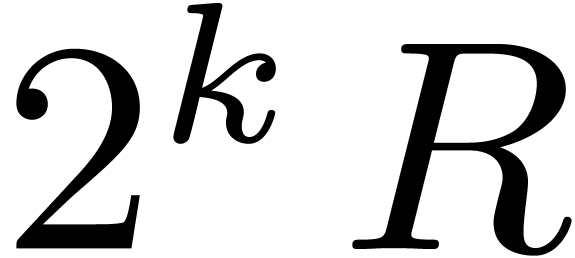 and
and 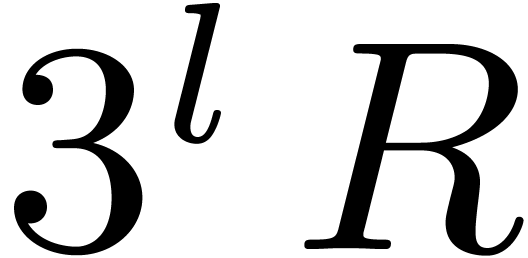 .
.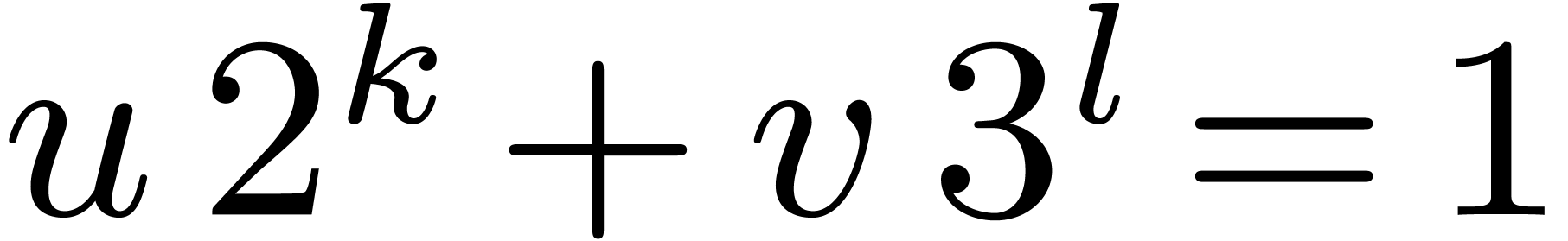 then we deduce
then we deduce  as
as
 .
. gives rise to an
additional overhead of
gives rise to an
additional overhead of 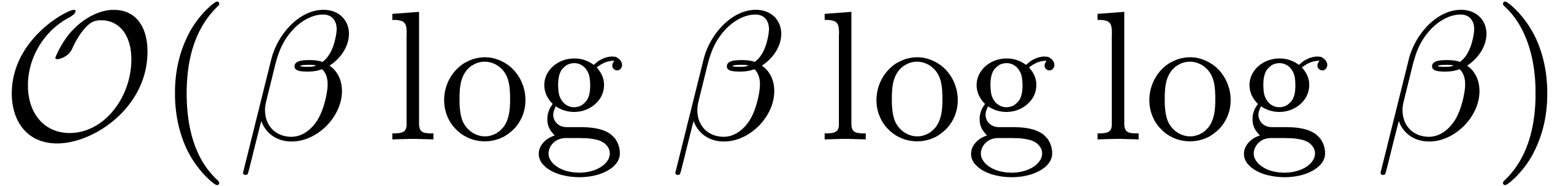 with respect to the
complexity analysis from the proof of Theorem
with respect to the
complexity analysis from the proof of Theorem 
 for a
sufficiently large constant
for a
sufficiently large constant 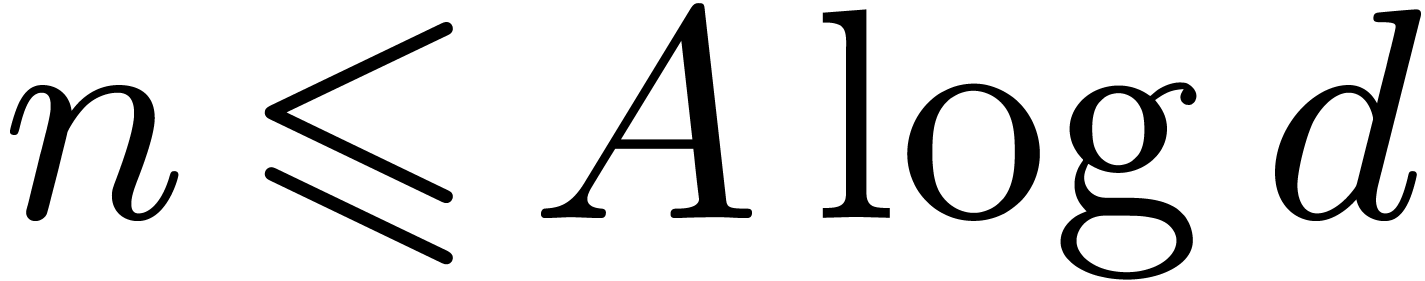 .
. such that
such that
 for
for 
 be the unique positive zero of
be the unique positive zero of  ,
,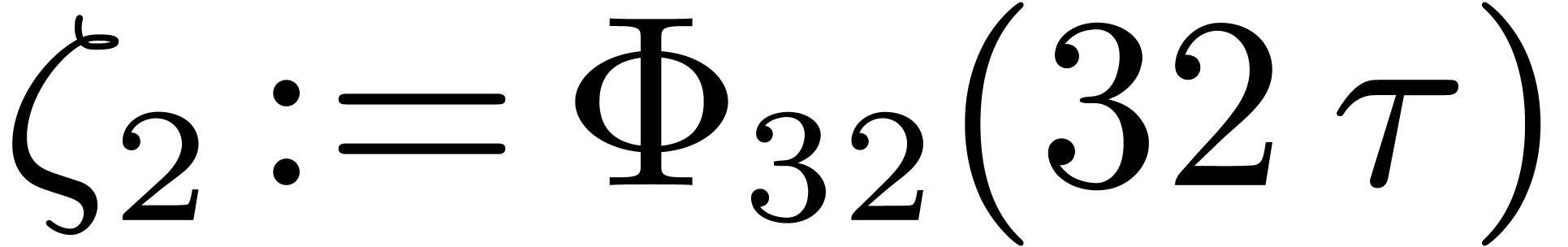 .
. and
and  .
.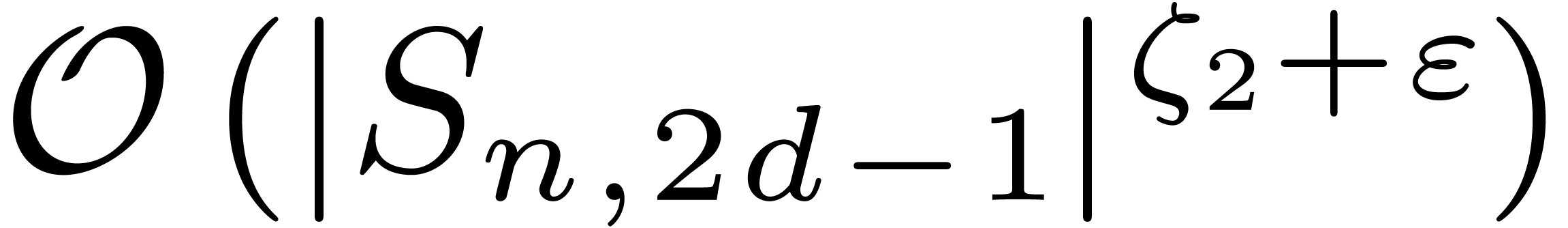 operations in
operations in 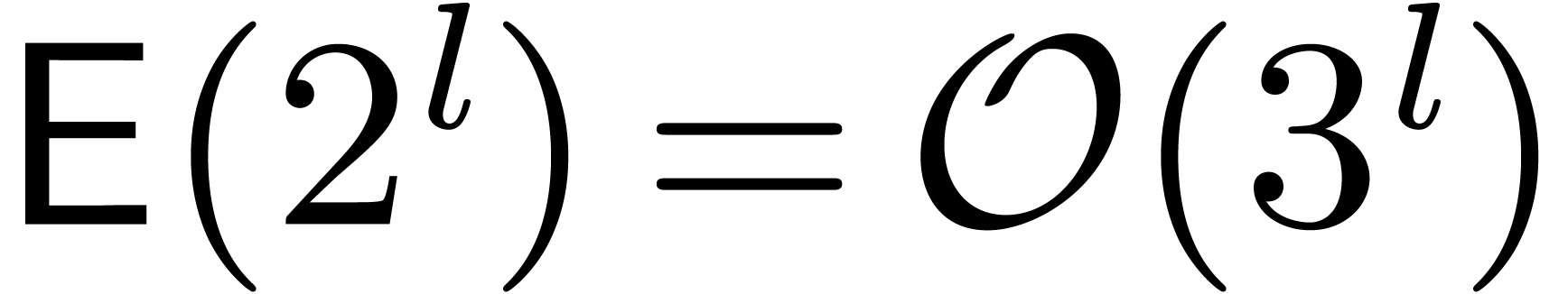 for
all
for
all  .
.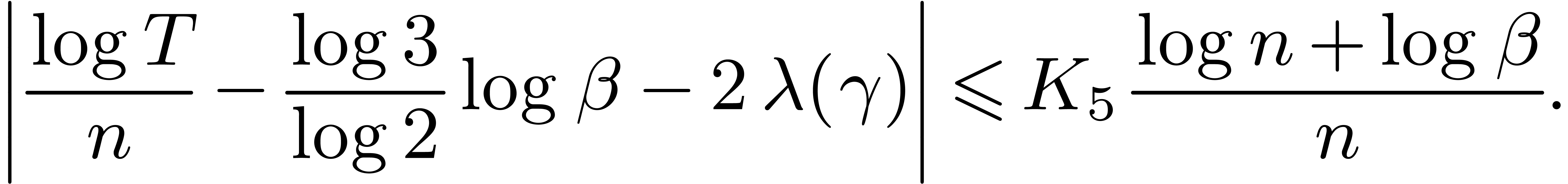
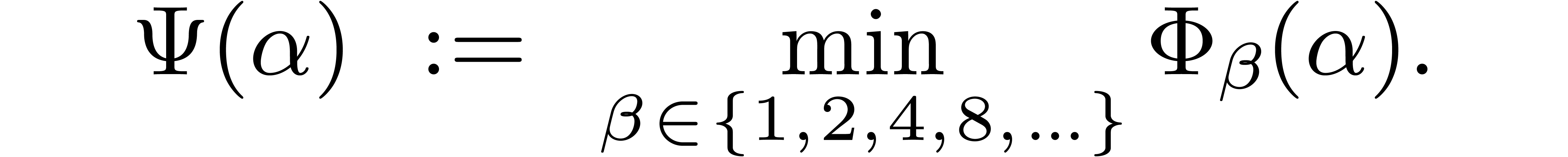
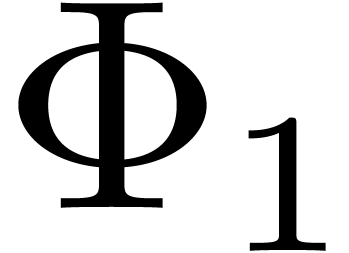 when
when  is
is  is the same as the one of
is the same as the one of
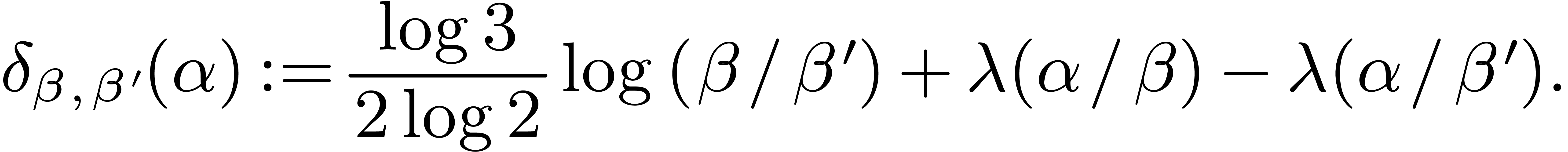
 ,
,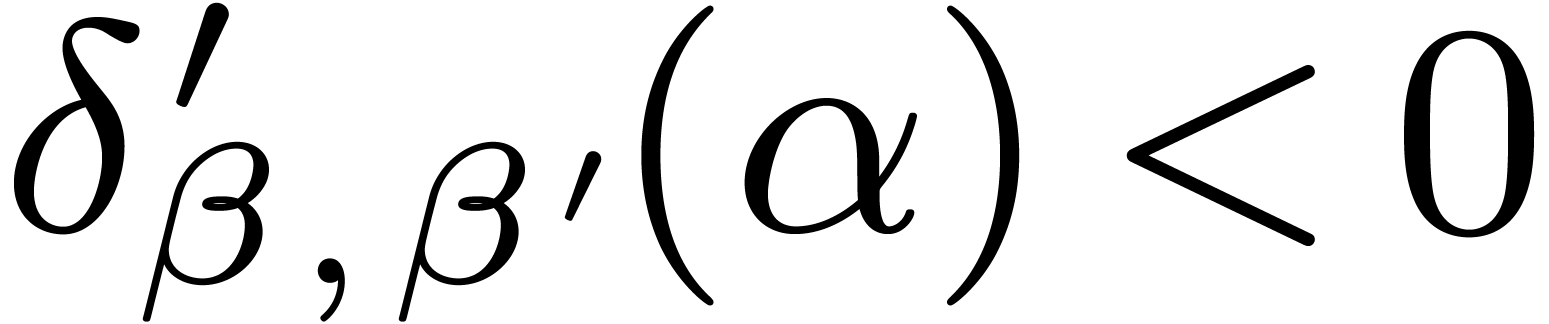 and
and 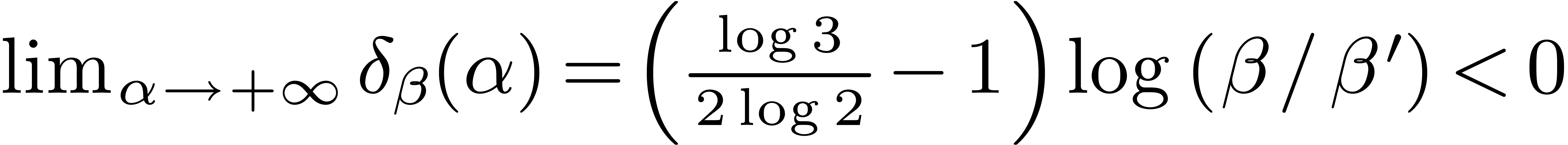 ,
, .
.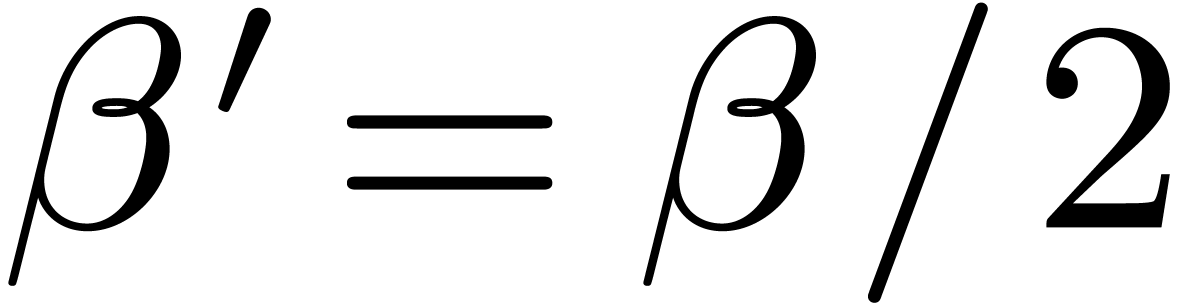 ,
,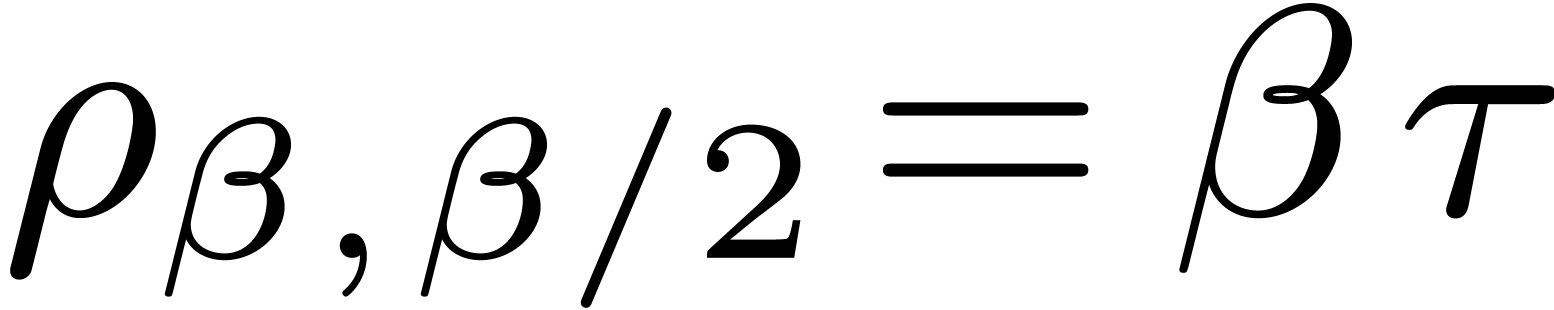 .
. ,
,
 holds for all
holds for all 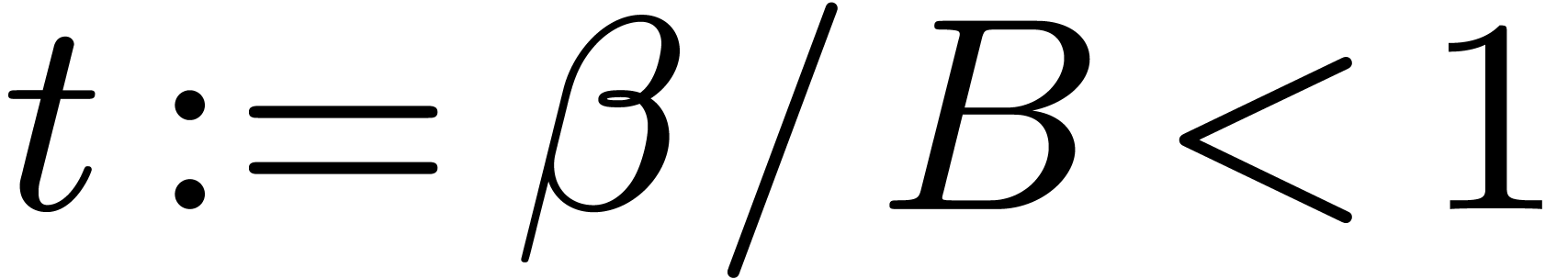 ,
, for all
for all 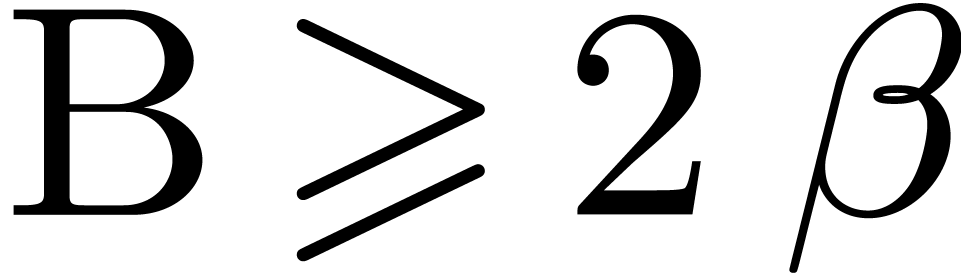 .
.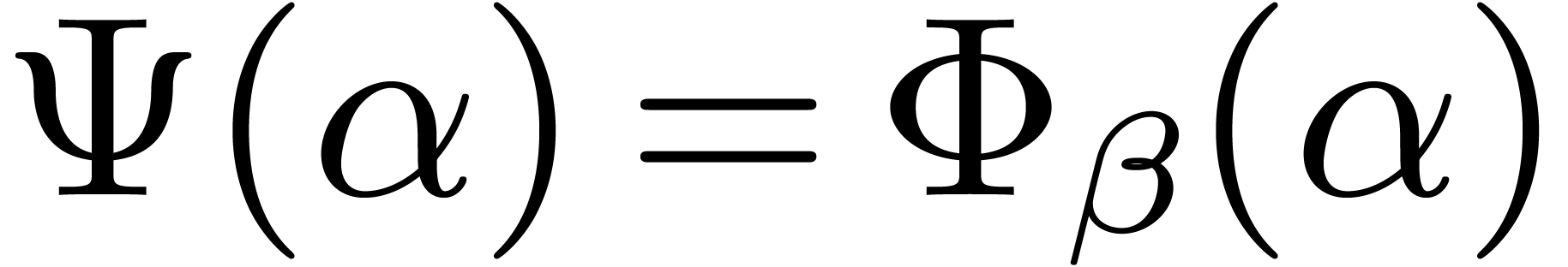 with
with  (with the convention that
(with the convention that 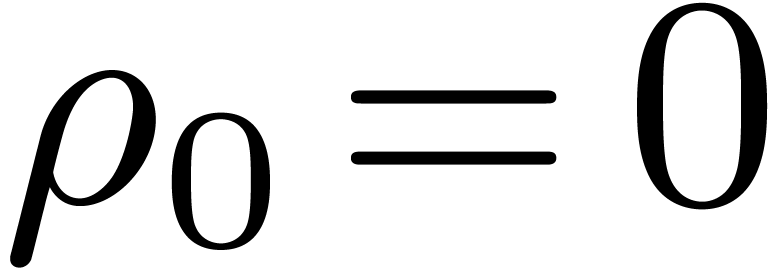 ).
).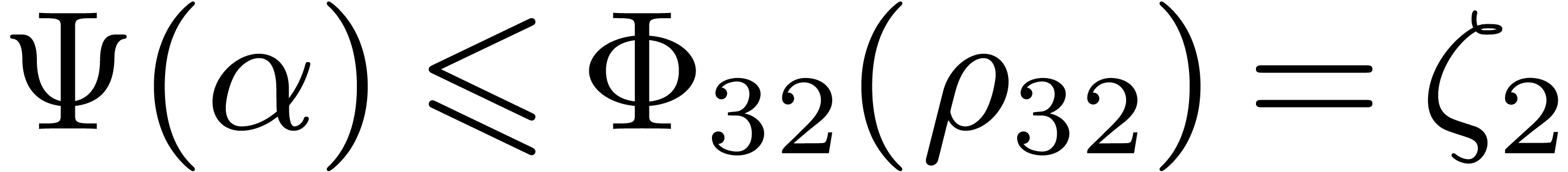 .
.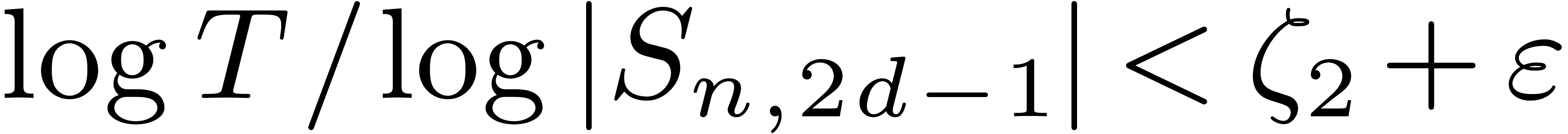 for all
for all 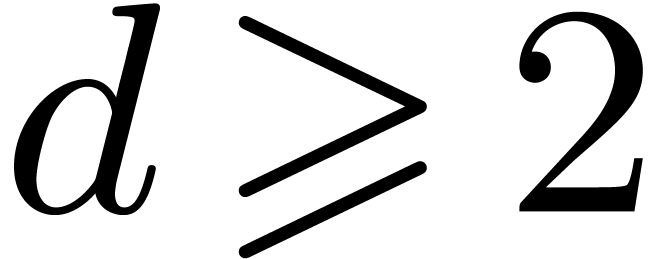 and
and 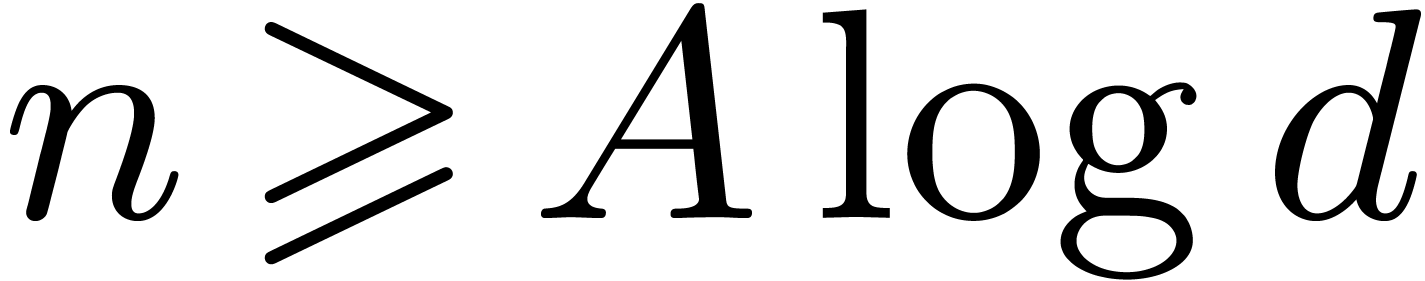 ,
, and
and 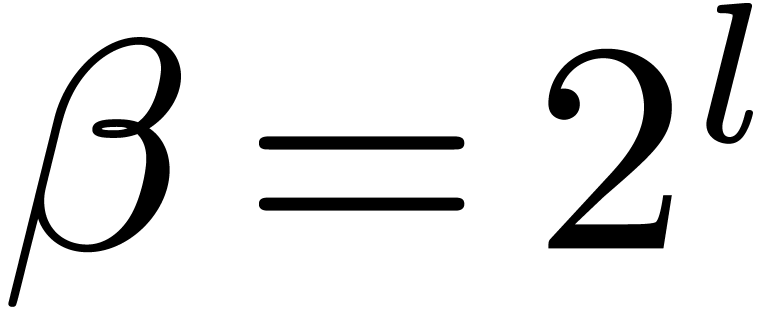 with
with 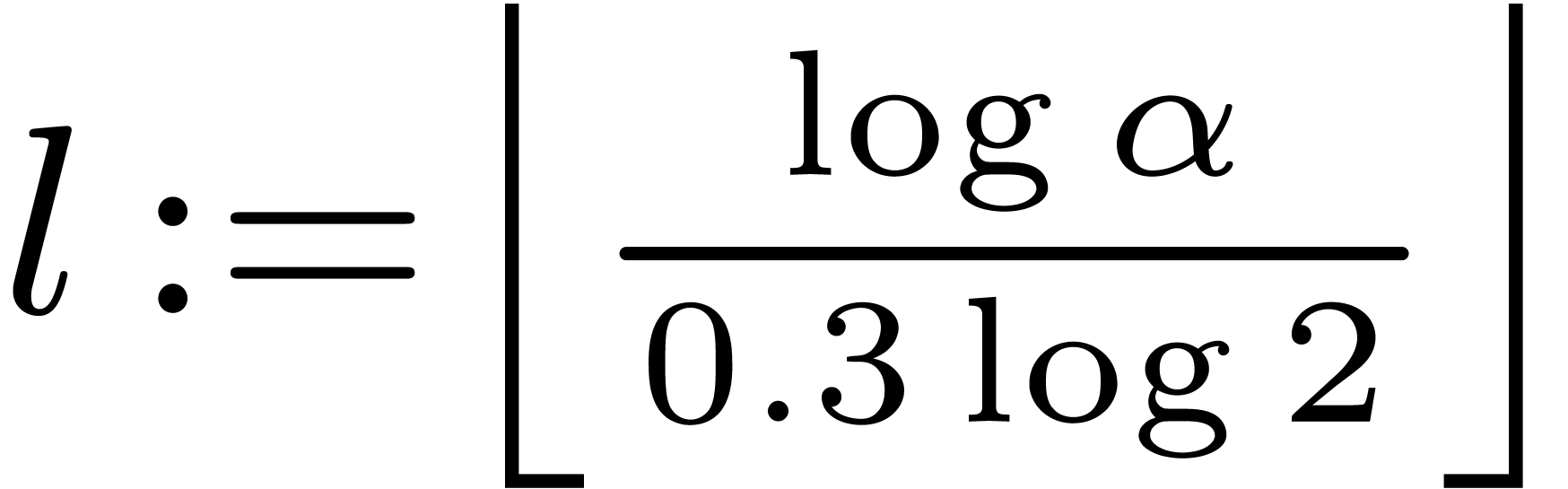 ,
,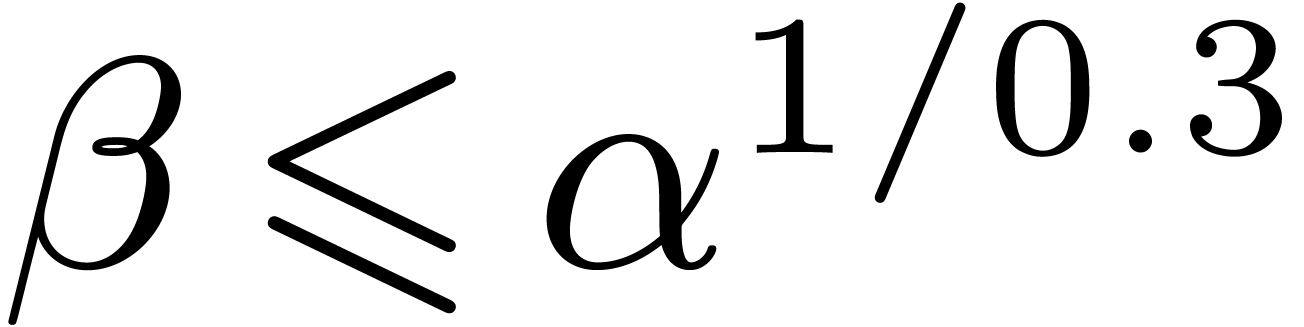 .
.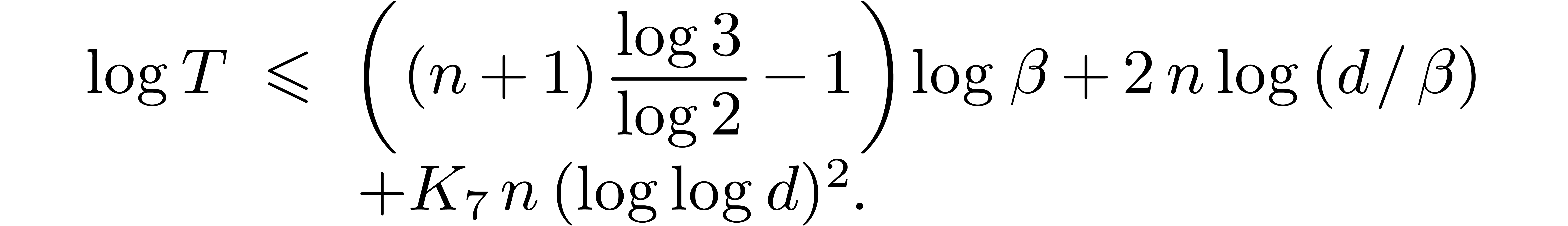
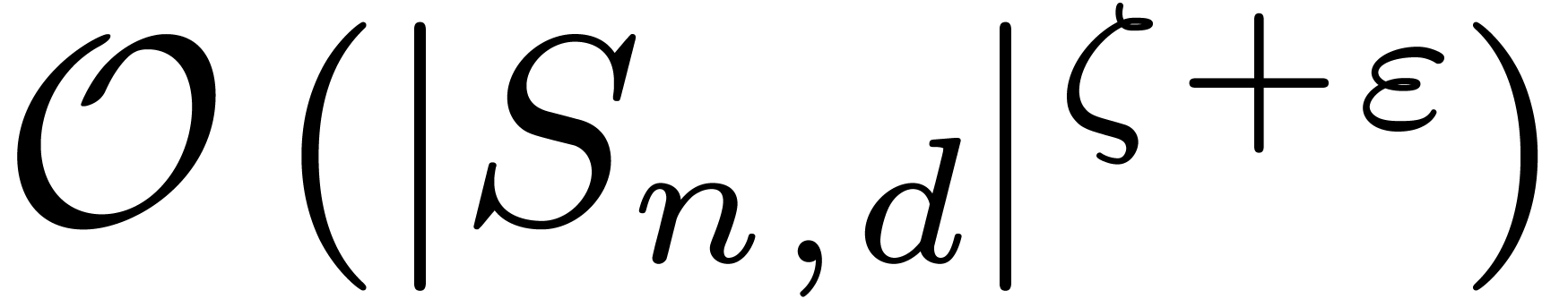 operations in
operations in 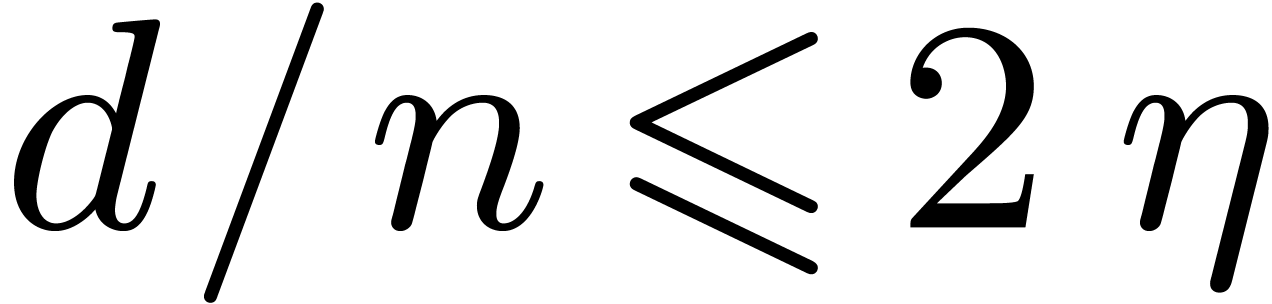 ,
,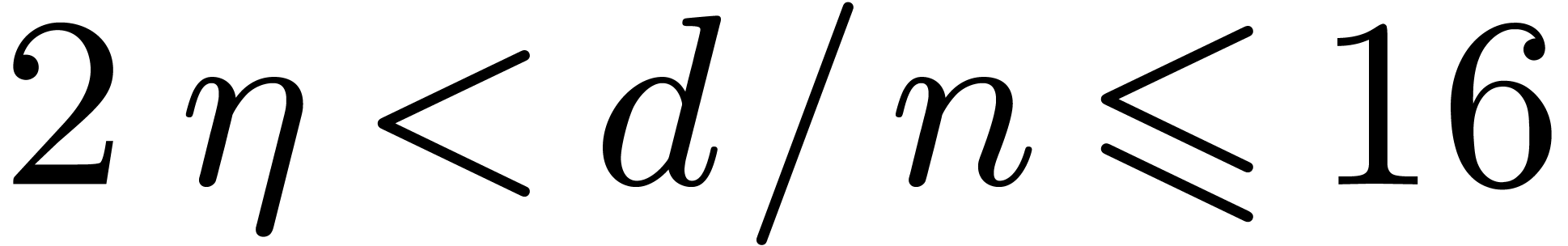 ,
,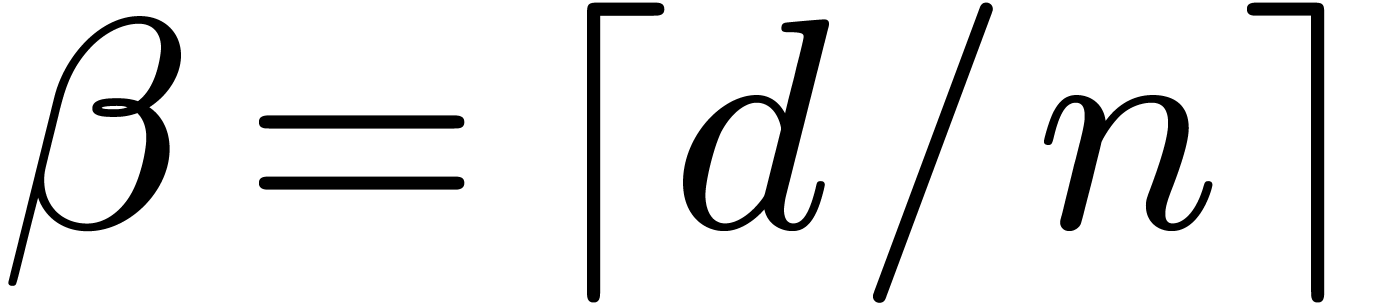 ,
,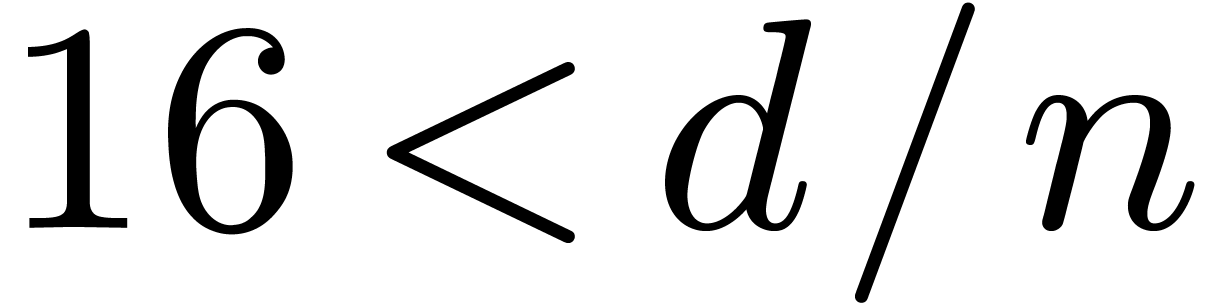 .
.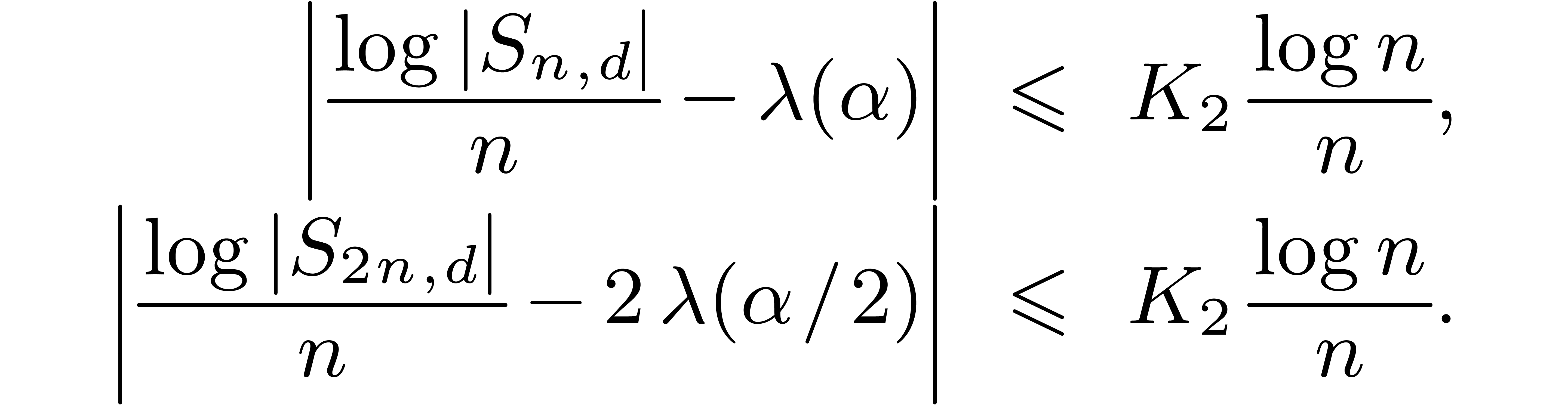
 and
and  .
.
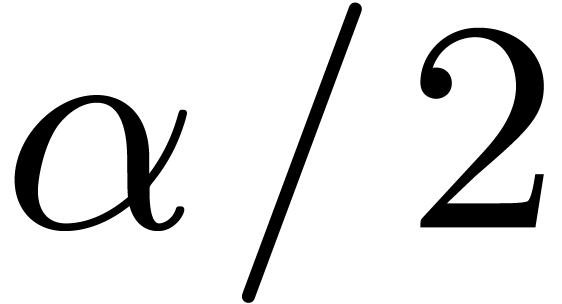 instead of
instead of 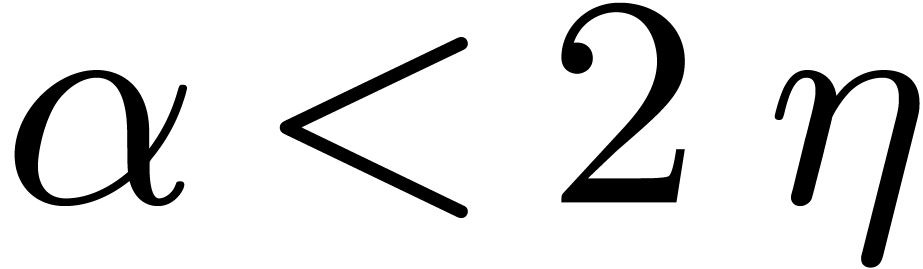 ,
, and
and 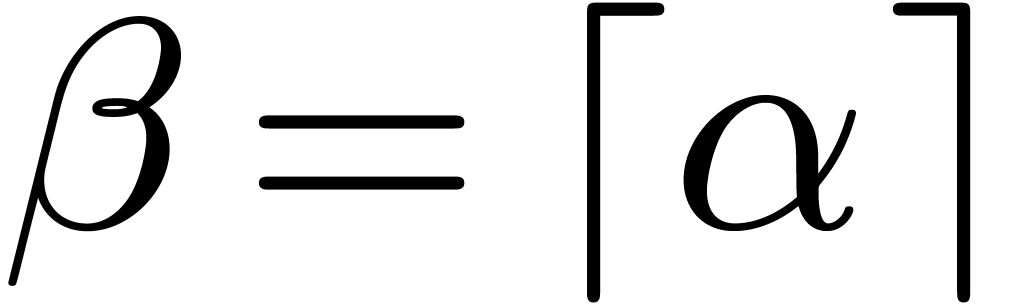 for larger
for larger 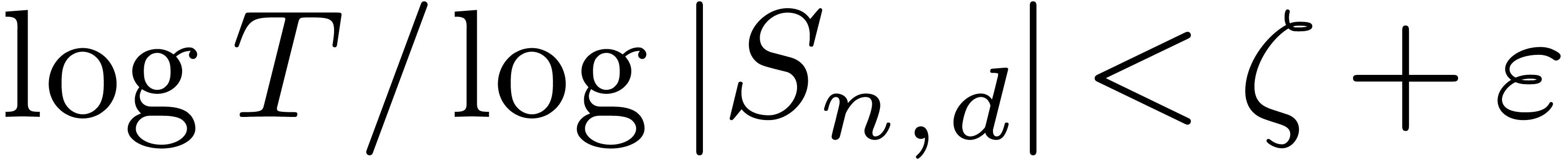 for all
for all 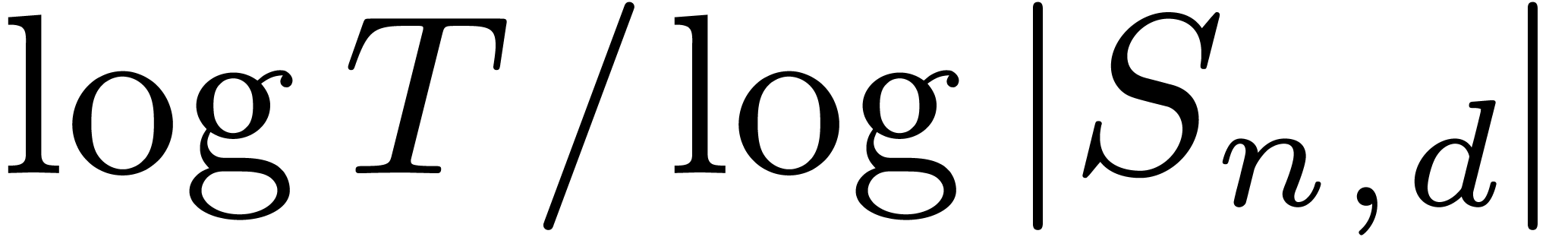 for
for 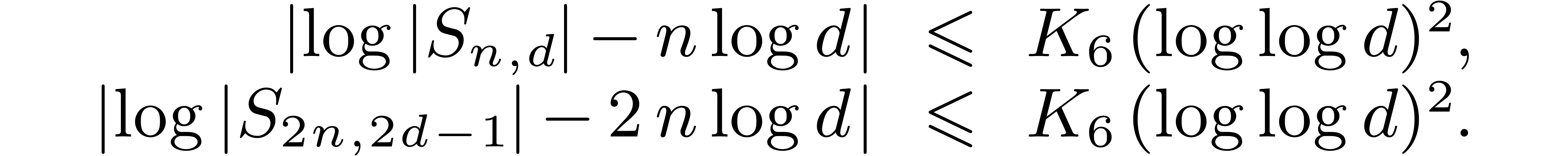
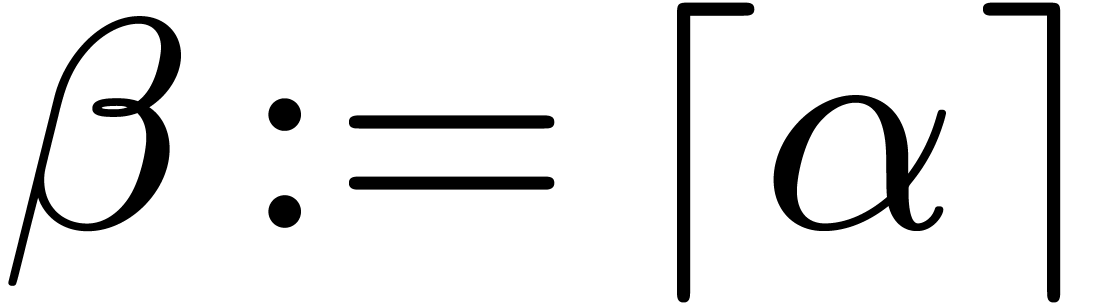 ,
,
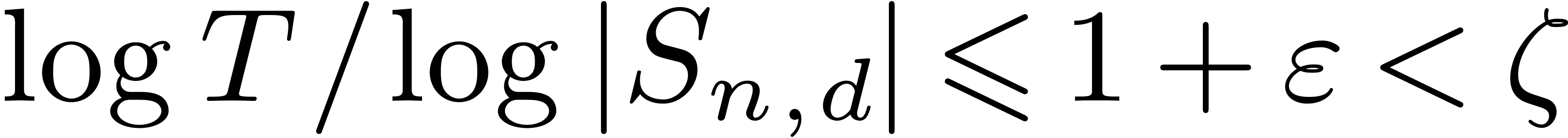 for
for 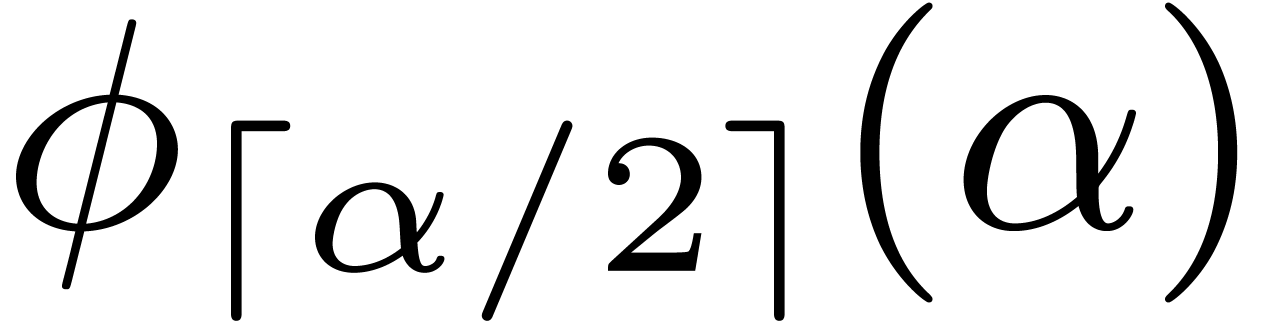 and
and 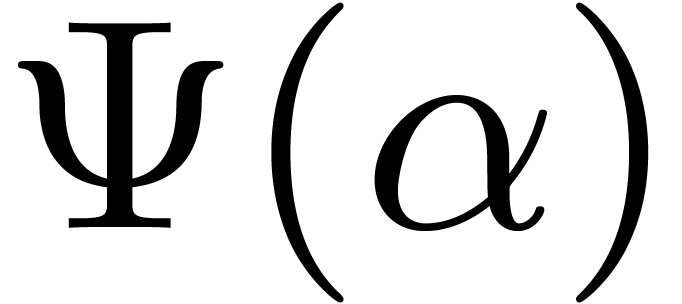 used in Section
used in Section  and
and 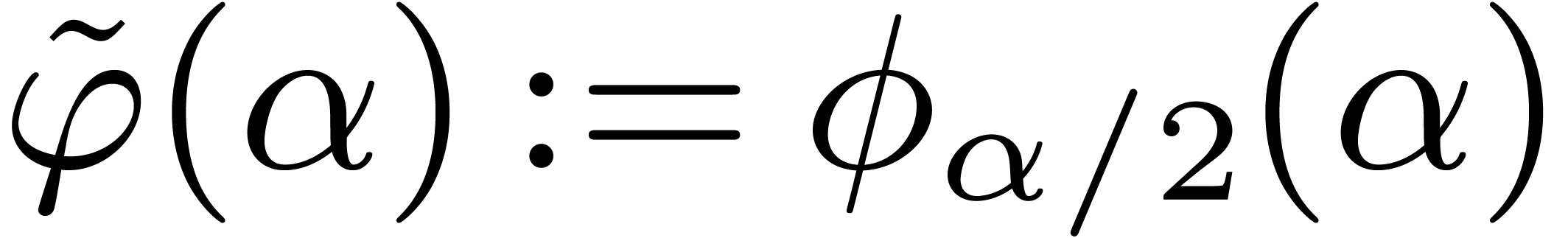 .
.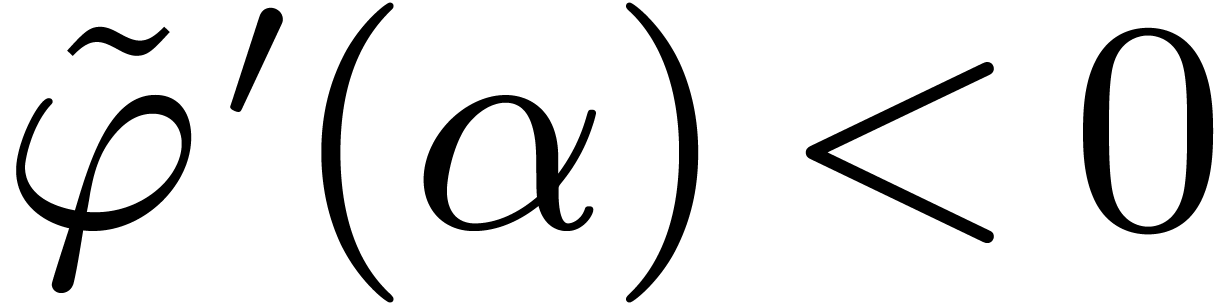 for all
for all  .
.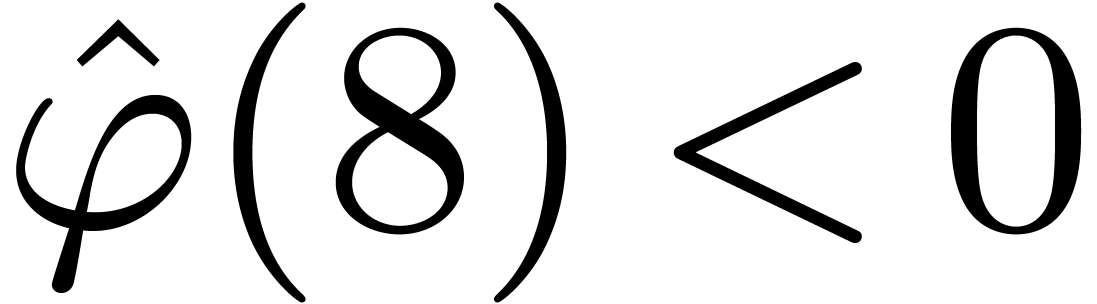 ,
,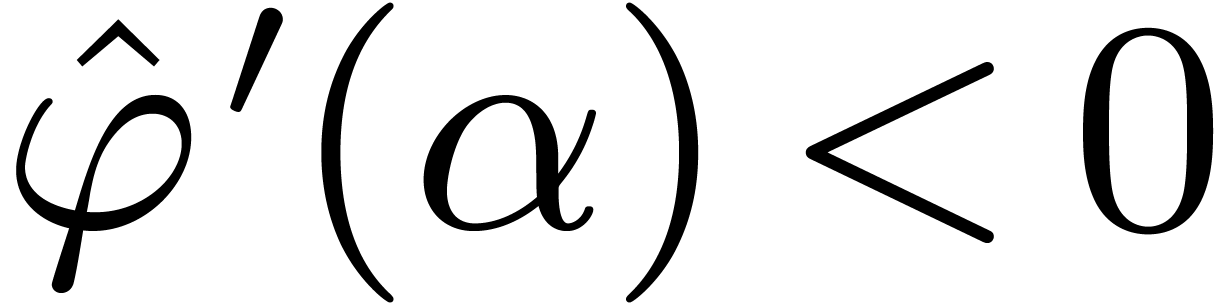 .
. ,
,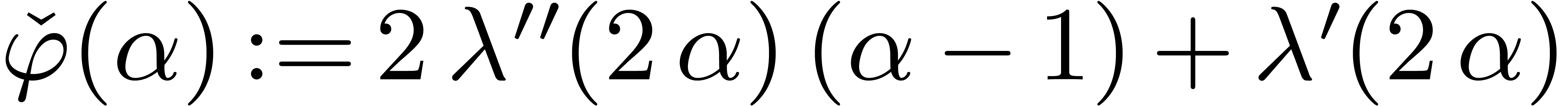 ,
,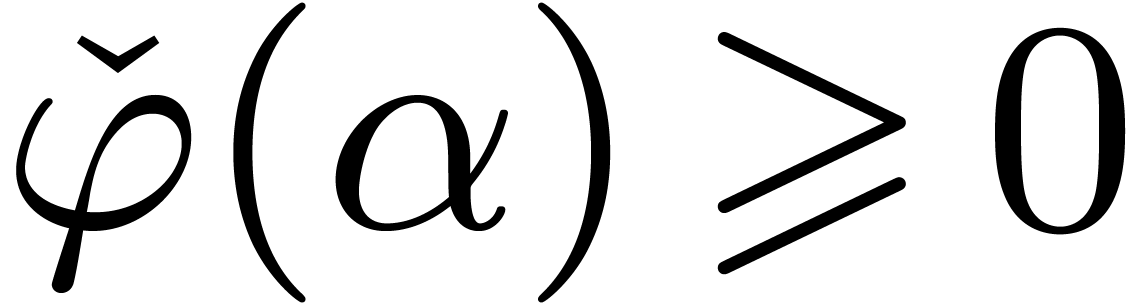 .
.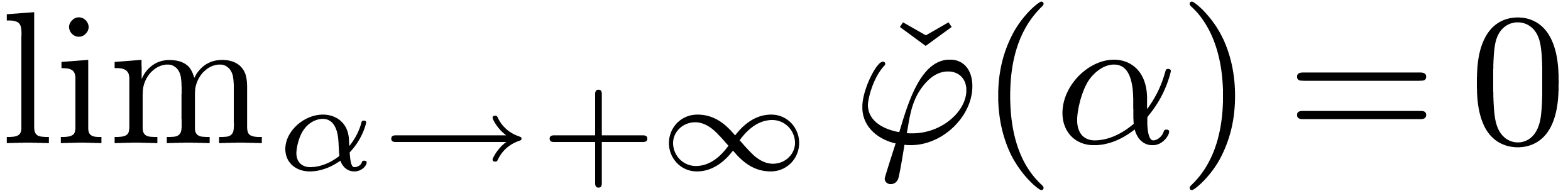 ,
,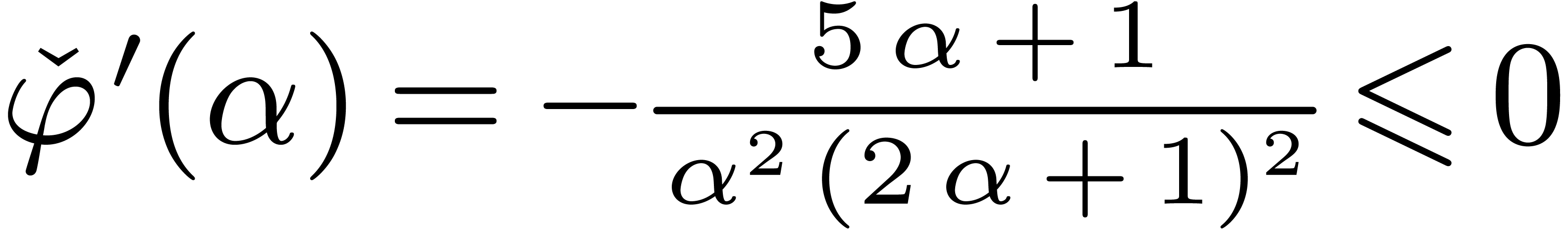 for
for  .
. we have
we have
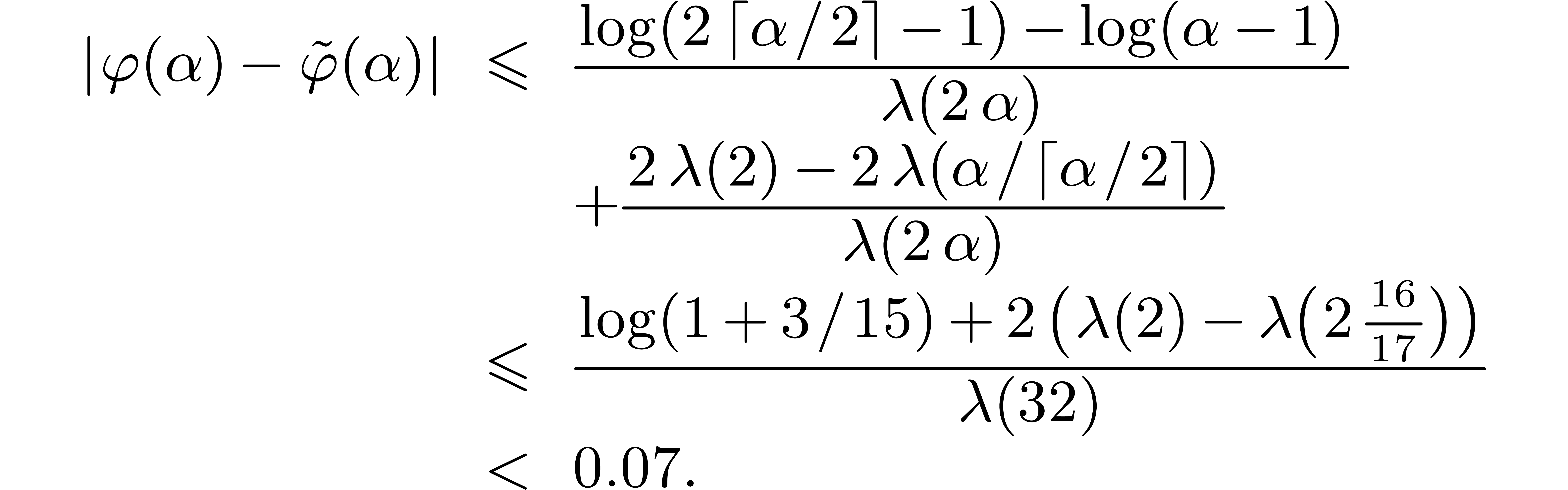
 ,
,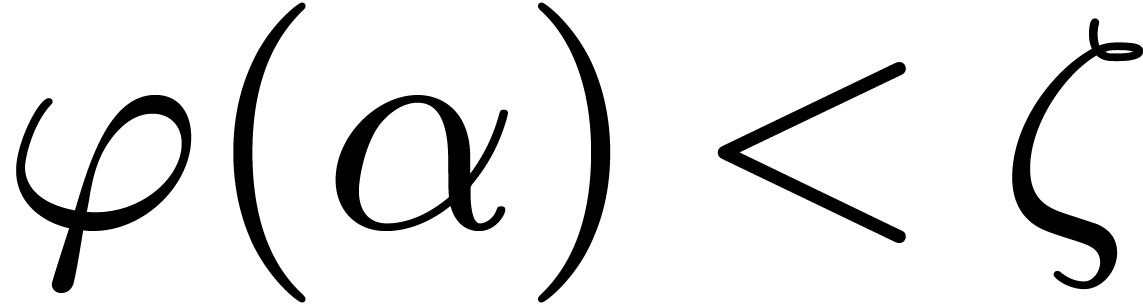 for
for 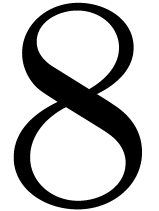 and
and  ,
,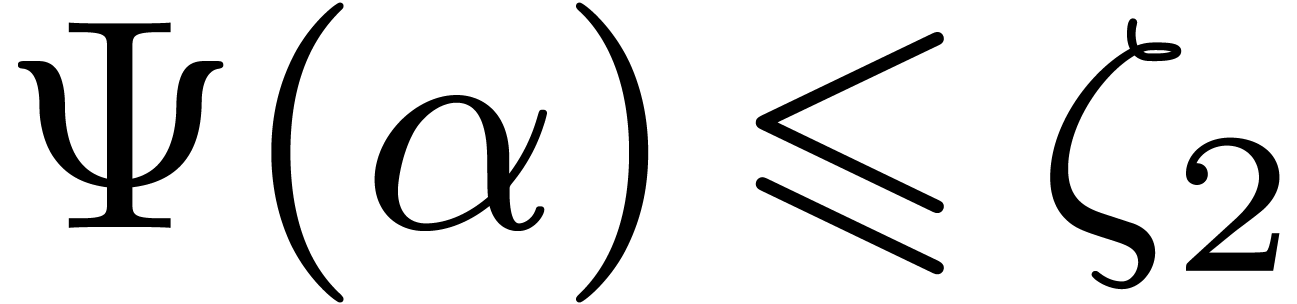 .
.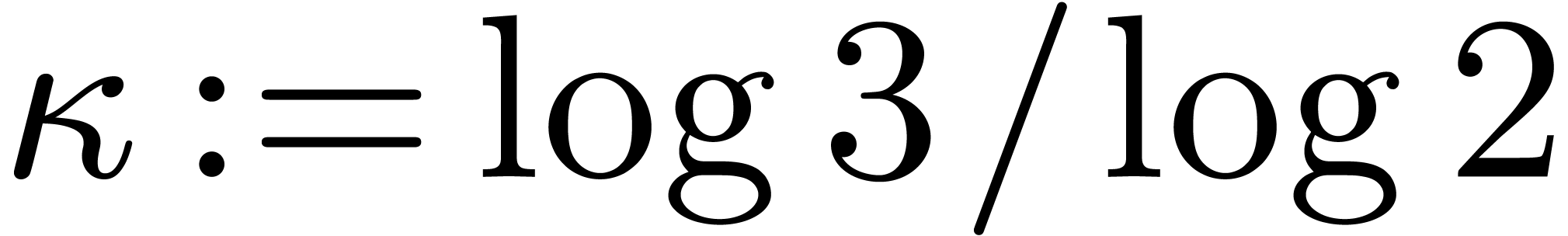 ,
,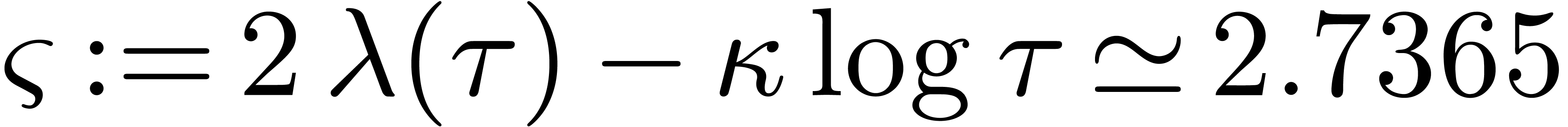 .
.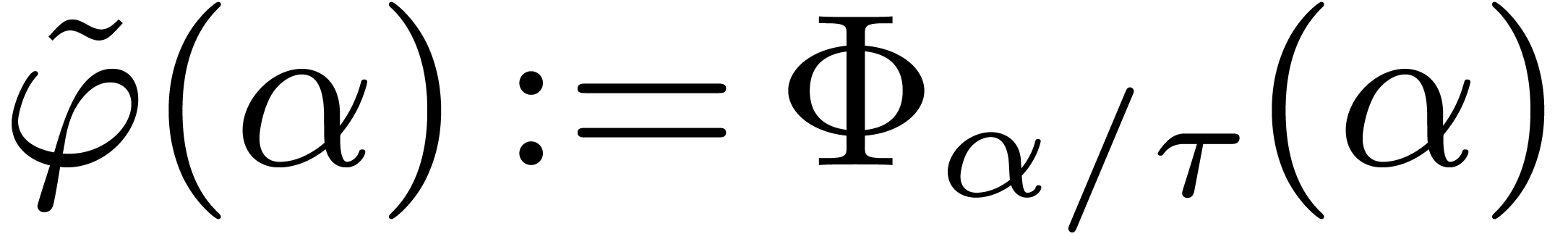 .
.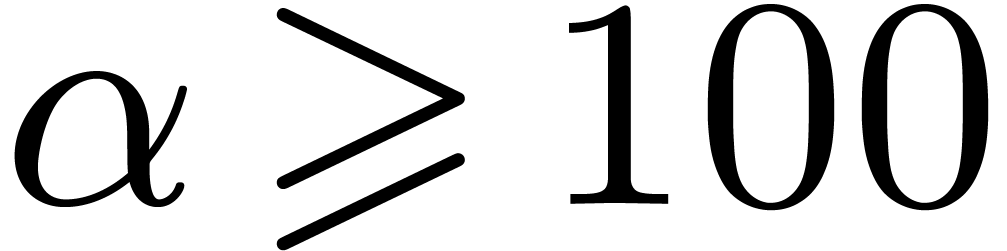 .
.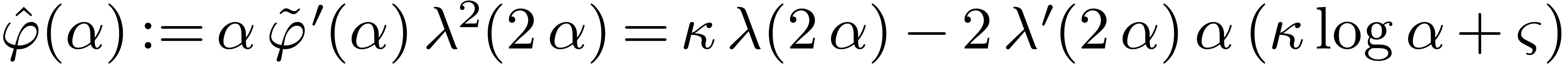 .
.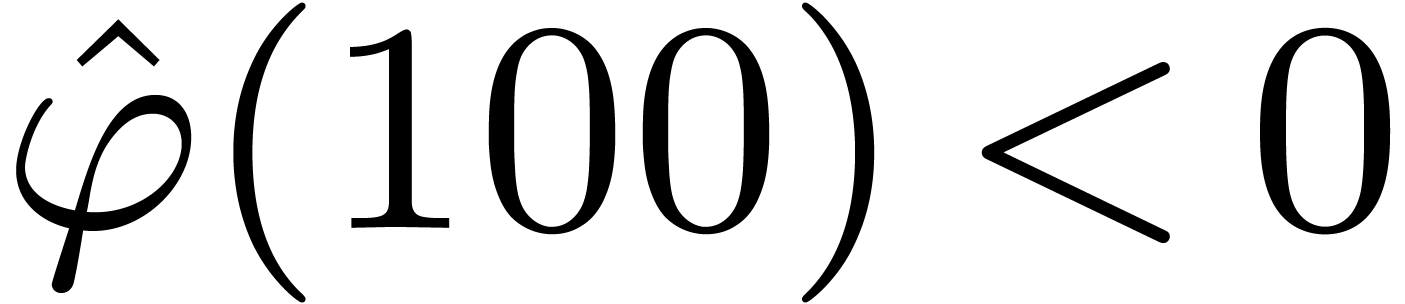 ,
,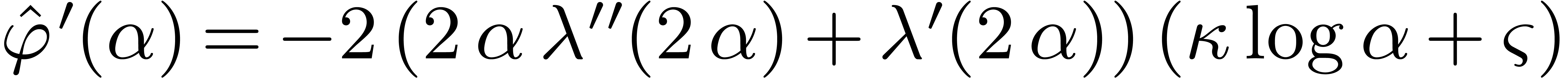 ,
,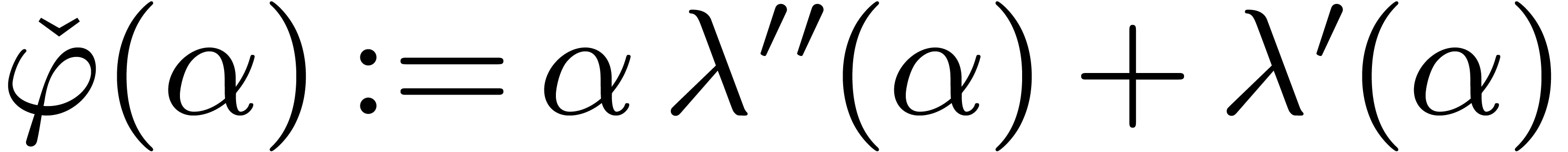 ,
,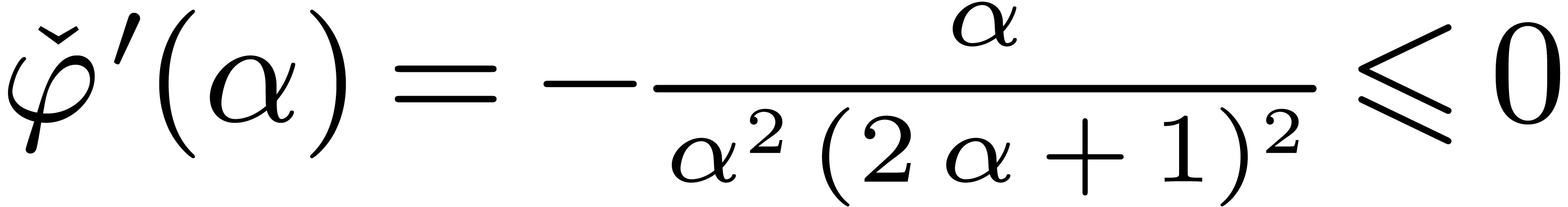 .
.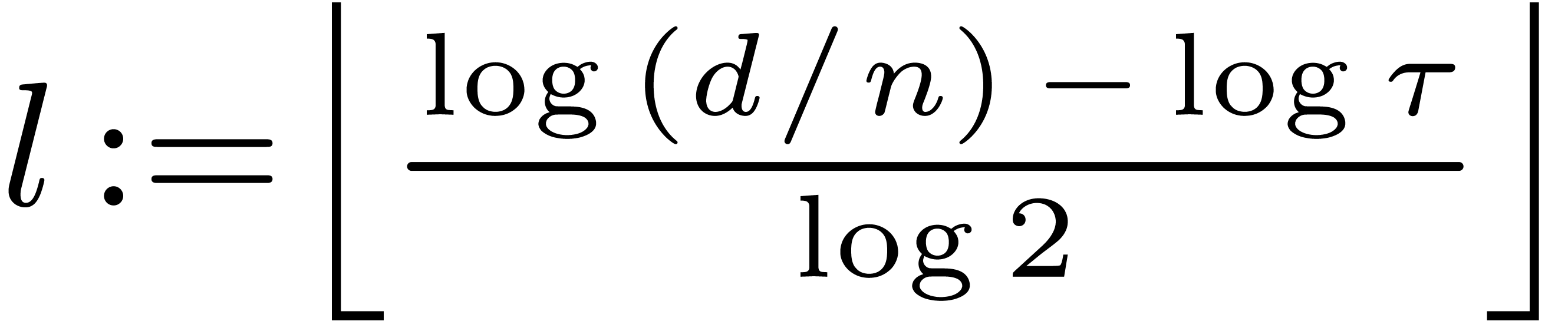 and
and 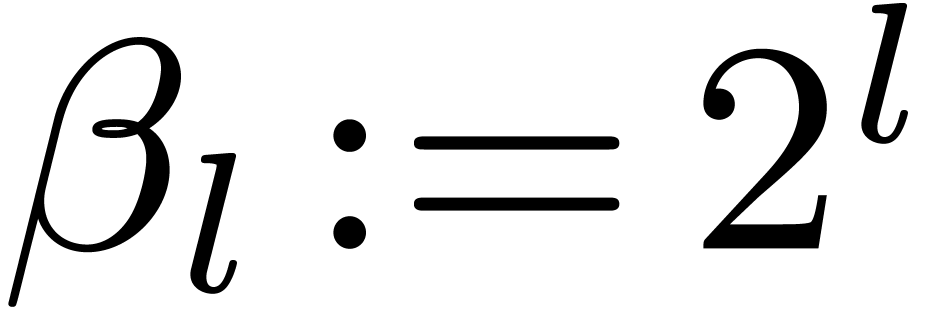 .
.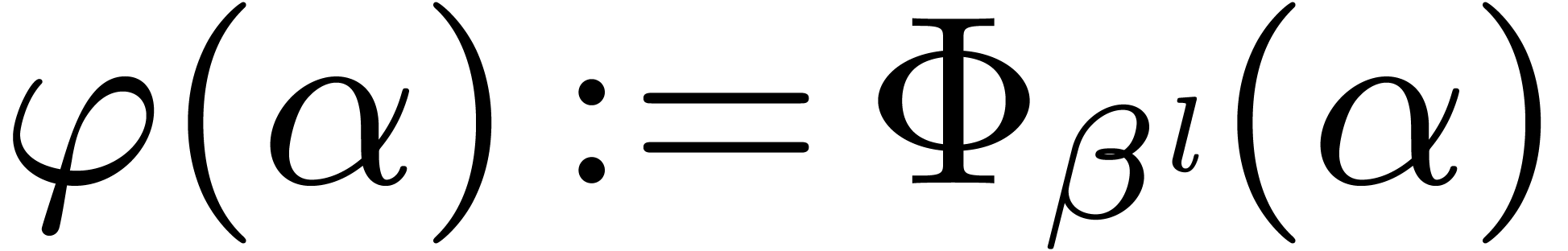 .
.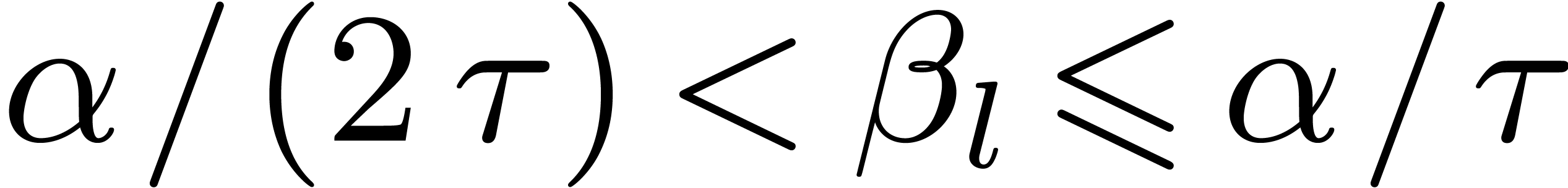 ,
,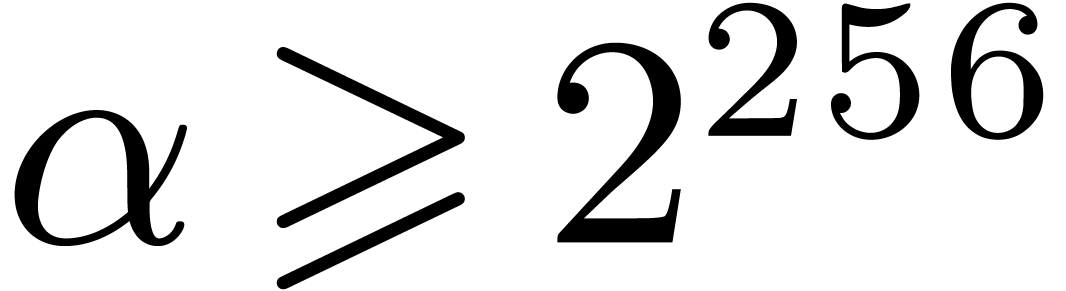 ,
,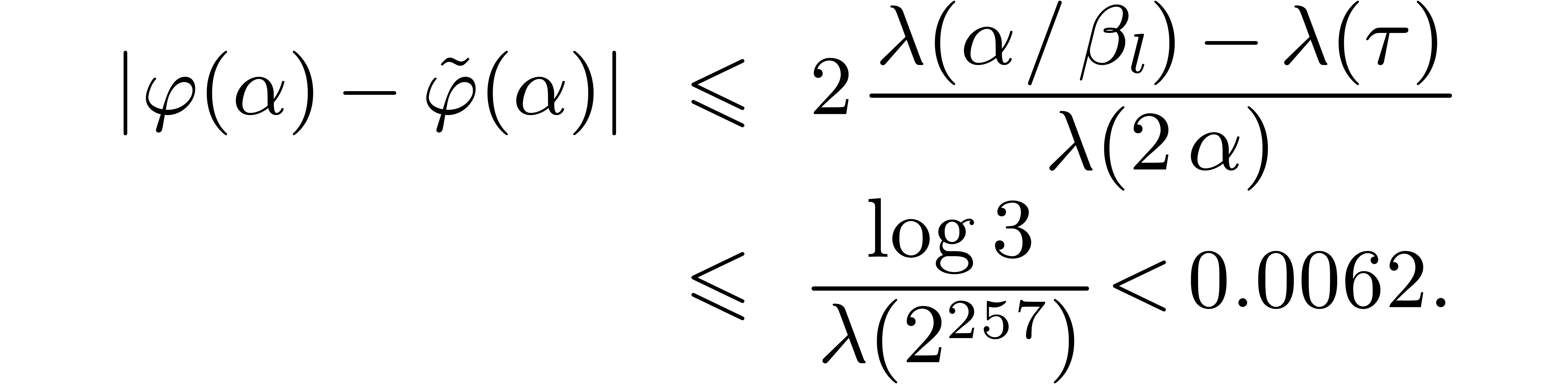
 ,
,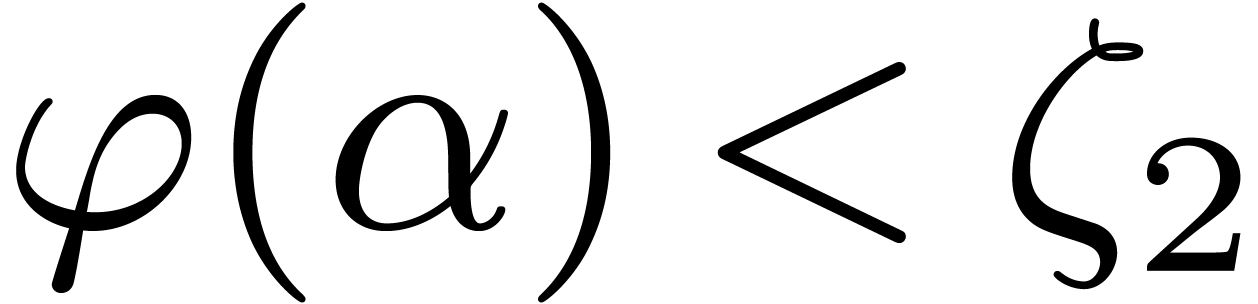 for
for 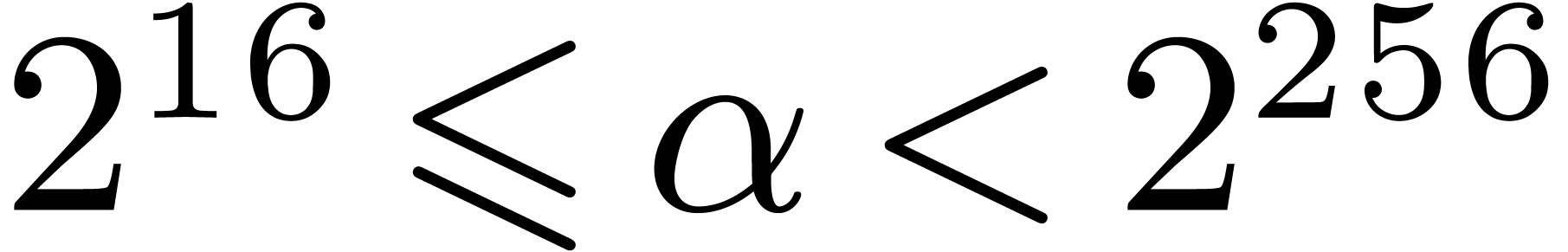 ,
,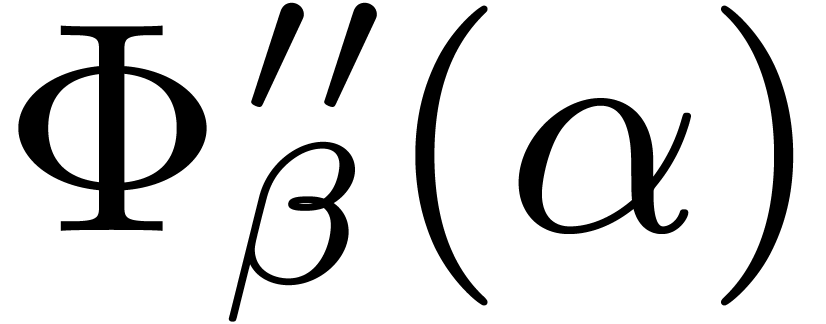 and straightforwardly lower bounded it
by a function
and straightforwardly lower bounded it
by a function 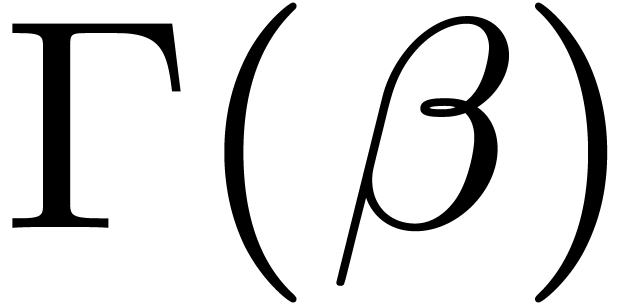 in the domain
in the domain 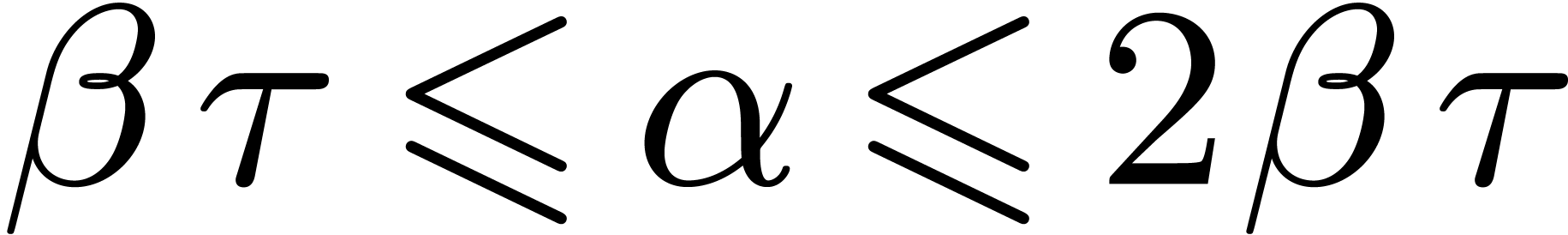 .
.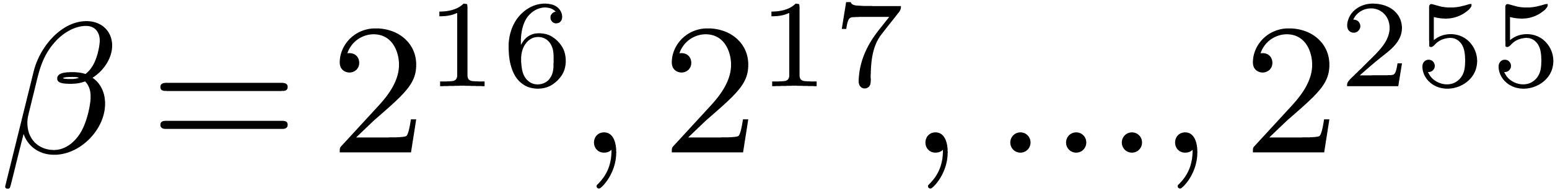 ,
, .
. whenever
whenever 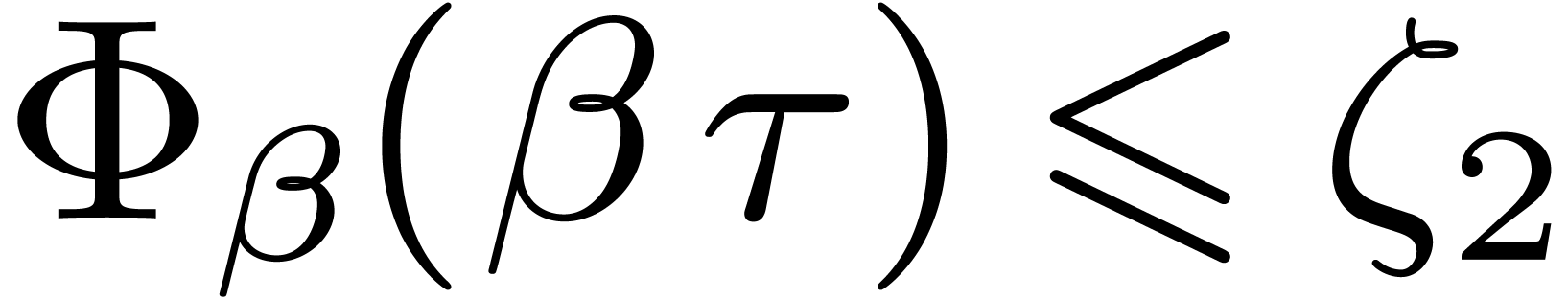 for all
for all 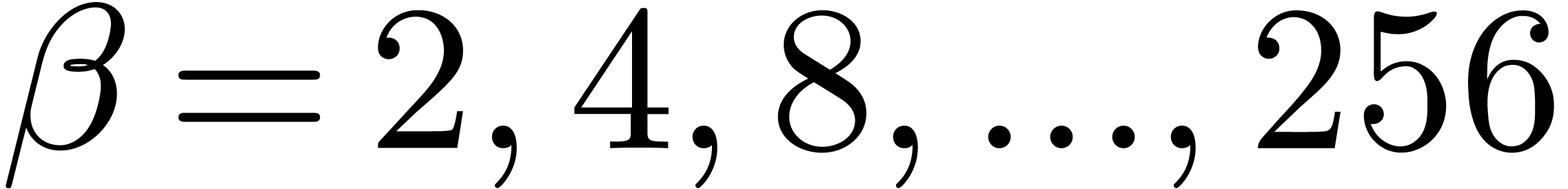 ,
,