Efficient certification of
numeric
solutions to eigenproblems |
|
|
Laboratoire d'informatique, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau
France
Email: vdhoeven@lix.polytechnique.fr
|
|
|
|
Inria Sophia Antipolis
Méditerranée
AROMATH
2004 route des Lucioles
06902 Sophia Antipolis
France
|
|
Email:
Bernard.Mourrain@inria.fr
|
|
|
|
In this paper, we present an efficient algorithm for the
certification of numeric solutions to eigenproblems. The algorithm
relies on a mixture of ball arithmetic, a suitable Newton
iteration, and clustering of eigenvalues that are close.
Keywords: Ball arithmetic, interval
arithmetic, reliable computing, computable analysis
A.M.S. subject classification: 65G20,
03F60, 65F99
|
1.Introduction
Let  be the set of floating point numbers for a
fixed precision and a fixed exponent range. We will denote
be the set of floating point numbers for a
fixed precision and a fixed exponent range. We will denote 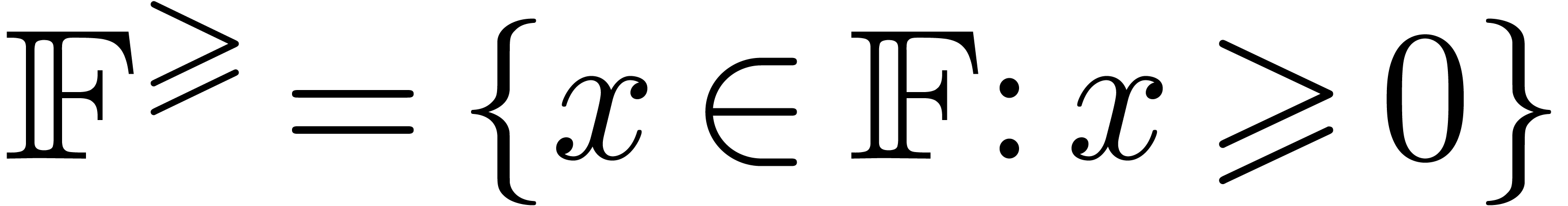 . Consider an
. Consider an  matrix
matrix
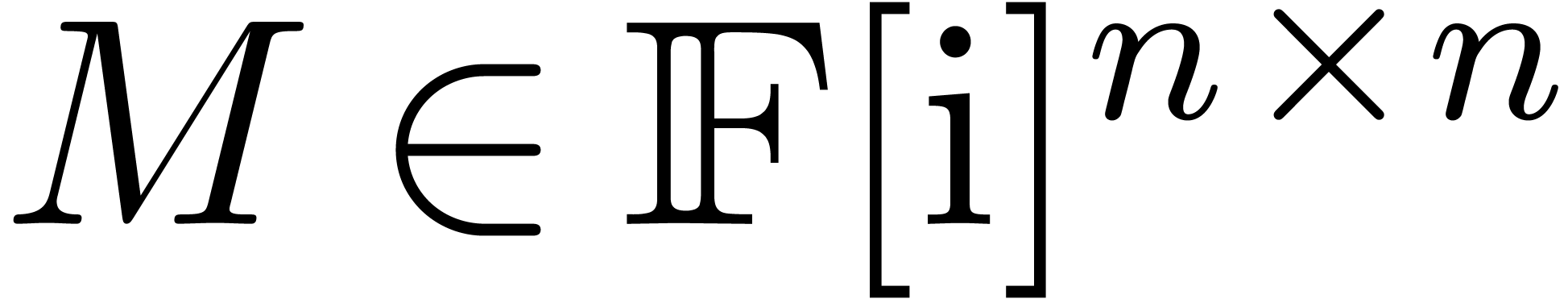 with complex floating entries. The numeric
eigenproblem associated to
with complex floating entries. The numeric
eigenproblem associated to 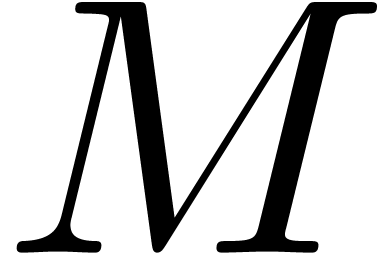 is to
compute a transformation matrix
is to
compute a transformation matrix 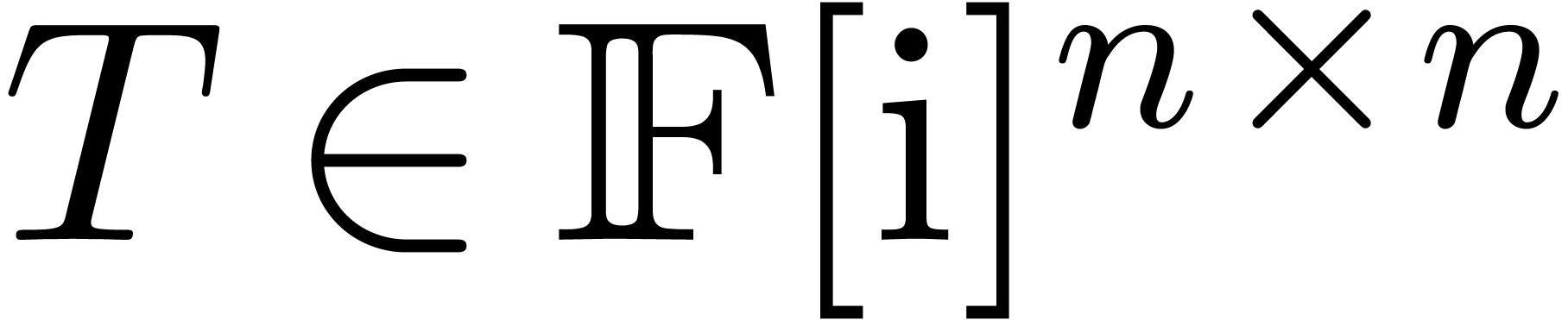 and a diagonal
matrix
and a diagonal
matrix 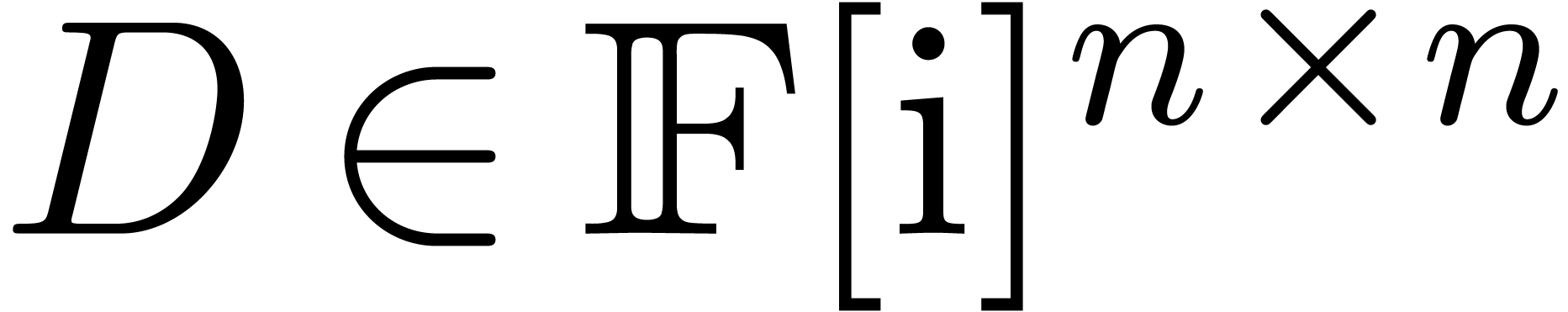 such that
such that
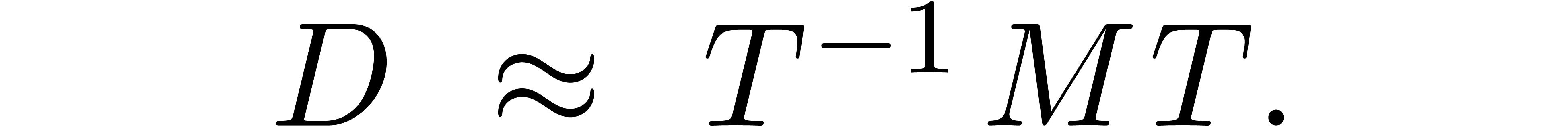 |
(1) |
The entries of 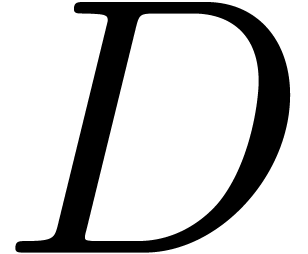 are the approximate eigenvalues
and the columns of
are the approximate eigenvalues
and the columns of  are the approximate
eigenvectors of
are the approximate
eigenvectors of 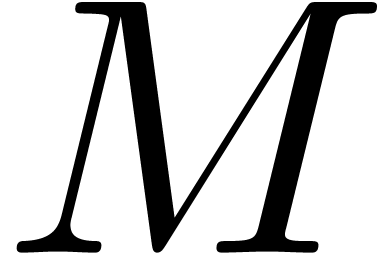 . In
addition, we might require that
. In
addition, we might require that  is normalized.
For instance, each of the columns might have unit norm. Alternatively,
the norm of the
is normalized.
For instance, each of the columns might have unit norm. Alternatively,
the norm of the 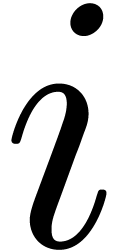 -th column
may be required to be the same as the norm of the
-th column
may be required to be the same as the norm of the 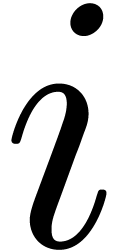 -th row of
-th row of 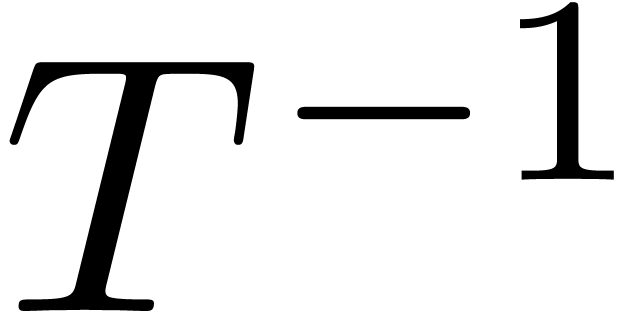 ,
for each
,
for each 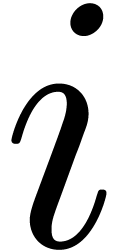 . There are several
well-known algorithms for solving the numeric eigenproblem [6].
. There are several
well-known algorithms for solving the numeric eigenproblem [6].
Unfortunately, (1) is only an approximate equality. It is
sometimes important to have rigourous bounds for the distance between
the approximate eigenvalues and/or eigenvectors and the genuine ones.
More precisely, we may ask for a diagonal matrix  and a matrix
and a matrix  such that there exists a matrix
such that there exists a matrix
 for which
for which
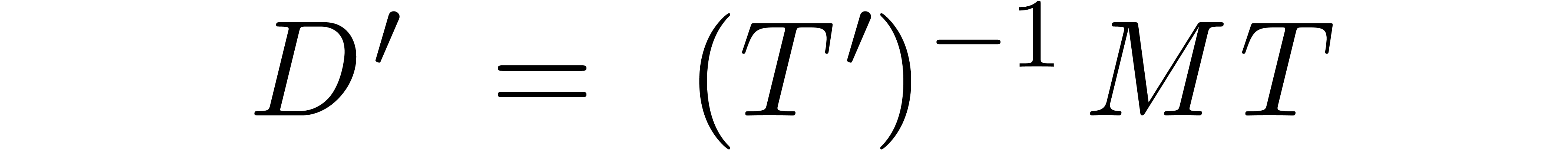
is diagonal and
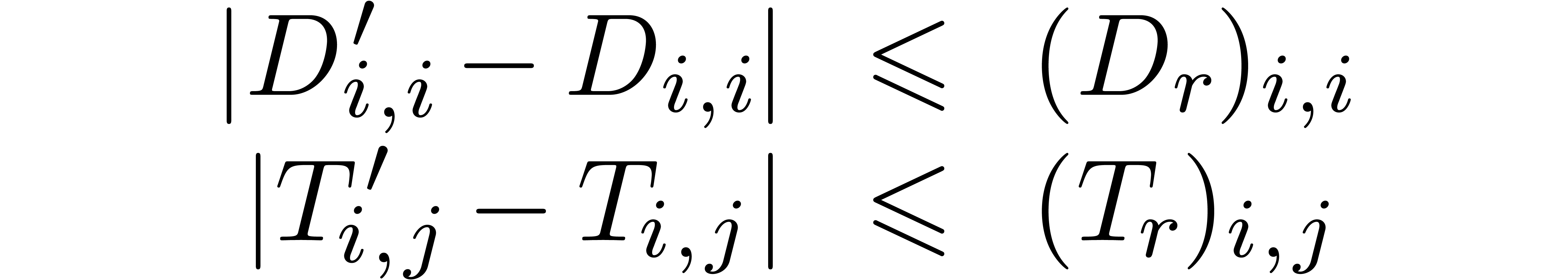
for all  . This task will be
called the certification problem of the numeric solution
. This task will be
called the certification problem of the numeric solution 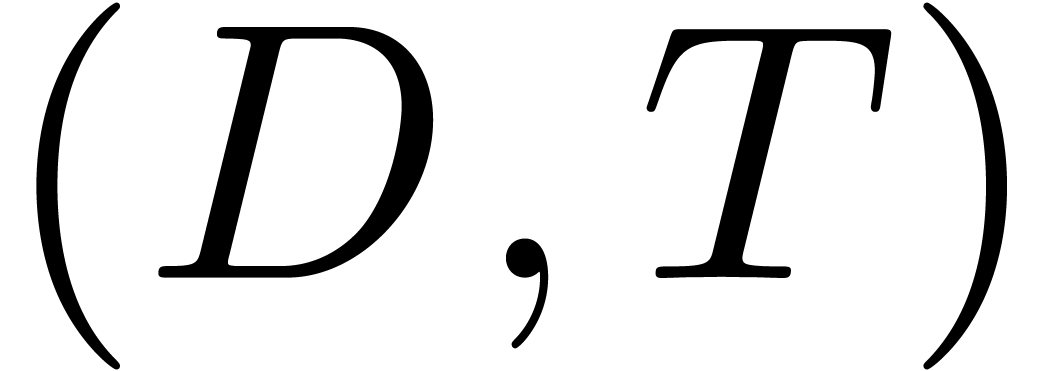 to the eigenproblem for
to the eigenproblem for 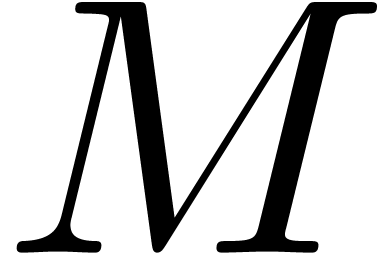 .
The matrices
.
The matrices 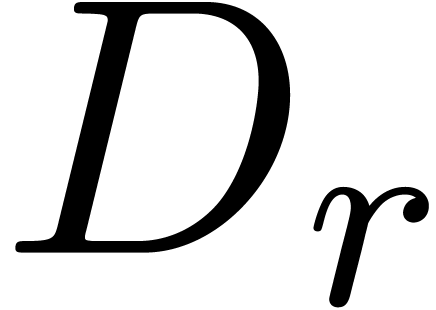 and
and 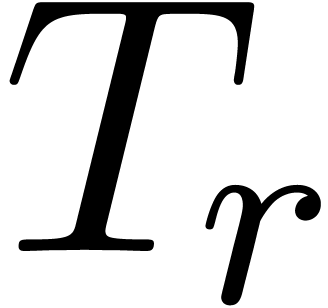 can be
thought of as reliable error bounds for the numerical solution
can be
thought of as reliable error bounds for the numerical solution 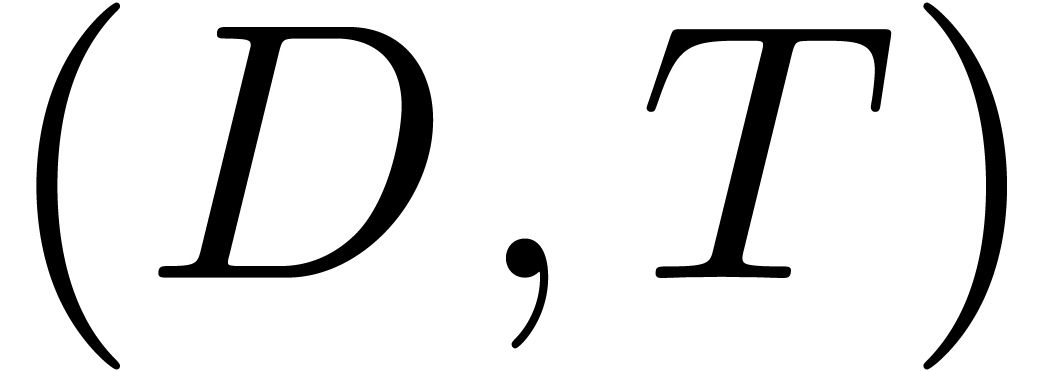 of the eigenproblem.
of the eigenproblem.
It will be convenient to rely on ball arithmetic [11,
14], which is a systematic technique for this kind of bound
computations. When computing with complex numbers, ball arithmetic is
more accurate than more classical interval arithmetic [17,
1, 18, 13, 15, 21], especially in multiple precision contexts. We will write
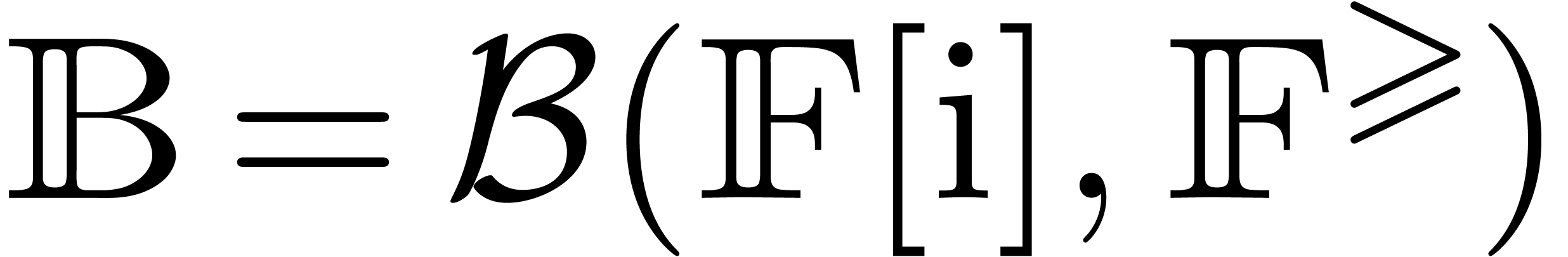 for the set of balls
for the set of balls 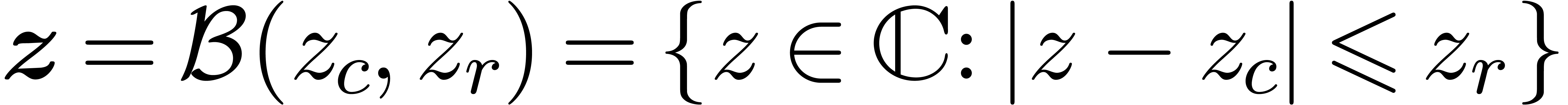 with centers
with centers  in
in  and
radii
and
radii 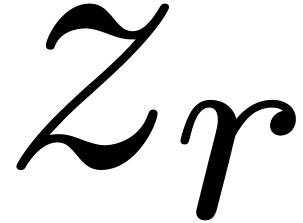 in
in 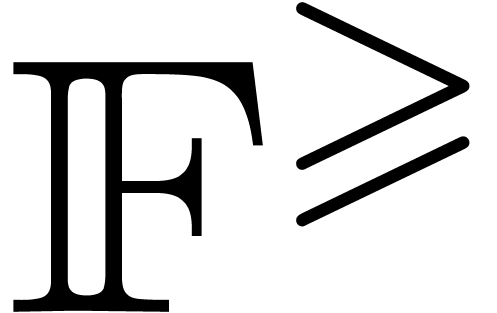 .
In a similar way, we may consider matricial balls
.
In a similar way, we may consider matricial balls  : given a center matrix
: given a center matrix 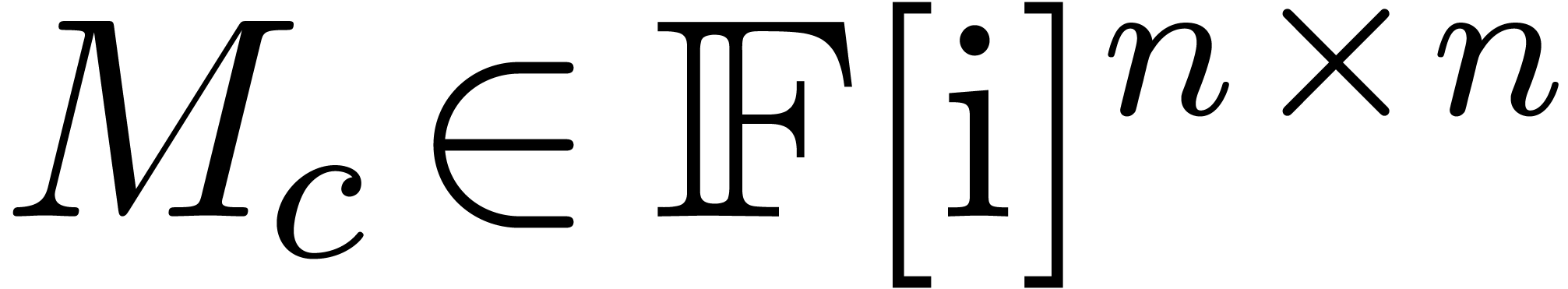 and
a radius matrix
and
a radius matrix 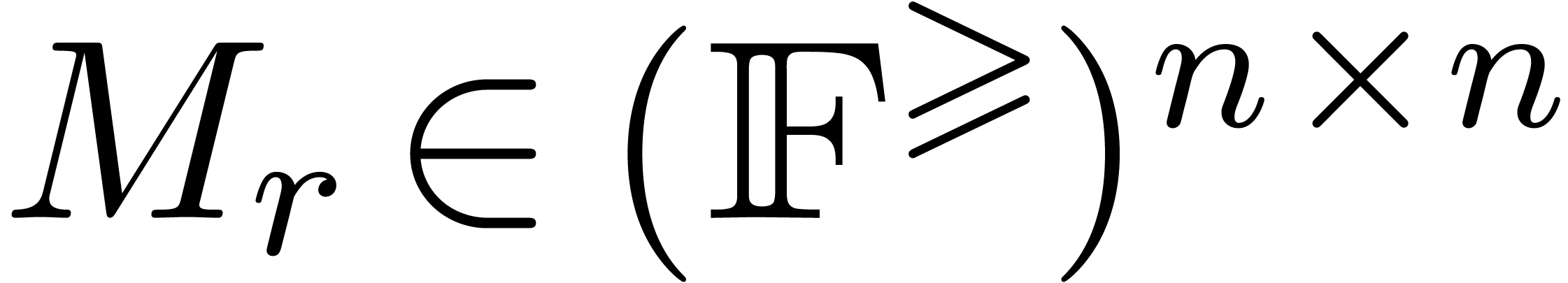 , we have
, we have
Alternatively, we may regard  as the set of
matrices in
as the set of
matrices in 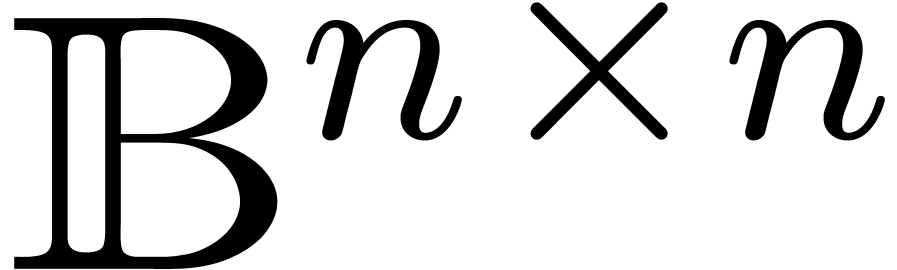 with ball coefficients:
with ball coefficients:
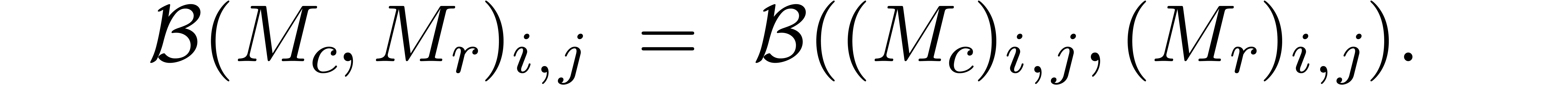
Standard arithmetic operations on balls are carried out in a reliable
way. For instance, if 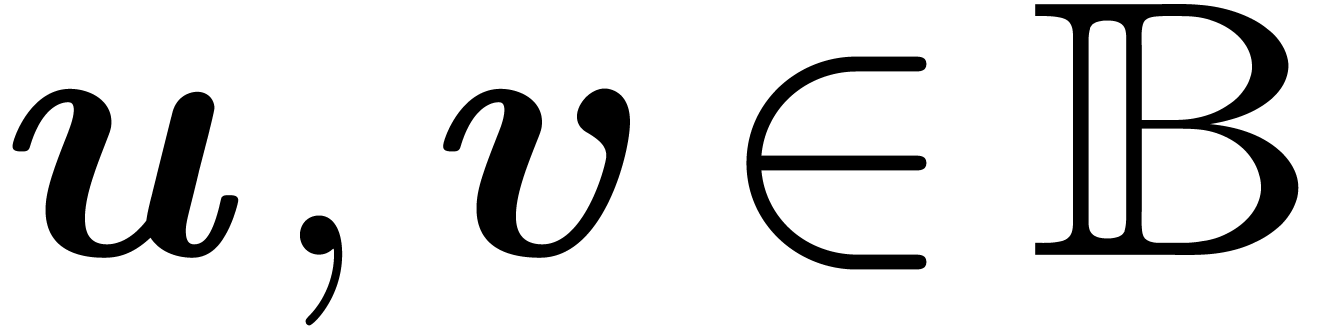 , then
the computation of the product
, then
the computation of the product 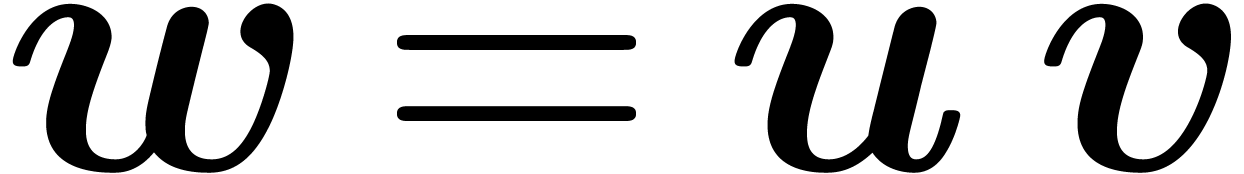 using ball
arithmetic has the property that
using ball
arithmetic has the property that  for any
for any  and
and  .
Given a ball
.
Given a ball 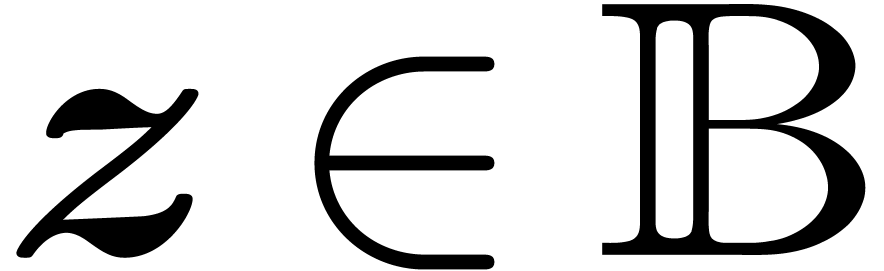 , it will
finally be convenient to write
, it will
finally be convenient to write  and
and  for certified lower and upper bounds of
for certified lower and upper bounds of  in
in  .
.
In the language of ball arithmetic, it is natural to allow for small
errors in the input and replace the numeric input 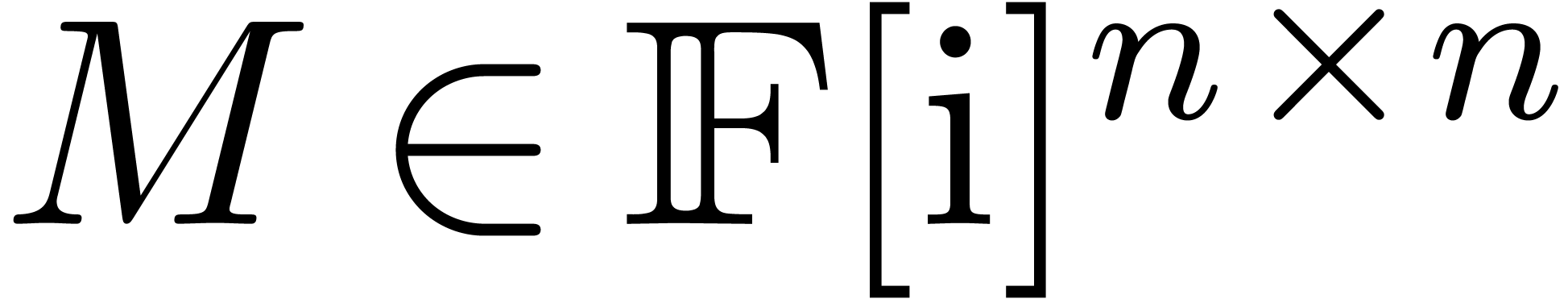 by a ball input
by a ball input 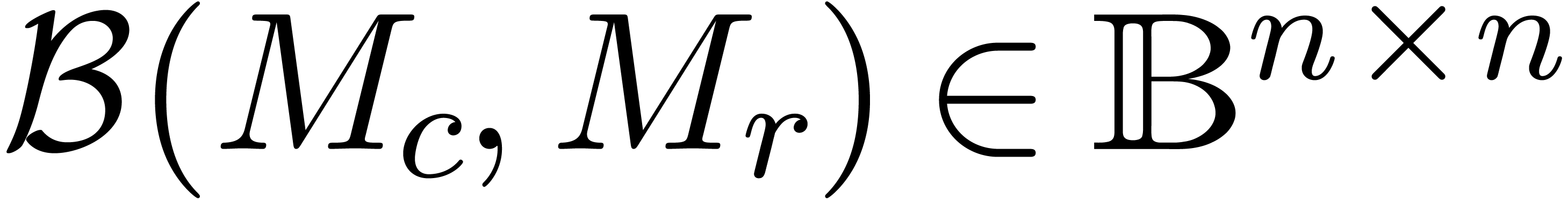 . Then we may
still compute a numeric solution
. Then we may
still compute a numeric solution
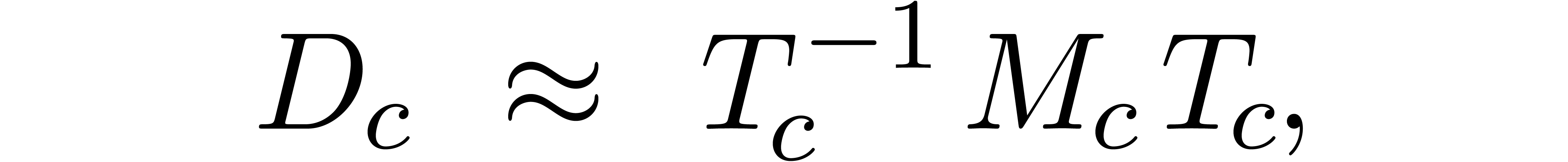 |
(2) |
for the eigenproblem associated to the center 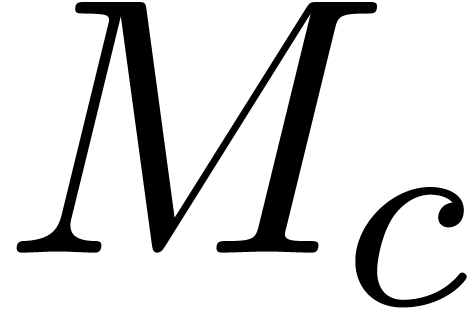 . Assume that the matrices in
. Assume that the matrices in 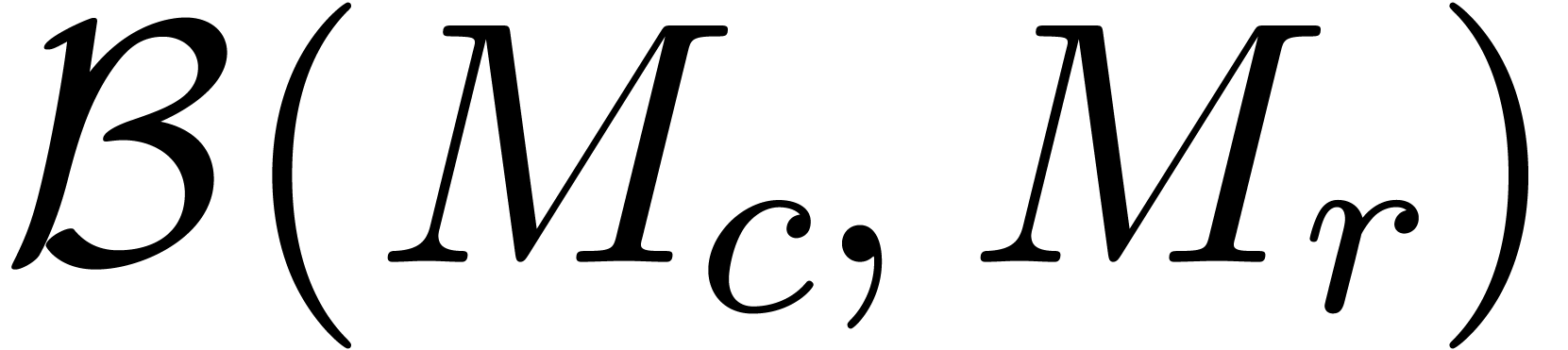 are all diagonalizable. The generalized certification problem
now consists of the computation of a diagonal matrix
are all diagonalizable. The generalized certification problem
now consists of the computation of a diagonal matrix  and a matrix
and a matrix  such that, for every
such that, for every 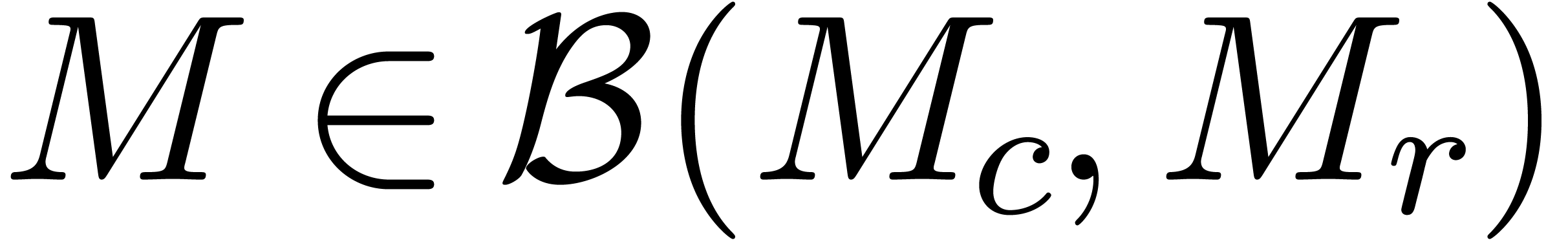 , there exist
, there exist 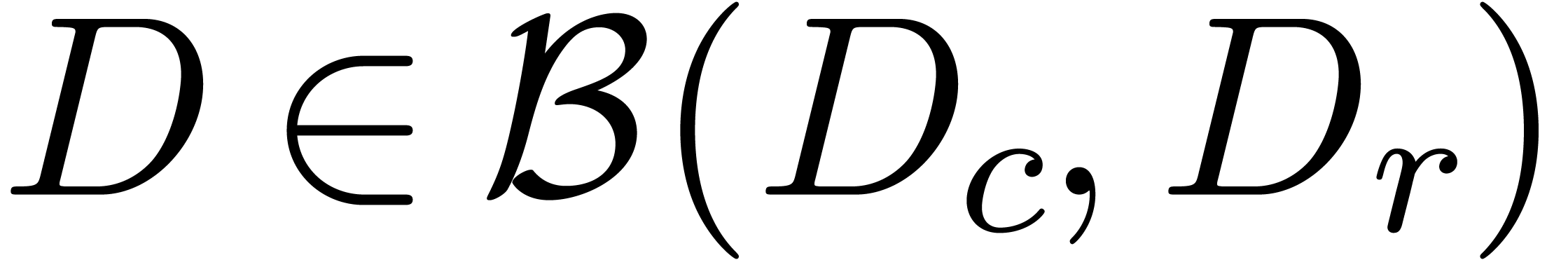 and
and 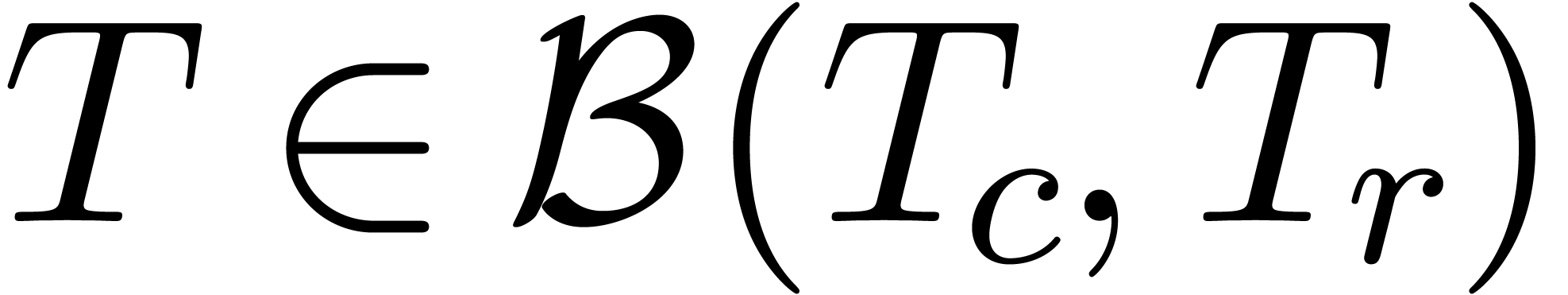 with
with
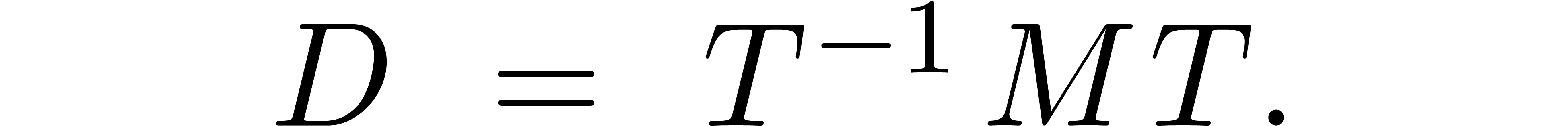
In absence of multiple eigenvalues, known algorithms for solving this
problem such as [23, 20] proceed by the
individual certification of each eigenvector, which results in an 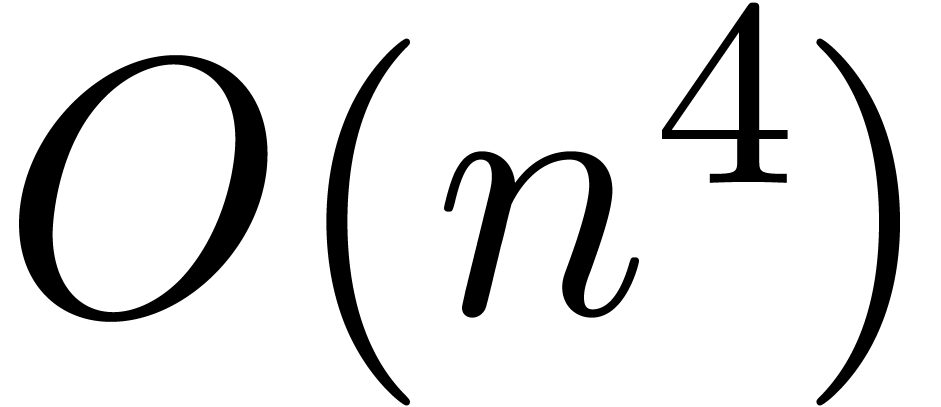 running time. From the more theoretical perspective
of
running time. From the more theoretical perspective
of  -theory [3],
we also refer to [2] for numerically stable, strongly
accurate, and theoretically efficient algorithms for solving
eigenproblems.
-theory [3],
we also refer to [2] for numerically stable, strongly
accurate, and theoretically efficient algorithms for solving
eigenproblems.
Extensions to a cluster of eigenvalues and the corresponding
eigenvectors have been considered in [4, 22],
with similar 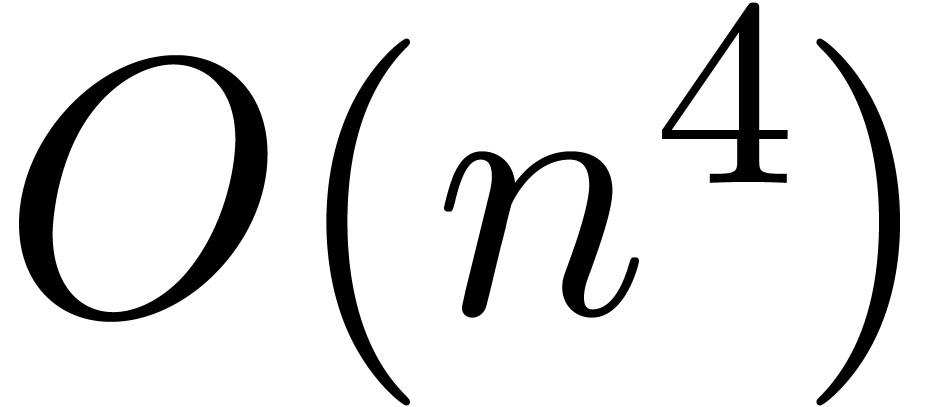 complexity bounds. Fixed points
theorem based on interval arithmetic are used to prove the existence of
a matrix with a given Jordan block in the matrix interval domain. Such
an approach has been exploited for the analysis of multiple roots in [7, 19]. A test that provides an enclosing of all
the eigenvalues has been proposed in [16]. Its
certification relies on interval and ball arithmetics. The complexity of
the test is in
complexity bounds. Fixed points
theorem based on interval arithmetic are used to prove the existence of
a matrix with a given Jordan block in the matrix interval domain. Such
an approach has been exploited for the analysis of multiple roots in [7, 19]. A test that provides an enclosing of all
the eigenvalues has been proposed in [16]. Its
certification relies on interval and ball arithmetics. The complexity of
the test is in 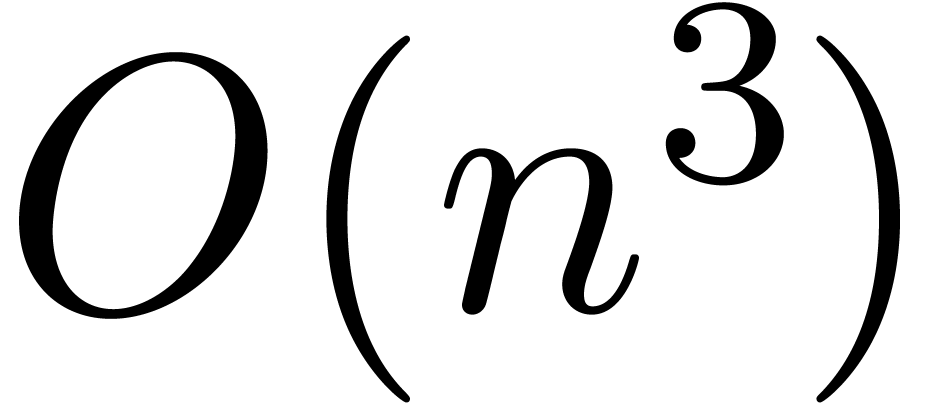 but no iteration converging to
the solution of the eigenproblem is described.
but no iteration converging to
the solution of the eigenproblem is described.
In this paper, we present a new algorithm of time complexity 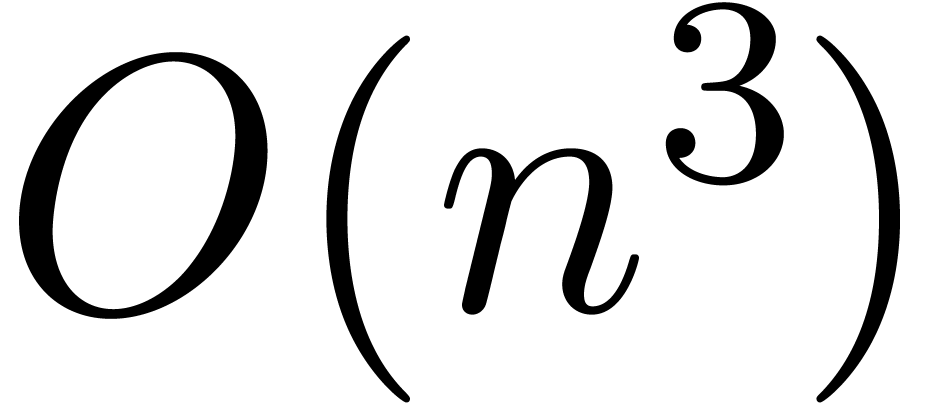 for certifying and enclosing clusters of eigenvectors and
eigenvalues in a single step. We also provide an iterative procedure
that converges geometrically to clusters of solutions. This convergence
is quadratic in the case of single eigenvalues. Our algorithm extends a
previous algorithm from [11] to the case of multiple
eigenvalues. This yields an efficient test for approximate
eigenvalues.
for certifying and enclosing clusters of eigenvectors and
eigenvalues in a single step. We also provide an iterative procedure
that converges geometrically to clusters of solutions. This convergence
is quadratic in the case of single eigenvalues. Our algorithm extends a
previous algorithm from [11] to the case of multiple
eigenvalues. This yields an efficient test for approximate
eigenvalues.
From a more theoretical bit complexity point of view, our algorithm
essentially reduces the certification problem to a constant number of
numeric matrix multiplications. When using a precision of 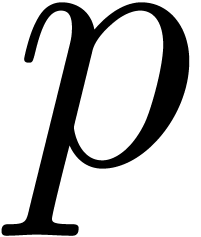 bits for numerical computations, it has recently been
shown [9] that two
bits for numerical computations, it has recently been
shown [9] that two  matrices can be
multiplied in time
matrices can be
multiplied in time  . Here
. Here
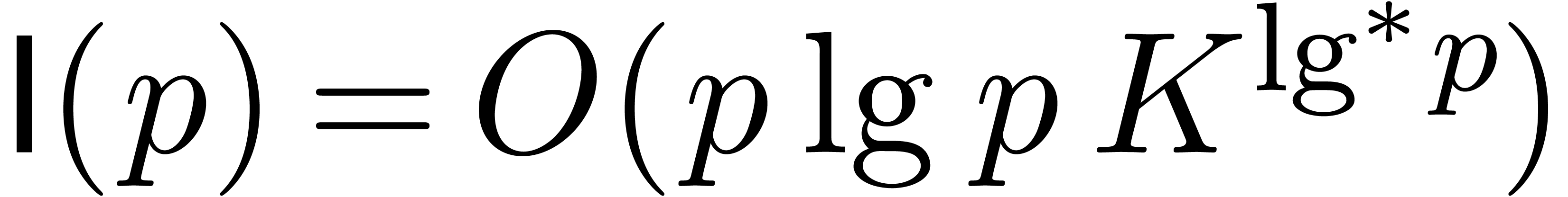 with
with 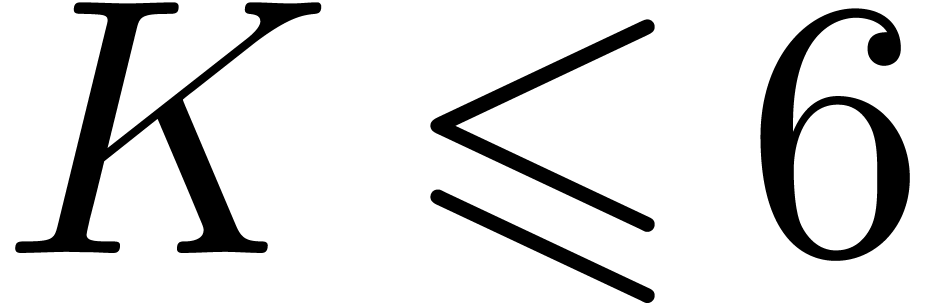 is the cost of
is the cost of
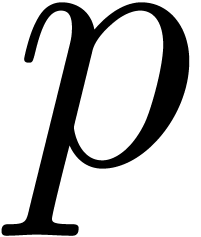 -bit integer multiplication
[10, 8] and
-bit integer multiplication
[10, 8] and  is the
exponent of matrix multiplication [5]. If
is the
exponent of matrix multiplication [5]. If 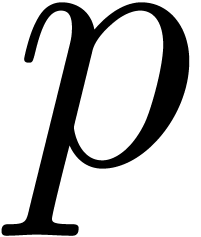 is large enough with respect to the log of the condition number, then
is large enough with respect to the log of the condition number, then
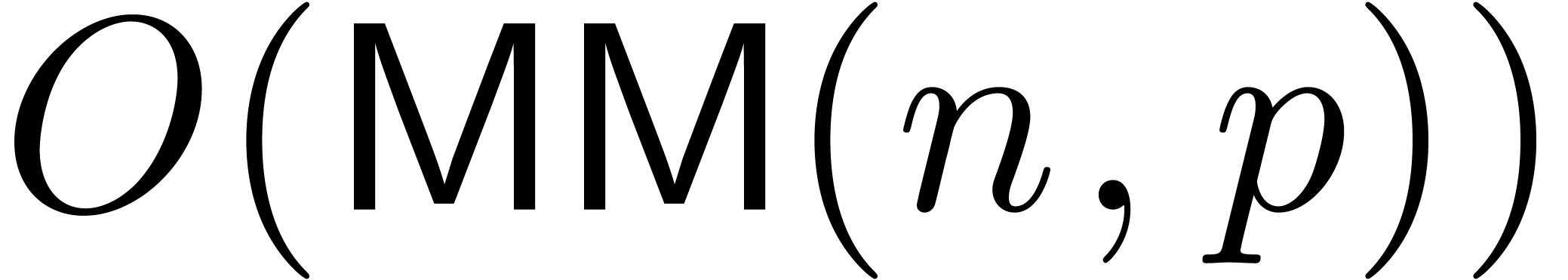 yields an asymptotic bound for the bit
complexity of our certification problem.
yields an asymptotic bound for the bit
complexity of our certification problem.
We recall that it is very unlikely that the numeric matrix 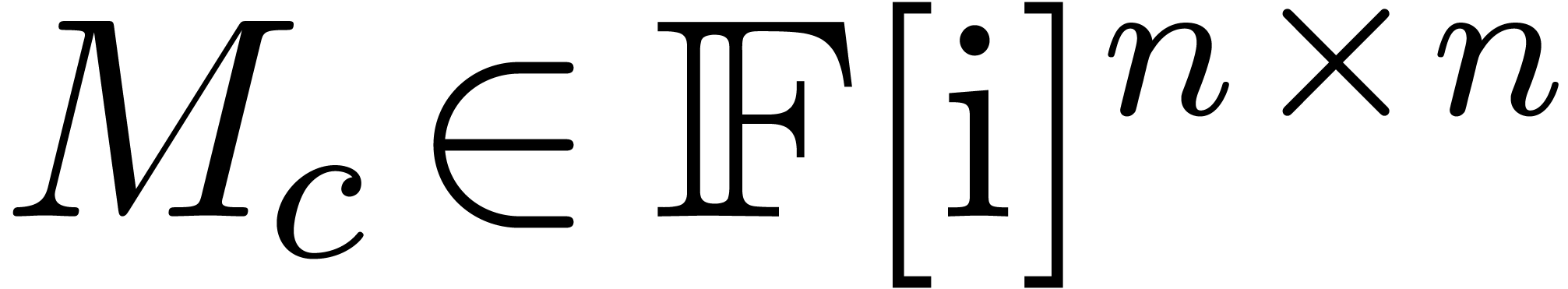 with complex floating point coefficients has multiple
eigenvalues. Indeed, small perturbations of matrices with multiple
eigenvalues, as induced by rounding errors, generically only have simple
eigenvalues. Consequently, we may assume without loss of generality that
the numeric eigenproblem (2) has a reasonably accurate
solution (if necessary, we may slightly perturb
with complex floating point coefficients has multiple
eigenvalues. Indeed, small perturbations of matrices with multiple
eigenvalues, as induced by rounding errors, generically only have simple
eigenvalues. Consequently, we may assume without loss of generality that
the numeric eigenproblem (2) has a reasonably accurate
solution (if necessary, we may slightly perturb 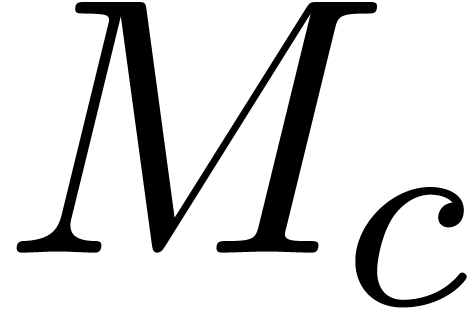 and increase
and increase  accordingly). Using ball
arithmetic, it is straightforward to compute the matricial ball
accordingly). Using ball
arithmetic, it is straightforward to compute the matricial ball
If our numerical algorithm is accurate, then the non diagonal entries of
 tend to be small, whence
tend to be small, whence  can be considered as a small perturbation of a diagonal matrix. If we
can estimate how far eigenvalues and eigenvectors of diagonal matrices
can drift away under small perturbations, we thus obtain a solution to
the original certification problem.
can be considered as a small perturbation of a diagonal matrix. If we
can estimate how far eigenvalues and eigenvectors of diagonal matrices
can drift away under small perturbations, we thus obtain a solution to
the original certification problem.
Section 2 introduces notations. In Section 3, we perform a
detailed study of the eigenproblem for small perturbations 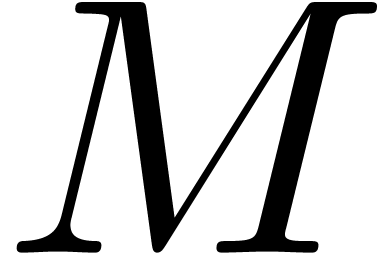 of diagonal matrices. We exhibit a Newton iteration for
finding the solutions. This iteration has quadratic convergence in the
absence of multiple eigenvalues and is also an efficient tool for
doubling the precision of a solution. However, in the case of multiple
eigenvalues, the eigenproblem is ill-posed. Indeed, by a well-known
observation, any vector occurs as the eigenvector of a small
perturbation of the
of diagonal matrices. We exhibit a Newton iteration for
finding the solutions. This iteration has quadratic convergence in the
absence of multiple eigenvalues and is also an efficient tool for
doubling the precision of a solution. However, in the case of multiple
eigenvalues, the eigenproblem is ill-posed. Indeed, by a well-known
observation, any vector occurs as the eigenvector of a small
perturbation of the  identity matrix. The best we
can hope for is to group eigenvectors with close eigenvalues together in
“clusters” (see also [22]) and only require
identity matrix. The best we
can hope for is to group eigenvectors with close eigenvalues together in
“clusters” (see also [22]) and only require
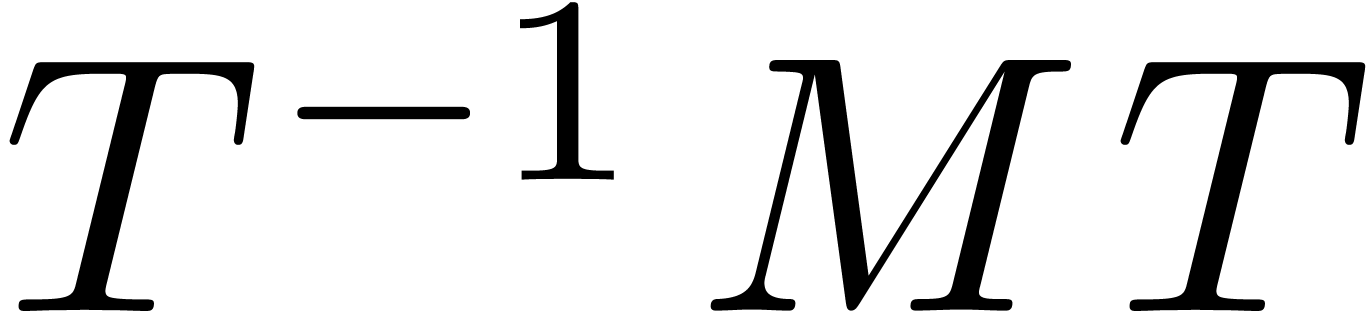 to be block diagonal. For this reason, we
present our Newton iteration in a sufficiently general setting which
encompasses block matrices. We will show that the iteration still admits
geometric convergence for sufficiently small perturbations and that the
blockwise certification is still sufficient for the computation of
rigourous error bounds for the eigenvalues. In Section 4,
we will present explicit algorithms for clustering and the overall
certification problem.
to be block diagonal. For this reason, we
present our Newton iteration in a sufficiently general setting which
encompasses block matrices. We will show that the iteration still admits
geometric convergence for sufficiently small perturbations and that the
blockwise certification is still sufficient for the computation of
rigourous error bounds for the eigenvalues. In Section 4,
we will present explicit algorithms for clustering and the overall
certification problem.
In absence of multiple eigenvalues, the Analyziz
library of the Mathemagix system [12]
contains an efficient implementation of our algorithm. The new algorithm
from this paper has still to be integrated.
2.Notations
2.1.Matrix norms
Throughout this paper, we will use the max norm for vectors and the
corresponding matrix norm. More precisely, given a vector 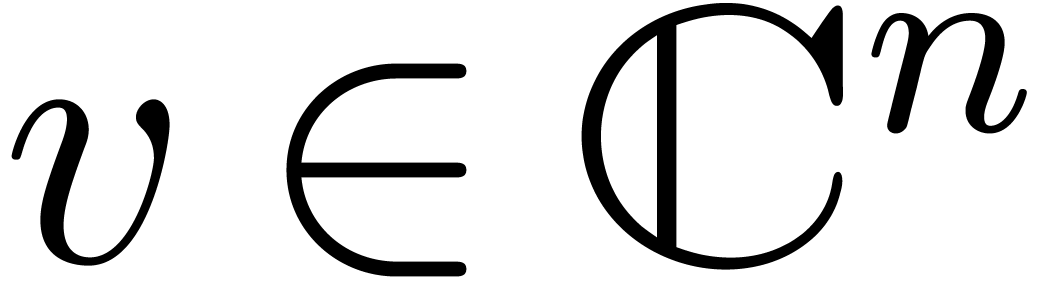 and an
and an  matrix
matrix  , we set
, we set
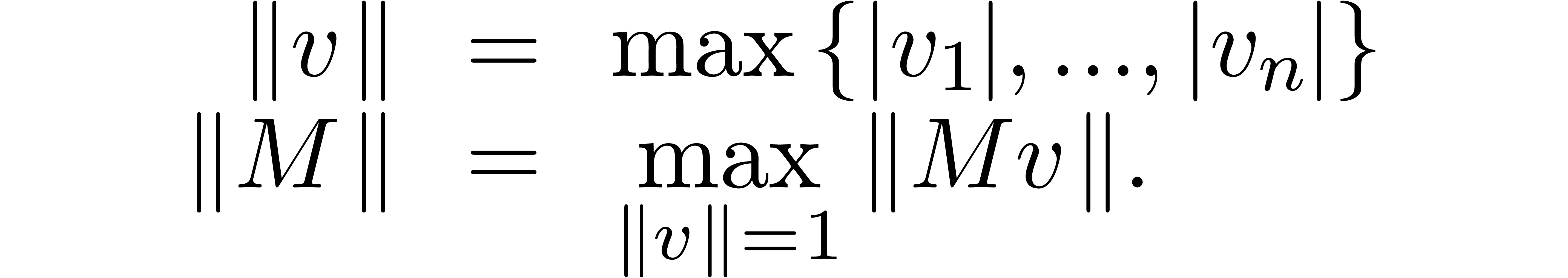
For a second matrix  , we
clearly have
, we
clearly have

Explicit machine computation of the matrix norm is easy using the
formula
 |
(3) |
In particular, when changing certain entries of a matrix 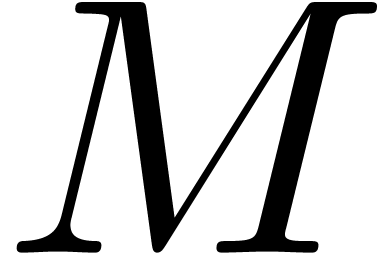 to zero, its matrix norm
to zero, its matrix norm 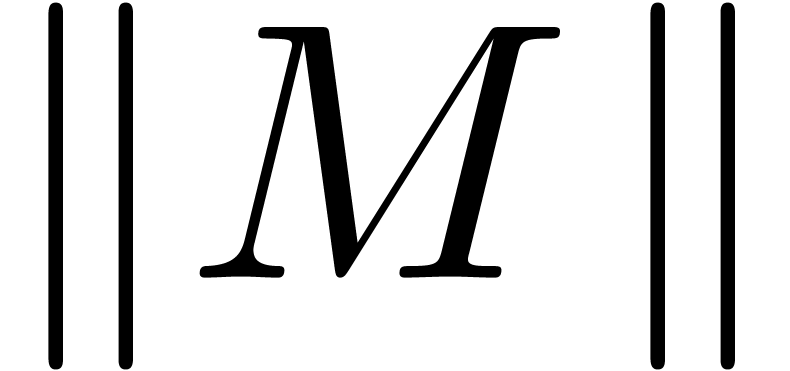 can only
decrease.
can only
decrease.
2.2.Clustering
Assume that we are given a partition
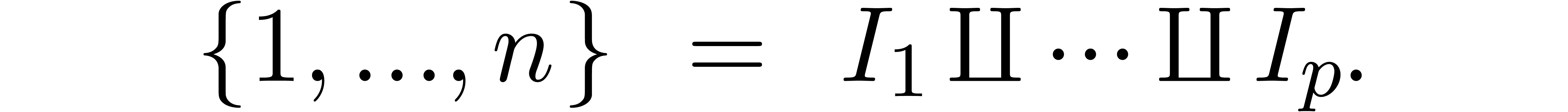 |
(4) |
Such a partition will also be called a clustering and denoted
by  . Two indices
. Two indices  are said to belong to the same cluster if there
exists a
are said to belong to the same cluster if there
exists a  with
with 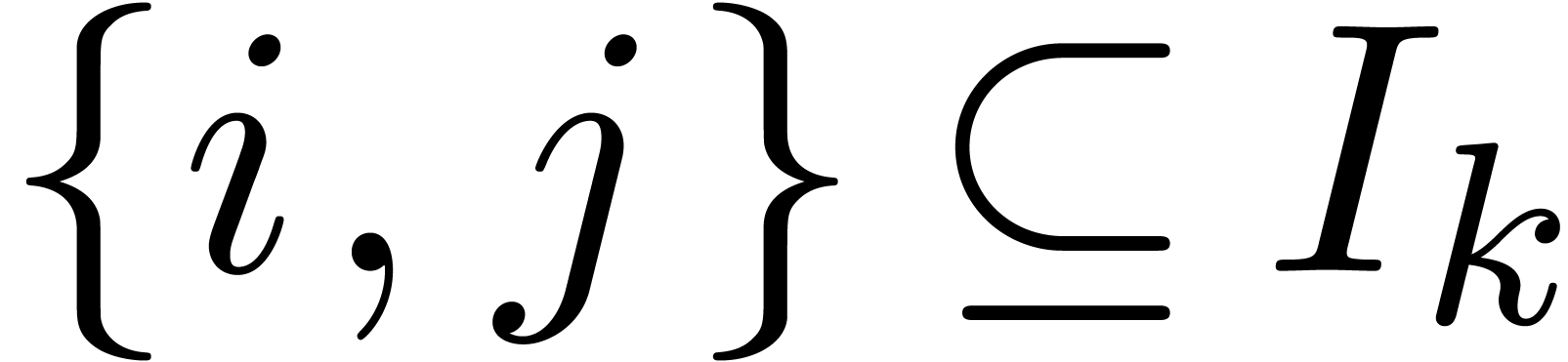 and we
will write
and we
will write  . Two entries
. Two entries 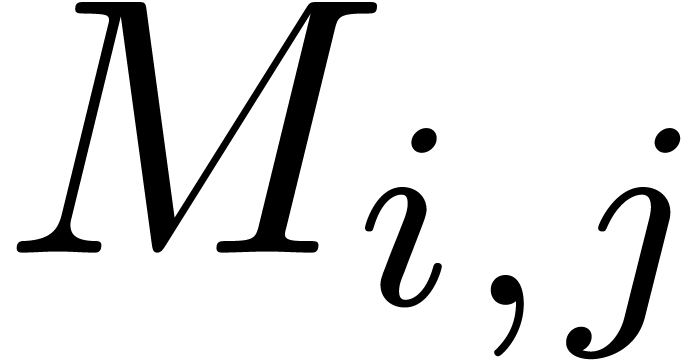 and
and 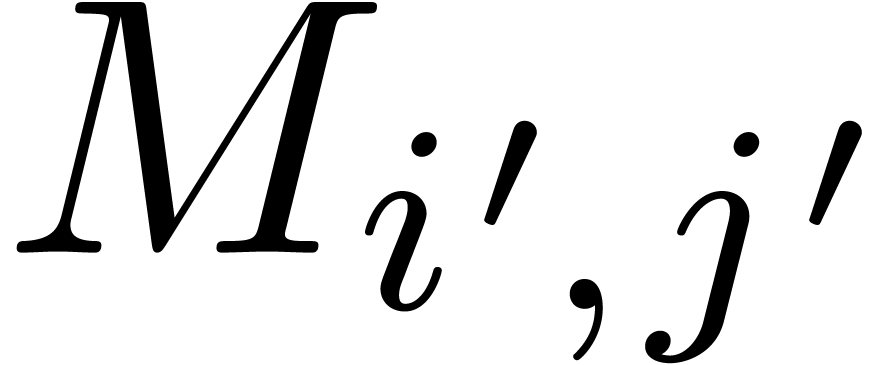 of a matrix
of a matrix  are said to belong to the same block if
are said to belong to the same block if  and
and  . We thus
regard
. We thus
regard  as a generalized block matrix, for which
the rows and columns of the blocks are not necessarily contiguous inside
as a generalized block matrix, for which
the rows and columns of the blocks are not necessarily contiguous inside
 .
.
A matrix  is said to be block diagonal
(relative to the clustering) if
is said to be block diagonal
(relative to the clustering) if 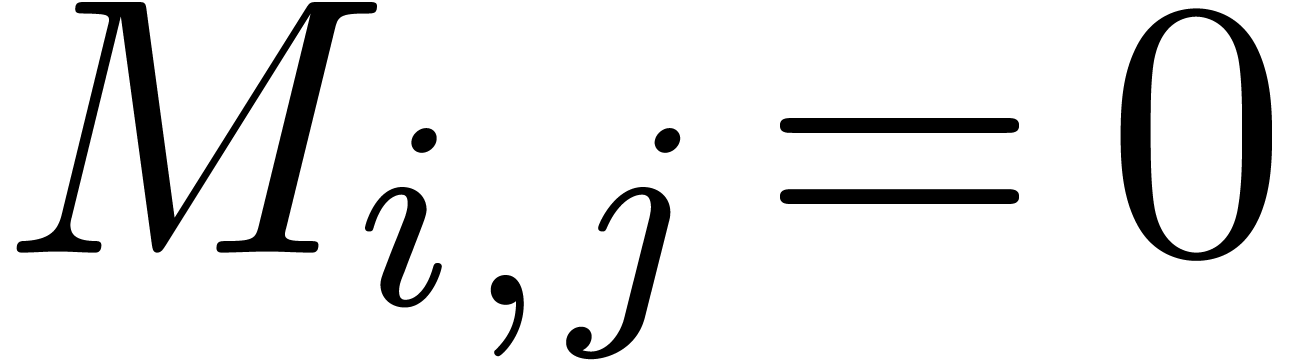 whenever
whenever  . Similarly, we say that
. Similarly, we say that  is off block diagonal if
is off block diagonal if 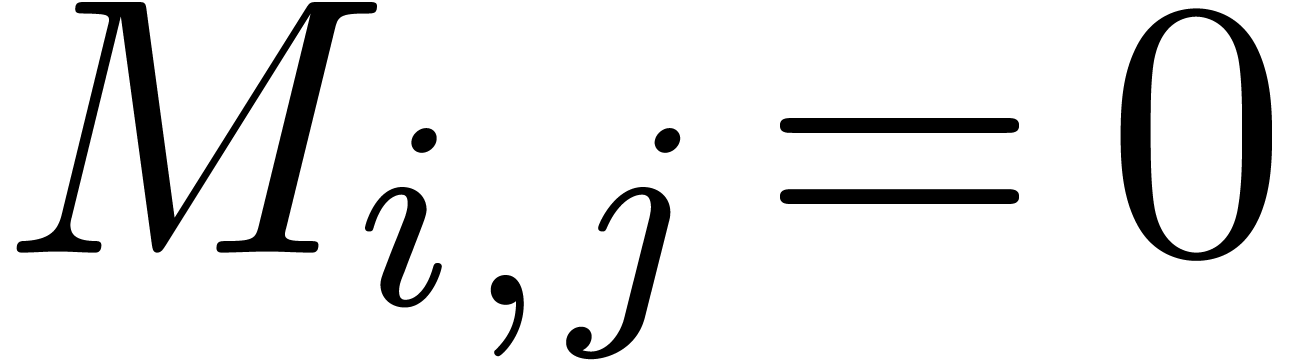 whenever
whenever  . For a general
. For a general
 , we define its block
diagonal and off block diagonal projections
, we define its block
diagonal and off block diagonal projections 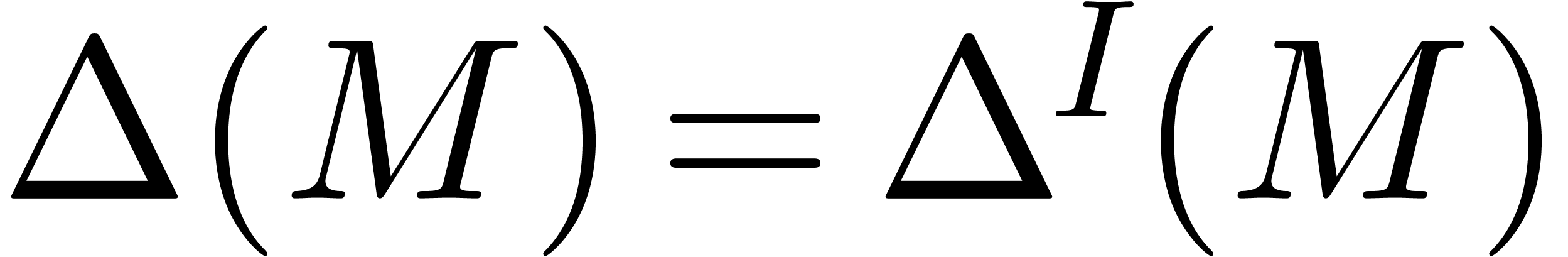 and
and
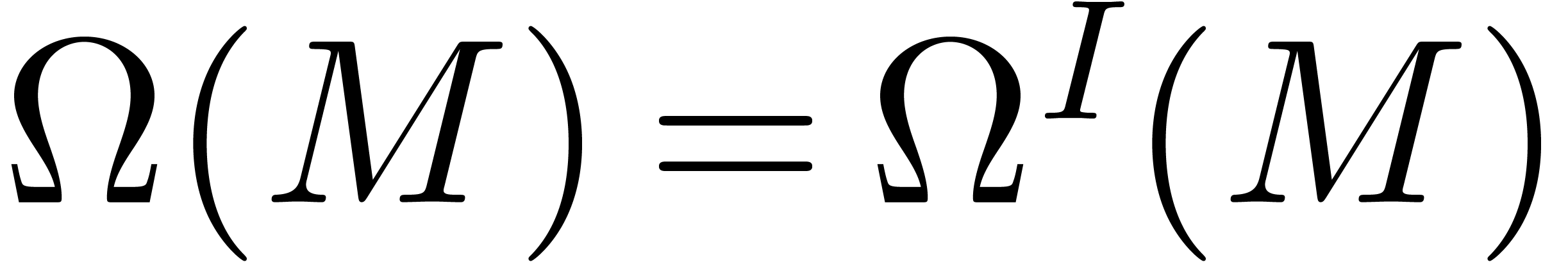 by
by

By our observation at the end of section 2.1, we have

For the trivial clustering 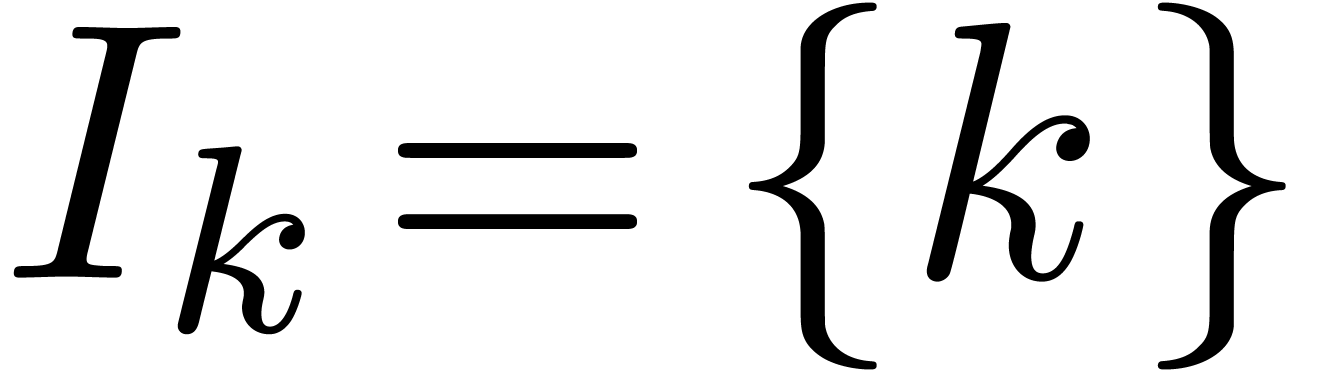 ,
the matrices
,
the matrices 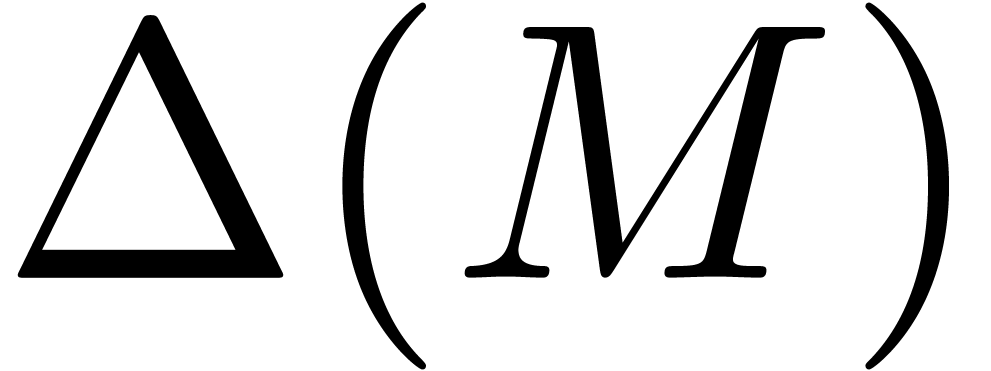 and
and 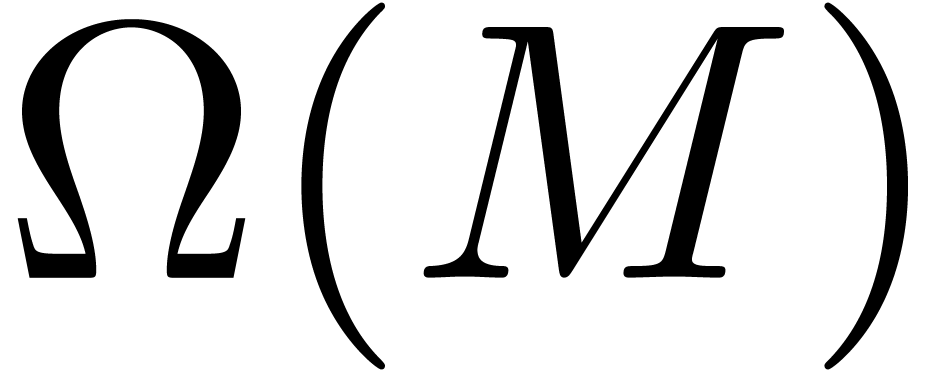 are
simply the diagonal and off diagonal projections of
are
simply the diagonal and off diagonal projections of  . In that case we will also write
. In that case we will also write 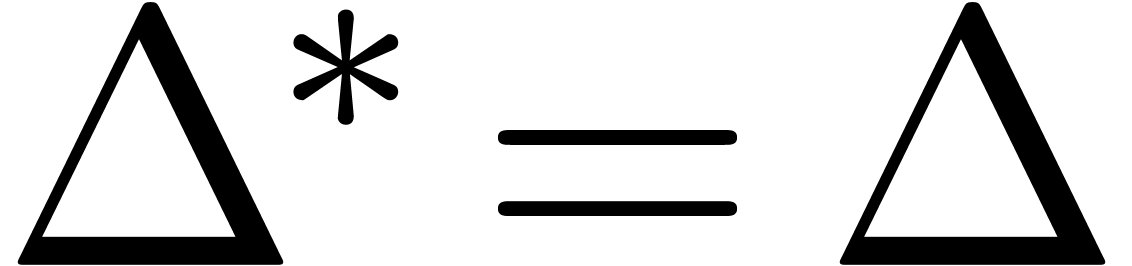 and
and 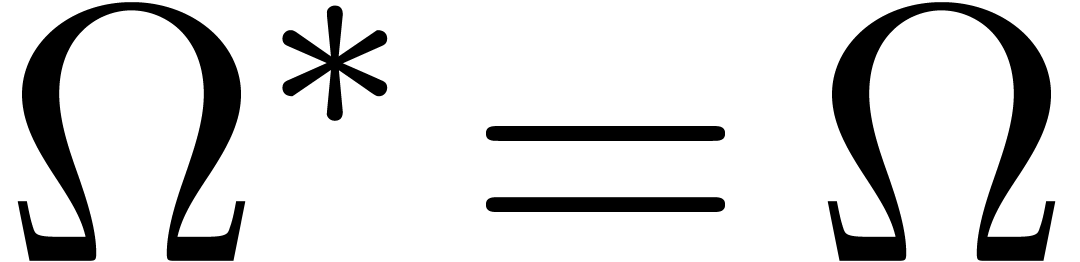 .
.
2.3.Diagonal matrices
Below, we will study eigenproblems for perturbations of a given diagonal
matrix
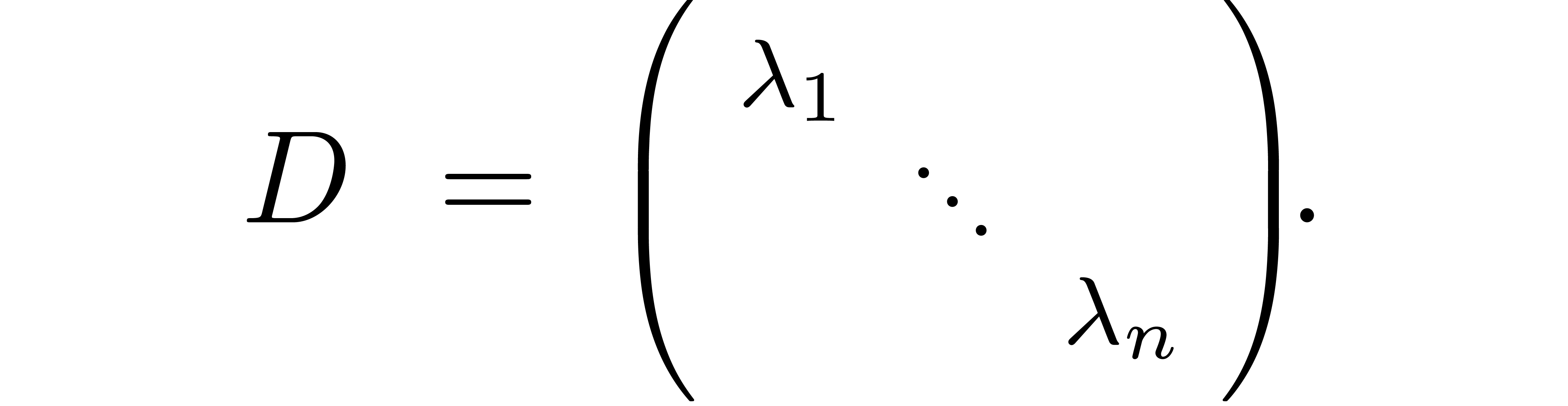 |
(5) |
It follows from (3) that the matrix norm 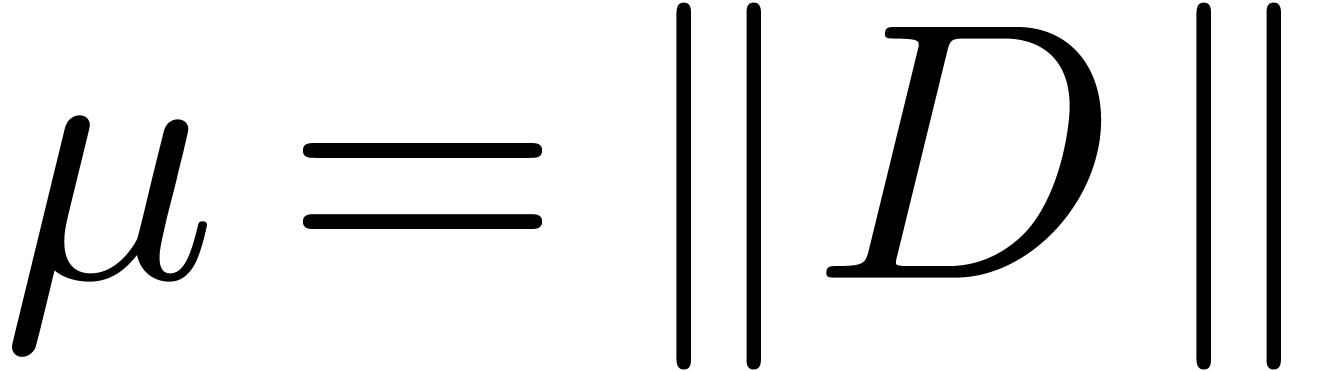 of a diagonal matrix
of a diagonal matrix 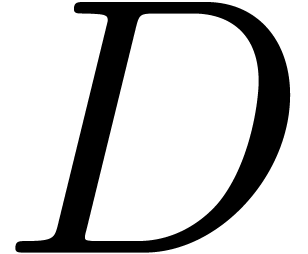 is given by
is given by
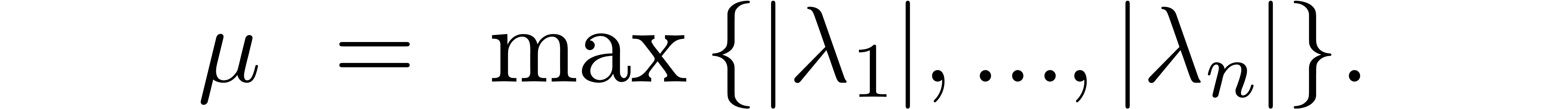
It will also be useful to define the separation number 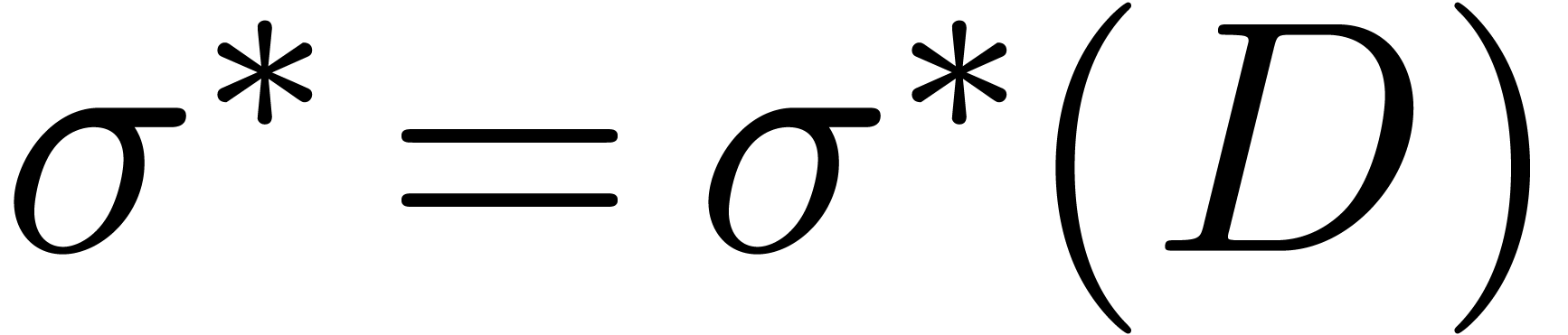 by
by
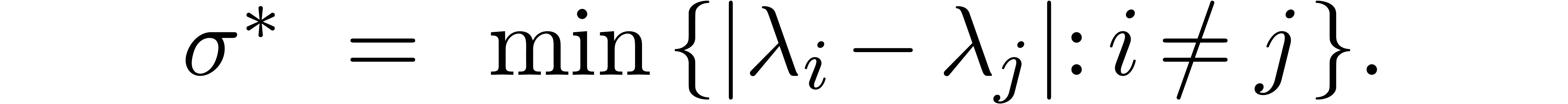
More generally, given a clustering as in the previous subsection, we
also define the block separation number 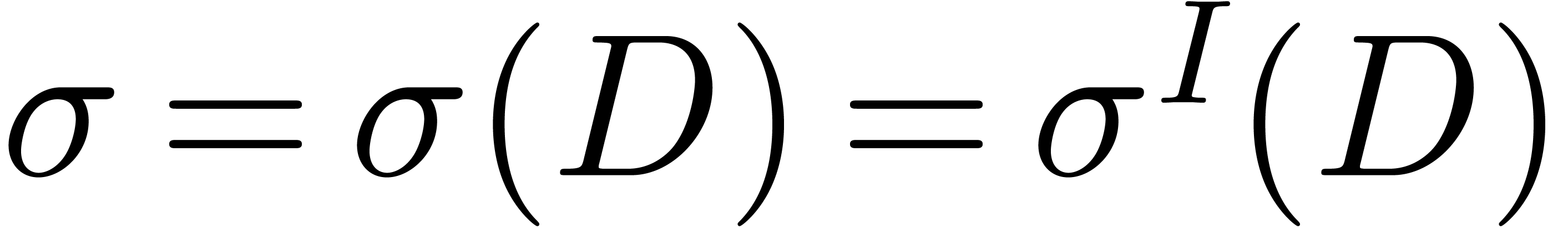 by
by
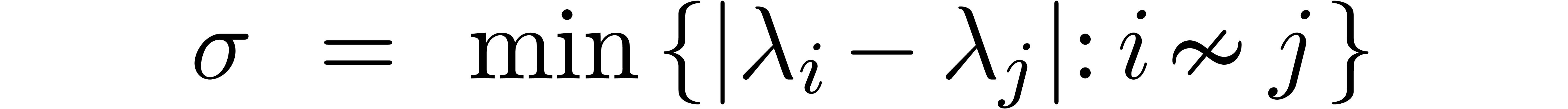
This number  remains high if the clustering is
chosen in such a way that the indices
remains high if the clustering is
chosen in such a way that the indices  of any two
“close” eigenvalues
of any two
“close” eigenvalues 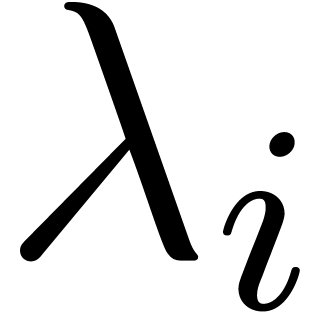 and
and 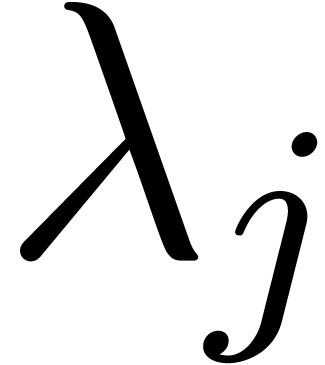 belong to the same cluster. In particular, if
belong to the same cluster. In particular, if 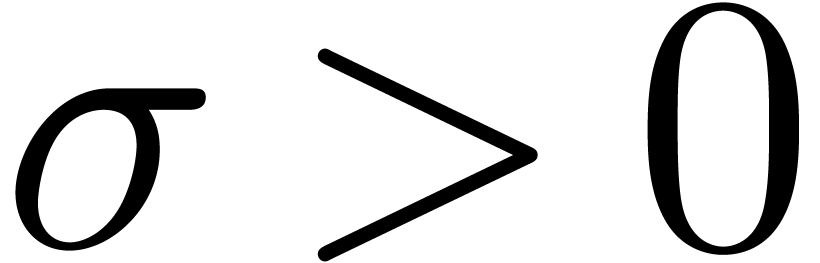 , then
, then 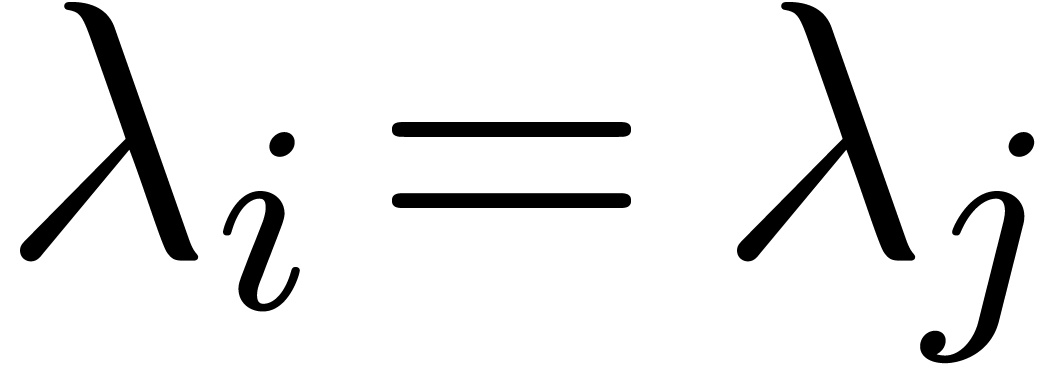 implies
implies  .
.
3.Eigenproblems for perturbed
diagonal matrices
3.1.The linearized equation
Let 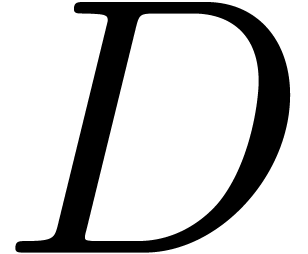 be a diagonal matrix (5). Given
a small perturbation
be a diagonal matrix (5). Given
a small perturbation
of 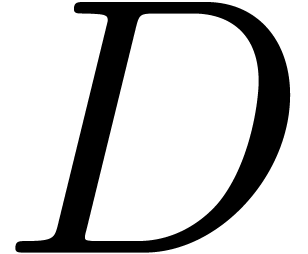 , where
, where  is an off diagonal matrix, the aim of this section is to find a small
matrix
is an off diagonal matrix, the aim of this section is to find a small
matrix  for which
for which
is block diagonal. In other words, we need to solve the equation
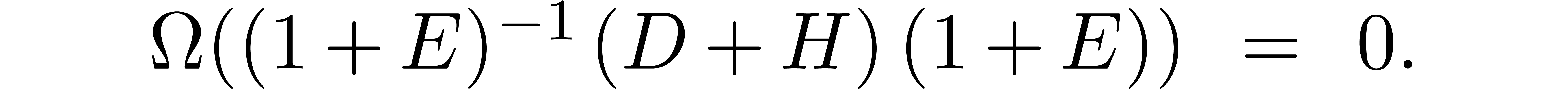
When linearizing this equation in  and
and  , we obtain
, we obtain
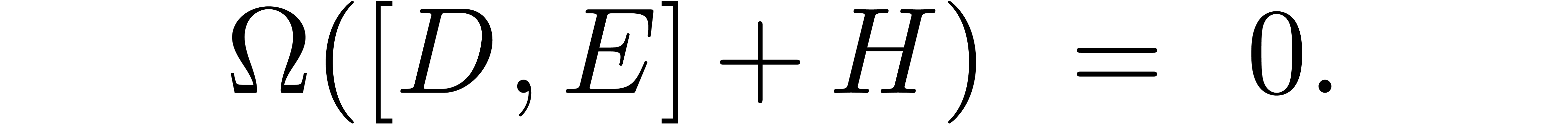
If  is strongly off diagonal, then so is
is strongly off diagonal, then so is 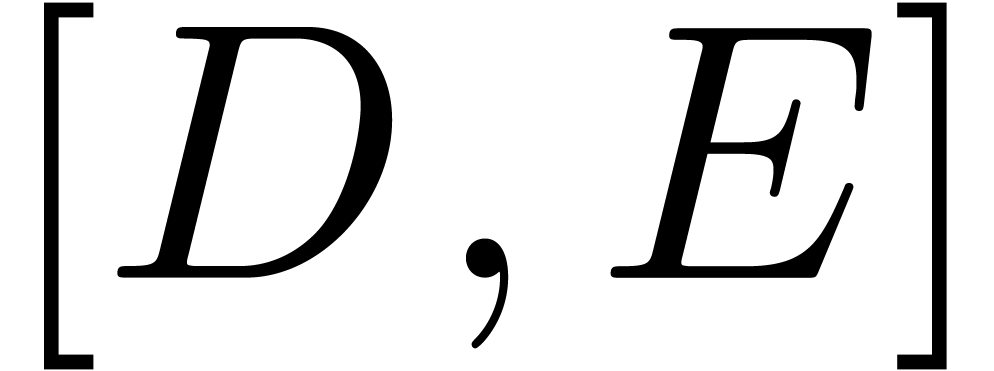 , and the equation further reduces
to
, and the equation further reduces
to
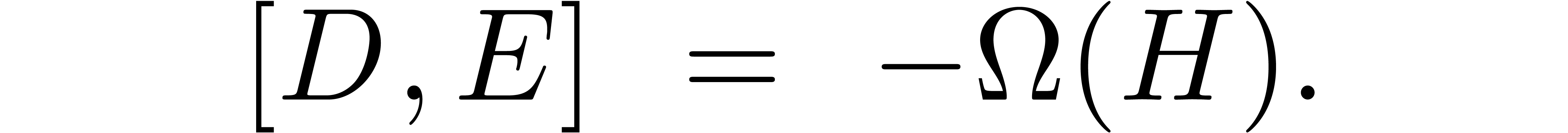
This equation can be solved using the following lemma:
Proof. The inequality follows from (3)
and the definition of  . One
may check (6) using a straightforward computation.
. One
may check (6) using a straightforward computation.
3.2.The fundamental iteration
In view of the lemma, we now consider the iteration

where
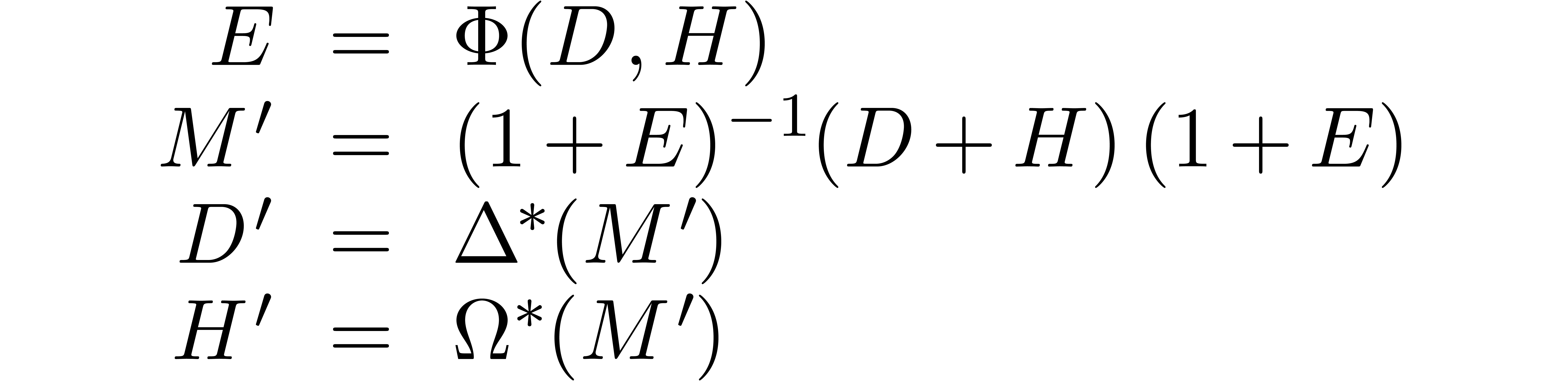
In order to study the convergence of this iteration, we introduce the
quantities
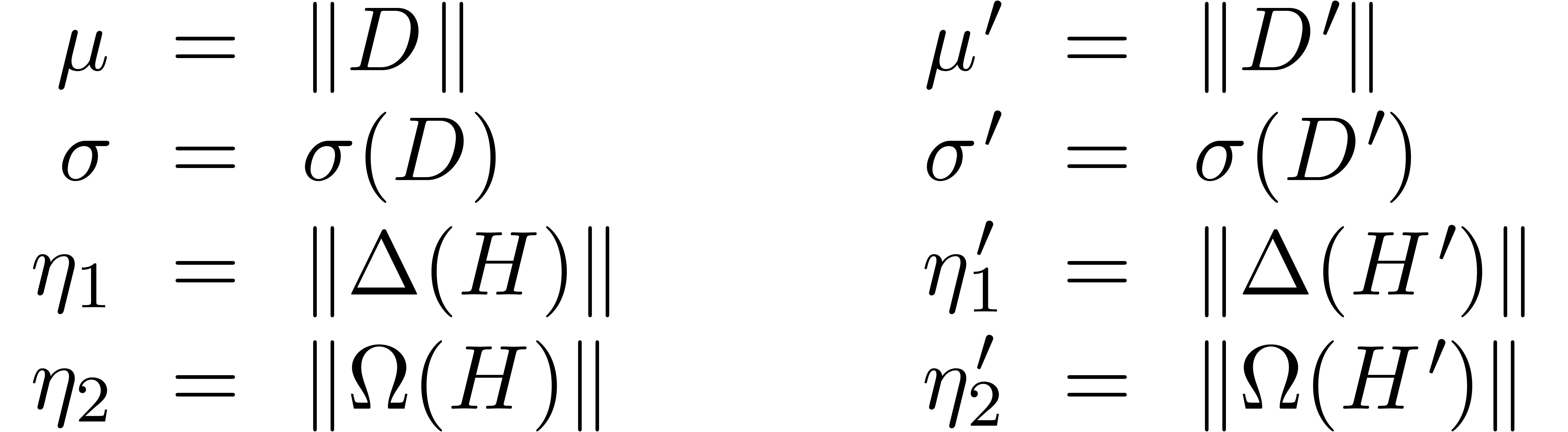
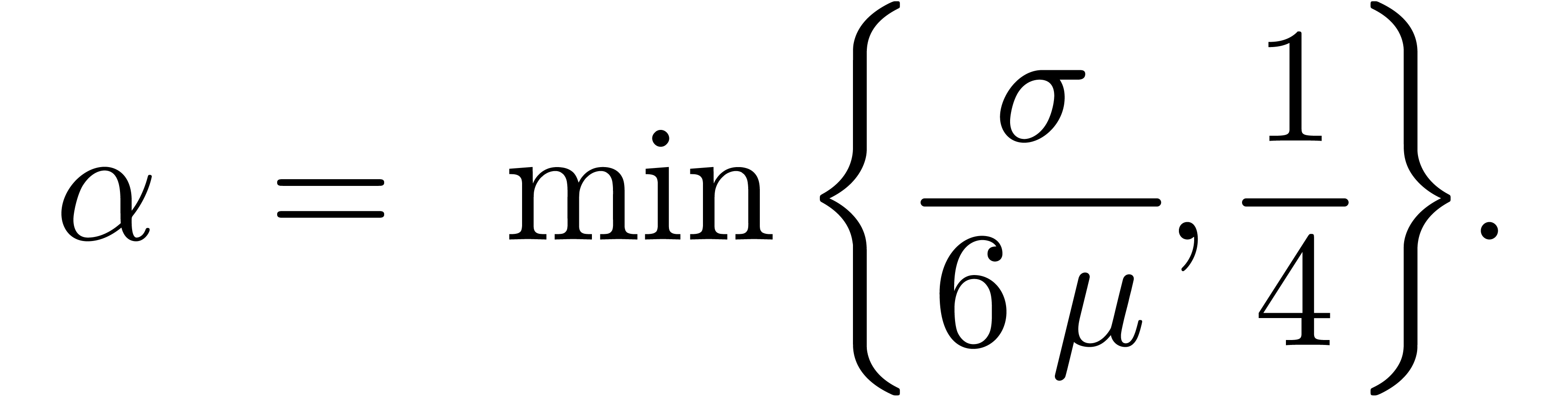
Lemma 2. For
 , assume that
, assume that
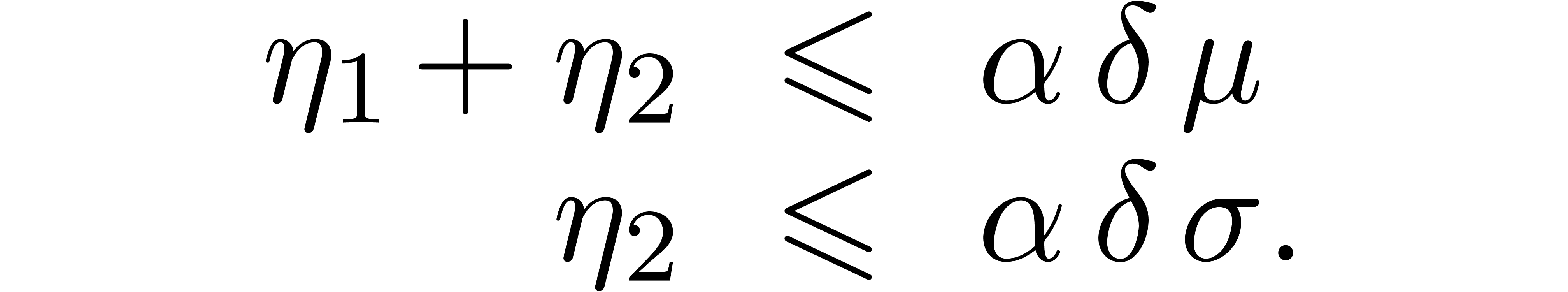
Then 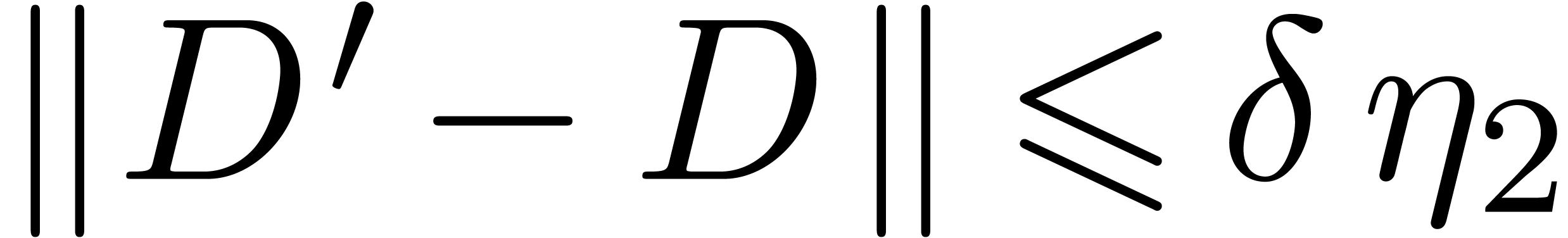 and
and
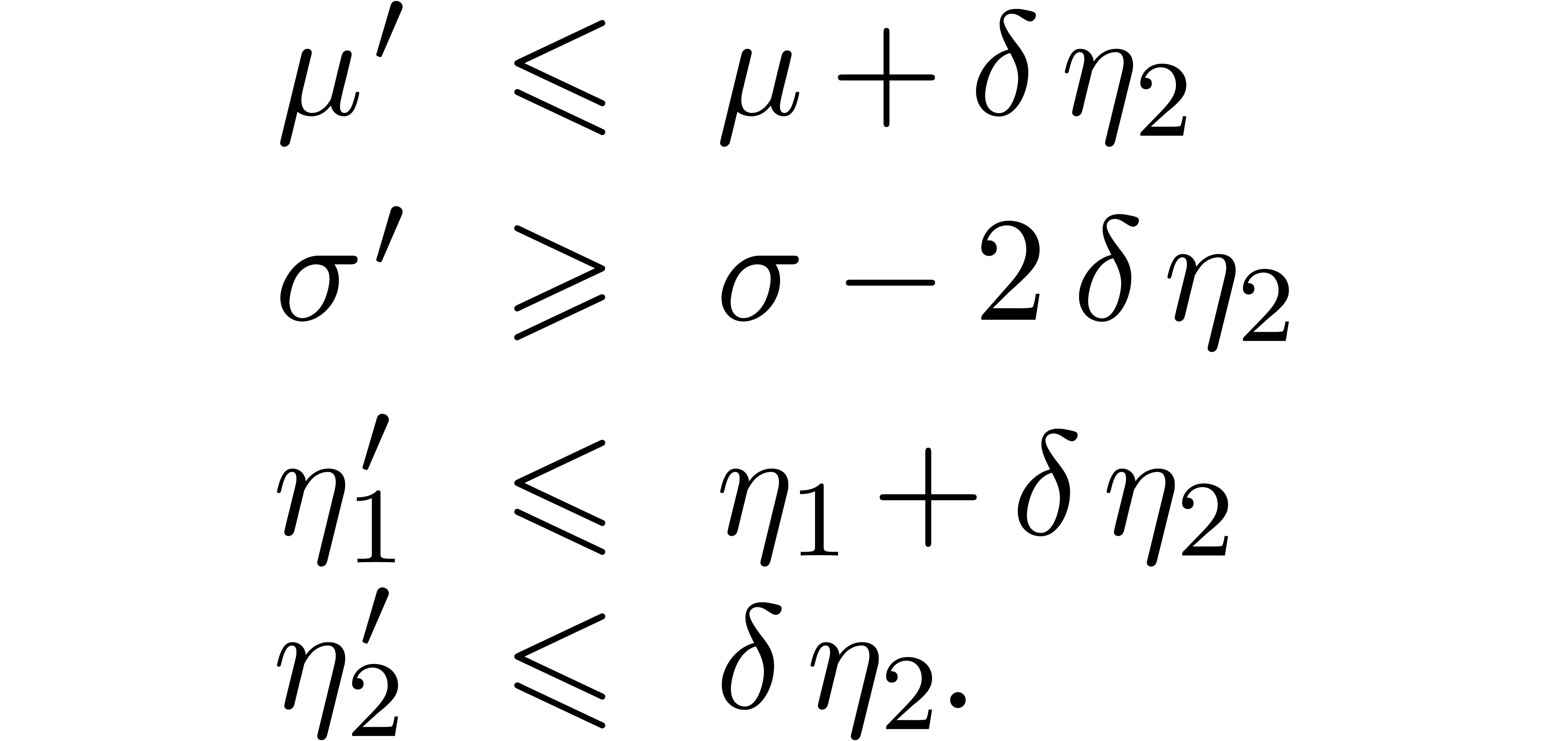
Proof. We have
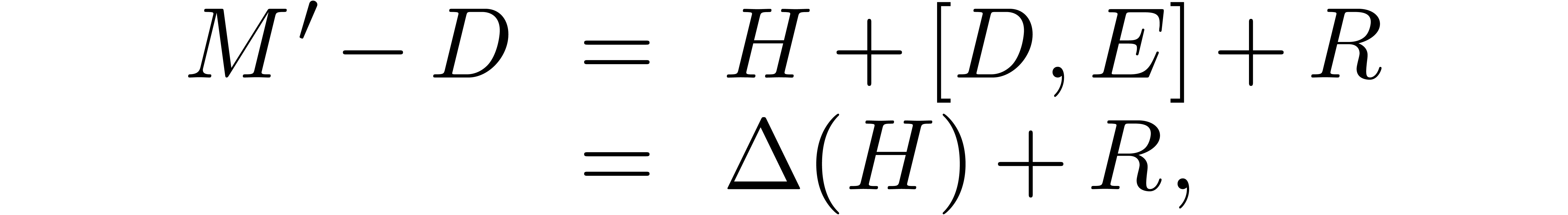
where
Setting 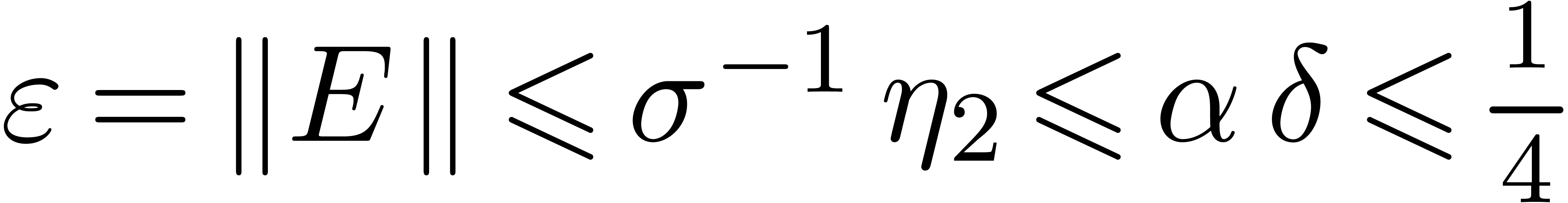 , the remainder
, the remainder  is bounded by
is bounded by
Consequently,
The inequalities 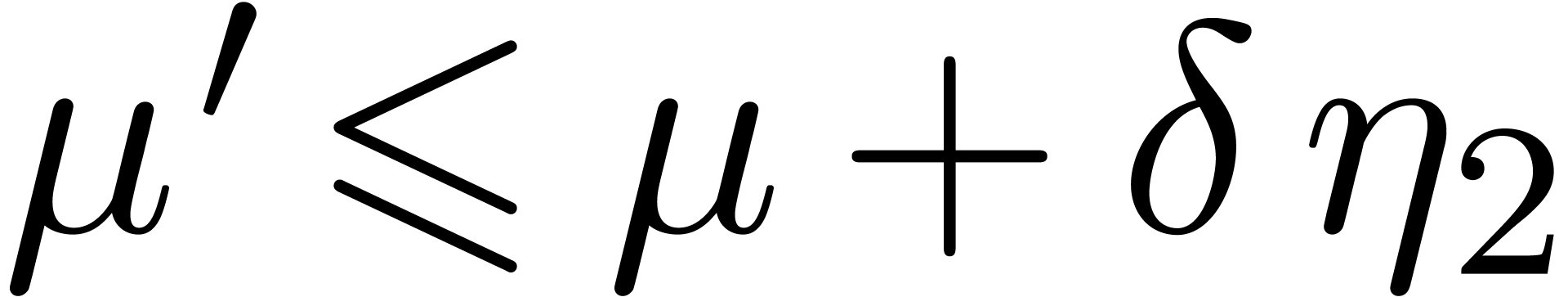 and
and 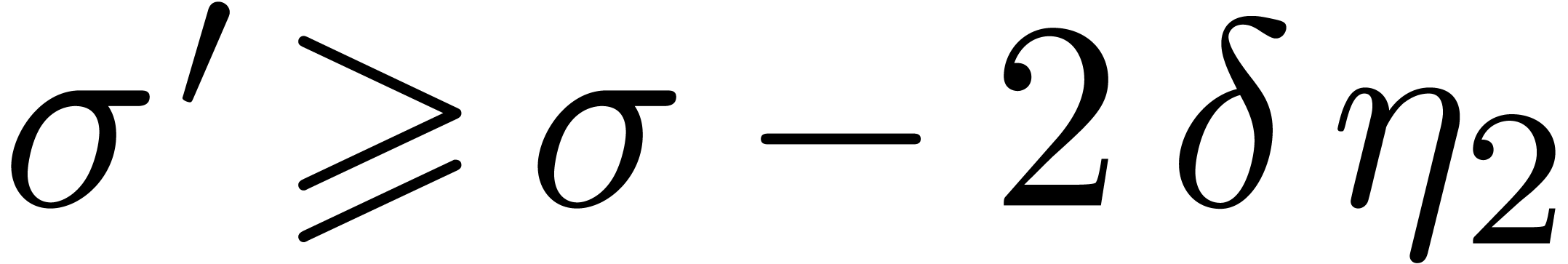 follow from
follow from 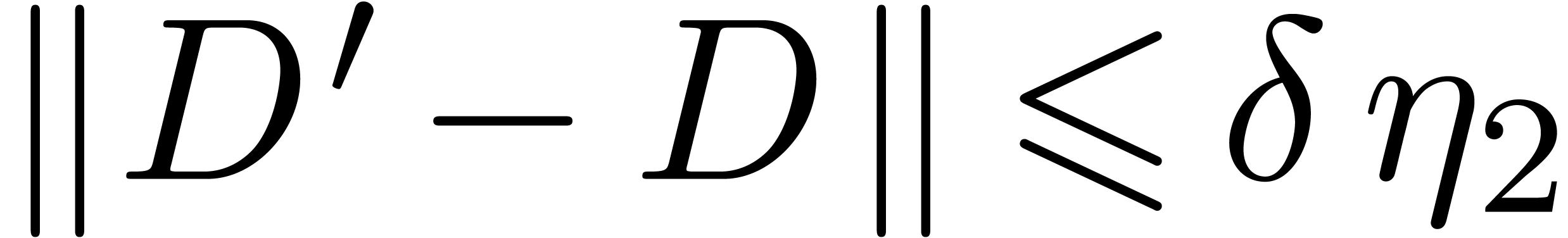 .
.
3.3.Convergence of the fundamental
iteration
Proof. Let 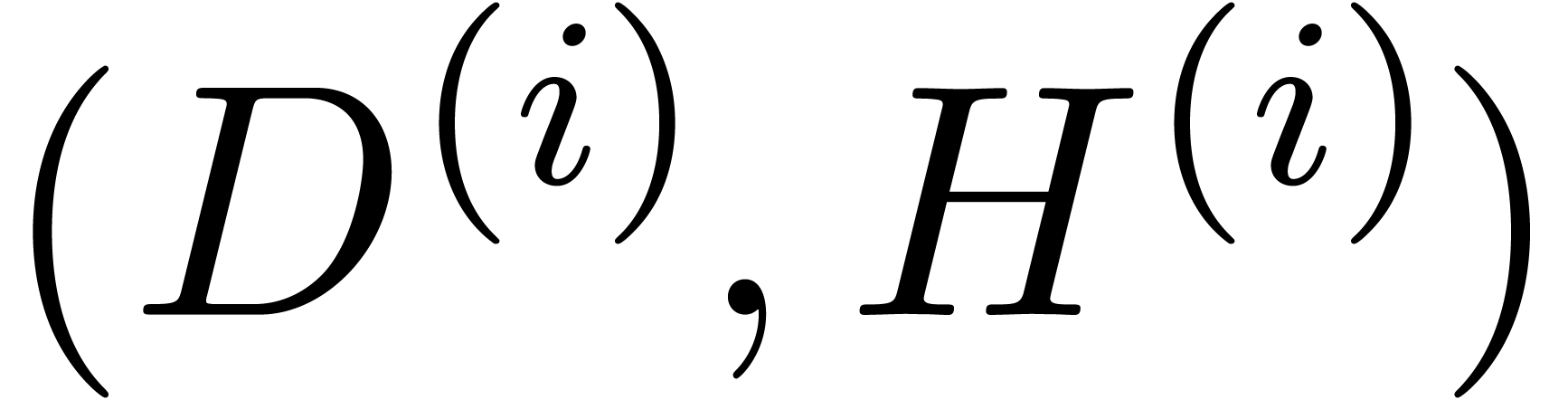 stand for the
stand for the
 -th fundamental iterate of
-th fundamental iterate of
 and
and  .
Denote
.
Denote 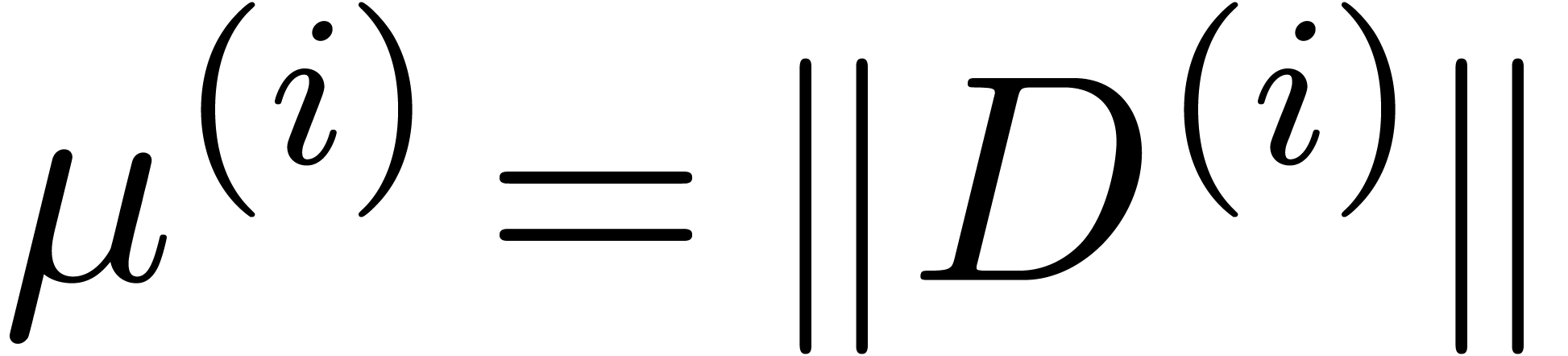 ,
, 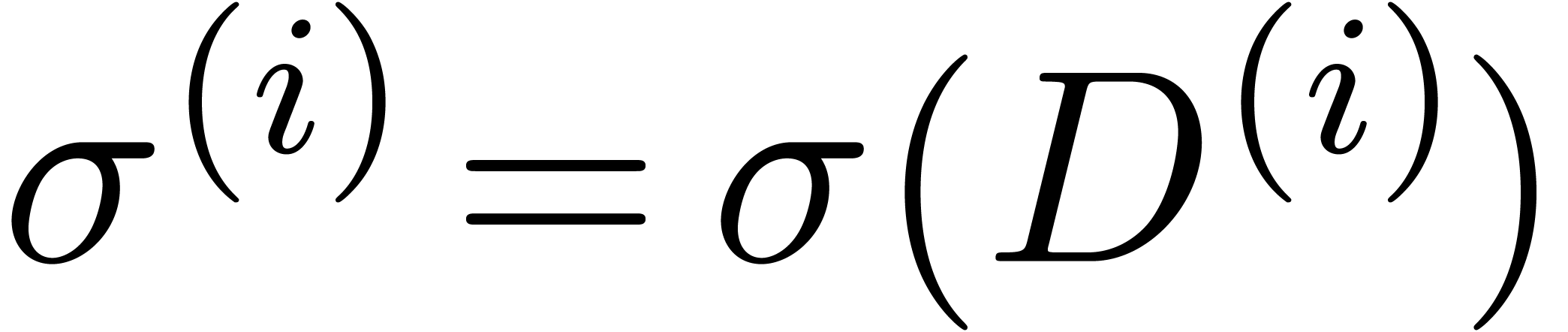 ,
, 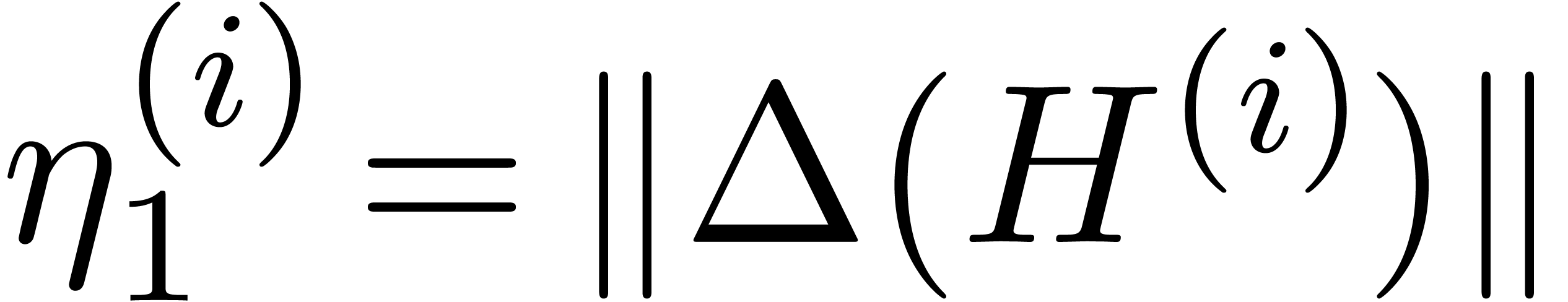 and
and 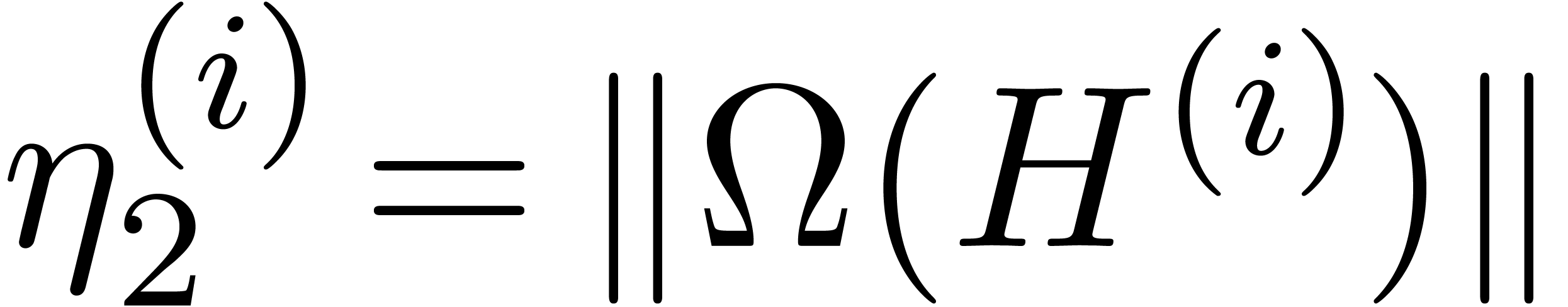 . Let us show by induction over
. Let us show by induction over 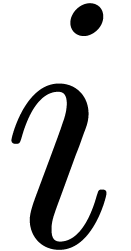 that
that
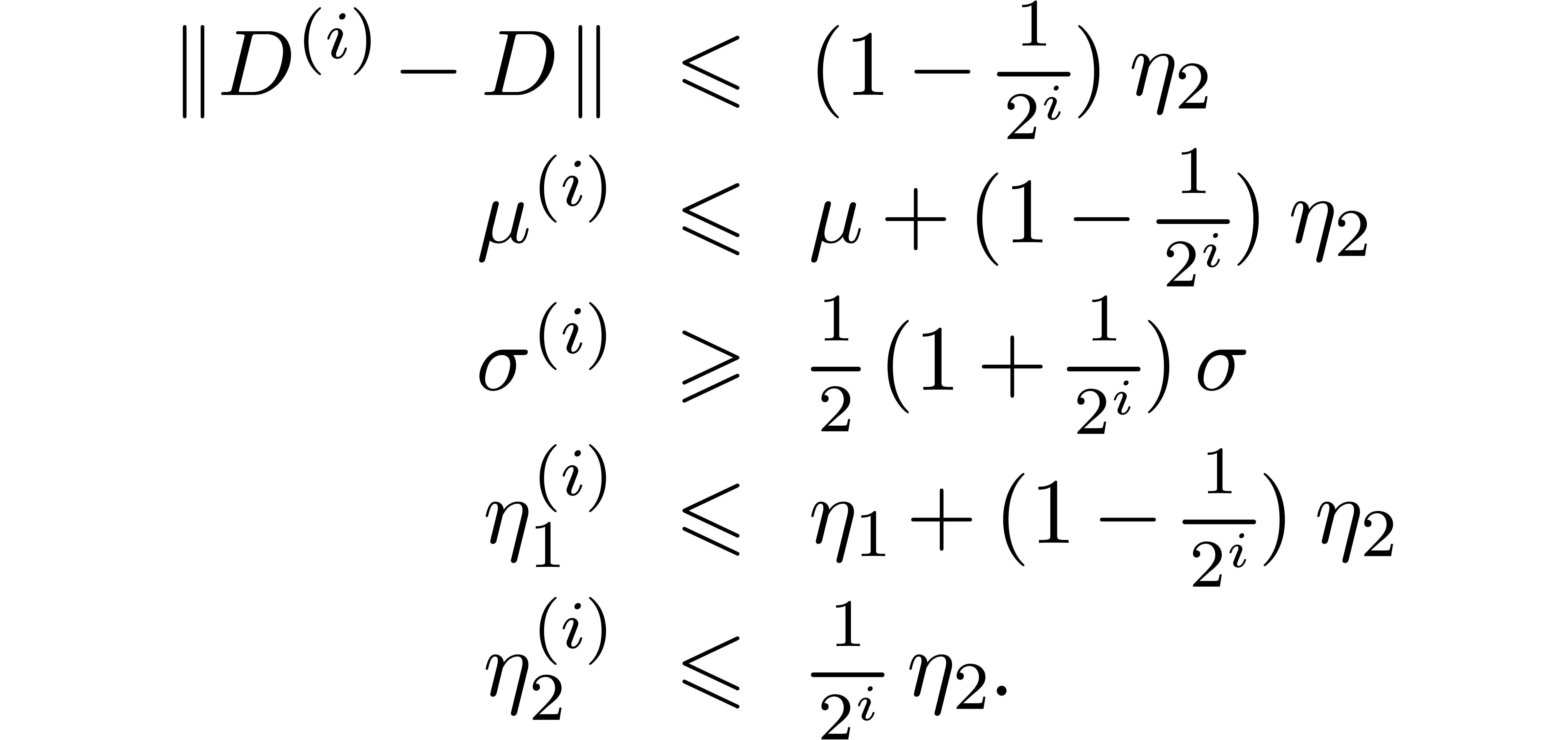
This is clear for 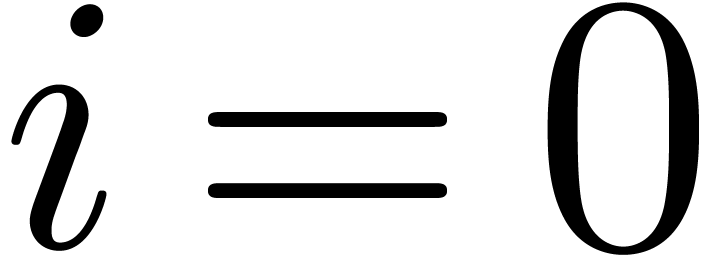 . Assume
that the induction hypothesis holds for a given
. Assume
that the induction hypothesis holds for a given 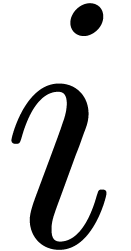 and let
and let
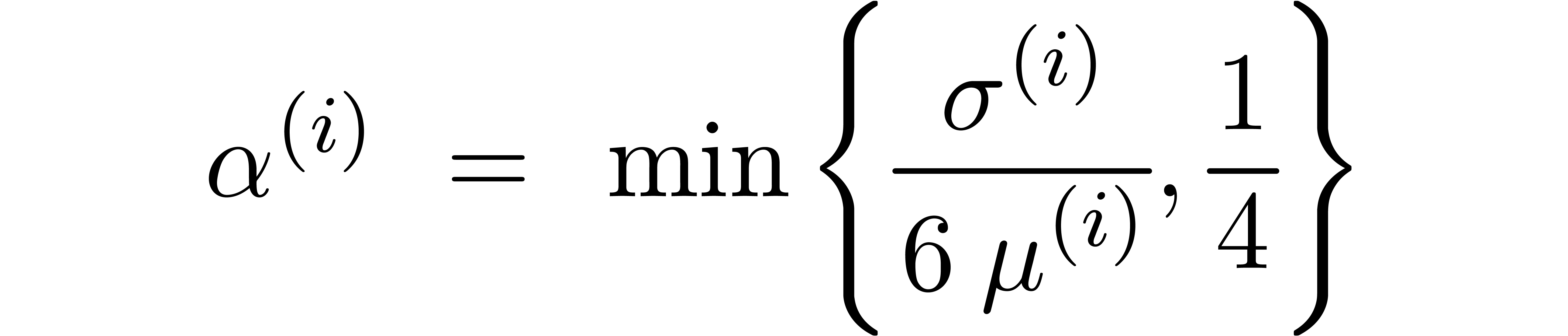
Since 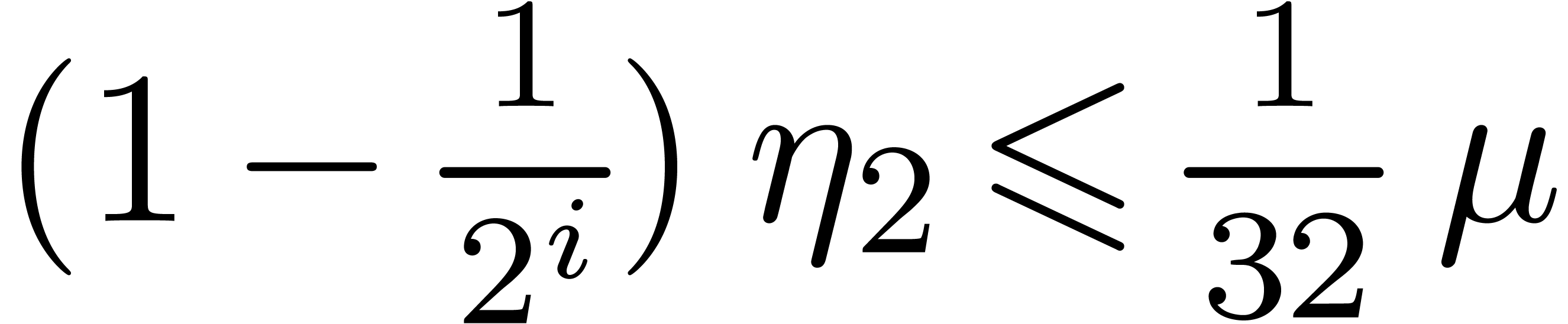 , the induction
hypothesis implies
, the induction
hypothesis implies
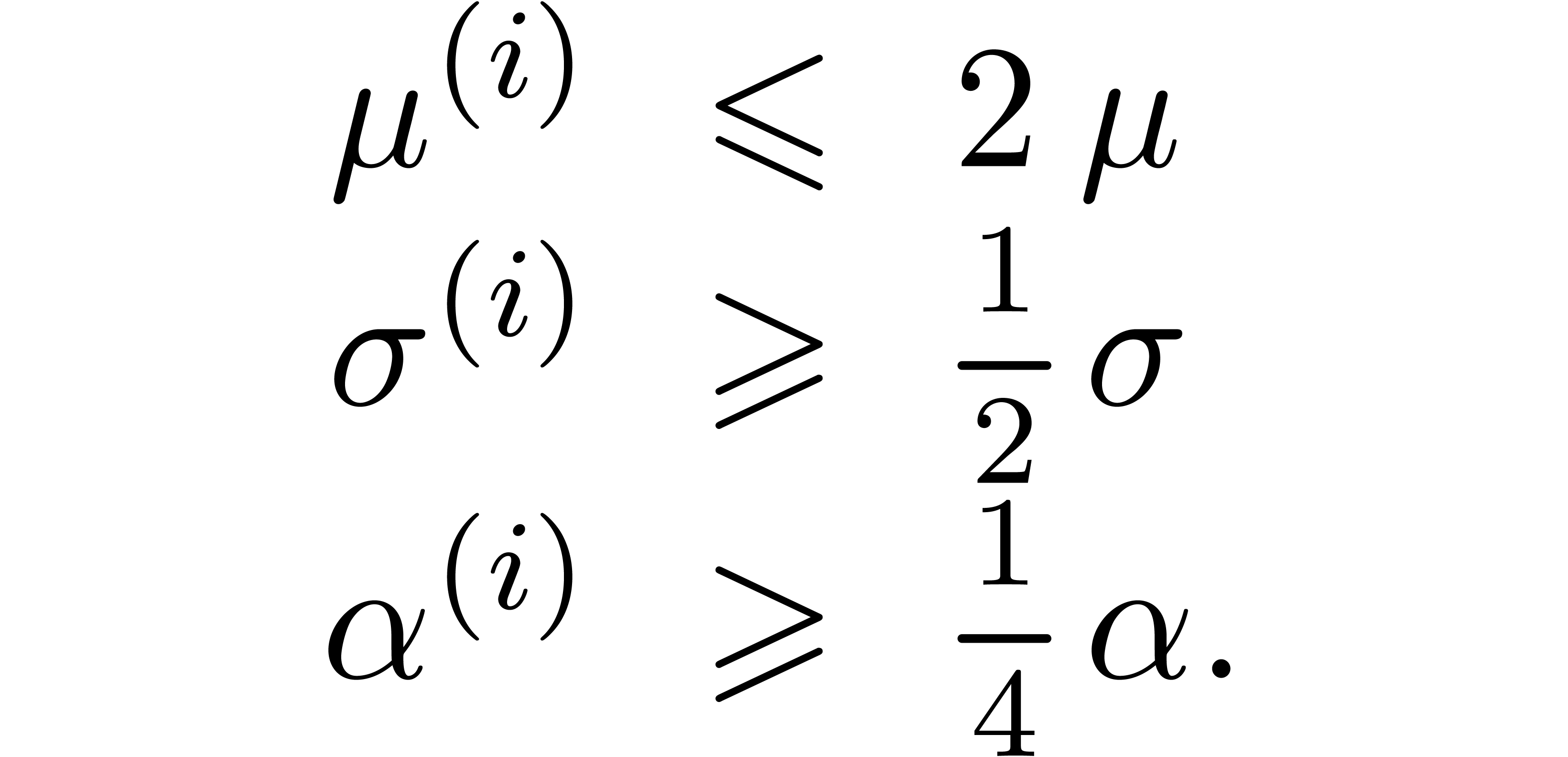
Applying Lemma 2 for  and
and 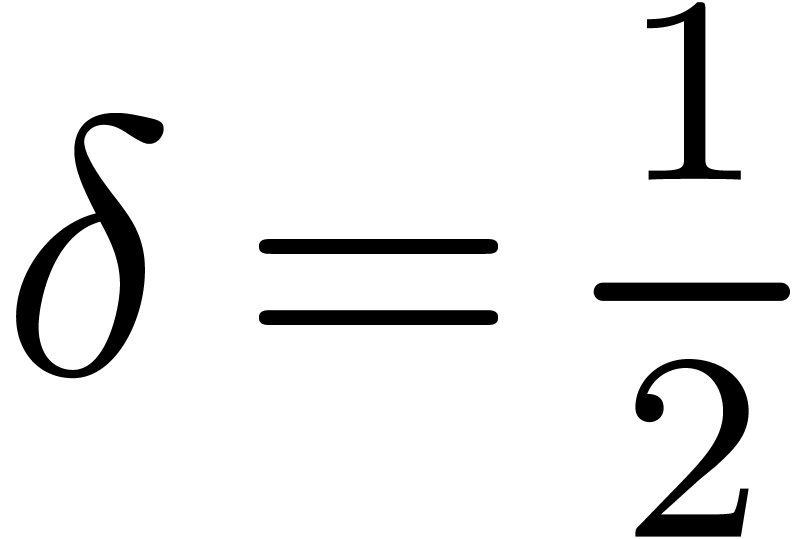 , we thus find
, we thus find
This completes the induction.
Applying the induction to the sequence starting at 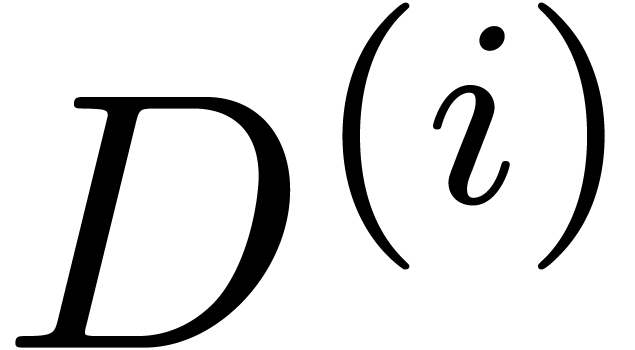 , we have for every
, we have for every 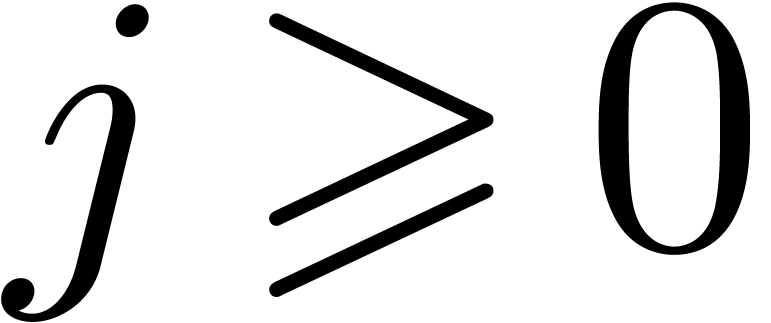 ,
,
This shows that 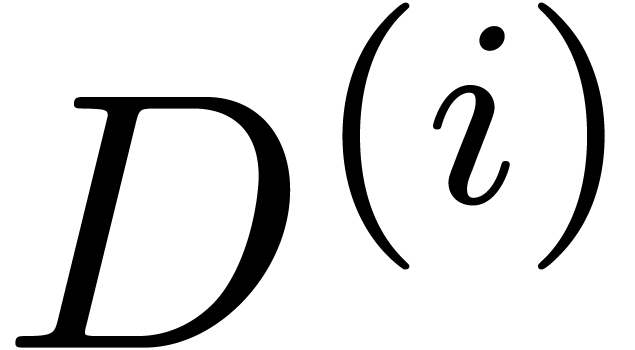 is a Cauchy sequence that tends
to a limit
is a Cauchy sequence that tends
to a limit 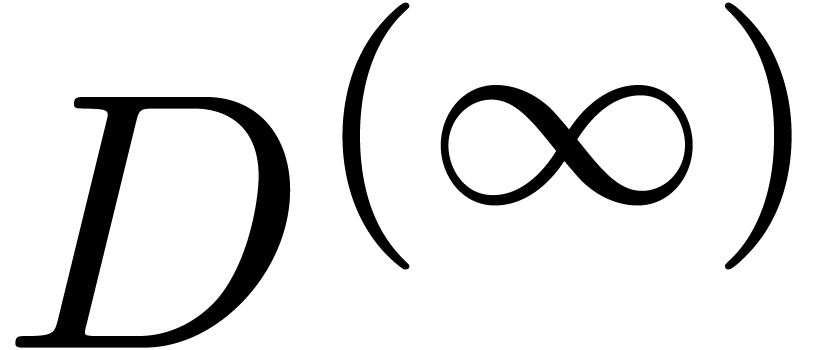 with
with 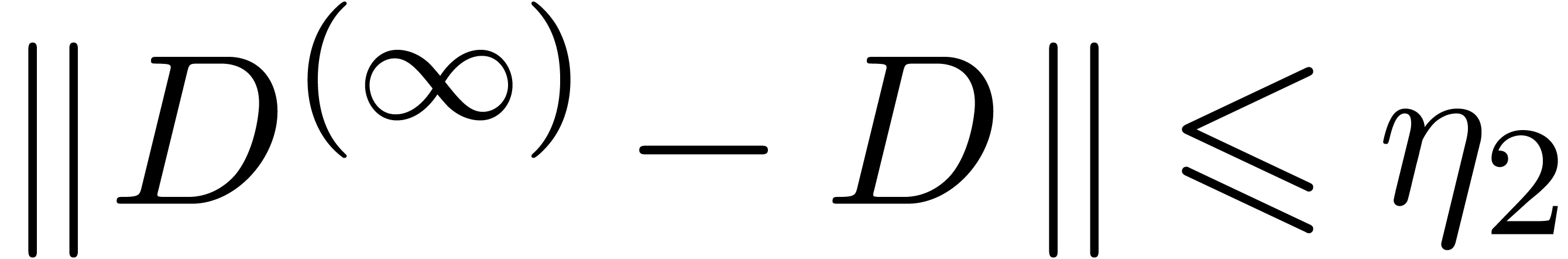 .
From this inequality, we also deduce that
.
From this inequality, we also deduce that 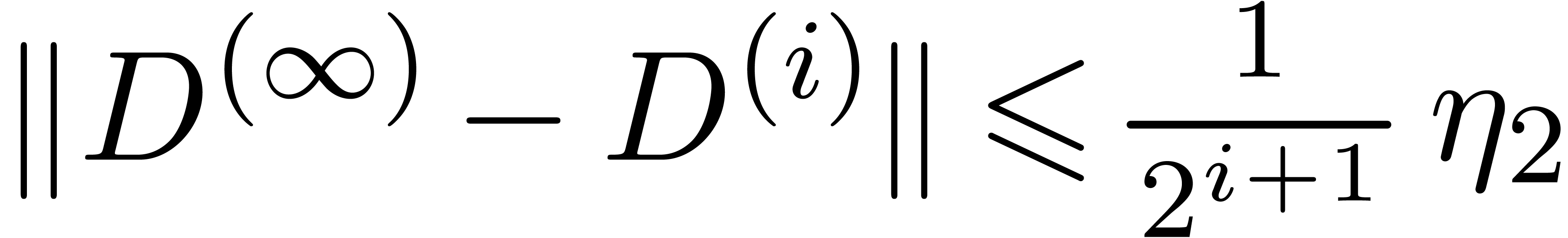 ,
so
,
so 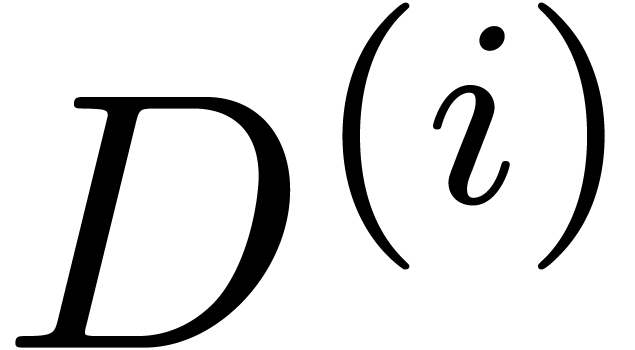 converges geometrically to
converges geometrically to 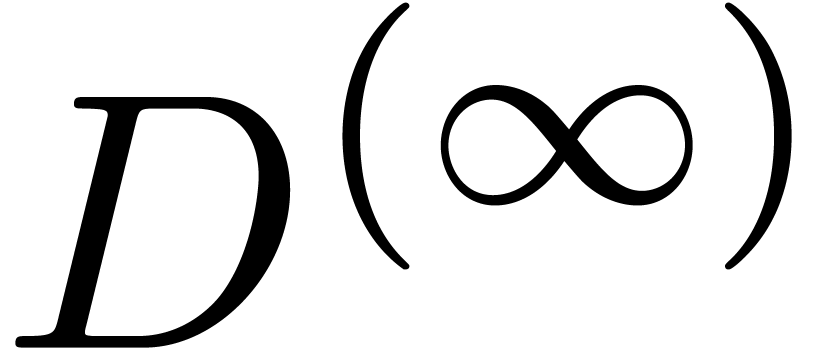 .
.
Moreover, for each  , we have
, we have
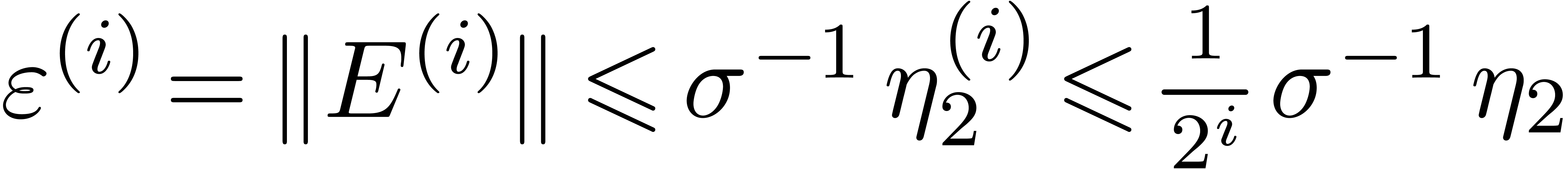 . Hence, the matrix
. Hence, the matrix
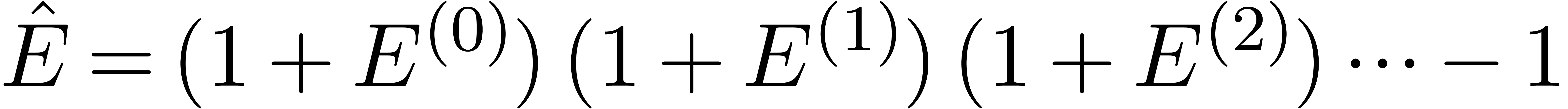
is well defined, and
We deduce that
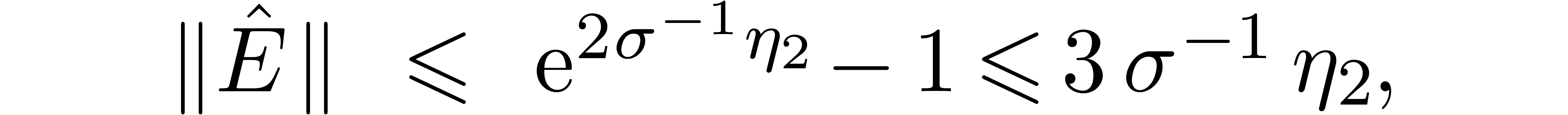
since 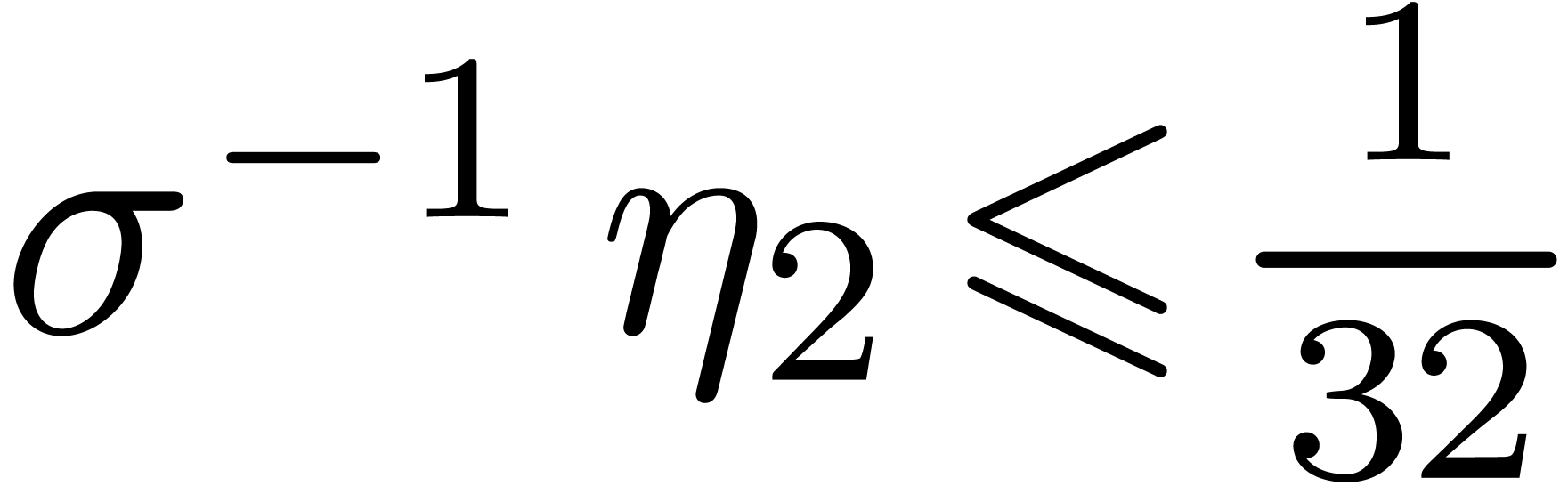 .
.
We claim that 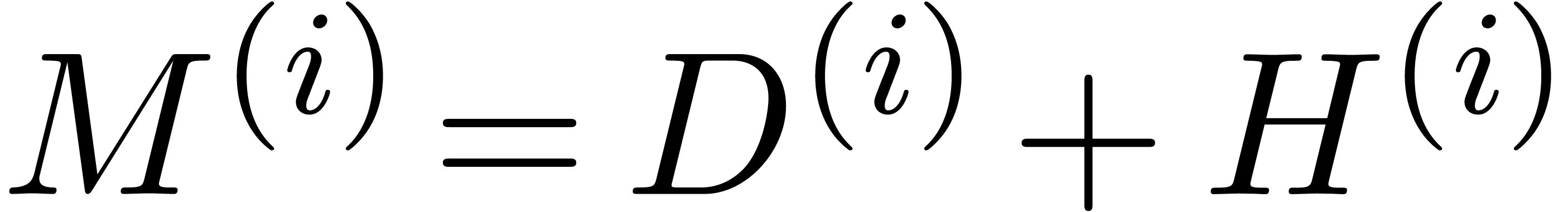 converges geometrically to
converges geometrically to
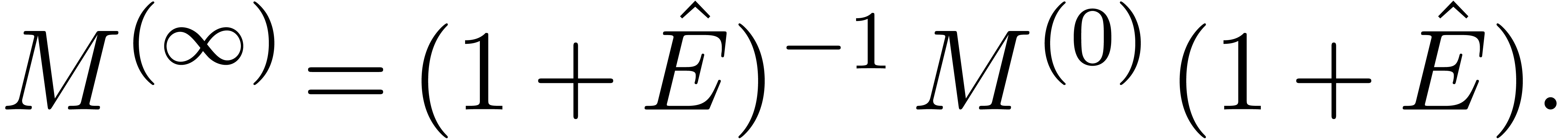
For any matrix  with
with 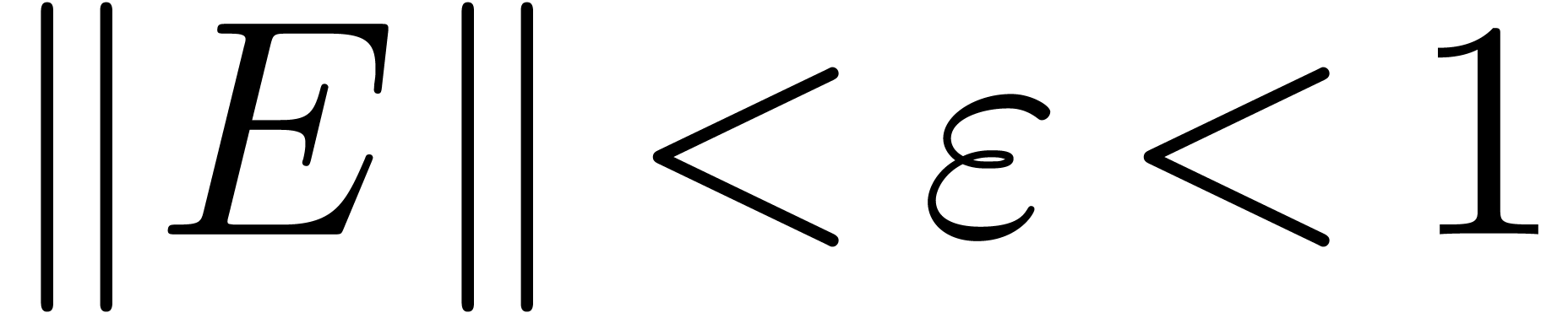 , we have
, we have
Let 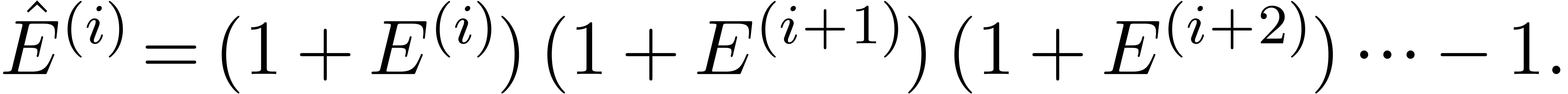 By the same arguments as above, we have
By the same arguments as above, we have
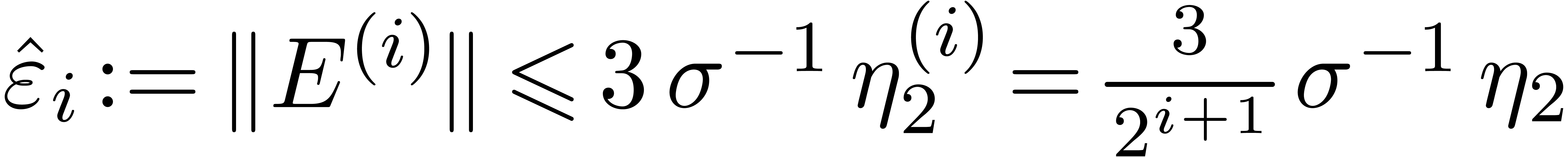 . Since
. Since 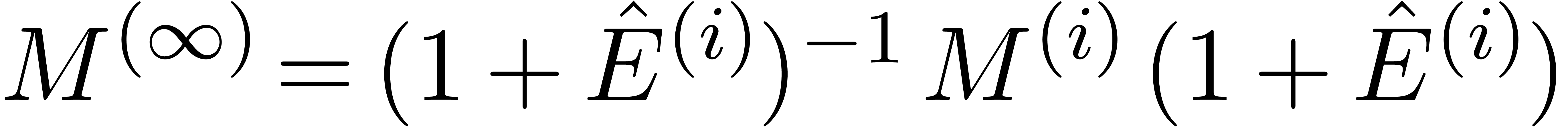 , the inequality (7)
implies
, the inequality (7)
implies
This shows that 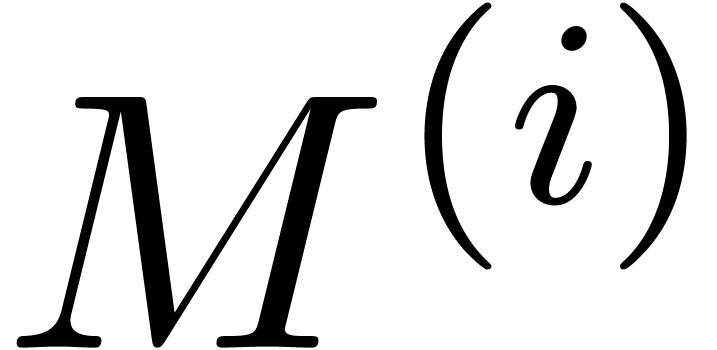 converges geometrically to
converges geometrically to 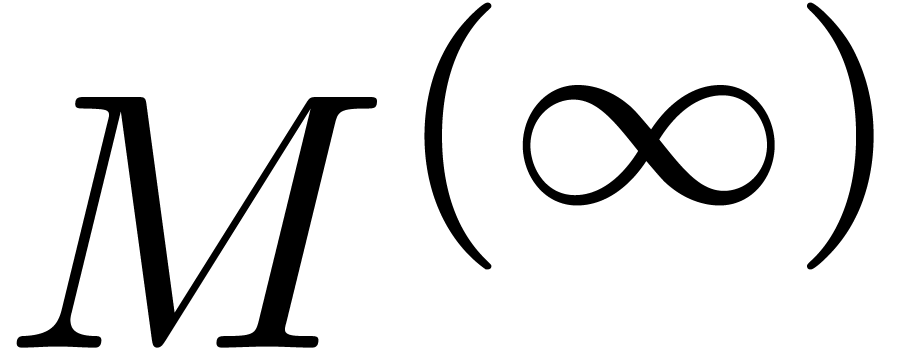 . We deduce that the sequence
. We deduce that the sequence  also converges geometrically to a limit
also converges geometrically to a limit 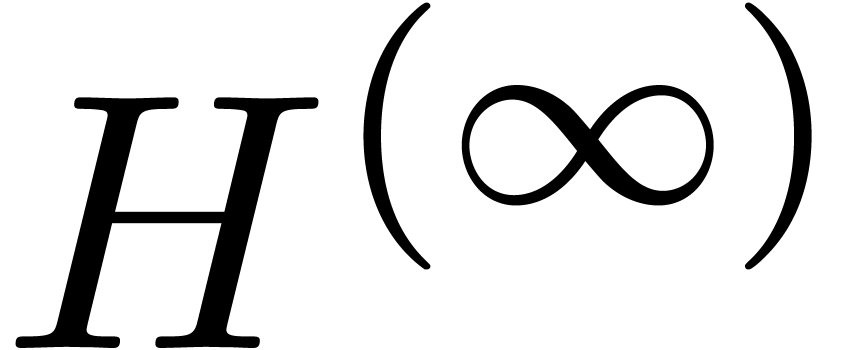 with
with 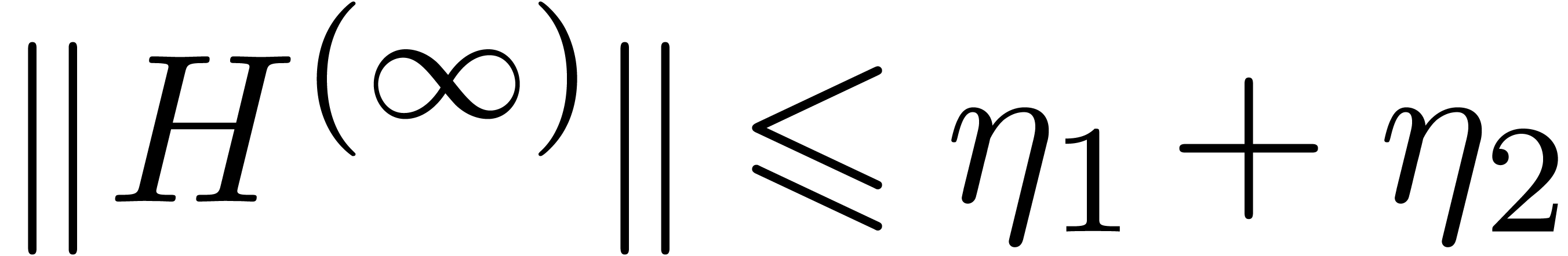 . Since
. Since
 , we finally observe that
, we finally observe that
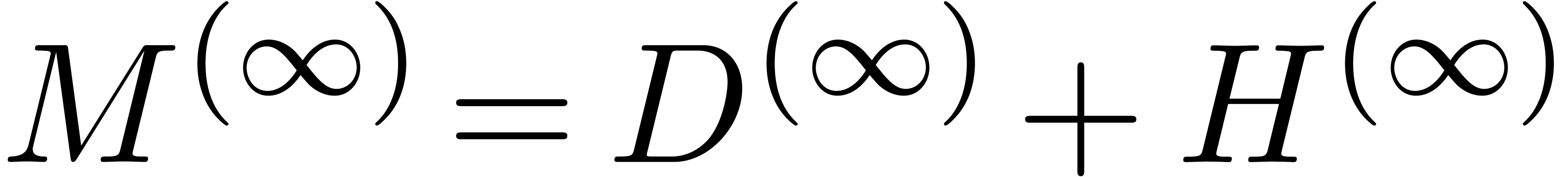 is block diagonal.
is block diagonal.
Proof. The extra assumption implies that 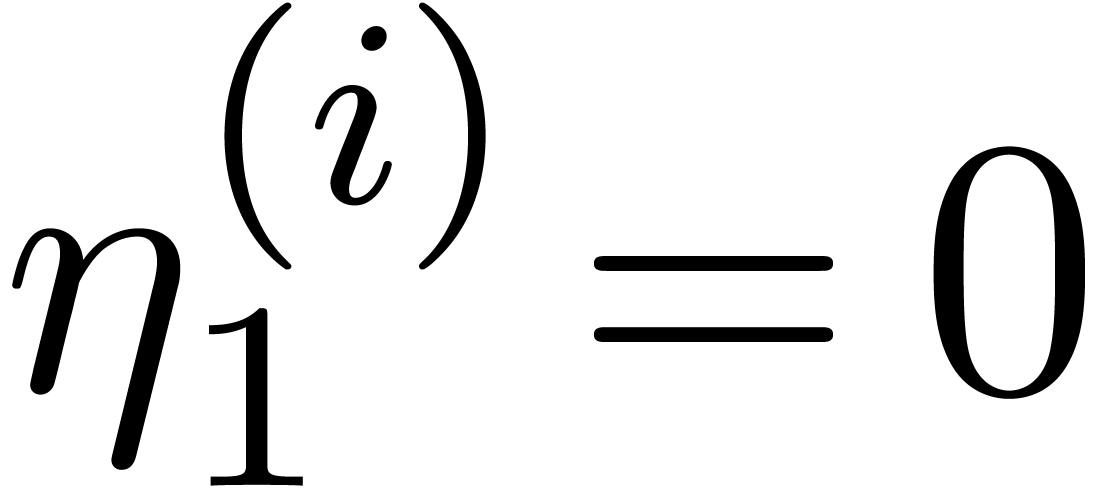 for all
for all 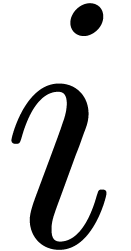 .
Let us show by induction over
.
Let us show by induction over  that we now have
that we now have
This is clear for 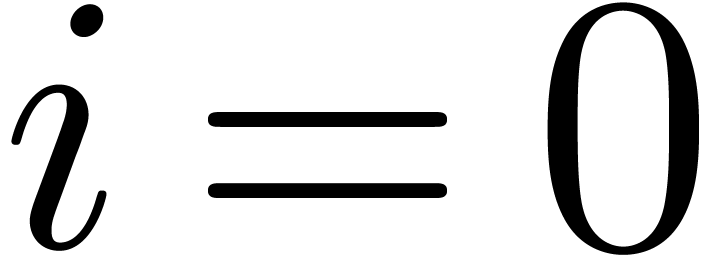 . Assume
that the result holds for a given
. Assume
that the result holds for a given 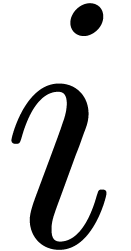 .
Then we may apply Lemma 2 to
.
Then we may apply Lemma 2 to 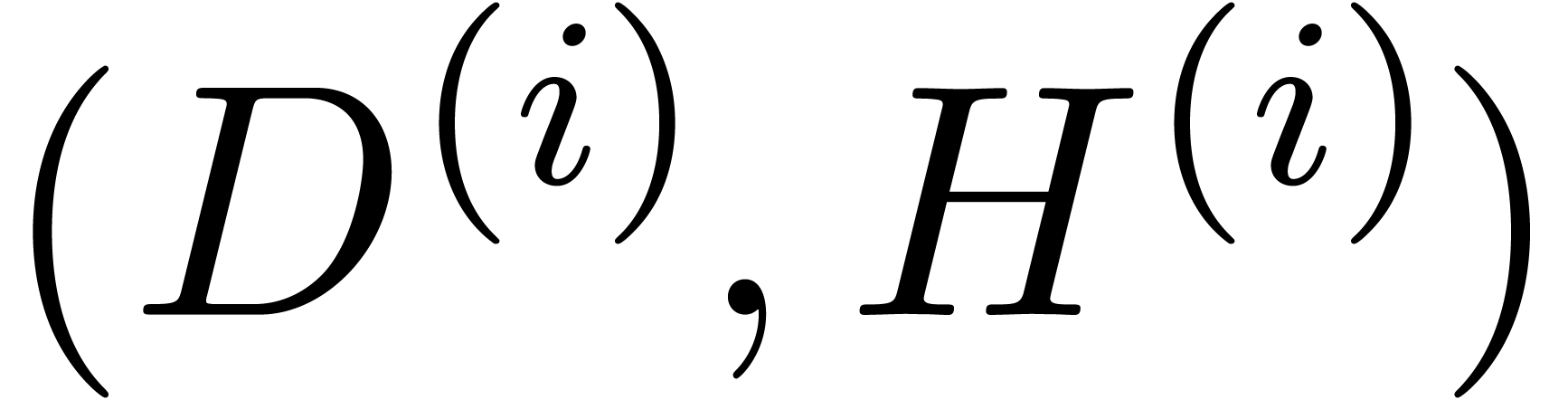 for
for
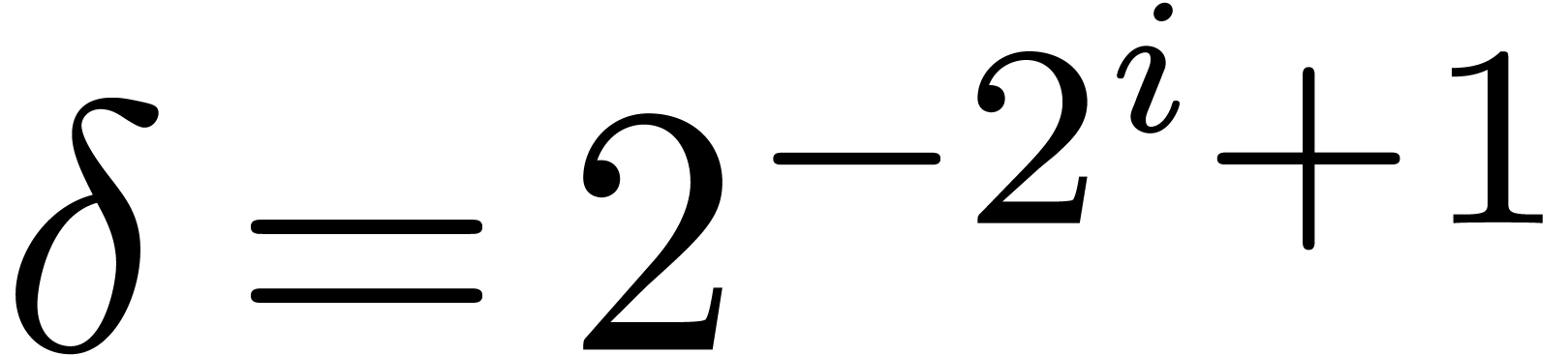 , and obtain
, and obtain
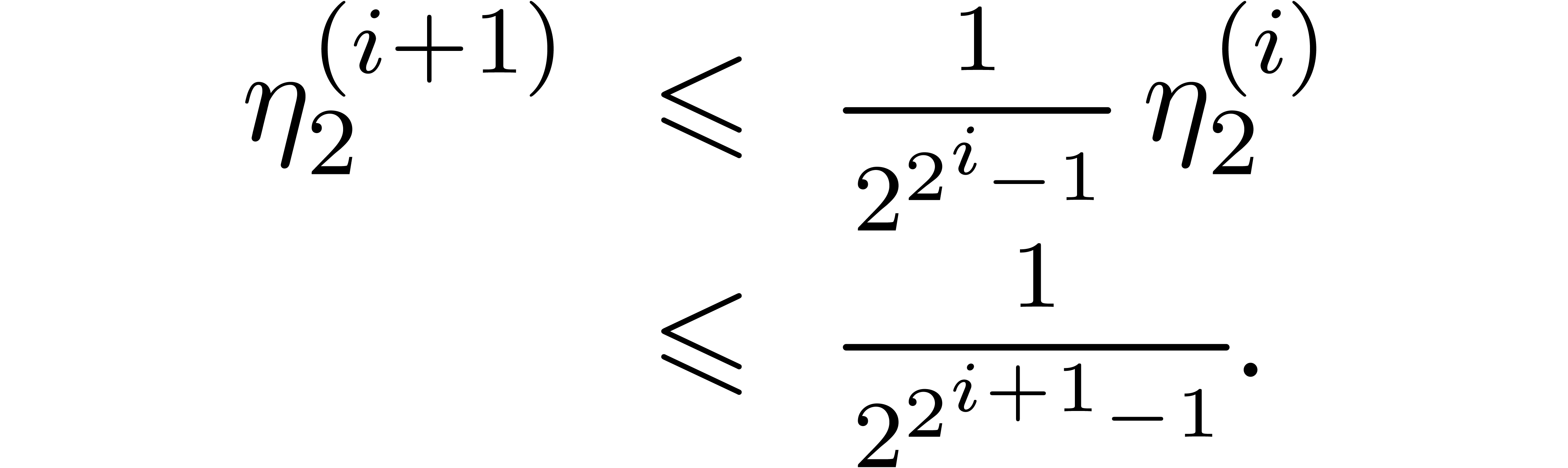
Since 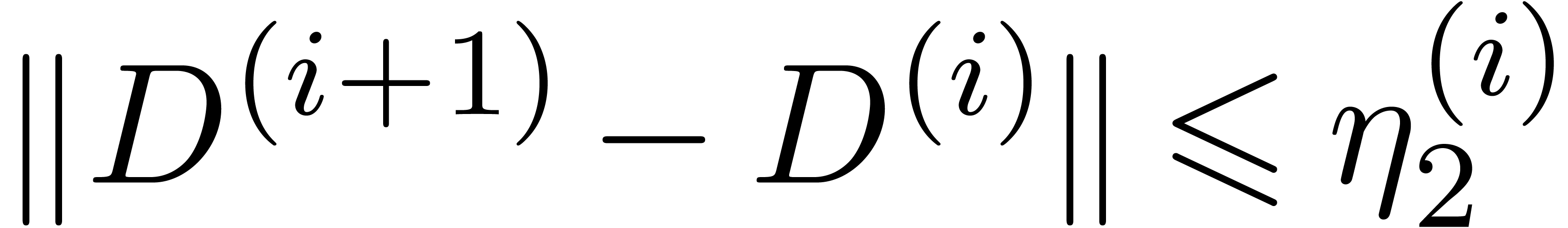 , this establishes the
quadratic convergence.
, this establishes the
quadratic convergence.
4.Algorithms
4.1.Clustering
Let 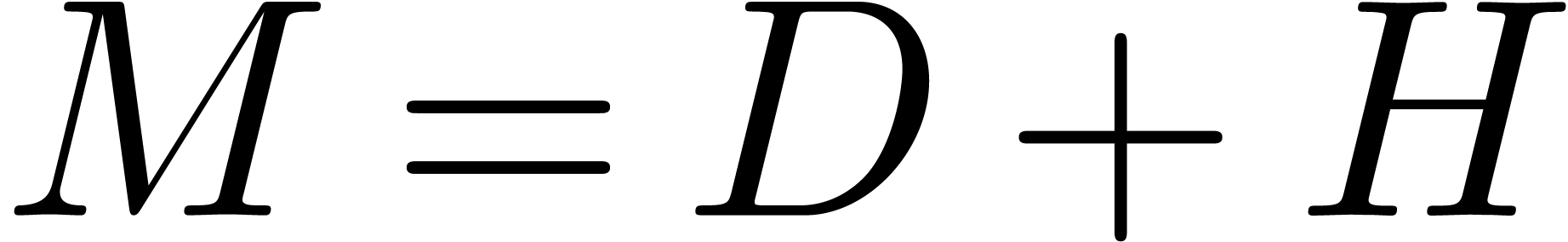 be the perturbation of a diagonal matrix (5) as in the previous section. In order to apply theorem 3, we first have to find a suitable clustering (4).
For a given threshold separation
be the perturbation of a diagonal matrix (5) as in the previous section. In order to apply theorem 3, we first have to find a suitable clustering (4).
For a given threshold separation  ,
we will simply take the finest clustering (i.e. for which
,
we will simply take the finest clustering (i.e. for which
 is maximal) with the property that
is maximal) with the property that 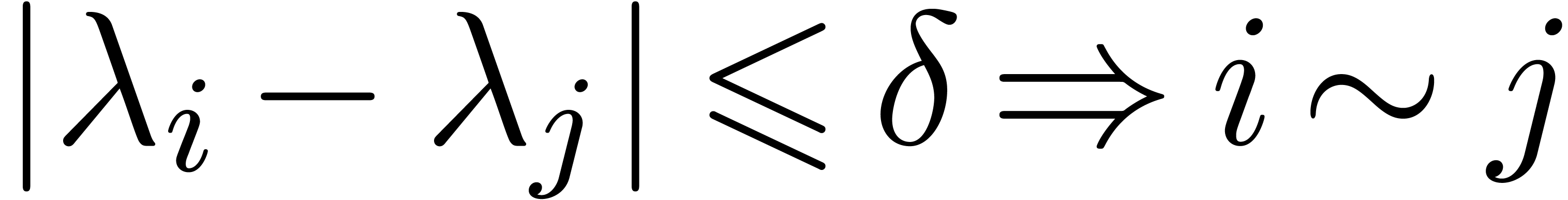 . This clustering can be computed using the
algorithm Cluster below.
. This clustering can be computed using the
algorithm Cluster below.
Algorithm Cluster
| Input: |
eigenvalues 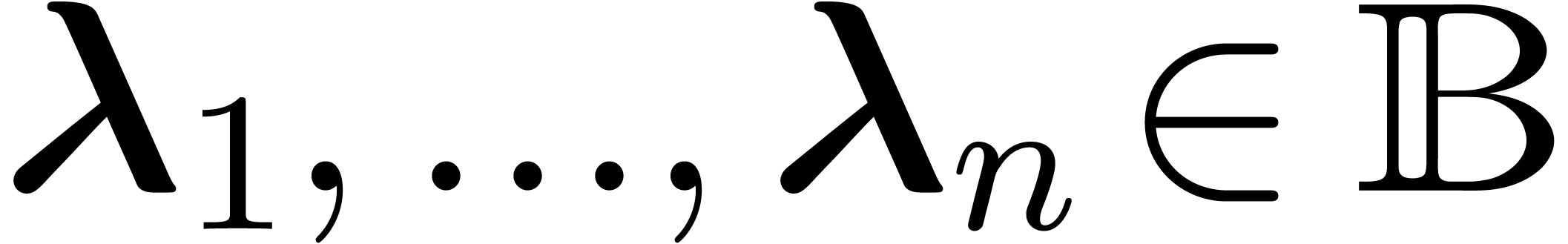 and and 
|
| Output: |
the finest clustering (4) with 
|
|
|
4.2.Certification in the case of perturbed
diagonal matrices
In order to apply theorem 3, it now remains to find a
suitable threshold 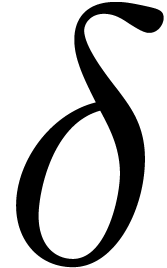 for which the conditions of
the theorem hold. Starting with
for which the conditions of
the theorem hold. Starting with 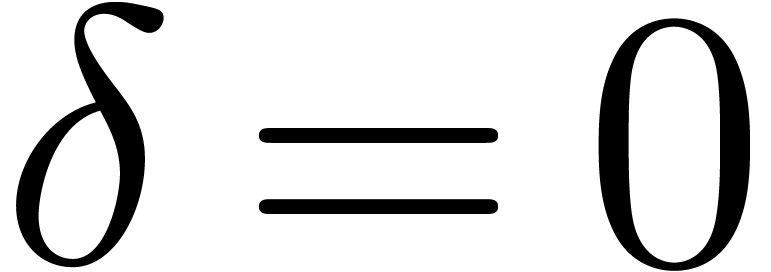 ,
we will simply increase
,
we will simply increase 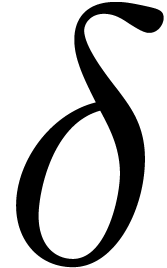 to
to 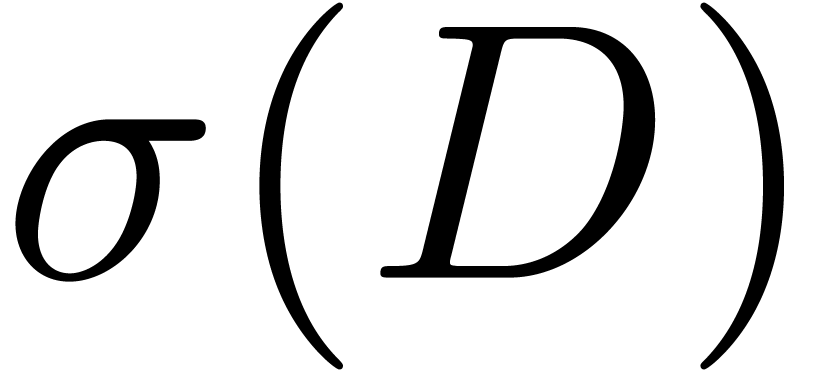 whenever the conditions are not satisfied. This will force the number
whenever the conditions are not satisfied. This will force the number
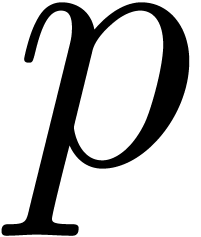 of clusters to decrease by at least one at every
iteration, whence the algorithm terminates. Notice that the workload of
one iteration is
of clusters to decrease by at least one at every
iteration, whence the algorithm terminates. Notice that the workload of
one iteration is 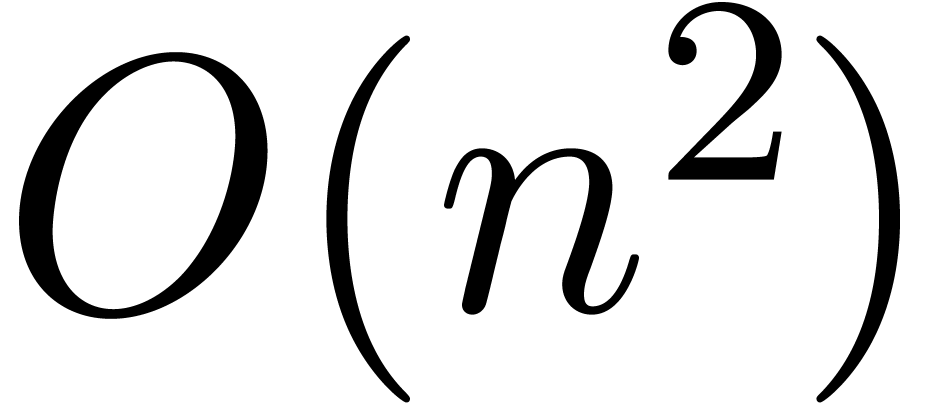 , so the
total running time remains bounded by
, so the
total running time remains bounded by 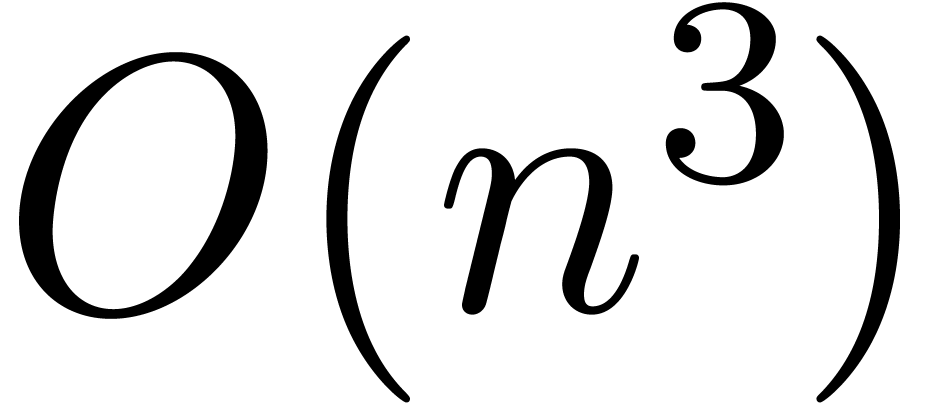 .
.
Algorithm DiagonalCertify
|
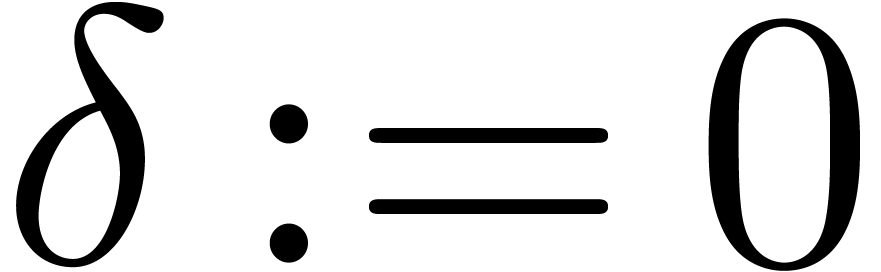
Repeat
Let 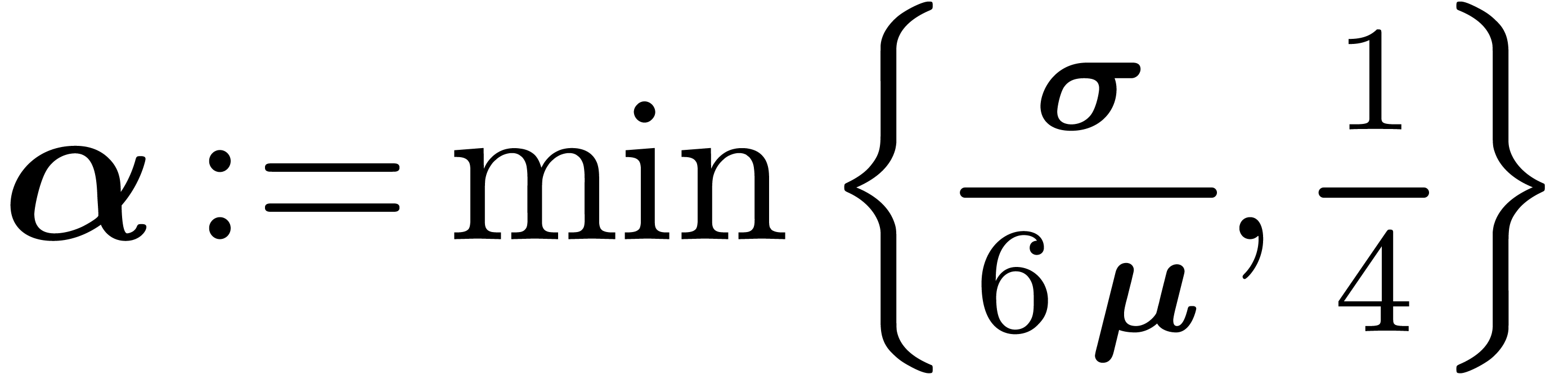
Set 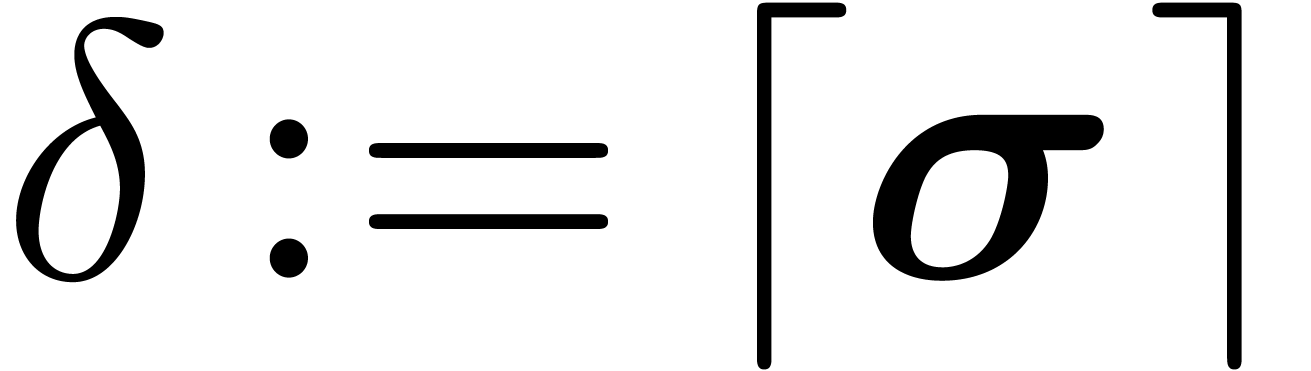
|
4.3.Certification of approximate eigenvectors
and eigenvalues
Let us now return to the original problem of certifying a numerical
solution to an eigenproblem. We will denote by 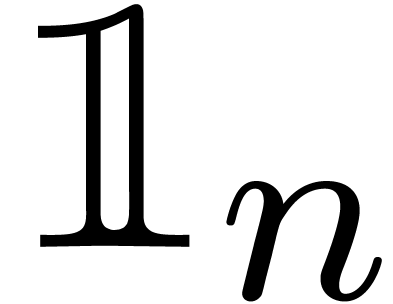 the
the  matrix of which all entries are one.
matrix of which all entries are one.
Algorithm EigenvectorCertify
|
Compute 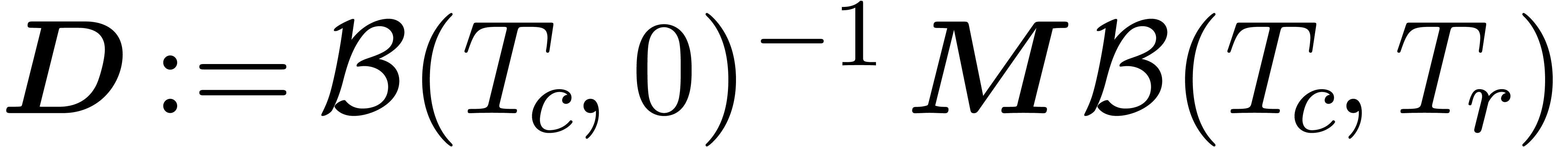
Let 
Let 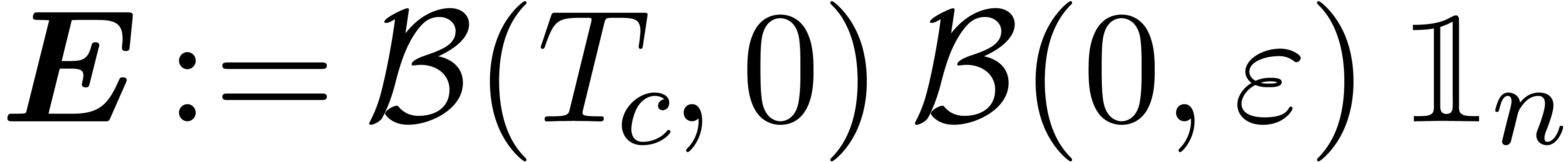
Let 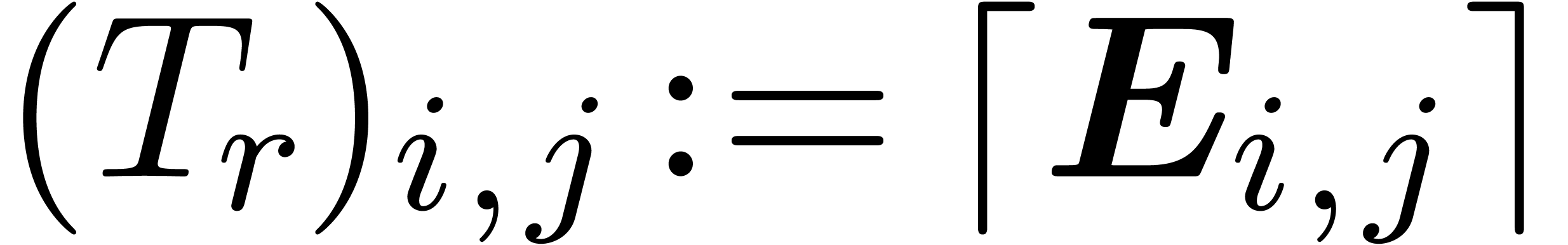 for all for all 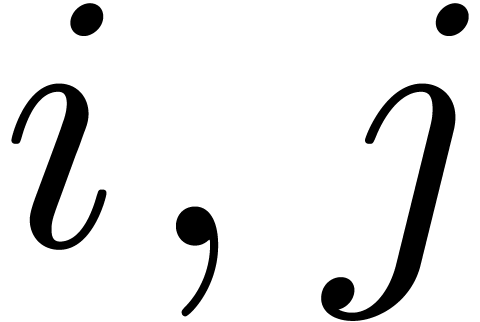
Return 
|
Obviously, any eigenvalue 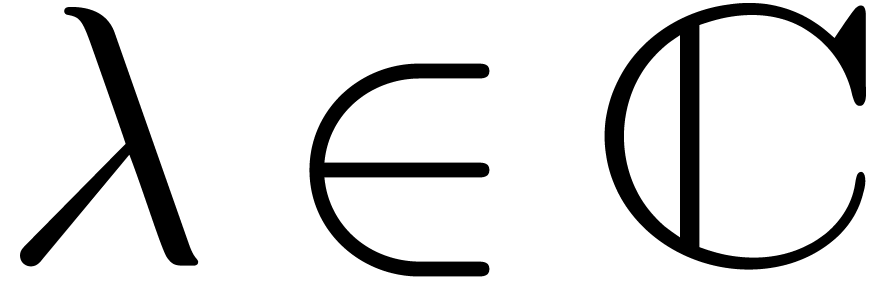 of a matrix
of a matrix  satisfies
satisfies 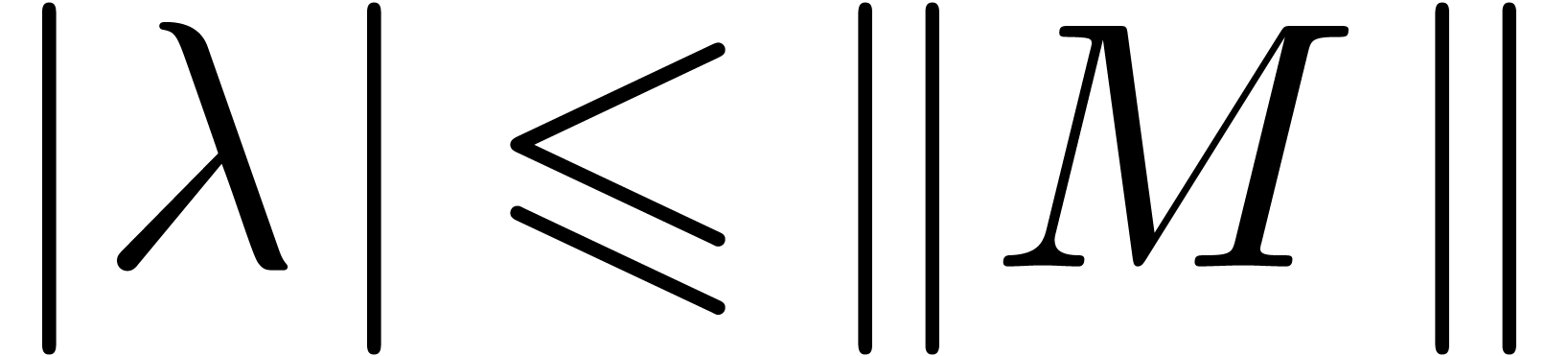 . We
may thus use the following modification of
EigenvectorCertify in order to compute enclosures for the
eigenvalues of
. We
may thus use the following modification of
EigenvectorCertify in order to compute enclosures for the
eigenvalues of  .
.
Algorithm EigenvalueCertify
| Input: |
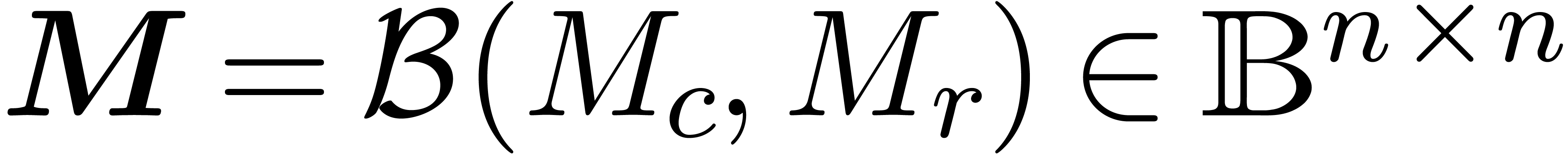 and and 
such that  is approximately
diagonal is approximately
diagonal
|
| Output: |
ball enclosures 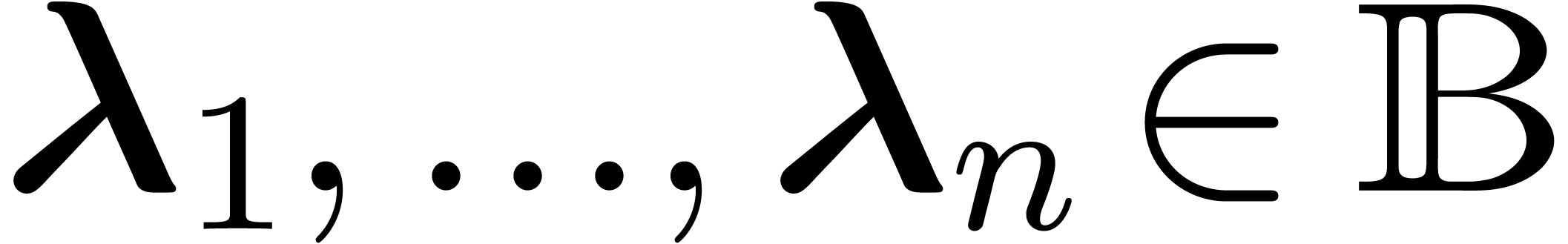 for the
eigenvalues of for the
eigenvalues of  , ,
with the appropriate multiplicities in cases of
overlapping
|
|
Compute 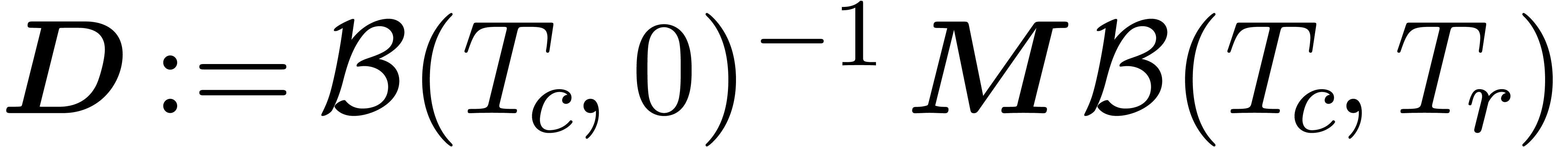
Let 
Let 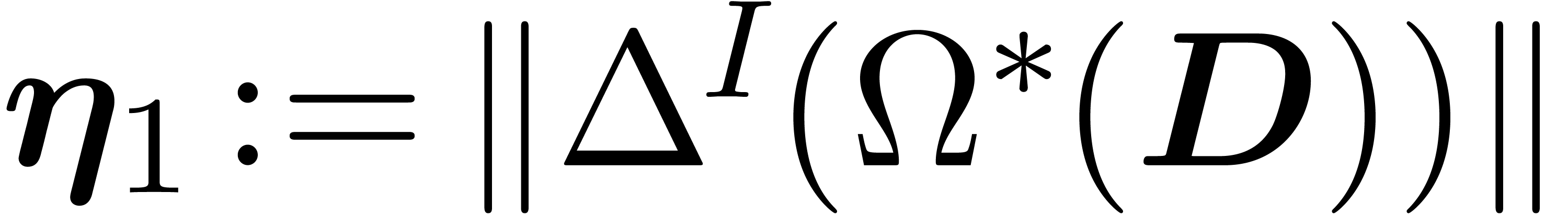 and and 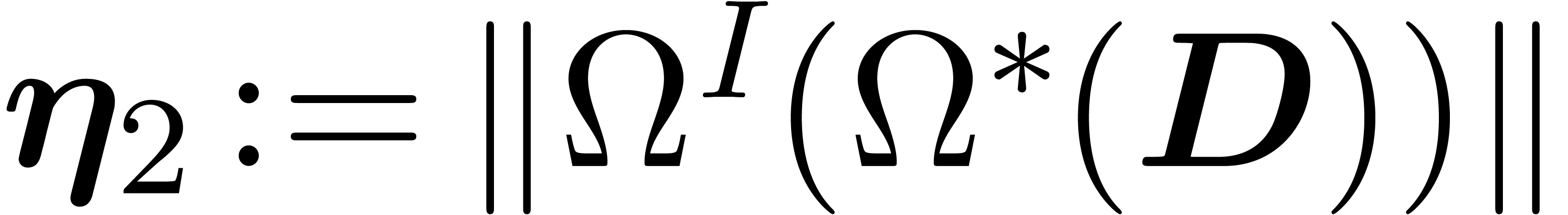
For each 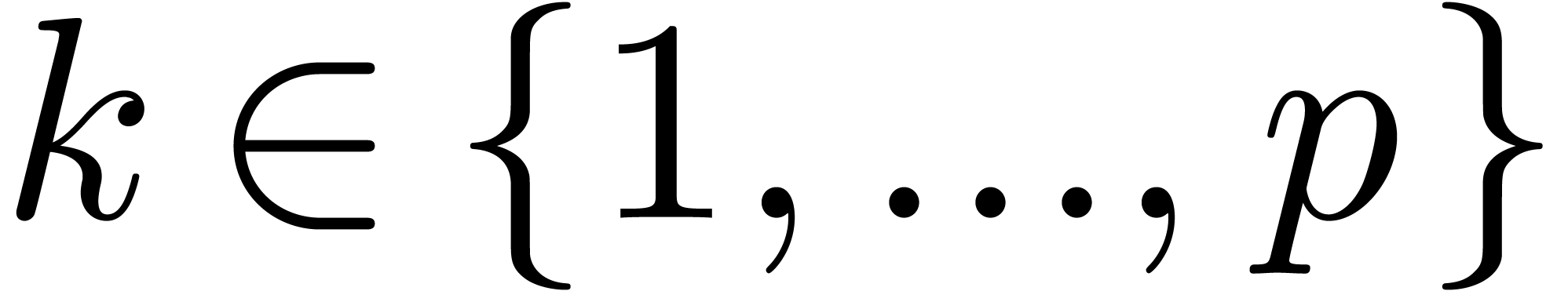 do do
Let  for all for all 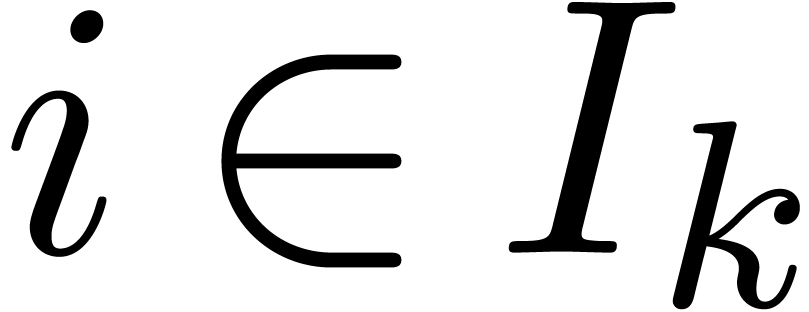
Return 
|
5.Possible extensions
Let  be a matrix with a (numerically) multiple
eigenvalue
be a matrix with a (numerically) multiple
eigenvalue 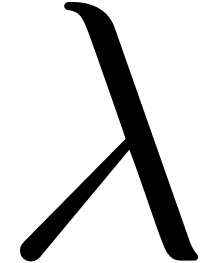 . We have already
stressed that it is generally impossible to provide non trivial
certifications for the corresponding eigenvectors. Nevertheless, two
observations should be made:
. We have already
stressed that it is generally impossible to provide non trivial
certifications for the corresponding eigenvectors. Nevertheless, two
observations should be made:
More precisely, in these two cases, we may search for ball enclosures
for orthonormal bases of the vector spaces 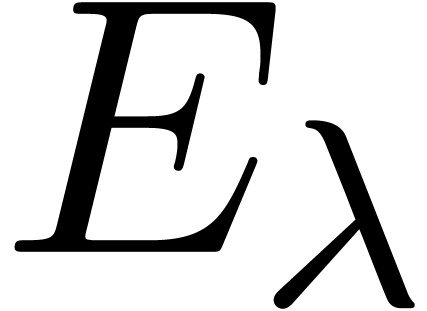 resp.
resp. 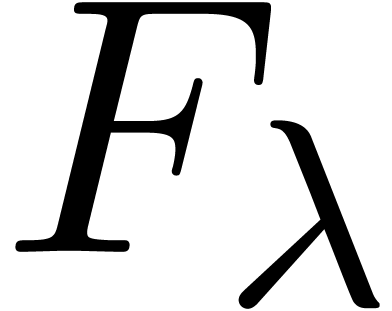 , which do
not contain the zero vector.
, which do
not contain the zero vector.
When considering the numeric solution (1) of the
eigenproblem for 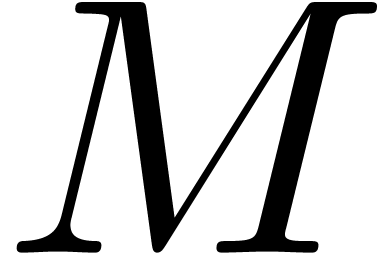 , the column
vectors which generate
, the column
vectors which generate 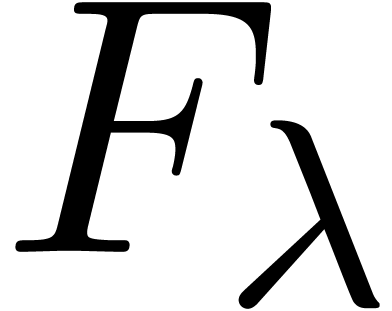 are usually far from
being orthogonal. Orthonormalization can only be done at the expense of
making
are usually far from
being orthogonal. Orthonormalization can only be done at the expense of
making 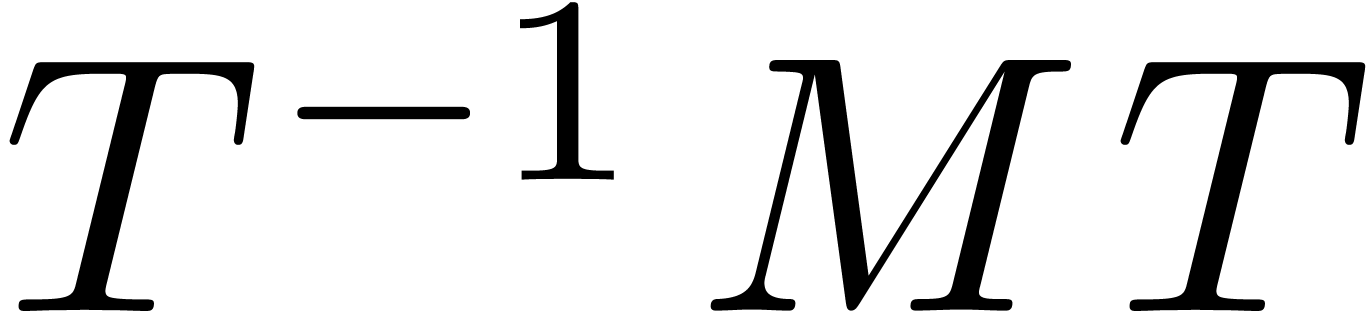 only upper triangular. Moreover, the
orthogonalization implies a big loss of accuracy, which requires the
application of a correction method for restoring the accuracy. It seems
that the fundamental Newton iteration from Section 3.2 can
actually be used as a correction method. For instance, for small
perturbations of the matrix
only upper triangular. Moreover, the
orthogonalization implies a big loss of accuracy, which requires the
application of a correction method for restoring the accuracy. It seems
that the fundamental Newton iteration from Section 3.2 can
actually be used as a correction method. For instance, for small
perturbations of the matrix
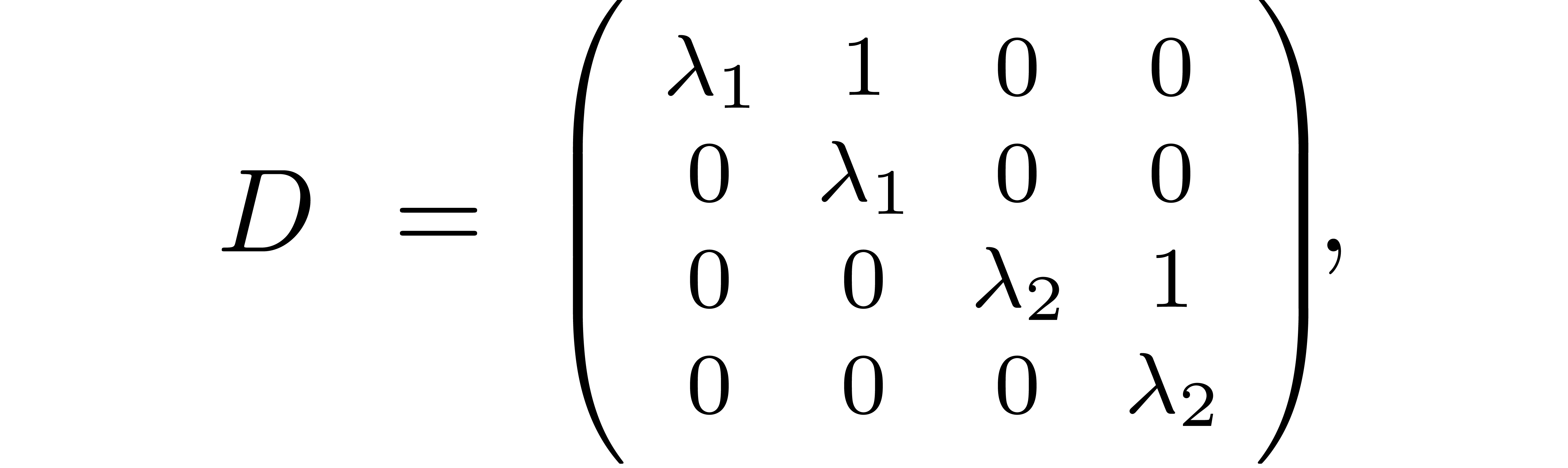
it can be shown that the fundamental iteration still converges. However,
for more general block diagonal matrices with triangular blocks, the
details are quite technical and yet to be worked out.
Yet another direction for future investigations concerns the quadratic
convergence. As a refinement of Lemma 1, we might replace
 by a block diagonal matrix with entries
by a block diagonal matrix with entries  . Instead of taking
. Instead of taking 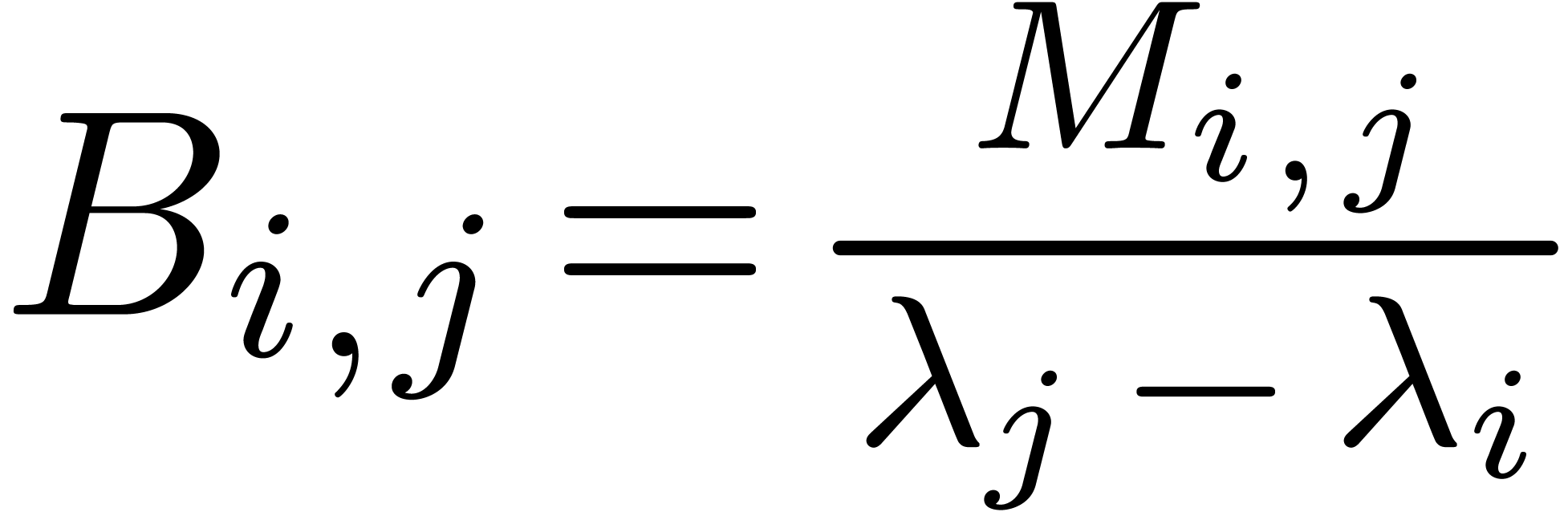 , we then have to solve equations of the form
, we then have to solve equations of the form
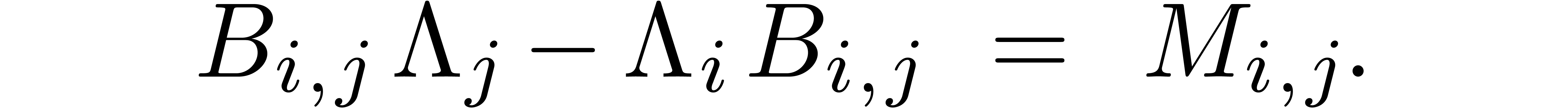
If the 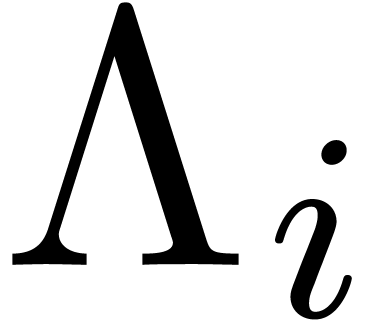 are sufficiently close to
are sufficiently close to 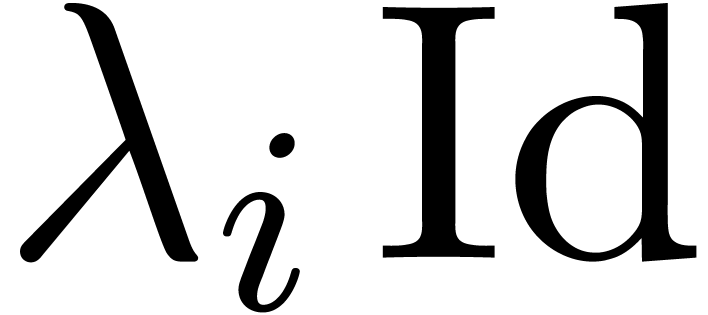 , it might then be possible to adapt the
fundamental iteration accordingly so as to achieve quadratic convergence
for the strongly off diagonal part.
, it might then be possible to adapt the
fundamental iteration accordingly so as to achieve quadratic convergence
for the strongly off diagonal part.
Bibliography
-
[1]
-
G. Alefeld and J. Herzberger. Introduction to
interval analysis. Academic Press, New York, 1983.
-
[2]
-
D. Armentano, C. Beltrán, P. Bürgisser,
F. Cucker, and M. Shub. A stable, polynomial-time algorithm for
the eigenpair problem. Technical report, ArXiv, 2014. http://arxiv.org/abs/1505.03290.
-
[3]
-
L. Blum, F. Cucker, M. Shub, and S. Smale.
Complexity and real computation. Springer-Verlag, 1998.
-
[4]
-
J. J. Dongarra, C. B. Moler, and J. H. Wilkinson.
Improving the accuracy of computed eigenvalues and eigenvectors.
SIAM Journal on Numerical Analysis, 20(1):23–45,
1983.
-
[5]
-
F. Le Gall. Powers of tensors and fast matrix
multiplication. In Proc. ISSAC 2014, pages 296–303,
Kobe, Japan, July 23–25 2014.
-
[6]
-
G. H. Golub and F. Van Loan. Matrix
Computations. JHU Press, 1996.
-
[7]
-
S. Graillat and Ph. Trébuchet. A new algorithm
for computing certified numerical approximations of the roots of
a zero-dimensional system. In Proc. ISSAC '09, pages
167–174. ACM Press, 2009.
-
[8]
-
D. Harvey. Faster truncated integer multiplication.
https://arxiv.org/abs/1703.00640, 2017.
-
[9]
-
D. Harvey and J. van der Hoeven. On the complexity of
integer matrix multiplication. Technical report, HAL, 2014. http://hal.archives-ouvertes.fr/hal-01071191,
accepted for publication in JSC.
-
[10]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Even
faster integer multiplication. Journal of Complexity,
36:1–30, 2016.
-
[11]
-
J. van der Hoeven. Ball arithmetic. Technical report,
HAL, 2009. http://hal.archives-ouvertes.fr/hal-00432152.
-
[12]
-
J. van der Hoeven, G. Lecerf, B. Mourrain, et al.
Mathemagix, 2002. http://www.mathemagix.org.
-
[13]
-
L. Jaulin, M. Kieffer, O. Didrit, and E. Walter.
Applied interval analysis. Springer, London, 2001.
-
[14]
-
F. Johansson. Arb: A c library for ball arithmetic.
ACM Commun. Comput. Algebra, 47(3/4):166–169, 2014.
-
[15]
-
U. W. Kulisch. Computer Arithmetic and Validity.
Theory, Implementation, and Applications. Number 33 in
Studies in Mathematics. de Gruyter, 2008.
-
[16]
-
S. Miyajima. Fast enclosure for all eigenvalues in
generalized eigenvalue problems. Journal of Computational and
Applied Mathematics, 233(11):2994–3004, 2010.
-
[17]
-
R. E. Moore. Interval Analysis. Prentice Hall,
Englewood Cliffs, N.J., 1966.
-
[18]
-
A. Neumaier. Interval methods for systems of
equations. Cambridge university press, Cambridge, 1990.
-
[19]
-
S. Rump and S. Graillat. Verified error bounds for
multiple roots of systems of nonlinear equations. Num.
Algs., 54:359–377, 2010.
-
[20]
-
S. M. Rump. Guaranteed inclusions for the complex
generalized eigenproblem. Computing, 42(2):225–238,
1989.
-
[21]
-
S. M. Rump. INTLAB - INTerval LABoratory. In Tibor
Csendes, editor, Developments in Reliable Computing,
pages 77–104. Kluwer Academic Publishers, Dordrecht, 1999.
http://www.ti3.tu-harburg.de/rump/.
-
[22]
-
S. M. Rump. Computational error bounds for multiple
or nearly multiple eigenvalues. Linear algebra and its
applications, 324(1-3):209–226, 2001.
-
[23]
-
T. Yamamoto. Error bounds for computed eigenvalues
and eigenvectors. Numerische Mathematik,
34(2):189–199, 1980.
 be the set of floating point numbers for a
fixed precision and a fixed exponent range. We will denote
be the set of floating point numbers for a
fixed precision and a fixed exponent range. We will denote 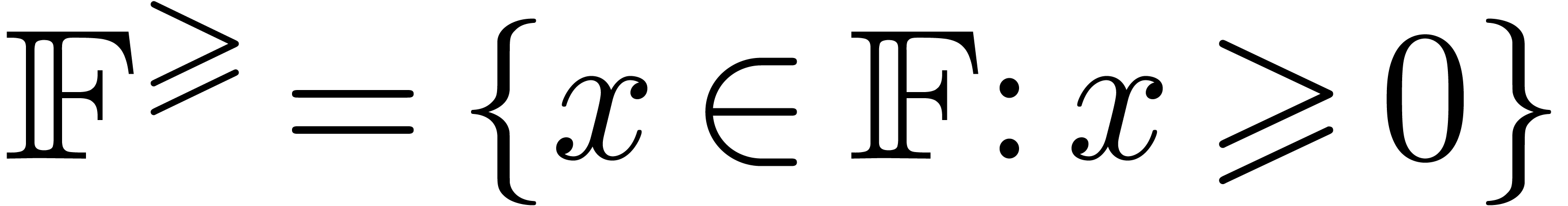 . Consider an
. Consider an  matrix
matrix
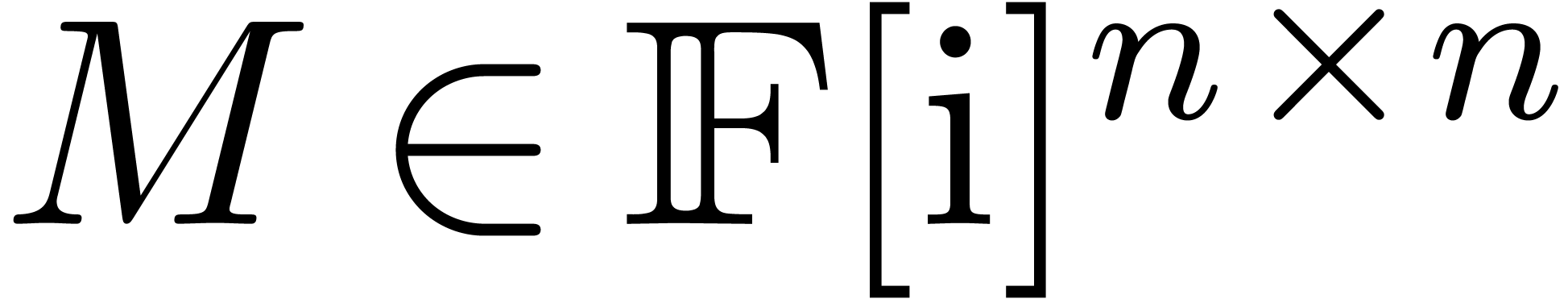 with complex floating entries. The numeric
eigenproblem associated to
with complex floating entries. The numeric
eigenproblem associated to 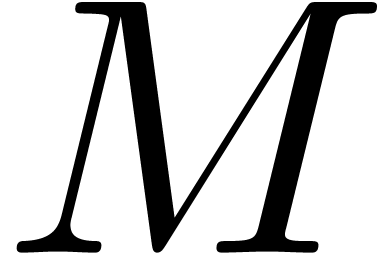 is to
compute a transformation matrix
is to
compute a transformation matrix 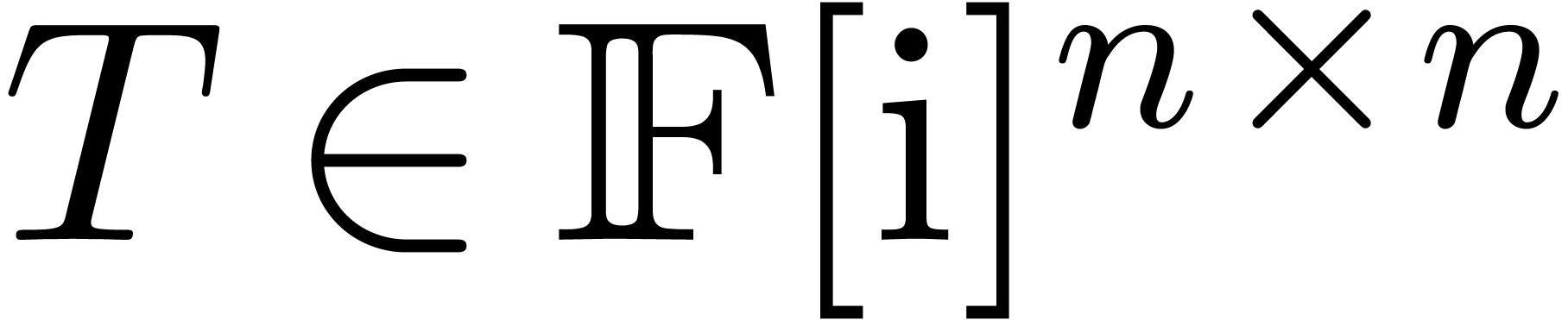 and a diagonal
matrix
and a diagonal
matrix 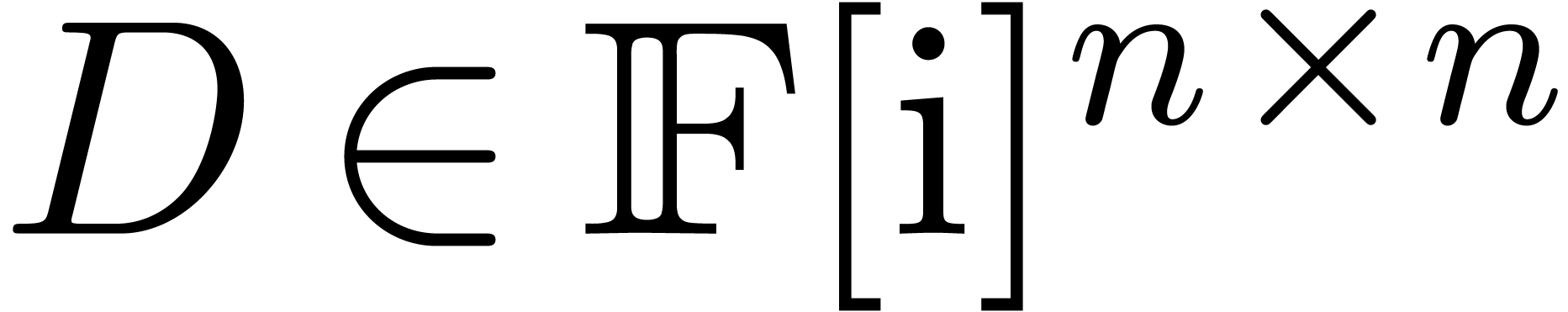 such that
such that
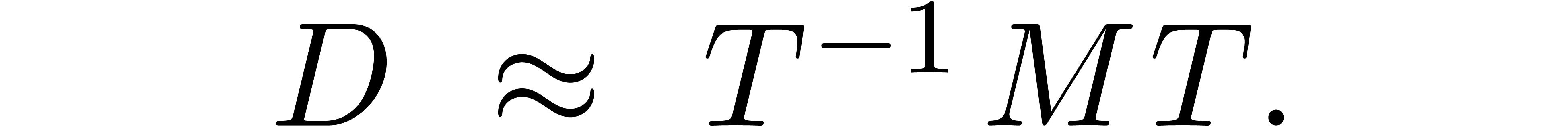
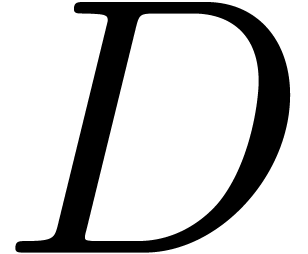 are the approximate eigenvalues
and the columns of
are the approximate eigenvalues
and the columns of  are the approximate
eigenvectors of
are the approximate
eigenvectors of 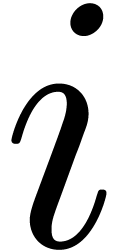 -th
-th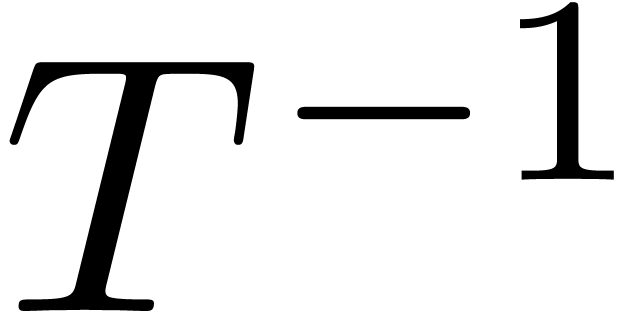 ,
, and a matrix
and a matrix  such that there exists a matrix
such that there exists a matrix
 for which
for which
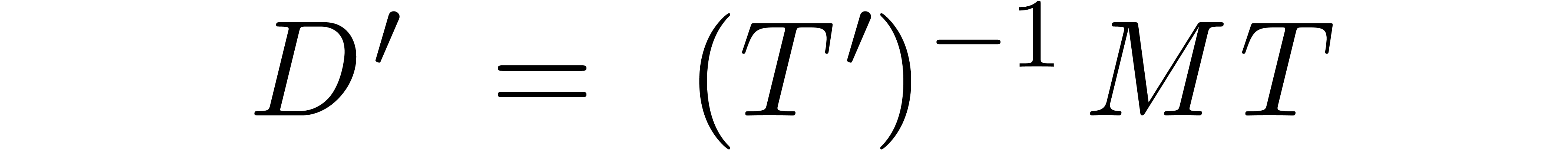
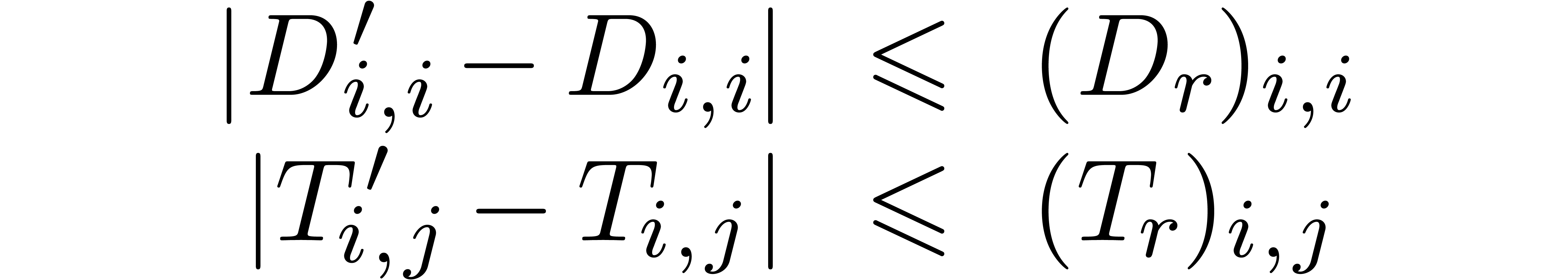
 .
.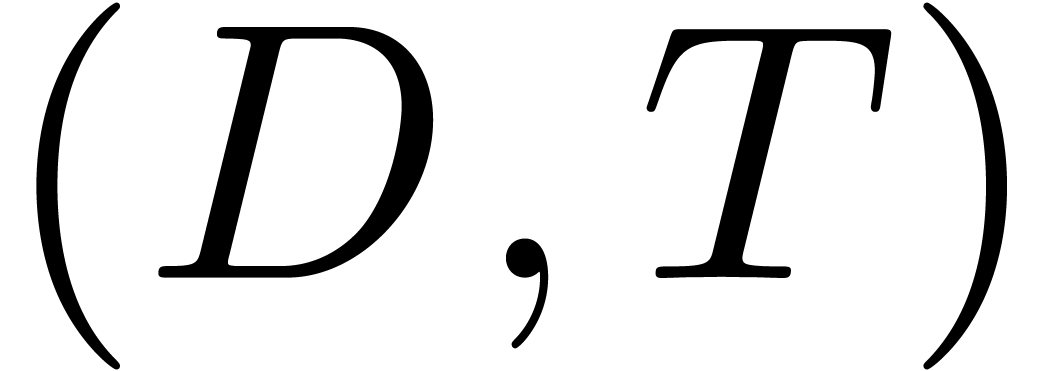 to the eigenproblem for
to the eigenproblem for 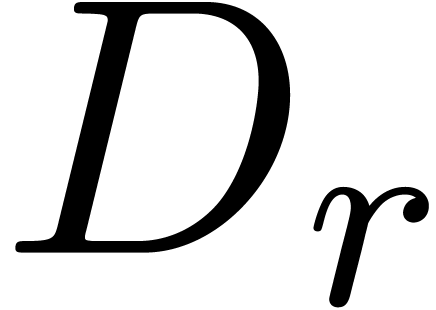 and
and  can be
thought of as reliable error bounds for the numerical solution
can be
thought of as reliable error bounds for the numerical solution 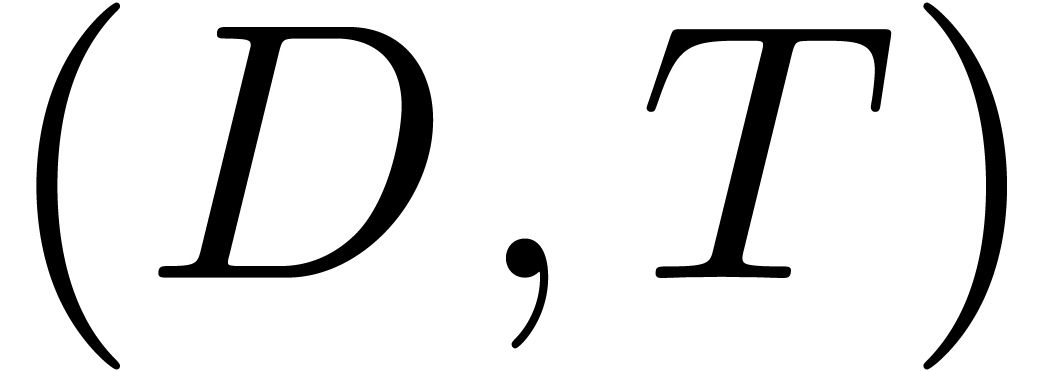 of the eigenproblem.
of the eigenproblem.
 for the set of balls
for the set of balls 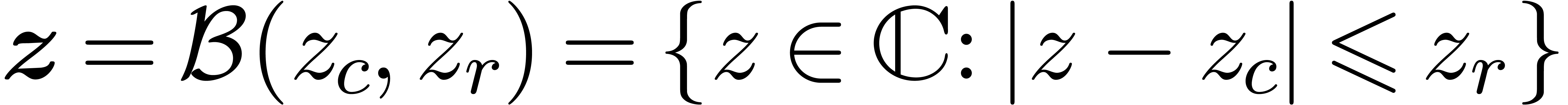 with centers
with centers  in
in  and
radii
and
radii  in
in  .
.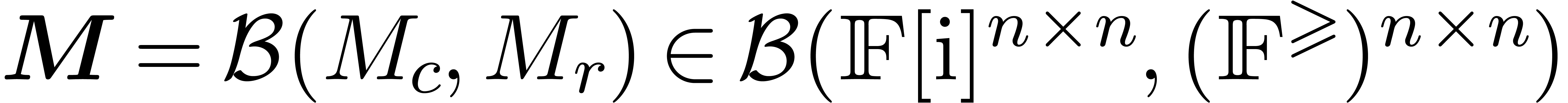 :
: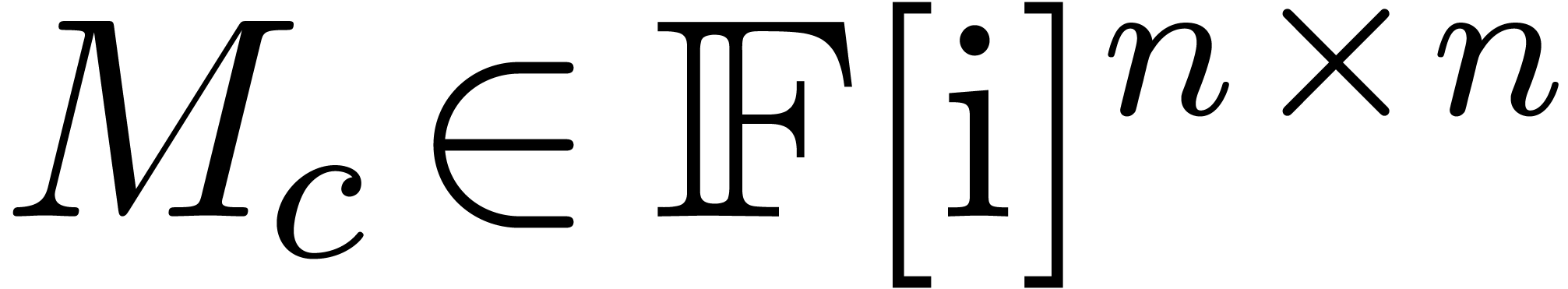 and
a radius matrix
and
a radius matrix 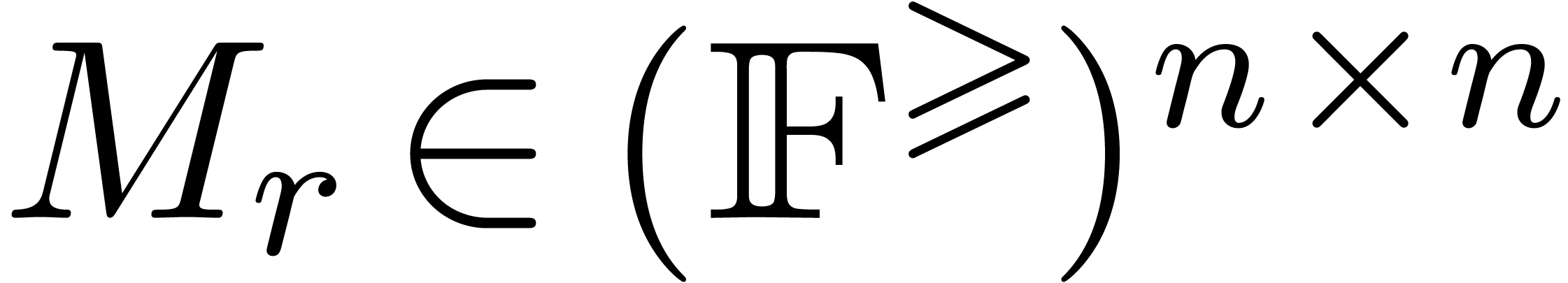 ,
,
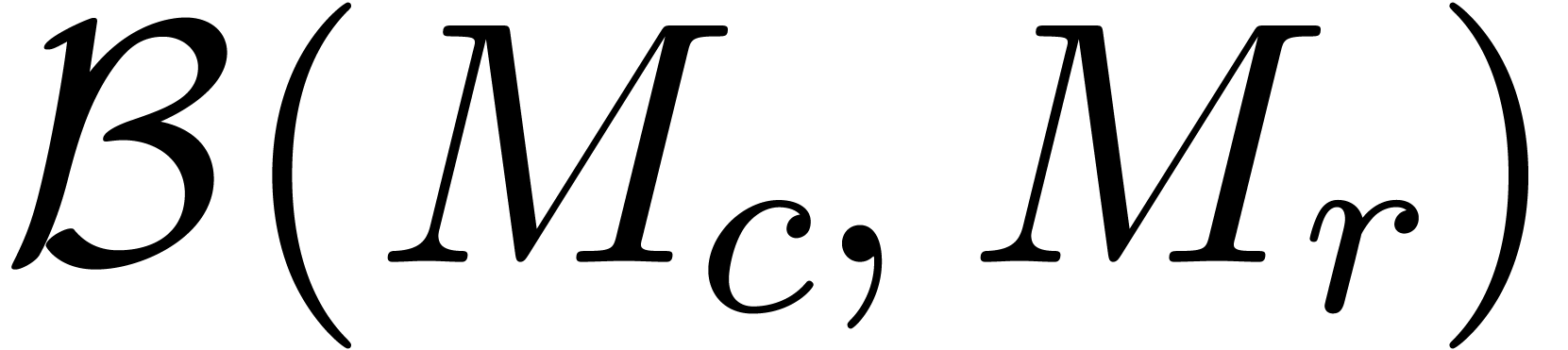 as the set of
matrices in
as the set of
matrices in 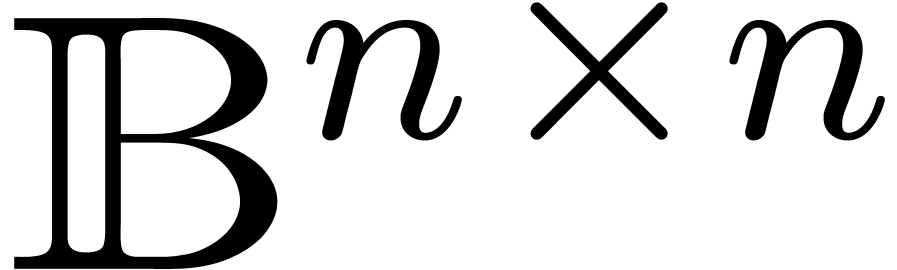 with ball coefficients:
with ball coefficients:
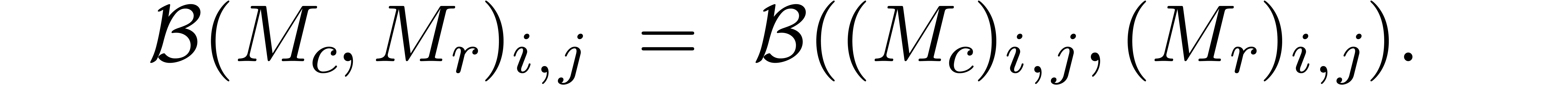
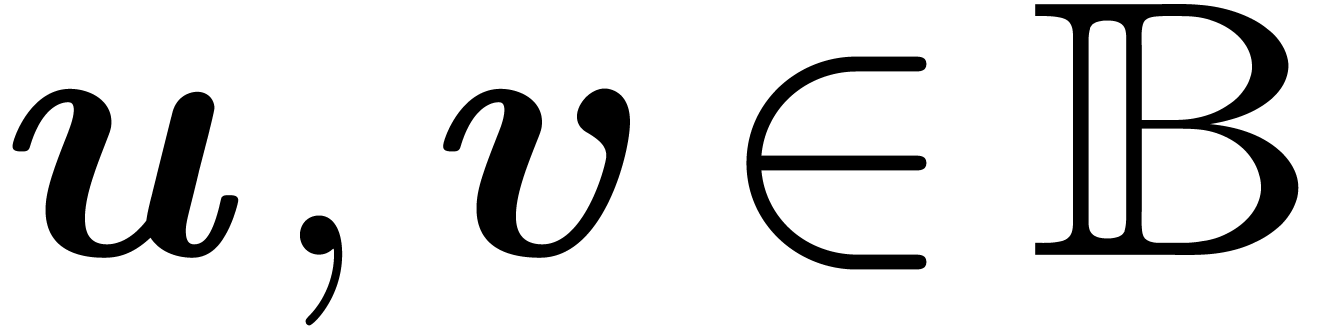 ,
,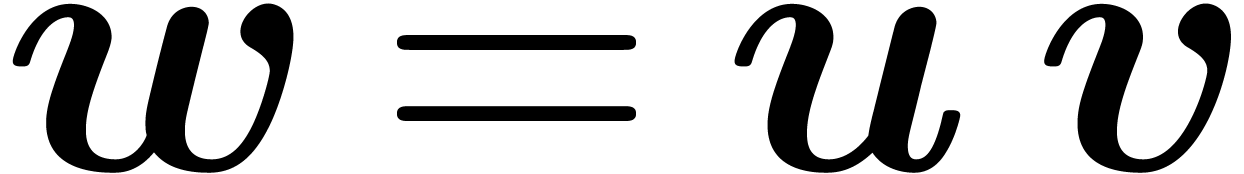 using ball
arithmetic has the property that
using ball
arithmetic has the property that  for any
for any  and
and  .
.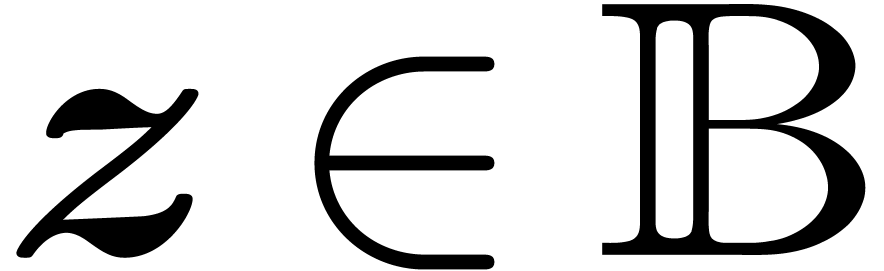 ,
, and
and  for certified lower and upper bounds of
for certified lower and upper bounds of  in
in 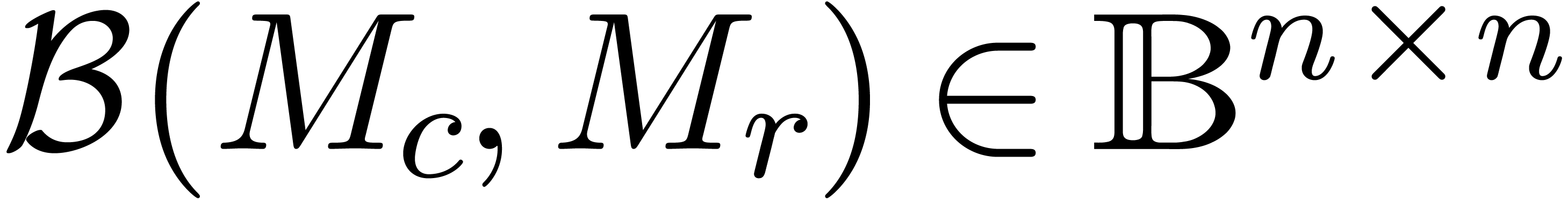 .
.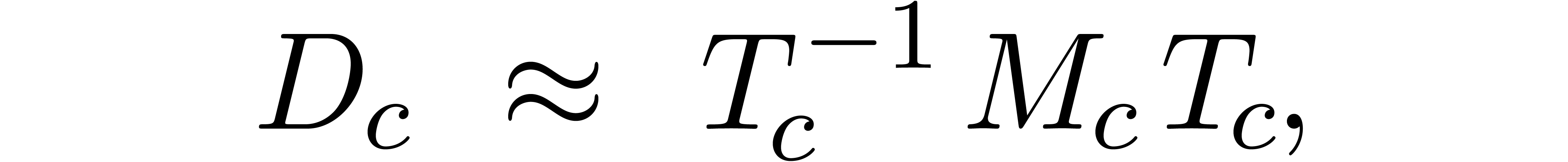
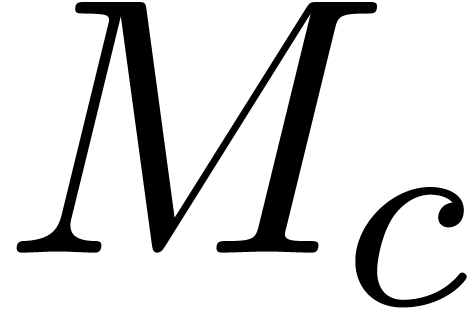 .
.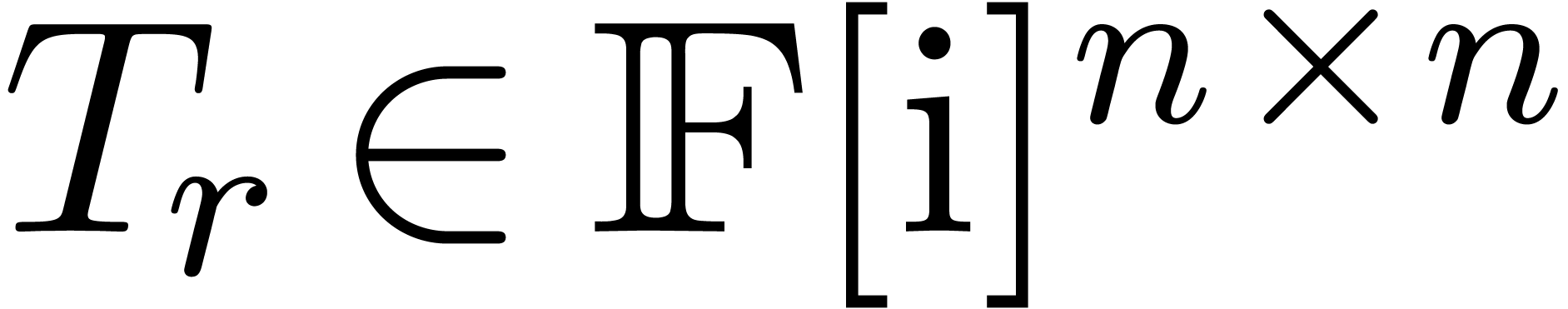 such that, for every
such that, for every 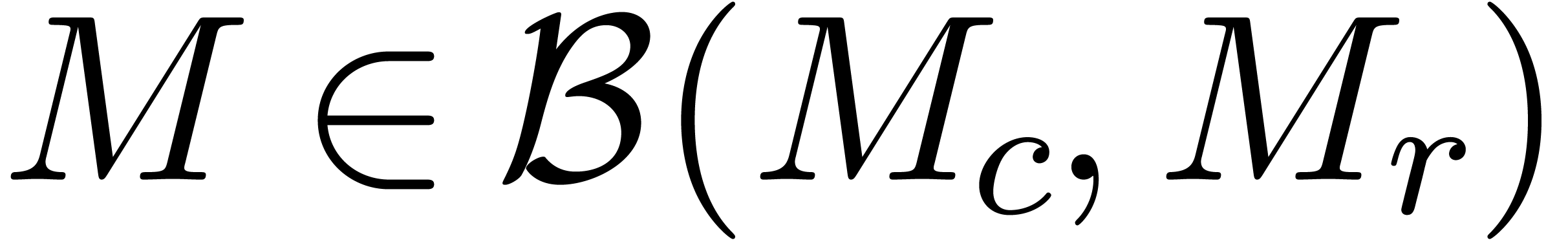 ,
, and
and 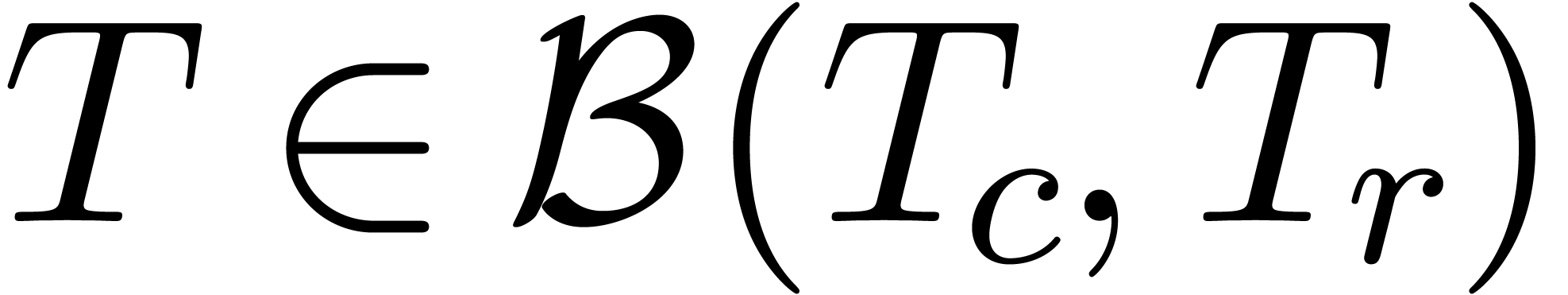 with
with
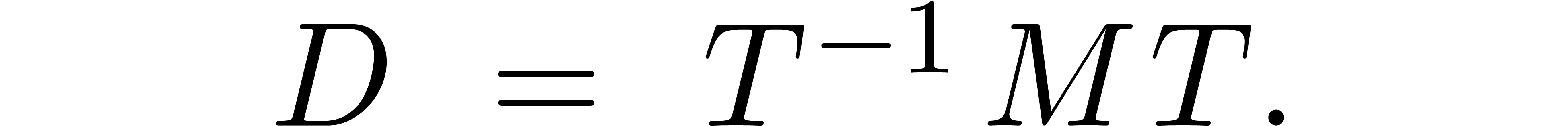
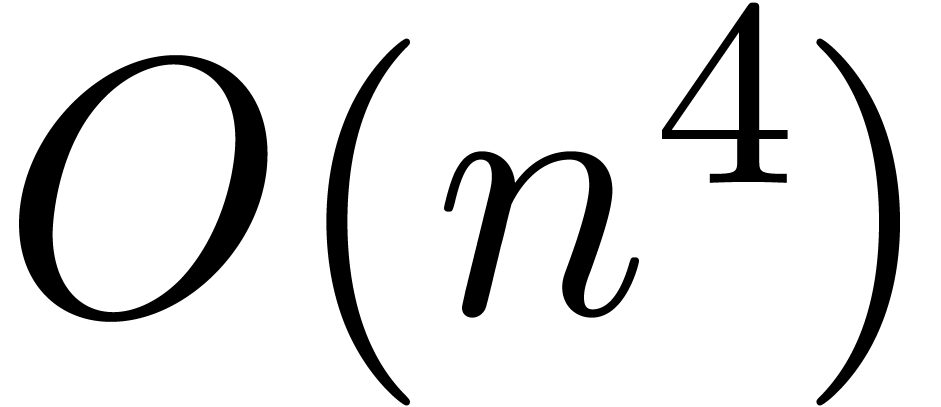 running time. From the more theoretical perspective
of
running time. From the more theoretical perspective
of  -theory
-theory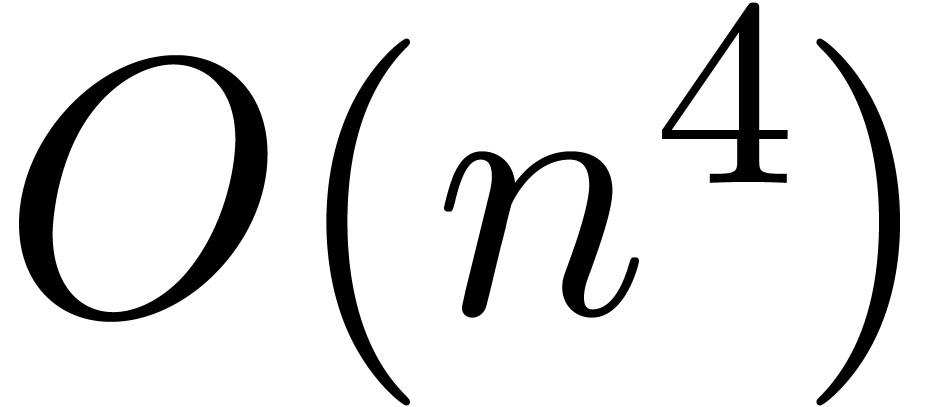 complexity bounds. Fixed points
theorem based on interval arithmetic are used to prove the existence of
a matrix with a given Jordan block in the matrix interval domain. Such
an approach has been exploited for the analysis of multiple roots in [
complexity bounds. Fixed points
theorem based on interval arithmetic are used to prove the existence of
a matrix with a given Jordan block in the matrix interval domain. Such
an approach has been exploited for the analysis of multiple roots in [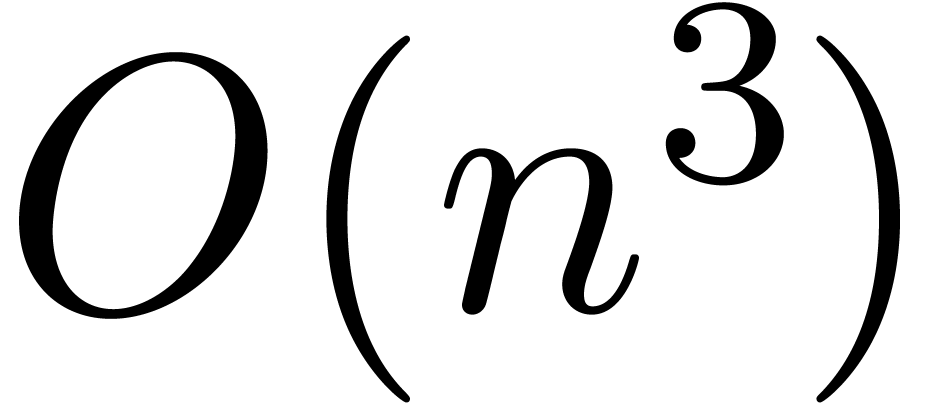 but no iteration converging to
the solution of the eigenproblem is described.
but no iteration converging to
the solution of the eigenproblem is described.
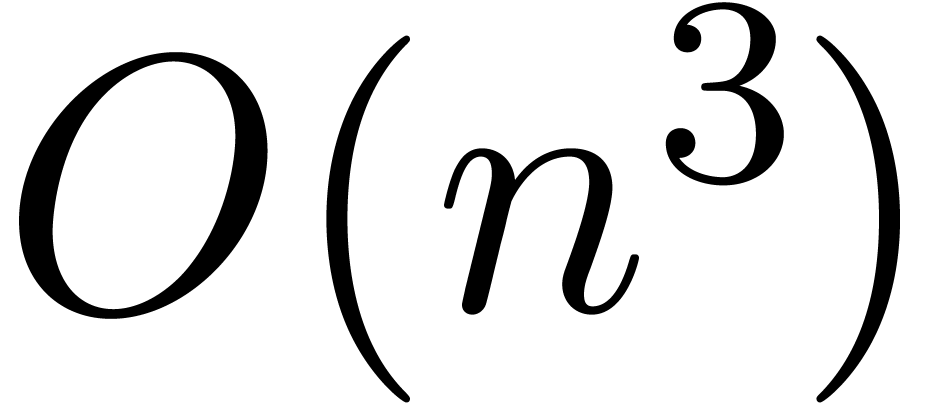 for certifying and enclosing clusters of eigenvectors and
eigenvalues in a single step. We also provide an iterative procedure
that converges geometrically to clusters of solutions. This convergence
is quadratic in the case of single eigenvalues. Our algorithm extends a
previous algorithm from [
for certifying and enclosing clusters of eigenvectors and
eigenvalues in a single step. We also provide an iterative procedure
that converges geometrically to clusters of solutions. This convergence
is quadratic in the case of single eigenvalues. Our algorithm extends a
previous algorithm from [ bits for numerical computations, it has recently been
shown [
bits for numerical computations, it has recently been
shown [ .
.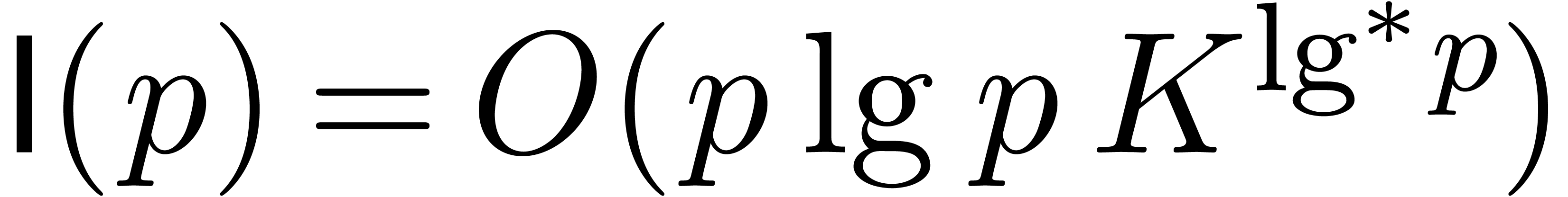 with
with  is the cost of
is the cost of
 is the
exponent of matrix multiplication [
is the
exponent of matrix multiplication [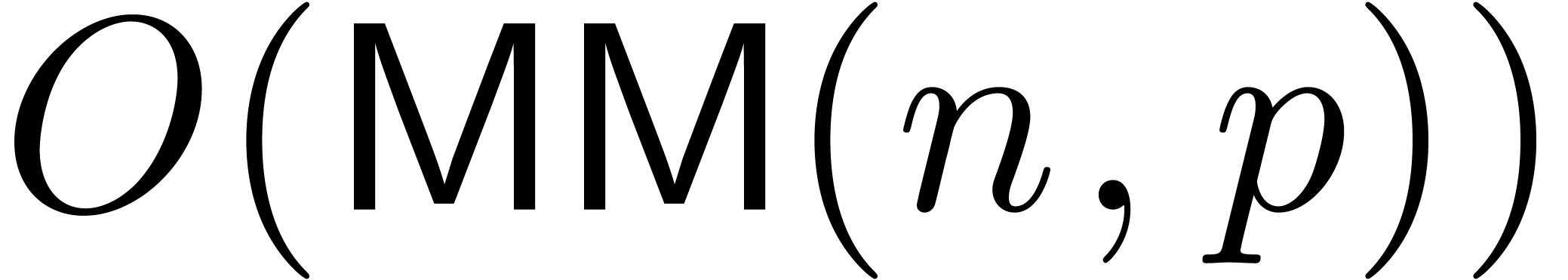 yields an asymptotic bound for the bit
complexity of our certification problem.
yields an asymptotic bound for the bit
complexity of our certification problem.
 accordingly). Using ball
arithmetic, it is straightforward to compute the matricial ball
accordingly). Using ball
arithmetic, it is straightforward to compute the matricial ball
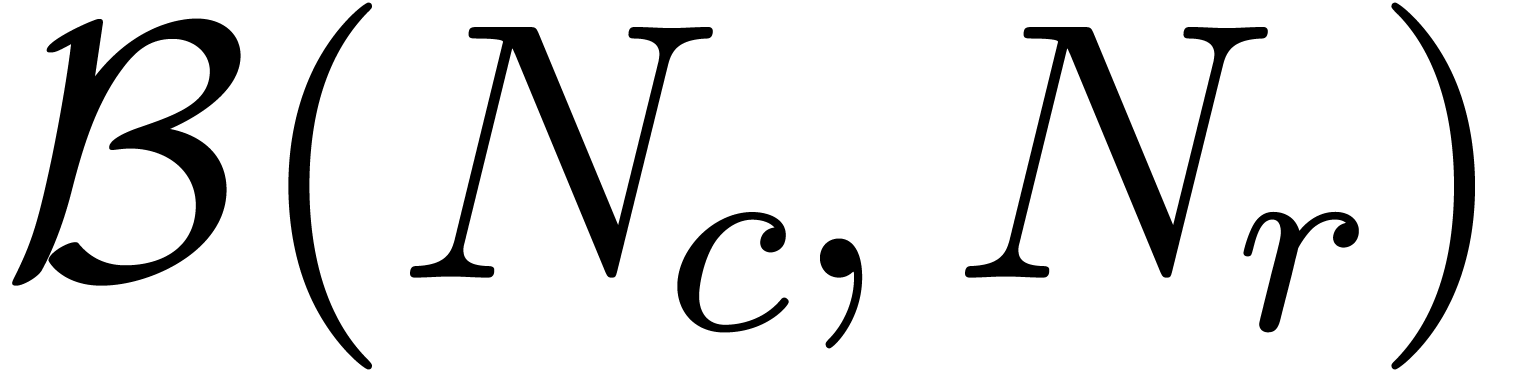 tend to be small, whence
tend to be small, whence  identity matrix. The best we
can hope for is to group eigenvectors with close eigenvalues together in
“clusters” (see also [
identity matrix. The best we
can hope for is to group eigenvectors with close eigenvalues together in
“clusters” (see also [ to be block diagonal. For this reason, we
present our Newton iteration in a sufficiently general setting which
encompasses block matrices. We will show that the iteration still admits
geometric convergence for sufficiently small perturbations and that the
blockwise certification is still sufficient for the computation of
rigourous error bounds for the eigenvalues. In Section
to be block diagonal. For this reason, we
present our Newton iteration in a sufficiently general setting which
encompasses block matrices. We will show that the iteration still admits
geometric convergence for sufficiently small perturbations and that the
blockwise certification is still sufficient for the computation of
rigourous error bounds for the eigenvalues. In Section  and an
and an  ,
,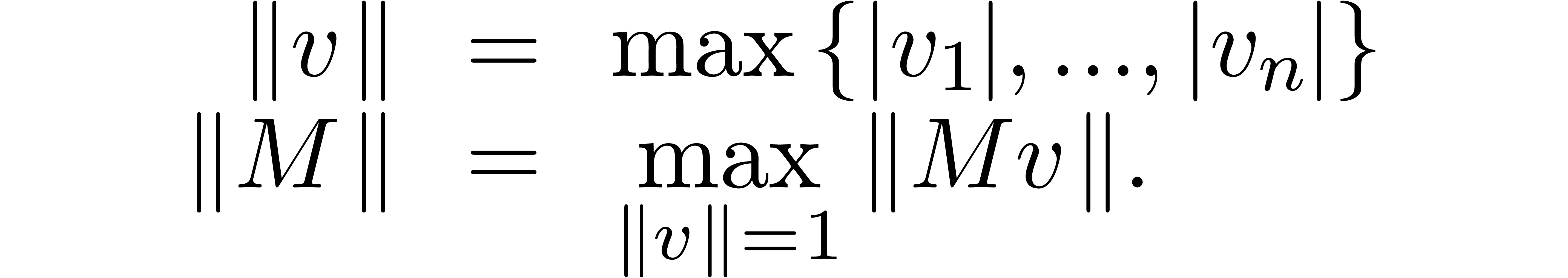
 ,
,
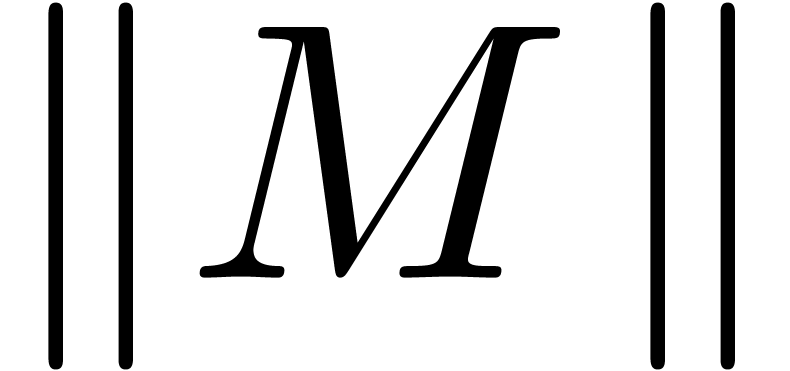 can only
decrease.
can only
decrease.
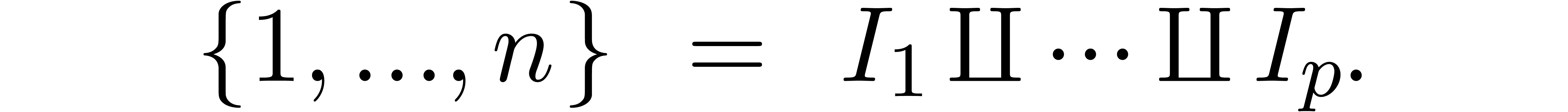
 .
.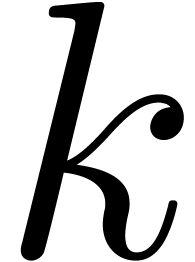 with
with 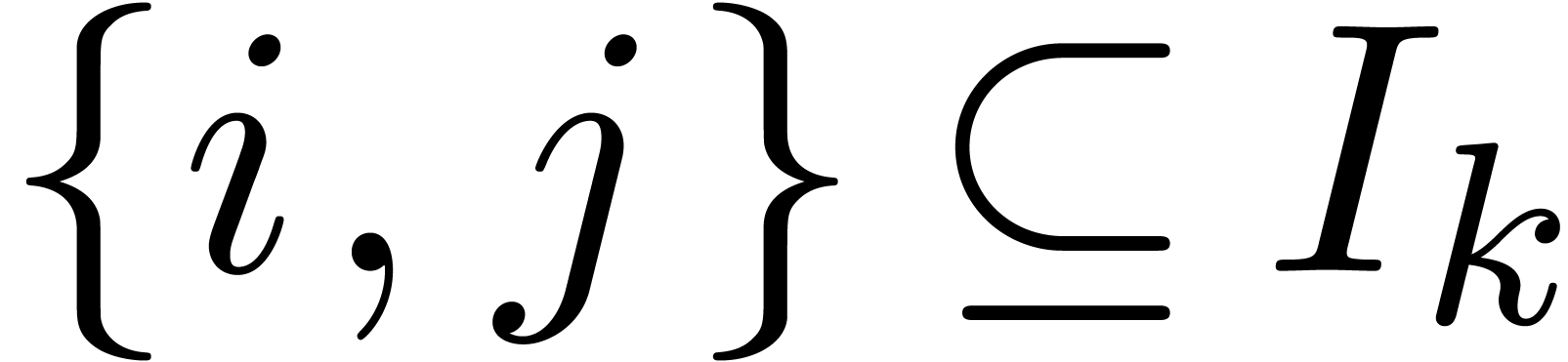 and we
will write
and we
will write  .
.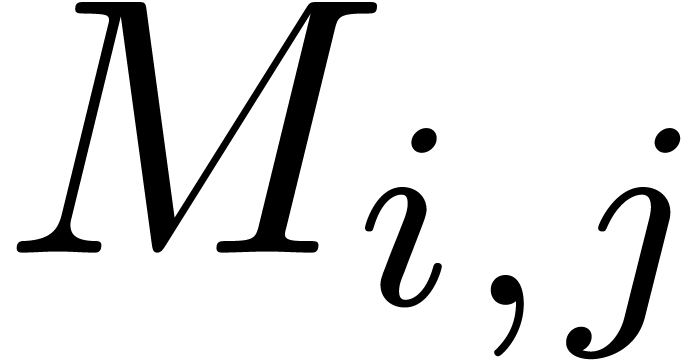 and
and 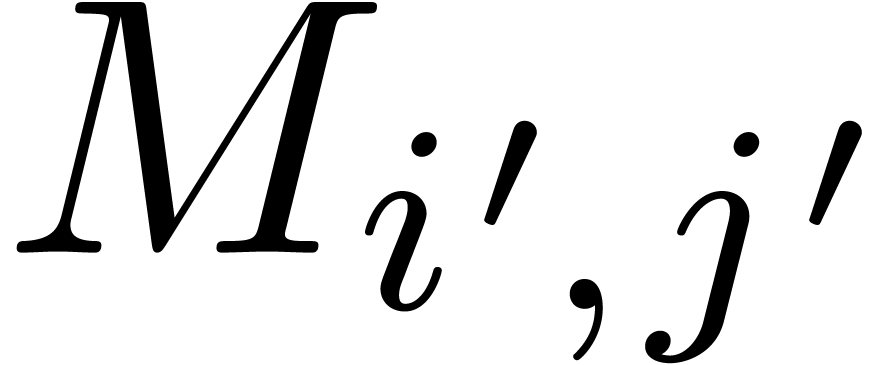 of a matrix
of a matrix  .
.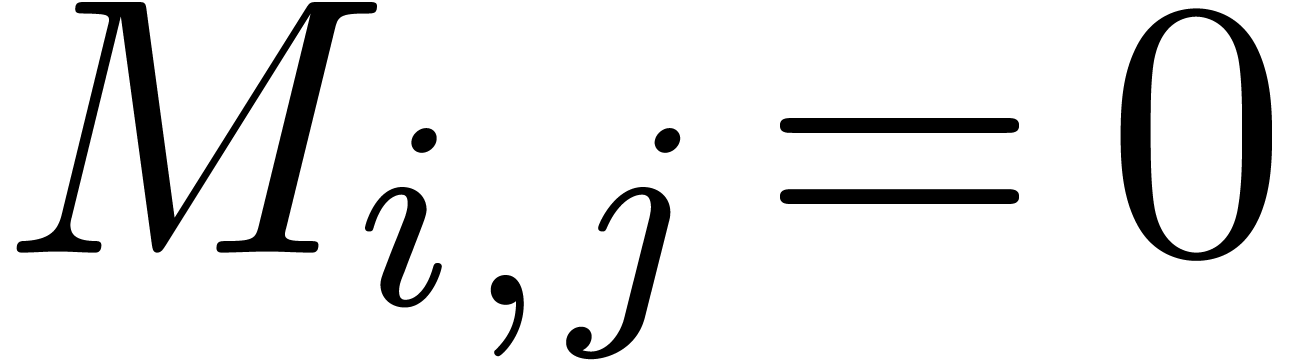 whenever
whenever  .
.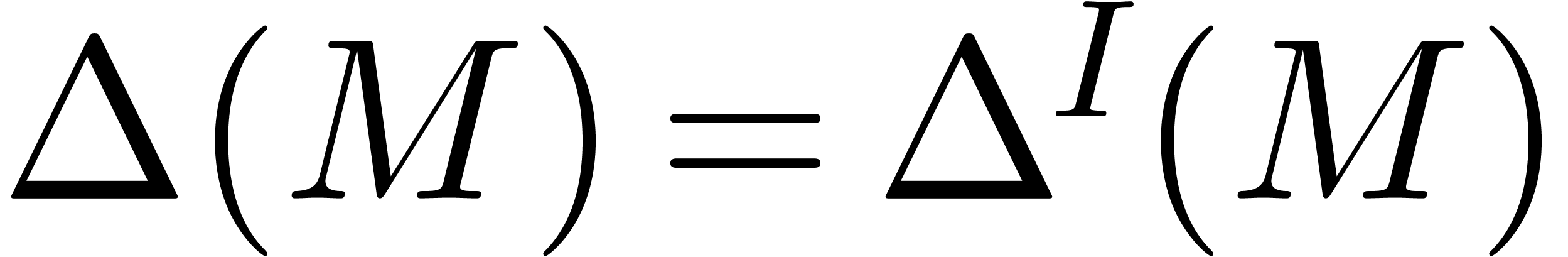 and
and
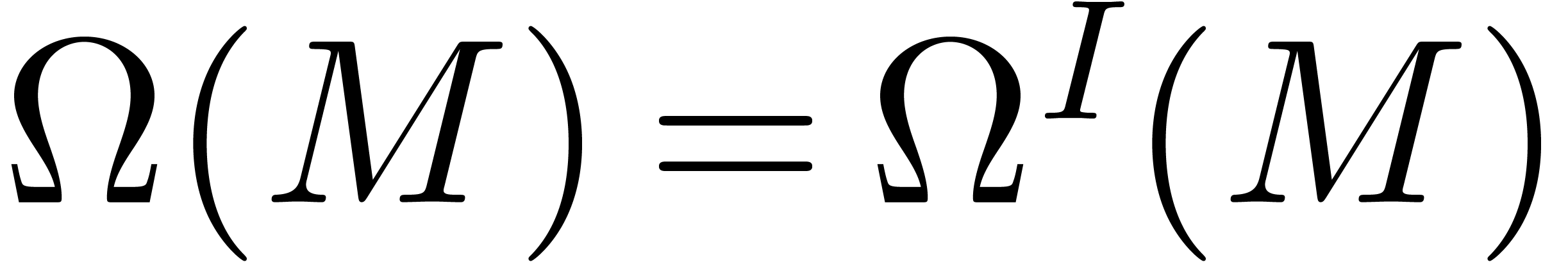 by
by


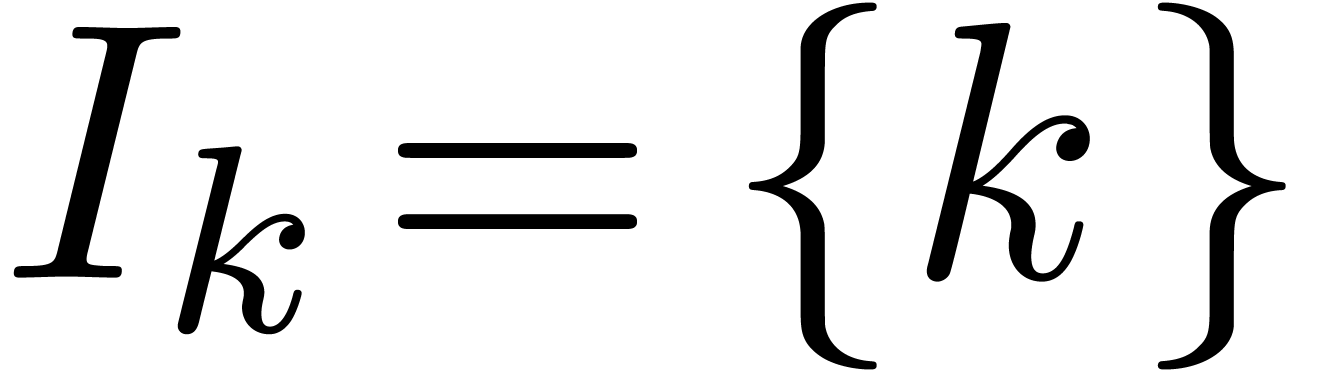 ,
,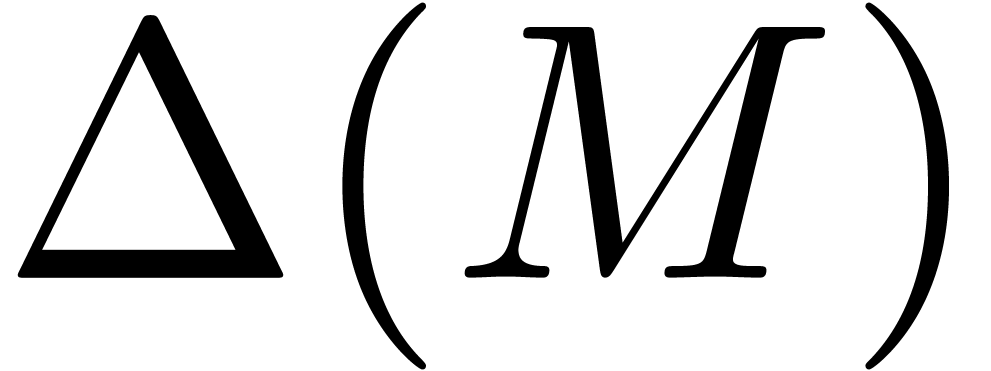 and
and 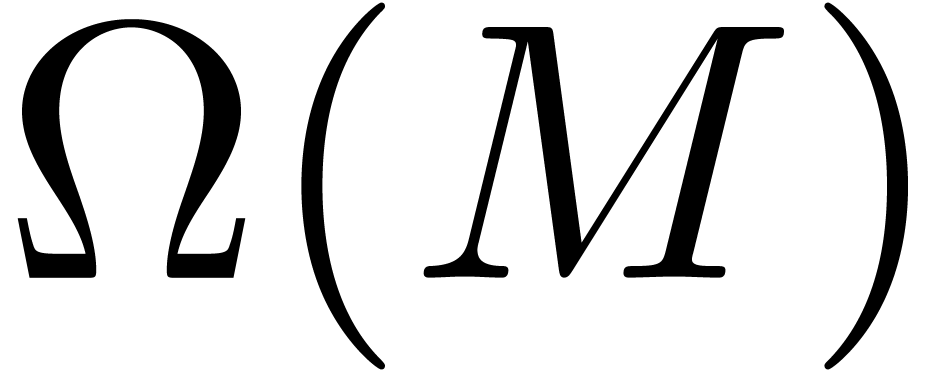 are
simply the diagonal and off diagonal projections of
are
simply the diagonal and off diagonal projections of 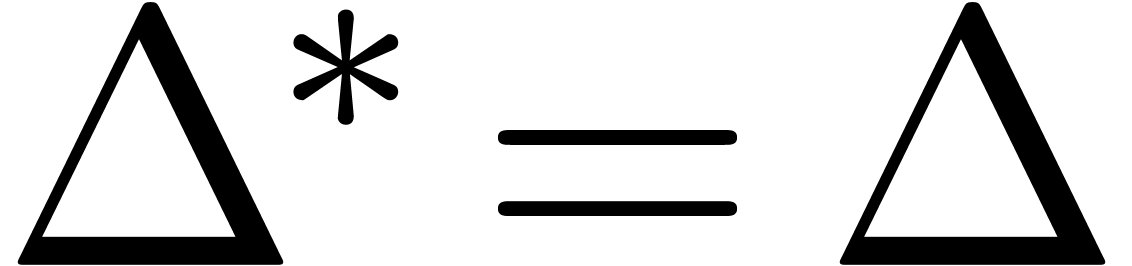 and
and 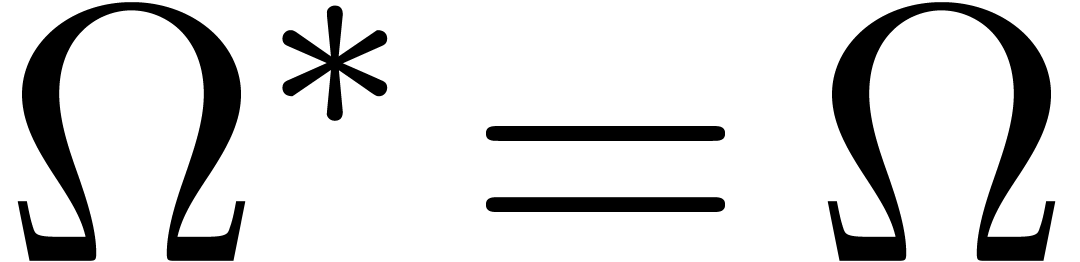 .
.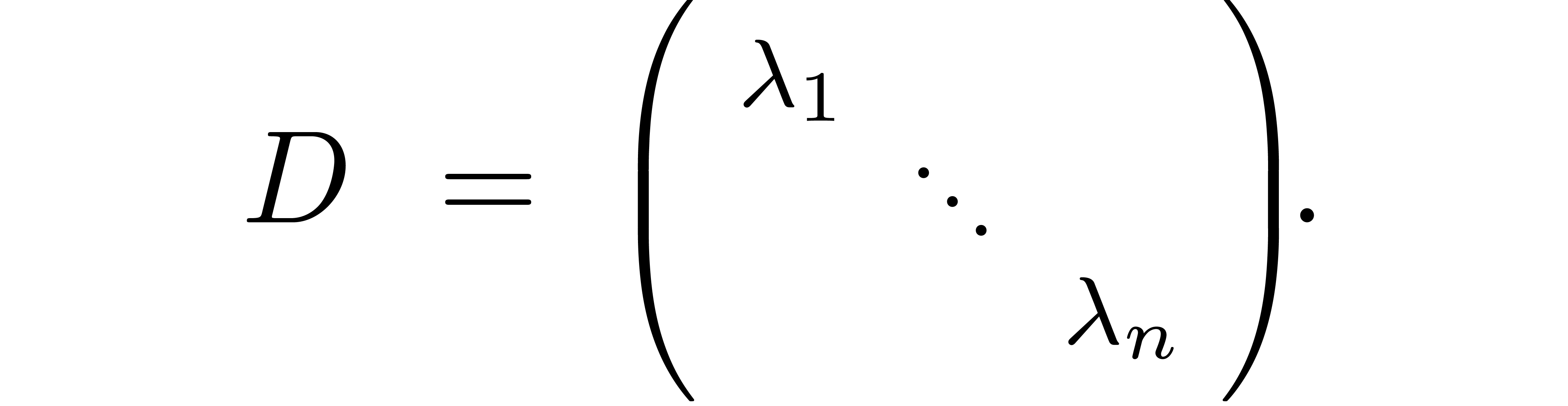
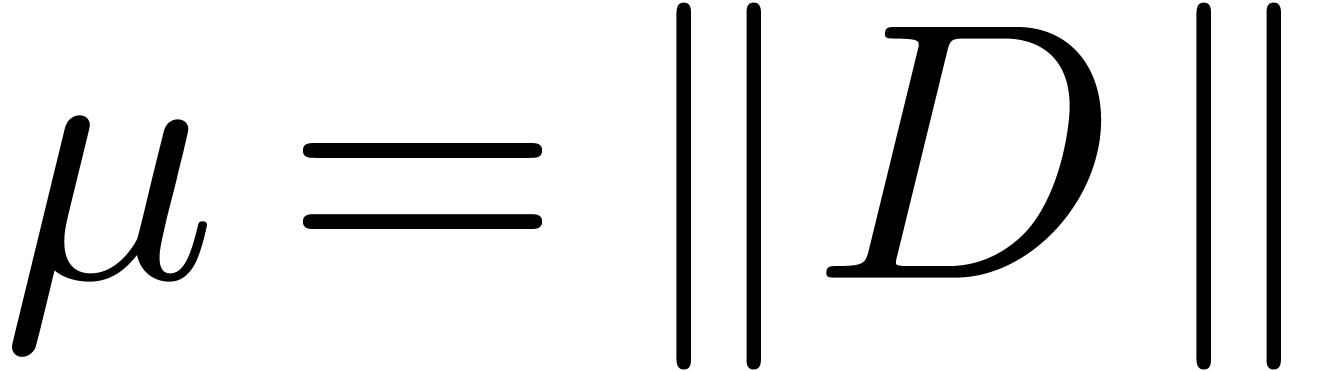 of a diagonal matrix
of a diagonal matrix 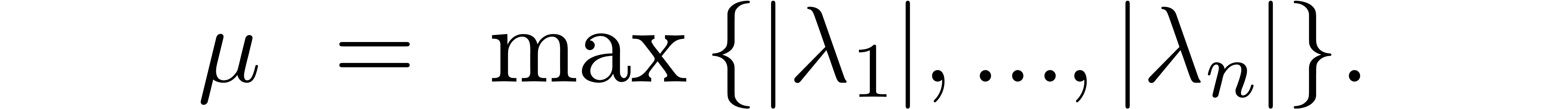
 by
by
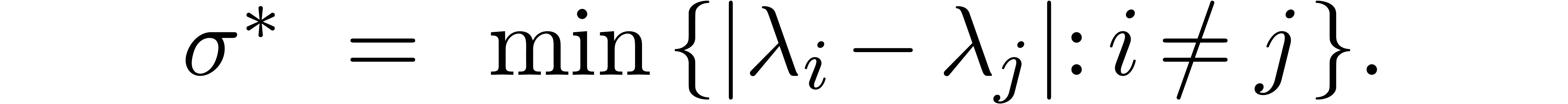
 by
by
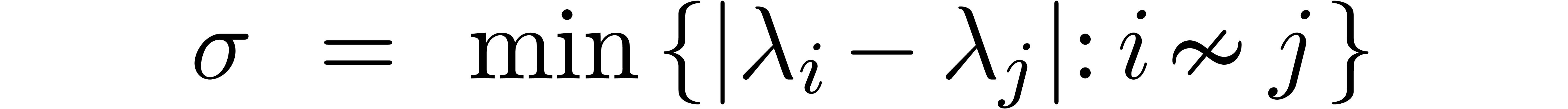
 remains high if the clustering is
chosen in such a way that the indices
remains high if the clustering is
chosen in such a way that the indices  and
and  belong to the same cluster. In particular, if
belong to the same cluster. In particular, if  ,
,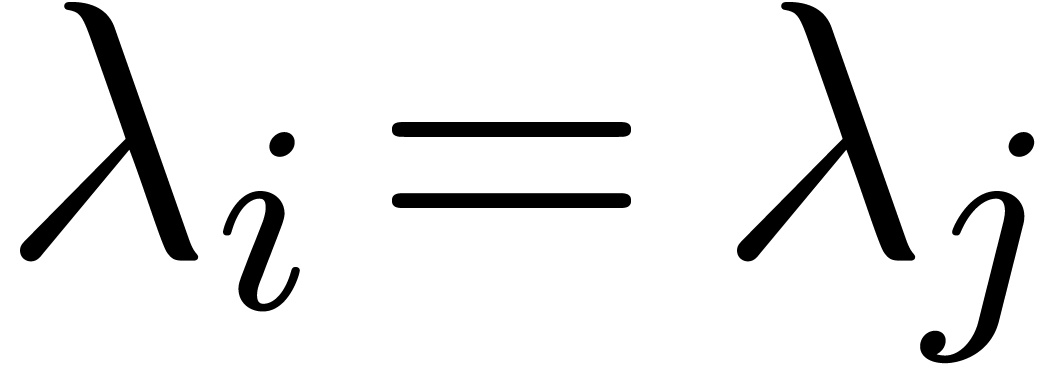 implies
implies 
 is an off diagonal matrix, the aim of this section is to find a small
matrix
is an off diagonal matrix, the aim of this section is to find a small
matrix  for which
for which
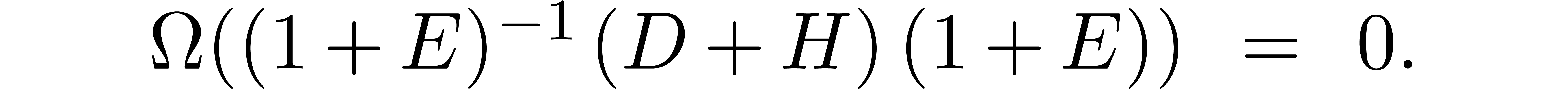
 and
and 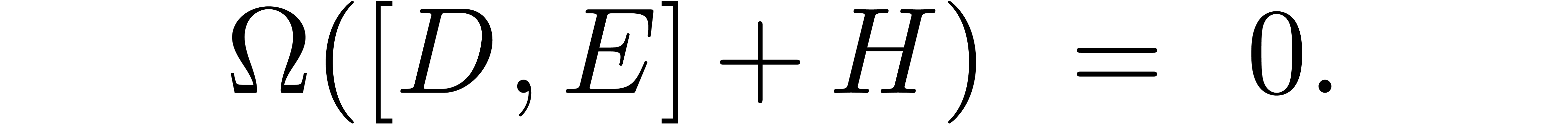
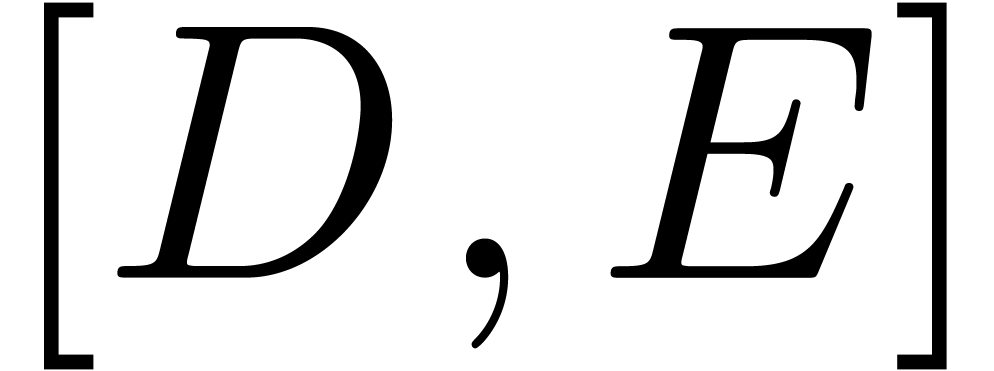 ,
,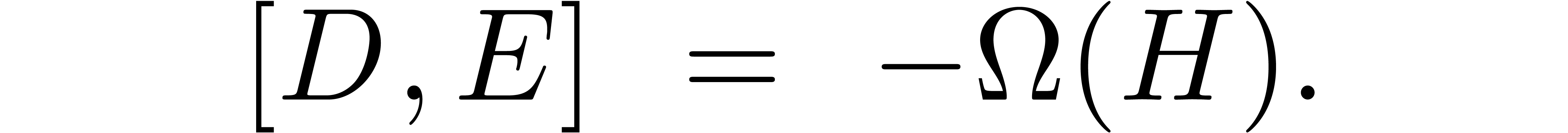
 and a diagonal matrix
and a diagonal matrix 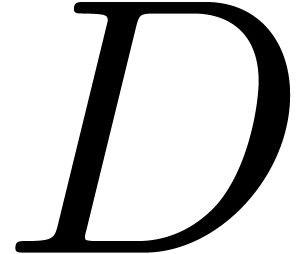 with entries
with entries  ,
,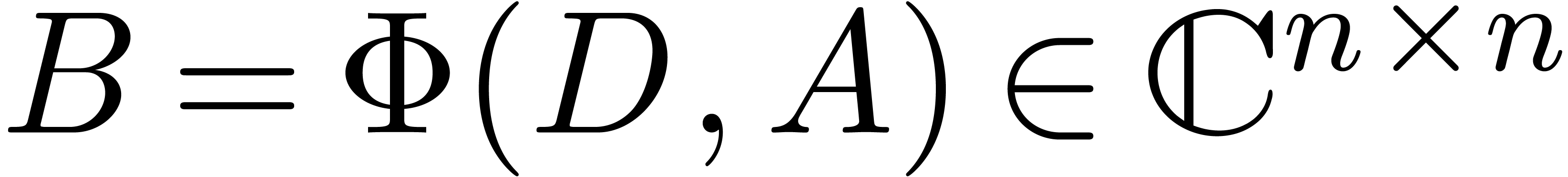 be the strongly off diagonal matrix
with
be the strongly off diagonal matrix
with
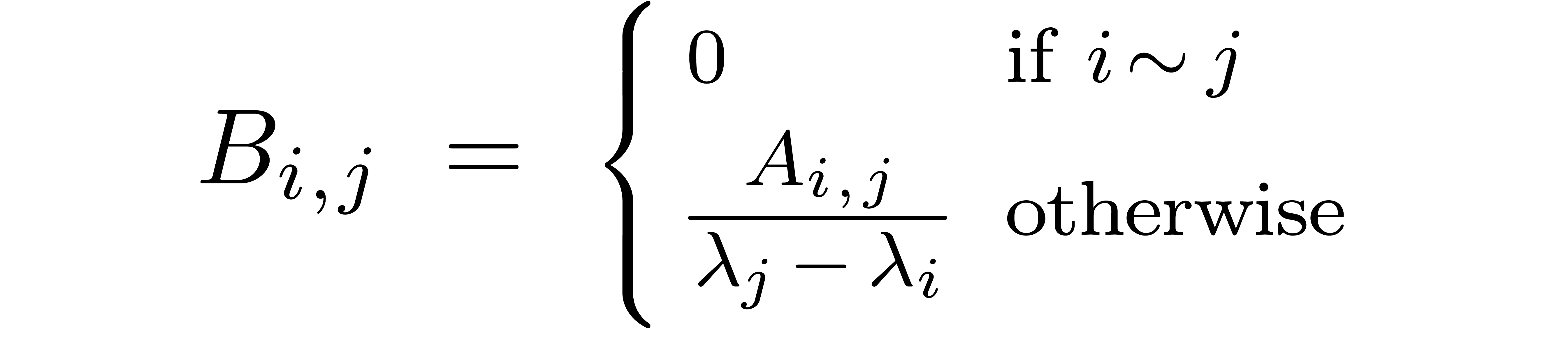
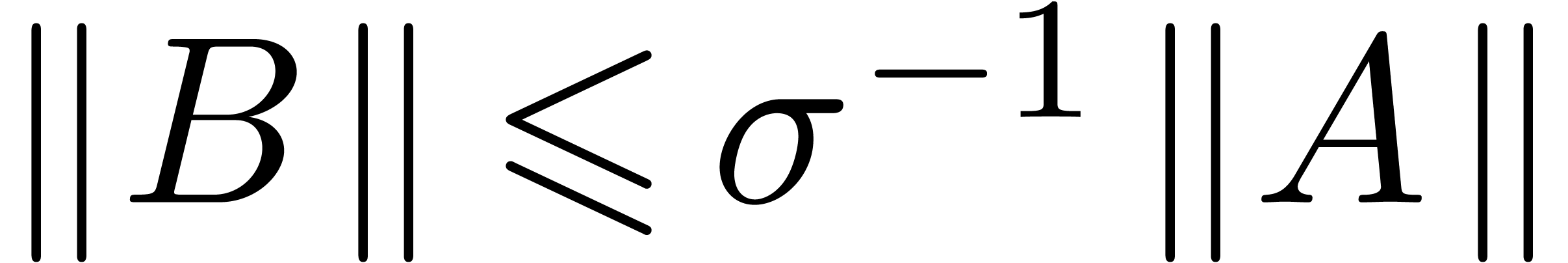 and
and
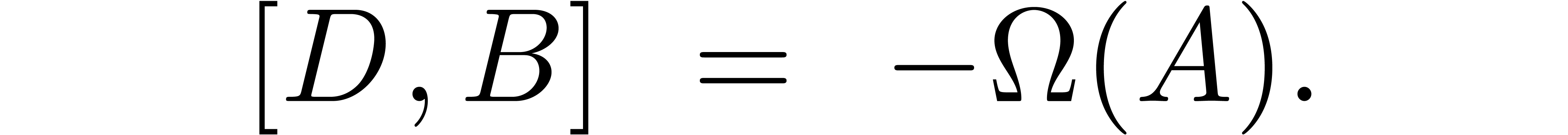
 .
.

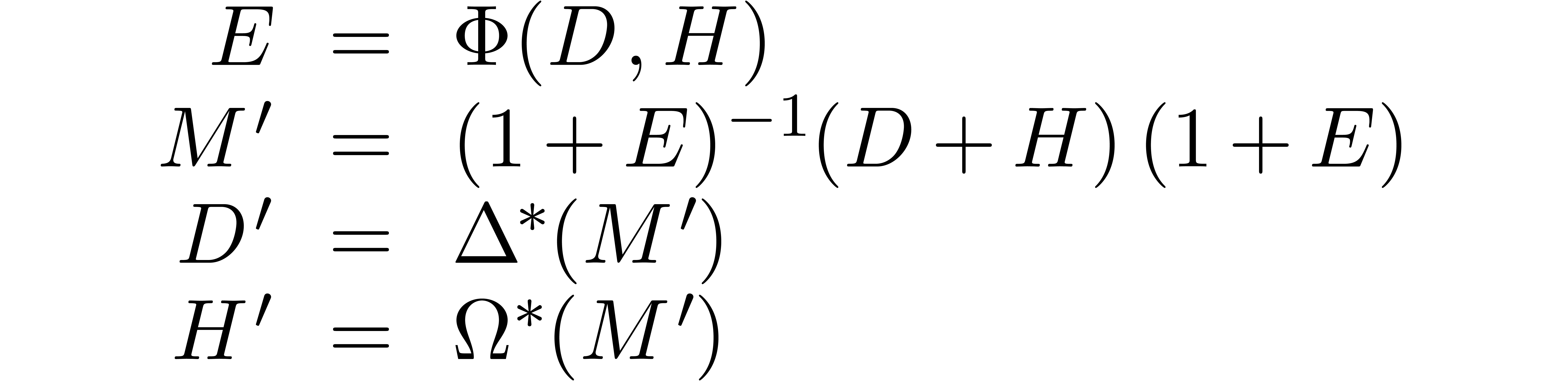
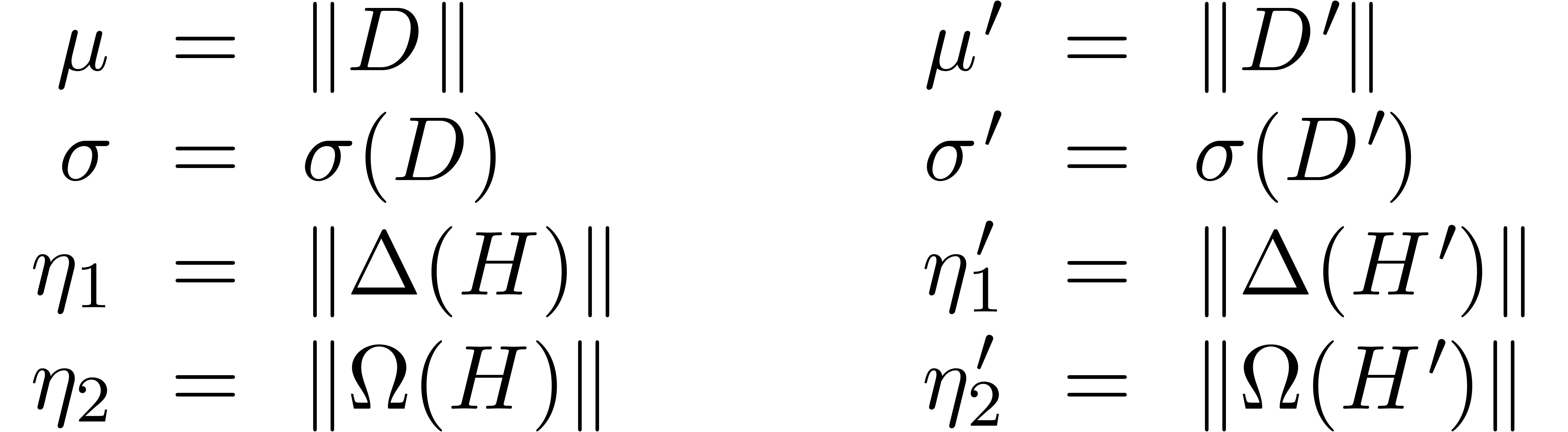
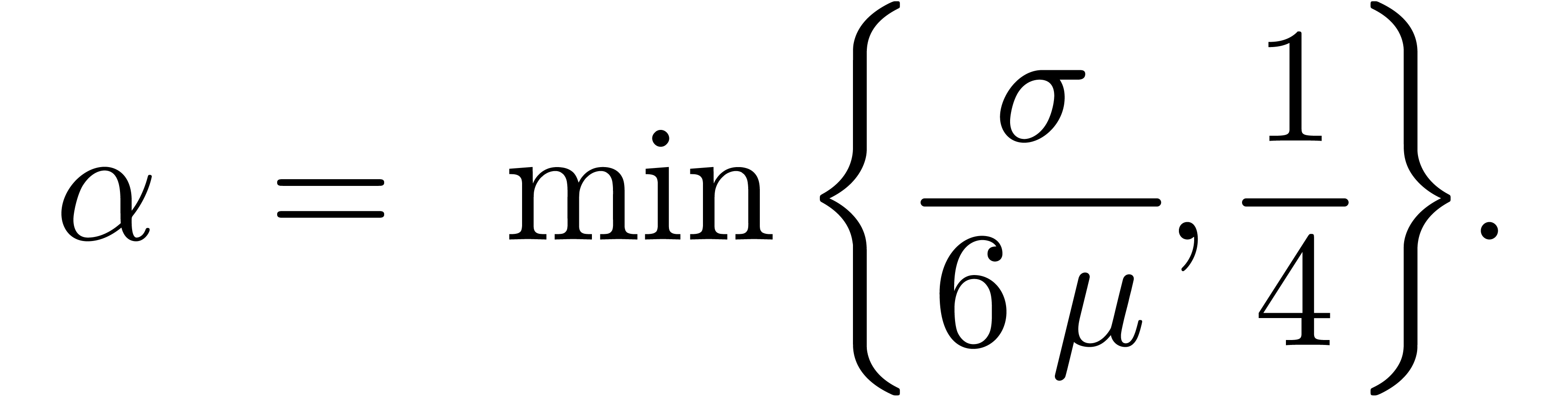
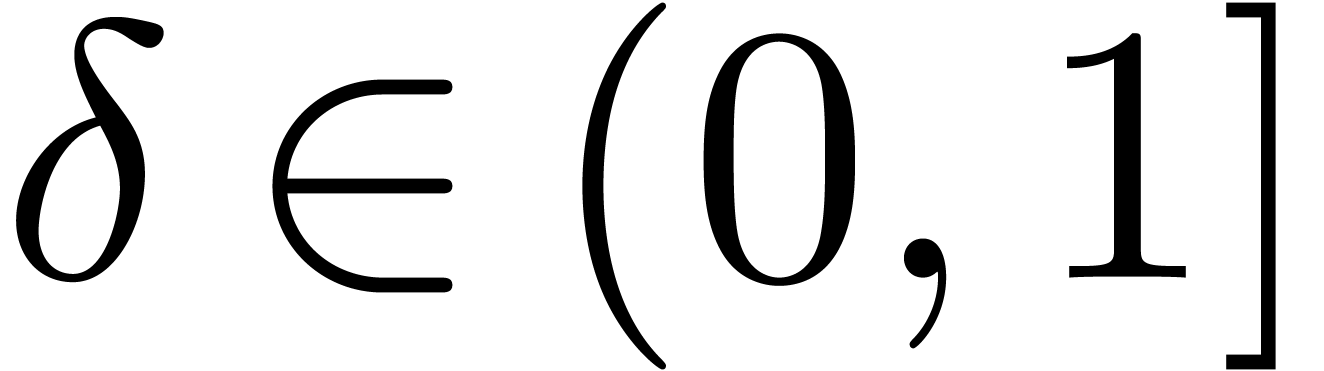 ,
,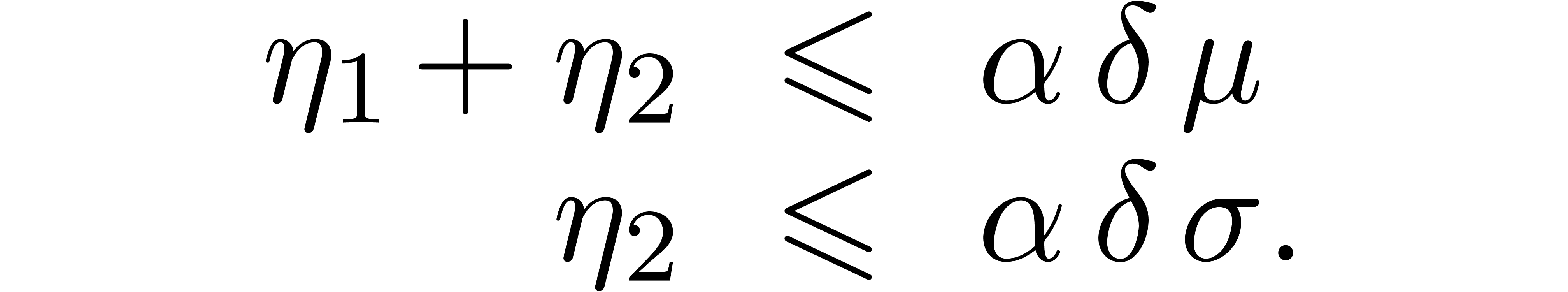
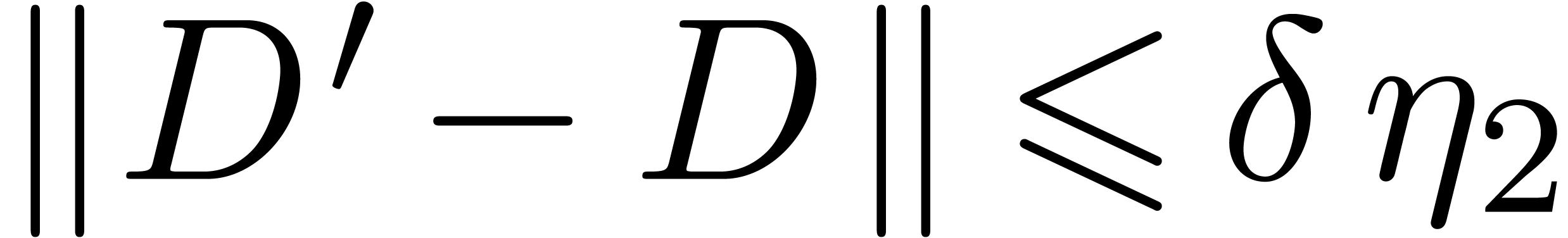 and
and
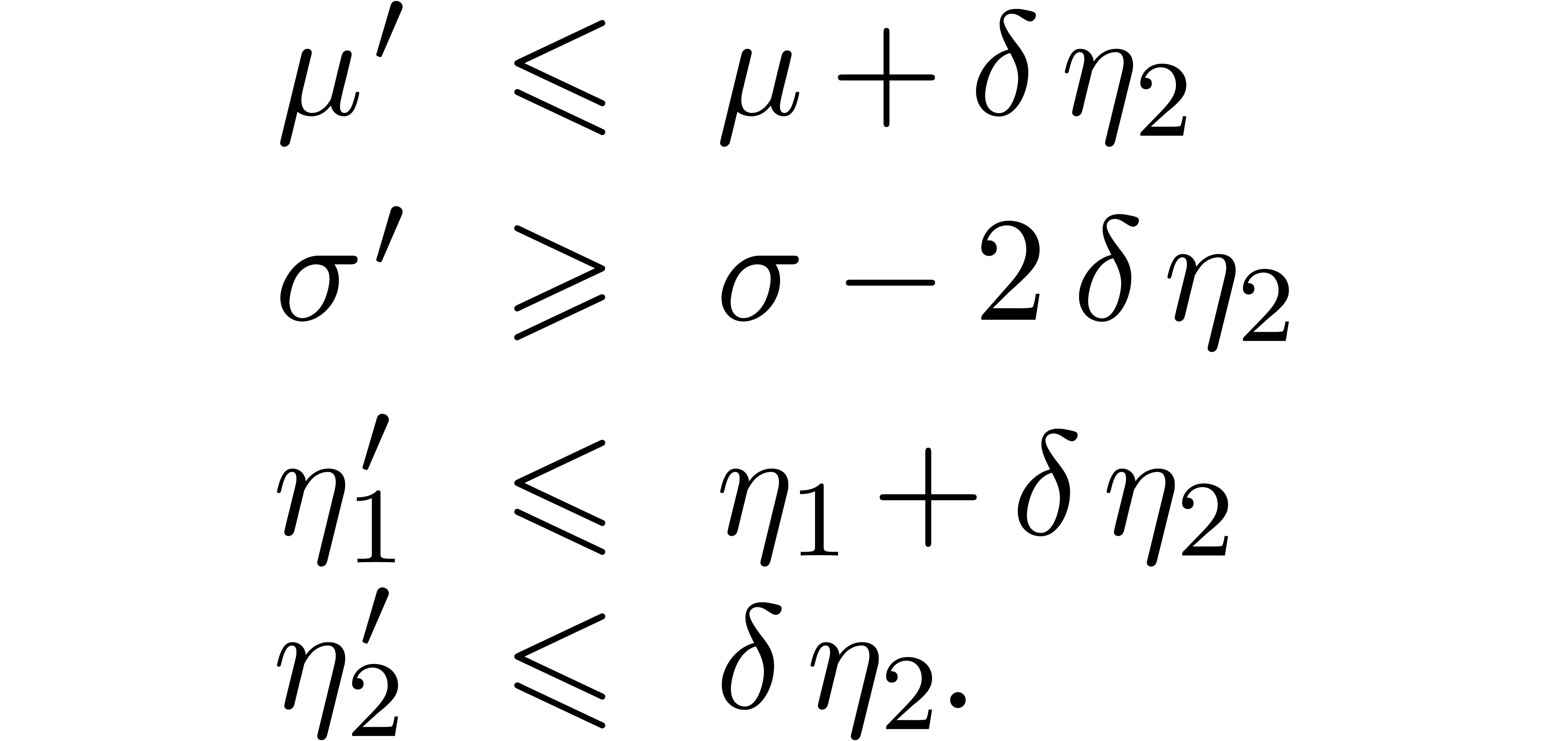
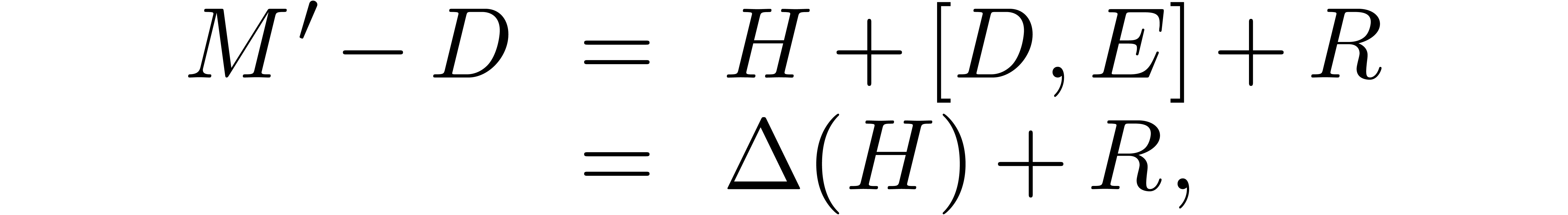
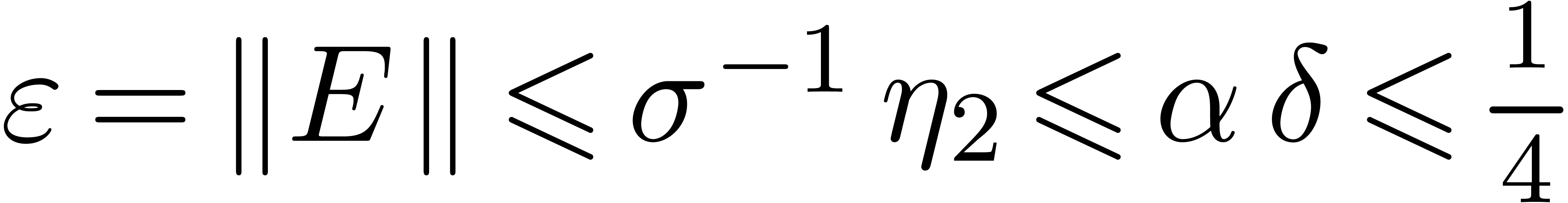 ,
, is bounded by
is bounded by
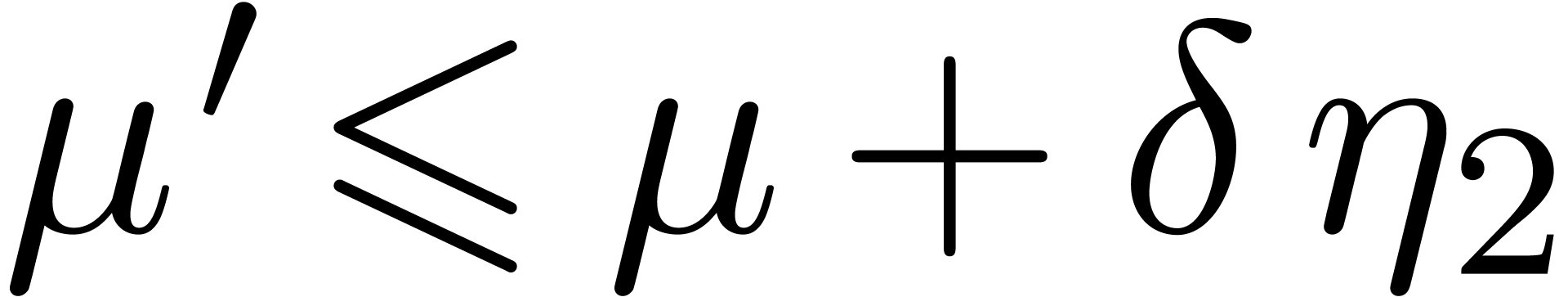 and
and 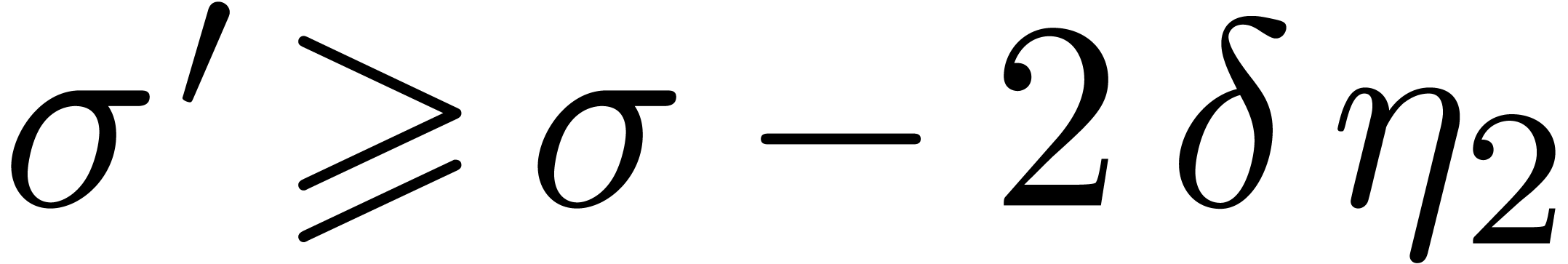 follow from
follow from 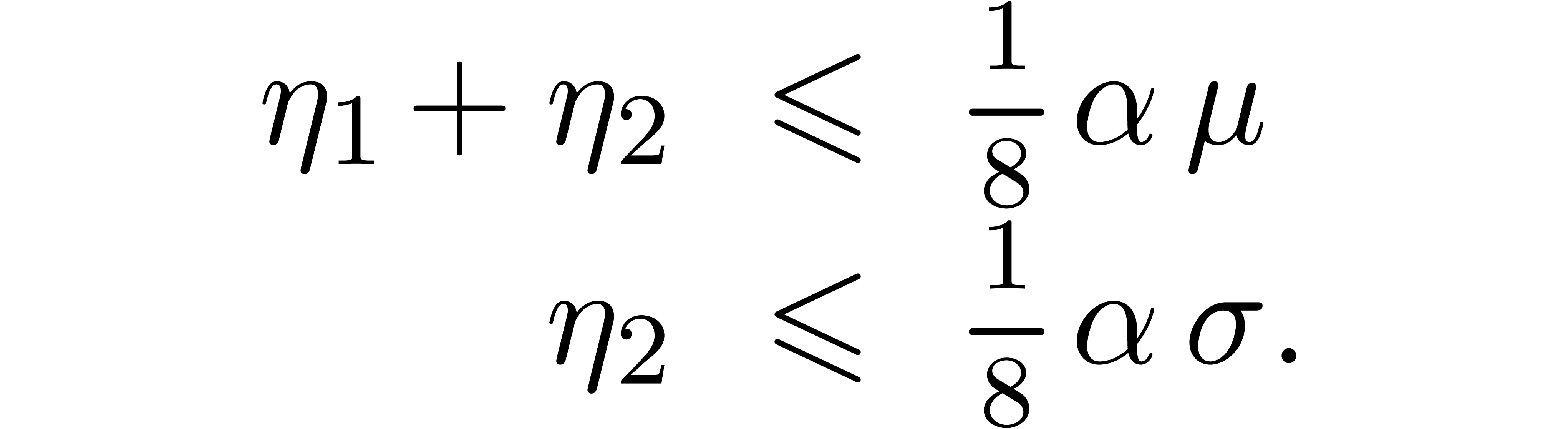
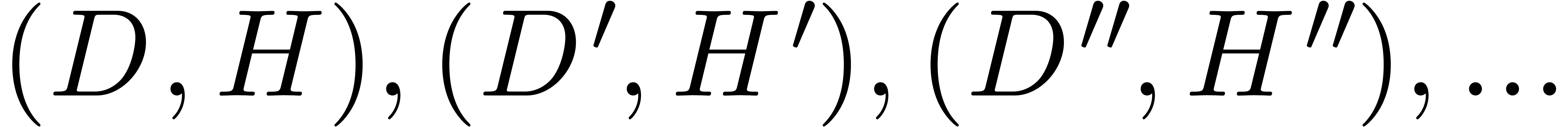
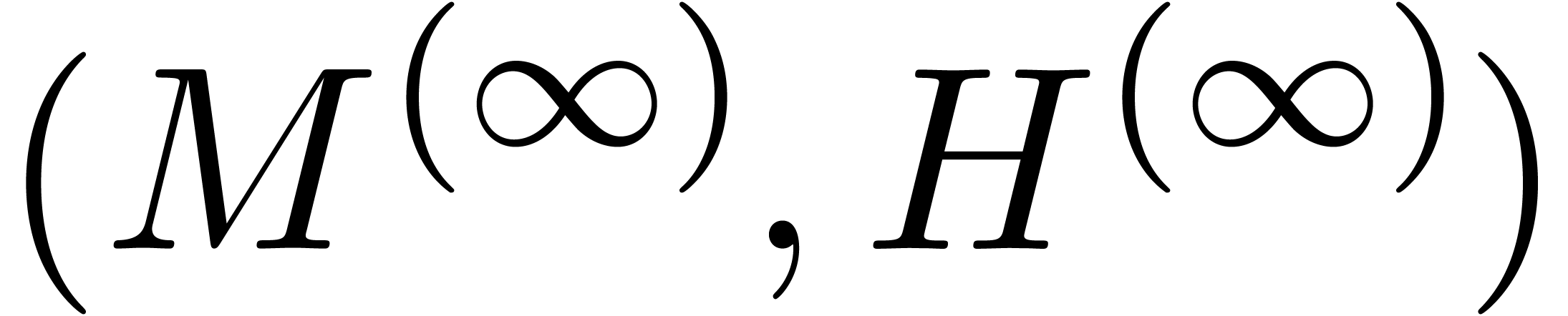 with
with
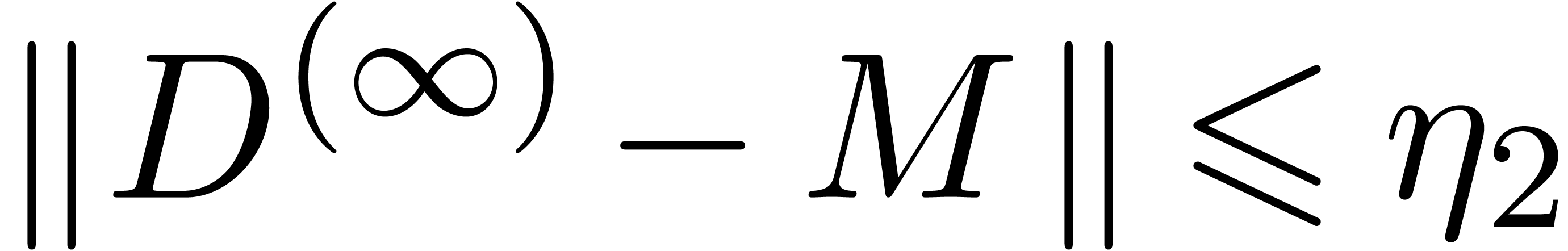 and
and 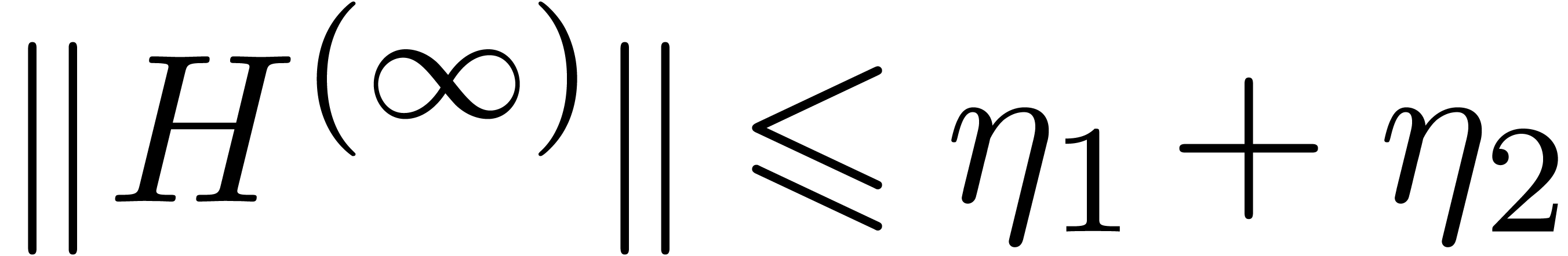 .
. is block diagonal and there exists
a matrix
is block diagonal and there exists
a matrix 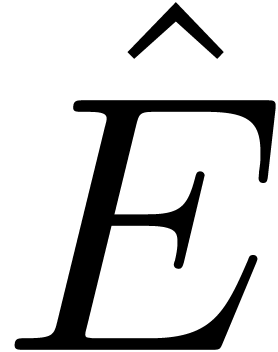 with
with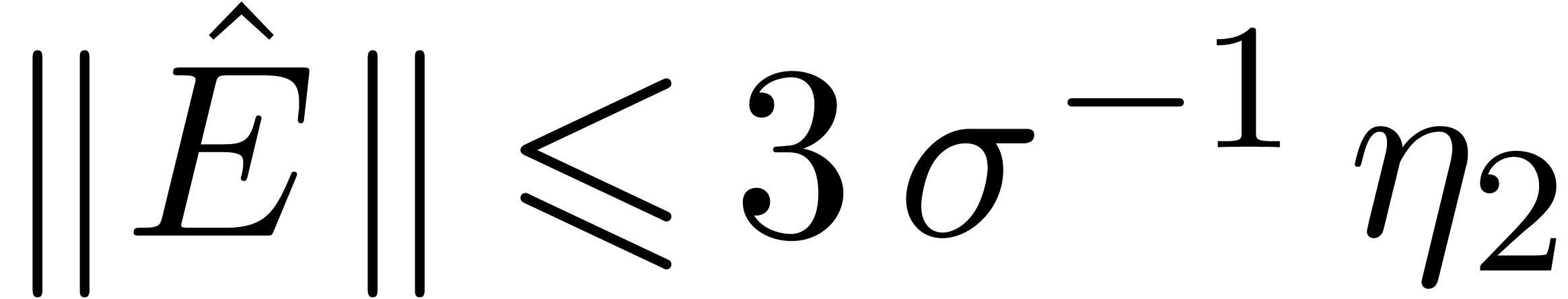 ,
,
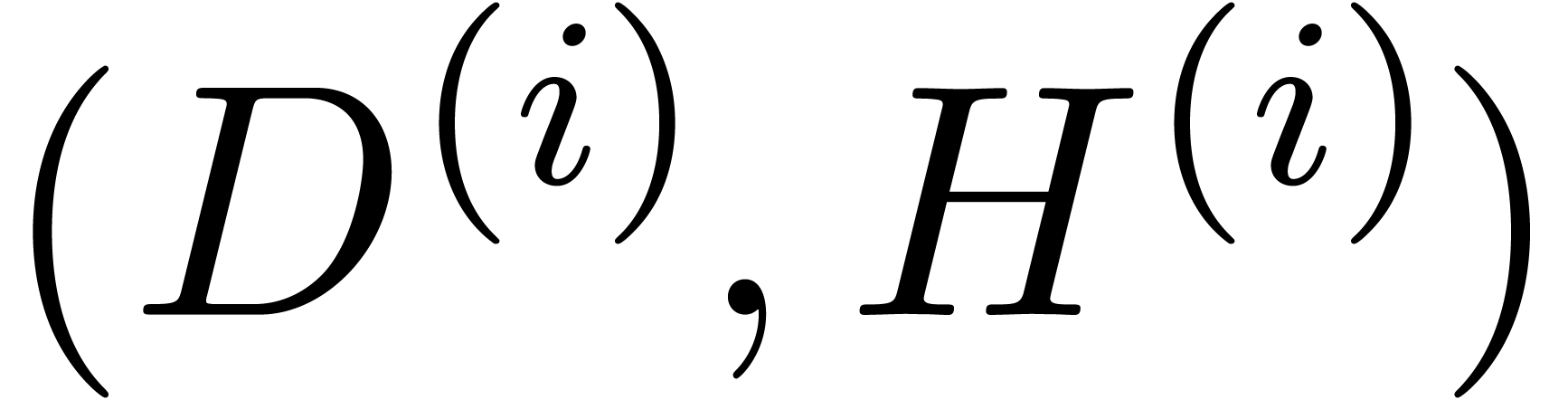 stand for the
stand for the
 -th
-th and
and  .
.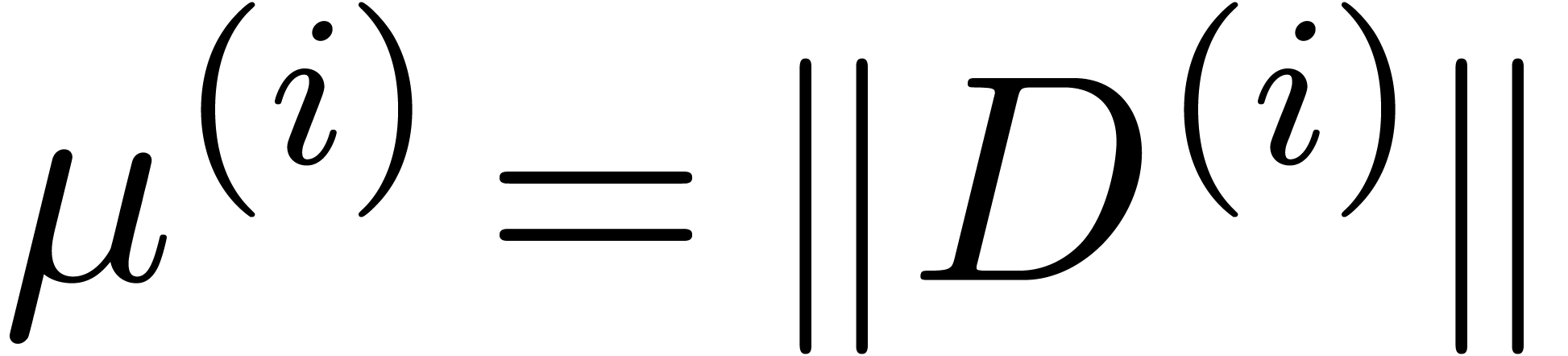 ,
,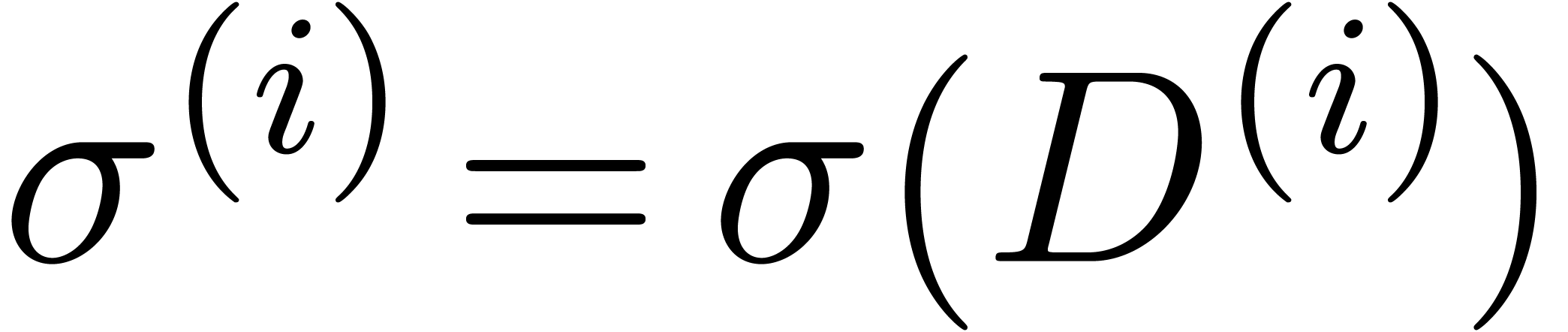 ,
,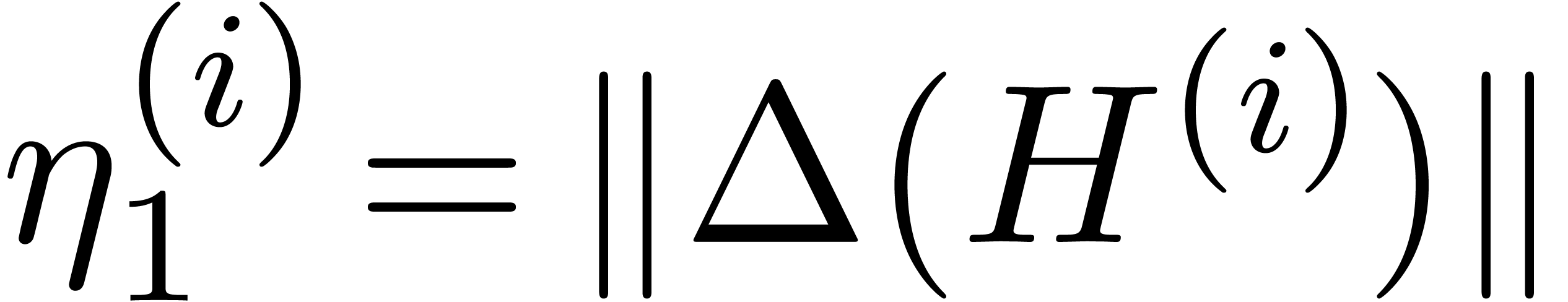 and
and 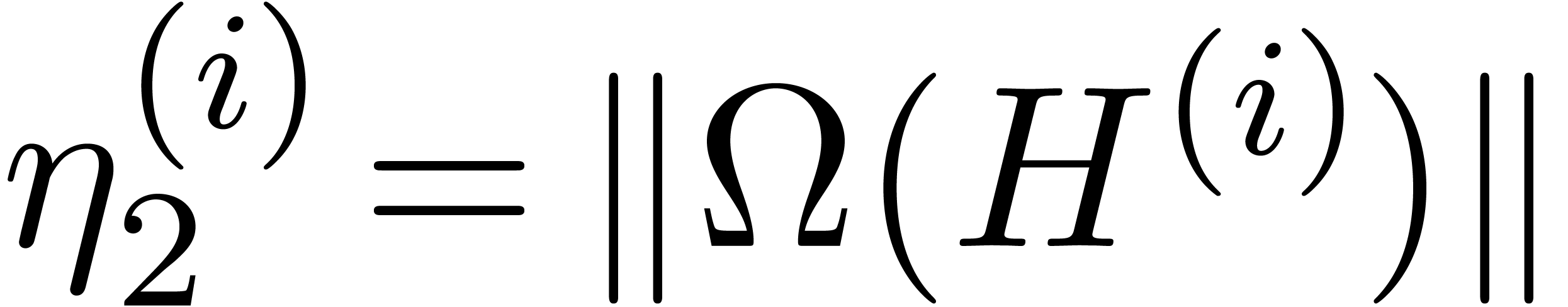 .
.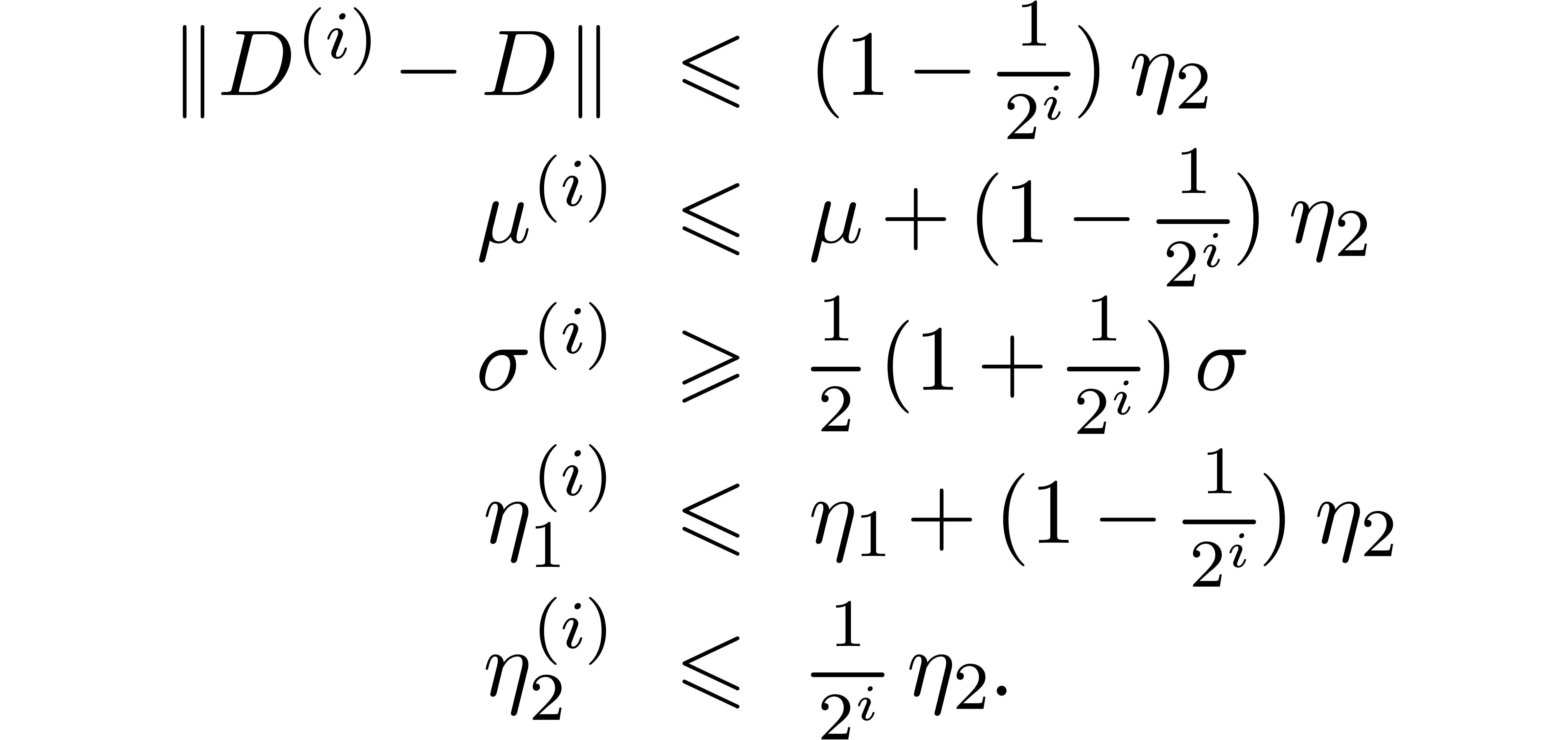
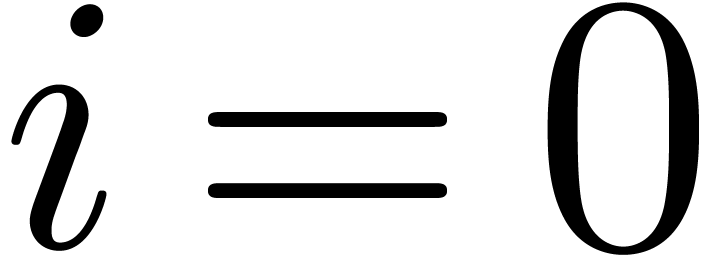 .
.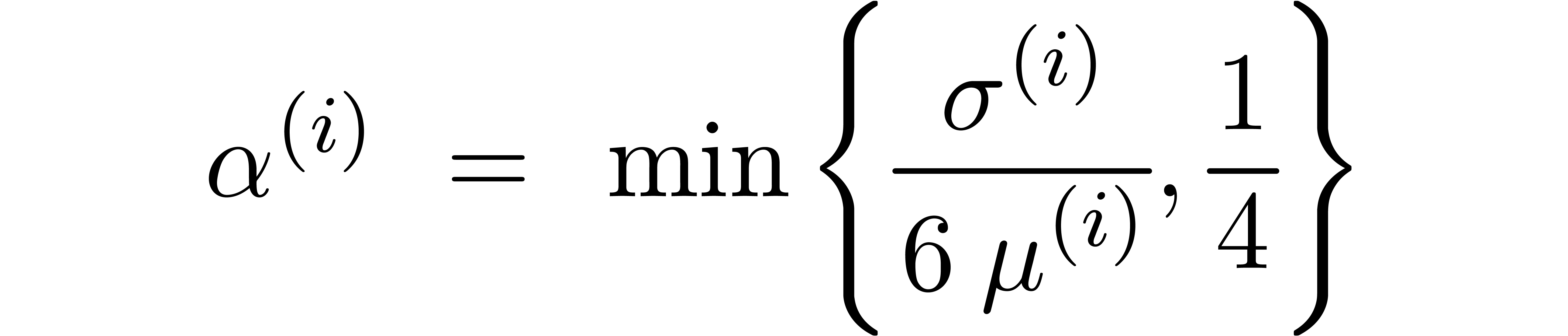
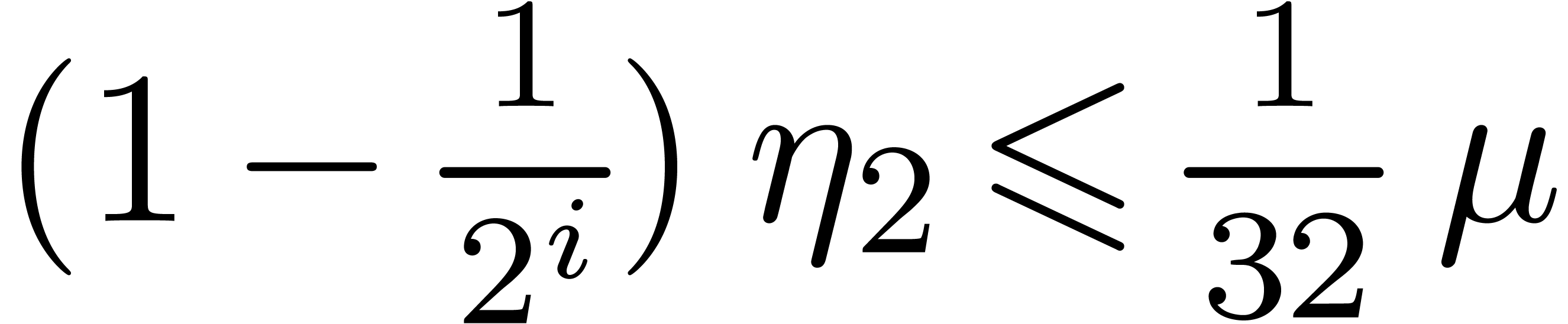 ,
,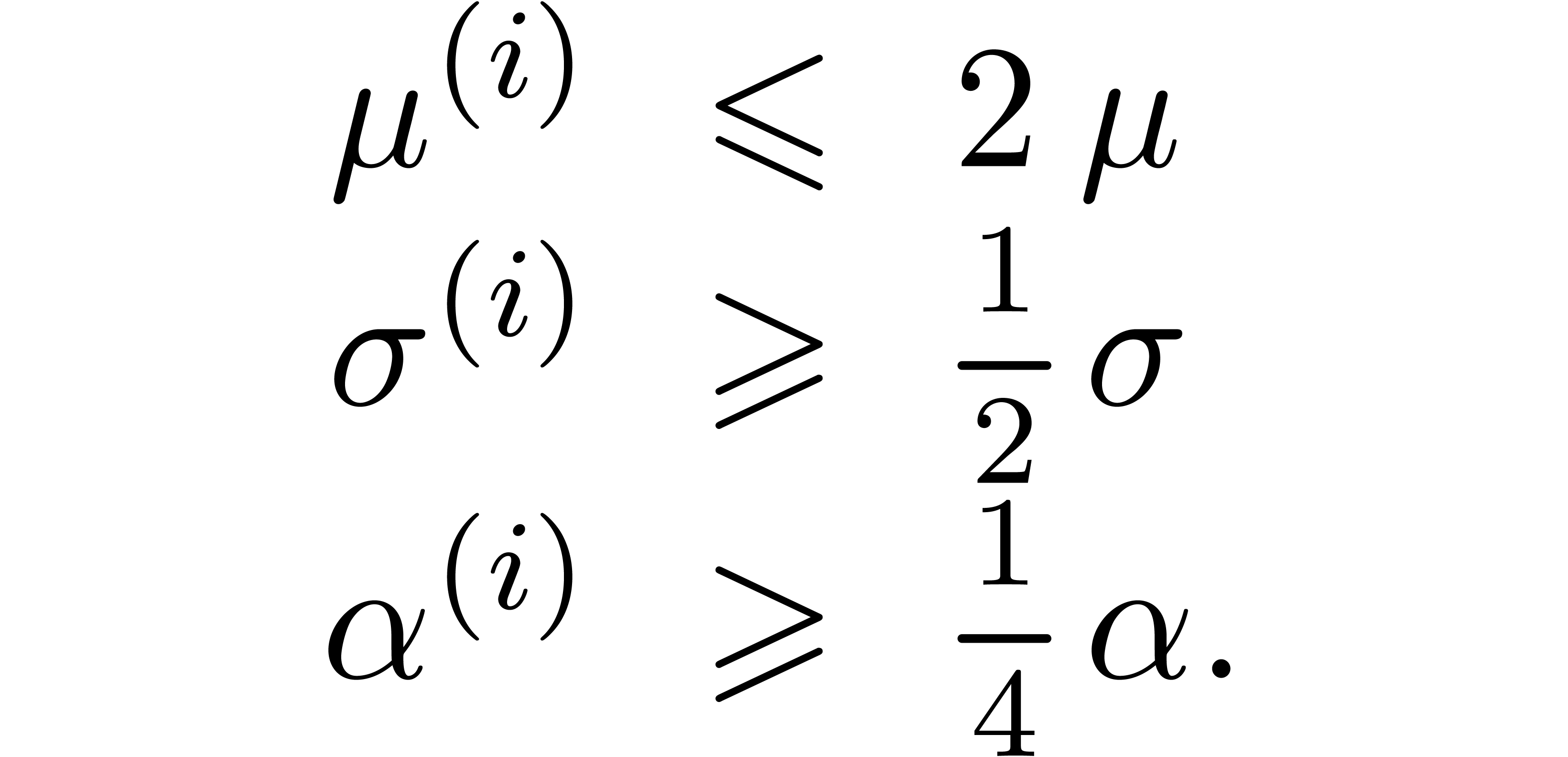
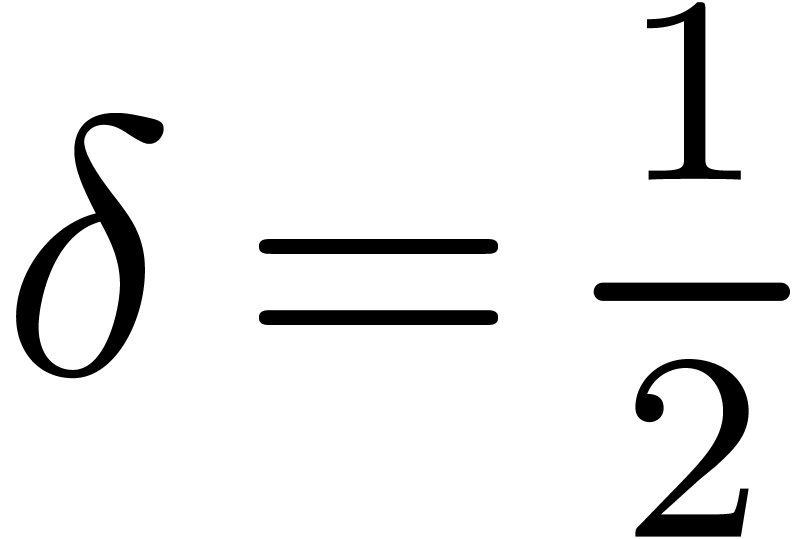 ,
,
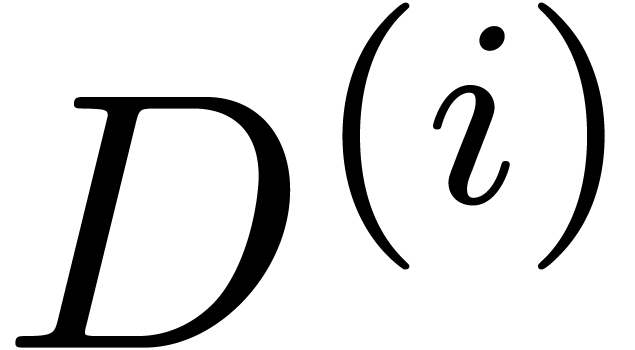 ,
,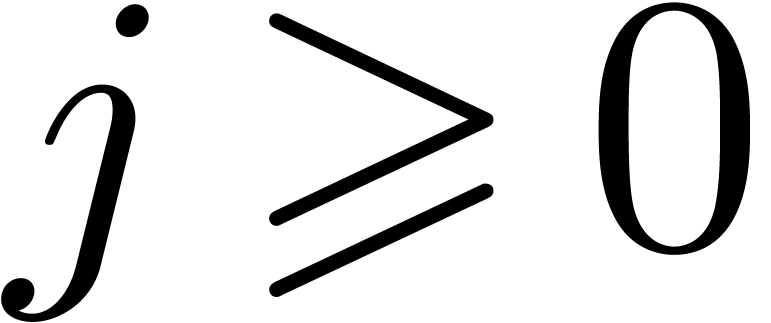 ,
,
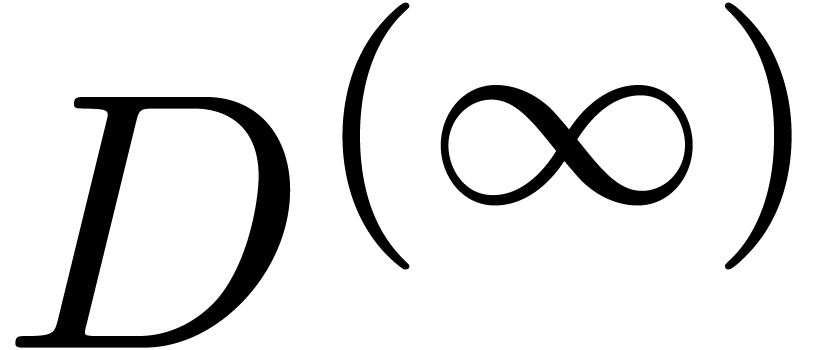 with
with 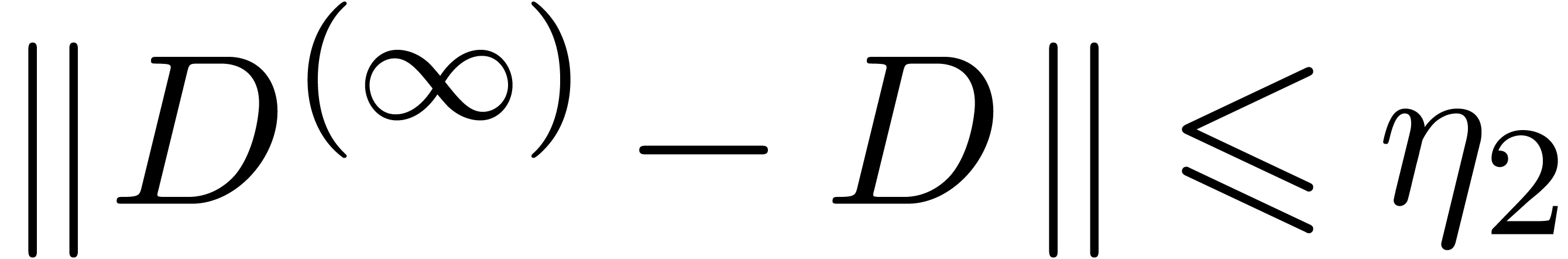 .
.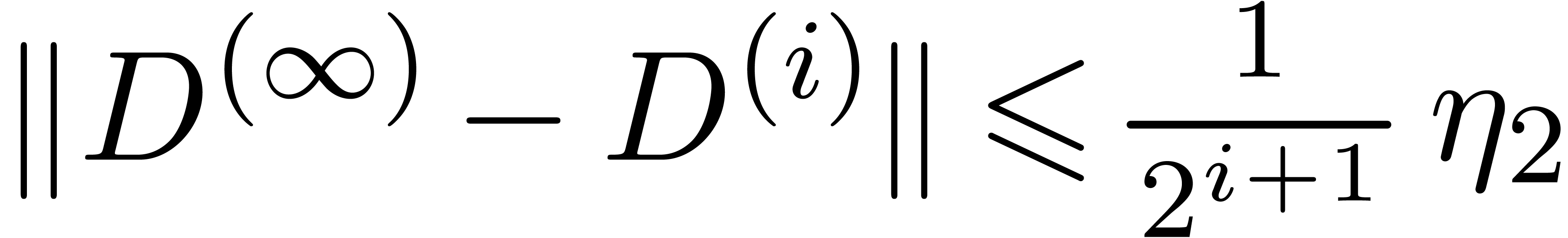 ,
,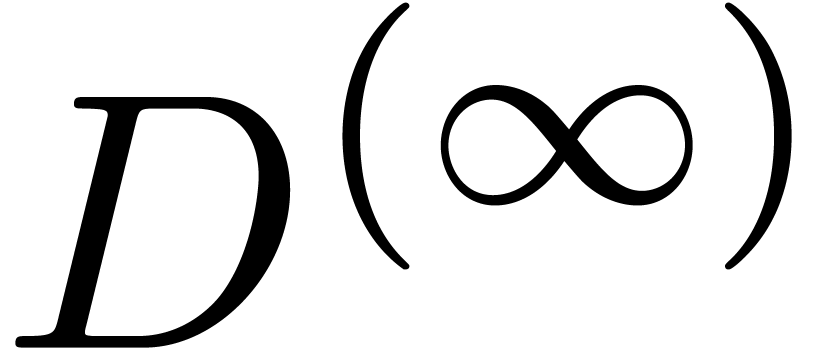 .
.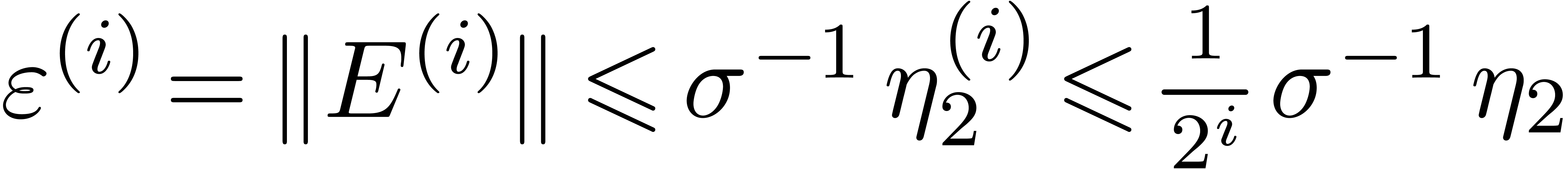 .
.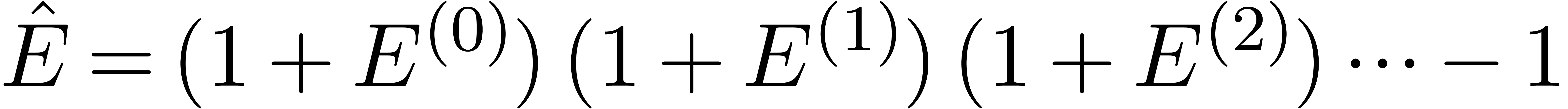
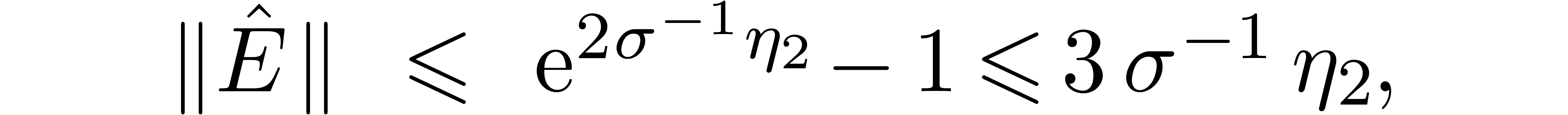
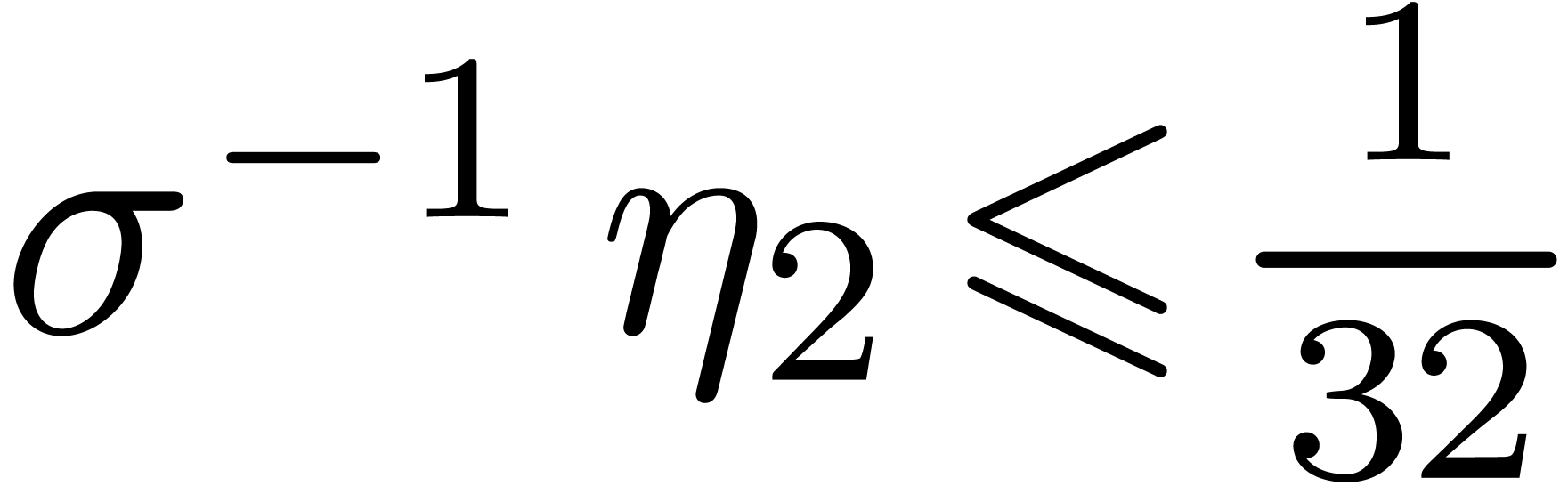 .
.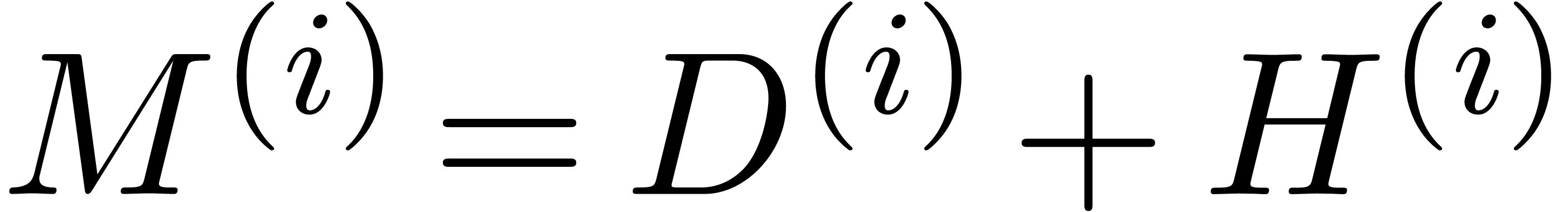 converges geometrically to
converges geometrically to
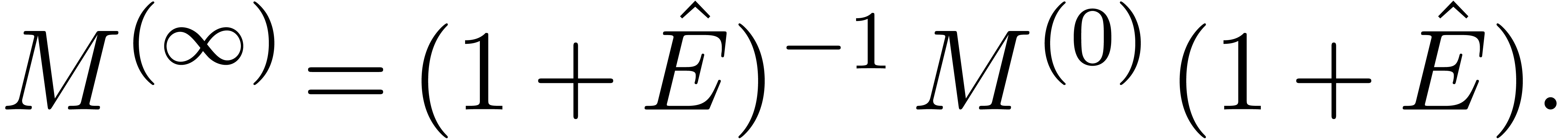
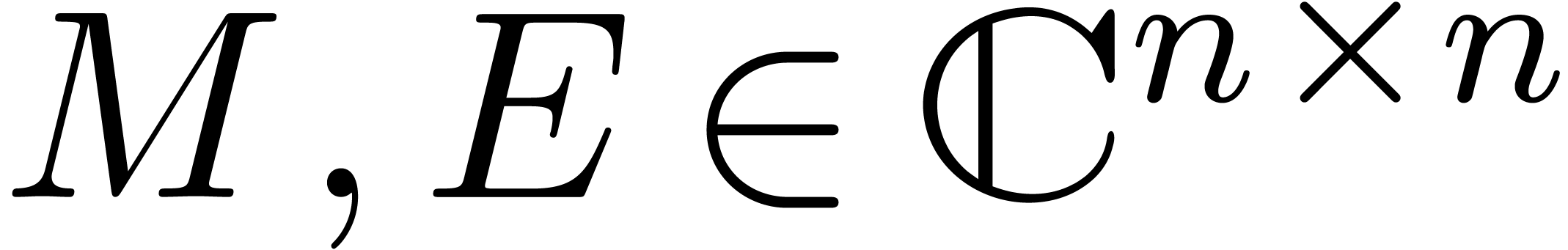 with
with 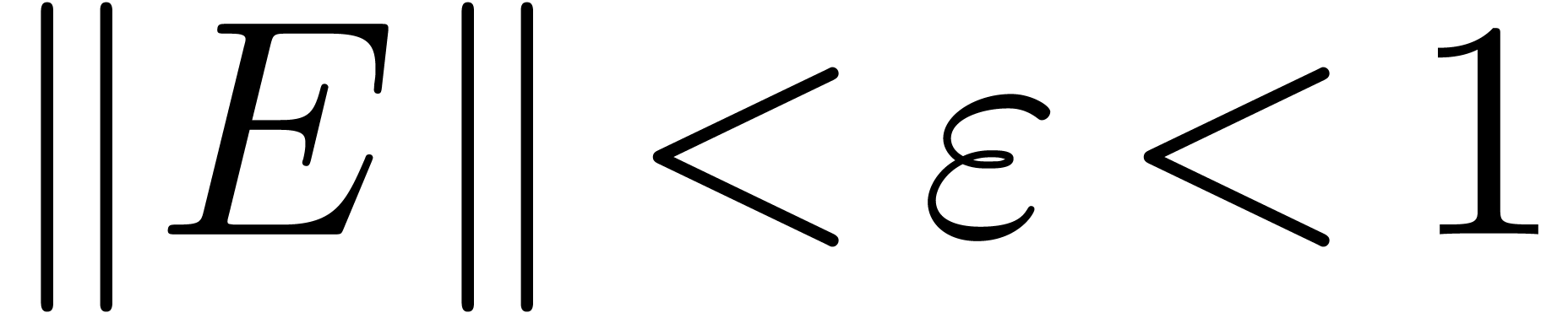 ,
,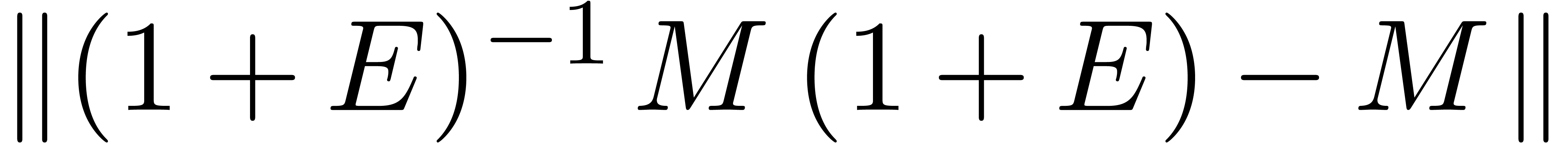
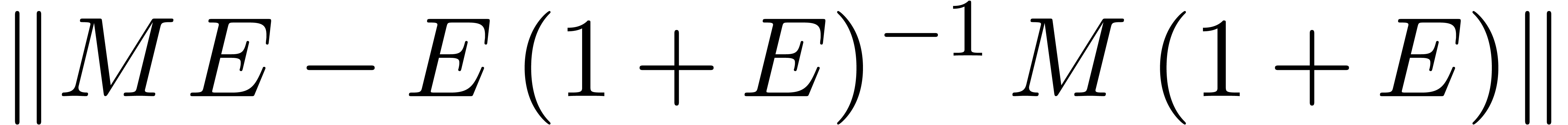
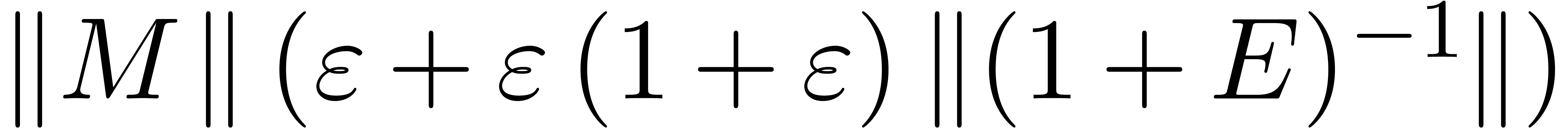
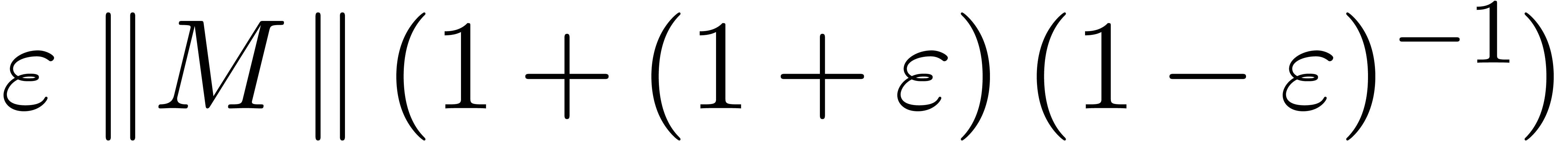
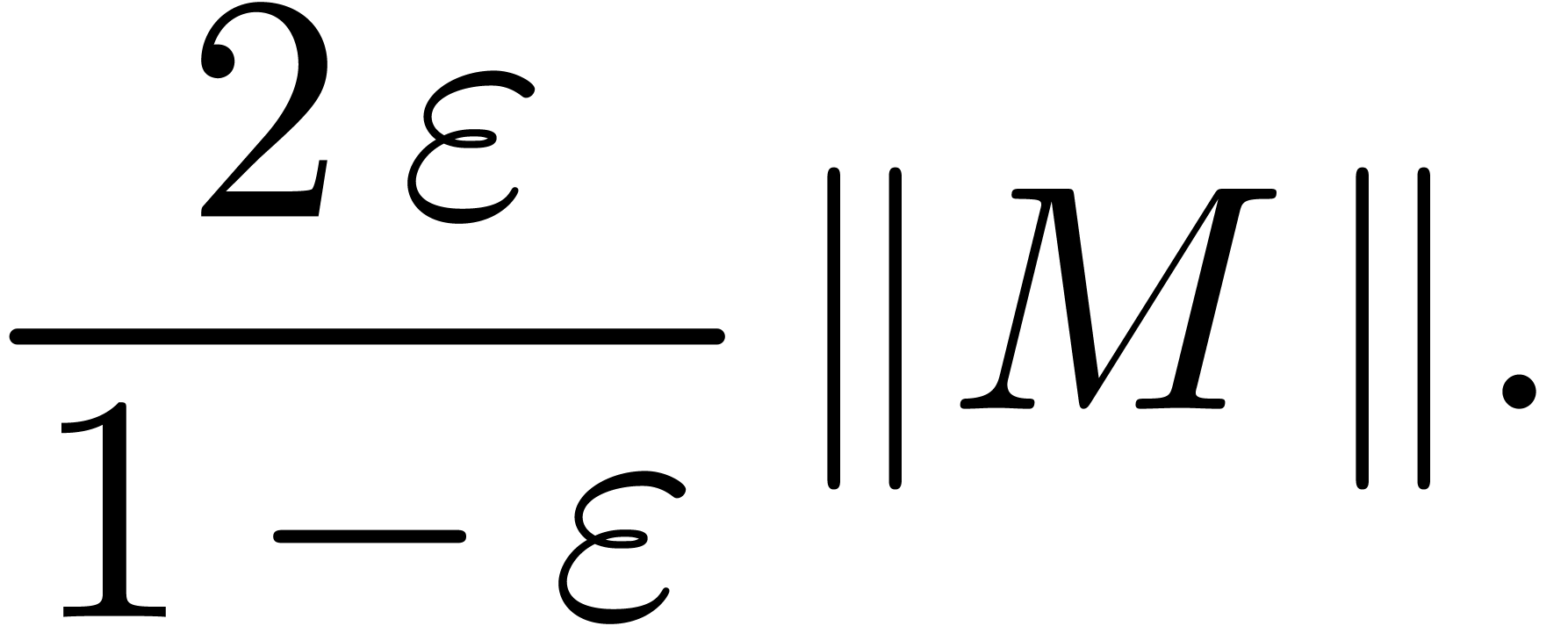
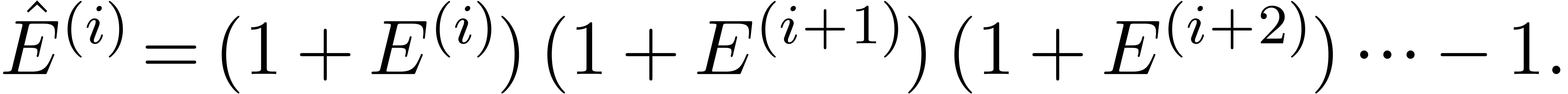 By the same arguments as above, we have
By the same arguments as above, we have
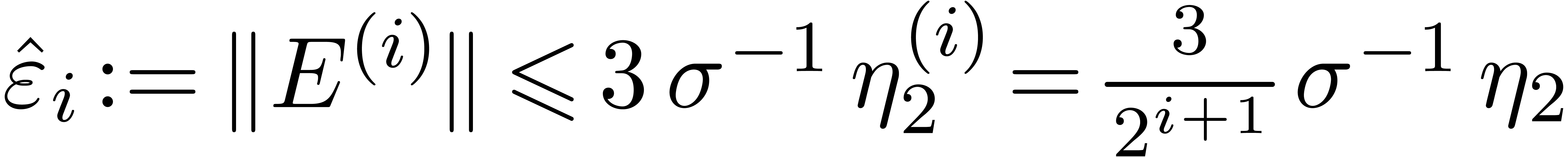 .
.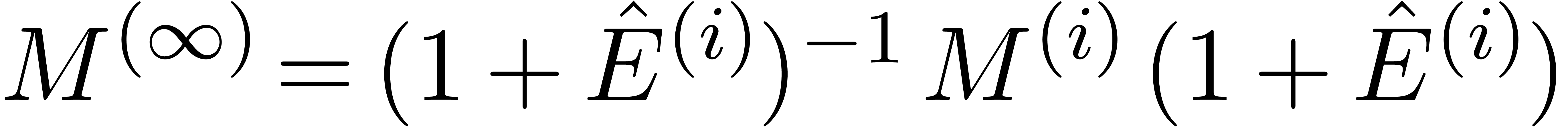 ,
,
 converges geometrically to
converges geometrically to  .
.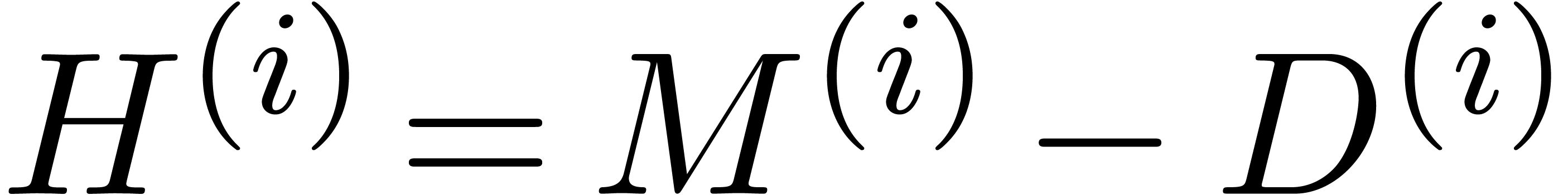 also converges geometrically to a limit
also converges geometrically to a limit 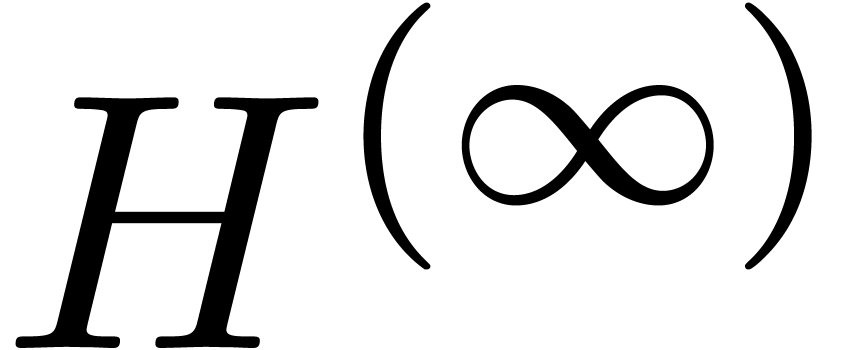 with
with 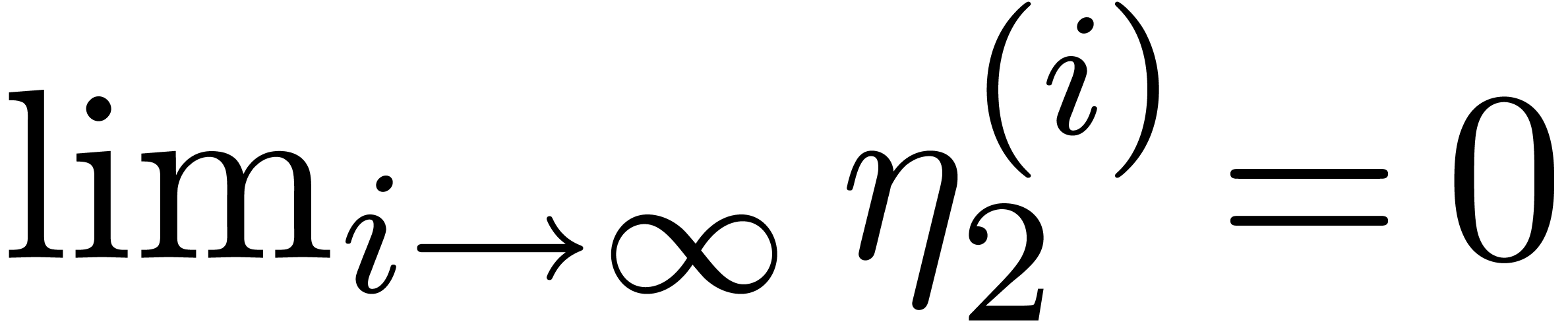 ,
,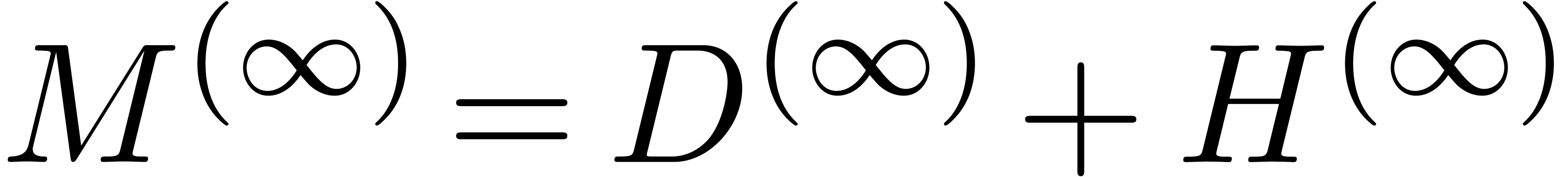 is block diagonal.
is block diagonal. .
.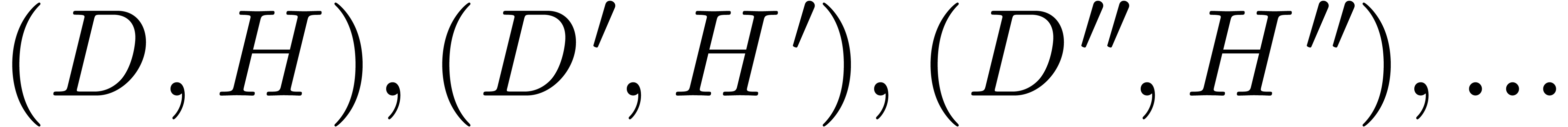 converges
quadratically to
converges
quadratically to 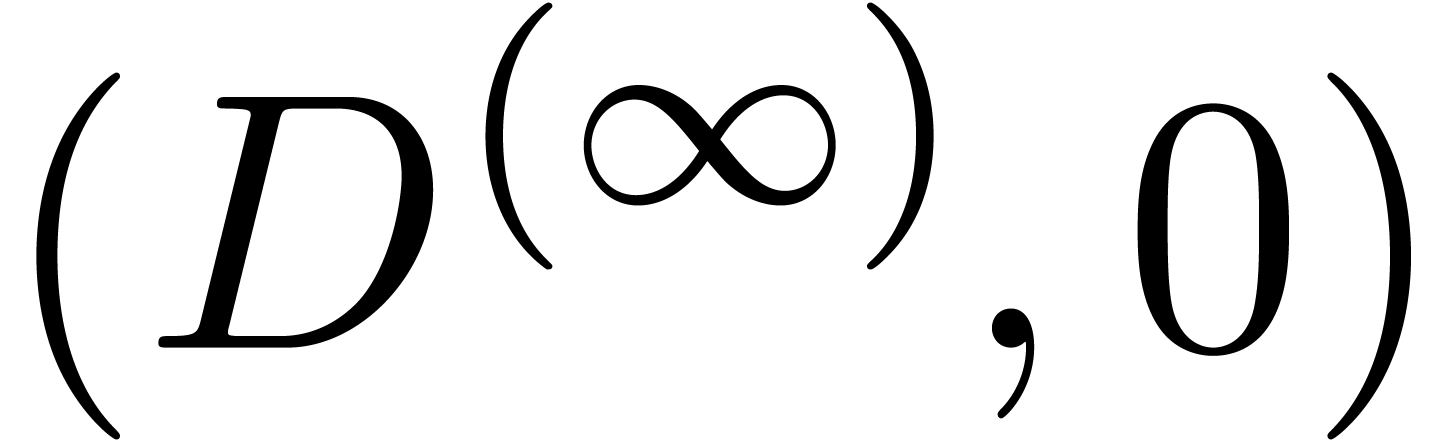 .
.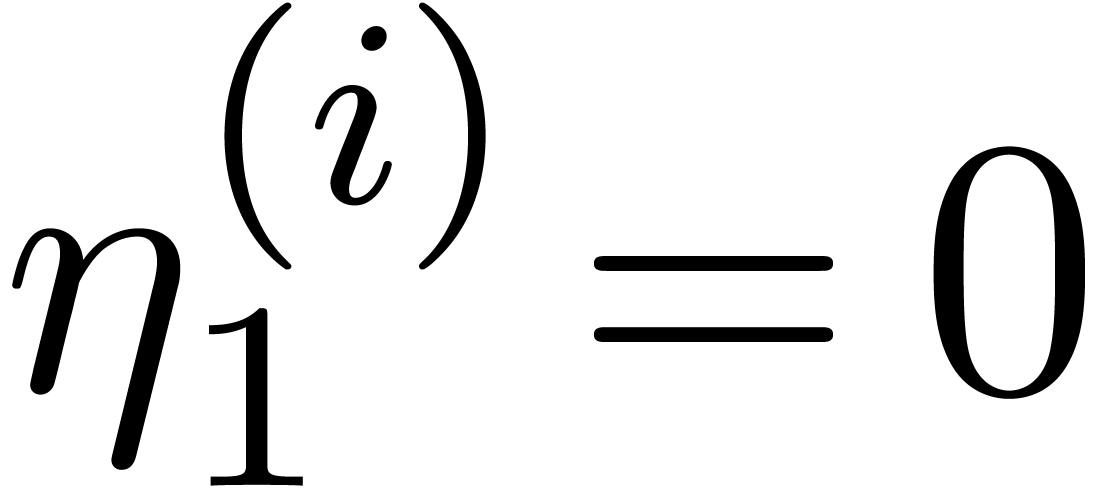 for all
for all 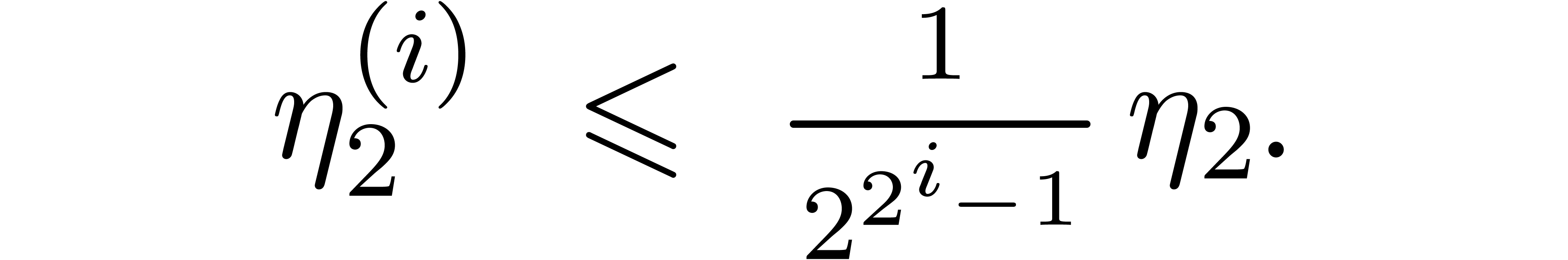
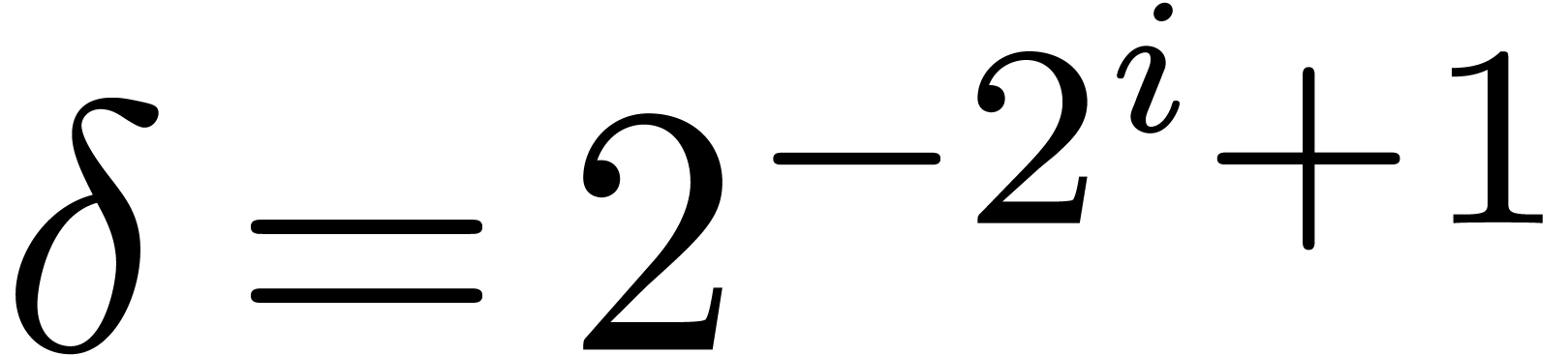 ,
,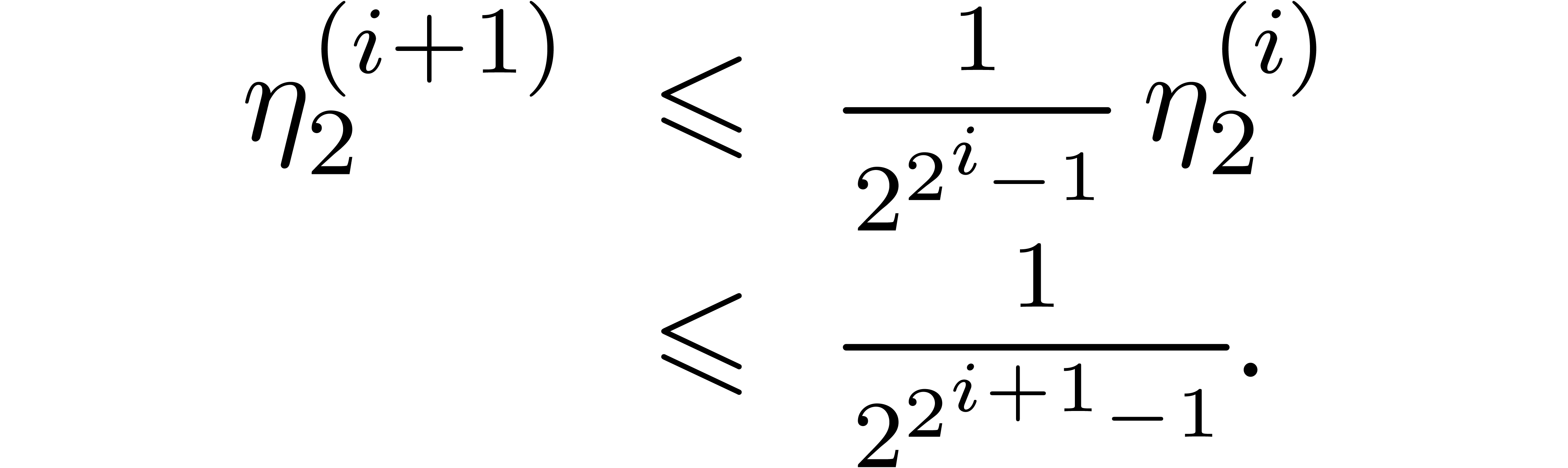
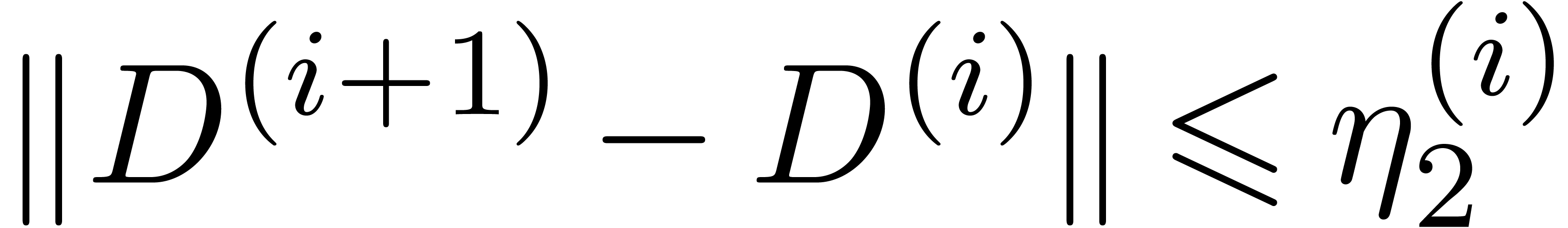 ,
, be the perturbation of a diagonal matrix (
be the perturbation of a diagonal matrix (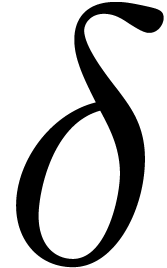 ,
,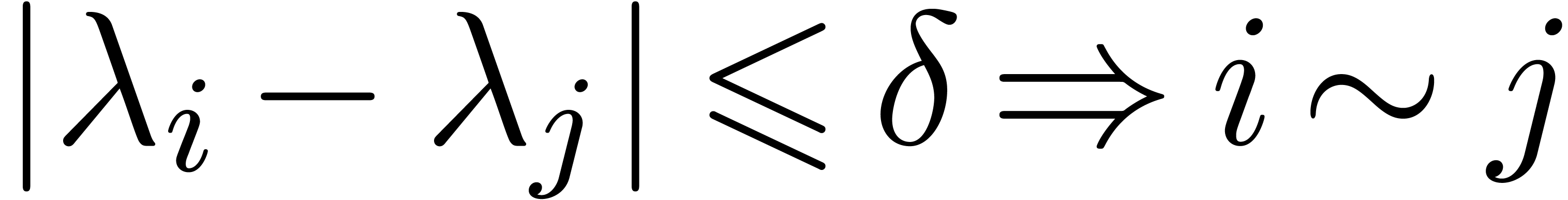 .
.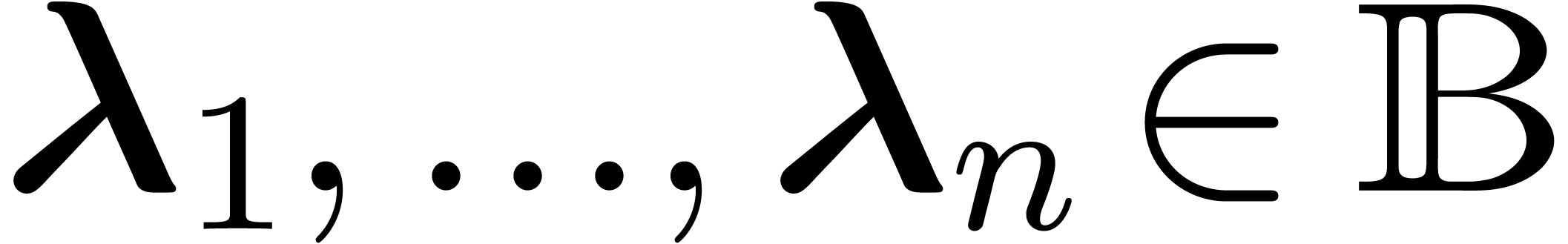 and
and 

 be the graph with vertices
be the graph with vertices
 and such that
and such that  are connected if and only if
are connected if and only if
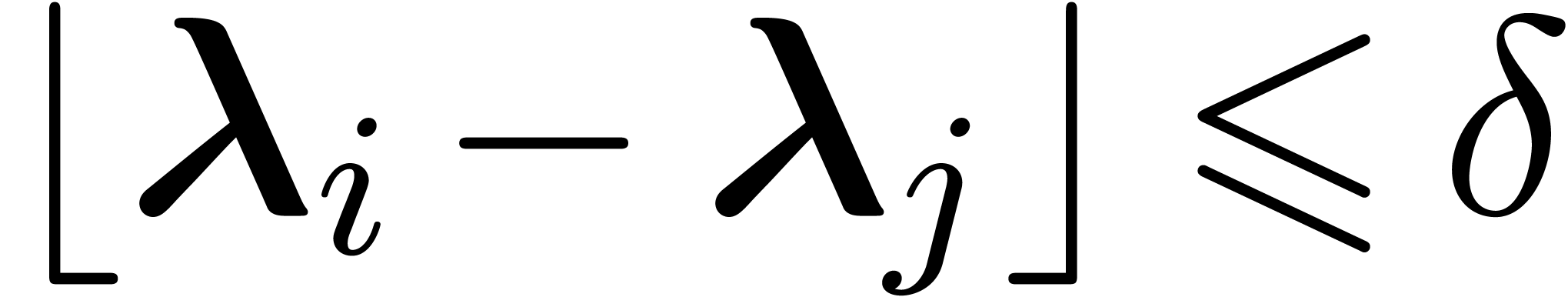 .
. the connected components of
the connected components of
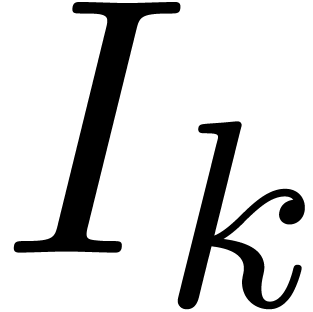 be the set of vertices of
be the set of vertices of
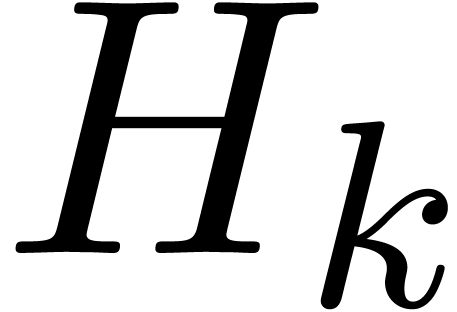 for each
for each 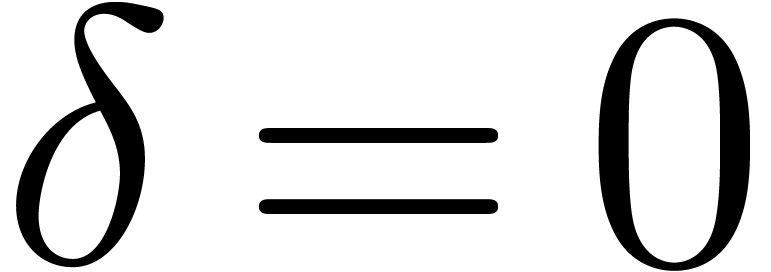 ,
,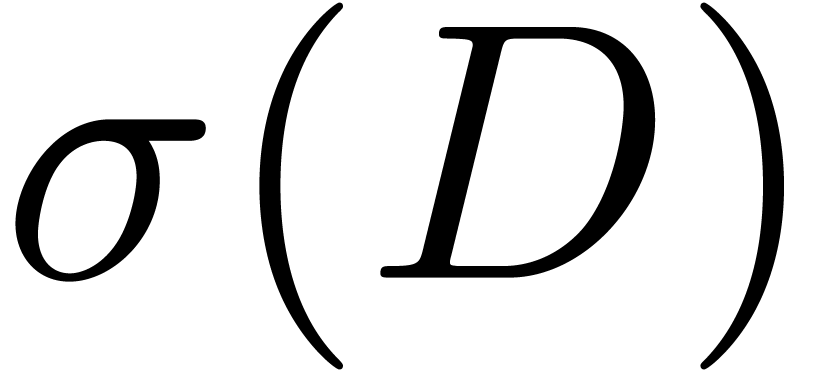 whenever the conditions are not satisfied. This will force the number
whenever the conditions are not satisfied. This will force the number
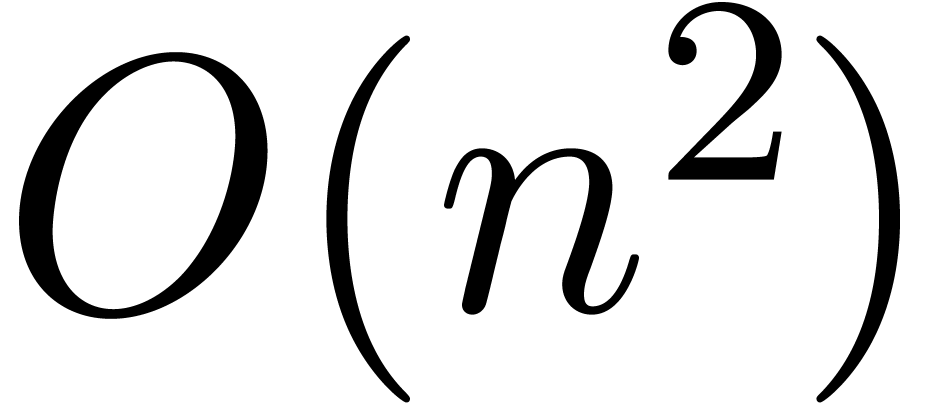 ,
, with
entries
with
entries  and
and
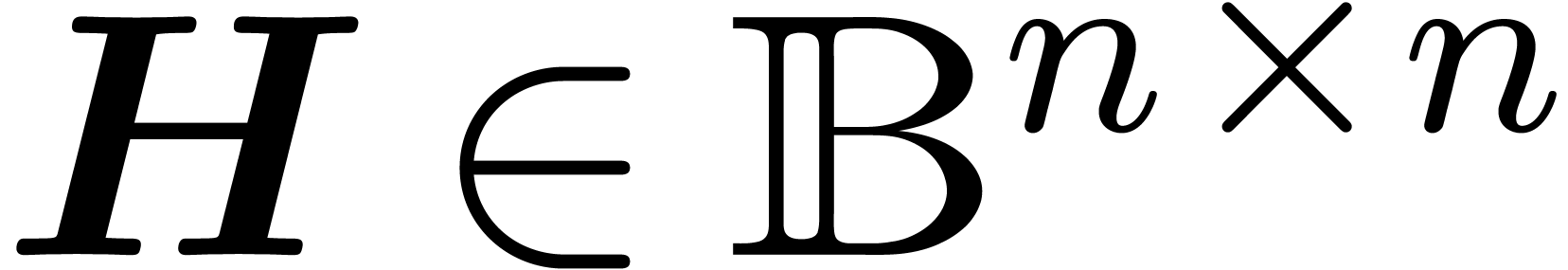
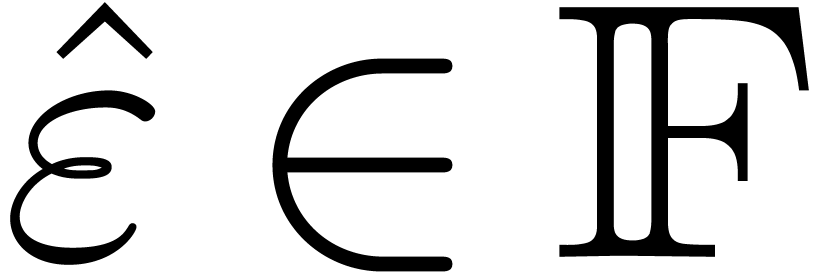 such that, for any
such that, for any 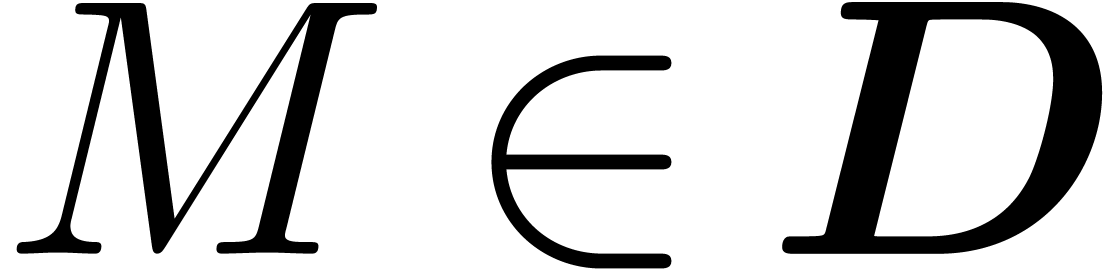 and
and 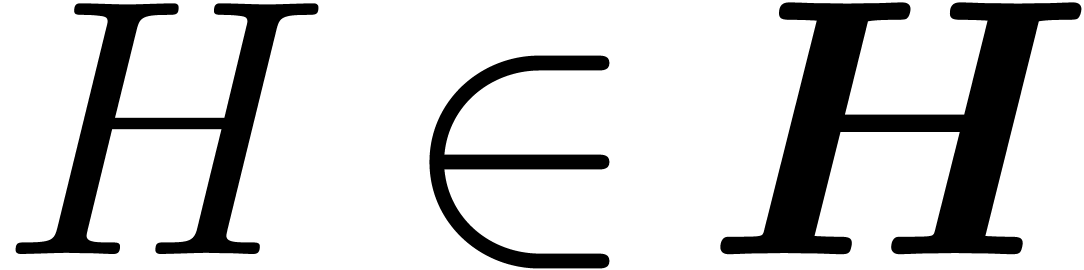 ,
,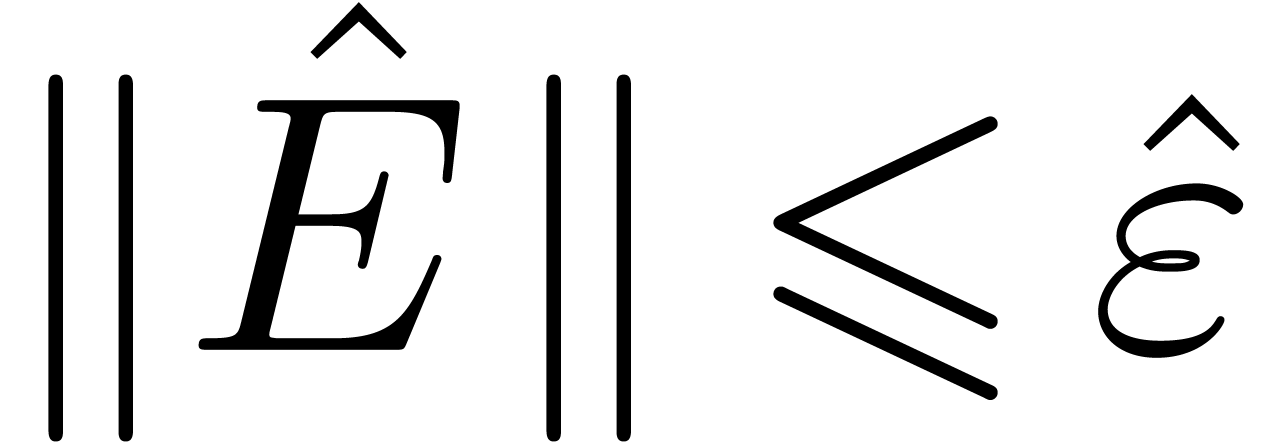
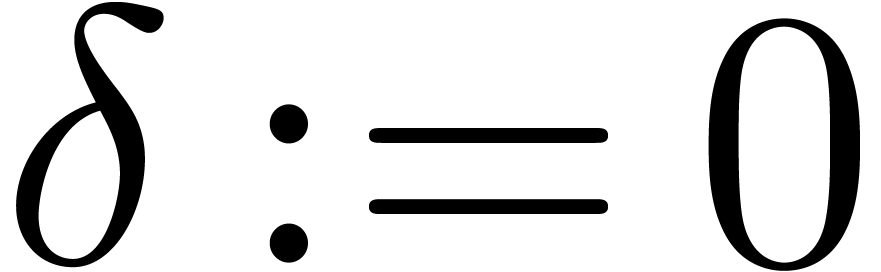
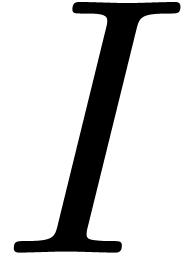 for
for  using
Cluster
using
Cluster
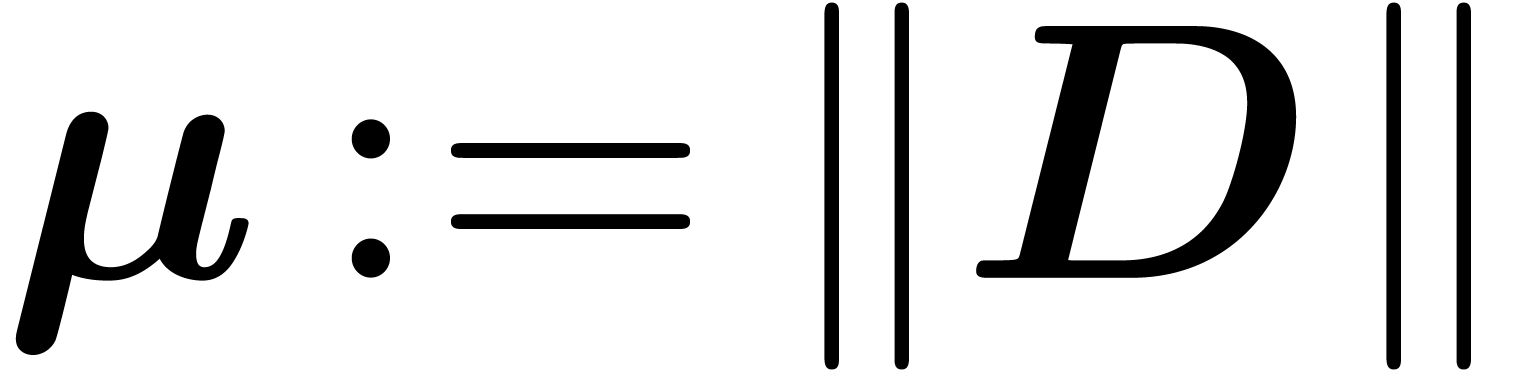 ,
,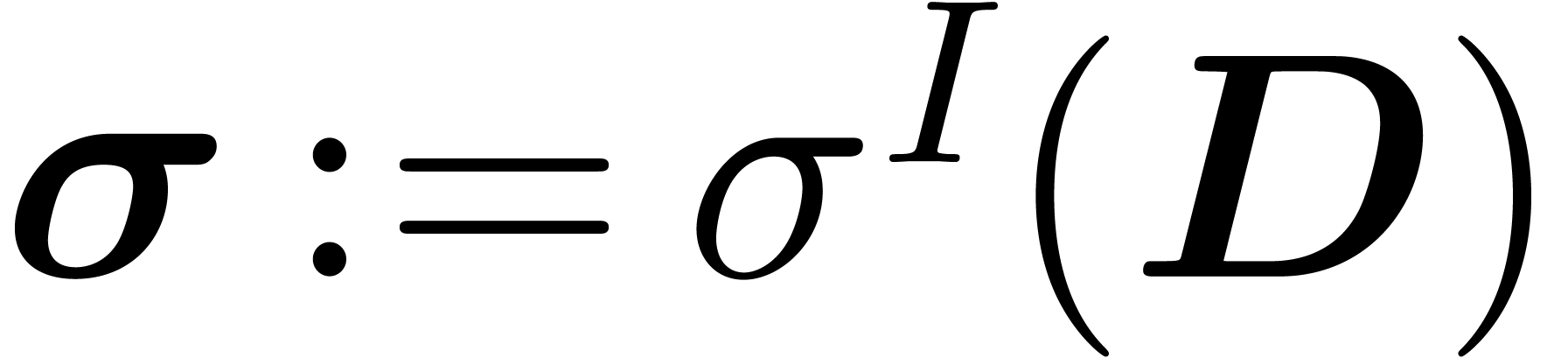 ,
, and
and 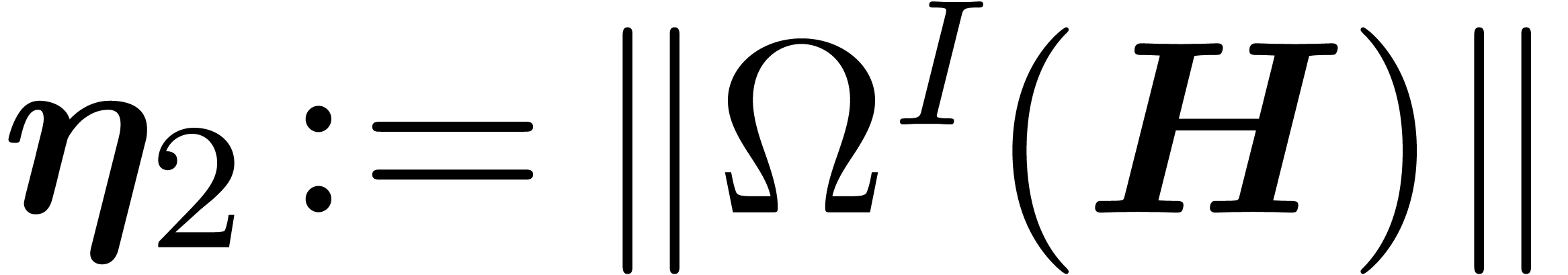
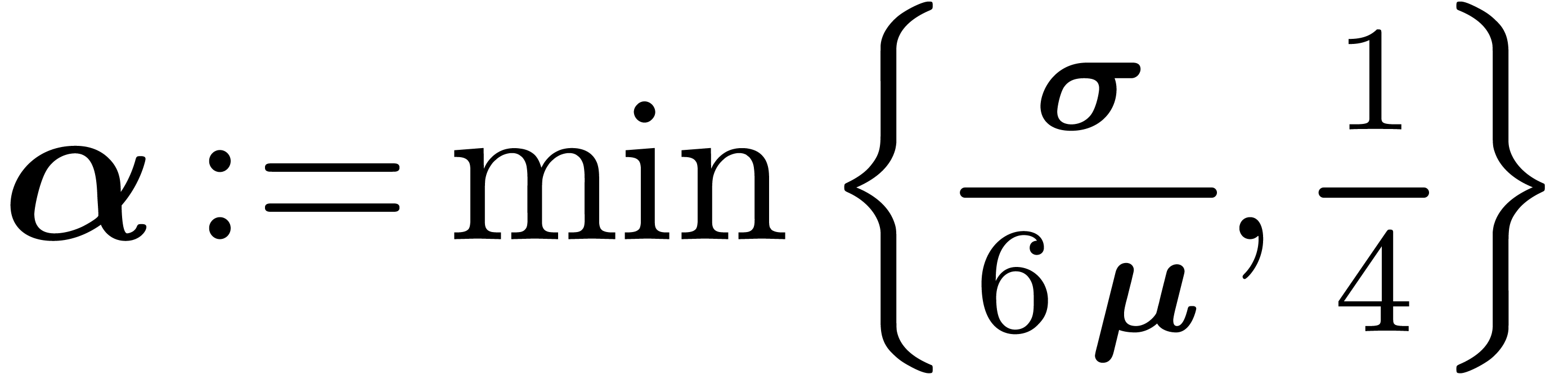
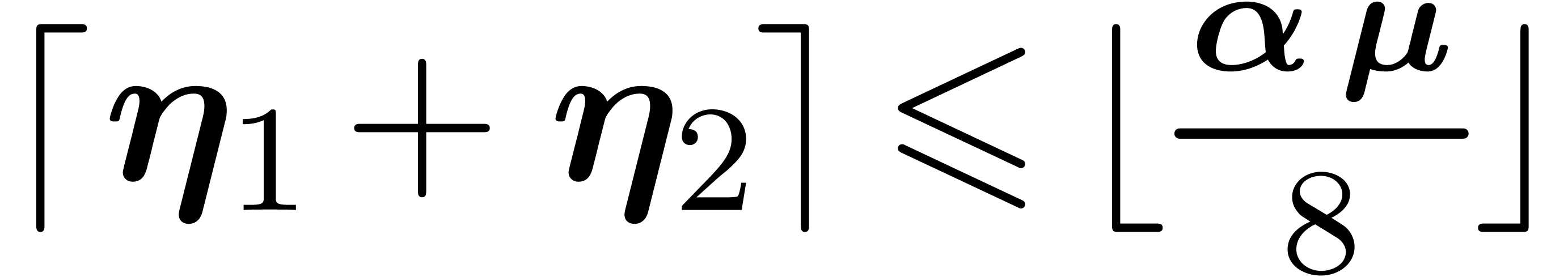 and
and 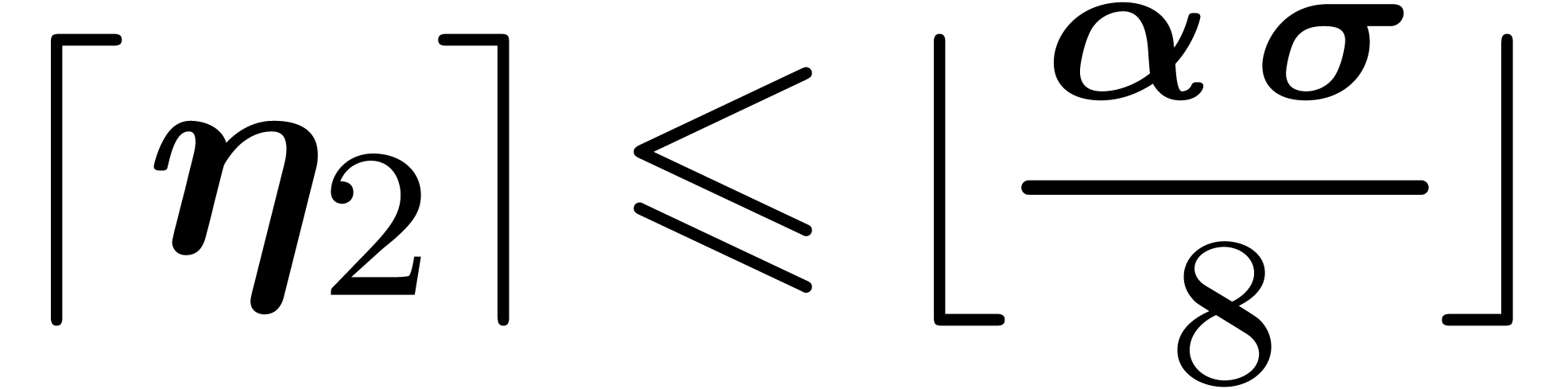 ,
,
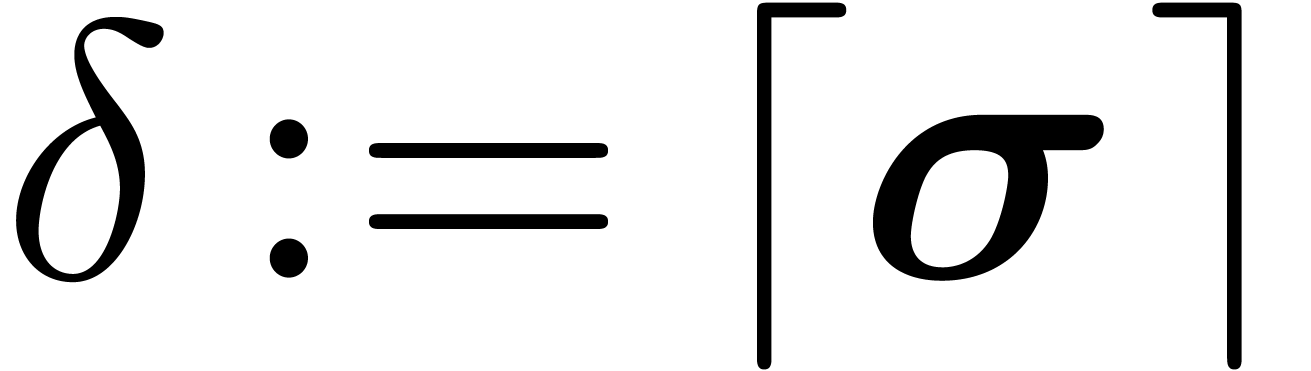
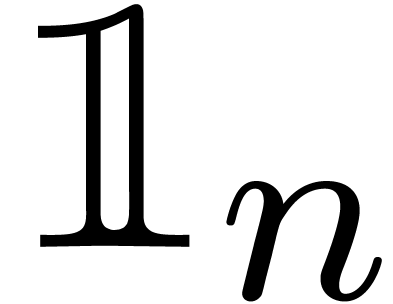 the
the 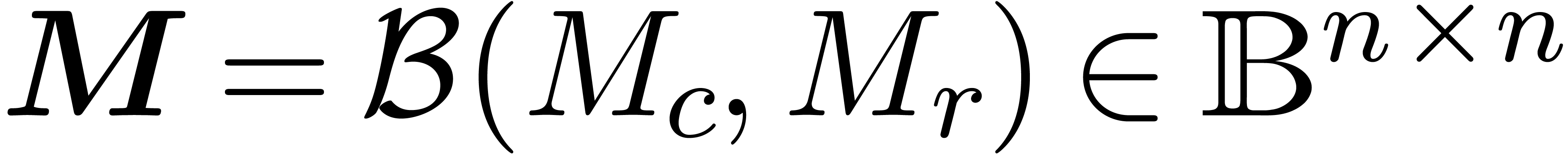 and
and 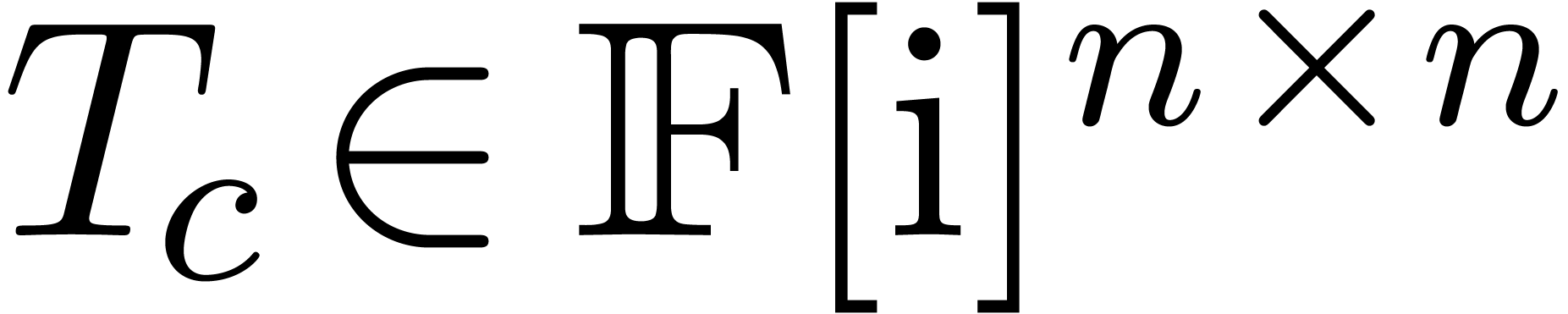
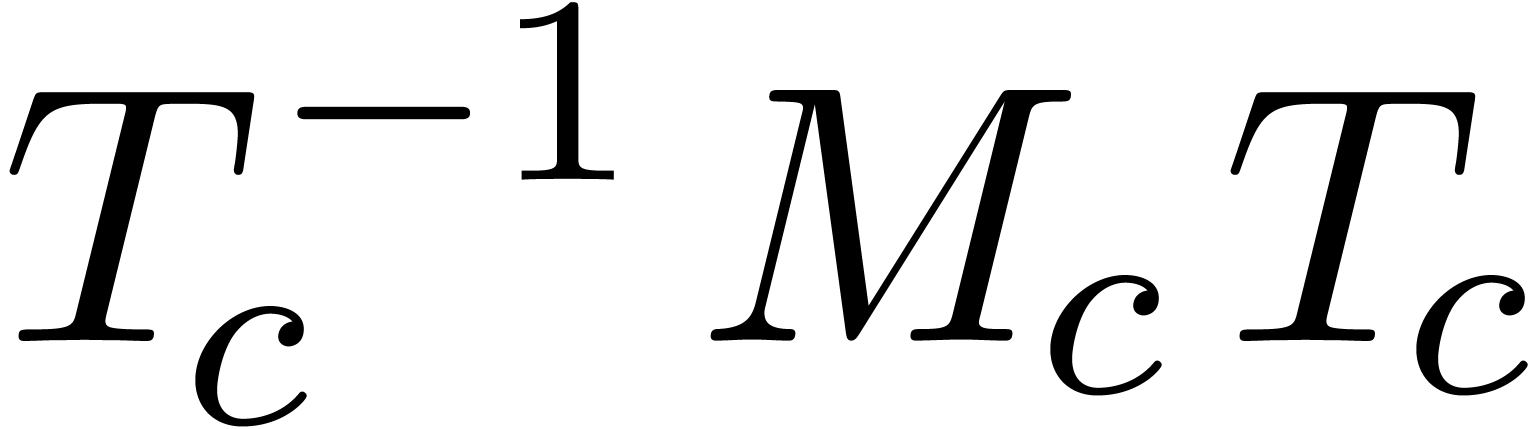 is approximately
diagonal
is approximately
diagonal
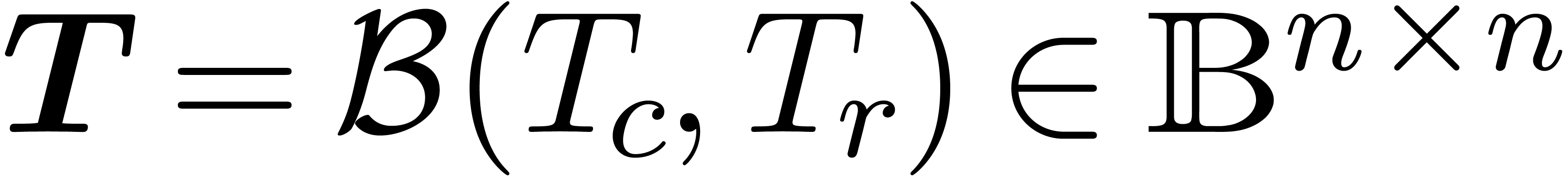 such that for any
such that for any 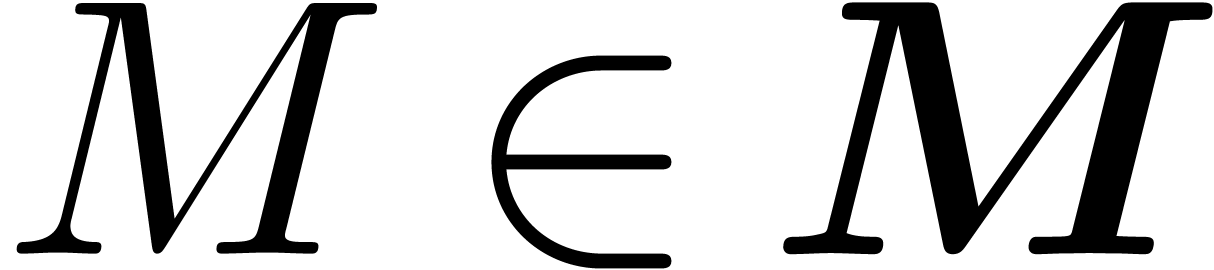 ,
, for which
for which 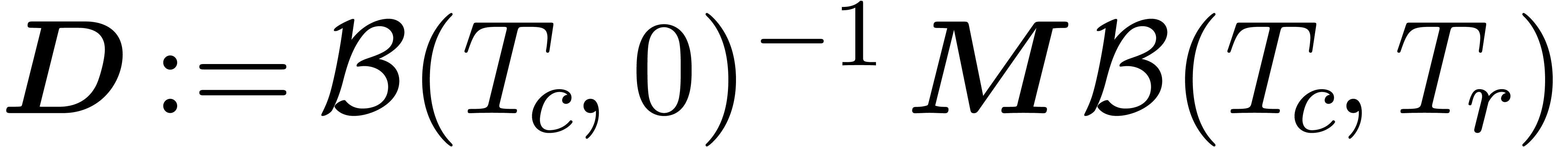

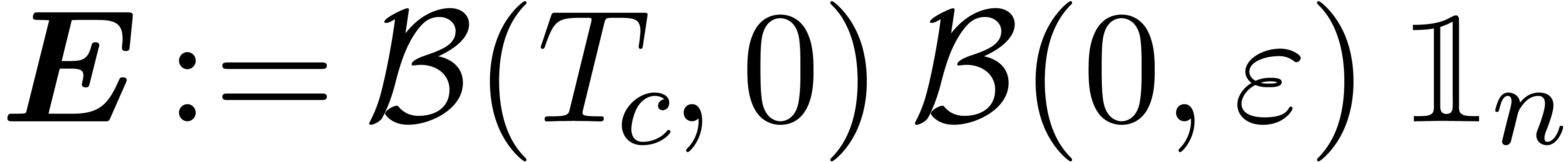
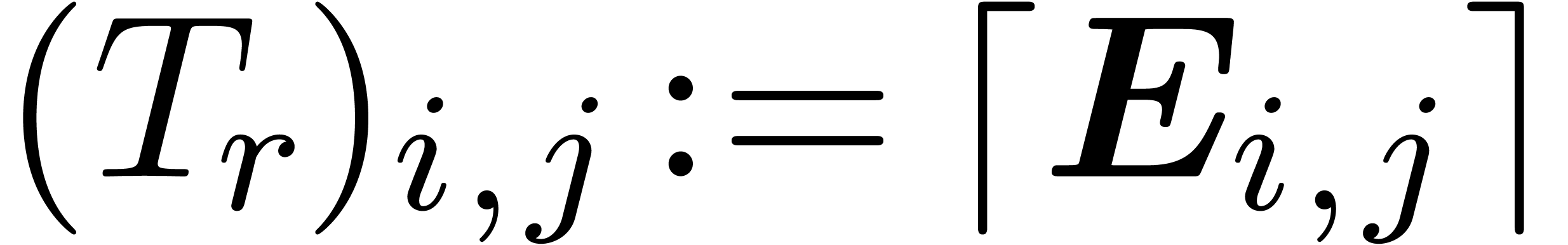 for all
for all 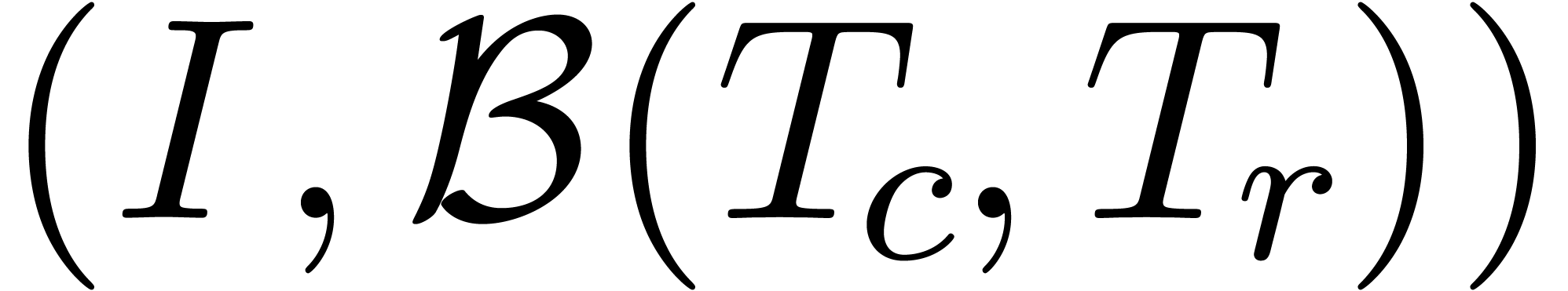
 of a matrix
of a matrix  .
. .
.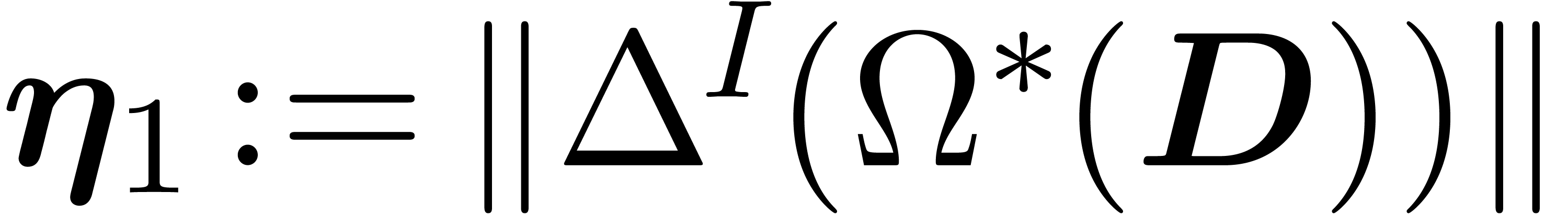 and
and 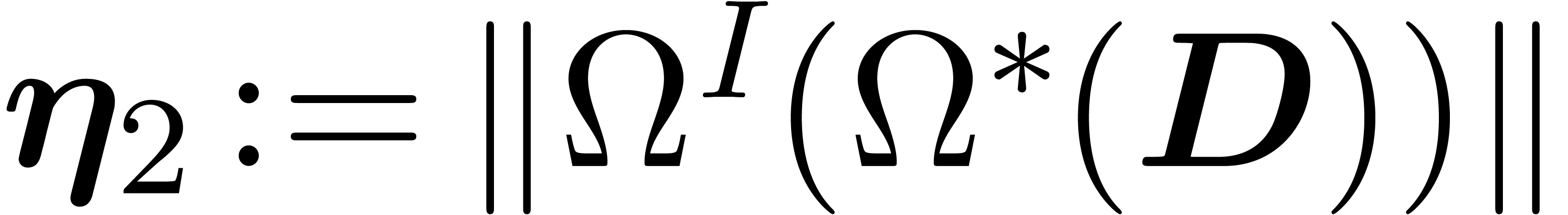
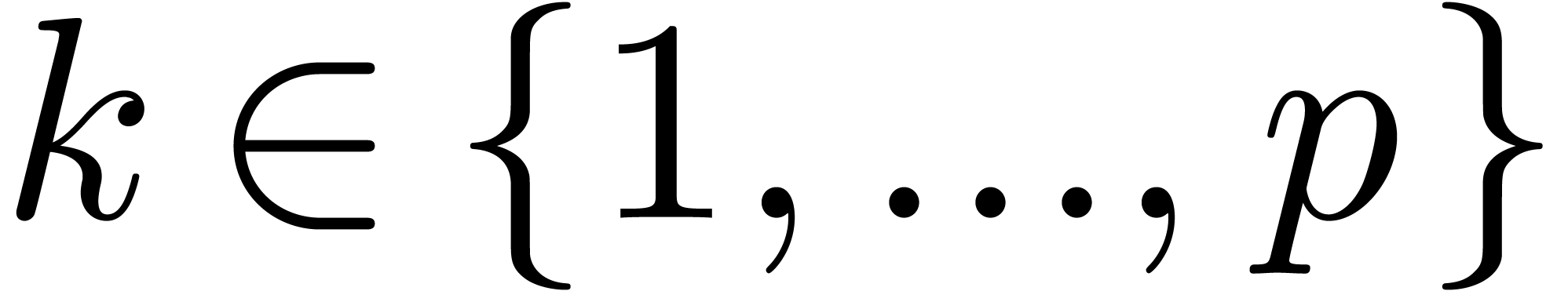 do
do
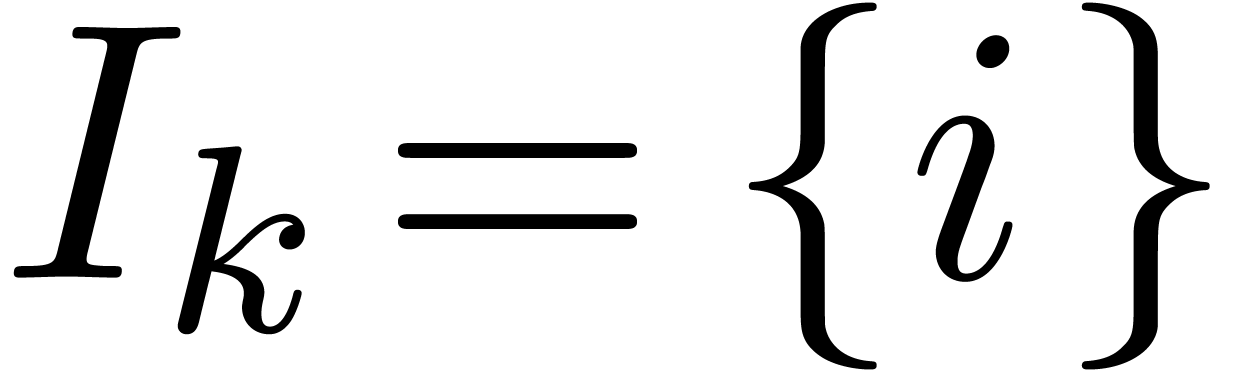 for some
for some 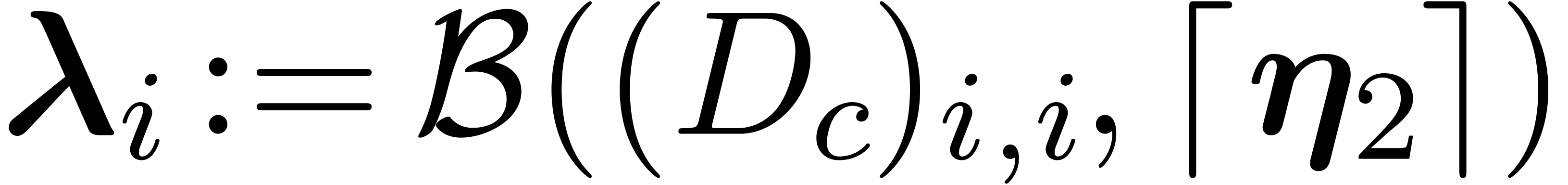
 be the barycenter of the
be the barycenter of the 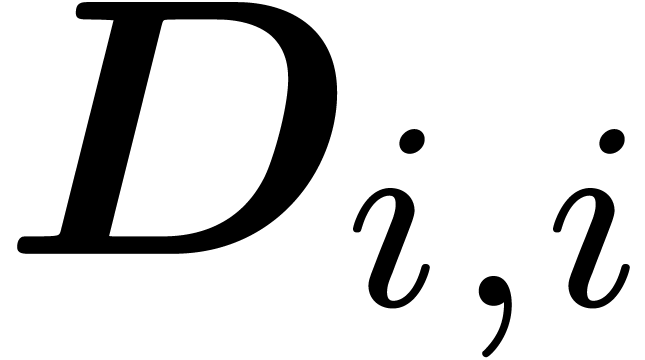 with
with 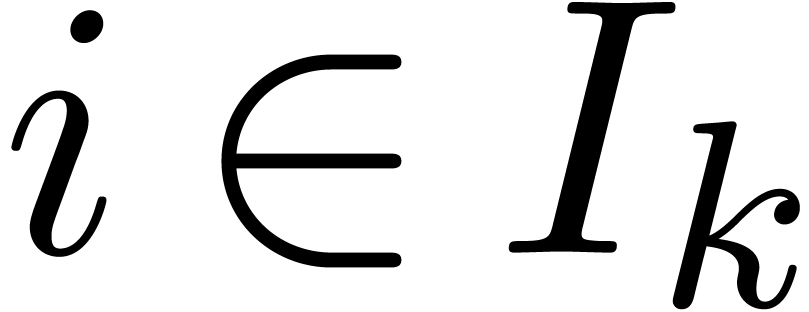
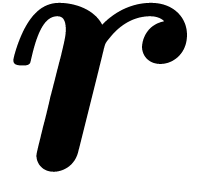 be the maximum of
be the maximum of 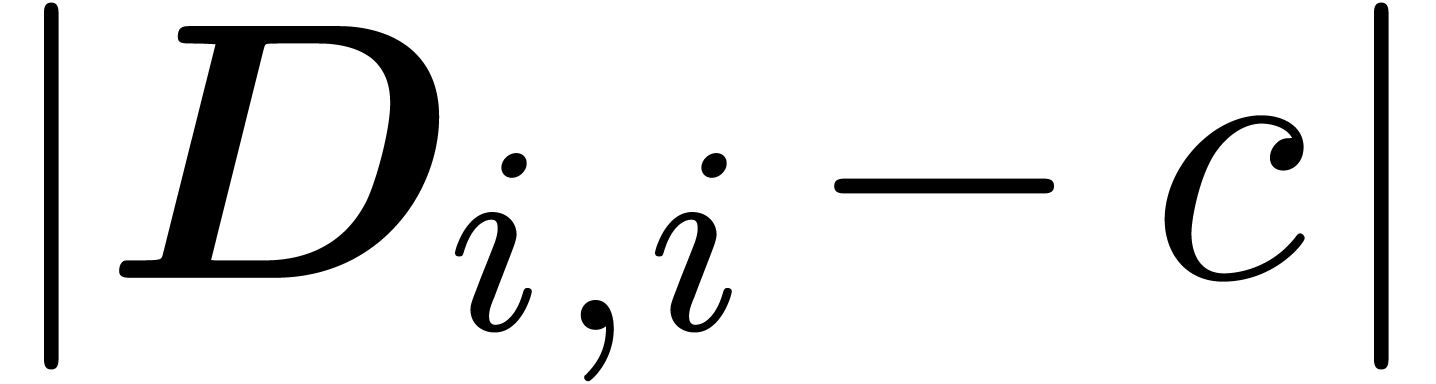 for
for  for all
for all 
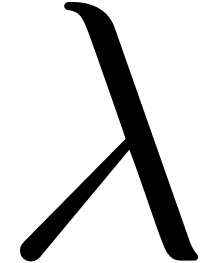 .
.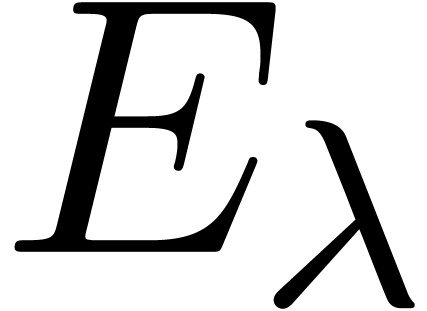 corresponding to
corresponding to  ,
, denote the full invariant subspace
associated to the eigenvalue
denote the full invariant subspace
associated to the eigenvalue 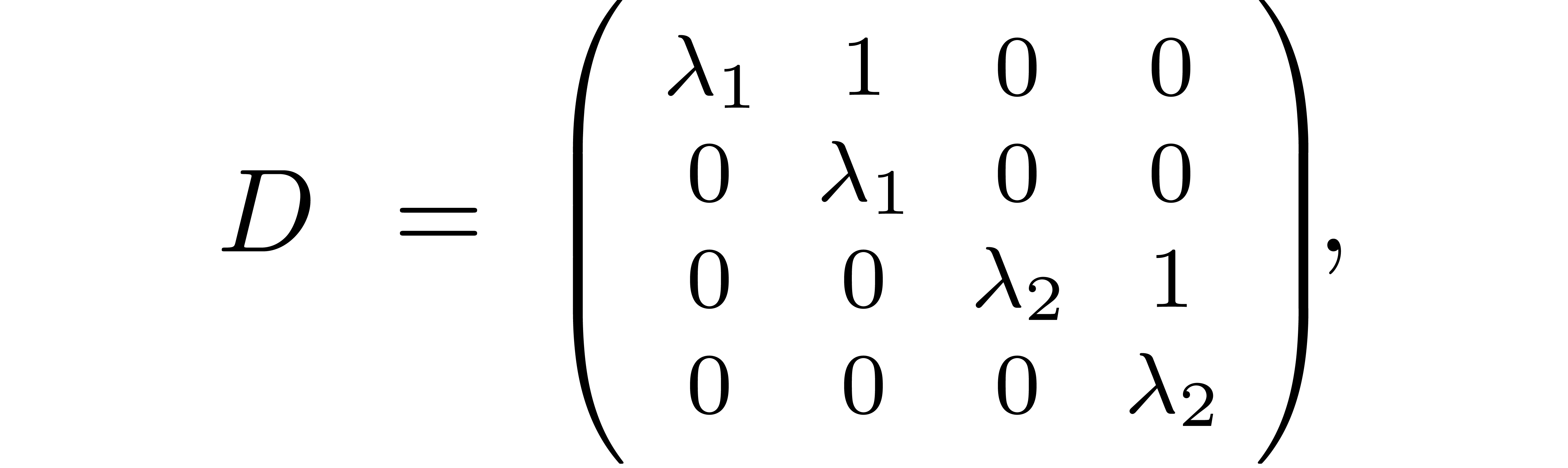
 .
. ,
,
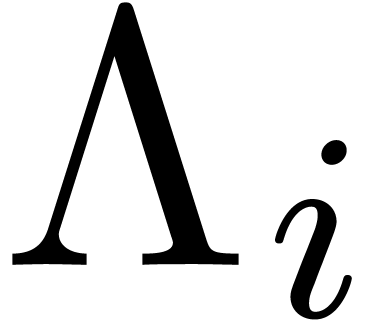 are sufficiently close to
are sufficiently close to 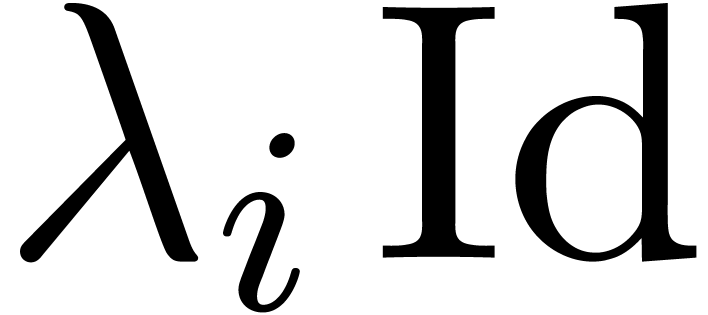 ,
,