| Fast Chinese remaindering in
practice |
|
Laboratoire d'informatique, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau
|
|
|
The Chinese remainder theorem is a key tool for the
design of efficient multi-modular algorithms. In this paper, we study
the case when the moduli  are fixed and can
even be chosen by the user. If
are fixed and can
even be chosen by the user. If  is small or
moderately large, then we show how to choose gentle moduli
that allow for speedier Chinese remaindering. The multiplication of
integer matrices is one typical application where we expect practical
gains for various common matrix dimensions and bitsizes of the
coefficients.
is small or
moderately large, then we show how to choose gentle moduli
that allow for speedier Chinese remaindering. The multiplication of
integer matrices is one typical application where we expect practical
gains for various common matrix dimensions and bitsizes of the
coefficients.
Keywords: Chinese remainder theorem,
algorithm, complexity, integer matrix multiplication
1Introduction
Modular reduction is an important tool for speeding up computations in
computer arithmetic, symbolic computation, and elsewhere. The technique
allows to reduce a problem that involves large integer or polynomial
coefficients to one or more similar problems that only involve small
modular coefficients. Depending on the application, the solution to the
initial problem is reconstructed via the Chinese remainder
theorem or Hensel's lemma. We refer to [9, chapter 5] for a
gentle introduction to this topic.
In this paper, we will mainly be concerned with multi-modular algorithms
over the integers that rely on the Chinese remainder theorem. Given 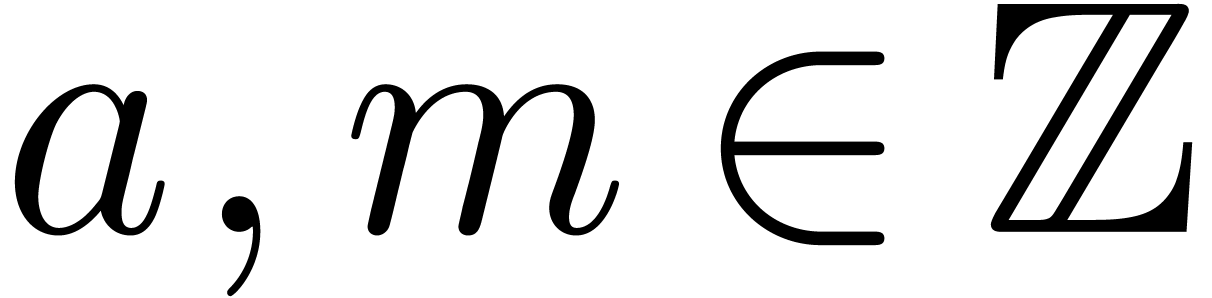 with
with 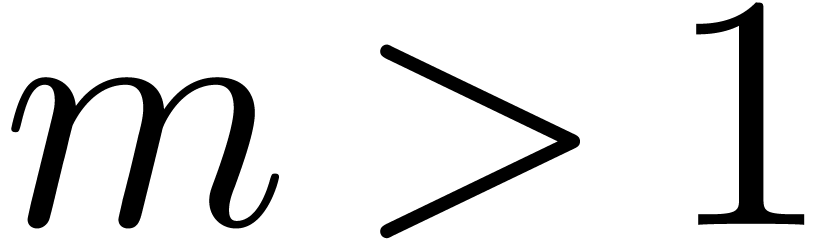 , we
will denote by
, we
will denote by 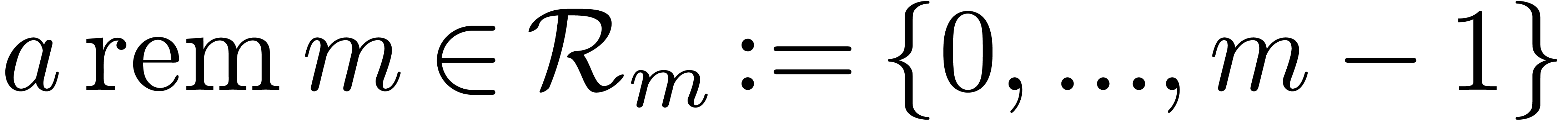 the remainder of the Euclidean
division of
the remainder of the Euclidean
division of  by
by  .
Given an
.
Given an  matrix
matrix  with
integer coefficients, we will also denote
with
integer coefficients, we will also denote 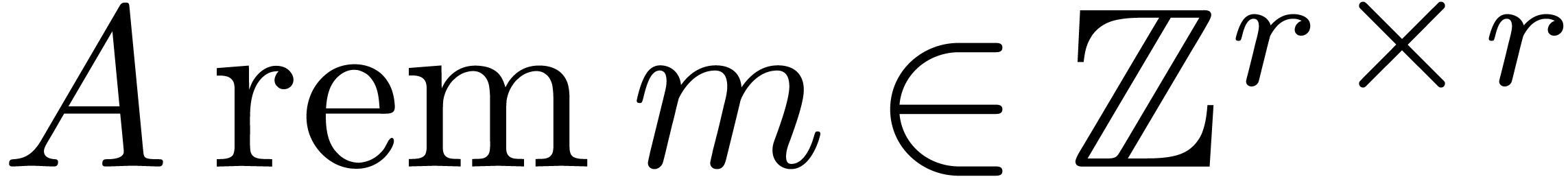 for
the matrix with coefficients
for
the matrix with coefficients 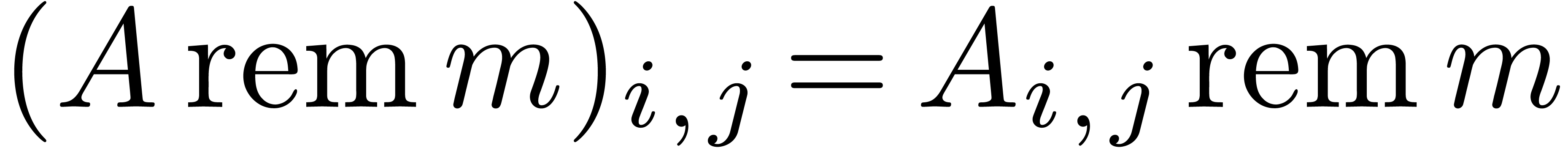 .
.
One typical application of Chinese remaindering is the multiplication of
 integer matrices
integer matrices  .
Assuming that we have a bound
.
Assuming that we have a bound 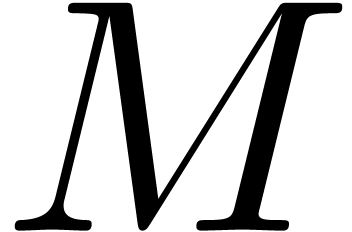 with
with  for all
for all  , we
proceed as follows:
, we
proceed as follows:
-
Select moduli  with
with 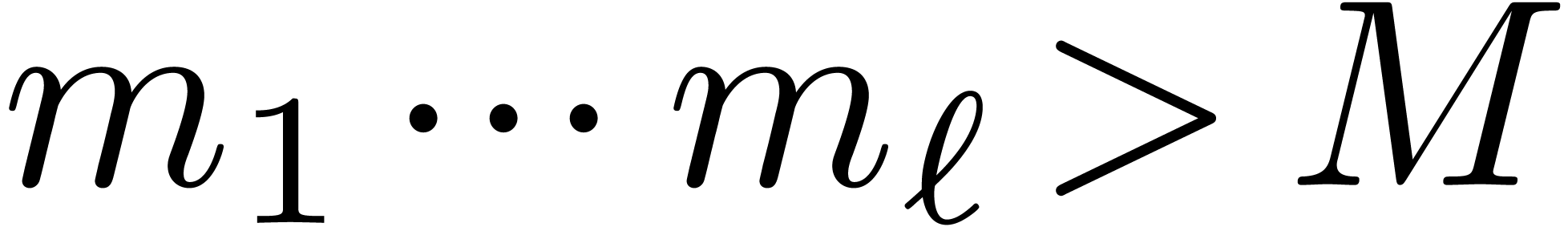 that are mutually coprime.
that are mutually coprime.
-
Compute  and
and 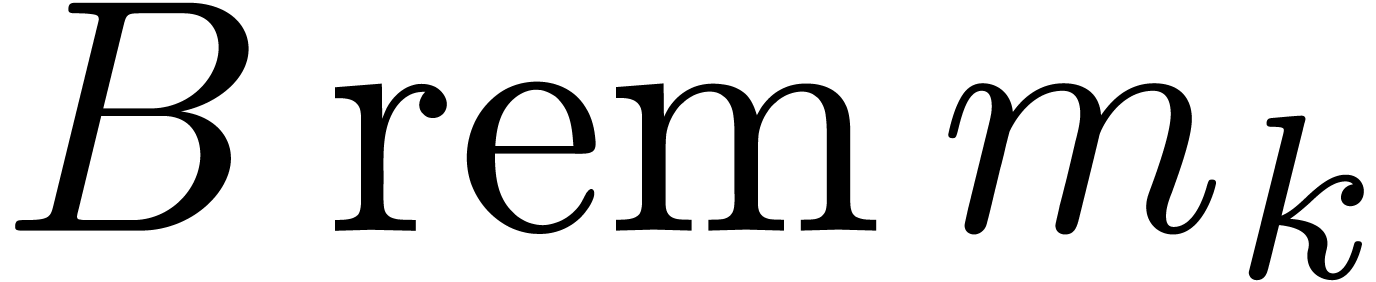 for
for
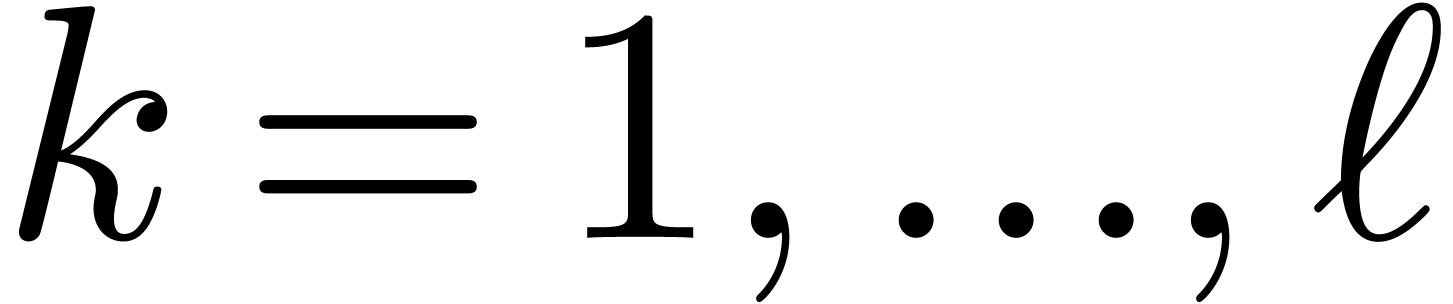 .
.
-
Multiply 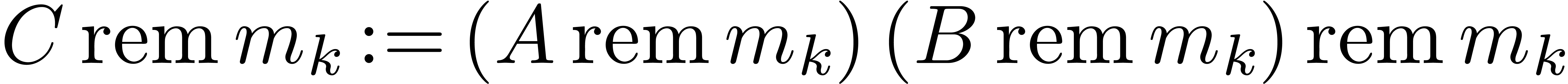 for
for 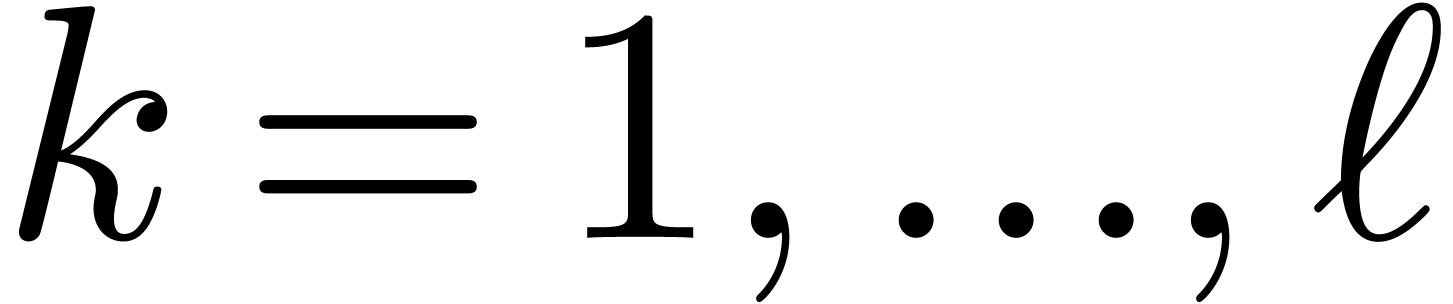 .
.
-
Reconstruct  from the
from the 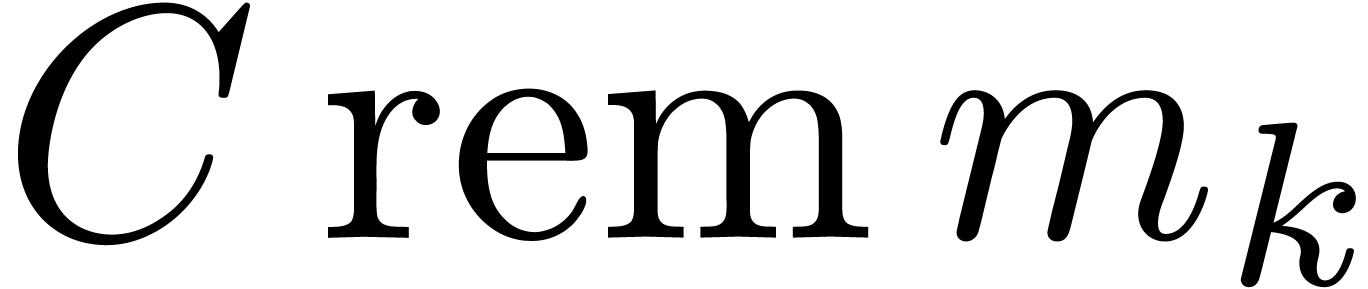 with
with 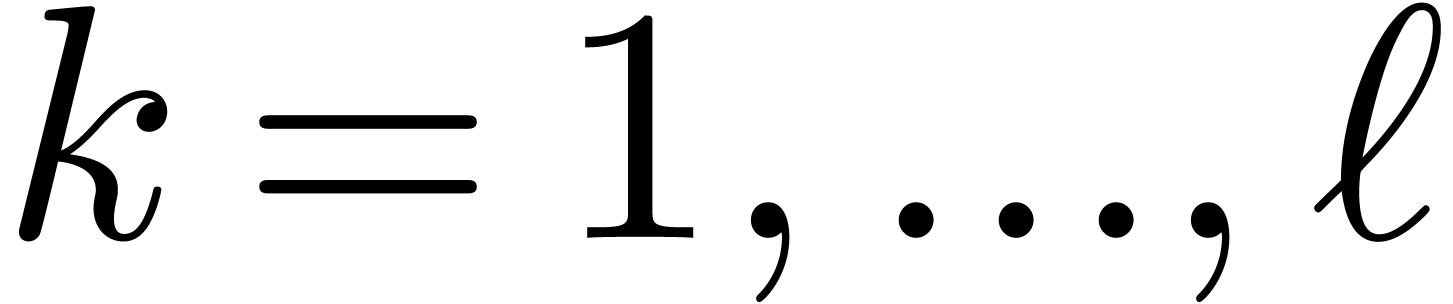 .
.
The simultaneous computation of  from
from 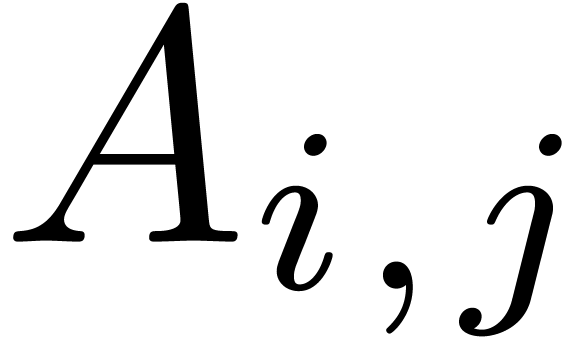 for all
for all 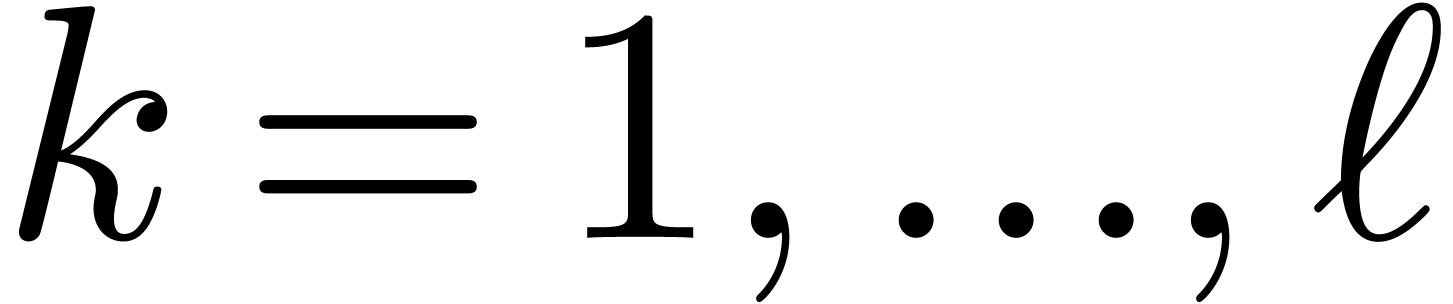 is called the problem of
multi-modular reduction. In step
is called the problem of
multi-modular reduction. In step  ,
we need to perform
,
we need to perform 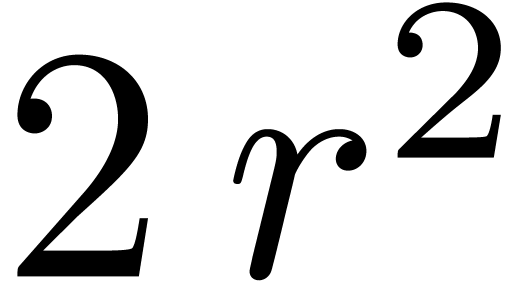 multi-modular reductions for
the coefficients of
multi-modular reductions for
the coefficients of  and
and  . The inverse problem of reconstructing
. The inverse problem of reconstructing  from the
from the  with
with 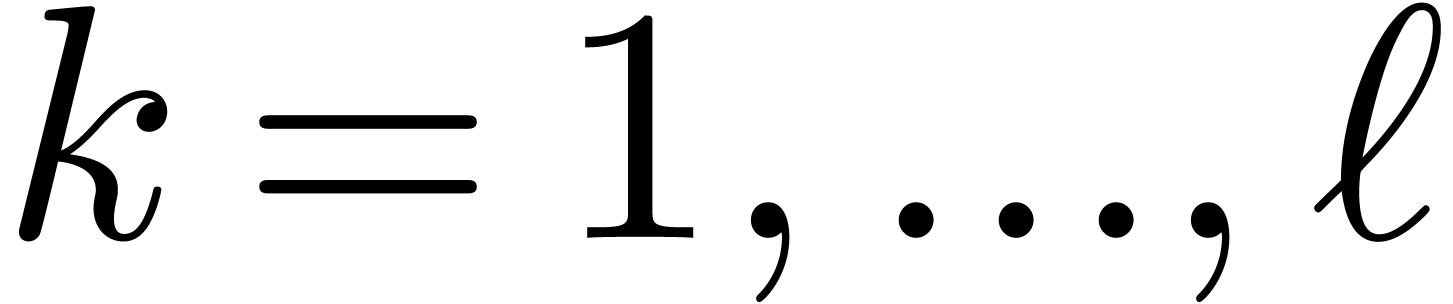 is called the problem of multi-modular reconstruction. We need
to perform
is called the problem of multi-modular reconstruction. We need
to perform 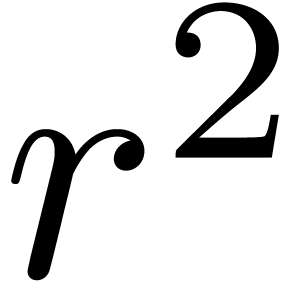 such reconstructions in step 3. Our
hypothesis on
such reconstructions in step 3. Our
hypothesis on 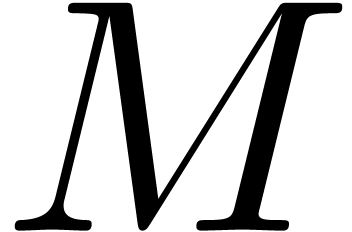 allows us to recover
allows us to recover  from
from  .
.
Let us quickly examine when and why the above strategy pays off. In this
paper, the number  should be small or moderately
large, say
should be small or moderately
large, say 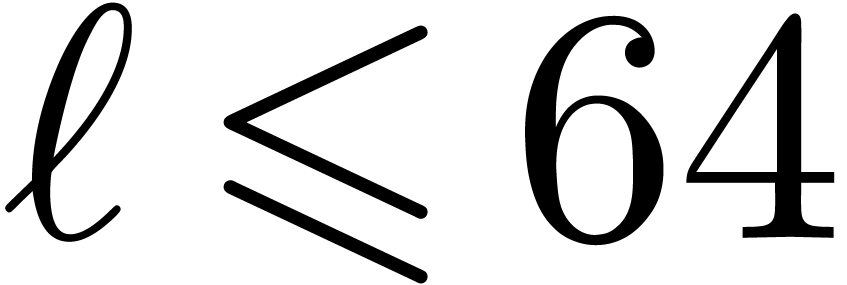 . The moduli
. The moduli  typically fit into a machine word. Denoting by
typically fit into a machine word. Denoting by 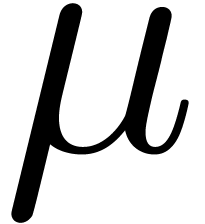 the bitsize of a machine word (say
the bitsize of a machine word (say 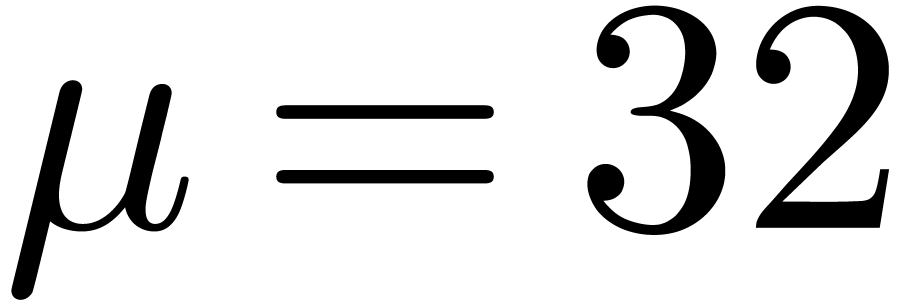 or
or 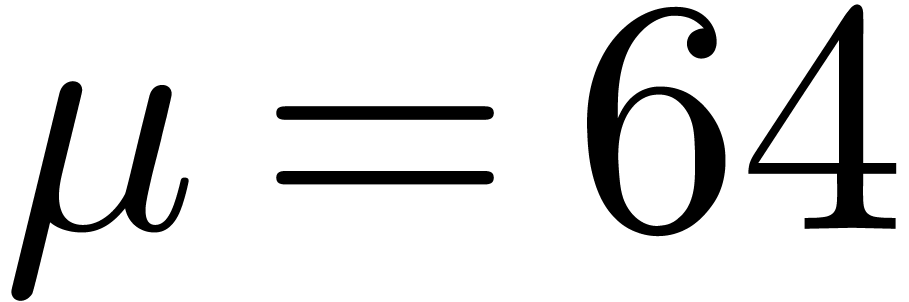 ), the coefficients of
), the coefficients of
 and
and  should therefore be
of bitsize
should therefore be
of bitsize 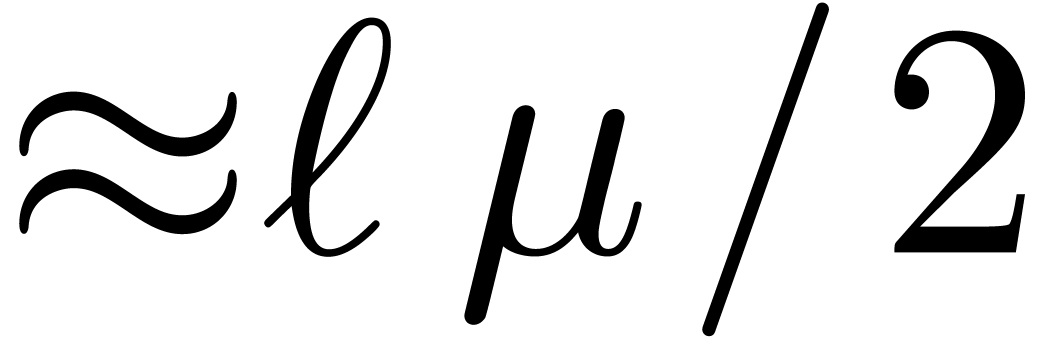 .
.
For small  , integer
multiplications of bitsize
, integer
multiplications of bitsize 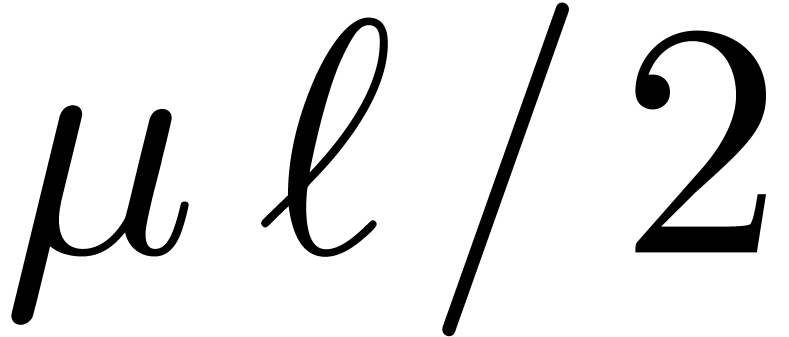 are usually carried
out using a naive algorithm, of complexity
are usually carried
out using a naive algorithm, of complexity 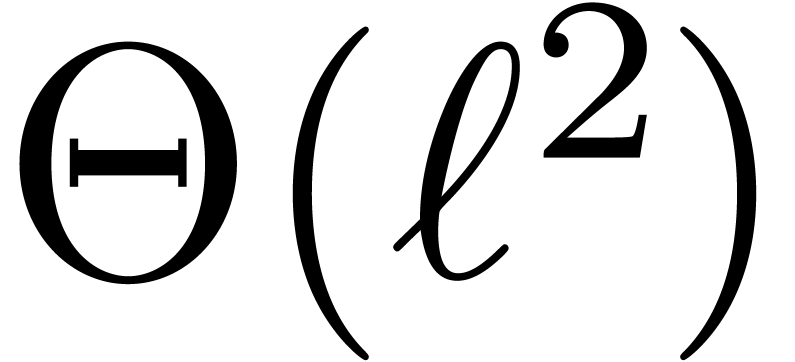 .
If we directly compute the product
.
If we directly compute the product 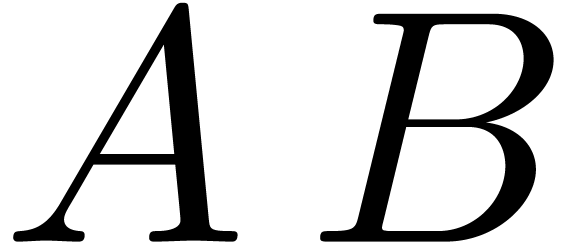 using
using 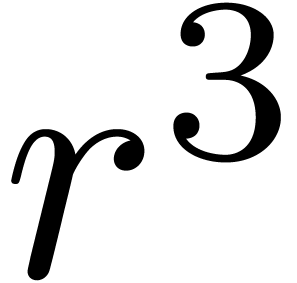 naive integer multiplications, the computation time
is therefore of order
naive integer multiplications, the computation time
is therefore of order 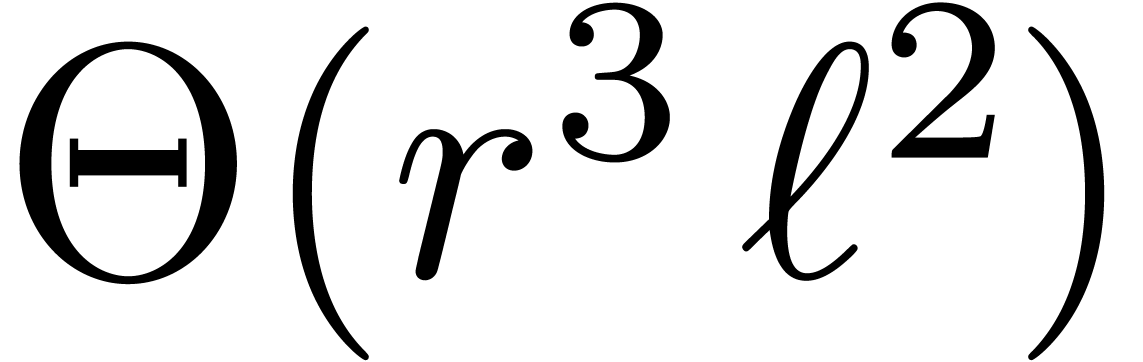 . In
comparison, as we will see, one naive multi-modular reduction or
reconstruction for
. In
comparison, as we will see, one naive multi-modular reduction or
reconstruction for  moduli roughly requires
moduli roughly requires 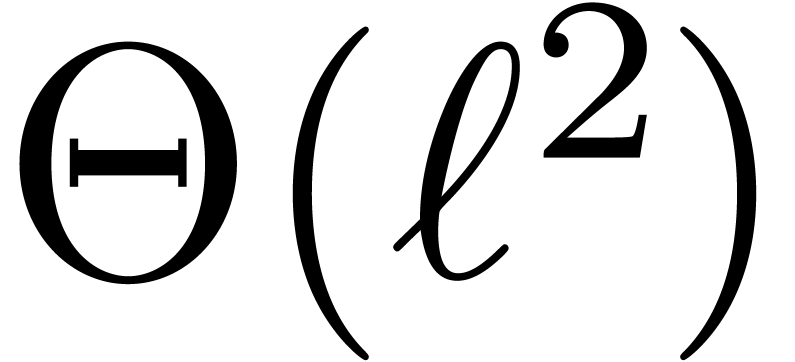 machine operations, whereas an
machine operations, whereas an  matrix multiplication modulo any of the
matrix multiplication modulo any of the 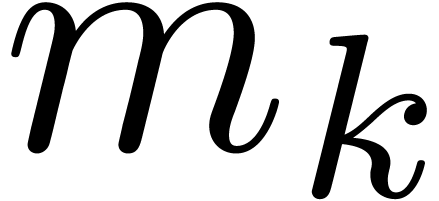 can be
done in time
can be
done in time 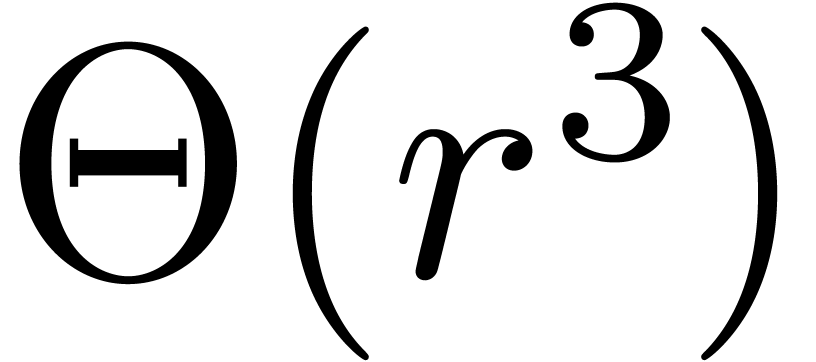 . Altogether,
this means that the above multi-modular algorithm for integer matrix
multiplication has running time
. Altogether,
this means that the above multi-modular algorithm for integer matrix
multiplication has running time 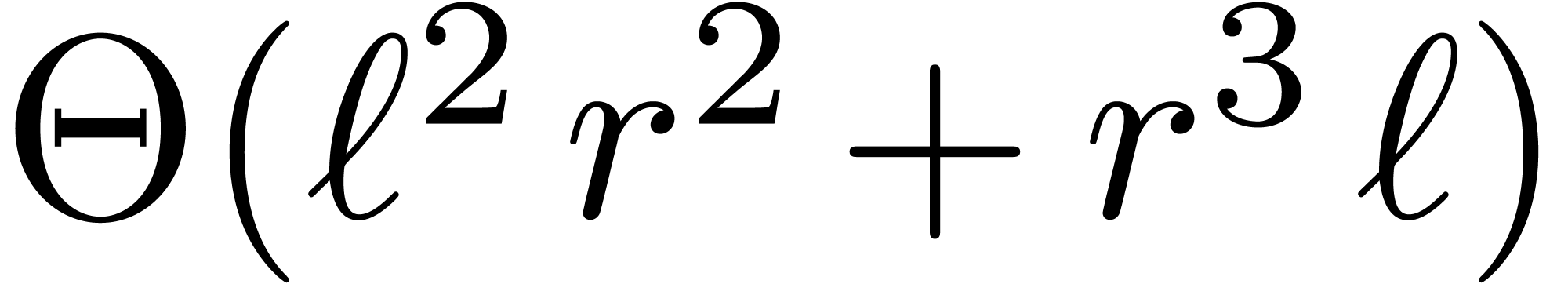 ,
which is
,
which is 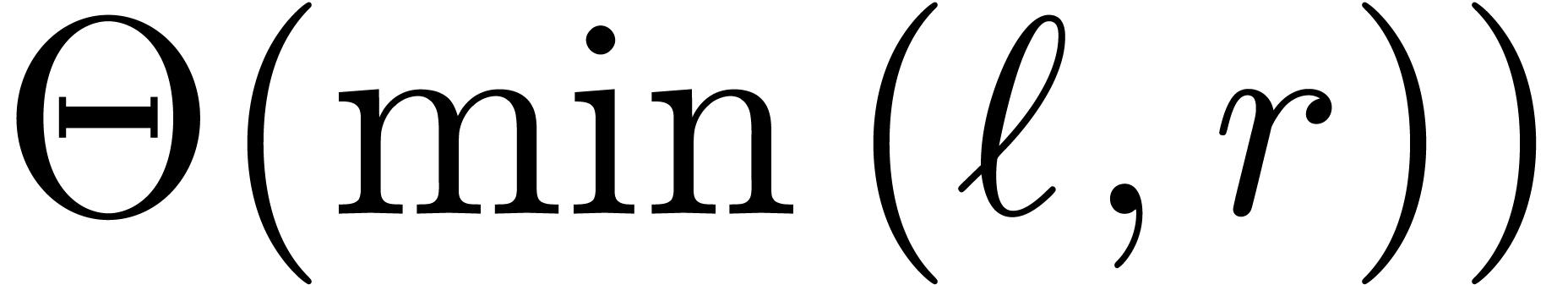 times faster than the naive algorithm.
times faster than the naive algorithm.
If 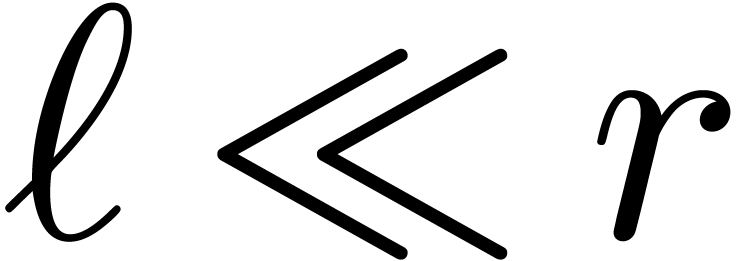 , then the cost
, then the cost 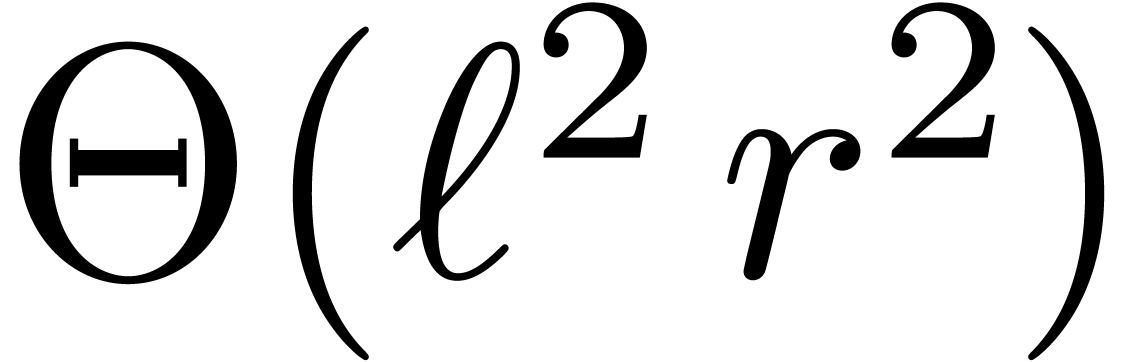 of steps 1 and 3 is negligible with respect to the cost
of steps 1 and 3 is negligible with respect to the cost
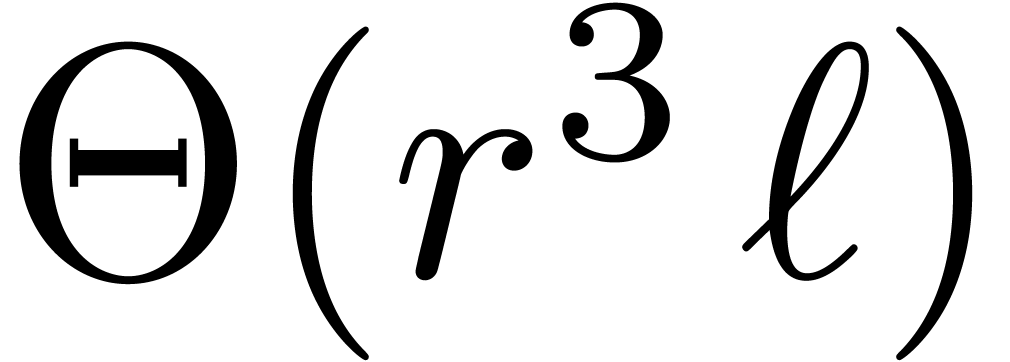 of step 2. However, if
of step 2. However, if  and
and 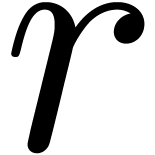 are of the same order of magnitude, then
Chinese remaindering may take an important part of the computation time;
the main purpose of this paper is to reduce this cost. If
are of the same order of magnitude, then
Chinese remaindering may take an important part of the computation time;
the main purpose of this paper is to reduce this cost. If 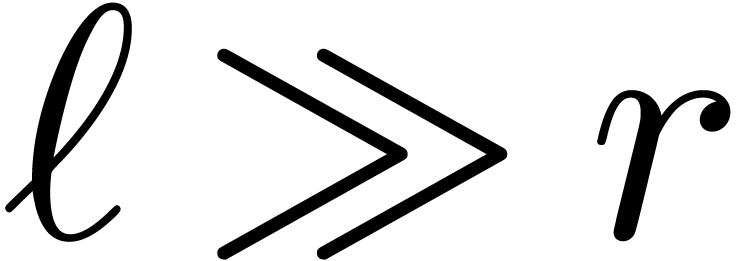 , then we notice that other algorithms for
matrix multiplication usually become faster, such as naive
multiplication for small
, then we notice that other algorithms for
matrix multiplication usually become faster, such as naive
multiplication for small  ,
Karatsuba multiplication [13] for larger
,
Karatsuba multiplication [13] for larger  , or FFT-based techniques [6] for
very large
, or FFT-based techniques [6] for
very large  .
.
Two observations are crucial for reducing the cost of Chinese
remaindering. First of all, the moduli  are the
same for all
are the
same for all 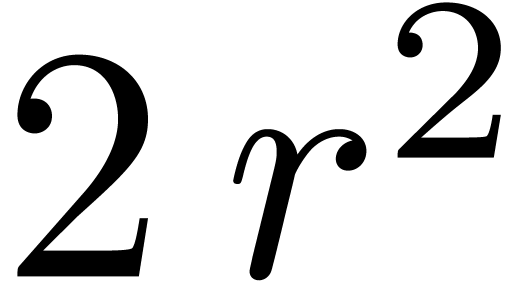 multi-modular reductions and
multi-modular reductions and 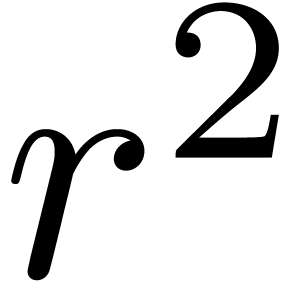 multi-modular reconstructions in steps
multi-modular reconstructions in steps 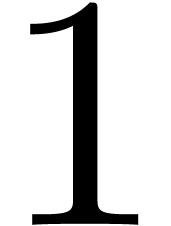 and
and  . If
. If 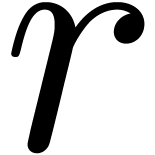 is large, then this means that we can essentially
assume that
is large, then this means that we can essentially
assume that  were fixed once and for all.
Secondly, we are free to choose
were fixed once and for all.
Secondly, we are free to choose  in any way that
suits us. We will exploit these observations by precomputing gentle
moduli for which Chinese remaindering can be performed more
efficiently than for ordinary moduli.
in any way that
suits us. We will exploit these observations by precomputing gentle
moduli for which Chinese remaindering can be performed more
efficiently than for ordinary moduli.
The first idea behind gentle moduli is to consider moduli  of the form
of the form 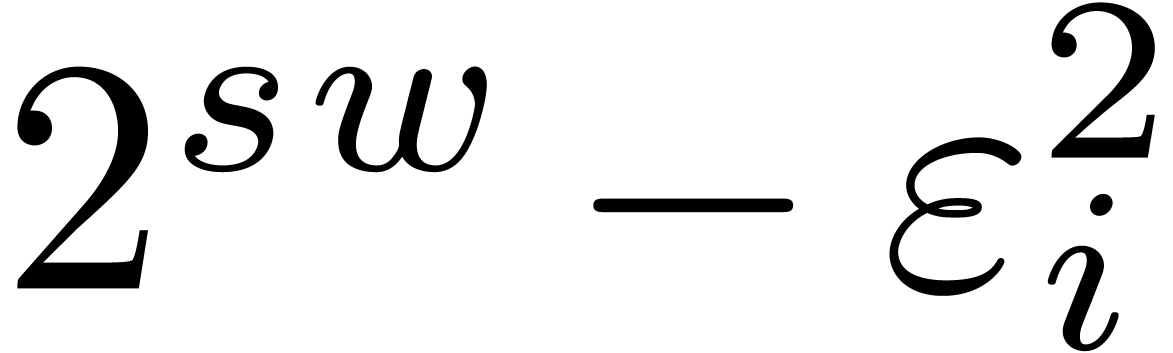 ,
where
,
where  is somewhat smaller than
is somewhat smaller than  , where
, where  is even, and
is even, and
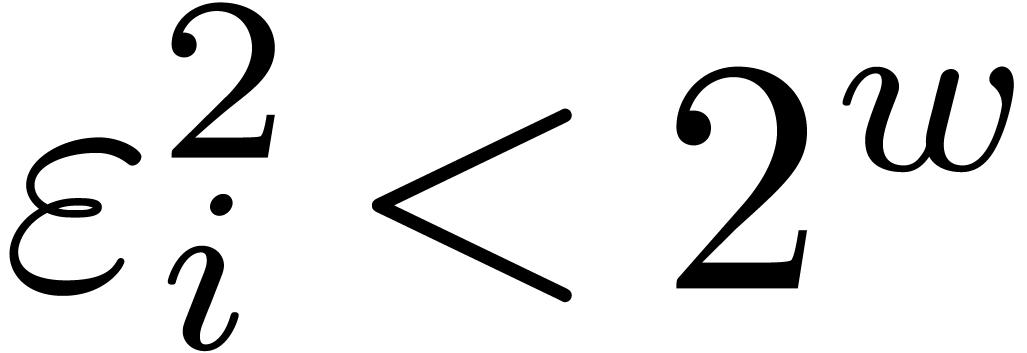 . In section 3.1,
we will show that multi-modular reduction and reconstruction both become
a lot simpler for such moduli. Secondly, each
. In section 3.1,
we will show that multi-modular reduction and reconstruction both become
a lot simpler for such moduli. Secondly, each  can be factored as
can be factored as 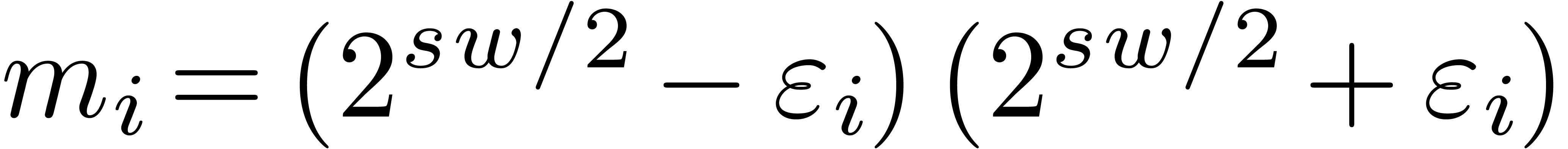 and, if we are lucky, then
both
and, if we are lucky, then
both 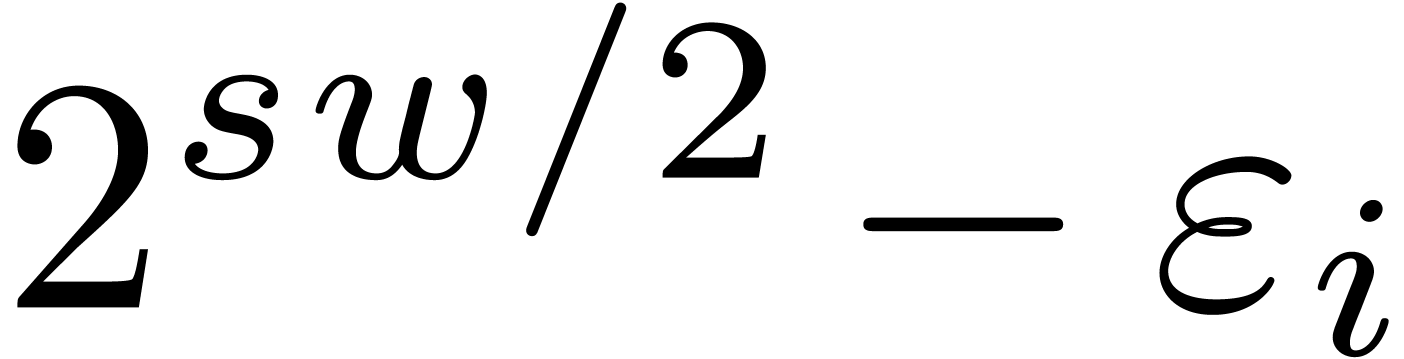 and
and 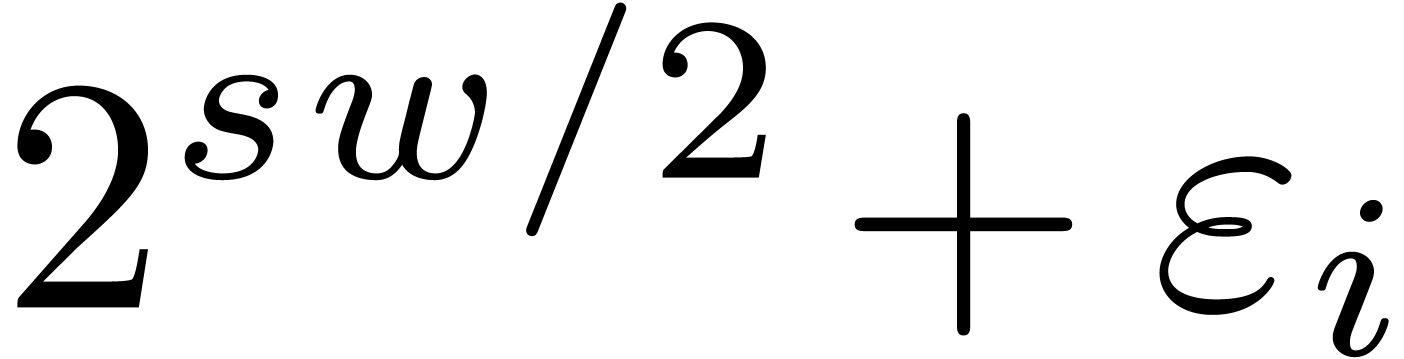 can be factored
into
can be factored
into 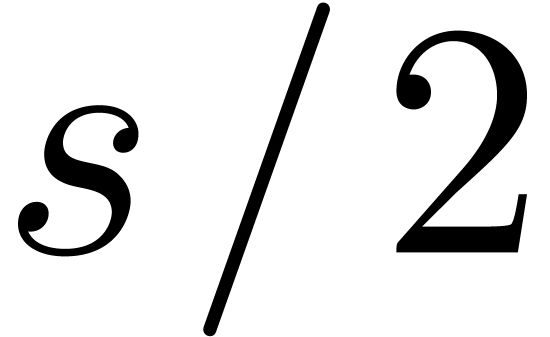 moduli of bitsize
moduli of bitsize 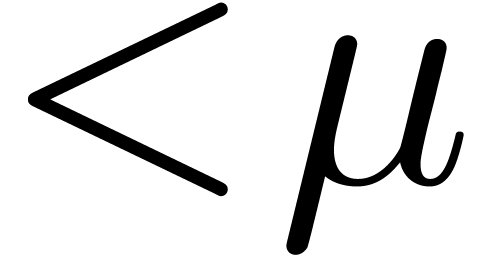 . If we are very lucky, then this allows us to
obtain
. If we are very lucky, then this allows us to
obtain 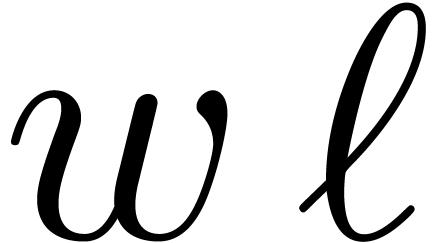 moduli
moduli 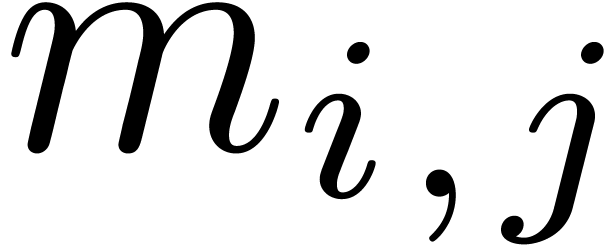 of bitsize
of bitsize
 that are mutually coprime and for which Chinese
remaindering can be implemented efficiently.
that are mutually coprime and for which Chinese
remaindering can be implemented efficiently.
Let us briefly outline the structure of this paper. In section 2,
we rapidly recall basic facts about Chinese remaindering and naive
algorithms for this task. In section 3, we introduce gentle
moduli and describe how to speed up Chinese remaindering with respect to
such moduli. The last section 4 is dedicated to the brute
force search of gentle moduli for specific values of  and
and  . We implemented a
sieving method in Mathemagix which allowed us to
compute tables with gentle moduli. For practical purposes, it turns out
that gentle moduli exist in sufficient number for
. We implemented a
sieving method in Mathemagix which allowed us to
compute tables with gentle moduli. For practical purposes, it turns out
that gentle moduli exist in sufficient number for  . We expect our technique to be efficient for
. We expect our technique to be efficient for  , but this still needs to be
confirmed via an actual implementation. The application to
integer matrix multiplication in section 4.3 also has not
been implemented yet.
, but this still needs to be
confirmed via an actual implementation. The application to
integer matrix multiplication in section 4.3 also has not
been implemented yet.
Let us finally discuss a few related results. In this paper, we have
chosen to highlight integer matrix multiplication as one typical
application in computer algebra. Multi-modular methods are used in many
other areas and the operations of multi-modular reduction and
reconstruction are also known as conversions between the positional
number system (PNS) and the residue number system (RNS). Asymptotically
fast algorithms are based on remainder trees [8,
14, 3], with recent improvements in [4,
2, 10]; we expect such algorithms to become
more efficient when  exceeds
exceeds 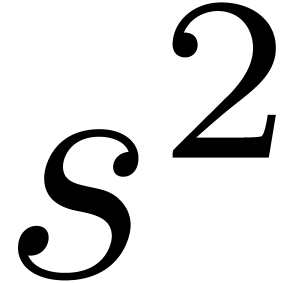 .
.
Special moduli of the form 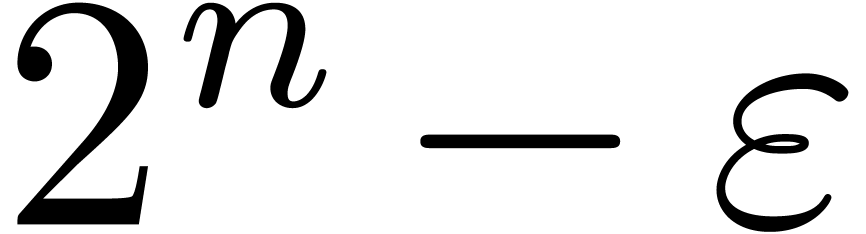 are also known as
pseudo-Mersenne moduli. They have been exploited before in
cryptography [1] in a similar way as in section 3.1,
but with a slightly different focus: whereas the authors of [1]
are keen on reducing the number of additions (good for circuit
complexity), we rather optimize the number of machine instructions on
recent general purpose CPUs (good for software implementations). Our
idea to choose moduli
are also known as
pseudo-Mersenne moduli. They have been exploited before in
cryptography [1] in a similar way as in section 3.1,
but with a slightly different focus: whereas the authors of [1]
are keen on reducing the number of additions (good for circuit
complexity), we rather optimize the number of machine instructions on
recent general purpose CPUs (good for software implementations). Our
idea to choose moduli 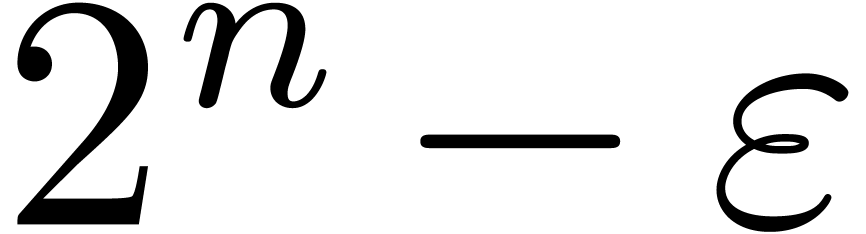 that can be factored into
smaller moduli is new.
that can be factored into
smaller moduli is new.
Other algorithms for speeding up multiple multi-modular reductions and
reconstructions for the same moduli (while allowing for additional
pre-computations) have recently been proposed in [7]. These
algorithms essentially replace all divisions by simple multiplications
and can be used in conjunction with our new algorithms for conversions
between residues modulo 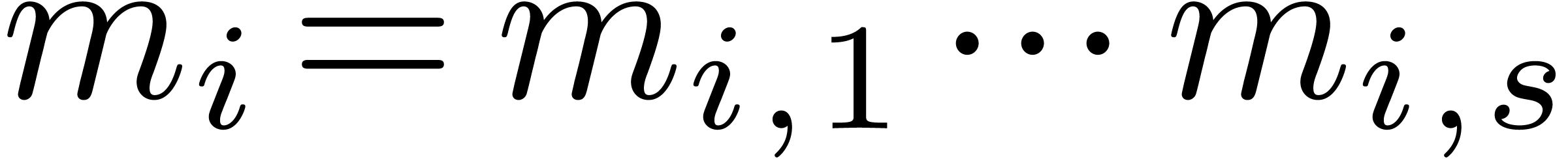 and residues modulo
and residues modulo
 .
.
2Chinese remaindering
2.1The Chinese remainder theorem
For any integer 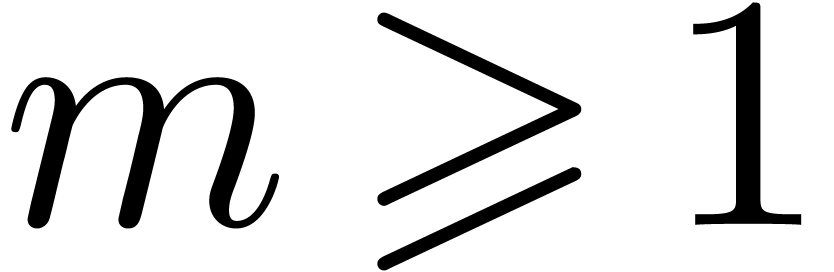 , we recall
that
, we recall
that  . For machine
computations, it is convenient to use the following effective version of
the Chinese remainder theorem:
. For machine
computations, it is convenient to use the following effective version of
the Chinese remainder theorem:
Chinese Remainder Theorem. Let  be positive integers that are mutually coprime and denote
be positive integers that are mutually coprime and denote 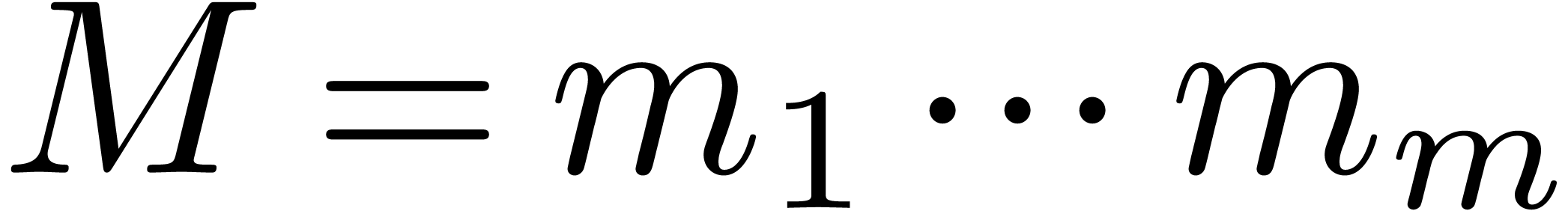 . There exist
. There exist 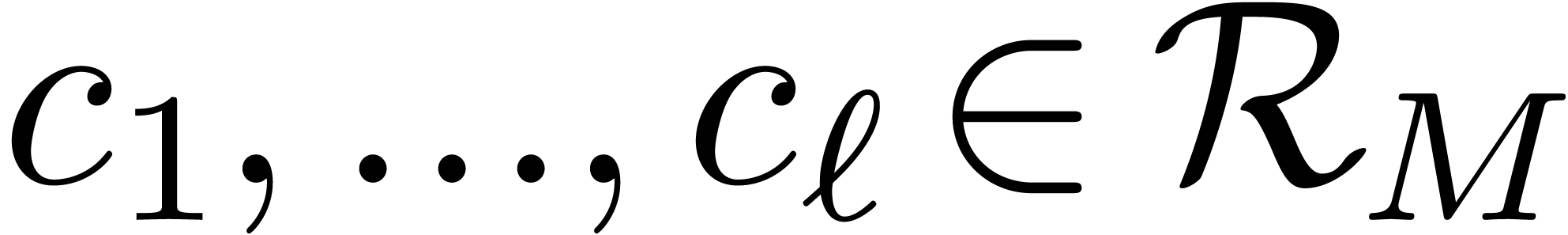 such that
for any
such that
for any  , the number
, the number

satisfies 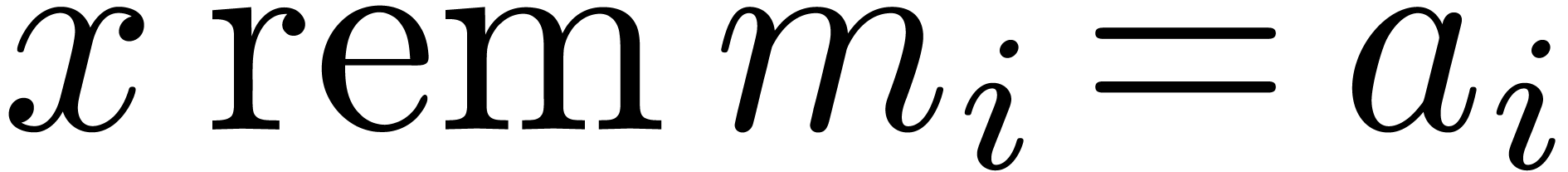 for
for 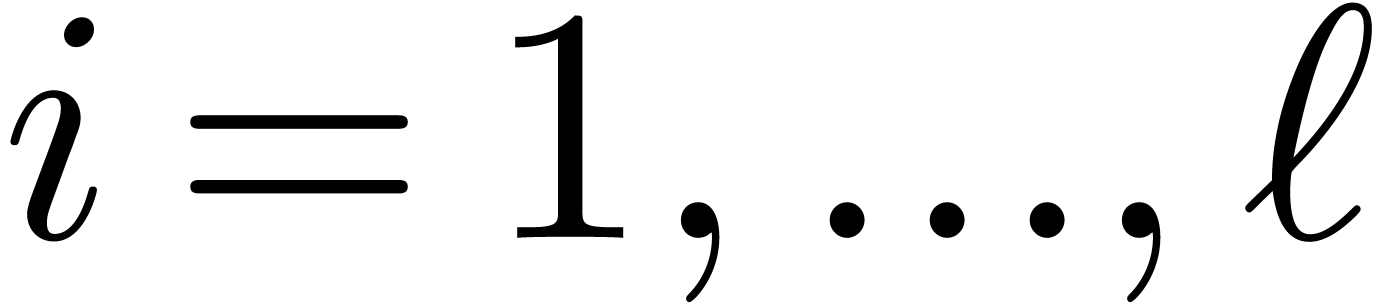 .
.
Proof. For each 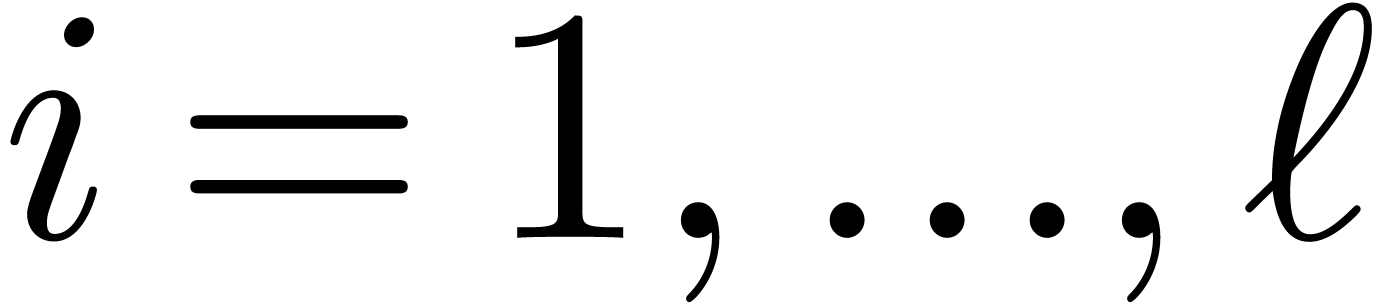 ,
let
,
let 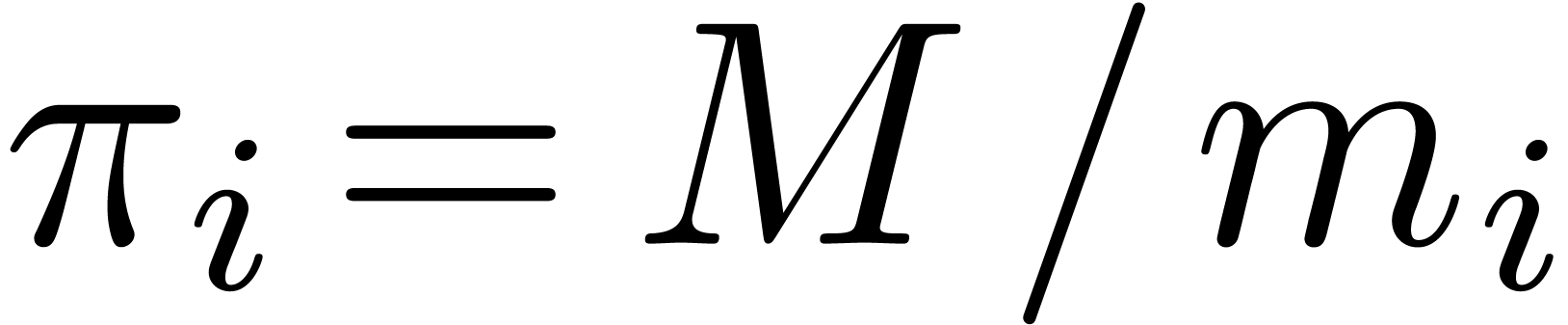 . Since
. Since  and
and  are coprime,
are coprime, 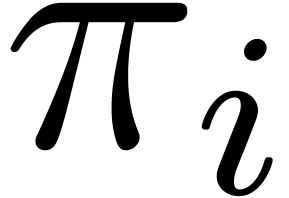 admits
an inverse
admits
an inverse 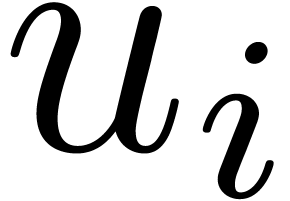 modulo
modulo  in
in
 . We claim that we may take
. We claim that we may take
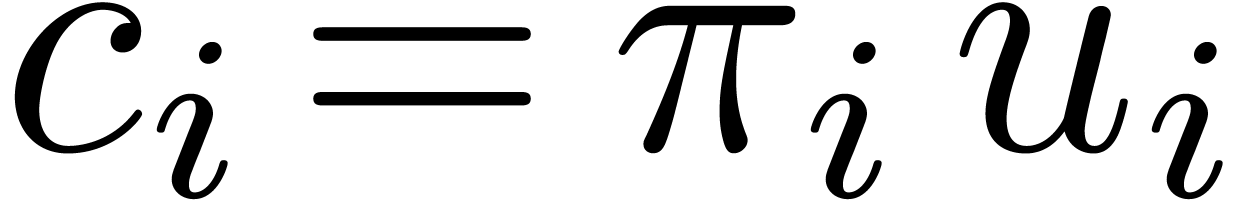 . Indeed, for
. Indeed, for 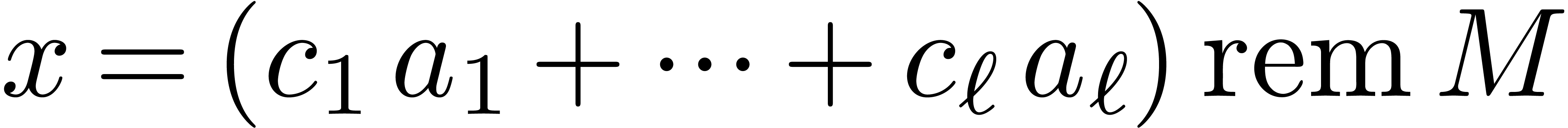 and any
and any 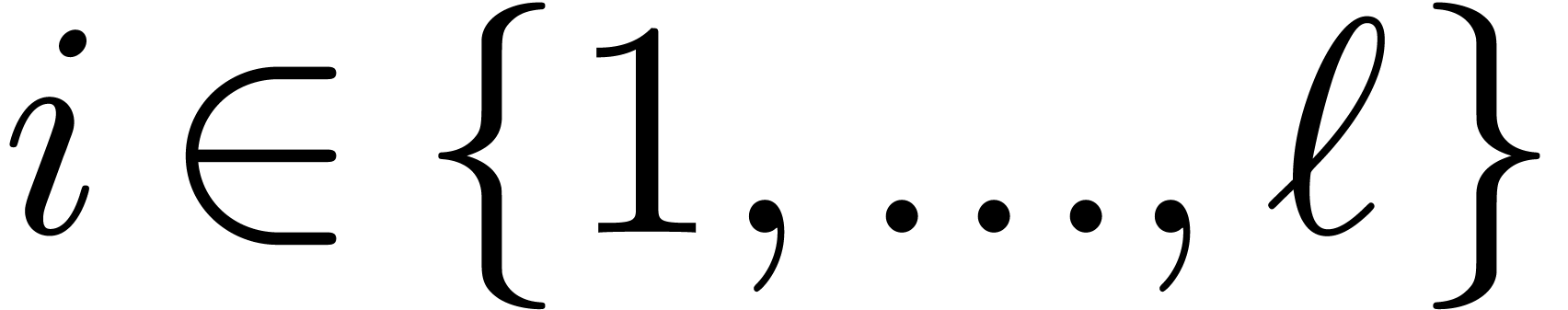 , we
have
, we
have

Since 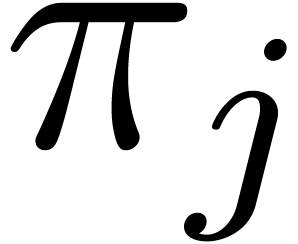 is divisible by
is divisible by  for all
for all 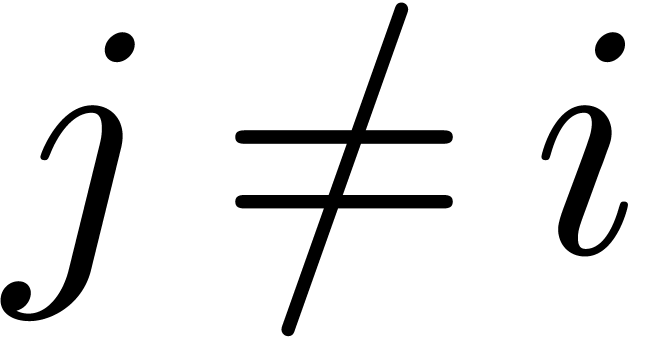 , this congruence
relation simplifies into
, this congruence
relation simplifies into
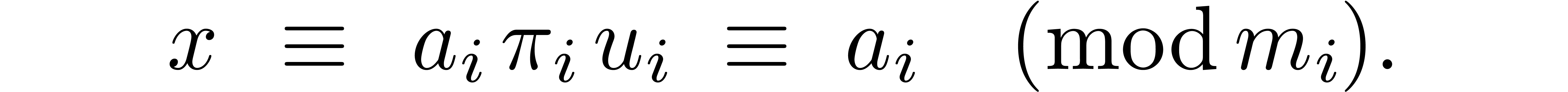
This proves our claim and the theorem.
Notation. We call  the
cofactors for
the
cofactors for  in
in  and
also denote these numbers by
and
also denote these numbers by  .
.
2.2Modular arithmetic
For practical computations, the moduli  are
usually chosen such that they fit into single machine words. Let
are
usually chosen such that they fit into single machine words. Let 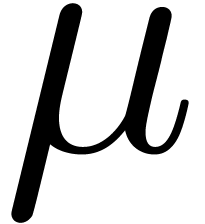 denote the bitsize of a machine word, so that we
typically have
denote the bitsize of a machine word, so that we
typically have 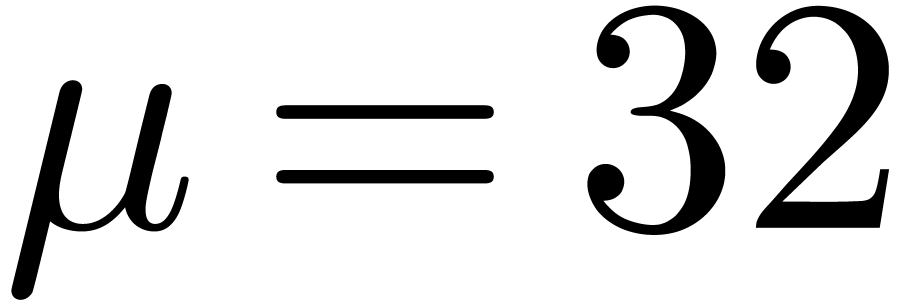 or
or 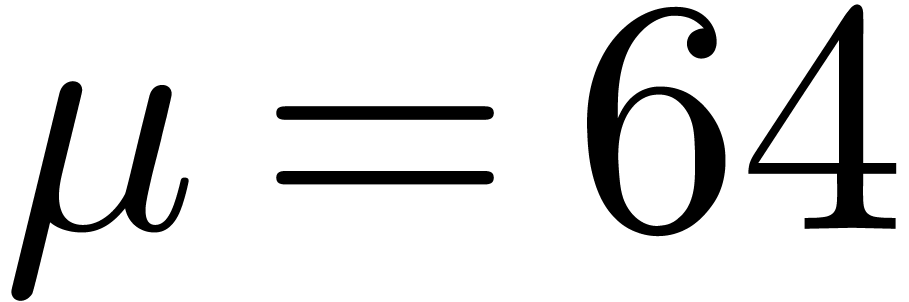 .
It depends on specifics of the processor how basic arithmetic operations
modulo
.
It depends on specifics of the processor how basic arithmetic operations
modulo  can be implemented most efficiently.
can be implemented most efficiently.
For instance, some processors have instructions for multiplying two
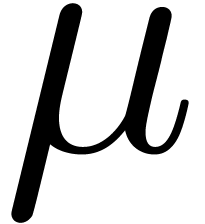 -bit integers and return the
exact
-bit integers and return the
exact 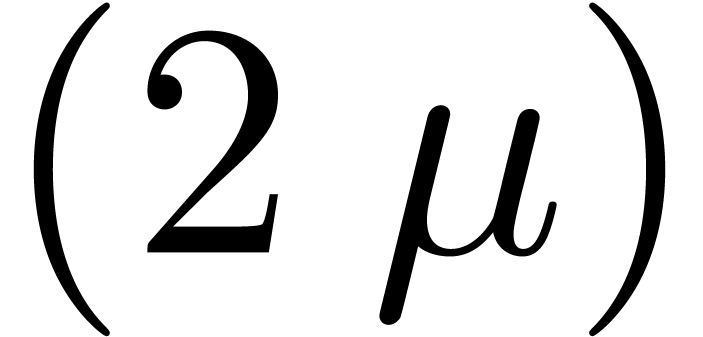 -bit product. If not,
then we rather have to assume that the moduli
-bit product. If not,
then we rather have to assume that the moduli  fit into
fit into 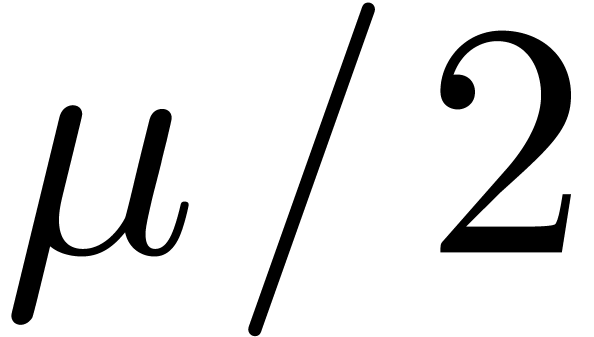 instead of
instead of 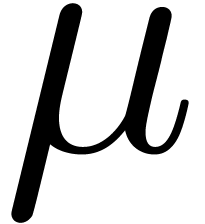 bits, or replace
bits, or replace 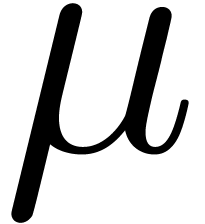 by
by 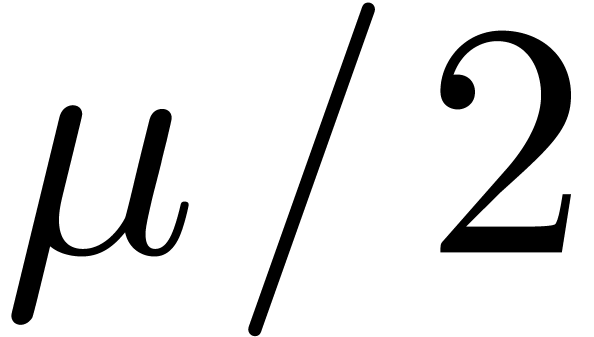 . Some processors do not provide efficient integer
arithmetic at all. In that case, one might rather wish to rely on
floating point arithmetic and take
. Some processors do not provide efficient integer
arithmetic at all. In that case, one might rather wish to rely on
floating point arithmetic and take 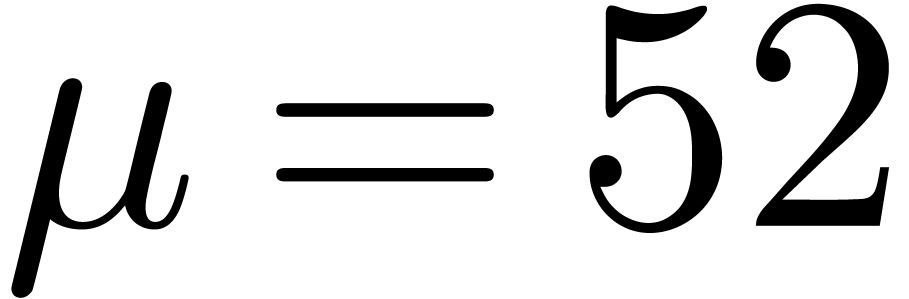 (assuming
that we have hardware support for double precision). For floating point
arithmetic it also matters whether the processor offers a
“fused-multiply-add” (FMA) instruction; this essentially
provides us with an efficient way to multiply two
(assuming
that we have hardware support for double precision). For floating point
arithmetic it also matters whether the processor offers a
“fused-multiply-add” (FMA) instruction; this essentially
provides us with an efficient way to multiply two 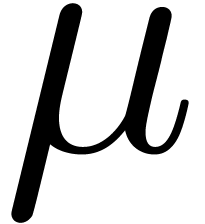 -bit integers exactly using floating point
arithmetic.
-bit integers exactly using floating point
arithmetic.
It is also recommended to choose moduli  that fit
into slightly less than
that fit
into slightly less than 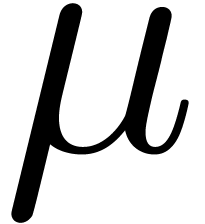 bits whenever possible.
Such extra bits can be used to significantly accelerate implementations
of modular arithmetic. For a more detailed survey of practically
efficient algorithms for modular arithmetic, we refer to [12].
bits whenever possible.
Such extra bits can be used to significantly accelerate implementations
of modular arithmetic. For a more detailed survey of practically
efficient algorithms for modular arithmetic, we refer to [12].
2.3Naive multi-modular reduction
and reconstruction
Let  ,
, 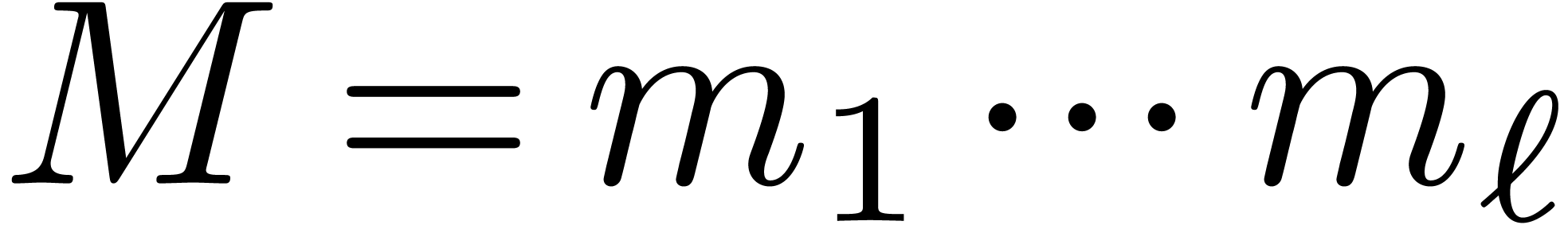 ,
,  and
and 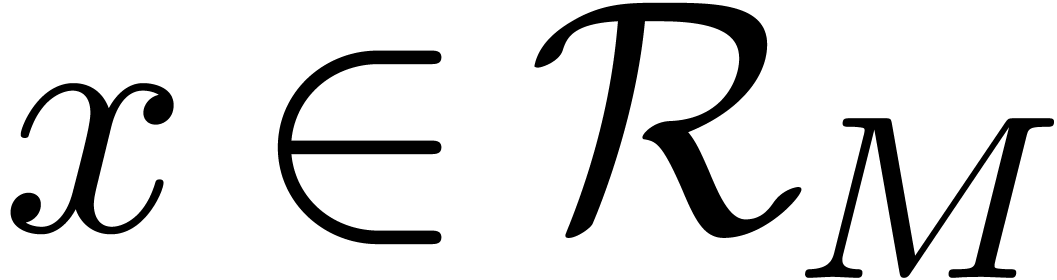 be as in the Chinese remainder theorem. We will refer to the computation
of
be as in the Chinese remainder theorem. We will refer to the computation
of  as a function of
as a function of 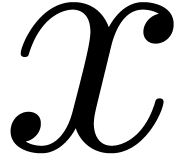 as
the problem of multi-modular reduction. The inverse problem is
called multi-modular reconstruction. In what follows, we assume
that
as
the problem of multi-modular reduction. The inverse problem is
called multi-modular reconstruction. In what follows, we assume
that  have been fixed once and for all.
have been fixed once and for all.
The simplest way to perform multi-modular reduction is to simply take
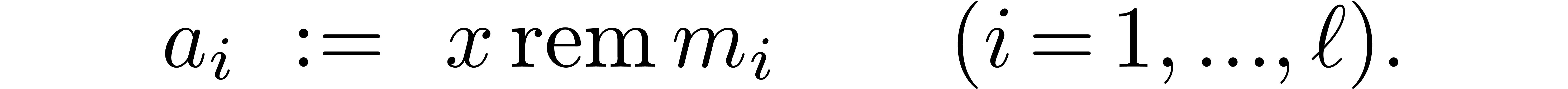 |
(1) |
Inversely, the Chinese remainder theorem provides us with a formula for
multi-modular reconstruction:
 |
(2) |
Since  are fixed, the computation of the
cofactors
are fixed, the computation of the
cofactors 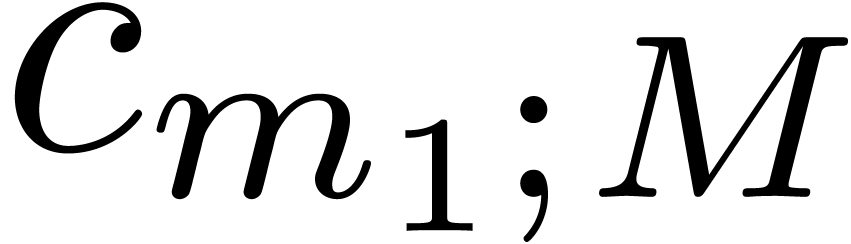 can be regarded as a precomputation.
can be regarded as a precomputation.
Assume that our hardware provides an instruction for the exact
multiplication of two integers that fit into a machine word. If  fits into a machine word, then so does the remainder
fits into a machine word, then so does the remainder
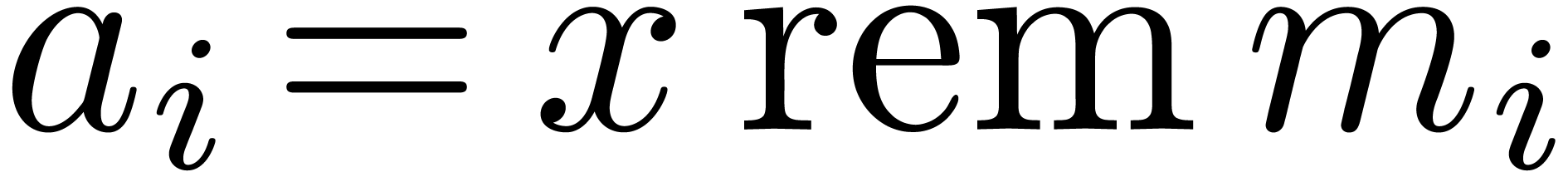 . Cutting
. Cutting 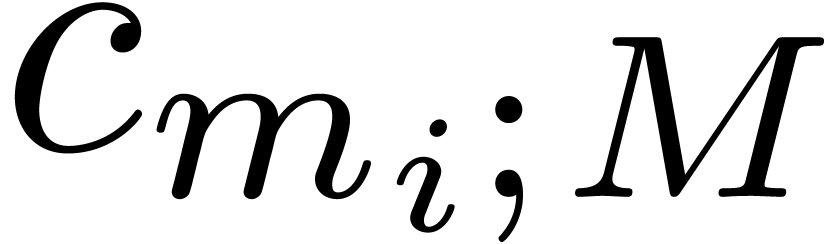 into
into  machine words, it follows that the product
machine words, it follows that the product
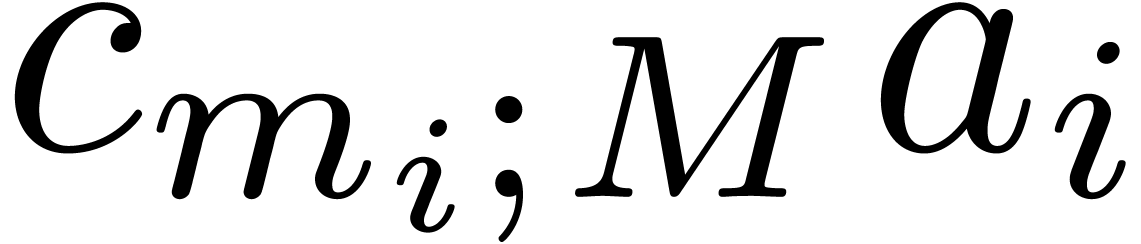 can be computed using
can be computed using  hardware products and
hardware products and  hardware additions.
Inversely, the Euclidean division of an
hardware additions.
Inversely, the Euclidean division of an  -word
integer
-word
integer 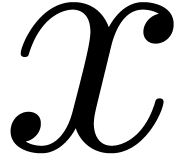 by
by  can be done
using
can be done
using 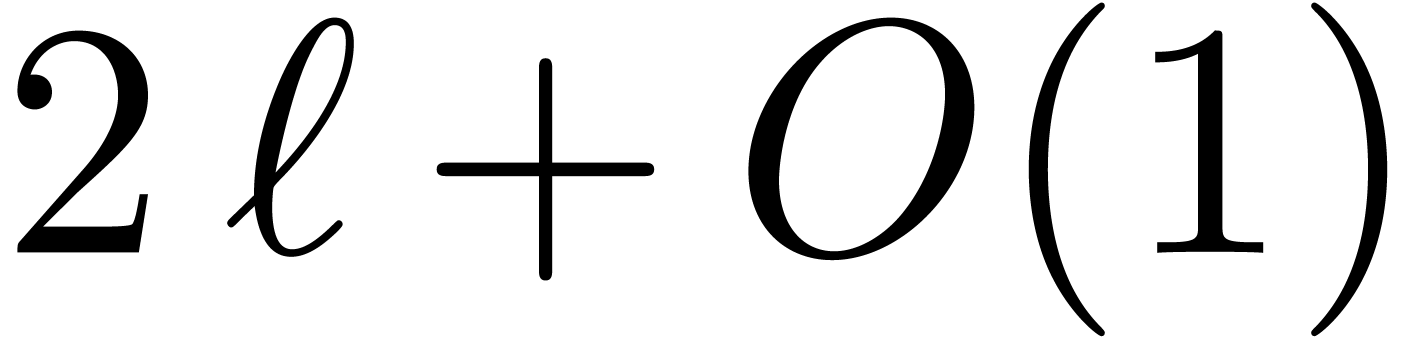 multiplications and
multiplications and 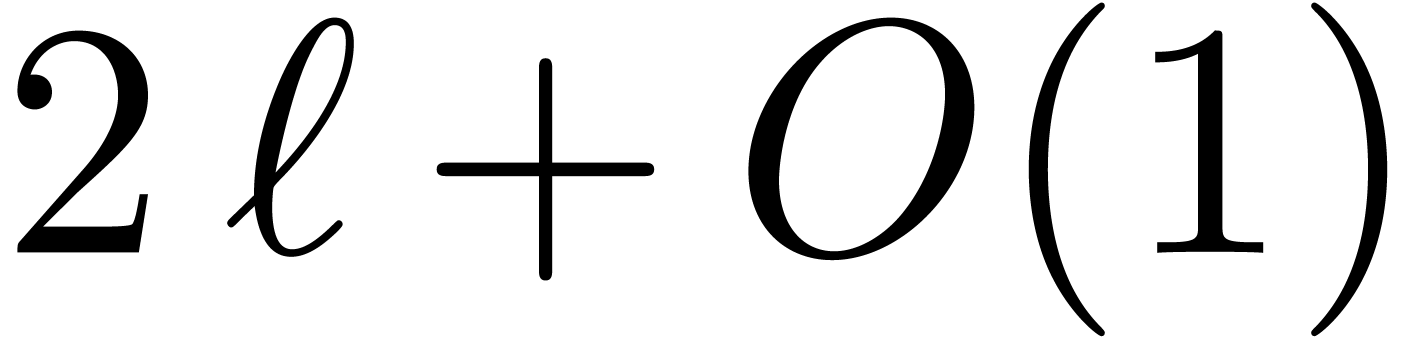 additions/subtractions: we essentially have to multiply the quotient by
additions/subtractions: we essentially have to multiply the quotient by
 and subtract the result from
and subtract the result from 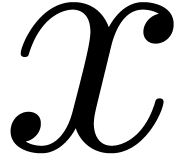 ; each next word of the quotient is obtained
through a one word multiplication with an approximate inverse of
; each next word of the quotient is obtained
through a one word multiplication with an approximate inverse of  .
.
The above analysis shows that the naive algorithm for multi-modular
reduction of 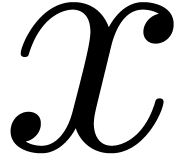 modulo
modulo  requires
requires 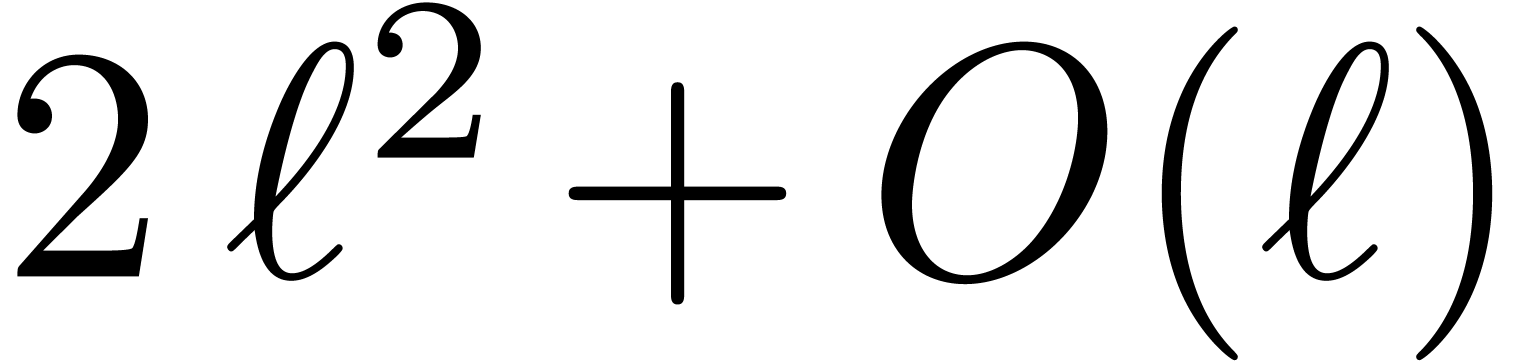 hardware multiplications and
hardware multiplications and 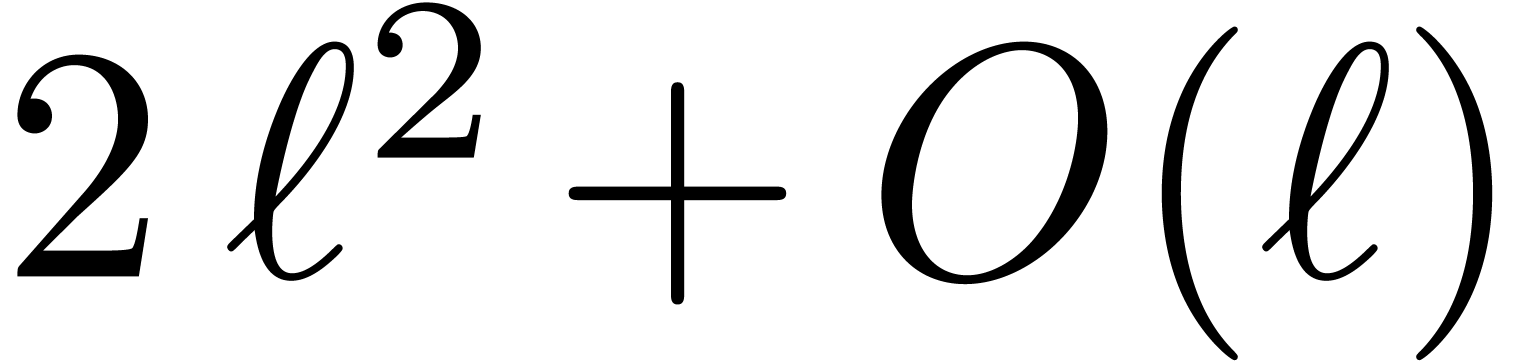 additions. The multi-modular reconstruction of
additions. The multi-modular reconstruction of  can be done using only
can be done using only 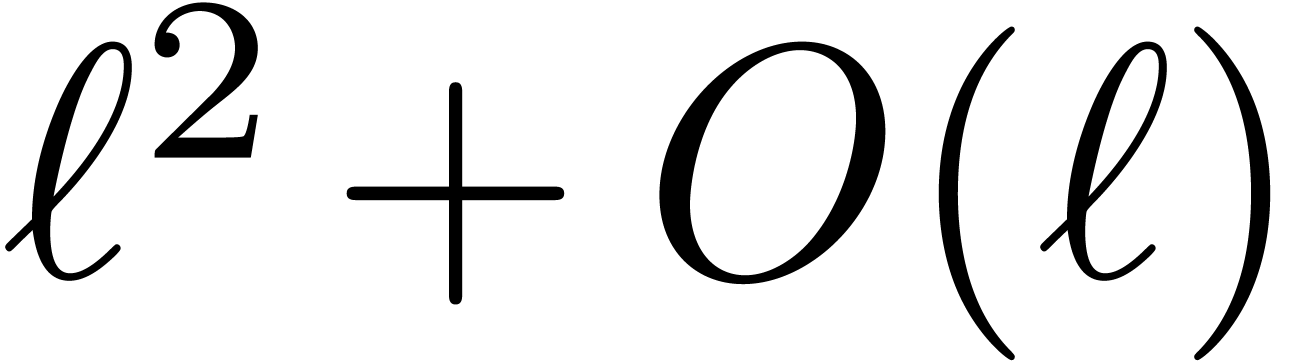 multiplications and
multiplications and 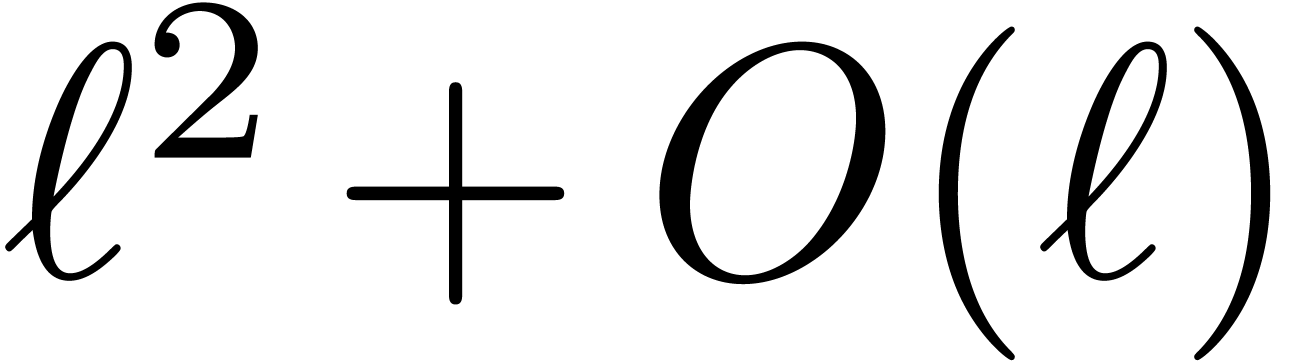 additions. Depending on the
hardware, the moduli
additions. Depending on the
hardware, the moduli  , and
the way we implement things,
, and
the way we implement things, 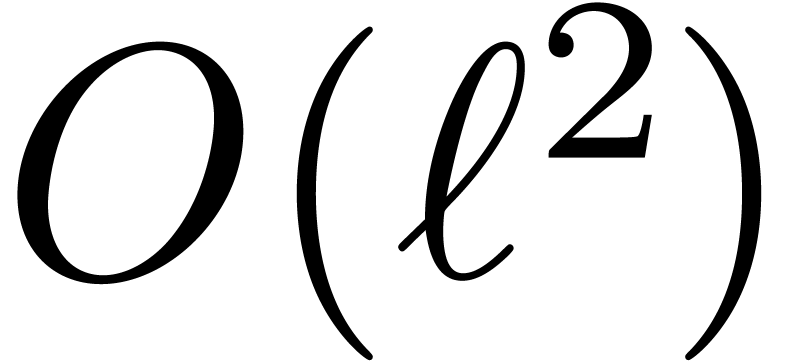 more operations may
be required for the carry handling—but it is beyond the scope of
this paper to go into this level of detail.
more operations may
be required for the carry handling—but it is beyond the scope of
this paper to go into this level of detail.
3Gentle moduli
3.1The naive algorithms revisited
for special moduli
Let us now reconsider the naive algorithms from section 2.3,
but in the case when the moduli  are all close to
a specific power of two. More precisely, we assume that
are all close to
a specific power of two. More precisely, we assume that
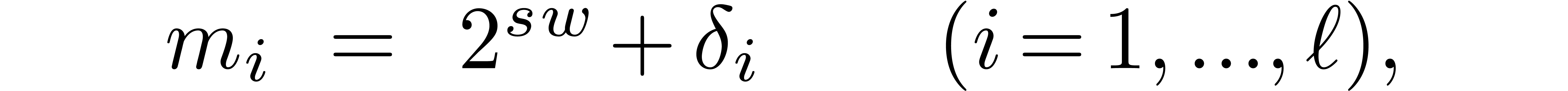 |
(3) |
where 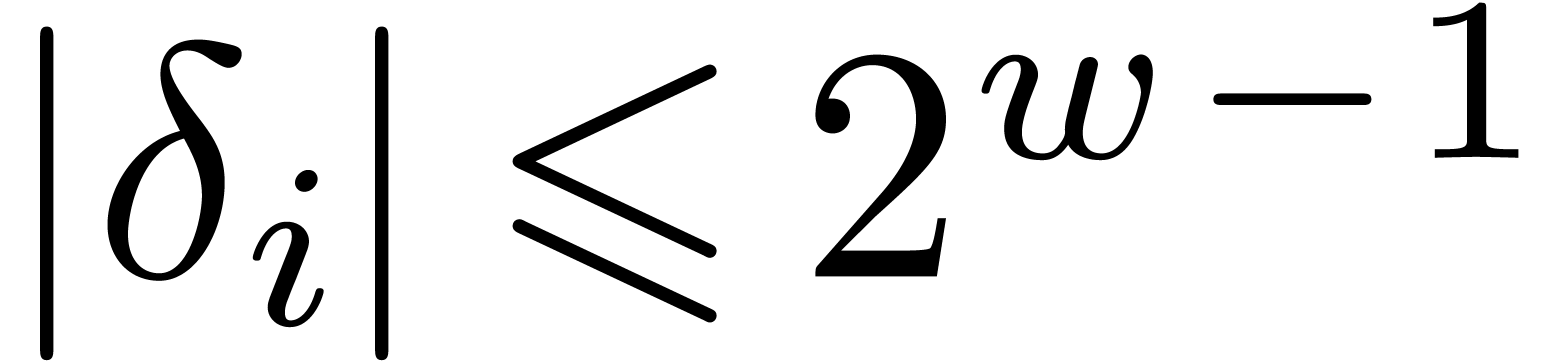 and
and 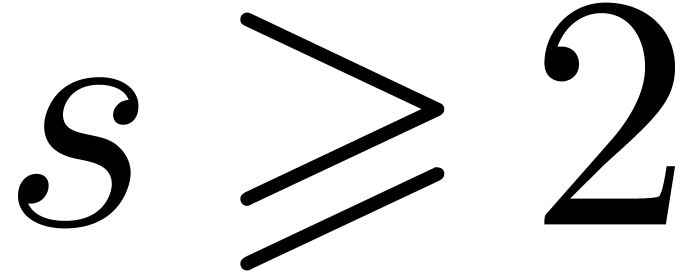 a small
number. As usual, we assume that the
a small
number. As usual, we assume that the  are
pairwise coprime and we let
are
pairwise coprime and we let 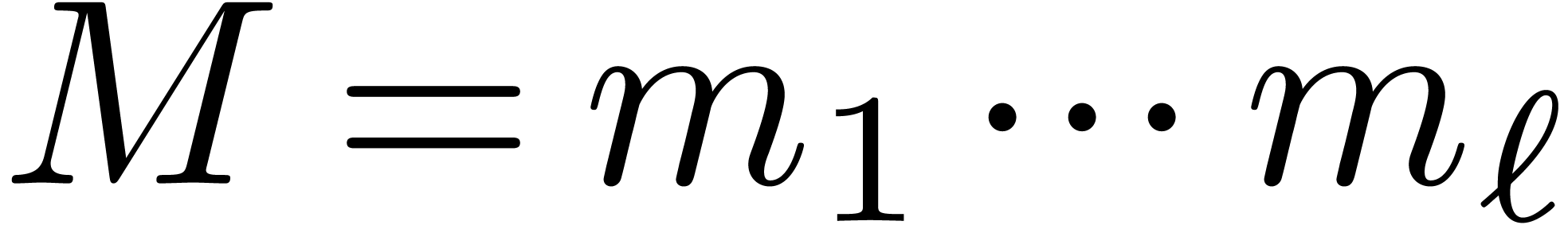 .
We also assume that
.
We also assume that  is slightly smaller than
is slightly smaller than
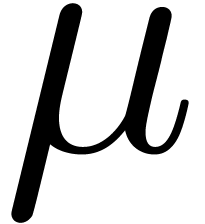 and that we have a hardware instruction for the
exact multiplication of
and that we have a hardware instruction for the
exact multiplication of 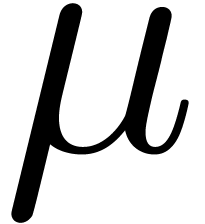 -bit
integers.
-bit
integers.
For moduli  as in (3), the naive
algorithm for the Euclidean division of a number
as in (3), the naive
algorithm for the Euclidean division of a number  by
by  becomes particularly simple and essentially
boils down to the multiplication of
becomes particularly simple and essentially
boils down to the multiplication of  with the
quotient of this division. In other words, the remainder can be computed
using
with the
quotient of this division. In other words, the remainder can be computed
using  hardware multiplications. In comparison,
the algorithm from section 2.3 requires
hardware multiplications. In comparison,
the algorithm from section 2.3 requires 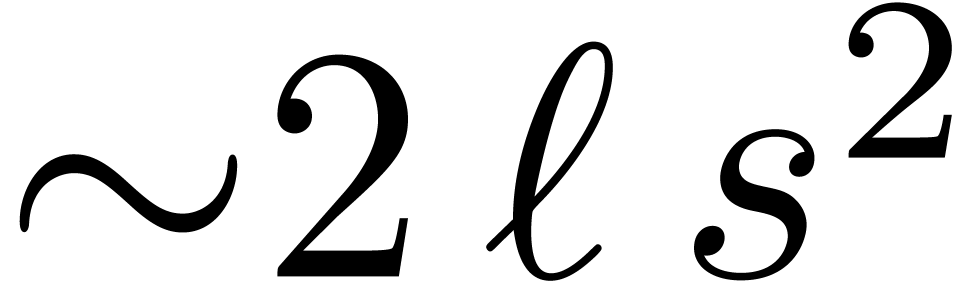 multiplication when applied to
multiplication when applied to  -bit
(instead of
-bit
(instead of  -bit) integers.
More generally, the computation of
-bit) integers.
More generally, the computation of  remainders
remainders
 can be done using
can be done using 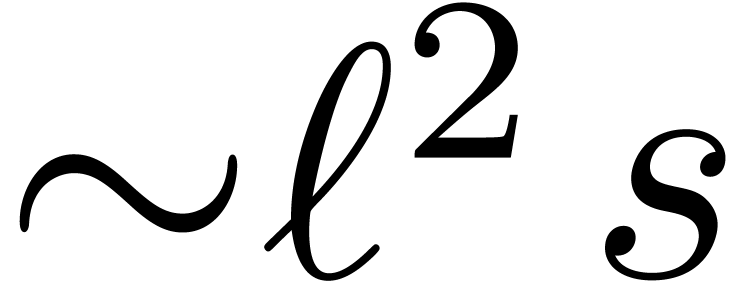 instead of
instead of  multiplications. This leads to a
potential gain of a factor
multiplications. This leads to a
potential gain of a factor 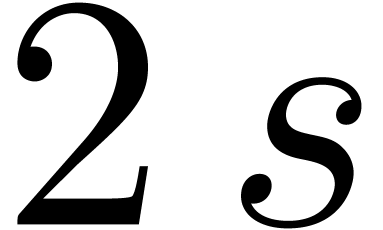 ,
although the remainders are
,
although the remainders are 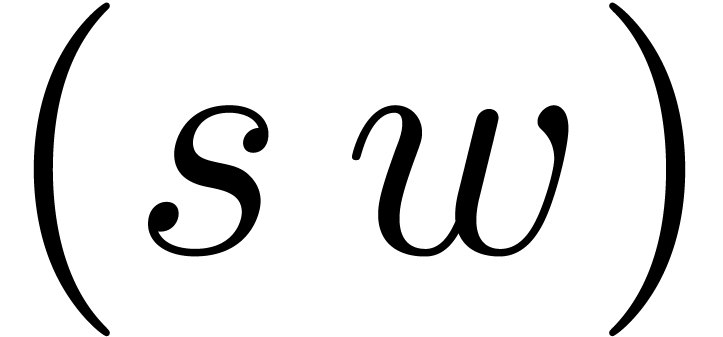 -bit
integers instead of
-bit
integers instead of  -bit
integers, for the time being.
-bit
integers, for the time being.
Multi-modular reconstruction can also be done faster, as follows, using
similar techniques as in [1, 5]. Let 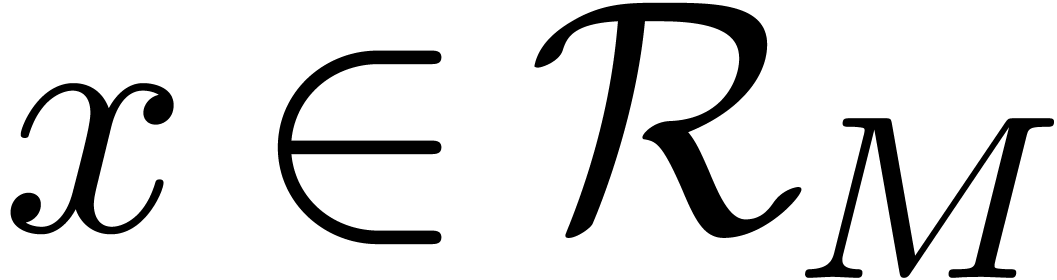 . Besides the usual binary
representation of
. Besides the usual binary
representation of 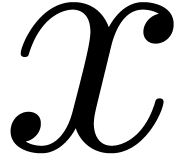 and the multi-modular
representation
and the multi-modular
representation  , it is also
possible to use the mixed radix representation (or Newton
representation)
, it is also
possible to use the mixed radix representation (or Newton
representation)
where 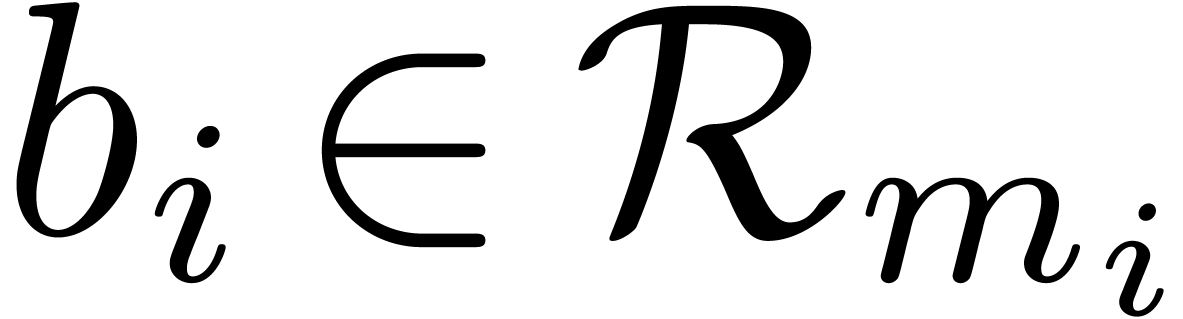 . Let us now show how
to obtain
. Let us now show how
to obtain  efficiently from
efficiently from  . Since
. Since 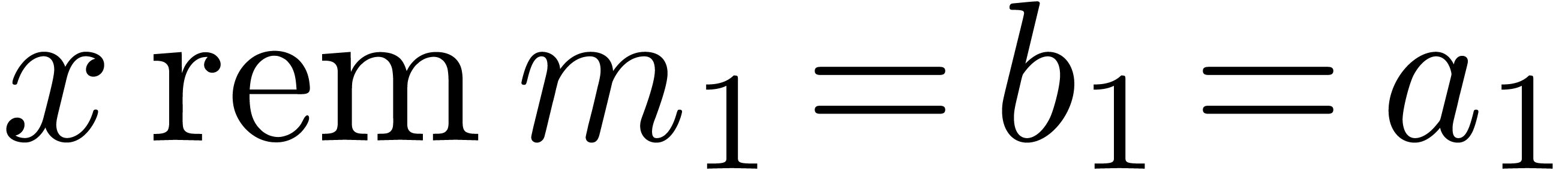 ,
we must take
,
we must take 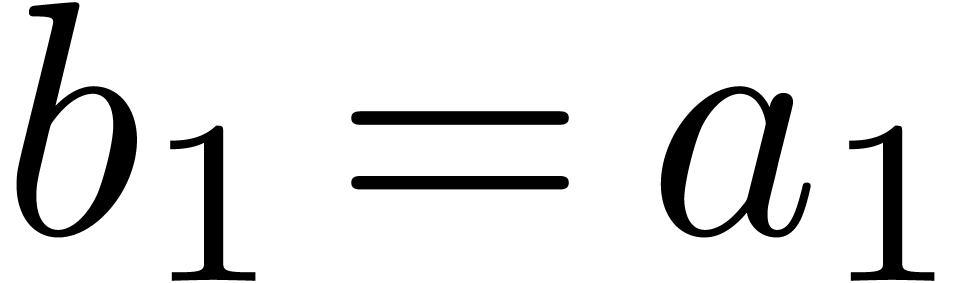 . Assume that
. Assume that
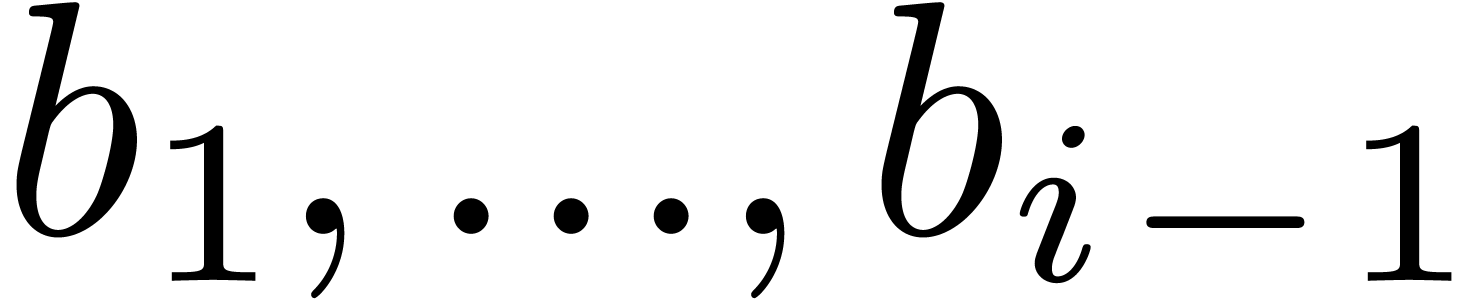 have been computed. For
have been computed. For 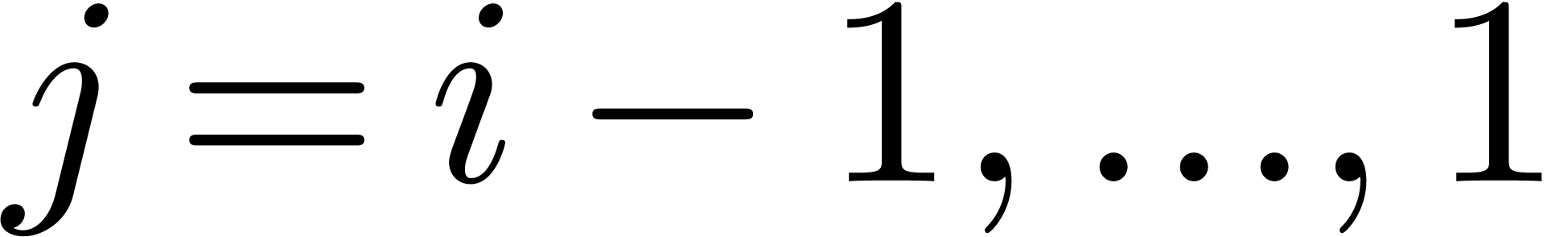 we next compute
we next compute
using 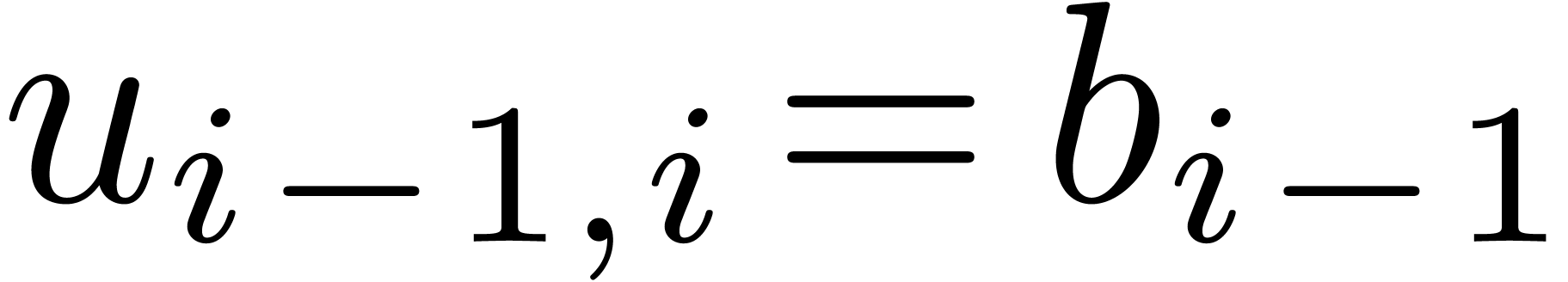 and
and
Notice that  can be computed using
can be computed using 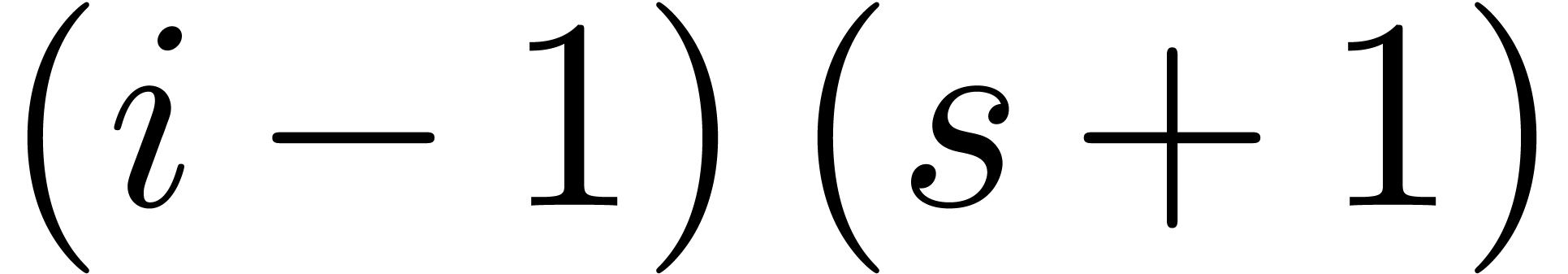 hardware multiplications. We have
hardware multiplications. We have
Now the inverse 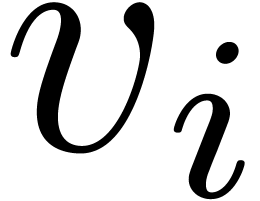 of
of 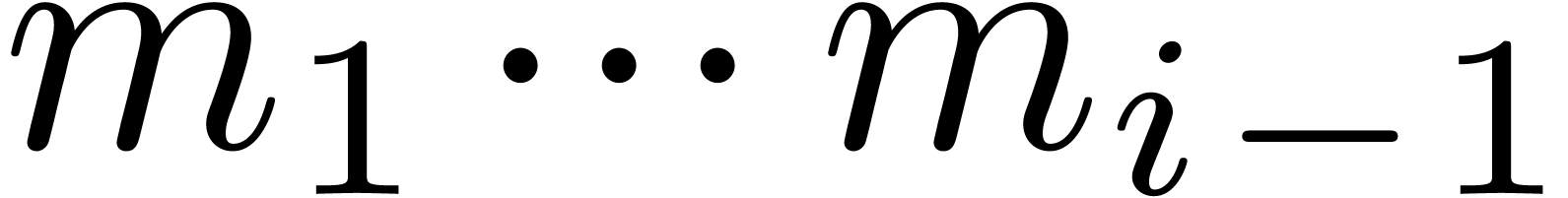 modulo
modulo  can be precomputed. We finally compute
can be precomputed. We finally compute
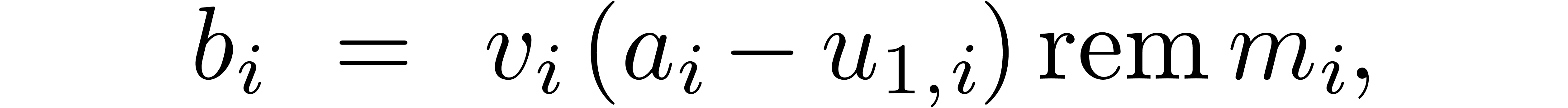
which requires 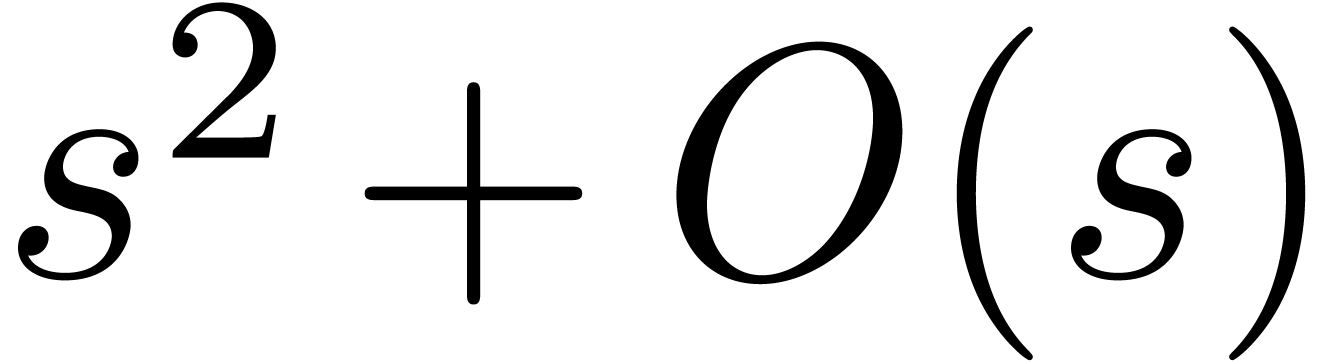 multiplications. For small
values of
multiplications. For small
values of  , we notice that it
may be faster to divide successively by
, we notice that it
may be faster to divide successively by  modulo
modulo
 instead of multiplying with
instead of multiplying with 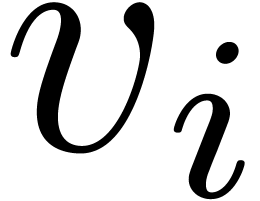 . In total, the computation of the mixed radix
representation
. In total, the computation of the mixed radix
representation  can be done using
can be done using 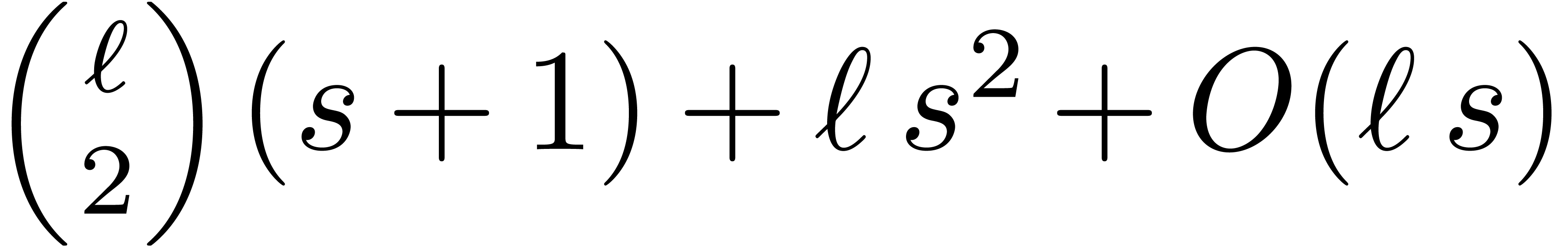 multiplications. Having computed the mixed radix
representation, we next compute
multiplications. Having computed the mixed radix
representation, we next compute
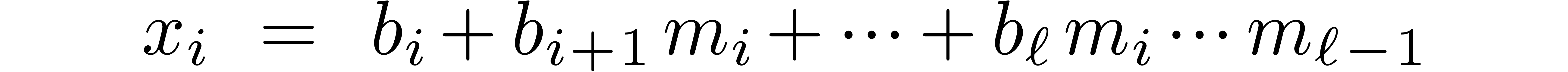
for 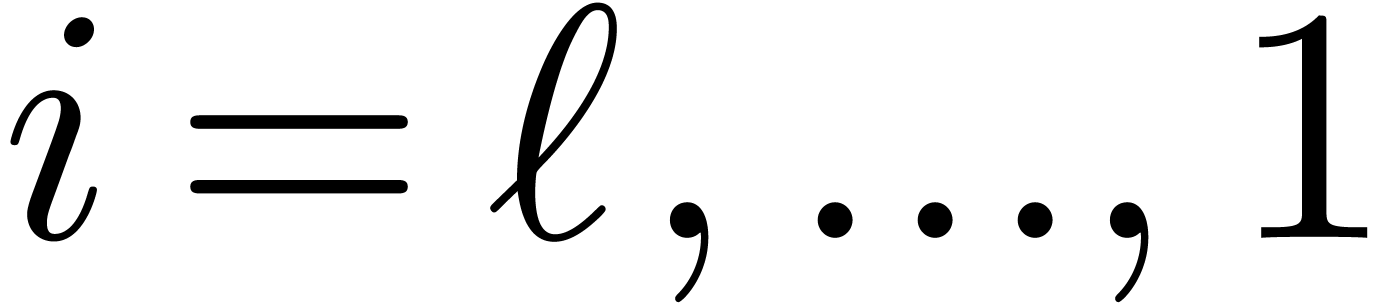 , using the recurrence
relation
, using the recurrence
relation

Since 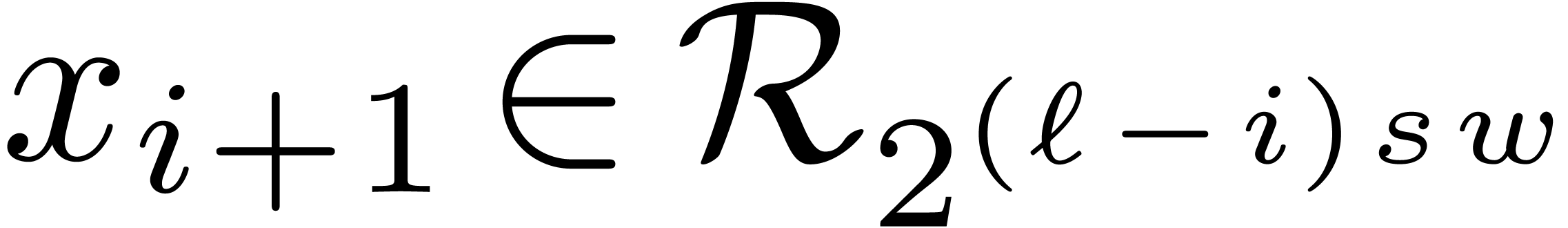 , the computation of
, the computation of
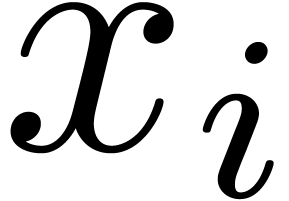 requires
requires 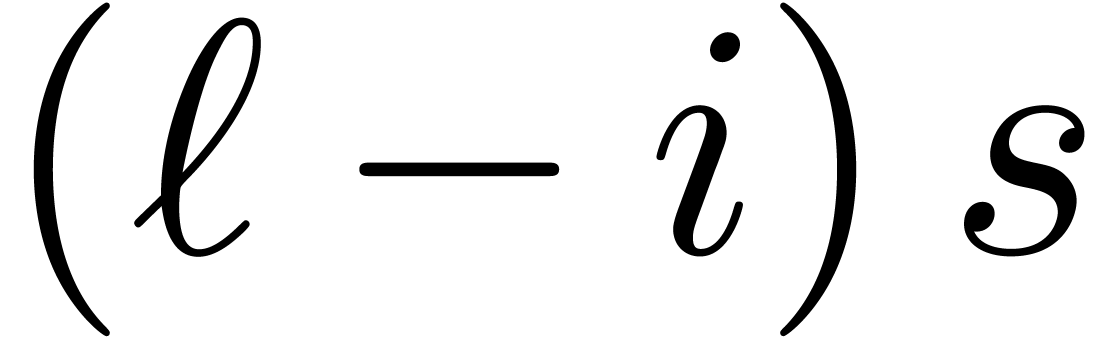 multiplications. Altogether, the computation of
multiplications. Altogether, the computation of  from
from  can therefore be done using
can therefore be done using 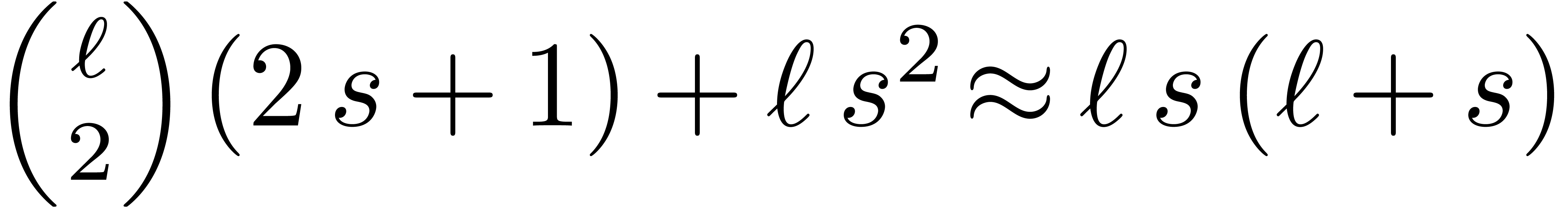 hardware multiplications.
hardware multiplications.
3.2Combining special moduli into
gentle moduli
For practical applications, we usually wish to work with moduli that fit
into one word (instead of  words). With the
words). With the  as in the previous subsection, this means that we
need to impose the further requirement that each modulus
as in the previous subsection, this means that we
need to impose the further requirement that each modulus  can be factored
can be factored
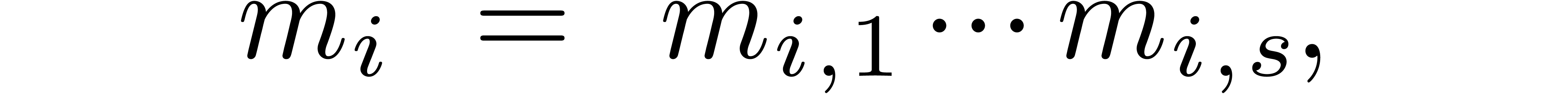
with 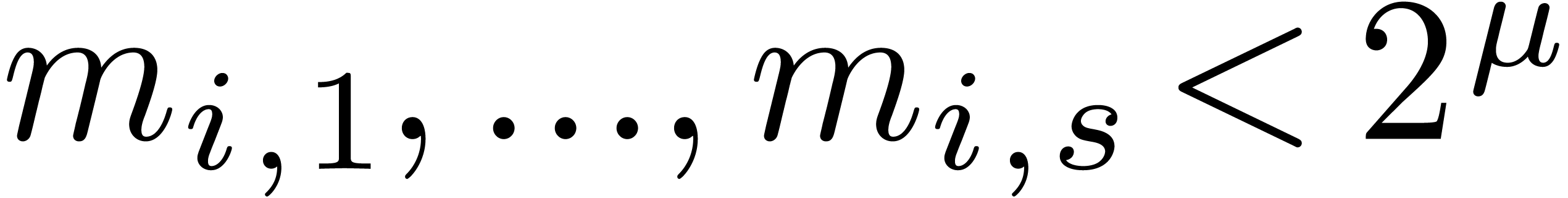 . If this is possible,
then the
. If this is possible,
then the  are called
are called  -gentle moduli. For given bitsizes
-gentle moduli. For given bitsizes  and
and  , the main
questions are now: do such moduli indeed exist? If so, then how to find
them?
, the main
questions are now: do such moduli indeed exist? If so, then how to find
them?
If 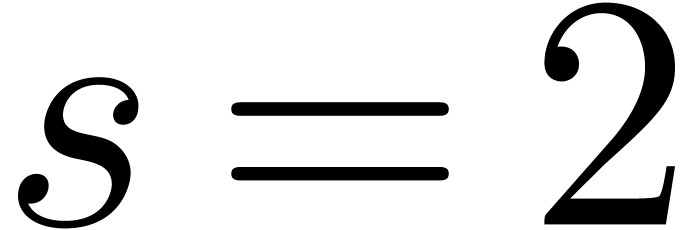 , then it is easy to
construct
, then it is easy to
construct  -gentle moduli
-gentle moduli 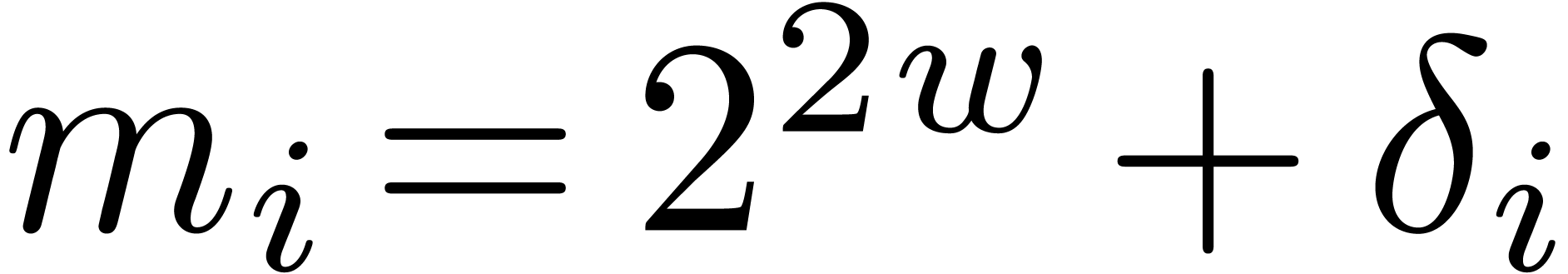 by taking
by taking 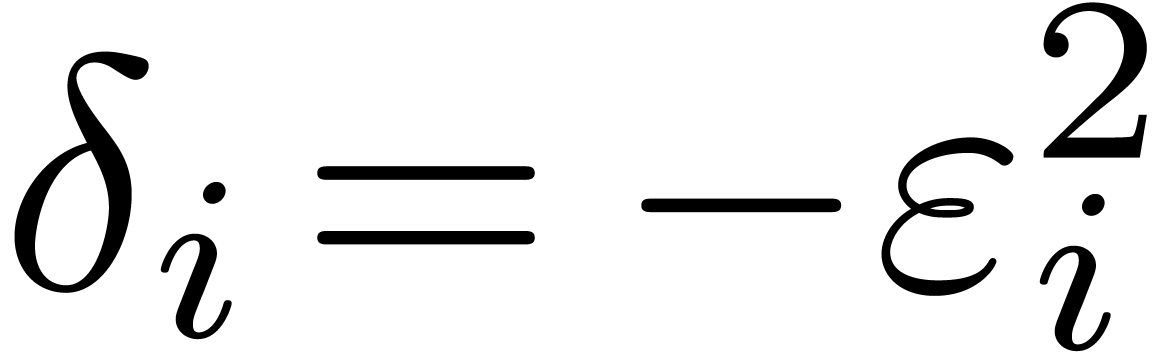 ,
where
,
where 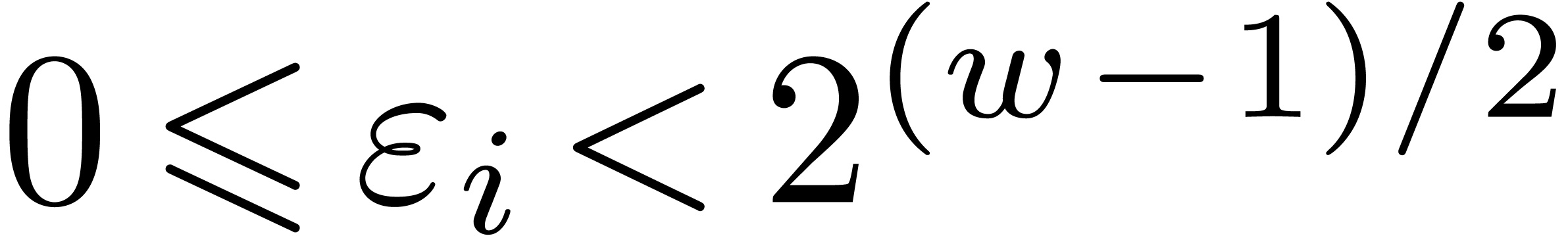 is odd. Indeed,
is odd. Indeed,
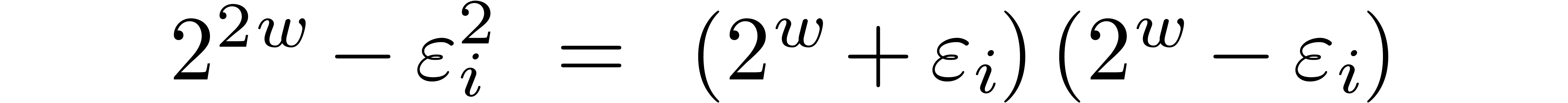
and  . Unfortunately, this
trick does not generalize to higher values
. Unfortunately, this
trick does not generalize to higher values 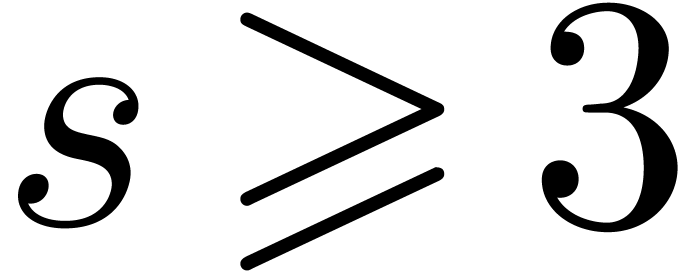 .
Indeed, consider a product
.
Indeed, consider a product
where  are small compared to
are small compared to 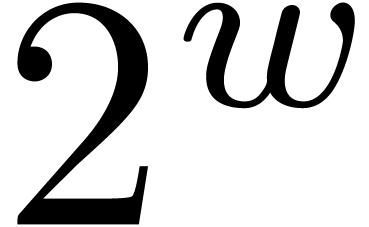 . If the coefficient
. If the coefficient  of
of
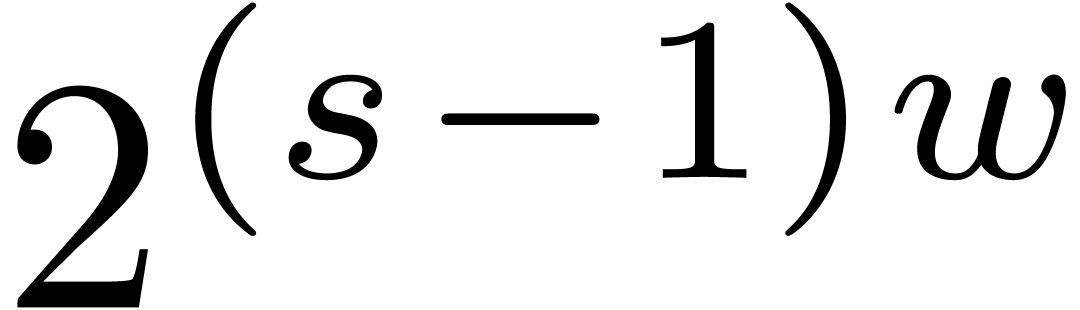 vanishes, then the coefficient of
vanishes, then the coefficient of 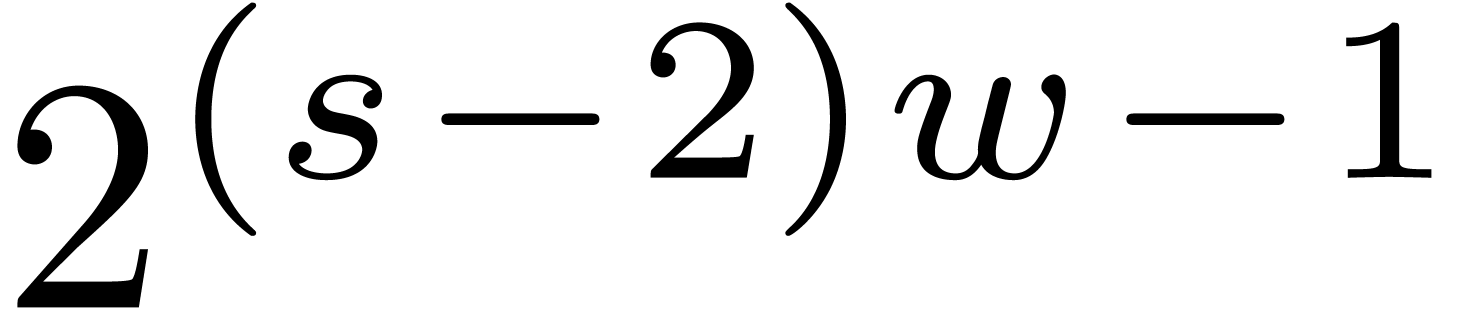 becomes the opposite
becomes the opposite 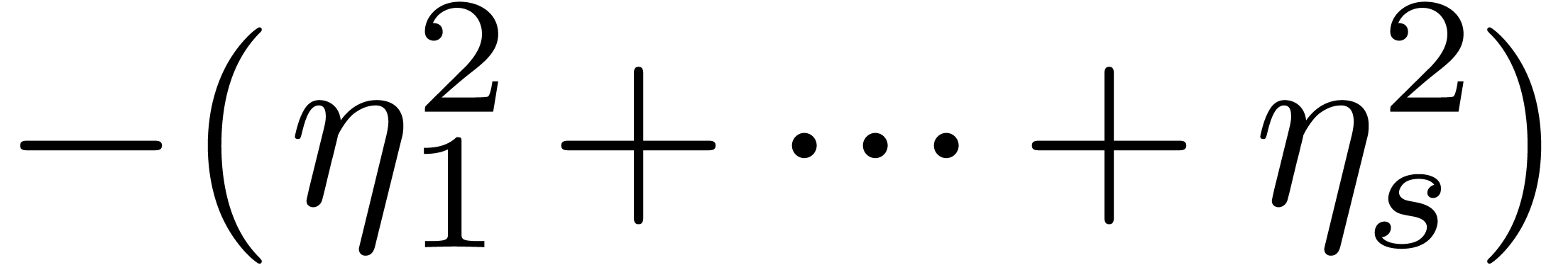 of a sum of
squares. In particular, both coefficients cannot vanish simultaneously,
unless
of a sum of
squares. In particular, both coefficients cannot vanish simultaneously,
unless 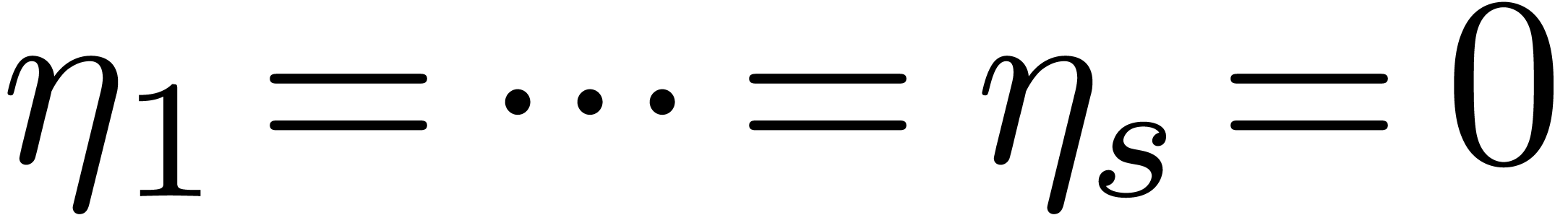 .
.
If  , then we are left with
the option to search
, then we are left with
the option to search  -gentle
moduli by brute force. As long as
-gentle
moduli by brute force. As long as  is
“reasonably small” (say
is
“reasonably small” (say  ),
the probability to hit an
),
the probability to hit an  -gentle
modulus for a randomly chosen
-gentle
modulus for a randomly chosen 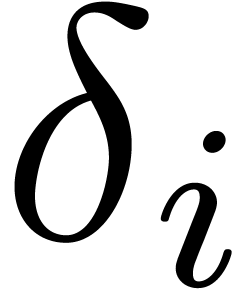 often remains
significantly larger than
often remains
significantly larger than 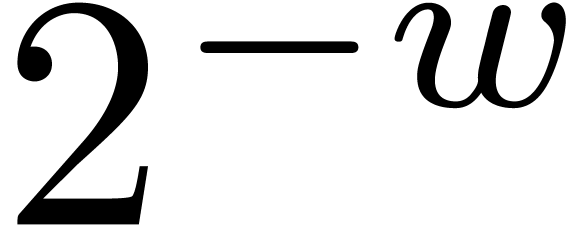 .
We may then use sieving to find such moduli. By what precedes, it is
also desirable to systematically take
.
We may then use sieving to find such moduli. By what precedes, it is
also desirable to systematically take 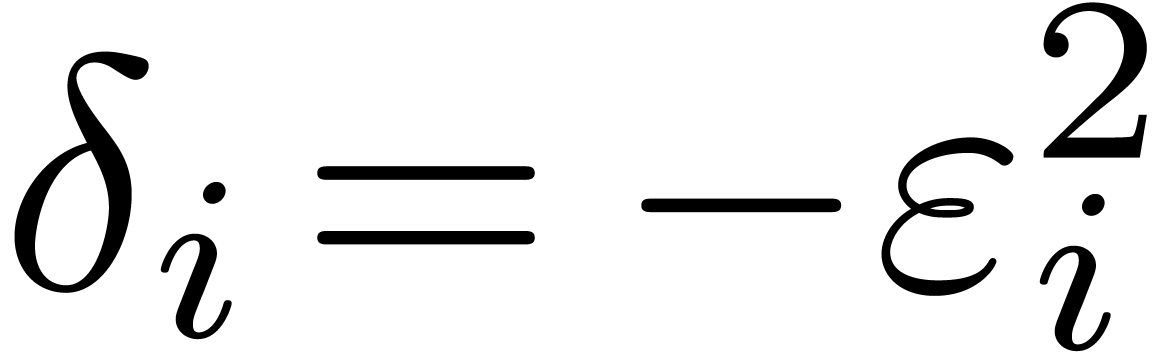 for
for 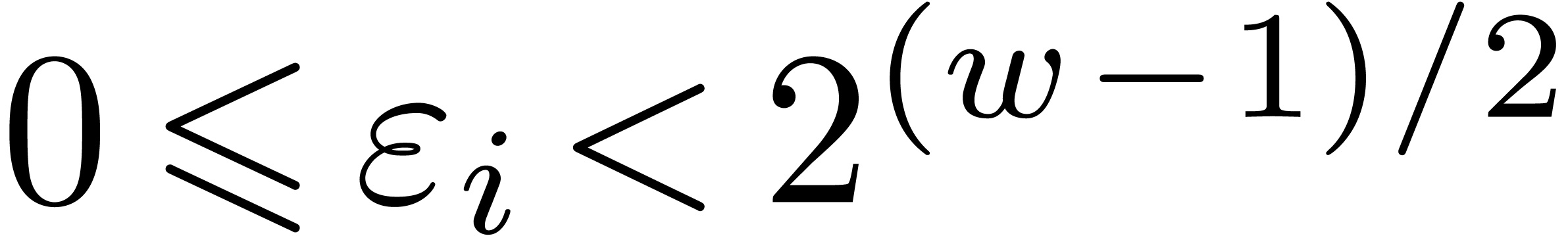 . This has the additional benefit
that we “only” have to consider
. This has the additional benefit
that we “only” have to consider 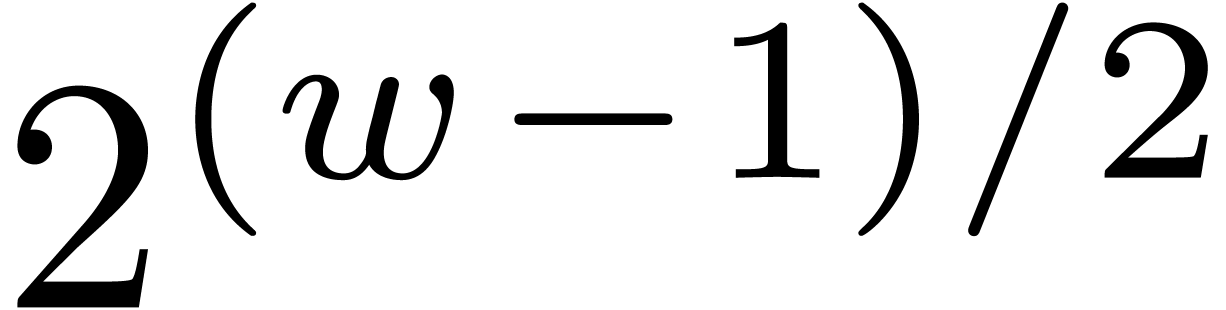 possibilities for
possibilities for  .
.
We will discuss sieving in more detail in the next section. Assuming
that we indeed have found  -gentle
moduli
-gentle
moduli  , we may use the naive
algorithms from section 2.3 to compute
, we may use the naive
algorithms from section 2.3 to compute  from
from 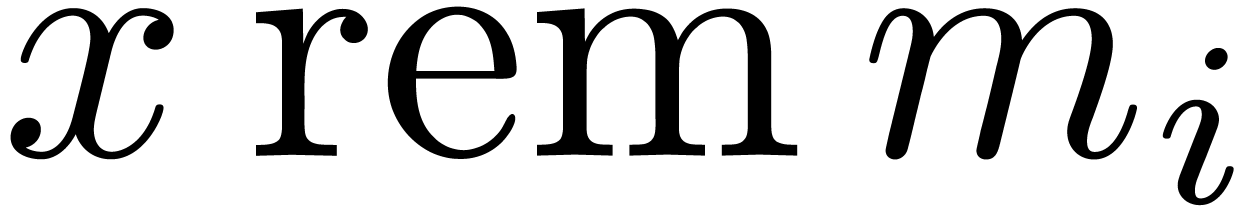 and vice versa for
and vice versa for 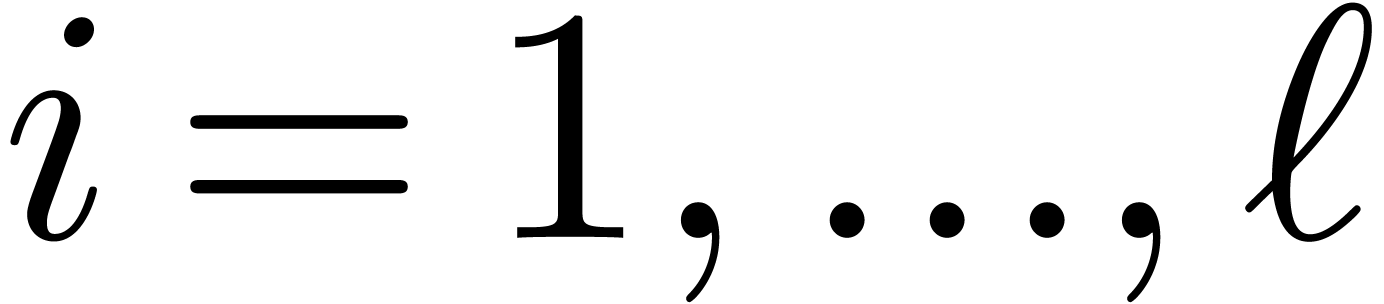 . Given
. Given 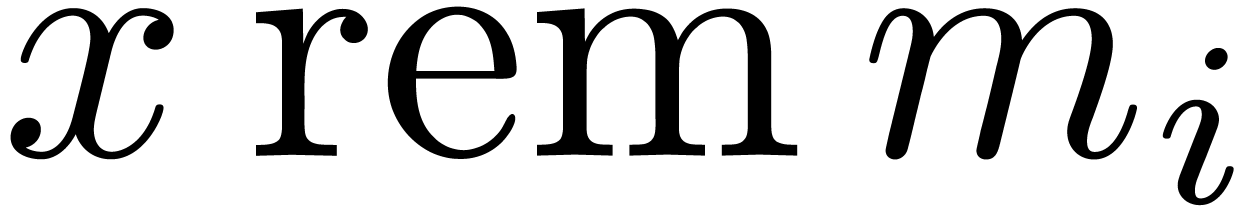 for all
for all 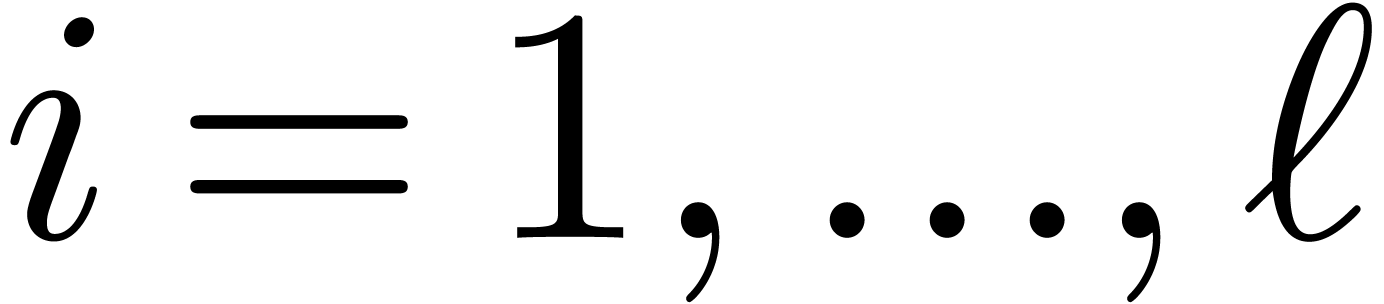 , this allows us to compute all
remainders
, this allows us to compute all
remainders  using
using 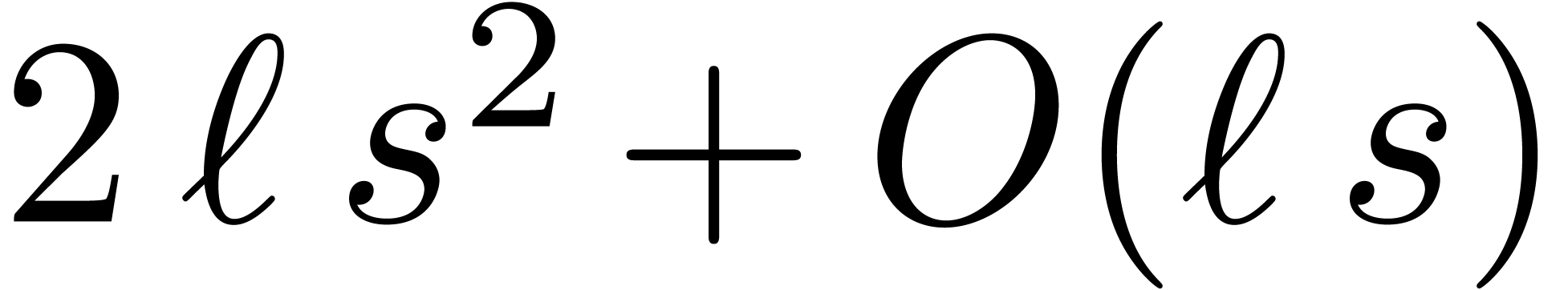 hardware multiplications, whereas the opposite conversion only requires
hardware multiplications, whereas the opposite conversion only requires
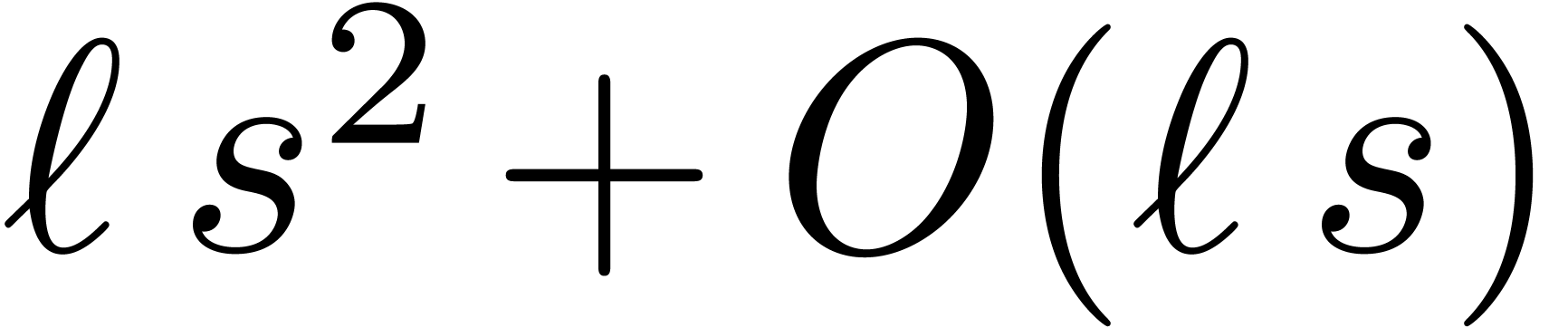 multiplications. Altogether, we may thus obtain
the remainders
multiplications. Altogether, we may thus obtain
the remainders  from
from  and
vice versa using
and
vice versa using 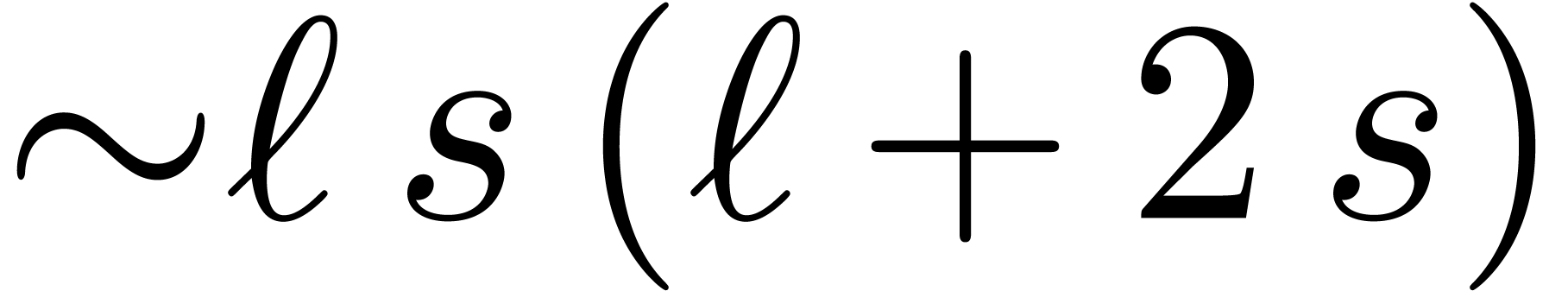 multiplications.
multiplications.
4The gentle modulus hunt
4.1The sieving procedure
We implemented a sieving procedure in Mathemagix
[11] that uses the Mpari package with
an interface to Pari-GP [15]. Given
parameters 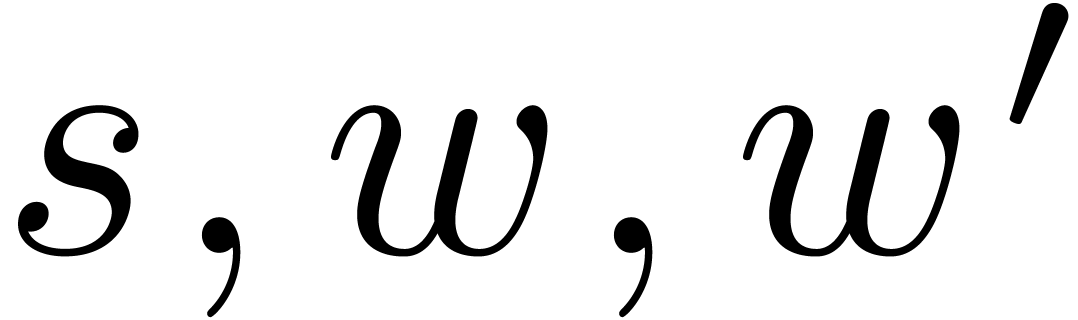 and
and 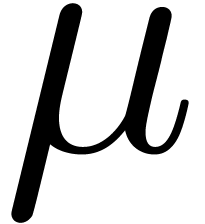 ,
the goal of our procedure is to find
,
the goal of our procedure is to find  -gentle
moduli of the form
-gentle
moduli of the form
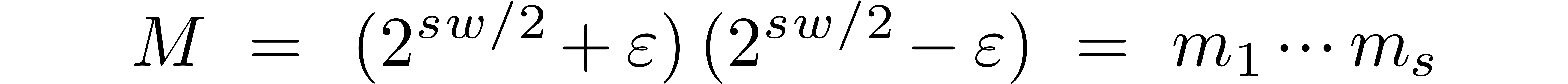
with the constraints that
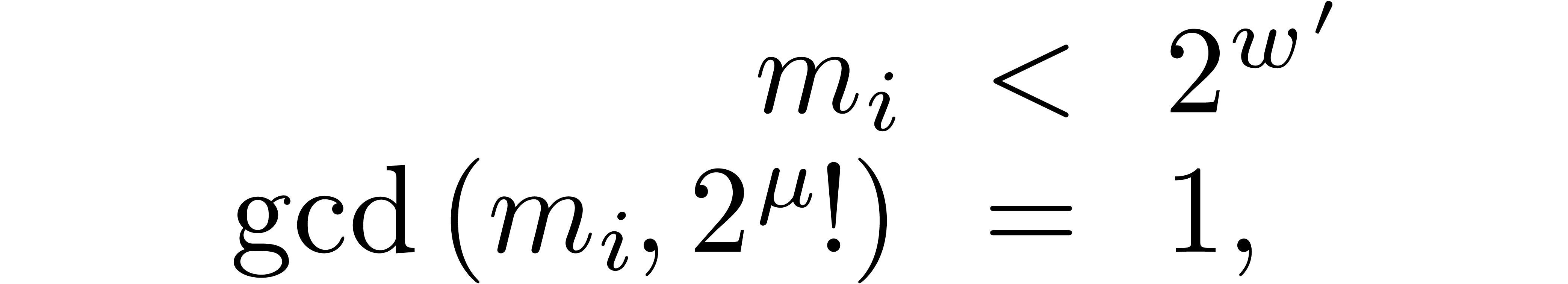
for 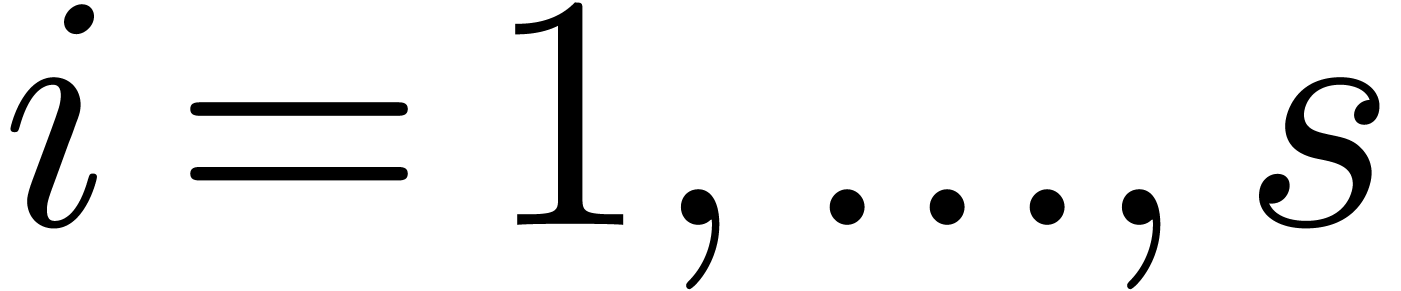 , and
, and  . The parameter
. The parameter  is
small and even. One should interpret
is
small and even. One should interpret  and
and 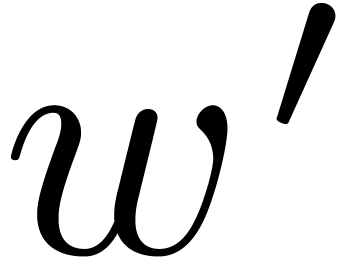 as the intended and maximal bitsize of the small
moduli
as the intended and maximal bitsize of the small
moduli  . The parameter
. The parameter 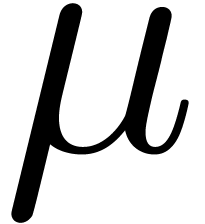 stands for the minimal bitsize of a prime factor of
stands for the minimal bitsize of a prime factor of
 . The parameter
. The parameter  should be such that
should be such that 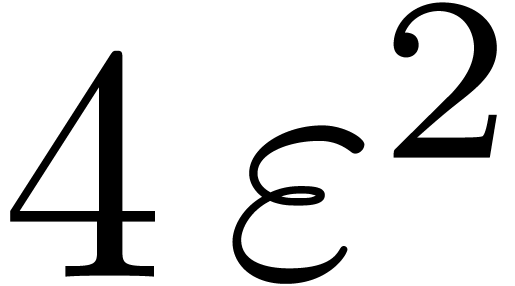 fits into a
machine word.
fits into a
machine word.
In Table 1 below we have shown some experimental results
for this sieving procedure in the case when 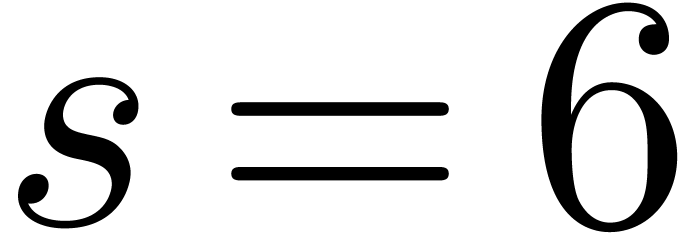 ,
, 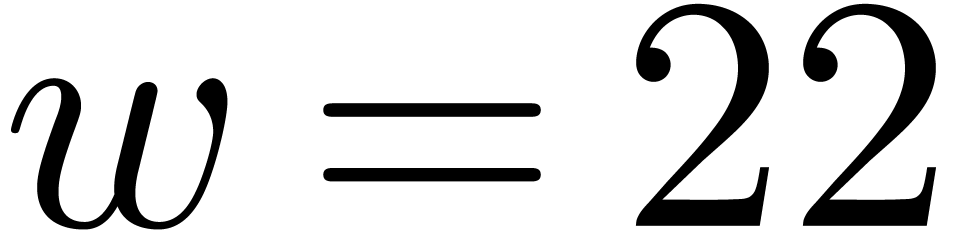 ,
, 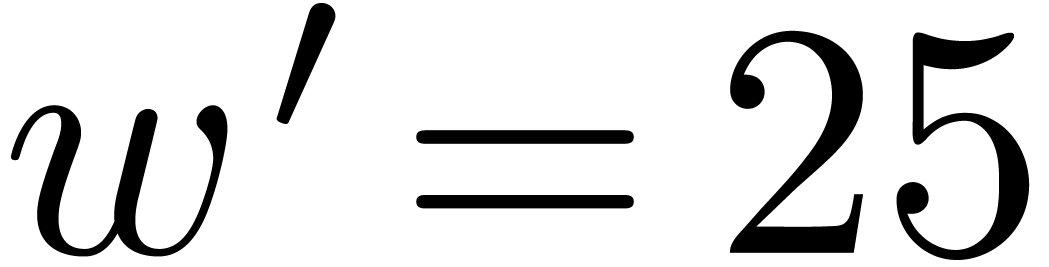 and
and 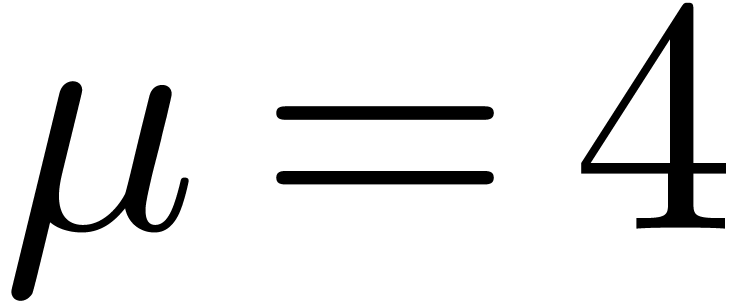 . For
. For
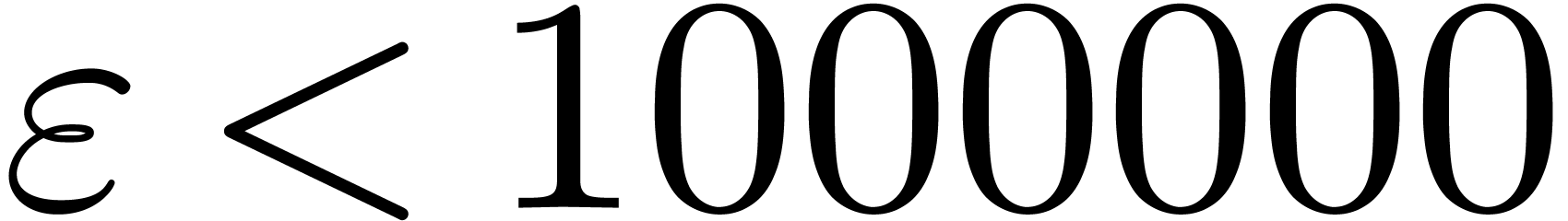 , the table provides us with
, the table provides us with
 , the moduli
, the moduli  , as well as the smallest prime power factors
of the product
, as well as the smallest prime power factors
of the product 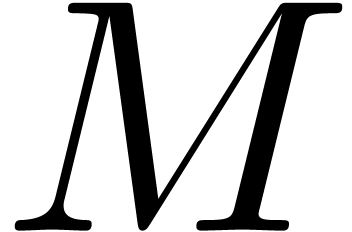 . Many hits
admit small prime factors, which increases the risk that different hits
are not coprime. For instance, the number
. Many hits
admit small prime factors, which increases the risk that different hits
are not coprime. For instance, the number  divides both
divides both 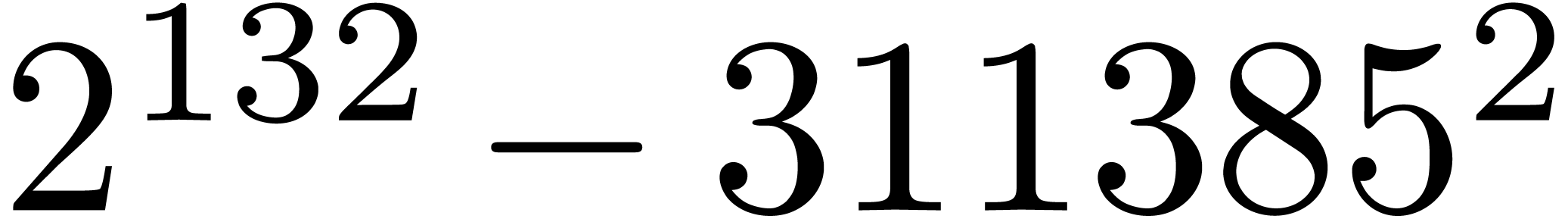 and
and 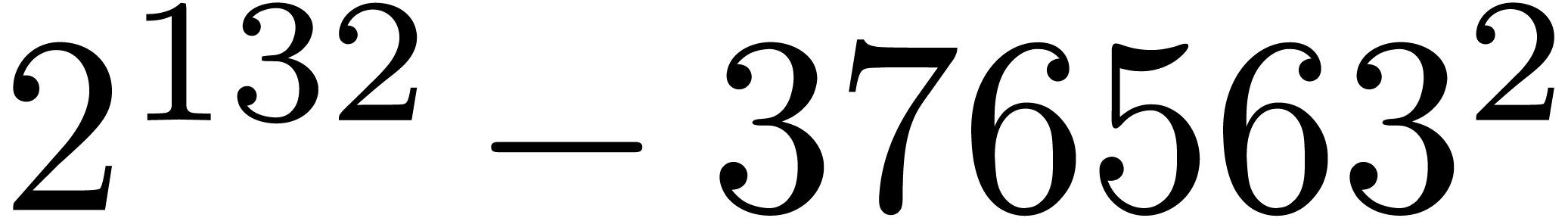 ,
whence these
,
whence these  -gentle moduli
cannot be selected simultaneously (except if one is ready to sacrifice a
few bits by working modulo
-gentle moduli
cannot be selected simultaneously (except if one is ready to sacrifice a
few bits by working modulo 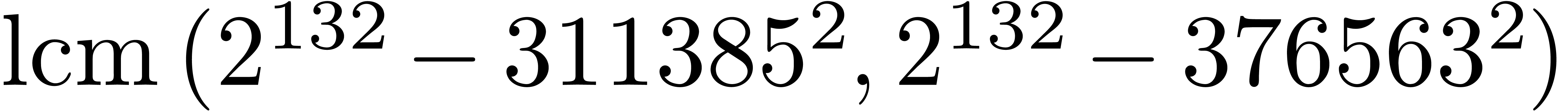 instead of
instead of  ).
).
In the case when we use multi-modular arithmetic for computations with
rational numbers instead of integers (see [9, section 5
and, more particularly, section 5.10]), then small prime factors should
completely be prohibited, since they increase the probability of
divisions by zero. For such applications, it is therefore desirable that
 are all prime. In our table, this occurs for
are all prime. In our table, this occurs for
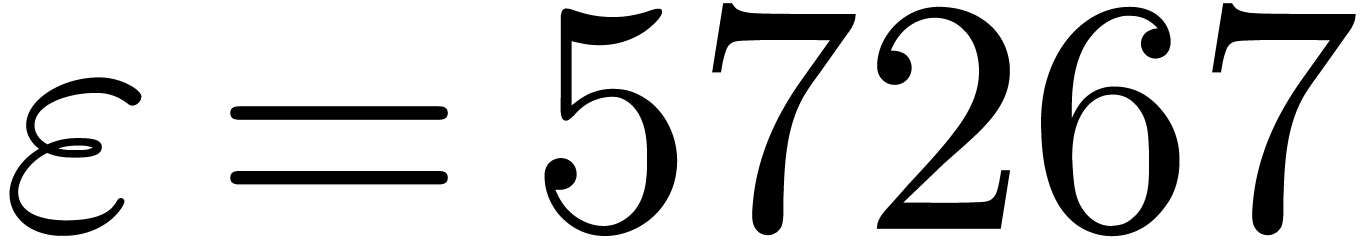 (we indicated this by highlighting the list of
prime factors of
(we indicated this by highlighting the list of
prime factors of 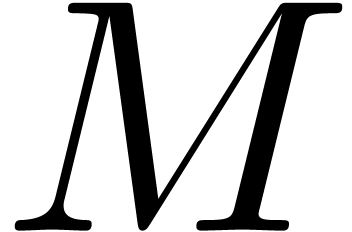 ).
).
In order to make multi-modular reduction and reconstruction as efficient
as possible, a desirable property of the moduli  is that they either divide
is that they either divide 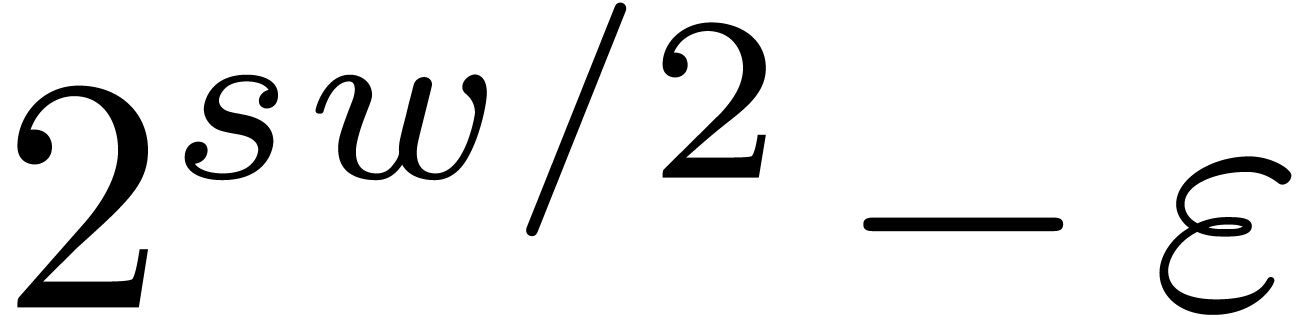 or
or 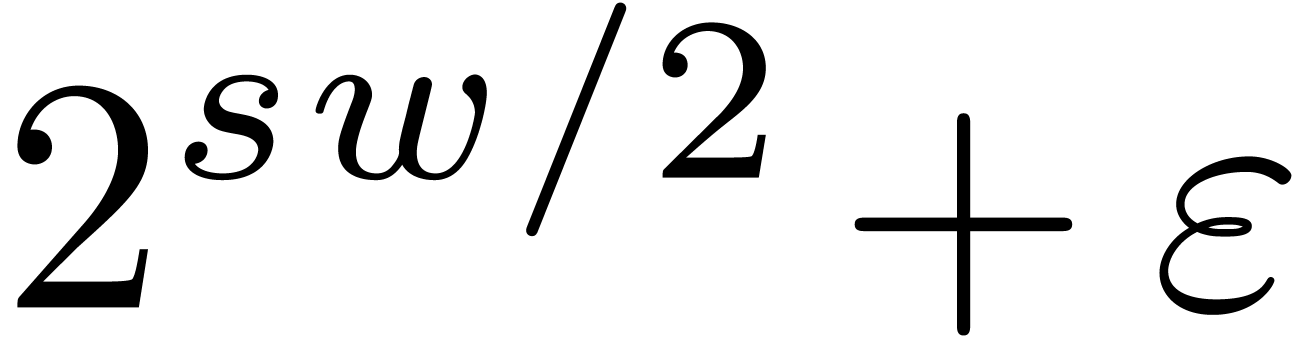 . In our table, we highlighted the
. In our table, we highlighted the  for which this happens. We notice that this is
automatically the case if
for which this happens. We notice that this is
automatically the case if  are all prime. If only
a small number of
are all prime. If only
a small number of  (say a single one) do not
divide either
(say a single one) do not
divide either 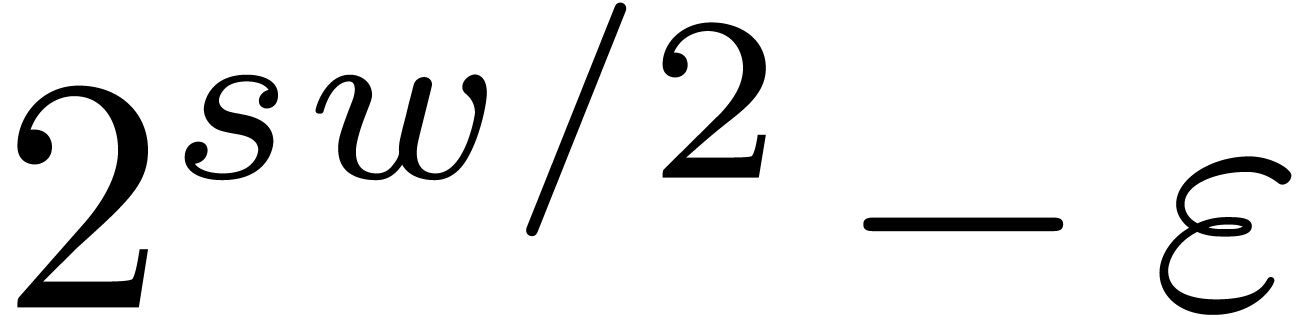 or
or 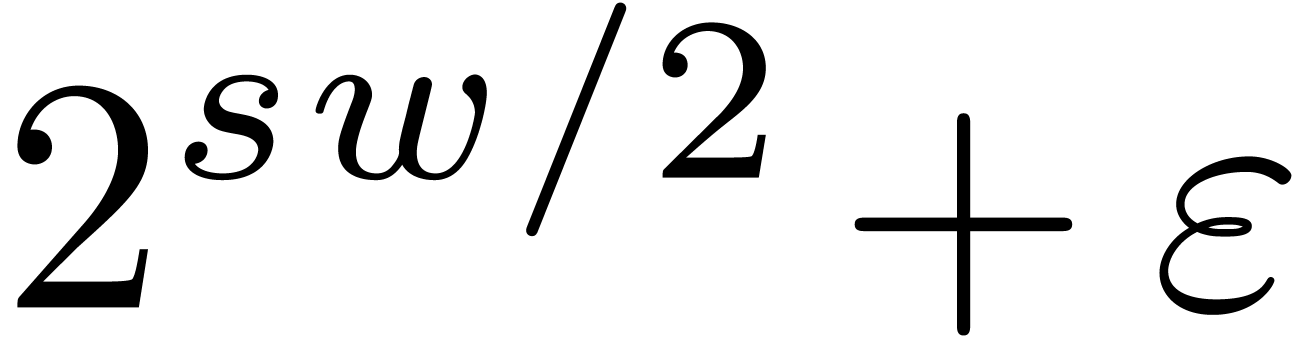 ,
then we remark that it should still be possible to design reasonably
efficient ad hoc algorithms for multi-modular reduction and
reconstruction.
,
then we remark that it should still be possible to design reasonably
efficient ad hoc algorithms for multi-modular reduction and
reconstruction.
Another desirable property of the moduli  is that
is that
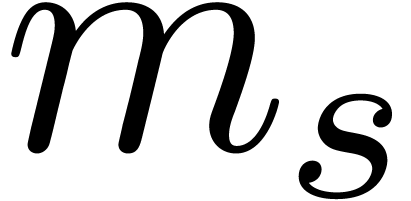 is as small as possible: the spare bits can for
instance be used to speed up matrix multiplication modulo
is as small as possible: the spare bits can for
instance be used to speed up matrix multiplication modulo 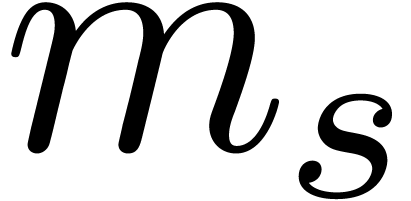 . Notice however that one
“occasional” large modulus
. Notice however that one
“occasional” large modulus 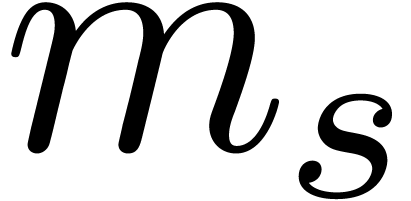 only
impacts on one out of
only
impacts on one out of  modular matrix products;
this alleviates the negative impact of such moduli. We refer to section
4.3 below for more details.
modular matrix products;
this alleviates the negative impact of such moduli. We refer to section
4.3 below for more details.
For actual applications, one should select gentle moduli that combine
all desirable properties mentioned above. If not enough such moduli can
be found, then it it depends on the application which criteria are most
important and which ones can be released.
 |
 |
 |
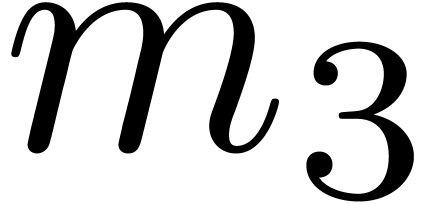 |
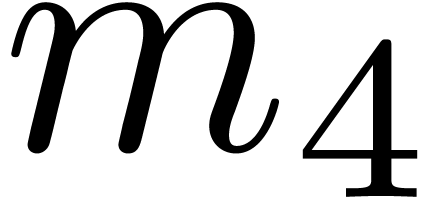 |
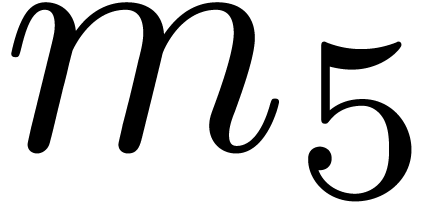 |
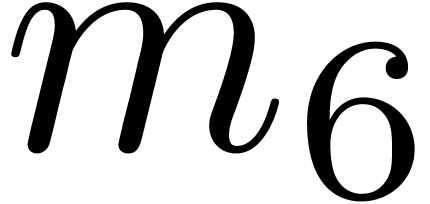 |
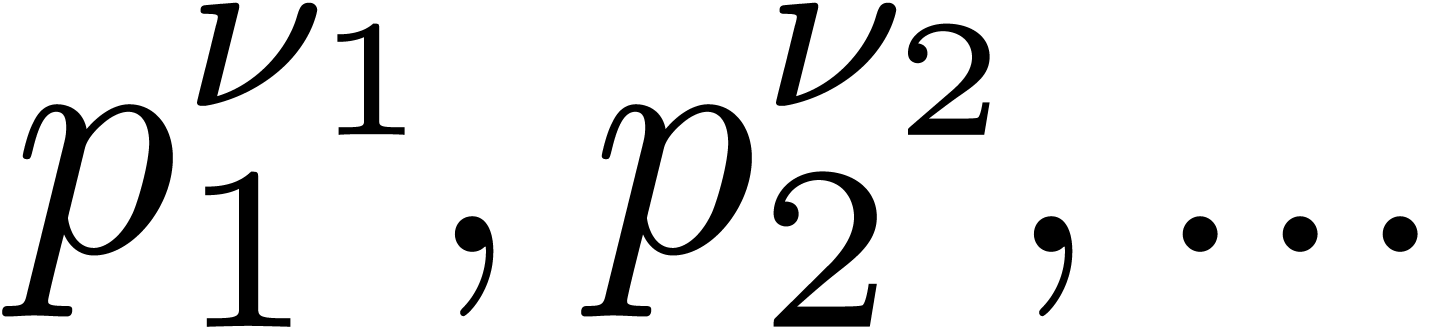 |
| 27657 |
28867 |
4365919 |
6343559 |
13248371 |
20526577 |
25042063 |
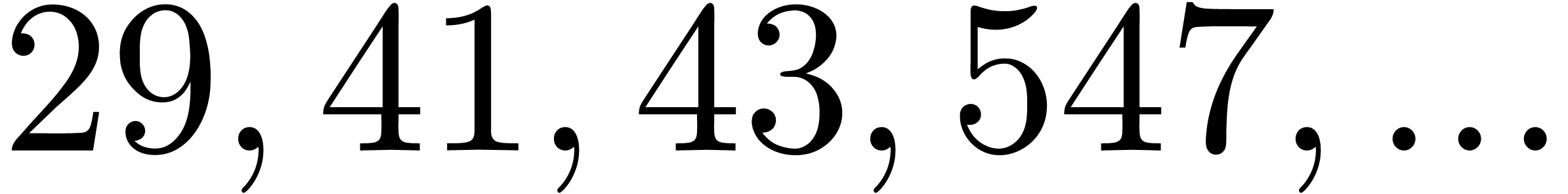 |
| 57267 |
416459 |
1278617 |
2041469 |
6879443 |
25754563 |
28268089 |
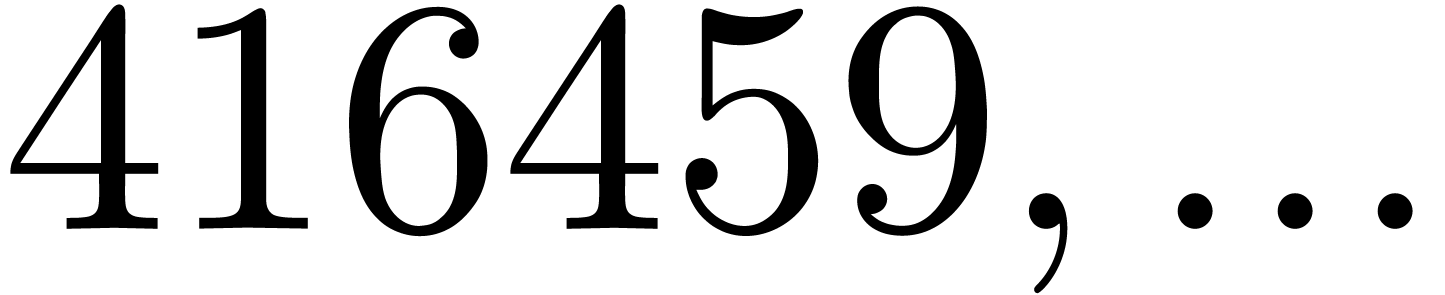 |
| 77565 |
7759 |
8077463 |
8261833 |
18751793 |
19509473 |
28741799 |
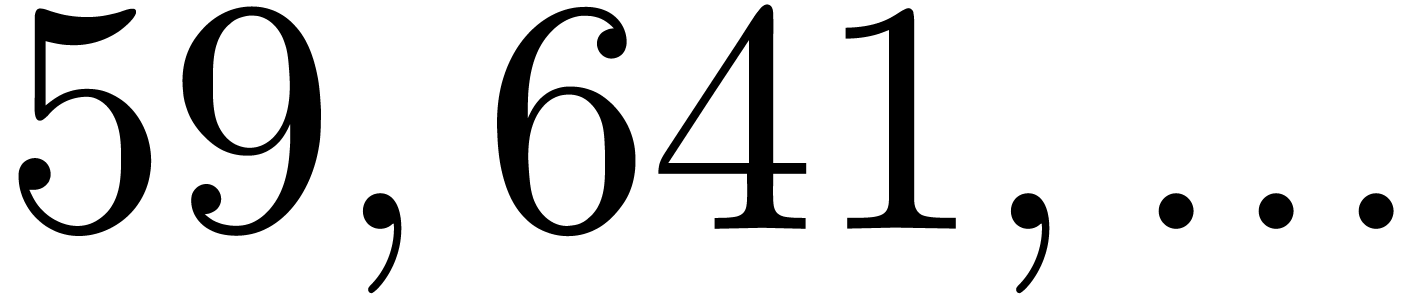 |
| 95253 |
724567 |
965411 |
3993107 |
4382527 |
19140643 |
23236813 |
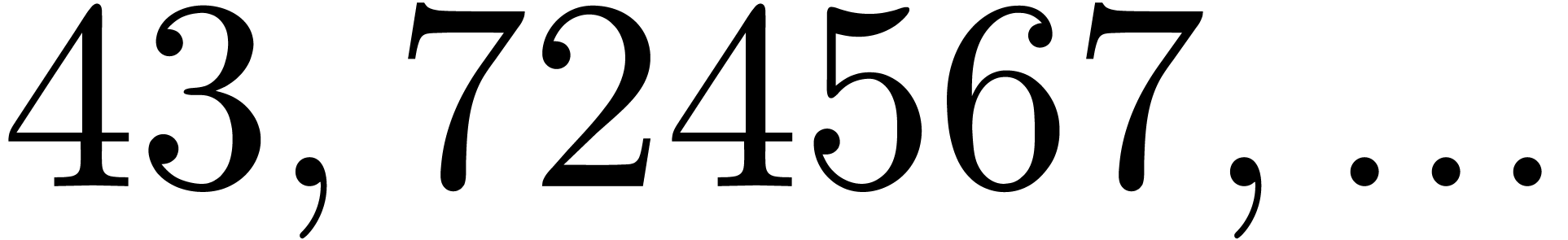 |
| 294537 |
190297 |
283729 |
8804561 |
19522819 |
19861189 |
29537129 |
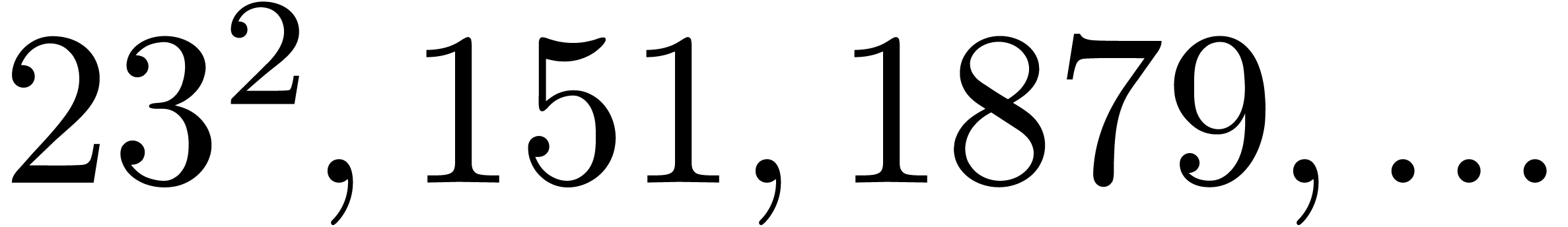 |
| 311385 |
145991 |
4440391 |
4888427 |
6812881 |
7796203 |
32346631 |
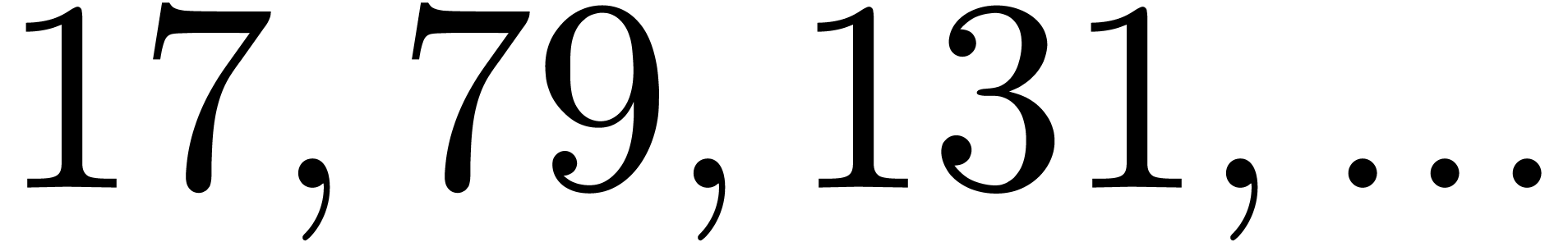 |
| 348597 |
114299 |
643619 |
6190673 |
11389121 |
32355397 |
32442427 |
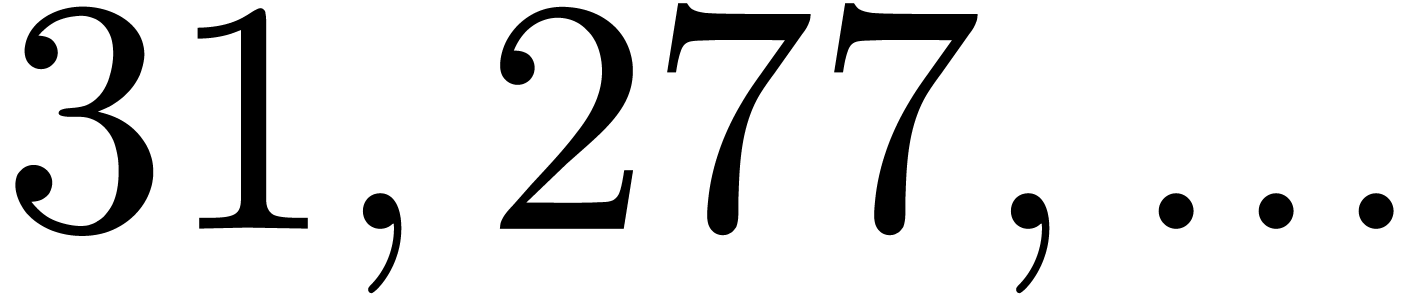 |
| 376563 |
175897 |
1785527 |
2715133 |
7047419 |
30030061 |
30168739 |
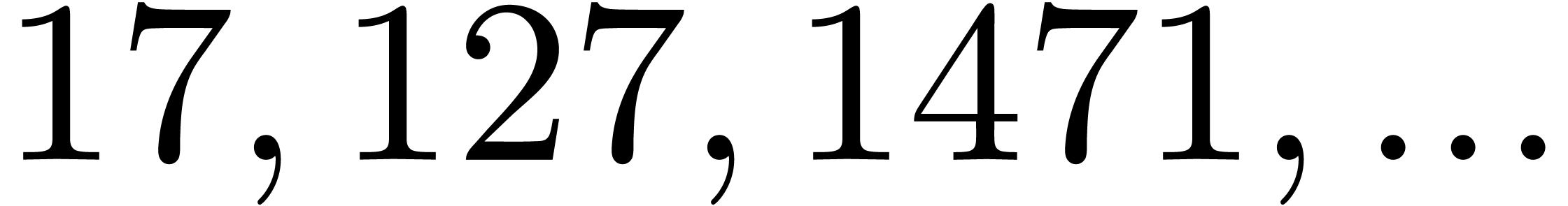 |
| 462165 |
39841 |
3746641 |
7550339 |
13195943 |
18119681 |
20203643 |
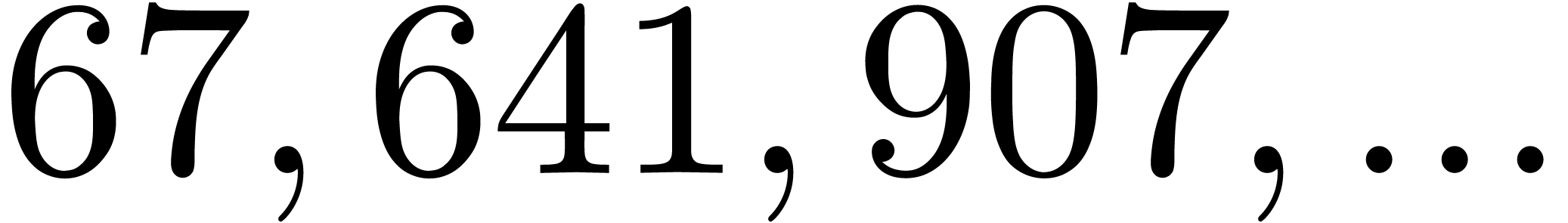 |
| 559713 |
353201 |
873023 |
2595031 |
11217163 |
18624077 |
32569529 |
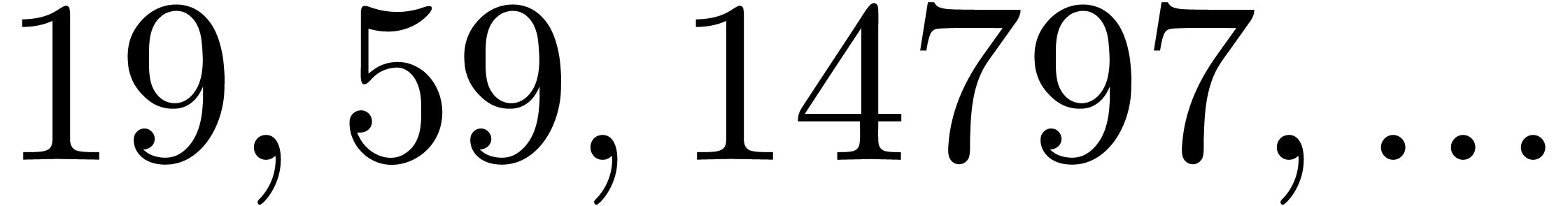 |
| 649485 |
21727 |
1186571 |
14199517 |
15248119 |
31033397 |
31430173 |
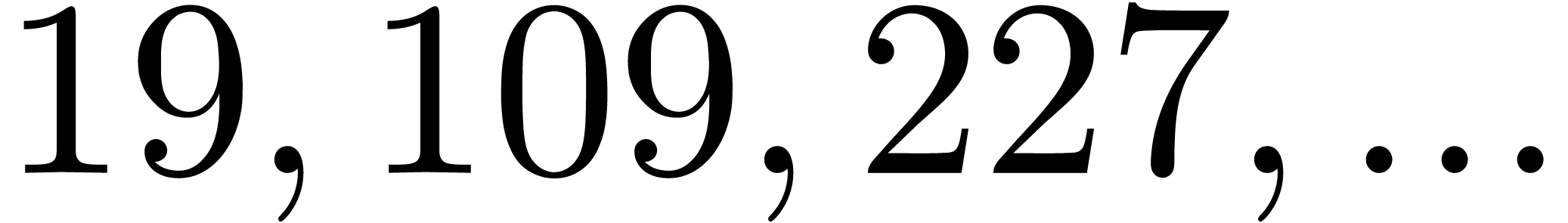 |
| 656997 |
233341 |
1523807 |
5654437 |
8563679 |
17566069 |
18001723 |
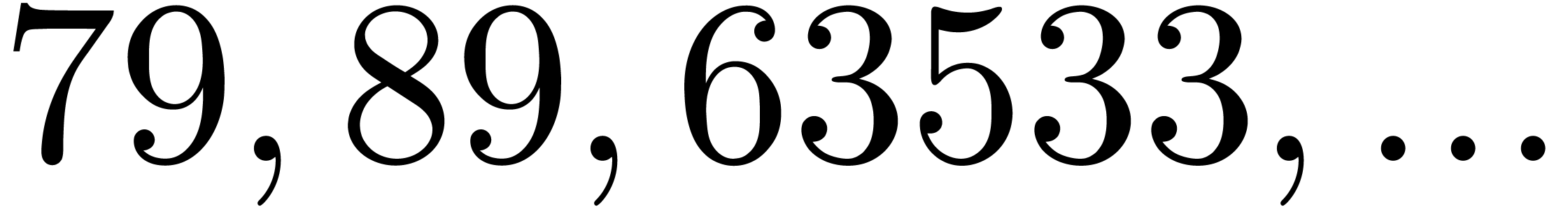 |
| 735753 |
115151 |
923207 |
3040187 |
23655187 |
26289379 |
27088541 |
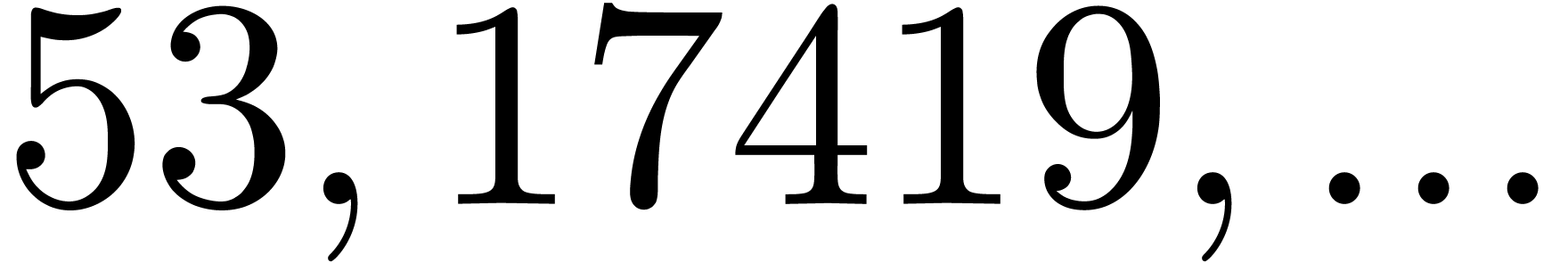 |
| 801687 |
873767 |
1136111 |
3245041 |
7357871 |
8826871 |
26023391 |
 |
| 826863 |
187177 |
943099 |
6839467 |
11439319 |
12923753 |
30502721 |
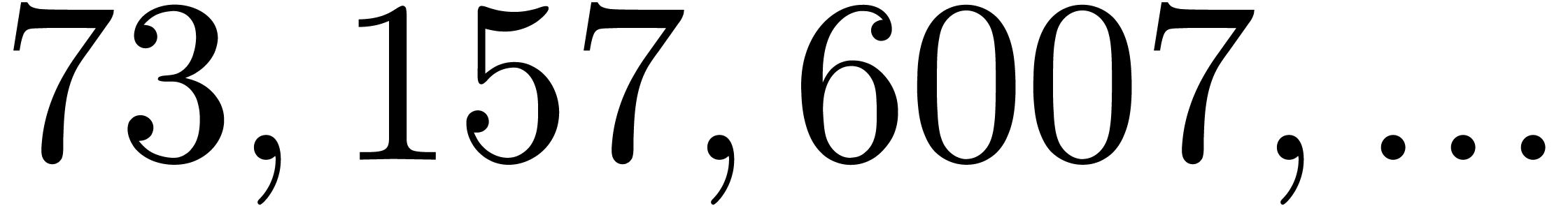 |
| 862143 |
15373 |
3115219 |
11890829 |
18563267 |
19622017 |
26248351 |
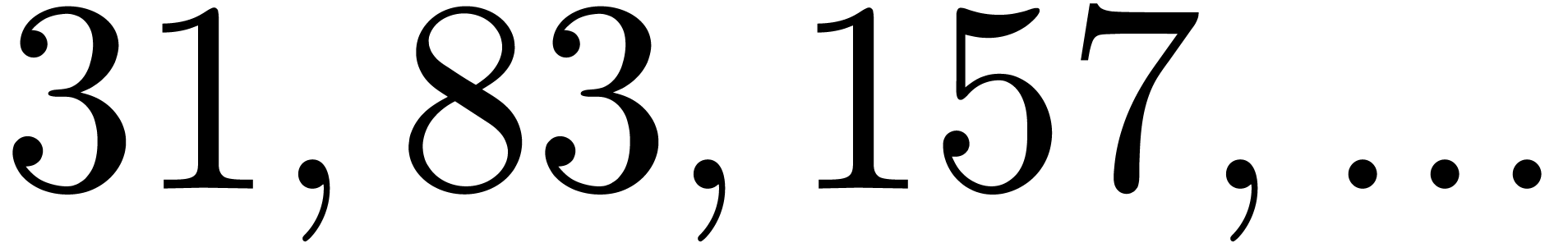 |
| 877623 |
514649 |
654749 |
4034687 |
4276583 |
27931549 |
33525223 |
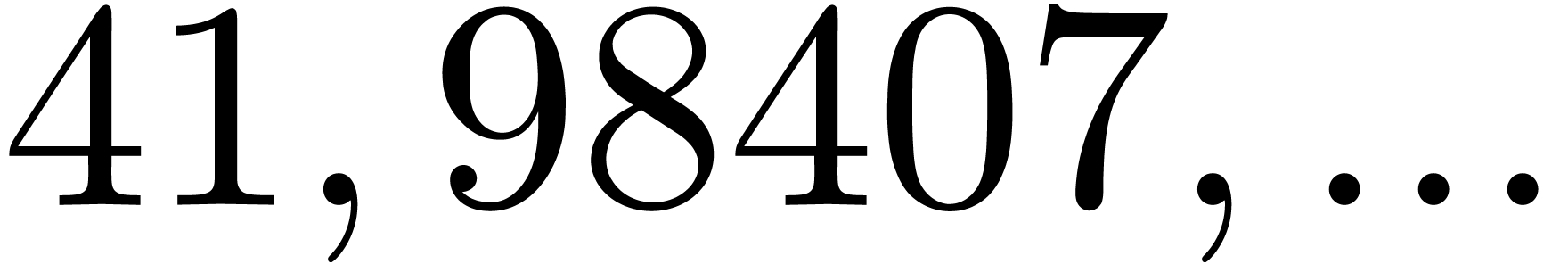 |
| 892455 |
91453 |
2660297 |
3448999 |
12237457 |
21065299 |
25169783 |
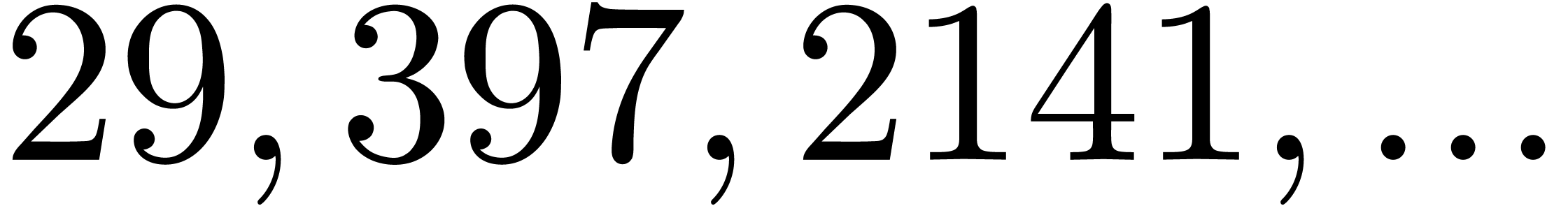 |
|
|
|
4.2Influence of the parameters  ,
,  and
and 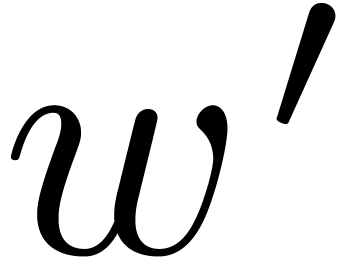
Ideally speaking, we want  to be as large as
possible. Furthermore, in order to waste as few bits as possible,
to be as large as
possible. Furthermore, in order to waste as few bits as possible, 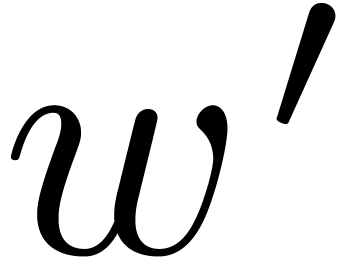 should be close to the word size (or half of it) and
should be close to the word size (or half of it) and
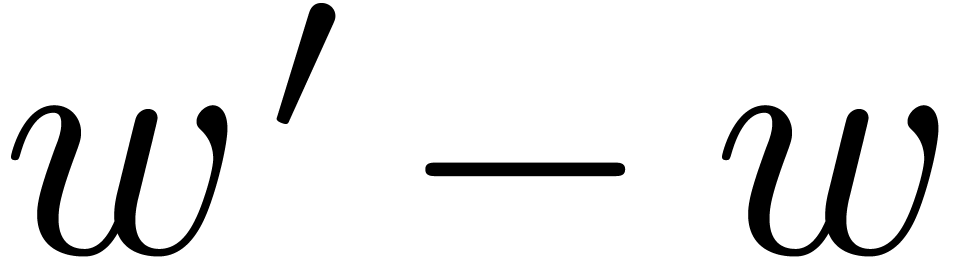 should be minimized. When using double precision
floating point arithmetic, this means that we wish to take
should be minimized. When using double precision
floating point arithmetic, this means that we wish to take 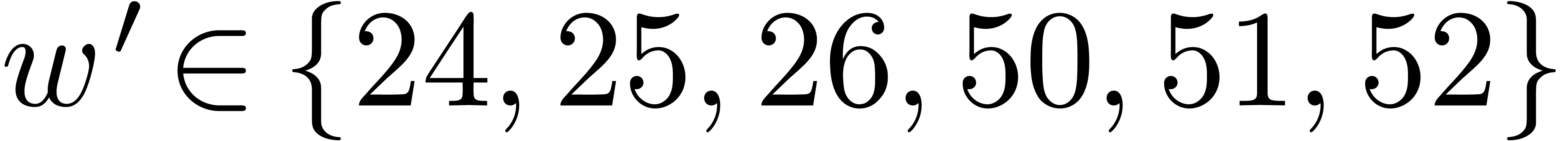 . Whenever we have efficient hardware support
for integer arithmetic, then we might prefer
. Whenever we have efficient hardware support
for integer arithmetic, then we might prefer  .
.
Let us start by studying the influence of 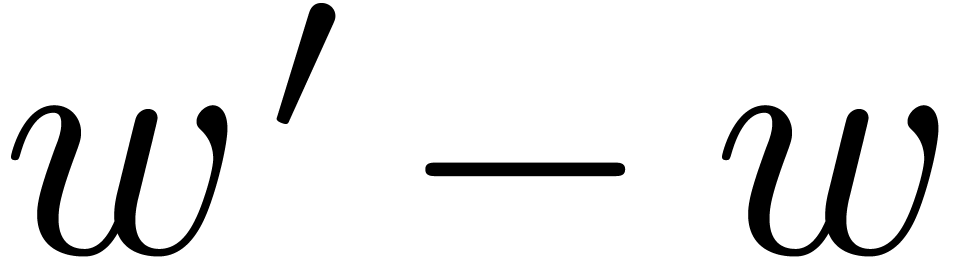 on the
number of hits. In Table 2, we have increased
on the
number of hits. In Table 2, we have increased  by one with respect to Table 1. This results
in an approximate
by one with respect to Table 1. This results
in an approximate 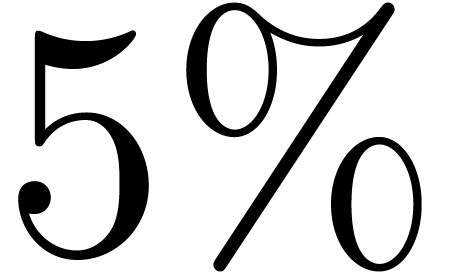 increase of the
“capacity”
increase of the
“capacity” 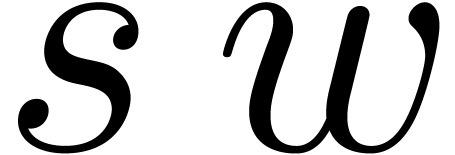 of the modulus
of the modulus 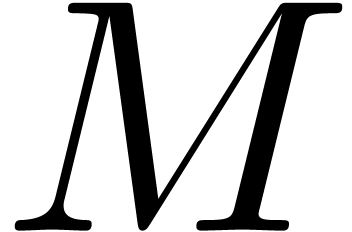 . On the one hand, we observe that
the hit rate of the sieve procedure roughly decreases by a factor of
thirty. On the other hand, we notice that the rare gentle moduli that we
do find are often of high quality (on four occasions the moduli
. On the one hand, we observe that
the hit rate of the sieve procedure roughly decreases by a factor of
thirty. On the other hand, we notice that the rare gentle moduli that we
do find are often of high quality (on four occasions the moduli  are all prime in Table 2).
are all prime in Table 2).
 |
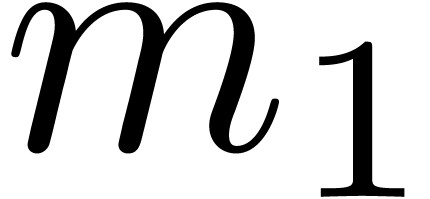 |
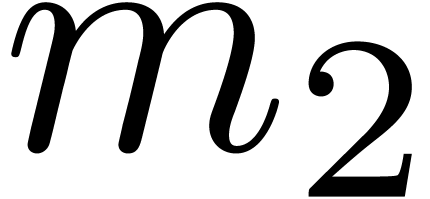 |
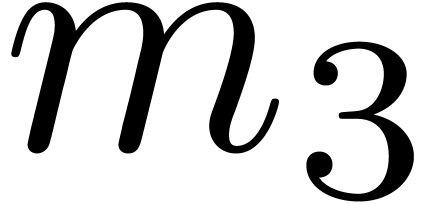 |
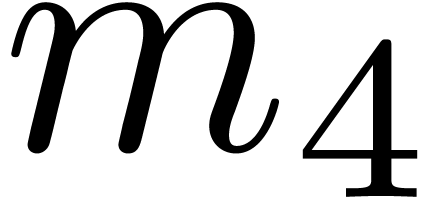 |
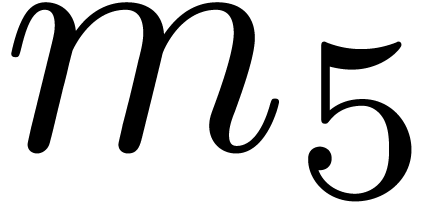 |
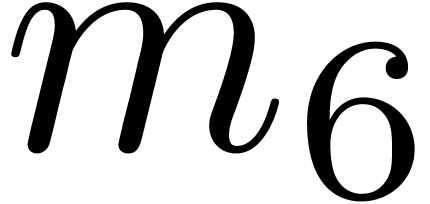 |
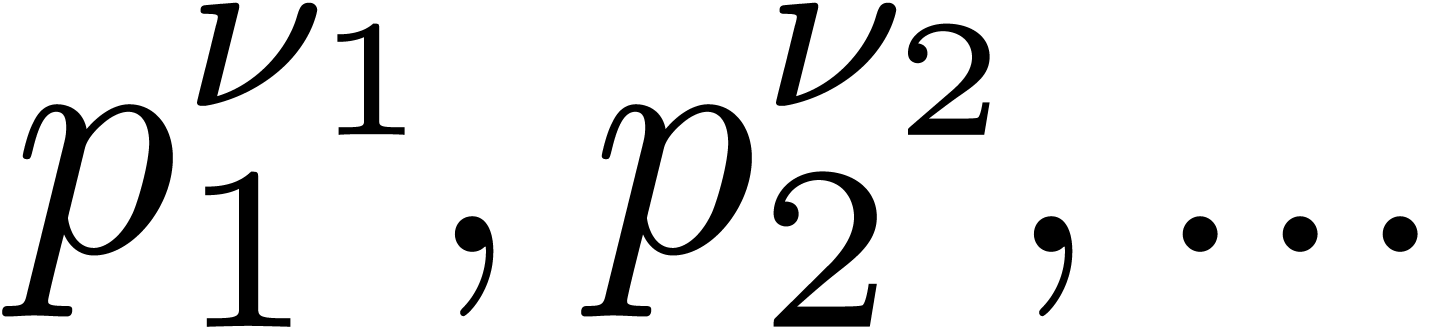 |
| 936465 |
543889 |
4920329 |
12408421 |
15115957 |
24645539 |
28167253 |
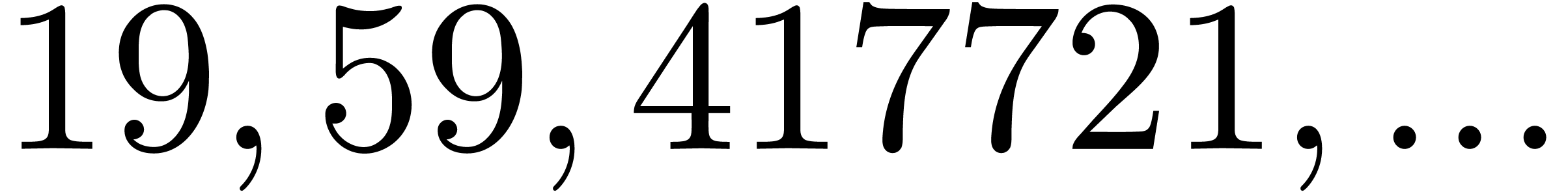 |
| 2475879 |
867689 |
4051001 |
11023091 |
13219163 |
24046943 |
28290833 |
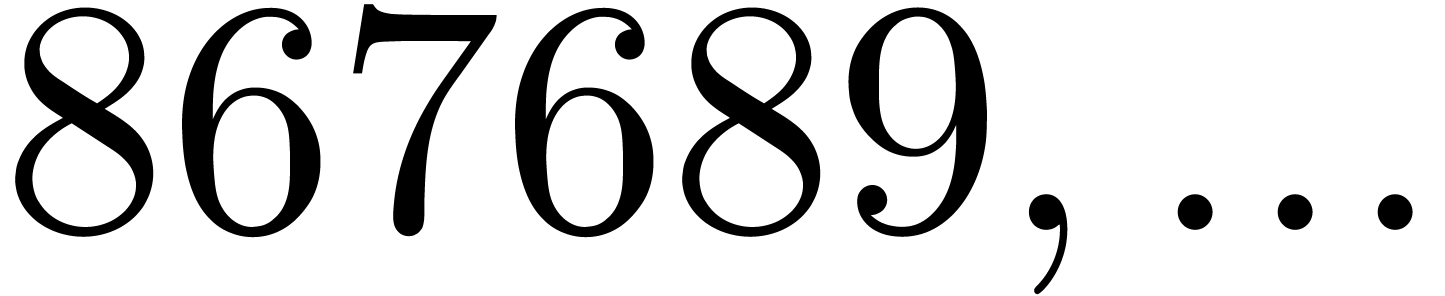 |
| 3205689 |
110161 |
12290741 |
16762897 |
22976783 |
25740731 |
25958183 |
 |
| 3932205 |
4244431 |
5180213 |
5474789 |
8058377 |
14140817 |
25402873 |
 |
| 5665359 |
241739 |
5084221 |
18693097 |
21474613 |
23893447 |
29558531 |
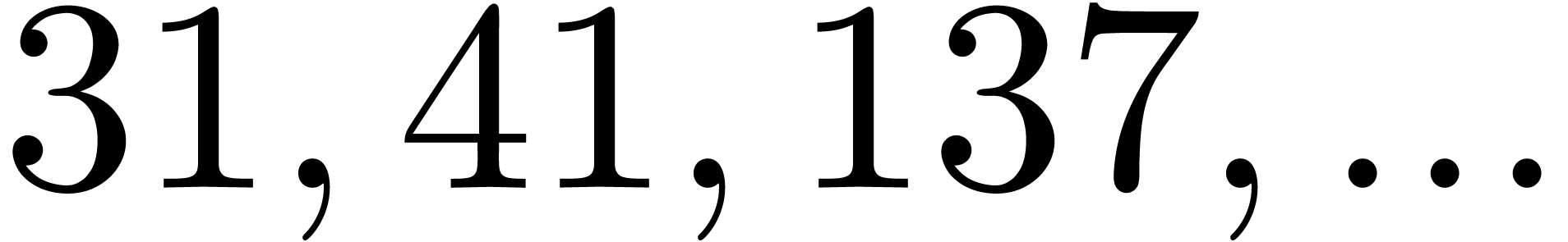 |
| 5998191 |
30971 |
21307063 |
21919111 |
22953967 |
31415123 |
33407281 |
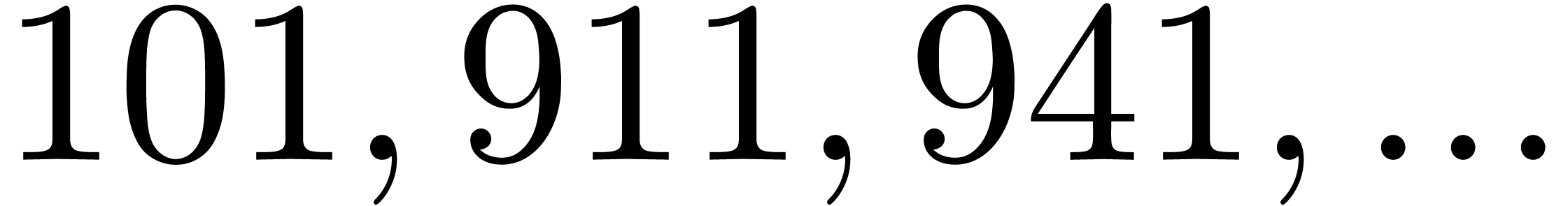 |
| 6762459 |
3905819 |
5996041 |
7513223 |
7911173 |
8584189 |
29160587 |
 |
| 9245919 |
2749717 |
4002833 |
8274689 |
9800633 |
15046937 |
25943587 |
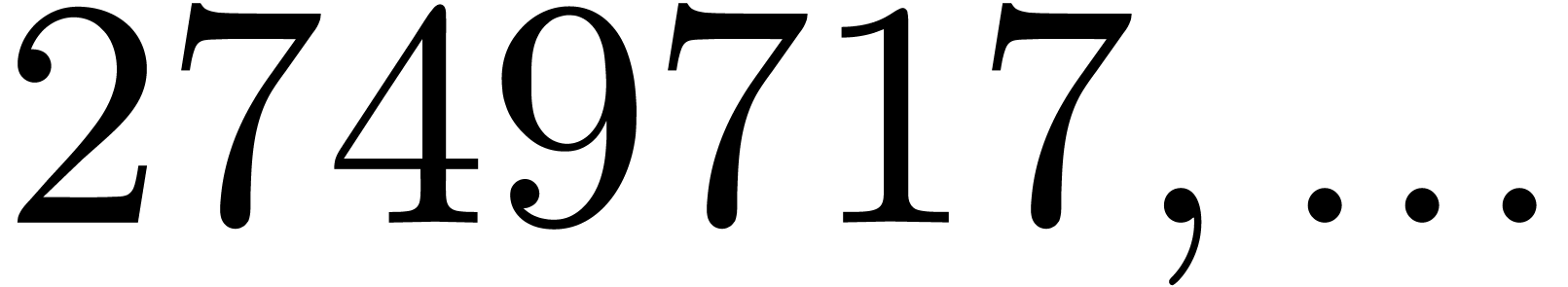 |
| 9655335 |
119809 |
9512309 |
20179259 |
21664469 |
22954369 |
30468101 |
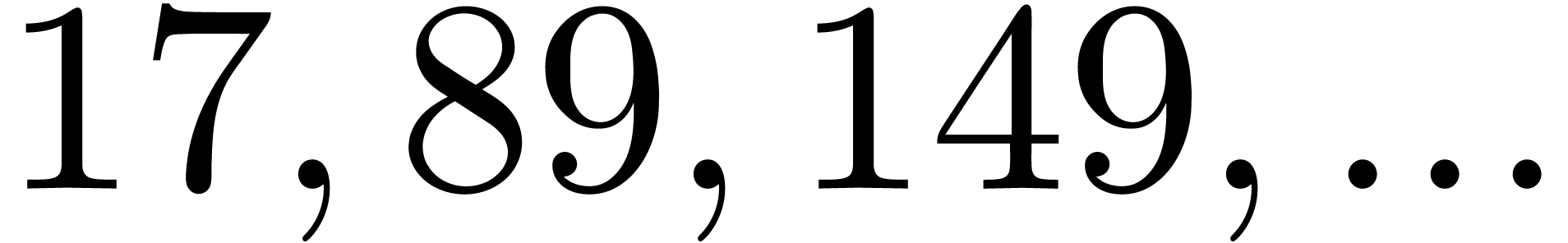 |
| 12356475 |
1842887 |
2720359 |
7216357 |
13607779 |
23538769 |
30069449 |
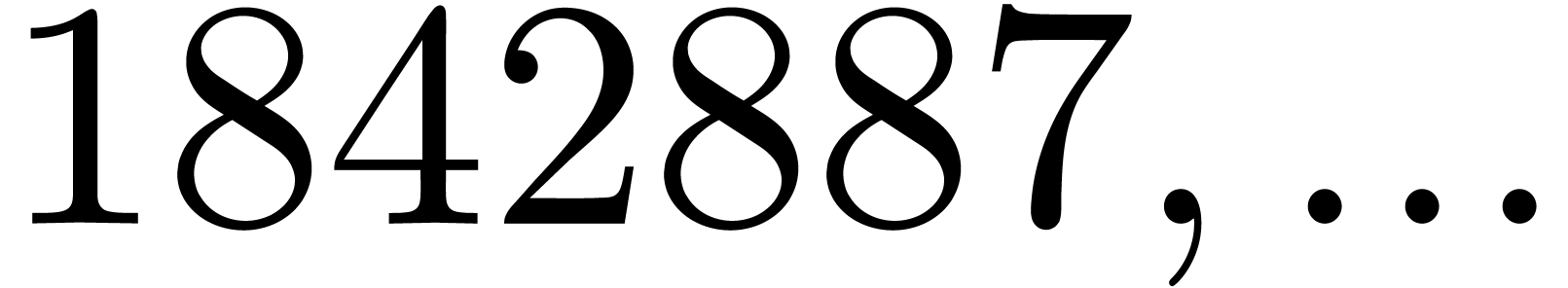 |
| 15257781 |
1012619 |
5408467 |
9547273 |
11431841 |
20472121 |
28474807 |
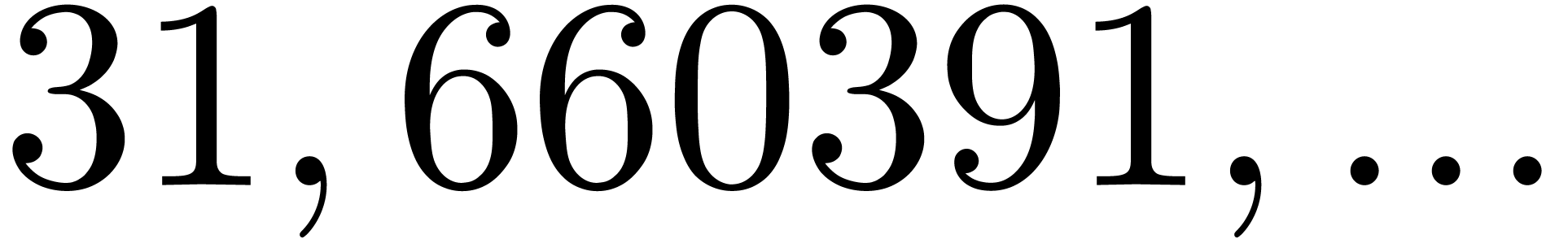 |
|
|
|
Without surprise, the hit rate also sharply decreases if we attempt to
increase  . The results for
. The results for
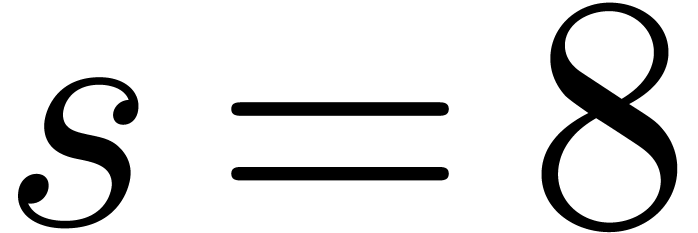 and
and 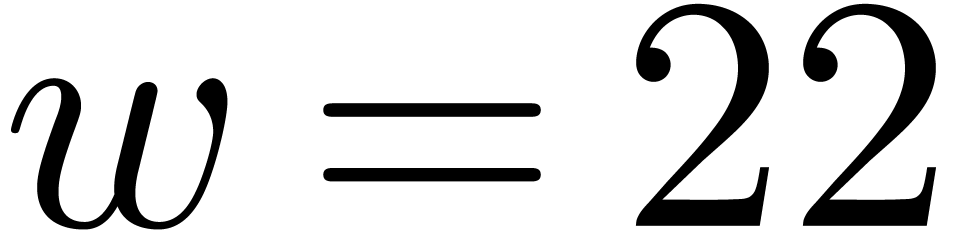 are shown in Table
3. A further infortunate side effect is that the quality of
the gentle moduli that we do find also decreases. Indeed, on the one
hand,
are shown in Table
3. A further infortunate side effect is that the quality of
the gentle moduli that we do find also decreases. Indeed, on the one
hand, 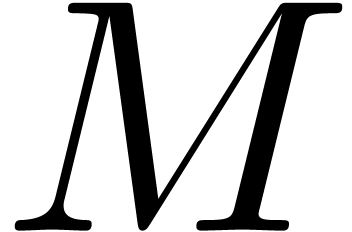 tends to systematically admit at least one
small prime factor. On the other hand, it is rarely the case that each
tends to systematically admit at least one
small prime factor. On the other hand, it is rarely the case that each
 divides either
divides either 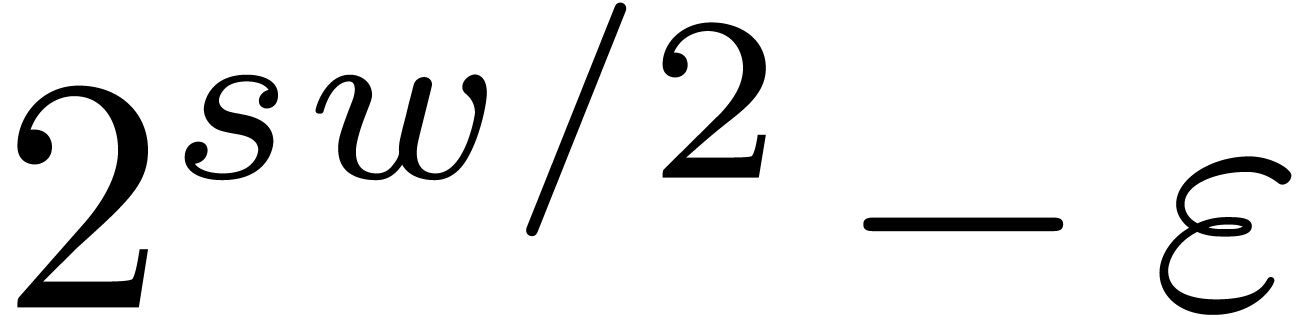 or
or 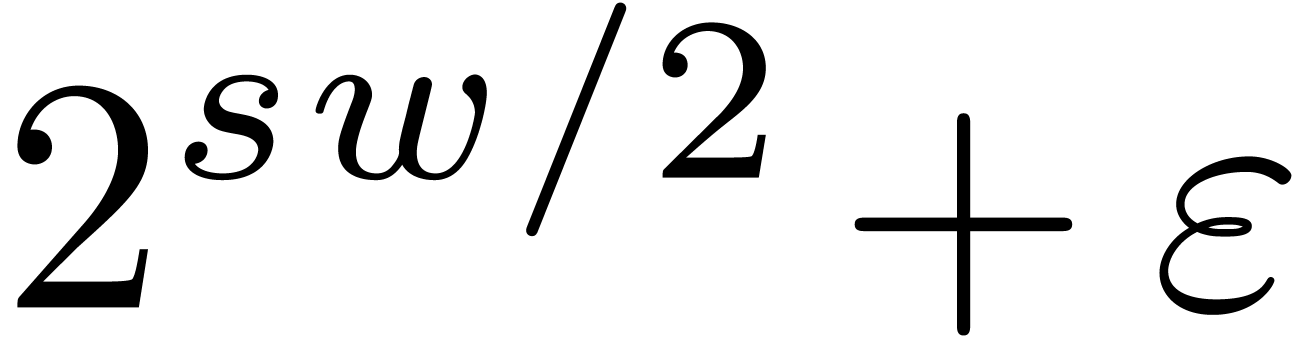 (this might nevertheless happen for other
recombinations of the prime factors of
(this might nevertheless happen for other
recombinations of the prime factors of 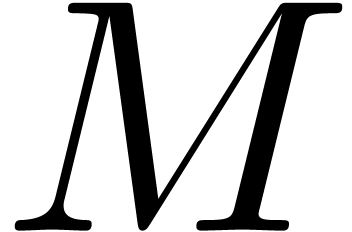 ,
but only modulo a further increase of
,
but only modulo a further increase of 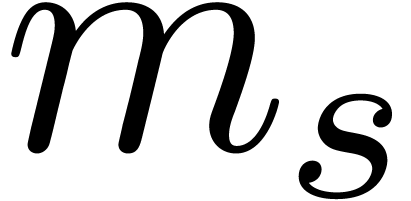 ).
).
 |
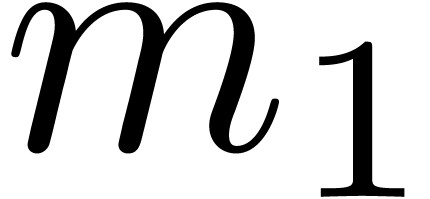 |
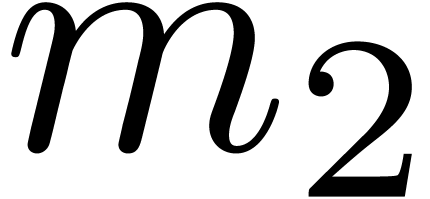 |
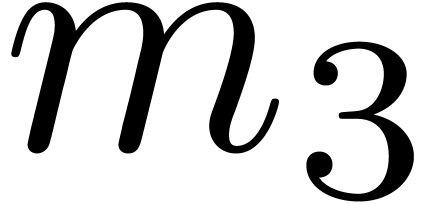 |
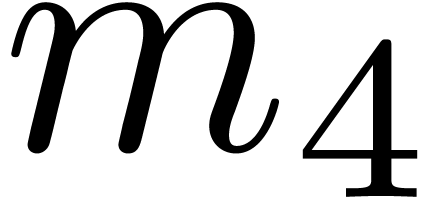 |
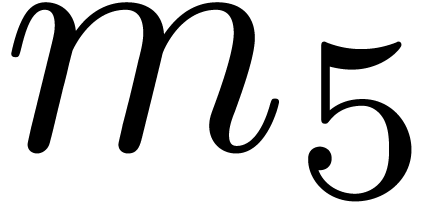 |
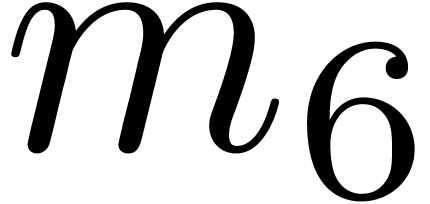 |
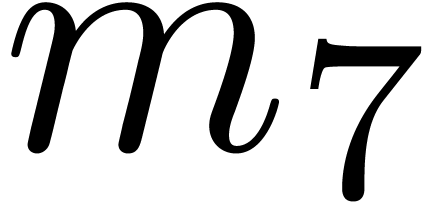 |
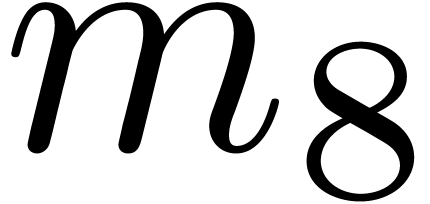 |
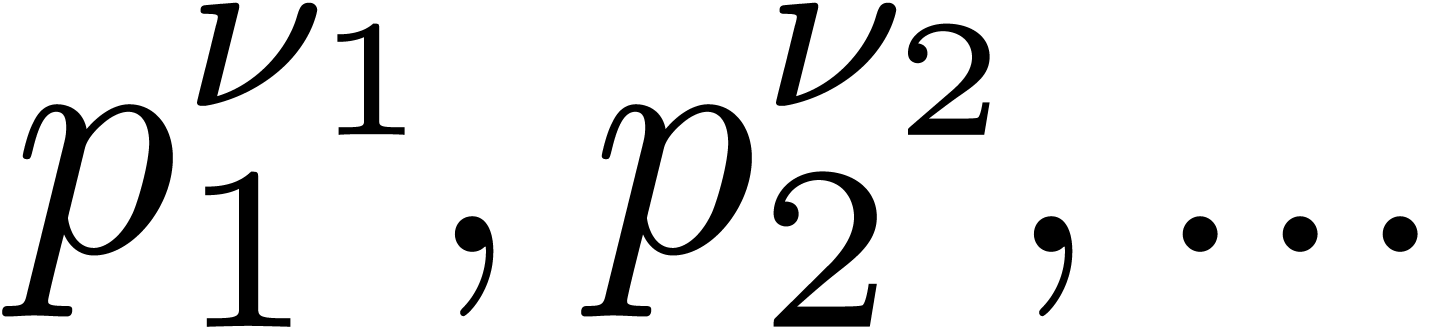 |
| 889305 |
50551 |
1146547 |
4312709 |
5888899 |
14533283 |
16044143 |
16257529 |
17164793 |
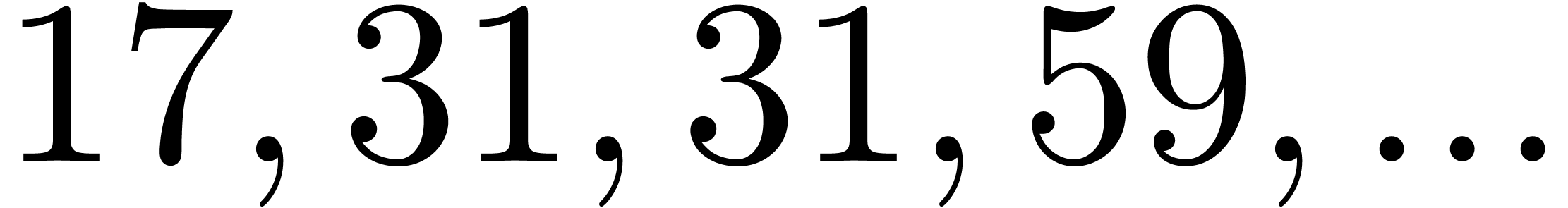 |
| 2447427 |
53407 |
689303 |
3666613 |
4837253 |
7944481 |
21607589 |
25976179 |
32897273 |
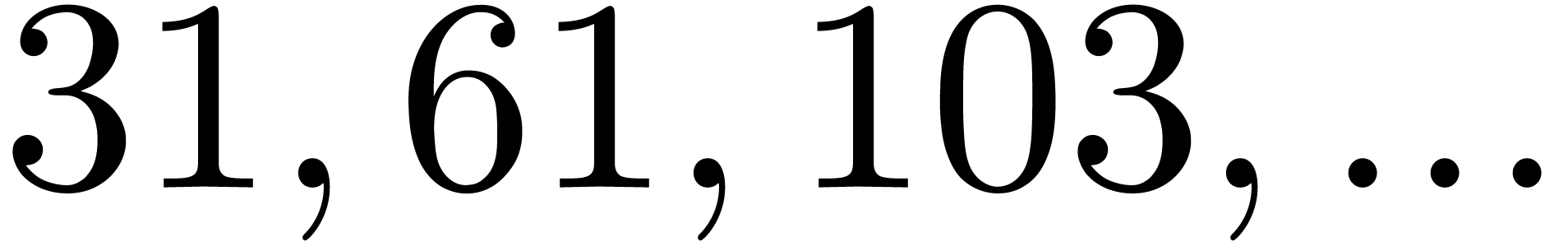 |
| 2674557 |
109841 |
1843447 |
2624971 |
5653049 |
7030883 |
8334373 |
18557837 |
29313433 |
 |
| 3964365 |
10501 |
2464403 |
6335801 |
9625841 |
10329269 |
13186219 |
17436197 |
25553771 |
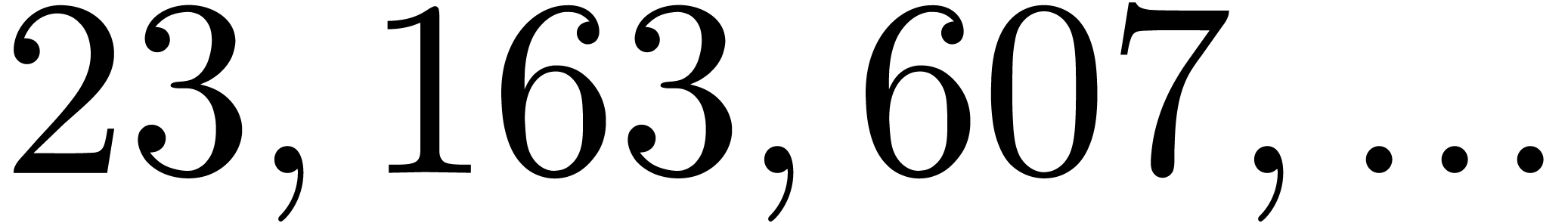 |
| 4237383 |
10859 |
3248809 |
5940709 |
6557599 |
9566959 |
11249039 |
22707323 |
28518509 |
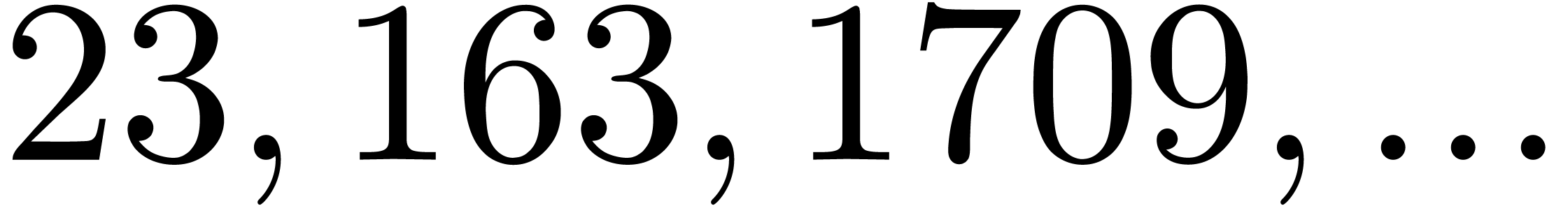 |
| 5312763 |
517877 |
616529 |
879169 |
4689089 |
9034687 |
11849077 |
24539909 |
27699229 |
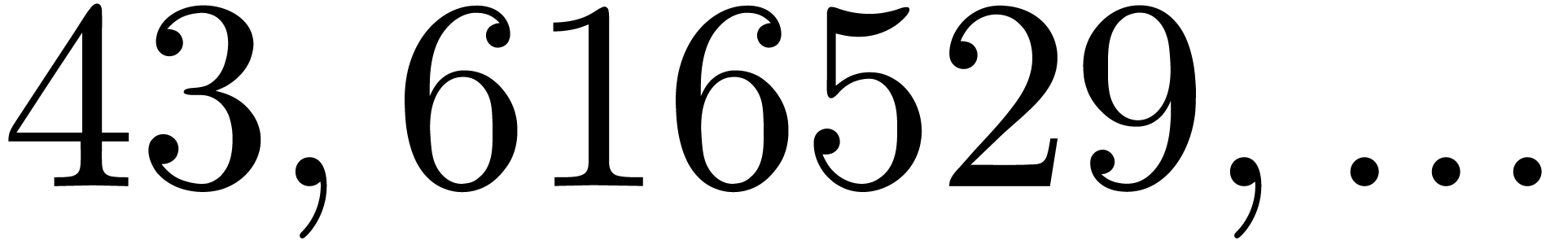 |
| 6785367 |
22013 |
1408219 |
4466089 |
7867589 |
9176941 |
12150997 |
26724877 |
29507689 |
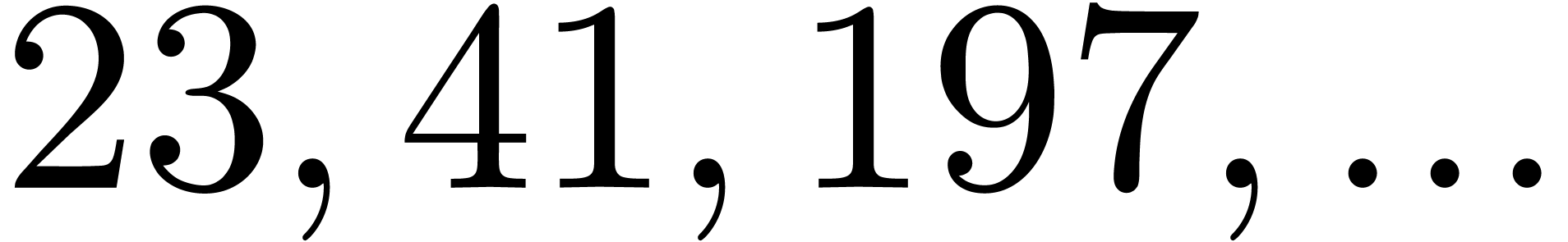 |
| 7929033 |
30781 |
730859 |
4756351 |
9404807 |
13807231 |
15433939 |
19766077 |
22596193 |
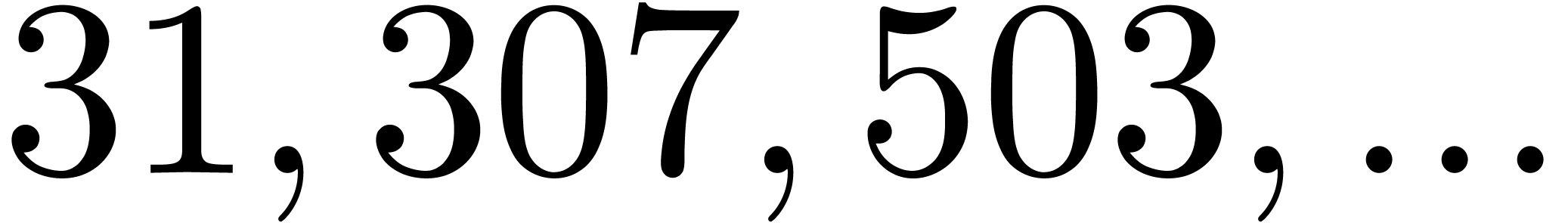 |
| 8168565 |
10667 |
3133103 |
3245621 |
6663029 |
15270019 |
18957559 |
20791819 |
22018021 |
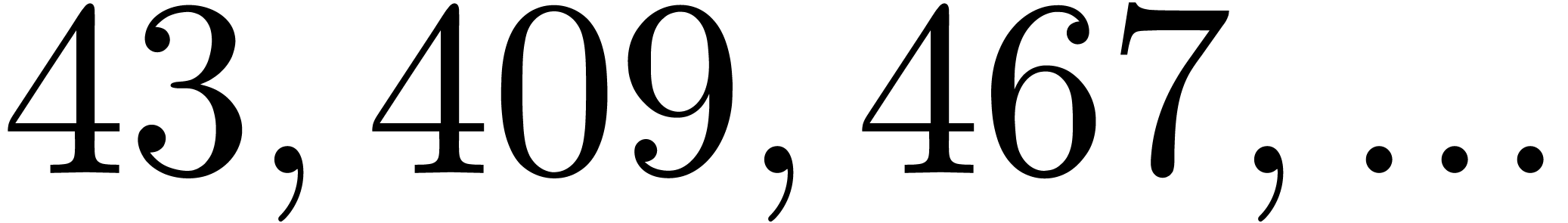 |
| 8186205 |
41047 |
2122039 |
2410867 |
6611533 |
9515951 |
14582849 |
16507739 |
30115277 |
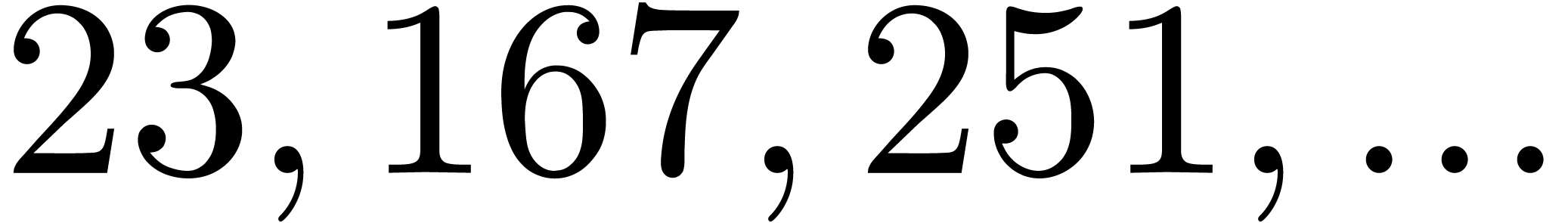 |
|
|
|
An increase of 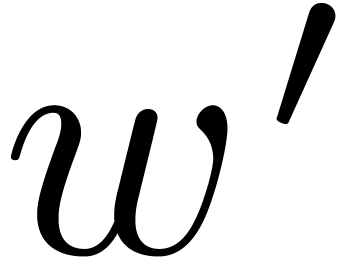 while maintaining
while maintaining  and
and 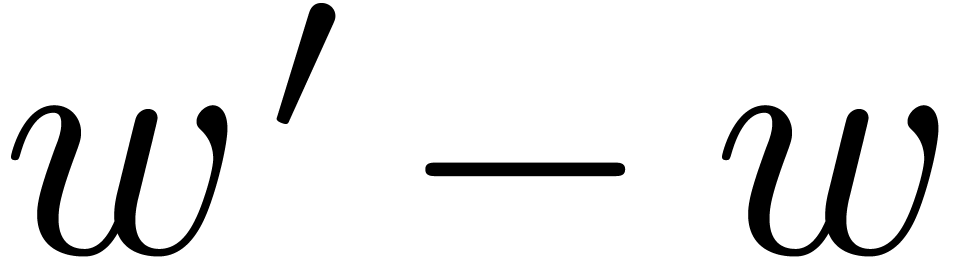 fixed also results in a
decrease of the hit rate. Nevertheless, when going from
fixed also results in a
decrease of the hit rate. Nevertheless, when going from 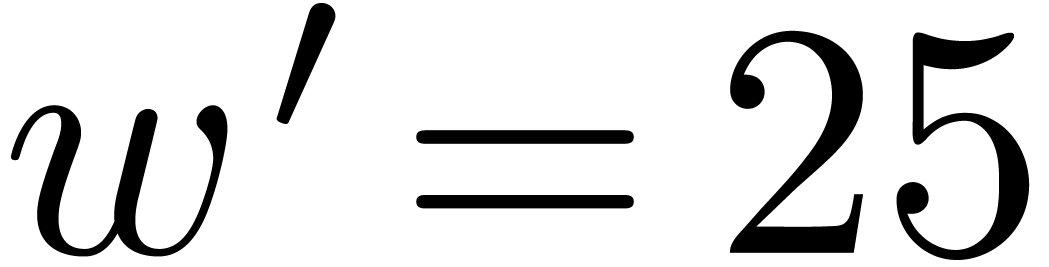 (floating point arithmetic) to
(floating point arithmetic) to 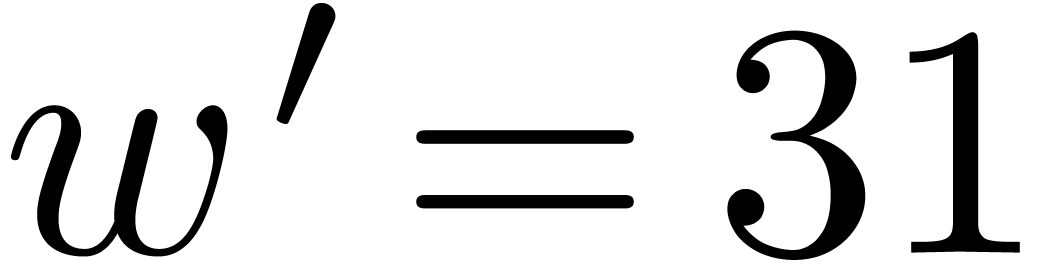 (integer
arithmetic), this is counterbalanced by the fact that
(integer
arithmetic), this is counterbalanced by the fact that  can also be taken larger (namely
can also be taken larger (namely 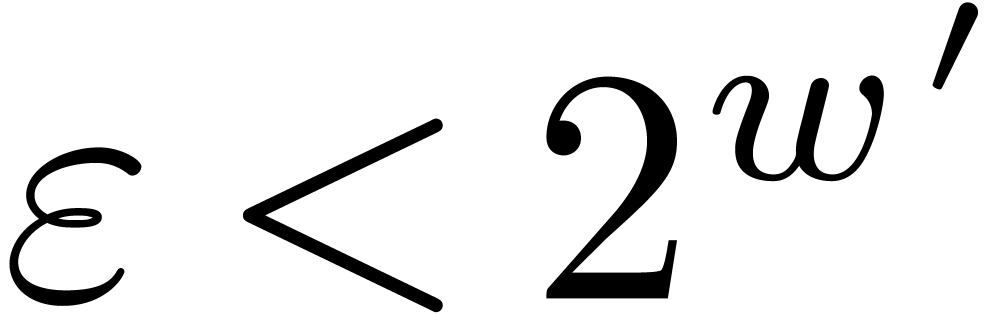 );
see Table 4 for a concrete example. When doubling
);
see Table 4 for a concrete example. When doubling  and
and 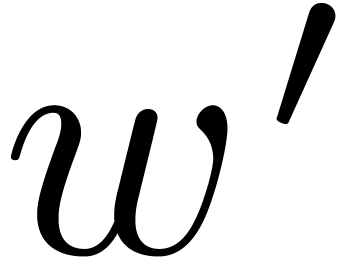 while keeping the same upper
bound for
while keeping the same upper
bound for  , the hit rate
remains more or less unchanged, but the rate of high quality hits tends
to decrease somewhat: see Table 5.
, the hit rate
remains more or less unchanged, but the rate of high quality hits tends
to decrease somewhat: see Table 5.
It should be possible to analyze the hit rate as a function of the
parameters  ,
,  ,
, 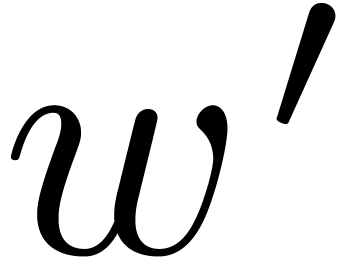 and
and 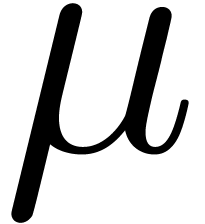 from a probabilistic point of view, using the idea that a random number
from a probabilistic point of view, using the idea that a random number
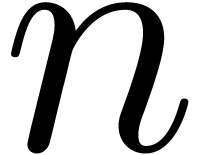 is prime with probability
is prime with probability 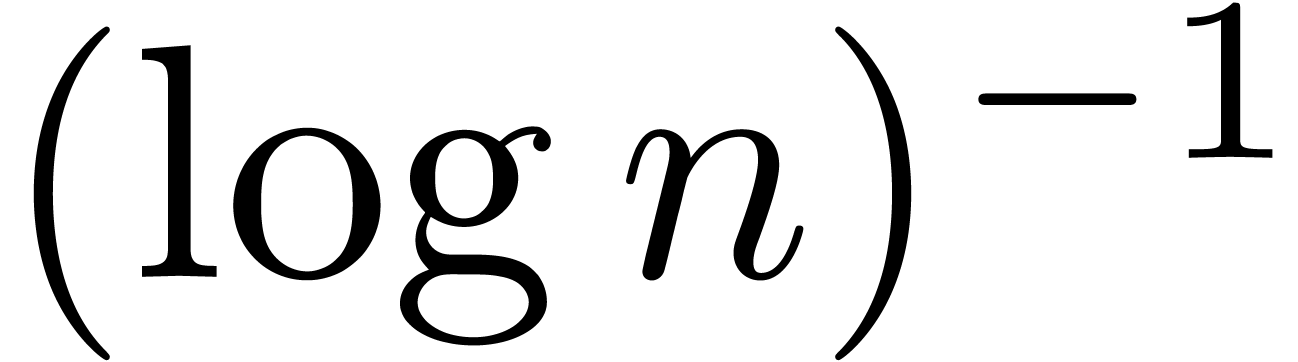 . However, from a practical perspective, the
priority is to focus on the case when
. However, from a practical perspective, the
priority is to focus on the case when 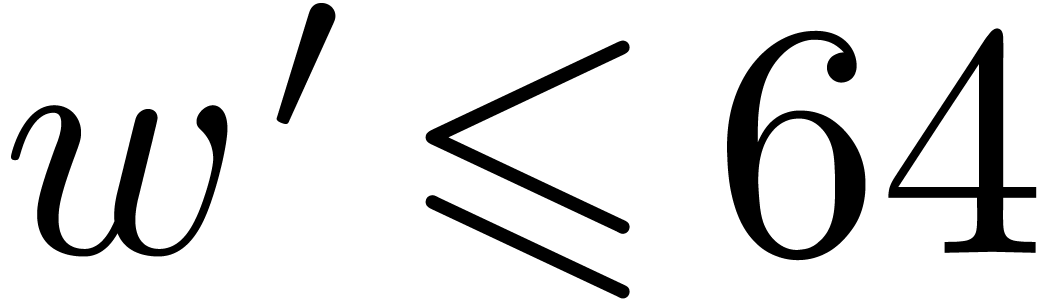 .
For the most significant choices of parameters
.
For the most significant choices of parameters 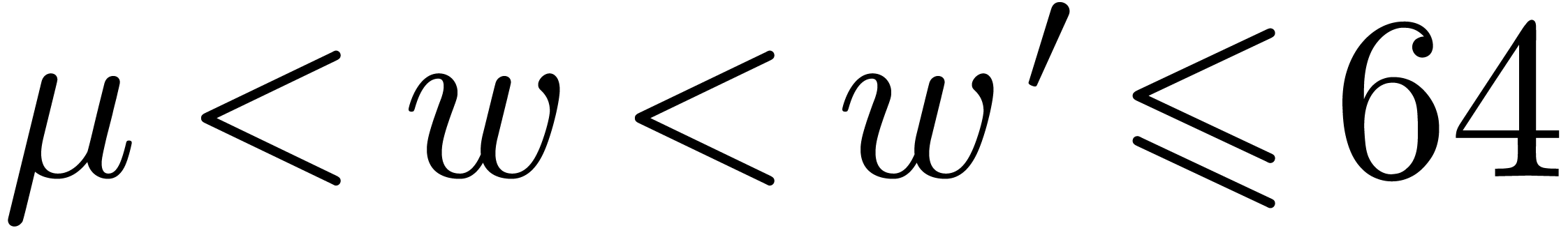 and
and  , it should be possible
to compile full tables of
, it should be possible
to compile full tables of  -gentle
moduli. Unfortunately, our current implementation is still somewhat
inefficient for
-gentle
moduli. Unfortunately, our current implementation is still somewhat
inefficient for  . A helpful
feature for upcoming versions of Pari would be a
function to find all prime factors of an integer below a specified
maximum
. A helpful
feature for upcoming versions of Pari would be a
function to find all prime factors of an integer below a specified
maximum 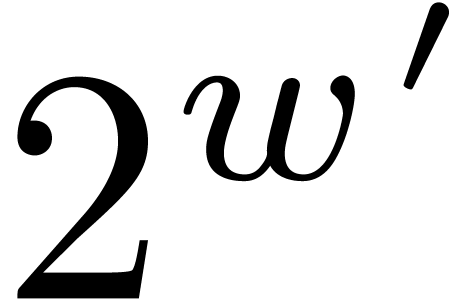 (the current version only does this for
prime factors that can be tabulated).
(the current version only does this for
prime factors that can be tabulated).
 |
 |
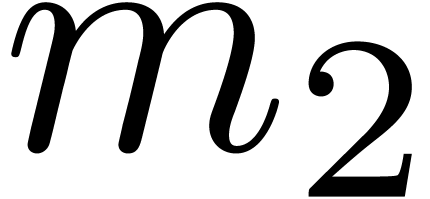 |
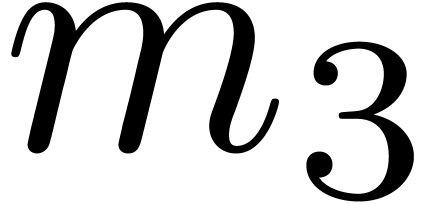 |
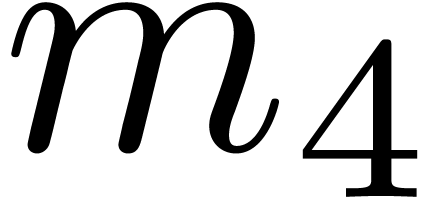 |
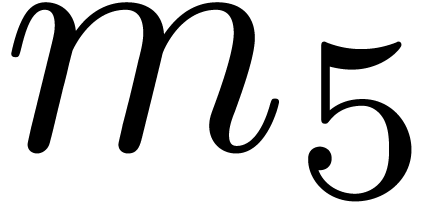 |
 |
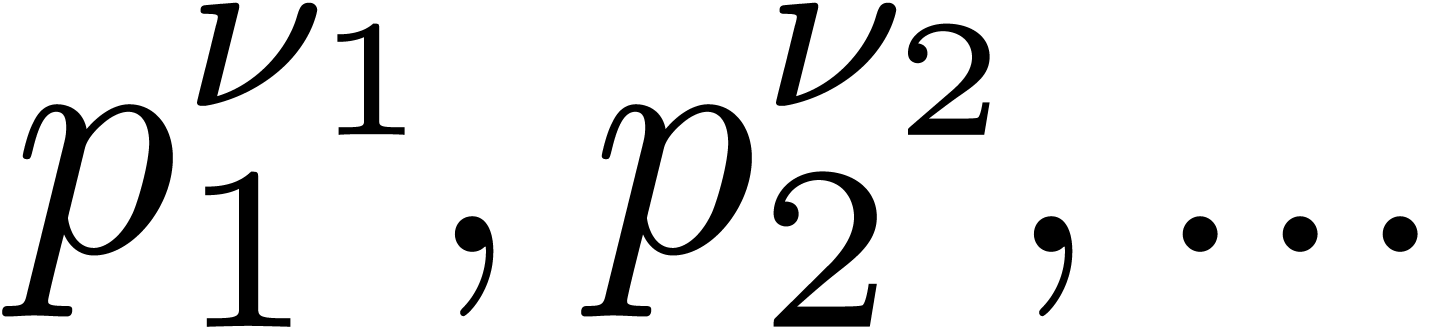 |
| 303513 |
42947057 |
53568313 |
331496959 |
382981453 |
1089261409 |
1176003149 |
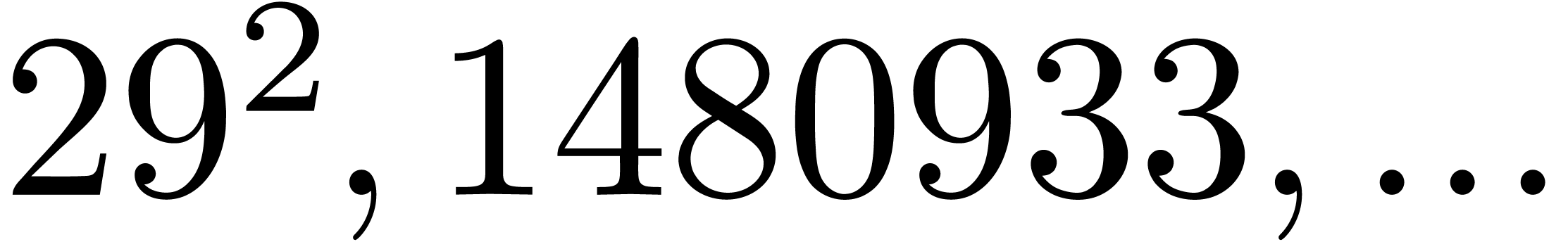 |
| 851463 |
10195123 |
213437143 |
470595299 |
522887483 |
692654273 |
1008798563 |
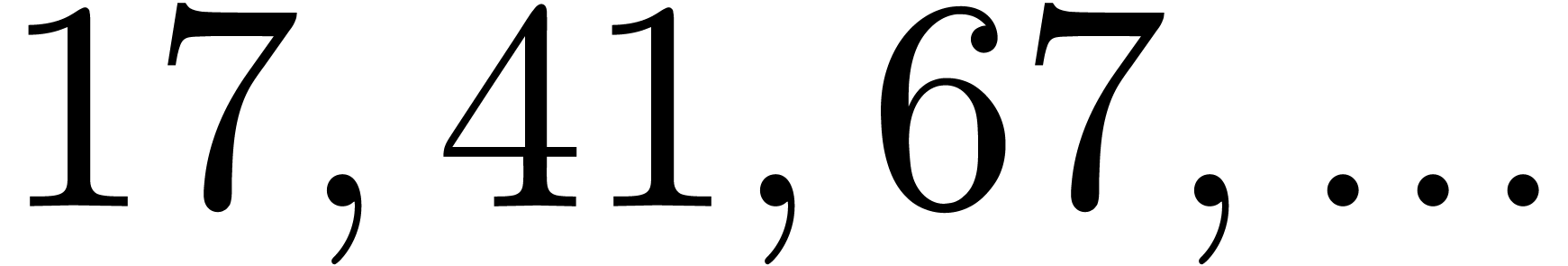 |
| 1001373 |
307261 |
611187931 |
936166801 |
1137875633 |
1196117147 |
1563634747 |
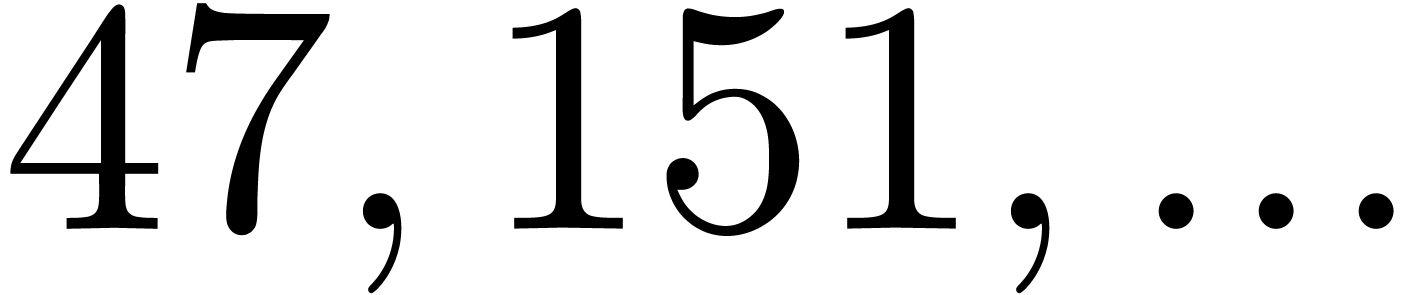 |
| 1422507 |
3950603 |
349507391 |
490215667 |
684876553 |
693342113 |
1164052193 |
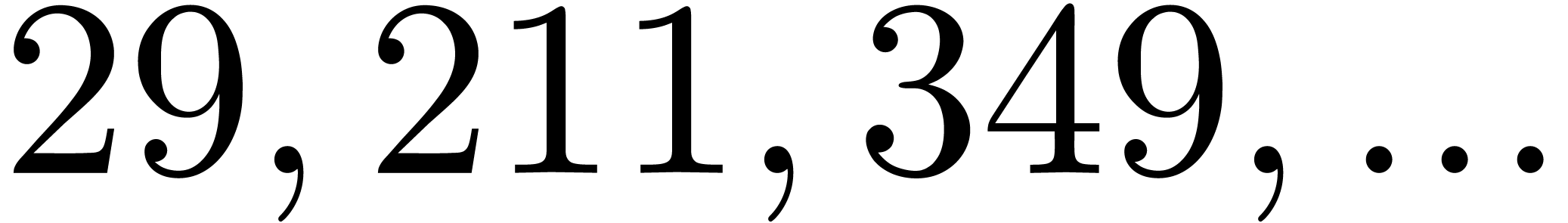 |
| 1446963 |
7068563 |
94667021 |
313871791 |
877885639 |
1009764377 |
2009551553 |
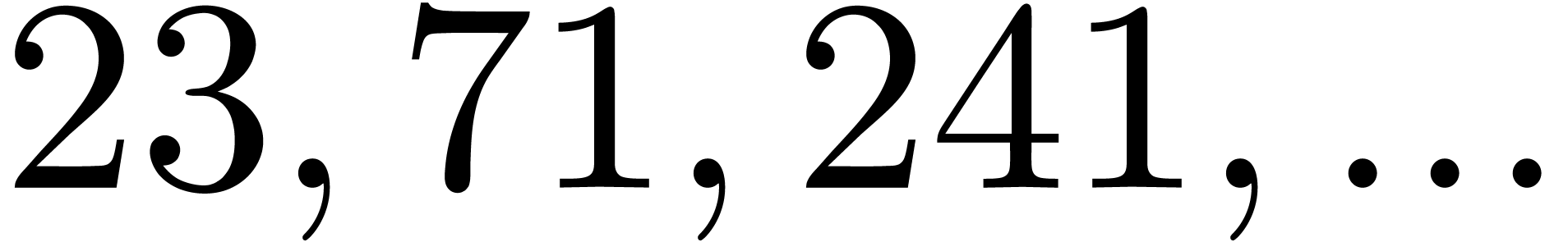 |
| 1551267 |
303551 |
383417351 |
610444753 |
1178193077 |
2101890797 |
2126487631 |
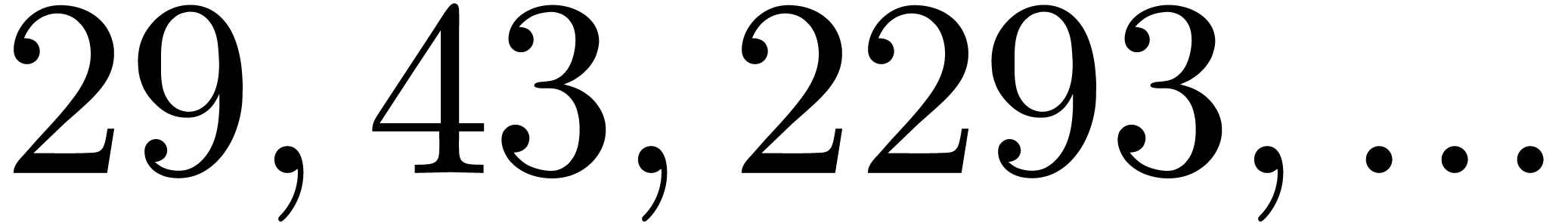 |
| 1555365 |
16360997 |
65165071 |
369550981 |
507979403 |
1067200639 |
1751653069 |
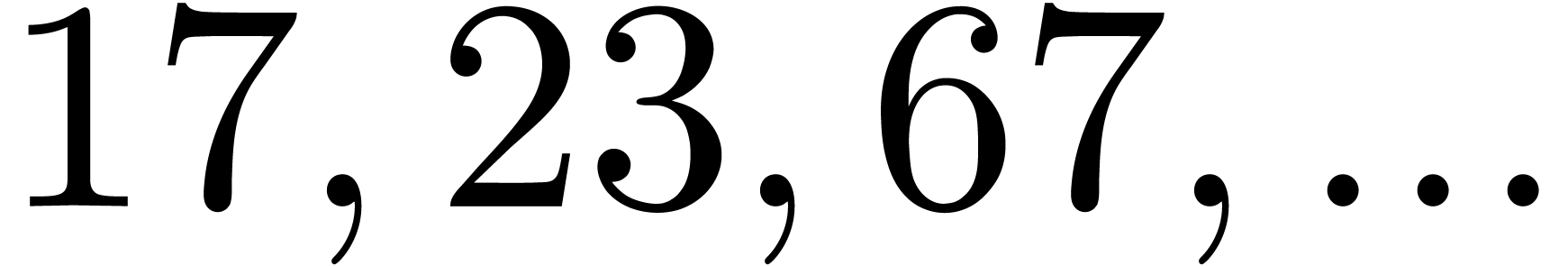 |
|
|
|
|
|
|
|
|
| 4003545 |
20601941 |
144707873 |
203956547 |
624375041 |
655374931 |
1503716491 |
 |
| 4325475 |
11677753 |
139113383 |
210843443 |
659463289 |
936654347 |
1768402001 |
 |
| 4702665 |
8221903 |
131321017 |
296701997 |
496437899 |
1485084431 |
1584149417 |
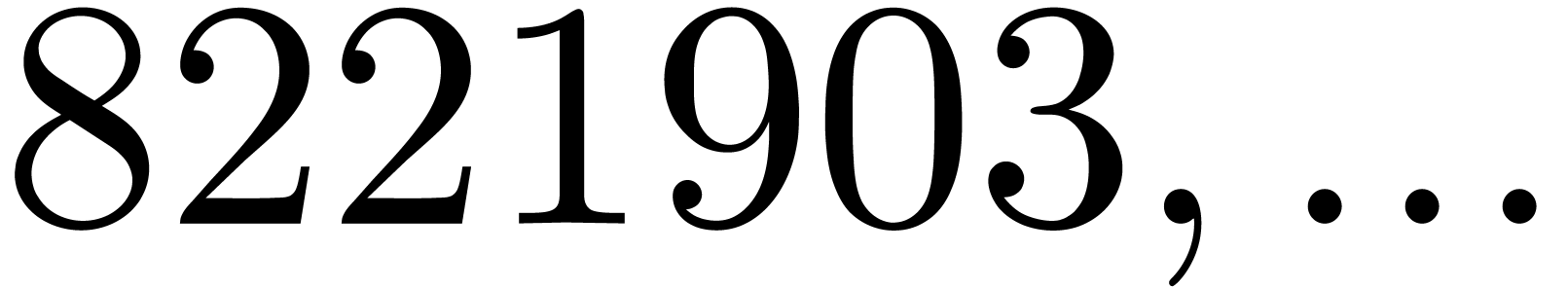 |
| 5231445 |
25265791 |
49122743 |
433700843 |
474825677 |
907918279 |
1612324823 |
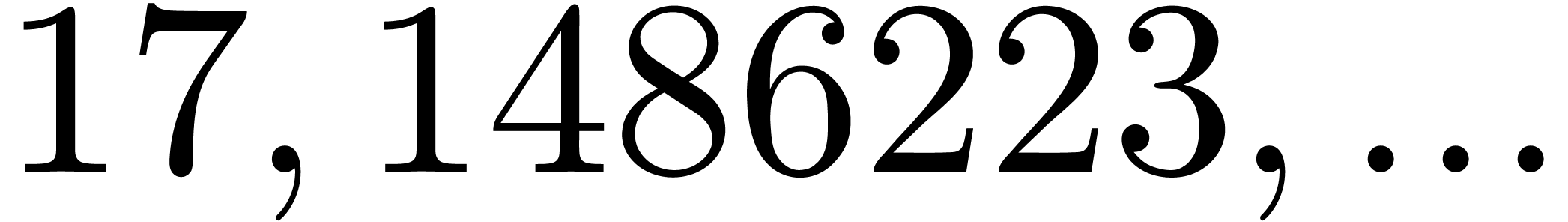 |
| 5425527 |
37197571 |
145692101 |
250849363 |
291039937 |
456174539 |
2072965393 |
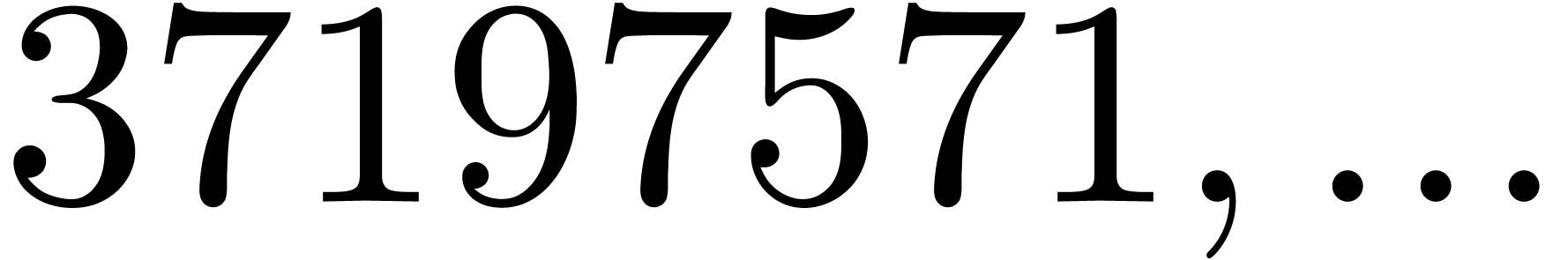 |
| 6883797 |
97798097 |
124868683 |
180349291 |
234776683 |
842430863 |
858917923 |
 |
| 7989543 |
4833137 |
50181011 |
604045619 |
638131951 |
1986024421 |
2015143349 |
 |
|
|
|
 |
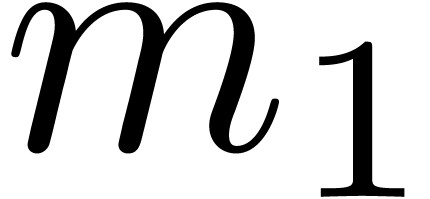 |
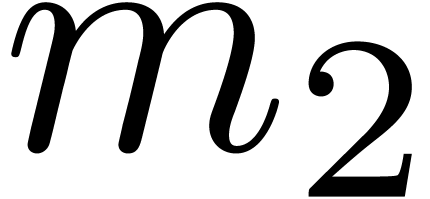 |
 |
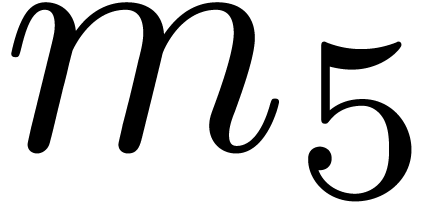 |
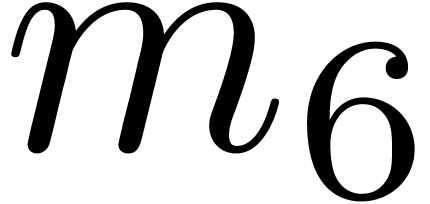 |
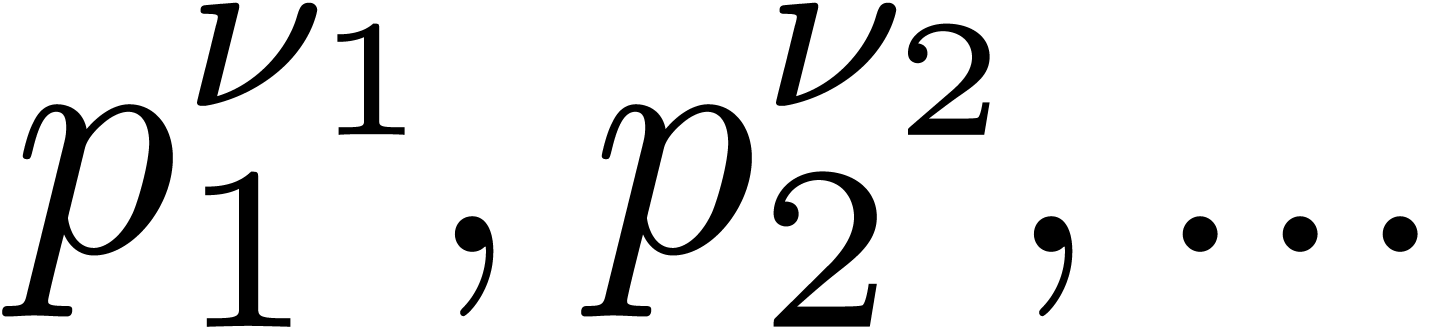 |
| 15123 |
380344780931 |
774267432193 |
 |
463904018985637 |
591951338196847 |
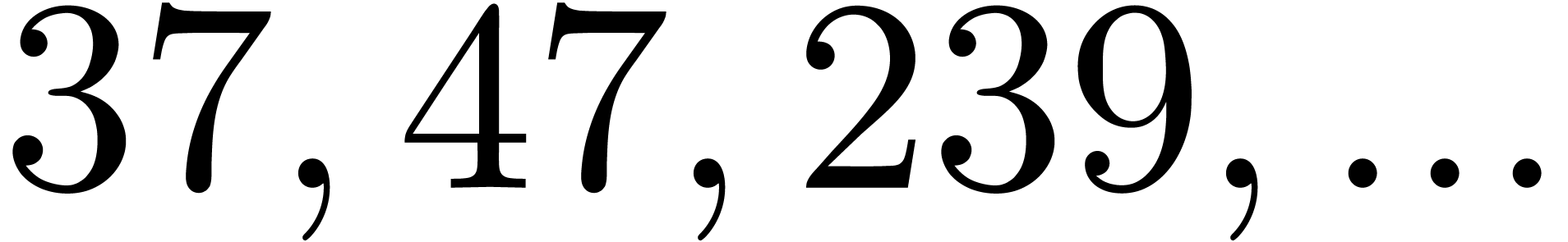 |
| 34023 |
9053503517 |
13181369695139 |
 |
680835893479031 |
723236090375863 |
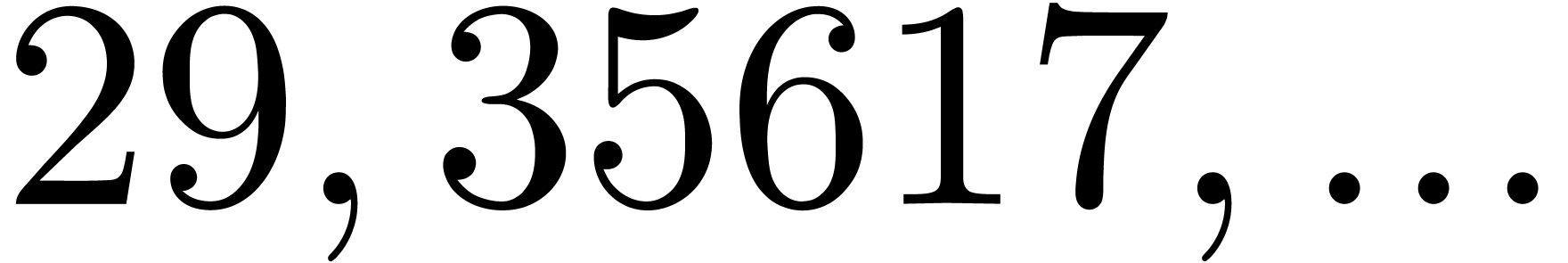 |
| 40617 |
3500059133 |
510738813367 |
 |
824394263006533 |
1039946916817703 |
 |
| 87363 |
745270007 |
55797244348441 |
 |
224580313861483 |
886387548974947 |
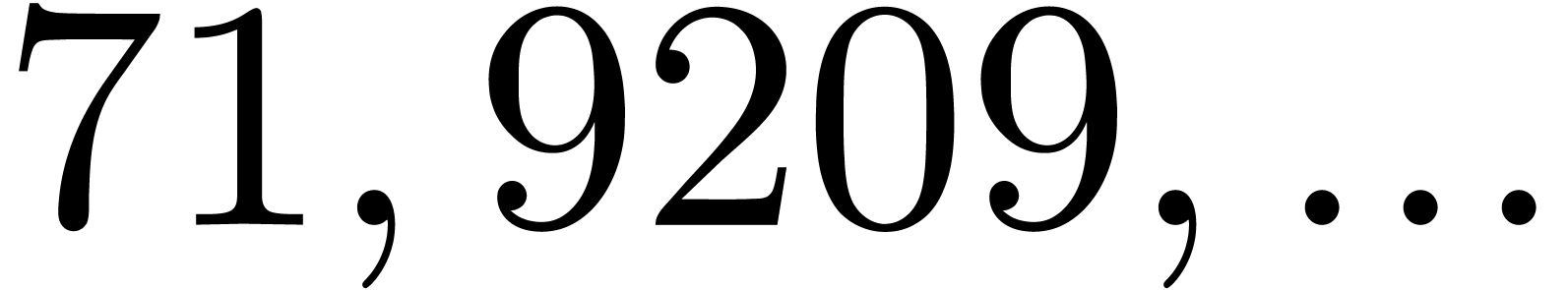 |
| 95007 |
40134716987 |
2565724842229 |
 |
130760921456911 |
393701833767607 |
 |
| 101307 |
72633113401 |
12070694419543 |
 |
95036720090209 |
183377870340761 |
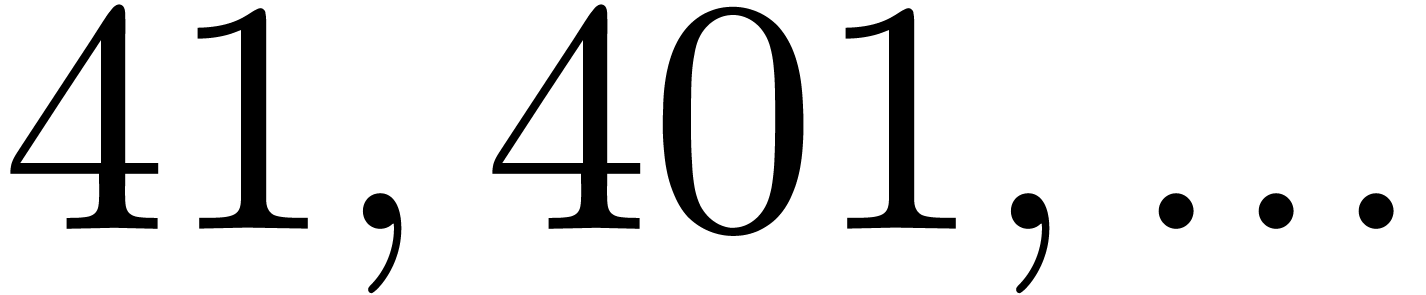 |
| 140313 |
13370367761 |
202513228811 |
 |
397041457462499 |
897476961701171 |
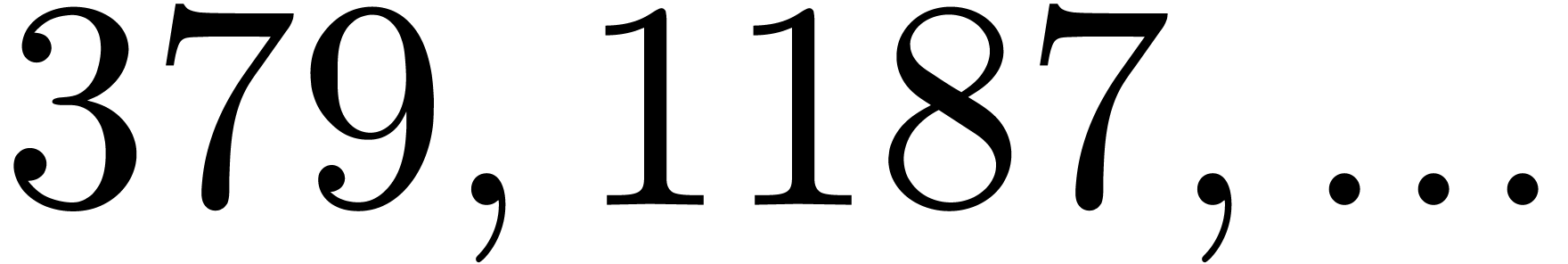 |
| 193533 |
35210831 |
15416115621749 |
 |
727365428298107 |
770048329509499 |
 |
|
|
|
|
|
|
|
| 519747 |
34123521053 |
685883716741 |
 |
705516472454581 |
836861326275781 |
 |
| 637863 |
554285276371 |
1345202287357 |
 |
344203886091451 |
463103013579761 |
 |
| 775173 |
322131291353 |
379775454593 |
 |
194236314135719 |
1026557288284007 |
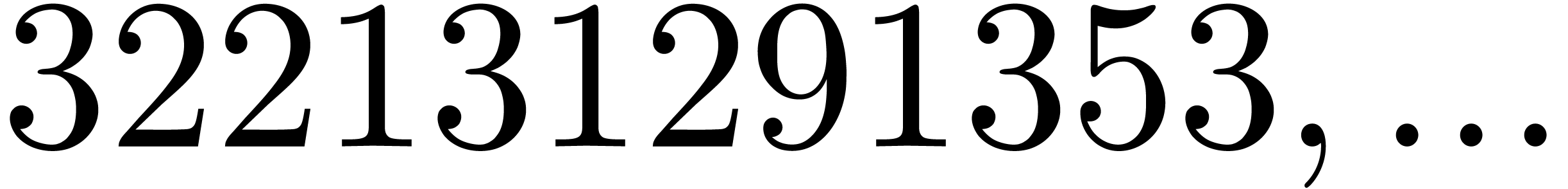 |
| 913113 |
704777248393 |
1413212491811 |
 |
217740328855369 |
261977228819083 |
 |
| 1400583 |
21426322331 |
42328735049 |
 |
411780268096919 |
626448556280293 |
 |
|
|
|
4.3Application to matrix
multiplication
Let us finally return to our favourite application of multi-modular
arithmetic to the multiplication of integer matrices  . From a practical point of view, the second
step of the algorithm from the introduction can be implemented very
efficiently if
. From a practical point of view, the second
step of the algorithm from the introduction can be implemented very
efficiently if 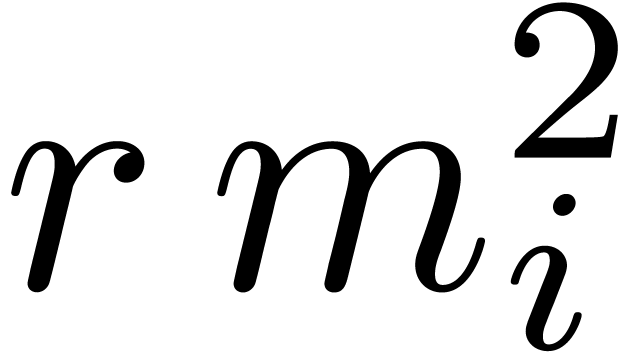 fits into the size of a word.
fits into the size of a word.
When using floating point arithmetic, this means that we should have
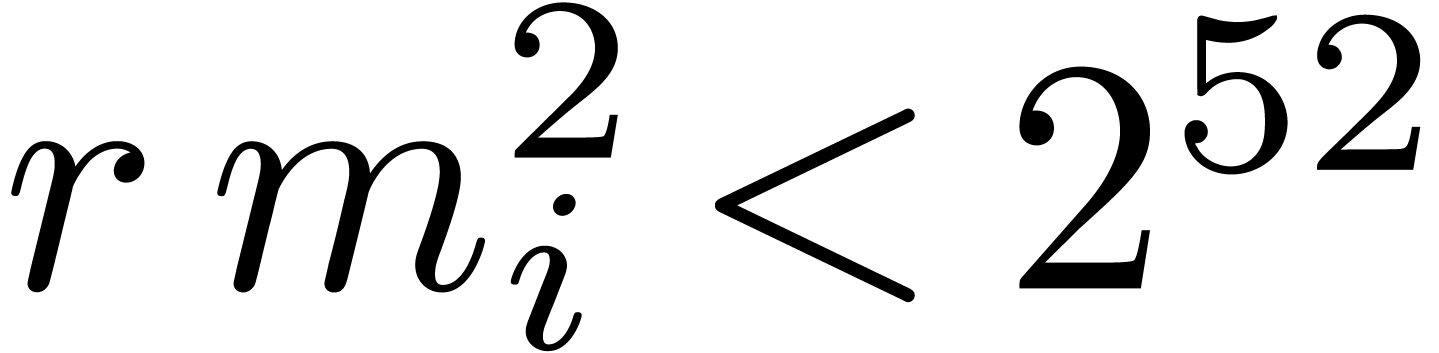 for all
for all  .
For large values of
.
For large values of  , this is
unrealistic; in that case, we subdivide the
, this is
unrealistic; in that case, we subdivide the  matrices into smaller
matrices into smaller  matrices with
matrices with 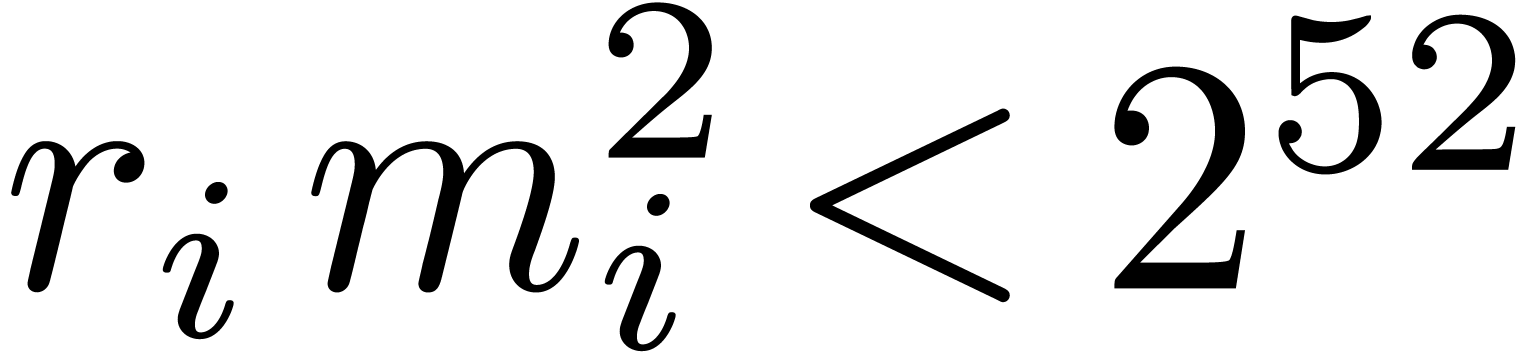 . The fact that
. The fact that 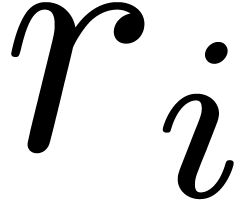 may
depend on
may
depend on 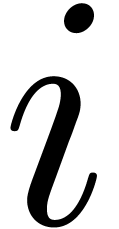 is very significant. First of all, the
larger we can take
is very significant. First of all, the
larger we can take 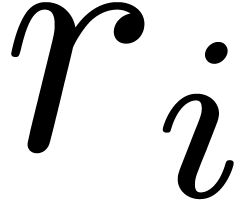 , the
faster we can multiply matrices modulo
, the
faster we can multiply matrices modulo  .
Secondly, the
.
Secondly, the  in the tables from the previous
sections often vary in bitsize. It frequently happens that we may take
all
in the tables from the previous
sections often vary in bitsize. It frequently happens that we may take
all 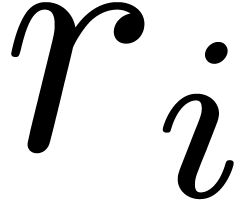 large except for the last modulus
large except for the last modulus  . The fact that matrix
multiplications modulo the worst modulus
. The fact that matrix
multiplications modulo the worst modulus  are
somewhat slower is compensated by the fact that they only account for
one out of every
are
somewhat slower is compensated by the fact that they only account for
one out of every  modular matrix products.
modular matrix products.
Several of the tables in the previous subsections were made with the
application to integer matrix multiplication in mind. Consider for
instance the modulus 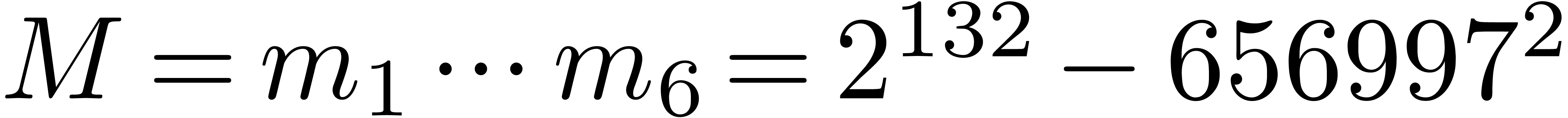 from Table 1.
When using floating point arithmetic, we obtain
from Table 1.
When using floating point arithmetic, we obtain  ,
, 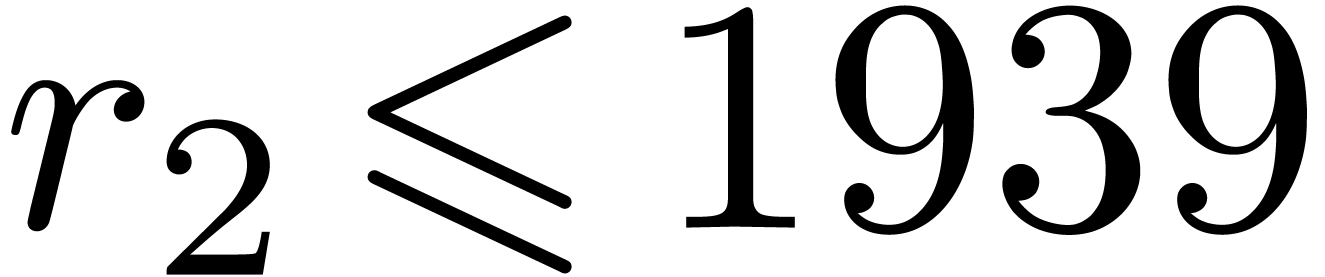 ,
, 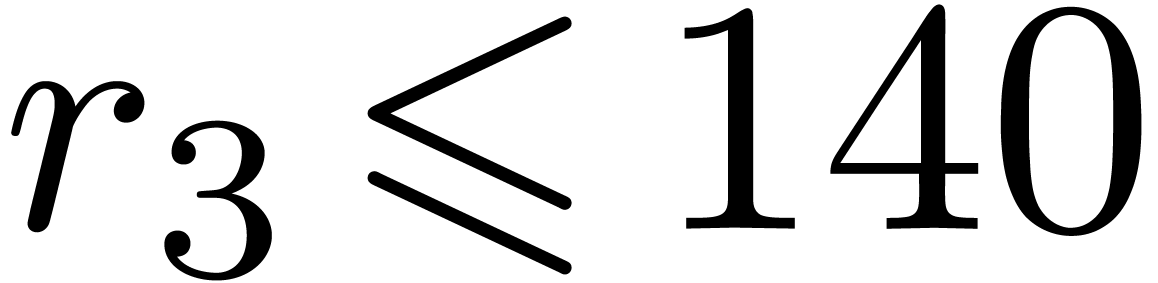 ,
, 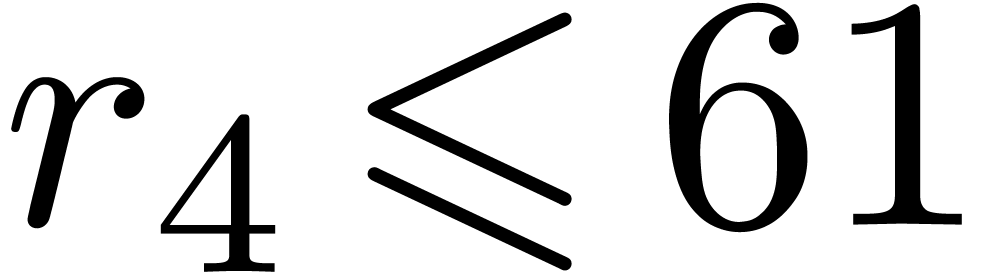 ,
,
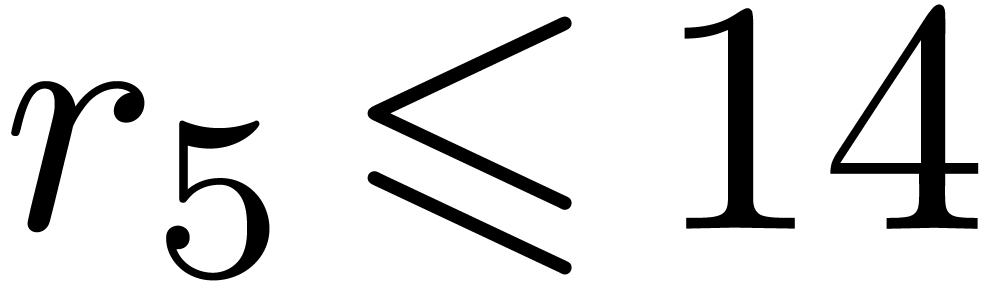 and
and 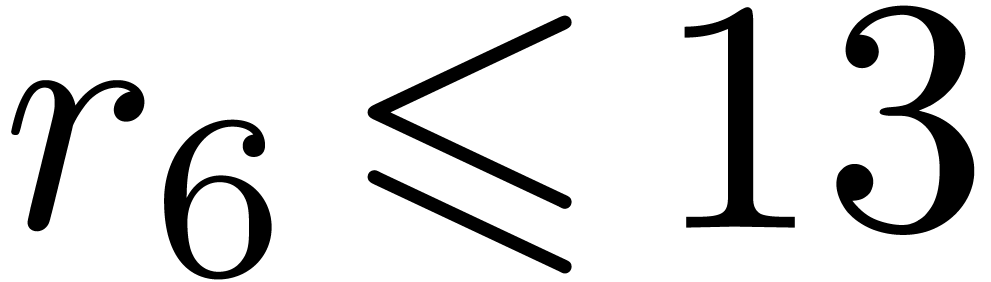 .
Clearly, there is a trade-off between the efficiency of the modular
matrix multiplications (high values of
.
Clearly, there is a trade-off between the efficiency of the modular
matrix multiplications (high values of 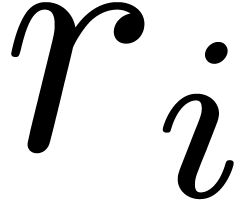 are
better) and the bitsize
are
better) and the bitsize  of
of 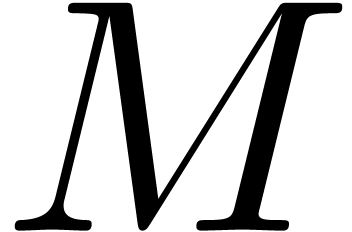 (larger capacities are better).
(larger capacities are better).
Bibliography
-
[1]
-
J.-C. Bajard, M. E. Kaihara, and T. Plantard.
Selected rns bases for modular multiplication. In Proc. of
the 19th IEEE Symposium on Computer Arithmetic, pages
25–32, 2009.
-
[2]
-
D. Bernstein. Scaled remainder trees. Available from
https://cr.yp.to/arith/scaledmod-20040820.pdf,
2004.
-
[3]
-
A. Borodin and R. T. Moenck. Fast modular transforms.
Journal of Computer and System Sciences, 8:366–386,
1974.
-
[4]
-
A. Bostan, G. Lecerf, and É. Schost.
Tellegen's principle into practice. In Proceedings of ISSAC
2003, pages 37–44. ACM Press, 2003.
-
[5]
-
A. Bostan and É. Schost. Polynomial evaluation
and interpolation on special sets of points. Journal of
Complexity, 21(4):420–446, August 2005. Festschrift
for the 70th Birthday of Arnold Schönhage.
-
[6]
-
J. W. Cooley and J. W. Tukey. An algorithm for the
machine calculation of complex Fourier series. Math.
Computat., 19:297–301, 1965.
-
[7]
-
J. Doliskani, P. Giorgi, R. Lebreton, and É.
Schost. Simultaneous conversions with the Residue Number System
using linear algebra. Technical Report https://hal-lirmm.ccsd.cnrs.fr/lirmm-01415472,
HAL, 2016.
-
[8]
-
C. M. Fiduccia. Polynomial evaluation via the
division algorithm: the fast fourier transform revisited. In A.
L. Rosenberg, editor, Fourth annual ACM symposium on theory
of computing, pages 88–93, 1972.
-
[9]
-
J. von zur Gathen and J. Gerhard. Modern Computer
Algebra. Cambridge University Press, New York, NY, USA, 3rd
edition, 2013.
-
[10]
-
J. van der Hoeven. Faster Chinese remaindering.
Technical report, HAL, 2016. http://hal.archives-ouvertes.fr/hal-01403810.
-
[11]
-
J. van der Hoeven, G. Lecerf, B. Mourrain, et al.
Mathemagix, 2002. http://www.mathemagix.org.
-
[12]
-
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular
SIMD arithmetic in Mathemagix. ACM Trans. Math. Softw.,
43(1):5:1–5:37, 2016.
-
[13]
-
A. Karatsuba and J. Ofman. Multiplication of
multidigit numbers on automata. Soviet Physics Doklady,
7:595–596, 1963.
-
[14]
-
R. T. Moenck and A. Borodin. Fast modular transforms
via division. In Thirteenth annual IEEE symposium on
switching and automata theory, pages 90–96, Univ.
Maryland, College Park, Md., 1972.
-
[15]
-
The PARI Group, Bordeaux. PARI/GP, 2012.
Software available from http://pari.math.u-bordeaux.fr.
 are fixed and can
even be chosen by the user. If
are fixed and can
even be chosen by the user. If  is small or
moderately large, then we show how to choose gentle moduli
that allow for speedier Chinese remaindering. The multiplication of
integer matrices is one typical application where we expect practical
gains for various common matrix dimensions and bitsizes of the
coefficients.
is small or
moderately large, then we show how to choose gentle moduli
that allow for speedier Chinese remaindering. The multiplication of
integer matrices is one typical application where we expect practical
gains for various common matrix dimensions and bitsizes of the
coefficients.
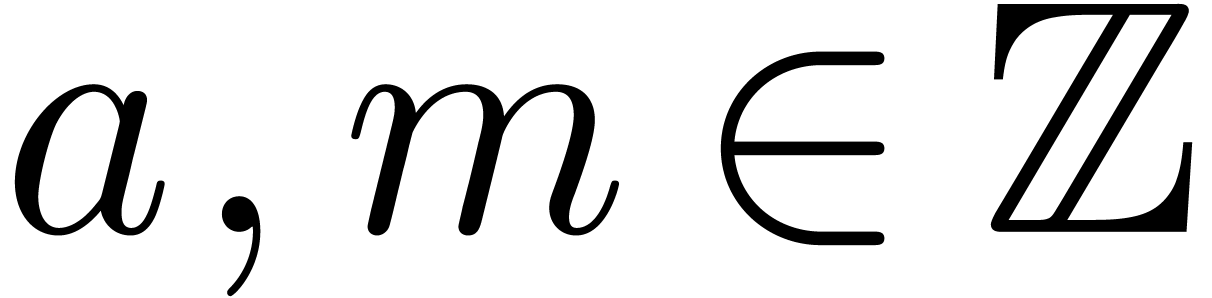 with
with 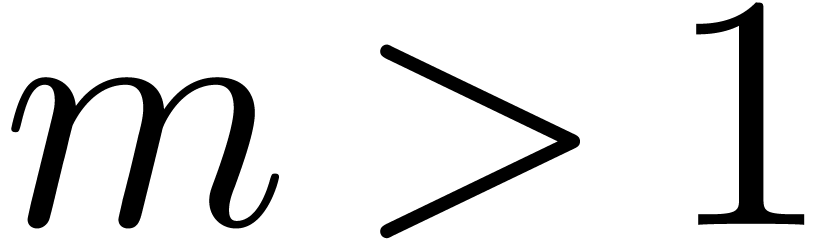 ,
,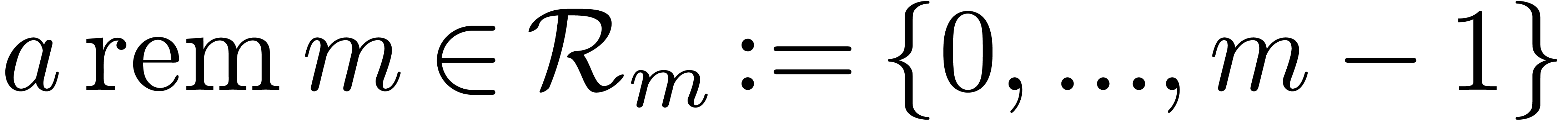 the remainder of the Euclidean
division of
the remainder of the Euclidean
division of  by
by  .
. matrix
matrix  with
integer coefficients, we will also denote
with
integer coefficients, we will also denote 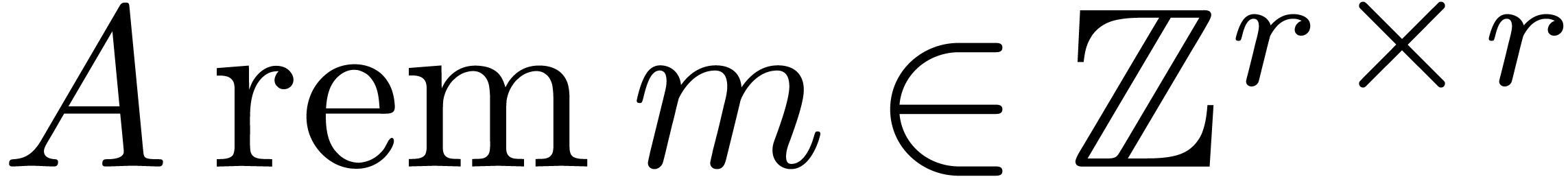 for
the matrix with coefficients
for
the matrix with coefficients 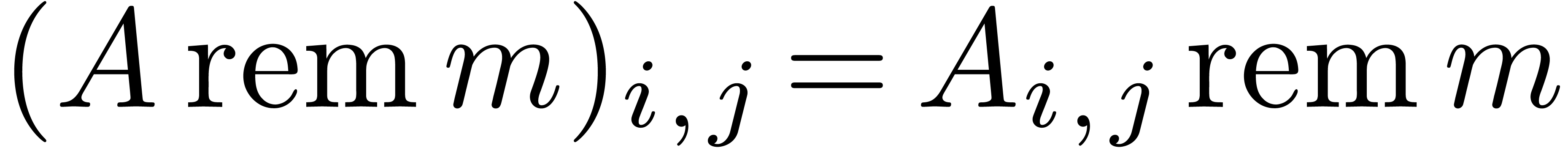 .
. .
.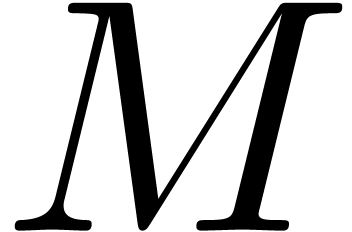 with
with 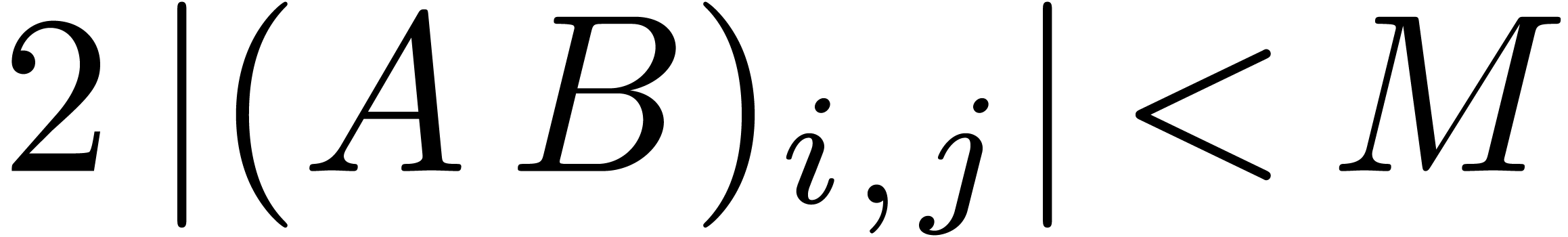 for all
for all  ,
,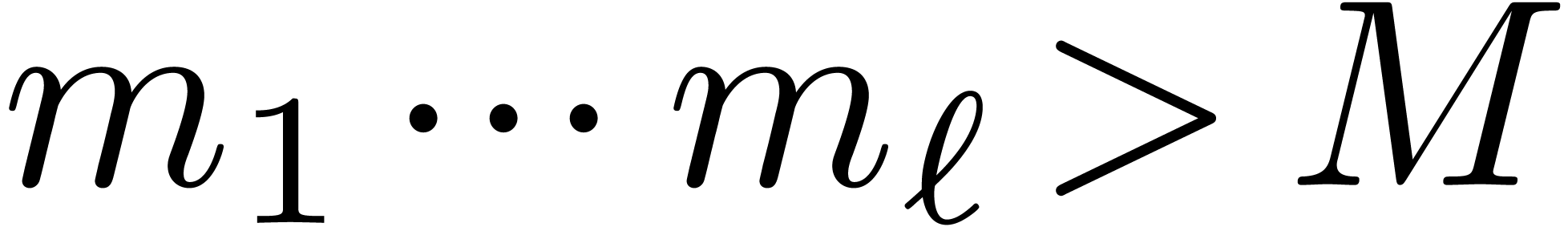 that are mutually coprime.
that are mutually coprime.
 and
and 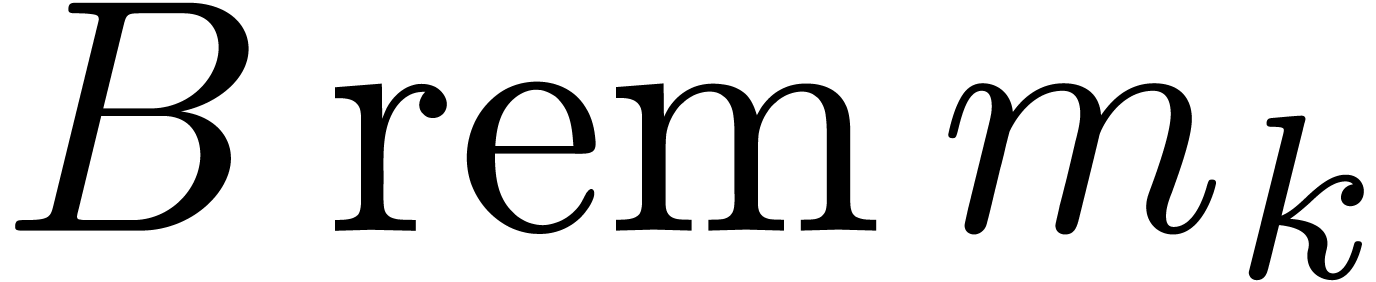 for
for
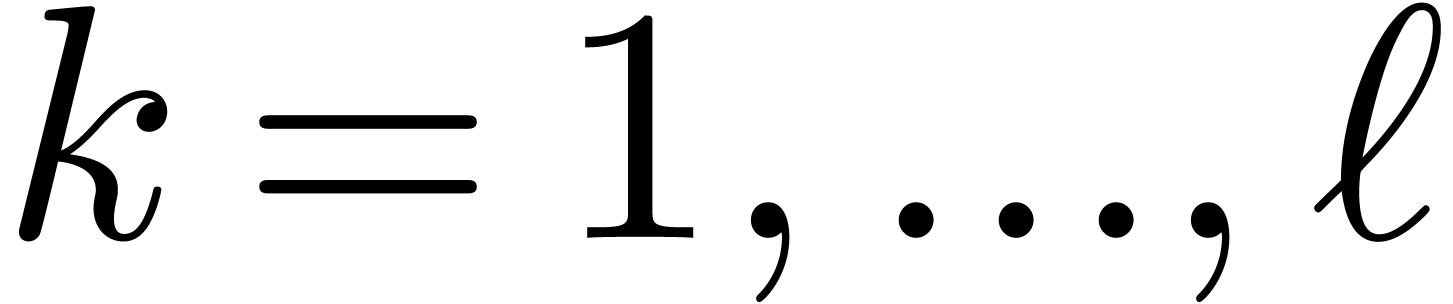 .
. for
for  from the
from the  with
with  from
from  for all
for all  ,
,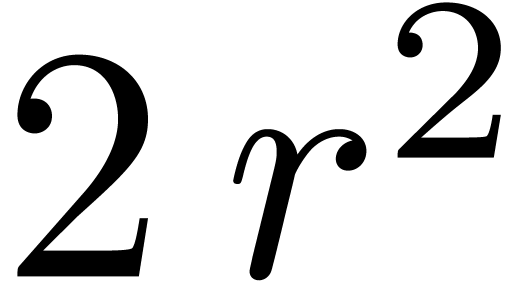 multi-modular reductions for
the coefficients of
multi-modular reductions for
the coefficients of  and
and  .
. from the
from the  with
with 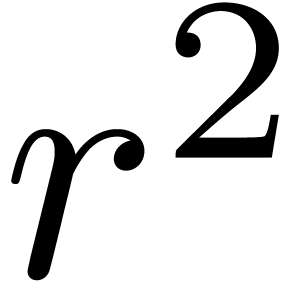 such reconstructions in step 3. Our
hypothesis on
such reconstructions in step 3. Our
hypothesis on  from
from  should be small or moderately
large, say
should be small or moderately
large, say 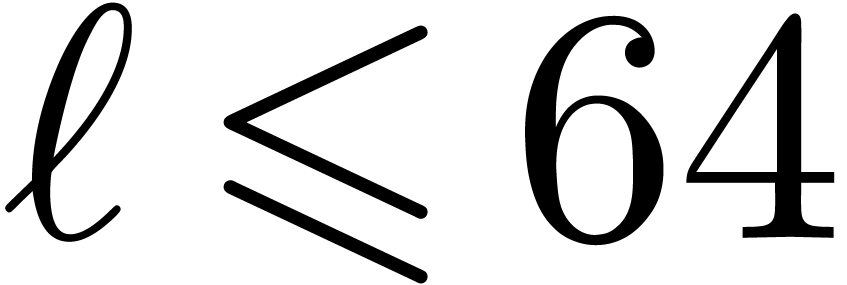 .
.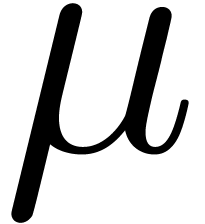 the bitsize of a machine word (say
the bitsize of a machine word (say 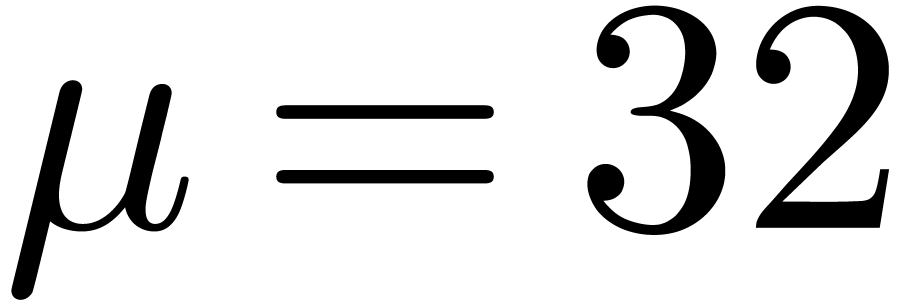 or
or 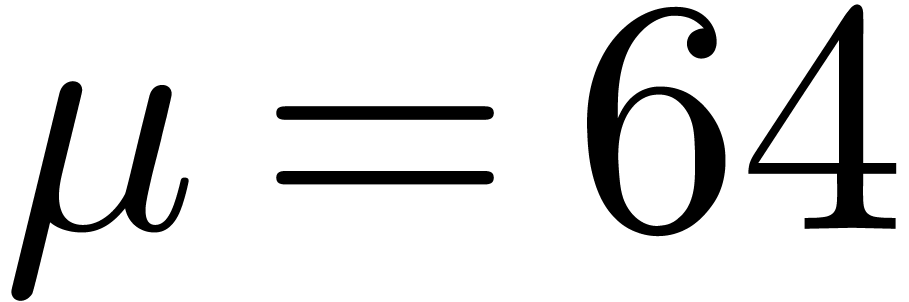 ),
), .
. are usually carried
out using a naive algorithm, of complexity
are usually carried
out using a naive algorithm, of complexity 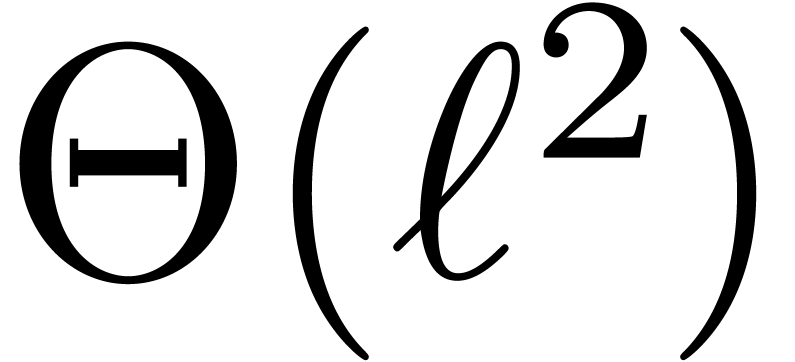 .
.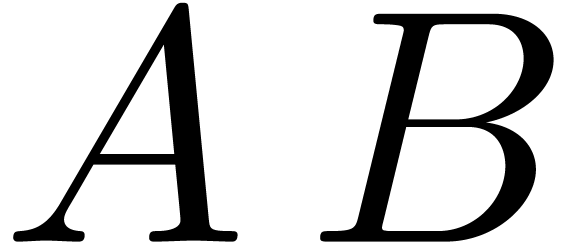 using
using 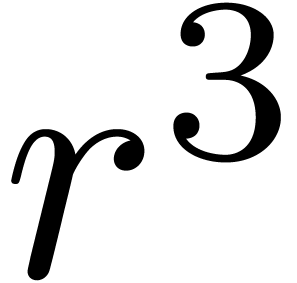 naive integer multiplications, the computation time
is therefore of order
naive integer multiplications, the computation time
is therefore of order 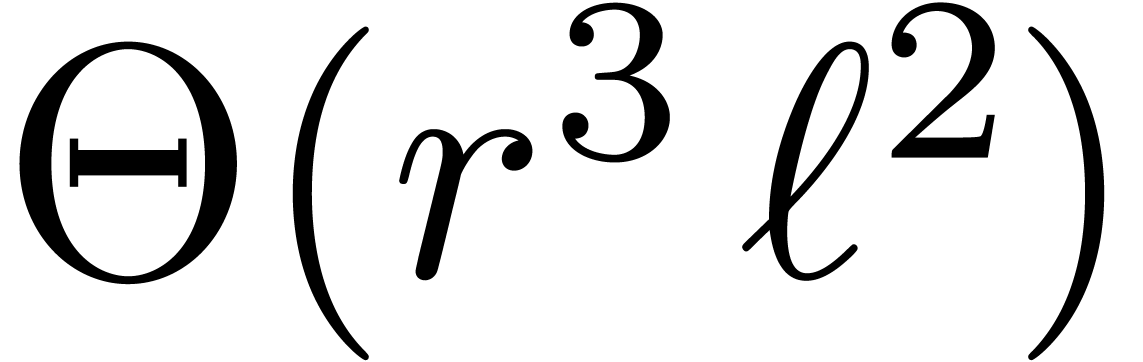 .
. can be
done in time
can be
done in time 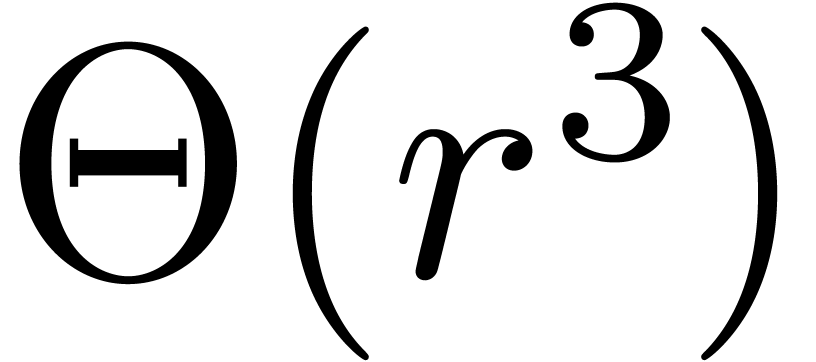 .
.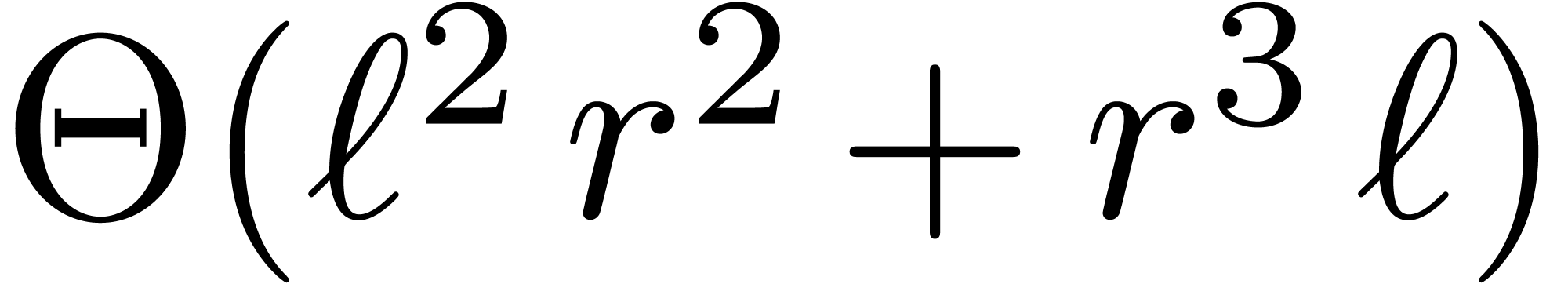 ,
,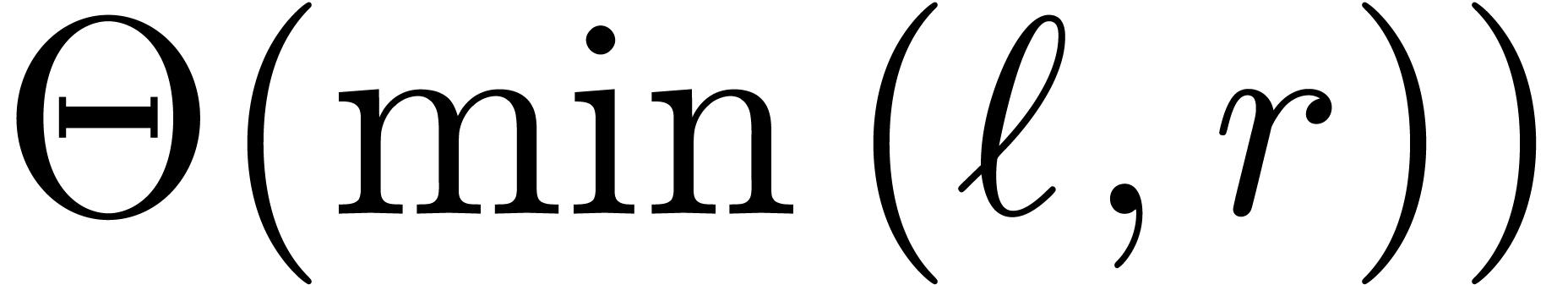 times faster than the naive algorithm.
times faster than the naive algorithm.
 ,
,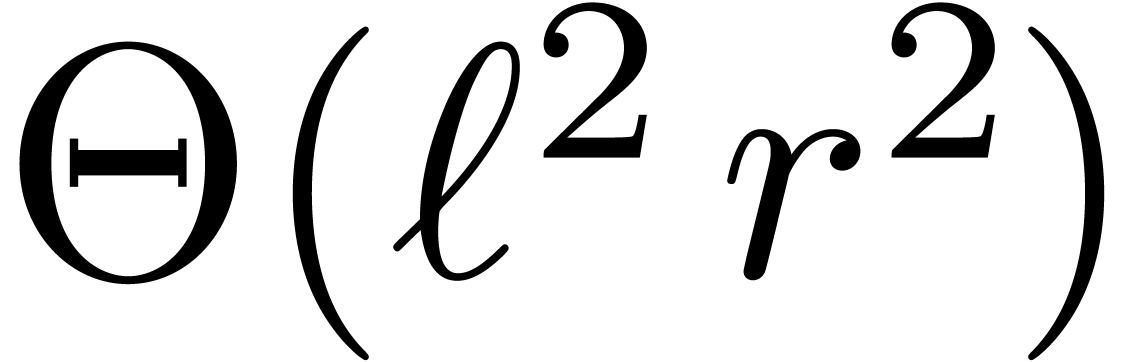 of steps 1 and 3 is negligible with respect to the cost
of steps 1 and 3 is negligible with respect to the cost
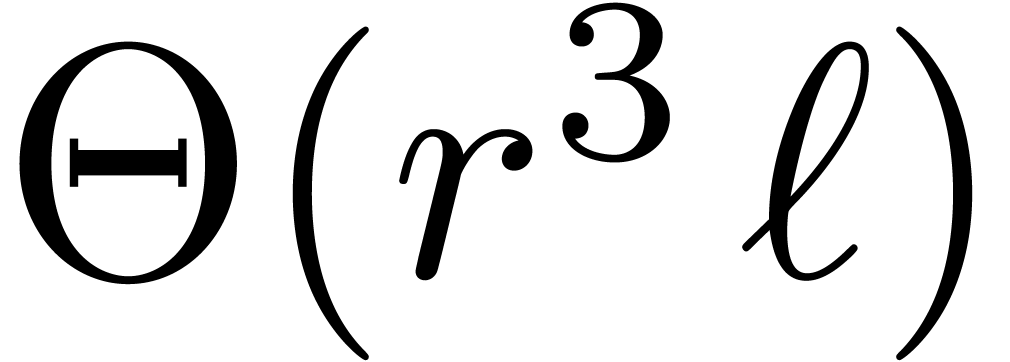 of step 2. However, if
of step 2. However, if  are of the same order of magnitude, then
Chinese remaindering may take an important part of the computation time;
the main purpose of this paper is to reduce this cost. If
are of the same order of magnitude, then
Chinese remaindering may take an important part of the computation time;
the main purpose of this paper is to reduce this cost. If  ,
, .
. of the form
of the form 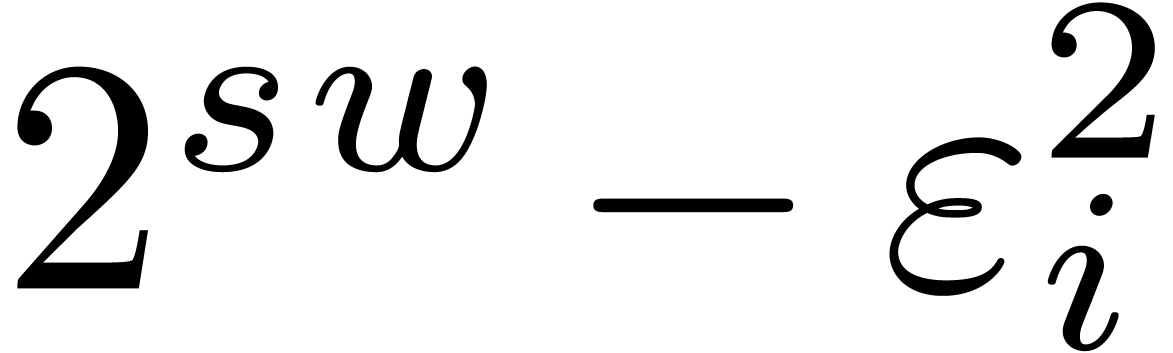 ,
, is somewhat smaller than
is somewhat smaller than  is even, and
is even, and
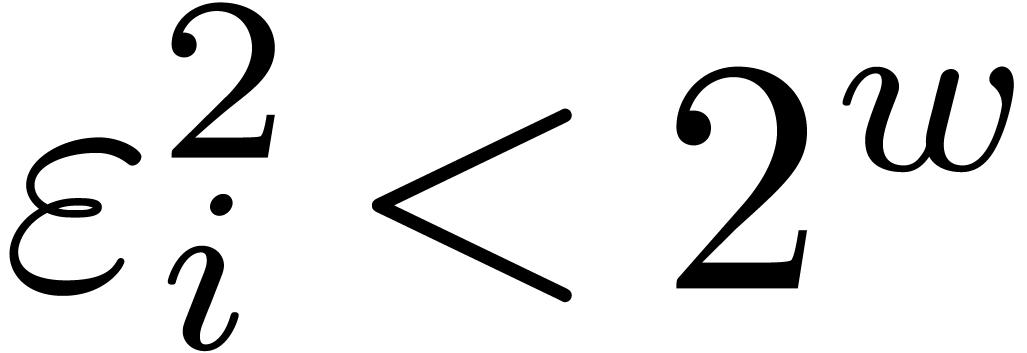 .
.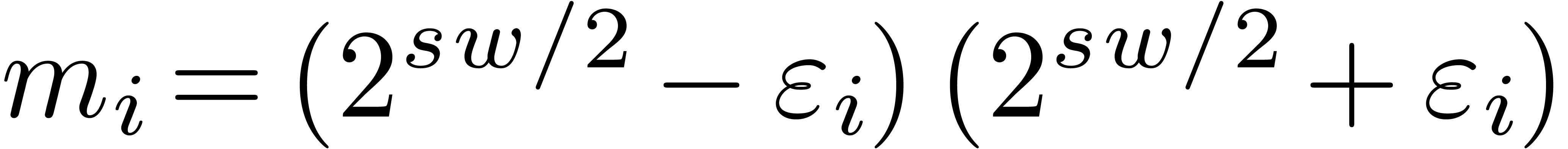 and, if we are lucky, then
both
and, if we are lucky, then
both 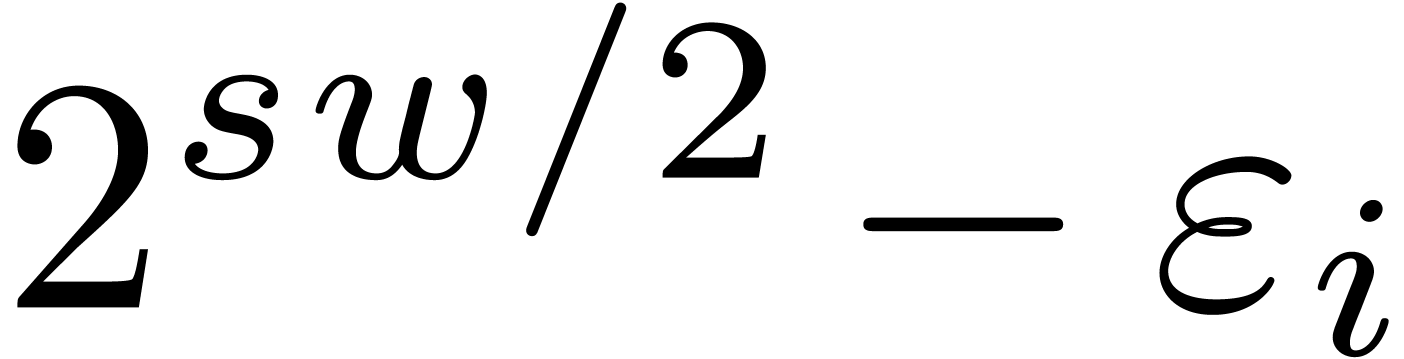 and
and 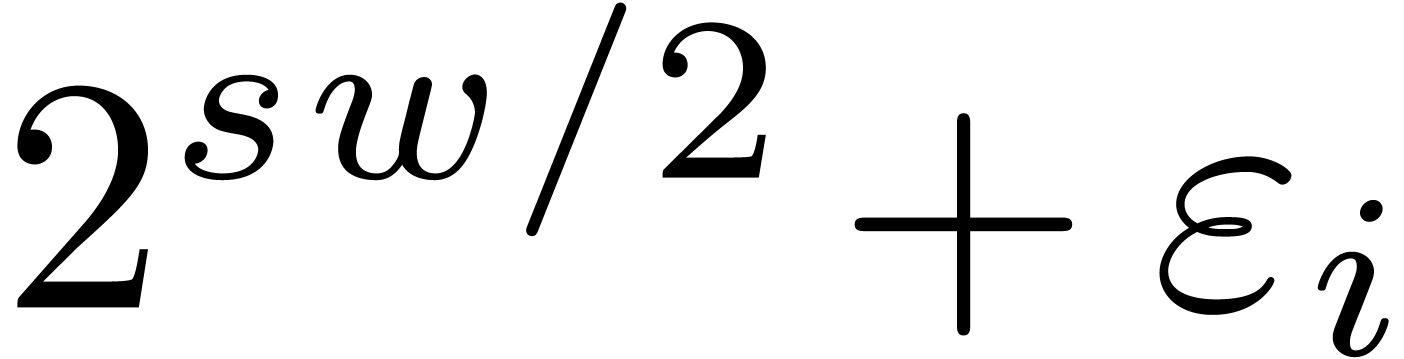 can be factored
into
can be factored
into 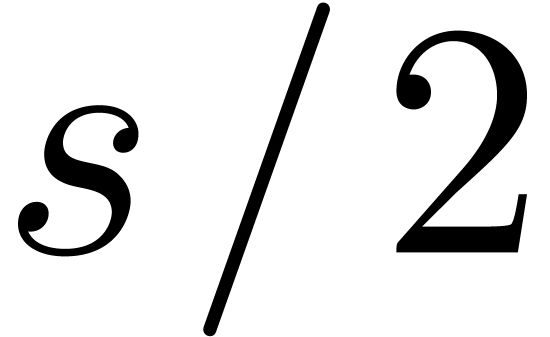 moduli of bitsize
moduli of bitsize 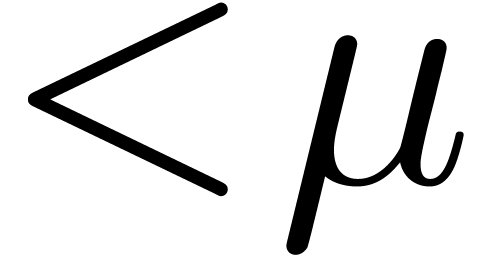 .
.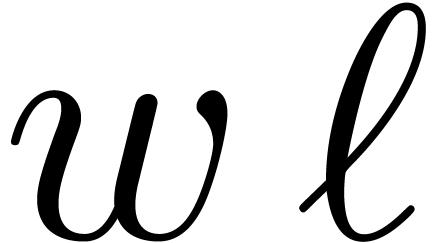 moduli
moduli 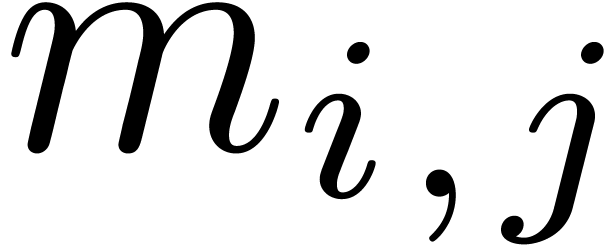 of bitsize
of bitsize
 that are mutually coprime and for which Chinese
remaindering can be implemented efficiently.
that are mutually coprime and for which Chinese
remaindering can be implemented efficiently.
 .
. ,
, .
. are also known as
pseudo-Mersenne moduli. They have been exploited before in
cryptography [
are also known as
pseudo-Mersenne moduli. They have been exploited before in
cryptography [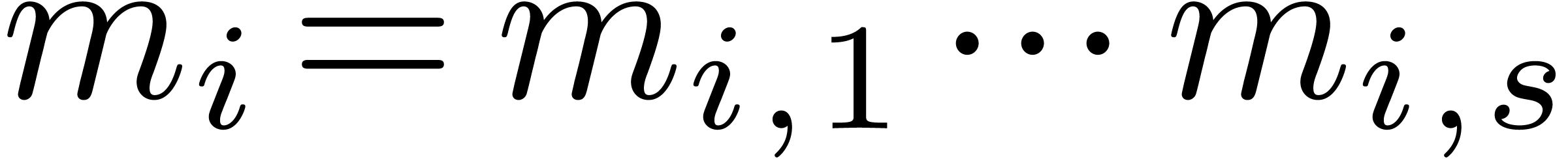 and residues modulo
and residues modulo
 .
.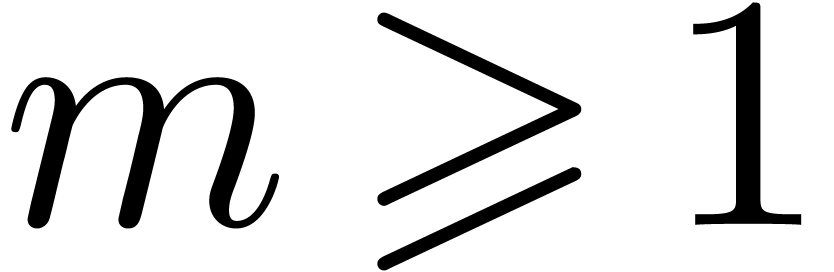 ,
, .
.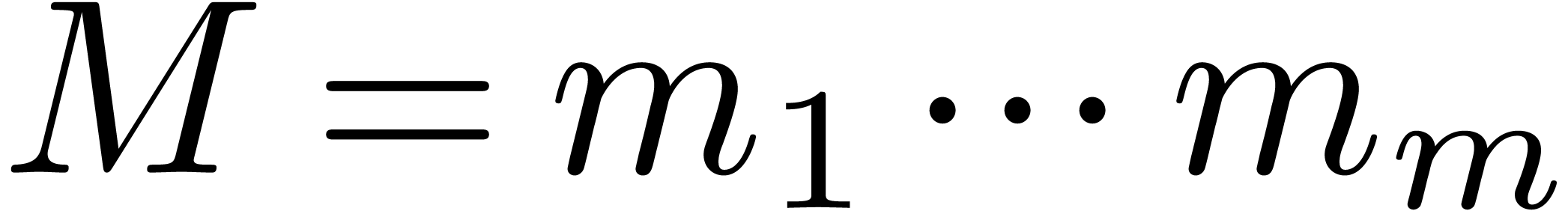 .
.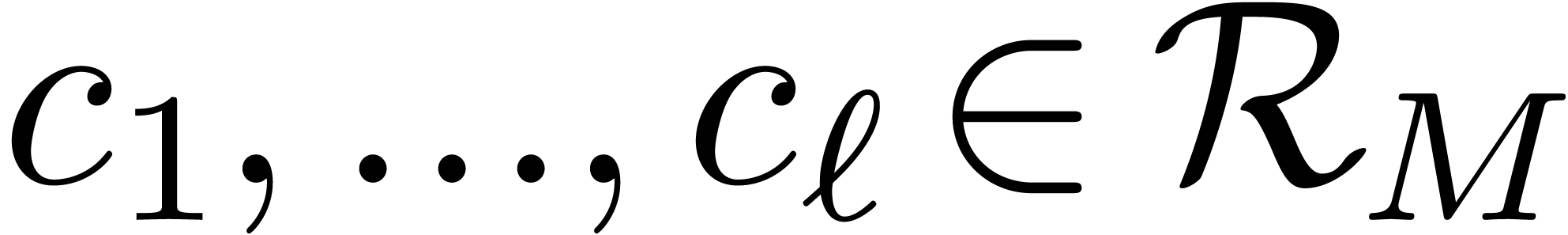 such that
for any
such that
for any  ,
,
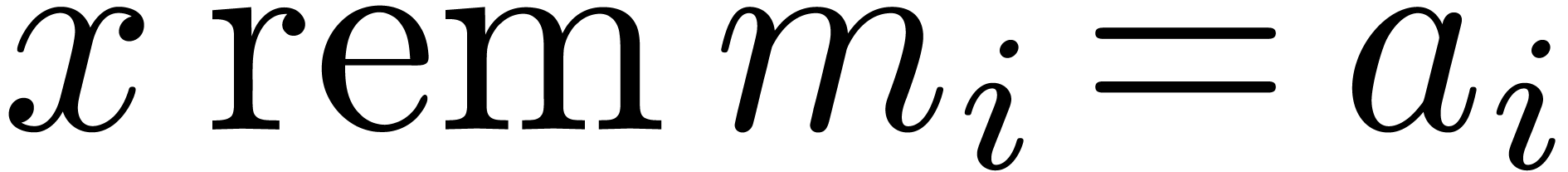 for
for 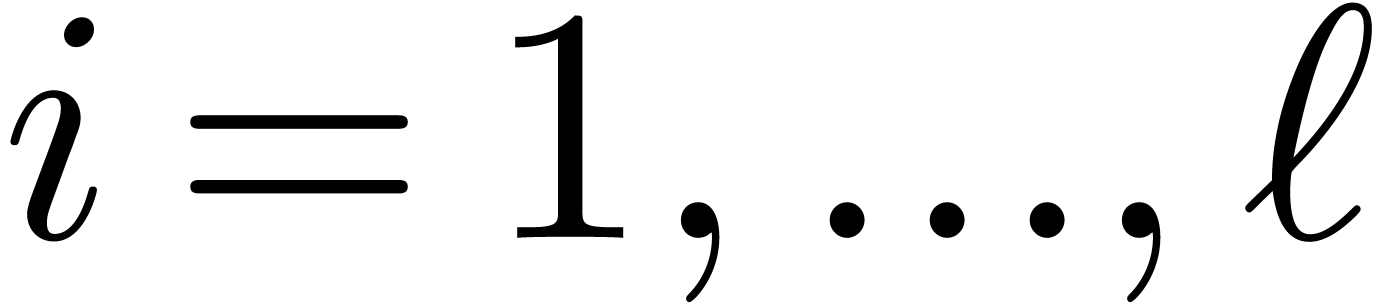 .
.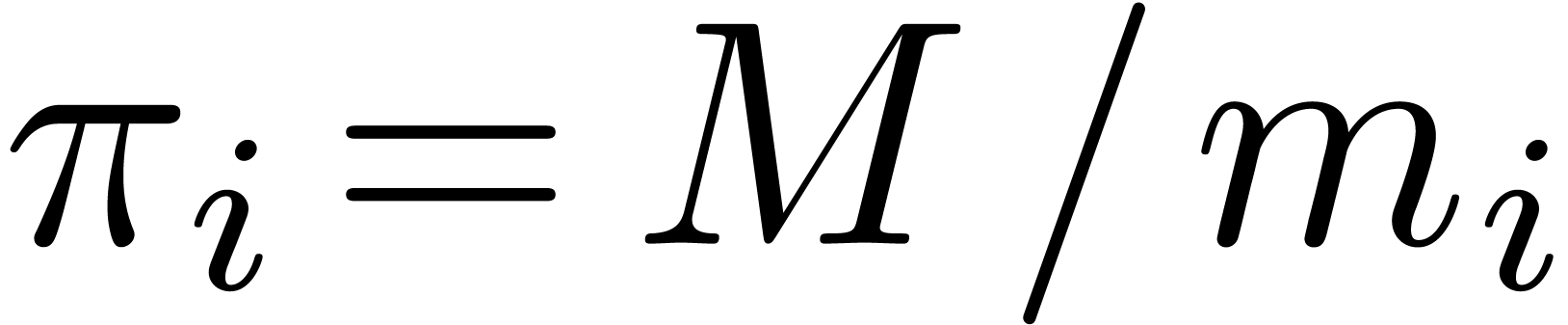 .
.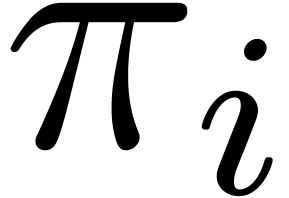 and
and 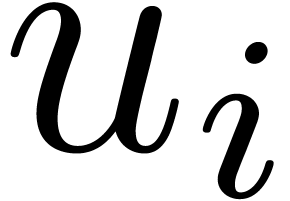 modulo
modulo  .
.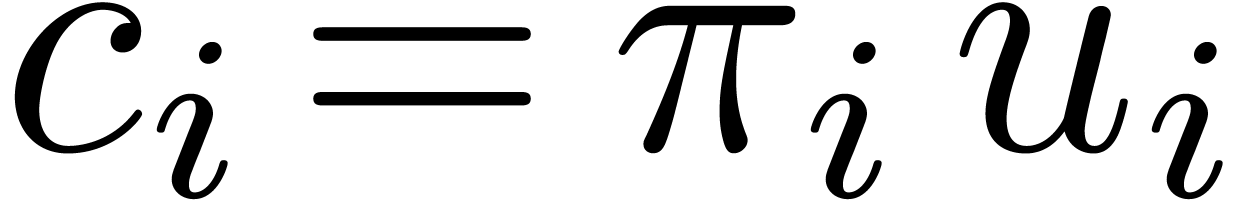 .
.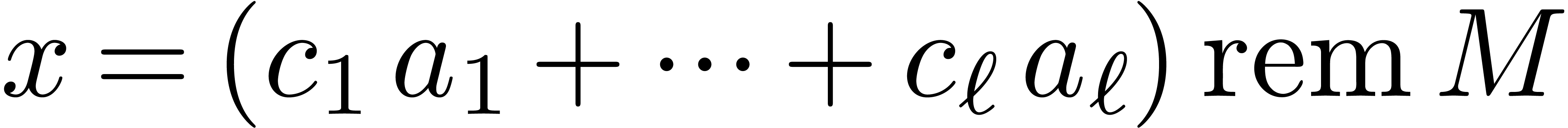 and any
and any  ,
,
 is divisible by
is divisible by  ,
,

 the
cofactors for
the
cofactors for  and
also denote these numbers by
and
also denote these numbers by  .
. -bit
-bit instead of
instead of  (assuming
that we have hardware support for double precision). For floating point
arithmetic it also matters whether the processor offers a
“fused-multiply-add” (FMA) instruction; this essentially
provides us with an efficient way to multiply two
(assuming
that we have hardware support for double precision). For floating point
arithmetic it also matters whether the processor offers a
“fused-multiply-add” (FMA) instruction; this essentially
provides us with an efficient way to multiply two  ,
,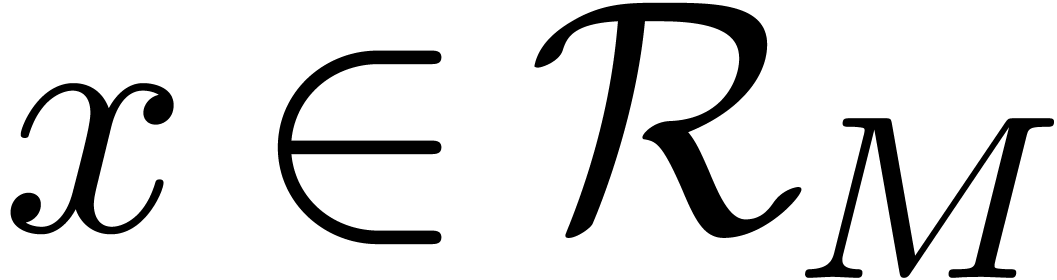 be as in the Chinese remainder theorem. We will refer to the computation
of
be as in the Chinese remainder theorem. We will refer to the computation
of  as a function of
as a function of 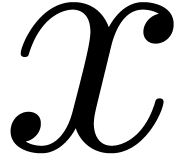 as
the problem of multi-modular reduction. The inverse problem is
called multi-modular reconstruction. In what follows, we assume
that
as
the problem of multi-modular reduction. The inverse problem is
called multi-modular reconstruction. In what follows, we assume
that 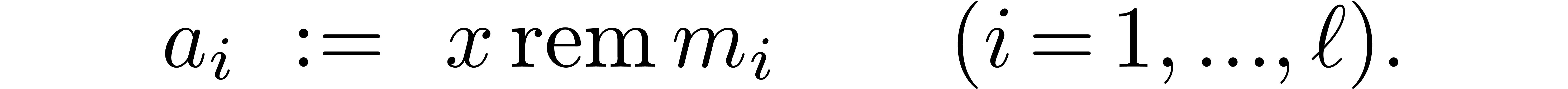

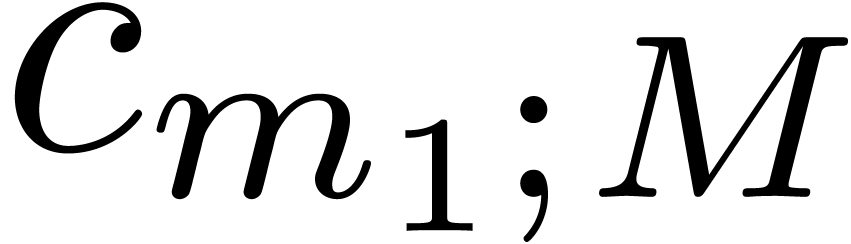 can be regarded as a precomputation.
can be regarded as a precomputation.
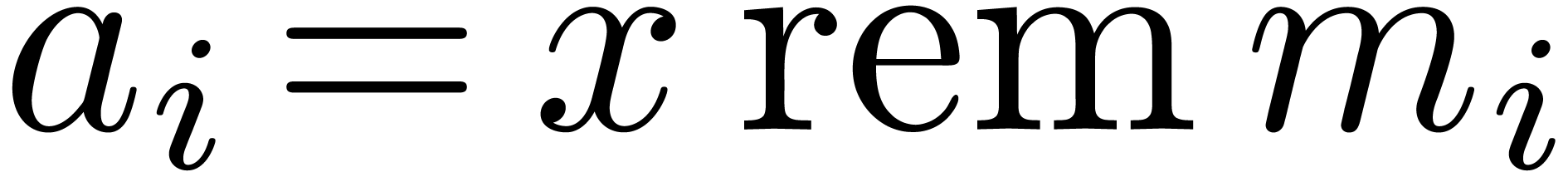 .
.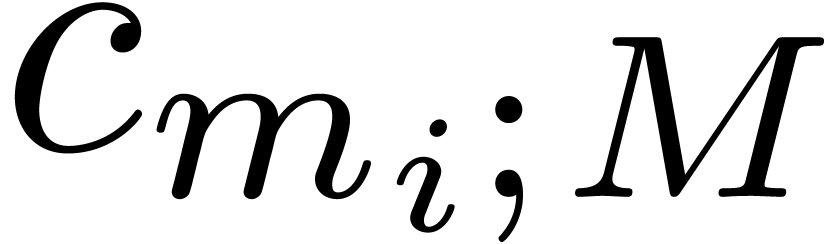 into
into 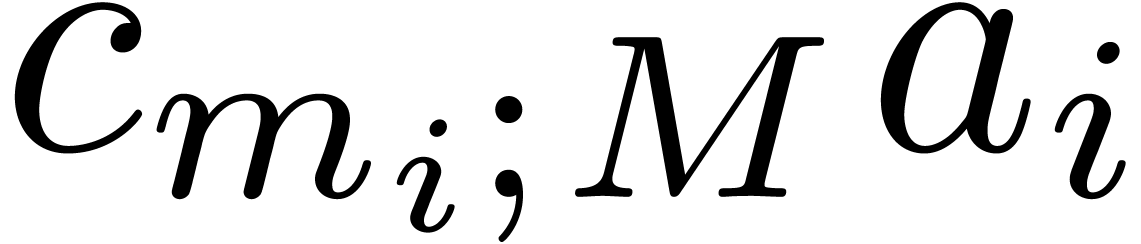 can be computed using
can be computed using 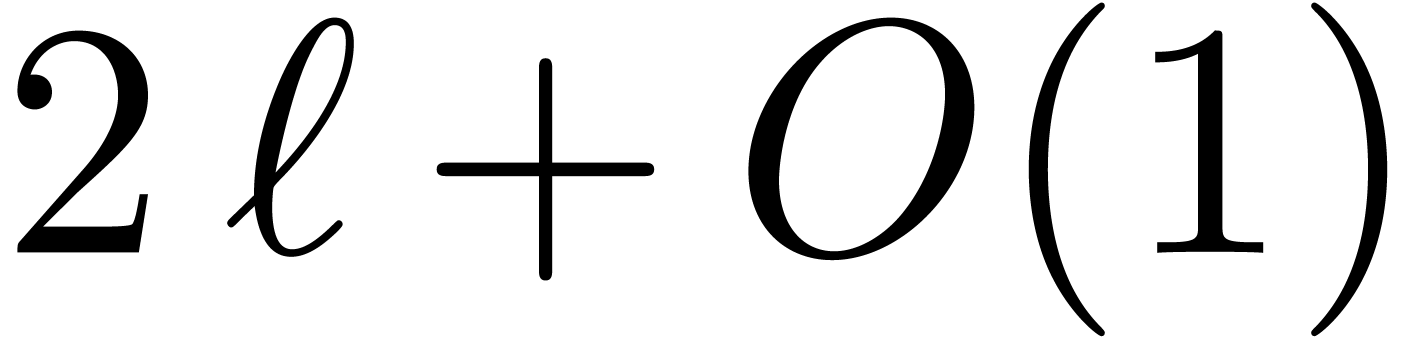 multiplications and
multiplications and 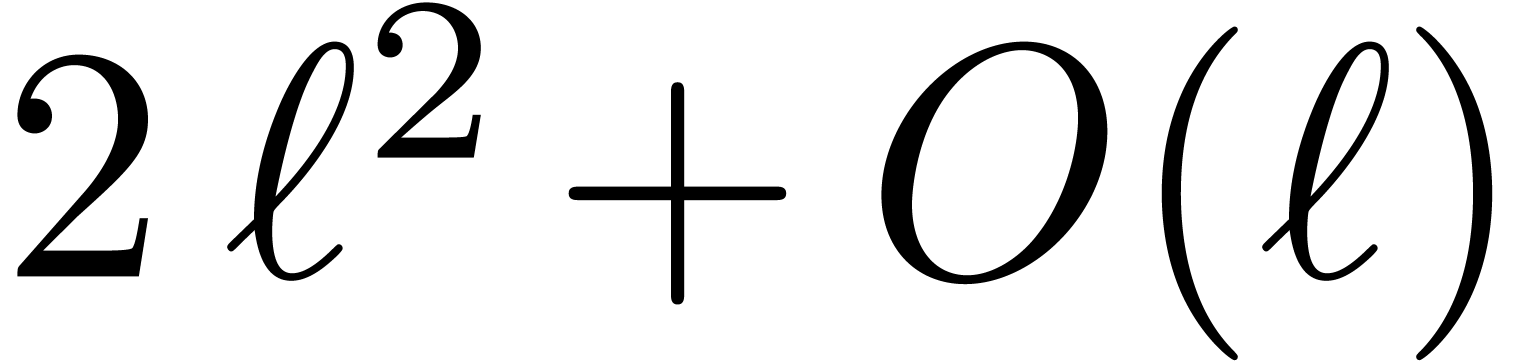 hardware multiplications and
hardware multiplications and  can be done using only
can be done using only 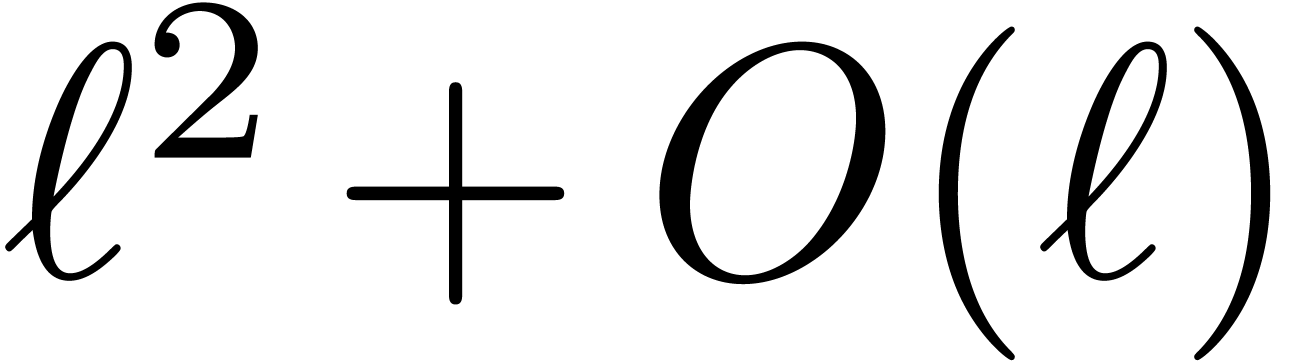 multiplications and
multiplications and 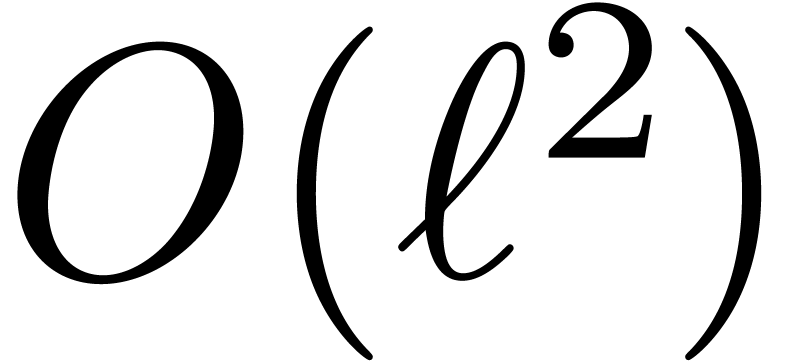 more operations may
be required for the carry handling—but it is beyond the scope of
this paper to go into this level of detail.
more operations may
be required for the carry handling—but it is beyond the scope of
this paper to go into this level of detail.
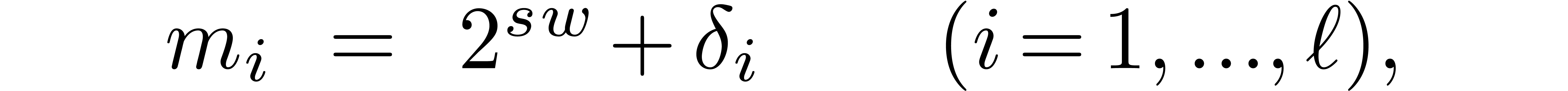
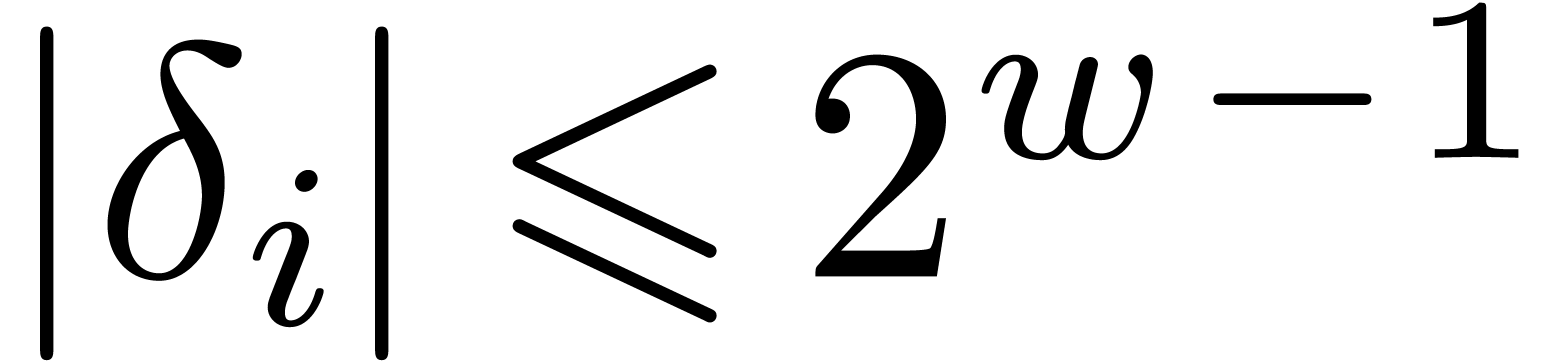 and
and  a small
number. As usual, we assume that the
a small
number. As usual, we assume that the  by
by  with the
quotient of this division. In other words, the remainder can be computed
using
with the
quotient of this division. In other words, the remainder can be computed
using  hardware multiplications. In comparison,
the algorithm from section
hardware multiplications. In comparison,
the algorithm from section 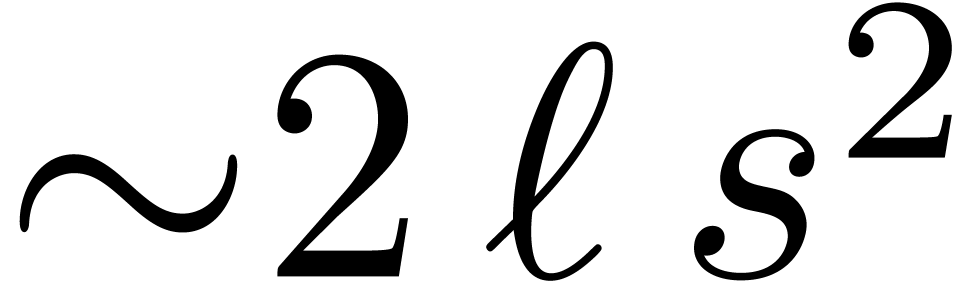 multiplication when applied to
multiplication when applied to  -bit
-bit can be done using
can be done using 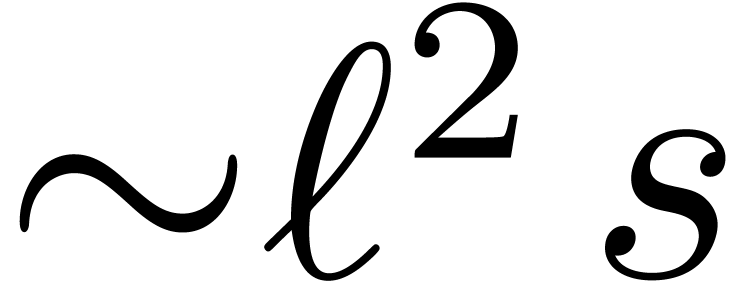 instead of
instead of 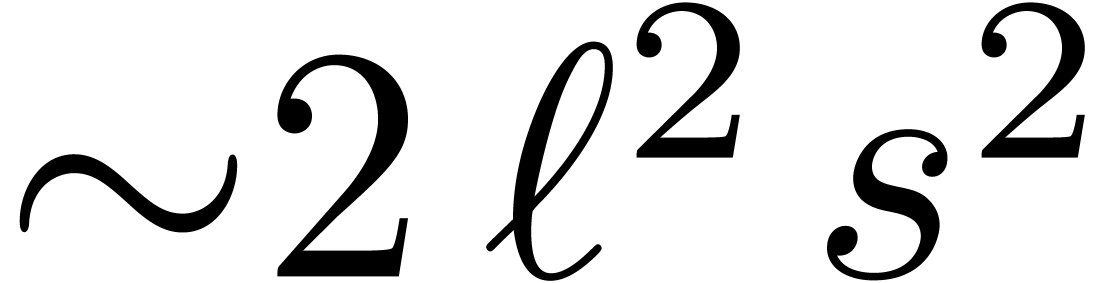 multiplications. This leads to a
potential gain of a factor
multiplications. This leads to a
potential gain of a factor 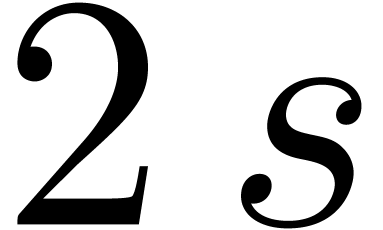 ,
, ,
,
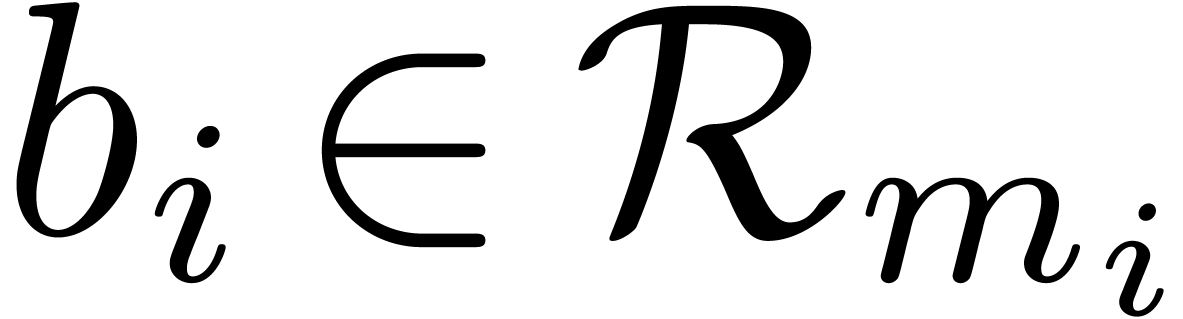 .
. efficiently from
efficiently from  .
. ,
,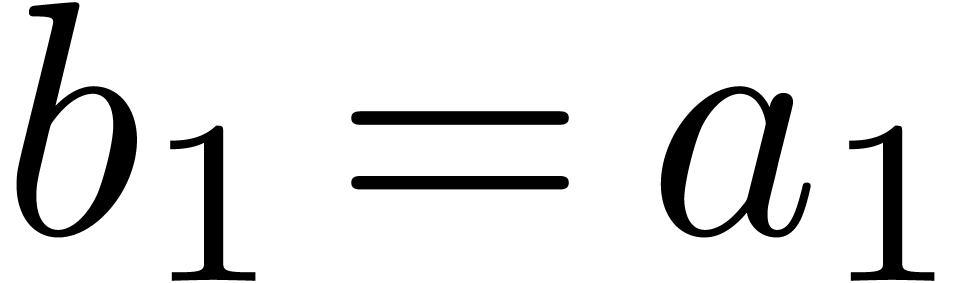 .
.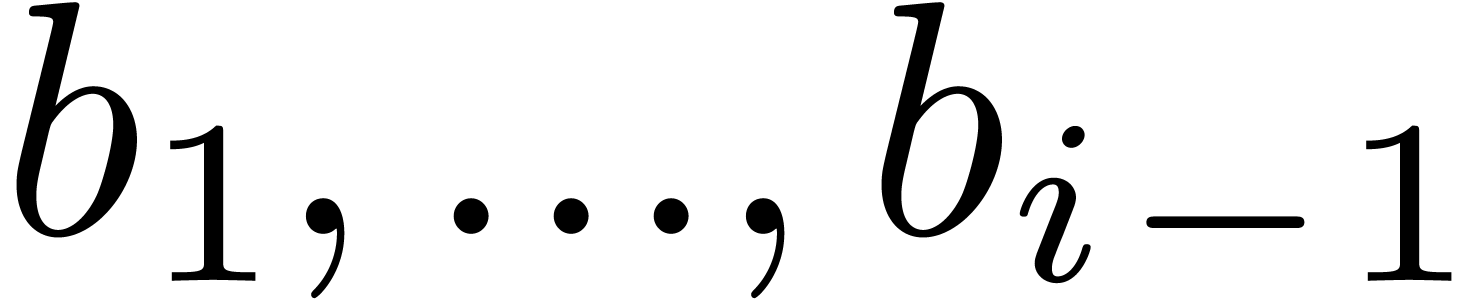 have been computed. For
have been computed. For 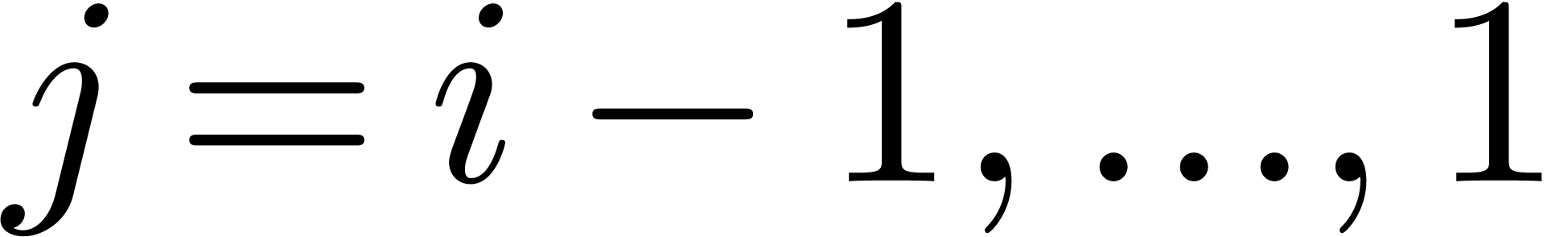 we next compute
we next compute
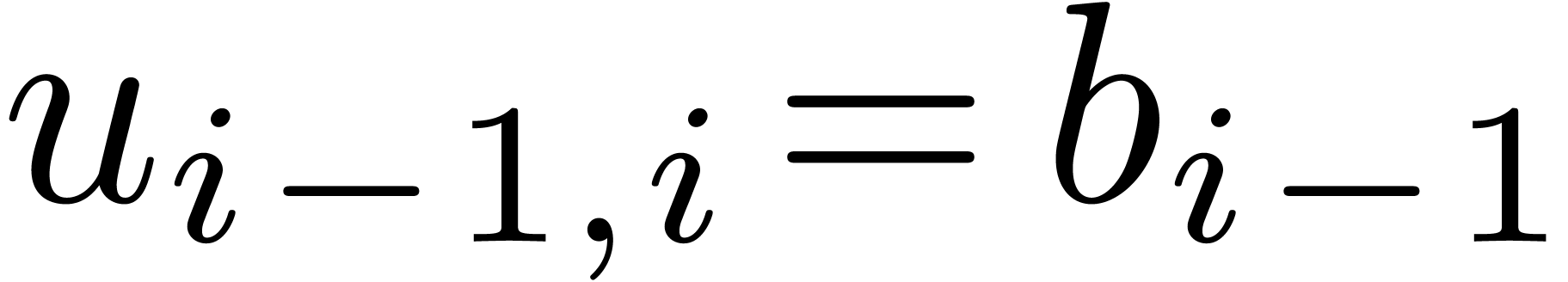 and
and
 can be computed using
can be computed using 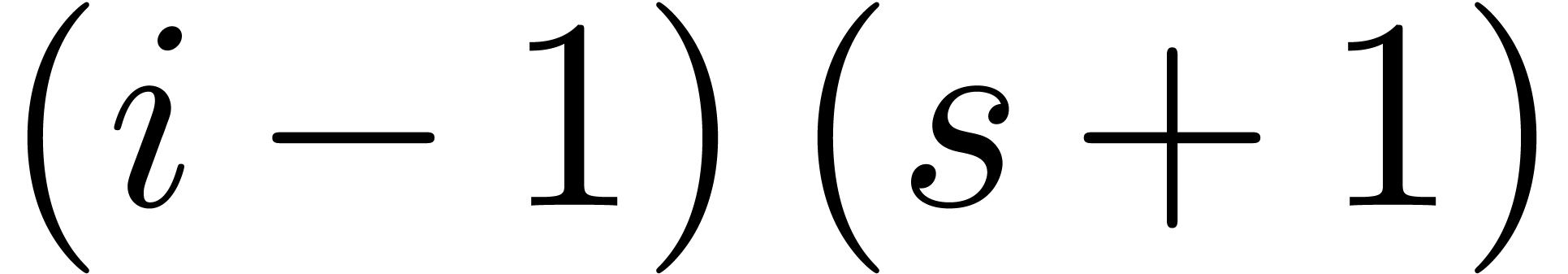 hardware multiplications. We have
hardware multiplications. We have
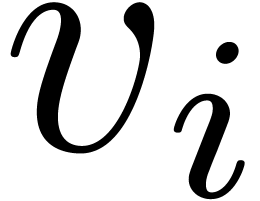 of
of  modulo
modulo 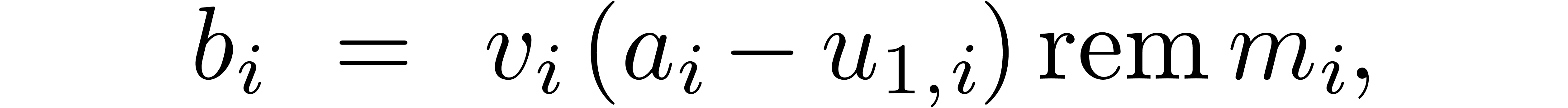
 multiplications. For small
values of
multiplications. For small
values of 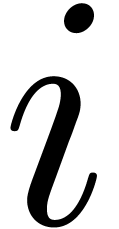 ,
, modulo
modulo
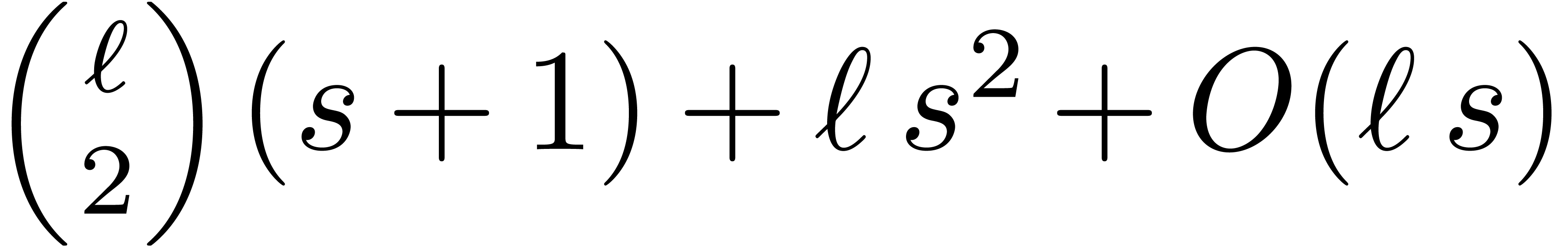 multiplications. Having computed the mixed radix
representation, we next compute
multiplications. Having computed the mixed radix
representation, we next compute
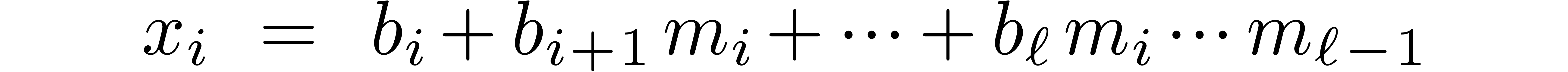
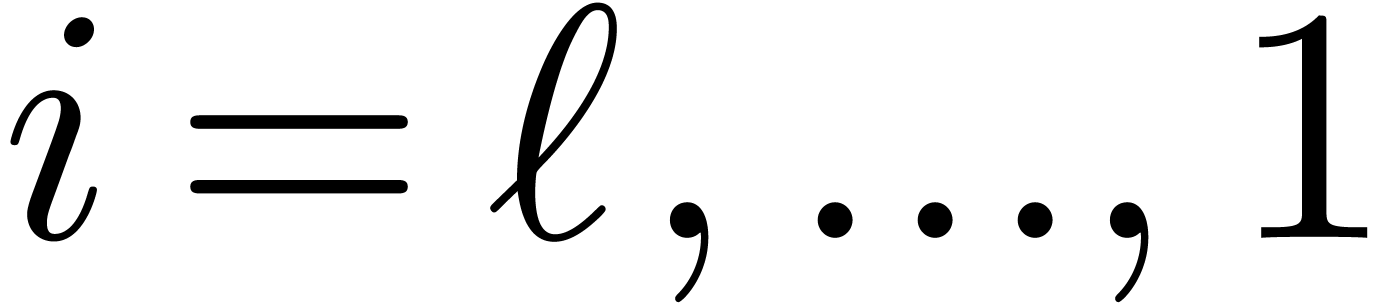 ,
,
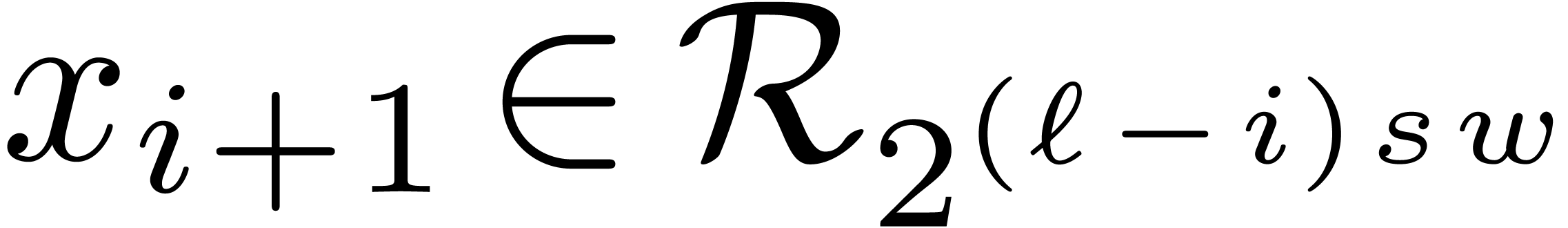 ,
,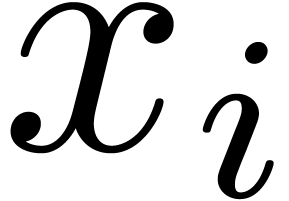 requires
requires 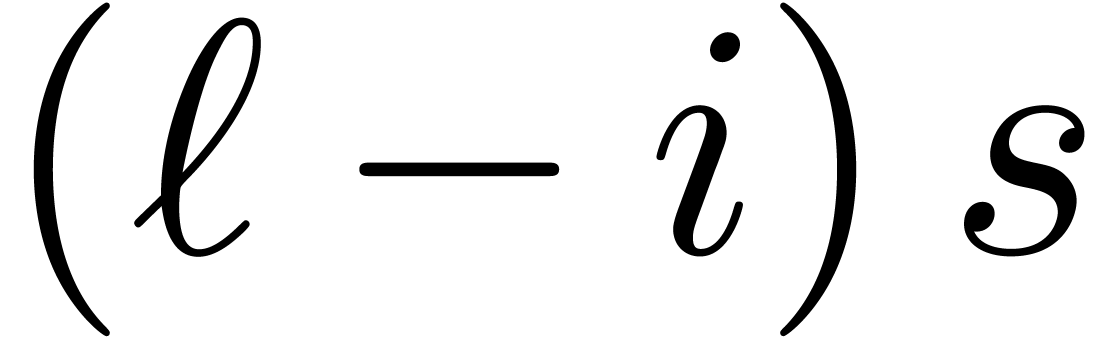 multiplications. Altogether, the computation of
multiplications. Altogether, the computation of 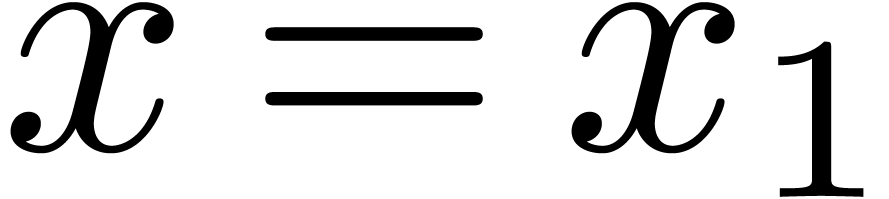 from
from 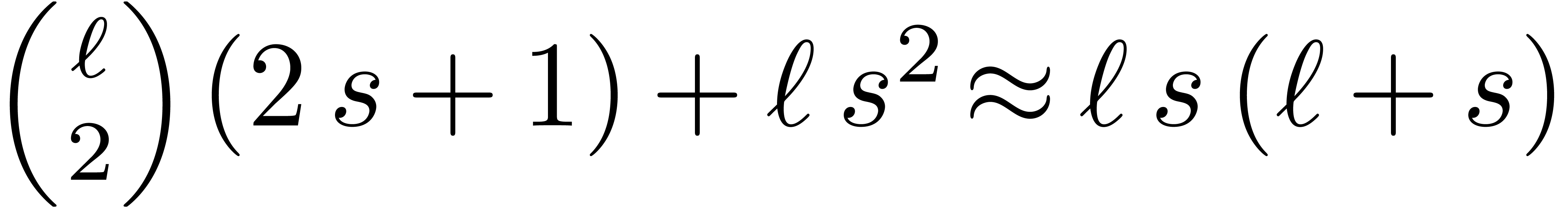 hardware multiplications.
hardware multiplications.
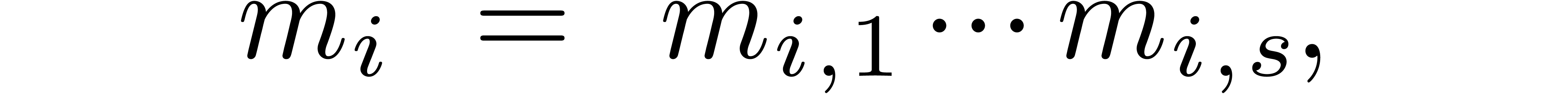
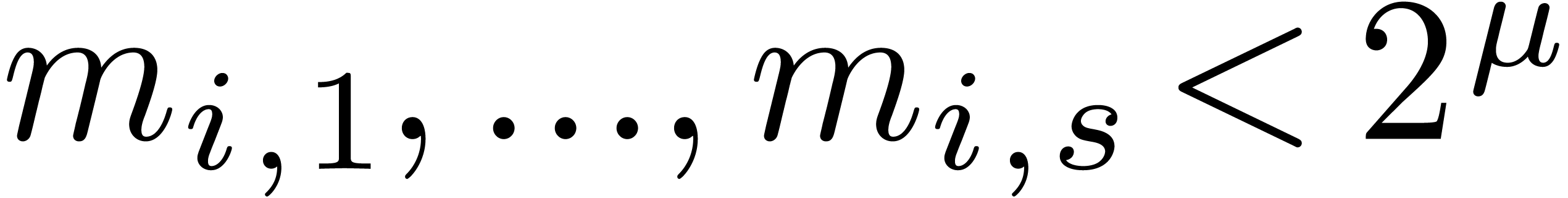 .
. ,
,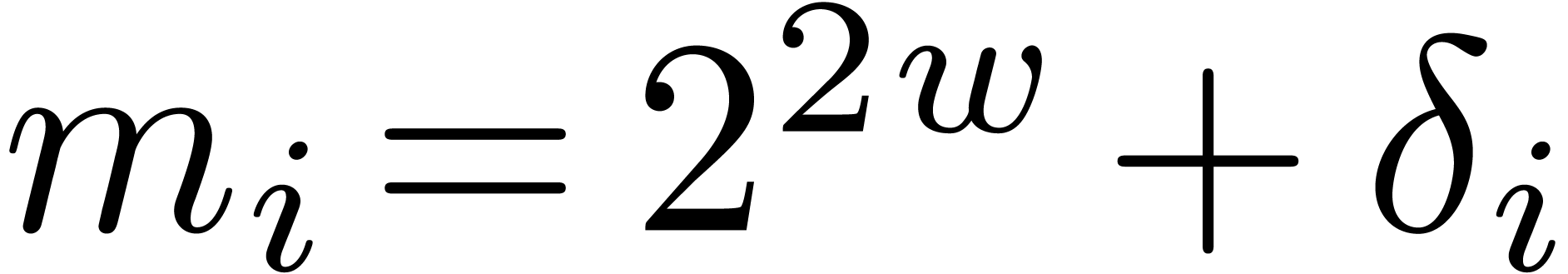 by taking
by taking 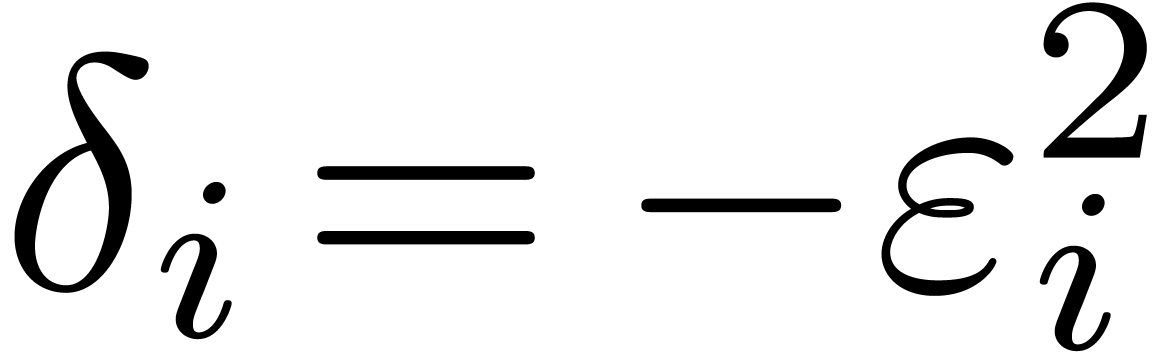 ,
,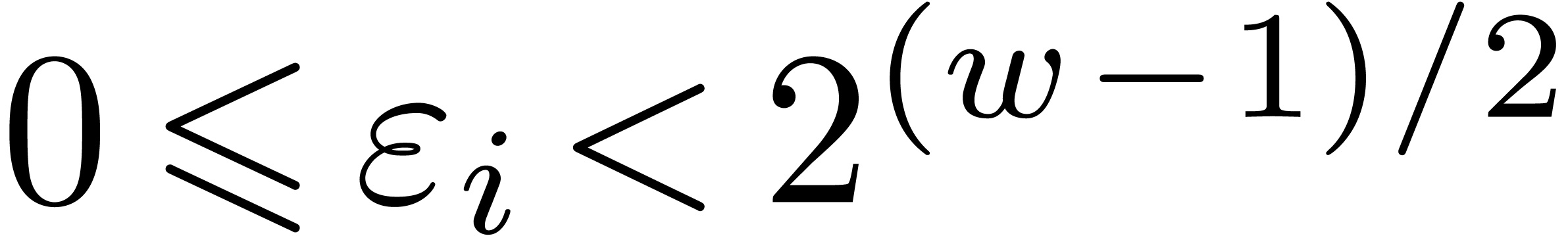 is odd. Indeed,
is odd. Indeed,
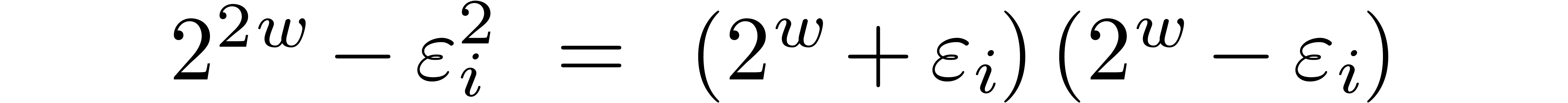
 .
. .
.
 are small compared to
are small compared to 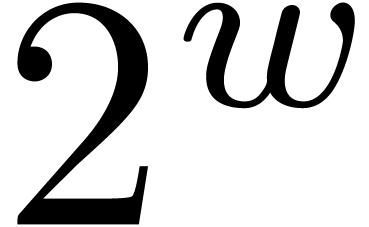 .
. of
of
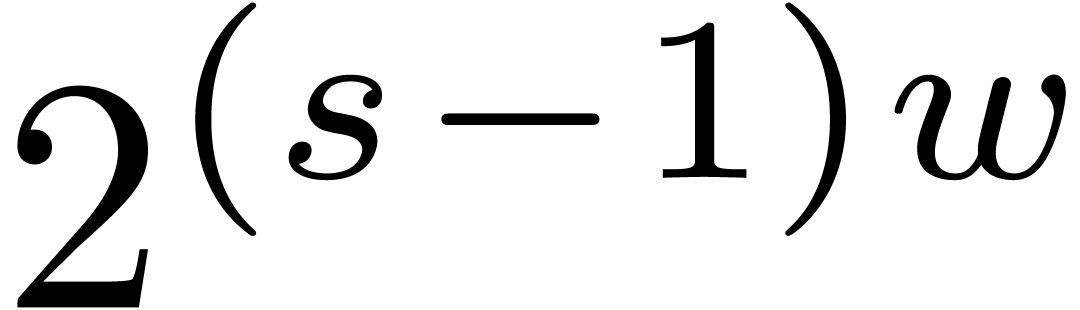 vanishes, then the coefficient of
vanishes, then the coefficient of 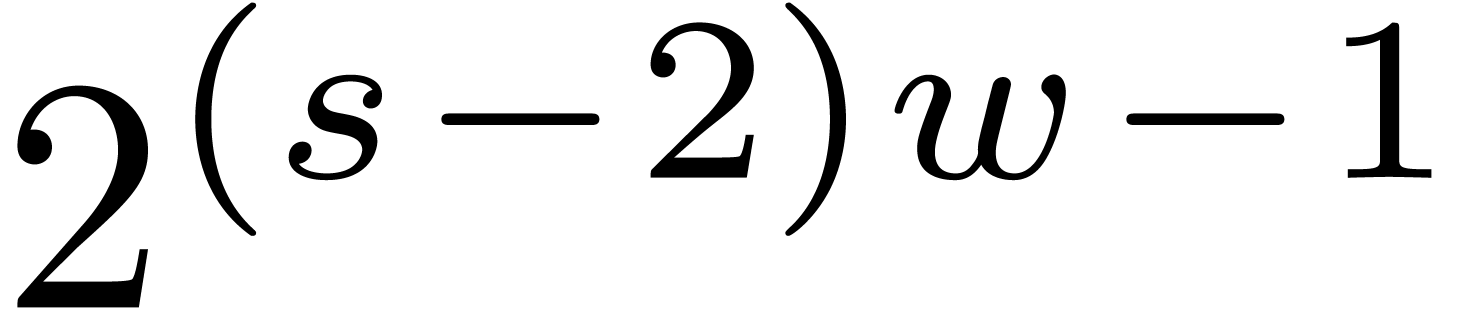 becomes the opposite
becomes the opposite 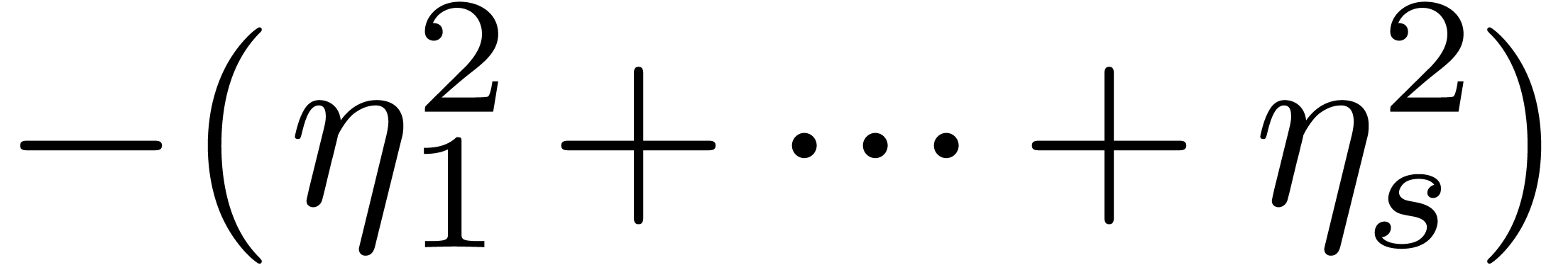 of a sum of
squares. In particular, both coefficients cannot vanish simultaneously,
unless
of a sum of
squares. In particular, both coefficients cannot vanish simultaneously,
unless 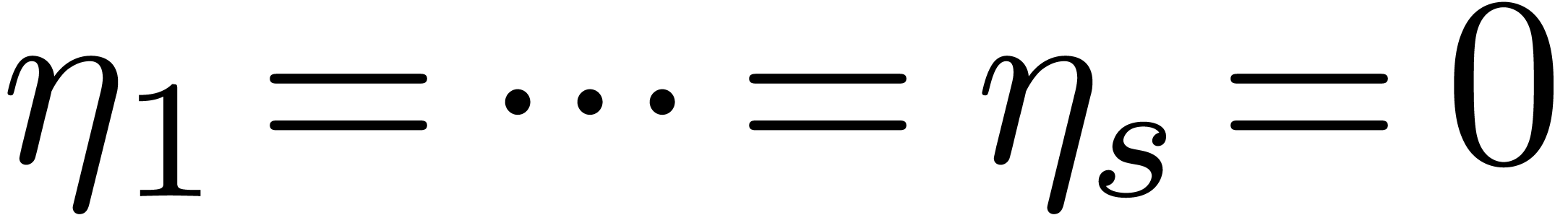 .
. ,
,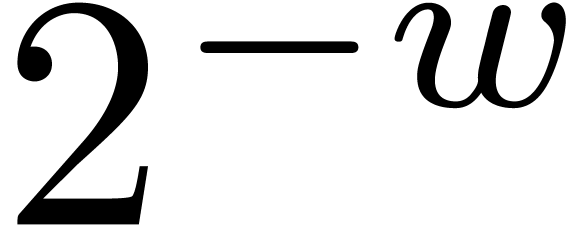 .
.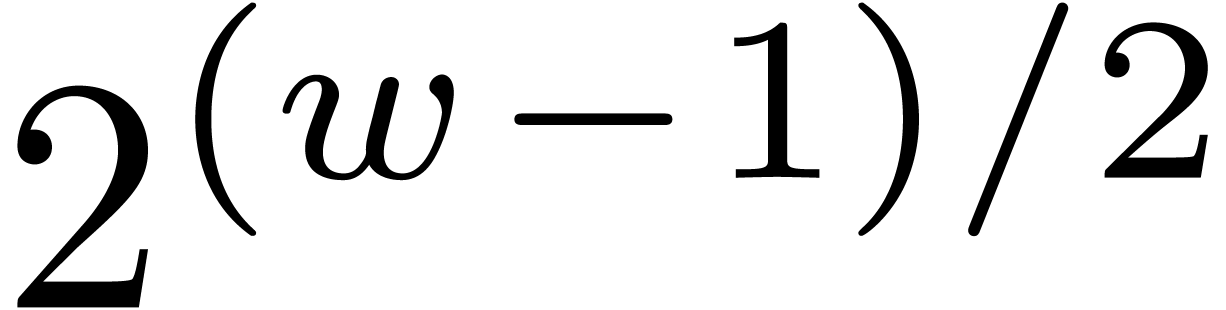 possibilities for
possibilities for  .
. from
from 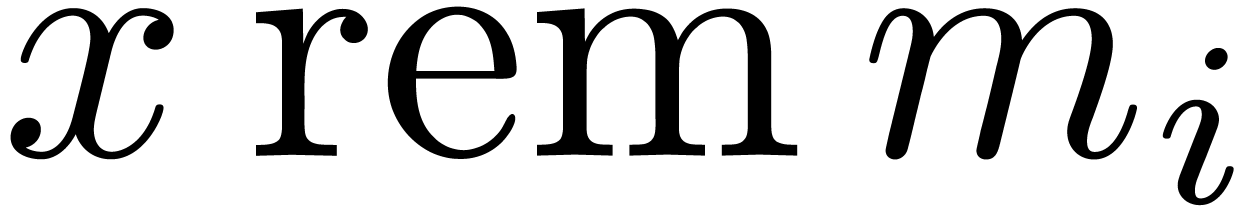 and vice versa for
and vice versa for 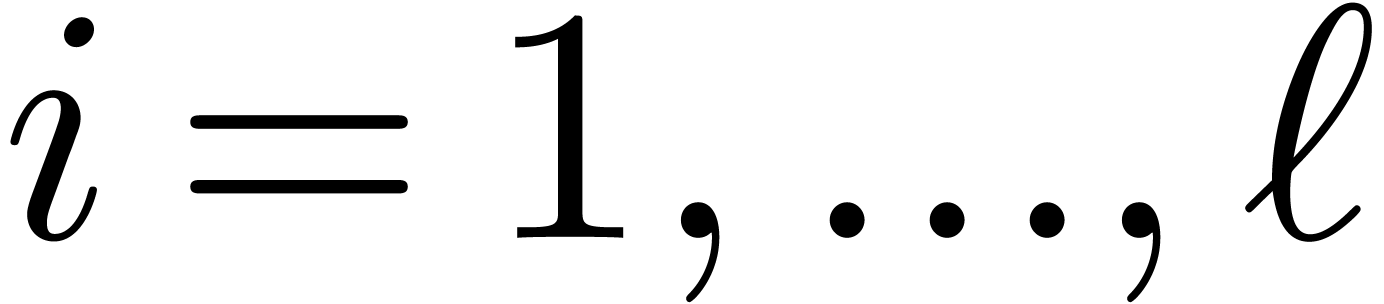 .
. using
using 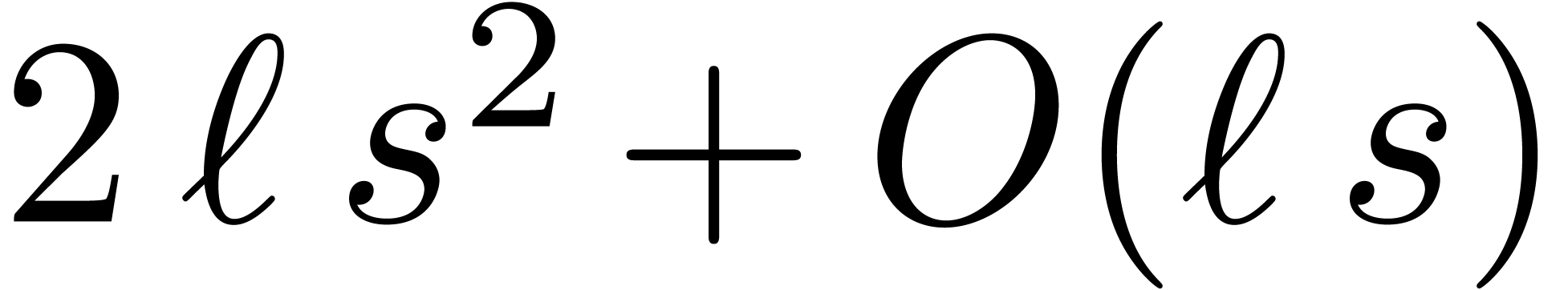 hardware multiplications, whereas the opposite conversion only requires
hardware multiplications, whereas the opposite conversion only requires
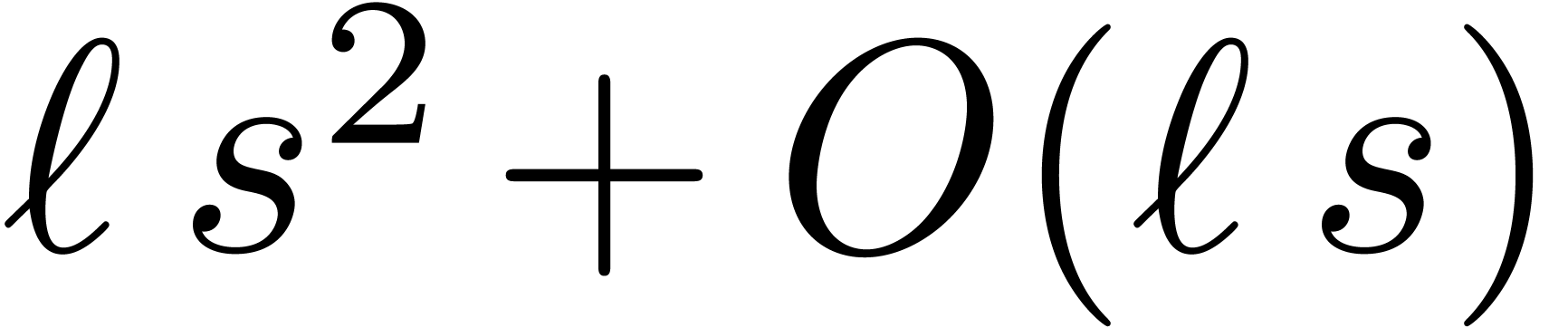 multiplications. Altogether, we may thus obtain
the remainders
multiplications. Altogether, we may thus obtain
the remainders 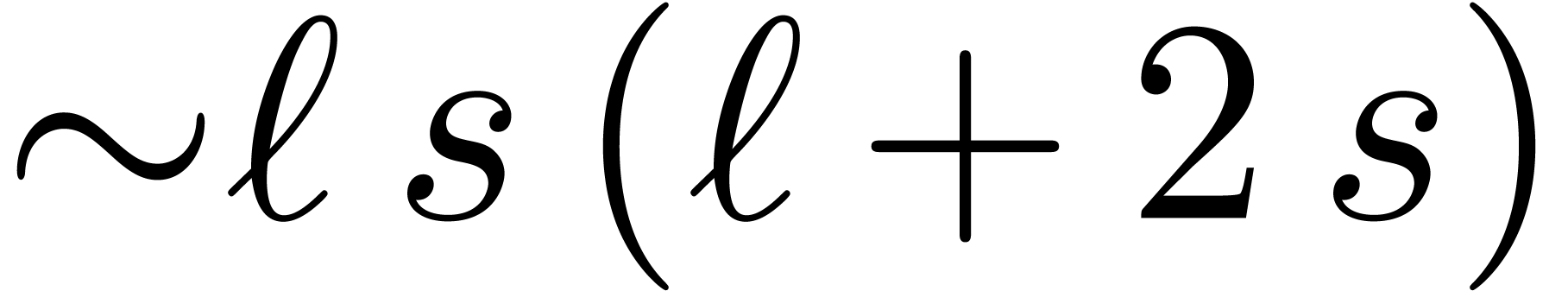 multiplications.
multiplications.
 and
and 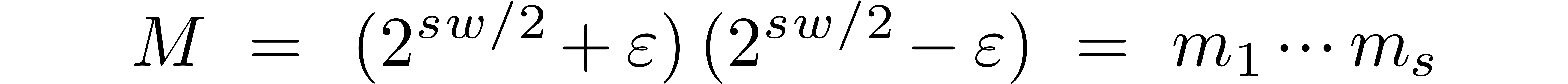
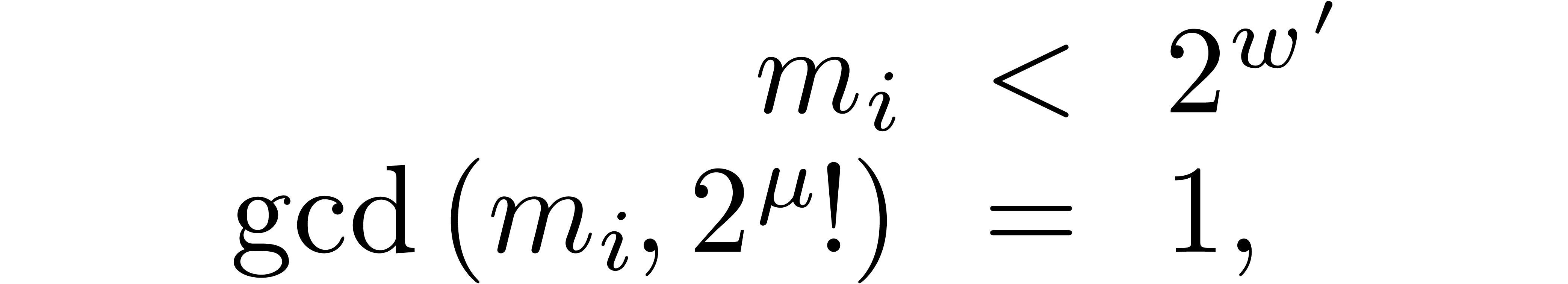
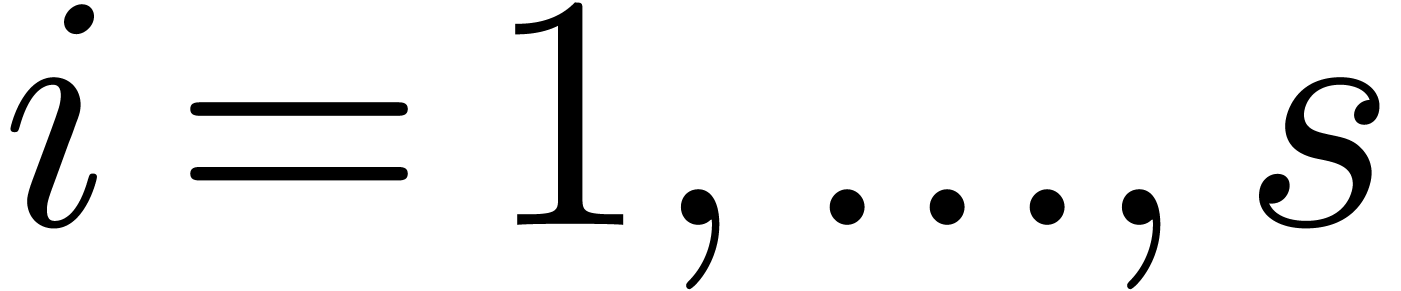 ,
, .
.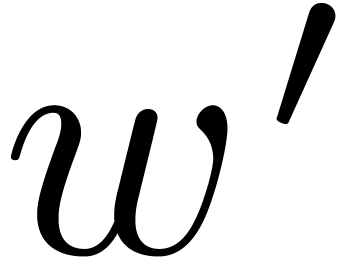 as the intended and maximal bitsize of the small
moduli
as the intended and maximal bitsize of the small
moduli  should be such that
should be such that 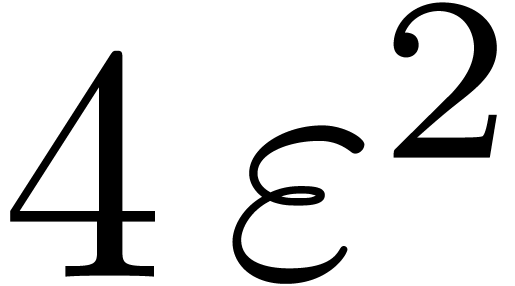 fits into a
machine word.
fits into a
machine word.
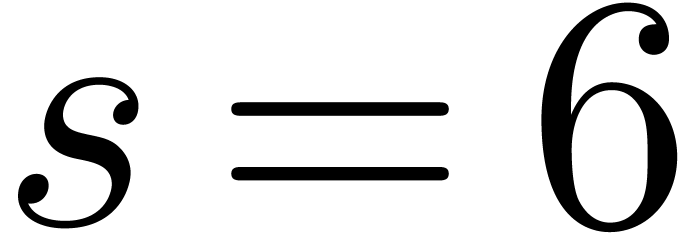 ,
,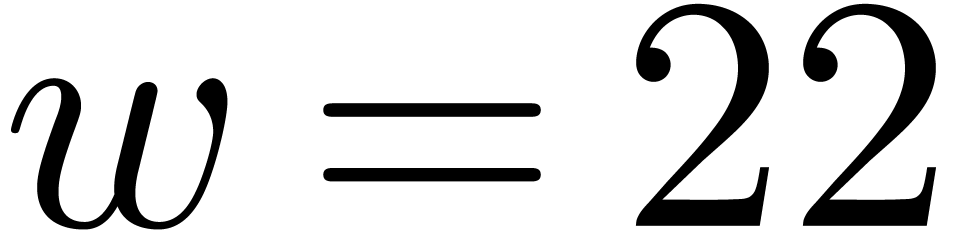 ,
,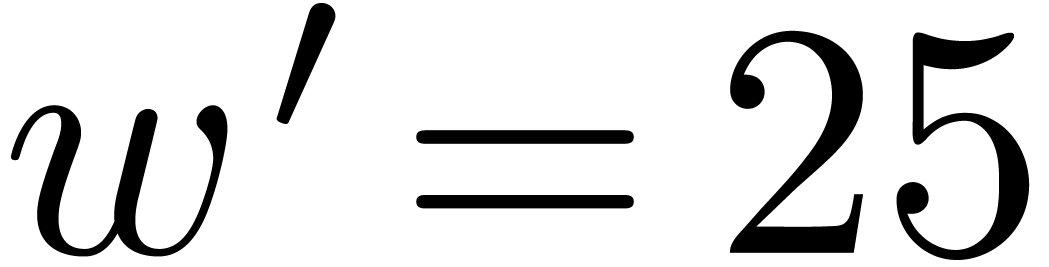 and
and 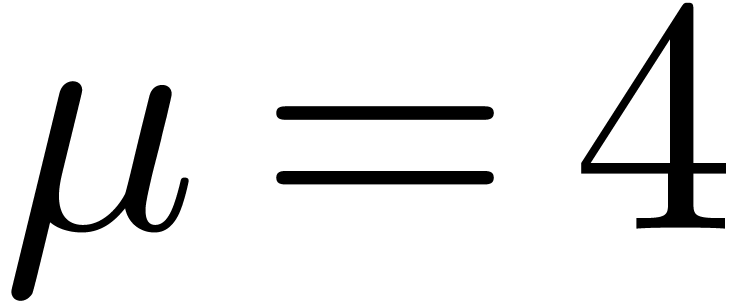 .
.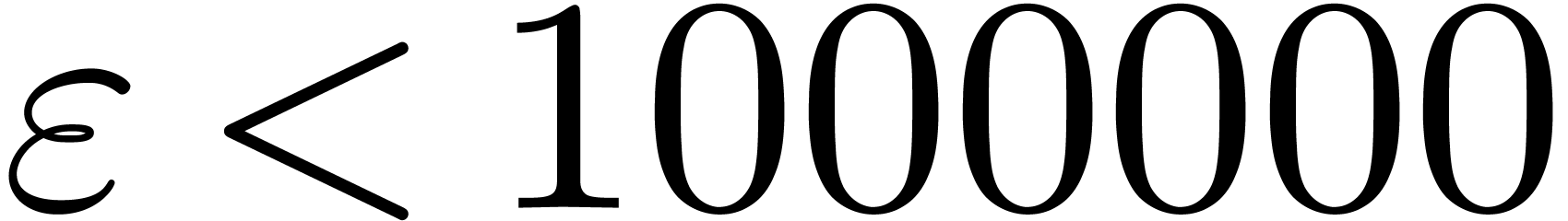 ,
, ,
, divides both
divides both 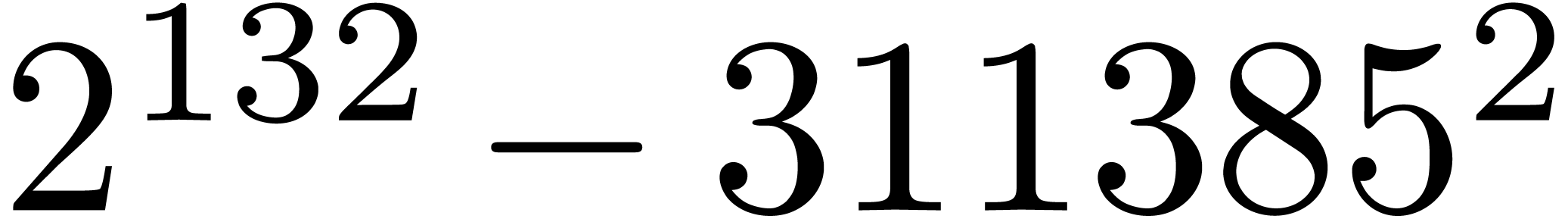 and
and 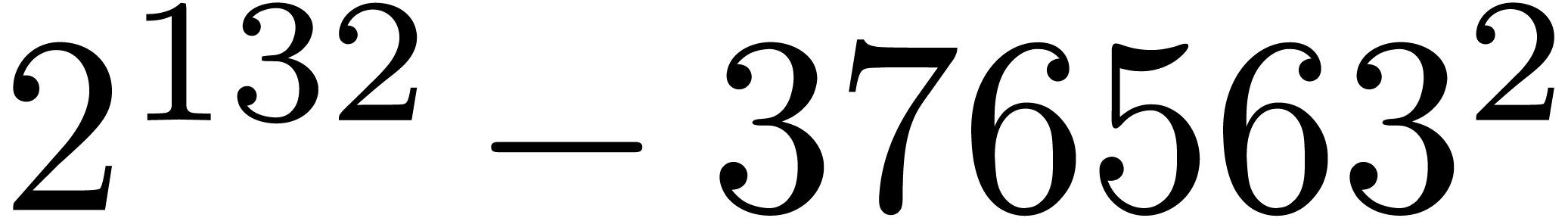 ,
, -gentle
-gentle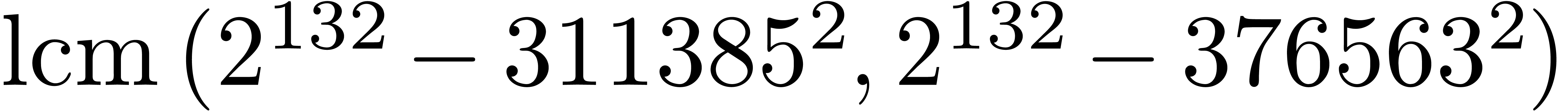 instead of
instead of  ).
).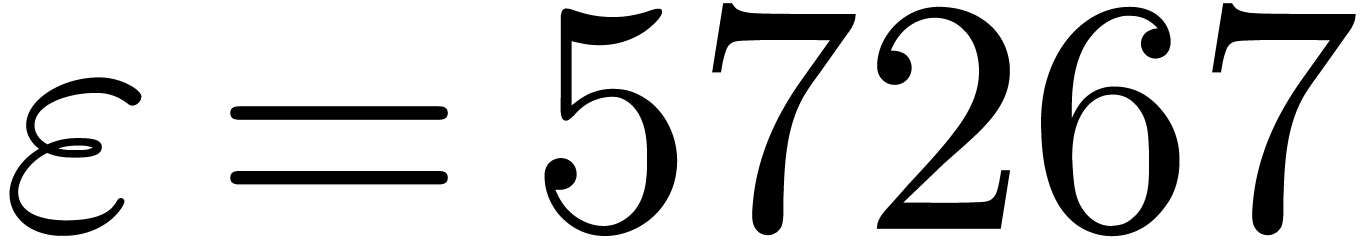 (we indicated this by highlighting the list of
prime factors of
(we indicated this by highlighting the list of
prime factors of 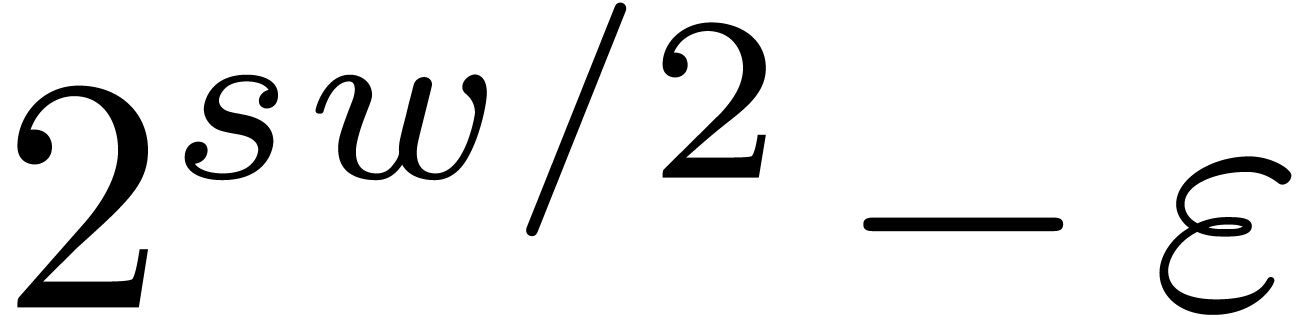 or
or 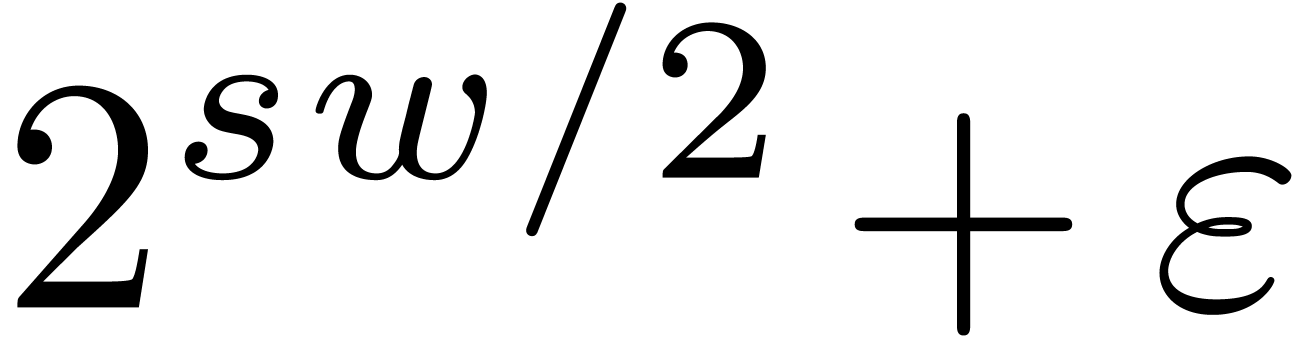 .
.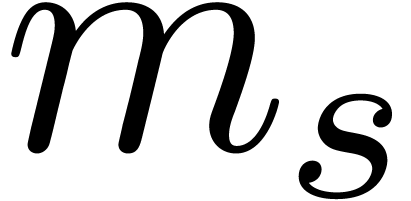 is as small as possible: the spare bits can for
instance be used to speed up matrix multiplication modulo
is as small as possible: the spare bits can for
instance be used to speed up matrix multiplication modulo 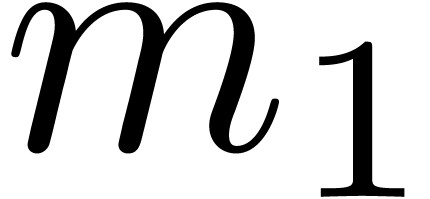
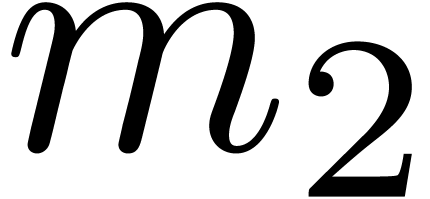
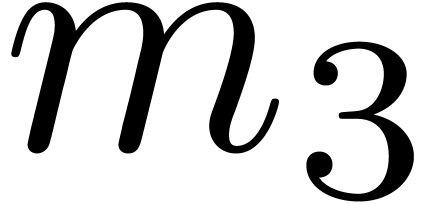
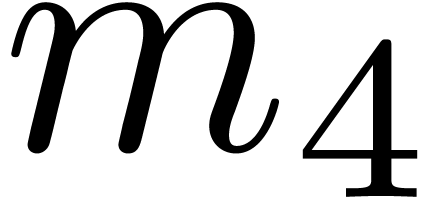
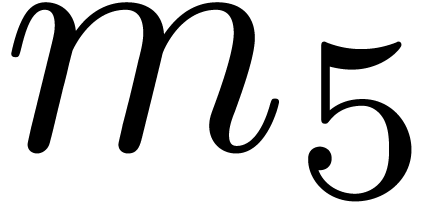
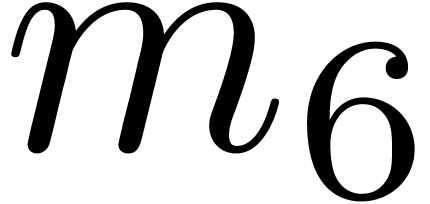
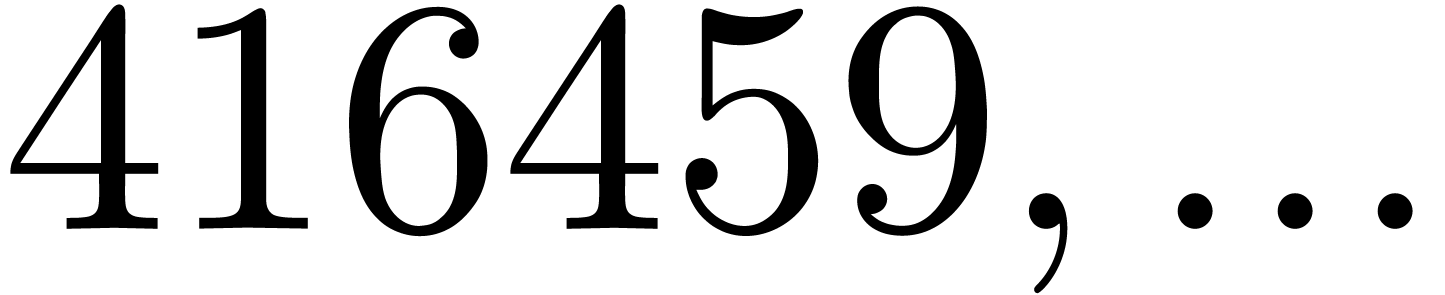
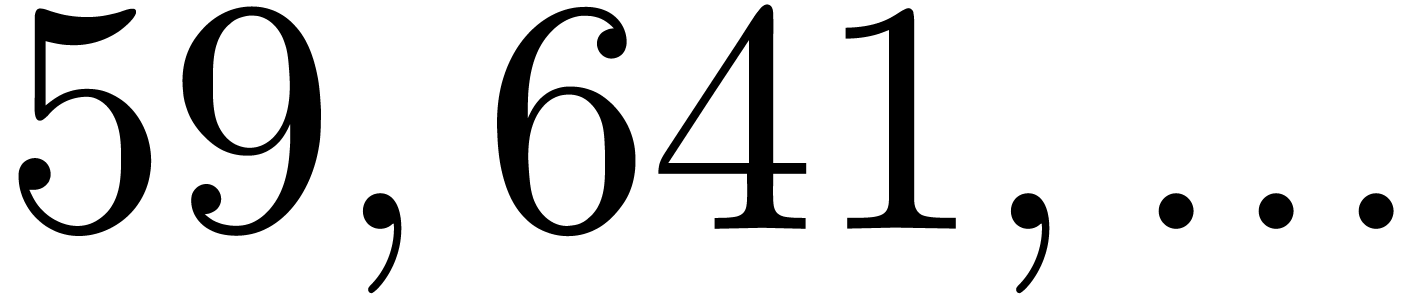
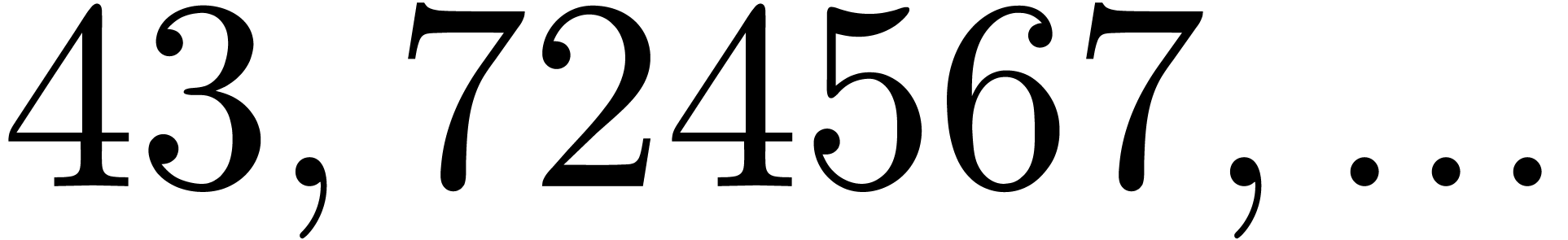
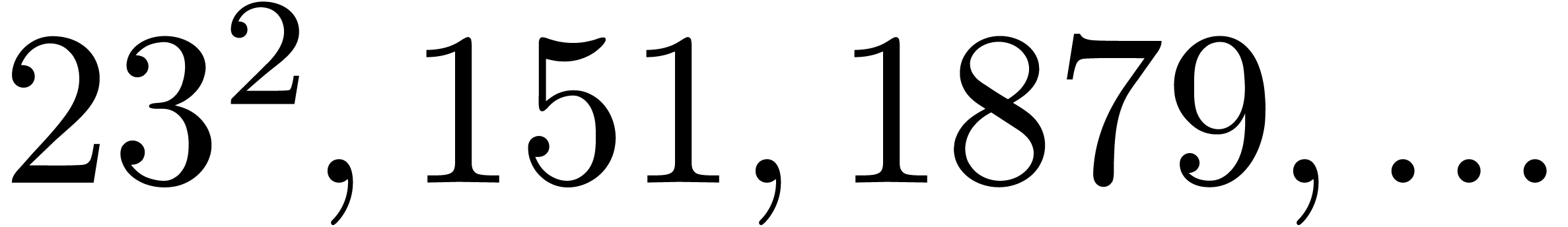
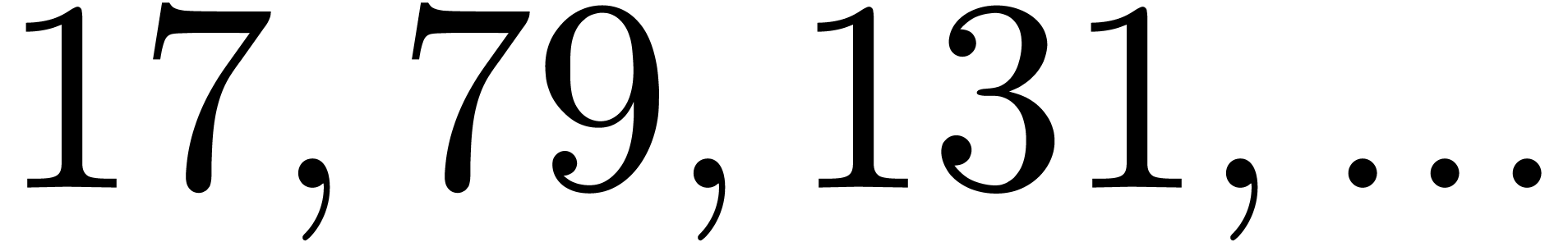
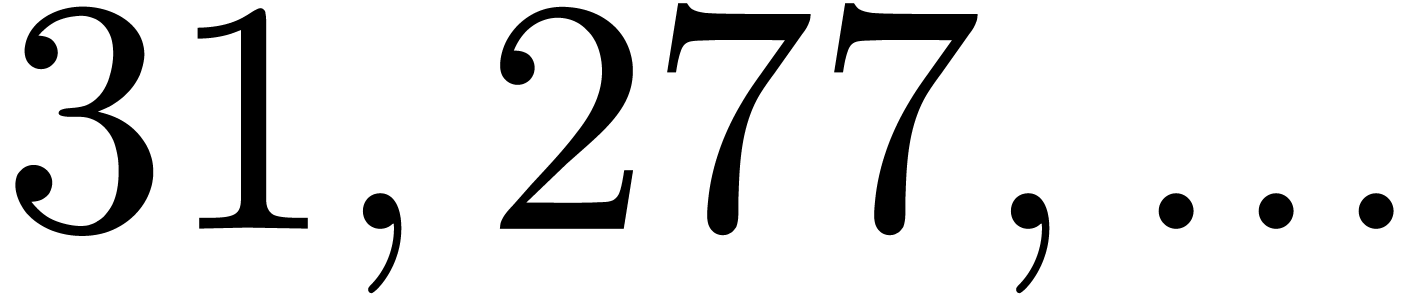
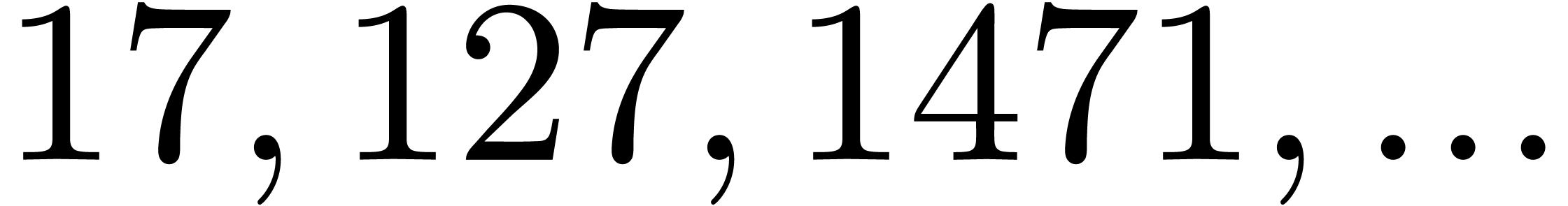
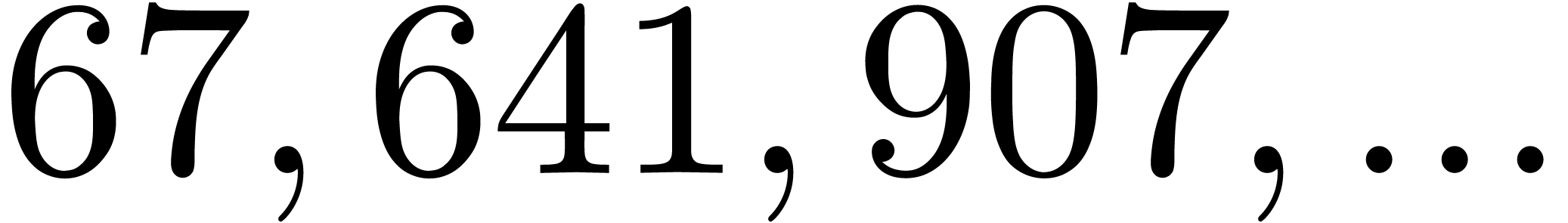
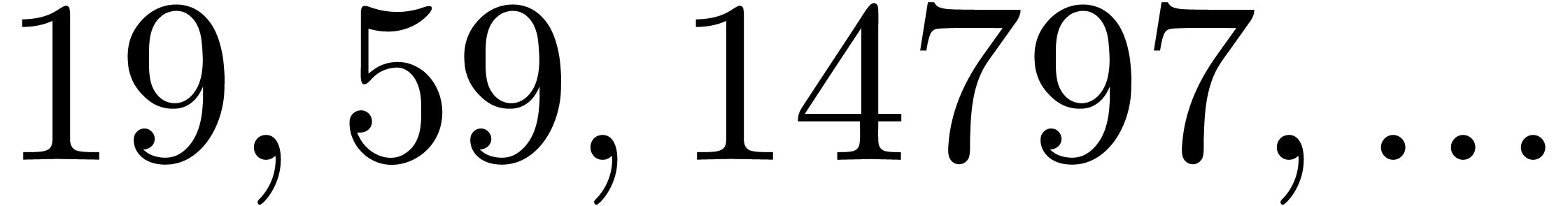
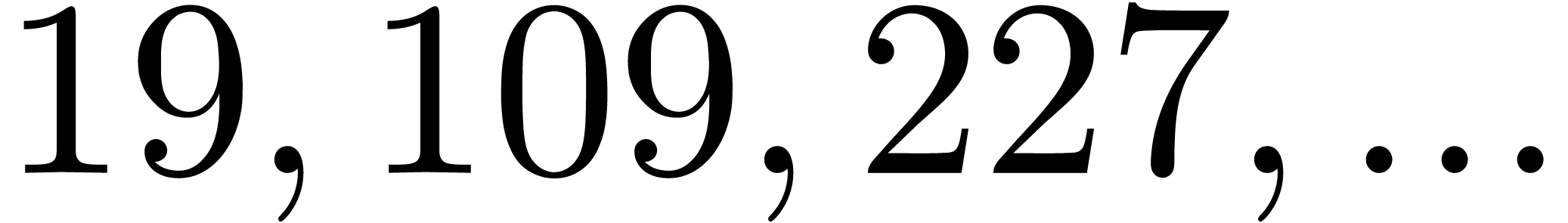
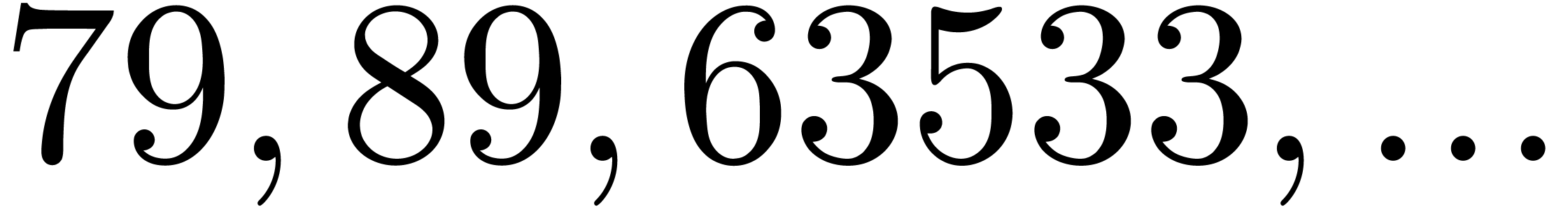
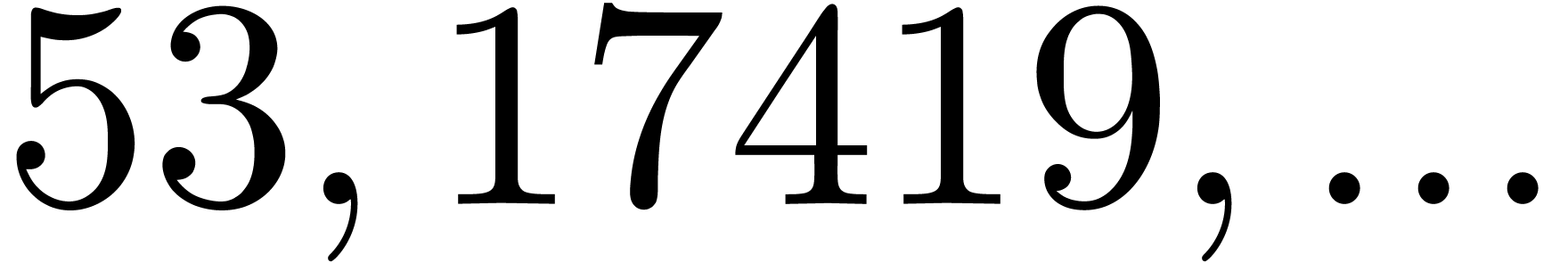

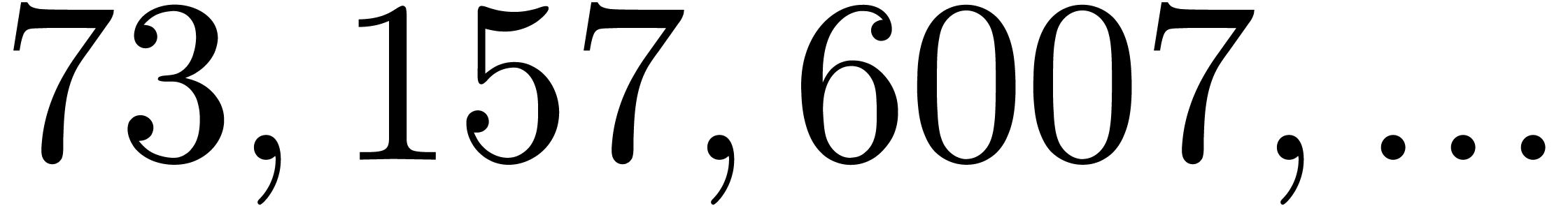
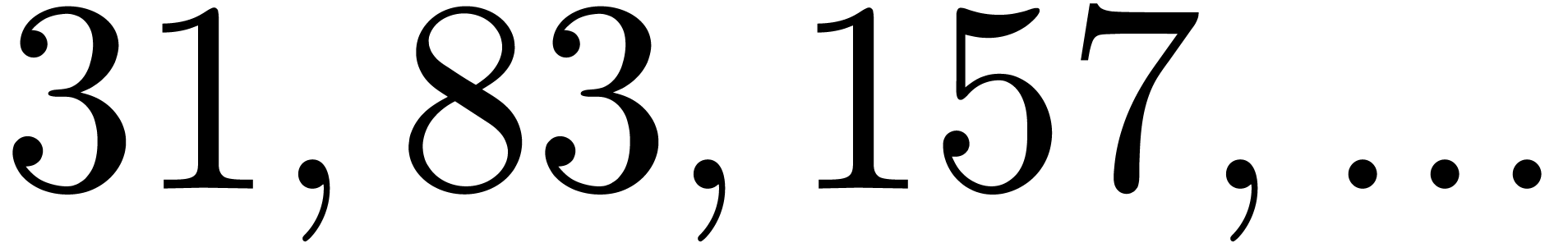
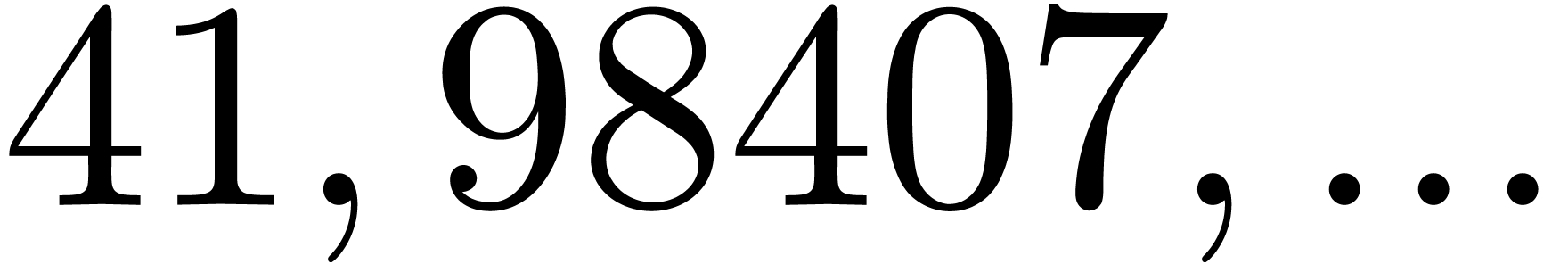
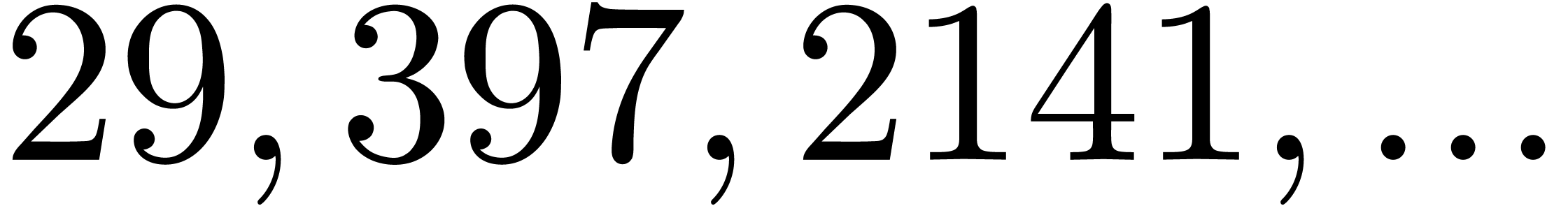
 -gentle
-gentle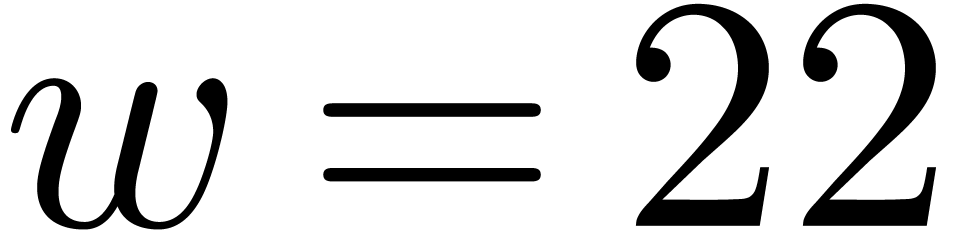 ,
,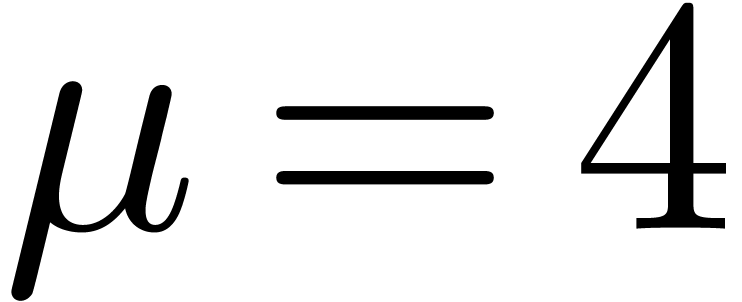 and
and 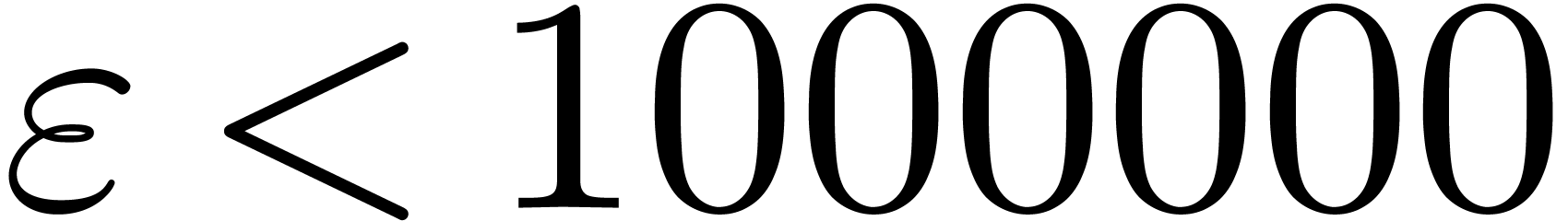 .
. should be minimized. When using double precision
floating point arithmetic, this means that we wish to take
should be minimized. When using double precision
floating point arithmetic, this means that we wish to take 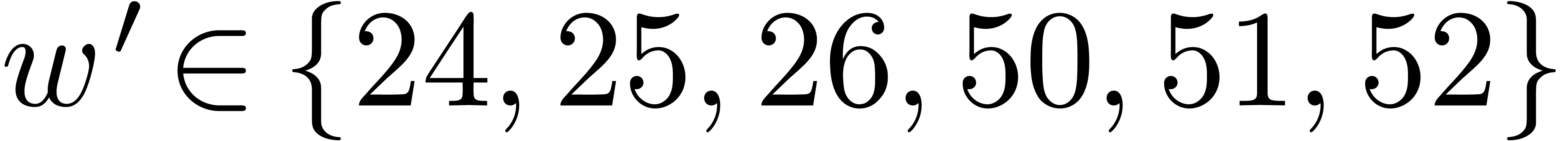 .
. .
.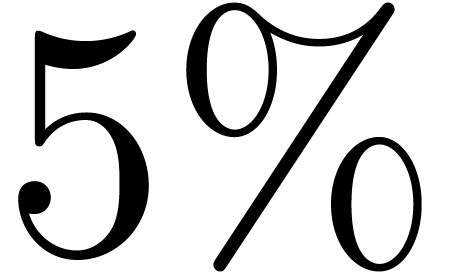 increase of the
“capacity”
increase of the
“capacity” 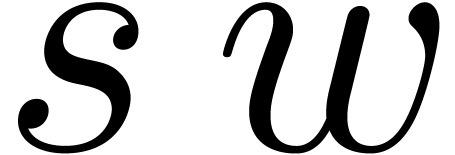 of the modulus
of the modulus 
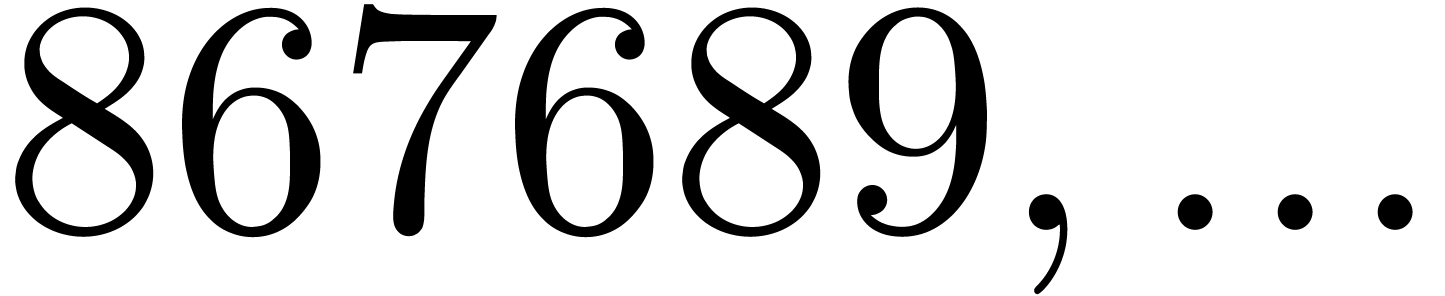


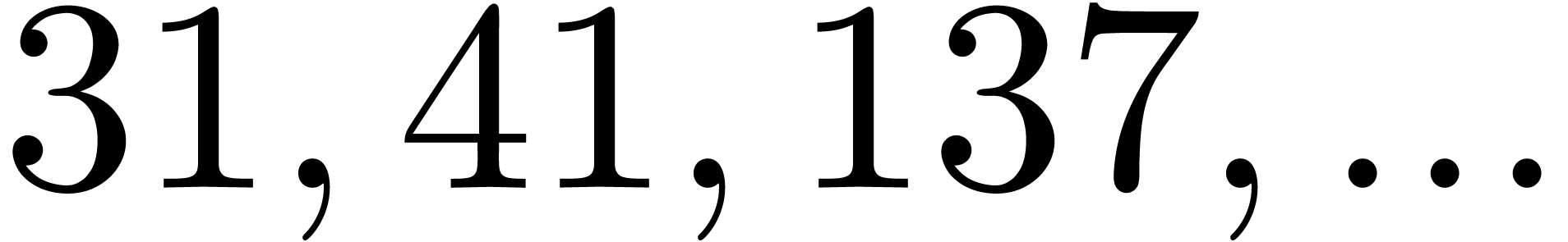
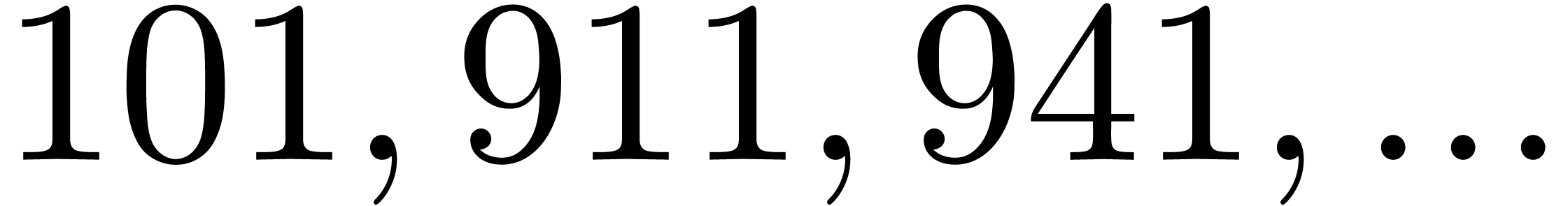

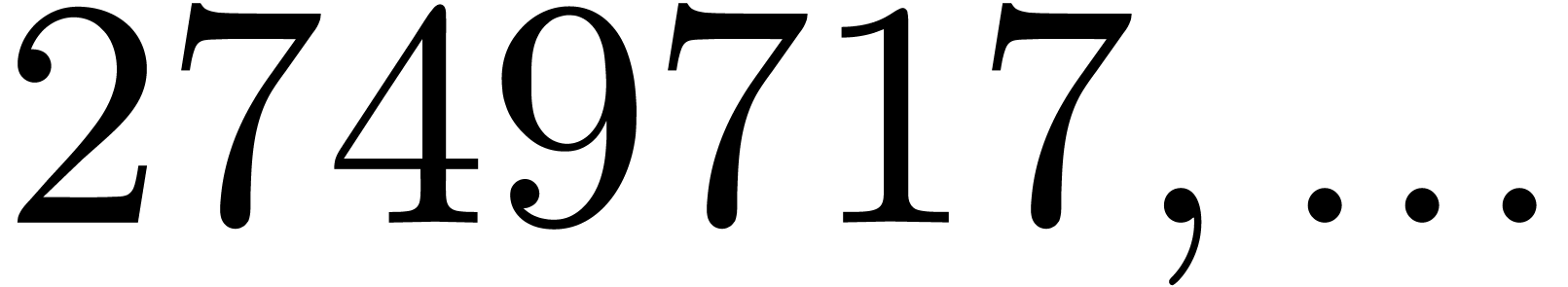
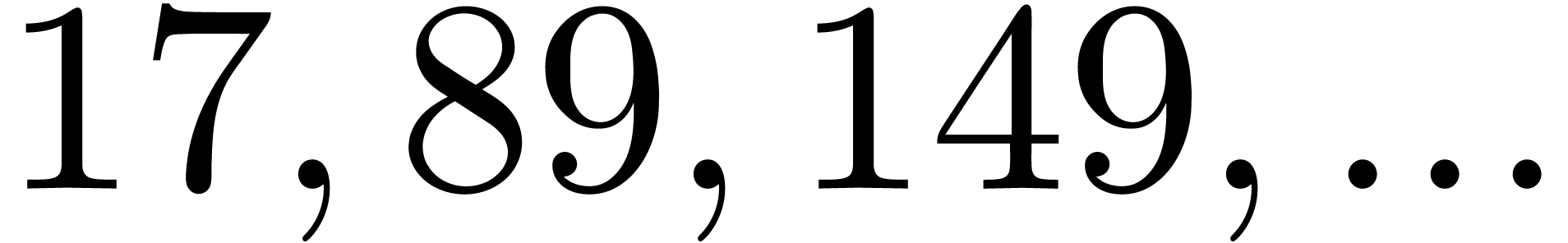
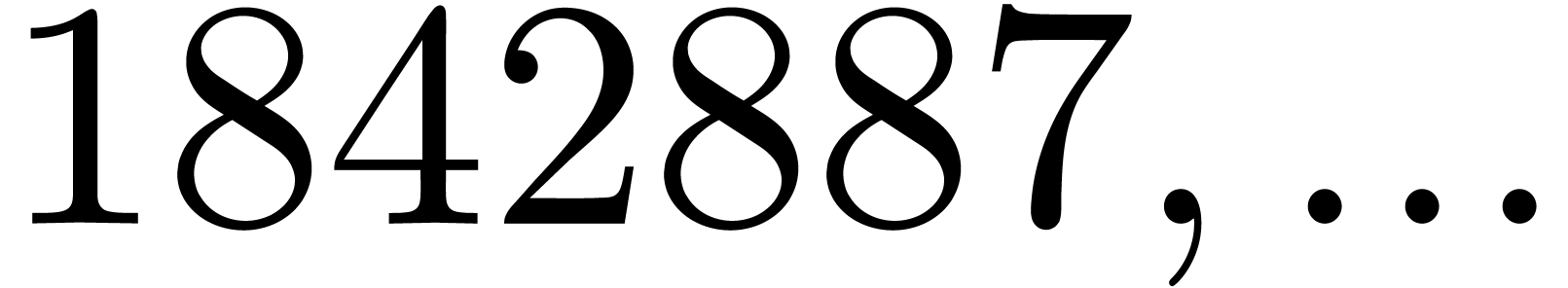
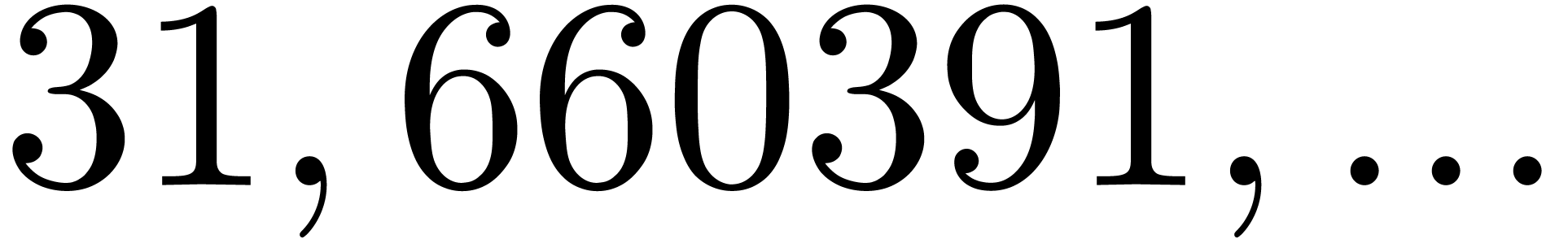
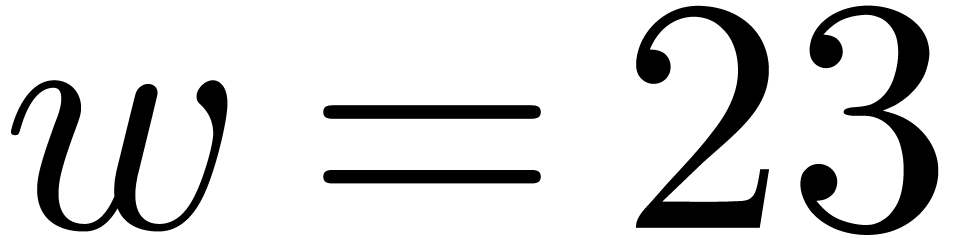 ,
,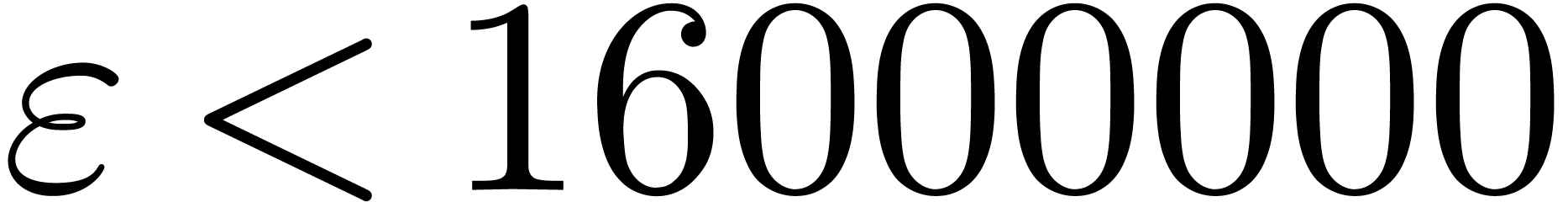 .
.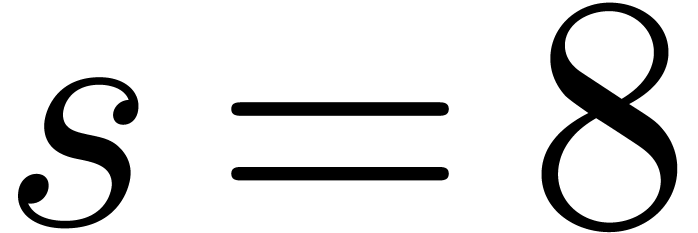 and
and 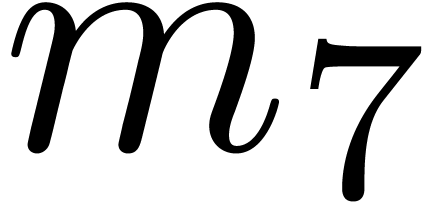
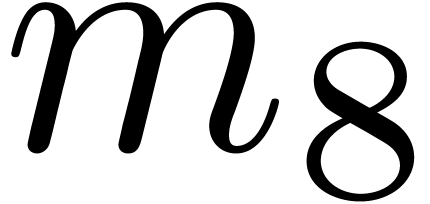
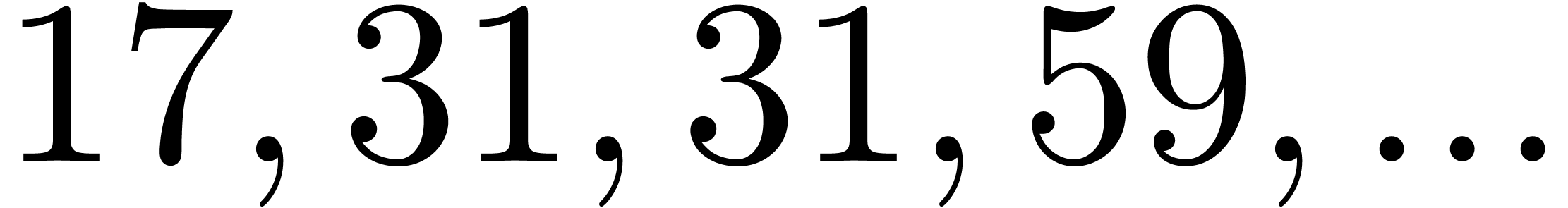
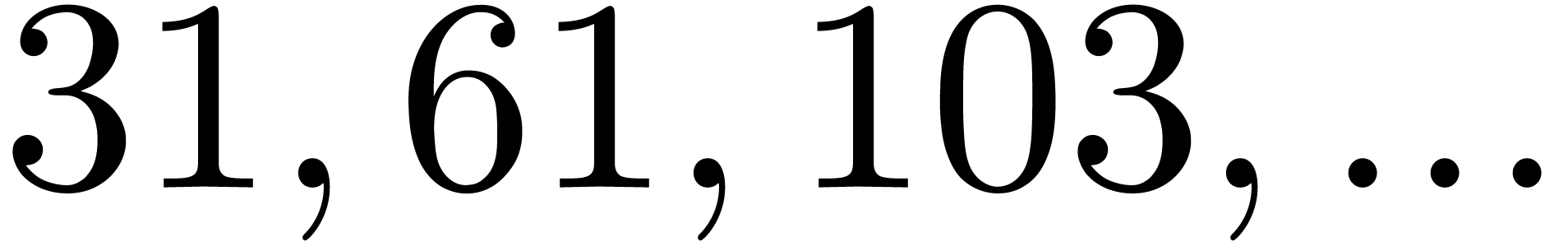

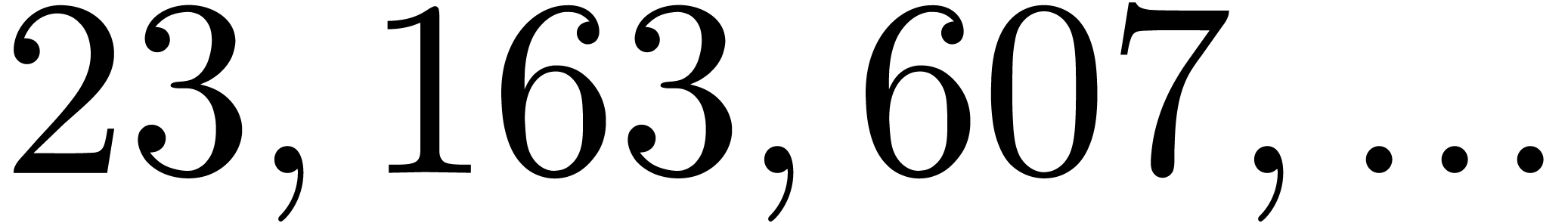
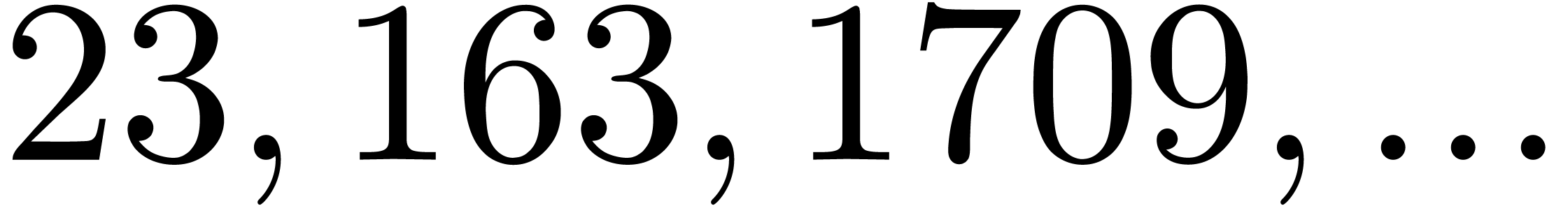
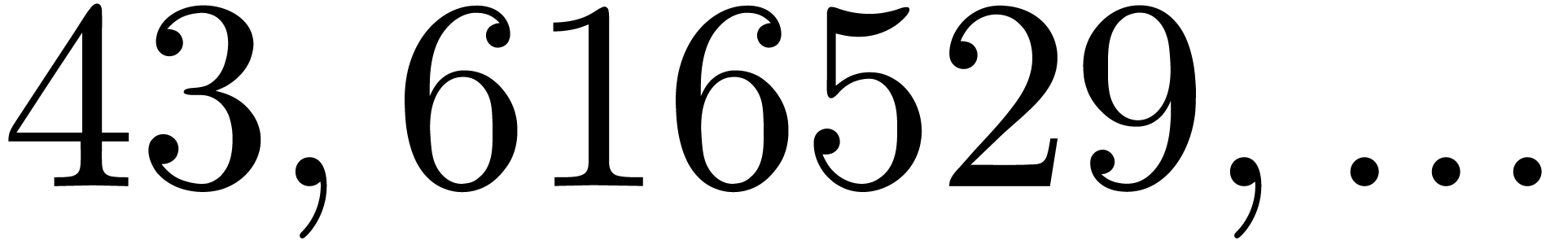
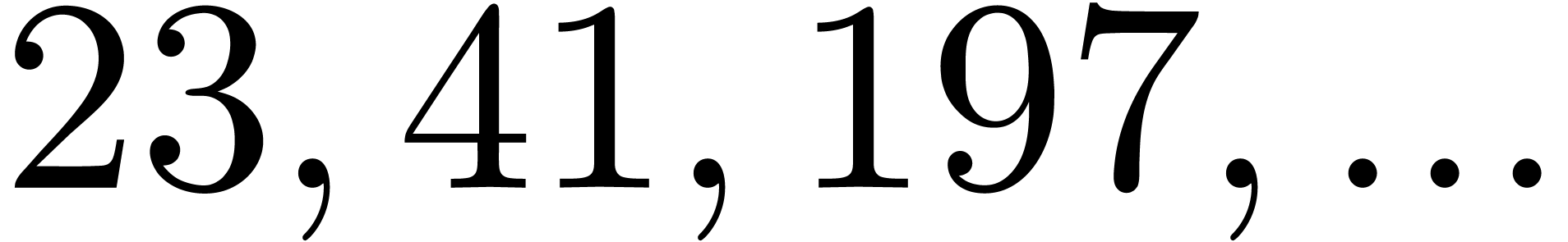
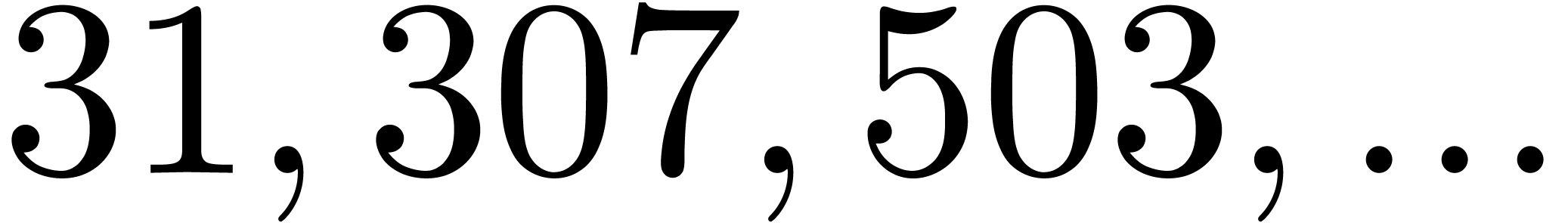
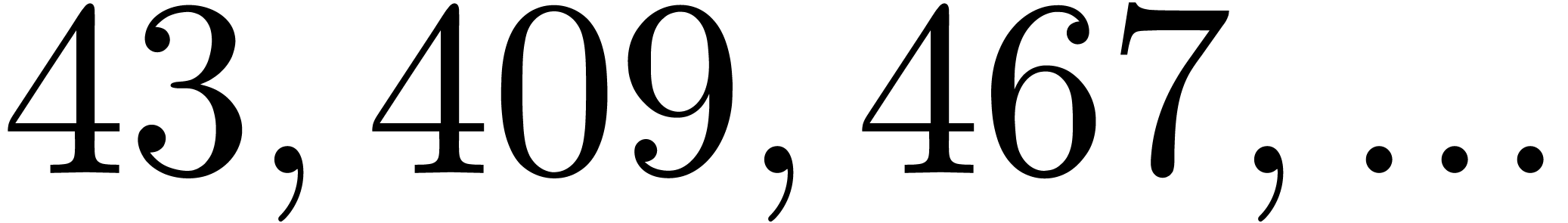
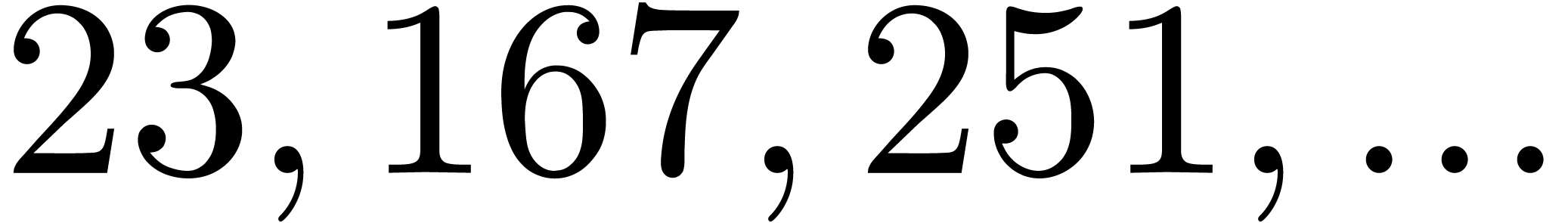
 -gentle
-gentle .
. (integer
arithmetic), this is counterbalanced by the fact that
(integer
arithmetic), this is counterbalanced by the fact that 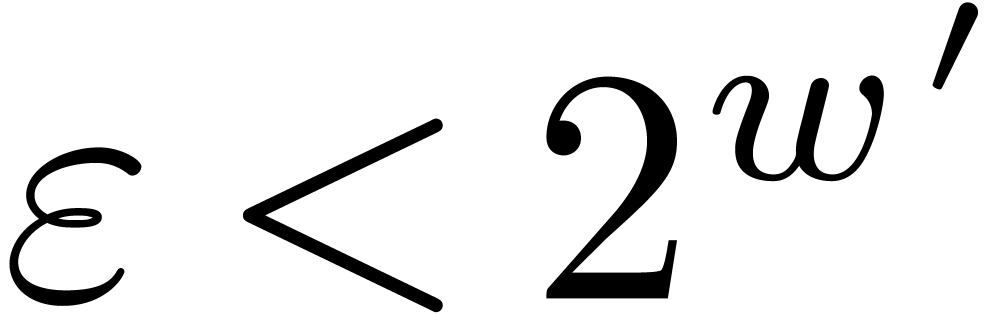 );
);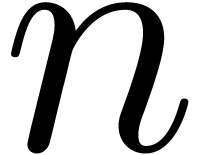 is prime with probability
is prime with probability 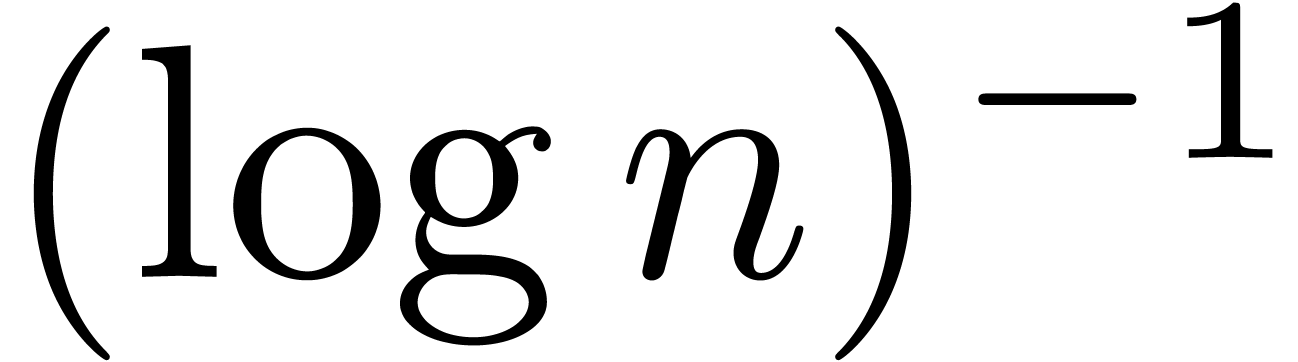 .
.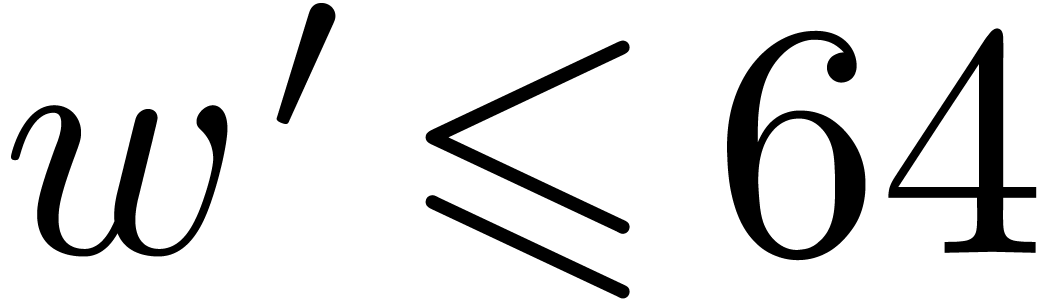 .
.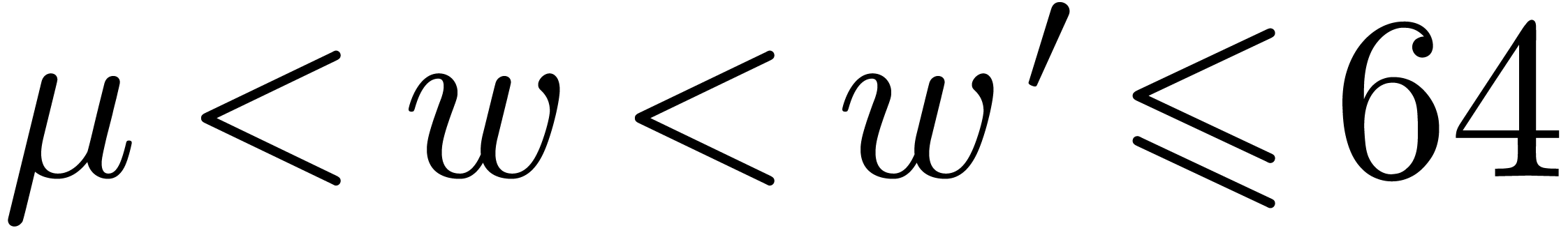 and
and  .
.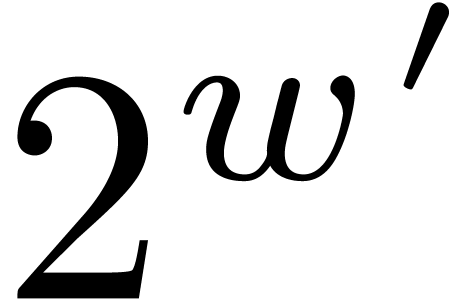 (the current version only does this for
prime factors that can be tabulated).
(the current version only does this for
prime factors that can be tabulated).
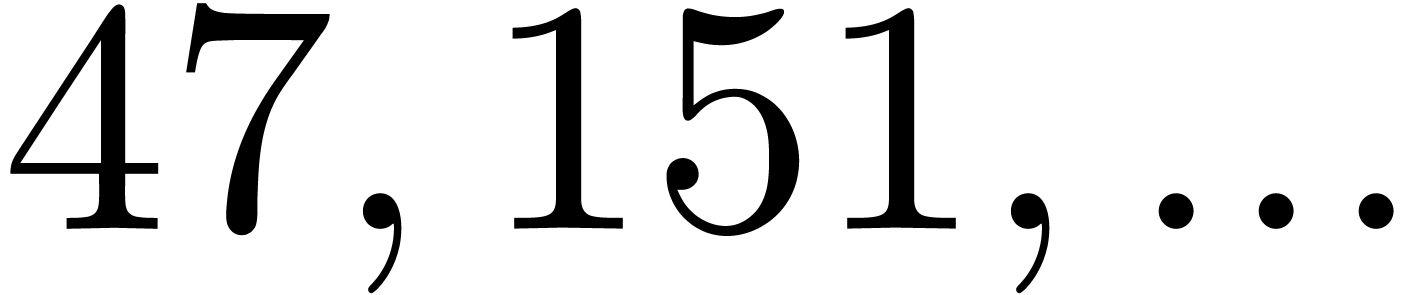
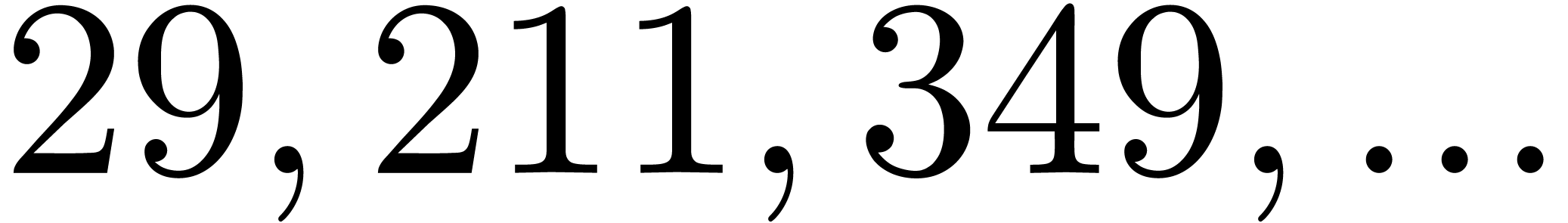
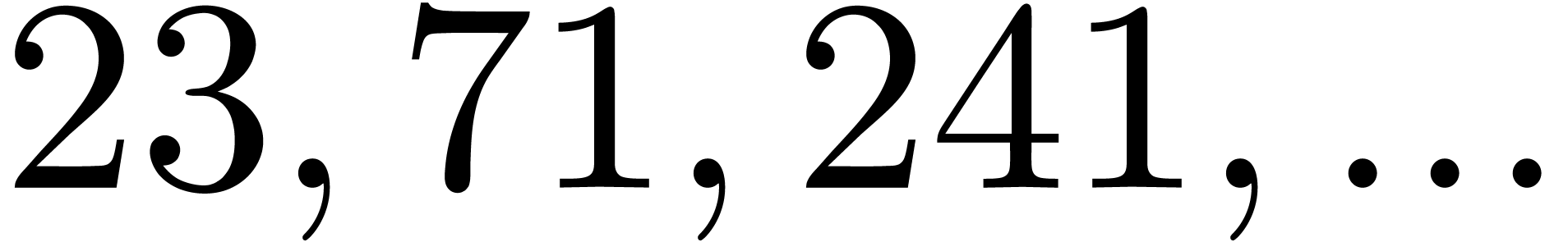
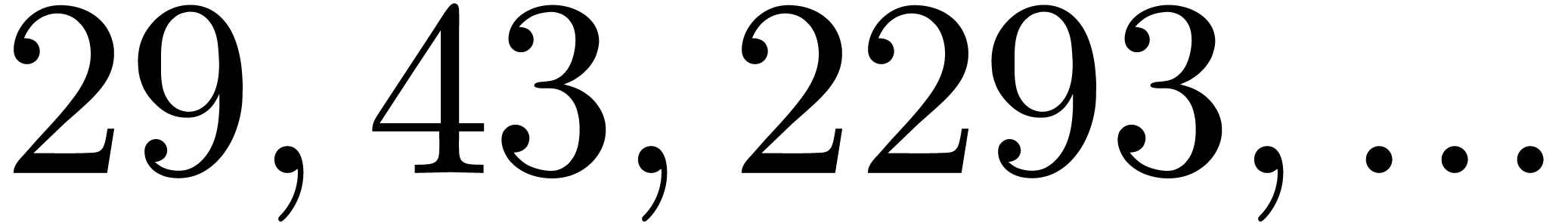
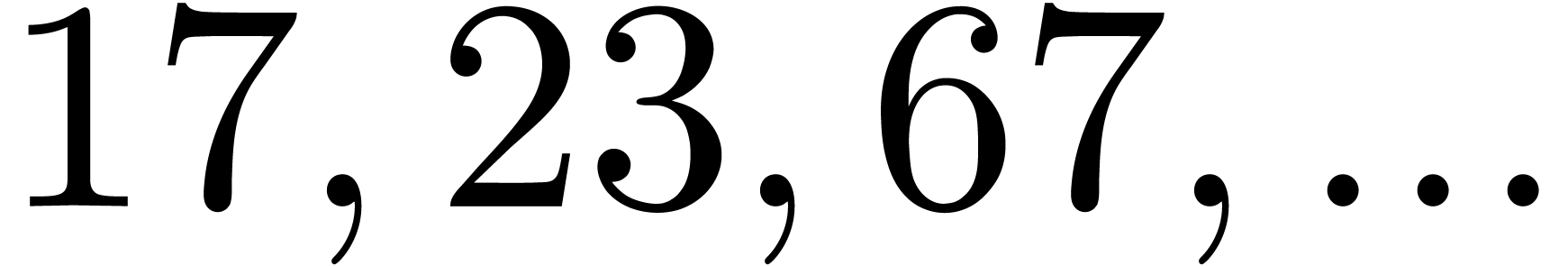


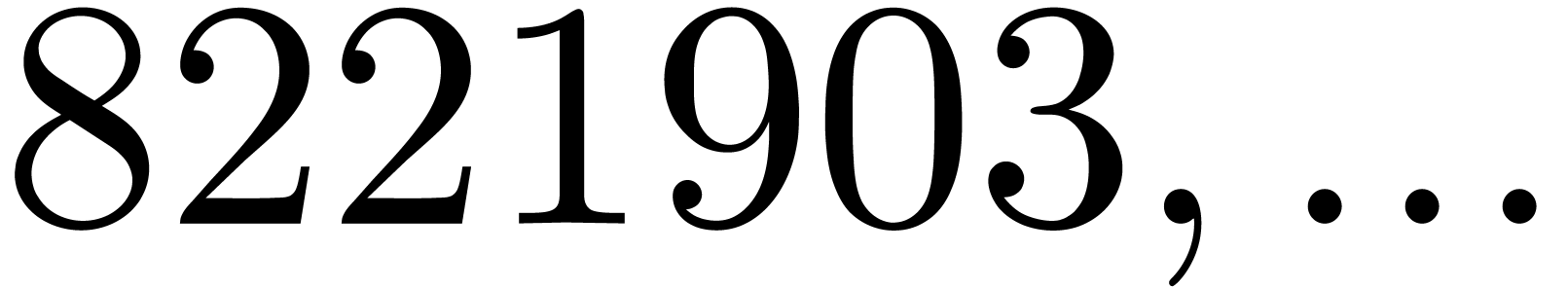
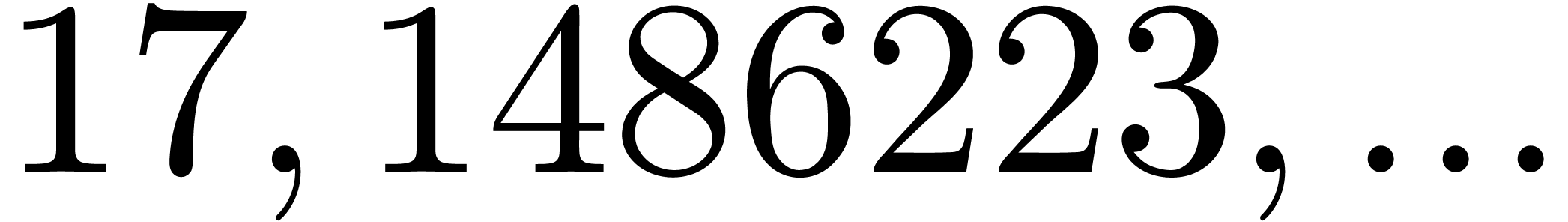
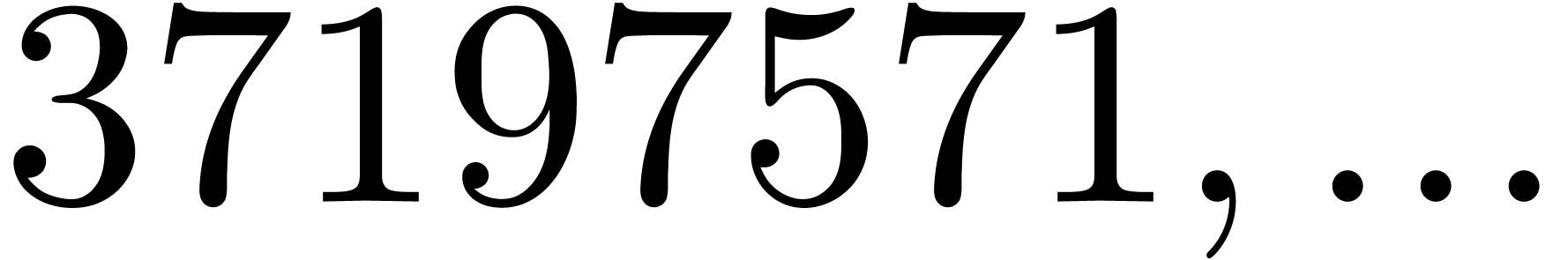
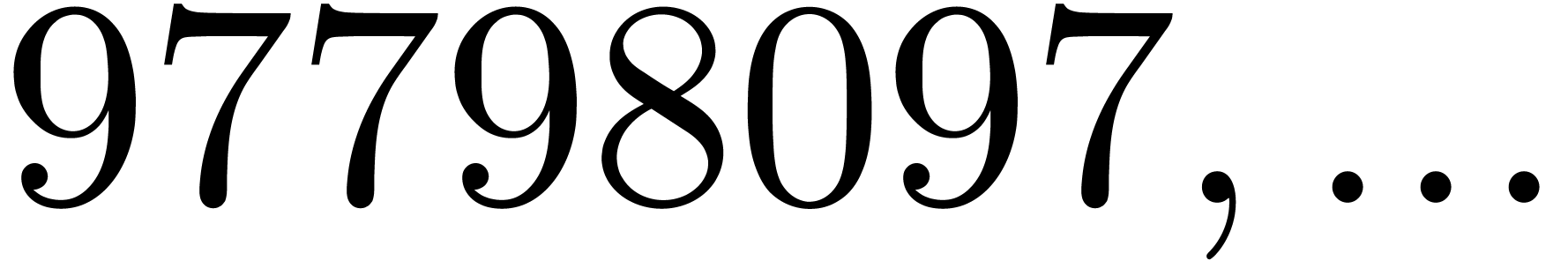
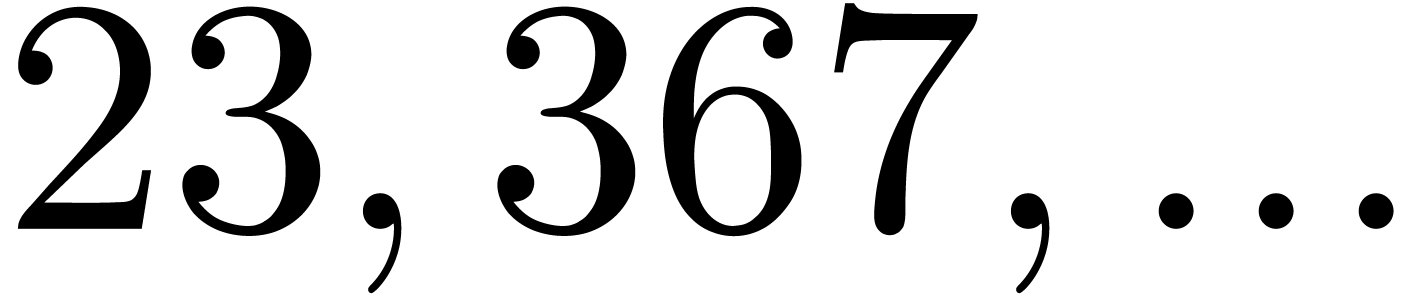
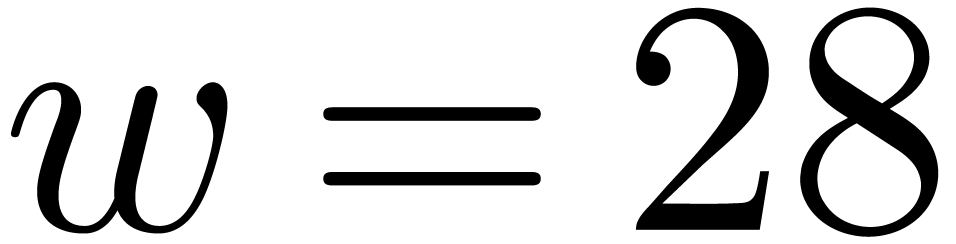 ,
,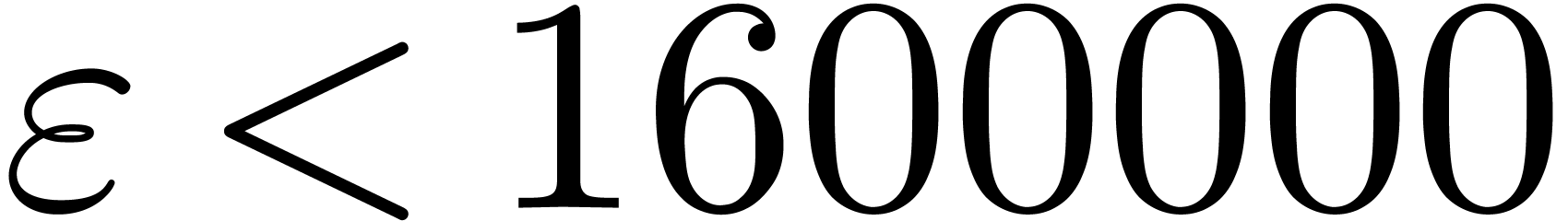 .
.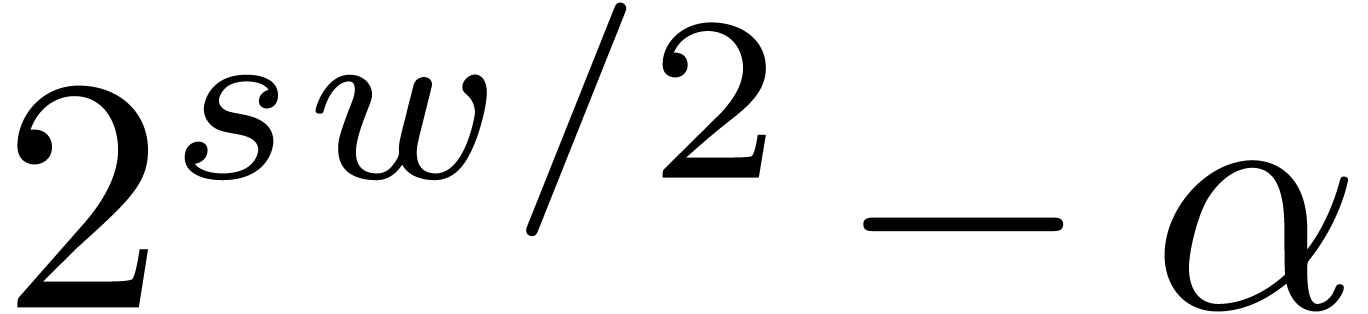 or
or
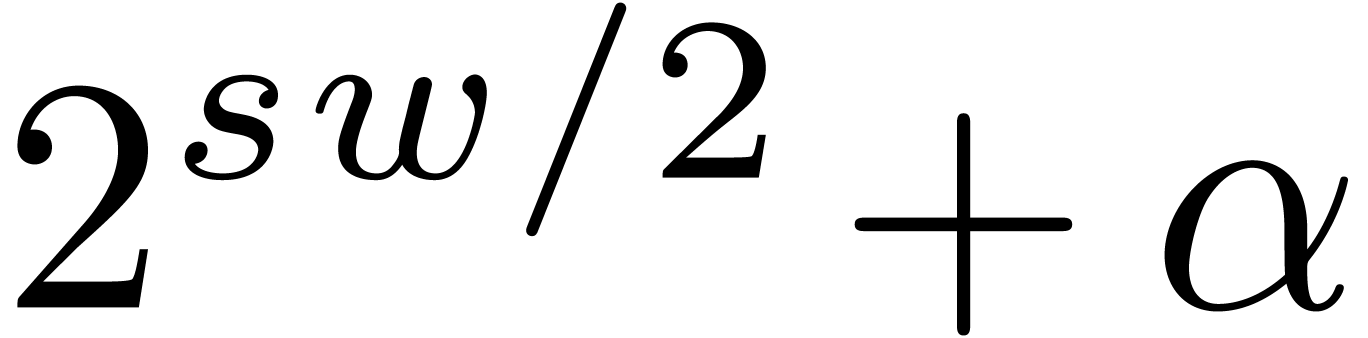 .
.
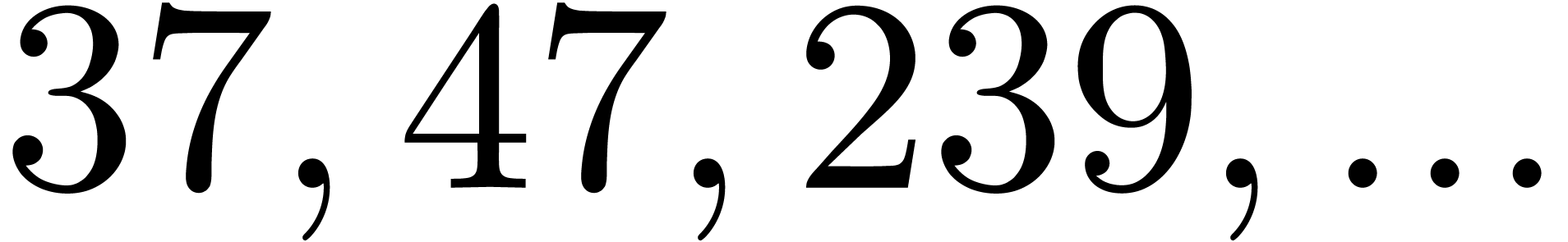
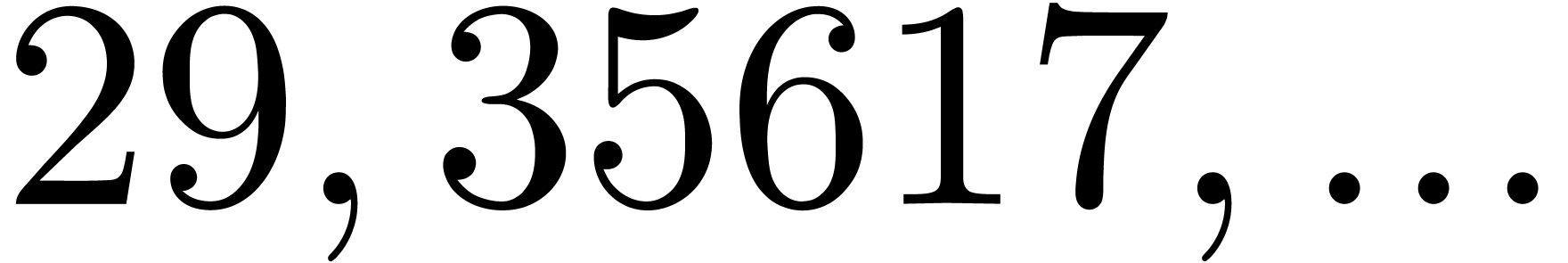

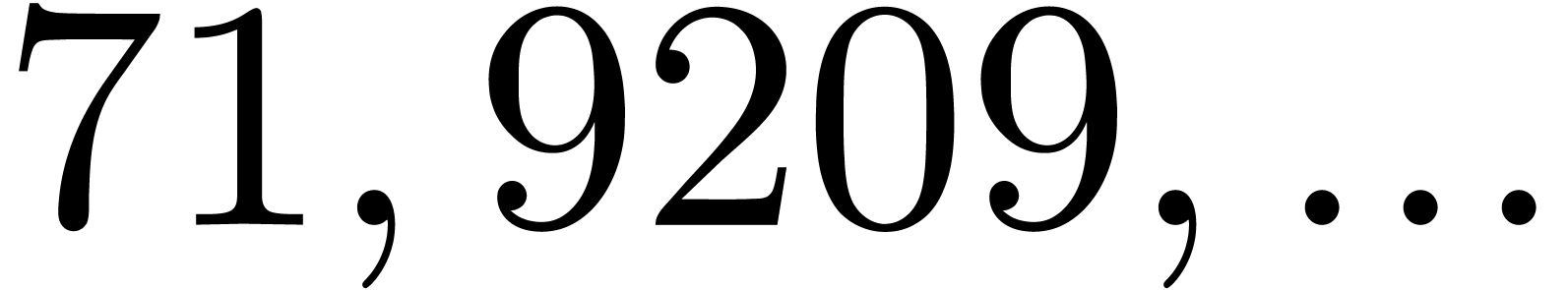

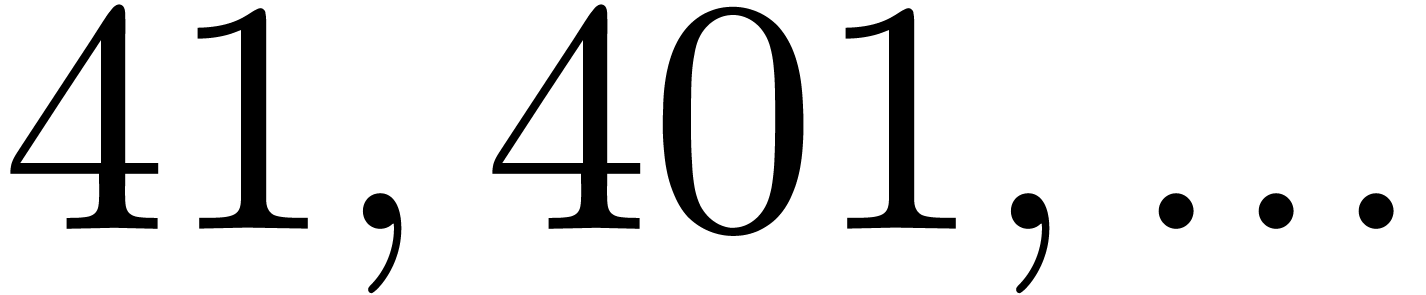
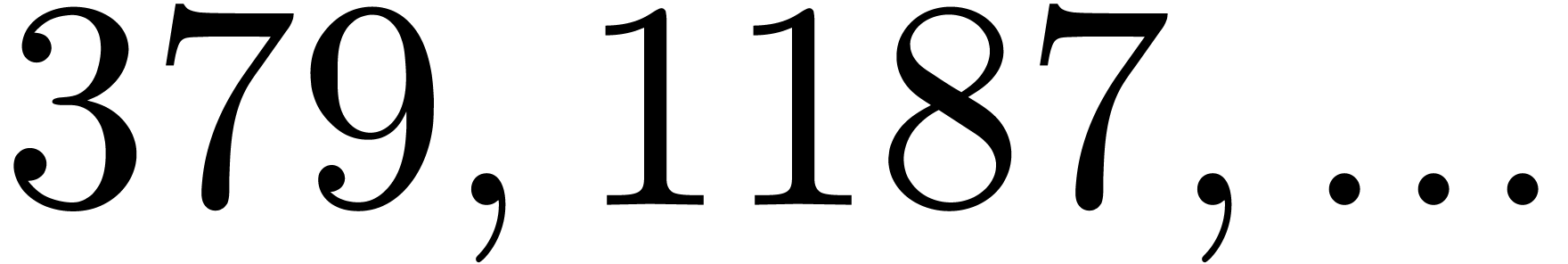



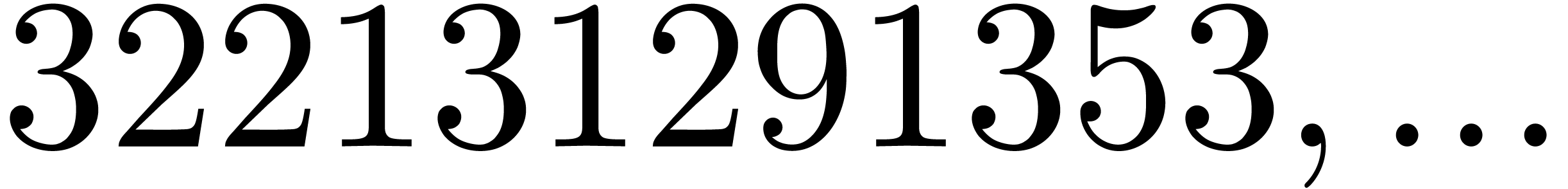
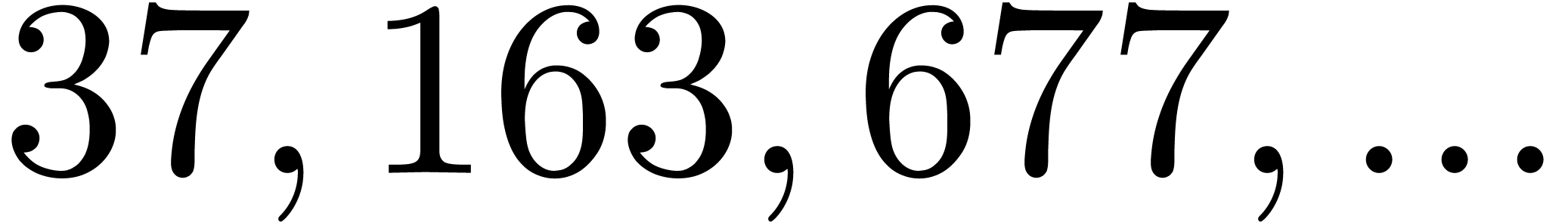
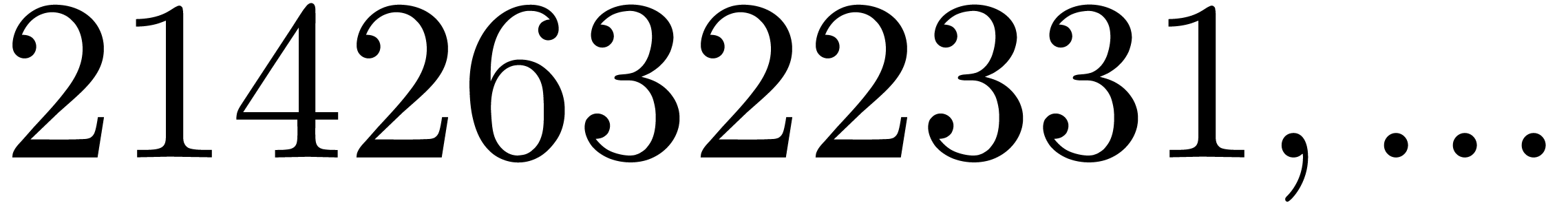
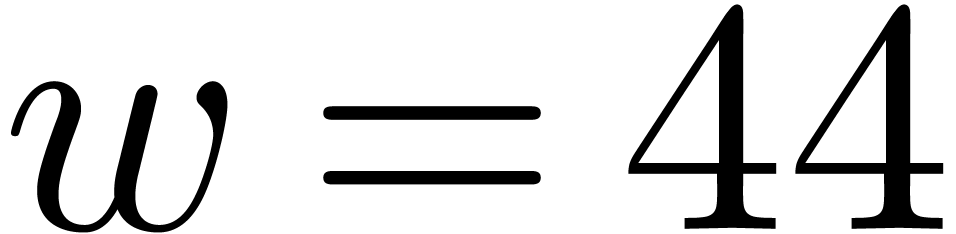 ,
,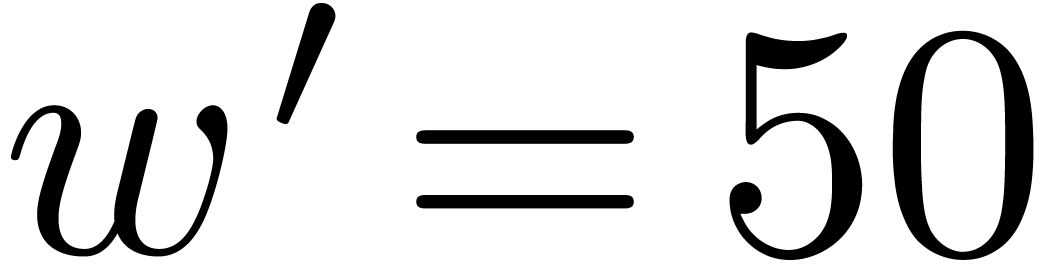 ,
,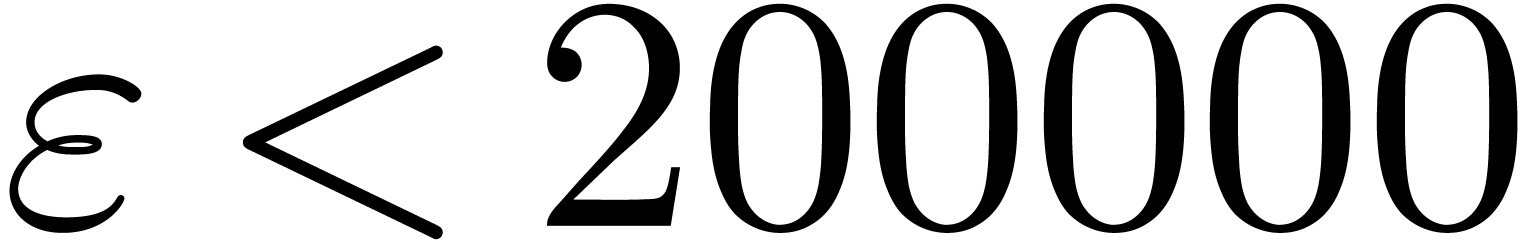 .
.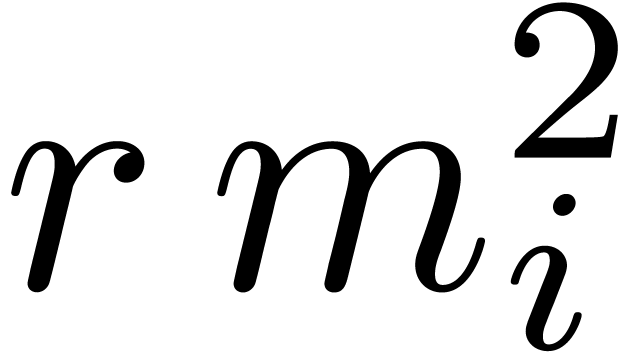 fits into the size of a word.
fits into the size of a word.
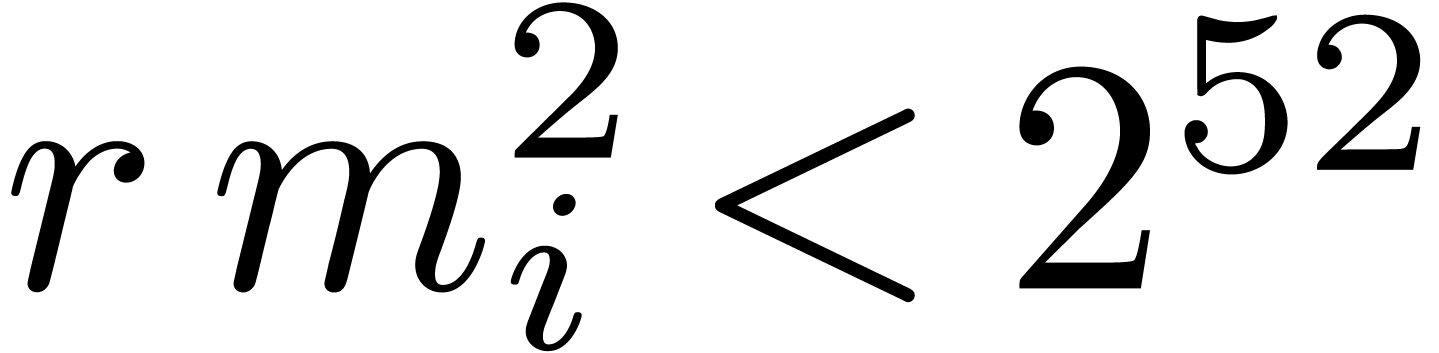 for all
for all  matrices with
matrices with 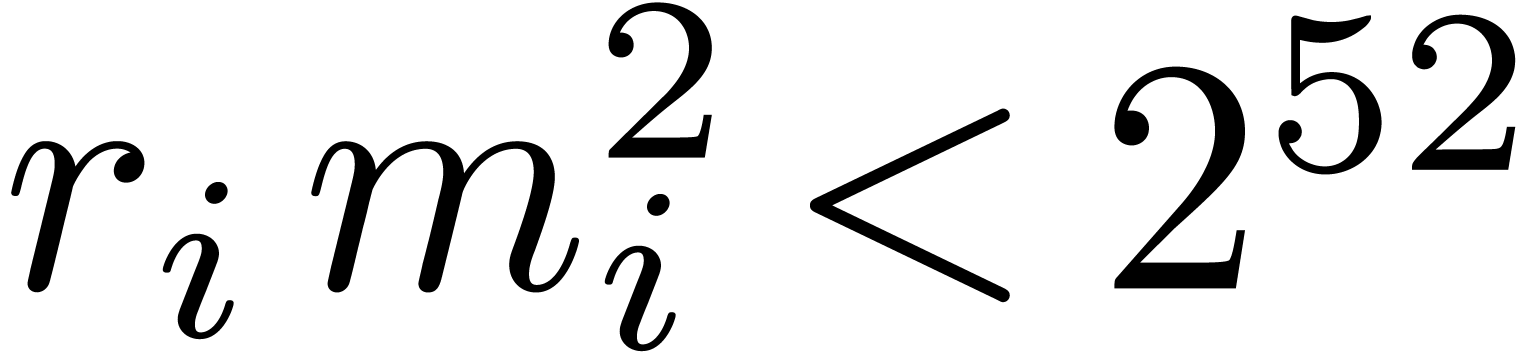 .
.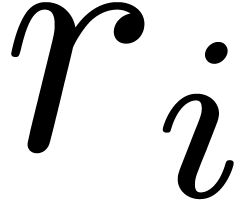 may
depend on
may
depend on 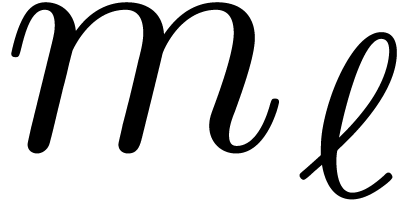 .
.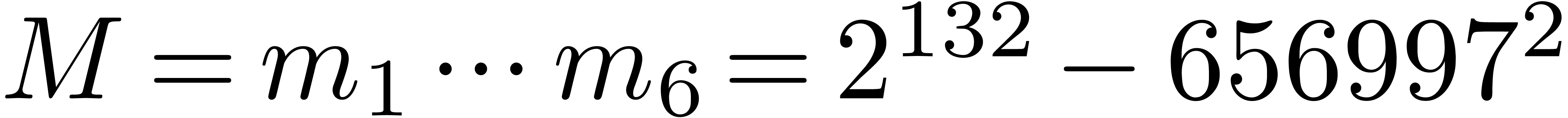 from Table
from Table  ,
,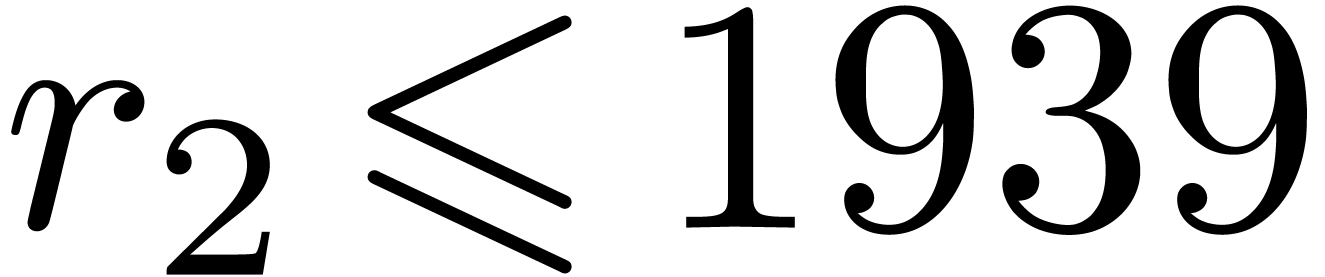 ,
,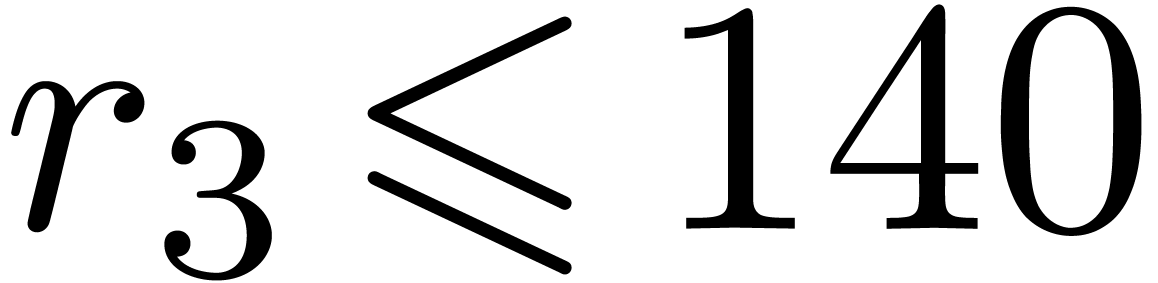 ,
, ,
, and
and  .
. of
of