The Chinese remainder theorem is a key tool for the design of
efficient multi-modular algorithms. In this paper, we study the
case when the moduli
|
|
The Chinese remainder theorem is a key tool for the design of
efficient multi-modular algorithms. In this paper, we study the
case when the moduli
|
Modular reduction is an important tool in computer algebra and elsewhere for speeding up computations. The technique allows to reduce a problem that involves large integer or polynomial coefficients to one or more similar problems that only involve small modular coefficients. Depending on the application, the solution to the initial problem is reconstructed via the Chinese remainder theorem or Hensel's lemma. We refer to [10, chapter 5] for a gentle introduction to this topic.
In this paper, we will mainly be concerned with multi-modular algorithms
over the integers that rely on the Chinese remainder theorem. The
archetype of such an algorithm works as follows. We start with a
polynomial function 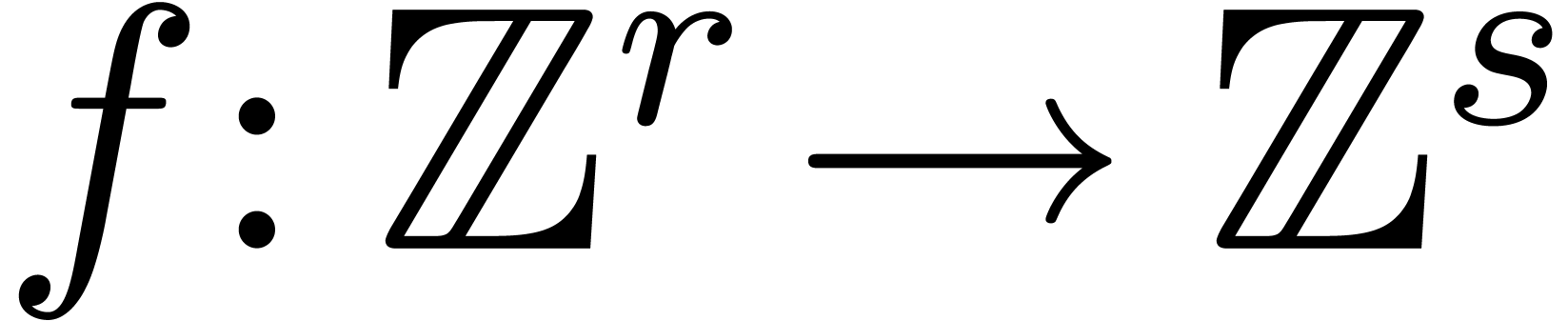 . For any
modulus
. For any
modulus  , reduction of
, reduction of  modulo
modulo  yields a new function
yields a new function
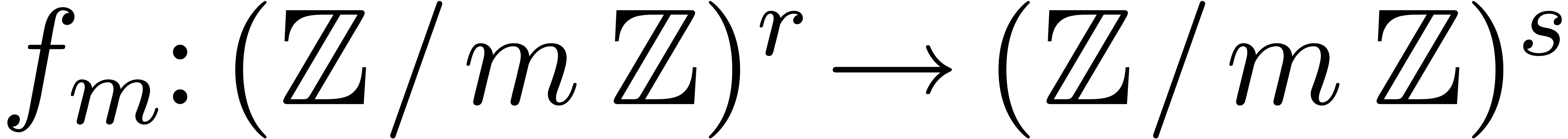 such that
such that
for all 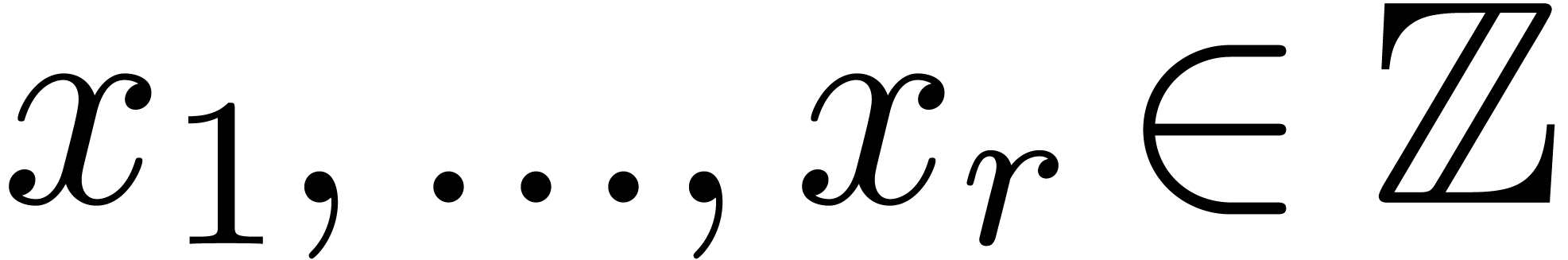 . Given an algorithm
to compute
. Given an algorithm
to compute  that only uses ring operations on
integers, it suffices to replace each ring operations by its reduction
modulo
that only uses ring operations on
integers, it suffices to replace each ring operations by its reduction
modulo  in order to obtain an algorithm that
computes
in order to obtain an algorithm that
computes  . Now given integers
. Now given integers
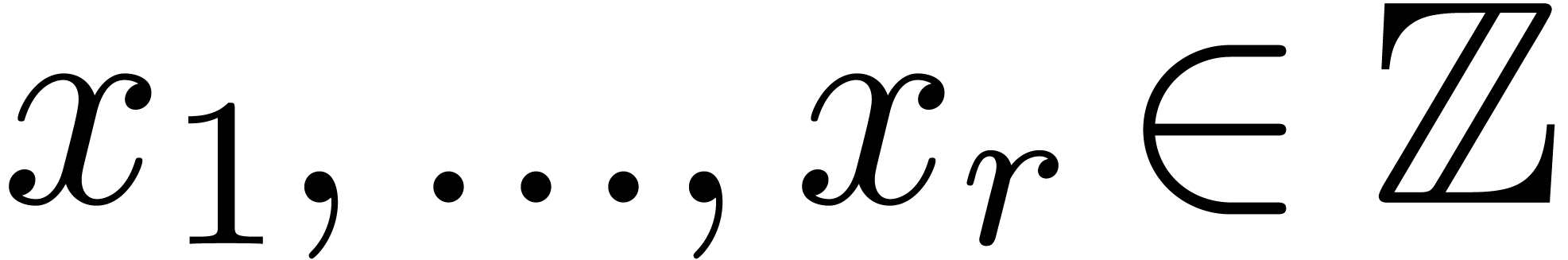 and
and 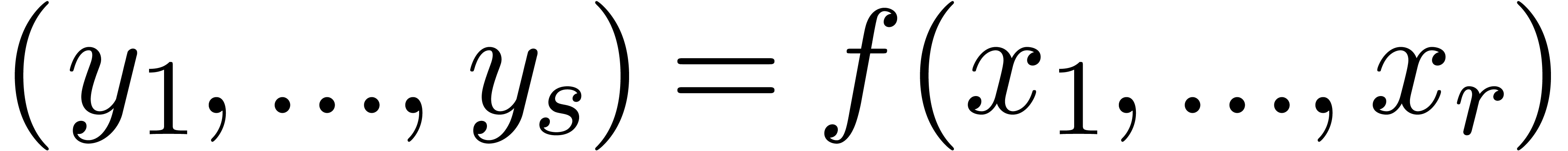 ,
assume that we know a bound
,
assume that we know a bound  with
with 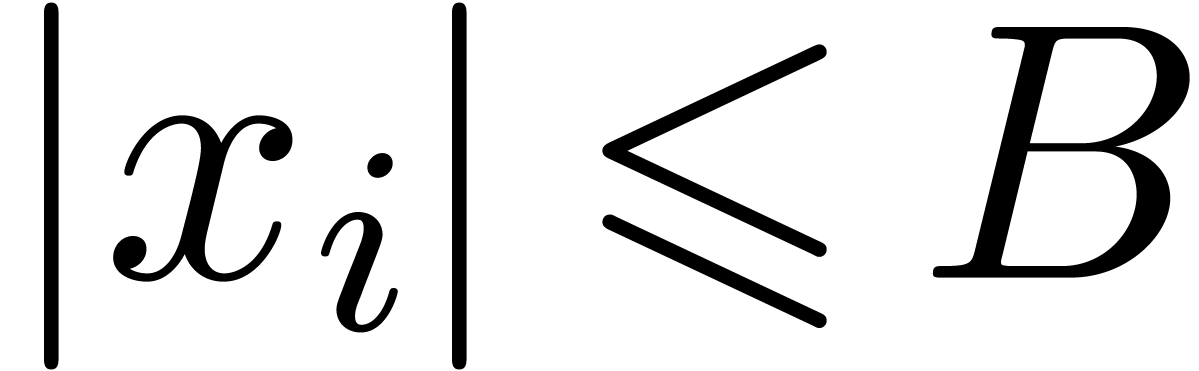 for
for 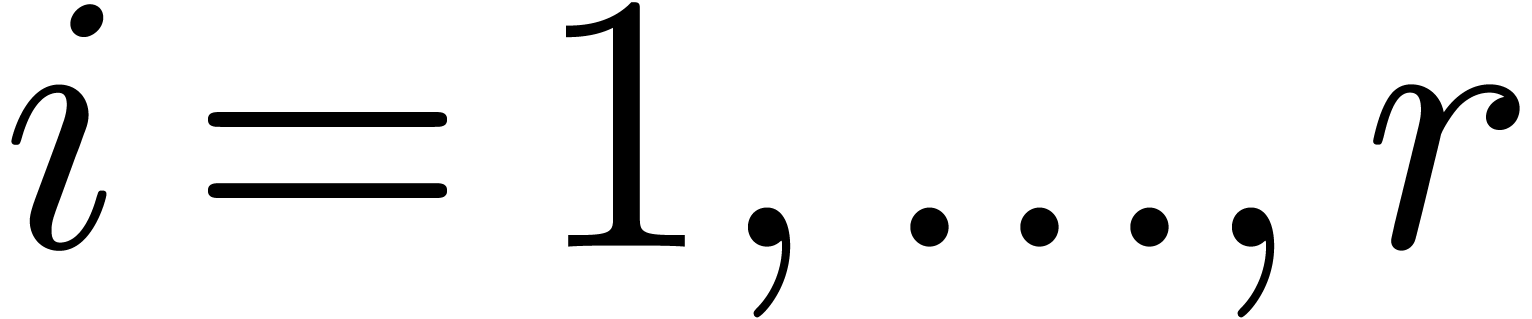 and
and 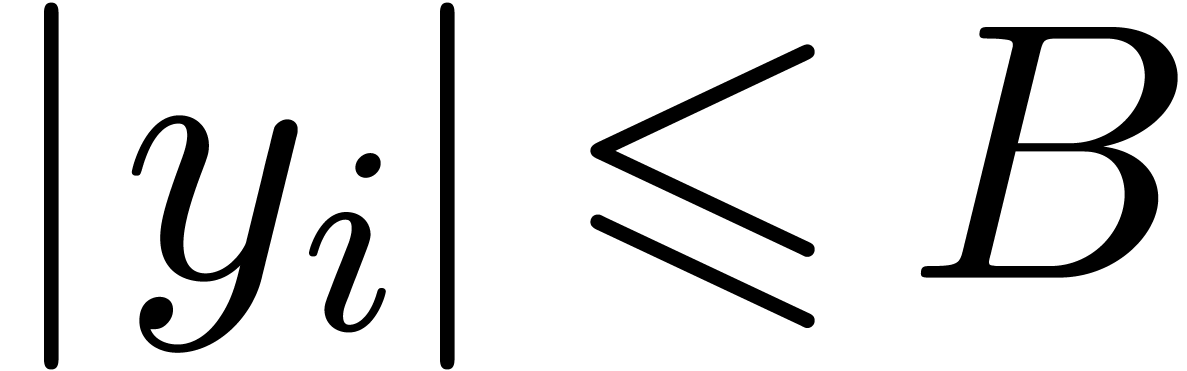 for
for 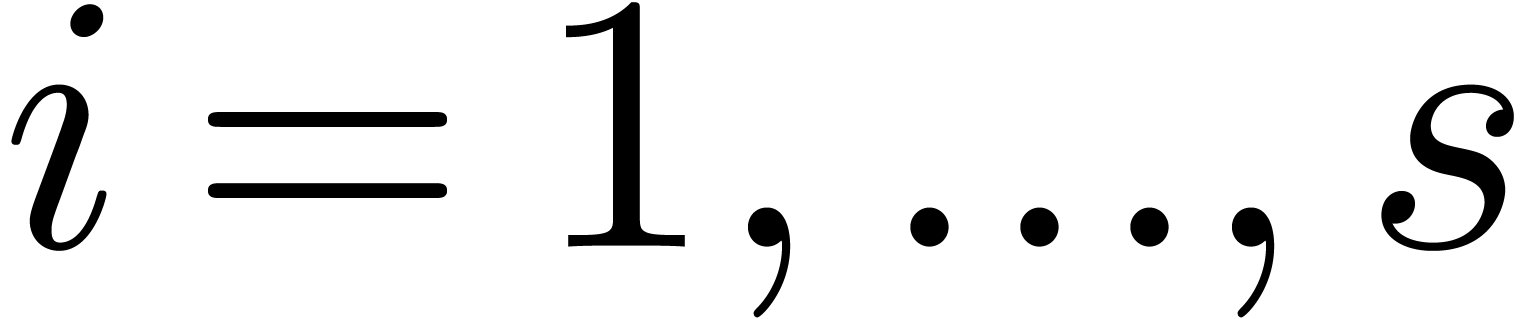 . Then the following
multi-modular algorithm provides with an alternative way to compute
. Then the following
multi-modular algorithm provides with an alternative way to compute
 :
:
Select moduli  with
with 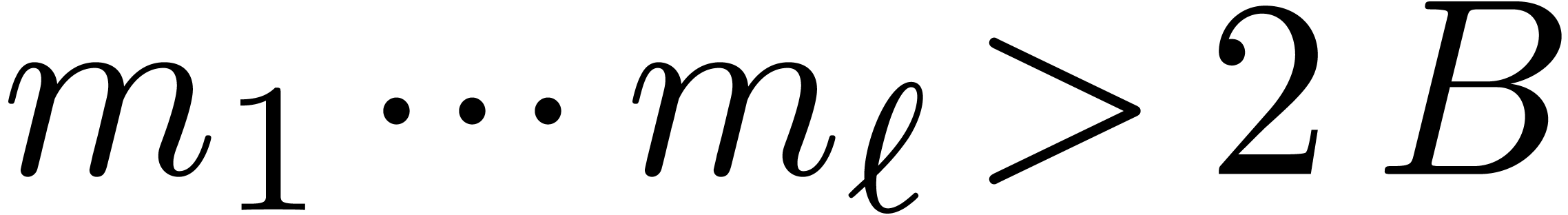 that are mutually coprime.
that are mutually coprime.
For 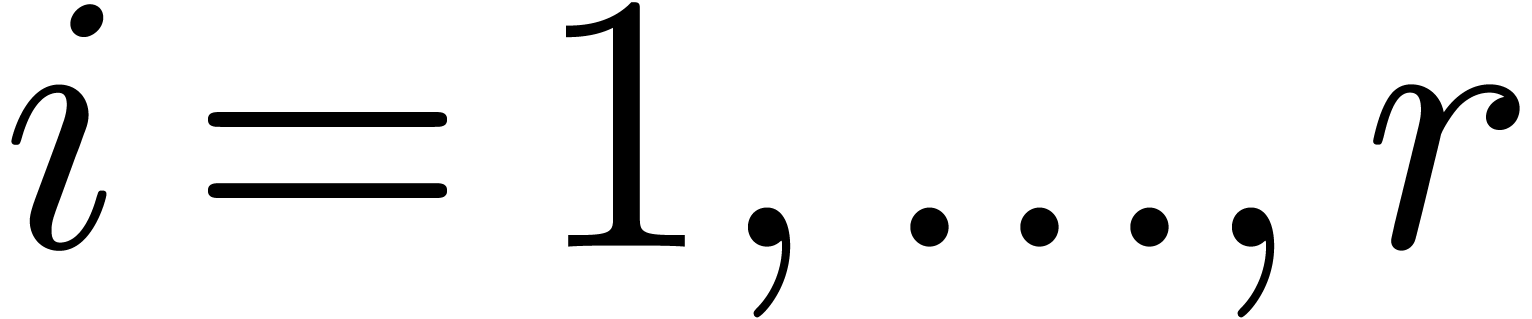 , compute
, compute 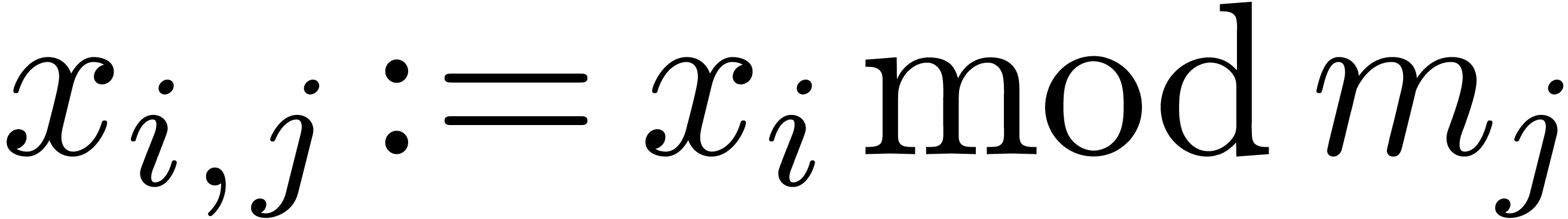 for
for 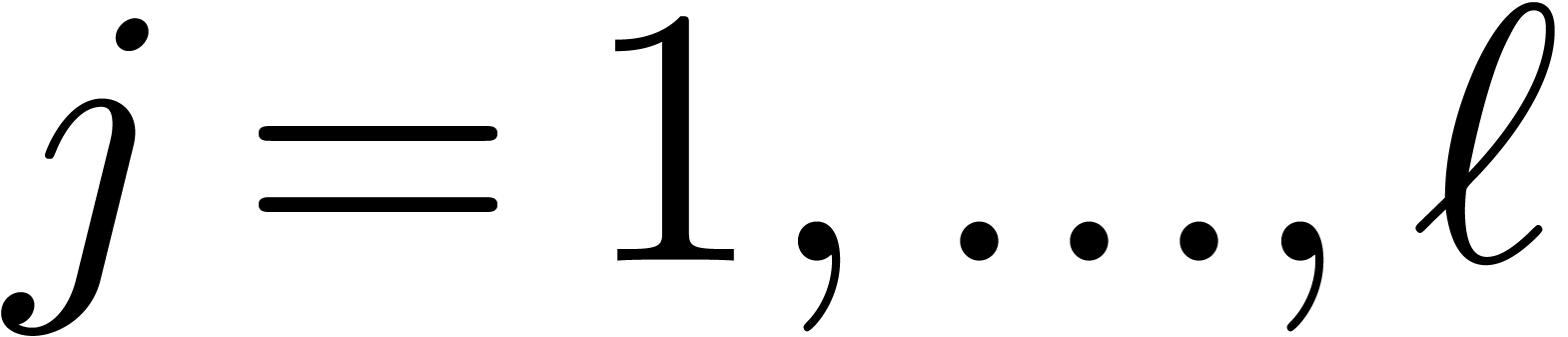 .
.
For 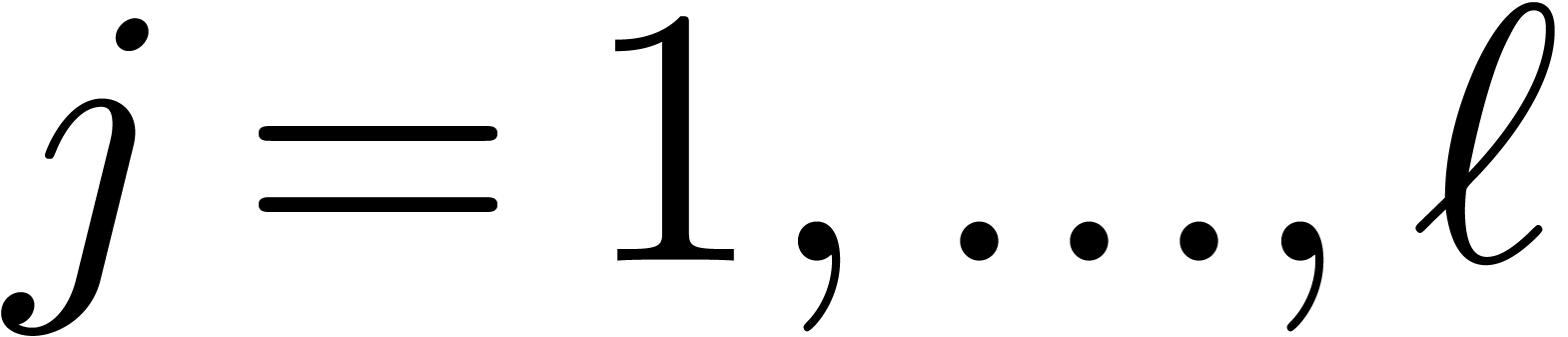 , compute
, compute 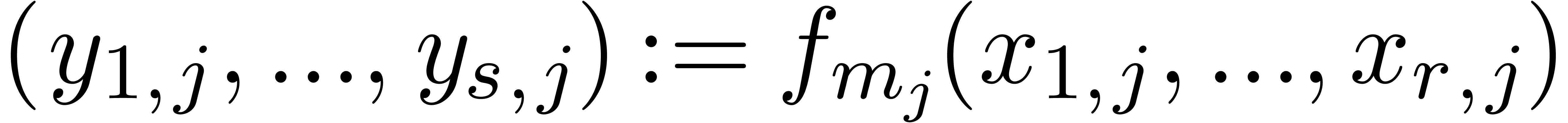 .
.
For 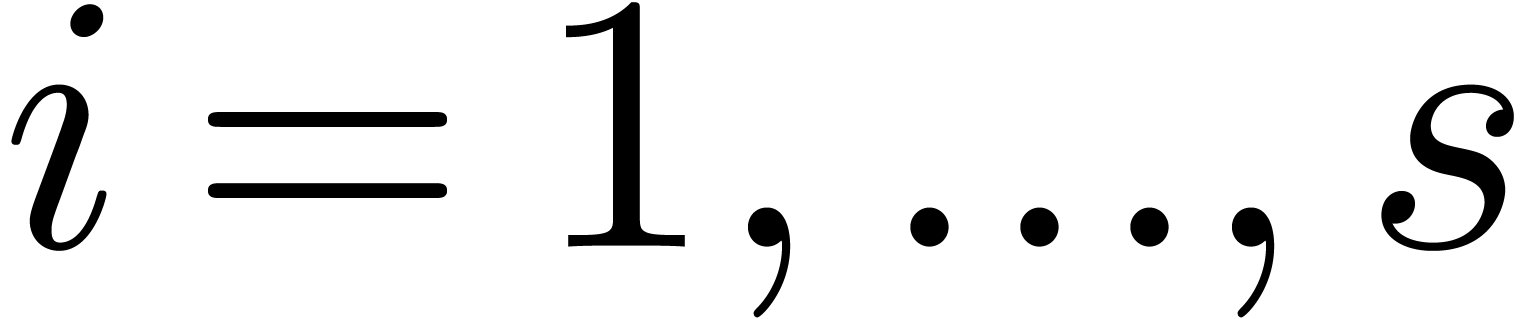 , reconstruct
, reconstruct 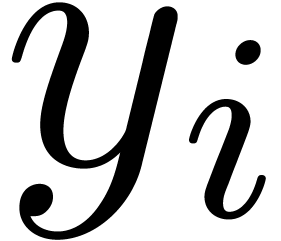 from the values
from the values 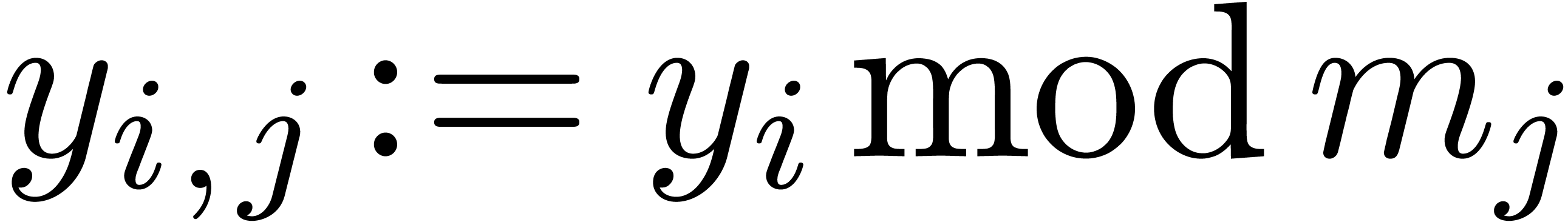 with
with
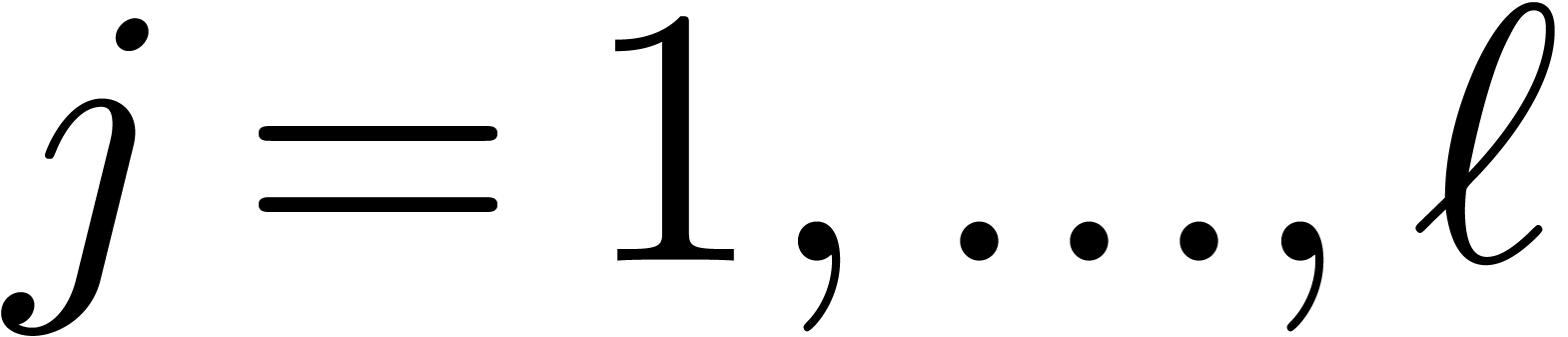 .
.
Step 1 consists of 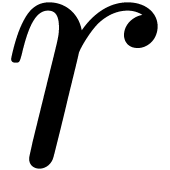 multi-modular
reductions (finding the
multi-modular
reductions (finding the 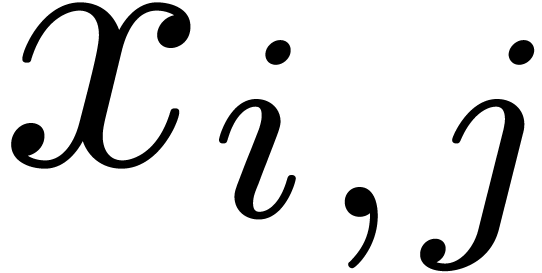 as a function of
as a function of
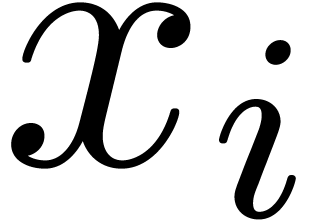 ) and step 3 of
) and step 3 of  multi-modular reconstructions (finding
multi-modular reconstructions (finding 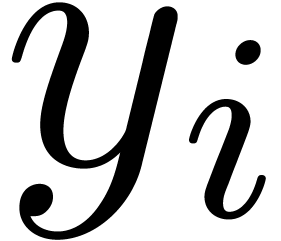 as a function the
as a function the 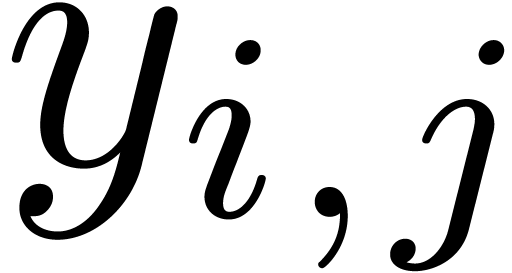 );
this is where the Chinese remainder theorem comes in. For a more
detailed example with an application to integer matrix multiplication,
we refer to section 4.5.
);
this is where the Chinese remainder theorem comes in. For a more
detailed example with an application to integer matrix multiplication,
we refer to section 4.5.
In favourable cases, the cost of steps 0, 1 and 3 is negligible with
respect to the cost of step 2. In such situations, the multi-modular
algorithm to compute 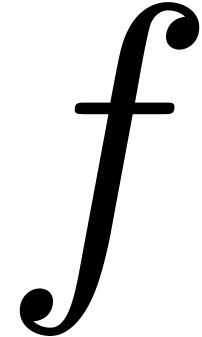 is usually much faster than
the original algorithm. In less favourable cases, the cost of steps 1
and 3 can no longer be neglected. This raises the question whether it is
possible to reduce the cost of these steps as much as possible.
is usually much faster than
the original algorithm. In less favourable cases, the cost of steps 1
and 3 can no longer be neglected. This raises the question whether it is
possible to reduce the cost of these steps as much as possible.
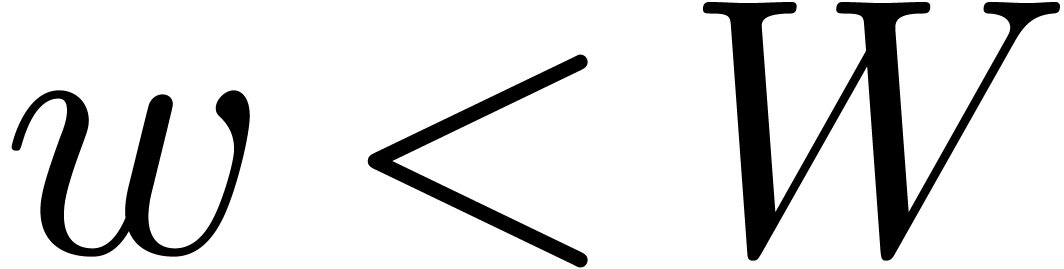
Two observations are crucial here. First of all, the moduli  are the same for all
are the same for all 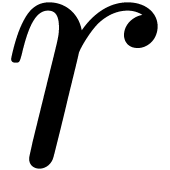 multi-modular
reductions and
multi-modular
reductions and  multi-modular reconstructions. If
multi-modular reconstructions. If
 is large, then this means that we can
essentially assume that
is large, then this means that we can
essentially assume that  were fixed once and for
all. Secondly, we are free to choose
were fixed once and for
all. Secondly, we are free to choose  in any way
that suits us. By making each
in any way
that suits us. By making each 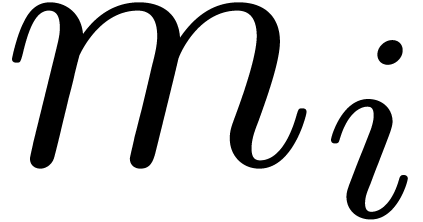 fit into a machine
word, one may ensure that every modular operation only takes a few
cycles. Special “FFT-moduli” are often used as well for
speeding up polynomial arithmetic.
fit into a machine
word, one may ensure that every modular operation only takes a few
cycles. Special “FFT-moduli” are often used as well for
speeding up polynomial arithmetic.
In this paper, we will show how to exploit both of the above
observations. For fixed moduli, we will show in section 3
how to make Chinese remaindering asymptotically more efficient by a
factor 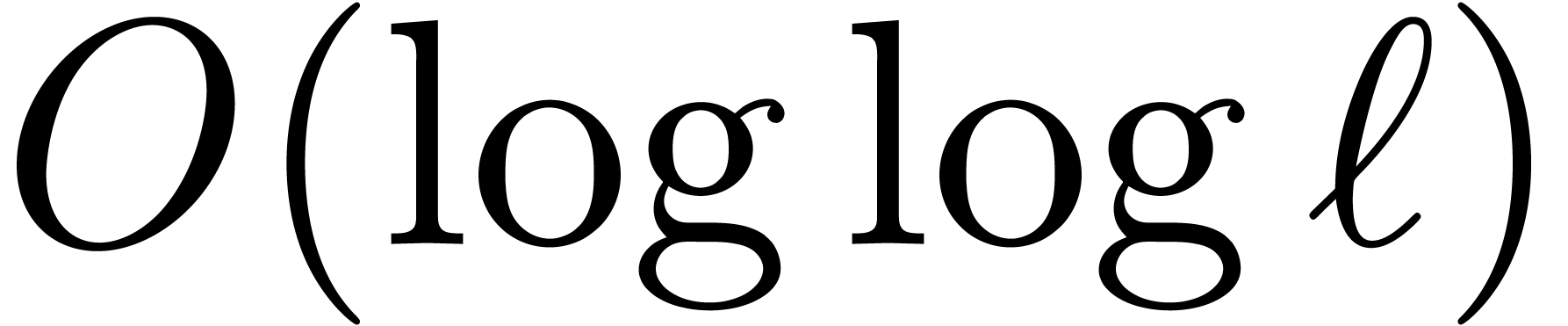 when
when  gets large.
In section 4, we show that it is possible to construct
“gentle modulo” that allow for speed-ups when
gets large.
In section 4, we show that it is possible to construct
“gentle modulo” that allow for speed-ups when  is small (
is small (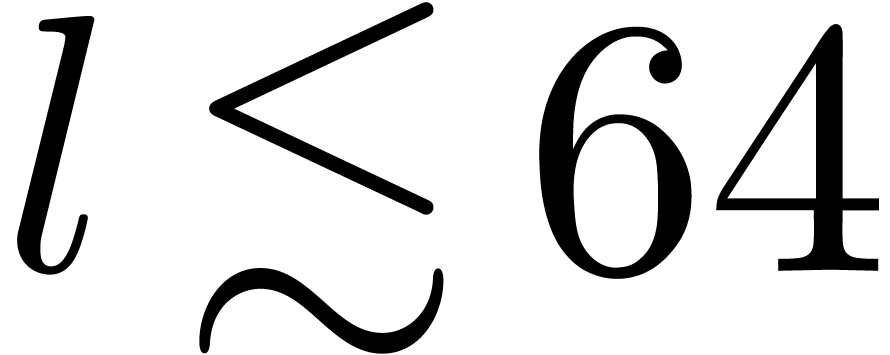 ).
Both results can be combined in order to accelerate Chinese remaindering
for all possible values of
).
Both results can be combined in order to accelerate Chinese remaindering
for all possible values of  .
.
The new asymptotic complexity bounds make heavy use of discrete Fourier
transforms. For our purposes, it is crucial to avoid
“synthetic” FFT schemes that require the adjunction of
artificial roots of unity as in Schönhage–Strassen
multiplication [24]. Instead, one should use
“inborn” FFT schemes that work with approximate roots of
unity in  or roots of unity with high smooth
orders in finite fields; see [24, section 3] and [23,
15]. Basic complexity properties of integer multiplication
and division based on fast Fourier techniques are recalled in section 2.
or roots of unity with high smooth
orders in finite fields; see [24, section 3] and [23,
15]. Basic complexity properties of integer multiplication
and division based on fast Fourier techniques are recalled in section 2.
Let 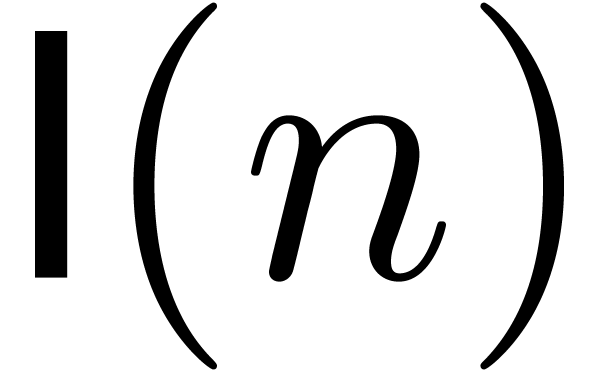 be the bit complexity for multiplying two
be the bit complexity for multiplying two
 -bit numbers. Given pairwise
comprime moduli
-bit numbers. Given pairwise
comprime moduli  of bit-size
of bit-size  , it is well known that multi-modular reduction
and reconstruction can be carried out in time
, it is well known that multi-modular reduction
and reconstruction can be carried out in time 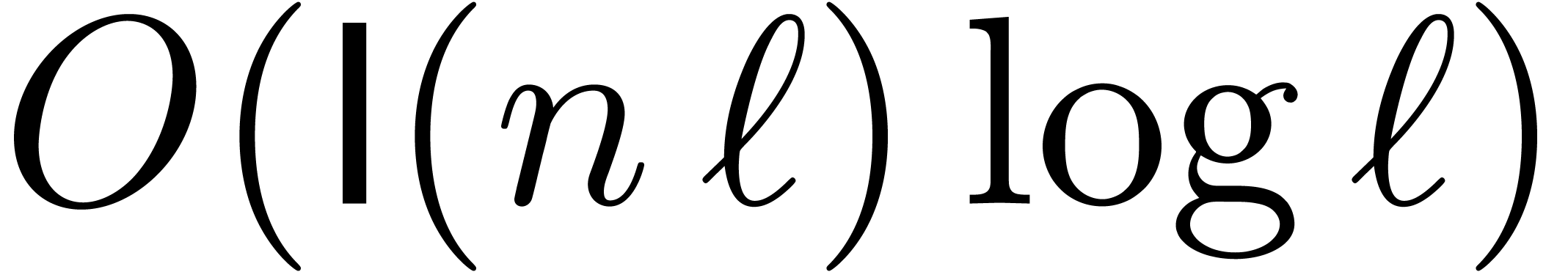 using so called remainder trees [8, 20,
3]. Recent improvements of this technique can be found in
[4, 2]. The main goal of section 3
is to show that this complexity essentially drops down to
using so called remainder trees [8, 20,
3]. Recent improvements of this technique can be found in
[4, 2]. The main goal of section 3
is to show that this complexity essentially drops down to 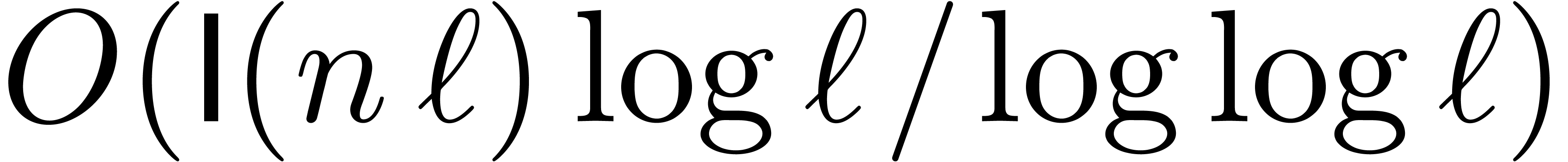 in the case when all moduli
in the case when all moduli  are
fixed; see Theorems 6 and 10 for more precise
statements. The main idea is to increase the arities of nodes in the
remainder tree, while performing the bulk of the computations at each
node using Fourier representations. This technique of trading faster
algorithms against faster representations was also used in [16],
where we called it FFT-trading; see also [1]. The
same approach can also be applied to the problem of base conversion (see
section 3.8) and for univariate polynomials instead of
integers (see section 3.9).
are
fixed; see Theorems 6 and 10 for more precise
statements. The main idea is to increase the arities of nodes in the
remainder tree, while performing the bulk of the computations at each
node using Fourier representations. This technique of trading faster
algorithms against faster representations was also used in [16],
where we called it FFT-trading; see also [1]. The
same approach can also be applied to the problem of base conversion (see
section 3.8) and for univariate polynomials instead of
integers (see section 3.9).
Having obtained a non trivial asymptotic speed-up for large  , we next turn our attention to the case when
, we next turn our attention to the case when
 is small (say
is small (say 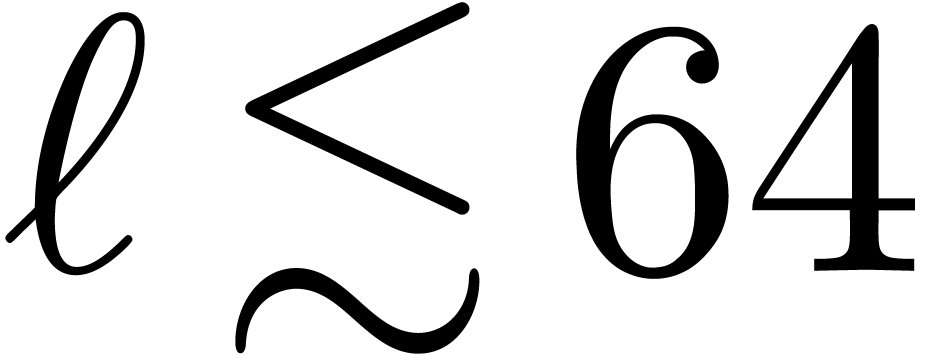 ).
The main goal of section 4 there is to exhibit the
existence of gentle moduli
).
The main goal of section 4 there is to exhibit the
existence of gentle moduli  for which
Chinese remaindering becomes more efficient than usual. The first idea
is to pick moduli
for which
Chinese remaindering becomes more efficient than usual. The first idea
is to pick moduli 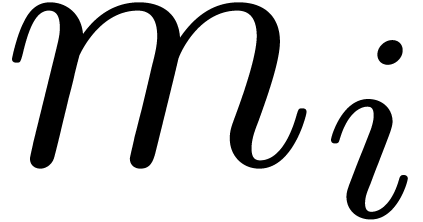 of the form
of the form 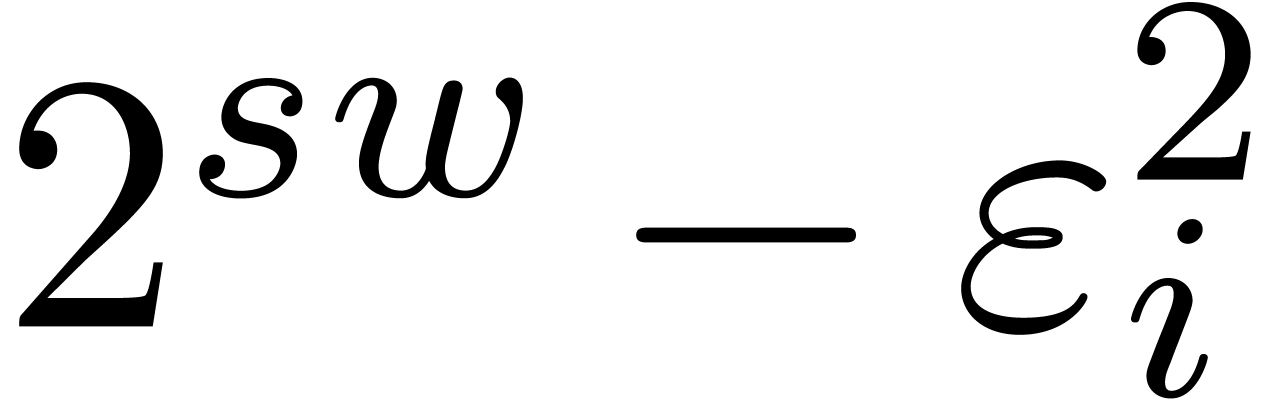 , where
, where  is somewhat
smaller than the hardware word size,
is somewhat
smaller than the hardware word size,  is even,
and
is even,
and 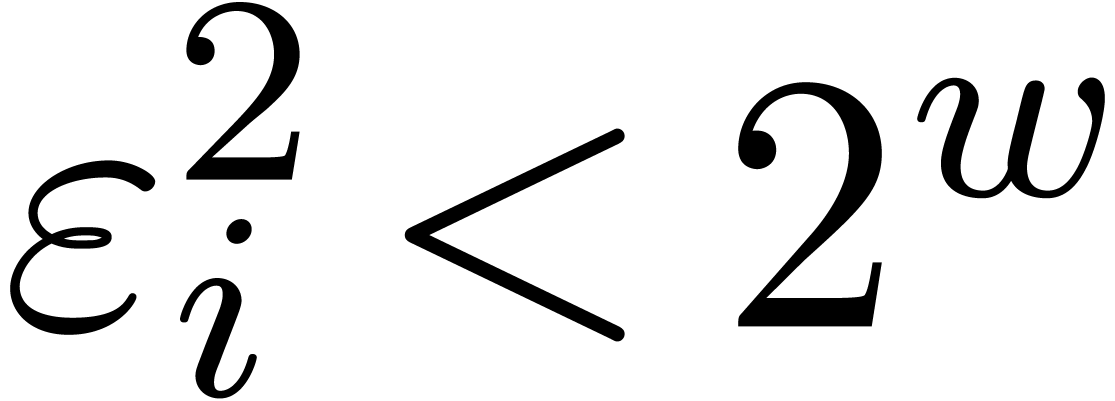 . In section 4.1,
we will show that multi-modular reduction and reconstruction both become
a lot simpler for such moduli. Secondly, each
. In section 4.1,
we will show that multi-modular reduction and reconstruction both become
a lot simpler for such moduli. Secondly, each 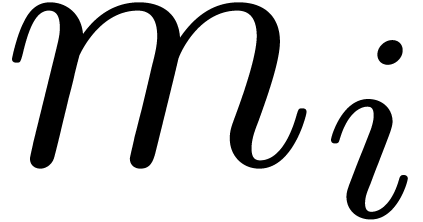 can be factored as
can be factored as 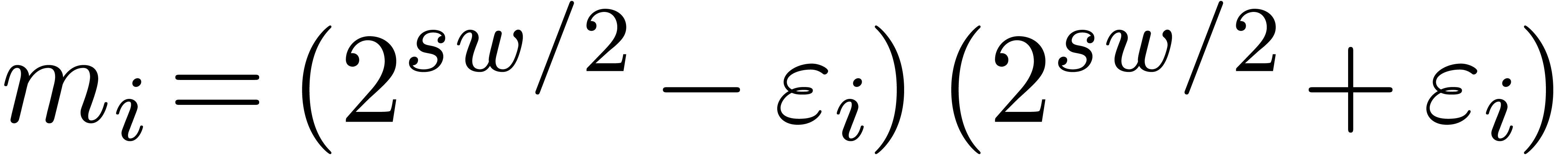 and, if we are lucky, then
both
and, if we are lucky, then
both 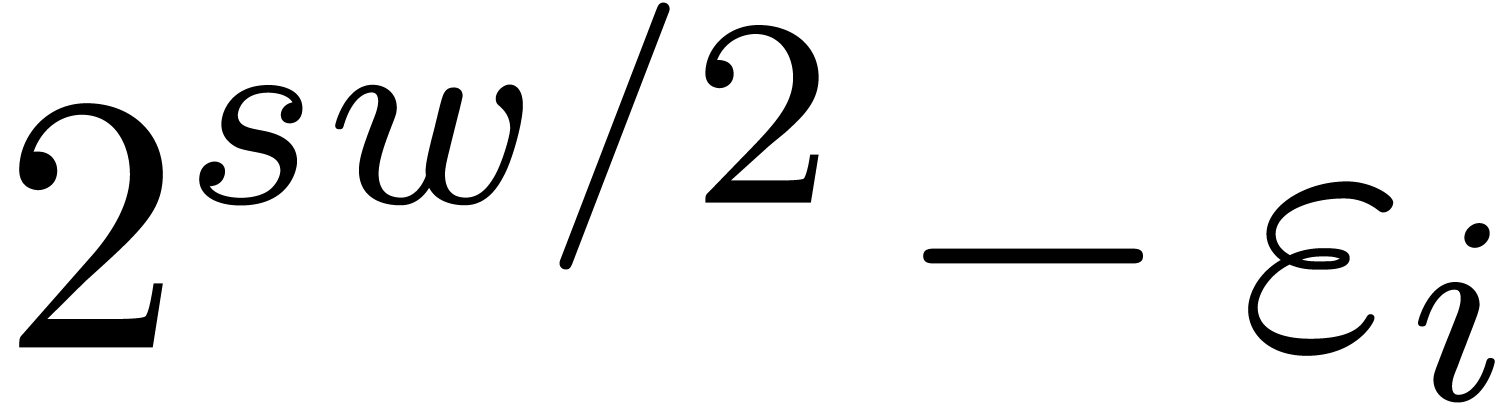 and
and 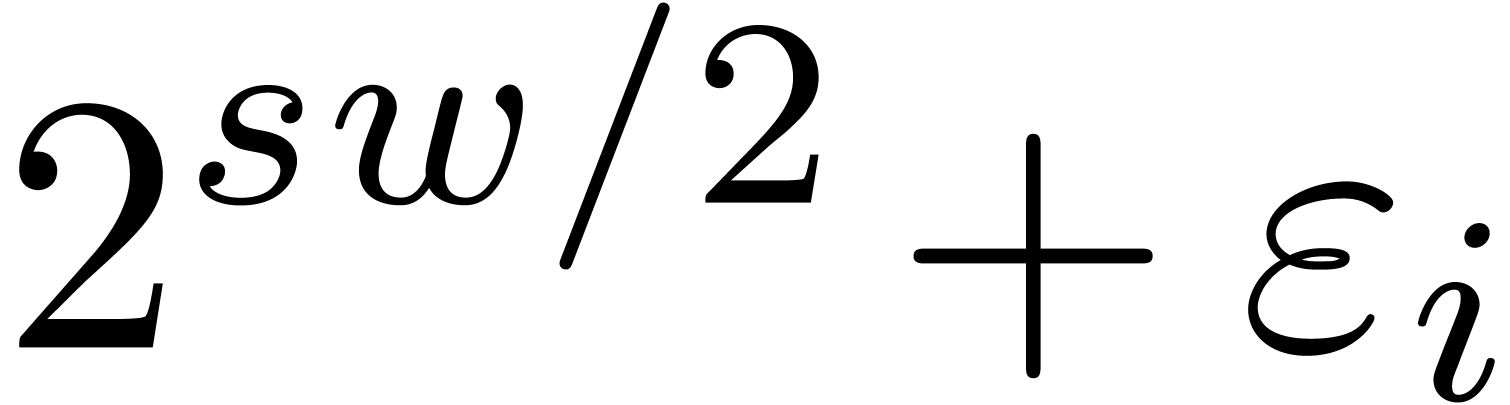 can be factored
into
can be factored
into 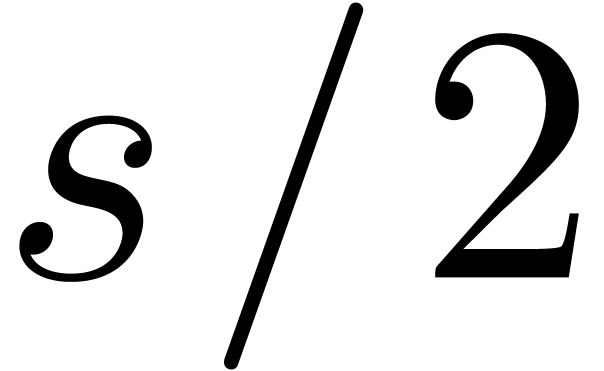 moduli that fit into machine words. If we
are very lucky, then this allows us to obtain
moduli that fit into machine words. If we
are very lucky, then this allows us to obtain  moduli
moduli  of bitsize
of bitsize  that
are mutually coprime and for which Chinese remaindering can be
implemented efficiently. Gentle moduli can be regarded as the integer
analogue of “special sets of points” that allowed for
speed-ups of multi-point evaluation and interpolation in [5].
that
are mutually coprime and for which Chinese remaindering can be
implemented efficiently. Gentle moduli can be regarded as the integer
analogue of “special sets of points” that allowed for
speed-ups of multi-point evaluation and interpolation in [5].
Acknowledgments. We would like to thank
Grégoire
Throughout this paper we will assuming the deterministic multitape
Turing model [21] in order to analyze the “bit
complexity” of our algorithms. We will denote by  the cost of
the cost of  -bit integer
multiplication. The best current bound [15] for
-bit integer
multiplication. The best current bound [15] for 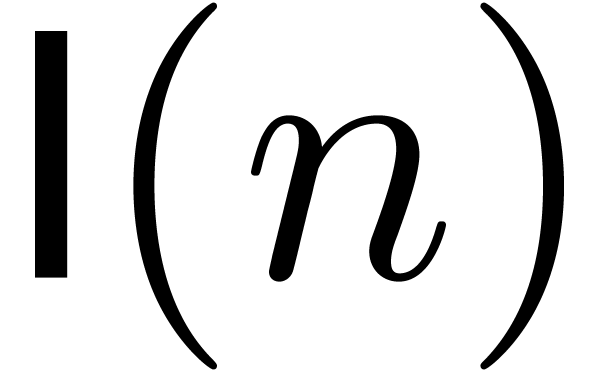 is
is
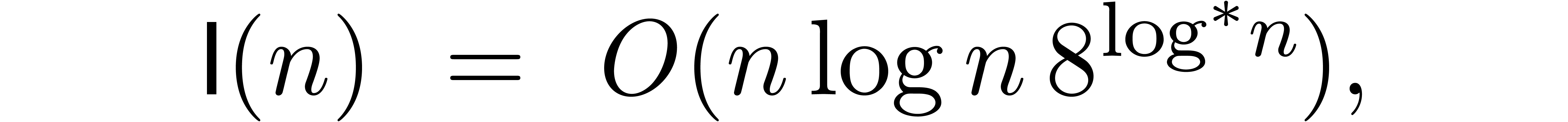
where 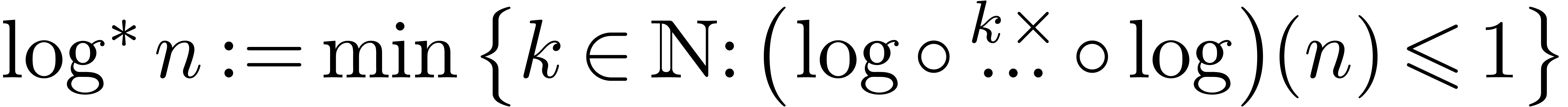 is called the iterator of the logarithm.
is called the iterator of the logarithm.
For large  , it is well known
that the fastest algorithms for integer multiplication [23,
24, 9, 15] are all based on the
discrete Fourier transform [7]: denoting by
, it is well known
that the fastest algorithms for integer multiplication [23,
24, 9, 15] are all based on the
discrete Fourier transform [7]: denoting by 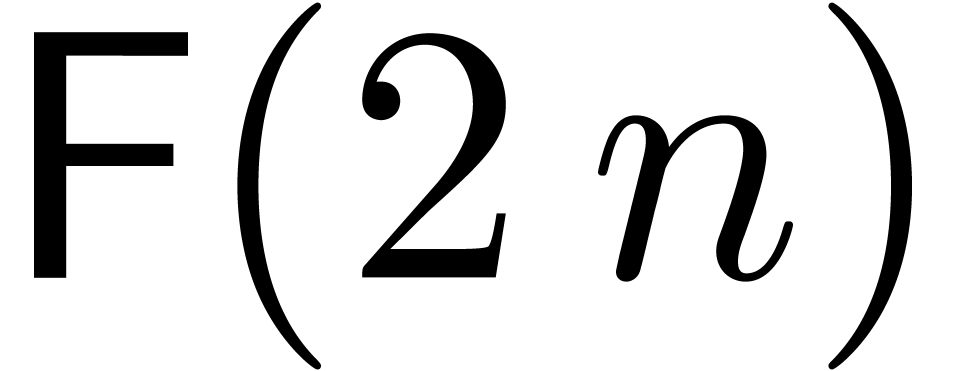 the cost of a “suitable Fourier transform” of
bitsize
the cost of a “suitable Fourier transform” of
bitsize 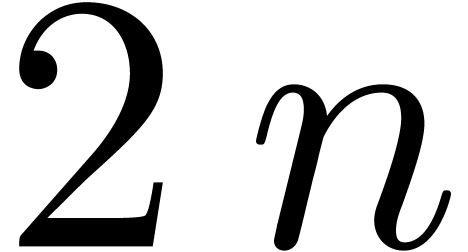 and by
and by 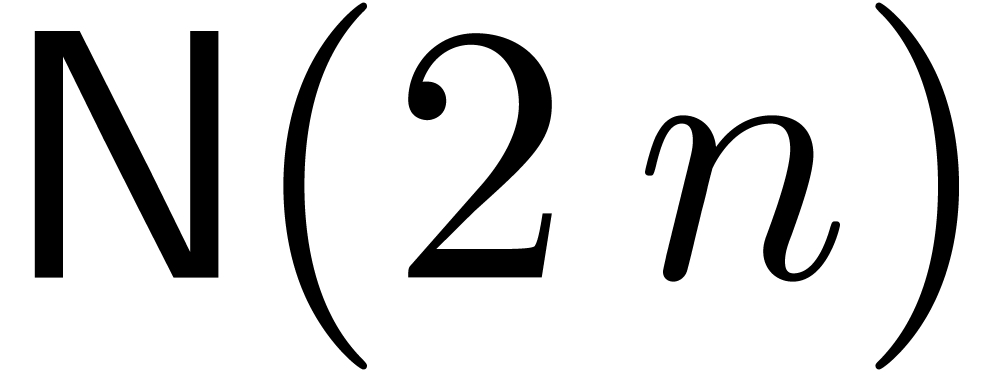 the cost
of the “inner multiplications” for this bitsize, one has
the cost
of the “inner multiplications” for this bitsize, one has
For the best current algorithm from [15], we have
One always has 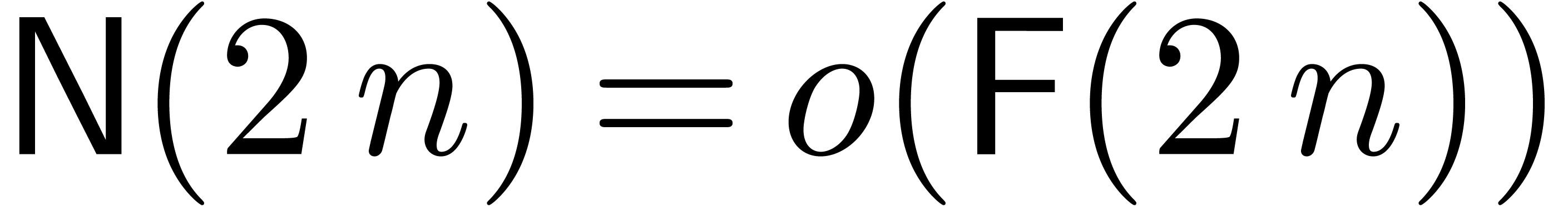 . The actual
size of Fourier transforms is usually somewhat restricted: for
efficiency reasons, it should be the product of powers of small prime
numbers only, such as
. The actual
size of Fourier transforms is usually somewhat restricted: for
efficiency reasons, it should be the product of powers of small prime
numbers only, such as 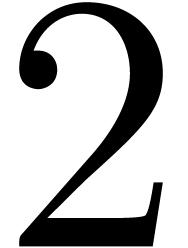 ,
,  and
and  .
Fortunately, for large numbers
.
Fortunately, for large numbers  ,
it is always possible to find
,
it is always possible to find 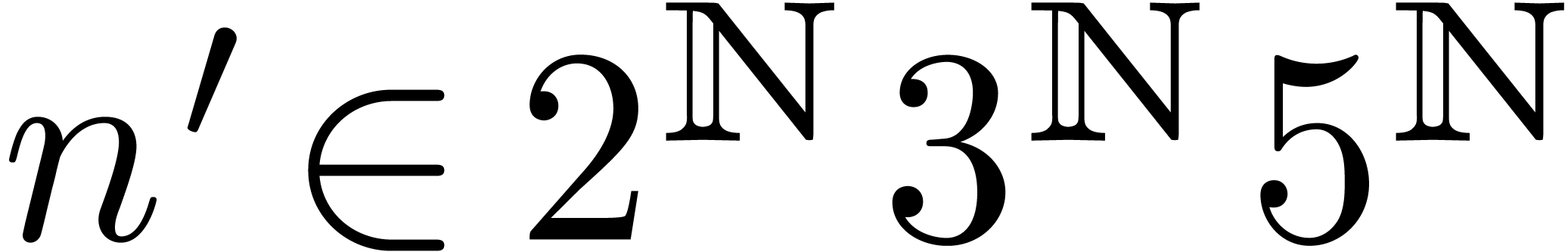 with
with  and
and  .
.
It is also well known that fast Fourier transforms allow for several
tricks. For instance, if one of the multiplicands of an  -bit integer product is fixed, then its Fourier
transform can be precomputed. This means that the cost of the
multiplication drops down to
-bit integer product is fixed, then its Fourier
transform can be precomputed. This means that the cost of the
multiplication drops down to
In particular, the complexity 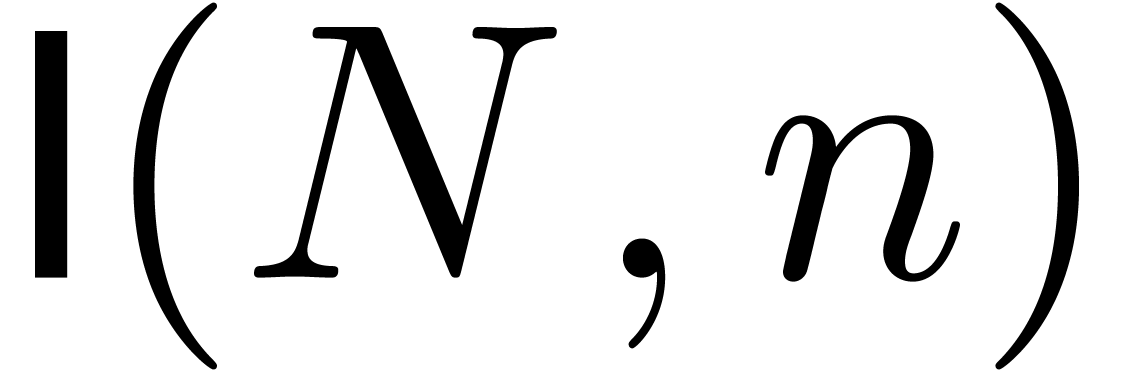 of multiplying an
of multiplying an
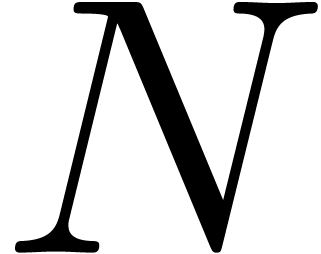 -bit integer with an
-bit integer with an  -bit one (for
-bit one (for 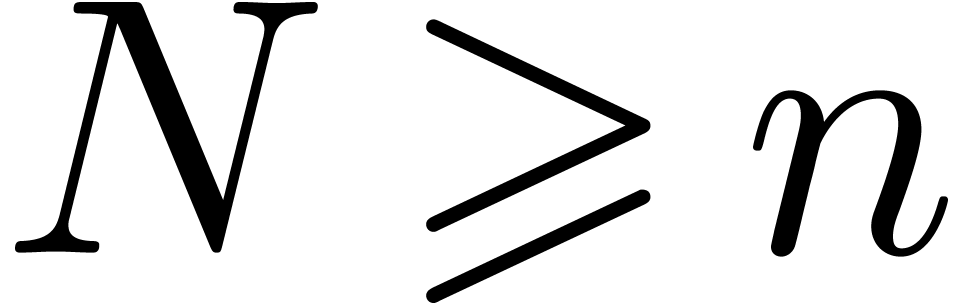 ) satisfies
) satisfies
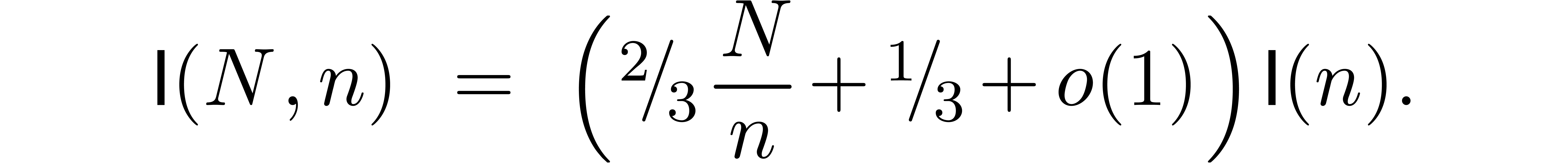
Squares of  -bit numbers can
be computed in time
-bit numbers can
be computed in time 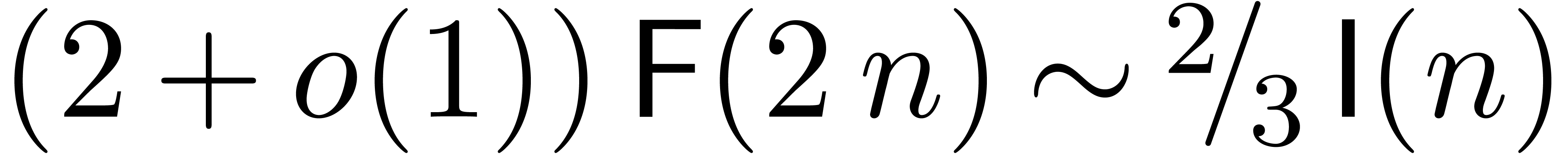 for the same reason. Yet
another example is the multiplication of two
for the same reason. Yet
another example is the multiplication of two  matrices with
matrices with 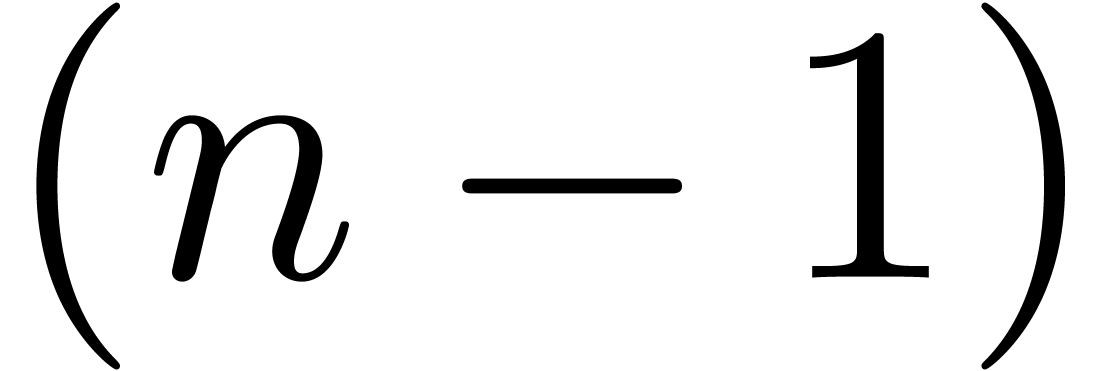 -bit integer
entries: such multiplications can be done in time
-bit integer
entries: such multiplications can be done in time 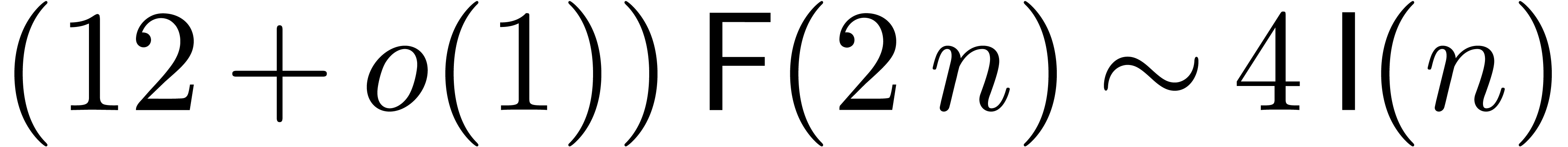 by transforming the input matrices, multiplying the transformed matrices
in the “Fourier model”, and then transforming the result
back.
by transforming the input matrices, multiplying the transformed matrices
in the “Fourier model”, and then transforming the result
back.
In the remainder of this paper, we will systematically assume that
asymptotically fast integer multiplication is based on fast Fourier
transforms. In particular, we have (1) for certain
functions 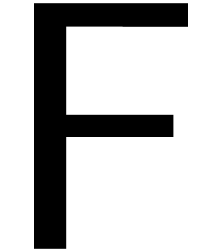 and
and  .
We will also assume that the functions
.
We will also assume that the functions 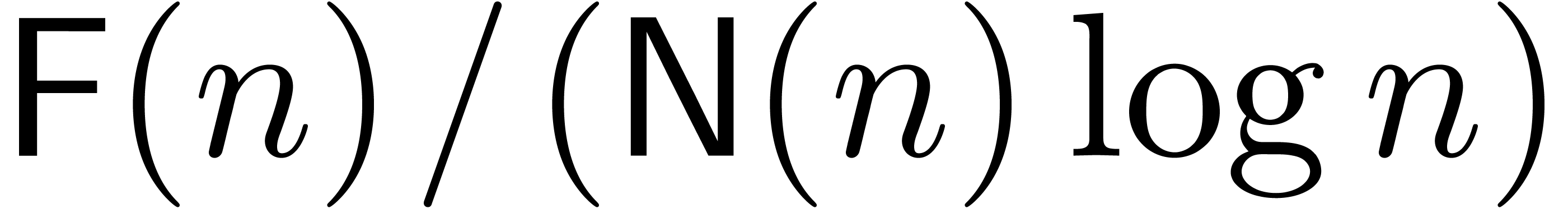 and
and 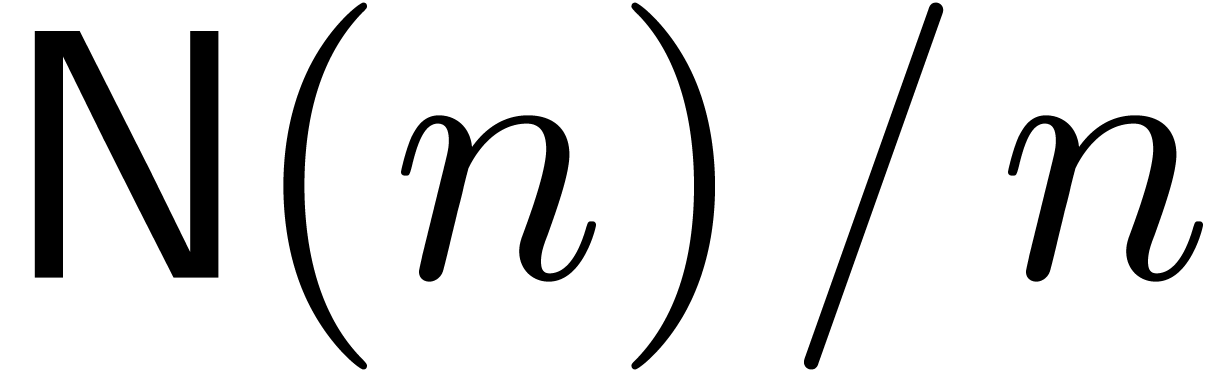 are (not necessarily strictly) increasing and that
are (not necessarily strictly) increasing and that
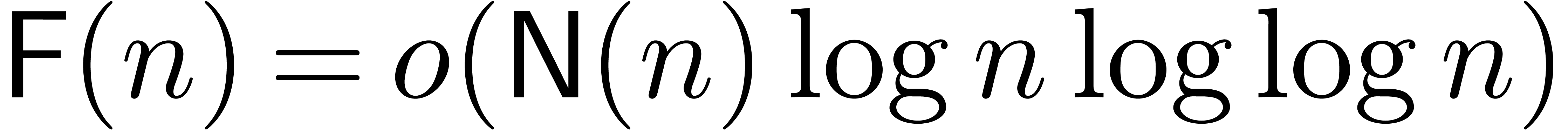 . These additional conditions
are satisfied for (2) and (3). The first
condition is violated whenever the FFT scheme requires the adjunction of
artificial roots of unity. This happens for
Schönhage–Strassen multiplication, in which case we have
. These additional conditions
are satisfied for (2) and (3). The first
condition is violated whenever the FFT scheme requires the adjunction of
artificial roots of unity. This happens for
Schönhage–Strassen multiplication, in which case we have 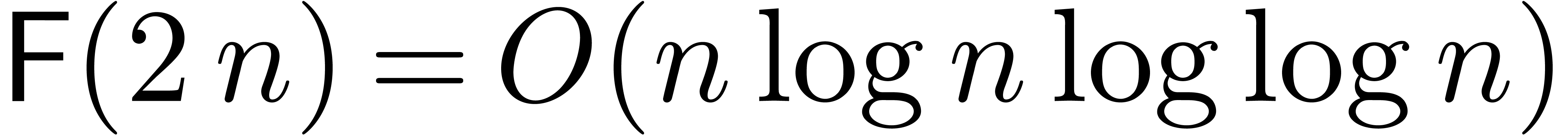 and
and  ). We
will say that an FFT-scheme is inborn if it satisfies our
additional requirements.
). We
will say that an FFT-scheme is inborn if it satisfies our
additional requirements.
For a hypothetical integer multiplication that runs in time 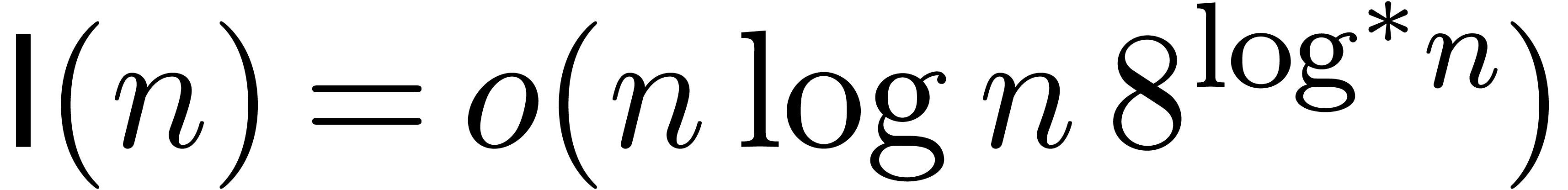 , but for which
, but for which 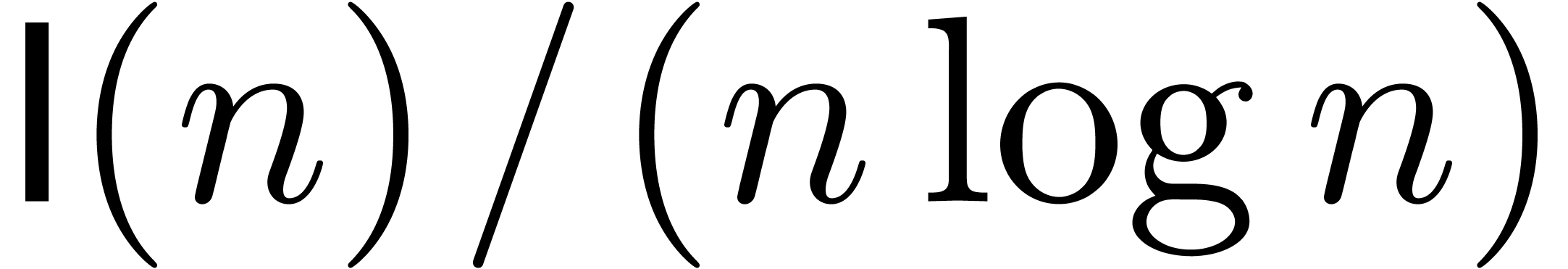 is (not
necessarily strictly) increasing, we also notice that it is possible to
design an inborn FFT-based integer multiplication method that runs in
time
is (not
necessarily strictly) increasing, we also notice that it is possible to
design an inborn FFT-based integer multiplication method that runs in
time 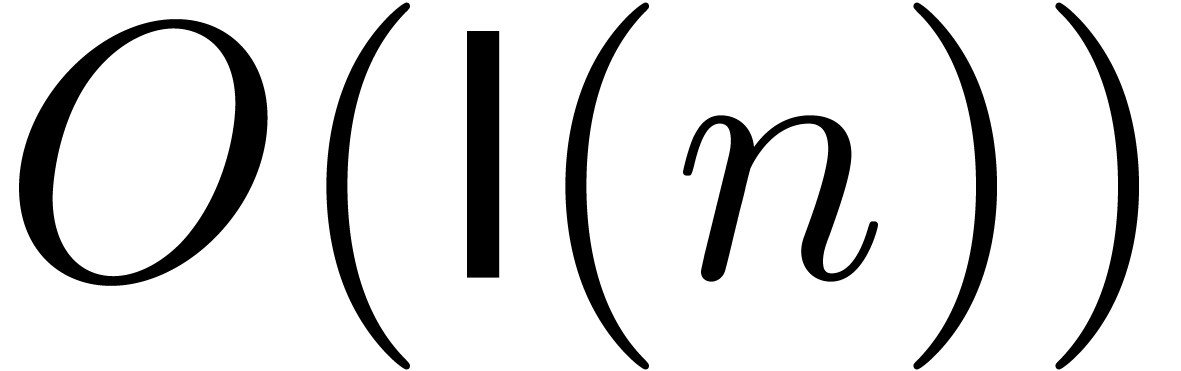 ; this is for instance
used in [13].
; this is for instance
used in [13].
Let  denote the cost of euclidean division with
remainder of an
denote the cost of euclidean division with
remainder of an 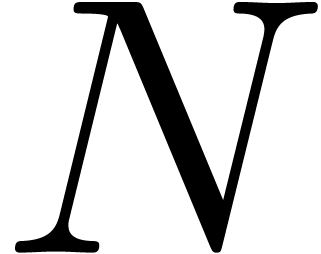 -bit integer
by an
-bit integer
by an  -bit one. In [16,
section 3.2], we gave an algorithm divide for the
euclidean division of a polynomial of degree
-bit one. In [16,
section 3.2], we gave an algorithm divide for the
euclidean division of a polynomial of degree 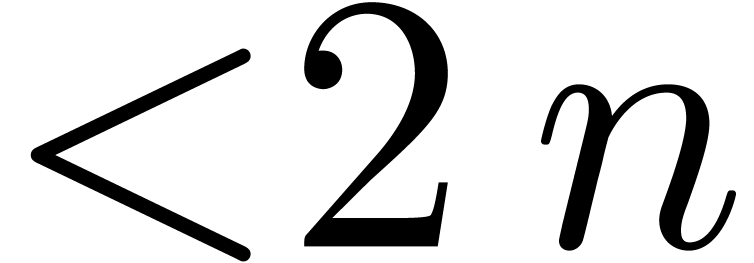 by
another polynomial of degree
by
another polynomial of degree 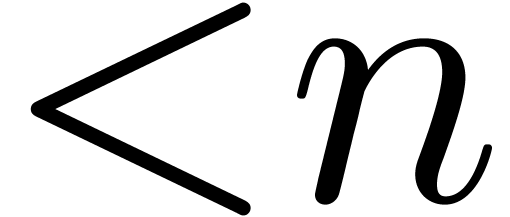 .
This algorithm is based on FFT trading, a technique that
consists of doing as much work as possible in the FFT-model even at the
expense of using naive, suboptimal algorithms in the FFT-model.
.
This algorithm is based on FFT trading, a technique that
consists of doing as much work as possible in the FFT-model even at the
expense of using naive, suboptimal algorithms in the FFT-model.
The straightforward adaptation of this division to integer arithmetic yields the asymptotic bound
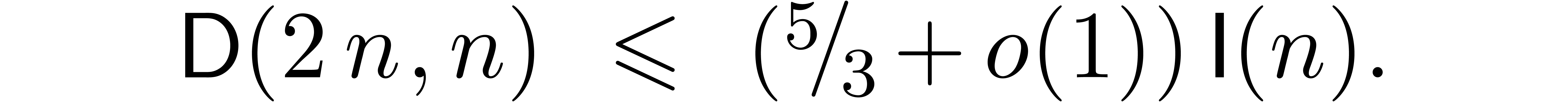
Furthermore, the discrete Fourier transforms for the dividend make up
for roughly one fifth of the total amount of transforms. For 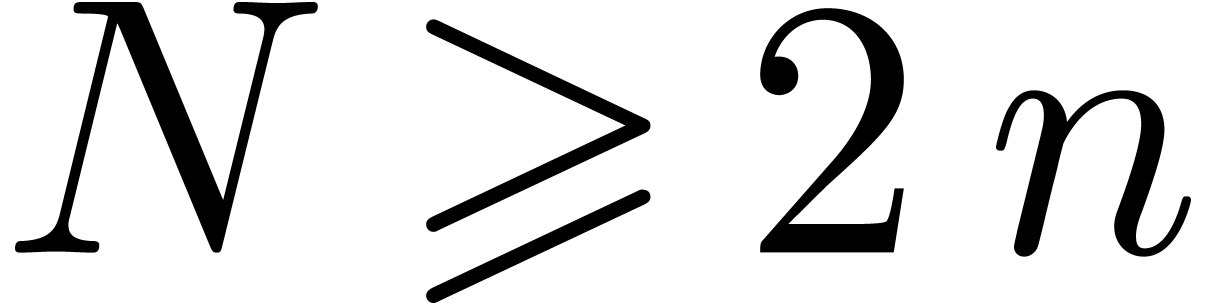 , the cost of the transforms for
the dividend does not grow with
, the cost of the transforms for
the dividend does not grow with 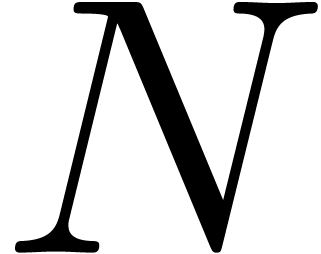 ,
which leads to the refinement
,
which leads to the refinement

Similarly, if 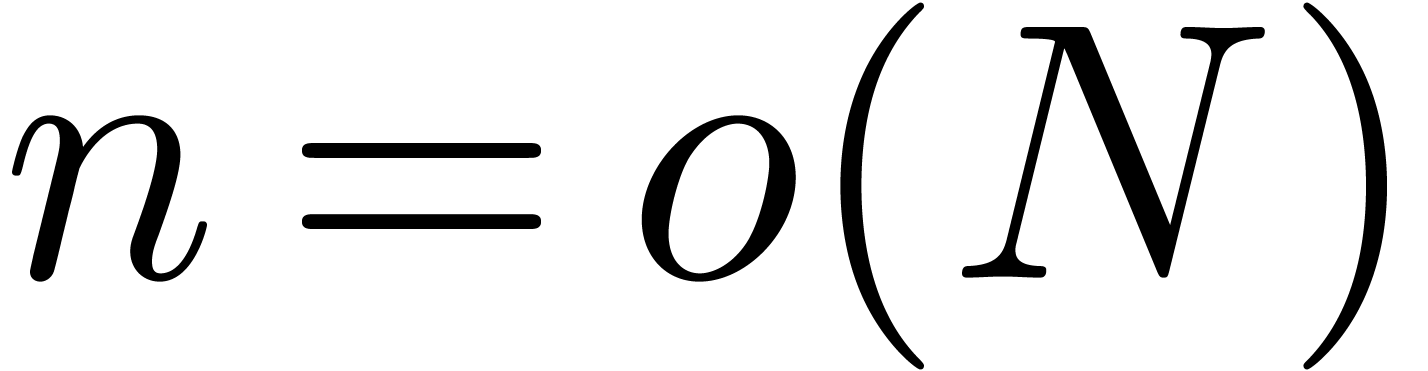 , then
, then
since the bulk of the computation consists of multiplying the
approximate  -bit quotient
with the
-bit quotient
with the 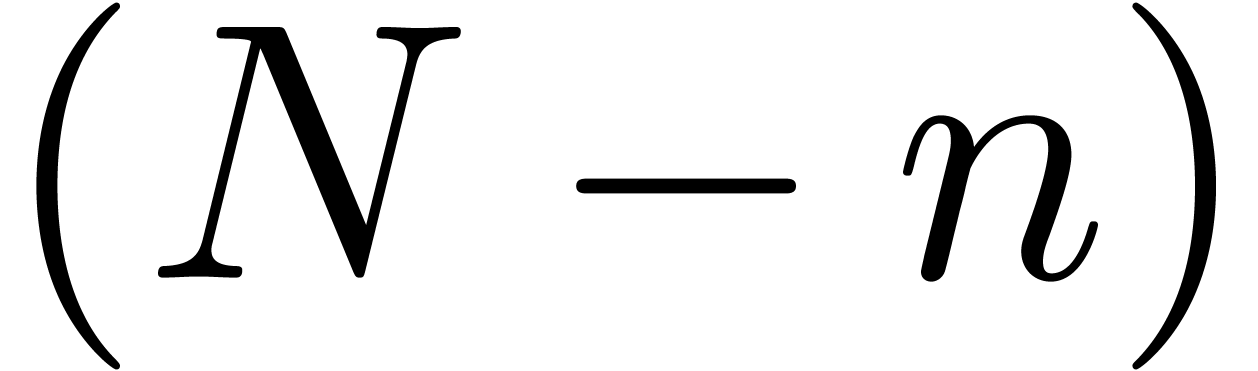 -bit dividend. If
the dividend is fixed, then we even get
-bit dividend. If
the dividend is fixed, then we even get
since the Fourier transforms for the dividend can be precomputed.
Let us start with a few definitions and notations. Given 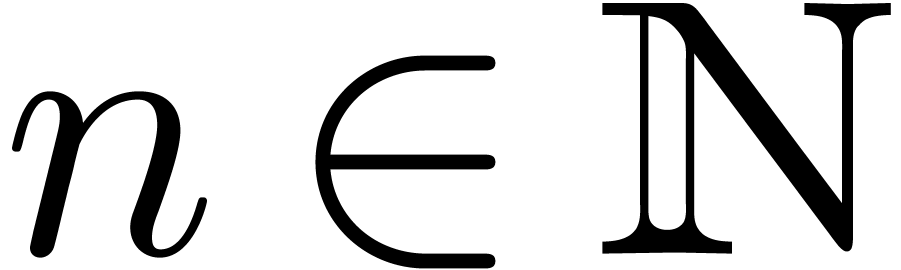 and
and 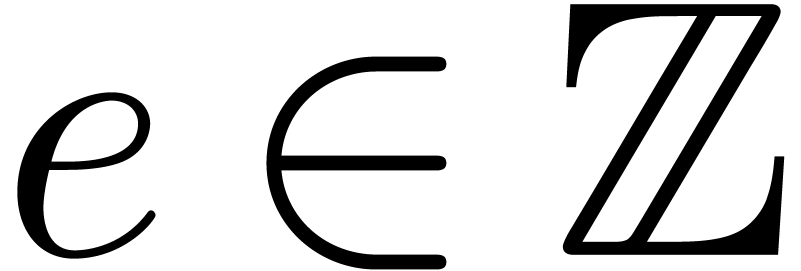 , we define
, we define
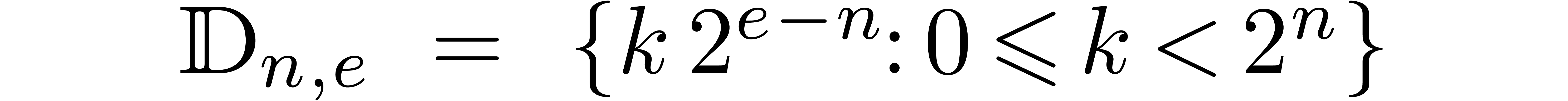
be the set of dyadic fixed point numbers of bitsize  and with exponent
and with exponent  . Given
. Given
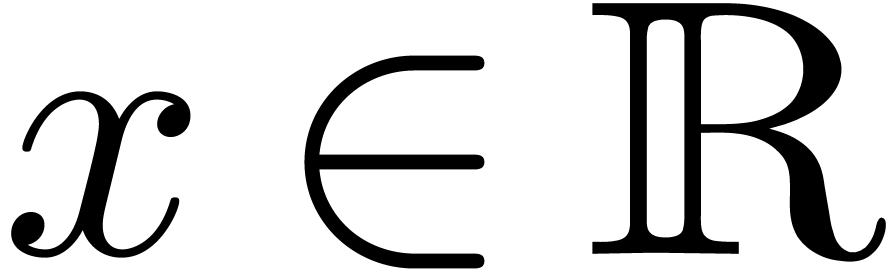 and
and 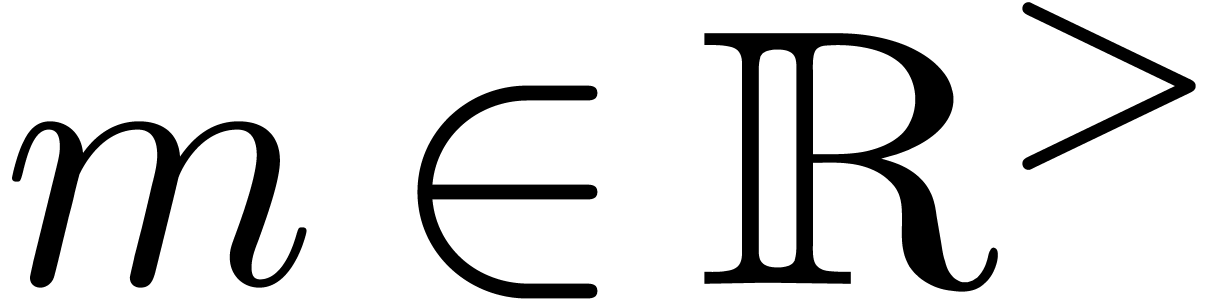 ,
we denote by
,
we denote by
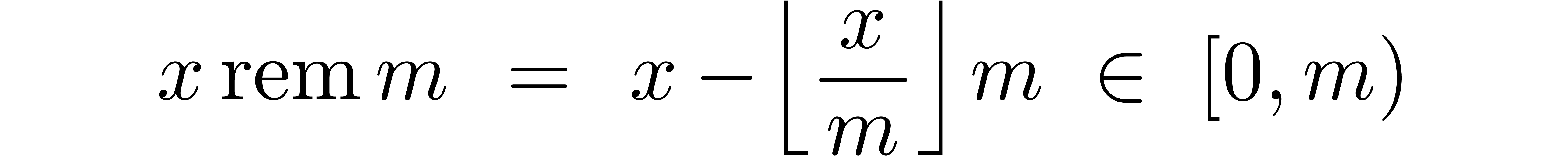
the remainder of the euclidean division of  by
by
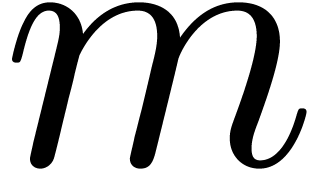 . Given
. Given 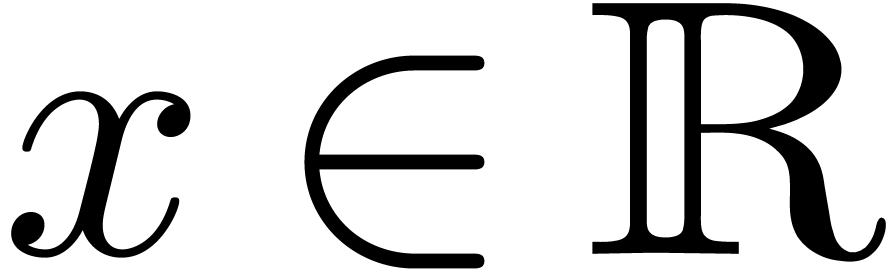 and
and  , we say that
, we say that 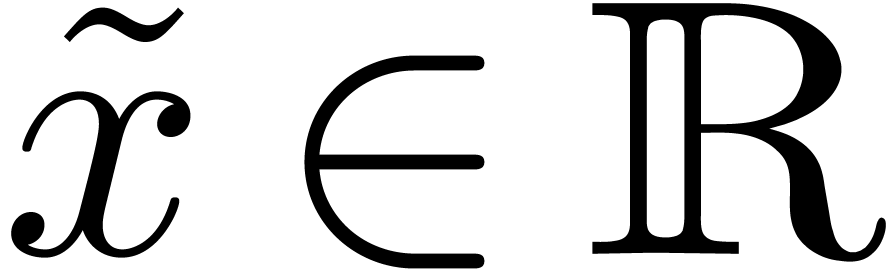 is an
is an  -approximation
of
-approximation
of  if
if 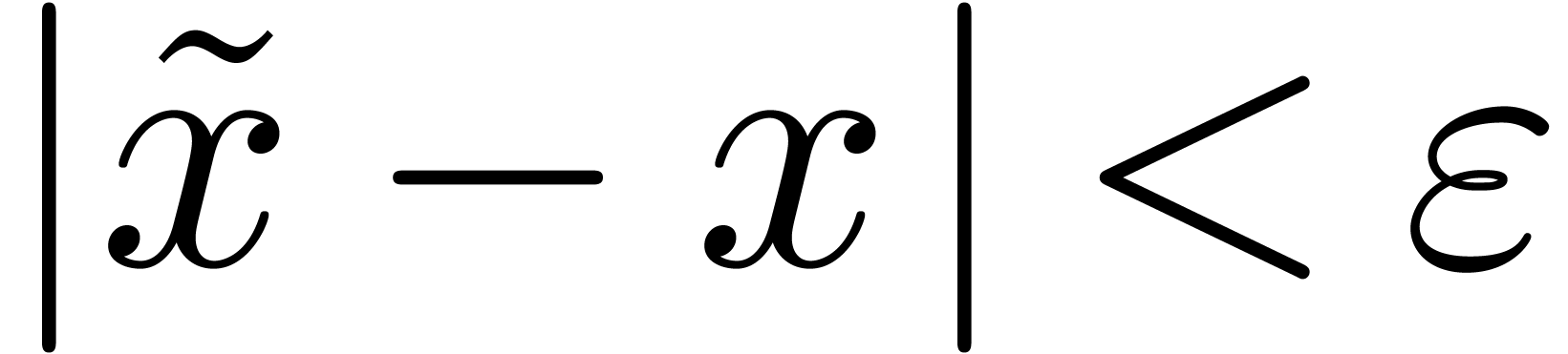 .
We also say that
.
We also say that  is a circular
is a circular  -approximation of
-approximation of  if
if 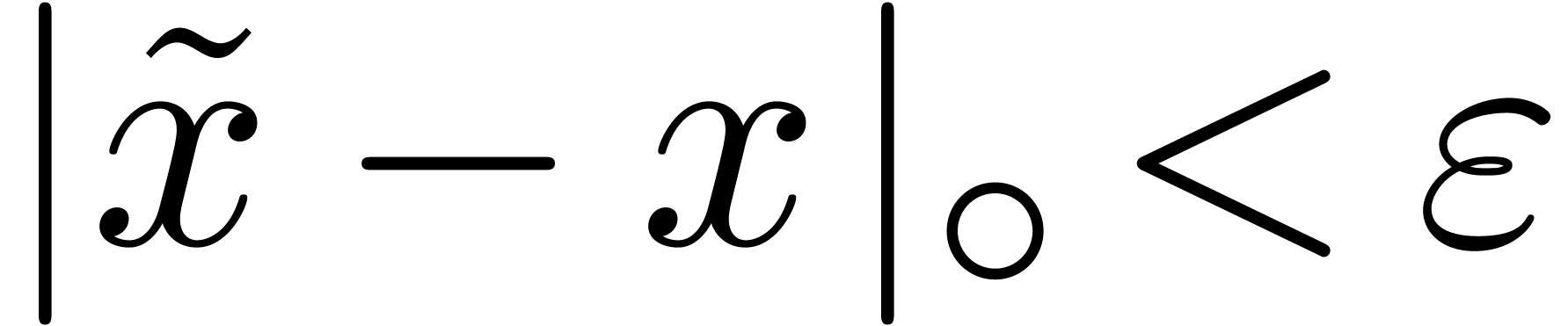 . Here
. Here 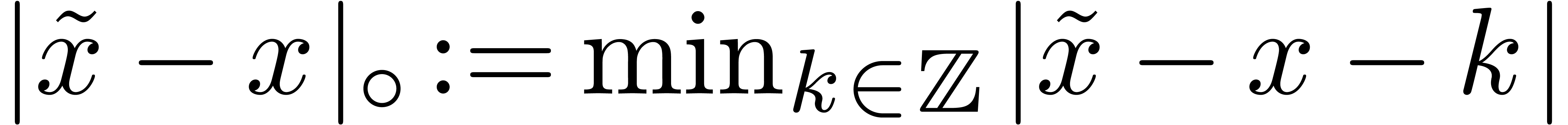 denotes the circular distance between
denotes the circular distance between  and
and  .
.
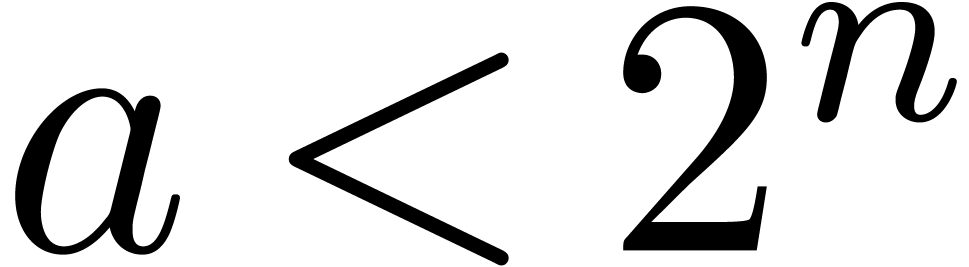
Let 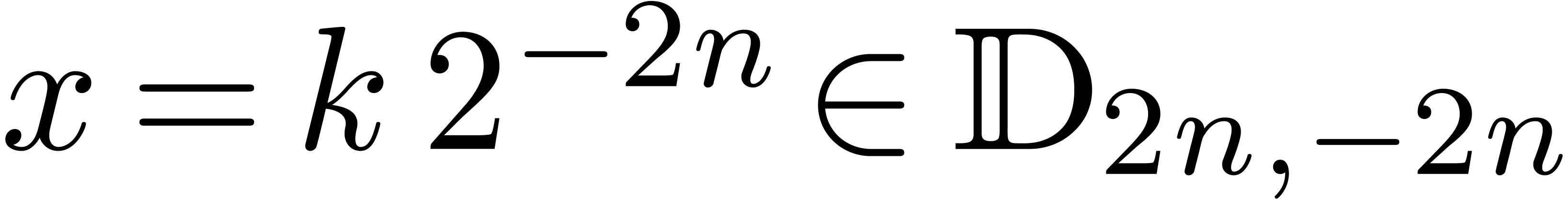 ,
, 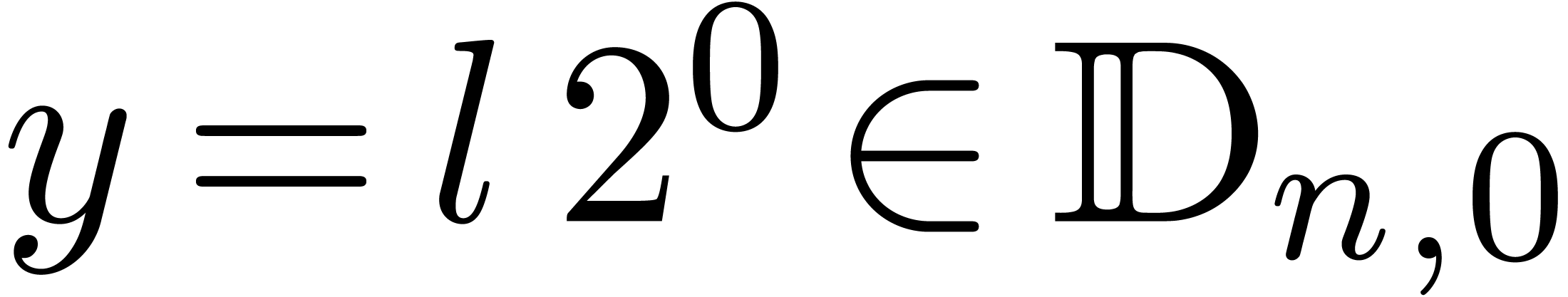 and
and 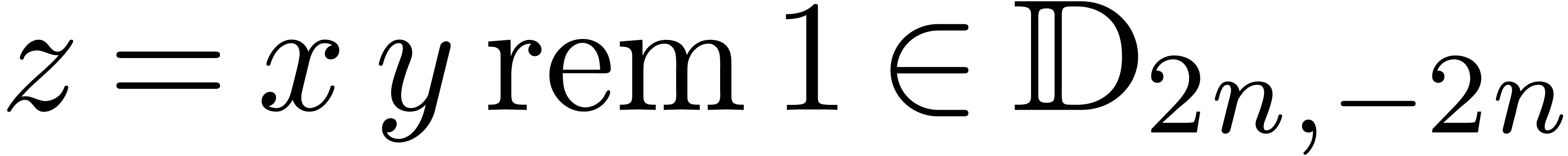 . Mutatis
mutandis, Bernstein observed in [2] that we may
compute a circular
. Mutatis
mutandis, Bernstein observed in [2] that we may
compute a circular  -approximation
-approximation
 for
for  as follows. We first
compute the product
as follows. We first
compute the product  of
of 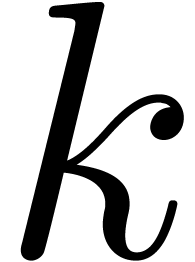 and
and  modulo
modulo 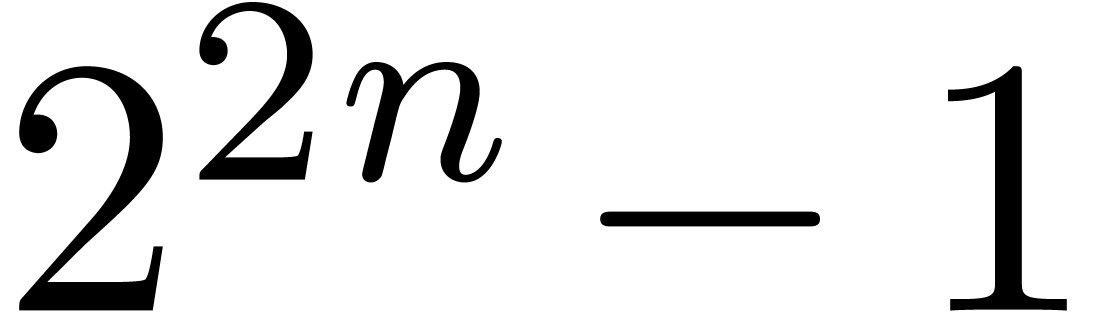 and then take
and then take
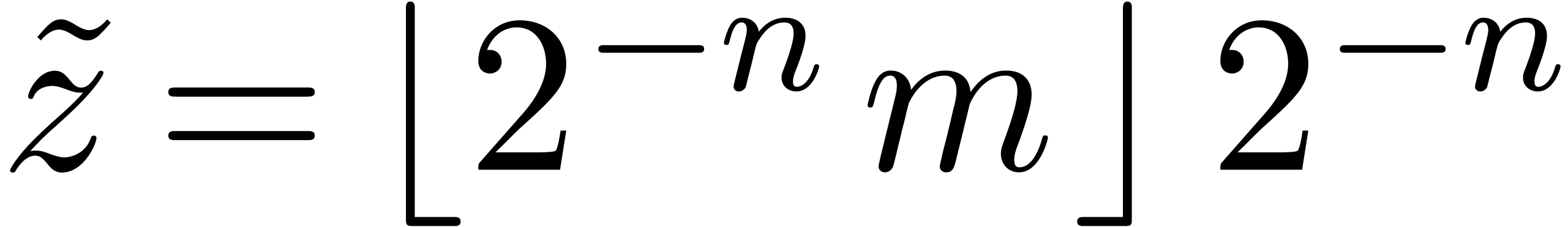 .
.
Let us show that  indeed satisfies the required
property. By construction, there exists an
indeed satisfies the required
property. By construction, there exists an 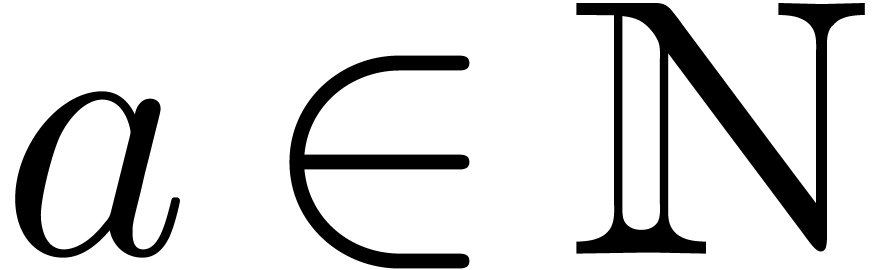 with
with
 such that
such that 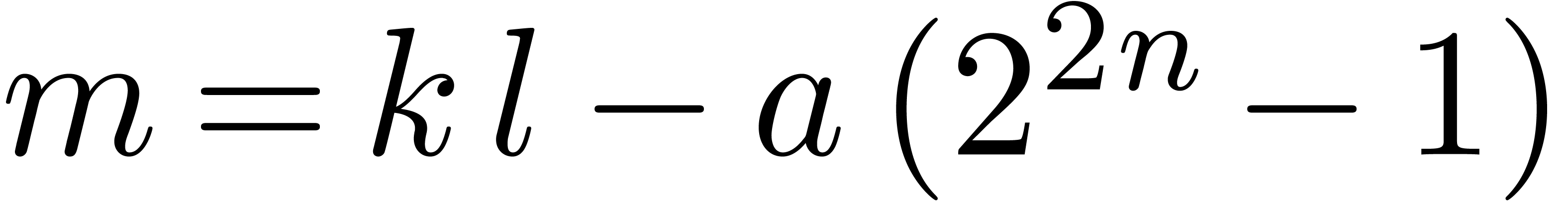 .
Therefore,
.
Therefore, 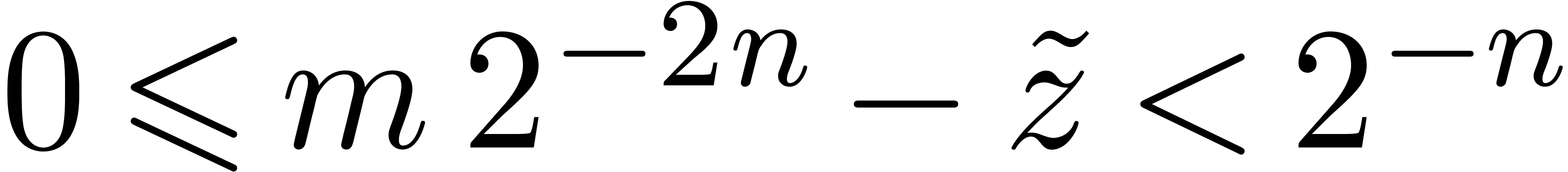 and
and 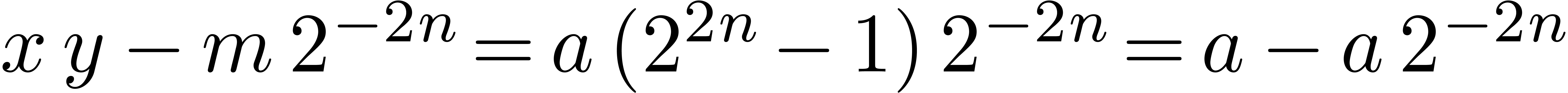 ,
whence
,
whence 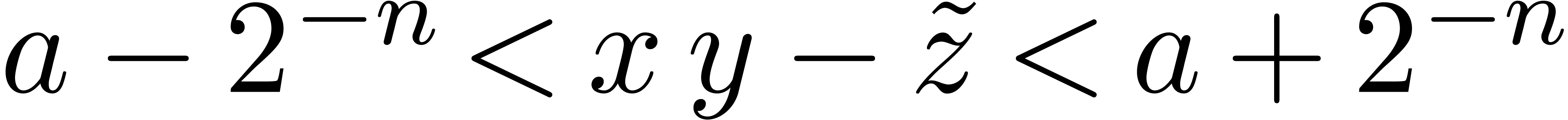 .
.
More generally, if we only have a circular 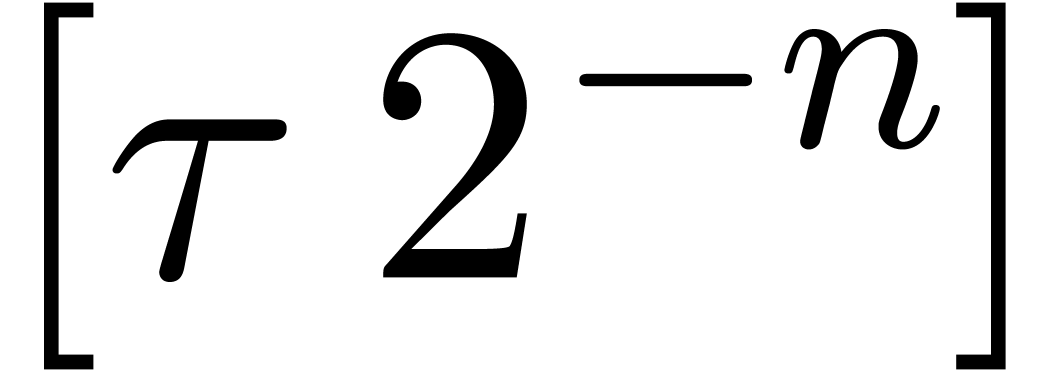 -approximation
-approximation
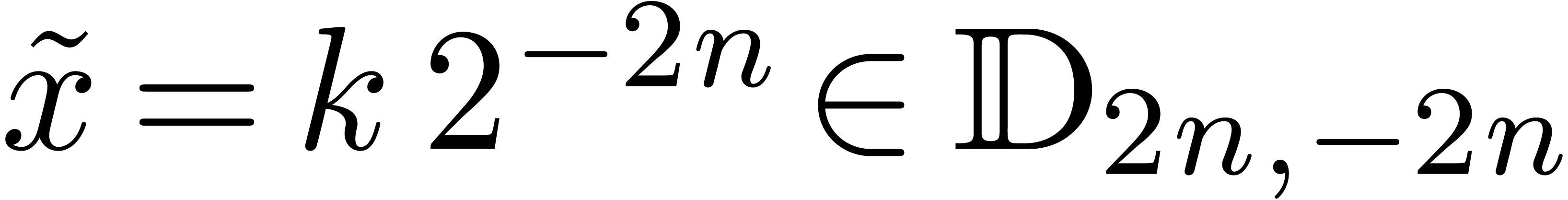 of a number
of a number 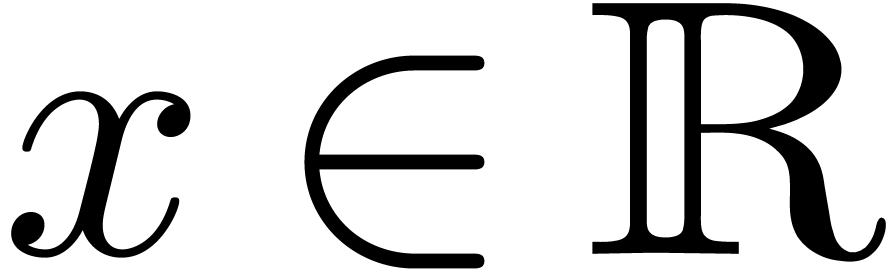 (instead of
a number
(instead of
a number 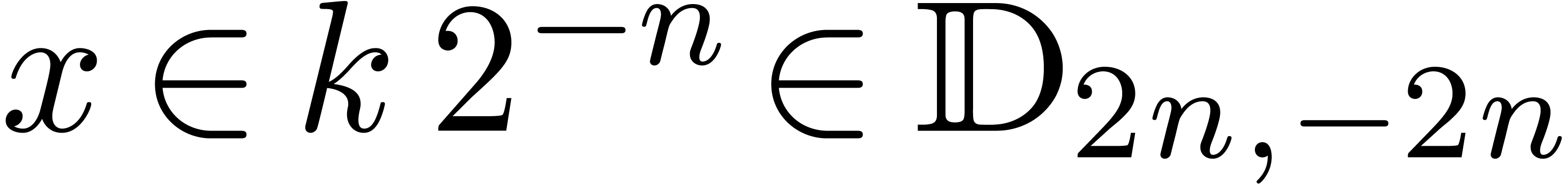 as above), then the algorithm computes
a circular
as above), then the algorithm computes
a circular 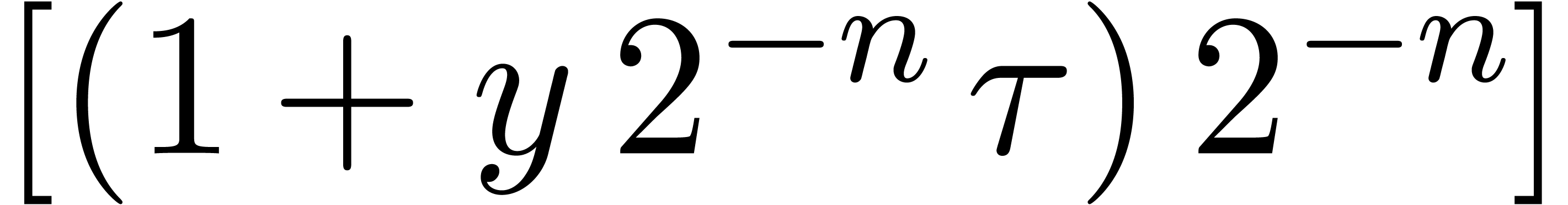 -approximation
-approximation
 of
of 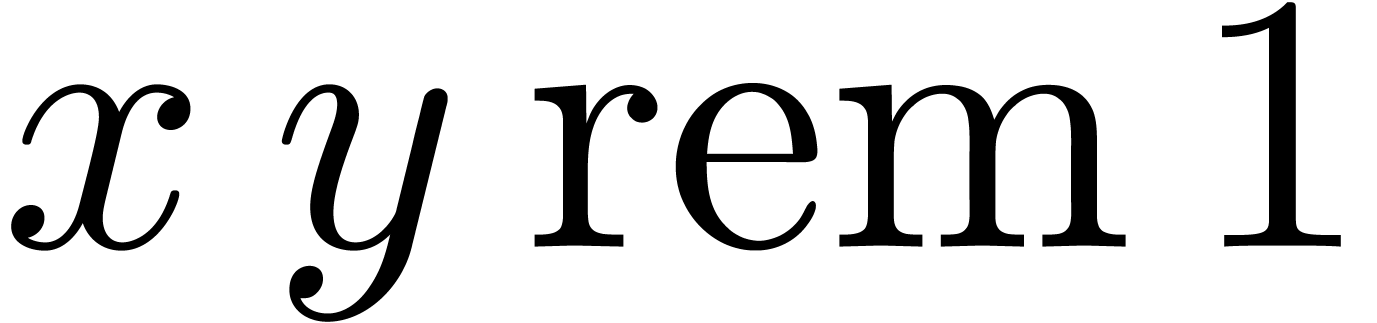 .
.
Bernstein's trick is illustrated in Figure 1: we are only
interested in the highlighted portion of the product. We notice that
these kinds of truncated products are reminiscent of the “middle
product” in the case of polynomials [12]; in our
setting, we also have to cope with carries and rounding errors. When
using FFT-multiplication, products modulo 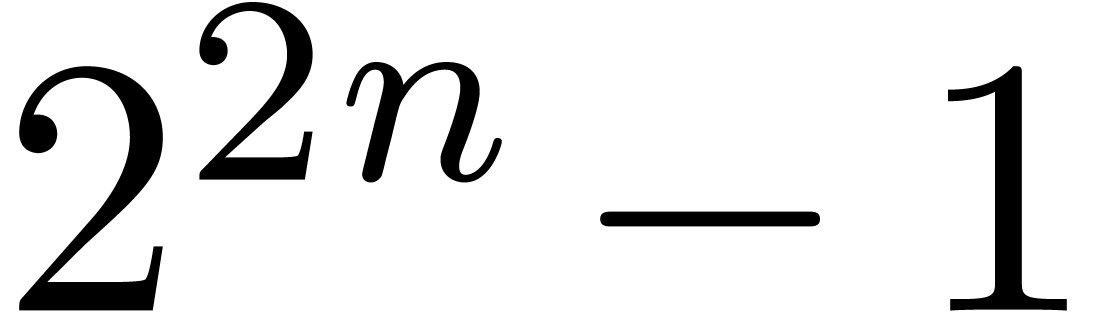 can be
computed using three discrete Fourier transforms of bitsize
can be
computed using three discrete Fourier transforms of bitsize 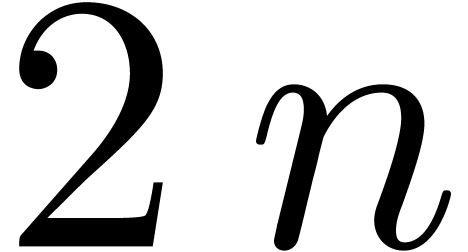 , so the cost is essentially the same as the
cost of an
, so the cost is essentially the same as the
cost of an  -bit integer
multiplication. If one of the arguments is fixed, then the cost becomes
asymptotic to
-bit integer
multiplication. If one of the arguments is fixed, then the cost becomes
asymptotic to 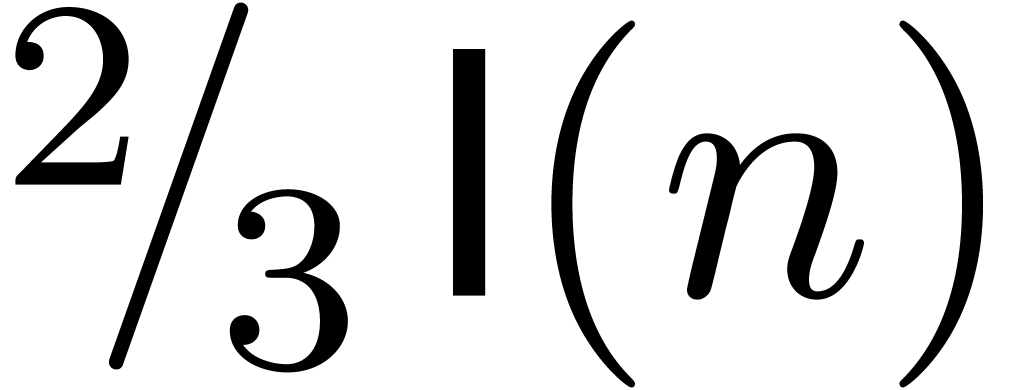 .
.
More generally, for 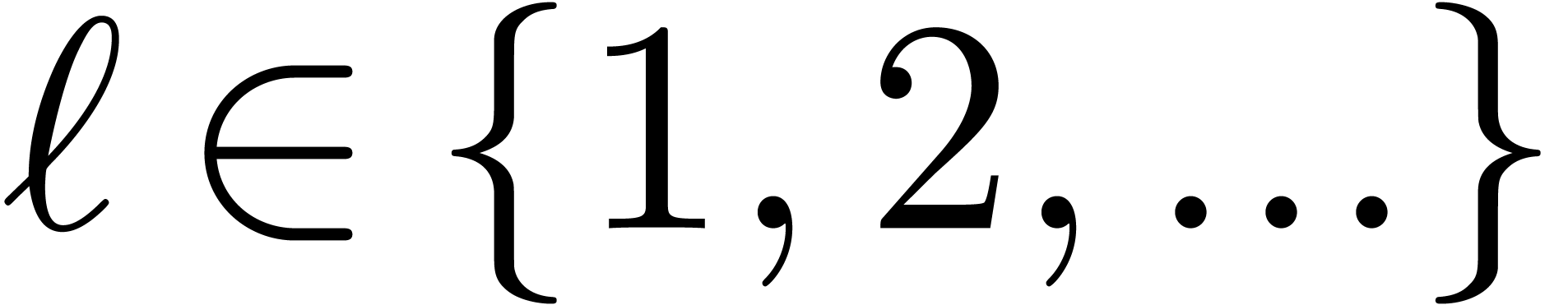 , let
, let
 be a circular
be a circular 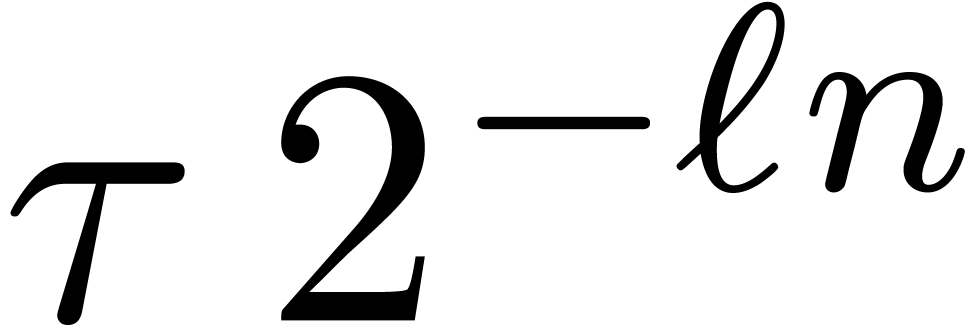 -approximation
of a number
-approximation
of a number  and let
and let 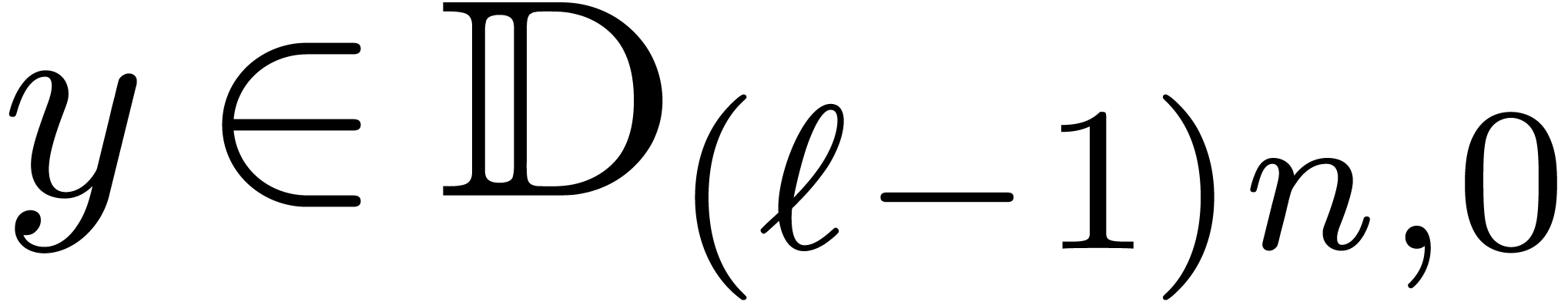 . Then we may compute a circular approximation
. Then we may compute a circular approximation  of
of  as follows. Consider the
expansions
as follows. Consider the
expansions
 |
(4) |
with  ; see Figure 2.
By what precedes, for
; see Figure 2.
By what precedes, for  , we
may compute circular
, we
may compute circular  -approximations
-approximations
 for
for
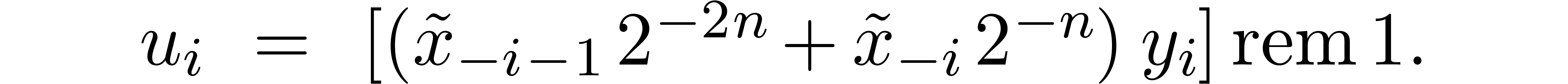
Setting
it follows that  , whereas
, whereas
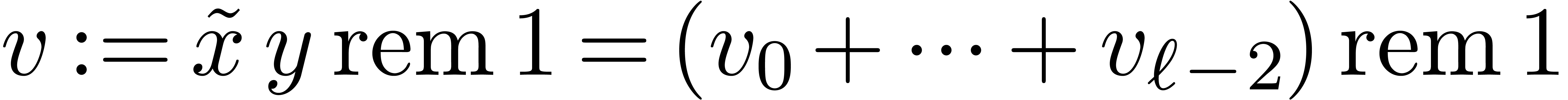 . Taking
. Taking  , it follows that
, it follows that 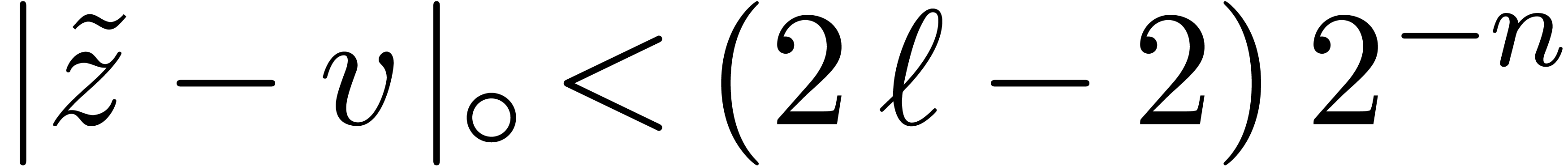 and
and
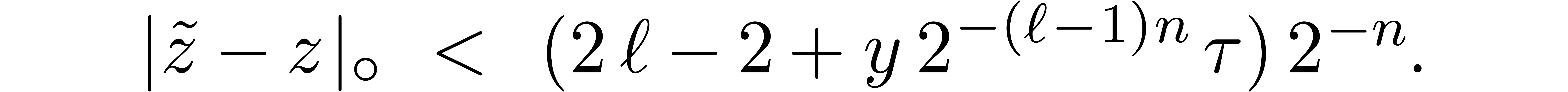
When using FFT-multiplication, we notice that the sum 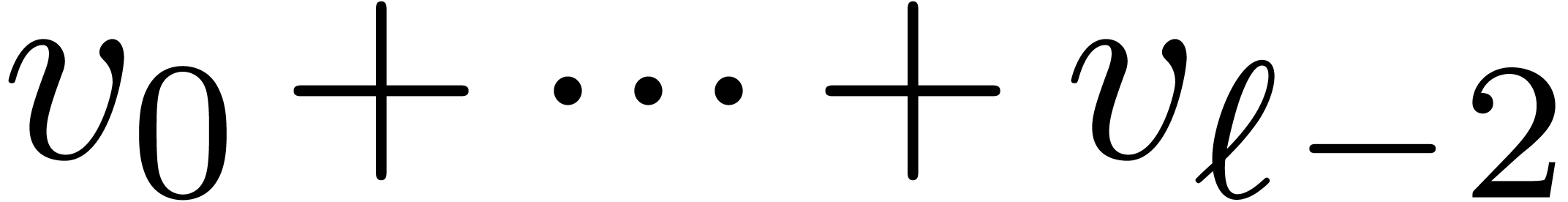 can be computed in the FFT-model, before being transformed back. In that
way, we only need
can be computed in the FFT-model, before being transformed back. In that
way, we only need 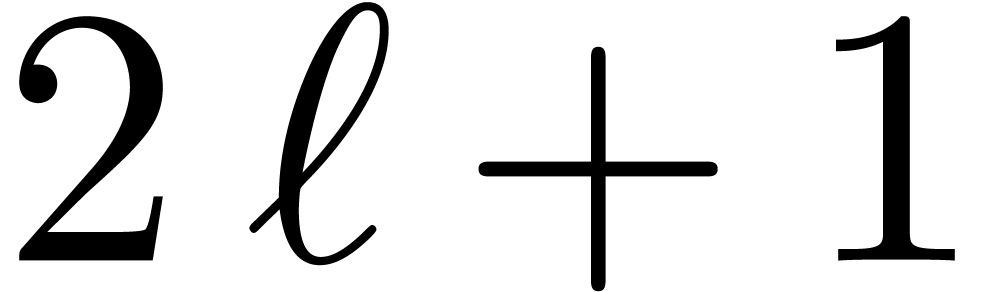 instead of
instead of 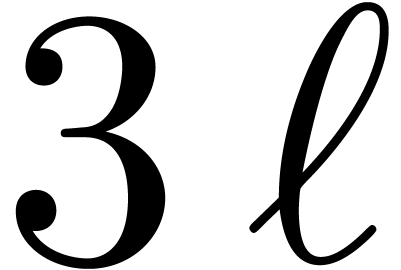 transforms of size
transforms of size 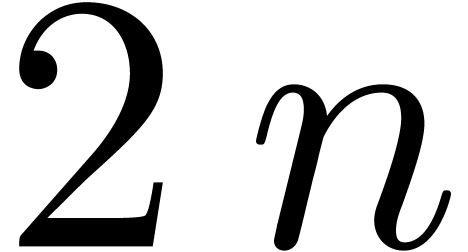 , for a
total cost of
, for a
total cost of  .
.
For actual machine implementations of large integer arithmetic, it is
customary to choose a base of the form  and to
perform all computations with respect to that base. We will call
and to
perform all computations with respect to that base. We will call  the soft word size. For processors that have
good hardware support for integer arithmetic, taking
the soft word size. For processors that have
good hardware support for integer arithmetic, taking  or
or  is usually most efficient. The GMP package
[11] uses this approach.
is usually most efficient. The GMP package
[11] uses this approach.
However, modern processors are often better at floating point
arithmetic. General purpose processors generally provide double
precision IEEE-768 compliant instructions, whereas GPUs are frequently
limited to single precision. The respective choices  and
and  are most adequate in these cases. It is good
to pick
are most adequate in these cases. It is good
to pick  slightly below the maximum bitsize of
the mantissa in order to accelerate carry handling. We refer to [17] for more details on the implementation of multiple
precision arithmetic based on floating point arithmetic.
slightly below the maximum bitsize of
the mantissa in order to accelerate carry handling. We refer to [17] for more details on the implementation of multiple
precision arithmetic based on floating point arithmetic.
Another particularity of recent processors is the availability of ever
wider SIMD (Single Instruction Multiple Data) instructions. For modern
implementations of large integer arithmetic, we therefore recommend to
focus on the problem of multiplying several ( ) large integers of a given bitsize instead of
a single one. We again refer to [17] for more details.
) large integers of a given bitsize instead of
a single one. We again refer to [17] for more details.
In what follows, when using integer arithmetic, we will denote by 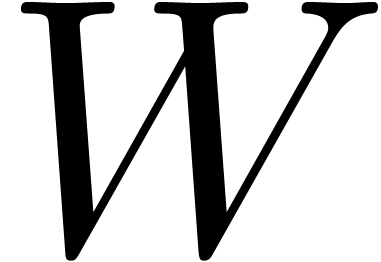 the maximal bitsize such that we have a hardware
instruction to multiply two integers of
the maximal bitsize such that we have a hardware
instruction to multiply two integers of 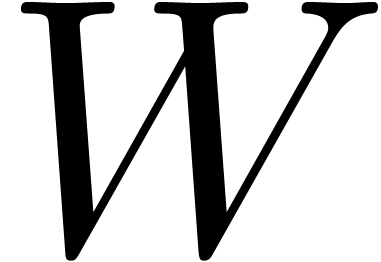 bits
(e.g.
bits
(e.g.  or
or  ). When using floating point arithmetic, we let
). When using floating point arithmetic, we let 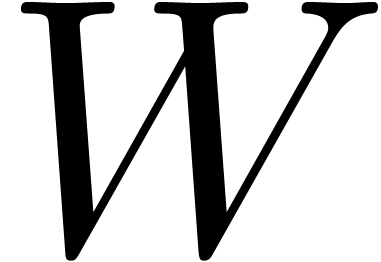 be the bitsize of a mantissa (i.e.
be the bitsize of a mantissa (i.e. 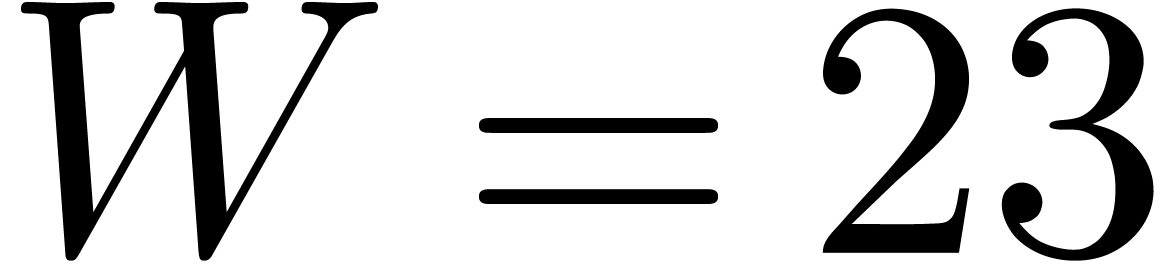 or
or 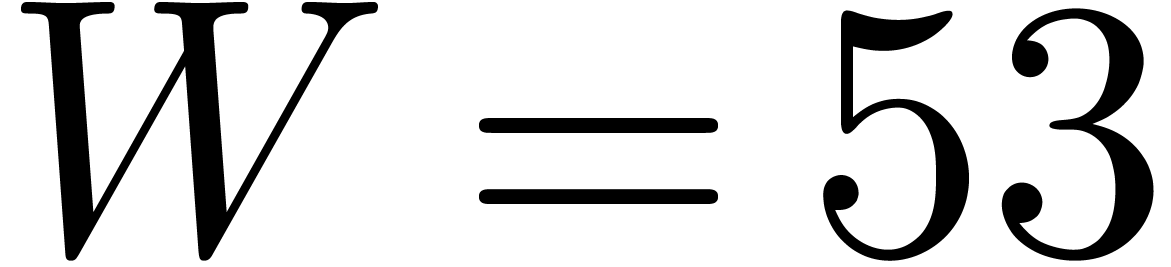 ). We
will call
). We
will call 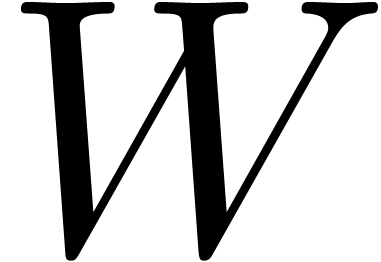 the machine word size. For
implementations of multiple precision arithmetic, we always have
the machine word size. For
implementations of multiple precision arithmetic, we always have 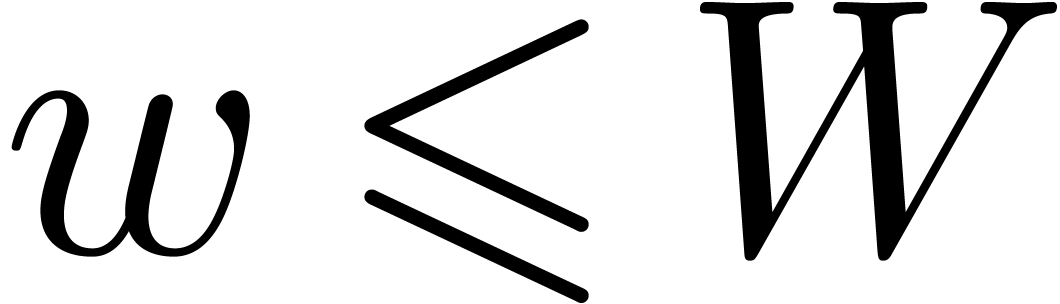 , but it can be interesting to take
, but it can be interesting to take
 .
.
For moduli 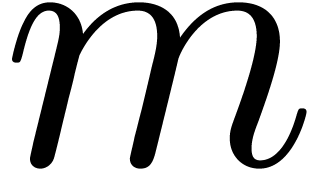 that fit into a machine word,
arithmetic modulo
that fit into a machine word,
arithmetic modulo 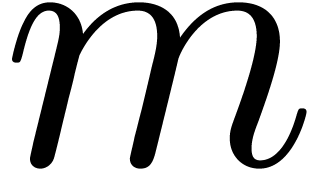 can be implemented efficiently
using hardware instructions. In this case, the available algorithms
again tend to be somewhat faster if the size of
can be implemented efficiently
using hardware instructions. In this case, the available algorithms
again tend to be somewhat faster if the size of 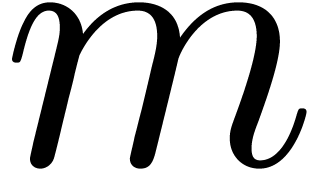 is a few bit smaller than
is a few bit smaller than  .
We refer to [19] for a survey of the best currently
available algorithms in various cases and how to exploit SIMD
instructions.
.
We refer to [19] for a survey of the best currently
available algorithms in various cases and how to exploit SIMD
instructions.
When using arithmetic modulo 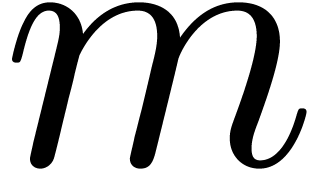 ,
it is often possible to delay the reductions modulo
,
it is often possible to delay the reductions modulo 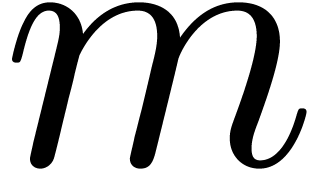 as much as possible. One typical example is modular matrix
multiplication. Assume that we have two
as much as possible. One typical example is modular matrix
multiplication. Assume that we have two  matrices
with coefficients modulo
matrices
with coefficients modulo 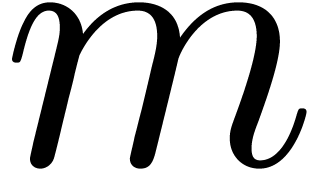 (represented by
integers between
(represented by
integers between 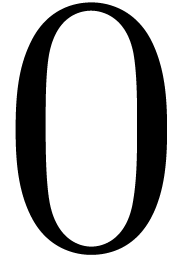 and
and 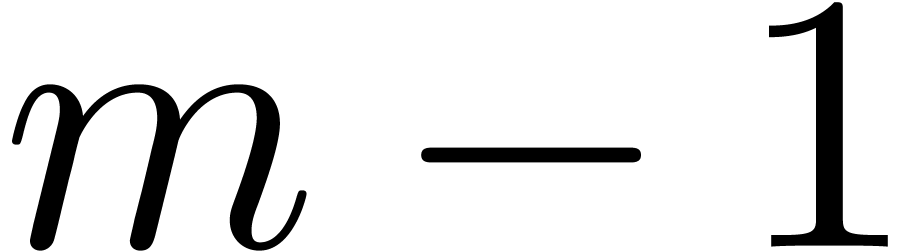 , say). If
, say). If 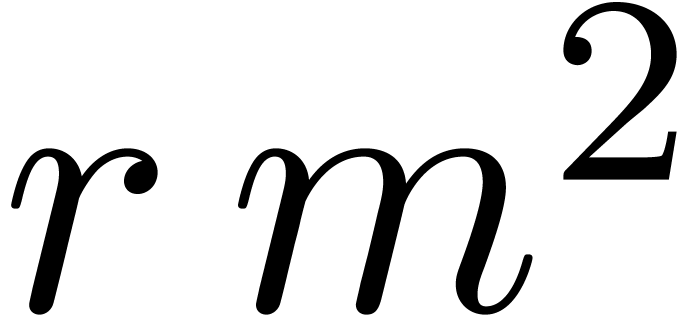 fits into a
machine word, then we may multiply the matrices using integer or
floating point arithmetic and reduce the result modulo
fits into a
machine word, then we may multiply the matrices using integer or
floating point arithmetic and reduce the result modulo 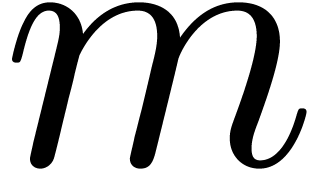 . This has the advantage that we may use
standard, highly optimized implementations of matrix multiplication. One
drawback is that the intermediate results before reduction require at
least twice as much space. Also, the bitsize of the modulus is at least
twice as small as
. This has the advantage that we may use
standard, highly optimized implementations of matrix multiplication. One
drawback is that the intermediate results before reduction require at
least twice as much space. Also, the bitsize of the modulus is at least
twice as small as  .
.
For any integer 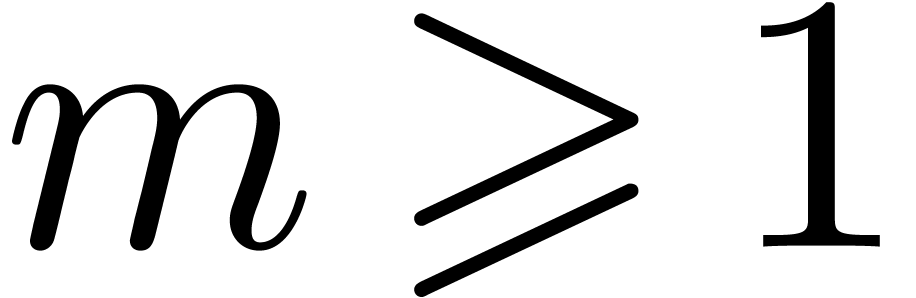 , we will
write
, we will
write  . We recall:
. We recall:
 be positive integers that are mutually coprime and
denote
be positive integers that are mutually coprime and
denote 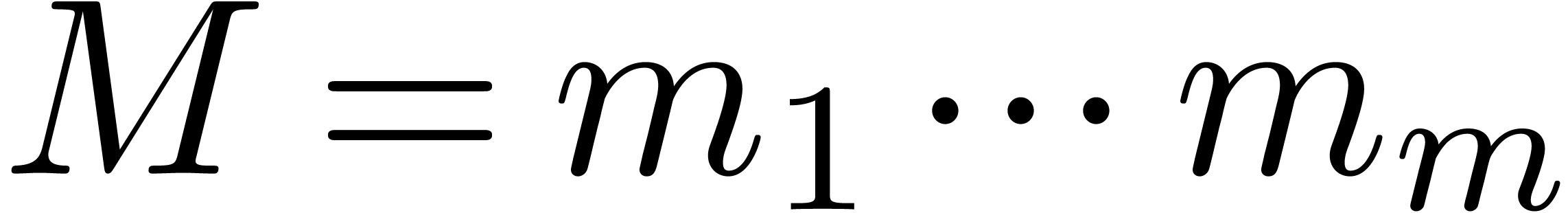 . Given
. Given  , there exists a unique
, there exists a unique 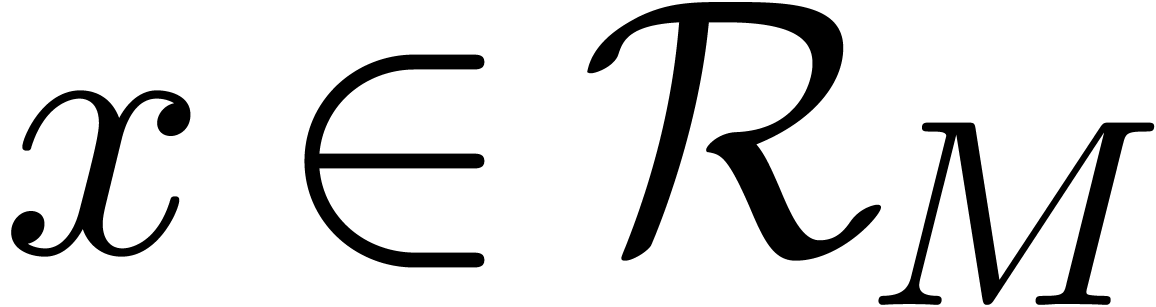 with
with 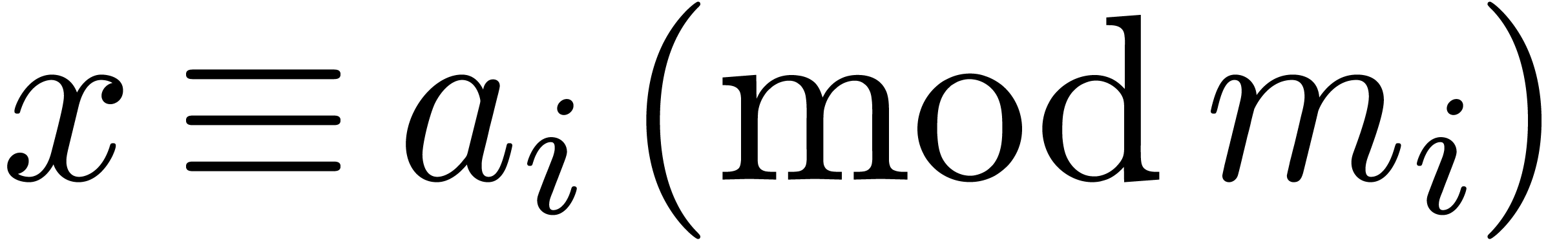 for
for 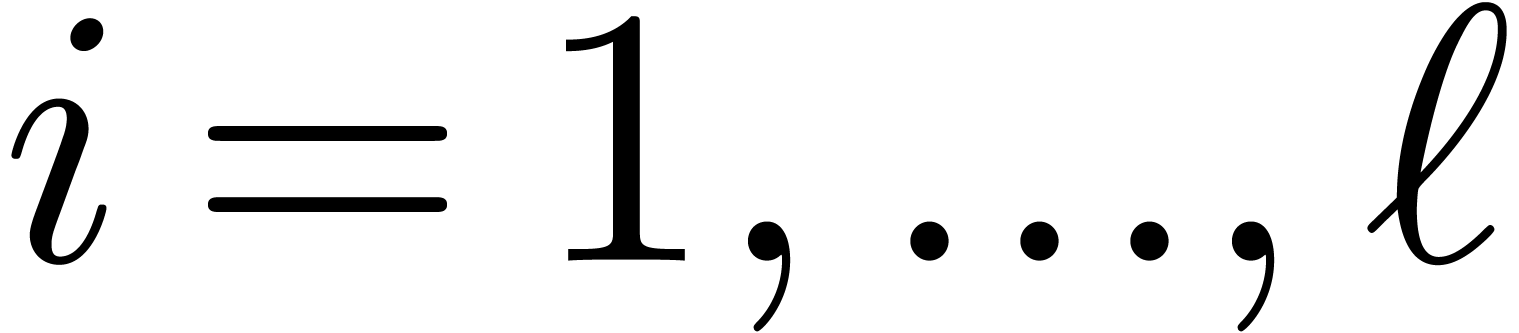 .
.
We will prove the following more constructive version of this theorem.
 be positive integers that are
mutually coprime and denote
be positive integers that are
mutually coprime and denote 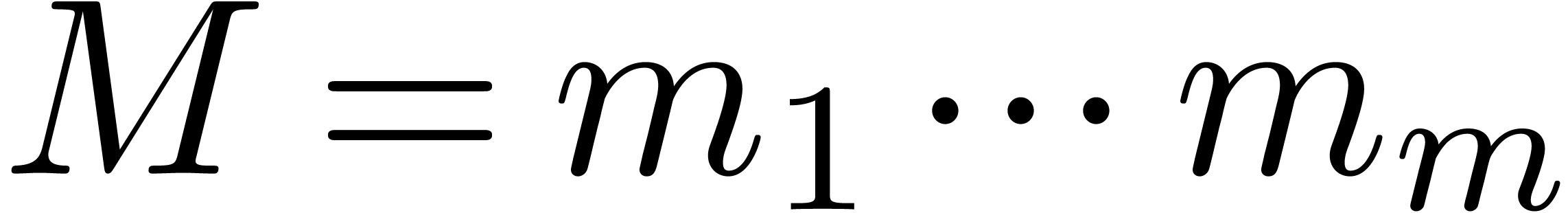 .
There exist
.
There exist 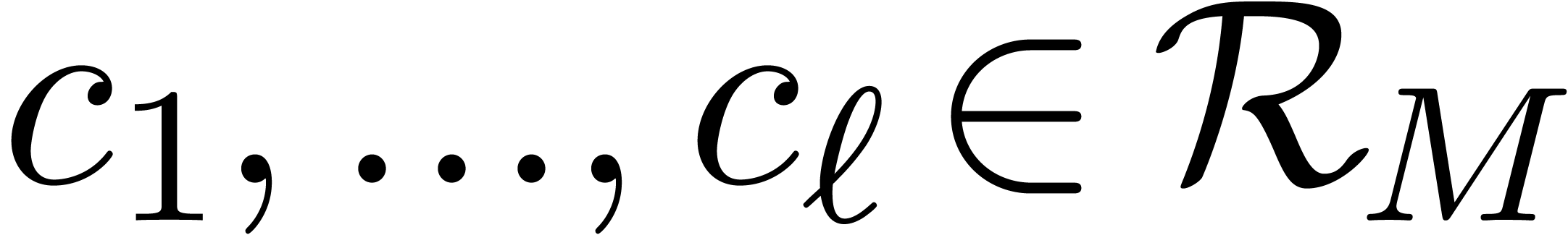 such that for any
such that for any  , the number
, the number

satisfies 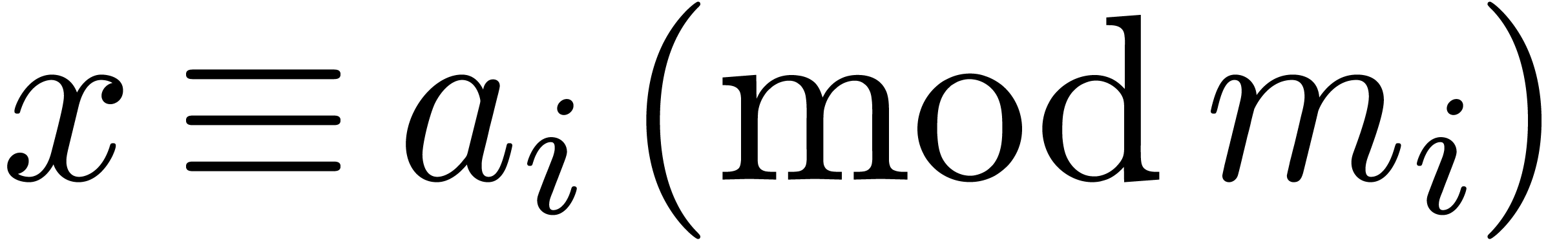 for
for 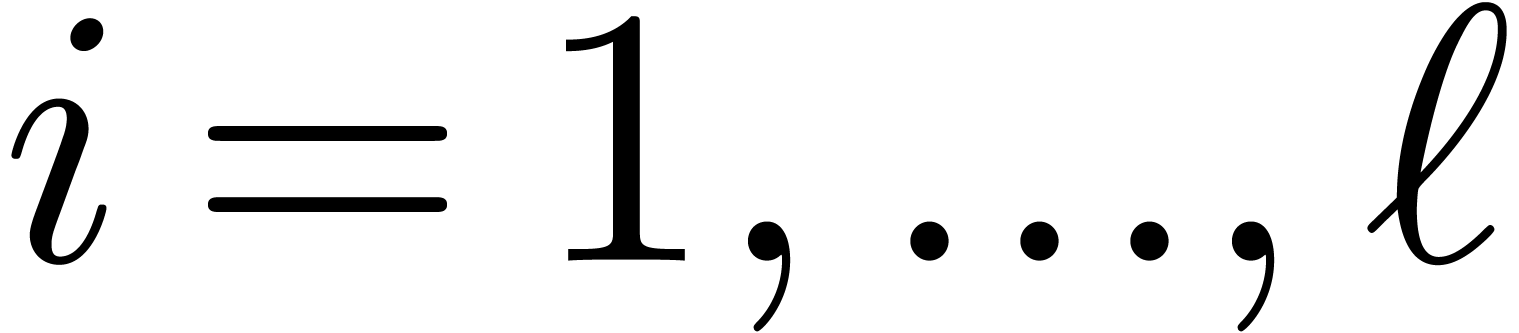 .
.
 the cofactors for
the cofactors for  in
in 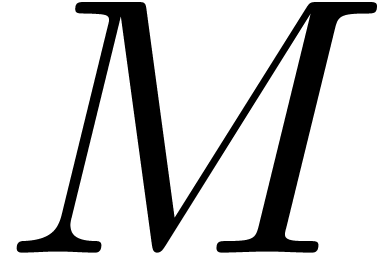 and also denote these numbers by
and also denote these numbers by  .
.
Proof. If 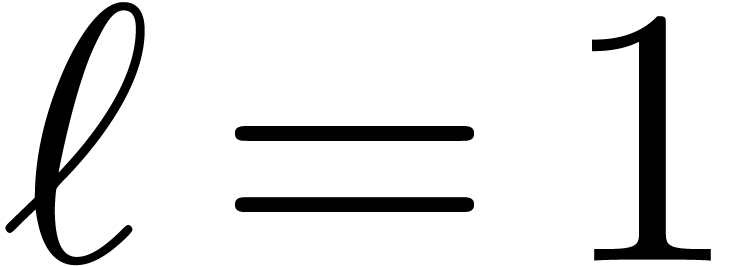 ,
then it suffices to take
,
then it suffices to take 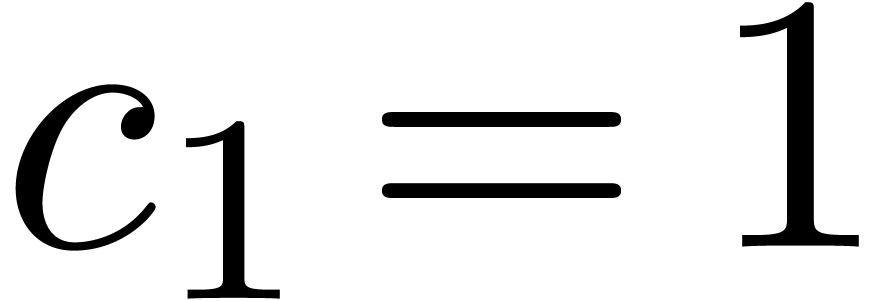 . If
. If
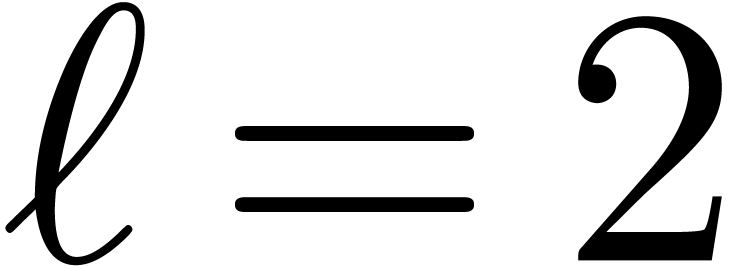 , then the extended Euclidean
algorithm allows us to compute a Bezout relation
, then the extended Euclidean
algorithm allows us to compute a Bezout relation
where 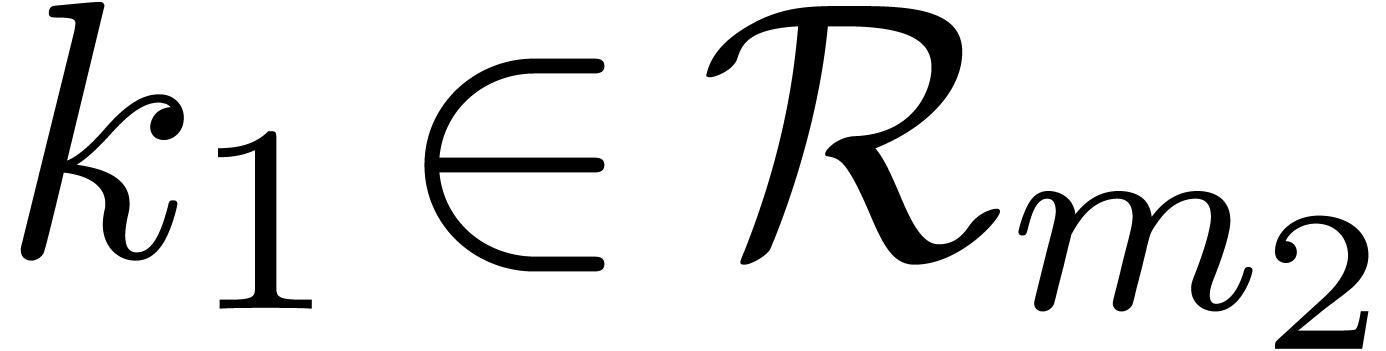 and
and 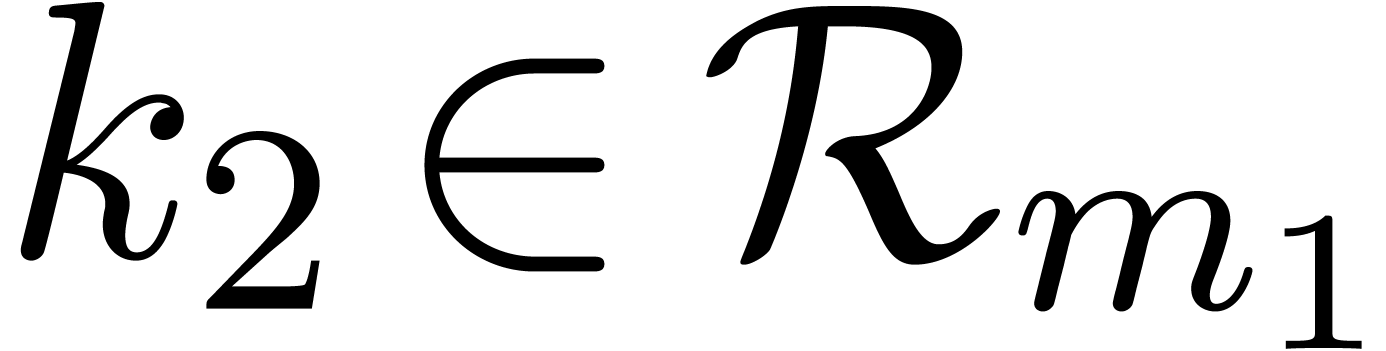 .
Let us show that we may take
.
Let us show that we may take
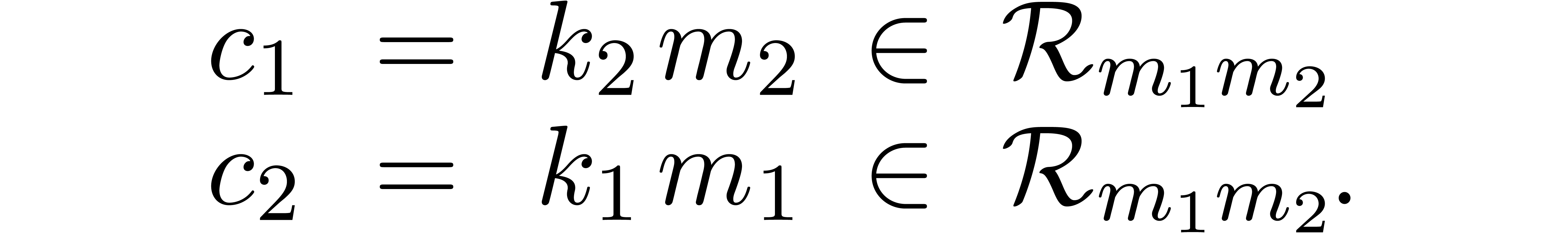
Indeed, given 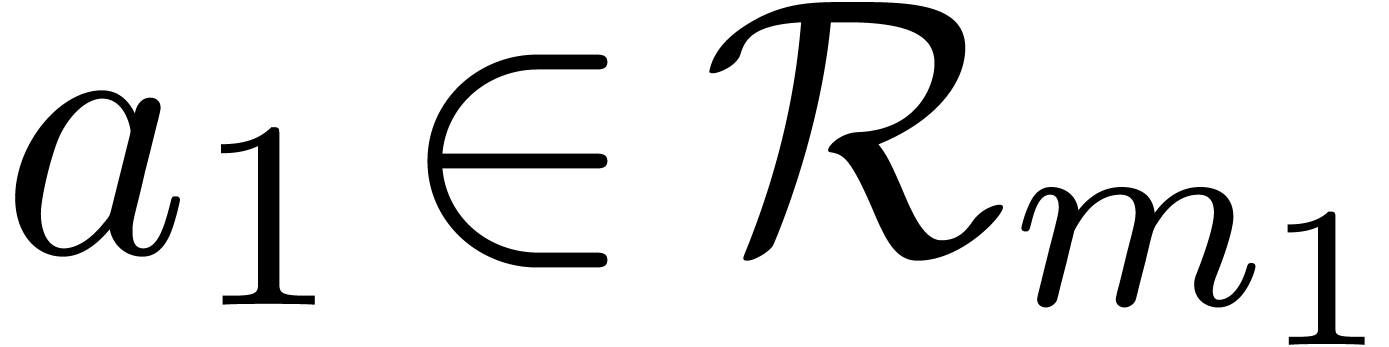 and
and 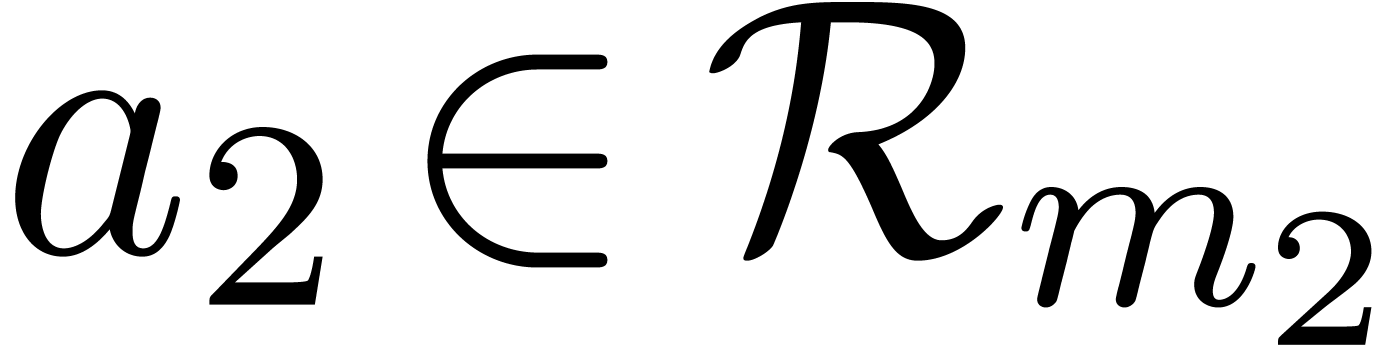 ,
we have
,
we have
In particular, 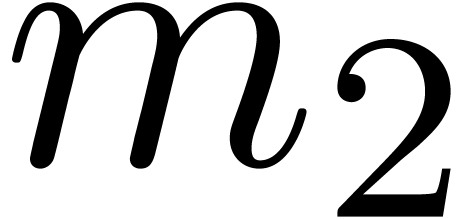 divides
divides 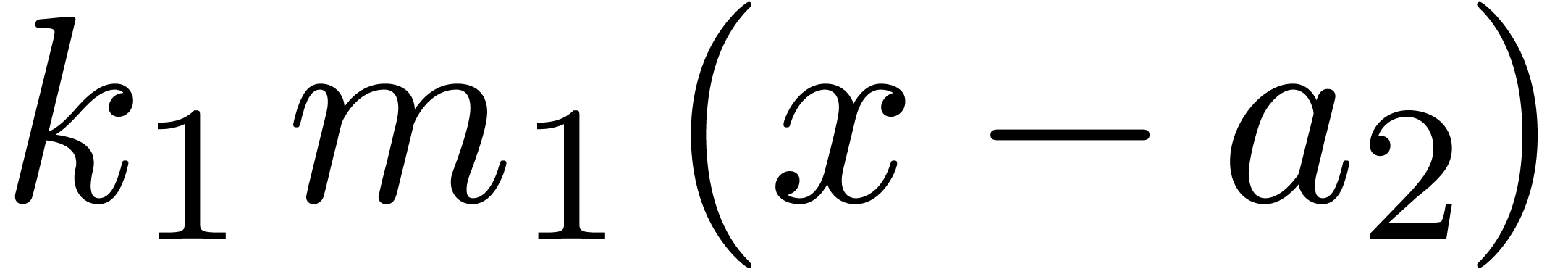 . Since (5) implies
. Since (5) implies 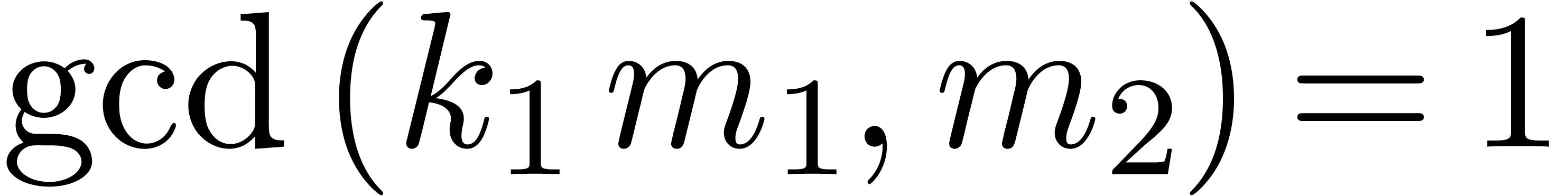 , it follows that
, it follows that 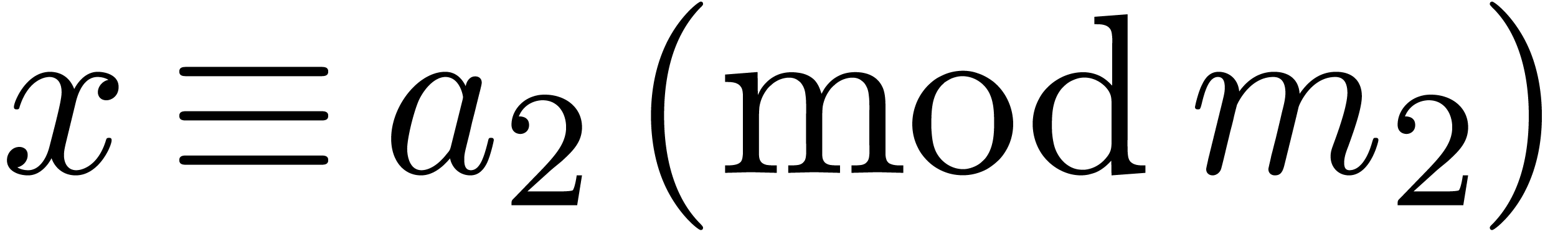 .
Similarly,
.
Similarly, 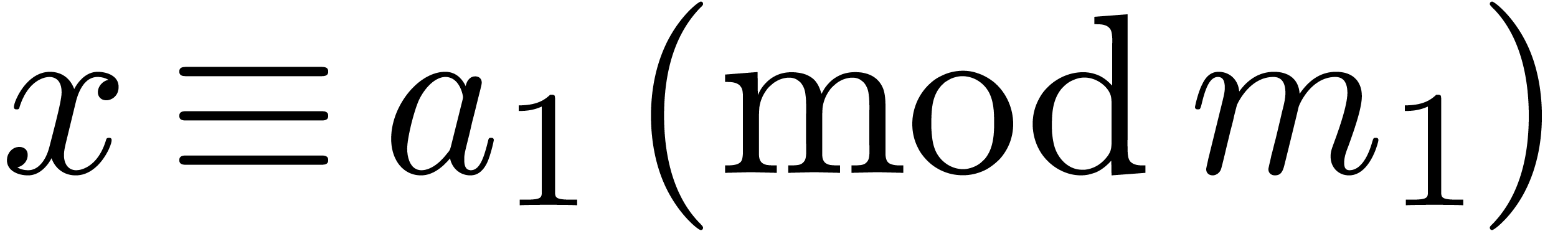 .
.
For 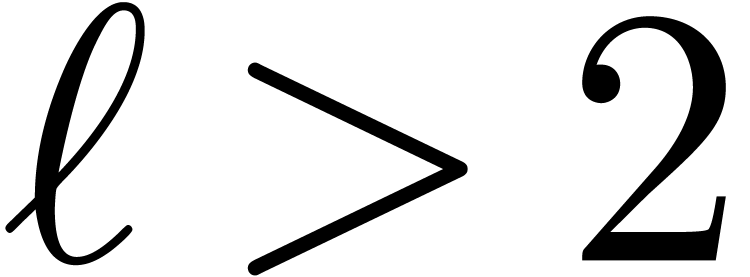 , we will use induction.
Let
, we will use induction.
Let 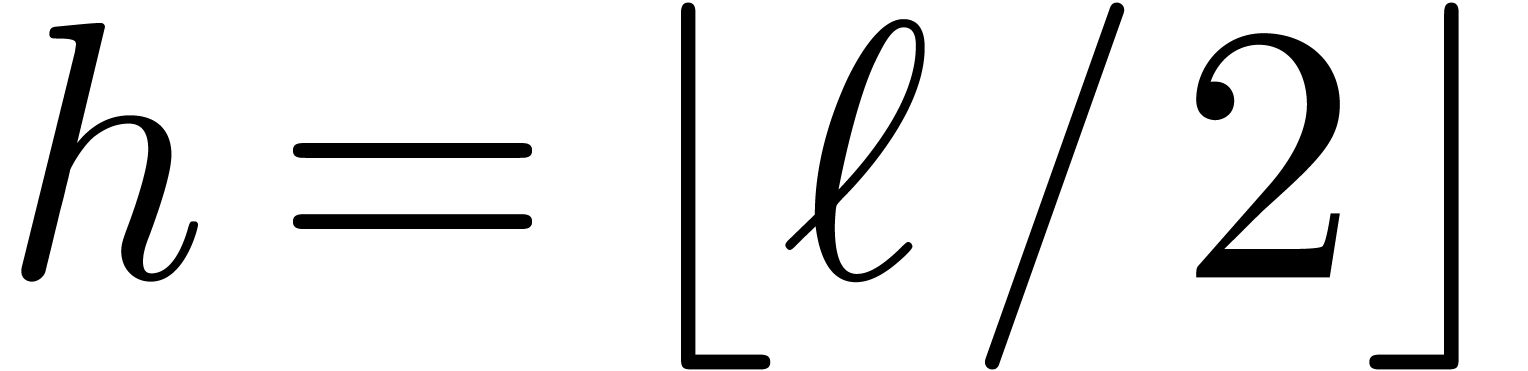 ,
, 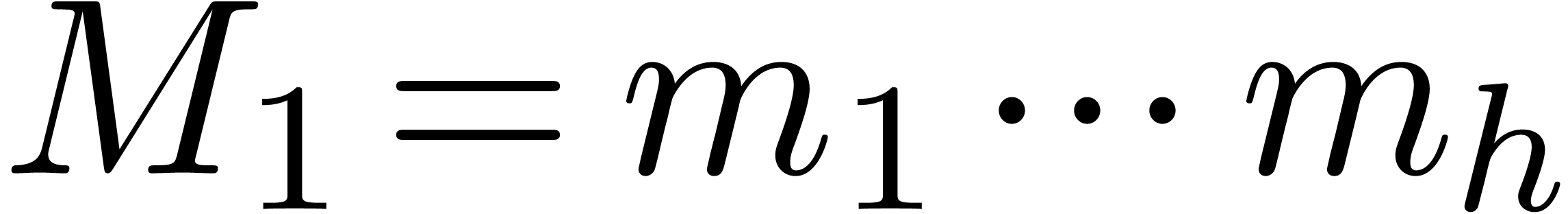 and
and 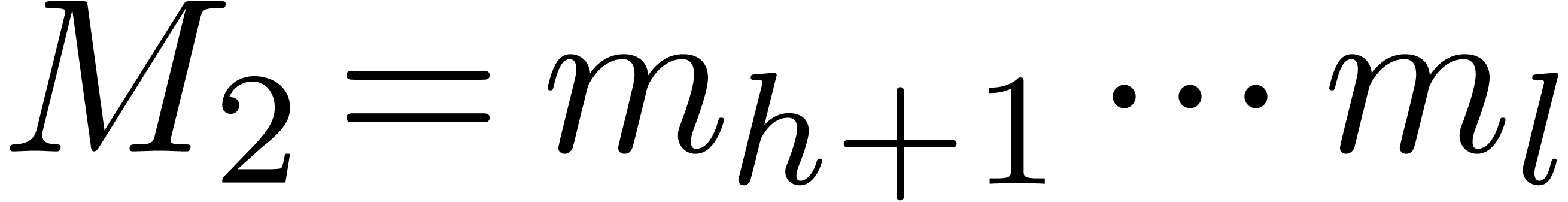 . By induction, we may
compute
. By induction, we may
compute 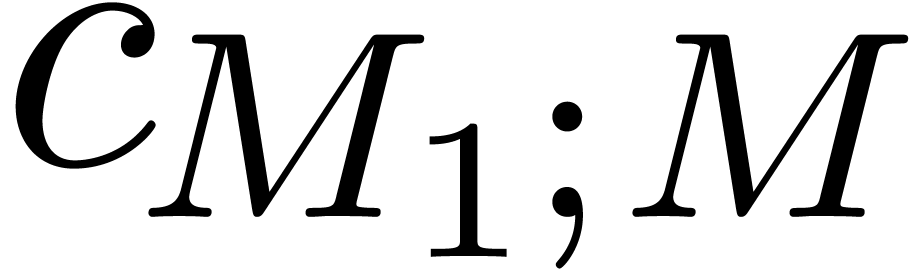 ,
, 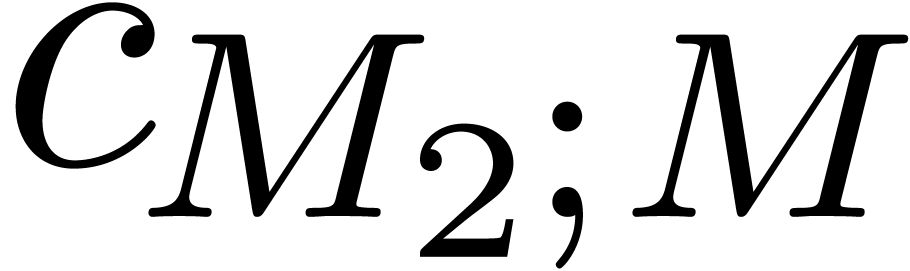 ,
,  and
and  . We claim that we may take
. We claim that we may take
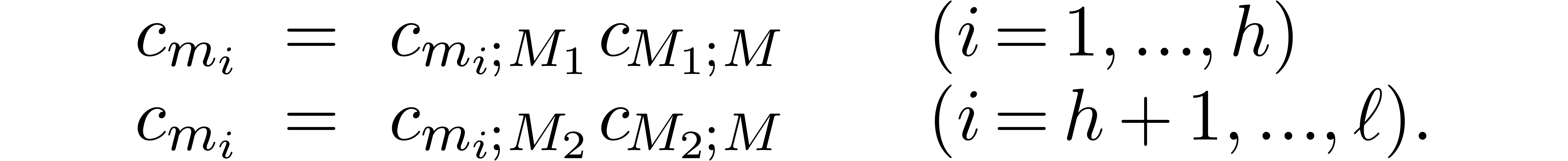
Indeed, for 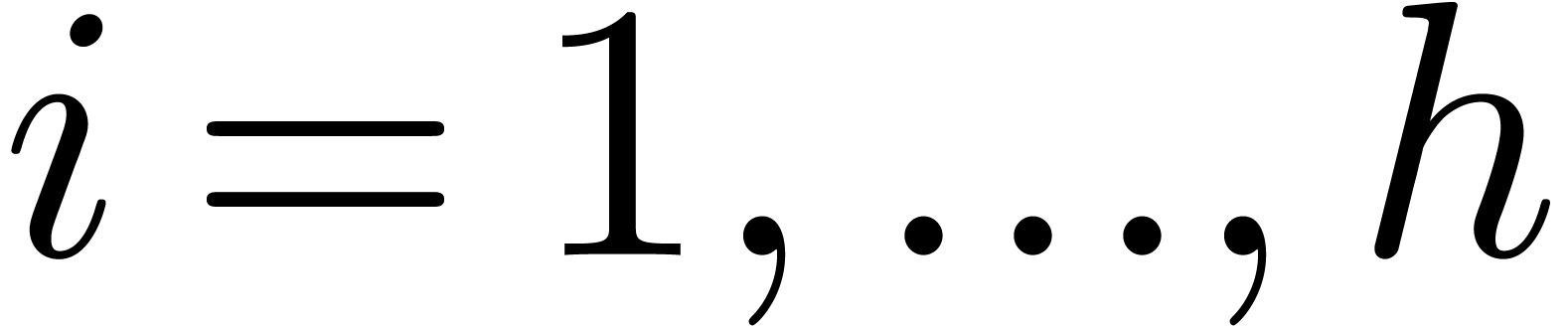 , we get
, we get
whence 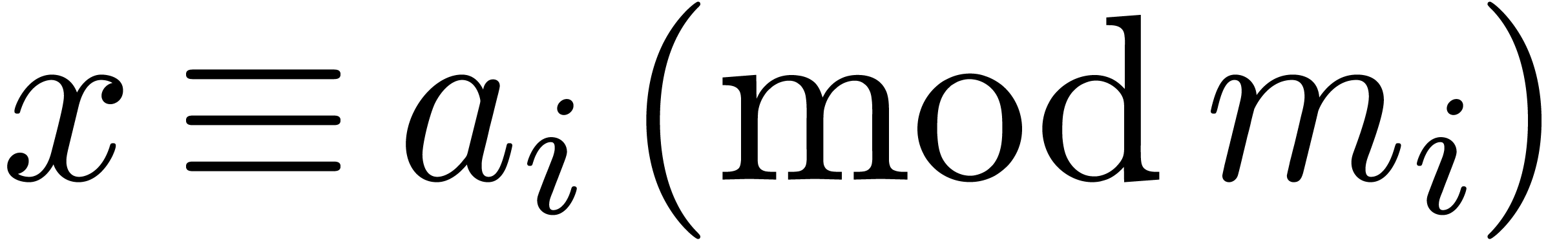 . For
. For 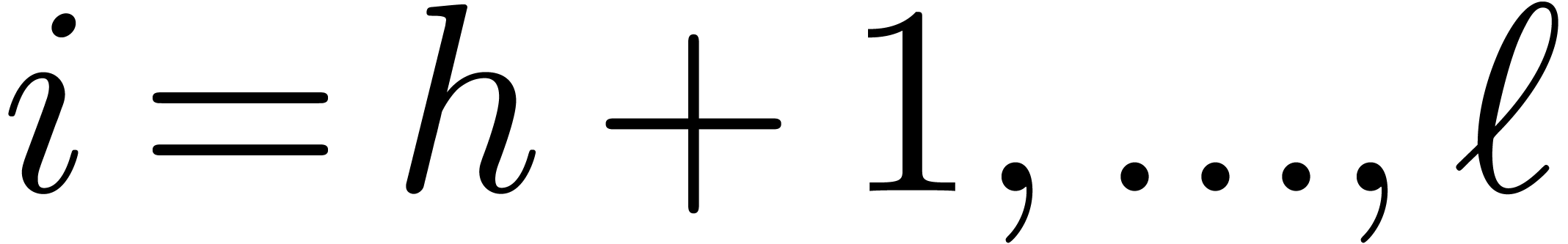 we obtain
we obtain 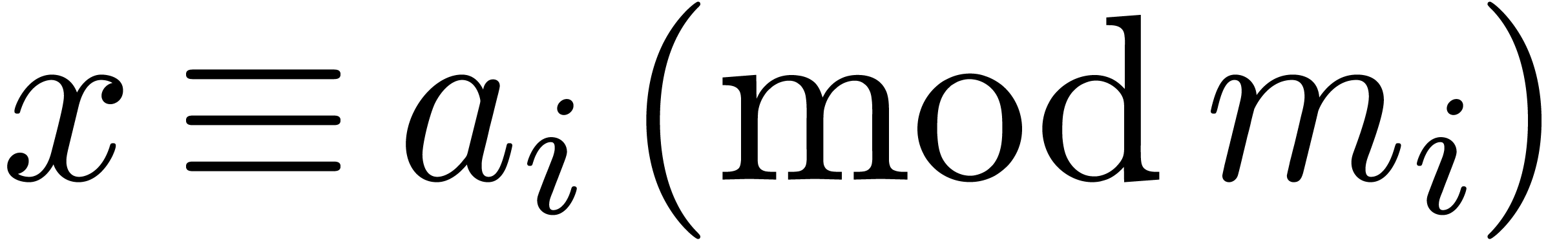 in a similar way.
in a similar way.
Let  ,
, 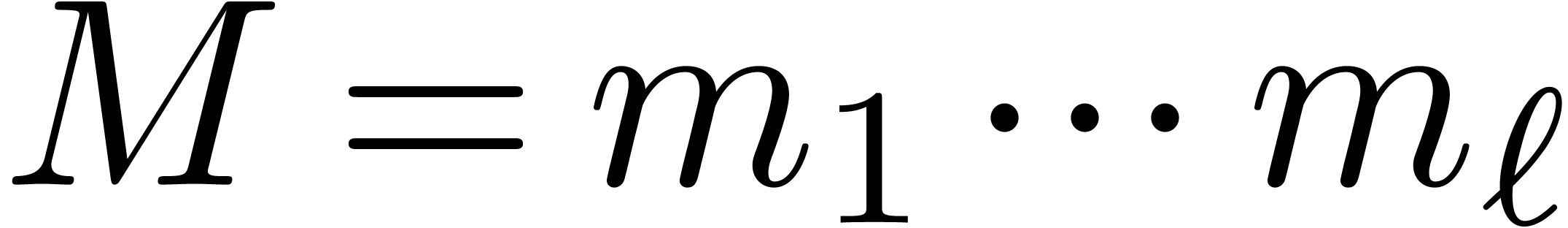 ,
,  and
and 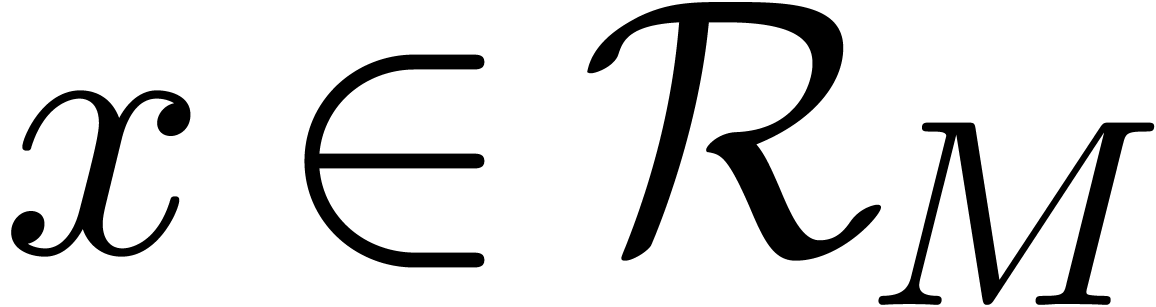 be as in the Chinese remainder theorem. We will refer to the computation
of
be as in the Chinese remainder theorem. We will refer to the computation
of  as a function of
as a function of  as
the problem of multi-modular reduction. The inverse problem is
called multi-modular reconstruction. In what follows, we assume
that
as
the problem of multi-modular reduction. The inverse problem is
called multi-modular reconstruction. In what follows, we assume
that  have been fixed once and for all.
have been fixed once and for all.
The simplest way to perform multi-modular reduction is to simply take
Inversely, Theorem 1 provides us with a formula for multi-modular reconstruction:
Since  are fixed, the computation of the
cofactors
are fixed, the computation of the
cofactors 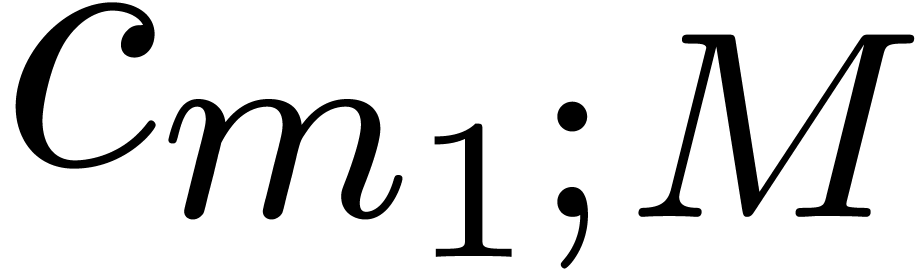 can be regarded as a pre-computation.
can be regarded as a pre-computation.
Let us analyze the cost of the above methods in terms of the complexity
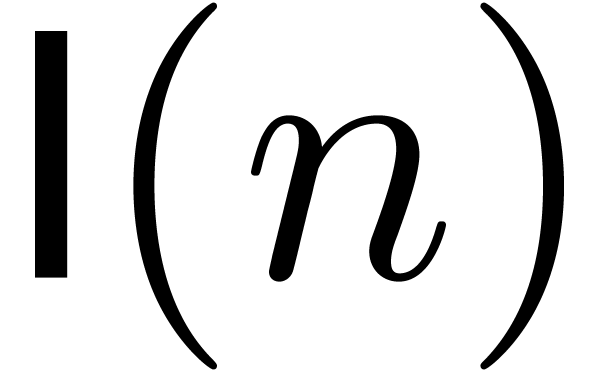 of
of  -bit
integer multiplication. Assume that
-bit
integer multiplication. Assume that 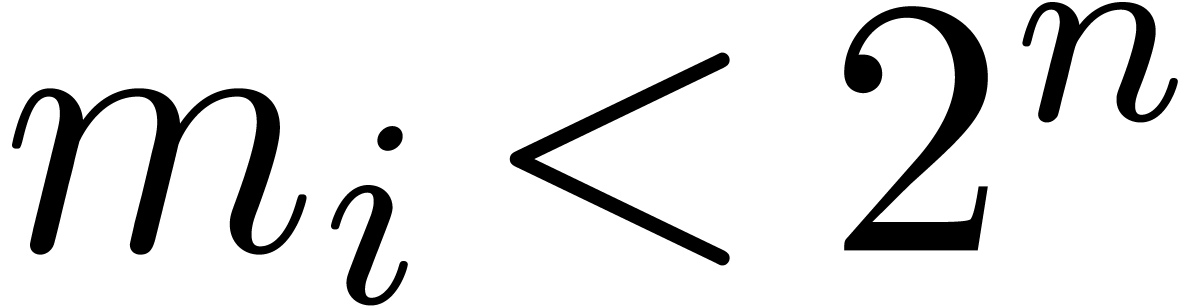 for
for 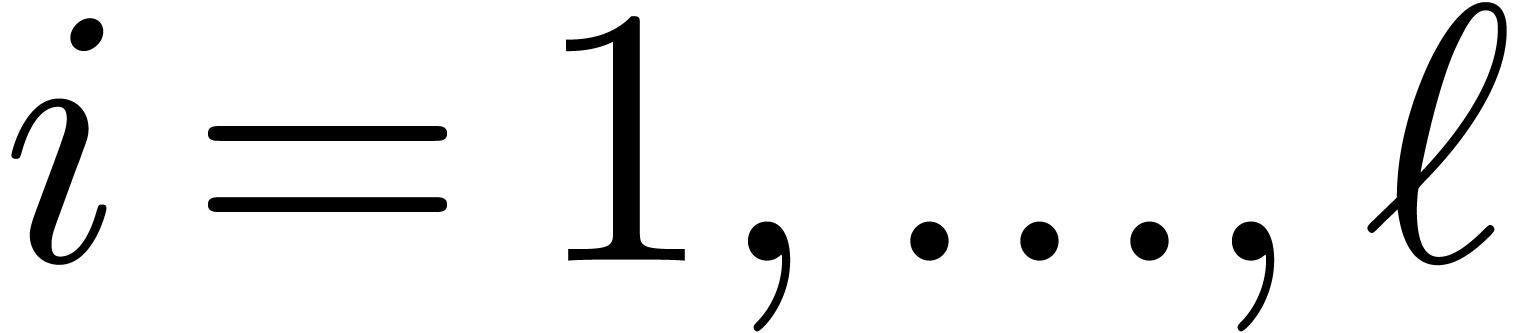 . Then multi-modular reduction can
clearly be done in time
. Then multi-modular reduction can
clearly be done in time 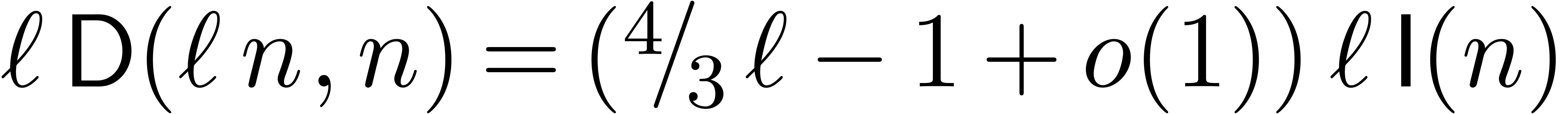 .
.
As to multi-modular reconstruction, assume that 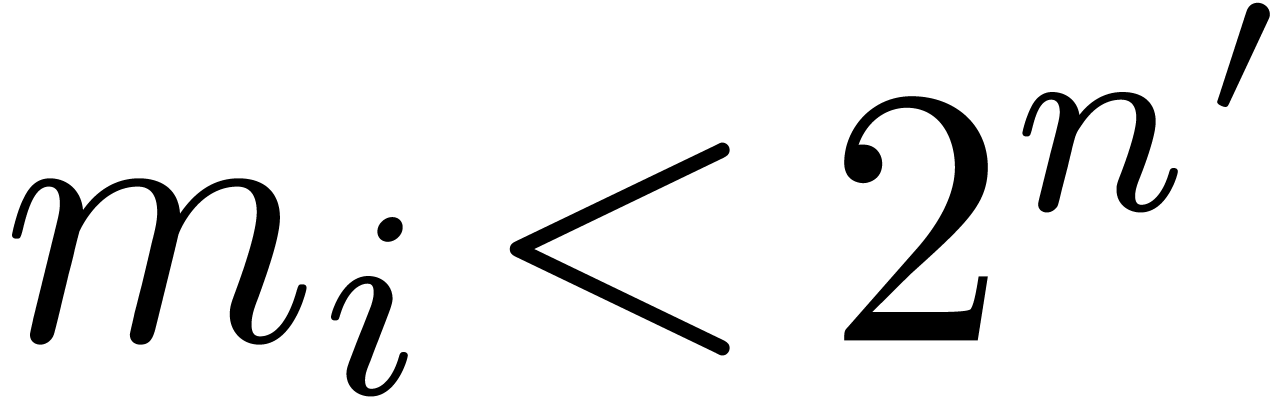 for
for 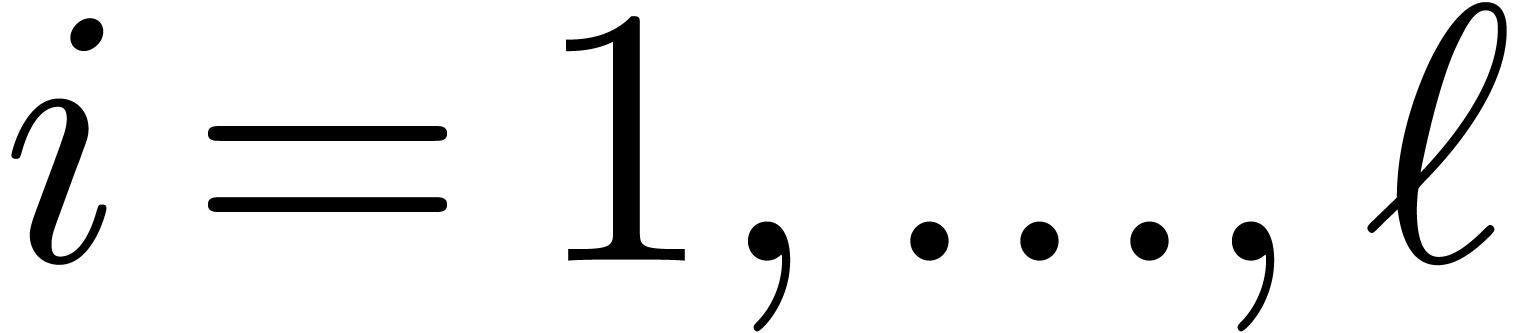 , where
, where 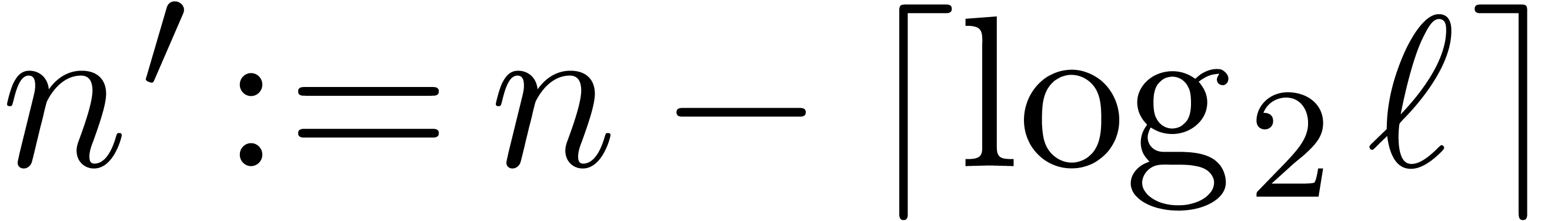 is such that
is such that 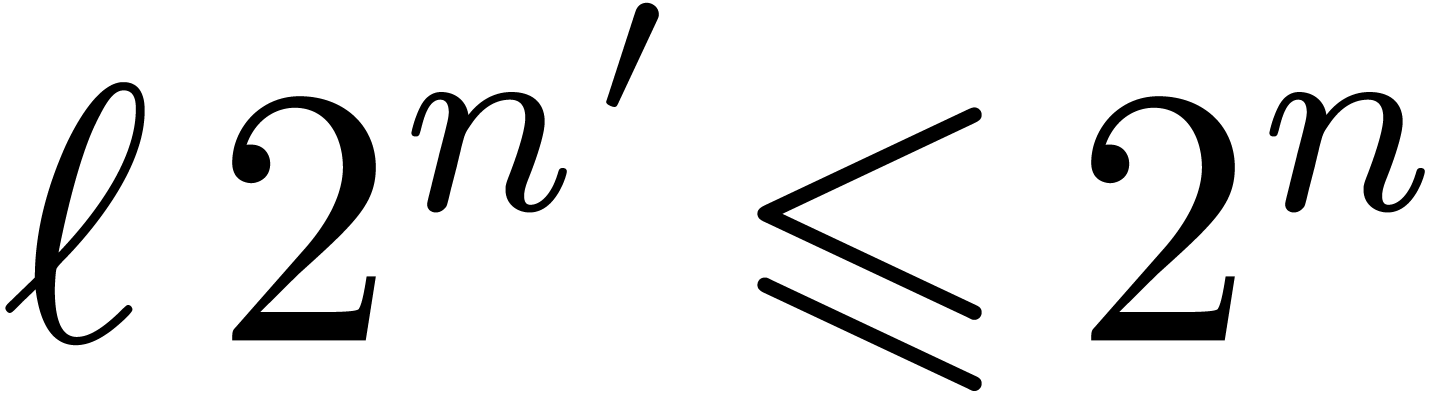 . Cutting the
cofactors in chunks of
. Cutting the
cofactors in chunks of  bits as in (4),
we precompute the Fourier transform of all obtained chunks. The Fourier
transforms of
bits as in (4),
we precompute the Fourier transform of all obtained chunks. The Fourier
transforms of  can be computed in time
can be computed in time 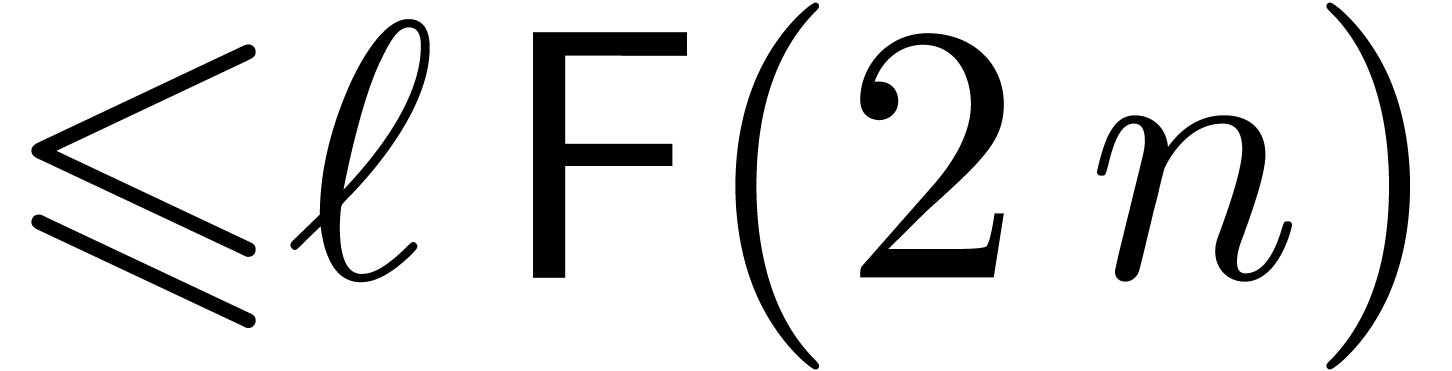 . The sum
. The sum  can be computed in the Fourier model in time
can be computed in the Fourier model in time 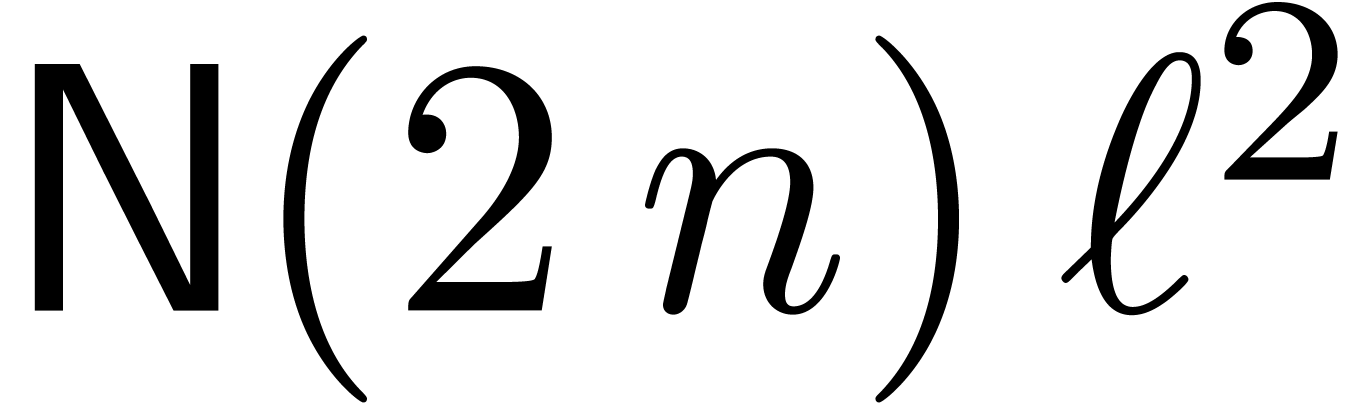 and
transformed back in time
and
transformed back in time 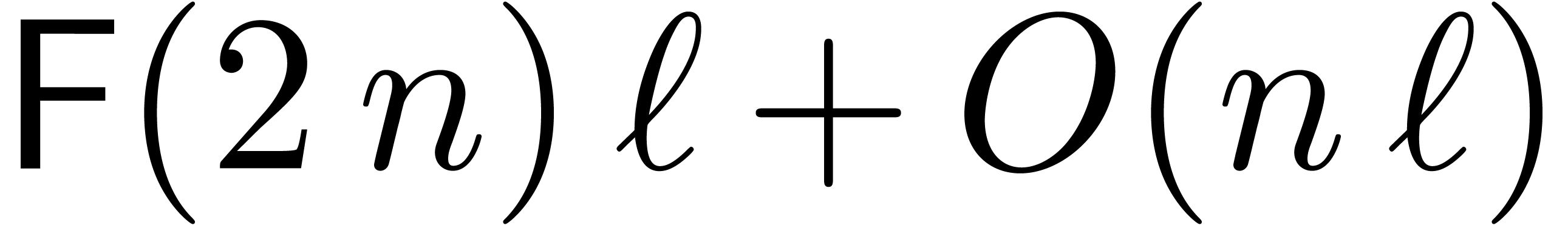 .
Our assumption that
.
Our assumption that 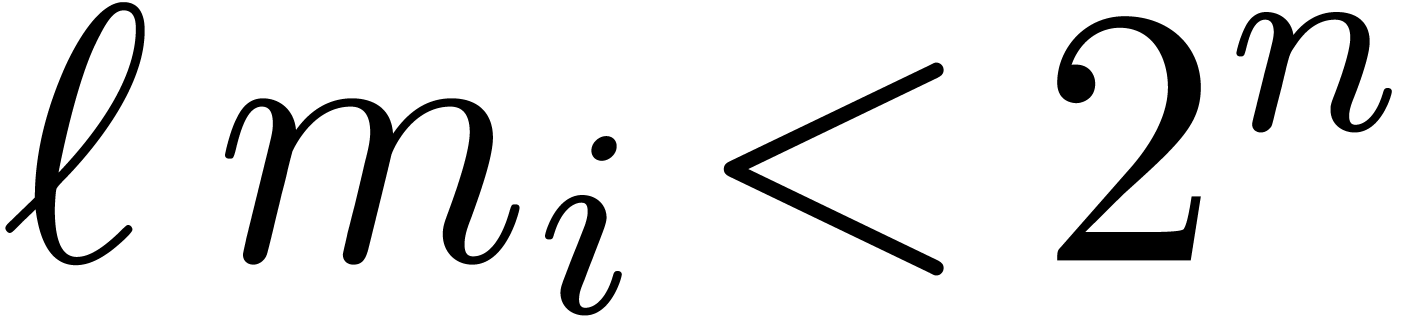 for
for 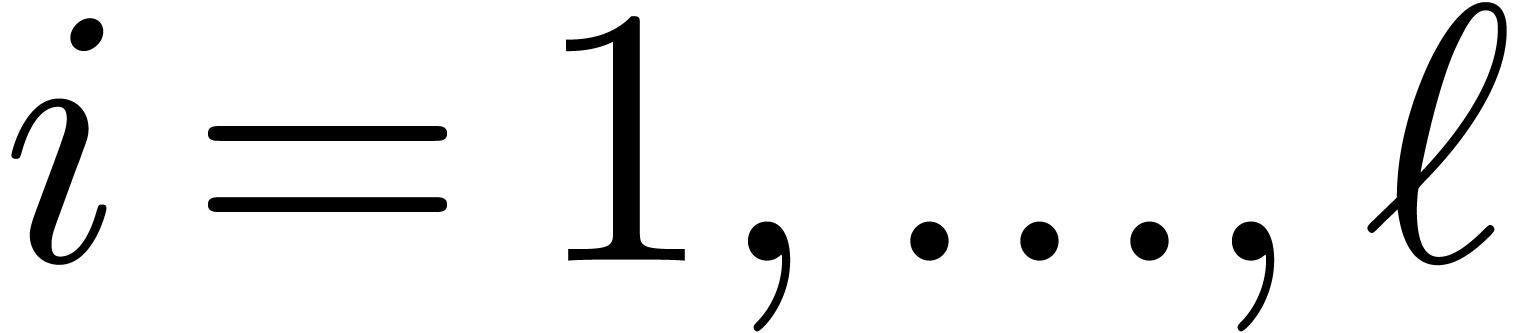 ensures that the computed sum is correct. The remainder
ensures that the computed sum is correct. The remainder  can be computed in time
can be computed in time  . The
total time of the reconstruction is therefore bounded by
. The
total time of the reconstruction is therefore bounded by
If we only assume that  , then
we need to increase the bitsize
, then
we need to increase the bitsize  by
by 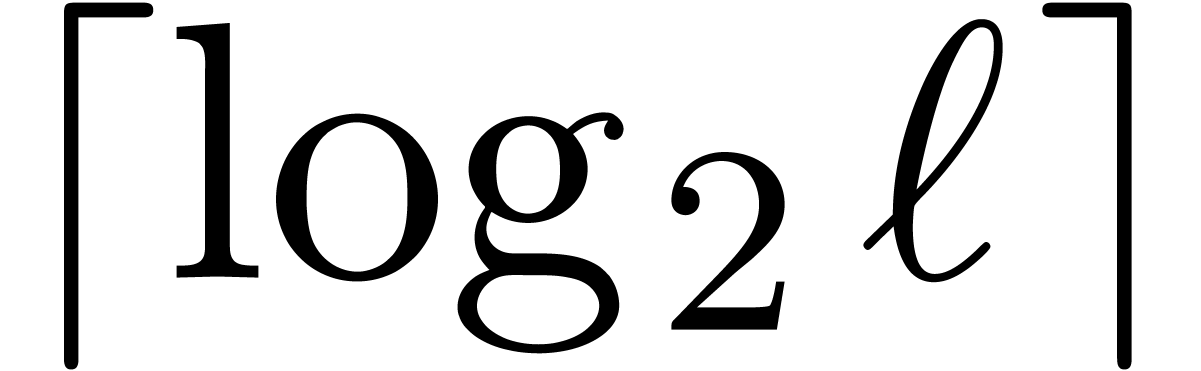 . If
. If 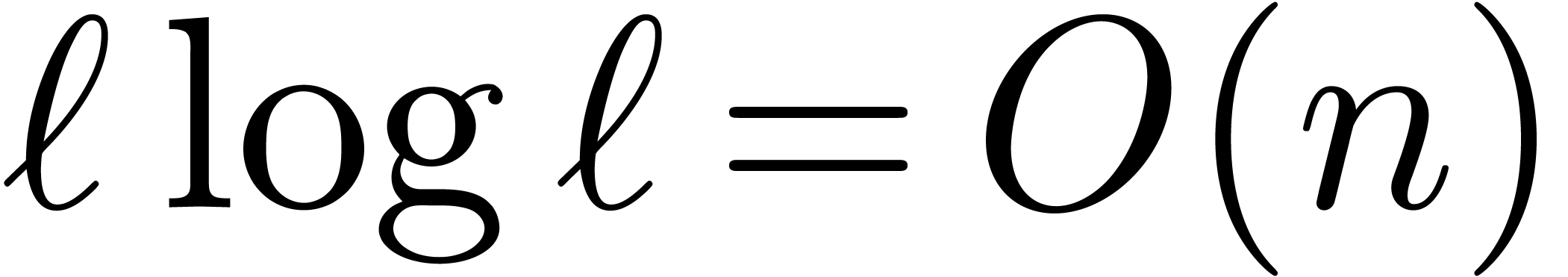 ,
then this means that we have to multiply the right-hand side of (8) by
,
then this means that we have to multiply the right-hand side of (8) by 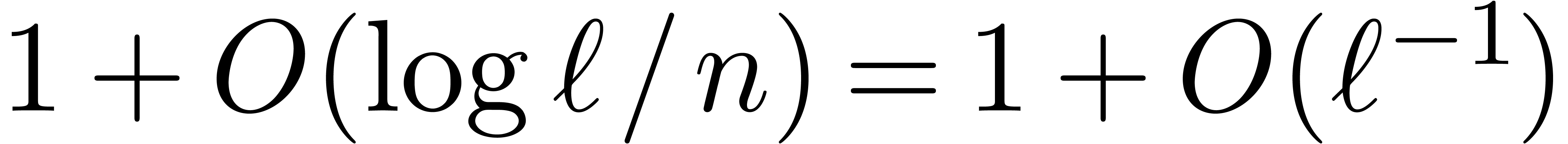 .
.
The above complexity analysis shows that naive multi-modular
recomposition can be done faster than naive multi-modular reduction. In
order to make the latter operation more efficient, one may work with
scaled remainders that were introduced in [2]. The
idea is that each remainder of the form  is
replaced by
is
replaced by  . The quotient
. The quotient
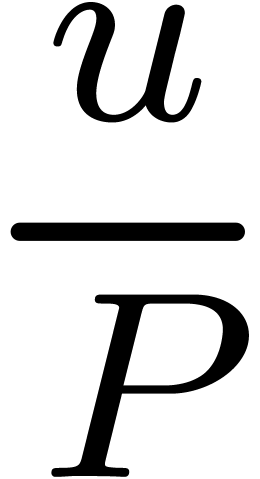 is regarded as a real number and its remainder
modulo
is regarded as a real number and its remainder
modulo 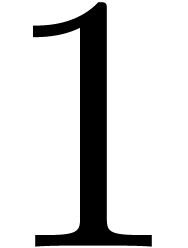 as a number in the interval
as a number in the interval 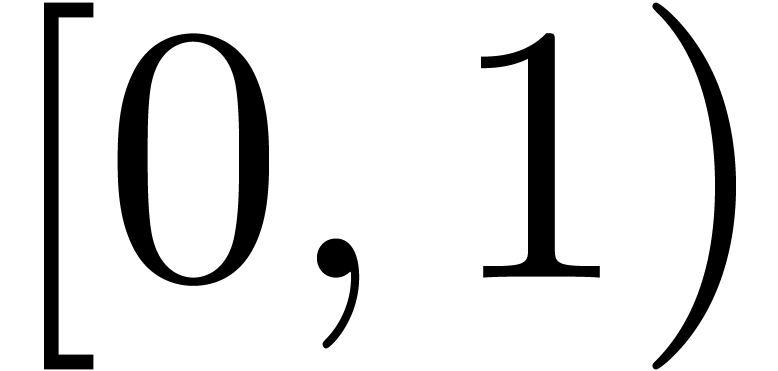 .
.
If we allow ourselves to compute with exact real numbers, then this leads us to replace the relation (6) by
and (7) by
For actual machine computations, we rather work with fixed point
approximations of the scaled remainders. In order to retrieve the actual
remainder  from the scaled one
from the scaled one  , we need a circular
, we need a circular 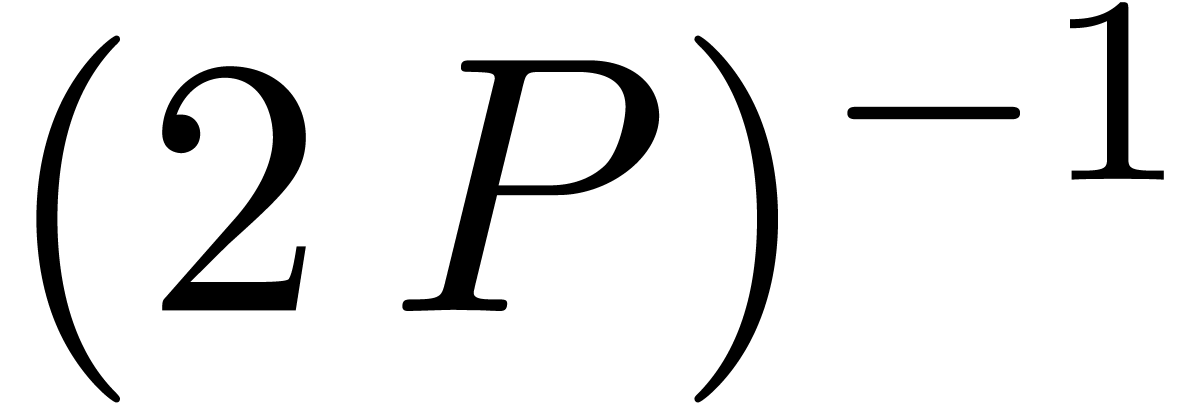 -approximation of
-approximation of  .
.
Now assume that 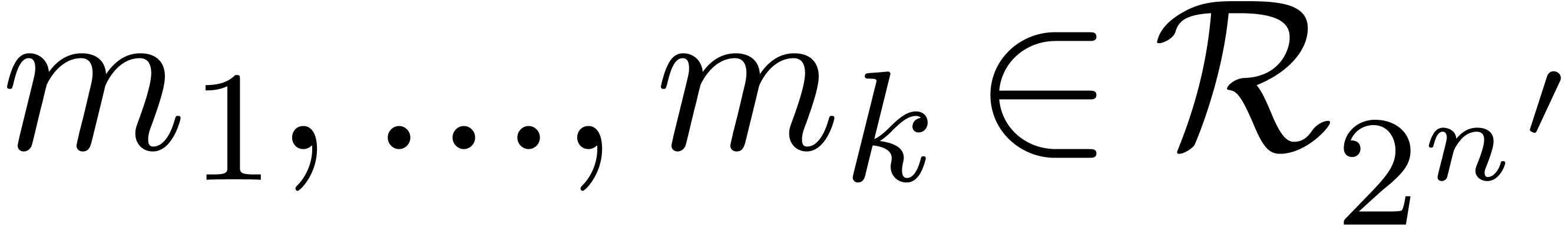 with
with
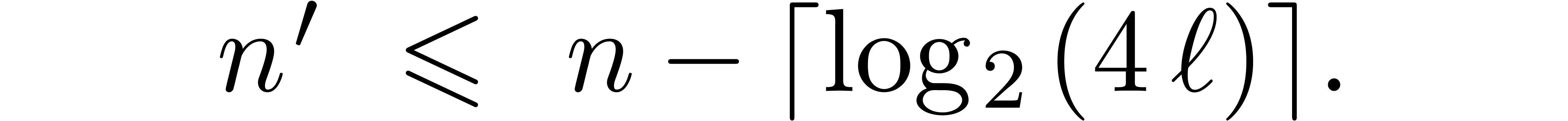
Given a circular  -approximation
of
-approximation
of 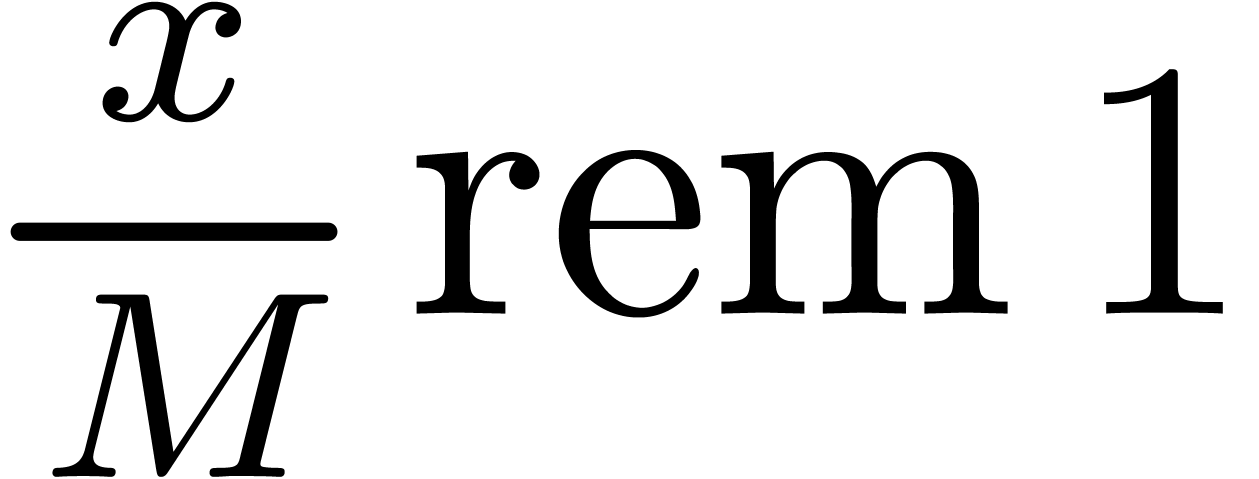 in
in 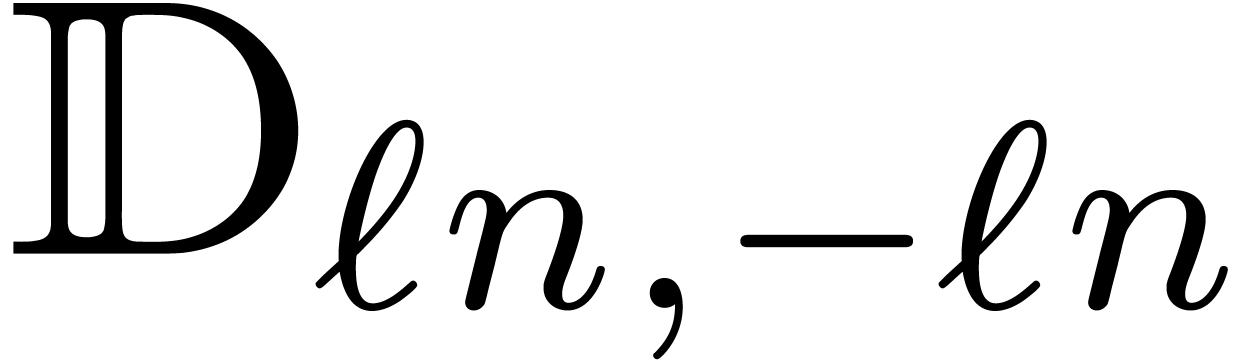 with
with
the algorithm at the end of section 2.3 allows us to
compute a circular  -approximation
modulo
-approximation
modulo  of
of 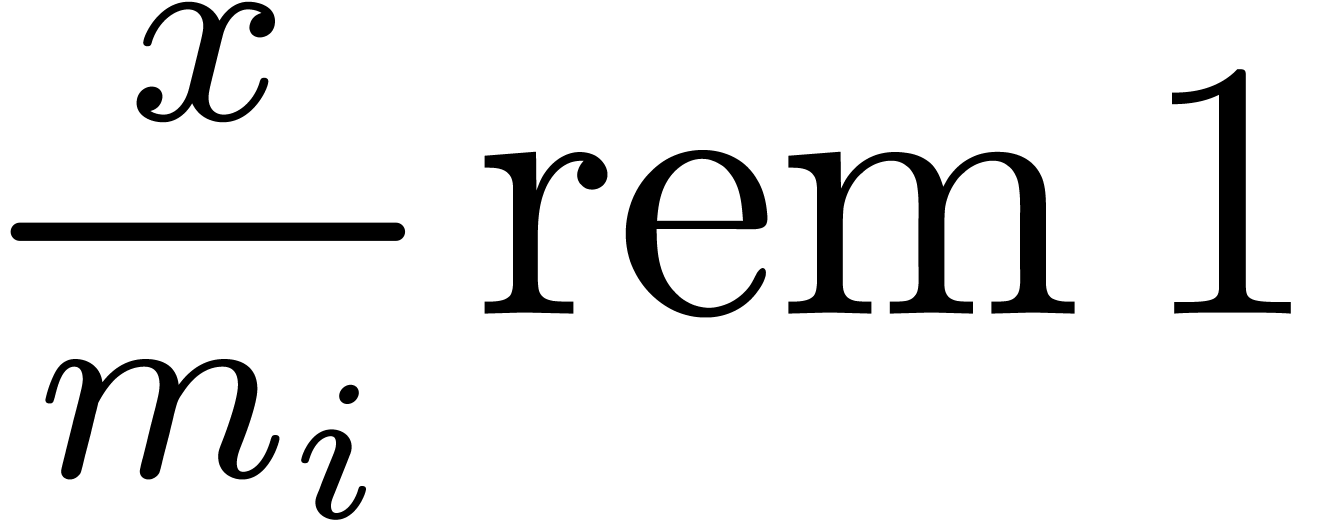 ,
by applying the formula (9). Since
,
by applying the formula (9). Since  , we may then recover the number
, we may then recover the number  using one final
using one final  -bit
multiplication. Moreover, in the FFT-model, the transforms for
-bit
multiplication. Moreover, in the FFT-model, the transforms for 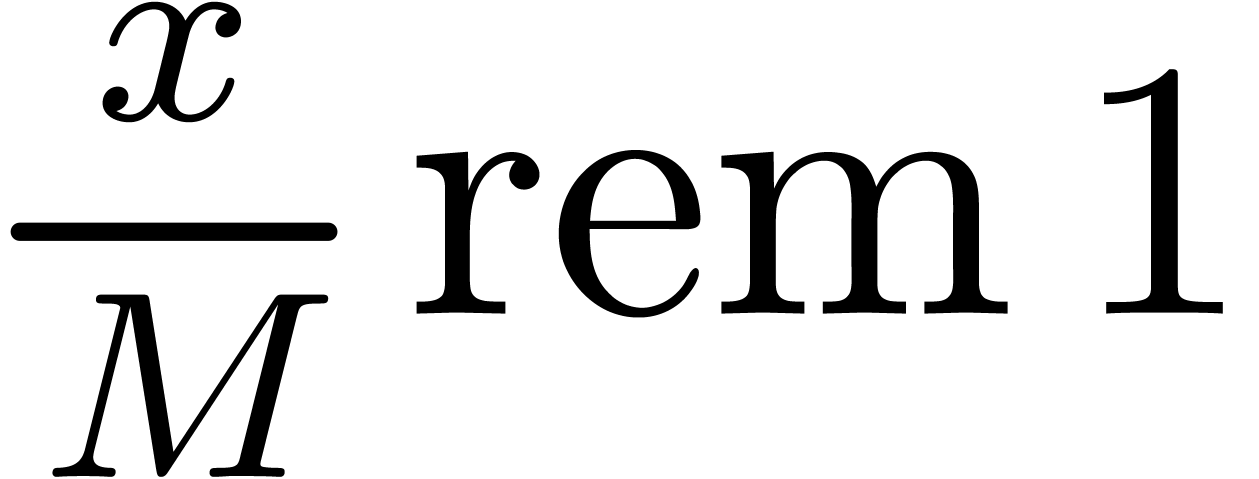 need to be computed only once and the transforms for the
numbers
need to be computed only once and the transforms for the
numbers 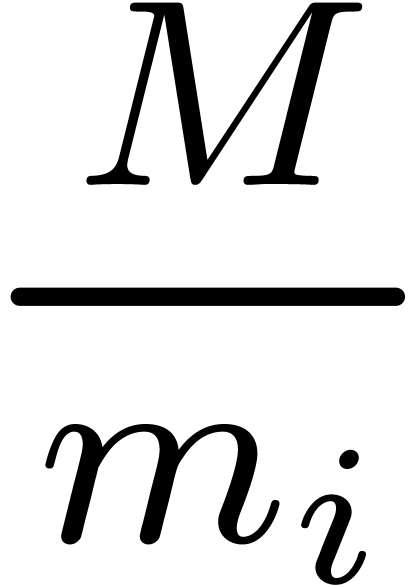 can be precomputed. In summary, given an
approximation for the scaled remainder
can be precomputed. In summary, given an
approximation for the scaled remainder 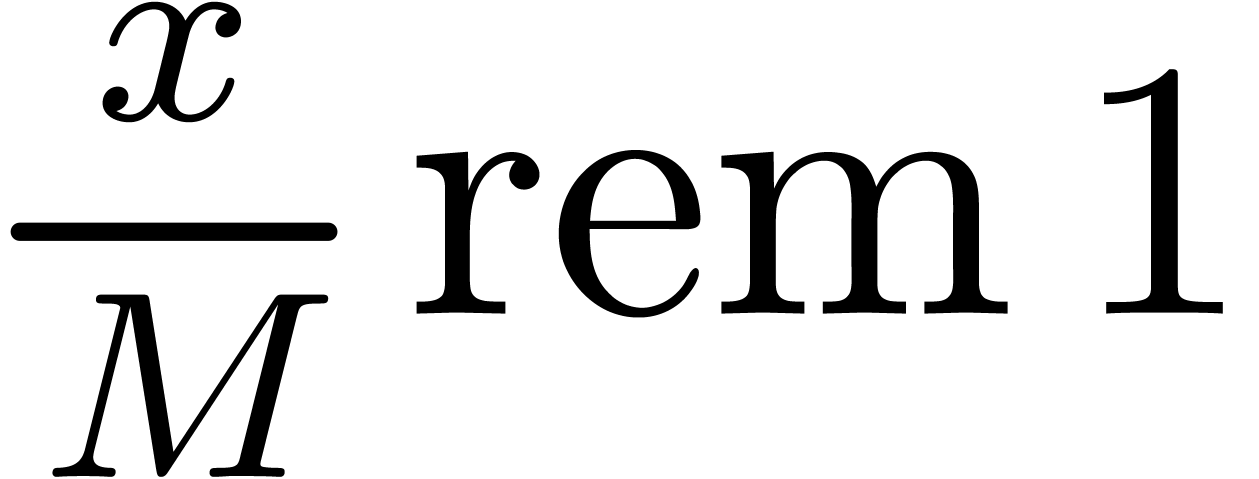 ,
we may thus compute approximations for the scaled remainders
,
we may thus compute approximations for the scaled remainders 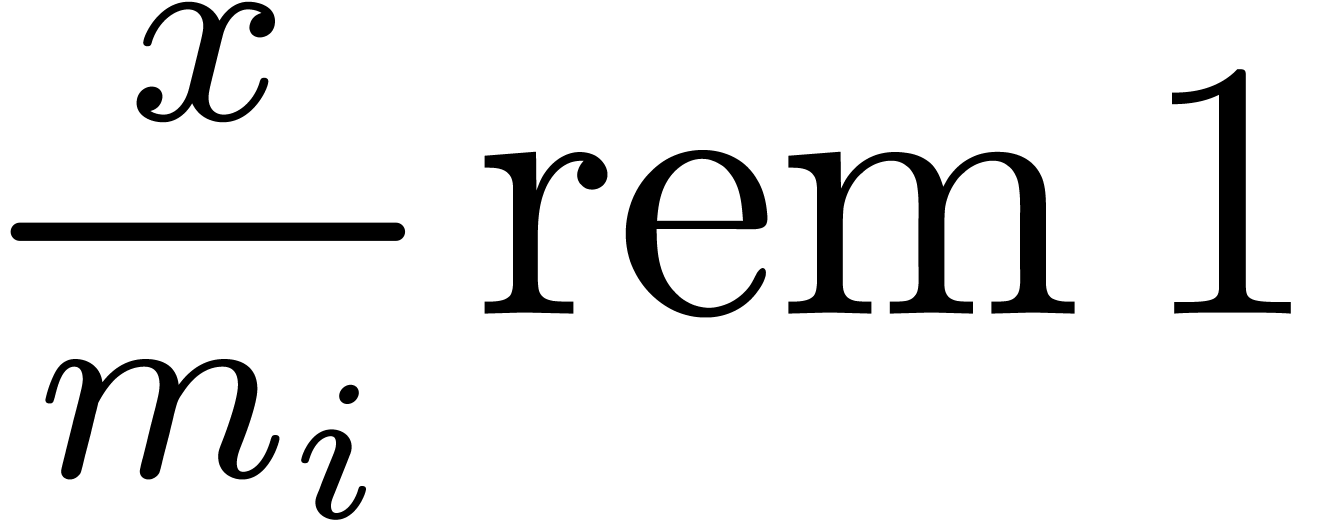 in time
in time
From this, we may recover the actual remainders  in time
in time 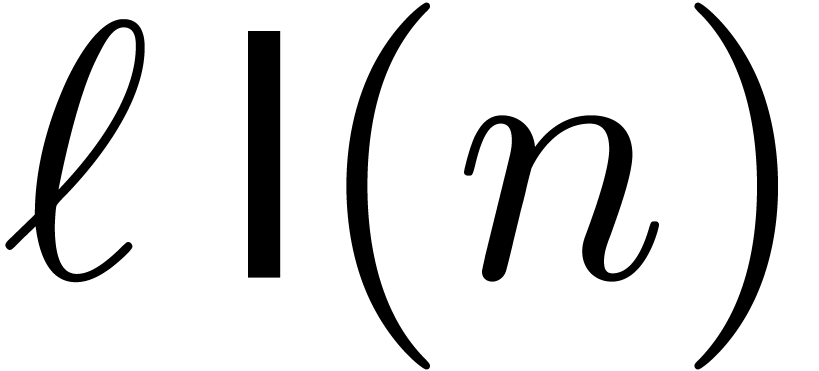 .
.
Scaled remainders can also be used for multi-modular reconstruction, but carry handling requires more care and the overall payoff is less when compared to the algorithm from the previous subsection.
It is well-known that Chinese remaindering can be accelerated using a
similar dichotomic technique as in the proof of Theorem 1.
This time, we subdivide 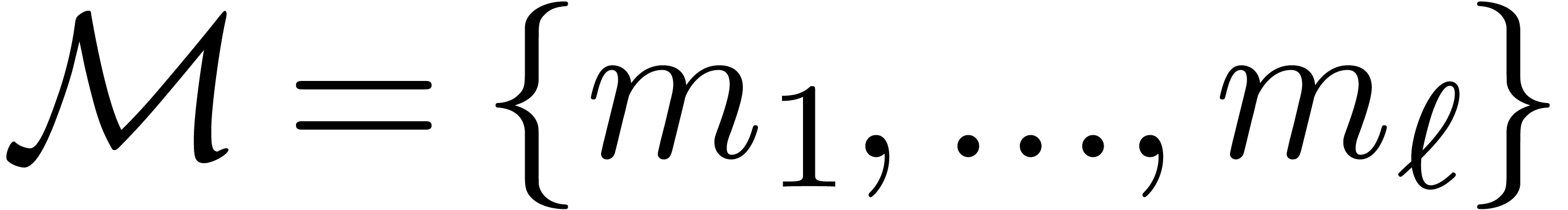 into
into  parts
parts  with
with 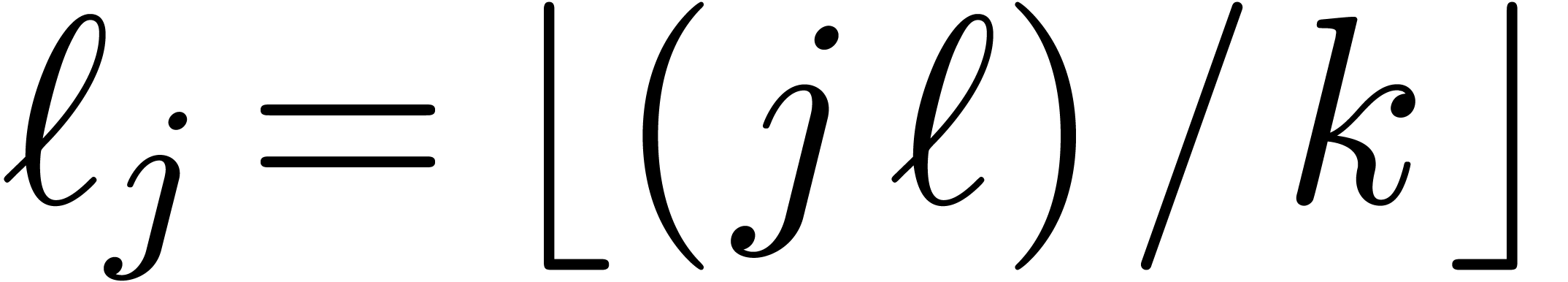 for
for 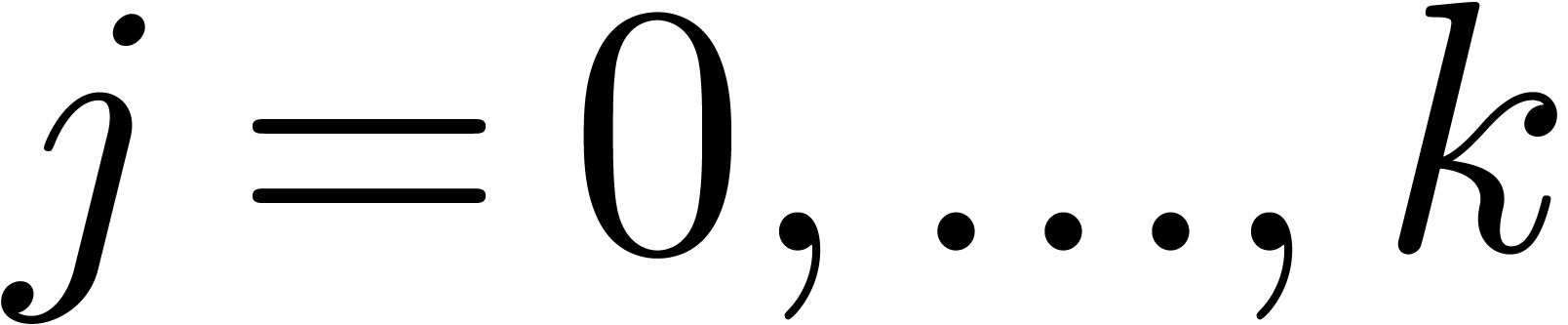 . We denote
. We denote 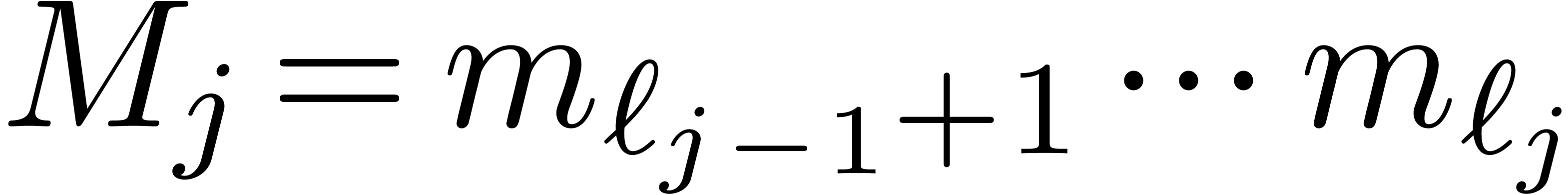 and assume that
and assume that 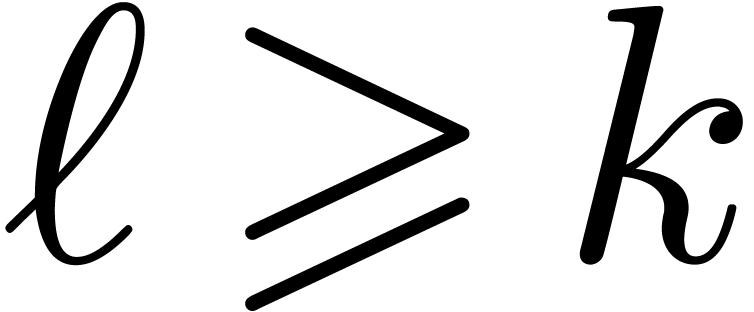 (if
(if 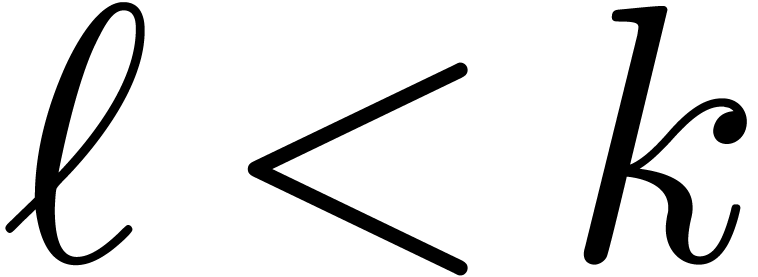 , then we apply the native algorithms from the
previous subsections).
, then we apply the native algorithms from the
previous subsections).
Fast multi-modular reduction proceeds as follows. We first compute
using the algorithm from the previous subsection. Next, we recursively apply fast multi-modular reduction to obtain
The computation process can be represented in the form of a so called
remainder tree; see Figure 3. The root of the tree
is labeled by 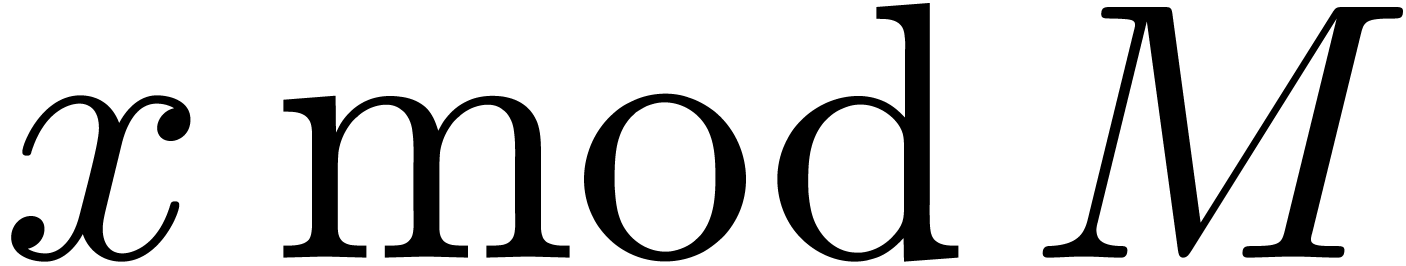 . The children
of the root are the remainder trees for
. The children
of the root are the remainder trees for 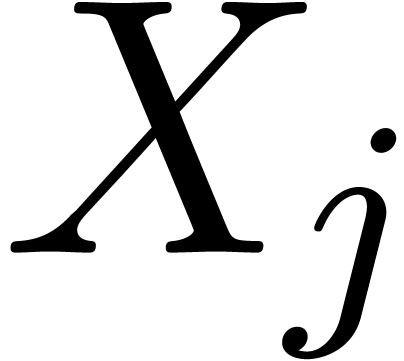 modulo
modulo
 , where
, where 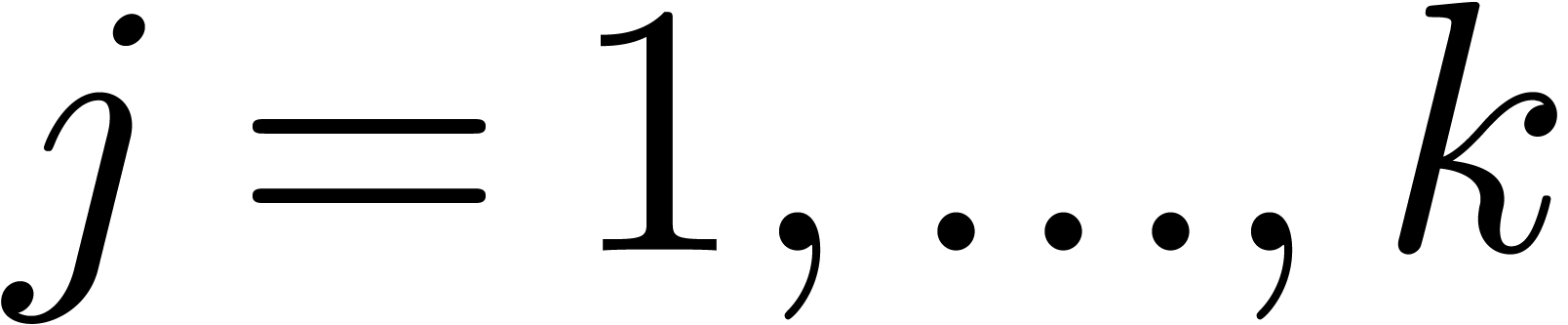 . If needed, then the arity
. If needed, then the arity  can be adjusted as a function of the bitsize of the moduli and
can be adjusted as a function of the bitsize of the moduli and  .
.
Fast multi-modular reconstruction is done in a similar way, following the opposite direction. We first reconstruct
followed by
The computation flow can again be represented using a tree, but this time the computations are done in a bottom-up way.
Following the approach from subsection 3.3, it is also
possible to systematically work with fixed point approximations of
scaled remainders  instead of usual remainders
instead of usual remainders
 . In that case, the
computation process gives rise to a scaled remainder tree as in
Figure 4. Of course, the precision of the approximations
has to be chosen with care. Before we come to this, let us first show
how to choose
. In that case, the
computation process gives rise to a scaled remainder tree as in
Figure 4. Of course, the precision of the approximations
has to be chosen with care. Before we come to this, let us first show
how to choose  .
.
|
|
Figure 4. The scaled remainder tree corresponding to Example 3, while using fixed point approximations for the scaled remainders. |
Let us first focus on multi-modular reconstruction. In order to make
this process as efficient as possible, the arity  should be selected as a function of
should be selected as a function of  and
and  so as to make
so as to make 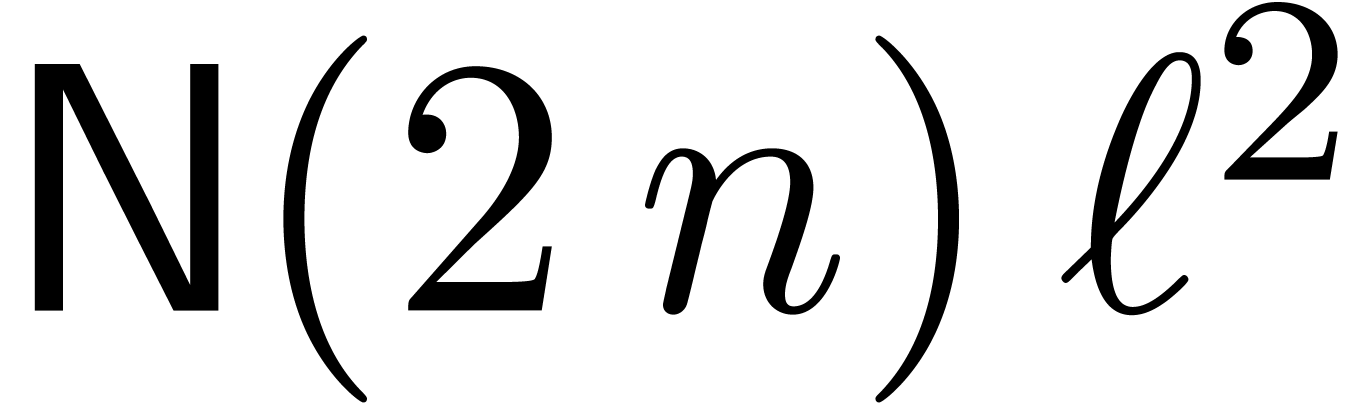 as large as
possible in (8), while remaining negligible with respect to
as large as
possible in (8), while remaining negligible with respect to
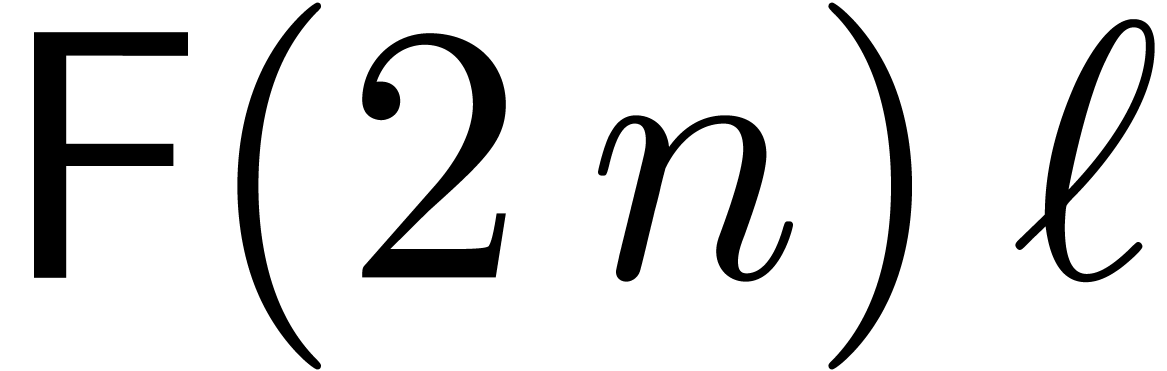 . Let
. Let
For inborn FFT schemes, we notice that
For the root of the remainder tree, we take
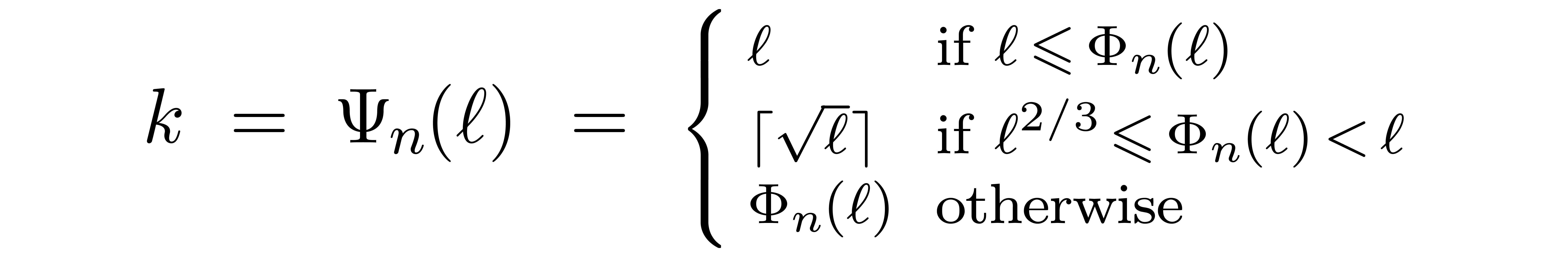
Using the same formula recursively for the other levels of the remainder
tree, it is natural to define the sequences 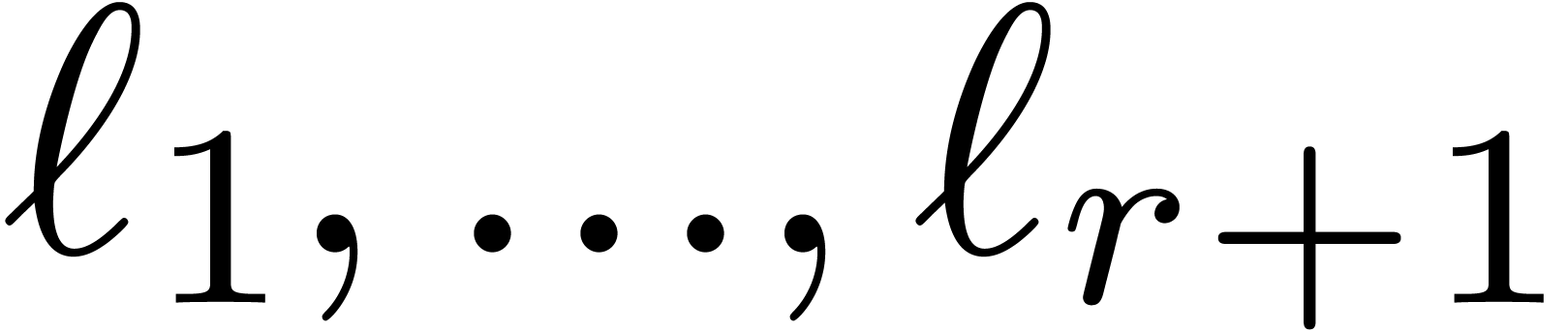 and
and
 by
by 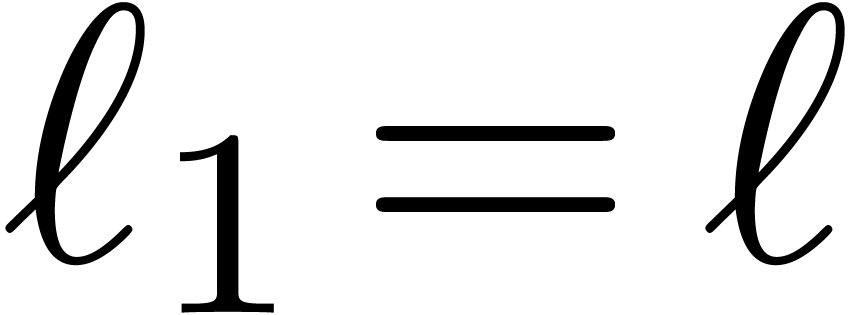 ,
,
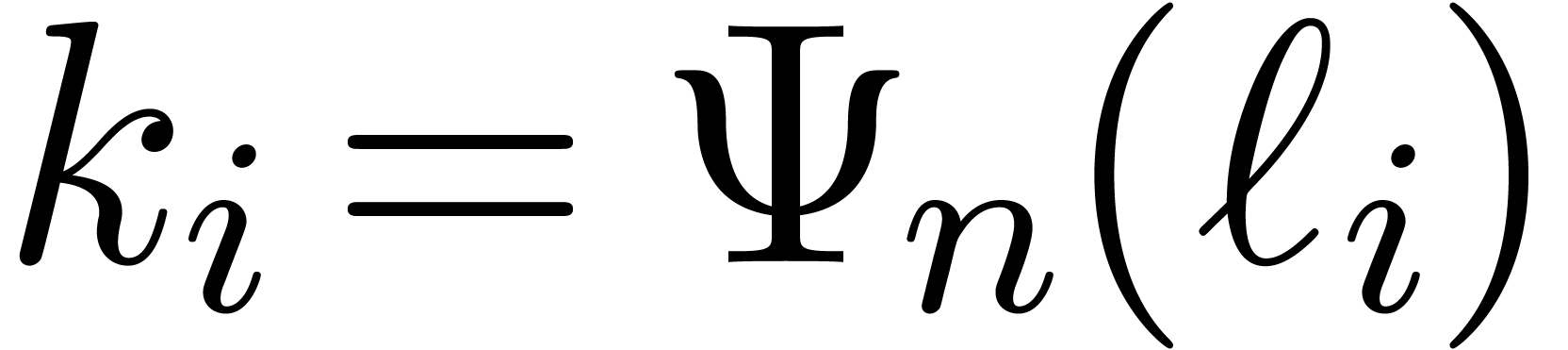 and
and 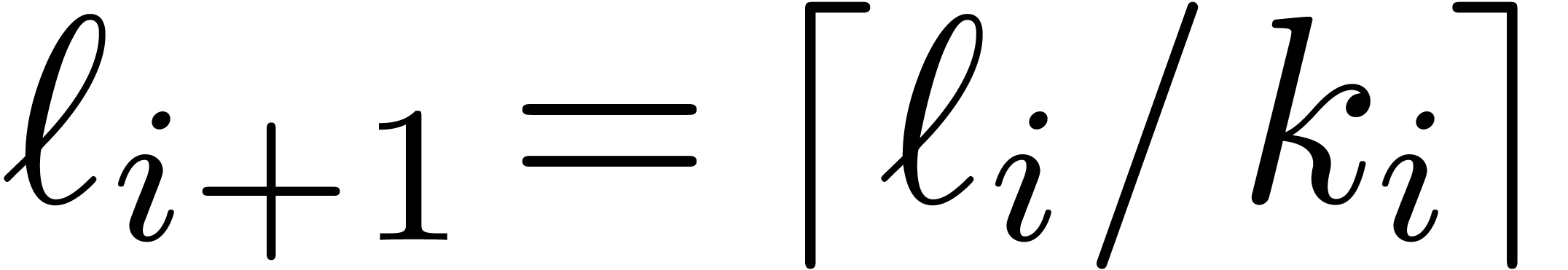 for
for 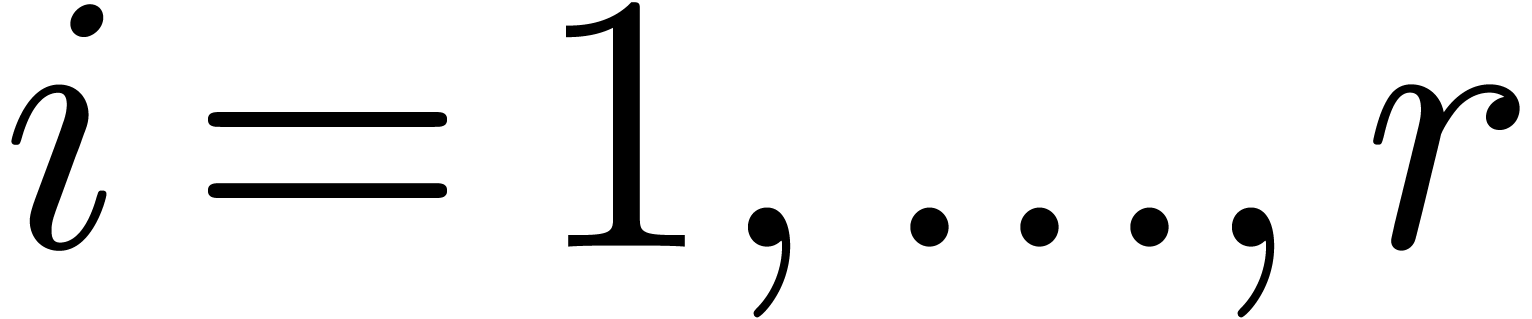 ; the construction stops as soon as
; the construction stops as soon as 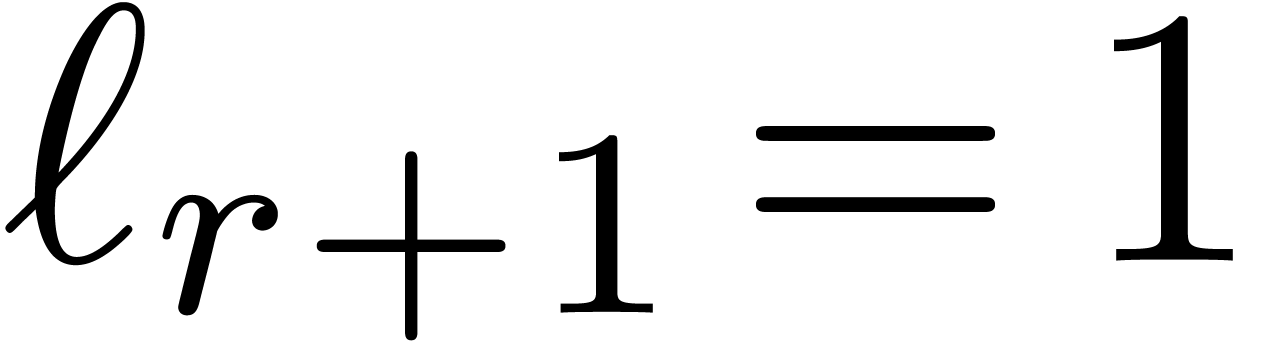 . Notice that we always have
. Notice that we always have  . The precise choice of
. The precise choice of 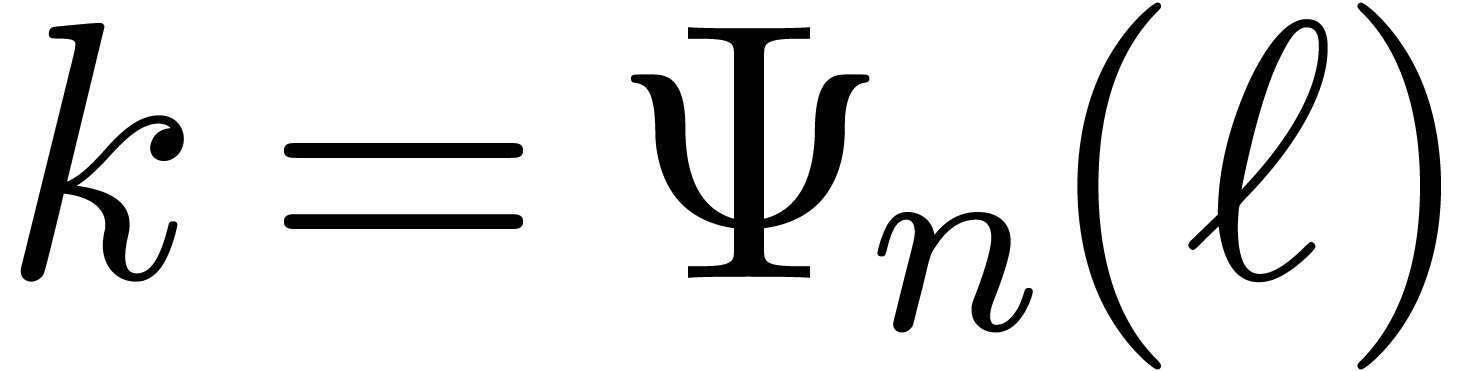 is motivated by the following lemmas.
is motivated by the following lemmas.
 , then
, then 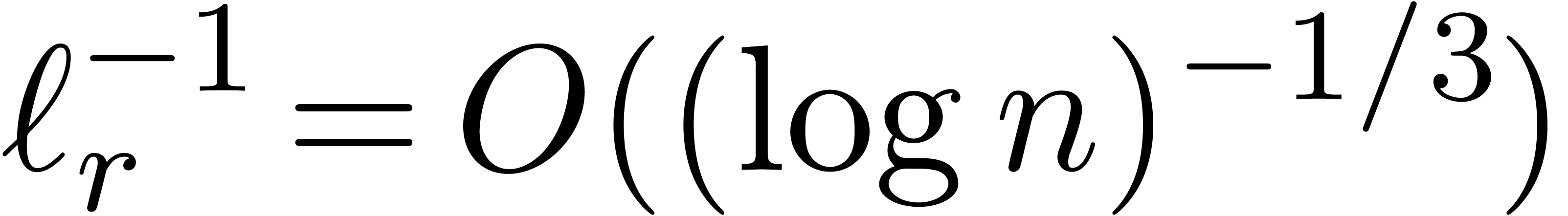 .
.
Proof. We clearly cannot have 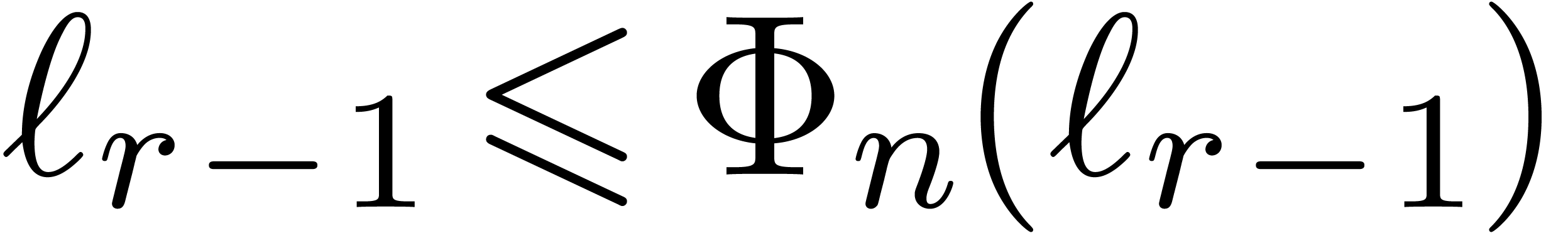 , since otherwise
, since otherwise  .
If
.
If 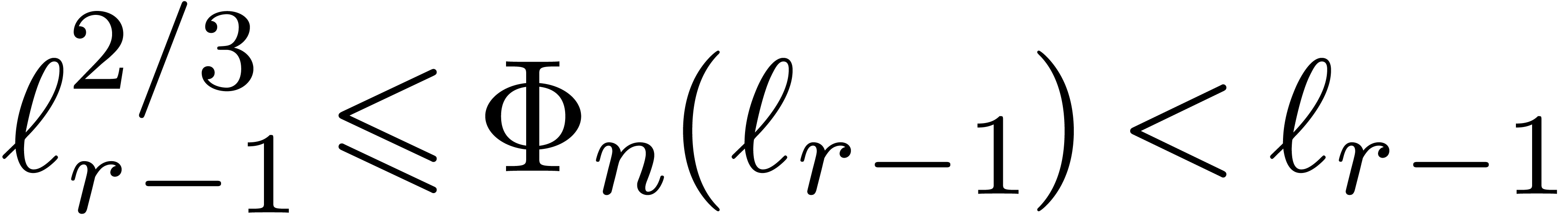 , then
, then
If 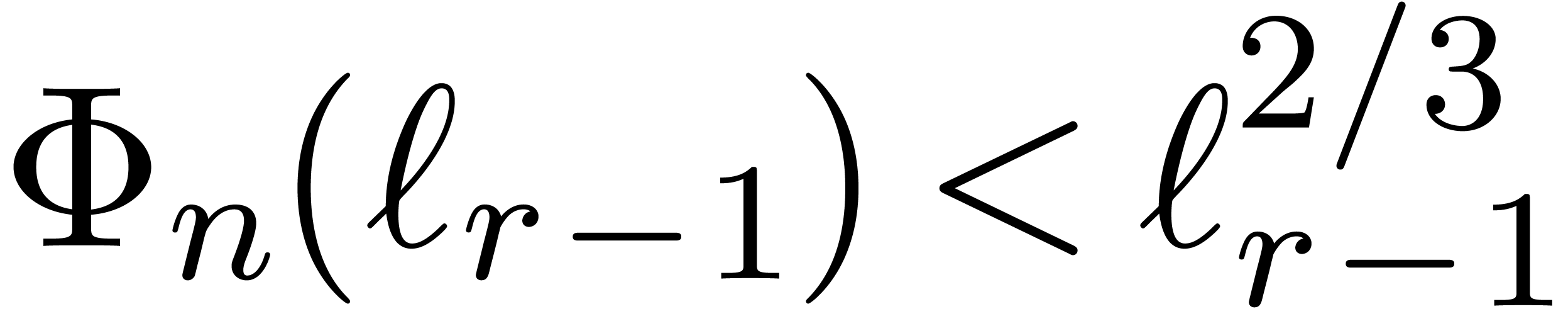 , then
, then
This proves the result in all cases.
 , then we have
, then we have 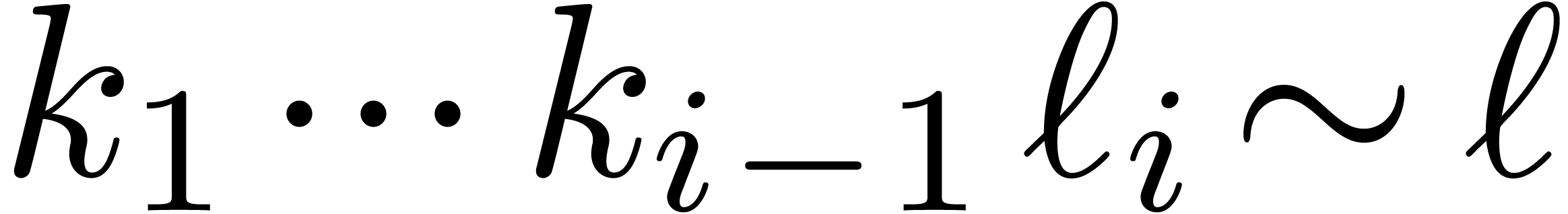 for
for  .
.
Proof. For  ,
we have
,
we have 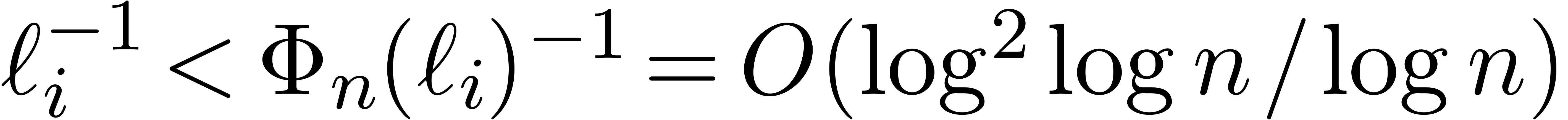 , so that
, so that 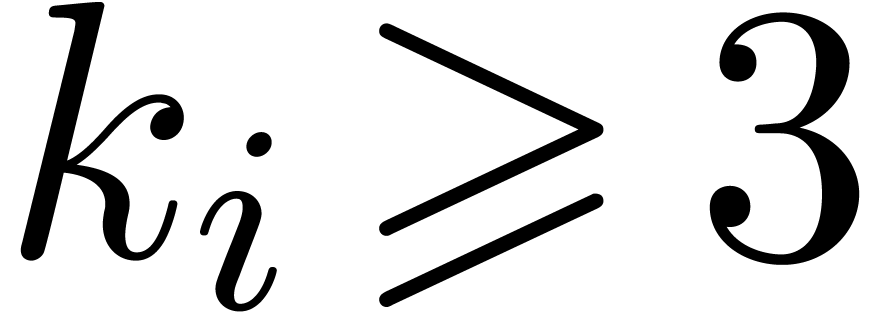 and
and 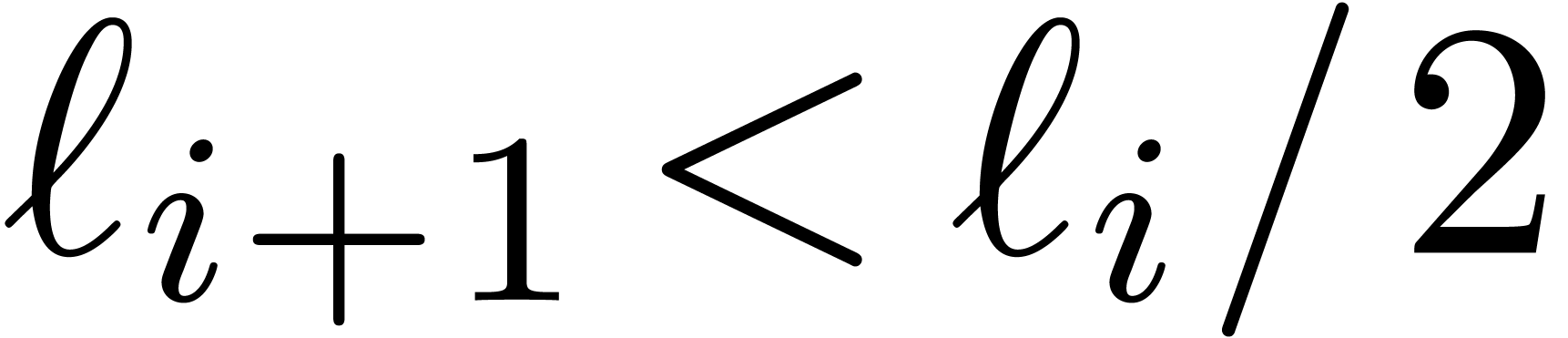 whenever
whenever  is sufficiently large. By construction, we also have
is sufficiently large. By construction, we also have
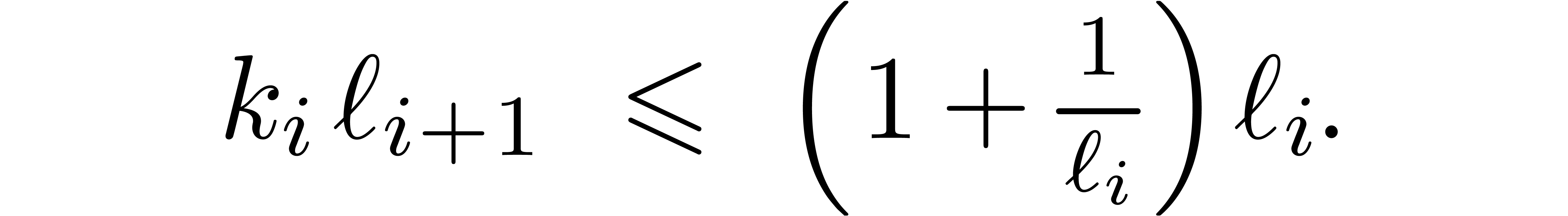
By induction, it follows that
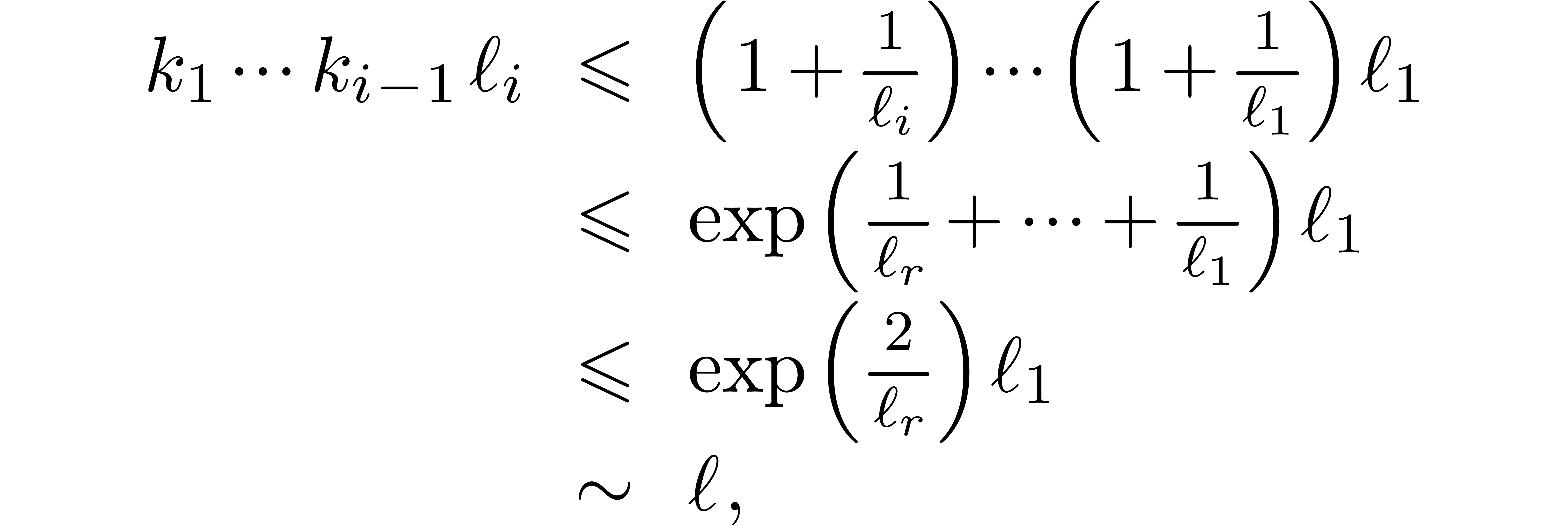
for  . We also have
. We also have 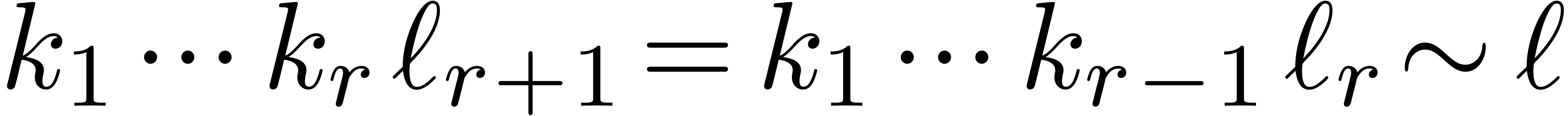 .
.
Proof. Let 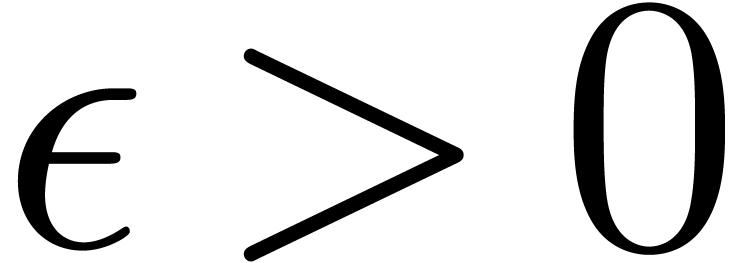 and let
and let  be smallest such that
be smallest such that 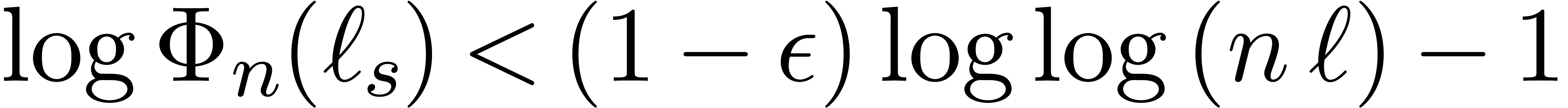 .
For all
.
For all 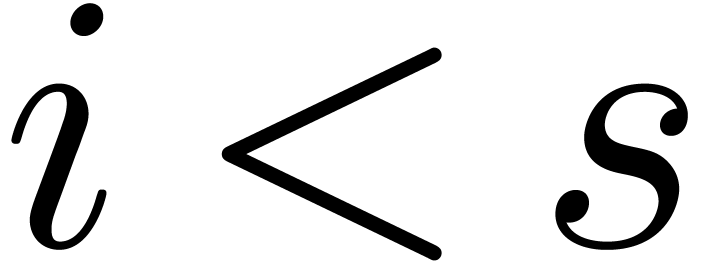 , we have
, we have 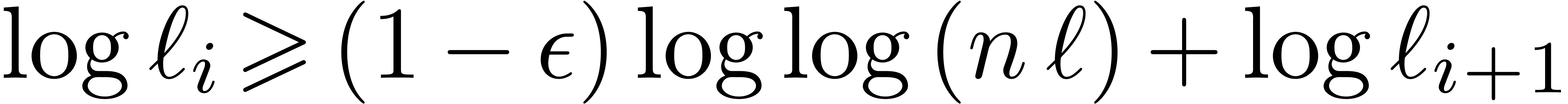 , whence
, whence
Let  be a constant such that
be a constant such that 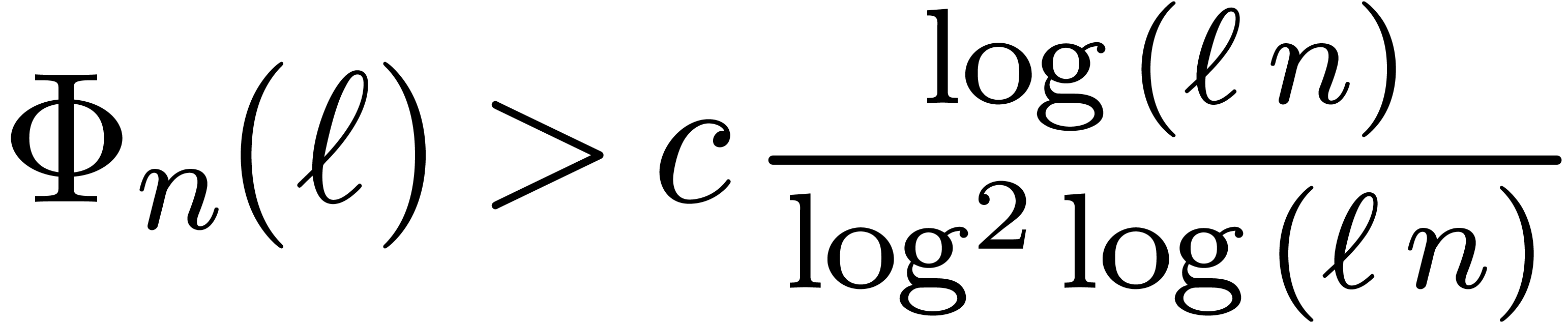 for all
for all  . We also have
. We also have
so that
Since 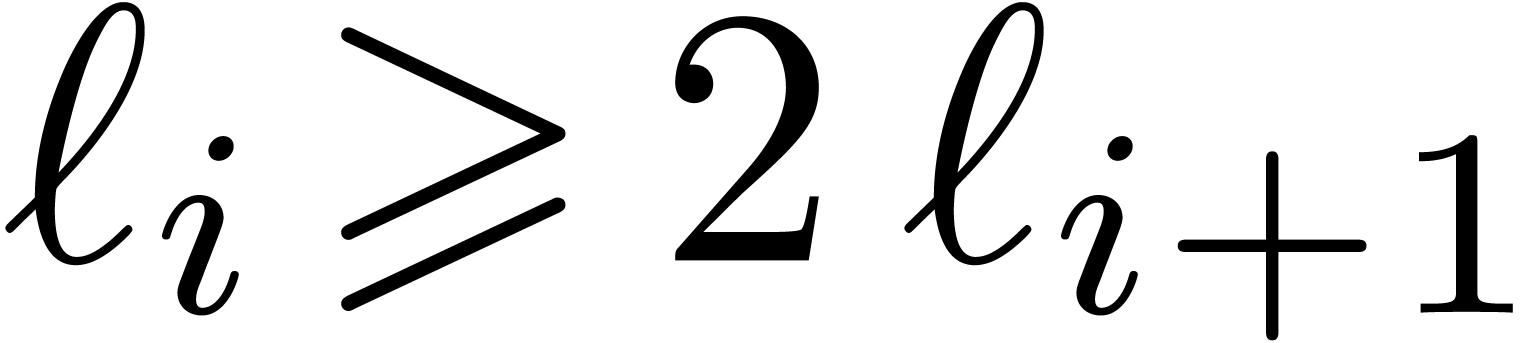 for all
for all 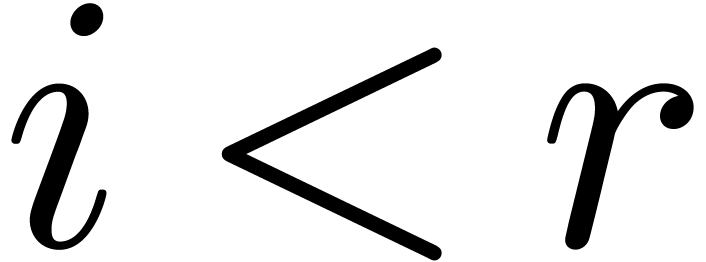 ,
it follows that
,
it follows that
Adding up (16) and (17) while letting  tend to zero, the result follows.
tend to zero, the result follows.
Proof. By construction, 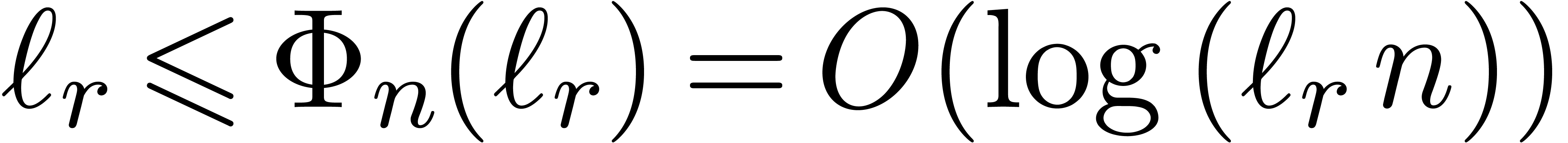 . For large
. For large  ,
this means that
,
this means that 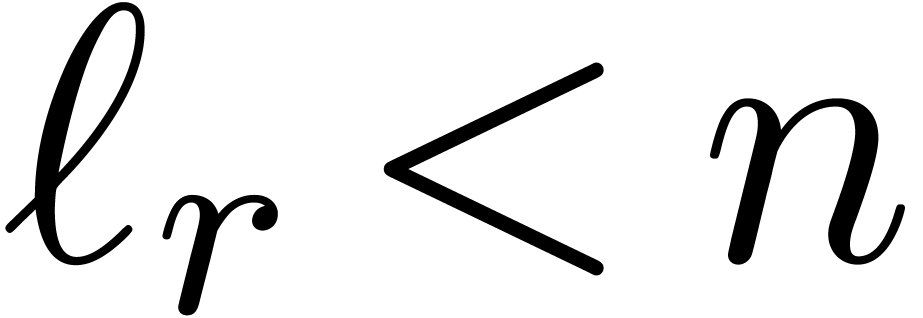 , since
otherwise
, since
otherwise 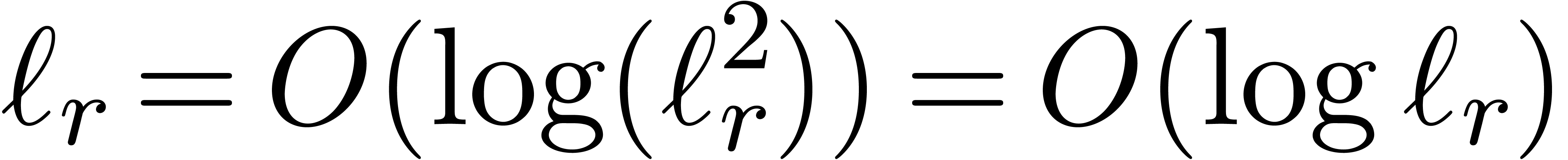 , which is
impossible. Consequently,
, which is
impossible. Consequently, 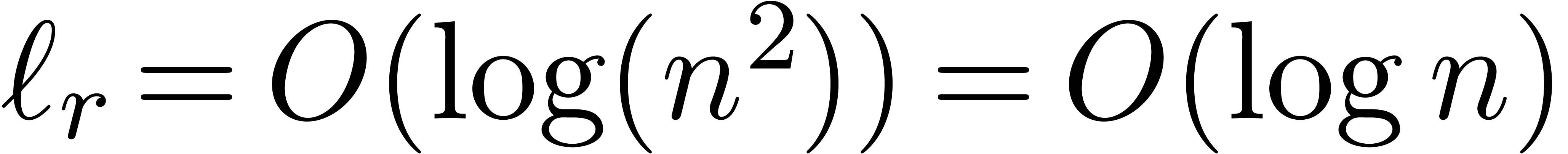 .
.
Let 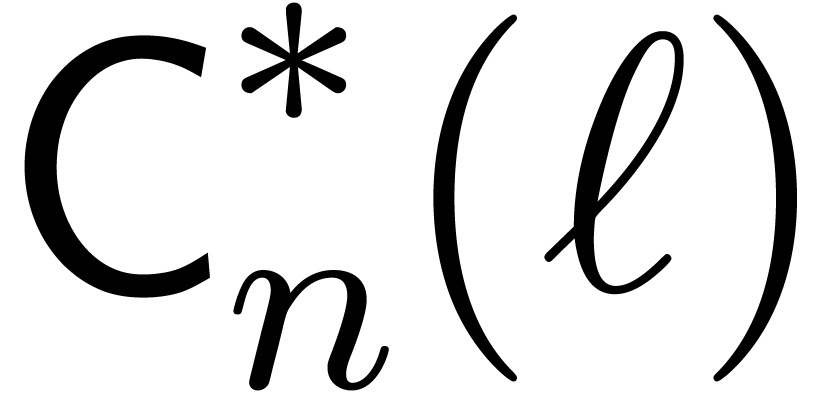 be the complexity multi-modular
reconstruction for fixed moduli
be the complexity multi-modular
reconstruction for fixed moduli  with
with  for
for 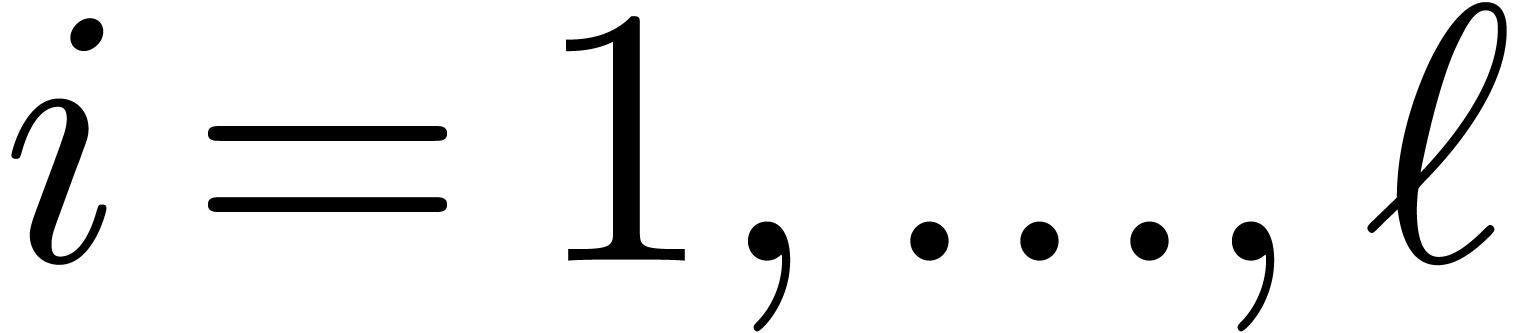 .
.
This bound holds uniformly in  for
for  .
.
Proof. In the special case when 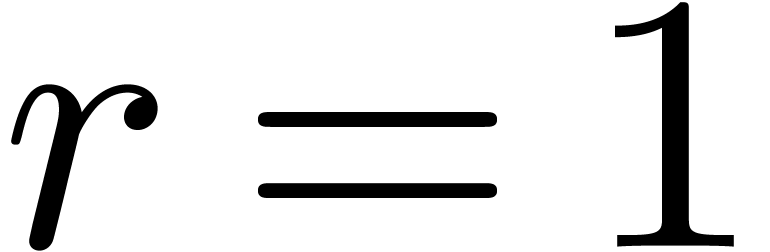 , the bound (8) yields
, the bound (8) yields
and we are done. If  , then
(8) implies
, then
(8) implies
for 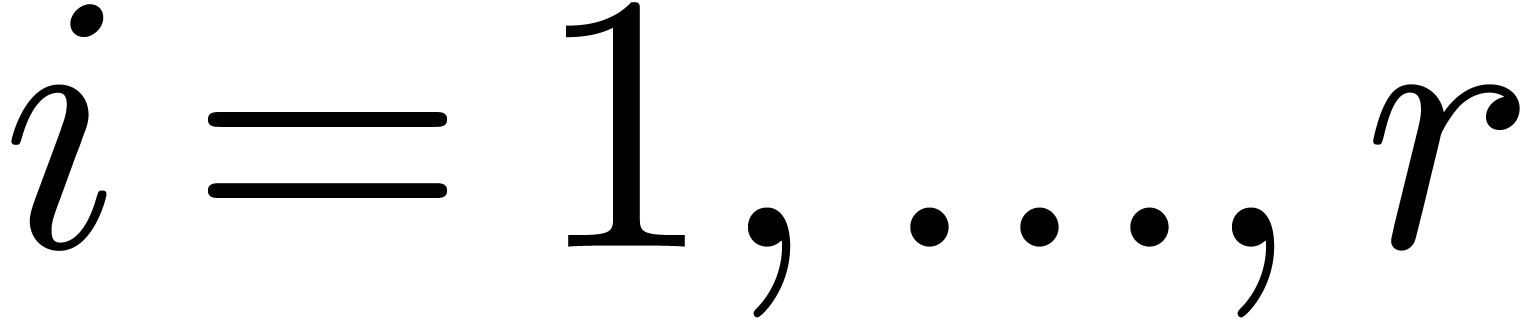 . By induction, and using
the fact that
. By induction, and using
the fact that 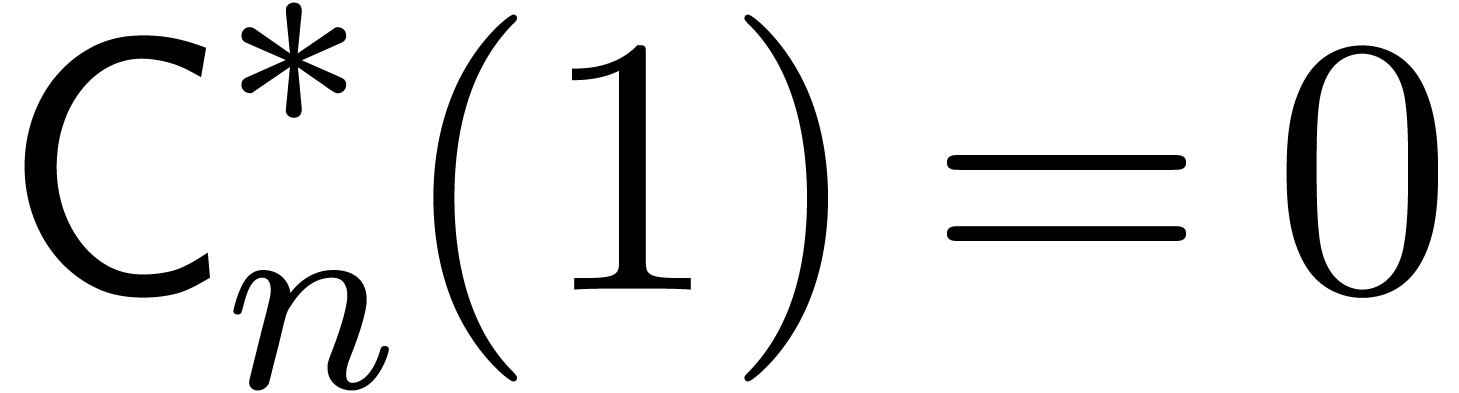 , we get
, we get
The result now follows from Lemma 4 and (1).
Remark 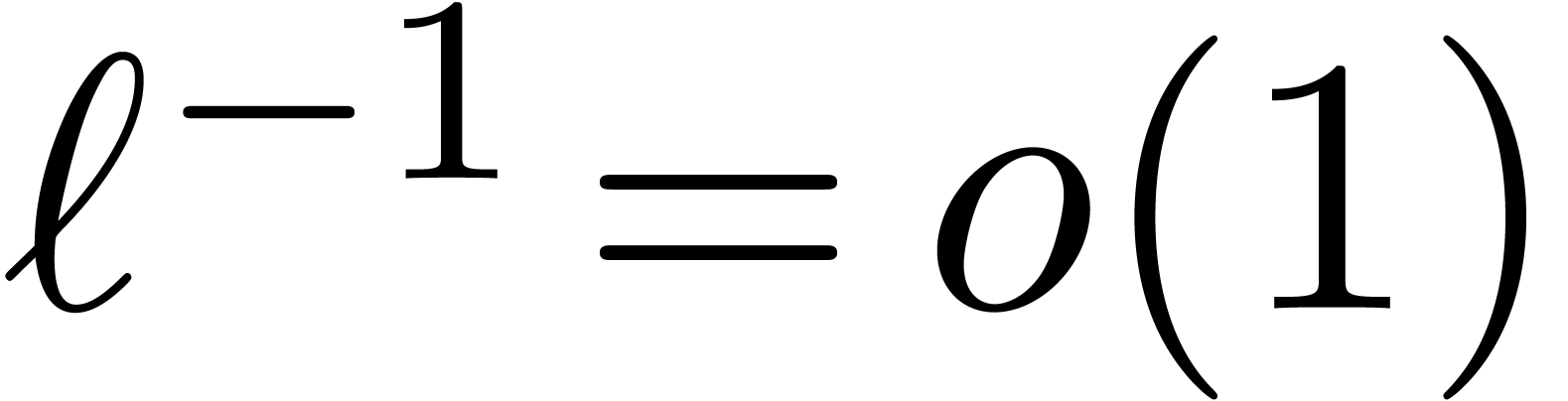 and
and 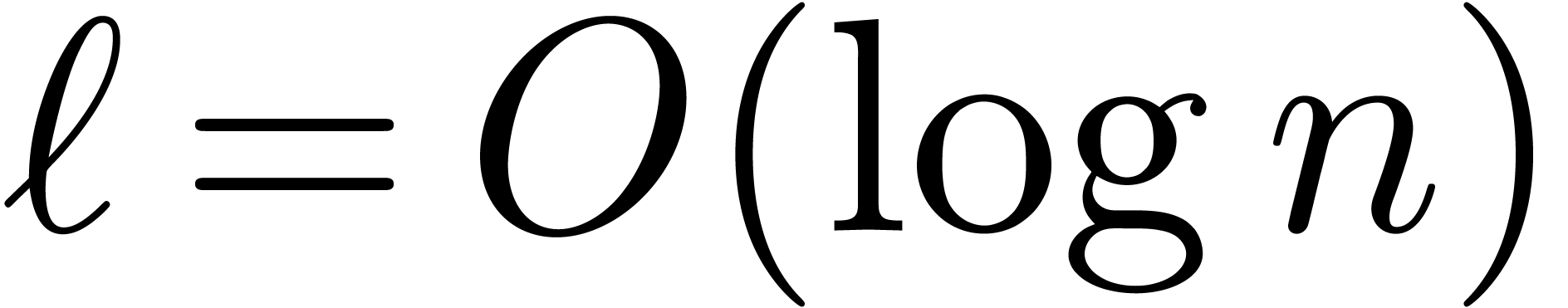 , the bound
(18) simplifies into
, the bound
(18) simplifies into
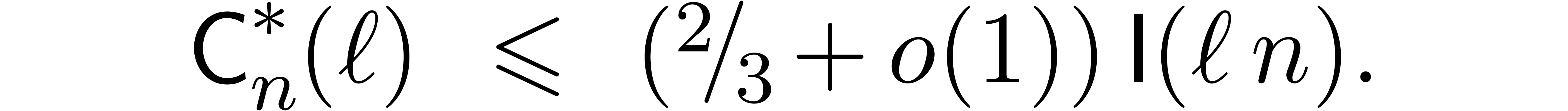
If 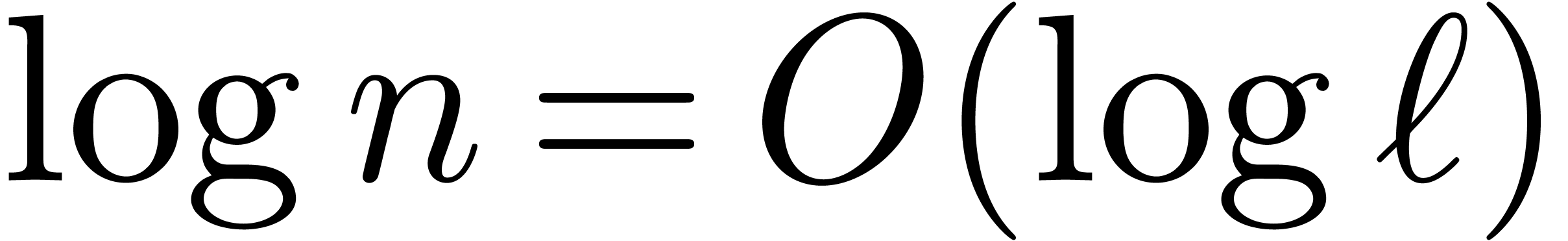 , then the bound becomes
, then the bound becomes
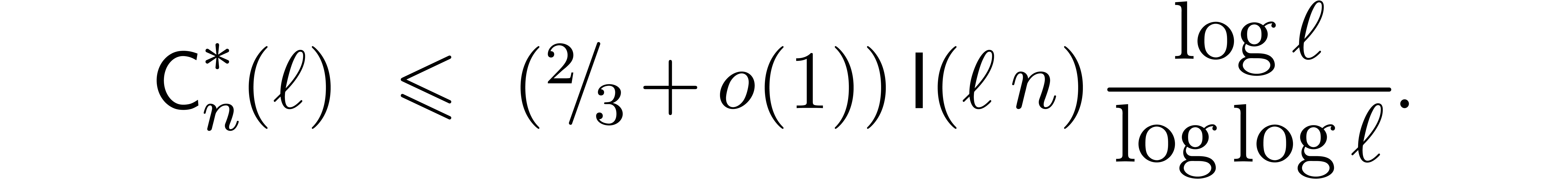
Remark  ,
,  and
and  . For a
node of the remainder tree at level
. For a
node of the remainder tree at level  ,
we essentially need to compute
,
we essentially need to compute  cofactors and
their transforms. This can be done in time
cofactors and
their transforms. This can be done in time 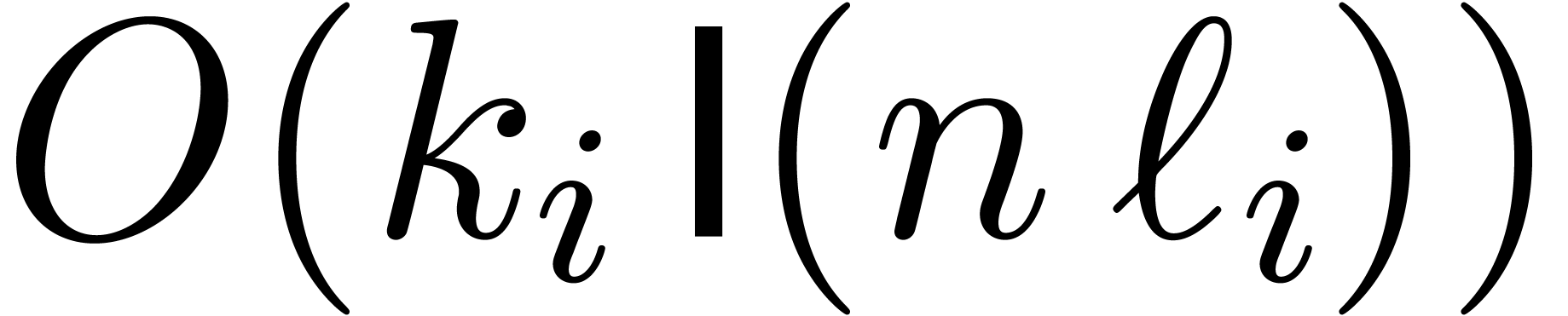 .
Since we have
.
Since we have 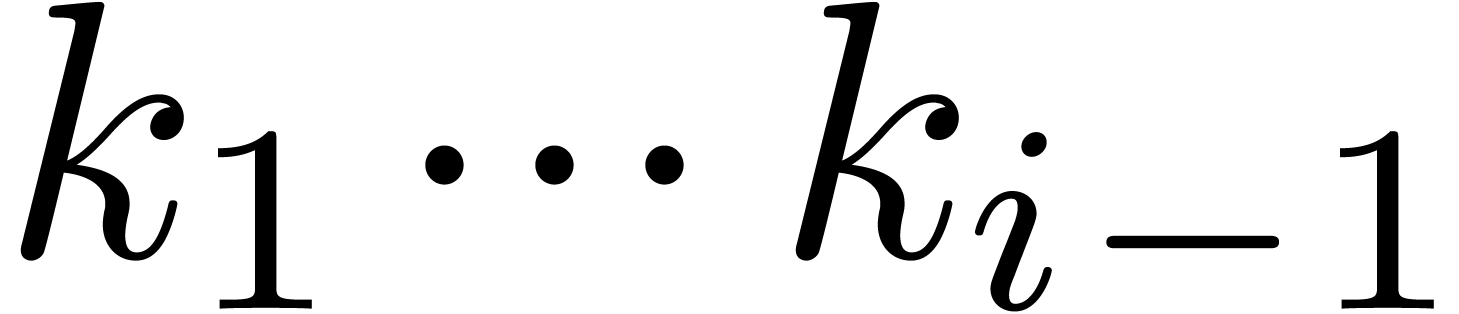 nodes at level
nodes at level  , the total precomputation time at level
, the total precomputation time at level  is therefore bounded by
is therefore bounded by 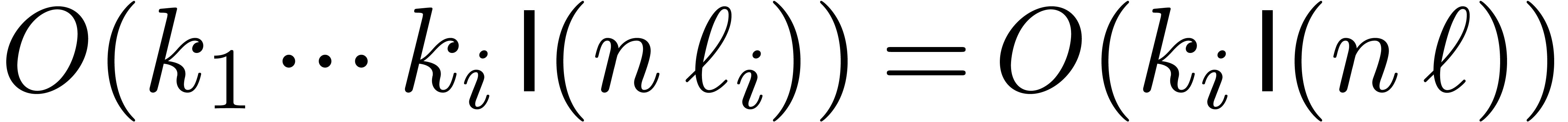 .
Now
.
Now  . Consequently, the total
precomputation time is bounded by
. Consequently, the total
precomputation time is bounded by
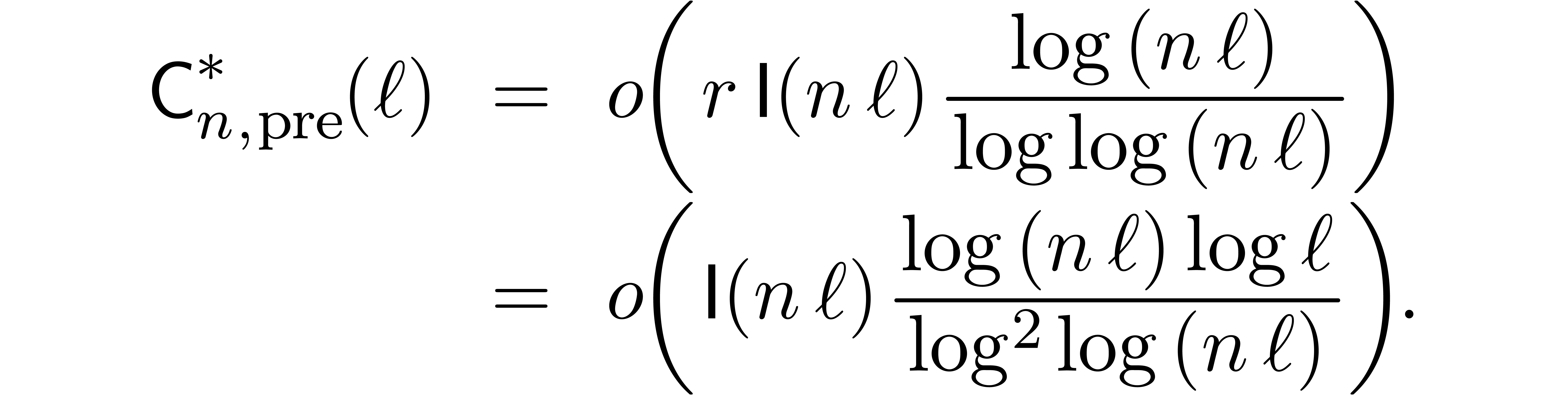
Let us now consider the complexity 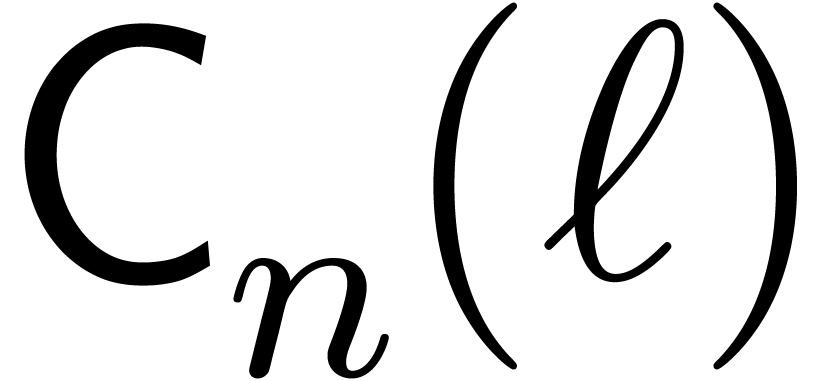 of
multi-modular reduction for fixed moduli
of
multi-modular reduction for fixed moduli  with
with
 for
for 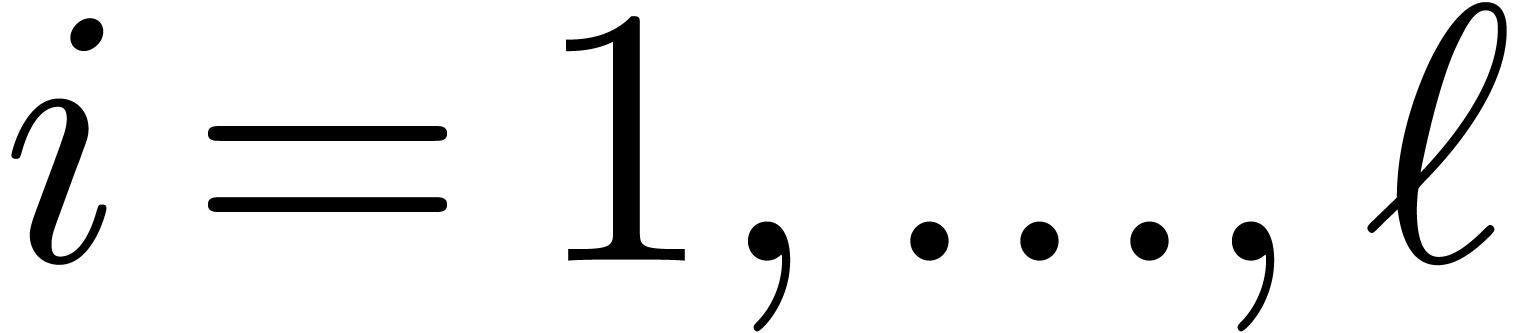 .
In this case, it is most efficient to work with scaled remainders, so
the algorithm contains three main steps:
.
In this case, it is most efficient to work with scaled remainders, so
the algorithm contains three main steps:
The initial conversion of  into (an
approximation of)
into (an
approximation of) 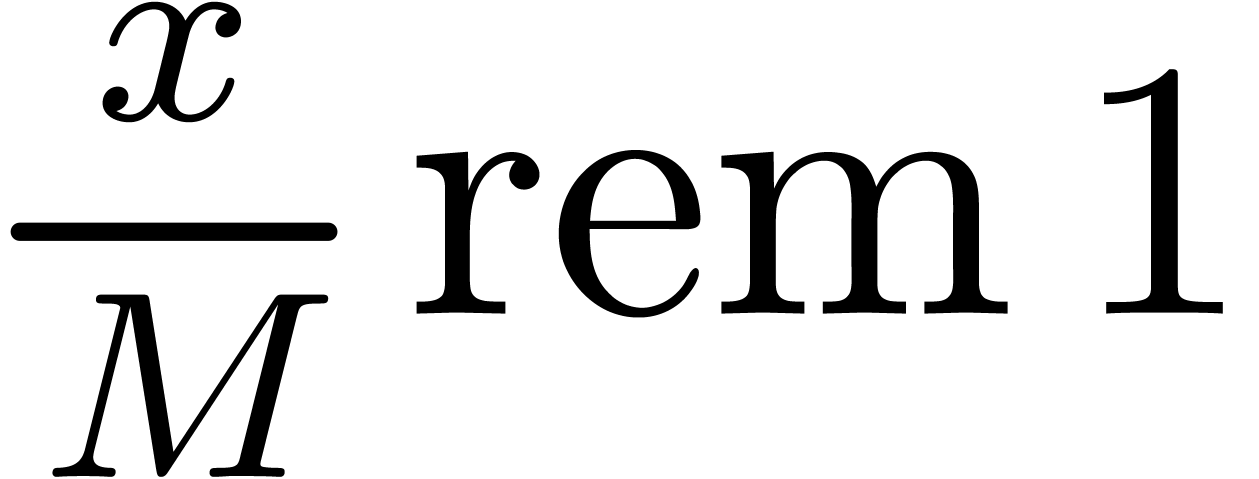 .
.
The computation of (approximations of) the scaled remainders 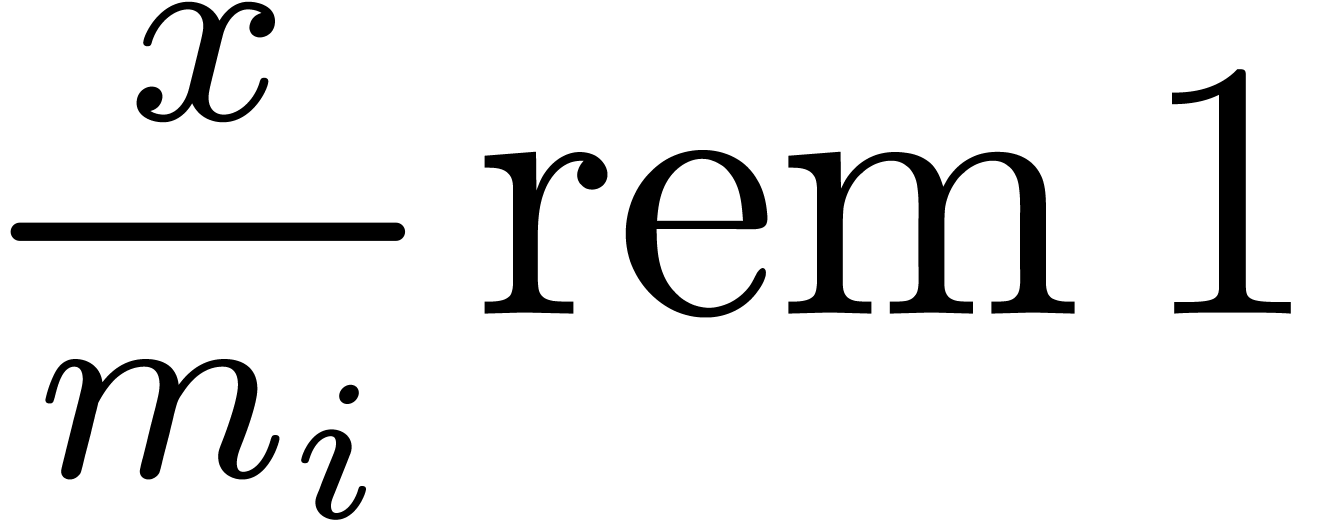 .
.
The final conversions of (approximations of) 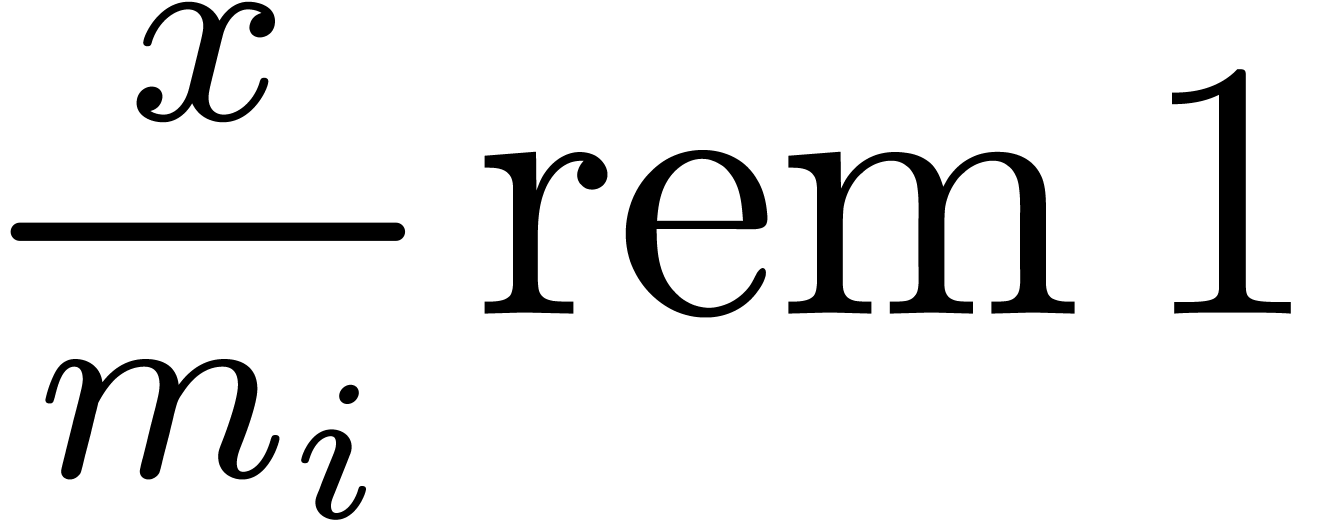 into
into  .
.
At a first stage, we will assume that  ,
where
,
where 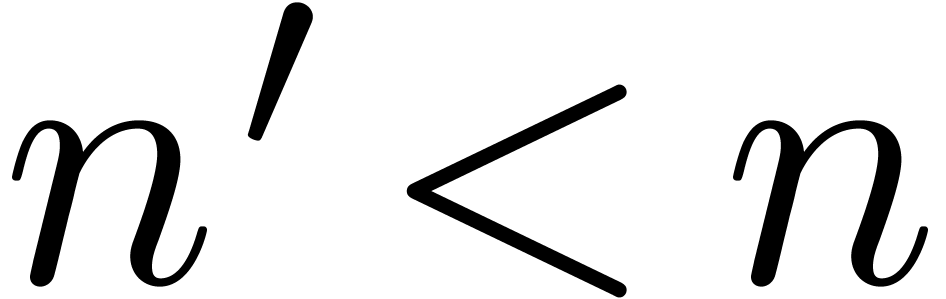 is sufficiently small such that the final
approximations of the scaled remainders
is sufficiently small such that the final
approximations of the scaled remainders 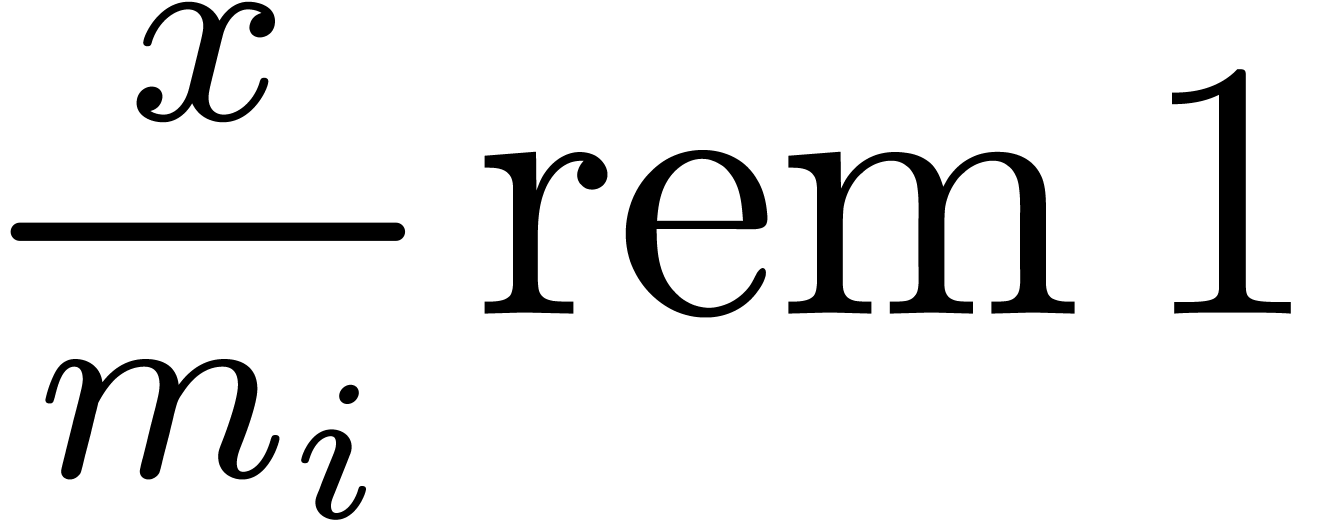 allow us
to recover the usual remainders
allow us
to recover the usual remainders  .
.
Let  denote the cost of step 2. The conversions
in steps 1 and 3 boil down to multiplications with fixed arguments, so
that
denote the cost of step 2. The conversions
in steps 1 and 3 boil down to multiplications with fixed arguments, so
that
For step 2, we use the scaled remainder tree algorithm from subsection
3.4, while taking the arities 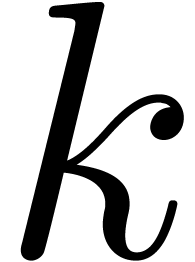 as in
subsection 3.5.
as in
subsection 3.5.
Our next task is to show that 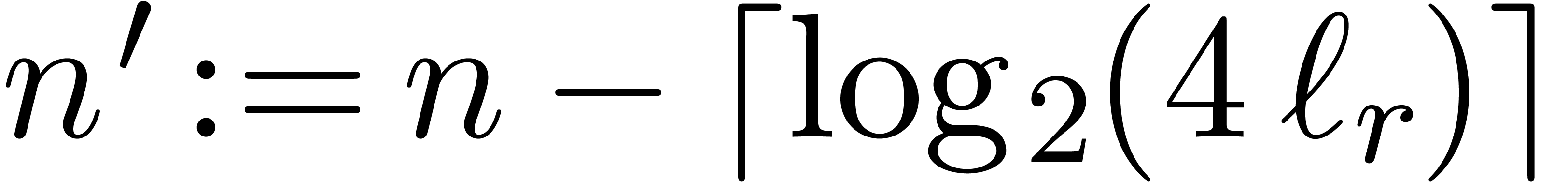 is small enough in
order to recover all remainders
is small enough in
order to recover all remainders  .
.
Proof. For 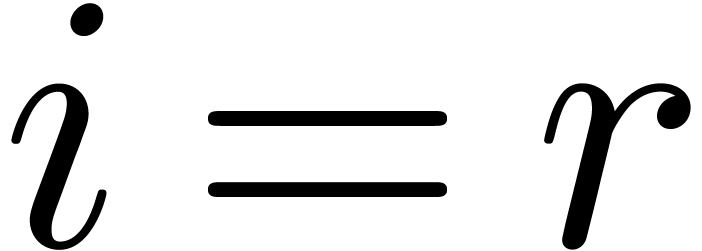 the result
clearly holds, so assume that
the result
clearly holds, so assume that  .
In particular, if
.
In particular, if  is sufficiently large, then it
follows that
is sufficiently large, then it
follows that 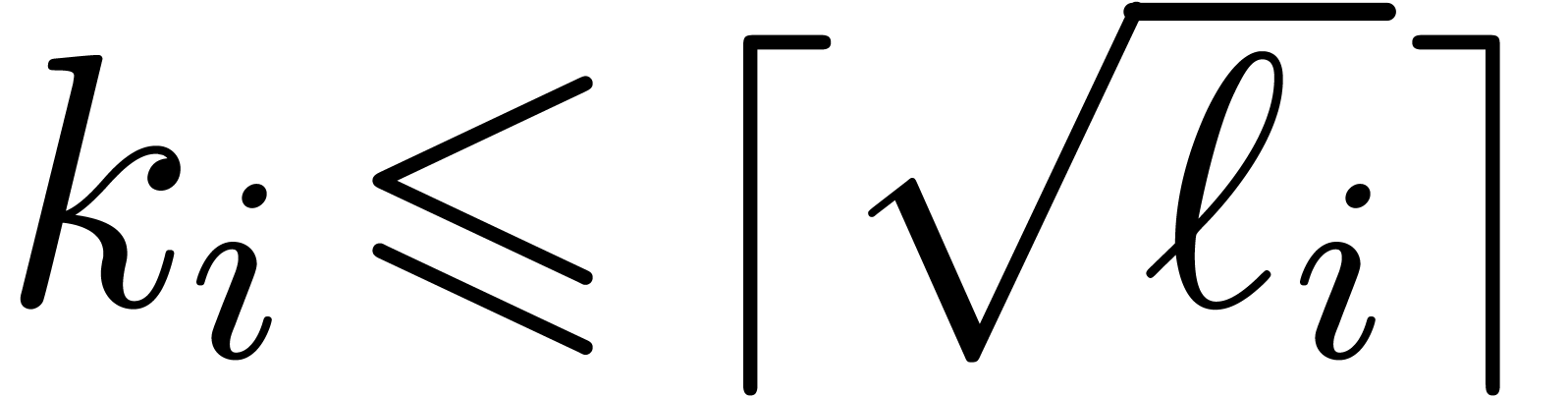 . Now assume for
contradiction that
. Now assume for
contradiction that 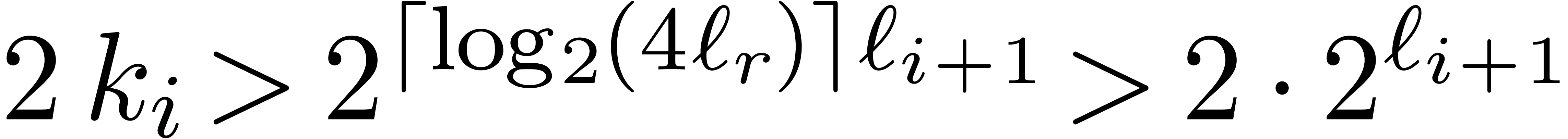 . Then we
would get
. Then we
would get 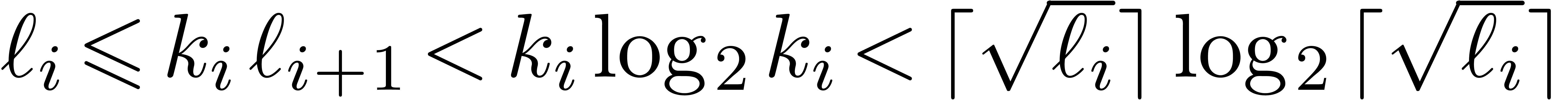 . This is
impossible for
. This is
impossible for 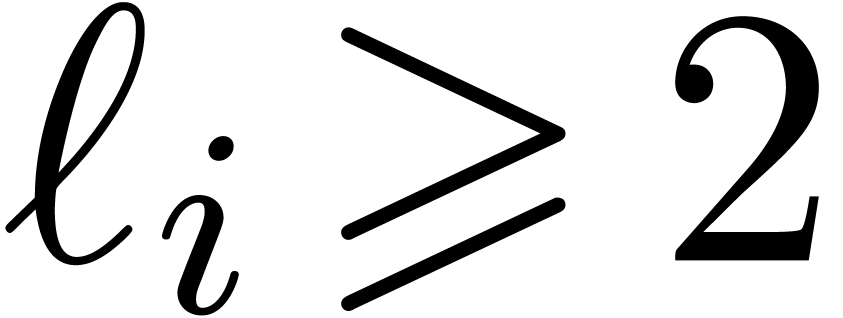 .
.
Now starting with a circular 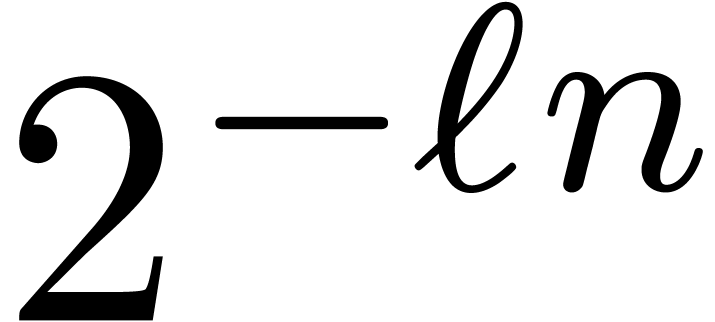 -approximation
of
-approximation
of 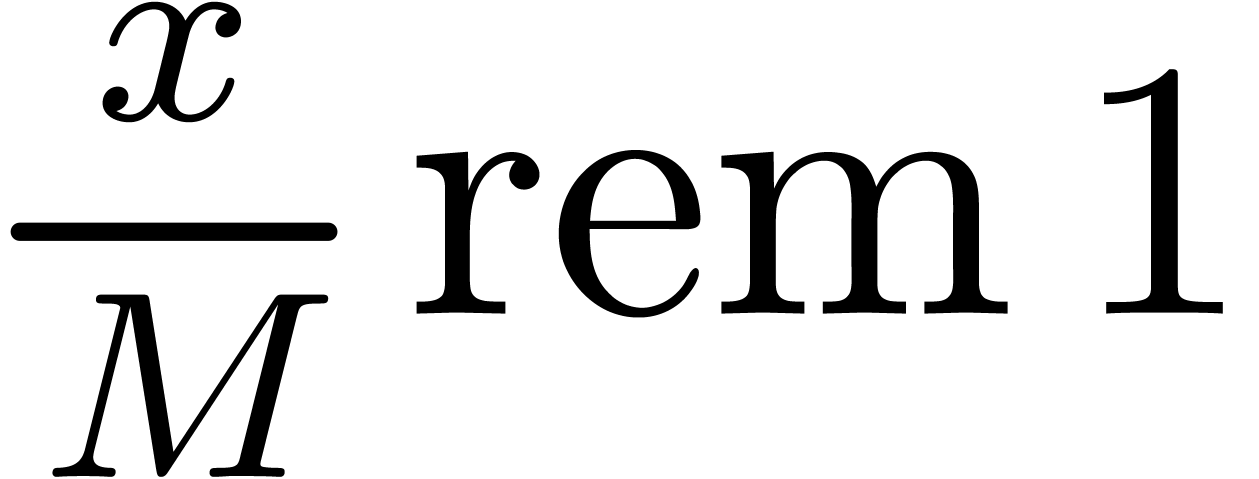 , the scaled reduction
algorithm from subsection 3.3 yields circular
, the scaled reduction
algorithm from subsection 3.3 yields circular  -approximations for the scaled remainders
-approximations for the scaled remainders 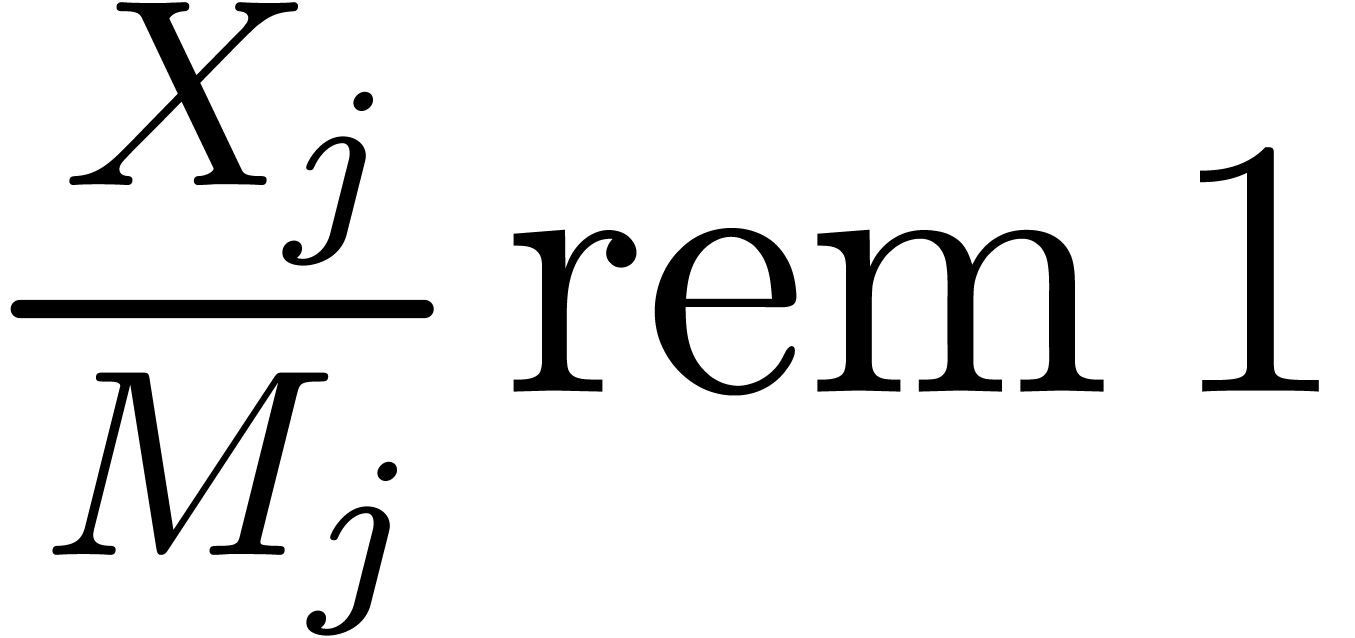 at level
at level 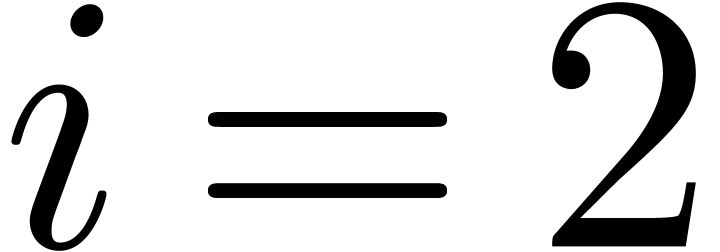 .
Lemma 9 now shows that
.
Lemma 9 now shows that 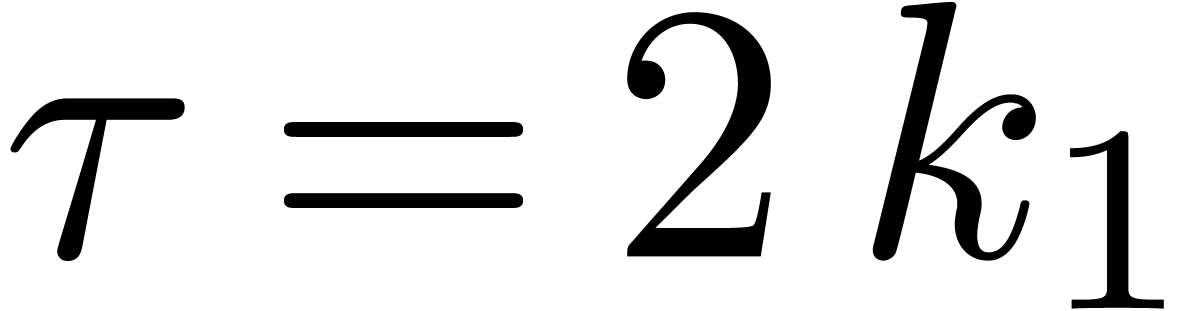 is
sufficiently small for a continued application of the same algorithm for
the next level. By induction over
is
sufficiently small for a continued application of the same algorithm for
the next level. By induction over 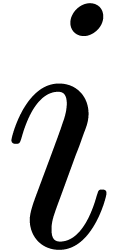 ,
the same reasoning shows that the scaled remainders at the
,
the same reasoning shows that the scaled remainders at the  -th level are computed with an error below
-th level are computed with an error below
At the very end, we obtain 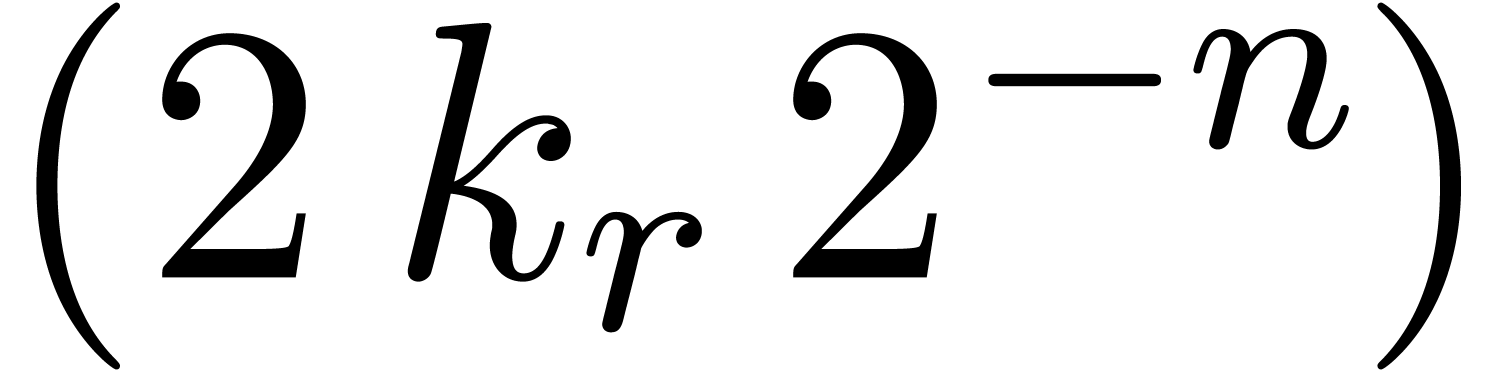 -approximations
for the scaled remainders
-approximations
for the scaled remainders 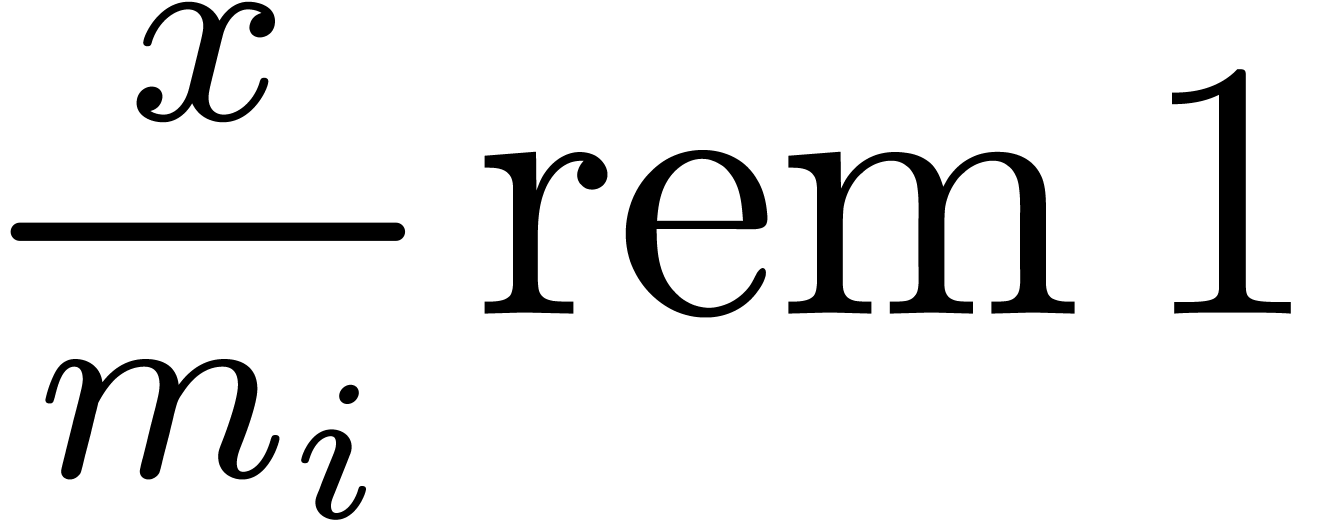 .
Since
.
Since 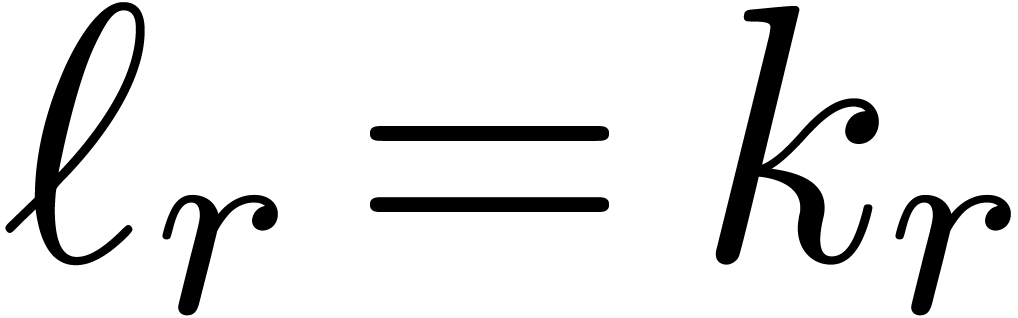 , this allows us to
reconstruct each remainder
, this allows us to
reconstruct each remainder  using a
multiplication by
using a
multiplication by 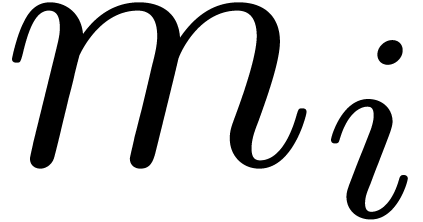 . This
shows that
. This
shows that 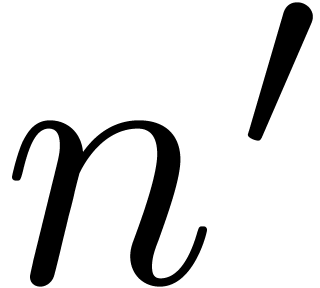 is indeed small enough for the
algorithm to work.
is indeed small enough for the
algorithm to work.
This bound holds uniformly in  for
for  .
.
Proof. A similar cost analysis as in the proof of Theorem 6 yields
when 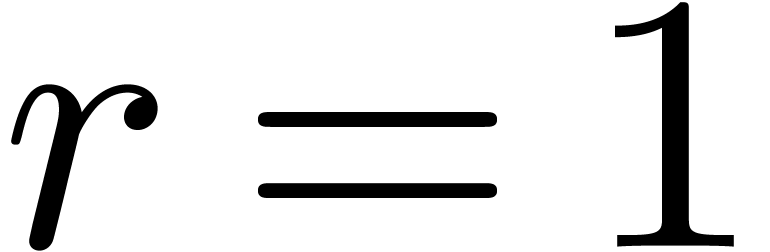 and
and
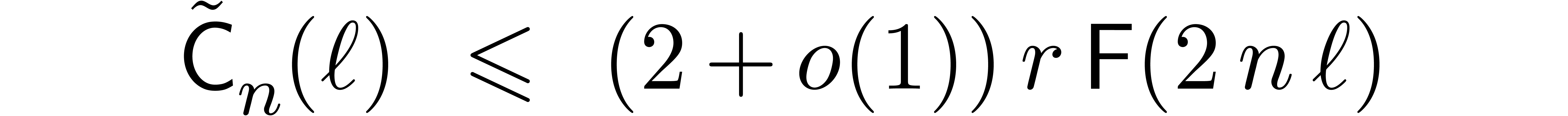
when  . In both cases,
combination with (19) yields
. In both cases,
combination with (19) yields
Notice also that 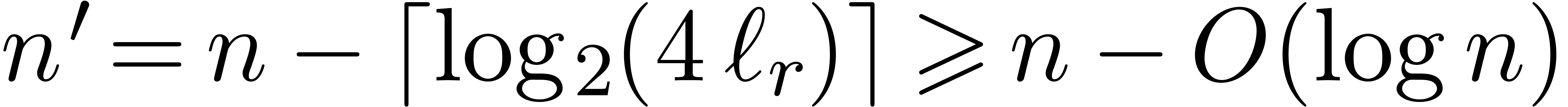 , by Lemma
5.
, by Lemma
5.
Given a number 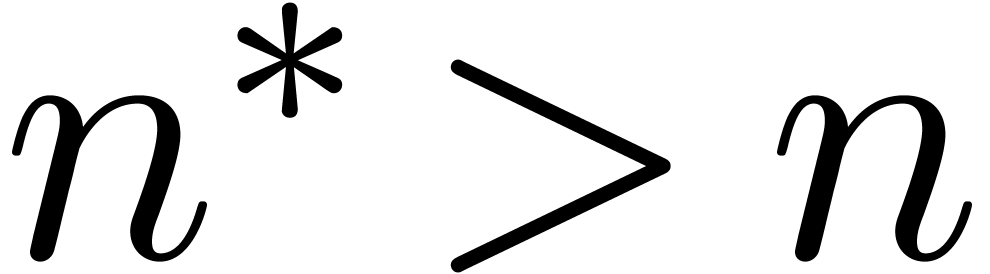 , we may
construct a similar sequence
, we may
construct a similar sequence 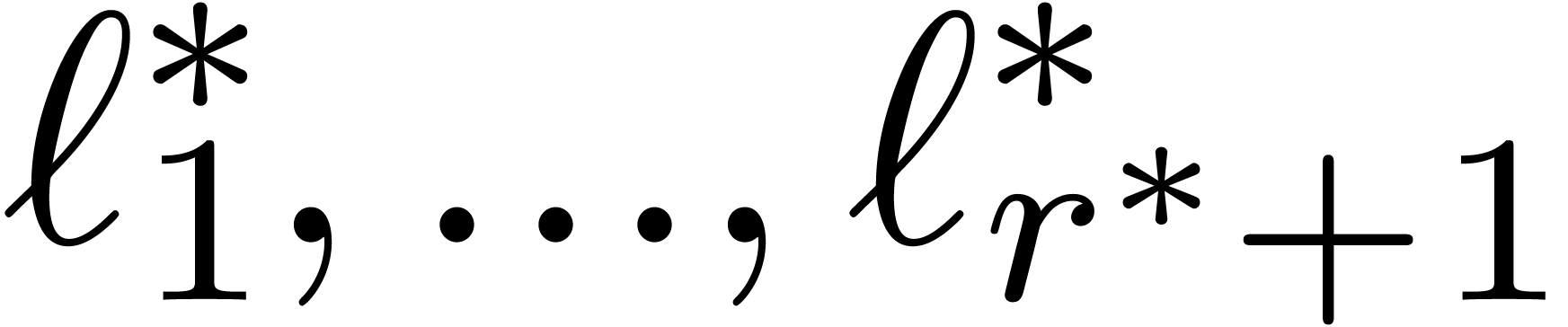 when using
when using 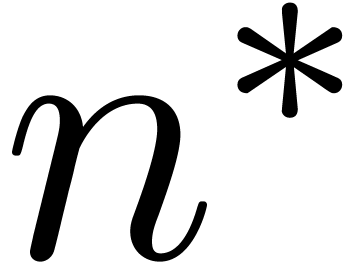 in the role of
in the role of 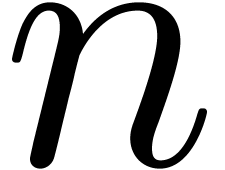 .
Taking
.
Taking 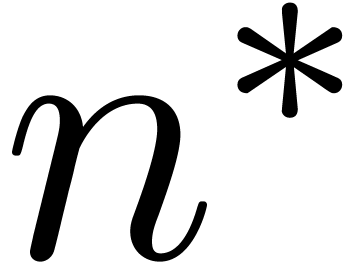 minimal such that
minimal such that 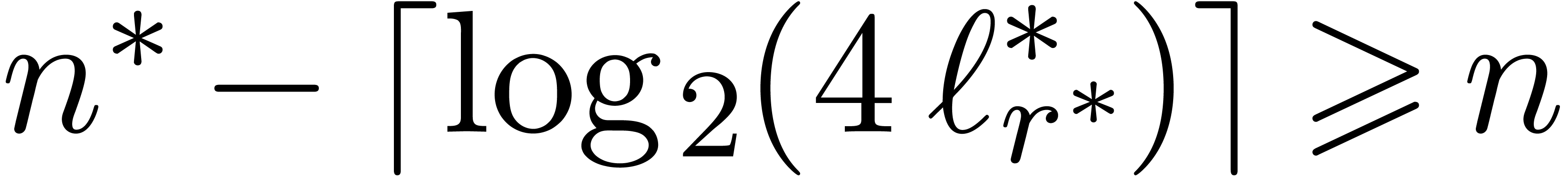 , we have
, we have
Moreover, 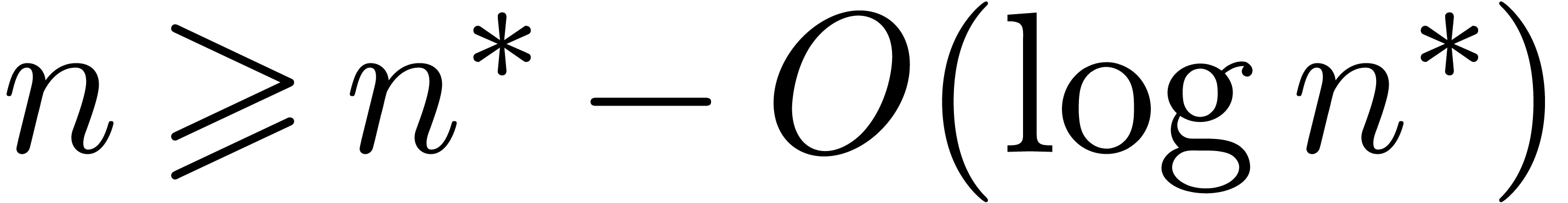 , which implies
, which implies
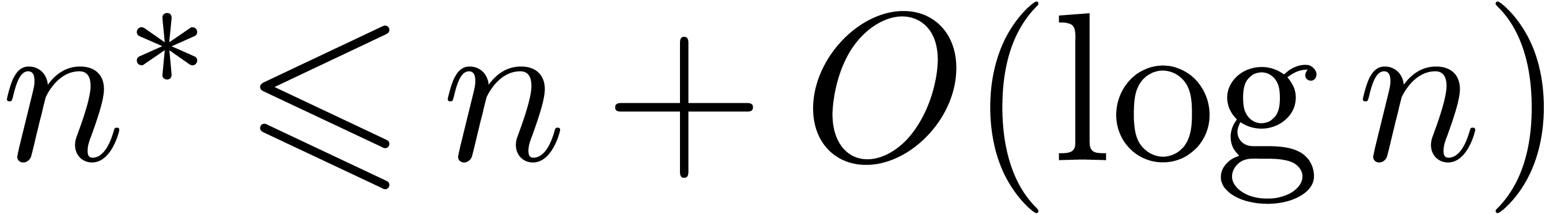 . Plugging this into (21), the result follows, since
. Plugging this into (21), the result follows, since 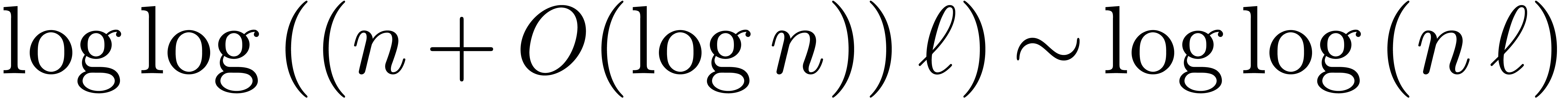 and the
assumption that
and the
assumption that 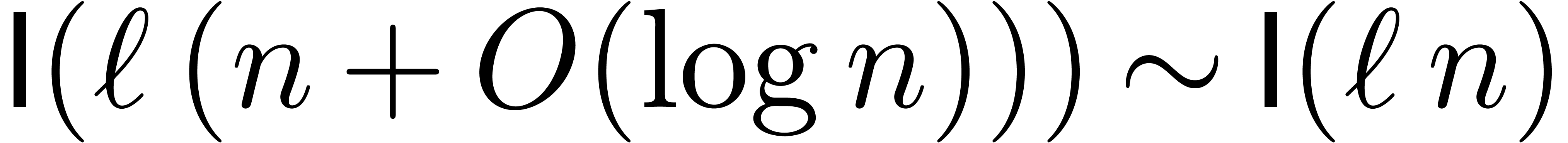 is increasing implies
is increasing implies 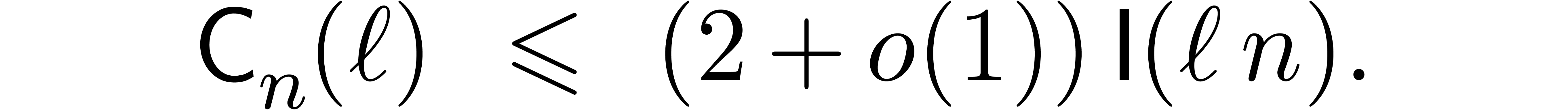 .
.
Remark 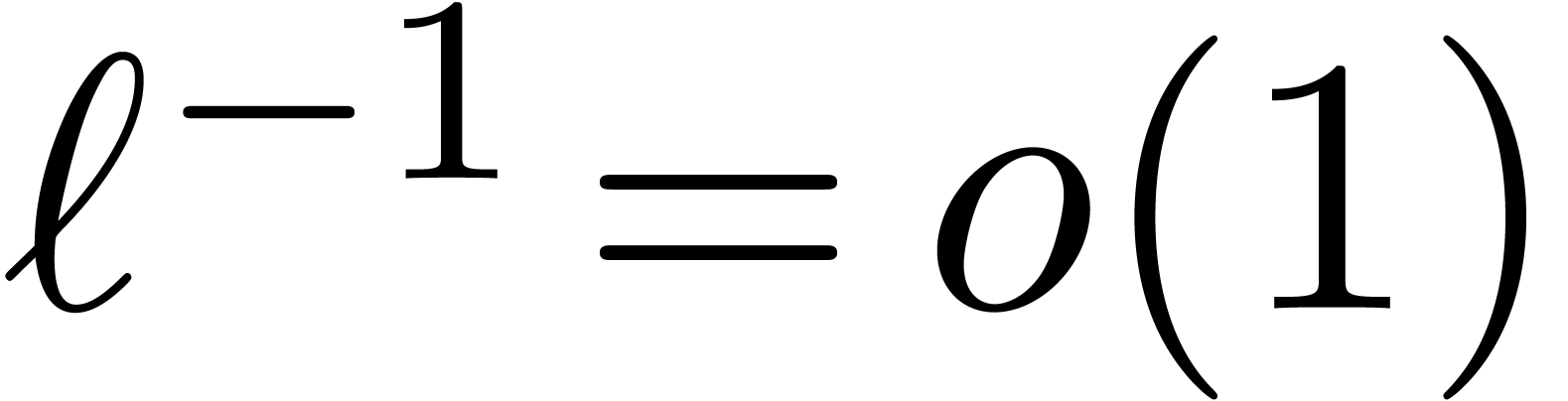 and
and 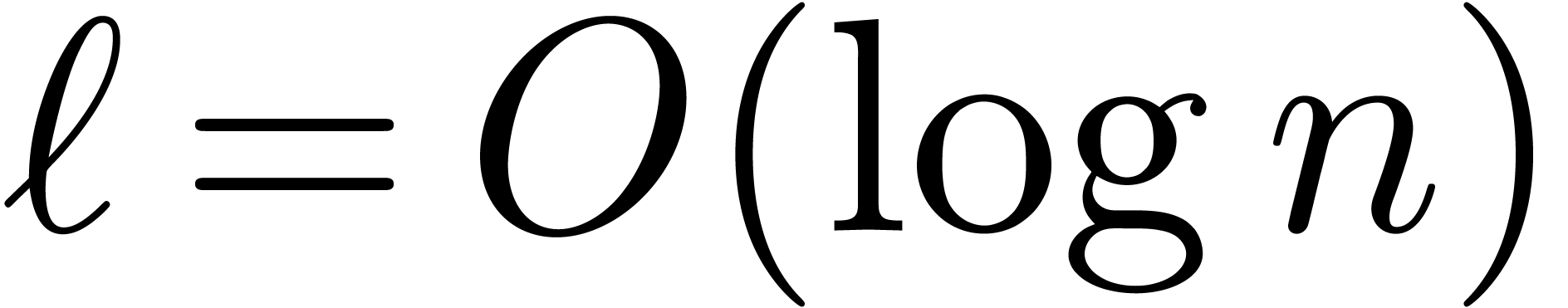 , the bound
(20) simplifies into
, the bound
(20) simplifies into
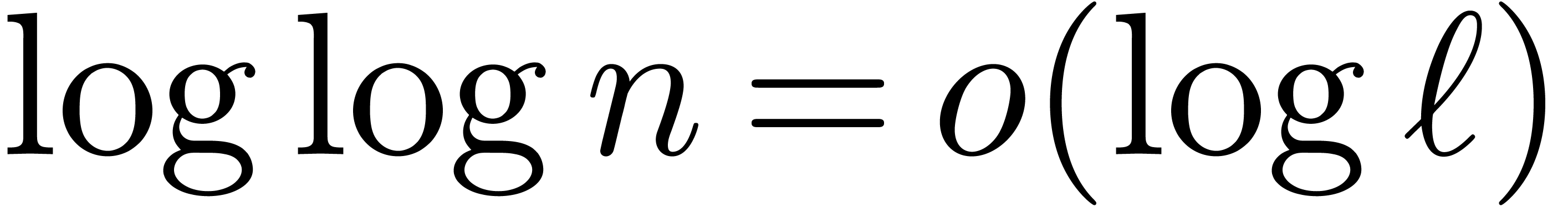
If 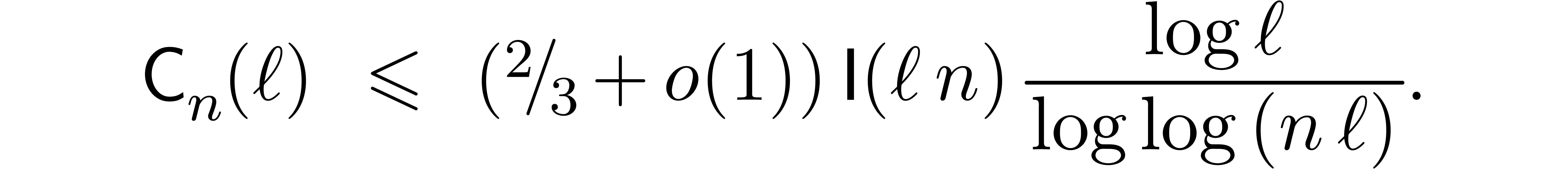 , then the bound (20)
becomes
, then the bound (20)
becomes
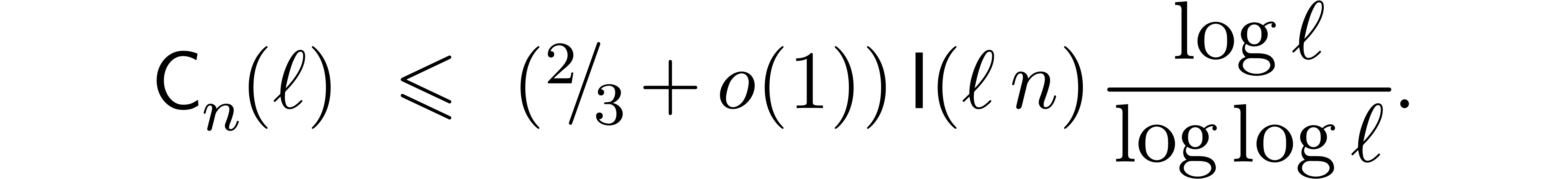
For very large  with
with 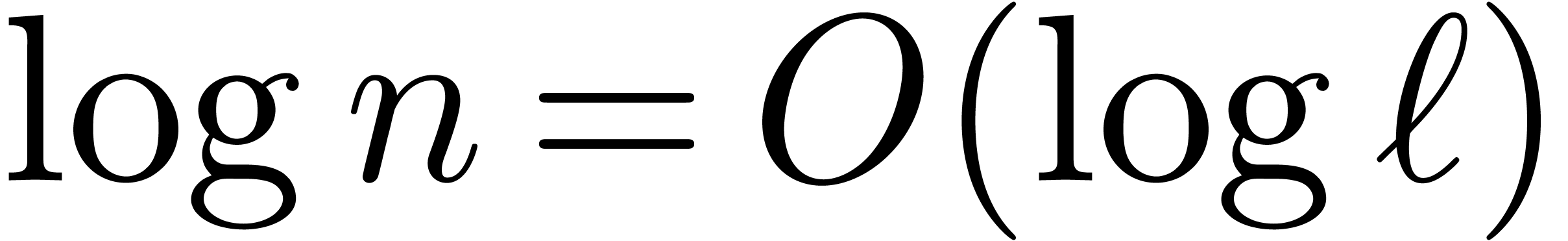 , this yields
, this yields
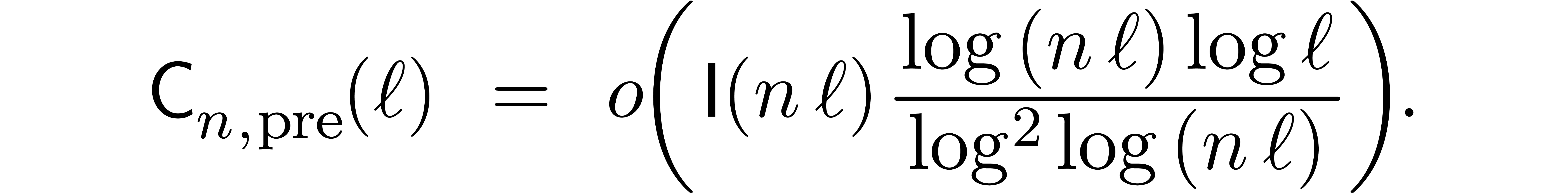
Remark 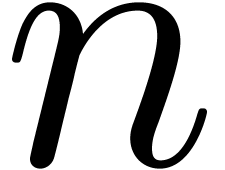 ,
,  and
and  is again bounded by
is again bounded by
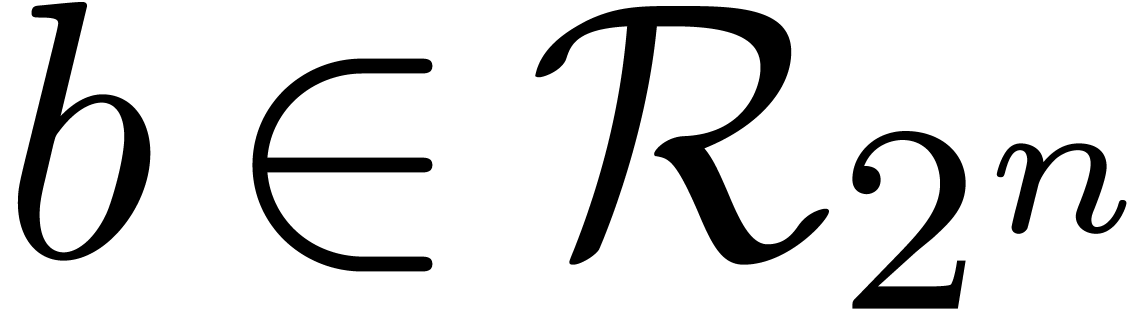
The approach of this section can also be used for the related problem
such as base conversion. Let 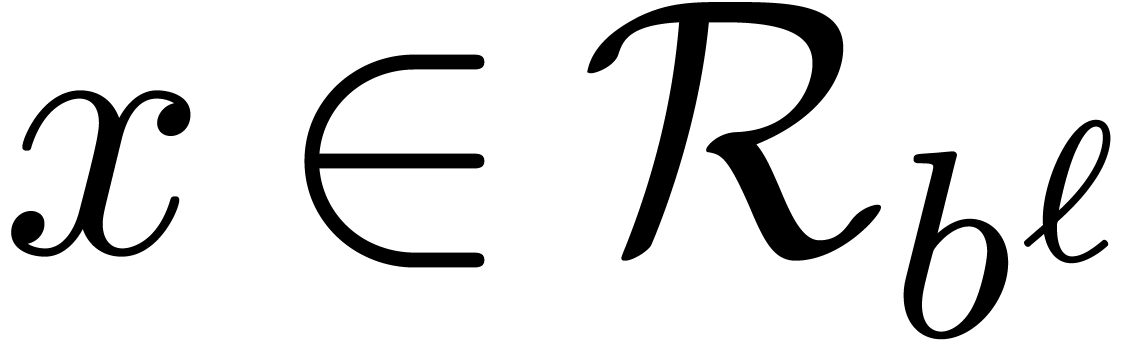 and
and  be a fixed base and order. Given a number
be a fixed base and order. Given a number 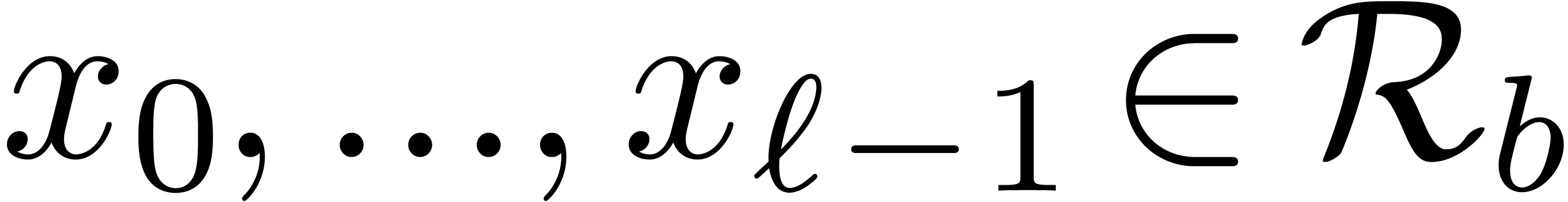 , the problem is to compute
, the problem is to compute 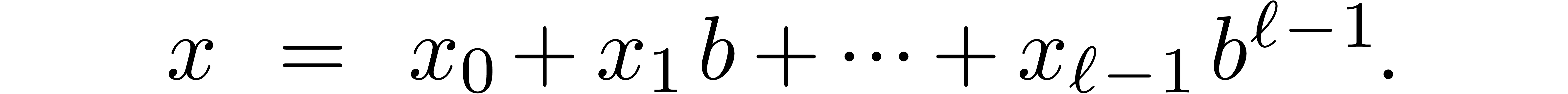 with
with
Inversely, one may wish to reconstruct  from
from
 . It is well known that both
problems can be solved using a similar remainder tree process as in the
case of Chinese remainders. The analogues for the formulas (7)
and (9) are (22) and
. It is well known that both
problems can be solved using a similar remainder tree process as in the
case of Chinese remainders. The analogues for the formulas (7)
and (9) are (22) and
The analogue of the recursive process of subsection 3.4
reduces a problem of size  to
to 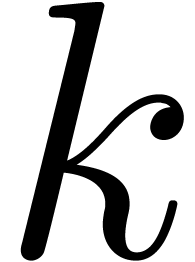 similar problems of size
similar problems of size 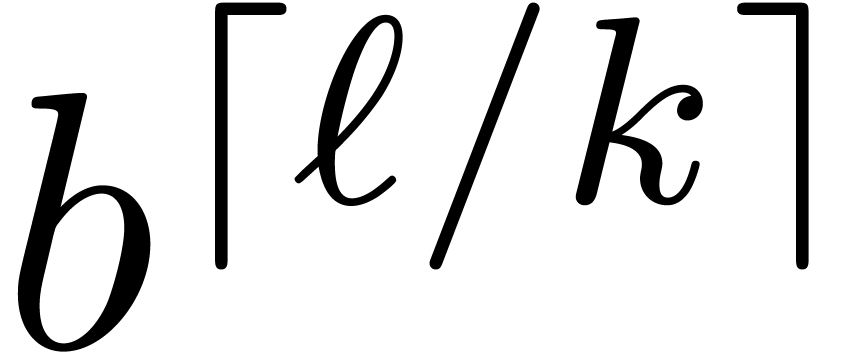 and one similar problem
of size
and one similar problem
of size 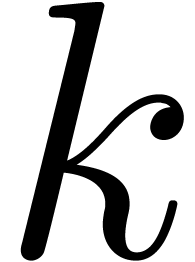 but for the base
but for the base 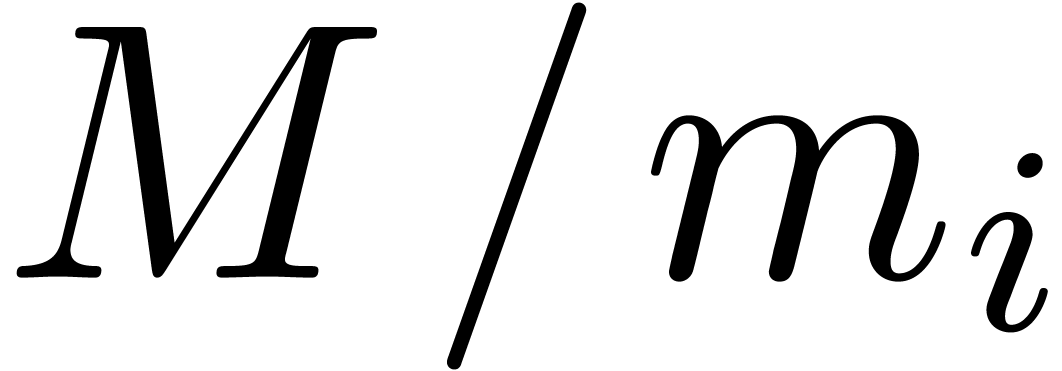 . A routine verification shows that the complexity
bounds (18) and (20) also apply in this
context.
. A routine verification shows that the complexity
bounds (18) and (20) also apply in this
context.
Moreover, for nodes of the remainder tree at the same level, the
analogues of the cofactors and the multiplicands  in (9) do not vary as a function of the node. For this
reason, the required precomputations as a function of
in (9) do not vary as a function of the node. For this
reason, the required precomputations as a function of 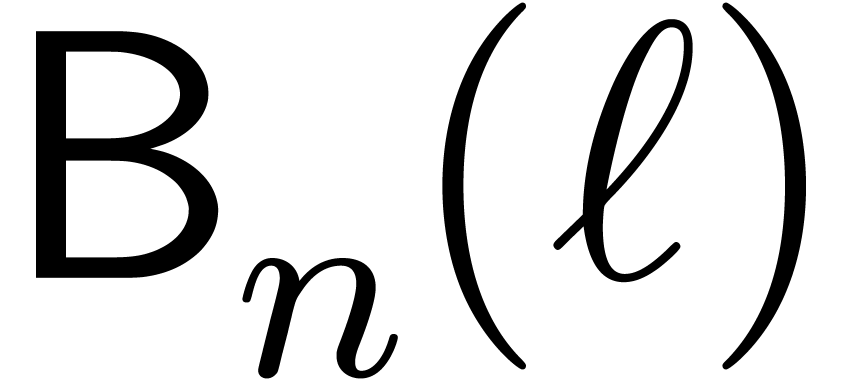 and
and  can actually be done much faster. This makes
it possible to drop the hypothesis that
can actually be done much faster. This makes
it possible to drop the hypothesis that 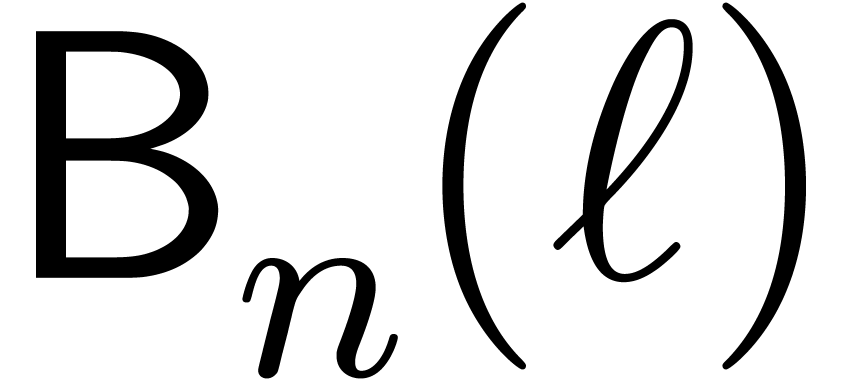 and
and  are fixed and consider these parameters as part of
the input. Let us denote by
are fixed and consider these parameters as part of
the input. Let us denote by 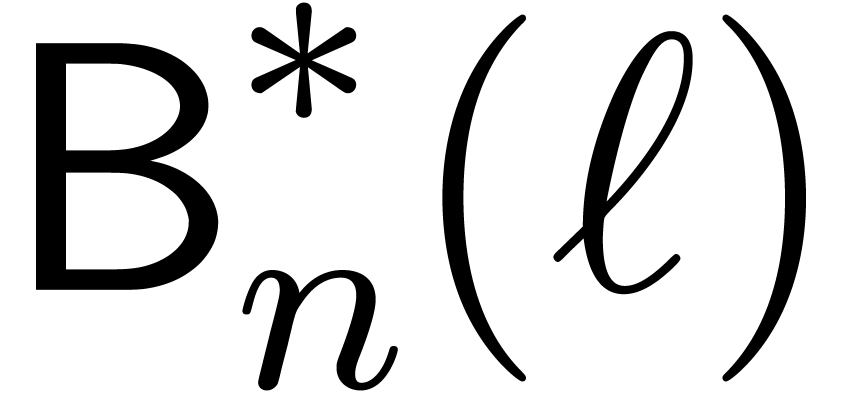 and
and 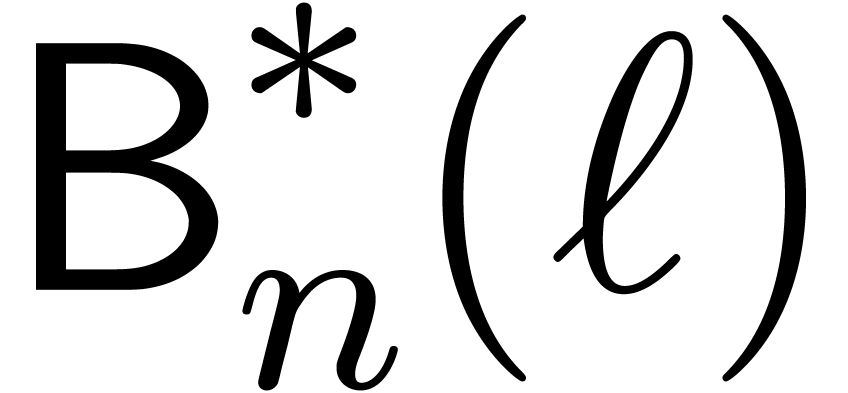 the complexities of computing
the complexities of computing  as a function of
as a function of
 and vice versa.
and vice versa.
These bound holds uniformly in  for
for  .
.
Proof. Let us estimate the cost of the
precomputations as a function of 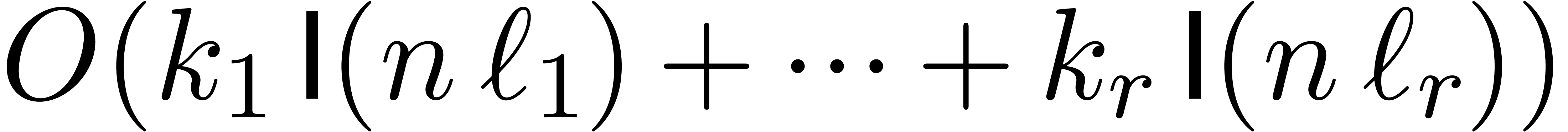 and
and  . The analysis is similar as in
Remark 8 except that we only have to do the precomputations
for a single node of the tree at each level
. The analysis is similar as in
Remark 8 except that we only have to do the precomputations
for a single node of the tree at each level 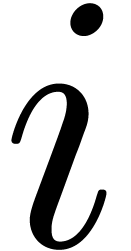 . Consequently, the precomputation time is now
bounded by
. Consequently, the precomputation time is now
bounded by 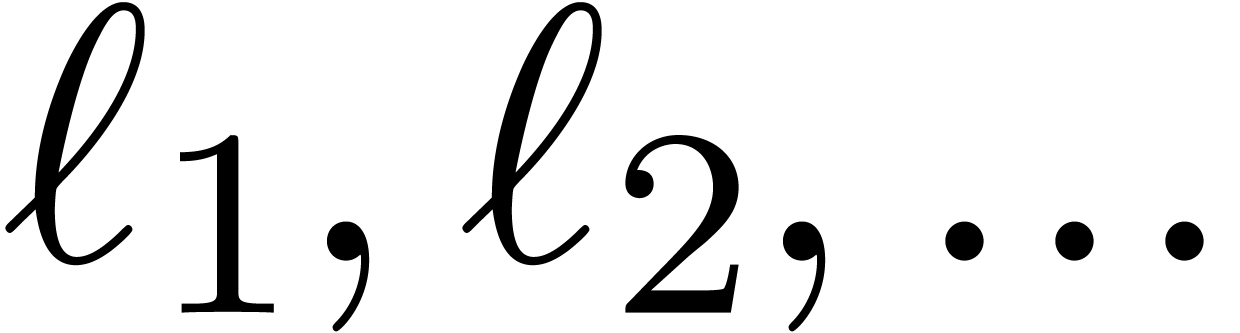 . Since the
. Since the 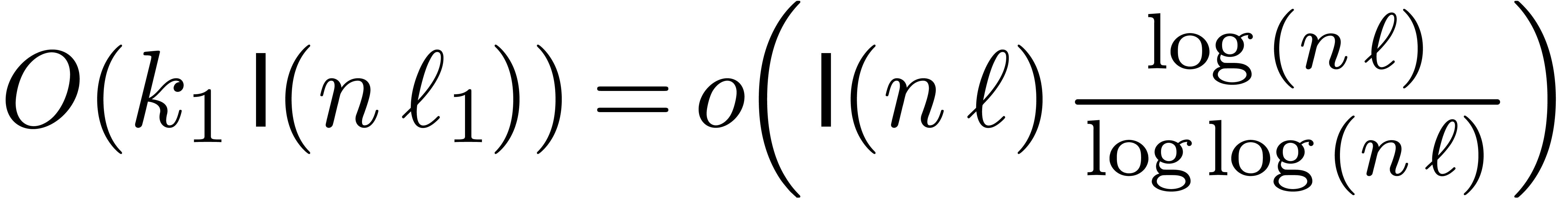 decrease with at least geometric speed, this cost is
dominated by
decrease with at least geometric speed, this cost is
dominated by 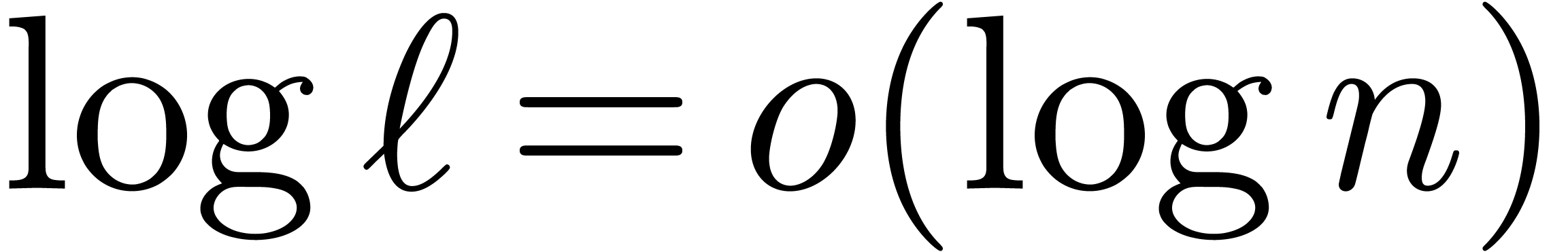 . This proves
the result under the condition that
. This proves
the result under the condition that 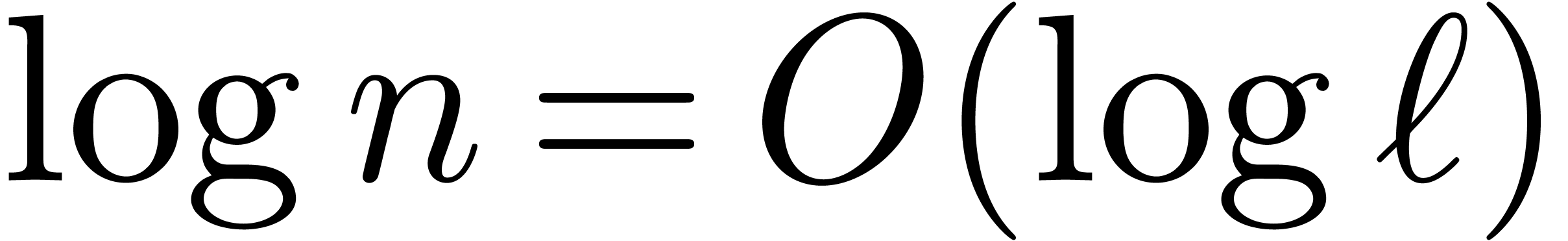 .
.
If 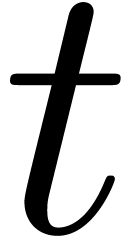 , then we need to
construct
, then we need to
construct  in a slightly different way. Assuming
that
in a slightly different way. Assuming
that 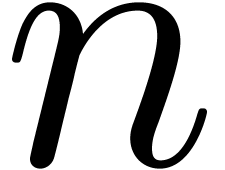 is sufficiently large, let
is sufficiently large, let 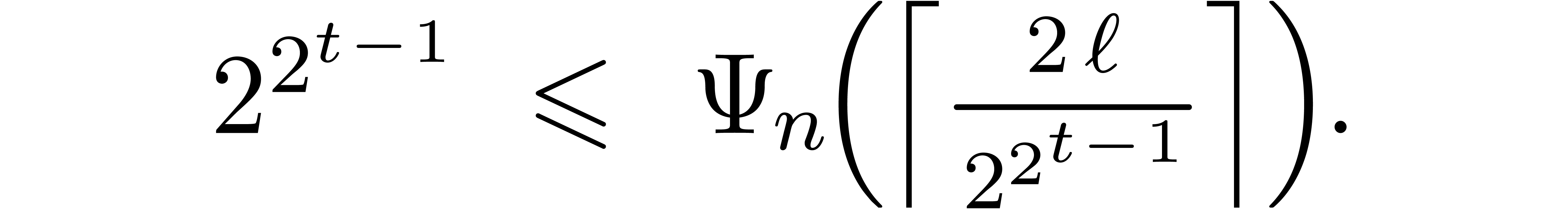 be maximal such that
be maximal such that
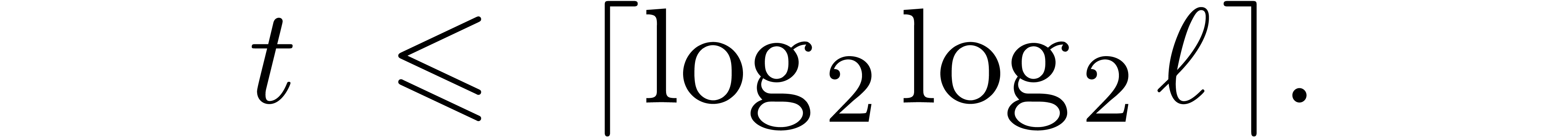
Notice that
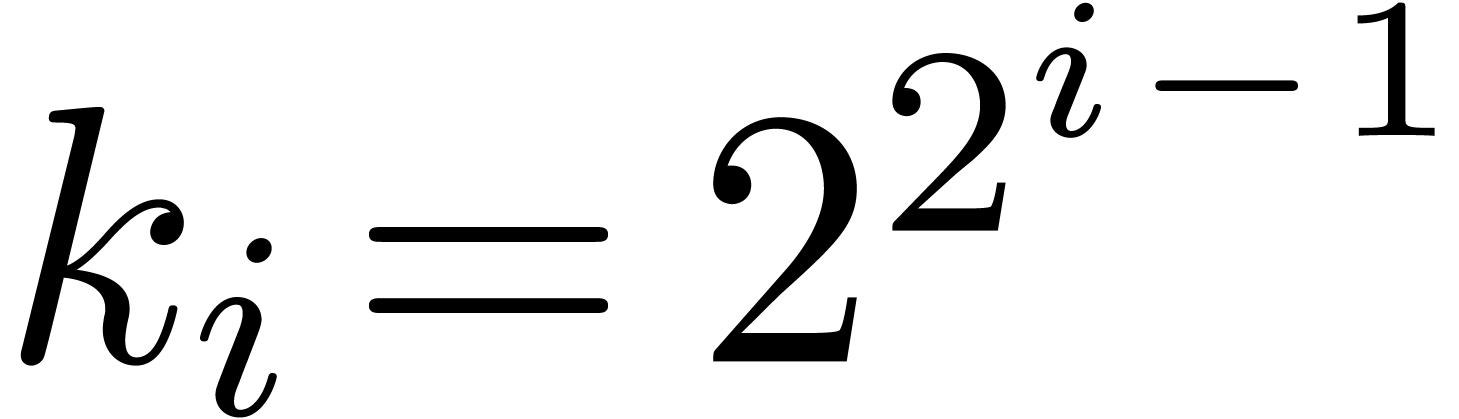
We again set 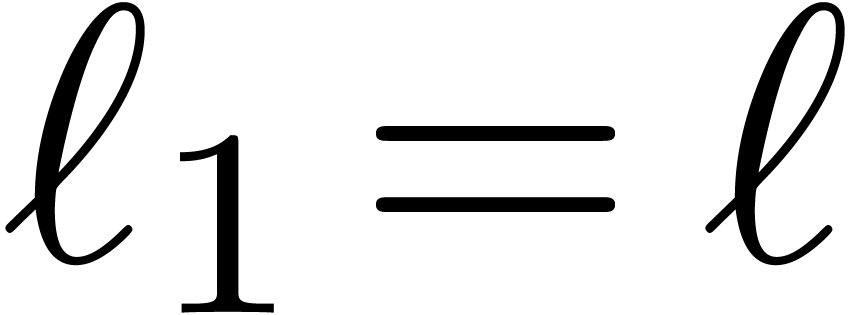 and
and 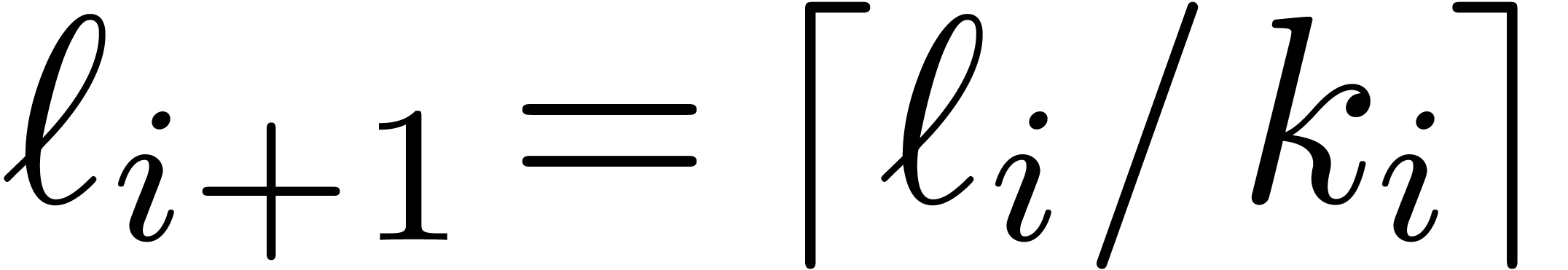 .
This time, we take
.
This time, we take 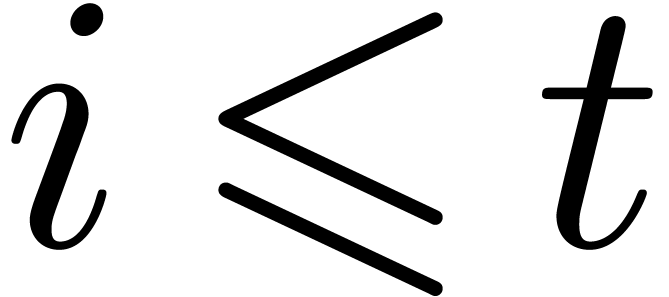 for
for 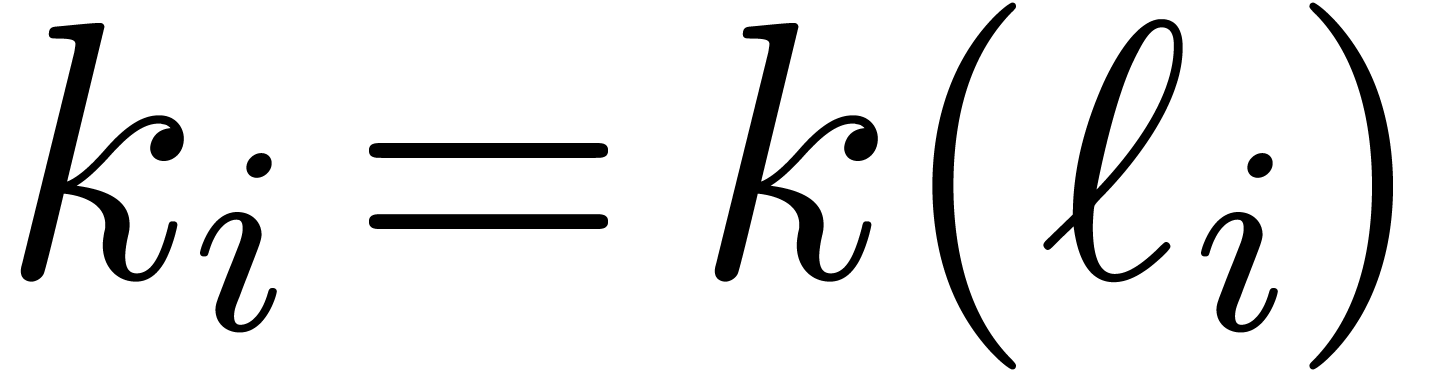 and proceed with the usual construction
and proceed with the usual construction  for
for
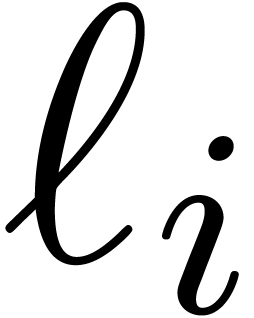 . It follows that
. It follows that
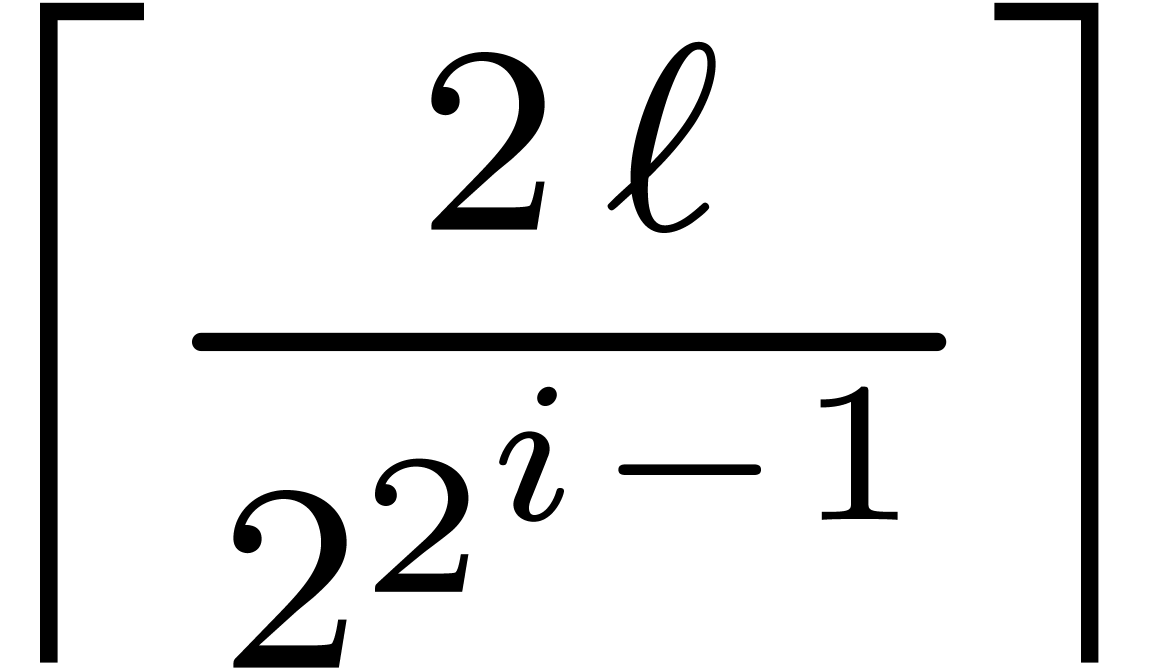 |
 |
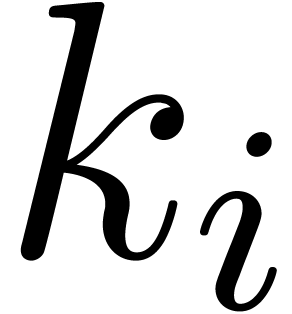 |
(i=1,…,t+1) |
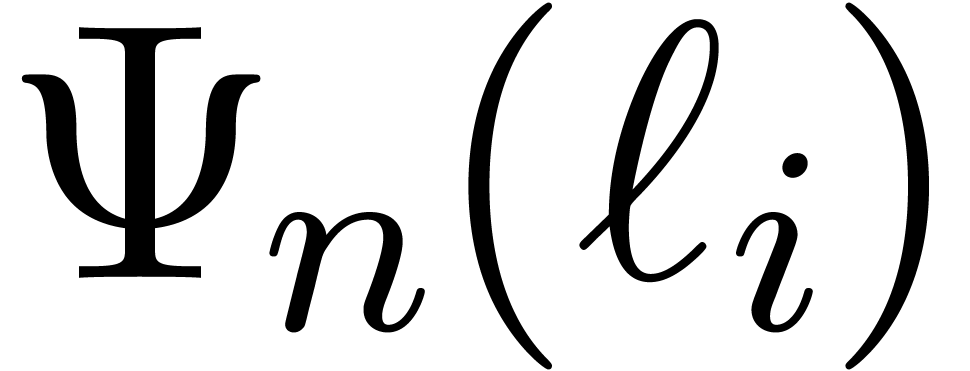 |
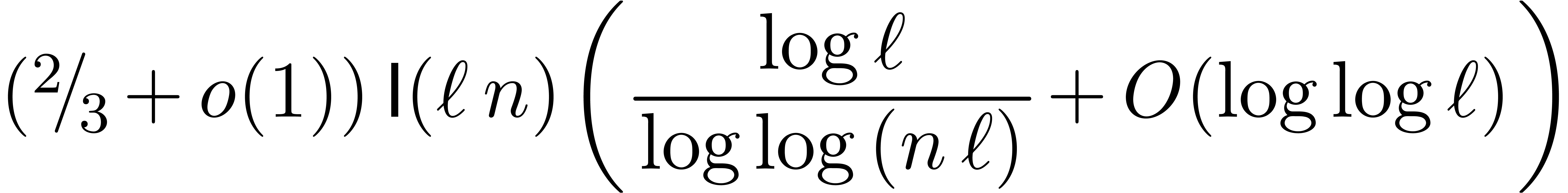 |
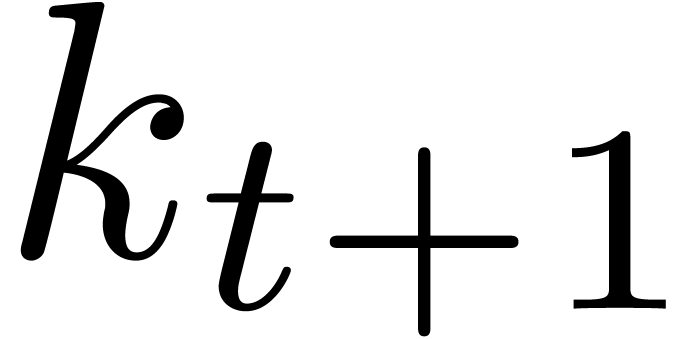 |
(i=1,…,t) |
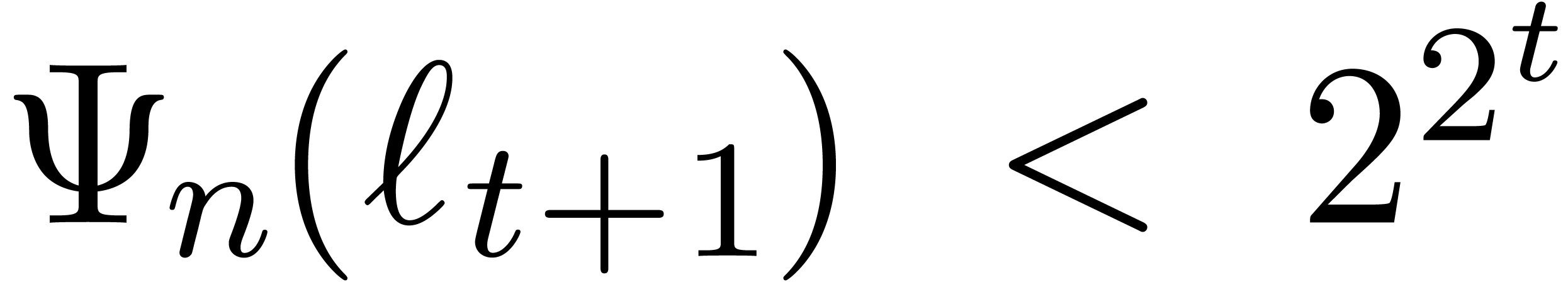 |
 |
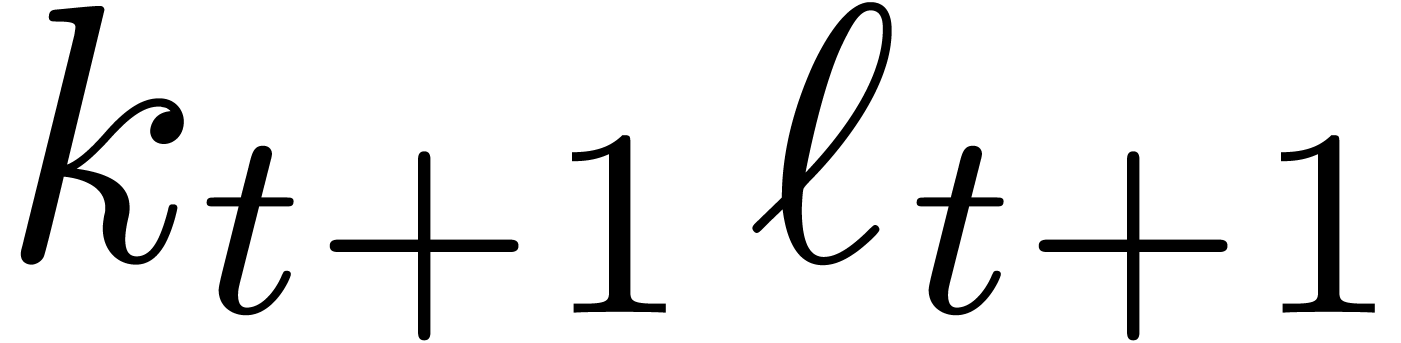 |
|
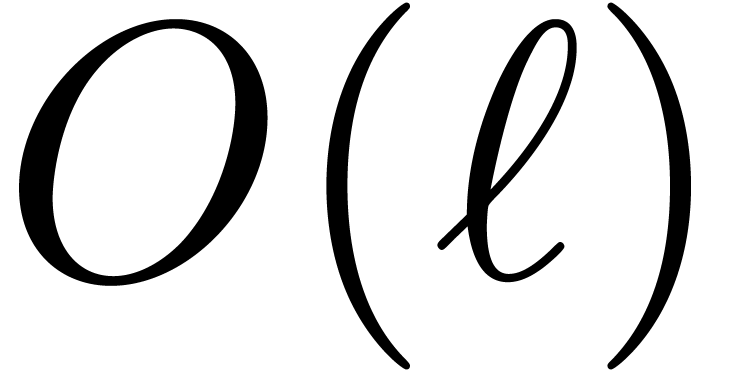 |
 |
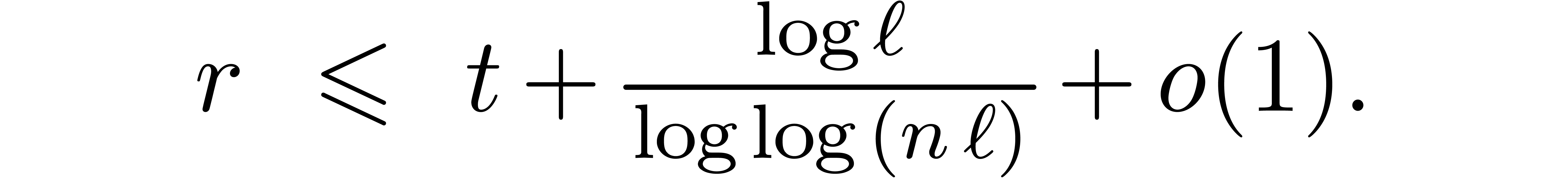 |
and
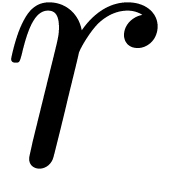
Using the new bound for  , a
similar complexity analysis as in the proofs of Theorems 6
and 10 yields the bounds (24) and (25)
when forgetting about the cost of the precomputations. Now the cost
, a
similar complexity analysis as in the proofs of Theorems 6
and 10 yields the bounds (24) and (25)
when forgetting about the cost of the precomputations. Now the cost  of the precomputations for the first
of the precomputations for the first 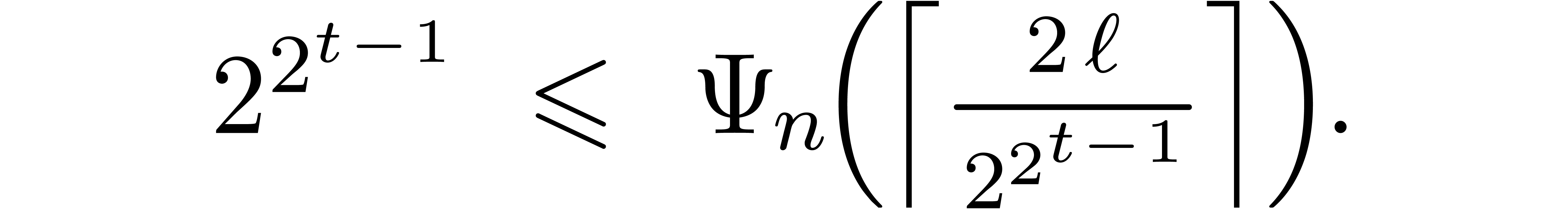 levels is bounded by
levels is bounded by

and the cost 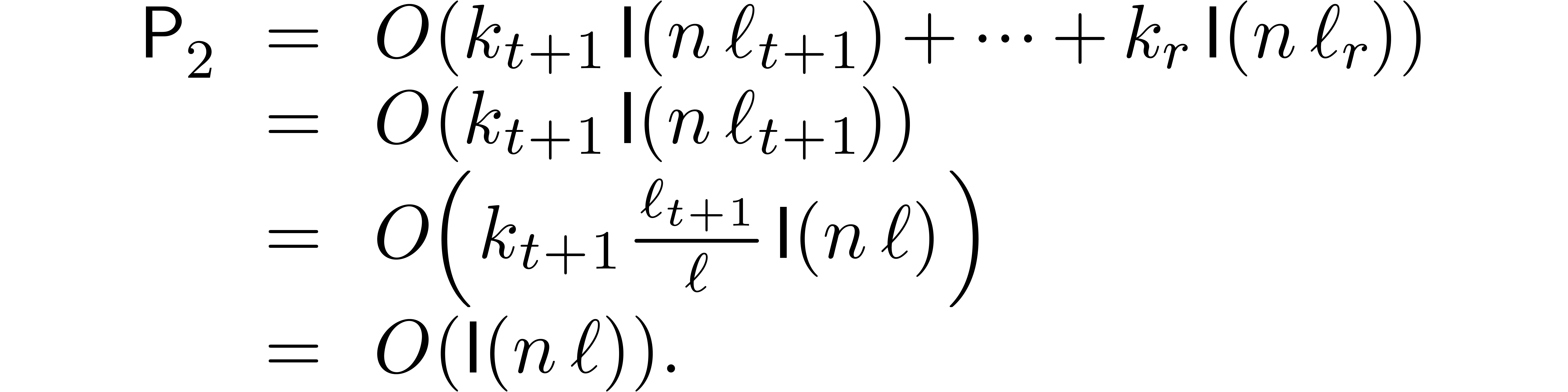 for the remaining levels by
for the remaining levels by

We conclude that the right-hand sides of (24) and (25)
absorb the cost 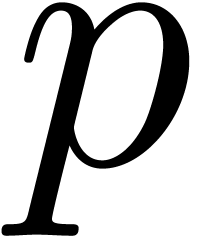 of the precomputations.
of the precomputations.
It is quite straightforward to adapt the theory of this section to
univariate polynomials instead of integers. An example of this kind of
adaptations can be found in [2]. In particular, this yields
efficient algorithms for multi-point evaluation and interpolation in the
case when the evaluation points are fixed. The analogues of our
algorithms for base conversion yield efficient methods for 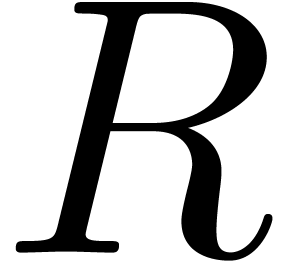 -adic expansions and reconstruction.
-adic expansions and reconstruction.
More precisely, let 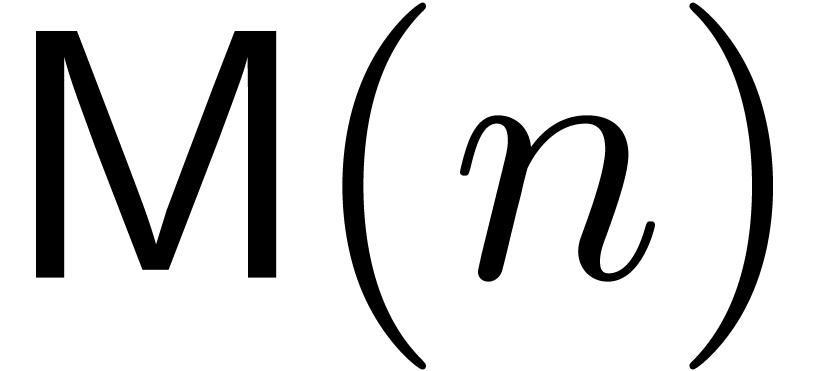 be an effective commutative
ring and let
be an effective commutative
ring and let 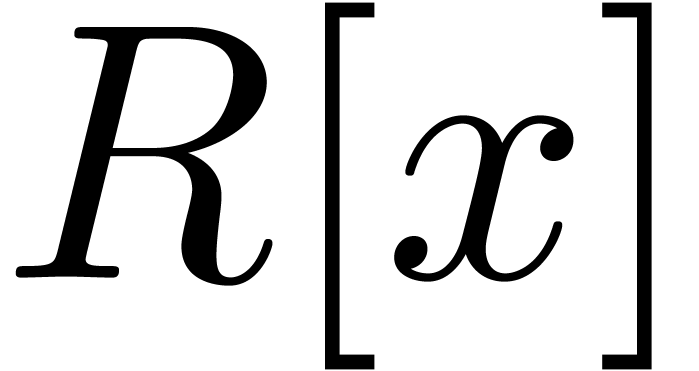 be the cost of multiplying two
polynomials of degree
be the cost of multiplying two
polynomials of degree 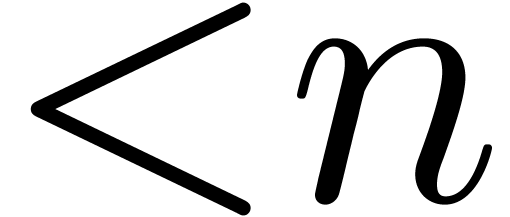 in
in 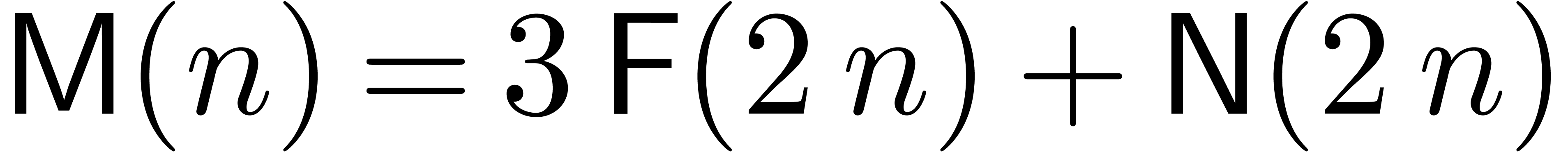 . Assume that
. Assume that 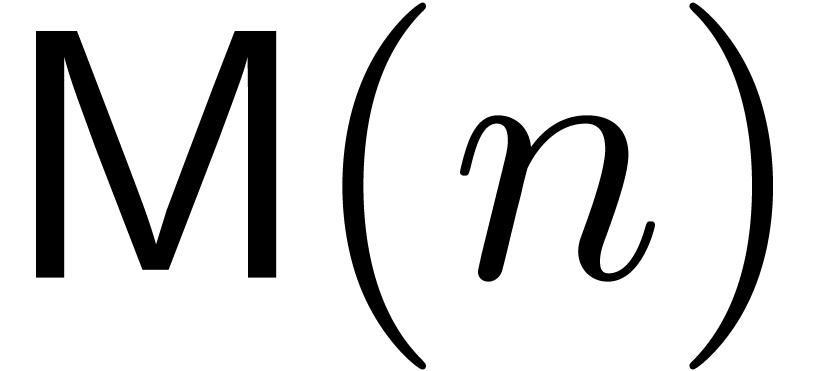 allows for
inborn FFT multiplication. Then
allows for
inborn FFT multiplication. Then  ,
where
,
where 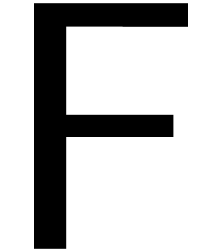 and
and  satisfy
similar properties as in the integer case. Let
satisfy
similar properties as in the integer case. Let 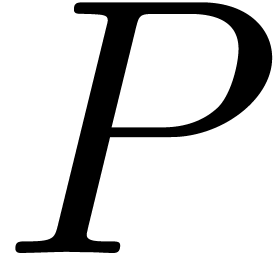 be
be  monic polynomials of degree
monic polynomials of degree  . Given a polynomial
. Given a polynomial 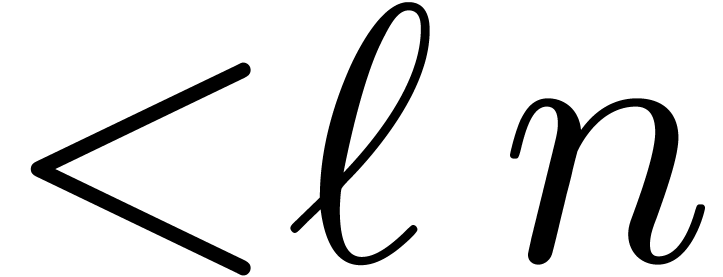 of
degree
of
degree  in
in  we may then
compute the remainders
we may then
compute the remainders  for
for 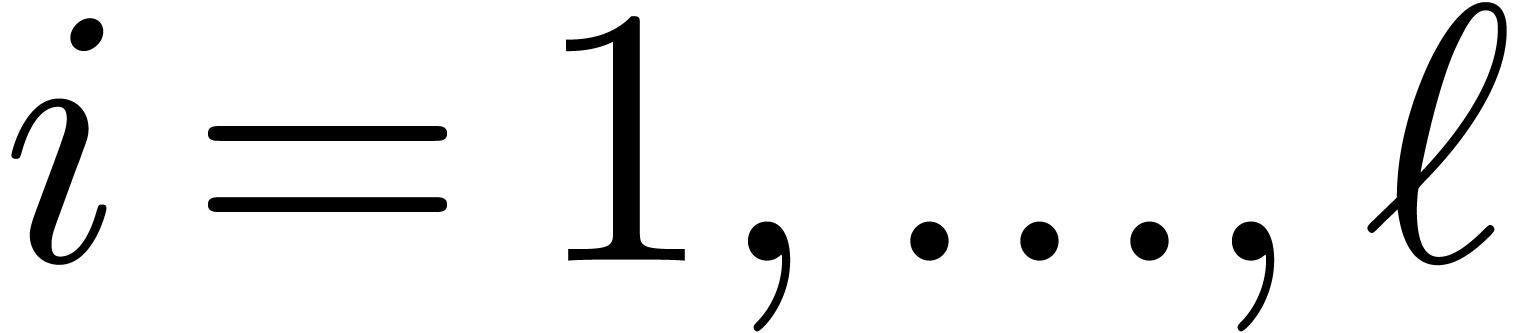 in time
in time
The reconstruction of 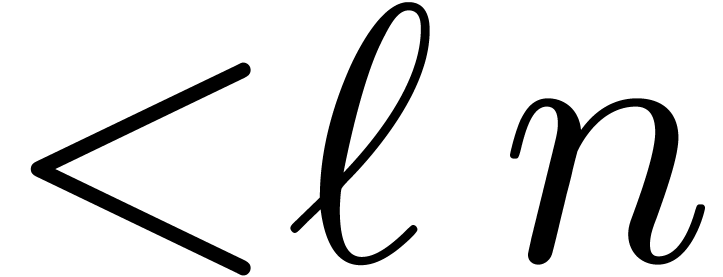 from these remainders can
be done in time
from these remainders can
be done in time
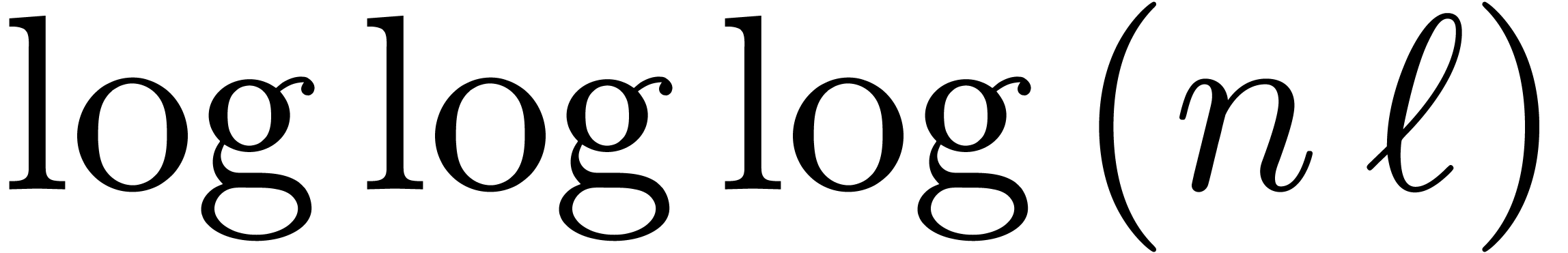
The assumption that 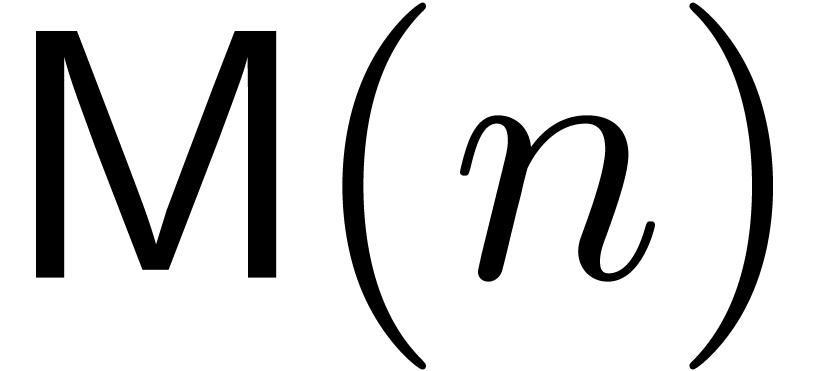 admits a suitable inborn FFT
scheme is in particular satisfied if
admits a suitable inborn FFT
scheme is in particular satisfied if 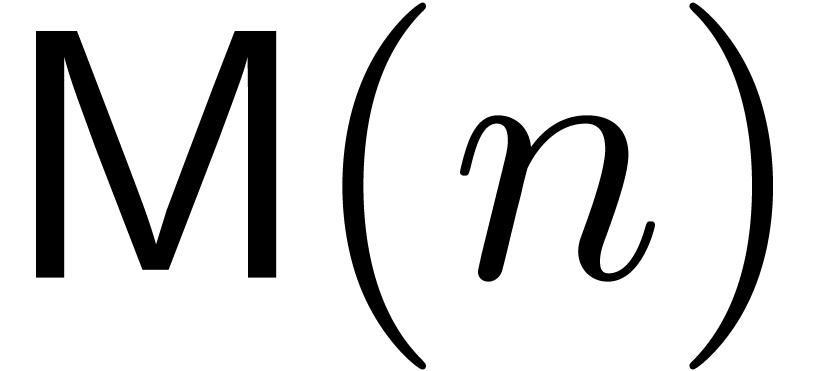 is a finite
field [14]. When working in an algebraic complexity model,
this is still the case if
is a finite
field [14]. When working in an algebraic complexity model,
this is still the case if 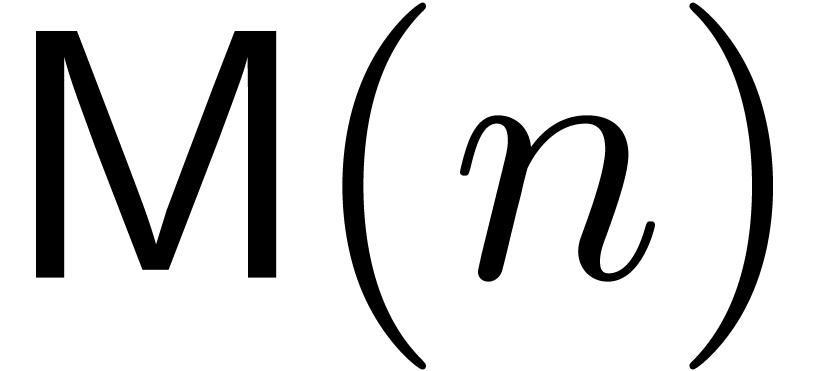 is any field of
positive characteristic [14]. For general fields of
characteristic zero, the best known FFT schemes rely on the adjunction
of artificial roots of unity [6]. In that case, our
techniques only result in an asymptotic speed-up by a factor
is any field of
positive characteristic [14]. For general fields of
characteristic zero, the best known FFT schemes rely on the adjunction
of artificial roots of unity [6]. In that case, our
techniques only result in an asymptotic speed-up by a factor 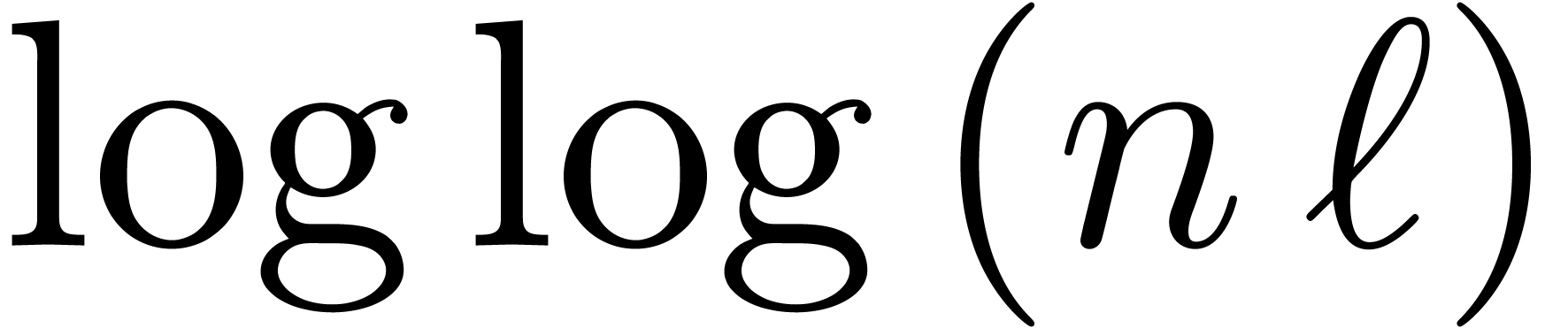 instead of
instead of  .
Nevertheless, the field of complex numbers does admit roots of unity of
any order, and our algorithms can be used for fixed point approximations
of complex numbers at any precision.
.
Nevertheless, the field of complex numbers does admit roots of unity of
any order, and our algorithms can be used for fixed point approximations
of complex numbers at any precision.
Multi-point evaluation has several interesting applications, but it is
important to keep in mind that our speed-ups only apply when the moduli
are fixed. For instance, assume that we computed approximate zeros 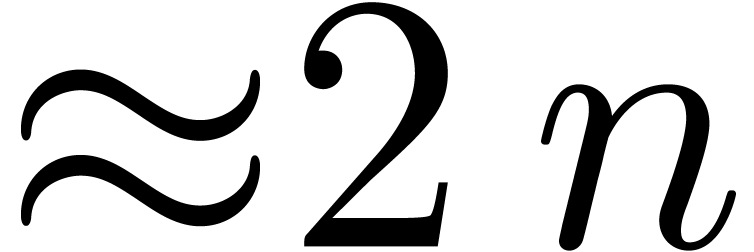 to a complex polynomial of degree
to a complex polynomial of degree  , using a bit-precision
, using a bit-precision  . Then we may use multi-point evaluation in order to
apply Newton's method simultaneously to all roots and find
approximations of bit-precision
. Then we may use multi-point evaluation in order to
apply Newton's method simultaneously to all roots and find
approximations of bit-precision 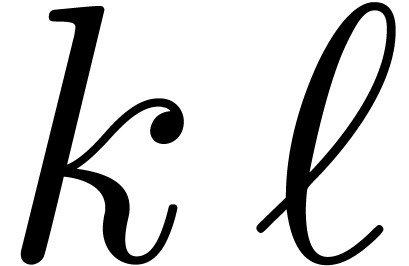 .
Unfortunately, our speed-up does not work in this case, since the
approximate zeros
.
Unfortunately, our speed-up does not work in this case, since the
approximate zeros 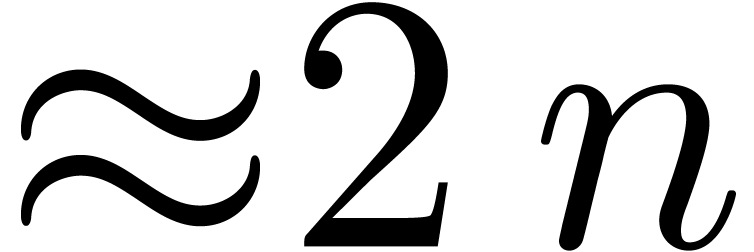 are not fixed. On the other
hand, if the polynomial has degree
are not fixed. On the other
hand, if the polynomial has degree 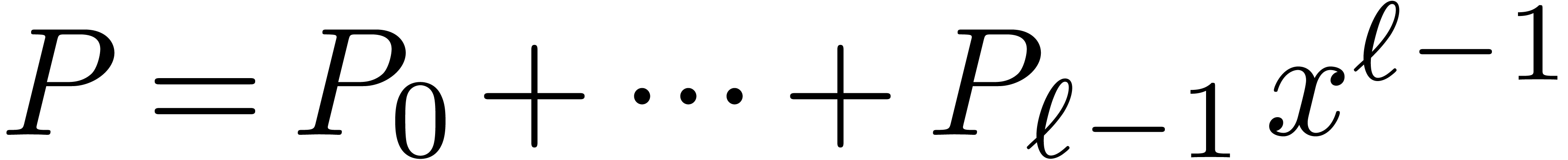 instead of
instead of
 and we are still given
and we are still given  approximate zeros
approximate zeros 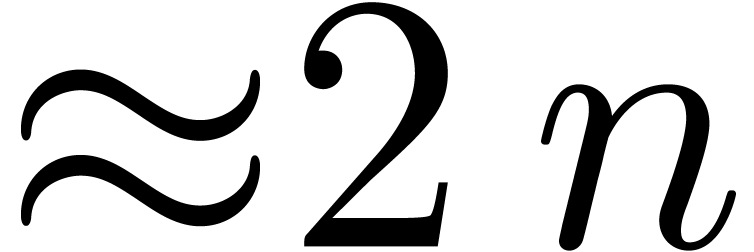 (say all zeros in some disk),
then the same moduli are used
(say all zeros in some disk),
then the same moduli are used 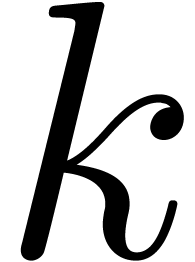 times, and one may
hope for some speed-up when using our methods.
times, and one may
hope for some speed-up when using our methods.
At another extremity, it is instructive to consider the approximate
evaluation of a fixed polynomial 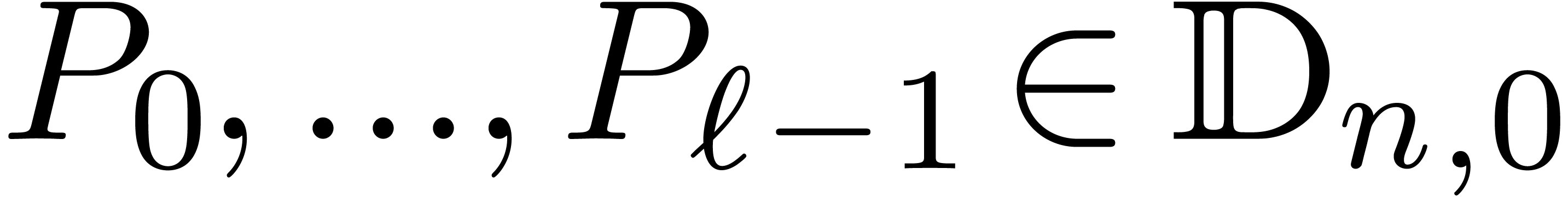 with fixed
point coefficients
with fixed
point coefficients  at a single point
at a single point 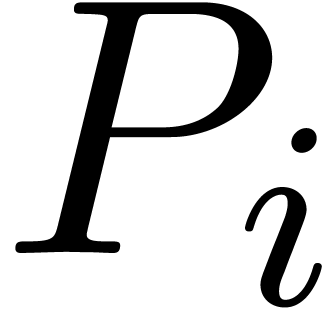 . We may thus assume that suitable
Fourier transforms of the
. We may thus assume that suitable
Fourier transforms of the 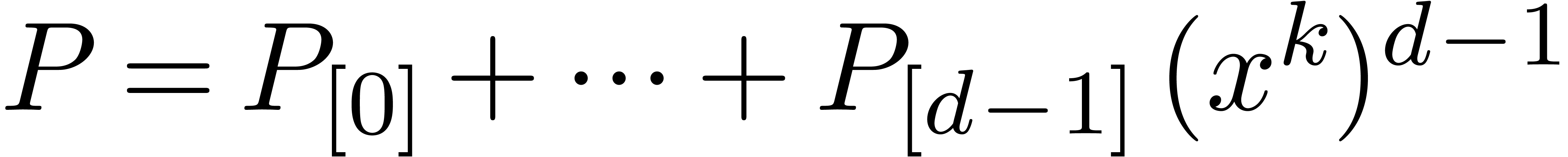 have been precomputed.
Now we rewrite
have been precomputed.
Now we rewrite 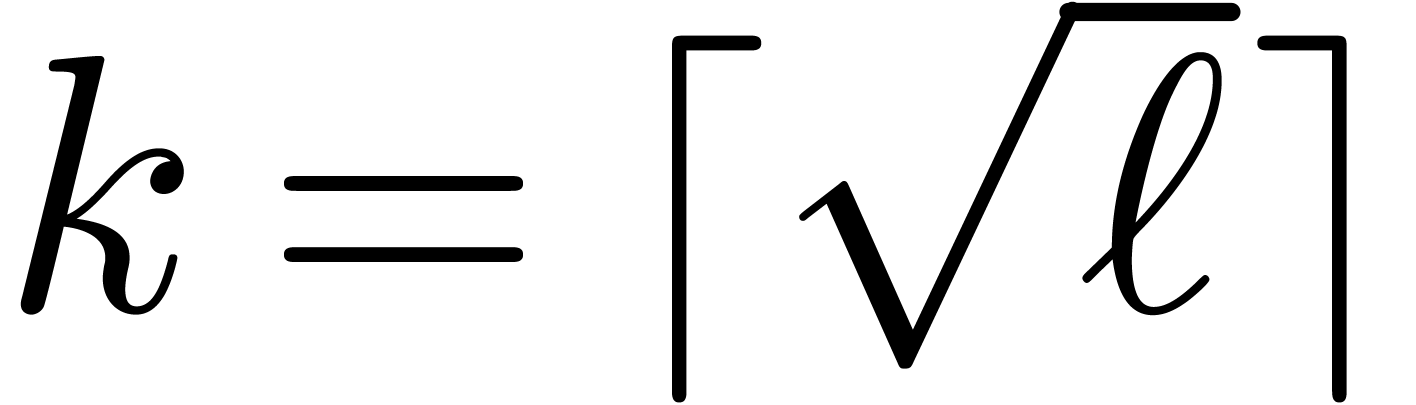 with
with  ,
, 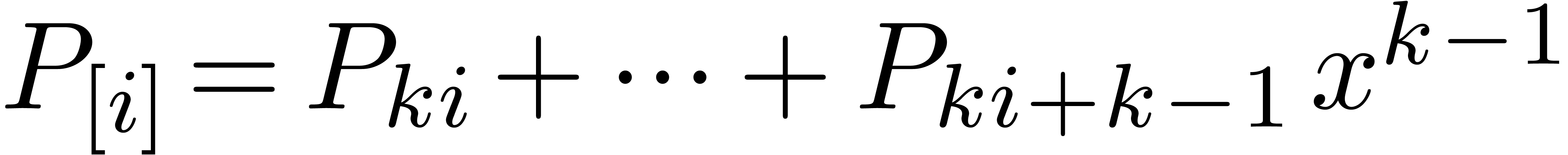 and
and 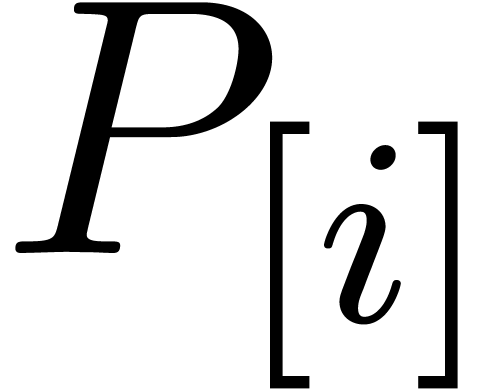 . In order to evaluate each of the
. In order to evaluate each of the  at
at  , it suffices to transform
the numbers
, it suffices to transform
the numbers  , to perform the
evaluations in the Fourier representation and then transform the results
back. This can be achieved in time
, to perform the
evaluations in the Fourier representation and then transform the results
back. This can be achieved in time 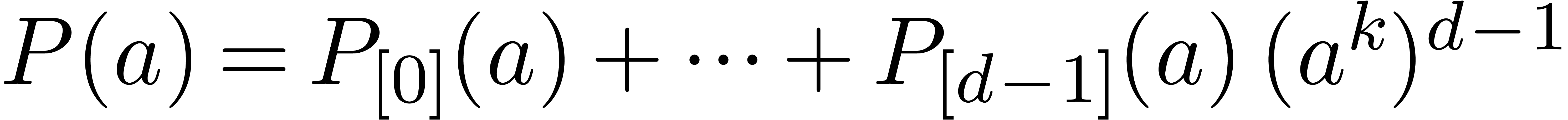 .
We may finally compute
.
We may finally compute  using Horner's method, in
time
using Horner's method, in
time  . For large
. For large  , the dominant term of the computation time is
, the dominant term of the computation time is
 .
.
Let us now reconsider the naive algorithms from section 3.2,
but in the case when the moduli  are all close to
a specific power of two. More precisely, we assume that
are all close to
a specific power of two. More precisely, we assume that
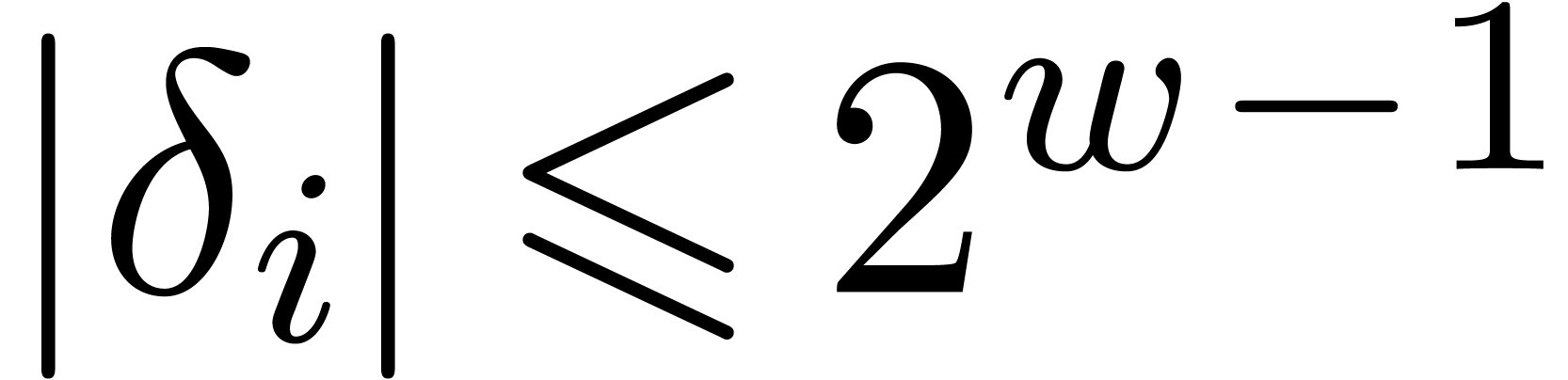
where 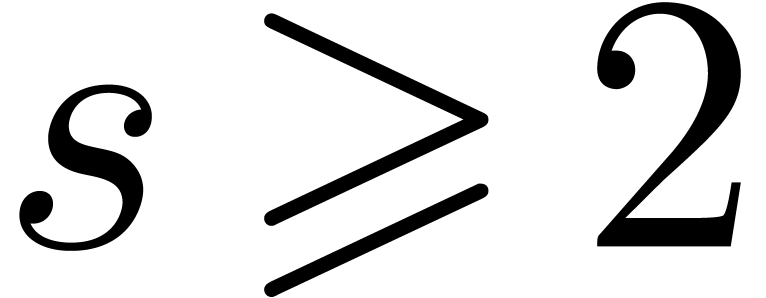 and
and 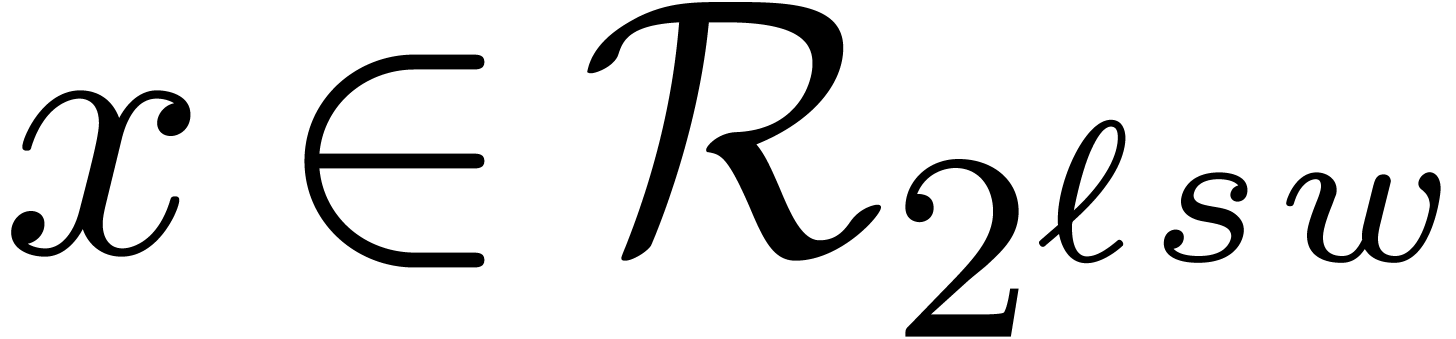 a small
number. As usual, we assume that the
a small
number. As usual, we assume that the 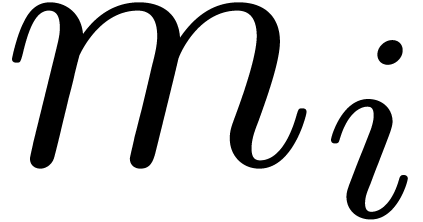 are
pairwise coprime and we let
are
pairwise coprime and we let 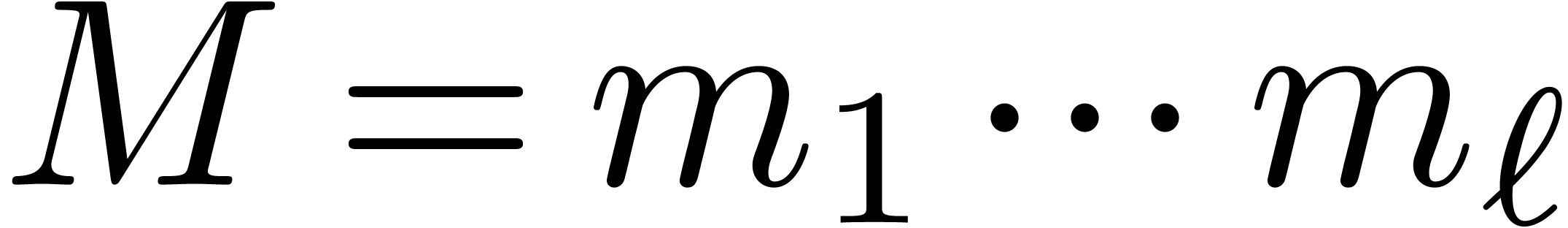 .
.
For such moduli, the naive algorithm for the euclidean division of a
number 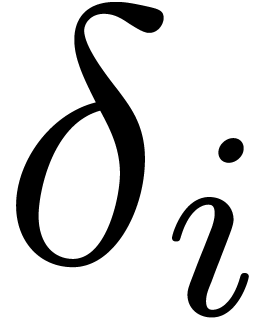 by
by 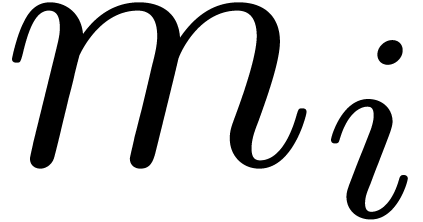 becomes
particularly simple and essentially boils down to the multiplication of
becomes
particularly simple and essentially boils down to the multiplication of
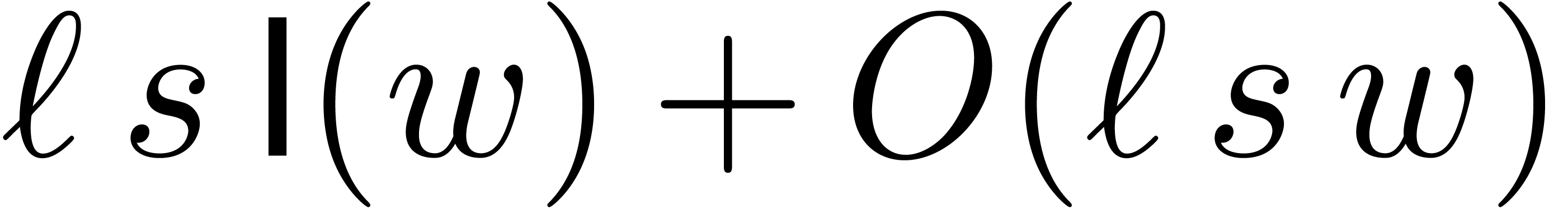 with the quotient of this division. In other
words, the remainder can be computed in time
with the quotient of this division. In other
words, the remainder can be computed in time  instead of
instead of  . For small values
of
. For small values
of  ,
,  and
and  , this gives rise to a
speedup by a factor
, this gives rise to a
speedup by a factor  at least. More generally,
the computation of
at least. More generally,
the computation of  remainders
remainders 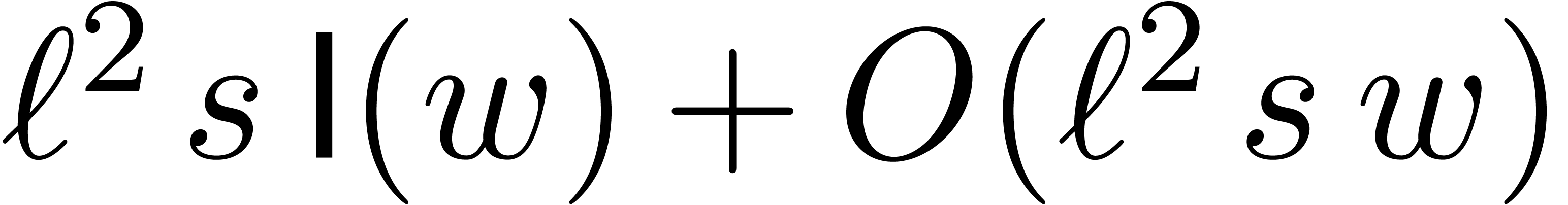 can be done in time
can be done in time  .
.
Multi-modular reconstruction can also be done faster, as follows, using
a similar technique as in [5]. Let 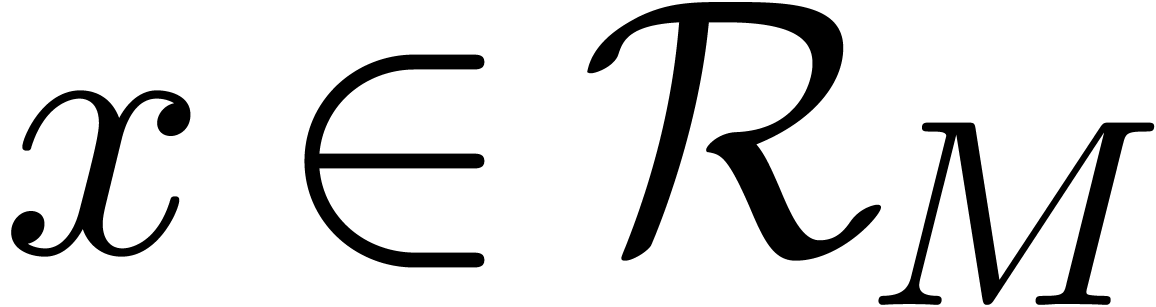 . Besides the usual binary representation of
. Besides the usual binary representation of  and the multi-modular representation
and the multi-modular representation  , it is also possible to use the Newton
representation
, it is also possible to use the Newton
representation
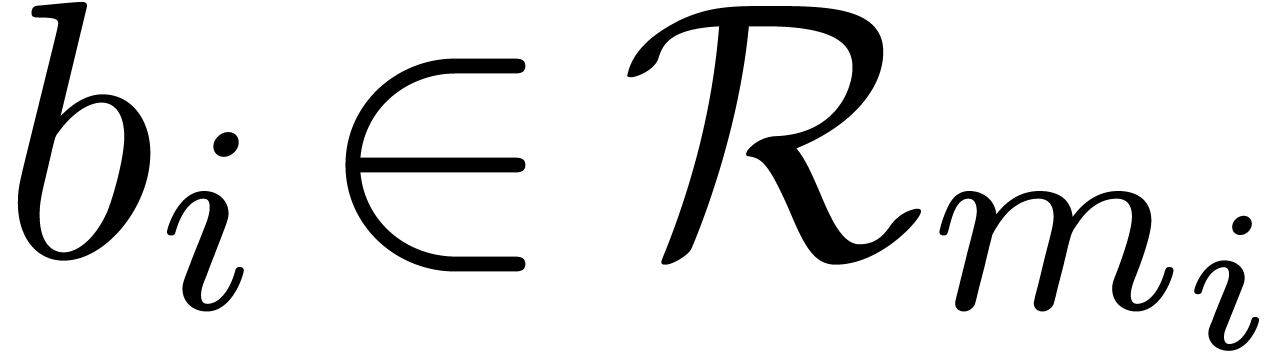
where  . Let us now show how
to obtain
. Let us now show how
to obtain  efficiently from
efficiently from 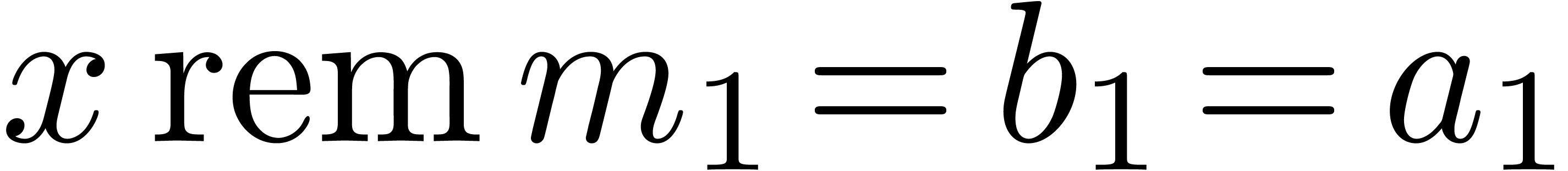 . Since
. Since 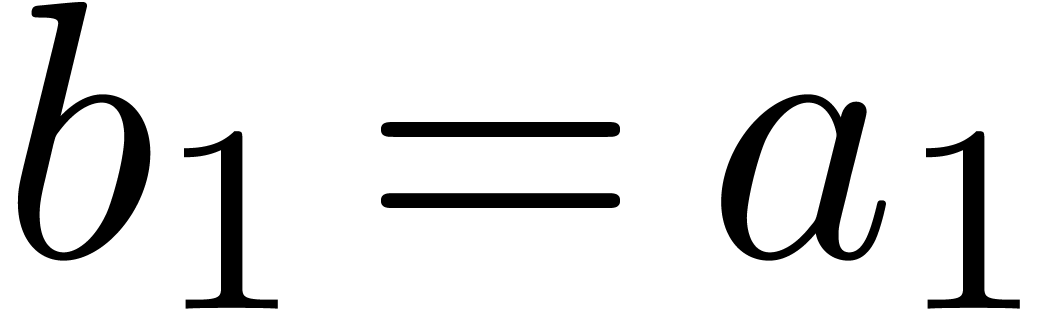 ,
we must take
,
we must take  . Assume that
. Assume that
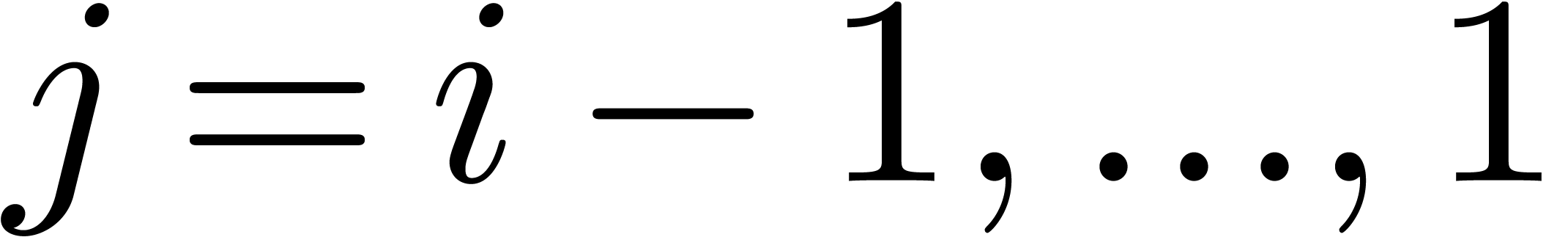 have been computed. For
have been computed. For  we next compute
we next compute
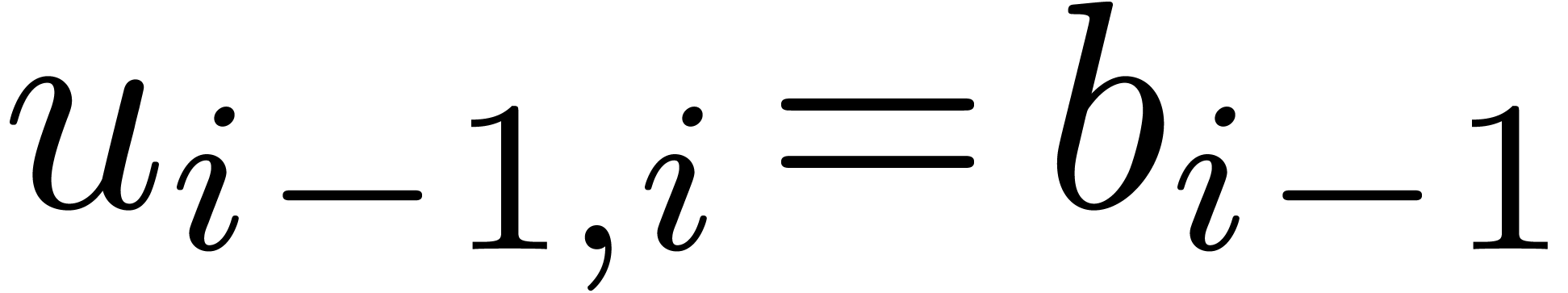
using  and
and

Notice that  can be computed in time
can be computed in time  . We have
. We have
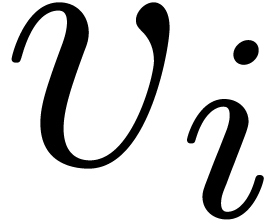
Now the inverse 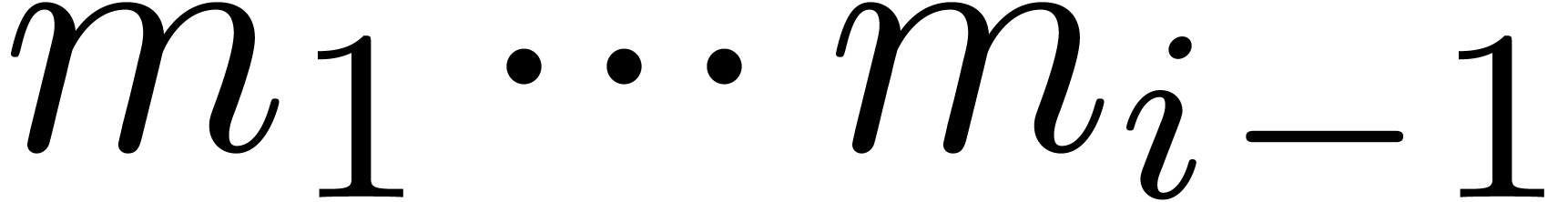 of
of 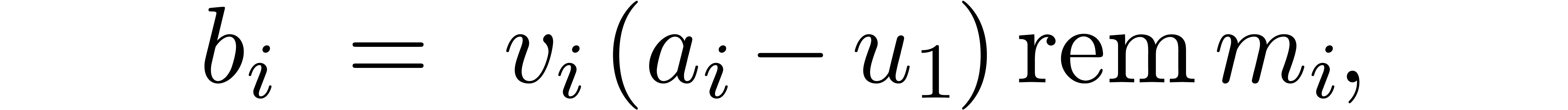 modulo
modulo 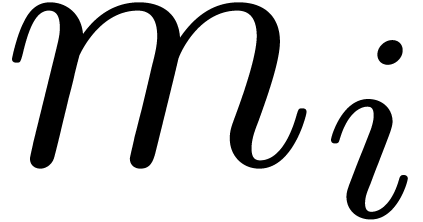 can be precomputed. We finally compute
can be precomputed. We finally compute
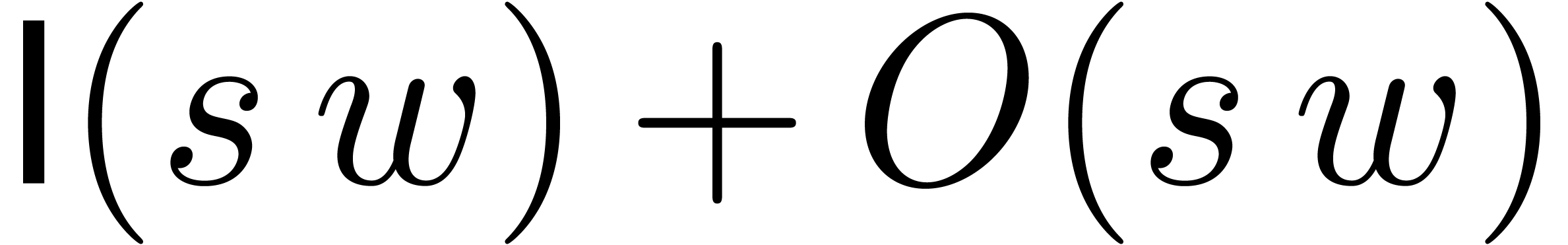
which can be done in time  .
For small values of
.
For small values of  , we
notice that it may be faster to divide successively by
, we
notice that it may be faster to divide successively by 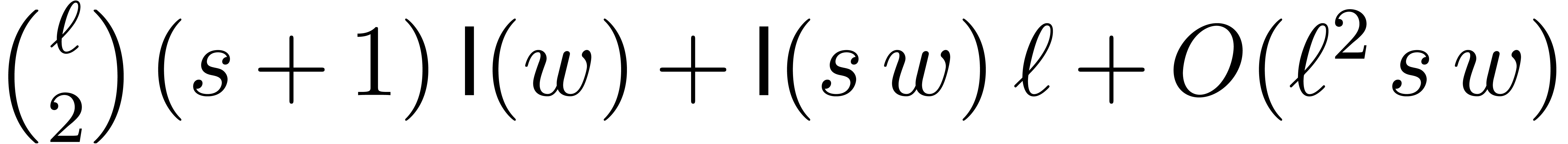 modulo
modulo  instead of multiplying with
instead of multiplying with 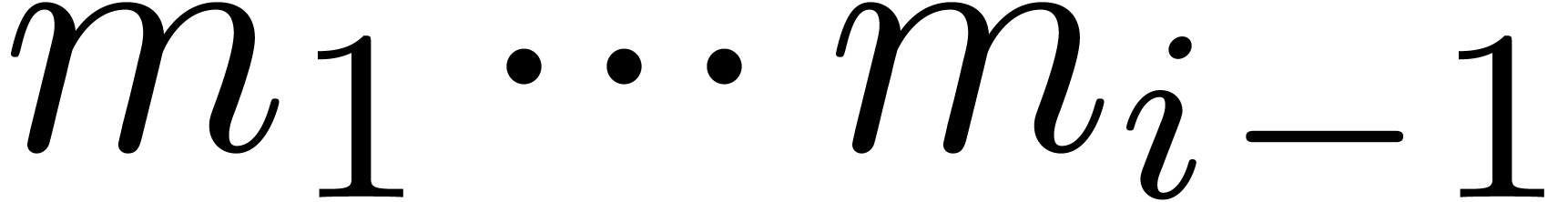 . In total, the computation of the Newton
representation
. In total, the computation of the Newton
representation  can be done in time
can be done in time 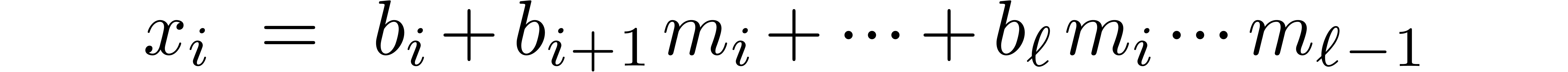 . Having computed the Newton representation, we
next compute
. Having computed the Newton representation, we
next compute
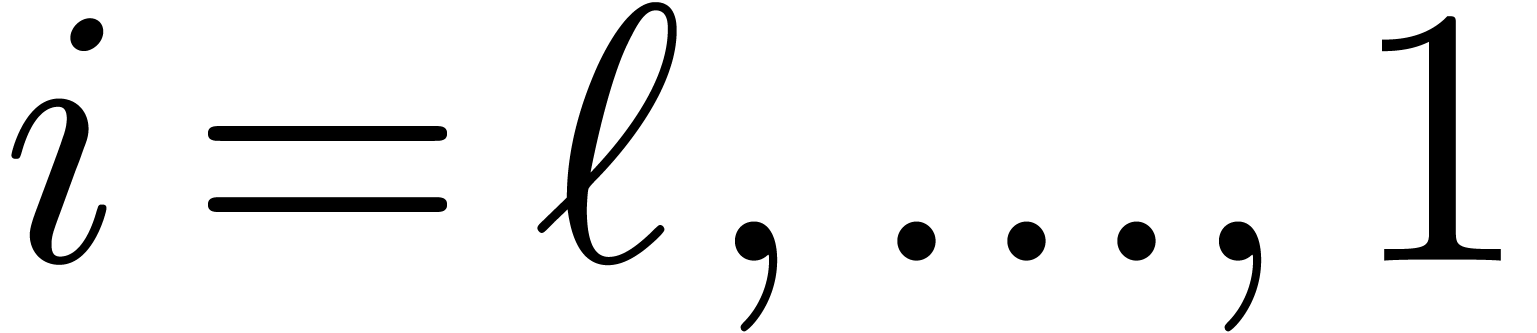
for  , using the recurrence
relation
, using the recurrence
relation
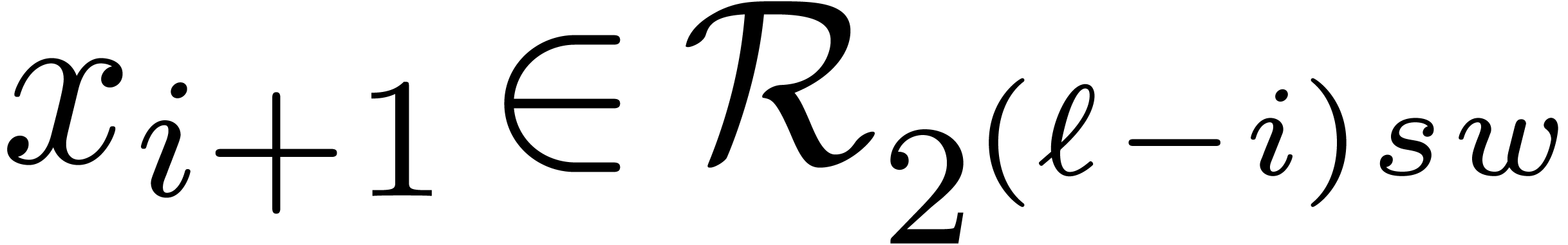
Since 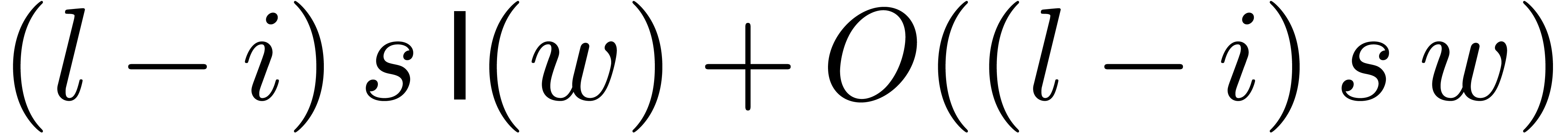 , the computation of
, the computation of
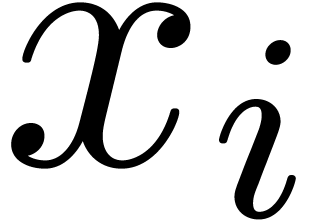 takes a time
takes a time  .
Altogether, the computation of
.
Altogether, the computation of 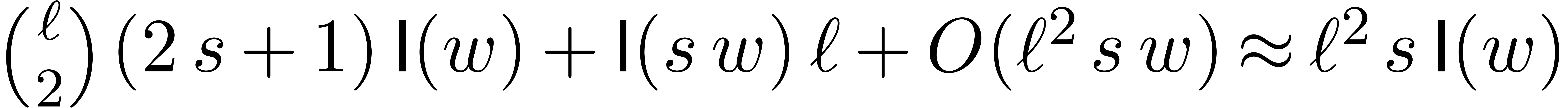 from
from 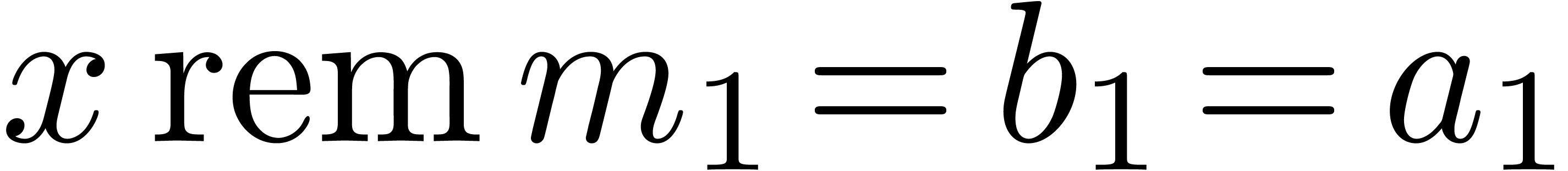 can therefore be done in time
can therefore be done in time 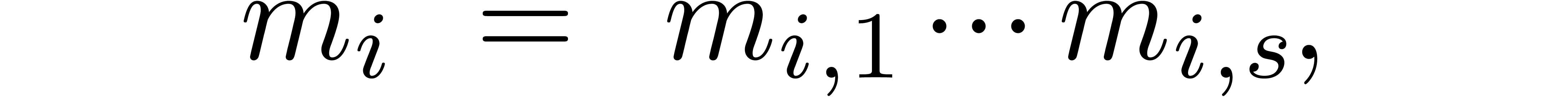 .
.
For practical applications, we usually wish to work with moduli that fit
into one word or half a word. Now the algorithm from the previous
subsection is particularly efficient if the numbers  also fit into one word or half a word. This means that we need to impose
the further requirement that each modulus
also fit into one word or half a word. This means that we need to impose
the further requirement that each modulus 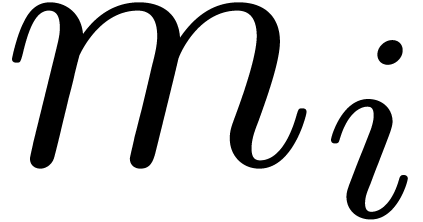 can be
factored
can be
factored
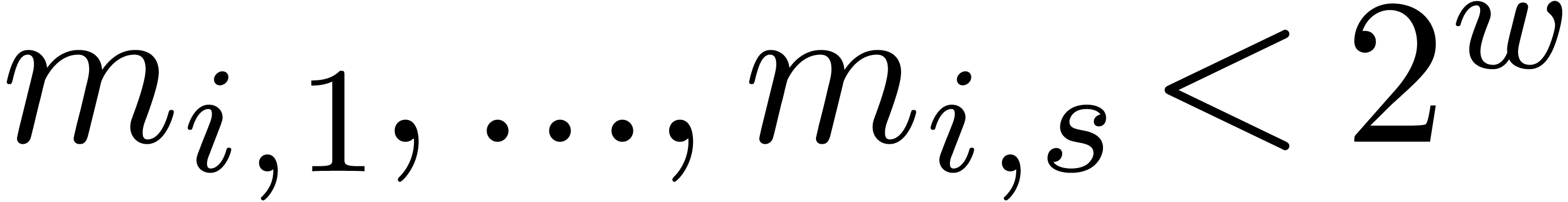
with 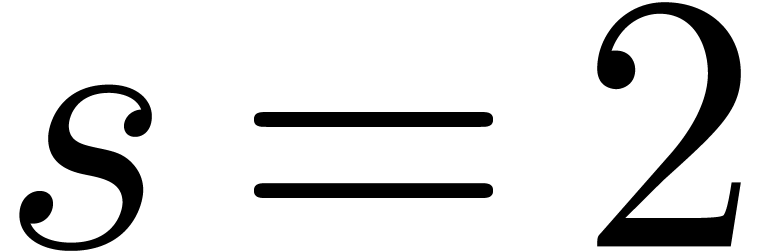 . If this is possible,
then the
. If this is possible,
then the 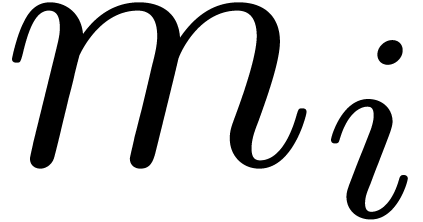 are called
are called  -gentle moduli. For given bitsizes
-gentle moduli. For given bitsizes  and
and 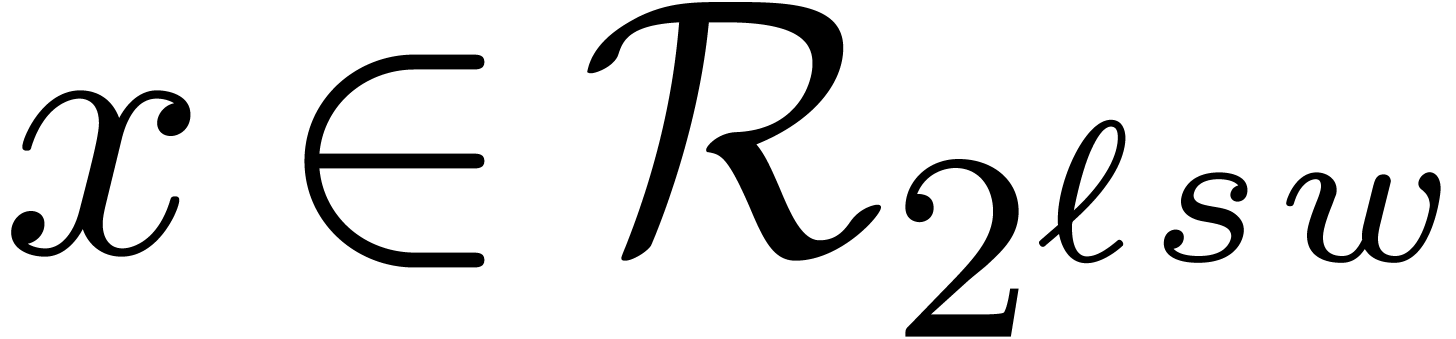 , the main
questions are now: do such moduli indeed exist? If so, then how to find
them?
, the main
questions are now: do such moduli indeed exist? If so, then how to find
them?
If 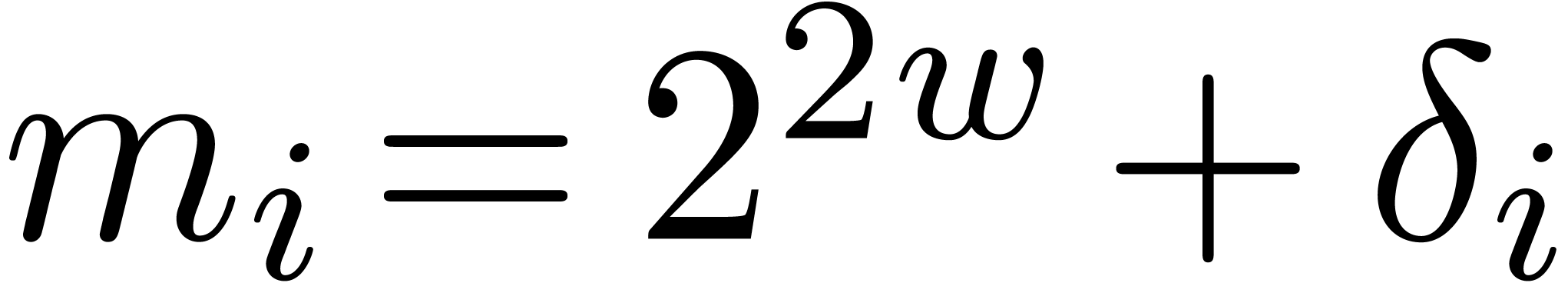 , then it is easy to
construct
, then it is easy to
construct  -gentle moduli
-gentle moduli 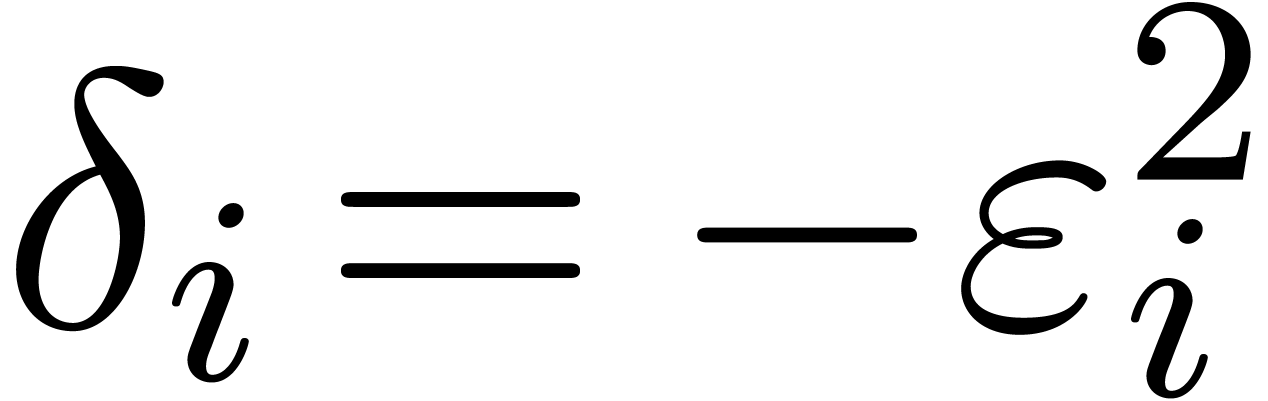 by taking
by taking 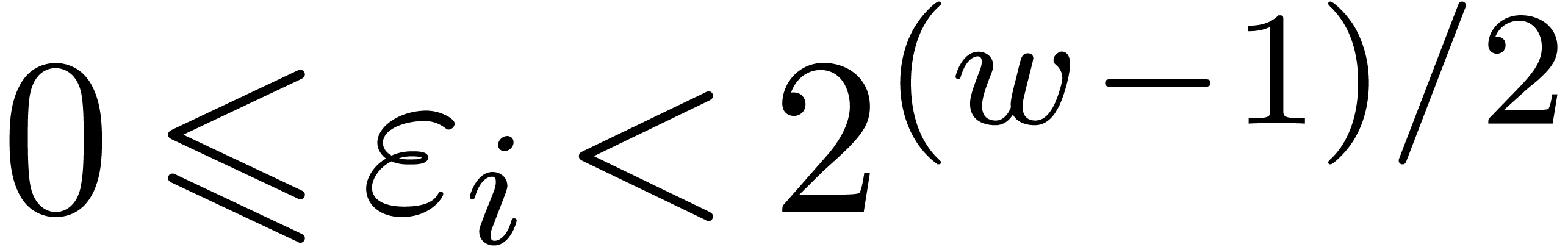 ,
where
,
where 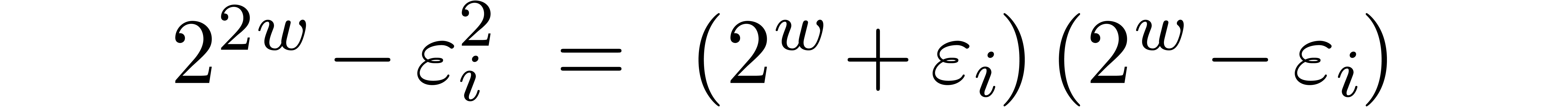 is odd. Indeed,
is odd. Indeed,
and 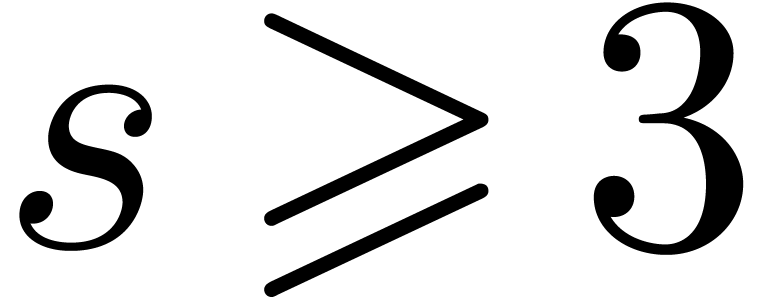 . Unfortunately, this
trick does not generalize to higher values
. Unfortunately, this
trick does not generalize to higher values  .
Indeed, consider a product
.
Indeed, consider a product

where  are small compared to
are small compared to 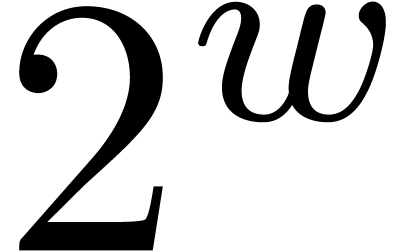 . If the coefficient
. If the coefficient 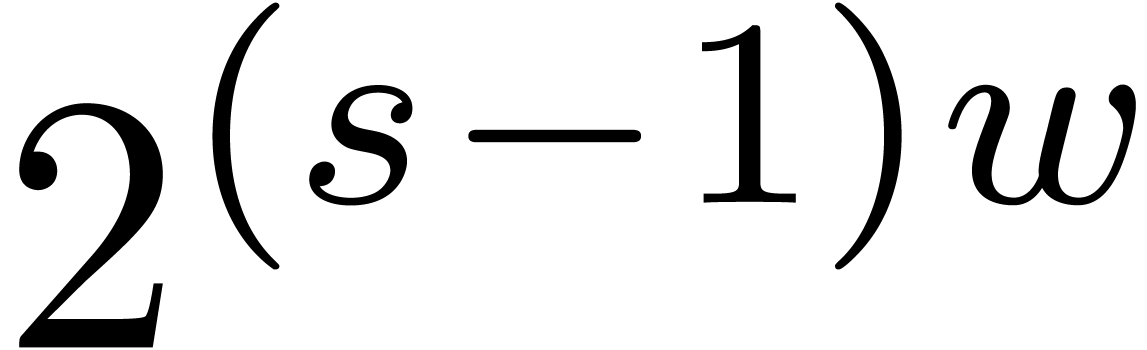 of
of
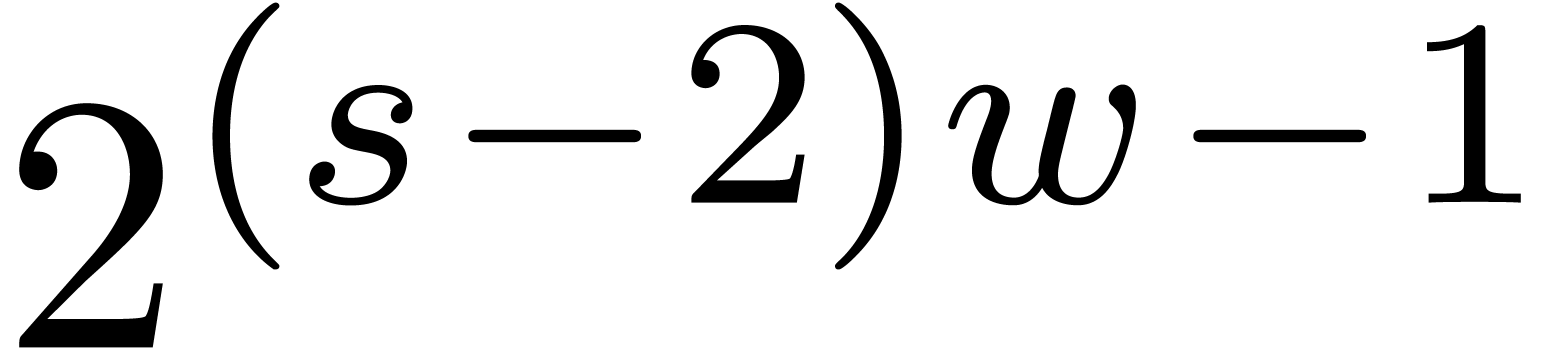 vanishes, then the coefficient of
vanishes, then the coefficient of 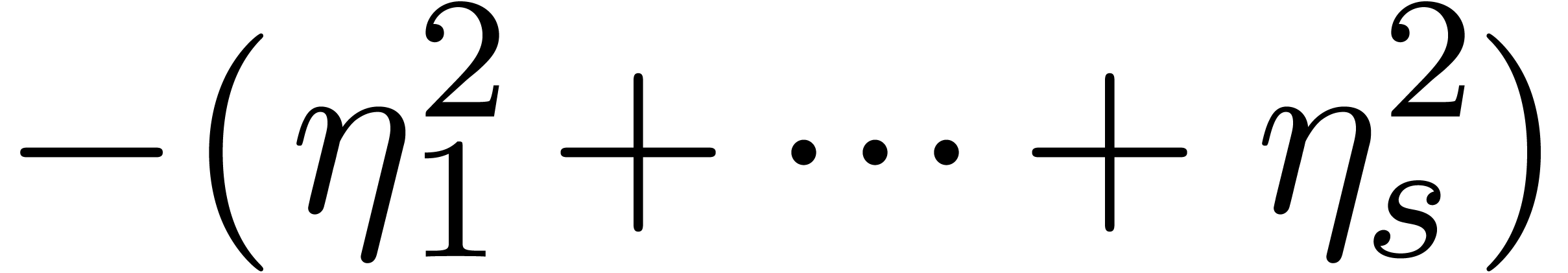 becomes the opposite
becomes the opposite  of a sum of
squares. In particular, both coefficients cannot vanish simultaneously,
unless
of a sum of
squares. In particular, both coefficients cannot vanish simultaneously,
unless  .
.
If 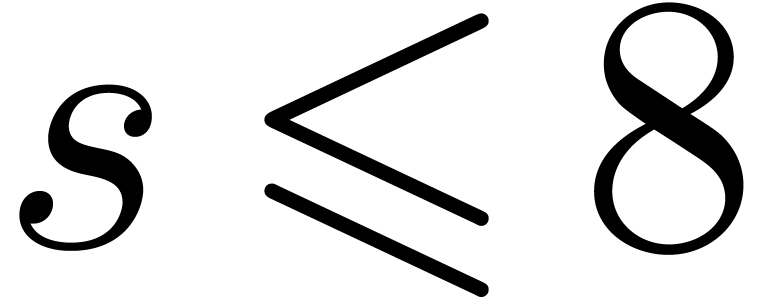 , then we are left with
the option to search
, then we are left with
the option to search  -gentle
moduli by brute force. As long as
-gentle
moduli by brute force. As long as  is
“reasonably small” (say
is
“reasonably small” (say 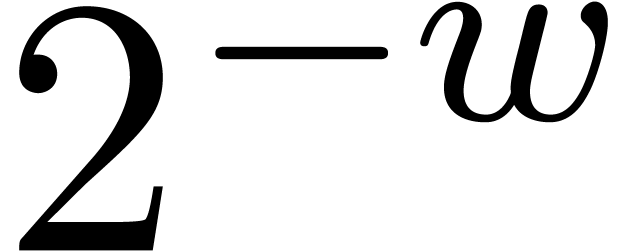 ),
the probability to hit an
),
the probability to hit an  -gentle
modulus for a randomly chosen
-gentle
modulus for a randomly chosen 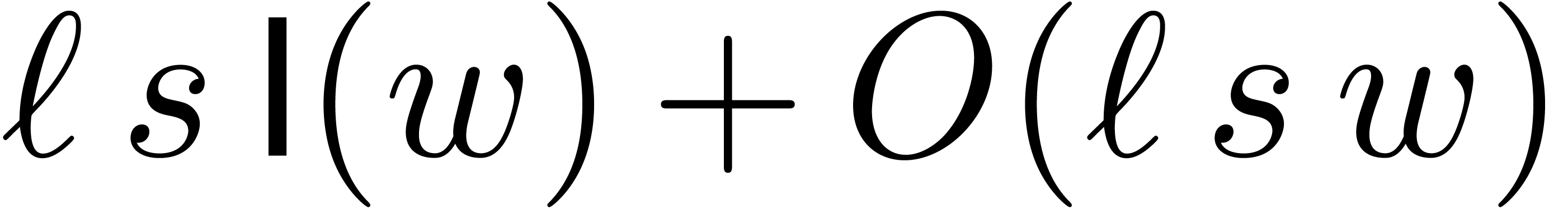 often remains
significantly larger than
often remains
significantly larger than 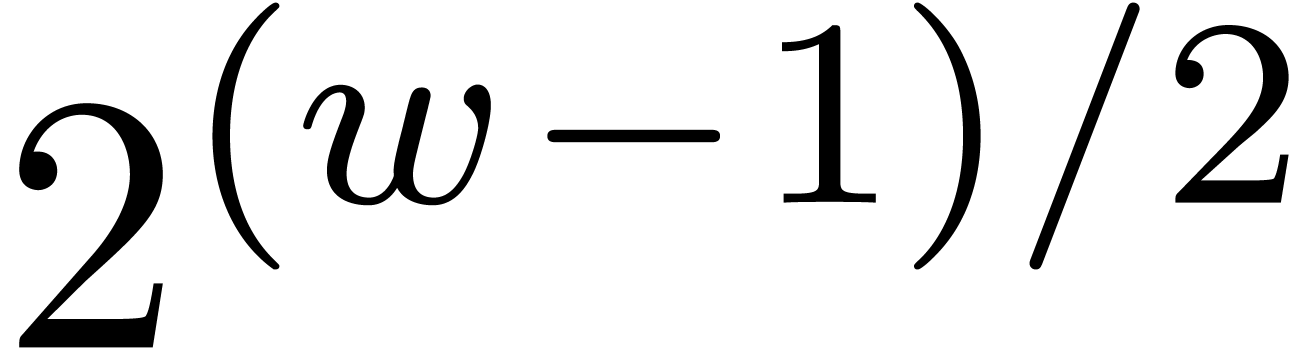 .
We may then use sieving to find such moduli. By what precedes, it is
also desirable to systematically take
.
We may then use sieving to find such moduli. By what precedes, it is
also desirable to systematically take 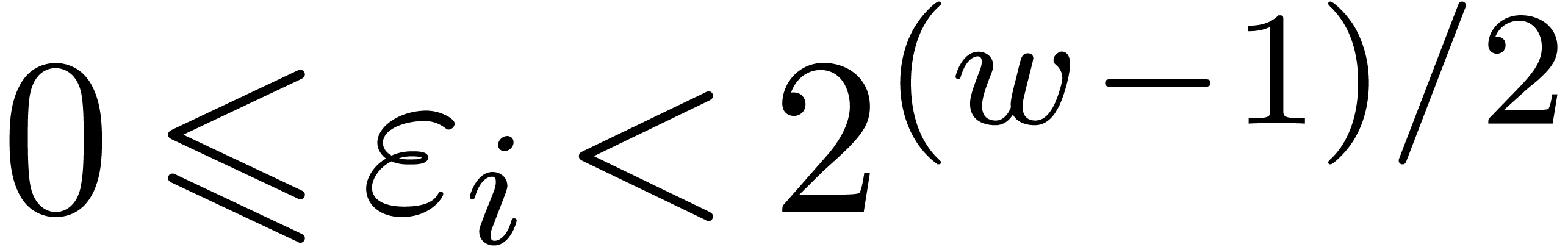 for
for 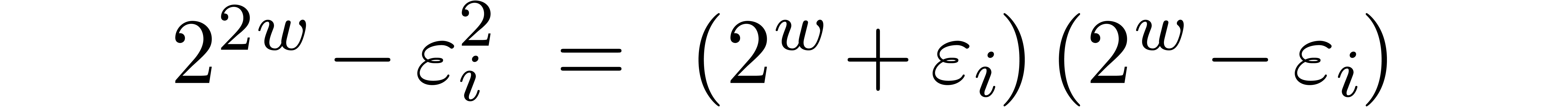 . This has the additional benefit
that we “only” have to consider
. This has the additional benefit
that we “only” have to consider  possibilities for
possibilities for  .
.
We implemented a sieving procedure in  and
and 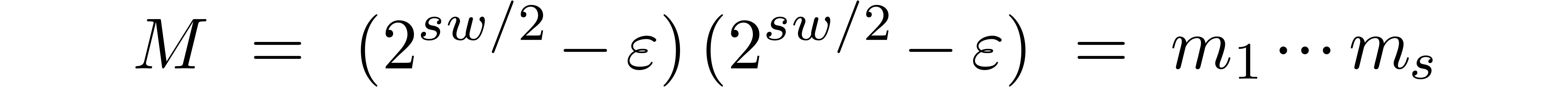 ,
the goal of our procedure is to find
,
the goal of our procedure is to find  -gentle
moduli of the form
-gentle
moduli of the form
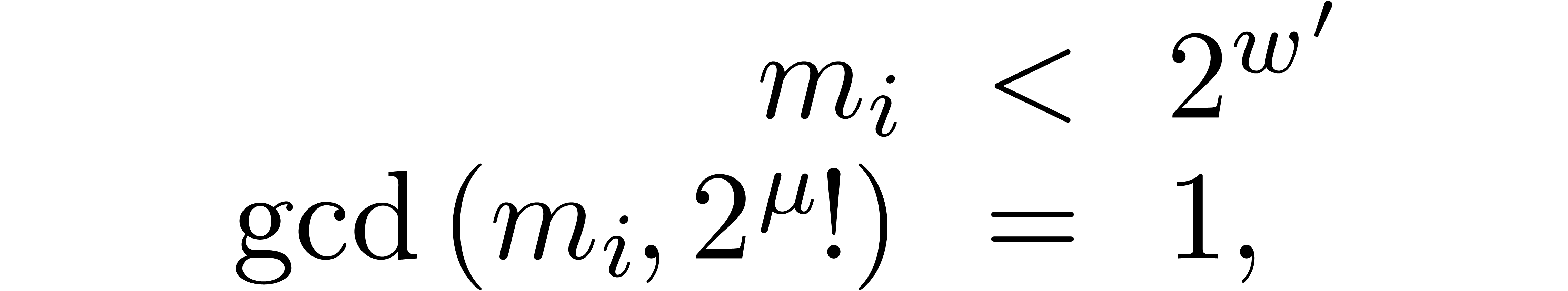
with the constraints that

for 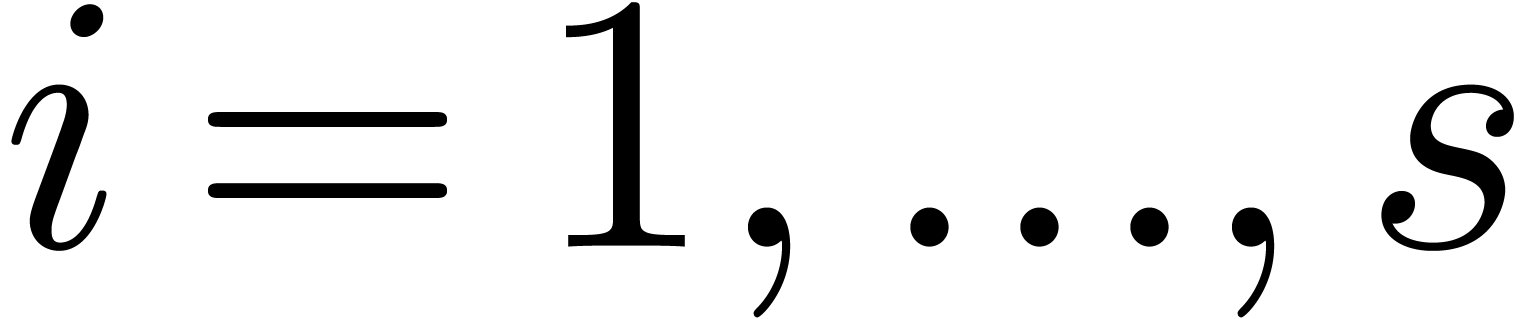 , and
, and 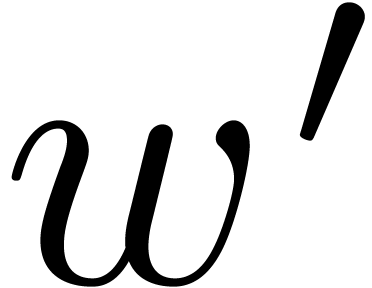 . The parameter
. The parameter  is
small and even. One should interpret
is
small and even. One should interpret  and
and 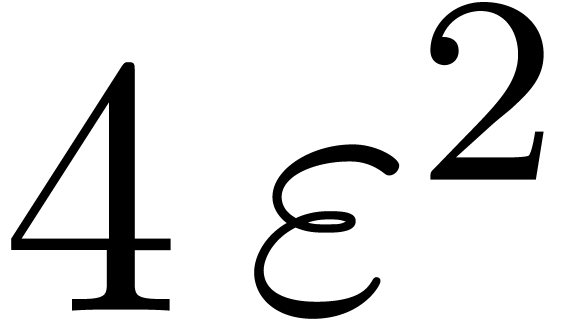 as the intended and maximal bitsize of the small
moduli
as the intended and maximal bitsize of the small
moduli 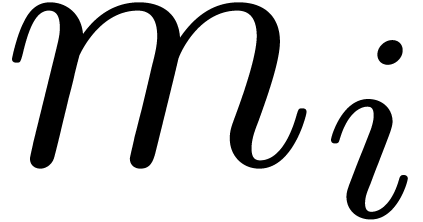 . The parameter
. The parameter  stands for the minimal bitsize of a prime factor of
stands for the minimal bitsize of a prime factor of
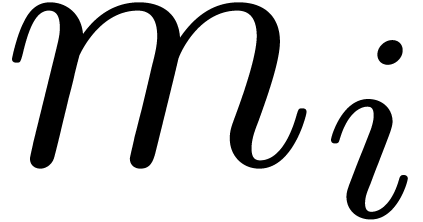 . The parameter
. The parameter  should be such that
should be such that 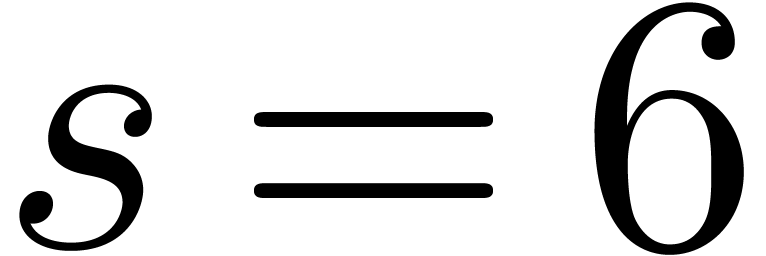 fits into a
machine word.
fits into a
machine word.
In Table 1 below we have shown some experimental results
for this sieving procedure in the case when 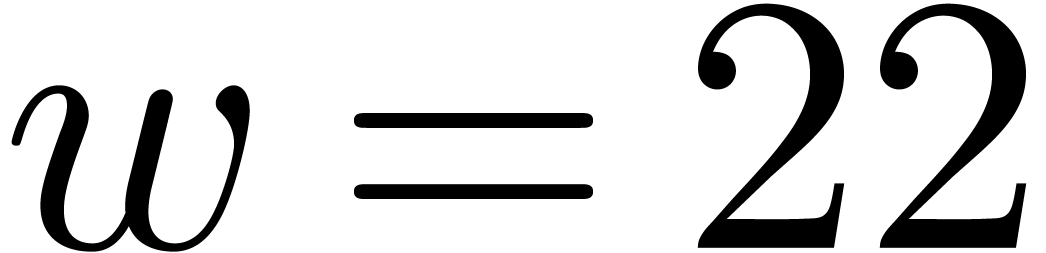 ,
, 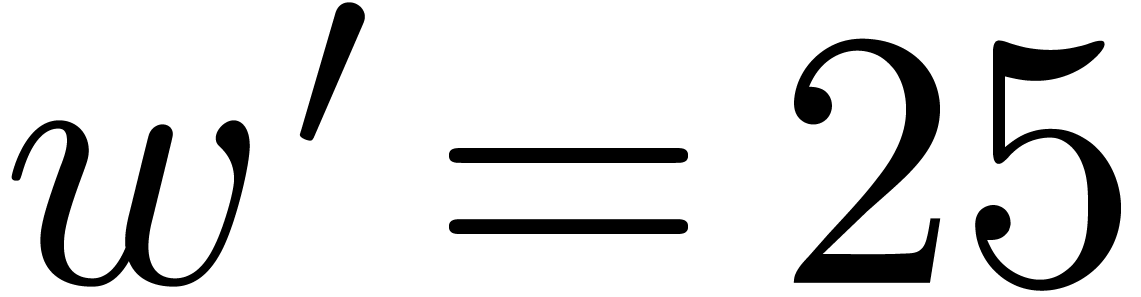 ,
, 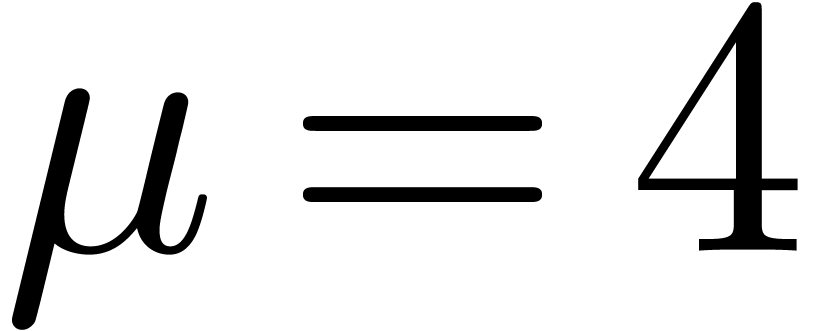 and
and 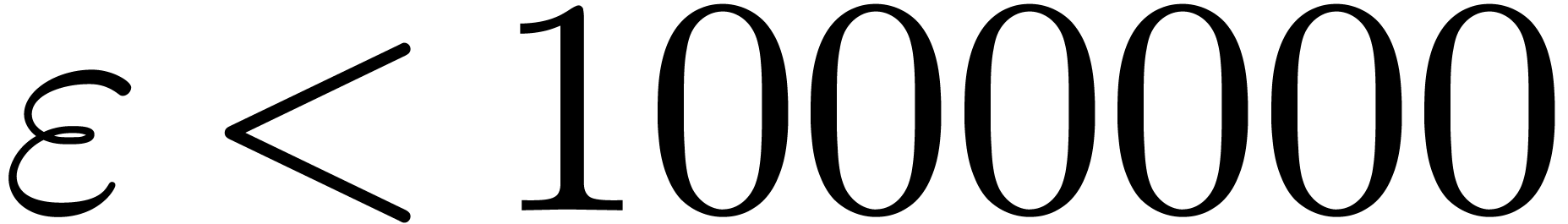 . For
. For
 , the table provides us with
, the table provides us with
 , the moduli
, the moduli 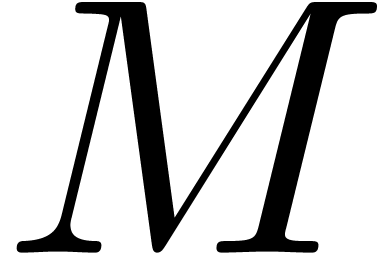 , as well as the smallest prime power factors
of the product
, as well as the smallest prime power factors
of the product  . Many hits
admit small prime factors, which increases the risk that different hits
are not coprime. For instance, the number
. Many hits
admit small prime factors, which increases the risk that different hits
are not coprime. For instance, the number 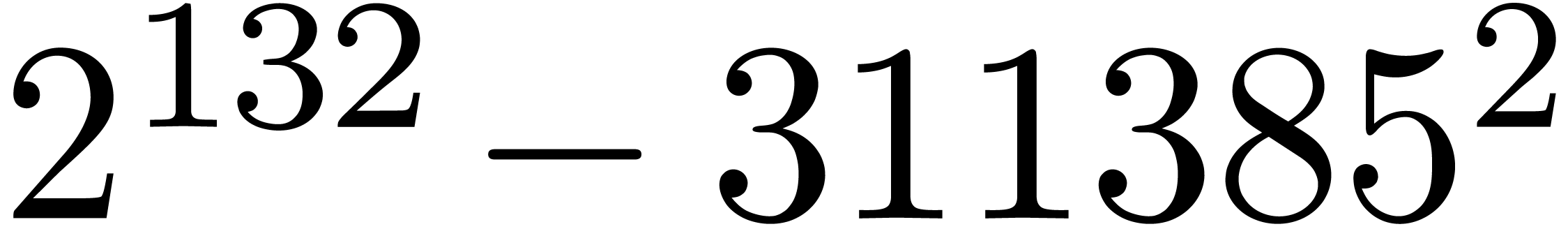 divides both
divides both  and
and  ,
whence these
,
whence these 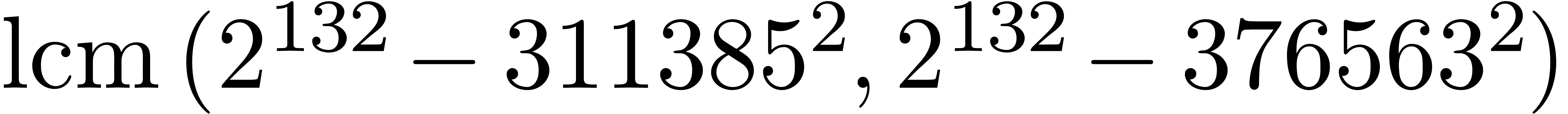 -gentle moduli
cannot be selected simultaneously (except if one is ready to sacrifice a
few bits by working modulo
-gentle moduli
cannot be selected simultaneously (except if one is ready to sacrifice a
few bits by working modulo  instead of
instead of 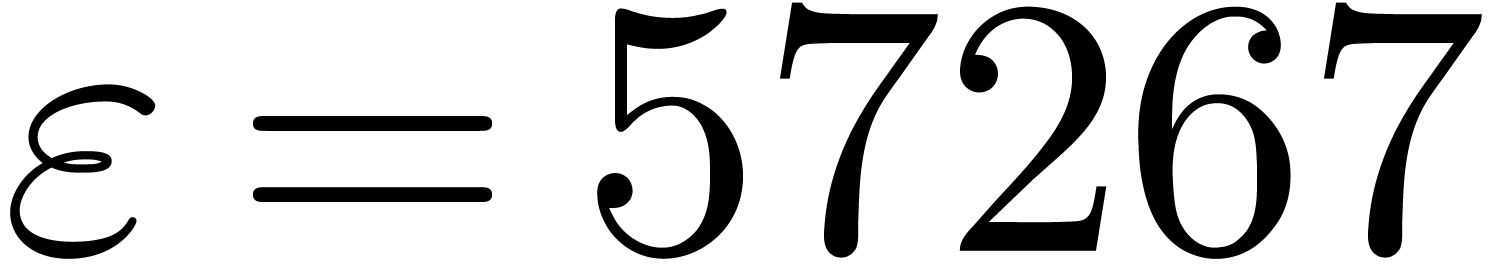 ).
).
In the case when we use multi-modular arithmetic for computations with
rational numbers instead of integers (see [10, section 5
and, more particularly, section 5.10]), then small prime factors should
completely be prohibited, since they increase the probability of
divisions by zero. For such applications, it is therefore desirable that
 are all prime. In our table, this occurs for
are all prime. In our table, this occurs for
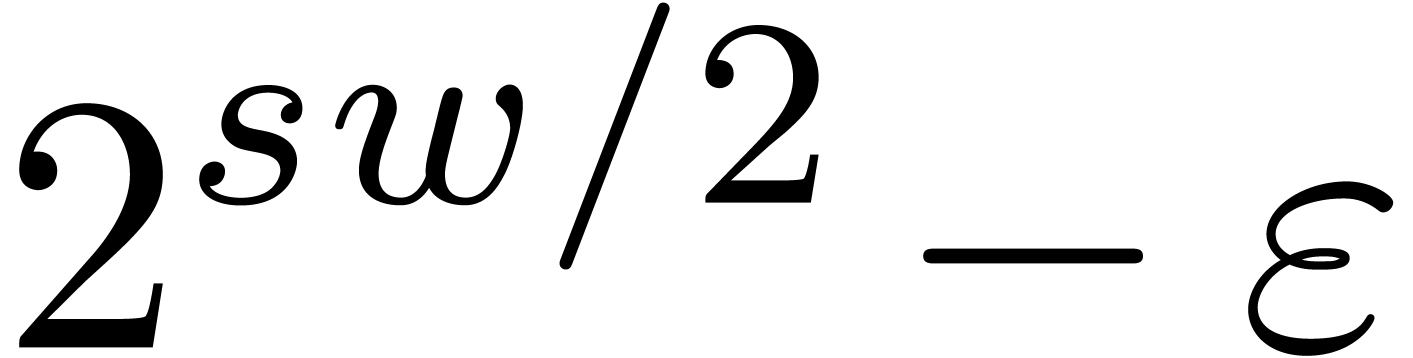 (we indicated this by highlighting the list of
prime factors of
(we indicated this by highlighting the list of
prime factors of  ).
).
In order to make multi-modular reduction and reconstruction as efficient
as possible, a desirable property of the moduli 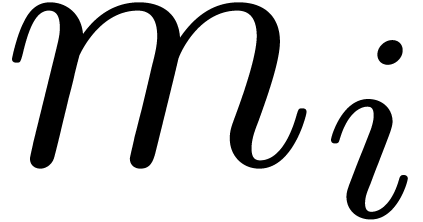 is that they either divide
is that they either divide 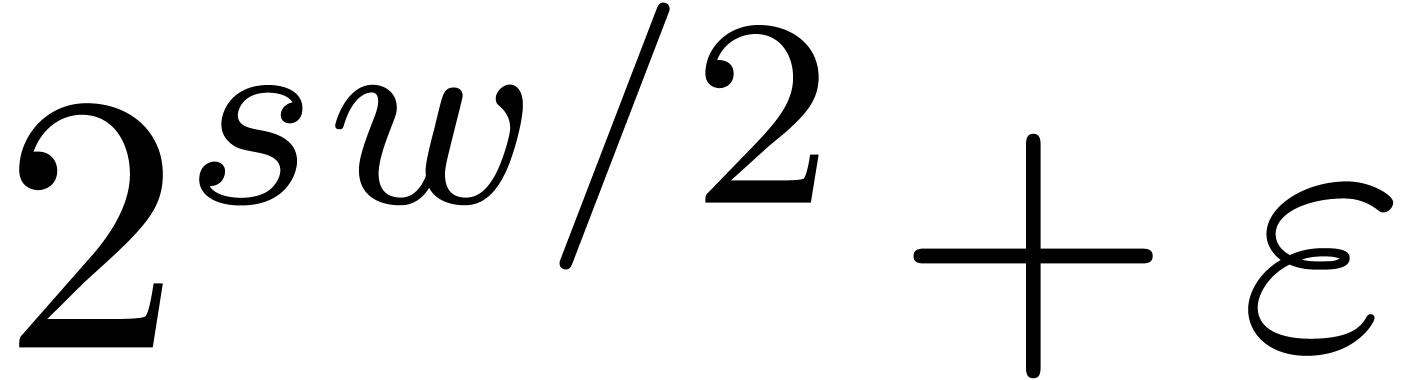 or
or 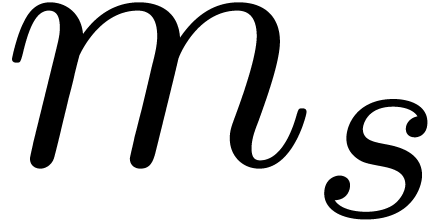 . In our table, we highlighted the
. In our table, we highlighted the  for which this happens. We notice that this is
automatically the case if
for which this happens. We notice that this is
automatically the case if 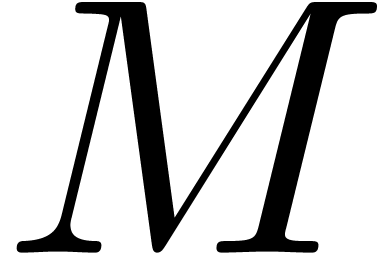 are all prime. If only
a small number of
are all prime. If only
a small number of 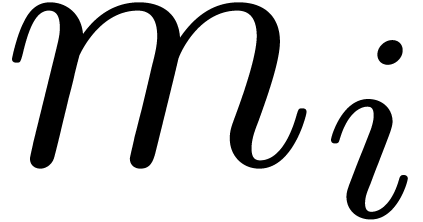 (say a single one) do not
divide either
(say a single one) do not
divide either 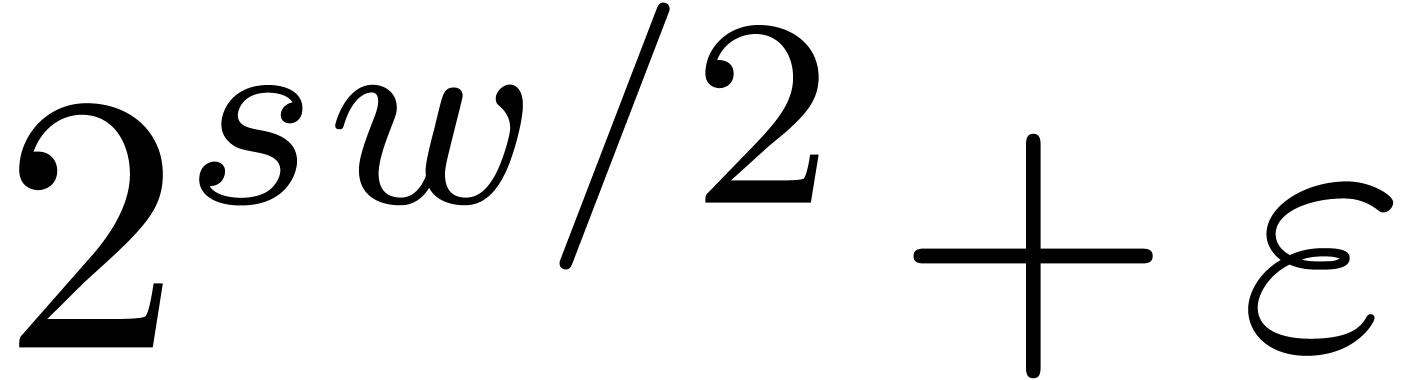 or
or 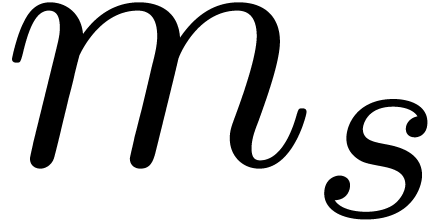 ,
then we remark that it should still be possible to design reasonably
efficient ad hoc algorithms for multi-modular reduction and
reconstruction.
,
then we remark that it should still be possible to design reasonably
efficient ad hoc algorithms for multi-modular reduction and
reconstruction.
Another desirable property of the moduli 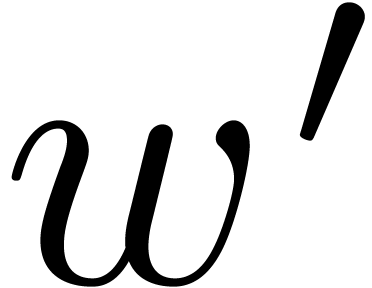 is that
is that
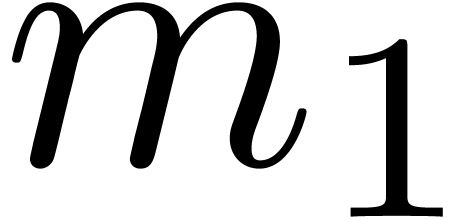 is as small as possible: the spare bits can for
instance be used to speed up matrix multiplication modulo
is as small as possible: the spare bits can for
instance be used to speed up matrix multiplication modulo 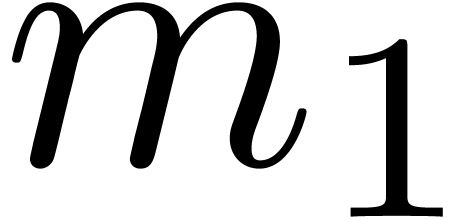 . Notice however that one
“occasional” large modulus
. Notice however that one
“occasional” large modulus 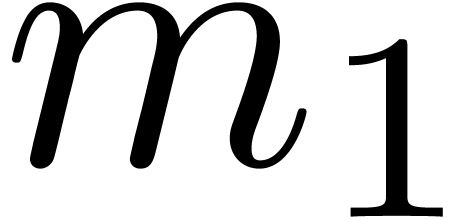 only
impacts on one out of
only
impacts on one out of  modular matrix products;
this alleviates the negative impact of such moduli. We refer to section
4.5 below for more details.
modular matrix products;
this alleviates the negative impact of such moduli. We refer to section
4.5 below for more details.
For actual applications, one should select gentle moduli that combine all desirable properties mentioned above. If not enough such moduli can be found, then it it depends on the application which criteria are most important and which ones can be released.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ,
,  and
and 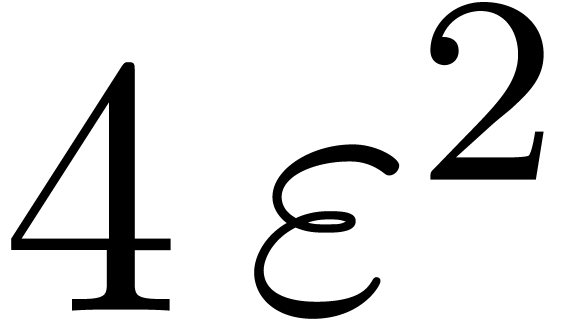
Ideally speaking, we want  to be as large as
possible. Furthermore, in order to waste as few bits as possible,
to be as large as
possible. Furthermore, in order to waste as few bits as possible, 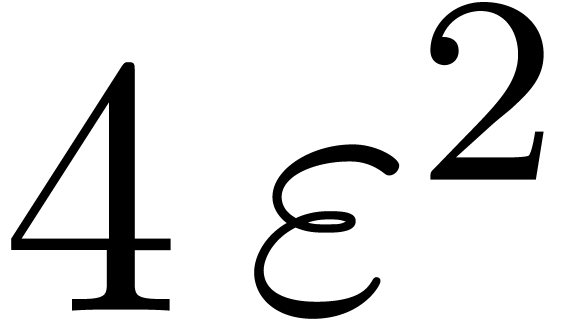 should be close to the word size (or half of it) and
should be close to the word size (or half of it) and
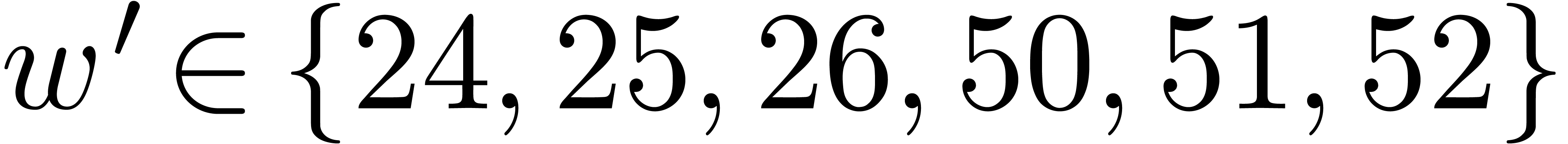 should be minimized. When using double precision
floating point arithmetic, this means that we wish to take
should be minimized. When using double precision
floating point arithmetic, this means that we wish to take  . Whenever we have efficient hardware support
for integer arithmetic, then we might prefer
. Whenever we have efficient hardware support
for integer arithmetic, then we might prefer  .
.
Let us start by studying the influence of 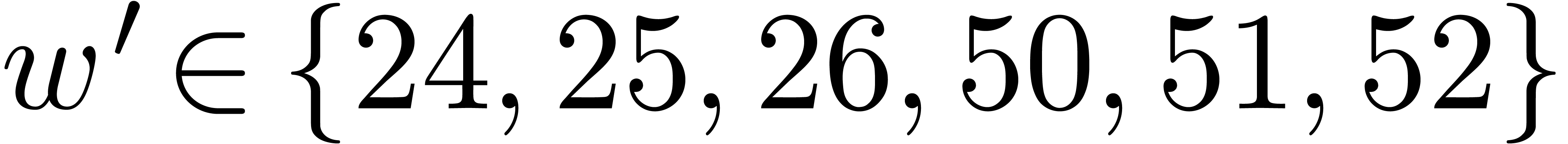 on the
number of hits. In Table 2, we have increased
on the
number of hits. In Table 2, we have increased  by one with respect to Table 1. This results
in an approximate
by one with respect to Table 1. This results
in an approximate  increase of the
“capacity”
increase of the
“capacity” 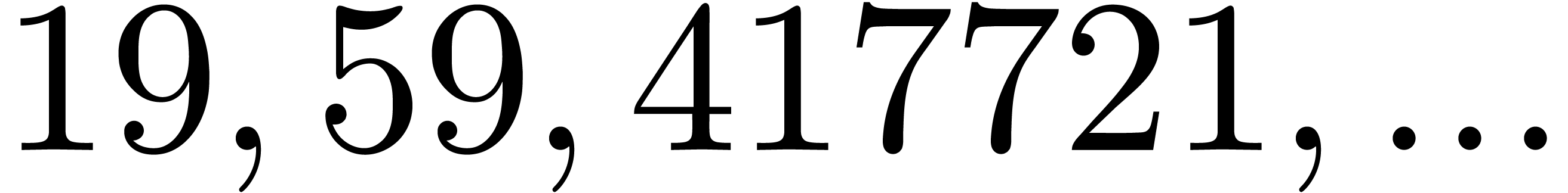 of the modulus
of the modulus  . On the one hand, we observe that
the hit rate of the sieve procedure roughly decreases by a factor of
thirty. On the other hand, we notice that the rare gentle moduli that we
do find are often of high quality (on four occasions the moduli
. On the one hand, we observe that
the hit rate of the sieve procedure roughly decreases by a factor of
thirty. On the other hand, we notice that the rare gentle moduli that we
do find are often of high quality (on four occasions the moduli  are all prime in Table 2).
are all prime in Table 2).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Without surprise, the hit rate also sharply decreases if we attempt to
increase  . The results for
. The results for
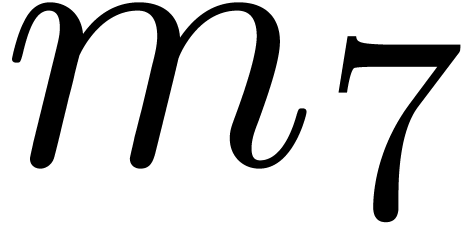 and
and 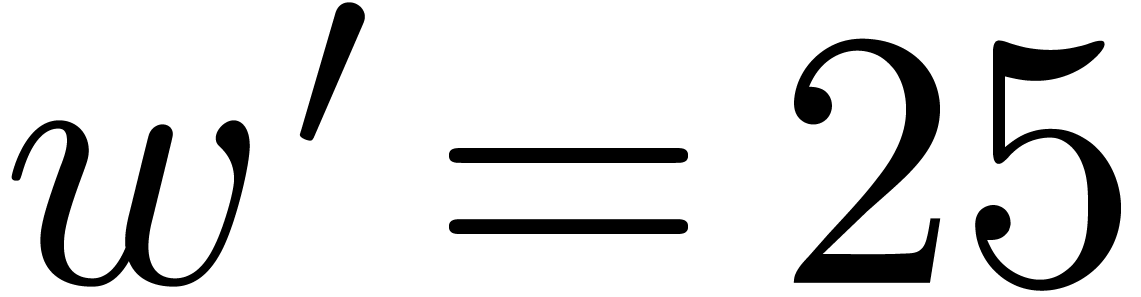 are shown in Table
3. A further infortunate side effect is that the quality of
the gentle moduli that we do find also decreases. Indeed, on the one
hand,
are shown in Table
3. A further infortunate side effect is that the quality of
the gentle moduli that we do find also decreases. Indeed, on the one
hand,  tends to systematically admit at least one
small prime factor. On the other hand, it is rarely the case that each
tends to systematically admit at least one
small prime factor. On the other hand, it is rarely the case that each
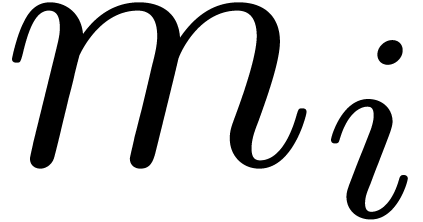 divides either
divides either 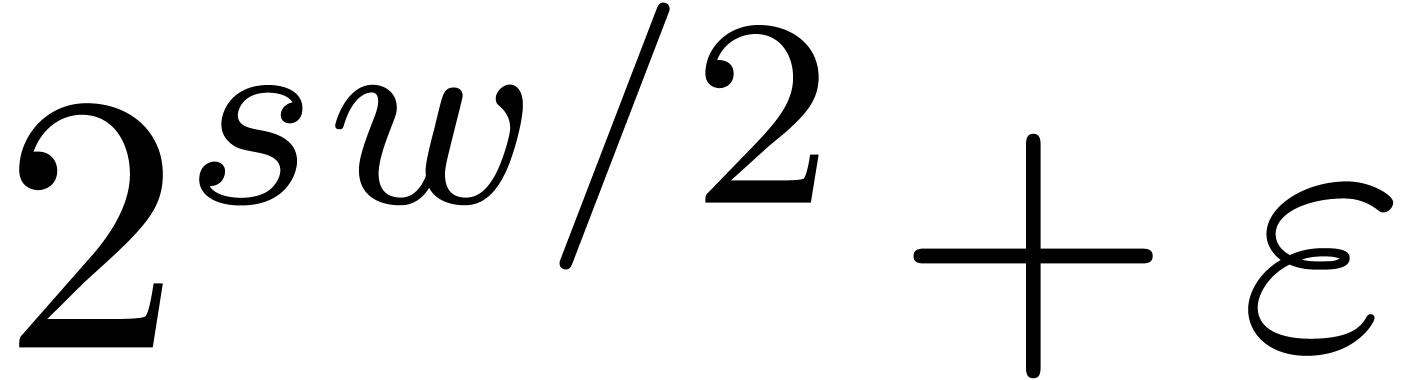 or
or 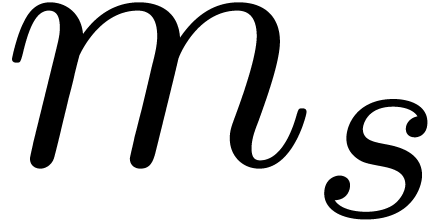 (this might nevertheless be the case for other
recombinations of the prime factors of
(this might nevertheless be the case for other
recombinations of the prime factors of  ,
but only modulo a further increase of
,
but only modulo a further increase of 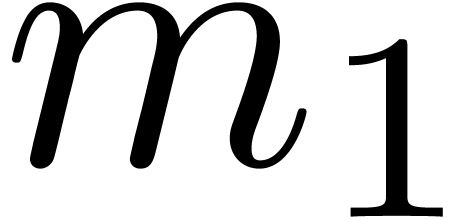 ).
).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
An increase of 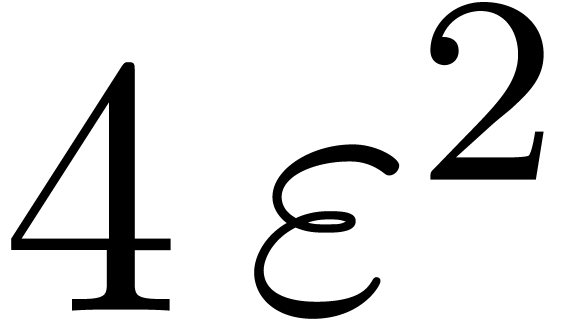 while maintaining
while maintaining  and
and 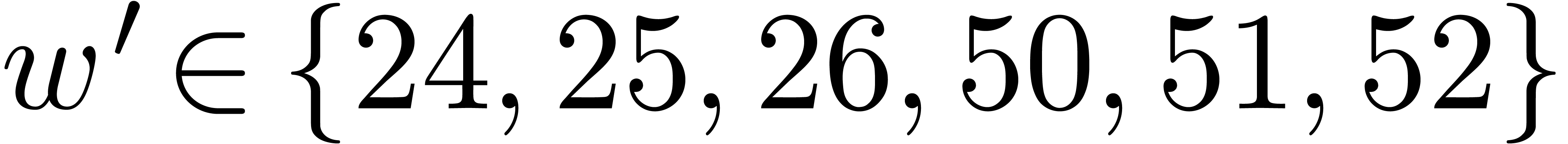 fixed also results in a
decrease of the hit rate. Nevertheless, when going from
fixed also results in a
decrease of the hit rate. Nevertheless, when going from 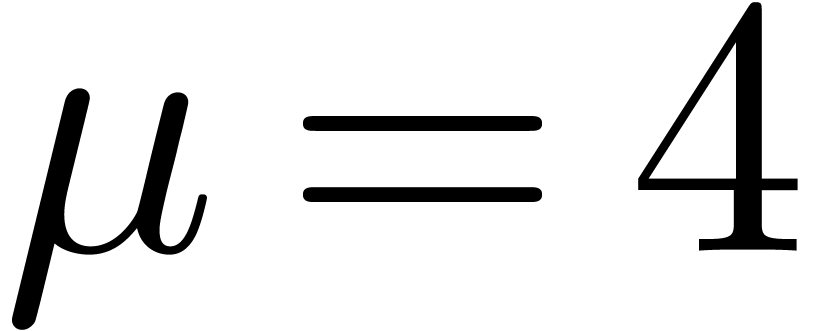 (floating point arithmetic) to
(floating point arithmetic) to 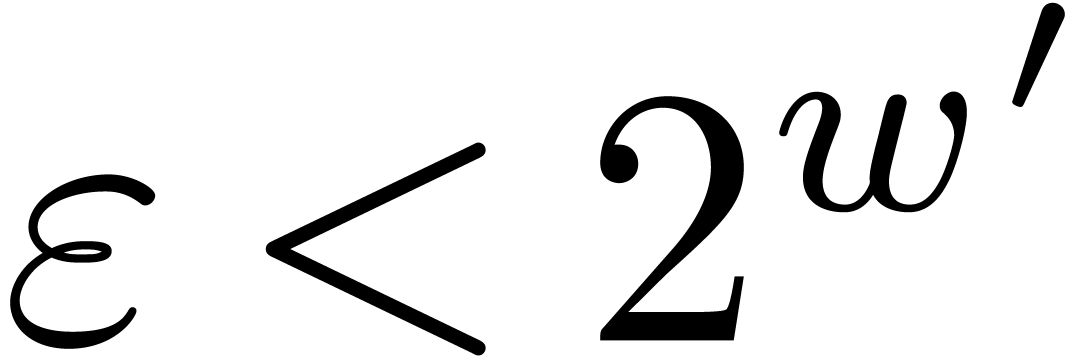 (integer
arithmetic), this is counterbalanced by the fact that
(integer
arithmetic), this is counterbalanced by the fact that  can also be taken larger (namely
can also be taken larger (namely 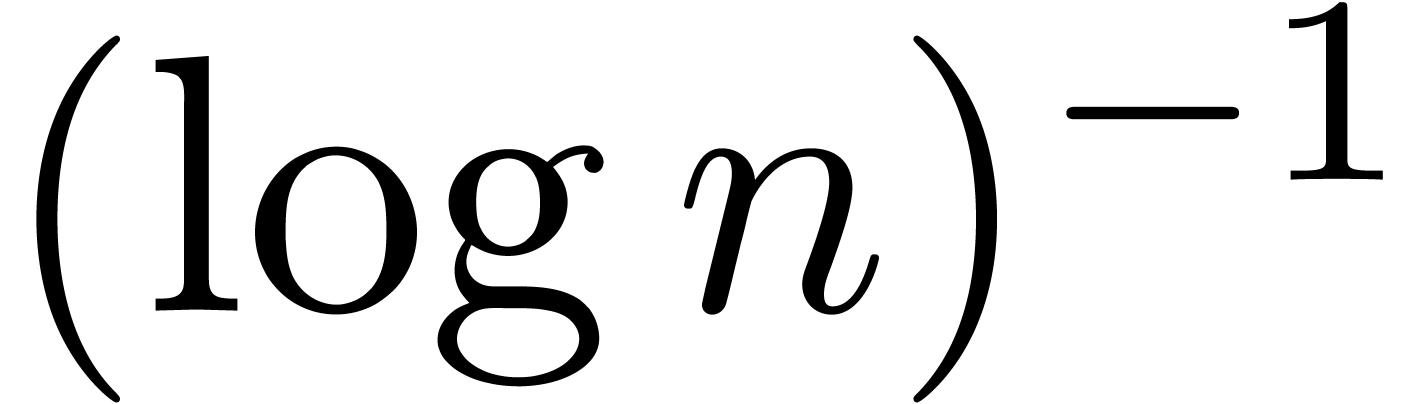 );
see Table 4 for a concrete example. When doubling
);
see Table 4 for a concrete example. When doubling  and
and 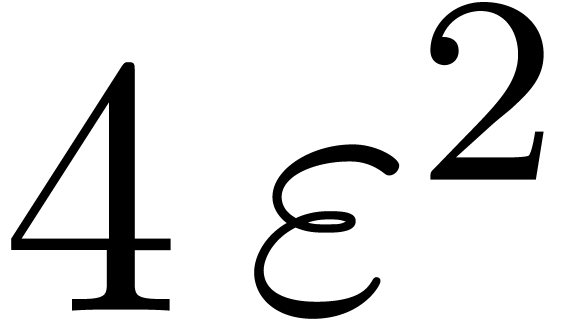 while keeping the same upper
bound for
while keeping the same upper
bound for  , the hit rate
remains more or less unchanged, but the rate of high quality hits tends
to decrease somewhat: see Table 5.
, the hit rate
remains more or less unchanged, but the rate of high quality hits tends
to decrease somewhat: see Table 5.
It should be possible to analyze the hit rate as a function of the
parameters  ,
,  ,
,  and
and  from a probabilistic point of view, using the idea that a random number
from a probabilistic point of view, using the idea that a random number
 is prime with probability
is prime with probability 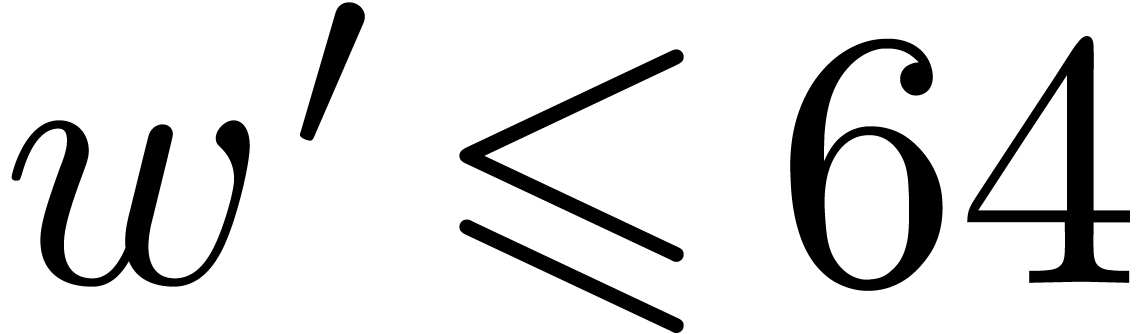 . However, from a practical point of view, the
priority is to focus on the case when
. However, from a practical point of view, the
priority is to focus on the case when 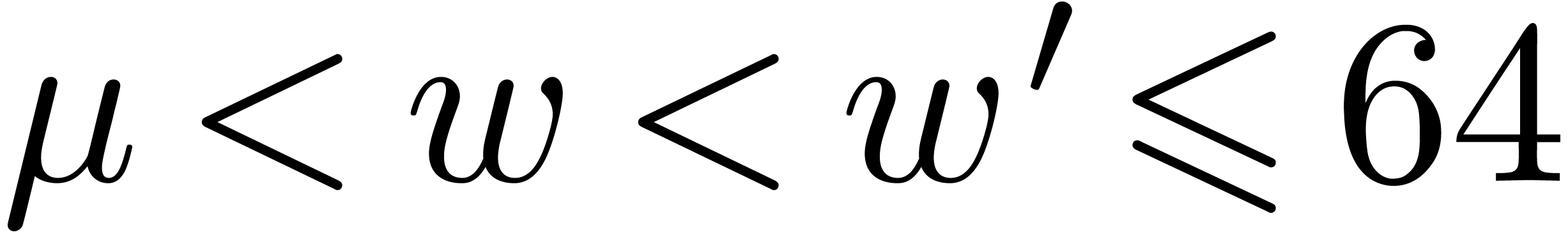 .
For the most significant choices of parameters
.
For the most significant choices of parameters 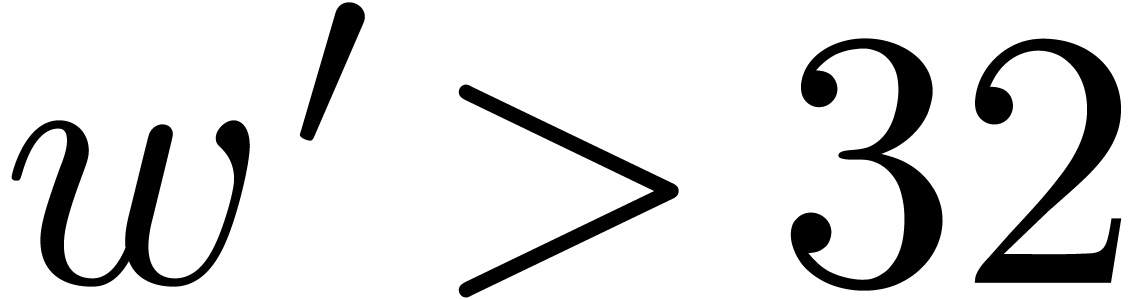 and
and  , it seems in principle
to be possible to compile full tables of
, it seems in principle
to be possible to compile full tables of  -gentle
moduli. Unfortunately, our current implementation is still somewhat
inefficient for
-gentle
moduli. Unfortunately, our current implementation is still somewhat
inefficient for 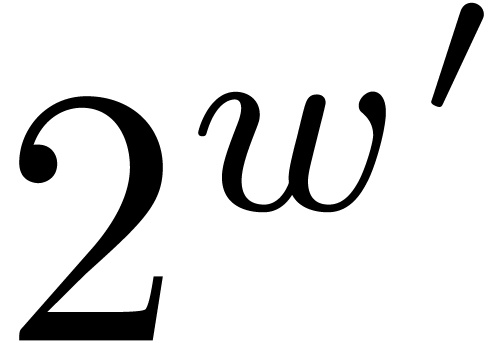 . A helpful
feature for upcoming versions of
. A helpful
feature for upcoming versions of 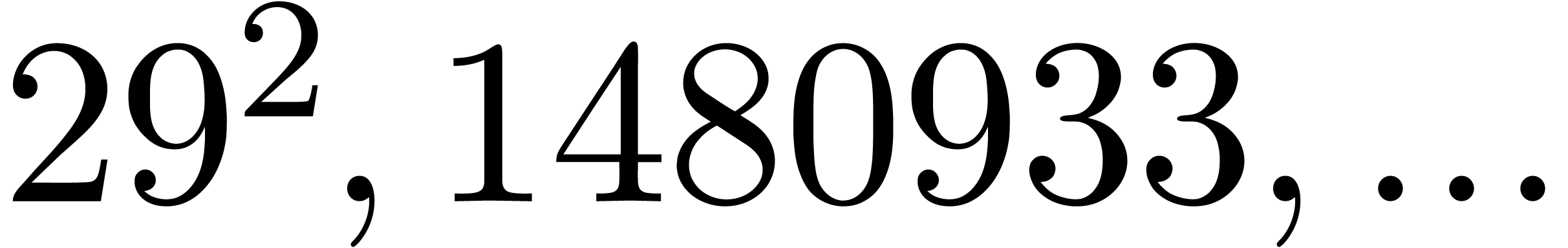 (the current version only does this for
prime factors that can be tabulated).
(the current version only does this for
prime factors that can be tabulated).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
One of our favourite applications of multi-modular arithmetic is the
multiplication of integer matrices  .
We proceed as follows:
.
We proceed as follows:
Compute 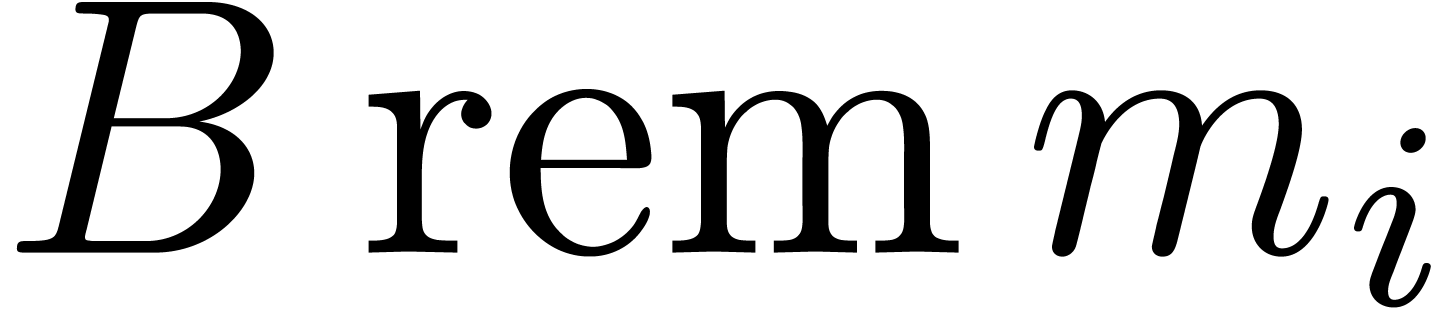 and
and 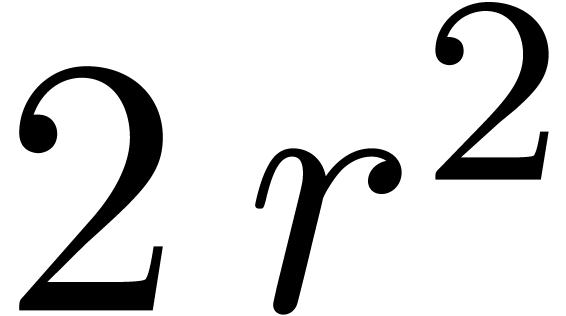 for
for
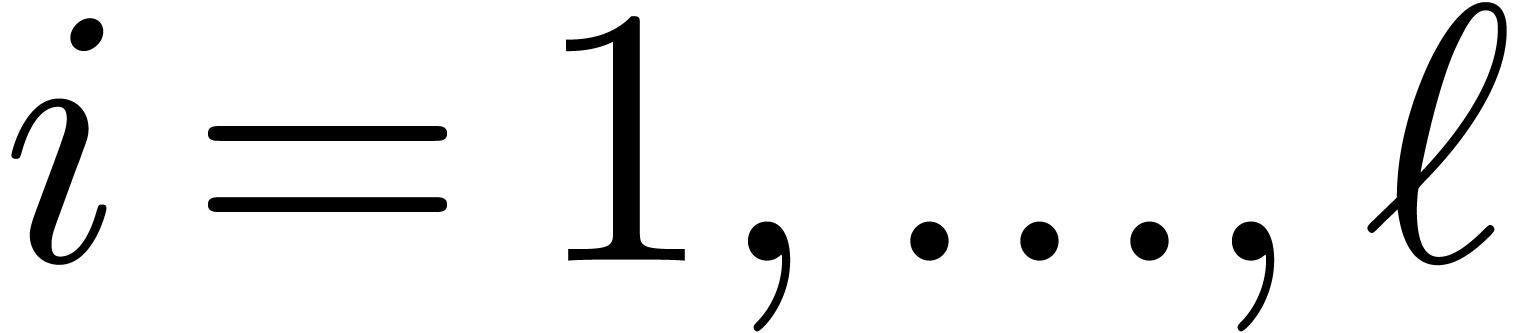 , using
, using 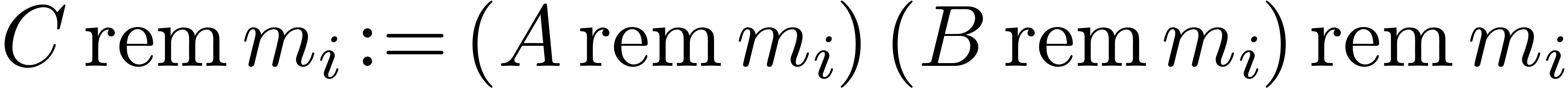 multi-modular reductions.
multi-modular reductions.
Multiply  for
for  .
.
Reconstruct  using
using  multi-modular reconstructions.
multi-modular reconstructions.
If  is larger than
is larger than  for
all
for
all 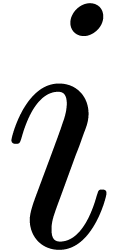 and
and  ,
then
,
then  can be read off from
can be read off from 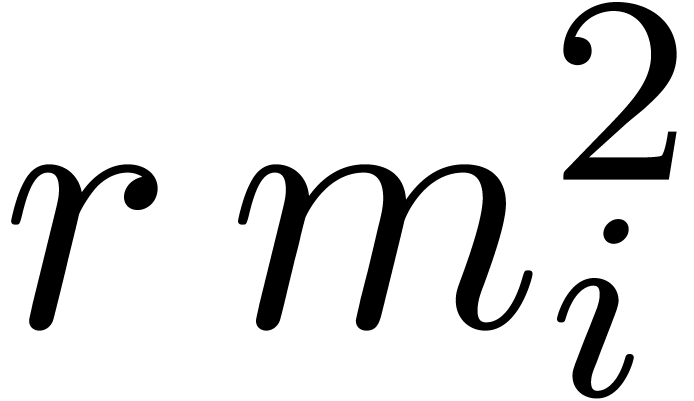 .
.
From a practical point of view, the second step can be implemented very
efficiently if 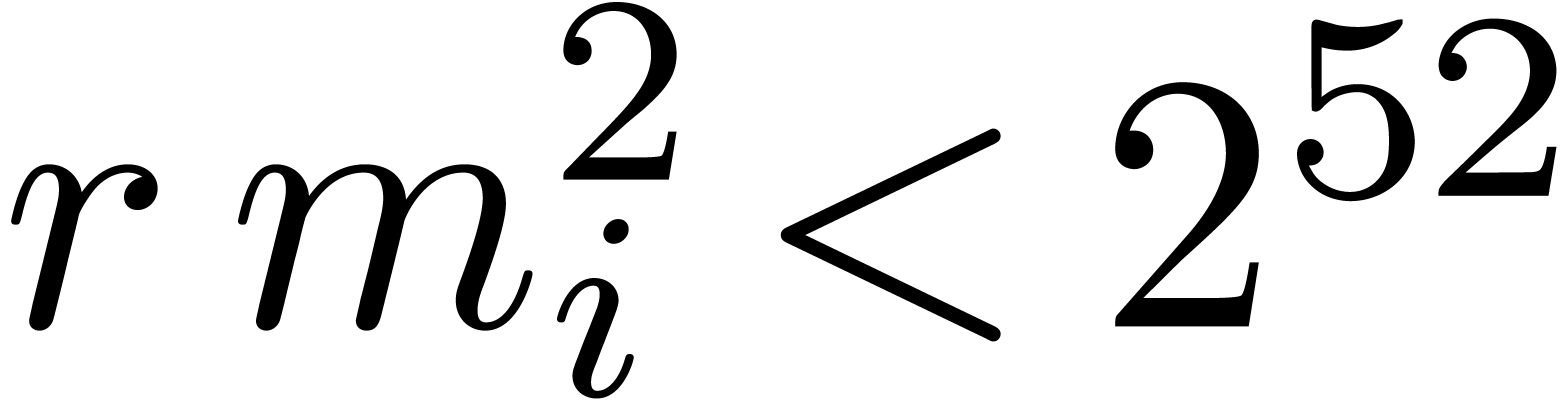 fits into the size of a word.
When using floating point arithmetic, this means that we should have
fits into the size of a word.
When using floating point arithmetic, this means that we should have
 for all
for all 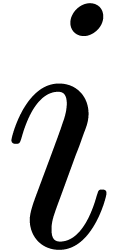 .
For large values of
.
For large values of 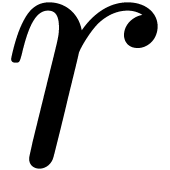 , this is
unrealistic; in that case, we subdivide the
, this is
unrealistic; in that case, we subdivide the  matrices into smaller
matrices into smaller 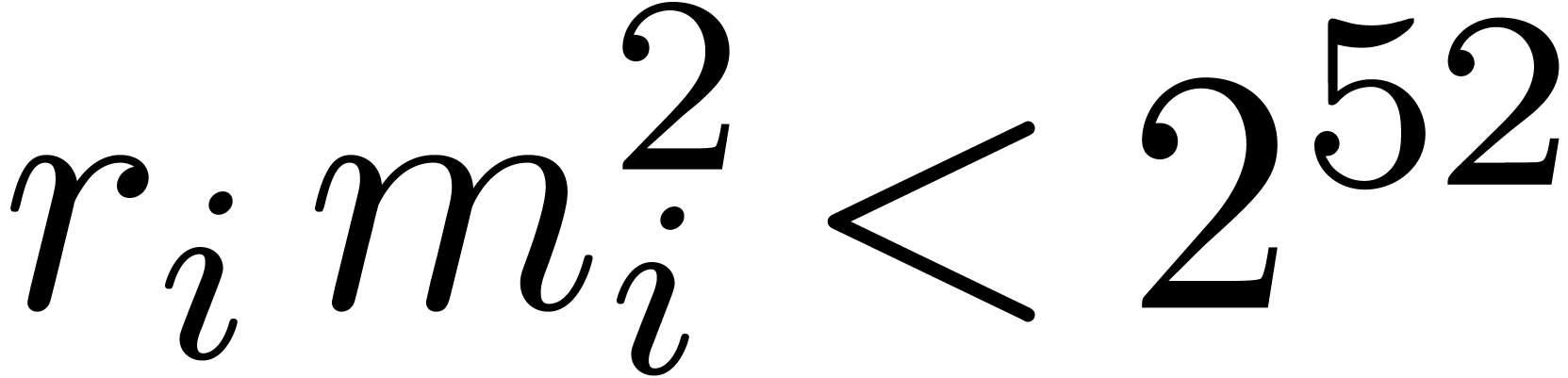 matrices with
matrices with 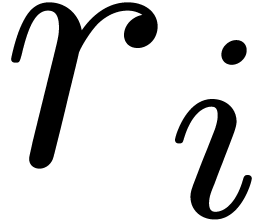 . The fact that
. The fact that 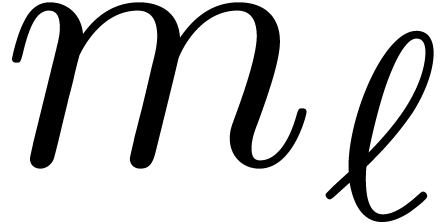 may
depend on
may
depend on 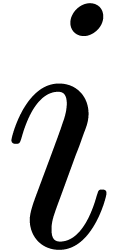 is very significant. First of all, the
larger we can take
is very significant. First of all, the
larger we can take 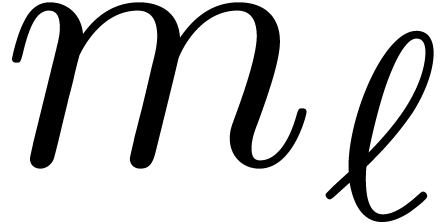 , the
faster we can multiply matrices modulo
, the
faster we can multiply matrices modulo 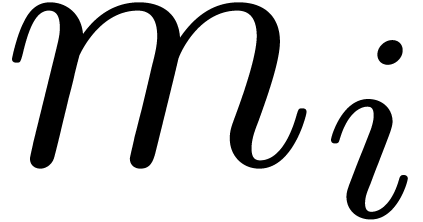 .
Secondly, the
.
Secondly, the 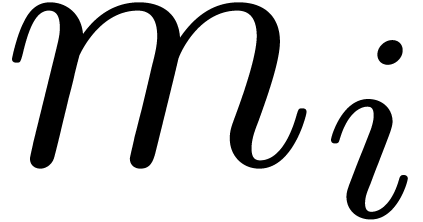 in the tables from the previous
sections often vary in bitsize. It frequently happens that we may take
all
in the tables from the previous
sections often vary in bitsize. It frequently happens that we may take
all 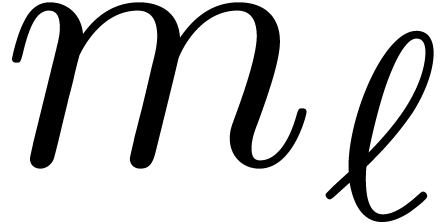 large except for the last modulus
large except for the last modulus  . The fact that matrix
multiplications modulo the worst modulus
. The fact that matrix
multiplications modulo the worst modulus  are
somewhat slower is compensated by the fact that they only account for
one out of every
are
somewhat slower is compensated by the fact that they only account for
one out of every  modular matrix products.
modular matrix products.
Several of the tables in the previous subsections were made with the
application to integer matrix multiplication in mind. Consider for
instance the modulus 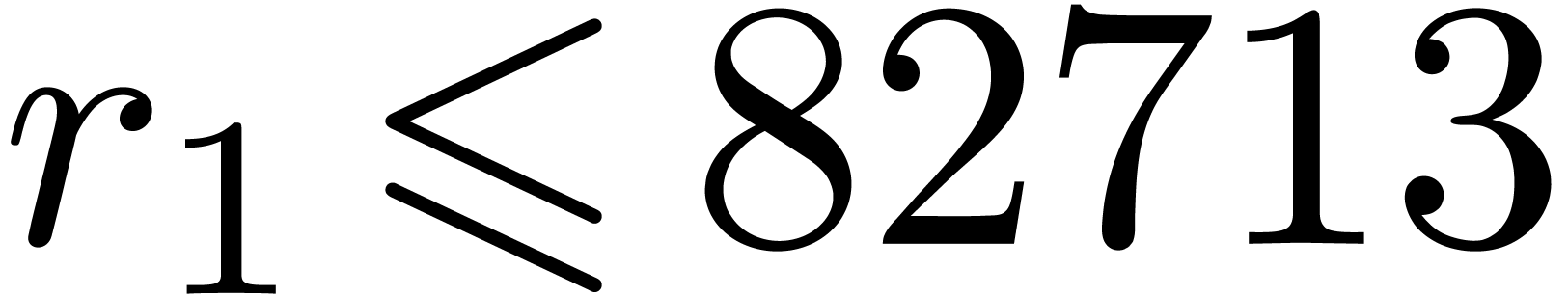 from Table 1.
When using floating point arithmetic, we obtain
from Table 1.
When using floating point arithmetic, we obtain 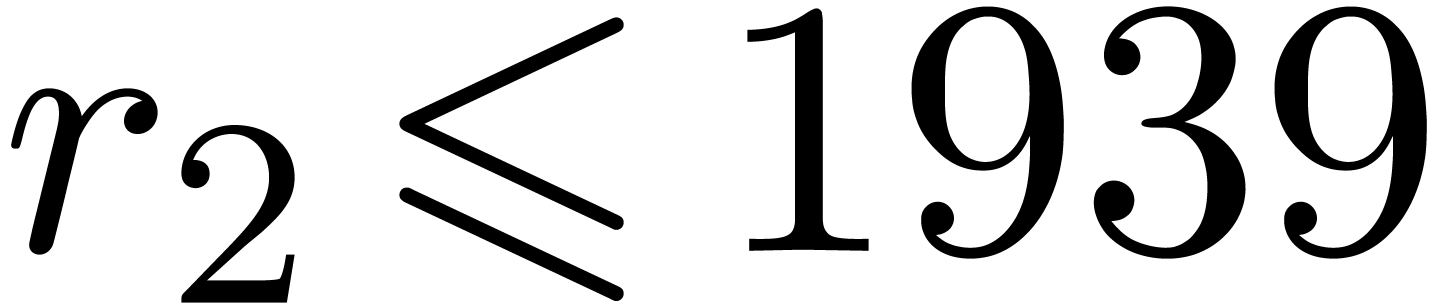 ,
, 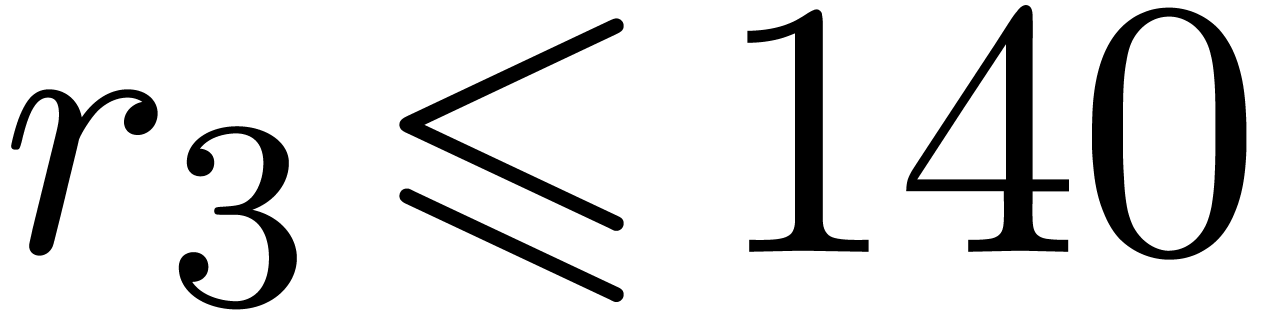 ,
, 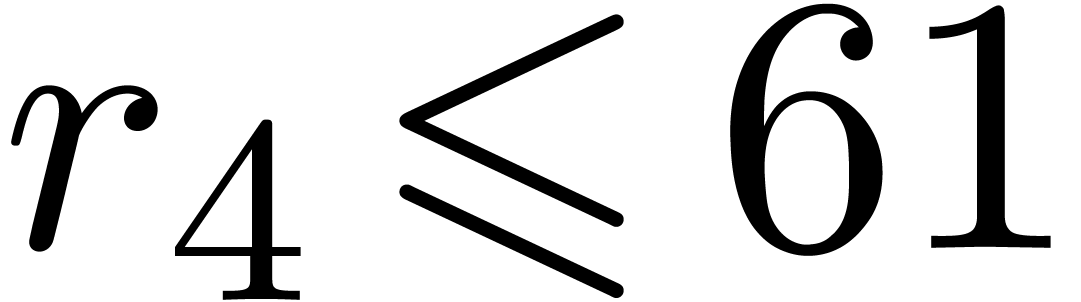 ,
, 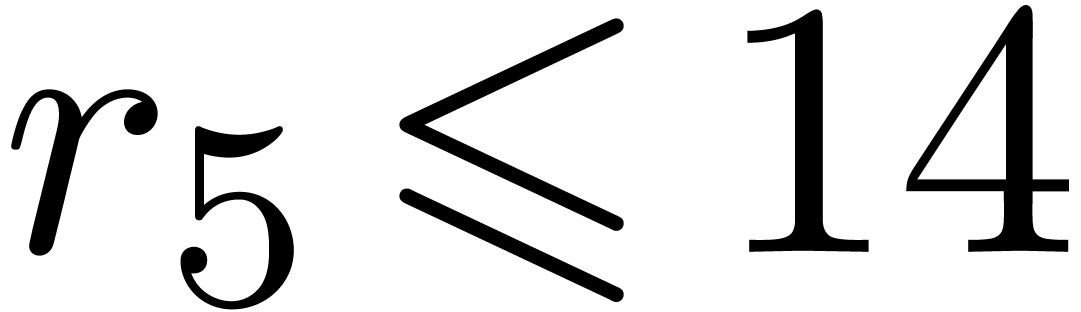 ,
,
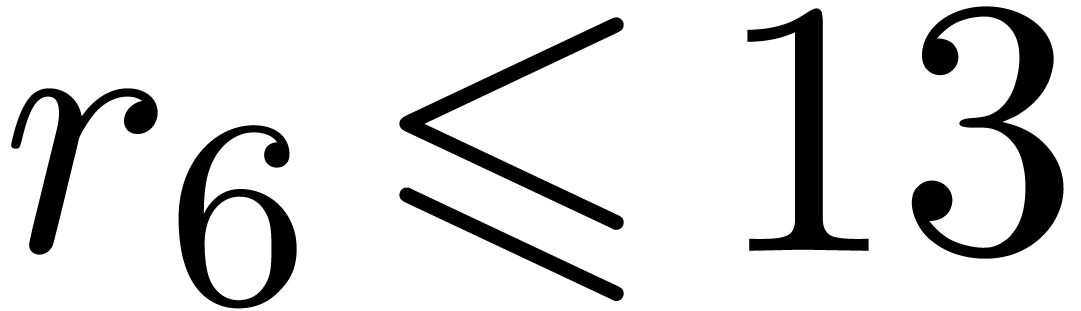 and
and  .
Clearly, there is a trade-off between the efficiency of the modular
matrix multiplications (high values of
.
Clearly, there is a trade-off between the efficiency of the modular
matrix multiplications (high values of  are
better) and the bitsize
are
better) and the bitsize 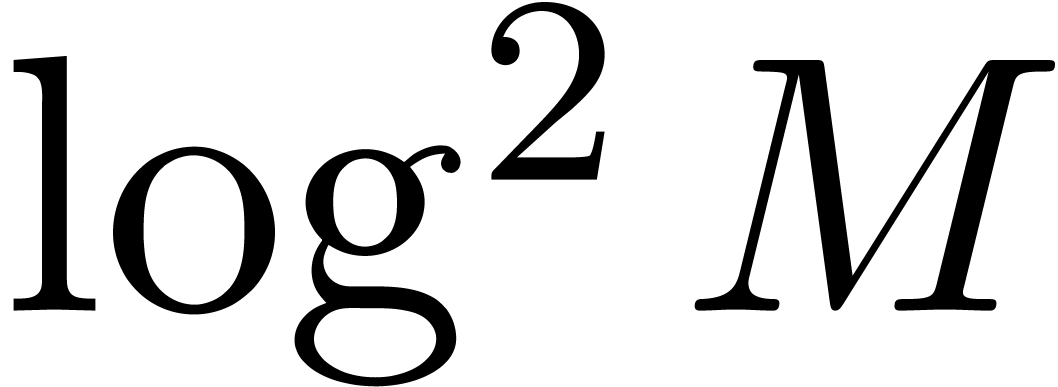 of
of  (larger capacities are better).
(larger capacities are better).
If 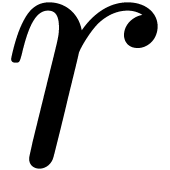 is large with respect to
is large with respect to 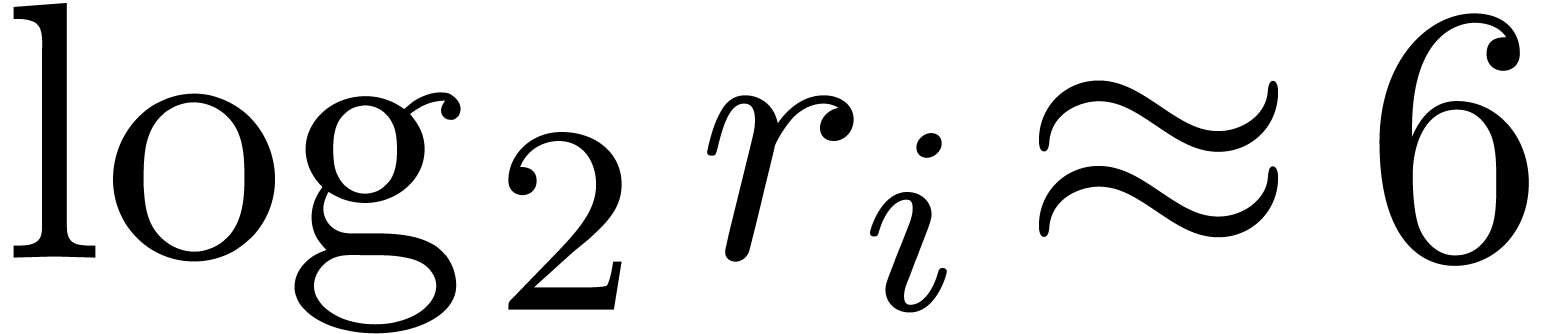 , then the modular matrix multiplication step
is the main bottleneck, so it is important to take all
, then the modular matrix multiplication step
is the main bottleneck, so it is important to take all 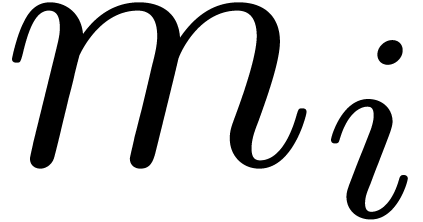 approximately of the same size (i.e.
approximately of the same size (i.e. 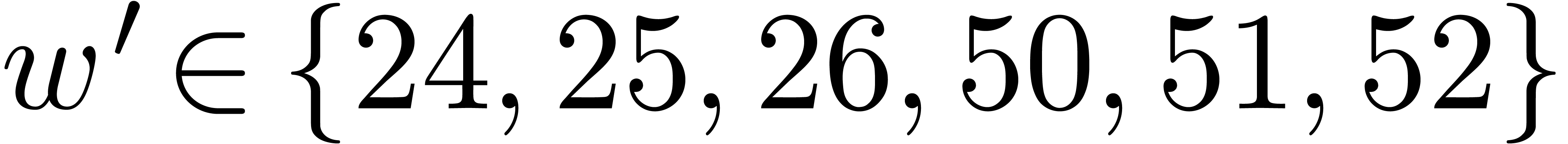 should be small) and in such a way that the corresponding
should be small) and in such a way that the corresponding 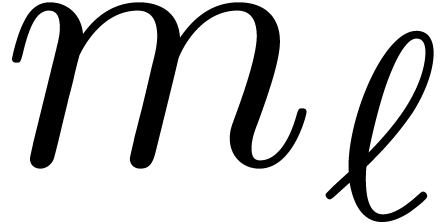 lead to the best complexity (
lead to the best complexity (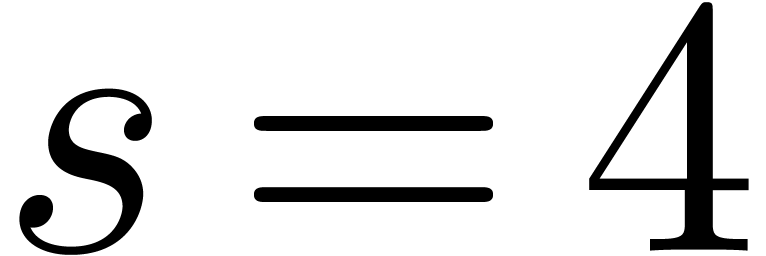 tends
to work well). This can often only be achieved by lowering
tends
to work well). This can often only be achieved by lowering  to
to 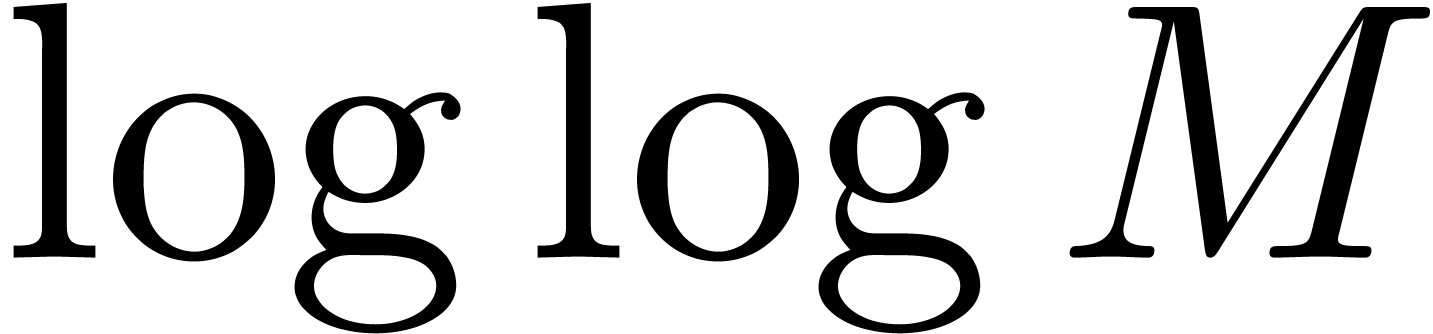 or
or 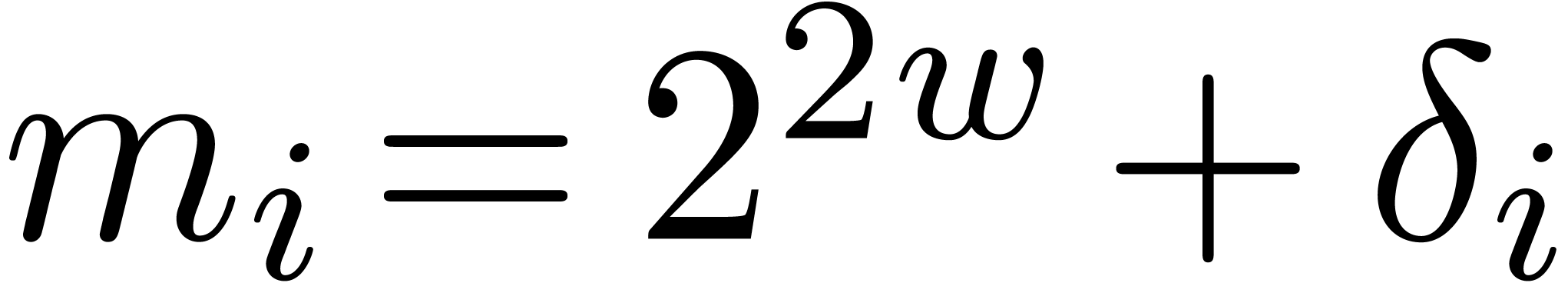 . For
. For 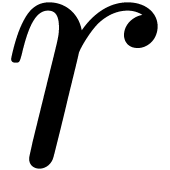 closer to
closer to 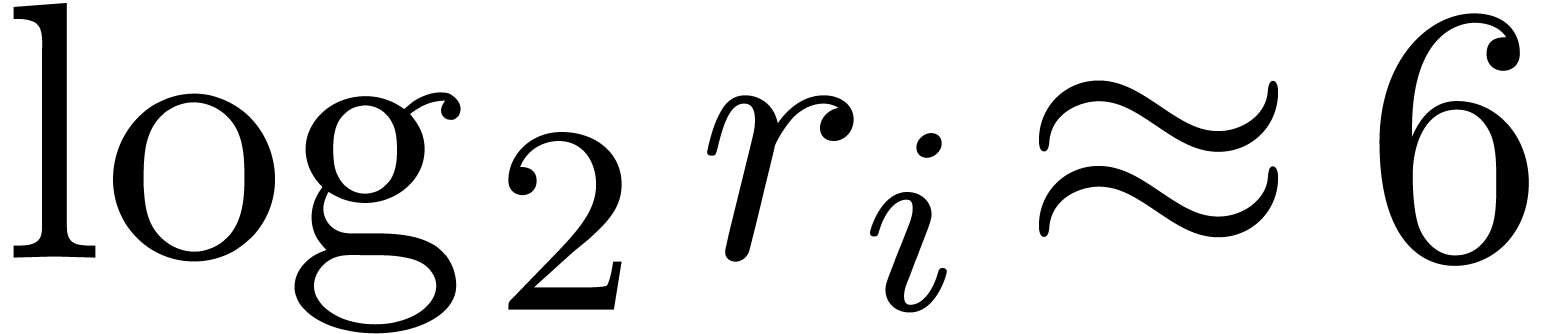 , the Chinese remaindering steps become more
and more expensive, which makes it interesting to consider larger values
of
, the Chinese remaindering steps become more
and more expensive, which makes it interesting to consider larger values
of  and to increase the difference
and to increase the difference  . For
. For 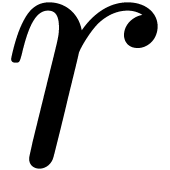 significantly
below
significantly
below  , we resort to
FFT-based matrix multiplication. This corresponds to taking roughly
twice as many moduli, but the transformations become approximately
, we resort to
FFT-based matrix multiplication. This corresponds to taking roughly
twice as many moduli, but the transformations become approximately 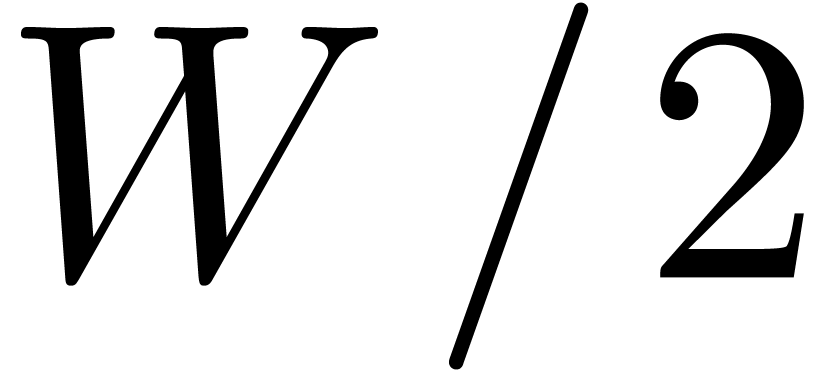 times less expensive.
times less expensive.
We have not yet implemented any of the algorithms in this paper. The
implementation that we envision selects appropriate code as a function
of the parameters  ,
, 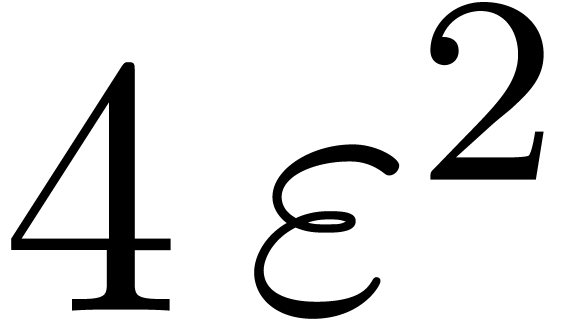 and
and  . The
parameters
. The
parameters  and
and 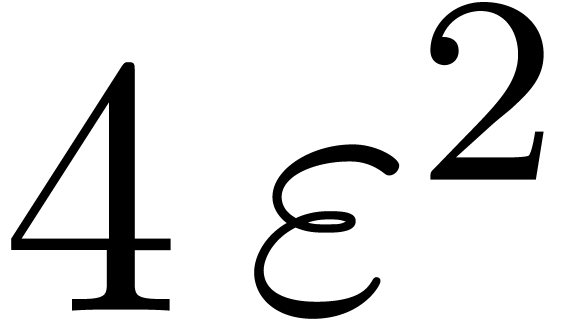 highly
depend on the application: see the above discussion in the case of
integer matrix multiplication. Generally speaking,
highly
depend on the application: see the above discussion in the case of
integer matrix multiplication. Generally speaking, 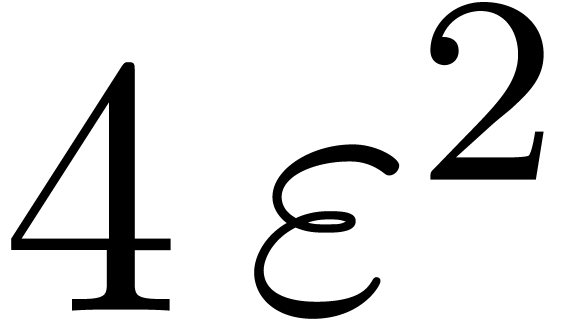 is bounded by the bitsize
is bounded by the bitsize 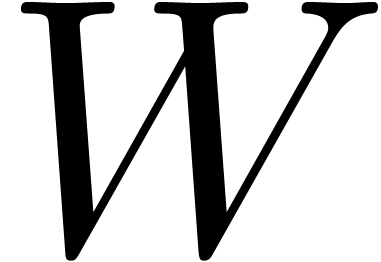 of a machine word or
by
of a machine word or
by  .
.
So far, we have described four main strategies for solving Chinese
remaindering problems for moduli 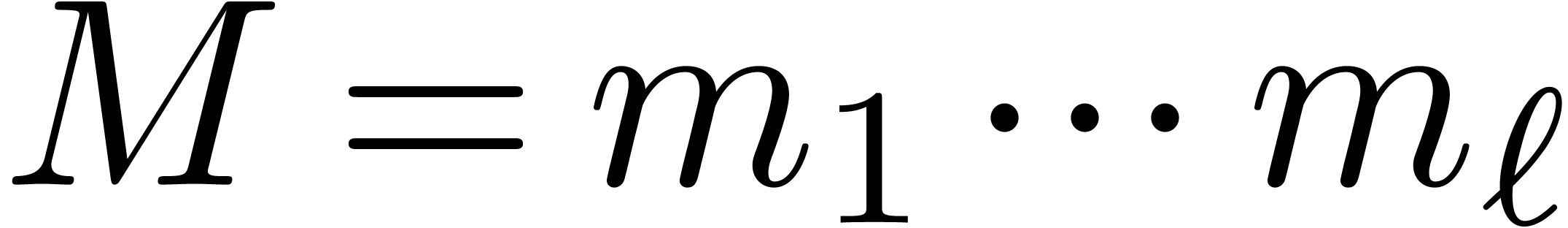 :
:
The “gentle modulus strategy” requires 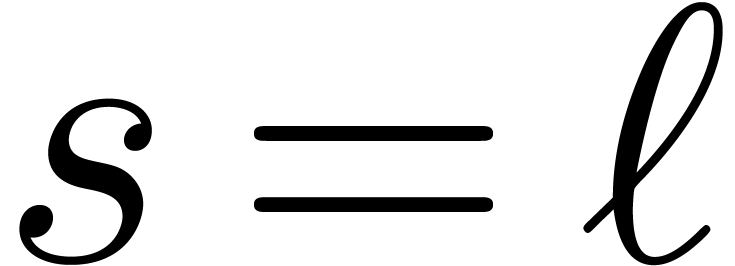 to be an
to be an  -gentle
modulus with
-gentle
modulus with 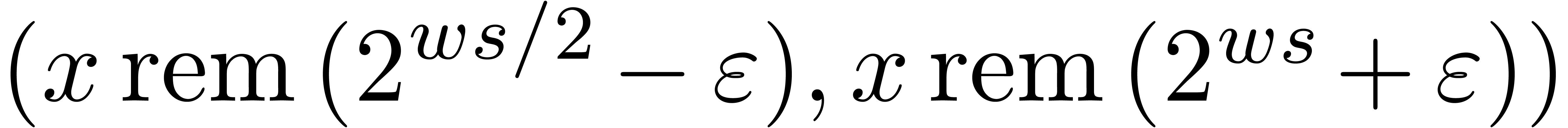 .
Conversions between
.
Conversions between  and
and  can be done fast. The further conversions from and to
can be done fast. The further conversions from and to 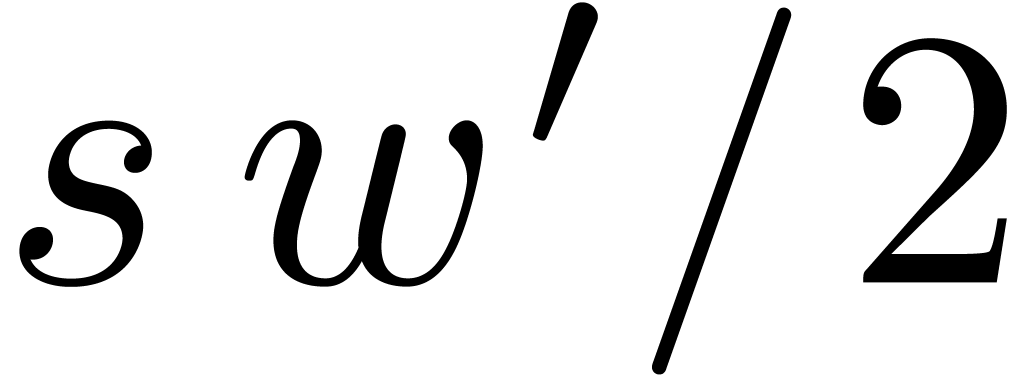 are done in a naive manner.
are done in a naive manner.
The “gentle product strategy” strategy requires  to be gentle moduli. We now perform the
multi-modular reductions and recombinations using the algorithms
from subsection 4.1.
to be gentle moduli. We now perform the
multi-modular reductions and recombinations using the algorithms
from subsection 4.1.
The “naive strategy” for Chinese remaindering has been described in subsections 3.2 and 3.3.
The asymptotically fast “FFT-based strategy” from Theorems 6 and 10, which attempts to do as much work as possible using Fourier representations.
The idea is now to apply each of these strategies at the appropriate levels of the remainder tree. At the very bottom, we use G, followed by P and N. At the top levels, we use F.
As a function of  , we need to
decide how much work we wish to perform at each of these levels. For
small
, we need to
decide how much work we wish to perform at each of these levels. For
small 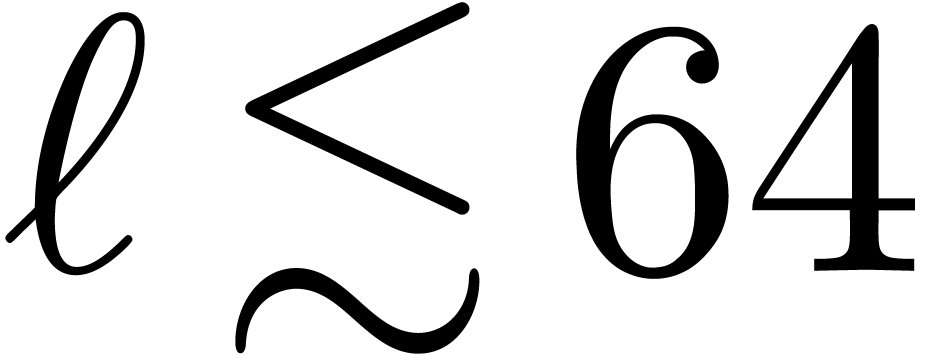 , it suffices to
combine the strategies G and P. As
soon as
, it suffices to
combine the strategies G and P. As
soon as 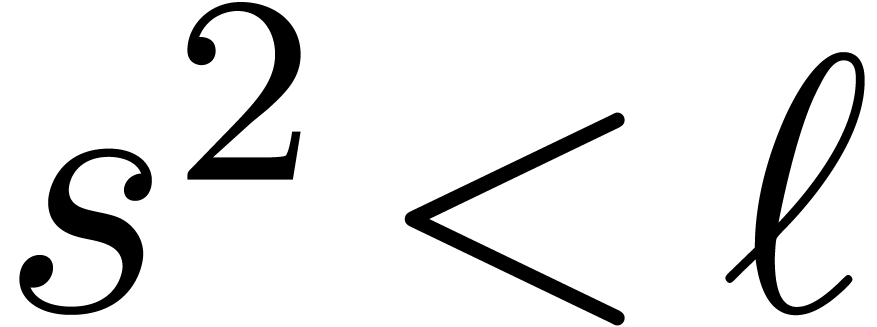 exceeds
exceeds  ,
some of the modular reductions in the strategy G may
become expensive. For this reason, it is generally better to let
P do a bit more work, i.e. to take
,
some of the modular reductions in the strategy G may
become expensive. For this reason, it is generally better to let
P do a bit more work, i.e. to take 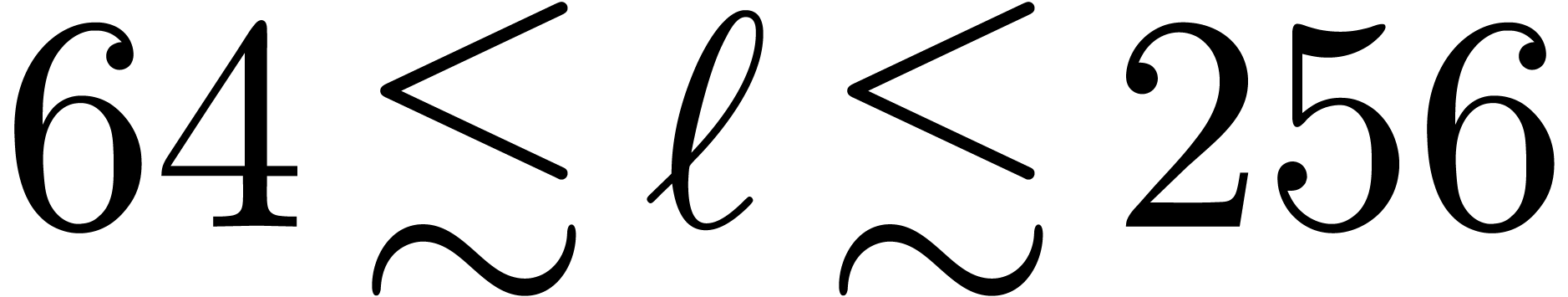 . It is also a good practice to use
. It is also a good practice to use
 as the “soft word size” for multiple
integer arithmetic (see subsection 2.4).
as the “soft word size” for multiple
integer arithmetic (see subsection 2.4).
As soon as  starts to get somewhat larger, say
starts to get somewhat larger, say
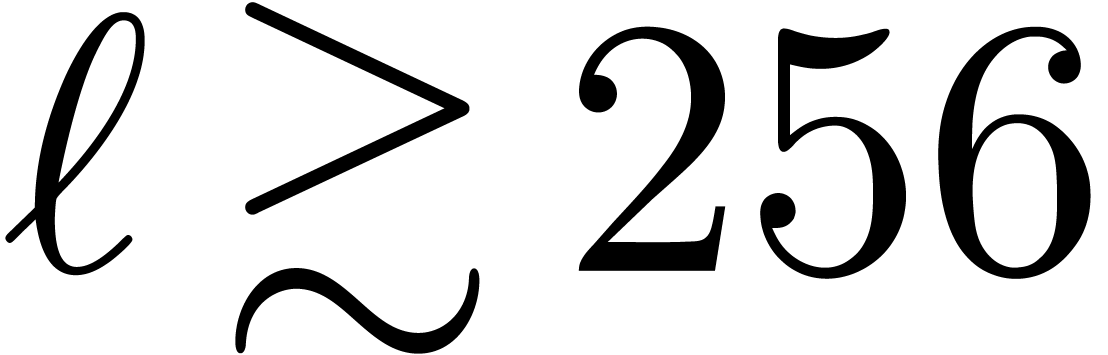 , then some intermediate
levels may be necessary before that FFT multiplication becomes plainly
efficient. For these levels, we use strategy N with
arity two. It still has to be found out how large this intermediate
region is, exactly. Indeed, the ability to do more work using the
Fourier representation often lowers the threshold at which such methods
become efficient. If one manages to design extremely efficient
implementations for the strategies G and
P (e.g. if multi-modular reduction and
reconstruction can approximately be done as fast as multiplication
itself), then one may also consider the use of Chinese remaindering
instead of Fourier transforms in F.
, then some intermediate
levels may be necessary before that FFT multiplication becomes plainly
efficient. For these levels, we use strategy N with
arity two. It still has to be found out how large this intermediate
region is, exactly. Indeed, the ability to do more work using the
Fourier representation often lowers the threshold at which such methods
become efficient. If one manages to design extremely efficient
implementations for the strategies G and
P (e.g. if multi-modular reduction and
reconstruction can approximately be done as fast as multiplication
itself), then one may also consider the use of Chinese remaindering
instead of Fourier transforms in F.
For large 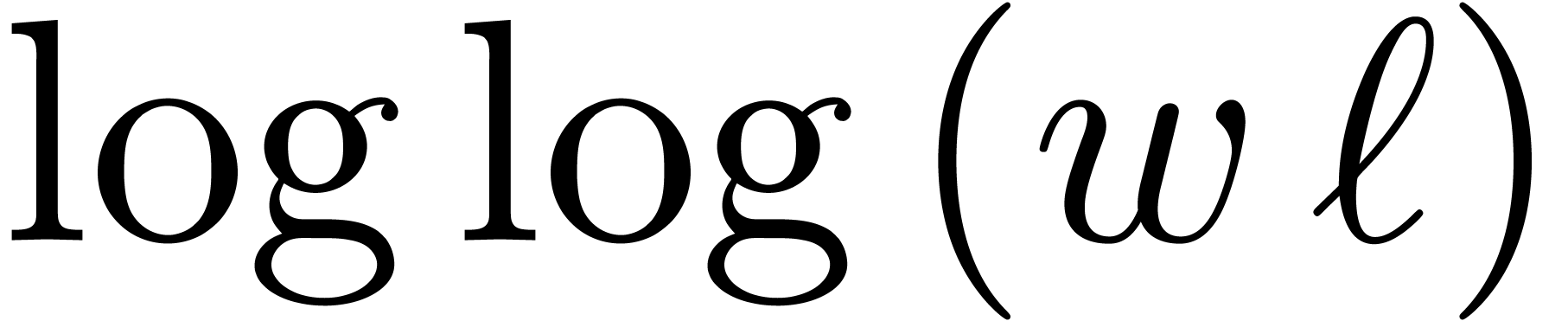 , the FFT-based
algorithms should become fastest and we expect that the theoretical
, the FFT-based
algorithms should become fastest and we expect that the theoretical 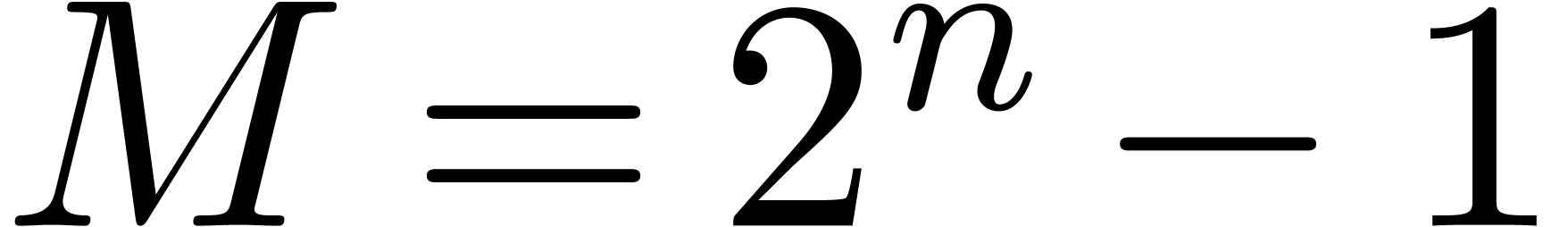 speed-up should result in practical gains of a factor
three at least. As emphasized before, it is crucial to rely on inborn
FFT strategies. For very large
speed-up should result in practical gains of a factor
three at least. As emphasized before, it is crucial to rely on inborn
FFT strategies. For very large  ,
we may also run out of
,
we may also run out of  -gentle
moduli. In that case, we may need to resort to lower values of
-gentle
moduli. In that case, we may need to resort to lower values of  , with the consequence that some of
the lower levels may become somewhat more expensive.
, with the consequence that some of
the lower levels may become somewhat more expensive.
A very intriguing question is whether it is possible to select moduli that allow for even faster Chinese remaindering. In the analogue case of polynomials, highly efficient algorithms exist for multi-point evaluation and interpolation at points that form a geometric sequence [5]. Geometric sequences of moduli do not work in our case, since they violate the mutual coprime requirement and they grow too fast anyway. Arithmetic progressions are more promising, although only algorithms with a better constant factor are known in the polynomial case [5], and the elements of such sequences generically admit small prime factors in common that have to be treated with care.
Another natural idea is to chose products 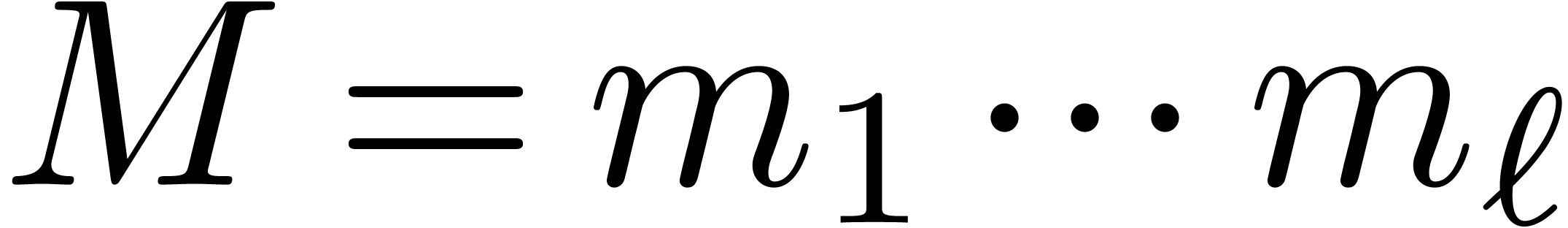 of the
form
of the
form 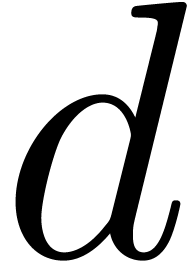 , where
, where  is highly composite. Each divisor
is highly composite. Each divisor 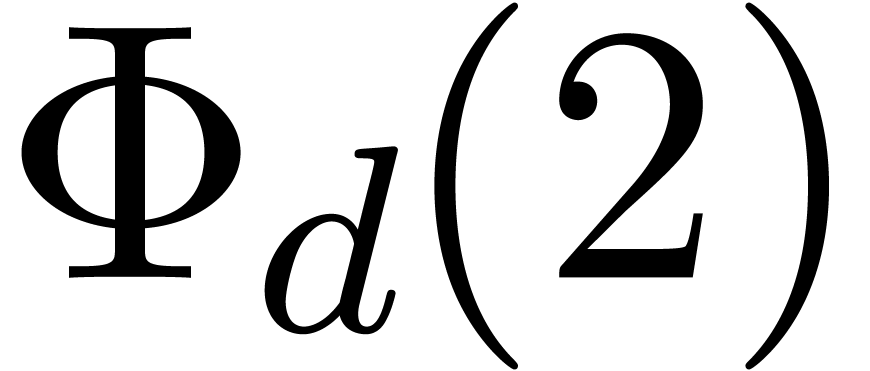 of
of  naturally induces a divisor
naturally induces a divisor 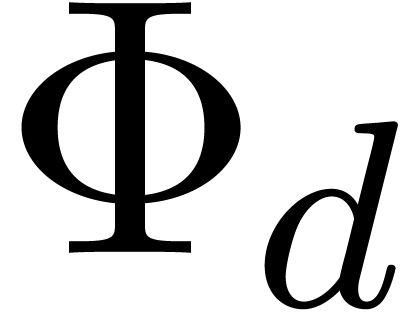 of
of
 , where
, where 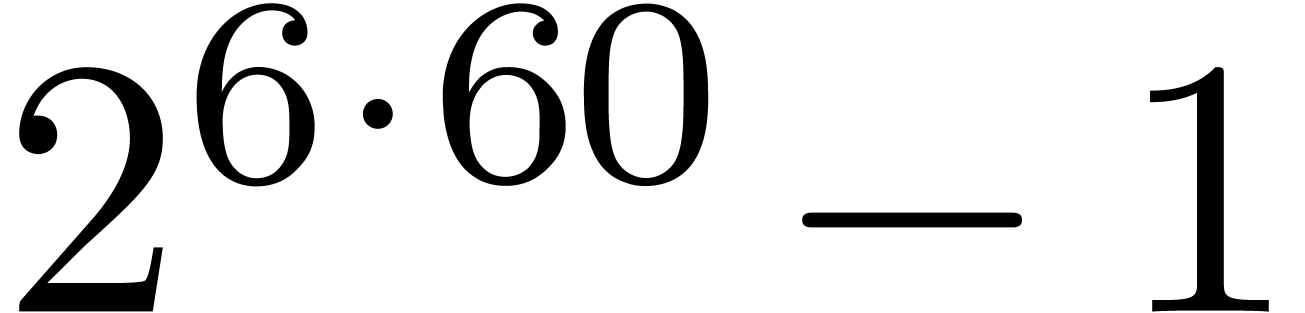 denotes the
denotes the 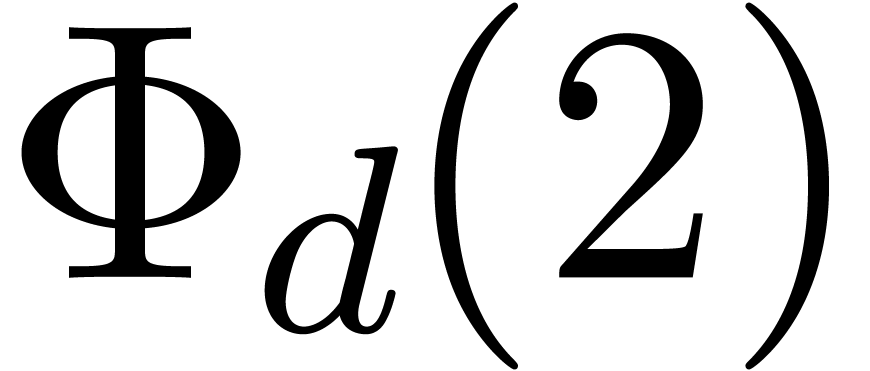 -th cyclotomic
polynomial. For instance, the number
-th cyclotomic
polynomial. For instance, the number 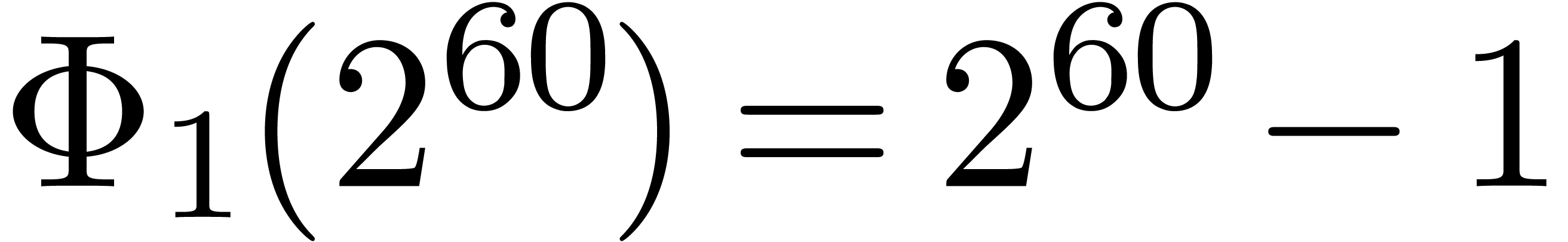 is
divisible by
is
divisible by 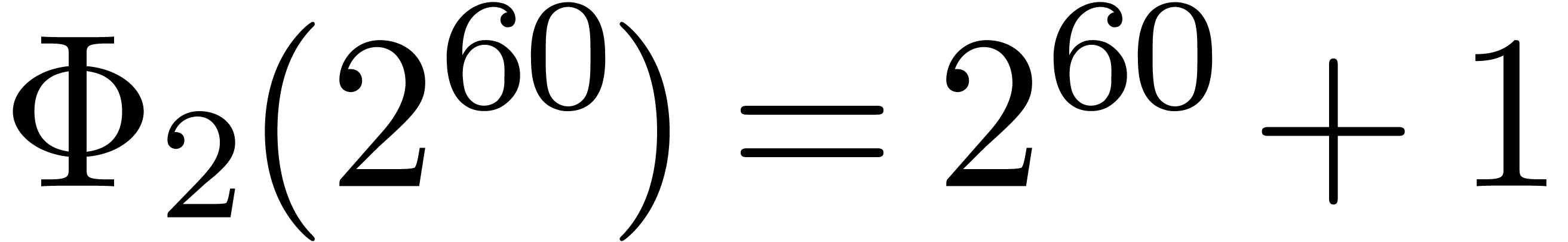 ,
, 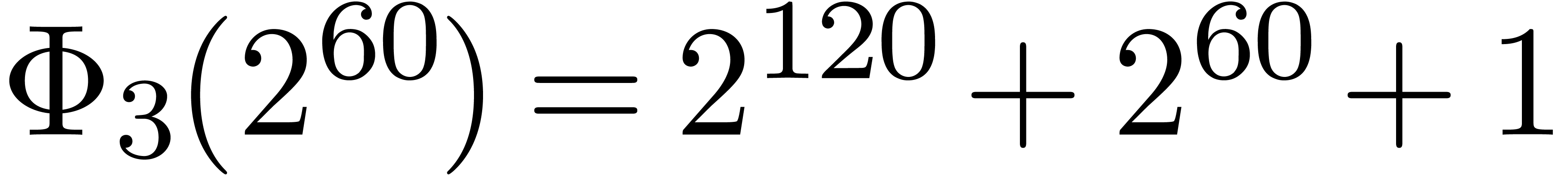 ,
, 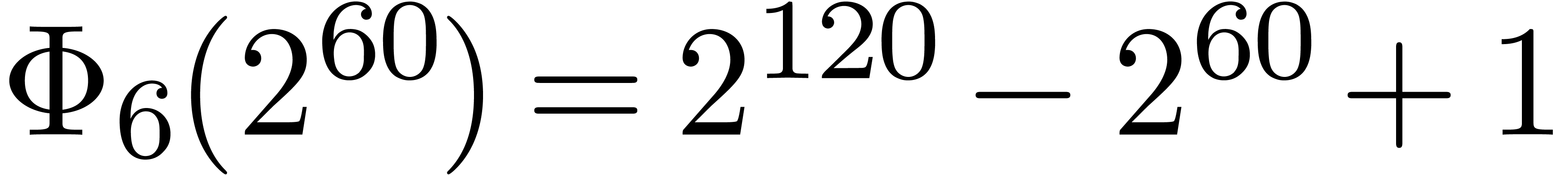 and
and  . Now euclidean division by
. Now euclidean division by 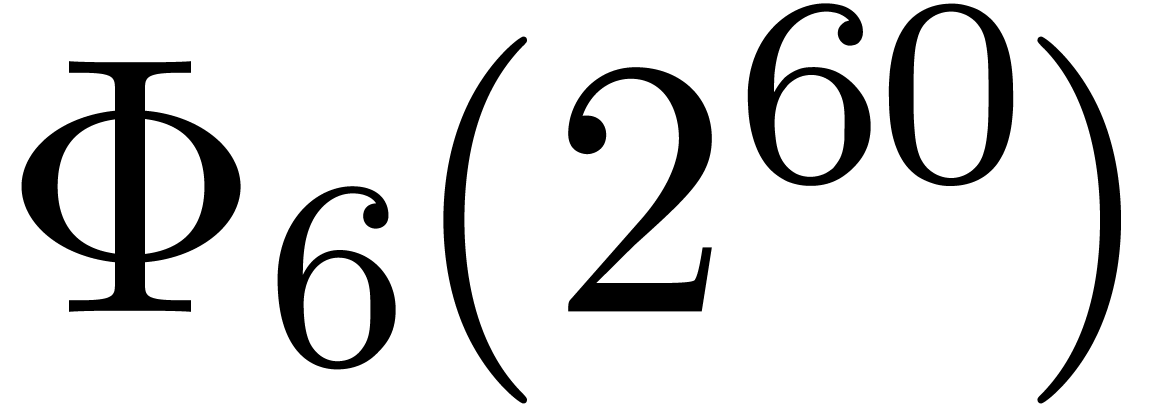 and
and 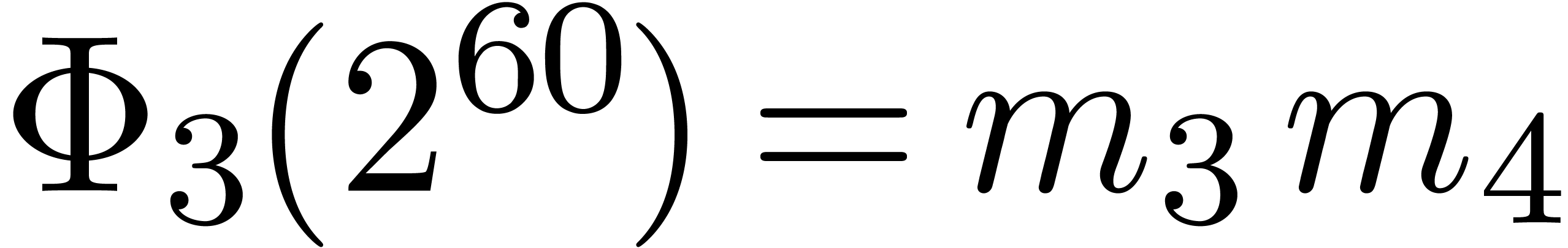 is easy since these numbers admit an
extremely sparse and regular binary representations. Furthermore, the
numbers
is easy since these numbers admit an
extremely sparse and regular binary representations. Furthermore, the
numbers 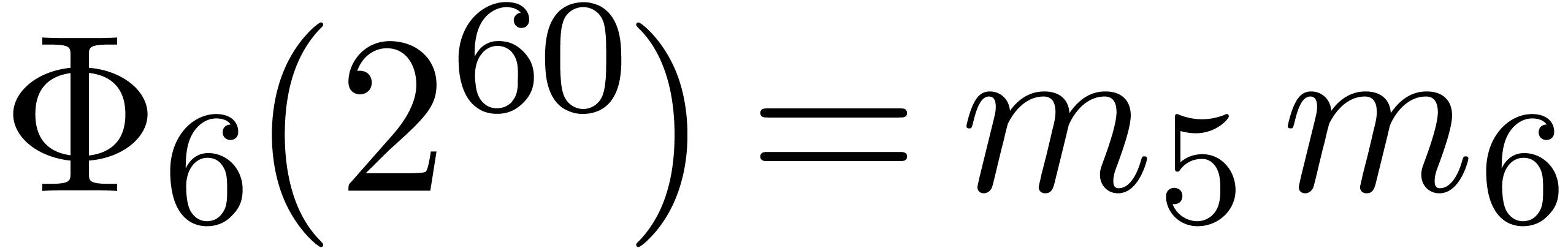 and
and  can both be
factored into products of two integers of less than
can both be
factored into products of two integers of less than  bits. Taking
bits. Taking  and
and 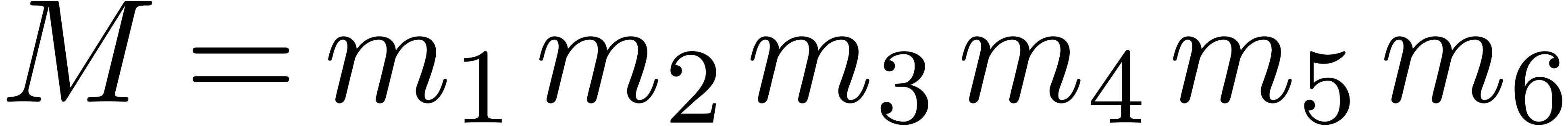 ,
it should therefore be possible to design a reasonably efficient Chinese
remaindering scheme for
,
it should therefore be possible to design a reasonably efficient Chinese
remaindering scheme for 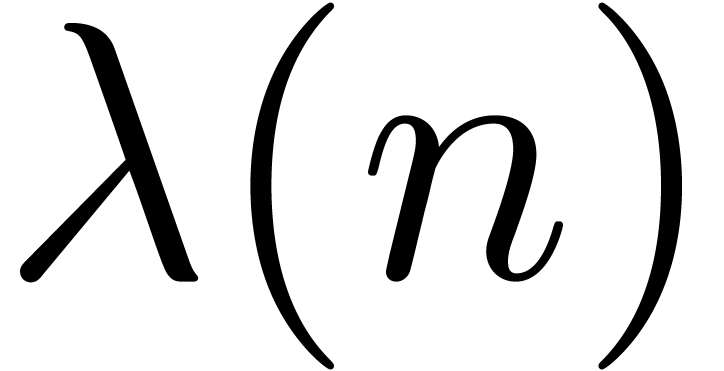 on a 64-bit
architecture.
on a 64-bit
architecture.
There are several downsides to this approach. Most importantly, the
largest prime divisor 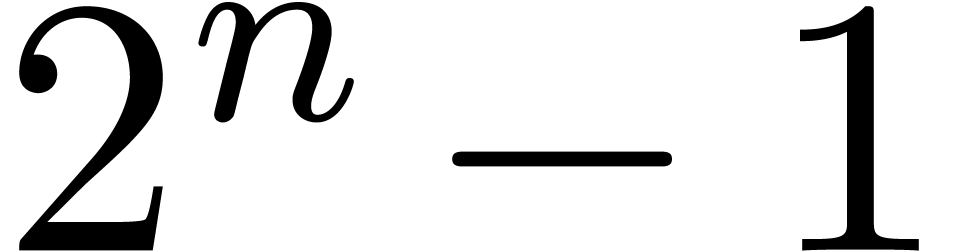 of
of 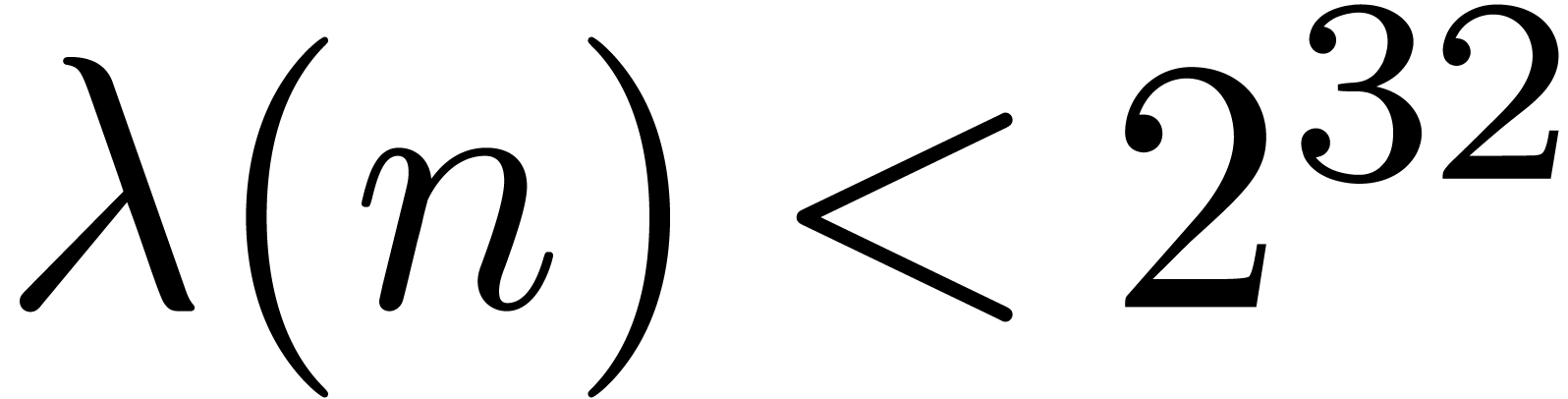 grows quite quickly with
grows quite quickly with  ,
even if
,
even if  is very smooth. For instance, the four
largest
is very smooth. For instance, the four
largest  for which
for which 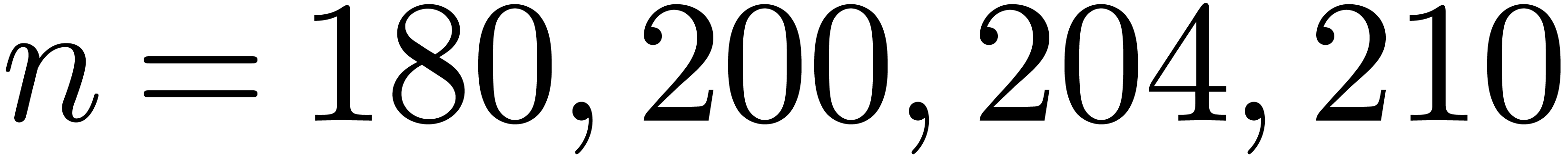 are
are
 and the four largest
and the four largest  for
which
for
which 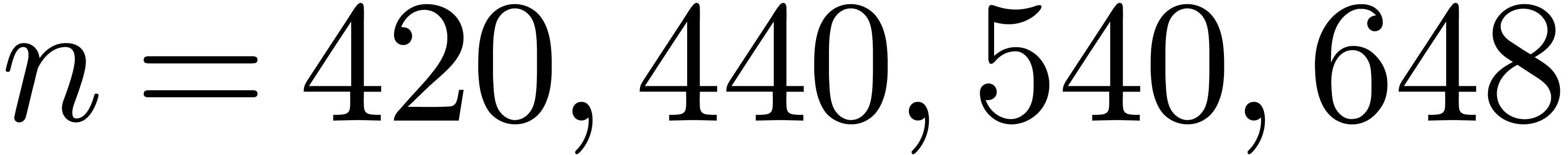 are
are 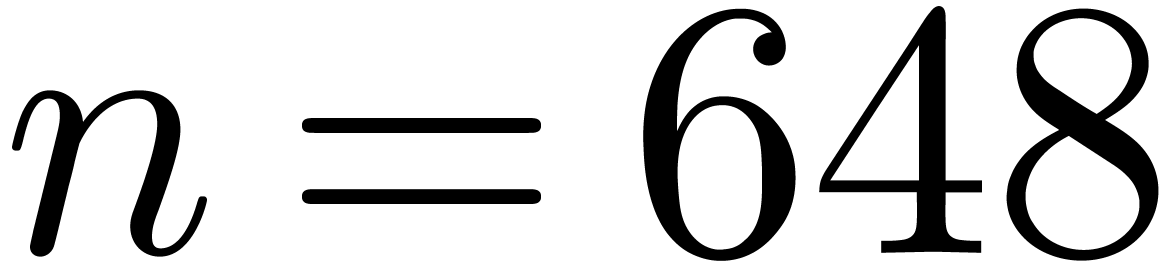 .
By construction, the number
.
By construction, the number 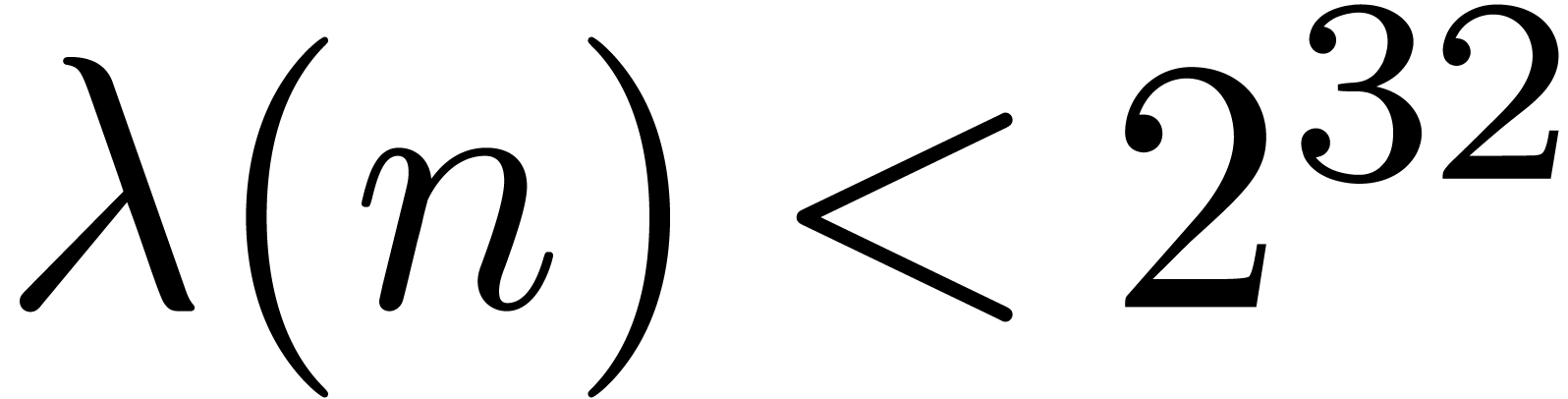 also admits many
divisors if
also admits many
divisors if  is smooth, so several moduli of this
type are generally not coprime. Both obstructions together imply that we
can only construct Chinese remaindering schemes with a small number of
moduli in this way. For instance, on a 64 bit architecture, one of the
best schemes would use
is smooth, so several moduli of this
type are generally not coprime. Both obstructions together imply that we
can only construct Chinese remaindering schemes with a small number of
moduli in this way. For instance, on a 64 bit architecture, one of the
best schemes would use  and twelve moduli of an
average size of
and twelve moduli of an
average size of  bits. In comparison, there are
many
bits. In comparison, there are
many  -gentle and
-gentle and 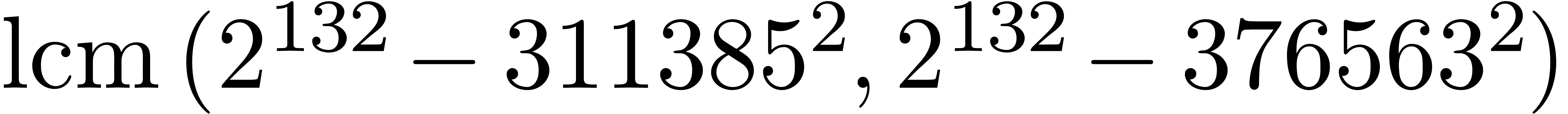 -gentle moduli that are products of prime
numbers of approximately
-gentle moduli that are products of prime
numbers of approximately  bits (or more), and
combining a few of them leads to efficient Chinese remaindering schemes
for twelve (or more) prime moduli of approximately
bits (or more), and
combining a few of them leads to efficient Chinese remaindering schemes
for twelve (or more) prime moduli of approximately  bits.
bits.
D. Bernstein. Removing redundancy in high precision Newton iteration. Available from http://cr.yp.to/fastnewton.html, 2000.
D. Bernstein. Scaled remainder trees. Available from https://cr.yp.to/arith/scaledmod-20040820.pdf, 2004.
A. Borodin and R.T. Moenck. Fast modular transforms. Journal of Computer and System Sciences, 8:366–386, 1974.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In Proceedings of ISSAC 2003, pages 37–44. ACM Press, 2003.
A. Bostan and É. Schost. Polynomial evaluation and interpolation on special sets of points. Journal of Complexity, 21(4):420–446, August 2005. Festschrift for the 70th Birthday of Arnold Schönhage.
D.G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
J.W. Cooley and J.W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
C.M. Fiduccia. Polynomial evaluation via the division algorithm: the fast fourier transform revisited. In A.L. Rosenberg, editor, Fourth annual ACM symposium on theory of computing, pages 88–93, 1972.
M. Fürer. Faster integer multiplication. SIAM J. Comp., 39(3):979–1005, 2009.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, New York, NY, USA, 3rd edition, 2013.
T. Granlund et al. GMP, the GNU multiple precision arithmetic library. http://www.swox.com/gmp, 1991.
G. Hanrot, M. Quercia, and P. Zimmermann. The middle product algorithm I. speeding up the division and square root of power series. Accepted for publication in AAECC, 2002.
D. Harvey and J. van der Hoeven. On the complexity of integer matrix multiplication. Technical report, HAL, 2014. http://hal.archives-ouvertes.fr/hal-01071191, accepted for publication in JSC.
D. Harvey, J. van der Hoeven, and G. Lecerf. Faster polynomial multiplication over finite fields. Technical report, ArXiv, 2014. http://arxiv.org/abs/1407.3361, accepted for publication in JACM.
D. Harvey, J. van der Hoeven, and G. Lecerf. Even faster integer multiplication. Journal of Complexity, 36:1–30, 2016.
J. van der Hoeven. Newton's method and FFT trading. JSC, 45(8):857–878, 2010.
J. van der Hoeven and G. Lecerf. Faster FFTs in medium precision. In 22nd Symposium on Computer Arithmetic (ARITH), pages 75–82, June 2015.
J. van der Hoeven, G. Lecerf, B. Mourrain, et al. Mathemagix, 2002. http://www.mathemagix.org.
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular SIMD arithmetic in Mathemagix. ACM Trans. Math. Softw., 43(1):5:1–5:37, 2016.
R.T. Moenck and A. Borodin. Fast modular transforms via division. In Thirteenth annual IEEE symposium on switching and automata theory, pages 90–96, Univ. Maryland, College Park, Md., 1972.
C.H. Papadimitriou. Computational Complexity. Addison-Wesley, 1994.
The PARI Group, Bordeaux. PARI/GP, 2012. Software available from http://pari.math.u-bordeaux.fr.
J.M. Pollard. The fast Fourier transform in a finite field. Mathematics of Computation, 25(114):365–374, 1971.
A. Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.