| Evaluating Straight-Line Programs over
Balls |
|
Joris van der Hoevena,
Grégoire Lecerfb
|
|
Laboratoire d'informatique de l'École
polytechnique
LIX, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau, France
|
|
a. Email:
vdhoeven@lix.polytechnique.fr
|
|
b. Email:
lecerf@lix.polytechnique.fr
|
|
|
Abstract—Interval arithmetic achieves numerical
reliability for a wide range of applications, at the price of a
performance penalty. For applications to homotopy continuation, one key
ingredient is the efficient and reliable evaluation of complex
polynomials represented by straight-line programs. This is best achieved
using ball arithmetic, a variant of interval arithmetic. In this
article, we describe strategies for reducing the performance penalty of
basic operations on balls. We also show how to bound the effect of
rounding errors at the global level of evaluating a straight-line
program. This allows us to introduce a new and faster
“transient” variant of ball arithmetic.
Index terms—ball arithmetic, polynomial evaluation,
software implementation
I.Introduction
Interval arithmetic is a classical tool for making numerical
computations reliable, by systematically computing interval enclosures
for the desired results instead of numerical approximations [1,
10, 11, 13, 14, 17, 24]. Interval arithmetic has been applied
with success in many areas, such as the resolution of systems of
equations, homotopy continuations, reliable integration of dynamical
systems, etc. There exist several variants of interval arithmetic such
as ball arithmetic, interval slope arithmetic, Taylor models, etc.
Depending on the context, these variants may be more efficient than
standard interval arithmetic and/or provide tighter enclosures.
In this paper, we will mainly focus on ball arithmetic (also
known as midpoint-radius interval arithmetic), which is
particularly useful for reliable computations with complex numbers and
multiple precision numbers [5]. One of our main motivations
is the implementation of reliable numerical homotopy methods for
polynomial system solving [2, 3, 6,
27–29]. One basic prerequisite for this
project concerns the efficient and reliable evaluation of multivariate
polynomials represented by so called straight-line programs
(SLPs).
Two classical disadvantages of interval arithmetic and its variants are
the additional computational overhead and possible overestimation of
errors. There is a trade-off between these two evils: it is always
possible to reduce the overestimation at the expense of a more costly
variant of interval arithmetic (such as high order Taylor models). For a
fixed variant, the computational overhead is usually finite, but it
remains an important issue for high performance applications to reduce
the involved constant factors as much as possible. In this paper, we
will focus on this “overhead problem” in the case of basic
ball arithmetic (and without knowledge about the derivatives of the
functions being evaluated).
About ten years ago, we started the implementation of a basic C++
template library for ball arithmetic in the Mathemagix
system [9]. However, comparing speed of operations over
complex numbers in double precision and over the corresponding balls was
quite discouraging. The overhead comes from extra computations of radii,
but also from changes of rounding mode, and the way the C++ compiler
generates executable code from C99 portable
sources. For our application to reliable homotopies, the critical part
to be optimized concerns the evaluation of input polynomials using ball
arithmetic. The goal of the present work is to minimize the overhead of
such evaluations with respect to their numeric counterparts.
Our contributions
In this article we investigate various strategies to reduce the overhead
involved when evaluating straight-line programs over balls. Our point of
view is pragmatic and directed towards the development of more efficient
implementations. We will not turn around the fact that the development
of efficient ball arithmetic admits a quite technical side: the optimal
answer greatly depends on available hardware features. We will consider
on the following situations, encountered for modern processors:
-
Without specific IEEE 754 compliant hardware (which is
frequently the case for GPUs), we may only assume faithful
rounding, specifying a bound on relative errors for each
operation, and that errors can be thrown on numerical exceptions.
-
For recent Intel-compatible processors
(integrating SSE or AVX technologies) it
is recommended to perform numerical computations using
SIMD (single instruction, multiple data) units.
Programming must be done mostly at the assembly code level with
specific builtin instructions called intrinsics.
Dynamically switching the rounding mode involves a rather small
overhead.
-
Recent AVX-512 processors propose floating point
instructions which directly incorporate a rounding mode, thereby
eliminating all need to switch rounding modes via the
status register and all resulting delays caused by broken pipelines.
As a general rule, modern processors have also become highly parallel.
For this reason, it is important to focus on algorithms that can easily
be vectorized. The first contribution of this paper concerns various
strategies for ball arithmetic as a function of the available hardware.
From the conceptual point of view, this will be done in Section 2,
whereas additional implementation details will be given in Section 4.
Our second main contribution is the introduction of transient
ball arithmetic in Section 2.5 and its application to the
evaluation of SLPs in Section 3. The idea is to not bother
about rounding errors occurring when computing centers and radii of
individual balls, which simplifies the implementation of the basic ring
operations. Provided that the radii of the input balls are not too small
and that neither overflow nor underflow occur, we will show that the
cumulated effect of the ignored rounding errors can be bounded for the
evaluation of a complete SLP. More precisely, we will show that the
relative errors due to rounding are essentially dominated by the depth
of the computation. Although it is most convenient to apply our result
to SLPs, much of it can be generalized to arbitrary programs, by
regarding the trace of the execution as an SLP. For such
generalizations, the main requirement is to have an a priori
bound for the (parallel) depth of the computation.
Most of our strategies have been implemented inside the Multimix
and Justinline libraries of Mathemagix
[9], in C++ and in the Mathemagix
language. In Section 4, we compare costs for naive,
statically compiled, and dynamically compiled polynomial evaluations.
Using our new theoretical ideas and various implementation tricks, we
managed to reduce the overhead of ball arithmetic to a small factor
between two and four. We also propose SSE and
AVX based functions for arithmetic operations on balls.
Dynamic compilation, also known as just in time
(JIT) compilation, is implemented from scratch in our
Runtime library, and turns out to reach high
performance for large polynomial functions.
Related Work
In the context of real midpoint-radius interval arithmetic, and
for specific calculations, such as matrix products, several authors
proposed dedicated solutions that mostly perform operations on centers
and then rely on fast bounds on radii [18–20,
23, 25]. In this case, the real gain comes
from the ability to exploit HPC (high performance
computing) solutions to linear algebra, and similar tricks
sometimes apply to classical interval methods [16, 21].
The use of SIMD instructions for intervals started in [30], and initially led to a rather modest speed-up, according
to the author. Changing the rounding mode for almost each arithmetic
operation seriously slows down computations, and might involve a serious
stall of a hundred of cycles by breaking FPU pipelines of
some hardware such as Intel x87.
To avoid switching rounding modes, the author of [26] uses
different independent rounding modes on the x87
and SSE units. Specific solutions to diminish the swap of
rounding modes also rely on the opposite trick in internal
computations or directly in the representation [4, 12,
30]. Modern wide SIMD processors tend to handle roundings
more efficiently and AVX-512 even features instructions that directly
integrate a rounding mode.
II.Different types of ball
arithmetic
A.Machine arithmetic
Throughout this paper, we denote by  the set of machine floating point numbers. We let
the set of machine floating point numbers. We let 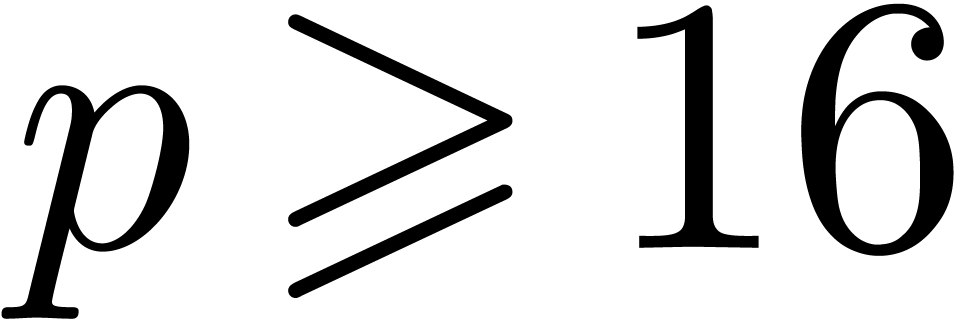 be the machine precision (which corresponds to the number of fractional
bits of the mantissa plus one), and let
be the machine precision (which corresponds to the number of fractional
bits of the mantissa plus one), and let  and
and  be the minimal and maximal exponents (included). For
IEEE 754 double precision numbers, this means that
be the minimal and maximal exponents (included). For
IEEE 754 double precision numbers, this means that 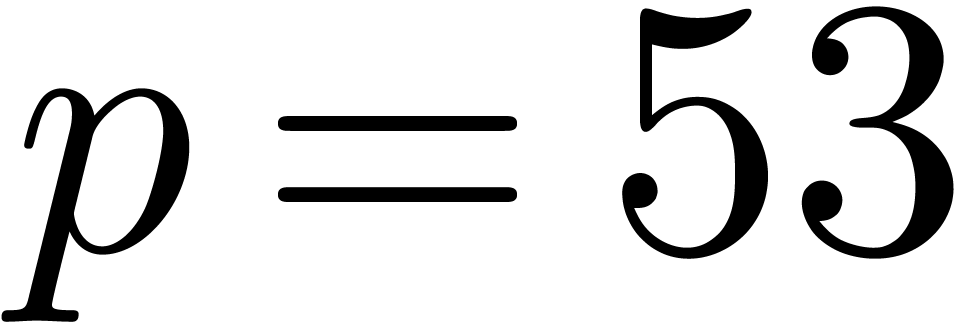 ,
, 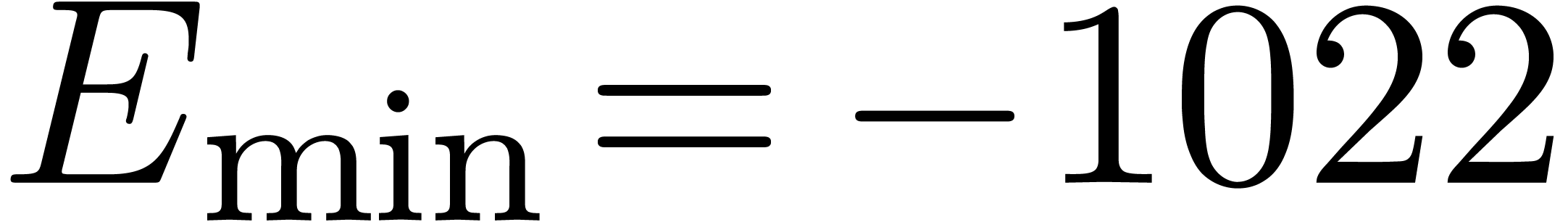 and
and 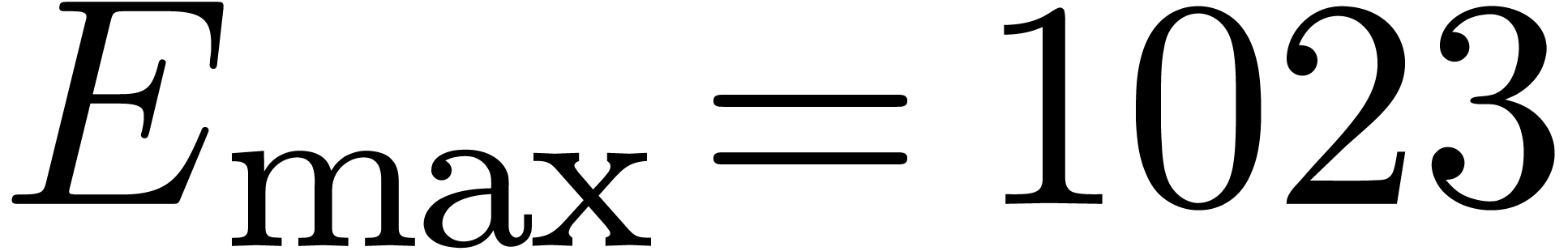 . We enlarge
. We enlarge  with symbols
with symbols  ,
, 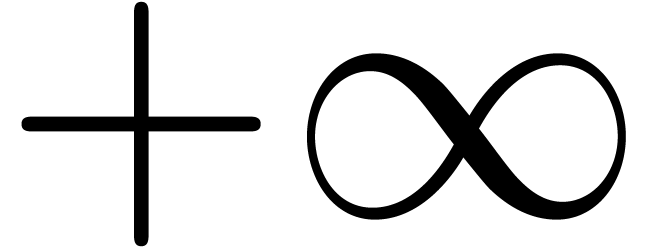 , and
, and  ,
with their standard meaning.
,
with their standard meaning.
For our basic arithmetic, we allow for various rounding modes written
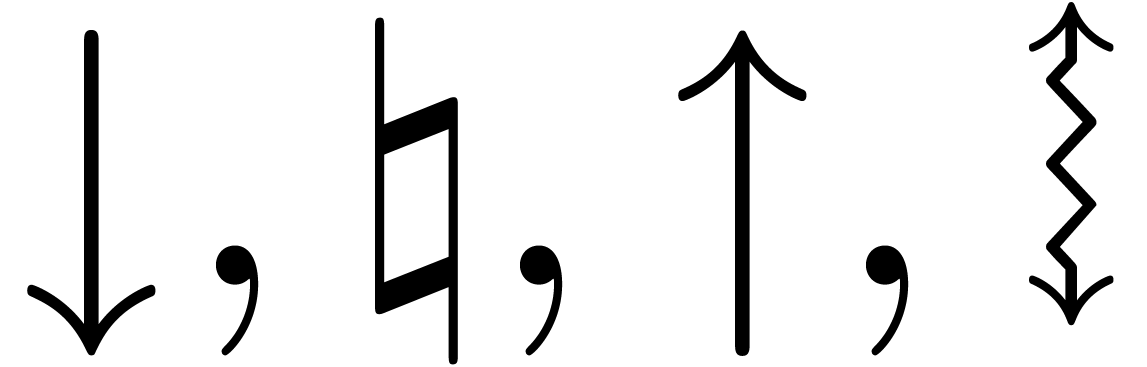 . The first three rounding
modes correspond to IEEE arithmetic with correct rounding
(downwards, to the nearest and upwards). The
rounding mode
. The first three rounding
modes correspond to IEEE arithmetic with correct rounding
(downwards, to the nearest and upwards). The
rounding mode  corresponds to faithful rounding
without any well specified direction. For
corresponds to faithful rounding
without any well specified direction. For 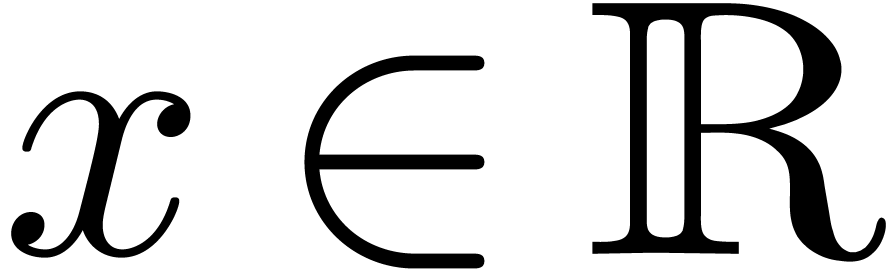 ,
we write
,
we write  for the approximation of
for the approximation of  in
in  with the specified rounding
mode
with the specified rounding
mode  . The quantity
. The quantity 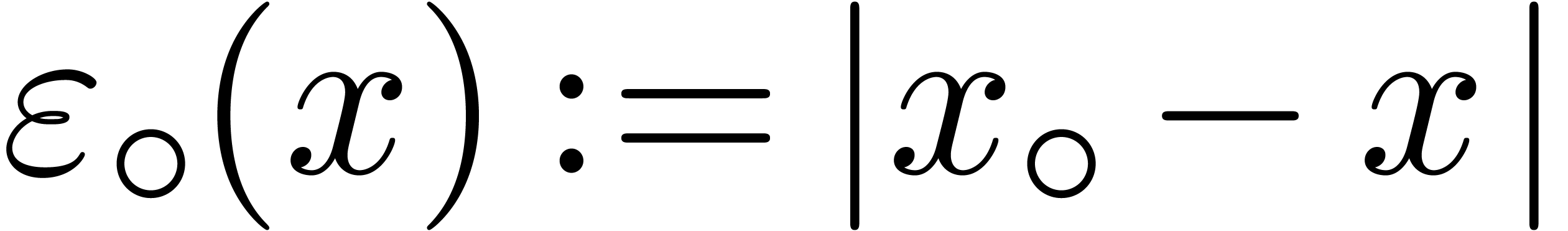 stands for the corresponding rounding error, that may be
stands for the corresponding rounding error, that may be
 . Given a single operation
. Given a single operation
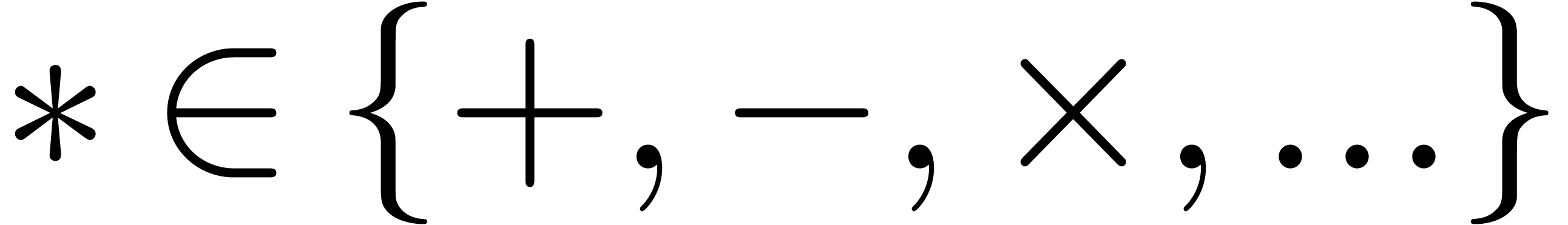 , it will be convenient to
write
, it will be convenient to
write 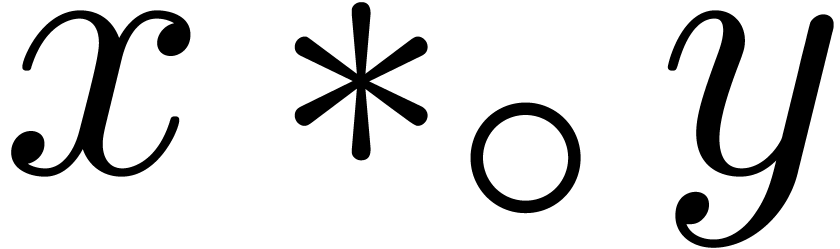 for
for 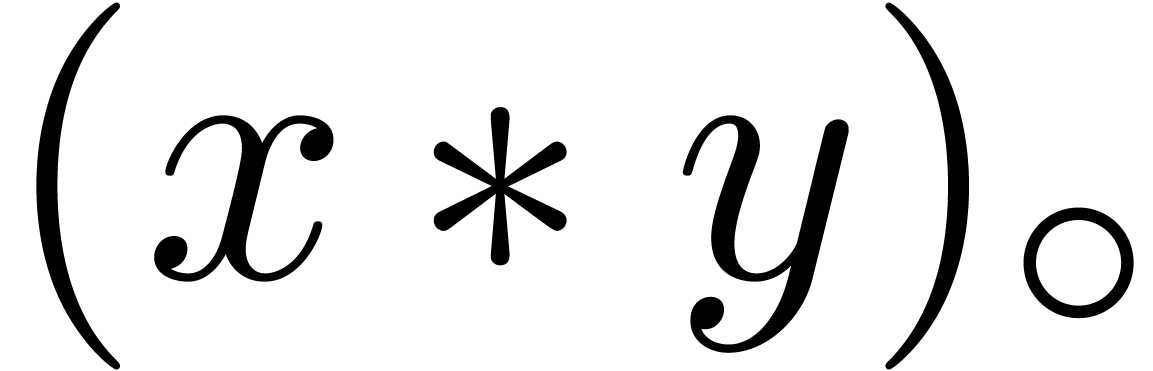 .
For compound expressions
.
For compound expressions  , we
will also write
, we
will also write 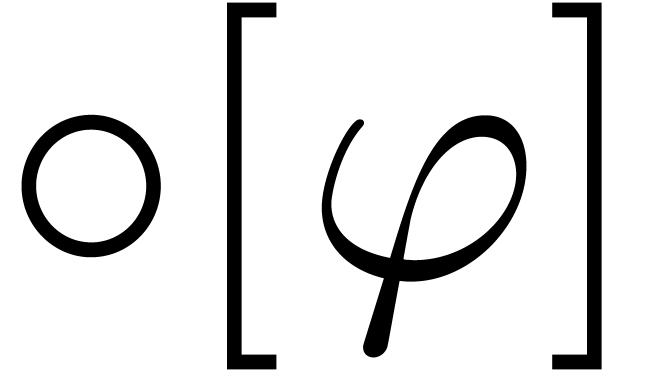 for the full evaluation of
for the full evaluation of  using the rounding mode
using the rounding mode  .
For instance,
.
For instance, 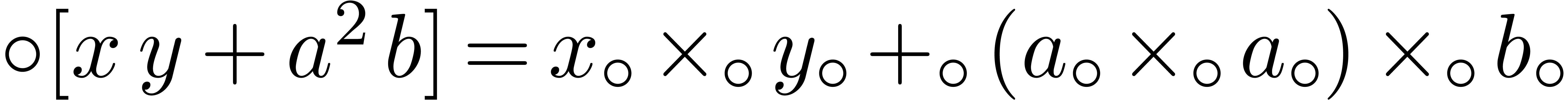 .
.
Modern processors usually support fused-multiply-add (fma) and
fused-multiply-subtract (fms) instructions, both for scalar and
SIMD vector operands: 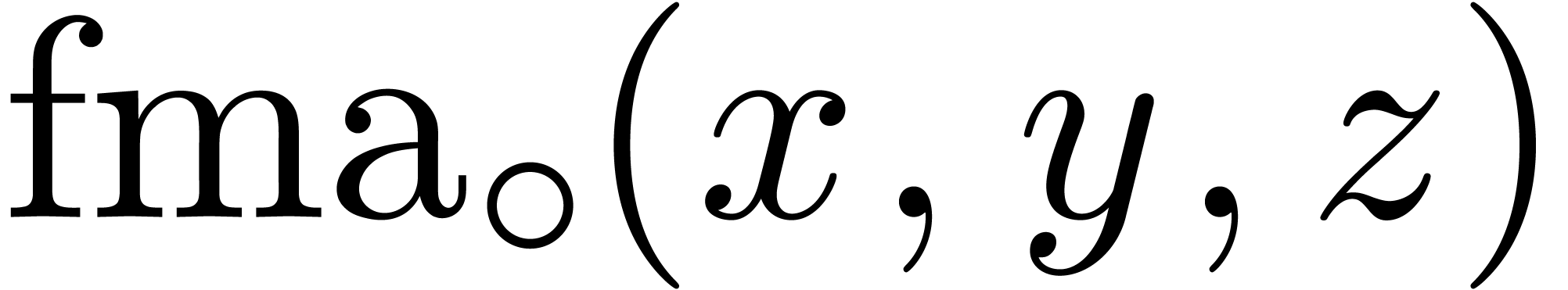 and
and 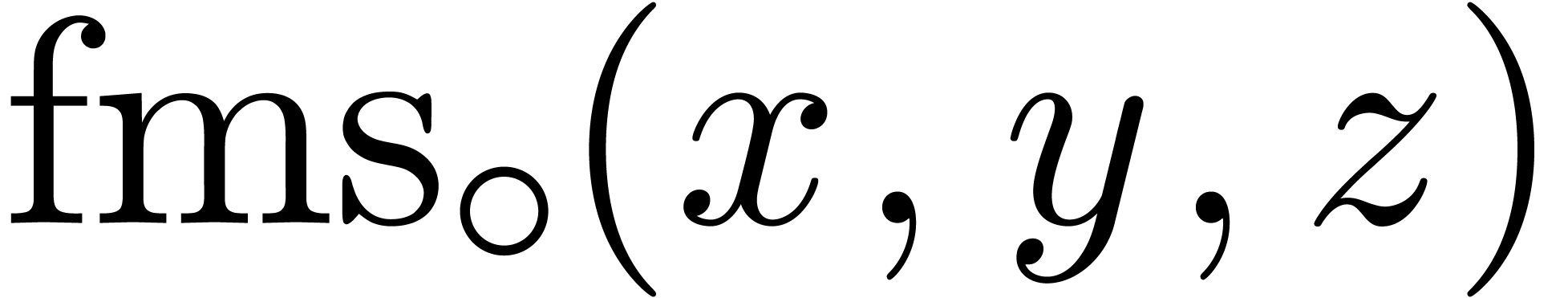 represent the roundings of
represent the roundings of 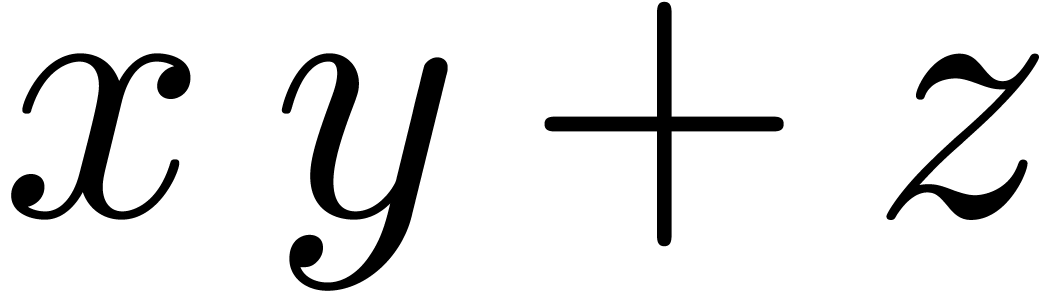 and
and
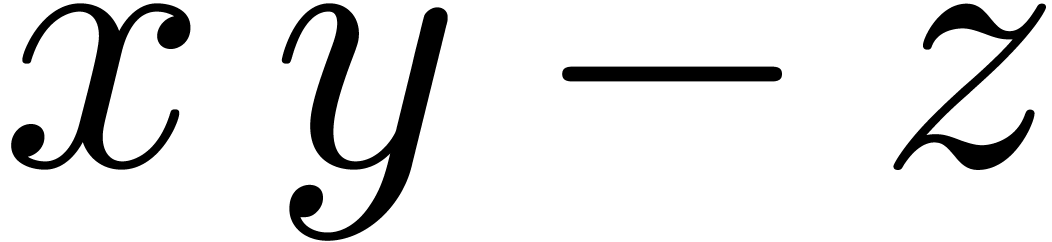 according to the mode
according to the mode  . For generalities about these instructions, we
refer the reader to the book [15] for instance.
. For generalities about these instructions, we
refer the reader to the book [15] for instance.
We will denote by  any upper bound function for
any upper bound function for
 that is easy to compute. In absence of
underflows/overflows, we claim that we may take
that is easy to compute. In absence of
underflows/overflows, we claim that we may take 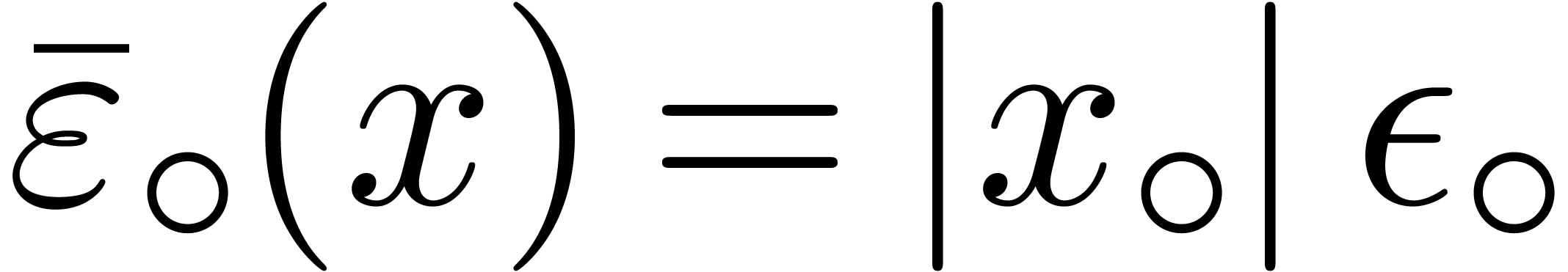 , with
, with 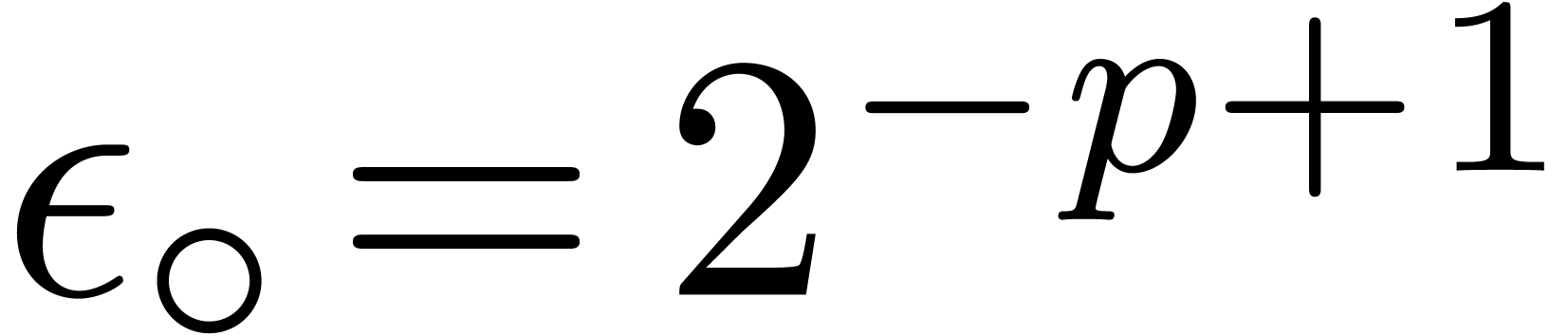 for
for  and
and 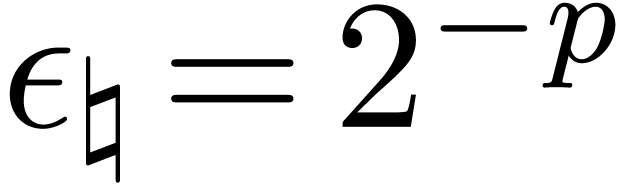 . Indeed, given
. Indeed, given 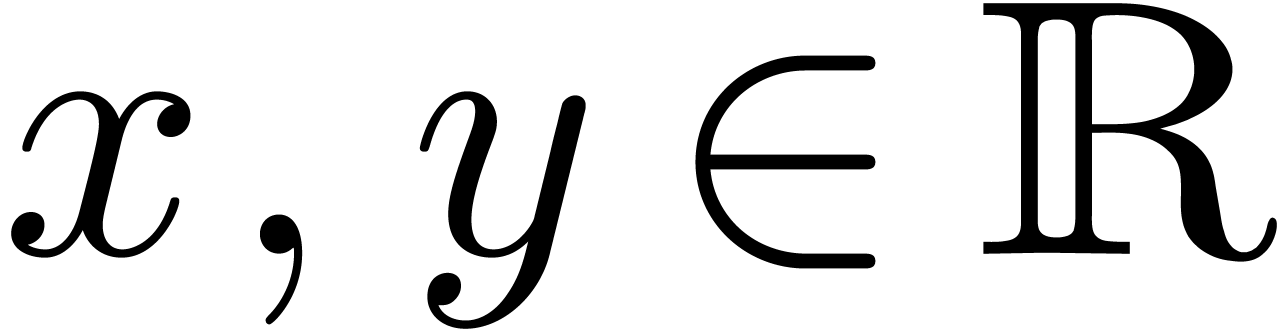 and
and 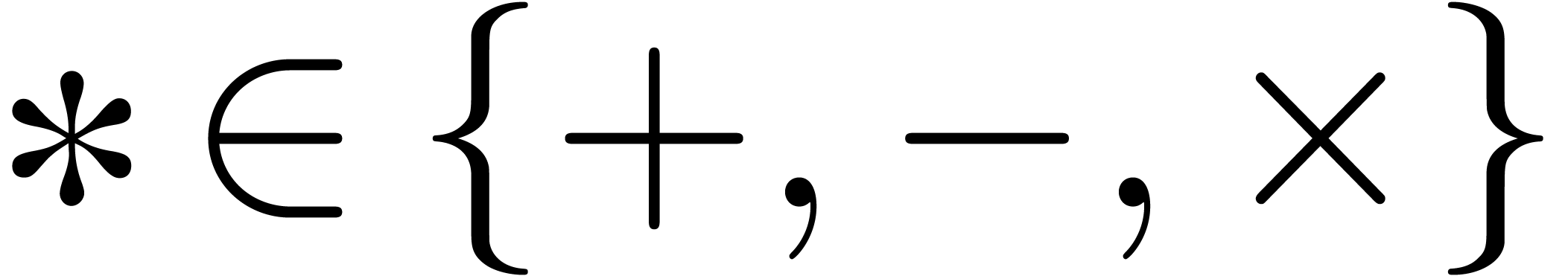 , let
, let  be the exponent of
be the exponent of 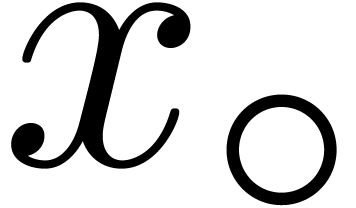 ,
so that
,
so that 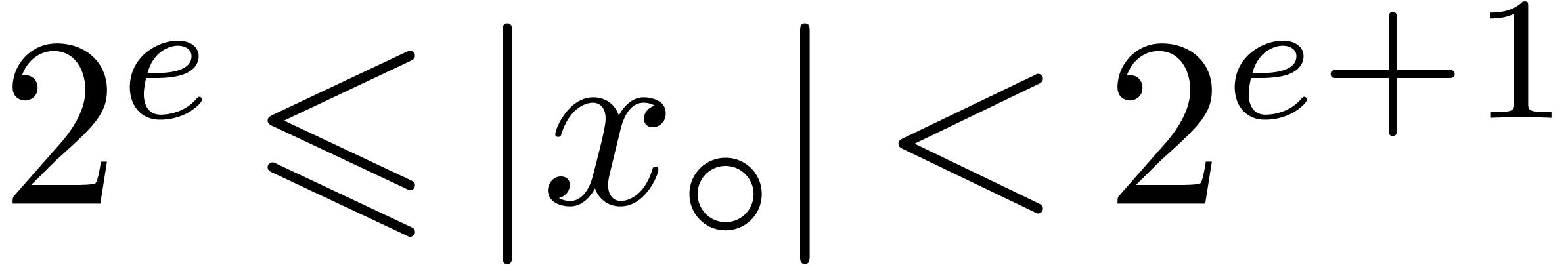 and
and  .
Then
.
Then 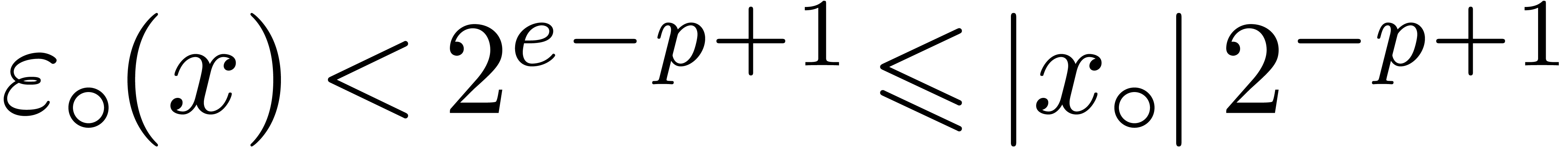 for all rounding modes, and
for all rounding modes, and 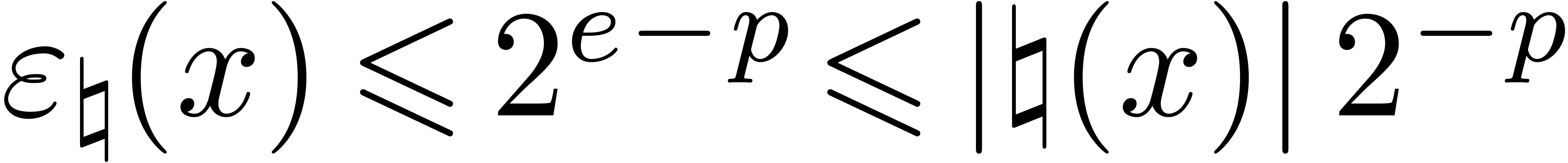 .
.
If we want to allow for underflows during computations, we may safely
take 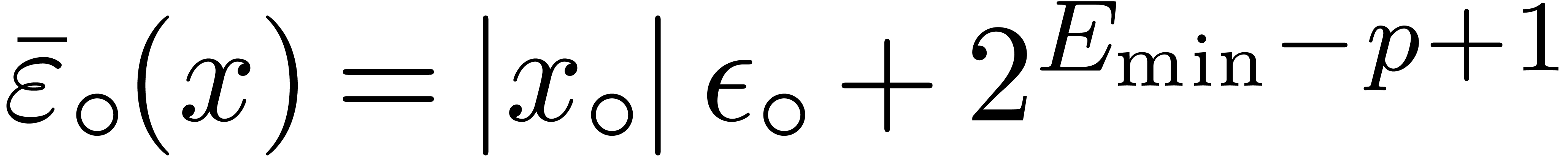 , where
, where 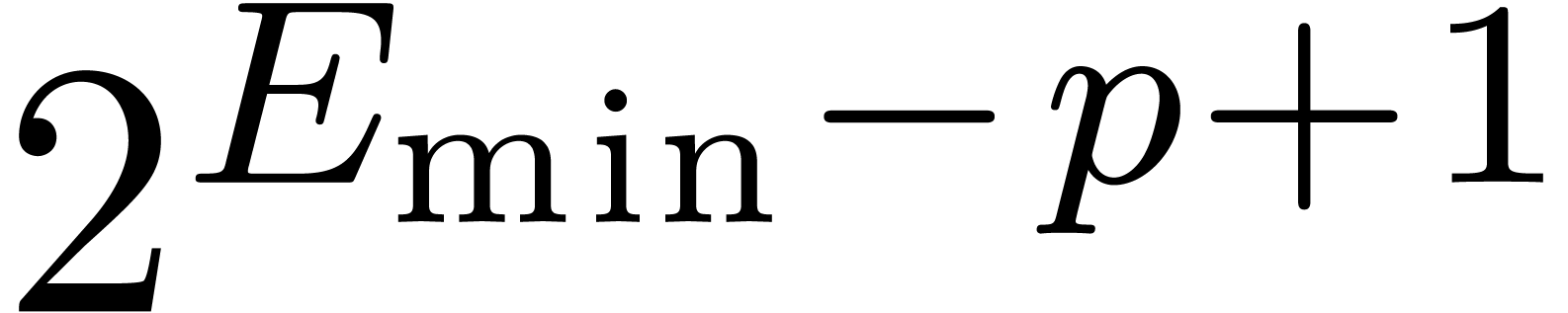 is the smallest positive subnormal number in
is the smallest positive subnormal number in  . Notice that if
. Notice that if 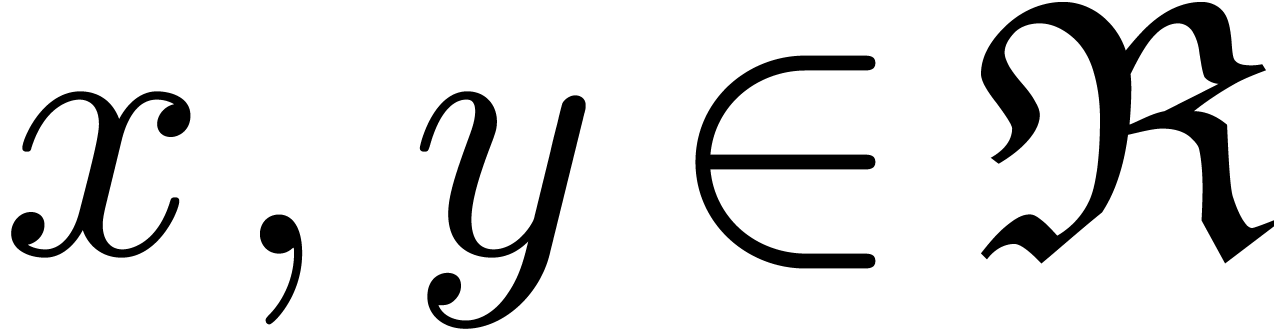 ,
then we may still take
,
then we may still take 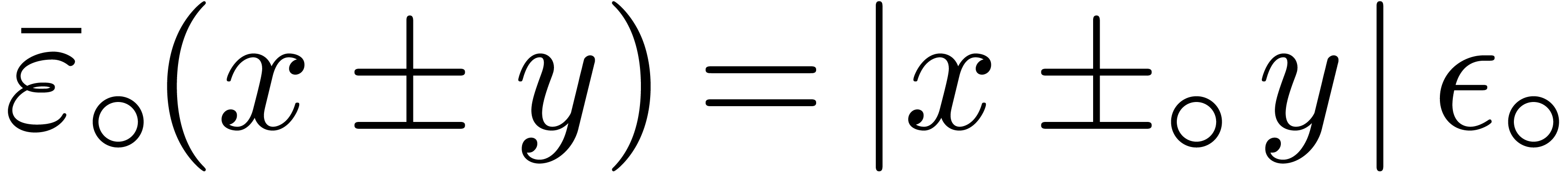 since no underflow occurs
in that special case. Underflows and overflows will be further discussed
in Section 3.3.
since no underflow occurs
in that special case. Underflows and overflows will be further discussed
in Section 3.3.
B.Complex arithmetic and
generalizations
In order to describe our algorithms in a flexible context,  denotes a Banach algebra over
denotes a Banach algebra over  , endowed with a norm written
, endowed with a norm written 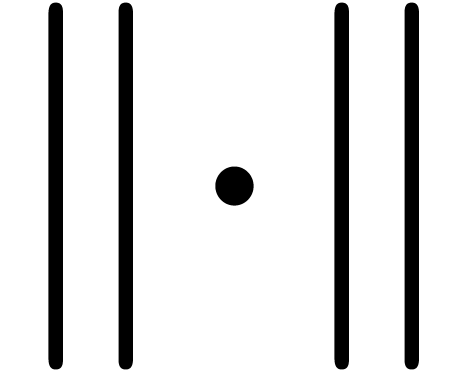 . The most common examples are
. The most common examples are 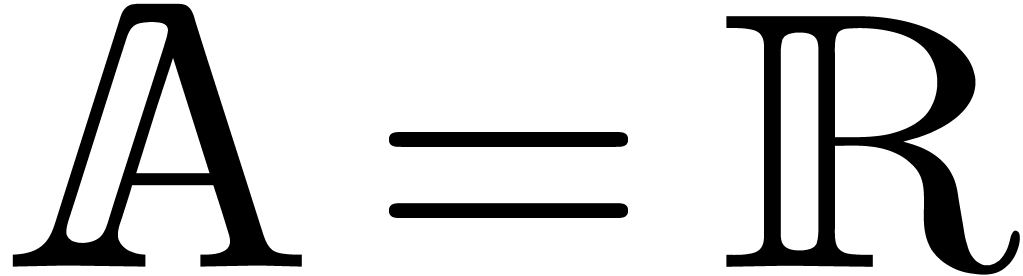 and
and 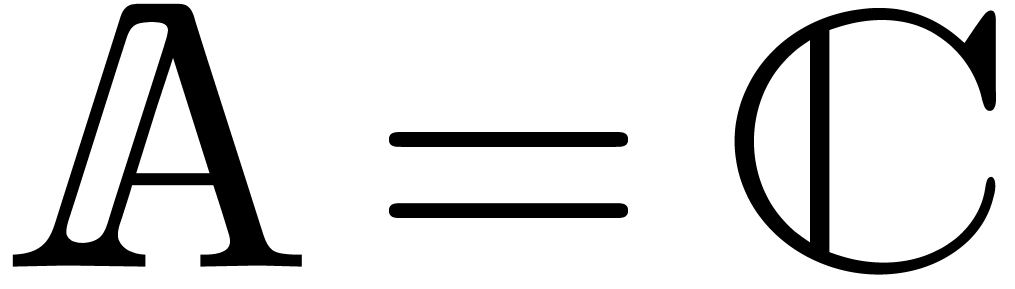 with
with 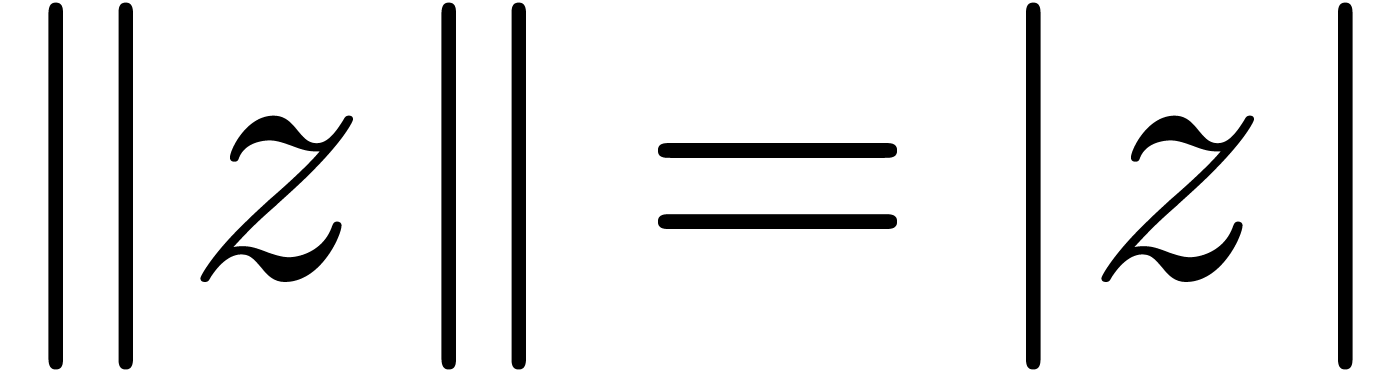 for all
for all 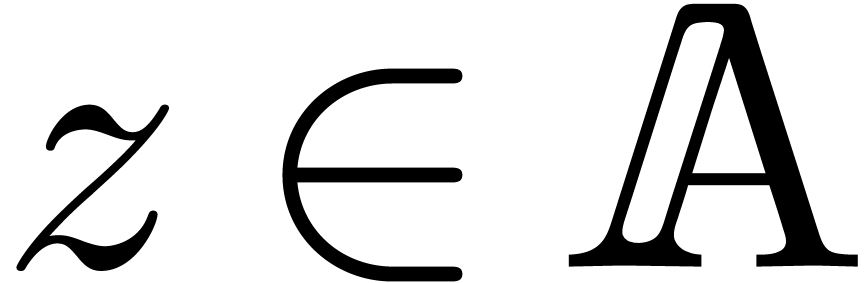 .
.
For actual machine computations, we will denote by  the counterpart of
the counterpart of  when
when  is replaced by
is replaced by  . For
instance, if
. For
instance, if 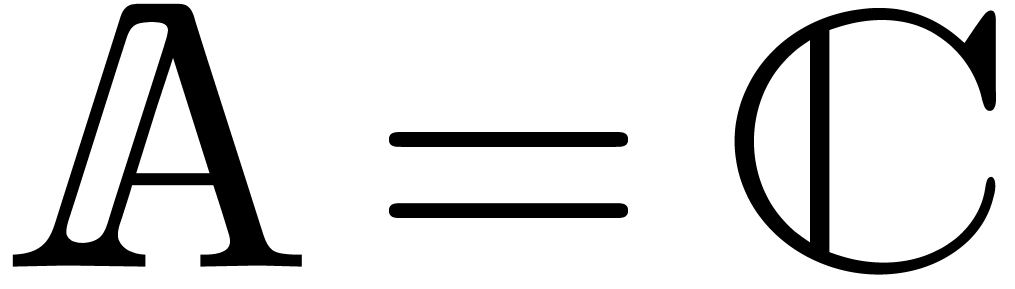 , then we may
take
, then we may
take 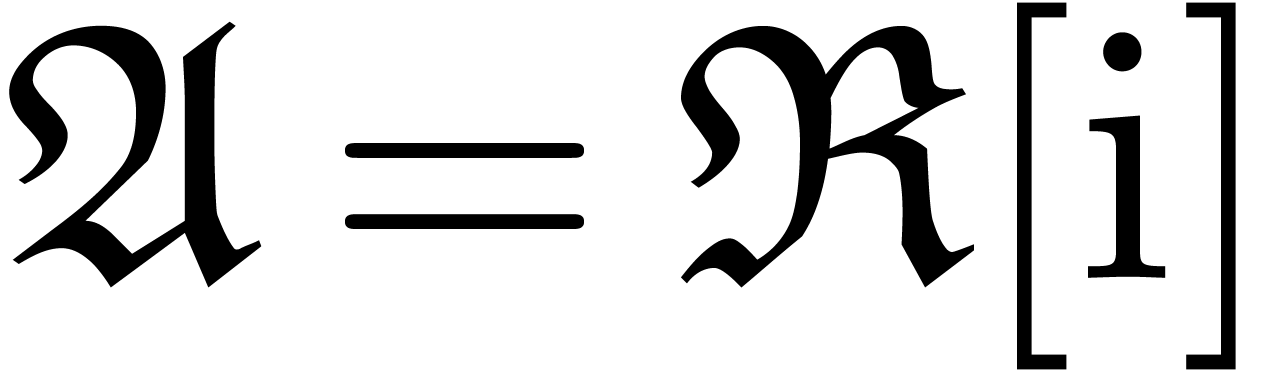 . In other words, if
. In other words, if
 is the C++ type double,
then we may take complex<double>
for
is the C++ type double,
then we may take complex<double>
for  , where complex represents the template type available from
the standard C++ library, or from the Numerix library of Mathemagix.
, where complex represents the template type available from
the standard C++ library, or from the Numerix library of Mathemagix.
For any rounding mode 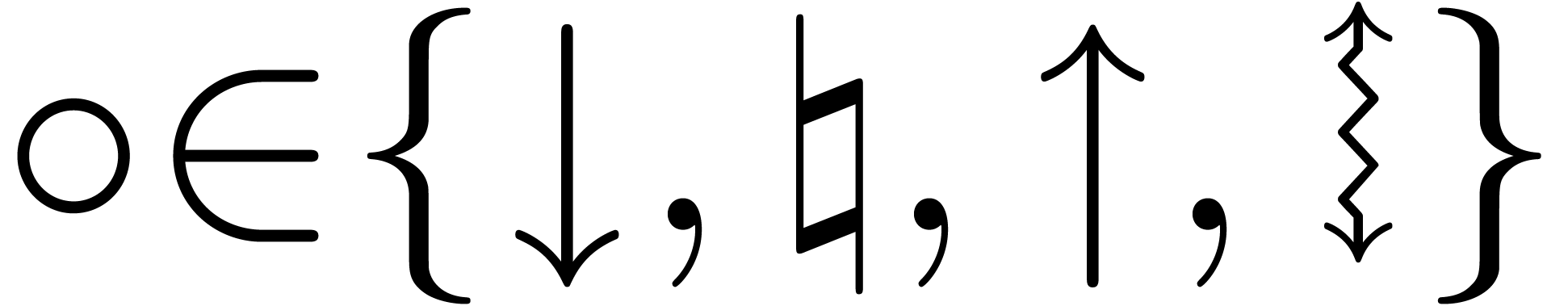 , the
notations from the previous section naturally extend to
, the
notations from the previous section naturally extend to  . For instance,
. For instance, 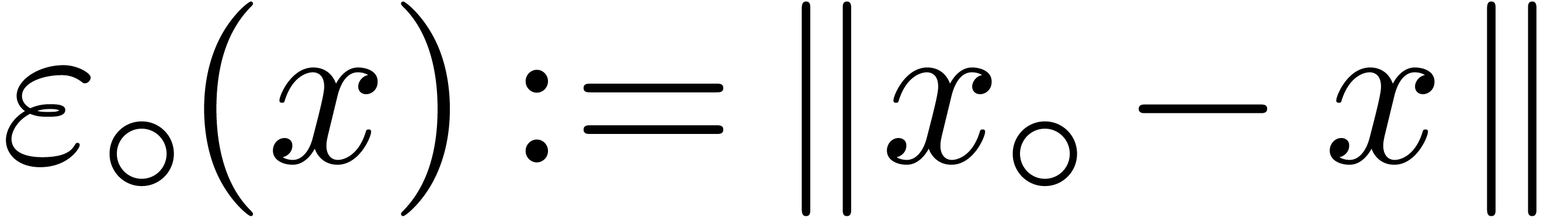 .
Similarly, if
.
Similarly, if 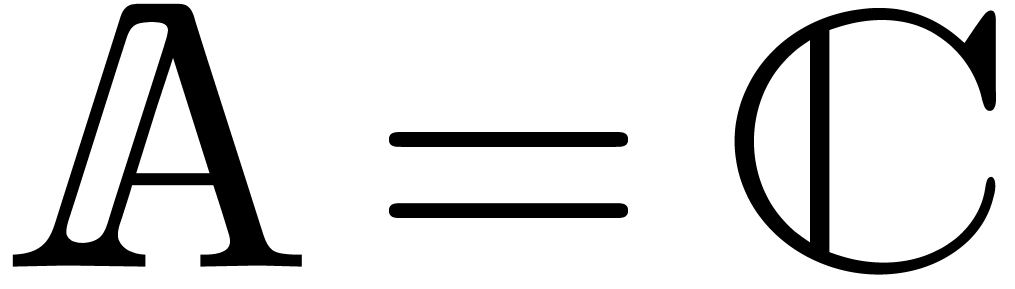 , then
, then 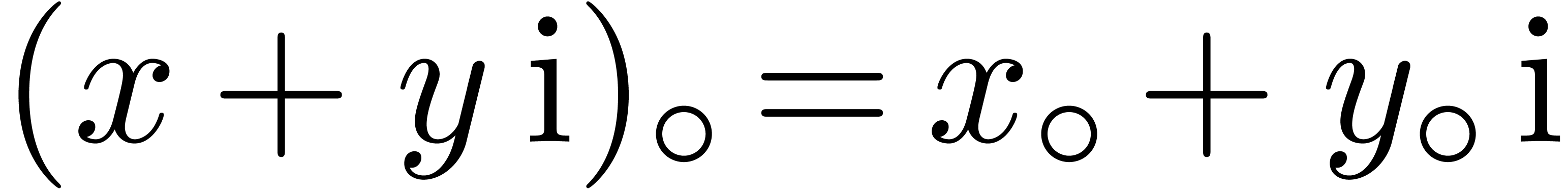 . For complex arithmetic we
consider the following implementation:
. For complex arithmetic we
consider the following implementation:
As for  we may clearly take
we may clearly take 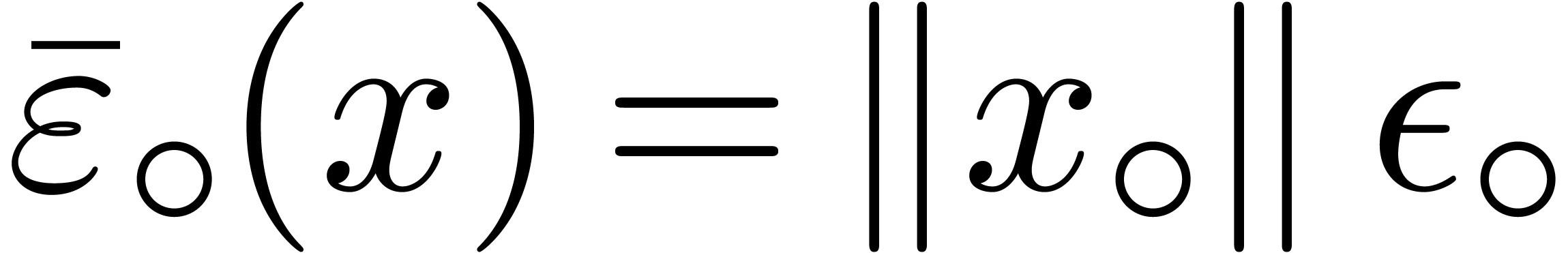 in absence of underflows/overflows, and
in absence of underflows/overflows, and  in
general.
in
general.
Remark 1. For applications to the
case when  , it is sometimes
interesting to replace computations of norms
, it is sometimes
interesting to replace computations of norms  by
computations of quick and rough upper bounds
by
computations of quick and rough upper bounds 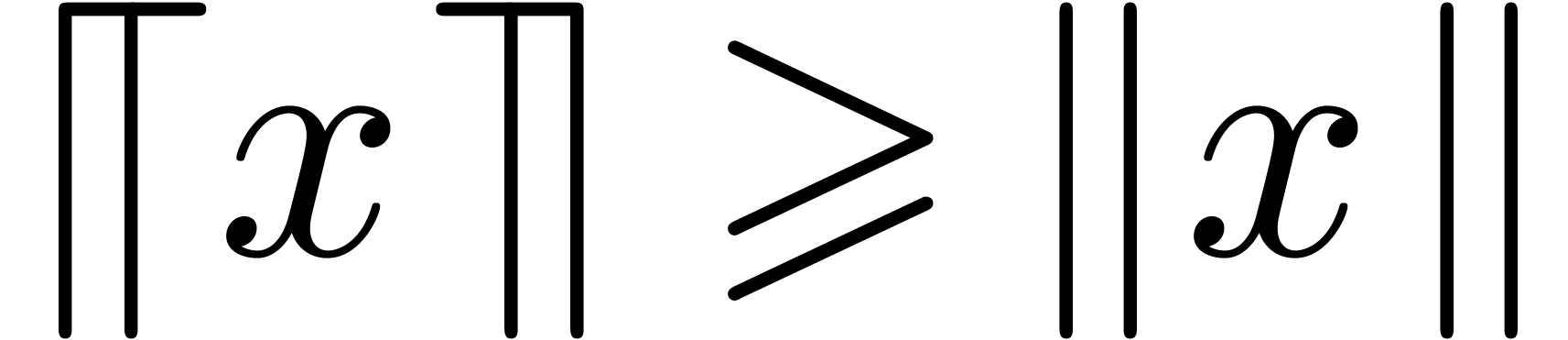 . For instance, on architectures where square roots
are expensive, one may use
. For instance, on architectures where square roots
are expensive, one may use
C.Exact ball arithmetic
Given  and
and  ,
we write
,
we write  for the closed ball with
center
for the closed ball with
center  and radius
and radius 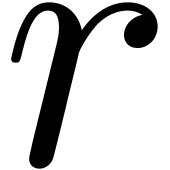 .
The set of such balls is denoted by
.
The set of such balls is denoted by  .
One may lift the ring operations
.
One may lift the ring operations 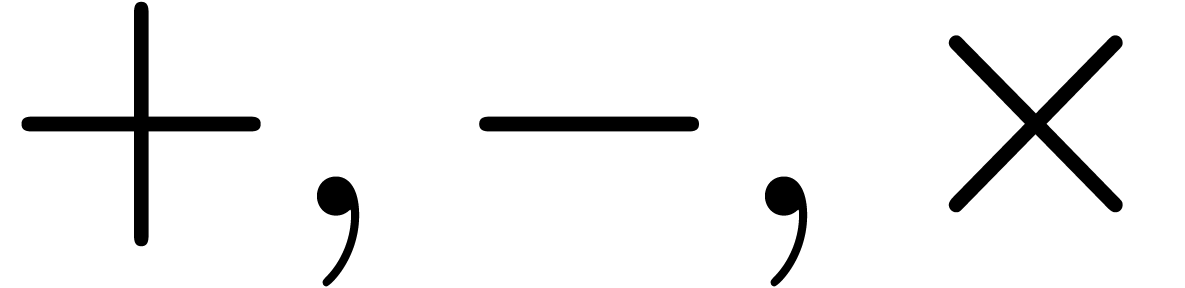 in
in  to balls in
to balls in  ,
by setting:
,
by setting:
These formulas are simplest so as to satisfy the so called inclusion
principle: given 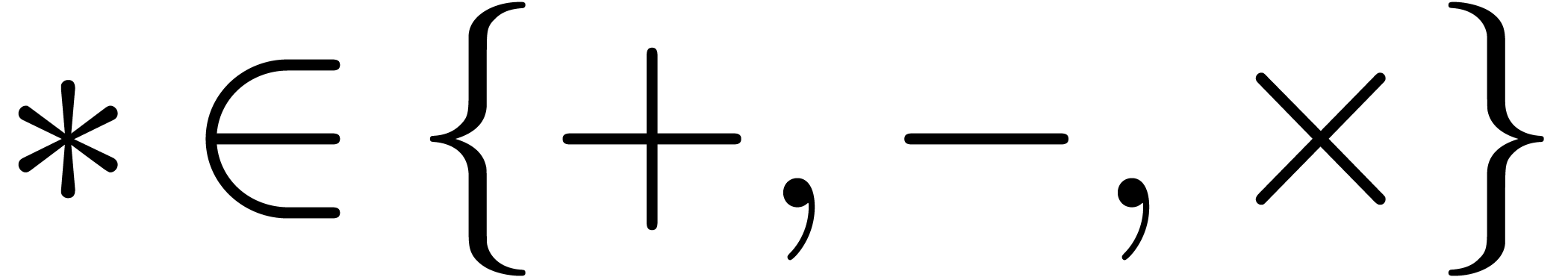 ,
, 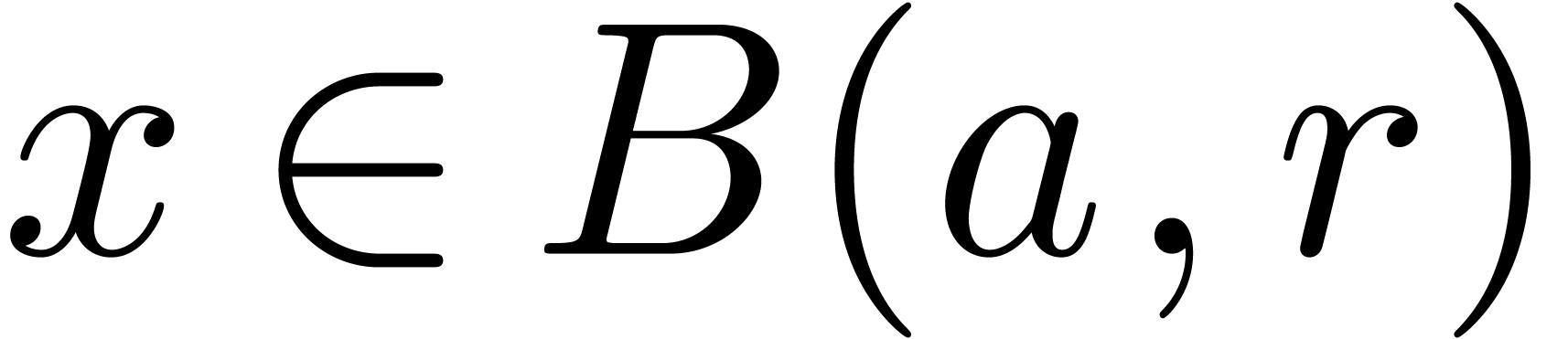 and
and 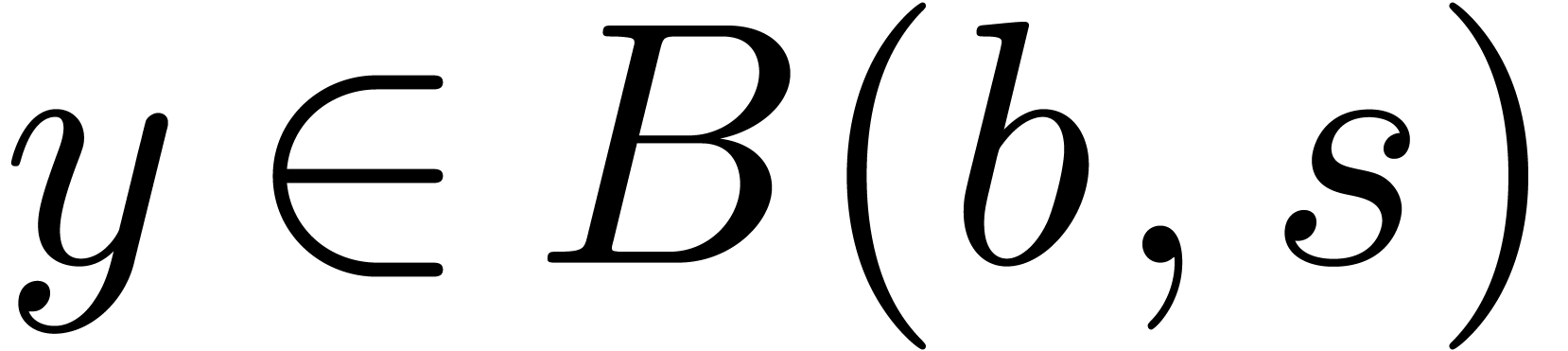 , we
have
, we
have 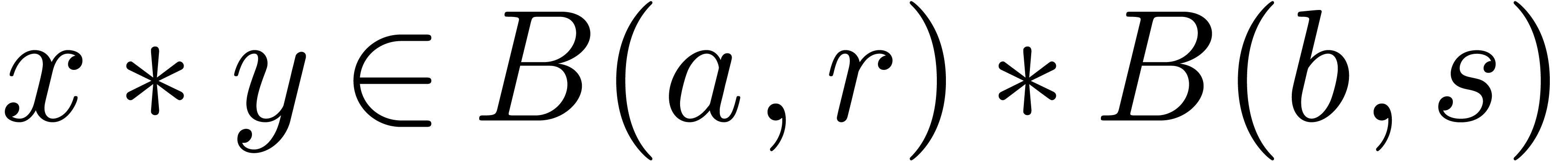 . This arithmetic for
computing with balls is called exact ball arithmetic. It
extends to other operations that might be defined on
. This arithmetic for
computing with balls is called exact ball arithmetic. It
extends to other operations that might be defined on  , as long as the ball lifts of operations
satisfy the inclusion principle. For instance, we may implement
fused-multiply-add and fused-multiply-subtract using
, as long as the ball lifts of operations
satisfy the inclusion principle. For instance, we may implement
fused-multiply-add and fused-multiply-subtract using
D.Certified machine ball
arithmetic
We will denote by  the set of balls with centers
in
the set of balls with centers
in  and radii in
and radii in  .
In order to implement machine ball arithmetic for
.
In order to implement machine ball arithmetic for  , we need to adjust formulas from the previous
section so as to take rounding errors into account. Indeed, the main
constraint is the inclusion principle, which should still hold for each
operation in such an implementation. The best way to achieve this
depends heavily on rounding modes used for operations on centers and
radii.
, we need to adjust formulas from the previous
section so as to take rounding errors into account. Indeed, the main
constraint is the inclusion principle, which should still hold for each
operation in such an implementation. The best way to achieve this
depends heavily on rounding modes used for operations on centers and
radii.
On processors that feature IEEE 754 style rounding, it is
most natural to perform operations on centers using any rounding mode
 (and preferably rounding to the nearest), and
operations on radii using upward rounding. This leads to the following
formulas:
(and preferably rounding to the nearest), and
operations on radii using upward rounding. This leads to the following
formulas:
For instance, when using 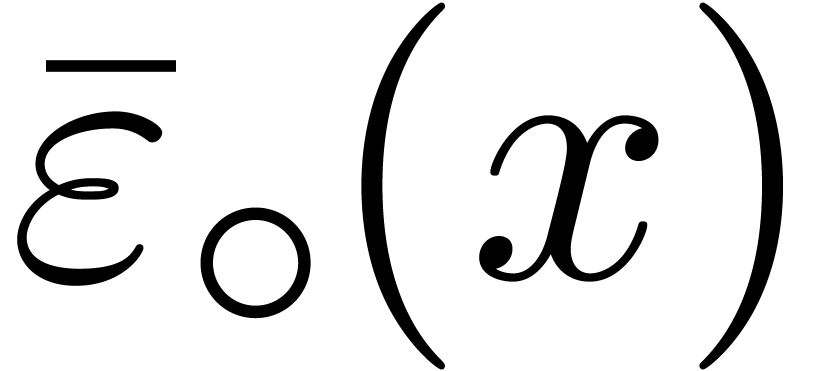 of the form
of the form 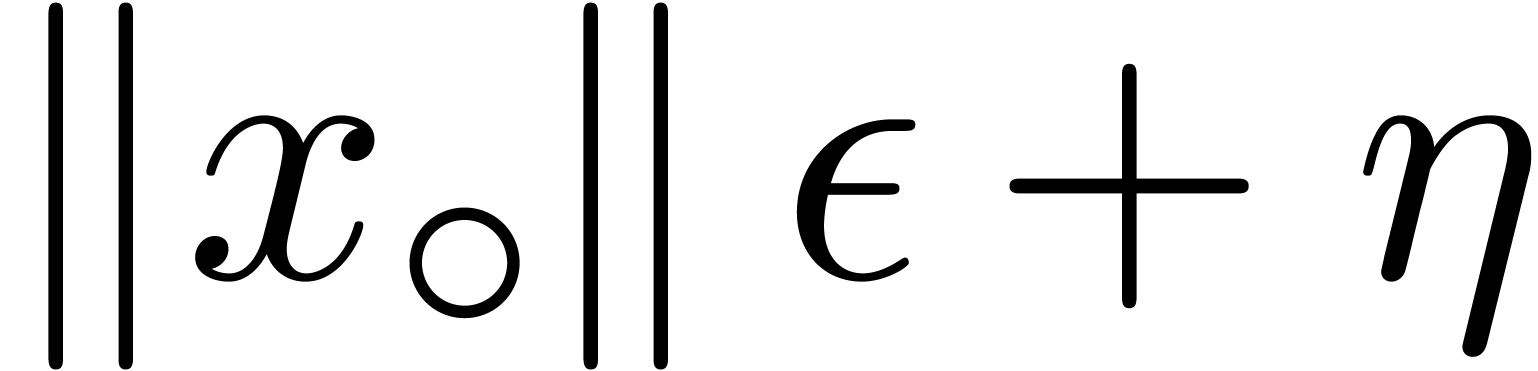 in the last case of fma/fms,
this means that three additional instructions are needed with respect to
the exact arithmetic from the previous subsection:
in the last case of fma/fms,
this means that three additional instructions are needed with respect to
the exact arithmetic from the previous subsection:
In practical implementations, unless  ,
the radius computations involve many roundings. The correctness of the
above formulas is justified by the fact that we systematically use
upward rounding for all bound computations; the rounding error for the
single operation on the centers is captured by
,
the radius computations involve many roundings. The correctness of the
above formulas is justified by the fact that we systematically use
upward rounding for all bound computations; the rounding error for the
single operation on the centers is captured by 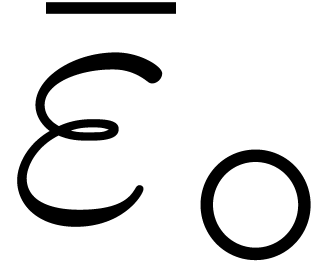 .
.
Remark 2. Unfortunately,
dynamically switching rounding modes may be expensive on some
processors. In that case, one approach is to reorganize computations in
such a way that we first perform sufficiently many operations on centers
using one rounding mode, and next perform all corresponding operations
on radii using upward rounding.
Another approach is to use the same rounding mode for computations on
centers and radii. If we take 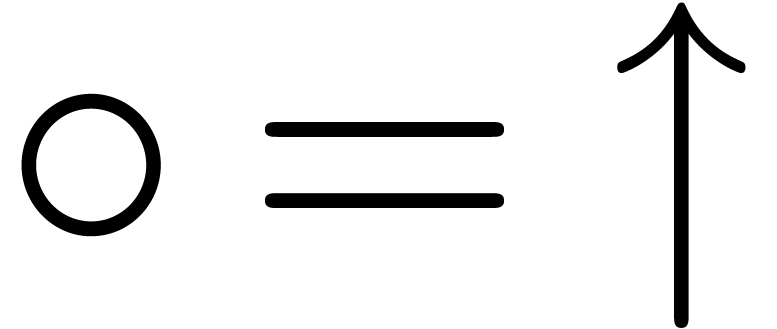 as the sole
rounding mode, then we may directly apply the above formulas, but the
quality of computations with centers degrades. If we take
as the sole
rounding mode, then we may directly apply the above formulas, but the
quality of computations with centers degrades. If we take 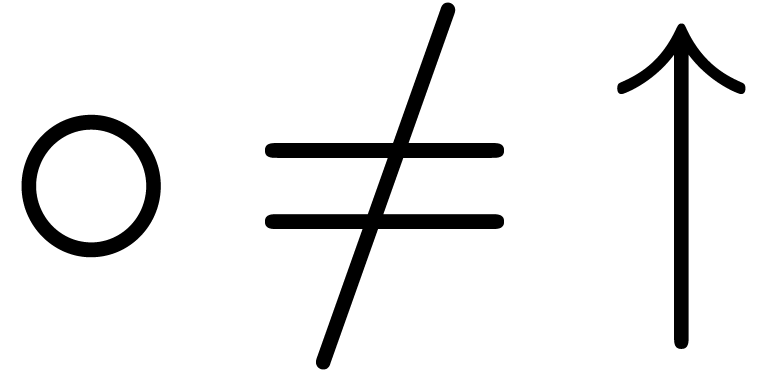 , then we have to further adjust the radii so
as to take into account the additional rounding errors that might occur
during radius computations. For instance, if
, then we have to further adjust the radii so
as to take into account the additional rounding errors that might occur
during radius computations. For instance, if 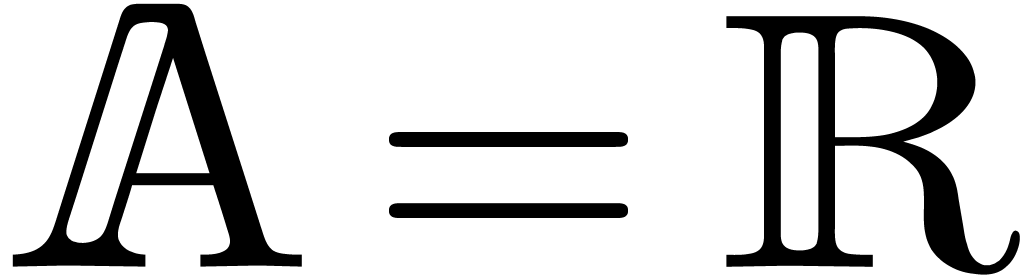 , in the cases of addition and subtraction, and in
absence of underflows/overflows, we may use
, in the cases of addition and subtraction, and in
absence of underflows/overflows, we may use
since we have  . This
arithmetic, sometimes called rough ball arithmetic, fits one of
the main recommendations of [22]: “Get free from the
rounding mode by bounding, roughly but robustly, errors with formulas
independent of the rounding mode if needed.”
. This
arithmetic, sometimes called rough ball arithmetic, fits one of
the main recommendations of [22]: “Get free from the
rounding mode by bounding, roughly but robustly, errors with formulas
independent of the rounding mode if needed.”
E.Transient ball arithmetic
The adjustments which where needed above in order to counter
the problem of rounding errors induce a non trivial computational
overhead, despite the fact that these adjustments are usually very
small. It is interesting to consider an alternative transient ball
arithmetic for which we simply ignore all rounding errors. In the
next Section 3, we will see that it is often possible to
treat these rounding errors at a more global level for a complete
computation instead of a single operation.
For any rounding mode  , we
will denote by
, we
will denote by  the corresponding “rounding
mode” for transient ball arithmetic; the basic operations are
defined as follows:
the corresponding “rounding
mode” for transient ball arithmetic; the basic operations are
defined as follows:
Of course, these formulas do not satisfy the inclusion principle. On
processors that allow for efficient switching of rounding modes, it is
also possible to systematically use upward rounding for radius
computations, with resulting simplifications in the error analysis
below.
Let us fix a rounding mode  .
We assume that we are given a suitable floating point number
.
We assume that we are given a suitable floating point number  in
in 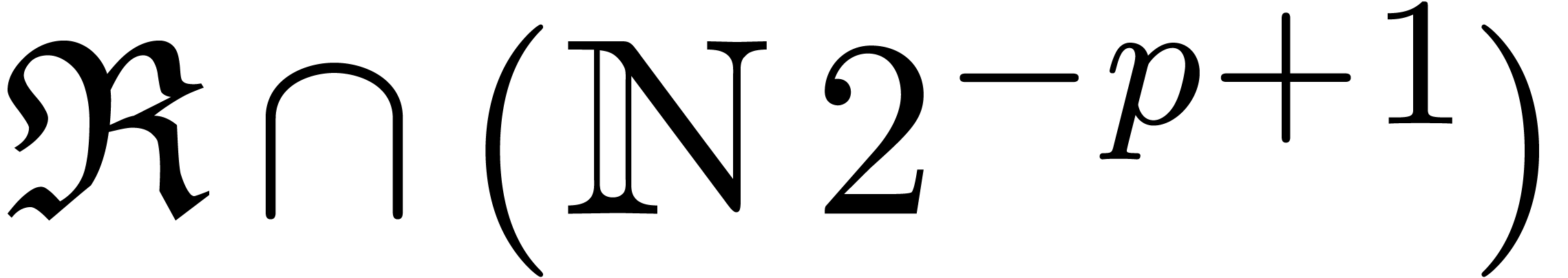 such that
such that 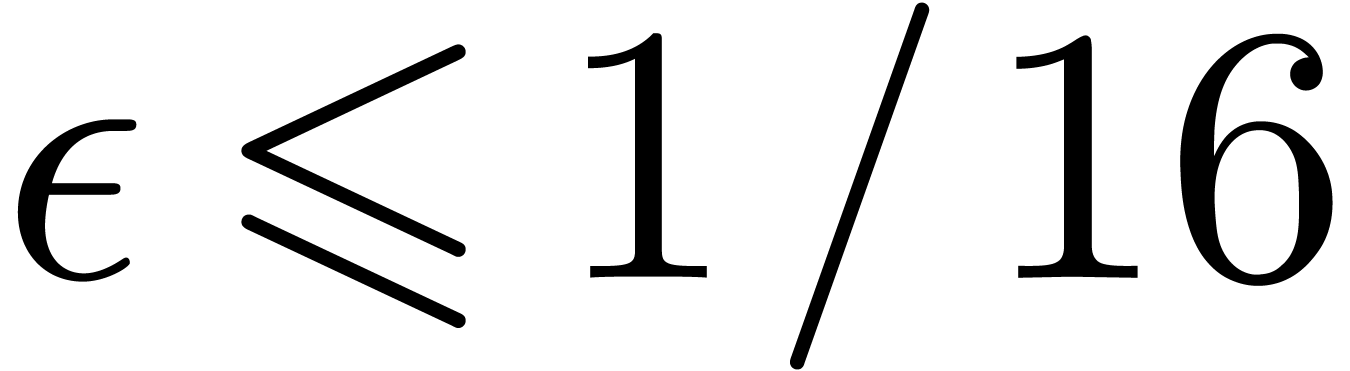 and
and
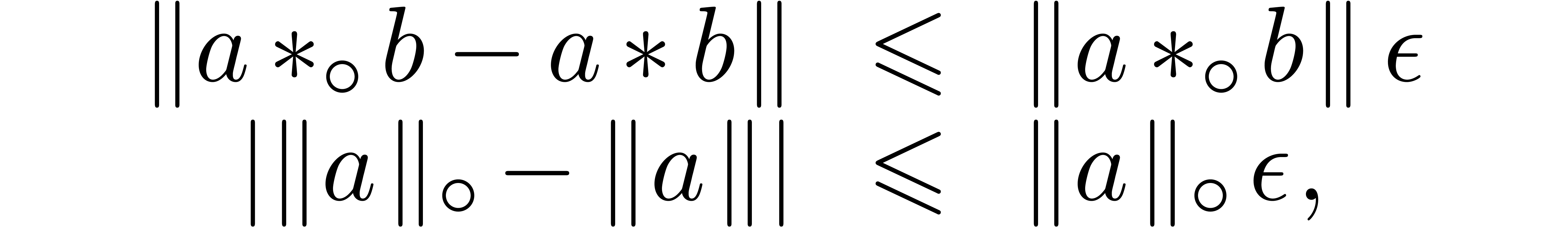
hold for all  and
and  ,
in absence of underflows and overflows. If
,
in absence of underflows and overflows. If 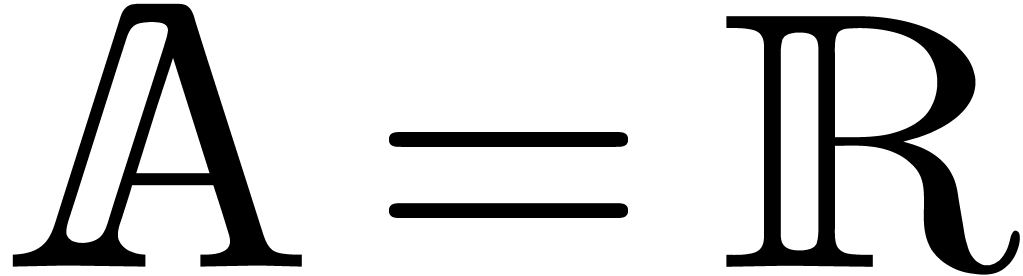 ,
then we may take
,
then we may take 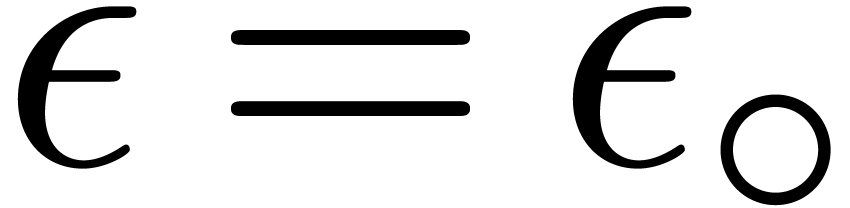 . If
. If 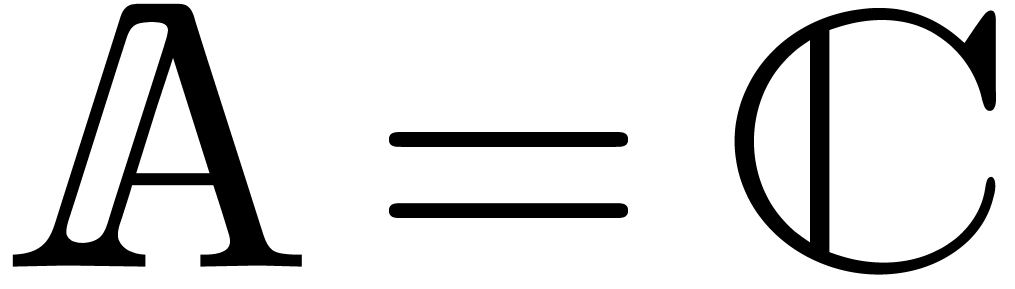 , and assuming that complex
arithmetic is implemented using (1–3),
then it can be checked that we may take
, and assuming that complex
arithmetic is implemented using (1–3),
then it can be checked that we may take 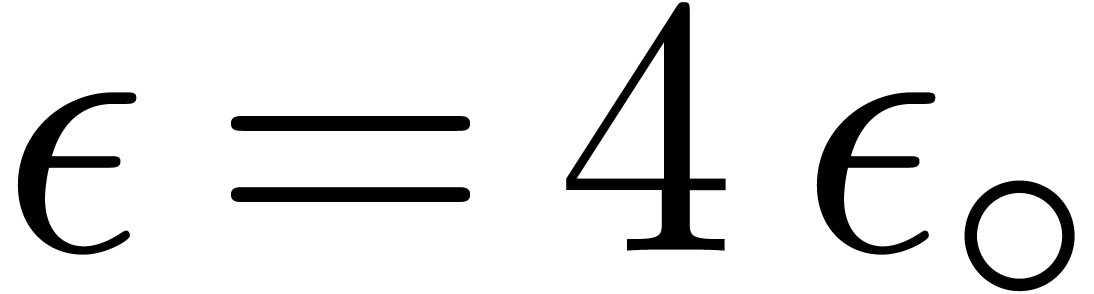 (see
Appendix A). The following lemma provides an error estimate
for the radius computation of a transient ball product.
(see
Appendix A). The following lemma provides an error estimate
for the radius computation of a transient ball product.
Lemma 3. For all
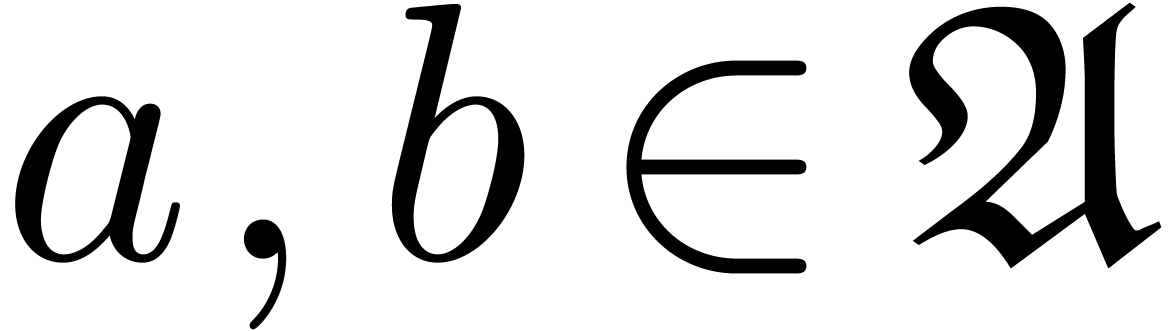 and
and  such that the
computation of
such that the
computation of
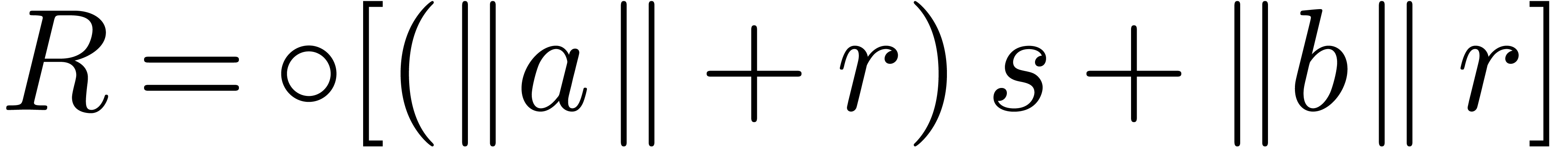
involves no underflow or overflow, we have 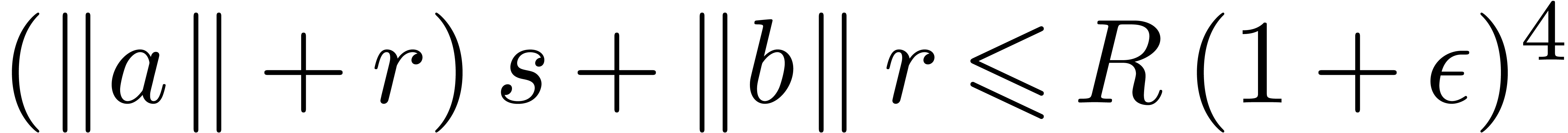 .
.
Proof. We have
III.Evaluation of SLPs
A.Straight-line programs
A straight-line program  over a ring
over a ring
 is a sequence
is a sequence  of
instructions of the form
of
instructions of the form
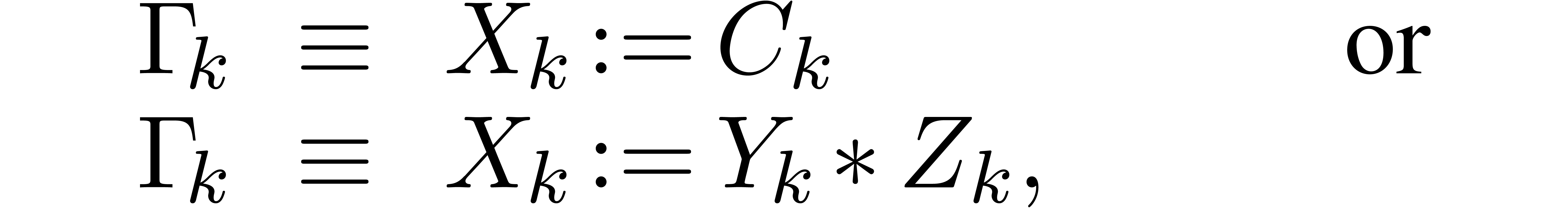
where 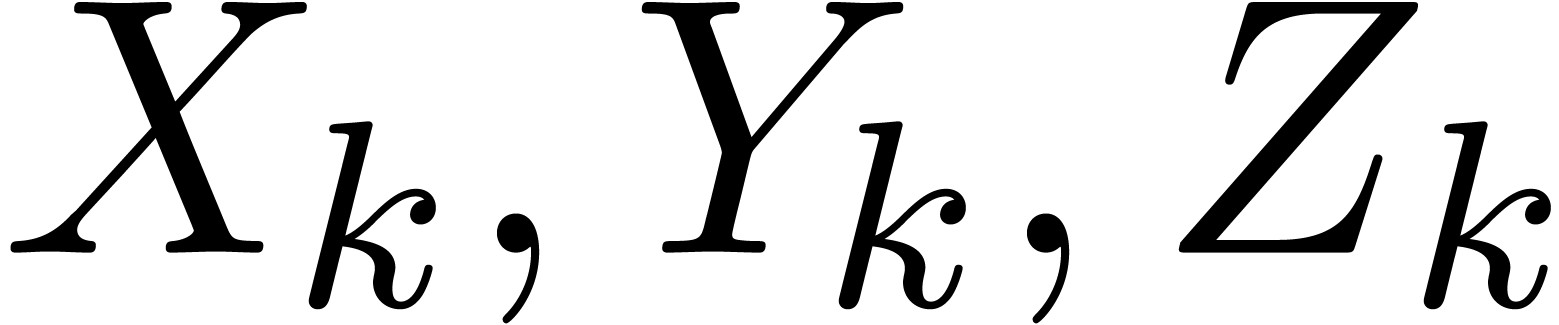 are variables in a finite ordered set
are variables in a finite ordered set
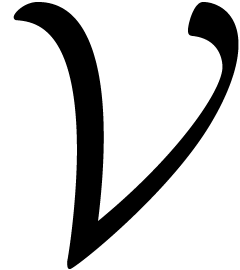 ,
, 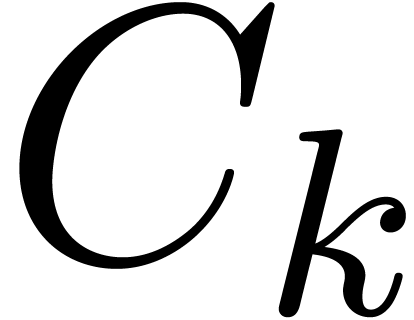 constants in
constants in  , and
, and 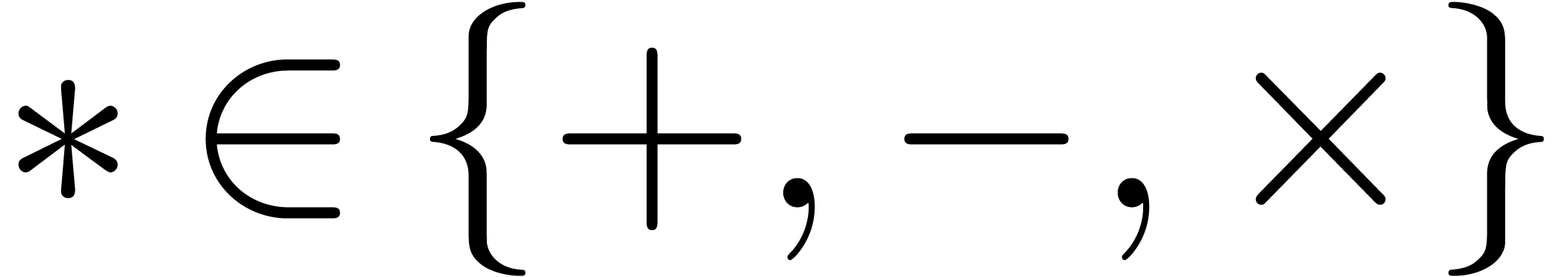 . Variables that appear for the
first time in the sequence in the right-hand side of an instruction are
called input variables. A distinguished subset of the set of
all variables occurring at the left-hand side of instructions is called
the set of output variables. Variables which are not used for
input or output are called temporary variables and determine
the amount of auxiliary memory needed to evaluate the program. The
length
. Variables that appear for the
first time in the sequence in the right-hand side of an instruction are
called input variables. A distinguished subset of the set of
all variables occurring at the left-hand side of instructions is called
the set of output variables. Variables which are not used for
input or output are called temporary variables and determine
the amount of auxiliary memory needed to evaluate the program. The
length 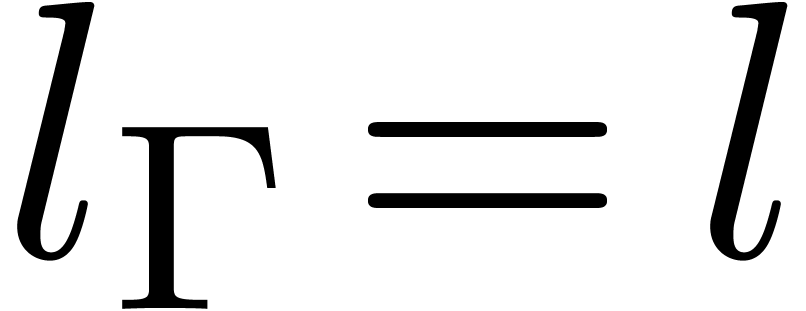 of the sequence is called the
length of
of the sequence is called the
length of  .
.
Let  be the input variables of
be the input variables of  and
and  the output variables, listed in increasing
order. Then we associate an evaluation function
the output variables, listed in increasing
order. Then we associate an evaluation function 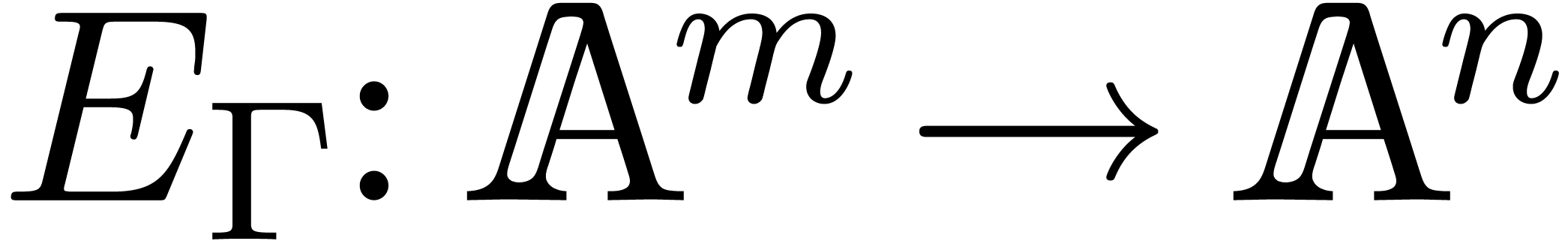 to
to  as follows: given
as follows: given 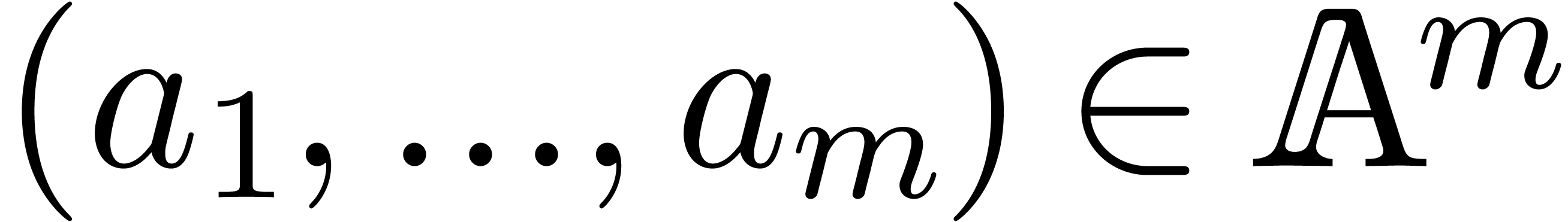 , we assign
, we assign  to
to 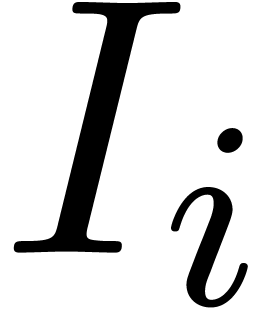 for
for 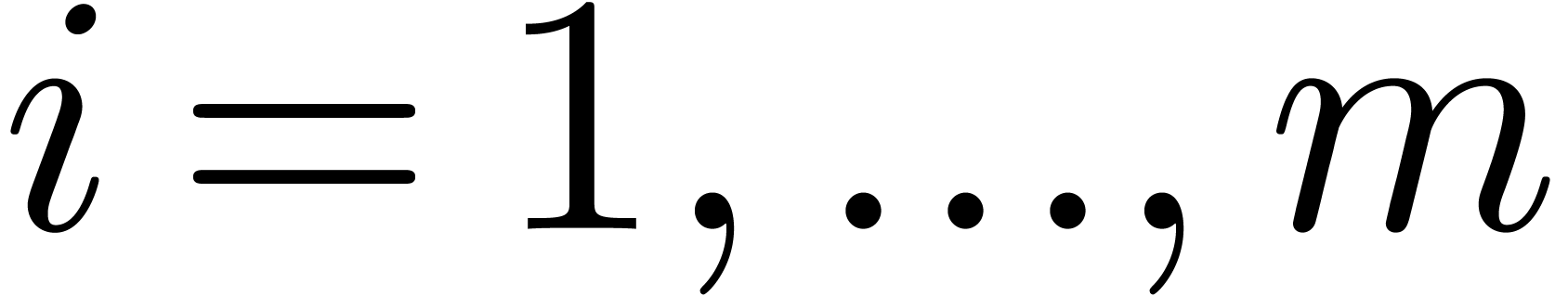 , then
evaluate the instructions of
, then
evaluate the instructions of  in sequence, and
finally read off the values of
in sequence, and
finally read off the values of  ,
which determine
,
which determine 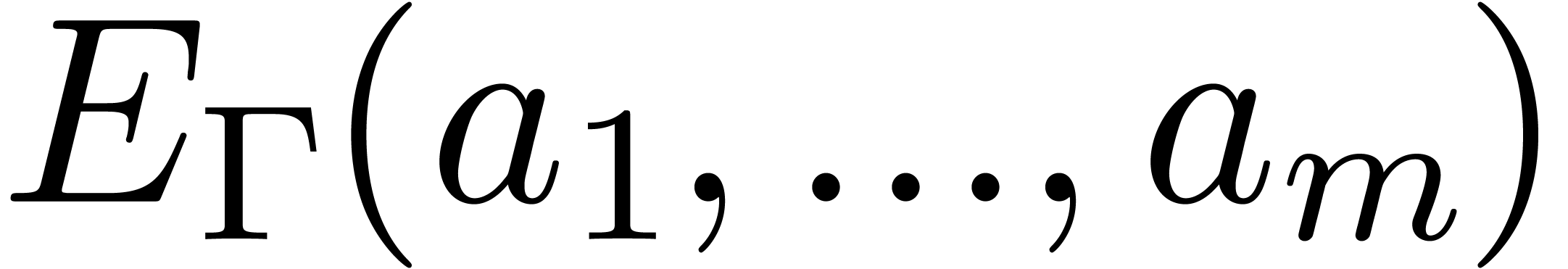 .
.
To each instruction 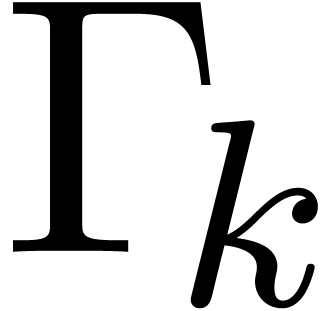 , one may
associate the remaining path lengths
, one may
associate the remaining path lengths 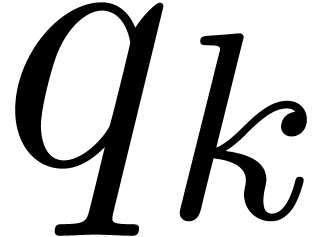 as
follows. Let
as
follows. Let 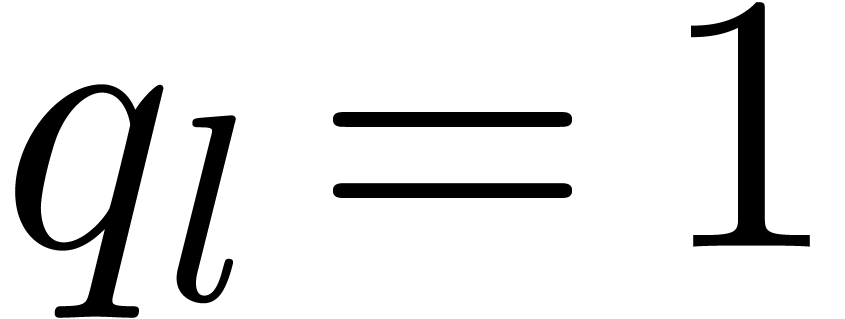 , and assume
that
, and assume
that  have been defined for some
have been defined for some 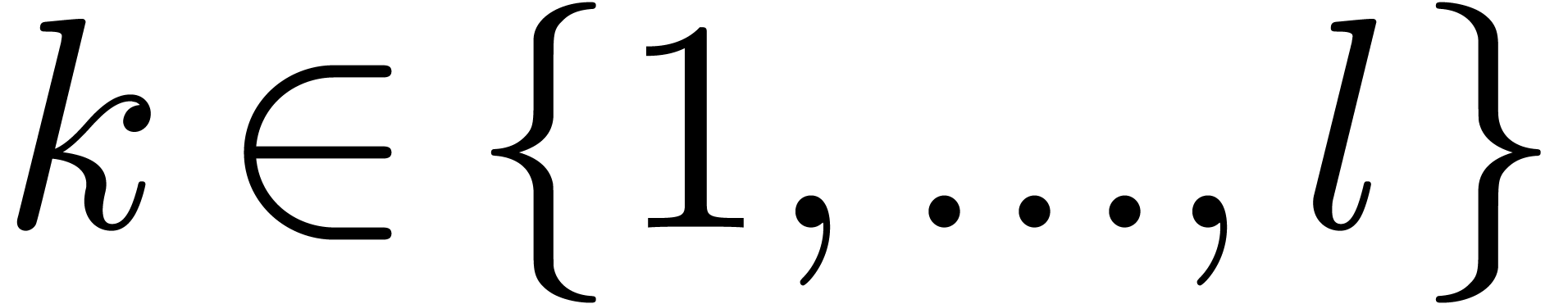 . Then we take
. Then we take 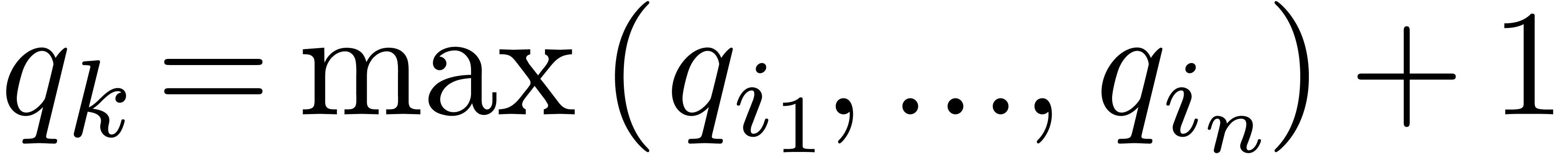 ,
where
,
where  are those indices
are those indices 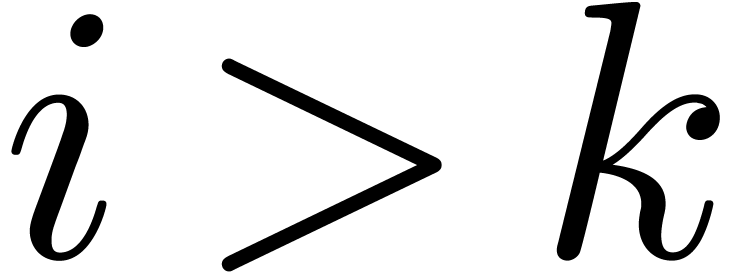 such that
such that 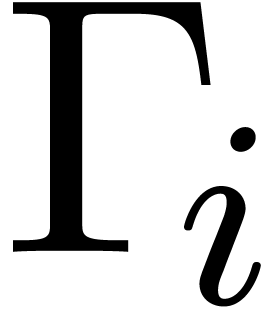 is of the form
is of the form 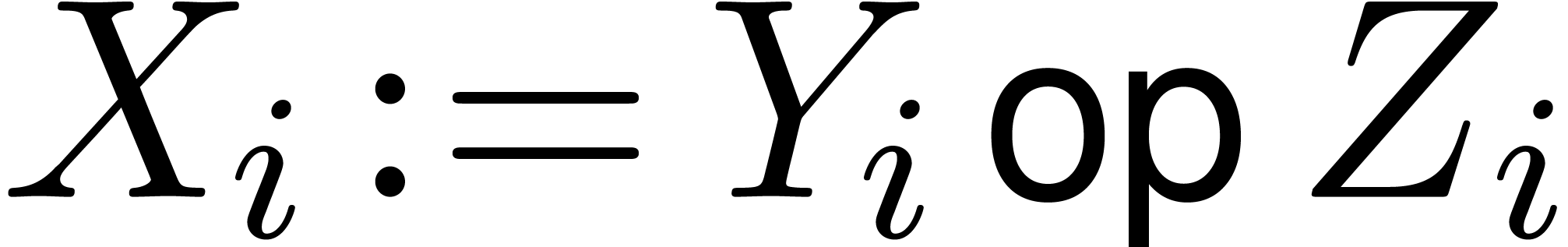 with
with 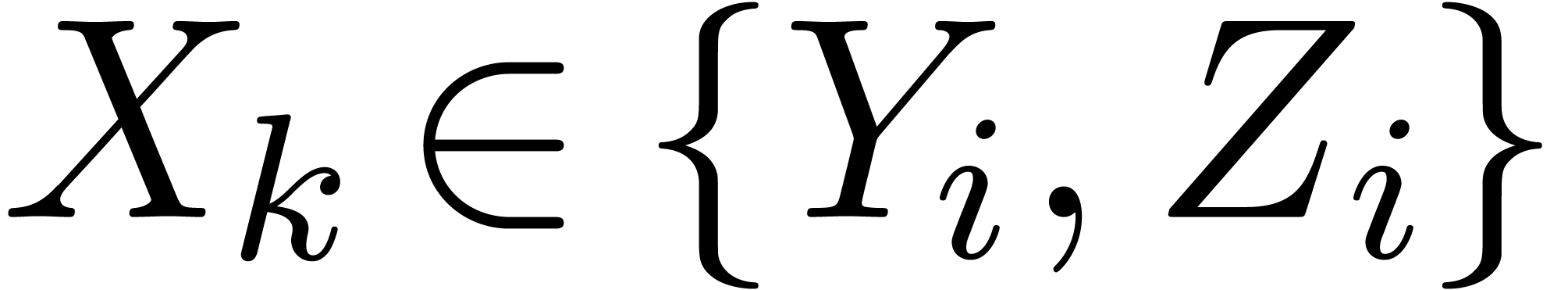 and
and 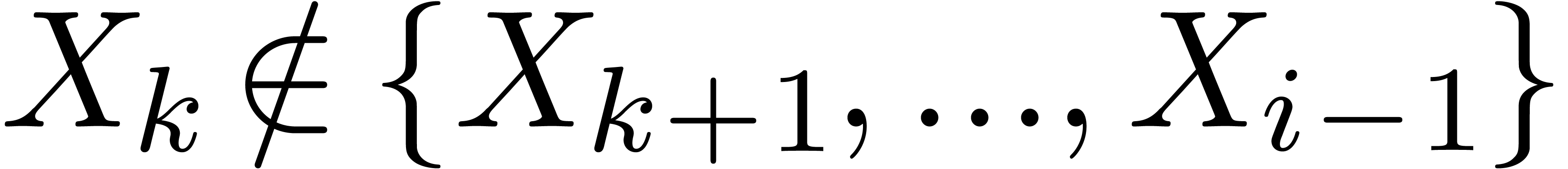 .
If no such indices
.
If no such indices 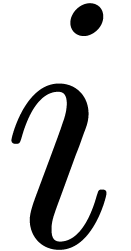 exist, then we set
exist, then we set  . Similarly, for each input
variable
. Similarly, for each input
variable 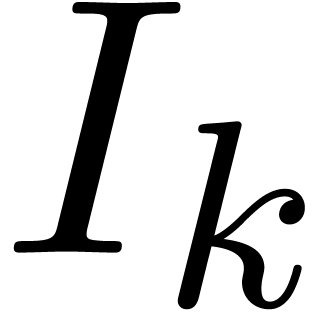 we define
we define 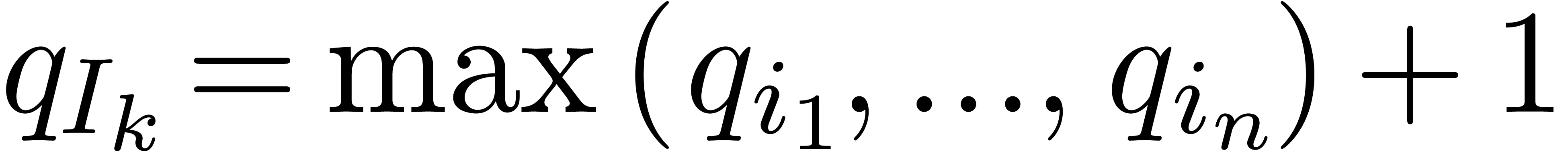 ,
where
,
where  are those indices such that
are those indices such that 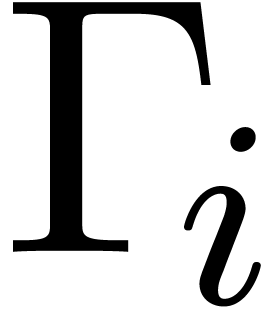 is of the form
is of the form  with
with  and
and  . We also
define
. We also
define  , where
, where  are the input variables of
are the input variables of  and
and
 all indices
all indices 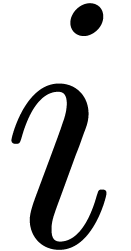 such that
such that
 is of the form
is of the form  .
.
Example 4. Let us
consider  , of length
, of length 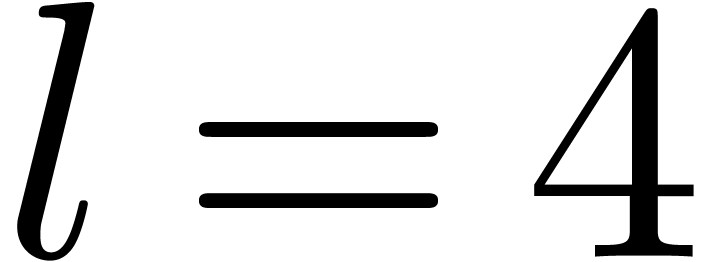 . The input variables are
. The input variables are 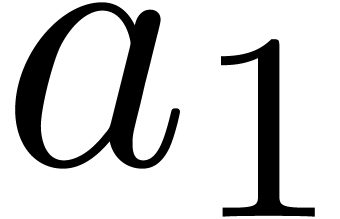 and
and 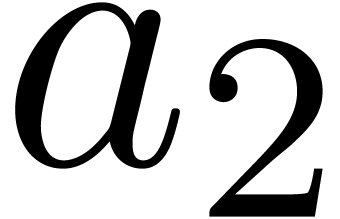 , and we
distinguish
, and we
distinguish 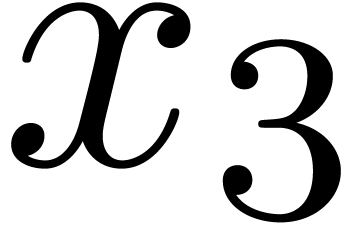 as the sole output variable. This
SLP thus computes the function
as the sole output variable. This
SLP thus computes the function 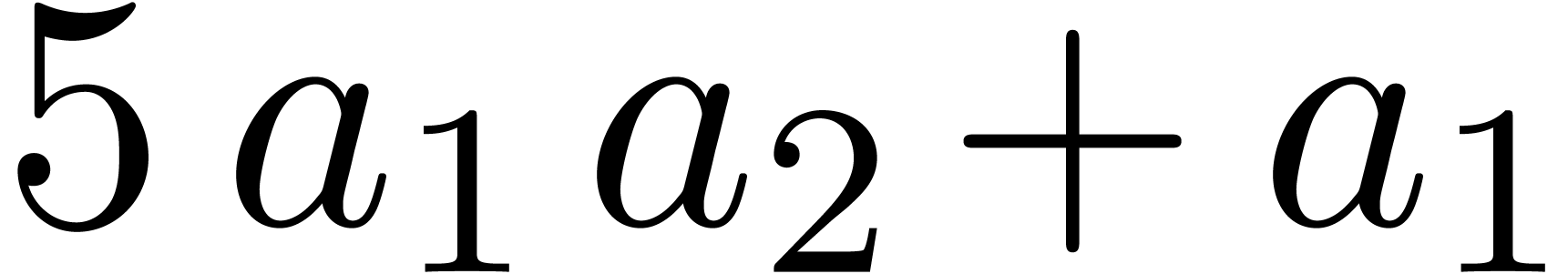 .
The associated computation graph, together with remaining path lengths
are as pictured:
.
The associated computation graph, together with remaining path lengths
are as pictured:

B.Transient evaluation
Consider the “semi-exact” ball arithmetic in which all
computations on centers are done using a given rounding mode  and all computations on radii are exact. More precisely,
we take
and all computations on radii are exact. More precisely,
we take
for any 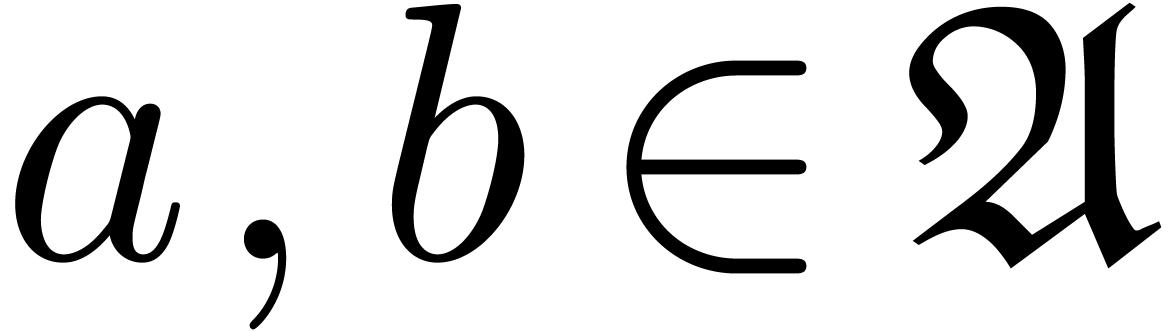 and
and 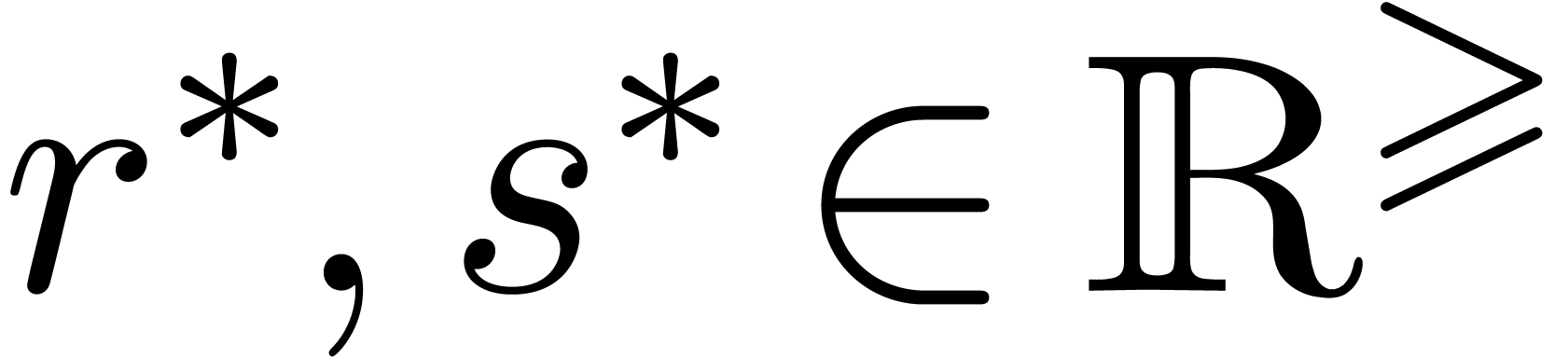 .
We wish to investigate how far the transient arithmetic from Section 2.5 can deviate from this idealized arithmetic (which
satisfies the inclusion principle). We will write
.
We wish to investigate how far the transient arithmetic from Section 2.5 can deviate from this idealized arithmetic (which
satisfies the inclusion principle). We will write 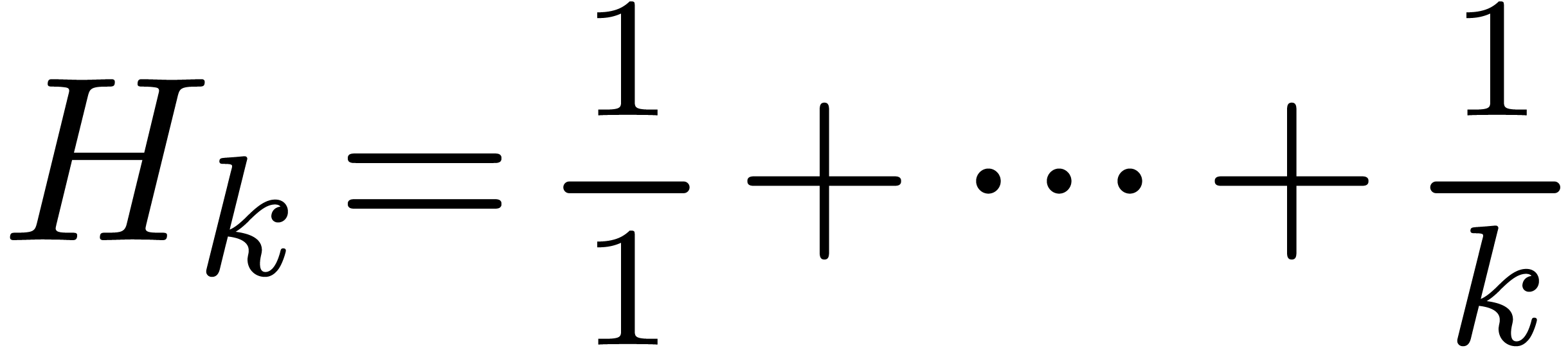 for the
for the 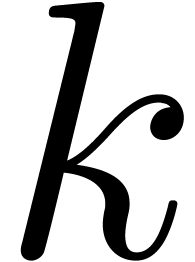 -th harmonic number
and
-th harmonic number
and 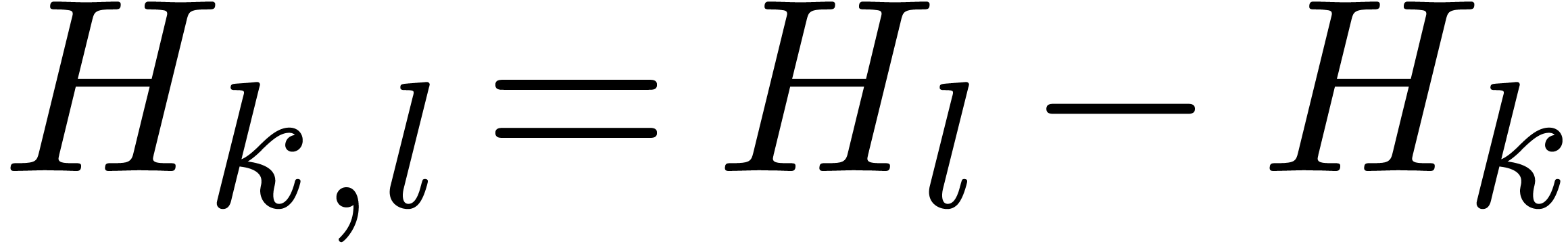 for all
for all 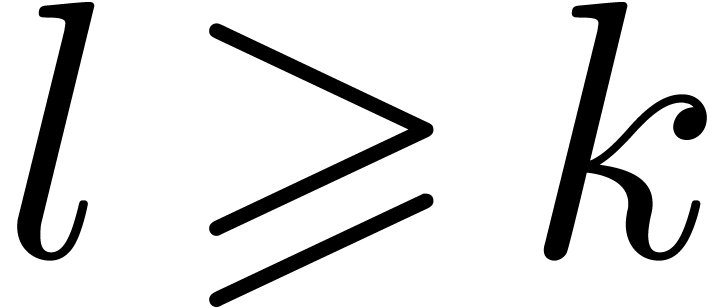 .
.
Theorem 5. Let  be a SLP of length
be a SLP of length  as above and let
as above and let  be an
arbitrary parameter such that
be an
arbitrary parameter such that 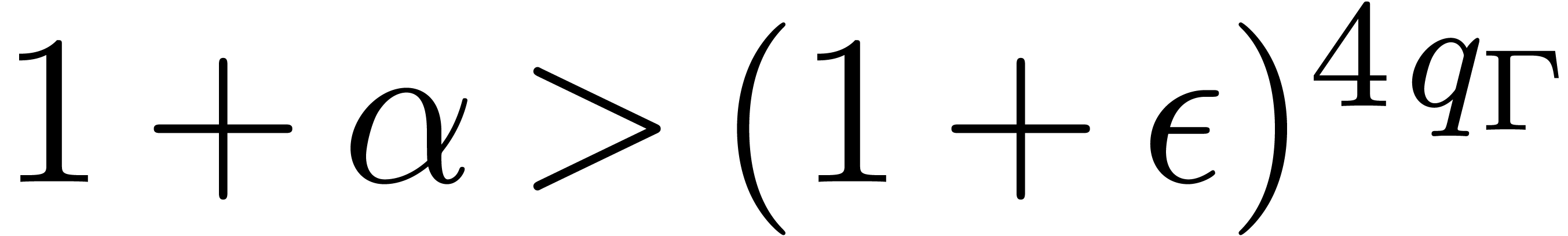 .
Consider two evaluations of
.
Consider two evaluations of  with two different
ball arithmetics. For the first evaluation, we use the above semi-exact
arithmetic with
with two different
ball arithmetics. For the first evaluation, we use the above semi-exact
arithmetic with 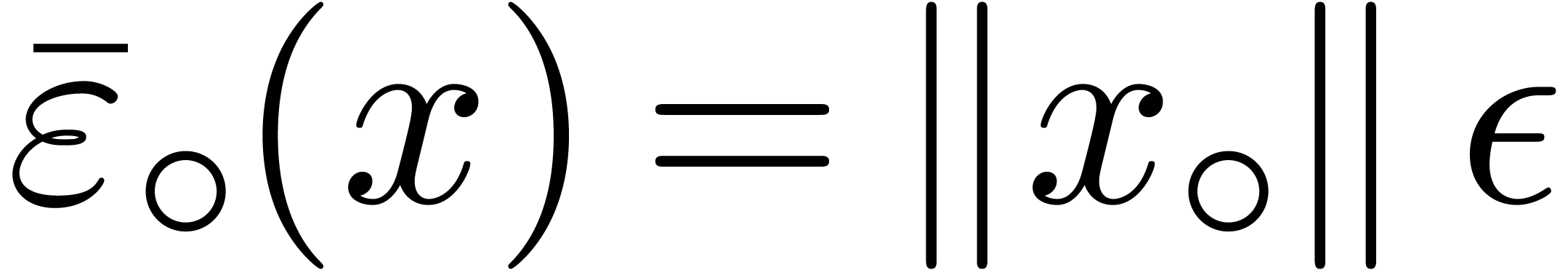 . For the
second evaluation, we use transient ball arithmetic with the same
arithmetic for centers, and the additional property that any input or
constant ball
. For the
second evaluation, we use transient ball arithmetic with the same
arithmetic for centers, and the additional property that any input or
constant ball  is replaced by a larger ball
is replaced by a larger ball 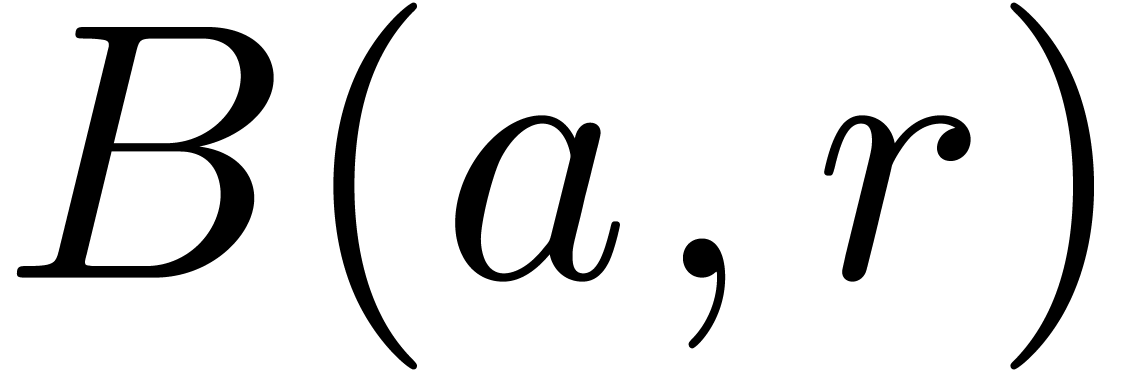 with
with
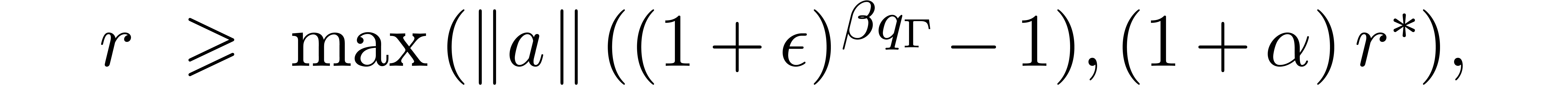
where
If no underflow or overflow occurs during the second evaluation, then
for all  in the output of the first evaluation
with corresponding entry
in the output of the first evaluation
with corresponding entry 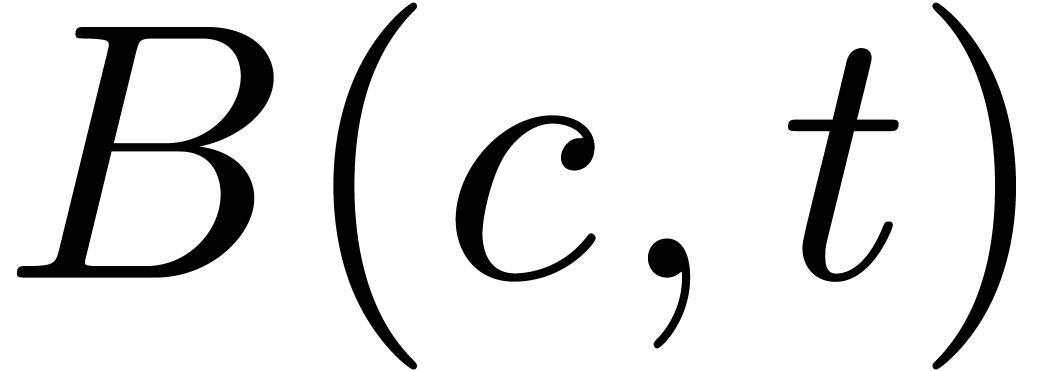 for the second
evaluation, we have
for the second
evaluation, we have 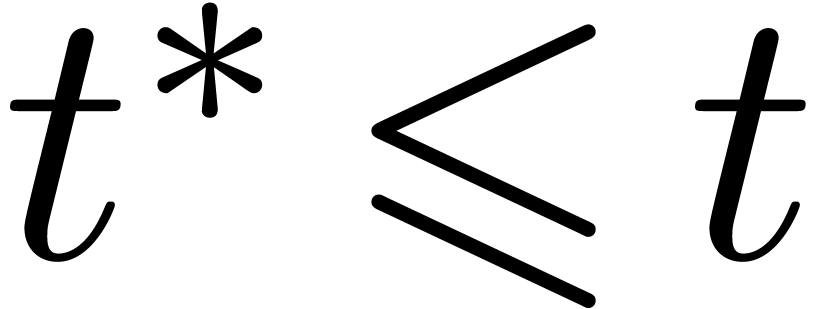 .
.
Proof. It will be convenient to systematically use the
star superscript for the semi-exact radius evaluation and no superscript
for the transient evaluation.
Let 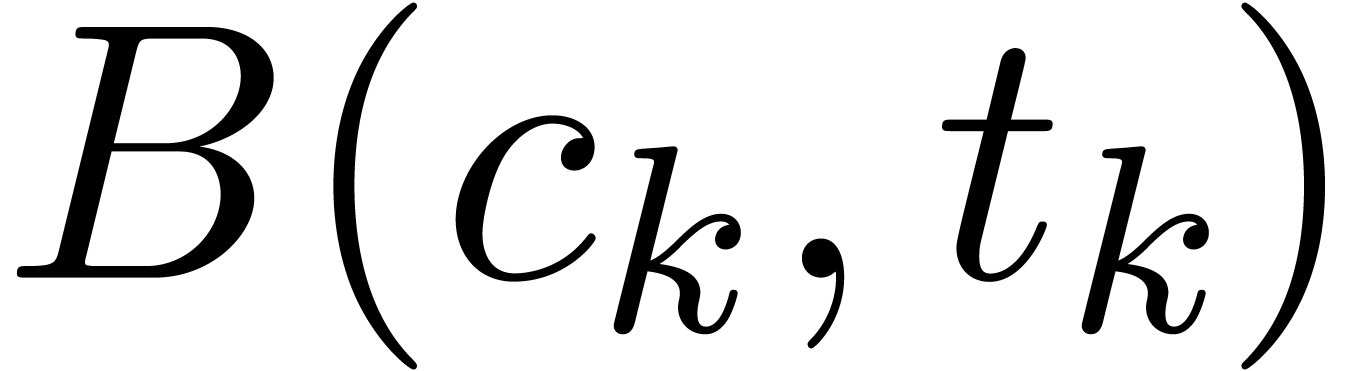 be the ball value of the variable
be the ball value of the variable 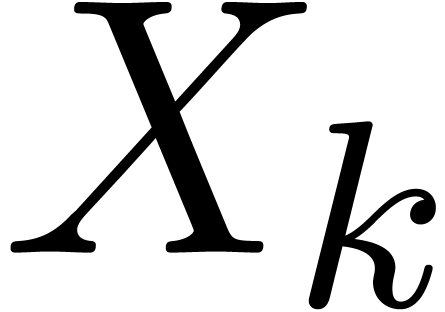 just after evaluation of
just after evaluation of  using
transient ball arithmetic. Let us show by induction over
using
transient ball arithmetic. Let us show by induction over 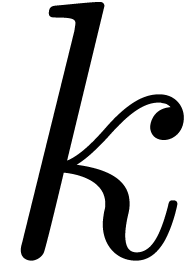 that
that
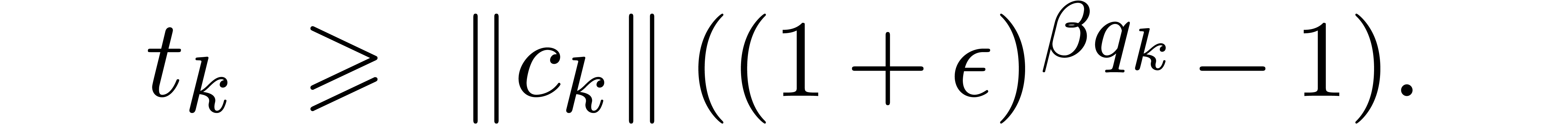
So assume that the hypothesis holds for all strictly smaller values of
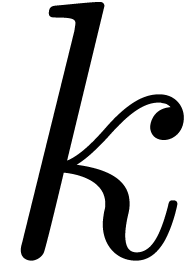 . If
. If 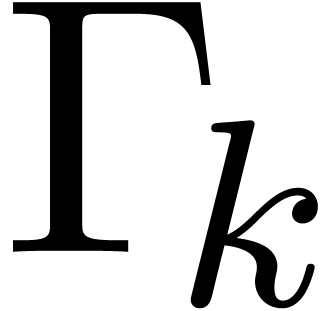 is of the form
is of the form 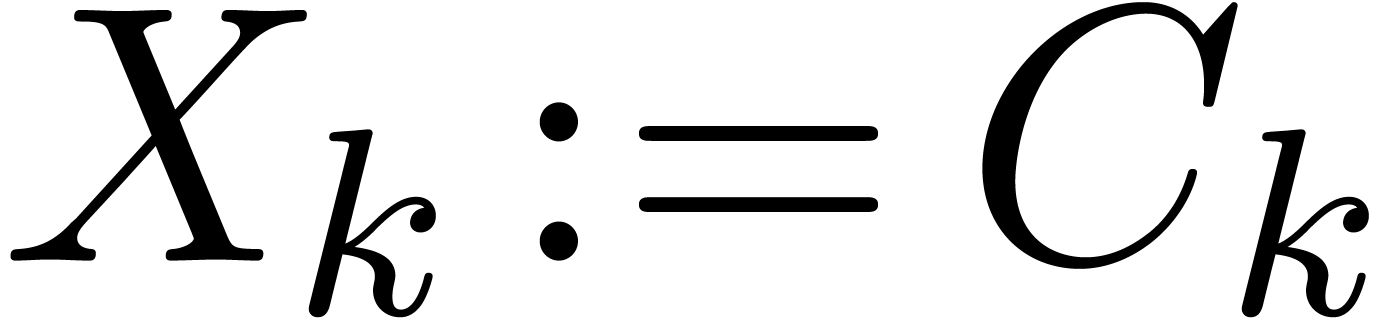 , then we are
done by assumption since
, then we are
done by assumption since 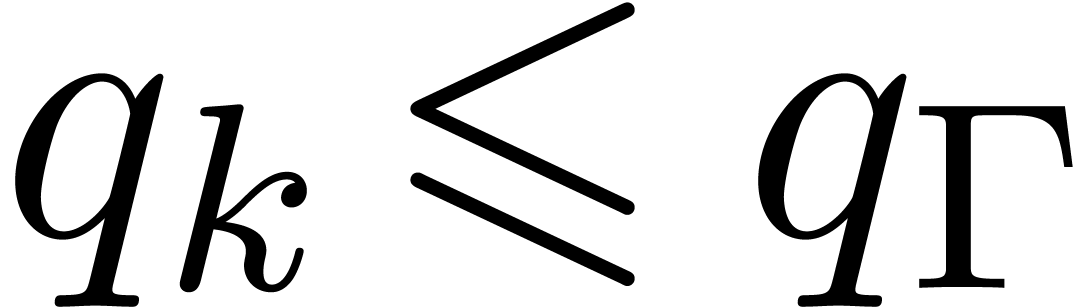 . If
. If
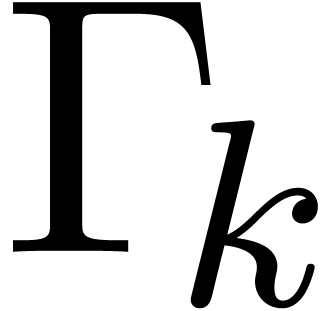 is of the form
is of the form 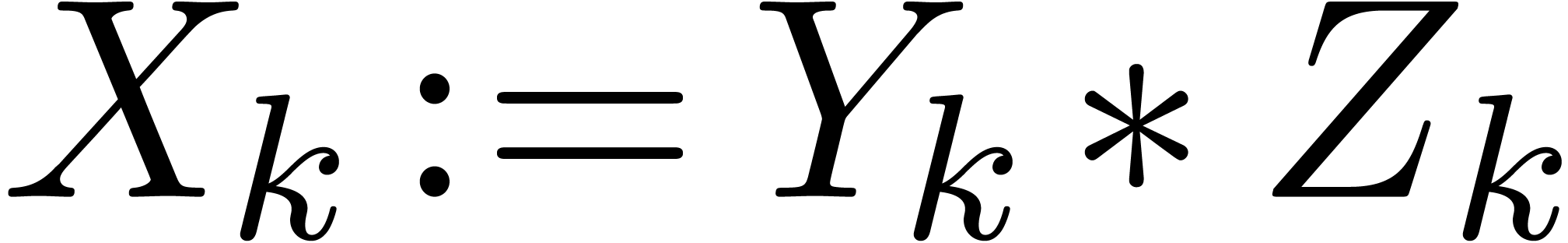 ,
then we claim that
,
then we claim that 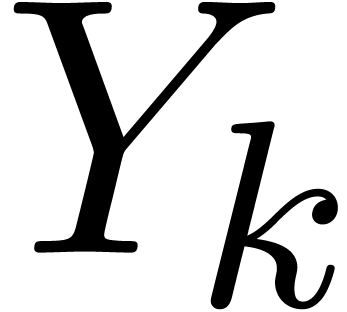 contains a ball
contains a ball  with
with
Indeed, this holds by assumption if 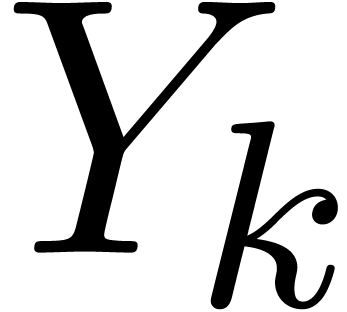 is an input
variable. Otherwise, let
is an input
variable. Otherwise, let 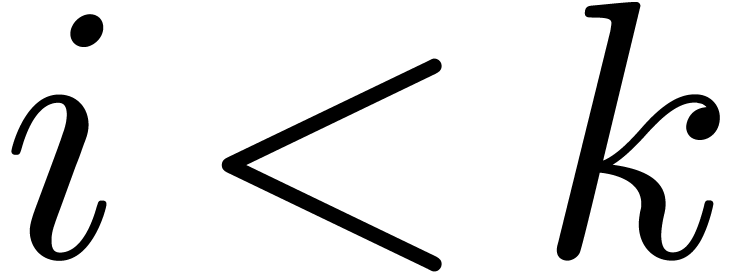 be largest with
be largest with 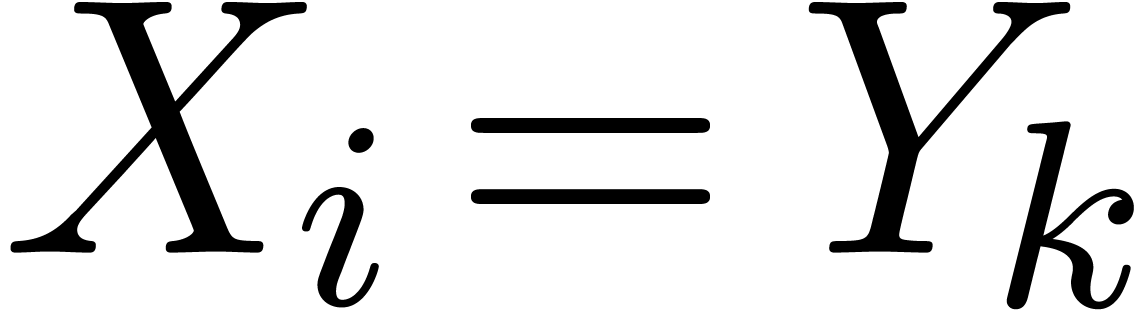 . Then
. Then  by
the construction of
by
the construction of  , whence
our claim follows by the induction hypothesis. In a similar way,
, whence
our claim follows by the induction hypothesis. In a similar way,  contains a ball
contains a ball  with
with 
Having shown our claim, let us first consider the case when  . Then we get
. Then we get
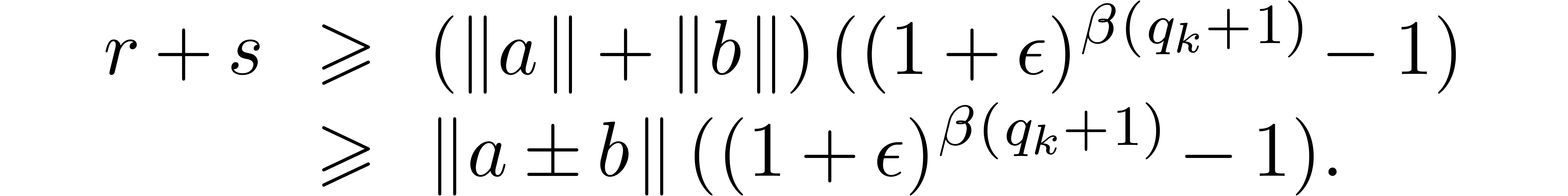
Using the inequalities 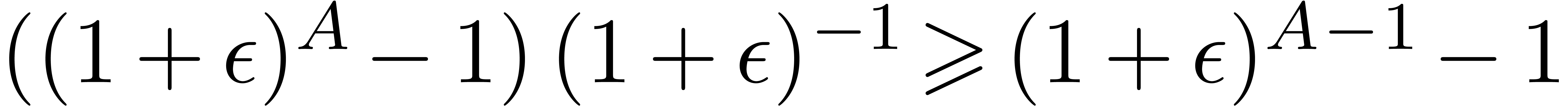 ,
,
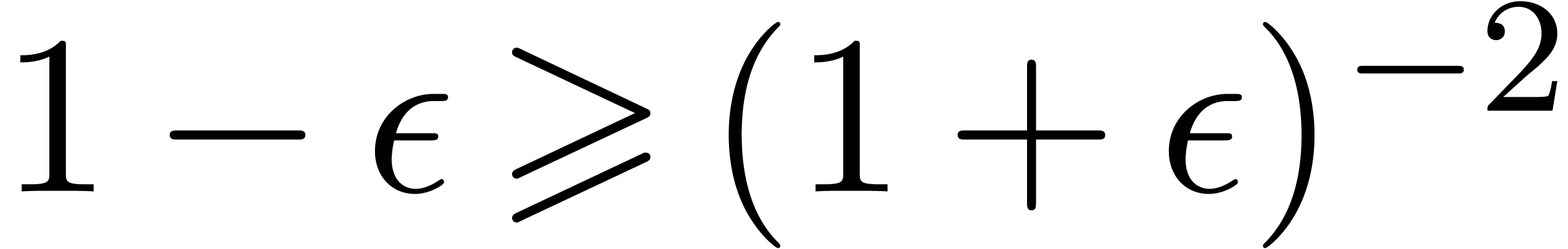 , and the fact that
, and the fact that 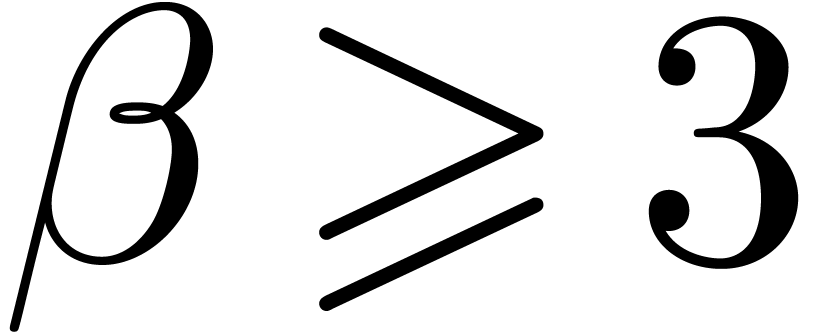 , we obtain:
, we obtain:
as desired. In the same way, if  ,
then
,
then
whence, using Lemma 3, and the fact that 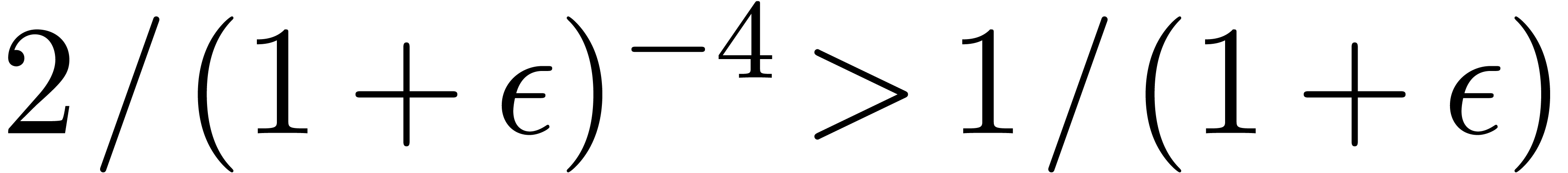 ,
,
which completes our claim by induction.
For all 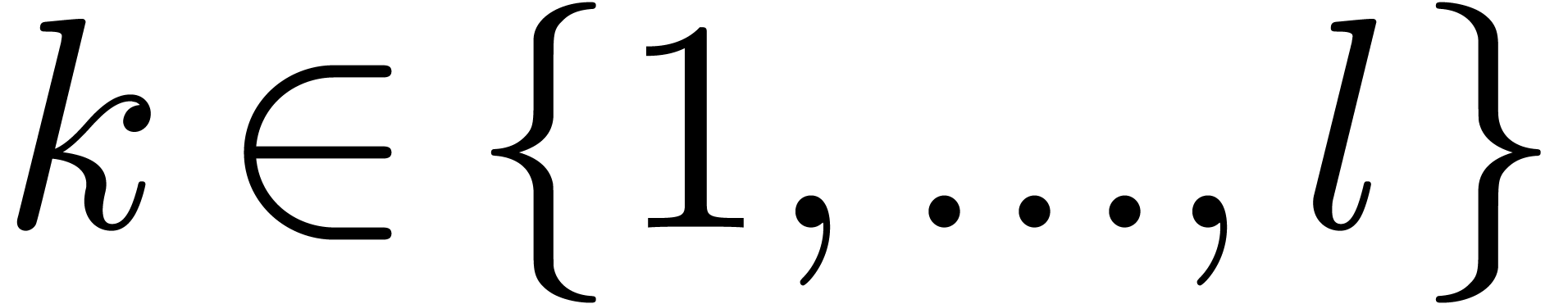 , we introduce
, we introduce
so that 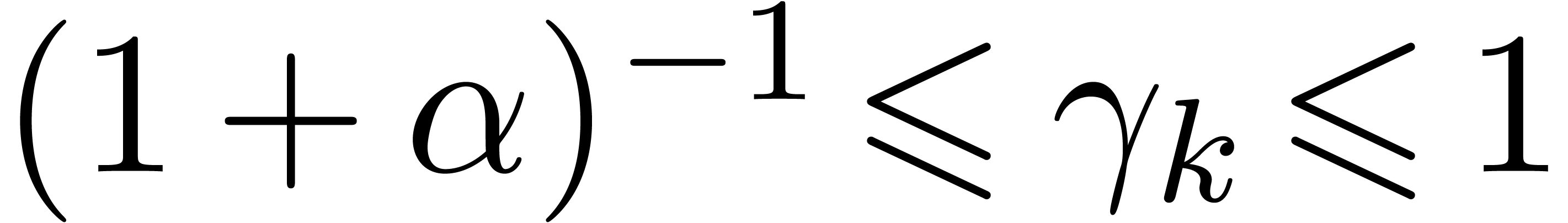 . Using a second
induction over
. Using a second
induction over  , let us next
prove that
, let us next
prove that
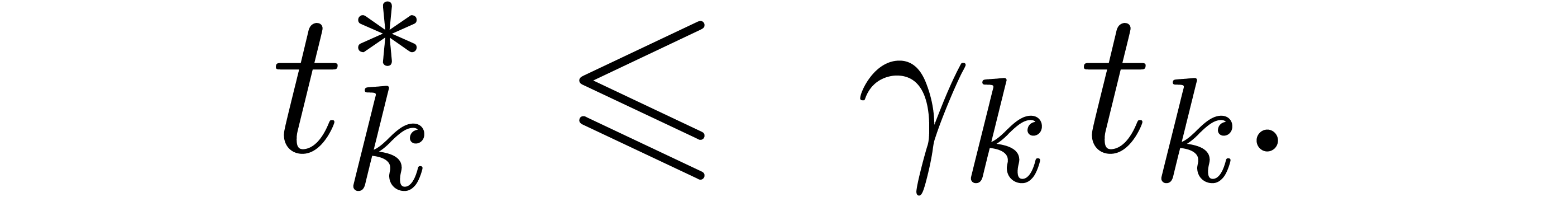
Assume that this inequality holds up until order  . If
. If 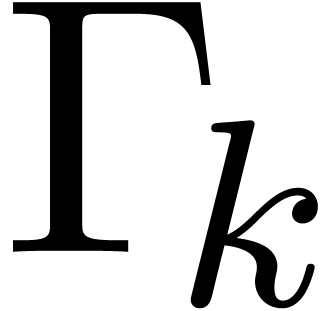 is of the form
is of the form 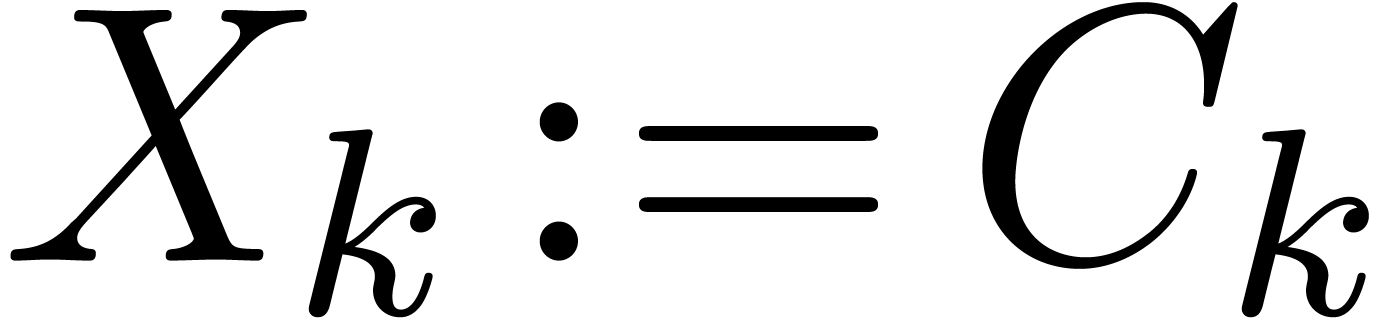 , then we are done by the fact that
, then we are done by the fact that
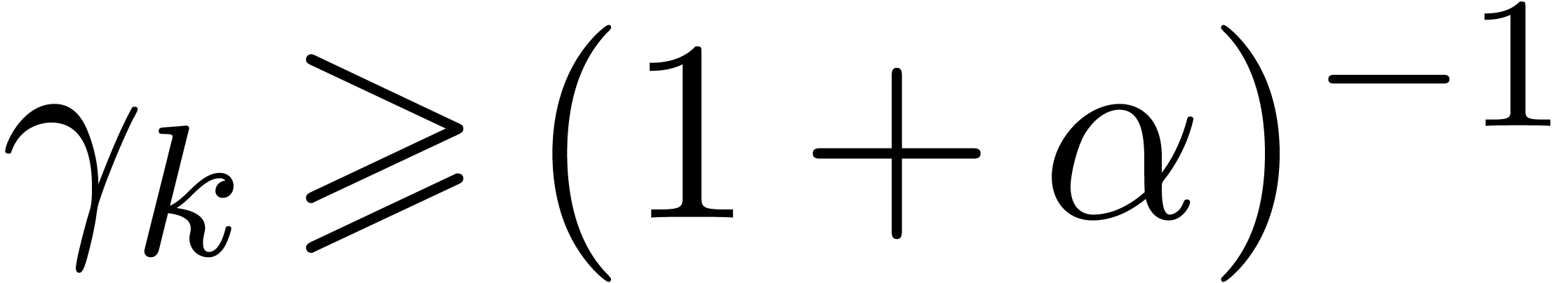 .
.
If 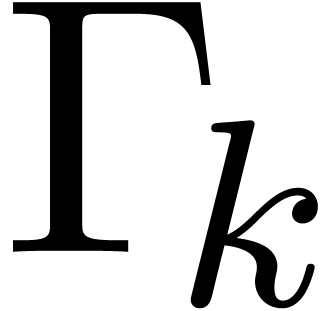 is of the form
is of the form 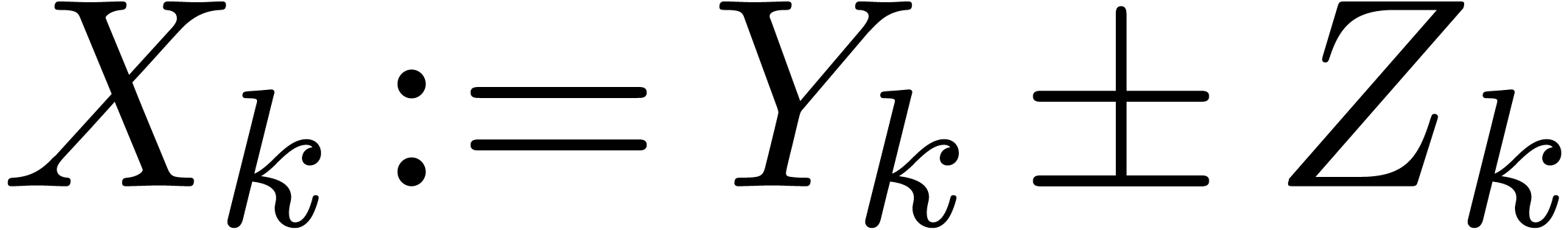 ,
then let
,
then let 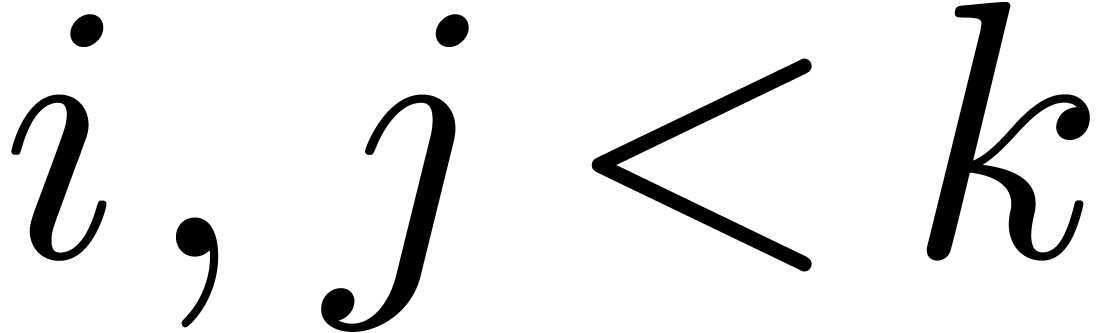 be largest with
be largest with 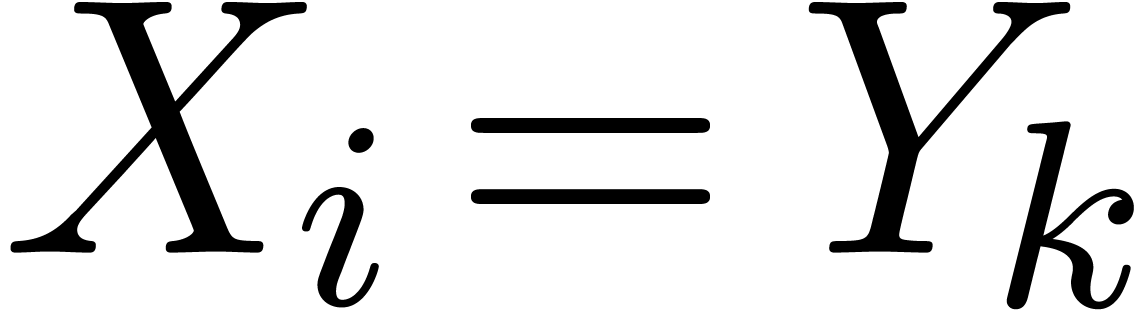 and
and 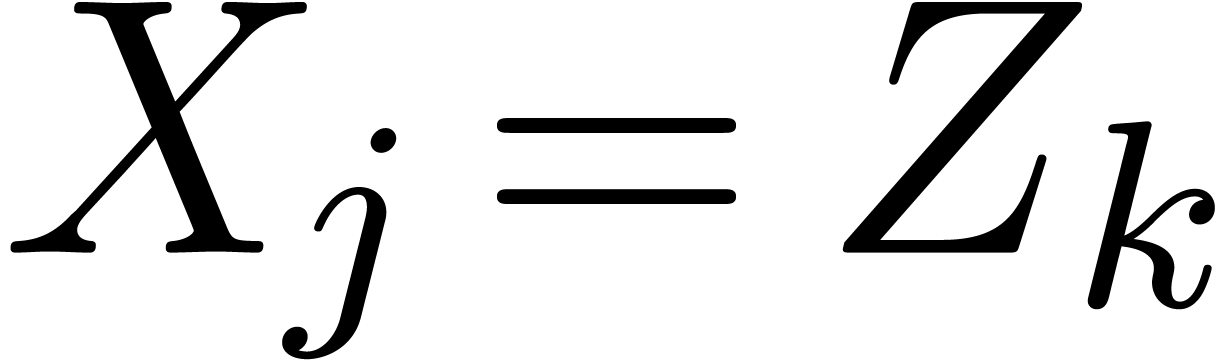 . Then
. Then 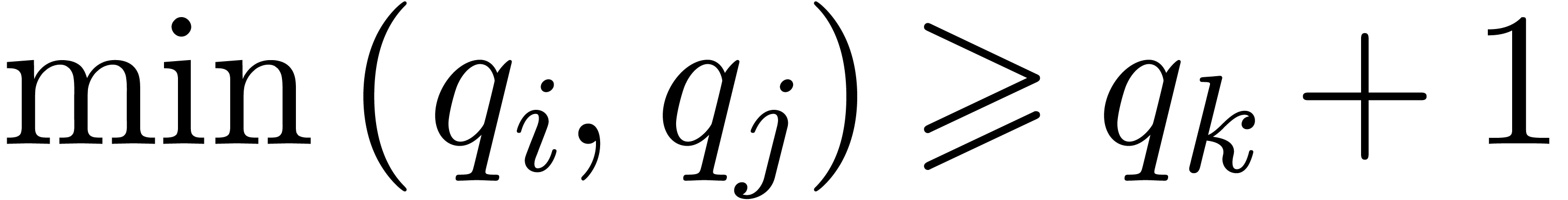 , and
, and
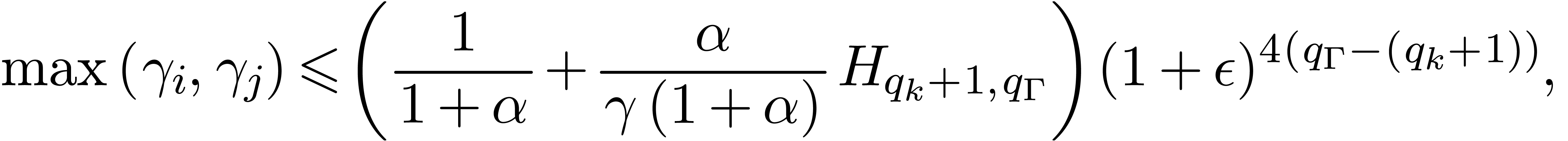
In particular, 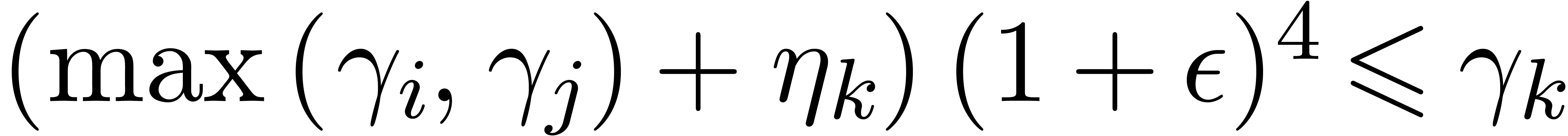 . With
. With  and
and  as above, it follows that
as above, it follows that
If  is of the form
is of the form  ,
then thanks to Lemma 3, a similar computation yields
,
then thanks to Lemma 3, a similar computation yields
This completes the second induction and the proof of this theorem.
For fixed  and
and  ,
we observe that
,
we observe that 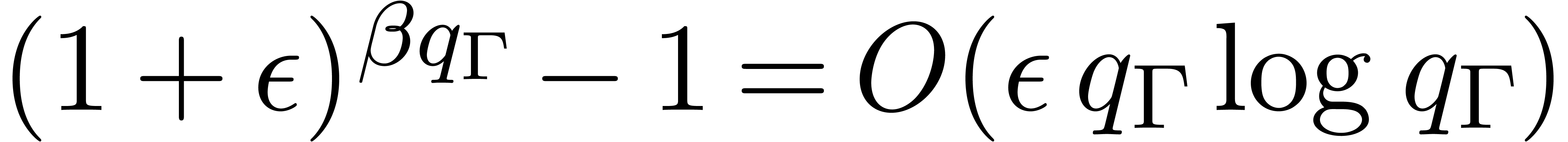 . The value
of the parameter
. The value
of the parameter  may be optimized for given SLPs
and inputs. Without entering details,
may be optimized for given SLPs
and inputs. Without entering details,  should be
taken large when inputs are accurate, and small when inputs are rough,
as encountered for instance within subdivision algorithms.
should be
taken large when inputs are accurate, and small when inputs are rough,
as encountered for instance within subdivision algorithms.
C.Managing underflows and
overflows
In Theorem 5, we have assumed the absence of underflows and
overflows. There are several strategies for managing such exceptions,
whose efficiencies heavily depend on the specific kind of hardware being
used.
One strategy to manage exceptions is to use the status register of an
IEEE 754 FPU. The idea is to simply clear the underflow and
overflow flags of the status register, then perform the evaluation, and
finally check both flags at the end. Whenever an overflow occurred
during the evaluation, then we may set the radii of all results to plus
infinity, thereby preserving the inclusion principle. If an underflow
occurred (which is quite unlikely), then we simply reevaluate the entire
SLP using a more expensive, fully certified ball arithmetic.
When performing all computations using the IEEE 754 rounding-to-nearest
mode  , we also notice that
consulting the status register can be avoided for managing overflows.
Indeed, denoting by
, we also notice that
consulting the status register can be avoided for managing overflows.
Indeed, denoting by  the largest positive finite
number in
the largest positive finite
number in  , we have
, we have 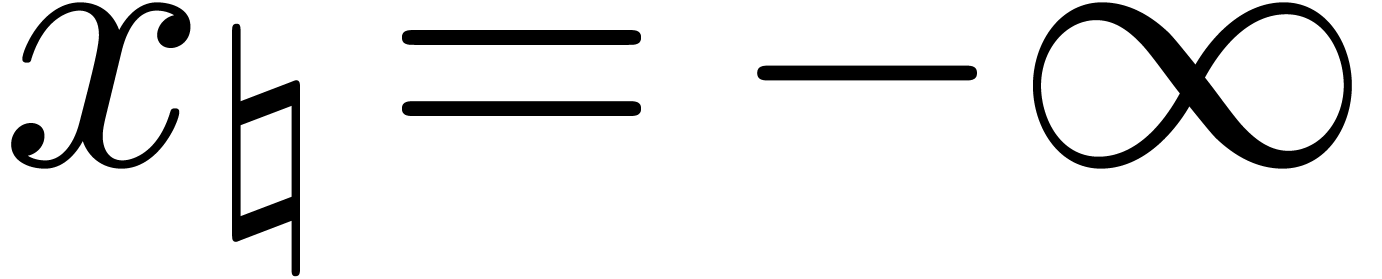 for all
for all 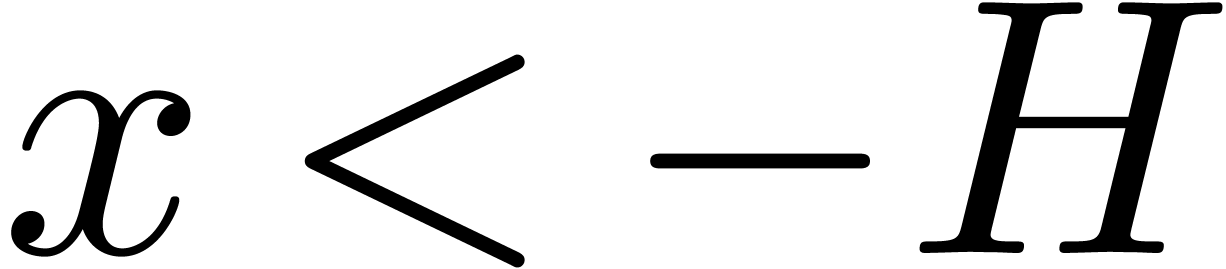 and
and 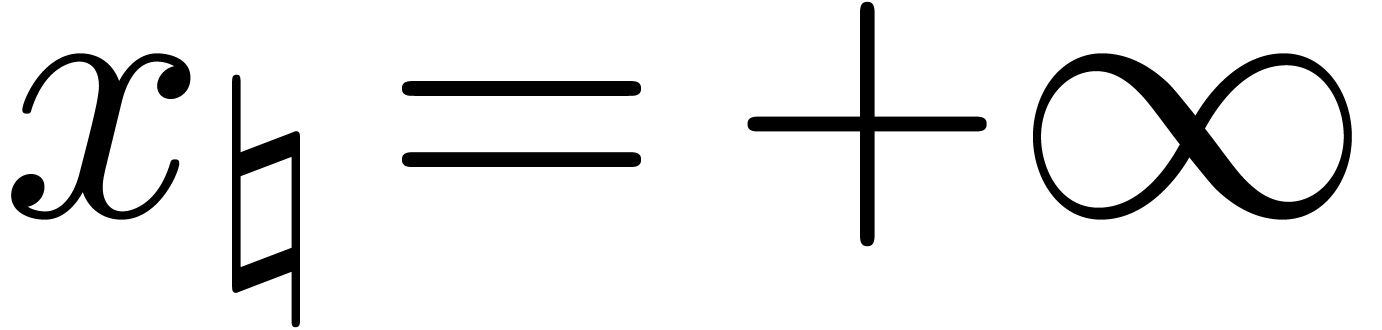 for all
for all 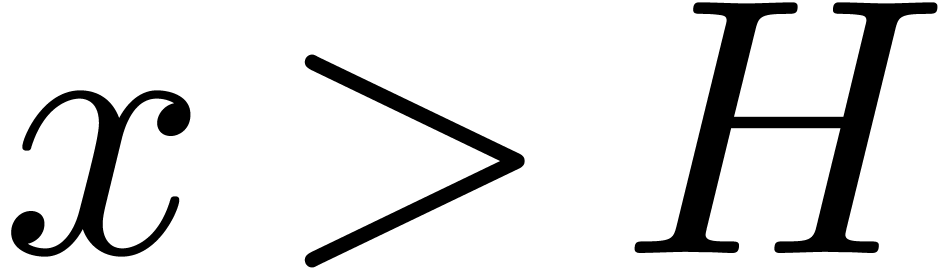 . Consequently,
whenever a computation on centers overflows, the corresponding radius
will be set to infinity.
. Consequently,
whenever a computation on centers overflows, the corresponding radius
will be set to infinity.
From now on, we assume the absence of overflows and we focus on
underflows. In addition to the constant  ,
we suppose given an other positive constant
,
we suppose given an other positive constant 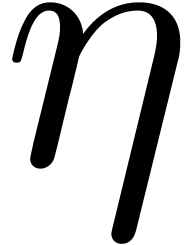 in
in
 such that
such that
for all 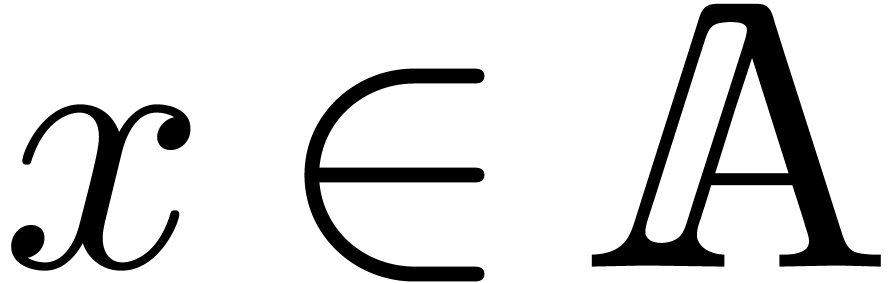 and
and 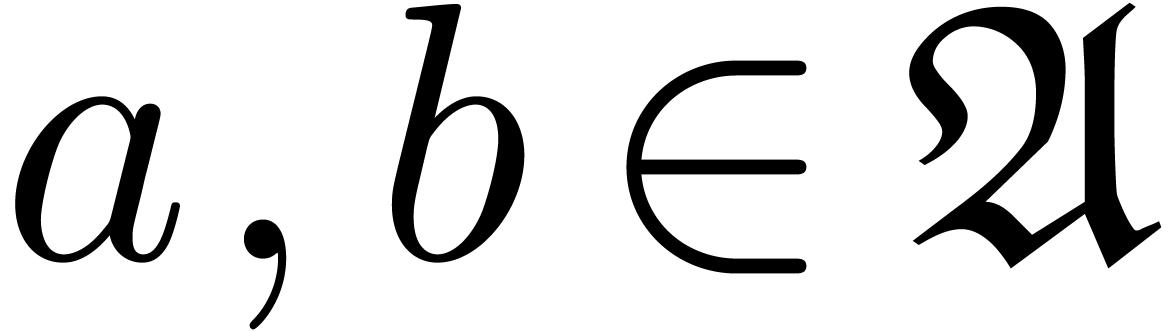 .
For instance, if
.
For instance, if 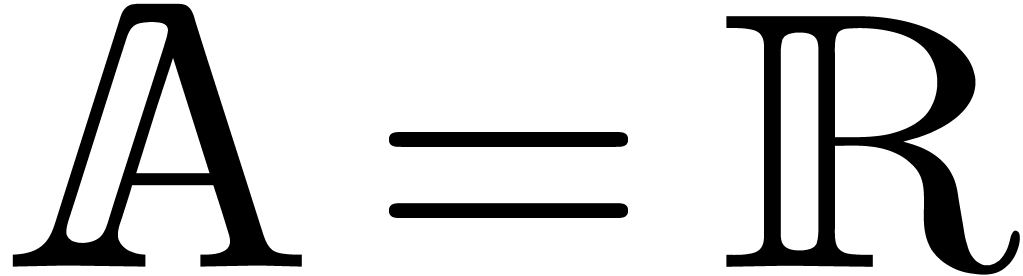 , then we
may take
, then we
may take 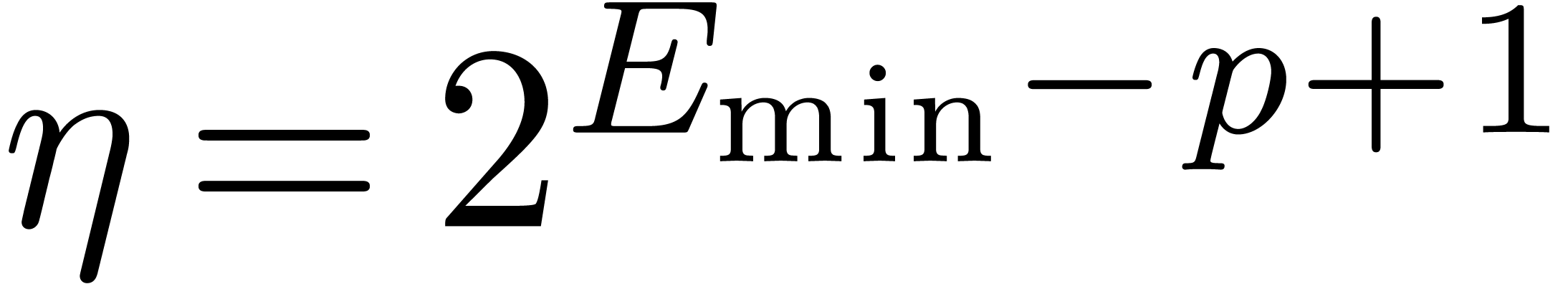 . If
. If 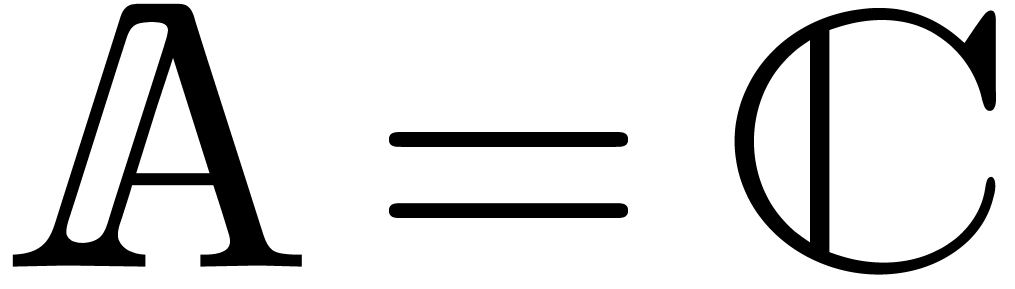 , and assuming the arithmetic from Section 2.2, then it is safe to take
, and assuming the arithmetic from Section 2.2, then it is safe to take 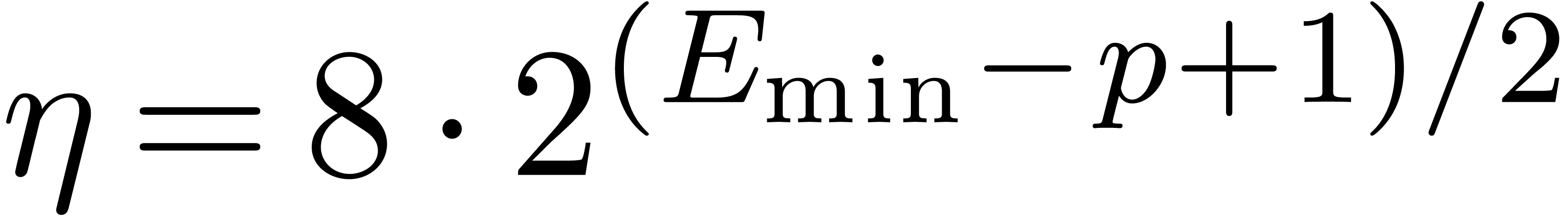 (see
Appendix A). In addition to the method based on the status
register, the following strategies can be used for managing underflows.
(see
Appendix A). In addition to the method based on the status
register, the following strategies can be used for managing underflows.
Using upward rounding for radii.
If it is possible to use different rounding modes for computations on
centers and radii, then we may round centers to the nearest and radii
upwards. In other words, we replace the transient arithmetic from
Section
2.5 by
This arithmetic makes Theorem 5 hold without the assumption
on the absence of underflows, and provided that
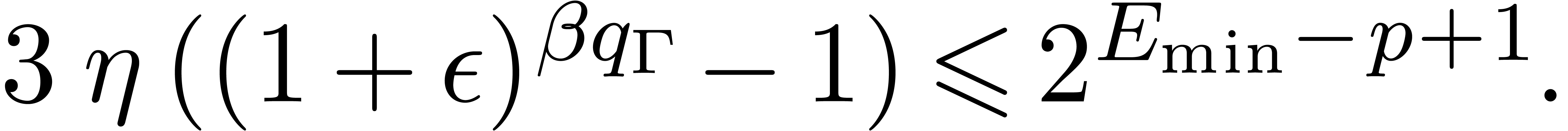 |
(13) |
Indeed, inequalities (5), (8), and (9)
immediately hold, even without extra factors  . It remains to prove that (6)
also holds. From
. It remains to prove that (6)
also holds. From  we have
we have 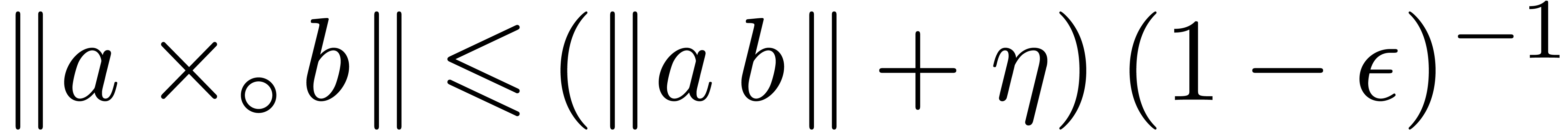 . Therefore, if
. Therefore, if 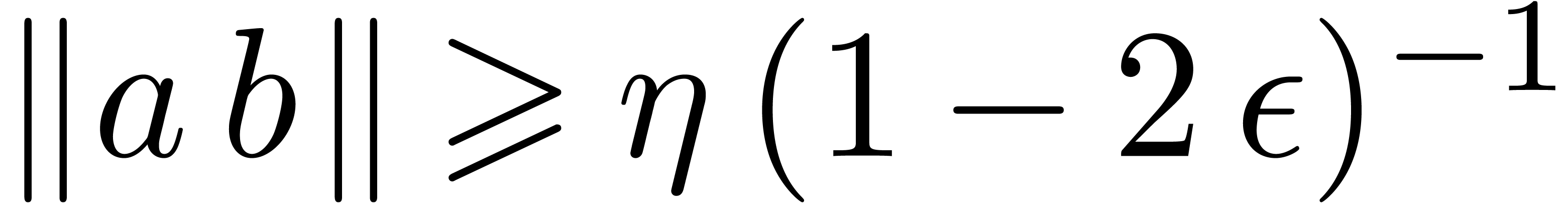 ,
then
,
then  holds, whence inequality (6). Otherwise
holds, whence inequality (6). Otherwise 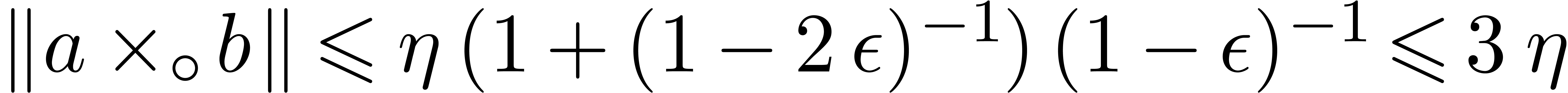 ,
and the extra assumption (13)
directly implies
,
and the extra assumption (13)
directly implies 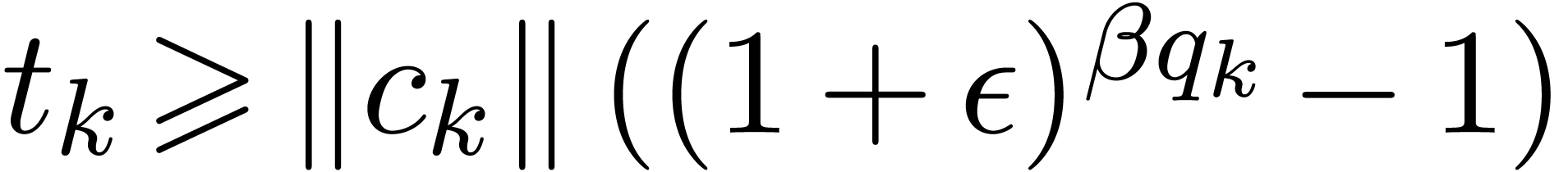 because
because 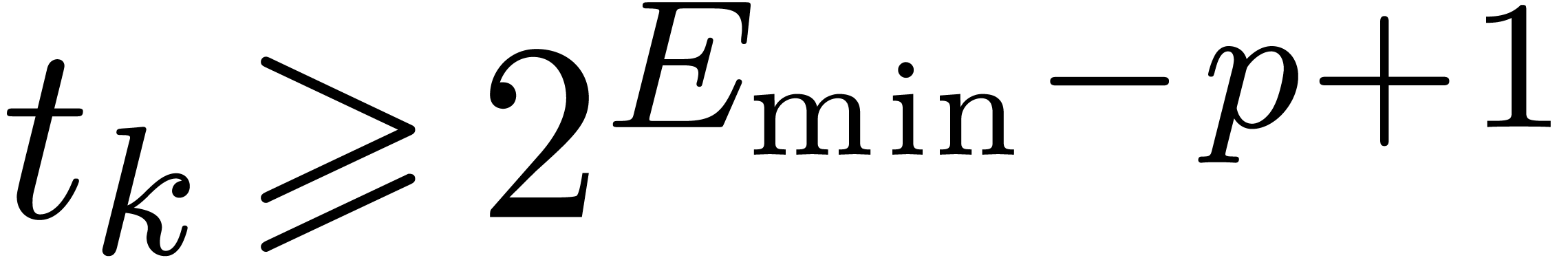 always holds by construction.
always holds by construction.
Adding corrective terms to the radii.
Another strategy is to manually counter underflows by adding
corrective terms to the radii. This yields the following arithmetic
which is half way between transient and certified:
No corrections are necessary for additions and subtractions which never
provoke underflows. As to multiplication, Lemma 3 admits
Lemma 6 below as its analogue in the case when  . Using this, it may again be shown that
Theorem 5 holds without the assumption on the absence of
underflows, and provided that
. Using this, it may again be shown that
Theorem 5 holds without the assumption on the absence of
underflows, and provided that
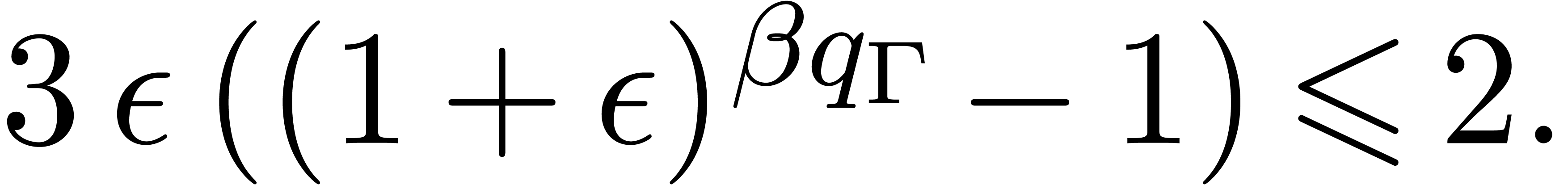 |
(14) |
Indeed, inequalities (5), (8), and (9)
immediately hold. It remains to prove that (6)
also holds. The case 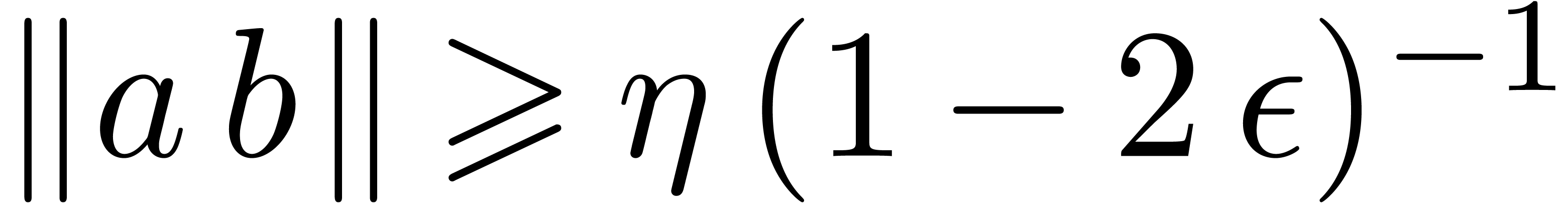 is handled as for the
previous strategy. Otherwise, we have
is handled as for the
previous strategy. Otherwise, we have 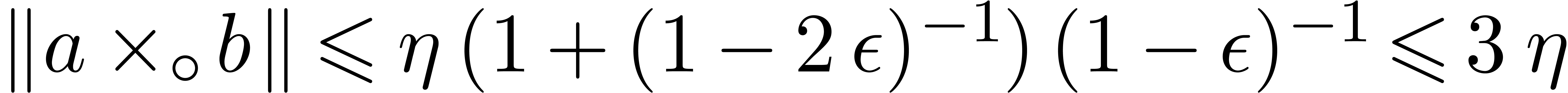 ,
and the extra assumption (14)
directly implies
,
and the extra assumption (14)
directly implies 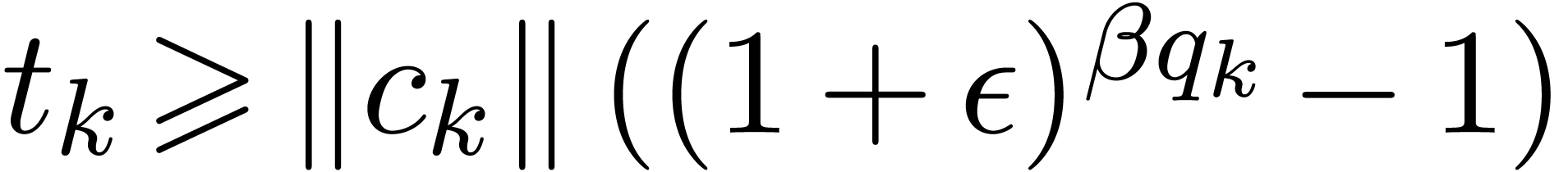 because
because 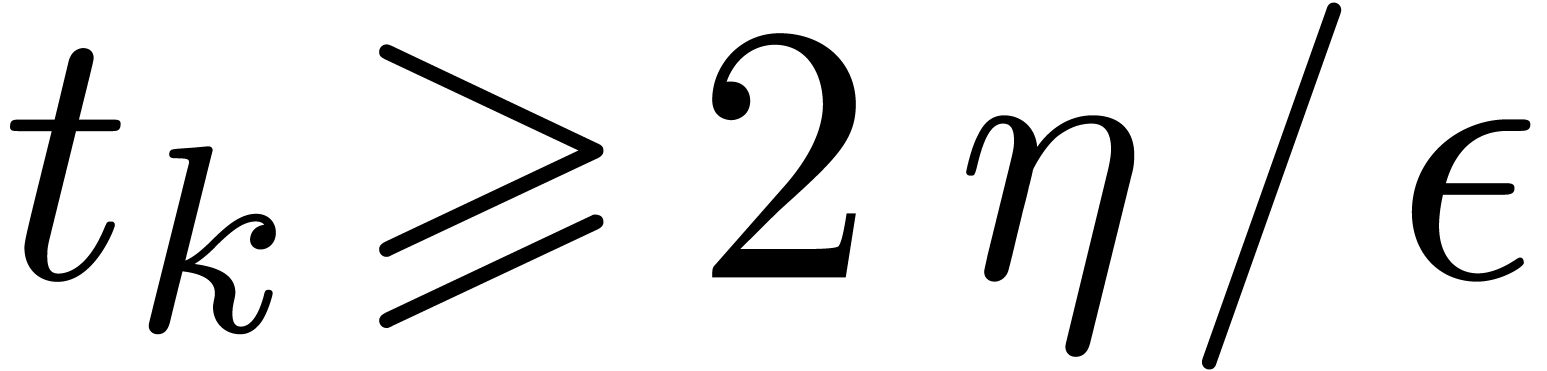 holds by construction.
holds by construction.
Lemma 6. For all
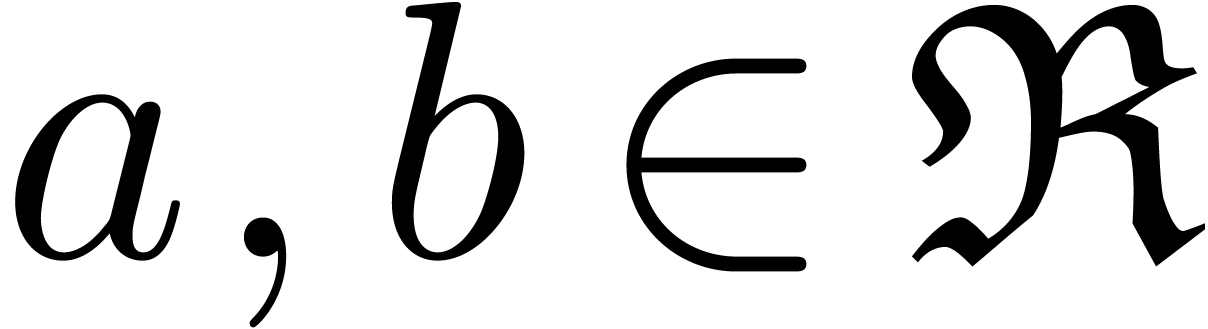 and
and  ,
letting
,
letting 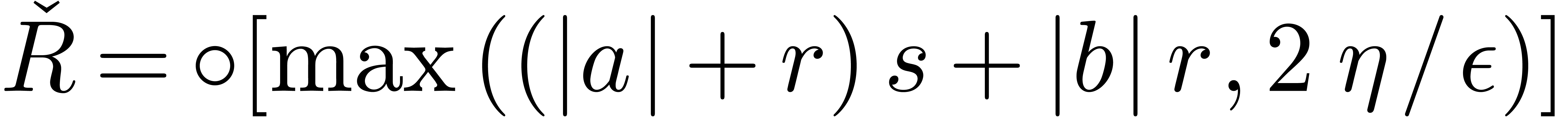 and
and 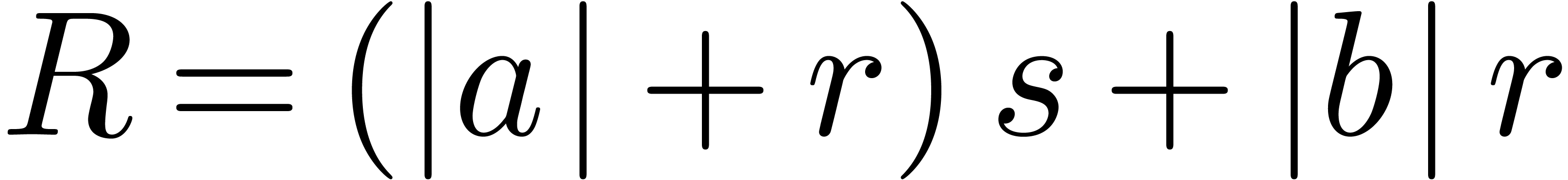 ,
we have
,
we have 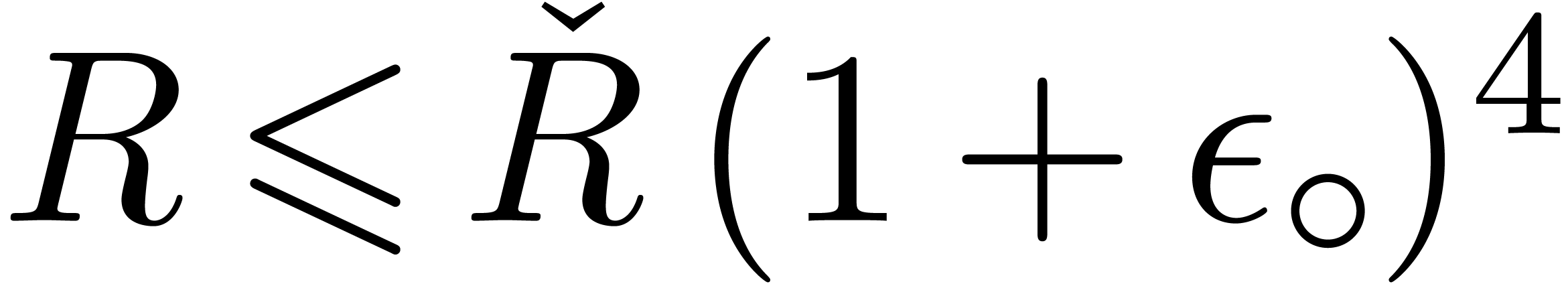 .
.
Proof. We have
It follows that 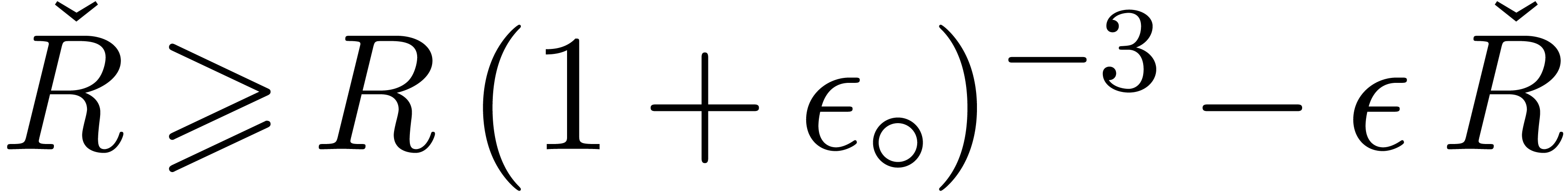 .
.
Remark 7. If 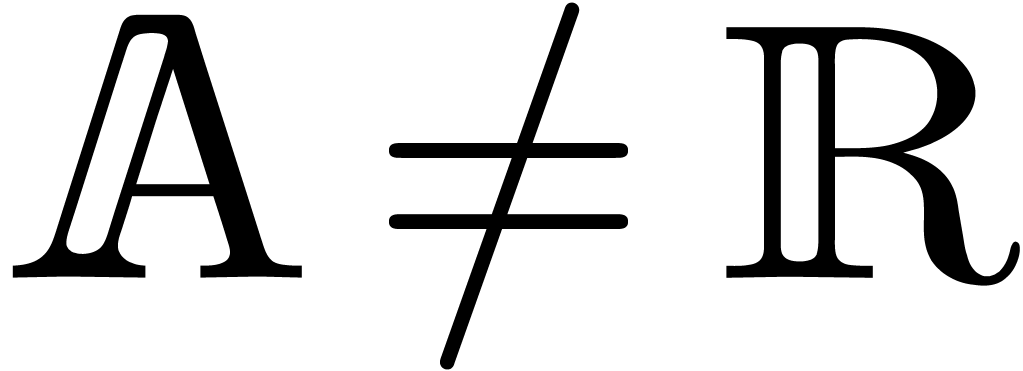 , then the above method still applies under the
condition that all norm computations are replaced by reliable upper
bounds. In other words, assuming that
, then the above method still applies under the
condition that all norm computations are replaced by reliable upper
bounds. In other words, assuming that 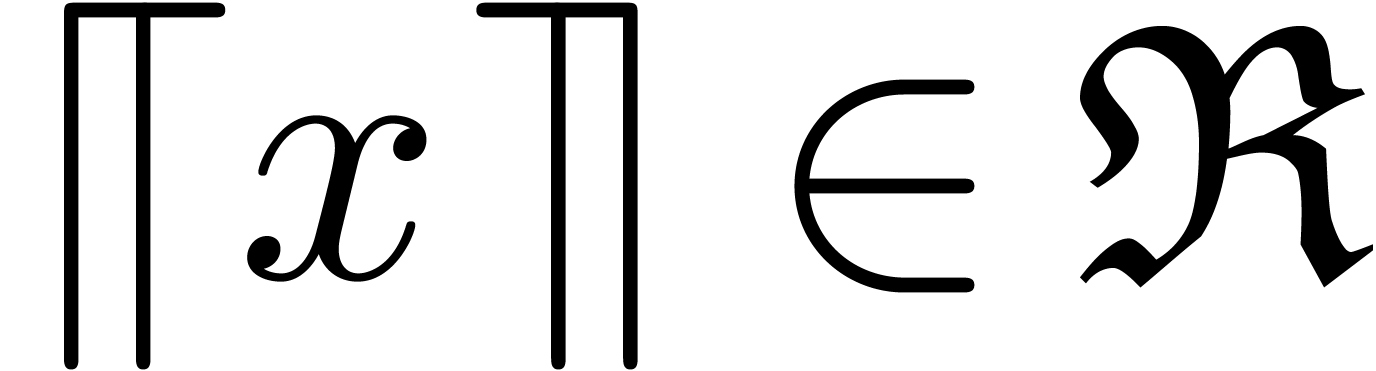 satisfies
satisfies
 for all
for all 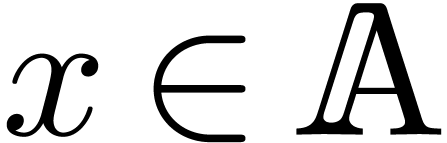 ,
we may take
,
we may take
Subnormal numbers.
On some processors, computations with subnormal numbers incur a
significant performance penalty. Such processors often support a
“fast math” mode in which subnormal numbers in input and
output are set to zero, which does not comply with the
IEEE 754 standard. For instance,
SSE and
AVX technologies include two flags in the
MXCSR control register dedicated to this purpose, namely
denormal-are-zero and
flush-to-zero. When setting
these two flags together, we must take
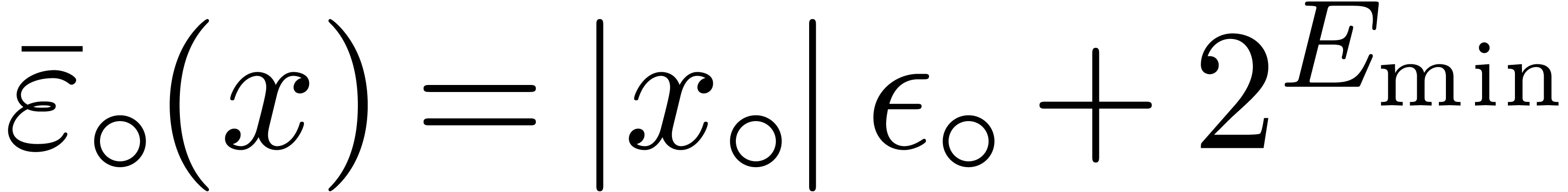
over

as a protection against this additional error,
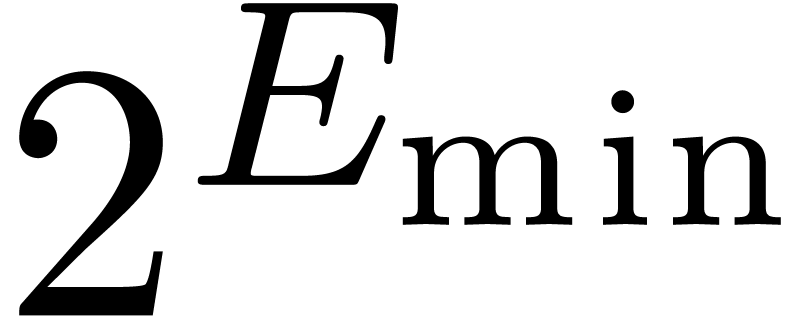
being the smallest positive normal number in
 .
. Roughly speaking, the
above strategies may be adapted by replacing
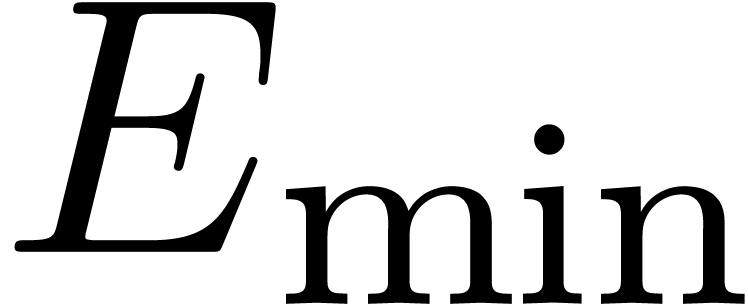
by
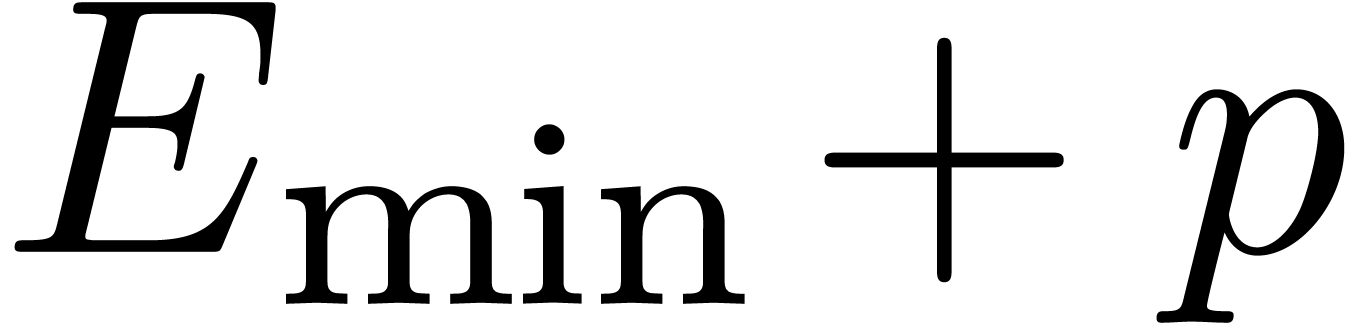
in the proofs.
IV.Implementation
Our new algorithms have been implemented in Mathemagix.
The source code, tests, and benchmark files are freely available from
the SVN server of Mathemagix
via http://gforge.inria.fr/projects/mmx/,
from revision 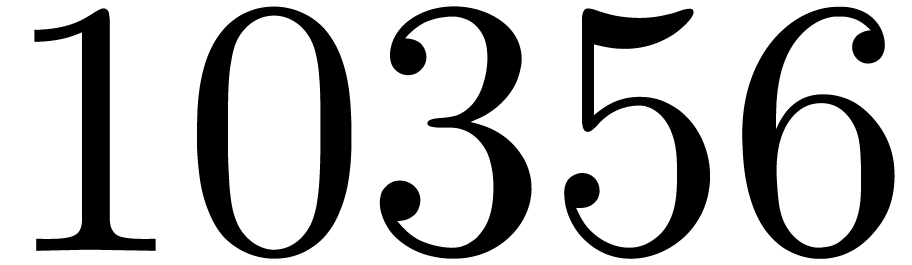 . In this
section, we briefly present our implementation. We first describe the
implemented strategies for evaluations over the standard numeric types
double and complex<double>.
We next consider balls over these types, and finally say a few words
about vectorized variants.
. In this
section, we briefly present our implementation. We first describe the
implemented strategies for evaluations over the standard numeric types
double and complex<double>.
We next consider balls over these types, and finally say a few words
about vectorized variants.
A.Software overview
Our implementation is divided into C++ and Mathemagix libraries. Import/export mechanisms between
these two languages are rather easy, as described in [7, 8]. The C++ library Multimix
contains several implementations of multivariate polynomials, including
SLPs (type slp_polynomial defined in slp_polynomial.hpp),
naive interpreted evaluation (slp_polynomial_naive.hpp),
compilation into dynamic libraries loaded via dlopen
(slp_polynomial_compiled.hpp), and fast JIT
compilation.
JIT compilation, is a classical technique, traditionally
used in scientific computing: when an expression such as a SLP needs to
be evaluated at many points, it pays off to compile the expression and
then perform the evaluations using fast executable code. When allowed by
the operating system, it suffices to compile SLPs into executable memory
regions, without temporary files. Since SLPs are very basic programs,
there is no special need to appeal to general purpose compilers. In
Multimix, such a compilation is supported for double coefficients, for SSE2 enabled
CPU, and System V amd64
application binary interface (ABI), which covers most
64-bit Unix-like platforms.
To develop a confortable JIT library dedicated to SLPs, we turned to the
Mathemagix language [8], from which
we benefit of extensible union types and fast pattern matching. Our
Runtime library provides basic facilities to
produce JIT executable code from assembly language. On the top of it,
our Justinline library defines a templated SLP
data type with additional JIT facilities. This includes common
subexpression simplification, constant simplification,
register allocation, and vectorization. Recall that
vectorization is the ability to transform a SLP over a given ring type
R to a SLP over vectors of R. This is
especially useful in order to exploit SIMD technologies.
B.Timings for numeric types
In order to estimate the concrete overhead of ball arithmetic, we first
focus on timings for double and complex<double>.
In the rest of this article, timings are measured on a platform equipped
with an Intel(R) Core(TM)
i7-4770 CPU at  GHz and 8 GB of
GHz and 8 GB of 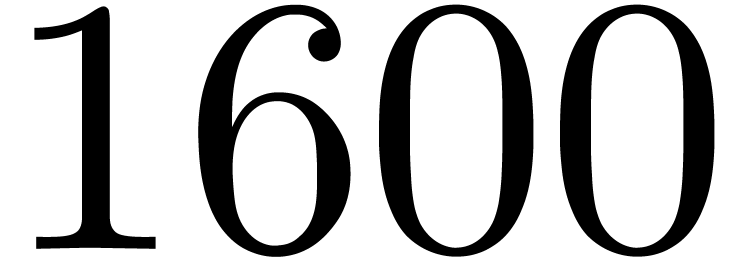 MHz DDR3, which includes
AVX2 and FMA technologies. The platform runs
the Jessie GNU Debian operating system with a 64
bit Linux kernel version 3.14. Care has been taken
for avoiding CPU throttling and Turbo Boost issues
while measuring timings. We compile with GCC [31] version 4.9.2 with options -O3 -mavx2
-mfma -mfpmath=sse.
MHz DDR3, which includes
AVX2 and FMA technologies. The platform runs
the Jessie GNU Debian operating system with a 64
bit Linux kernel version 3.14. Care has been taken
for avoiding CPU throttling and Turbo Boost issues
while measuring timings. We compile with GCC [31] version 4.9.2 with options -O3 -mavx2
-mfma -mfpmath=sse.
In Table 1, column “double”
displays timings for evaluating a multivariate polynomial over double, with 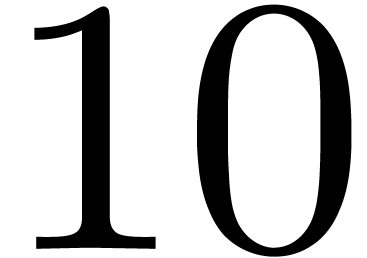 variables, made of 100
terms, built from random monomials of partial degrees at most 10. We
build the SLP using a dedicated algorithm implemented in multimix/dag_polynomial.hpp.
Support for this specific coefficient type may be found in multimix/slp_polynomial_double.hpp.
This example, with the corresponding functions to reproduce these
timings are available in multimix/bench/slp_polynomial_bench.cpp.
The evaluation of this SLP takes 1169 products and 100 sums.
variables, made of 100
terms, built from random monomials of partial degrees at most 10. We
build the SLP using a dedicated algorithm implemented in multimix/dag_polynomial.hpp.
Support for this specific coefficient type may be found in multimix/slp_polynomial_double.hpp.
This example, with the corresponding functions to reproduce these
timings are available in multimix/bench/slp_polynomial_bench.cpp.
The evaluation of this SLP takes 1169 products and 100 sums.
The first row corresponds to using the naive interpreted evaluation
available by default from Multimix. In the second
row, the SLP is printed into a C++ file, which is
then compiled into a dynamic library with options -O3
-fPIC -mavx2 -mfma -mfpmath=sse. The compilation and dynamic loading take
260ms, which corresponds to about 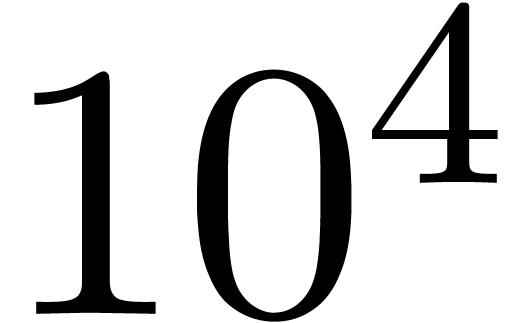 naive
evaluations.
naive
evaluations.
The third row concerns JIT compilation from Multimix,
which achieves compilation for SSE2 legacy scalar
instructions in 50μs, with no optimization and no register
allocation. Notice that this only corresponds to less than 30 naive
evaluations. However the lack of optimization implies a loss of a factor
more than two with respect to GCC.
The fourth row is for our JIT implementation in the Justinline library. Compilation performs register
allocation as sole optimization, and takes about 8ms: this is much
faster than with GCC, but still higher than in
Multimix. Nevertheless, the integration of more
powerful optimization features in the Mathemagix
compiler should progressively reduce this gap. The implementation of
additional optimizations in the Justinline library
should also make it possible to get closer to the evaluation performance
via GCC.
The second column of Table 1 shows similar timings for the
complex<double> type from the
Numerix library. We did not implement the
JIT strategy in Multimix. Of course,
the performance ratio between compiled and interpreted strategies is
much lower than for double.
|
double |
complex<double> |
| Multimix, naive |
2.1 |
3.4 |
| Multimix, compiled |
0.29 |
1.3 |
| Multimix, JIT |
0.84 |
N/A |
| Justinline, JIT |
0.43 |
1.4 |
|
|
Table 1. Polynomial evaluation with
100 terms of degree 10 in 10 variables, in μs.
|
C.Timings for balls
We are now interested in measuring the speed-up of our evaluation
strategies over balls. The first column of Table 2 shows
timings for balls over double (i.e. 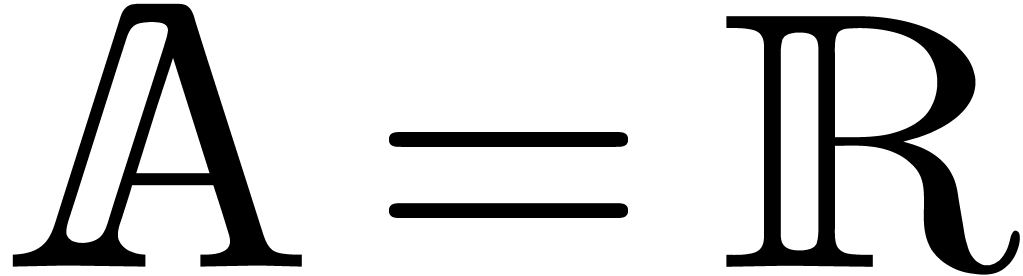 ). Early versions of the Mathemagix libraries already contained a C99
portable implementation of ball arithmetic in the Numerix
library (see numerix/ball.hpp and related files). The
first row of Table 2 is obtained with naive evaluation over
this portable arithmetic when rounding centers to the nearest and radii
upwards. We observe rather high timings involved by the compiler and the
mathematical library. The second row is similar but concerns the rough
ball arithmetic of Remark 2. The row “Naive,
transient” is the interpreted transient ball arithmetic from
Multimix. The next three rows correspond to
dynamic compilation via GCC and Justinline; they reveal the gain of the JIT
strategy.
). Early versions of the Mathemagix libraries already contained a C99
portable implementation of ball arithmetic in the Numerix
library (see numerix/ball.hpp and related files). The
first row of Table 2 is obtained with naive evaluation over
this portable arithmetic when rounding centers to the nearest and radii
upwards. We observe rather high timings involved by the compiler and the
mathematical library. The second row is similar but concerns the rough
ball arithmetic of Remark 2. The row “Naive,
transient” is the interpreted transient ball arithmetic from
Multimix. The next three rows correspond to
dynamic compilation via GCC and Justinline; they reveal the gain of the JIT
strategy.
Notice that we carefully tuned the assembly code generated by our SLP
compiler. For instance, if ymm0 contains 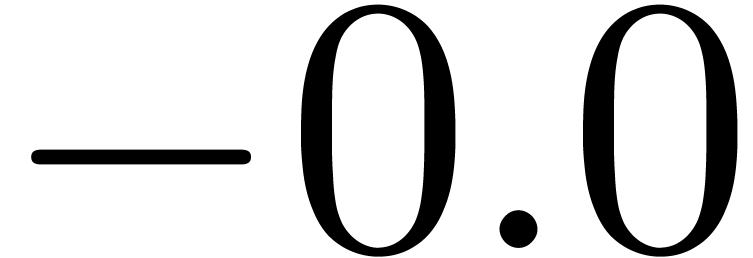 and if ymm1 contains a center
and if ymm1 contains a center  , then
, then 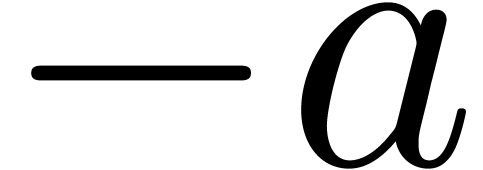 is obtained as
vxorpd ymm0 ymm1 ymm2, and
is obtained as
vxorpd ymm0 ymm1 ymm2, and  as
vandnpd ymm0 ymm1 ymm2. The latency and throughput of
both these instructions are a single cycle and no branchings are
required to compute
as
vandnpd ymm0 ymm1 ymm2. The latency and throughput of
both these instructions are a single cycle and no branchings are
required to compute  . In this
way, each transient addition/subtraction takes 2 cycles, and each
product 6 cycles. For rough arithmetic this increases to 5 and 9 cycles
respectively. The gain of the transient arithmetic is thus well
reflected in practice, since our example essentially performs products.
Comparing to Table 1, we observe that transient arithmetic
is just about 4 times slower than numeric arithmetic. This turns out to
be competitive with interval arithmetic, where each interval product
usually requires 8 machine multiplications and 6 min/max operations.
. In this
way, each transient addition/subtraction takes 2 cycles, and each
product 6 cycles. For rough arithmetic this increases to 5 and 9 cycles
respectively. The gain of the transient arithmetic is thus well
reflected in practice, since our example essentially performs products.
Comparing to Table 1, we observe that transient arithmetic
is just about 4 times slower than numeric arithmetic. This turns out to
be competitive with interval arithmetic, where each interval product
usually requires 8 machine multiplications and 6 min/max operations.
The second column of timings in Table 2 is similar to the
first one, but with balls over complex<double>.
The computation of norms is expensive in this case because the scalar
square root instruction takes 14 CPU cycles. In order to reduce this
cost, we rewrite SPLs so that norms of products are computed as products
of norms. Taking care of using or simulating upwards rounding, this
involves a slight loss in precision but does not invalidate the results.
At the end, comparing to Table 1, we are glad to observe
that our new transient arithmetic strategy is only about twice as
expensive as standard numeric evaluations.
|
Ball over
double
|
Ball over
complex<double>
|
| Naive, rounded, C99 |
62 |
130 |
| Naive, rough, C99 |
66 |
200 |
| Naive, transient |
14 |
18 |
| Compiled, transient |
2.0 |
4.0 |
| JIT, rough |
3.2 |
4.5 |
| JIT, transient |
1.8 |
3.1 |
|
|
Table 2. Polynomial evaluation with
100 terms of degree 10 in 10 variables, in μs.
|
D.Vectorization
In order to profit from SIMD technologies, we also
implemented vectorization in our Justinline
library, in the sense that the executable code runs over
SSE or AVX hardware vectors. The
expected speed-up of 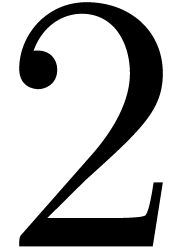 or
or  is easily observed for double, complex<double>,
and balls over double. For balls over complex<double>, a penalty occurs, because the
vectorial square root instruction is about twice slower than its scalar
counterpart. For instance, the evaluation of a univariate polynomial in
degree
is easily observed for double, complex<double>,
and balls over double. For balls over complex<double>, a penalty occurs, because the
vectorial square root instruction is about twice slower than its scalar
counterpart. For instance, the evaluation of a univariate polynomial in
degree 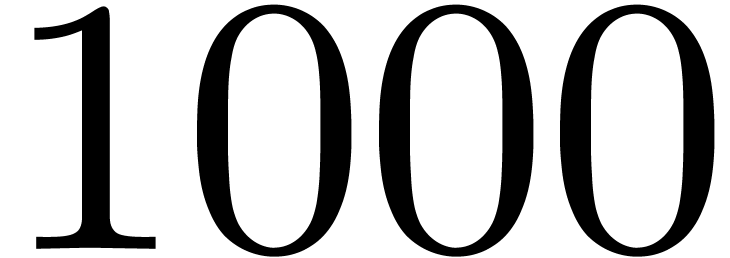 with Hörner's method takes about
5000 CPU cycles over double (each fma instruction takes
the expected latency), 13000 cycles over complex<double>,
and 16000 cycles for transient balls of double, with
both scalar and vectorial instructions. As for transient balls over complex<double>, scalar
instructions amount to about 17000 cycles, while vectorial ones take
about 28000 cycles.
with Hörner's method takes about
5000 CPU cycles over double (each fma instruction takes
the expected latency), 13000 cycles over complex<double>,
and 16000 cycles for transient balls of double, with
both scalar and vectorial instructions. As for transient balls over complex<double>, scalar
instructions amount to about 17000 cycles, while vectorial ones take
about 28000 cycles.
V.Conclusion
In this paper, we have shown how to implement highly efficient ball
arithmetic dedicated to polynomial evaluation. In the near future, we
expect significant speed-ups in our numerical system solvers implemented
within Mathemagix.
It is interesting to notice in Table 2 that the code
generated by our rather straightforward JIT compiler for SLPs is more
efficient than the code produced by GCC. This suggests that it might be
worthwhile to put more efforts into the development of specific JIT
compilers for SLPs dedicated to high performance computing.
We also plan to adapt the present results to standard intervals, that
are useful for real solving. In that case, we replace input and constant
intervals 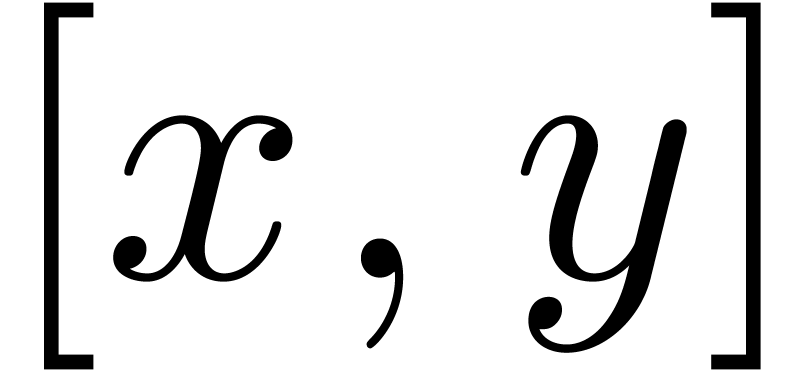 by intervals of the form
by intervals of the form 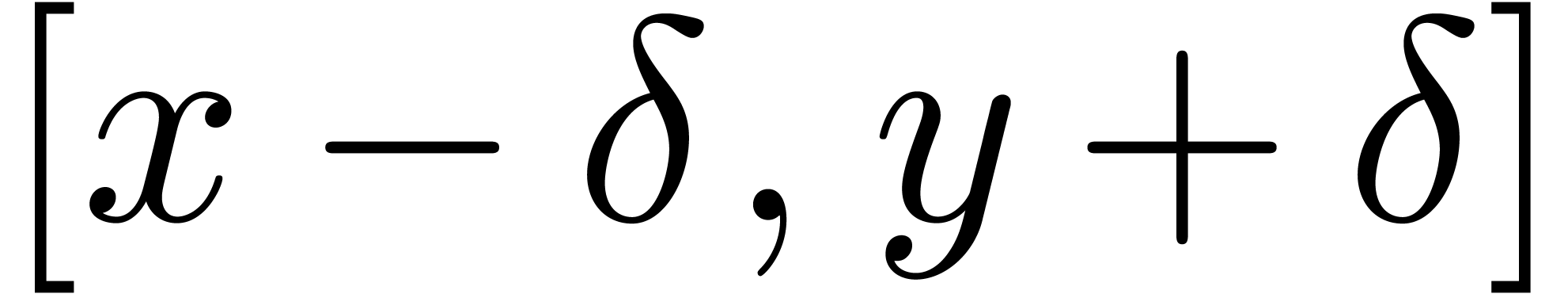 , where
, where 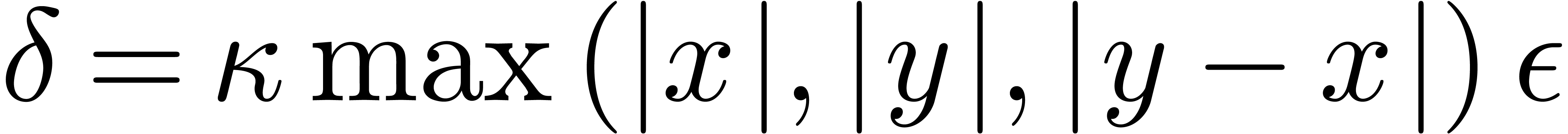 for suitable
for suitable
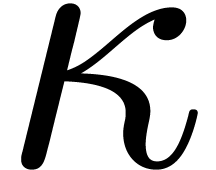 . We next proceed as usual,
but without any assumption on the rounding mode.
. We next proceed as usual,
but without any assumption on the rounding mode.
We finally notice that interval arithmetic benefits from hardware
accelerations on many current processors, as soon as IEEE 754 style
rounding is integrated in an efficient manner. An interesting question
is whether ball arithmetic might benefit from similar hardware
accelerations. In particular, is it possible to integrate rounding
errors more efficiently into error bounds (the radii of balls)? This
might for instance be achieved using an
accumulate-rounding-error instruction for computing a
guaranteed upper bound for 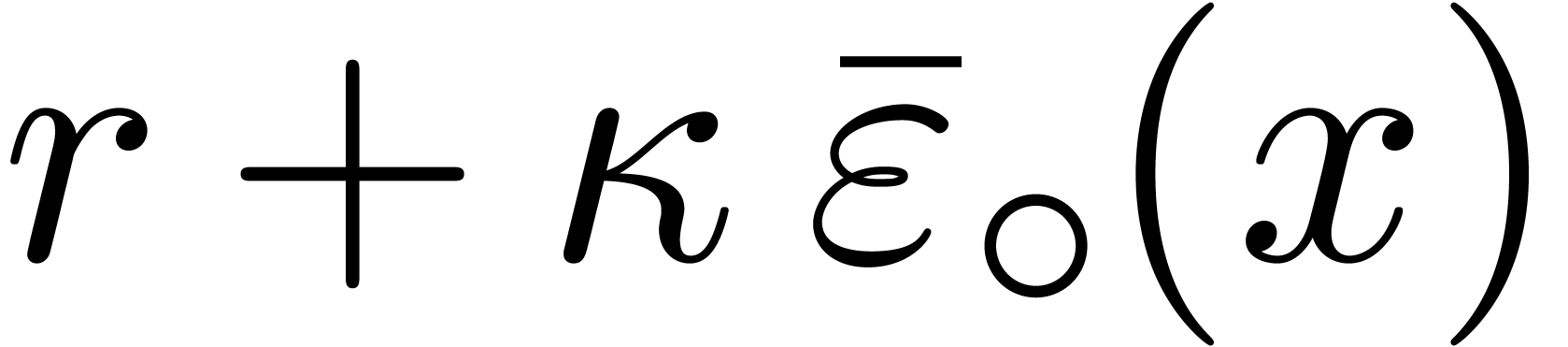 as a function of
as a function of
 .
.
Bibliography
-
[1]
-
G. Alefeld and J. Herzberger. Introduction to
interval analysis. Academic Press, New York, 1983.
-
[2]
-
D. Bates, J. Hauenstein, A. Sommese, and C. Wampler.
Bertini: software for numerical algebraic geometry. http://www.nd.edu/~sommese/bertini/,
2006.
-
[3]
-
C. Beltrán and A. Leykin. Certified numerical
homotopy tracking. Experiment. Math., 21(1):69–83,
2012.
-
[4]
-
F. Goualard. Fast and correct SIMD algorithms for
interval arithmetic. Technical Report, Université de
Nantes, 2008. https://hal.archives-ouvertes.fr/hal-00288456.
-
[5]
-
J. van der Hoeven. Ball arithmetic. In A. Beckmann,
Ch. Gaßner, and B. Löwe, editors, Logical
approaches to Barriers in Computing and Complexity, number 6
in Preprint-Reihe Mathematik, pages 179–208.
Ernst-Moritz-Arndt-Universität Greifswald, 2010.
International Workshop.
-
[6]
-
J. van der Hoeven. Reliable homotopy continuation.
Technical Report, CNRS & École polytechnique, 2011.
http://hal.archives-ouvertes.fr/hal-00589948.
-
[7]
-
J. van der Hoeven and G. Lecerf. Interfacing
Mathemagix with C++. In M. Monagan, G. Cooperman, and M.
Giesbrecht, editors, Proc. ISSAC '13, pages
363–370. ACM, 2013.
-
[8]
-
J. van der Hoeven and G. Lecerf. Mathemagix User
Guide. CNRS & École polytechnique, France, 2013.
http://hal.archives-ouvertes.fr/hal-00785549.
-
[9]
-
J. van der Hoeven, G. Lecerf, B. Mourrain et al.
Mathemagix. 2002. http://www.mathemagix.org.
-
[10]
-
L. Jaulin, M. Kieffer, O. Didrit, and E. Walter.
Applied interval analysis. Springer, London, 2001.
-
[11]
-
U. W. Kulisch. Computer Arithmetic and Validity.
Theory, Implementation, and Applications. Number 33 in
Studies in Mathematics. De Gruyter, 2008.
-
[12]
-
B. Lambov. Interval arithmetic using SSE-2. In P.
Hertling, C. M. Hoffmann, W. Luther, and N. Revol, editors,
Reliable Implementation of Real Number Algorithms: Theory and
Practice, volume 5045 of Lect. Notes Comput. Sci.,
pages 102–113. Springer Berlin Heidelberg, 2008.
-
[13]
-
R. E. Moore. Interval Analysis. Prentice Hall,
Englewood Cliffs, N.J., 1966.
-
[14]
-
R. E. Moore, R. B. Kearfott, and M. J. Cloud.
Introduction to Interval Analysis. SIAM Press, 2009.
-
[15]
-
J.-M. Muller, N. Brisebarre, F. de Dinechin, C.-P.
Jeannerod, V. Lefèvre, G. Melquiond, N. Revol, D.
Stehlé, and S. Torres. Handbook of Floating-Point
Arithmetic. Birkhäuser Boston, 2010.
-
[16]
-
Hong Diep Nguyen. Efficient algorithms for
verified scientific computing: numerical linear algebra using
interval arithmetic. PhD thesis, École Normale
Supérieure de Lyon, Université de Lyon, 2011.
-
[17]
-
A. Neumaier. Interval methods for systems of
equations. Cambridge university press, Cambridge, 1990.
-
[18]
-
T. Ogita and S. Oishi. Fast inclusion of interval
matrix multiplication. Reliab. Comput.,
11(3):191–205, 2005.
-
[19]
-
K. Ozaki, T. Ogita, and S. Oishi. Tight and efficient
enclosure of matrix multiplication by using optimized BLAS.
Numer. Linear Algebra Appl., 18:237–248, 2011.
-
[20]
-
K. Ozaki, T. Ogita, S. M. Rump, and S. Oishi. Fast
algorithms for floating-point interval matrix multiplication.
J. Comput. Appl. Math., 236(7):1795–1814, 2012.
-
[21]
-
N. Revol and Ph. Théveny. Parallel
implementation of interval matrix multiplication. Reliab.
Comput., 19(1):91–106, 2013.
-
[22]
-
N. Revol and Ph. Théveny. Numerical
reproducibility and parallel computations: issues for interval
algorithms. IEEE Trans. Comput., 63(8):1915–1924,
2014.
-
[23]
-
S. M. Rump. Fast and parallel interval arithmetic.
BIT, 39(3):534–554, 1999.
-
[24]
-
S. M. Rump. Verification methods: rigorous results
using floating-point arithmetic. Acta Numer.,
19:287–449, 2010.
-
[25]
-
S. M. Rump. Fast interval matrix multiplication.
Numer. Algor., 61(1):1–34, 2012.
-
[26]
-
N. Stolte. Arbitrary 3D resolution discrete ray
tracing of implicit surfaces. In E. Andres, G. Damiand, and P.
Lienhardt, editors, Discrete Geometry for Computer
Imagery, volume 3429 of Lect. Notes Comput. Sci.,
pages 414–426. Springer Berlin Heidelberg, 2005.
-
[27]
-
A. J. Sommese and C. W. Wampler. The Numerical
Solution of Systems of Polynomials Arising in Engineering and
Science. World Scientific, 2005.
-
[28]
-
J. Verschelde. Homotopy continuation methods for
solving polynomial systems. PhD thesis, Katholieke
Universiteit Leuven, 1996.
-
[29]
-
J. Verschelde. PHCpack: a general-purpose solver for
polynomial systems by homotopy continuation. ACM Trans. Math.
Software, 25(2):251–276, 1999. Algorithm 795.
-
[30]
-
J. W. Von Gudenberg. Interval arithmetic on
multimedia architectures. Reliab. Comput.,
8(4):307–312, 2002.
-
[31]
-
GCC, the GNU Compiler Collection. Software available
at http://gcc.gnu.org, from 1987.
Appendix A.Rounding errors for complex
arithmetic
Let 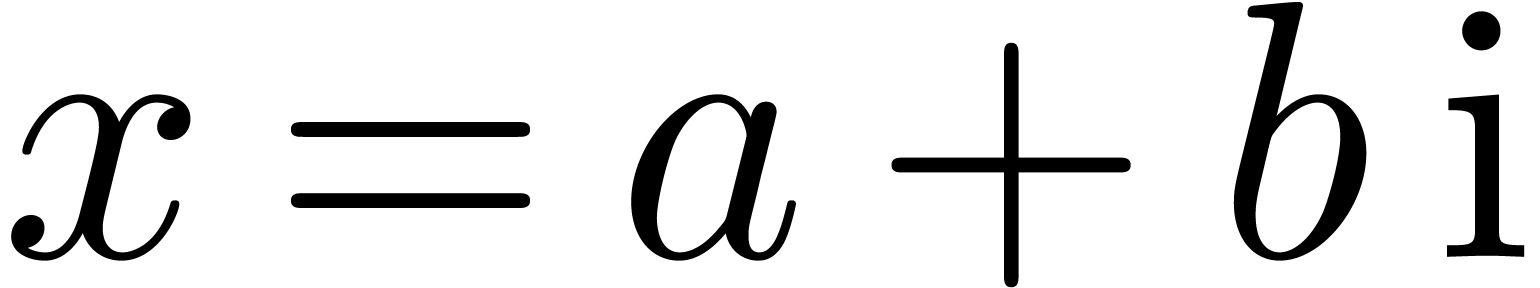 and
and 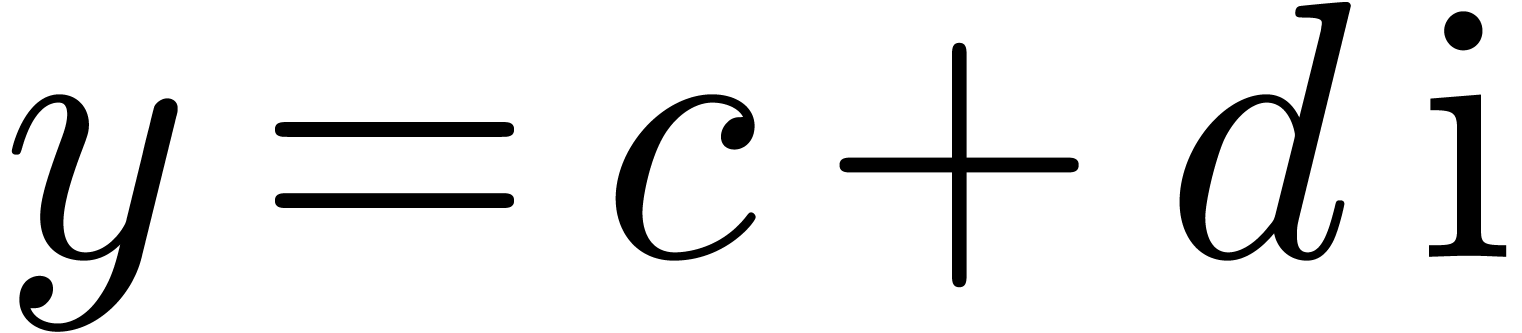 be
two complex numbers in
be
two complex numbers in  . We
will show that
. We
will show that
 |
(15) |
 |
(16) |
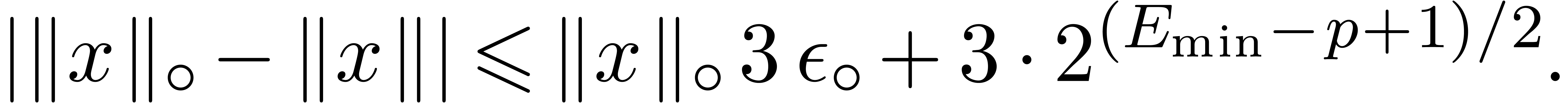 |
(17) |
In addition, in absence of underflows, the terms in 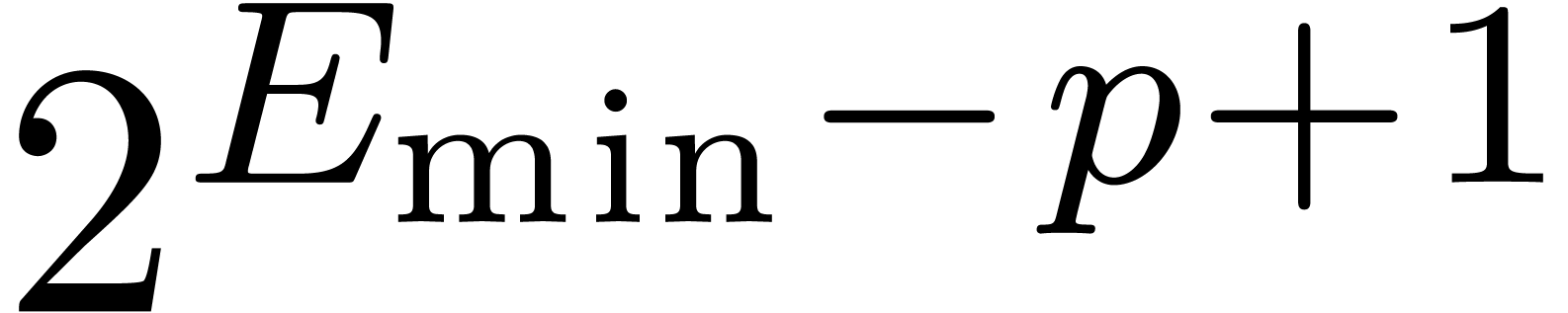 may be discarded.
may be discarded.
For short we set 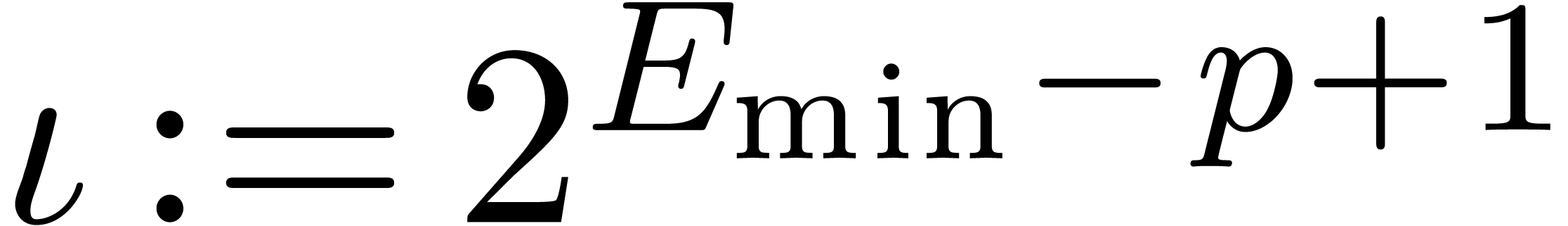 , and we
shall freely use the assumption
, and we
shall freely use the assumption 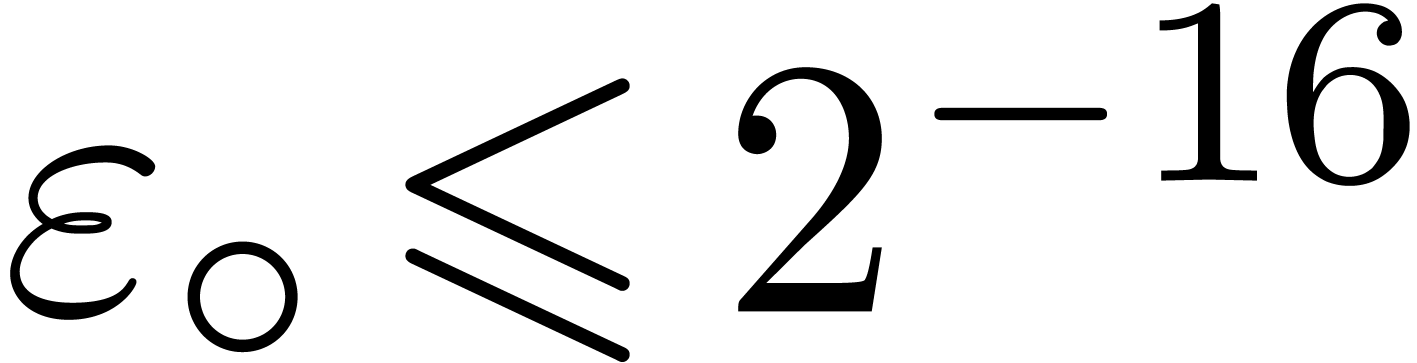 .
The first bound (15) is immediate. As
for the second one, it will be convenient to use the norm
.
The first bound (15) is immediate. As
for the second one, it will be convenient to use the norm 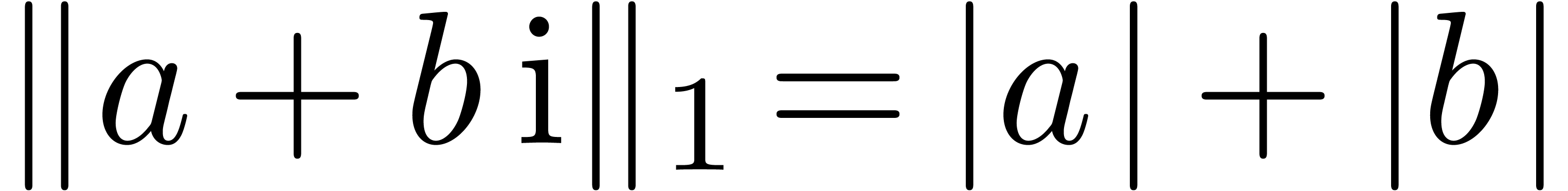 , that satisfies
, that satisfies 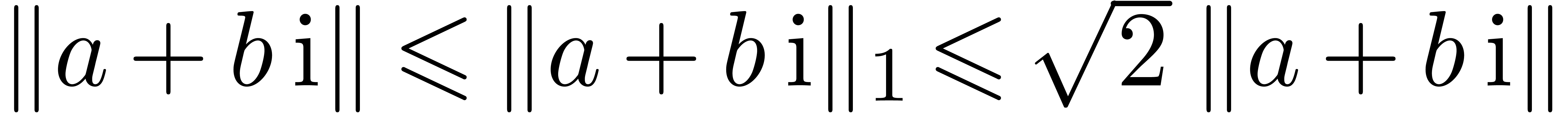 .
We begin with combining
.
We begin with combining
and
into

We deduce that
whence
which simplifies into

It follows that
which simplifies into (16).
As to (17), we begin with 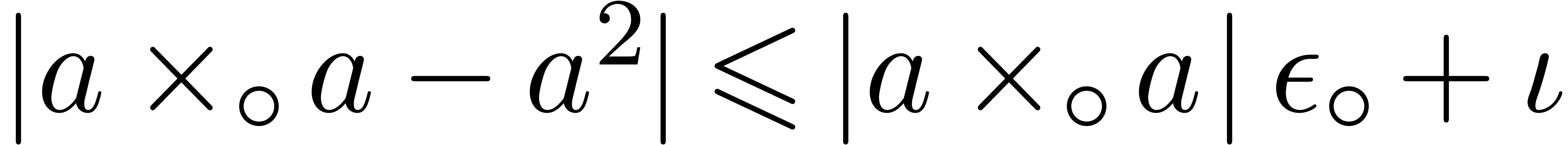 and
and  , that give
, that give
It follows that
from which we extract
We thus obtain that
We distinguish the two following cases:
 the set of machine floating point numbers. We let
the set of machine floating point numbers. We let  be the machine precision (which corresponds to the number of fractional
bits of the mantissa plus one), and let
be the machine precision (which corresponds to the number of fractional
bits of the mantissa plus one), and let 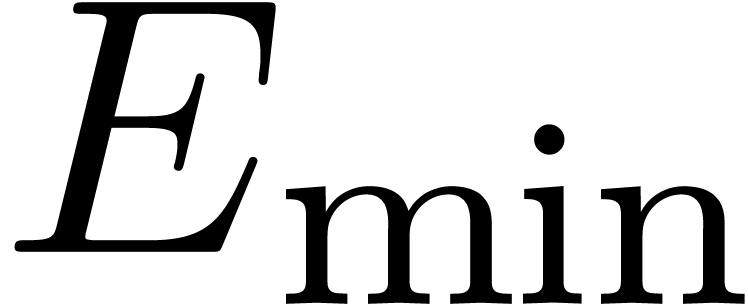 and
and 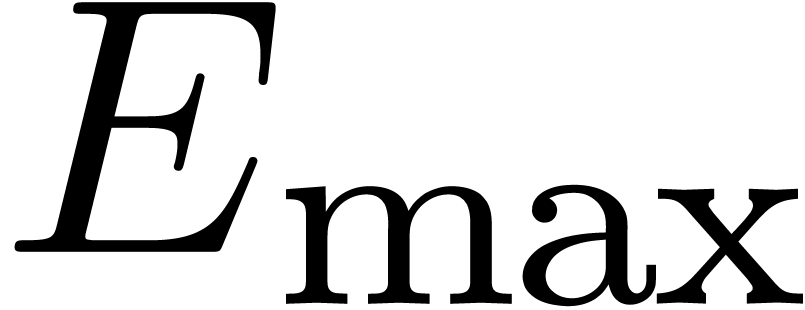 be the minimal and maximal exponents (included). For
IEEE 754 double precision numbers, this means that
be the minimal and maximal exponents (included). For
IEEE 754 double precision numbers, this means that 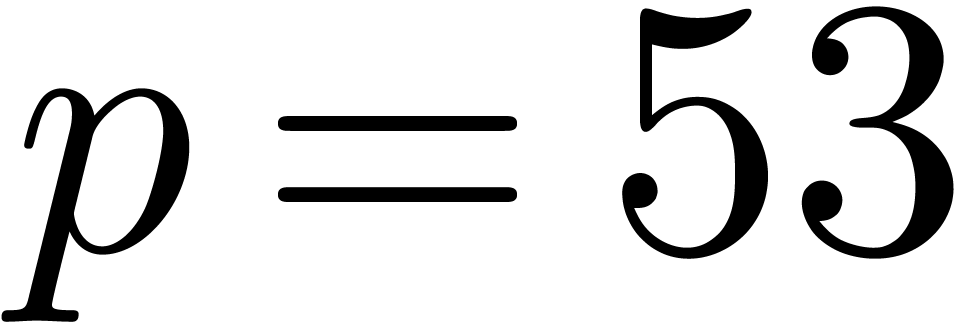 ,
, 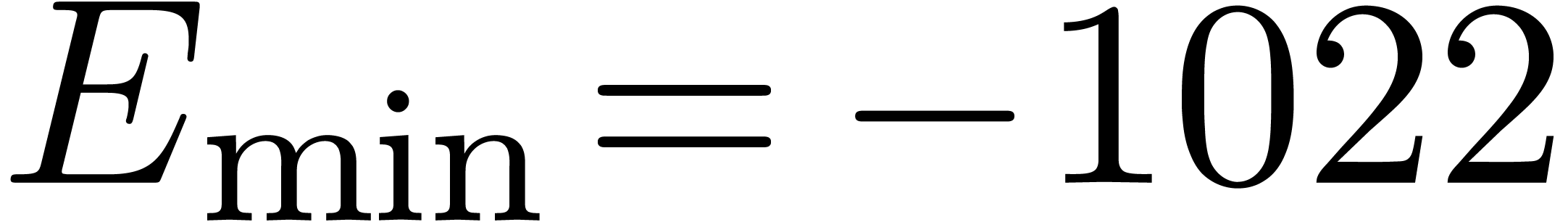 and
and 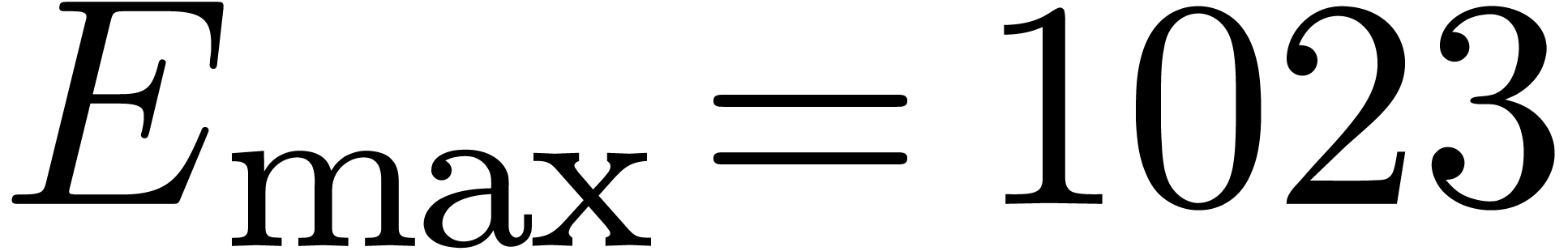 . We enlarge
. We enlarge  with symbols
with symbols  ,
, 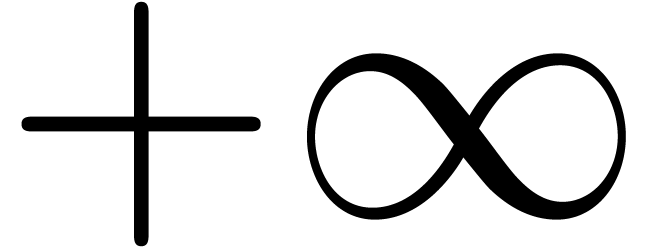 , and
, and  ,
with their standard meaning.
,
with their standard meaning.
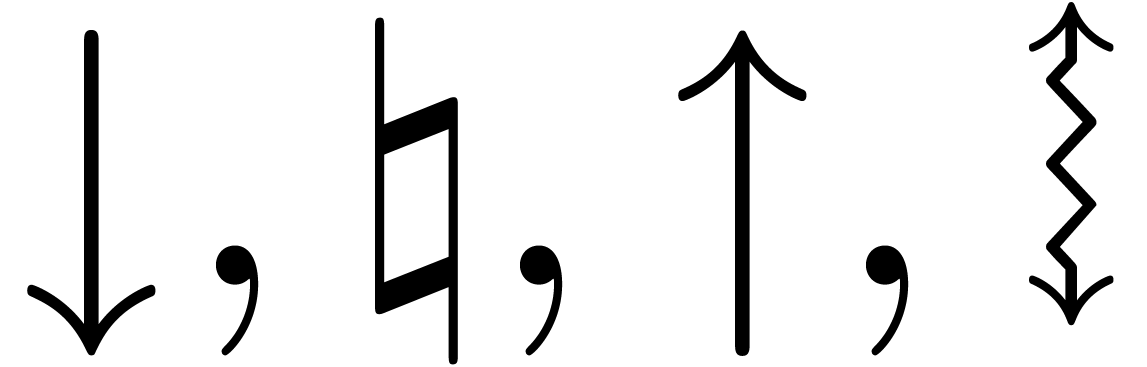 .
. corresponds to faithful rounding
without any well specified direction. For
corresponds to faithful rounding
without any well specified direction. For 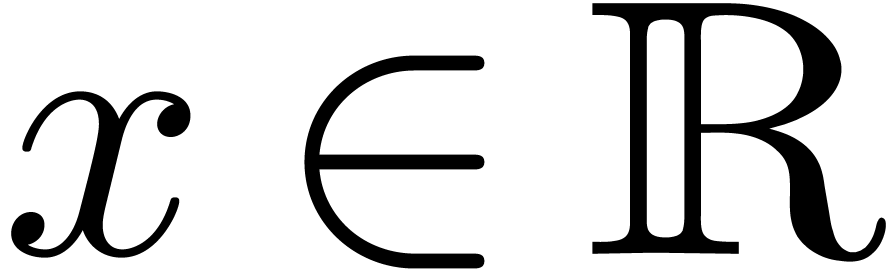 ,
, for the approximation of
for the approximation of  in
in  .
.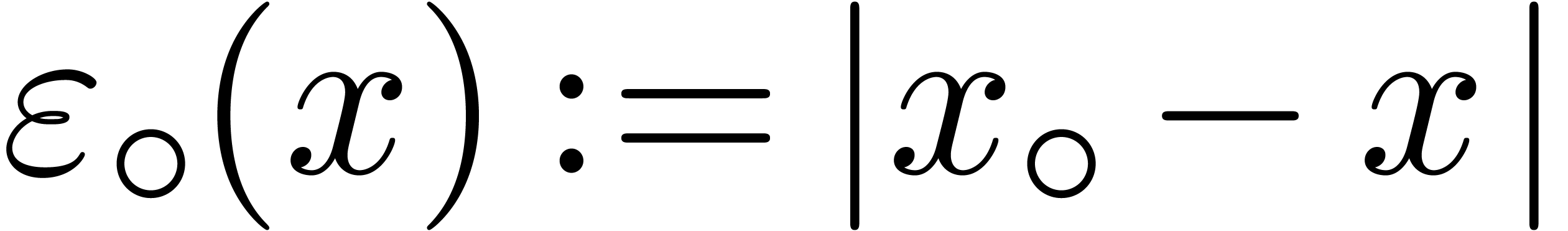 stands for the corresponding rounding error, that may be
stands for the corresponding rounding error, that may be
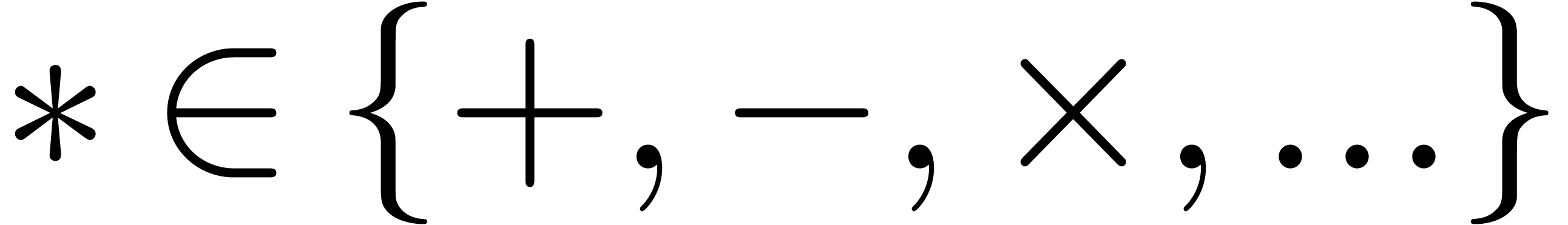 ,
, for
for  .
. ,
,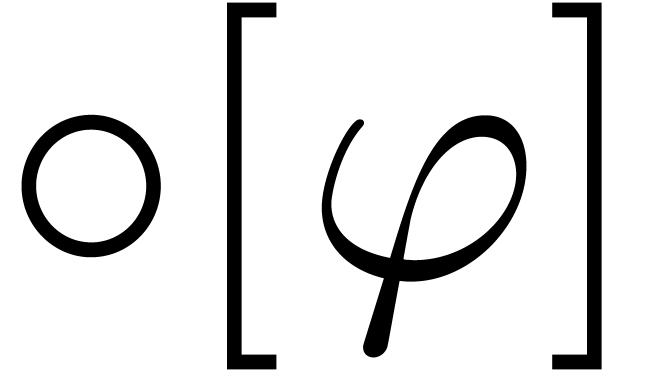 for the full evaluation of
for the full evaluation of  .
.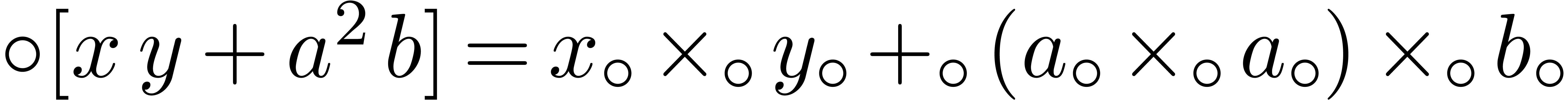 .
.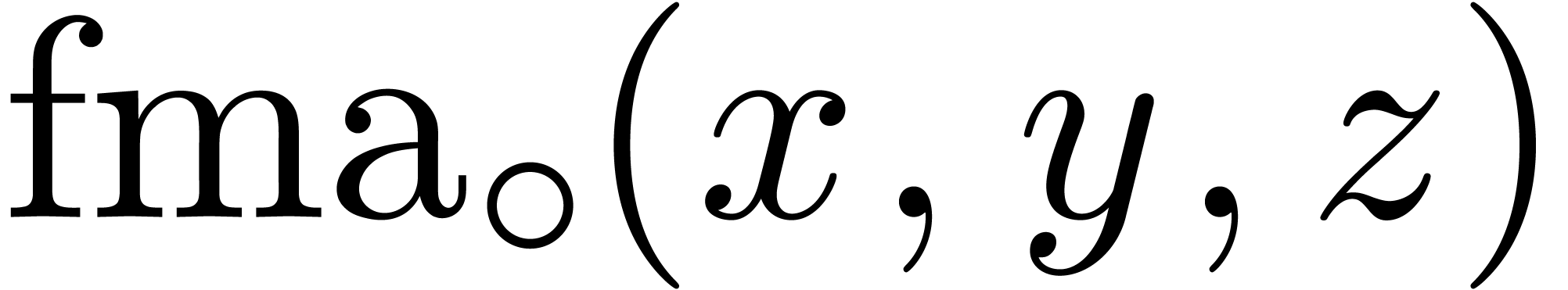 and
and 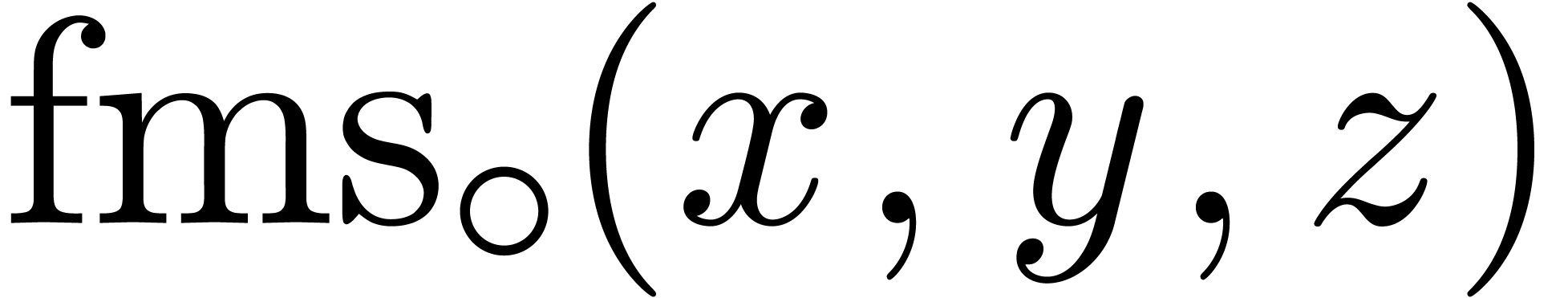 represent the roundings of
represent the roundings of 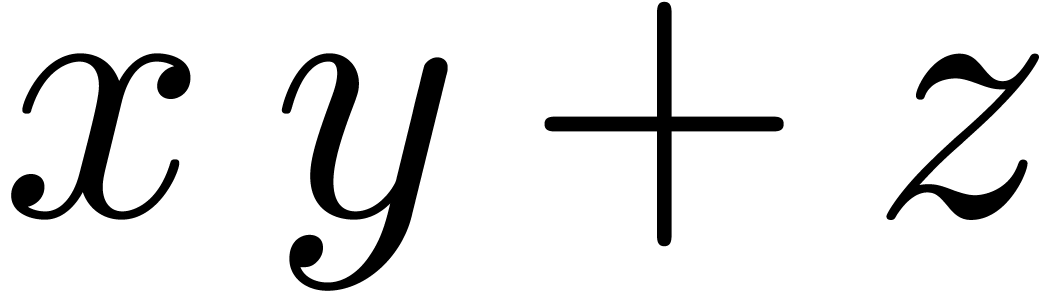 and
and
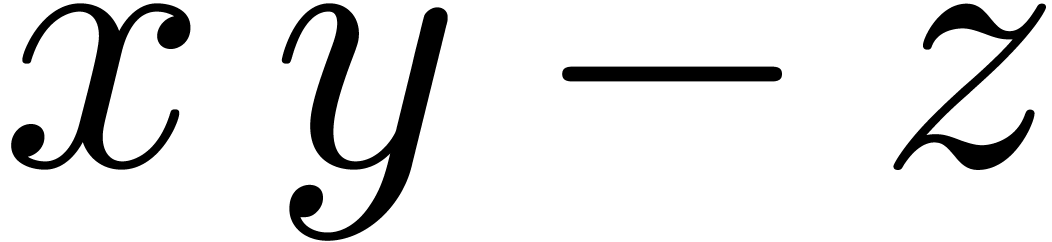 according to the mode
according to the mode 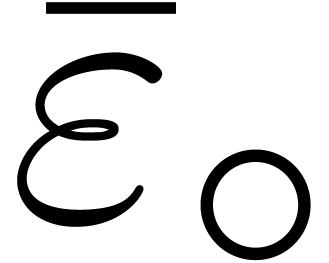 any upper bound function for
any upper bound function for
 that is easy to compute. In absence of
underflows/overflows, we claim that we may take
that is easy to compute. In absence of
underflows/overflows, we claim that we may take 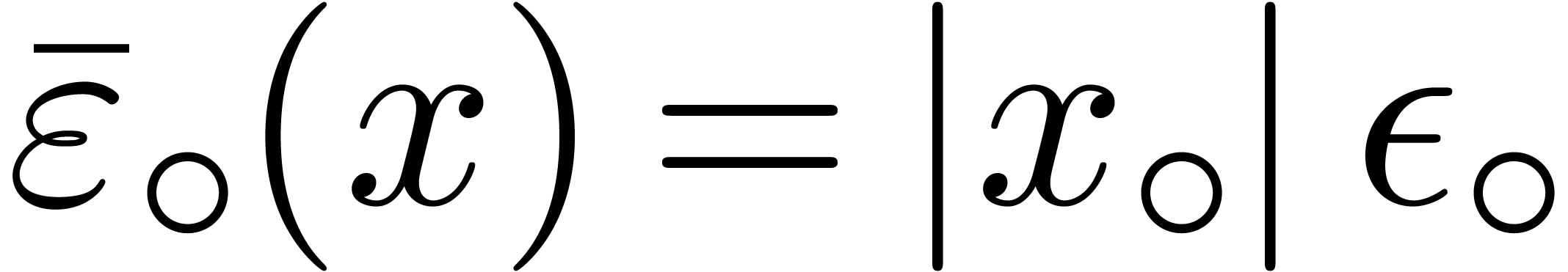 ,
,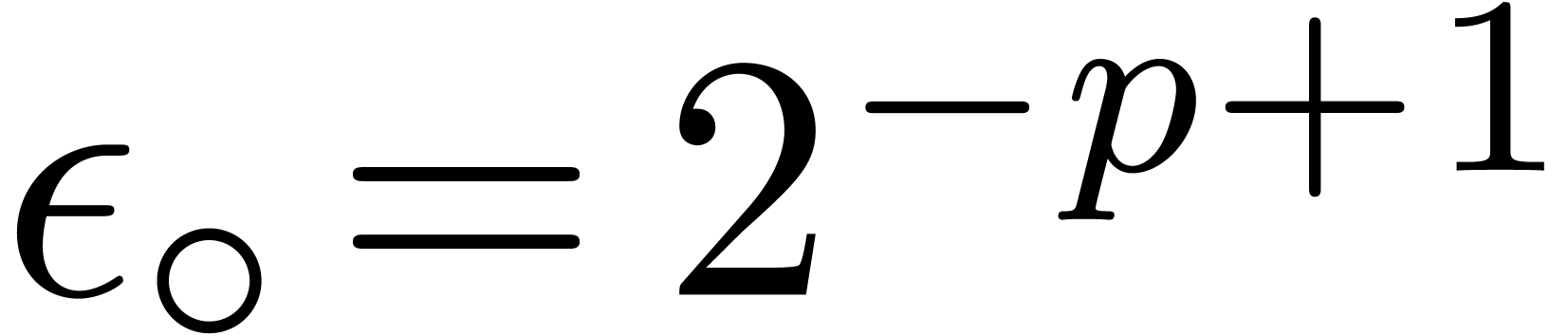 for
for  and
and 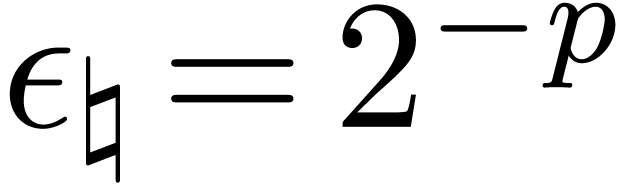 .
. and
and 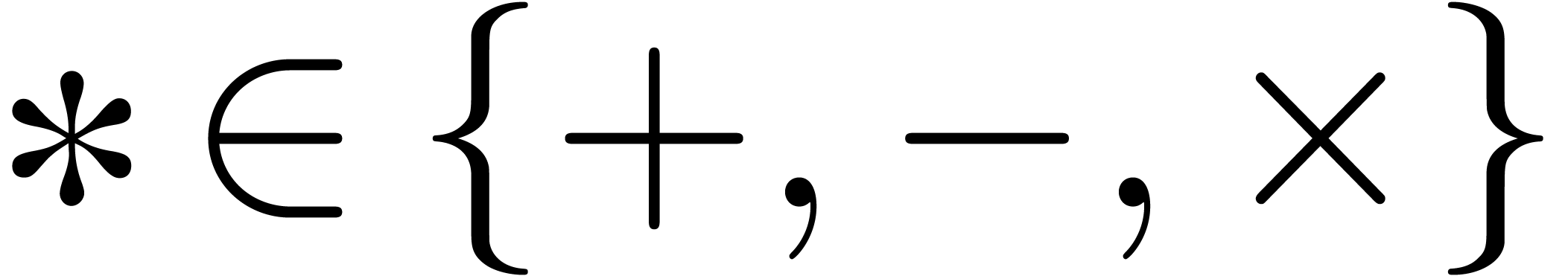 ,
, be the exponent of
be the exponent of 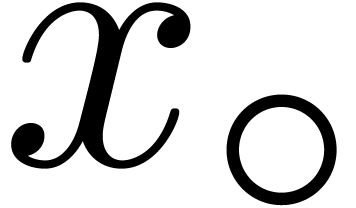 ,
,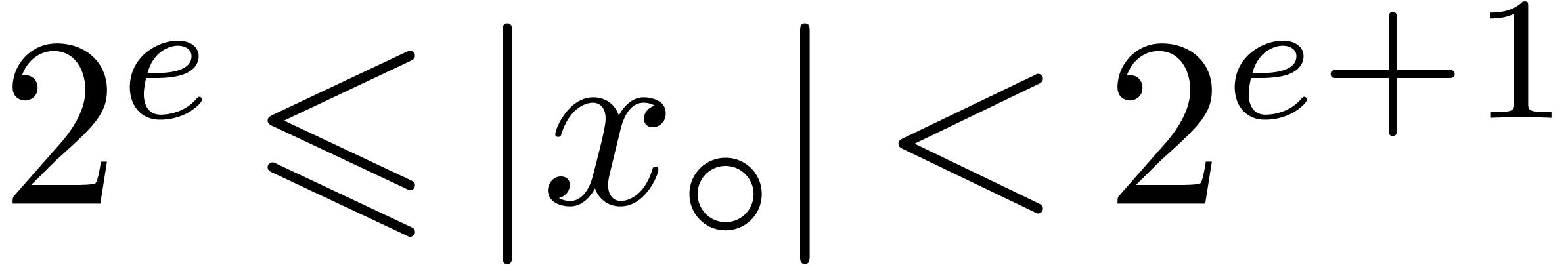 and
and 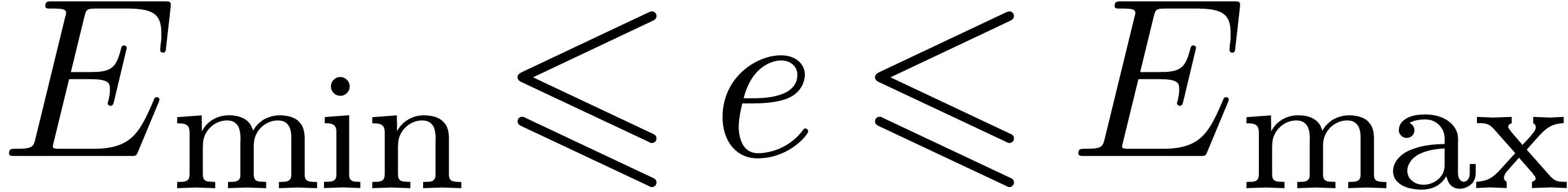 .
.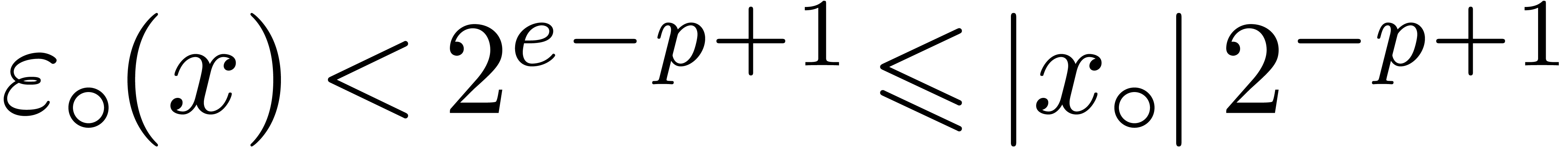 for all rounding modes, and
for all rounding modes, and 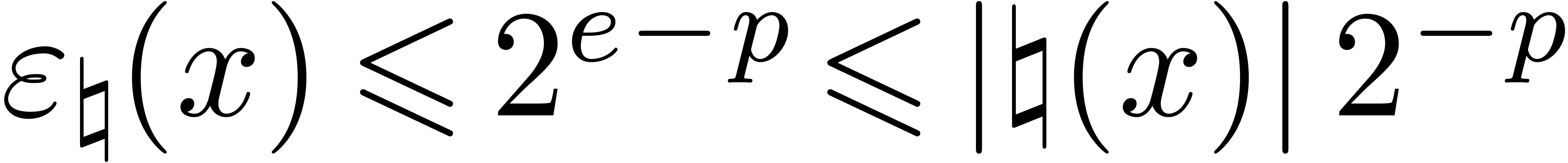 .
.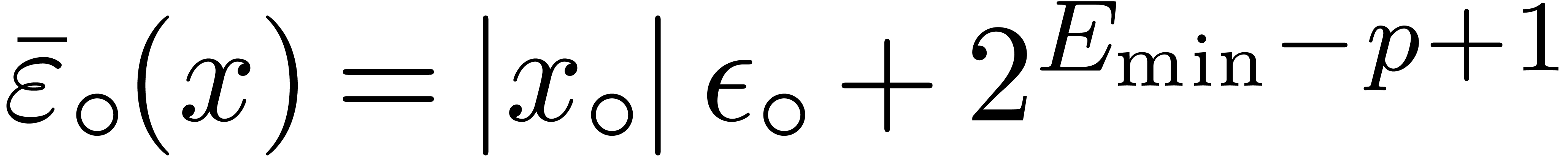 ,
,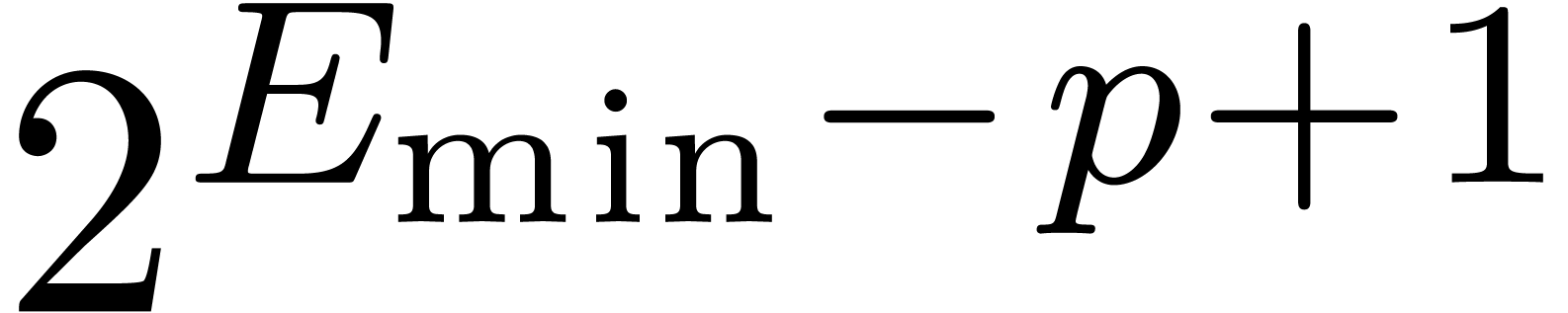 is the smallest positive subnormal number in
is the smallest positive subnormal number in 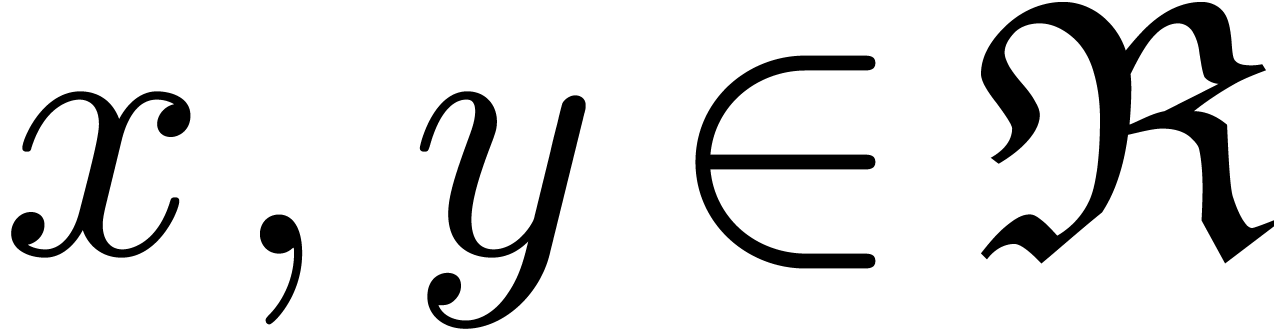 ,
,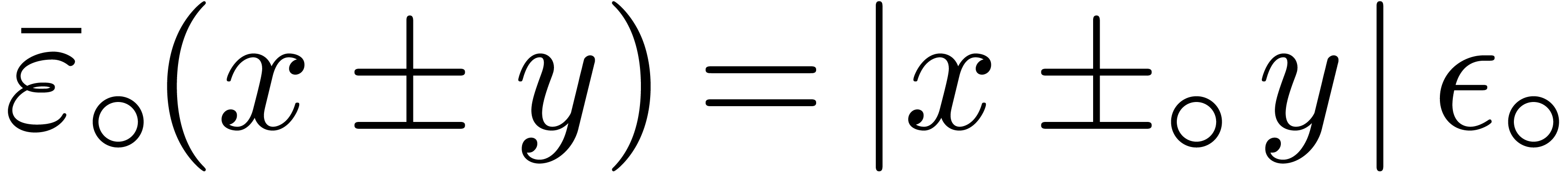 since no underflow occurs
in that special case. Underflows and overflows will be further discussed
in Section
since no underflow occurs
in that special case. Underflows and overflows will be further discussed
in Section  denotes a Banach algebra over
denotes a Banach algebra over  ,
, .
.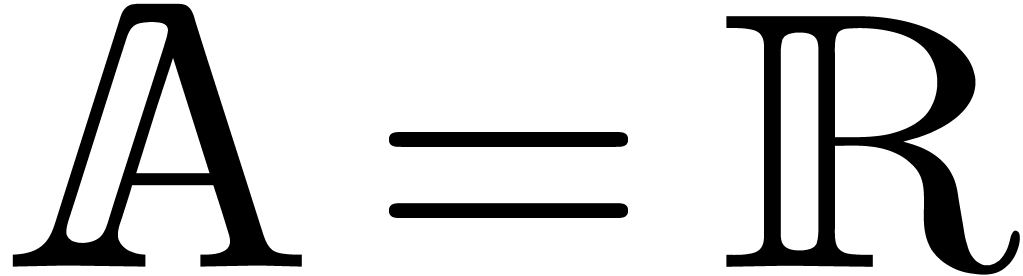 and
and 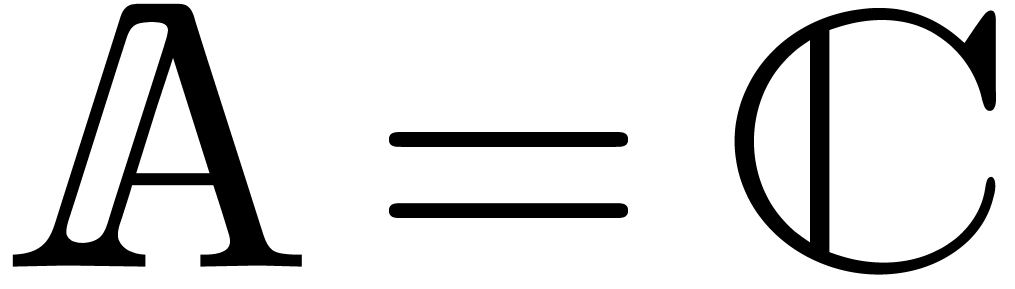 with
with 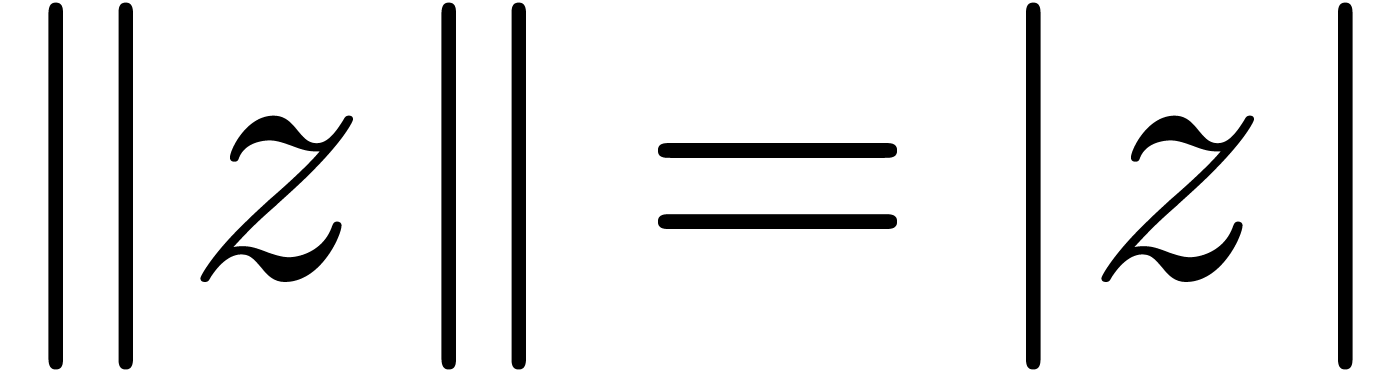 for all
for all 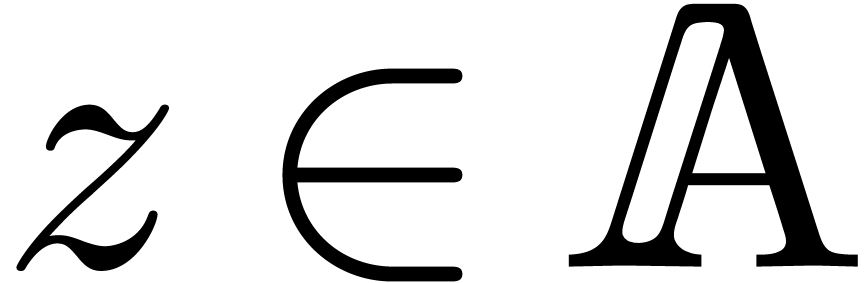 .
. the counterpart of
the counterpart of 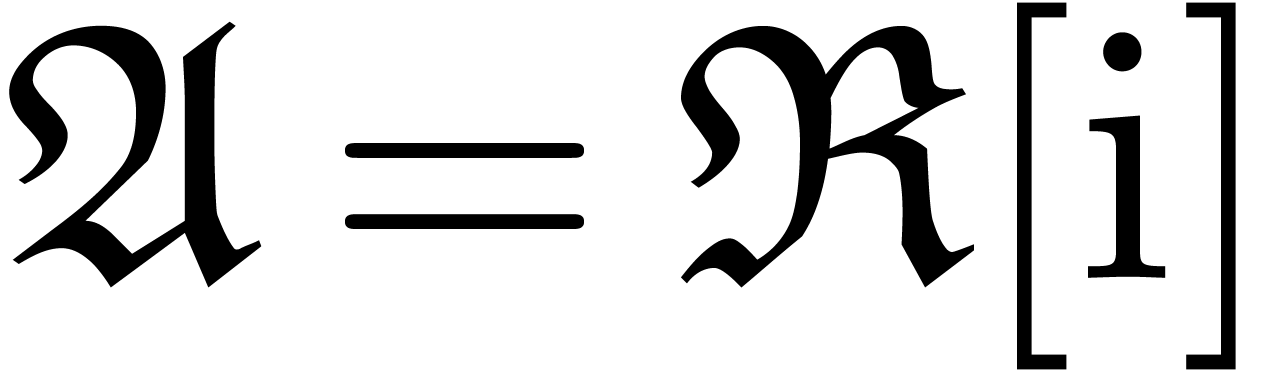 .
. ,
,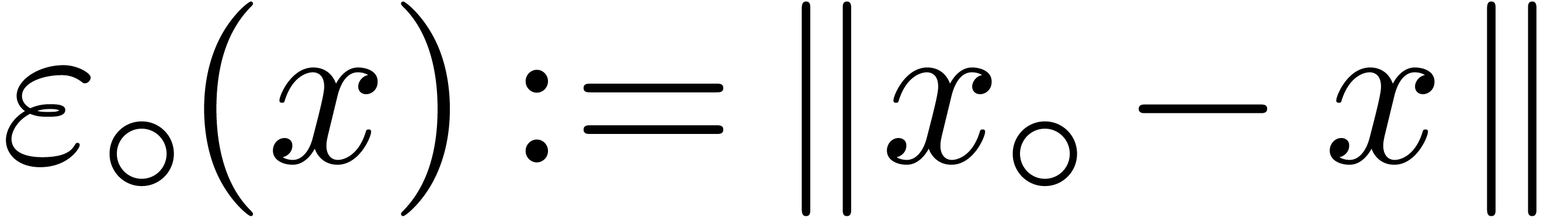 .
.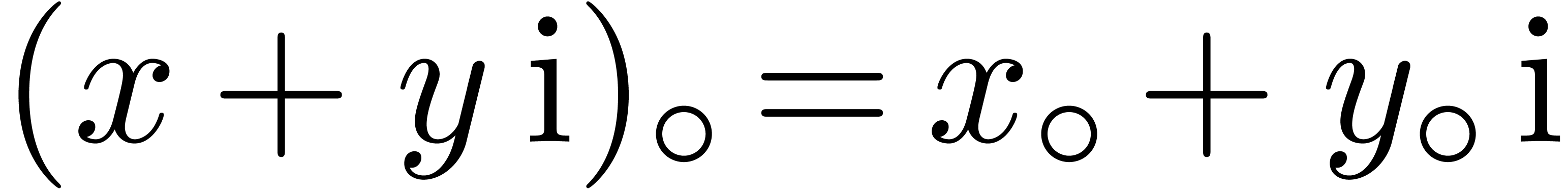 .
.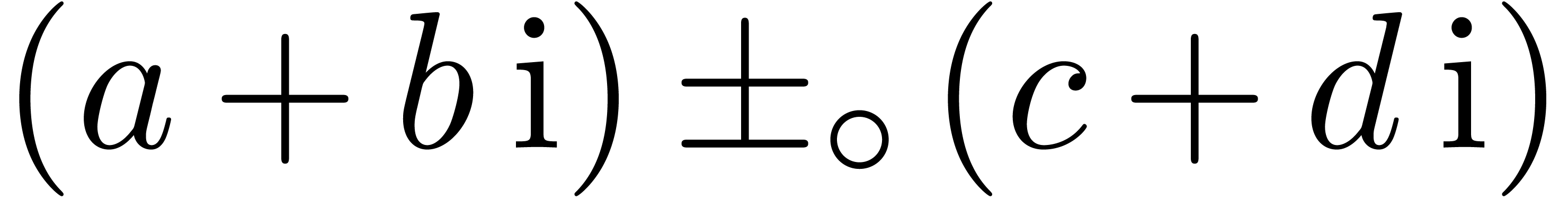
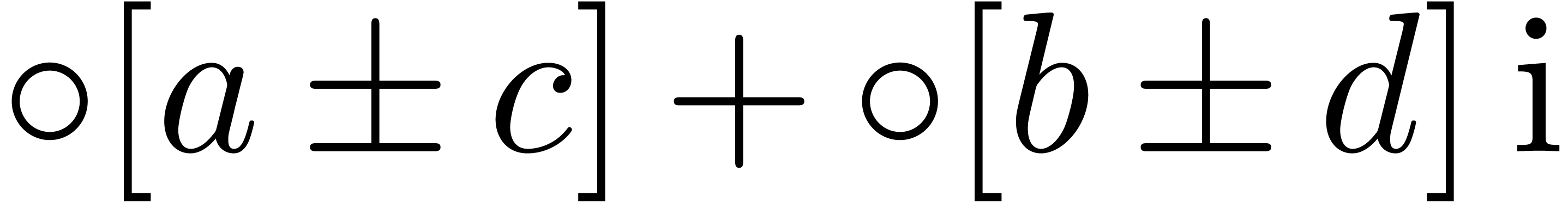
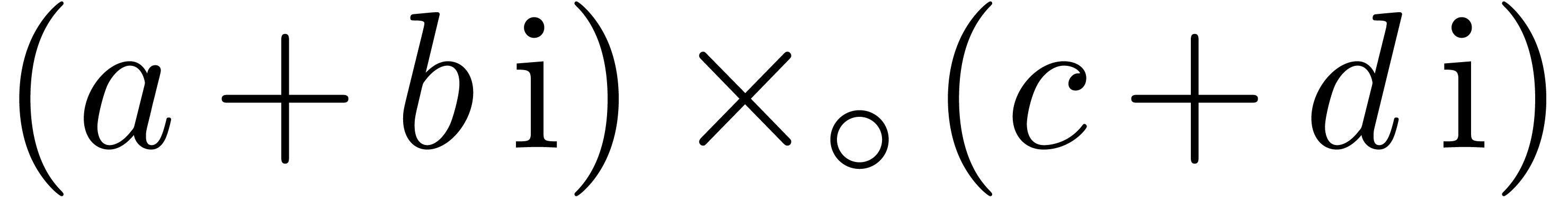
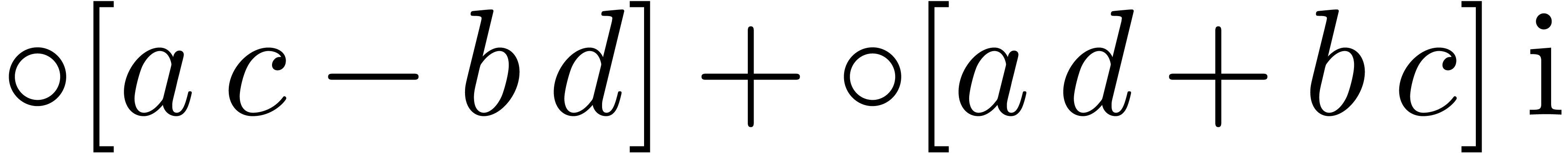
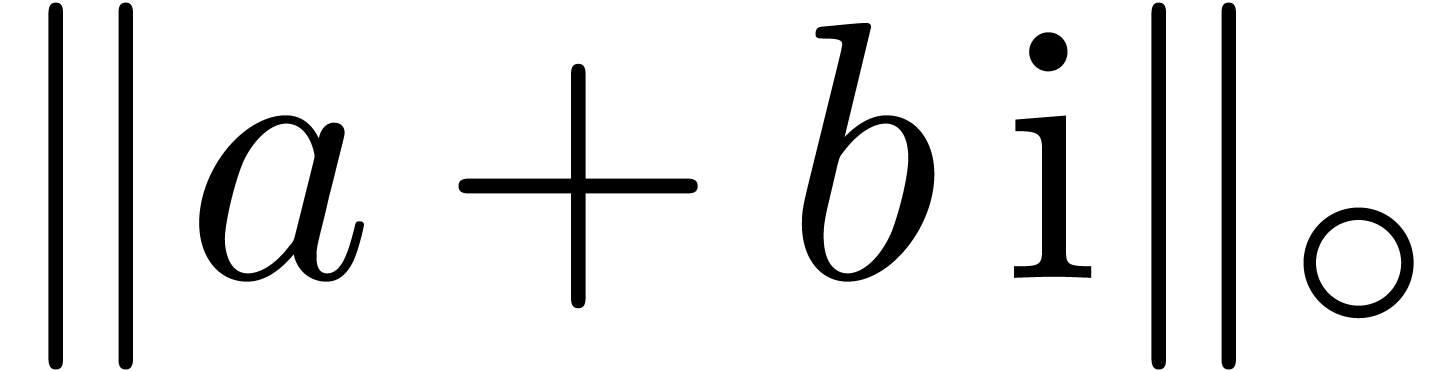
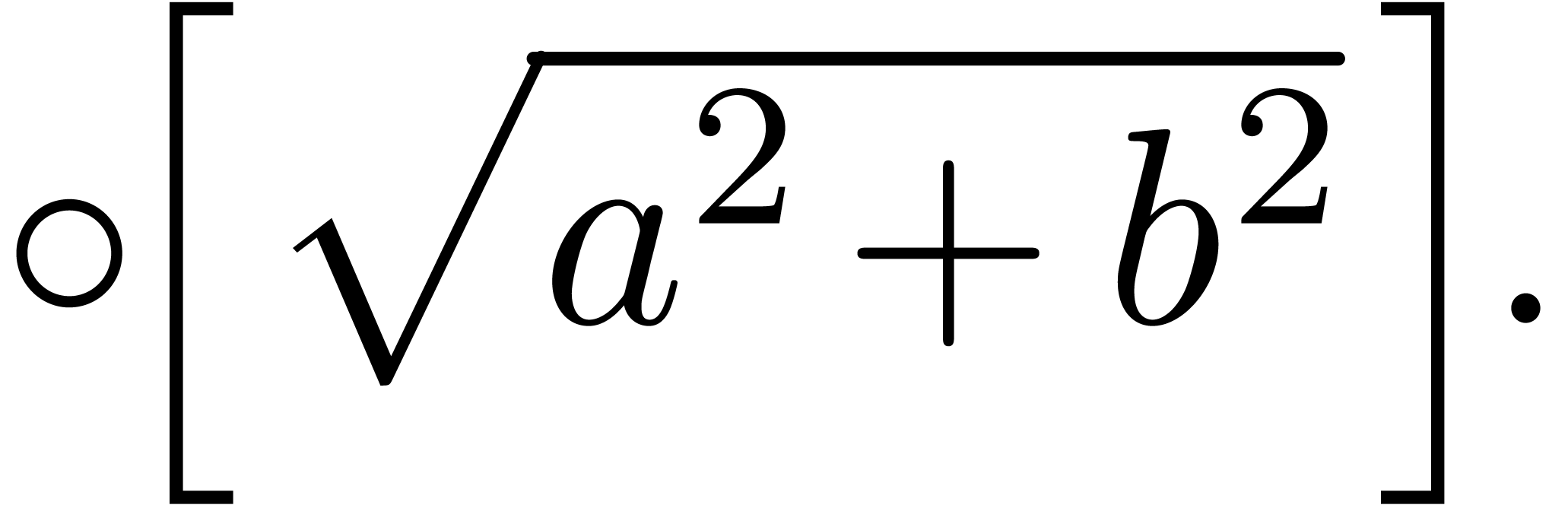
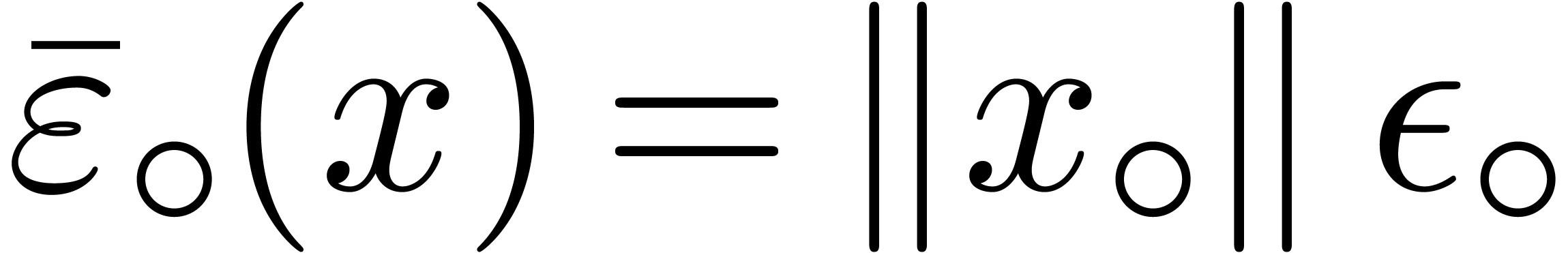 in absence of underflows/overflows, and
in absence of underflows/overflows, and  in
general.
in
general.
 ,
, by
computations of quick and rough upper bounds
by
computations of quick and rough upper bounds  .
.
 and
and  ,
, for the closed ball with
center
for the closed ball with
center  and radius
and radius  .
. .
. in
in 
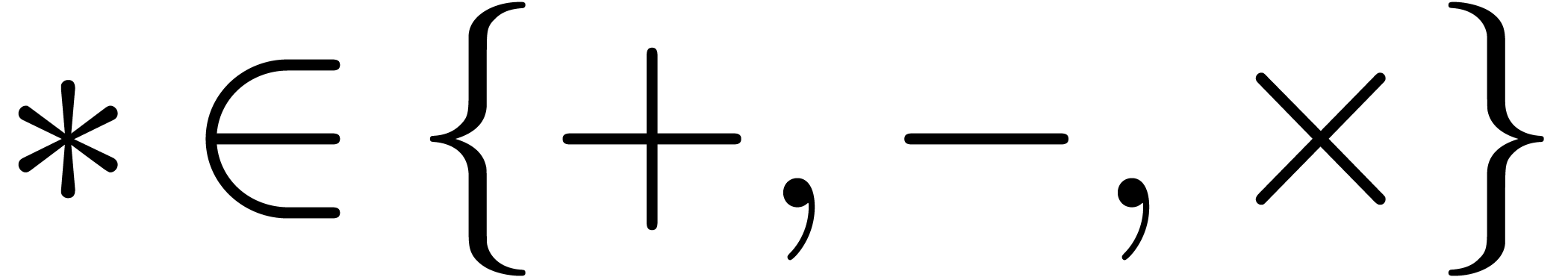 ,
,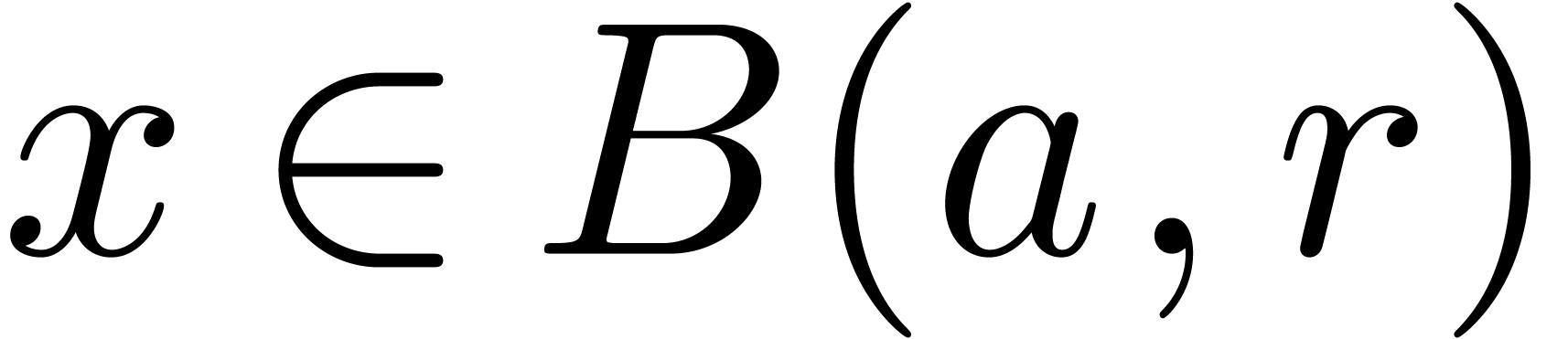 and
and 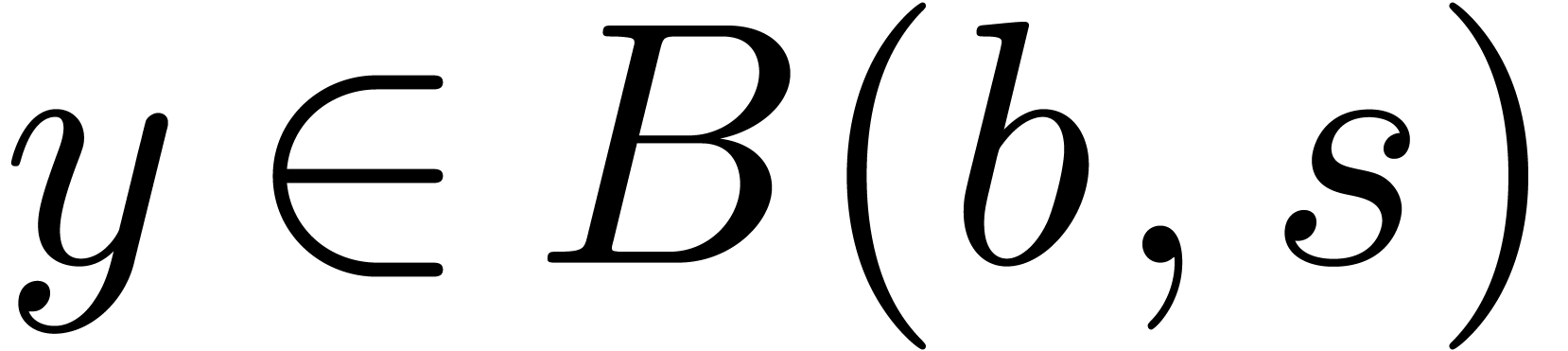 ,
,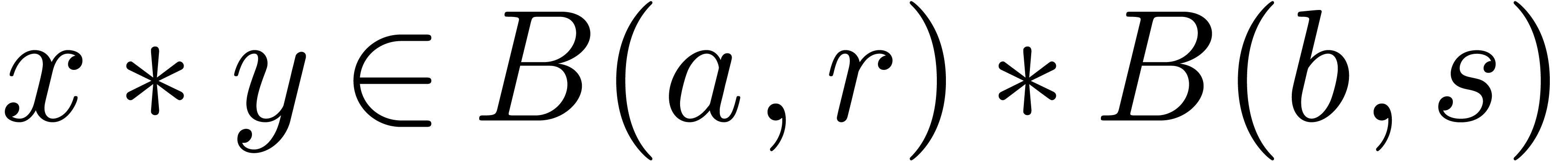 .
.
 the set of balls with centers
in
the set of balls with centers
in  (and preferably rounding to the nearest), and
operations on radii using upward rounding. This leads to the following
formulas:
(and preferably rounding to the nearest), and
operations on radii using upward rounding. This leads to the following
formulas:
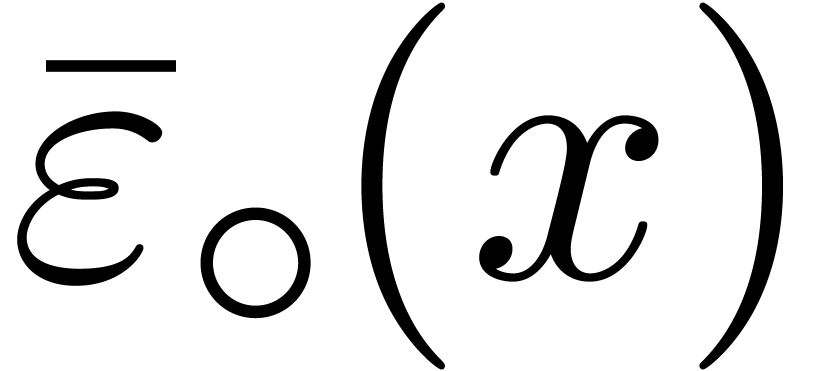 of the form
of the form 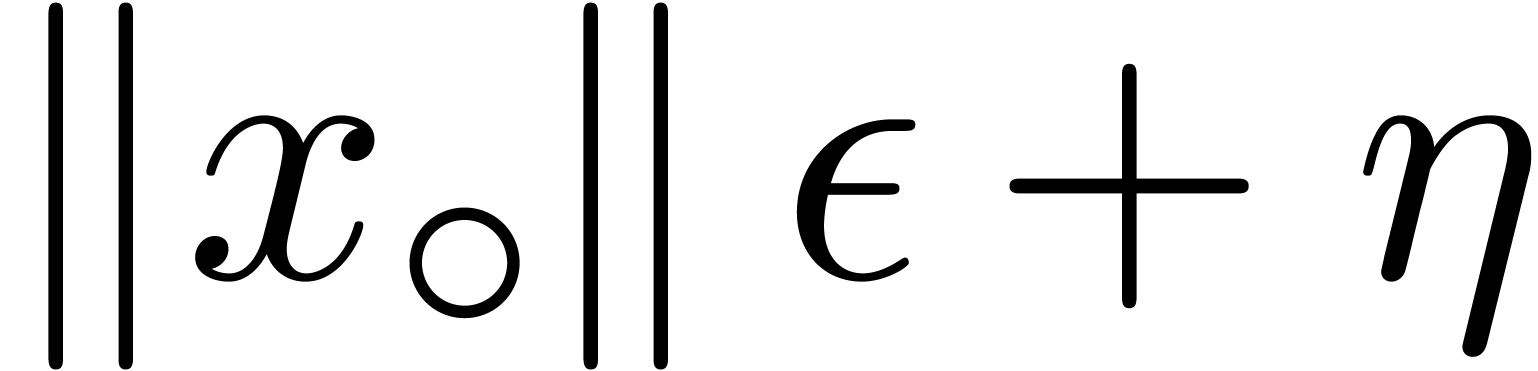 in the last case of fma/fms,
this means that three additional instructions are needed with respect to
the exact arithmetic from the previous subsection:
in the last case of fma/fms,
this means that three additional instructions are needed with respect to
the exact arithmetic from the previous subsection:
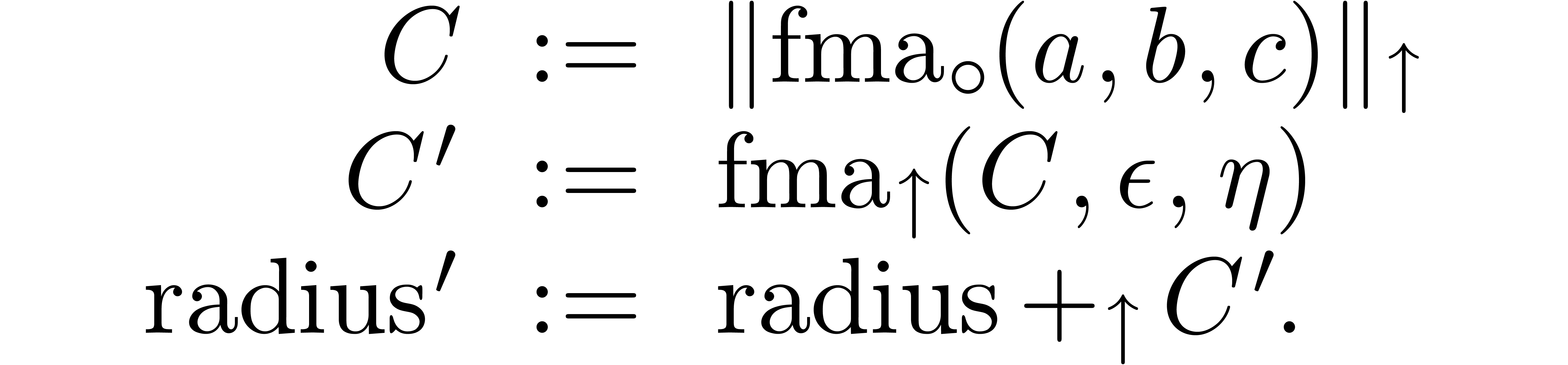
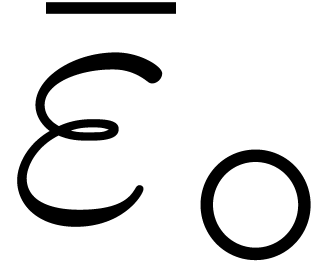 .
.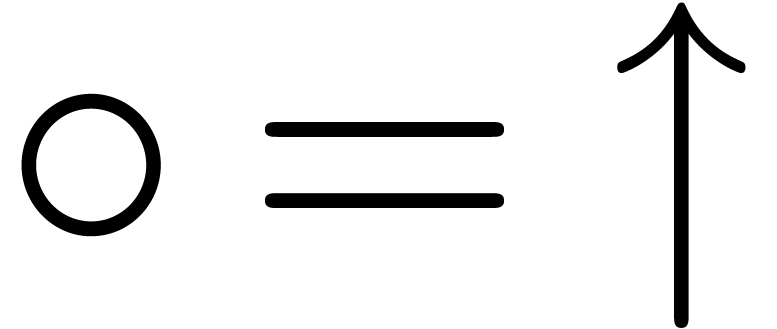 as the sole
rounding mode, then we may directly apply the above formulas, but the
quality of computations with centers degrades. If we take
as the sole
rounding mode, then we may directly apply the above formulas, but the
quality of computations with centers degrades. If we take  ,
, ,
,
 .
. the corresponding “rounding
mode” for transient ball arithmetic; the basic operations are
defined as follows:
the corresponding “rounding
mode” for transient ball arithmetic; the basic operations are
defined as follows:
 .
. in
in 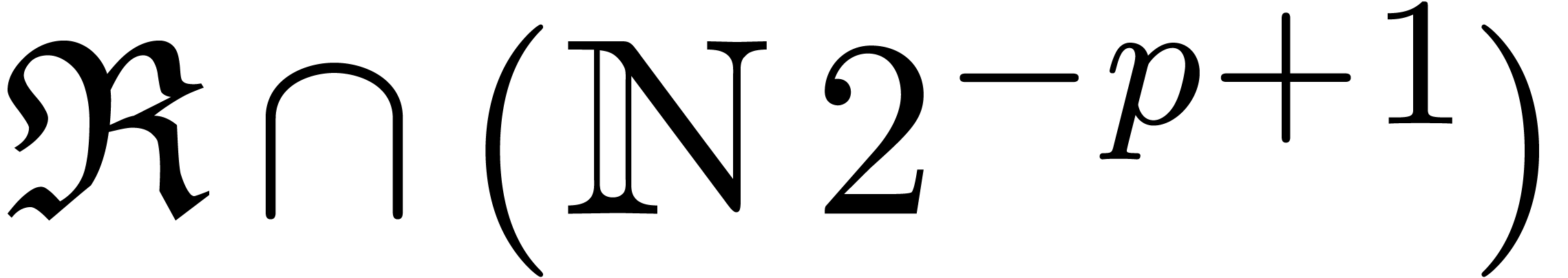 such that
such that 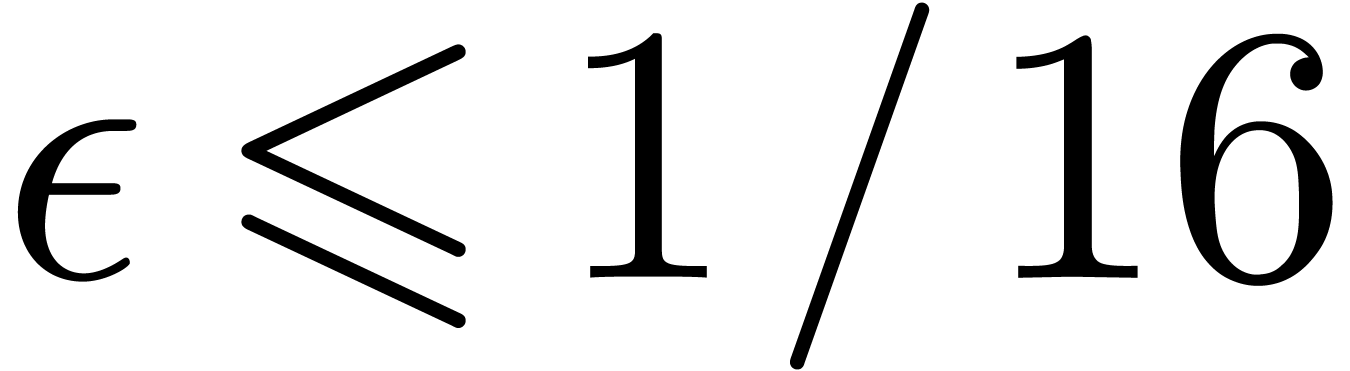 and
and
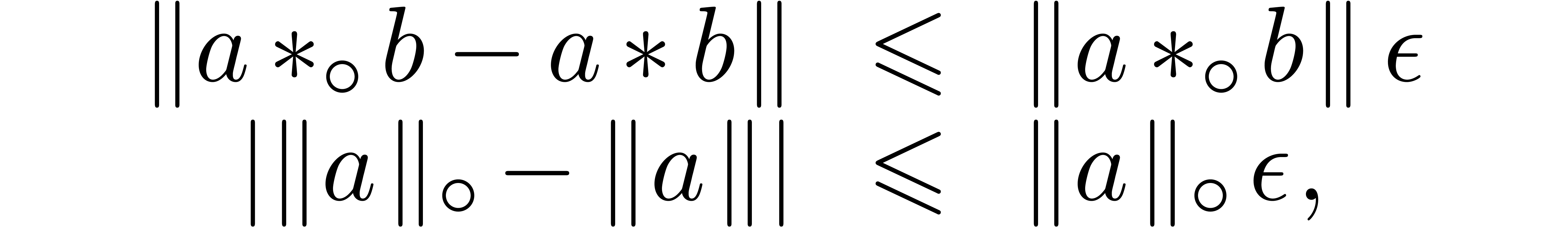
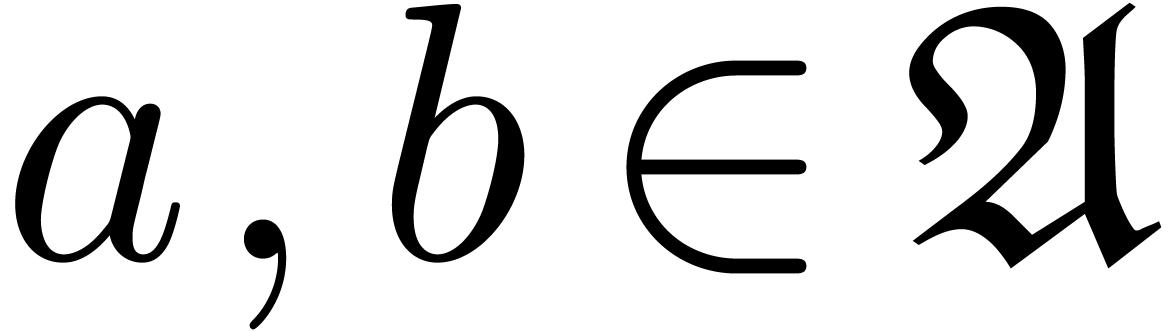 and
and 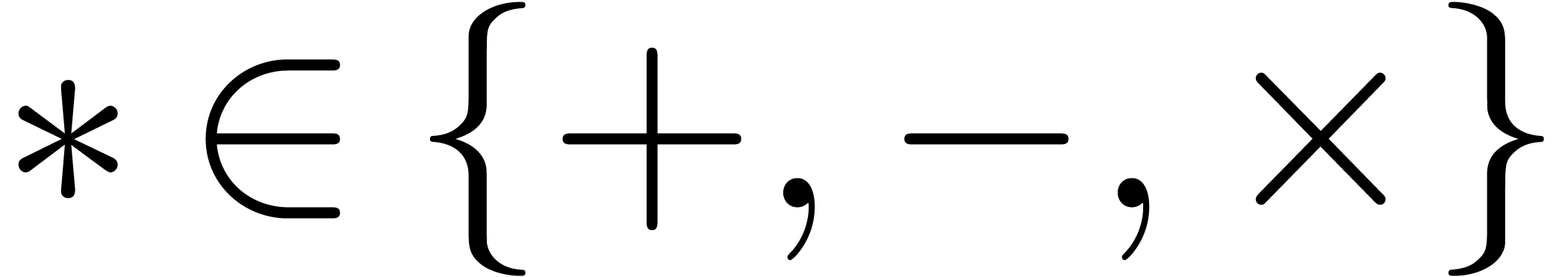 ,
,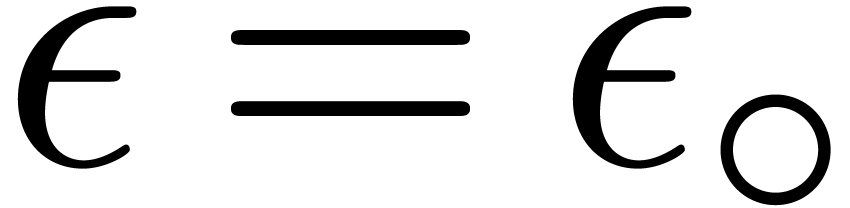 .
.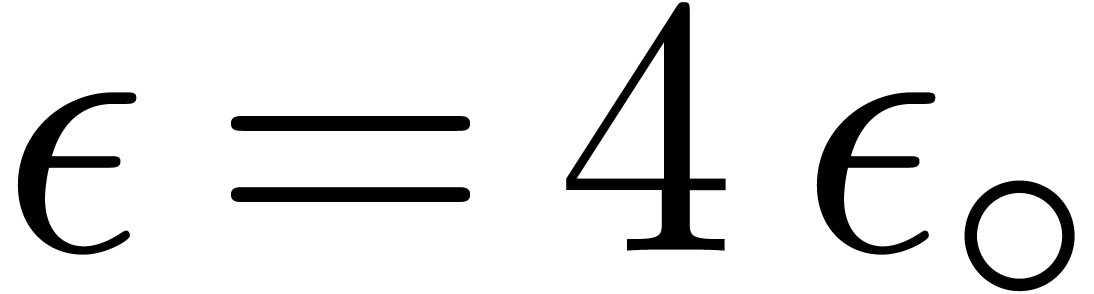 (see
Appendix
(see
Appendix 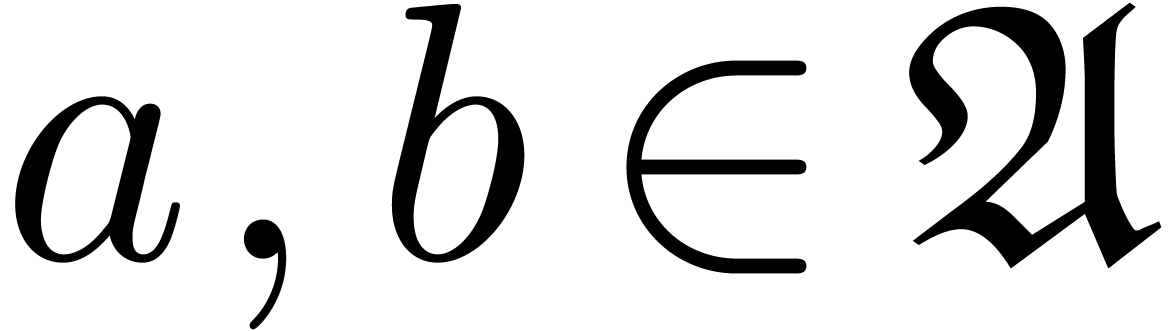 and
and  such that the
computation of
such that the
computation of
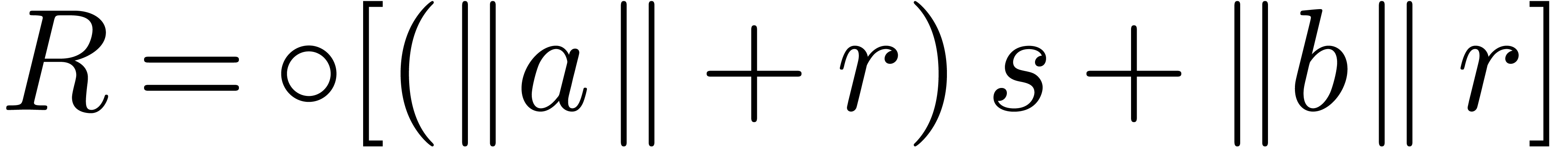
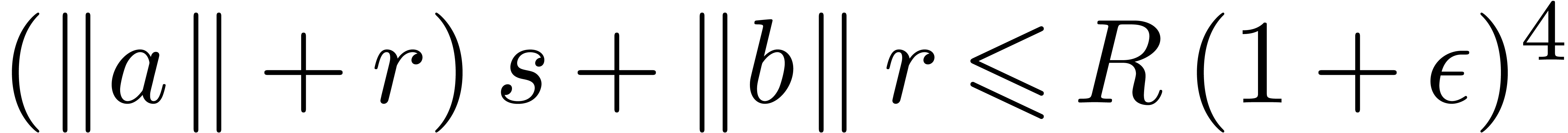 .
.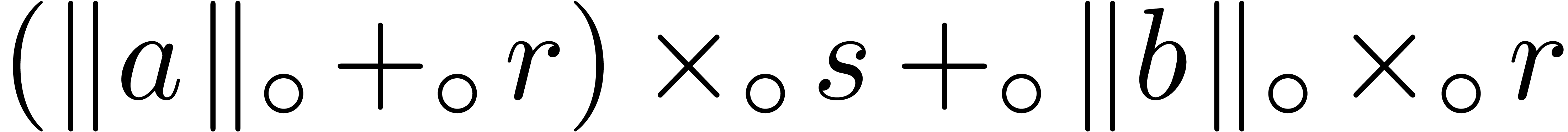
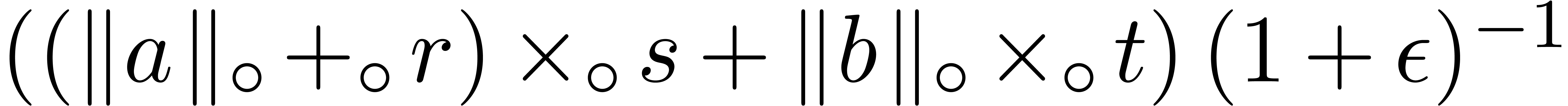
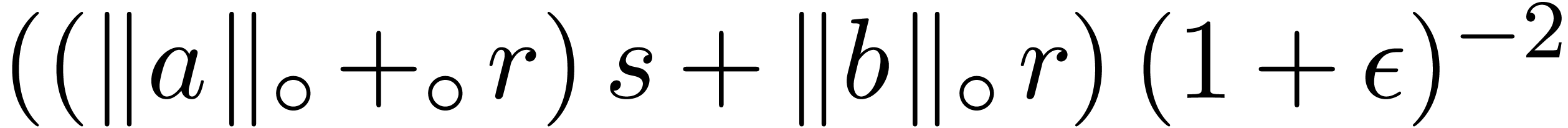
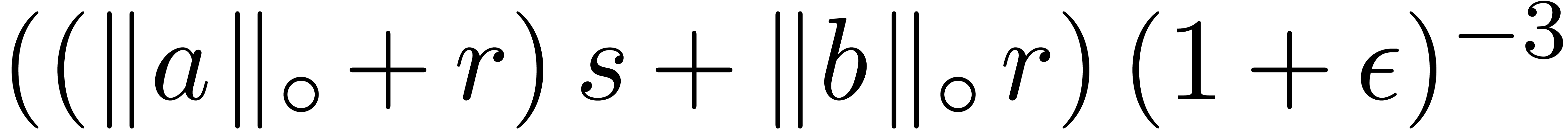
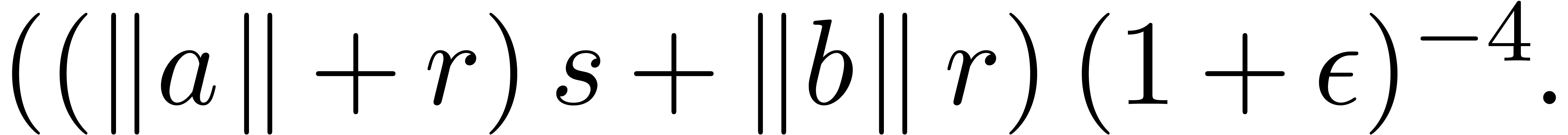
 over a ring
over a ring
 of
instructions of the form
of
instructions of the form
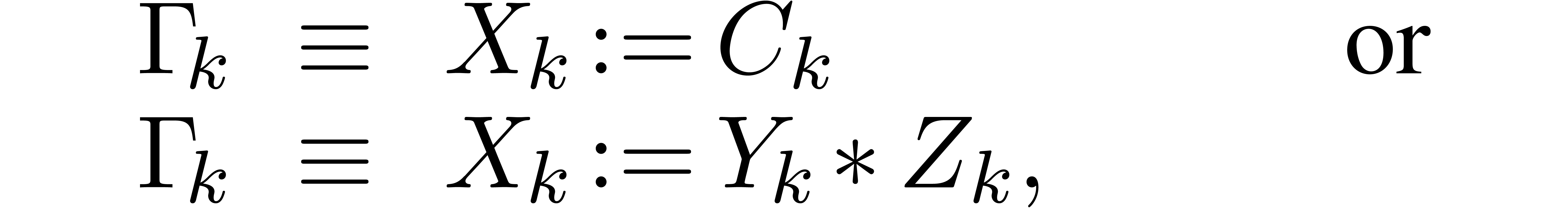
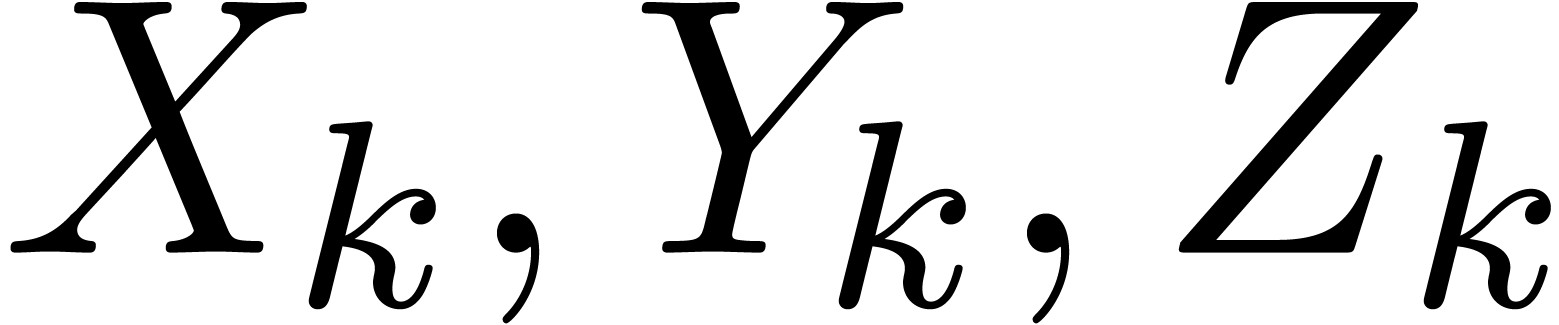 are variables in a finite ordered set
are variables in a finite ordered set
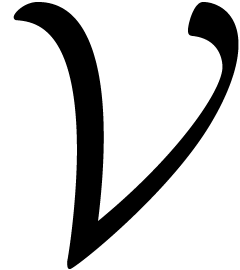 ,
,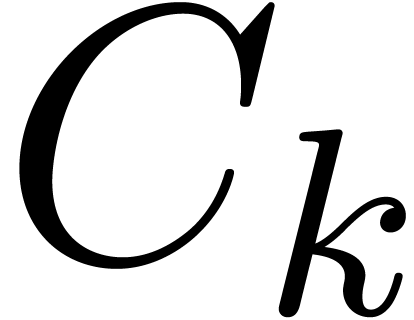 constants in
constants in 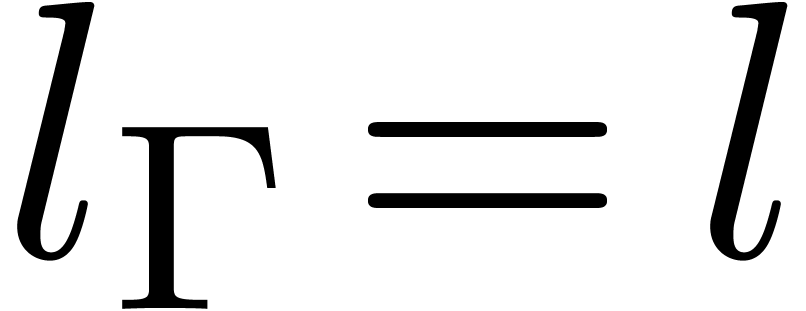 of the sequence is called the
length of
of the sequence is called the
length of  be the input variables of
be the input variables of  the output variables, listed in increasing
order. Then we associate an evaluation function
the output variables, listed in increasing
order. Then we associate an evaluation function 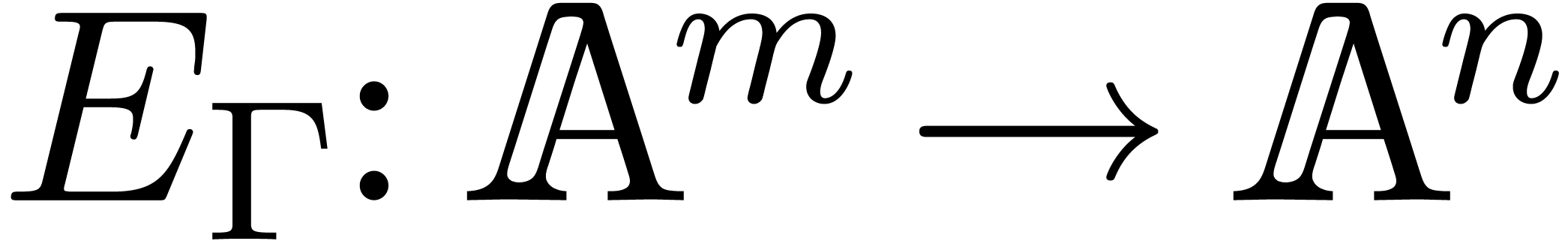 to
to 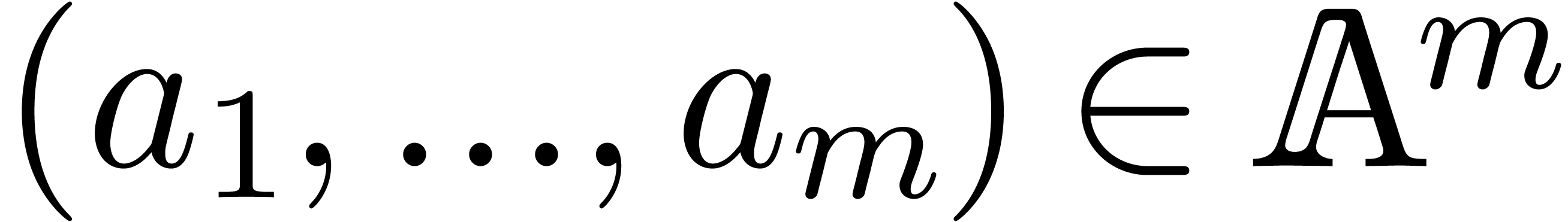 ,
,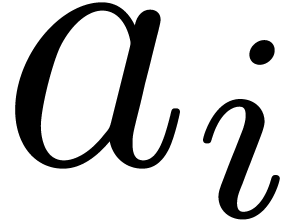 to
to 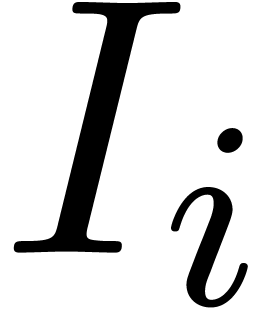 for
for 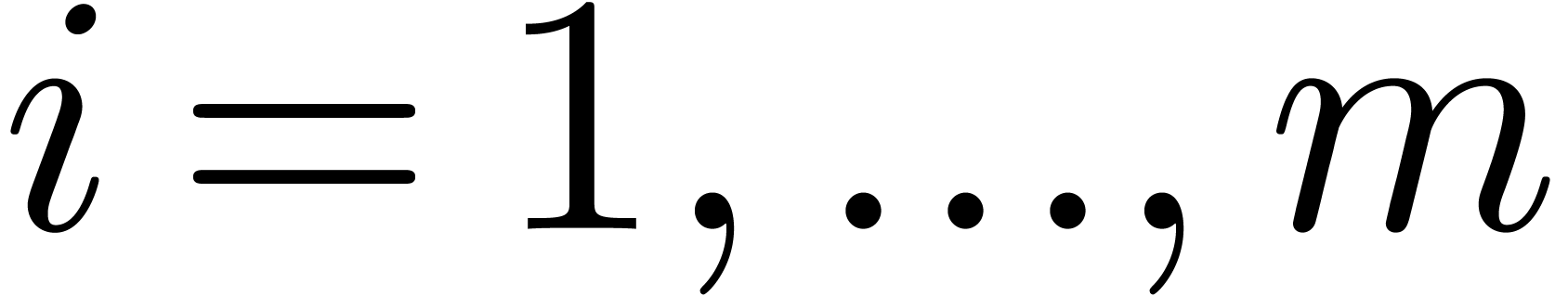 ,
,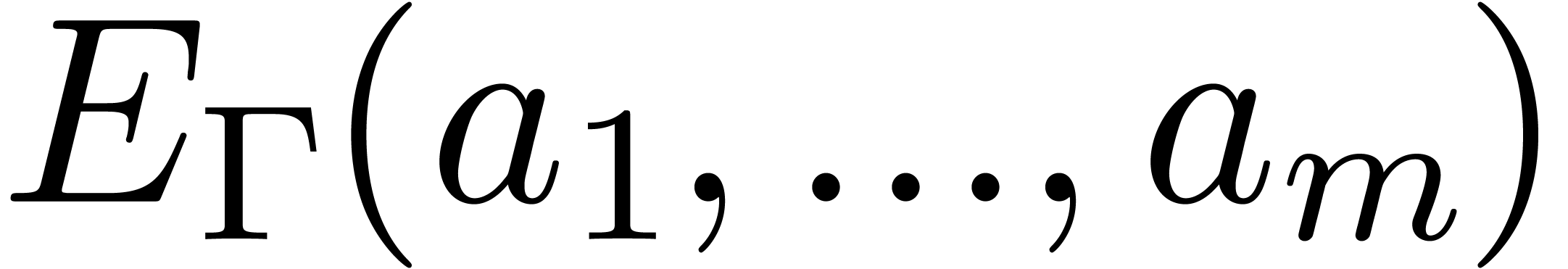 .
.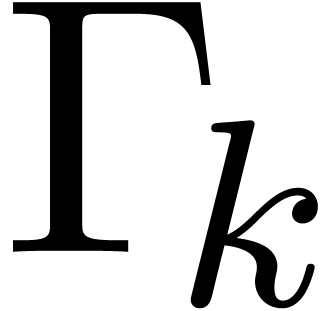 ,
,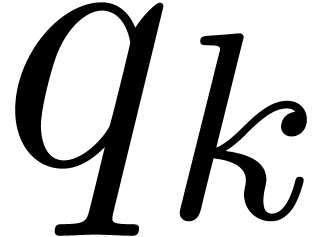 as
follows. Let
as
follows. Let  ,
, have been defined for some
have been defined for some  .
.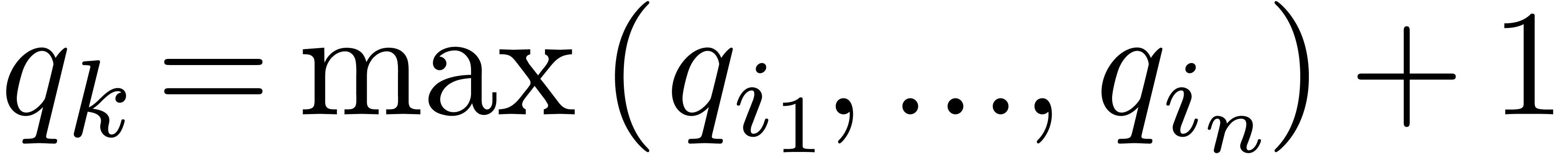 ,
, are those indices
are those indices  such that
such that 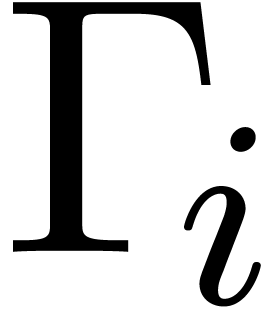 is of the form
is of the form 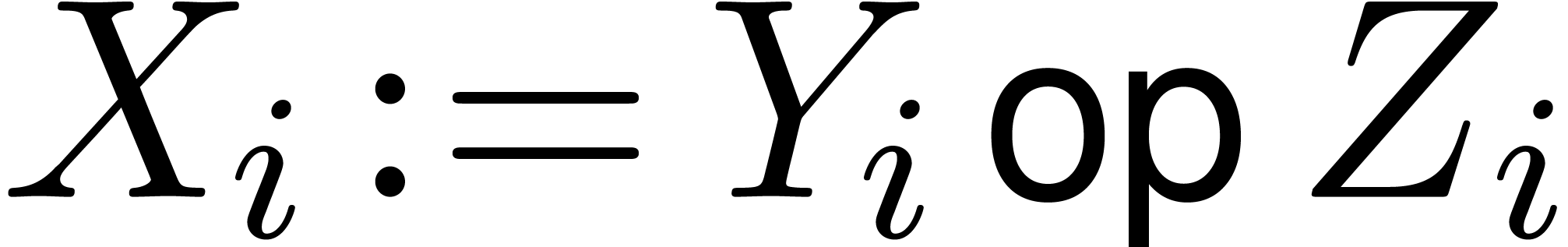 with
with 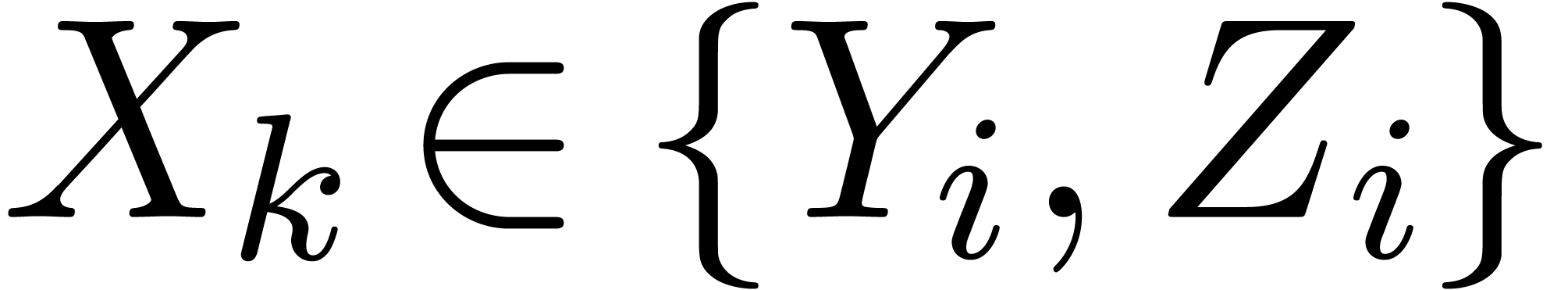 and
and 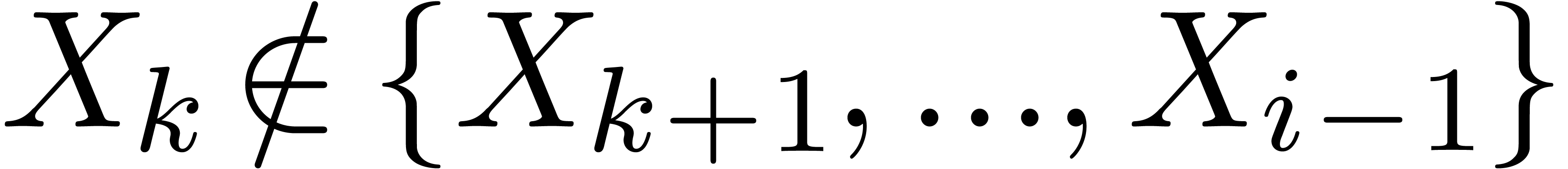 .
. exist, then we set
exist, then we set 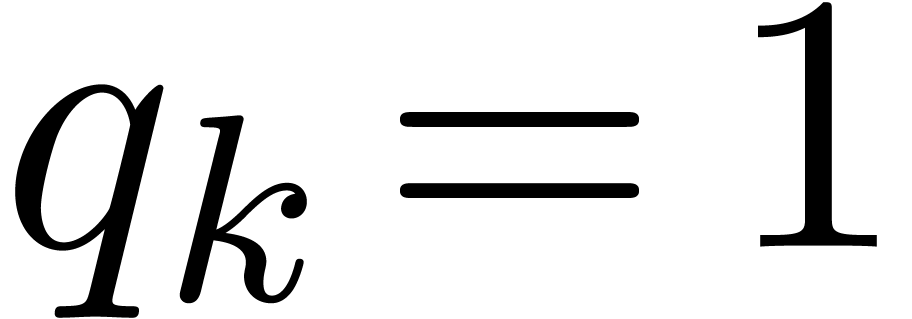 .
.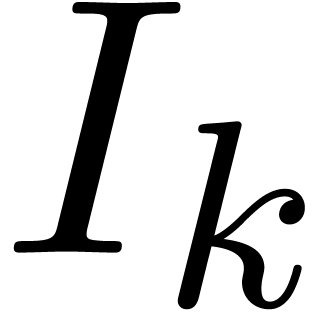 we define
we define 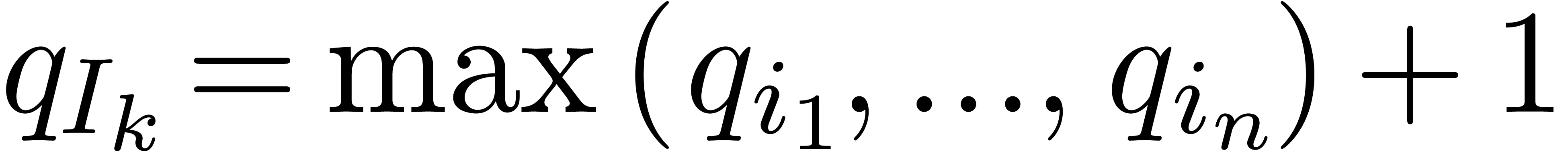 ,
,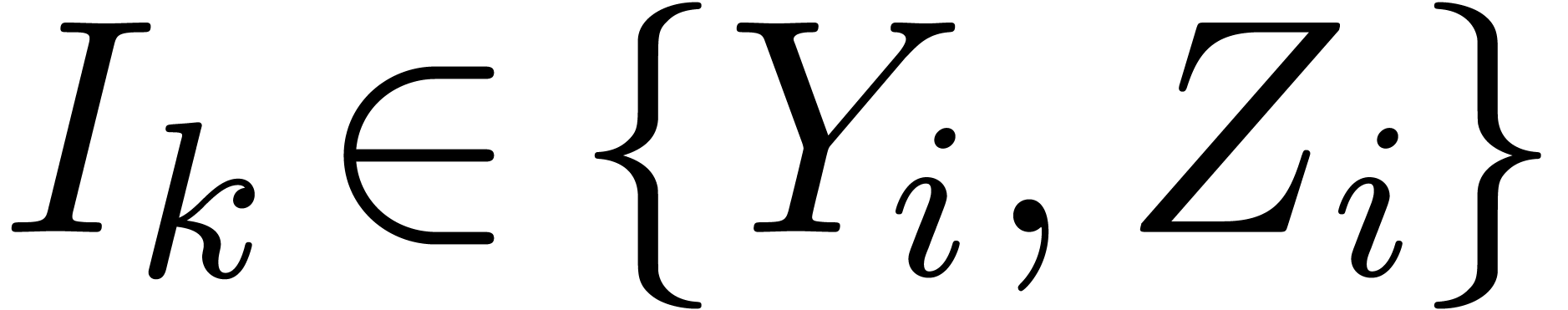 and
and  .
. ,
, all indices
all indices 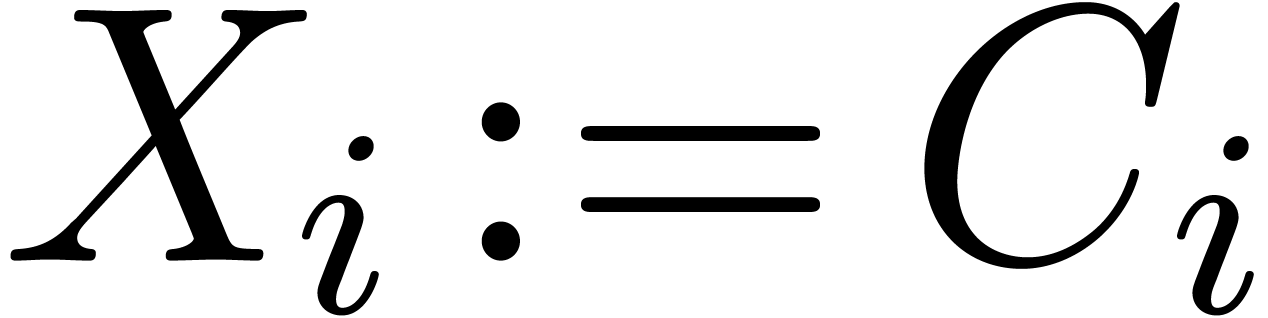 .
. ,
,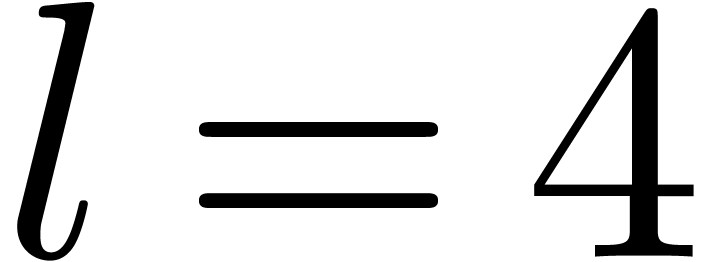 .
.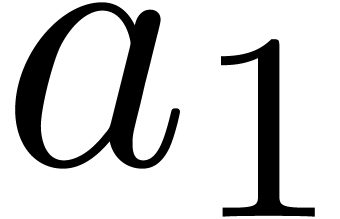 and
and 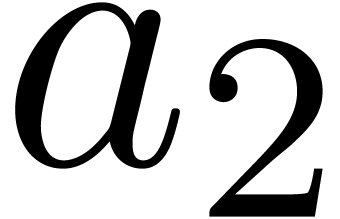 ,
,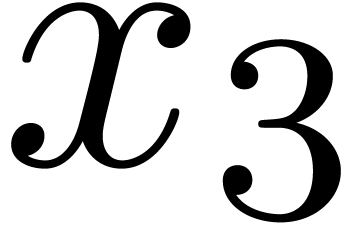 as the sole output variable. This
SLP thus computes the function
as the sole output variable. This
SLP thus computes the function 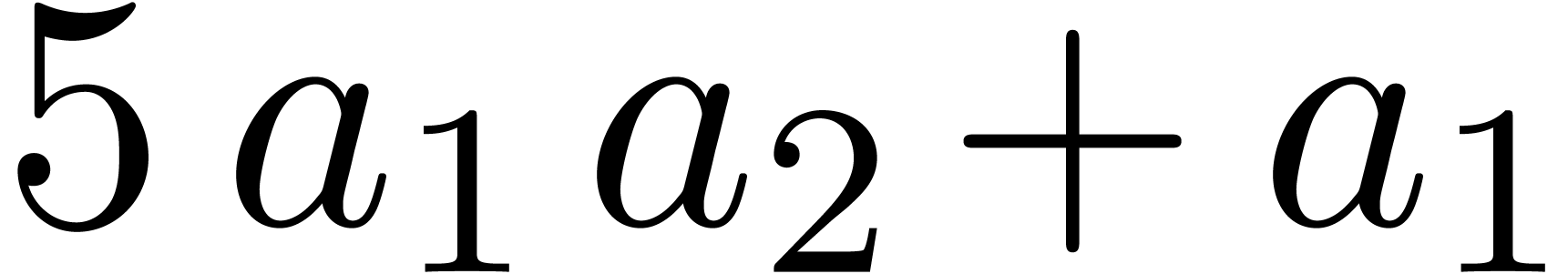 .
.
 .
.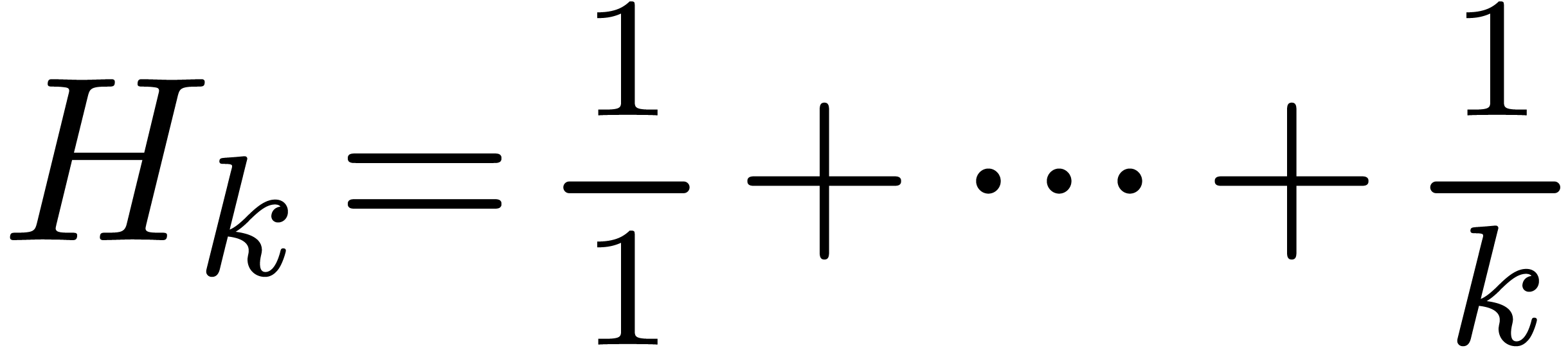 for the
for the 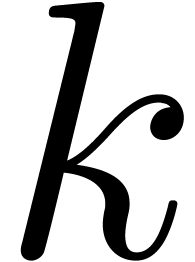 -th
-th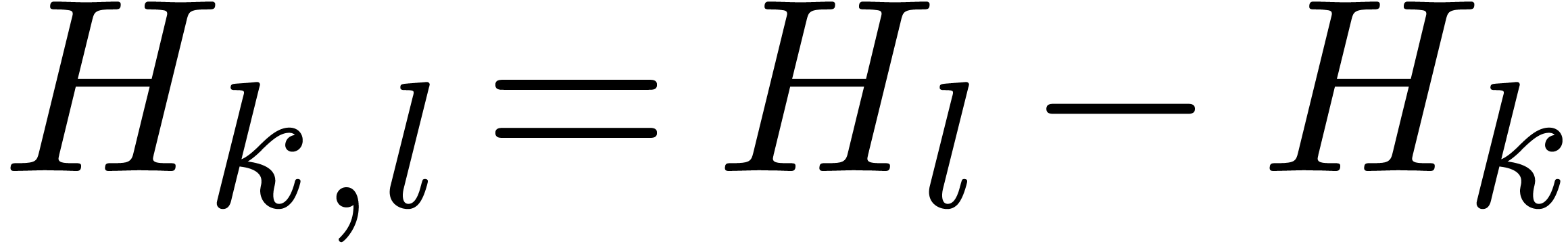 for all
for all 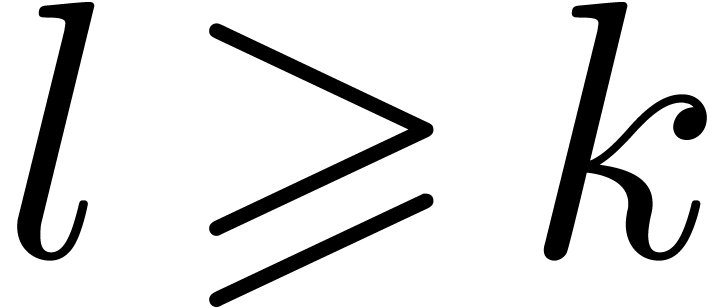 .
. be a SLP of length
be a SLP of length  as above and let
as above and let  be an
arbitrary parameter such that
be an
arbitrary parameter such that 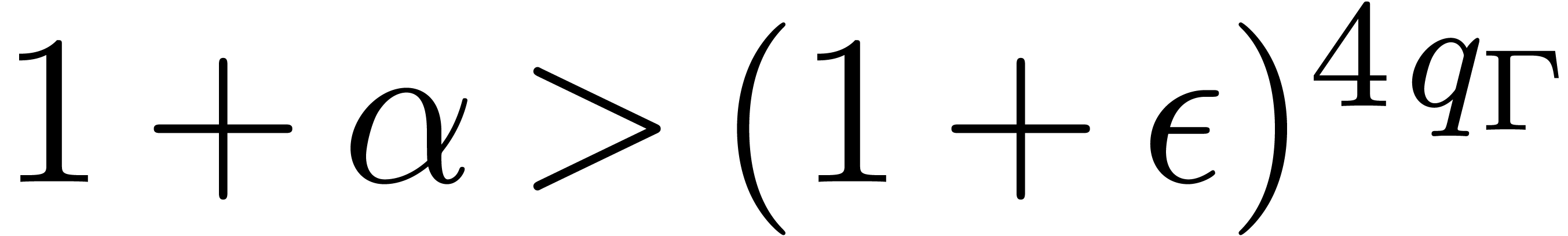 .
.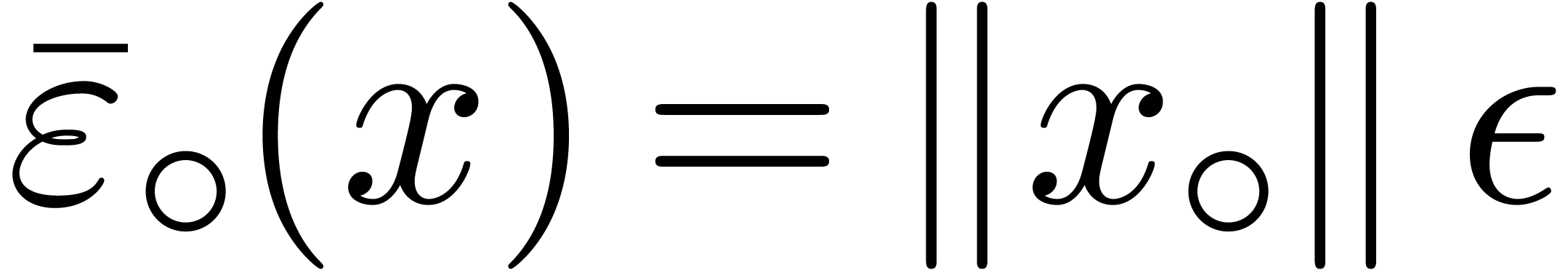 .
.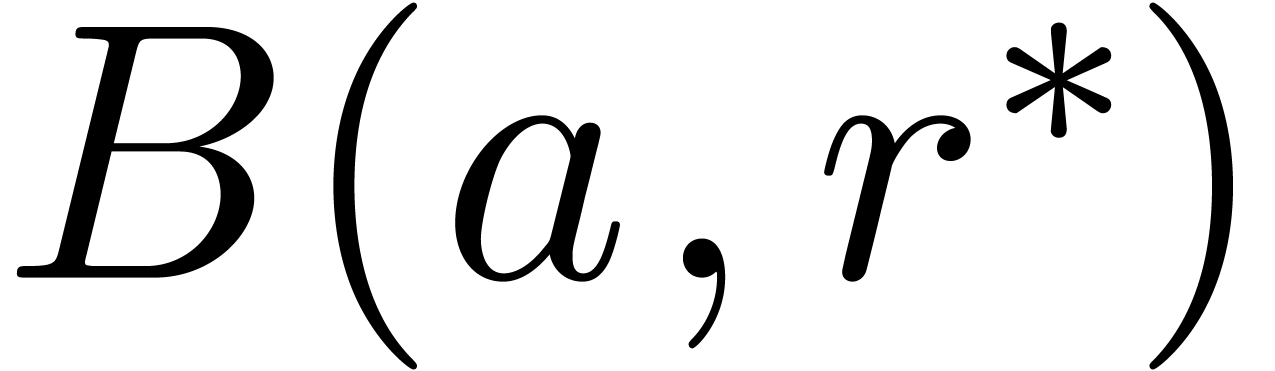 is replaced by a larger ball
is replaced by a larger ball 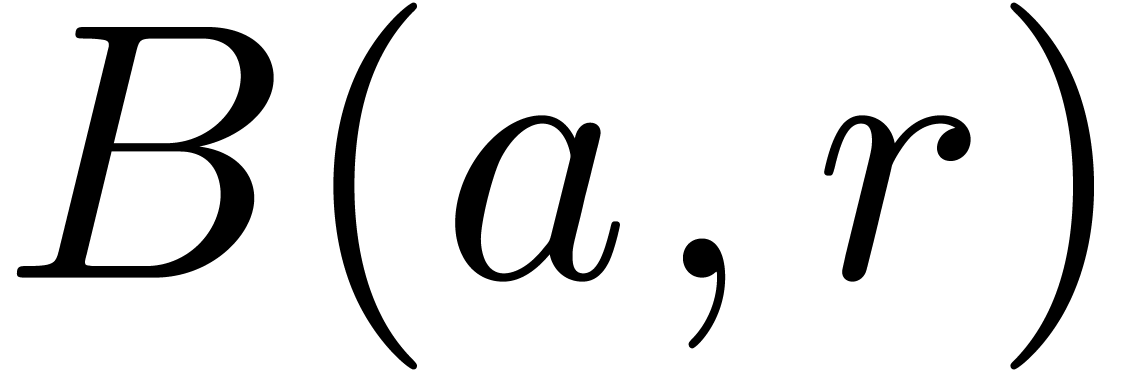 with
with
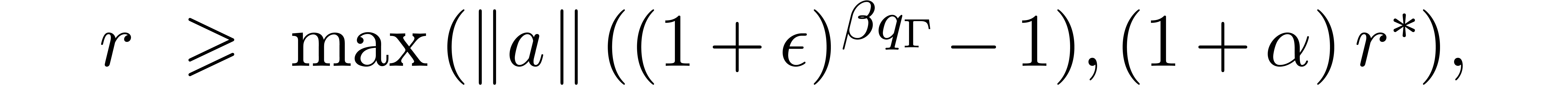
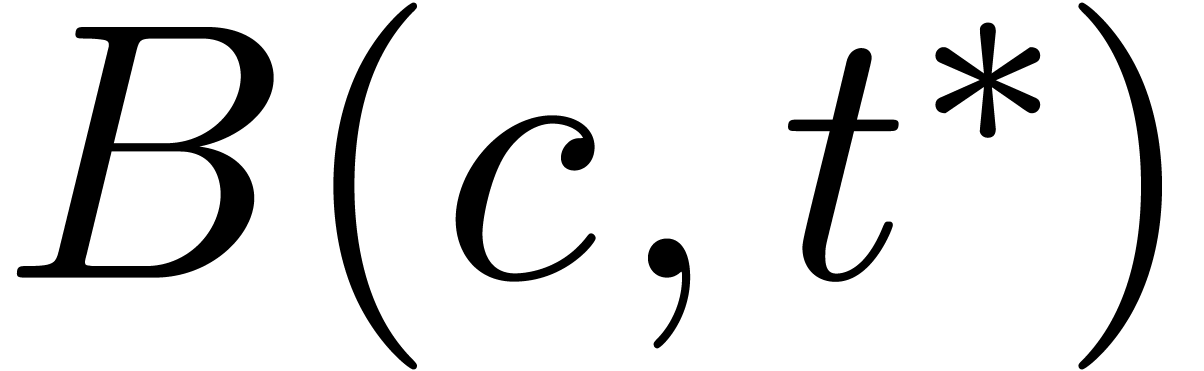 in the output of the first evaluation
with corresponding entry
in the output of the first evaluation
with corresponding entry 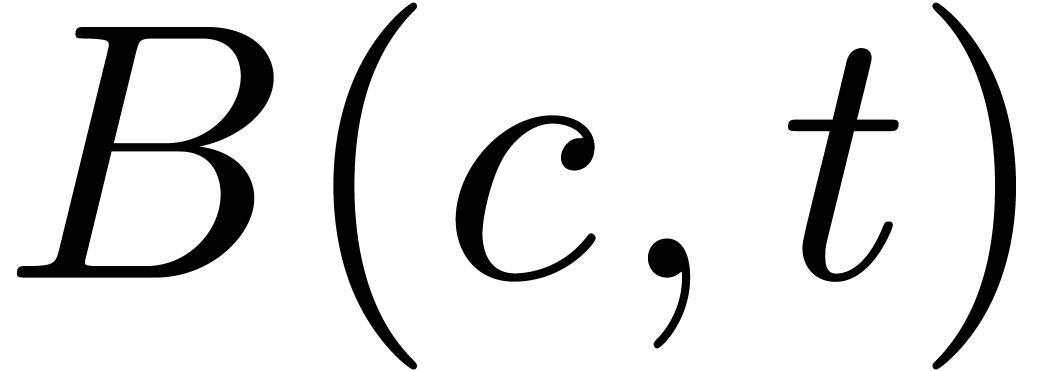 for the second
evaluation, we have
for the second
evaluation, we have  .
.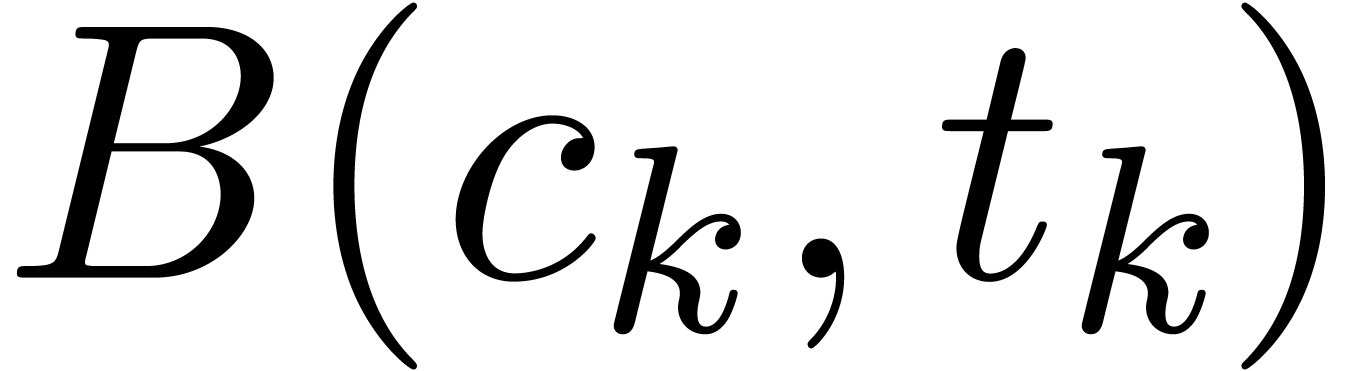 be the ball value of the variable
be the ball value of the variable 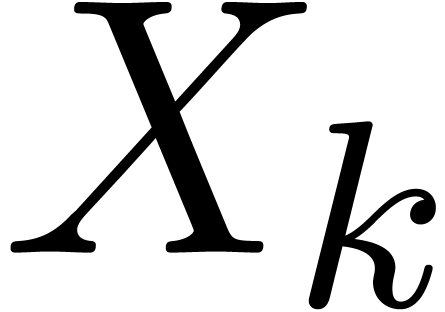 just after evaluation of
just after evaluation of  using
transient ball arithmetic. Let us show by induction over
using
transient ball arithmetic. Let us show by induction over  that
that
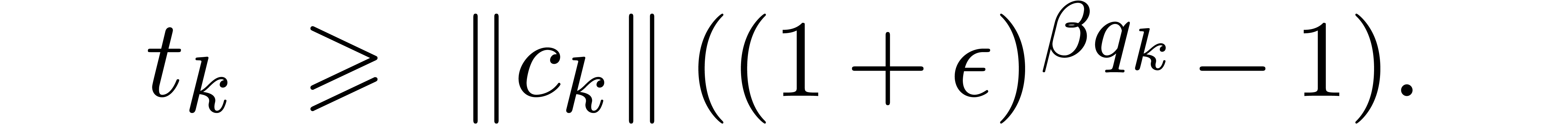
 ,
, .
.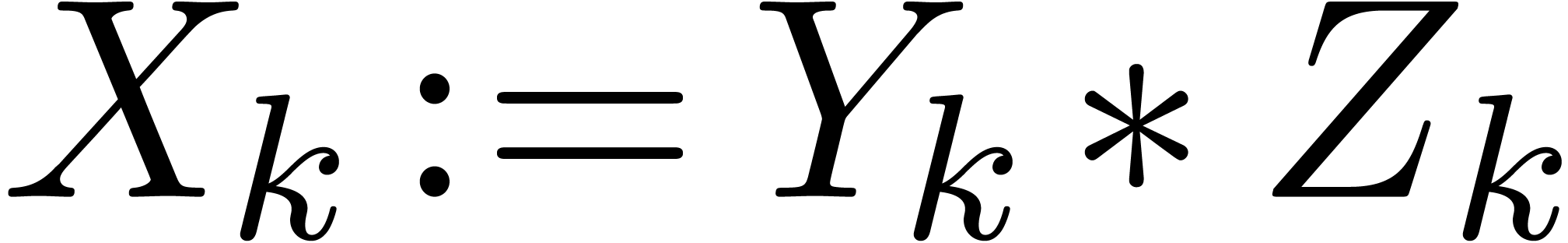 ,
,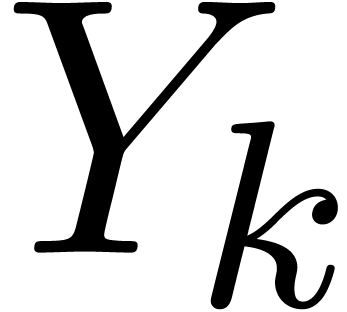 contains a ball
contains a ball 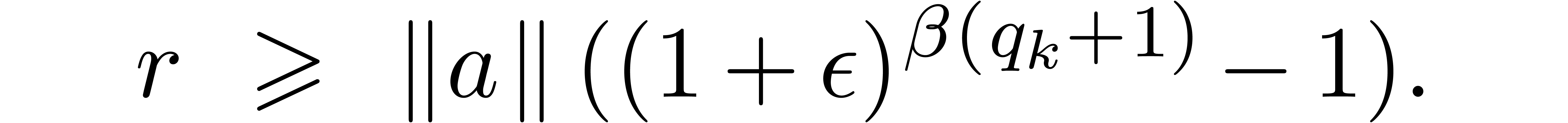
 be largest with
be largest with  .
.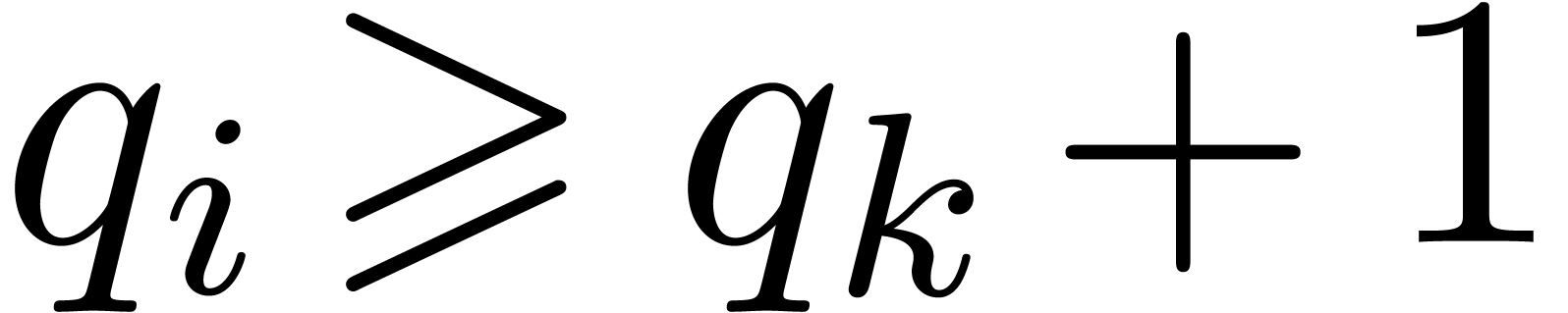 by
the construction of
by
the construction of 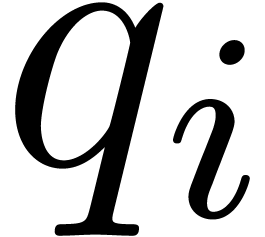 ,
, contains a ball
contains a ball  with
with 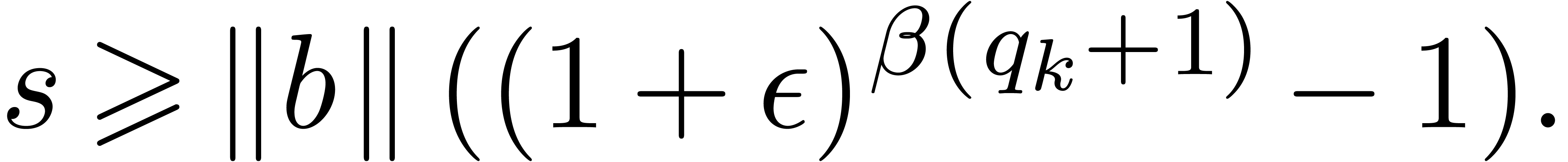
 .
.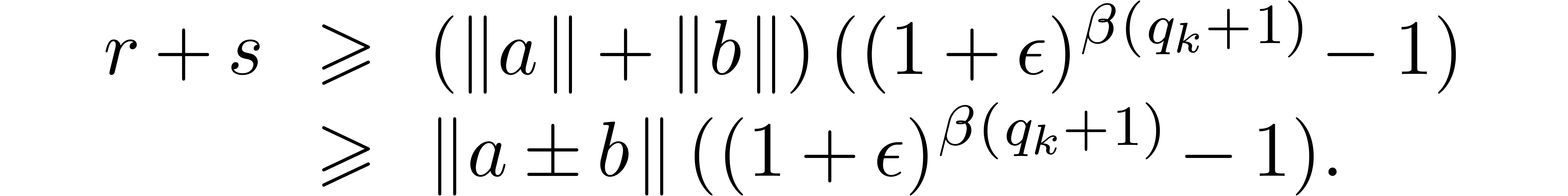
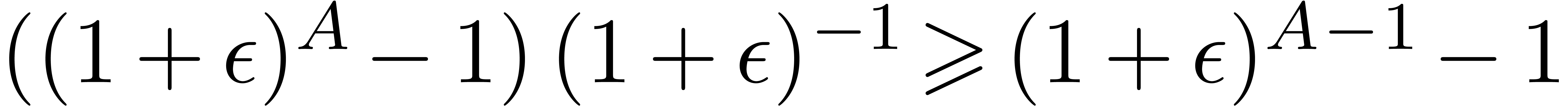 ,
,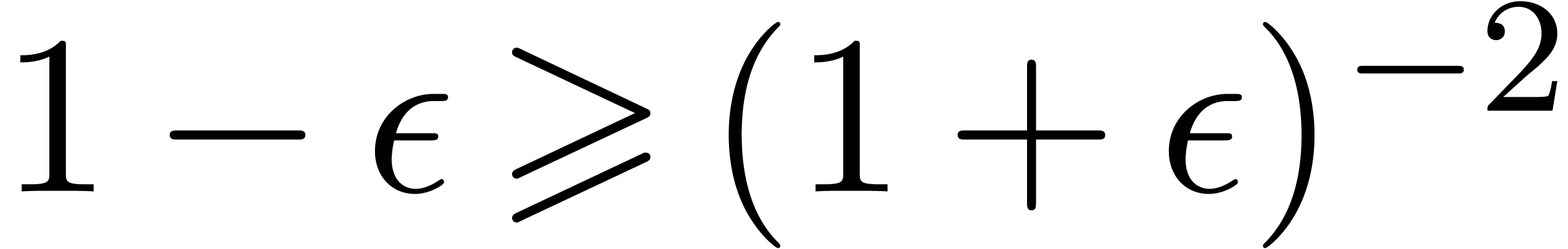 ,
, ,
,
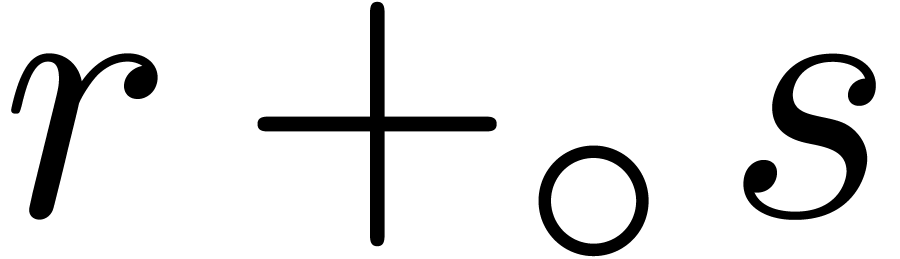
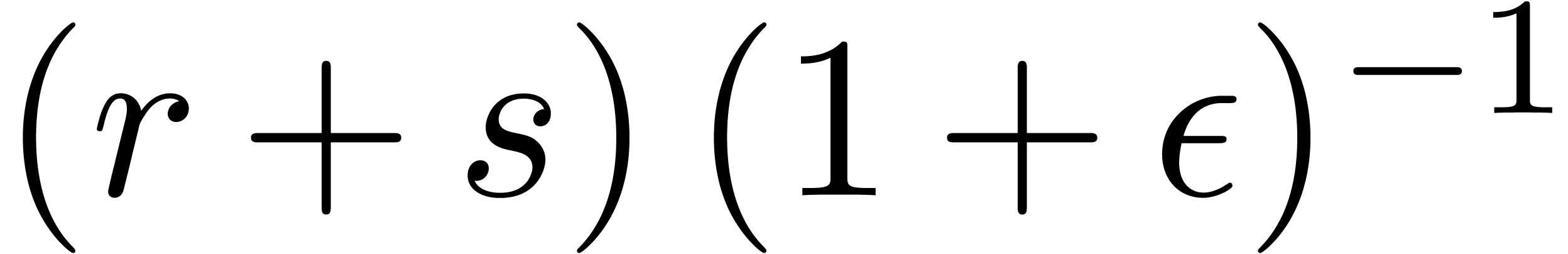
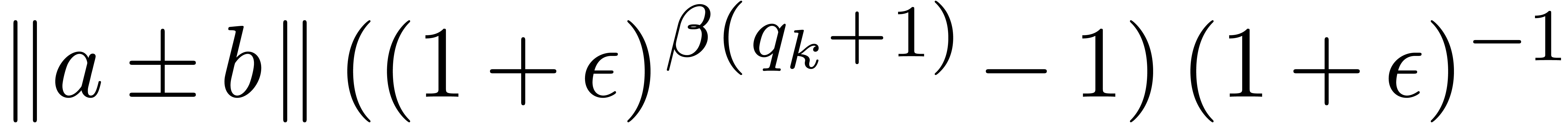
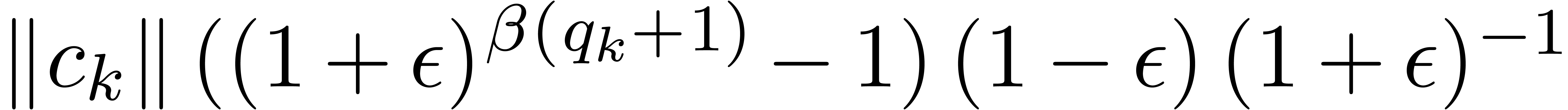
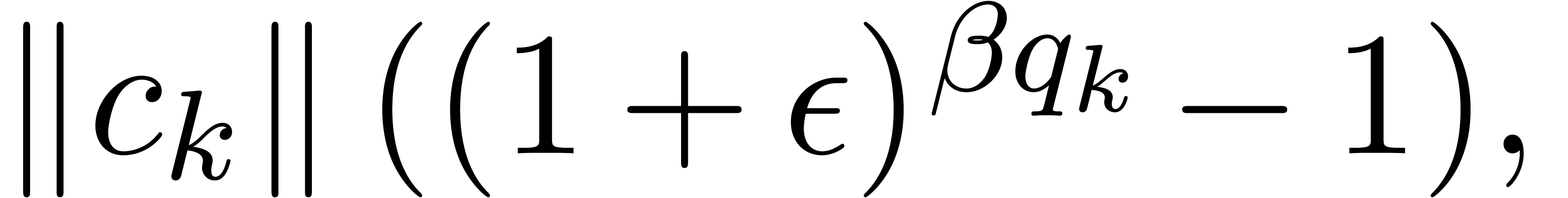
 ,
,
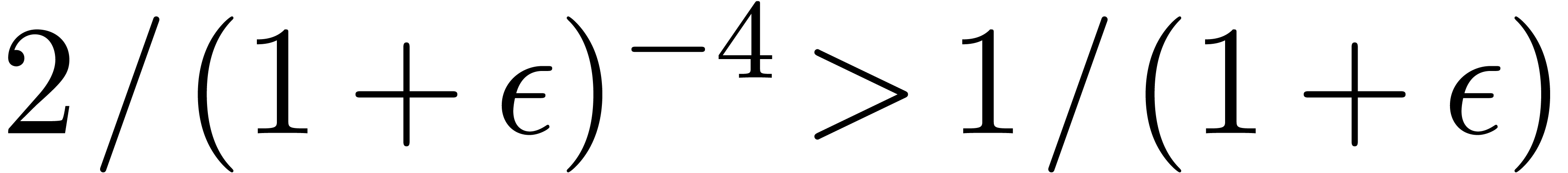 ,
,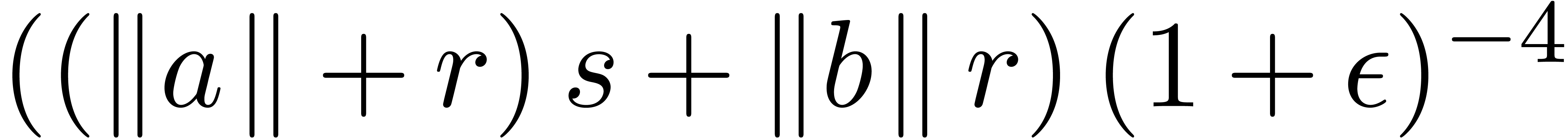
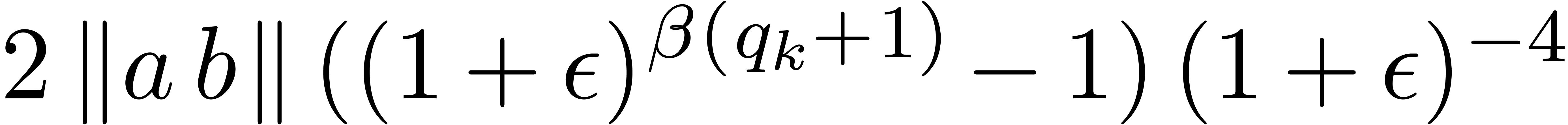
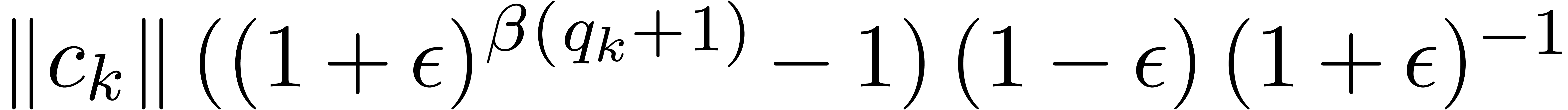
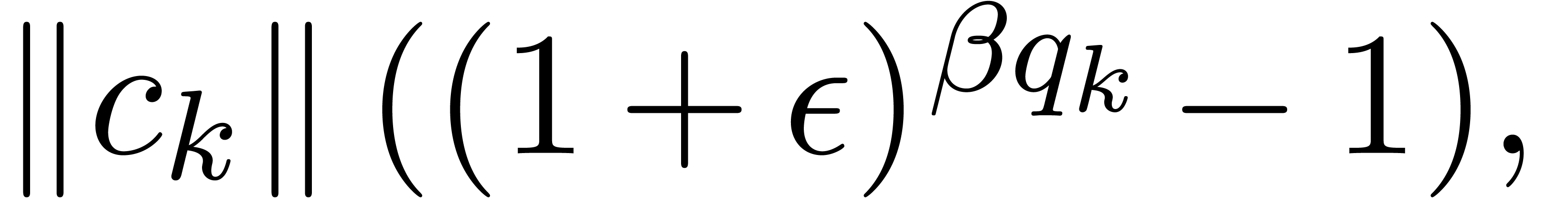
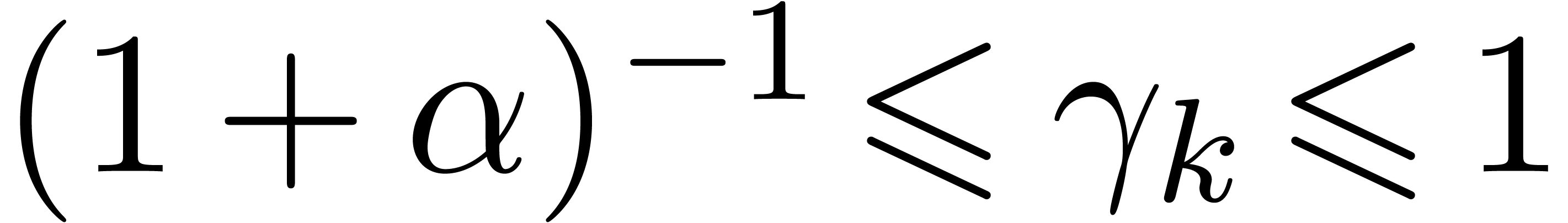 .
.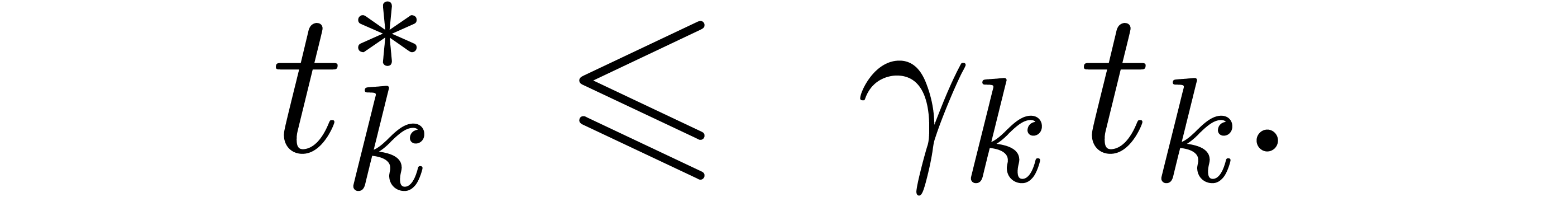
 .
.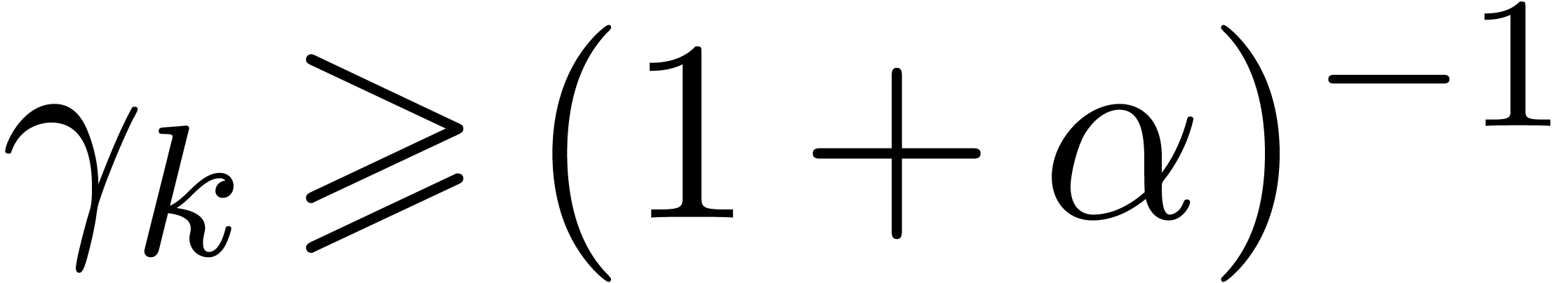 .
.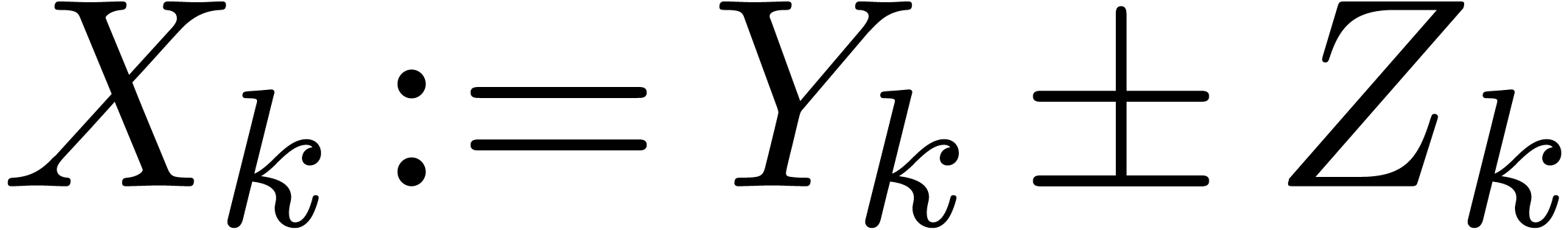 ,
, be largest with
be largest with 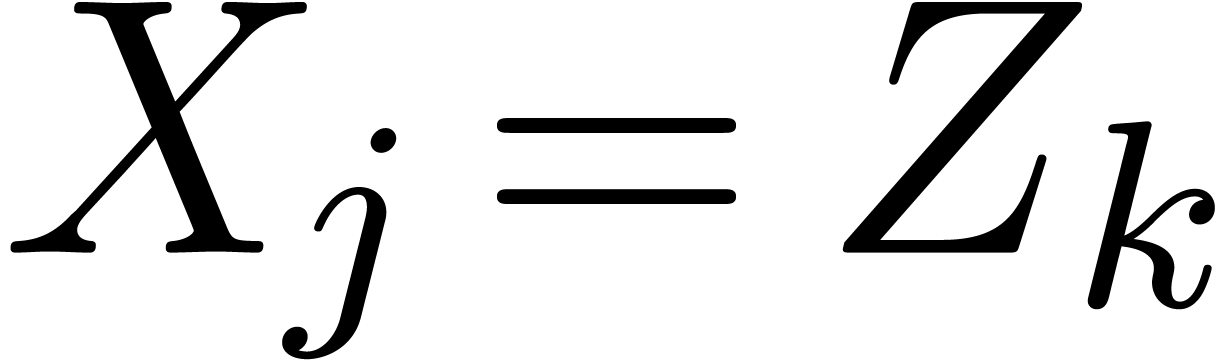 .
.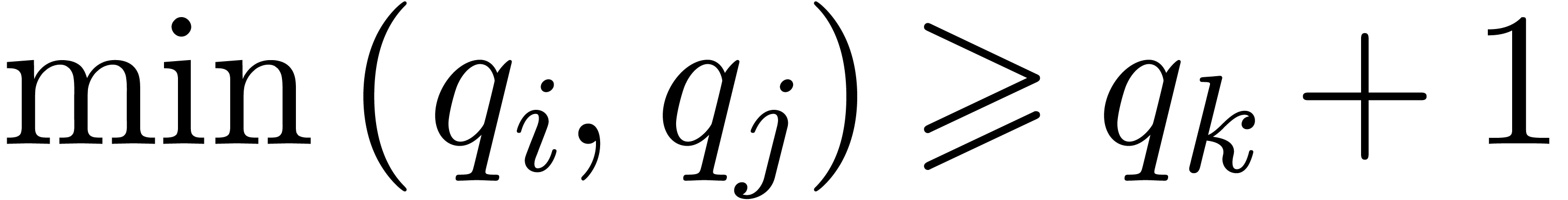 ,
,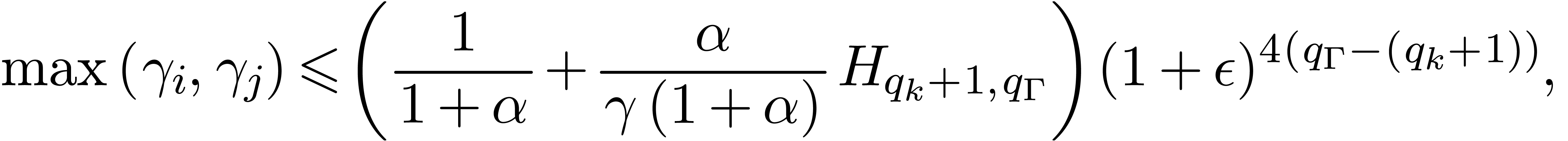
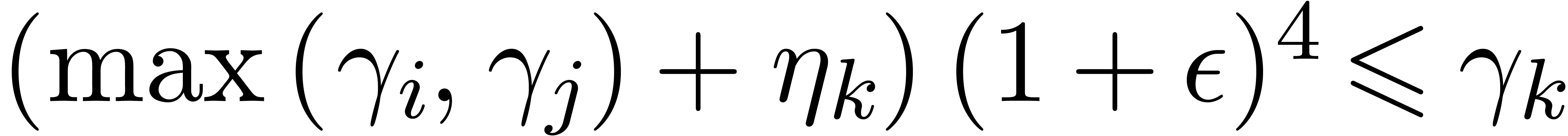 .
.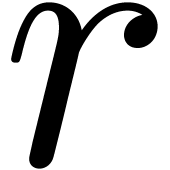 and
and  as above, it follows that
as above, it follows that
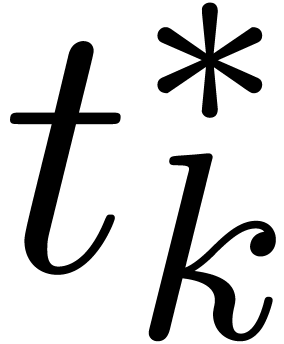
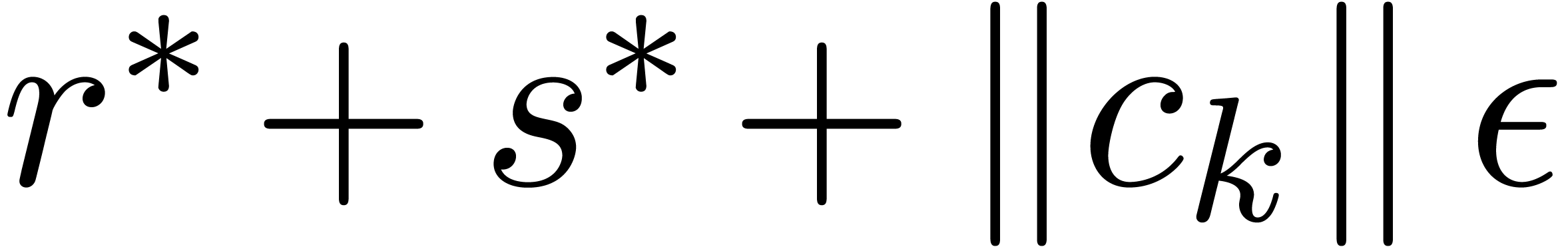
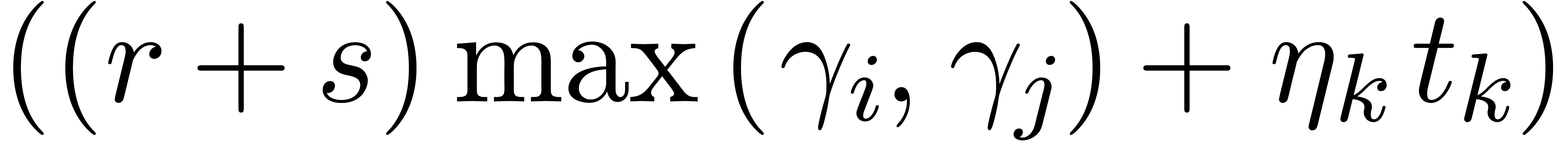

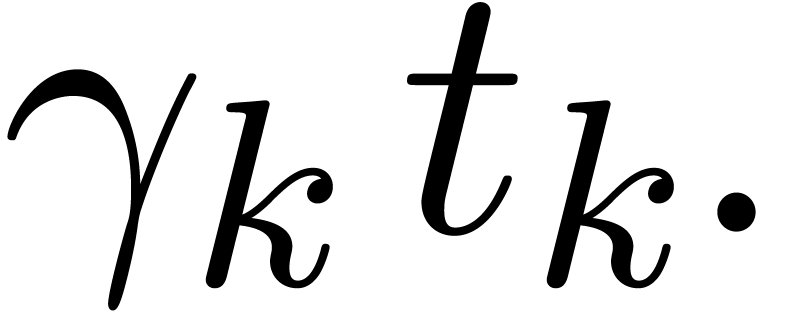
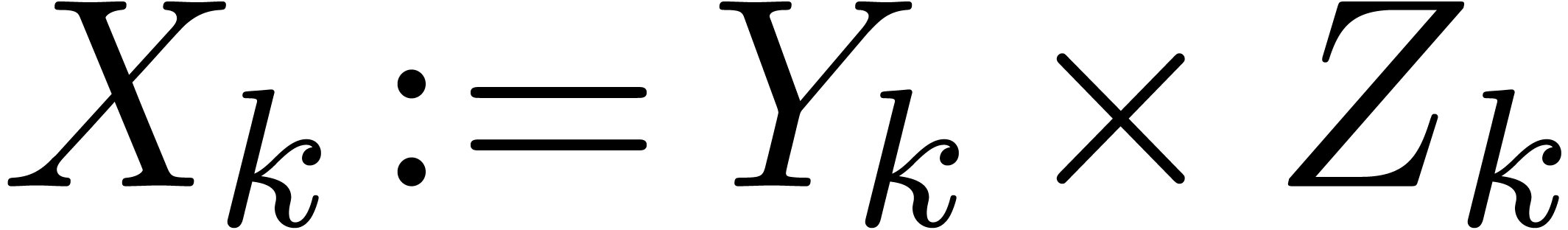 ,
,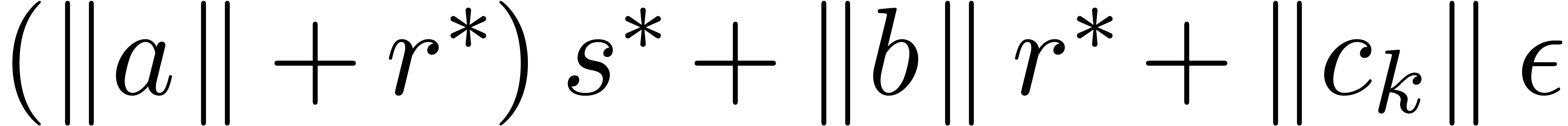
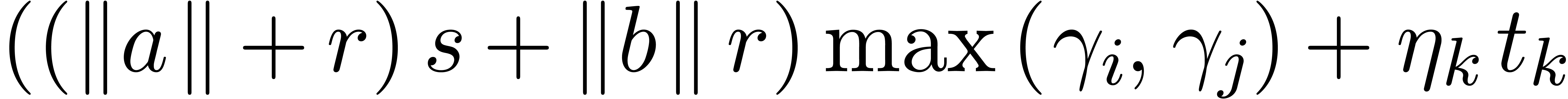
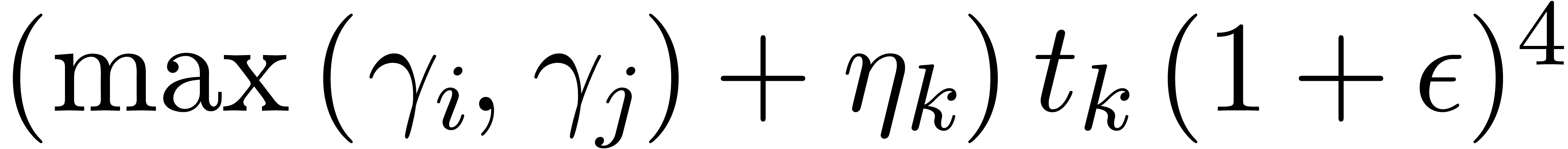

 and
and 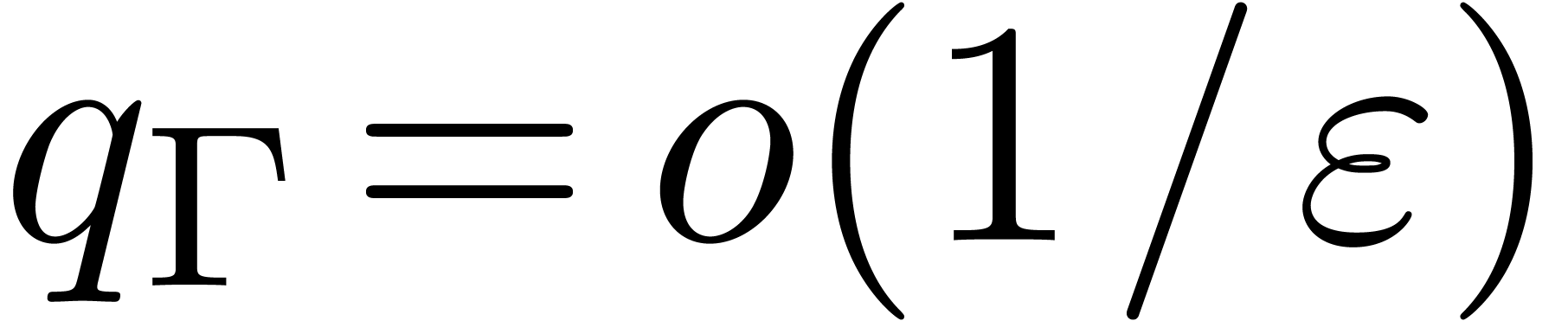 ,
,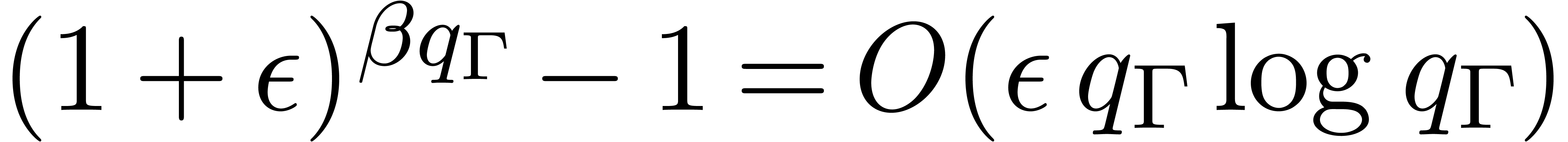 .
. ,
, the largest positive finite
number in
the largest positive finite
number in 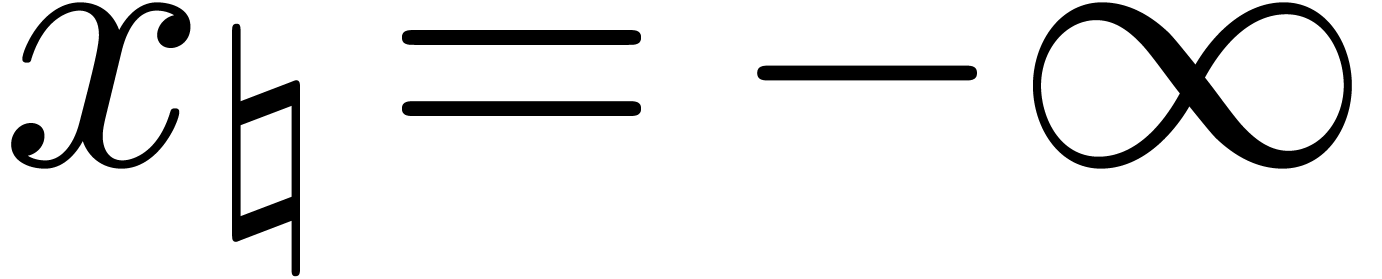 for all
for all 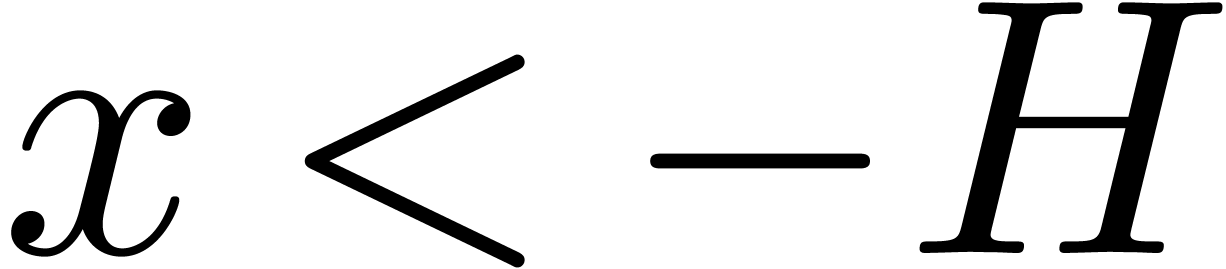 and
and 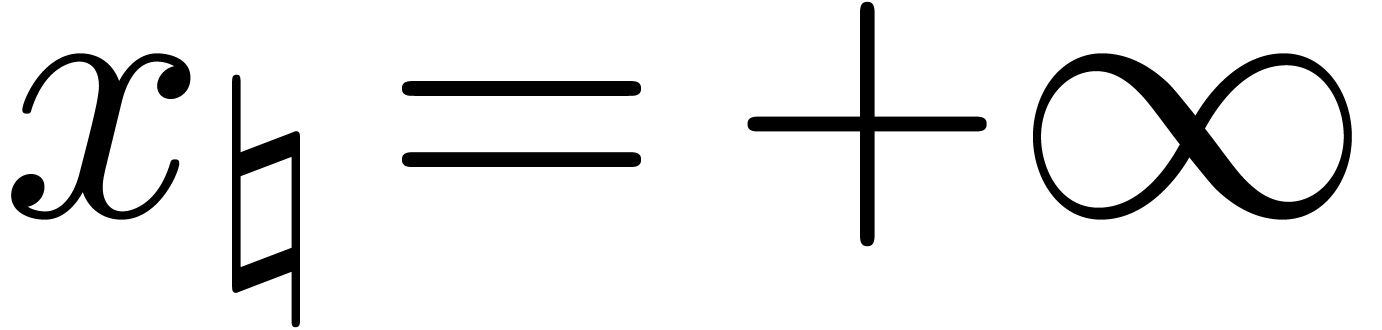 for all
for all  .
.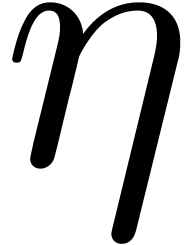 in
in
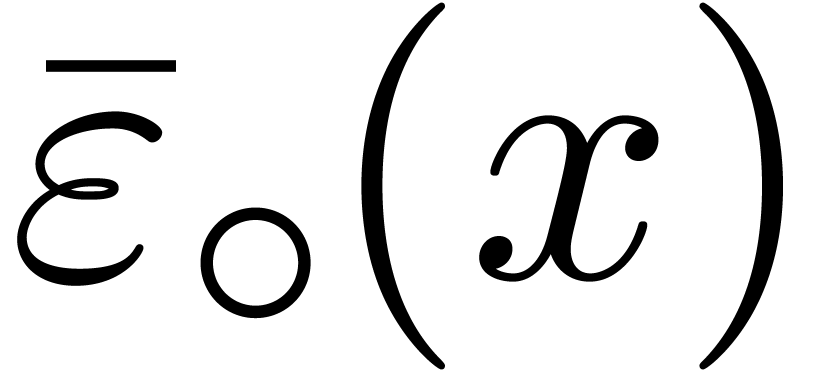
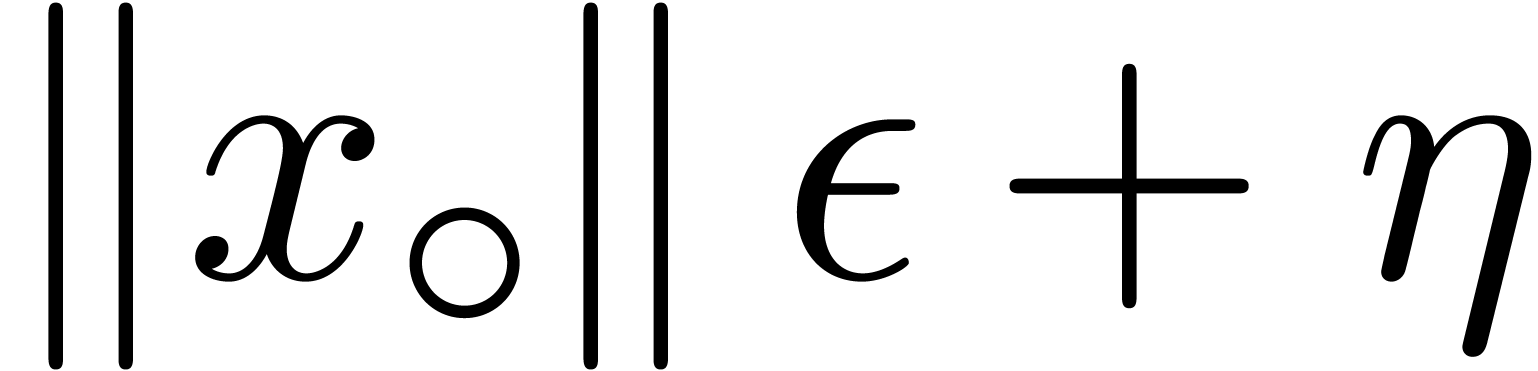
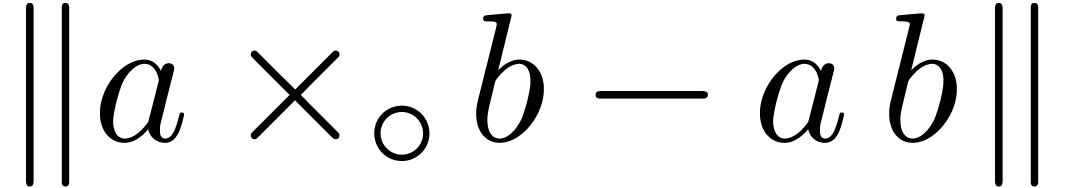
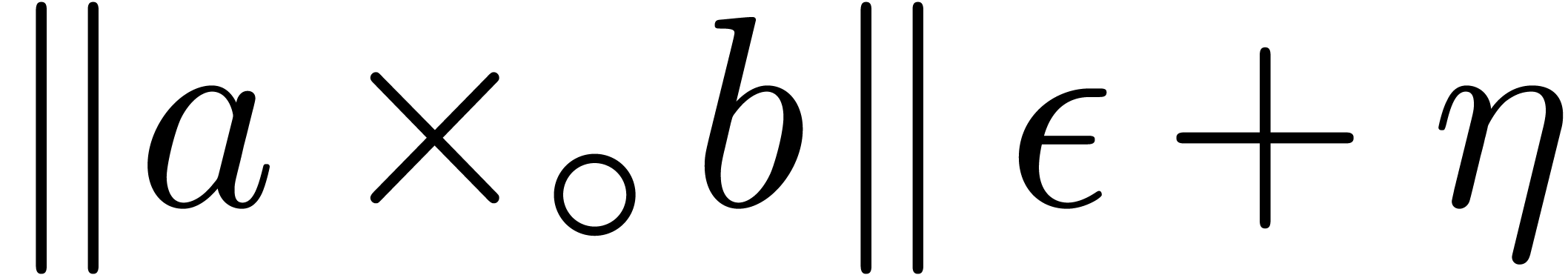
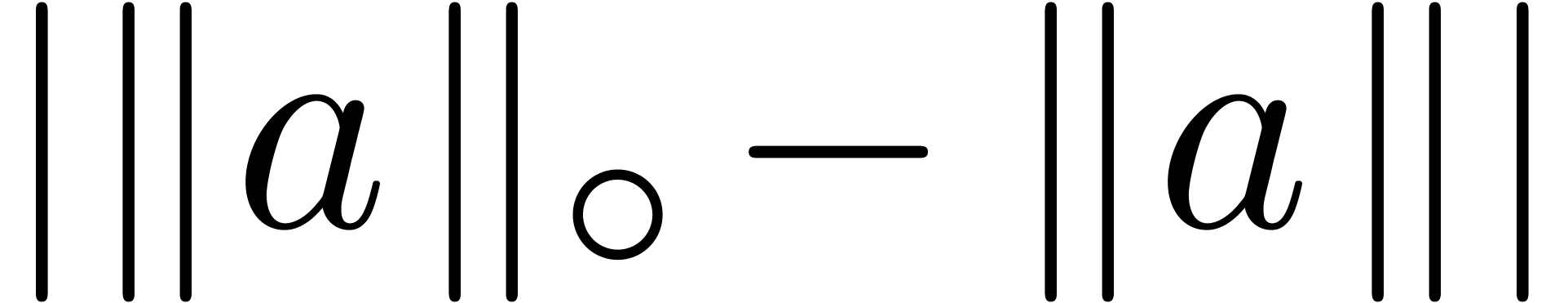
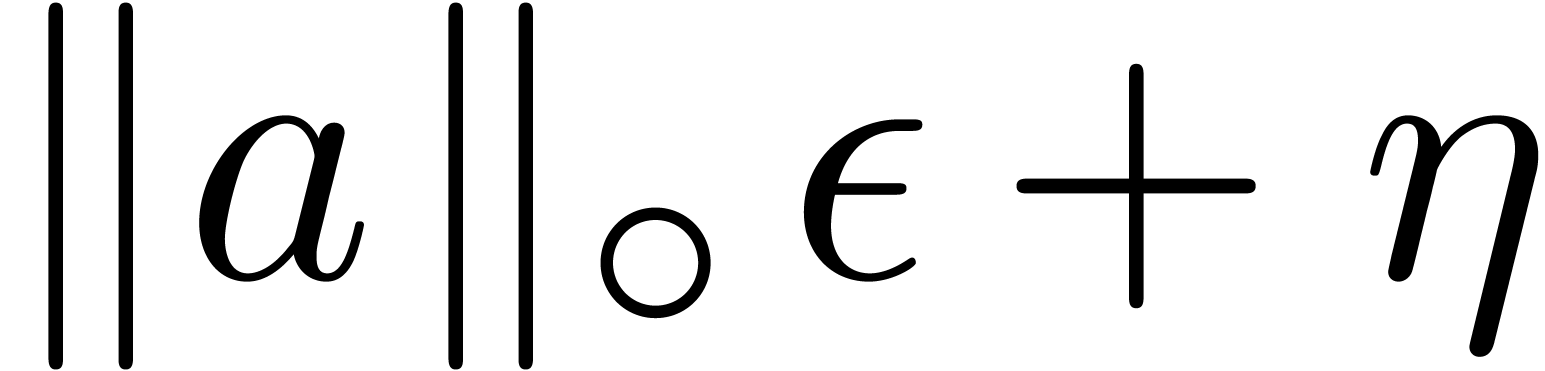
 and
and 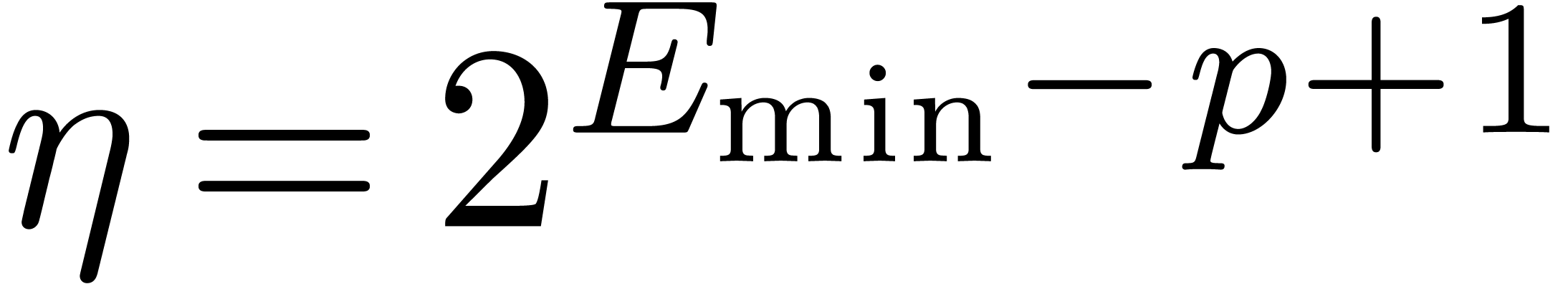 .
.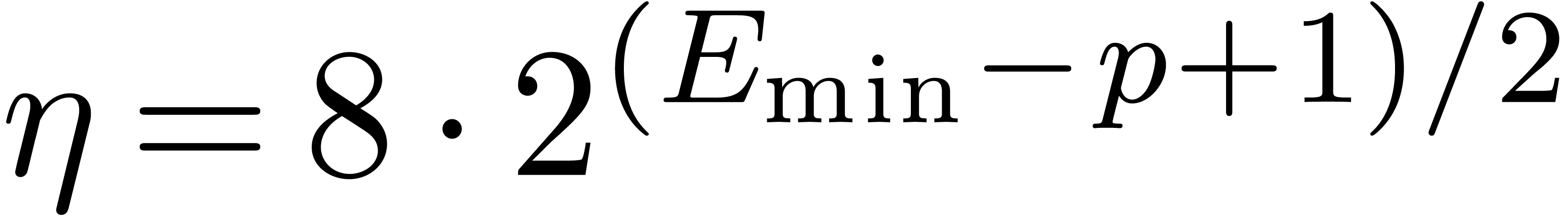 (see
Appendix
(see
Appendix 
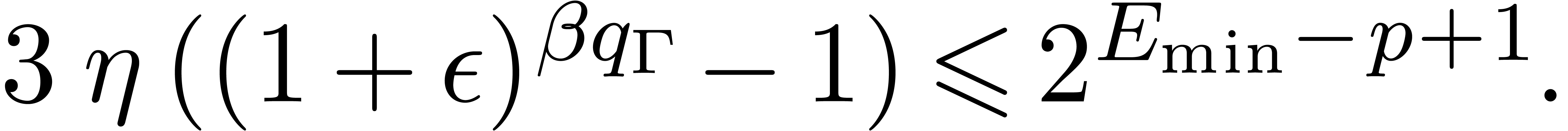
 .
. we have
we have 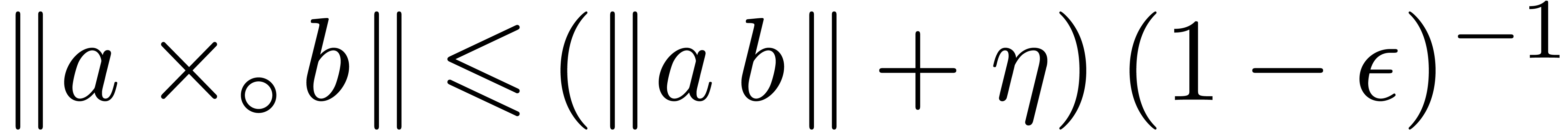 .
.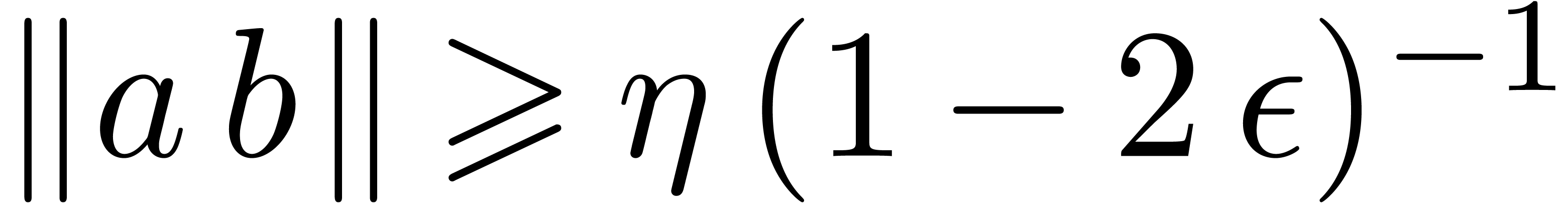 ,
, holds, whence inequality
holds, whence inequality 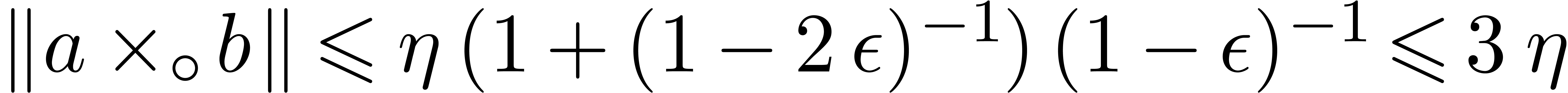 ,
,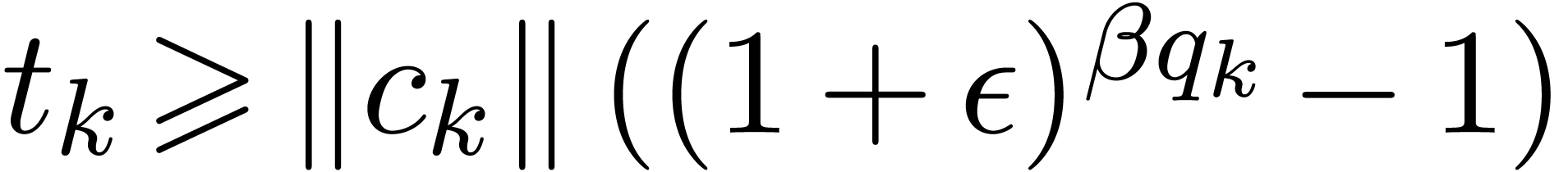 because
because 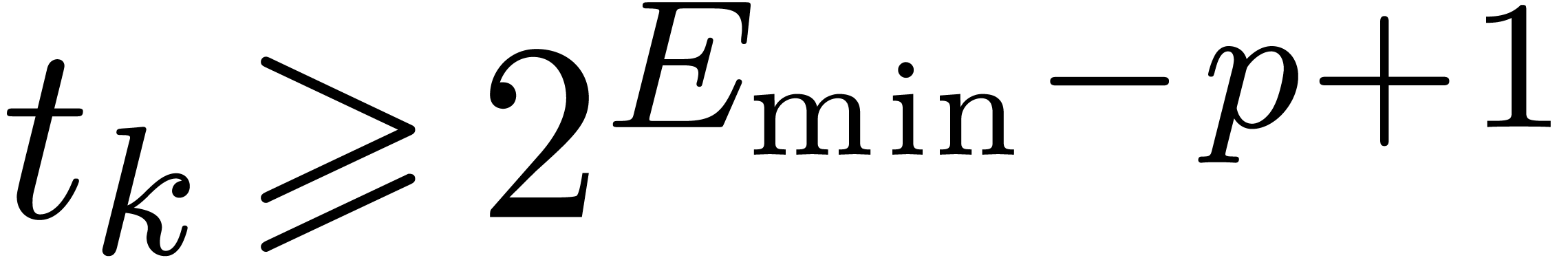 always holds by construction.
always holds by construction.
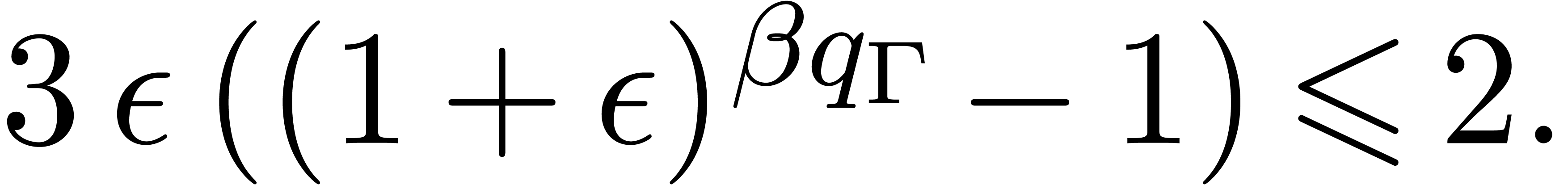
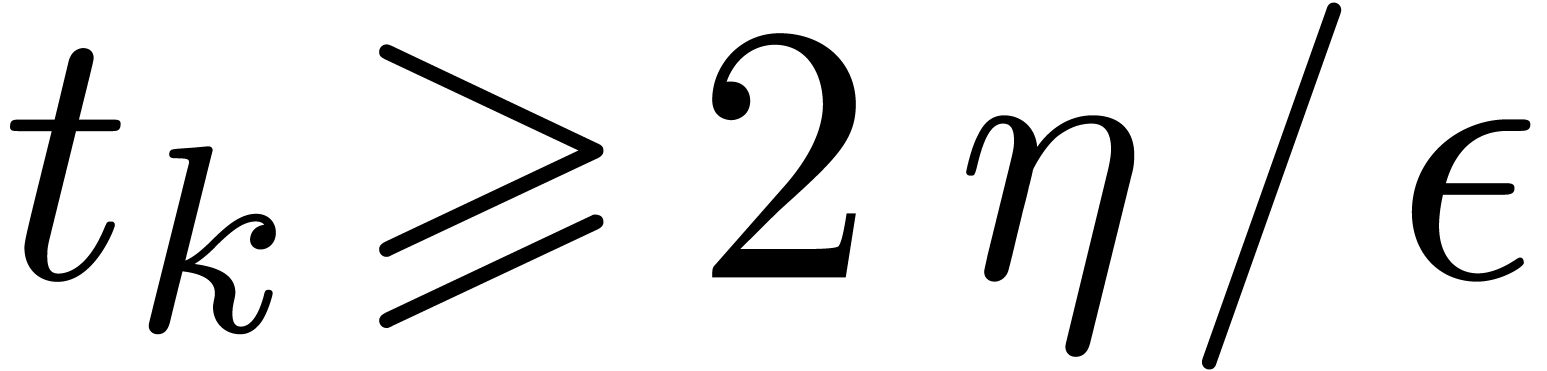 holds by construction.
holds by construction.
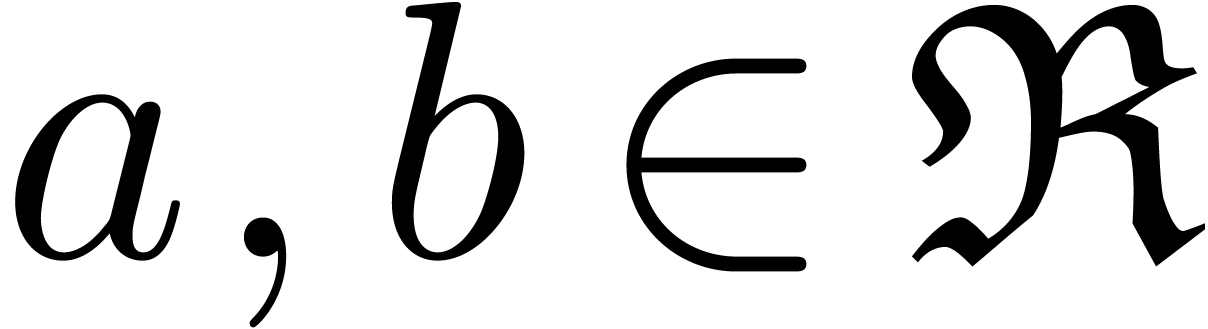 and
and 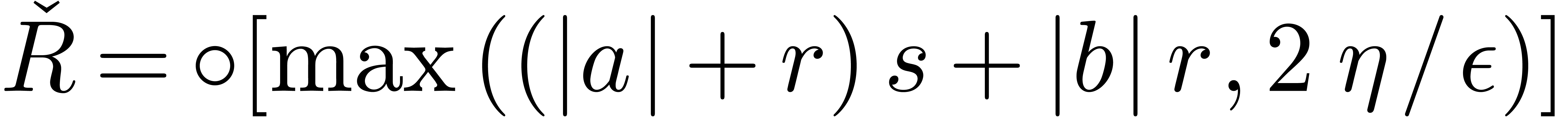 and
and 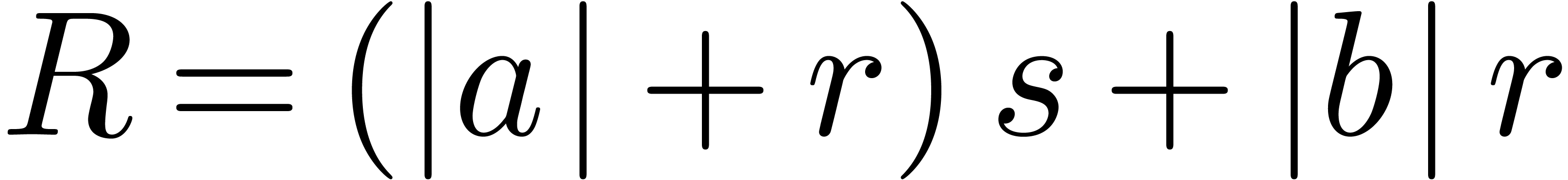 ,
,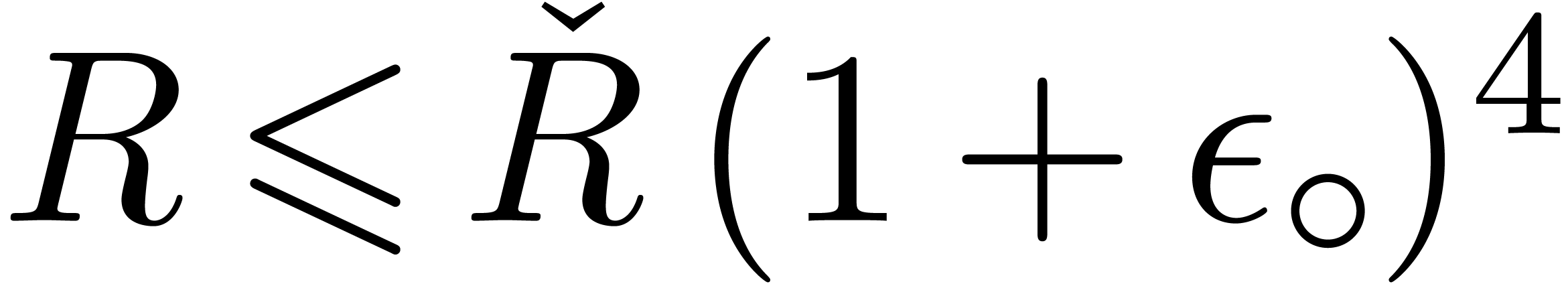 .
.
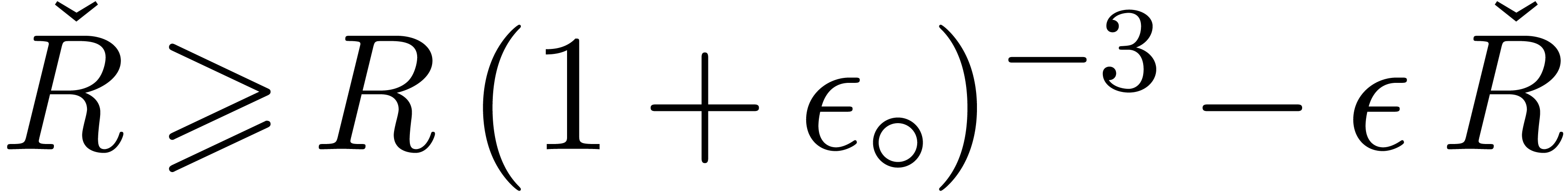 .
. ,
, satisfies
satisfies
 ,
,
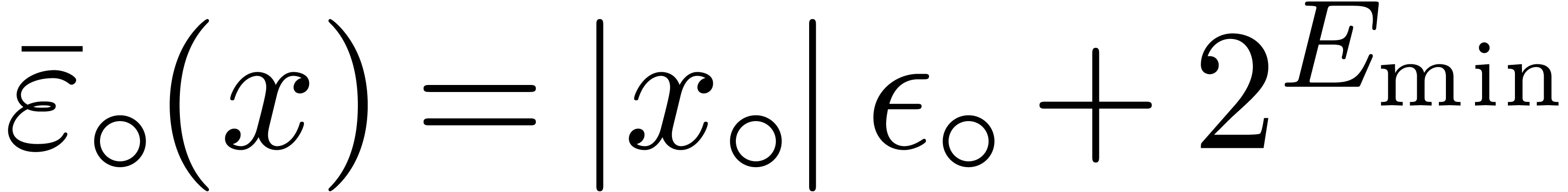 over
over
 being the smallest positive normal number in
being the smallest positive normal number in
 in the proofs.
in the proofs.
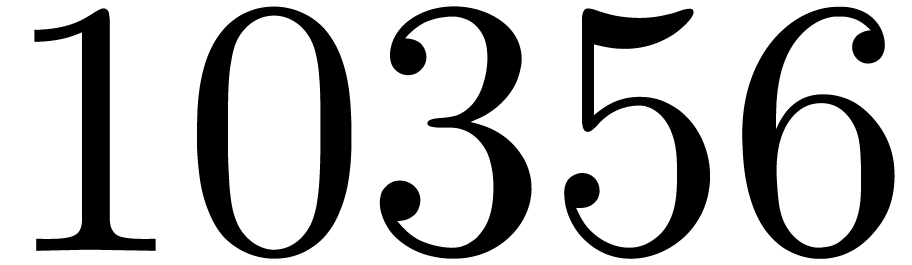 .
. GHz and 8 GB of
GHz and 8 GB of 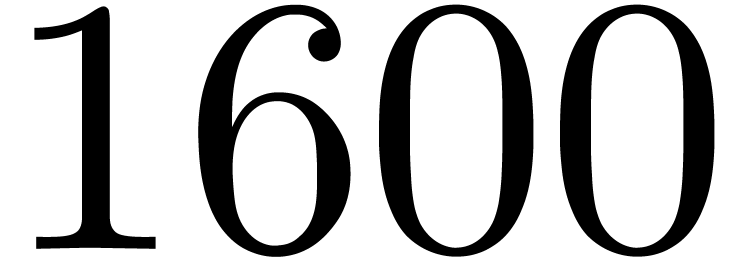 MHz DDR3, which includes
AVX2 and FMA technologies. The platform runs
the
MHz DDR3, which includes
AVX2 and FMA technologies. The platform runs
the 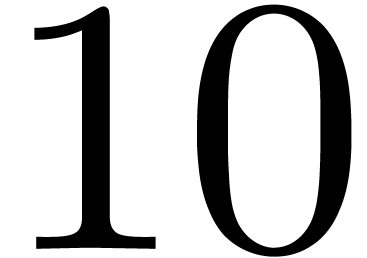 variables, made of 100
terms, built from random monomials of partial degrees at most 10. We
build the SLP using a dedicated algorithm implemented in multimix/dag_polynomial.hpp.
Support for this specific coefficient type may be found in multimix/slp_polynomial_double.hpp.
This example, with the corresponding functions to reproduce these
timings are available in multimix/bench/slp_polynomial_bench.cpp.
The evaluation of this SLP takes 1169 products and 100 sums.
variables, made of 100
terms, built from random monomials of partial degrees at most 10. We
build the SLP using a dedicated algorithm implemented in multimix/dag_polynomial.hpp.
Support for this specific coefficient type may be found in multimix/slp_polynomial_double.hpp.
This example, with the corresponding functions to reproduce these
timings are available in multimix/bench/slp_polynomial_bench.cpp.
The evaluation of this SLP takes 1169 products and 100 sums.
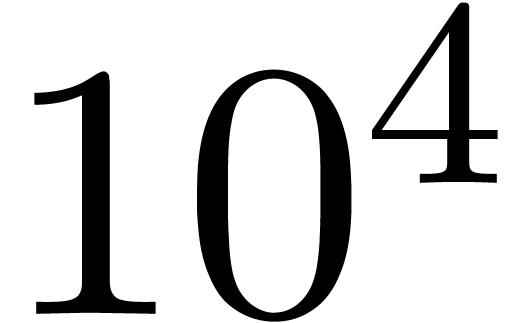 naive
evaluations.
naive
evaluations.
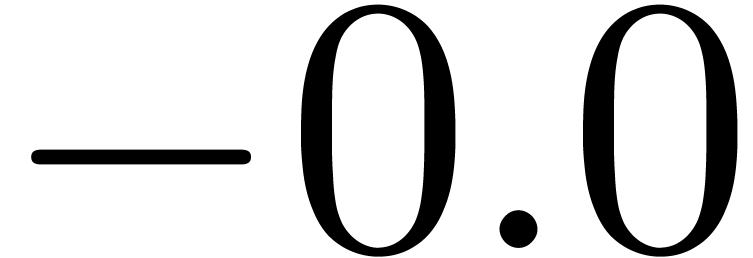 and if ymm1 contains a center
and if ymm1 contains a center 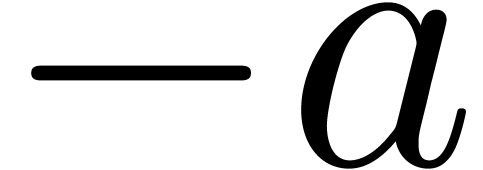 is obtained as
vxorpd ymm0 ymm1 ymm2, and
is obtained as
vxorpd ymm0 ymm1 ymm2, and  as
vandnpd ymm0 ymm1 ymm2. The latency and throughput of
both these instructions are a single cycle and no branchings are
required to compute
as
vandnpd ymm0 ymm1 ymm2. The latency and throughput of
both these instructions are a single cycle and no branchings are
required to compute 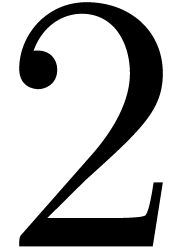 or
or  is easily observed for double, complex<double>,
and balls over double. For balls over complex<double>, a penalty occurs, because the
vectorial square root instruction is about twice slower than its scalar
counterpart. For instance, the evaluation of a univariate polynomial in
degree
is easily observed for double, complex<double>,
and balls over double. For balls over complex<double>, a penalty occurs, because the
vectorial square root instruction is about twice slower than its scalar
counterpart. For instance, the evaluation of a univariate polynomial in
degree 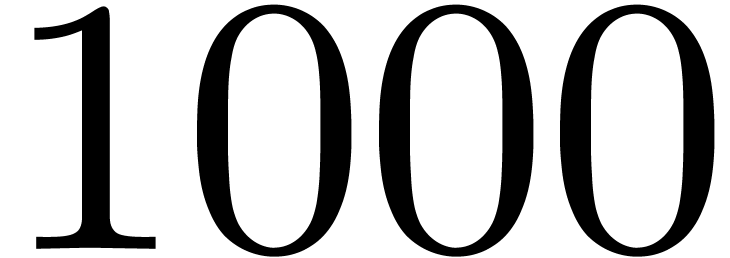 with Hörner's method takes about
5000 CPU cycles over double (each fma instruction takes
the expected latency), 13000 cycles over complex<double>,
and 16000 cycles for transient balls of double, with
both scalar and vectorial instructions. As for transient balls over complex<double>, scalar
instructions amount to about 17000 cycles, while vectorial ones take
about 28000 cycles.
with Hörner's method takes about
5000 CPU cycles over double (each fma instruction takes
the expected latency), 13000 cycles over complex<double>,
and 16000 cycles for transient balls of double, with
both scalar and vectorial instructions. As for transient balls over complex<double>, scalar
instructions amount to about 17000 cycles, while vectorial ones take
about 28000 cycles.
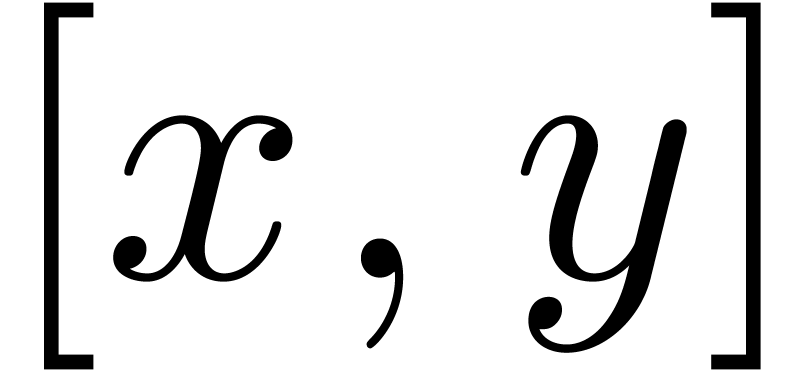 by intervals of the form
by intervals of the form 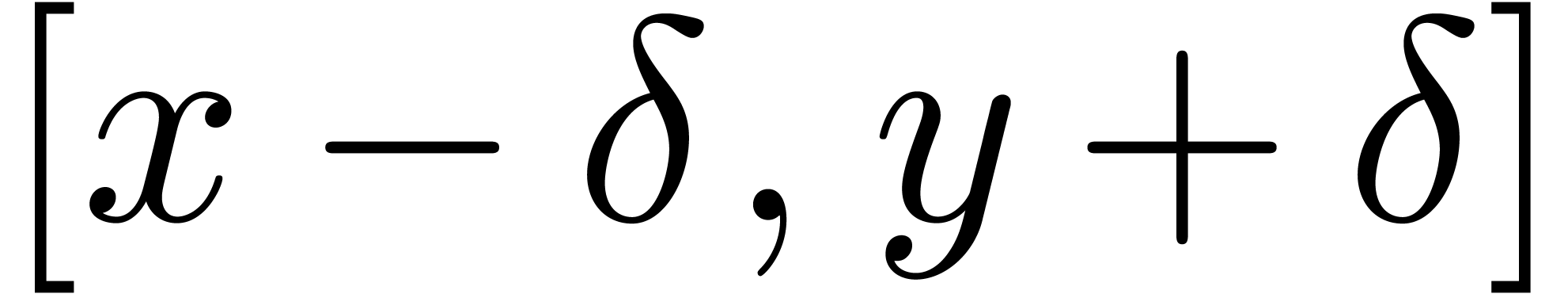 ,
,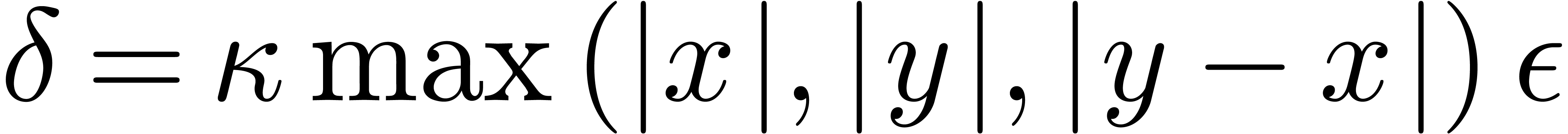 for suitable
for suitable
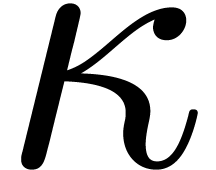 .
.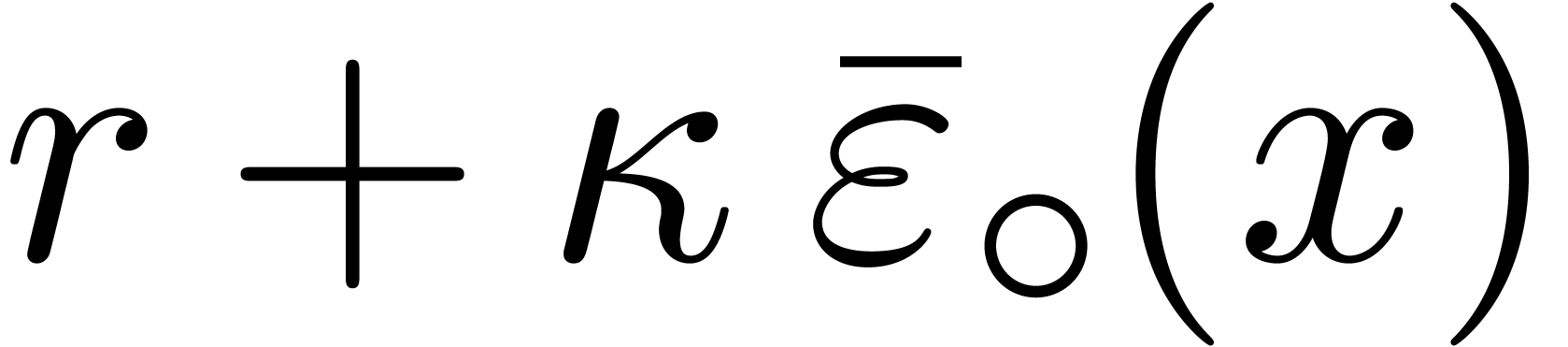 as a function of
as a function of
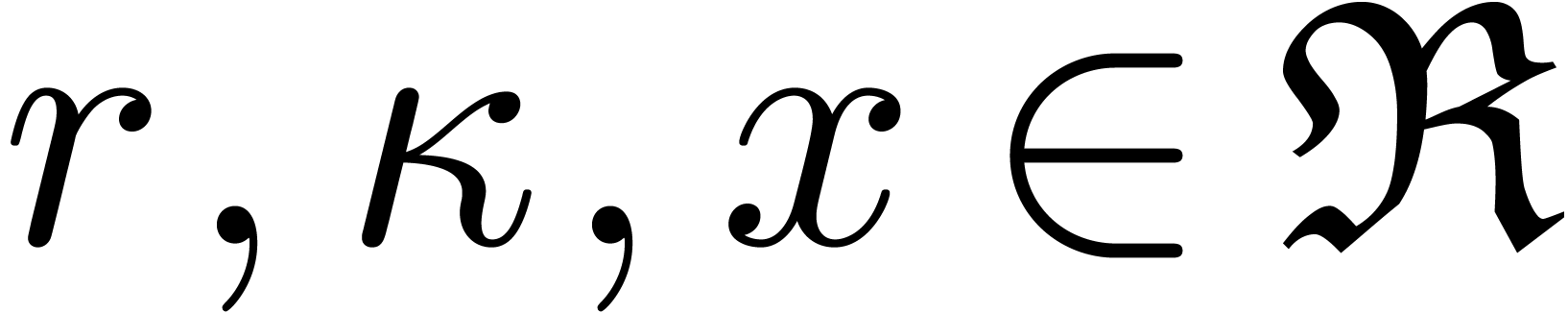 .
.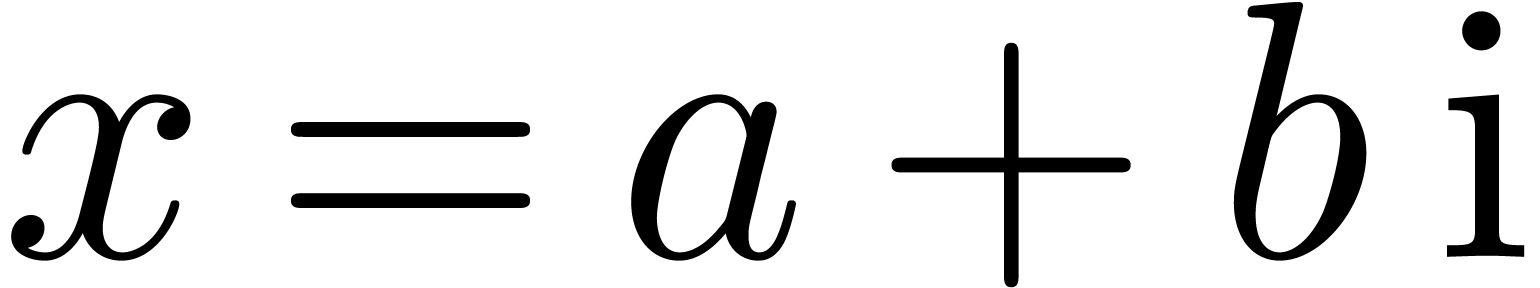 and
and 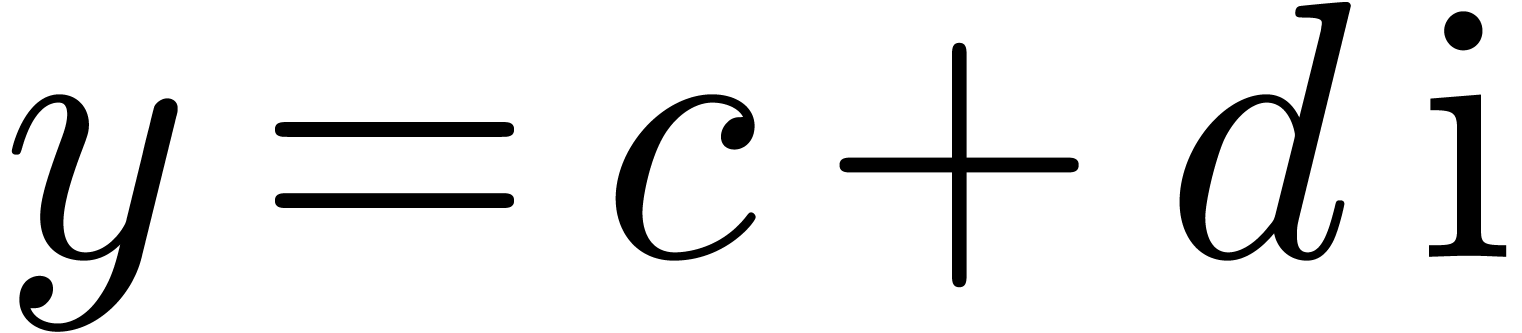 be
two complex numbers in
be
two complex numbers in  .
.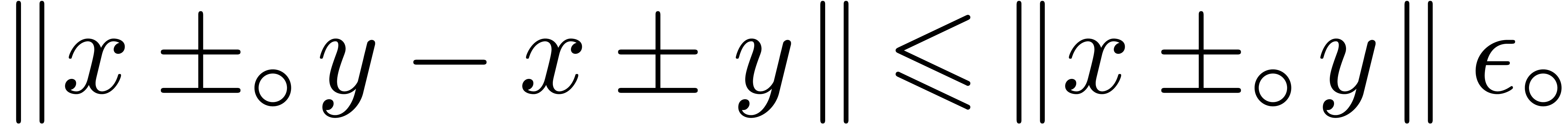
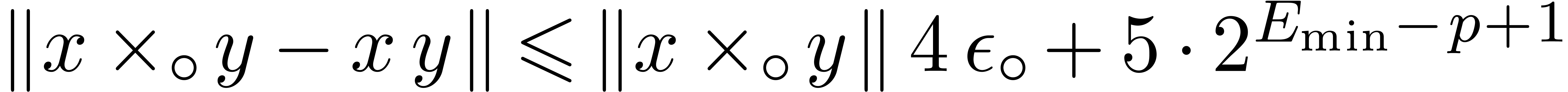
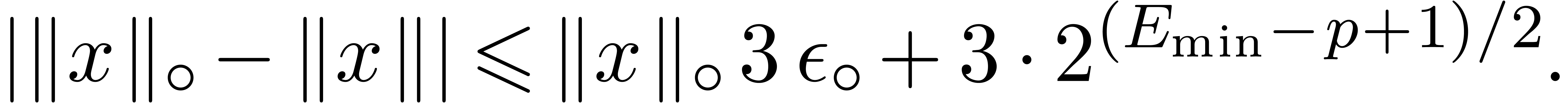
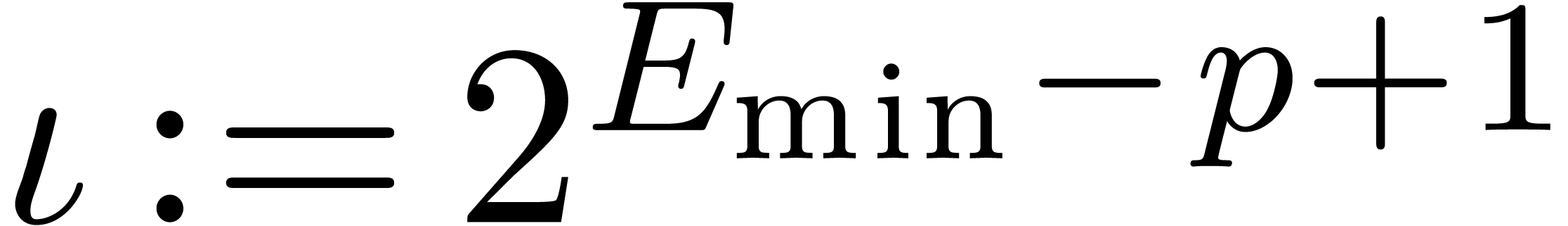 ,
, .
. ,
, .
.


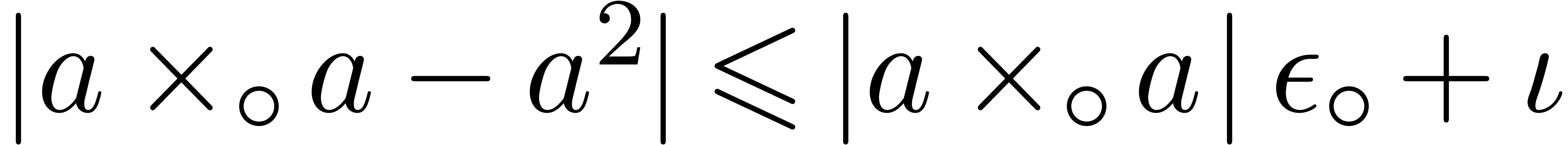 and
and  ,
,
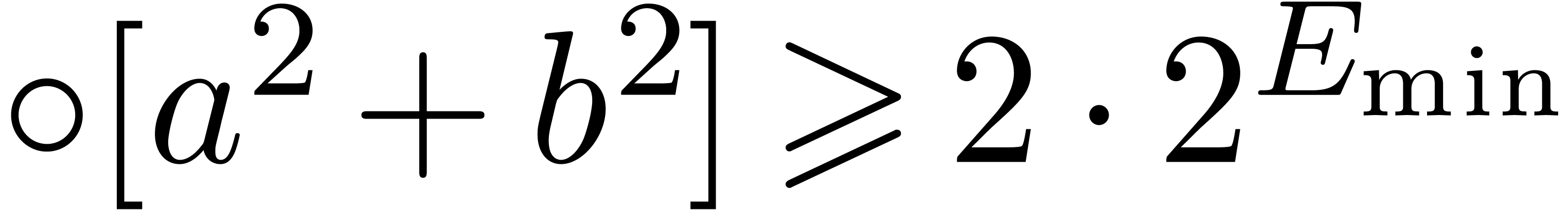 ,
,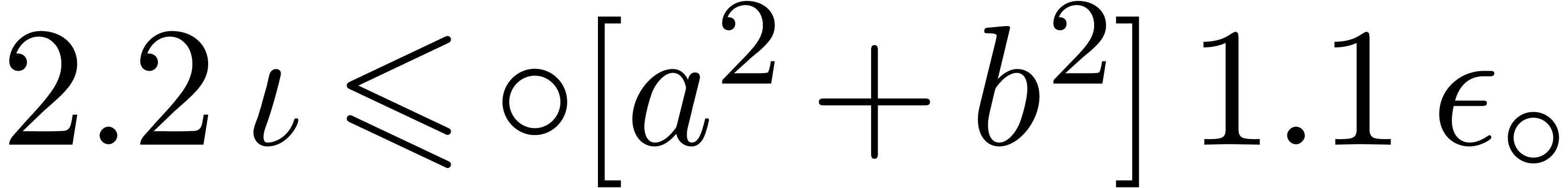 .
.
 ,
,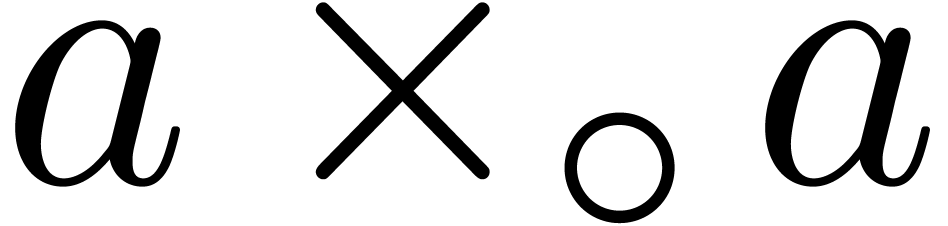 and
and 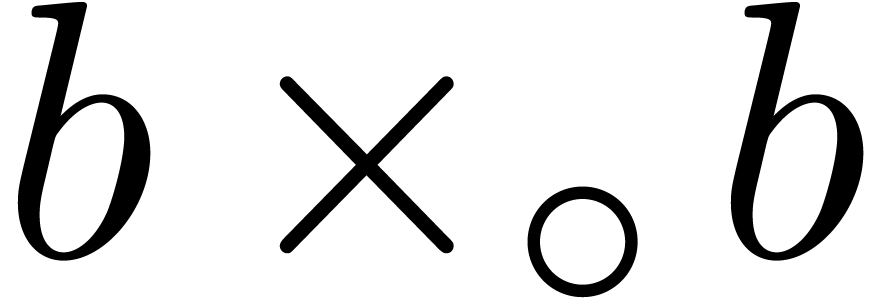 involve underflows. We restart the analysis from
involve underflows. We restart the analysis from
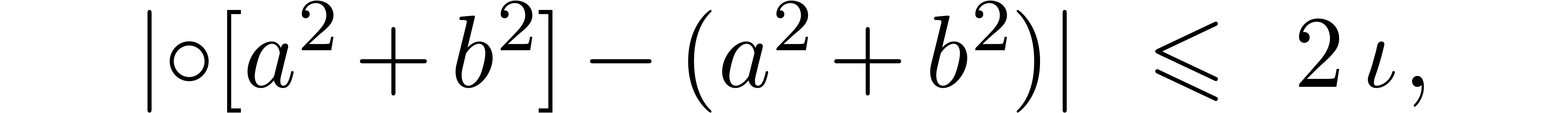
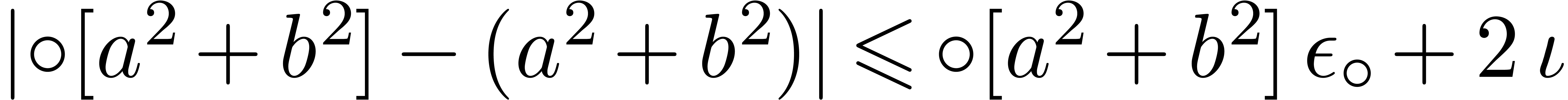 .
.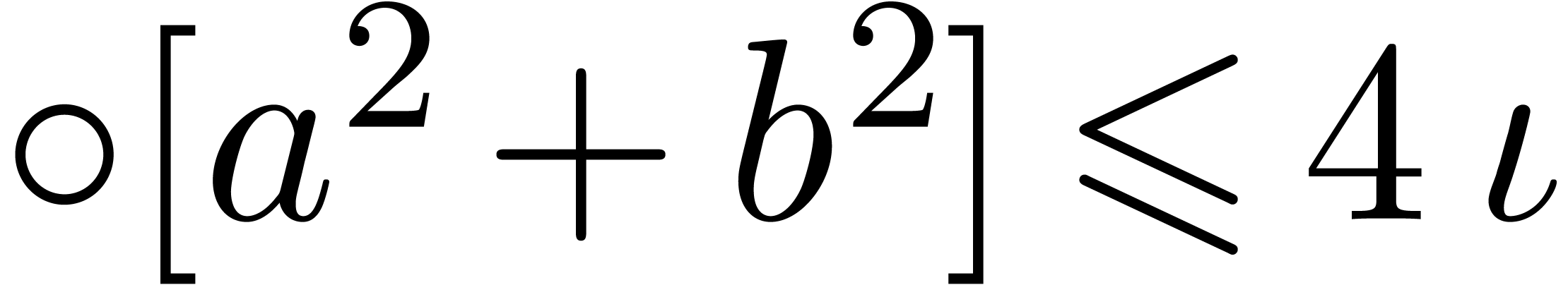 ,
,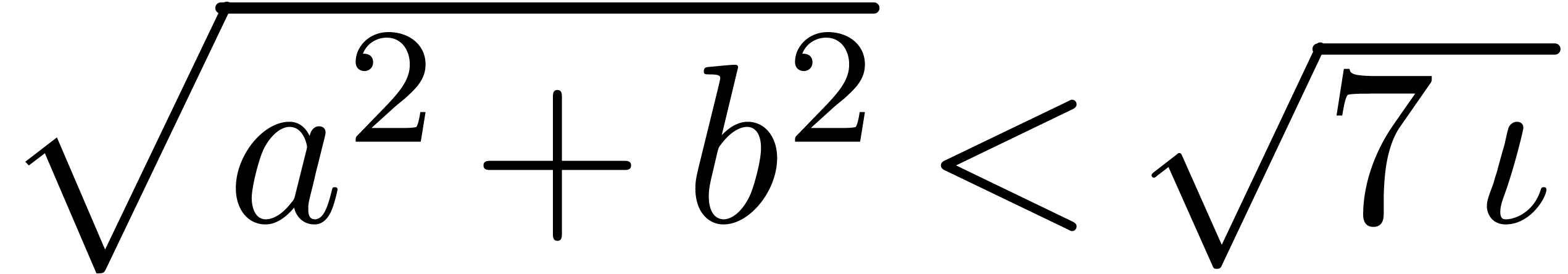 .
.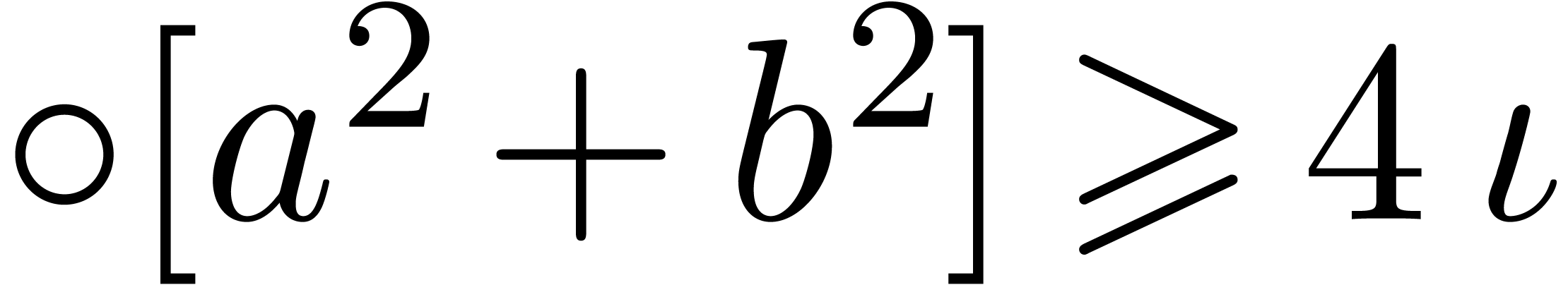 ,
,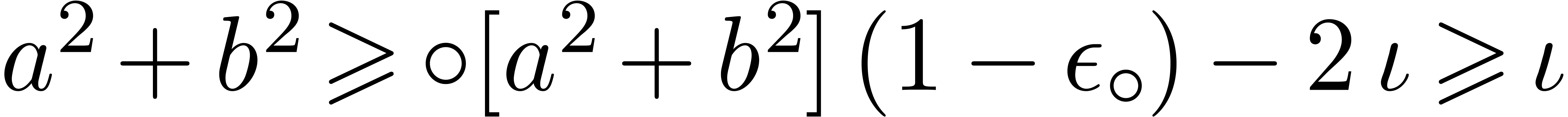 ,
,