A. Partially supported by a LIX–Qualcomm –Carnot
postdoctoral fellowship.
–Carnot
postdoctoral fellowship.
|
A. Partially supported by a LIX–Qualcomm –Carnot
postdoctoral fellowship.
–Carnot
postdoctoral fellowship.
We design new deterministic algorithms, based on Graeffe
transforms, to compute all the roots of a polynomial which splits
over a finite field |
Let  represent the finite field with
represent the finite field with 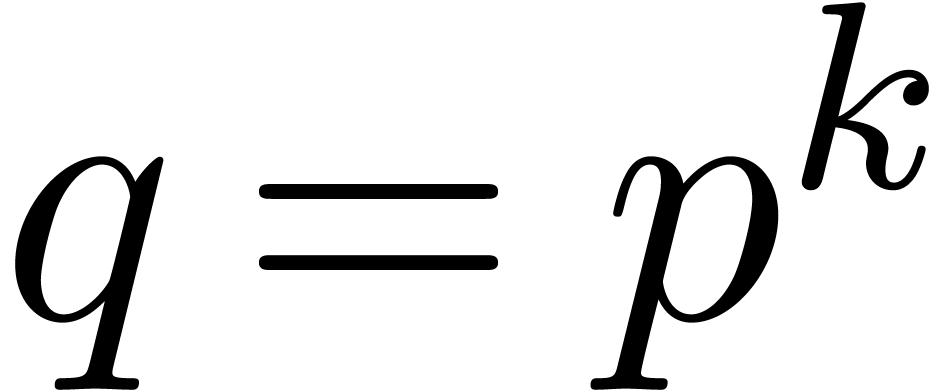 elements, where
elements, where 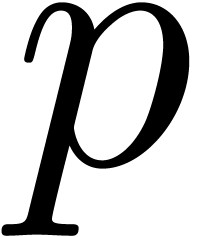 is a prime number,
and
is a prime number,
and 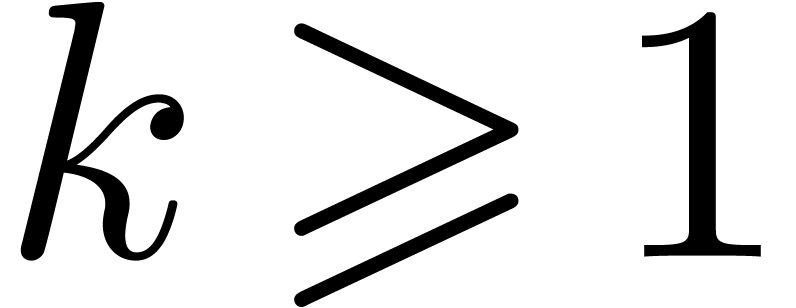 . Throughout this
article, such a field is supposed to be described as a quotient of
. Throughout this
article, such a field is supposed to be described as a quotient of 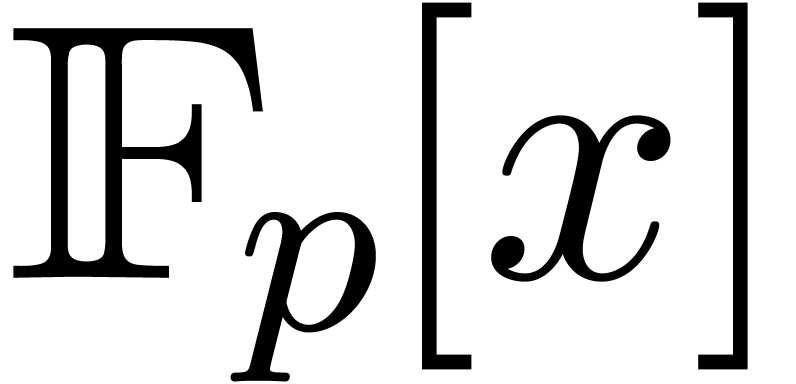 by a monic irreducible polynomial. Let
by a monic irreducible polynomial. Let 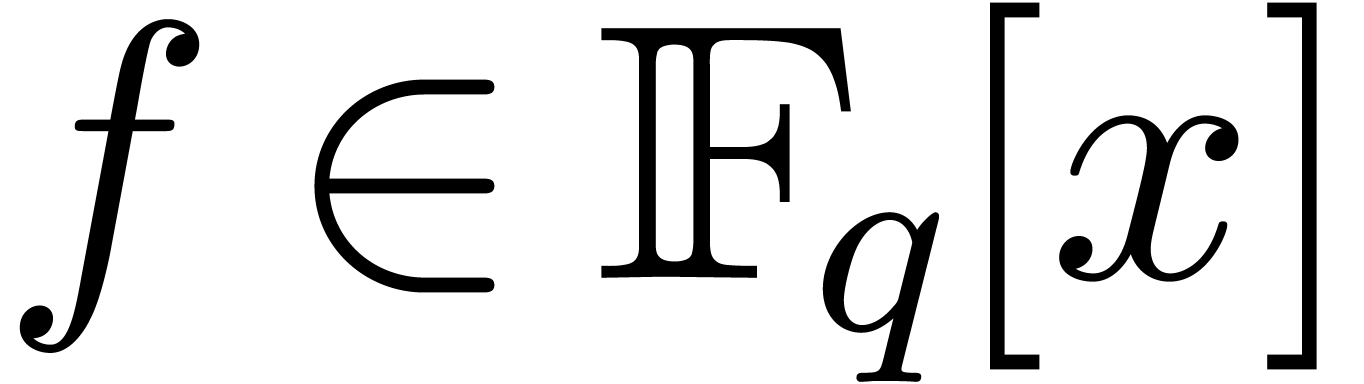 represent a separable monic polynomial of
degree
represent a separable monic polynomial of
degree 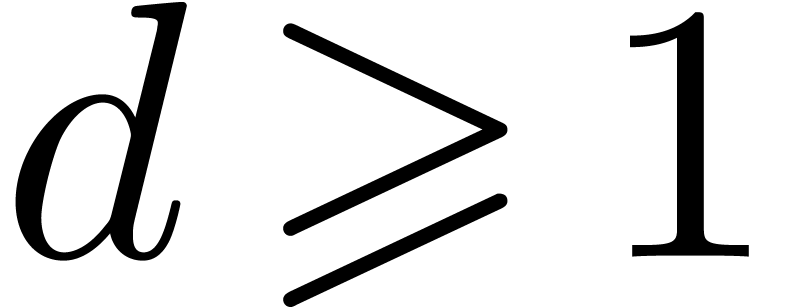 which splits over
which splits over  , which means that all its irreducible factors
have degree one and multiplicity one. In this article we are interested
in computing all the roots of
, which means that all its irreducible factors
have degree one and multiplicity one. In this article we are interested
in computing all the roots of 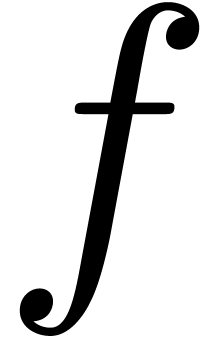 .
.
In a previous paper [20], we presented efficient randomized
root finding algorithms. Such algorithms were needed for the efficient
interpolation, into the standard monomial basis, of polynomials that are
given through evaluation functions. This latter problem is also known
under the name sparse interpolation, and root finding often
turns out to be a bottleneck, as indicated in [23]. In
fact, in this case, the ground field can be chosen to be 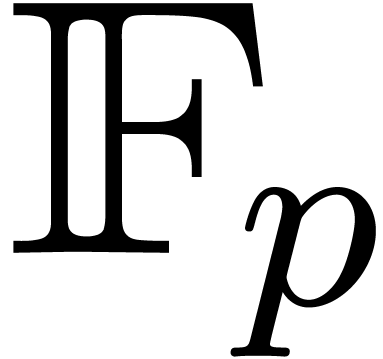 with
with 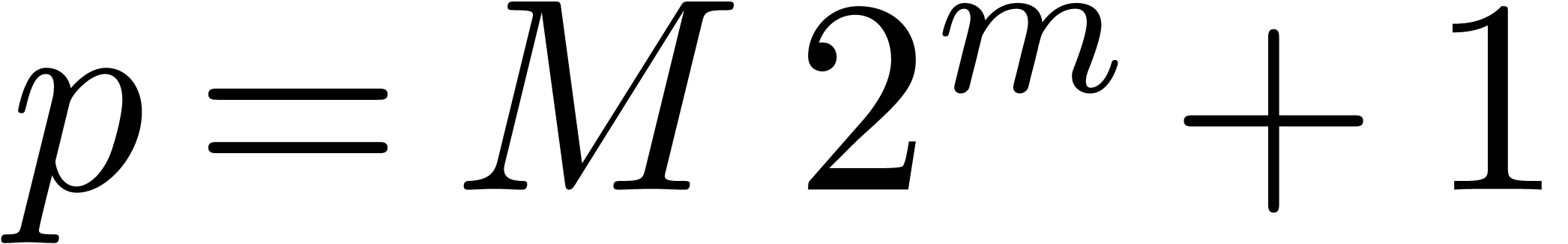 , and
where
, and
where 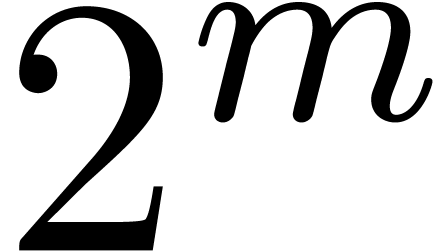 is taken to be much larger than the number
of terms to be discovered. In order to minimize the size of
is taken to be much larger than the number
of terms to be discovered. In order to minimize the size of 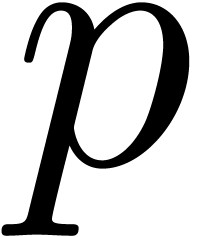 , making it fit into a machine register, we
usually take
, making it fit into a machine register, we
usually take 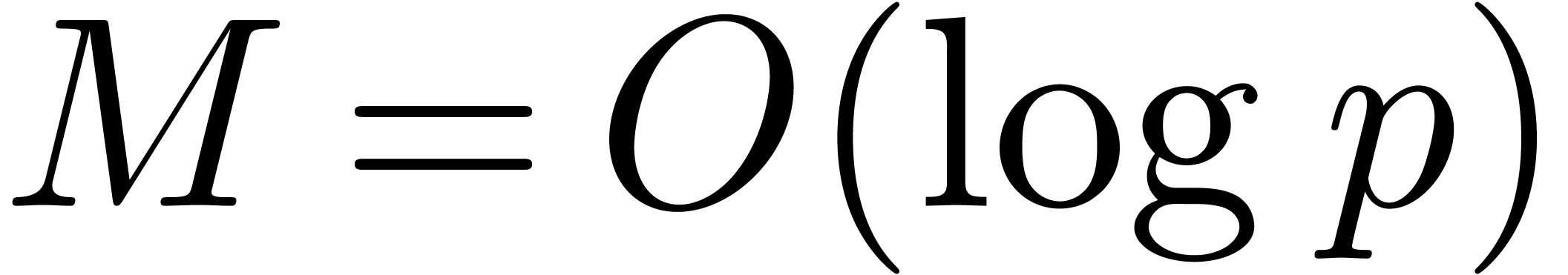 as small as possible. A typical
example is
as small as possible. A typical
example is 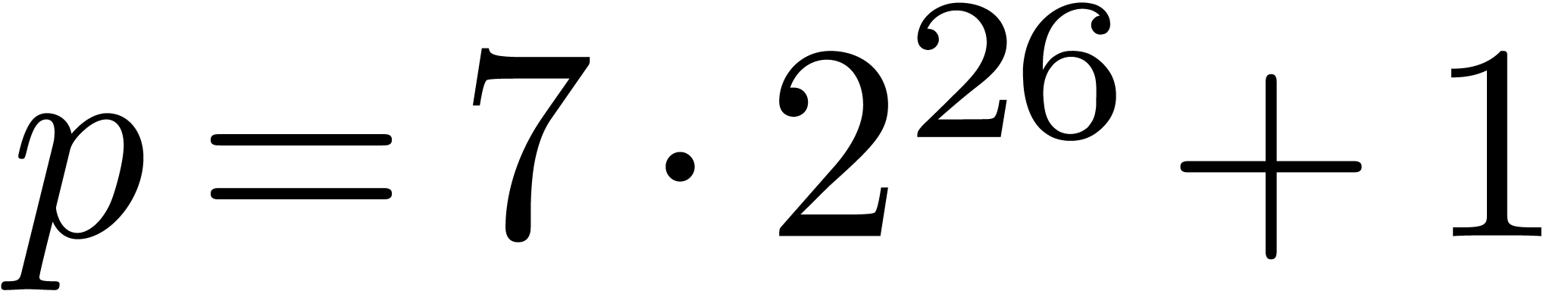 . We informally
refer to such primes as FFT primes.
. We informally
refer to such primes as FFT primes.
While working on [20], it turned out that some of the new
methods could also be used for the design of fast deterministic methods
for computing all the roots of  .
Even though randomized algorithms are more useful in practice, the
existence of efficient deterministic algorithms remains interesting from
a theoretical point of view. The goal of this paper is to report on our
progress on this issue.
.
Even though randomized algorithms are more useful in practice, the
existence of efficient deterministic algorithms remains interesting from
a theoretical point of view. The goal of this paper is to report on our
progress on this issue.
We will use the same notations as in [20], which we briefly
recall now. The multiplicative group 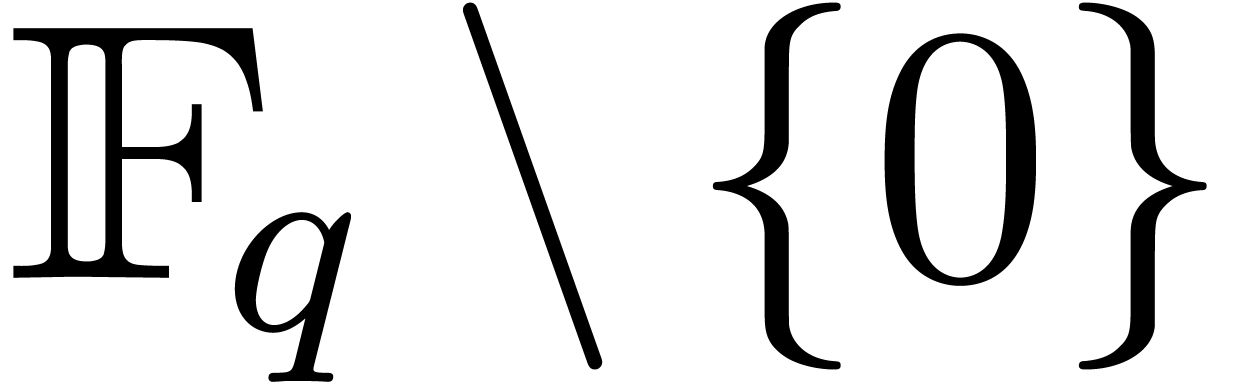 of
of
 is written
is written 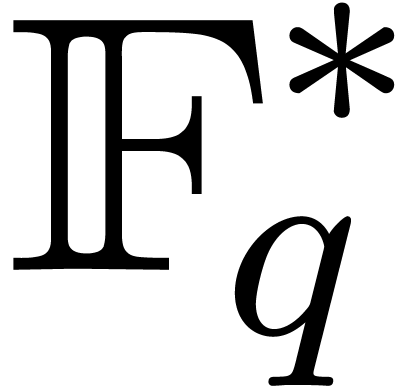 .
Complexity bounds will frequently be expressed using the
soft-Oh notation:
.
Complexity bounds will frequently be expressed using the
soft-Oh notation: 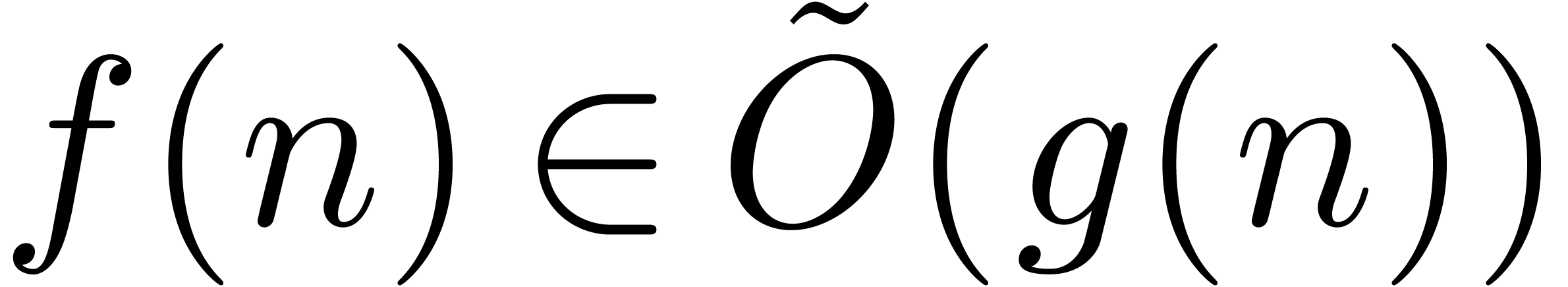 means that
means that 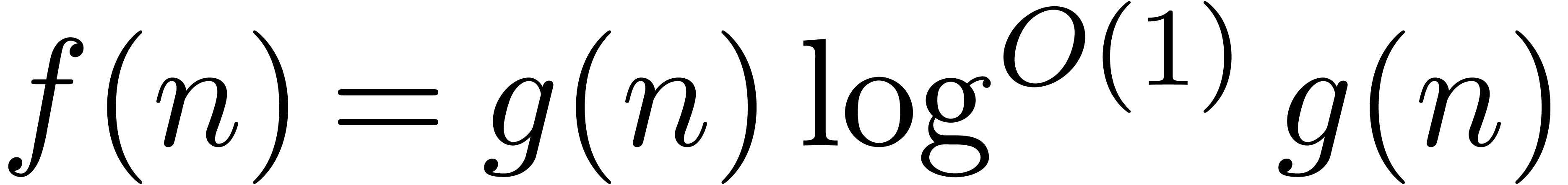 . Given
. Given 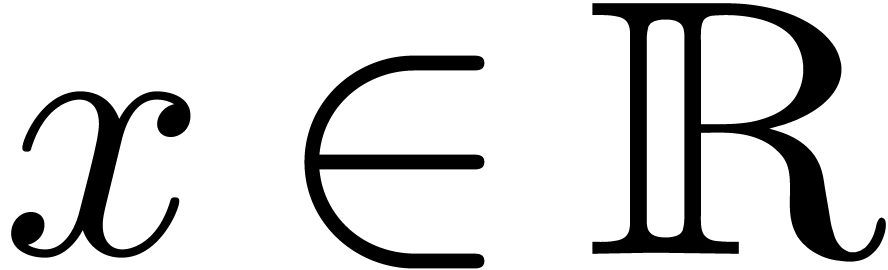 , we write
, we write 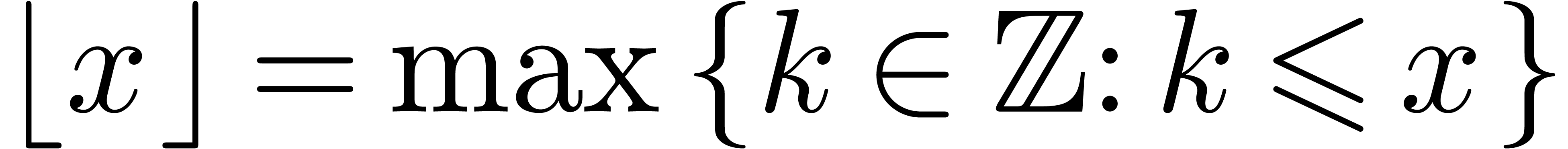 and
and 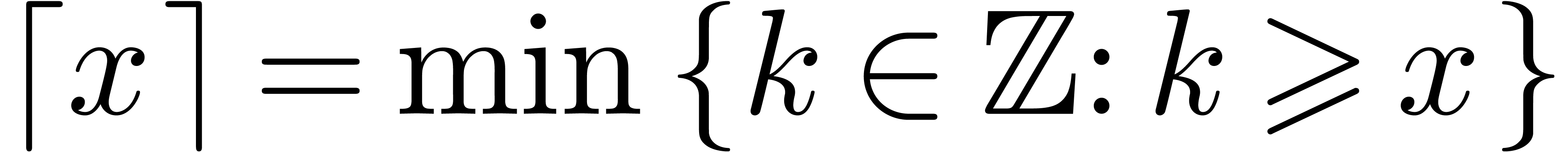 . The remainder of a division of
. The remainder of a division of  by
by 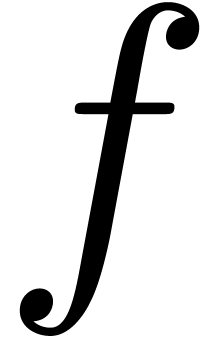 is denoted by
is denoted by 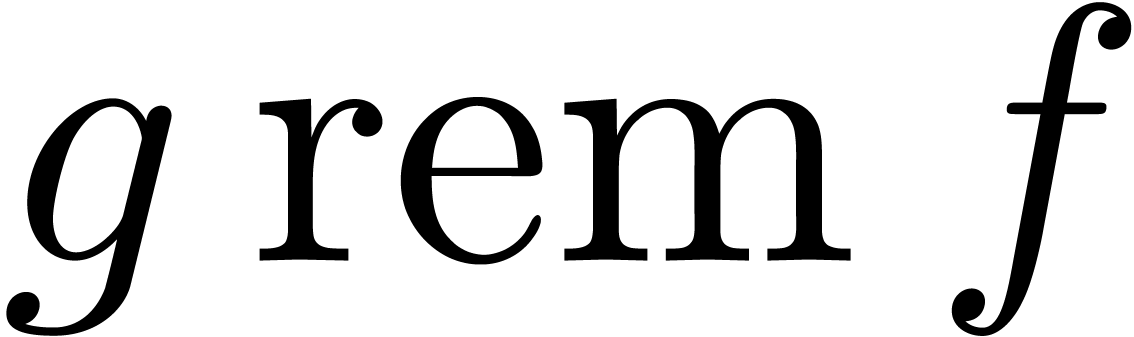 .
.
We write 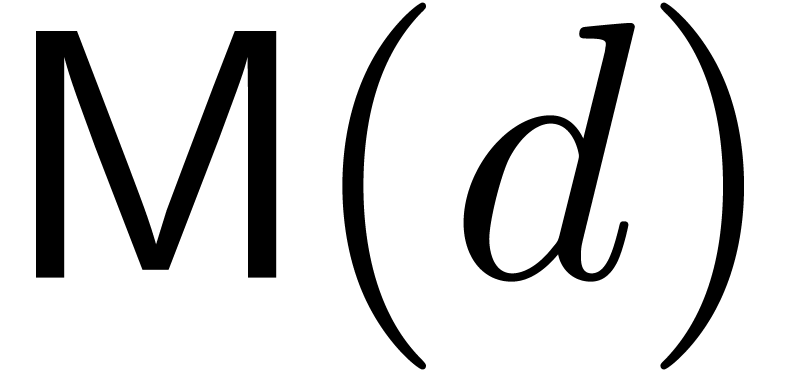 for the complexity of multiplication of
polynomials of degree
for the complexity of multiplication of
polynomials of degree 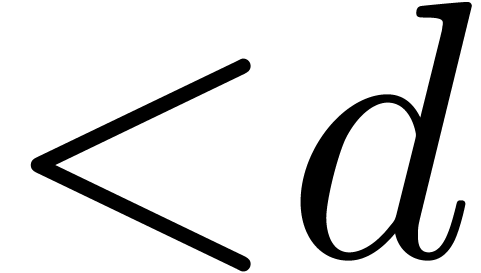 over an arbitrary ring. We
also write
over an arbitrary ring. We
also write 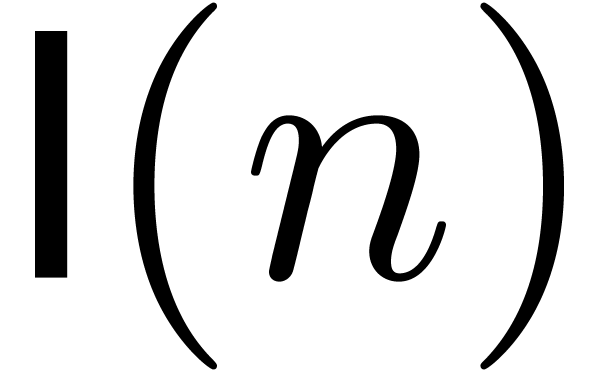 and
and 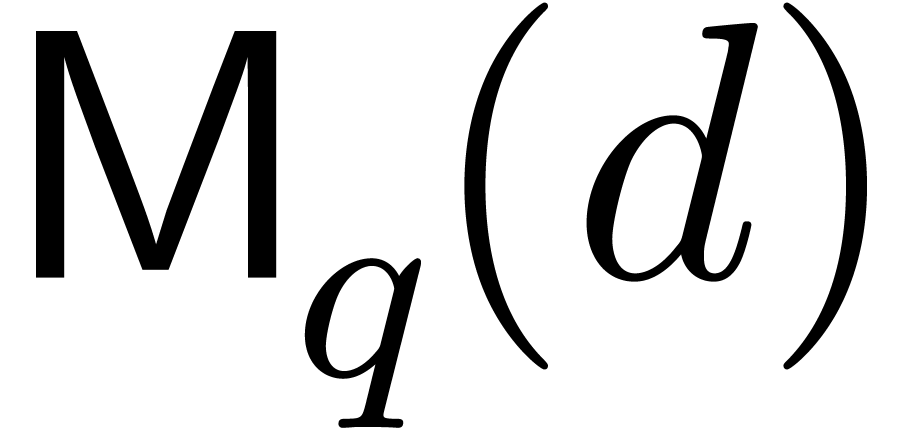 for the
bit complexities (in the Turing machine model) of
for the
bit complexities (in the Turing machine model) of 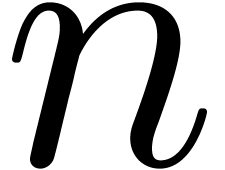 -bit integer multiplication and multiplication of
polynomials of degrees
-bit integer multiplication and multiplication of
polynomials of degrees 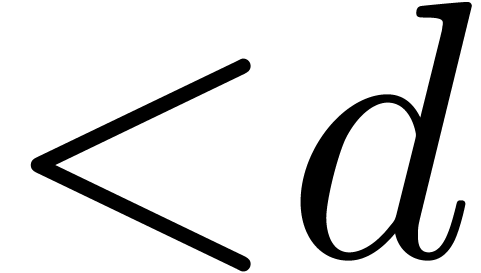 over
over  . We make the customary assumption that
. We make the customary assumption that 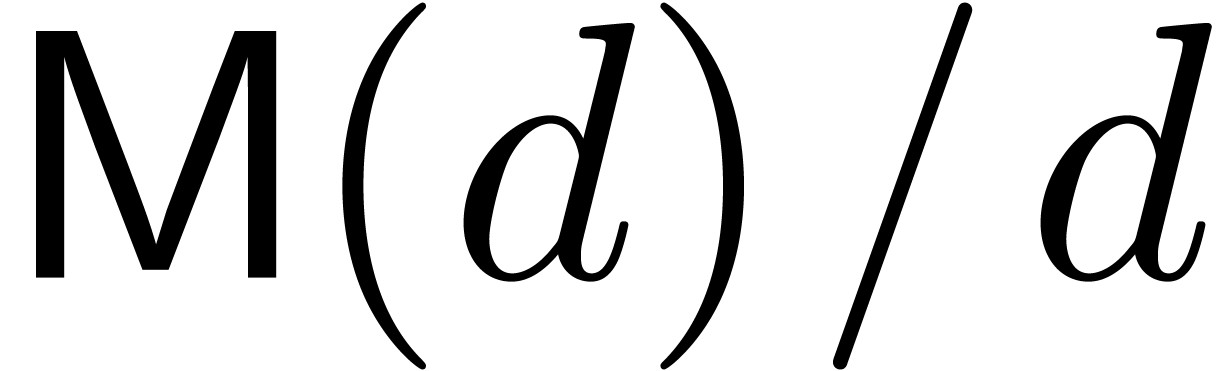 ,
, 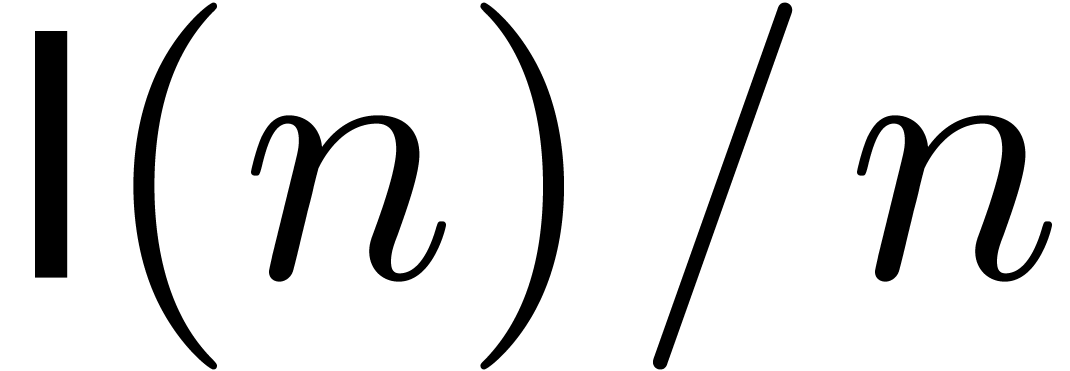 and
and 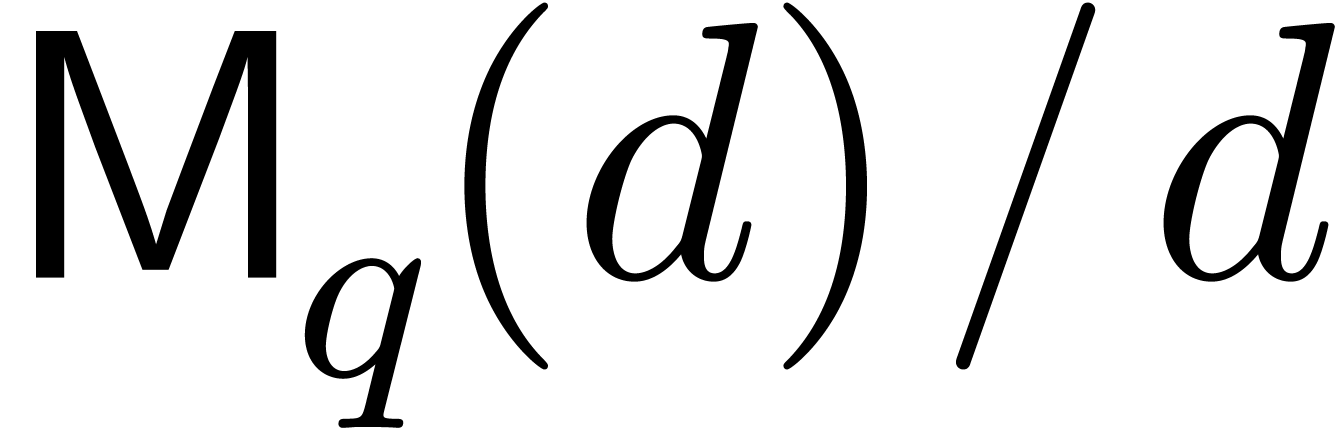 are increasing functions. Currently best known bounds
[10, 21, 22] are
are increasing functions. Currently best known bounds
[10, 21, 22] are 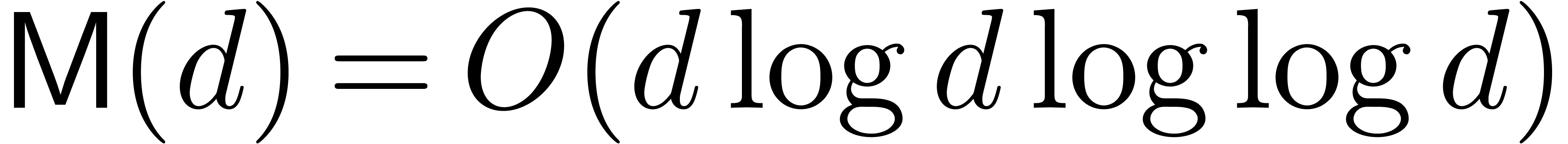 ,
, 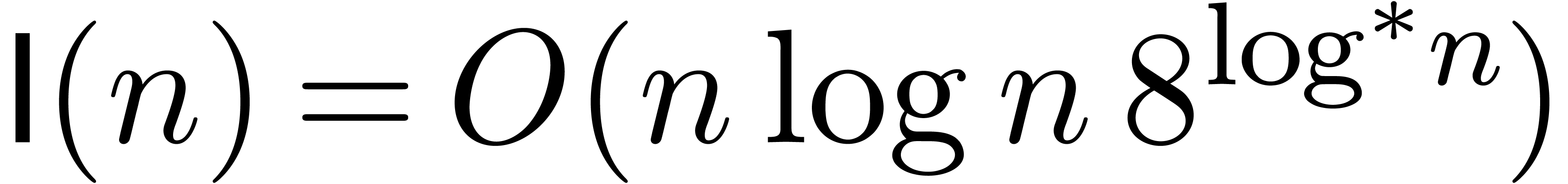 and
and 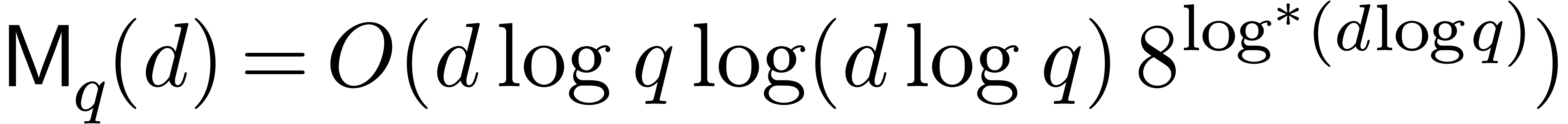 , where
, where 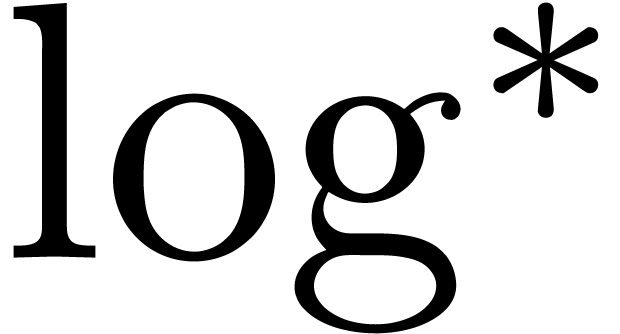 stands for the
iterated logarithm function
stands for the
iterated logarithm function 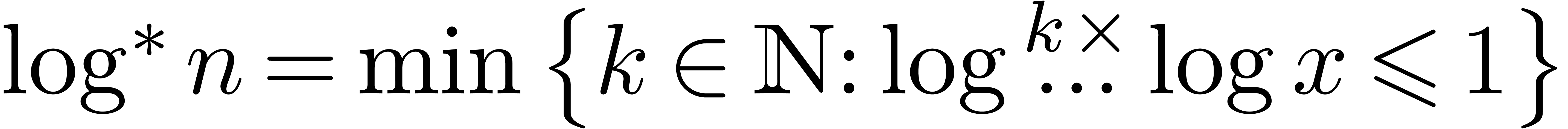 .
.
We freely use the following classical facts: ring operations in 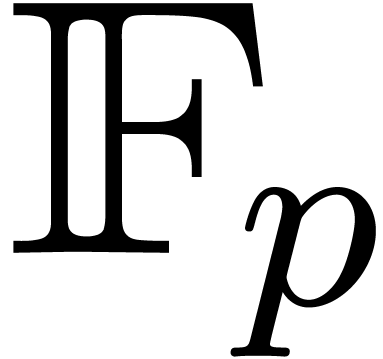 cost
cost 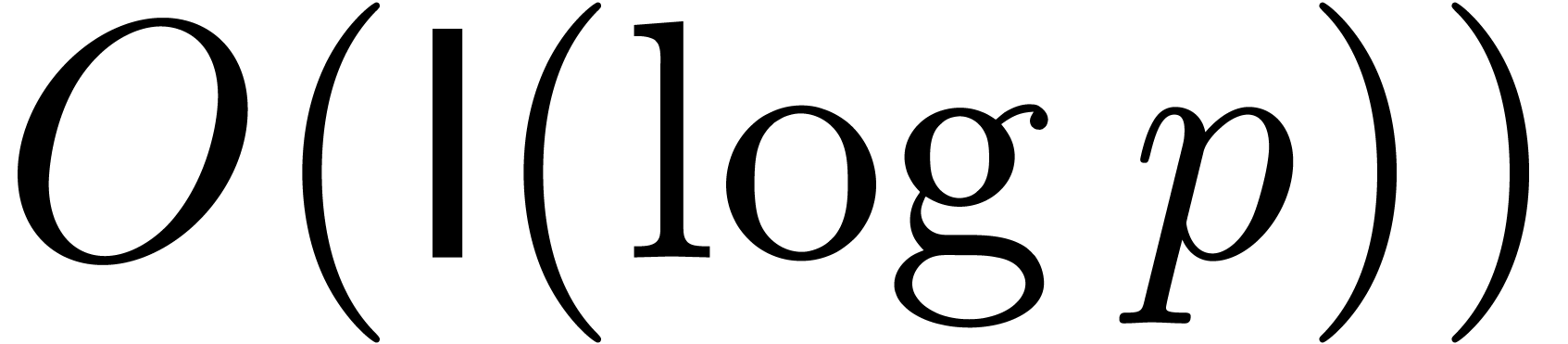 and one division or
inversion in
and one division or
inversion in 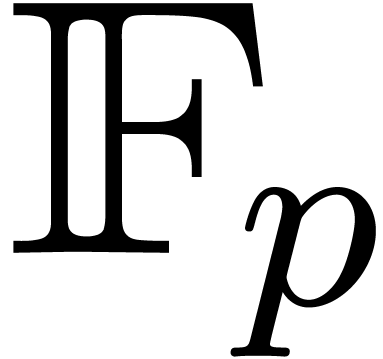 costs
costs 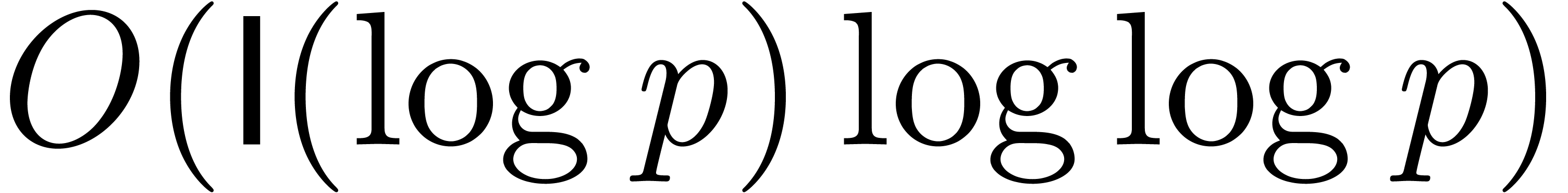 [17, Chapter 11]. The ring operations in
[17, Chapter 11]. The ring operations in  cost at most
cost at most 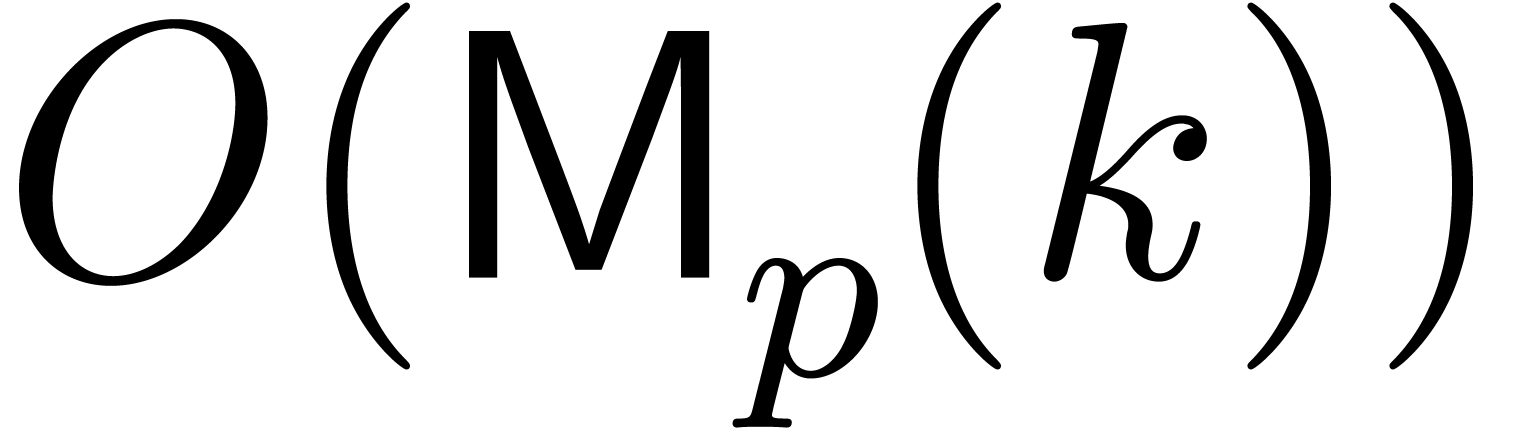 , and inversions
take at most
, and inversions
take at most 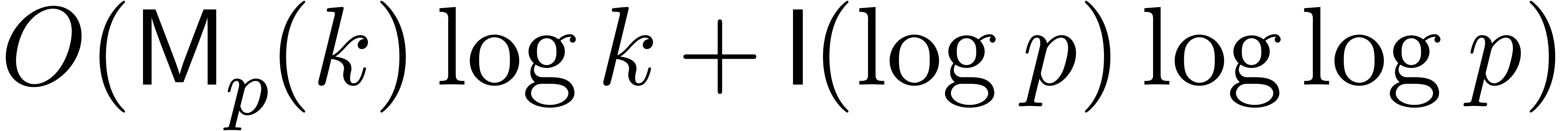 . For
convenience,
. For
convenience, 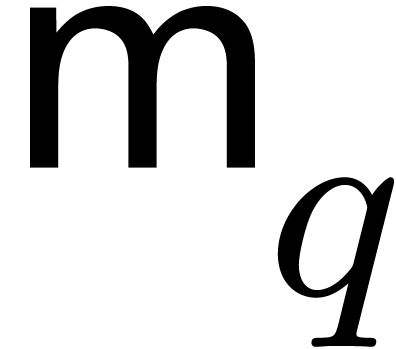 and
and 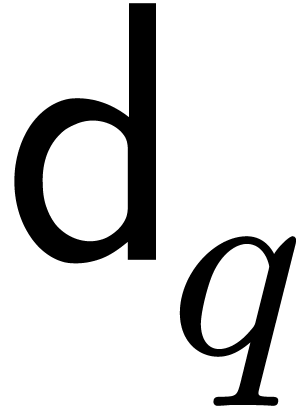 will
respectively denote cost functions for the product and the inverse in
will
respectively denote cost functions for the product and the inverse in
 . The gcd of two polynomials
of degrees at most
. The gcd of two polynomials
of degrees at most  over
over  can be computed in time
can be computed in time 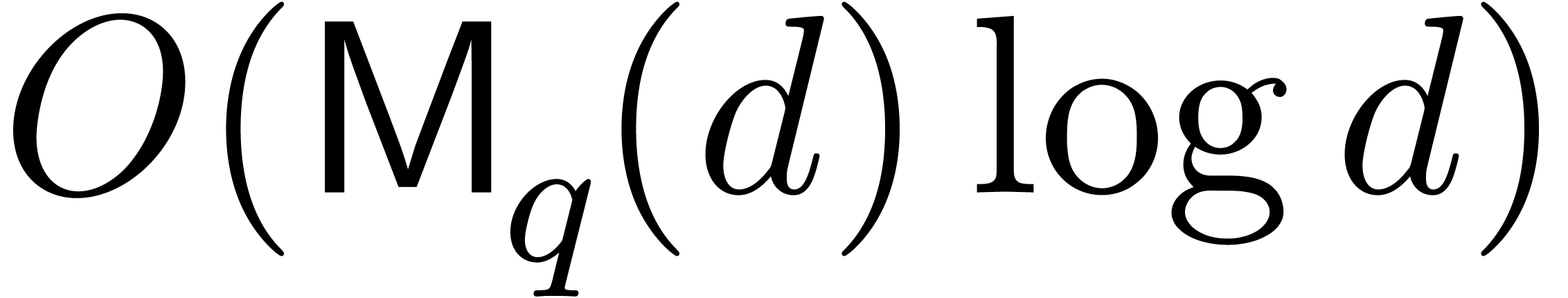 [17,
Algorithm 11.4]. Given polynomials
[17,
Algorithm 11.4]. Given polynomials  and
and  monic with
monic with 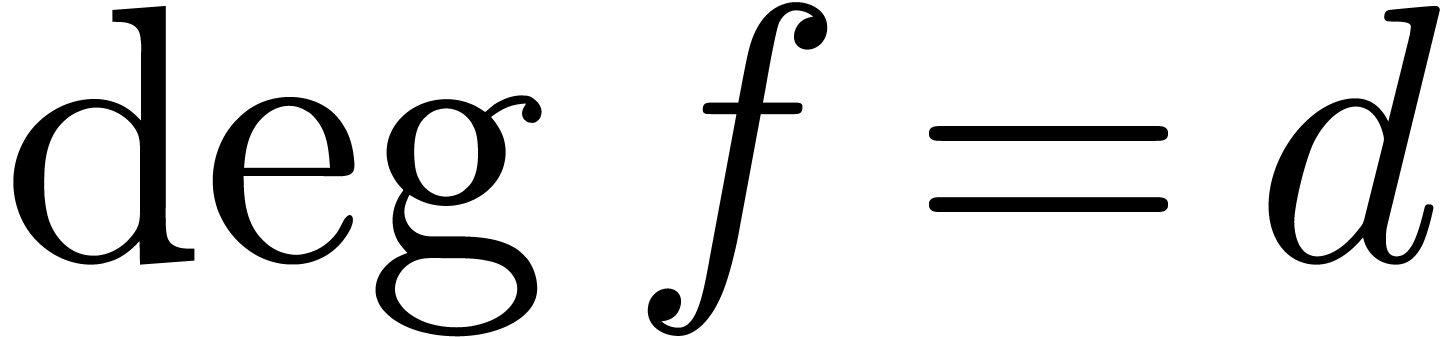 and
and 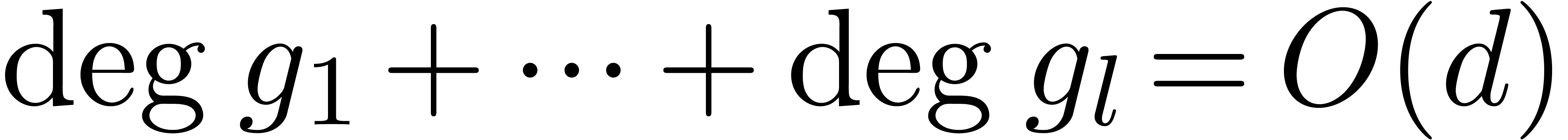 , all the remainders
, all the remainders 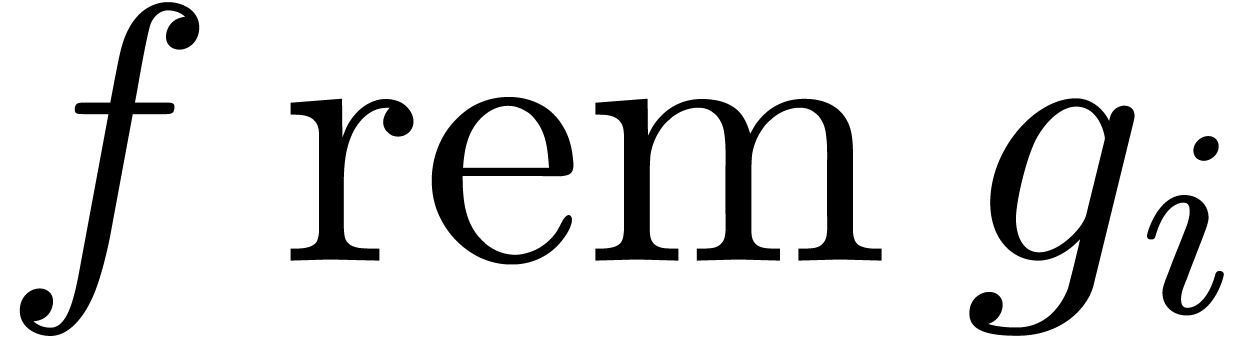 can be computed in time
can be computed in time 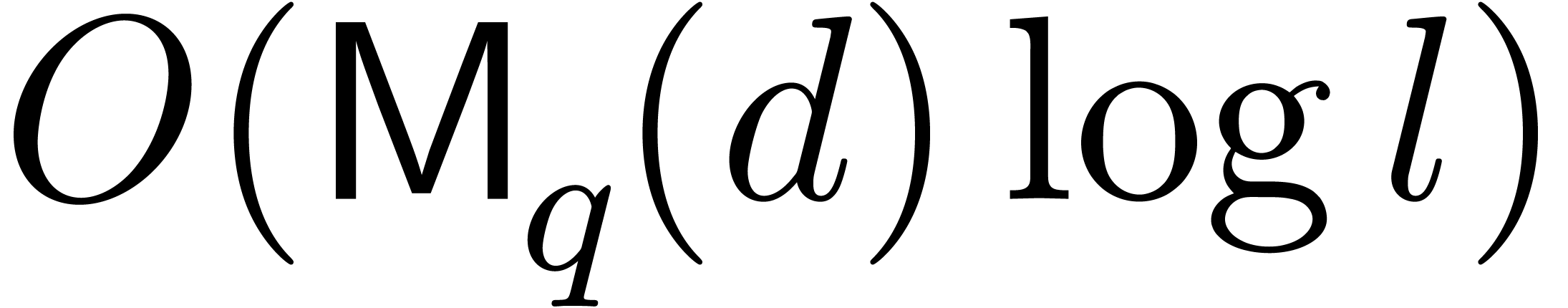 [17,
Chapter 10]. The inverse problem, called Chinese remaindering,
can be solved within a similar cost
[17,
Chapter 10]. The inverse problem, called Chinese remaindering,
can be solved within a similar cost 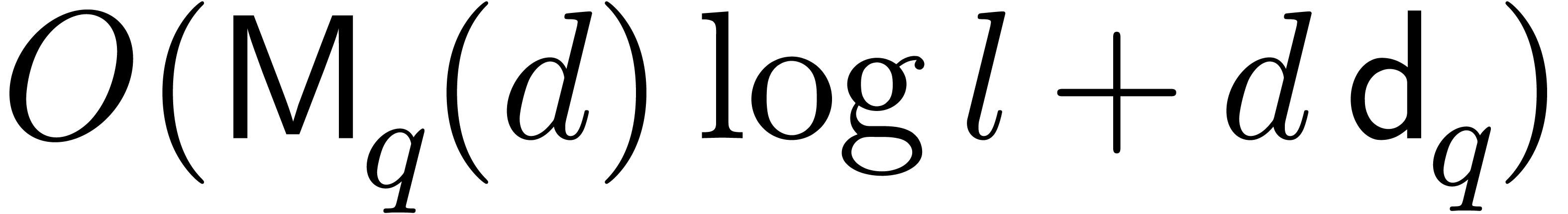 .
.
For an integer 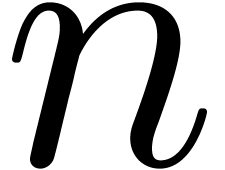 , the largest
prime dividing
, the largest
prime dividing 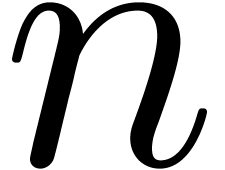 is written
is written 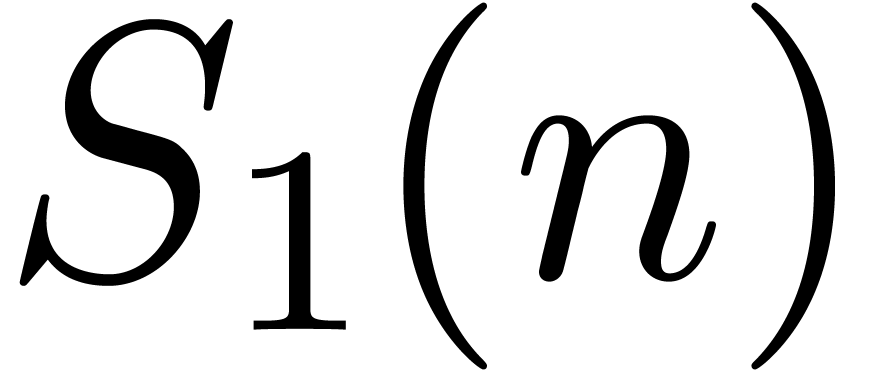 , and the second one
, and the second one 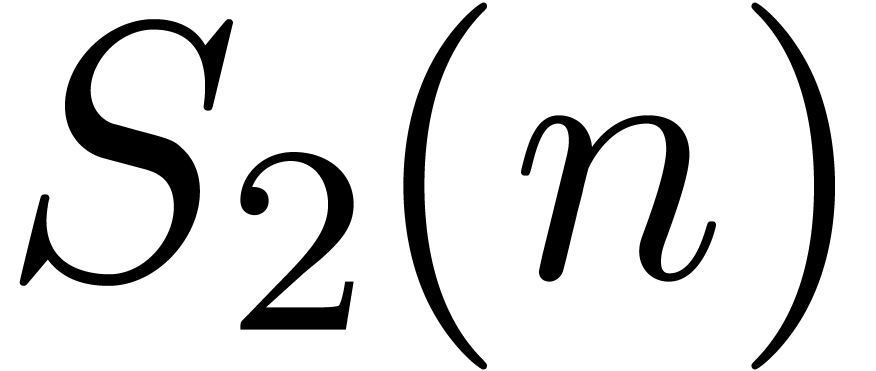 .
Pollard and Strassen have given a deterministic algorithm for factoring
.
Pollard and Strassen have given a deterministic algorithm for factoring
 , of bit complexity
, of bit complexity 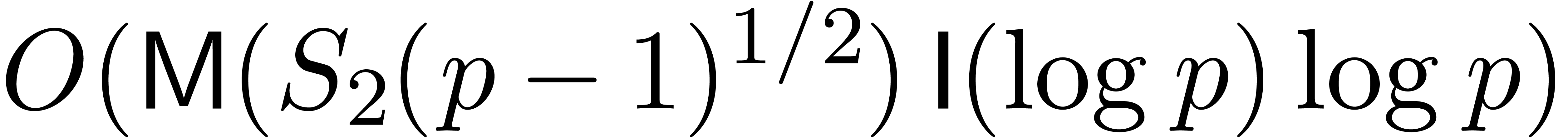 (see for instance [17, Corollary 19.4]).
Ignoring smoothness considerations, the latter result has been improved
into
(see for instance [17, Corollary 19.4]).
Ignoring smoothness considerations, the latter result has been improved
into 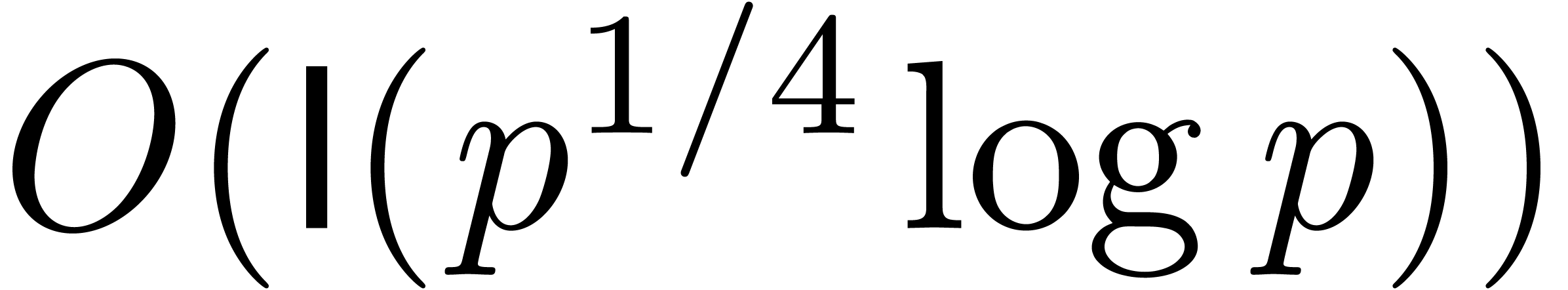 in [6], and further refined to
in [6], and further refined to
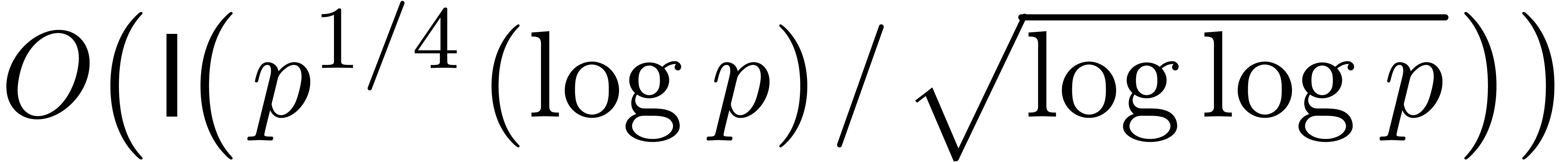 in [13].
in [13].
In this article, when needed, we consider that the factorization of 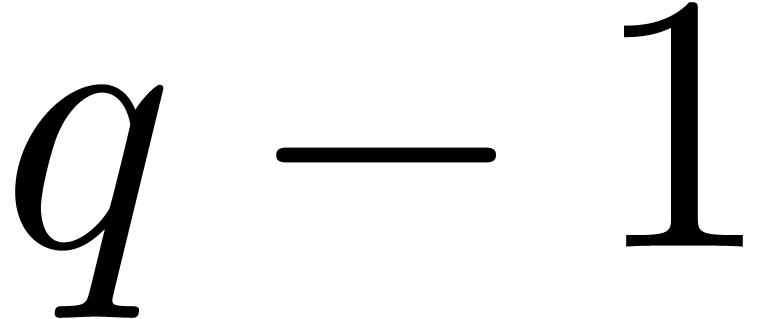 and a primitive element of
and a primitive element of 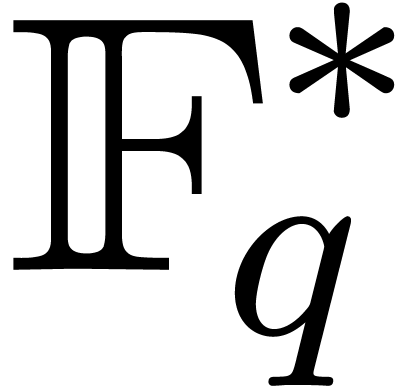 have been precomputed once, and we discard the necessary underlying
costs. In practice, if the factorization of
have been precomputed once, and we discard the necessary underlying
costs. In practice, if the factorization of 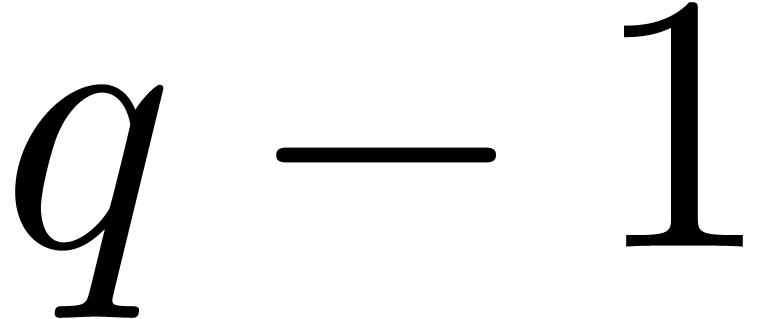 is
given, then it is straightforward to verify whether a given element is
primitive. For known complexity bounds and historical details on these
tasks, we refer to [2, 33, 44].
is
given, then it is straightforward to verify whether a given element is
primitive. For known complexity bounds and historical details on these
tasks, we refer to [2, 33, 44].
It is now classical that polynomial factorization over  reduces to finding roots over
reduces to finding roots over 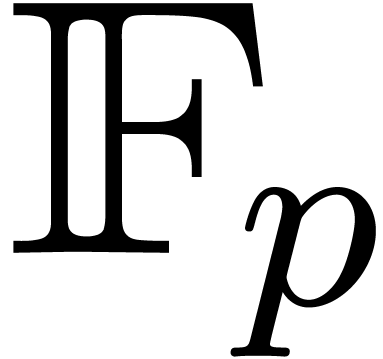 in deterministic
polynomial time, uniformly in
in deterministic
polynomial time, uniformly in 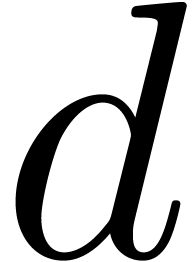 and
and 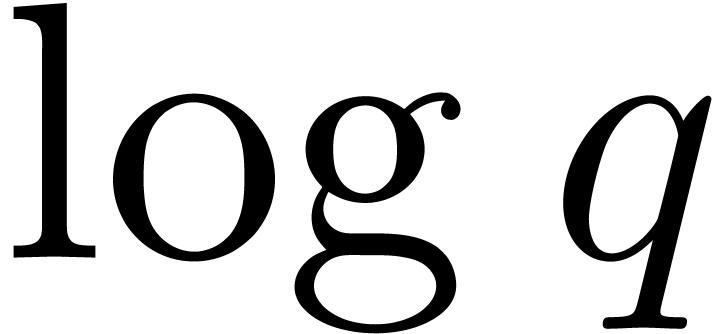 . But it is still unknown whether root finding
can be solved in deterministic polynomial time or not, even under
classical conjectures in number theory. This problem can nevertheless be
solved efficiently by randomized algorithms in average polynomial time.
Concerning related results and historical surveys on this topic, the
reader might consult [17, 18, 25,
33].
. But it is still unknown whether root finding
can be solved in deterministic polynomial time or not, even under
classical conjectures in number theory. This problem can nevertheless be
solved efficiently by randomized algorithms in average polynomial time.
Concerning related results and historical surveys on this topic, the
reader might consult [17, 18, 25,
33].
Seminal algorithms for polynomial factorization over finite fields are
classically attributed to Berlekamp [3, 4],
and Cantor and Zassenhaus [11], but central earlier ideas
can be found in works of Gauss, Galois, Arwins, Faddeev and Skopin.
Cantor–Zassenhaus' algorithm is randomized and well suited to
compute roots of polynomials of degree 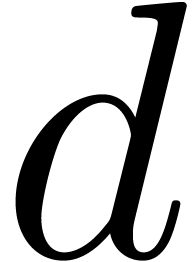 that
split over
that
split over  in average time
in average time 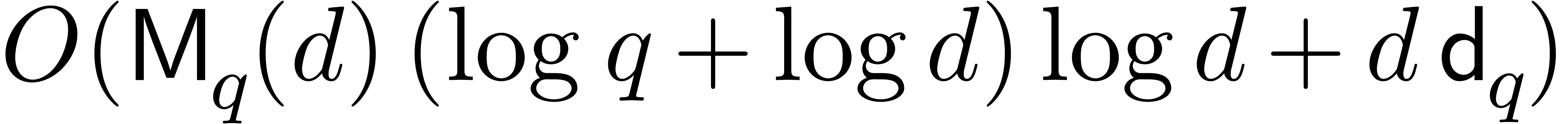 . Of course, if
. Of course, if 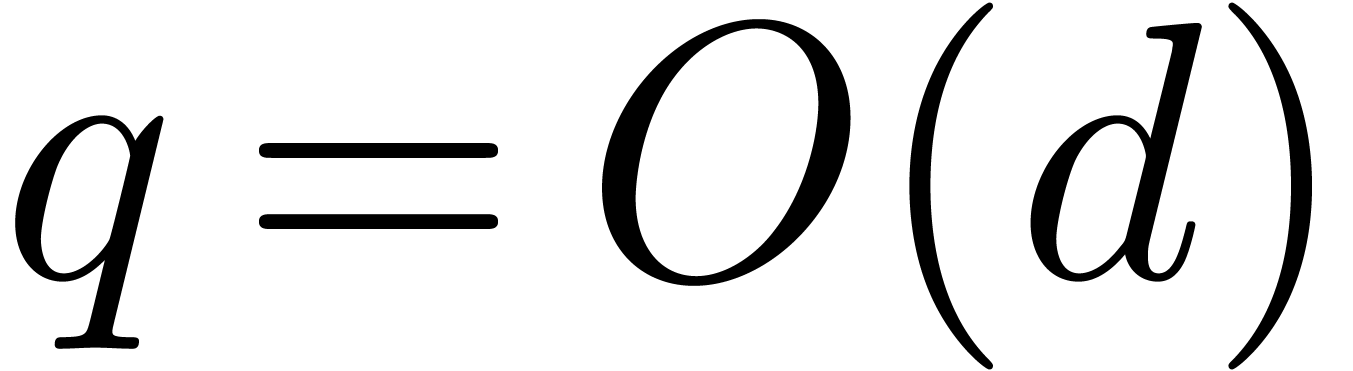 then an
exhaustive search can be naively performed in time
then an
exhaustive search can be naively performed in time 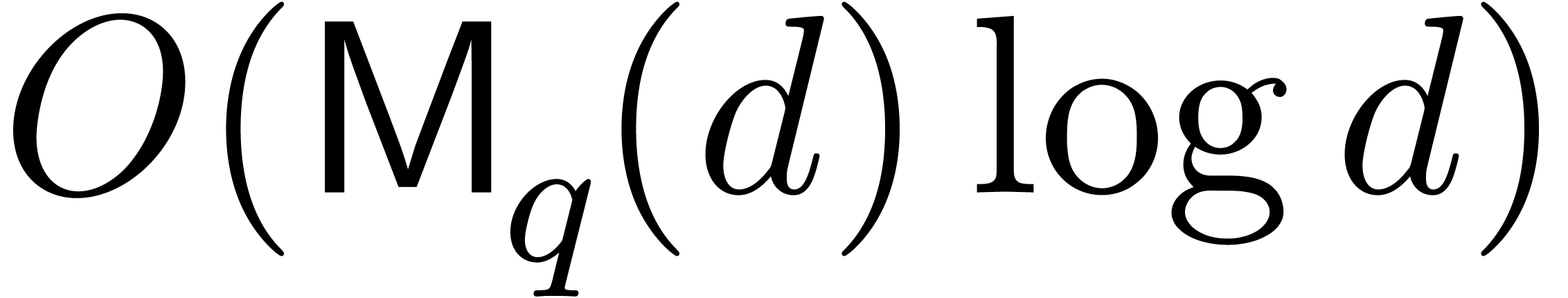 (the factor
(the factor 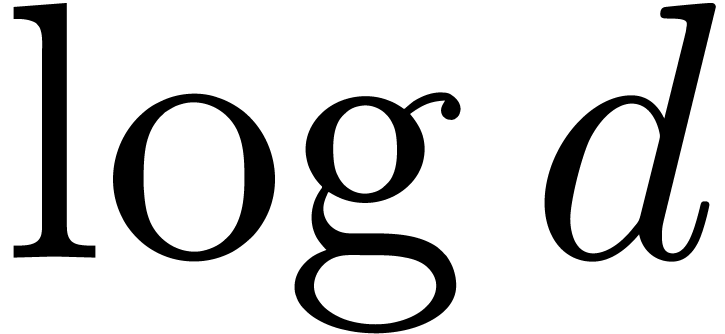 can be discarded if a primitive
element of
can be discarded if a primitive
element of 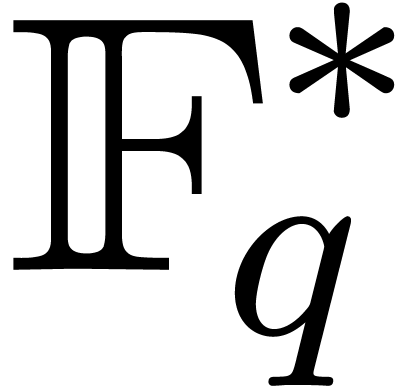 is given, by means of [8,
Proposition 3]), so that the cost of root finding simplifies to
is given, by means of [8,
Proposition 3]), so that the cost of root finding simplifies to 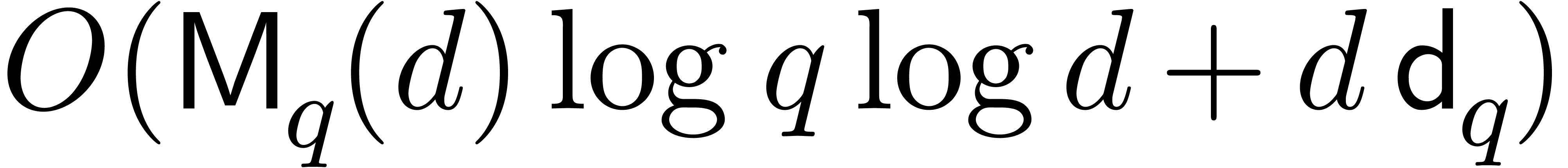 . This classical approach is for
instance implemented in the
. This classical approach is for
instance implemented in the
Deterministic polynomial time root finding has been tackled by several authors. Camion showed that, for a fixed finite field, one can pre-compute a suitable subset which allows to factor any polynomial in deterministic polynomial time [9]. Nevertheless the construction of such a subset is purely theoretical, and it is not clear that there exists an efficient algorithm to compute it, even for FFT prime fields.
Schoof, Rónyai, Huang, and Źrałek designed
different methods for particular types of input polynomials according to
their syntax or to properties of the Galois group of the lifted input
polynomial over  [24, 37,
38, 40, 46]. Some of their
algorithms require the general Riemann hypothesis (GRH) or the extended
Riemann hypothesis (ERH). Sub-exponential algorithms are also known from
the work of Evdokimov [14], which has recently led to new
conjectures in terms of graphs [1]. Other conjectural
algorithms can be found in [15, 39].
[24, 37,
38, 40, 46]. Some of their
algorithms require the general Riemann hypothesis (GRH) or the extended
Riemann hypothesis (ERH). Sub-exponential algorithms are also known from
the work of Evdokimov [14], which has recently led to new
conjectures in terms of graphs [1]. Other conjectural
algorithms can be found in [15, 39].
Another series of articles concern complexity bounds which are uniformly
polynomial in the degree and in 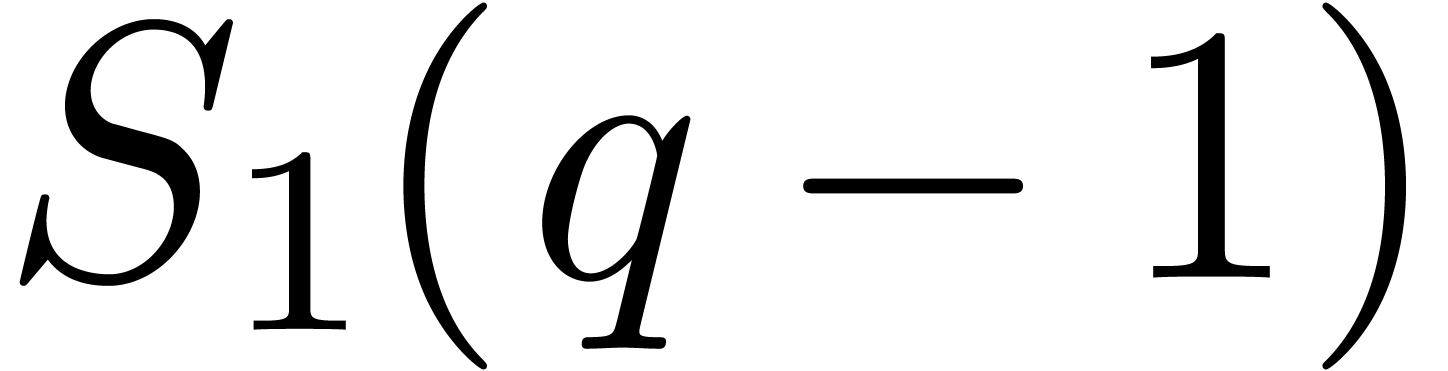 .
Such algorithms are practical when
.
Such algorithms are practical when 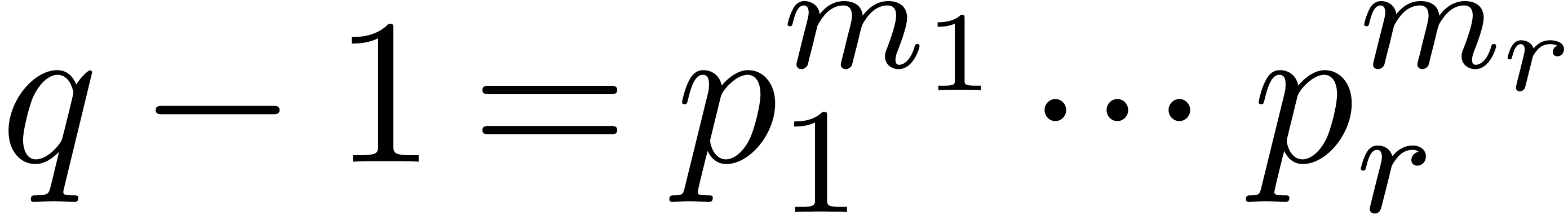 is
sufficiently smooth. Assuming a primitive element of
is
sufficiently smooth. Assuming a primitive element of 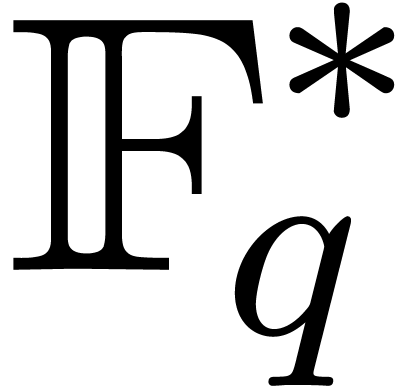 is given, Mignotte and Schnorr [31] proposed a method based
on a cascade of gcds, that needs
is given, Mignotte and Schnorr [31] proposed a method based
on a cascade of gcds, that needs 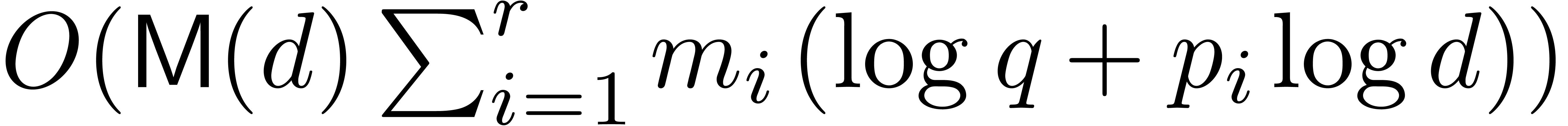 operations in
operations in
 . The computation of a
primitive element might of course be expensive but it can be seen as a
pre-computation. In fact, von zur Gathen proved the deterministic
polynomial time equivalence (in terms of
. The computation of a
primitive element might of course be expensive but it can be seen as a
pre-computation. In fact, von zur Gathen proved the deterministic
polynomial time equivalence (in terms of 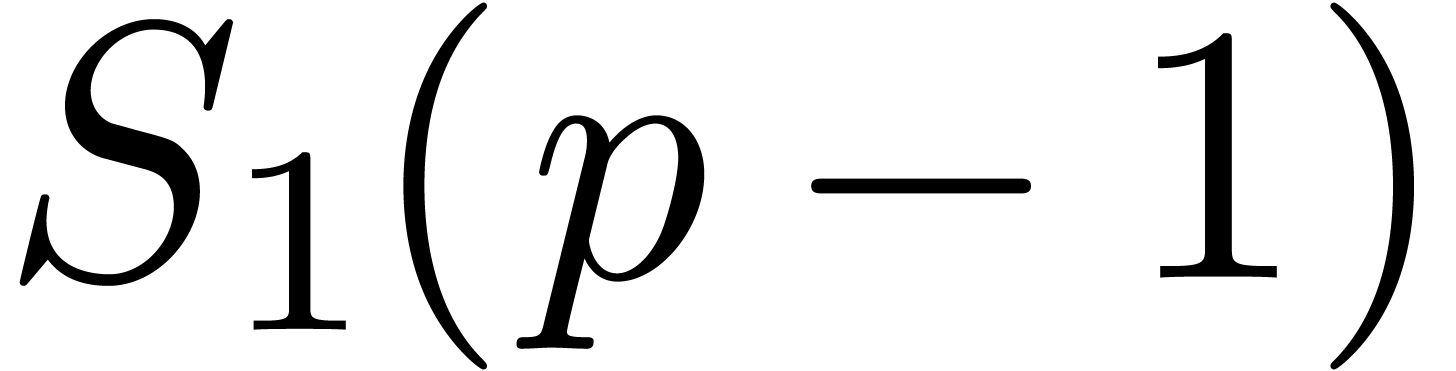 and
input size) between the computation of primitive elements and polynomial
factorization [16].
and
input size) between the computation of primitive elements and polynomial
factorization [16].
Rónyai [37] obtained a polynomial complexity bound
in 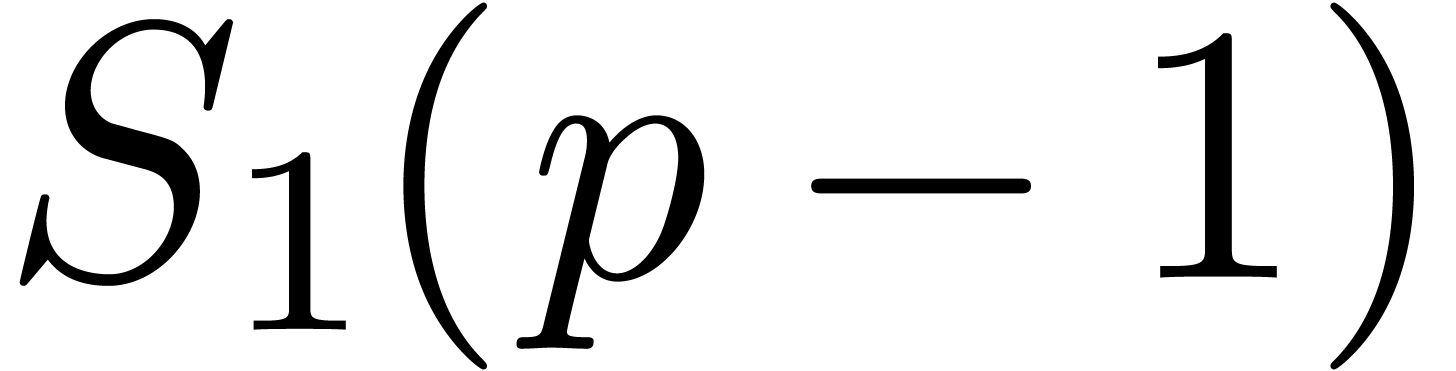 ,
, 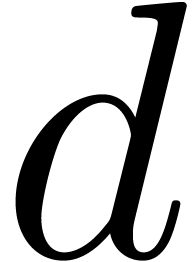 and
and 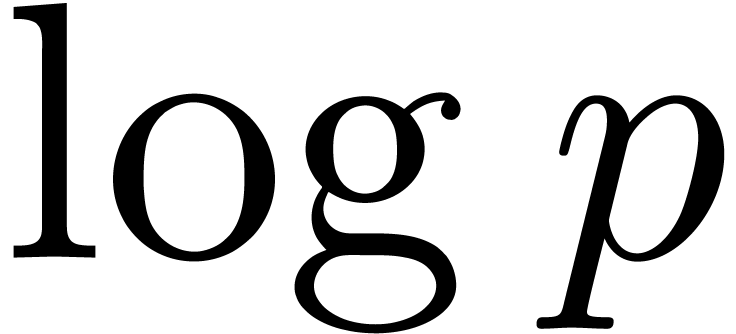 by means of linear algebra techniques, using
primitive roots of orders lower than in [16], but he did
not explicit the exponents in the bound. For
by means of linear algebra techniques, using
primitive roots of orders lower than in [16], but he did
not explicit the exponents in the bound. For 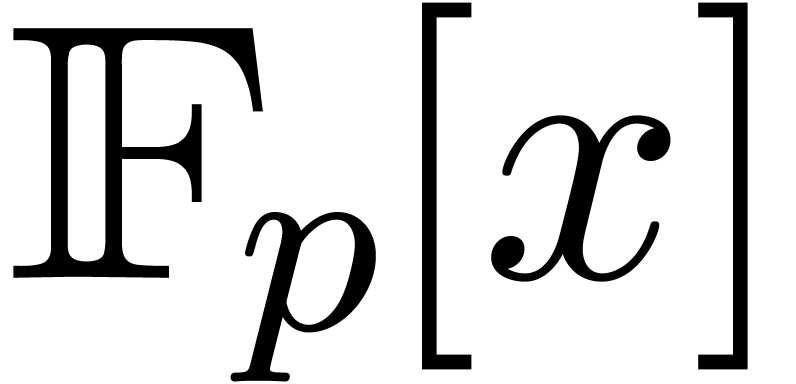 , Shoup [41] reached the bound
, Shoup [41] reached the bound 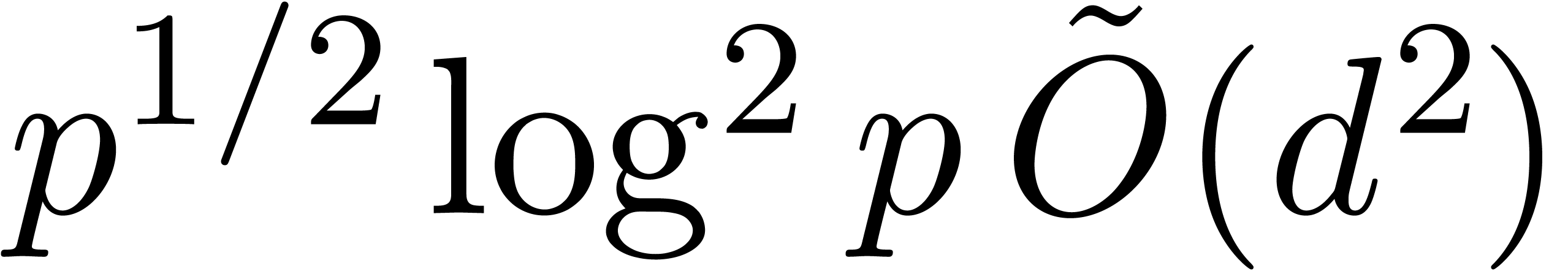 in terms of the number of operations in
in terms of the number of operations in  , and then refined it to
, and then refined it to 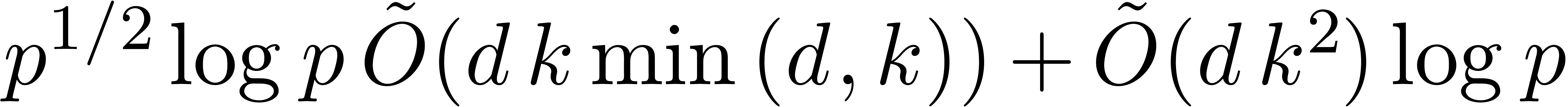 for
for 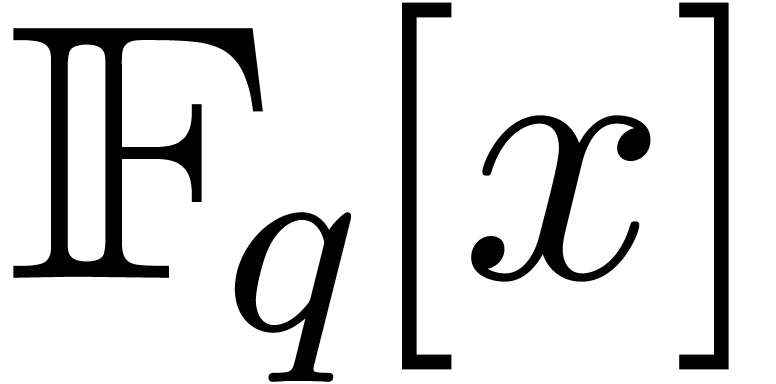 , still in terms of
operations in
, still in terms of
operations in 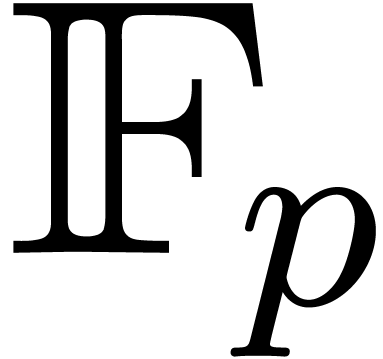 [42]. Finally Shoup
proved the bound
[42]. Finally Shoup
proved the bound 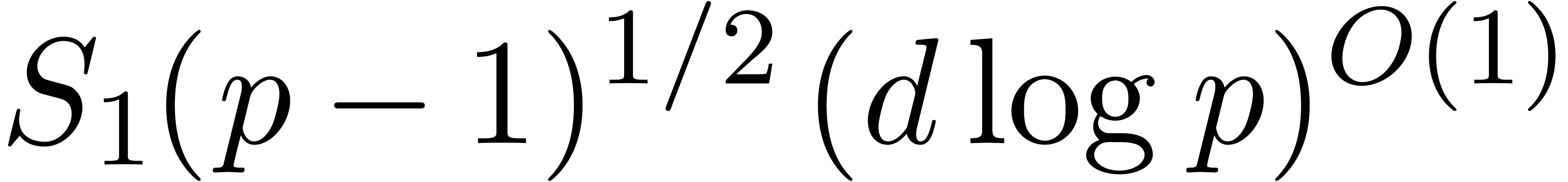 in
in 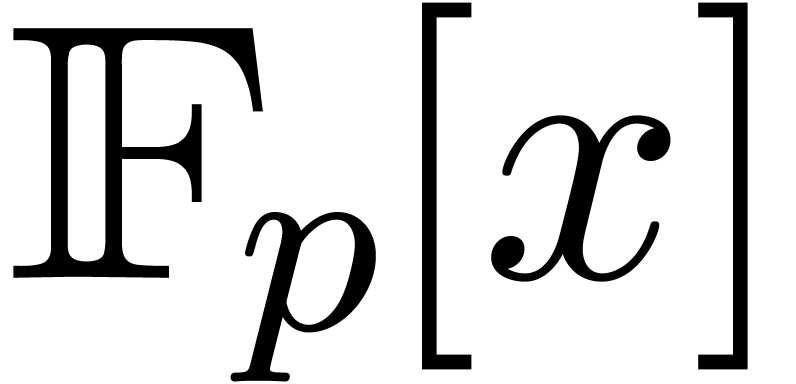 under ERH [43].
under ERH [43].
The main contribution of this article is an efficient deterministic root
finding method. The new algorithm is based on generalized Graeffe
transforms and it is particularly efficient for finite fields 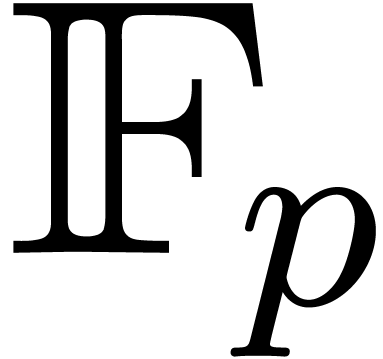 such that
such that 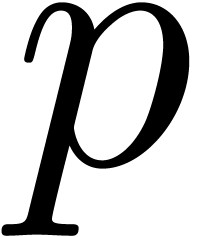 is an FFT prime. Roughly
speaking, the generalized Graeffe transform replaces modular exponention
as used in Cantor–Zassenhaus' algorithm, and gcd computations are
changed to multi-point evaluations.
is an FFT prime. Roughly
speaking, the generalized Graeffe transform replaces modular exponention
as used in Cantor–Zassenhaus' algorithm, and gcd computations are
changed to multi-point evaluations.
Thanks to a slight improvement of Shoup's adaptation of
Pollard–Strassen's algorithm to find roots deterministically [43], we obtain a new deterministic complexity bound in terms
of 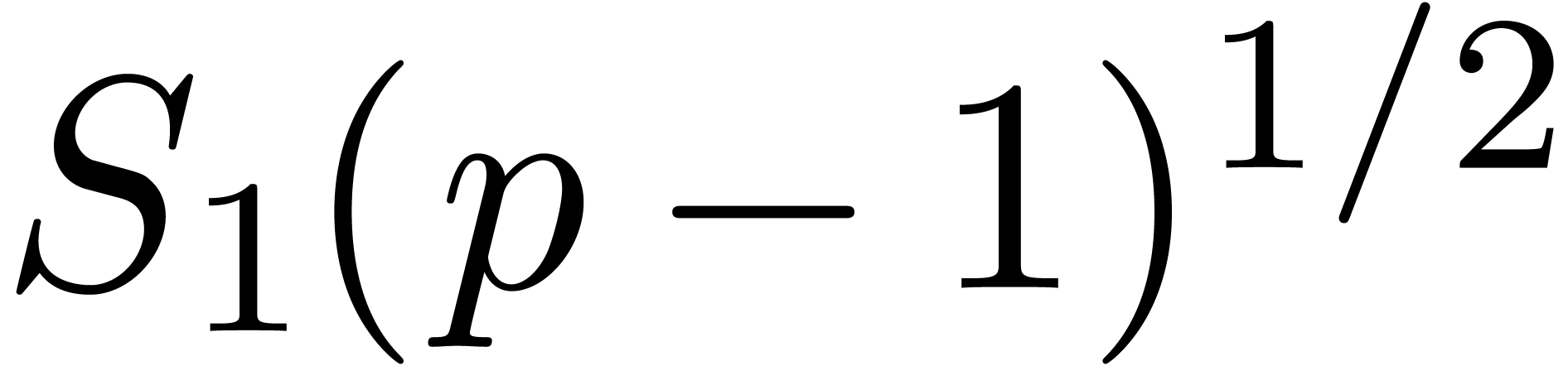 . In addition, in the
smooth case
. In addition, in the
smooth case 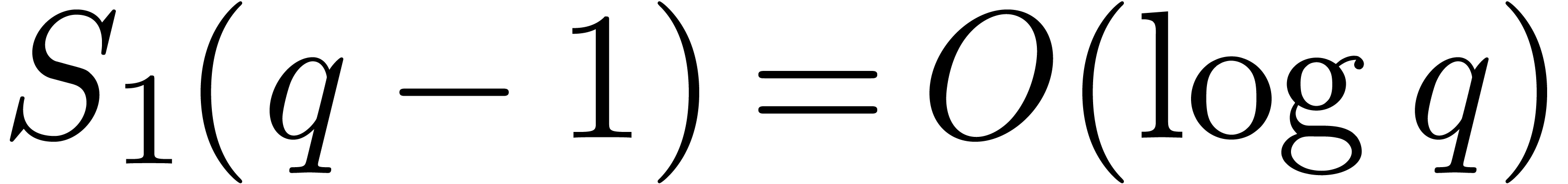 , the cost of our
deterministic algorithm is softly equivalent to the one of
Cantor–Zassenhaus.
, the cost of our
deterministic algorithm is softly equivalent to the one of
Cantor–Zassenhaus.
The complexity of generalized Graeffe transforms is studied in Section 2. A first ingredient is the transposed modular composition algorithm of Kedlaya and Umans [27], also called modular power projections algorithm. The second ingredient is a special variant for finite fields of Newton–Girard's formulas for recovering a polynomial from the power sums of its roots. Such a variant had been previously designed by Bostan, Gonzalez-Vega, Perdry and Schost [7] in the case of prime finite fields. We extend their results to finite fields from scratch, using very simple arguments, and independently of the framework designed in [12].
Classically, the Graeffe transform of a polynomial 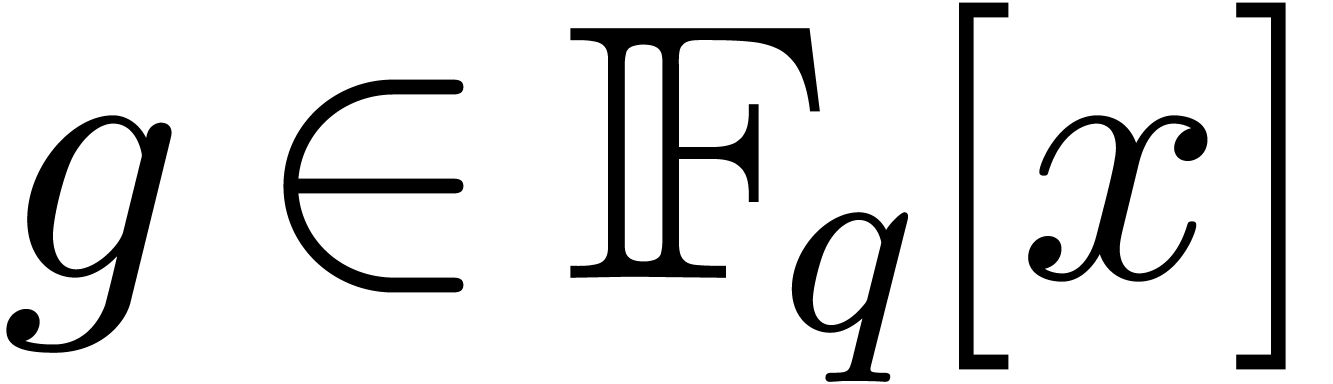 of degree
of degree 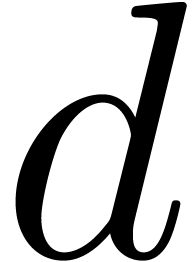 is the unique polynomial
is the unique polynomial
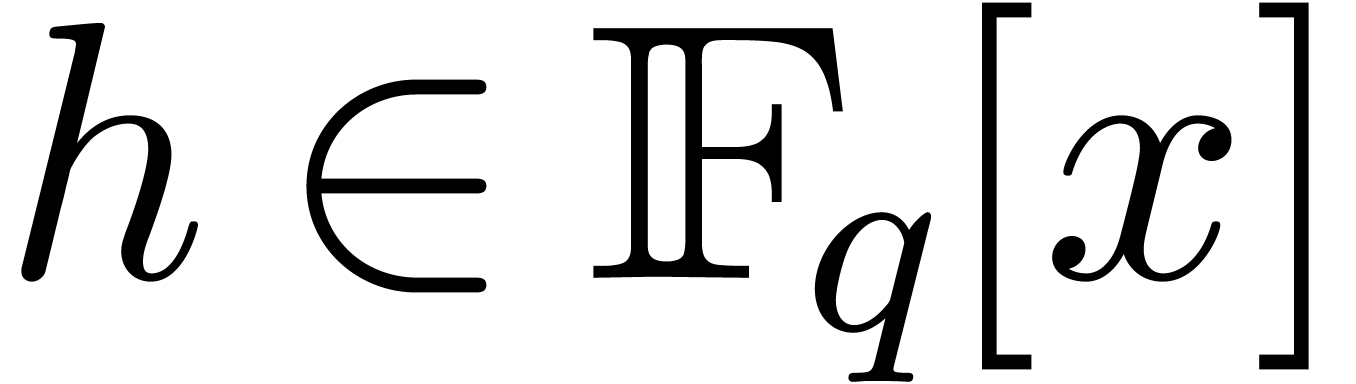 satisfying
satisfying 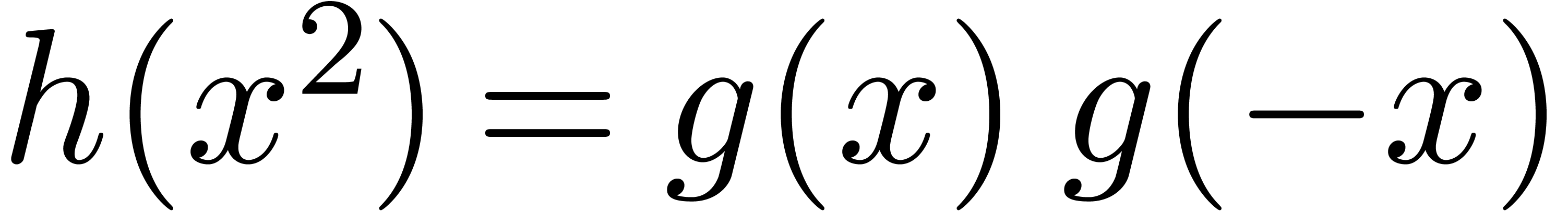 .
If
.
If 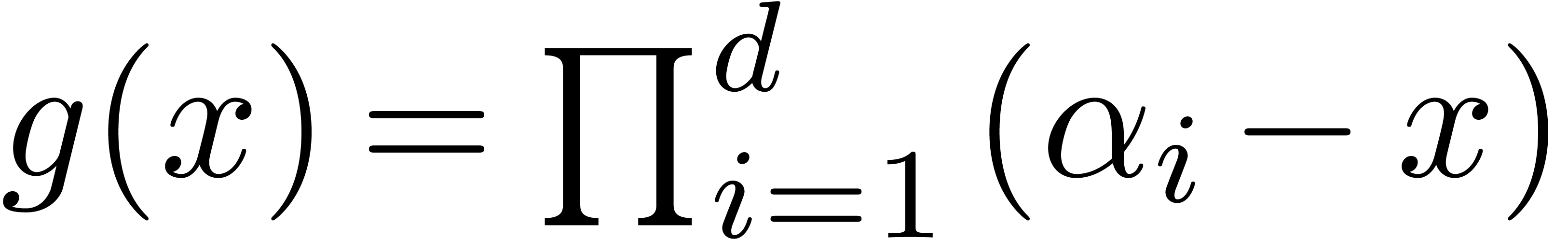 , then
, then 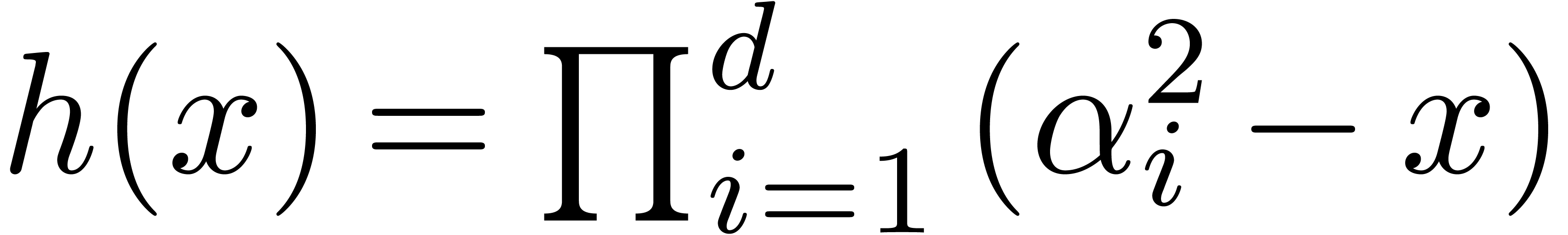 . This construction can be extended to higher
orders as follows: the generalized Graeffe transform of
. This construction can be extended to higher
orders as follows: the generalized Graeffe transform of  of order
of order  ,
written
,
written 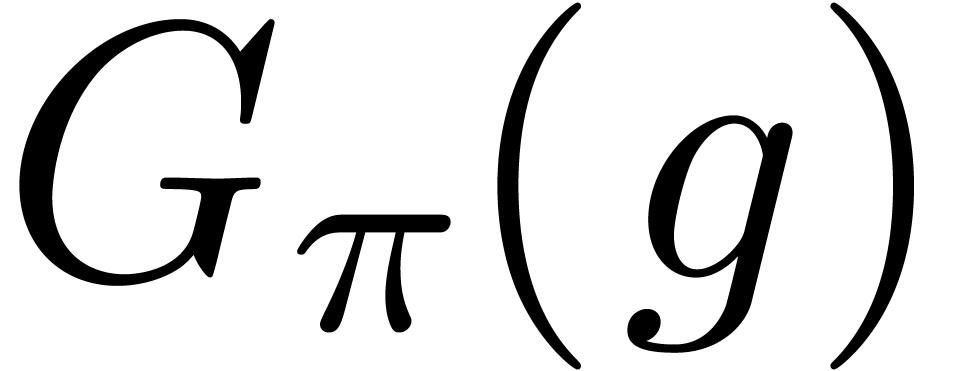 , is defined as the
resultant
, is defined as the
resultant
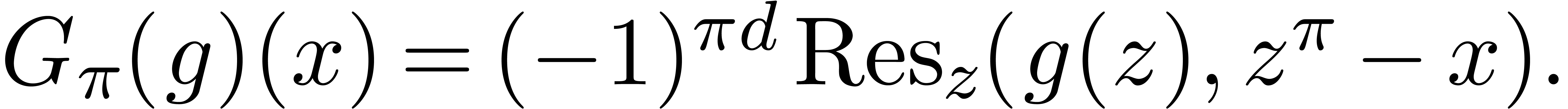
If 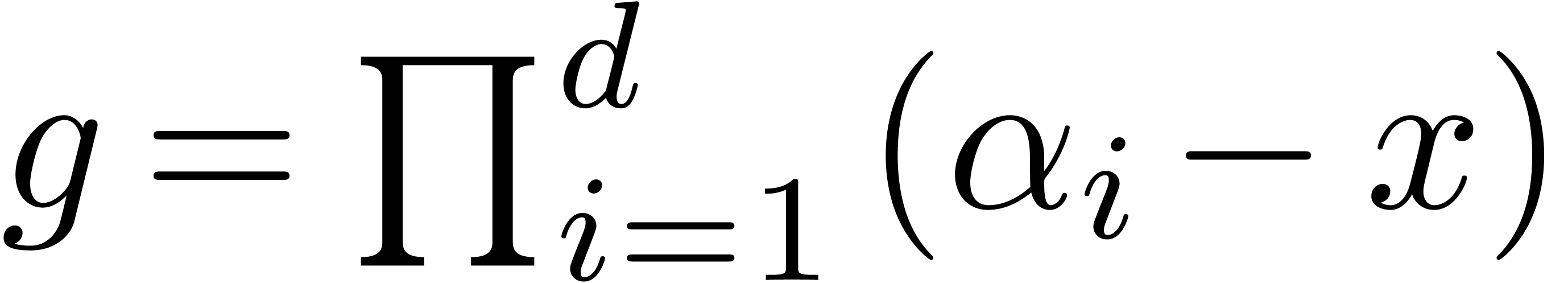 , then
, then 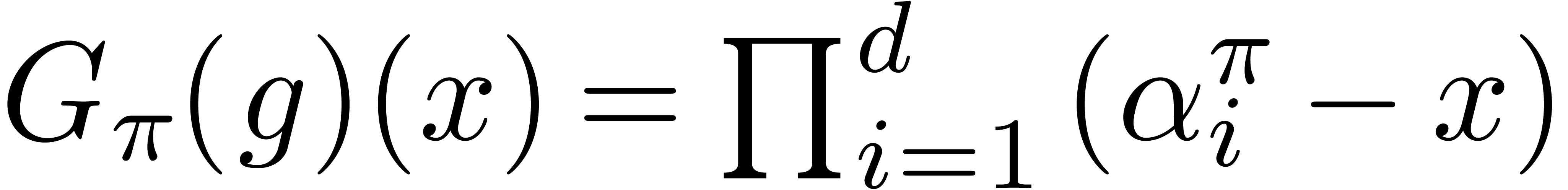 . Equivalently,
. Equivalently,  is the
characteristic polynomial of multiplication by
is the
characteristic polynomial of multiplication by  in
in  (up to the sign). In this section we show how
to compute Graeffe transforms efficiently. We start with a particularly
simple and efficient algorithm for the smooth case, repeated from [20].
(up to the sign). In this section we show how
to compute Graeffe transforms efficiently. We start with a particularly
simple and efficient algorithm for the smooth case, repeated from [20].
For our root finding algorithm, the most important case is when  is smooth and the order
is smooth and the order  of
the generalized Graeffe transform divides
of
the generalized Graeffe transform divides  .
.
 be integers
be integers  , such that
, such that 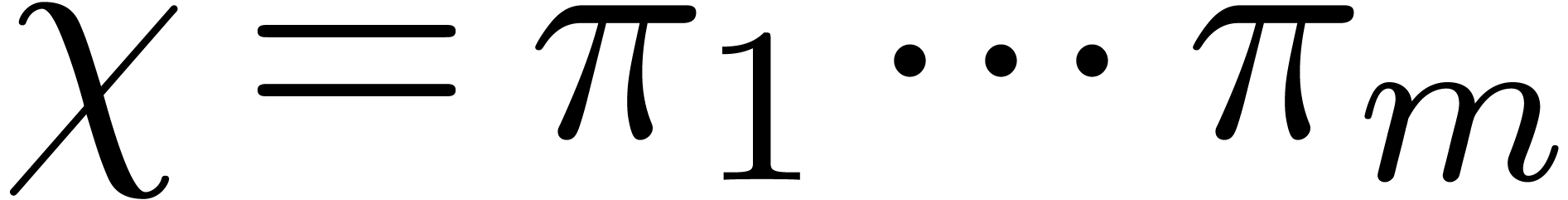 divides
divides 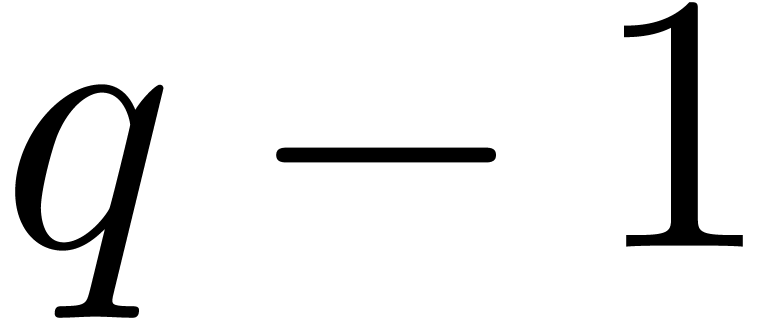 , and let
, and let  be given primitive roots of unity of order
be given primitive roots of unity of order 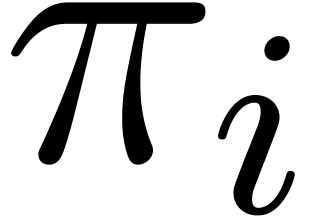 , for all
, for all  .
If
.
If  is a monic polynomial in
is a monic polynomial in 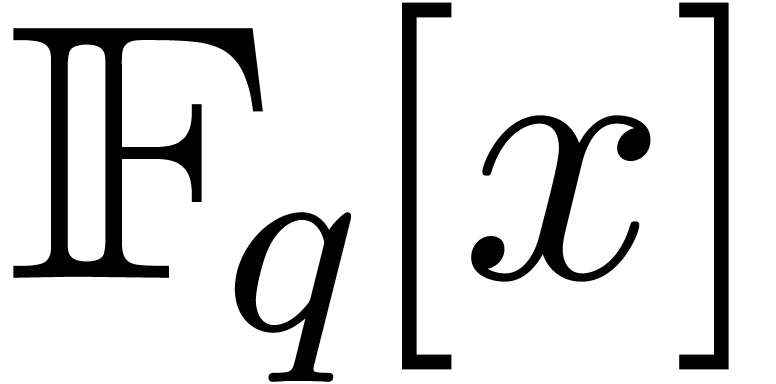 of degree
of degree 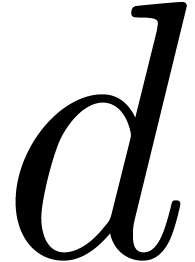 , then the
generalized Graeffe transforms of orders
, then the
generalized Graeffe transforms of orders 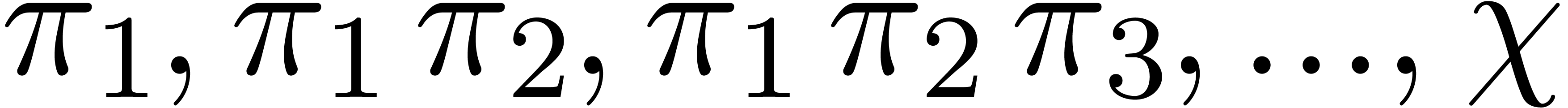 of
of
 can be computed in time
can be computed in time 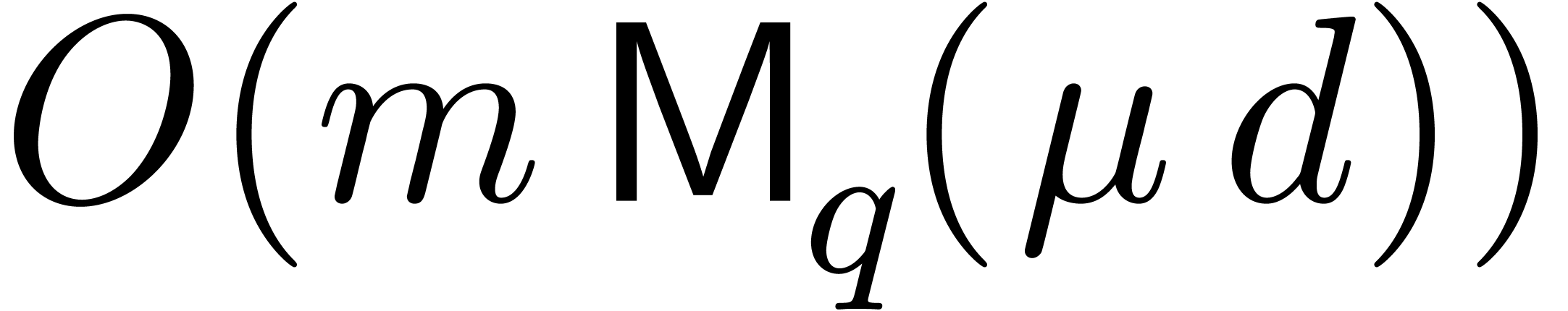 or
or 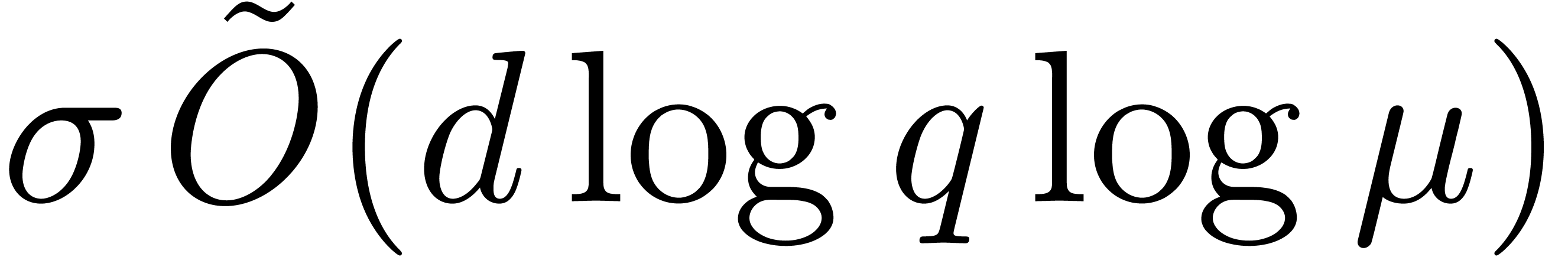 , where
, where  and
and 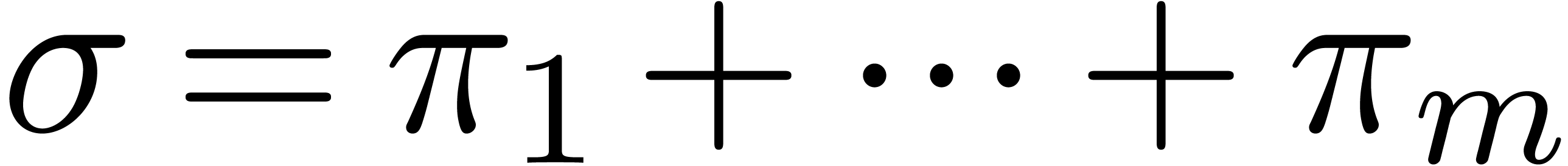 .
.
Proof. Writing 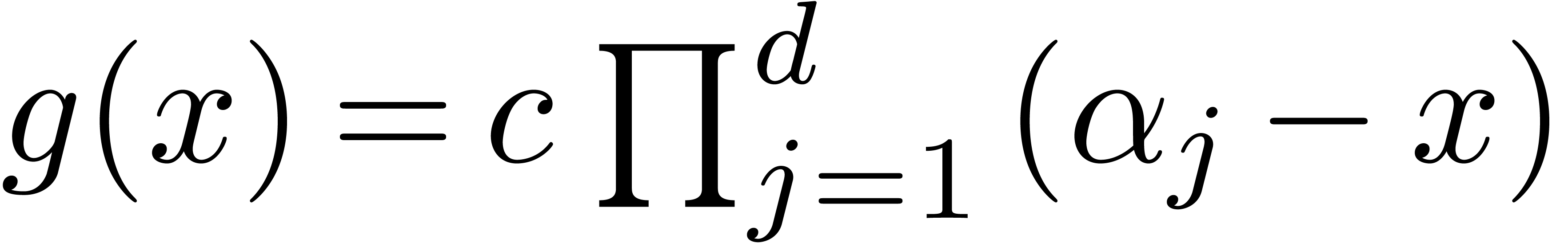 in an
algebraic closure of
in an
algebraic closure of  , the
Graeffe transform of
, the
Graeffe transform of  of order
of order 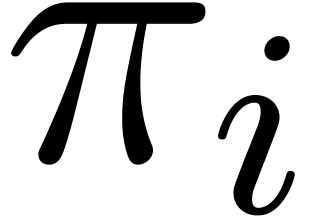 is
is 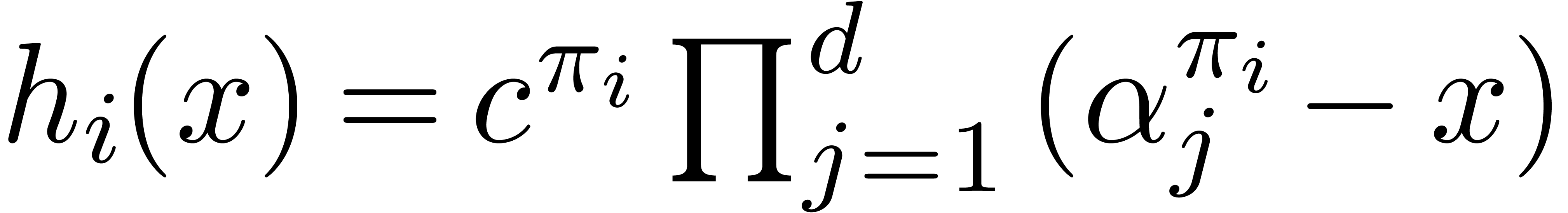 . Consequently this leads
to
. Consequently this leads
to 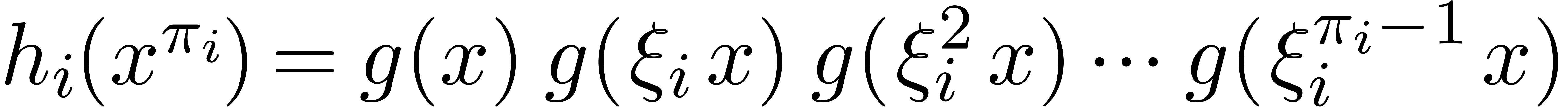 . Using the latter
formula, by Lemma 2 below, the transform can be obtained in
time
. Using the latter
formula, by Lemma 2 below, the transform can be obtained in
time 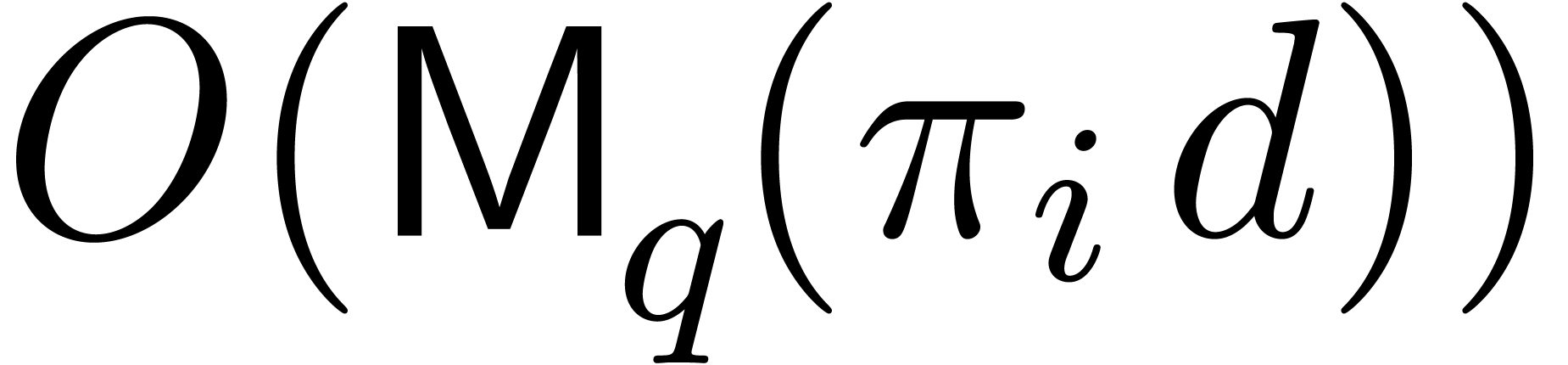 . Taking the sum over
. Taking the sum over
 concludes the proof.
concludes the proof.
 be a polynomial of degree
be a polynomial of degree 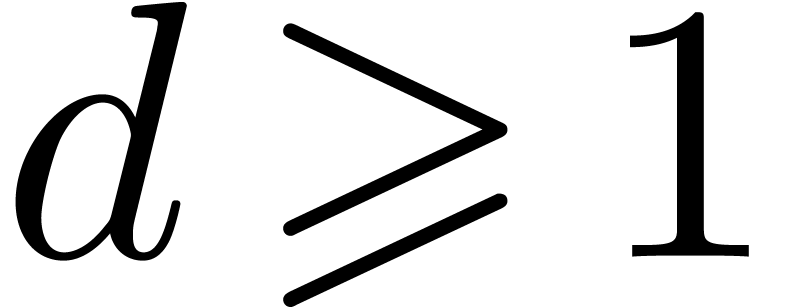 in
in 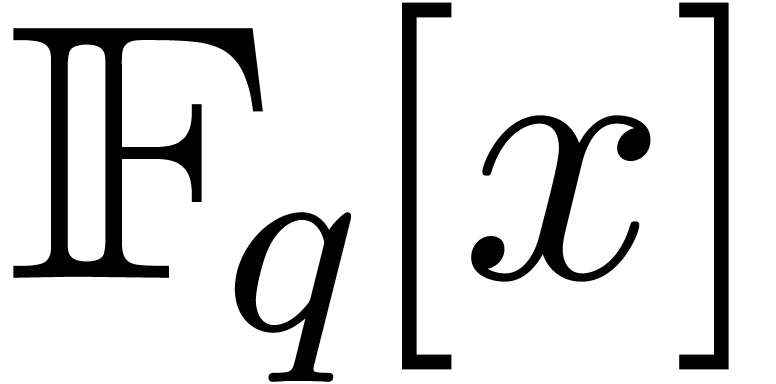 , let
, let 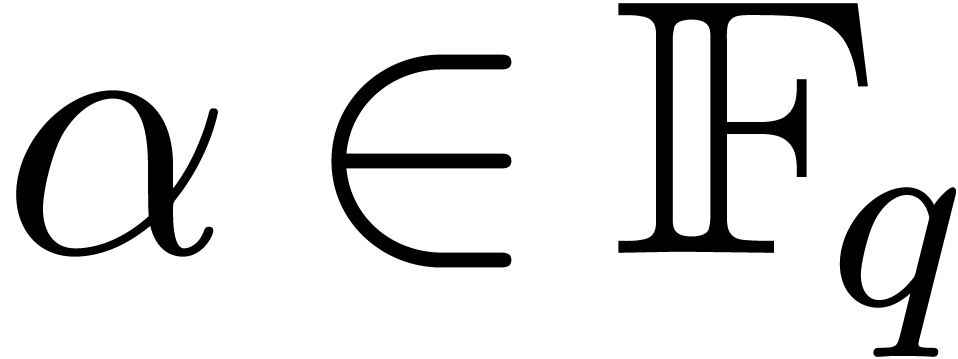 , and let
, and let  be an
integer. Then the product
be an
integer. Then the product 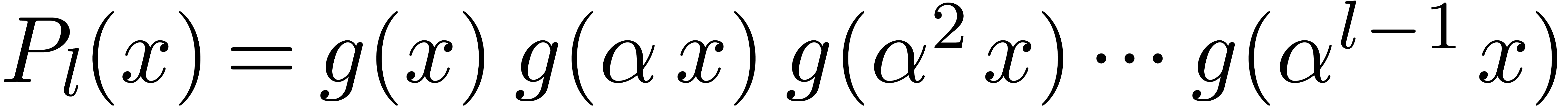 can be computed in
time
can be computed in
time 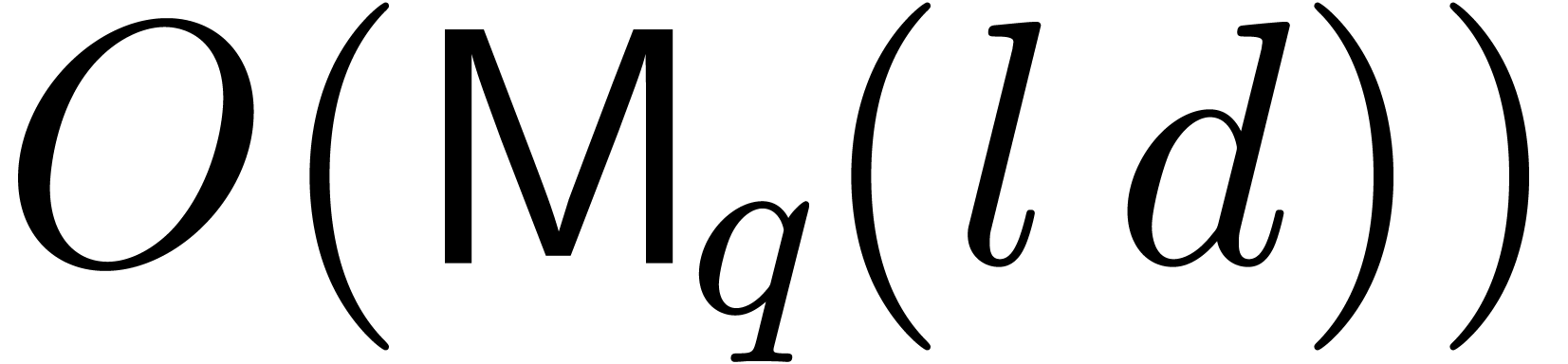 .
.
Proof. Let 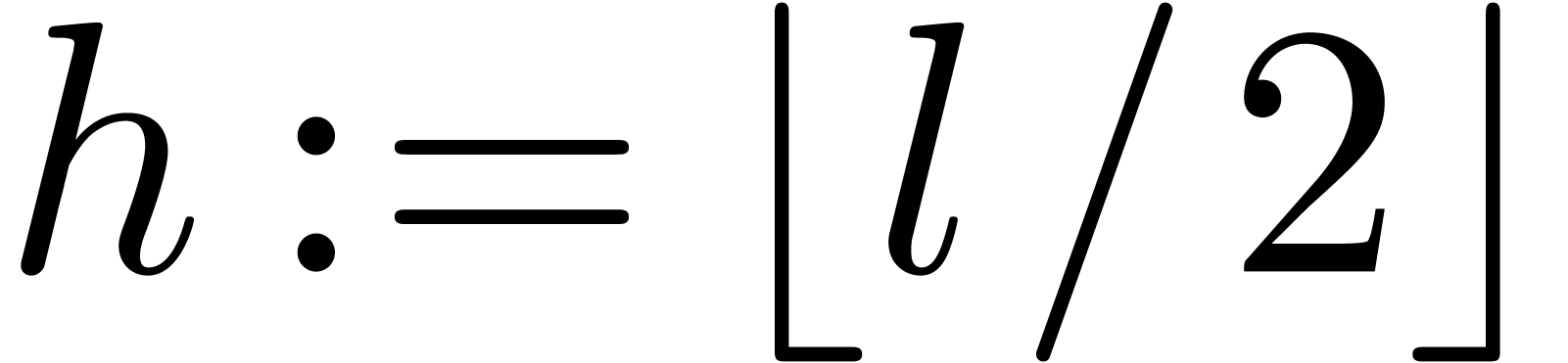 .
If
.
If 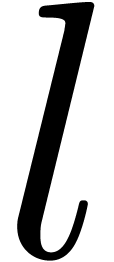 is even, then
is even, then 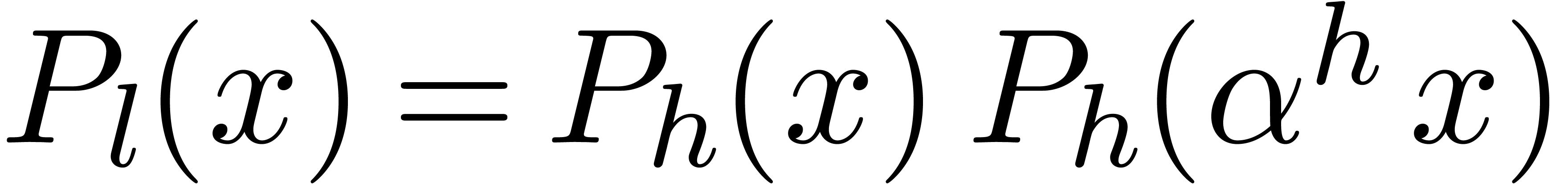 ,
otherwise we have
,
otherwise we have 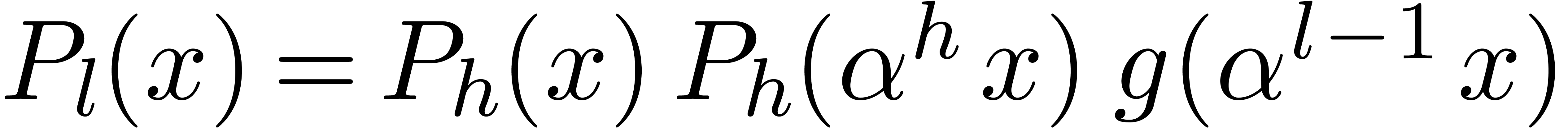 . These
formulas lead to an algorithm with the claimed cost.
. These
formulas lead to an algorithm with the claimed cost.
Notice that this lemma generalizes to arbitrary fields.
In the general case, let 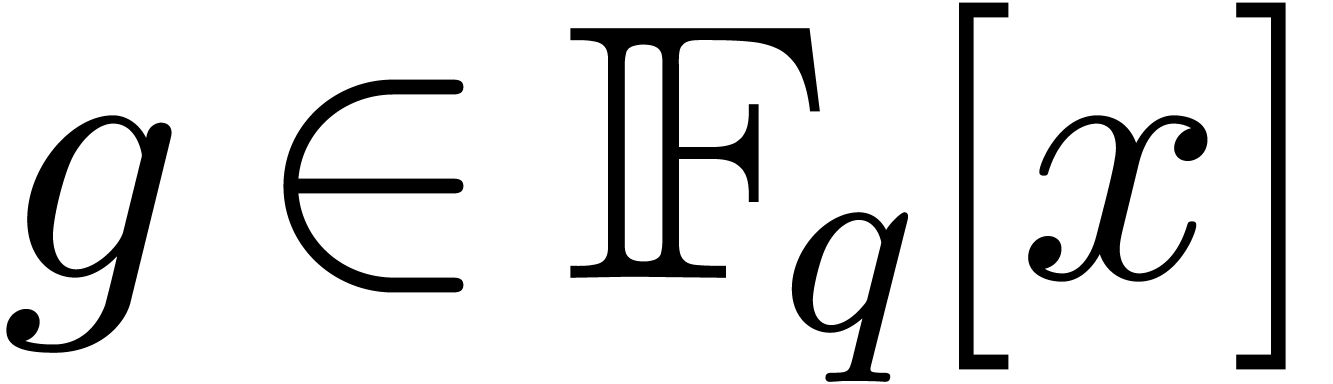 be monic of degree
be monic of degree
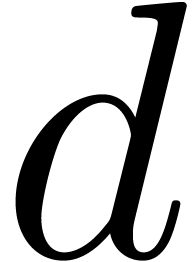 . Given a polynomial
. Given a polynomial  of degree
of degree 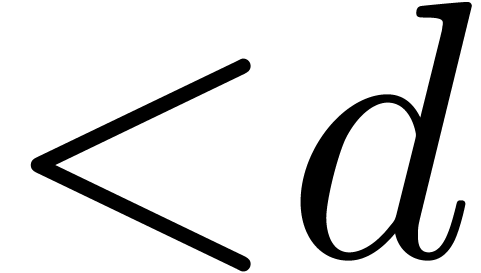 ,
we are interested in computing the characteristic polynomial
,
we are interested in computing the characteristic polynomial 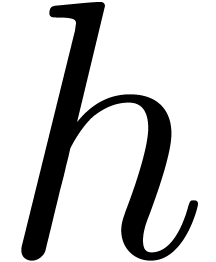 of the multiplication by
of the multiplication by  in
in 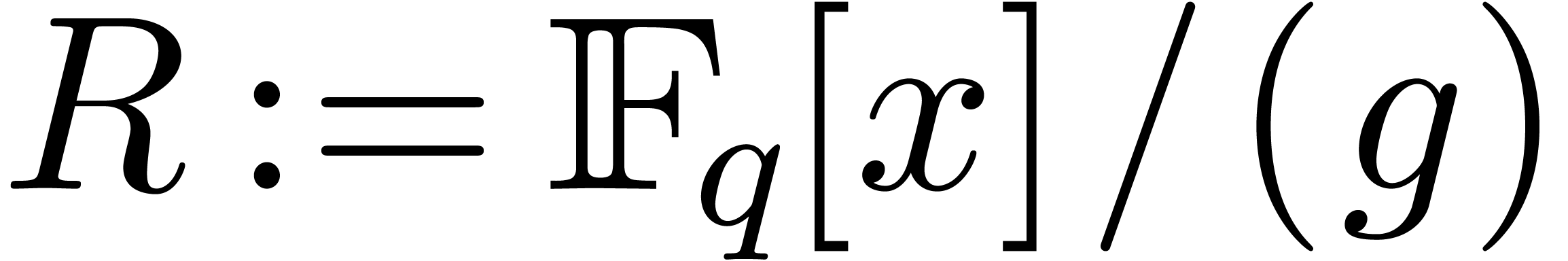 . Our strategy essentially follows
Le Verrier's method: we first compute the traces
. Our strategy essentially follows
Le Verrier's method: we first compute the traces 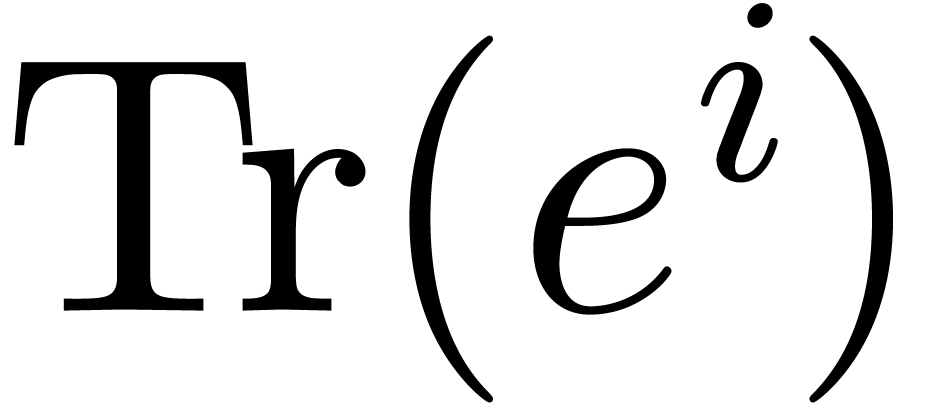 of the multiplication by
of the multiplication by 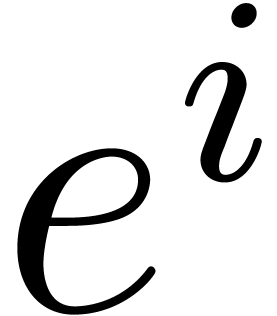 in
in  for all
for all 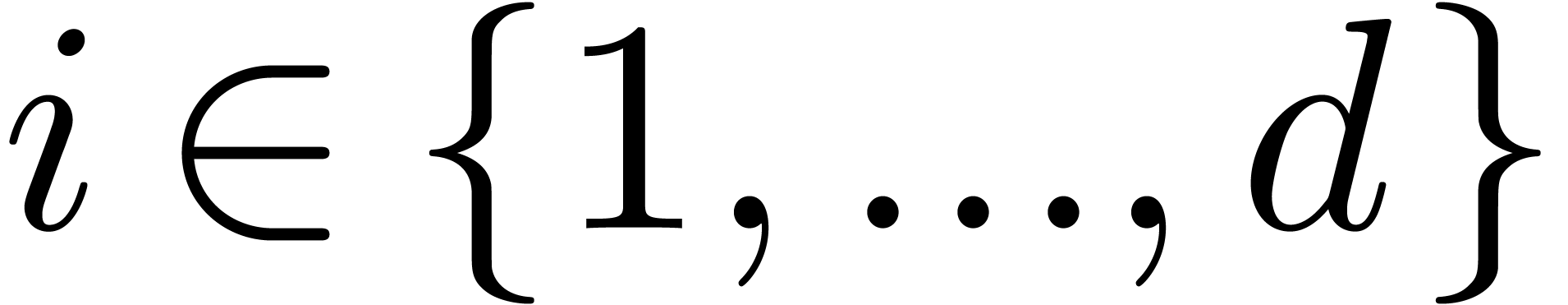 , which are also
called the power sums of the roots of the characteristic
polynomial
, which are also
called the power sums of the roots of the characteristic
polynomial  . The generating
series
. The generating
series 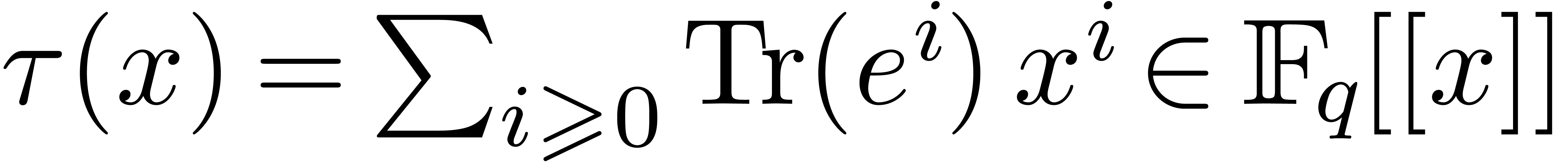 of these power sums relates to the
logarithmic derivative of the reverse polynomial
of these power sums relates to the
logarithmic derivative of the reverse polynomial 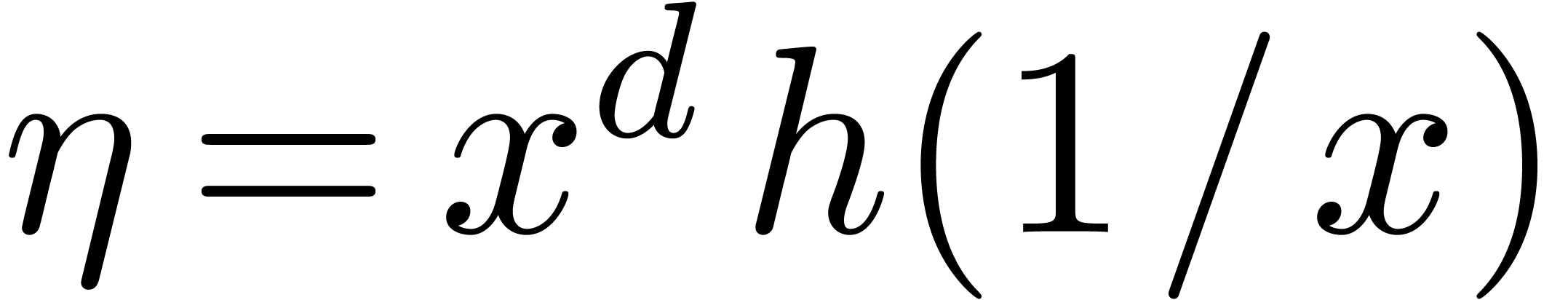 of
of 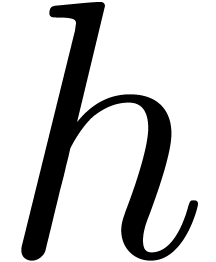 via a first order
differential equation
via a first order
differential equation
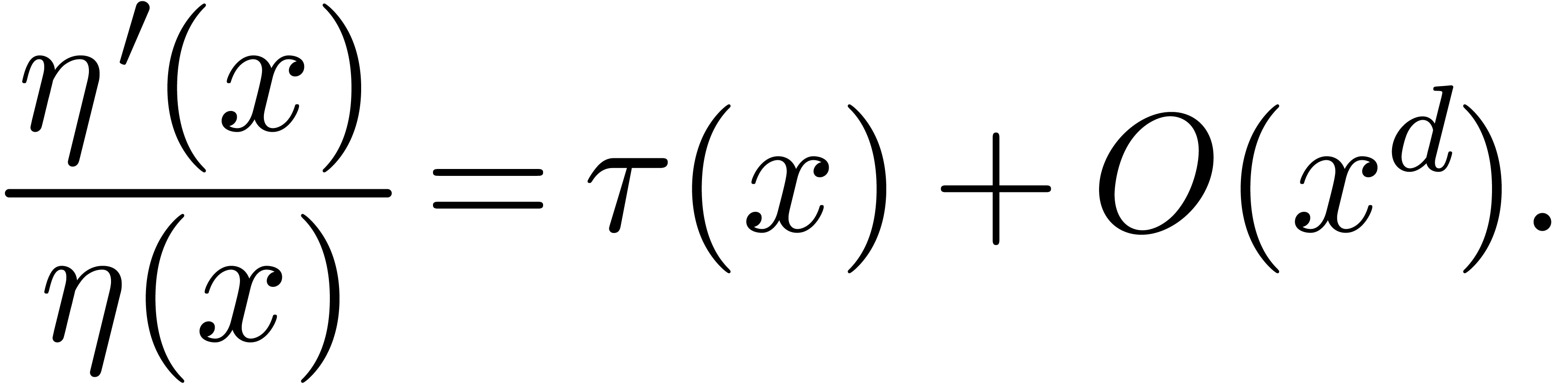 |
(1) |
This equation can be seen as a compact form of the classical
Newton–Girard identities which relate power sums and symmetric
polynomials. After computing  it thus suffices to
solve this equation in order to deduce
it thus suffices to
solve this equation in order to deduce 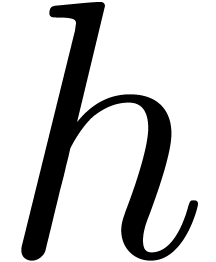 .
If
.
If 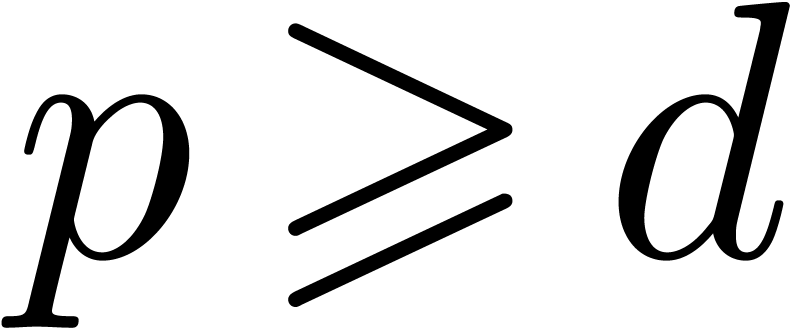 , then this method is
classical. If
, then this method is
classical. If 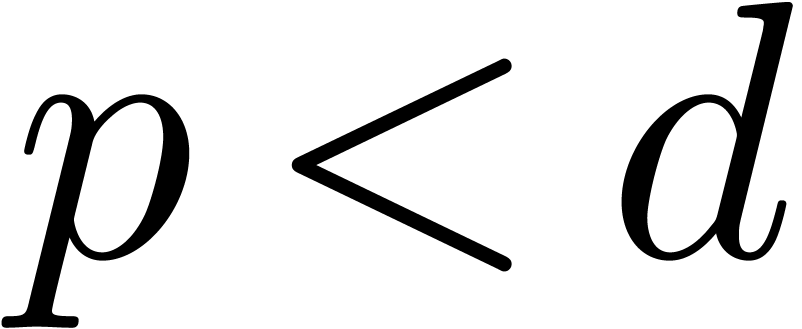 , then
, then 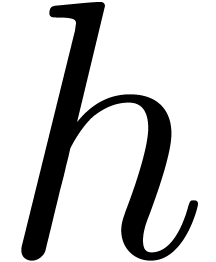 cannot directly be retrieved in this way [35,
Fact 2.1]. In the rest of this section, we will overcome this problem by
computing with
cannot directly be retrieved in this way [35,
Fact 2.1]. In the rest of this section, we will overcome this problem by
computing with 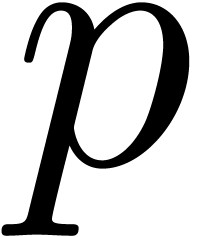 -adic integers
at a suitable finite precision
-adic integers
at a suitable finite precision 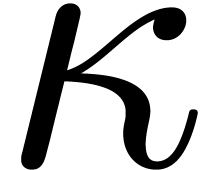 .
.
Let  be the ring of truncated
be the ring of truncated 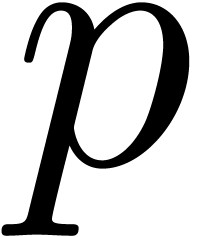 -adic integers at precision
-adic integers at precision 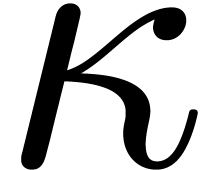 . It is convenient to write
. It is convenient to write 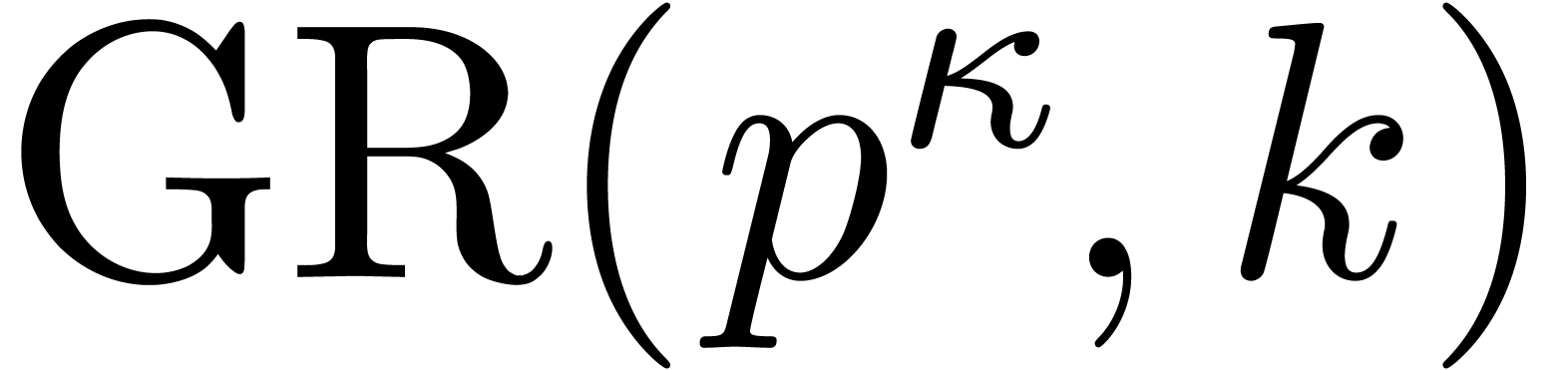 for the Galois ring of characteristic
for the Galois ring of characteristic 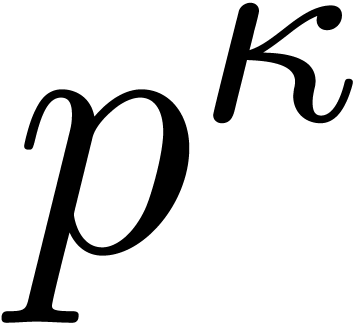 and degree
and degree 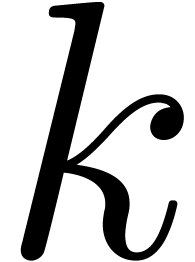 , which is
classically defined as
, which is
classically defined as 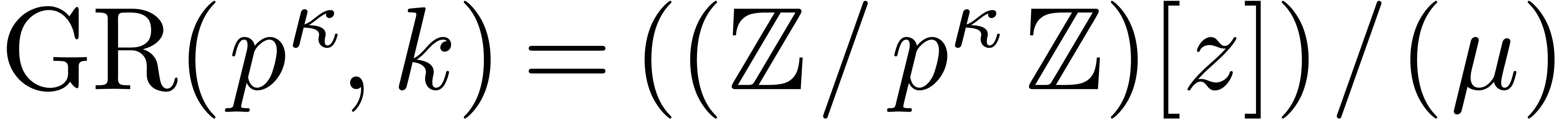 ,
where
,
where 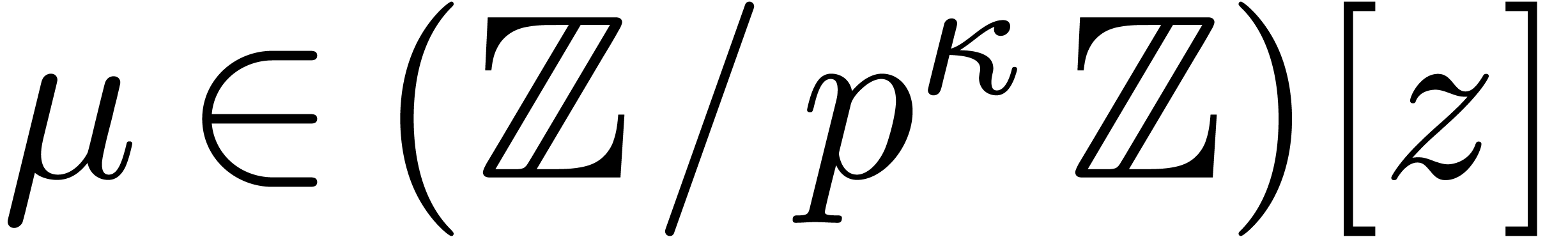 is a monic polynomial of degree
is a monic polynomial of degree 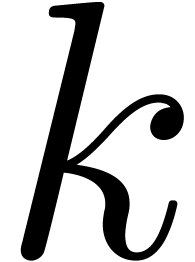 and is irreducible modulo
and is irreducible modulo 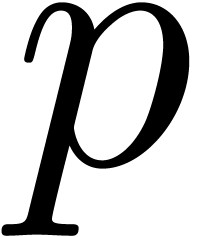 .
.
Let  represent a given monic polynomial of degree
represent a given monic polynomial of degree
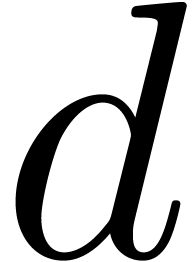 , let
, let 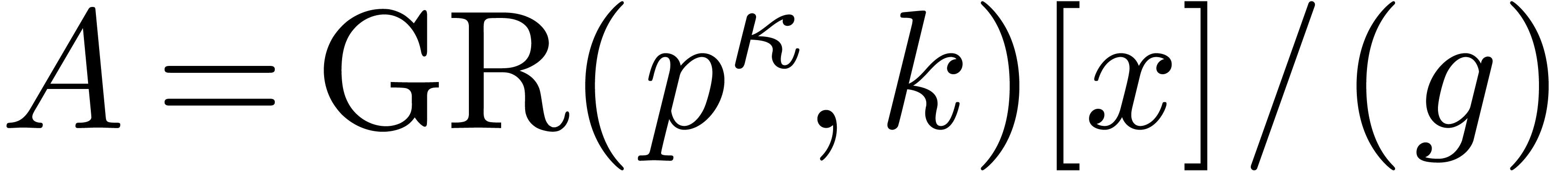 . We write
. We write 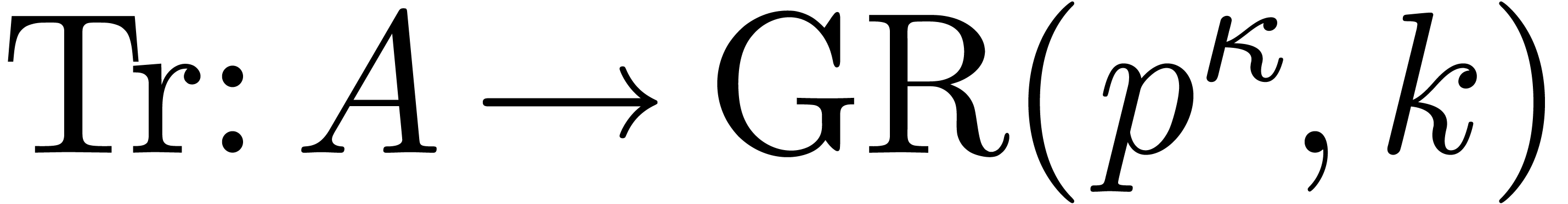 the classical
trace function on
the classical
trace function on  . In order
to compute the power sums
. In order
to compute the power sums 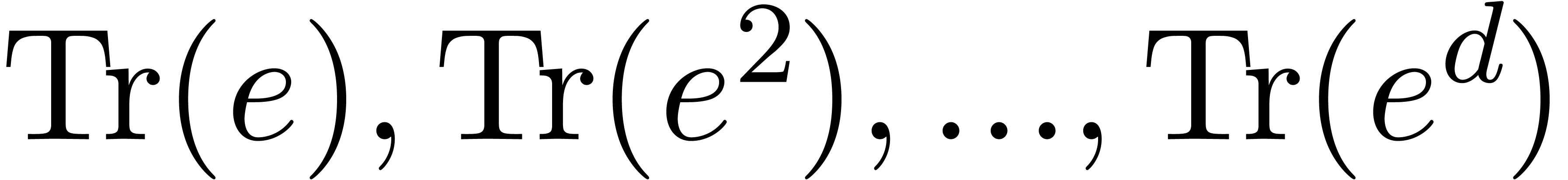 ,
we will use the following proposition, which is essentially a
consequence of a result due to Kedlaya and Umans in [26, 27]:
,
we will use the following proposition, which is essentially a
consequence of a result due to Kedlaya and Umans in [26, 27]:
Proof. Let 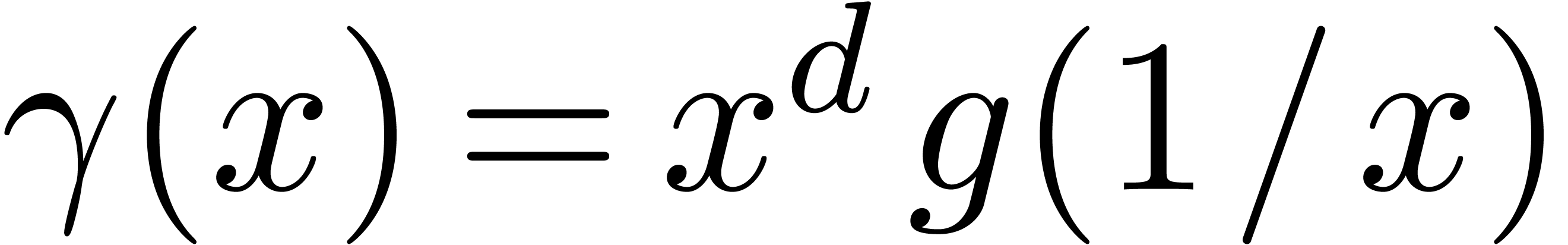 denote the
reverse polynomial of
denote the
reverse polynomial of  . Since
. Since
 is monic we have
is monic we have 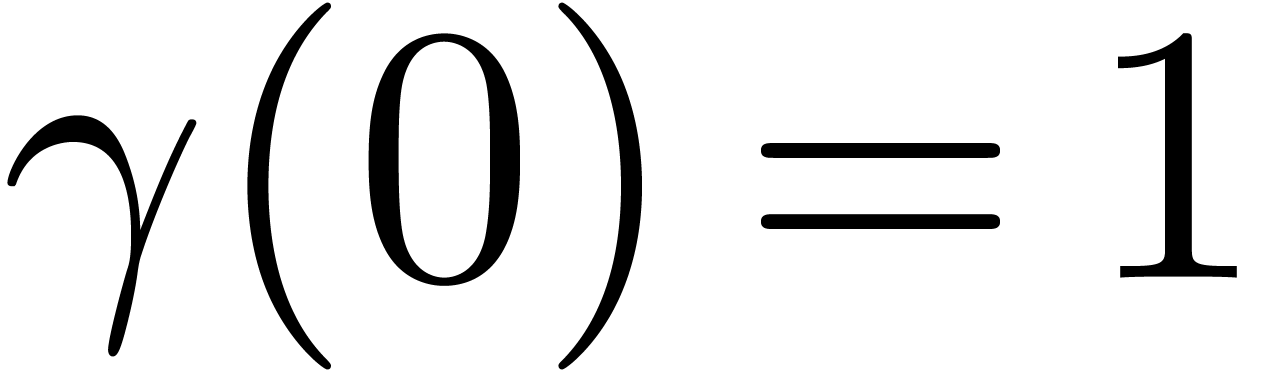 .
In the canonical basis made of the classes of
.
In the canonical basis made of the classes of  in
in
 , the trace function can be
computed as the first
, the trace function can be
computed as the first 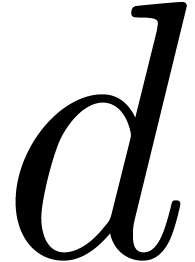 terms of the generating
series
terms of the generating
series
in softly linear time, namely 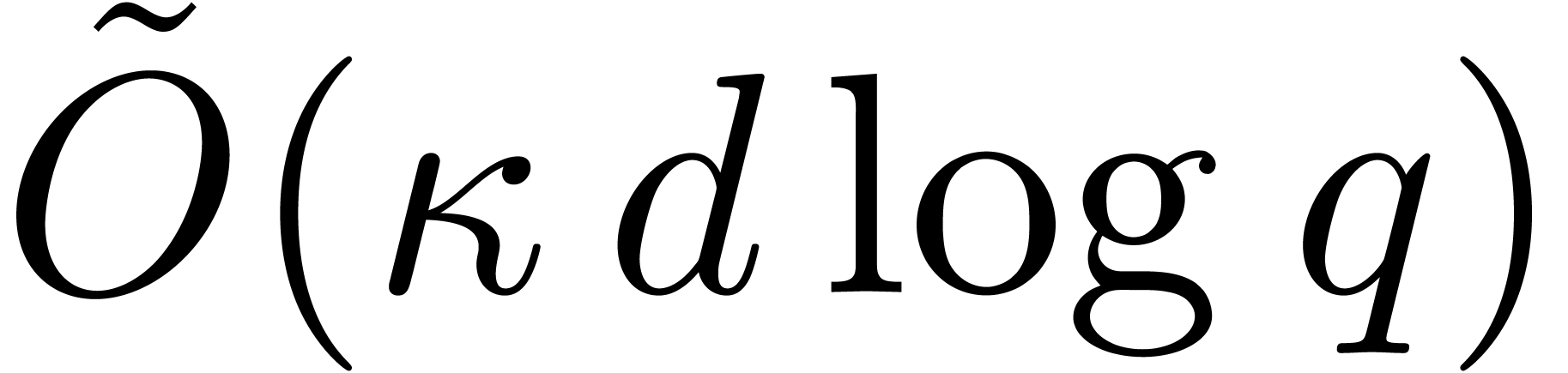 .
.
The cardinality of  is
is 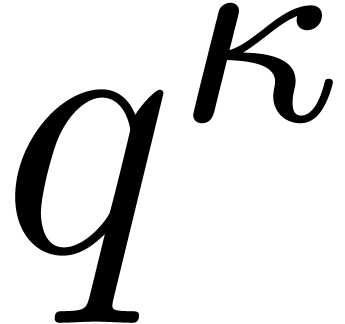 , and
, and  contains at least
contains at least  invertible elements. Then, for every constant
invertible elements. Then, for every constant 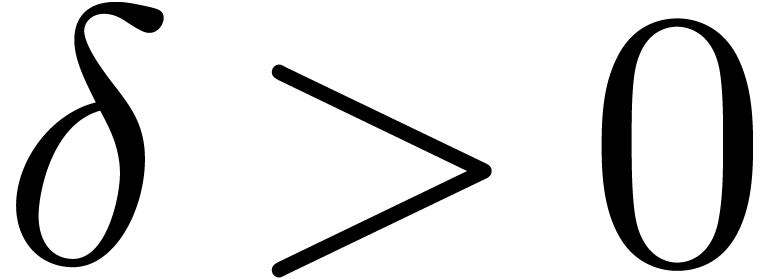 such that
such that 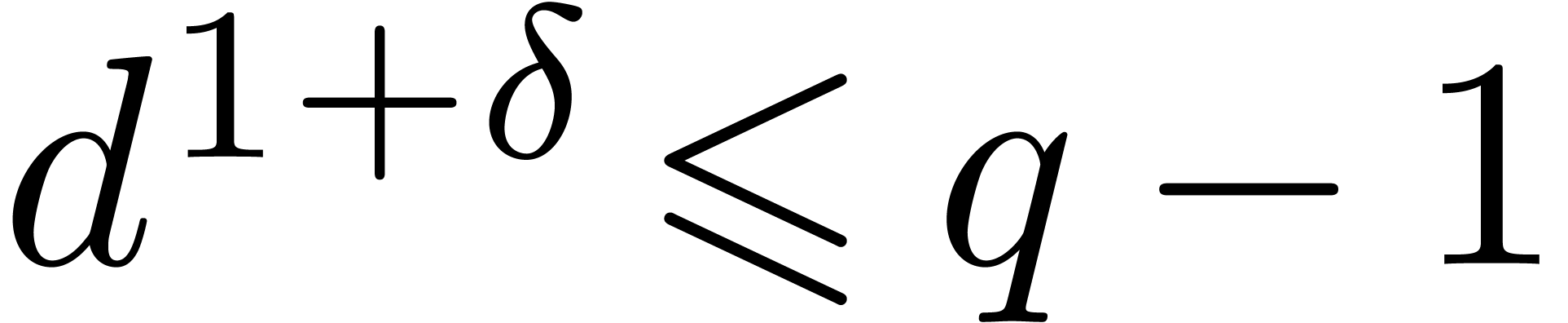 ,
Theorem 7.7 of [27, p. 1792] provides us with an algorithm
to compute
,
Theorem 7.7 of [27, p. 1792] provides us with an algorithm
to compute 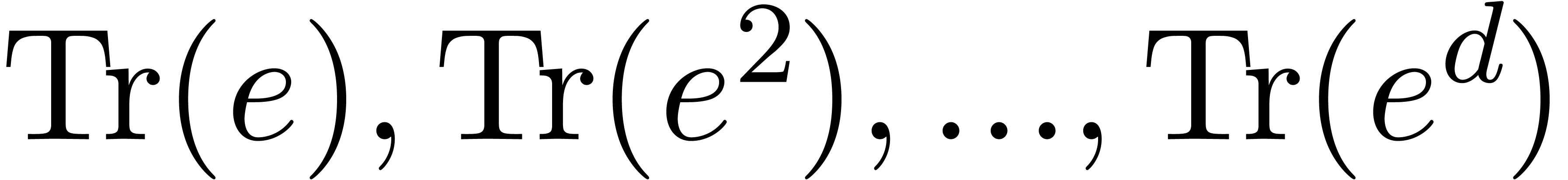 in time
in time 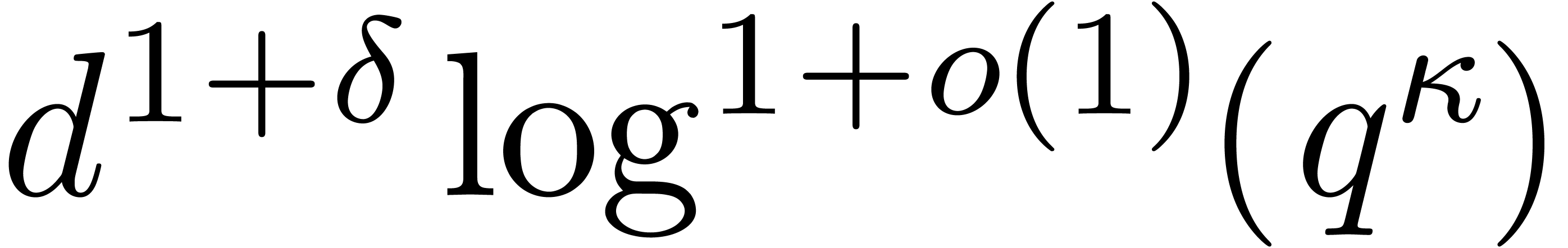 .
.
Remark 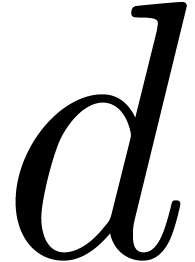 close to
close to  the proposition does not
apply. A simple solution is to lift the computations in
the proposition does not
apply. A simple solution is to lift the computations in 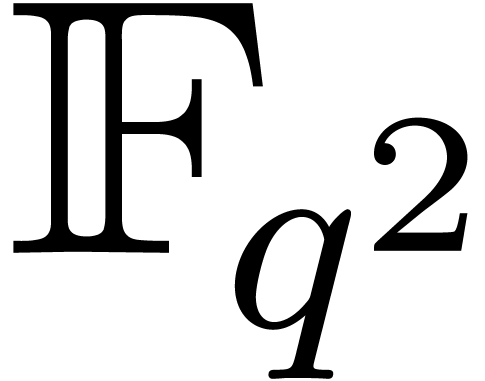 . Nevertheless, for finding the roots of
. Nevertheless, for finding the roots of  , this case is in fact favorable:
it suffices to evaluate
, this case is in fact favorable:
it suffices to evaluate  at all the elements of
at all the elements of
 . Therefore we will not need
to work in
. Therefore we will not need
to work in 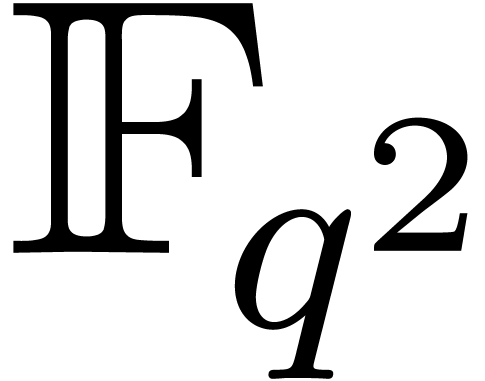 .
.
We carry on with the notations of the previous subsection. Let  be a given element in
be a given element in  ,
and let
,
and let 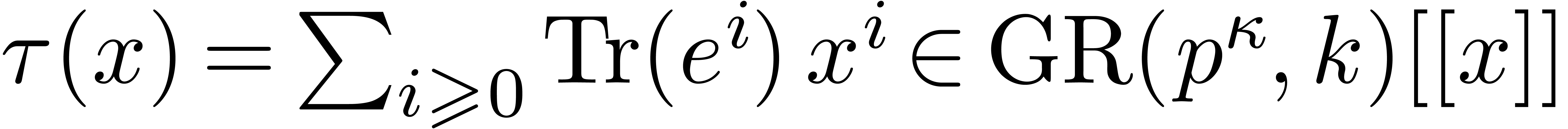 represent the generating series of the
power sums of the roots of the characteristic polynomial
represent the generating series of the
power sums of the roots of the characteristic polynomial 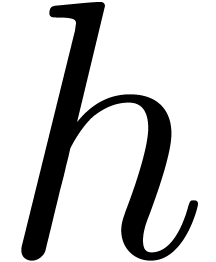 of
of  . If
. If  , then
, then  can
be deduced from
can
be deduced from 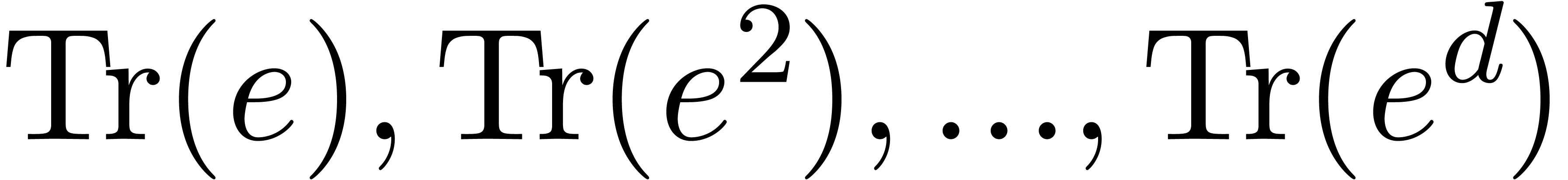 in softly linear time, using
Newton–Girard's identities (1), as for instance in
[5, Corollary 1]. If
in softly linear time, using
Newton–Girard's identities (1), as for instance in
[5, Corollary 1]. If  ,
then Theorem 1 of [7] solves the equation modulo
,
then Theorem 1 of [7] solves the equation modulo  whenever
whenever 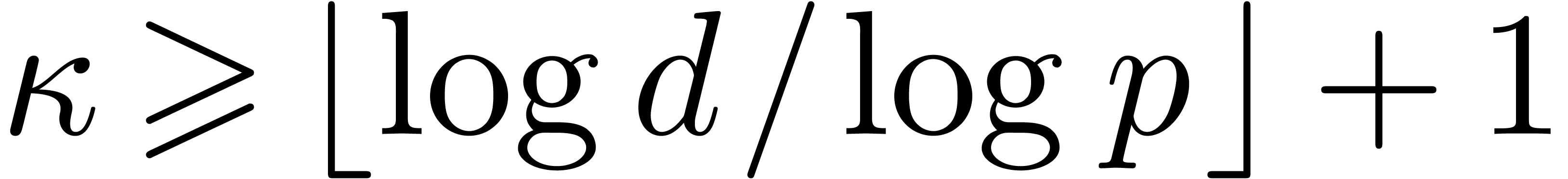 . This
subsection is dedicated to the remaining case when
. This
subsection is dedicated to the remaining case when  and
and 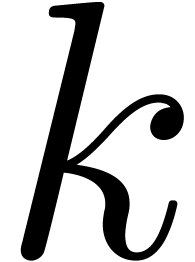 is general. Our new alternative proofs are
also shorter than in [7].
is general. Our new alternative proofs are
also shorter than in [7].
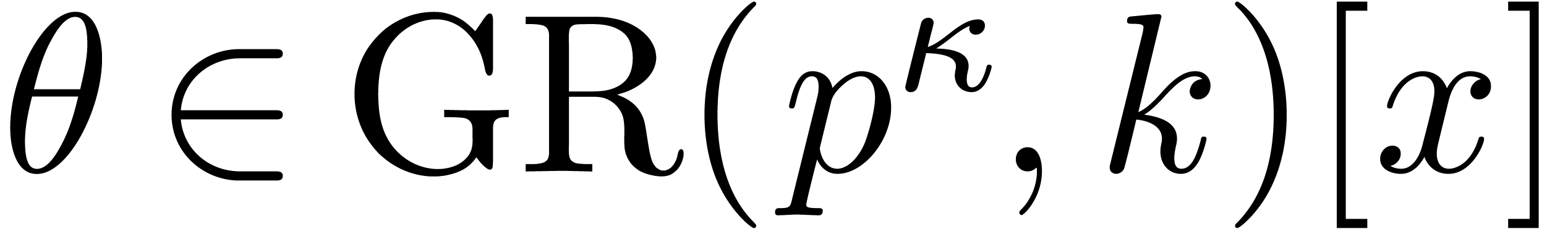 be of degree
be of degree 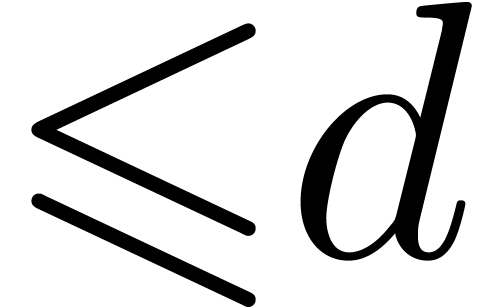 satisfying
satisfying 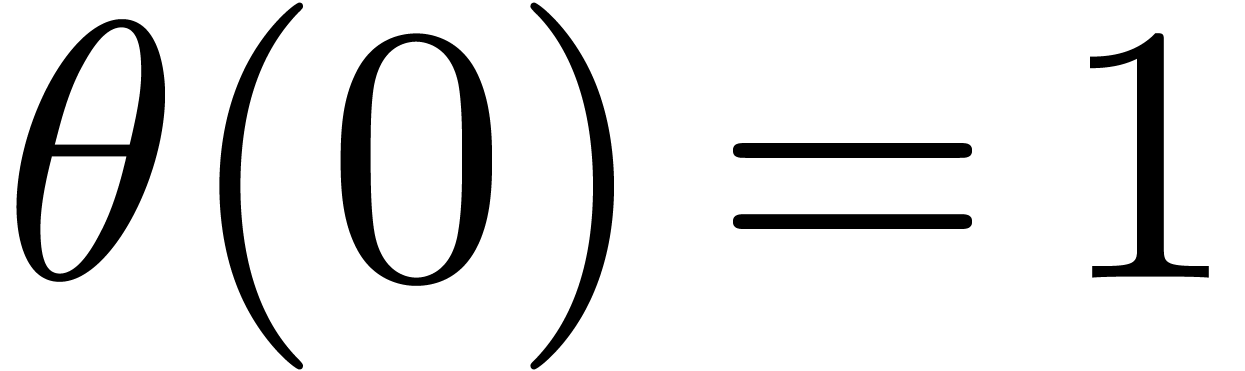 , and
, and 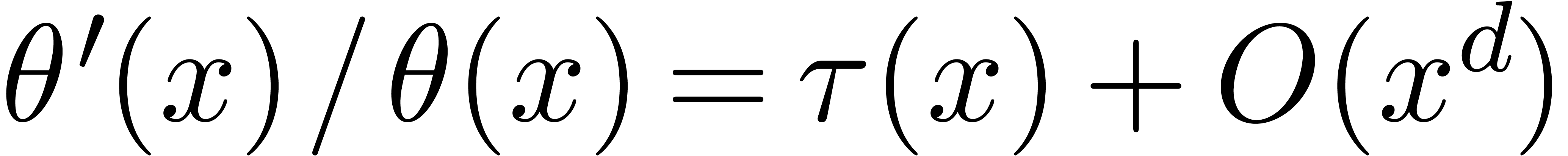 . If
. If 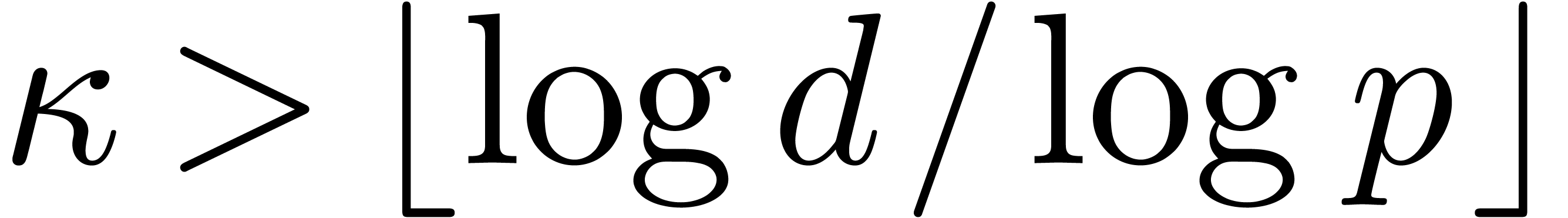 , then
, then 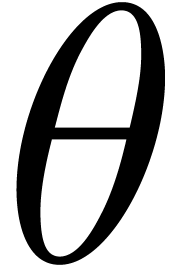 coincides with
coincides with 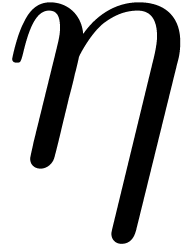 modulo
modulo 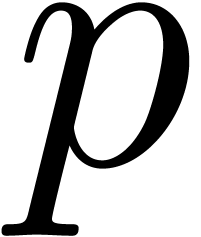 at precision
at precision  .
.
Proof. Let  .
Writing
.
Writing  as
as 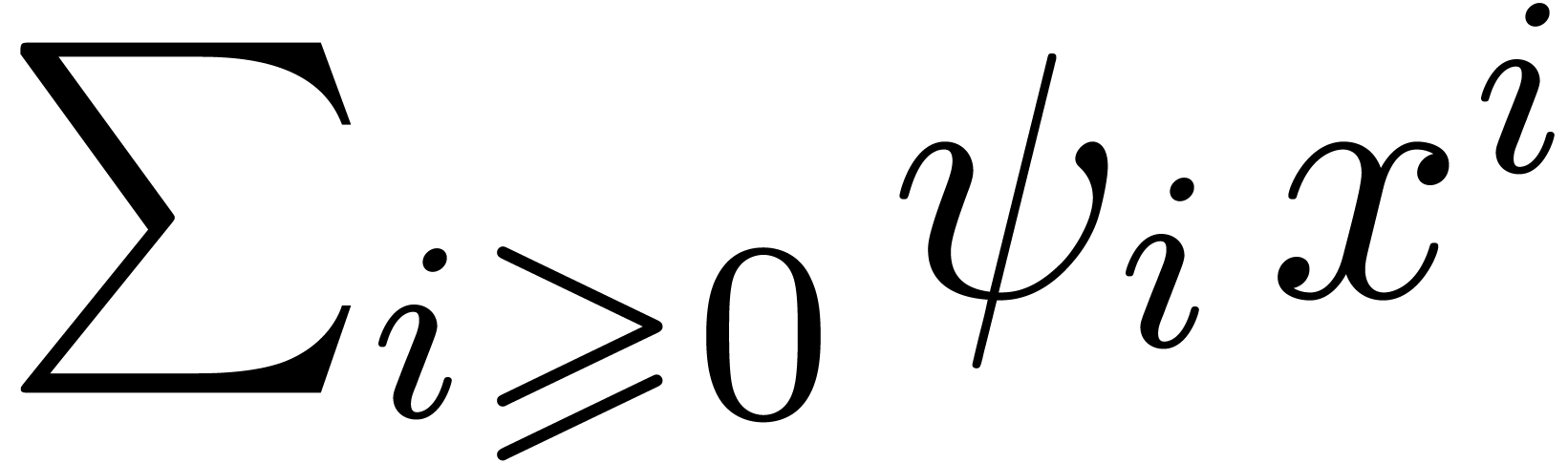 ,
we deduce from
,
we deduce from 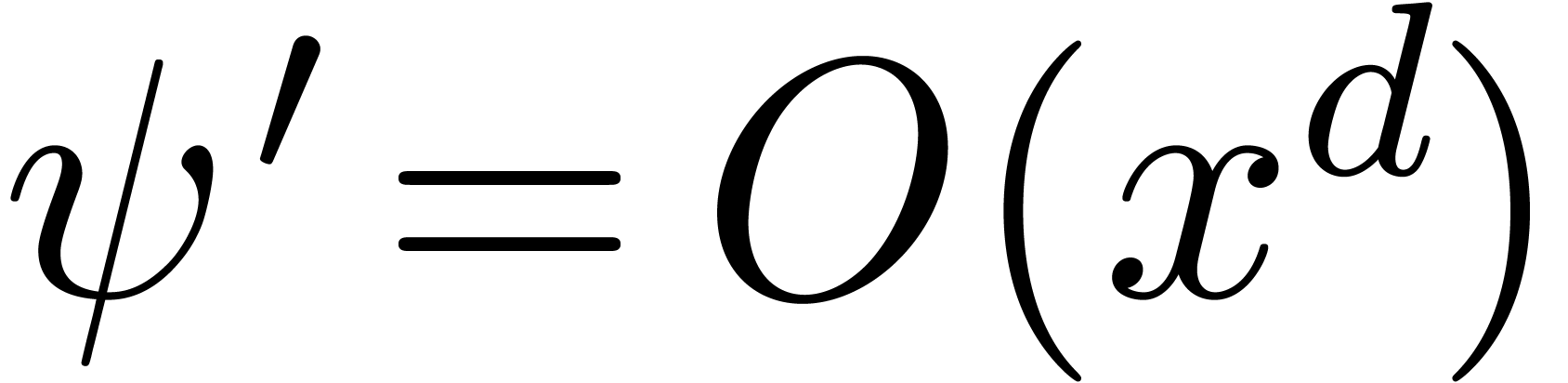 that
that 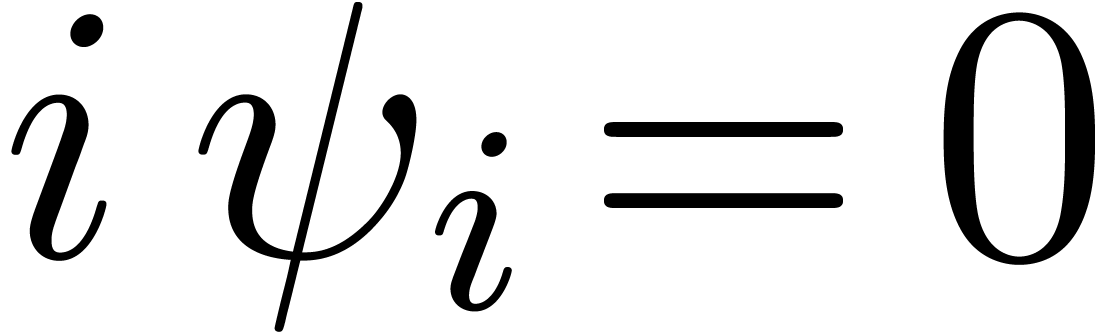 for
all
for
all 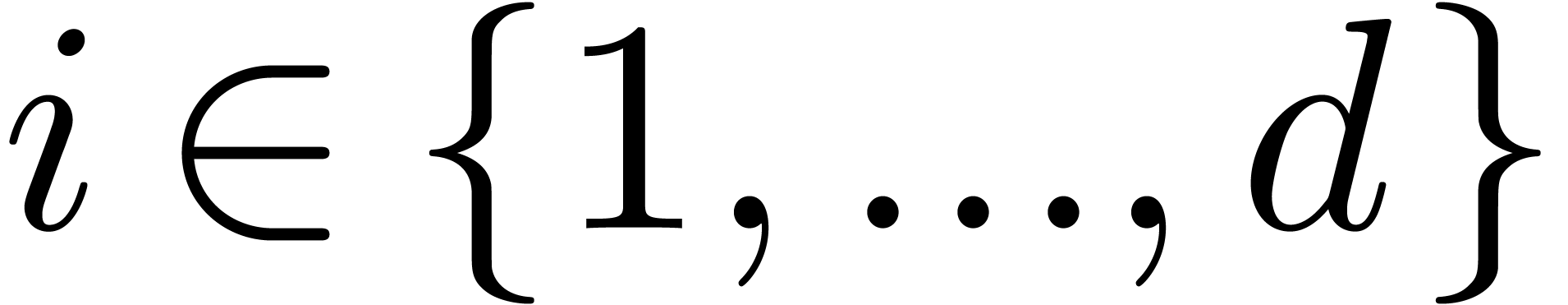 , whence
, whence 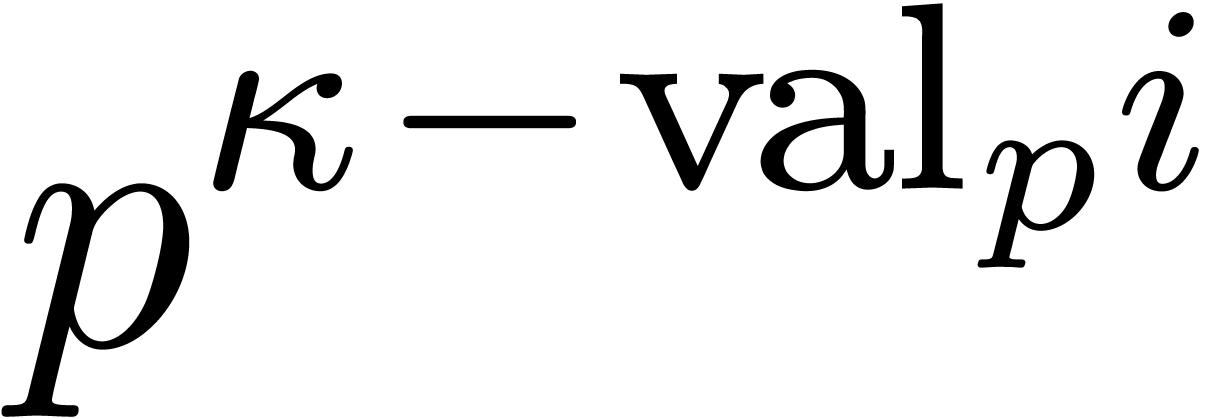 divides
divides 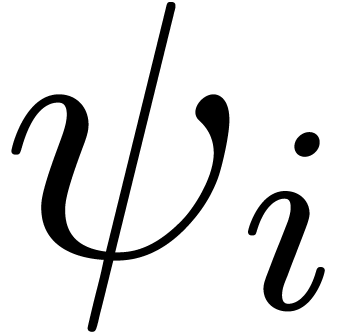 , where
, where 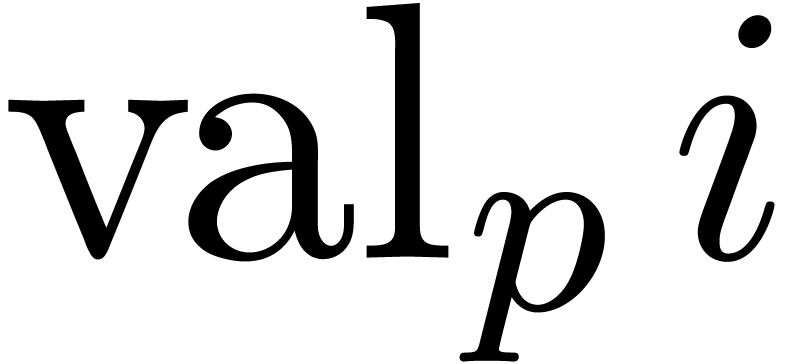 denotes the
denotes the 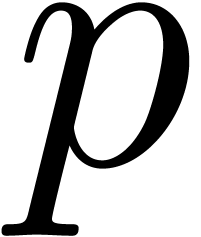 -adic
valuation of
-adic
valuation of 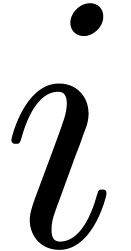 . Since
. Since 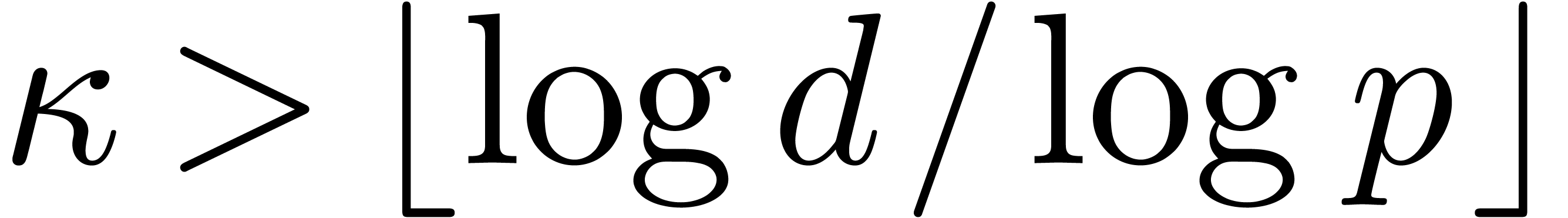 is equivalent to
is equivalent to 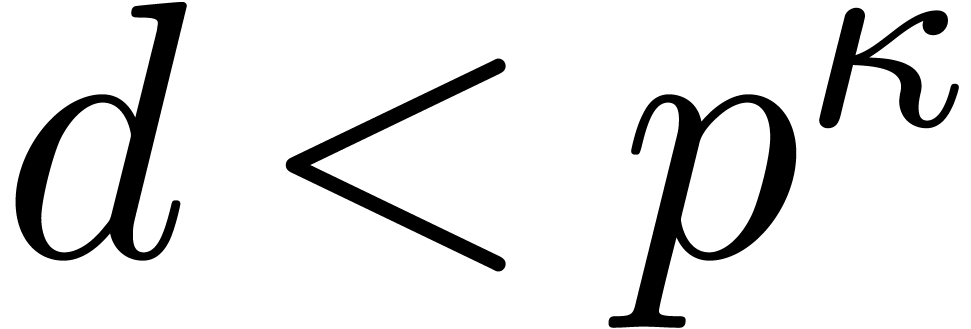 ,
we have
,
we have 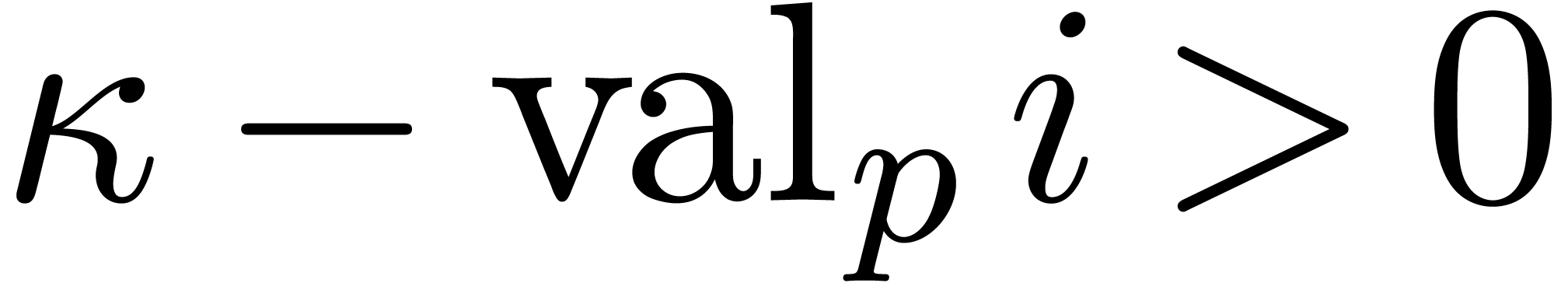 , which concludes the
proof.
, which concludes the
proof.
Denote cost of multiplication in 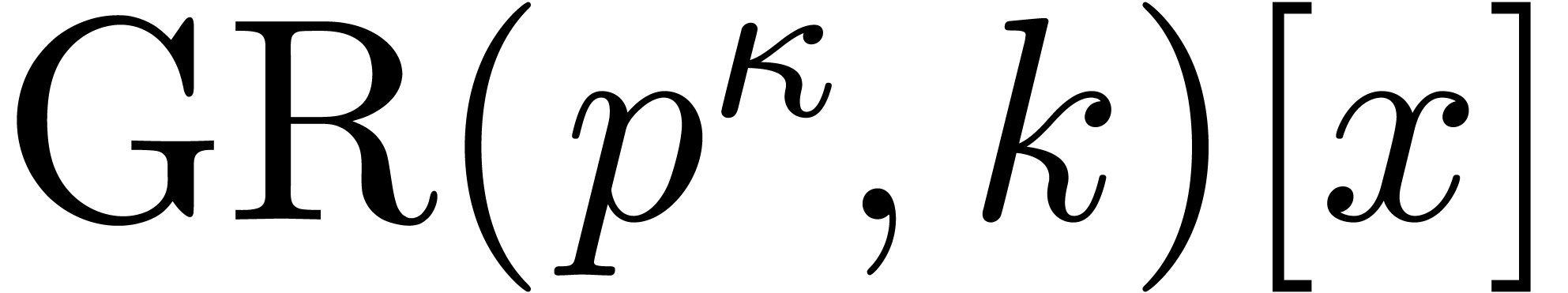 of polynomials
of degrees
of polynomials
of degrees 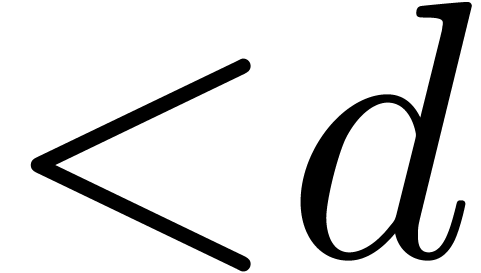 by
by 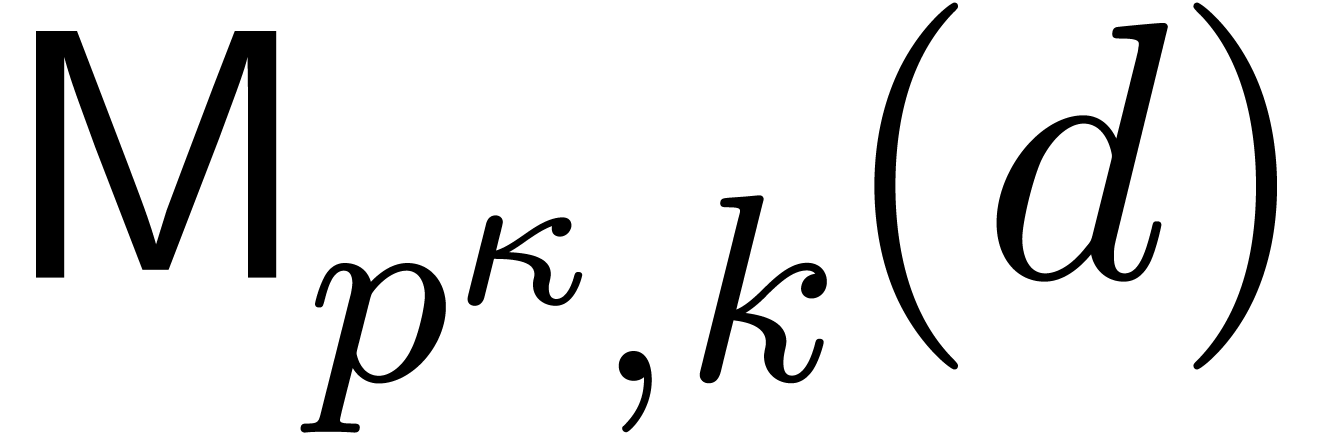 .
We have
.
We have  according to [22].
according to [22].
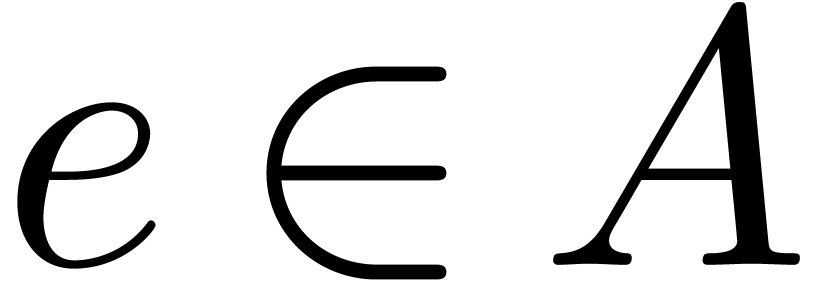 ,
and let
,
and let 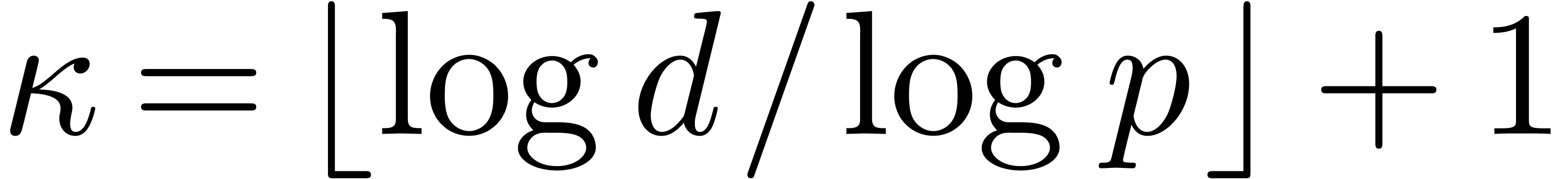 . From
. From  , we can compute the characteristic
polynomial
, we can compute the characteristic
polynomial 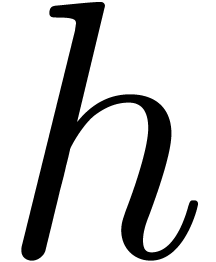 of
of  modulo
modulo
 in time
in time 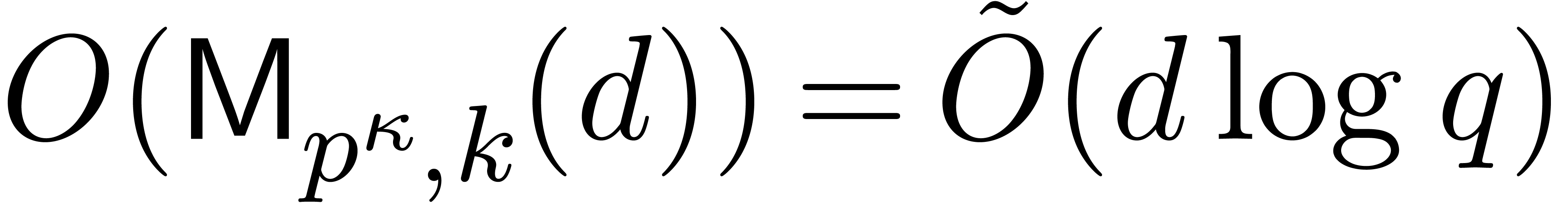 .
.
Proof. We will show how to compute a series 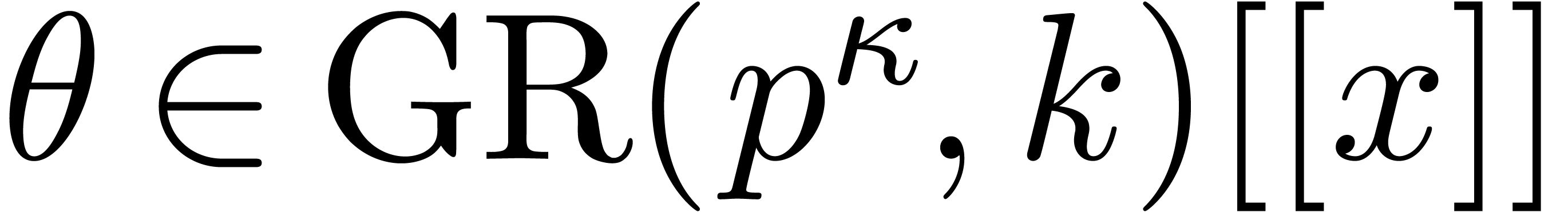 satisfying
satisfying 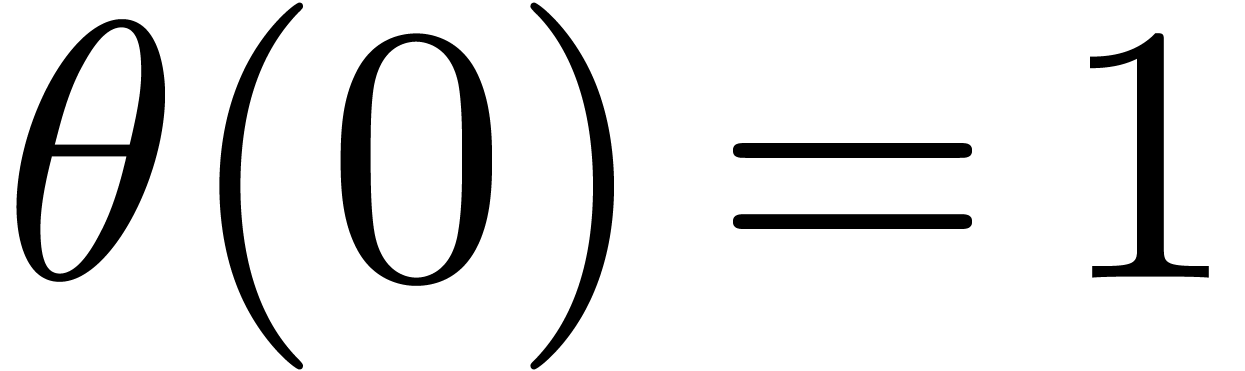 and
and 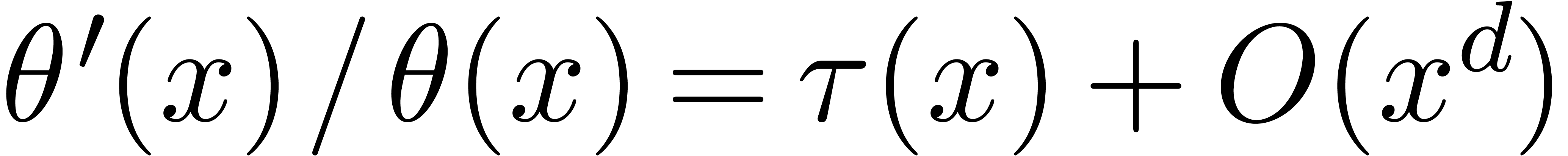 , using Newton's method. In view of the above
lemma, this will yield
, using Newton's method. In view of the above
lemma, this will yield  followed by
followed by  modulo
modulo  .
.
Suppose that we are given 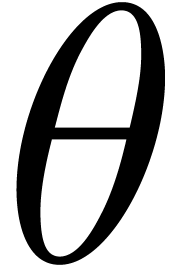 such that
such that 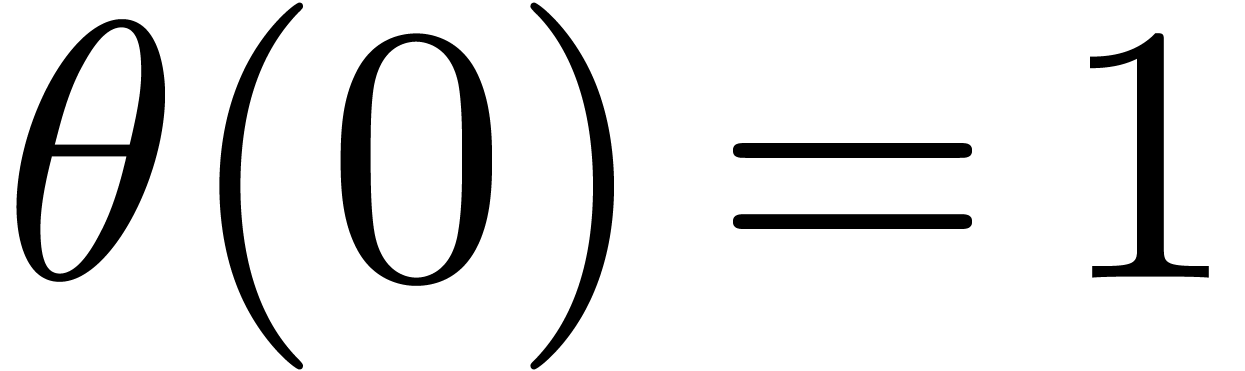 and
and 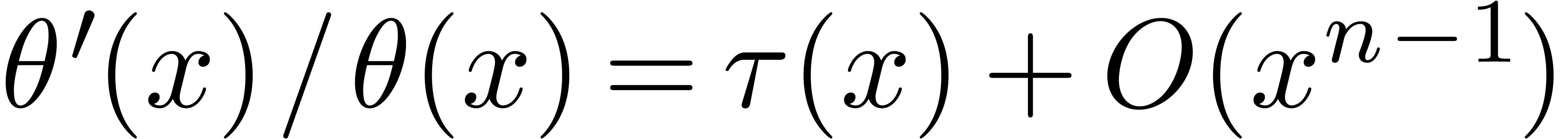 for some integer
for some integer 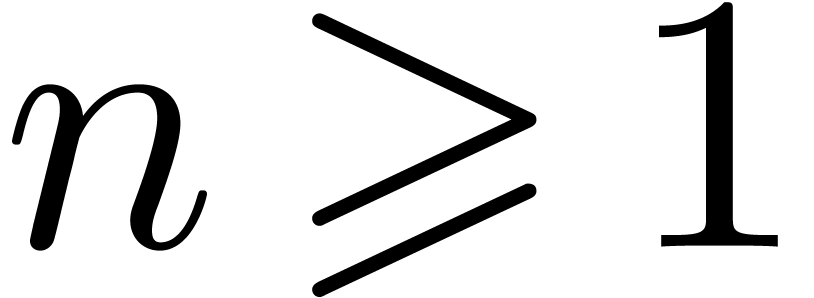 . Then we claim that there exists
. Then we claim that there exists 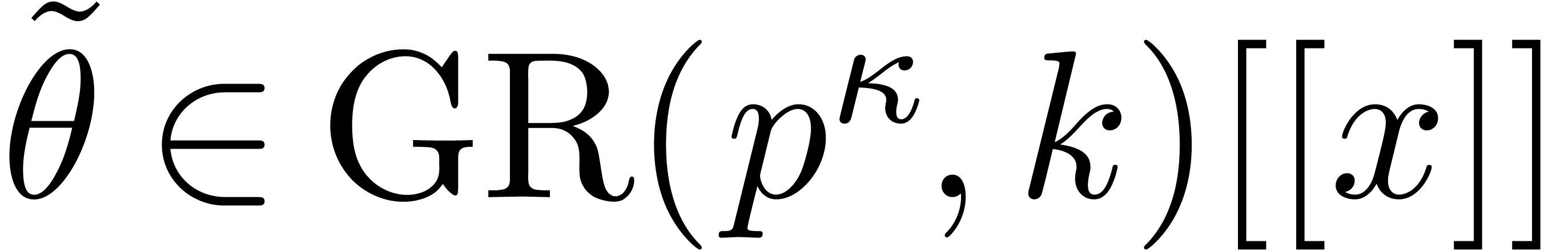 of valuation in
of valuation in  at least
at least 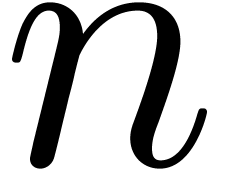 and such that
and such that
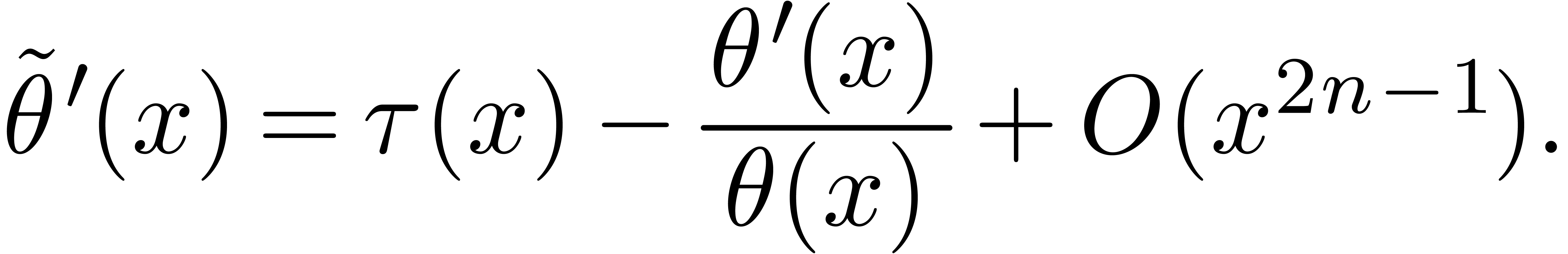 |
(2) |
Indeed, using that 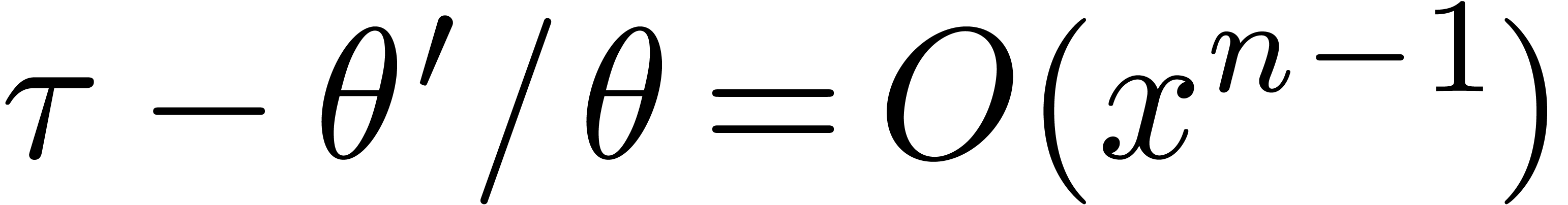 and
and 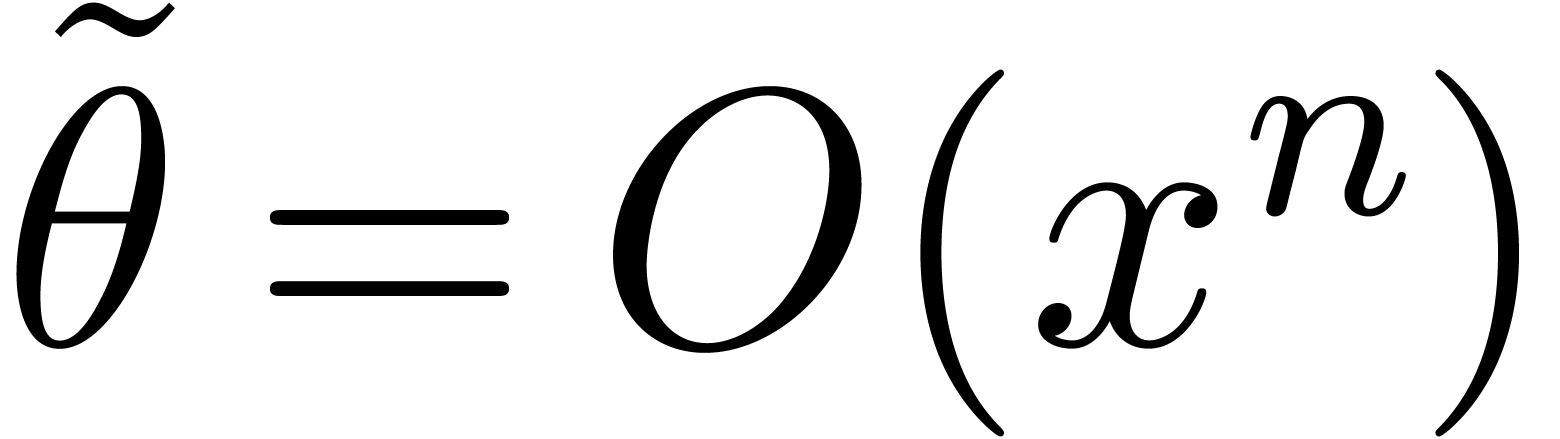 , this equation is equivalent to
, this equation is equivalent to
and therefore equivalent to
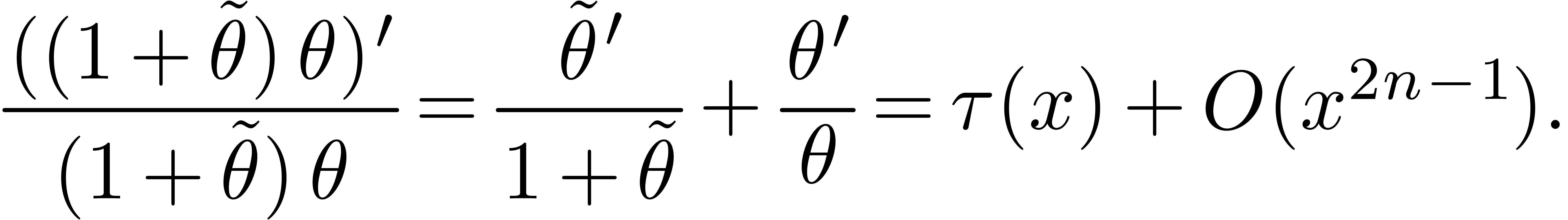
This latter equation admits 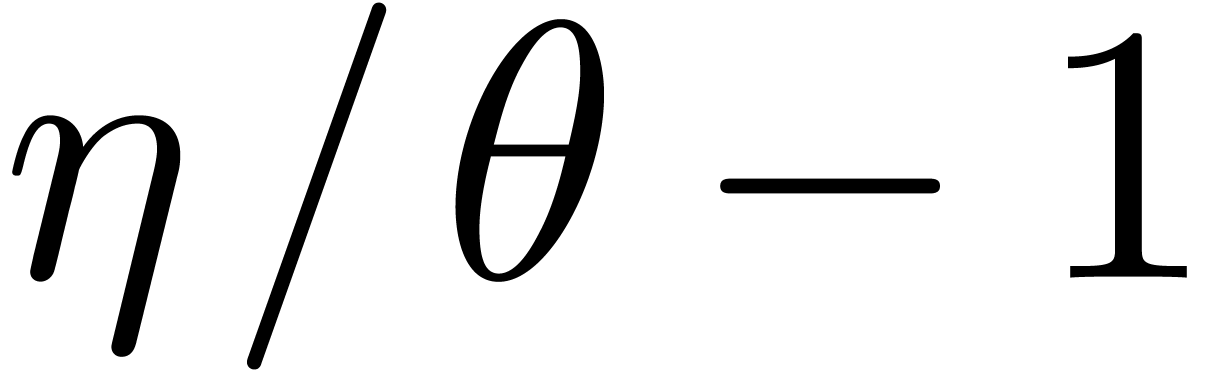 as a solution.
Having proved our claim, we can compute
as a solution.
Having proved our claim, we can compute  as being
any integral of
as being
any integral of 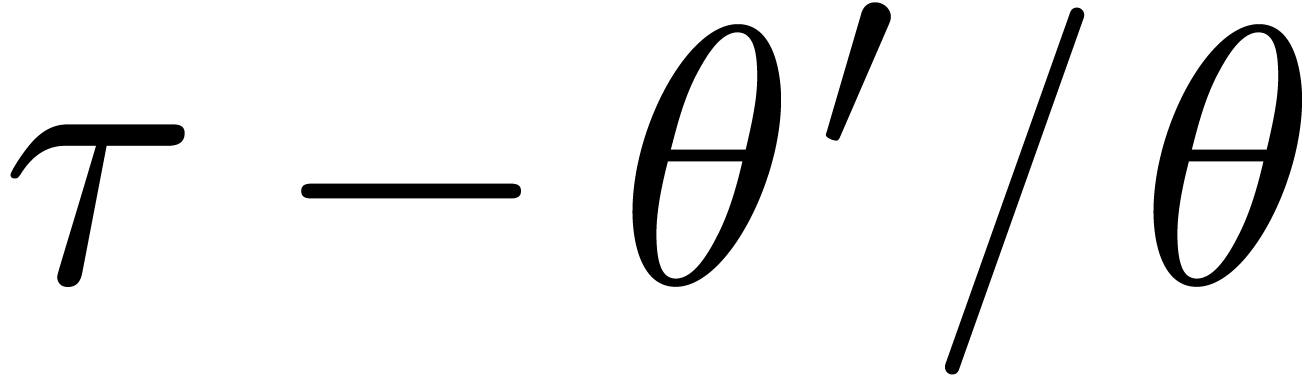 modulo
modulo 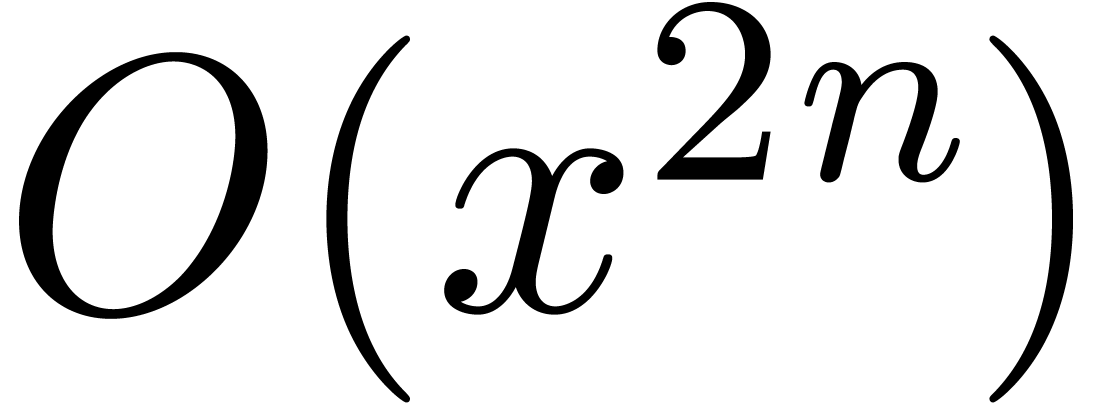 , and observe that
, and observe that 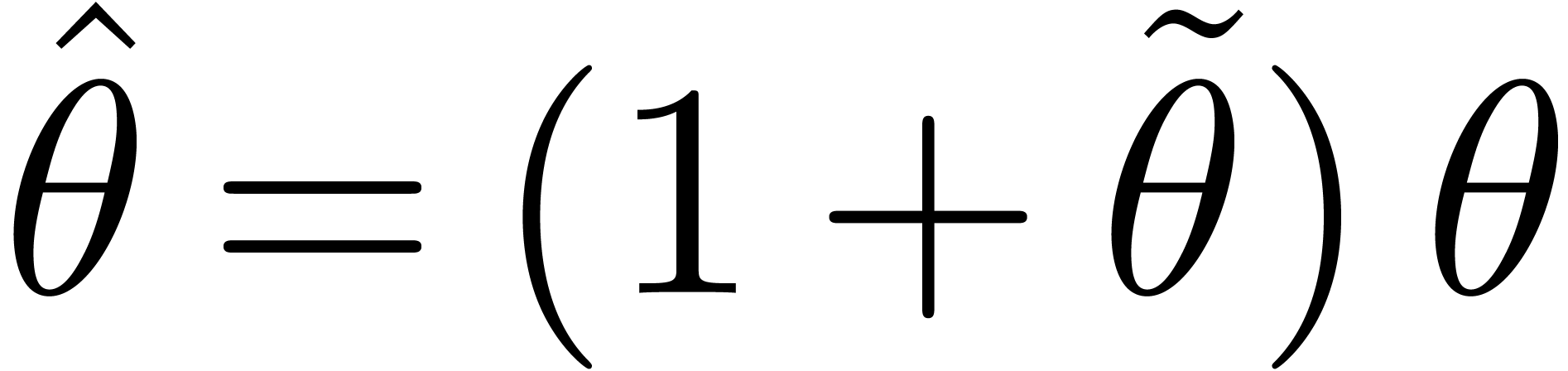 satisfies
satisfies
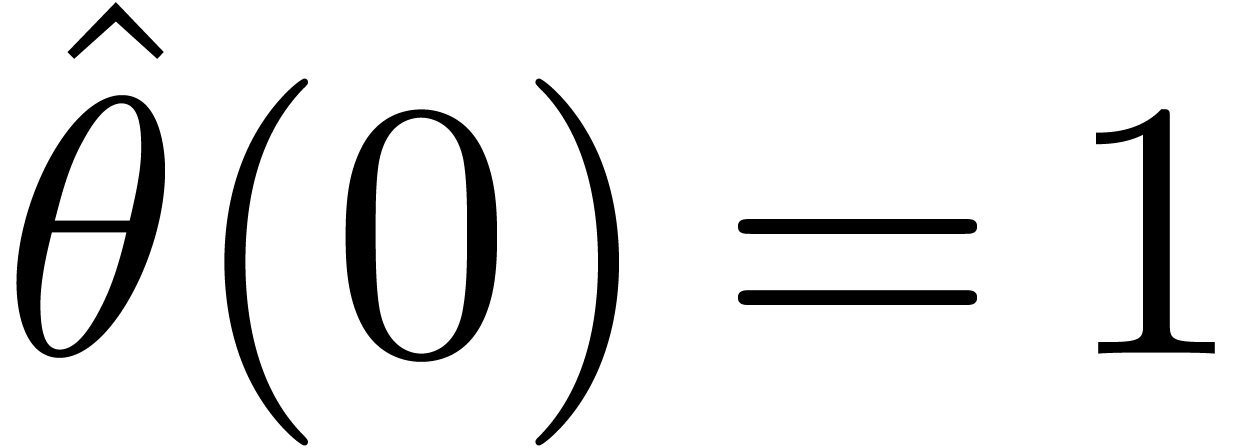 and
and 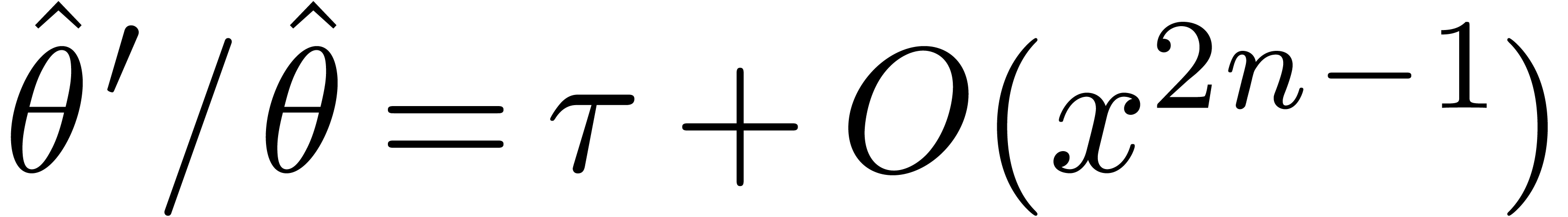 .
.
The cost of one iteration (2) is bounded by 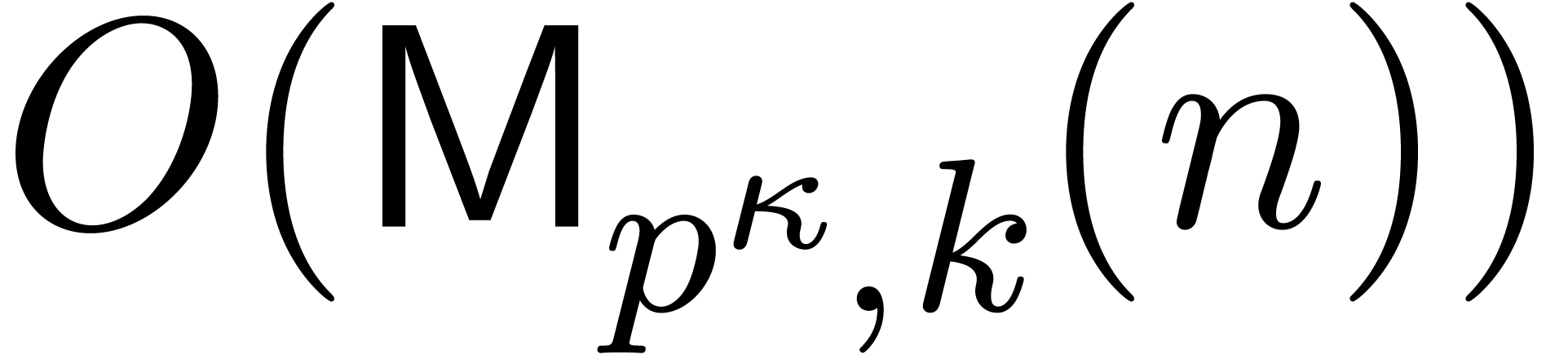 . Starting with
. Starting with 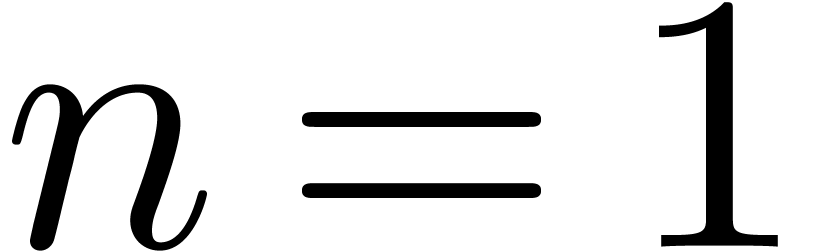 and
and
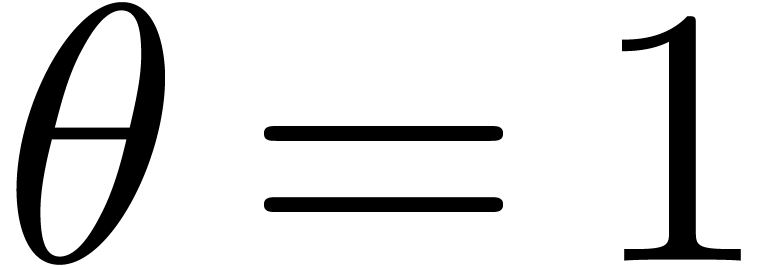 , we recursively apply the
iteration for
, we recursively apply the
iteration for 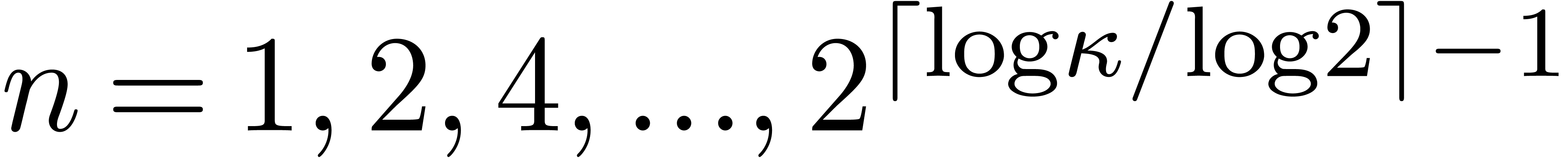 , the end
result being a
, the end
result being a 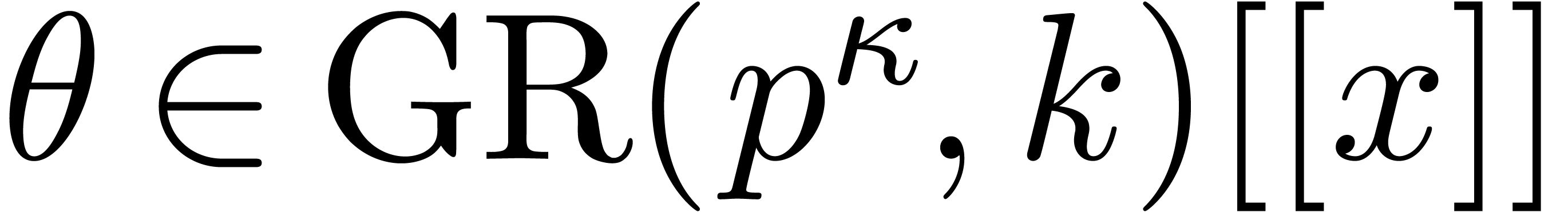 with
with 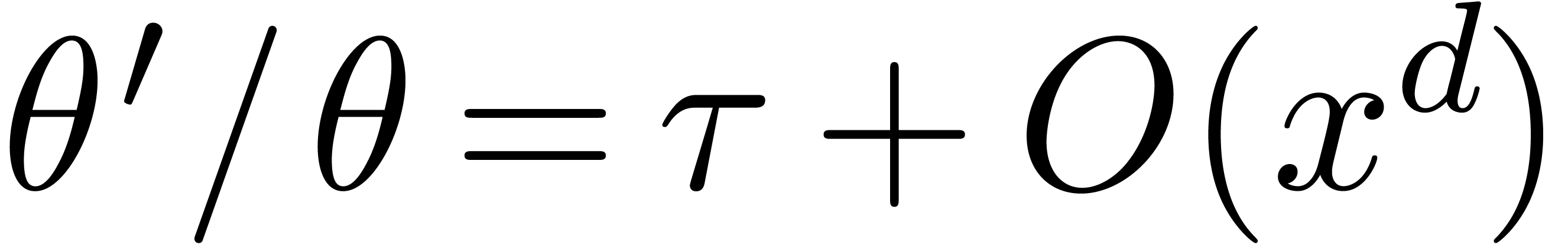 . It is classical that the cost of the last
iteration dominates the total cost, which is therefore bounded by
. It is classical that the cost of the last
iteration dominates the total cost, which is therefore bounded by 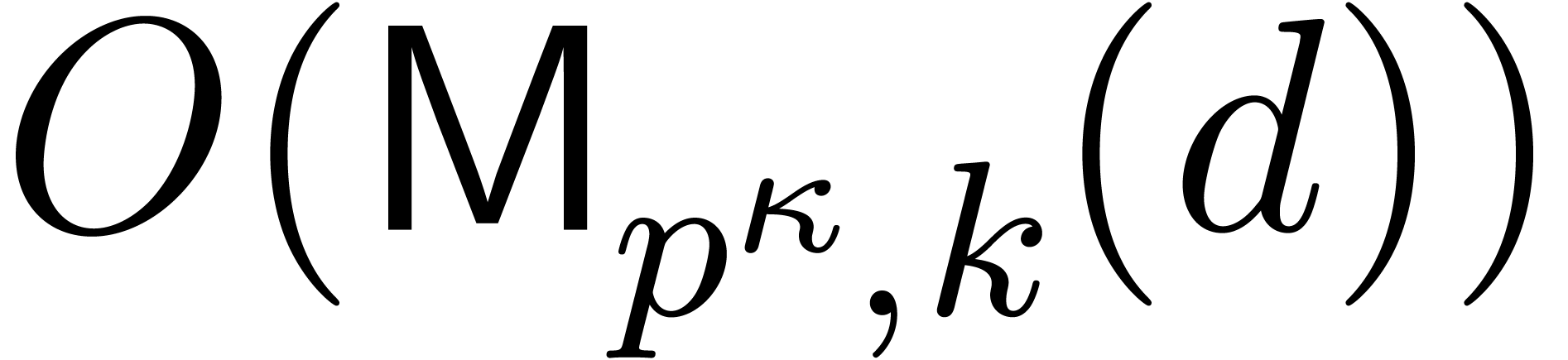 .
.
Now we come back to the original computational problem over  .
.
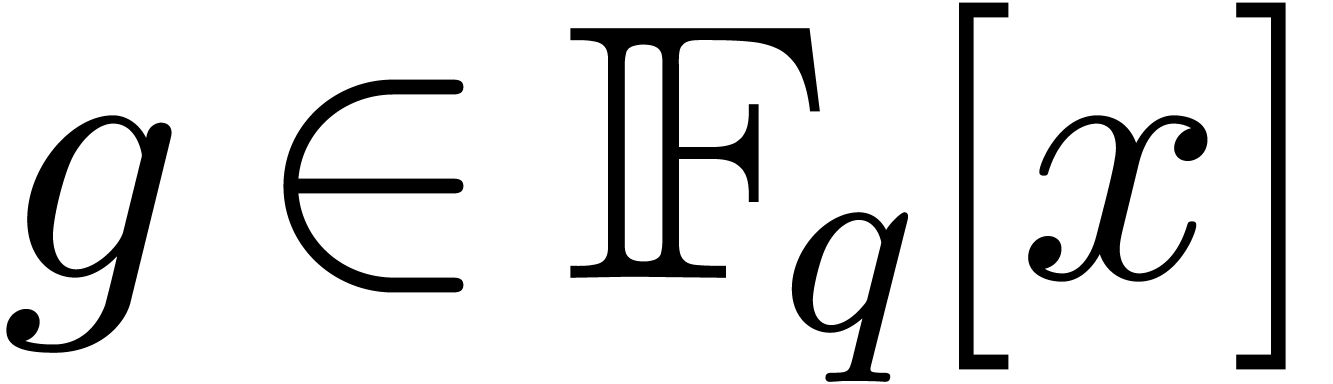 be a monic polynomial of degree
be a monic polynomial of degree
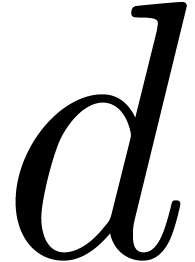 , and let
, and let 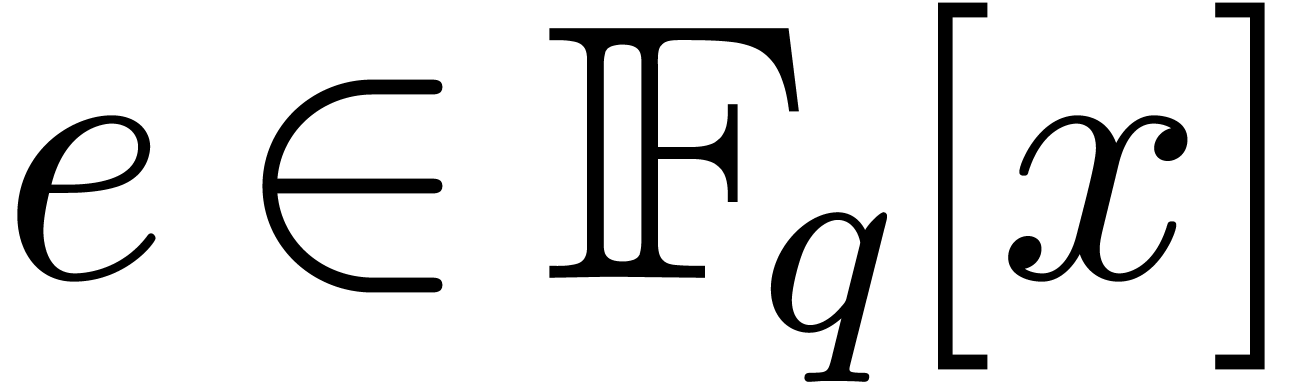 be of degree
be of degree 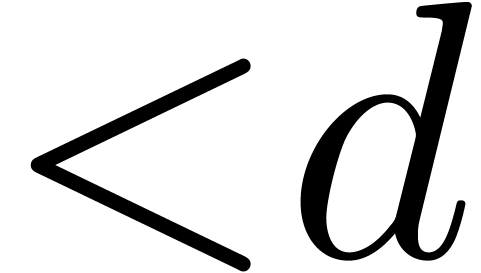 . For every
constant
. For every
constant  such that
such that  , the characteristic polynomial
, the characteristic polynomial 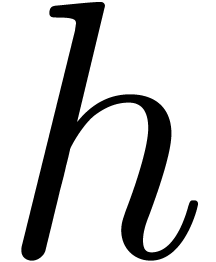 of the multiplication by
of the multiplication by  in
in 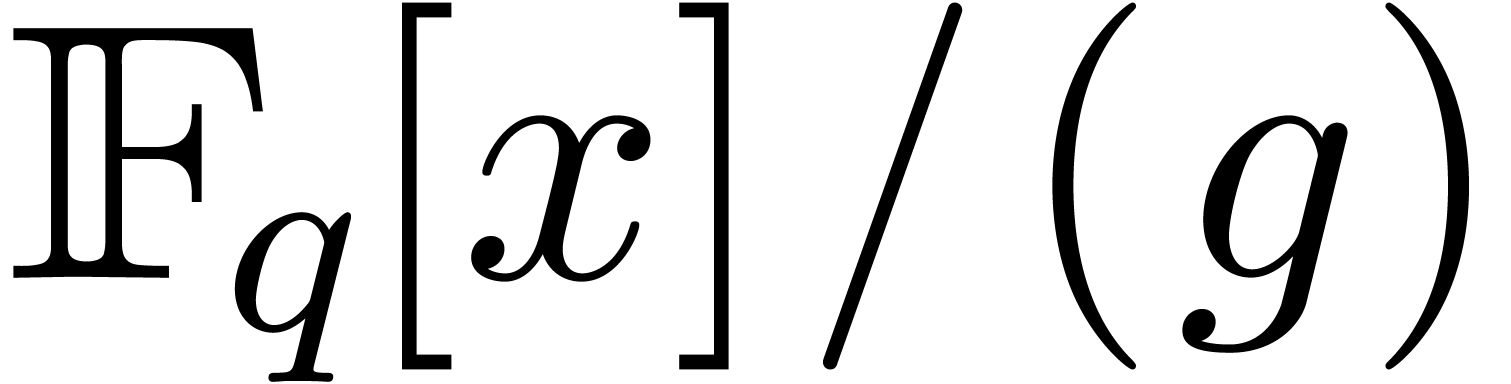 can be computed in time
can be computed in time 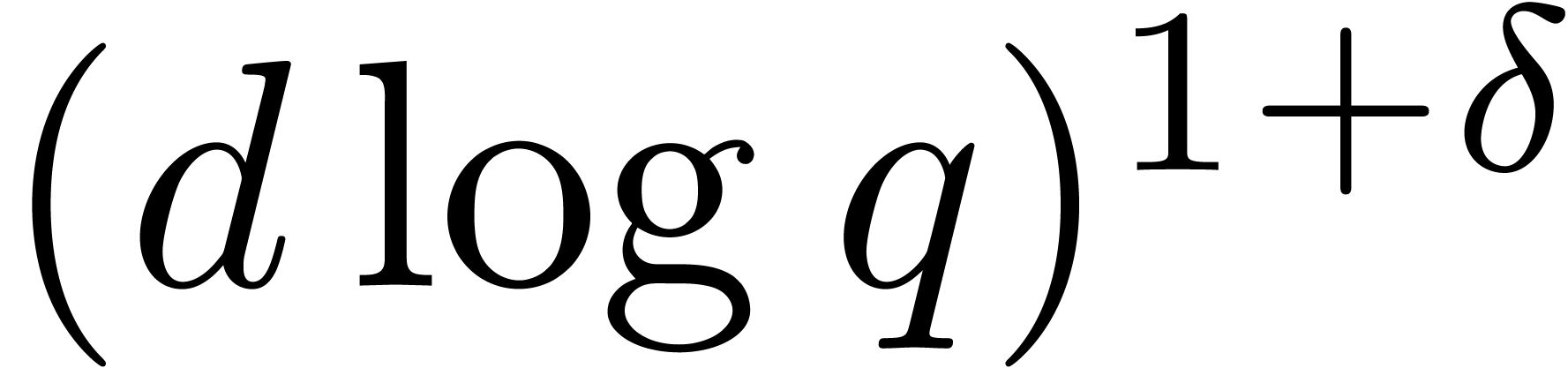 .
.
Proof. We embed 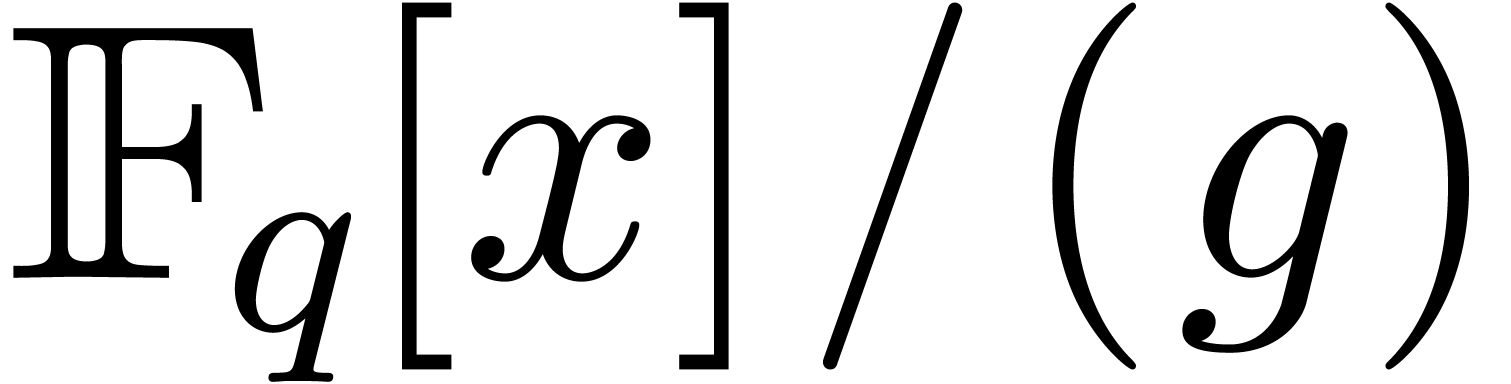 into
into
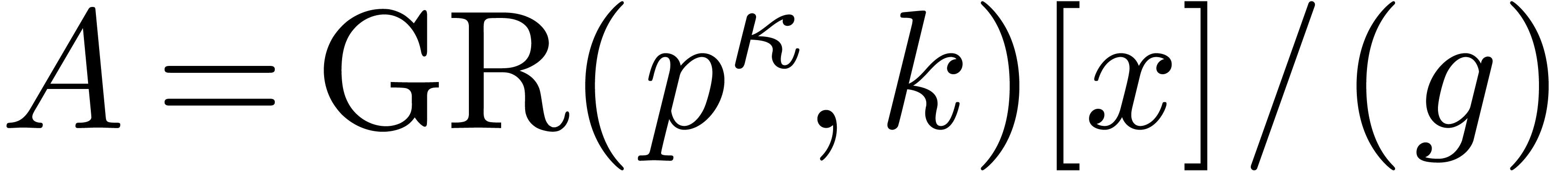 , where
, where 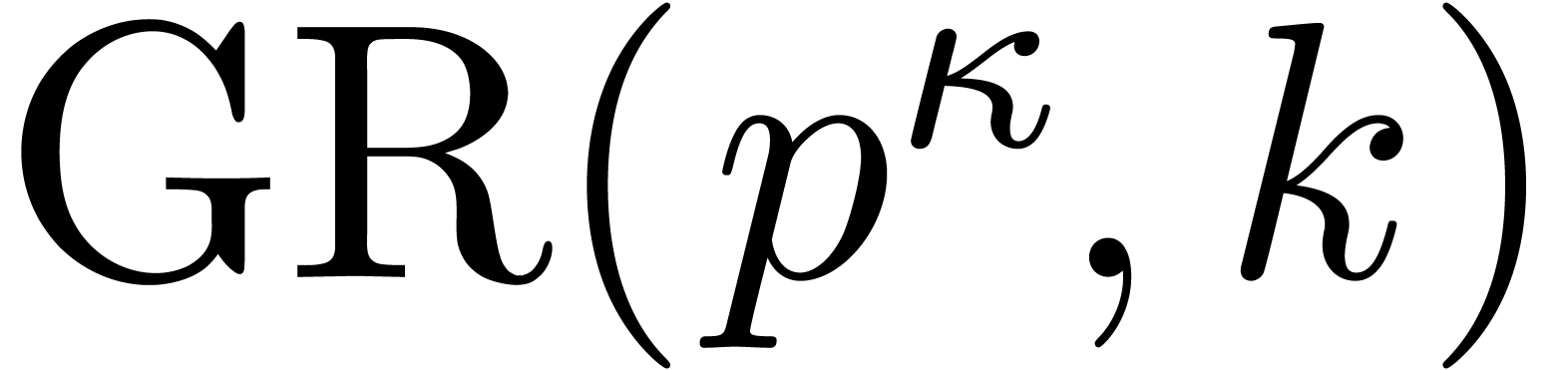 is constructed from
is constructed from 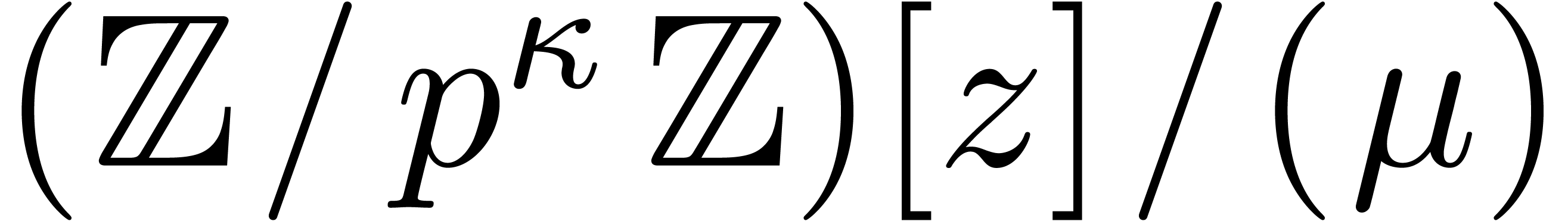 , and
, and
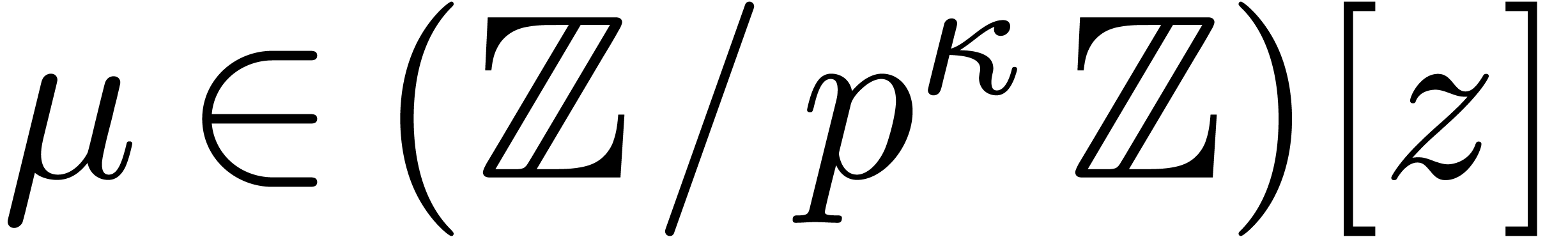 is the monic defining polynomial of degree
is the monic defining polynomial of degree 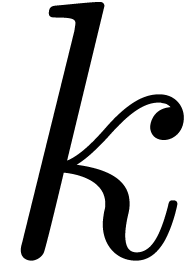 of
of  over
over 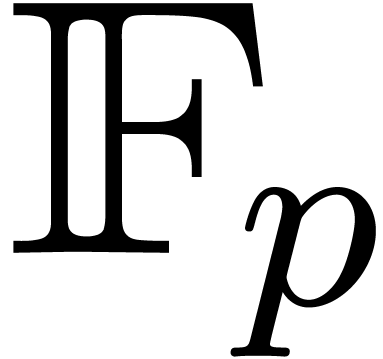 .
.
Let  be such that
be such that  .
Proposition 3 allows us to compute the traces of the
successive powers of
.
Proposition 3 allows us to compute the traces of the
successive powers of  seen in
seen in  in time
in time 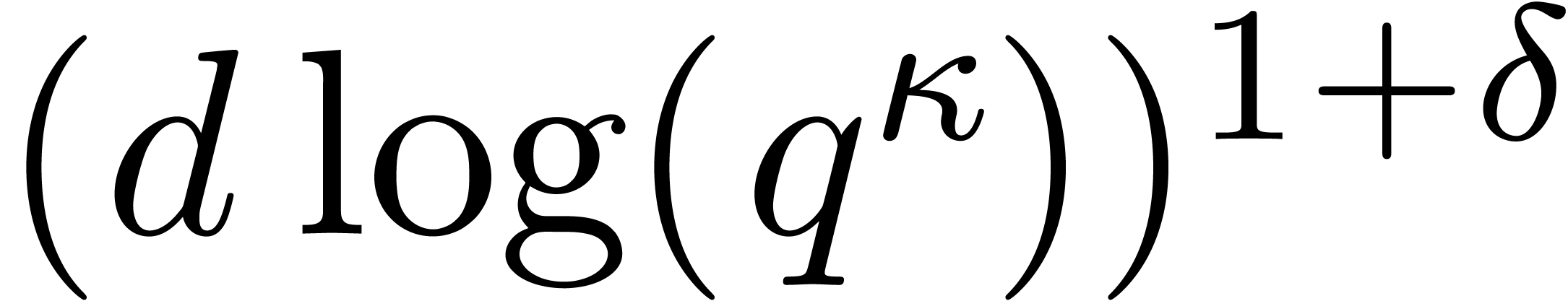 . Then Proposition 6 allows to deduce
. Then Proposition 6 allows to deduce 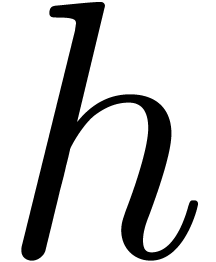 modulo
modulo 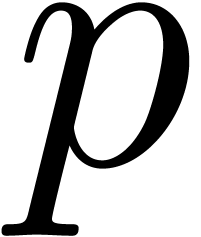 in softly linear time.
in softly linear time.
Remark 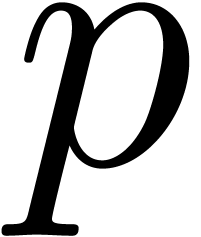 is larger than the multiplicities
of the roots of
is larger than the multiplicities
of the roots of 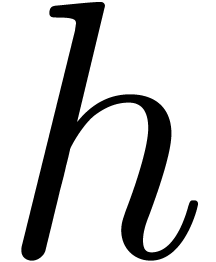 , then Pan's
algorithm [35] does not involve
, then Pan's
algorithm [35] does not involve 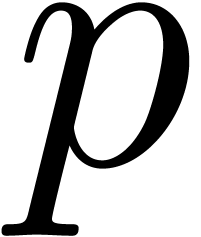 -adic arithmetic, but may require higher order
traces.
-adic arithmetic, but may require higher order
traces.
 be a monic polynomial in
be a monic polynomial in 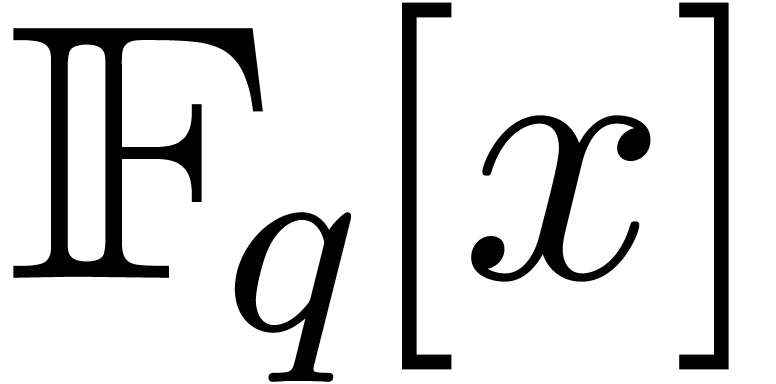 of degree
of degree 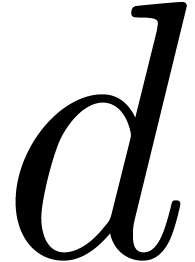 .
For every constant
.
For every constant  such that
such that  , the generalized Graeffe transform
, the generalized Graeffe transform 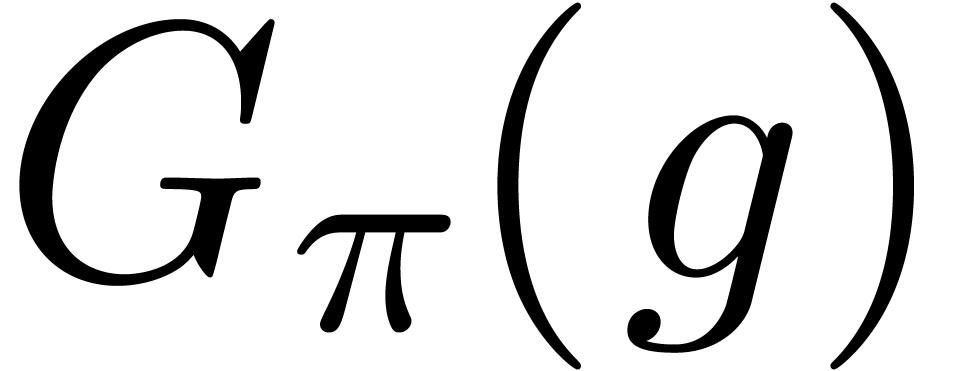 can be computed in time
can be computed in time 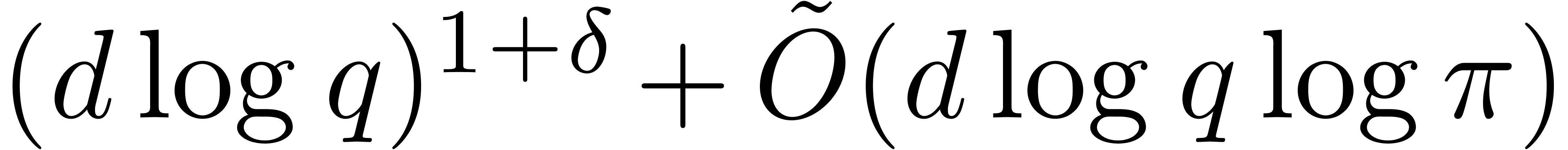 .
.
Proof. We apply the latter theorem to 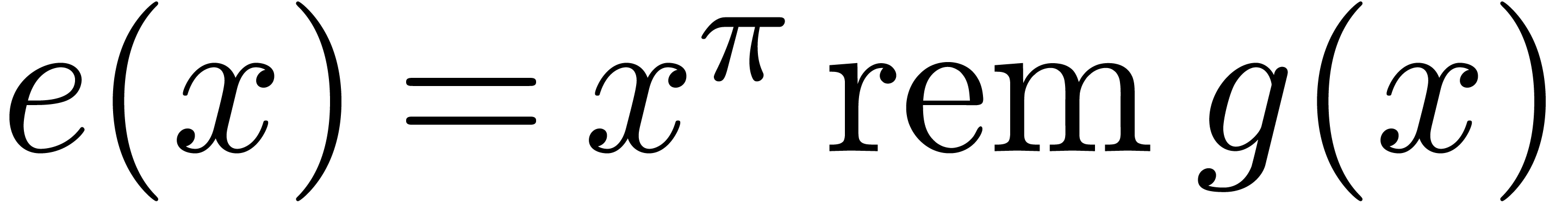 , that can be computed in time
, that can be computed in time
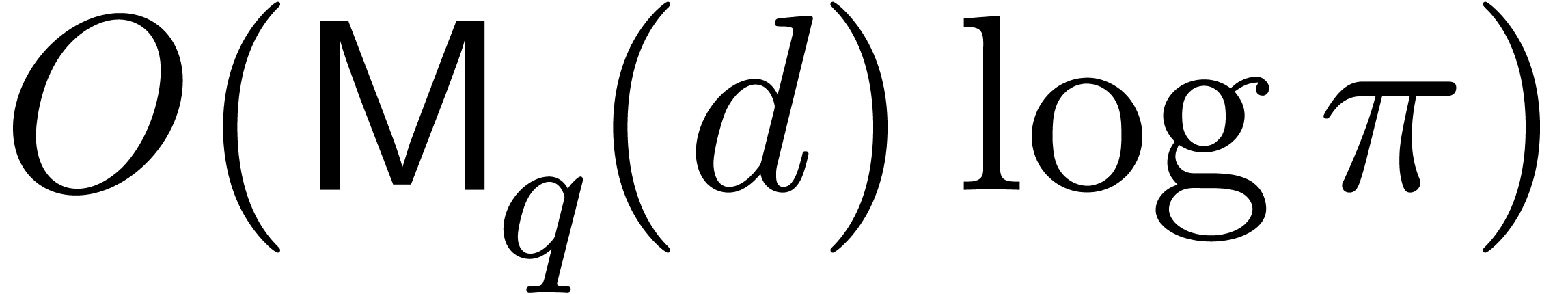 .
.
Whenever a Graeffe transform preserves the number of distinct simple roots, the so called tangent Graeffe transform can be used to directly recover the original simple roots from the simple roots of the transformed polynomial. Our randomized root finding algorithms from [20] heavily rely on this fact. Unfortunately, we have not found a way to exploit tangent Graeffe transforms in the deterministic setting. For completeness, we will nevertheless show that the results of this section extend to the tangent case.
Introducing a formal parameter  with
with 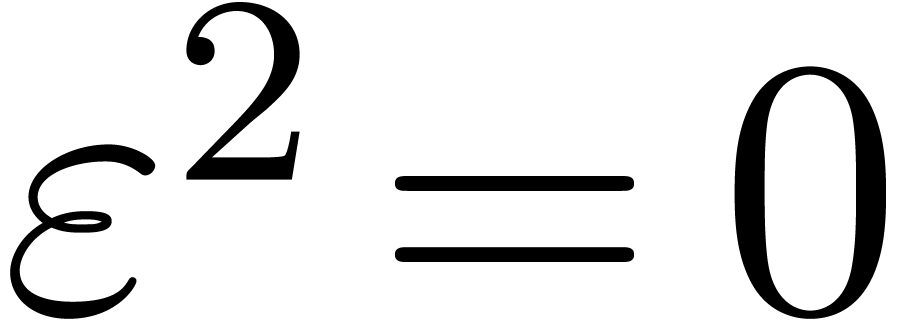 , we define the generalized tangent Graeffe
transform of
, we define the generalized tangent Graeffe
transform of  of order
of order  as being
as being 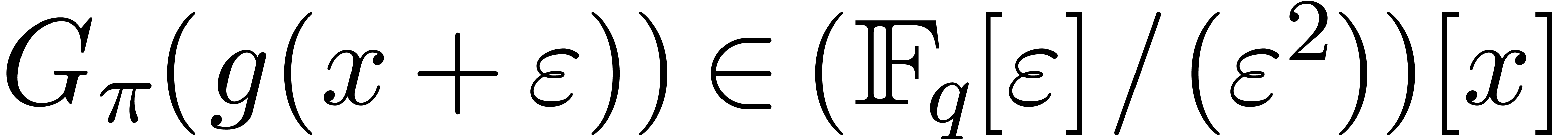 . For any ring
. For any ring 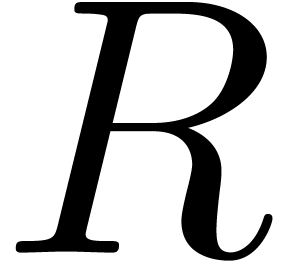 , computations with “tangent
numbers” in
, computations with “tangent
numbers” in  can be done with constant
overhead with respect to computations in
can be done with constant
overhead with respect to computations in 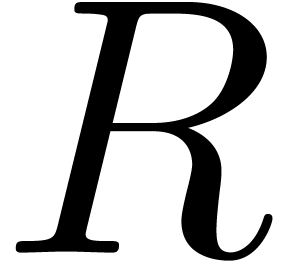 (in the
FFT model, the overhead is asymptotically limited to a factor of two).
(in the
FFT model, the overhead is asymptotically limited to a factor of two).
In the context of the Graeffe method, the tangent transform is classical
(for instance, see [30, 34] for history,
references, and use in numerical algorithms). The generalized tangent
Graeffe transform can also be seen as the tangent characteristic
polynomial of 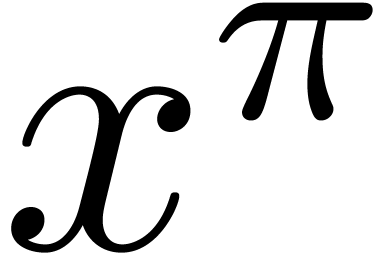 modulo
modulo 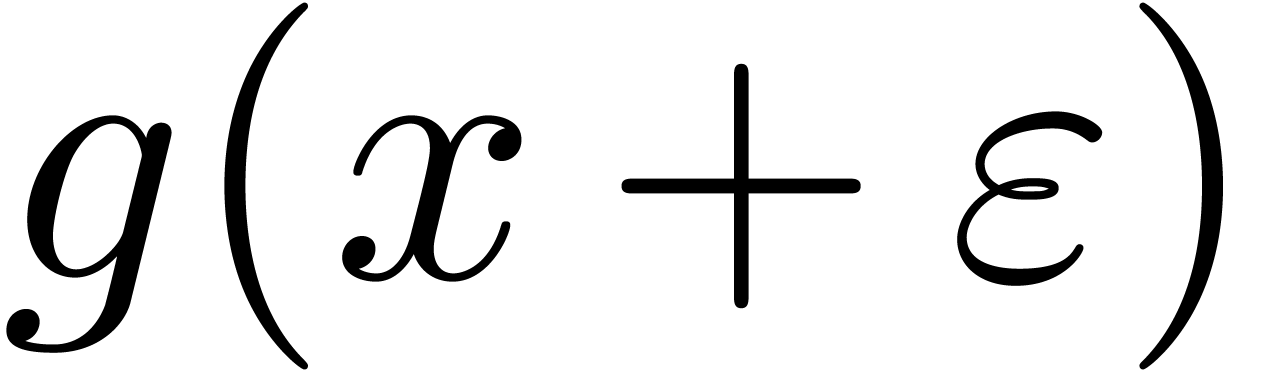 , and this construction is attributed to Kronecker
in algebraic geometry [19, 28].
, and this construction is attributed to Kronecker
in algebraic geometry [19, 28].
Proposition 1 from Section 2.1 admits a
straightforward generalization to tangent Graeffe transforms with a
constant overhead. In order to generalize Proposition 3, we
introduce 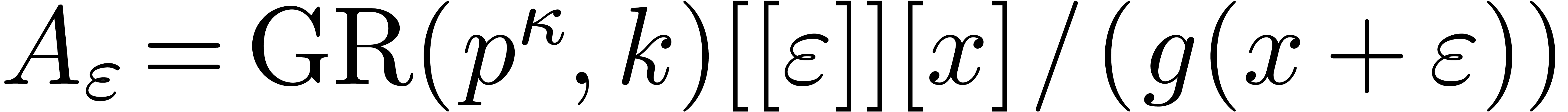 , where
, where 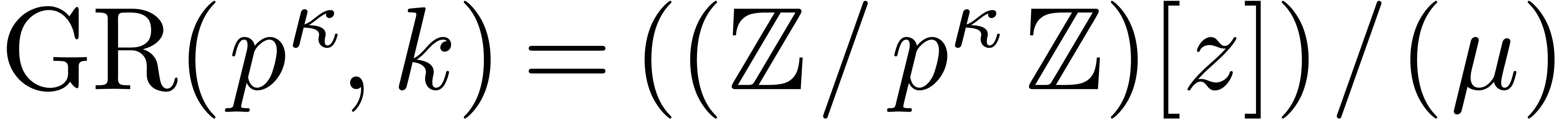 , where
, where 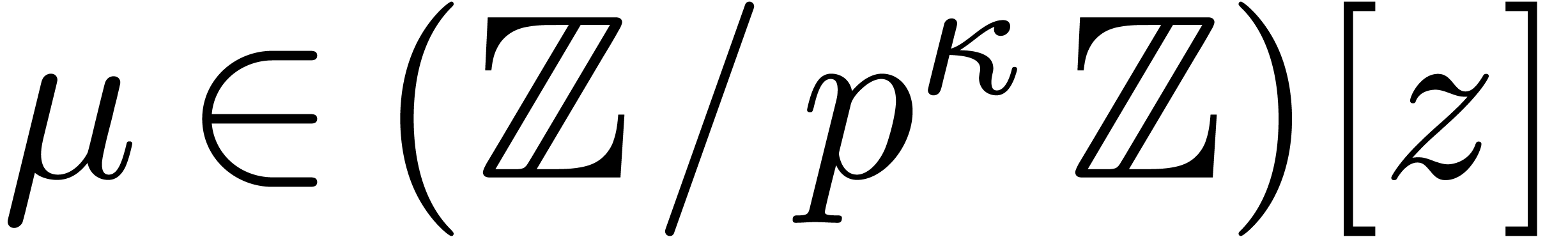 is
monic of degree
is
monic of degree 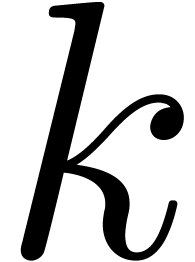 and irreducible modulo
and irreducible modulo 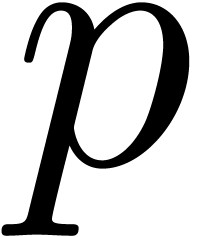 . Let
. Let 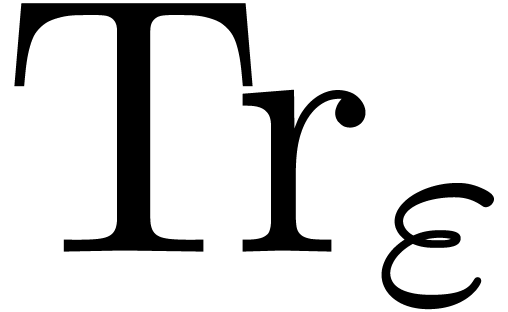 represent the trace function in
represent the trace function in  .
.
 be a fixed constant.
If
be a fixed constant.
If  , then the traces
, then the traces 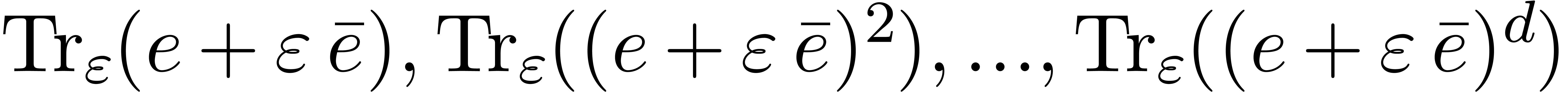 modulo
modulo  ,
for a given
,
for a given 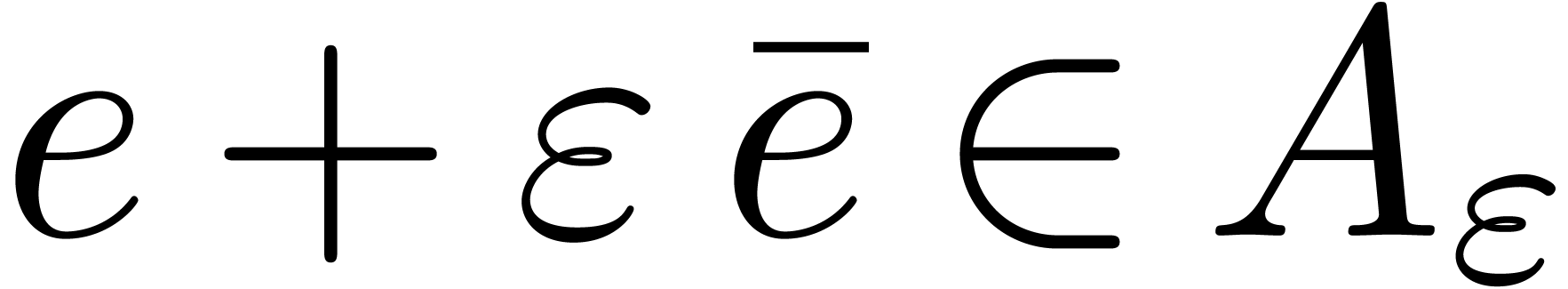 , can be
computed in time
, can be
computed in time  .
.
Proof. The value 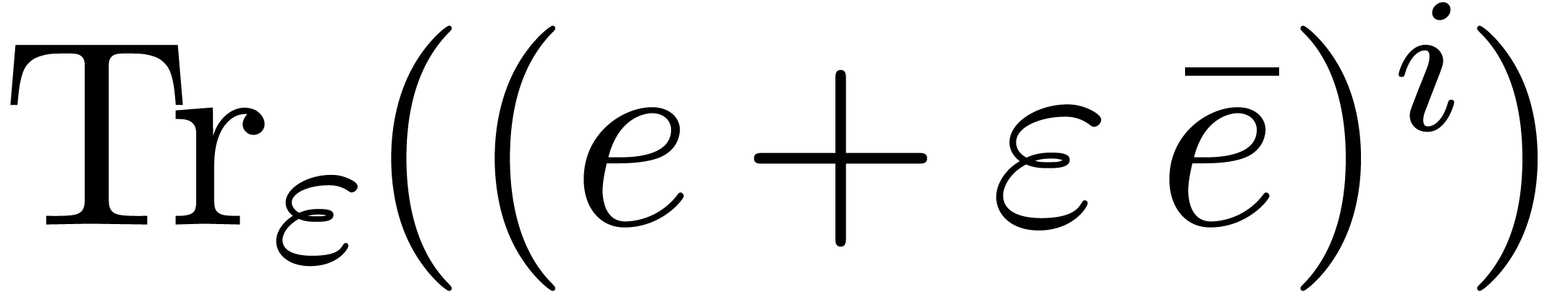 equals
the trace of
equals
the trace of 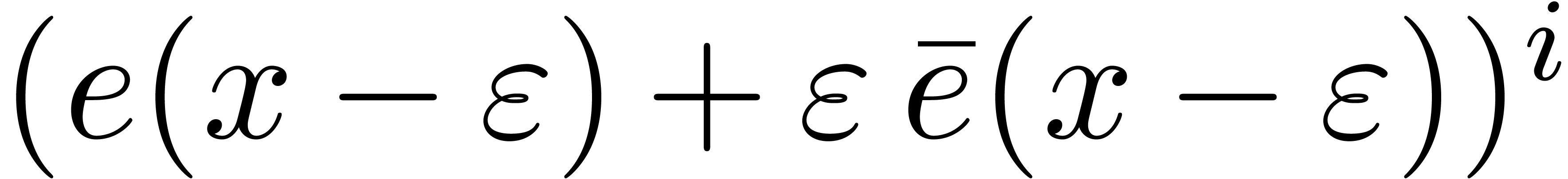 computed in
computed in 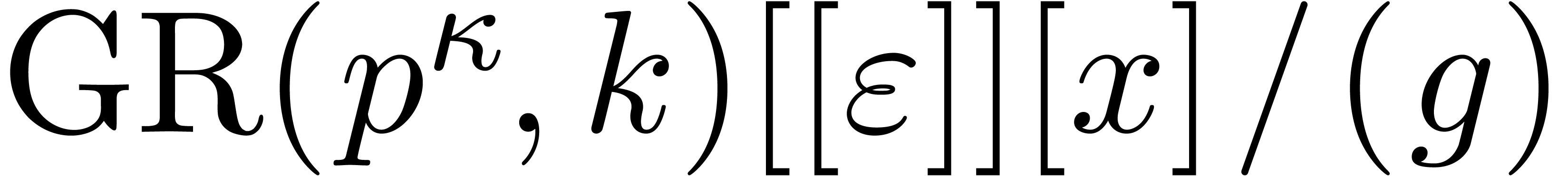 . Therefore we obtain:
. Therefore we obtain:
We therefore use Theorem 7.7 of [27, p. 1792] twice over
 : once with
: once with  , and once for
, and once for  ,
where
,
where  is the product by
is the product by 

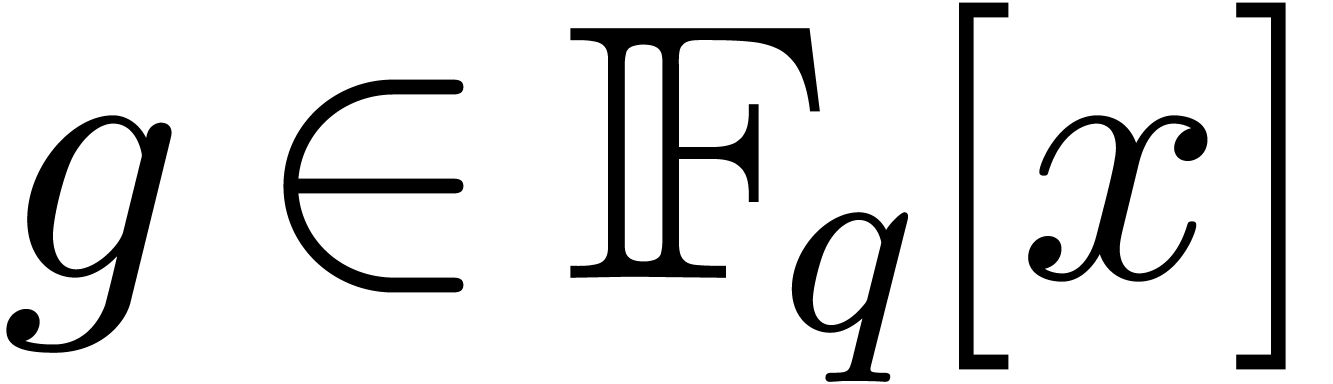 be a monic polynomial of degree
be a monic polynomial of degree
 , and let
, and let 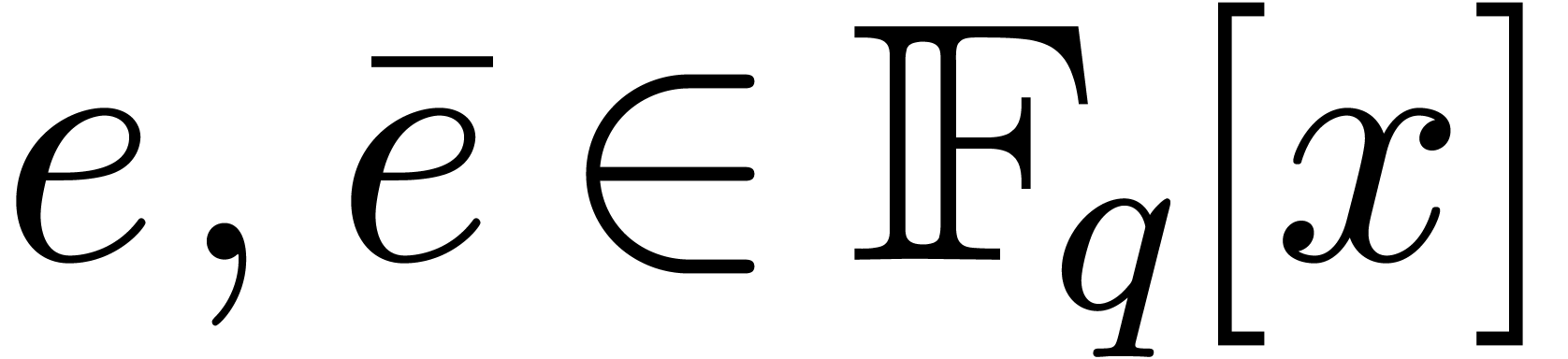 be of degrees
be of degrees 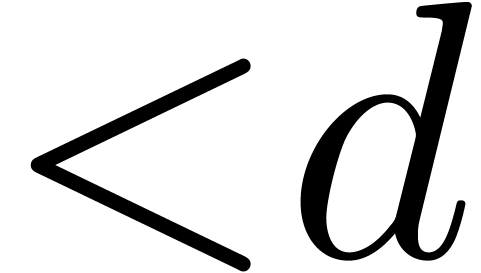 . For every
constant
. For every
constant  such that
such that  , the characteristic polynomial
, the characteristic polynomial  of the multiplication by
of the multiplication by  in
in 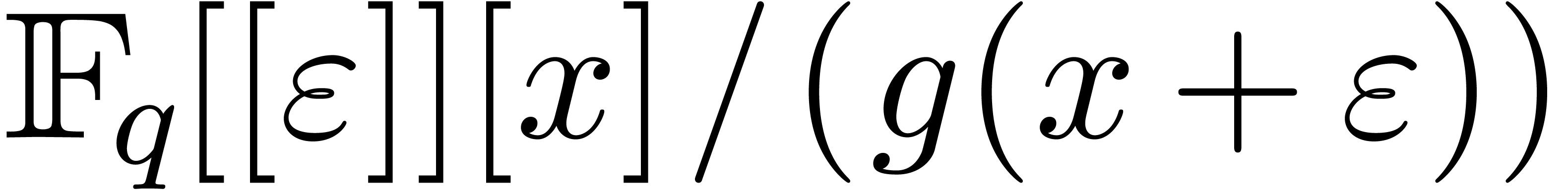 can be computed in time
can be computed in time 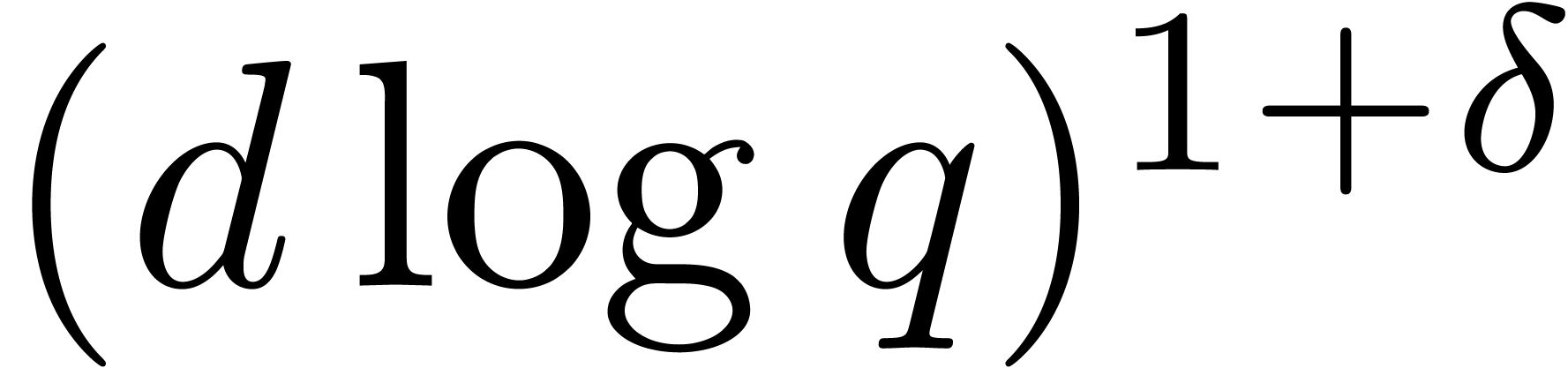 .
.
Proof. We embed 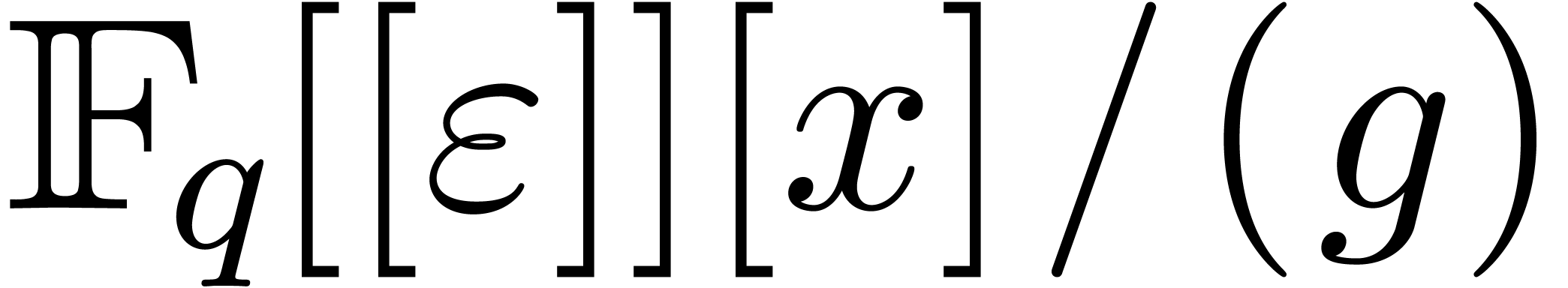 into
into
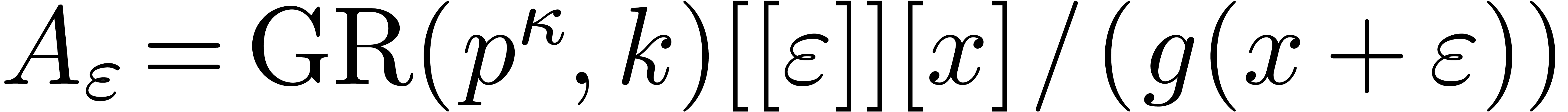 , where
, where 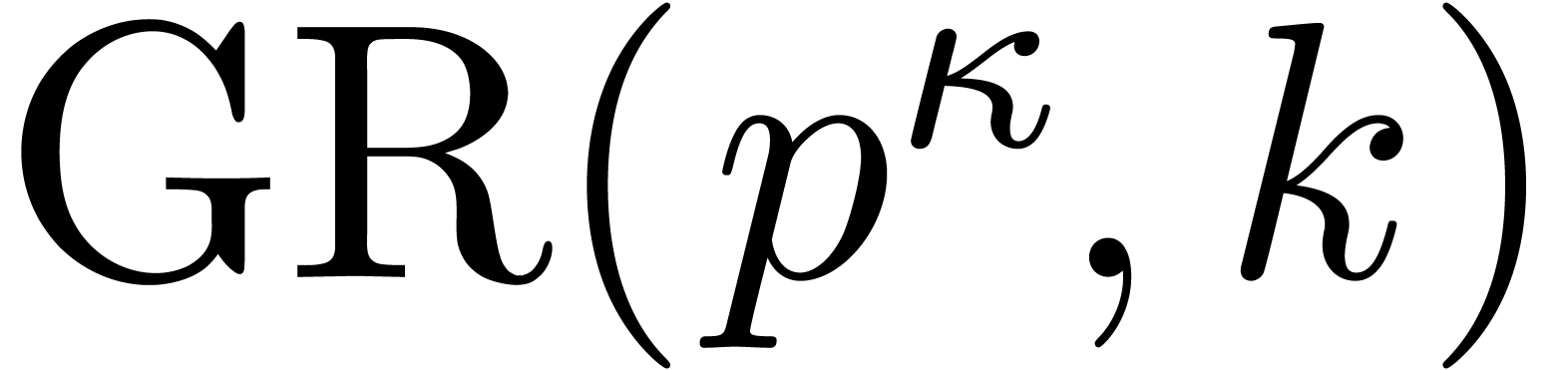 is constructed from
is constructed from 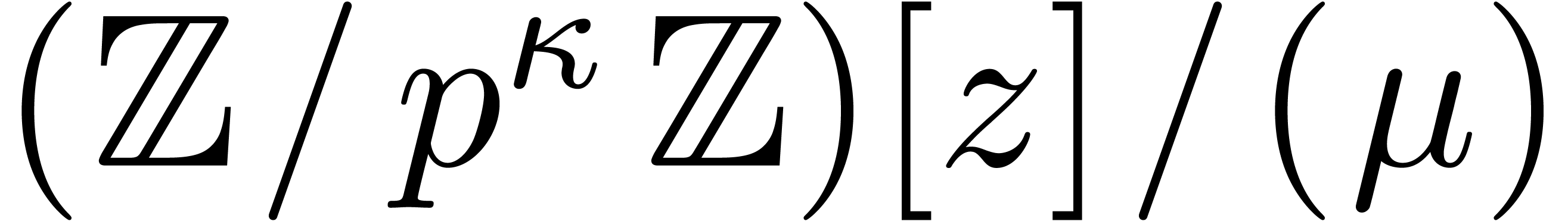 , and
, and
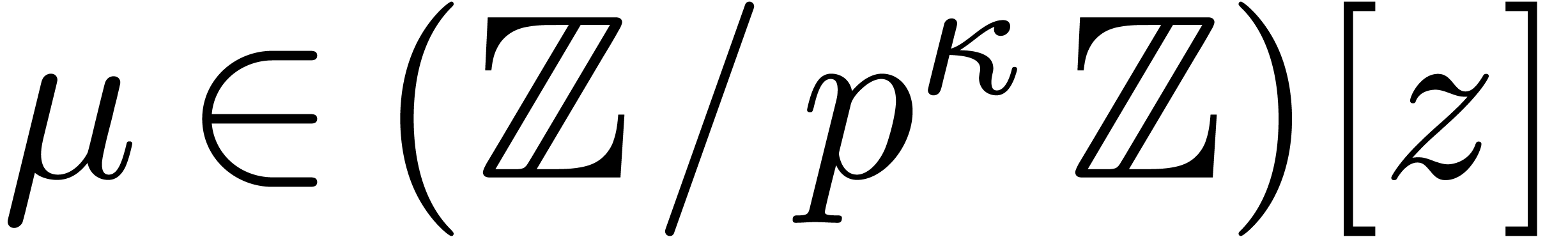 is the monic defining polynomial of degree
is the monic defining polynomial of degree 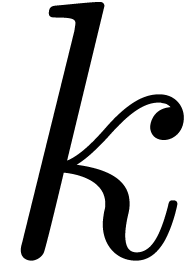 of
of  over
over  .
.
Let  be such that
be such that  .
Proposition 10 allows us to compute the traces of the
successive powers of
.
Proposition 10 allows us to compute the traces of the
successive powers of  seen in
seen in  in time
in time  . Then Proposition 6 allows us to deduce
. Then Proposition 6 allows us to deduce  modulo
modulo 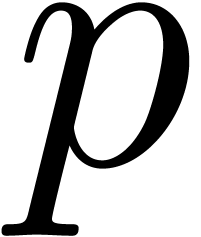 in softly linear time, mutatis mutandis.
in softly linear time, mutatis mutandis.
 be a monic polynomial in
be a monic polynomial in 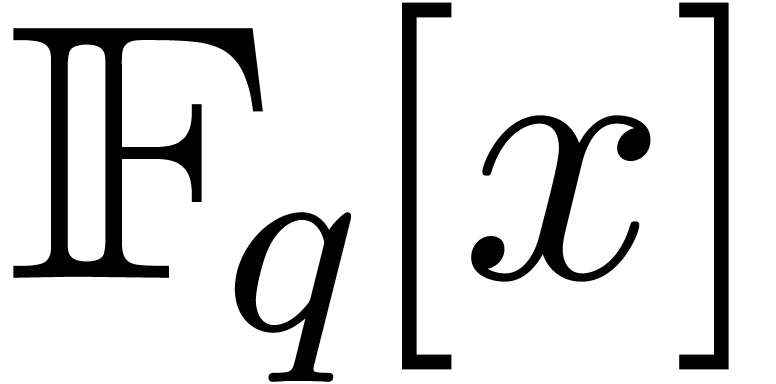 of degree
of degree 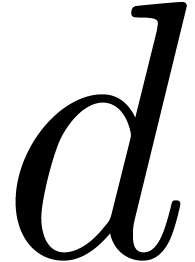 .
For every constant
.
For every constant  such that
such that  , the generalized tangent Graeffe transform
, the generalized tangent Graeffe transform
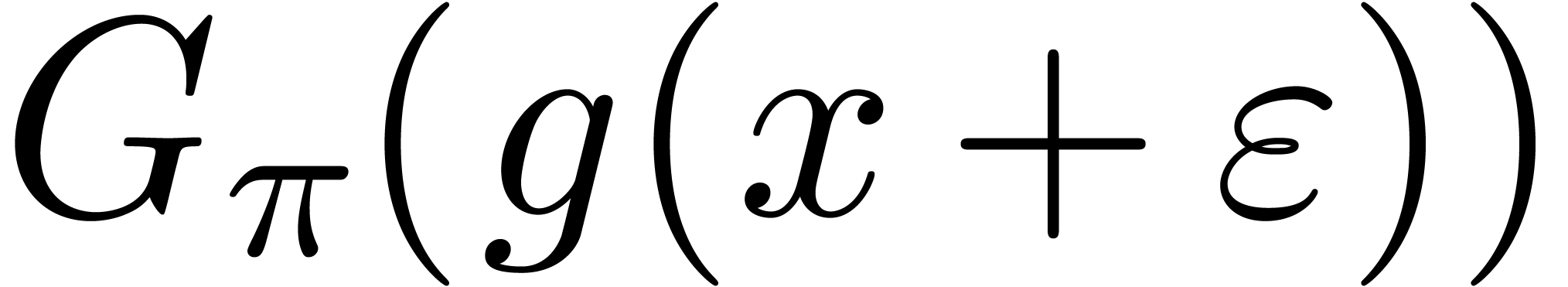 can be computed in time
can be computed in time 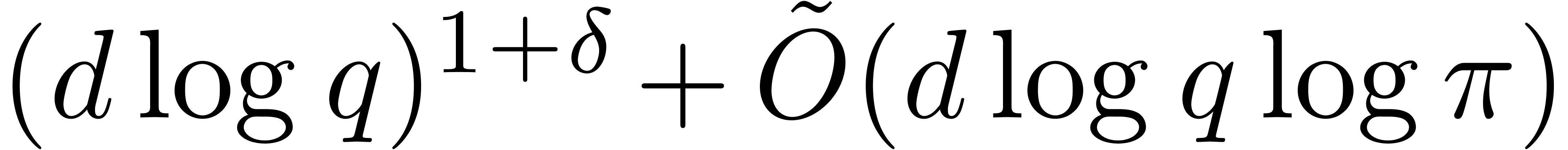 .
.
Proof. We apply the latter theorem to 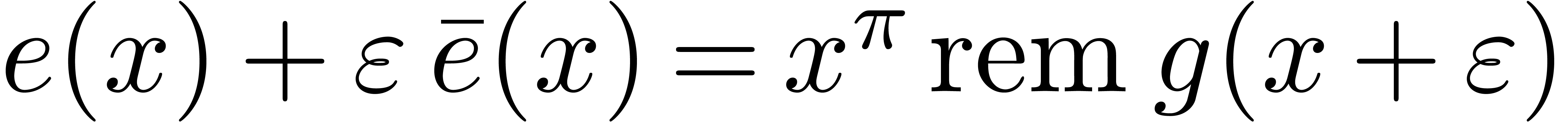 , that can be computed in time
, that can be computed in time
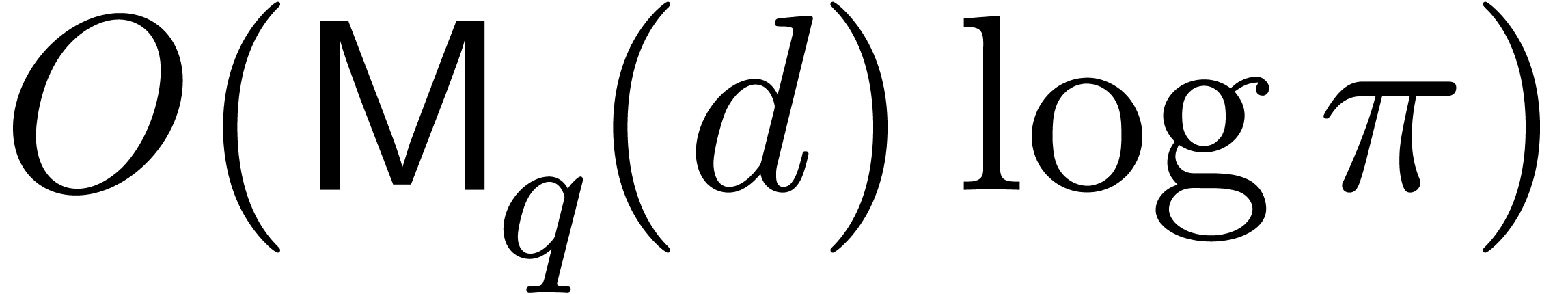 .
. 
Our new root finding algorithm is technically reminiscent of numerical
solvers: we make use of the Graeffe transform instead of the modular
exponentiation, and replace gcds by multi-point evaluations. We begin
this section with a first simple version of the algorithm, and then
introduce new ingredients in order to improve it. Throughout this
section, the quantity 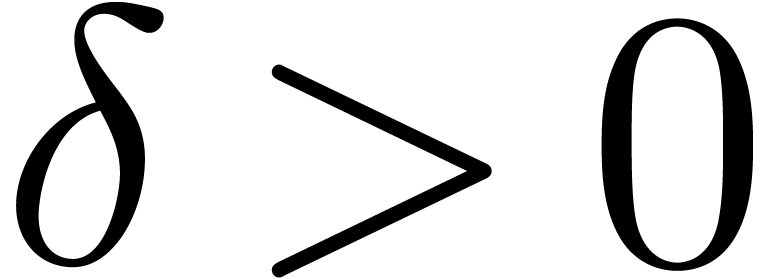 represents a constant that
can be fixed arbitrarily small.
represents a constant that
can be fixed arbitrarily small.
We assume given integers 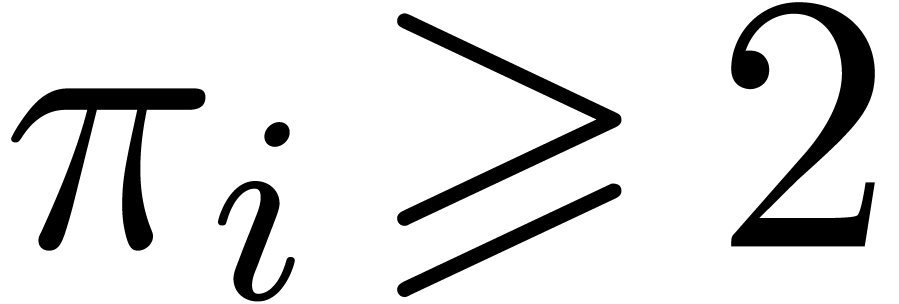 such that
such that 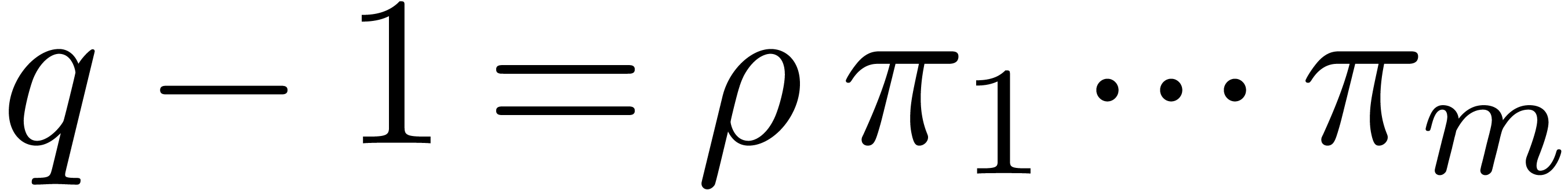 . We let
. We let 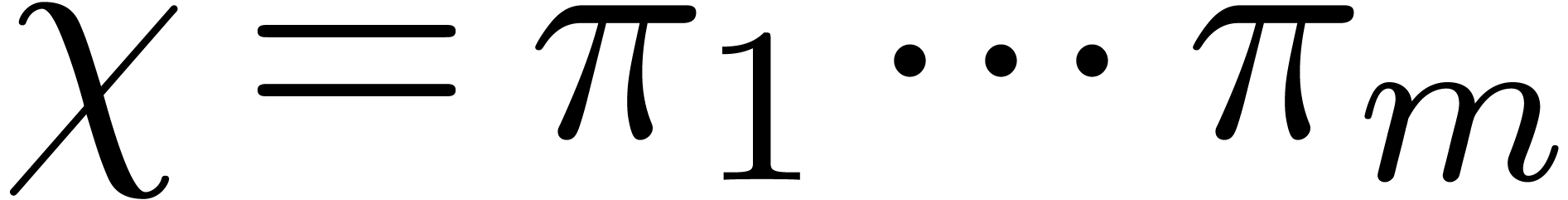 ,
and
,
and 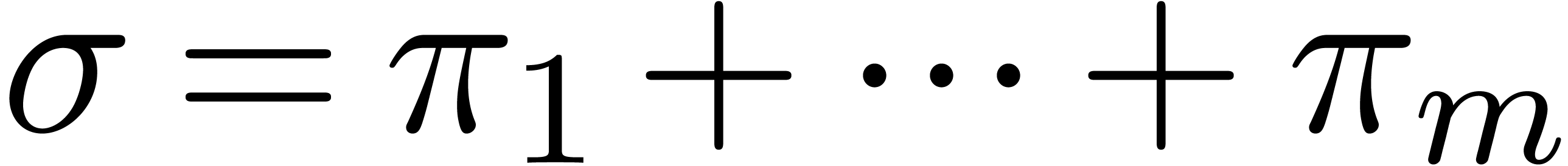 as previously. The core algorithm of this
section computes a sequence of Graeffe transforms, and then deduces
inductively their roots starting from the last transform and finishing
to the input polynomial.
as previously. The core algorithm of this
section computes a sequence of Graeffe transforms, and then deduces
inductively their roots starting from the last transform and finishing
to the input polynomial.
Algorithm
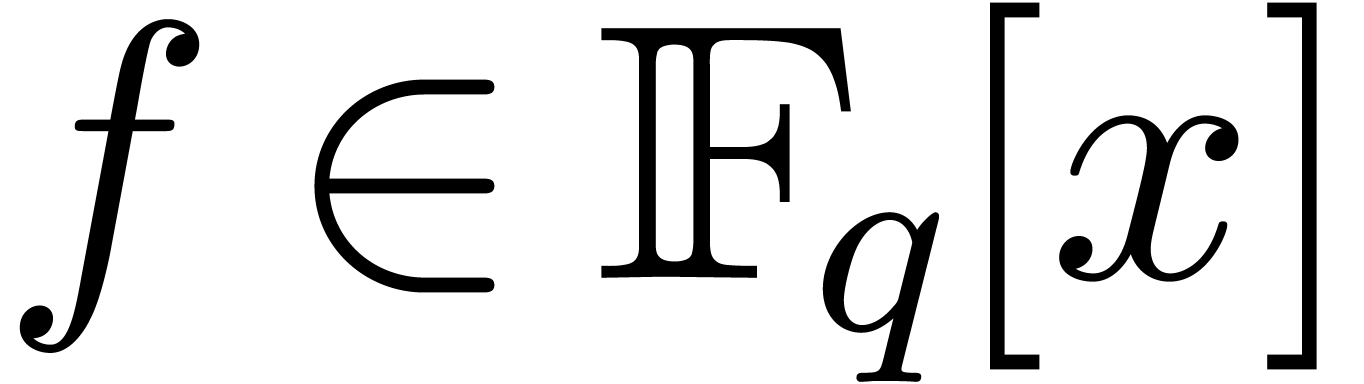 of degree
of degree
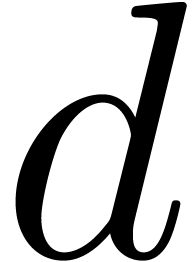 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
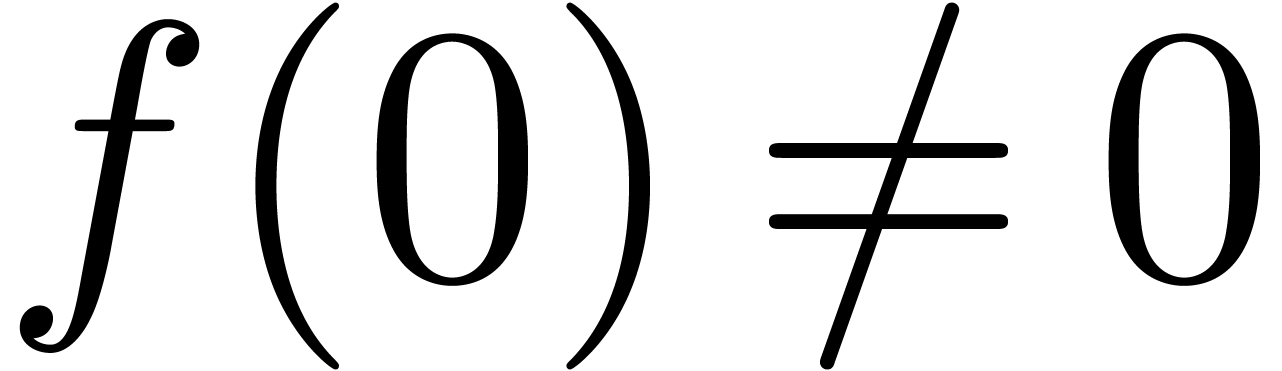 ;
a primitive root
;
a primitive root
 of unity of order
of unity of order
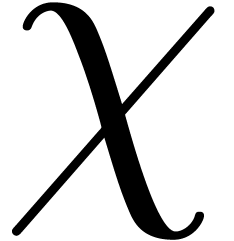 .
.
 in
in 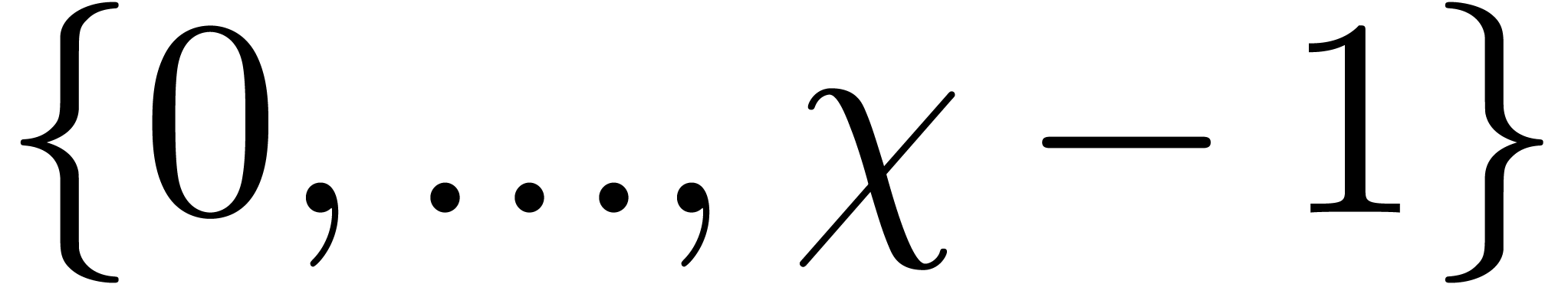 ,
such that
,
such that  divides
divides 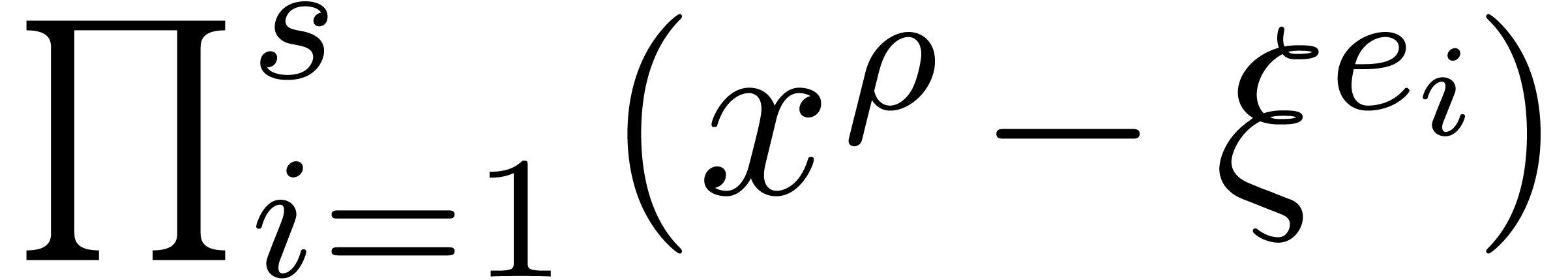 .
.
Compute the Graeffe transform 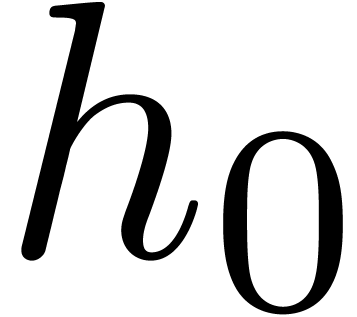 of order
of order 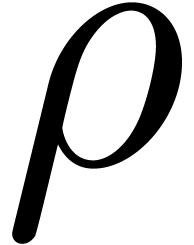 of
of 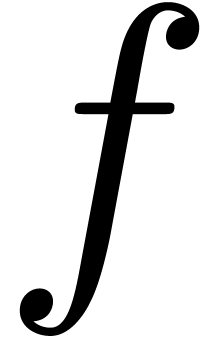 ,
and recursively compute
,
and recursively compute 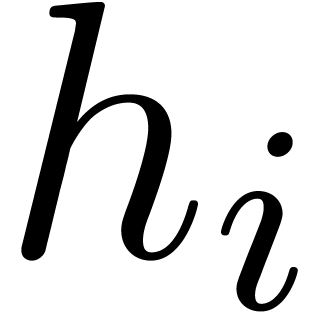 as the Graeffe
transform of order
as the Graeffe
transform of order 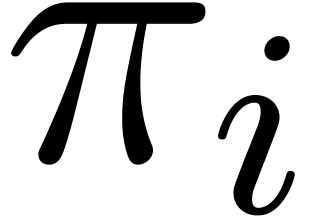 of
of 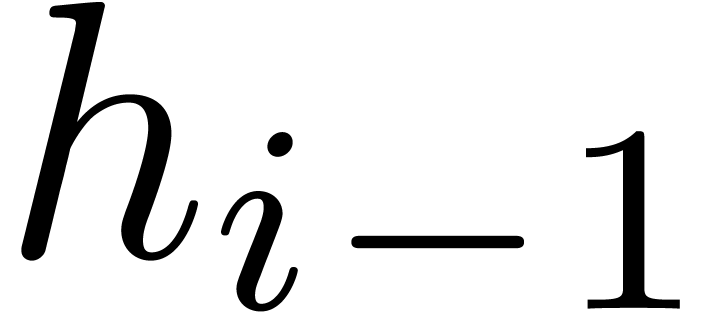 , for all
, for all 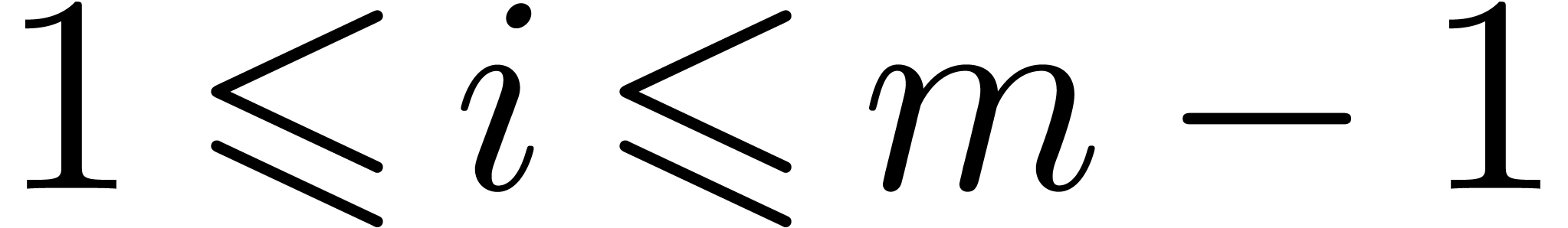 .
.
Initialize  with the list
with the list  .
.
For 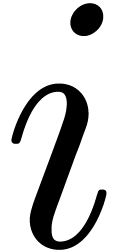 from
from 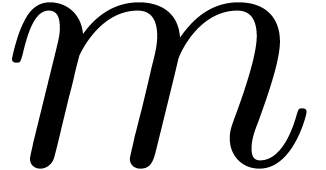 down to
down to
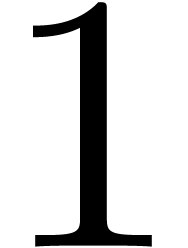 do
do
Replace  by the concatenation of
by the concatenation of 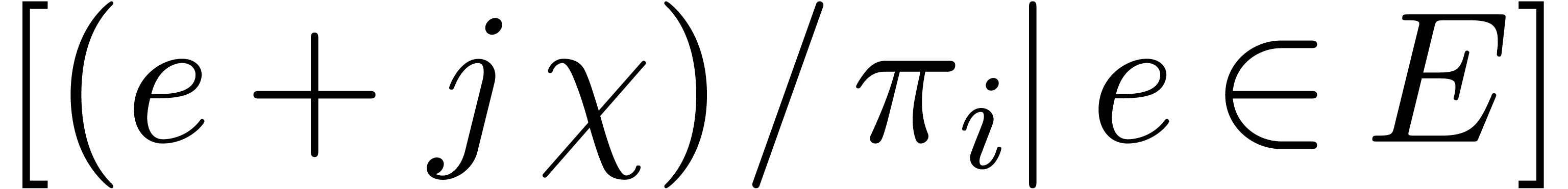 for
for  from
from 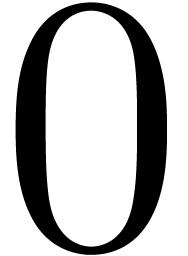 to
to 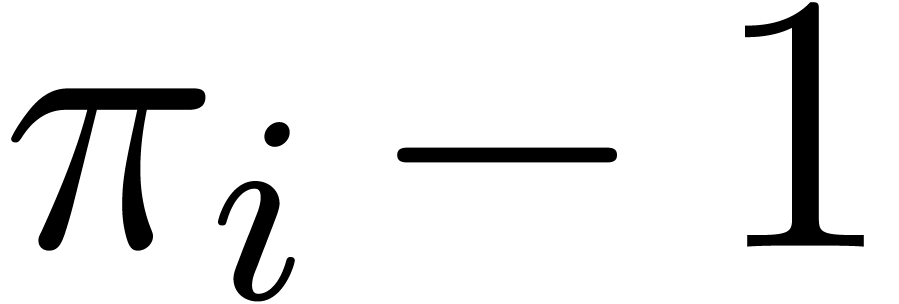 .
.
If  has cardinality more than
has cardinality more than 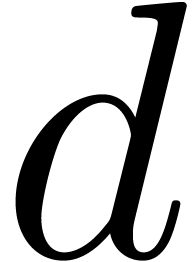 then remove the elements
then remove the elements  from
from  such that
such that 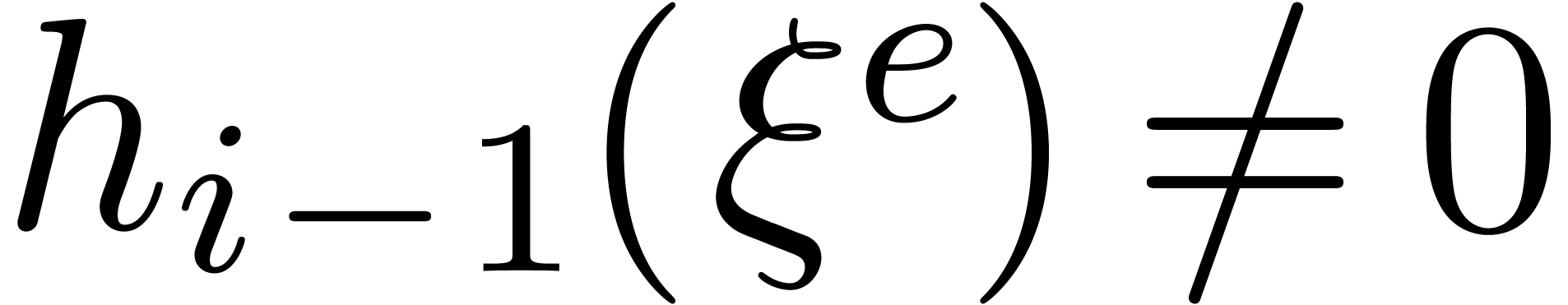 , using a multi-point evaluation to compute
the
, using a multi-point evaluation to compute
the 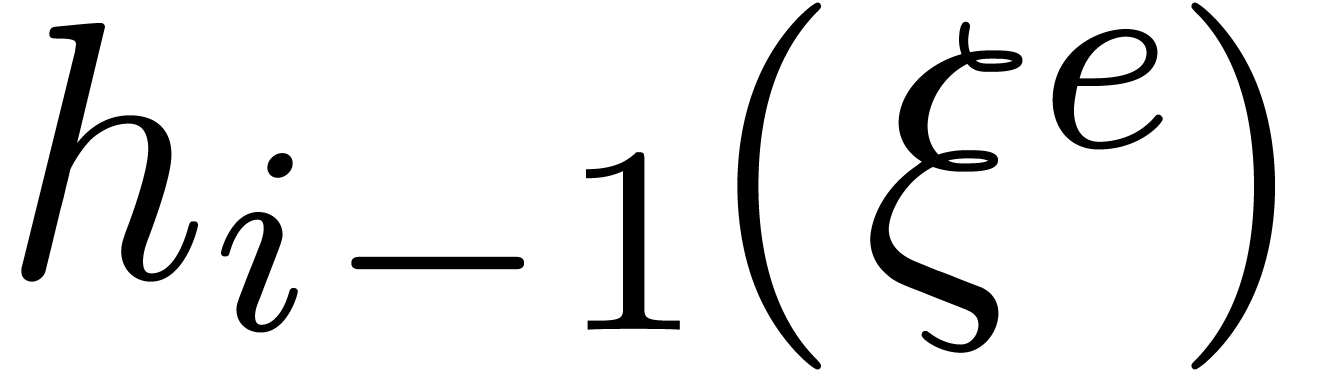 .
.
Return  .
.
 then it costs
then it costs  .
Whenever a primitive root of unity of order
.
Whenever a primitive root of unity of order 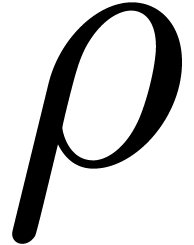 is
given, and
is
given, and  , this bound
further reduces to
, this bound
further reduces to 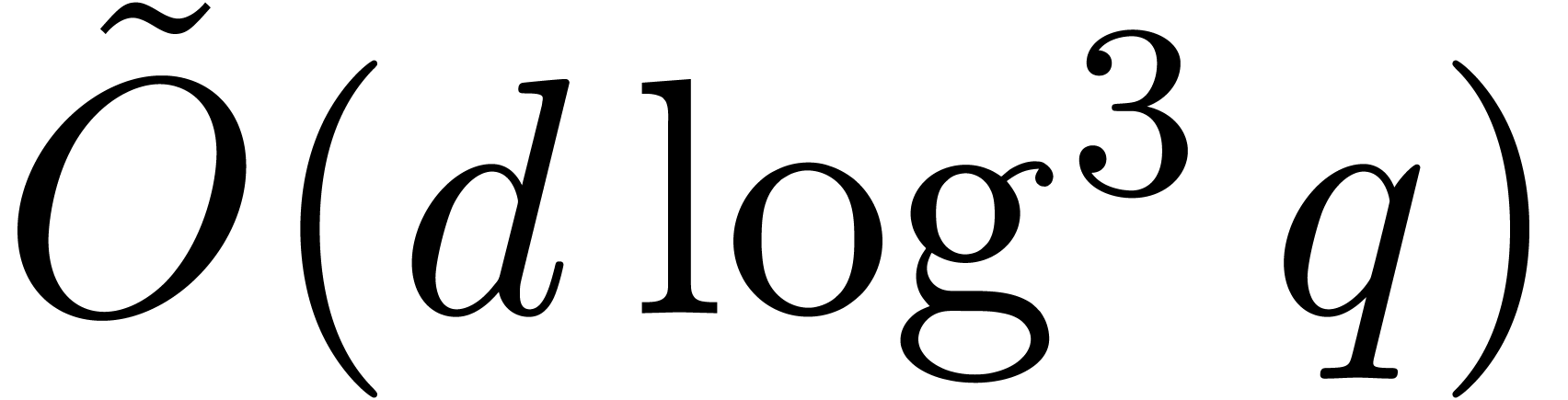 .
.
Proof. We prove the correctness by descending
induction on 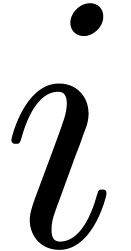 from
from  down
to
down
to 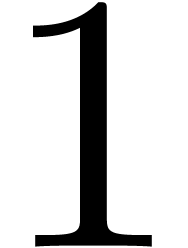 . At the end of iteration
. At the end of iteration
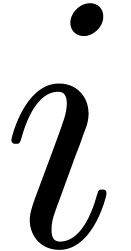 of the loop of step 3, we claim that
of the loop of step 3, we claim that 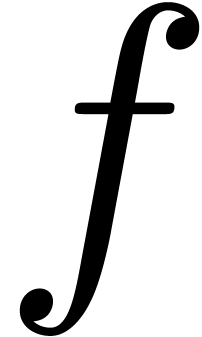 divides
divides 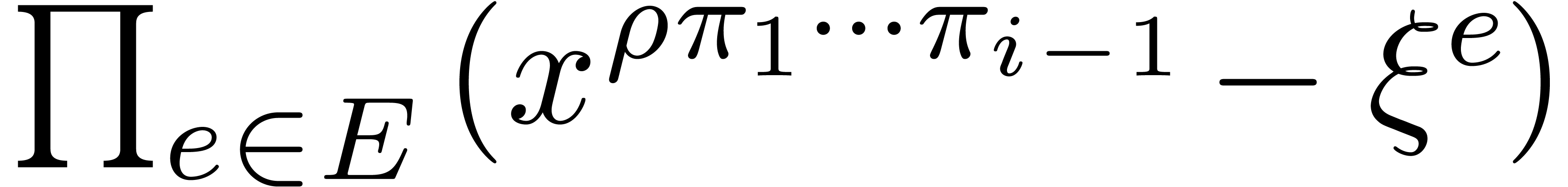 , and
that the integers
, and
that the integers  in
in  are
in
are
in 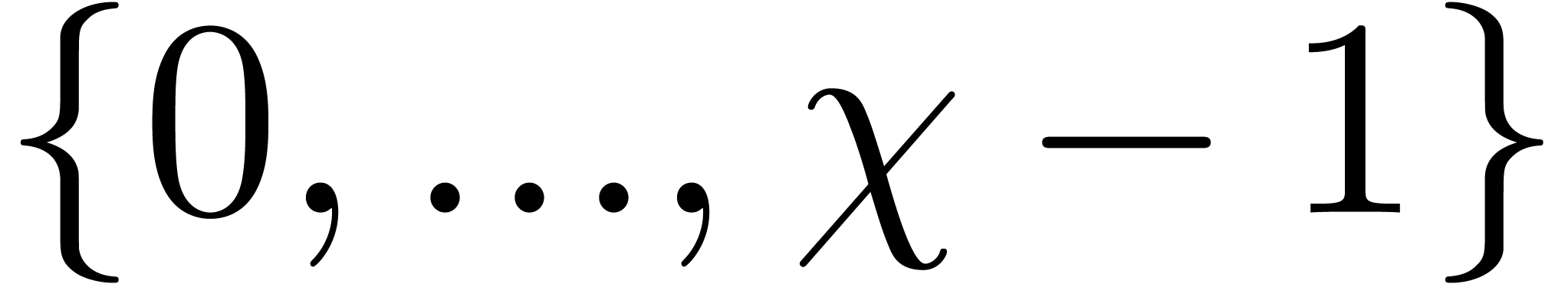 and are divisible by
and are divisible by  . These properties all hold for
. These properties all hold for 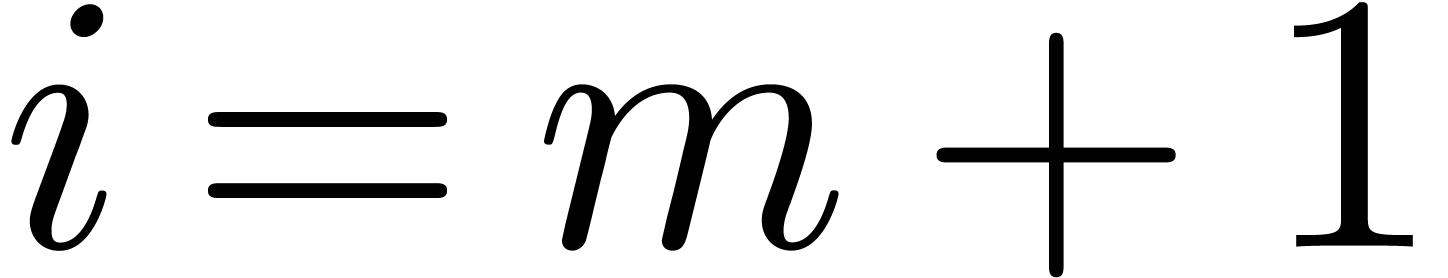 when entering step 3. By induction, we may assume that these properties
hold with
when entering step 3. By induction, we may assume that these properties
hold with 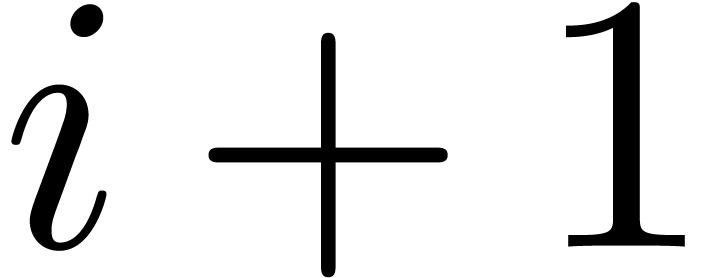 when entering the loop at level
when entering the loop at level 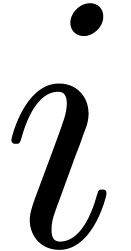 . Let
. Let 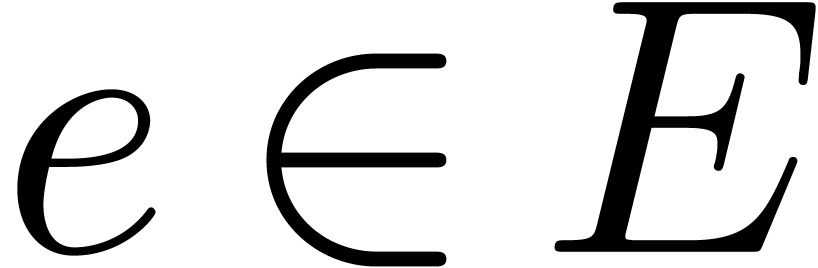 ,
and let
,
and let  be a root of
be a root of  such that
such that  . Since
. Since  is divisible by
is divisible by  ,
there exists
,
there exists  such that
such that 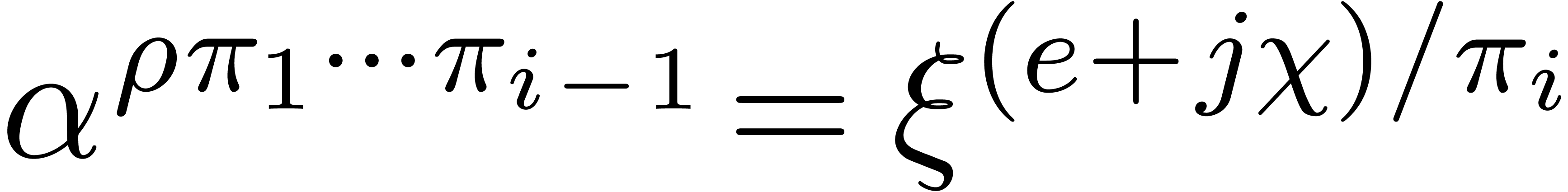 . This proves the correctness.
. This proves the correctness.
From now on we assume that  .
As to the complexity, we can compute the
.
As to the complexity, we can compute the 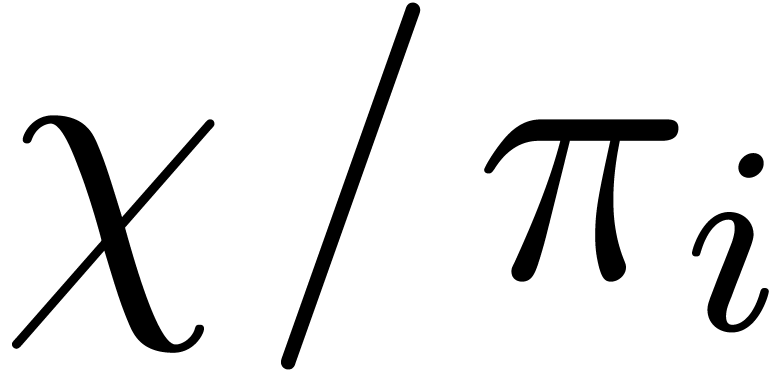 for
for
 in time
in time 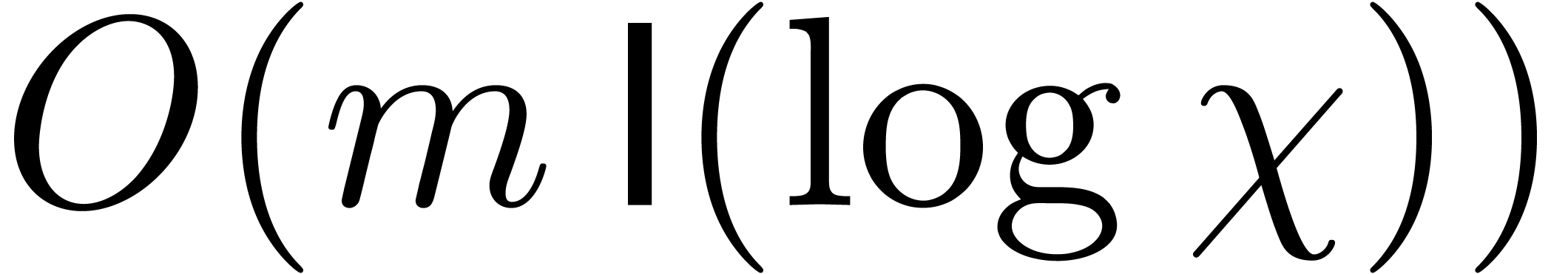 as follows: we
first compute
as follows: we
first compute 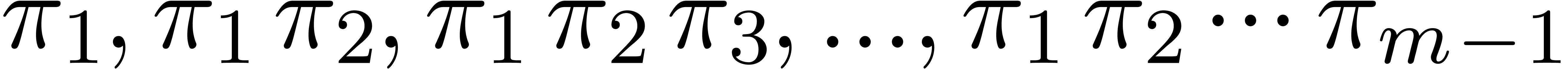 , and
, and 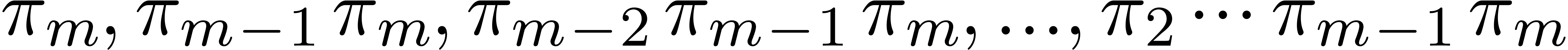 , and then deduce each
, and then deduce each 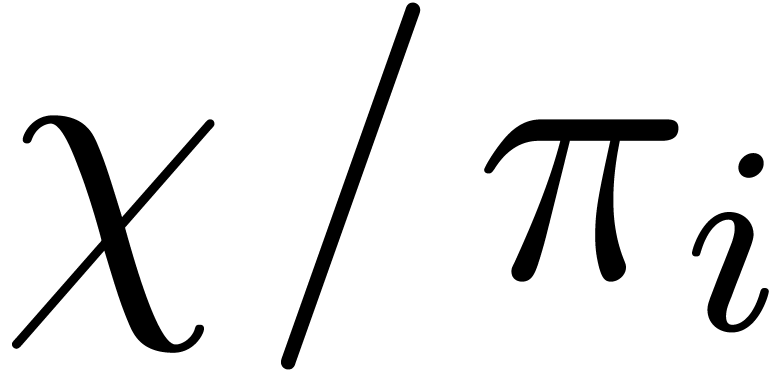 by multiplying
by multiplying  and
and  .
.
Step 1 requires time 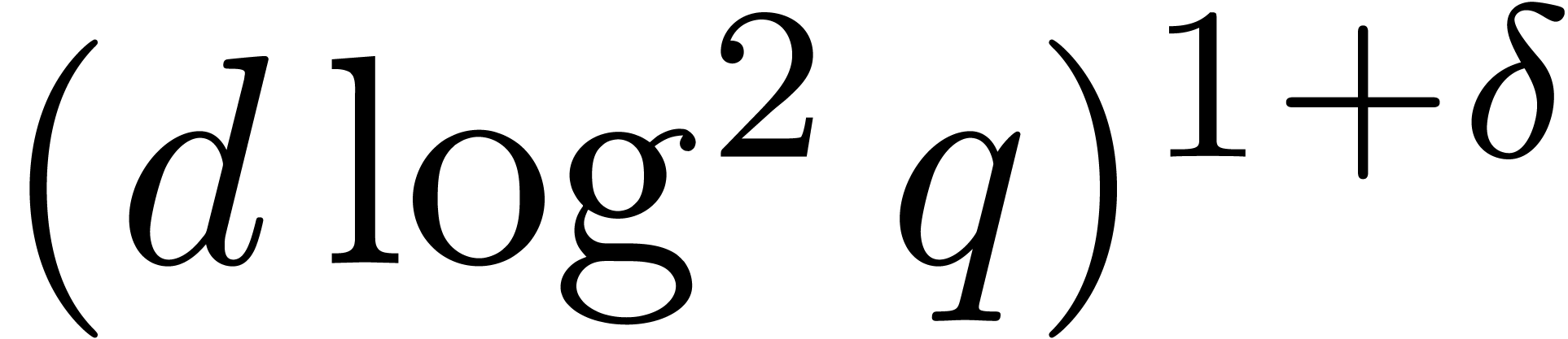 by Corollary 9.
In step 3.a, we compute all the
by Corollary 9.
In step 3.a, we compute all the 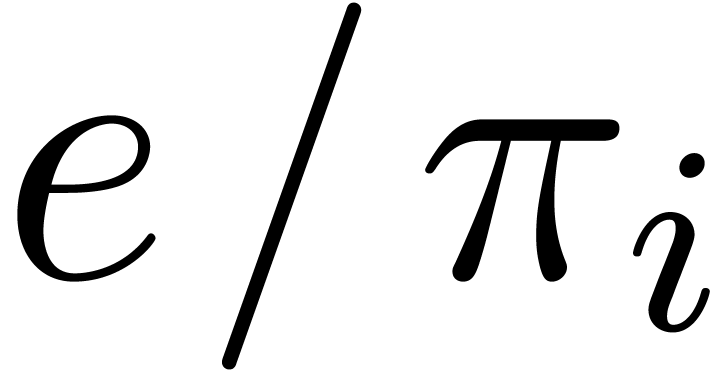 in time
in time 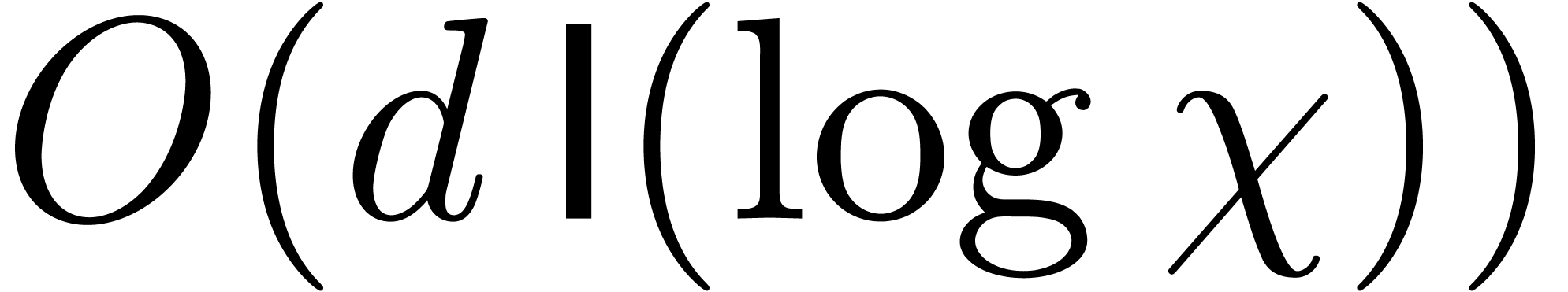 , and then all the
, and then all the 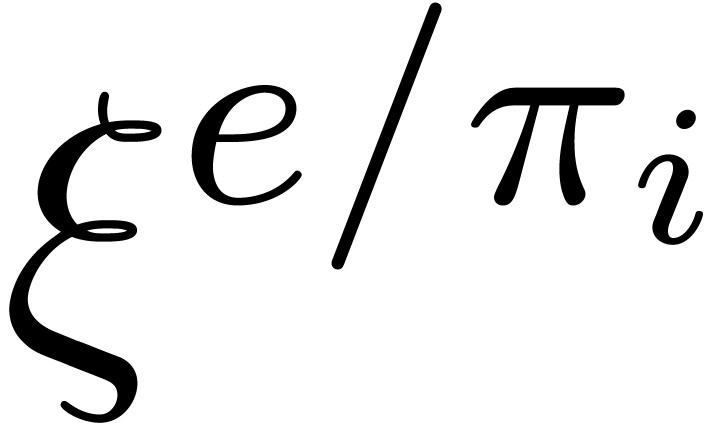 and
and 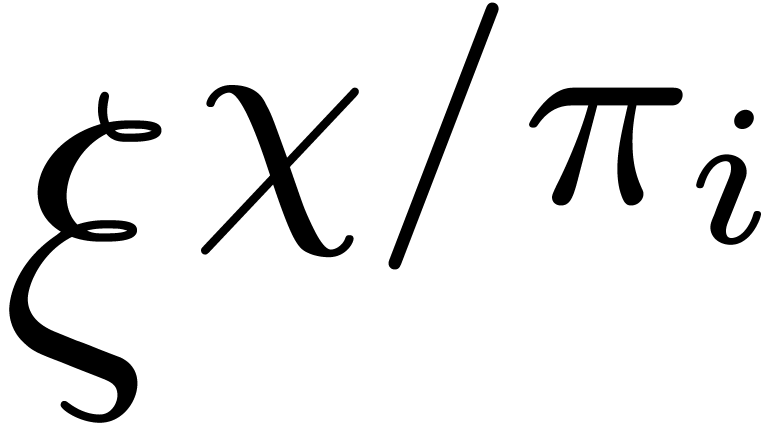 by means of
by means of 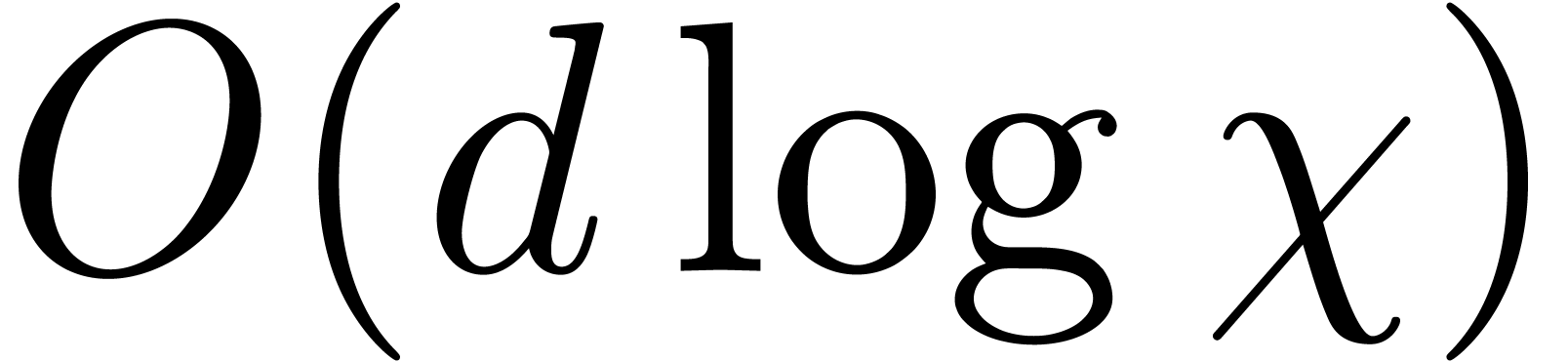 operations in
operations in  . Deducing all
the
. Deducing all
the 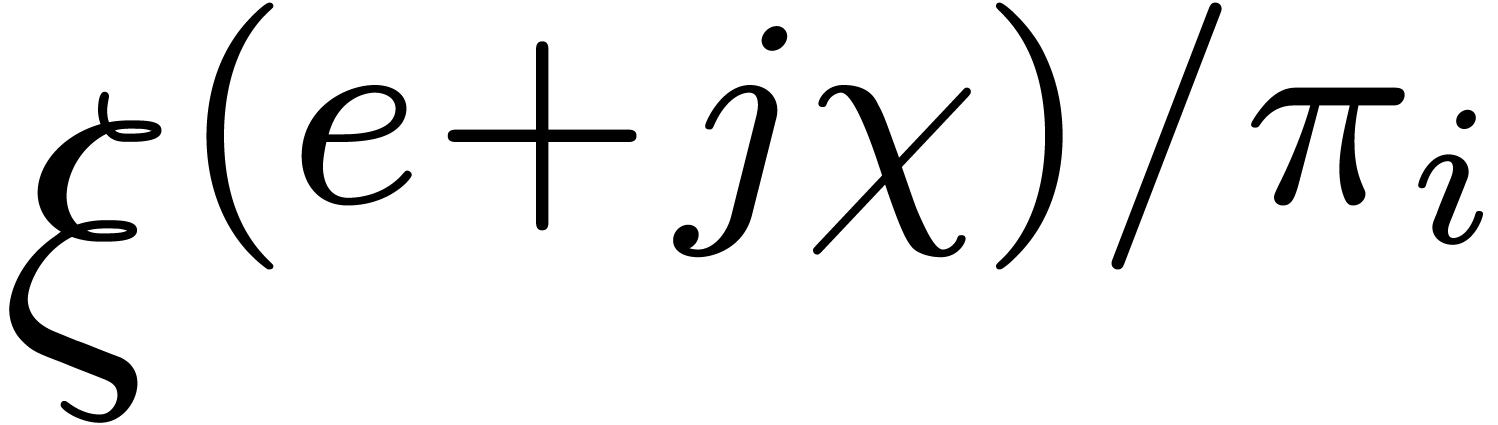 takes
takes  additional
products in
additional
products in  . The multi-point
evaluations can be done in time
. The multi-point
evaluations can be done in time 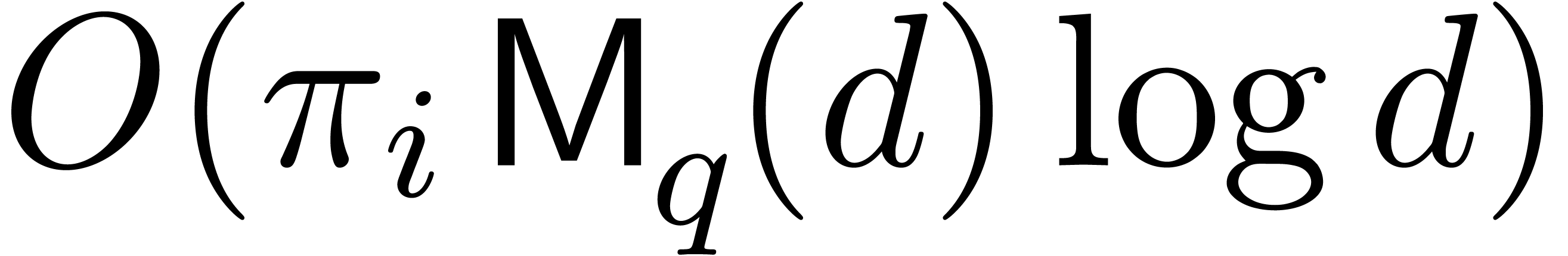 .
.
Finally, when 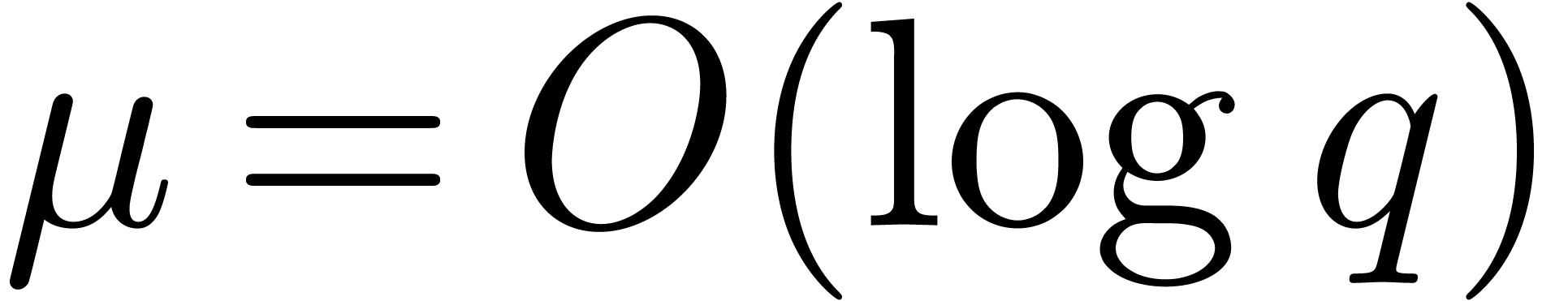 , the term
, the term 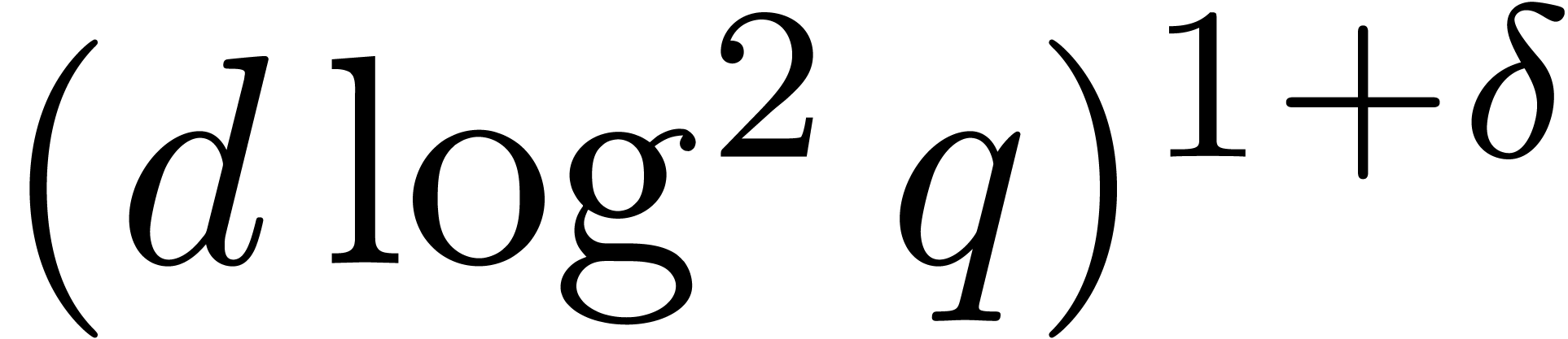 can be replaced by
can be replaced by  in view of
Proposition 1.
in view of
Proposition 1.
The cost in the latter proposition is asymptotically higher than the one
of Mignotte–Schnorr's algorithm [20, Section 2],
because of the term 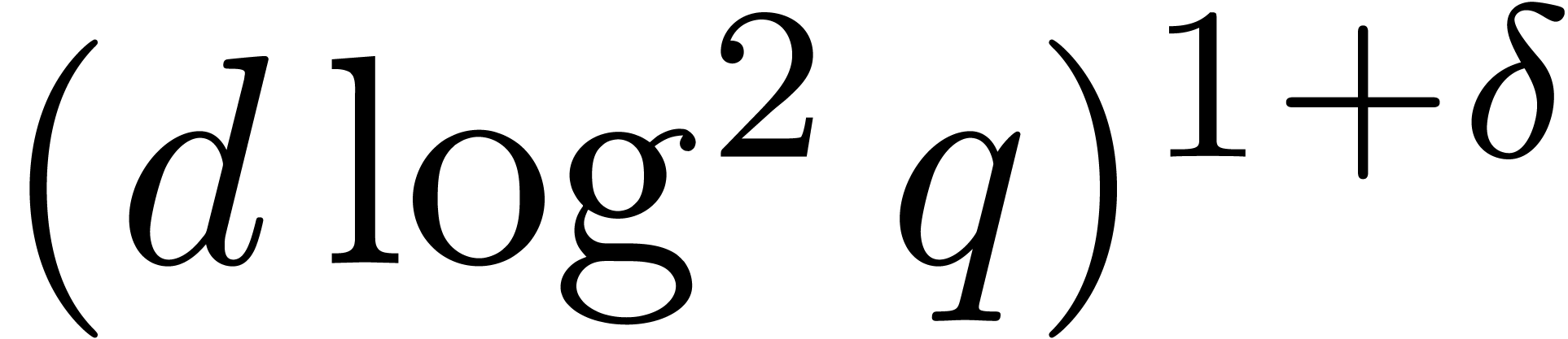 . In the
smooth case when
. In the
smooth case when 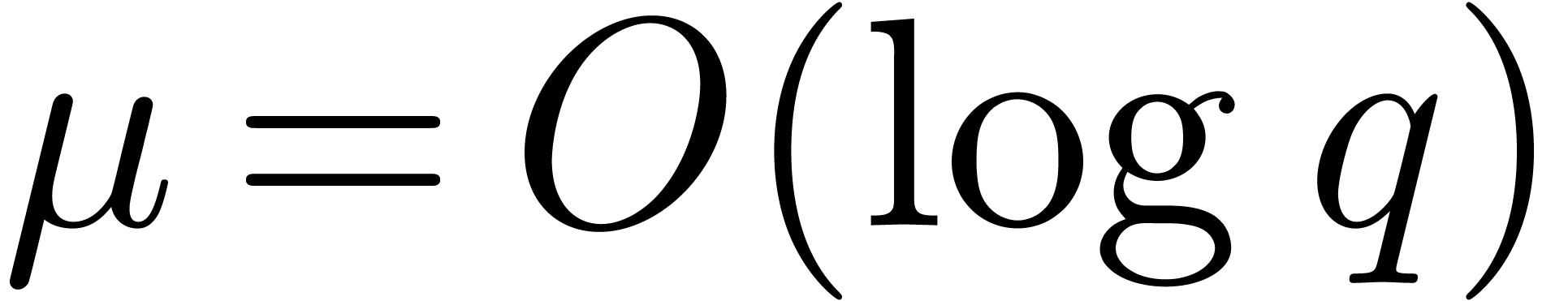 , the
asymptotic complexity bounds become similar.
, the
asymptotic complexity bounds become similar.
The rest of this section is devoted to improve Algorithm 13.
In order to diminish the dependence on 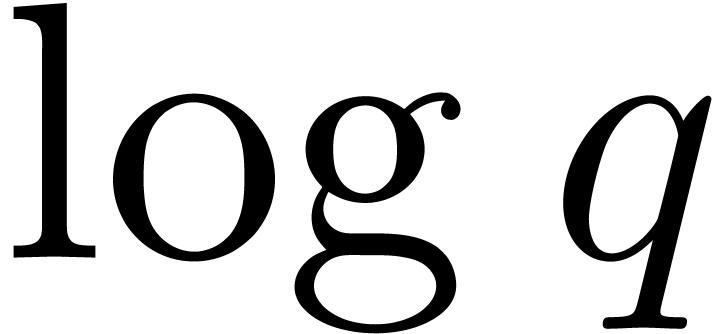 ,
we stop representing roots by their logarithms as in
Mignotte–Schnorr's algorithm. Instead we shall compute discrete
logarithms only when necessary. Furthermore, we will show how to
decrease the dependence on the
,
we stop representing roots by their logarithms as in
Mignotte–Schnorr's algorithm. Instead we shall compute discrete
logarithms only when necessary. Furthermore, we will show how to
decrease the dependence on the 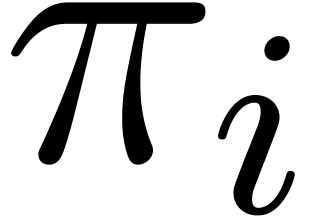 to
to  , by using the “baby-step
giant-step” technique.
, by using the “baby-step
giant-step” technique.
Let  be a monic polynomial which splits over
be a monic polynomial which splits over
 . Once the roots
. Once the roots  of the Graeffe transform of order
of the Graeffe transform of order  of
of  have been recovered, we may decompose
have been recovered, we may decompose  into
into 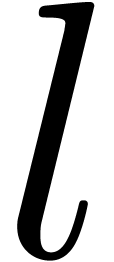 factors
factors  such that the
such that the  -th powers of
the roots of
-th powers of
the roots of 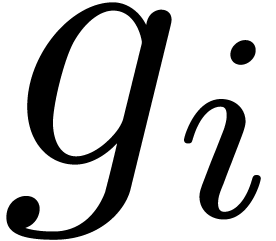 all coincide to
all coincide to 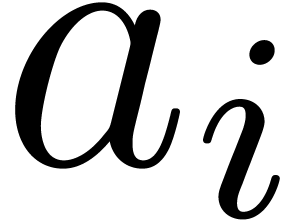 , for all
, for all 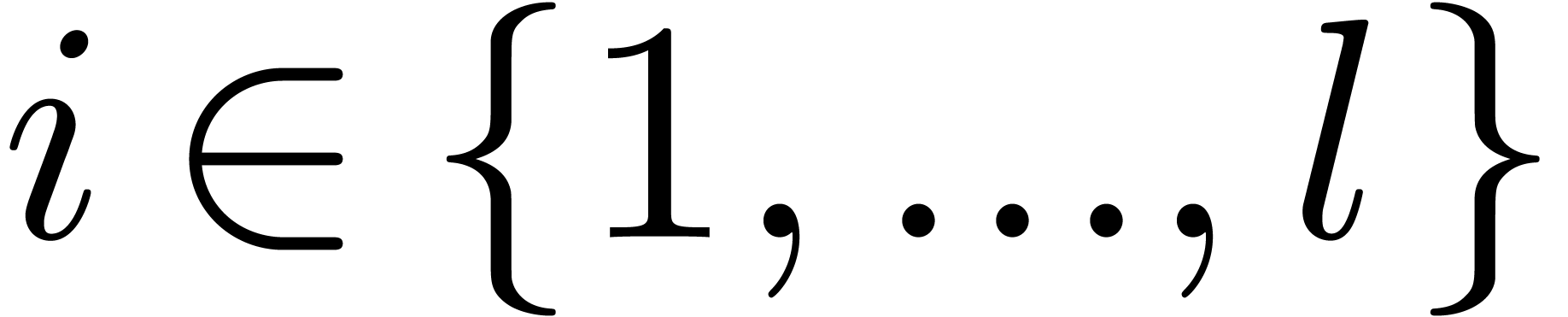 .
In short, we have
.
In short, we have 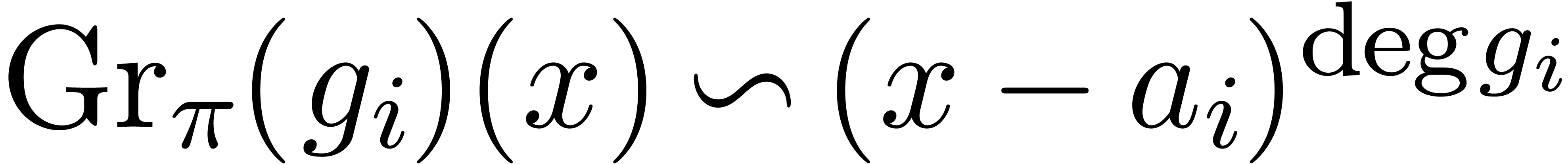 . This
decomposition may be achieved efficiently via the following
divide and conquer algorithm.
. This
decomposition may be achieved efficiently via the following
divide and conquer algorithm.
Algorithm
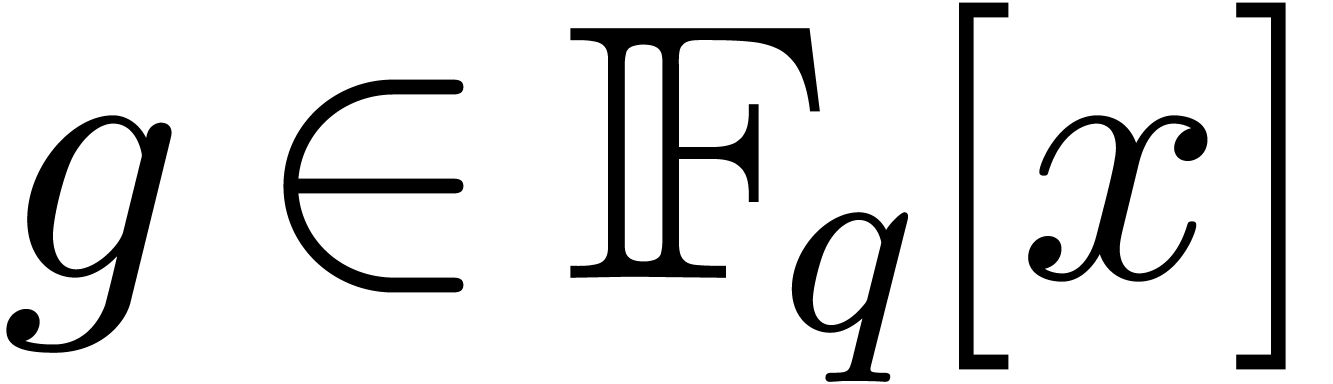 of degree
of degree
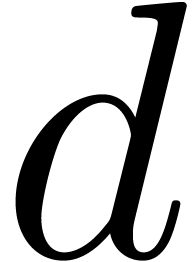 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
and such that
,
and such that
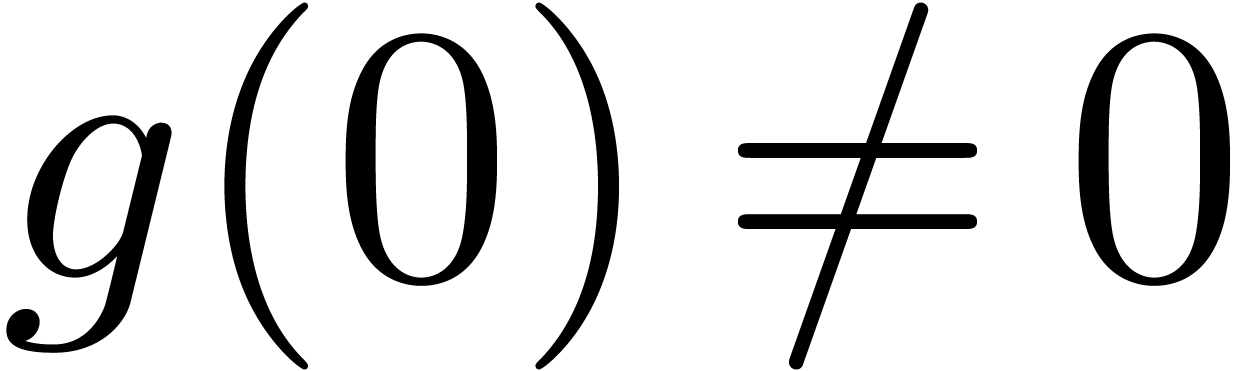 ;
the pairwise distinct roots
;
the pairwise distinct roots
 of the Graeffe transform of a given order
of the Graeffe transform of a given order
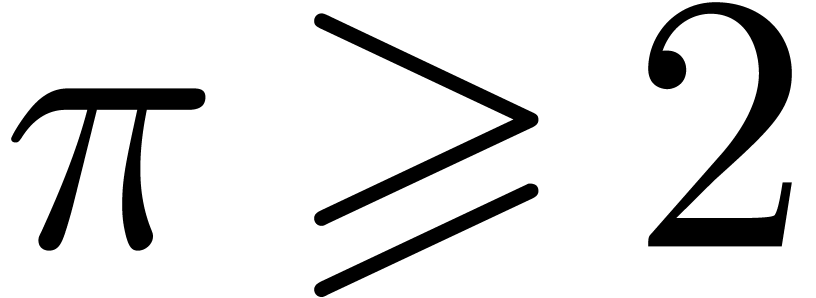 of
of
 .
.
The sequence of the monic 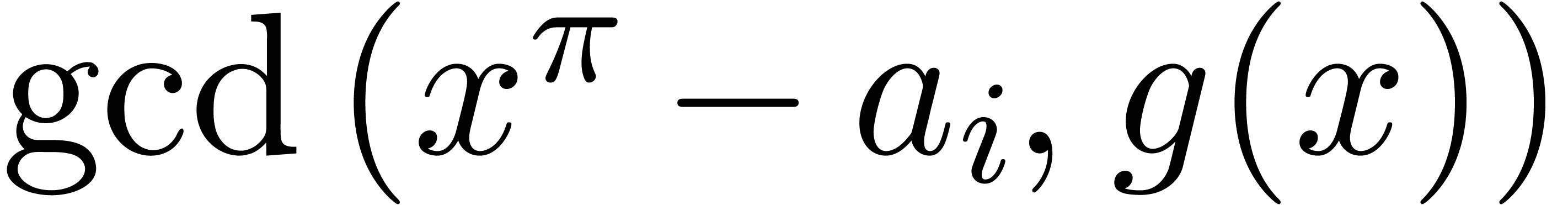 for all
for all 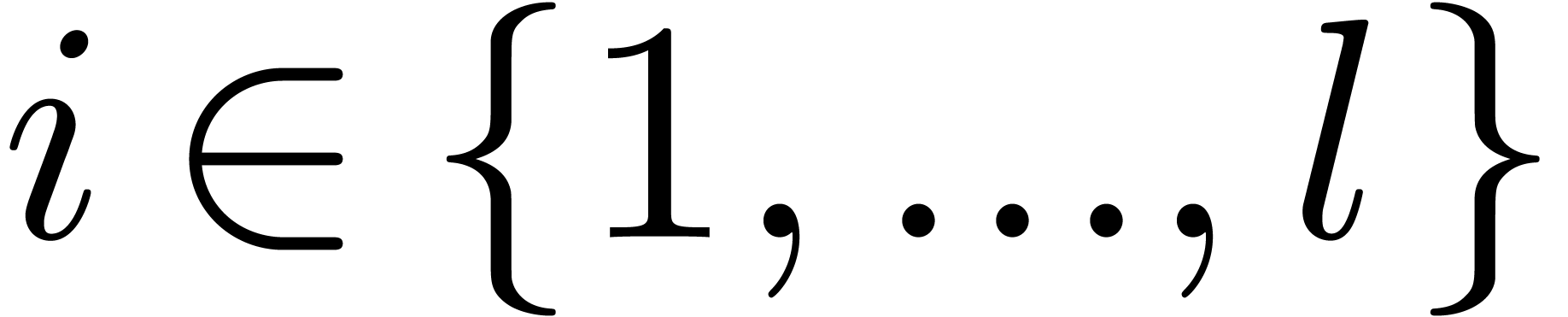 .
.
If 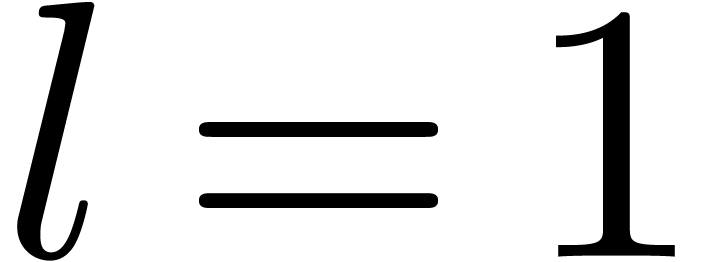 then return
then return  .
.
Let 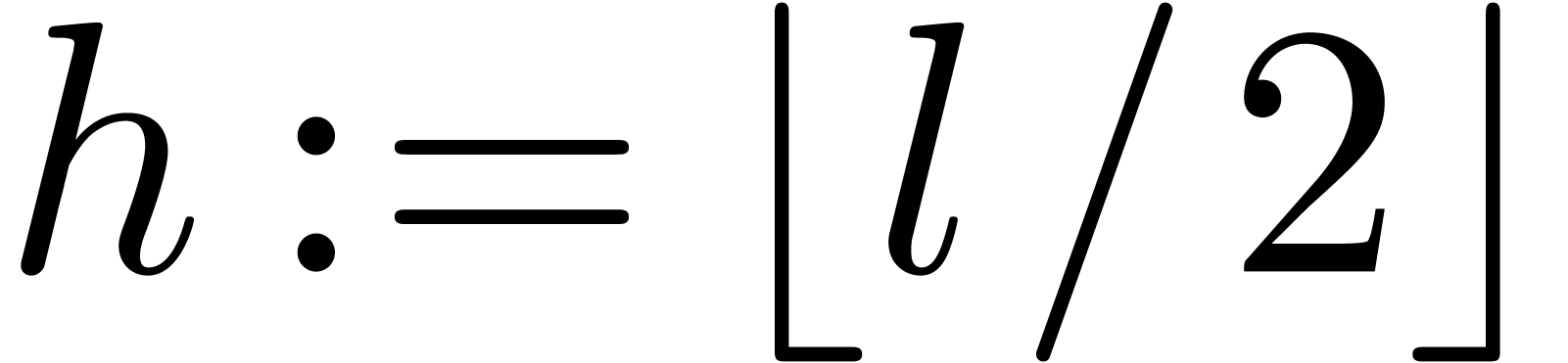 .
.
Compute 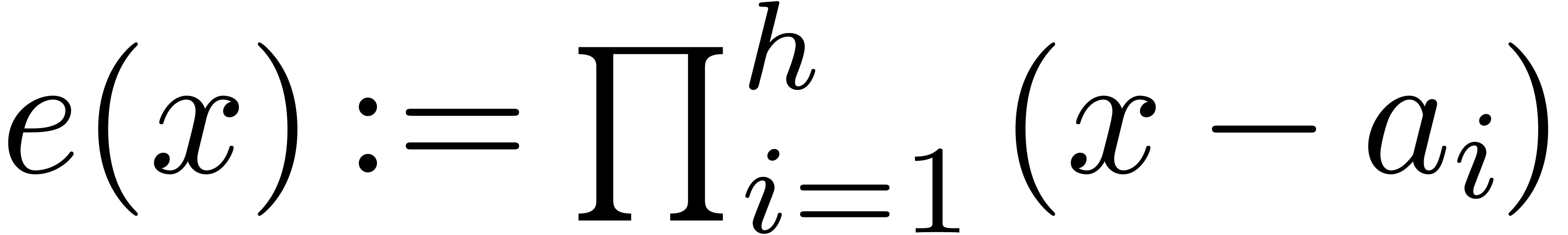 .
.
Compute 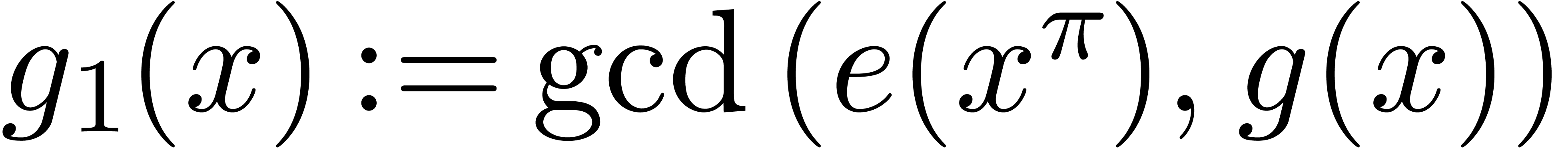 and
and 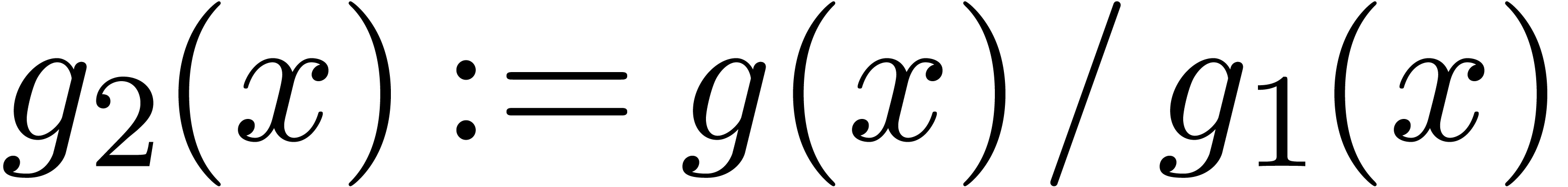 .
.
Call recursively the algorithm with input 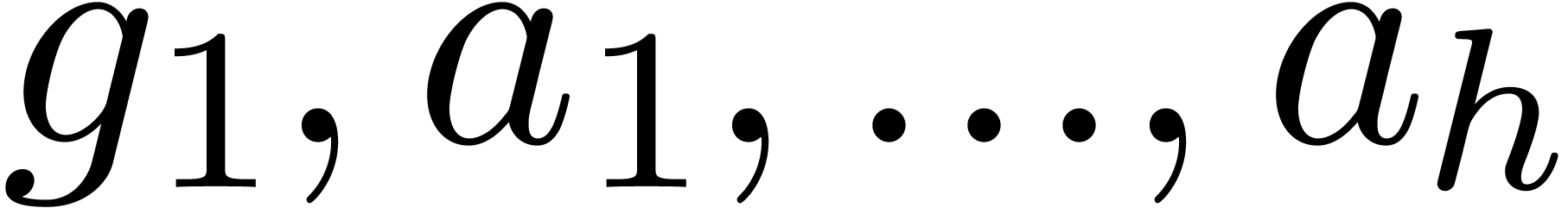 and
and 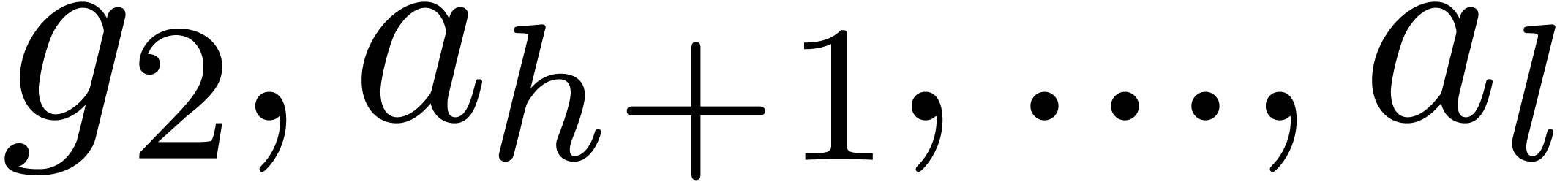 , and return the
concatenation of the polynomial sequences returned so.
, and return the
concatenation of the polynomial sequences returned so.
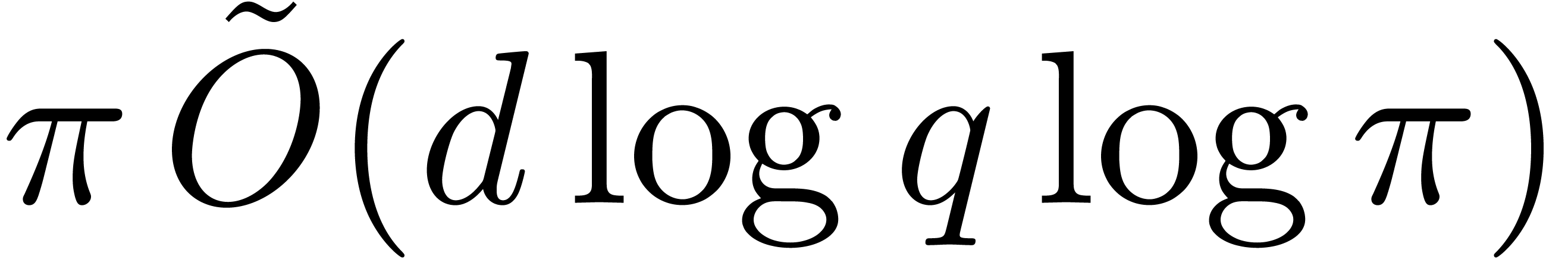 or
or 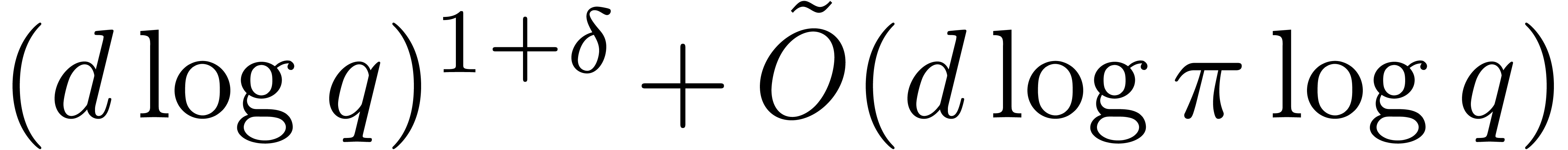 ,
for any constant
,
for any constant  .
.
Proof. If 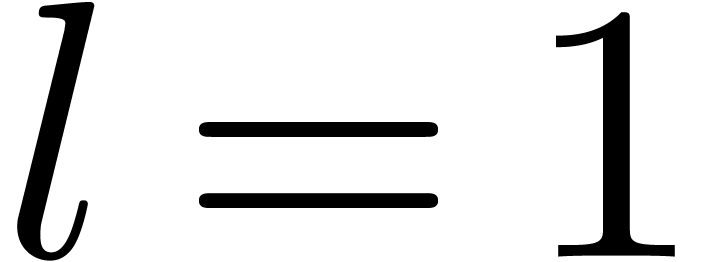 ,
then the
,
then the  -th powers of the
roots of
-th powers of the
roots of  are all equal to
are all equal to 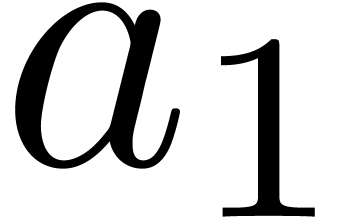 , whence the correctness. If
, whence the correctness. If 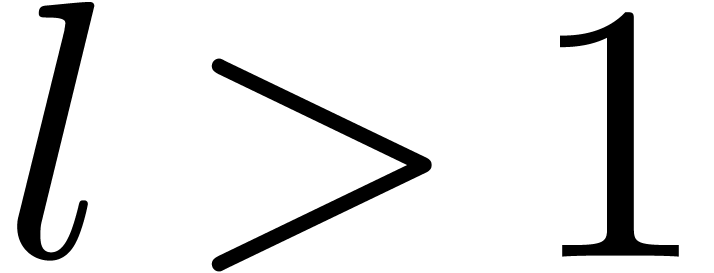 , then the roots of
, then the roots of 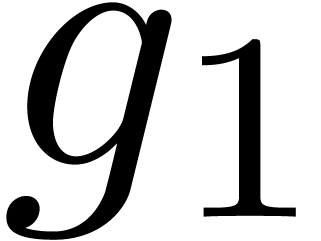 are
exactly those of
are
exactly those of  whose
whose  -th powers are in the set
-th powers are in the set  . Consequently, the
. Consequently, the  -th
powers of the roots of
-th
powers of the roots of 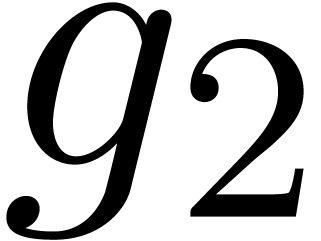 are all in the set
are all in the set 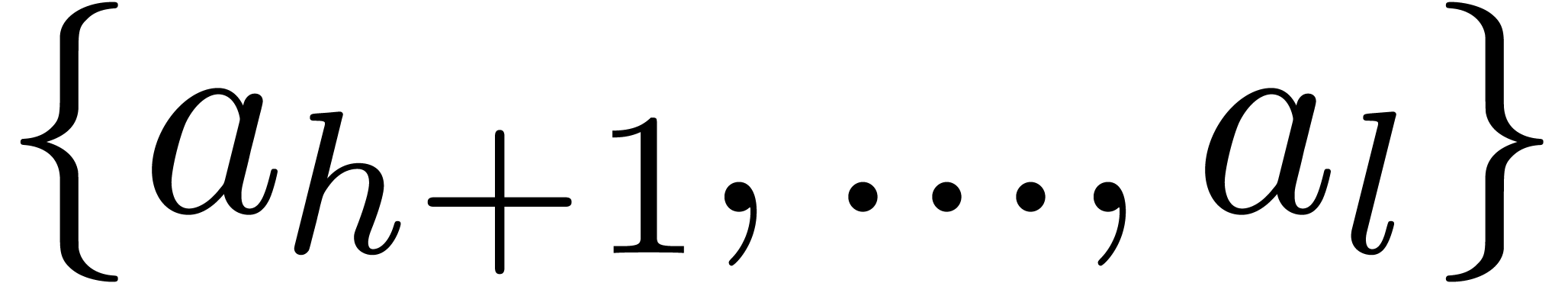 . This completes the proof of the
correctness by induction.
. This completes the proof of the
correctness by induction.
Step 3 can be performed in softly linear time by the subproduct tree technique (for the sake of efficiency the subproduct tree should be shared between all the recursive calls).
On the one hand, computing 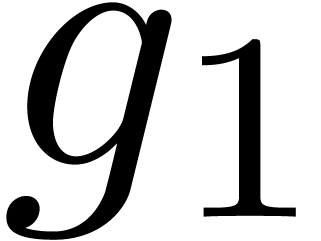 can be done naively
in time
can be done naively
in time 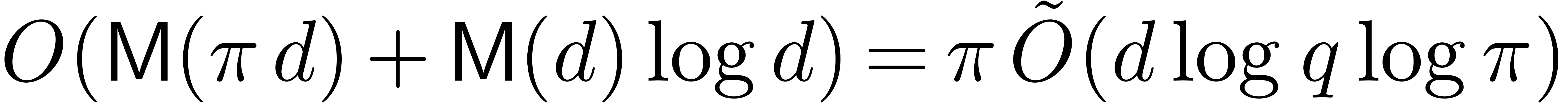 . On the other hand,
one may proceed as follows: compute
. On the other hand,
one may proceed as follows: compute 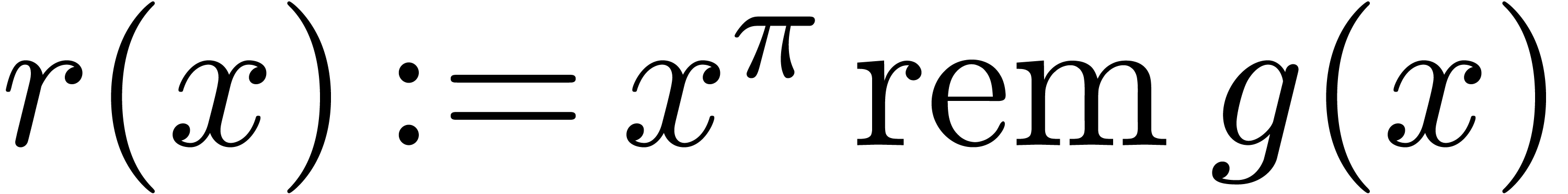 in time
in time
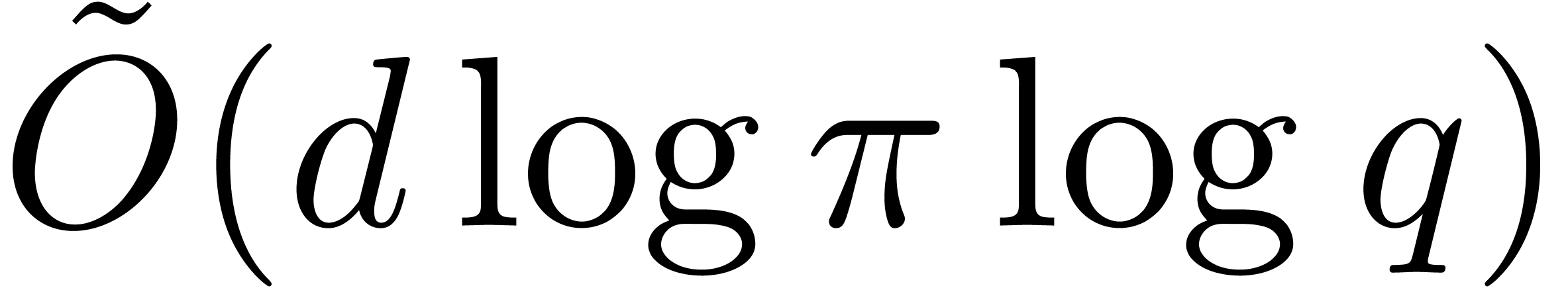 , and then use [27,
Corollary 7.2, p. 1789] to obtain
, and then use [27,
Corollary 7.2, p. 1789] to obtain 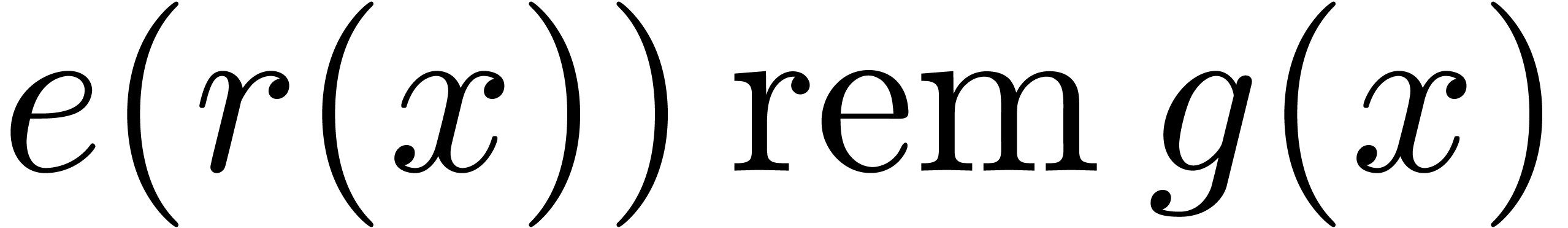 in time
in time 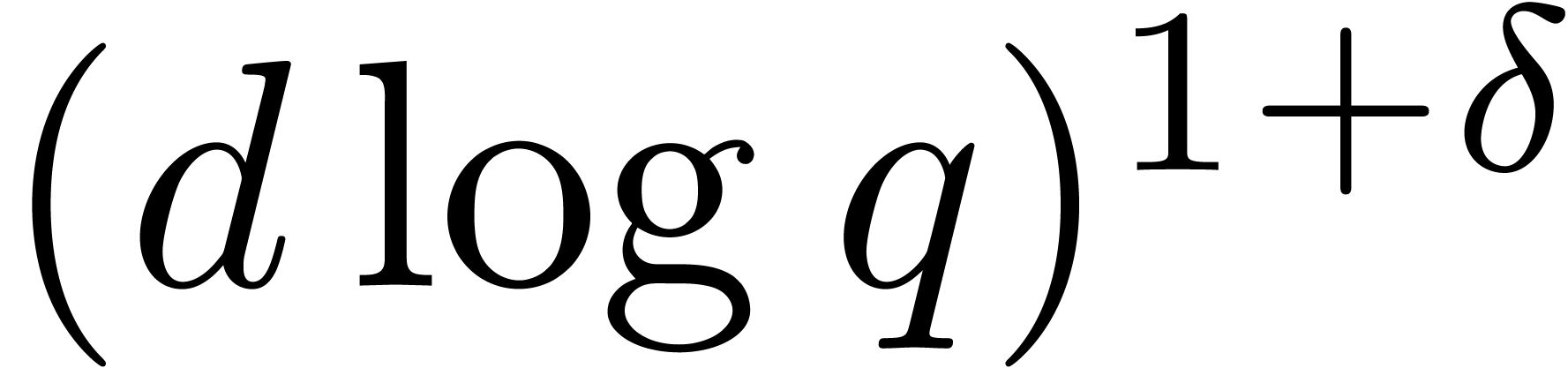 .
.
The sum of the degrees of the input polynomials  at the same depth of the recursive calls is at most
at the same depth of the recursive calls is at most 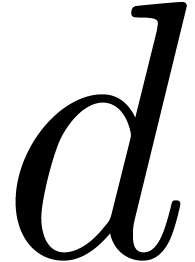 , and the maximal depth is
, and the maximal depth is 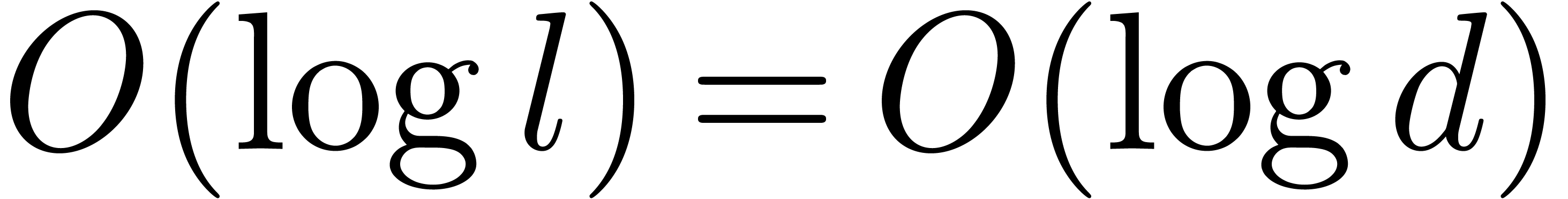 . This yields the complexity bounds of the
algorithm.
. This yields the complexity bounds of the
algorithm.
Let  be polynomials of respective degrees
be polynomials of respective degrees  , and let
, and let  . For given subset
. For given subset  of
of  of cardinality
of cardinality 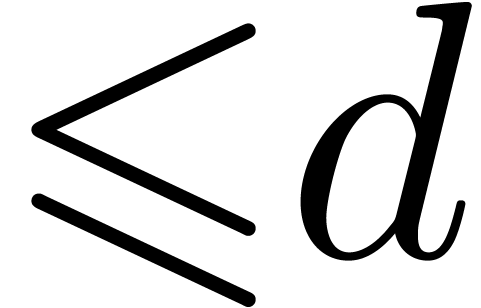 ,
we are interested in finding the roots of
,
we are interested in finding the roots of 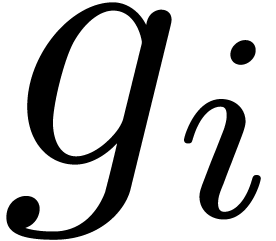 in
in
 for each
for each 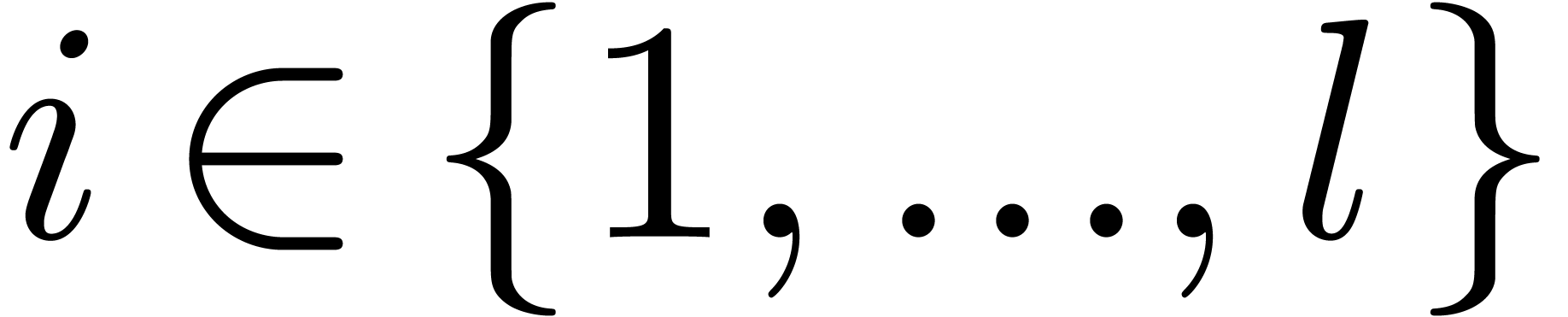 simultaneously.
We do not make additional assumptions, and in particular the
simultaneously.
We do not make additional assumptions, and in particular the 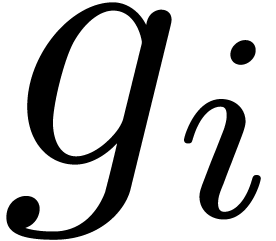 are allowed to share common roots. A natural divide and
conquer approach applies, as explained in the following algorithm.
are allowed to share common roots. A natural divide and
conquer approach applies, as explained in the following algorithm.
Algorithm
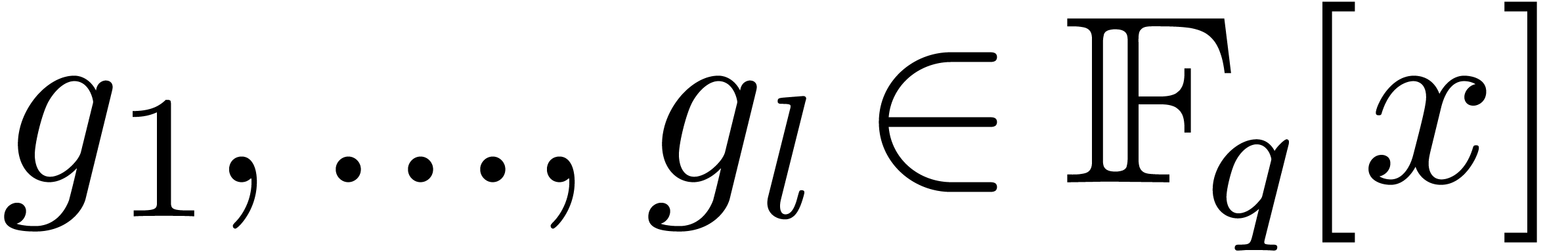 of degrees
of degrees
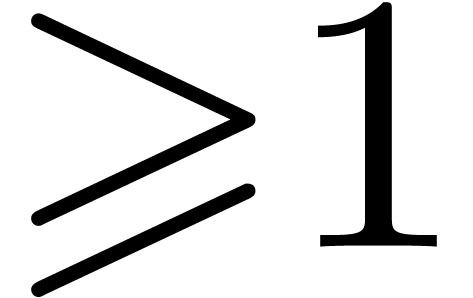 ;
a subset
;
a subset
 of
of
 of cardinality at most
of cardinality at most
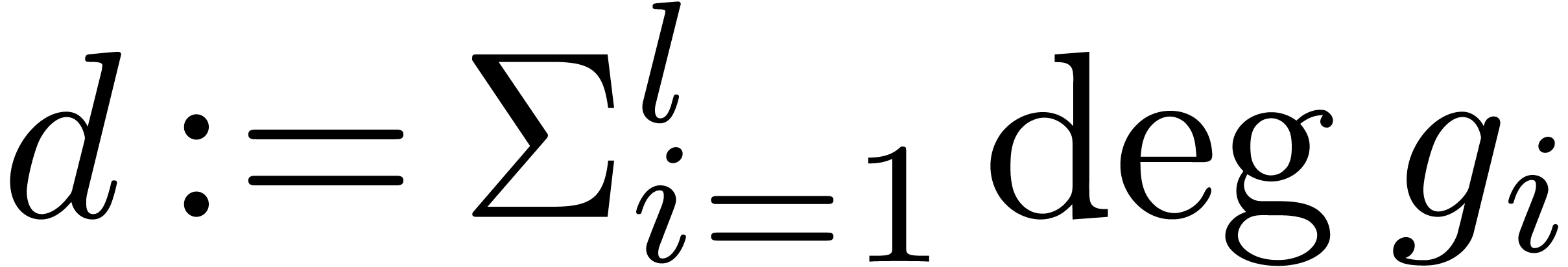 .
.
The sequence of the sets of the roots of  in
in  .
.
If 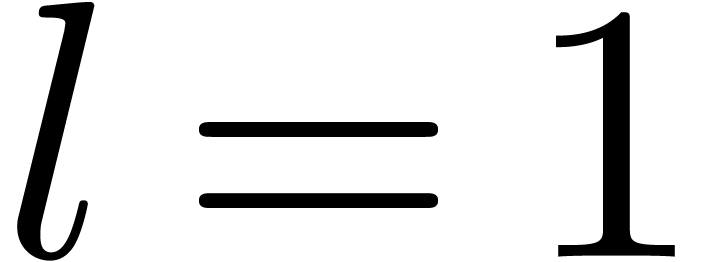 , then evaluate
, then evaluate 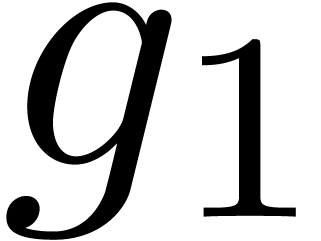 at all the points of
at all the points of  , and return those which are roots.
, and return those which are roots.
Let 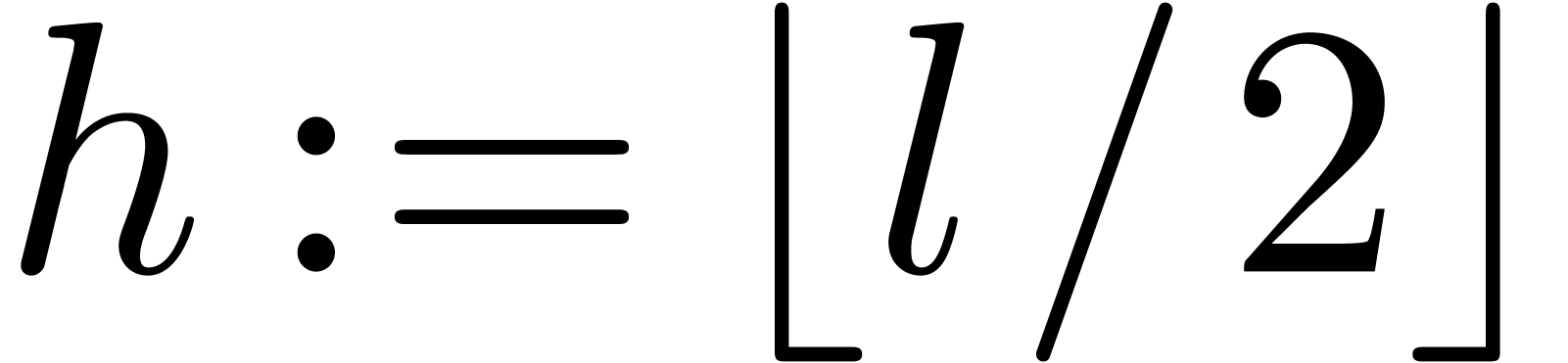 .
.
Compute 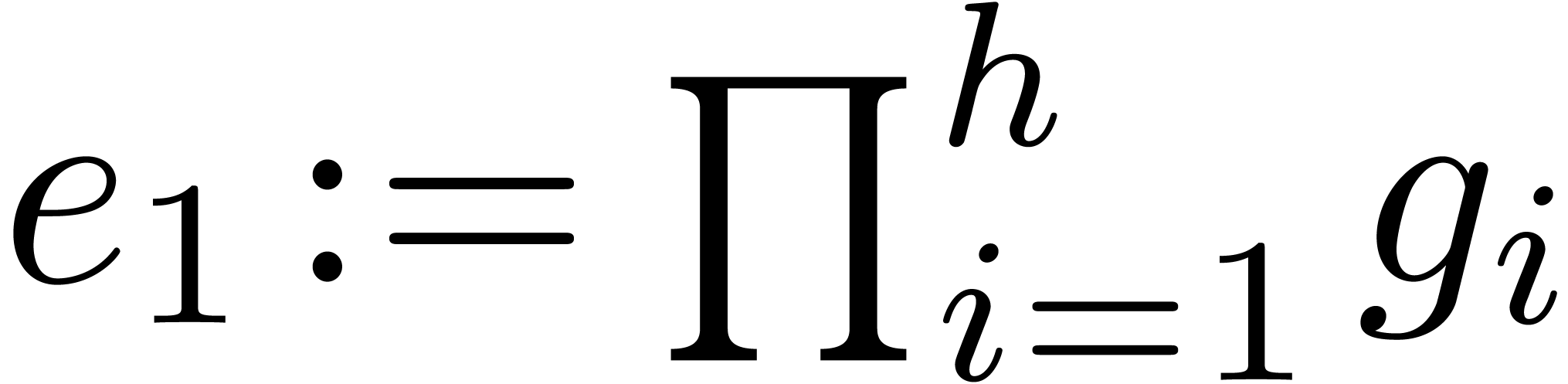 and
and 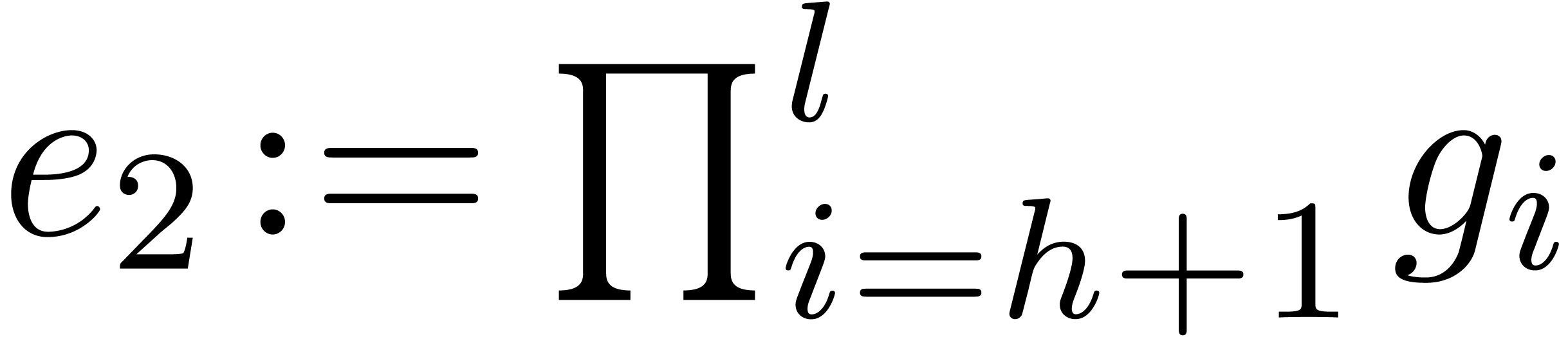 .
.
Compute the subset 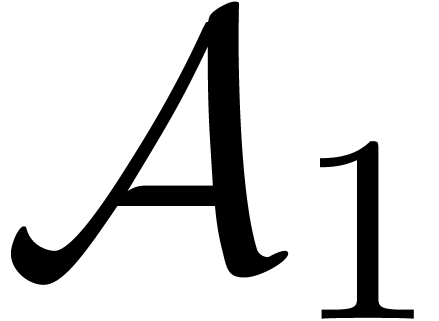 of points of
of points of  which are roots of
which are roots of 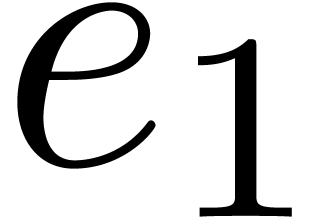 .
.
Compute the subset 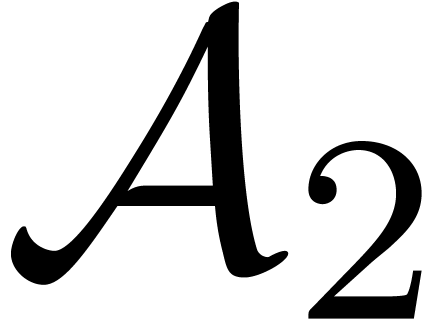 of points of
of points of  which are roots of
which are roots of 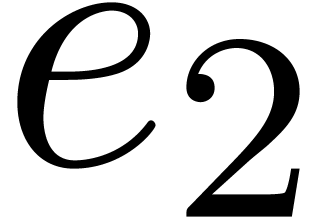 .
.
Call recursively the algorithm with input 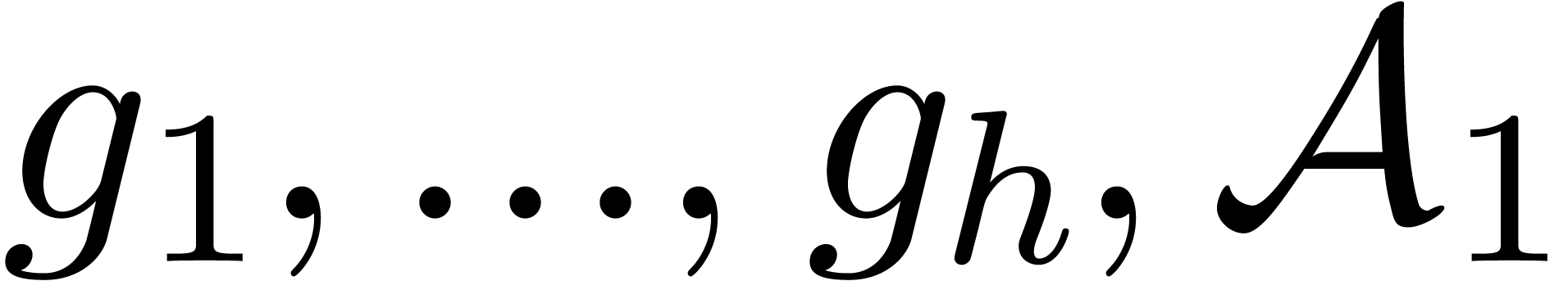 and
and  , and return the
concatenation of the returned sequences of sets of roots.
, and return the
concatenation of the returned sequences of sets of roots.
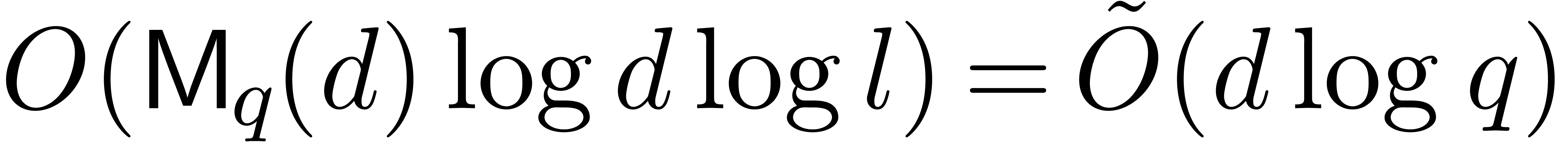 .
.
Proof. For the correctness, it is clear that the
roots of  in
in  are to be
found in
are to be
found in 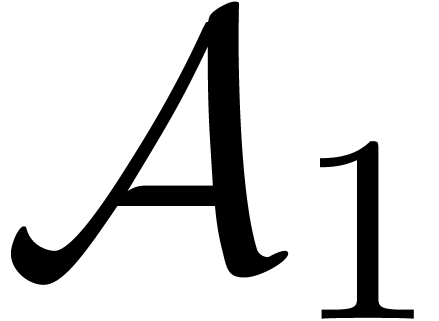 — idem for
— idem for 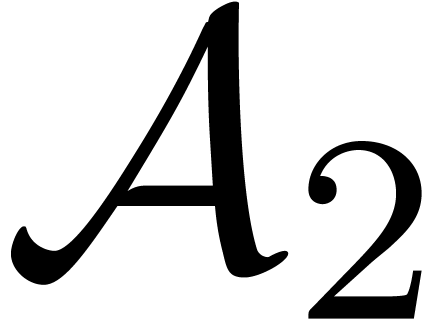 . The recursive calls are legitimate since the
cardinality of
. The recursive calls are legitimate since the
cardinality of 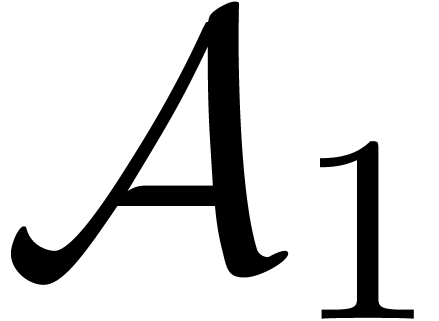 (resp. of
(resp. of 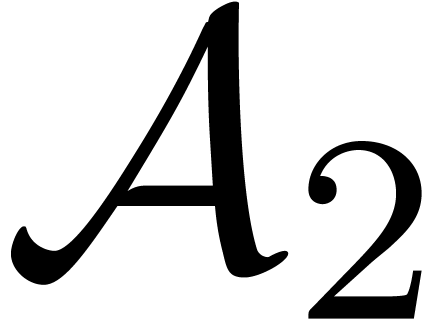 ) cannot exceed
) cannot exceed 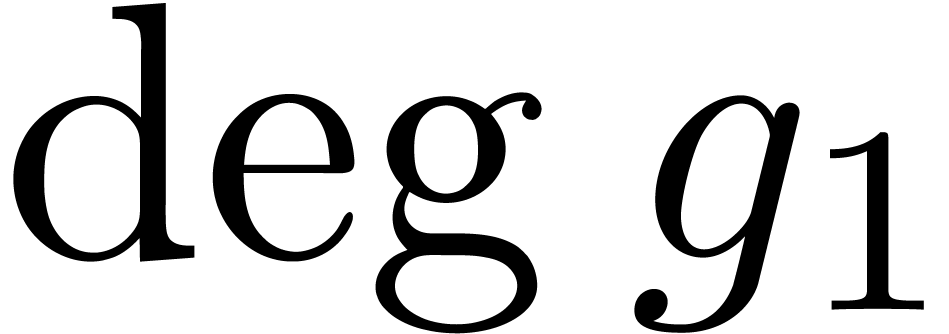 (resp.
(resp. 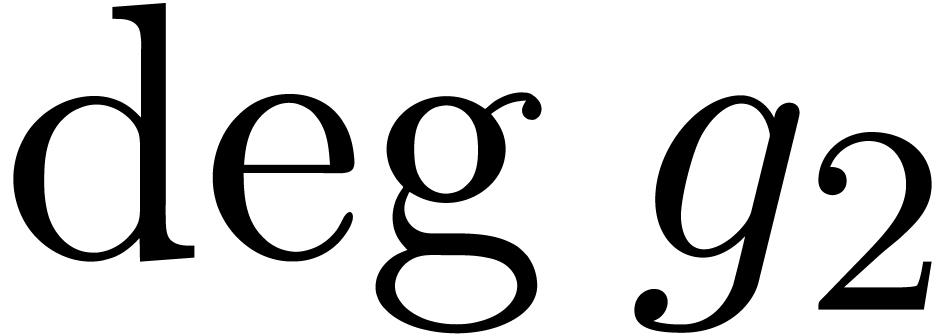 ).
).
Steps 1 to 5 take 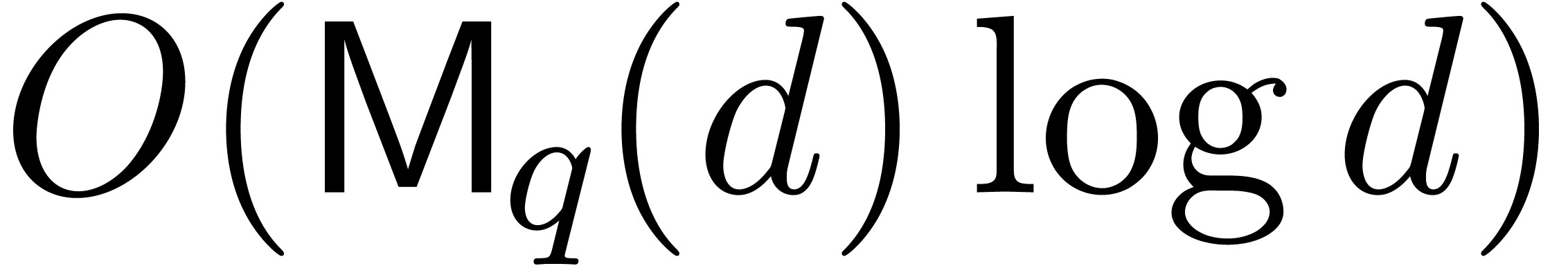 . The sum
of the degrees of the input polynomials at the same depth of the
recursive calls is at most
. The sum
of the degrees of the input polynomials at the same depth of the
recursive calls is at most 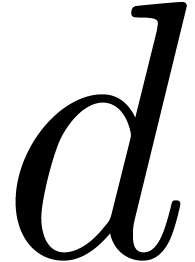 ,
and the maximal depth is
,
and the maximal depth is 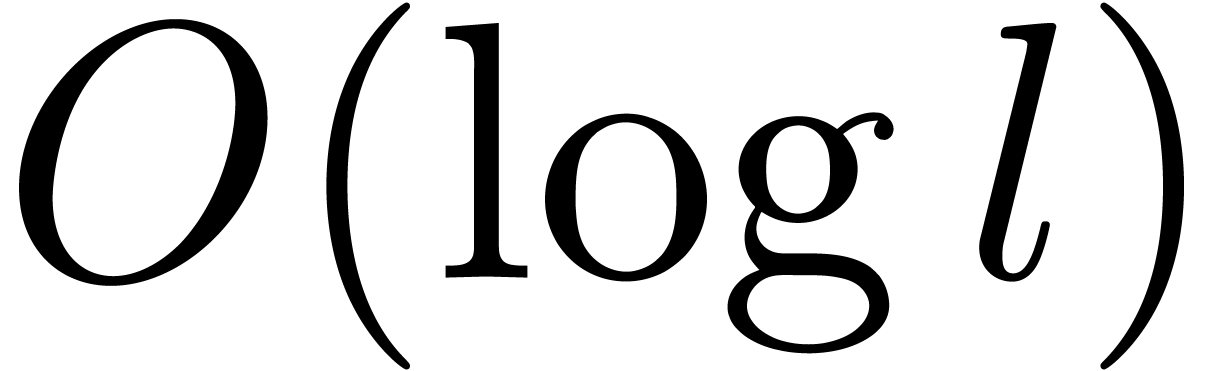 .
This yields the complexity bound, thanks to the super-additivity of
.
This yields the complexity bound, thanks to the super-additivity of
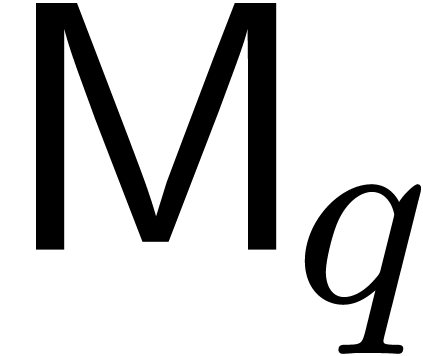 .
.
Notice that this lemma generalizes to arbitrary fields.
Instead of using multi-point evaluations in step 3.b of Algorithm 13, we may split the separable part of 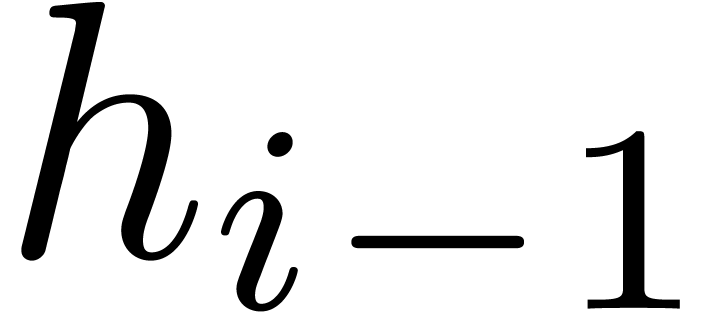 thanks to Algorithm 15. We will detail later how this
situation further reduces to computing all the roots of several
polynomials of degree sum at most
thanks to Algorithm 15. We will detail later how this
situation further reduces to computing all the roots of several
polynomials of degree sum at most  ,
and having roots of order dividing
,
and having roots of order dividing  .
To perform efficient root finding in this case, we adapt
Pollard–Strassen's aforementioned strategy for integer factoring
as follows.
.
To perform efficient root finding in this case, we adapt
Pollard–Strassen's aforementioned strategy for integer factoring
as follows.
Algorithm
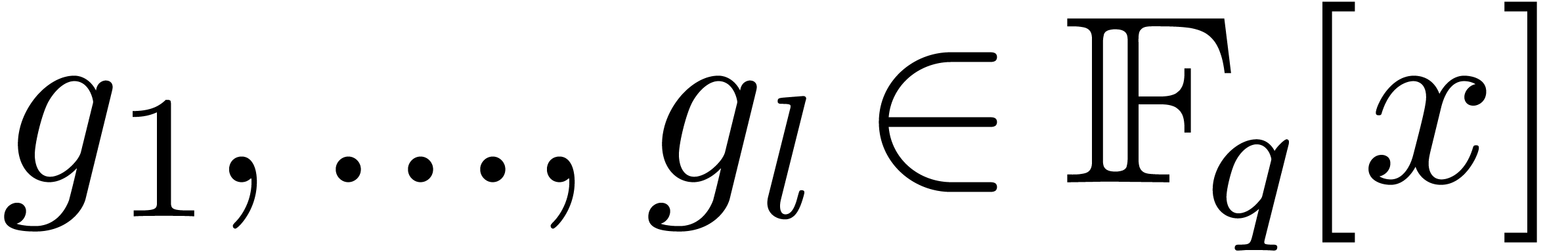 of degrees
of degrees
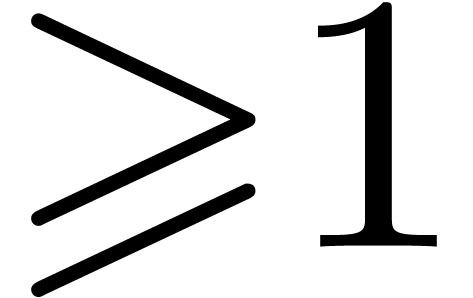 ,
monic, separable, which split over
,
monic, separable, which split over
 ,
and such that
,
and such that
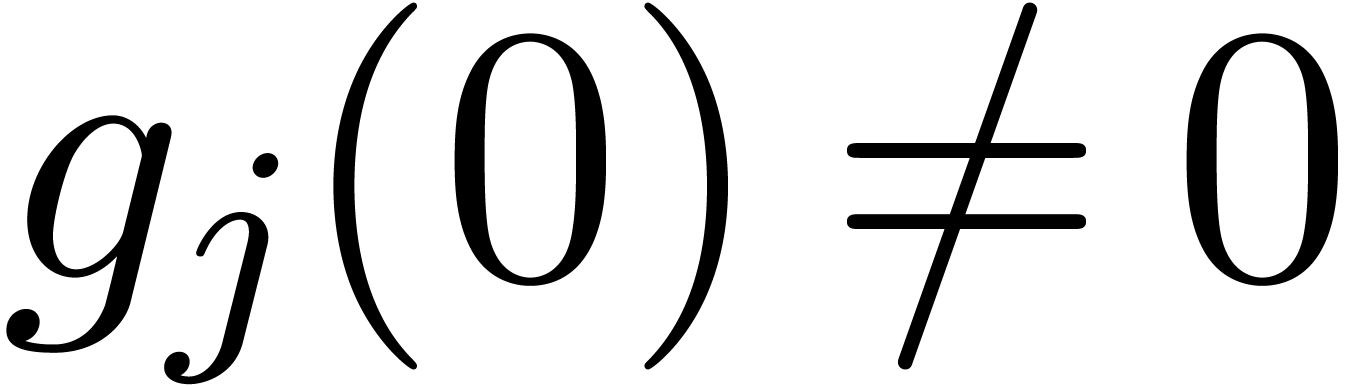 holds for all
holds for all
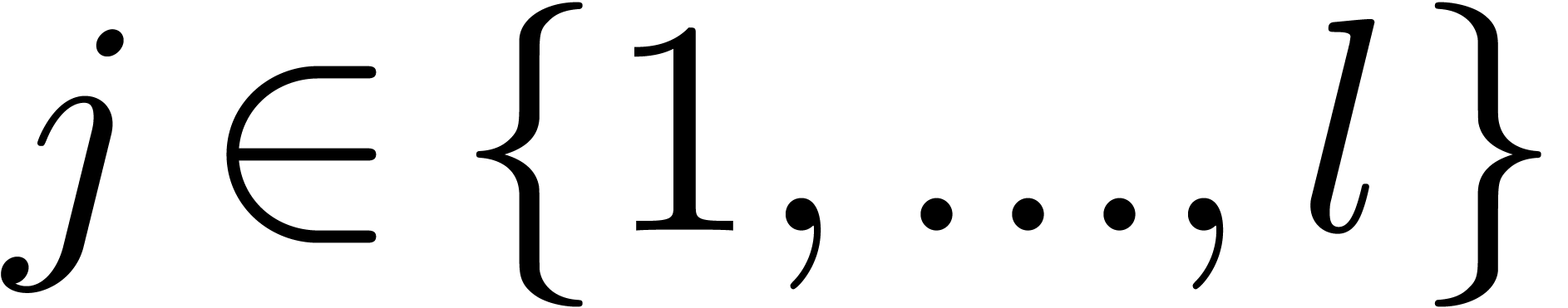 ;
a multiple
;
a multiple
 of the orders of the roots of all the
of the orders of the roots of all the
 ;
a primitive root
;
a primitive root
 of unity of order
of unity of order
 .
.
The sets 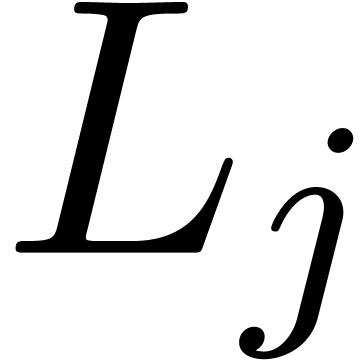 of the
of the  -logarithms of the roots of
-logarithms of the roots of  for all
for all 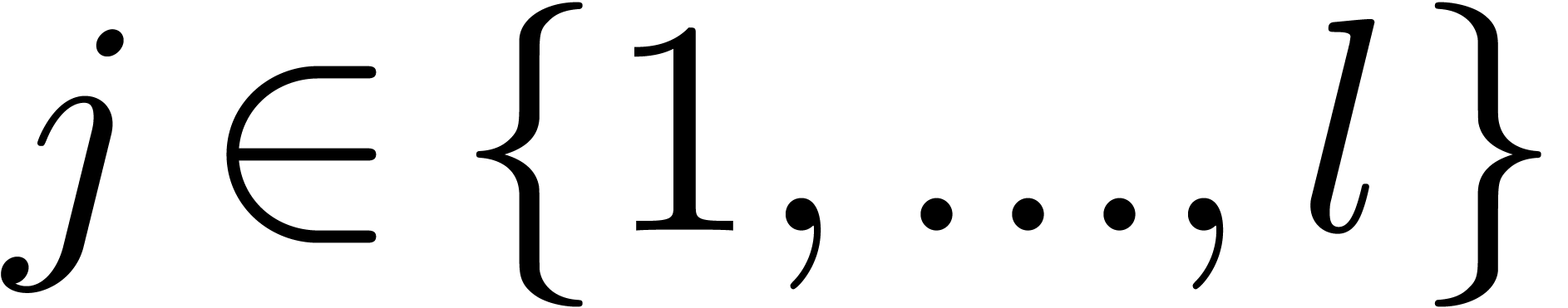 .
.
Let  , let
, let 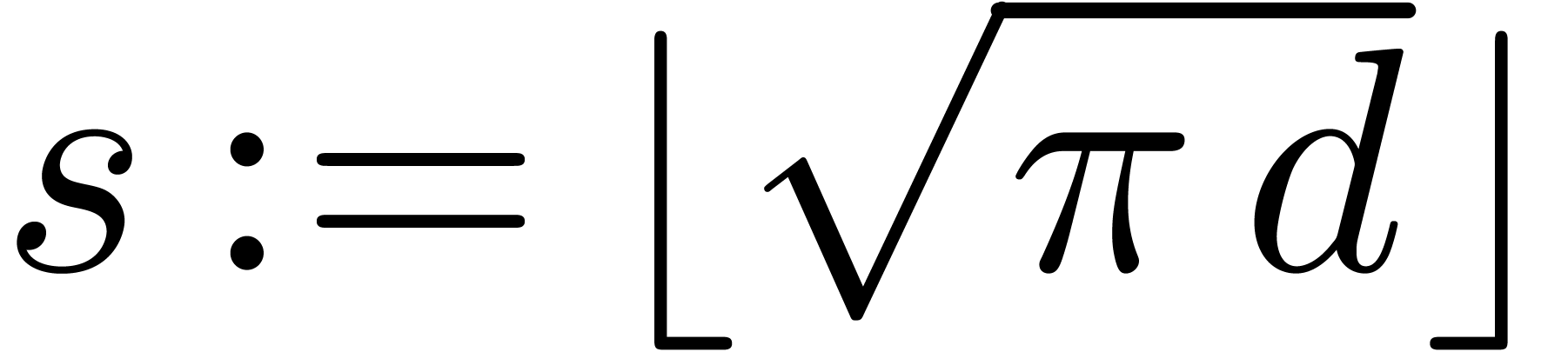 , and
, and  .
.
Compute 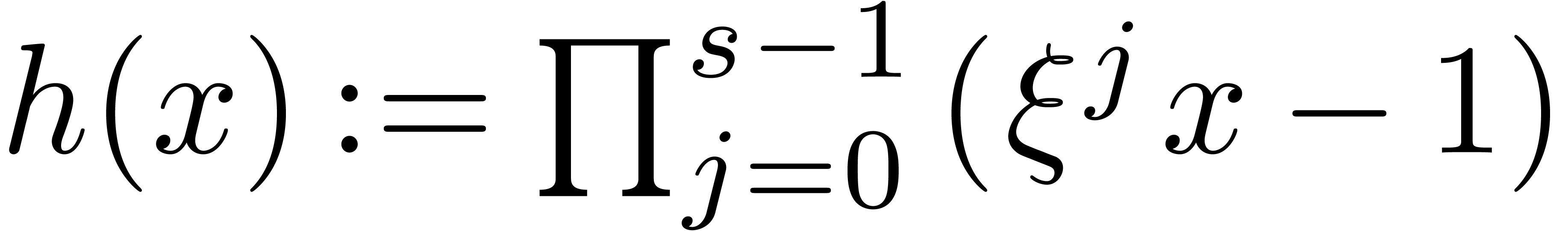 .
.
For all 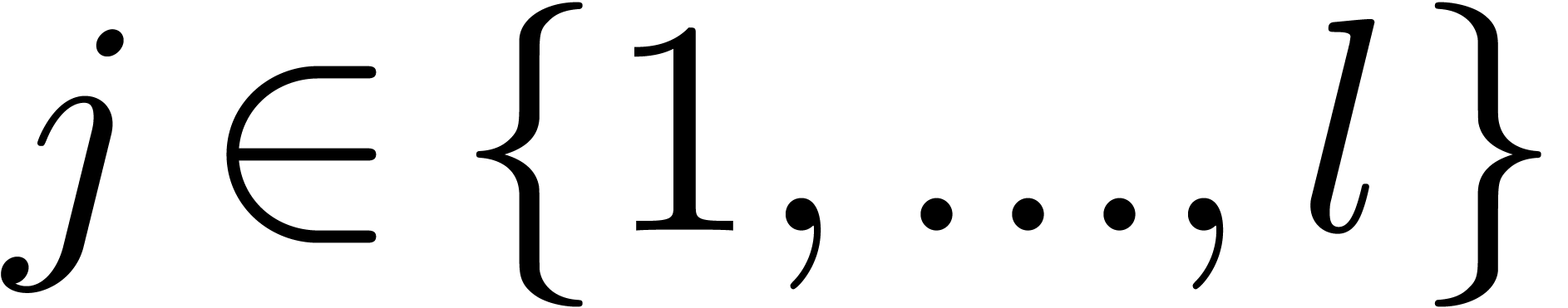 and all
and all  , compute
, compute 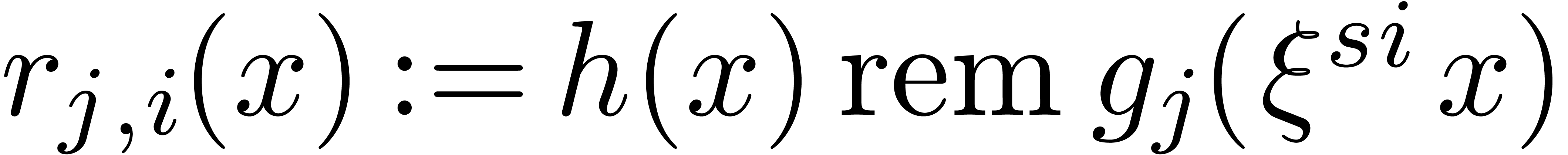 .
.
For all 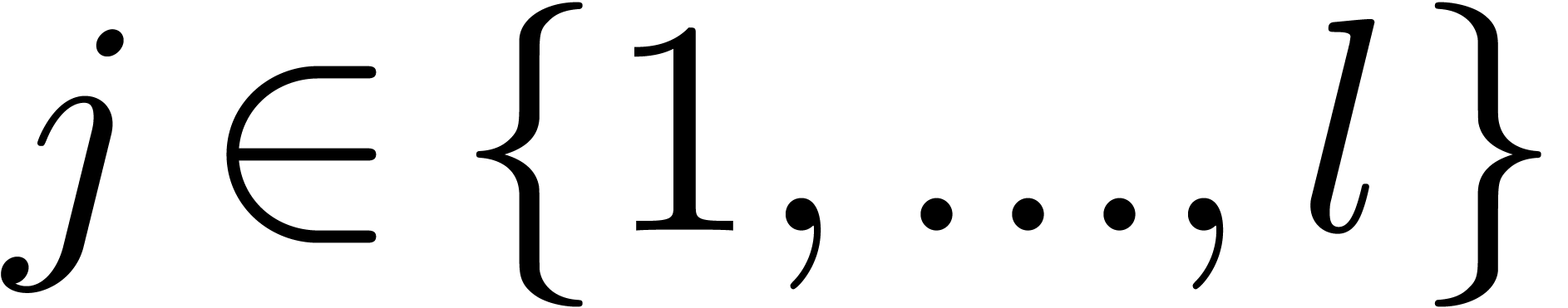 , compute the set
, compute the set
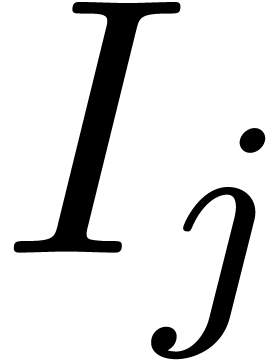 of indices
of indices  such that
such that
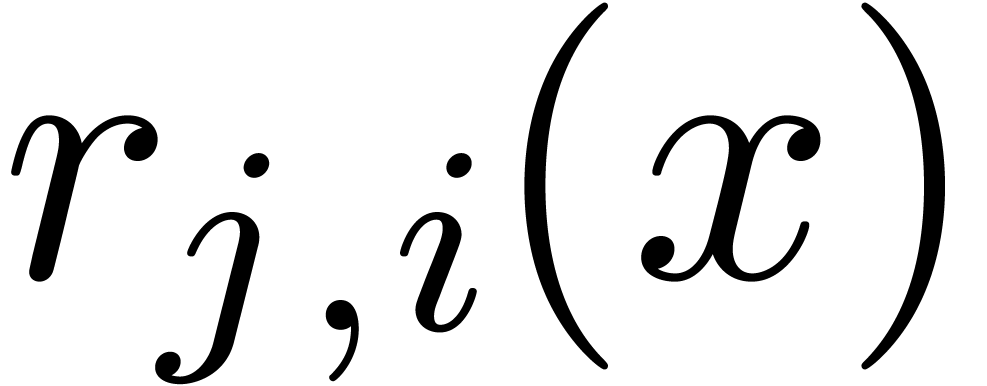 has a proper gcd
has a proper gcd 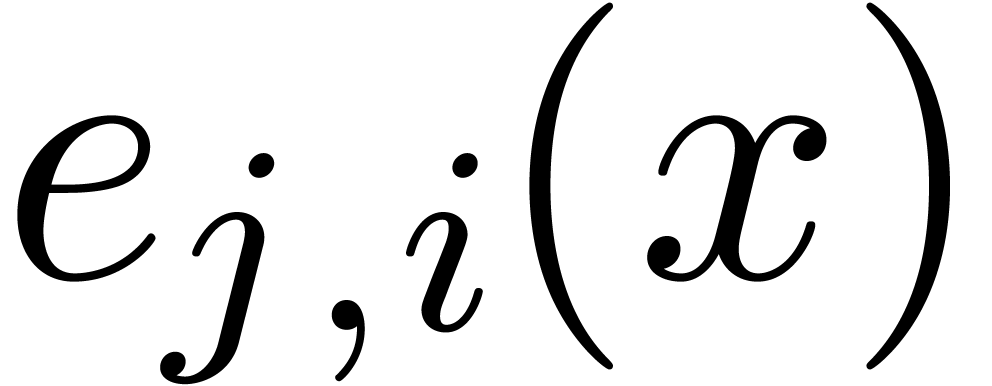 with
with 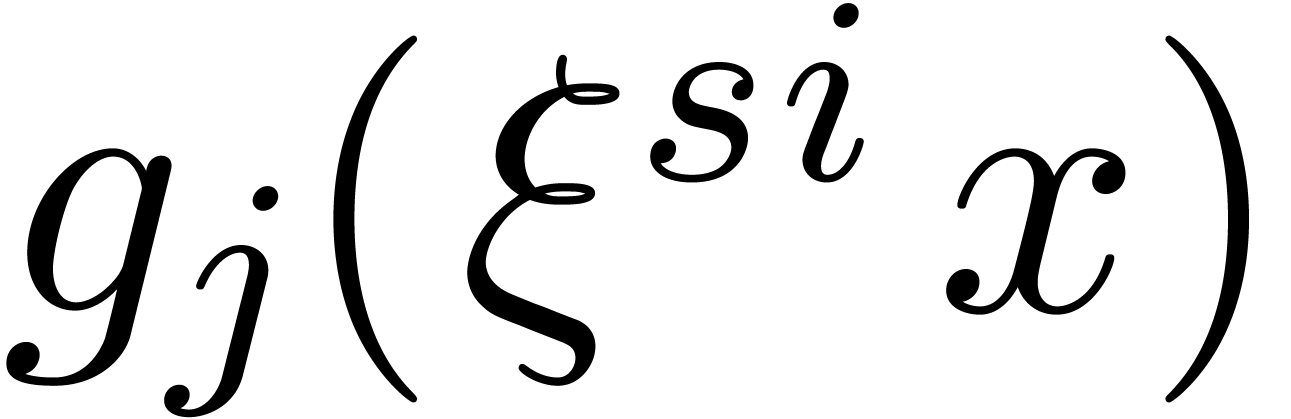 .
.
For all 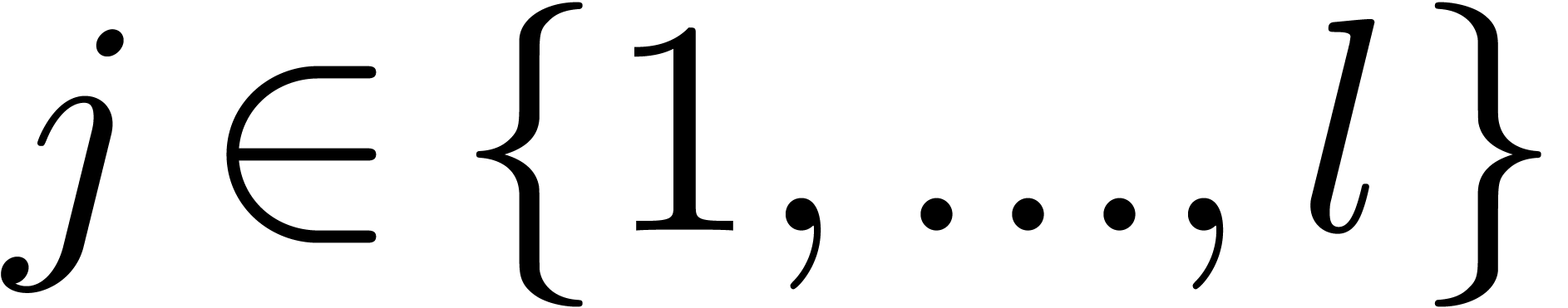 and all
and all 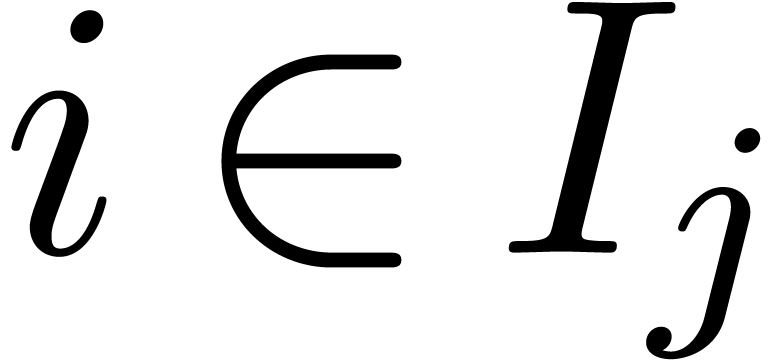 , compute all the
, compute all the  -logarithms
-logarithms
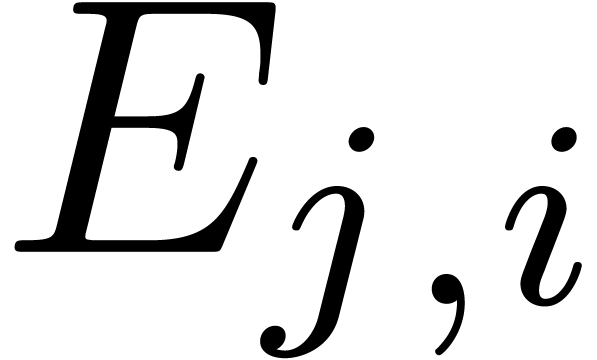 of the roots of
of the roots of 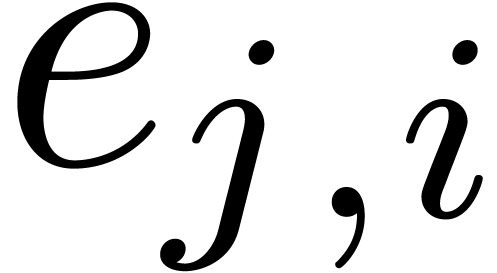 in
in
 by calling Algorithm 17
by calling Algorithm 17 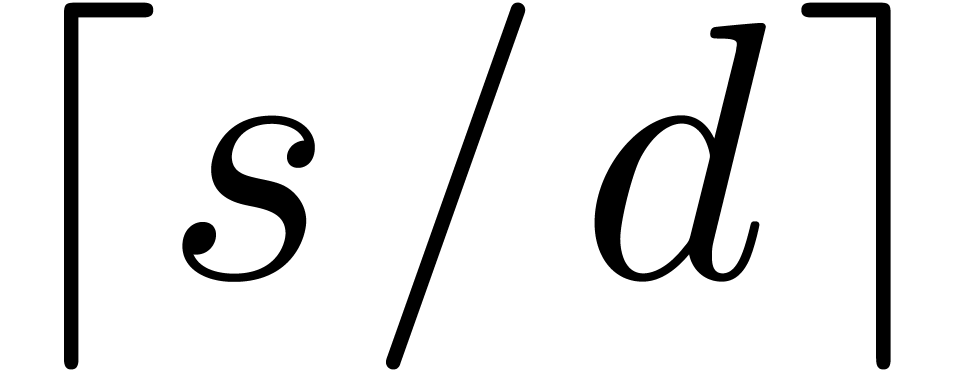 times on subsets of
times on subsets of  of
cardinalities at most
of
cardinalities at most 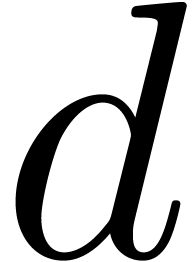 .
.
Return the sets 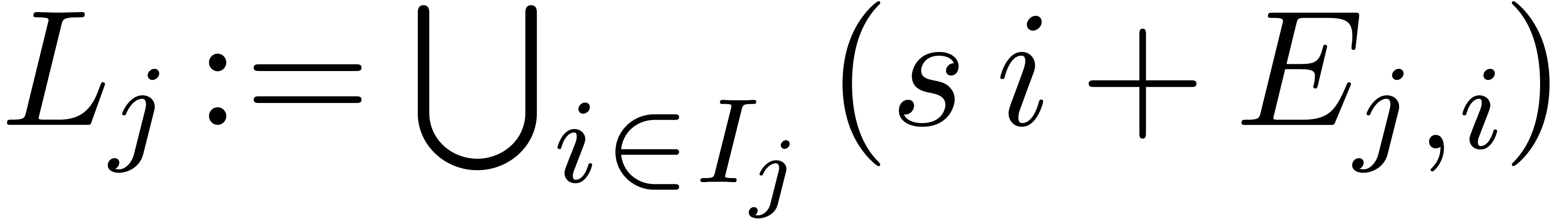 , for all
, for all
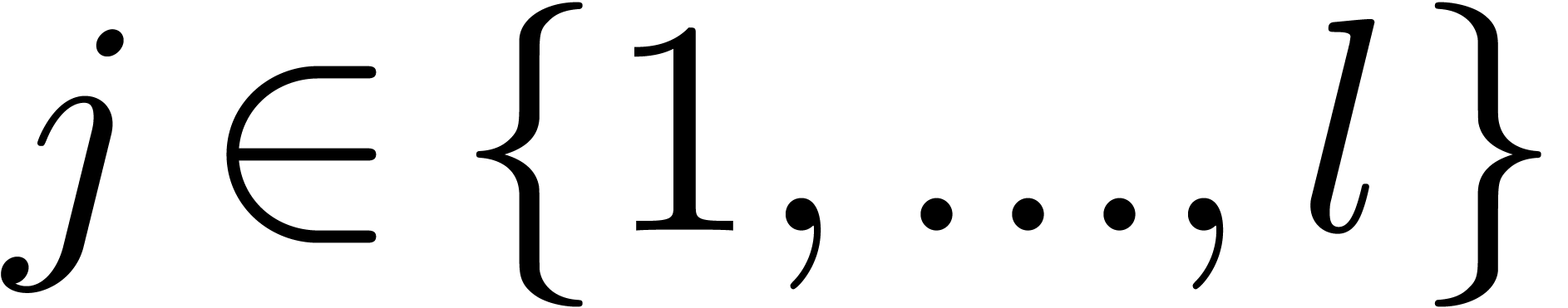 .
.
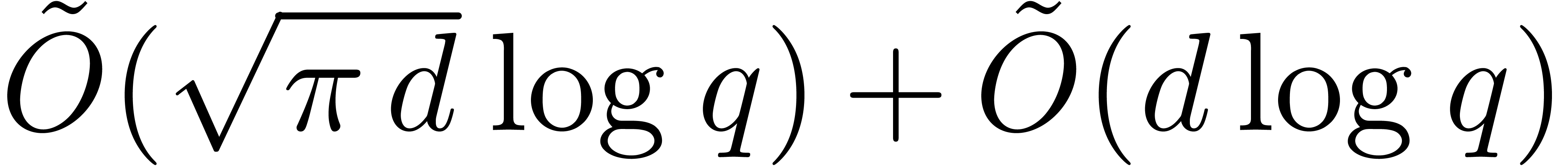 .
.
Proof. Of course, the returned values in 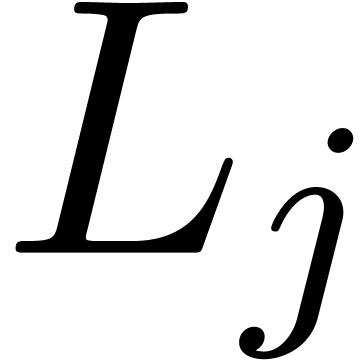 are
are  -logarithms
of roots of
-logarithms
of roots of  . Conversely, let
. Conversely, let
 be a root of
be a root of  with
with  . There exists a unique
. There exists a unique 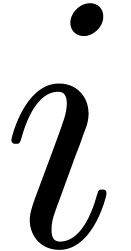 in
in 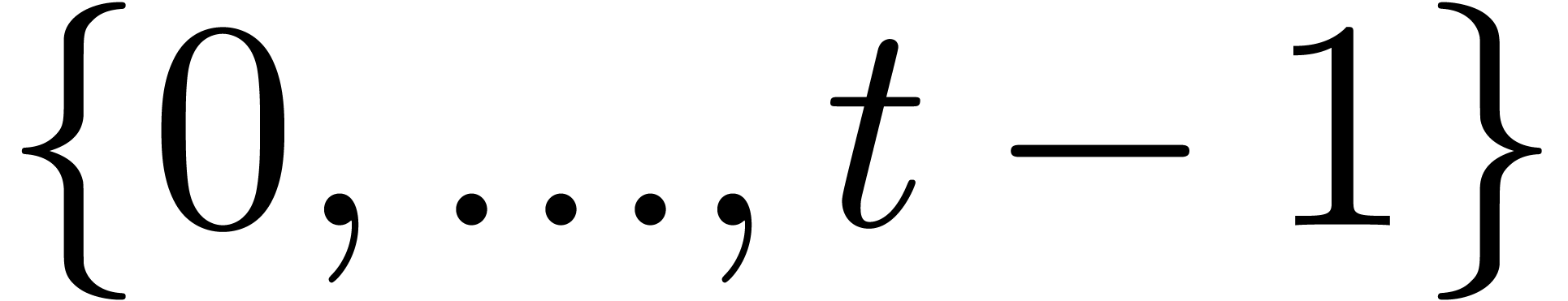 such that
such that 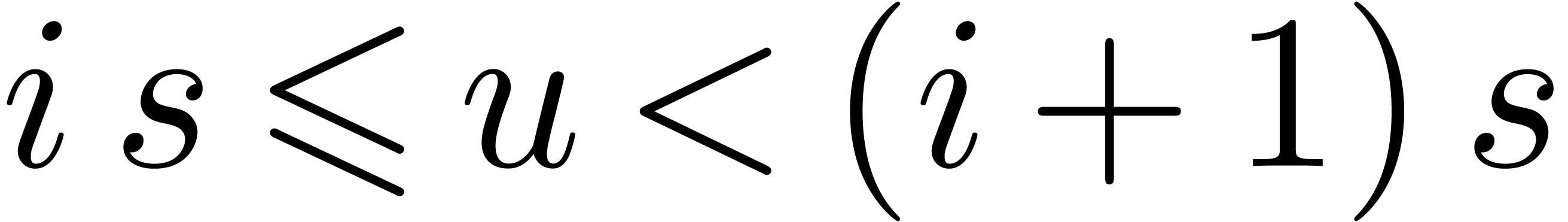 , since
, since 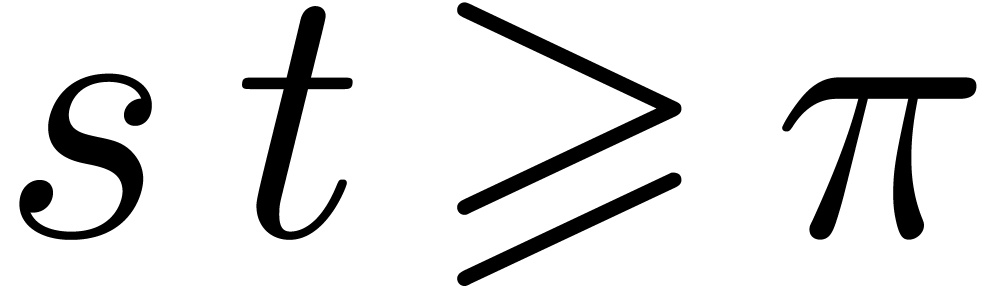 .
Then
.
Then 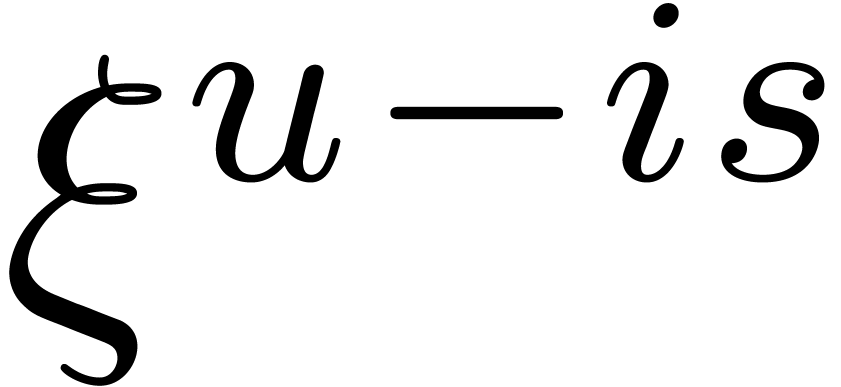 is a common root of
is a common root of 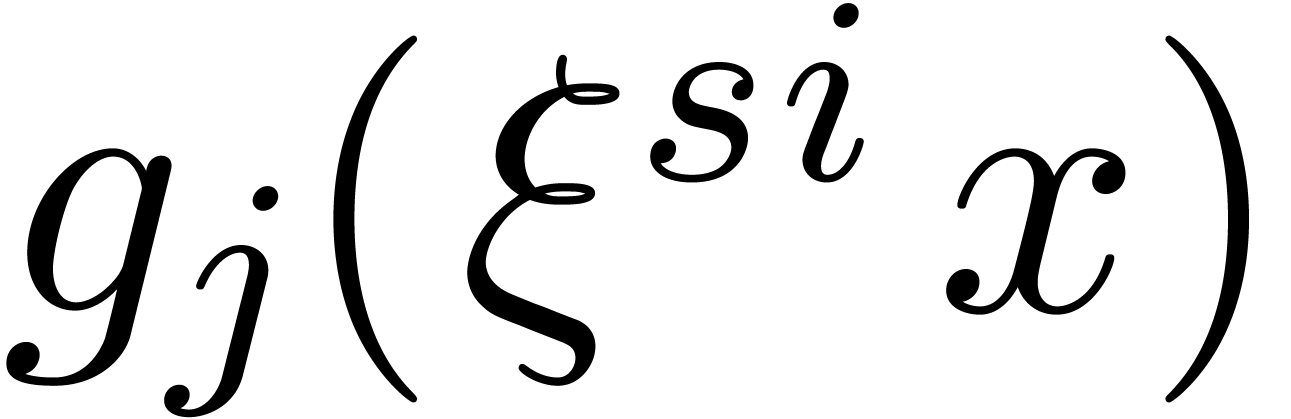 and
and  . This proves the
correctness.
. This proves the
correctness.
By Lemma 2, step 2 executes in time 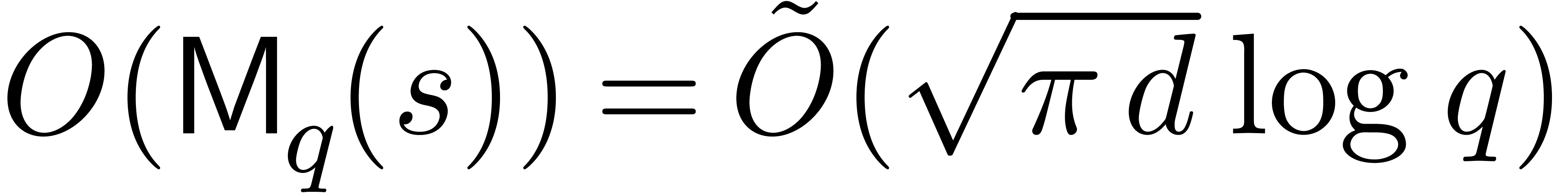 . Since
. Since 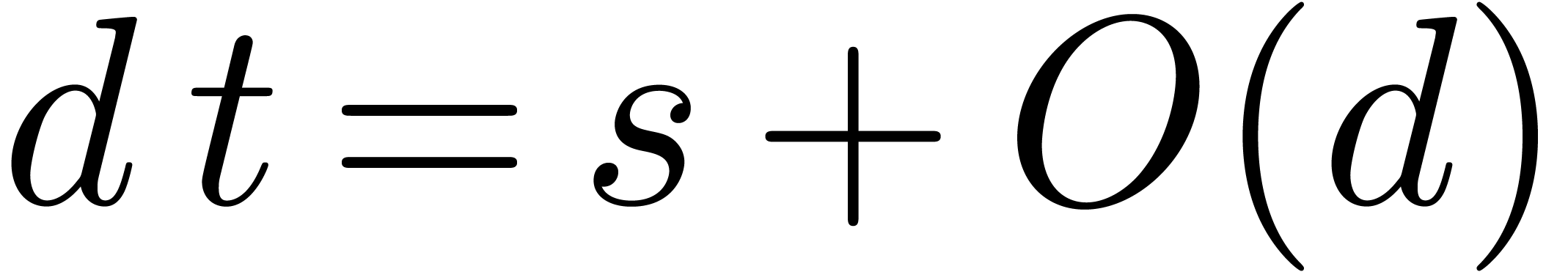 ,
step 3 costs
,
step 3 costs
Using the super-additivity of 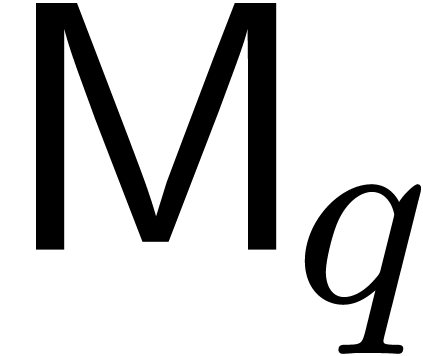 ,
step 4 needs
,
step 4 needs 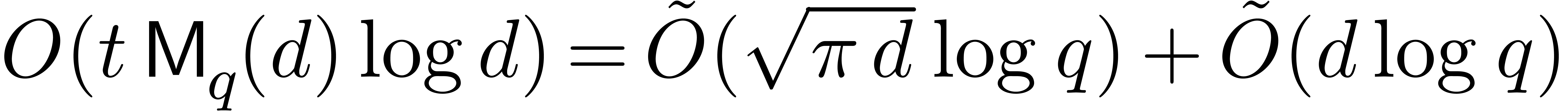 . Since the sum
of the degrees of all the polynomials
. Since the sum
of the degrees of all the polynomials 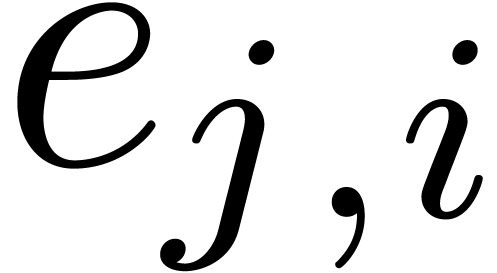 is at most
is at most
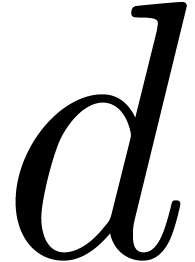 , Proposition 18
implies a cost
, Proposition 18
implies a cost 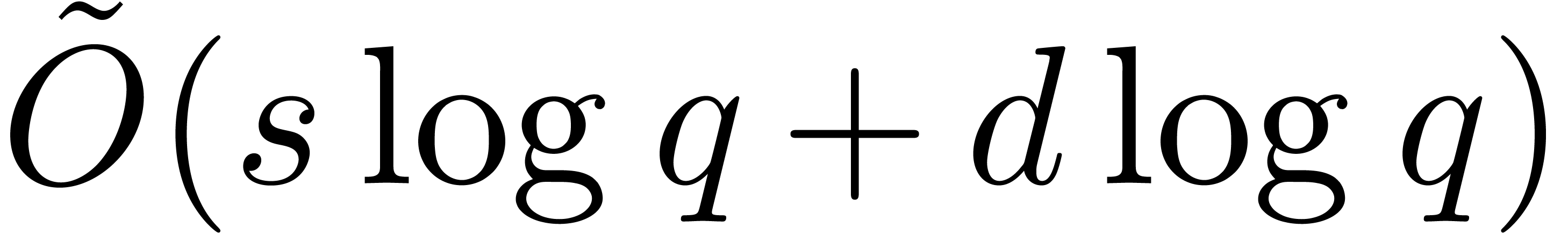 for step 5.
for step 5.
If 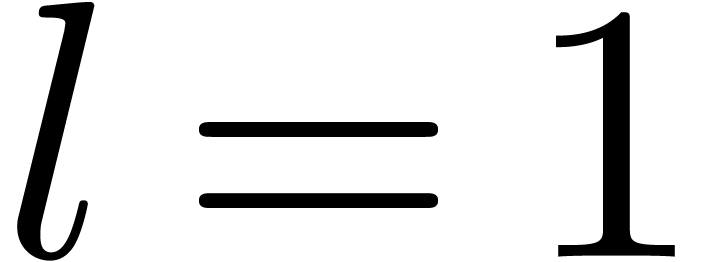 , then Algorithm 19
slightly improves Shoup's variant of Pollard–Strassen's algorithm
described in [43], which takes
, then Algorithm 19
slightly improves Shoup's variant of Pollard–Strassen's algorithm
described in [43], which takes 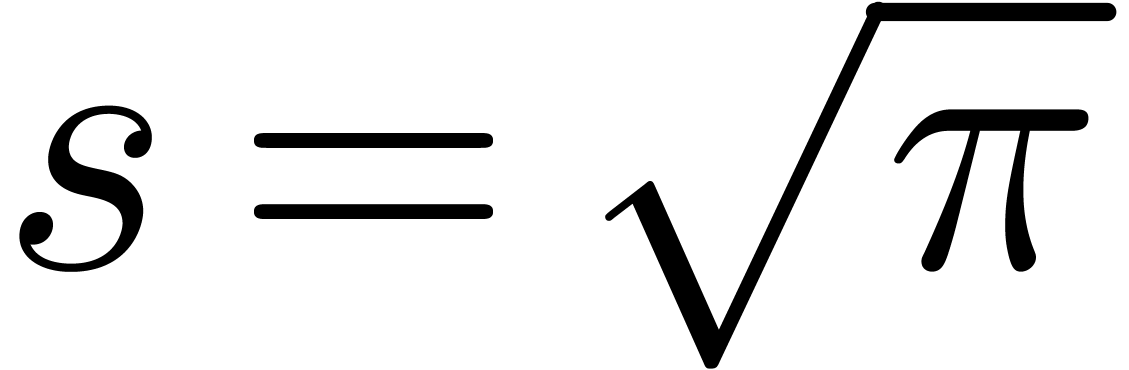 independently of
independently of 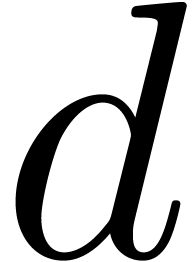 ; taking
; taking
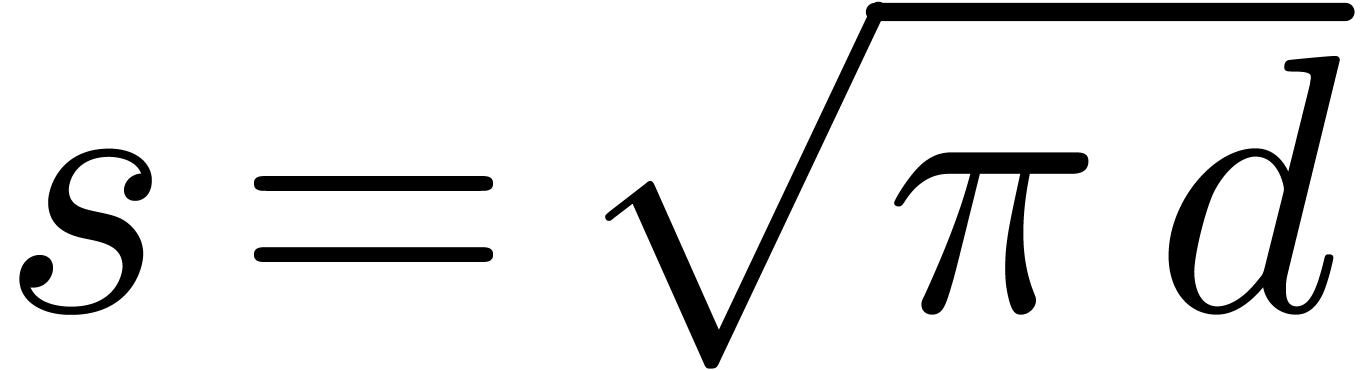 turns out to be a better trade-off between the
baby steps and the giant steps. We also notice that this trade-off might
be further improved by introducing logarithm factors in
turns out to be a better trade-off between the
baby steps and the giant steps. We also notice that this trade-off might
be further improved by introducing logarithm factors in  .
.
Let us recall that the term 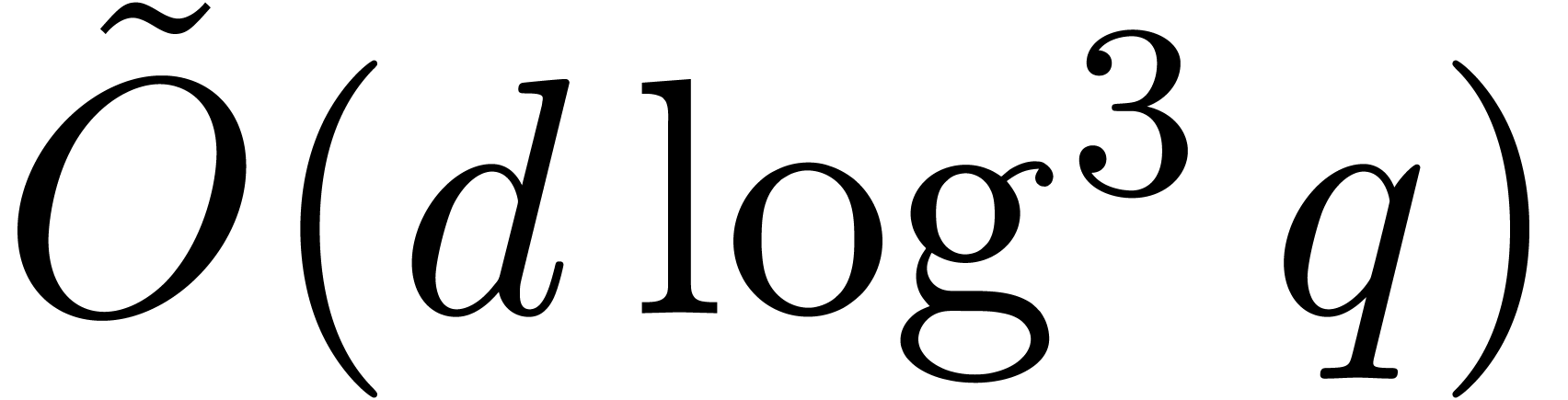 in the complexity of
Algoritm 13 is due to computing roots from their
logarithms. In the next subsection we will proceed differently and will
compute logarithms only when needed. This is why we now address the
discrete logarithm problem. Let us recall that the seminal discrete
logarithm method in the smooth case of
in the complexity of
Algoritm 13 is due to computing roots from their
logarithms. In the next subsection we will proceed differently and will
compute logarithms only when needed. This is why we now address the
discrete logarithm problem. Let us recall that the seminal discrete
logarithm method in the smooth case of 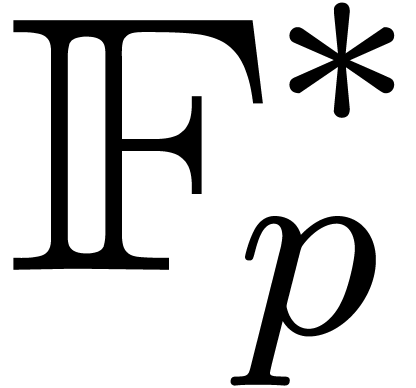 goes back
to [36] and performs
goes back
to [36] and performs 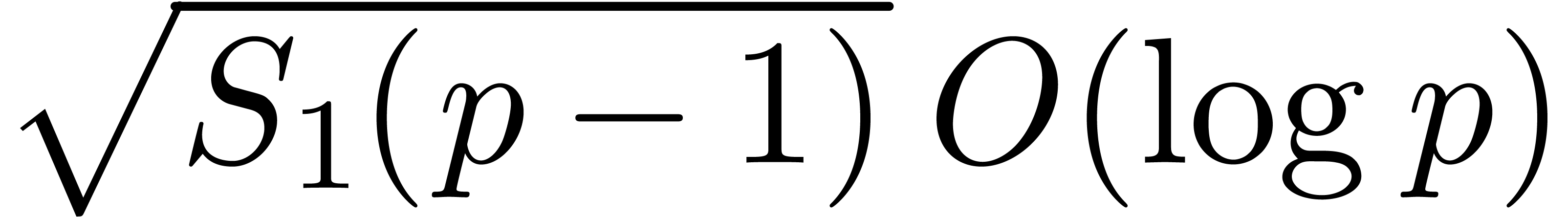 operations in
operations in
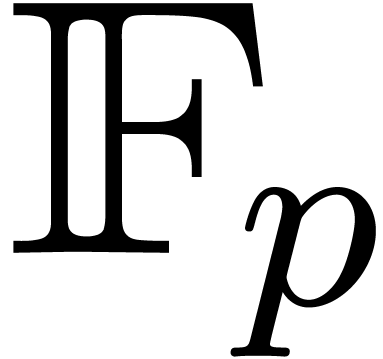 , making use internally of
Shanks' baby-step giant-step paradigm. We recall this algorithm for
completeness, adapting it to our context of Turing machines.
, making use internally of
Shanks' baby-step giant-step paradigm. We recall this algorithm for
completeness, adapting it to our context of Turing machines.
Algorithm
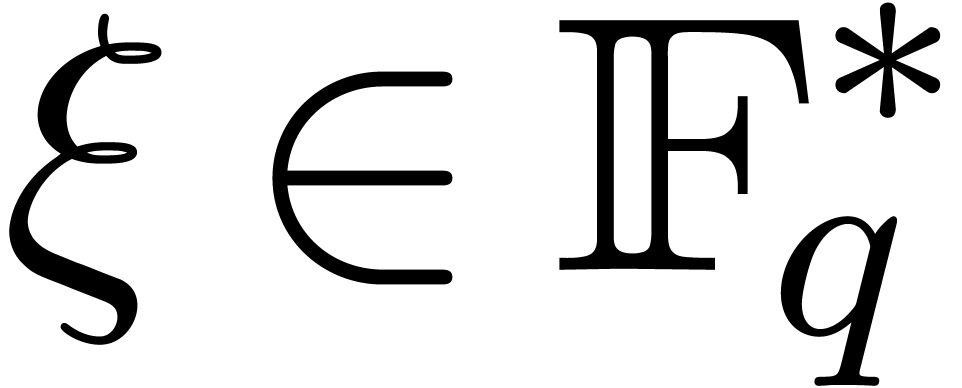 of order
of order
 of unity;
of unity;
 in the multiplicative subgroup generated by
in the multiplicative subgroup generated by
 .
.
The  -logarithm of
-logarithm of  in
in 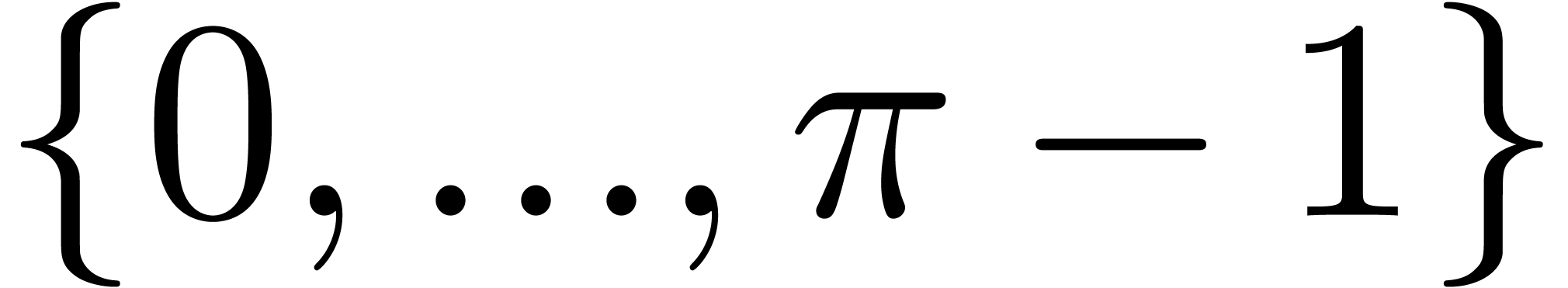 .
.
Let 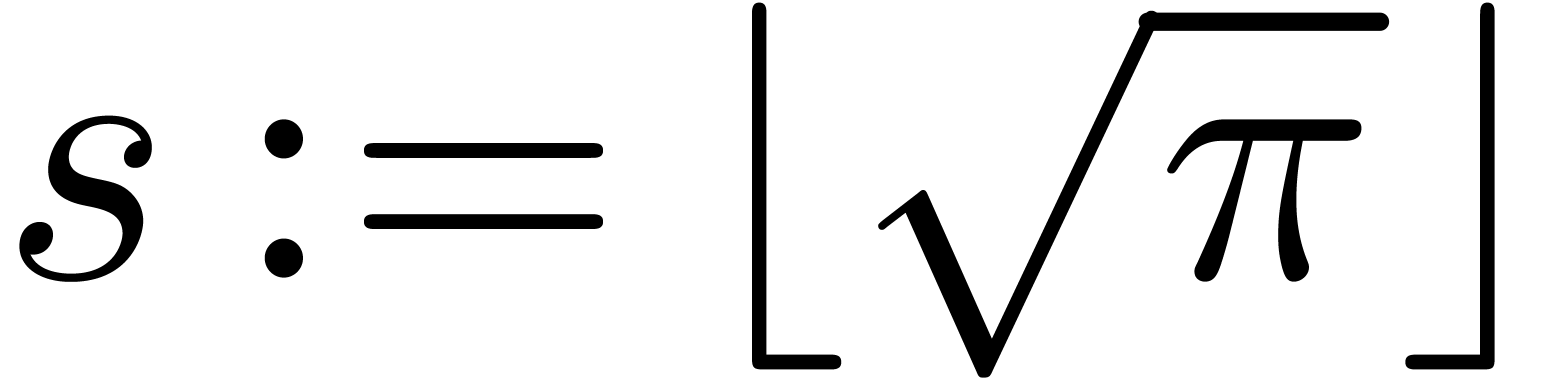 and
and  .
.
Compute 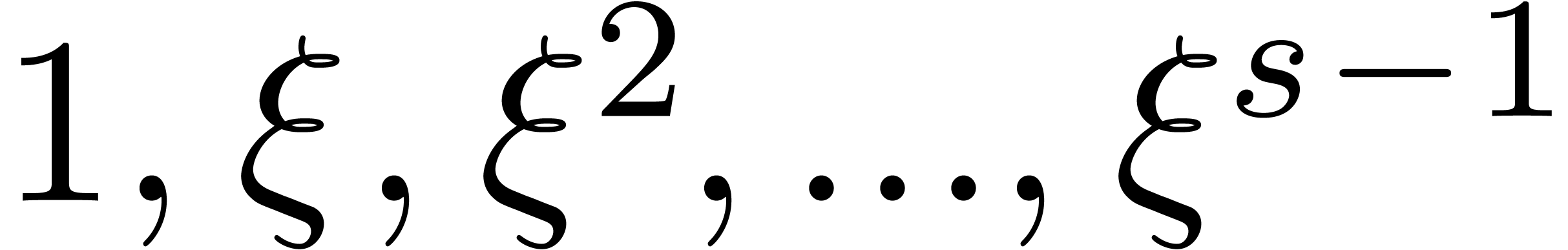 .
.
Compute 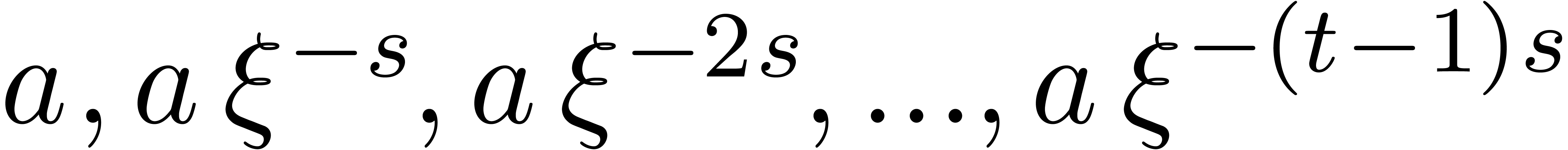 .
.
Sort the array made of the pairs 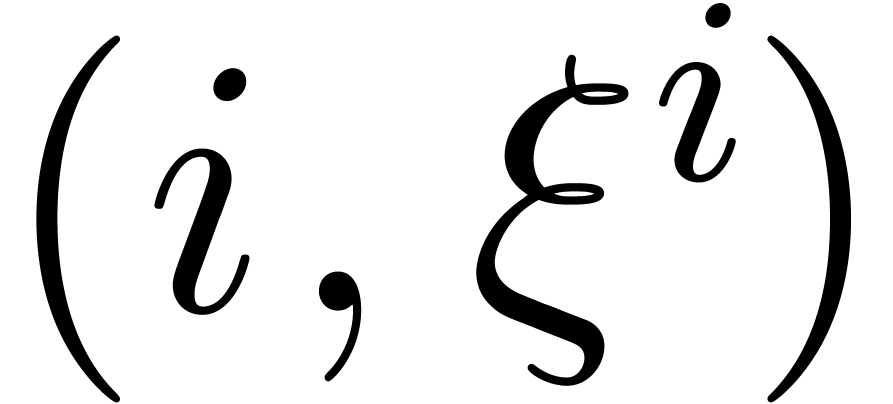 for
for  and
and 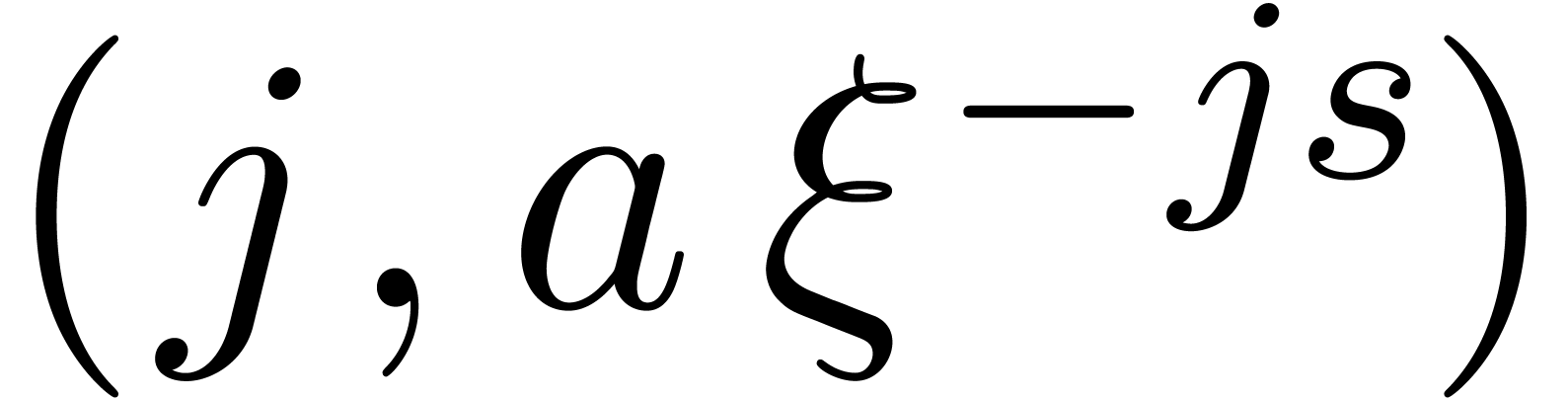 for
for  , accordingly to the lexicographic order of
the second entries of the pairs seen as
, accordingly to the lexicographic order of
the second entries of the pairs seen as 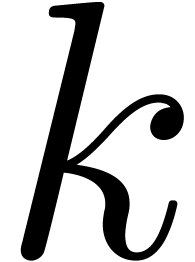 -tuples in
-tuples in 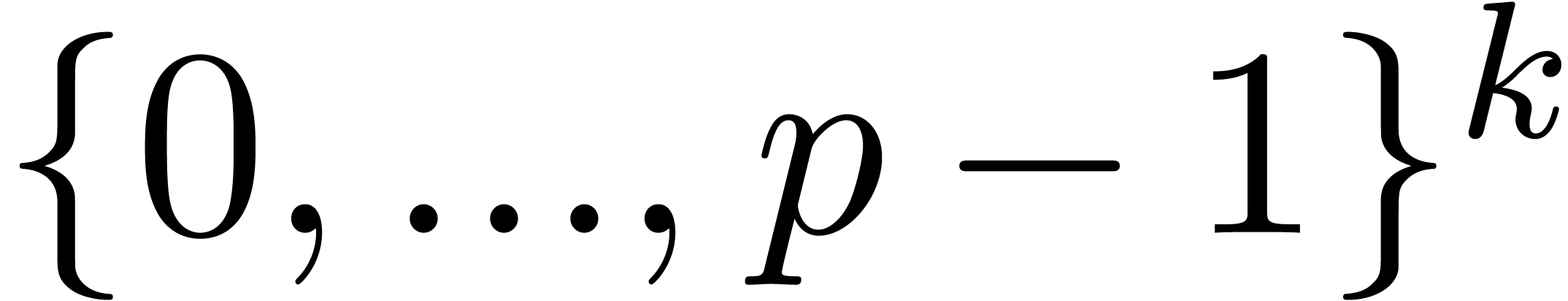 .
.
Find the first two consecutive pairs  and
and
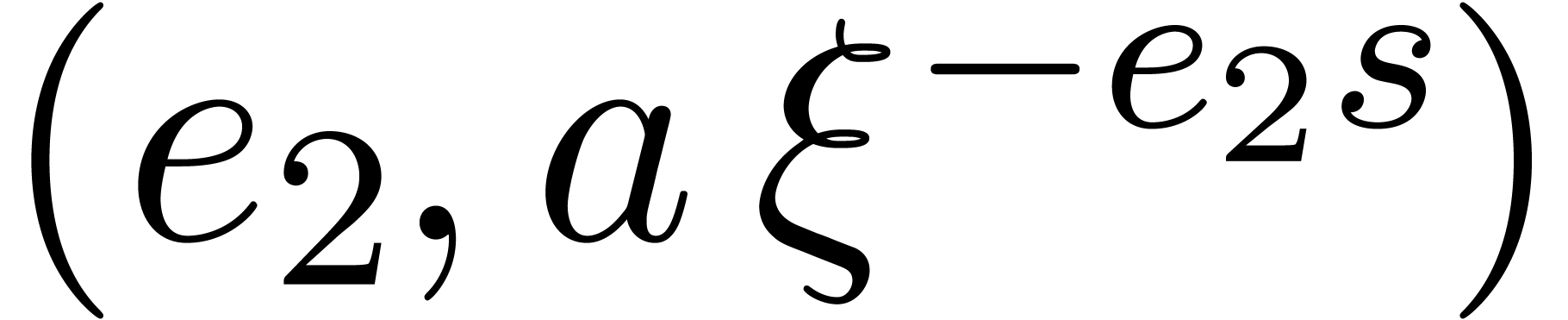 whose second entries coincide.
whose second entries coincide.
Return 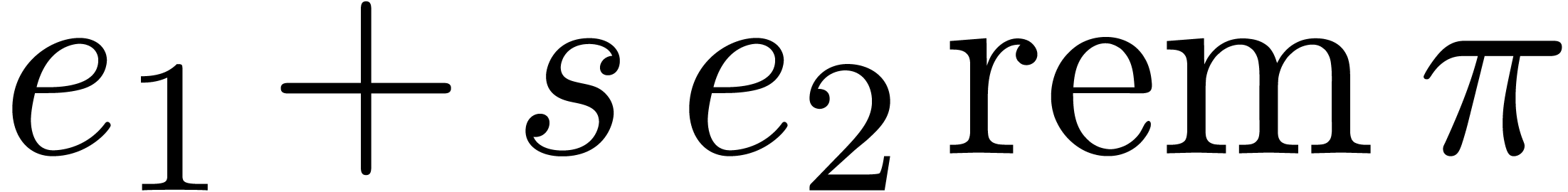 .
.
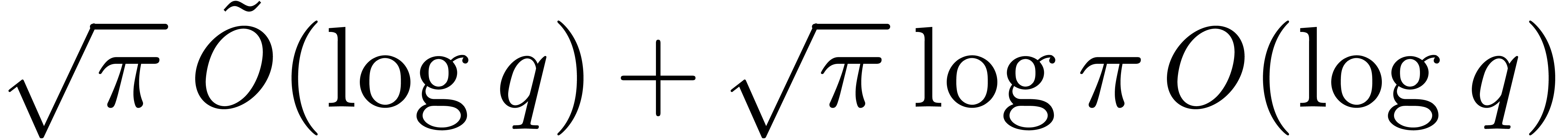 .
.
Proof. Since 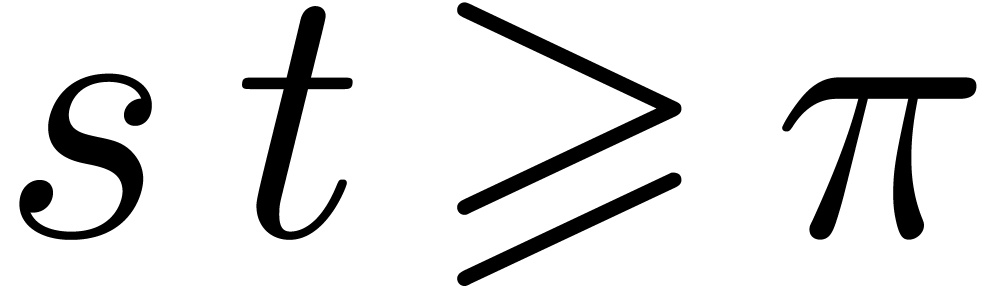 ,
the discrete logarithm
,
the discrete logarithm 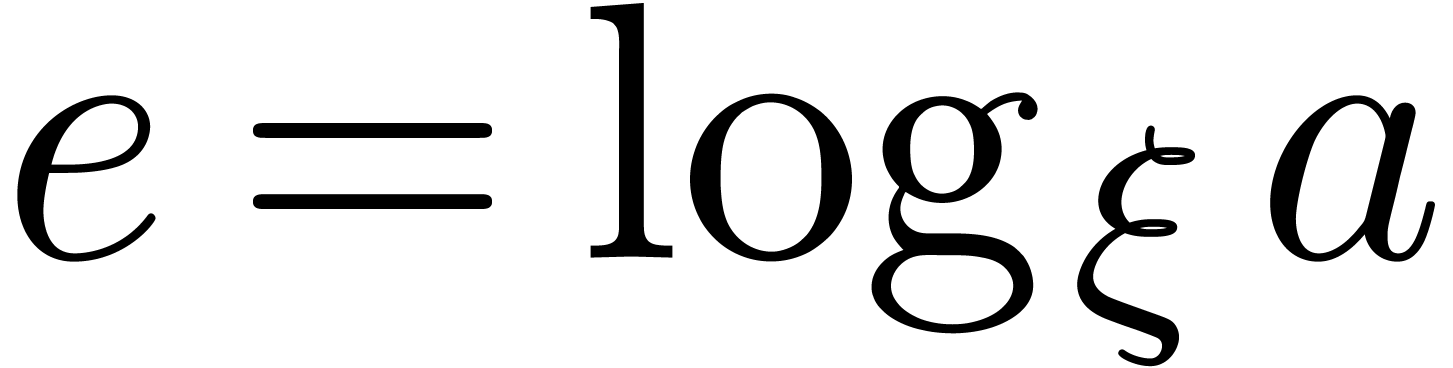 can be uniquely written
as
can be uniquely written
as 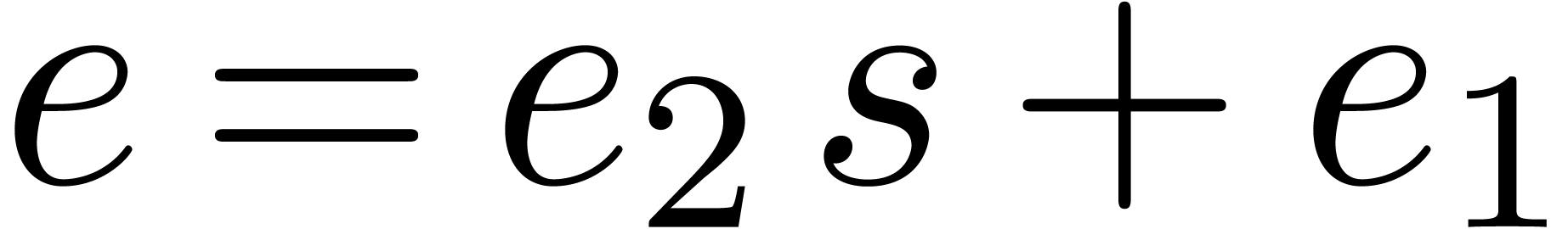 with
with 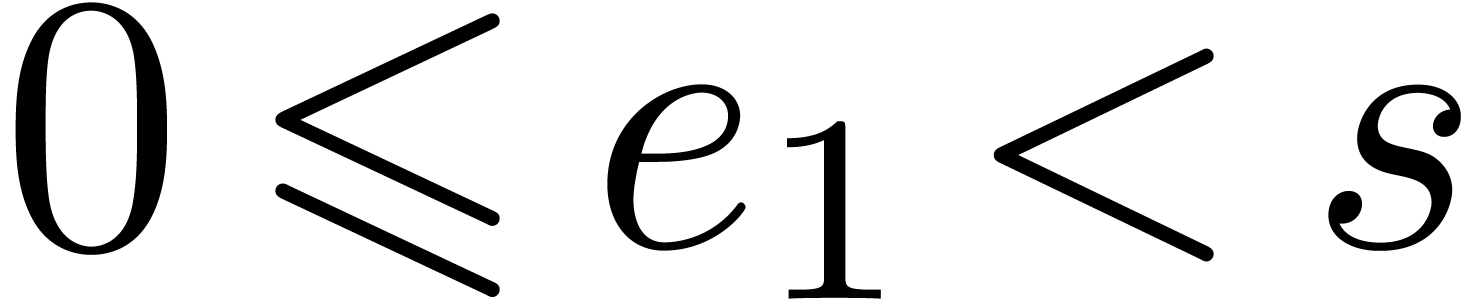 and
and 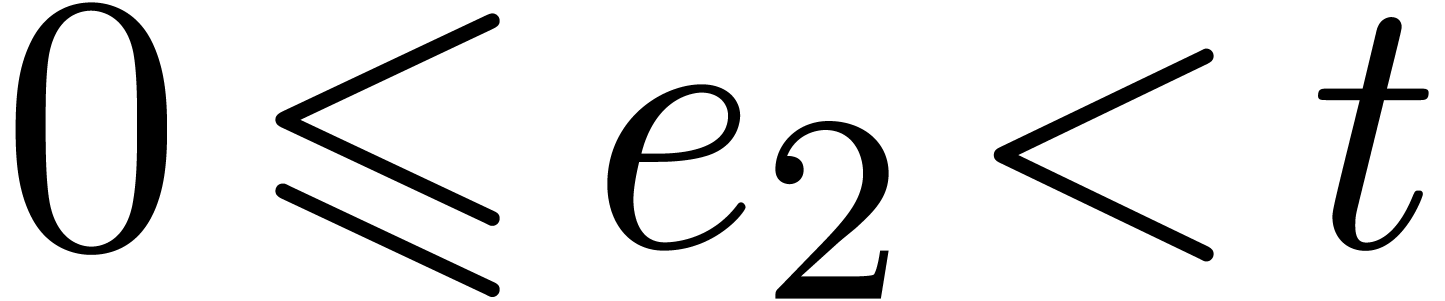 . This proves the correctness.
. This proves the correctness.
Steps 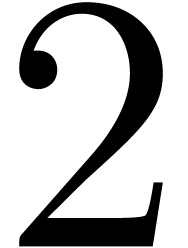 and
and  perform
perform 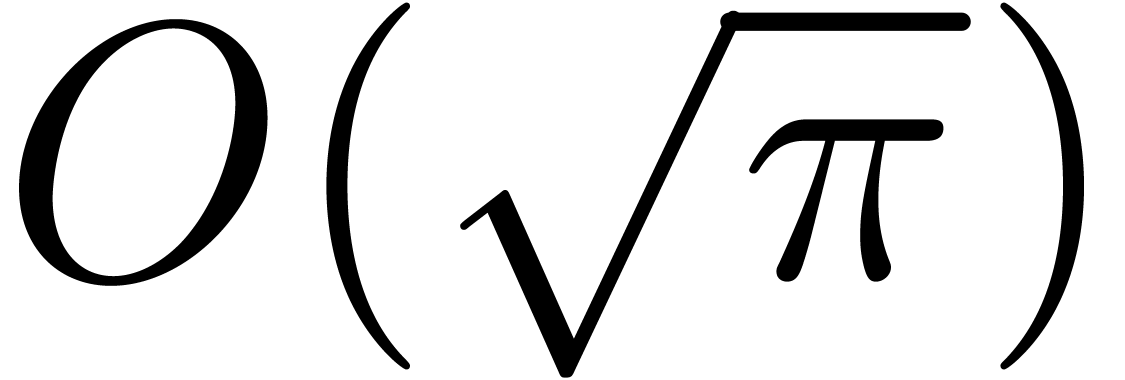 products in
products in  and one
inversion. Using the merge-sort algorithm, step 4 costs
and one
inversion. Using the merge-sort algorithm, step 4 costs 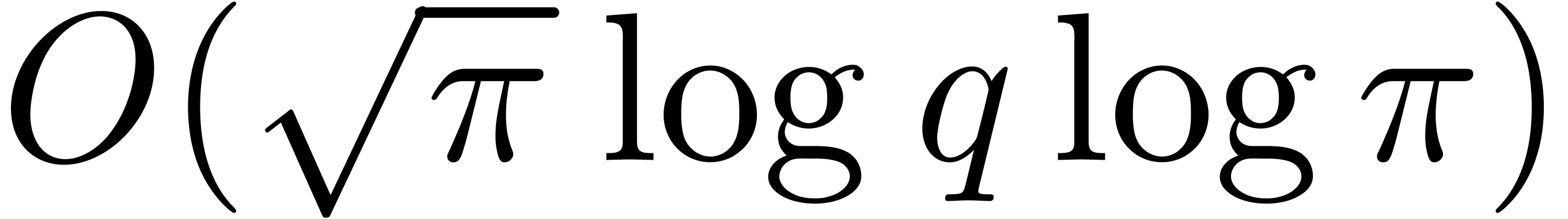 .
.
The following divide and conquer approach allows us to compute
logarithms for composite orders 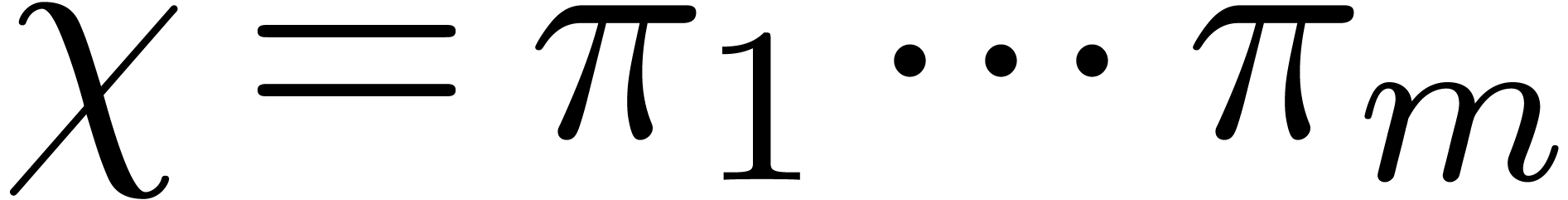 .
Independently from the previous algorithm, it leads to a good complexity
bound in terms of
.
Independently from the previous algorithm, it leads to a good complexity
bound in terms of 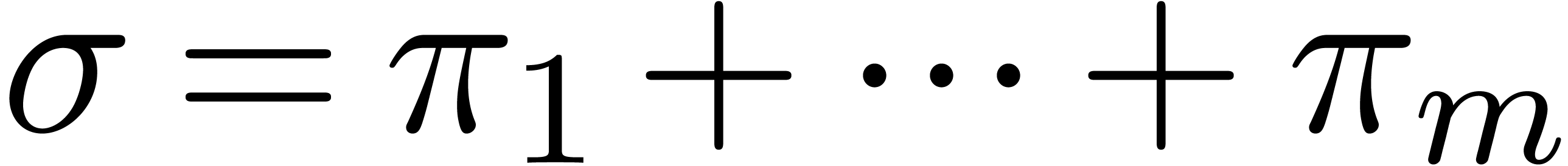 . This
approach might already be known, but we could not find a reference to it
in the literature.
. This
approach might already be known, but we could not find a reference to it
in the literature.
Algorithm
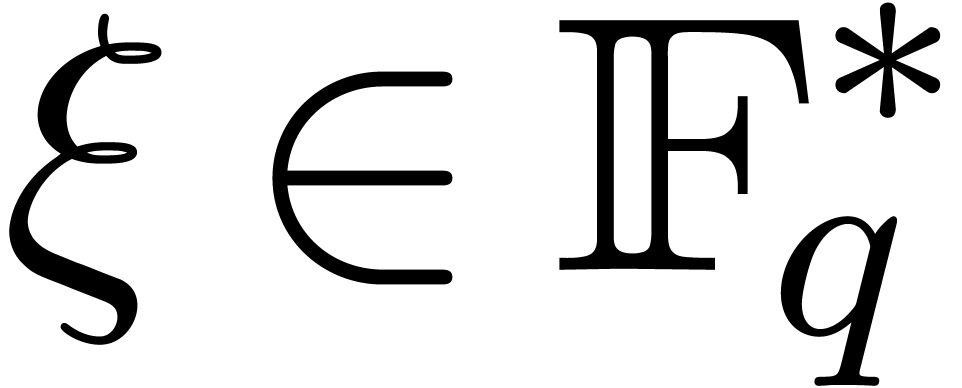 of order
of order
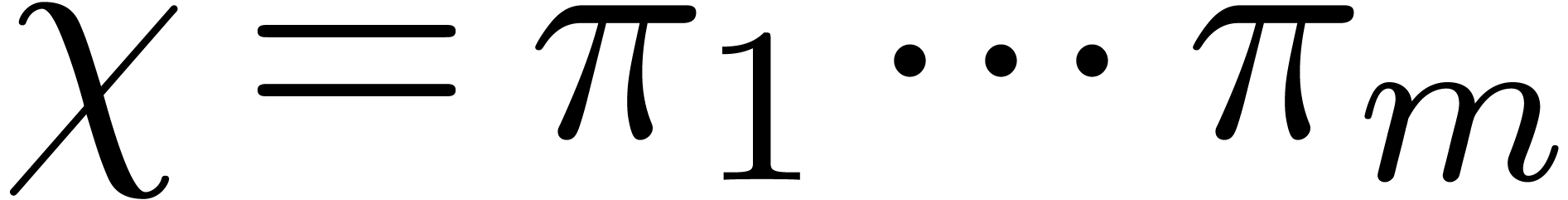 ,
with given
,
with given
 ;
;
 in the multiplicative subgroup generated by
in the multiplicative subgroup generated by
 .
.
The  -logarithm of
-logarithm of  in
in 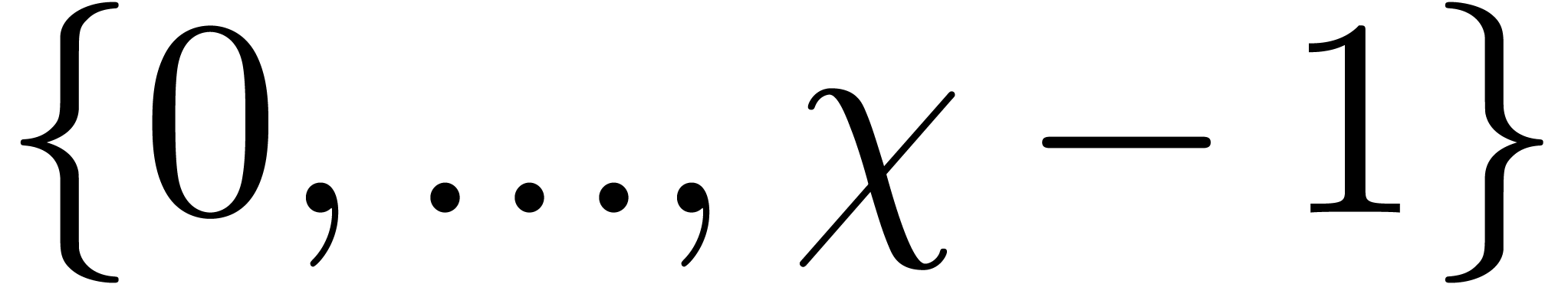 .
.
If 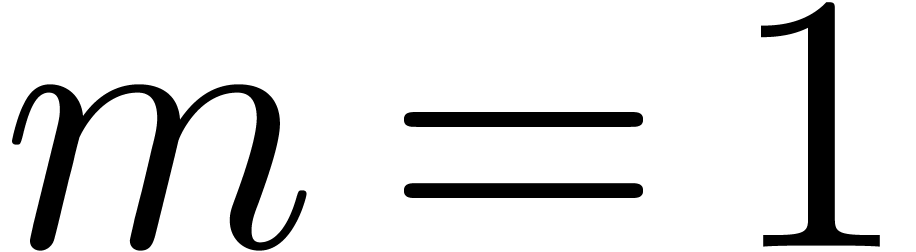 , then find and return
, then find and return
 such that
such that 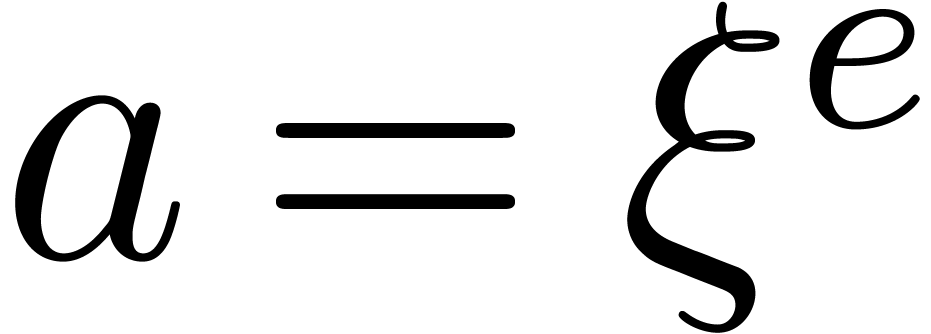 .
.
Let 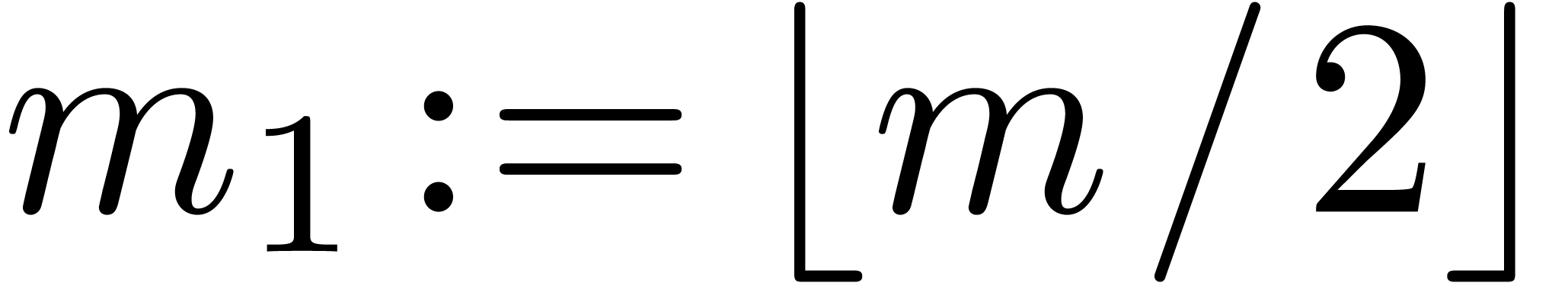 ,
, 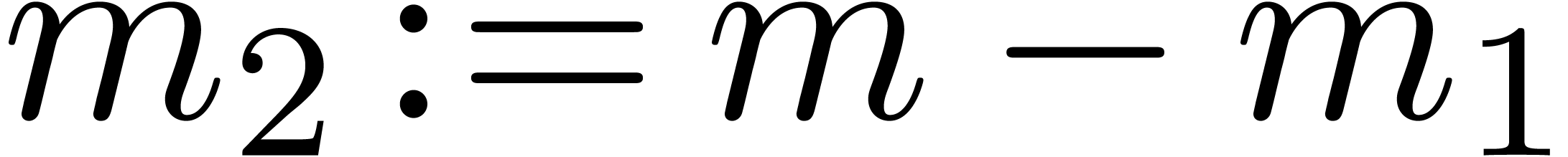 ,
, 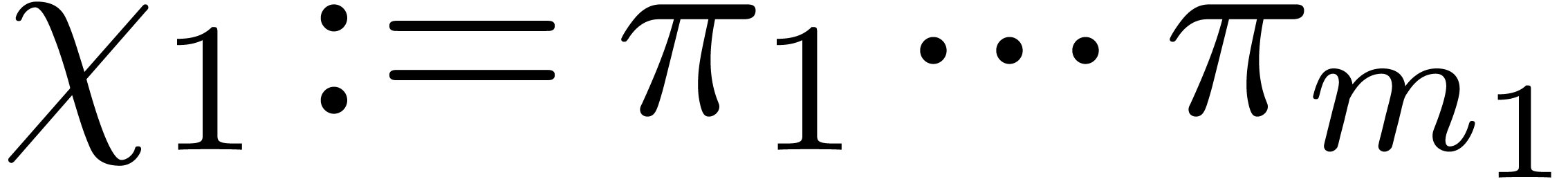 and
and 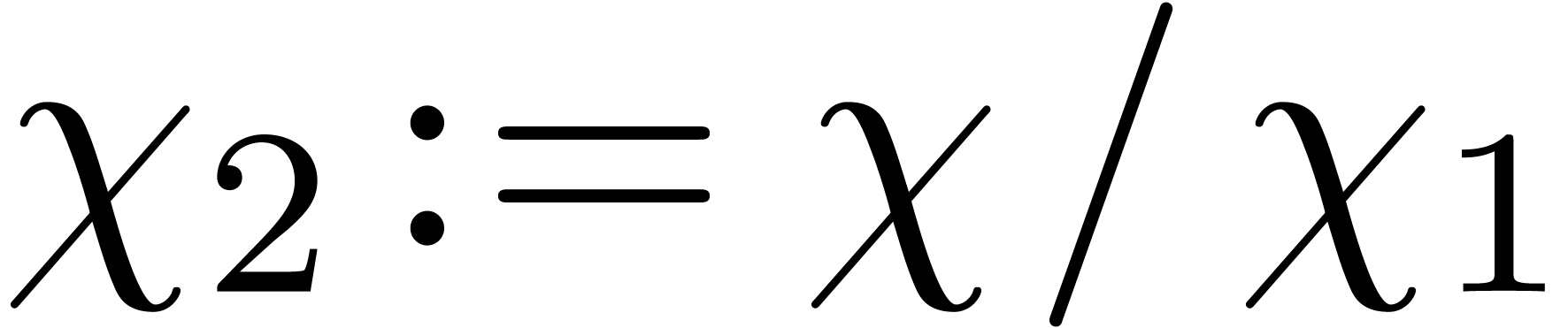 .
.
Recursively compute 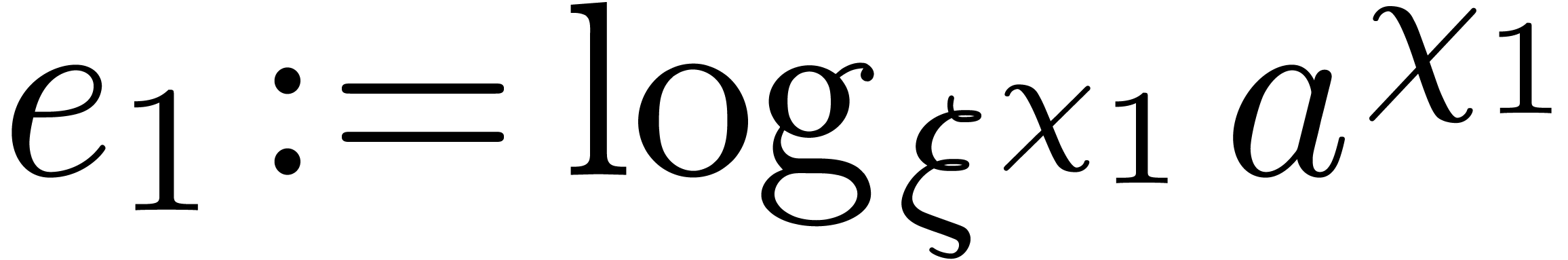 .
.
Recursively compute 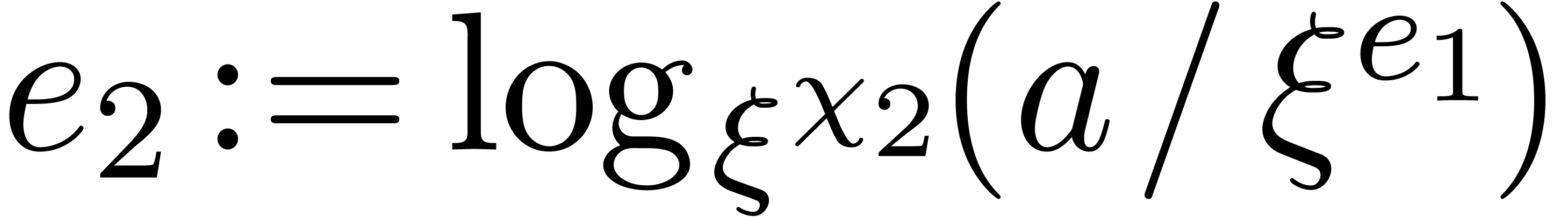 .
.
Return 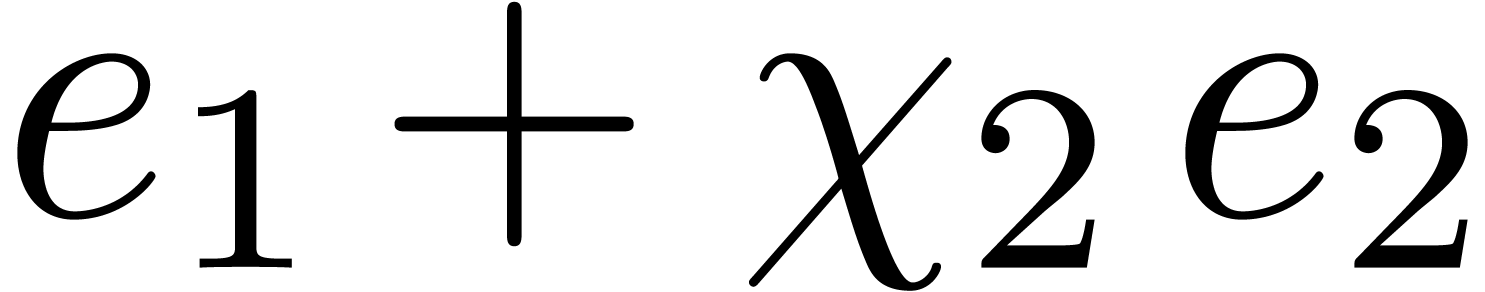 .
.
 . By using
Algorithm 21 in step 1, the cost becomes
. By using
Algorithm 21 in step 1, the cost becomes 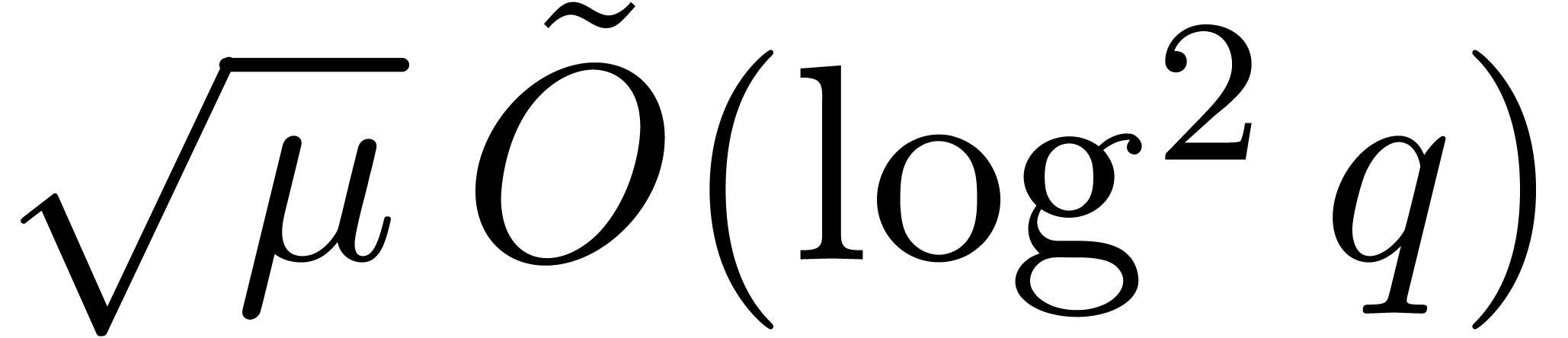 , where
, where  .
.
Proof. We prove the correctness by induction.
The case 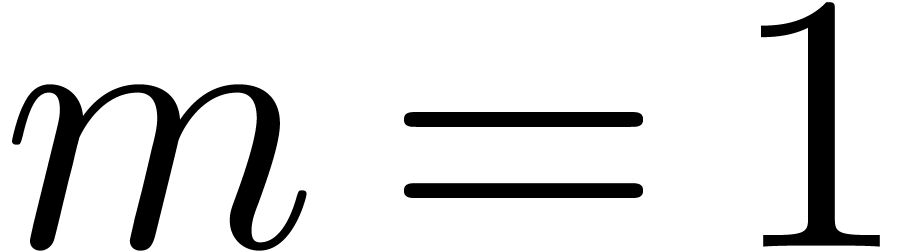 is clear. Assume
is clear. Assume 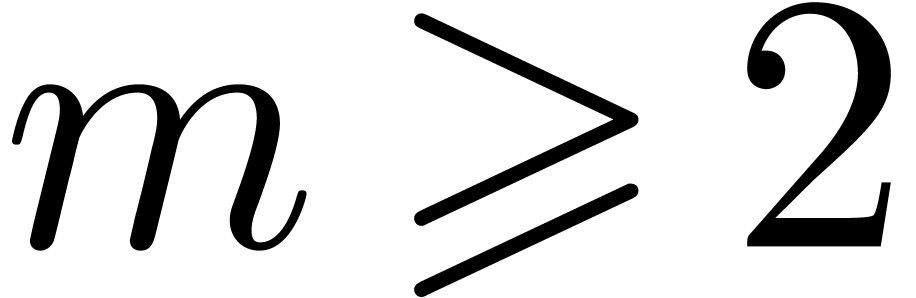 . In step 3, we have
. In step 3, we have  .
By definition of
.
By definition of 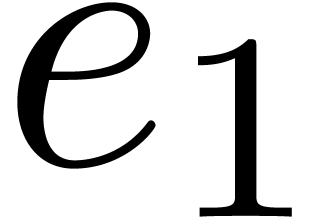 , we have
, we have
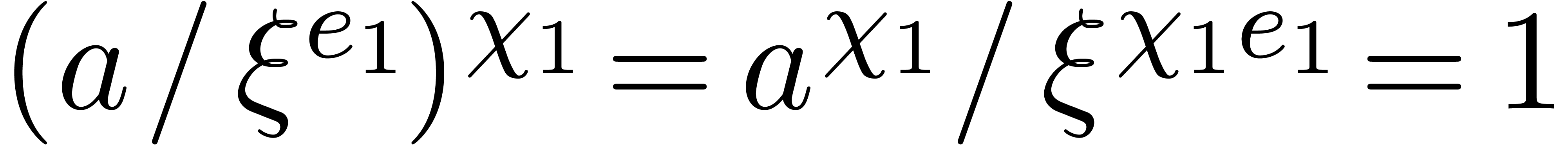 in step 4, whence
in step 4, whence  indeed
lies in the multiplicative subgroup of order
indeed
lies in the multiplicative subgroup of order 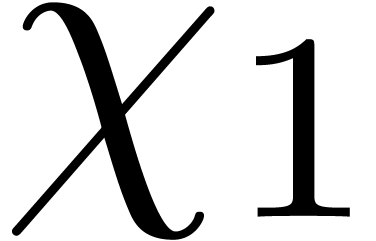 generated by
generated by 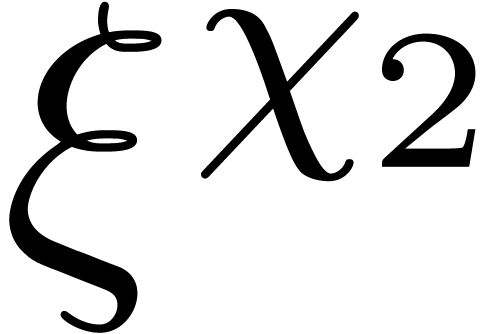 . By definition
of
. By definition
of 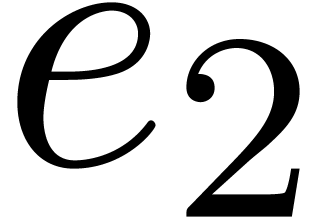 , we have
, we have 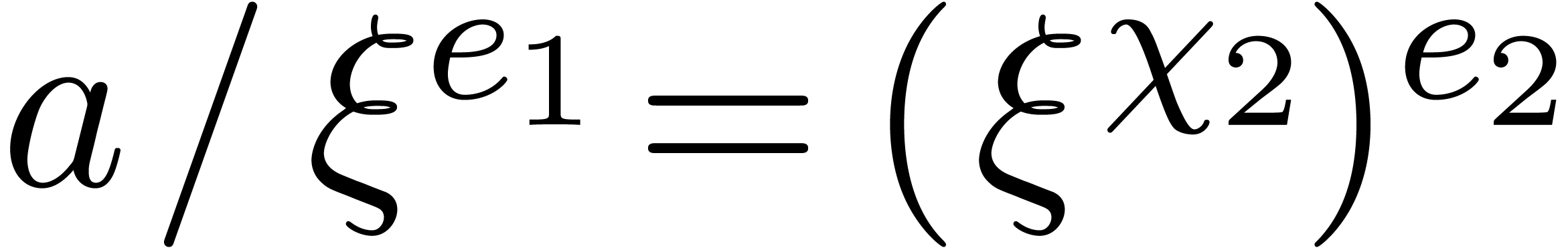 , whence
, whence 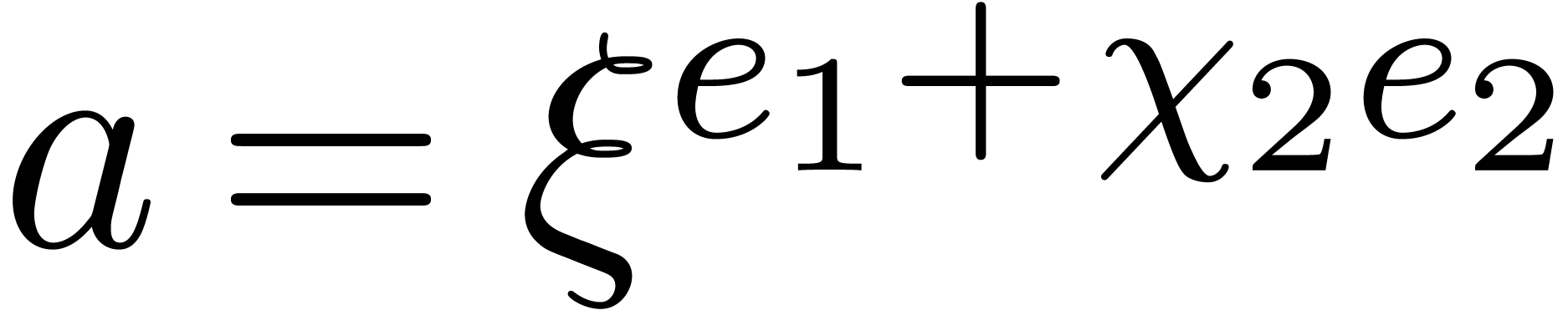 ,
which completes the induction.
,
which completes the induction.
As to the complexity bound, let 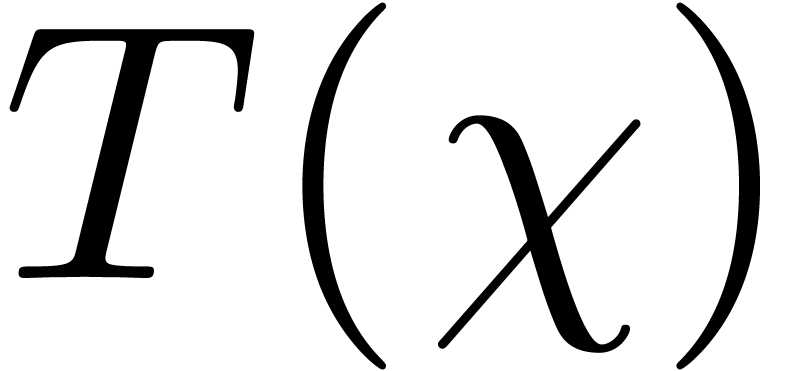 denote the cost
of the algorithm. We share the subproduct tree built from
denote the cost
of the algorithm. We share the subproduct tree built from  , in time
, in time 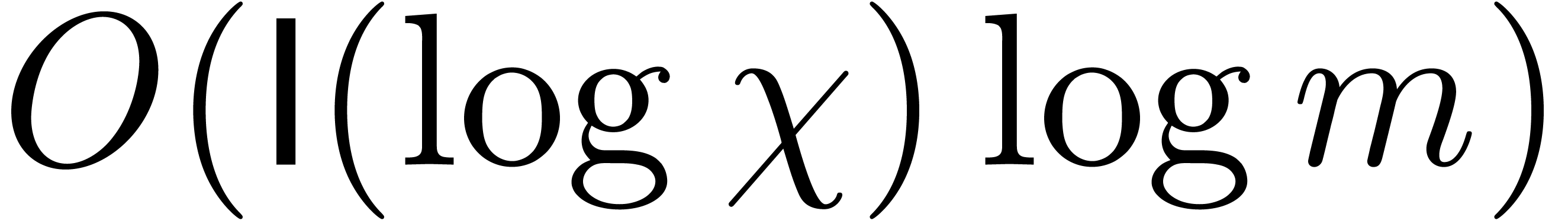 ,
between the recursive calls. Using binary powering in steps 3 and 4, we
obtain the recursion relation
,
between the recursive calls. Using binary powering in steps 3 and 4, we
obtain the recursion relation
which leads to the bound 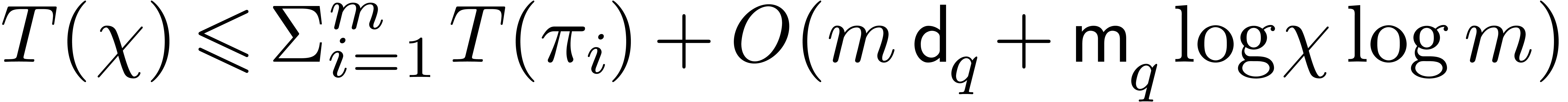 .
.
Using a naive exhaustive search in step 1 yields 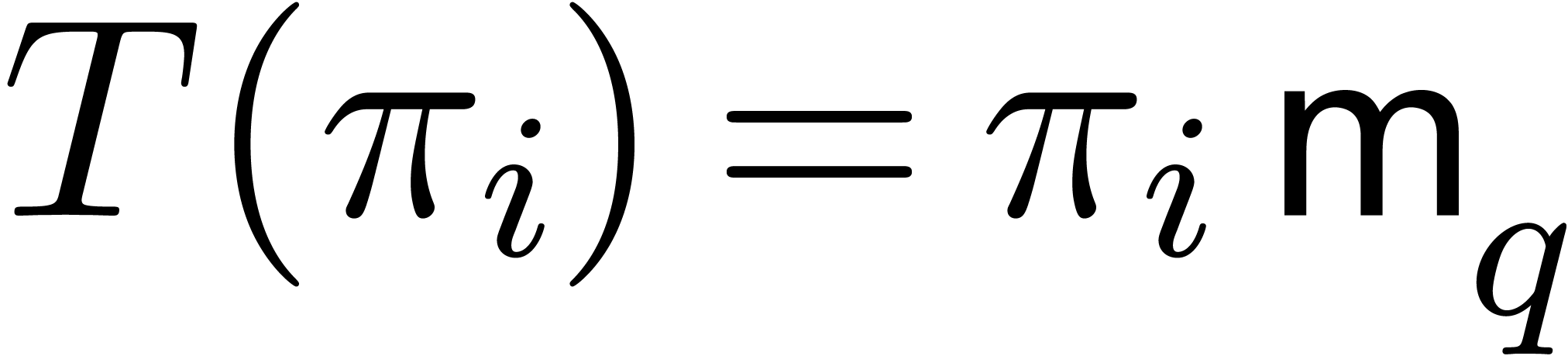 , whence
, whence  .
The first bound thus follows using
.
The first bound thus follows using 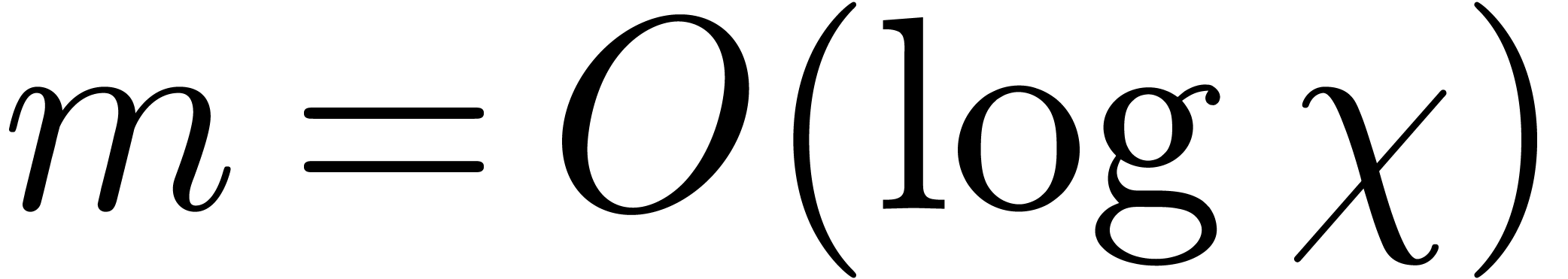 .
The second bound follows from Proposition 22 that gives
.
The second bound follows from Proposition 22 that gives
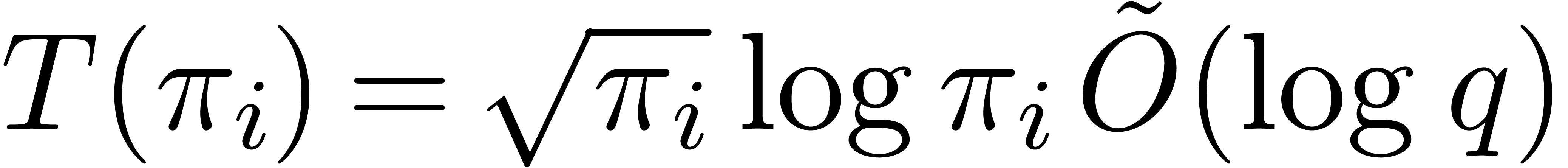 .
.
Remark  of order
of order 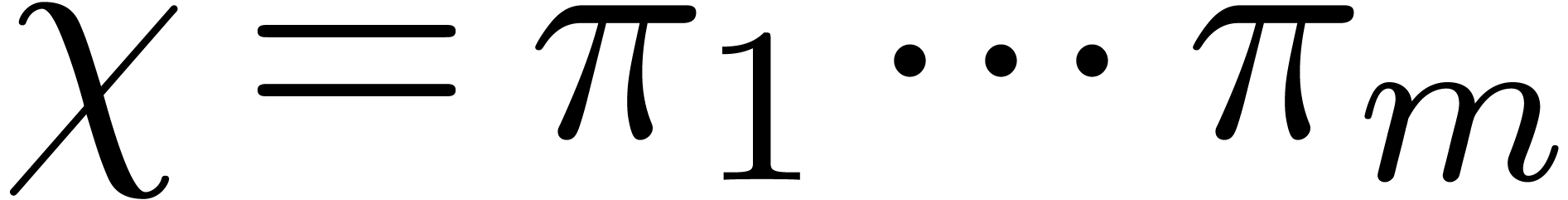 , where the
, where the 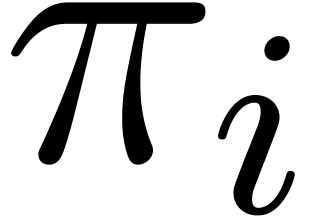 are given
integers
are given
integers 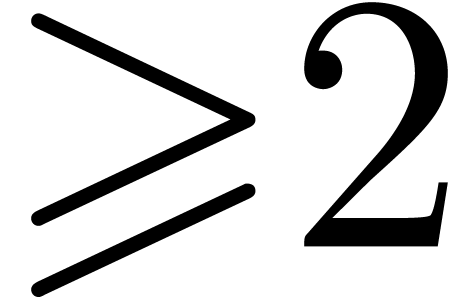 , one may compute
primitive roots of unity
, one may compute
primitive roots of unity  for all orders
for all orders 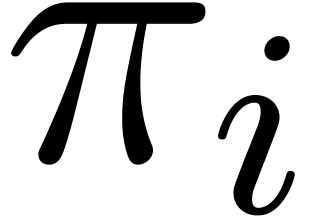 in time
in time 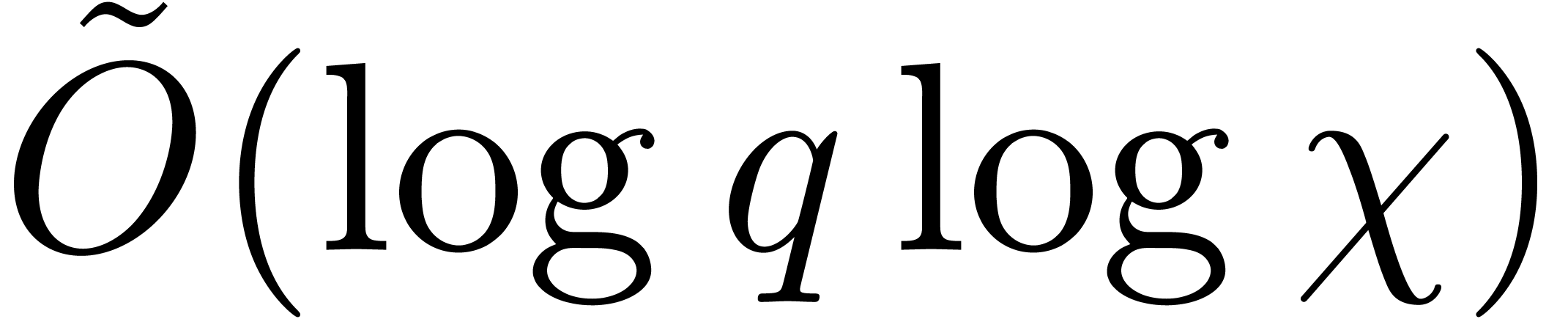 .
.
Over any field  the separable factorization of a
univariate polynomial
the separable factorization of a
univariate polynomial  of degree
of degree 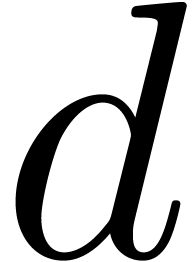 can computed by means of
can computed by means of 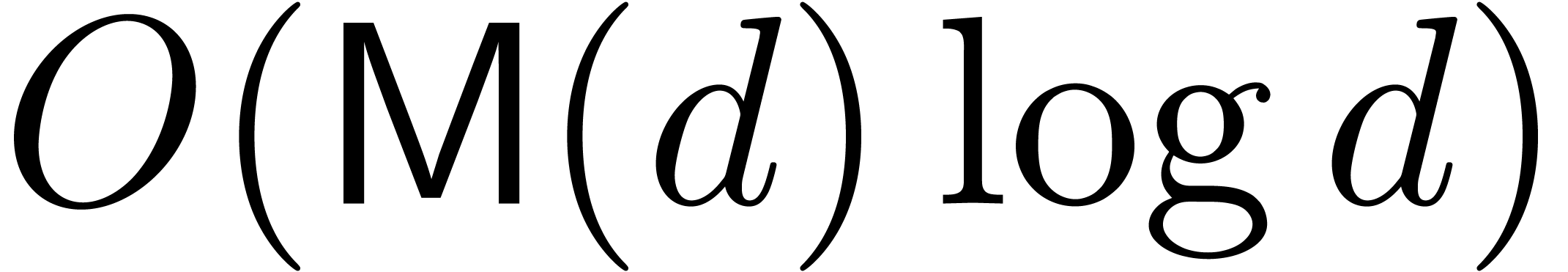 operations in
operations in  [29]. If
[29]. If  is the
finite field
is the
finite field  then it is possible to deduce the
squarefree factorization of
then it is possible to deduce the
squarefree factorization of  with
with 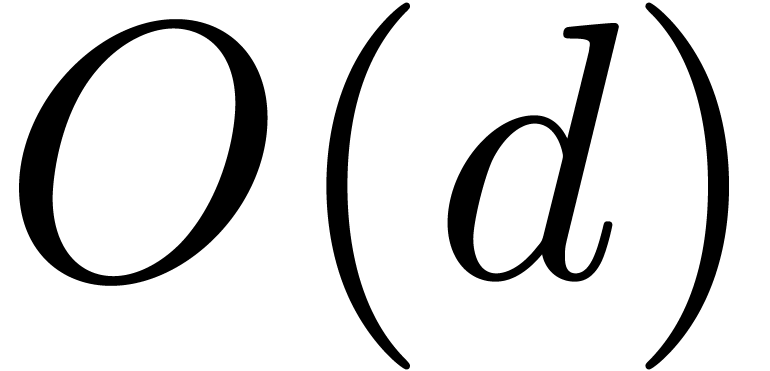 additional extractions of
additional extractions of 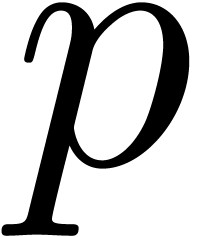 -th
roots [29, Section 4]. This result is also left as an
exercise in [17, Chapter 14, Exercise 14.30]. In the
special case when
-th
roots [29, Section 4]. This result is also left as an
exercise in [17, Chapter 14, Exercise 14.30]. In the
special case when 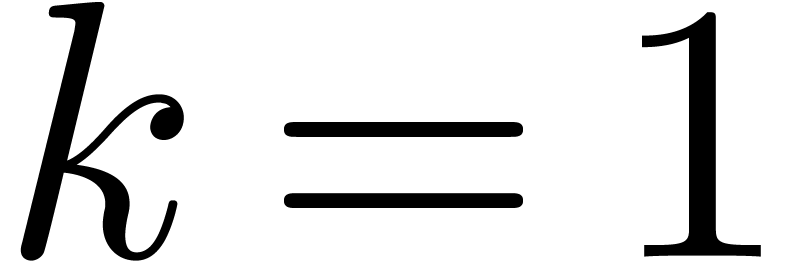 and
and  , no root extraction is necessary and the squarefree
part of
, no root extraction is necessary and the squarefree
part of  is obtained as
is obtained as 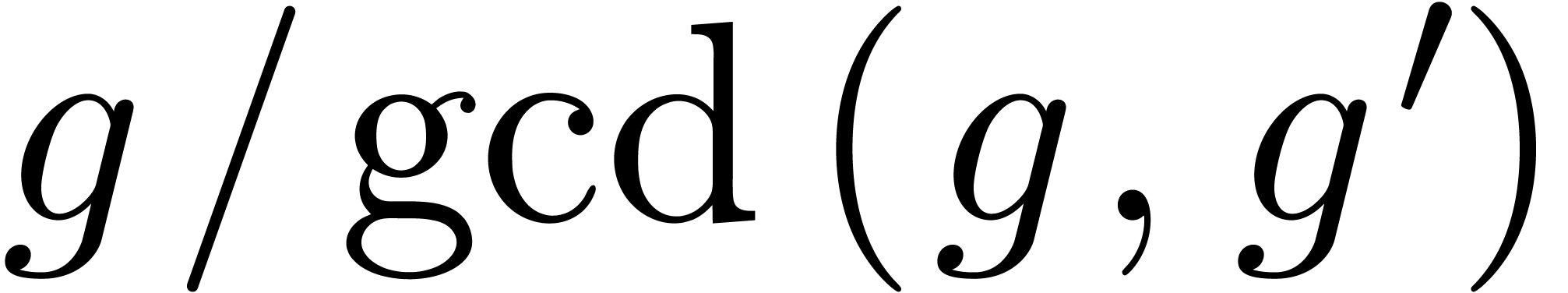 . In the next subsection we will need the following
bound, taking the number of simple and multiple roots into account.
. In the next subsection we will need the following
bound, taking the number of simple and multiple roots into account.
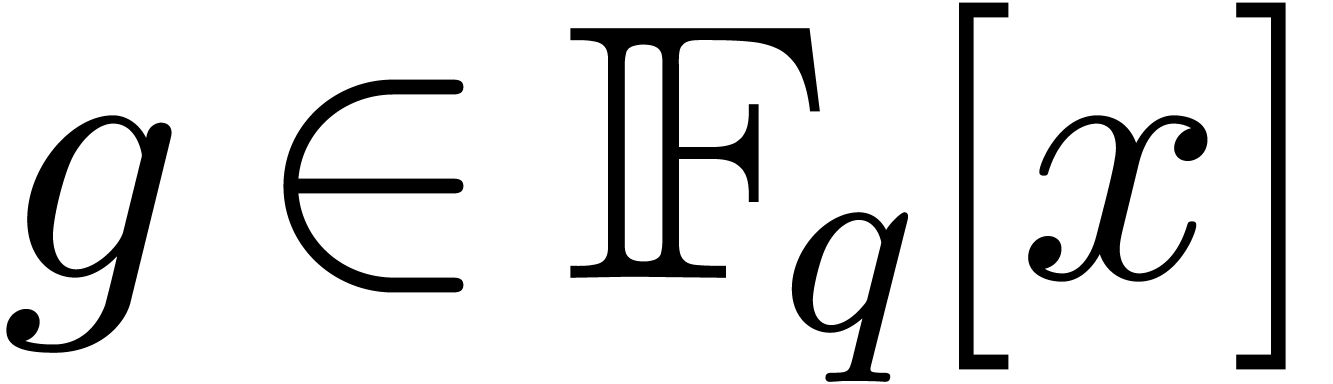 be of degree
be of degree 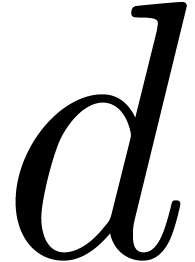 . In an algebraic closure of
. In an algebraic closure of
 , let
, let 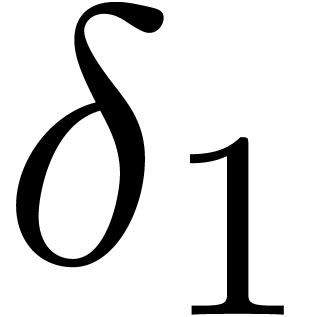 be the number of simple roots of
be the number of simple roots of  ,
let
,
let 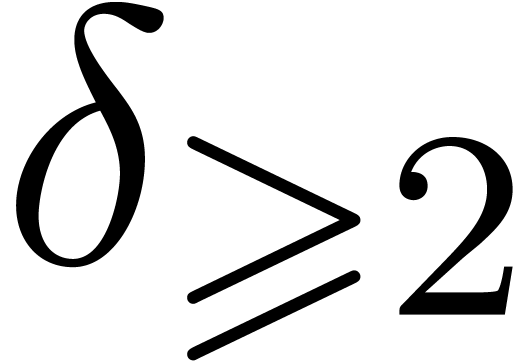 be the number of its multiple roots, and
let
be the number of its multiple roots, and
let 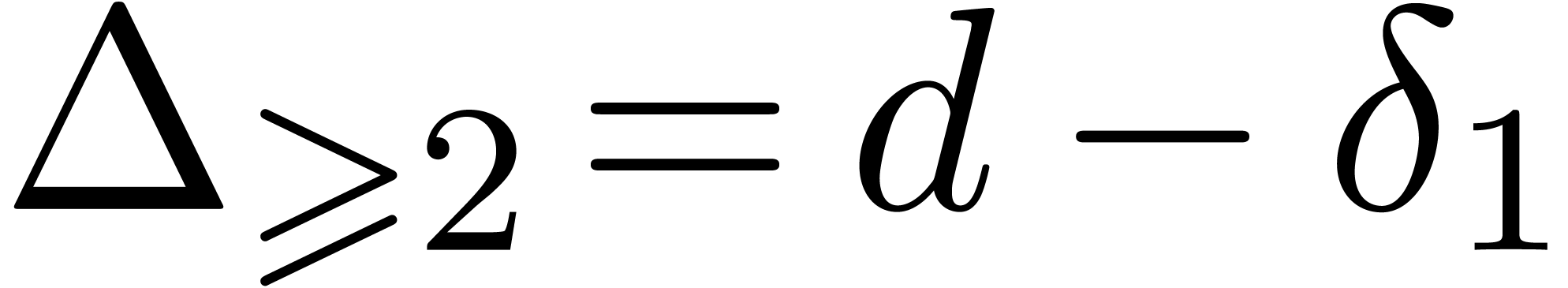 be the number of multiple roots counted
with multiplicities. Then the squarefree factorization and the
squarefree part of
be the number of multiple roots counted
with multiplicities. Then the squarefree factorization and the
squarefree part of 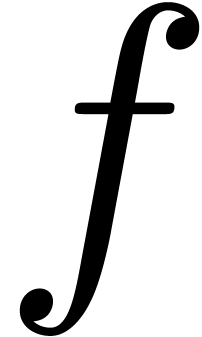 may be computed in time
may be computed in time

Proof. Let  in
in 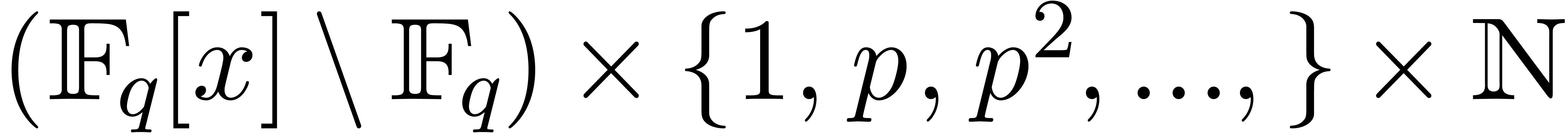 represent the separable factorization of
represent the separable factorization of  [29, Introduction], so that we have
[29, Introduction], so that we have 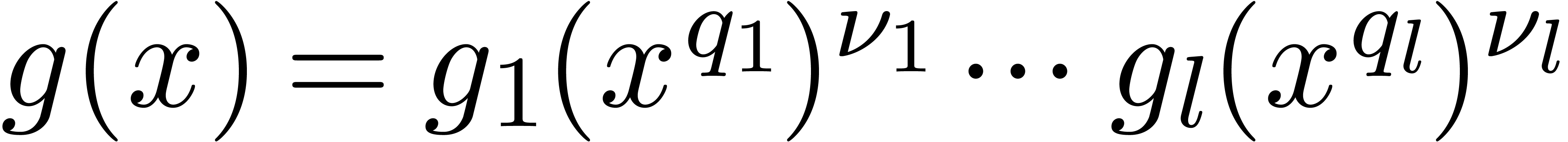 . Since
. Since  is perfect, the
factors
is perfect, the
factors 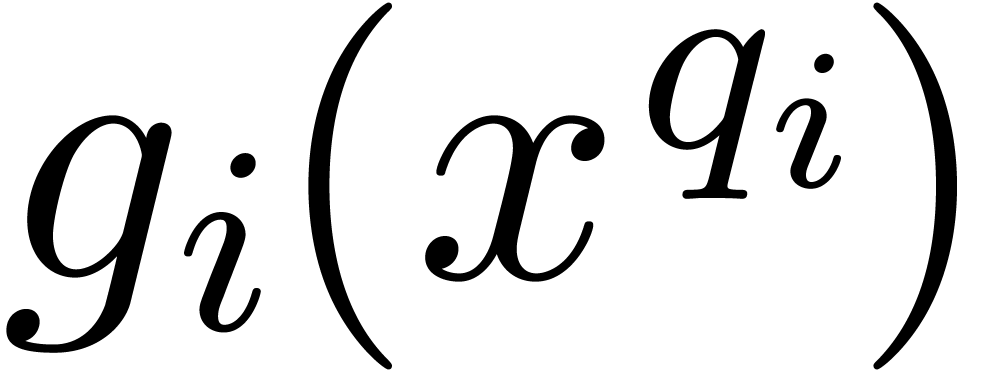 with
with 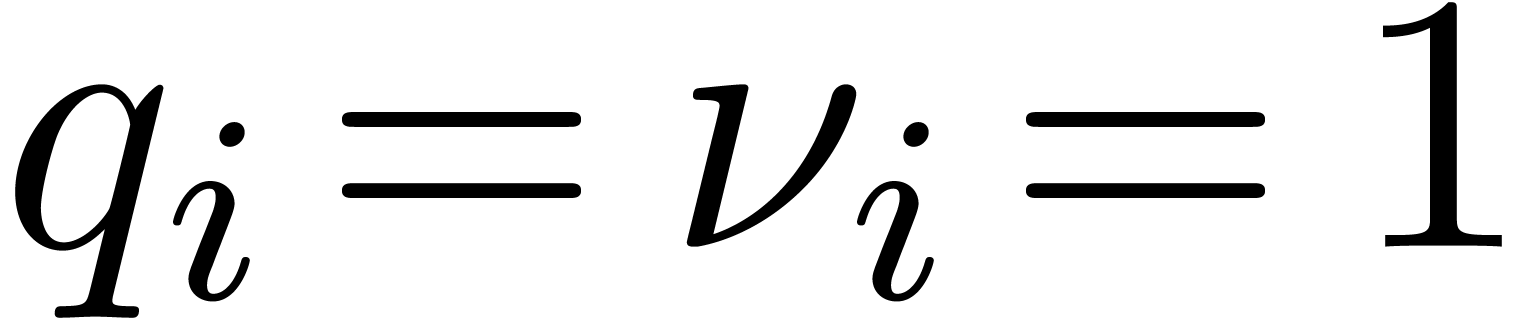 contain all
the simple roots of
contain all
the simple roots of  . Letting
. Letting
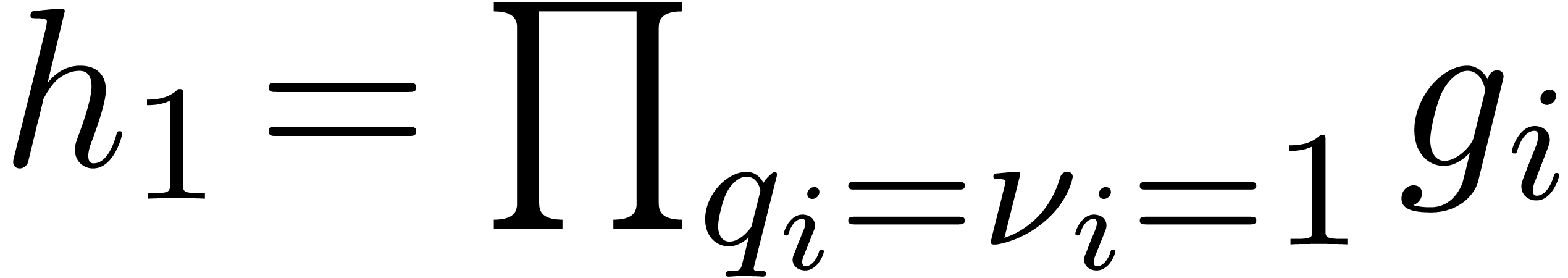 and
and 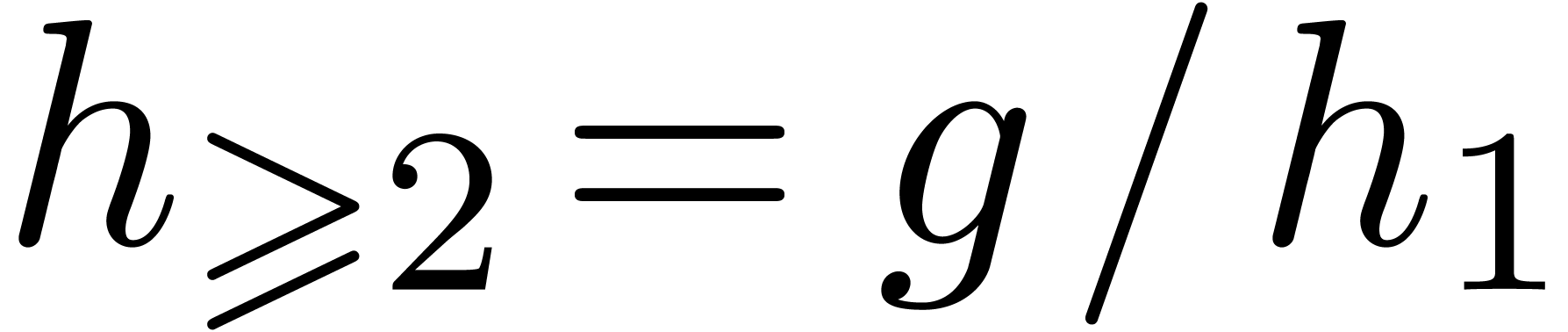 ,
we have
,
we have 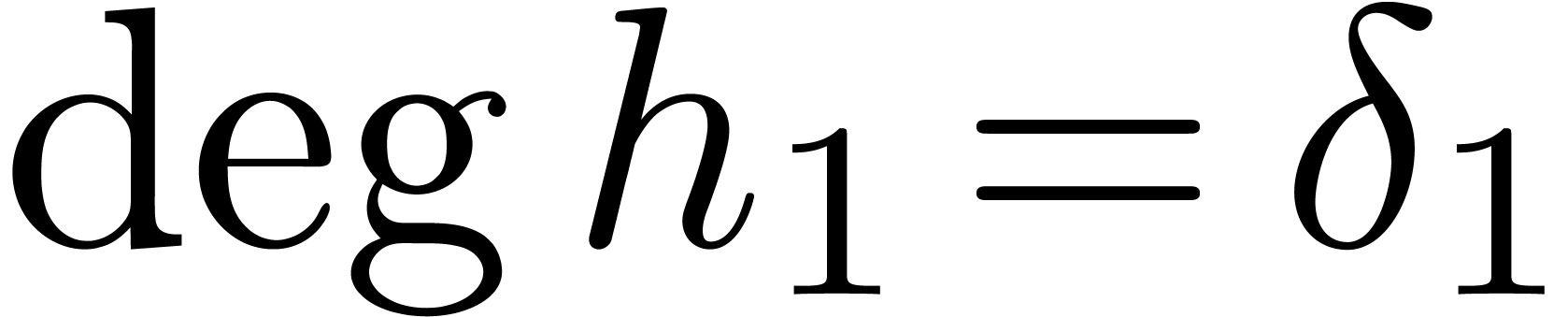 and
and 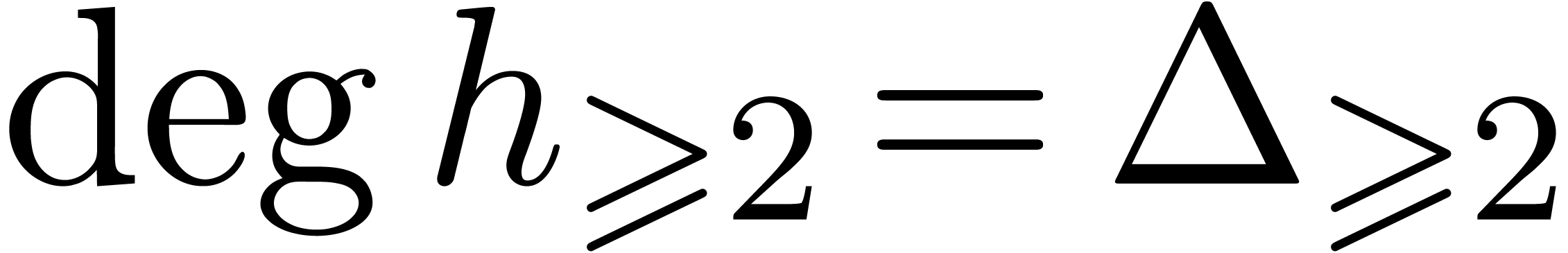 .
Following [29, Section 4], the actual number of
.
Following [29, Section 4], the actual number of 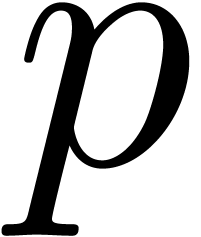 -th root extractions is
-th root extractions is 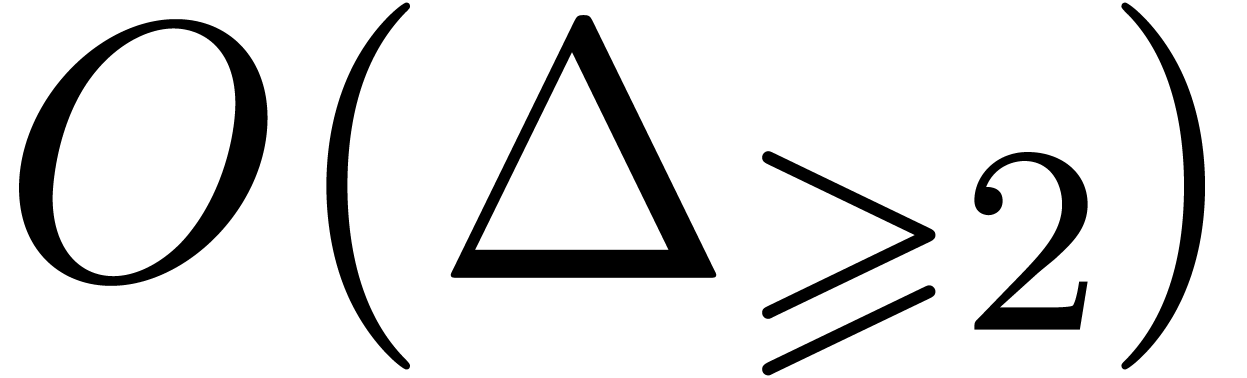 . Each such extraction amounts to
. Each such extraction amounts to
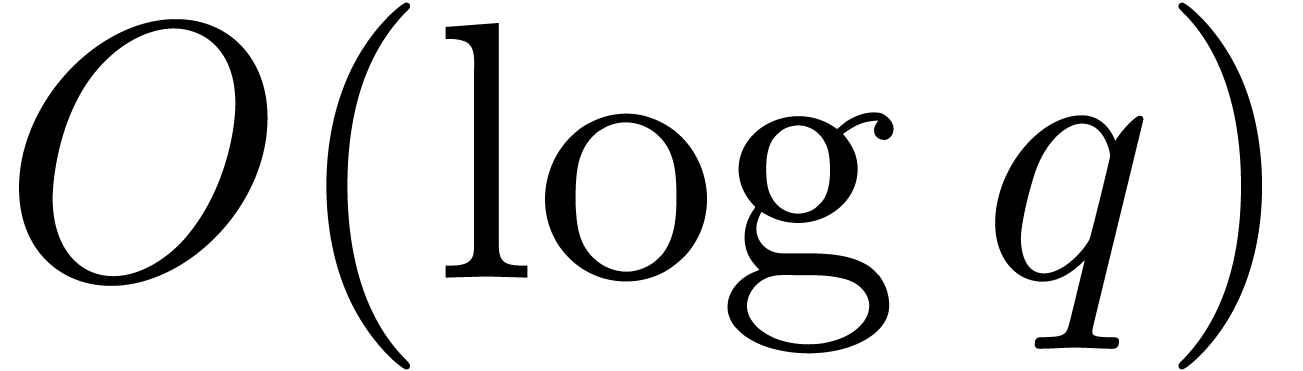 products in
products in  .
In this way we obtain the squarefree factorization of
.
In this way we obtain the squarefree factorization of  .
.
We are now ready to combine all the previous algorithms of this section
in order to improve Algorithm 13. Recall that we are given
integers  such that
such that 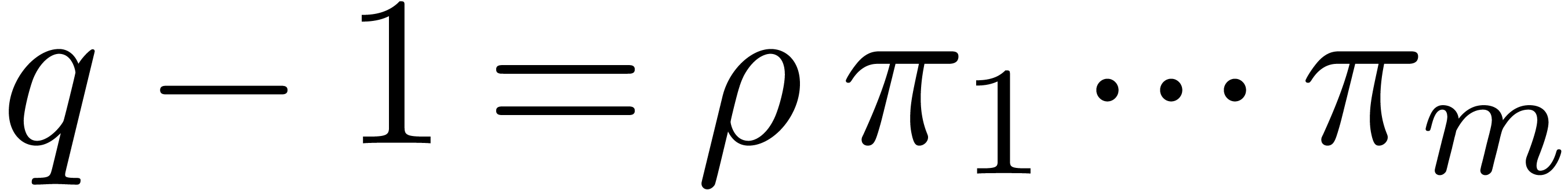 ,
and that we let
,
and that we let 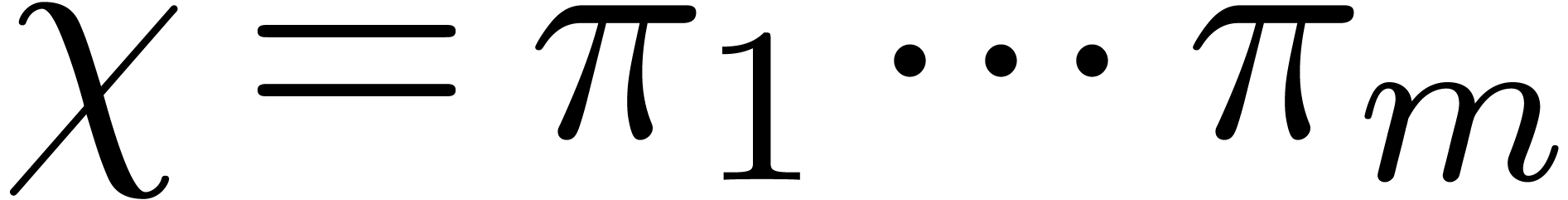 . The
following algorithm is parametrized by subroutines used internally. We
distinguish three cases of use, leading to complexity bounds in terms of
. The
following algorithm is parametrized by subroutines used internally. We
distinguish three cases of use, leading to complexity bounds in terms of
 , of
, of  , and in the smooth case of
, and in the smooth case of 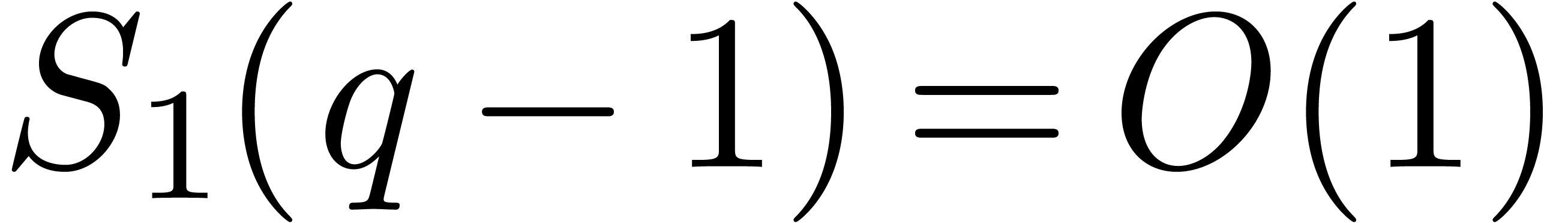 .
.
Algorithm
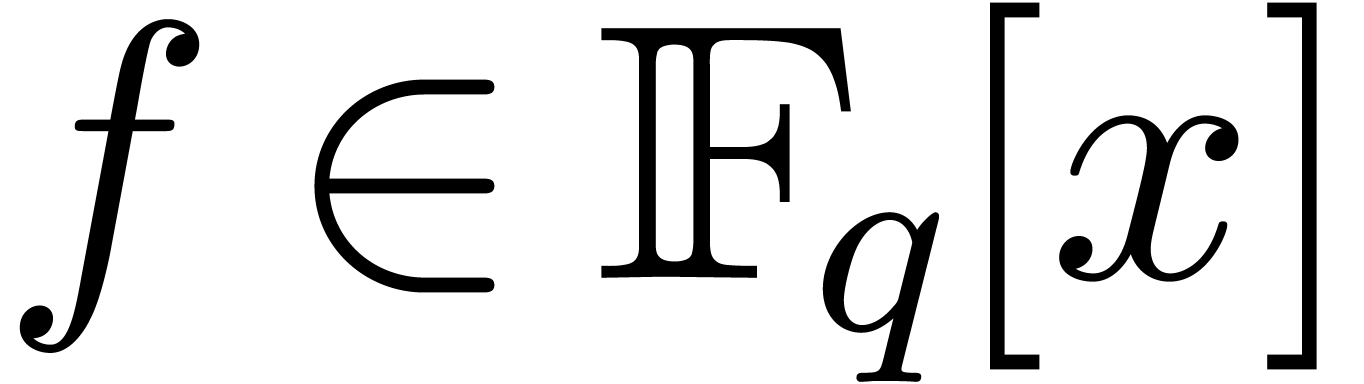 ,
monic, separable, which splits over
,
monic, separable, which splits over
 ,
of degree
,
of degree
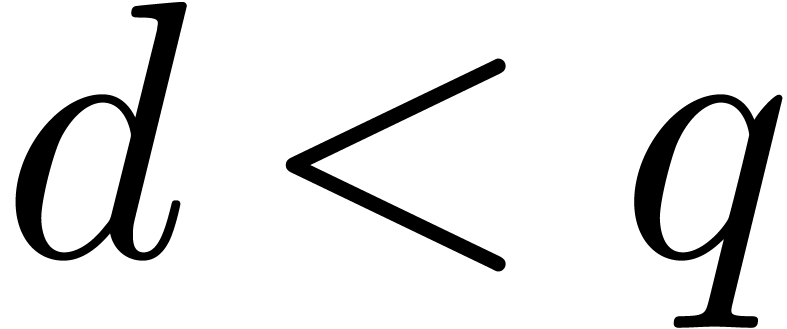 ,
such that
,
such that
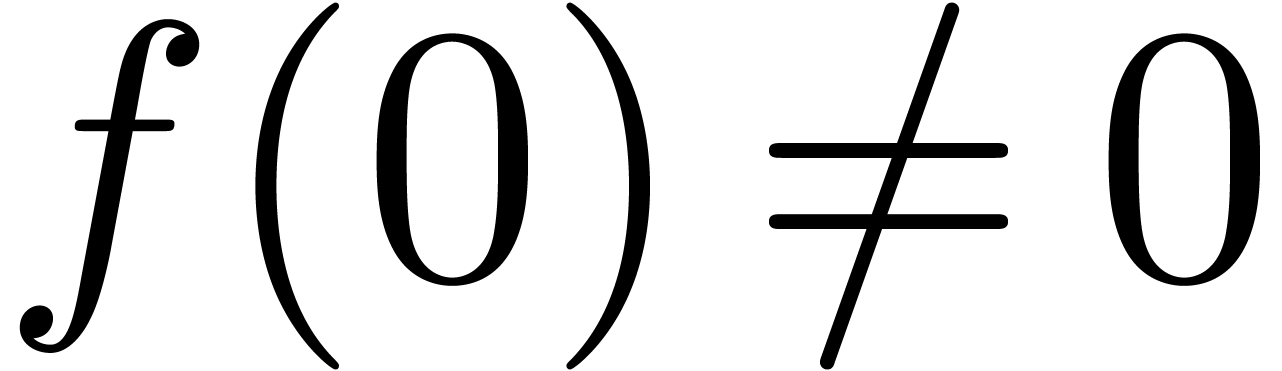 ;
a primitive root
;
a primitive root
 of
of
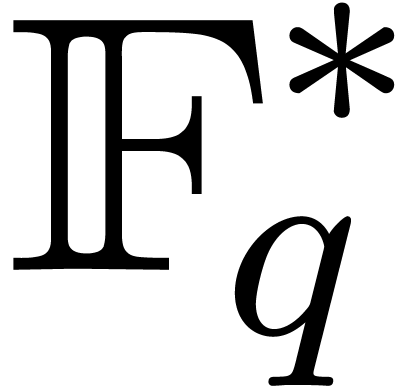 .
.
The roots of 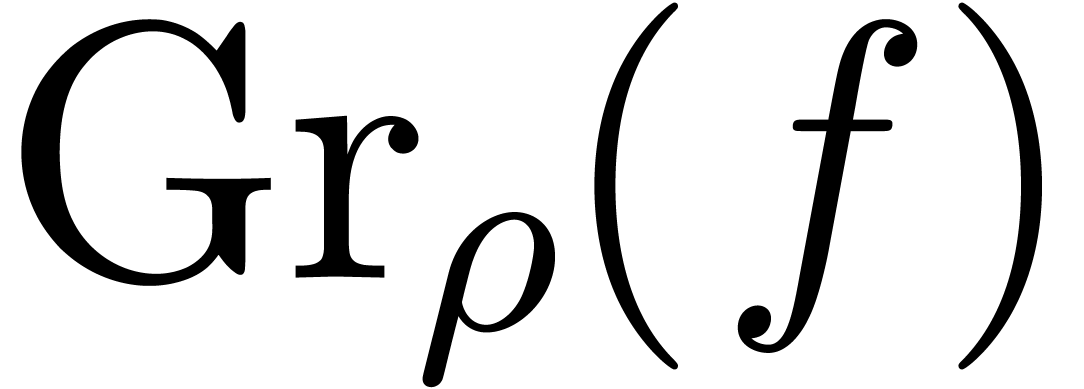 .
.
Compute  as the Graeffe transform of
as the Graeffe transform of 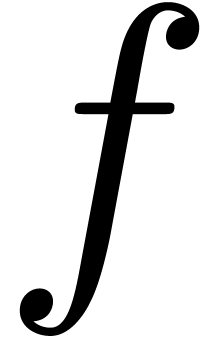 of order
of order 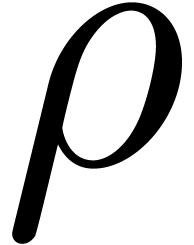 .
Compute
.
Compute 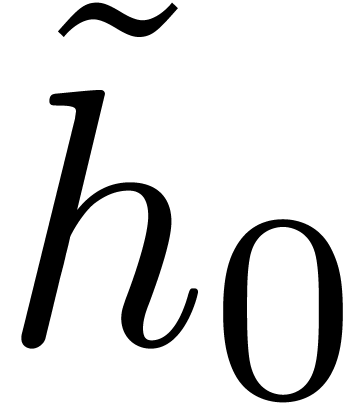 as the squarefree part of
as the squarefree part of 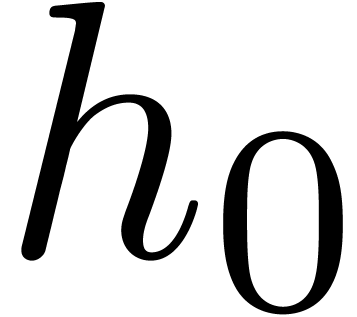 . Recursively compute
. Recursively compute 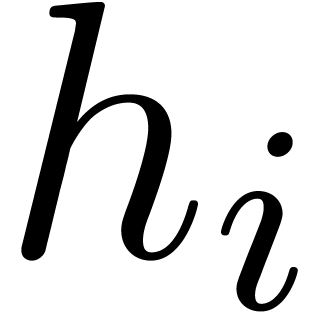 as the Graeffe transform of order
as the Graeffe transform of order 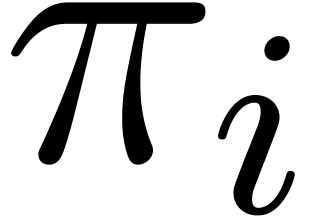 of
of 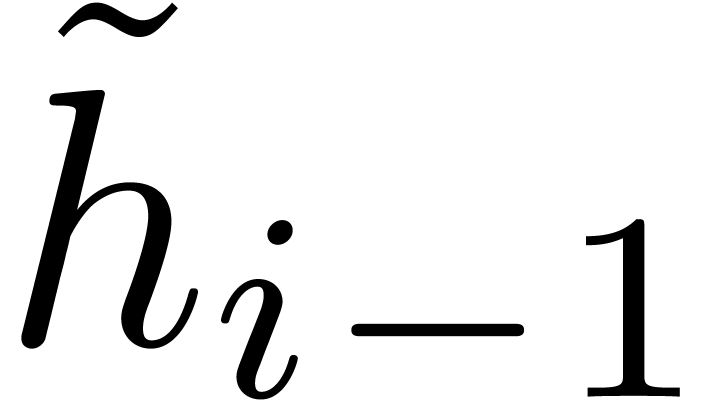 , and
, and  as the squarefree part of
as the squarefree part of  ,
for all
,
for all  from
from 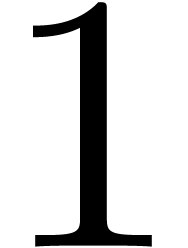 to
to
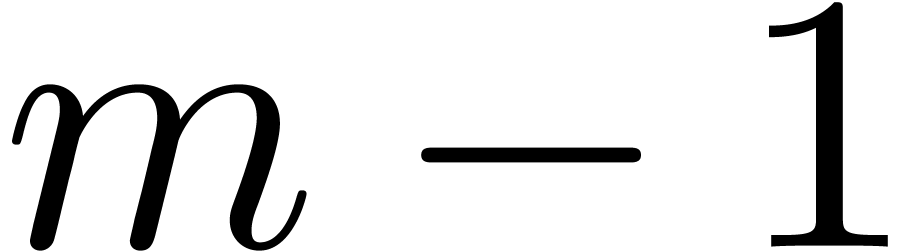 .
.
Initialize  with
with  , and compute
, and compute 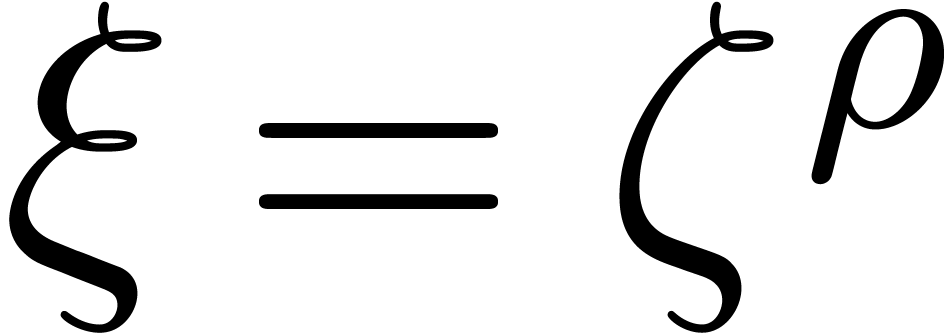 .
.
For 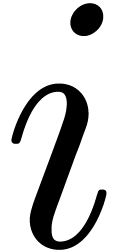 from
from  down to
down to
 do
do
Use Algorithm 15 with input 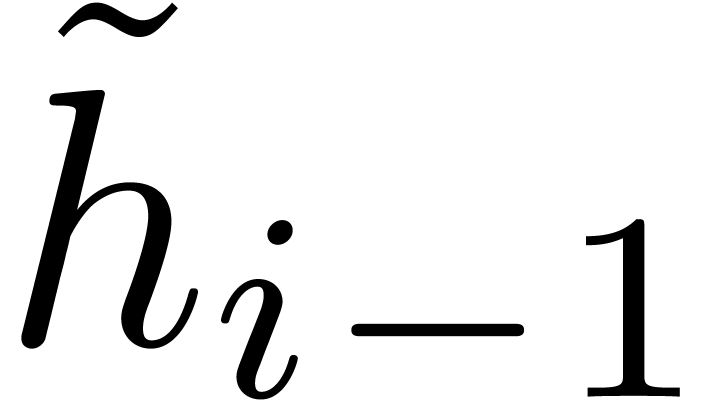 and
and  , and let
, and let  be the polynomials obtained in return.
be the polynomials obtained in return.
Initialize 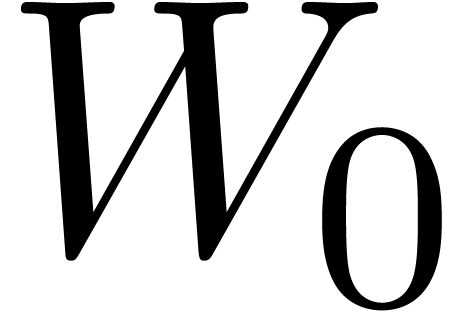 with the roots of all the
with the roots of all the
 of degree
of degree 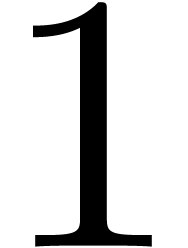 ,
for
,
for 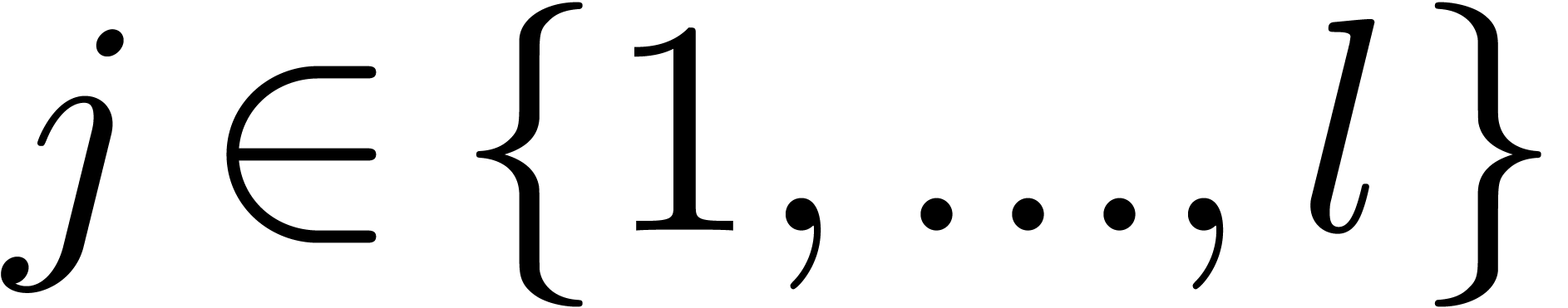 .
.
For all 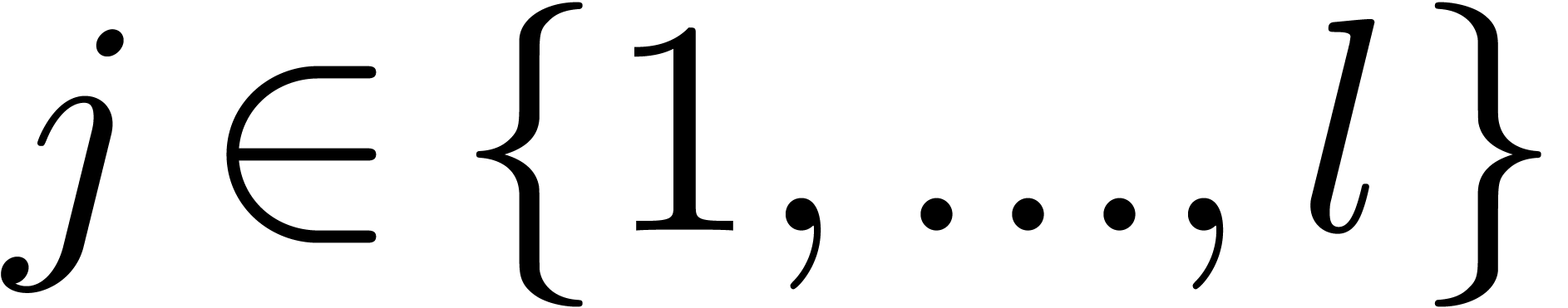 such that
such that 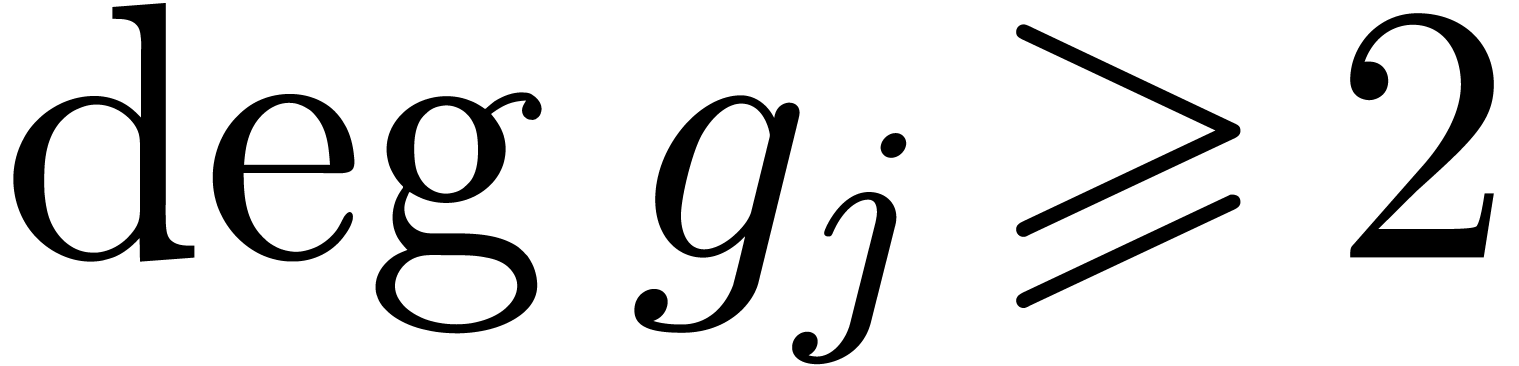 , compute the
, compute the  -logarithm
-logarithm
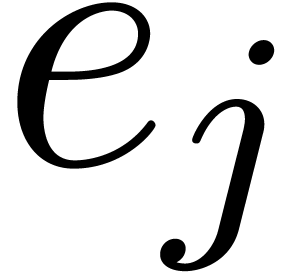 of
of 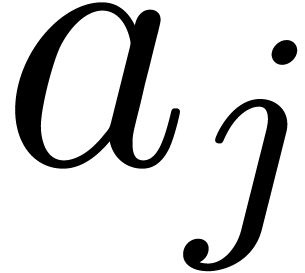 with
Algorithm 23 (resp. with Algorithms 23 and 21).
with
Algorithm 23 (resp. with Algorithms 23 and 21).
Use Algorithm 17 (resp. Algorithm 19) to compute the sets of roots 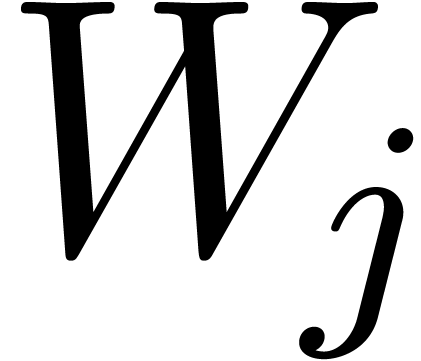 of
of 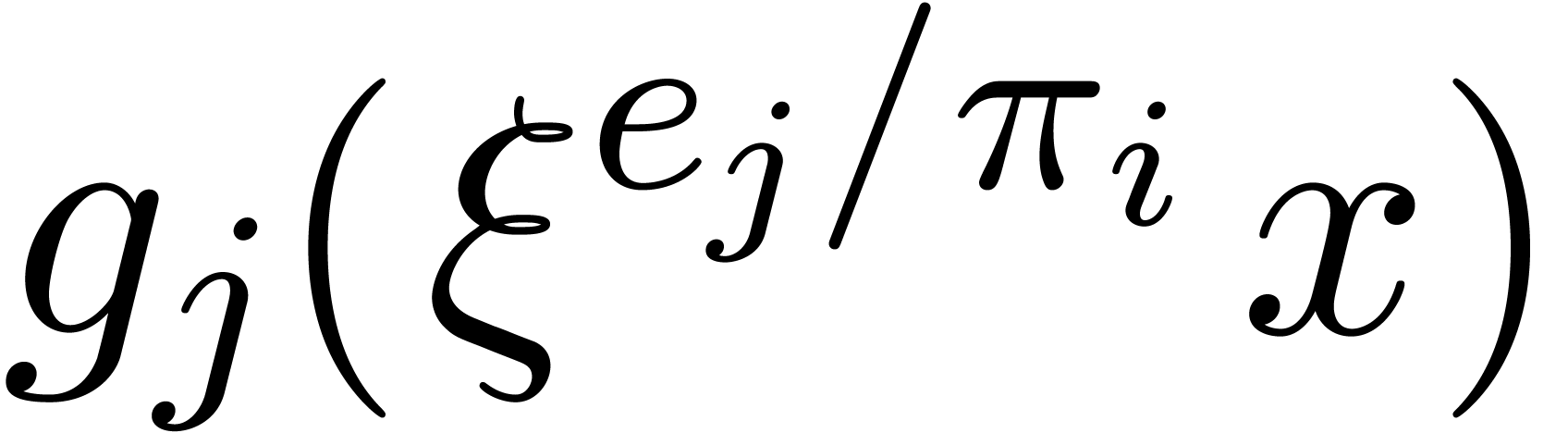 for all
for all 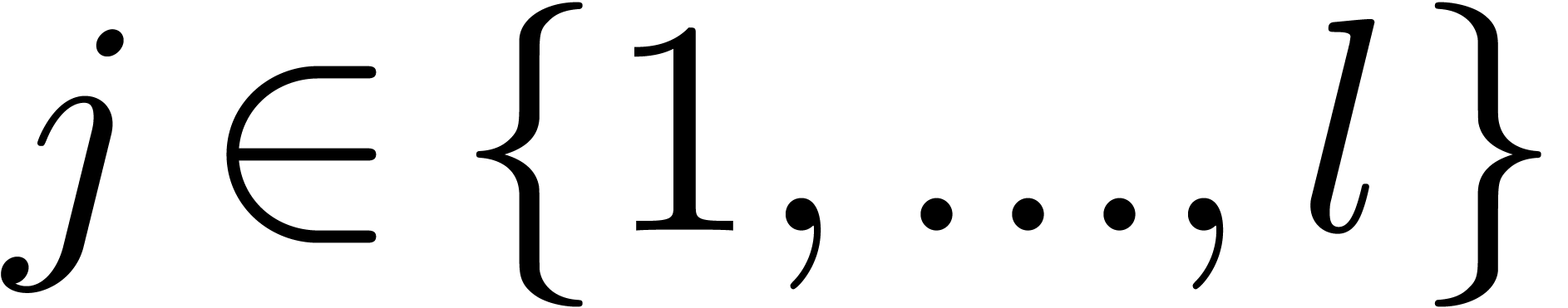 such
that
such
that 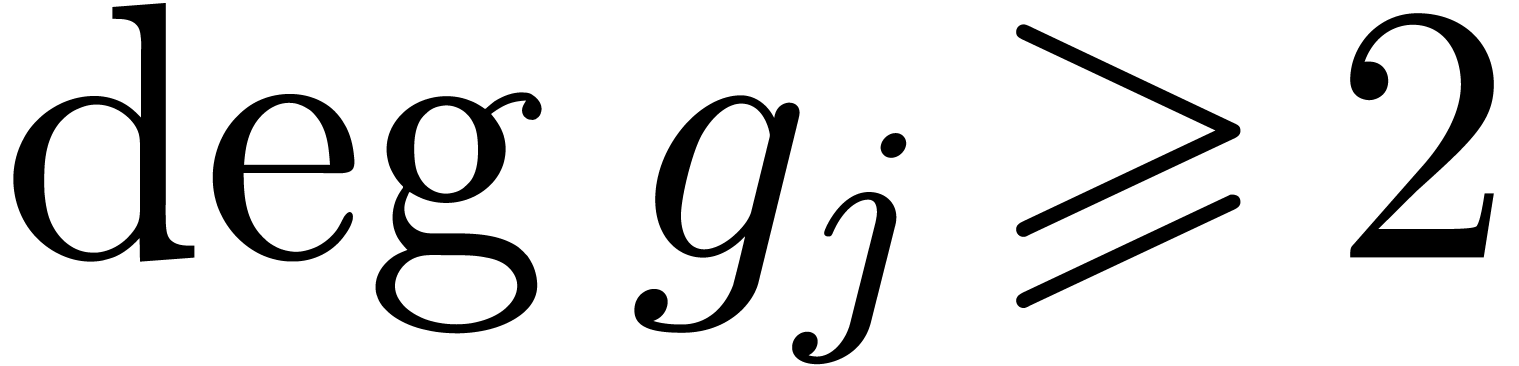 .
.
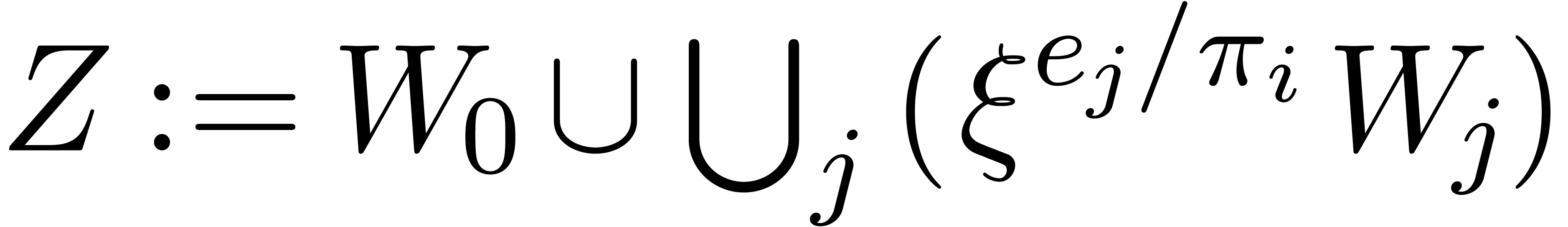 .
.
Return  .
.
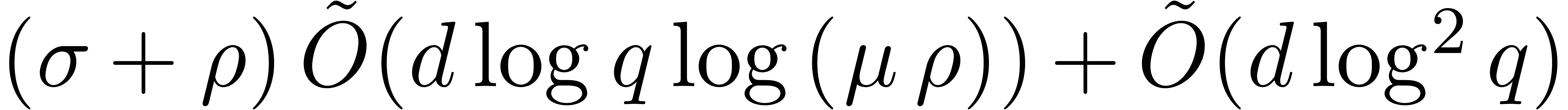 . In addition, for any
fixed
. In addition, for any
fixed  , the cost is also
bounded by
, the cost is also
bounded by 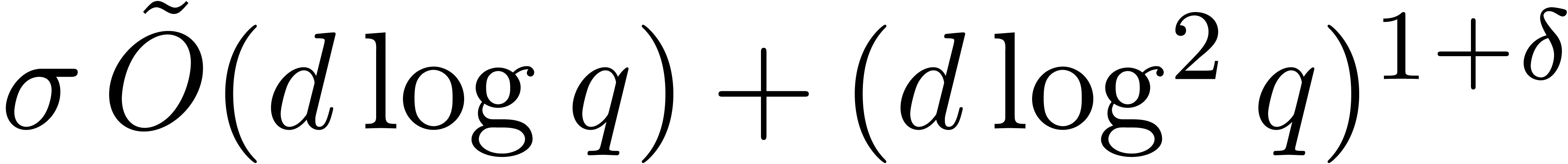 or
or 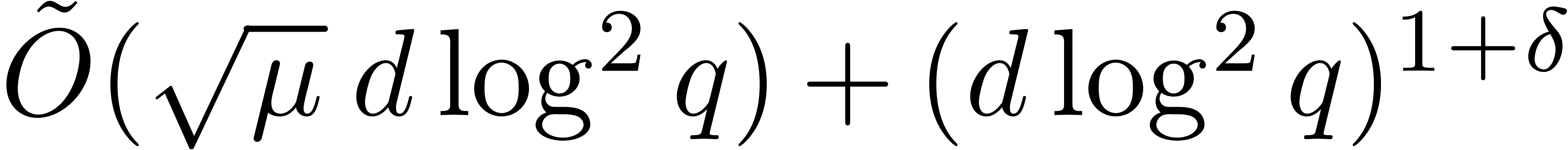 ,
whenever
,
whenever  and where
and where  .
.
Proof. Let introduce 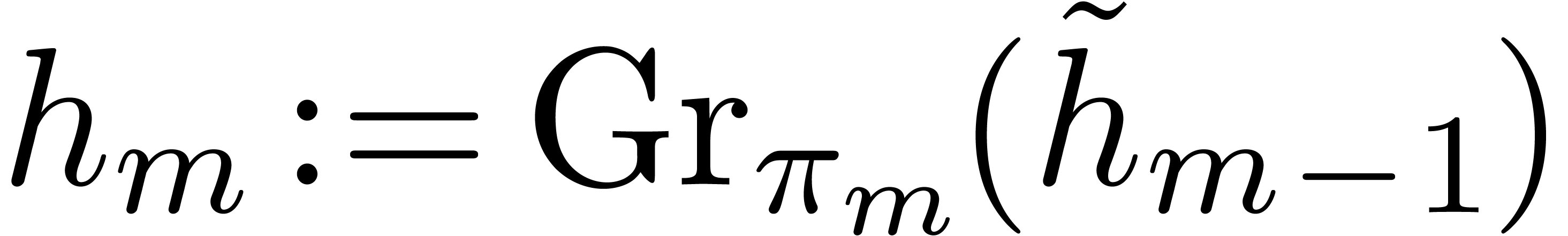 , which does not need to be computed. When entering
the loop in step 3, the set
, which does not need to be computed. When entering
the loop in step 3, the set  contains the single
root of
contains the single
root of 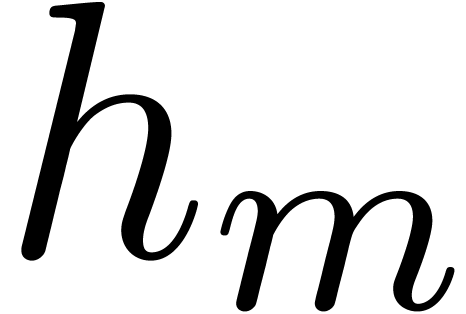 . We prove by
descending induction on
. We prove by
descending induction on 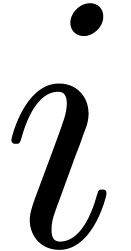 from
from 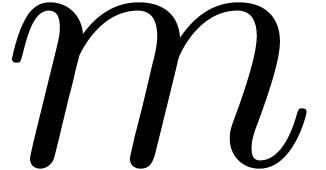 down to
down to 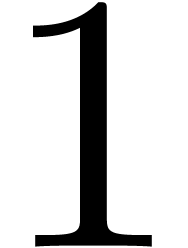 that
that  contains
the roots of
contains
the roots of 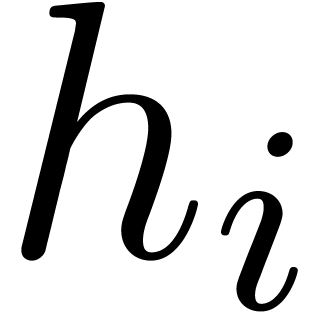 when entering step
when entering step 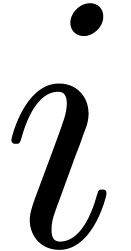 of the loop. Assuming this hypothesis holds for
of the loop. Assuming this hypothesis holds for 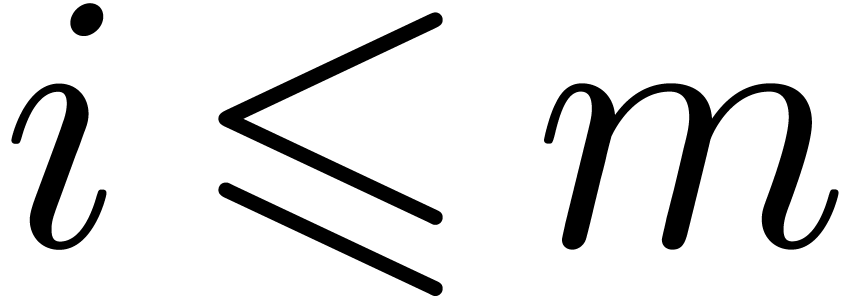 , conditions of Algorithm 15 are met,
and finding the roots of
, conditions of Algorithm 15 are met,
and finding the roots of 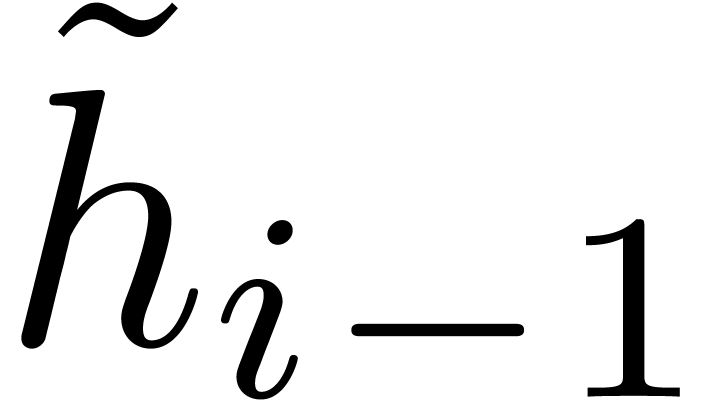 reduces to finding the
roots of
reduces to finding the
roots of  . The
. The  of degree
of degree 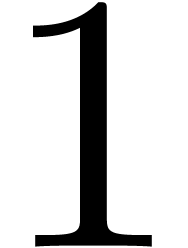 contribute to roots of
contribute to roots of
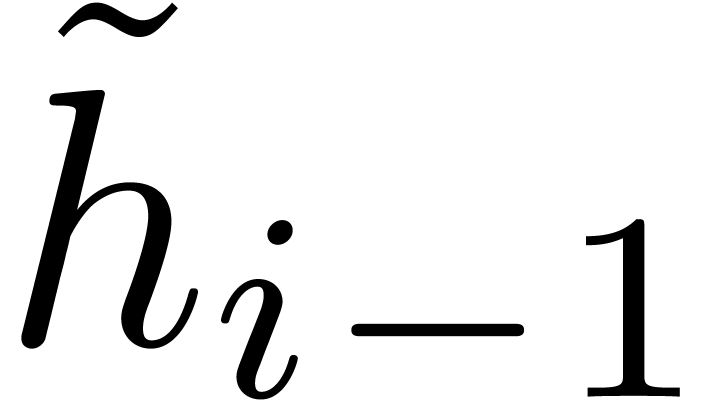 in a straightforward manner. For the other
in a straightforward manner. For the other  , of degree at least
, of degree at least 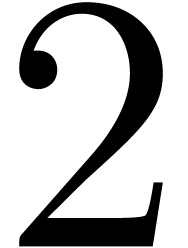 , it turns out that the roots of
, it turns out that the roots of 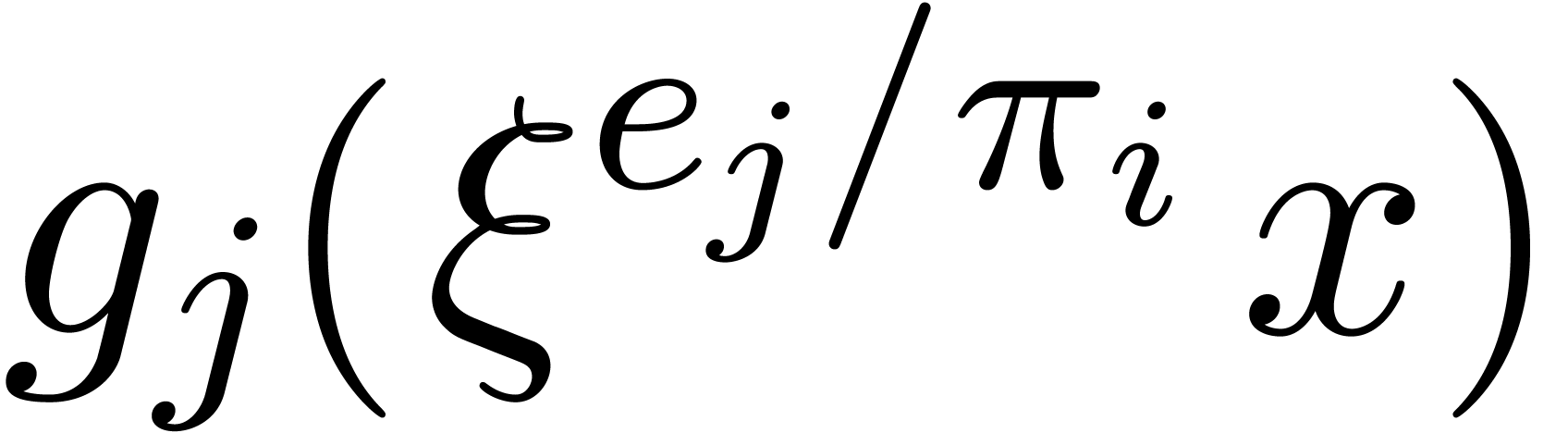 have order dividing
have order dividing 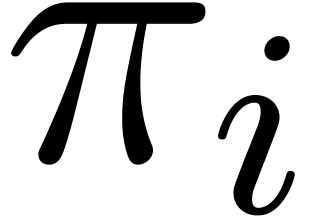 ,
and thus Algorithms 17 or 19 produce the
remaining roots of
,
and thus Algorithms 17 or 19 produce the
remaining roots of 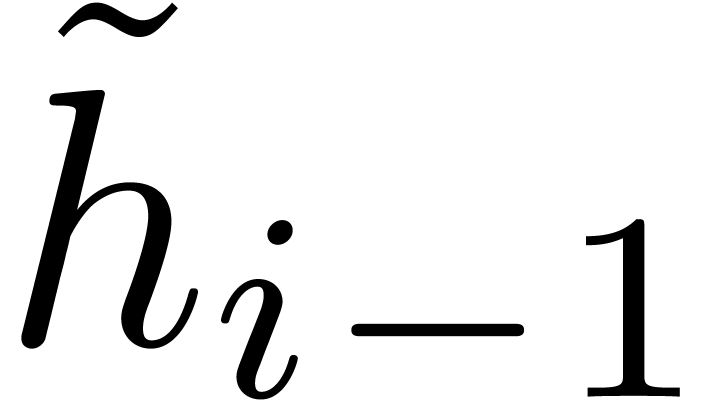 . This
shows the correctness.
. This
shows the correctness.
First all, the primitive roots of unity of orders 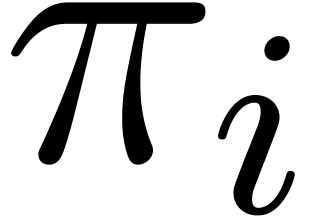 and
and  needed during the execution of the algorithm
can be obtained in time
needed during the execution of the algorithm
can be obtained in time 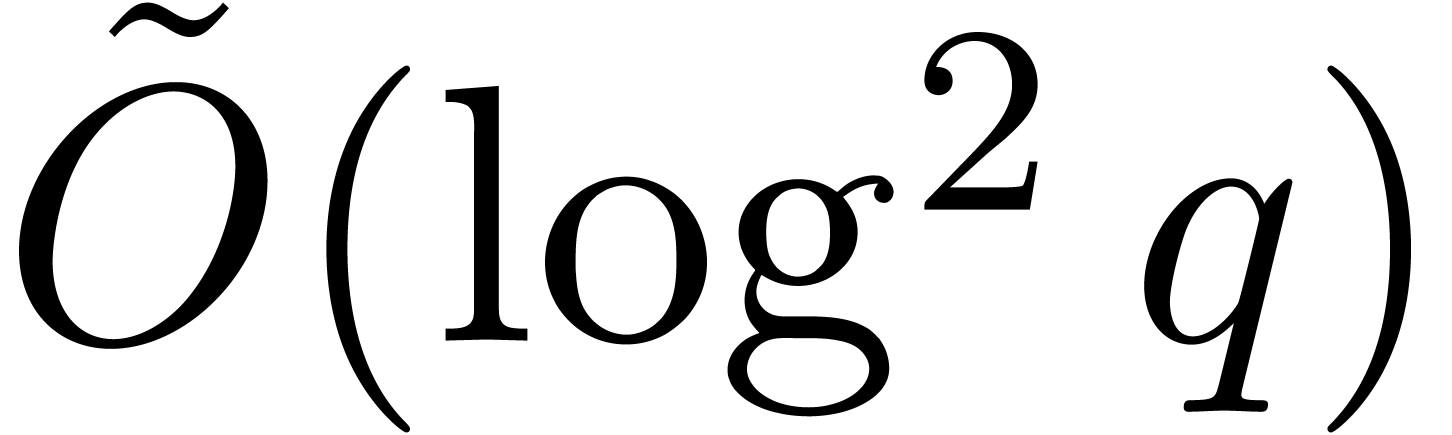 by Remark 25.
The Graeffe transforms in step 1 may execute in time
by Remark 25.
The Graeffe transforms in step 1 may execute in time 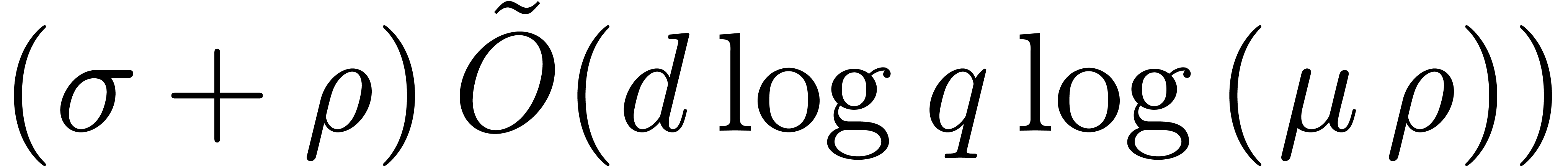 by Proposition 1.
by Proposition 1.
Let 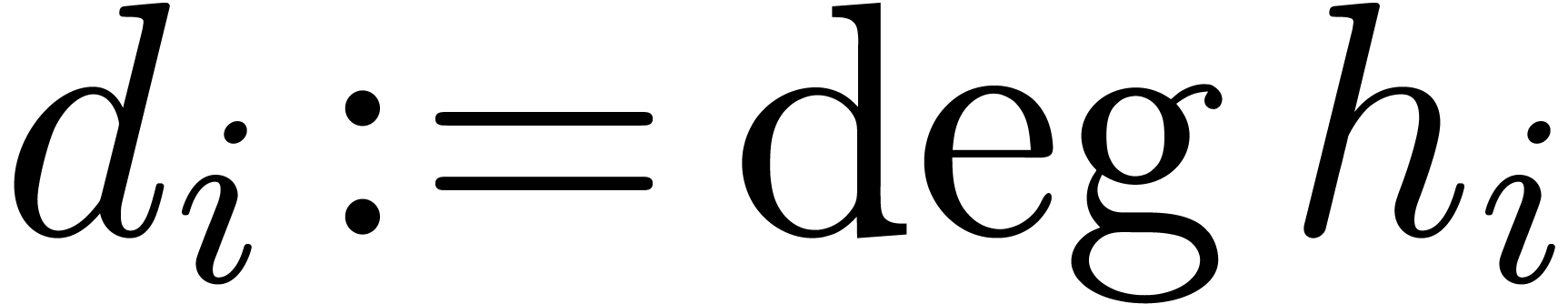 , let
, let 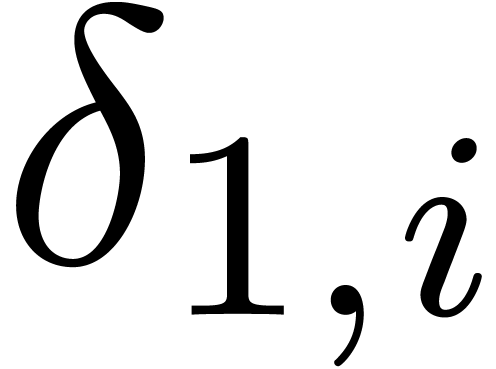 be the number of simple roots of
be the number of simple roots of 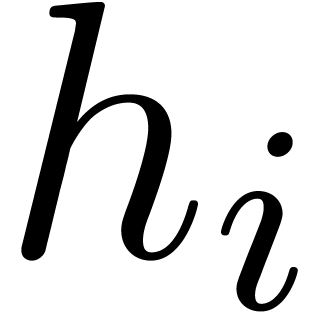 ,
let
,
let 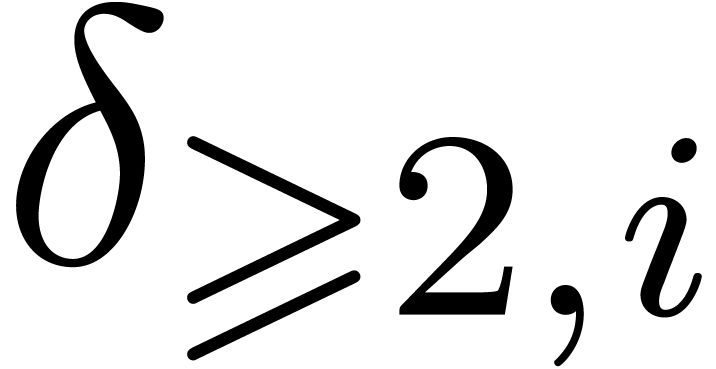 be the number of multiple roots of
be the number of multiple roots of 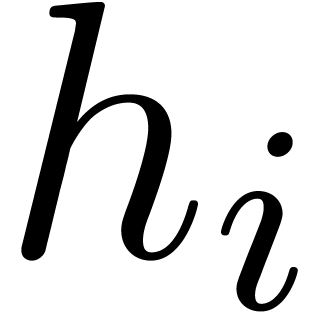 , and let
, and let 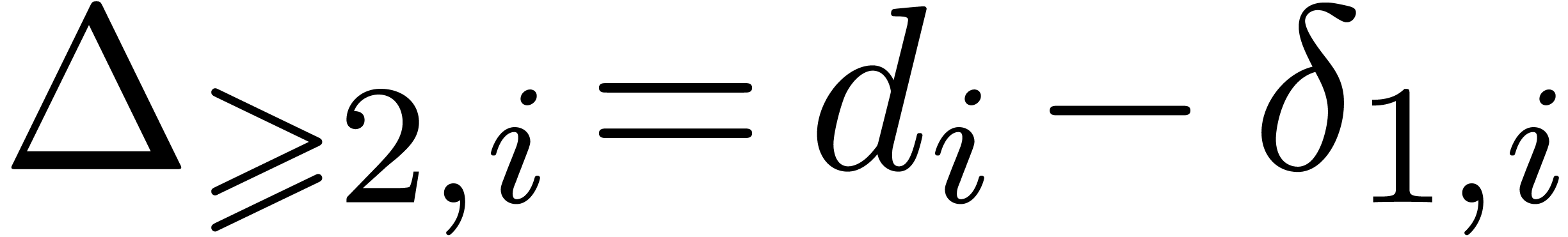 be the number of multiple roots of
be the number of multiple roots of 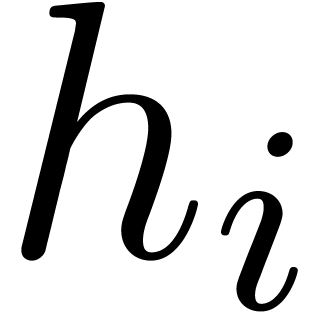 counted with
multiplicities. By Proposition 26, computing the squarefree
part
counted with
multiplicities. By Proposition 26, computing the squarefree
part 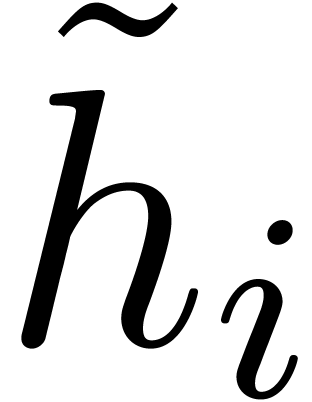 of
of 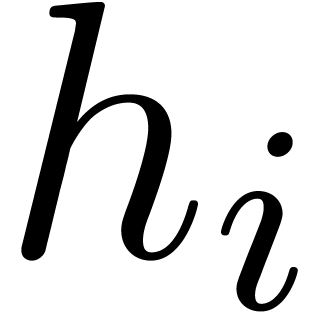 takes time
takes time 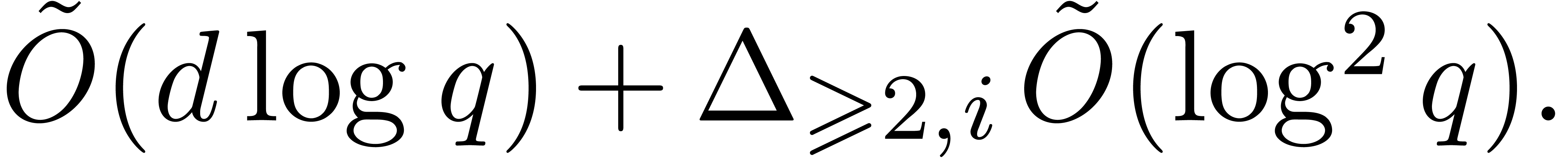 From
From 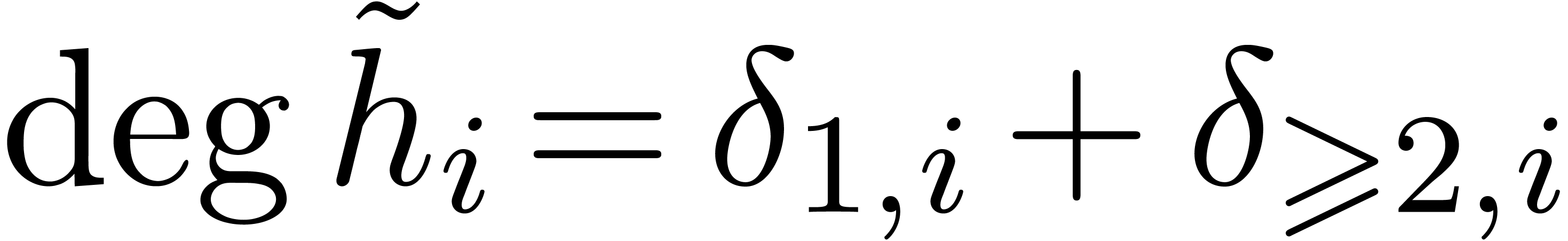 and
and 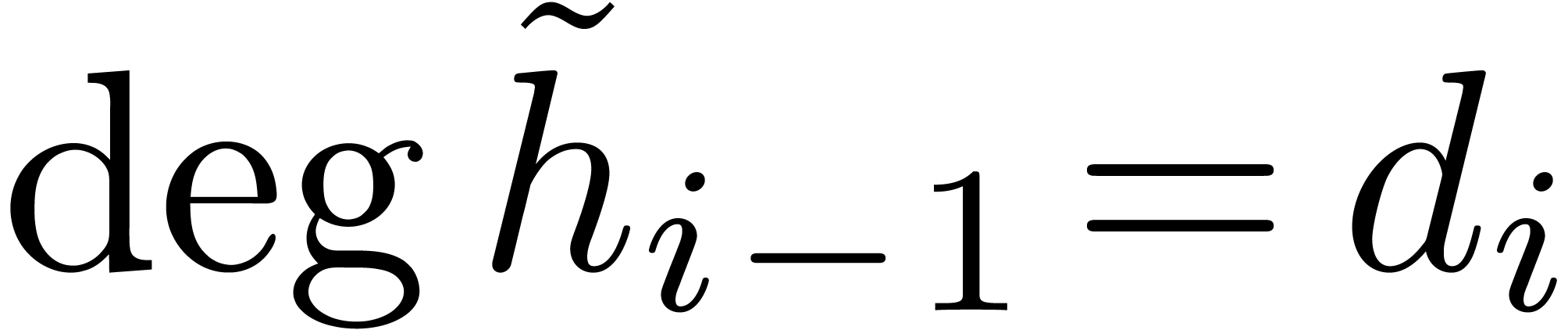 , we obtain
, we obtain 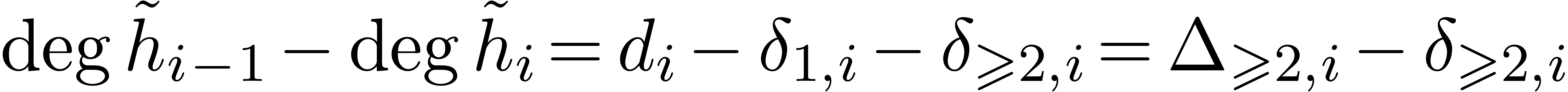 .
Summing these equalities over
.
Summing these equalities over  leads to
leads to 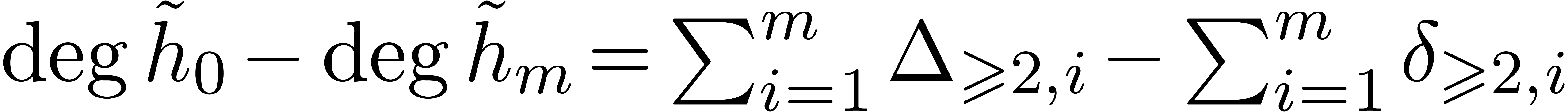 . Using
. Using 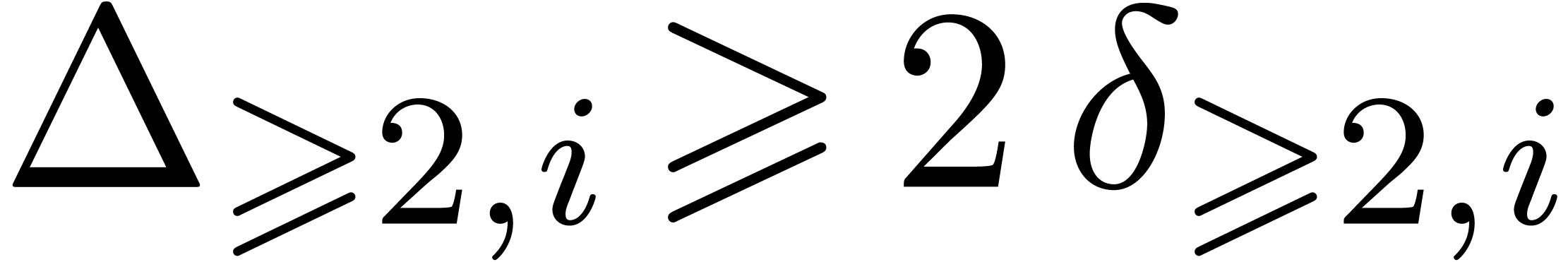 ,
, 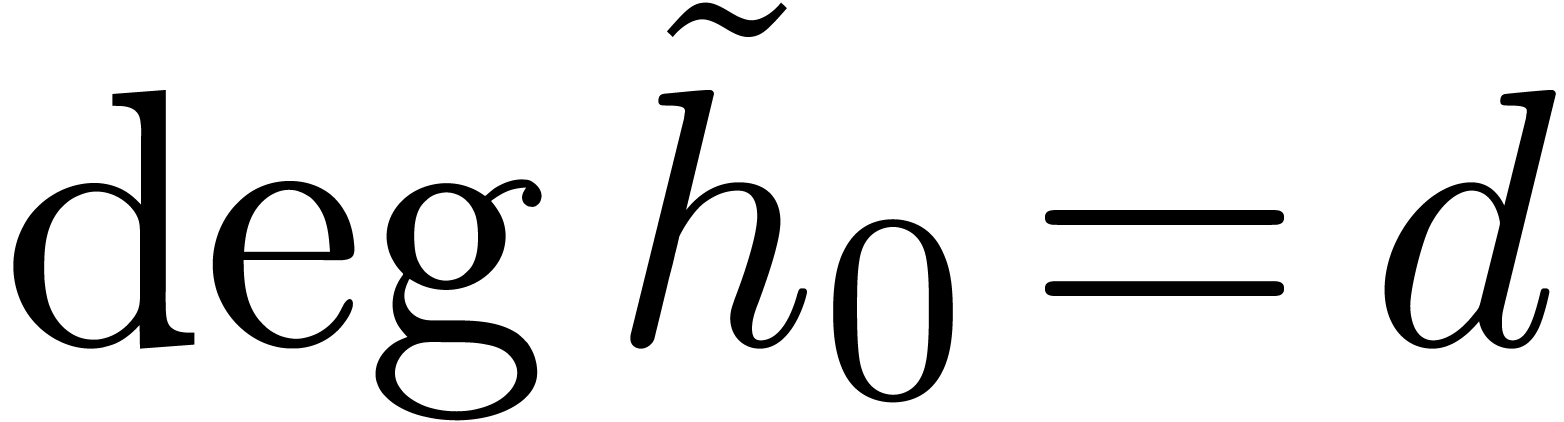 , and
, and
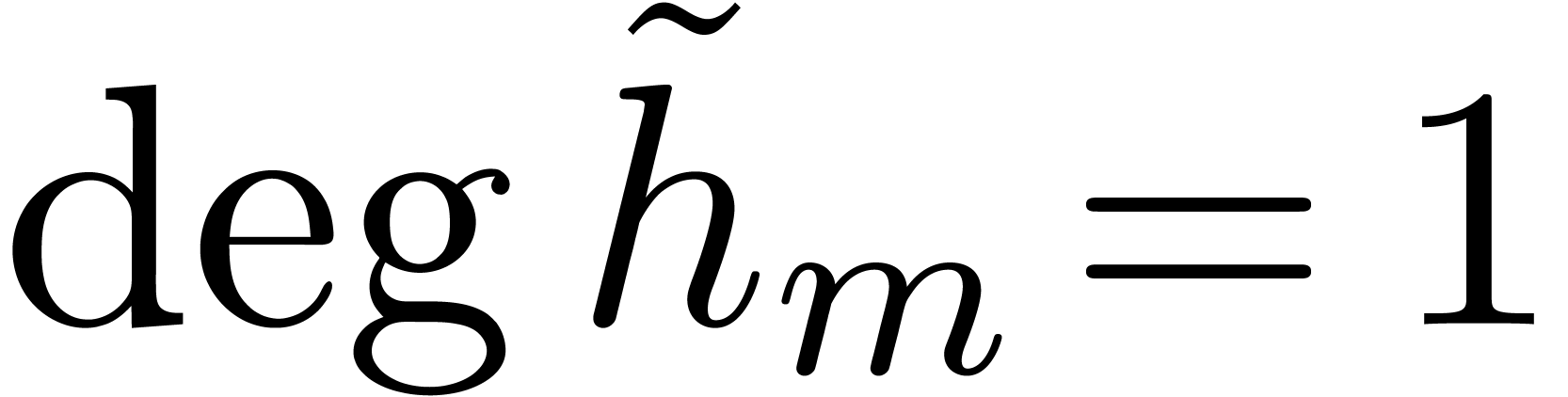 , we deduce that
, we deduce that 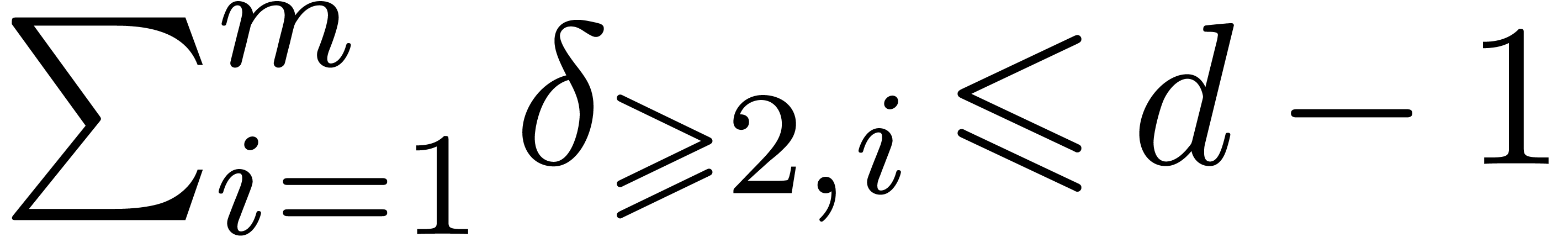 , and then that
, and then that 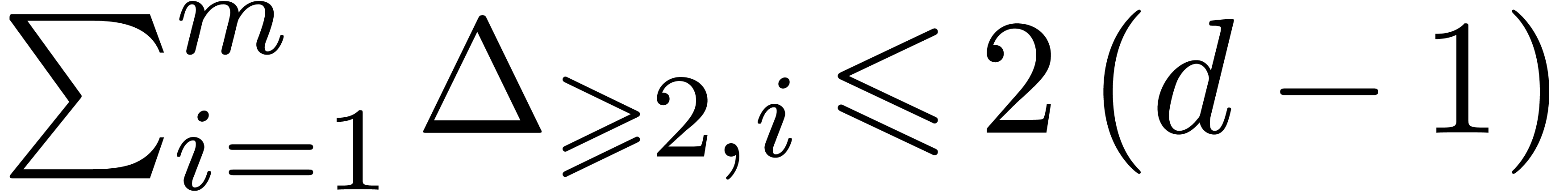 .
Consequently, the total cost for computing all the squarefree parts
drops to
.
Consequently, the total cost for computing all the squarefree parts
drops to 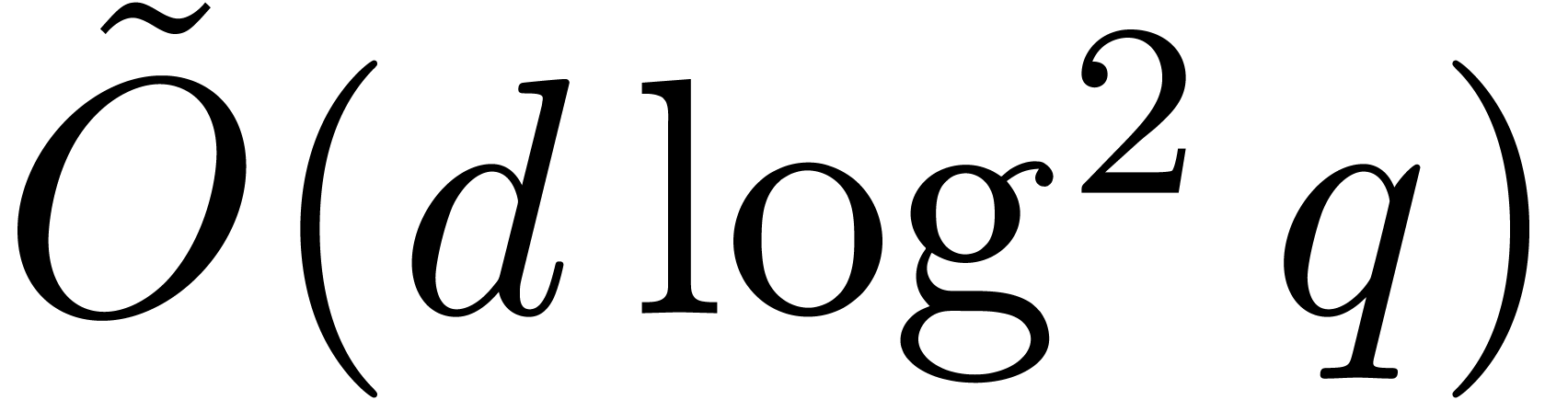 .
.
Step 3.a may take 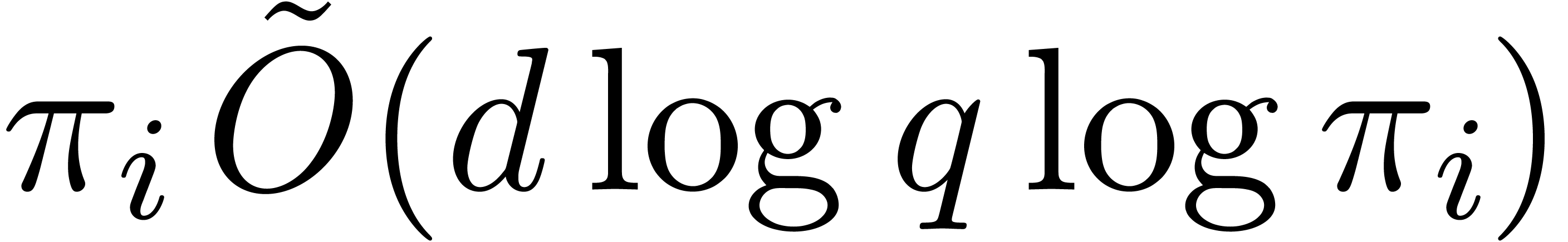 by Proposition 16,
which yields a total cost
by Proposition 16,
which yields a total cost 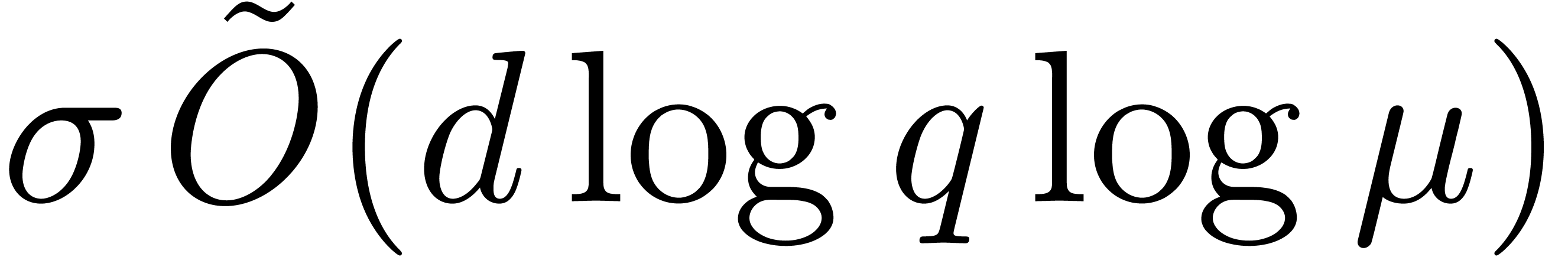 .
In step 3.c, Algorithm 23 is called
.
In step 3.c, Algorithm 23 is called 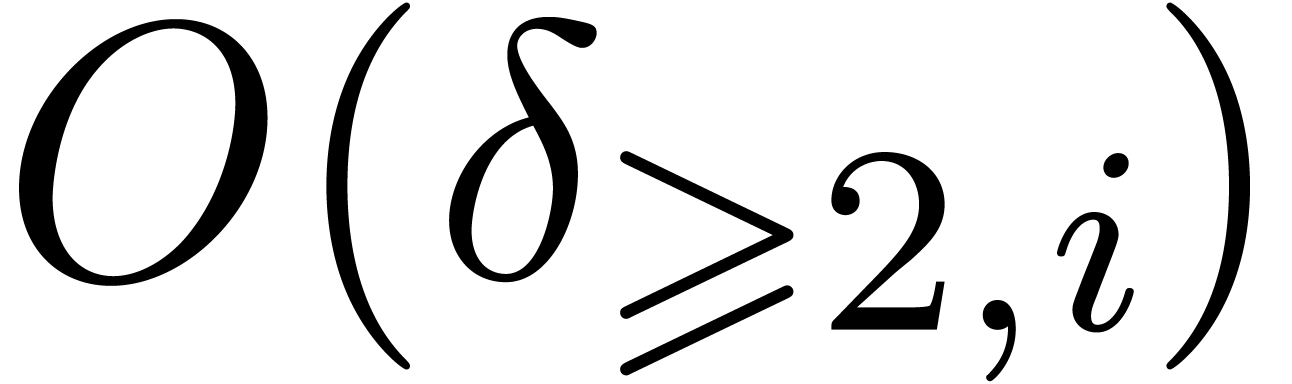 times. Consequently, the total cost of this step is
times. Consequently, the total cost of this step is 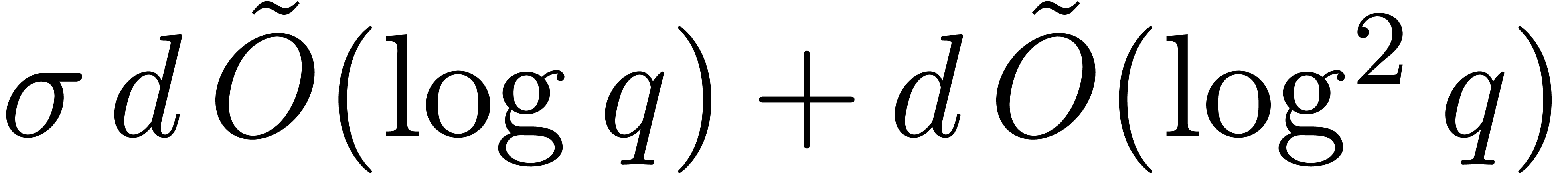 by Proposition 24. If we use Algorithm 17 in
step 3.d, then the cost is
by Proposition 24. If we use Algorithm 17 in
step 3.d, then the cost is  by Proposition 18. The sum of these costs is bounded by
by Proposition 18. The sum of these costs is bounded by 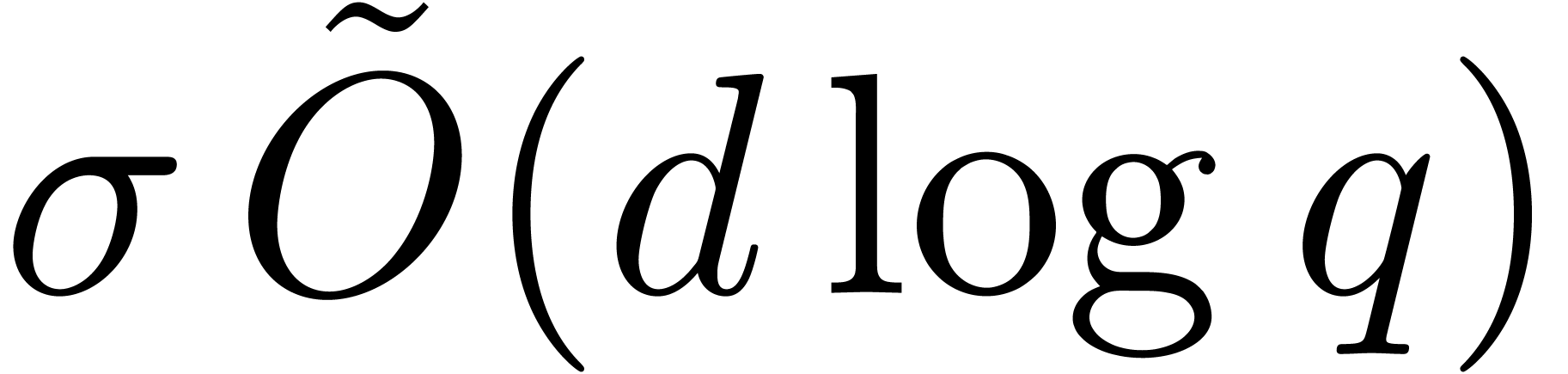 . So far, this establishes the first complexity
bound.
. So far, this establishes the first complexity
bound.
From now on assume that  . The
cost for the Graeffe transforms in step 1 may drop into
. The
cost for the Graeffe transforms in step 1 may drop into 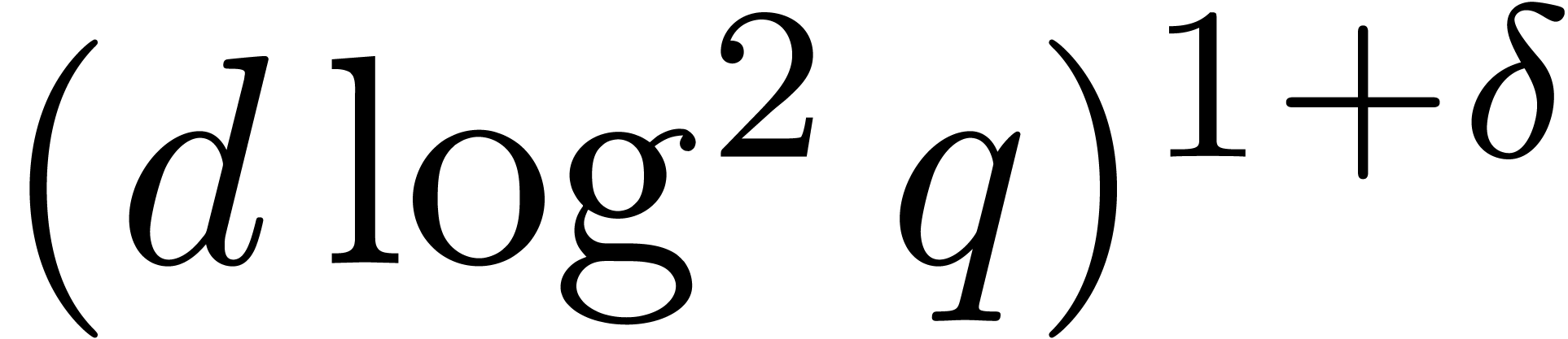 by Corollary 9. Step 3.a may run in time
by Corollary 9. Step 3.a may run in time 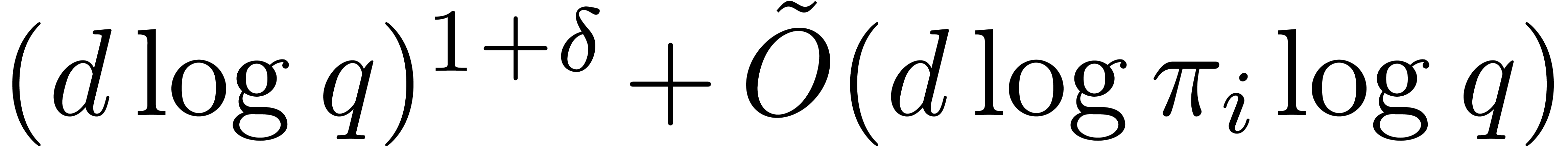 by Proposition 16. The total cost of this step thus amounts
to
by Proposition 16. The total cost of this step thus amounts
to 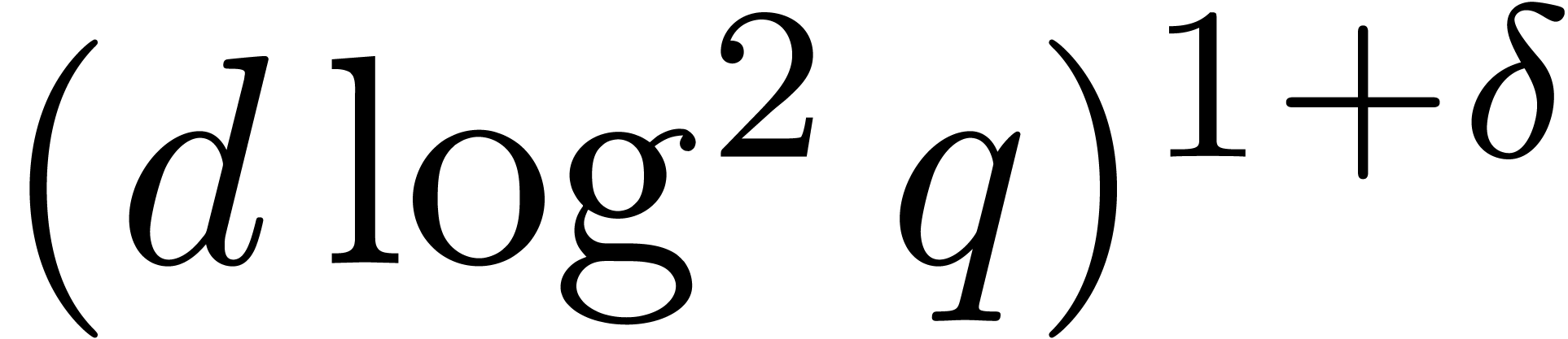 . Putting these bounds
together yields the second complexity.
. Putting these bounds
together yields the second complexity.
For the third complexity bound, we use Algorithm 23
combined with Algorithm 21 in step 3.c, so that Proposition
24 ensures a time 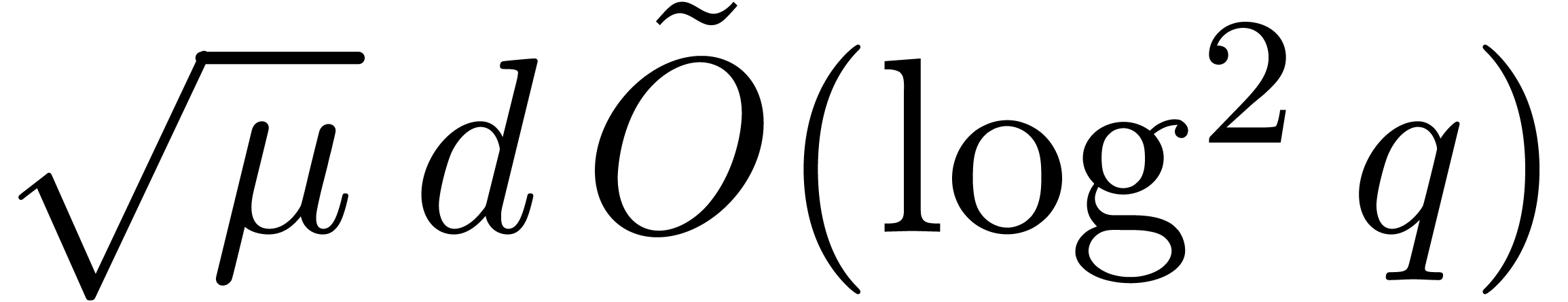 .
In addition we use Algorithm 19 in step 3.d, and
Proposition 20 gives a total cost
.
In addition we use Algorithm 19 in step 3.d, and
Proposition 20 gives a total cost 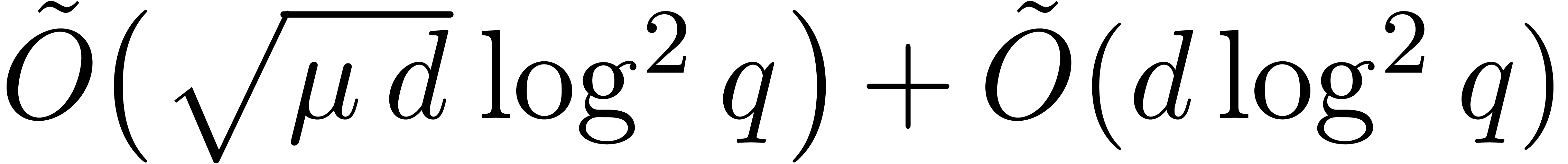 .
.
Recall that 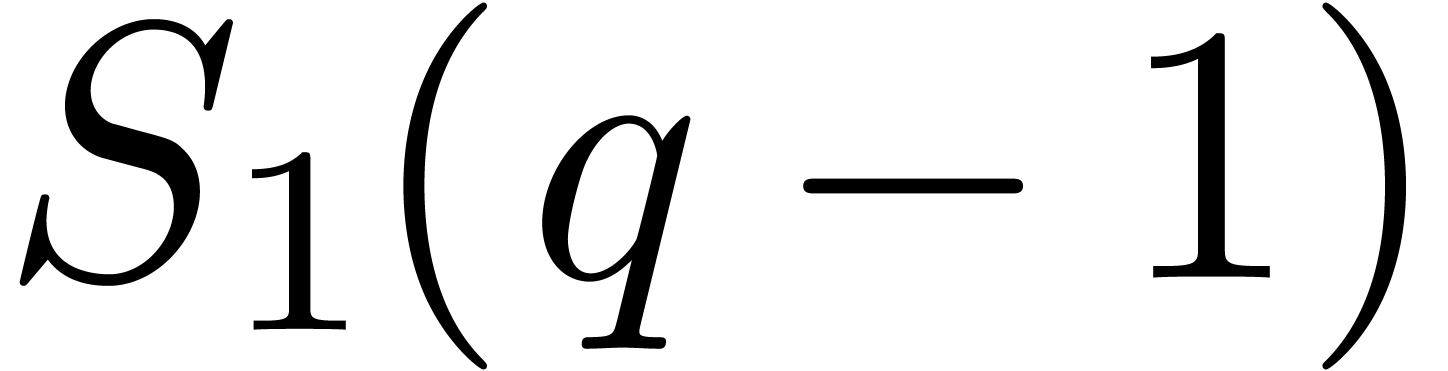 represents the largest prime number
in the irreducible factorization of
represents the largest prime number
in the irreducible factorization of 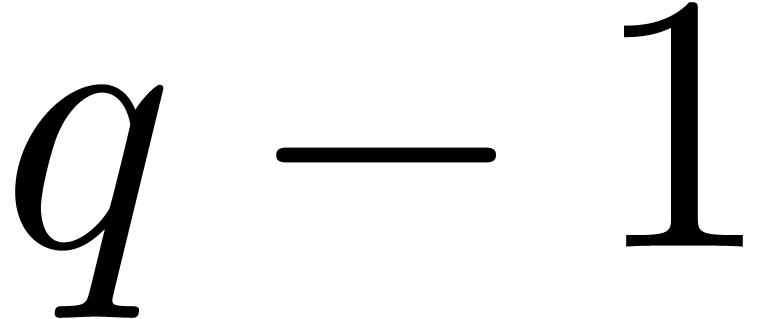 .
If
.
If 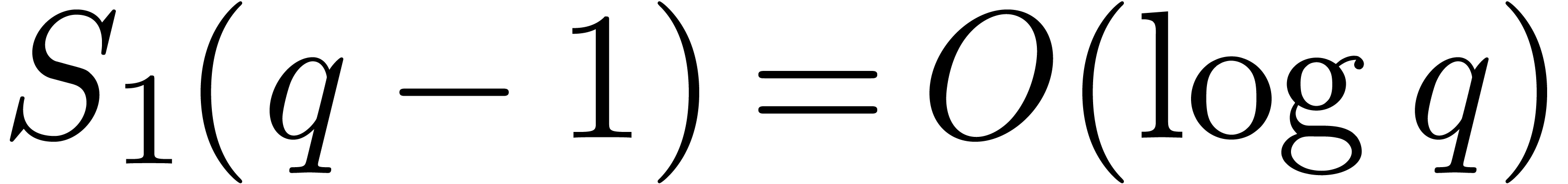 and if
and if 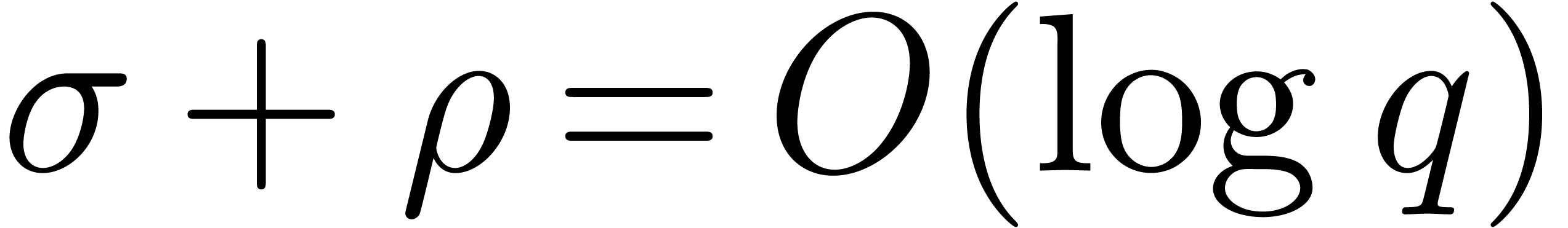 ,
then the first complexity bound of Proposition 28 rewrites
into
,
then the first complexity bound of Proposition 28 rewrites
into 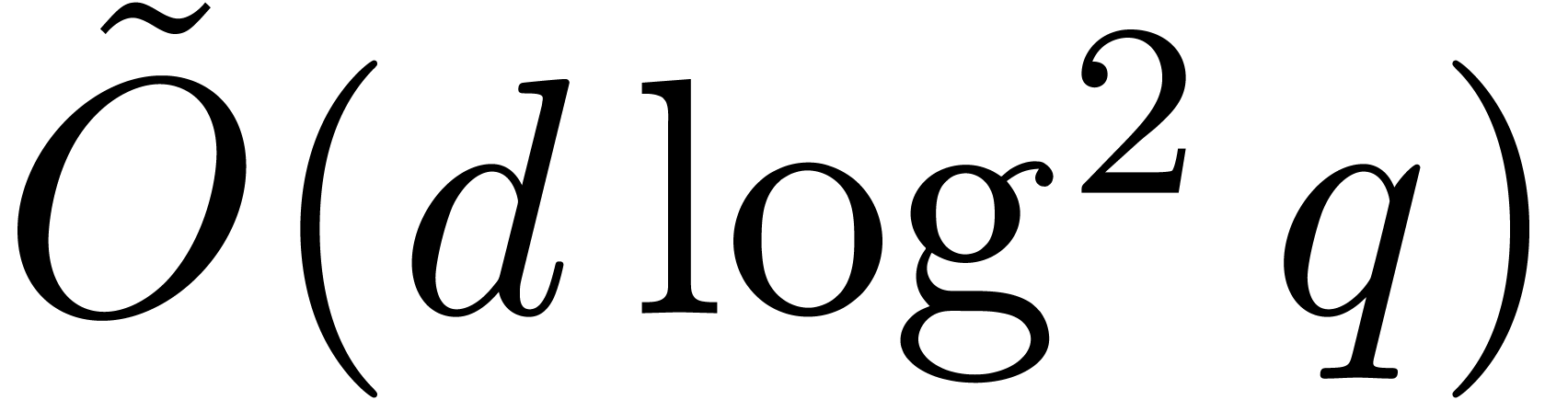 , which is thus softly
equivalent to the average cost of Cantor–Zassenhaus' algorithm. We
are now able to state the main result of this section.
, which is thus softly
equivalent to the average cost of Cantor–Zassenhaus' algorithm. We
are now able to state the main result of this section.
 ,
the irreducible factorization of
,
the irreducible factorization of 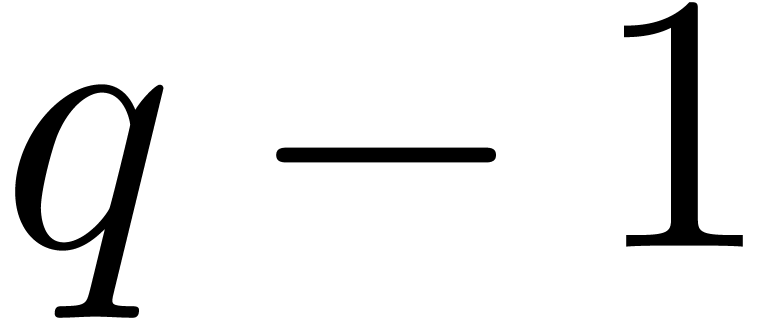 ,
a primitive element of
,
a primitive element of 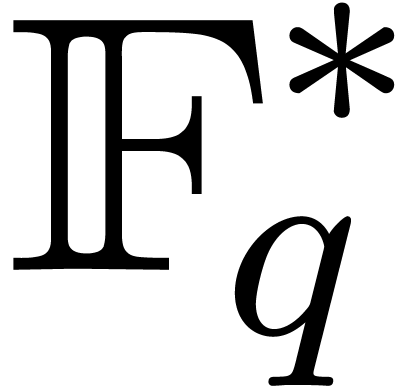 ,
and
,
and 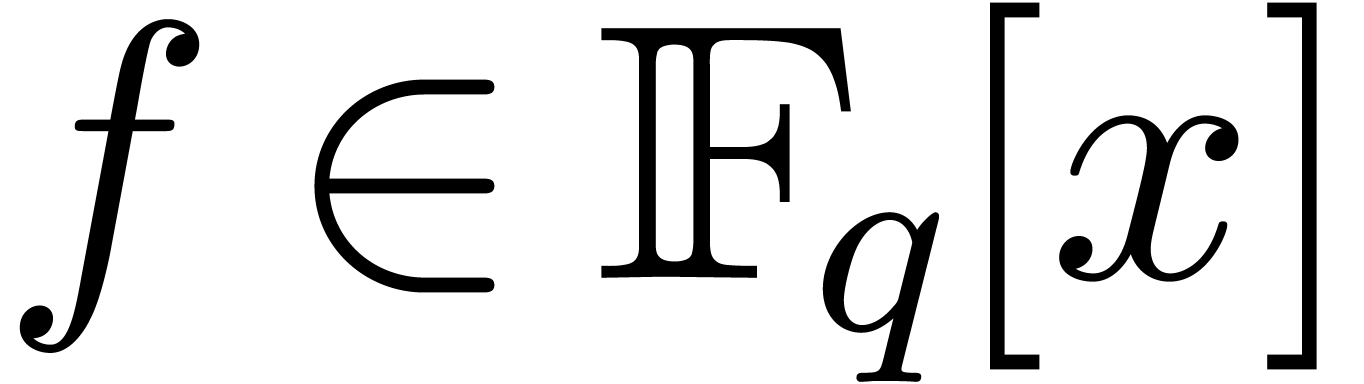 of degree
of degree 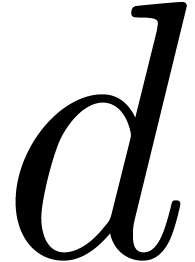 ,
monic, separable, which splits over
,
monic, separable, which splits over  ,
the roots of
,
the roots of 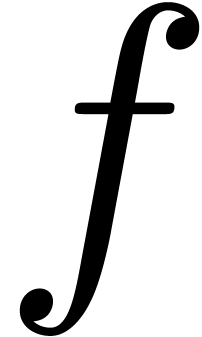 can be computed in time
can be computed in time 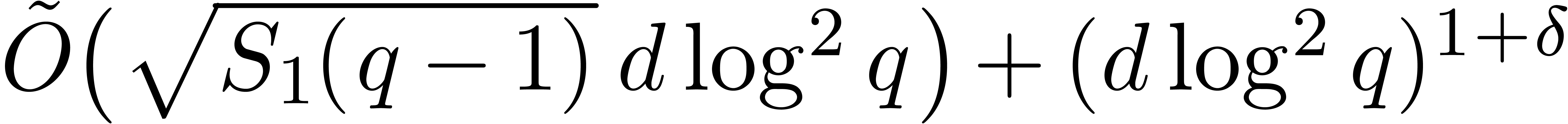 .
.
Proof. Without loss of generality we can assume
that 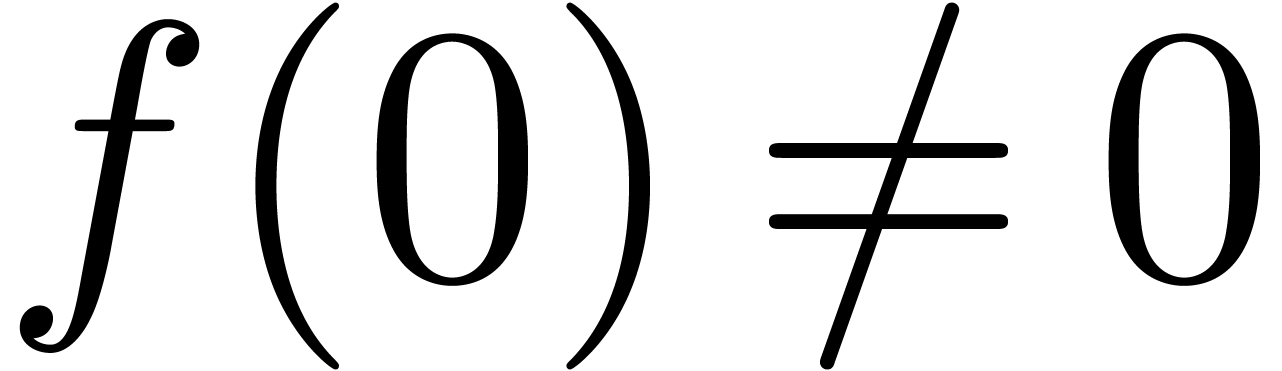 and that
and that 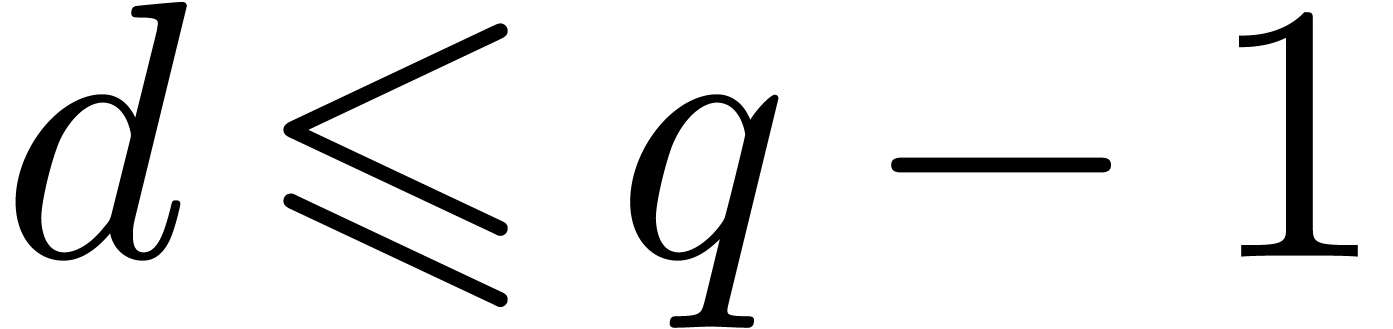 .
If
.
If  , then it suffices to
evaluate
, then it suffices to
evaluate 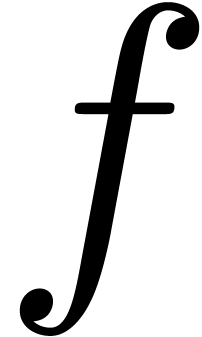 at all the elements of
at all the elements of  in time
in time 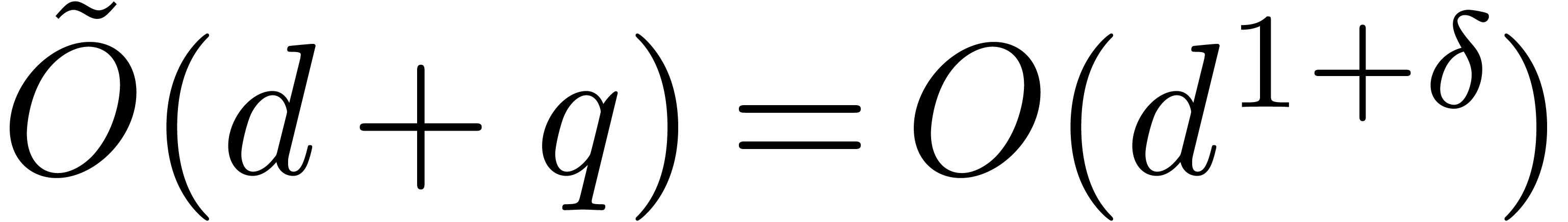 . Consequently, for
when
. Consequently, for
when  , we appeal to the
preceding proposition.
, we appeal to the
preceding proposition.
Let us finally mention that, in general, the present method improves [16, Theorem 4.1] (see complexity details at the end of the
proof). Nevertheless, if  ,
and if
,
and if  is close to
is close to 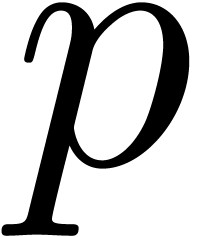 ,
then Theorem 29 does not improve [42, Theorem
4.1(2)].
,
then Theorem 29 does not improve [42, Theorem
4.1(2)].
M. Arora, G. Ivanyos, M. Karpinski, and N. Saxena. Deterministic polynomial factoring and association schemes. LMS J. Comput. Math., 17(1):123–140, 2014.
E. Bach. Comments on search procedures for primitive roots. Math. Comp., 66:1719–1727, 1997.
E. R. Berlekamp. Factoring polynomials over finite fields. Bell System Tech. J., 46:1853–1859, 1967.
E. R. Berlekamp. Factoring polynomials over large finite fields. Math. Comp., 24:713–735, 1970.
A. Bostan, Ph. Flajolet, B. Salvy, and É. Schost. Fast computation of special resultants. J. Symbolic Comput., 41(1):1–29, 2006.
A. Bostan, P. Gaudry, and É. Schost. Linear recurrences with polynomial coefficients and application to integer factorization and Cartier-Manin operator. SIAM J. Comput., 36(6):1777–1806, 2007.
A. Bostan, L. Gonzales-Vega, H. Perdry, and É. Schost. Complexity issues on Newton sums of polynomials. Distributed in the digital proceedings of MEGA'05, 2005.
A. Bostan and É. Schost. Polynomial evaluation and interpolation on special sets of points. J. Complexity, 21(4):420–446, 2005.
P. Camion. A deterministic algorithm for factorizing
polynomials of 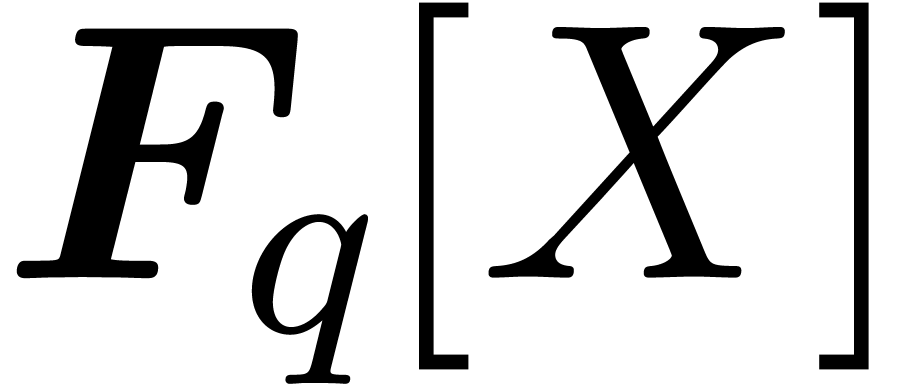 . In
Combinatorial mathematics (Marseille-Luminy, 1981),
volume 75 of North-Holland Math. Stud., pages
149–157. North-Holland, Amsterdam, 1983.
. In
Combinatorial mathematics (Marseille-Luminy, 1981),
volume 75 of North-Holland Math. Stud., pages
149–157. North-Holland, Amsterdam, 1983.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Infor., 28(7):693–701, 1991.
D. G. Cantor and H. Zassenhaus. A new algorithm for factoring polynomials over finite fields. Math. Comp., 36(154):587–592, 1981.
X. Caruso, D. Roe, and T. Vaccon. Tracking 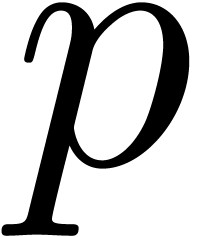 -adic precision. LMS J.
Comput. Math., 17:274–294, 2014. Special Issue A,
Algorithmic Number Theory Symposium XI.
-adic precision. LMS J.
Comput. Math., 17:274–294, 2014. Special Issue A,
Algorithmic Number Theory Symposium XI.
E. Costa and D. Harvey. Faster deterministic integer factorization. Math. Comp., 83(285):339–345, 2014.
S. Evdokimov. Factorization of polynomials over finite fields in subexponential time under GRH. In Algorithmic number theory (Ithaca, NY, 1994), volume 877 of Lecture Notes in Comput. Sci., pages 209–219. Springer, Berlin, 1994.
Shuhong Gao. On the deterministic complexity of factoring polynomials. J. Symbolic Comput., 31(1–2):19 – 36, 2001.
J. von zur Gathen. Factoring polynomials and primitive elements for special primes. Theoret. Comput. Sci., 52(1-2):77–89, 1987.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, 2nd edition, 2003.
J. von zur Gathen and D. Panario. Factoring polynomials over finite fields: A survey. J. Symbolic Comput., 31(1–2):3–17, 2001.
M. Giusti, G. Lecerf, and B. Salvy. A Gröbner free alternative for polynomial system solving. J. Complexity, 17(1):154–211, 2001.
B. Grenet, J. van der Hoeven, and G. Lecerf. Randomized root finding over finite fields using tangent Graeffe transforms. Technical report, École polytechnique, 2015.
D. Harvey, J. van der Hoeven, and G. Lecerf. Even faster integer multiplication. http://arxiv.org/abs/1407.3360, 2014.
D. Harvey, J. van der Hoeven, and G. Lecerf. Faster polynomial multiplication over finite fields. http://arxiv.org/abs/1407.3361, 2014.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation in practice. ACM Commun. Comput. Algebra, 48(4), 2014. In section "ISSAC 2014 Software Presentations".
Ming-Deh A. Huang. Generalized Riemann hypothesis and factoring polynomials over finite fields. J. Algorithms, 12(3):464–481, 1991.
E. Kaltofen. Polynomial factorization: a success story. In Hoon Hong, editor, ISSAC '03: Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, pages 3–4. ACM Press, 2003.
K. S. Kedlaya and C. Umans. Fast modular composition in any characteristic. In A. Z. Broder et al., editors, 49th Annual IEEE Symposium on Foundations of Computer Science 2008 (FOCS '08), pages 146–155. IEEE, 2008.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
L. Kronecker. Grundzüge einer arithmetischen Theorie der algebraischen Grössen. J. reine angew. Math., 92:1–122, 1882.
G. Lecerf. Fast separable factorization and applications. Appl. Alg. Eng. Comm. Comp., 19(2):135–160, 2008.
G. Malajovich and J. P. Zubelli. Tangent Graeffe iteration. Numer. Math., 89(4):749–782, 2001.
M. Mignotte and C. Schnorr. Calcul déterministe des racines d'un polynôme dans un corps fini. C. R. Acad. Sci. Paris Sér. I Math., 306(12):467–472, 1988.
R. T. Moenck. On the efficiency of algorithms for polynomial factoring. Math. Comp., 31:235–250, 1977.
G. L. Mullen and D. Panario. Handbook of Finite Fields. Discrete Mathematics and Its Applications. Chapman and Hall/CRC, 2013.
V. Pan. Solving a polynomial equation: Some history and recent progress. SIAM Rev., 39(2):187–220, 1997.
V. Pan. New techniques for the computation of linear recurrence coefficients. Finite Fields Appl., 6:93–118, 2000.
S. C. Pohlig and M. E. Hellman. An improved algorithm
for computing logarithms over GF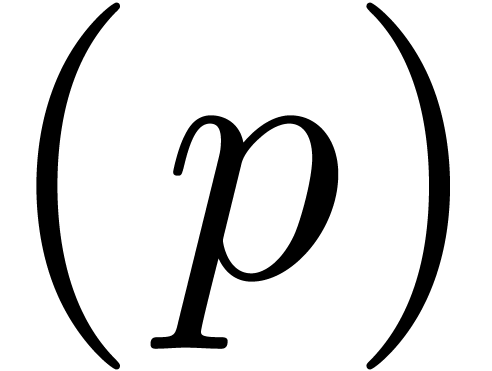 and its
cryptographic significance (corresp.). IEEE Trans. Inform.
Theory, 24(1):106–110, 1978.
and its
cryptographic significance (corresp.). IEEE Trans. Inform.
Theory, 24(1):106–110, 1978.
L. Rónyai. Factoring polynomials modulo special primes. Combinatorica, 9(2):199–206, 1989.
L. Rónyai. Galois groups and factoring polynomials over finite fields. SIAM J. Disc. Math., 5(3):345–365, 1992.
Chandan Saha. Factoring polynomials over finite fields using balance test. In S. Albers and P. Weil, editors, 25th International Symposium on Theoretical Aspects of Computer Science, volume 1 of Leibniz International Proceedings in Informatics (LIPIcs), pages 609–620, Dagstuhl, Germany, 2008. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik. http://drops.dagstuhl.de/opus/volltexte/2008/1323.
R. Schoof. Elliptic curves over finite fields and the
computation of square roots mod 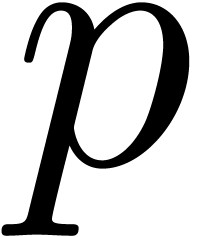 .
Math. Comp., 44(170):483–494, 1985.
.
Math. Comp., 44(170):483–494, 1985.
V. Shoup. On the deterministic complexity of factoring polynomials over finite fields. Inform. Process. Lett., 33(5):261–267, 1990.
V. Shoup. A fast deterministic algorithm for factoring polynomials over finite fields of small characteristic. In S. M. Watt, editor, ISSAC '91: Proceedings of the 1991 International Symposium on Symbolic and Algebraic Computation, pages 14–21. ACM Press, 1991.
V. Shoup. Smoothness and factoring polynomials over finite fields. Inform. Process. Lett., 38(1):39–42, 1991.
V. Shoup. Searching for primitive roots in finite fields. Math. Comp., 58:369–380, 1992.
V. Shoup. NTL: A Library for doing Number Theory, 2014. Software, version 8.0.0. http://www.shoup.net/ntl.
B. Źrałek. Using partial smoothness of
 for factoring polynomials modulo
for factoring polynomials modulo 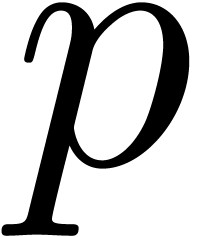 . Math. Comp.,
79:2353–2359, 2010.
. Math. Comp.,
79:2353–2359, 2010.