Faster relaxed
multiplication |
|
CNRS, Laboratoire d'informatique
École polytechnique
91128 Palaiseau Cedex
France
Email: joris@texmacs.org
|
|
|
Abstract
In previous work, we have introduced several fast algorithms for relaxed
power series multiplication (also known under the name on-line
multiplication) up to a given order 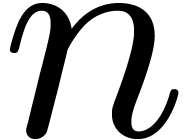 .
The fastest currently known algorithm works over an effective base field
.
The fastest currently known algorithm works over an effective base field
 with sufficiently many
with sufficiently many 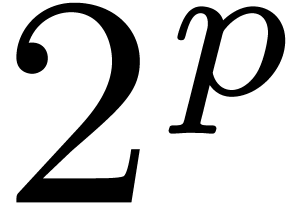 -th roots of unity and has algebraic time complexity
-th roots of unity and has algebraic time complexity
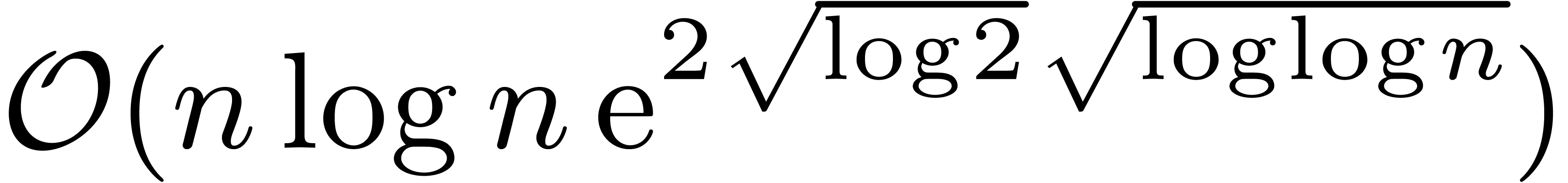 . In this paper, we will
generalize this algorithm to the cases when
. In this paper, we will
generalize this algorithm to the cases when  is
replaced by an effective ring of positive characteristic or by an
effective ring of characteristic zero, which is also torsion-free as a
is
replaced by an effective ring of positive characteristic or by an
effective ring of characteristic zero, which is also torsion-free as a
 -module and comes with an
additional algorithm for partial division by integers. In particular, we
may take
-module and comes with an
additional algorithm for partial division by integers. In particular, we
may take  to be any effective field. We will also
present an asymptotically faster algorithm for relaxed multiplication of
to be any effective field. We will also
present an asymptotically faster algorithm for relaxed multiplication of
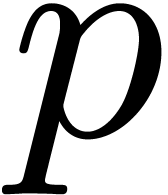 -adic numbers.
-adic numbers.
Keywords: power series, multiplication, on-line
algorithm, FFT, computer algebra
A.M.S. subject classification: 68W30, 30B10, 68W25, 33F05, 11Y55,
42-04
1Introduction
1.1Relaxed resolution of recursive
equations
Let  be an effective (possibly non-commutative)
ring; i.e., we assume data structures for representing the
elements of
be an effective (possibly non-commutative)
ring; i.e., we assume data structures for representing the
elements of  and algorithms for performing the
ring operations
and algorithms for performing the
ring operations  ,
,  and
and  . The aim
of algebraic complexity theory is to study the cost of basic or more
complex algebraic operations over
. The aim
of algebraic complexity theory is to study the cost of basic or more
complex algebraic operations over  (such as the
multiplication of polynomials or matrices) in terms of the number of
operations in
(such as the
multiplication of polynomials or matrices) in terms of the number of
operations in  .
.
The algebraic complexity usually does not coincide with the bit
complexity, which also takes into account the potential growth of the
actual coefficients in  .
Nevertheless, understanding the algebraic complexity usually constitutes
a first useful step towards understanding the bit complexity. Of course,
in the special case when
.
Nevertheless, understanding the algebraic complexity usually constitutes
a first useful step towards understanding the bit complexity. Of course,
in the special case when  is a finite field, both
complexities coincide up to a constant factor.
is a finite field, both
complexities coincide up to a constant factor.
One of the most central operations is polynomial multiplication. We will
denote by 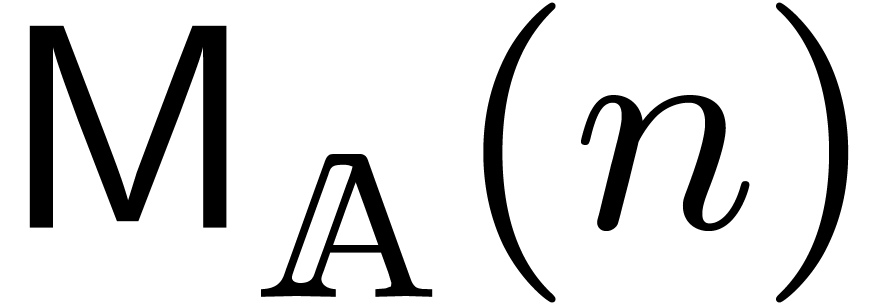 the number of operations required to
multiply two polynomials of degrees
the number of operations required to
multiply two polynomials of degrees 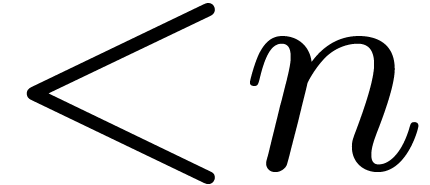 in
in 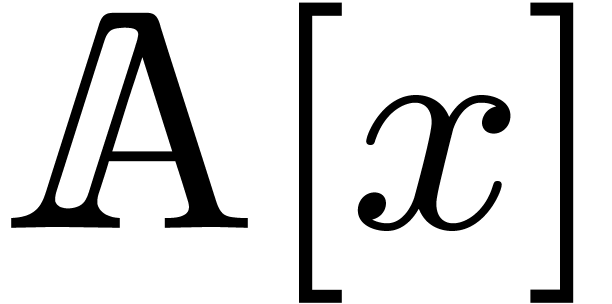 . If
. If  admits
primitive
admits
primitive 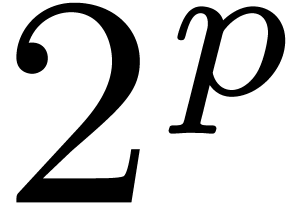 -th roots of unity
for all
-th roots of unity
for all 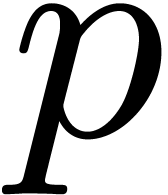 , then we have
, then we have 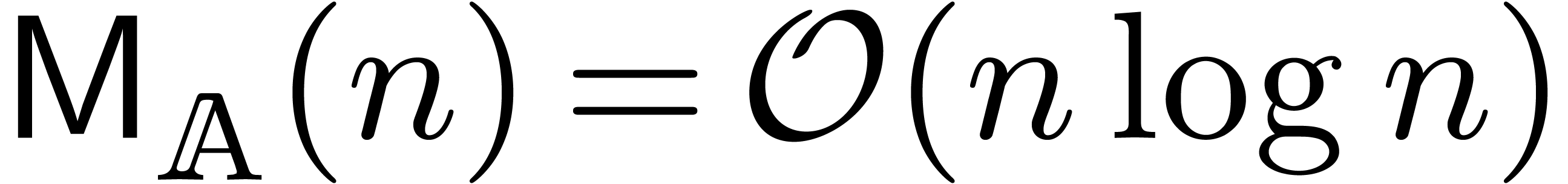 using FFT multiplication, which is based on the fast
Fourier transform [12]. In general, it has been shown [28, 10] that
using FFT multiplication, which is based on the fast
Fourier transform [12]. In general, it has been shown [28, 10] that 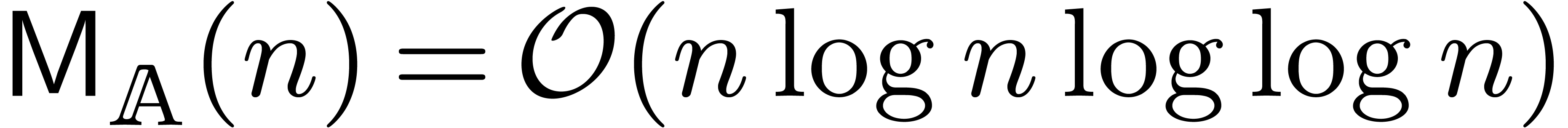 .
The complexities of most other operations (division, Taylor shift,
extended g.c.d., multipoint evaluation, interpolation,
etc.) can be expressed in terms of
.
The complexities of most other operations (division, Taylor shift,
extended g.c.d., multipoint evaluation, interpolation,
etc.) can be expressed in terms of 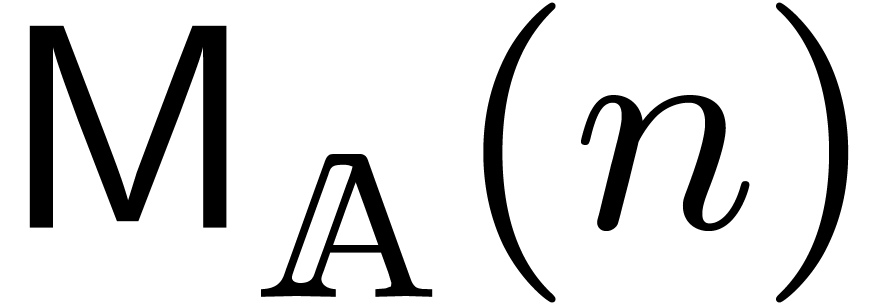 . Often, the cost of such other operations is simply
. Often, the cost of such other operations is simply
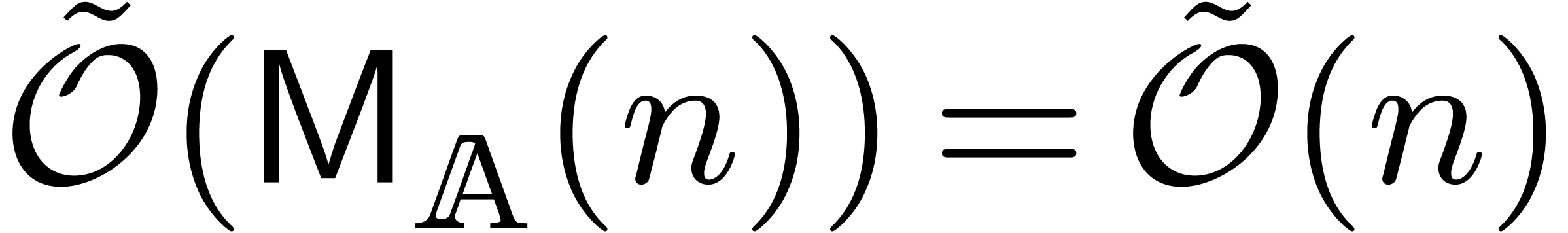 , where
, where 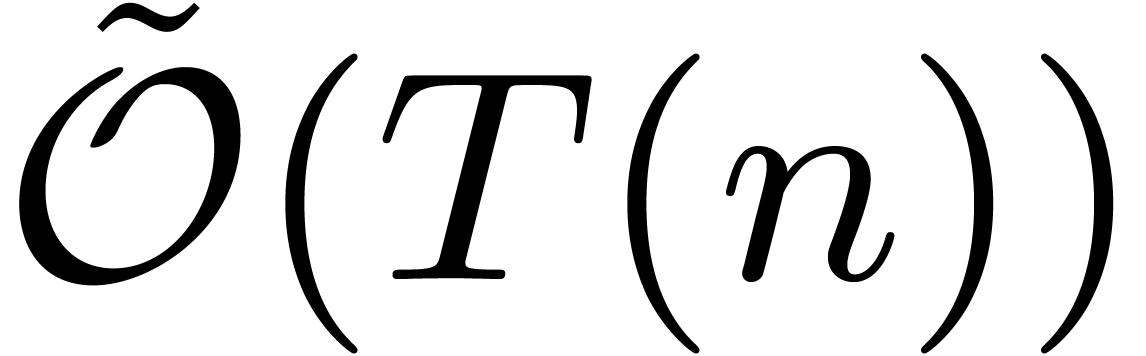 stands for
stands for 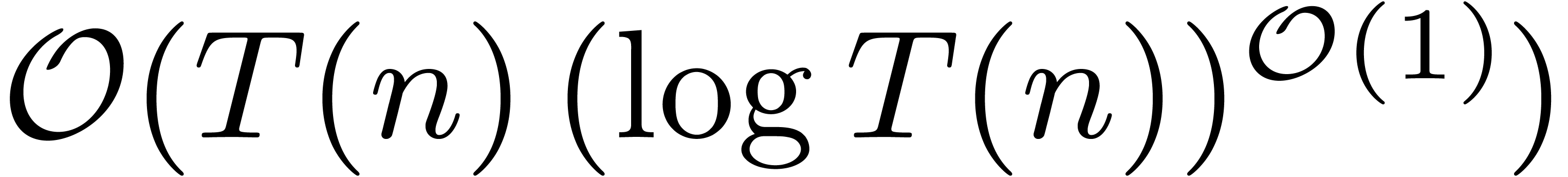 ; see [2,
6, 15] for some classical results along these
lines.
; see [2,
6, 15] for some classical results along these
lines.
The complexity of polynomial multiplication is fundamental for studying
the cost of operations on formal power series in 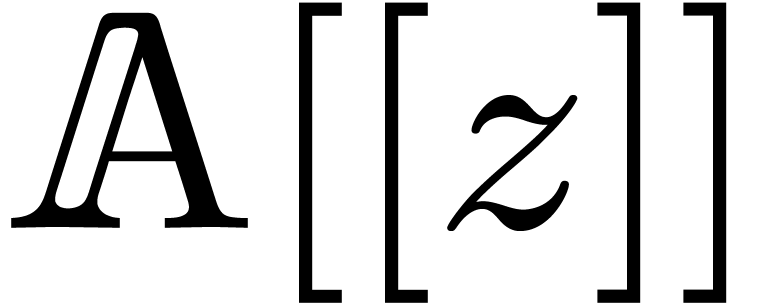 up to a given truncation order
up to a given truncation order  .
Clearly, it is possible to perform the multiplication up to order
.
Clearly, it is possible to perform the multiplication up to order  in time
in time  :
it suffices to multiply the truncated power series at order
:
it suffices to multiply the truncated power series at order  and truncate the result. Using Newton's method, and
assuming that
and truncate the result. Using Newton's method, and
assuming that 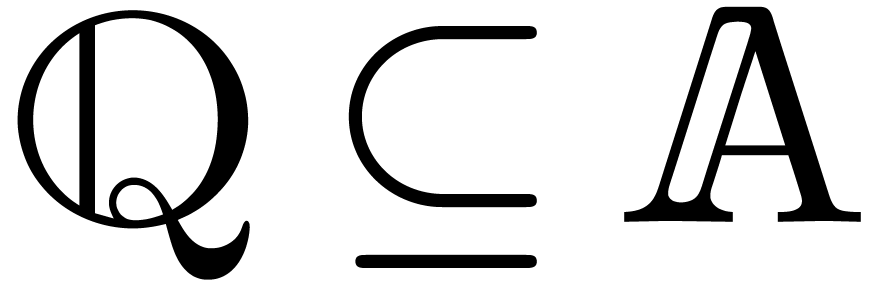 , it is also
possible to compute
, it is also
possible to compute  ,
,  , etc. up to order
, etc. up to order
 in time
in time  .
More generally, it has been shown in [9, 17,
29, 23] that the power series solutions of
algebraic differential equations with coefficients in
.
More generally, it has been shown in [9, 17,
29, 23] that the power series solutions of
algebraic differential equations with coefficients in 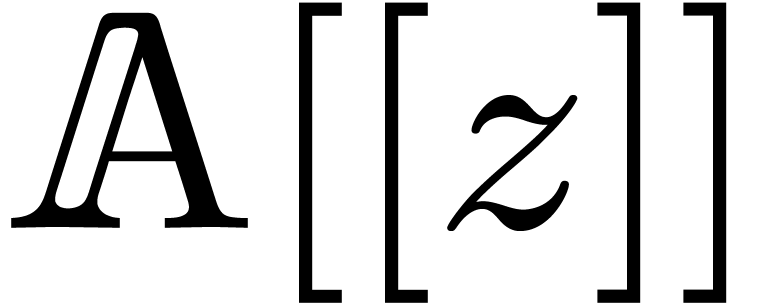 can be computed up to order
can be computed up to order 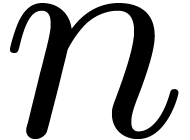 in time
in time  . However, in this case, the “
. However, in this case, the “ ” hides a non-trivial
constant factor which depends on the expression size of the equation
that one wants to solve.
” hides a non-trivial
constant factor which depends on the expression size of the equation
that one wants to solve.
The relaxed approach for computations with formal power series
makes it possible to solve equations in quasi-optimal time with respect
to the sparse expression size of the equations. The idea is to consider
power series  as streams of coefficients
as streams of coefficients 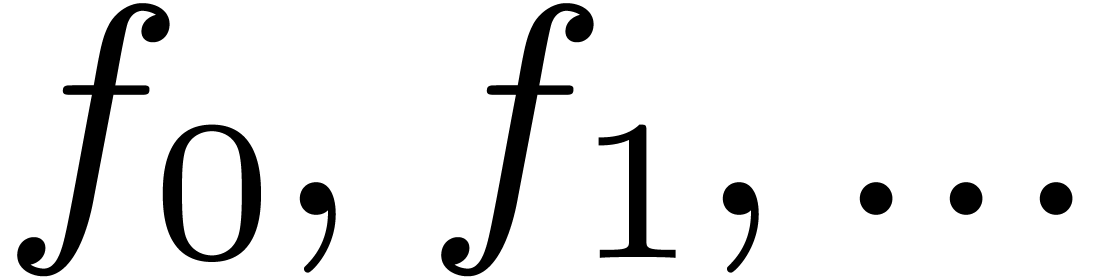 and to require that all operations are performed
“without delay” on these streams. For instance, for a
multiplication
and to require that all operations are performed
“without delay” on these streams. For instance, for a
multiplication 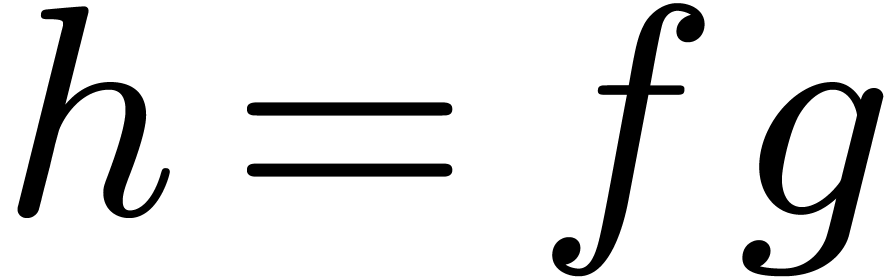 of two power series
of two power series 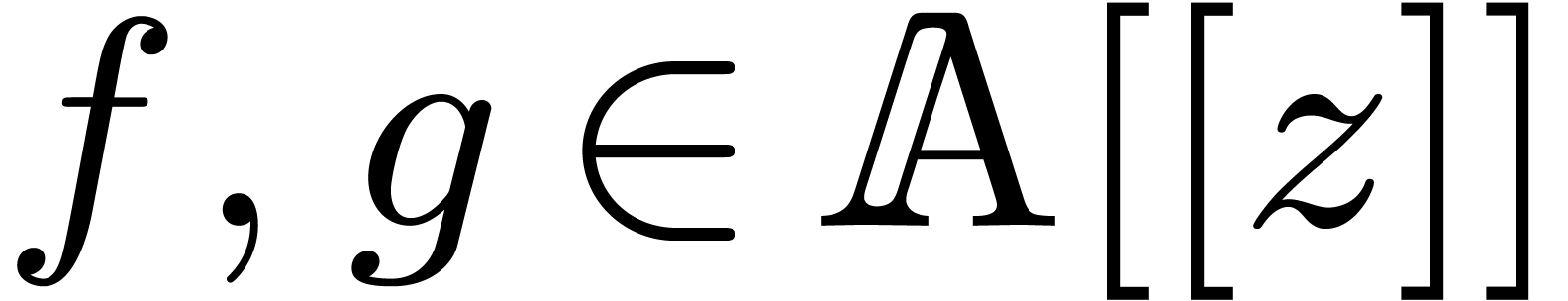 , we require that
, we require that 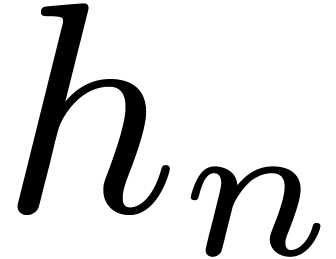 is
computed as soon as
is
computed as soon as  are known. Any
algorithm which has this property will be called a relaxed or
on-line algorithm for multiplication.
are known. Any
algorithm which has this property will be called a relaxed or
on-line algorithm for multiplication.
Given a relaxed algorithm for multiplication, it is possible to let the
later coefficients 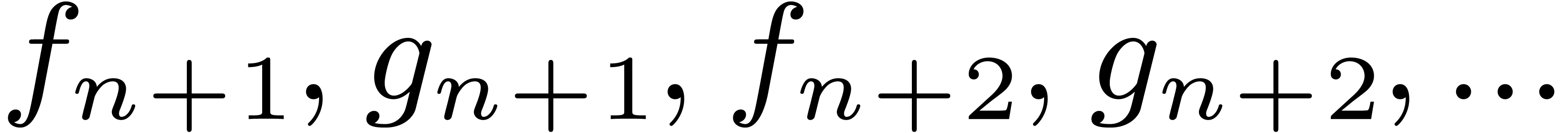 of the input depend
on the known coefficients
of the input depend
on the known coefficients  of the output. For
instance, given a power series
of the output. For
instance, given a power series  with
with  , we may compute
, we may compute  using
the formula
using
the formula
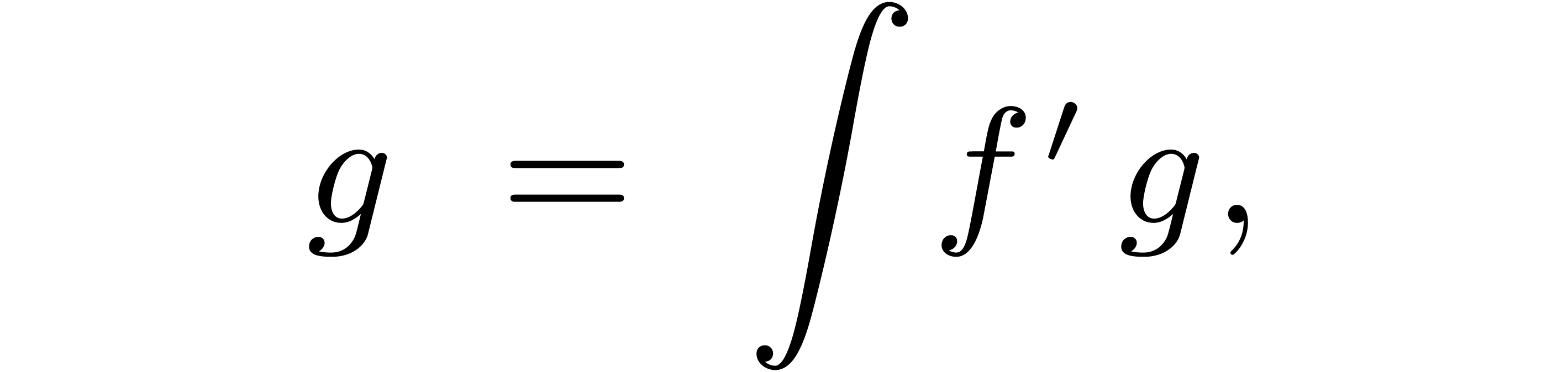 |
(1) |
provided that  . Indeed,
extraction of the coefficient of
. Indeed,
extraction of the coefficient of  in
in  and
and 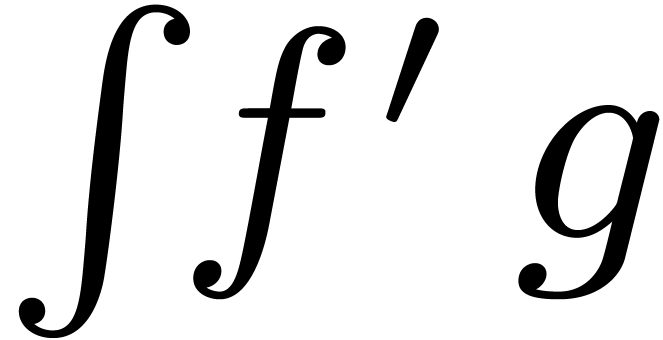 yields
yields
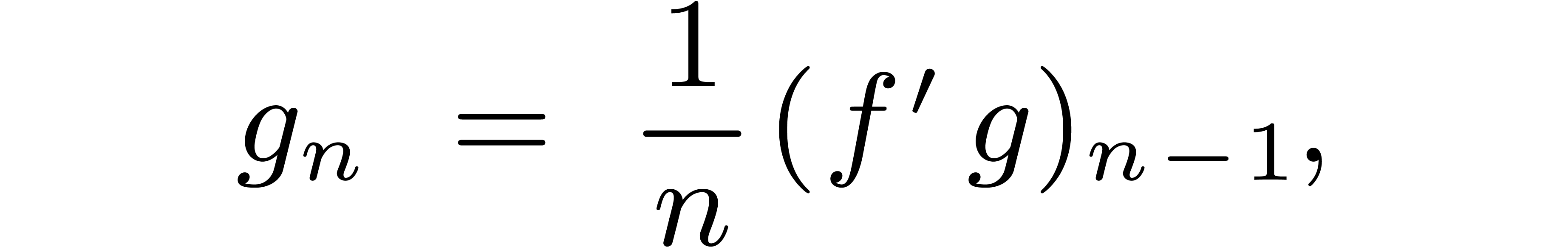
and 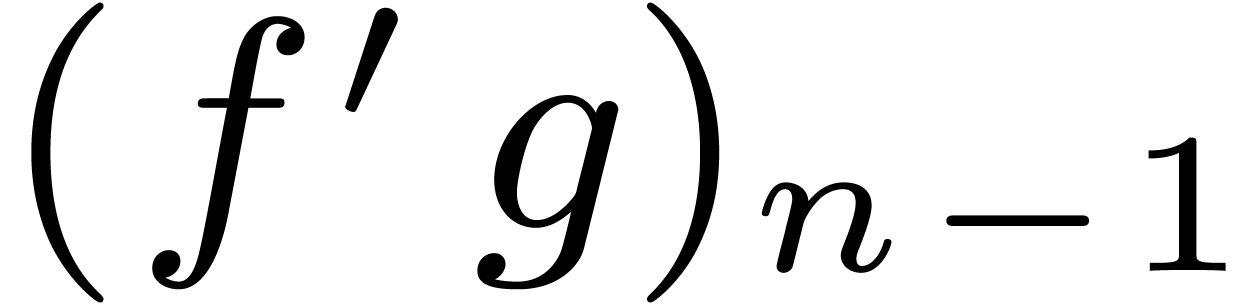 only depends on
only depends on 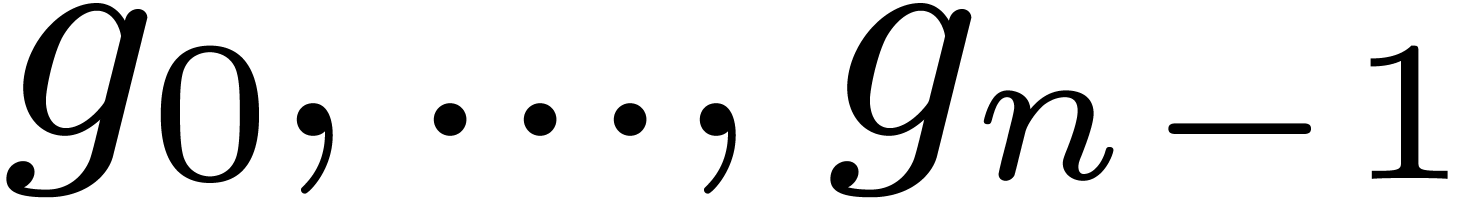 . More generally, we define an equation of the form
. More generally, we define an equation of the form
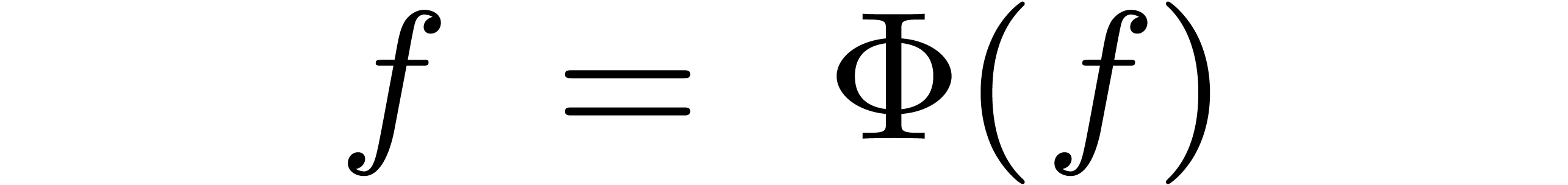 |
(2) |
to be recursive, if 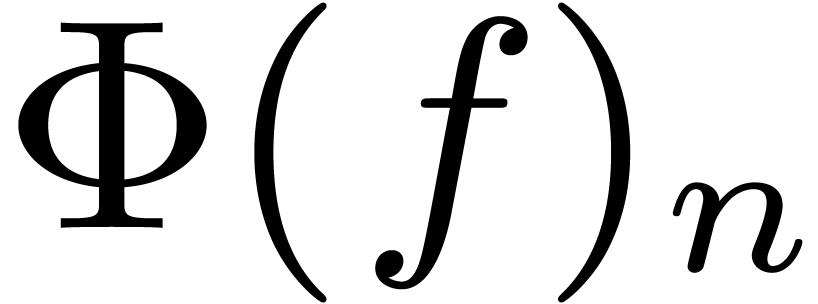 only depends on
only depends on
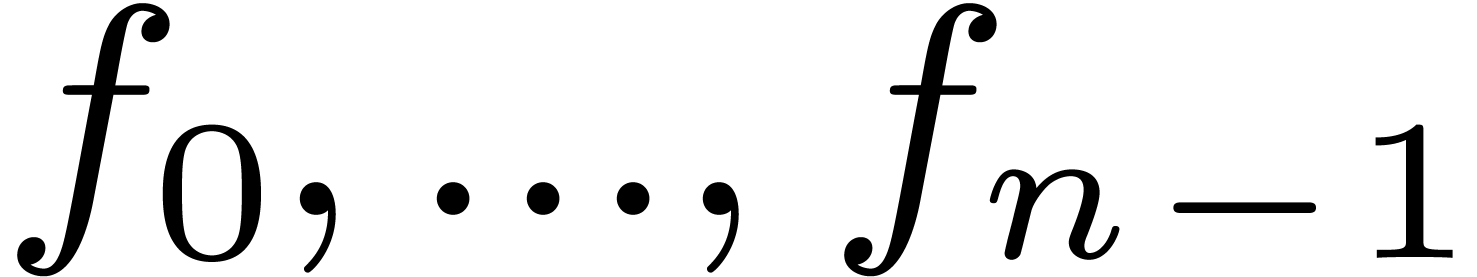 . Replacing
. Replacing  by
by  , we notice that the same
terminology applies to systems of
, we notice that the same
terminology applies to systems of  equations. In
the case of an implicit equation, special rewriting techniques can be
implied in order to transform the input equation into a recursive
equation [24, 22, 5].
equations. In
the case of an implicit equation, special rewriting techniques can be
implied in order to transform the input equation into a recursive
equation [24, 22, 5].
Let 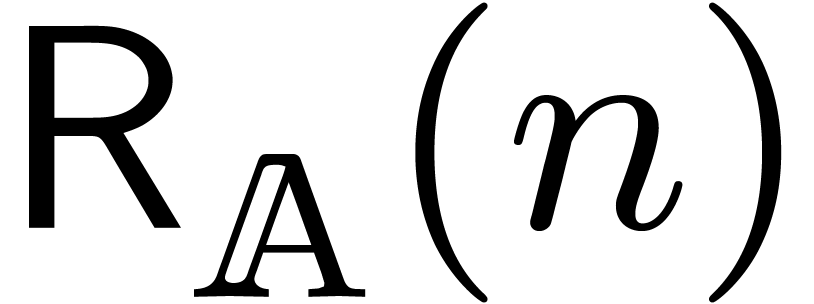 denote the cost of performing a relaxed
multiplication up to order
denote the cost of performing a relaxed
multiplication up to order 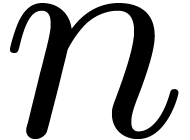 .
If
.
If  is an expression which involves
is an expression which involves  multiplications and
multiplications and 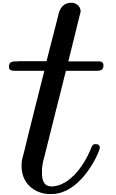 other
“linear time” operations (additions, integrations, etc.),
then it follows that (2) can be solved up to order
other
“linear time” operations (additions, integrations, etc.),
then it follows that (2) can be solved up to order 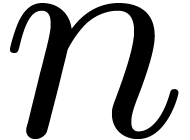 in time
in time 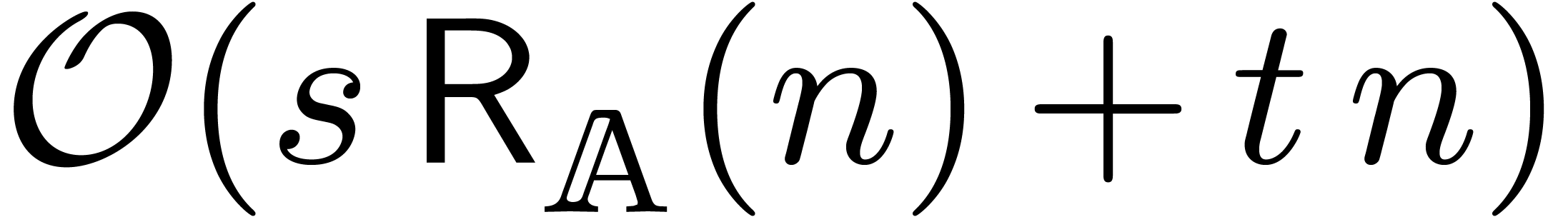 .
If we had
.
If we had  , then this would
yield an optimal algorithm for solving (2) in the sense
that the computation of the solution would essentially require the same
time as its verification.
, then this would
yield an optimal algorithm for solving (2) in the sense
that the computation of the solution would essentially require the same
time as its verification.
1.2Known algorithms for relaxed
multiplication
The naive  algorithm for computing
algorithm for computing 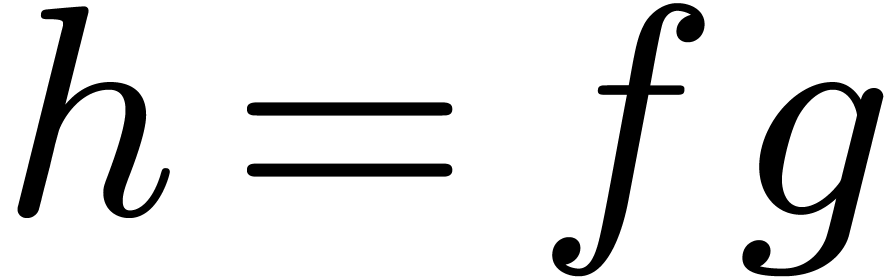 , based on the formula
, based on the formula
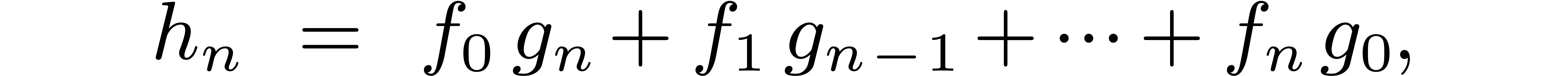
is clearly relaxed. Unfortunately, FFT multiplication is not
relaxed, since  are computed simultaneously as a
function of
are computed simultaneously as a
function of  , in this case.
, in this case.
In [16, 17] it was remarked that Karatsuba's
 algorithm [25] for multiplying
polynomials can be rewritten in a relaxed manner. Karatsuba
multiplication and its relaxed version thus require exactly the
same number of operations. In [16, 17], an
additional fast relaxed algorithm was presented with time complexity
algorithm [25] for multiplying
polynomials can be rewritten in a relaxed manner. Karatsuba
multiplication and its relaxed version thus require exactly the
same number of operations. In [16, 17], an
additional fast relaxed algorithm was presented with time complexity
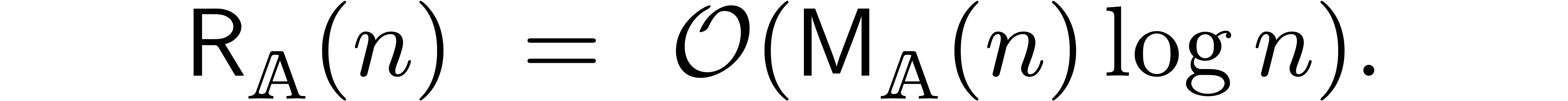 |
(3) |
We were recently made aware of the fact that a similar algorithm was
first published in [13]. However, this early paper was
presented in a different context of on-line (relaxed) multiplication of
integers (instead of power series), and without the application to the
resolution of recursive equations (which is quite crucial from our
perspective).
An interesting question remained: can the bound (3) be
lowered further, be it by a constant factor? In [18], it
was first noticed that an approximate factor of two can be gained if one
of the multiplicands is known beforehand. For instance, if we want to
compute 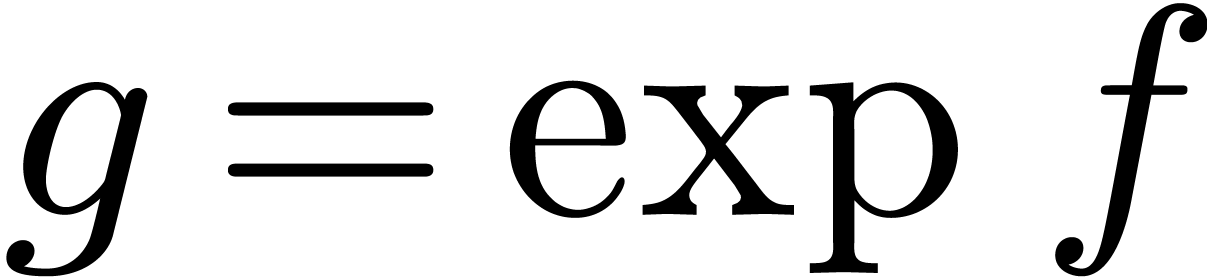 for a known series
for a known series 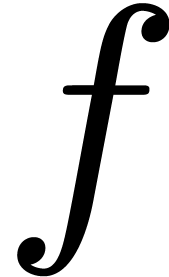 with
with 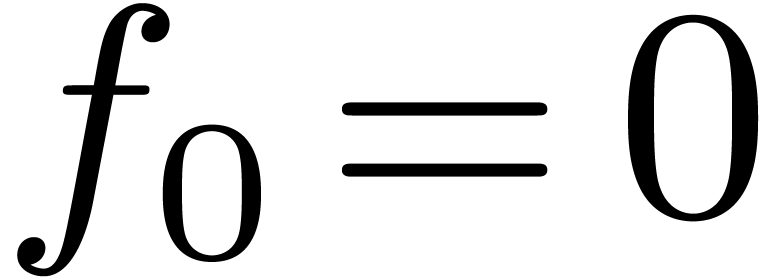 , then the coefficients
of
, then the coefficients
of 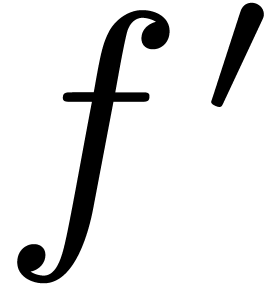 are already known in the product
are already known in the product 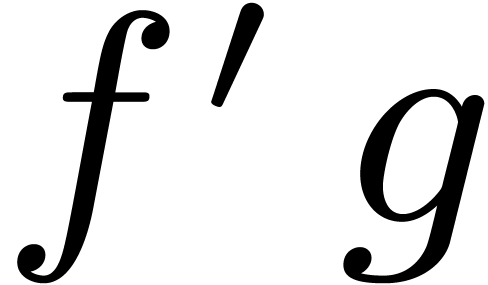 in (1), so only one of the inputs depends on
the output. An algorithm for the computation of
in (1), so only one of the inputs depends on
the output. An algorithm for the computation of  is said to be semi-relaxed, if
is said to be semi-relaxed, if  is
written to the output as soon as
is
written to the output as soon as  are known, but
all coefficients of
are known, but
all coefficients of  are known beforehand. We
will denote by
are known beforehand. We
will denote by 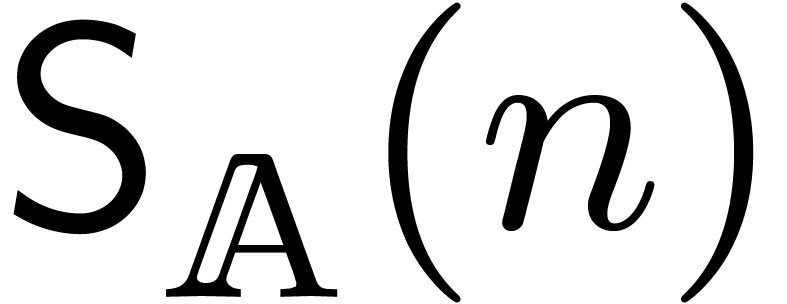 the complexity of semi-relaxed
multiplication. We recall from [21] (see also Section 3) that relaxed multiplication reduces to semi-relaxed
multiplication:
the complexity of semi-relaxed
multiplication. We recall from [21] (see also Section 3) that relaxed multiplication reduces to semi-relaxed
multiplication:

It has recently been pointed out [26] that the factor  that was gained in the case of semi-relaxed
multiplication can also be gained in the general case.
that was gained in the case of semi-relaxed
multiplication can also be gained in the general case.
The first reduction of (3) by a non-constant factor was
published in [21], and uses the technique of FFT
blocking (which has also been used for the multiplication of
multivariate polynomials and power series in [17, Section
6.3], and for speeding up Newton iterations in [3, 23]).
Under the assumption that  admits primitive
admits primitive 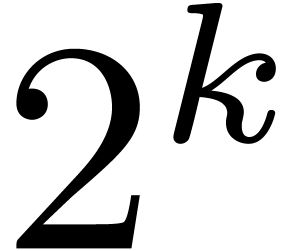 -th roots of unity for all
-th roots of unity for all  (or at least for all
(or at least for all  with
with
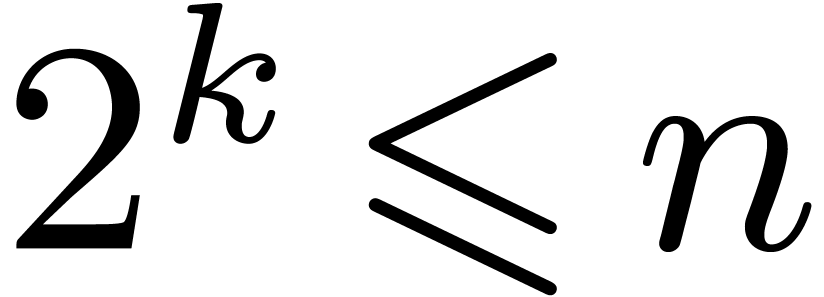 ), we showed that
), we showed that
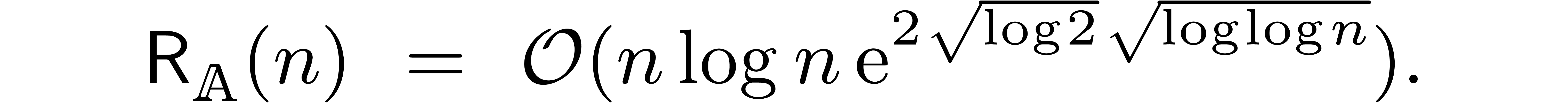 |
(4) |
The function 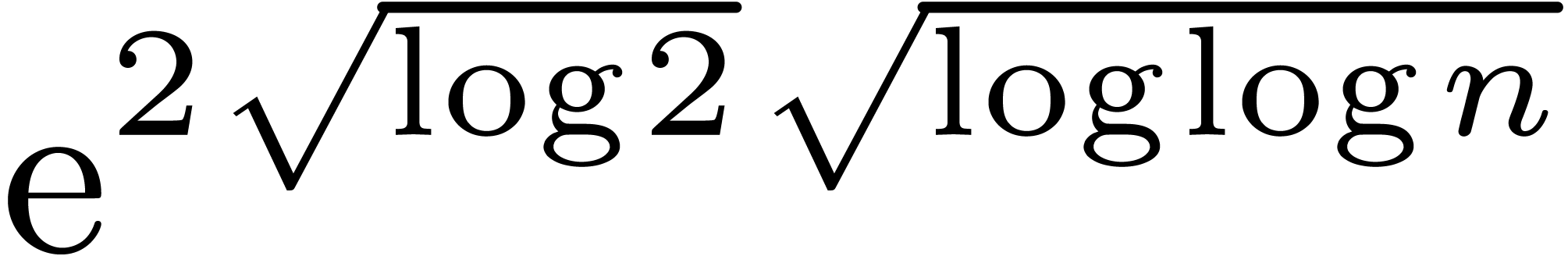 has slower growth than any strictly
positive power of
has slower growth than any strictly
positive power of  . It is
convenient to write
. It is
convenient to write  whenever
whenever 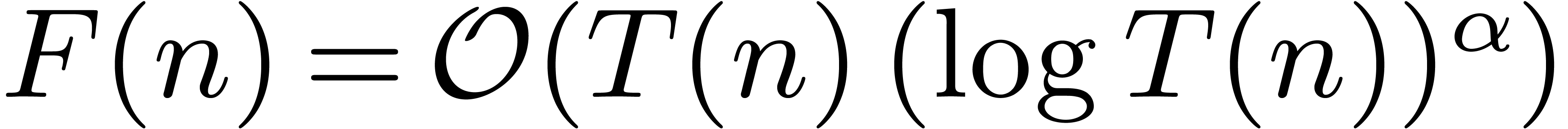 for all
for all 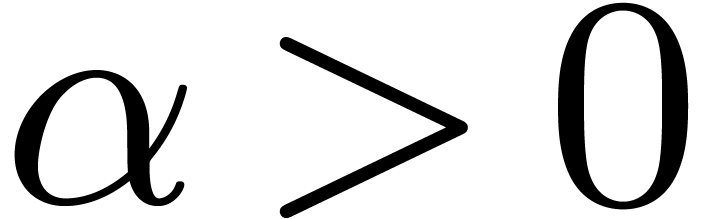 . In particular, it
follows that
. In particular, it
follows that

In Section 3, we will recall the main ideas from [21]
which lead to the complexity bound (4).
In fact, in Section 4, we will see that the complexity
bound from [21] can be further reduced to
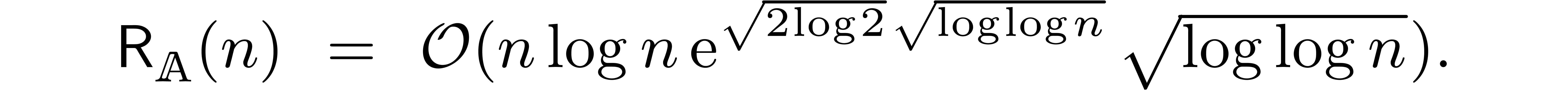
Since such complexity bounds involve rather complex expressions, it will
be convenient to use the following abbreviations:
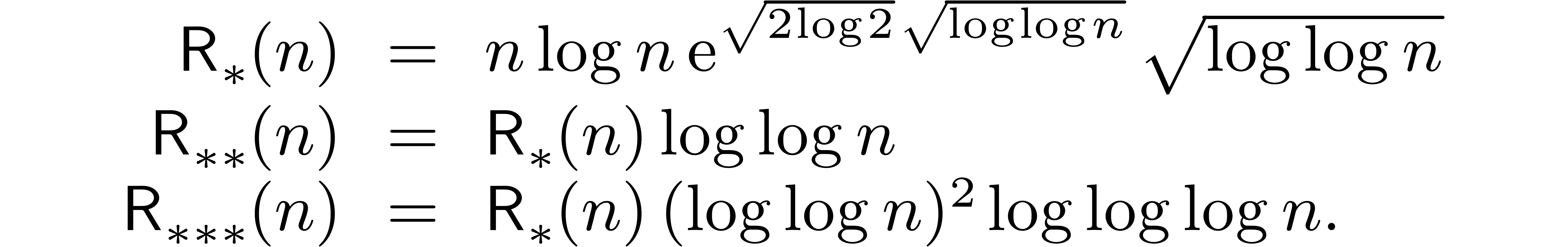
Clearly, 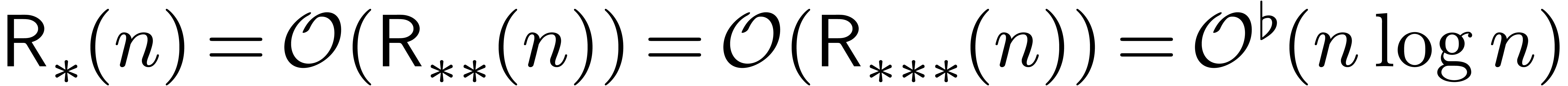 .
.
1.3Improved complexity bounds
We recall that the characteristic of a ring  is
the integer
is
the integer 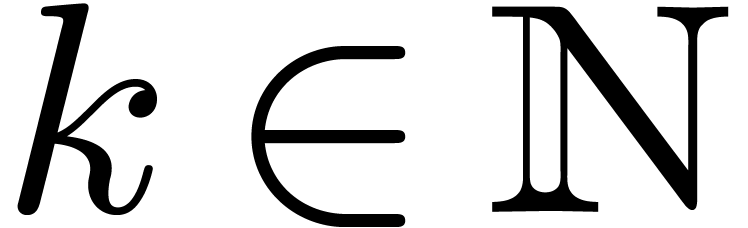 such that the canonical ring
homomorphism
such that the canonical ring
homomorphism 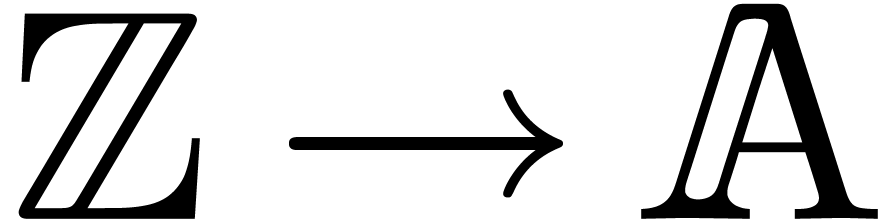 has kernel
has kernel 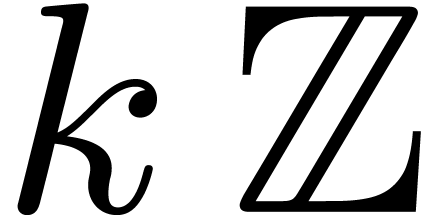 . If
. If  is torsion-free as a
is torsion-free as a
 -module (i.e.
-module (i.e.
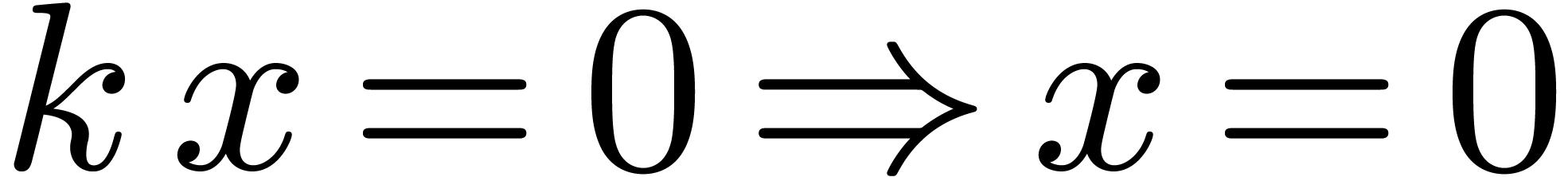 for any
for any 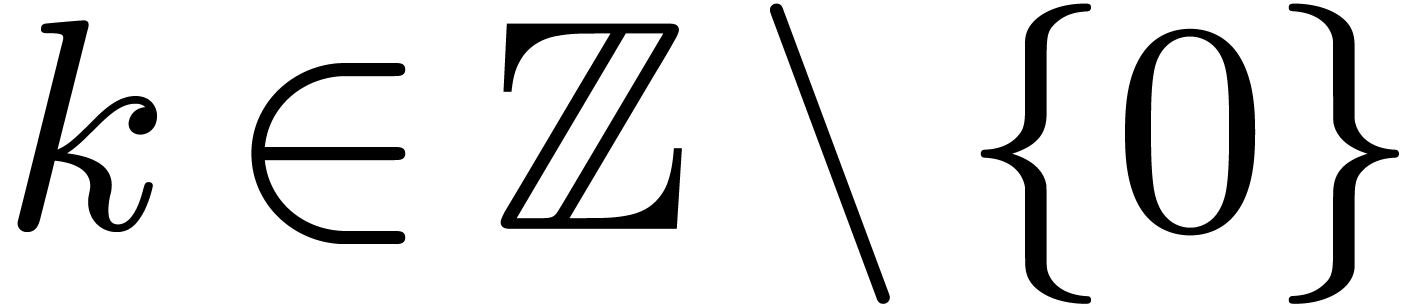 and
and  ), then we will say that
), then we will say that  admits an effective partial division by integers if there exists an
algorithm which takes
admits an effective partial division by integers if there exists an
algorithm which takes 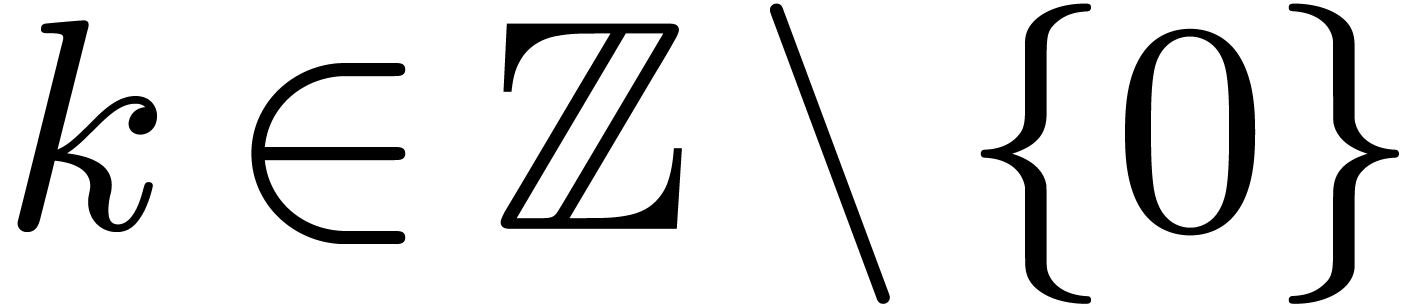 and
and 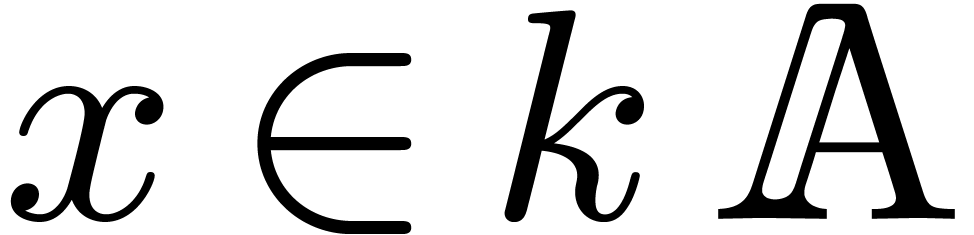 on input and which returns the unique
on input and which returns the unique 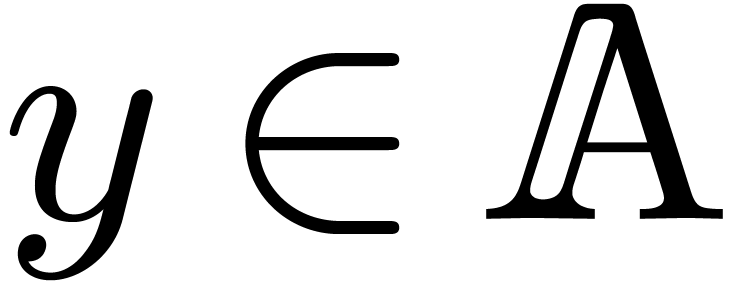 with
with  on output. We will count a unit cost for such
divisions. The main result of this paper is:
on output. We will count a unit cost for such
divisions. The main result of this paper is:
Theorem 1. Assume
that one of the following two holds:
-
 is an effective ring of characteristic zero,
which is torsion-free as a
is an effective ring of characteristic zero,
which is torsion-free as a  -module,
and which admits an effective partial division by integers.
-module,
and which admits an effective partial division by integers.
-
 is an effective ring of positive
characteristic.
is an effective ring of positive
characteristic.
Then we have
 |
(5) |
We notice that the theorem holds in particular if  is an effective field. In Section 8, we will also consider
the relaxed multiplication of
is an effective field. In Section 8, we will also consider
the relaxed multiplication of 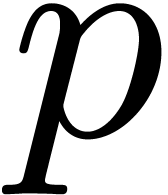 -adic
numbers, with
-adic
numbers, with 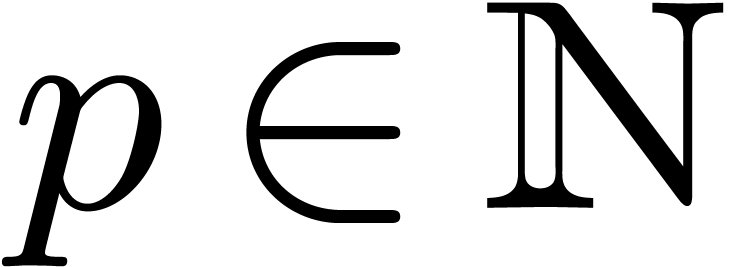 and
and 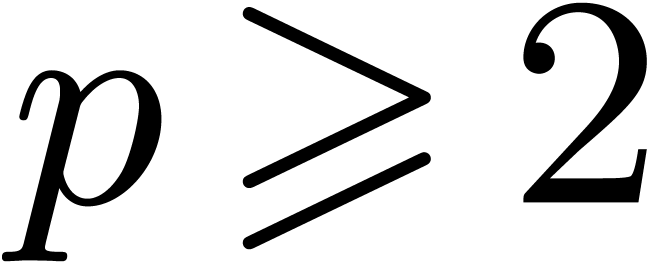 .
If we denote by
.
If we denote by 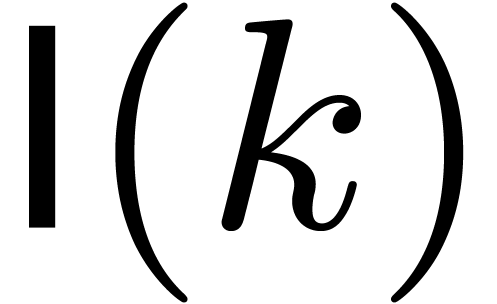 the bit complexity of
multiplying two
the bit complexity of
multiplying two 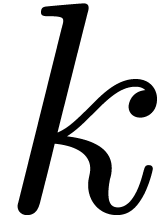 -bit
integers, then [13] essentially provided an algorithm of
bit complexity
-bit
integers, then [13] essentially provided an algorithm of
bit complexity 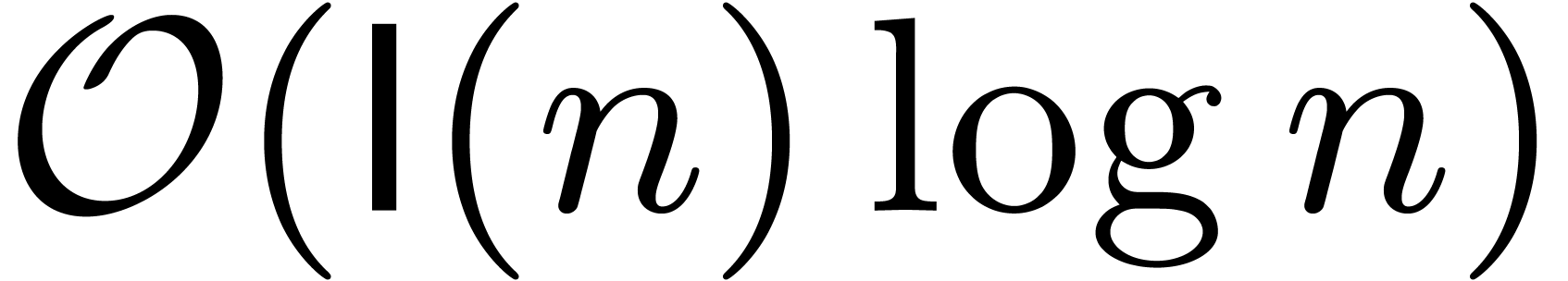 for the relaxed multiplication of
for the relaxed multiplication of
 -adic numbers at order
-adic numbers at order 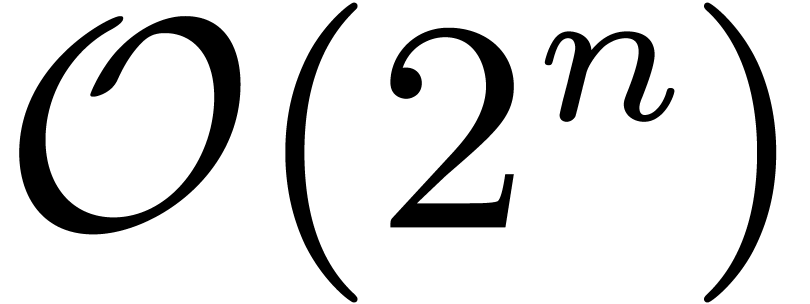 . Various algorithms and benchmarks
for more general
. Various algorithms and benchmarks
for more general 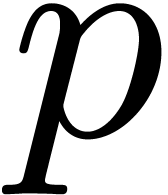 were presented in [4].
It is also well known [33, 11, 28,
14] that
were presented in [4].
It is also well known [33, 11, 28,
14] that 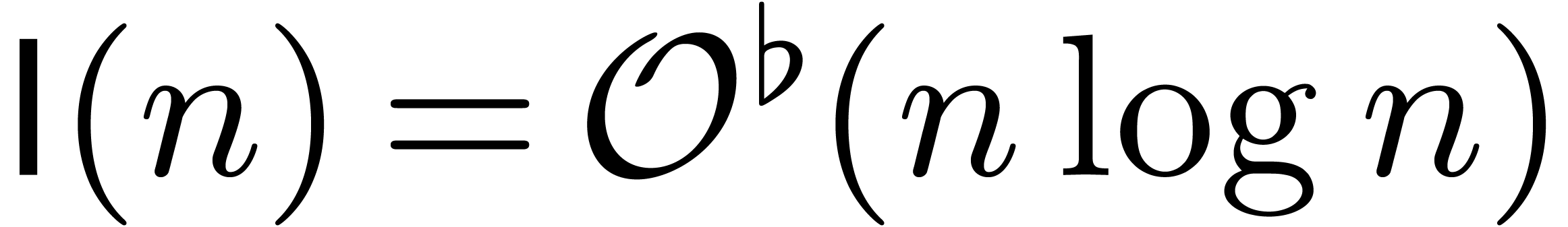 . Let
. Let
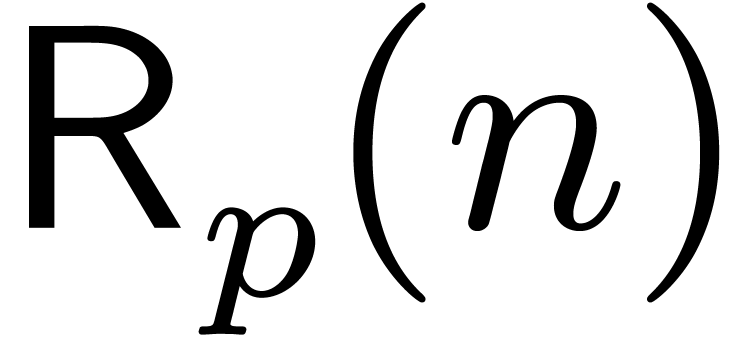 denote the bit complexity of the relaxed
multiplication of two
denote the bit complexity of the relaxed
multiplication of two 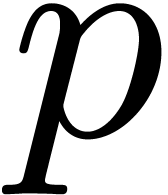 -adic
numbers modulo
-adic
numbers modulo 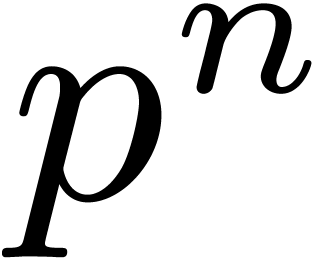 . In Section
8, we will prove the following new result:
. In Section
8, we will prove the following new result:
Theorem 2. Let 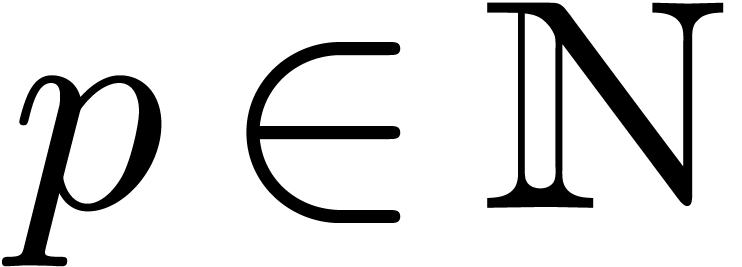 with
with 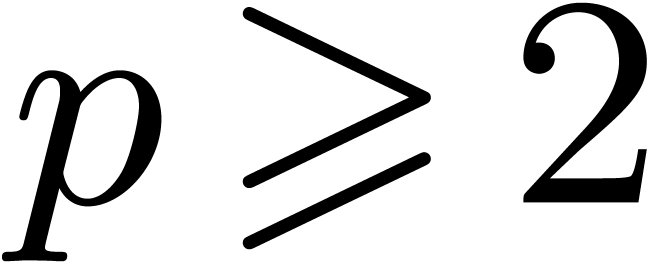 .
Then we have
.
Then we have
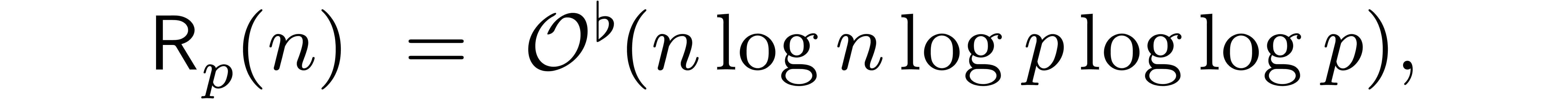
uniformly in 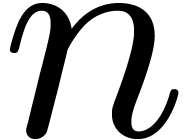 and
and 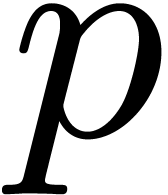 .
.
For comparison, the best previously known bound for relaxed
multiplication in 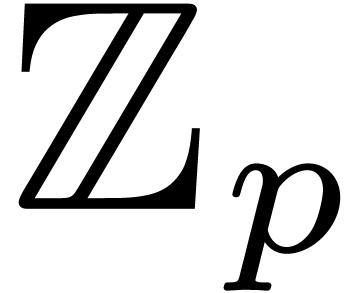 was
was
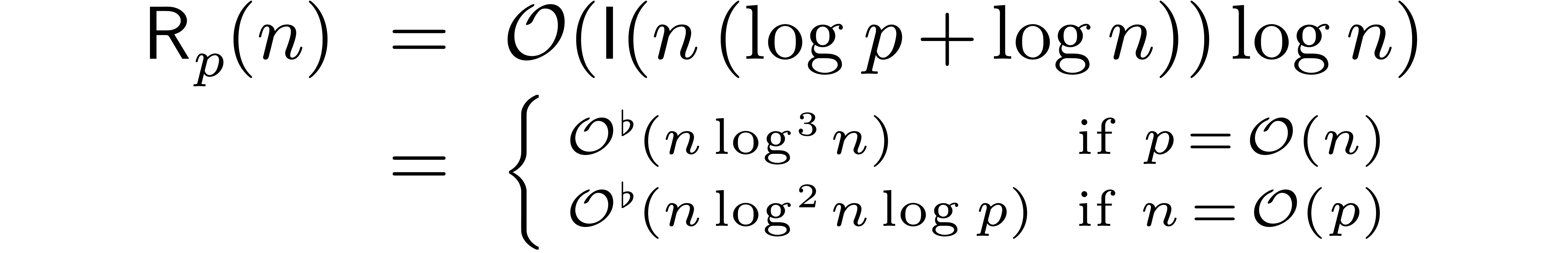
We thus improved the previous bound by a factor 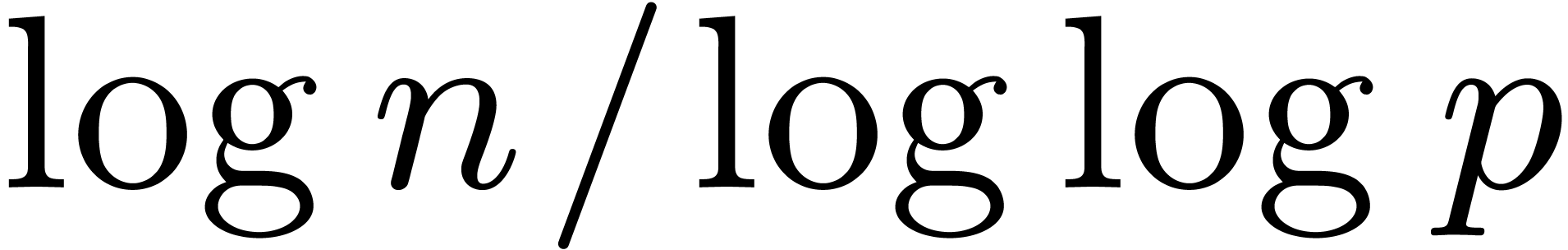 at least, up to sublogarithmic terms.
at least, up to sublogarithmic terms.
The main idea which allows for the present generalizations is quite
straightforward. In our original algorithm from [21], the
presence of sufficiently many primitive 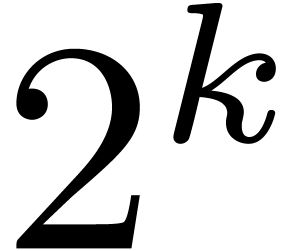 -th
roots of unity in
-th
roots of unity in  gives rise to a quasi-optimal
evaluation-interpolation strategy for the multiplication of polynomials.
More precisely, given two polynomials of degrees
gives rise to a quasi-optimal
evaluation-interpolation strategy for the multiplication of polynomials.
More precisely, given two polynomials of degrees 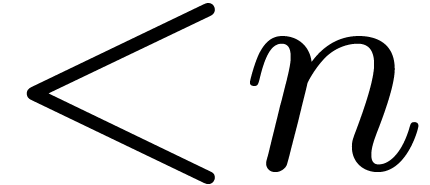 , their FFT-multiplication only requires
, their FFT-multiplication only requires  evaluation and interpolation points, and both the
evaluation and interpolation steps can be performed efficiently, using
only
evaluation and interpolation points, and both the
evaluation and interpolation steps can be performed efficiently, using
only  operations. Now it has recently been shown
[8] that quasi-optimal evaluation-interpolation strategies
still exist if we evaluate and interpolate at points in geometric
progressions instead of roots of unity. This result is the key to our
new complexity bounds, although further technical details have to be
dealt with in order to make things work for various types of effective
rings
operations. Now it has recently been shown
[8] that quasi-optimal evaluation-interpolation strategies
still exist if we evaluate and interpolate at points in geometric
progressions instead of roots of unity. This result is the key to our
new complexity bounds, although further technical details have to be
dealt with in order to make things work for various types of effective
rings  . We also notice that
the main novelty of [8] concerns the interpolation step.
Fast evaluation at geometric progressions was possible before using the
so called chirp transform [27, 7].
For effective rings
. We also notice that
the main novelty of [8] concerns the interpolation step.
Fast evaluation at geometric progressions was possible before using the
so called chirp transform [27, 7].
For effective rings  of positive characteristic,
this would actually have been sufficient for the proving the bound (5).
of positive characteristic,
this would actually have been sufficient for the proving the bound (5).
Our paper is structured as follows. Since the algorithms of [8]
were presented in the case when  is an effective
field, Section 2 starts with their generalization to more
general effective rings
is an effective
field, Section 2 starts with their generalization to more
general effective rings  .
These generalizations are purely formal and contain no essentially new
ideas. In Section 3, we give a short survey of the
algorithm from [21], but we recommend reading the original
paper for full technical details. In Section 4, we sharpen
the complexity analysis for the algorithm from [21]. In
Section 5, we prove Theorem 1 in the case when
.
These generalizations are purely formal and contain no essentially new
ideas. In Section 3, we give a short survey of the
algorithm from [21], but we recommend reading the original
paper for full technical details. In Section 4, we sharpen
the complexity analysis for the algorithm from [21]. In
Section 5, we prove Theorem 1 in the case when
 has characteristic zero. In Section 6,
we turn our attention to the case when
has characteristic zero. In Section 6,
we turn our attention to the case when  has prime
characteristic
has prime
characteristic 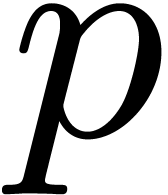 . If the
characteristic is sufficiently large, then we may find sufficiently
large geometric progressions in
. If the
characteristic is sufficiently large, then we may find sufficiently
large geometric progressions in  in order to
generalize the results from Section 5. Otherwise, we have
to work over
in order to
generalize the results from Section 5. Otherwise, we have
to work over 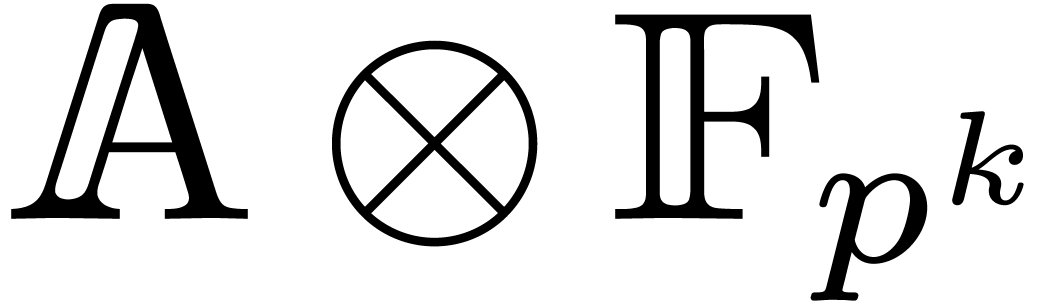 for some sufficiently large
for some sufficiently large 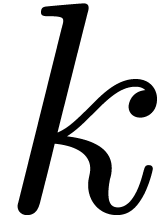 . In Section 7, we
complete the proof of Theorem 1; the case when the
characteristic is a prime power is a refinement of the result from
Section 6. The remaining case is done via Chinese
remaindering. In Section 8, we will prove Theorem 2.
. In Section 7, we
complete the proof of Theorem 1; the case when the
characteristic is a prime power is a refinement of the result from
Section 6. The remaining case is done via Chinese
remaindering. In Section 8, we will prove Theorem 2.
Acknowledgments. I am grateful to the referees for
their detailed comments and suggestions. A special thanks goes to the
referee who made a crucial suggestion for the improved complexity
analysis in Section 4.
2Multipoint evaluation and
interpolation
Let 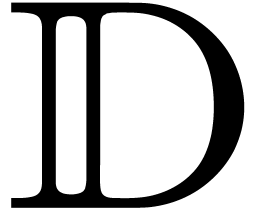 be a (commutative) effective integral domain
and let
be a (commutative) effective integral domain
and let  be its quotient field. Assume that
be its quotient field. Assume that  has characteristic zero. Let
has characteristic zero. Let  be an effective torsion-free
be an effective torsion-free  -module
and
-module
and 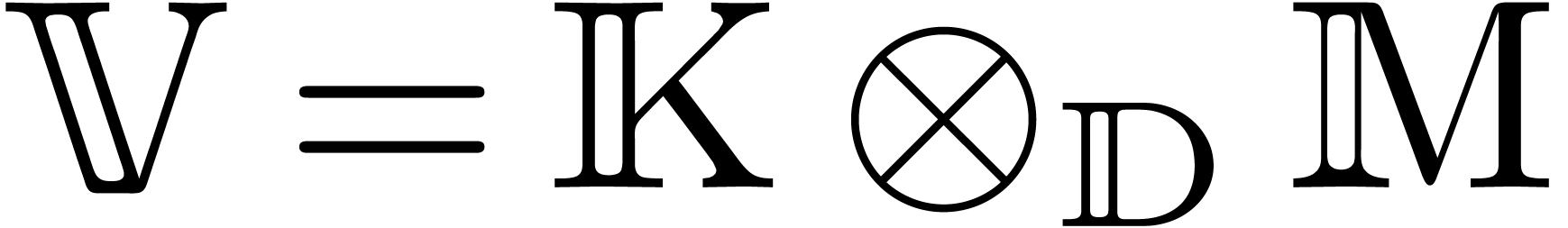 . Elements of
. Elements of  and
and  are fractions
are fractions 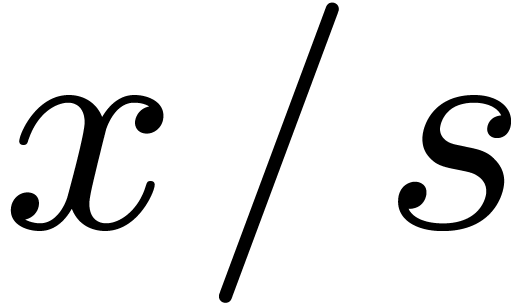 with
with 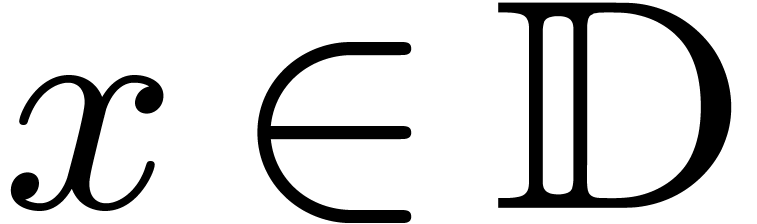 (resp.
(resp. 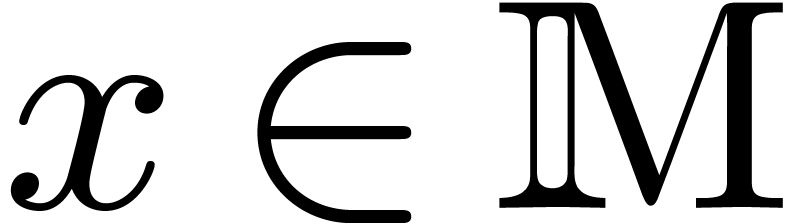 ) and
) and  ,
and the operations
,
and the operations  on such fractions are as
usual:
on such fractions are as
usual:
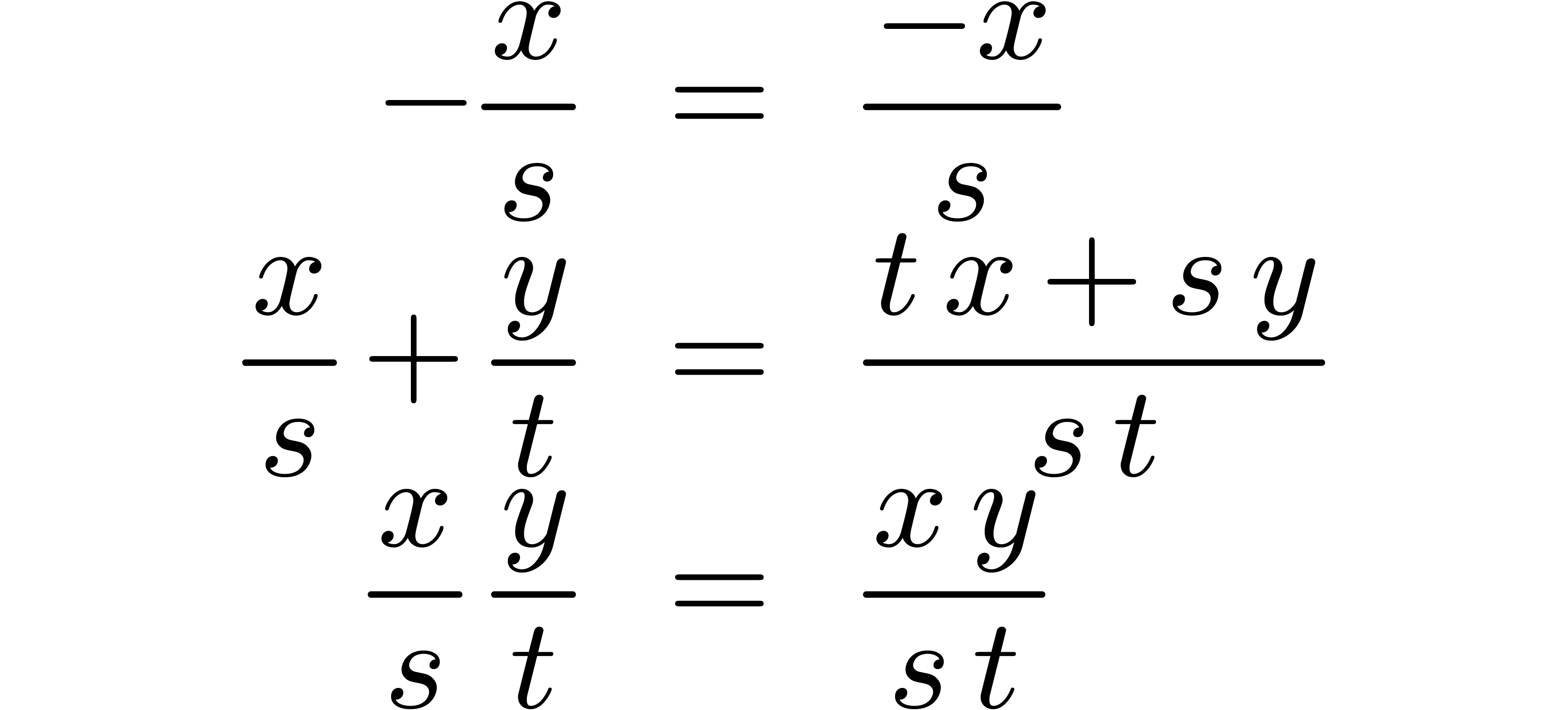
For 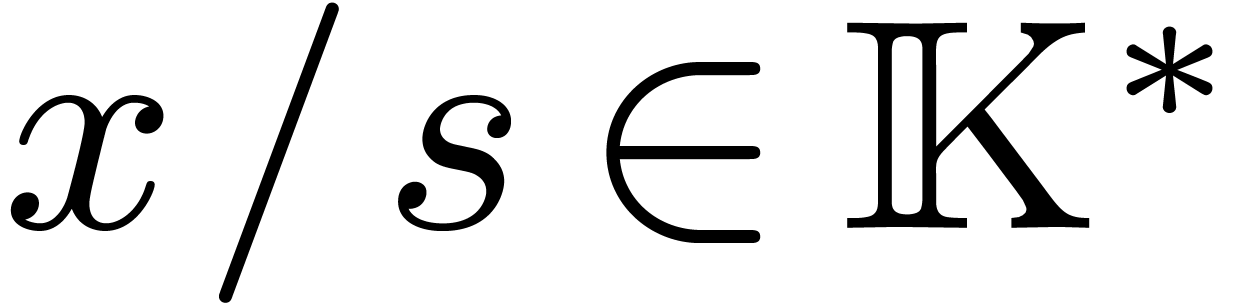 , we also have
, we also have 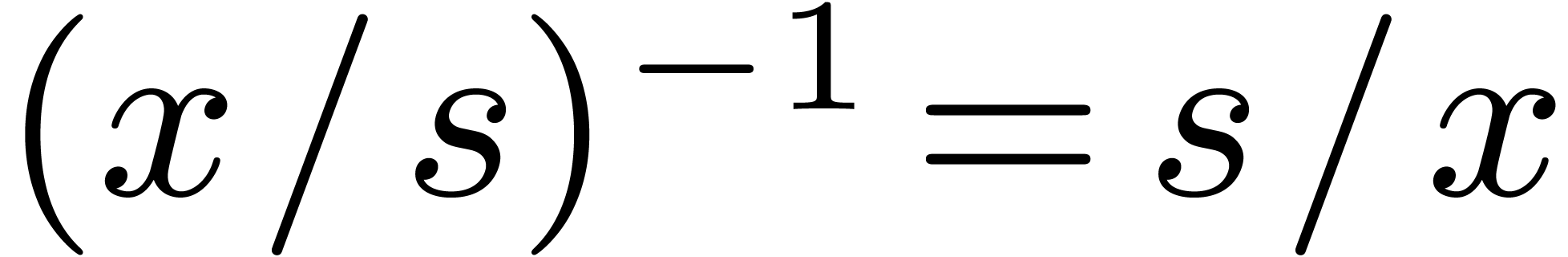 . It follows that
. It follows that  is an effetive field and
is an effetive field and  an effective
an effective  -vector space. Moreover, all field
operations in
-vector space. Moreover, all field
operations in  (and all vector space operations
in
(and all vector space operations
in  ) can be performed using
only
) can be performed using
only 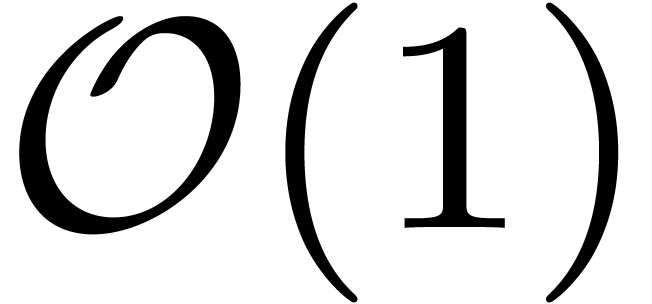 operations in
operations in  (resp.
(resp.  or
or  ).
).
We will say that  admits an effective partial
division, if for every
admits an effective partial
division, if for every  and
and 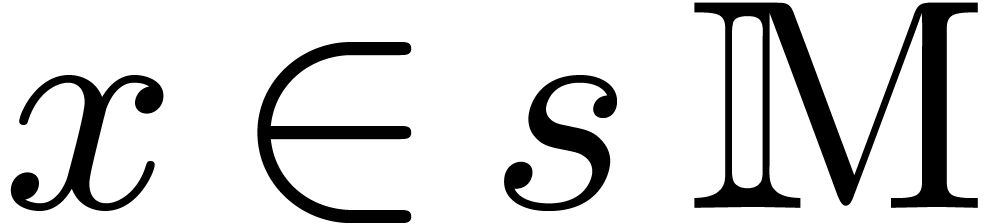 , we can compute the unique
, we can compute the unique 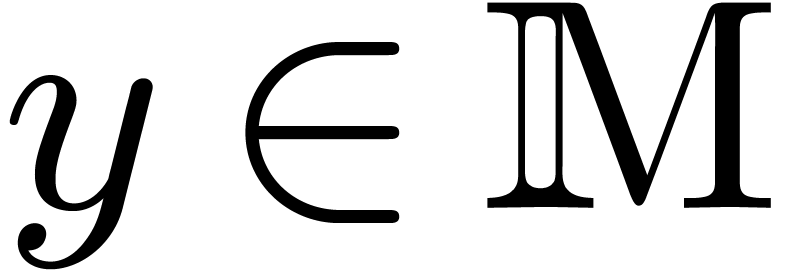 with
with  . In that case, and we
will count any division of the above kind as one operation in
. In that case, and we
will count any division of the above kind as one operation in  . Similarly, given a fixed
. Similarly, given a fixed  , we say that
, we say that  admits an effective partial division by
admits an effective partial division by 
 , we can compute the unique
, we can compute the unique 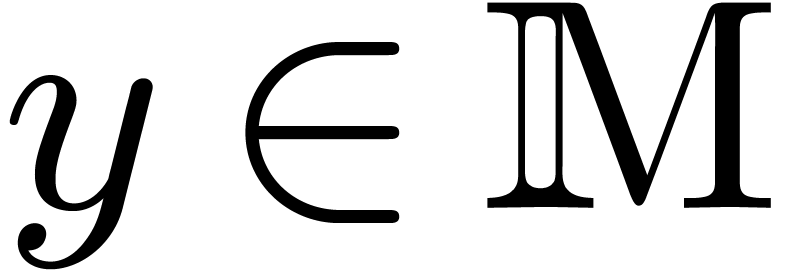 with
with 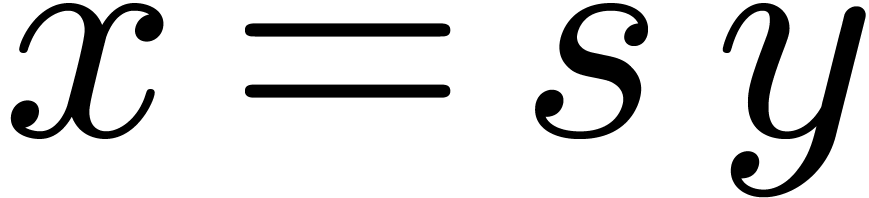 .
Given
.
Given 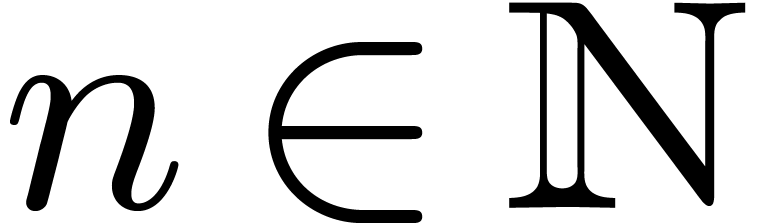 , we define
, we define
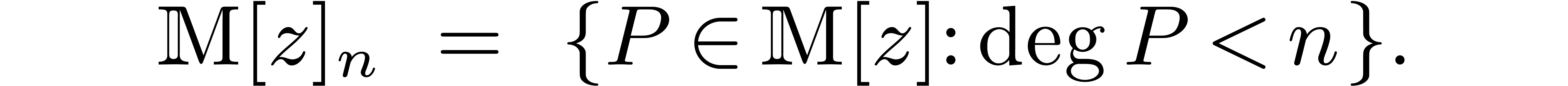
Given  and
and 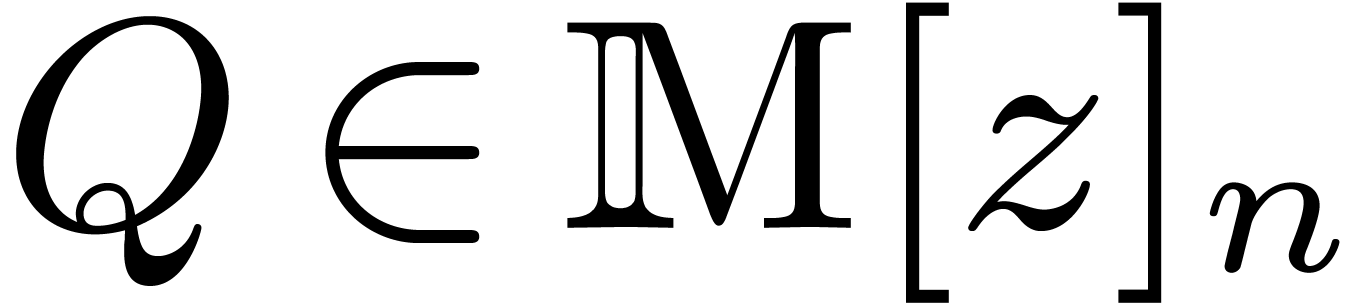 ,
we will denote by
,
we will denote by 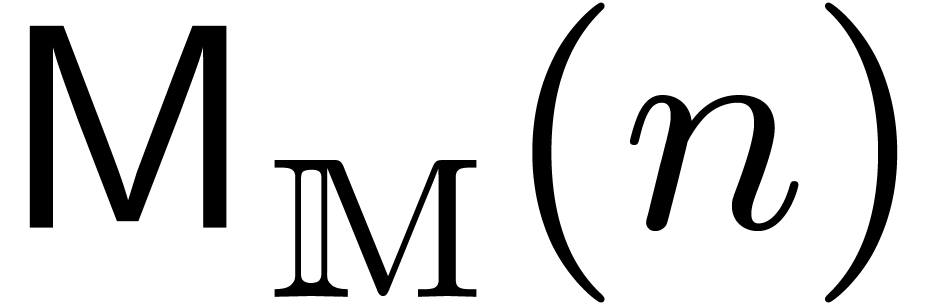 the number of operations in
the number of operations in
 and
and  which are needed in
order to compute the product
which are needed in
order to compute the product 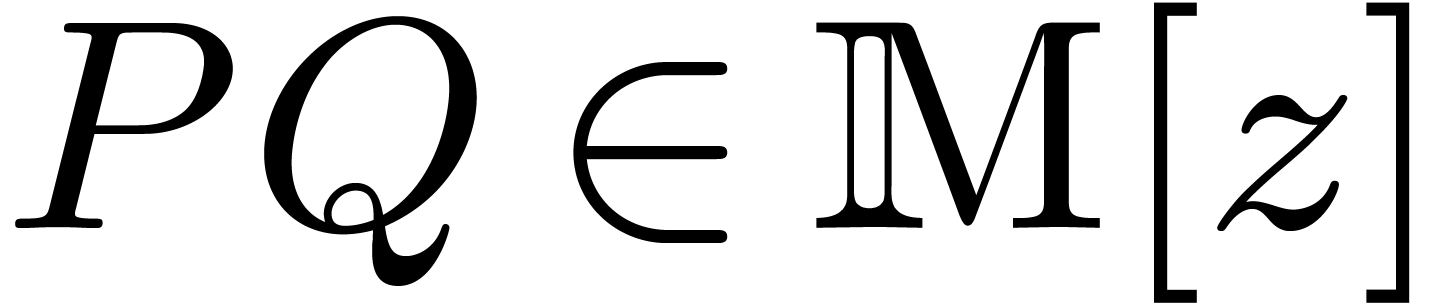 .
.
Lemma 3. Let  be an effective integral domain and
be an effective integral domain and  an effective torsion-free
an effective torsion-free  -module.
There exists a constant
-module.
There exists a constant  ,
such that the following holds: for any
,
such that the following holds: for any  ,
,
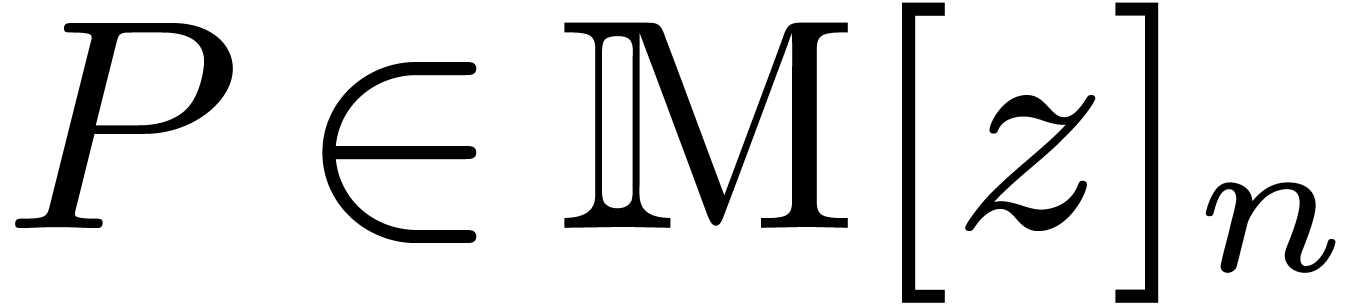 and
and  such that
such that  are pairwise distinct, and such that
are pairwise distinct, and such that  admits effective divisions by
admits effective divisions by  and
and 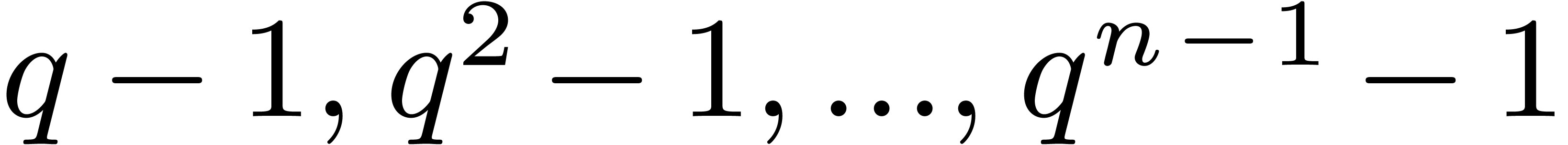 , we have:
, we have:
Proof. In the case when  is a
field and
is a
field and  , this result was
first proven in [8]. More precisely, the conversions can be
done using the algorithms NewtonEvalGeom,
NewtonInterpGeom, NewtonToMonomialGeom
and MonomialToNewtonGeom in that paper. Examining these
algorithms, we observe that general elements in
, this result was
first proven in [8]. More precisely, the conversions can be
done using the algorithms NewtonEvalGeom,
NewtonInterpGeom, NewtonToMonomialGeom
and MonomialToNewtonGeom in that paper. Examining these
algorithms, we observe that general elements in  are only multiplied with elements in
are only multiplied with elements in 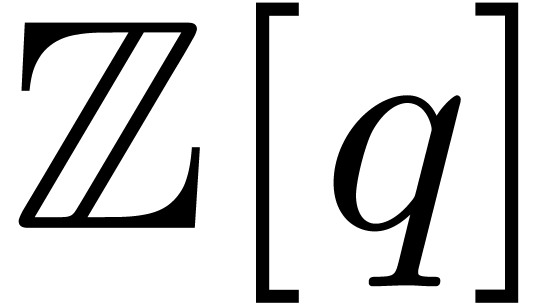 and divided
by elements of the set
and divided
by elements of the set 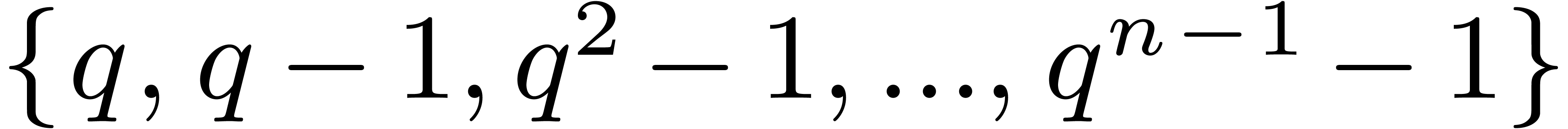 . In
particular, the algorithms can still be applied in the more general case
when
. In
particular, the algorithms can still be applied in the more general case
when  is a field and
is a field and 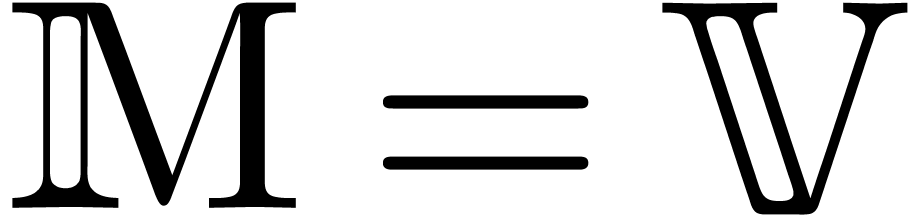 a
vector space.
a
vector space.
If  is only an effective integral domain and
is only an effective integral domain and  an effective torsion-free
an effective torsion-free  -module with an effective partial division, then we
define the effective field
-module with an effective partial division, then we
define the effective field  and the effective
vector space
and the effective
vector space  as above, and we may still apply
the generalized algorithms for multipoint evaluation and interpolation
in
as above, and we may still apply
the generalized algorithms for multipoint evaluation and interpolation
in  . In particular, both
multipoint evaluation and interpolation can still be done using
. In particular, both
multipoint evaluation and interpolation can still be done using 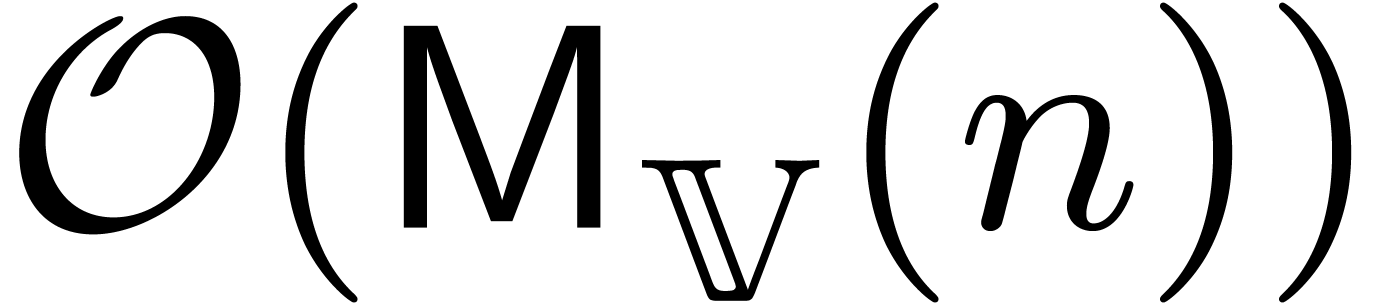 operations in
operations in  and
and  , whence
, whence 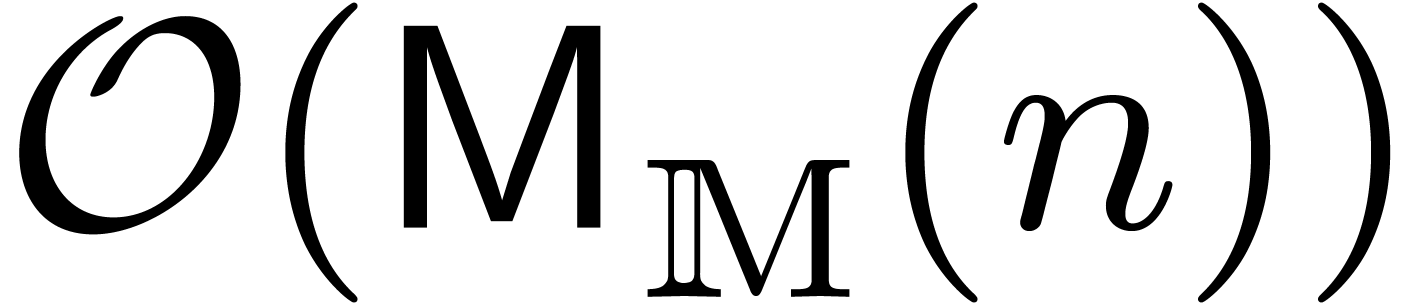 operations in
operations in  and
and  .
If we know that the end-results of these algorithms are really
in the subspace
.
If we know that the end-results of these algorithms are really
in the subspace 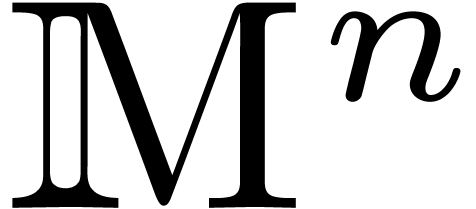 of
of  (or
in the submodule
(or
in the submodule  of
of  ), then we use the partial division in
), then we use the partial division in  to replace their representations in
to replace their representations in 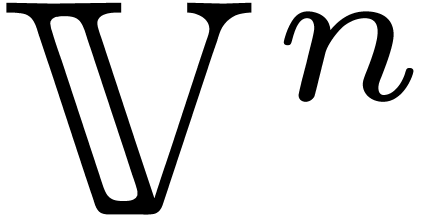 (or
(or 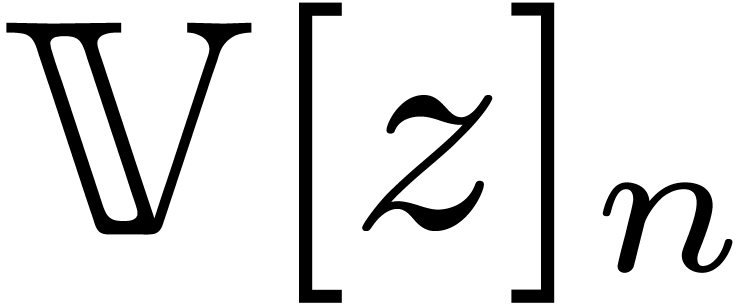 ) by representations in
) by representations in
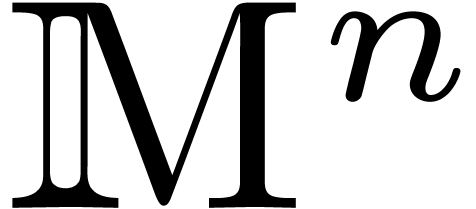 (or
(or 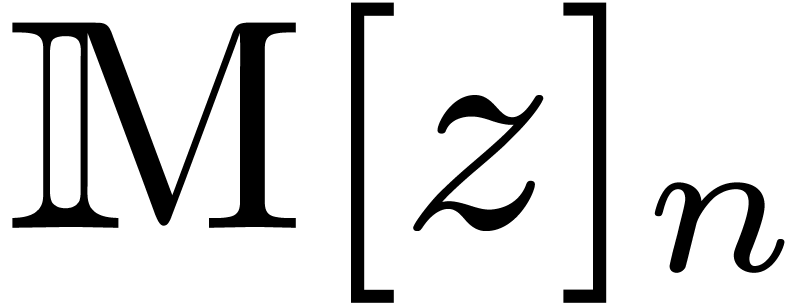 ).
).
3Survey of blockwise relaxed
multiplication
Let  be an effective (possibly non-commutative)
ring and recall that
be an effective (possibly non-commutative)
ring and recall that

Given a power series  and
and 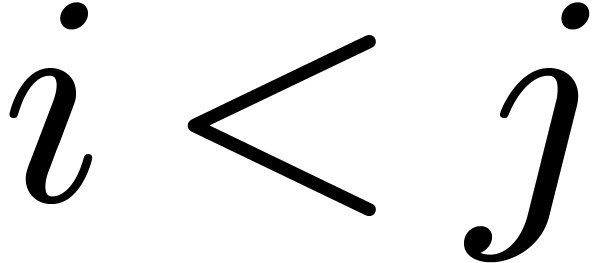 , we will also use the notations
, we will also use the notations
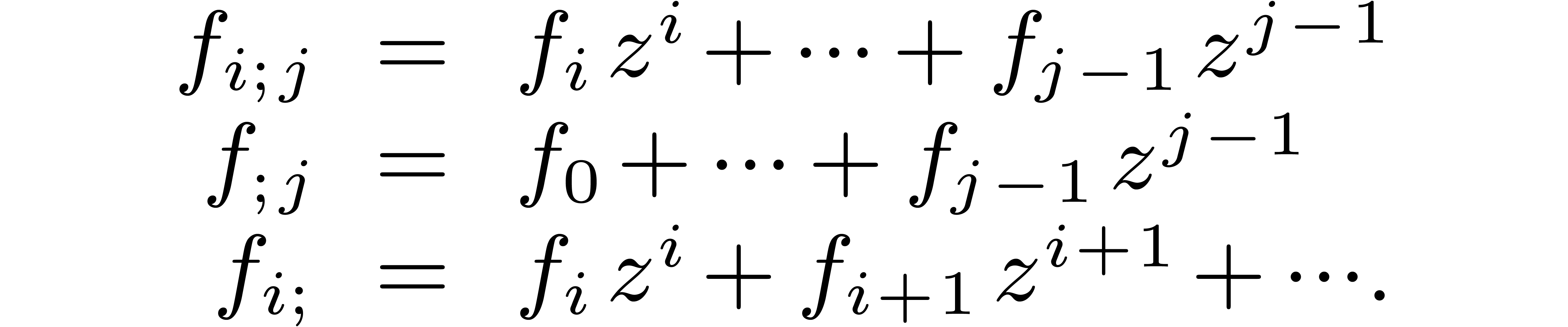
The fast relaxed algorithms from [21] are all based on two
main changes of representation: “blocking” and the fast
Fourier transform. Let us briefly recall these transformations and how
to use them for the design of fast algorithms for relaxed
multiplication.
Blocking and unblocking.
Given a block size
 ,
, the
first operation of
blocking rewrites a power series

as a series in
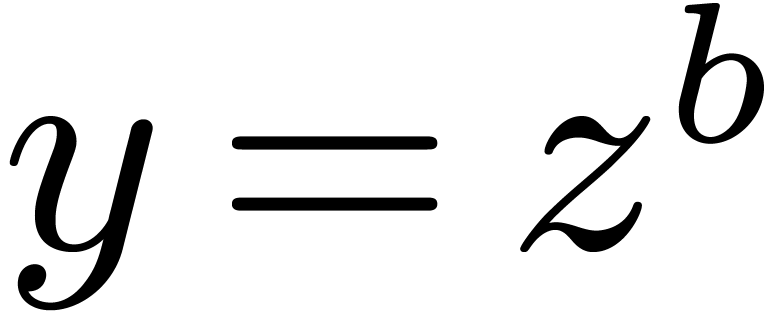
with coefficients
in
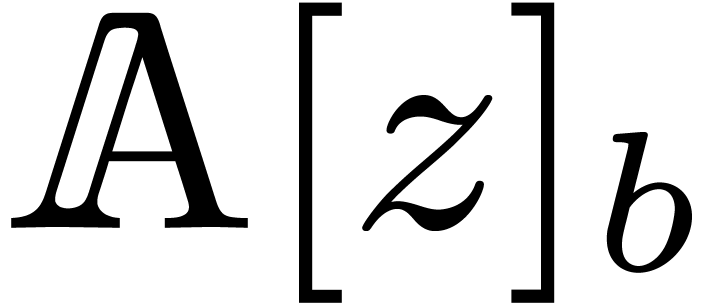
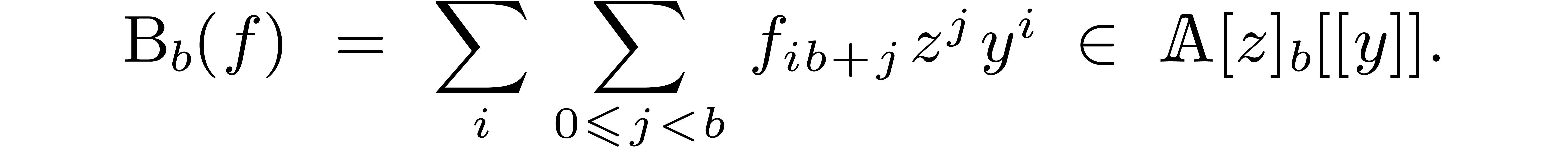
Given 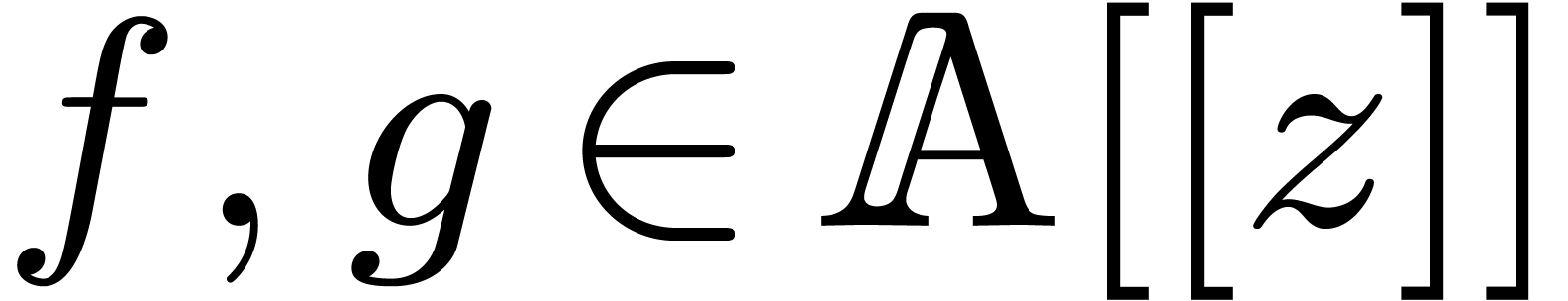 , we may then compute
, we may then compute
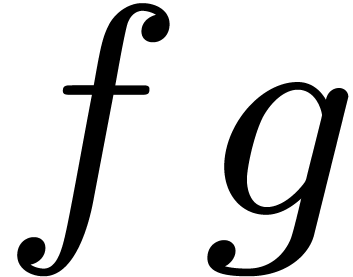 using
using

where 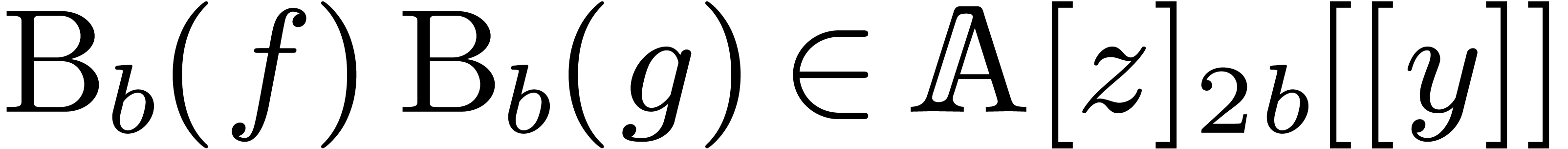 and
and
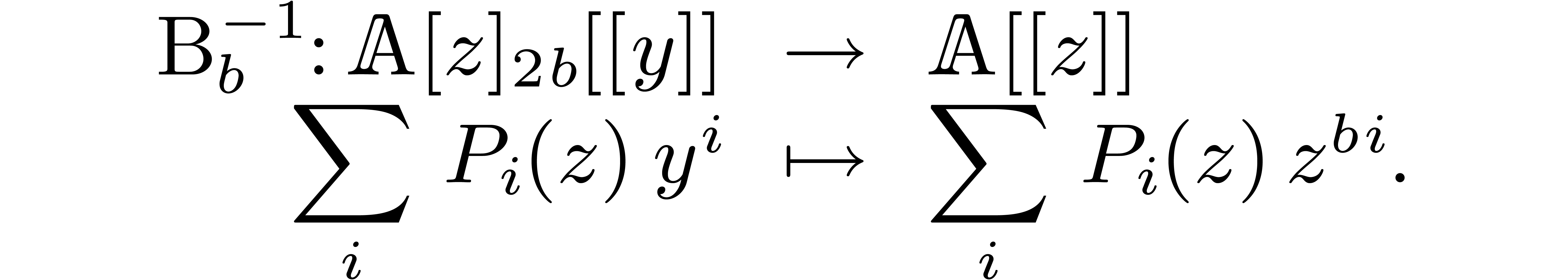
Discrete Fourier transforms.
Assume now that
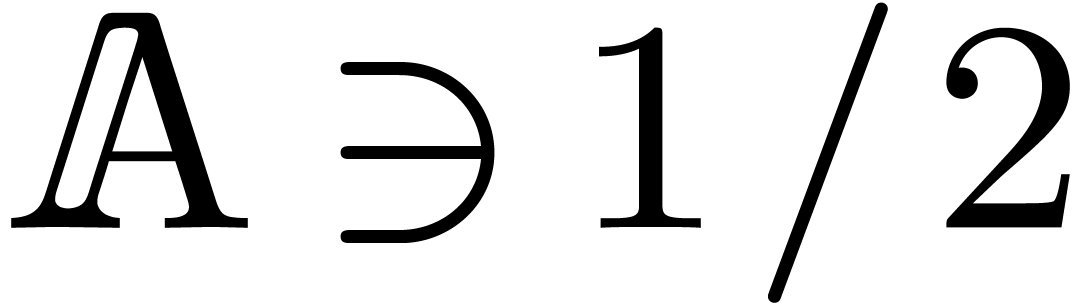 ,
, that
 ,
, and that

admits a primitive
 -th
-th root
of unity
 .
. Then the
discrete Fourier transform provides us with an isomorphism
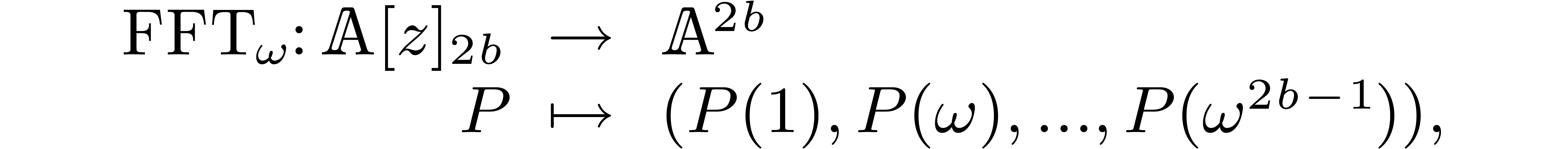
and it is classical [12] that both  and
and 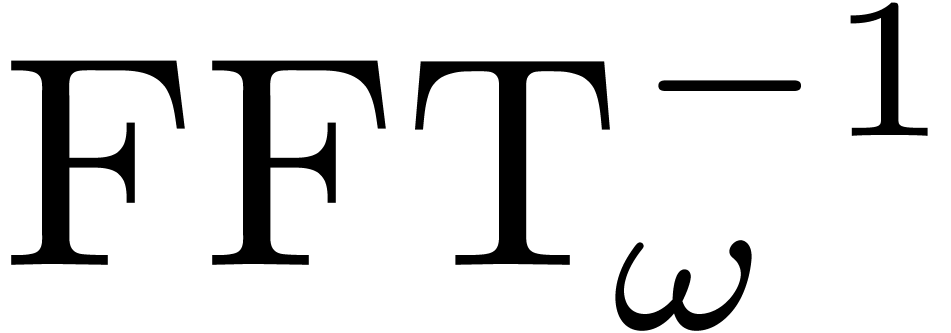 can be computed using
can be computed using 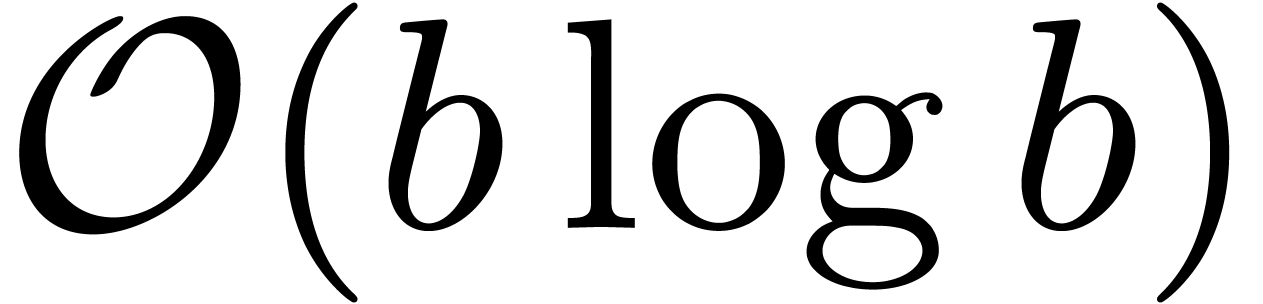 operations in
operations in  . The
operations
. The
operations  and
and 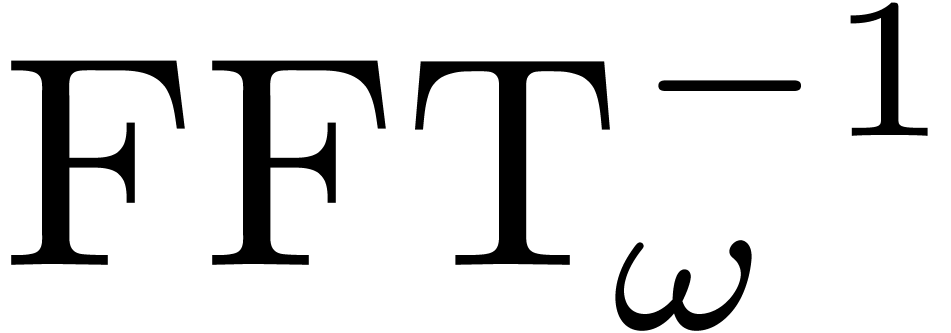 extend
naturally to
extend
naturally to 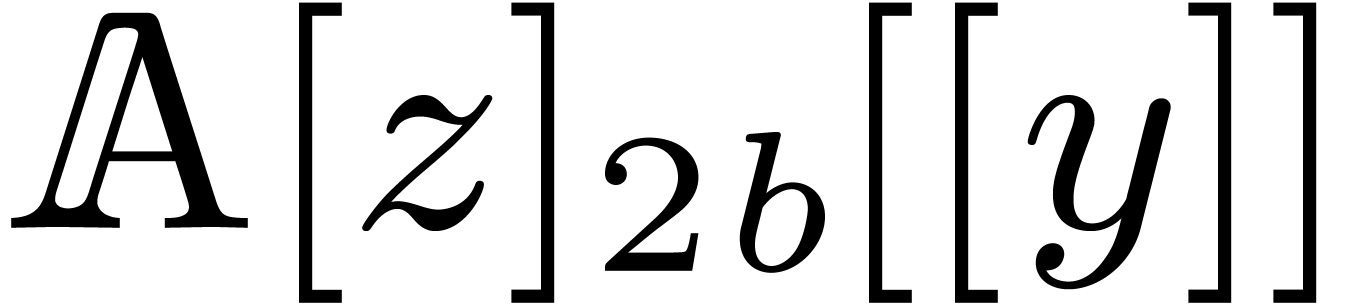 via
via
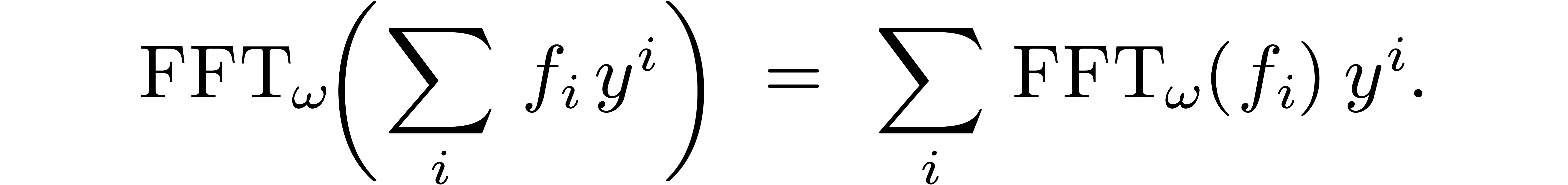
Given 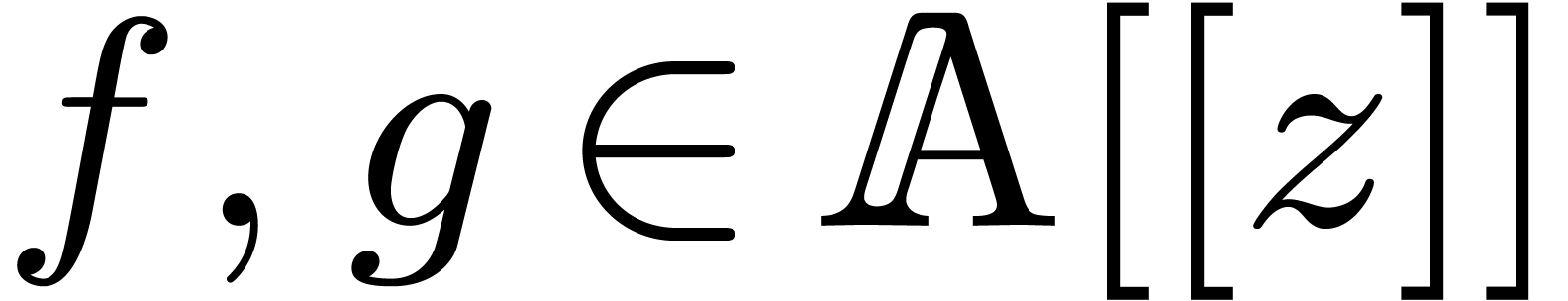 , this allows us to
compute
, this allows us to
compute  using the formula
using the formula
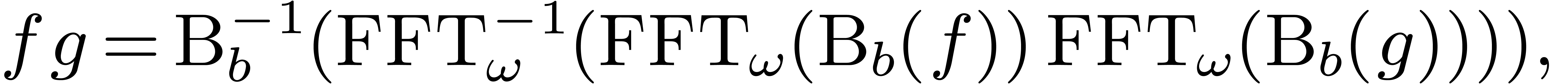 |
(6) |
where 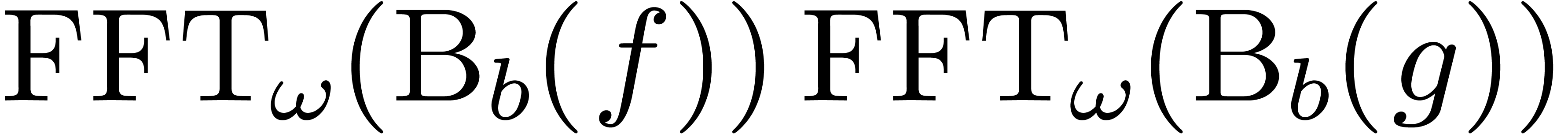 is a pointwise product in
is a pointwise product in  . The first
. The first  coefficients of
coefficients of  can be computed using at most
can be computed using at most
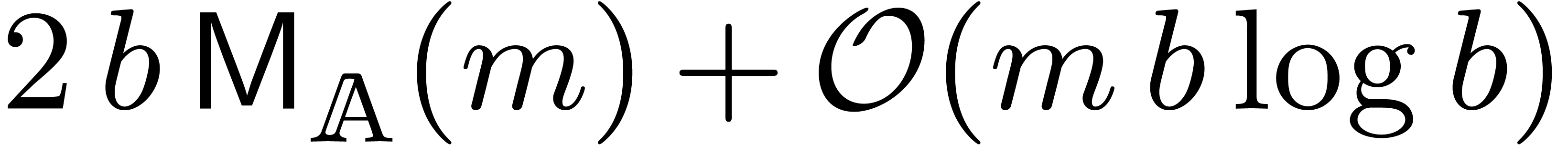 operations in
operations in  .
.
Relaxed multiplication.
In formula (
6) the
 -th
-th
coefficient of the right hand side may depend on the
 -th
-th coefficients of
and
 .
. In order to make (
6) suitable for relaxed multiplication, we have to treat the
first
coefficients of
and

separately. Indeed, the formula
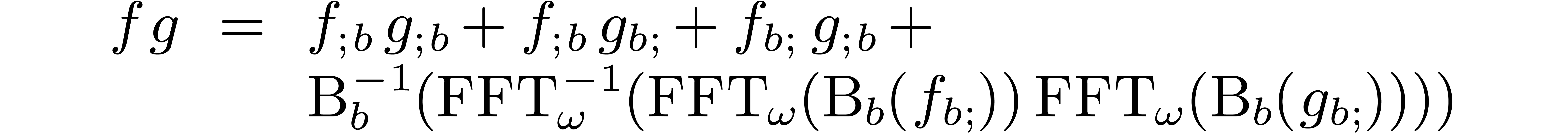
allows for the relaxed computation of 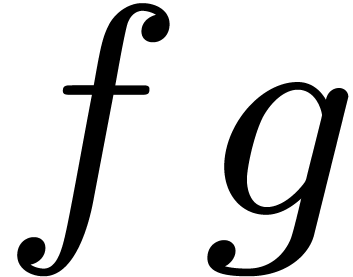 at order
at order
 using at most
using at most
operations in  . Similarly,
the formula
. Similarly,
the formula
allows for the semi-relaxed computation of 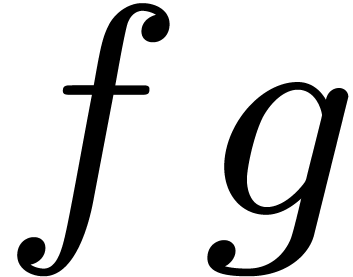 at
order
at
order  using at most
using at most
 |
(8) |
operations in  . For a given
expansion order
. For a given
expansion order  , one may
take
, one may
take  , and use the above
formula in a recursive manner. This yields [21, Theorem 11]
, and use the above
formula in a recursive manner. This yields [21, Theorem 11]
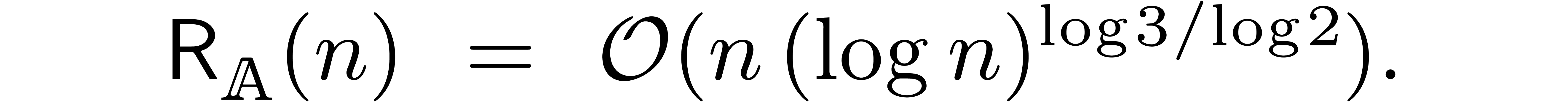
Remark 4. Since the block size
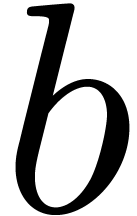 is chosen as a function of
is chosen as a function of 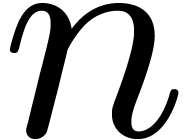 , the above method really describes a relaxed
algorithm for computing the product up to an order
, the above method really describes a relaxed
algorithm for computing the product up to an order 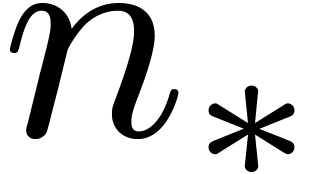 which is specified in advance. In fact, such an algorithm automatically
yields a genuine relaxed algorithm with the same complexity (up to a
constant factor), by doubling the order
which is specified in advance. In fact, such an algorithm automatically
yields a genuine relaxed algorithm with the same complexity (up to a
constant factor), by doubling the order 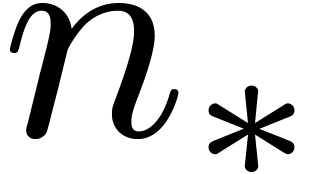 each
time when needed.
each
time when needed.
Reduction to semi-relaxed multiplication.
In the above discussion, we both provided bounds for
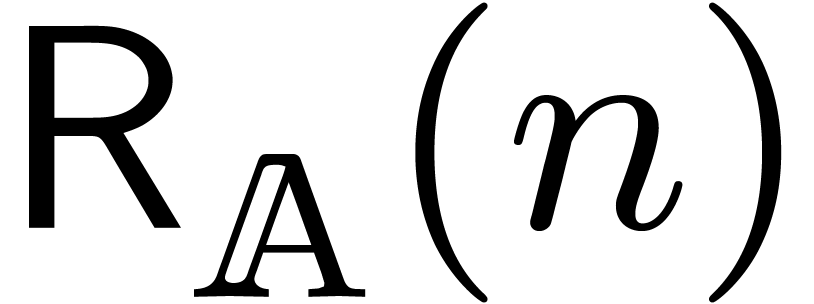
and
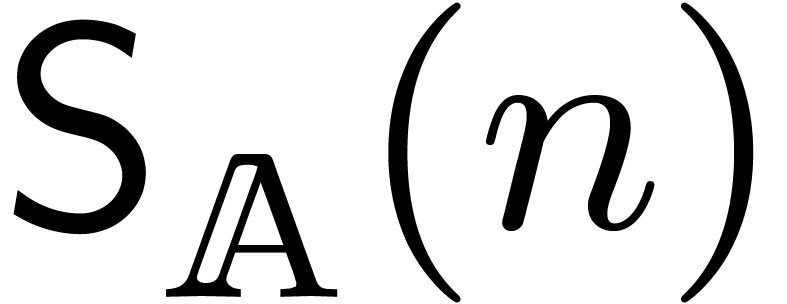 .
. In fact, there exists
a straightforward reduction of relaxed multiplication to semi-relaxed
multiplication. First of all, the relaxed multiplication of two power
series
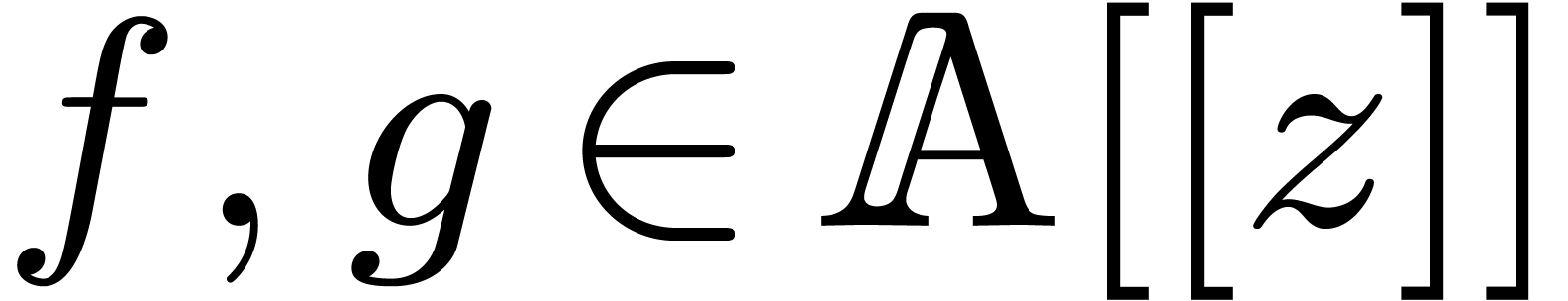
up to order
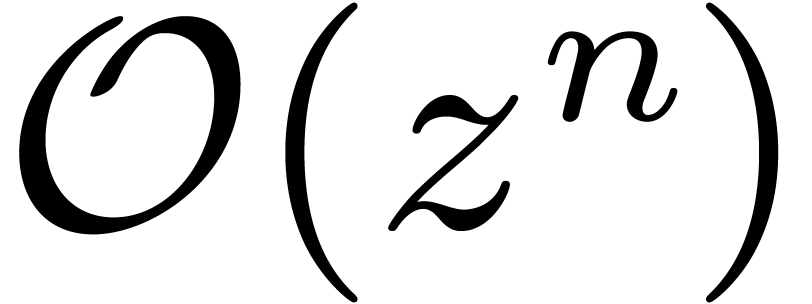
clearly reduces to the relaxed multiplication of the two polynomials
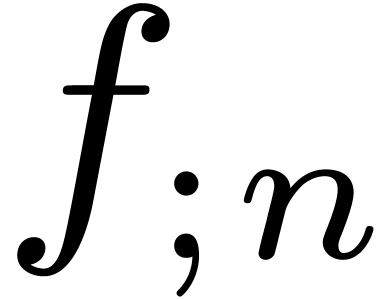
and
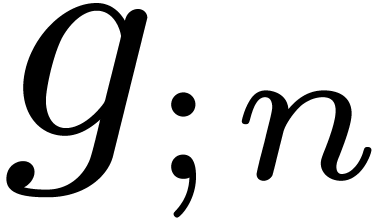
up to order
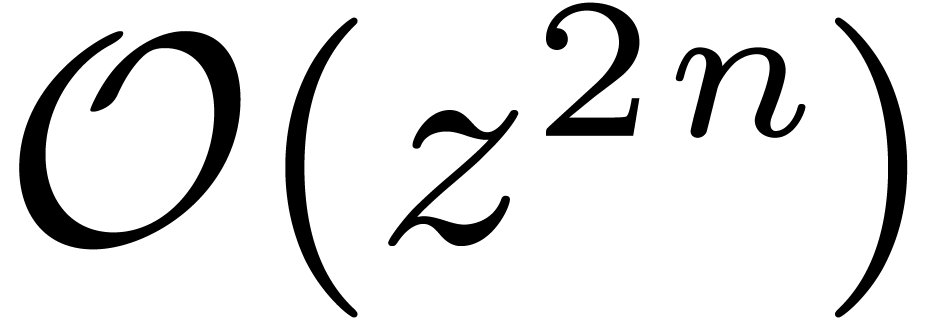 .
. Now the formula
shows that a relaxed product of two polynomials 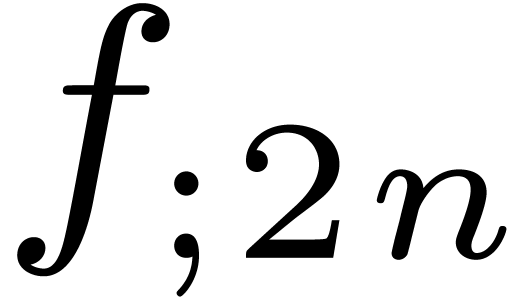 and
and 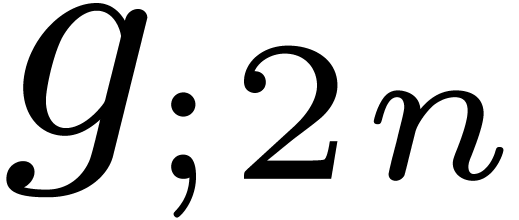 of degrees
of degrees 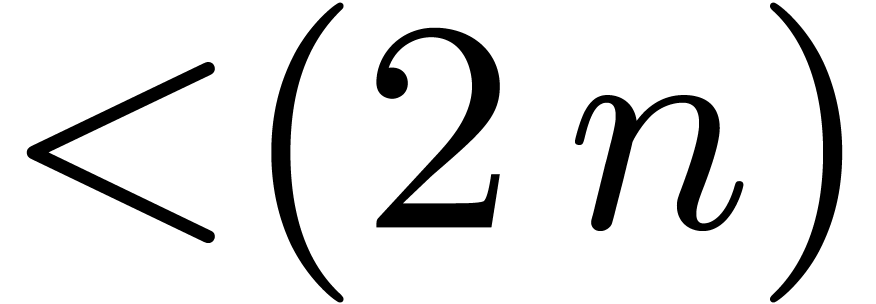 reduces
to a relaxed product
reduces
to a relaxed product 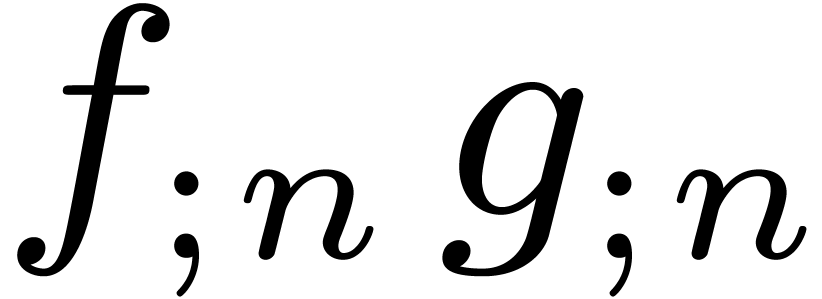 of half the size, two
semi-relaxed products
of half the size, two
semi-relaxed products 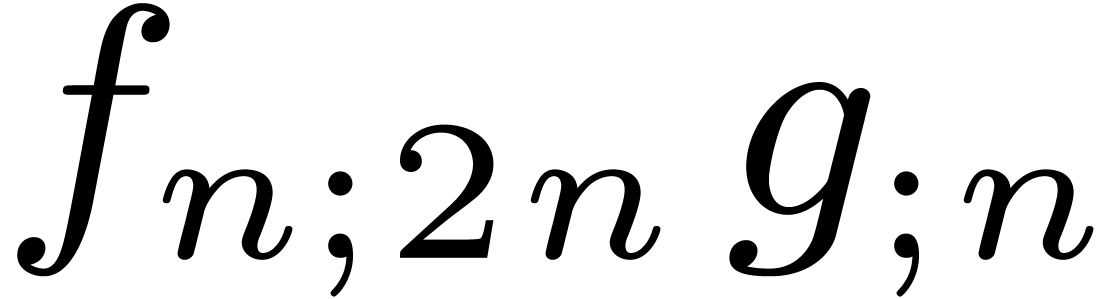 ,
, 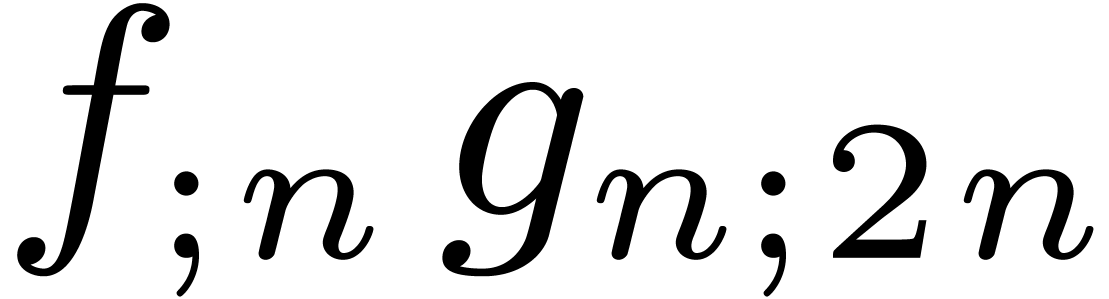 , and one non-relaxed product
, and one non-relaxed product 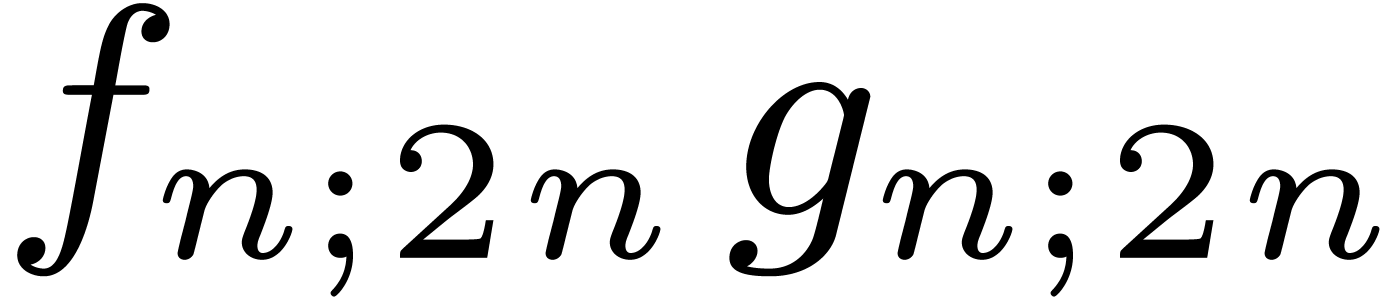 . Under the assumptions that
. Under the assumptions that 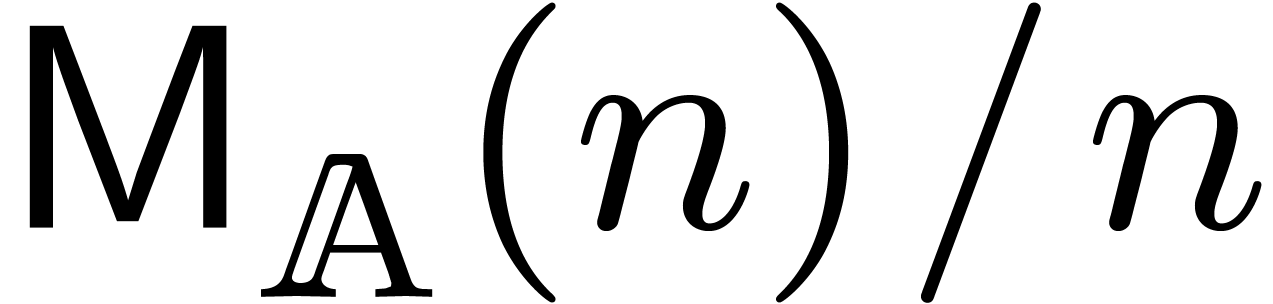 and
and 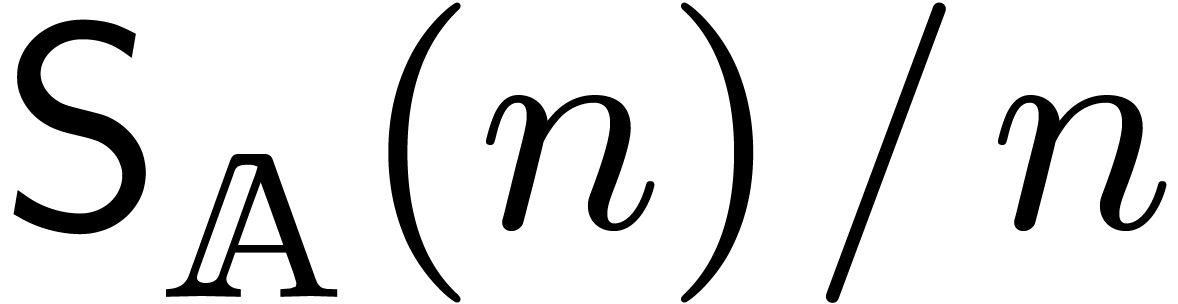 are increasing, a routine
calculation thus yields
are increasing, a routine
calculation thus yields

Multiple block sizes.
Instead of using a single block size
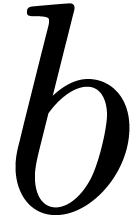 ,
,
one may use several block sizes. Applying this technique, we proved in
[
21, Theorem 12] that
4Improved complexity analysis
One of the referees suggested to take 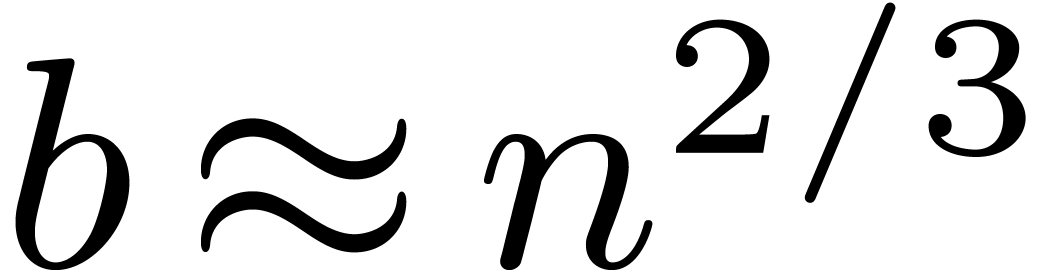 instead of
instead of
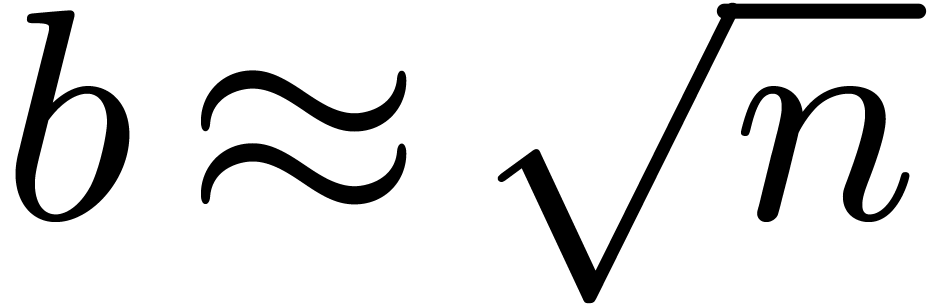 in (8). As a matter of fact, it is
even better to take
in (8). As a matter of fact, it is
even better to take 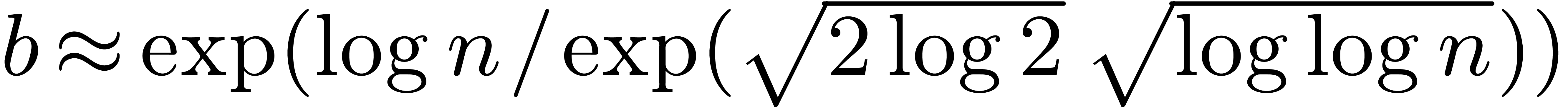 . In this
section, we will show that this leads to the bound
. In this
section, we will show that this leads to the bound

which further improves on (9). We will prove a slightly
more general result, which is useful for the analysis of algorithms
which satisfy complexity bounds similar to (8).
Lemma 5. Let  be an increasing function with
be an increasing function with 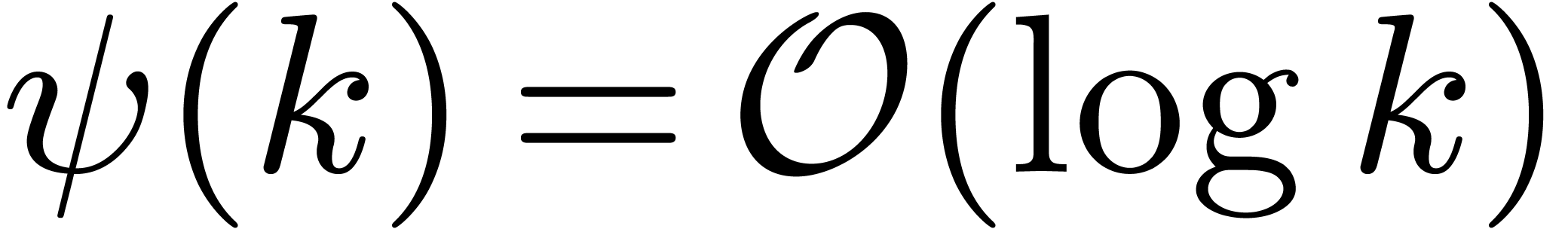 and let
and let
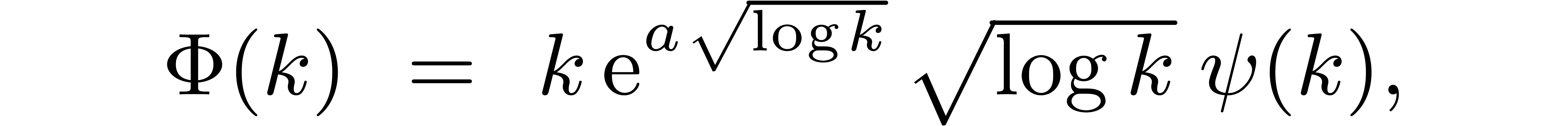
where 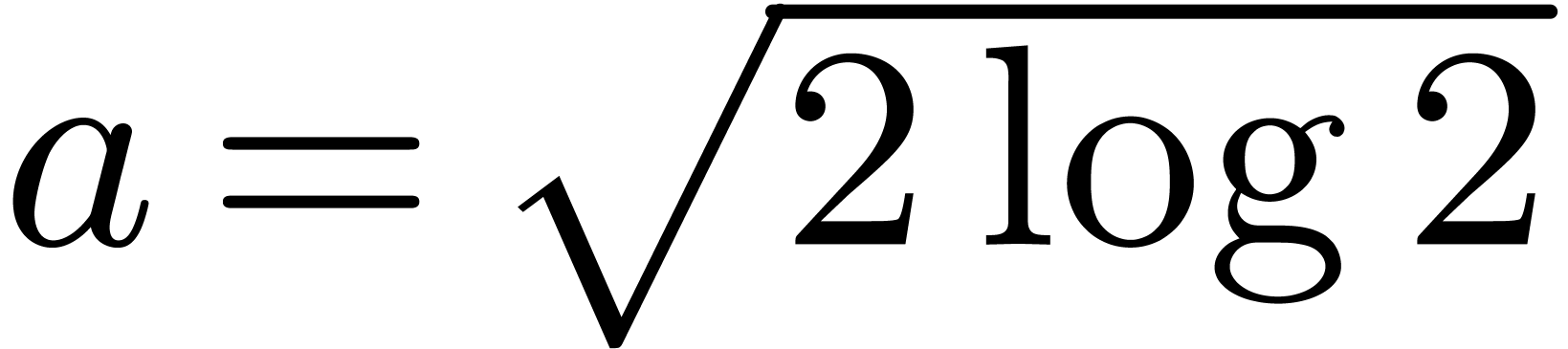 . Then there exist
constants
. Then there exist
constants 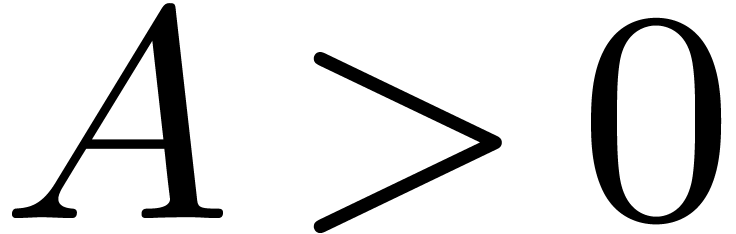 and
and 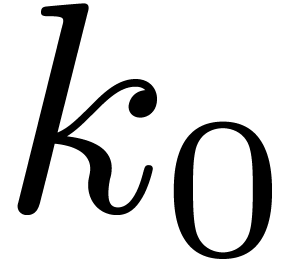 such that
for all
such that
for all 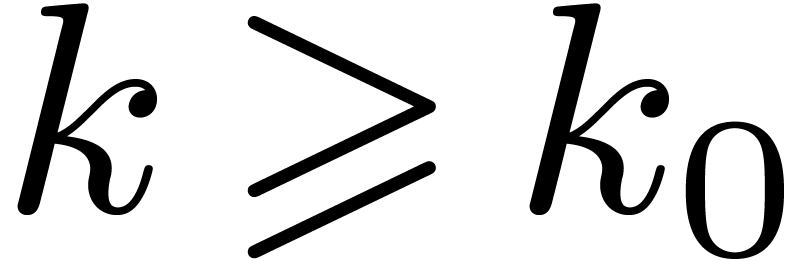 ,
, 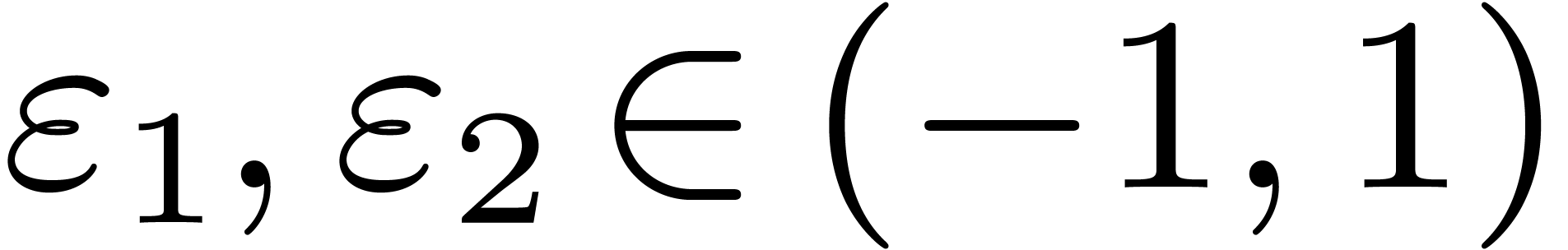 , and
, and 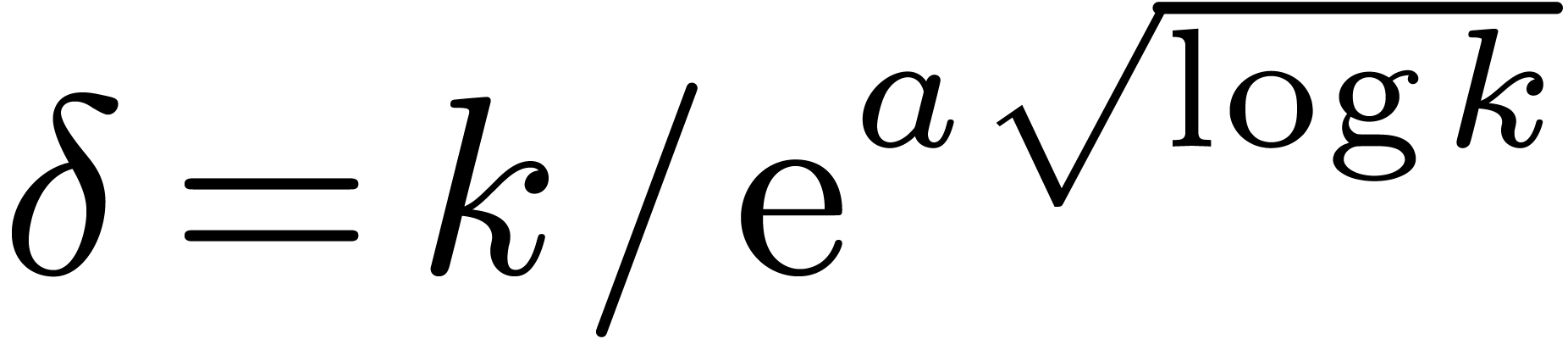 ,
we have
,
we have
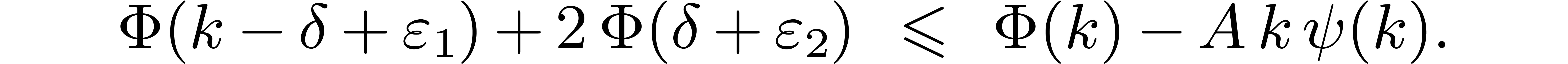
Proof. Notice that 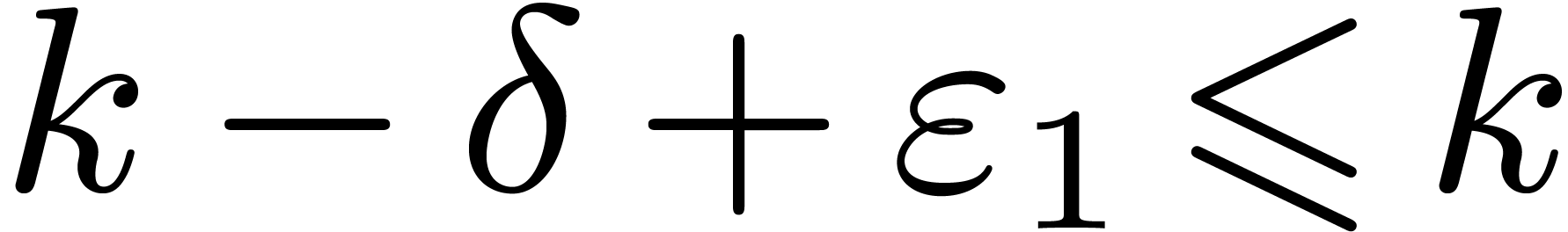 and
and 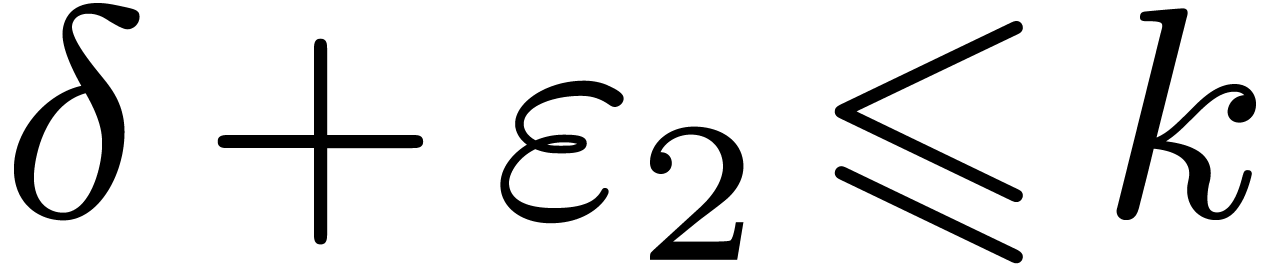 for sufficiently large
for sufficiently large  .
We have
.
We have
For a suitable constant  and all sufficiently
large
and all sufficiently
large  , it follows that
, it follows that
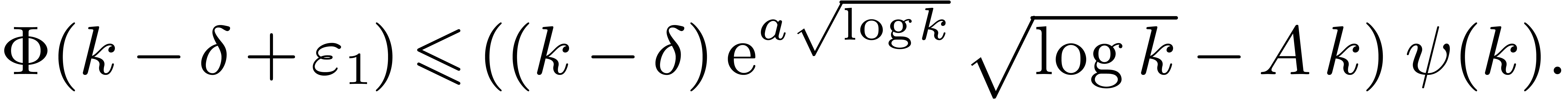 |
(10) |
We also have
whence
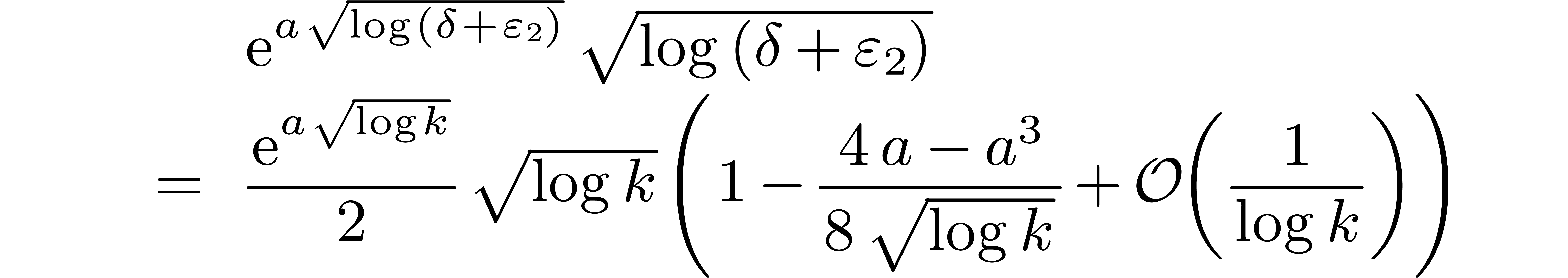
For all sufficiently large  ,
it follows that
,
it follows that
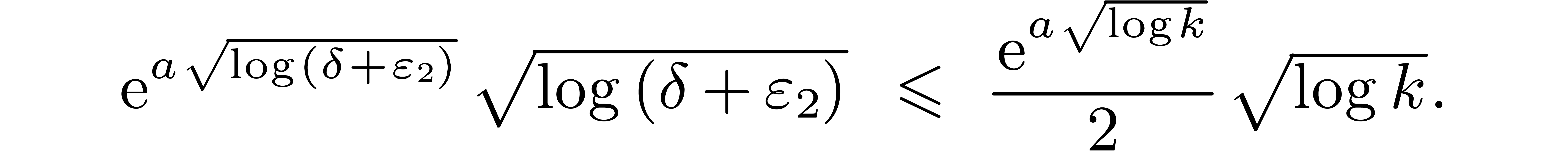
Consequently,
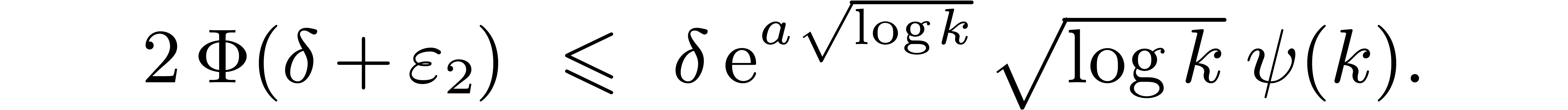 |
(11) |
Adding up (10) and (11), we obtain
for all sufficiently large 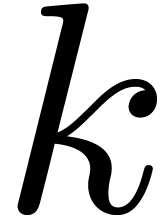 .
.
Theorem 6. Let  be an increasing function with
be an increasing function with 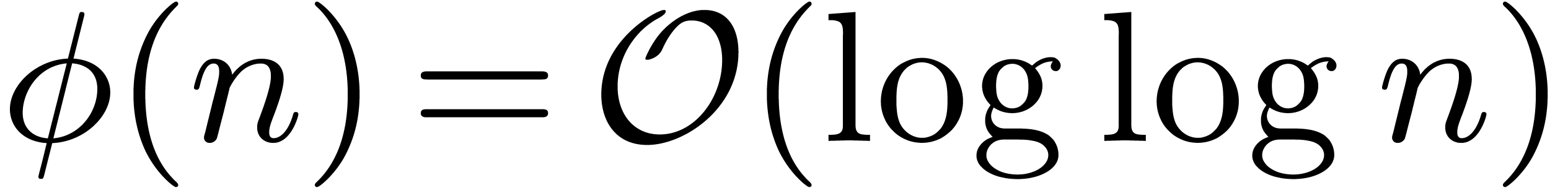 . Assume that
. Assume that
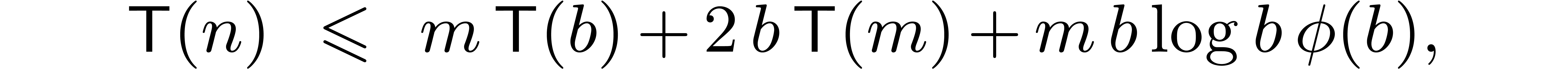 |
(12) |
for all sufficiently large 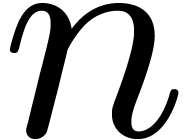 ,
where
,
where
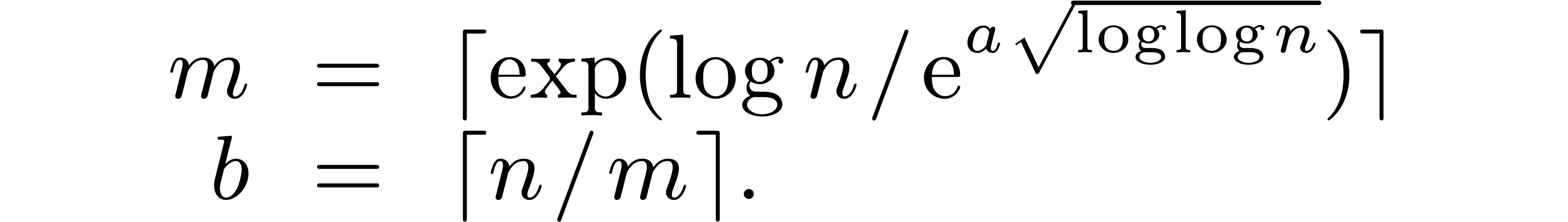
Then
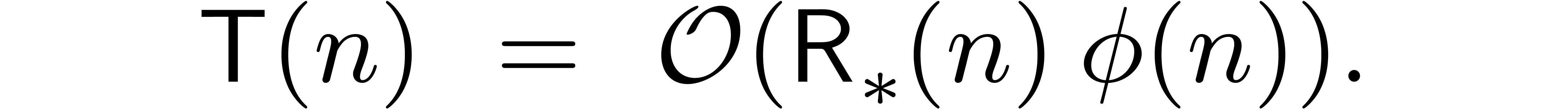
Proof. We define functions 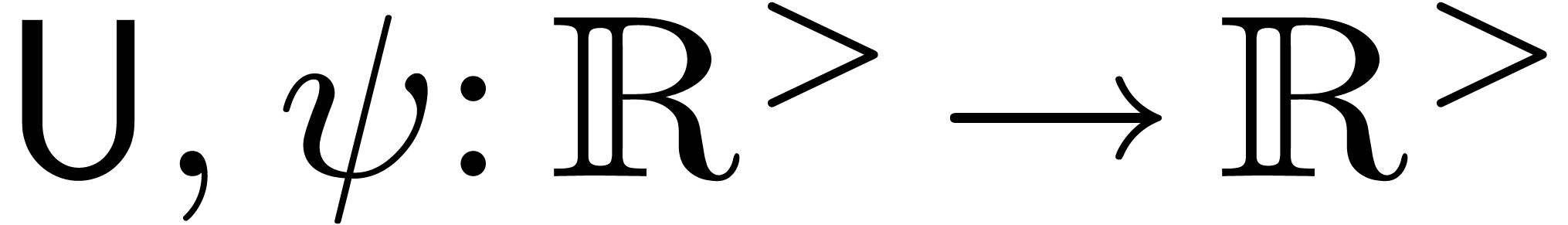 by
by
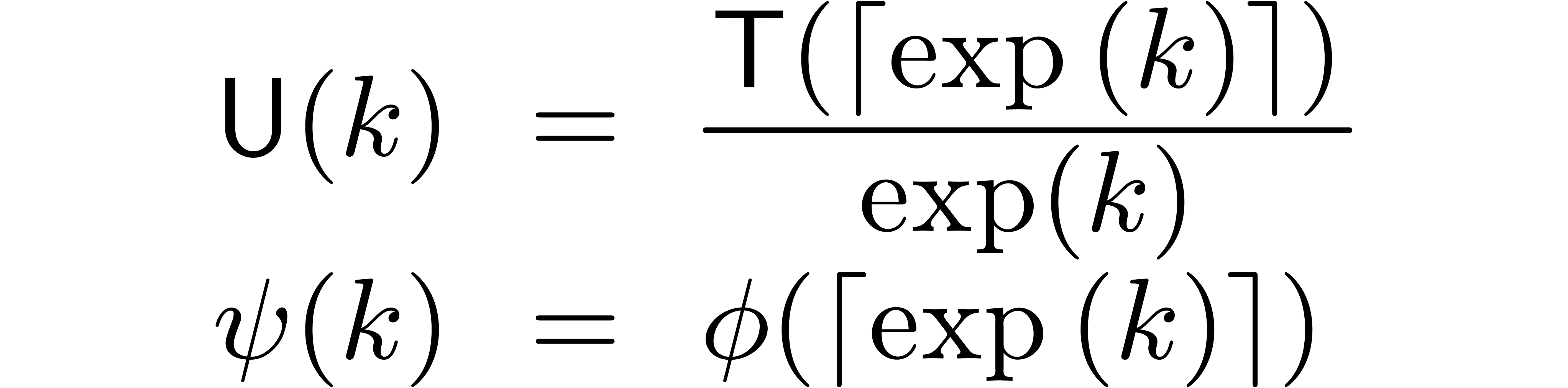
and let  ,
,  and
and 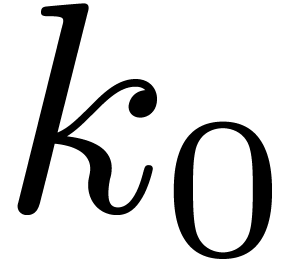 be as in Lemma 5. Without loss
of generality, we may pick
be as in Lemma 5. Without loss
of generality, we may pick 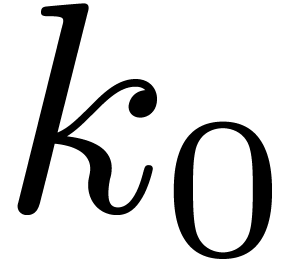 sufficiently large
such that
sufficiently large
such that 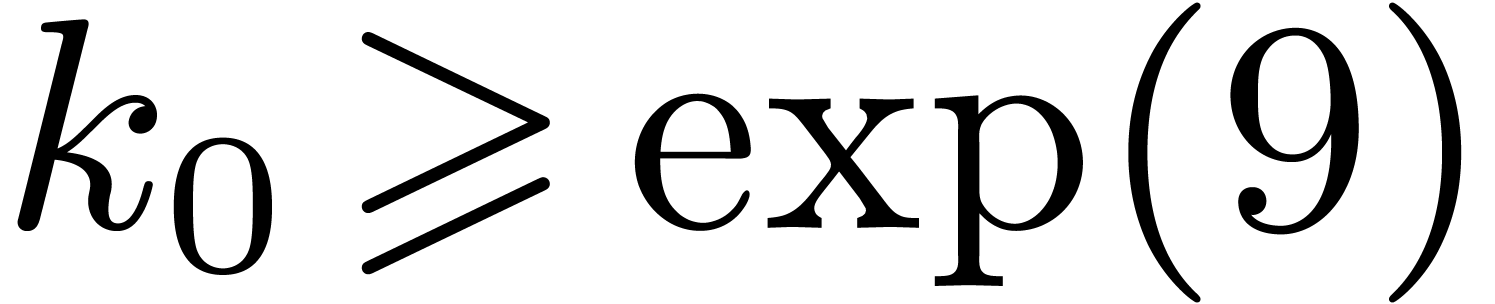 and such that (12) holds
for
and such that (12) holds
for 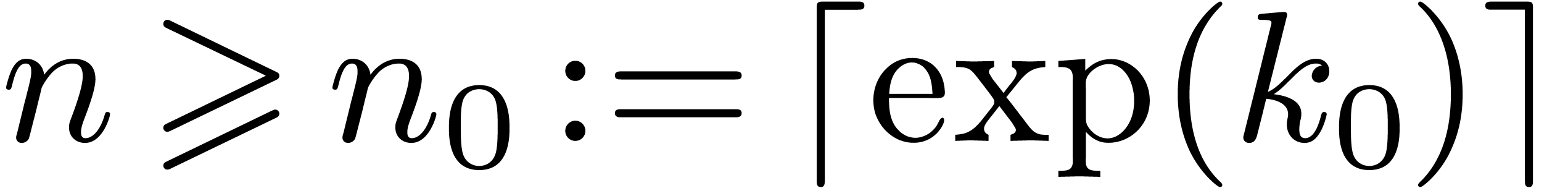 . Let
. Let 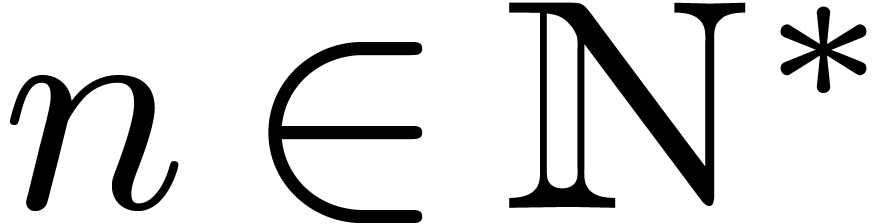 be such that
be such that 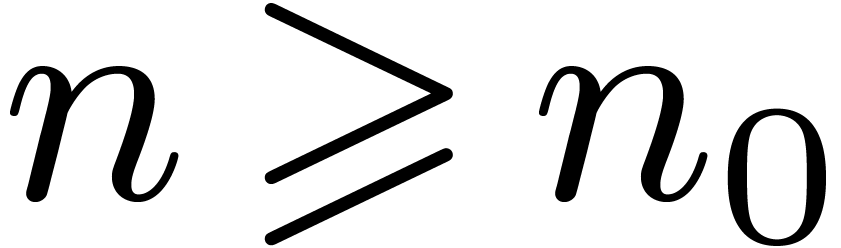 and denote
and denote 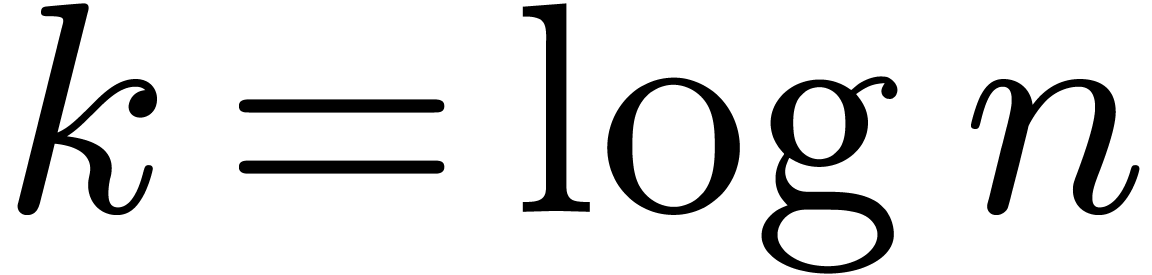 and
and 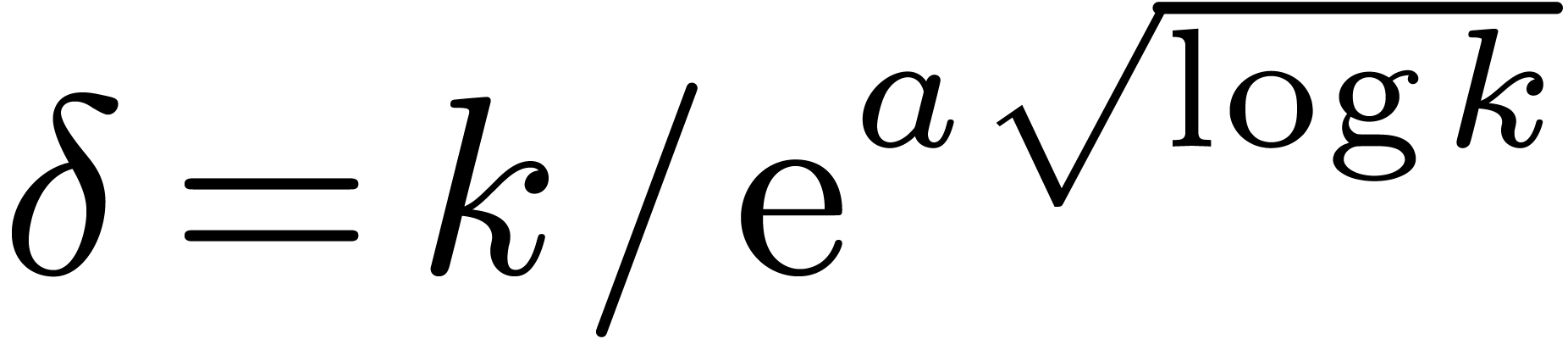 . For certain
. For certain 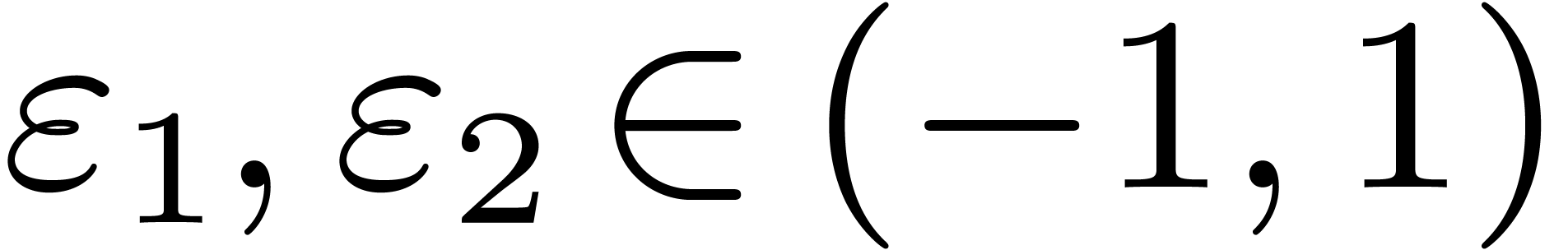 , we have
, we have 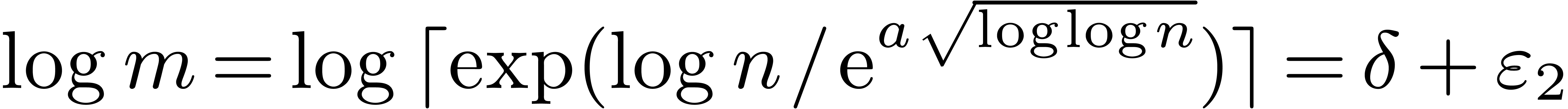 and
and 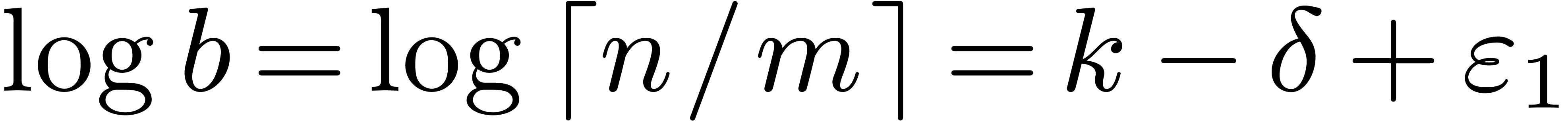 . Now (12)
implies
. Now (12)
implies
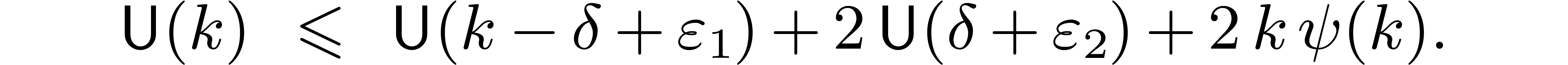
Let 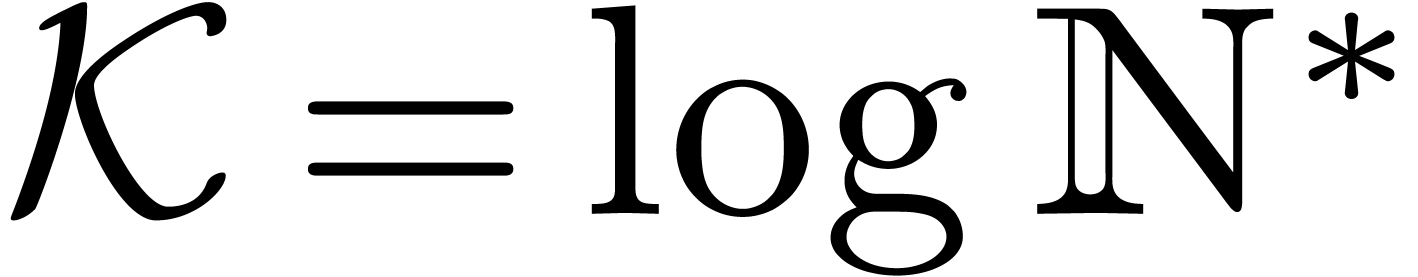 and
and  .
Let us prove by induction that
.
Let us prove by induction that  for all
for all  . This is clear for
. This is clear for  . Assume now that
. Assume now that  and
and
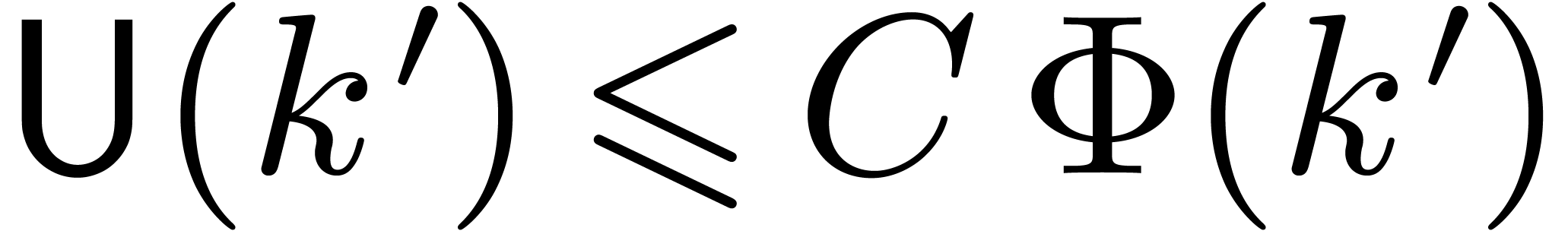 for all
for all 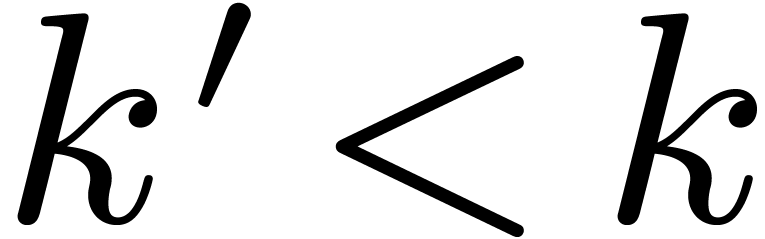 .
Then, with the above notations,
.
Then, with the above notations, 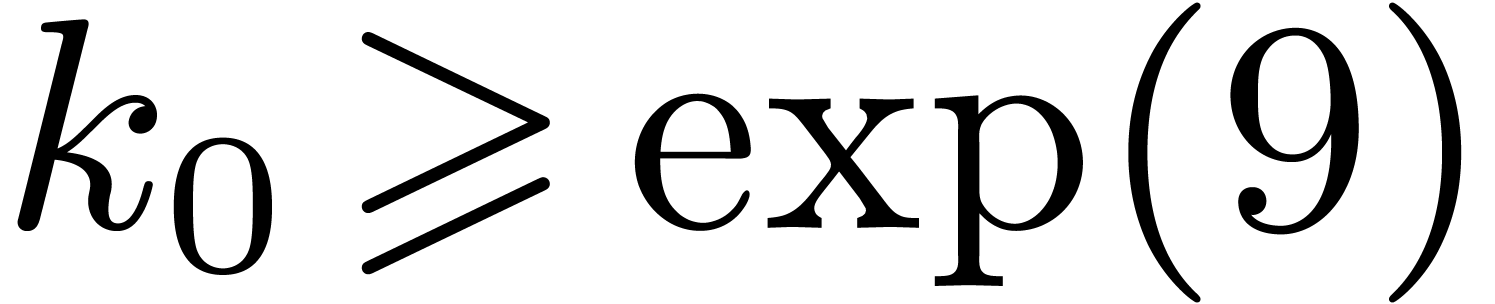 implies
implies 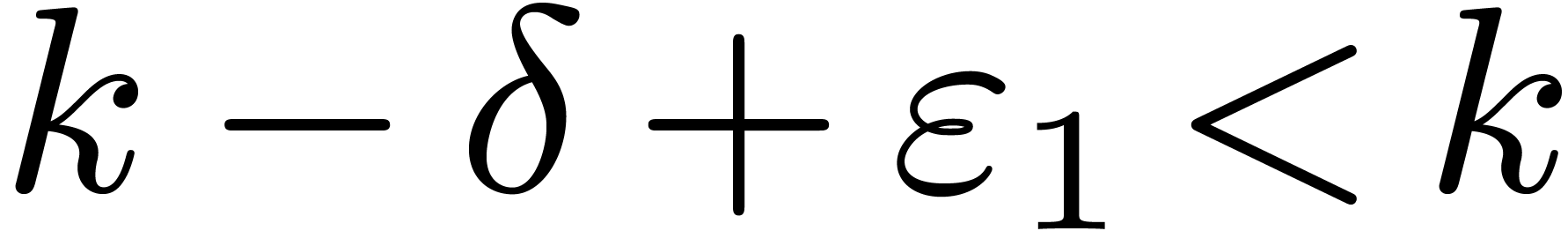 and
and  ,
whence
,
whence
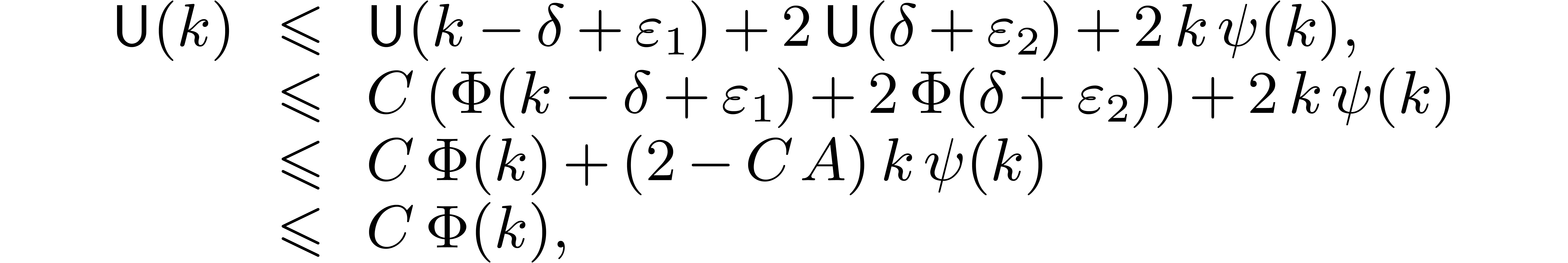
as desired. For all 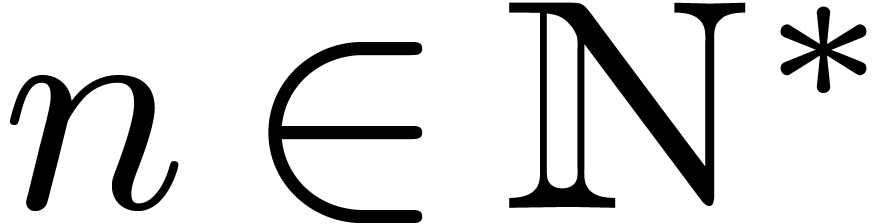 , we have
thus shown that
, we have
thus shown that 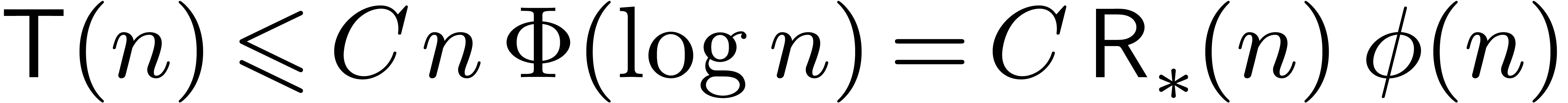 .
.
5Relaxed multiplication in
characteristic zero
Let us now consider the less favourable case when  is an effective ring which does not necessarily contain primitive
is an effective ring which does not necessarily contain primitive 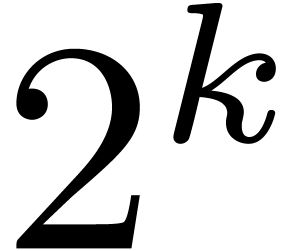 -th roots of unity for arbitrarily
high
-th roots of unity for arbitrarily
high 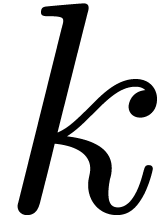 . In this section, we
will first consider the case when
. In this section, we
will first consider the case when  is
torsion-free as a
is
torsion-free as a  -module and
also admits a partial algorithm for division by integers.
-module and
also admits a partial algorithm for division by integers.
Given a block size 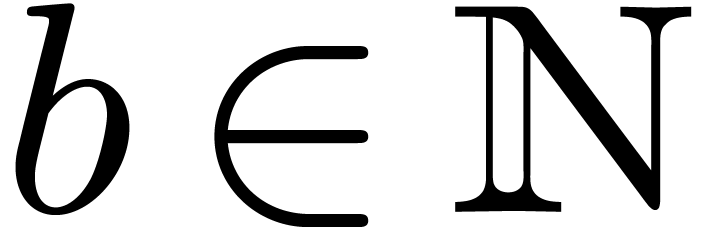 and
and 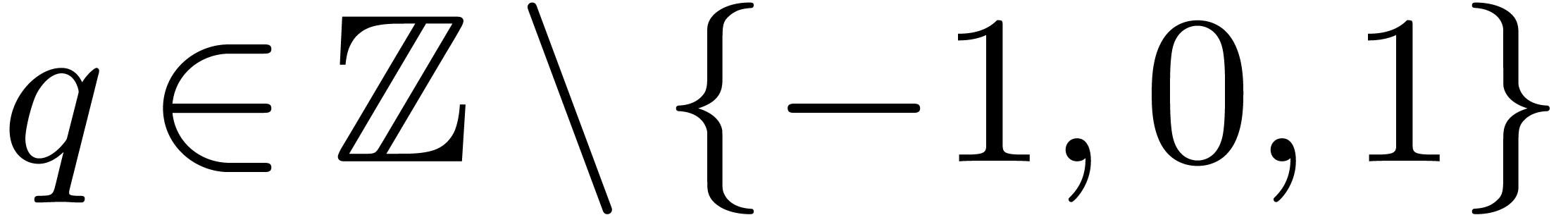 (say
(say 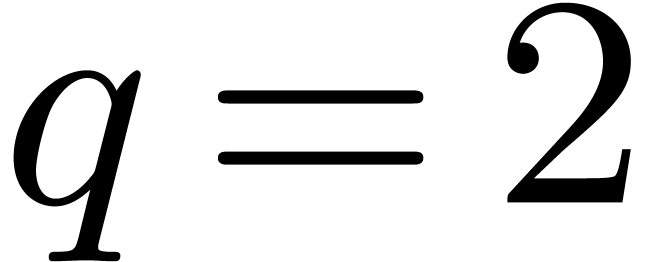 ), we will replace the
discrete Fourier transform
), we will replace the
discrete Fourier transform  at a
at a 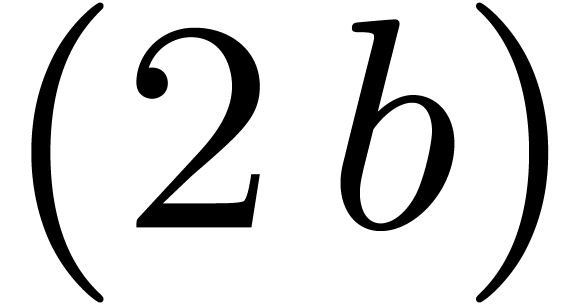 -th primitive root of unity by multipoint
evaluation at
-th primitive root of unity by multipoint
evaluation at 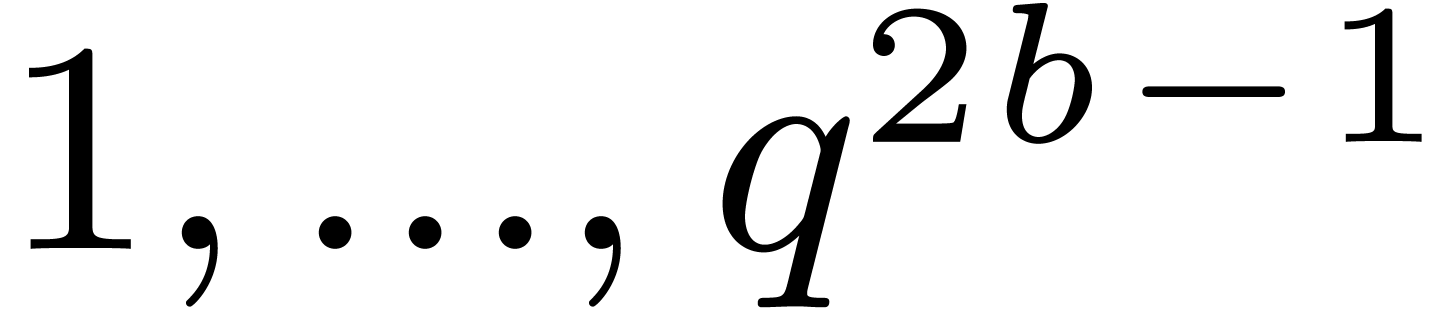 . More
precisely, we define
. More
precisely, we define
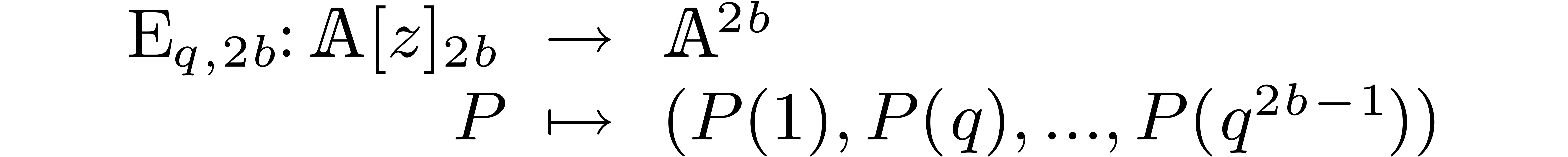
and the inverse transform 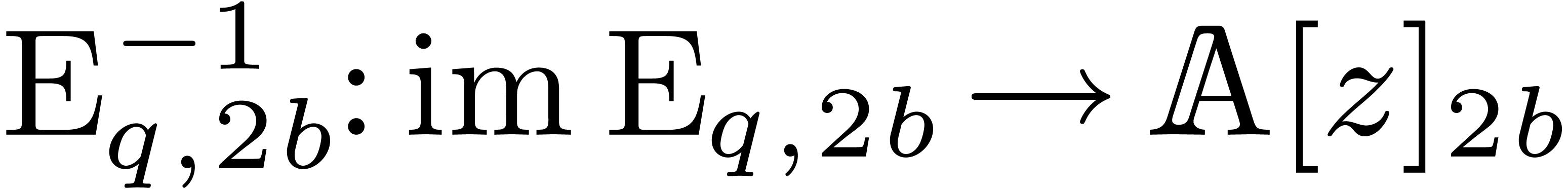 .
By Lemma 3, these transforms can both be computed using
.
By Lemma 3, these transforms can both be computed using
 operations in
operations in  .
In a similar way as for
.
In a similar way as for  and
and 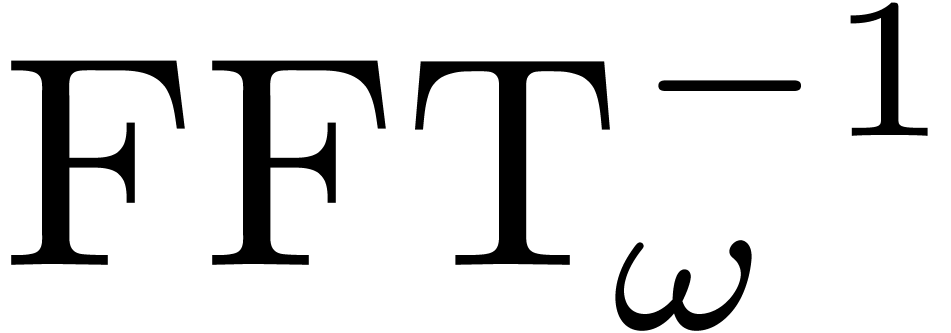 , we extend
, we extend 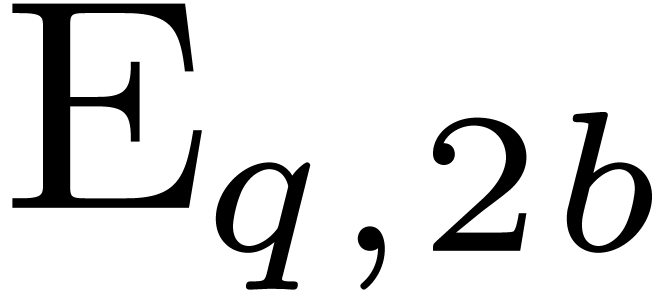 and
and 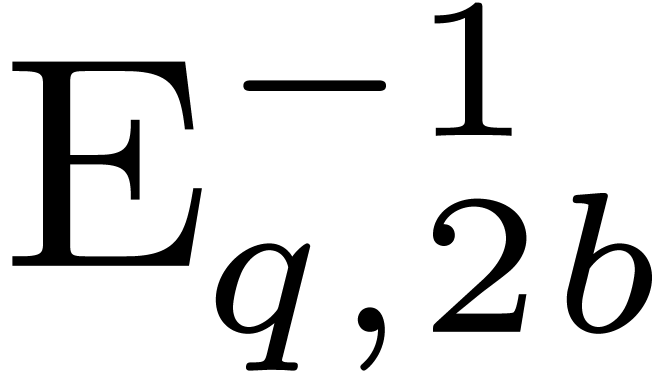 to power series in
to power series in  .
.
Theorem 7. Let  both be an effective ring and an effective
torsion-free
both be an effective ring and an effective
torsion-free  -module with an
effective partial division by elements in
-module with an
effective partial division by elements in 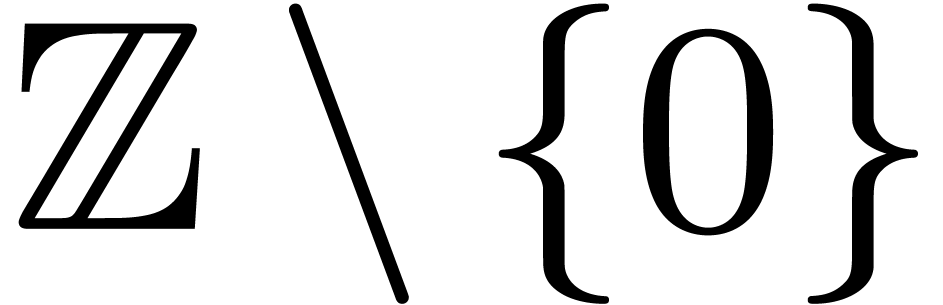 .
Then
.
Then

Proof. It suffices to prove the complexity bound for
semi-relaxed multiplication. Instead of (7), we now compute
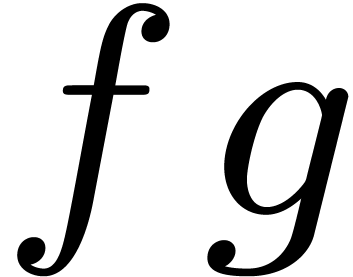 using
using
The bound (8) then has to be replaced by
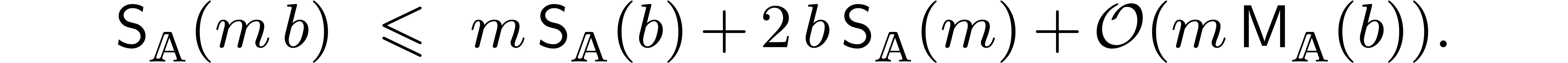 |
(14) |
Plugging in the bound 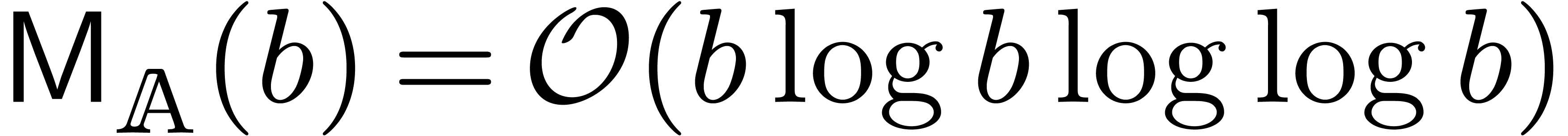 from [10] and
applying Theorem 6, the result follows.
from [10] and
applying Theorem 6, the result follows.
6Relaxed multiplication in prime
characteristic
Let  now be an effective ring of prime
characteristic
now be an effective ring of prime
characteristic 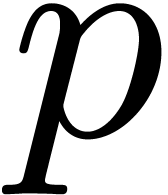 . For
expansion orders
. For
expansion orders 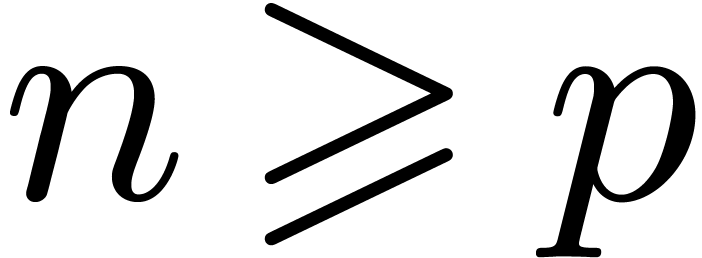 , the ring
, the ring
 does not necessarily contain
does not necessarily contain 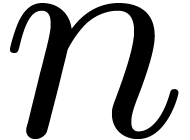 distinct points in geometric progression. Therefore, in order to apply
Lemma 3, we will first replace
distinct points in geometric progression. Therefore, in order to apply
Lemma 3, we will first replace  by a
suitable extension, in which we can find sufficiently large geometric
progressions.
by a
suitable extension, in which we can find sufficiently large geometric
progressions.
Given 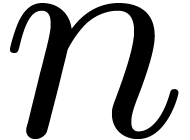 , let
, let 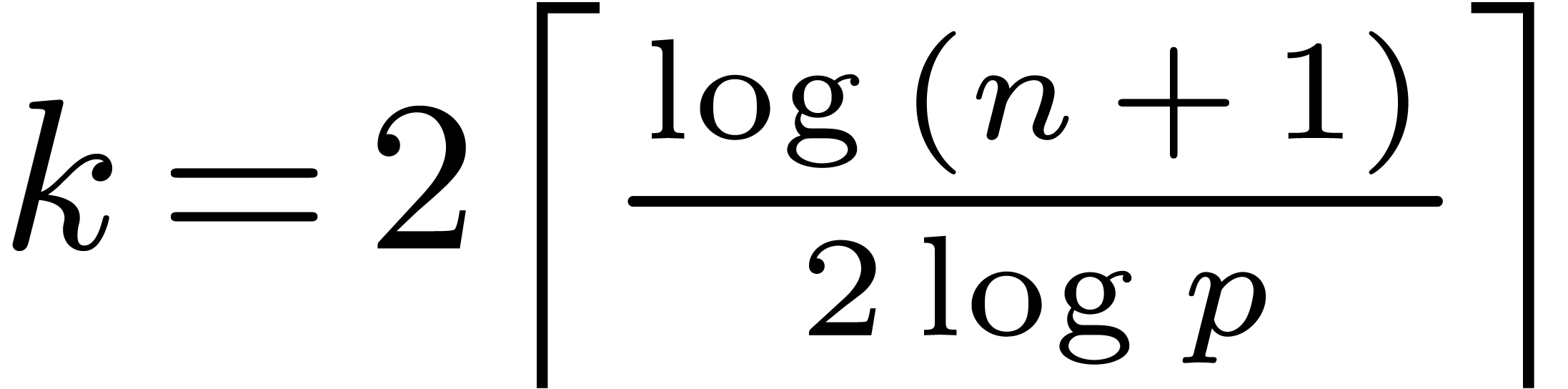 be even with
be even with 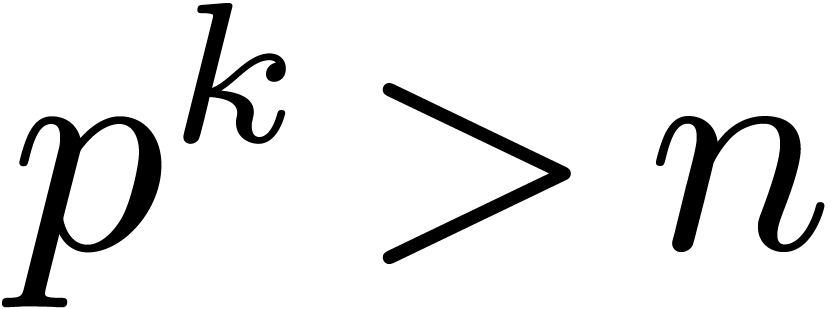 . Let
. Let 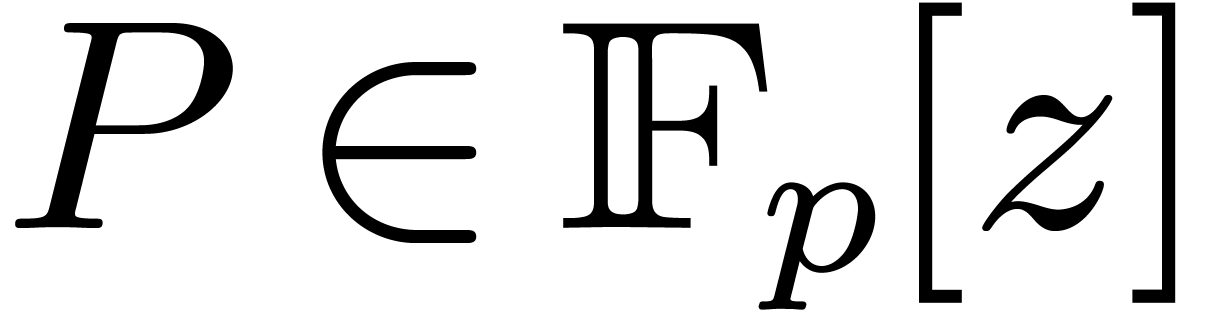 be such that the finite field
be such that the finite field 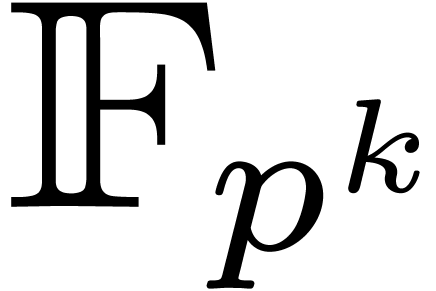 is
isomorphic to
is
isomorphic to 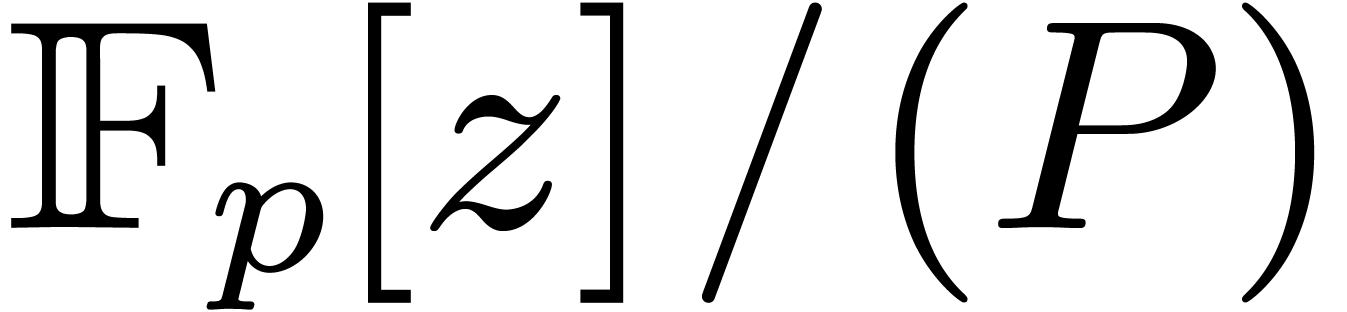 . Then the ring
. Then the ring

has dimension 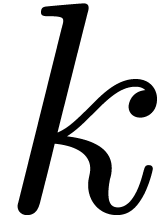 over
over  as a
vector space, so we have a natural
as a
vector space, so we have a natural  -linear
bijection
-linear
bijection
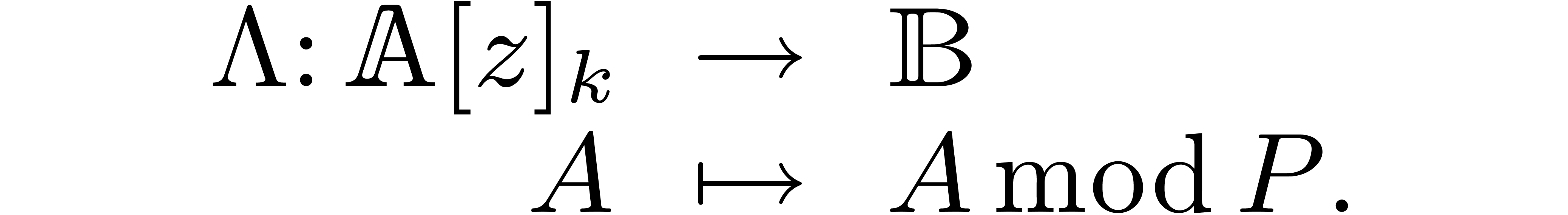
The ring  is an effective ring and one addition
or subtraction in
is an effective ring and one addition
or subtraction in  corresponds to
corresponds to 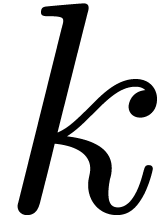 additions or subtractions in
additions or subtractions in  .
Similarly, one multiplication in
.
Similarly, one multiplication in  can be done
using
can be done
using  operations in
operations in  .
.
In order to multiply two series 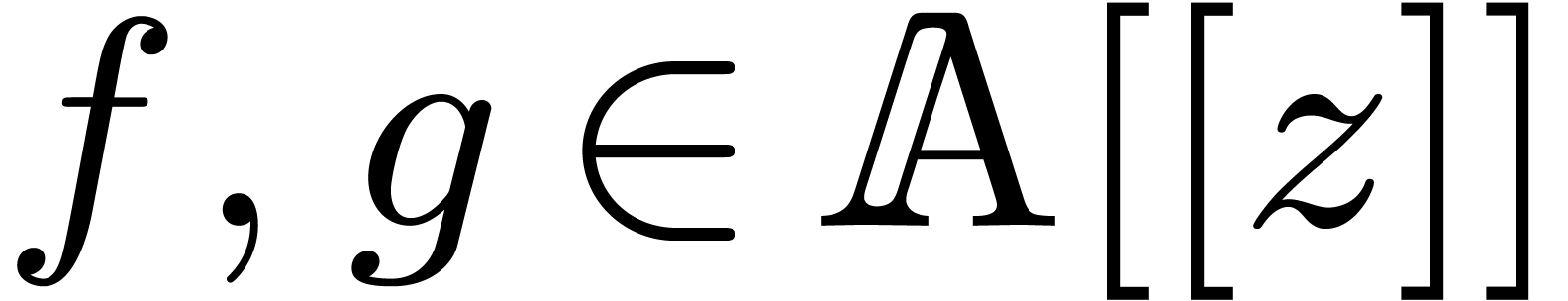 up to order
up to order
 , the idea is now to rewrite
, the idea is now to rewrite
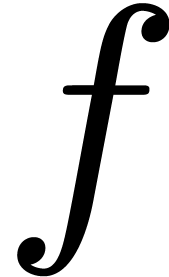 and
and  as series in
as series in 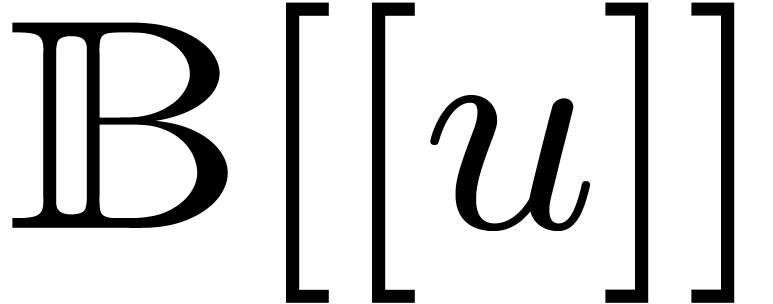 with
with 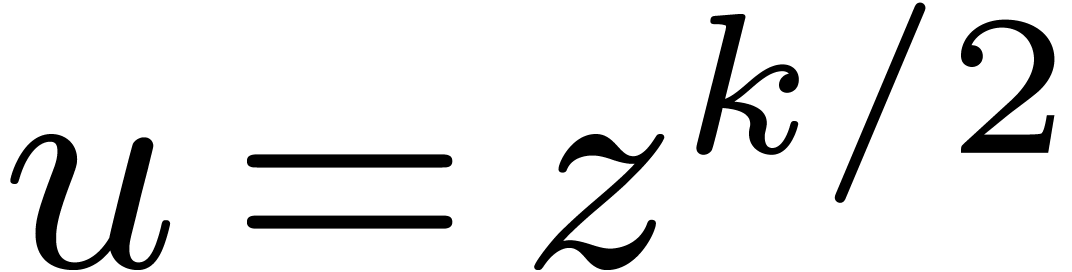 . If
we want to compute the relaxed product, then we also have to treat the
first
. If
we want to compute the relaxed product, then we also have to treat the
first  coefficients apart, as we did before for
the blocking strategy. More precisely, we will compute the semi-relaxed
product
coefficients apart, as we did before for
the blocking strategy. More precisely, we will compute the semi-relaxed
product  using the formula
using the formula
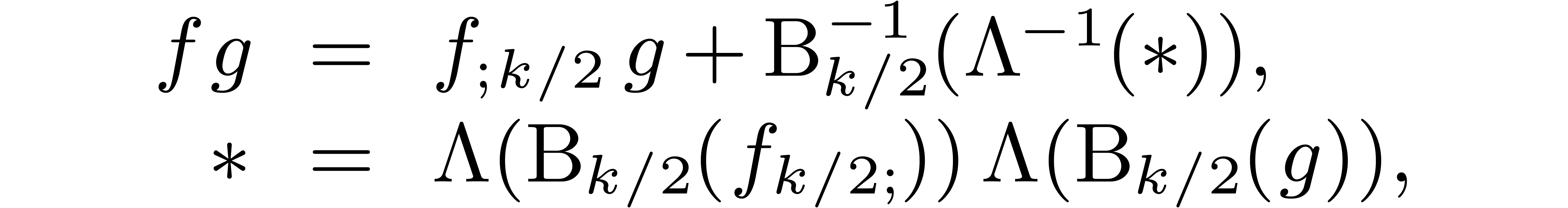
where we extended  to
to 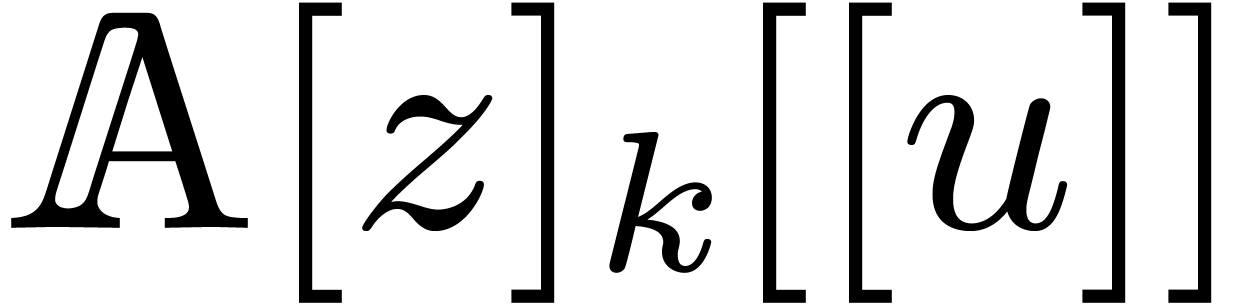 in
the natural way:
in
the natural way:
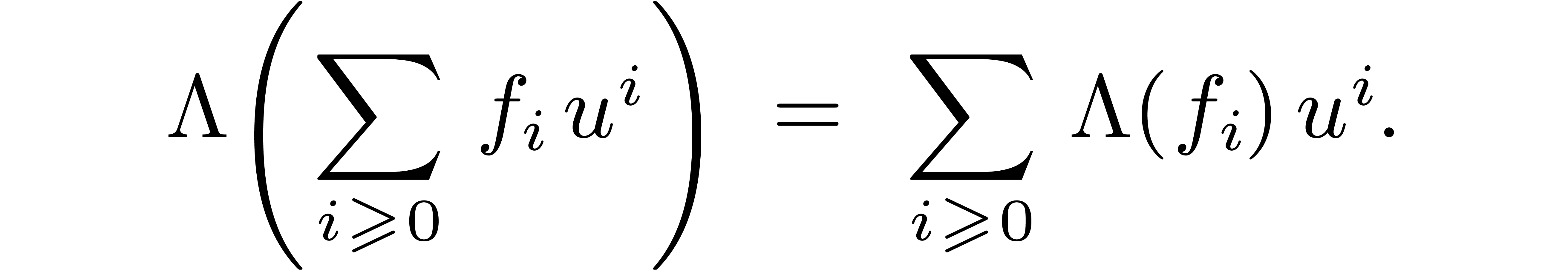
From the complexity point of view, we get
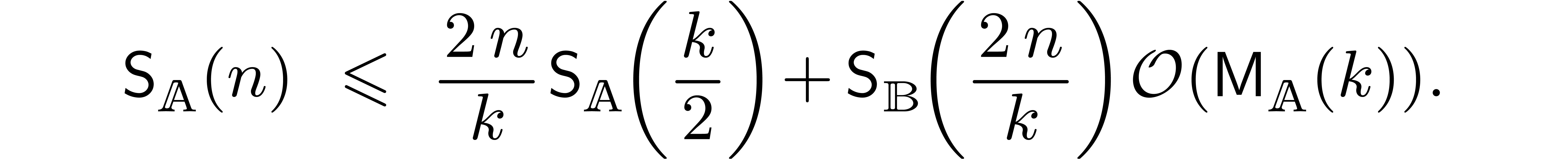 |
(15) |
Since  contains a copy of
contains a copy of 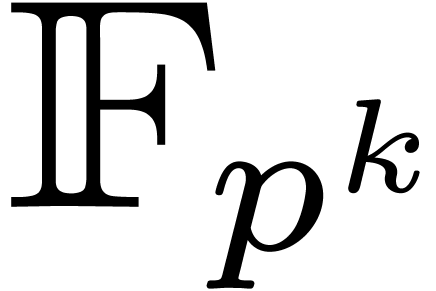 , it also contains at least
, it also contains at least 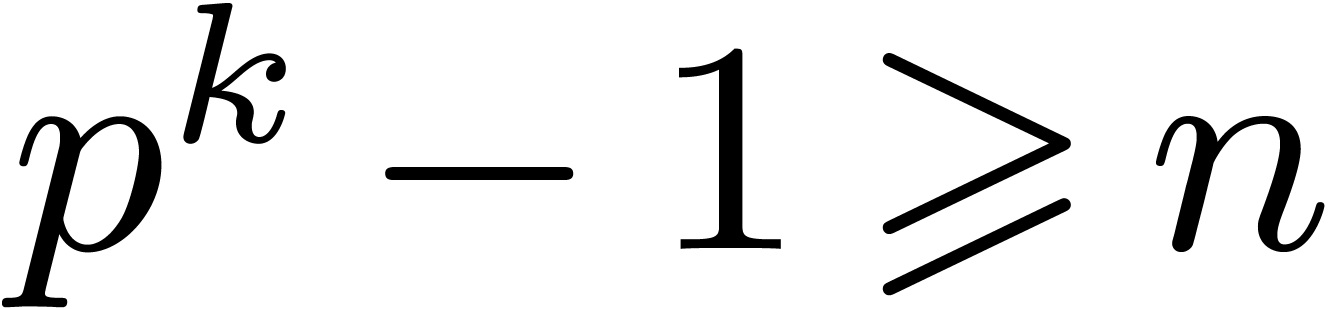 points in geometric progression. For the multiplication up to order
points in geometric progression. For the multiplication up to order 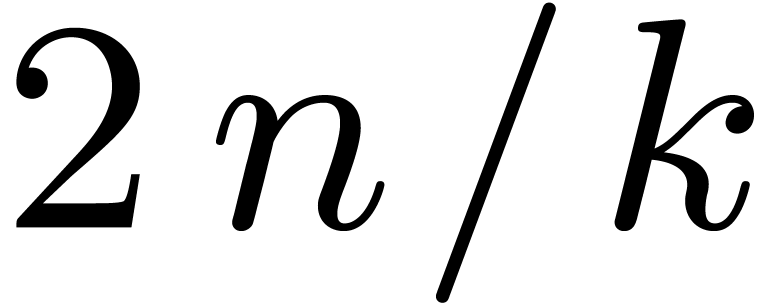 of two series with coefficients in
of two series with coefficients in  , we may thus use the blocking strategy
combined with multipoint evaluation and interpolation.
, we may thus use the blocking strategy
combined with multipoint evaluation and interpolation.
Theorem 8. Let  be an effective ring of prime characteristic
be an effective ring of prime characteristic 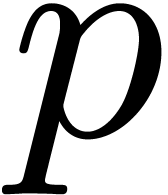 . Then
. Then

Proof. With the notations from above, we may find a
primitive 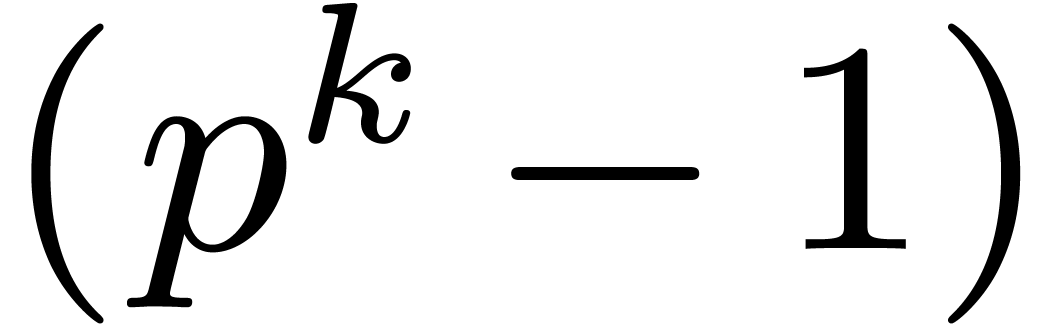 -th root of unity
-th root of unity
 in
in 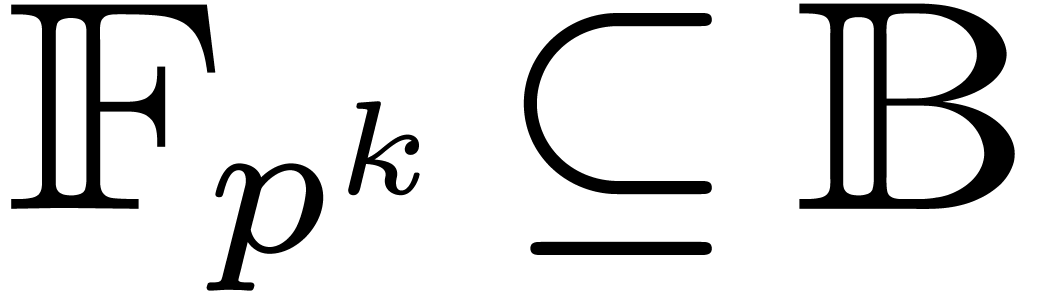 .
We may thus use formula (13) for the semi-relaxed
multiplication of two series in
.
We may thus use formula (13) for the semi-relaxed
multiplication of two series in 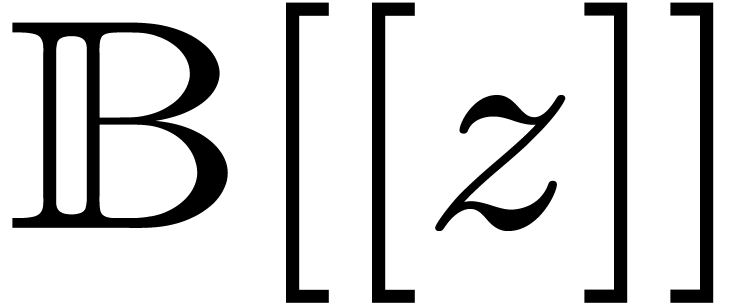 up to order
up to order
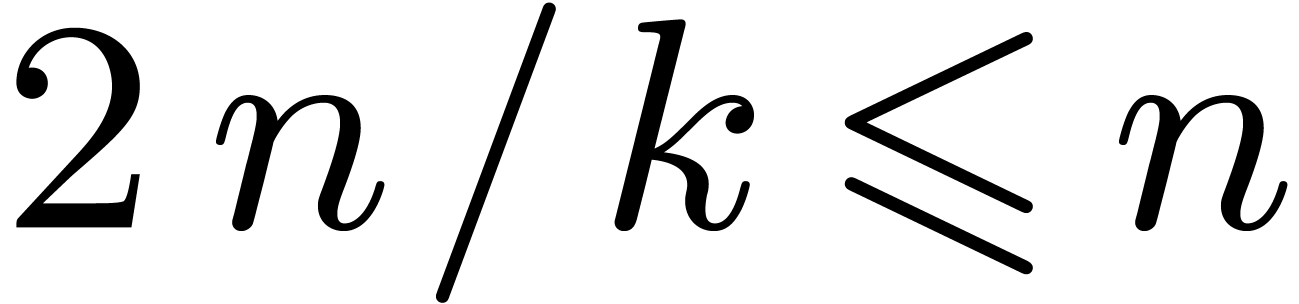 . In a similar way as in the
proof of Theorem 7, we thus get
. In a similar way as in the
proof of Theorem 7, we thus get
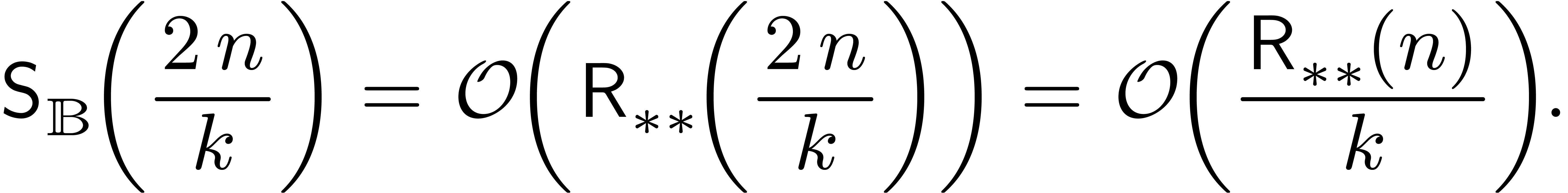
Using classical fast relaxed multiplication [16, 17,
13], we also have
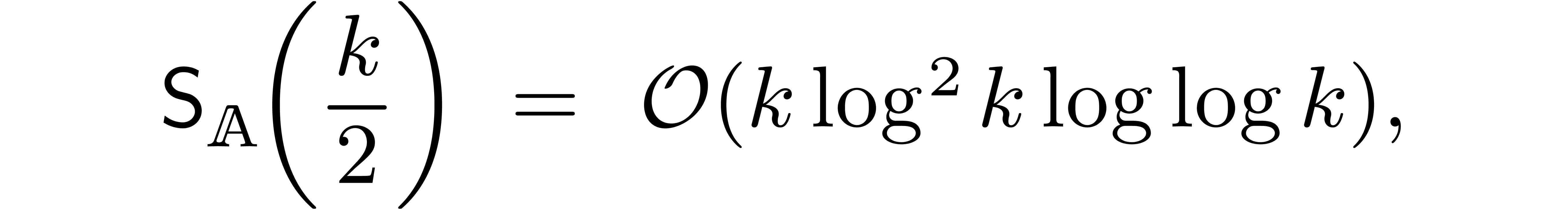
whence (15) simplifies to
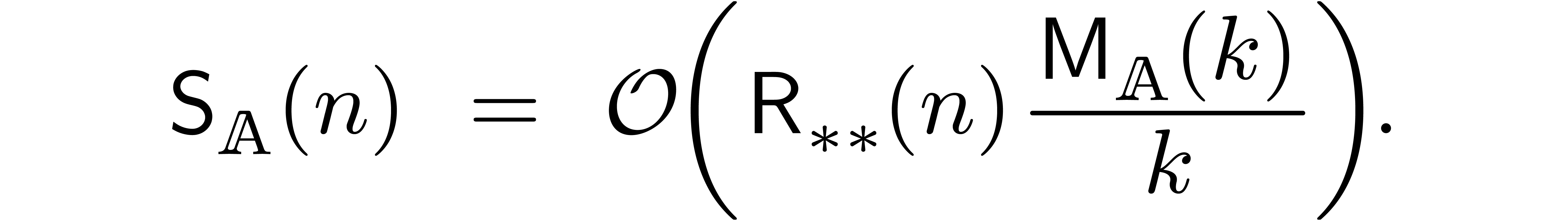 |
(16) |
Since 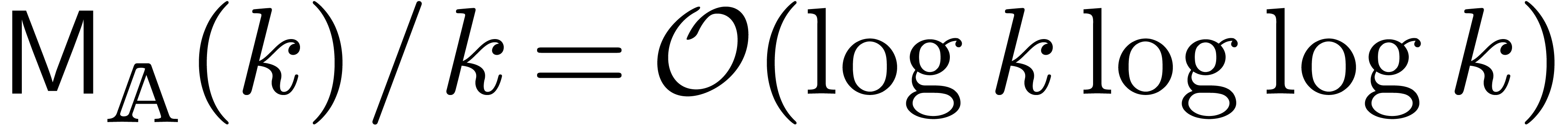 and
and 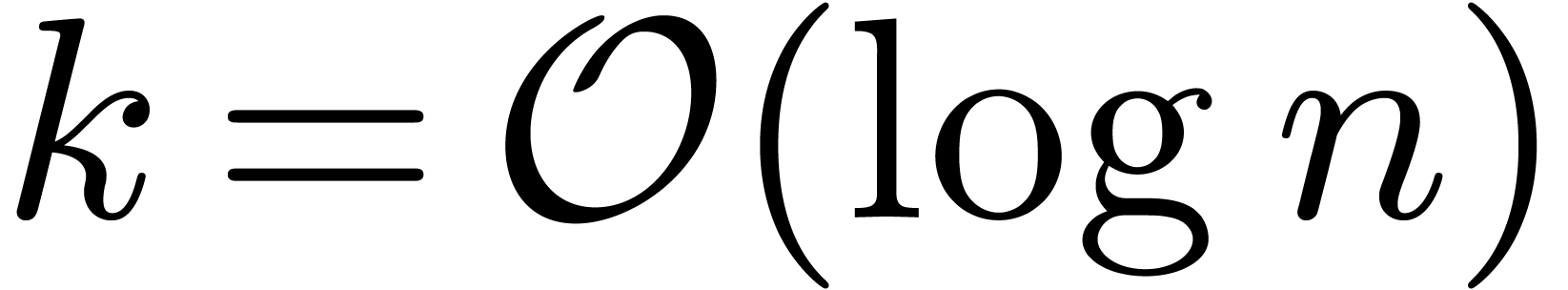 ,
the result follows.
,
the result follows.
Remark 9. As long as
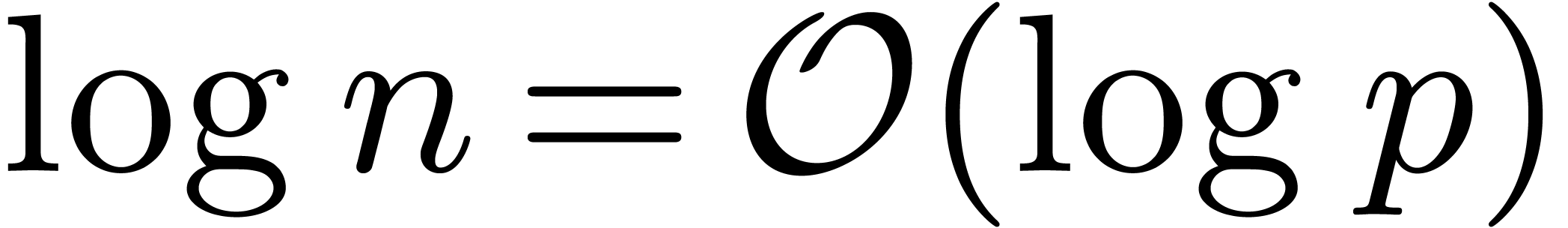 , then
, then 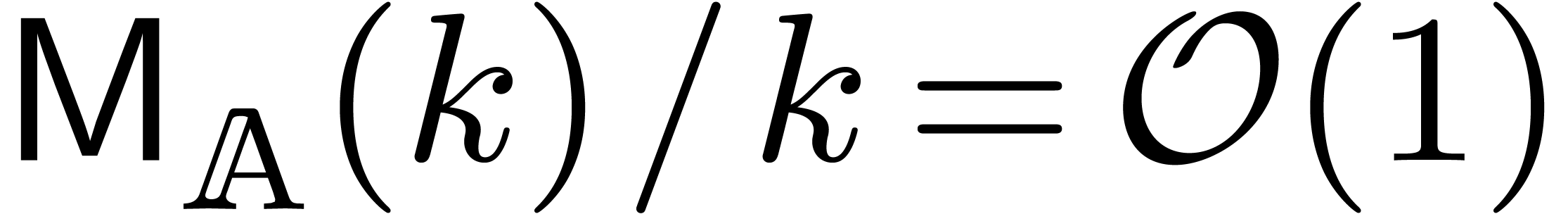 in (16), so the bound further reduces into
in (16), so the bound further reduces into

Remark 10. In our complexity
analysis, we have not taken into account the computation of the
polynomial 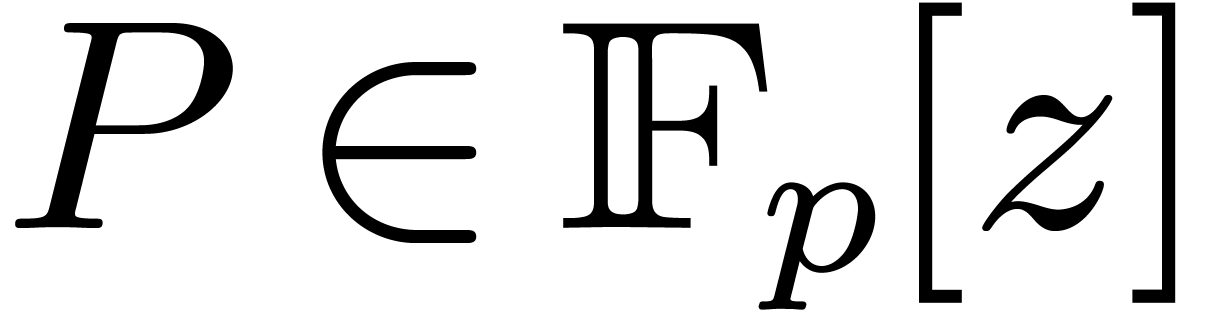 with
with 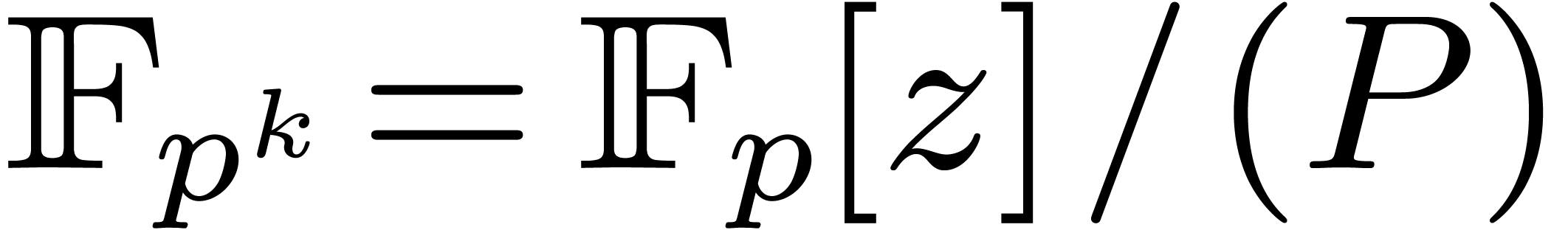 .
Using a randomized algorithm, such a polynomial can be computed in time
.
Using a randomized algorithm, such a polynomial can be computed in time
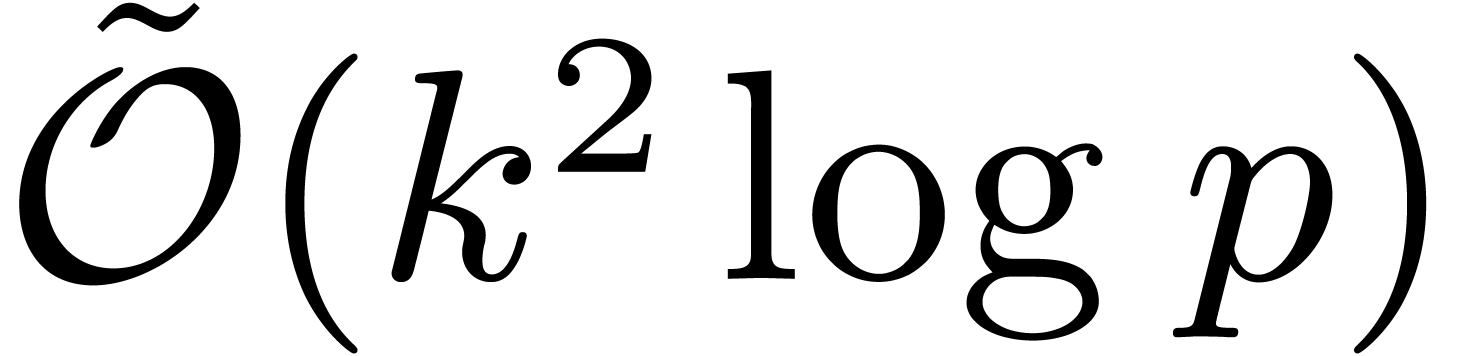 ; see [15,
Corollary 14.44]. If
; see [15,
Corollary 14.44]. If 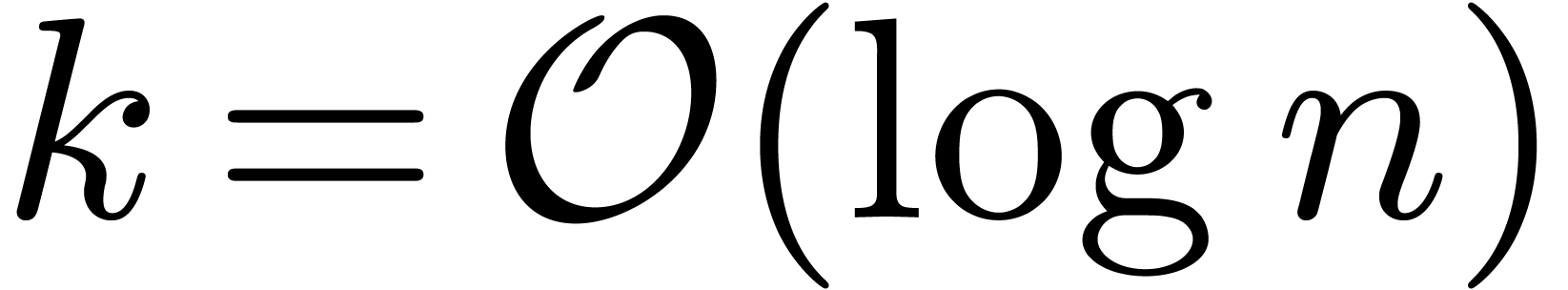 , then
this is really a precomputation of negligible cost
, then
this is really a precomputation of negligible cost 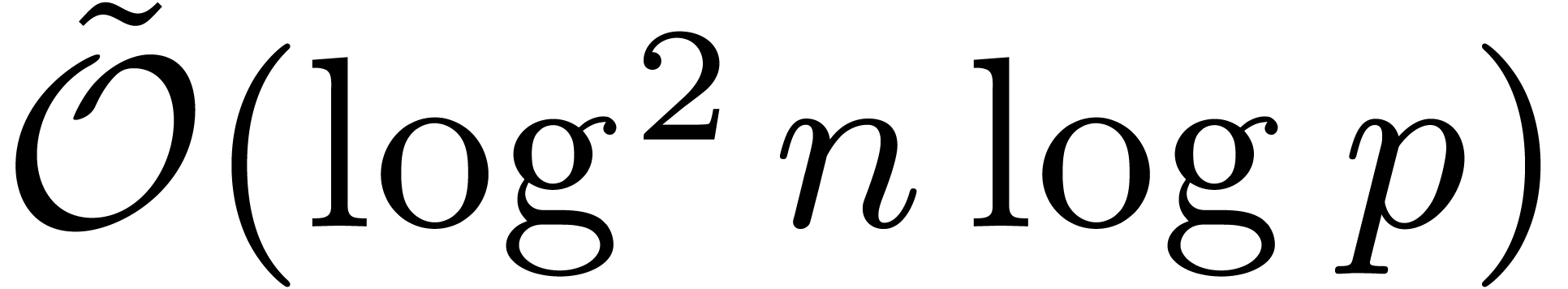 .
.
If we insist on computing 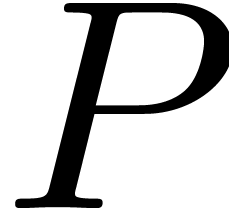 in a deterministic
way, then one may use [30, Theorem 3.2], which provides us
with an algorithm of time complexity
in a deterministic
way, then one may use [30, Theorem 3.2], which provides us
with an algorithm of time complexity 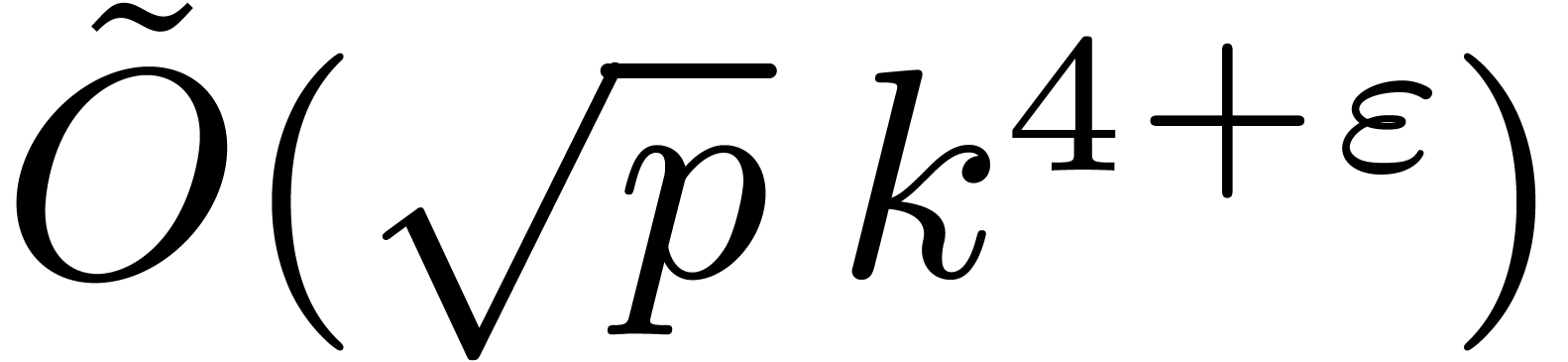 .
.
Similarly, there both exist randomized and deterministic algorithms [32, 31] for the efficient computation of
primitive 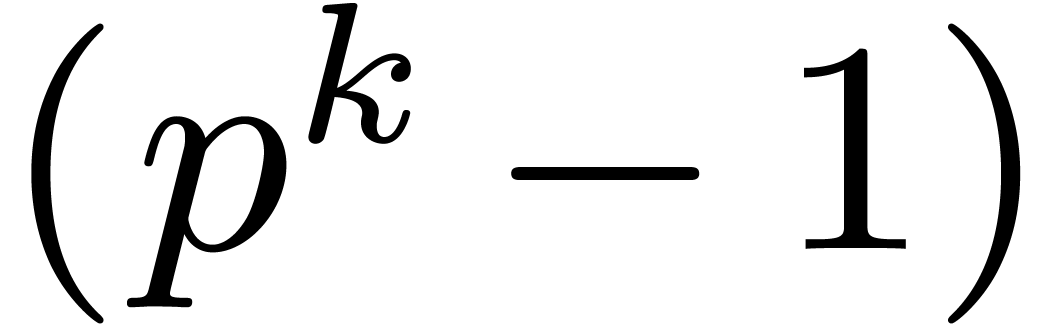 -th roots of unity
in
-th roots of unity
in 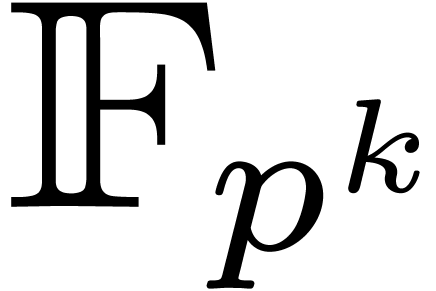 . In particular, thanks to
[31, Theorem 1] such a primitive root of unity can always
be computed in time
. In particular, thanks to
[31, Theorem 1] such a primitive root of unity can always
be computed in time  , when
using a naive algorithm for factoring
, when
using a naive algorithm for factoring 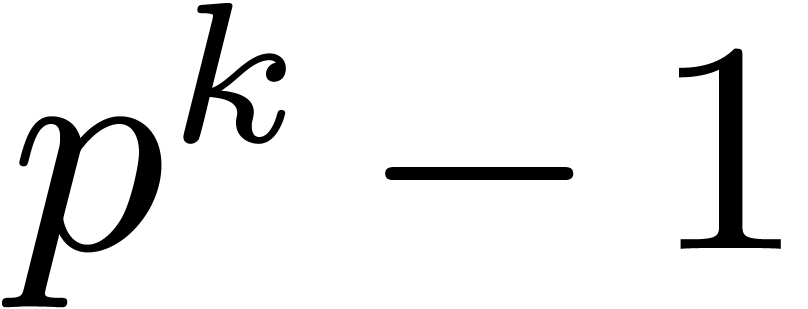 .
.
7Relaxed multiplication in positive
characteristic
Let us now show that the technique from the previous section actually
extends to the case when  is an arbitrary
effective ring of positive characteristic. We first show that the
algorithm still applies when the characteristic of
is an arbitrary
effective ring of positive characteristic. We first show that the
algorithm still applies when the characteristic of  is a prime power. We then conclude by showing how to apply Chinese
remaindering in our setting.
is a prime power. We then conclude by showing how to apply Chinese
remaindering in our setting.
Theorem 11. Let
 be an effective ring of prime power
characteristic
be an effective ring of prime power
characteristic 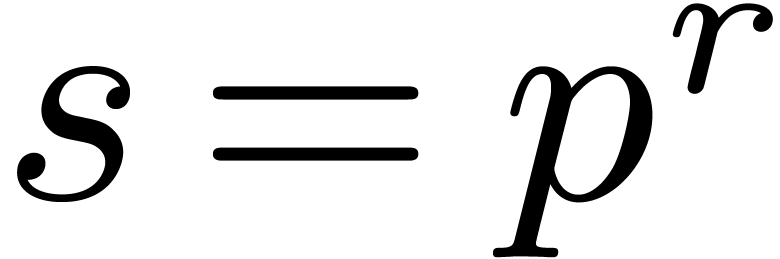 . Then
. Then

Proof. Taking 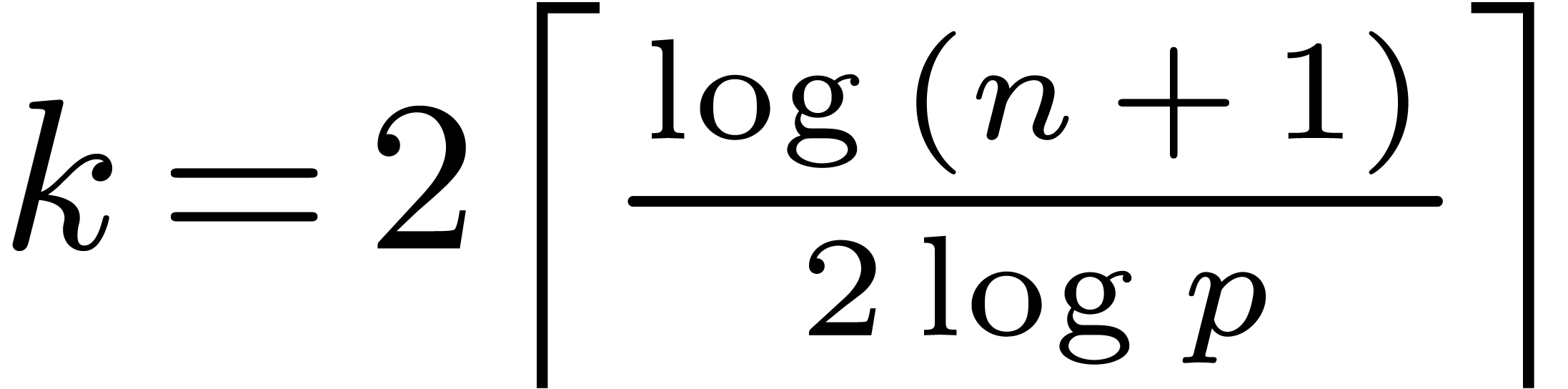 ,
let
,
let  of degree
of degree  be as in
the previous section and pick a monic polynomial
be as in
the previous section and pick a monic polynomial  of degree
of degree  in
in 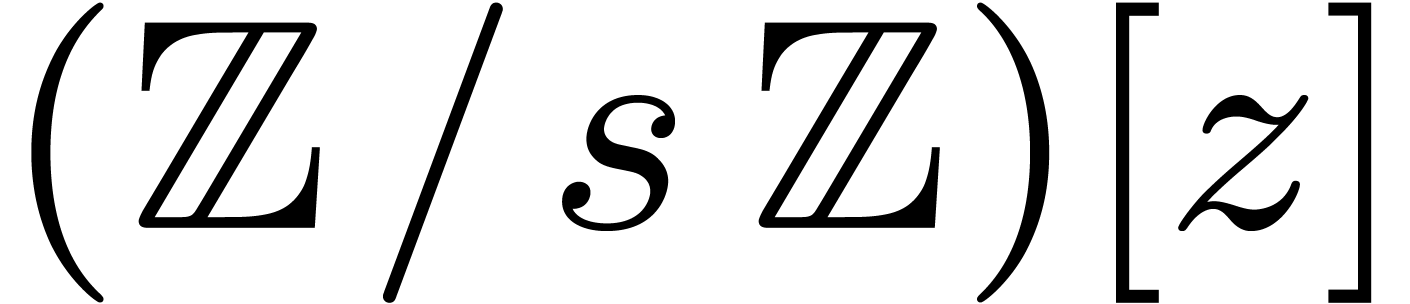 such that
the reduction
such that
the reduction  of
of  modulo
modulo
 yields
yields  .
Then we get a natural commutative diagram
.
Then we get a natural commutative diagram
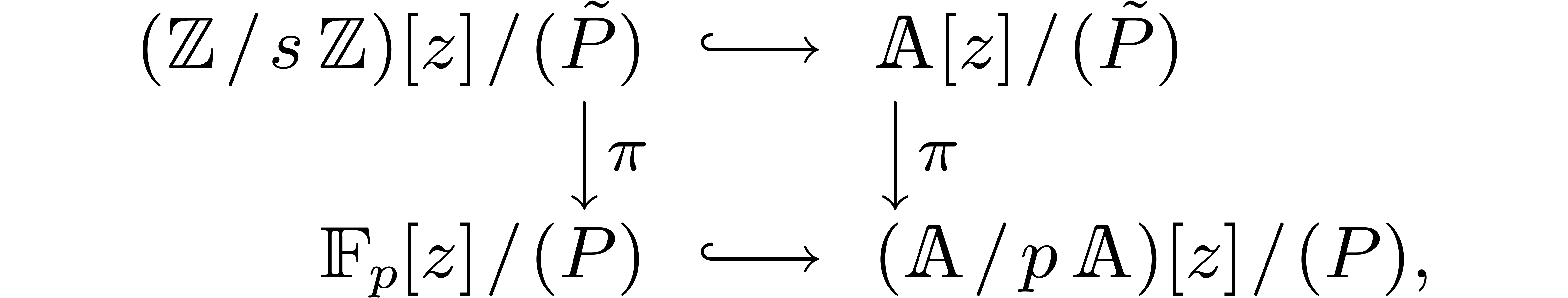
where  stands for reduction modulo
stands for reduction modulo 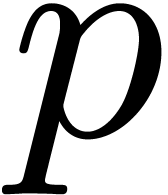 . In particular, we have an epimorphism
. In particular, we have an epimorphism
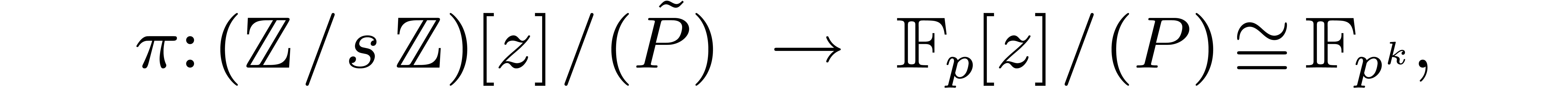
with 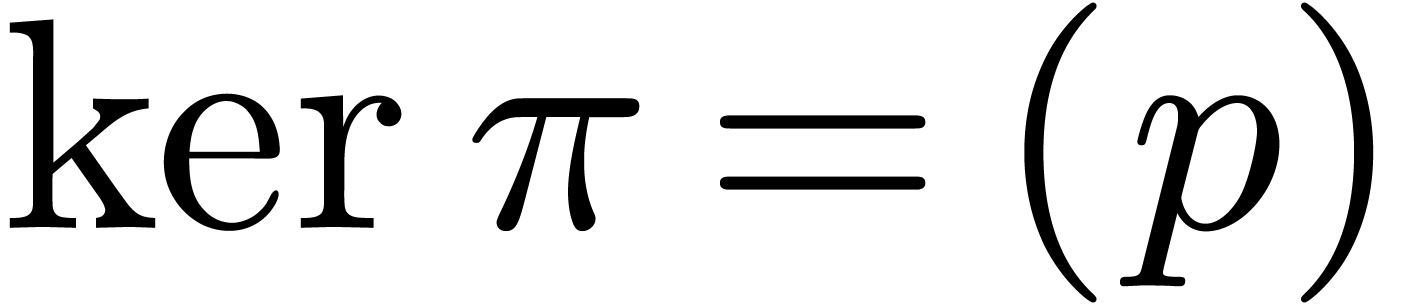 .
.
Now let  be an element in
be an element in 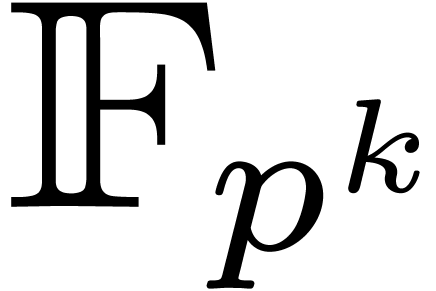 of order
of order 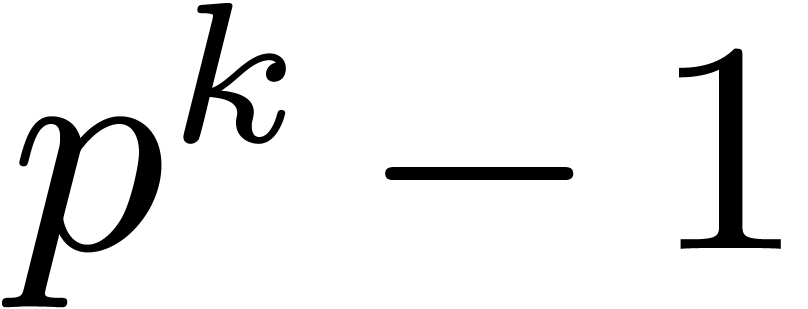 . Then any lift
. Then any lift 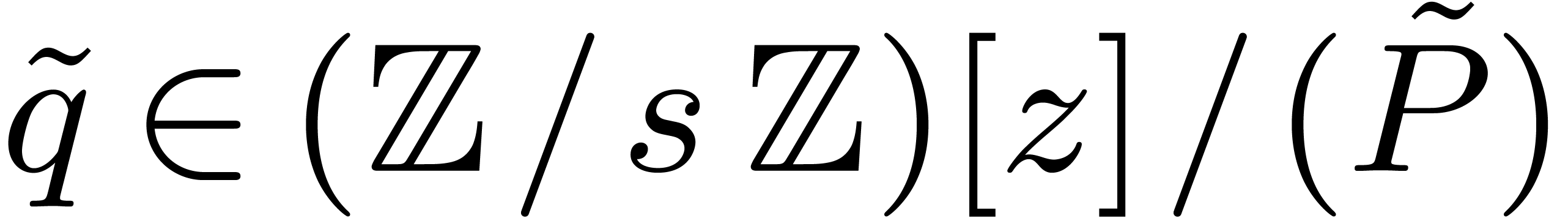 of
of  with
with 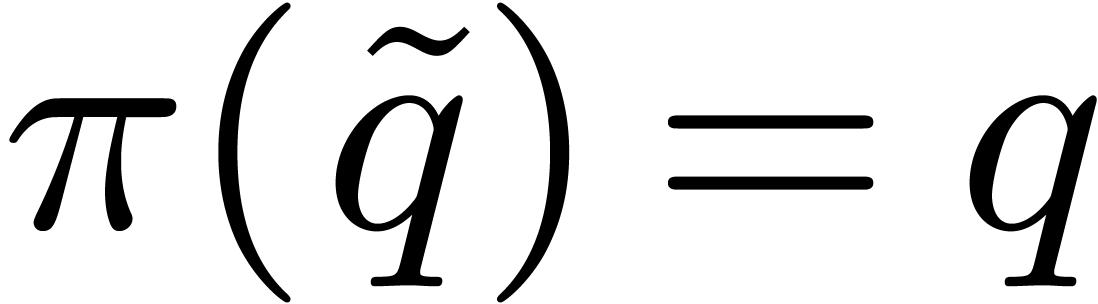 has order at least
has order at least 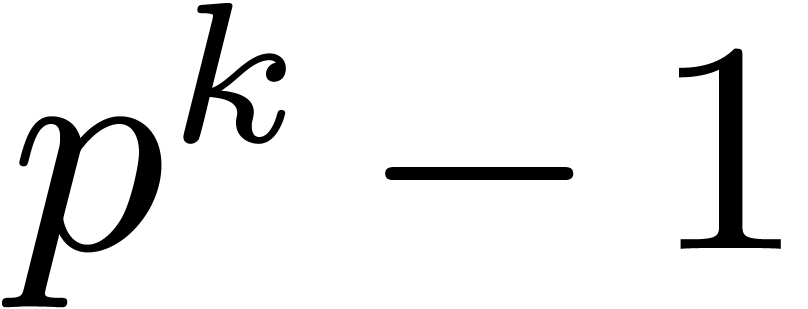 .
Moreover,
.
Moreover, 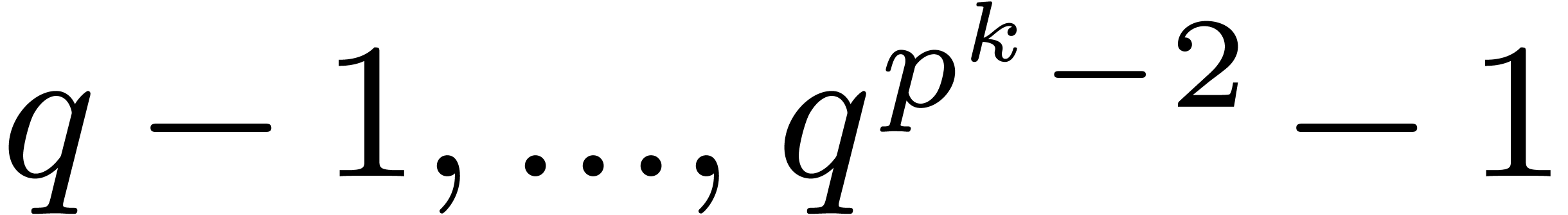 and
and  are all
invertible. Consequently,
are all
invertible. Consequently, 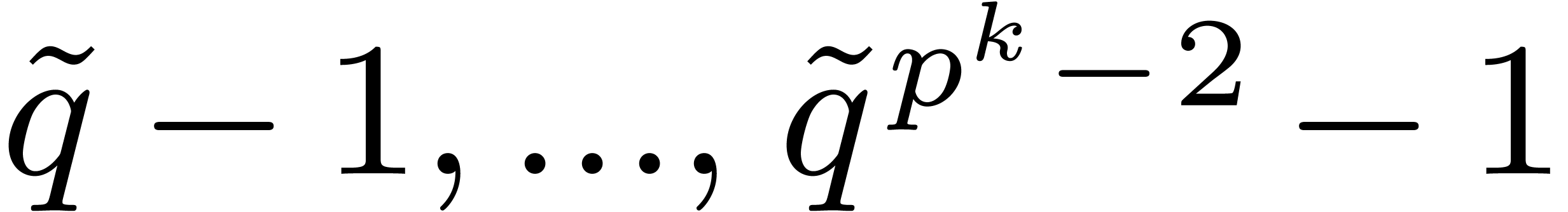 and
and  do not lie in
do not lie in 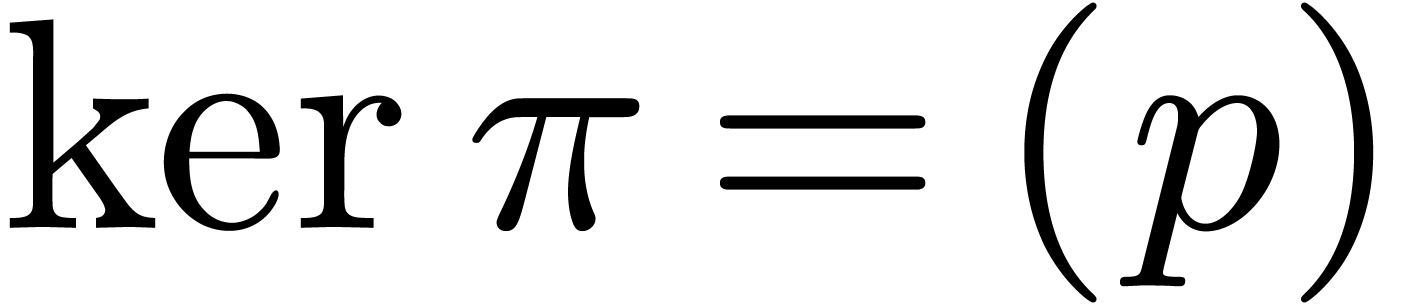 , whence they
are invertible as well. It follows that we may still apply multipoint
evaluation and interpolation in
, whence they
are invertible as well. It follows that we may still apply multipoint
evaluation and interpolation in 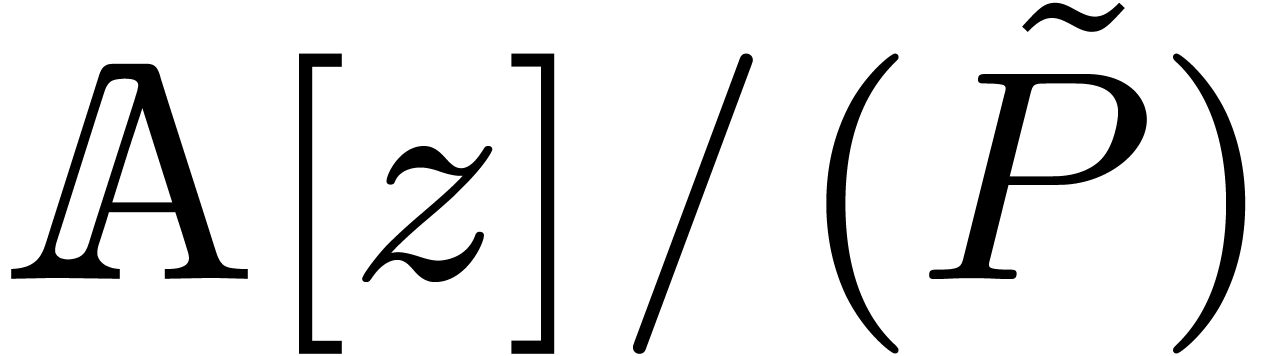 at the sequence
at the sequence
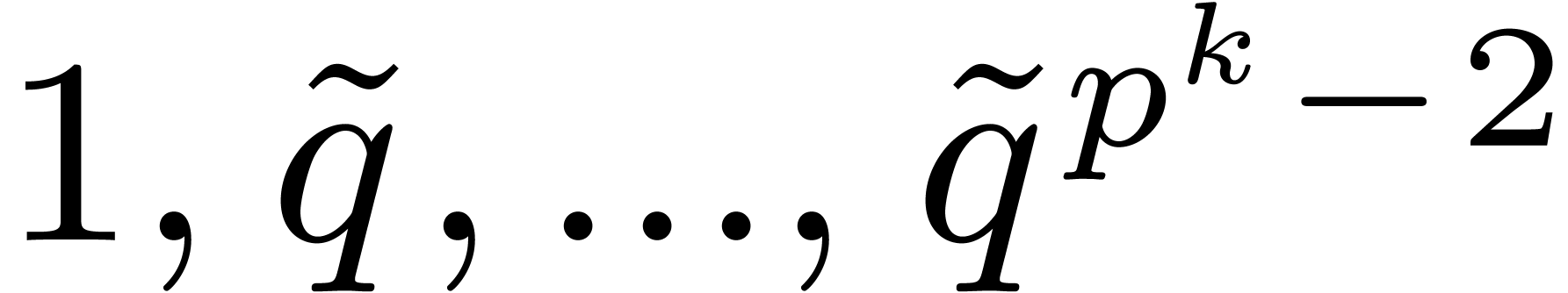 , whence Theorem 8
generalizes to the present case.
, whence Theorem 8
generalizes to the present case.
Remark 12. For a fixed
prime number 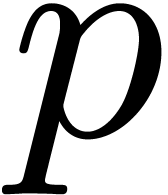 , we notice that
the complexity bound is uniform in the following sense: there exists a
constant
, we notice that
the complexity bound is uniform in the following sense: there exists a
constant 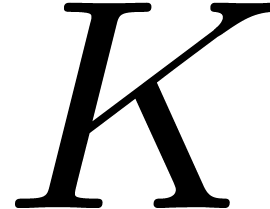 such that for all effective rings of
characteristic
such that for all effective rings of
characteristic 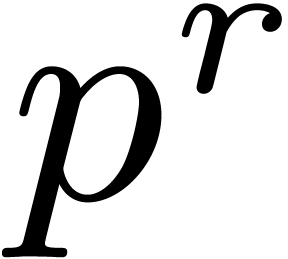 with
with 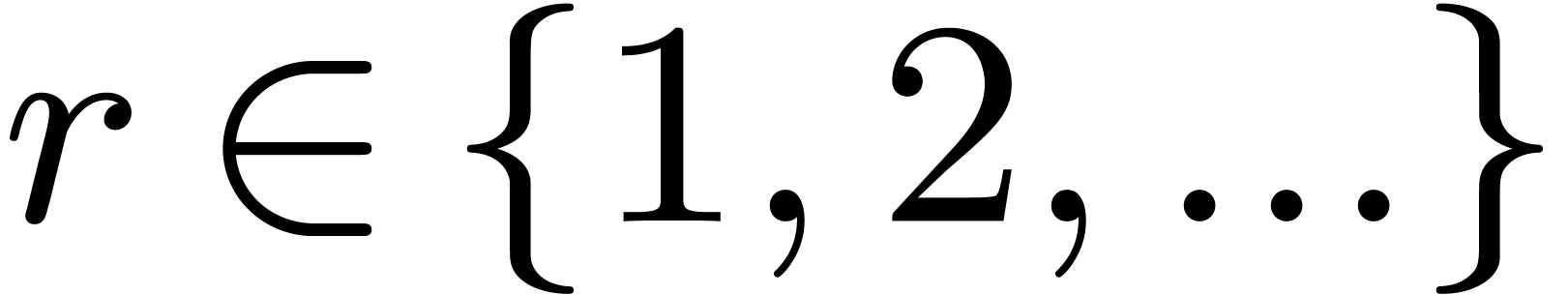 , we have
, we have 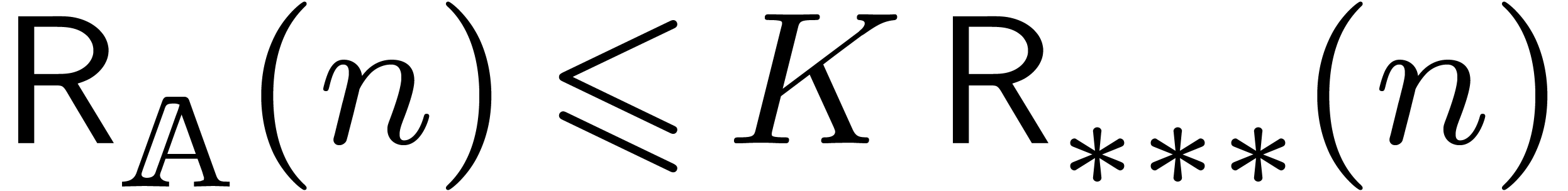 .
Indeed, the choice of
.
Indeed, the choice of 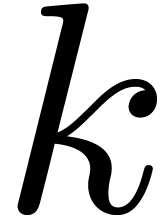 only depends on
only depends on 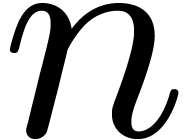 and
and 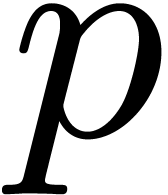 , and any
operation in
, and any
operation in 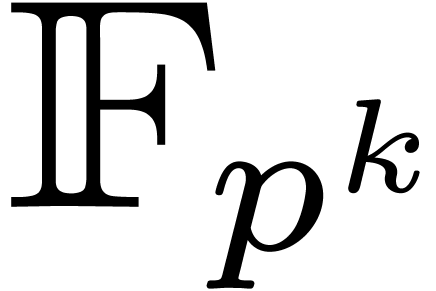 or
or 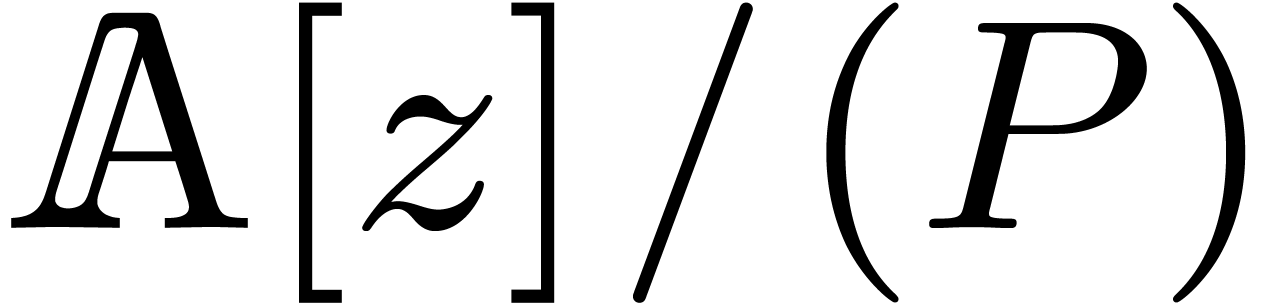 in the
case
in the
case 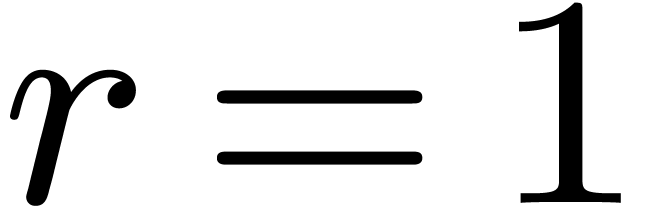 corresponds to exactly one lifted operation
in
corresponds to exactly one lifted operation
in 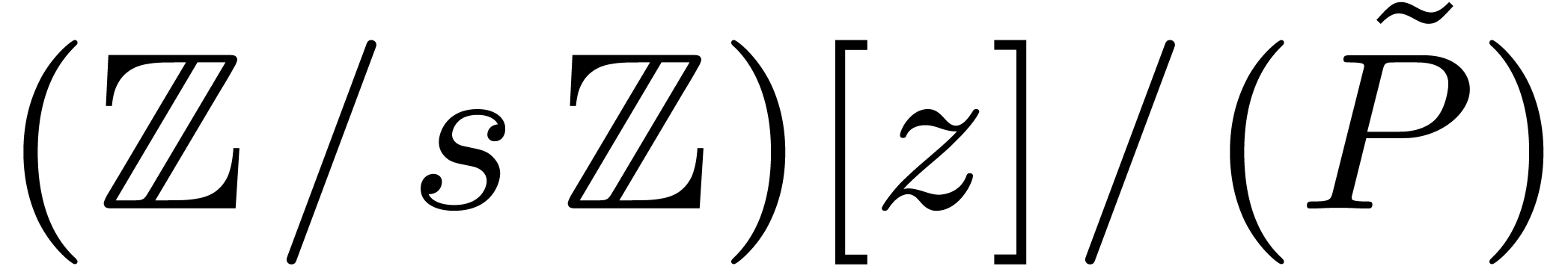 or
or 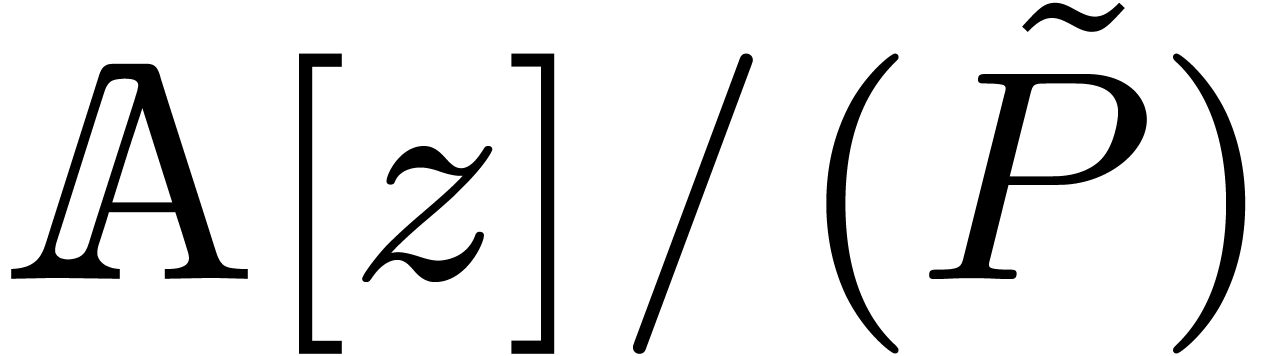 in the general
case.
in the general
case.
Remark 13. Similarly
as in Remark 9, the hypothesis 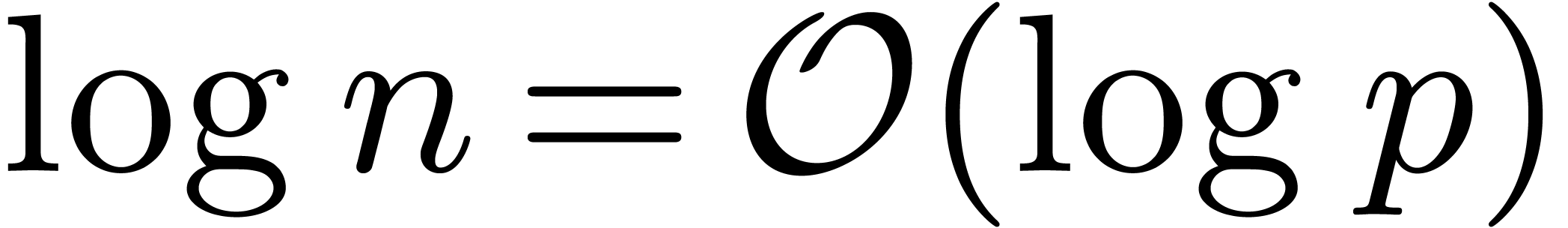 leads to the improved bound
leads to the improved bound

This bound is uniform in a similar way as in Remark 12.
Theorem 14. Let
 be an effective ring of non-zero characteristic
be an effective ring of non-zero characteristic
 . Then
. Then

Proof. We will prove the theorem by induction on the
number of prime divisors of  .
If
.
If  is a prime power, then we are done. So assume
that
is a prime power, then we are done. So assume
that  , where
, where  and
and  are relatively prime, and let
are relatively prime, and let 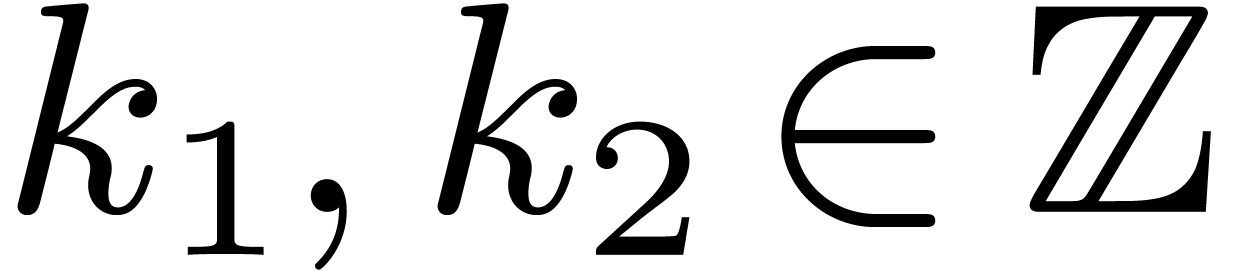 be such that
be such that
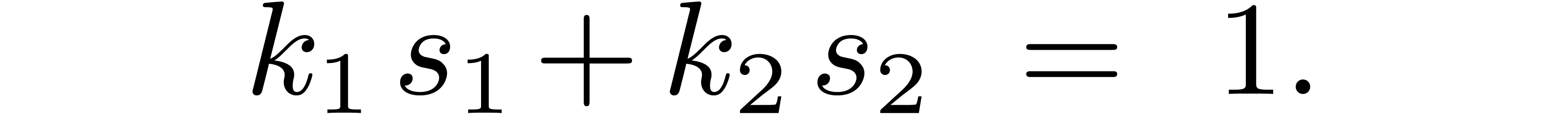
Then we may consider the rings
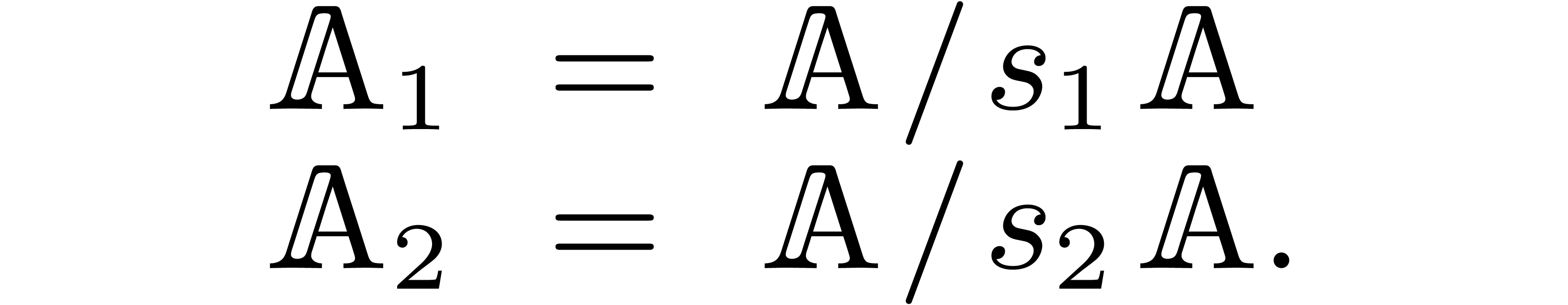
These rings are effective, when representing their elements by elements
of  and transporting the operations from
and transporting the operations from  . Of course, the representation of
an element
. Of course, the representation of
an element 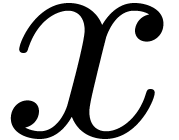 of
of  (or
(or  ) is not unique, since we may
replace it by
) is not unique, since we may
replace it by  for any
for any  (or
(or  ). But this is not a
problem, since our definition of effective ring did not require unique
representability or the existence of an equality test.
). But this is not a
problem, since our definition of effective ring did not require unique
representability or the existence of an equality test.
Now let  and let
and let 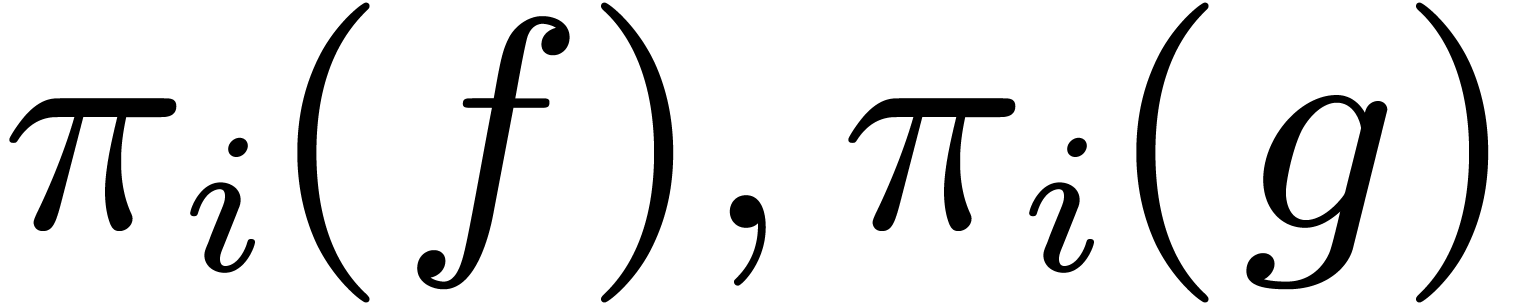 be their
projections in
be their
projections in 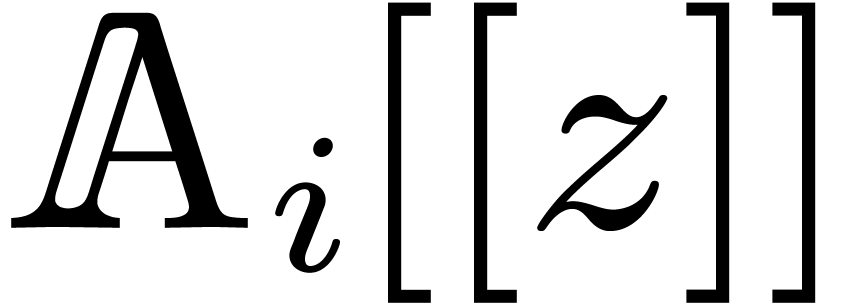 , for
, for 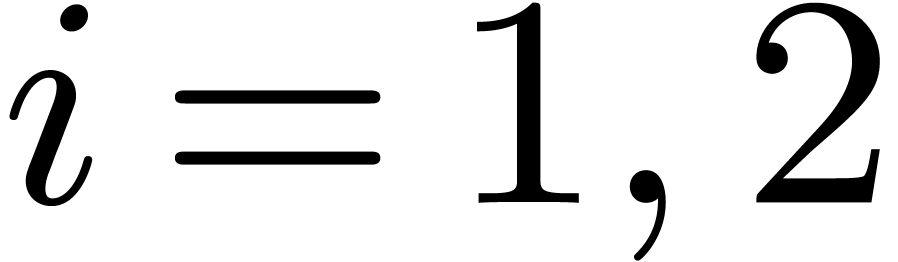 . Consider the relaxed products
. Consider the relaxed products
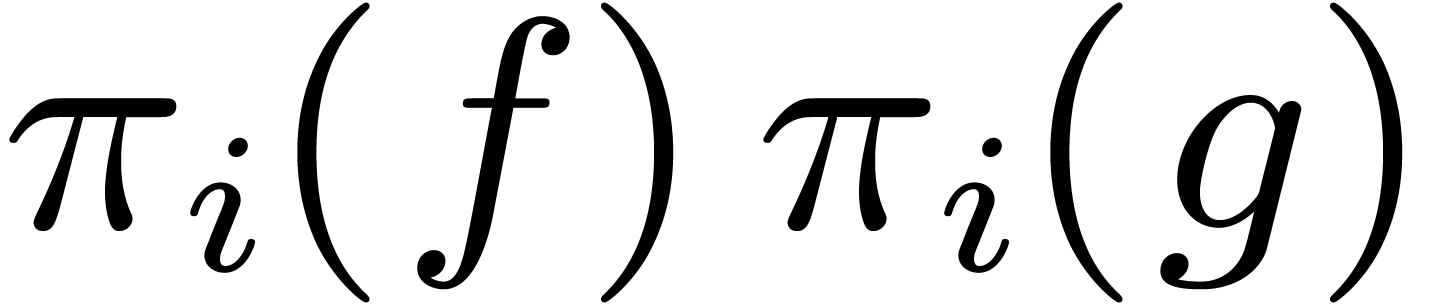 , for
, for 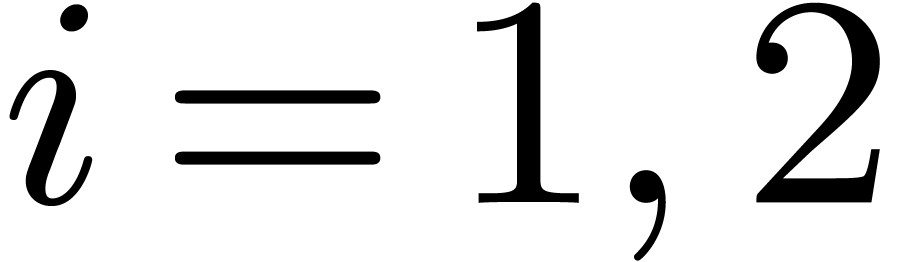 . These products are represented by relaxed series
. These products are represented by relaxed series
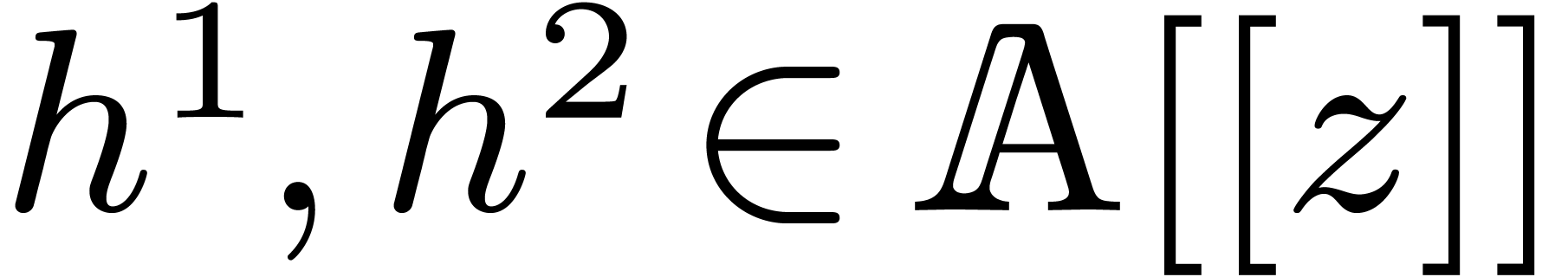 via
via 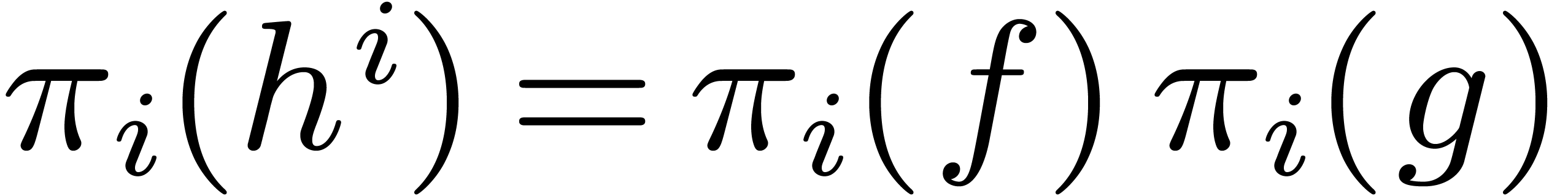 ,
for
,
for 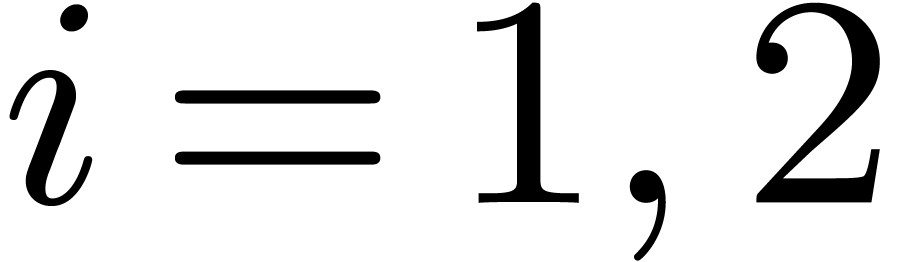 . By the induction
hypotheses, we may compute
. By the induction
hypotheses, we may compute 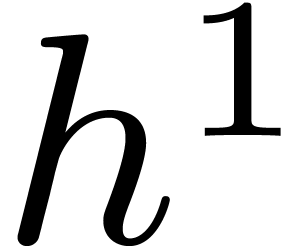 and
and 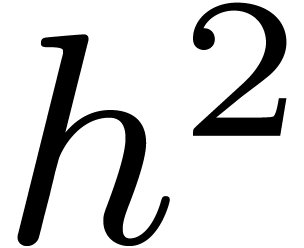 at order
at order 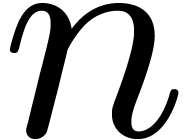 using
using 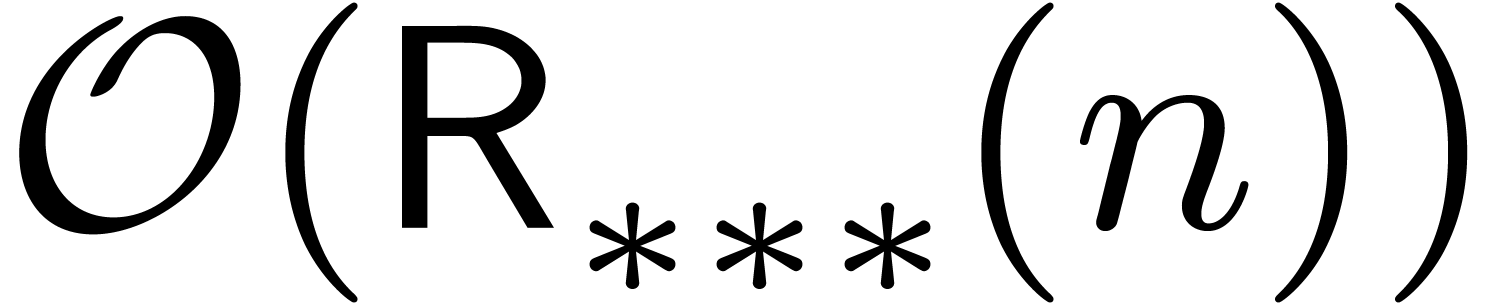 operations in
operations in  . The linear
combination
. The linear
combination 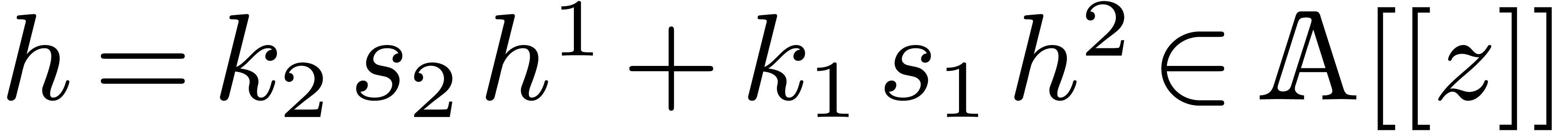 can still be expanded up to order
can still be expanded up to order
 with the same complexity. We claim that
with the same complexity. We claim that 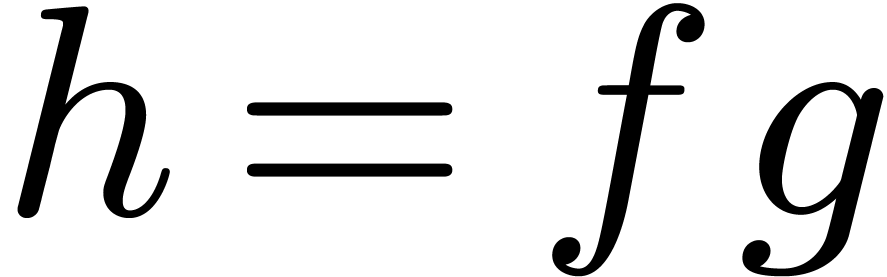 . Indeed,
. Indeed,
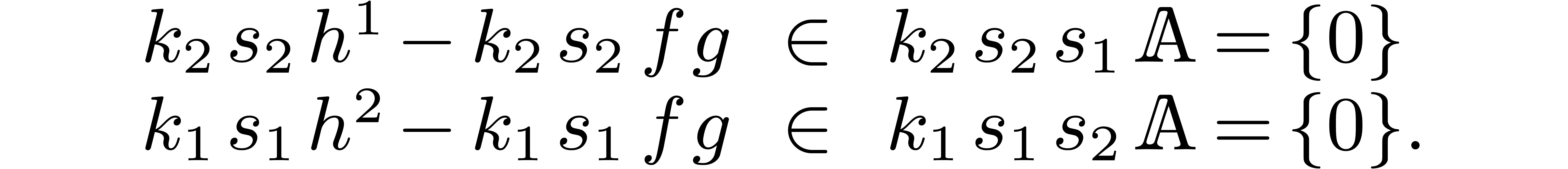
Summing both relations, our claim follows.
Remark 15. A uniform bound
interms of  can be given along similar lines as
in Remark 12. This time, such a bound depends linearly on
the number of prime factors of
can be given along similar lines as
in Remark 12. This time, such a bound depends linearly on
the number of prime factors of  .
.
8Relaxed multiplication of  -adic numbers
-adic numbers
Let  be an integer, not necessarily a prime
number, and denote
be an integer, not necessarily a prime
number, and denote  . We will
regard
. We will
regard  -adic numbers
-adic numbers 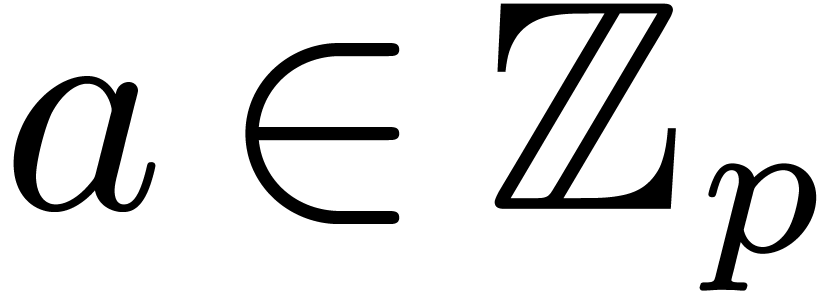 as series
as series  with
with 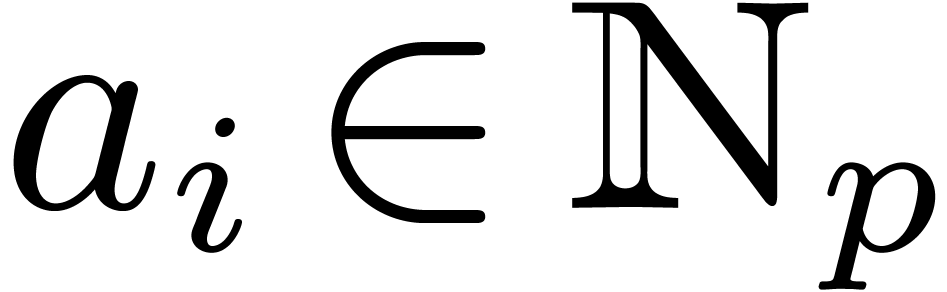 , and such that the basic ring operations
, and such that the basic ring operations  ,
,  and
and  require an additional carry treatment.
require an additional carry treatment.
In order to multiply two relaxed 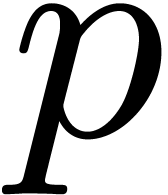 -adic
numbers
-adic
numbers 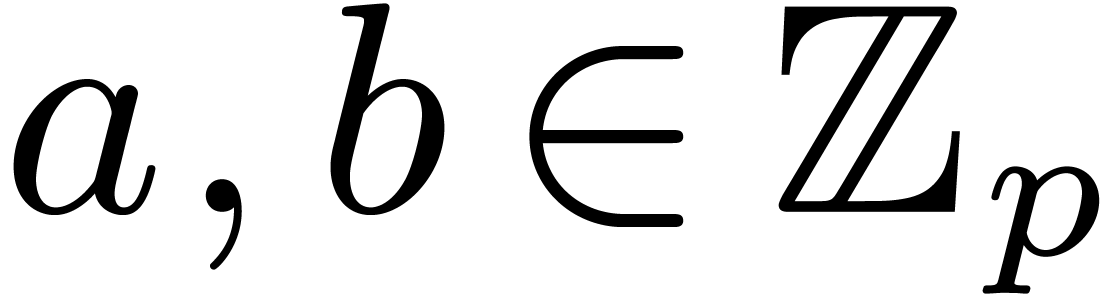 , we may rewrite them
as series
, we may rewrite them
as series 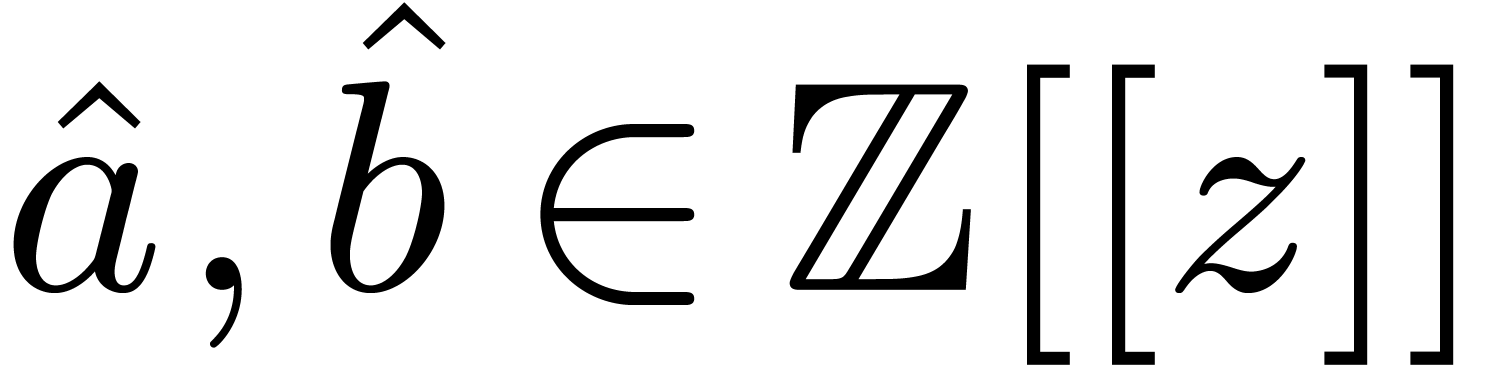 , multiply these
series
, multiply these
series 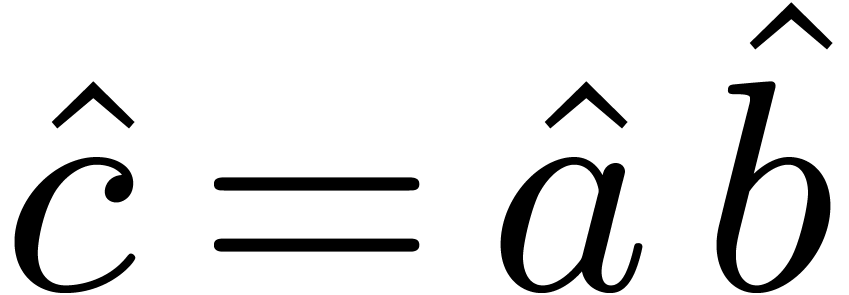 , and recover the
product
, and recover the
product 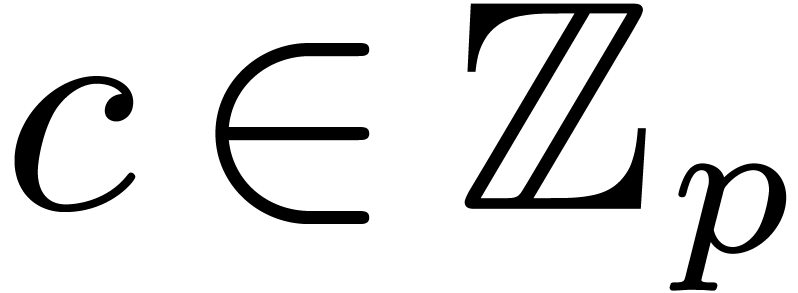 from the result. Of course, the
coefficients of
from the result. Of course, the
coefficients of 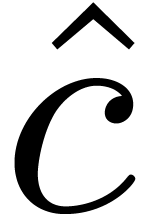 may exceed
may exceed 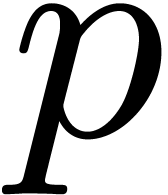 , so some relaxed carry handling is required in
order to recover
, so some relaxed carry handling is required in
order to recover  from
from 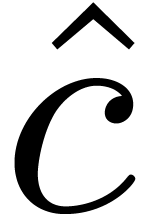 . We refer to [4, Section 2.7] for
details. In particular, we prove there that
. We refer to [4, Section 2.7] for
details. In particular, we prove there that  can
be computed up to order
can
be computed up to order 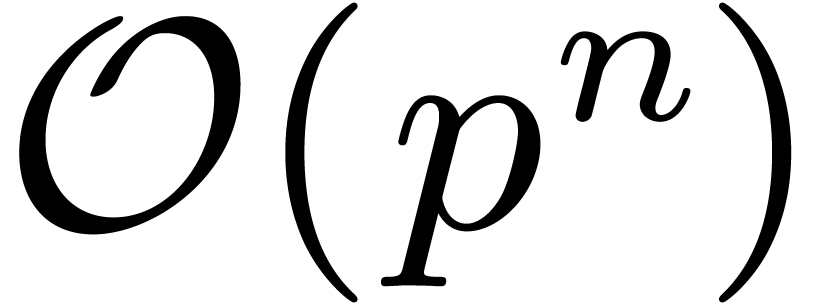 using
using  ring operations in
ring operations in  of bit size
of bit size 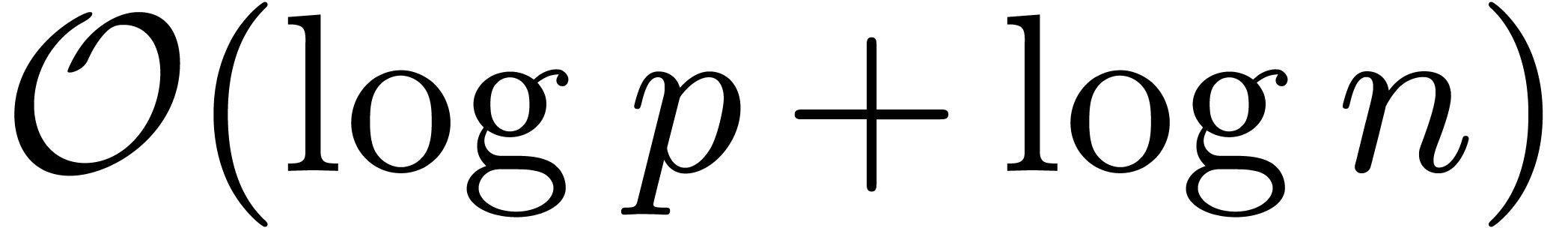 .
.
Given  , let
, let 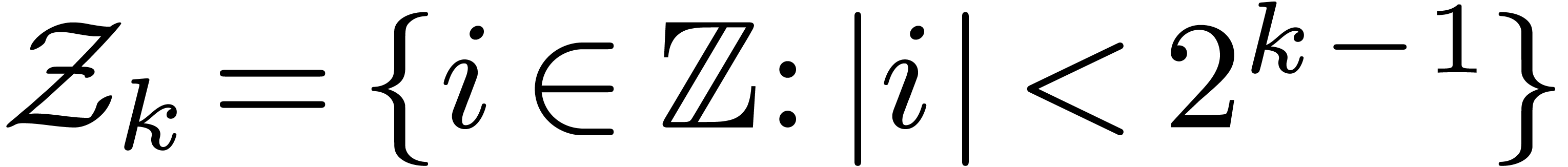 , and consider two power series
, and consider two power series 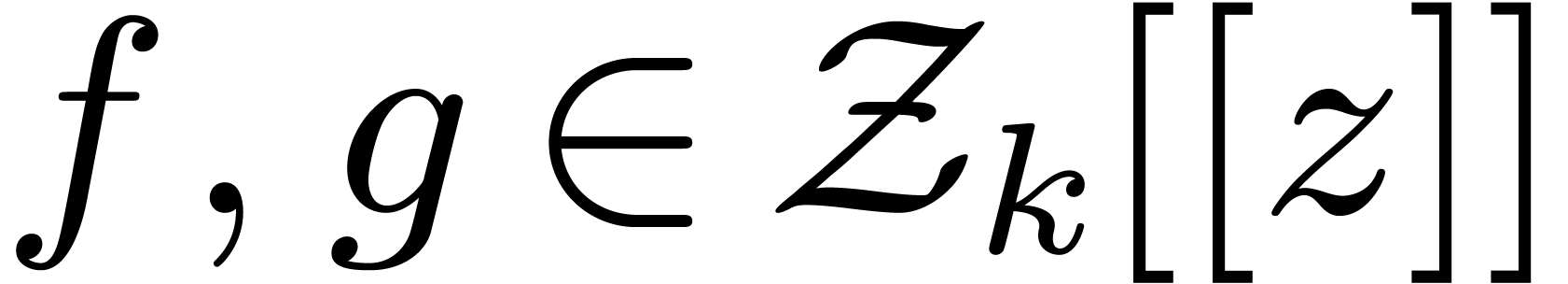 . We will denote by
. We will denote by 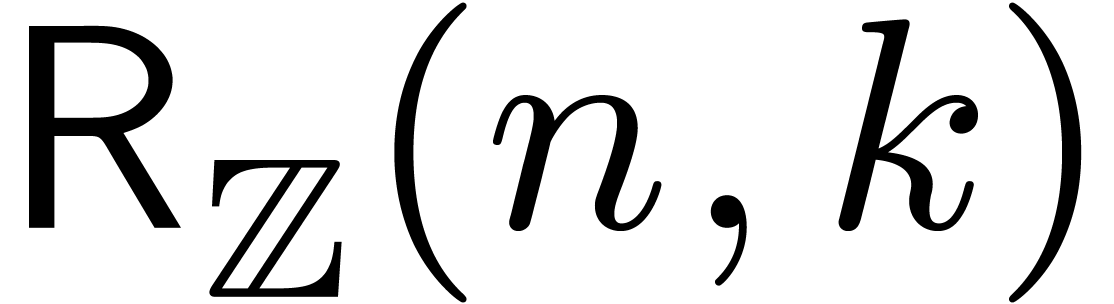 (resp.
(resp. 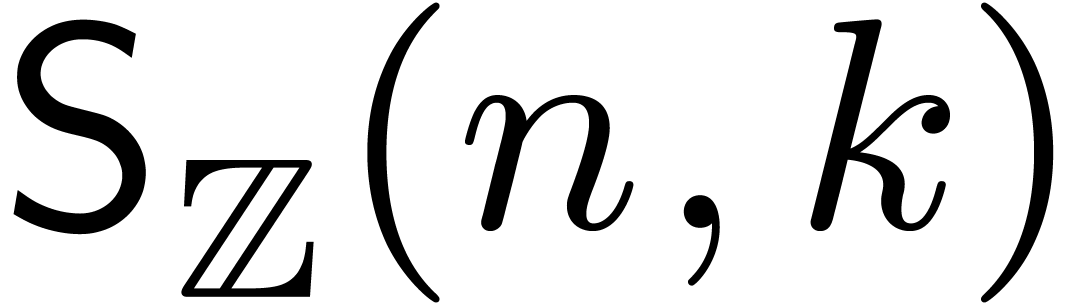 ) the bit
complexity of multiplying
) the bit
complexity of multiplying 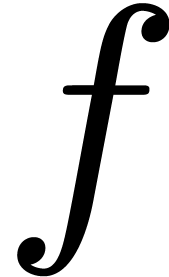 and
and  up to order
up to order 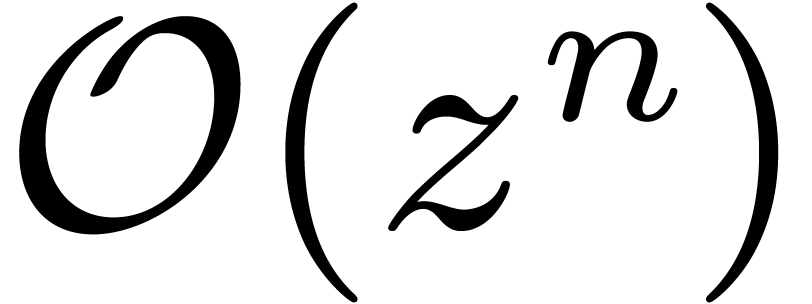 using a relaxed (resp.
semi-relaxed) algorithm.
using a relaxed (resp.
semi-relaxed) algorithm.
Lemma 16. We
have

Proof. Let  be a prime number
with
be a prime number
with  . Such a prime
. Such a prime  can be computed in time
can be computed in time 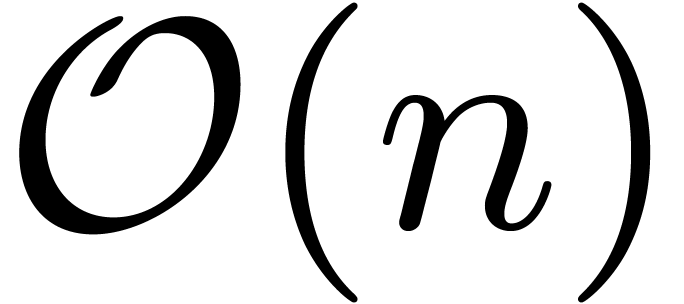 using the
polynomial time polynomial primality test from [1],
together with the Bertrand-Chebychev theorem.
using the
polynomial time polynomial primality test from [1],
together with the Bertrand-Chebychev theorem.
Let 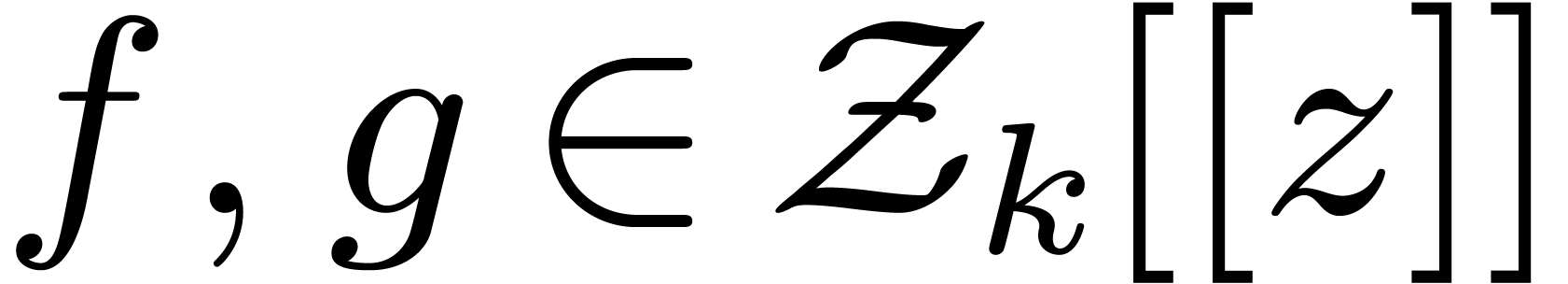 and consider
and consider 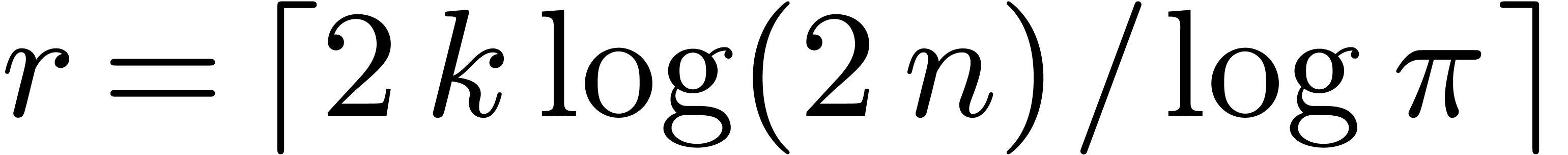 such
that
such
that 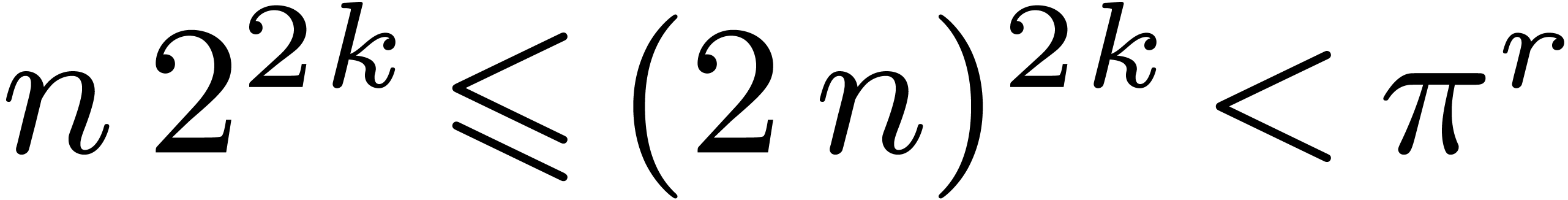 . Let
. Let 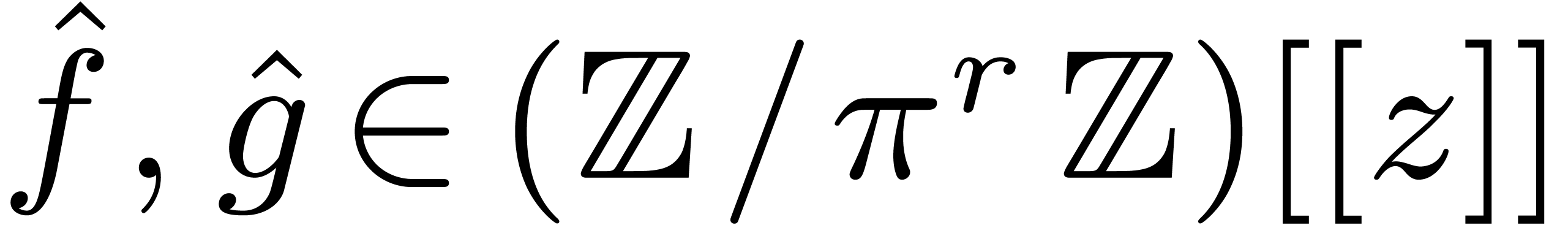 be the reductions of
be the reductions of  modulo
modulo  . Then
. Then  may be
reconstructed up to order
may be
reconstructed up to order  from the product
from the product  . We thus get
. We thus get
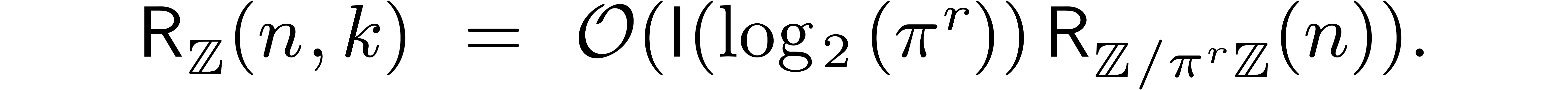
By Theorem 11 and Remarks 12 and 13,
while using the fact that 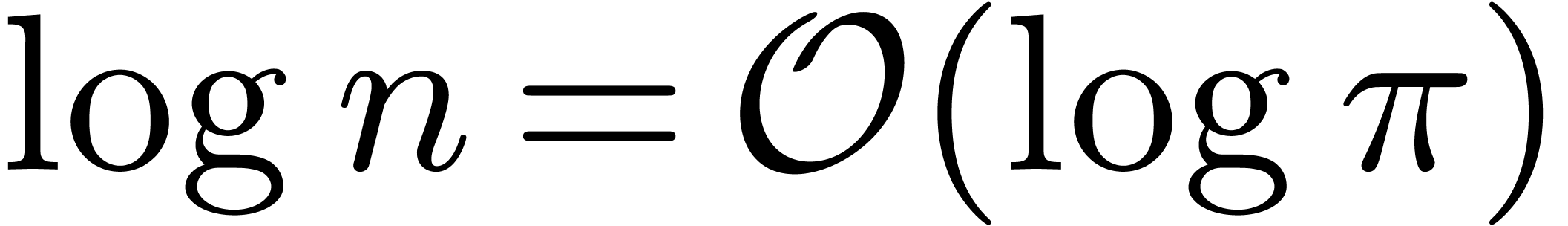 ,
we have
,
we have
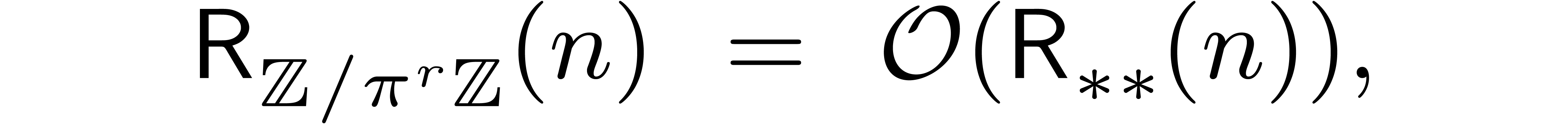
and this bound is uniform in  .
Since
.
Since 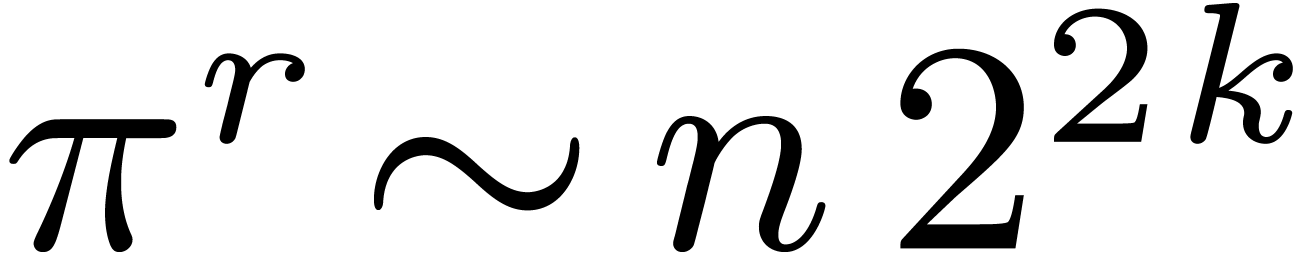 , the result
follows.
, the result
follows.
For the above strategy to be efficient, it is important that 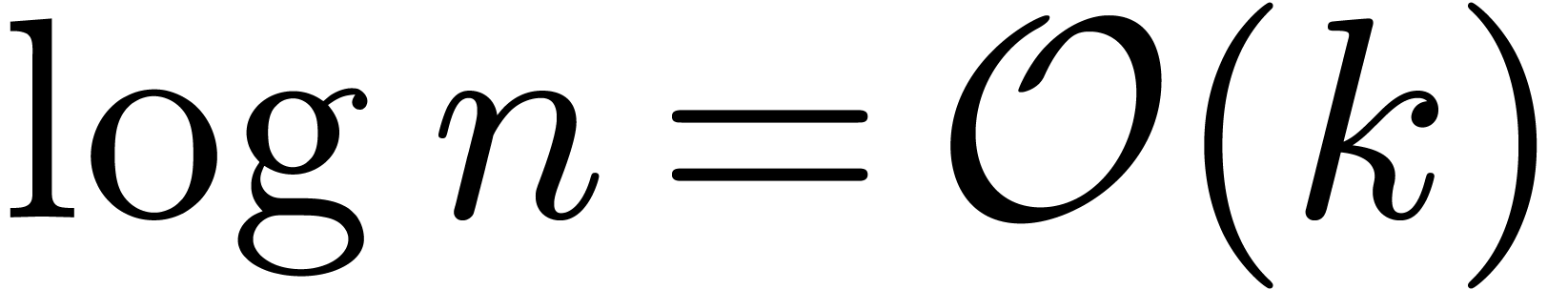 . This can be achieved by combining
it with the technique of
. This can be achieved by combining
it with the technique of 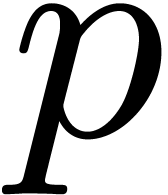 -adic
blocking. More precisely, given a
-adic
blocking. More precisely, given a 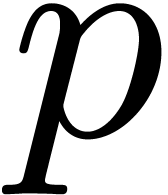 -adic
block size
-adic
block size  , then any
, then any 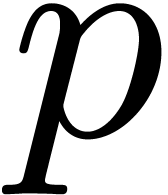 -adic number in
-adic number in 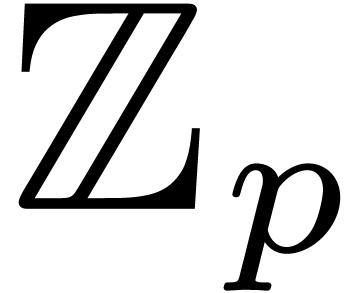 can naturally be considered as a
can naturally be considered as a 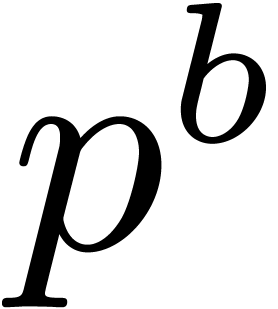 -adic
number in
-adic
number in 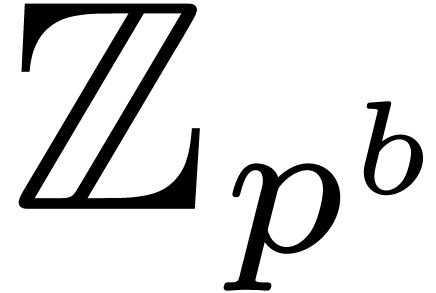 , and vice
versa. Assuming that numbers in
, and vice
versa. Assuming that numbers in 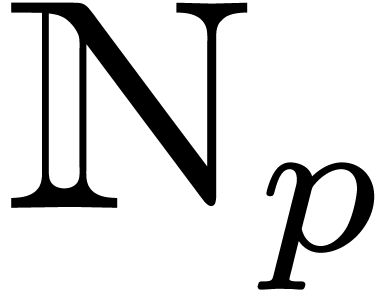 are written
in base
are written
in base  , the conversion is
trivial if
, the conversion is
trivial if 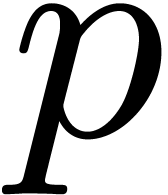 is a power of two. Otherwise, the
conversion involves base conversions and we refer to [4,
Section 4] for more details. In particular, the conversions in both
directions up to order
is a power of two. Otherwise, the
conversion involves base conversions and we refer to [4,
Section 4] for more details. In particular, the conversions in both
directions up to order 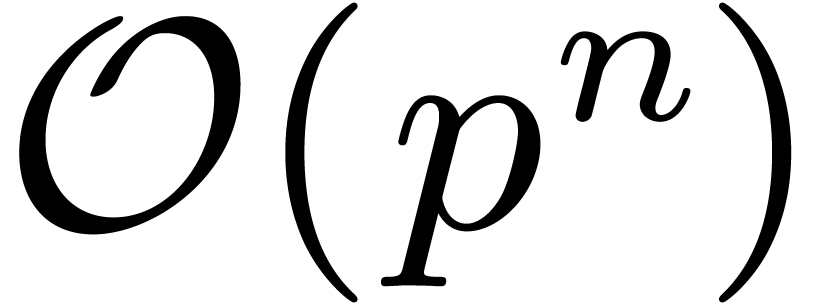 can be done in time
can be done in time 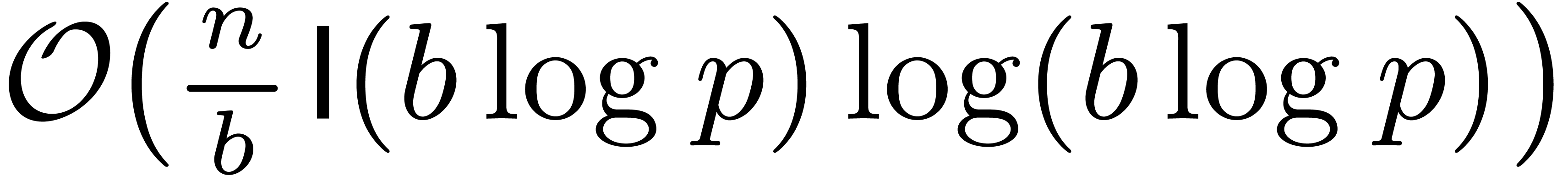 .
.
Let 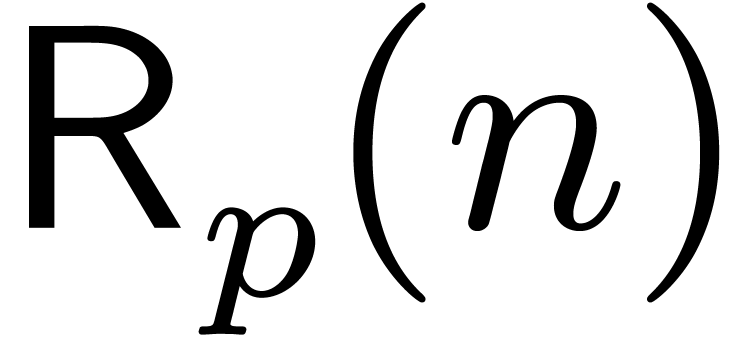 (resp.
(resp. 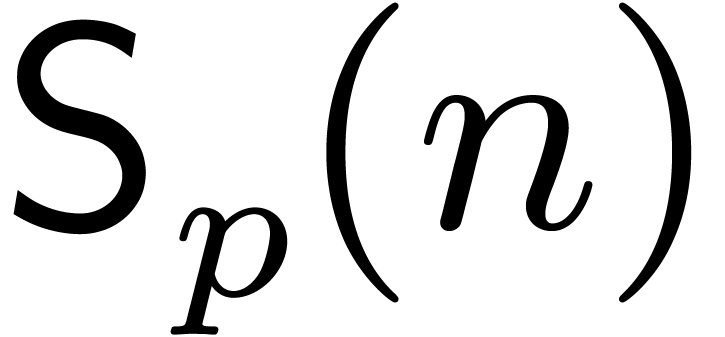 ) the complexity of relaxed (resp.
semi-relaxed) multiplication in
) the complexity of relaxed (resp.
semi-relaxed) multiplication in 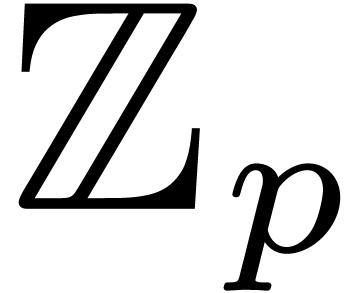 up to order
up to order
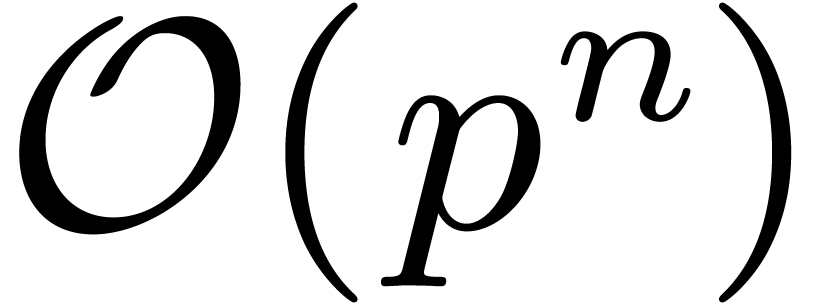 .
.
Theorem 17. Setting 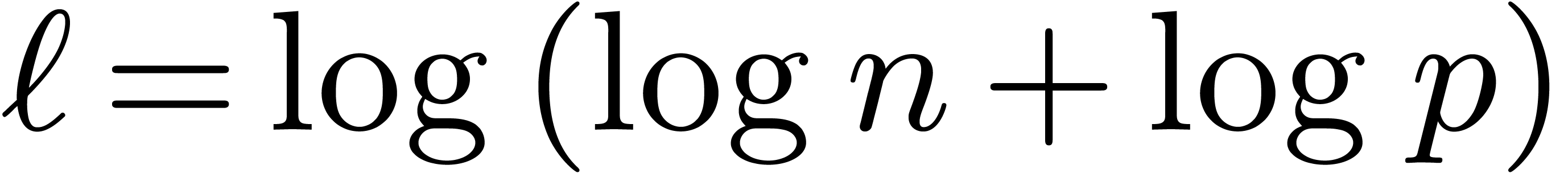 , we have
, we have
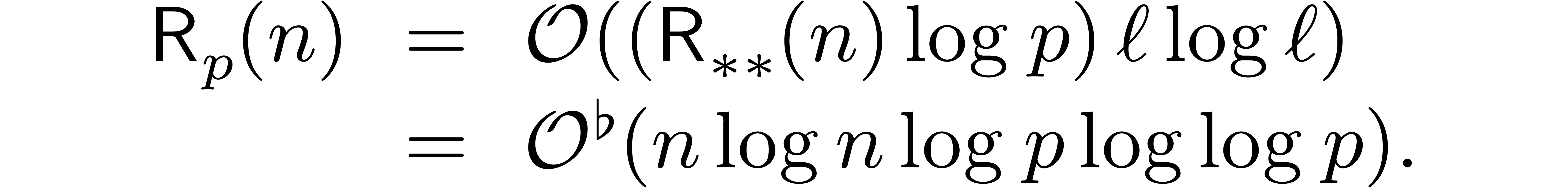
Proof. Let 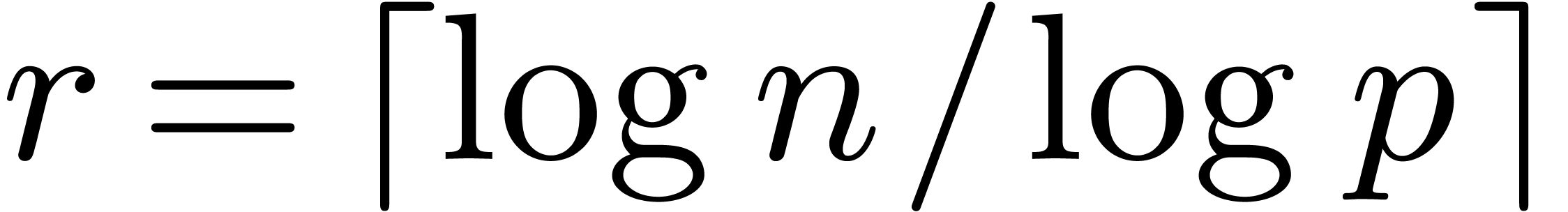 ,
so that
,
so that
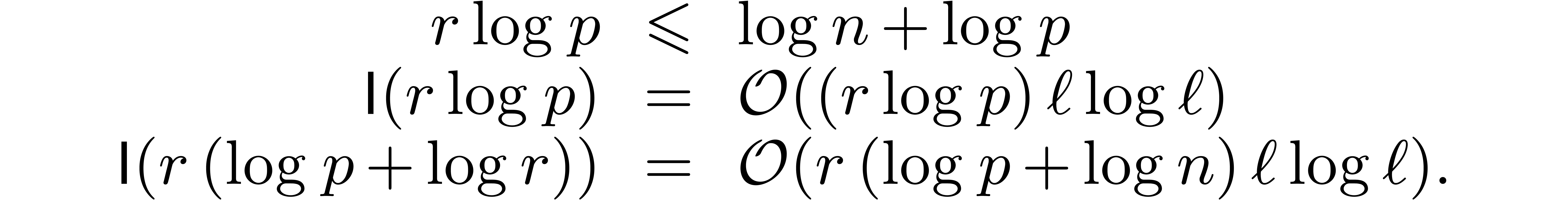
Using the strategy of 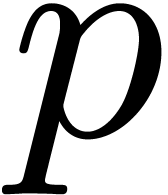 -adic
blocking, a semi-relaxed product in
-adic
blocking, a semi-relaxed product in 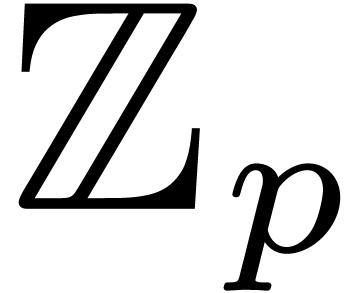 may then be
reduced to one semi-relaxed product in
may then be
reduced to one semi-relaxed product in 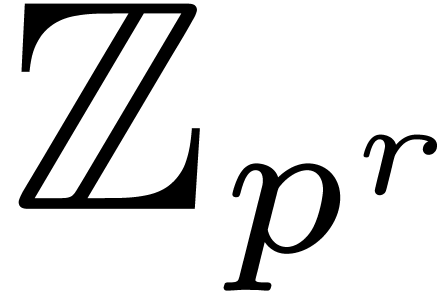 and one
relaxed multiplication with an integer in
and one
relaxed multiplication with an integer in 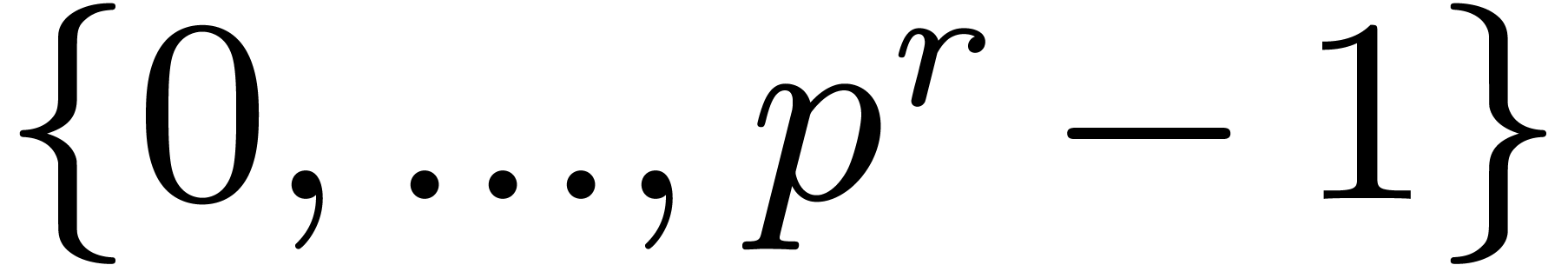 .
In other words,
.
In other words,
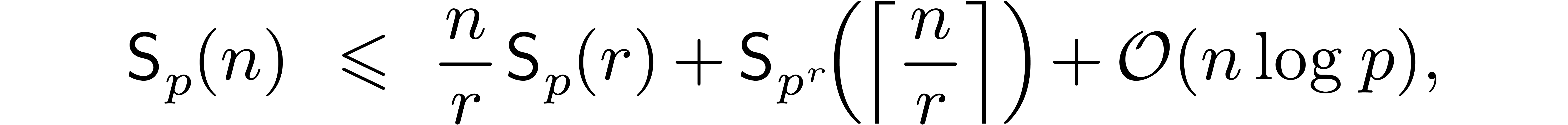
where 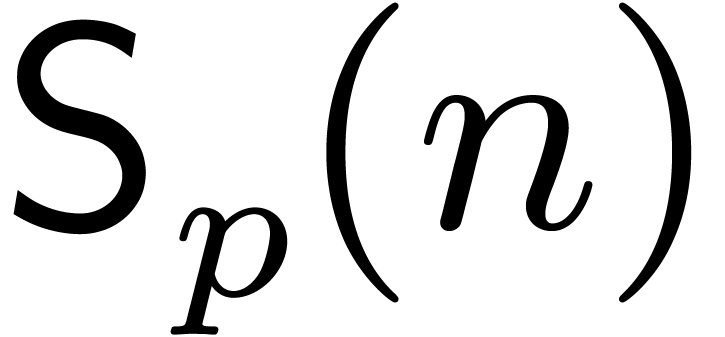 stands for the cost of semi-relaxed
multiplication of two
stands for the cost of semi-relaxed
multiplication of two 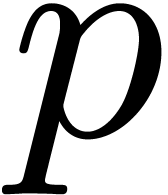 -adic
numbers in
-adic
numbers in  up to order
up to order  . By [4, Proposition 4], we have
. By [4, Proposition 4], we have
By Lemma 16, we also have
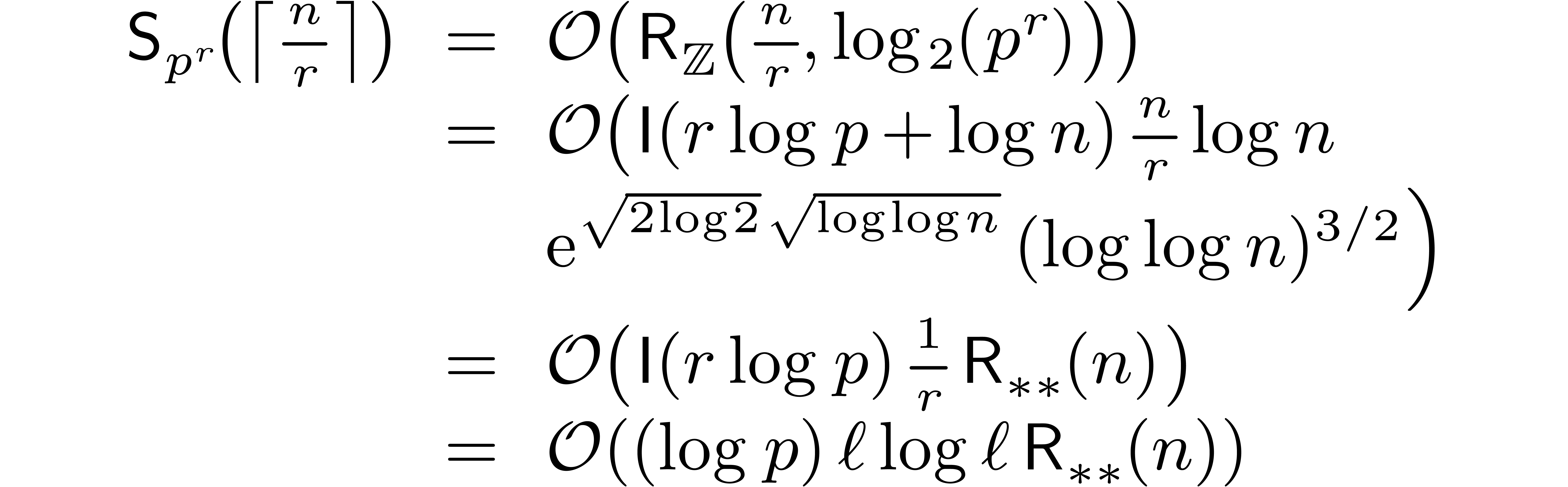
Notice that
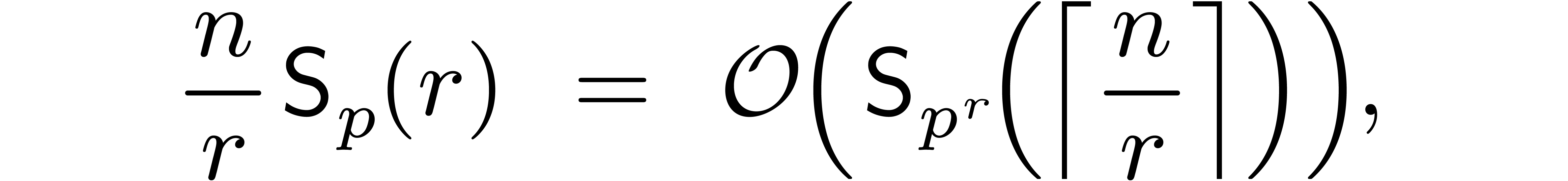
which completes the proof of the theorem.
9Final remarks
For the moment, we have not implemented any of the new algorithms in
practice. Nevertheless, our old implementation of the algorithm from [21] allowed us to gain some insight on the practical
usefulness of blockwise relaxed multiplication. Let us briefly discuss
the potential impact of the new results for practical purposes.
Characteristic zero.
In characteristic zero, our focus on algebraic complexity makes the
complexity bounds more or less irrelevant from a practical point of
view. In practice, two cases are of particular interest: floating
point coefficients (which were already considered in [
21])
and integer coefficients (rational coefficients can be dealt with
similarly after multiplying by the common denominator).
In the case of integer coefficients, it is best to re-encode the
integers as polynomials in 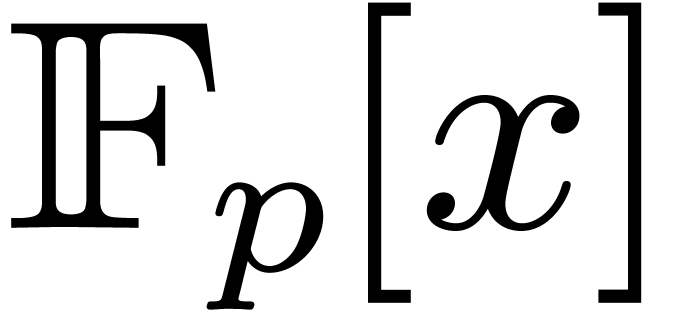 for a prime number
which fits into a machine word and such that
for a prime number
which fits into a machine word and such that 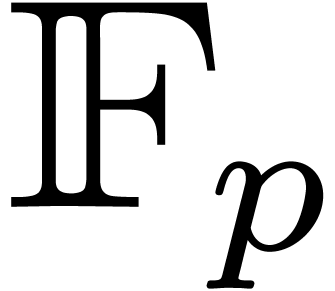 admits many
admits many 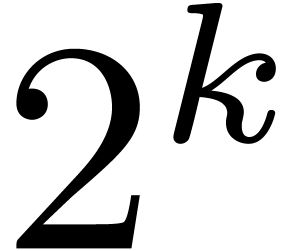 -th roots of
unity (it is also possible to take several primes
-th roots of
unity (it is also possible to take several primes 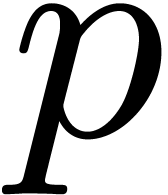 and use Chinese remaindering). After that, one may again use the old
algorithm from [21]. Also, integer coefficients usually
grow in size with
and use Chinese remaindering). After that, one may again use the old
algorithm from [21]. Also, integer coefficients usually
grow in size with 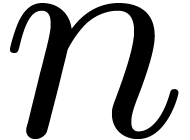 , so one
really should see the power series as a bivariate power series in
, so one
really should see the power series as a bivariate power series in 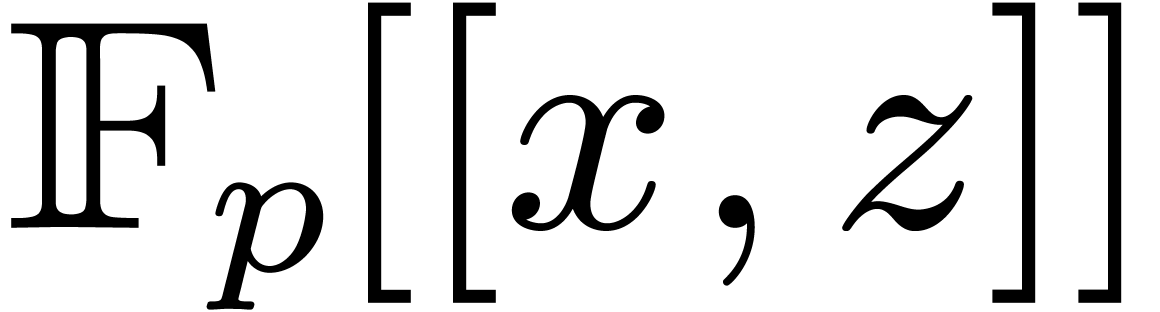 with a triangular support. One may then want to use
TFT-style multiplication [19, 20] in order to
gain another constant factor.
with a triangular support. One may then want to use
TFT-style multiplication [19, 20] in order to
gain another constant factor.
Finite fields.
For large finite fields, it is easy to find large geometric
progressions, so the algorithms of this paper can be applied without
the need to consider field extensions. Moreover, for finite fields of
the form
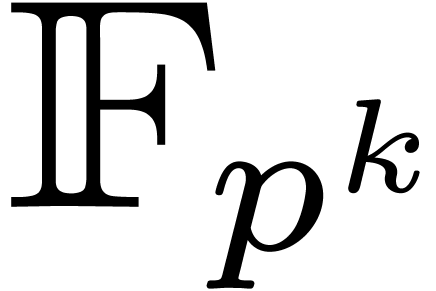
with
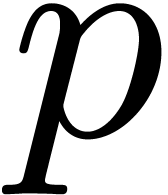
sufficiently large and
 ,
, it
is possible to choose
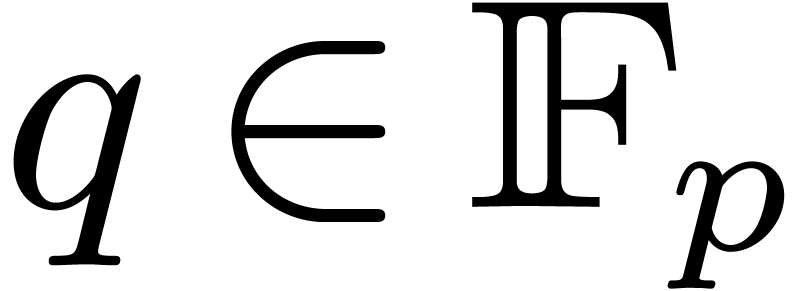 ,
,
thereby speeding up evaluation and interpolation. For small finite
fields of the form
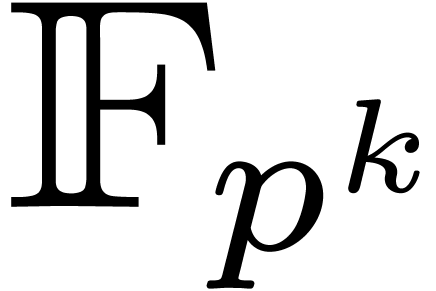 ,
, it is
generally necessary to make the
initial investment of working
in a larger ring with sufficiently large geometric progressions. Of
course, instead of the ring extensions considered in Section
6,
we may directly use field extensions of the form
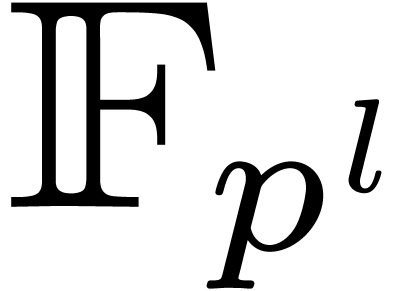
with
 .
.
Semi-relaxed multiplication.
In principle, a factor 2 can be gained in the semi-relaxed
(
resp. general) case using the technique from [
18]
(
resp. [
26]). Unfortunately, the middle
product (
resp. the FFT-trick used in [
26])
is not always easy to implement. For instance, if we rely on Kronecker
substitution for multiplications in
 ,
,
then we will need to implement an
ad hoc analogue for the
middle product. Since we did not use a fast algorithm for middle
products for our benchmarks in [
21, Section 5], the
timings for the semi-relaxed product in were only about
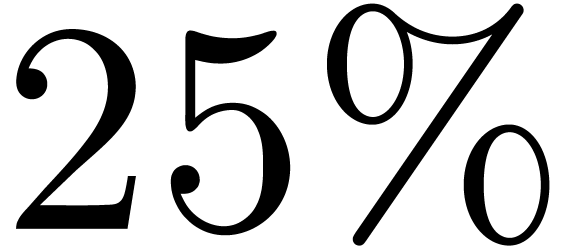
instead of
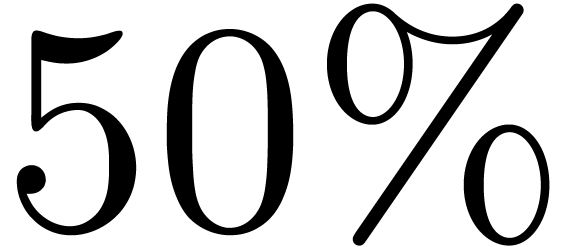
better than the
timings for the fully relaxed product. Nevertheless, modulo increased
implementation efforts, we stress that a
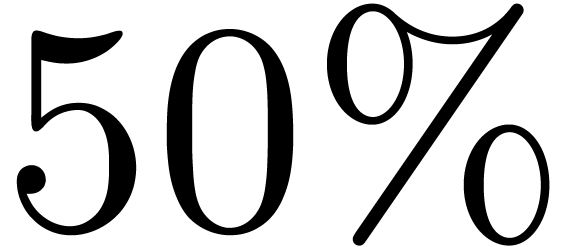
gain
should be achievable.
Cache friendliness.
So far, we have not investigated the cache friendliness of blockwise
relaxed multiplication, and it can be feared that a lot of additional
work is required in order to make our algorithms really efficient from
this point of view.
Bilinear maps.
In order to keep the presentation reasonably simple, we have focussed
on the case when

is an effective ring. In
fact, a more general setting for relaxed multiplication is to consider
a bilinear mapping
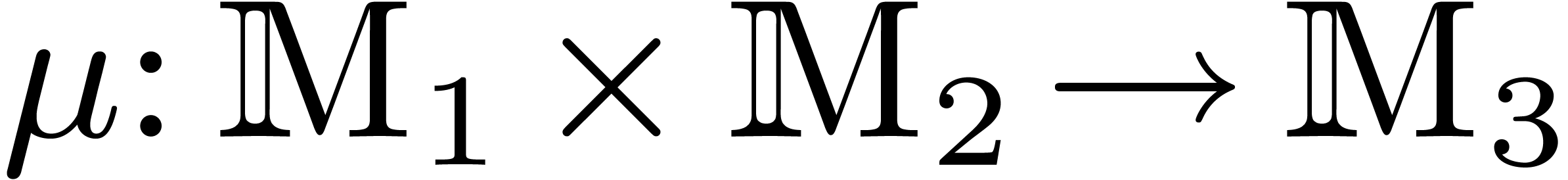 ,
, where
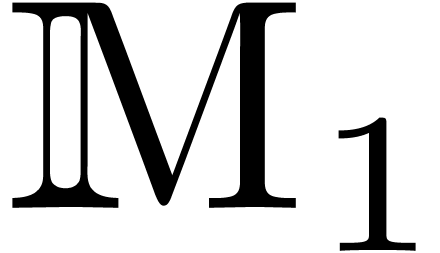 ,
, 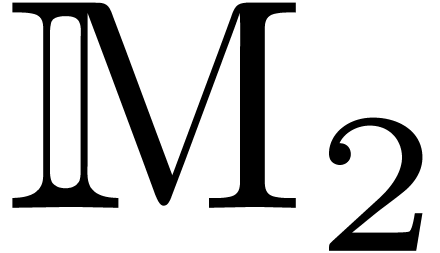
and
are effective
 -modules,
-modules, and extend it into a mapping
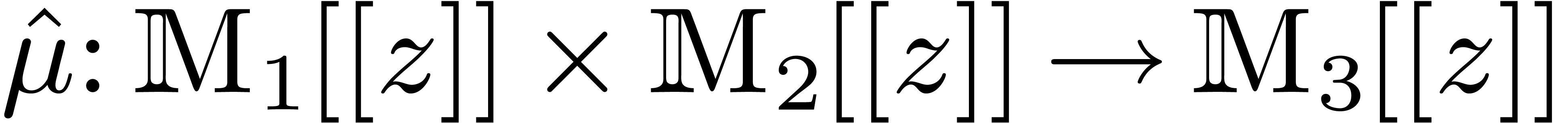
by
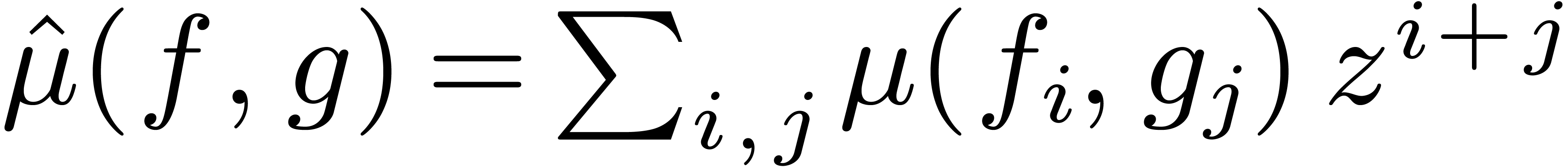 .
. Under
suitable hypothesis, the algorithms in this paper generalize to this
setting.
Skew series.
The relaxed approach can also be generalized to the case when the
coefficients of the power series are operators which commute with
monomials
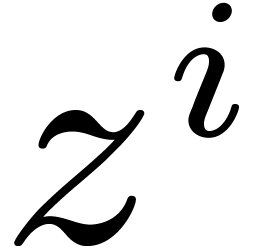
in a non-trivial way. More
precisely, assume that we have an effective ring homomorphism
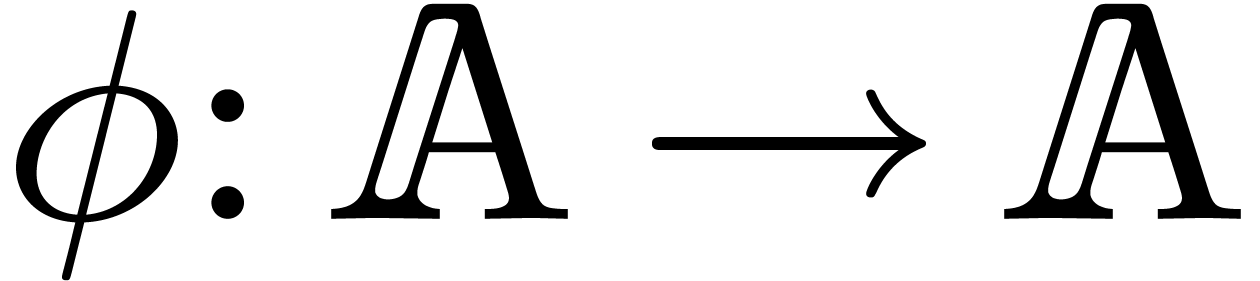
such that
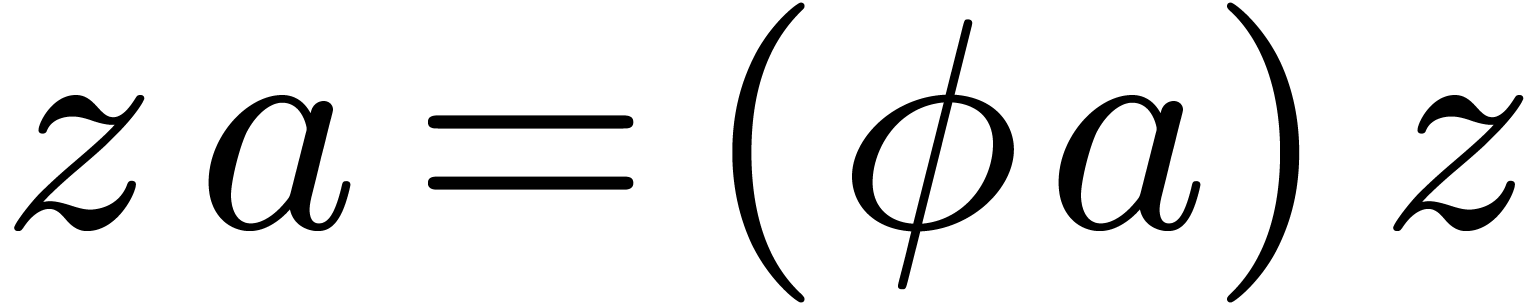
for all
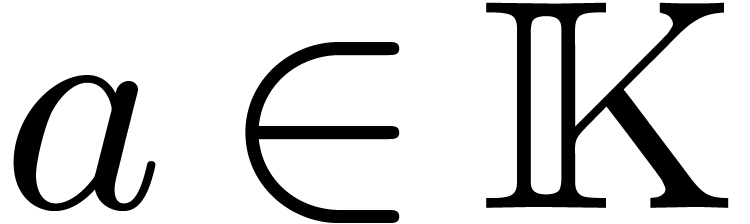 .
. For instance, one may take
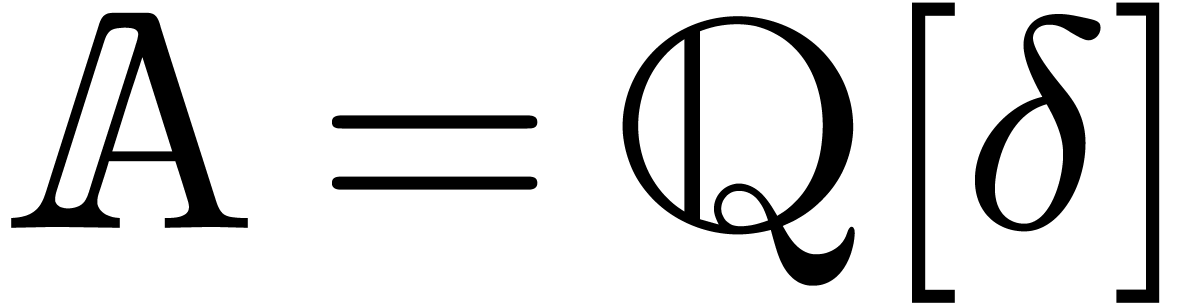
with
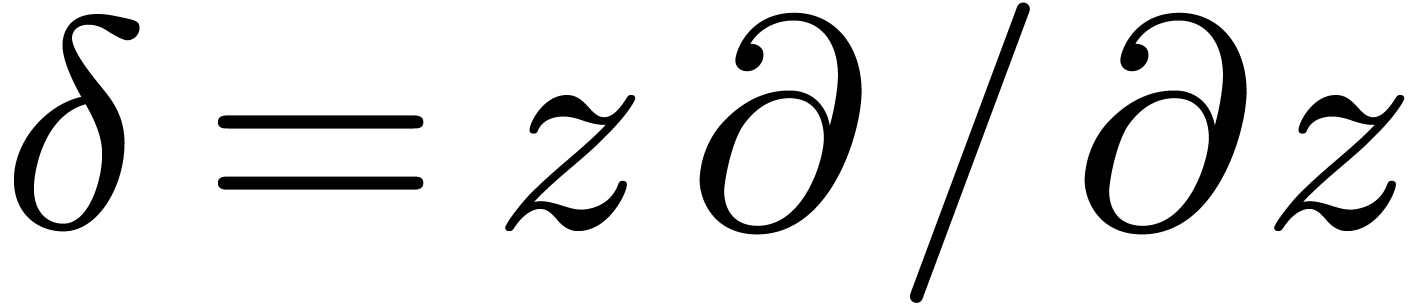 ,
,
so that
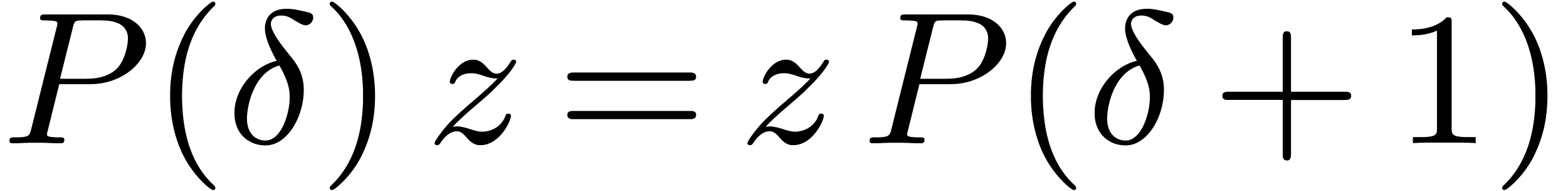 .
. Given a
commutation rule of this kind, we define a skew multiplication on
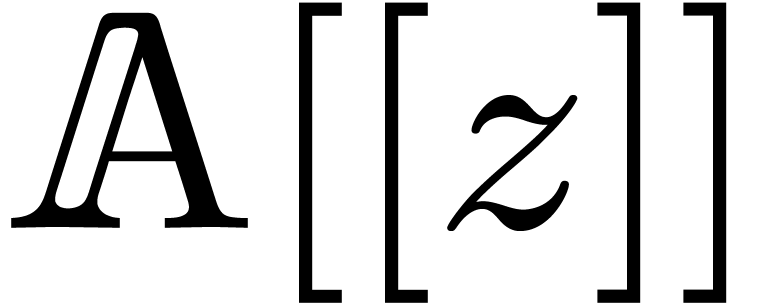
by
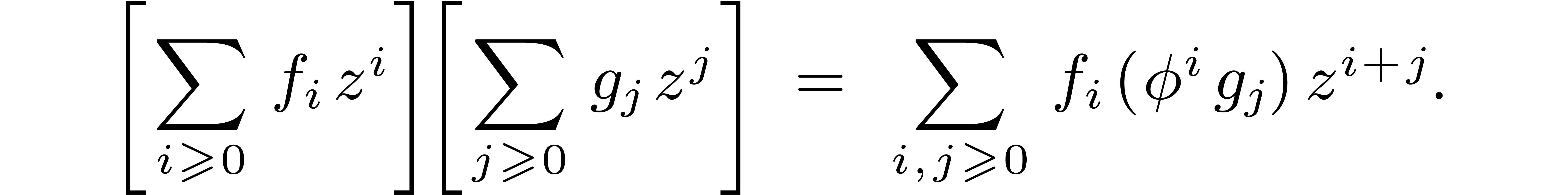
If 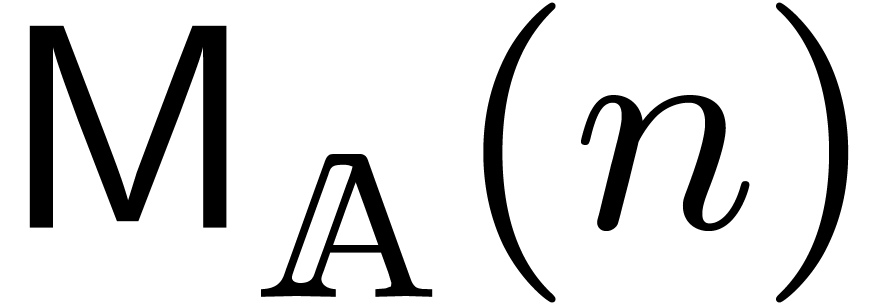 denotes the cost of multiplying two
polynomials
denotes the cost of multiplying two
polynomials 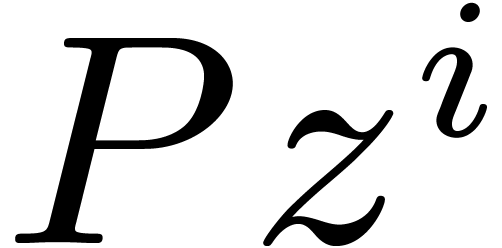 and
and 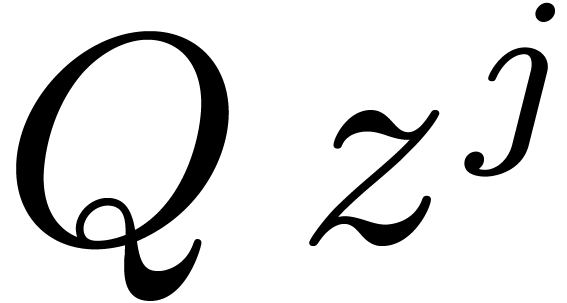 in
in 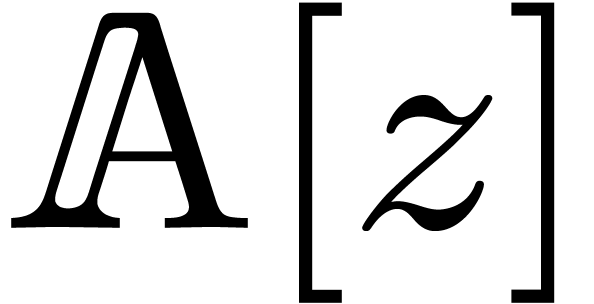 with
with 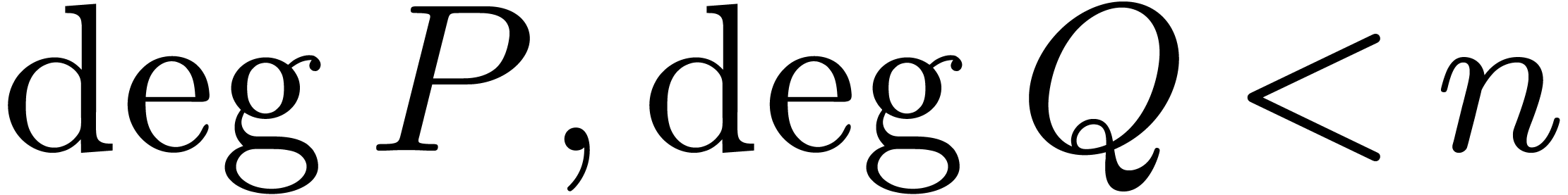 ,
then the classical fast relaxed multiplication algorithm from [17,
13] generalizes and still admits the time complexity
,
then the classical fast relaxed multiplication algorithm from [17,
13] generalizes and still admits the time complexity 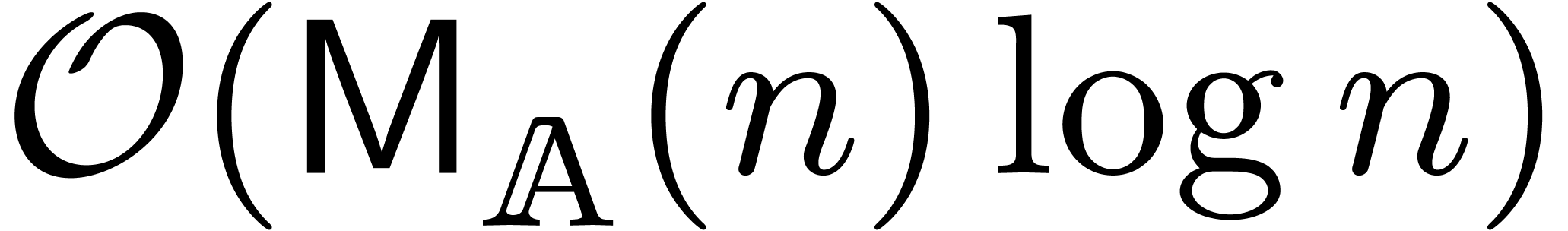 . However, the blockwise algorithm
from this paper does not generalize to this setting, at least not in a
straightforward way.
. However, the blockwise algorithm
from this paper does not generalize to this setting, at least not in a
straightforward way.
Bibliography
-
[1]
-
M. Agrawal, N. Kayal, and N. Saxena. PRIMES is in P.
Annals of Mathematics, 160(2):781–793, 2004.
-
[2]
-
A. Aho, J. Hopcroft, and J. Ullman. The Design and
Analysis of Computer Algorithms. Addison-Wesley, Reading,
Massachusetts, 1974.
-
[3]
-
D. Bernstein. Removing redundancy in high precision
Newton iteration. Available from http://cr.yp.to/fastnewton.html,
2000.
-
[4]
-
J. Berthomieu, J. van der Hoeven, and G. Lecerf.
Relaxed algorithms for 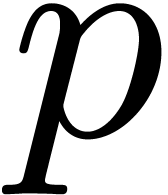 -adic
numbers. Journal de Théorie des Nombres de
Bordeaux, 23(3):541–577, 2011.
-adic
numbers. Journal de Théorie des Nombres de
Bordeaux, 23(3):541–577, 2011.
-
[5]
-
J. Berthomieu and R. Lebreton. Relaxed 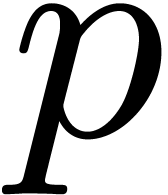 -adic hensel lifting for algebraic
systems. In J. van der Hoeven and M. van Hoeij, editors,
Proc. ISSAC '12, pages 59–66, Grenoble, France,
July 2012.
-adic hensel lifting for algebraic
systems. In J. van der Hoeven and M. van Hoeij, editors,
Proc. ISSAC '12, pages 59–66, Grenoble, France,
July 2012.
-
[6]
-
D. Bini and V.Y. Pan. Polynomial and matrix
computations. Vol. 1. Birkhäuser Boston Inc., Boston,
MA, 1994. Fundamental algorithms.
-
[7]
-
Leo I. Bluestein. A linear filtering approach to the
computation of discrete Fourier transform. IEEE Transactions
on Audio and Electroacoustics, 18(4):451–455, 1970.
-
[8]
-
A. Bostan and É. Schost. Polynomial evaluation
and interpolation on special sets of points. Journal of
Complexity, 21(4):420–446, August 2005. Festschrift
for the 70th Birthday of Arnold Schönhage.
-
[9]
-
R.P. Brent and H.T. Kung. Fast algorithms for
manipulating formal power series. Journal of the ACM,
25:581–595, 1978.
-
[10]
-
D.G. Cantor and E. Kaltofen. On fast multiplication
of polynomials over arbitrary algebras. Acta Informatica,
28:693–701, 1991.
-
[11]
-
S. A. Cook. On the minimum computation time of
functions. PhD thesis, Harvard University, 1966.
-
[12]
-
J.W. Cooley and J.W. Tukey. An algorithm for the
machine calculation of complex Fourier series. Math.
Computat., 19:297–301, 1965.
-
[13]
-
M. J. Fischer and L. J. Stockmeyer. Fast on-line
integer multiplication. Proc. 5th ACM Symposium on Theory of
Computing, 9:67–72, 1974.
-
[14]
-
M. Fürer. Faster integer multiplication. In
Proceedings of the Thirty-Ninth ACM Symposium on Theory of
Computing (STOC 2007), pages 57–66, San Diego,
California, 2007.
-
[15]
-
J. von zur Gathen and J. Gerhard. Modern Computer
Algebra. Cambridge University Press, first edition, 1999.
-
[16]
-
J. van der Hoeven. Lazy multiplication of formal
power series. In W. W. Küchlin, editor, Proc. ISSAC
'97, pages 17–20, Maui, Hawaii, July 1997.
-
[17]
-
J. van der Hoeven. Relax, but don't be too lazy.
JSC, 34:479–542, 2002.
-
[18]
-
J. van der Hoeven. Relaxed multiplication using the
middle product. In Manuel Bronstein, editor, Proc. ISSAC
'03, pages 143–147, Philadelphia, USA, August 2003.
-
[19]
-
J. van der Hoeven. The truncated Fourier transform
and applications. In J. Gutierrez, editor, Proc. ISSAC
2004, pages 290–296, Univ. of Cantabria, Santander,
Spain, July 4–7 2004.
-
[20]
-
J. van der Hoeven. Notes on the Truncated Fourier
Transform. Technical Report 2005-5, Université Paris-Sud,
Orsay, France, 2005.
-
[21]
-
J. van der Hoeven. New algorithms for relaxed
multiplication. JSC, 42(8):792–802, 2007.
-
[22]
-
J. van der Hoeven. Relaxed resolution of implicit
equations. Technical report, HAL, 2009. http://hal.archives-ouvertes.fr/hal-00441977.
-
[23]
-
J. van der Hoeven. Newton's method and FFT trading.
JSC, 45(8):857–878, 2010.
-
[24]
-
J. van der Hoeven. From implicit to recursive
equations. Technical report, HAL, 2011. http://hal.archives-ouvertes.fr/hal-00583125.
-
[25]
-
A. Karatsuba and J. Ofman. Multiplication of
multidigit numbers on automata. Soviet Physics Doklady,
7:595–596, 1963.
-
[26]
-
R. Lebreton and É. Schost. A simple and fast
online power series multiplication and its analysis. Technical
report, LIRMM, 2013. http://hal-lirmm.ccsd.cnrs.fr/lirmm-00867279.
-
[27]
-
L.R. Rabiner, R.W. Schafer, and C.M. Rader. The chirp
z-transform algorithm and its application. Bell System Tech.
J., 48:1249–1292, 1969.
-
[28]
-
A. Schönhage and V. Strassen. Schnelle
Multiplikation großer Zahlen. Computing,
7:281–292, 1971.
-
[29]
-
Alexandre Sedoglavic. Méthodes
seminumériques en algèbre différentielle ;
applications à l'étude des
propriétés structurelles de systèmes
différentiels algébriques en automatique. PhD
thesis, École polytechnique, 2001.
-
[30]
-
V. Shoup. New algorithms for finding irreducible
polynomials over finite fields. Math. Comp.,
54:535–447, 1990.
-
[31]
-
V. Shoup. Searching for primitive roots in finite
fields. Math. Comp., 58:369–380, 1992.
-
[32]
-
I. Shparlinski. On primitive elements in finite
fields and on elliptic curves. Mat. Sbornik,
181(9):1196–1206, 1990.
-
[33]
-
A.L. Toom. The complexity of a scheme of functional
elements realizing the multiplication of integers. Soviet
Mathematics, 4(2):714–716, 1963.

 . This work has been partly supported
by the French ANR-09-JCJC-0098-01
. This work has been partly supported
by the French ANR-09-JCJC-0098-01 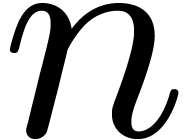 .
. with sufficiently many
with sufficiently many 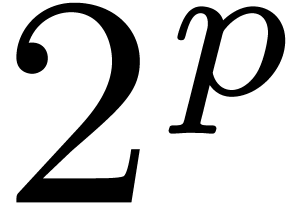 -th
-th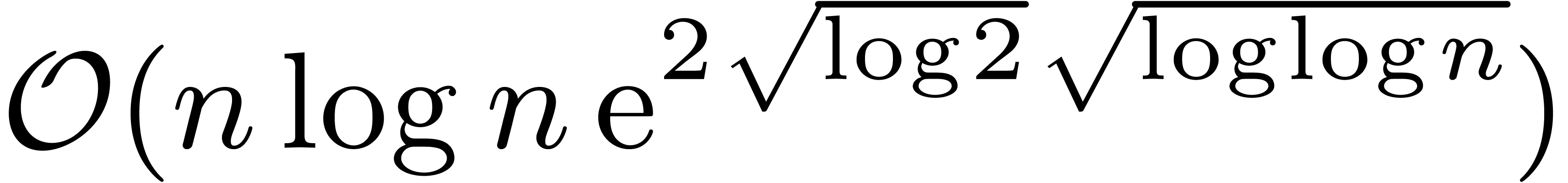 .
. -module
-module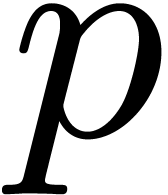 -adic
-adic be an effective (possibly non-commutative)
ring; i.e., we assume data structures for representing the
elements of
be an effective (possibly non-commutative)
ring; i.e., we assume data structures for representing the
elements of  ,
, and
and  .
.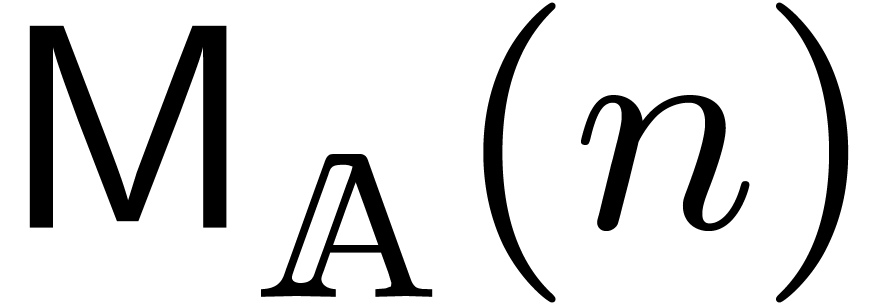 the number of operations required to
multiply two polynomials of degrees
the number of operations required to
multiply two polynomials of degrees 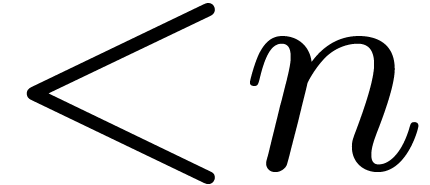 in
in 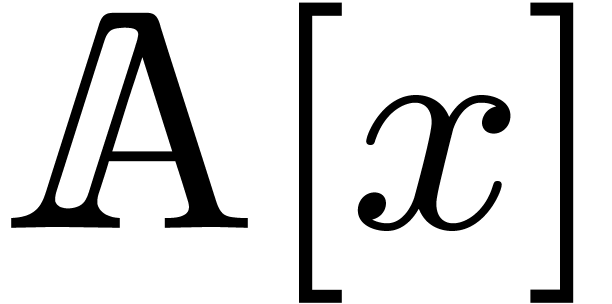 .
. ,
,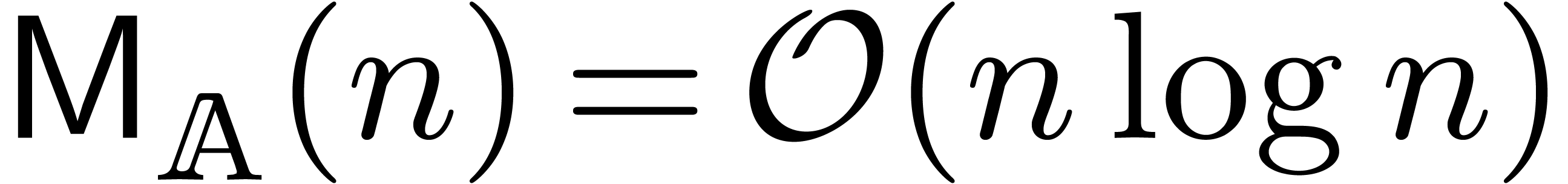 using FFT multiplication, which is based on the fast
Fourier transform [
using FFT multiplication, which is based on the fast
Fourier transform [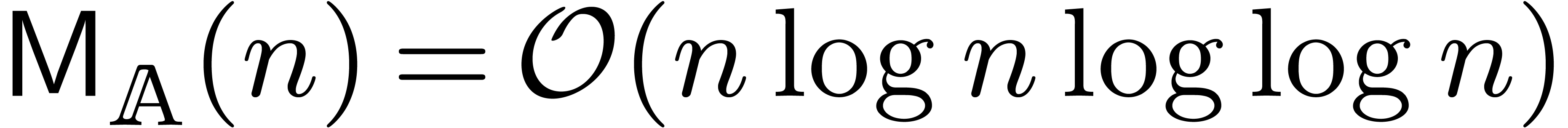 .
. ,
,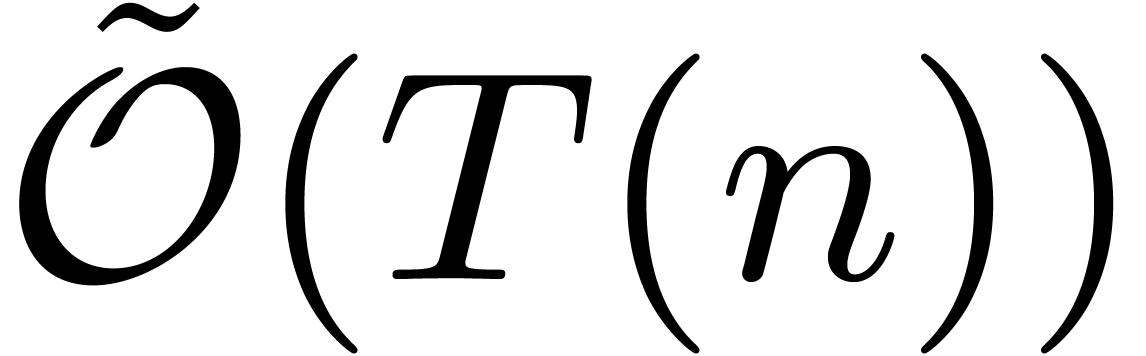 stands for
stands for 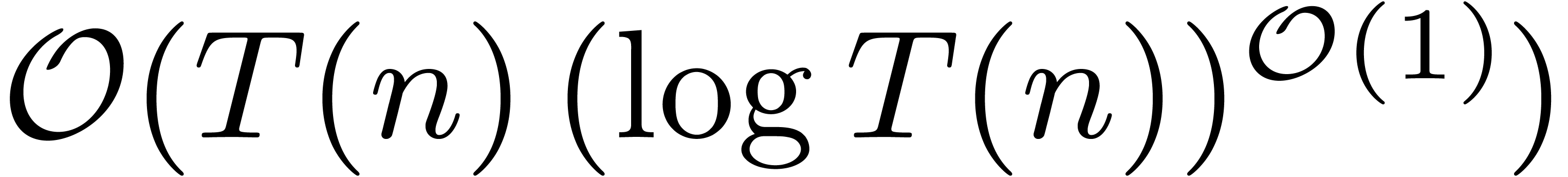 ;
;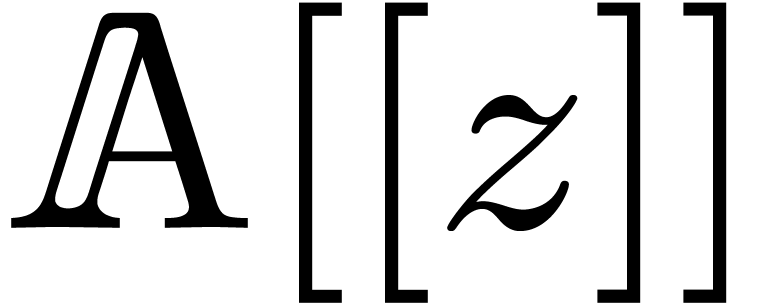 up to a given truncation order
up to a given truncation order  .
. :
: ,
,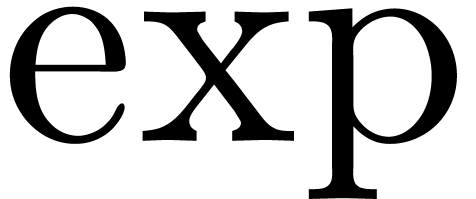 ,
, ,
, ”
” as streams of coefficients
as streams of coefficients 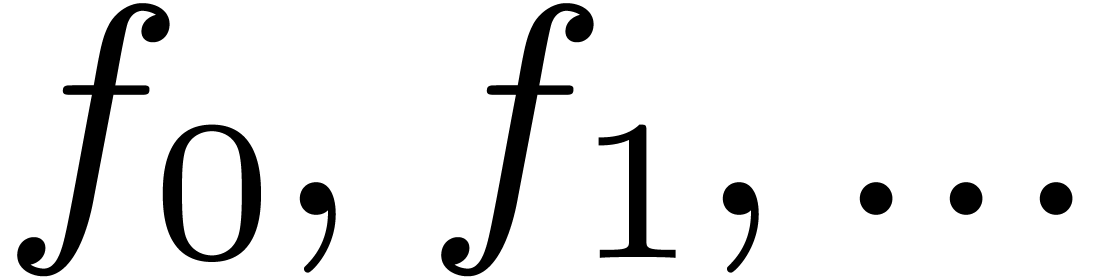 and to require that all operations are performed
“without delay” on these streams. For instance, for a
multiplication
and to require that all operations are performed
“without delay” on these streams. For instance, for a
multiplication  of two power series
of two power series 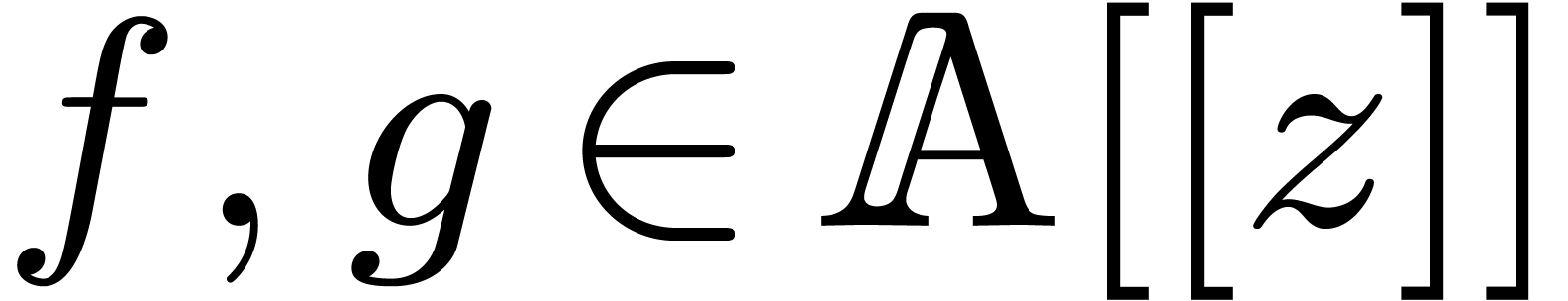 ,
,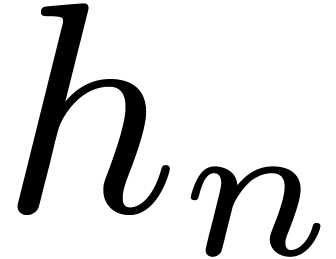 is
computed as soon as
is
computed as soon as  are known. Any
algorithm which has this property will be called a relaxed or
on-line algorithm for multiplication.
are known. Any
algorithm which has this property will be called a relaxed or
on-line algorithm for multiplication.
 of the input depend
on the known coefficients
of the input depend
on the known coefficients  of the output. For
instance, given a power series
of the output. For
instance, given a power series  with
with  ,
,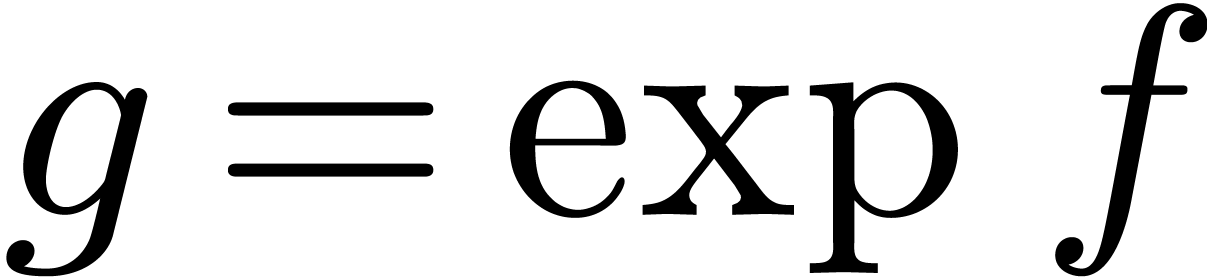 using
the formula
using
the formula
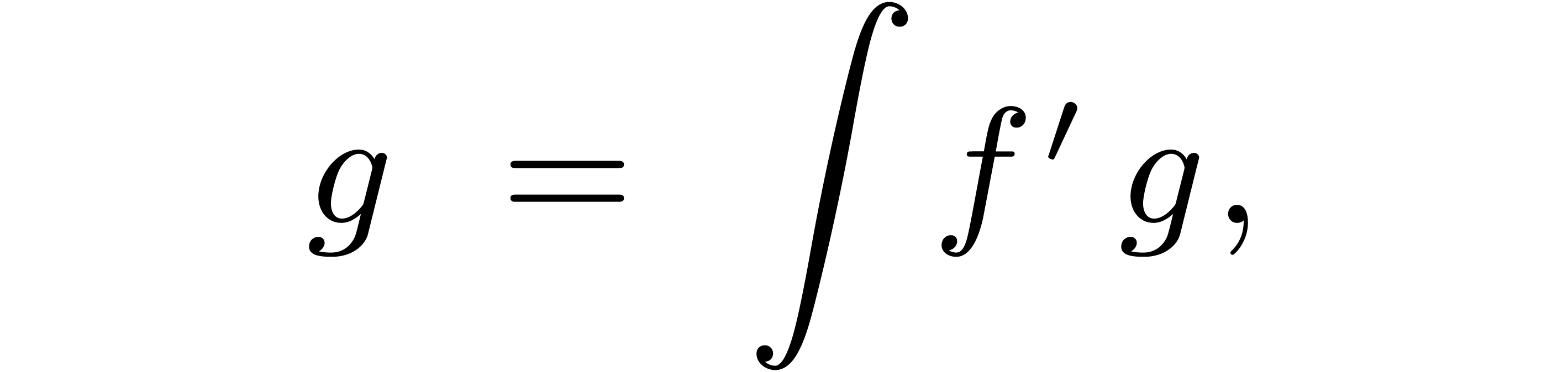
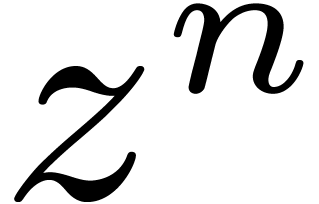 in
in  and
and 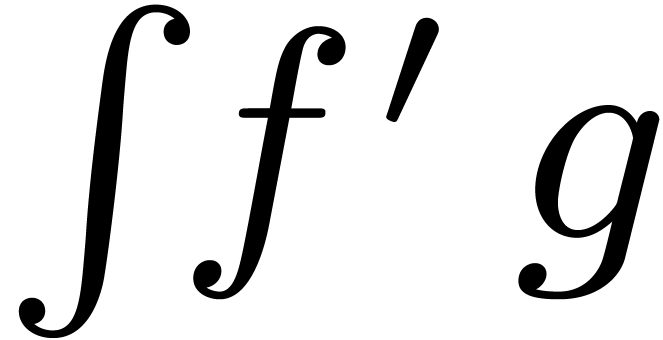 yields
yields
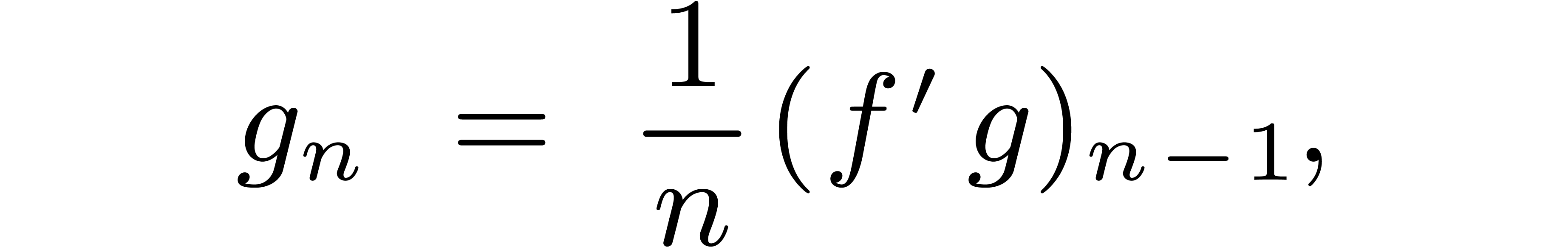
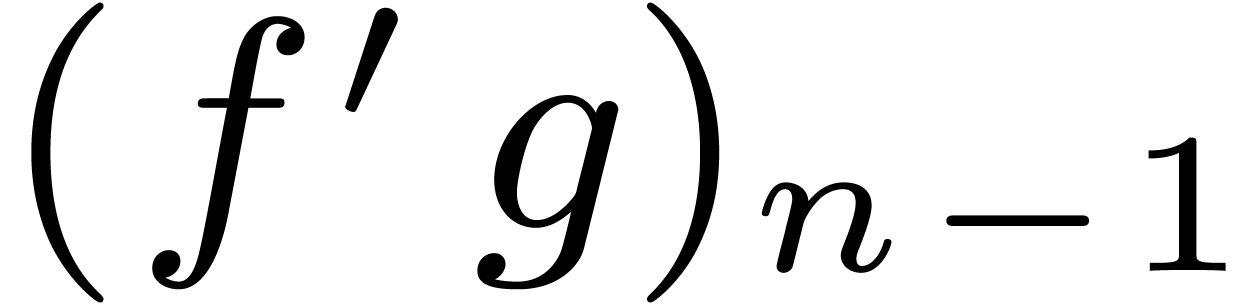 only depends on
only depends on  .
.
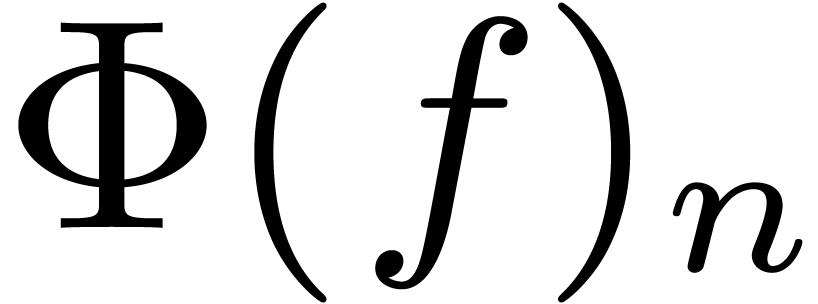 only depends on
only depends on
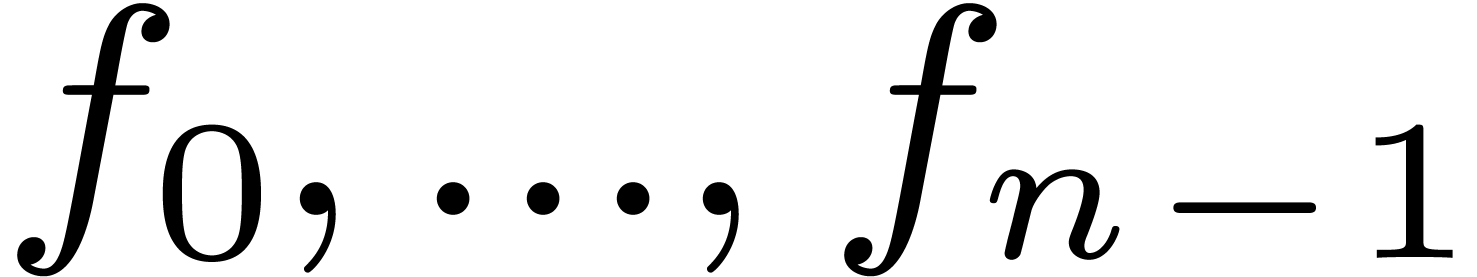 .
. ,
,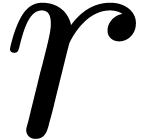 equations. In
the case of an implicit equation, special rewriting techniques can be
implied in order to transform the input equation into a recursive
equation [
equations. In
the case of an implicit equation, special rewriting techniques can be
implied in order to transform the input equation into a recursive
equation [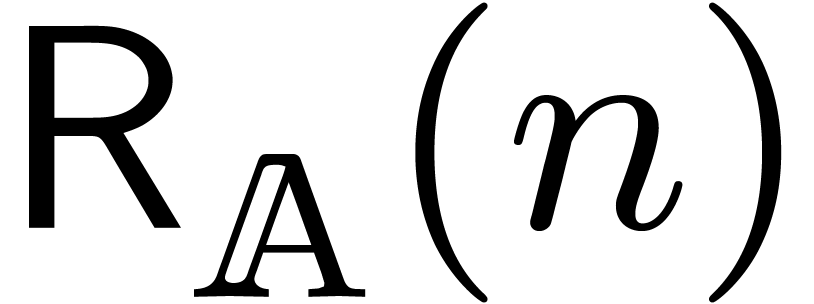 denote the cost of performing a relaxed
multiplication up to order
denote the cost of performing a relaxed
multiplication up to order  is an expression which involves
is an expression which involves  multiplications and
multiplications and 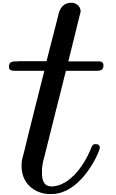 other
“linear time” operations (additions, integrations, etc.),
then it follows that (
other
“linear time” operations (additions, integrations, etc.),
then it follows that (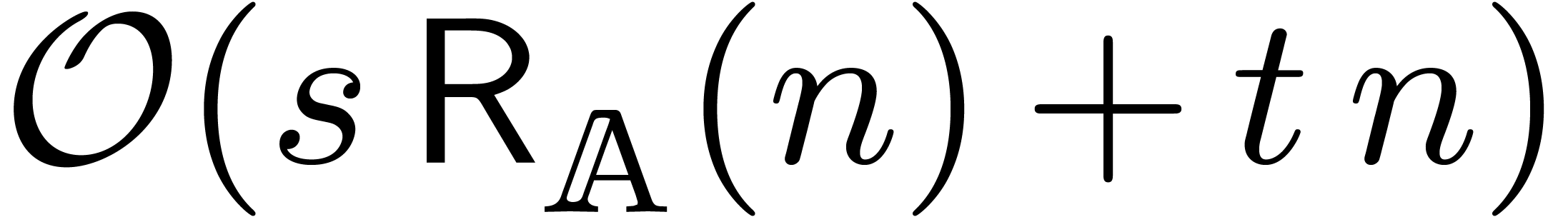 .
. ,
,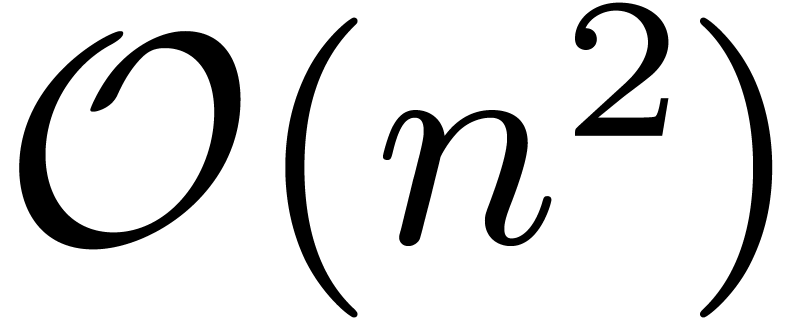 algorithm for computing
algorithm for computing 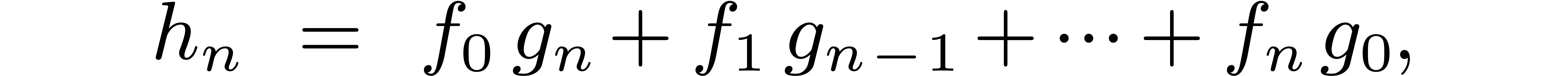
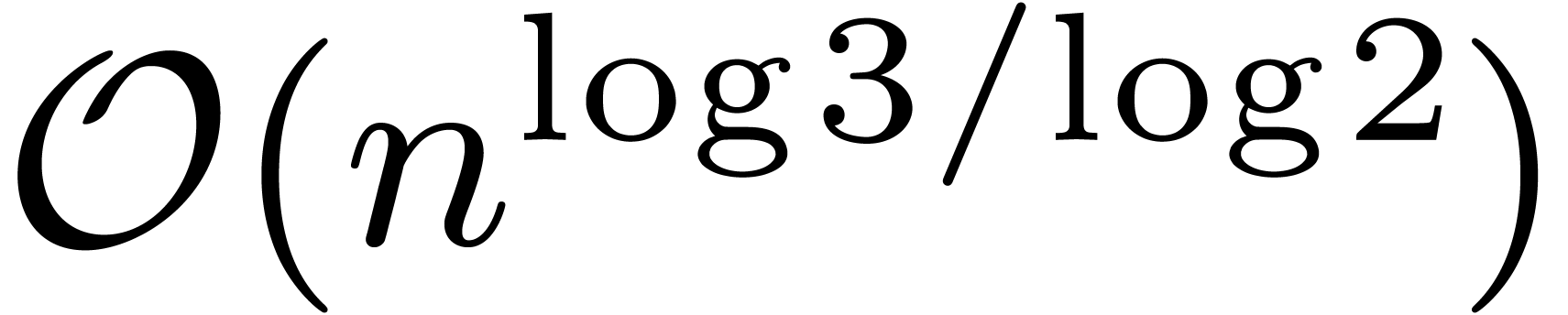 algorithm [
algorithm [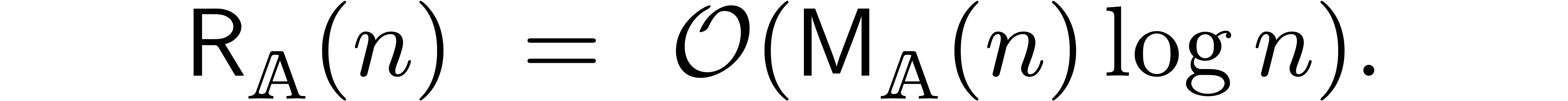
 with
with  are already known in the product
are already known in the product 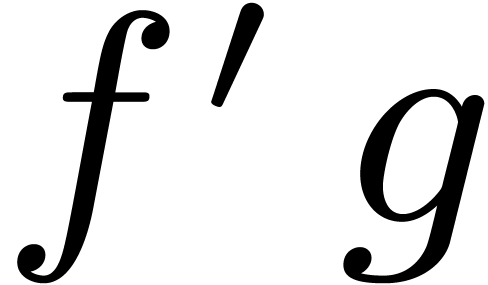 in (
in ( are known, but
all coefficients of
are known, but
all coefficients of 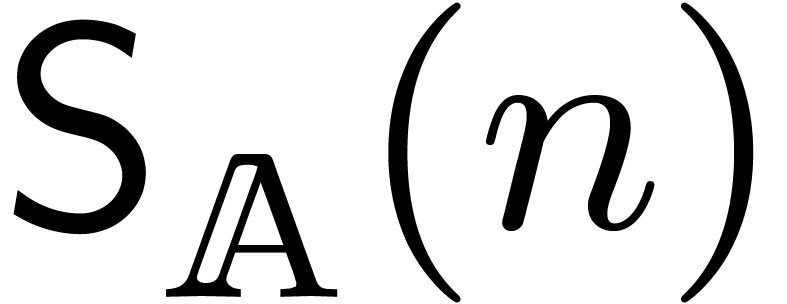 the complexity of semi-relaxed
multiplication. We recall from [
the complexity of semi-relaxed
multiplication. We recall from [
 that was gained in the case of semi-relaxed
multiplication can also be gained in the general case.
that was gained in the case of semi-relaxed
multiplication can also be gained in the general case.
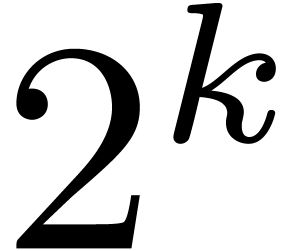 -th
-th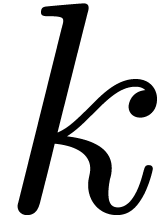 (or at least for all
(or at least for all 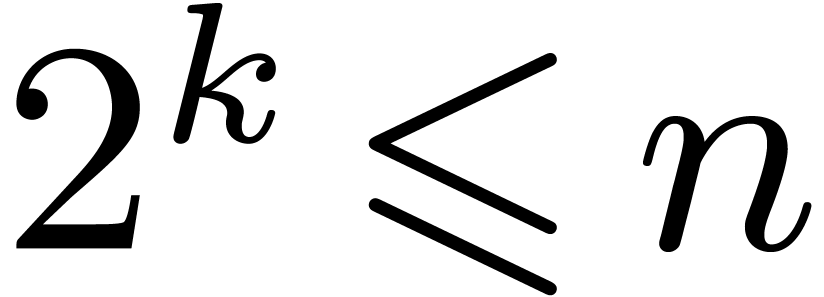 ),
),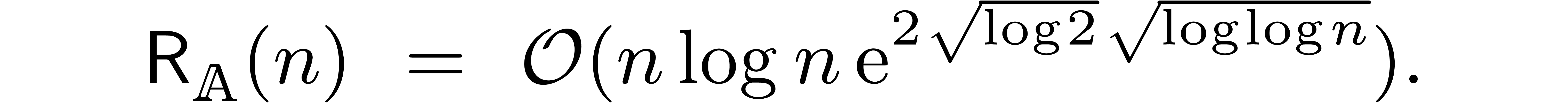
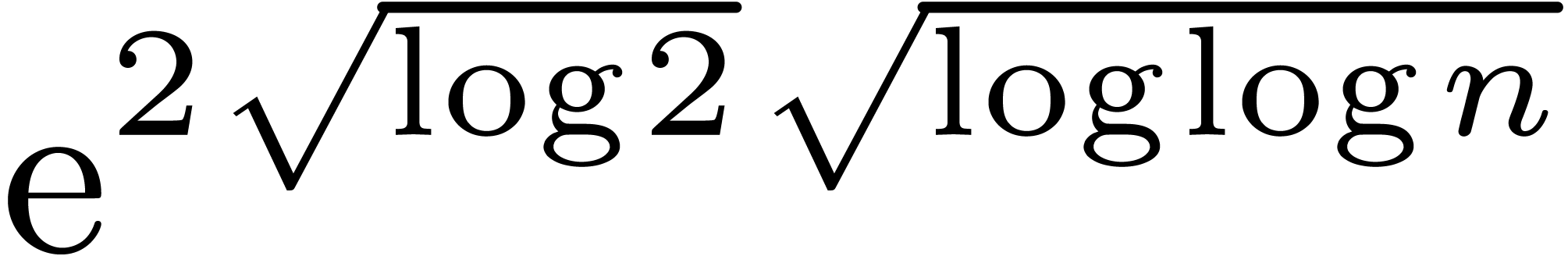 has slower growth than any strictly
positive power of
has slower growth than any strictly
positive power of 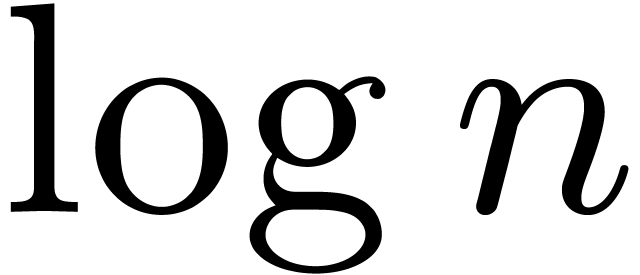 .
. whenever
whenever 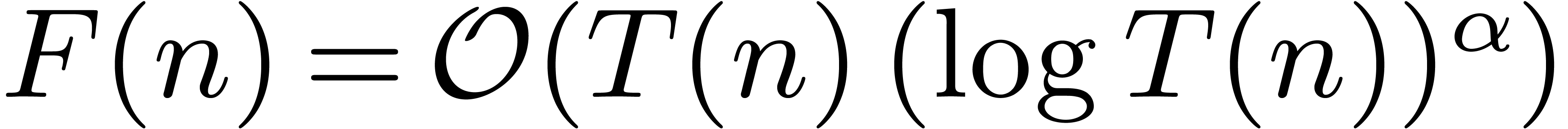 for all
for all 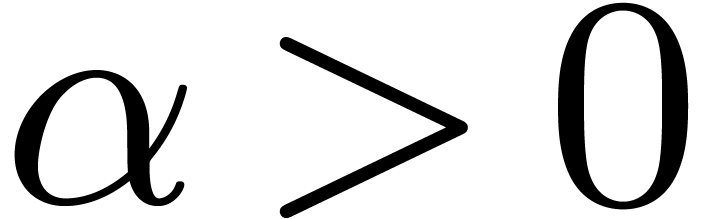 .
.
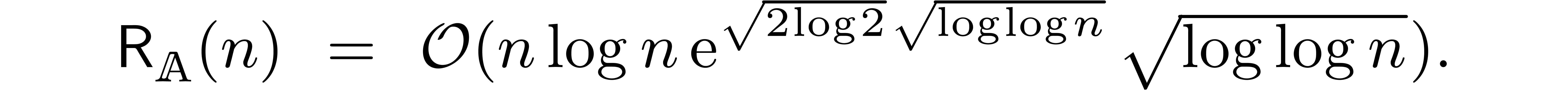
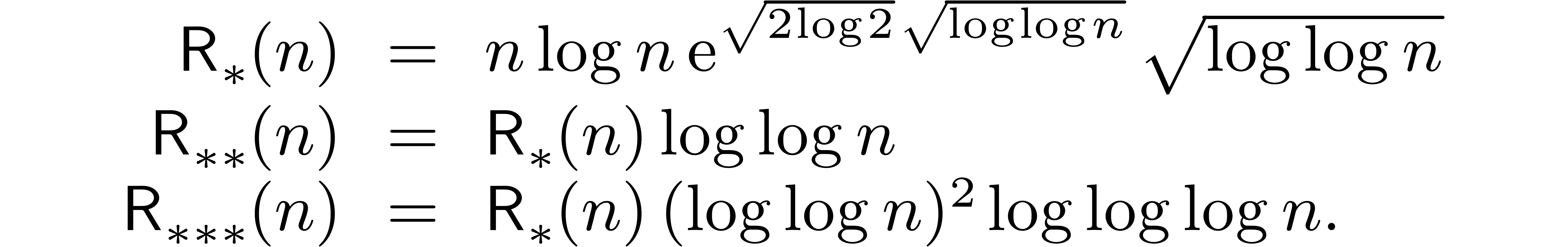
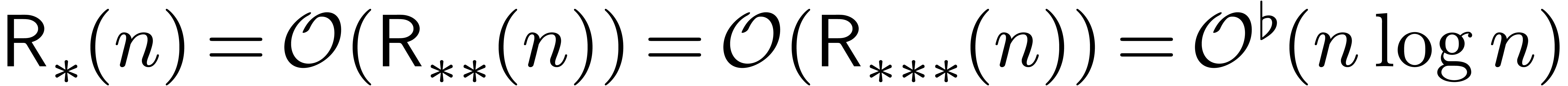 .
.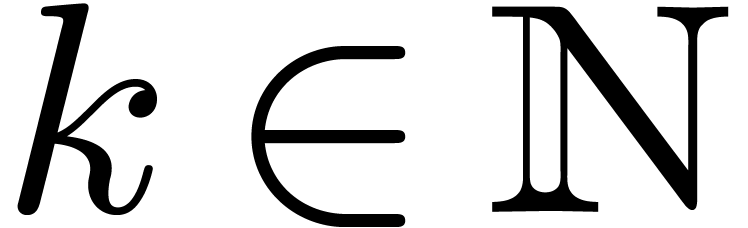 such that the canonical ring
homomorphism
such that the canonical ring
homomorphism  has kernel
has kernel 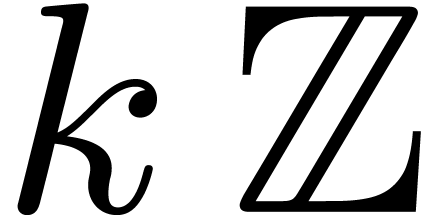 .
. -module
-module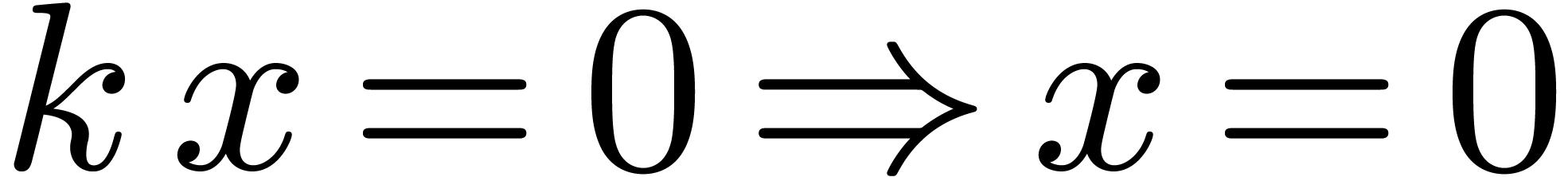 for any
for any 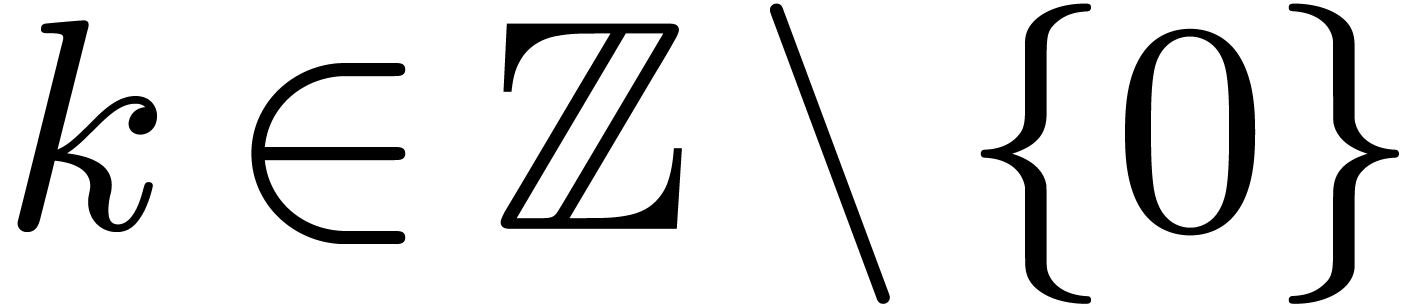 and
and 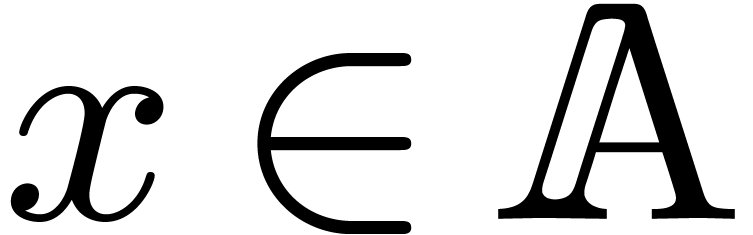 ),
),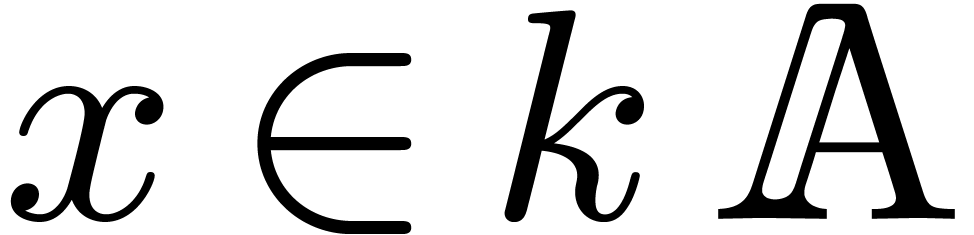 on input and which returns the unique
on input and which returns the unique 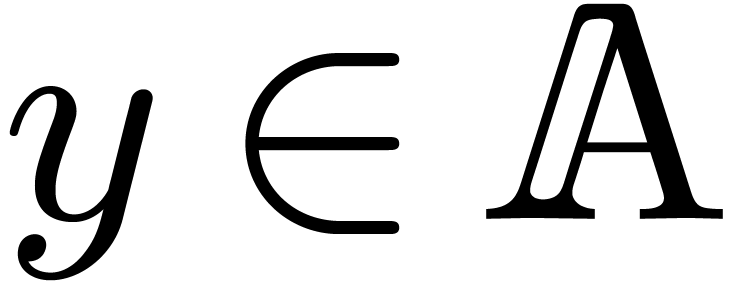 with
with 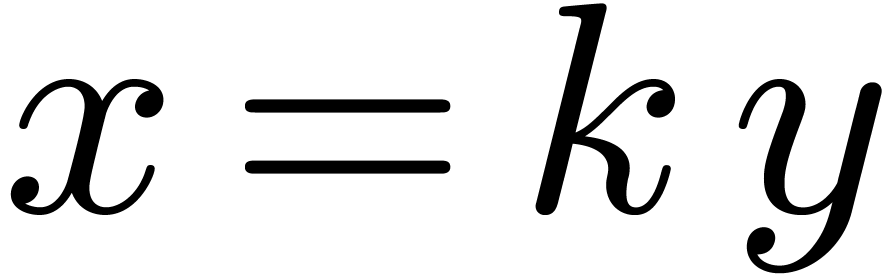 on output. We will count a unit cost for such
divisions. The main result of this paper is:
on output. We will count a unit cost for such
divisions. The main result of this paper is:

 and
and  .
.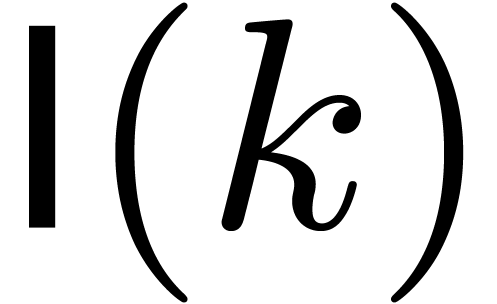 the bit complexity of
multiplying two
the bit complexity of
multiplying two 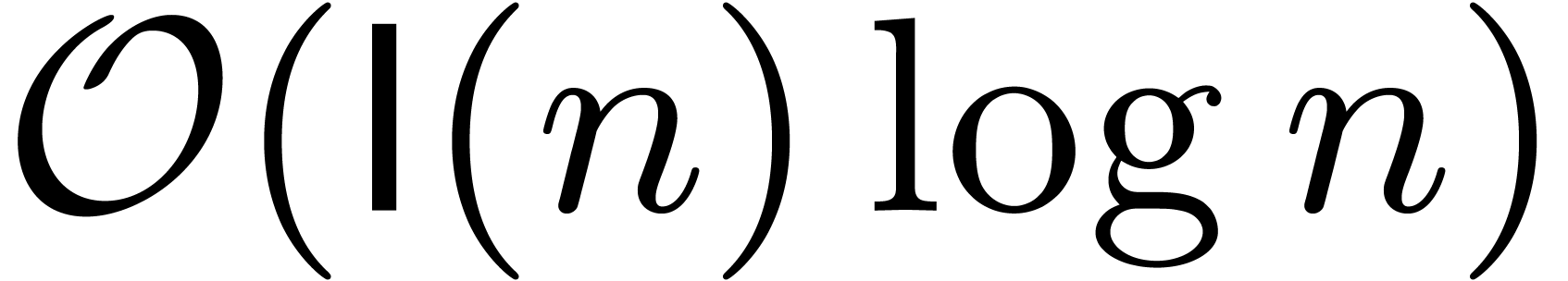 for the relaxed multiplication of
for the relaxed multiplication of
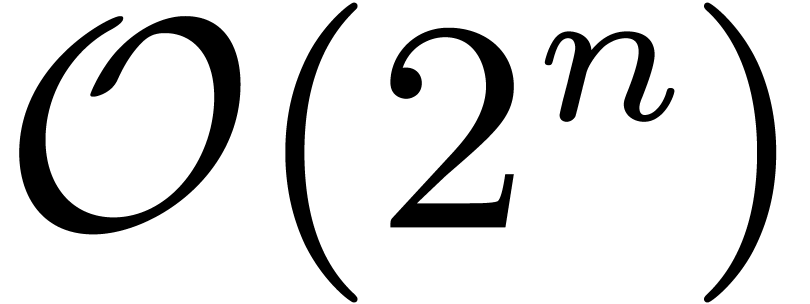 .
.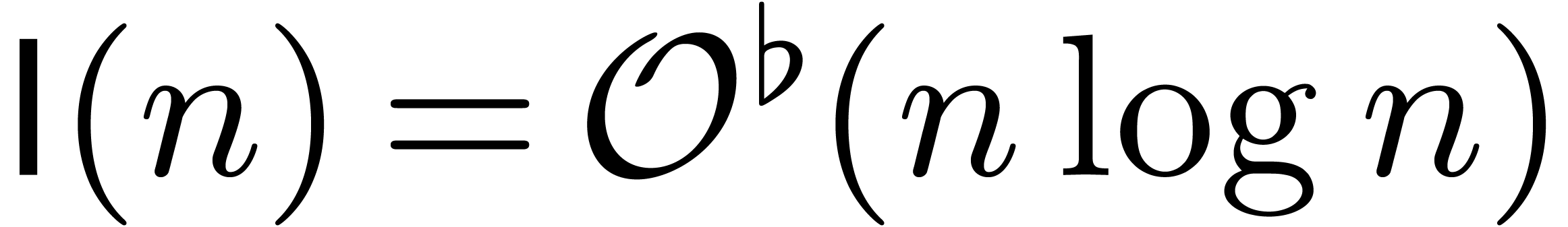 .
.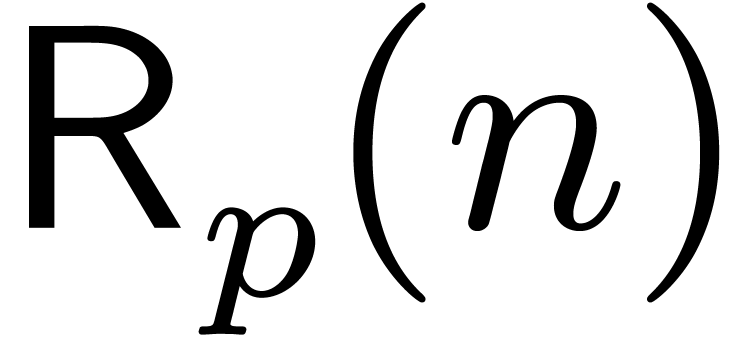 denote the bit complexity of the relaxed
multiplication of two
denote the bit complexity of the relaxed
multiplication of two 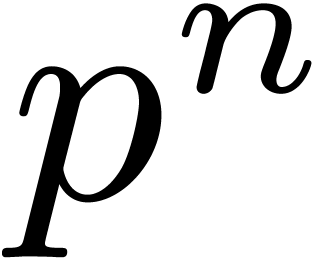 .
.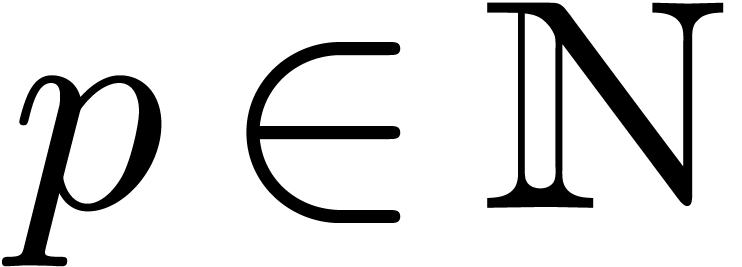 with
with  .
.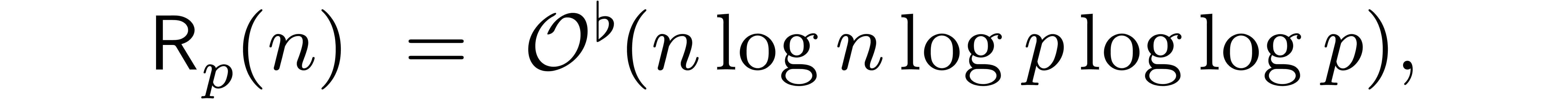
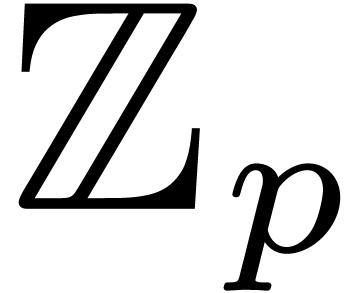 was
was
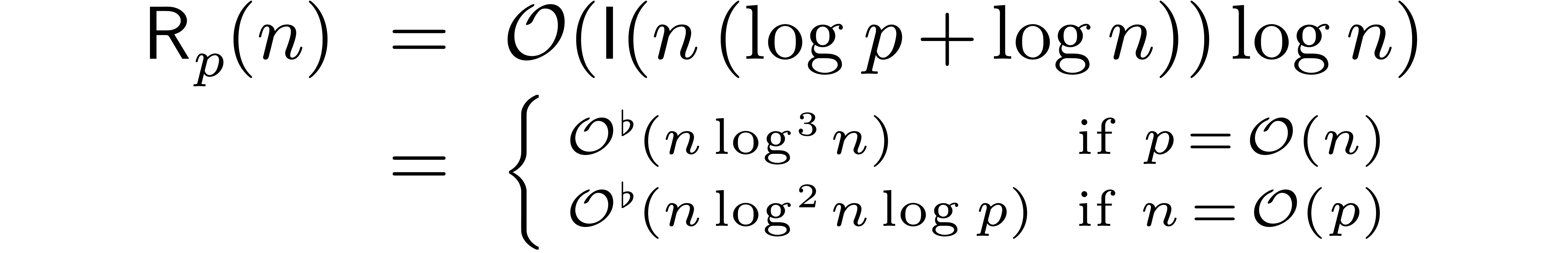
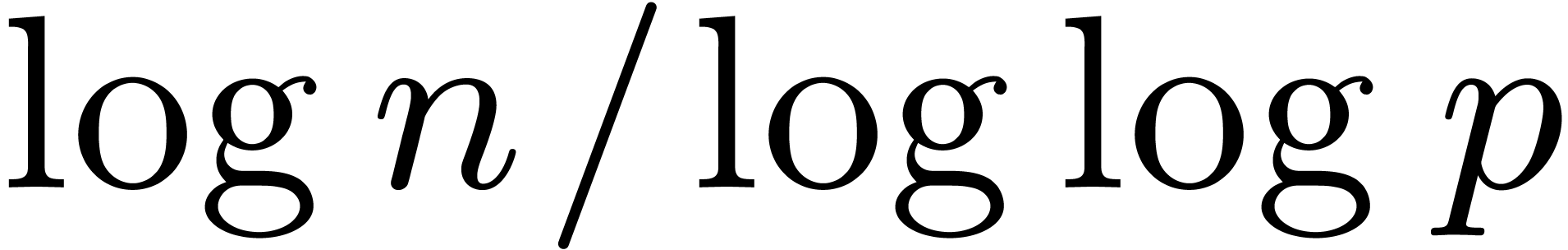 at least, up to sublogarithmic terms.
at least, up to sublogarithmic terms.
 evaluation and interpolation points, and both the
evaluation and interpolation steps can be performed efficiently, using
only
evaluation and interpolation points, and both the
evaluation and interpolation steps can be performed efficiently, using
only  operations. Now it has recently been shown
[
operations. Now it has recently been shown
[ in order to
generalize the results from Section
in order to
generalize the results from Section  for some sufficiently large
for some sufficiently large  be a (commutative) effective integral domain
and let
be a (commutative) effective integral domain
and let  be its quotient field. Assume that
be its quotient field. Assume that  be an effective torsion-free
be an effective torsion-free 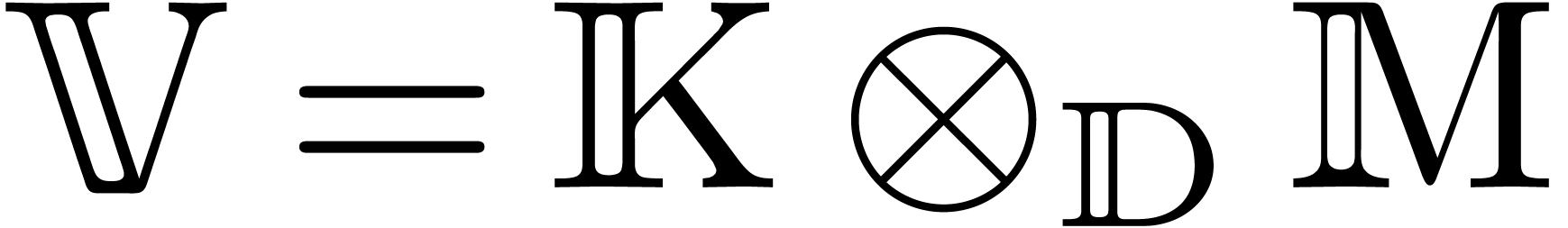 .
. are fractions
are fractions 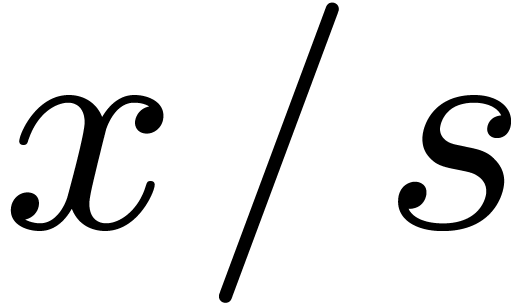 with
with  (resp.
(resp.  )
) ,
, on such fractions are as
usual:
on such fractions are as
usual:
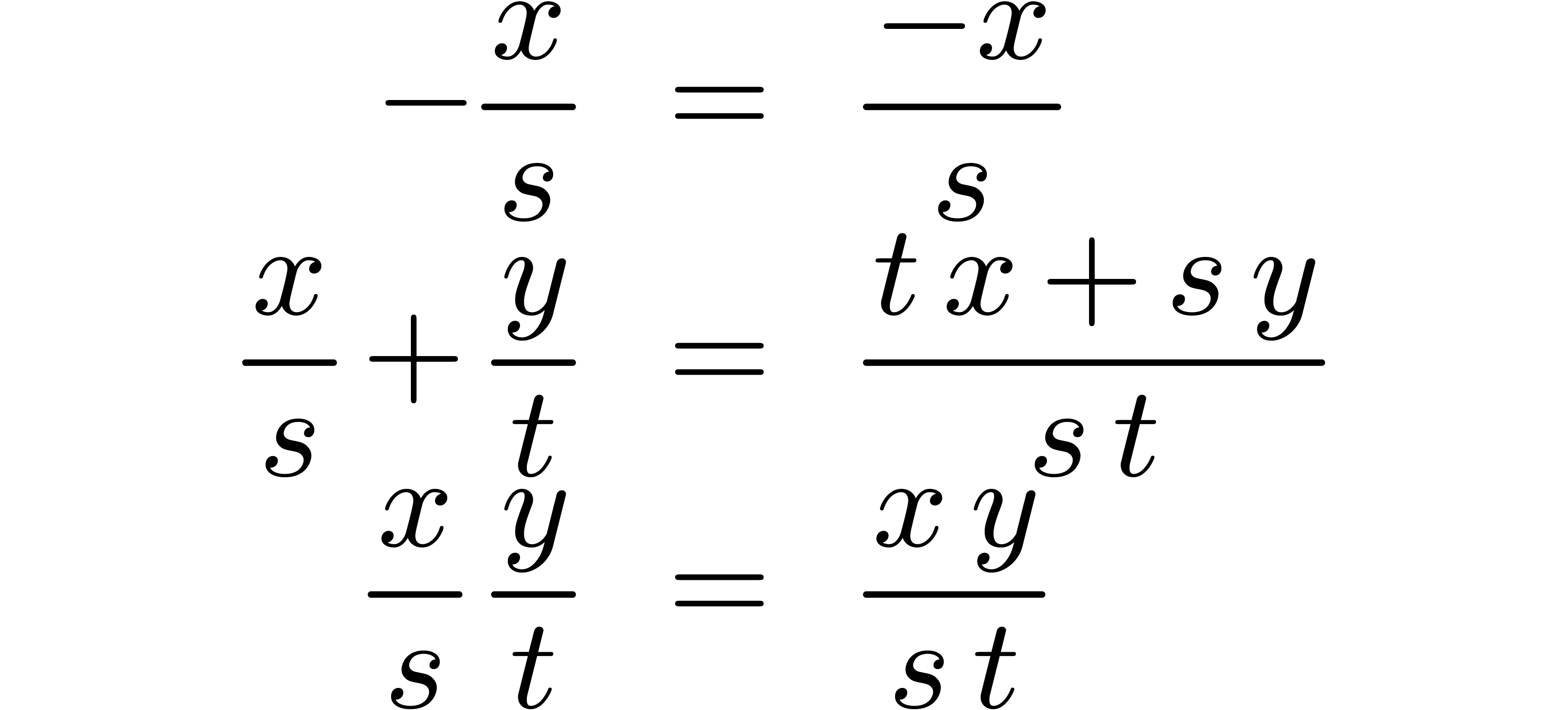
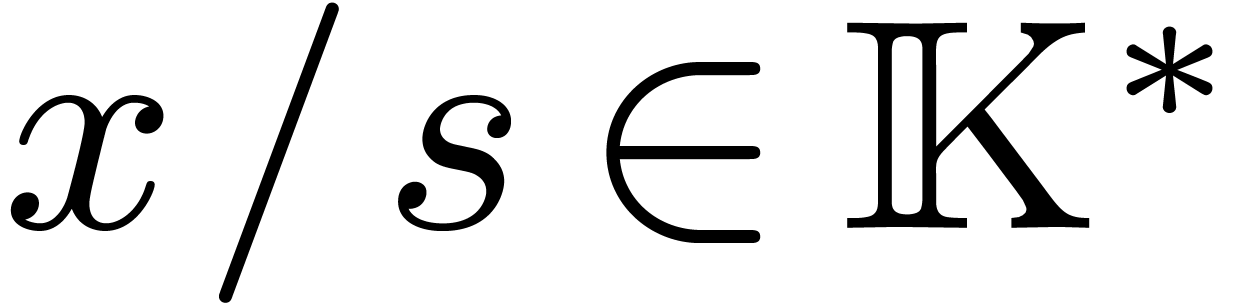 ,
,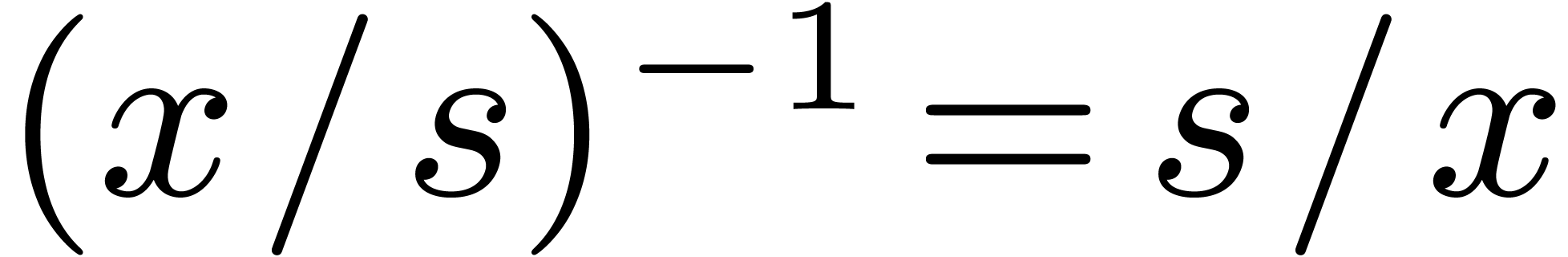 .
. operations in
operations in 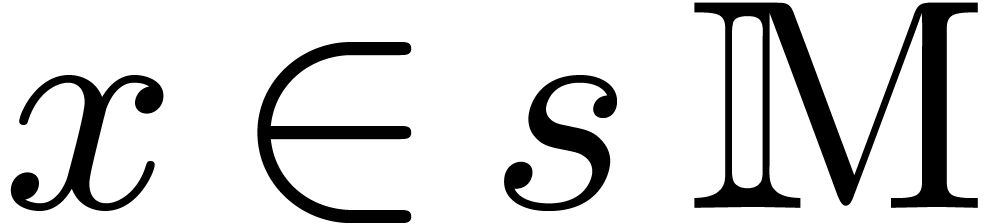 ,
,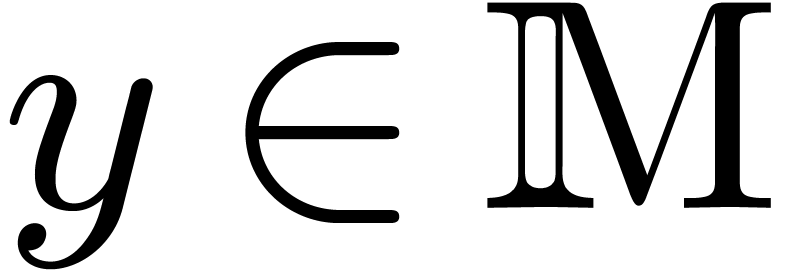 with
with 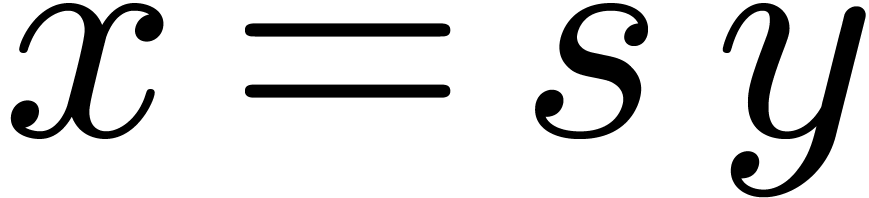 .
.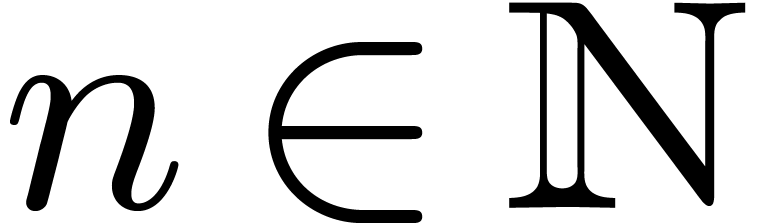 ,
,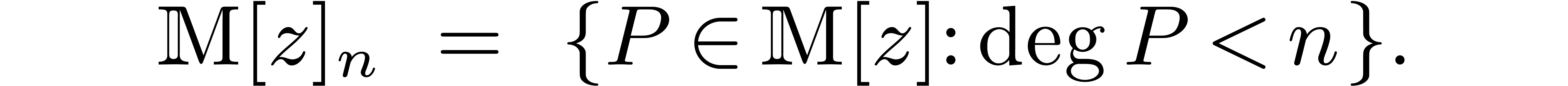
 and
and 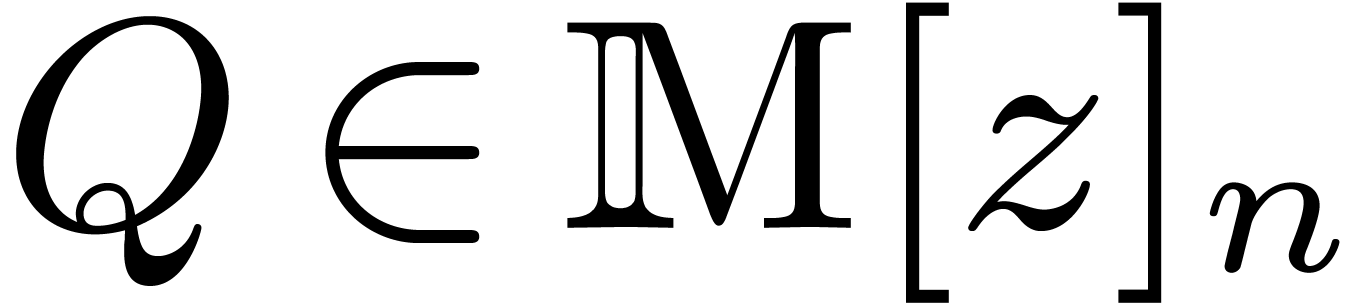 ,
,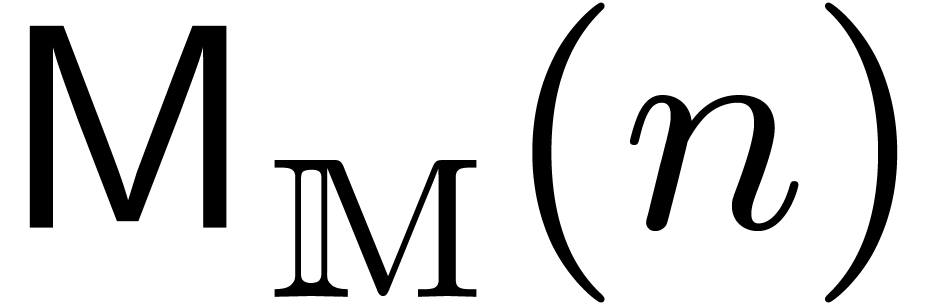 the number of operations in
the number of operations in
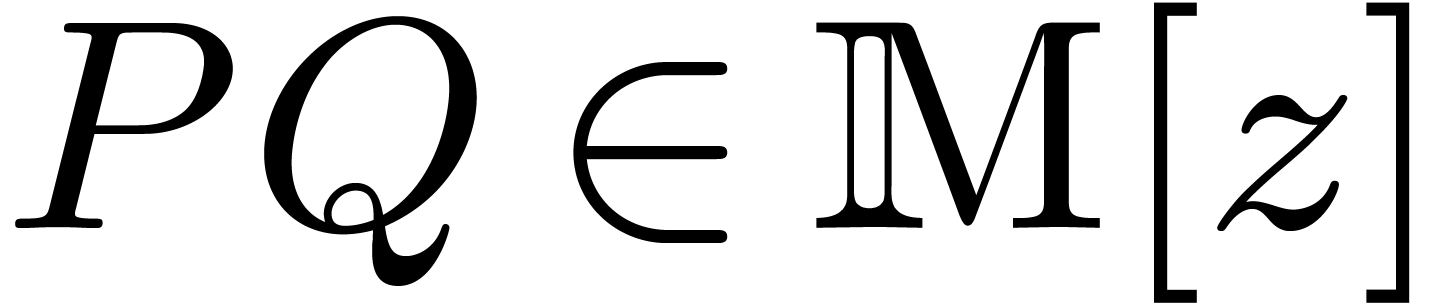 .
. be an effective integral domain and
be an effective integral domain and  an effective torsion-free
an effective torsion-free  ,
, ,
,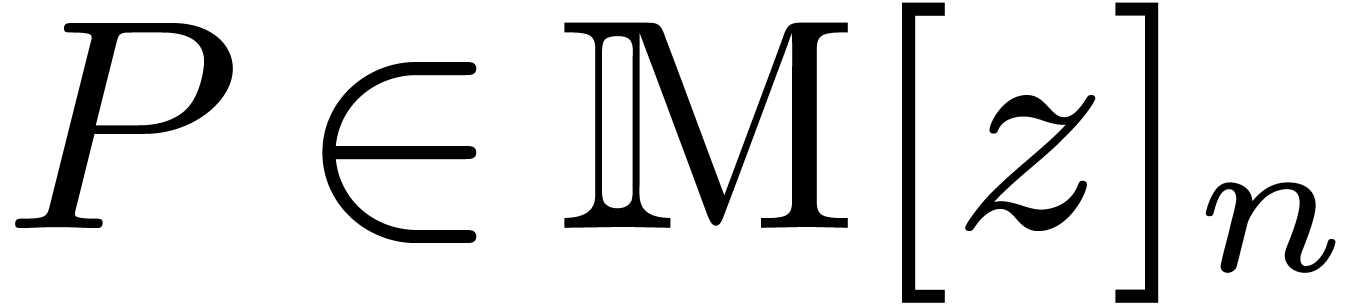 and
and  such that
such that  are pairwise distinct, and such that
are pairwise distinct, and such that  and
and  ,
, from
from  using
using  operations in
operations in  is a
field and
is a
field and  ,
, and divided
by elements of the set
and divided
by elements of the set  .
.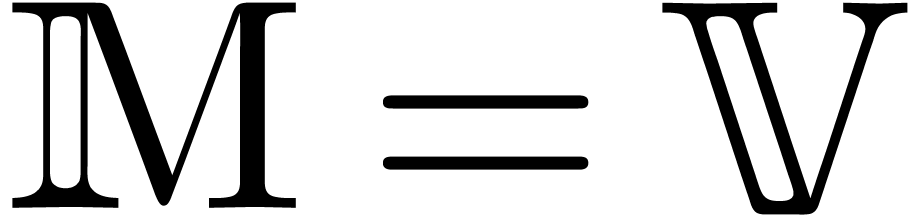 a
vector space.
a
vector space.
 as above, and we may still apply
the generalized algorithms for multipoint evaluation and interpolation
in
as above, and we may still apply
the generalized algorithms for multipoint evaluation and interpolation
in 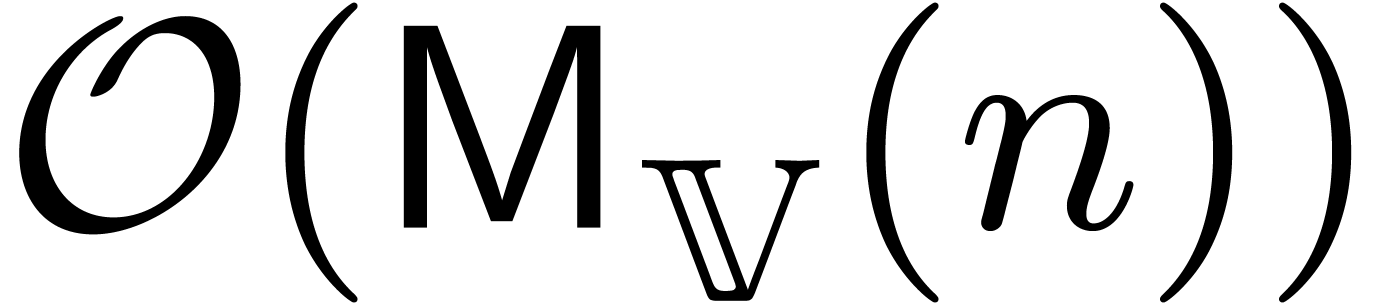 operations in
operations in 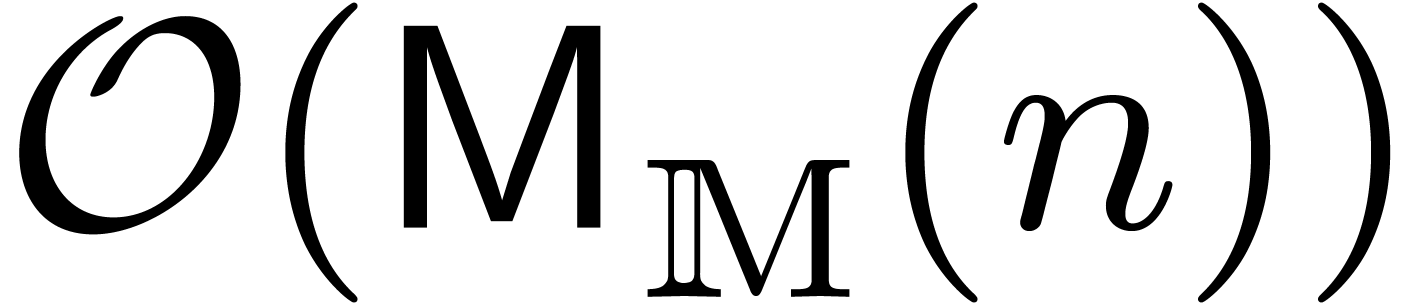 operations in
operations in 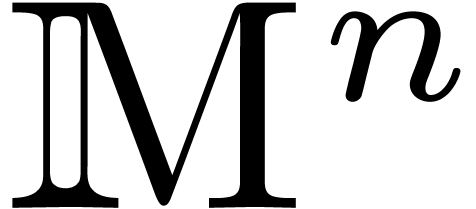 of
of 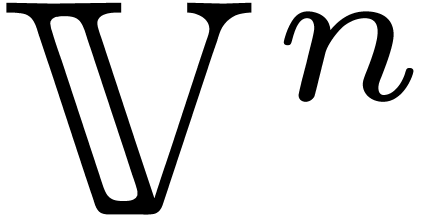 (or
in the submodule
(or
in the submodule 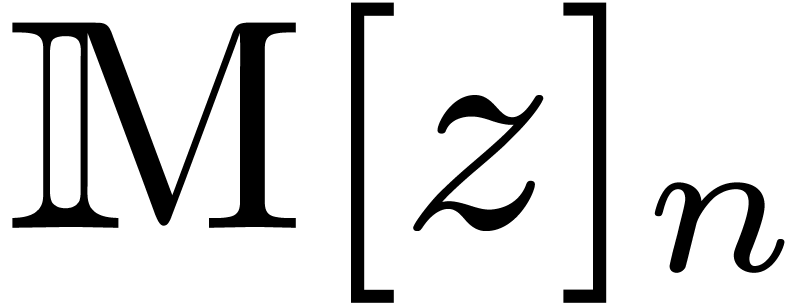 of
of 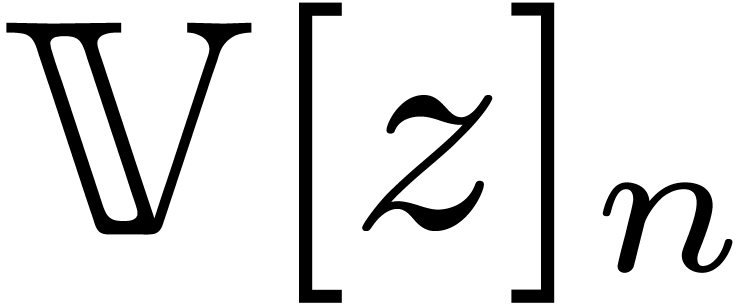 ),
),

 ,
,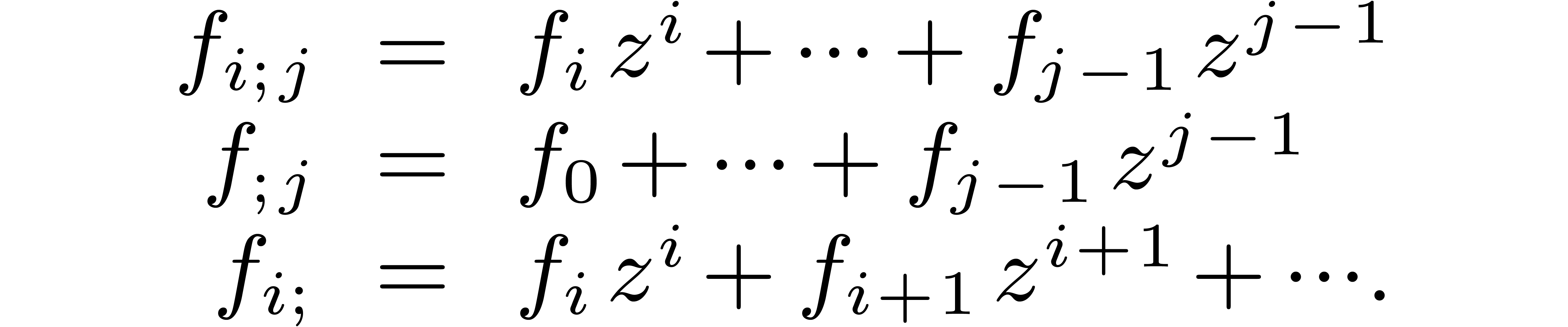
 ,
, with coefficients
in
with coefficients
in 
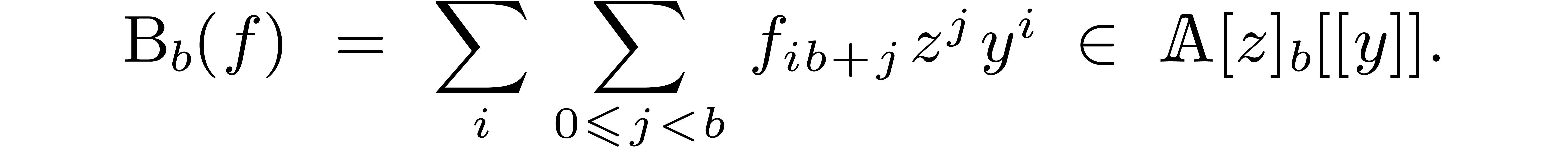
 using
using

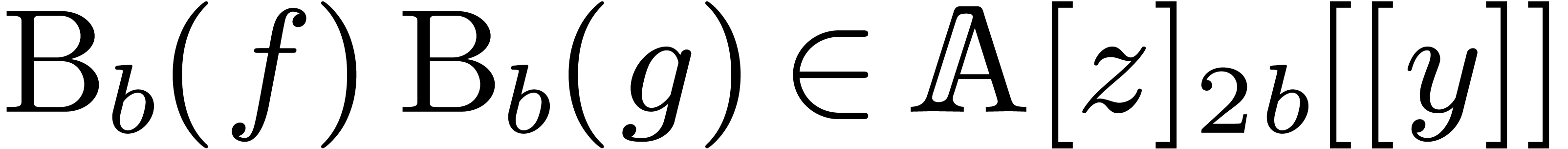 and
and
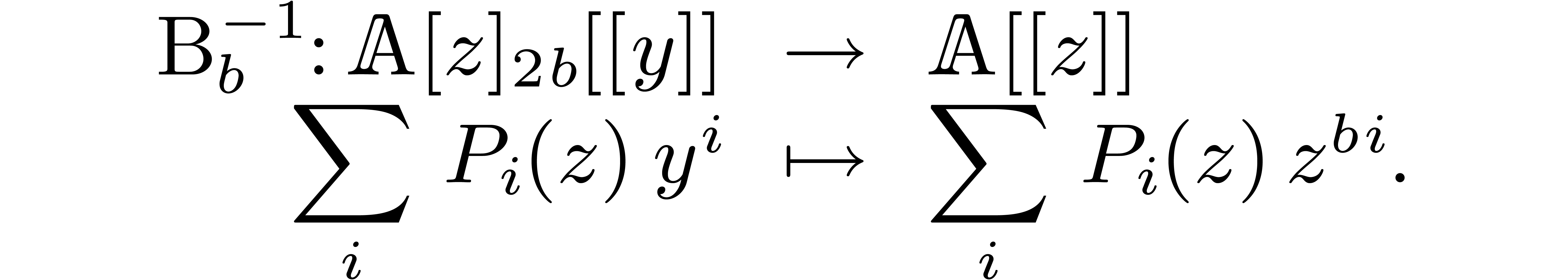
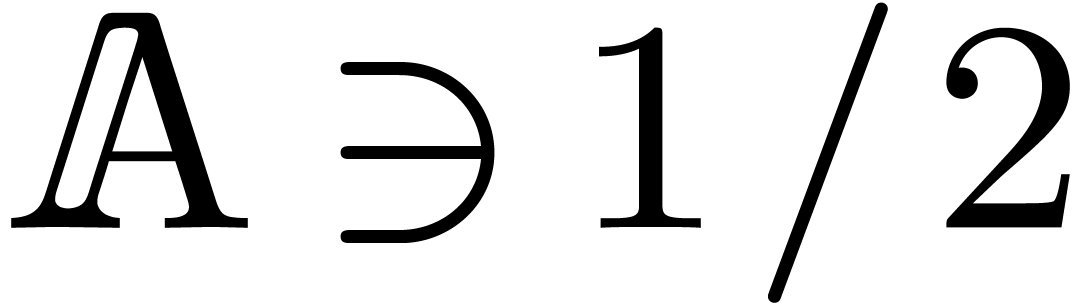 ,
,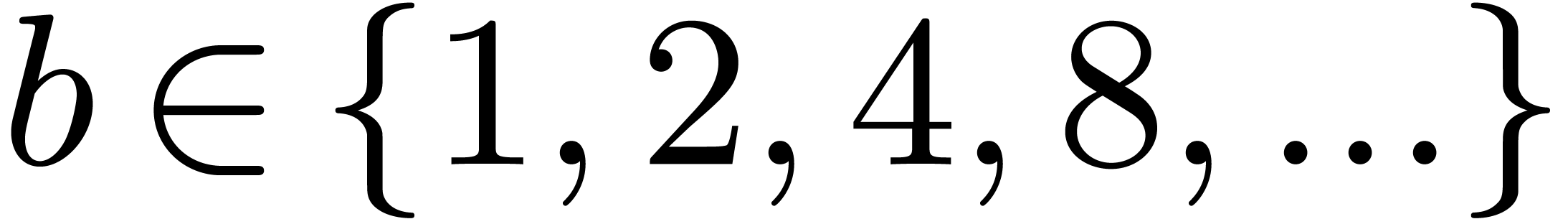 ,
, -th
-th .
.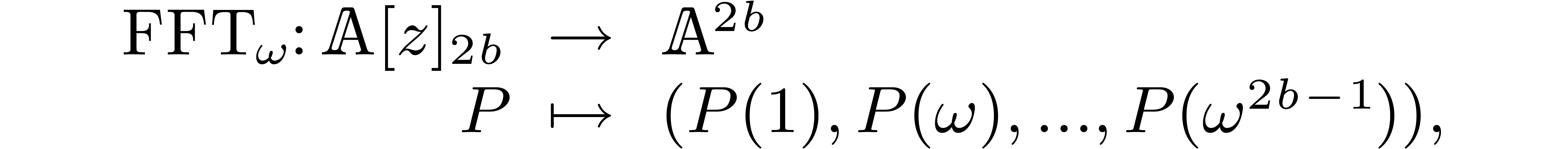
 and
and 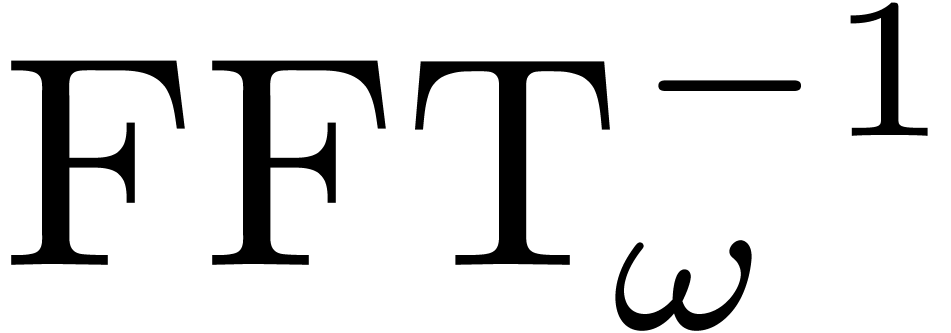 can be computed using
can be computed using  operations in
operations in  via
via
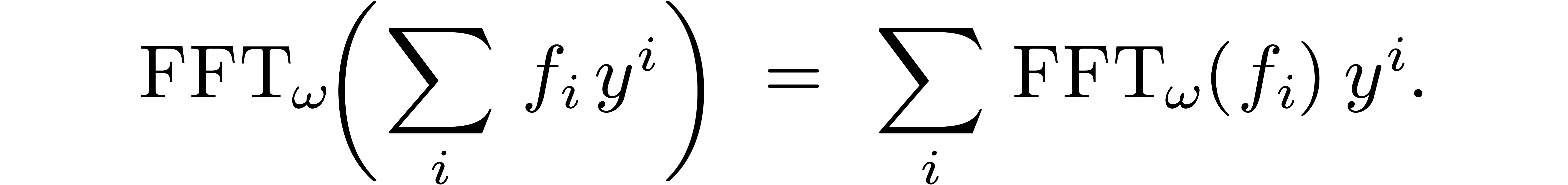
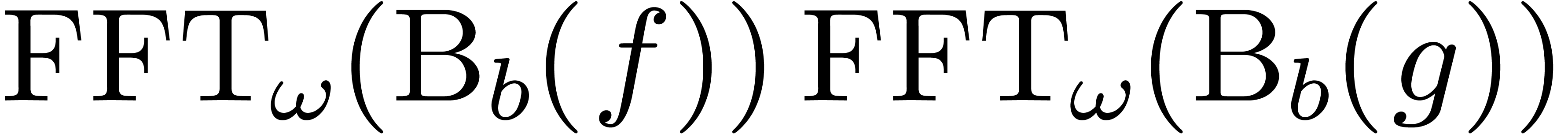 is a pointwise product in
is a pointwise product in  .
. coefficients of
coefficients of  operations in
operations in  -th
-th -th
-th coefficients of
coefficients of 
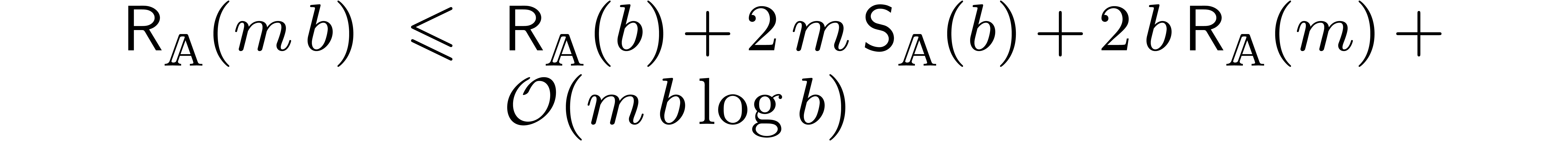
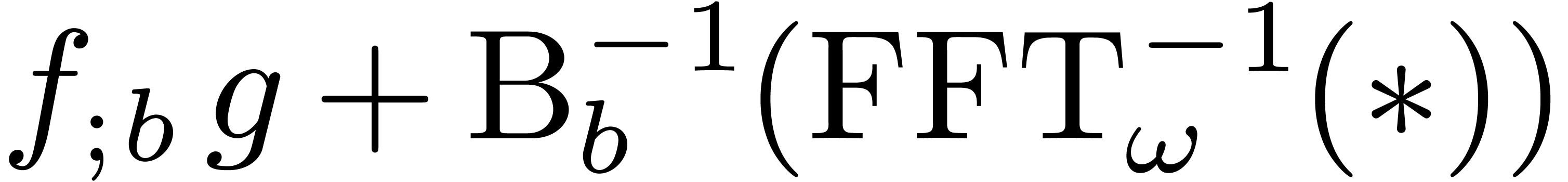

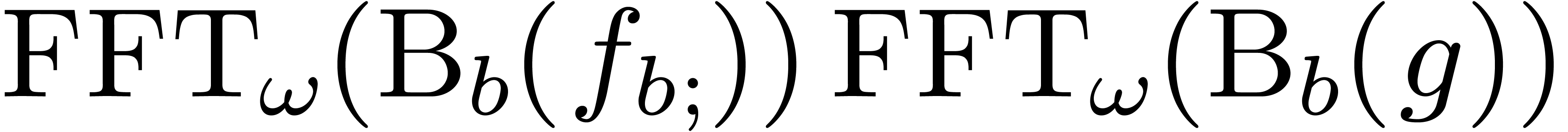
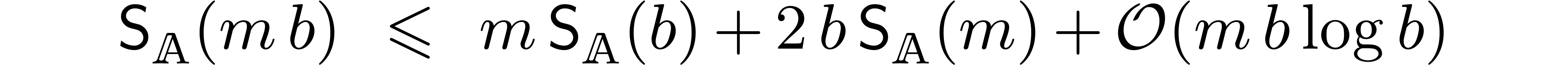
 ,
,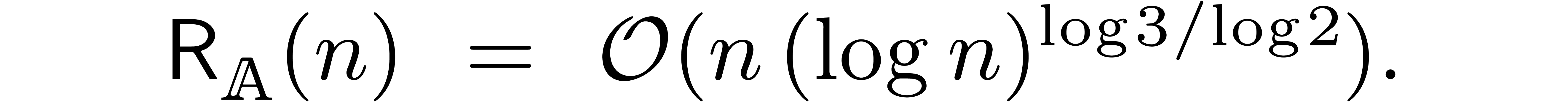
 is chosen as a function of
is chosen as a function of  which is specified in advance. In fact, such an algorithm automatically
yields a genuine relaxed algorithm with the same complexity (up to a
constant factor), by doubling the order
which is specified in advance. In fact, such an algorithm automatically
yields a genuine relaxed algorithm with the same complexity (up to a
constant factor), by doubling the order  clearly reduces to the relaxed multiplication of the two polynomials
clearly reduces to the relaxed multiplication of the two polynomials
 and
and 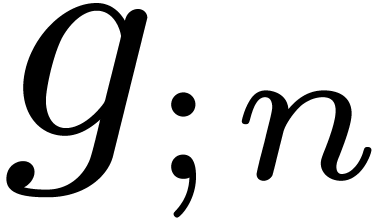 up to order
up to order 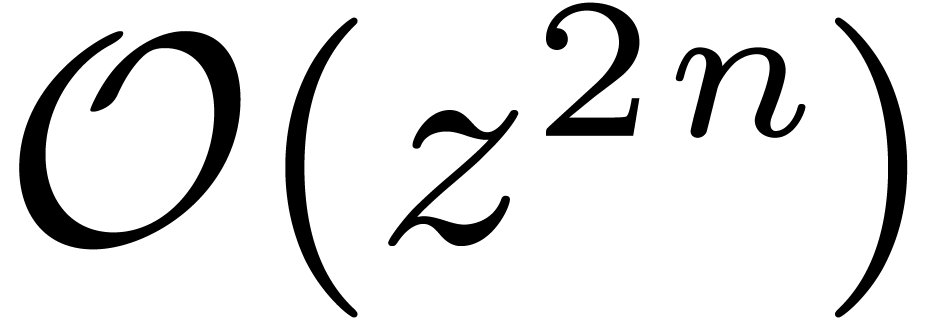 .
.
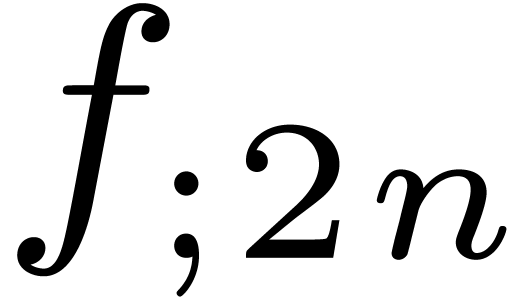 and
and 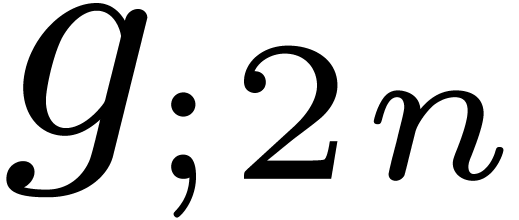 of degrees
of degrees 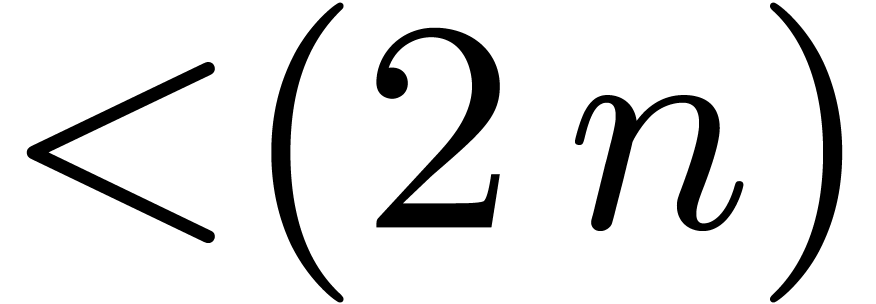 reduces
to a relaxed product
reduces
to a relaxed product  of half the size, two
semi-relaxed products
of half the size, two
semi-relaxed products  ,
,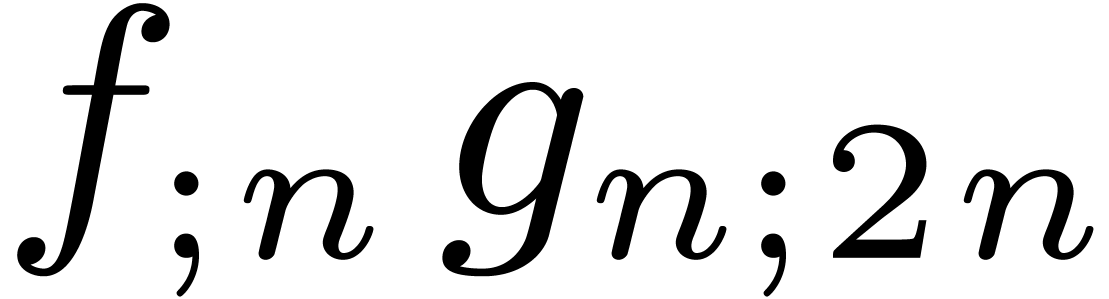 ,
,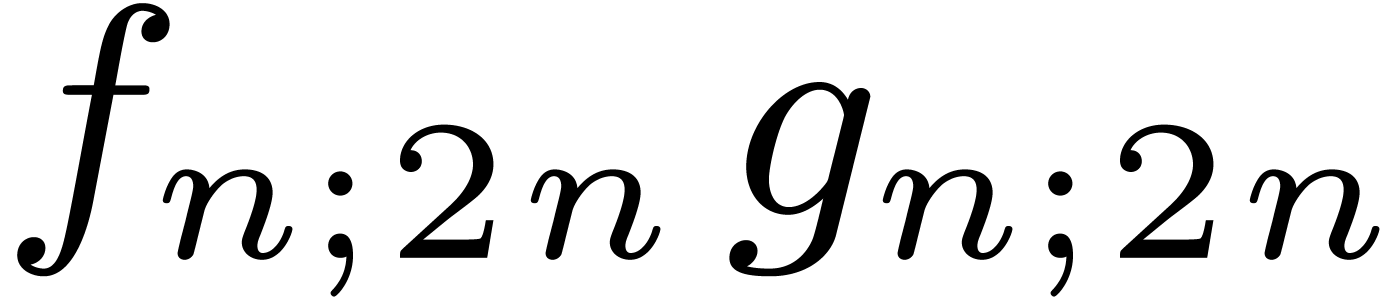 .
.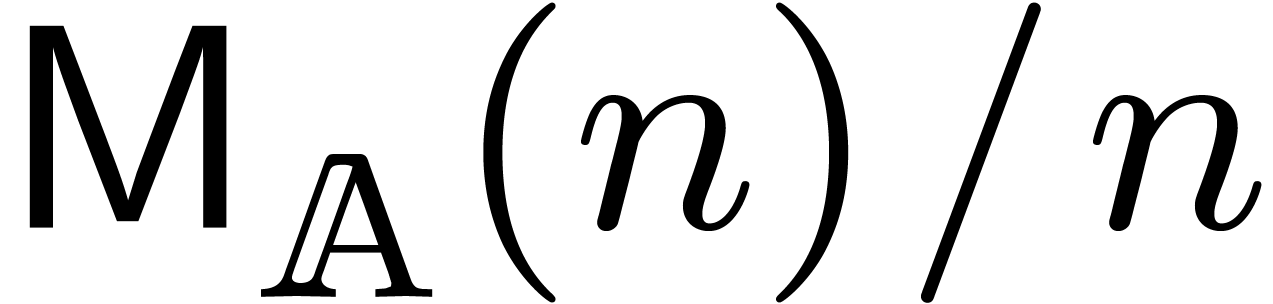 and
and 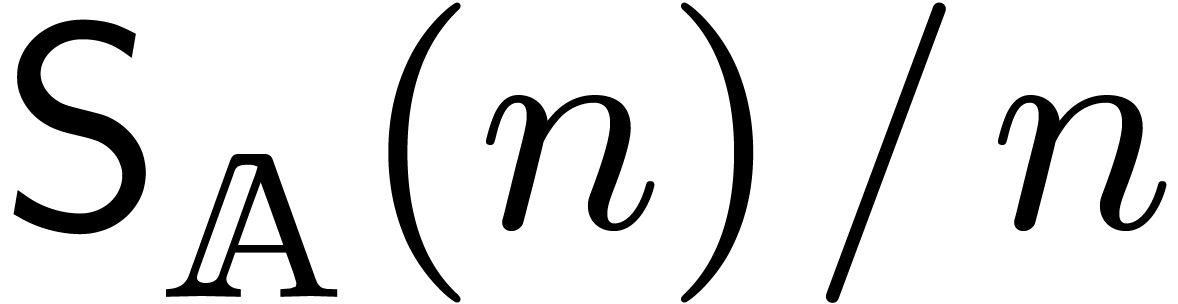 are increasing, a routine
calculation thus yields
are increasing, a routine
calculation thus yields
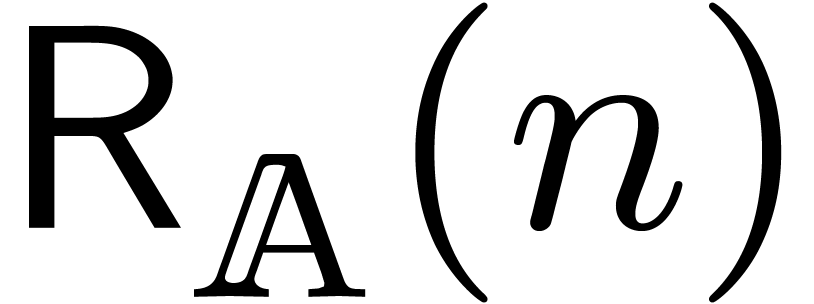

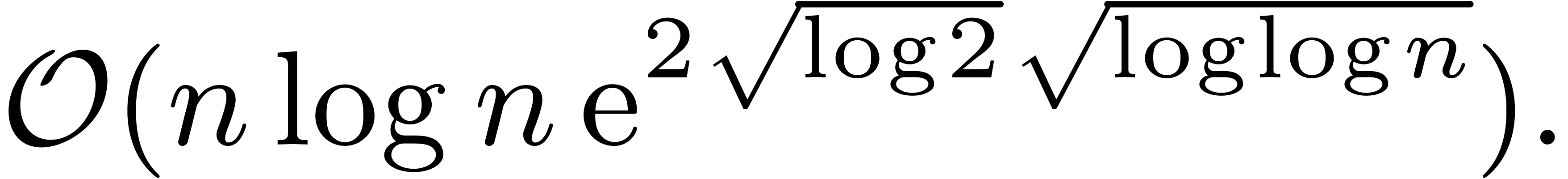
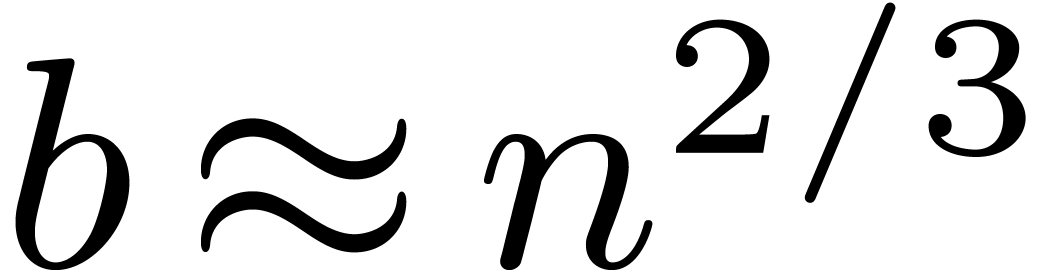 instead of
instead of
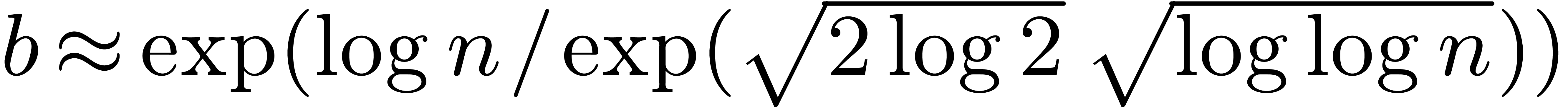 .
.
 be an increasing function with
be an increasing function with 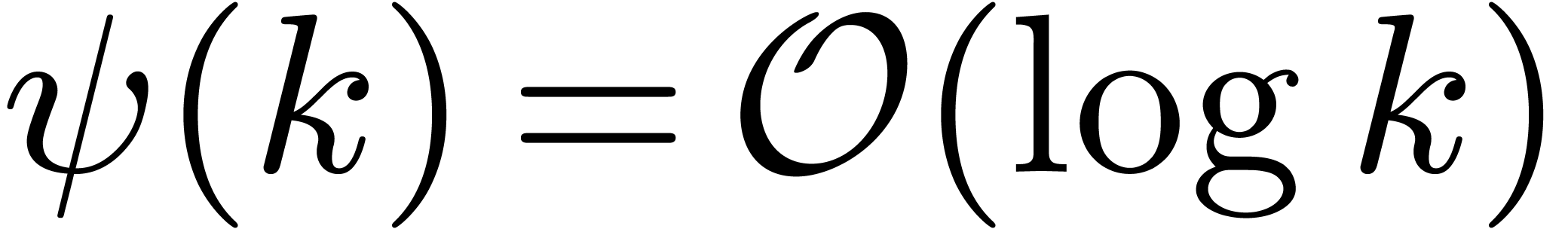 and let
and let
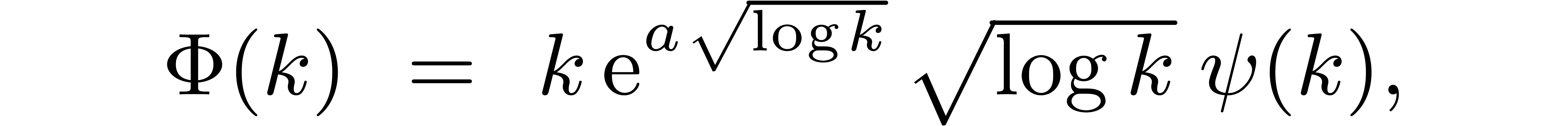
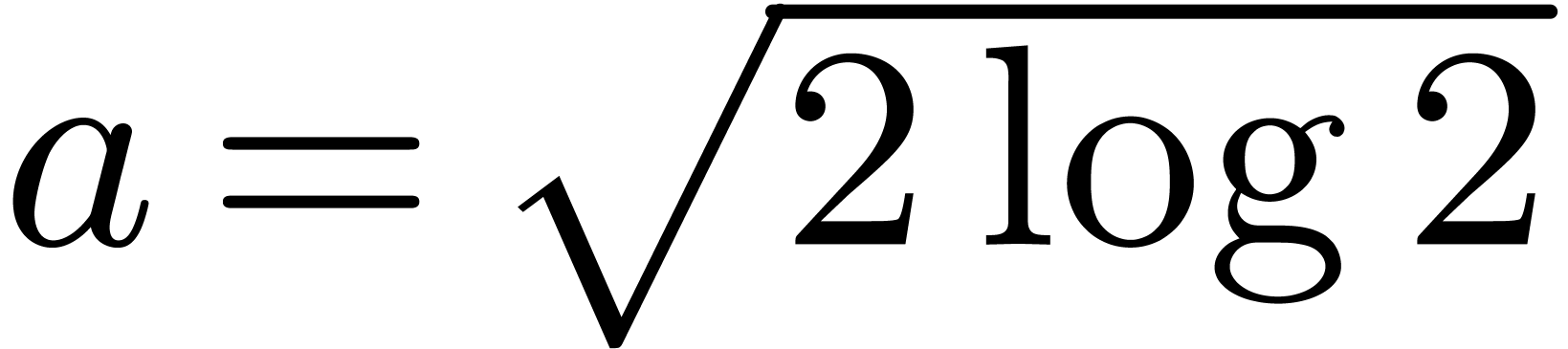 .
.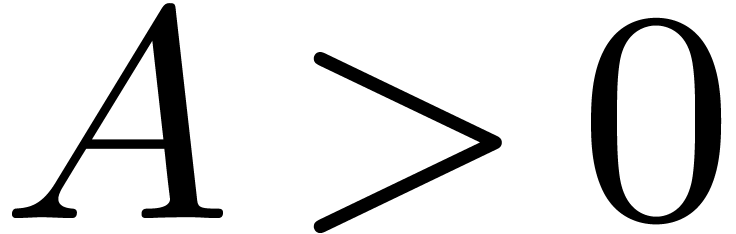 and
and 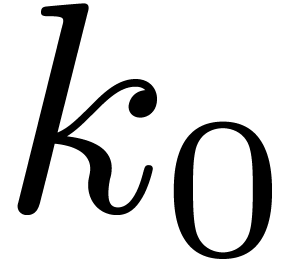 such that
for all
such that
for all  ,
,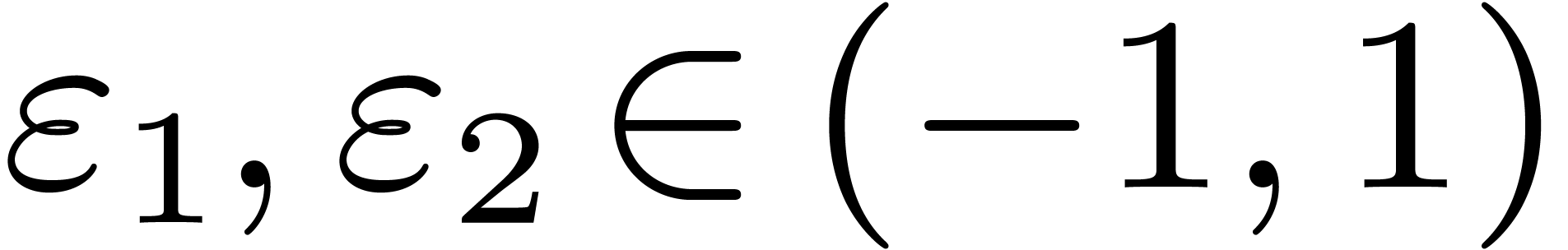 ,
,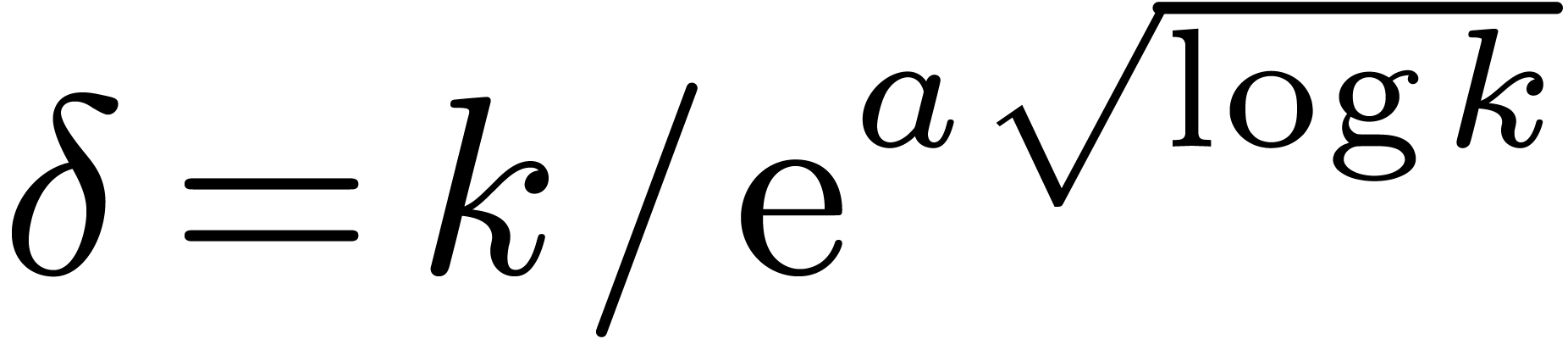 ,
,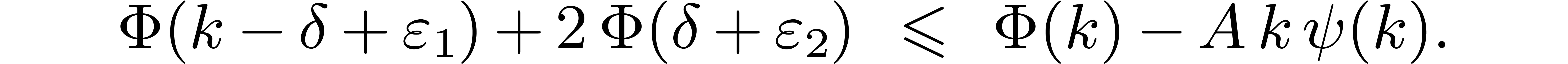
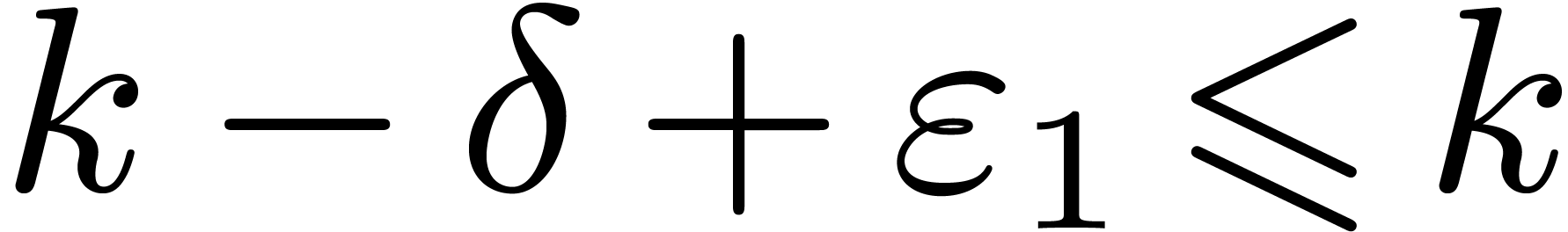 and
and 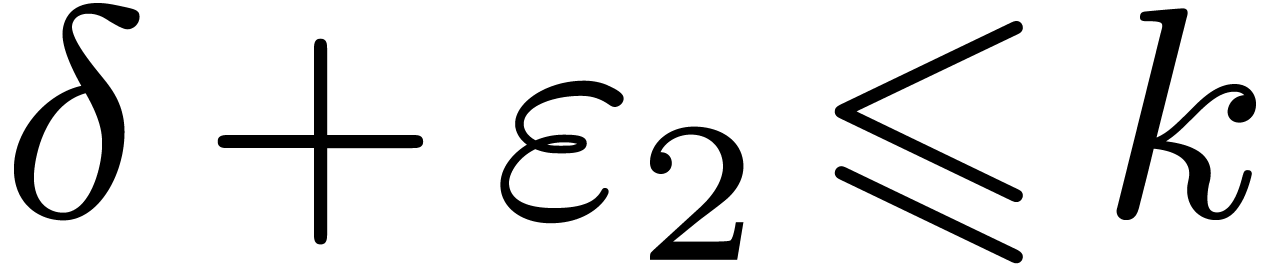 for sufficiently large
for sufficiently large 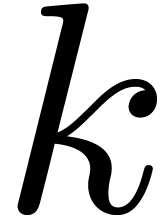 .
.
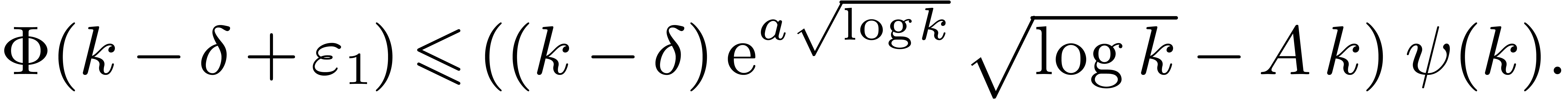
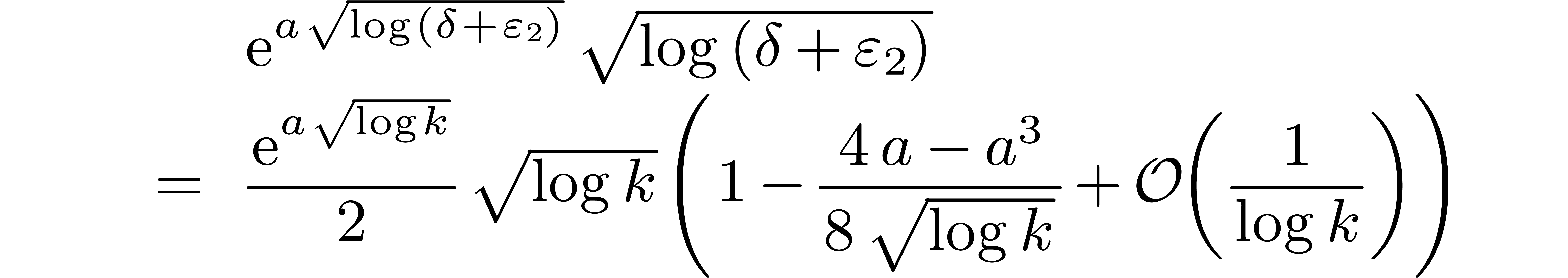
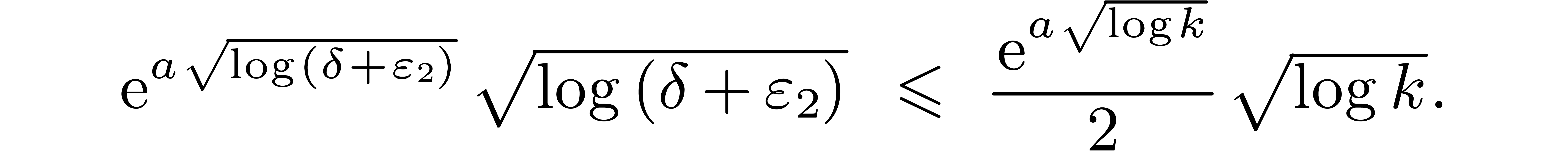
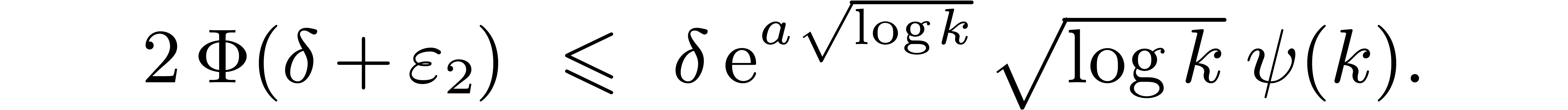
 be an increasing function with
be an increasing function with 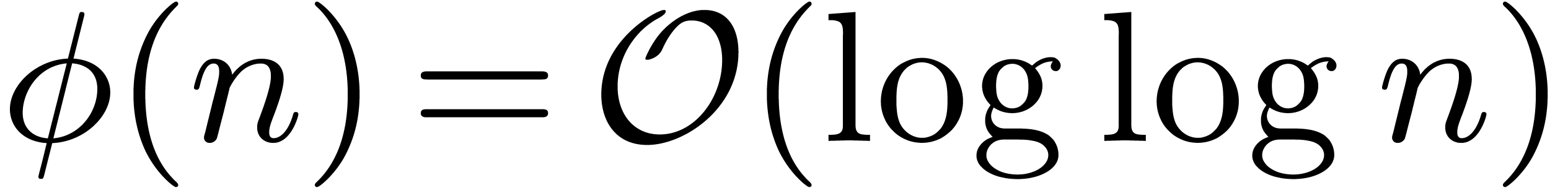 .
.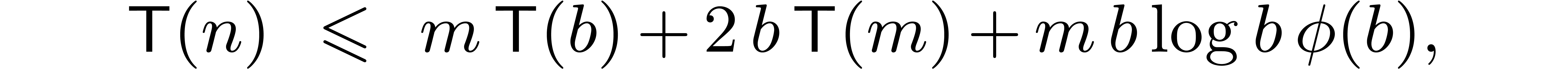
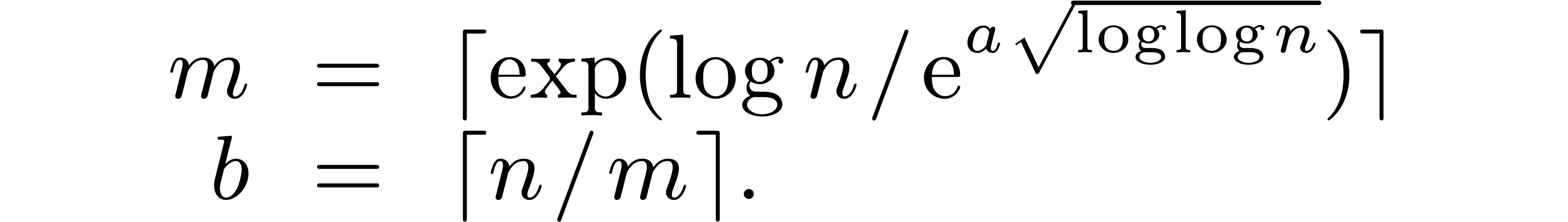
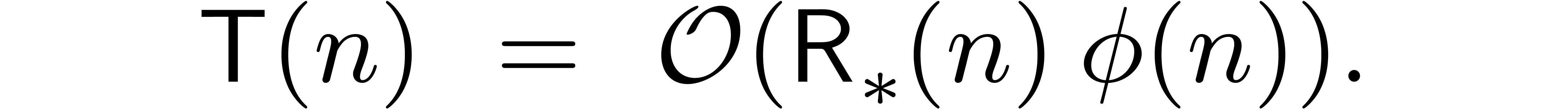
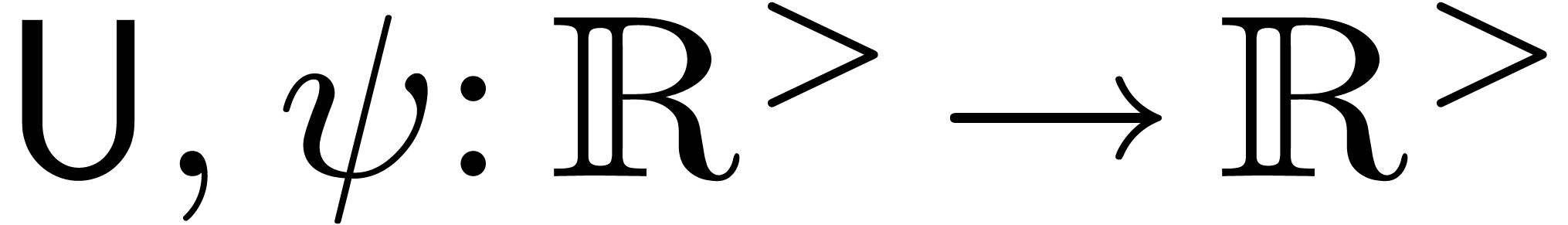 by
by
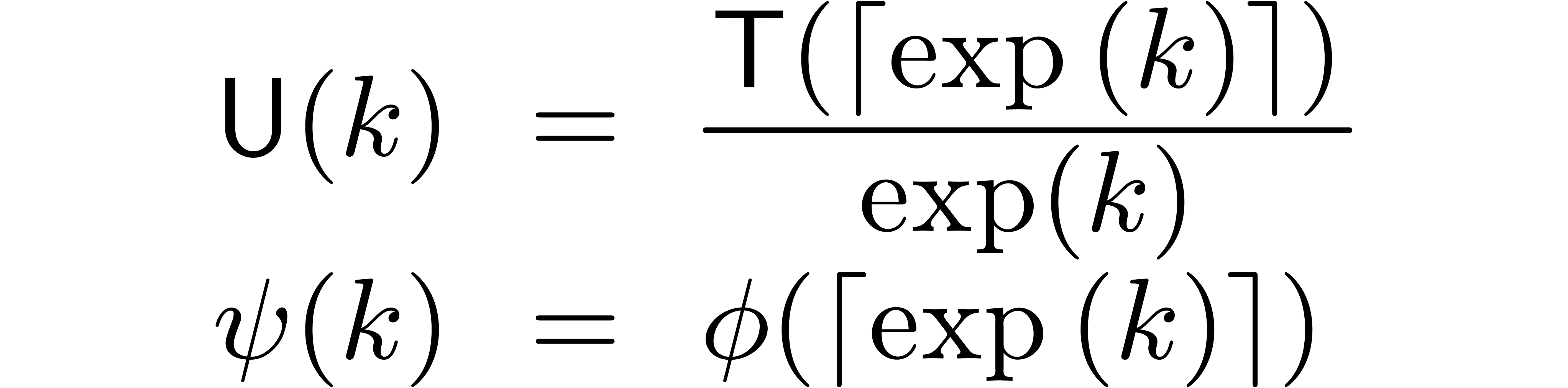
 ,
, and
and 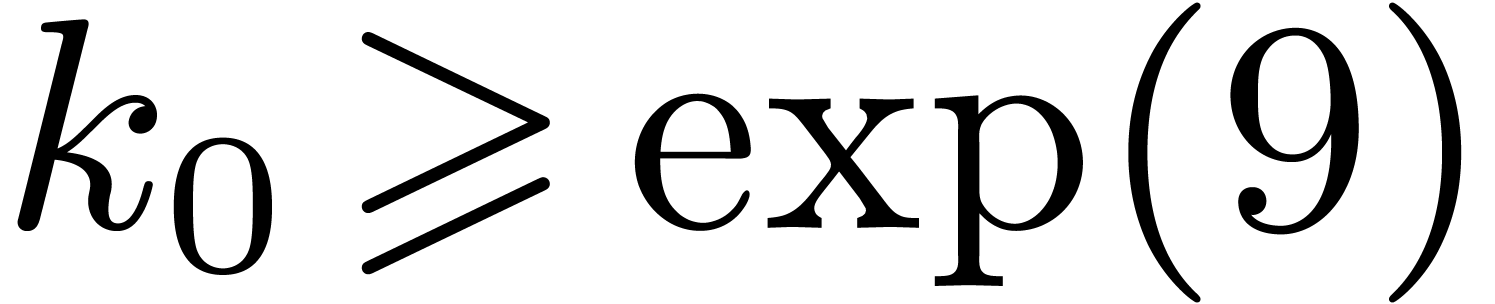 and such that (
and such that (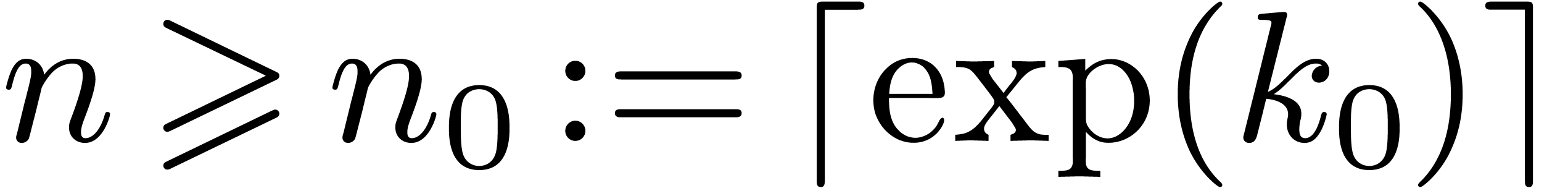 .
.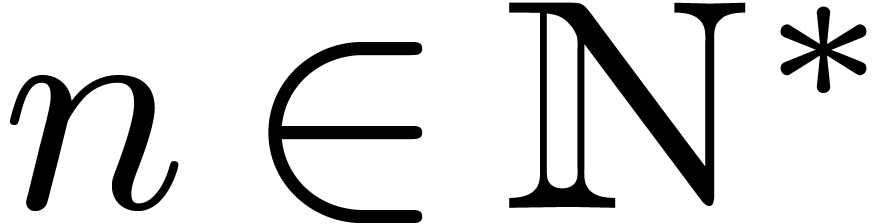 be such that
be such that  and denote
and denote 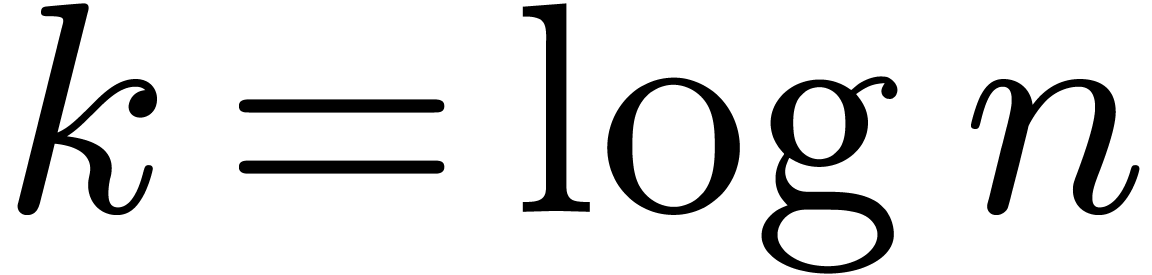 and
and 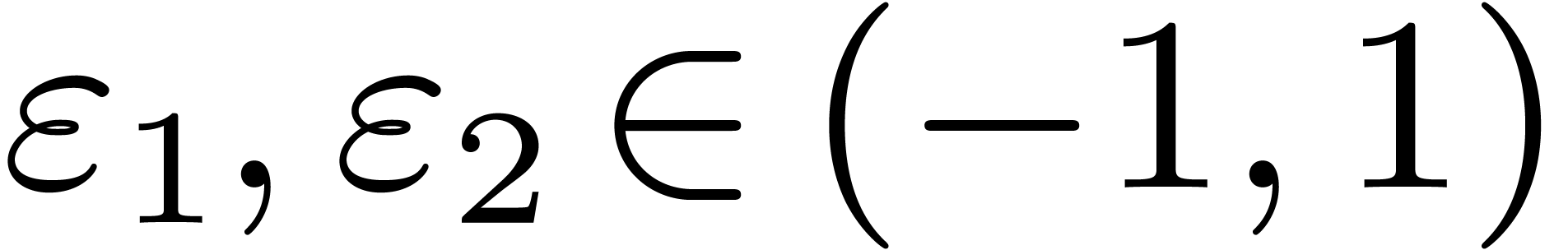 ,
,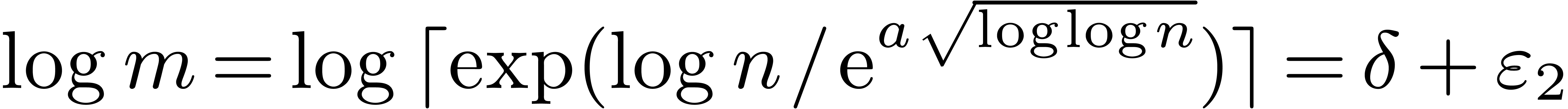 and
and 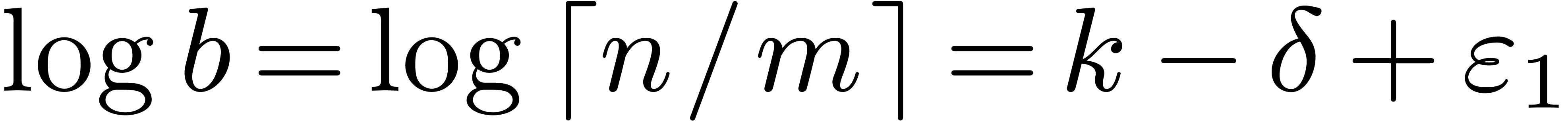 .
.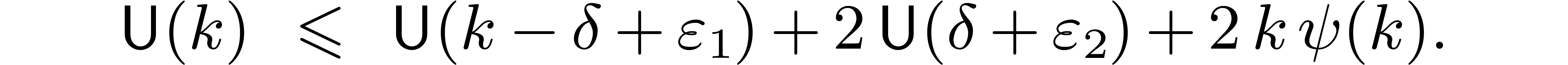
 and
and  .
. for all
for all  .
. .
.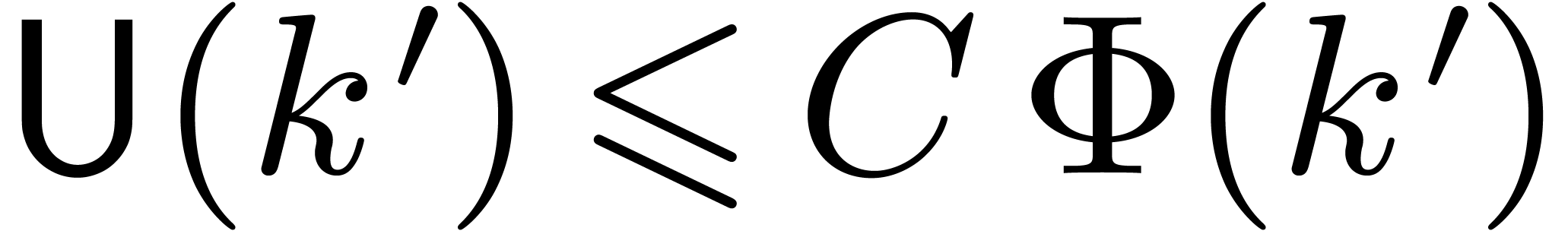 for all
for all  .
.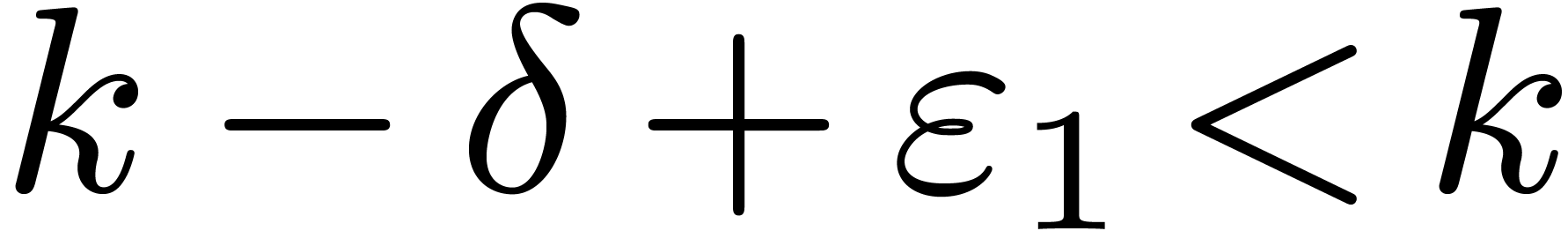 and
and  ,
,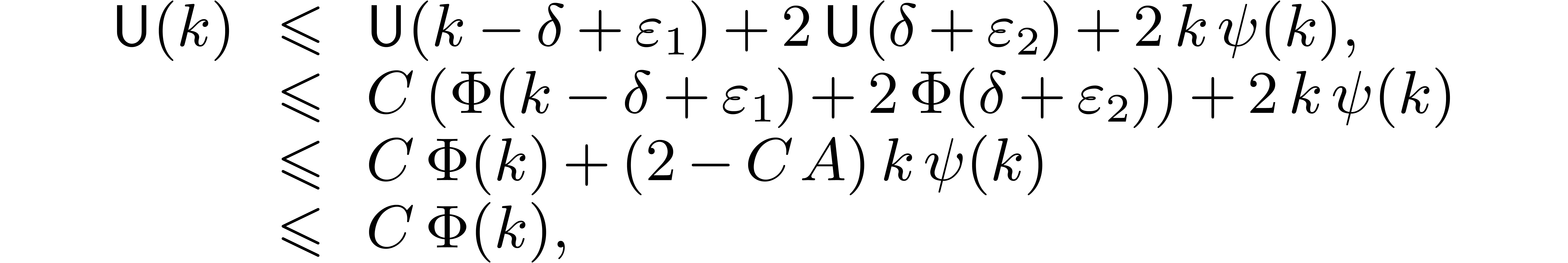
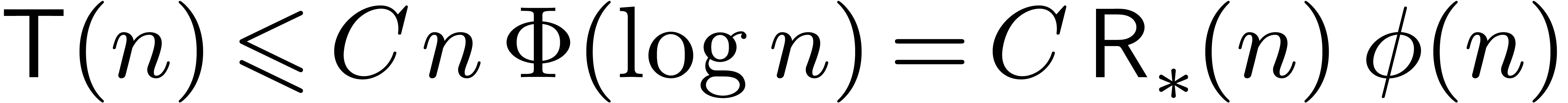 .
.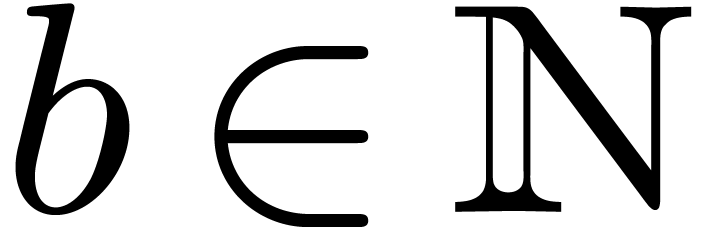 and
and 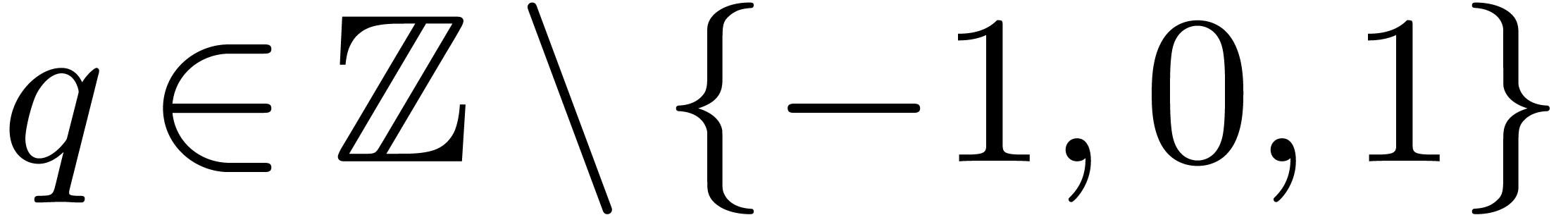 (say
(say 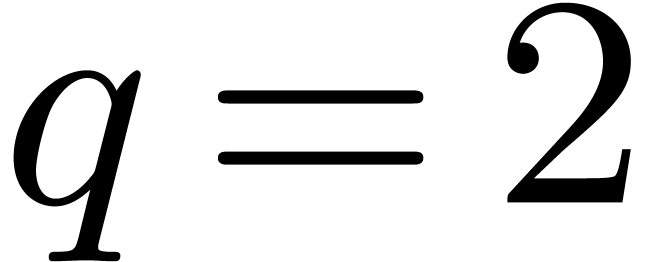 ),
),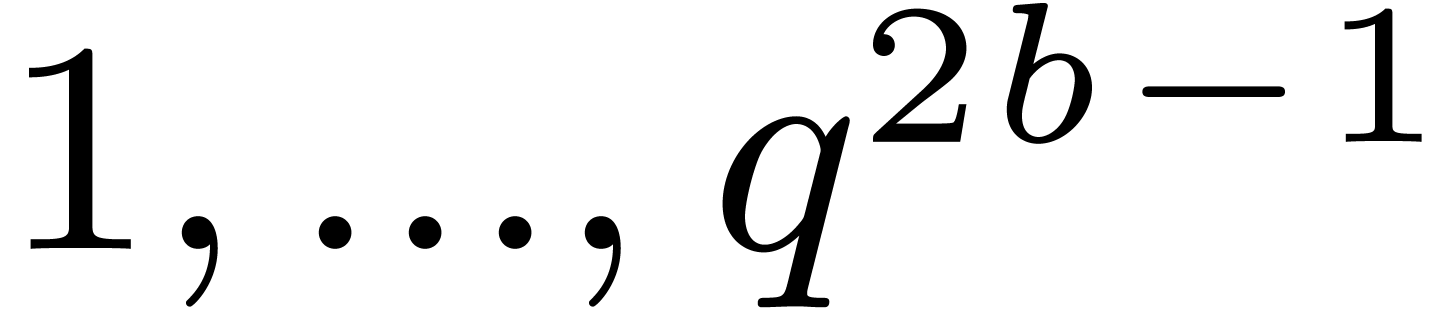 .
.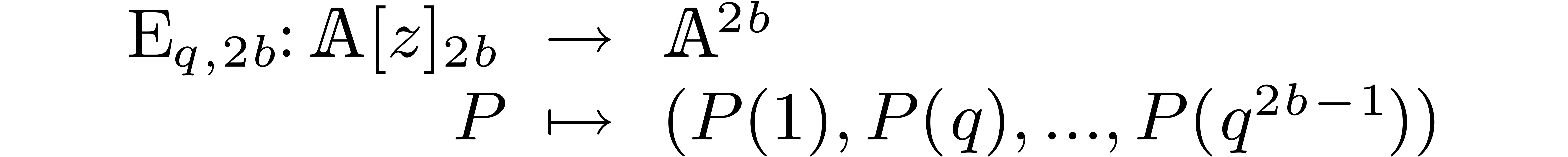
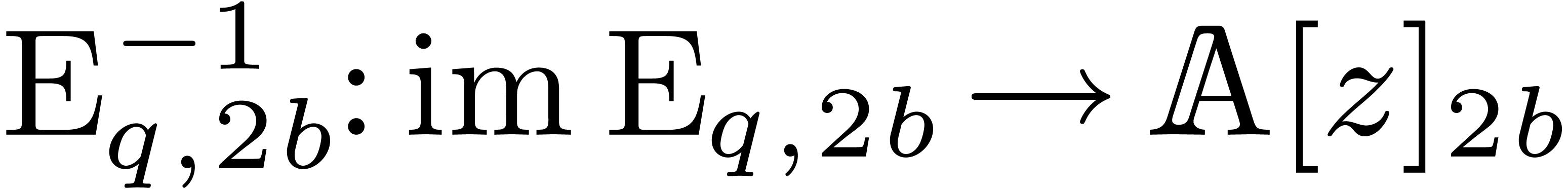 .
. operations in
operations in 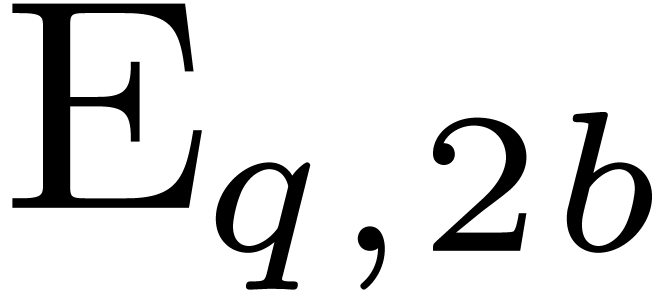 and
and 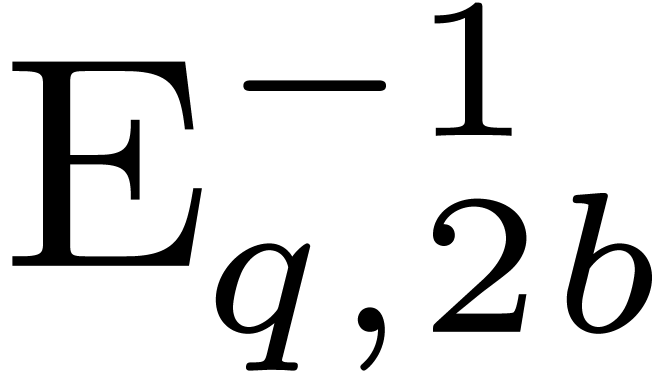 to power series in
to power series in 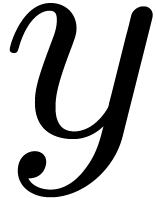 .
. both be an effective ring and an effective
torsion-free
both be an effective ring and an effective
torsion-free 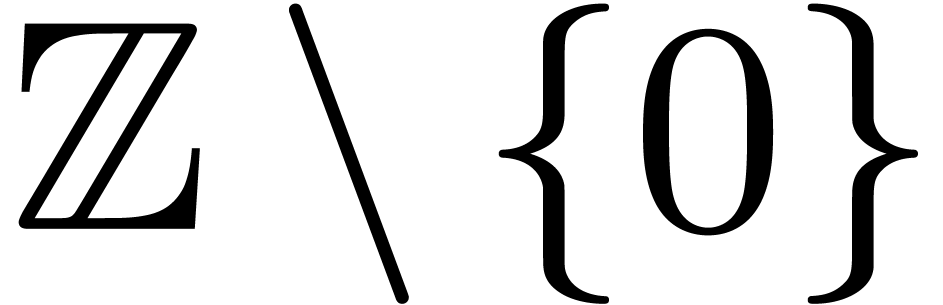 .
.
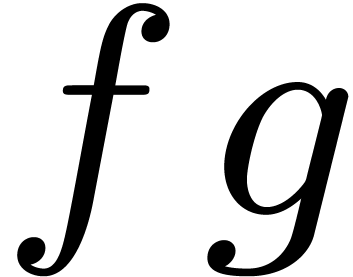 using
using
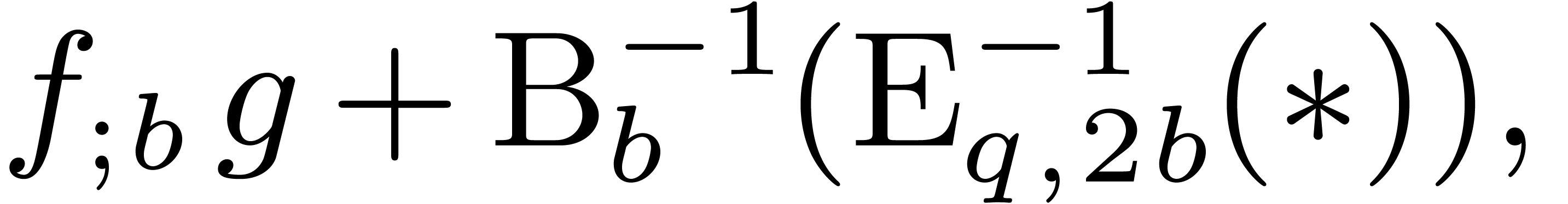
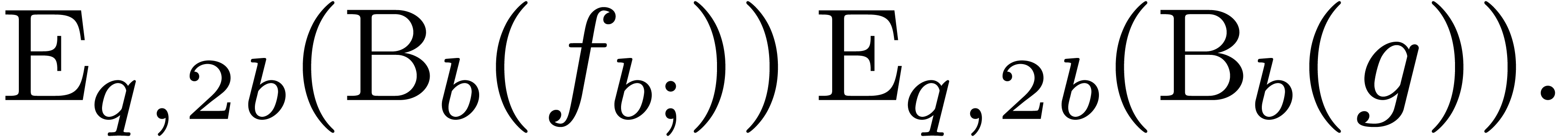
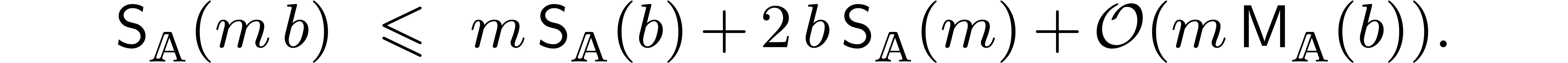
 from [
from [ ,
, be even with
be even with 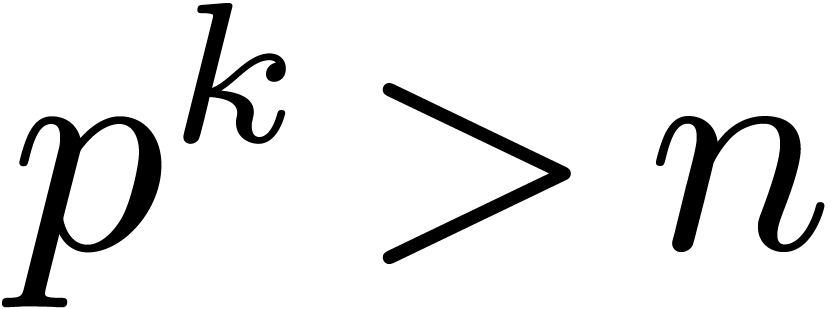 .
.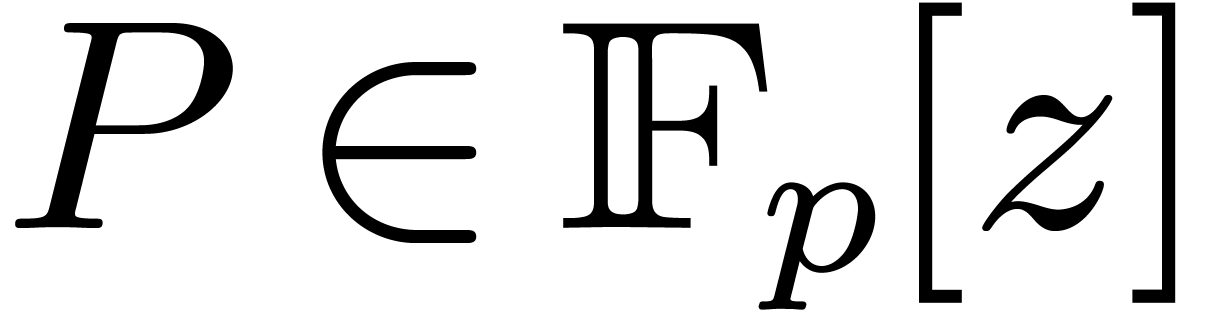 be such that the finite field
be such that the finite field 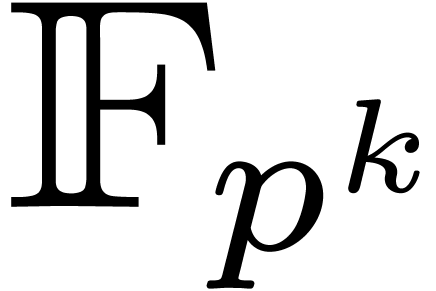 is
isomorphic to
is
isomorphic to 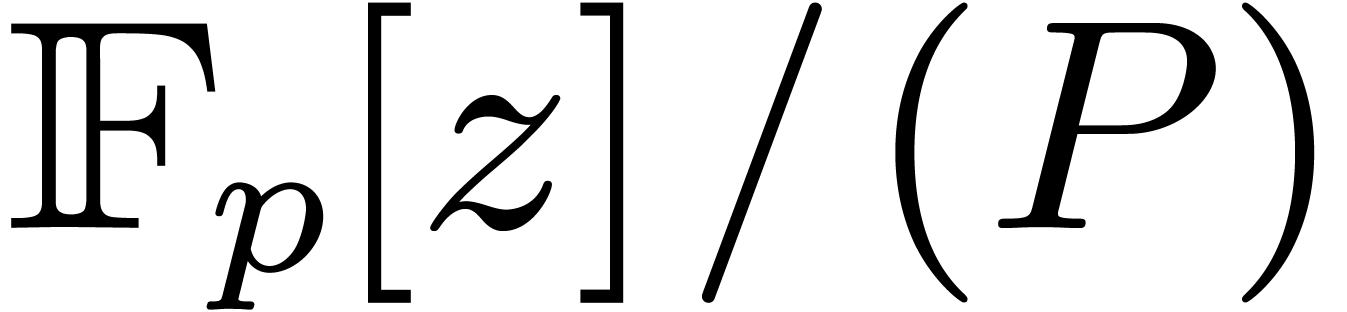 .
.
 is an effective ring and one addition
or subtraction in
is an effective ring and one addition
or subtraction in  operations in
operations in 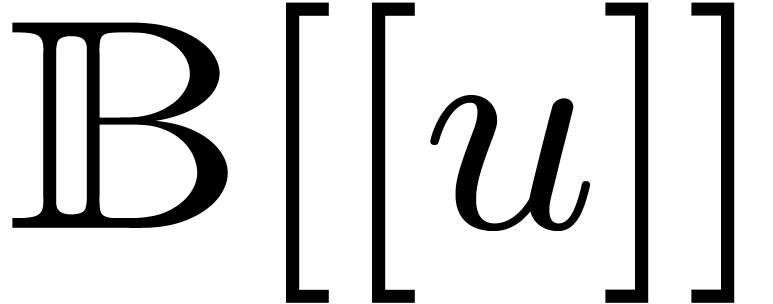 with
with 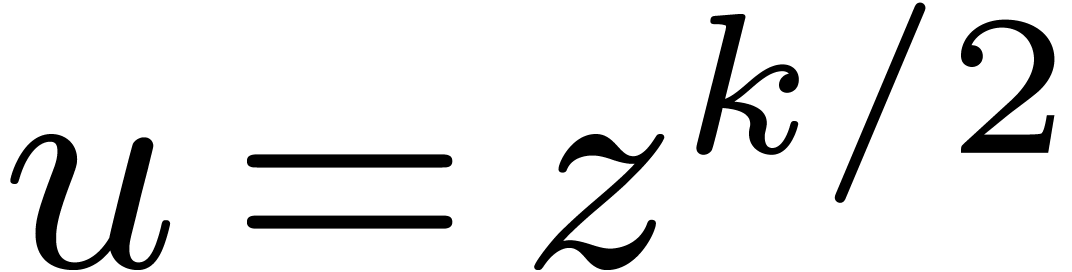 .
. coefficients apart, as we did before for
the blocking strategy. More precisely, we will compute the semi-relaxed
product
coefficients apart, as we did before for
the blocking strategy. More precisely, we will compute the semi-relaxed
product 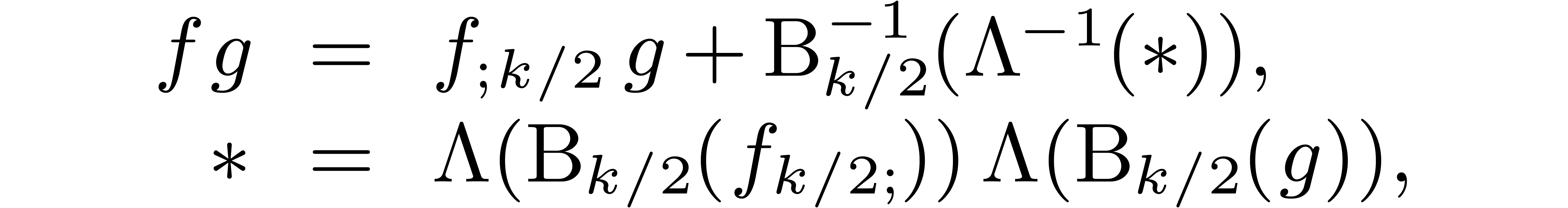
 to
to 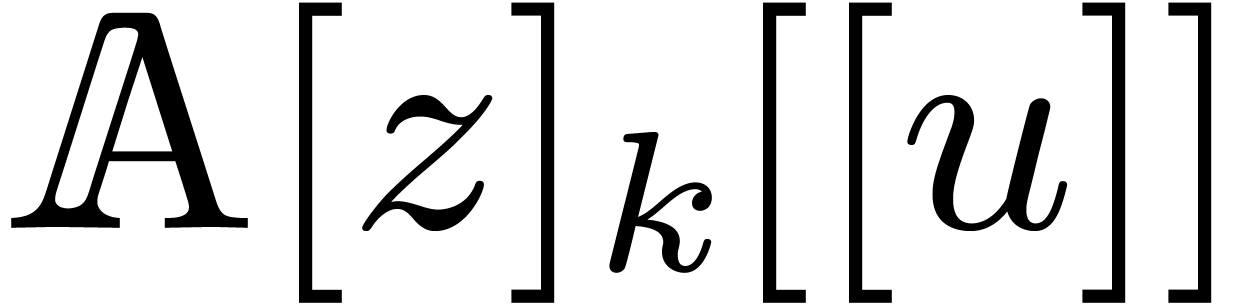 in
the natural way:
in
the natural way:
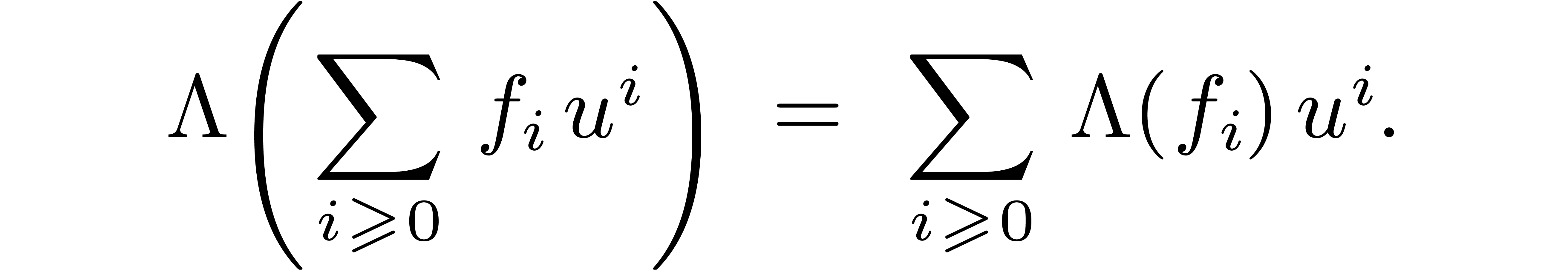
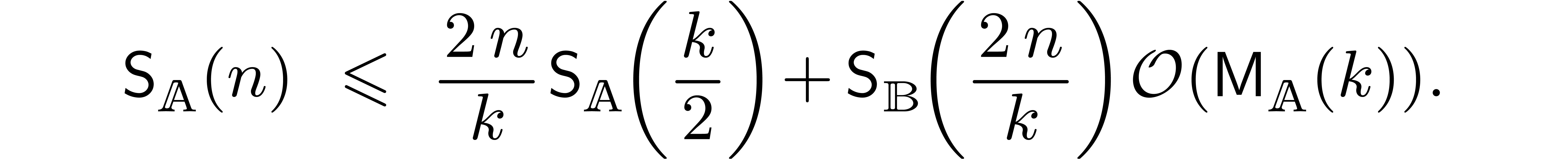
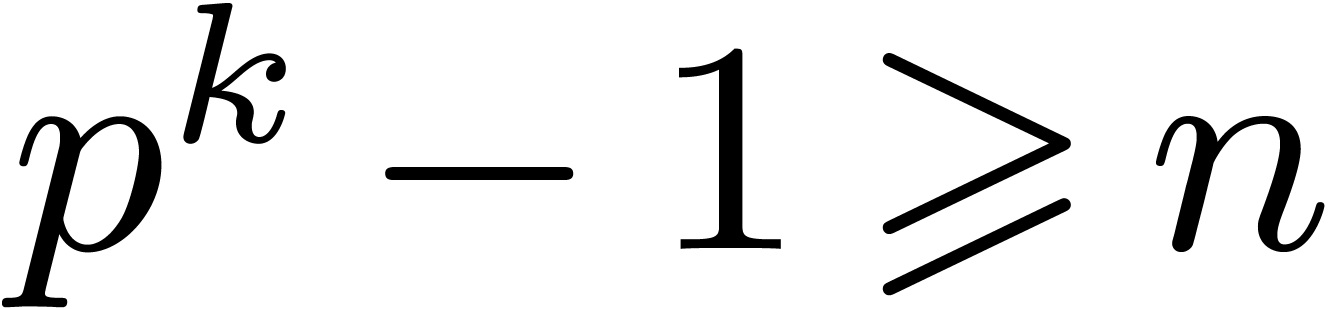 points in geometric progression. For the multiplication up to order
points in geometric progression. For the multiplication up to order 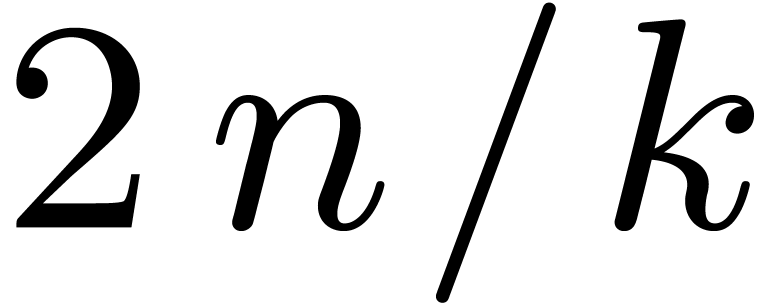 of two series with coefficients in
of two series with coefficients in 
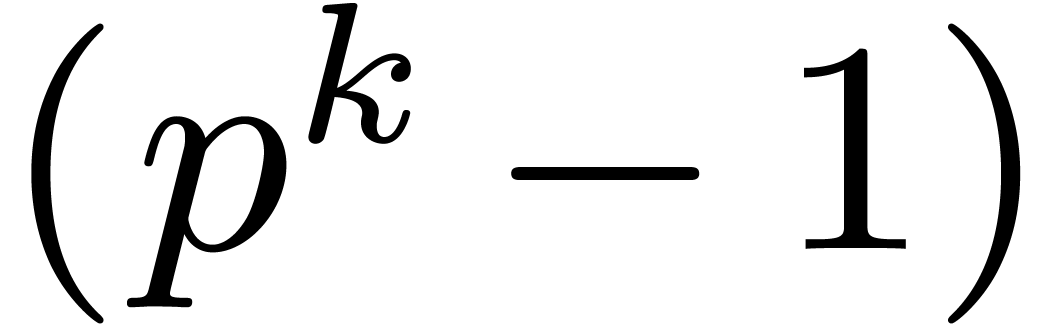 -th
-th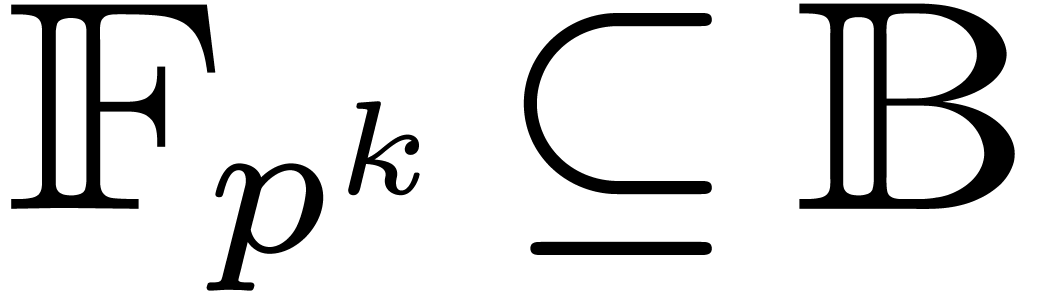 .
.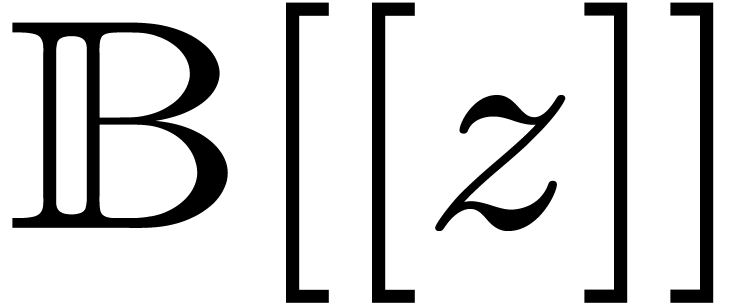 up to order
up to order
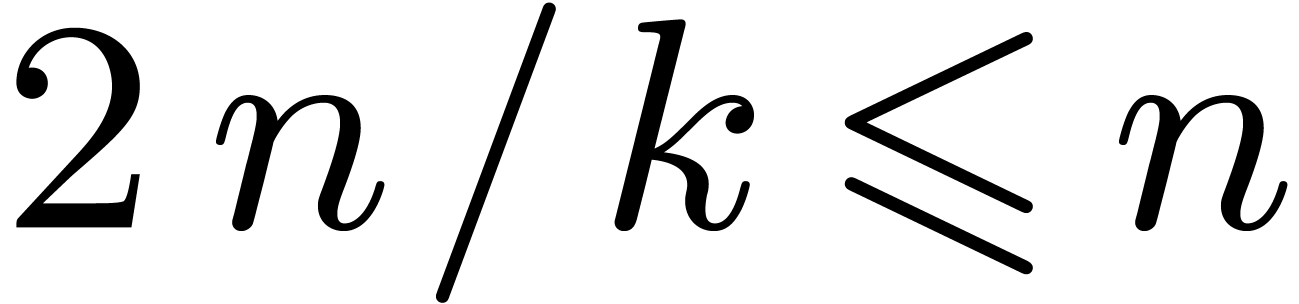 .
.
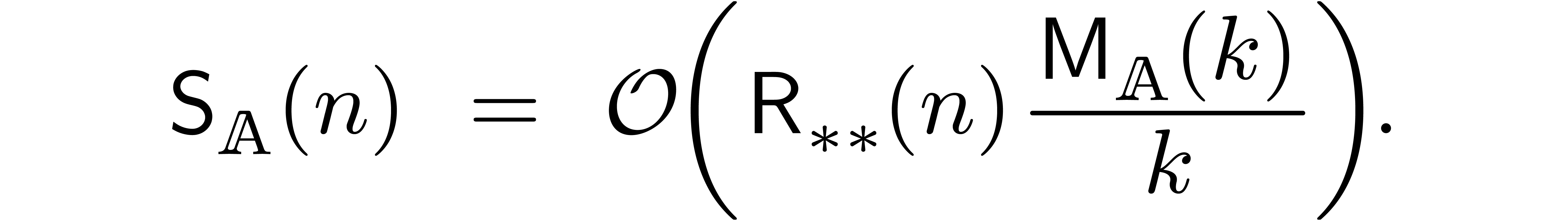
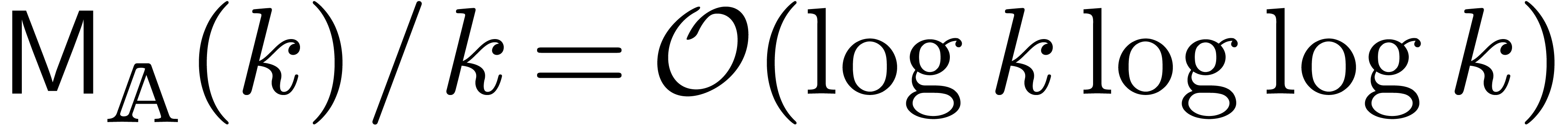 and
and 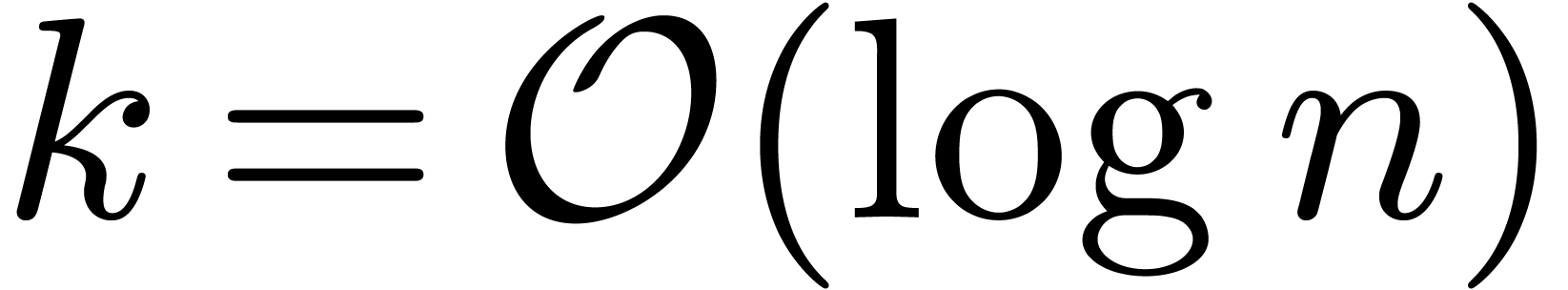 ,
,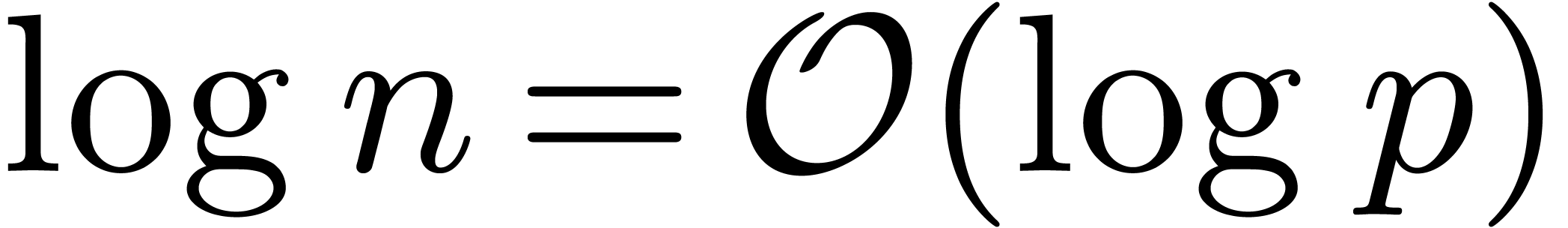 ,
,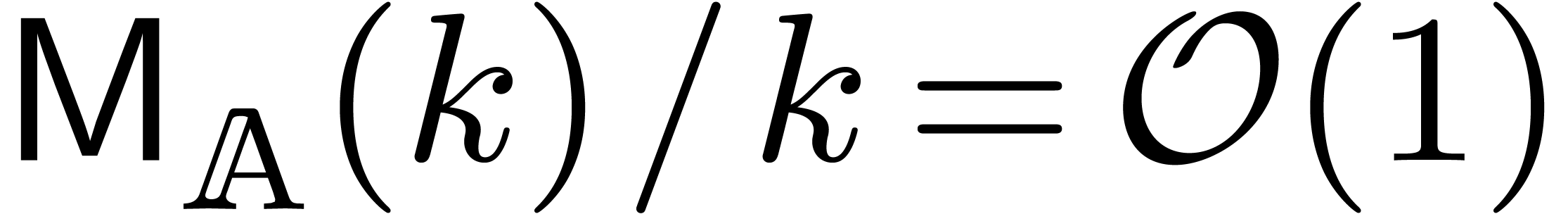 in (
in (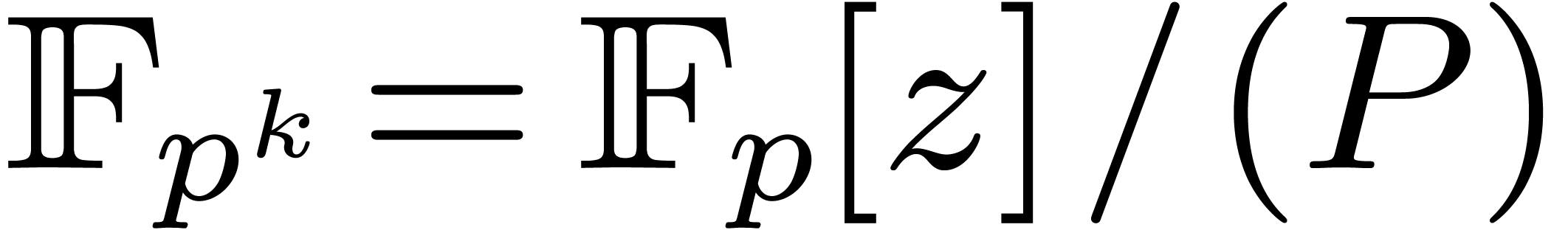 .
.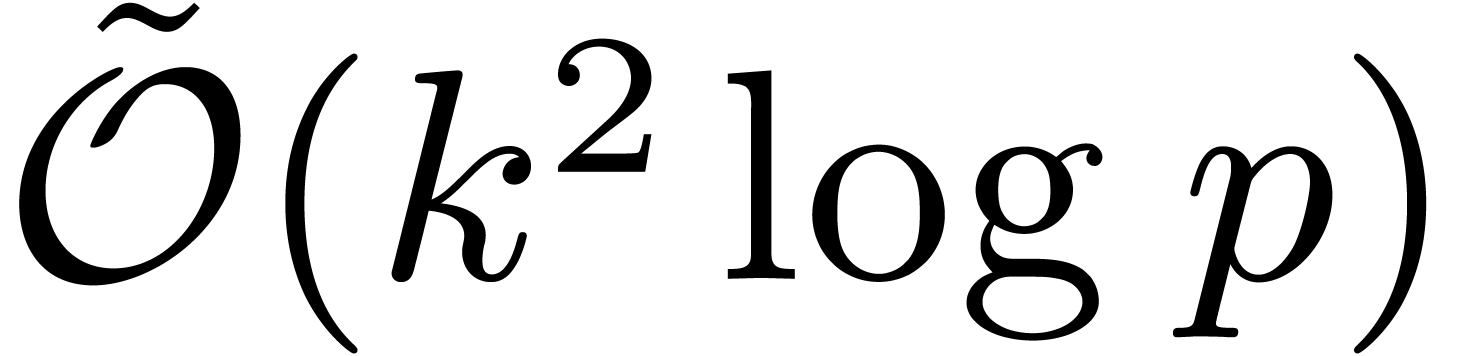 ;
;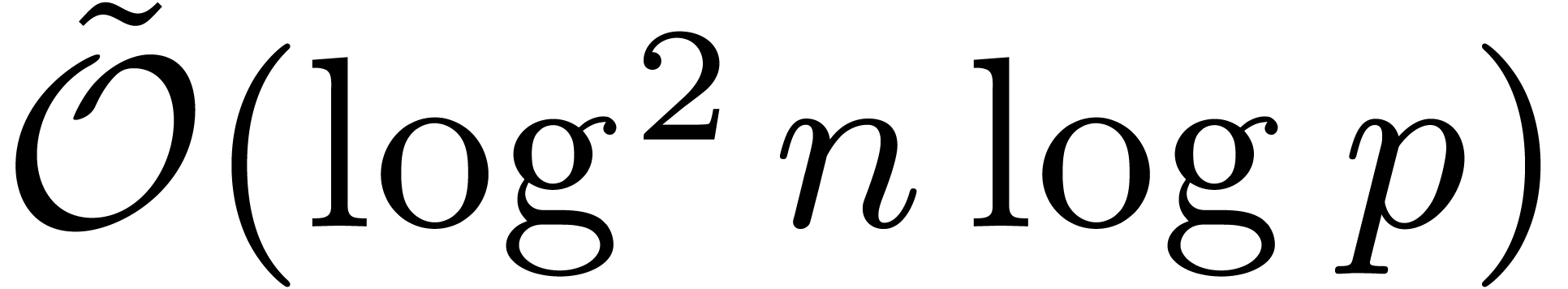 .
. in a deterministic
way, then one may use [
in a deterministic
way, then one may use [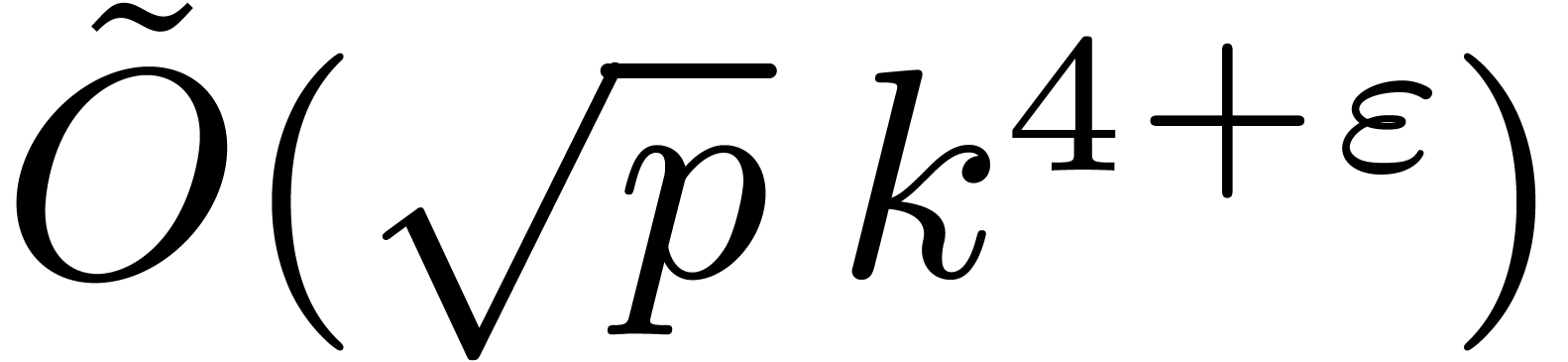 .
. ,
, .
. .
.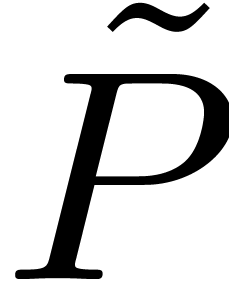 of degree
of degree 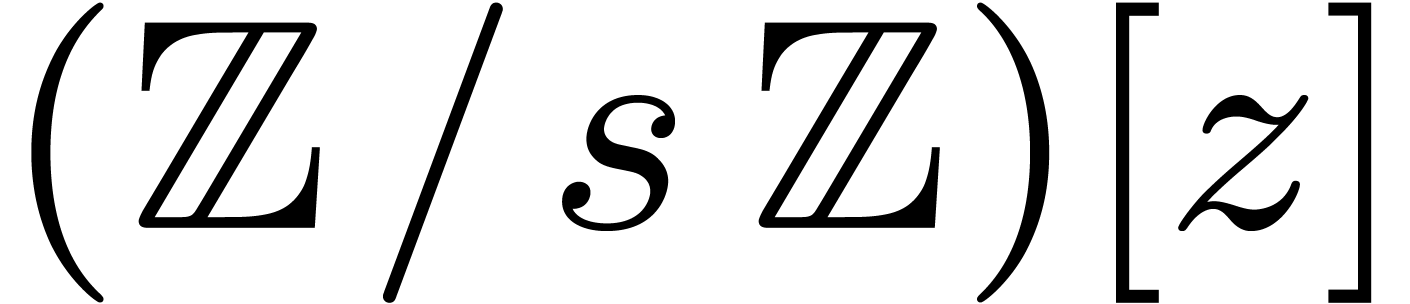 such that
the reduction
such that
the reduction 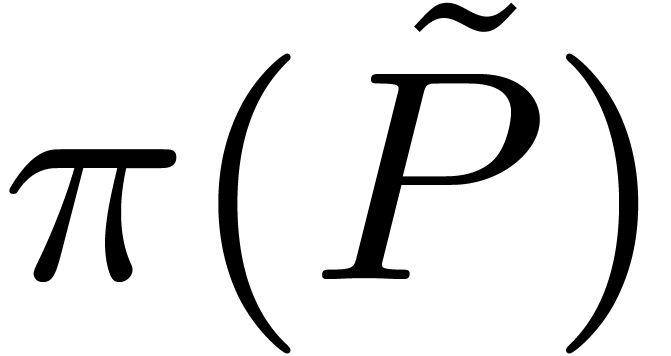 of
of 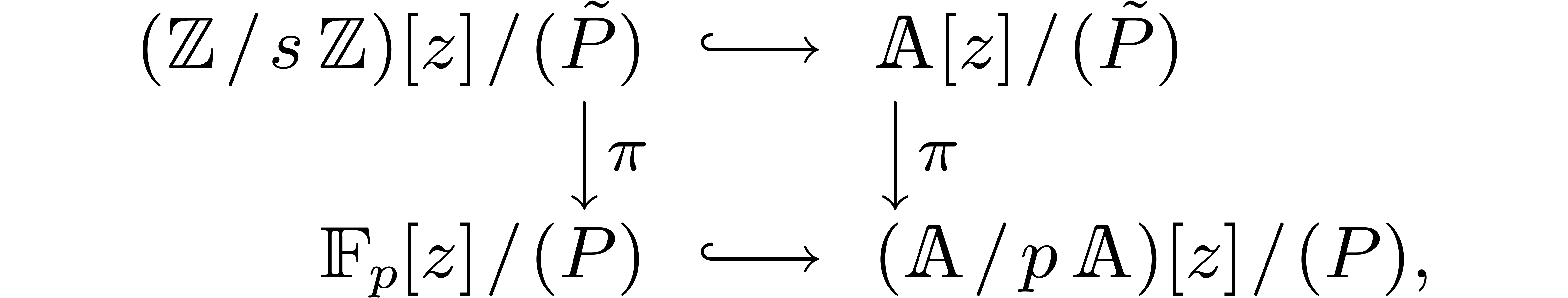
 stands for reduction modulo
stands for reduction modulo 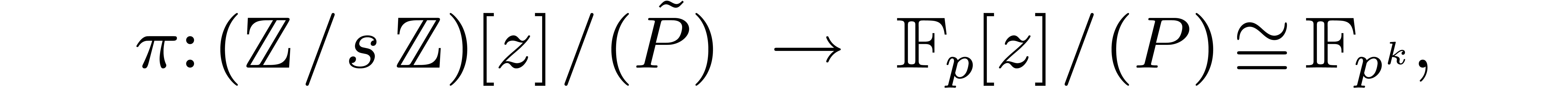
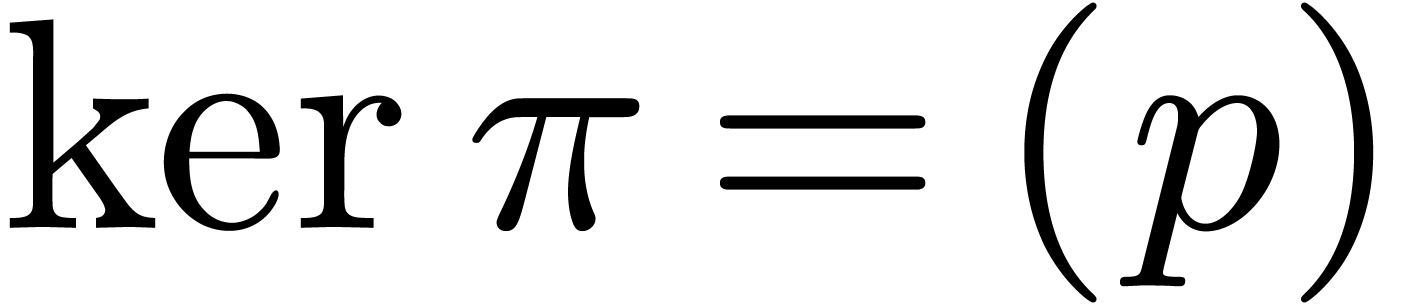 .
. of
of  has order at least
has order at least 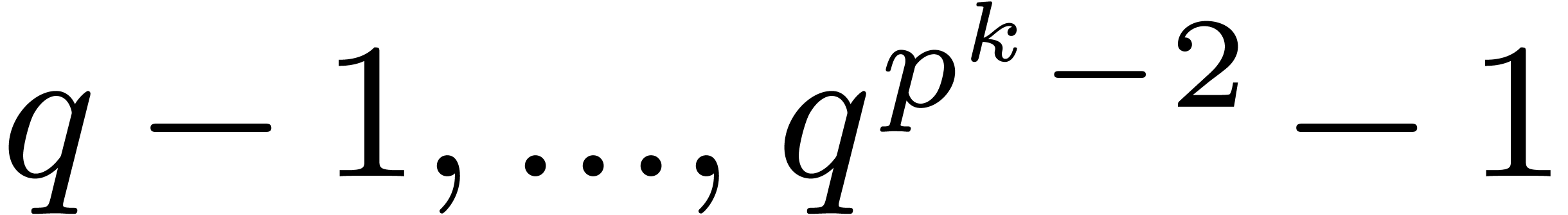 and
and 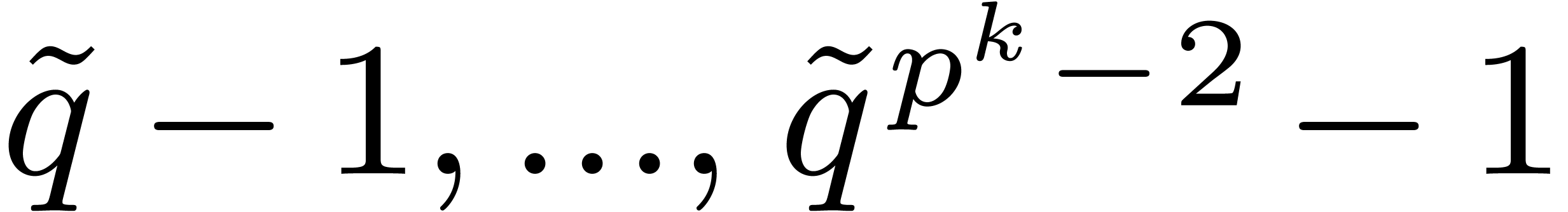 and
and  do not lie in
do not lie in 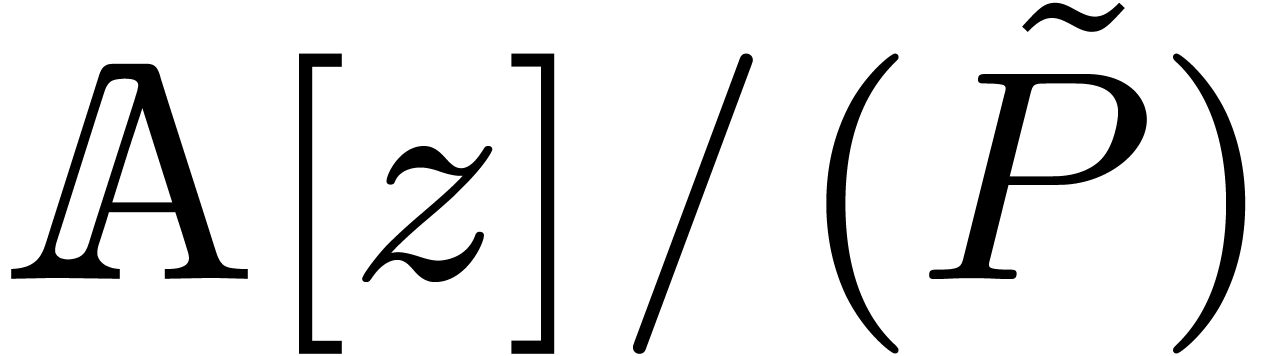 at the sequence
at the sequence
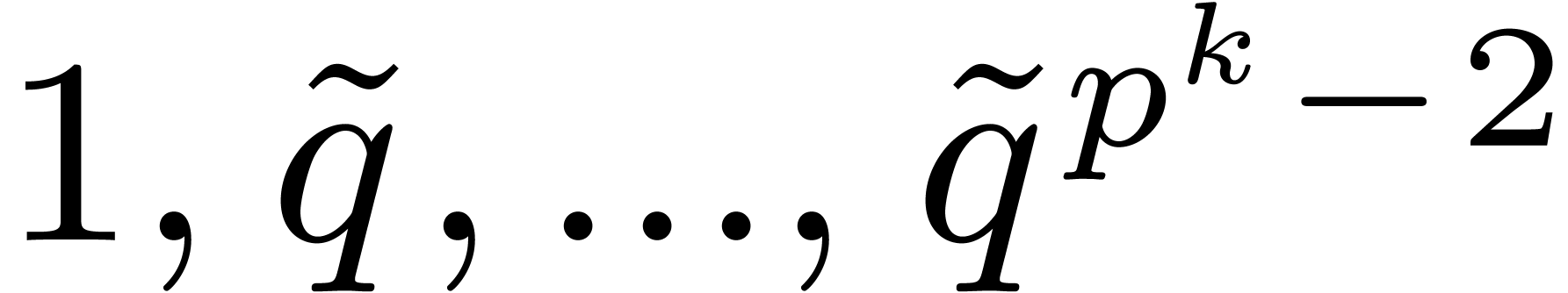 ,
, with
with 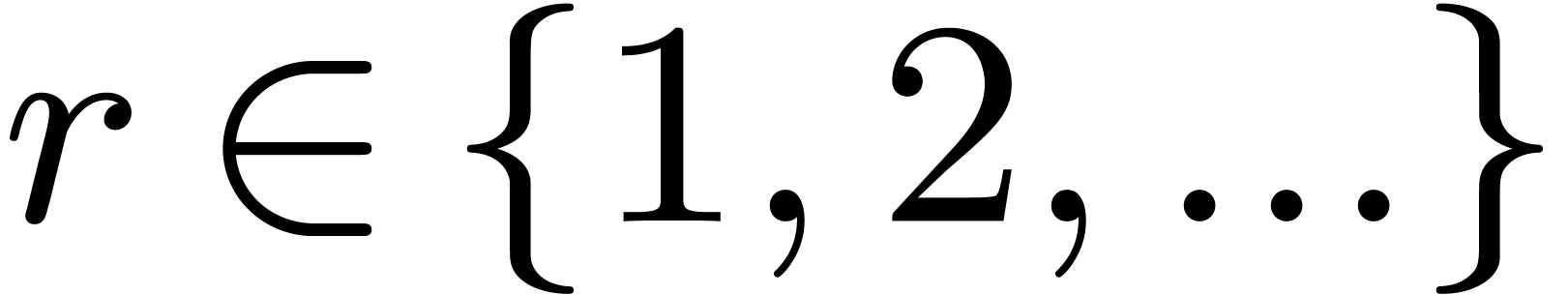 ,
,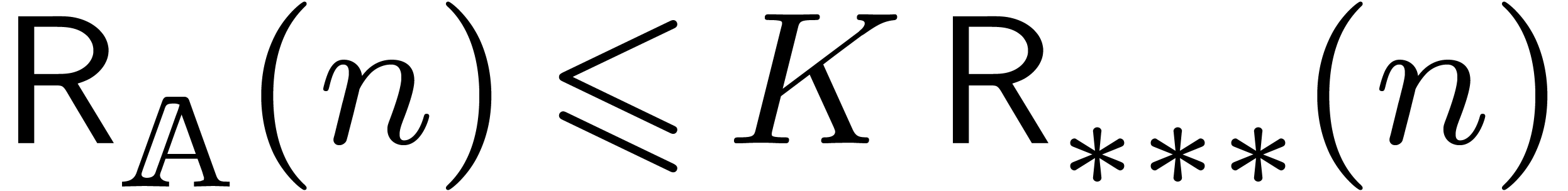 .
.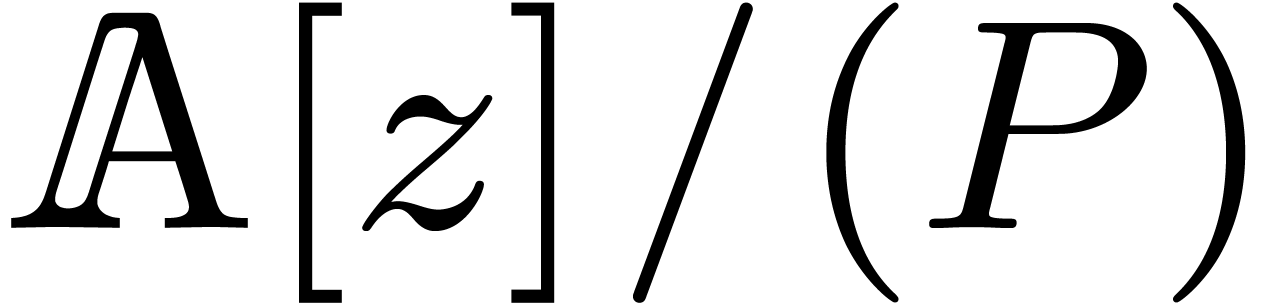 in the
case
in the
case 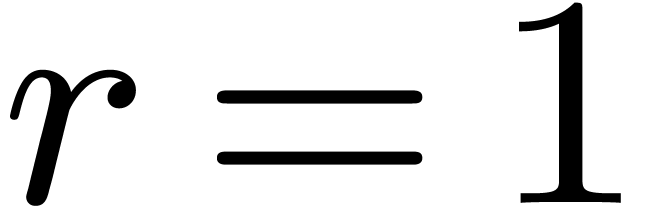 corresponds to exactly one lifted operation
in
corresponds to exactly one lifted operation
in 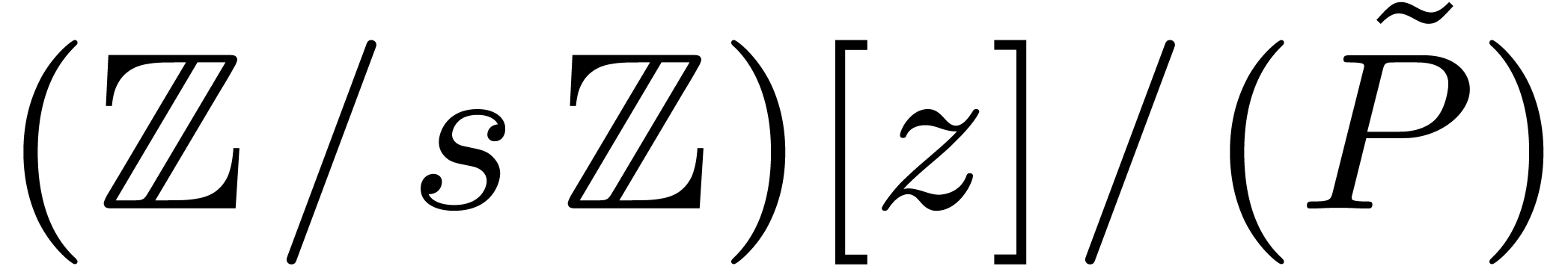 or
or  .
. ,
, and
and  are relatively prime, and let
are relatively prime, and let 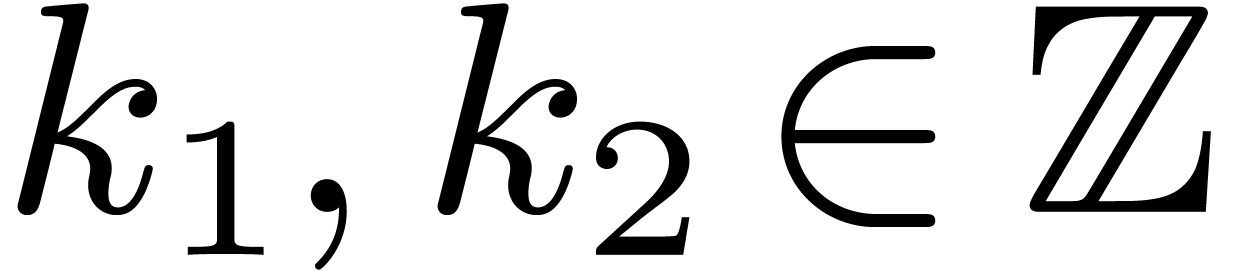 be such that
be such that
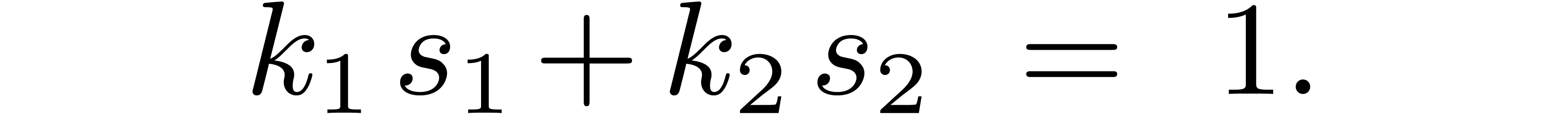
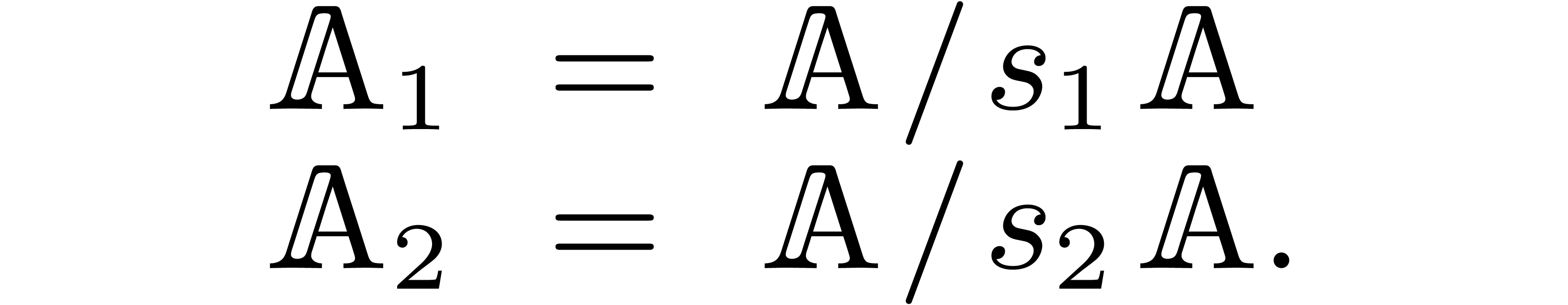
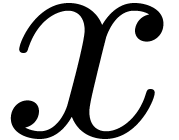 of
of  (or
(or  )
) for any
for any 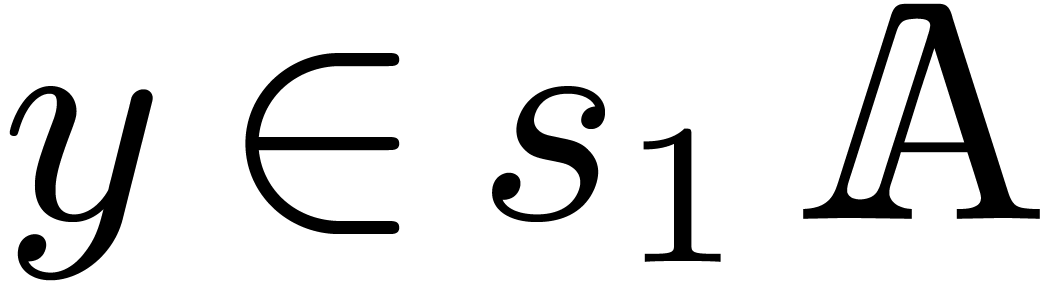 (or
(or 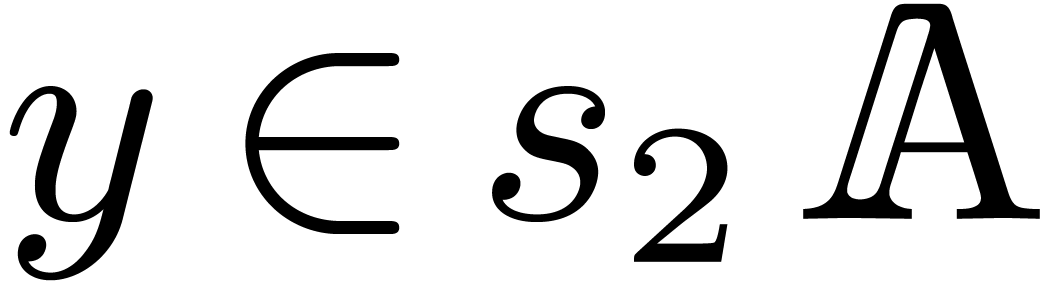 ).
).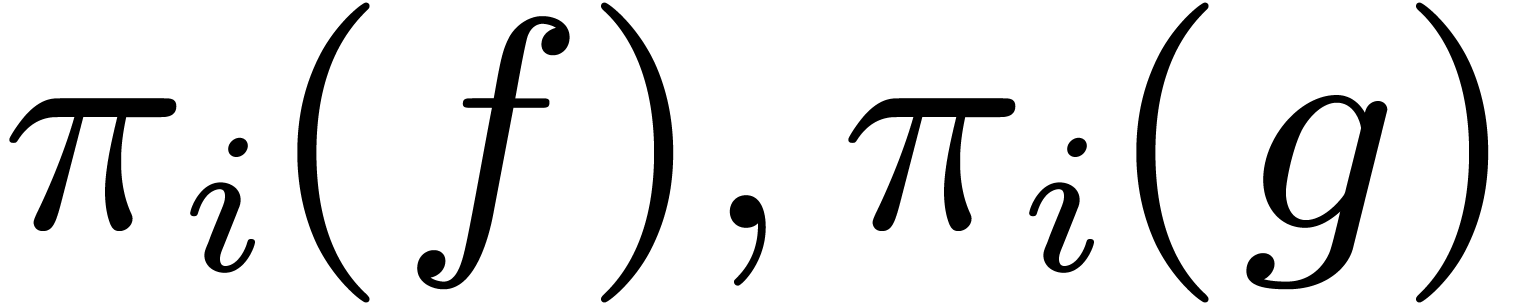 be their
projections in
be their
projections in 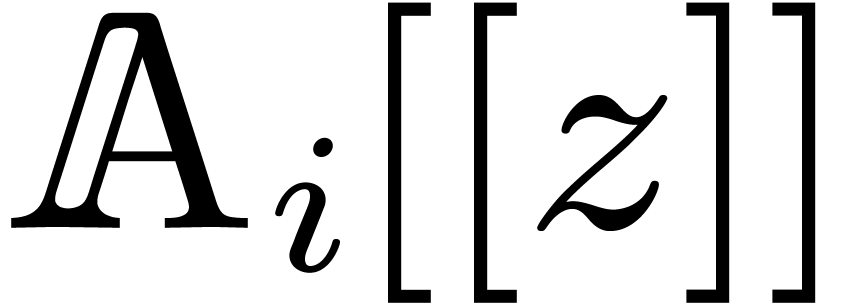 ,
,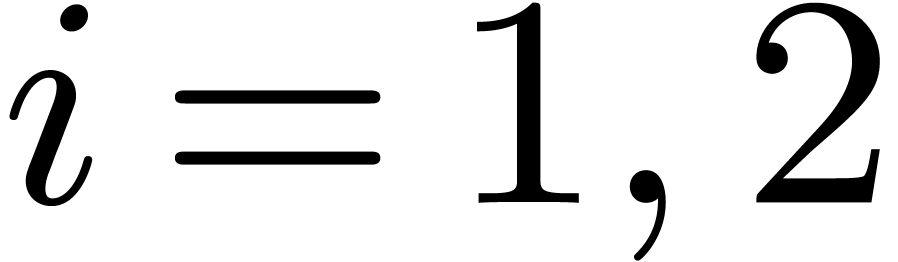 .
.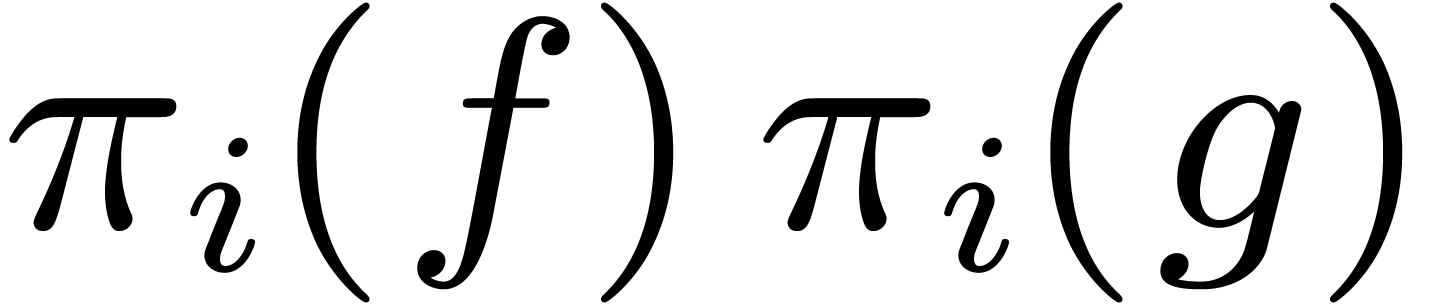 ,
,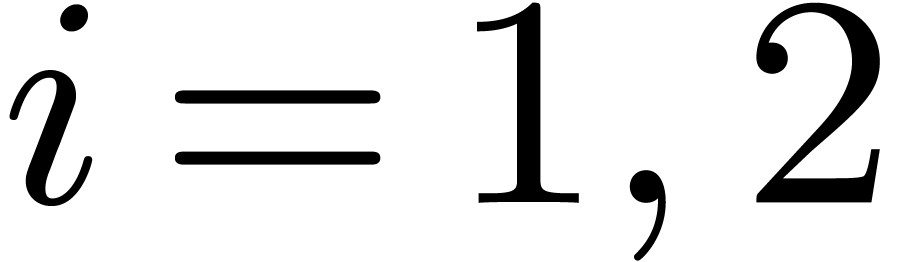 .
.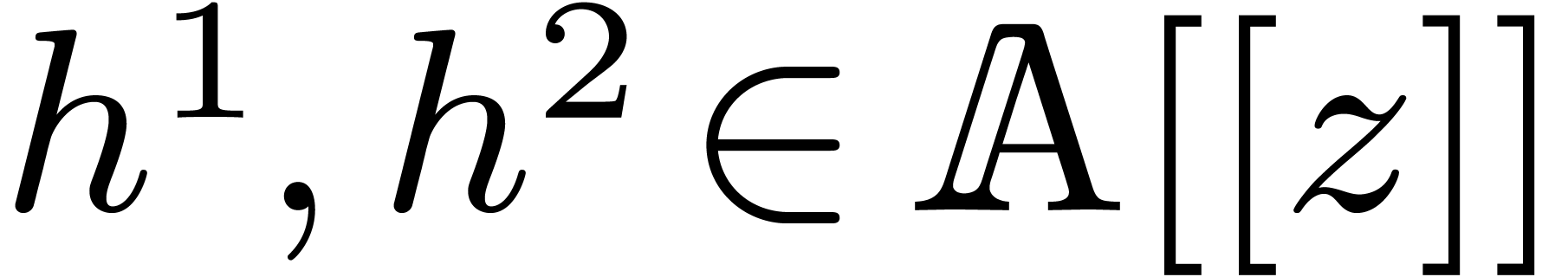 via
via 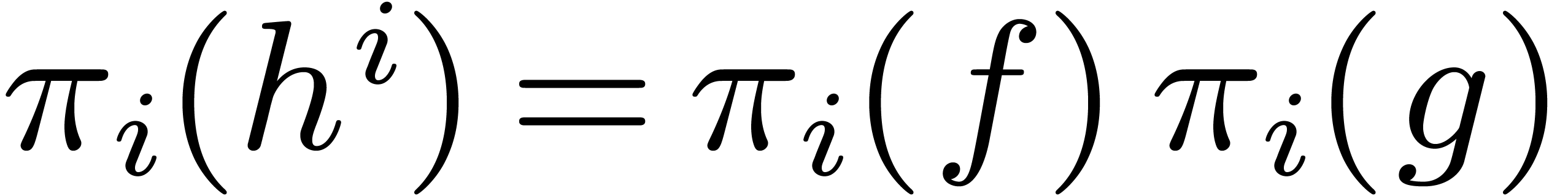 ,
,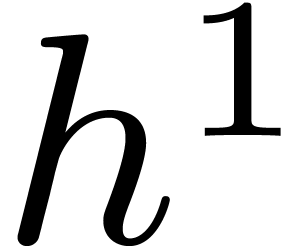 and
and 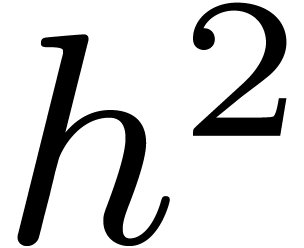 at order
at order  operations in
operations in 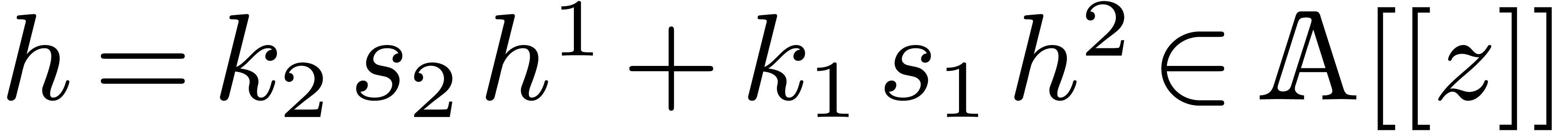 can still be expanded up to order
can still be expanded up to order
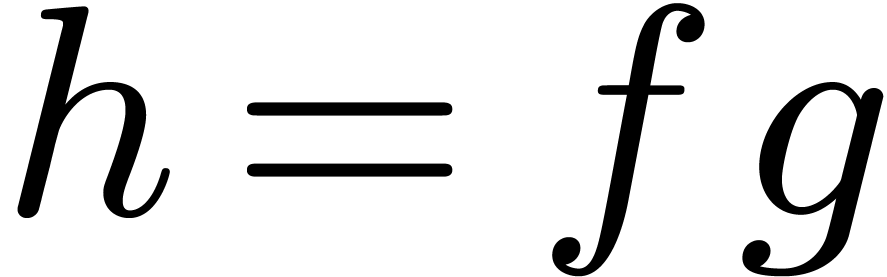 .
.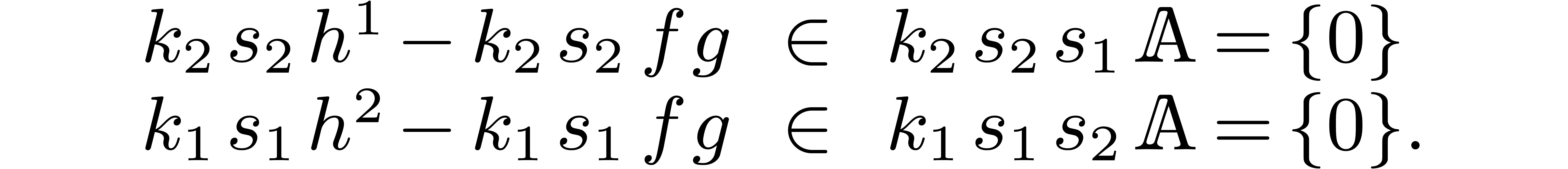
 be an integer, not necessarily a prime
number, and denote
be an integer, not necessarily a prime
number, and denote  .
.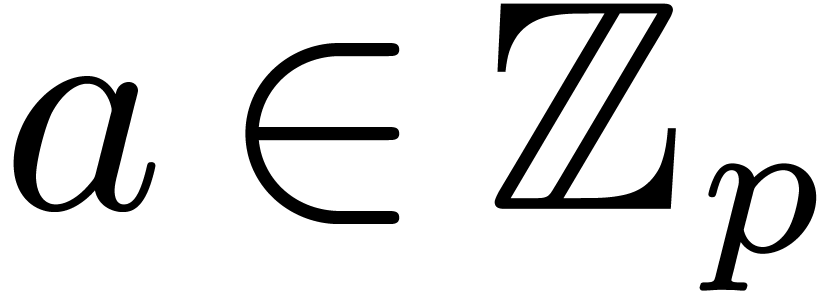 as series
as series 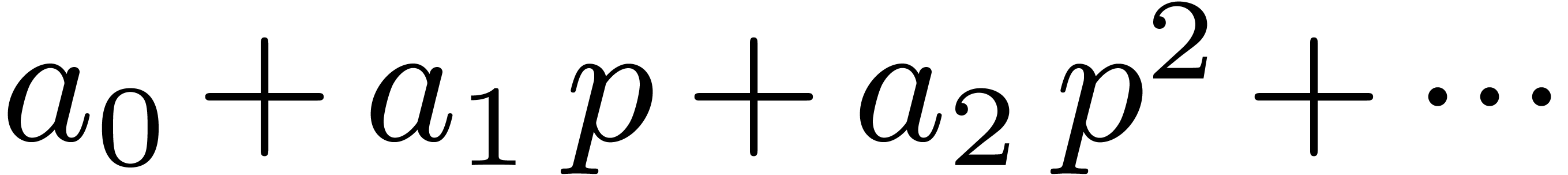 with
with 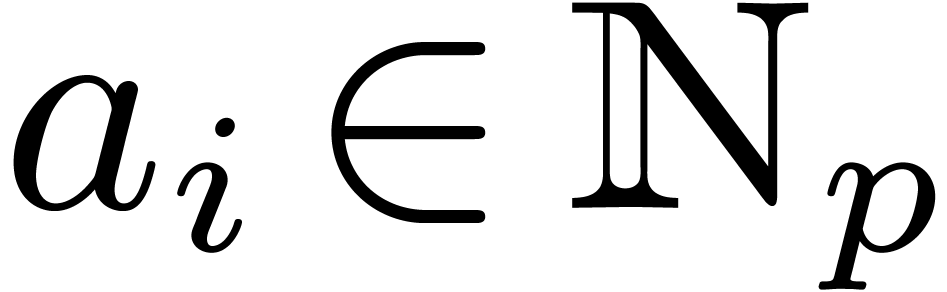 ,
,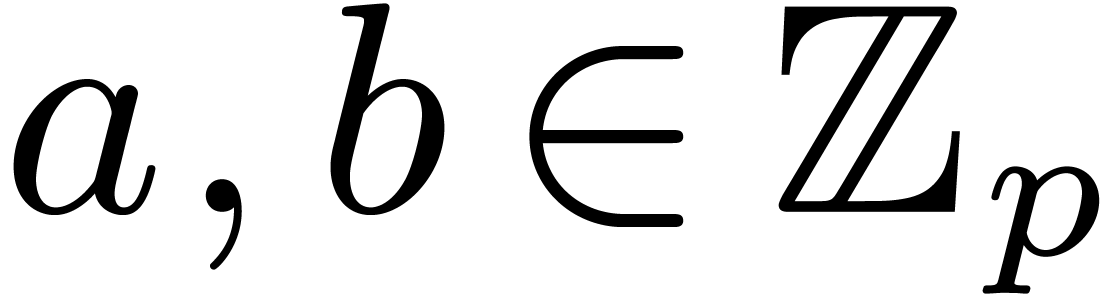 ,
, ,
, ,
,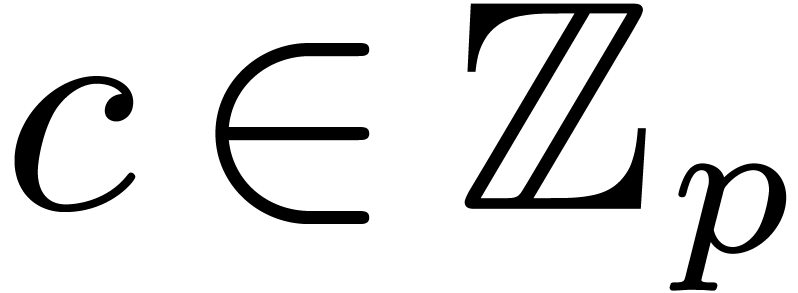 from the result. Of course, the
coefficients of
from the result. Of course, the
coefficients of  may exceed
may exceed  from
from  using
using  ring operations in
ring operations in 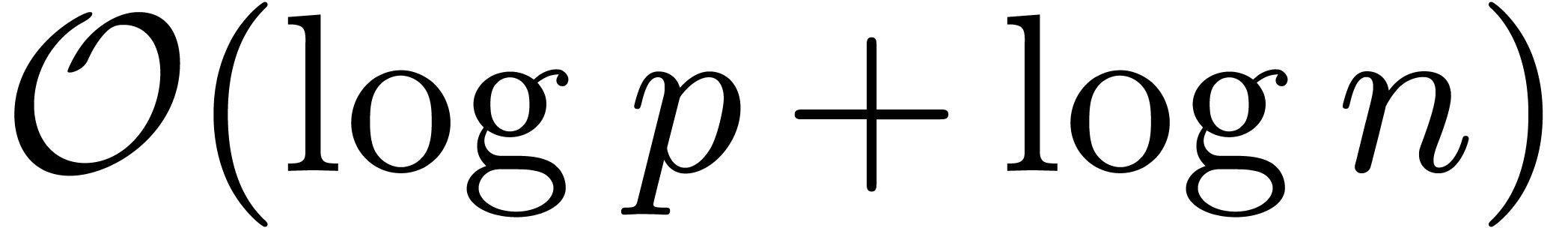 .
. ,
,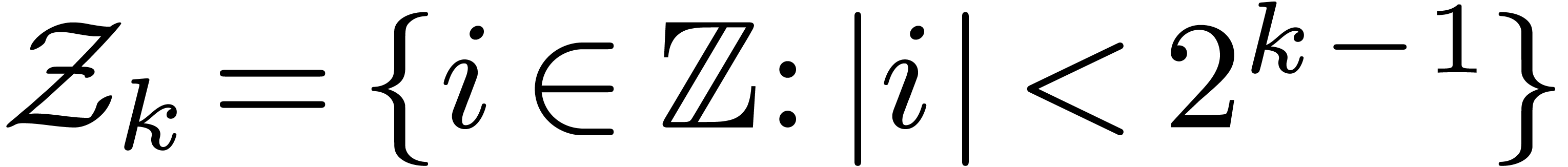 ,
,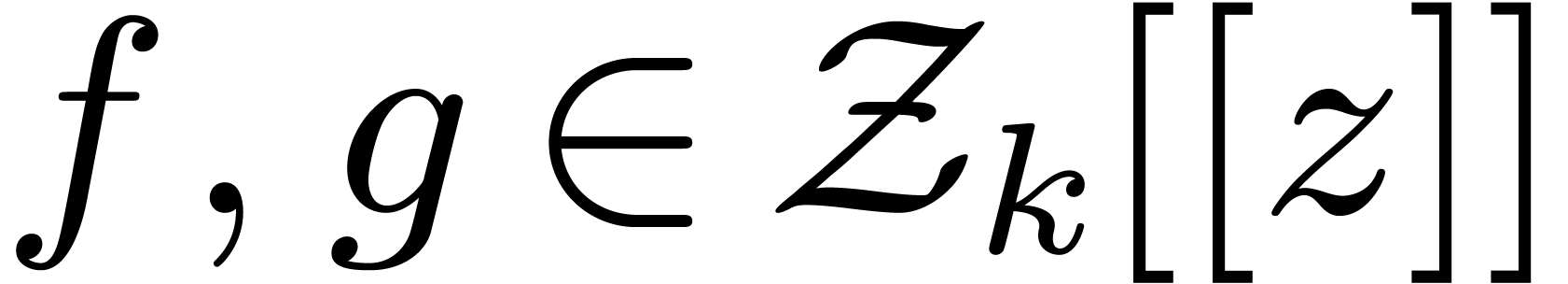 .
.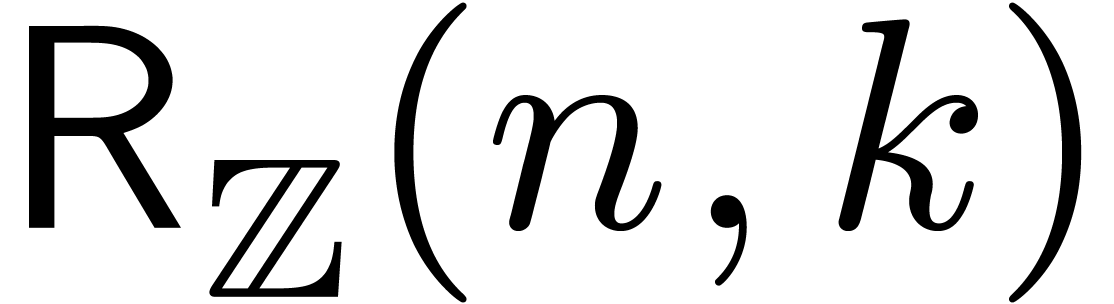 (resp.
(resp. 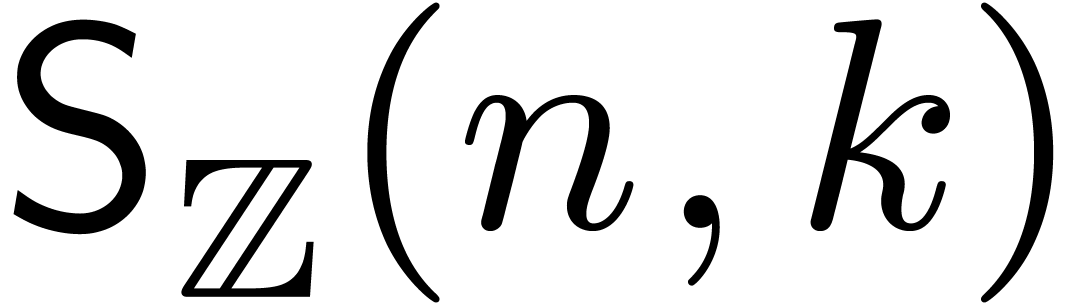 )
)
 .
.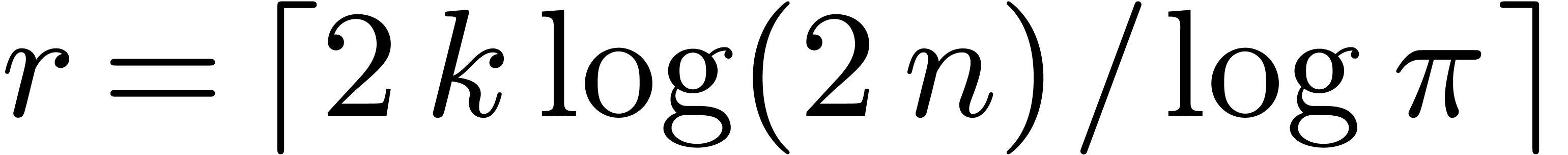 such
that
such
that 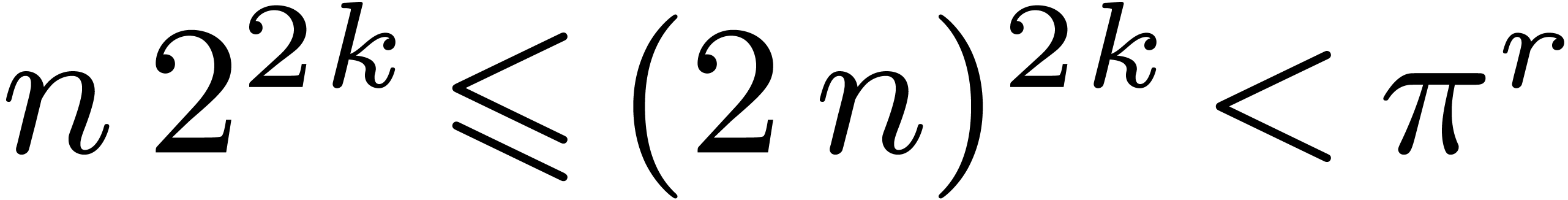 .
. be the reductions of
be the reductions of  modulo
modulo  .
. .
.
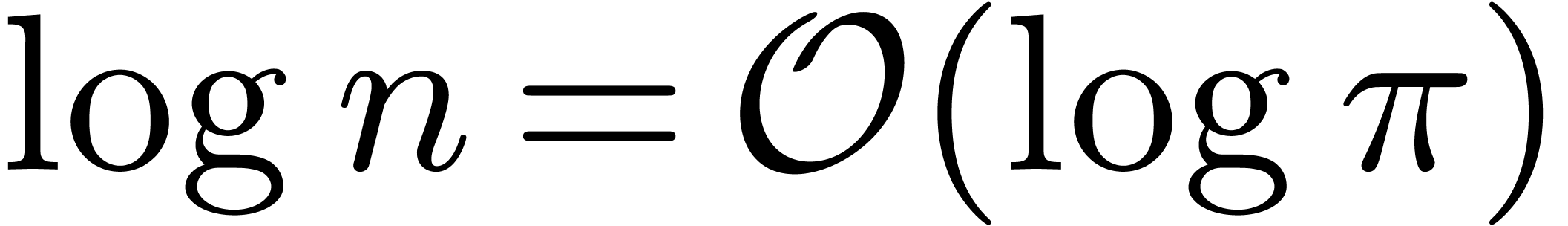 ,
,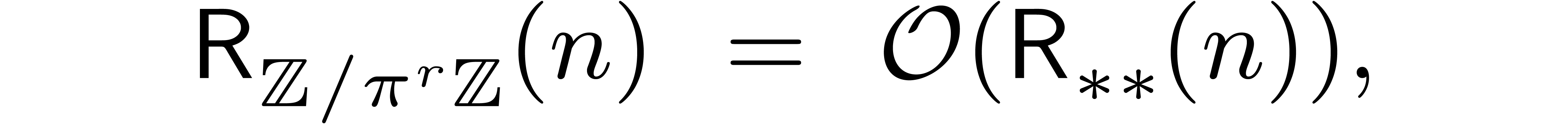
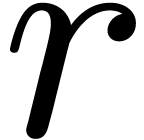 .
.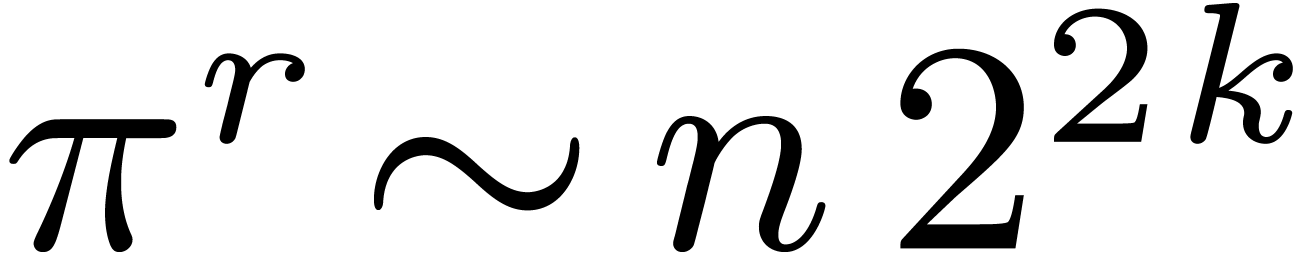 ,
,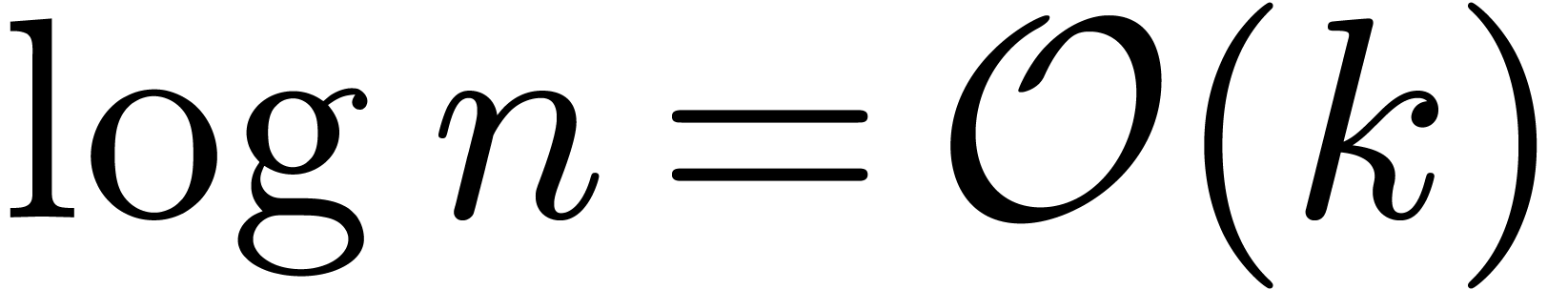 .
. ,
,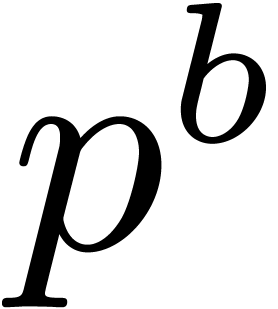 -adic
-adic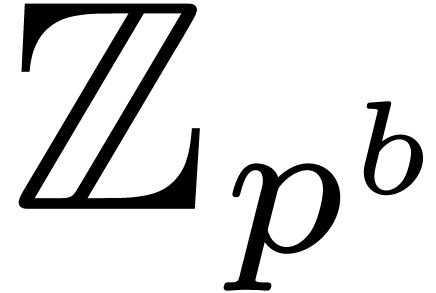 ,
,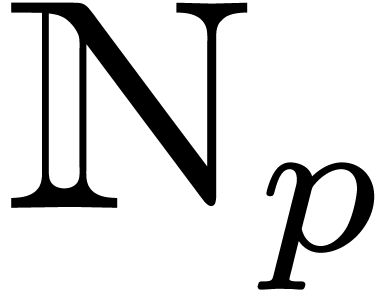 are written
in base
are written
in base 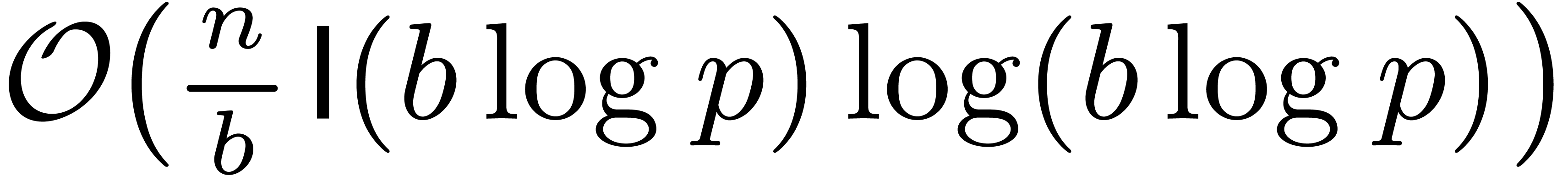 .
.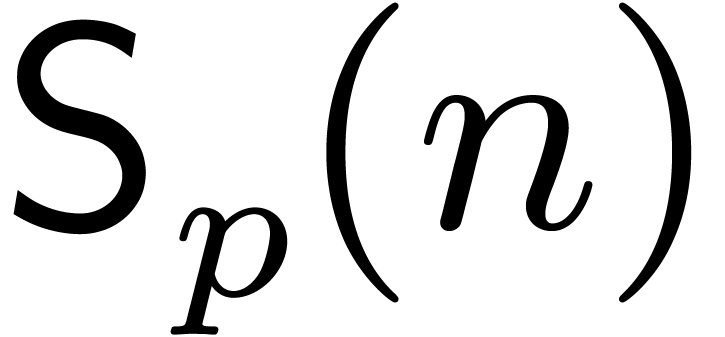 )
)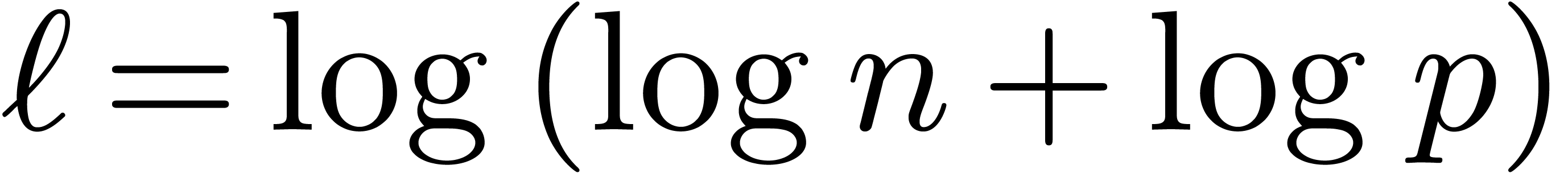 ,
,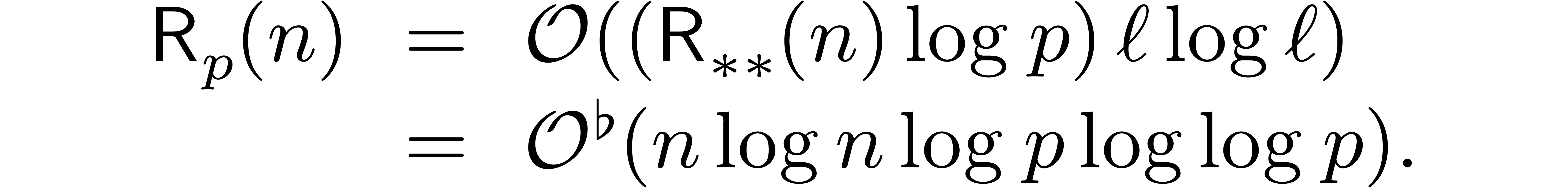
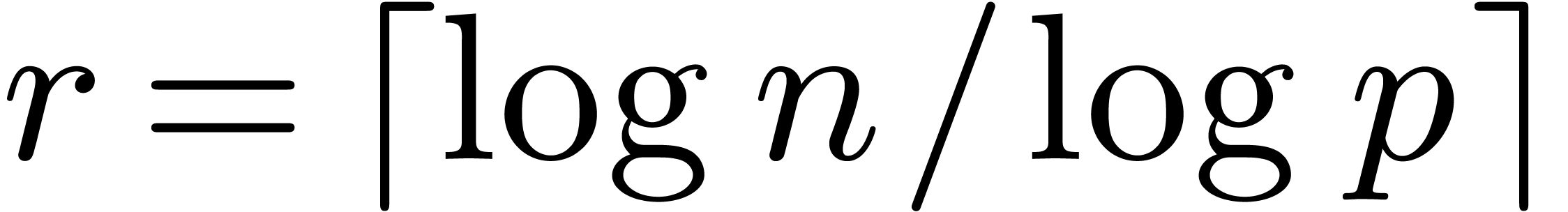 ,
,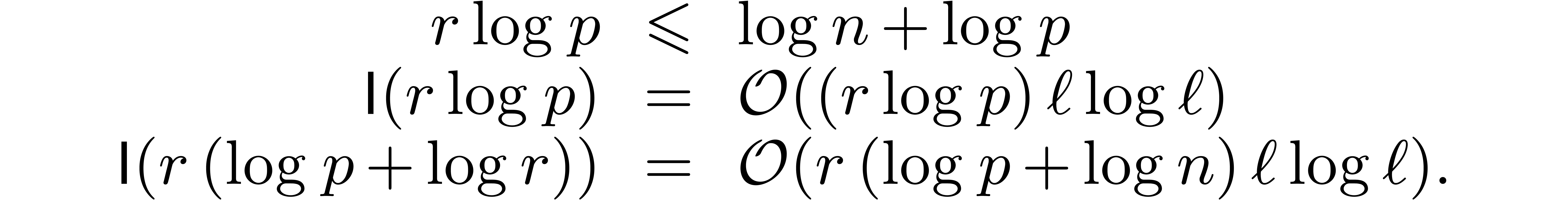
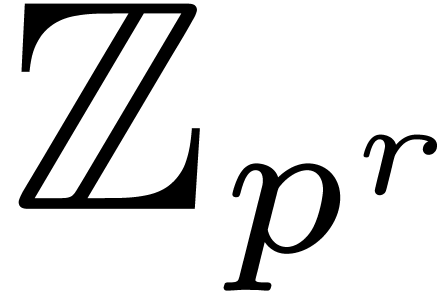 and one
relaxed multiplication with an integer in
and one
relaxed multiplication with an integer in  .
.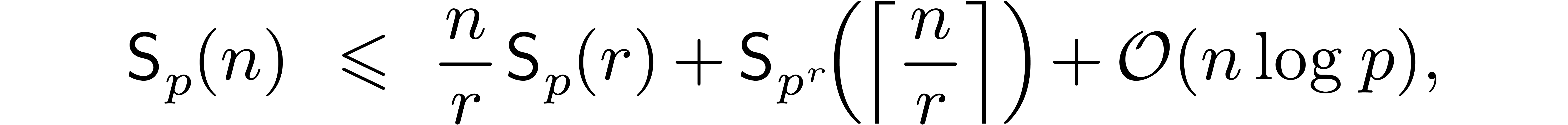
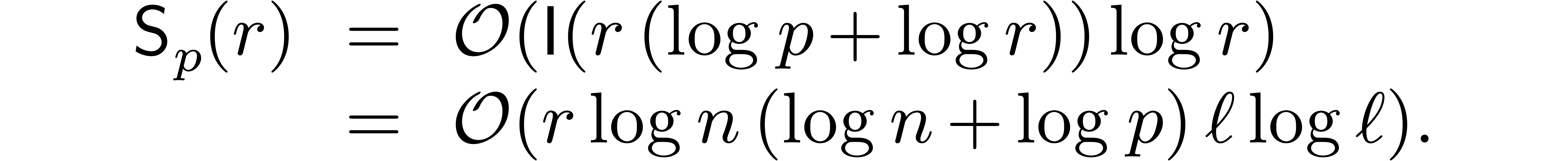
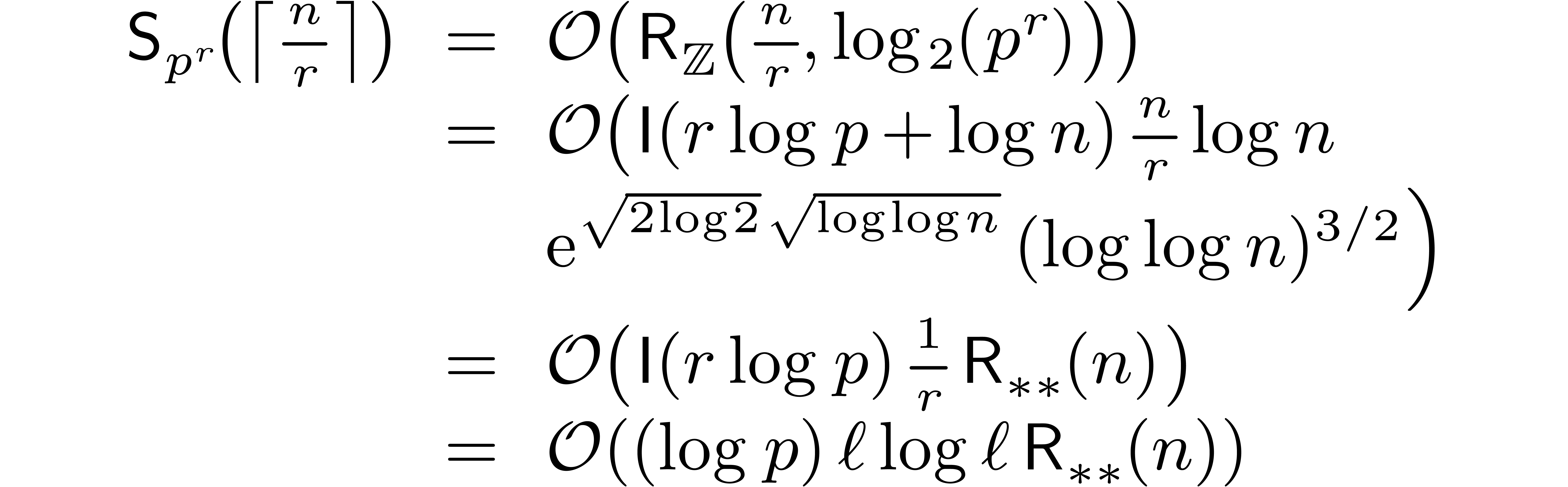
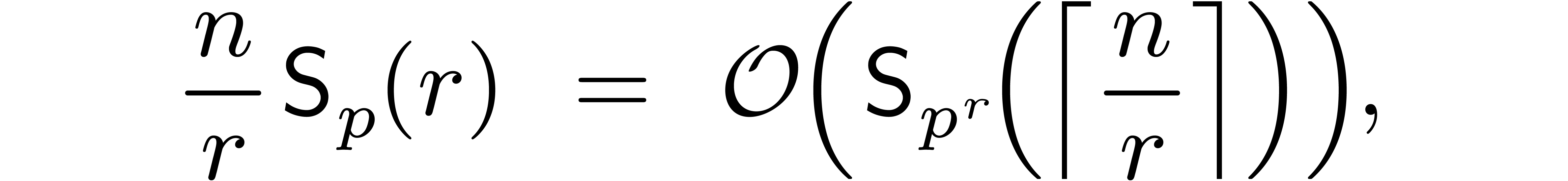
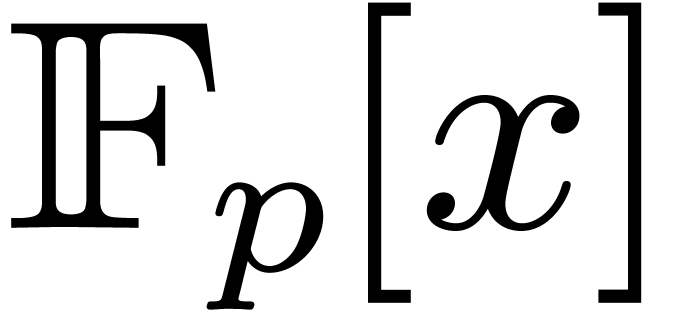 for a prime number
which fits into a machine word and such that
for a prime number
which fits into a machine word and such that  admits many
admits many 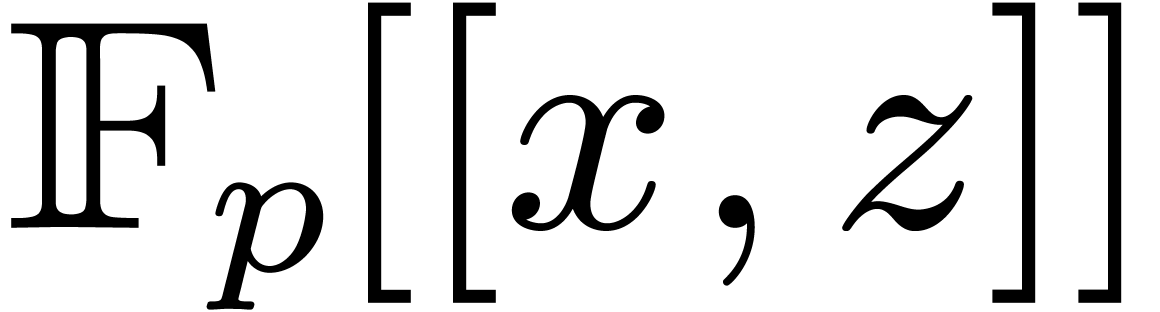 with a triangular support. One may then want to use
TFT-style multiplication [
with a triangular support. One may then want to use
TFT-style multiplication [ ,
, ,
, with
with  .
. ,
, instead of
instead of  better than the
timings for the fully relaxed product. Nevertheless, modulo increased
implementation efforts, we stress that a
better than the
timings for the fully relaxed product. Nevertheless, modulo increased
implementation efforts, we stress that a 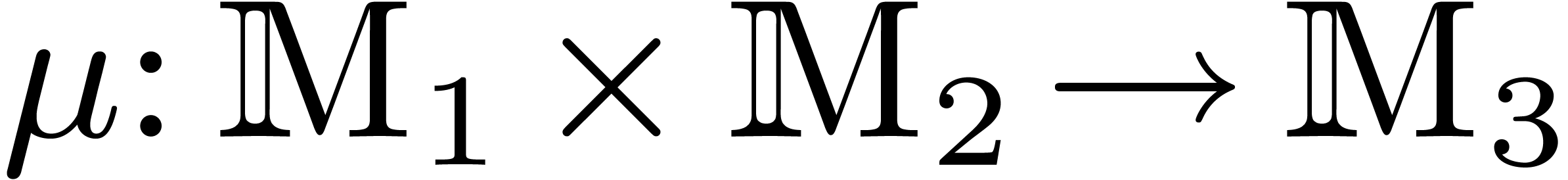 ,
, ,
, and
and  are effective
are effective 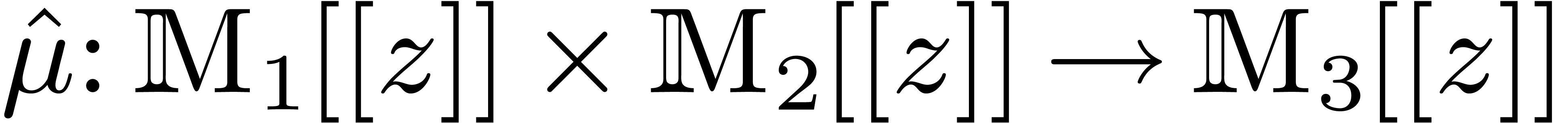 by
by 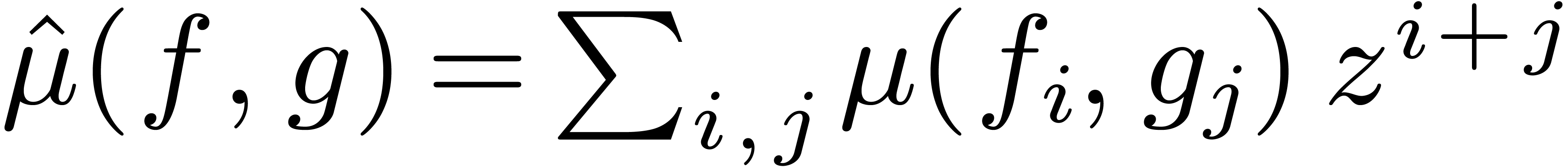 .
.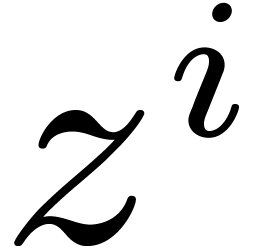 in a non-trivial way. More
precisely, assume that we have an effective ring homomorphism
in a non-trivial way. More
precisely, assume that we have an effective ring homomorphism  such that
such that 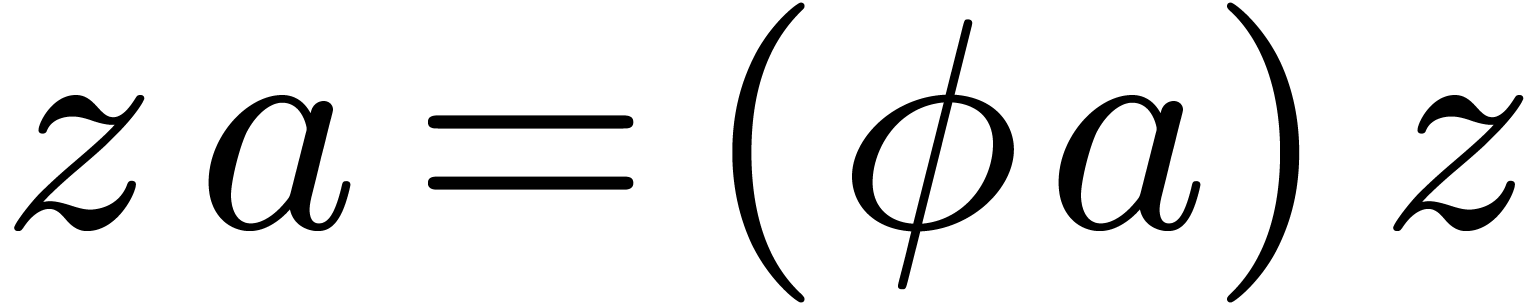 for all
for all  .
. with
with 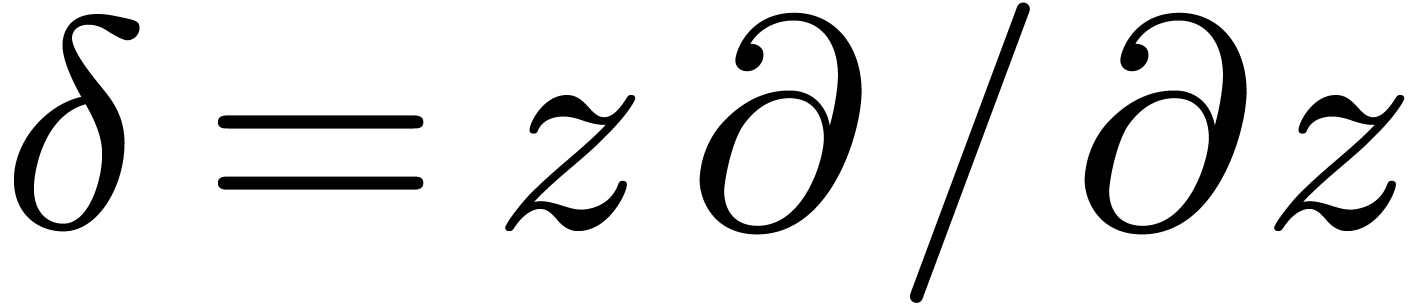 ,
,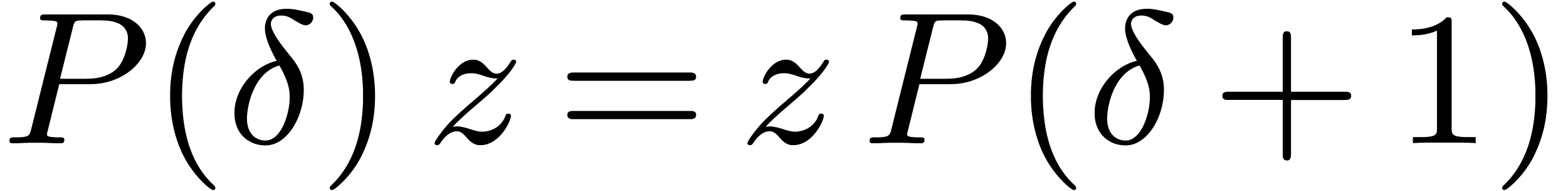 .
.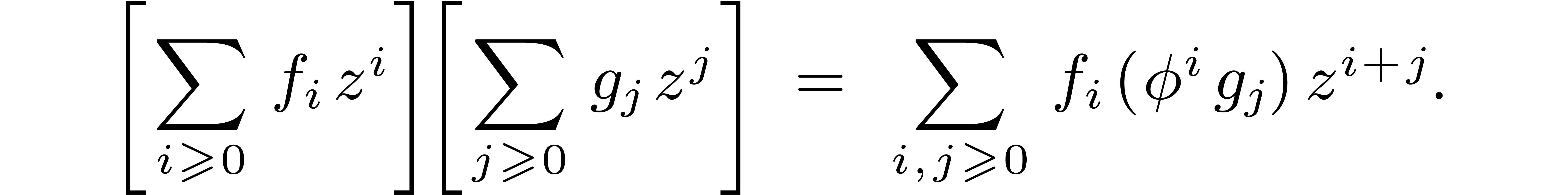
 and
and  in
in  with
with  ,
, .
.