Abstract
Consider a multivariate polynomial 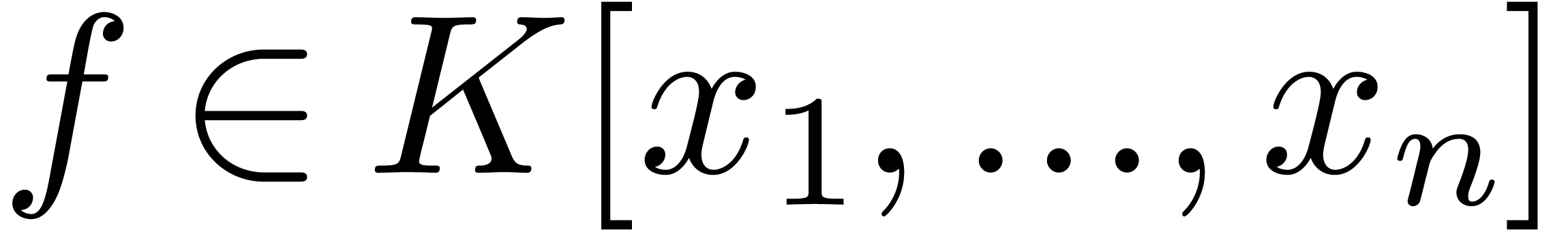 over a field
over a field 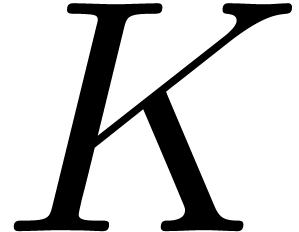 , which is given
through a black box capable of evaluating
, which is given
through a black box capable of evaluating 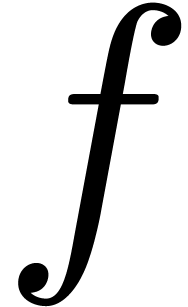 at points in
at points in 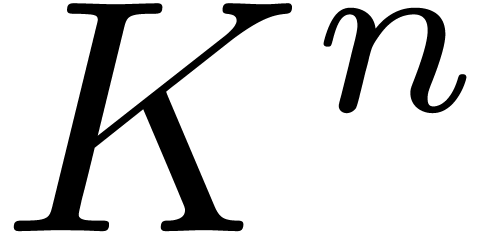 , or possibly at
points in
, or possibly at
points in 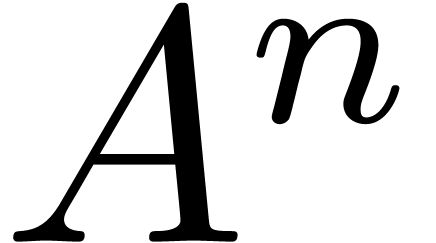 for any
for any 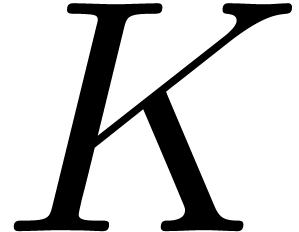 -algebra
-algebra  . The problem of sparse interpolation is to express
. The problem of sparse interpolation is to express
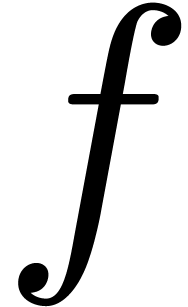 in its usual form with
respect to the monomial basis. We analyze the complexity of various old
and new algorithms for this task in terms of bounds
in its usual form with
respect to the monomial basis. We analyze the complexity of various old
and new algorithms for this task in terms of bounds 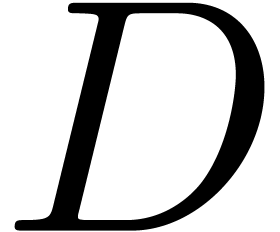 and
and  for the total degree of
for the total degree of 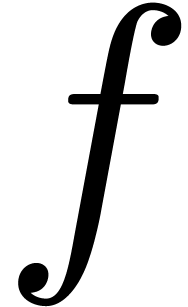 and
its number of terms. We mainly focus on the case when
and
its number of terms. We mainly focus on the case when 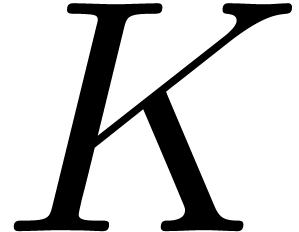 is a finite field and explore possible
speed-ups under suitable heuristic assumptions.
is a finite field and explore possible
speed-ups under suitable heuristic assumptions.
Authors: Joris van der Hoeven,
Grégoire Lecerf
View: Html, TeXmacs, Pdf,
BibTeX
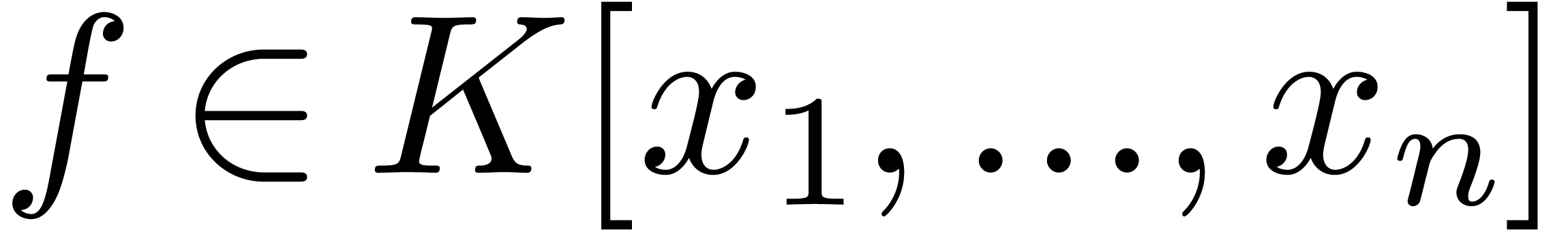 over a field
over a field 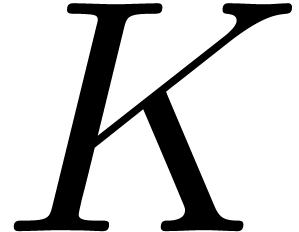 , which is given
through a black box capable of evaluating
, which is given
through a black box capable of evaluating 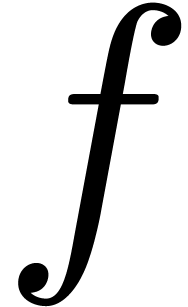 at points in
at points in 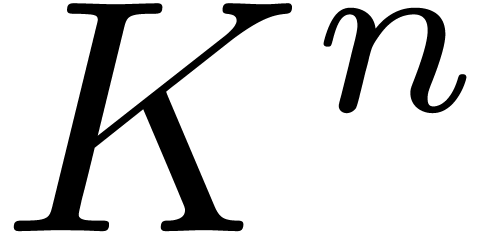 , or possibly at
points in
, or possibly at
points in 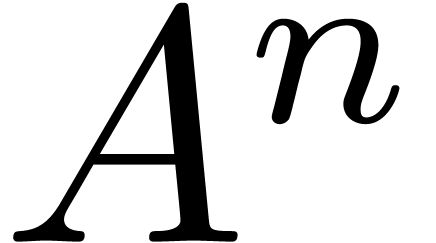 for any
for any 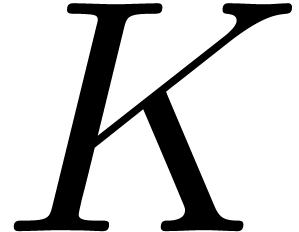 -algebra
-algebra  . The problem of sparse interpolation is to express
. The problem of sparse interpolation is to express
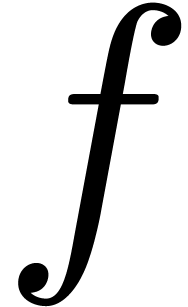 in its usual form with
respect to the monomial basis. We analyze the complexity of various old
and new algorithms for this task in terms of bounds
in its usual form with
respect to the monomial basis. We analyze the complexity of various old
and new algorithms for this task in terms of bounds 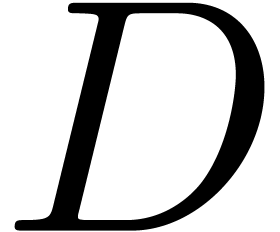 and
and  for the total degree of
for the total degree of 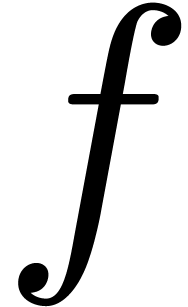 and
its number of terms. We mainly focus on the case when
and
its number of terms. We mainly focus on the case when 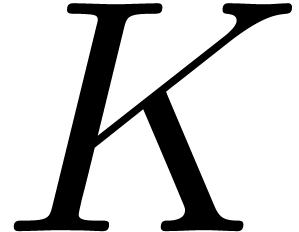 is a finite field and explore possible
speed-ups under suitable heuristic assumptions.
is a finite field and explore possible
speed-ups under suitable heuristic assumptions.