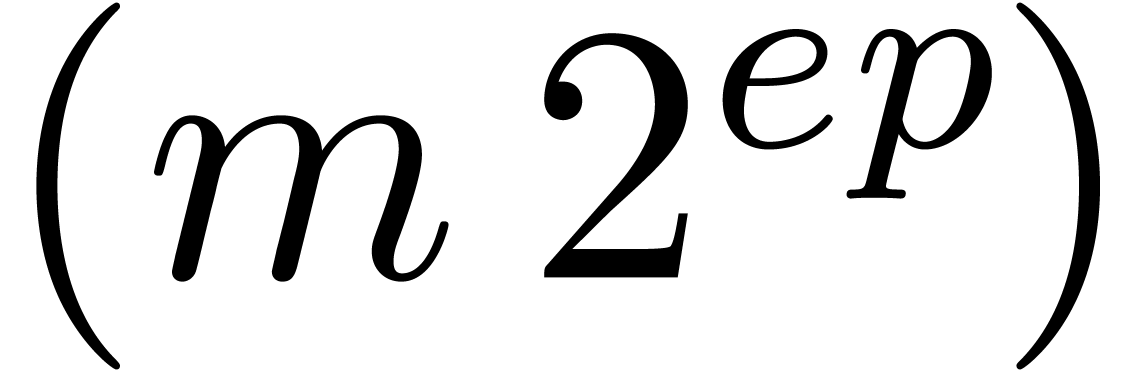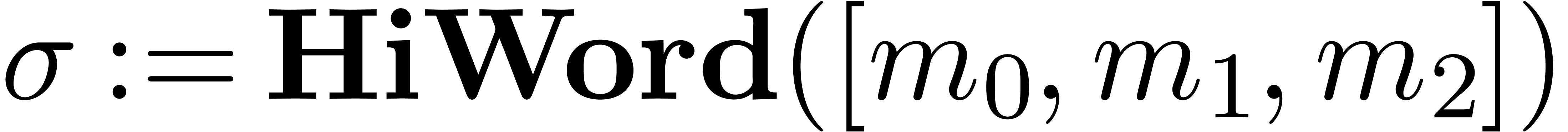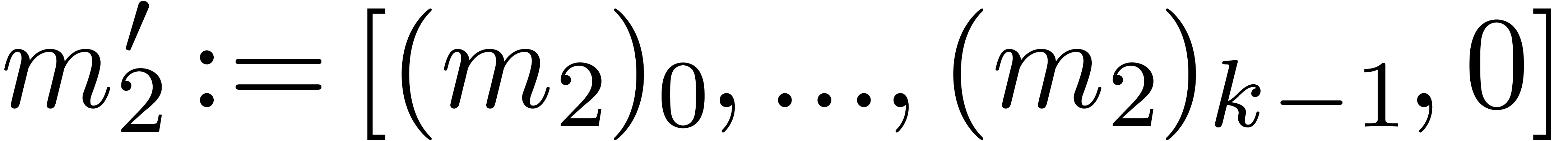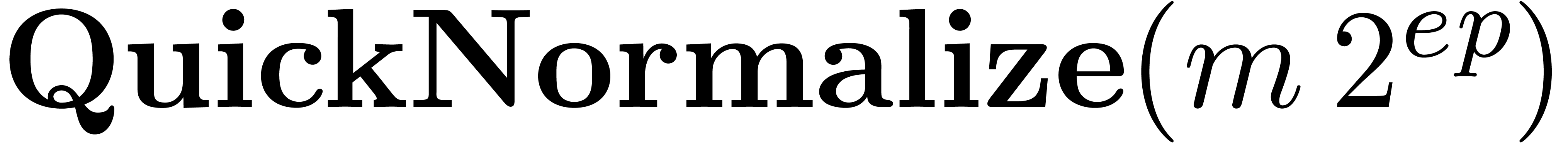| Multiple precision floating-point
arithmetic on SIMD processors |
|
|
Laboratoire d'informatique, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau
|
|
Email:
vdhoeven@lix.polytechnique.fr
|
|
|
|
Current general purpose libraries for multiple precision
floating-point arithmetic such as Mpfr
suffer from a large performance penalty with respect to hard-wired
instructions. The performance gap tends to become even larger with
the advent of wider SIMD arithmetic in both CPUs and GPUs. In this
paper, we present efficient algorithms for multiple precision
floating-point arithmetic that are suitable for implementations on
SIMD processors.
Keywords: floating-point arithmetic,
multiple precision, SIMD
A.C.M. subject classification:
G.1.0 Computer-arithmetic
A.M.S. subject classification: 65Y04,
65T50, 68W30
|
1.Introduction
Multiple precision arithmetic [3] is crucial in areas such
as computer algebra and cryptography, and increasingly useful in
mathematical physics and numerical analysis [1]. Early
multiple precision libraries appeared in the seventies [2],
and nowadays GMP [7] and MPFR [6] are
typically very efficient for large precisions of more than, say, 1000
bits. However, for precisions that are only a few times larger than the
machine precision, these libraries suffer from a large overhead. For
instance, the MPFR library for arbitrary precision and IEEE-style
standardized floating-point arithmetic is typically about a factor 100
slower than double precision machine arithmetic.
This overhead of multiple precision libraries tends to further increase
with the advent of wider SIMD (Single Instruction, Multiple
Data) arithmetic in modern processors, such as Intel's
AVX technology. Indeed, it is hard to take advantage of wide SIMD
instructions when implementing basic arithmetic for individual numbers
of only a few words. In order to fully exploit SIMD instructions, one
should rather operate on suitably represented SIMD vectors of multiple
precision numbers. A second problem with current SIMD arithmetic is that
CPU vendors tend to favor wide floating-point arithmetic over wide
integer arithmetic, whereas faster integer arithmetic is most useful for
speeding up multiple precision libraries.
In order to make multiple precision arithmetic more useful in areas such
as numerical analysis, it is a major challenge to reduce the overhead of
multiple precision arithmetic for small multiples of the machine
precision, and to build libraries with direct SIMD arithmetic for
multiple precision floating-point numbers.
One existing approach is based on the
“TwoSum” and
“TwoProduct” operations [4, 13] that allow for the exact computation of sums and products
of two machine floating-point numbers. The results of these operations
are represented as sums  where
where  and
and  have no “overlapping bits”
(e.g.
have no “overlapping bits”
(e.g. 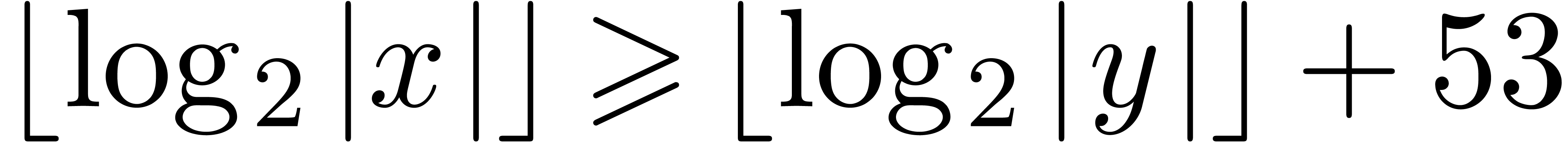 or
or 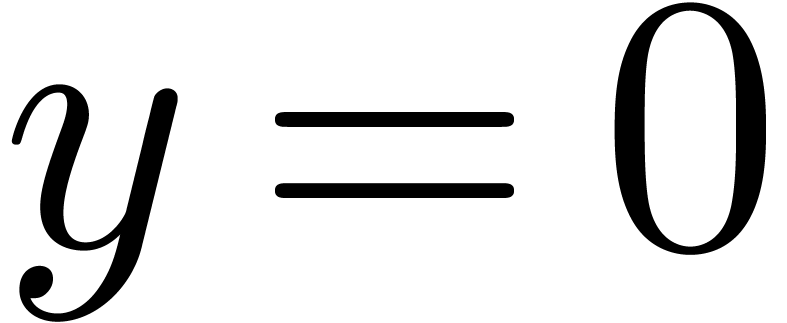 ). The TwoProduct operation can be
implemented using only two instructions when hardware offers the
fused-multiply-add (FMA) and fused-multiply-subtract
(FMS) instructions, as is for instance the case for AVX2 enabled
processors. The TwoSum operation could be done using
only two instructions as well if we had similar fused-add-add and
fused-add-subtract instructions. Unfortunately, this is not the case for
current hardware.
). The TwoProduct operation can be
implemented using only two instructions when hardware offers the
fused-multiply-add (FMA) and fused-multiply-subtract
(FMS) instructions, as is for instance the case for AVX2 enabled
processors. The TwoSum operation could be done using
only two instructions as well if we had similar fused-add-add and
fused-add-subtract instructions. Unfortunately, this is not the case for
current hardware.
It is well known that double machine precision arithmetic can be
implemented reasonably efficiently in terms of the
TwoSum and TwoProduct algorithms [4, 13, 15]. The approach has been
further extended in [17, 14] to higher
precisions. Specific algorithms are also described in [12]
for triple-double precision, and in [9] for
quadruple-double precision. But these approaches tend to become
inefficient for large precisions.
An alternative approach is to represent floating-point numbers by
products 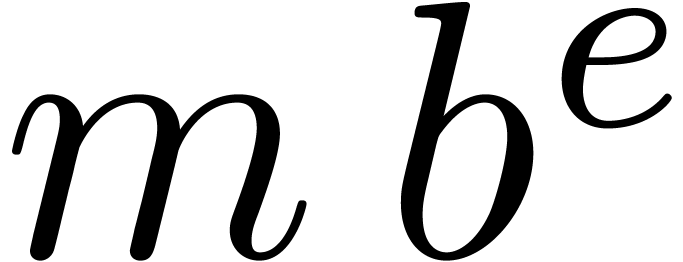 , where
, where 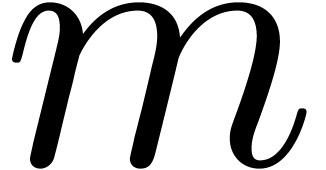 is a fixed-point mantissa,
is a fixed-point mantissa,  an
exponent, and
an
exponent, and 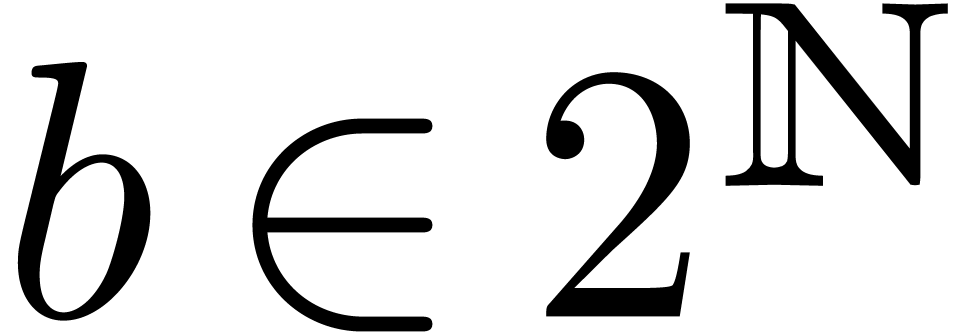 the base. This representation is
used in most of the existing multi-precision libraries such as Gmp [7] and Mpfr [6]. However, the authors are only aware of sequential
implementations of this approach. In this paper we examine the
efficiency of this approach on SIMD processors. As in [10],
we systematically work with vectors of multiple precision numbers rather
than with vectors of “digits” in base
the base. This representation is
used in most of the existing multi-precision libraries such as Gmp [7] and Mpfr [6]. However, the authors are only aware of sequential
implementations of this approach. In this paper we examine the
efficiency of this approach on SIMD processors. As in [10],
we systematically work with vectors of multiple precision numbers rather
than with vectors of “digits” in base  . We refer to [19, 5] for
some other recent approaches.
. We refer to [19, 5] for
some other recent approaches.
Our paper is structured as follows. In section 2, we detail
the representation of fixed-point numbers and basic arithmetic
operations. We follow a similar approach as in [10], but
slightly adapt the representation and corresponding algorithms to allow
for larger bit precisions of the mantissa. As in [10], we
rely on standard IEEE-754 compliant floating-point arithmetic that is
supported by most recent processors and GPUs. For processors with
efficient SIMD integer arithmetic, it should be reasonably easy to adapt
our algorithms to this kind of arithmetic. Let  be the bit precision of our machine floating-point numbers minus one (so
that
be the bit precision of our machine floating-point numbers minus one (so
that 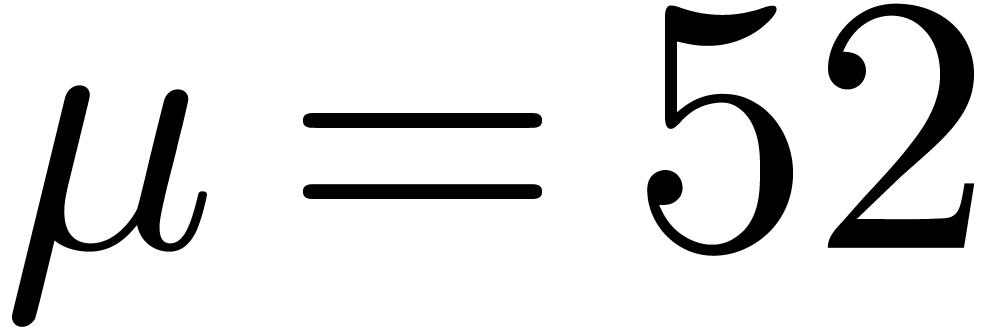 for IEEE-754 double precision numbers).
Throughout this paper, we represent fixed-point numbers in base
for IEEE-754 double precision numbers).
Throughout this paper, we represent fixed-point numbers in base 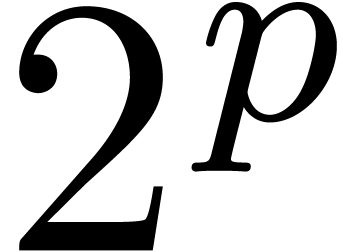 by
by 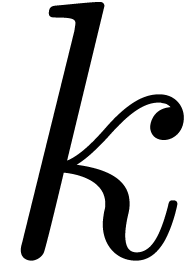 -tuplets
of machine floating-point numbers, where
-tuplets
of machine floating-point numbers, where 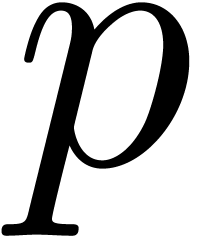 is
slightly smaller than
is
slightly smaller than 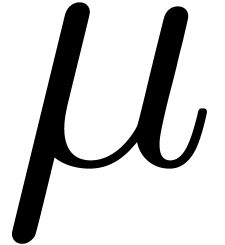 and
and 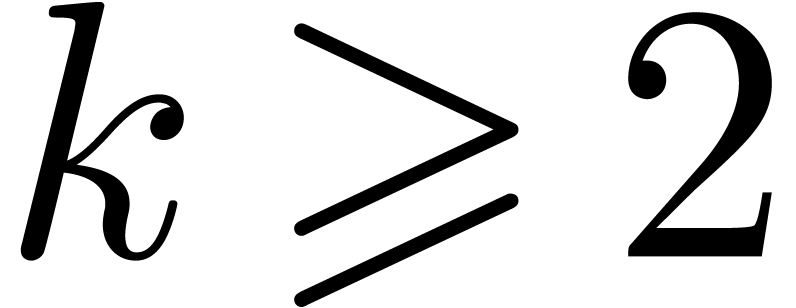 .
.
The main bottleneck for the implementation of floating-point arithmetic
on top of fixed-point arithmetic is shifting. This operation is
particularly crucial for addition, since every addition requires three
shifts. Section 3 is devoted to this topic and we will show
how to implement reasonably efficient shifting algorithms for SIMD
vectors of fixed-point numbers. More precisely, small shifts (of less
than  bits) can be done in parallel using
approximately
bits) can be done in parallel using
approximately 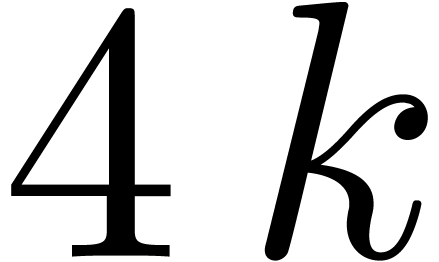 operations, whereas arbitrary
shifts require approximately
operations, whereas arbitrary
shifts require approximately 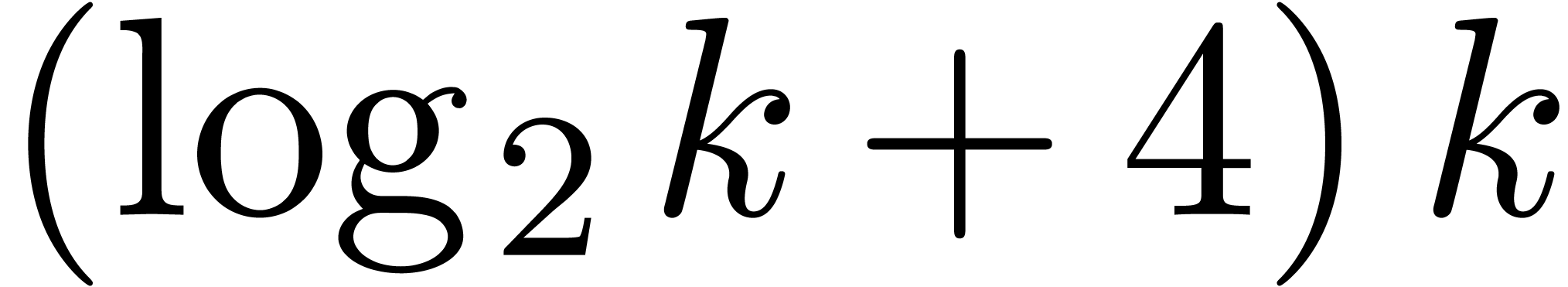 operations.
operations.
In section 4, we show how to implement arbitrary precision
floating-point arithmetic in base  .
Our approach is fairly standard. On the one hand, we use the “left
shifting” procedures from section 3 in order to
normalize floating-point numbers (so that mantissas of non zero numbers
are always “sufficiently large” in absolute value). On the
other hand, the “right shifting” procedures are used to work
with respect to a common exponent in the cases of addition and
subtraction. We also discuss a first strategy to reduce the cost of
shifting and summarize the corresponding operation counts in Table 2. In section 5, we perform a similar analysis
for arithmetic in base
.
Our approach is fairly standard. On the one hand, we use the “left
shifting” procedures from section 3 in order to
normalize floating-point numbers (so that mantissas of non zero numbers
are always “sufficiently large” in absolute value). On the
other hand, the “right shifting” procedures are used to work
with respect to a common exponent in the cases of addition and
subtraction. We also discuss a first strategy to reduce the cost of
shifting and summarize the corresponding operation counts in Table 2. In section 5, we perform a similar analysis
for arithmetic in base 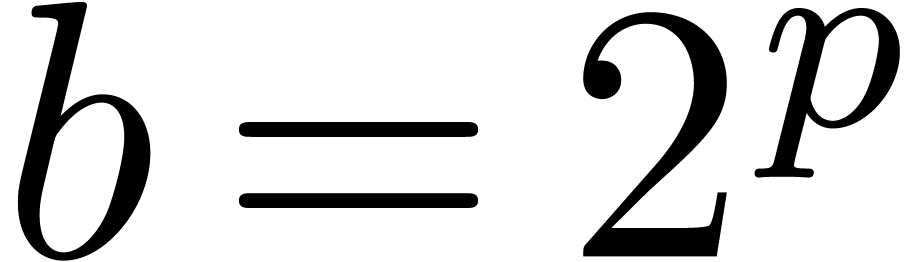 . This
leads to slightly less compact representations, but shifting is reduced
to multiple word shifting in this setting. The resulting operation
counts can be found in Table 3.
. This
leads to slightly less compact representations, but shifting is reduced
to multiple word shifting in this setting. The resulting operation
counts can be found in Table 3.
The operation counts in Tables 2 and 3 really
represent the worst case scenario in which our implementations for basic
arithmetic operations are required to be “black boxes”.
Multiple precision arithmetic can be made far more efficient if we allow
ourselves to open up these boxes when needed. For instance, any number
of floating-pointing numbers can be added using a single function call
by generalizing the addition algorithms from sections 4 and
5 to take more than two arguments; this can become almost
thrice as efficient as the repeated use of ordinary additions. A similar
approach can be applied to entire algorithms such as the FFT [10]:
we first shift the inputs so that they all admit the same exponent and
then use a fixed-point algorithm for computing the FFT. We intend to
come back to this type of optimizations in a forthcoming paper.
So far, we only checked the correctness of our algorithms using a
prototype implementation. Our operation count analysis indicates that
our approach should outperform others as soon as 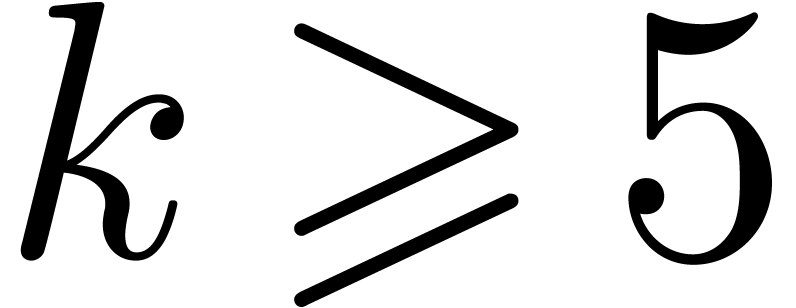 and maybe even for
and maybe even for 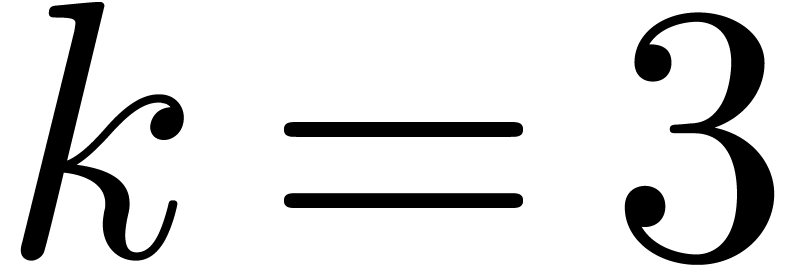 and
and 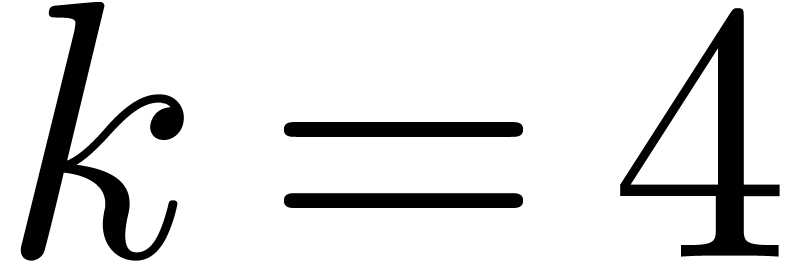 . Another direction of future investigations
concerns correct rounding and full compliance with the IEEE standard,
taking example on Mpfr [6].
. Another direction of future investigations
concerns correct rounding and full compliance with the IEEE standard,
taking example on Mpfr [6].
Notations
Throughout this paper, we assume IEEE arithmetic with correct rounding
and we denote by  the set of machine
floating-point numbers. We let
the set of machine
floating-point numbers. We let 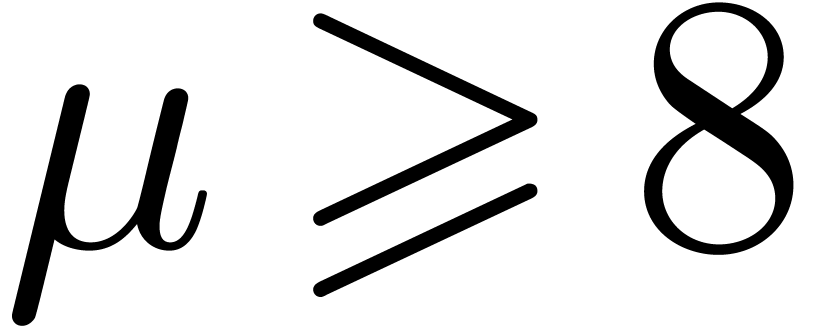 be the machine
precision minus one (which corresponds to the number of fractional bits
of the mantissa) and let
be the machine
precision minus one (which corresponds to the number of fractional bits
of the mantissa) and let 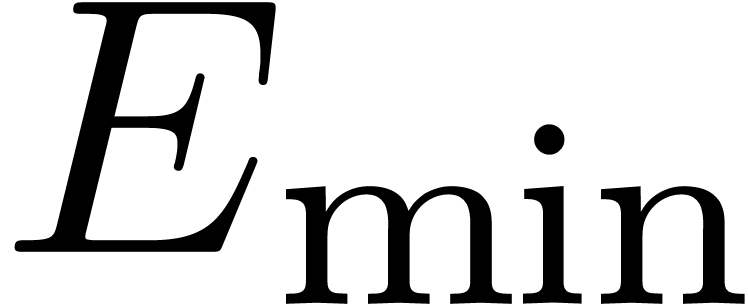 and
and 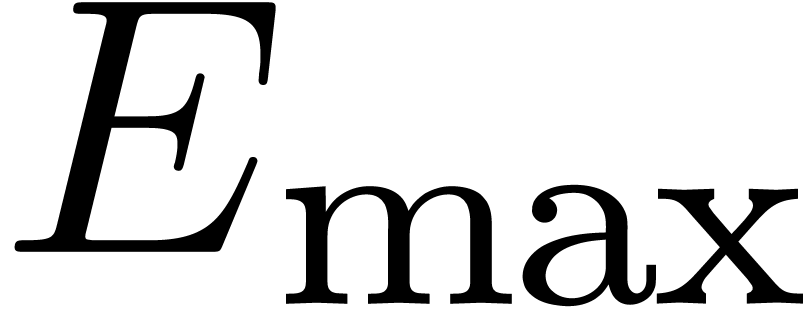 be the minimal and maximal exponents of machine floating-point numbers.
For IEEE double precision numbers, this means that
be the minimal and maximal exponents of machine floating-point numbers.
For IEEE double precision numbers, this means that 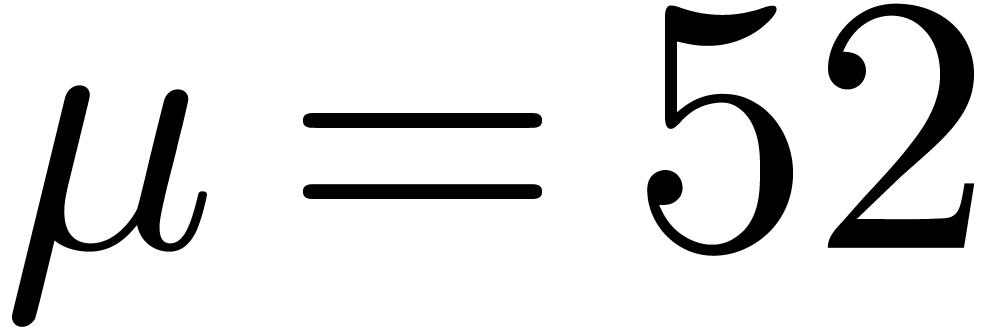 ,
, 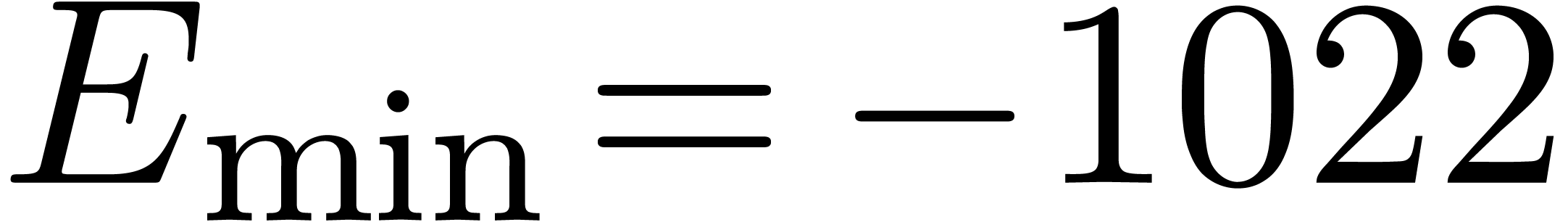 and
and 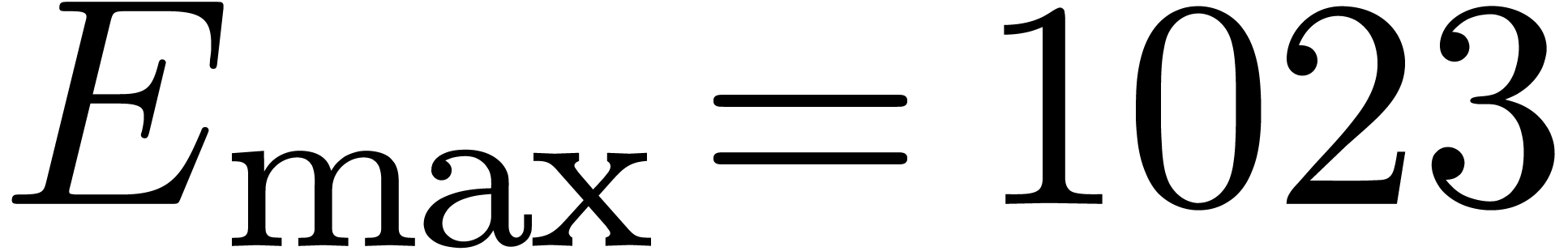 .
.
In this paper, and contrary to [10], the rounding mode is
always assume to be “round to nearest”. Given 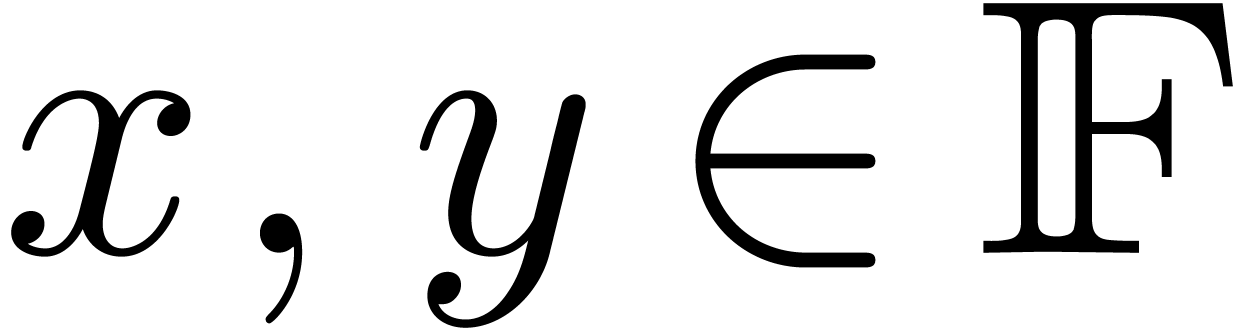 and
and  , we denote
by
, we denote
by 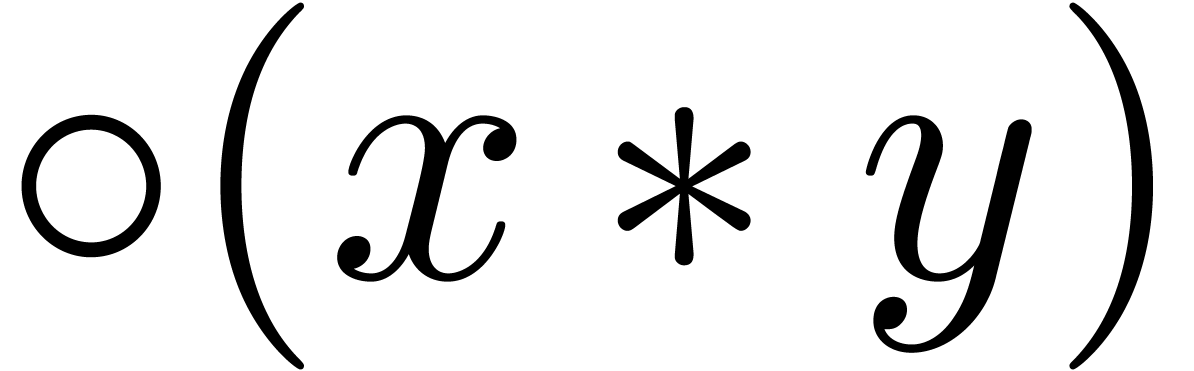 the rounding of
the rounding of  to
the nearest. For convenience of the reader, we denote
to
the nearest. For convenience of the reader, we denote  whenever the result
whenever the result  is provably exact in the
given context. If
is provably exact in the
given context. If  is the exponent of
is the exponent of  and
and  (i.e. in absence
of overflow and underflow), then we notice that
(i.e. in absence
of overflow and underflow), then we notice that 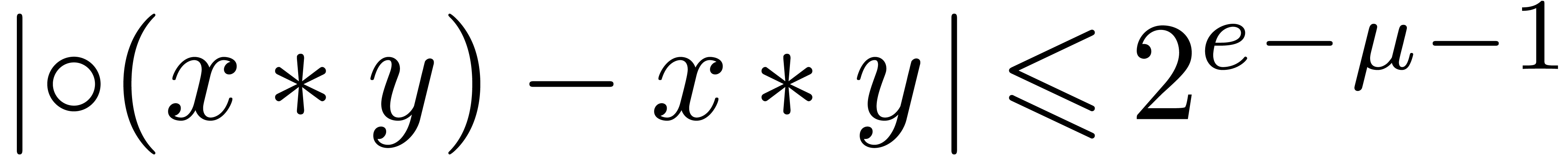 . For efficiency reasons, the algorithms in this
paper do not attempt to check for underflows, overflows, and other
exceptional cases.
. For efficiency reasons, the algorithms in this
paper do not attempt to check for underflows, overflows, and other
exceptional cases.
Modern processors usually support fused-multiply-add (FMA) and
fused-multiply-subtract (FMS) instructions, both for scalar and SIMD
vector operands. Throughout this paper, we assume that these
instructions are indeed present, and we denote by 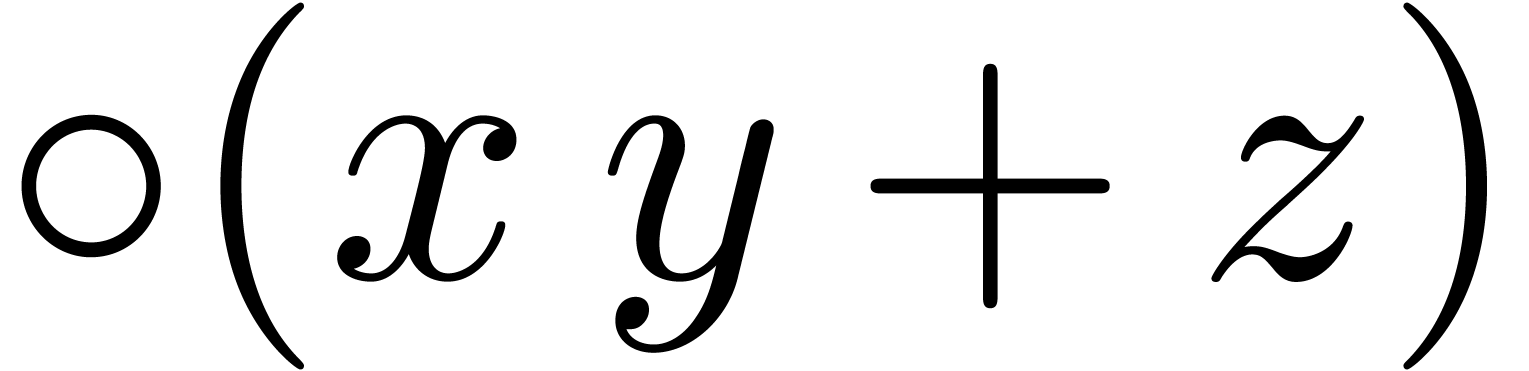 and
and 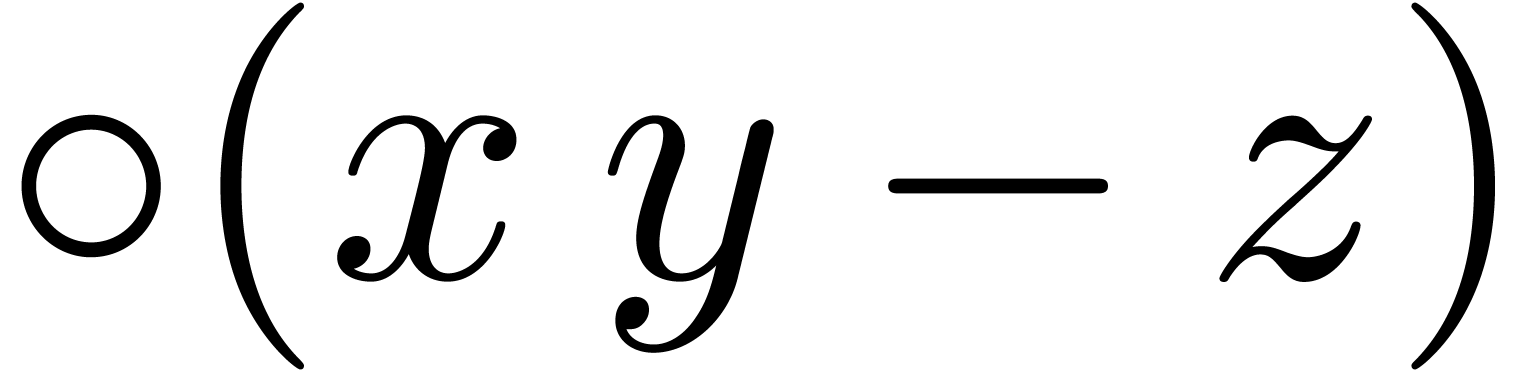 the roundings of
the roundings of 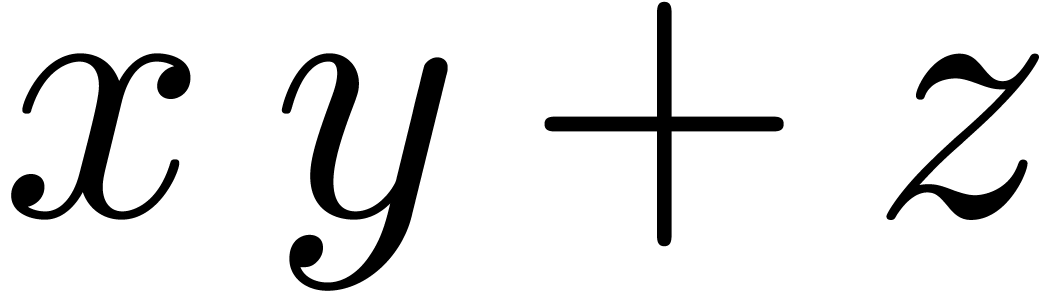 and
and
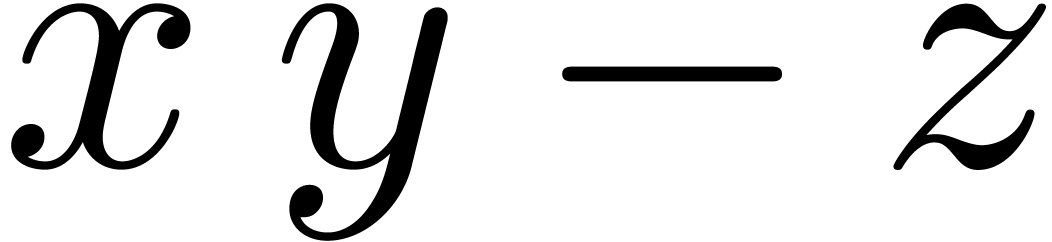 to the nearest.
to the nearest.
Acknowledgment. We are very grateful to the
third referee for various suggestions and for drawing our attention to
several more or less serious errors in an earlier version of this paper.
2.Fixed-point arithmetic
Let  and
and 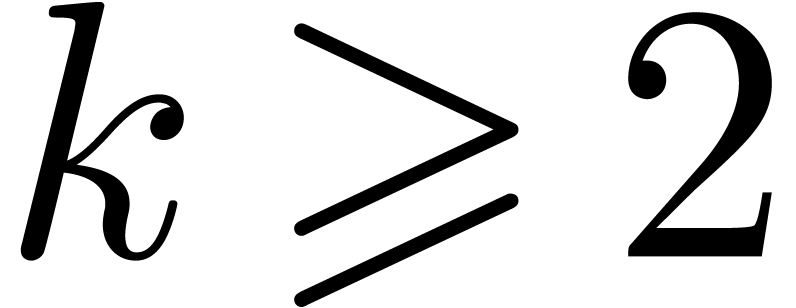 .
In this section, we start with a survey of efficient fixed-point
arithmetic at bit precision
.
In this section, we start with a survey of efficient fixed-point
arithmetic at bit precision 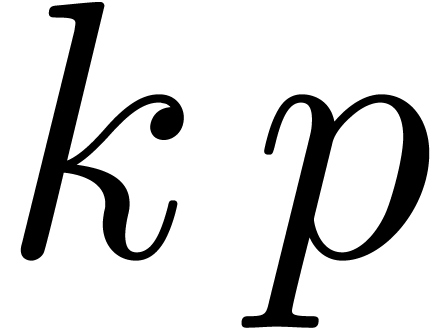 .
We recall the approach from [10], but use a slightly
different representation in order to allow for high precisions
.
We recall the approach from [10], but use a slightly
different representation in order to allow for high precisions 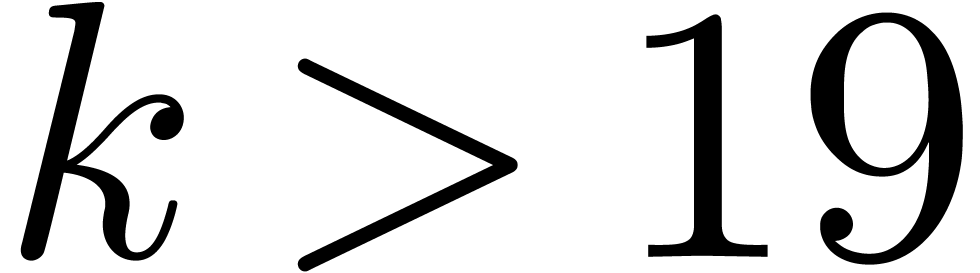 . We adapted the algorithms from
[10] accordingly and explicitly state the adapted versions.
Allowing
. We adapted the algorithms from
[10] accordingly and explicitly state the adapted versions.
Allowing 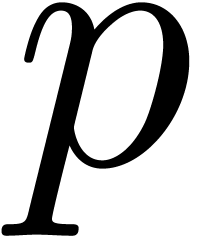 to be smaller than
to be smaller than 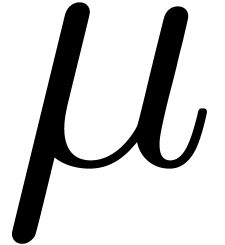 corresponds to using a redundant number representation that makes it
possible to efficiently handle carries during intermediate computations.
We denote by
corresponds to using a redundant number representation that makes it
possible to efficiently handle carries during intermediate computations.
We denote by 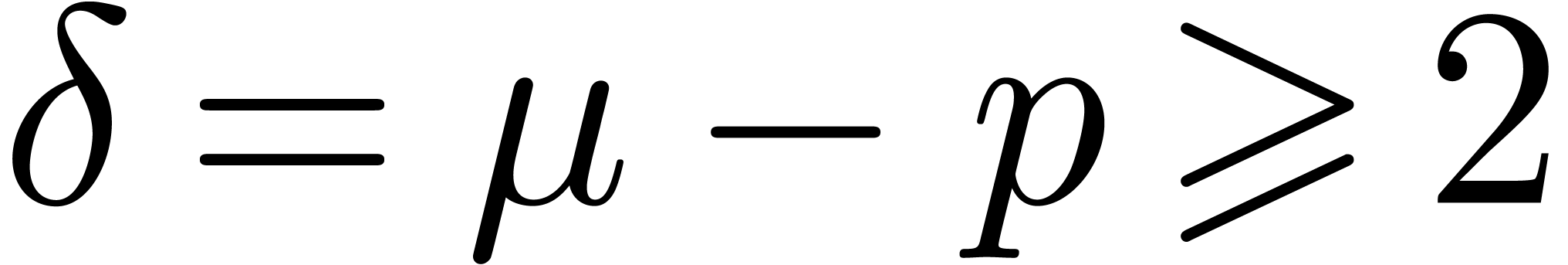 the number of extra carry bits
(these bits are sometimes called “nails”, following GMP [7]). We refer to section 3.5 for a table that
recapitulates the operation counts for the algorithms in this section.
the number of extra carry bits
(these bits are sometimes called “nails”, following GMP [7]). We refer to section 3.5 for a table that
recapitulates the operation counts for the algorithms in this section.
2.1.Representation of fixed-point numbers
Given  and an integer
and an integer 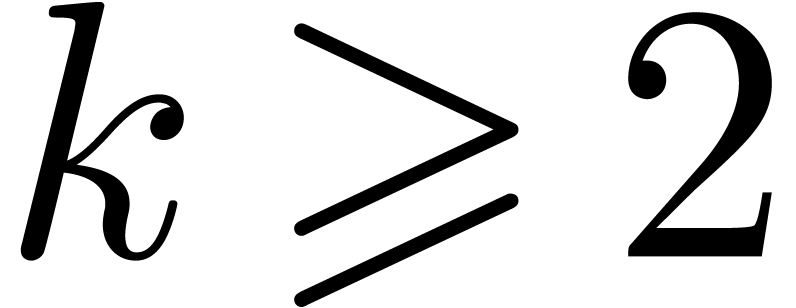 , we denote by
, we denote by 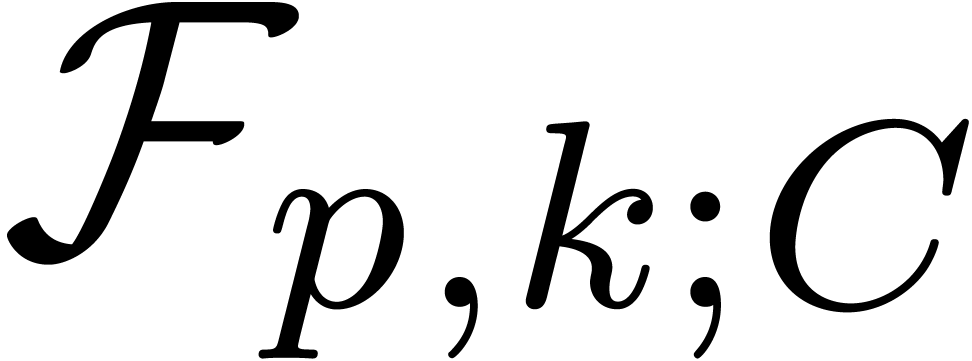 the set of
numbers of the form
the set of
numbers of the form
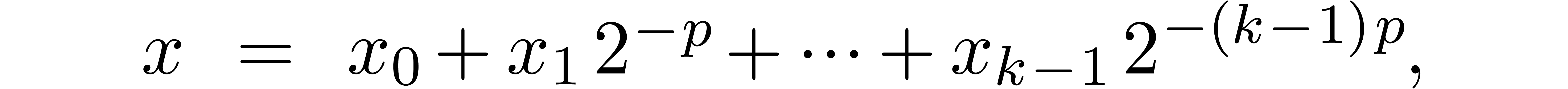 |
(1) |
where 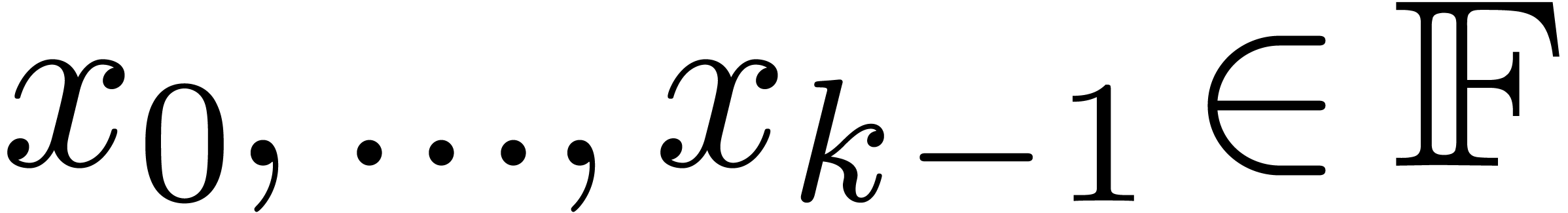 are such that
are such that
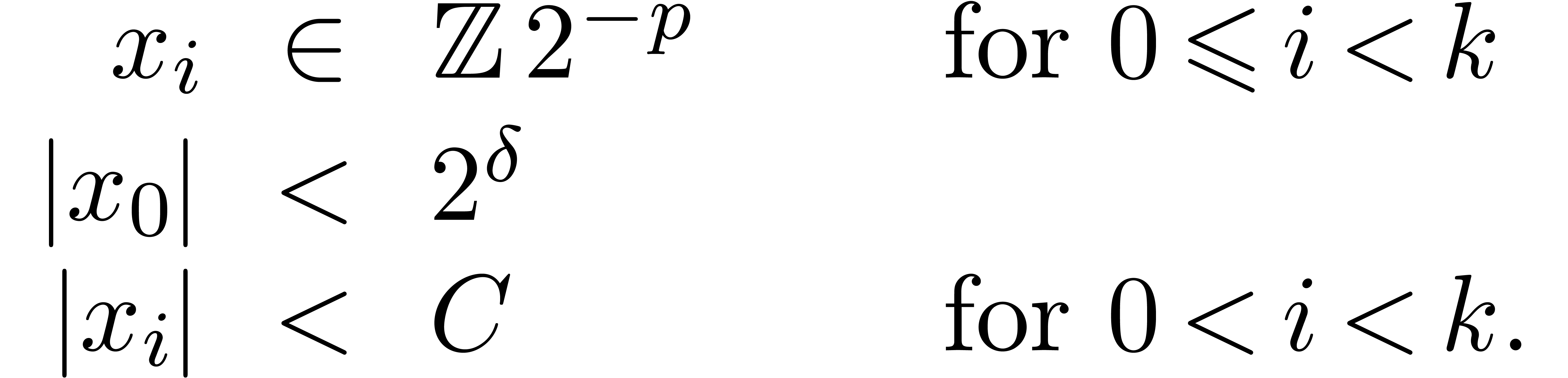
We write 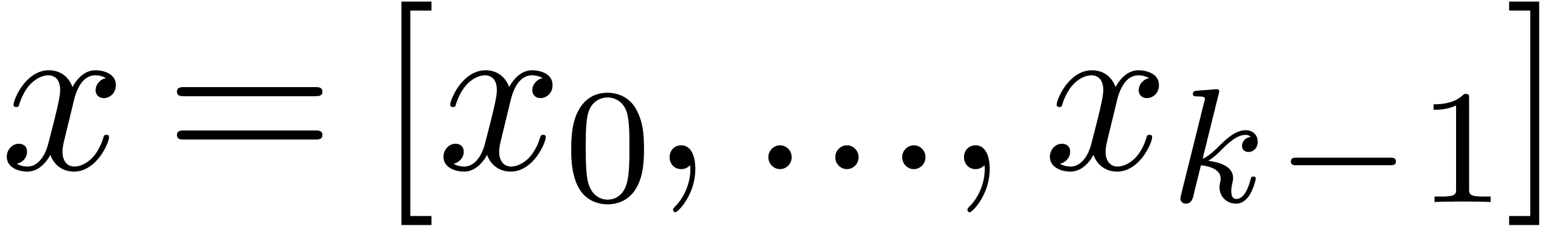 for numbers of the above form and
abbreviate
for numbers of the above form and
abbreviate 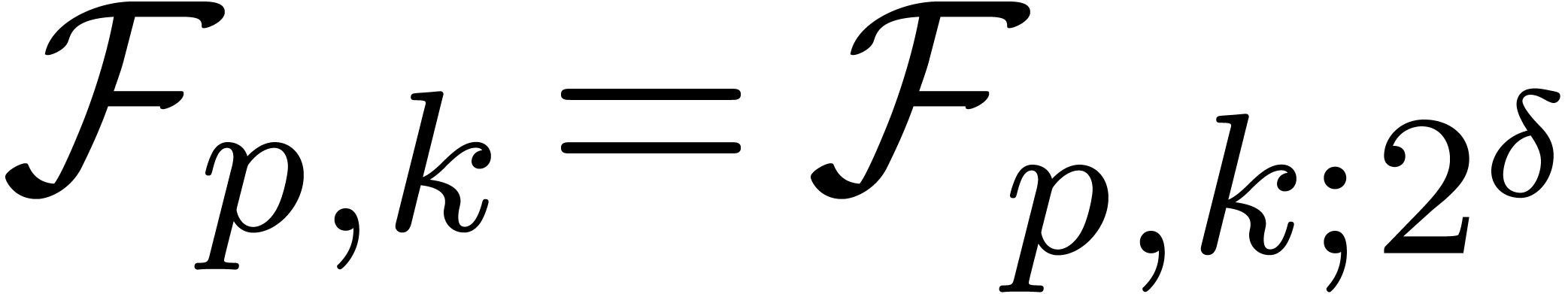 . Numbers in
. Numbers in 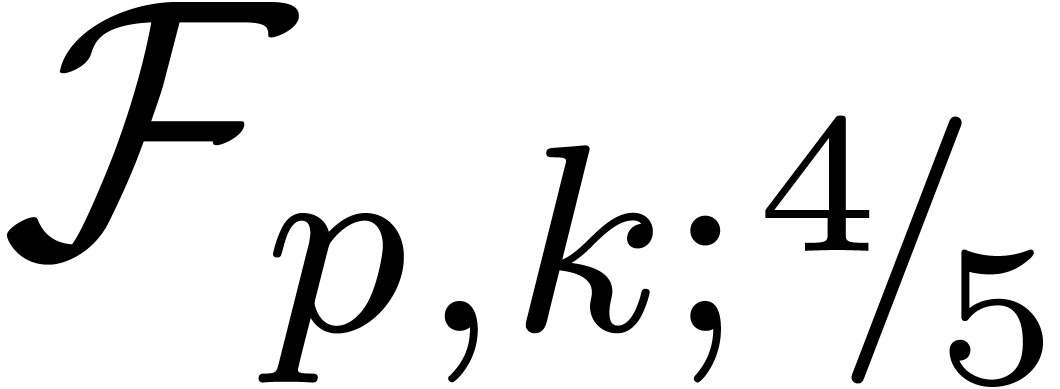 are said to be in carry normal form.
are said to be in carry normal form.
Remark 1. The paper [10] rather uses the representation  with
with 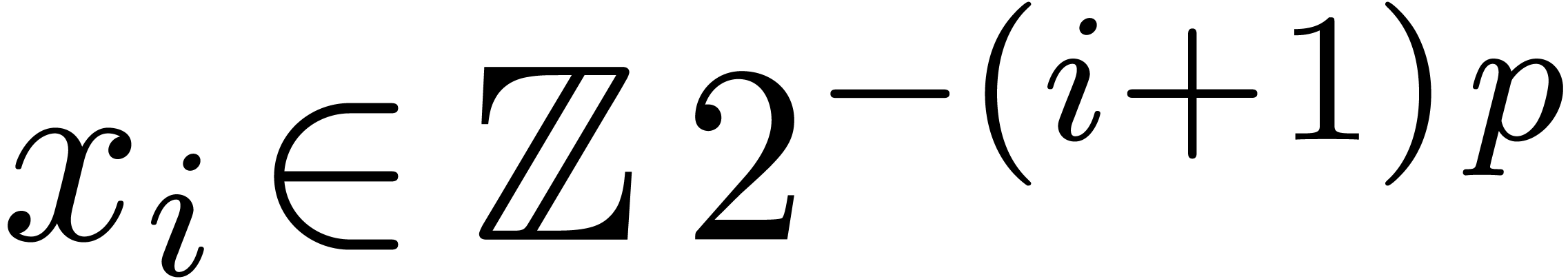 and
and 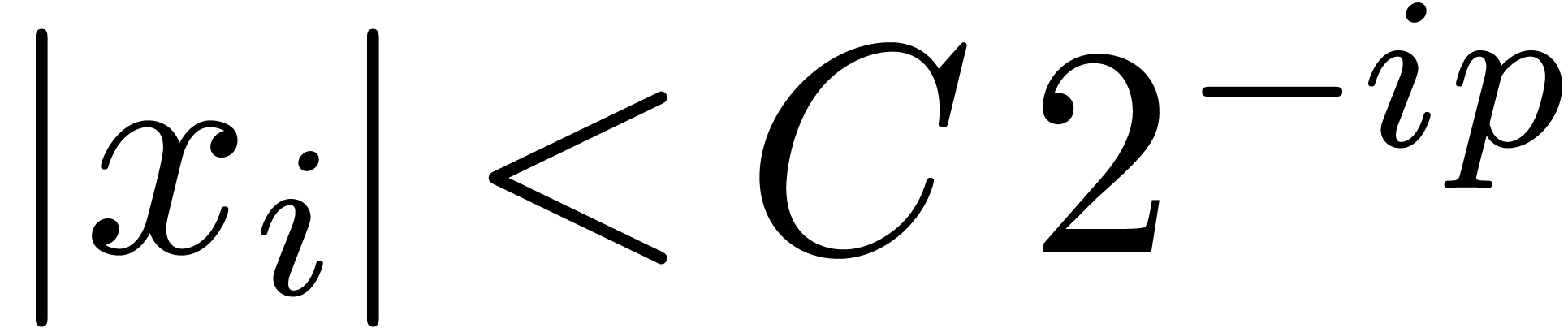 .
This representation is slightly more efficient for small
.
This representation is slightly more efficient for small 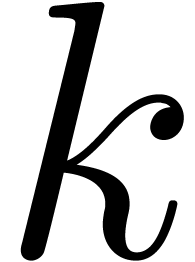 , since it allows one to save one operation in
the implementation of the multiplication algorithm. However, it is
limited to small values of
, since it allows one to save one operation in
the implementation of the multiplication algorithm. However, it is
limited to small values of 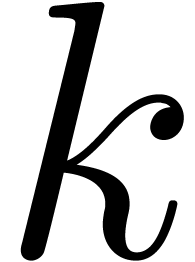 (typically
(typically 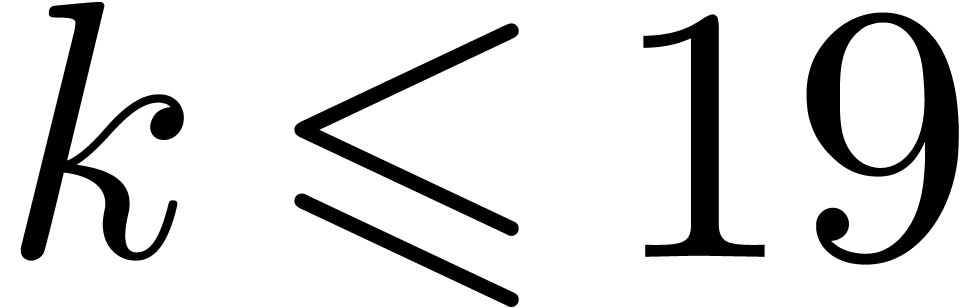 ), since
), since 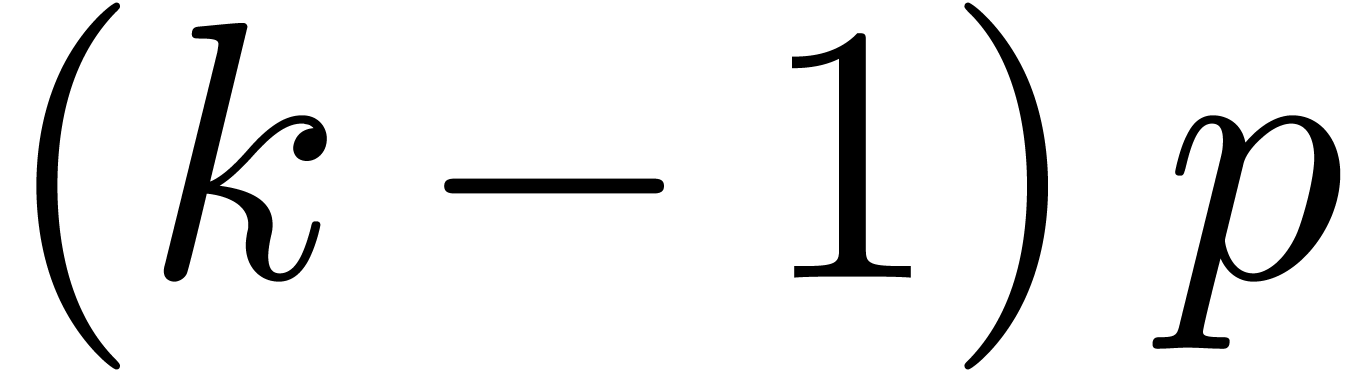 must required to be smaller than
must required to be smaller than  .
The representation (1) also makes it easier to implement
efficient multiplication algorithms at high precisions
.
The representation (1) also makes it easier to implement
efficient multiplication algorithms at high precisions  , such as Karatsuba's algorithm [11]
or FFT-based methods [16, 18, 8].
We intend to return to this issue in a forthcoming paper.
, such as Karatsuba's algorithm [11]
or FFT-based methods [16, 18, 8].
We intend to return to this issue in a forthcoming paper.
Remark 2. Another minor
change with respect to [10] is that we also require  to hold for the last index
to hold for the last index 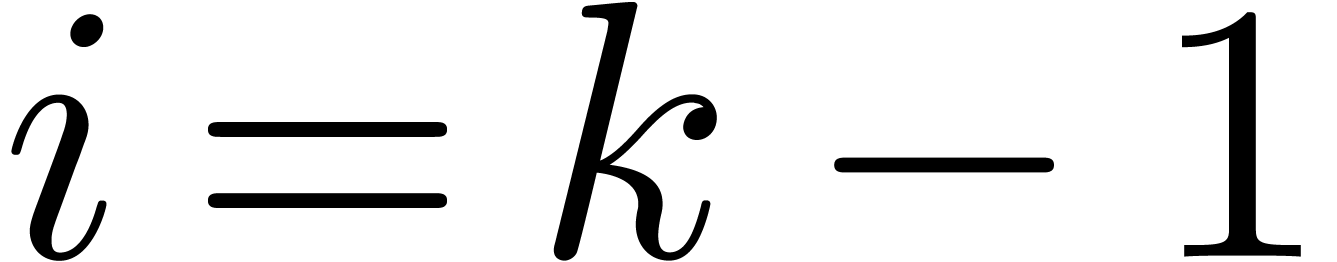 . In order to meet this additional requirement, we
need two additional instructions at the end of the multiplication
routine in section 2.6 below.
. In order to meet this additional requirement, we
need two additional instructions at the end of the multiplication
routine in section 2.6 below.
2.2.Splitting numbers at a given exponent
An important subalgorithm for efficient fixed-point arithmetic computes
the truncation of a floating-point number at a given exponent:
Proposition 1 from [10] becomes as follows for
“rounding to nearest”:
2.3.Carry propagation
Numbers can be rewritten in carry normal form using carry propagition.
This can be achieved as follows (of course, the loop being unrolled in
practice):
Algorithm CarryNormalize( ) )
|
for 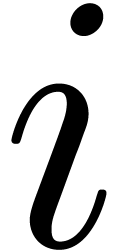 from from
 down to down to 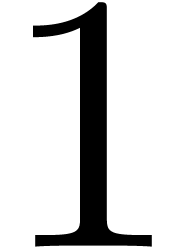 do
do
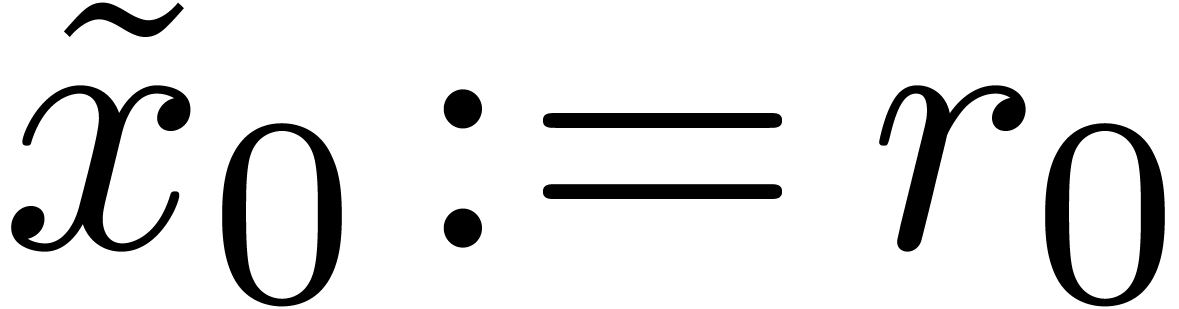
return 
|
A straightforward adaptation of [10, Proposition 2] yields:
2.4.Addition and subtraction
Non normalized addition and subtraction of fixed-point numbers is
straightforward:
Algorithm Add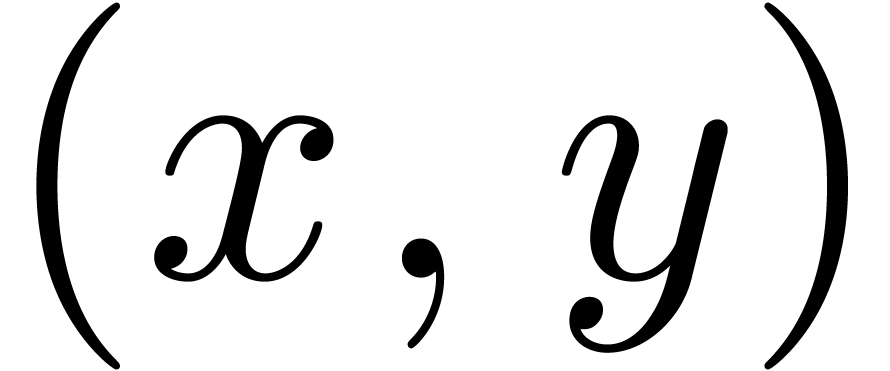
|
return 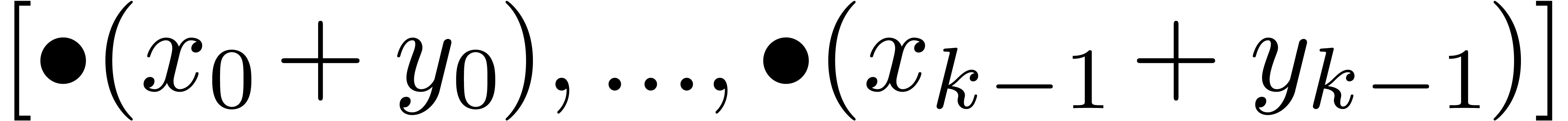
|
|
|
Algorithm Subtract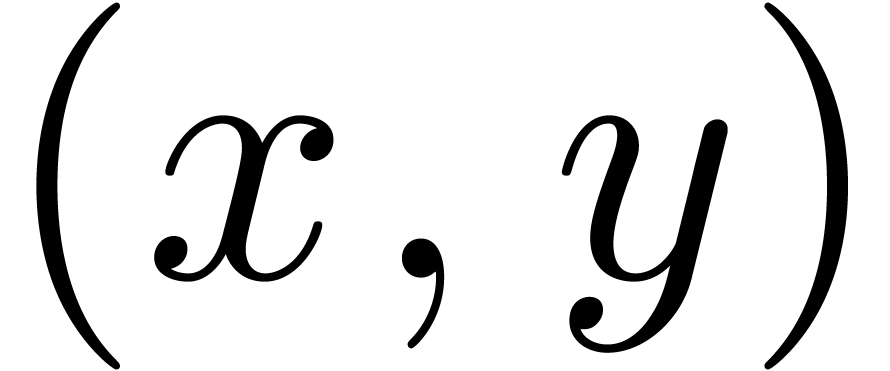
|
return 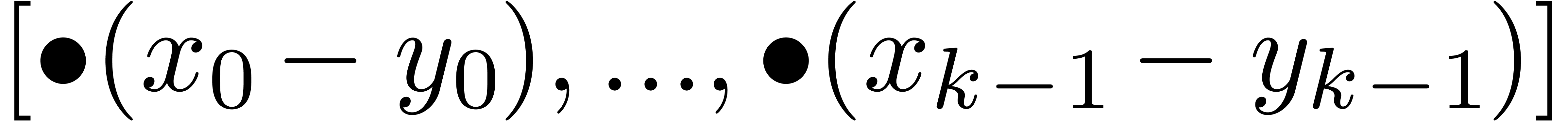
|
|
Proposition 9 from [10] now becomes:
2.5.Double length multiplication
The multiplication algorithm of fixed-point numbers is based on a
subalgorithm LongMul that computes the exact product of two numbers
that computes the exact product of two numbers 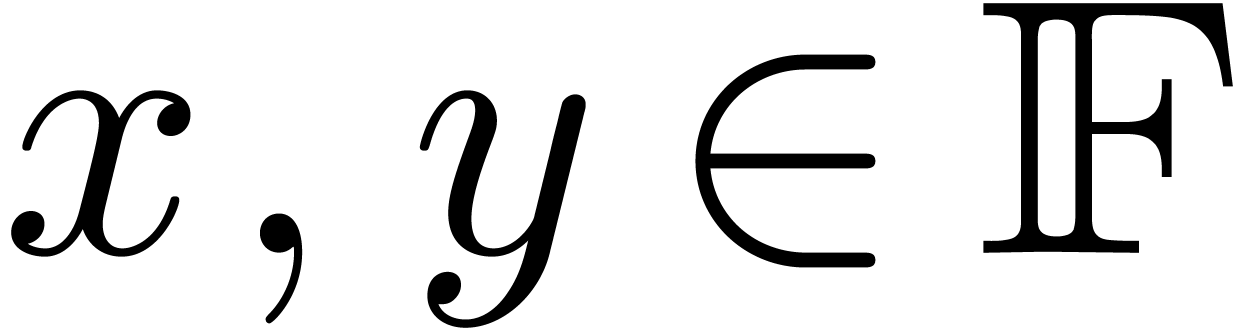 in the form of a sum
in the form of a sum 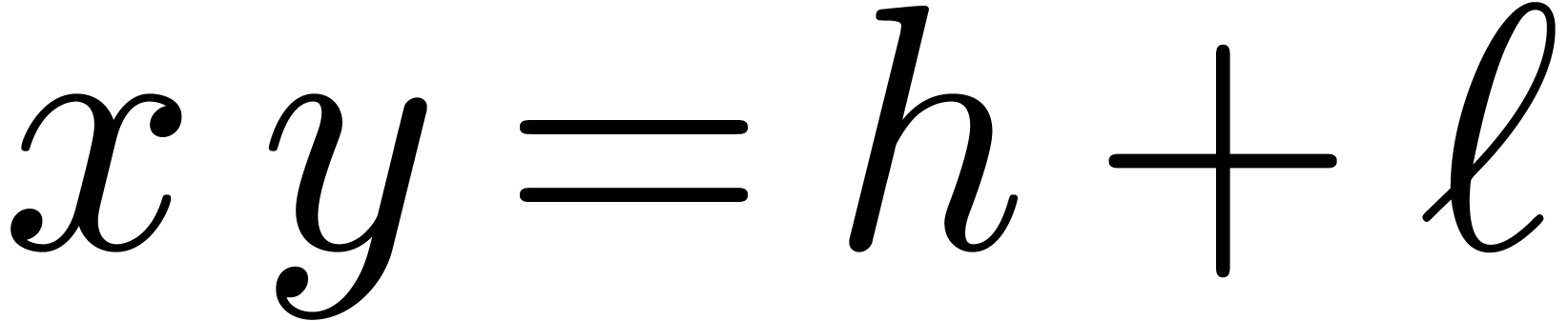 , with
the additional constraint that
, with
the additional constraint that 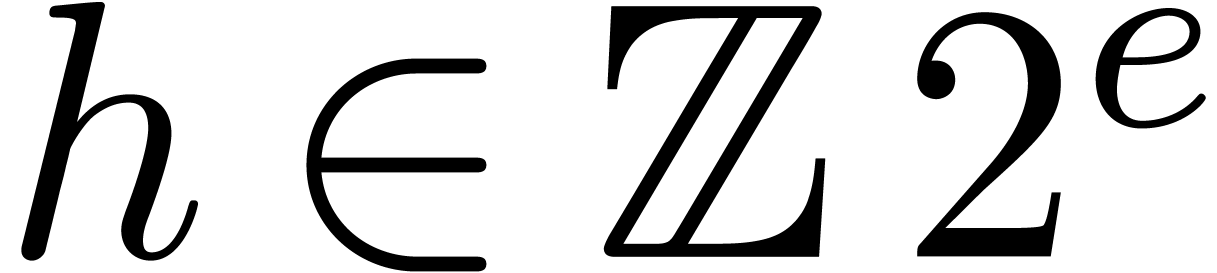 .
Without this additional constraint (and in absence of overflow and
underflow),
.
Without this additional constraint (and in absence of overflow and
underflow),  and
and  can be
computed using the well known “Two Product” algorithm:
can be
computed using the well known “Two Product” algorithm: 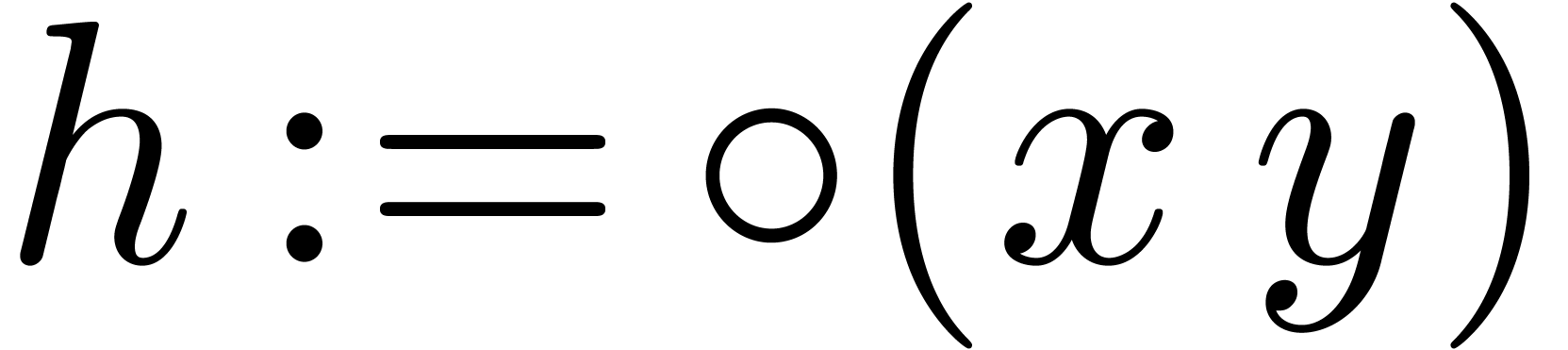 ,
, 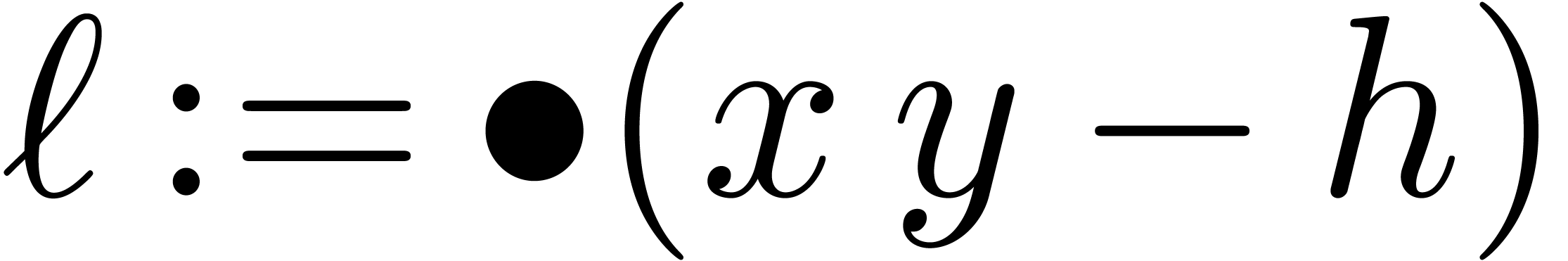 .
The LongMul
.
The LongMul algorithm
exploits the FMA and FMS instructions in a similar way.
algorithm
exploits the FMA and FMS instructions in a similar way.
Proposition 4 from [10] becomes as follows for
“rounding to nearest”:
2.6.General fixed-point
multiplication
For  large enough as a function of
large enough as a function of 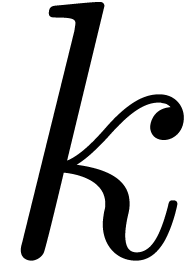 , one may use the following algorithm for
multiplication (all loops again being unrolled in practice):
, one may use the following algorithm for
multiplication (all loops again being unrolled in practice):
Notice that we need the additional line  at the
end with respect to [10] in order to ensure that
at the
end with respect to [10] in order to ensure that 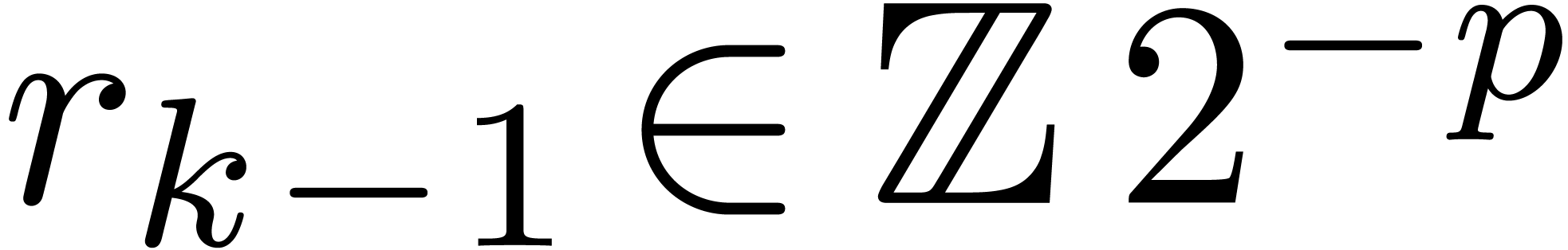 . Adapting [10,
Proposition 10], we obtain:
. Adapting [10,
Proposition 10], we obtain:
3.Fast parallel shifting
In this section, we discuss several routines for shifting fixed-point
numbers. All algorithms were designed to be naturally parallel. More
precisely, we logically operate on SIMD vectors 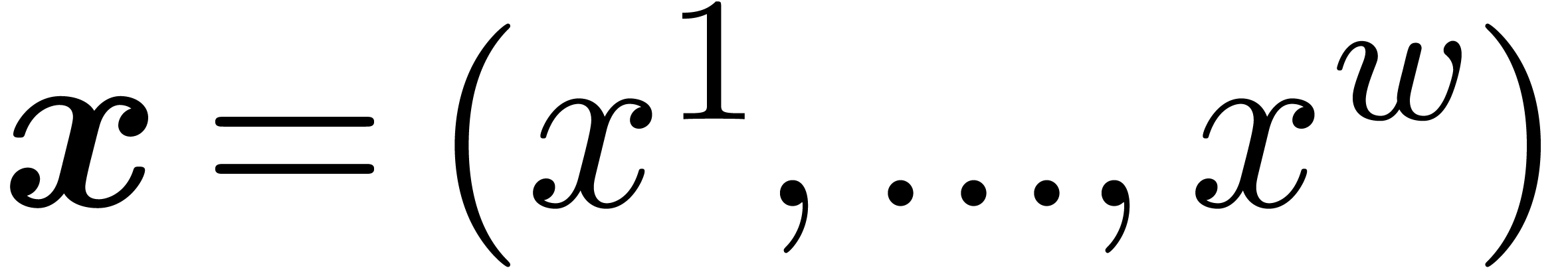 of fixed-point numbers
of fixed-point numbers 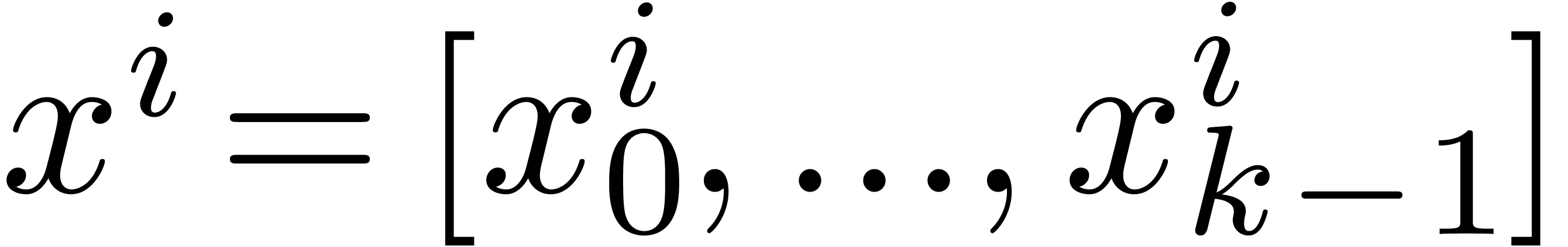 .
Internally, we rather work with fixed point numbers
.
Internally, we rather work with fixed point numbers 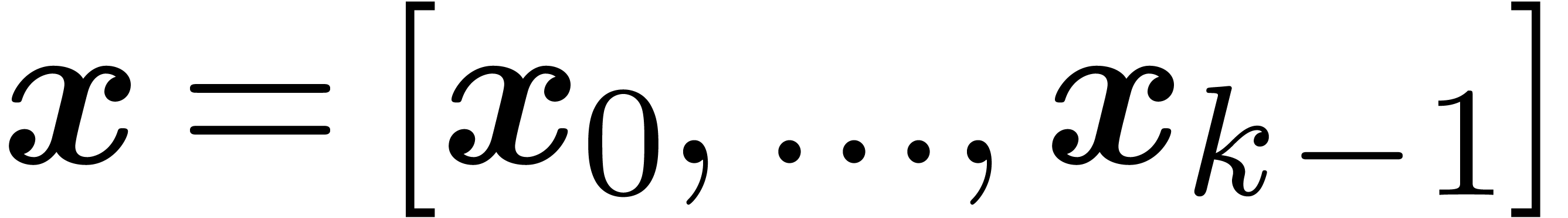 whose “coefficients” are machine SIMD vectors
whose “coefficients” are machine SIMD vectors 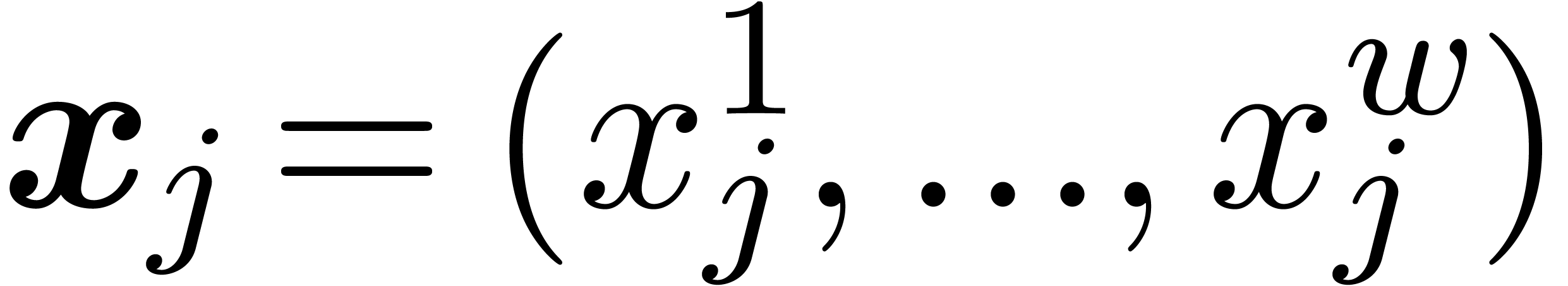 . All arithmetic operations can then simply be
performed in SIMD fashion using hardware instructions. For compatibility
with the notations from the previous section, we omit the bold face for
SIMD vectors, except if we want to stress their SIMD nature. For actual
implementations for a given
. All arithmetic operations can then simply be
performed in SIMD fashion using hardware instructions. For compatibility
with the notations from the previous section, we omit the bold face for
SIMD vectors, except if we want to stress their SIMD nature. For actual
implementations for a given 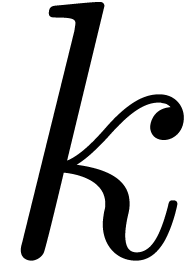 ,
we also understand that we systematically use in-place versions of our
algorithms and that all loops and function calls are completely
expanded.
,
we also understand that we systematically use in-place versions of our
algorithms and that all loops and function calls are completely
expanded.
3.1.Small parallel shifts
Let 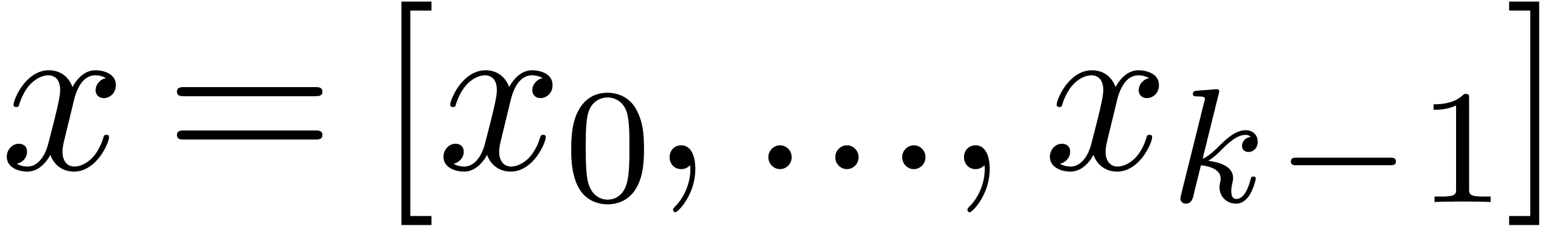 be a fixed-point number. Left shifts
be a fixed-point number. Left shifts 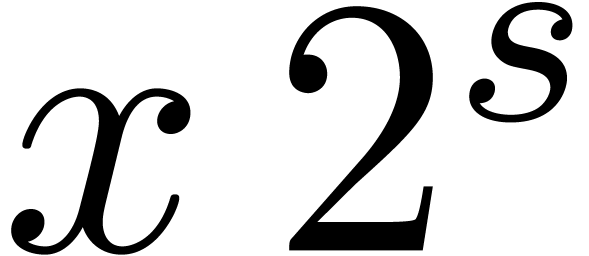 and right shifts
and right shifts 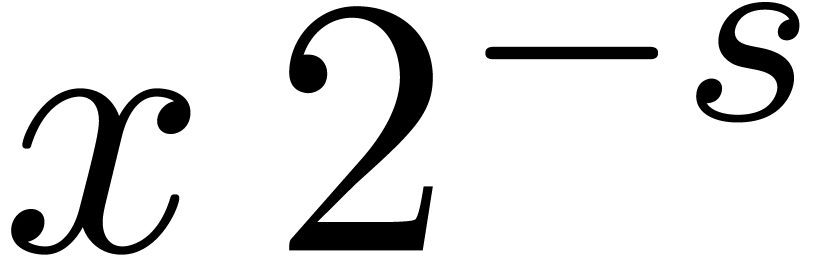 of
of  with
with  can be computed by cutting
the shifted coefficients
can be computed by cutting
the shifted coefficients 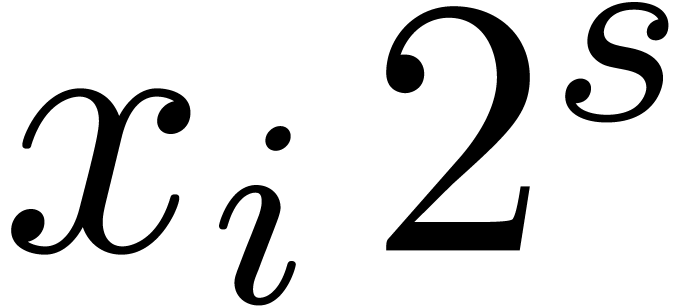 resp.
resp. 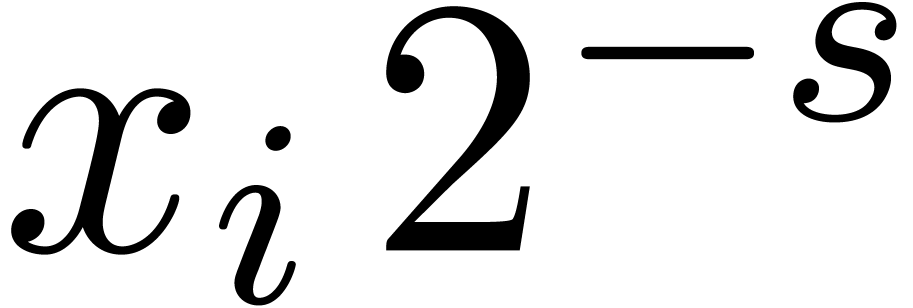 using the routine
using the routine  and
reassembling the pieces. The shift routines behave very much like
generalizations of the routine for carry normalization.
and
reassembling the pieces. The shift routines behave very much like
generalizations of the routine for carry normalization.
Algorithm SmallShiftLeft( ) )
|
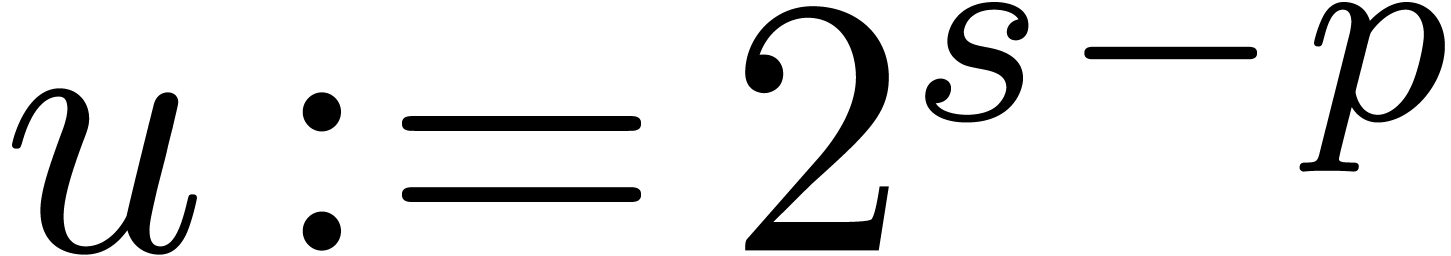

for  from
from  to
to  do
do

return 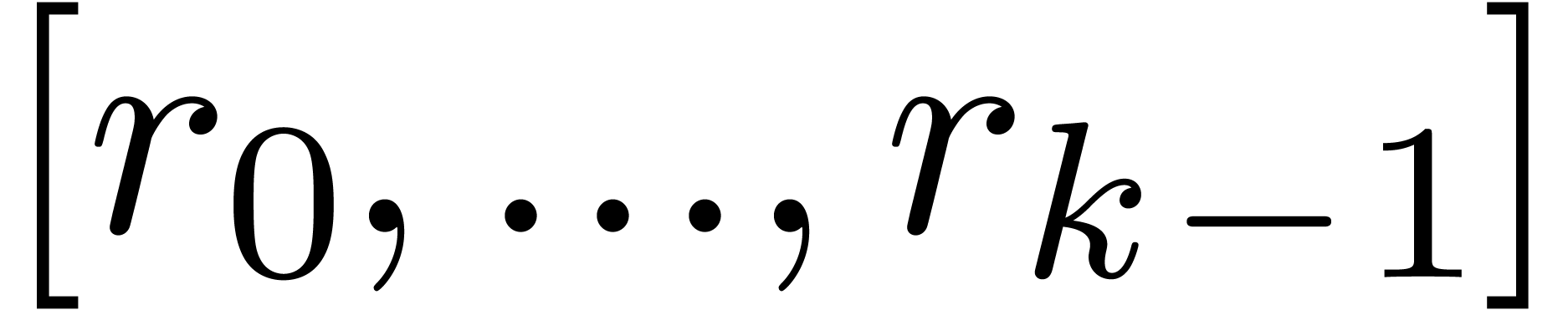
|
|
|
Algorithm SmallShiftRight( ) )
|
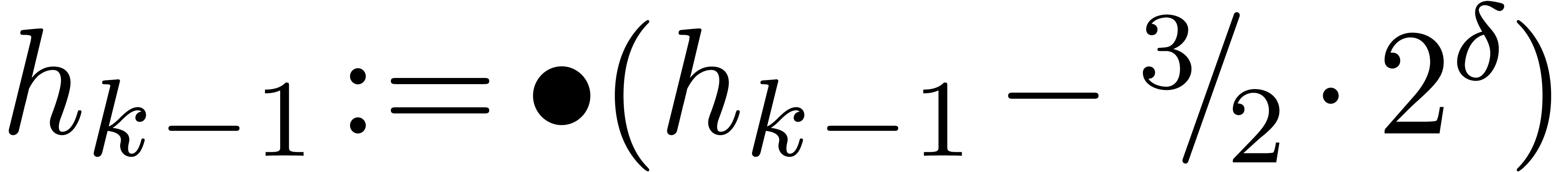
for 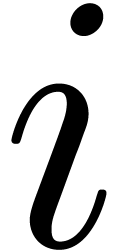 from
from  down
to down
to  do do
return 
|
|
Proof. In the main loop, we observe that  and
and  . The
assumption
. The
assumption 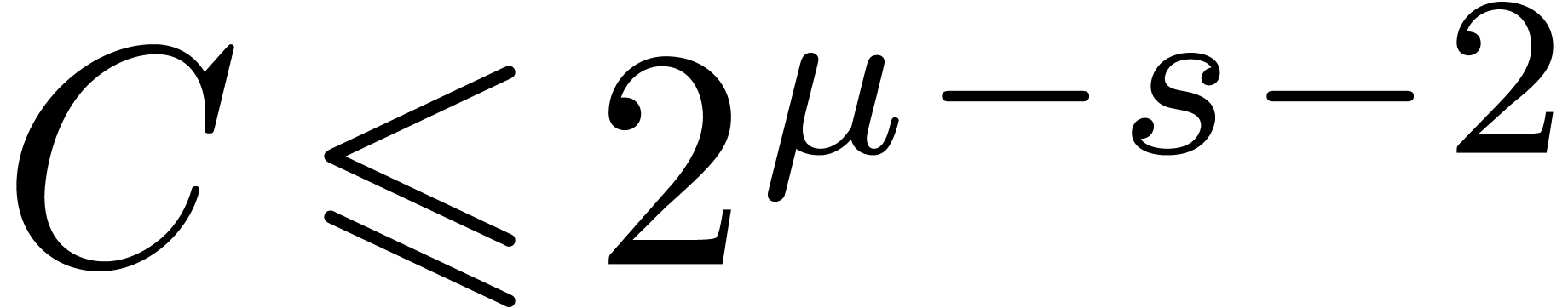 guarantees that Proposition 3
applies, so that
guarantees that Proposition 3
applies, so that  and
and 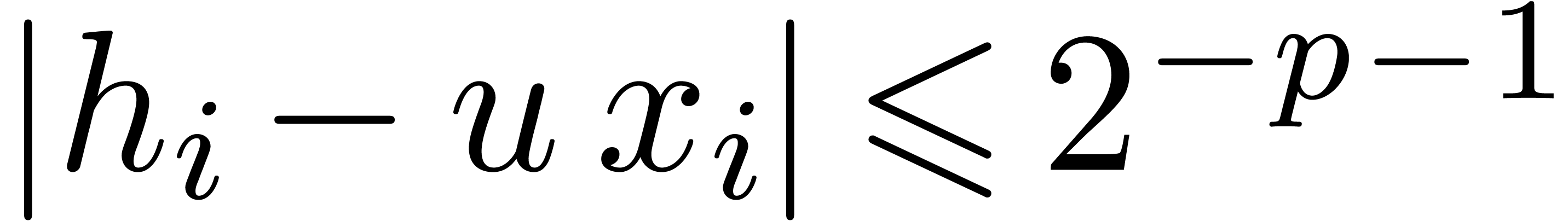 . The operation
. The operation 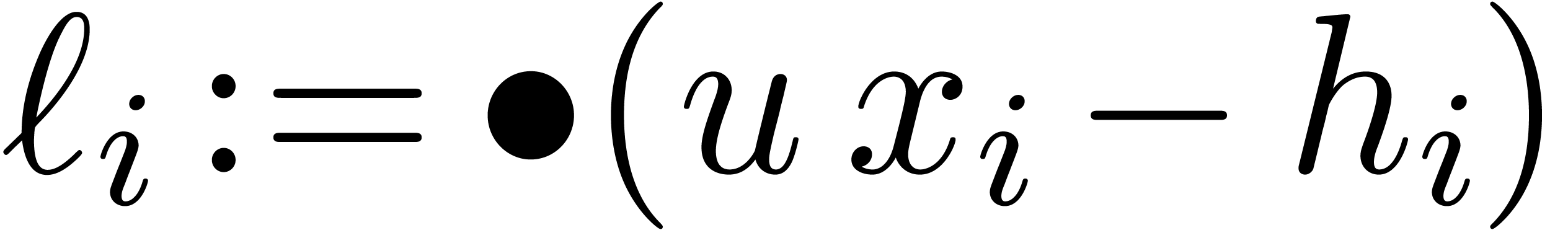 is therefore
exact, so that
is therefore
exact, so that 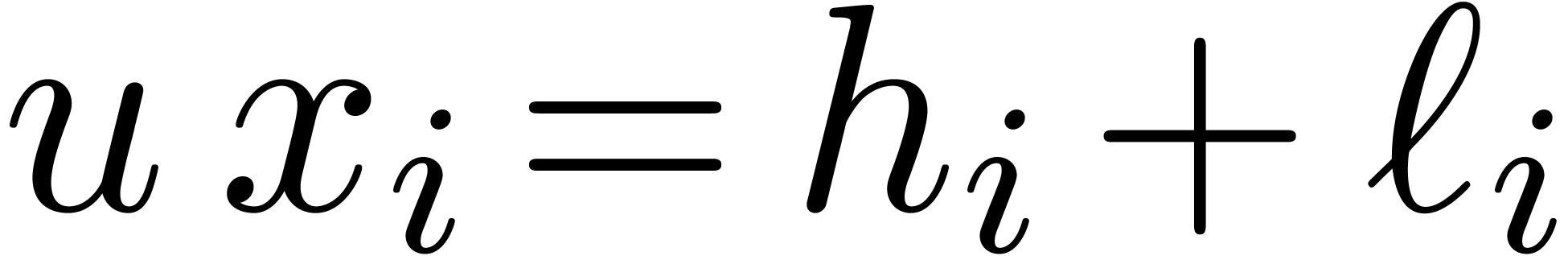 ,
,  , and
, and 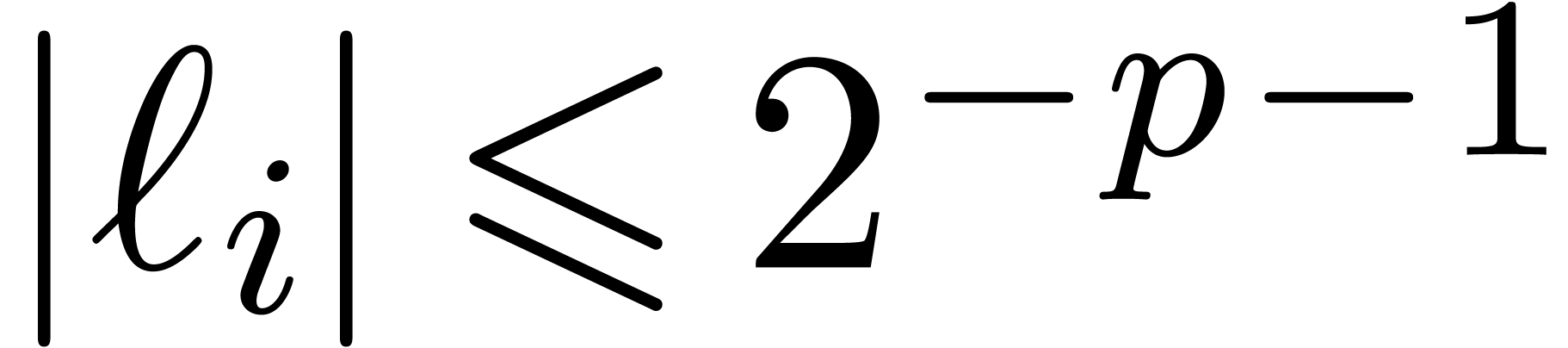 .
Since
.
Since 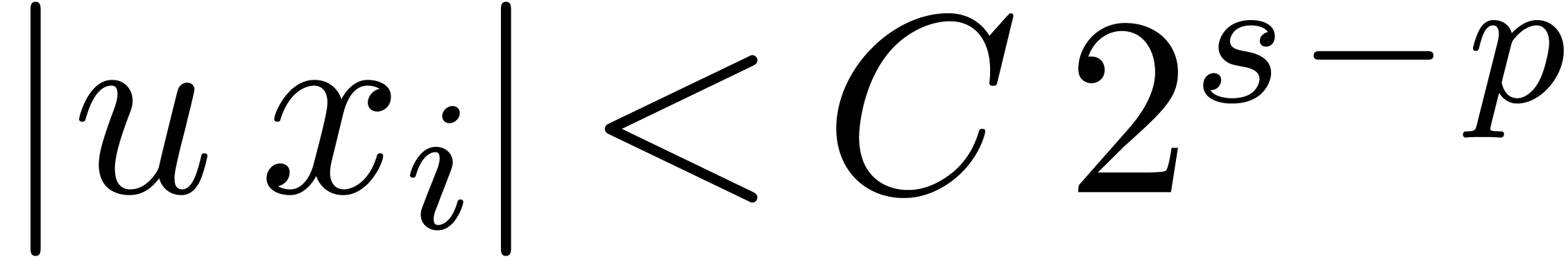 , we also have
, we also have 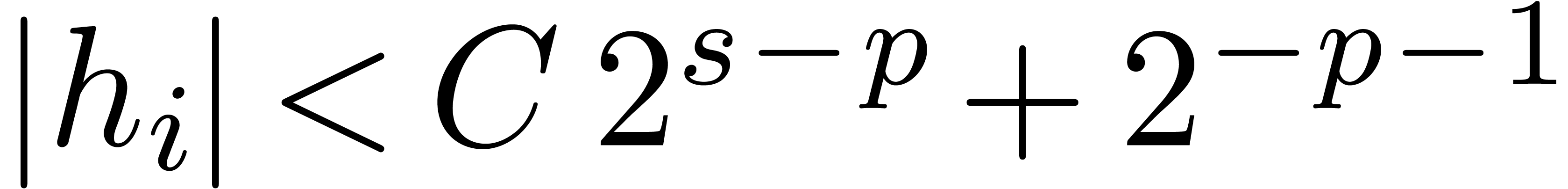 . Now
. Now 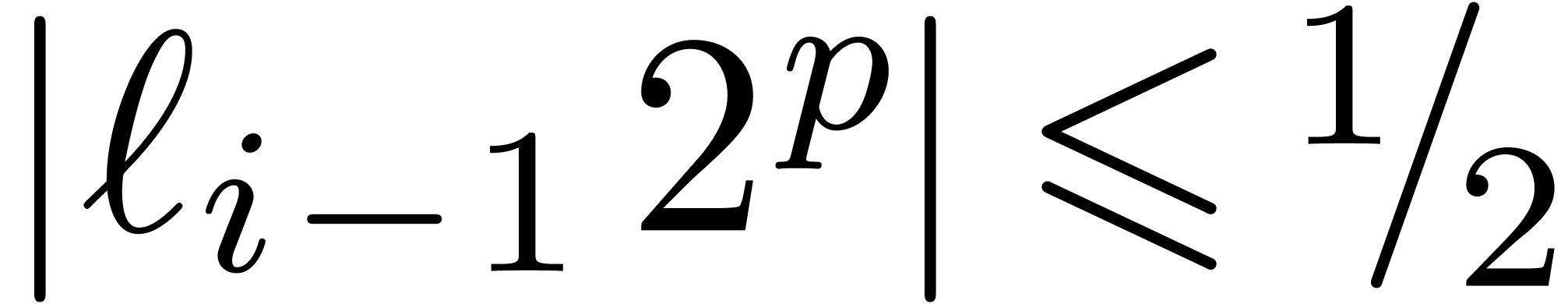 if
if
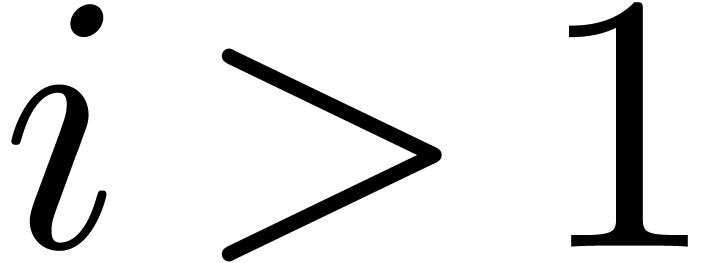 and
and 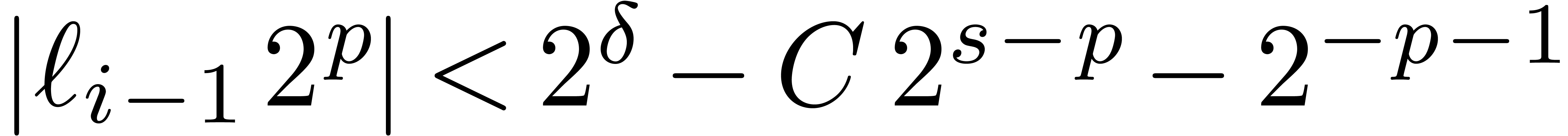 if
if 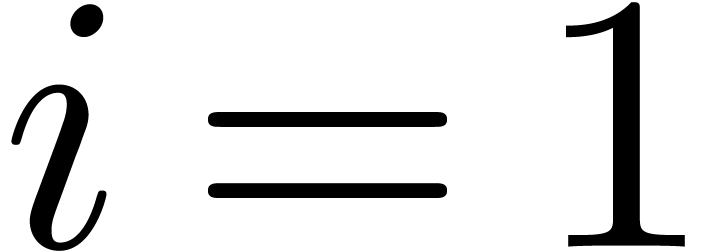 . Combined with the facts that
. Combined with the facts that 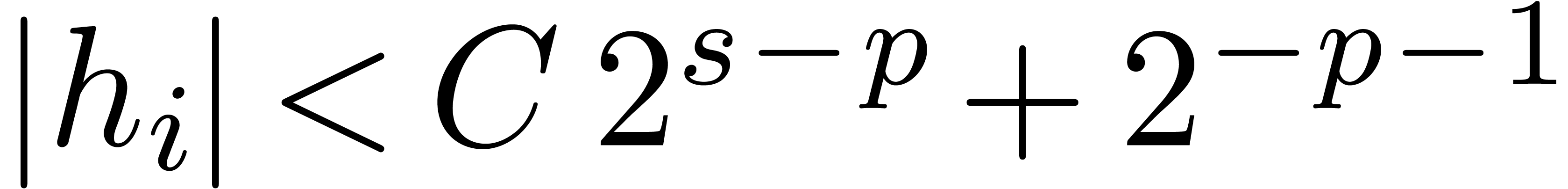 and
and 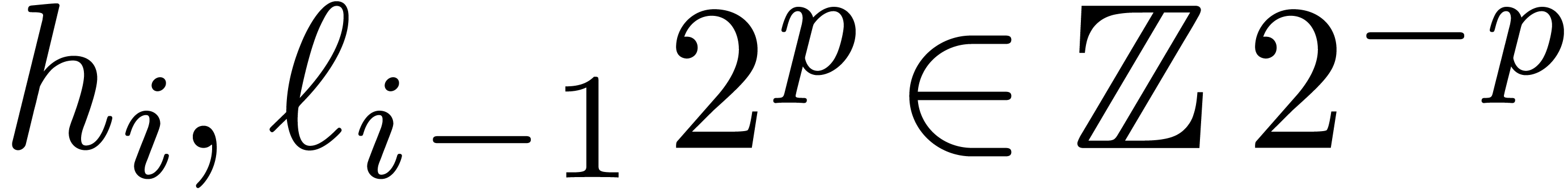 , it follows that the
operation
, it follows that the
operation 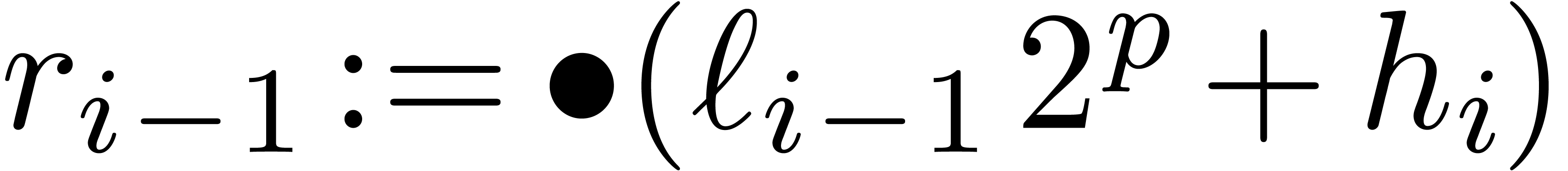 is also exact. Moreover,
is also exact. Moreover, 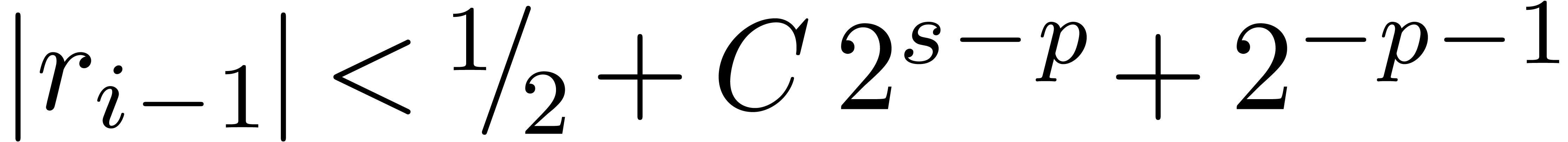 if
if  and
and 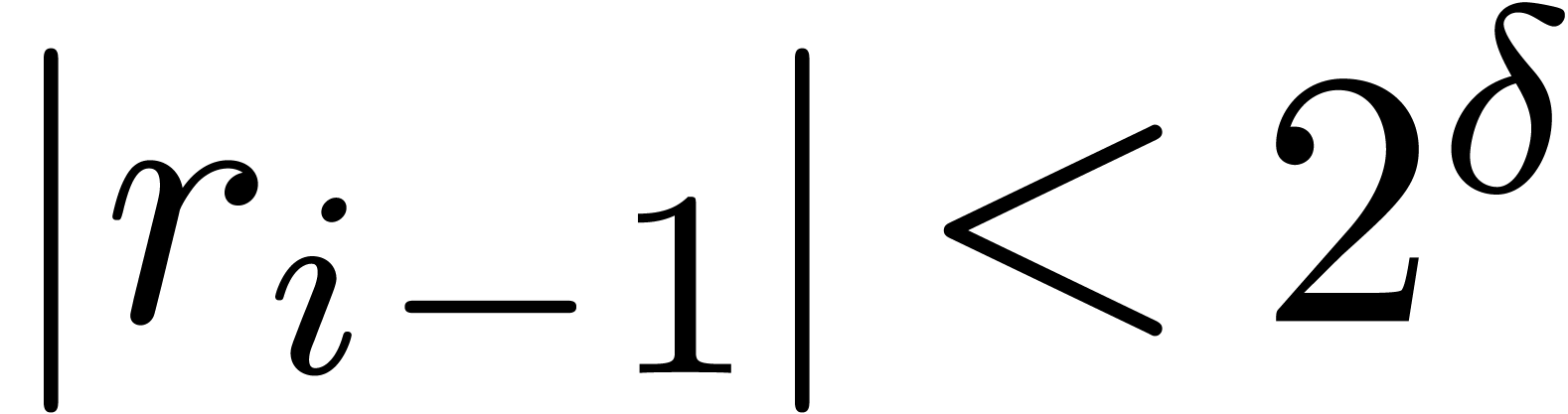 if
if
 . The last operation
. The last operation  is clearly exact and
is clearly exact and 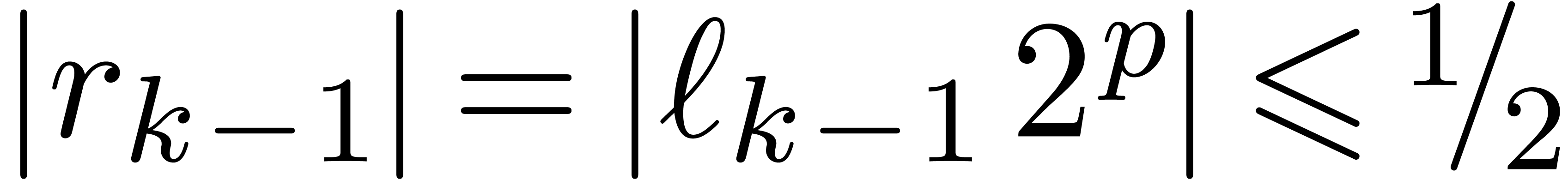 .
Finally,
.
Finally,
This proves that 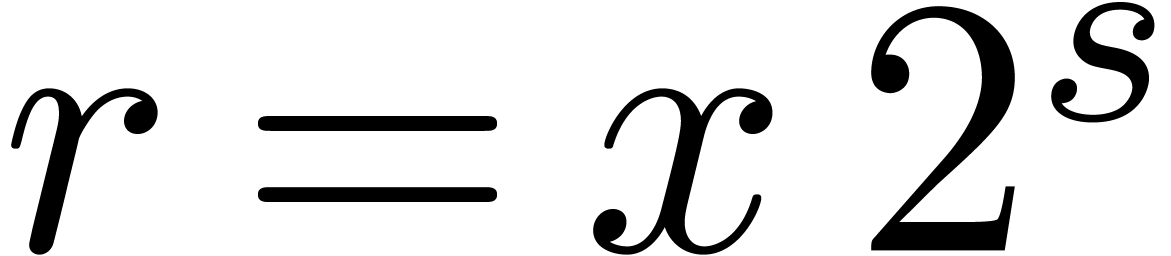 .□
.□
Proof. Similar to the proof of Proposition 8.□
3.2.Large parallel shifts
For shifts by 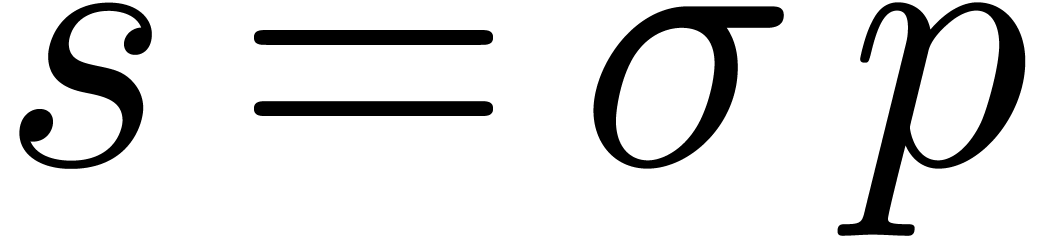 bits with
bits with 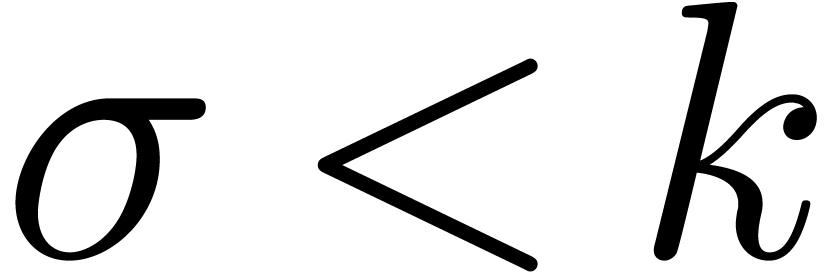 , we may directly shift the coefficients
, we may directly shift the coefficients  of the operand. Let
of the operand. Let 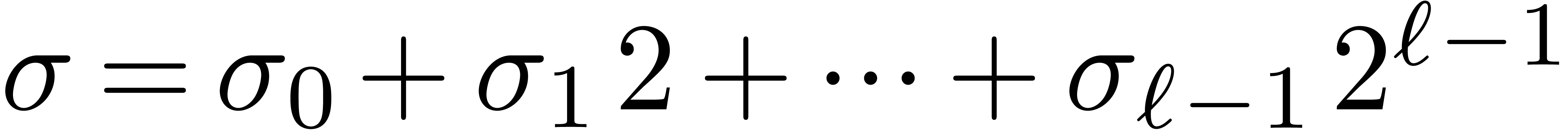 be the binary
representation of
be the binary
representation of  with
with 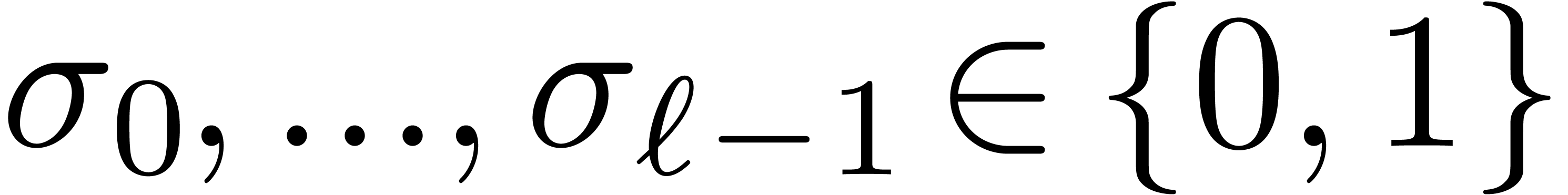 . Then we decompose a shift by
. Then we decompose a shift by  bits as the composition of
bits as the composition of  shifts by either
shifts by either  or
or 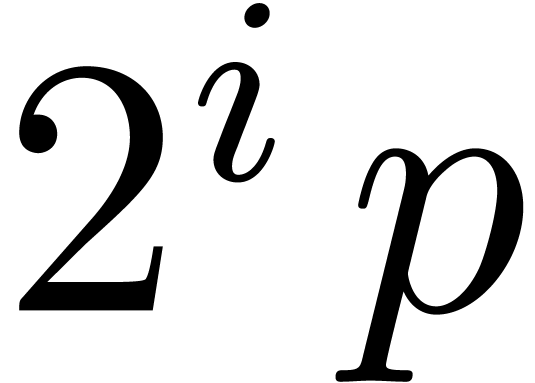 bits for
bits for  , depending on whether
, depending on whether 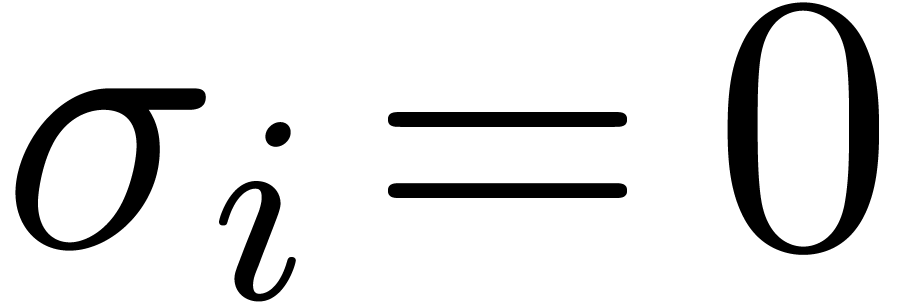 or
or 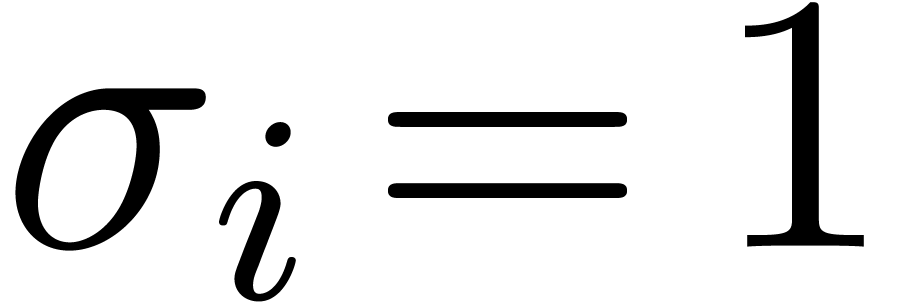 . This way of proceeding
has the advantage of being straightforward to parallelize, assuming that
we have an instruction to extract a new SIMD vector from two given SIMD
vectors according to a mask. On Intel processors,
there are several “blend” instructions for this purpose. In
the pseudo-code below, we simply used “if expressions”
instead.
. This way of proceeding
has the advantage of being straightforward to parallelize, assuming that
we have an instruction to extract a new SIMD vector from two given SIMD
vectors according to a mask. On Intel processors,
there are several “blend” instructions for this purpose. In
the pseudo-code below, we simply used “if expressions”
instead.
Algorithm LargeShiftLeft( ) )
|
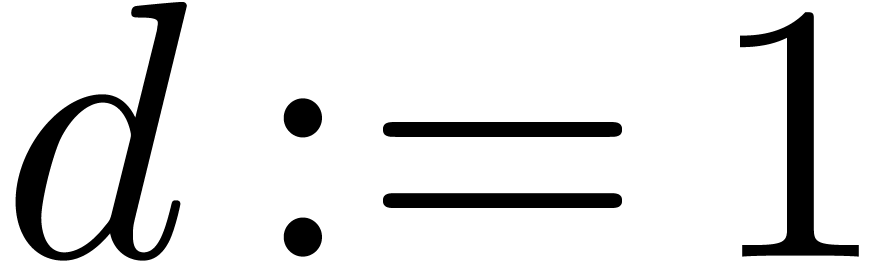
while 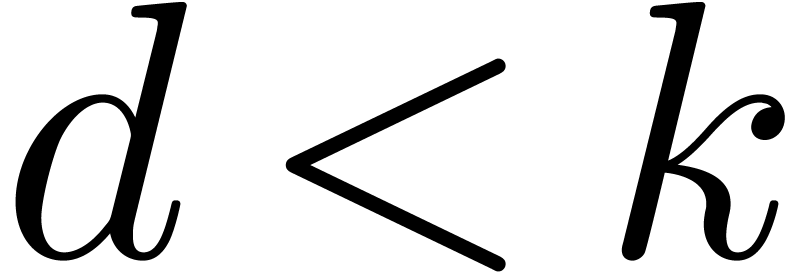 do
do
return 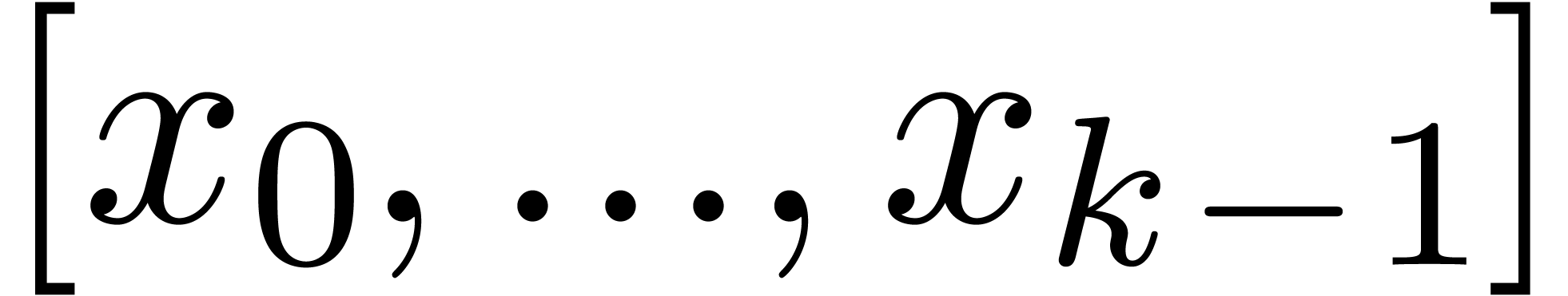
|
|
|
Algorithm LargeShiftRight( ) )
|
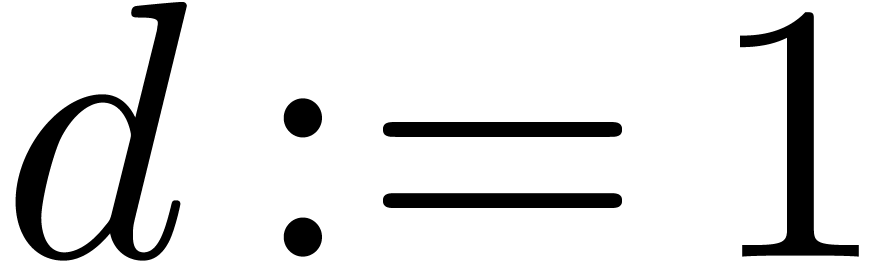
while  do
do
return 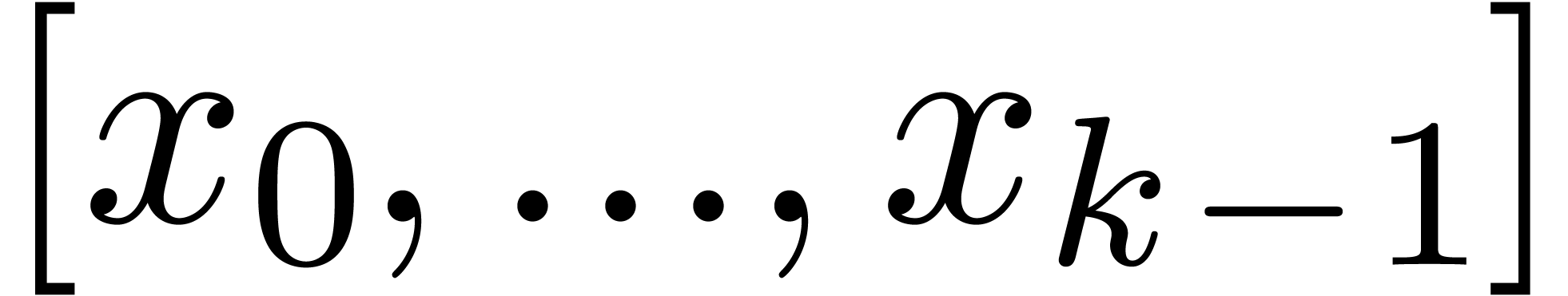
|
|
The following propositions are straightforward to prove.
Combining with the algorithms from the previous subsection, we obtain
the routines ShiftLeft and ShiftRight
below for general shifts. Notice that we shift by at most 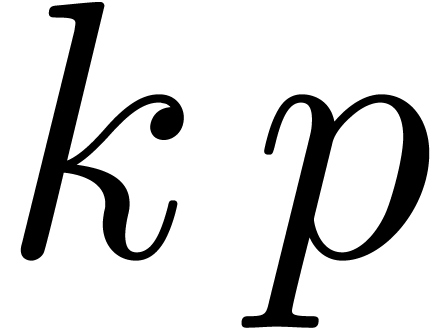 bits. Due to the fact that we allow for nail bits, the
maximal error is bounded by
bits. Due to the fact that we allow for nail bits, the
maximal error is bounded by 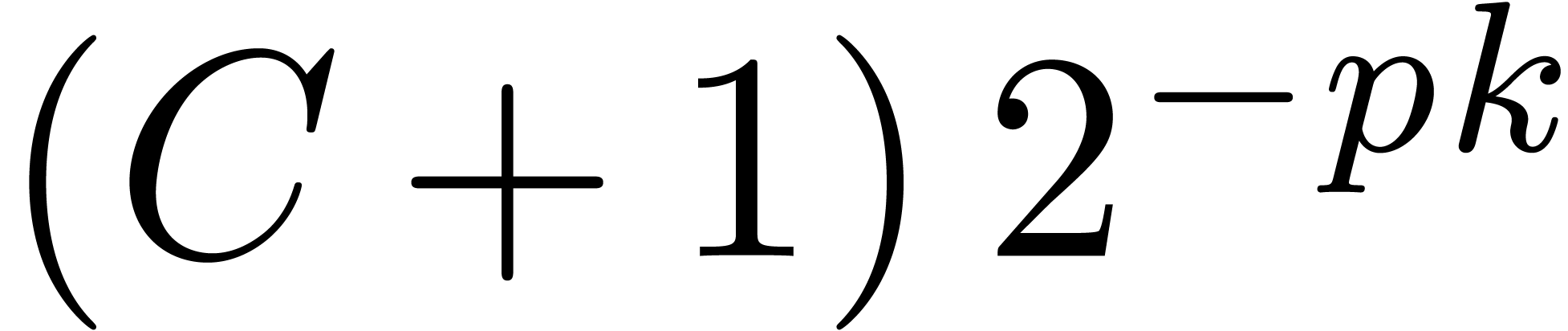 .
.
Algorithm ShiftLeft( ) )
|
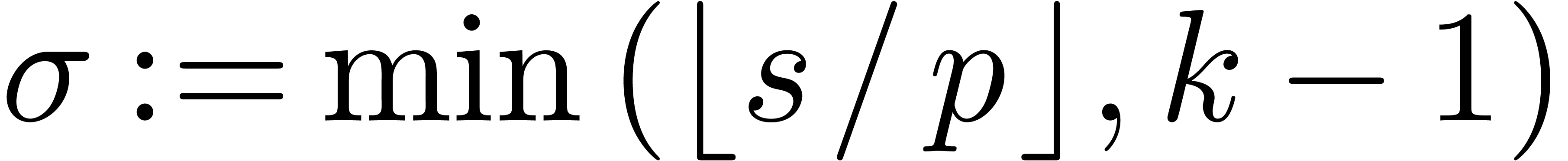
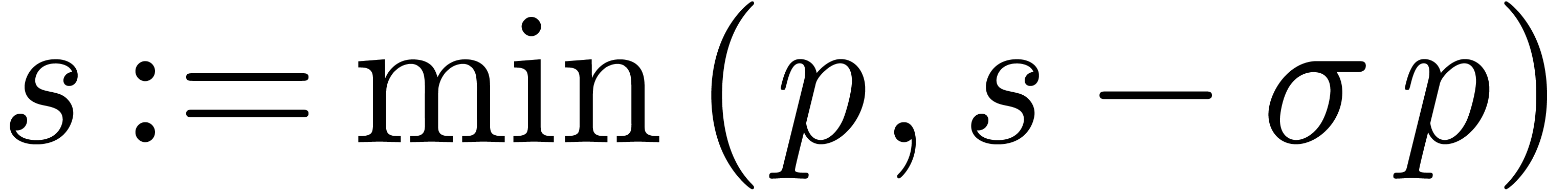


return 
|
|
|
Algorithm ShiftRight( ) )
|
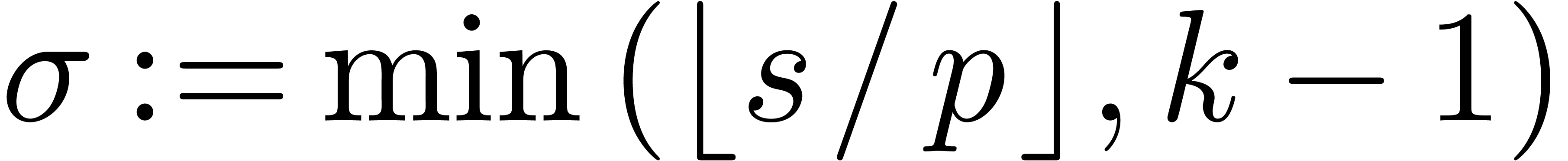
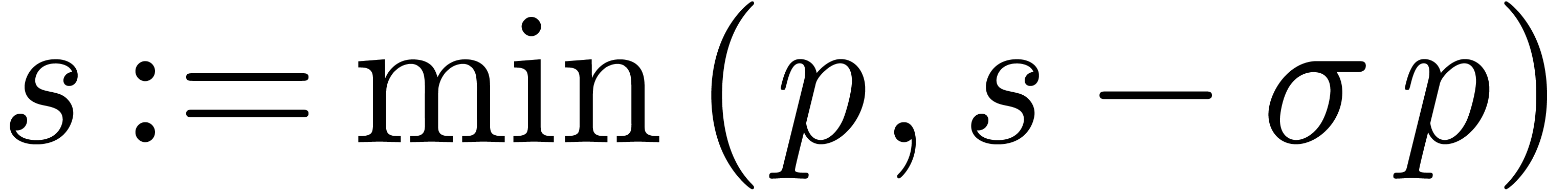


return 
|
|
3.3.Uniform parallel shifts
The routines LargeShiftLeft and
LargeShiftRight were designed to work for SIMD vectors
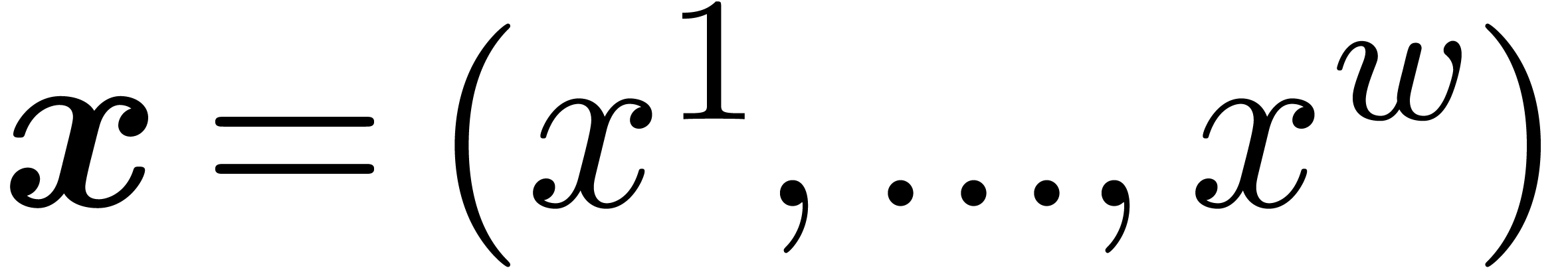 of fixed-point numbers and shift amounts
of fixed-point numbers and shift amounts 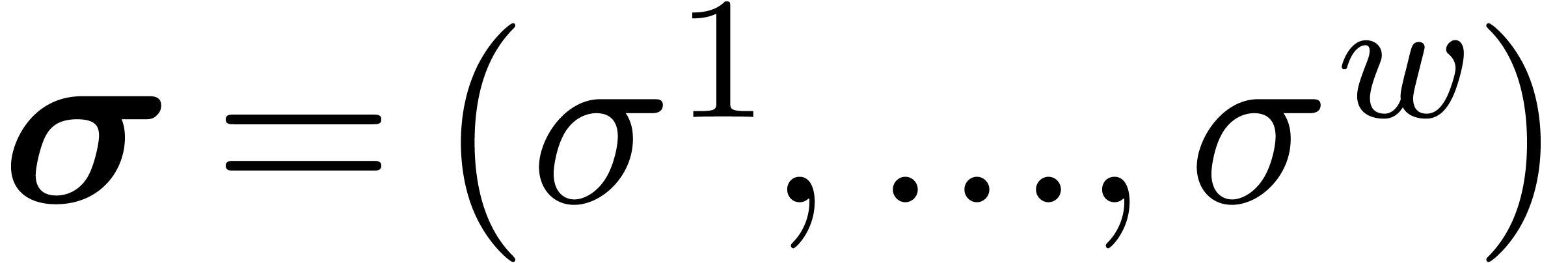 . If the number of bits by which we
shift is the same
. If the number of bits by which we
shift is the same 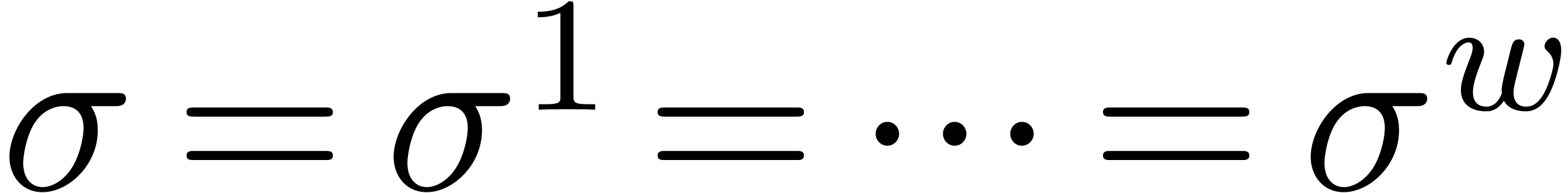 for all entries, then we may
use the following routines instead:
for all entries, then we may
use the following routines instead:
3.4.Retrieving the exponent
The IEEE-754 standard provides an operation 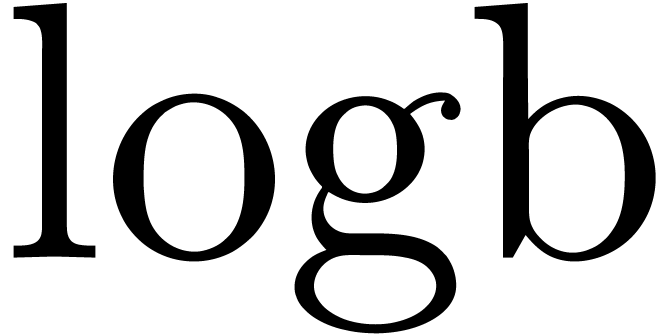 for
retrieving the exponent
for
retrieving the exponent  of a machine number
of a machine number
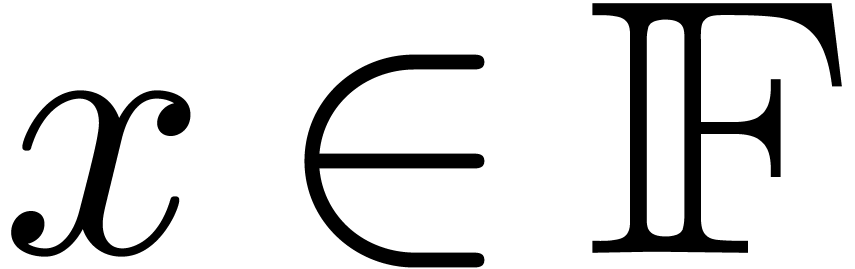 : if
: if 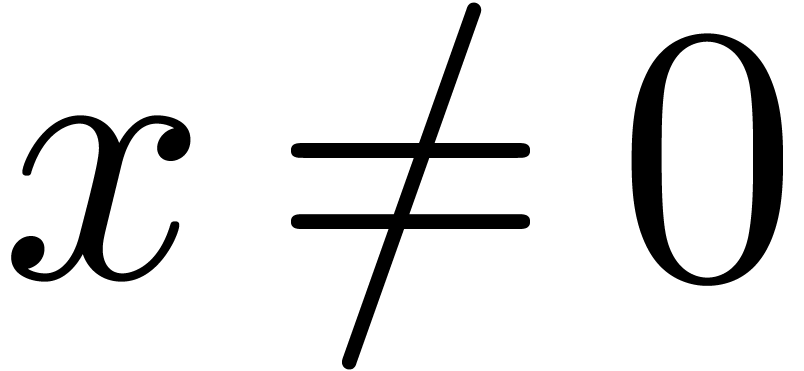 , then
, then 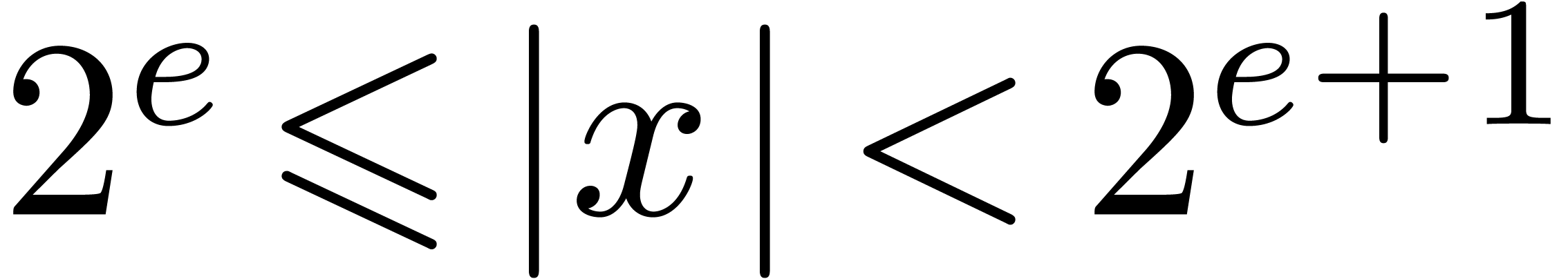 .
It is natural to ask for a similar function on
.
It is natural to ask for a similar function on 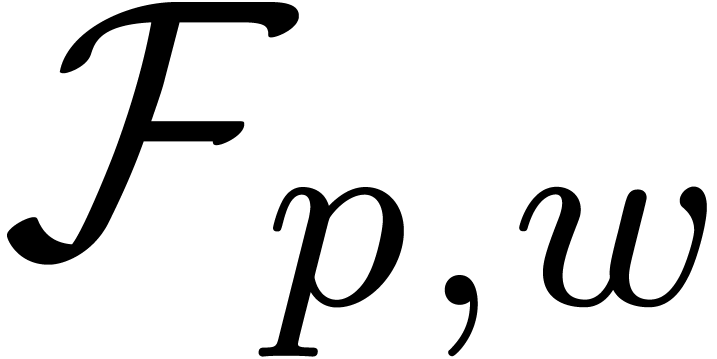 , as well as a similar function
, as well as a similar function 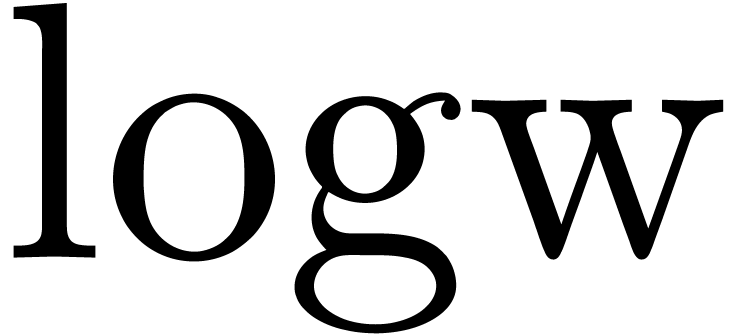 in base
in base 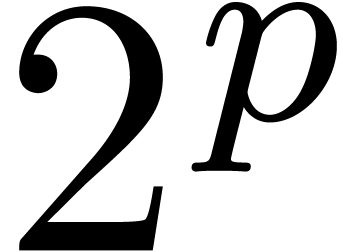 (that returns the exponent
(that returns the exponent  with
with 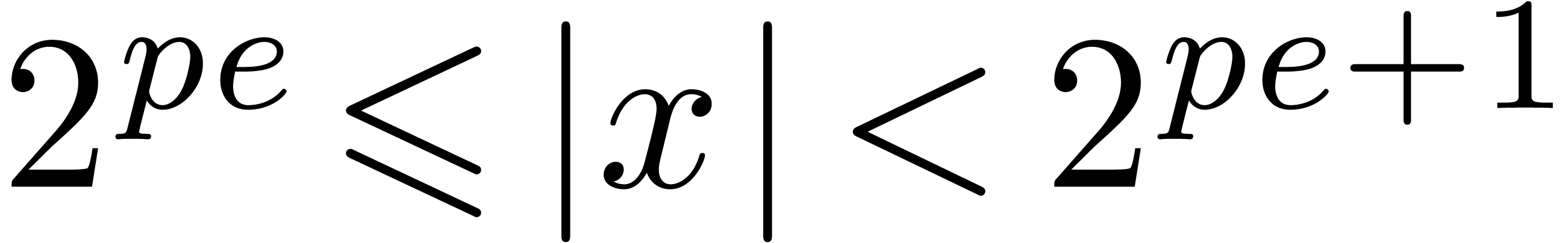 for every
for every 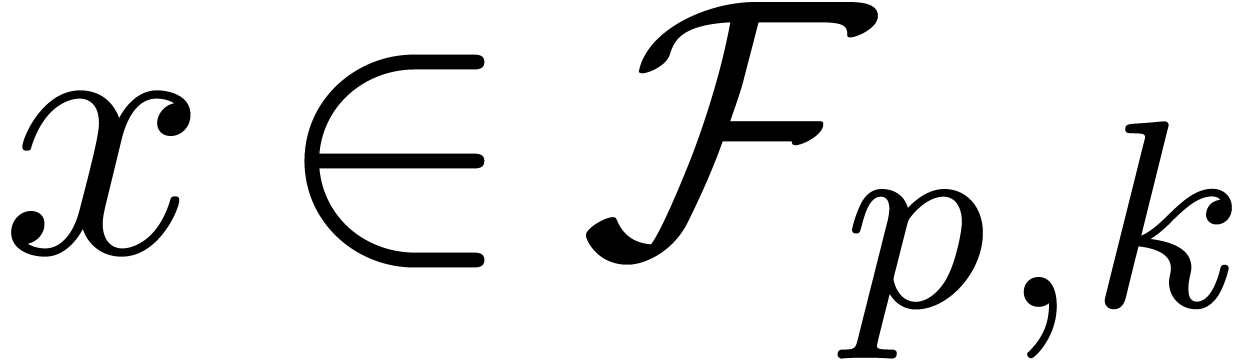 with
with 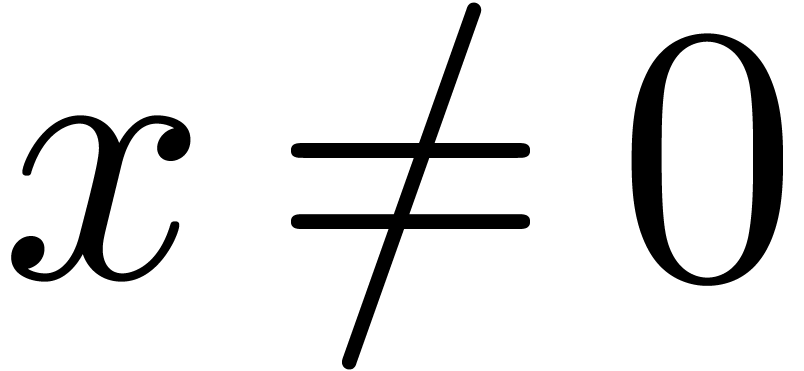 ). For
). For 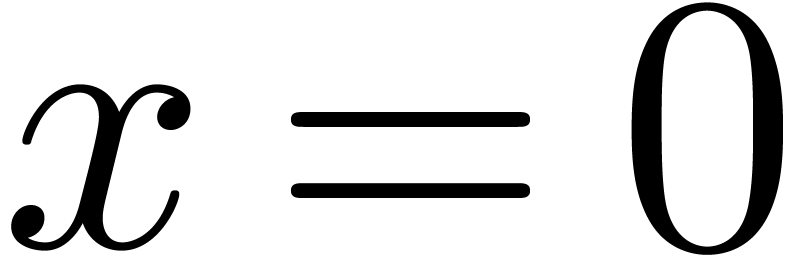 , we understand that
, we understand that 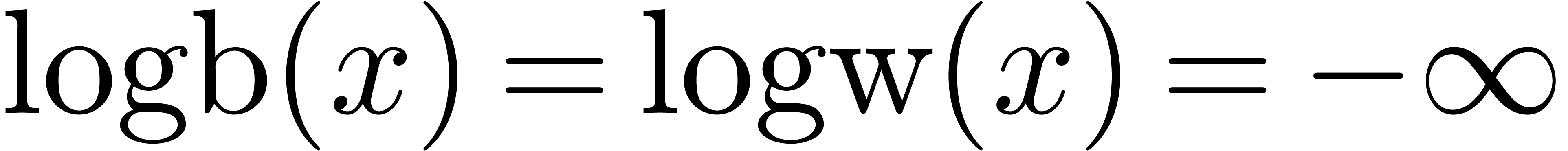 .
.
The functions LogB and LogW below are
approximations for such functions 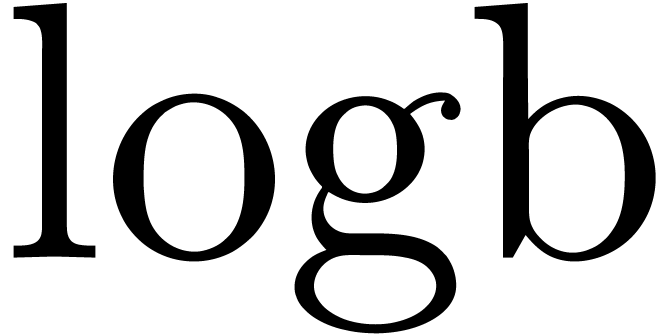 and
and 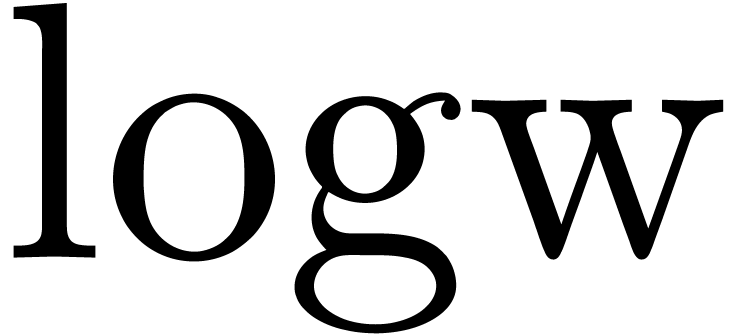 . More precisely, for all
. More precisely, for all 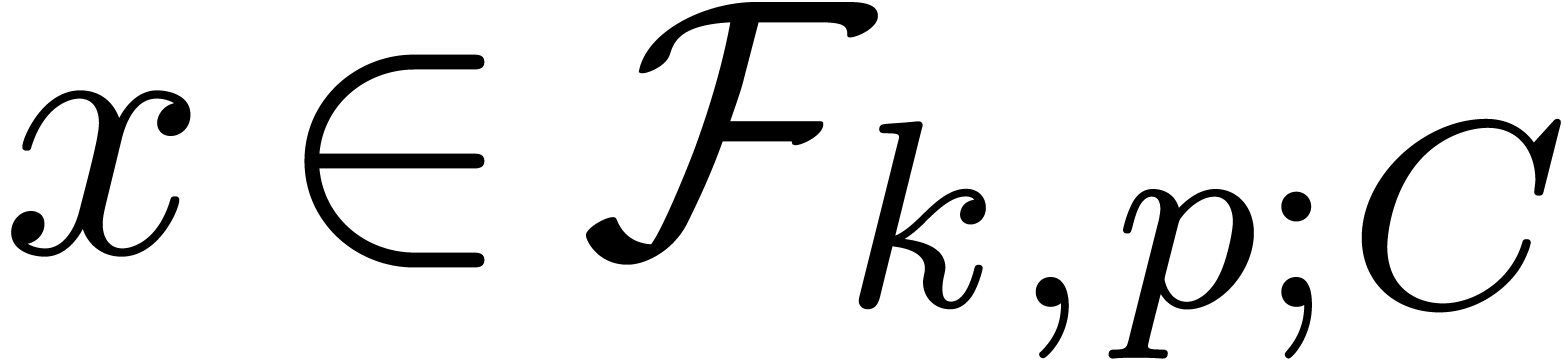 in carry normal form with
in carry normal form with 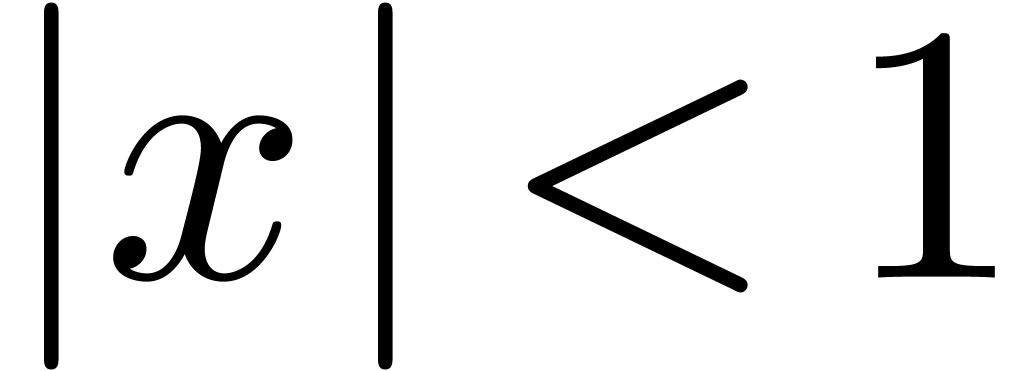 ,
we have
,
we have
The routine LogB relies on the computation of a number
 with
with  that only works
under the assumption that
that only works
under the assumption that 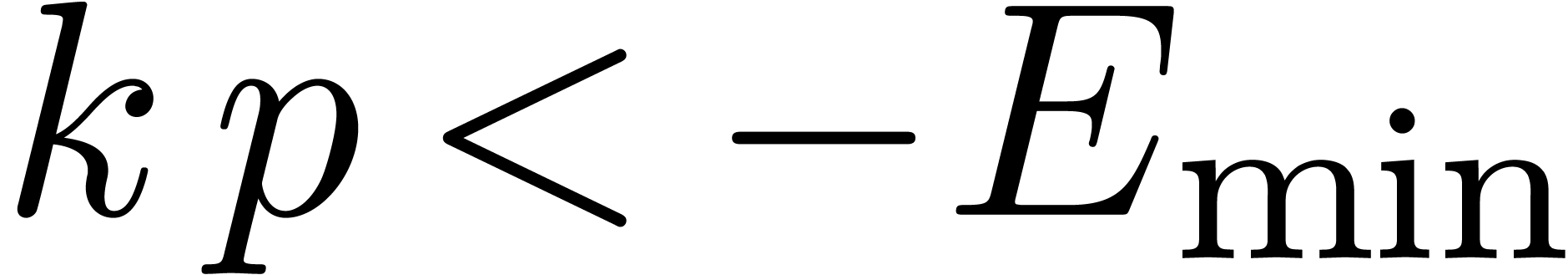 .
It is nevertheless easy to adapt the routine to higher precisions by
cutting
.
It is nevertheless easy to adapt the routine to higher precisions by
cutting  into chunks of
into chunks of  machine numbers. The routine LogW relies on a routine
HiWord that determines the smallest index
machine numbers. The routine LogW relies on a routine
HiWord that determines the smallest index 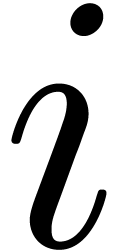 with
with  .
.
Algorithm Compress( ) )
|
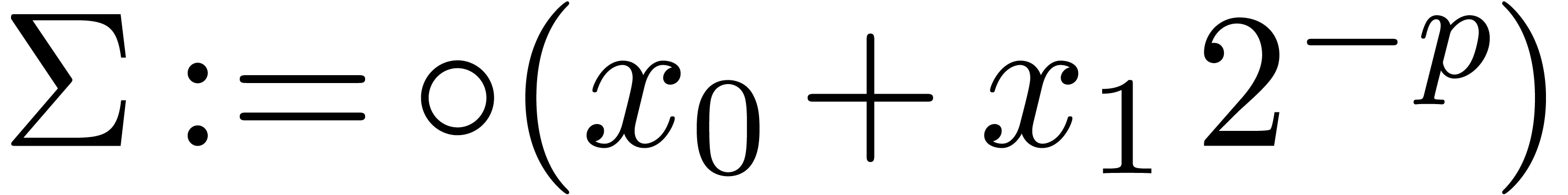
for  from
from  to
to  do
do
return 
|
|
|
Algorithm HiWord( ) )
|

for  from
from  down
to down
to 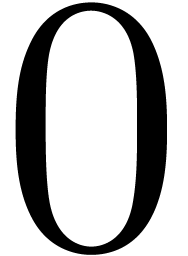 do do
return 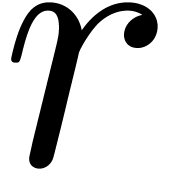
|
|
|
|
|
Algorithm LogB( ) )
|
return 
|
|
|
Algorithm LogW( ) )
|
return 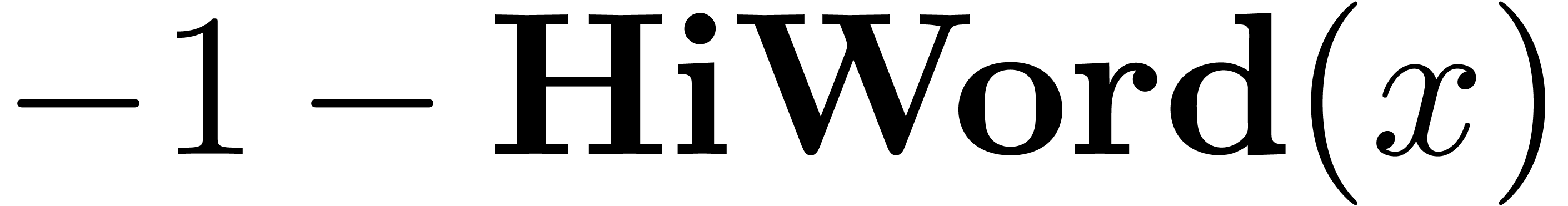
|
|
Proposition 12.
The routines Compress,
HiWord, LogB
and LogW are correct.
Proof. In Compress, let 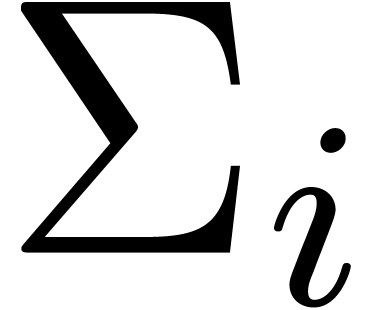 be the value of
be the value of  after adding
after adding
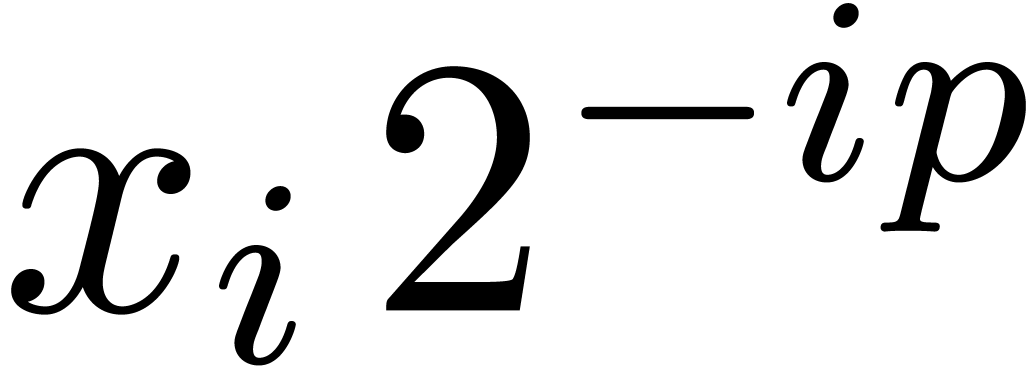 and notice that
and notice that  for all
for all
 . If
. If 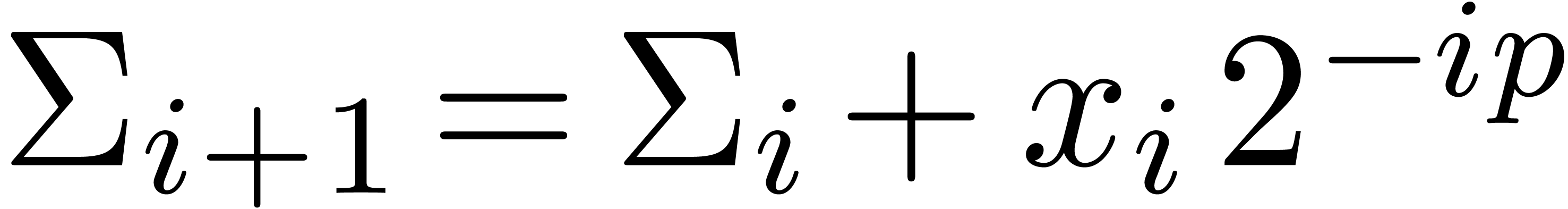 for all
for all  , then
, then  and Compress returns an exact result.
Otherwise, let
and Compress returns an exact result.
Otherwise, let  be minimal such that
be minimal such that 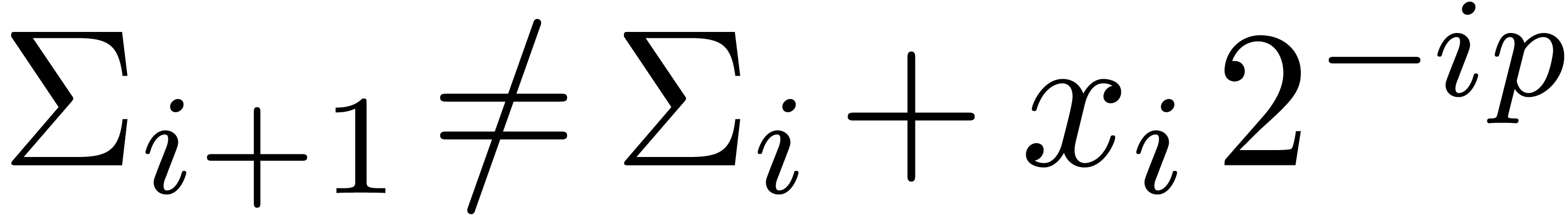 . Then
. Then 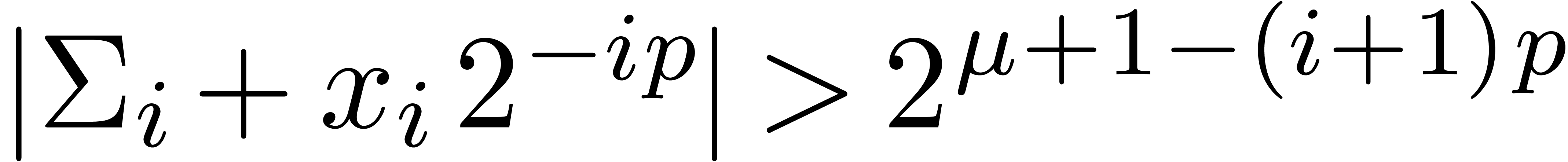 and
and 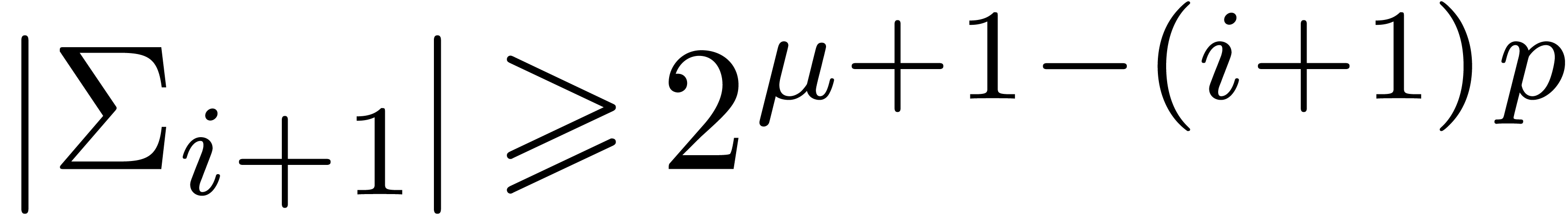 , whence
, whence 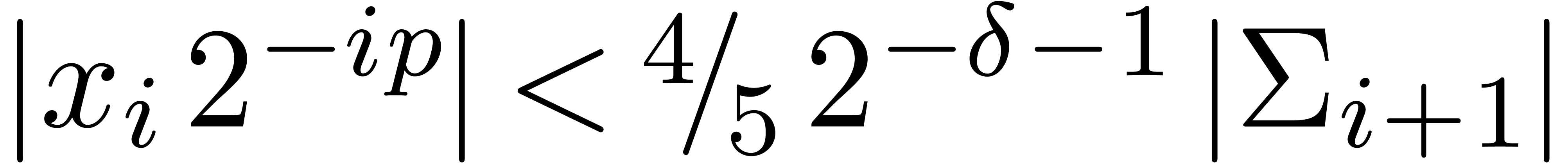 and
and 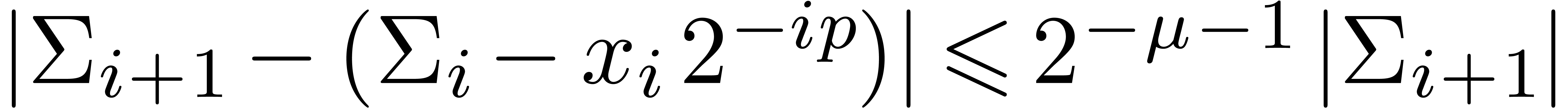 . Moreover, the exponent
. Moreover, the exponent  of
of  is at least
is at least  . For
. For  ,
we have
,
we have 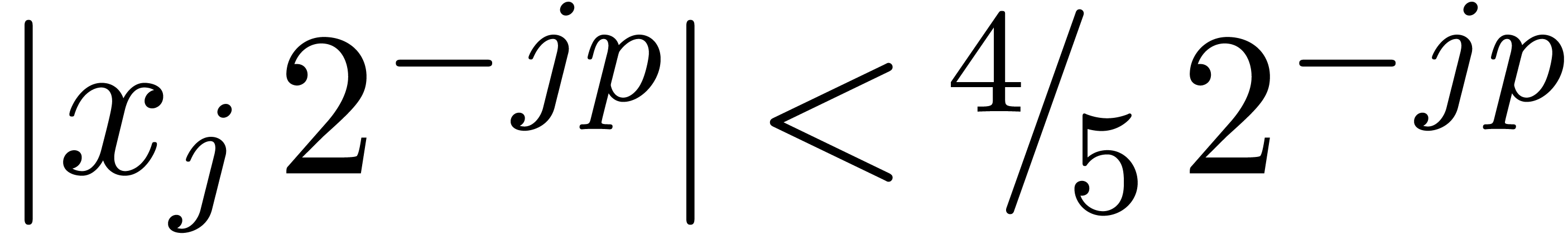 , whence the exponent
, whence the exponent
 of
of 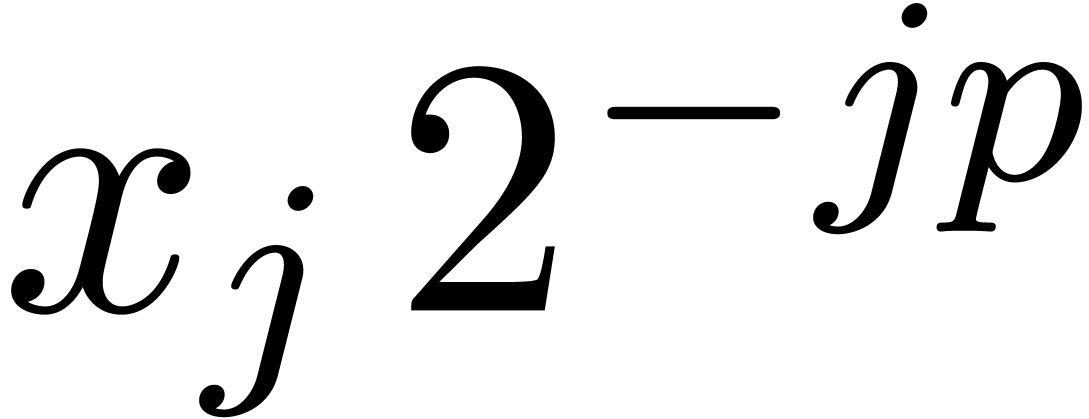 is at most
is at most 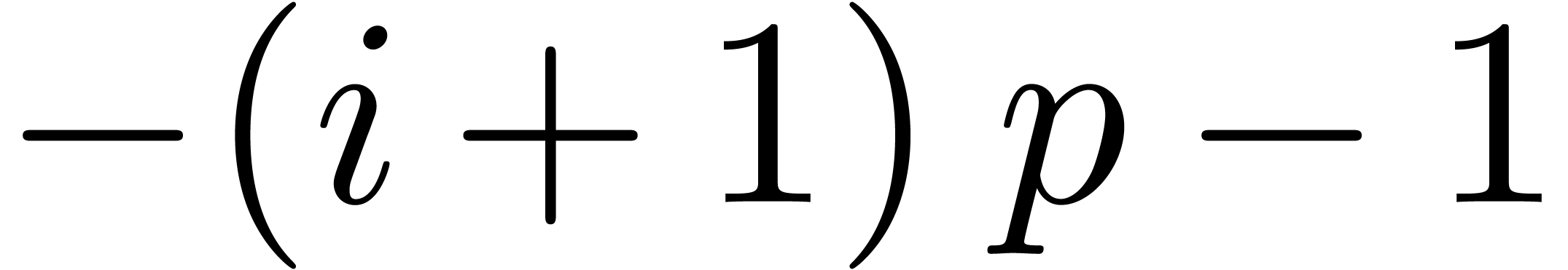 . This means that
. This means that 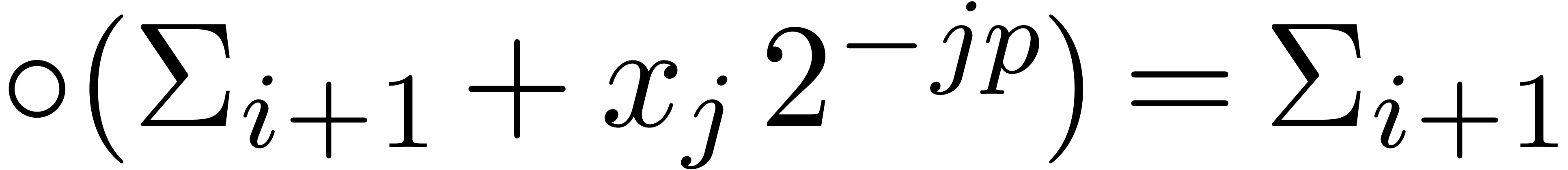 , whence
, whence 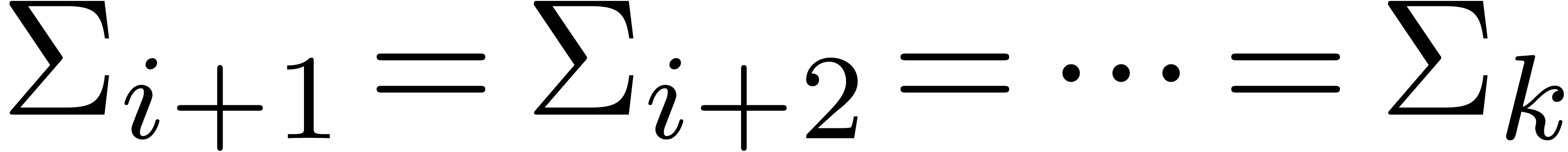 and
and  . The bound (2)
directly follows.
. The bound (2)
directly follows.
The algorithm HiWord is clearly correct. Assume that
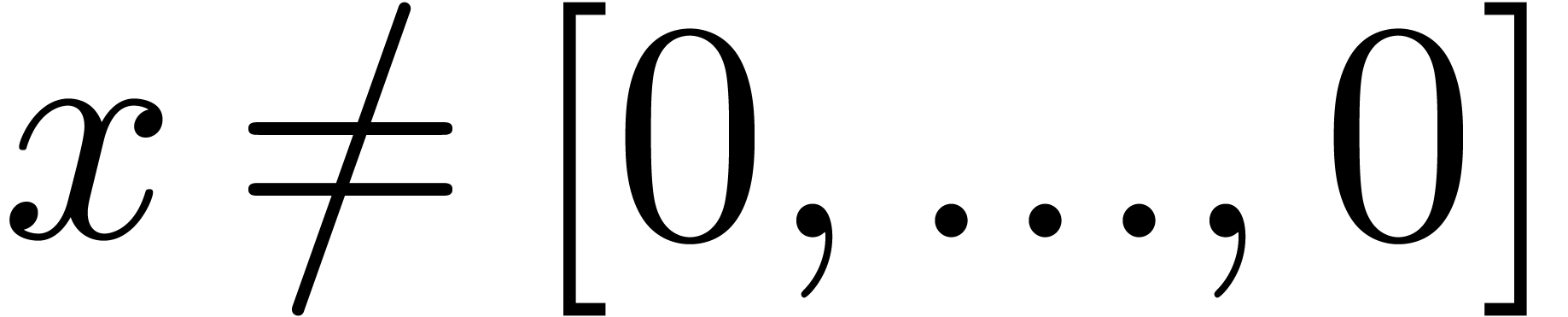 and let
and let  be minimal with
be minimal with
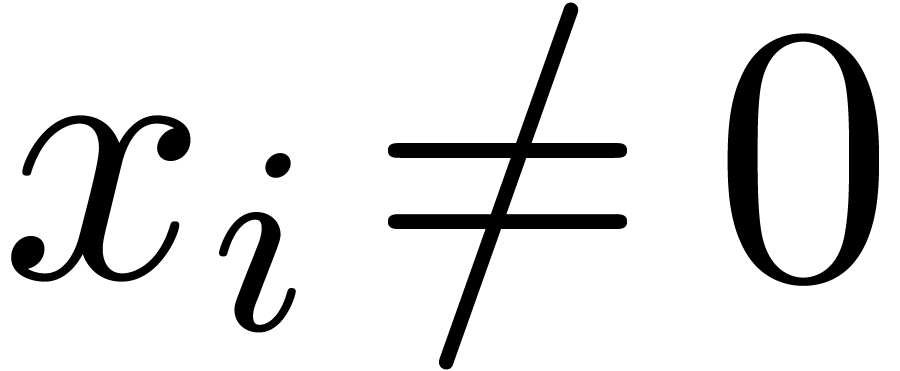 . Then we have
. Then we have 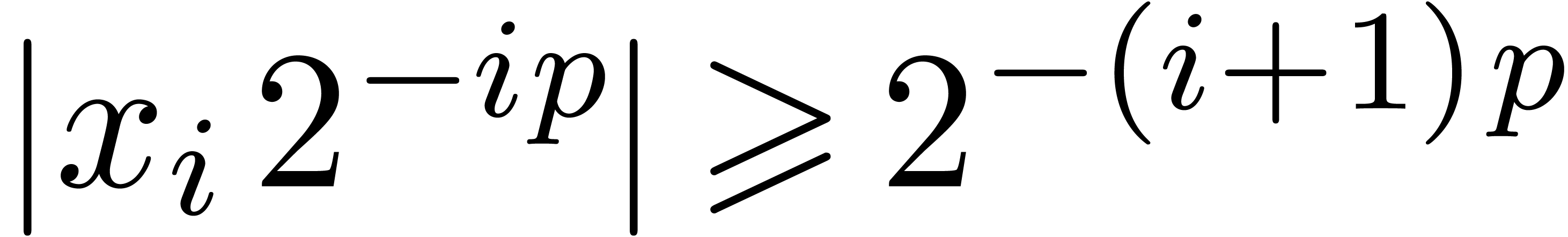 , whereas
, whereas 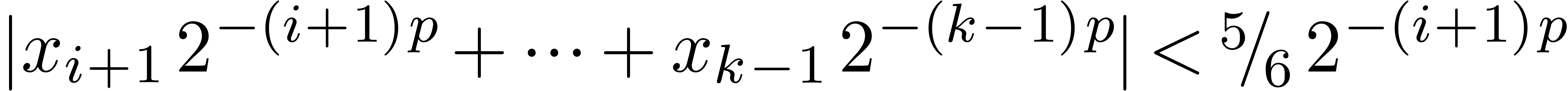 ,
so that
,
so that 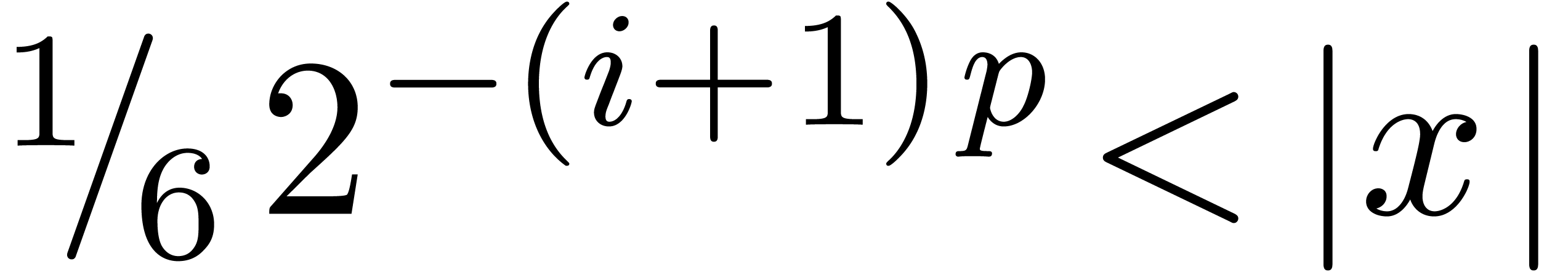 . If
. If 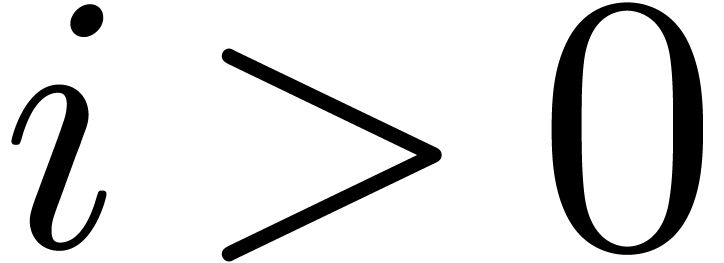 , then we also get
, then we also get  , whence
, whence 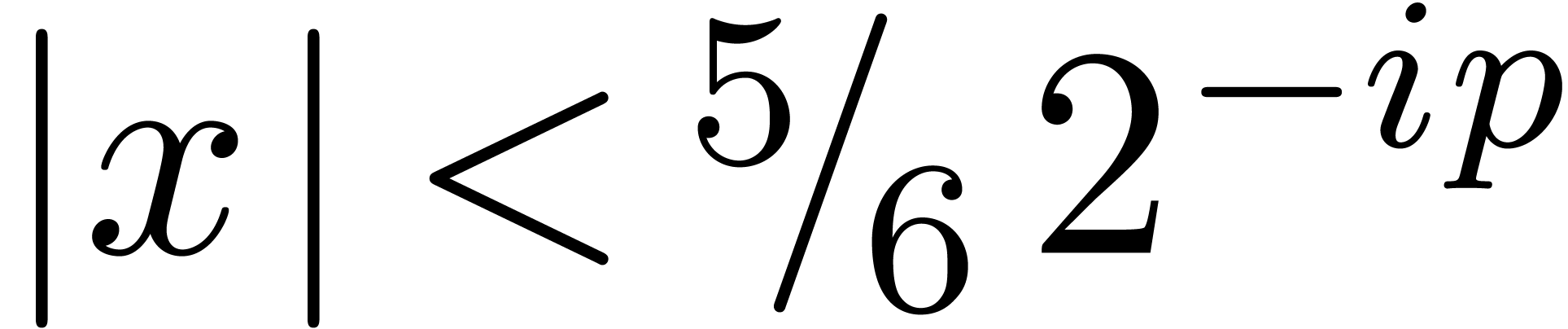 .
If
.
If 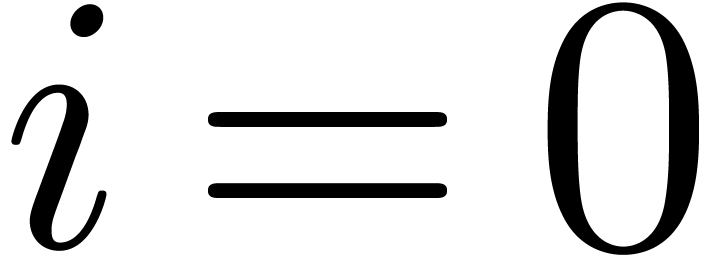 , then
, then  by assumption. This shows that (3) holds as well.□
by assumption. This shows that (3) holds as well.□
3.5.Operation counts
In Table 1 below, we have shown the number of machine
operations that are required for the fixed-point operations from this
and the previous section, as a function of  .
Of course, the actual time complexity of the algorithms also depends on
the latency and throughput of machine instructions. We count an
assignment
.
Of course, the actual time complexity of the algorithms also depends on
the latency and throughput of machine instructions. We count an
assignment  as a single instruction.
as a single instruction.
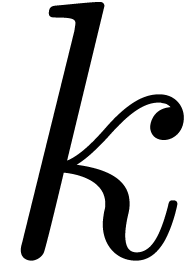 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Carry normalize |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
| Add/subtract |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Multiply |
8 |
18 |
33 |
53 |
78 |
108 |
143 |
183 |
228 |
278 |
333 |
| Small shift |
7 |
11 |
15 |
19 |
23 |
27 |
31 |
35 |
39 |
43 |
47 |
| Large shift |
3 |
8 |
10 |
18 |
21 |
24 |
27 |
40 |
44 |
48 |
52 |
| General shift |
12 |
21 |
27 |
39 |
45 |
53 |
60 |
77 |
85 |
92 |
100 |
| Uniform shift |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
| Bit exponent |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| Highest word |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
Table 1. Operation counts in terms
of machine instructions (the results are not necessarily
normalized).
|
4.Floating-point arithmetic in base
Let 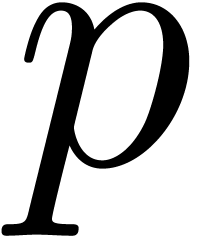 ,
, 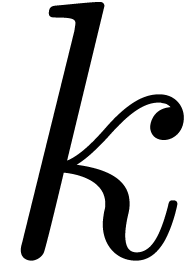 and
and  be as in section 2. We will
represent floating-point numbers as products
be as in section 2. We will
represent floating-point numbers as products
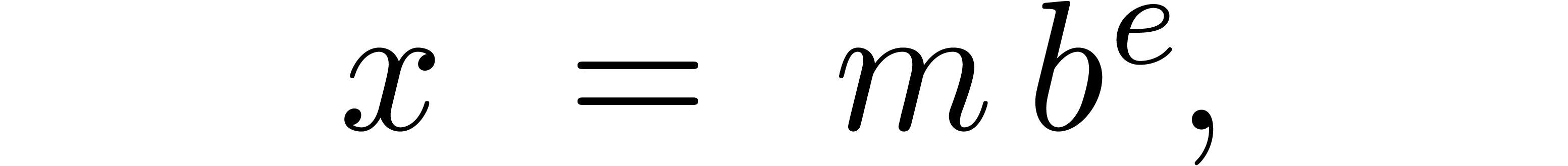
where 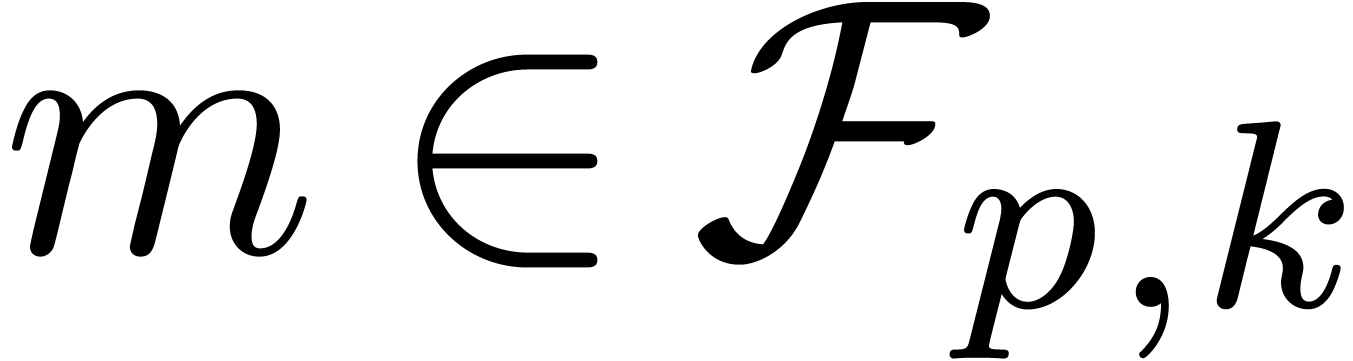 is the mantissa of
is the mantissa of  and
and 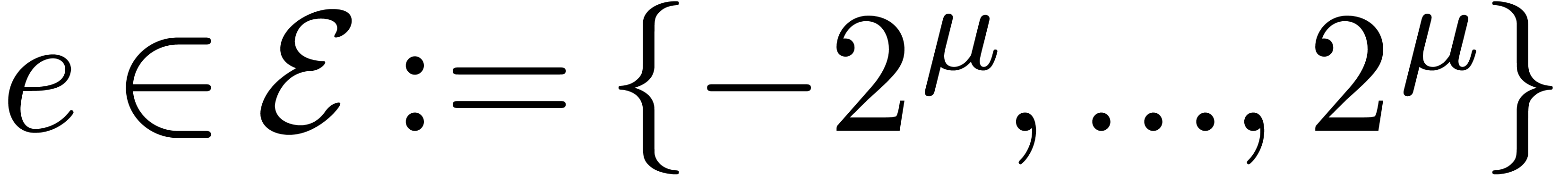 its exponent in base
its exponent in base
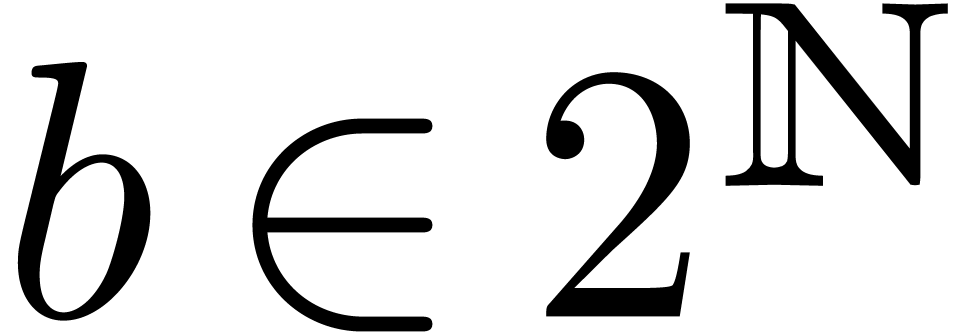 . We denote by
. We denote by 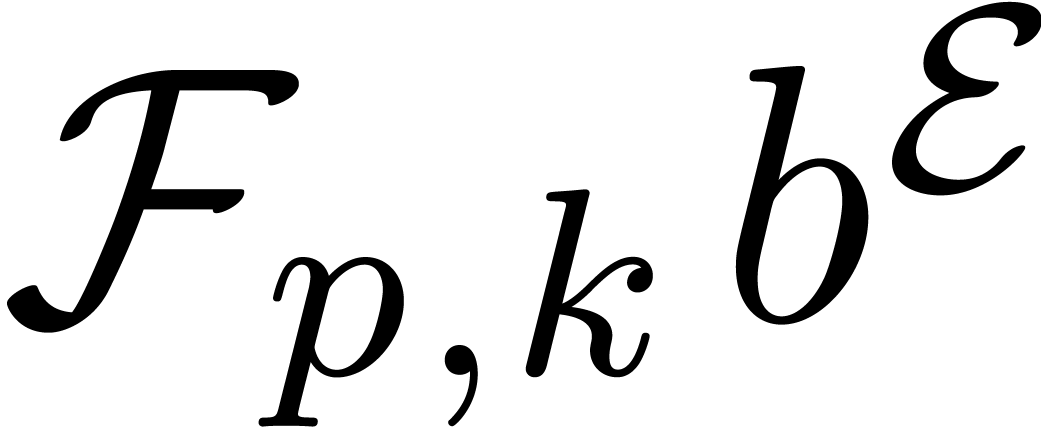 the set of all such floating-point numbers. We assume that
the exponents in
the set of all such floating-point numbers. We assume that
the exponents in 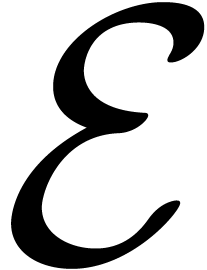 can be represented exactly, by
machine integers or numbers in
can be represented exactly, by
machine integers or numbers in  .
As in most existing multiple precision libraries, we use an extended
exponent range. For multiple precision arithmetic, it is indeed natural
to support exponents of at least as many bits as the precision itself.
.
As in most existing multiple precision libraries, we use an extended
exponent range. For multiple precision arithmetic, it is indeed natural
to support exponents of at least as many bits as the precision itself.
In this section, we assume that 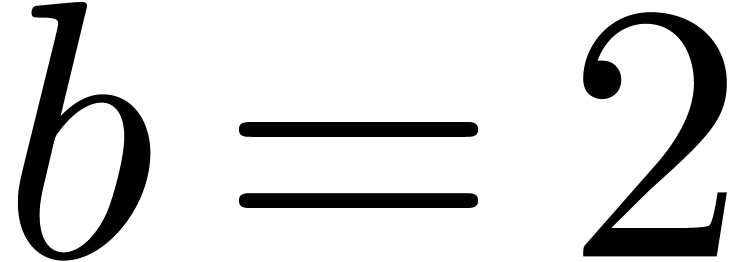 .
The main advantage of this base is that floating-point numbers can be
represented in a compact way. The main disadvantage is that
normalization involves expensive shifts by general numbers of bits that
are not necessarily multiples of
.
The main advantage of this base is that floating-point numbers can be
represented in a compact way. The main disadvantage is that
normalization involves expensive shifts by general numbers of bits that
are not necessarily multiples of 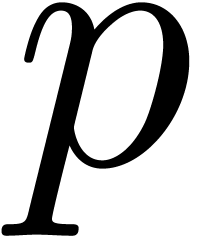 .
Notice that
.
Notice that 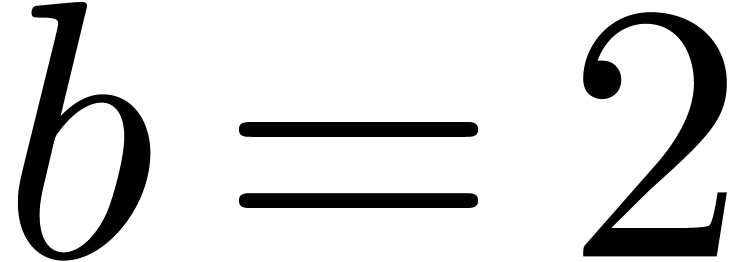 is also used in the Mpfr
library for multiple precision floating-point arithmetic [6].
is also used in the Mpfr
library for multiple precision floating-point arithmetic [6].
4.1.Normalization
Given  , we denote
, we denote 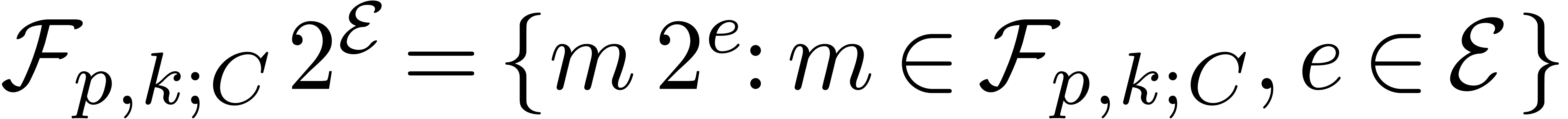 . Numbers in
. Numbers in  are again said to be in carry normal form and the routine
CarryNormalize extends to
are again said to be in carry normal form and the routine
CarryNormalize extends to 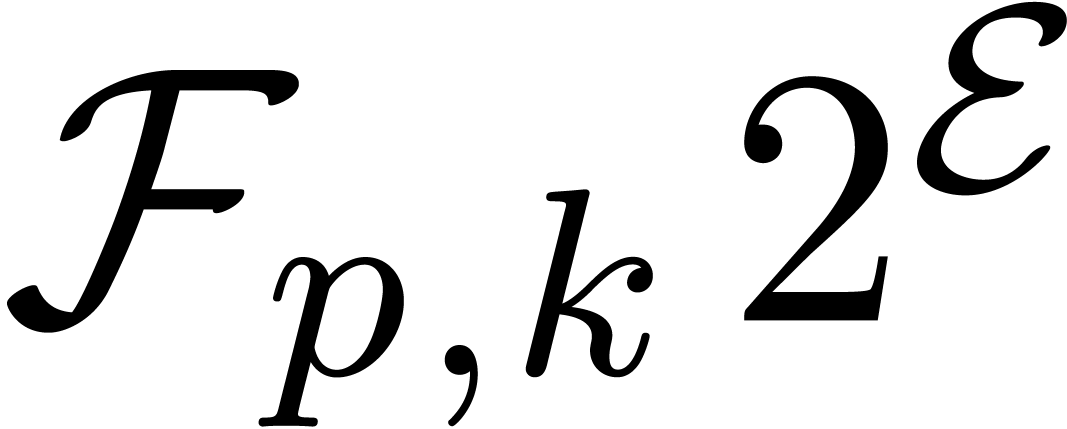 by
applying it to the mantissa. We say that a floating-point number
by
applying it to the mantissa. We say that a floating-point number 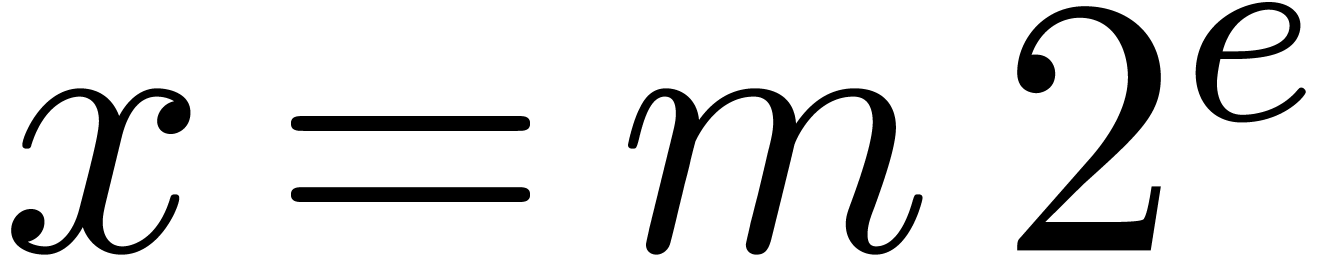 with
with 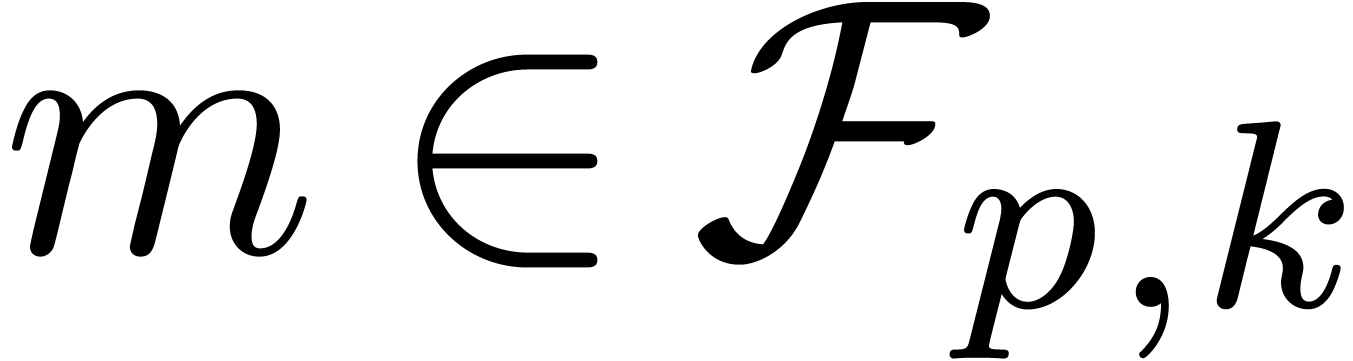 is in dot normal
form if we either have
is in dot normal
form if we either have 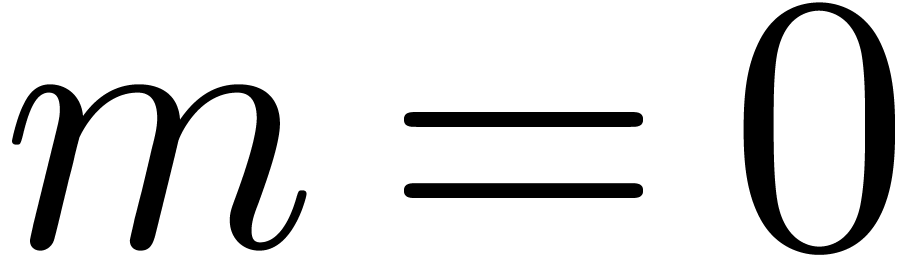 or
or  . If
. If  is also in carry
normal form, then we simply say that
is also in carry
normal form, then we simply say that  is in
normal form. In absence of overflows, normalizations can be
computed using the routine Normalize below. In the case
when the number to be normalized is the product of two normalized
floating-point numbers, we need to shift the mantissa by at most two
bits, and it is faster to use the variant
QuickNormalize.
is in
normal form. In absence of overflows, normalizations can be
computed using the routine Normalize below. In the case
when the number to be normalized is the product of two normalized
floating-point numbers, we need to shift the mantissa by at most two
bits, and it is faster to use the variant
QuickNormalize.
Algorithm Normalize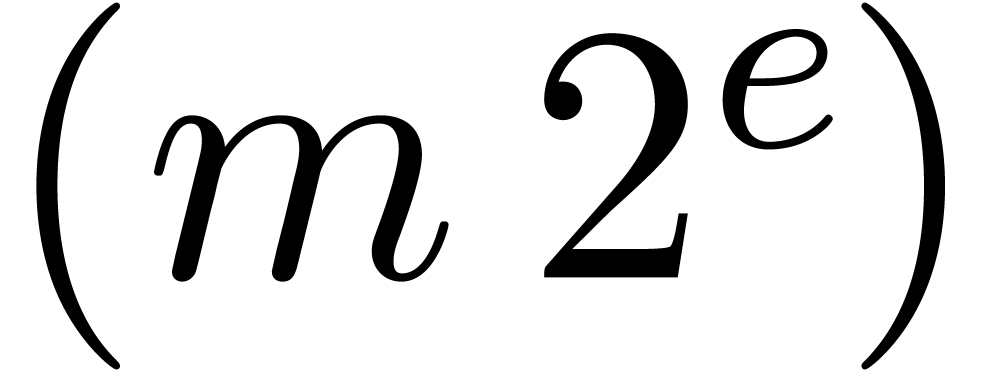
|

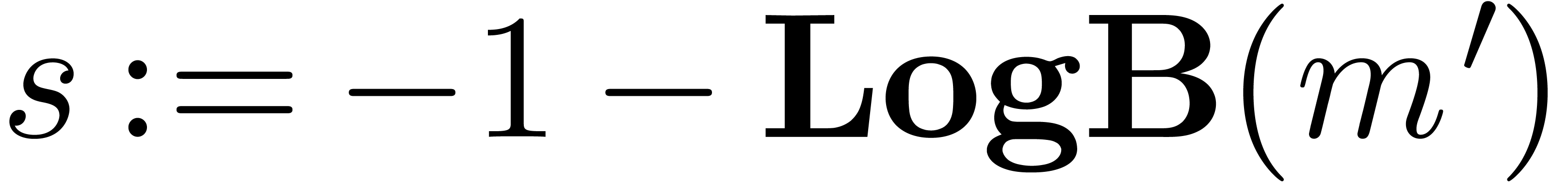
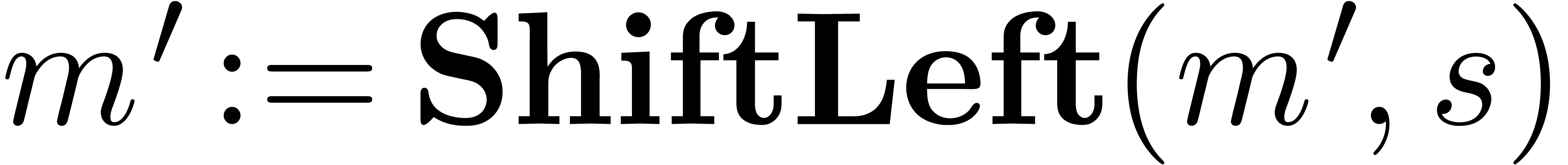
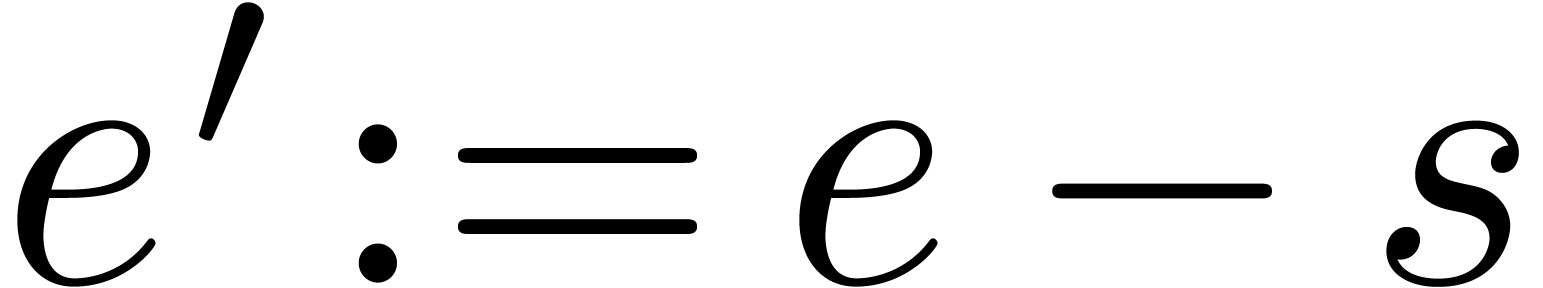
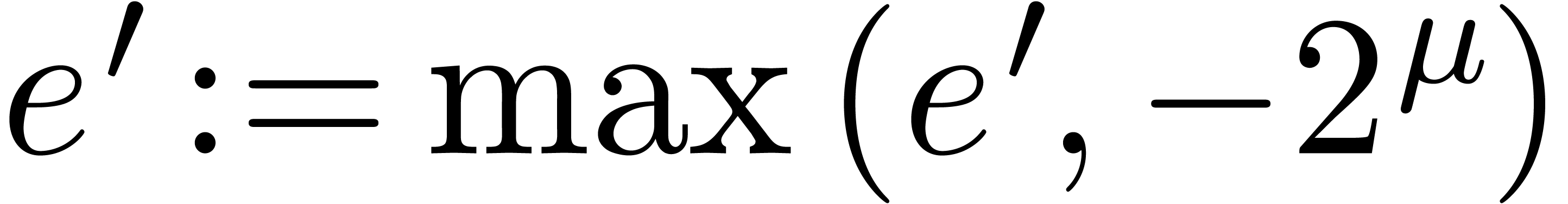

return 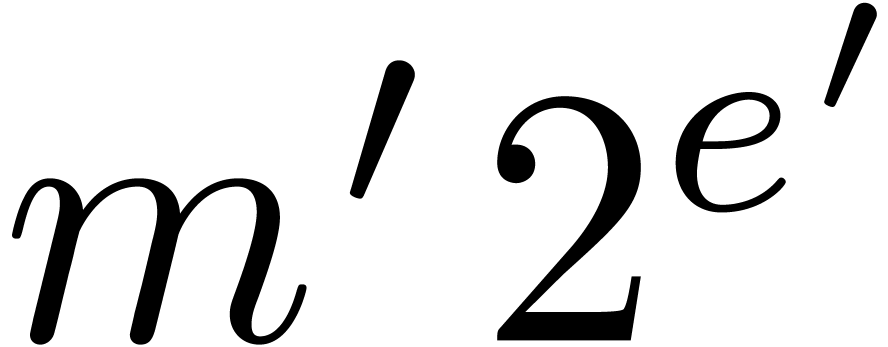
|
|
|
Algorithm QuickNormalize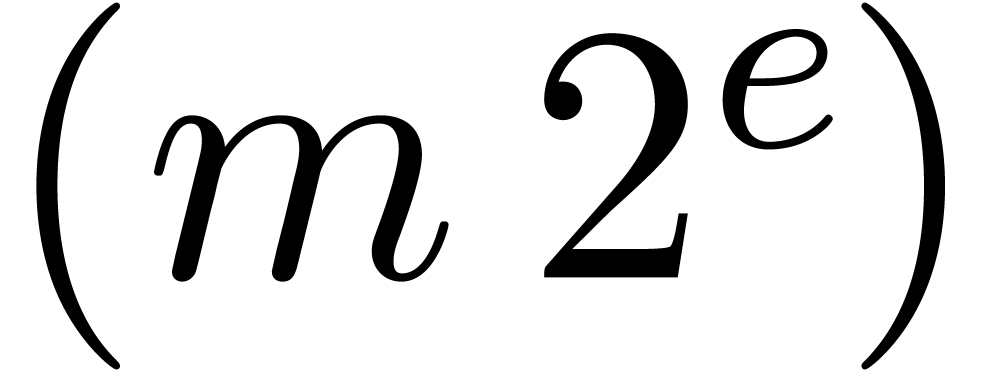
|

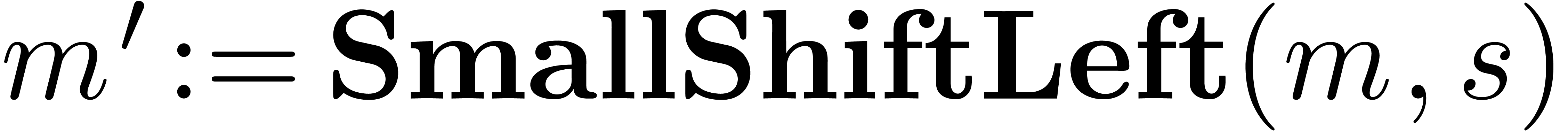
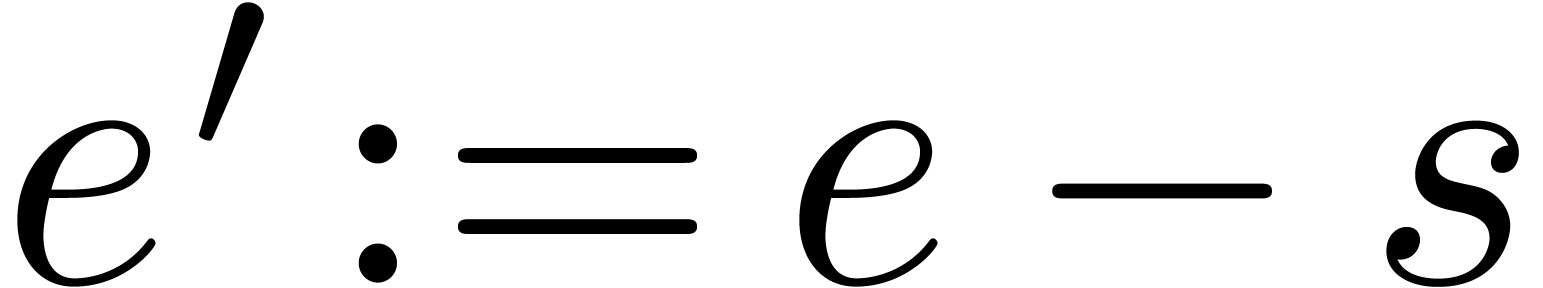
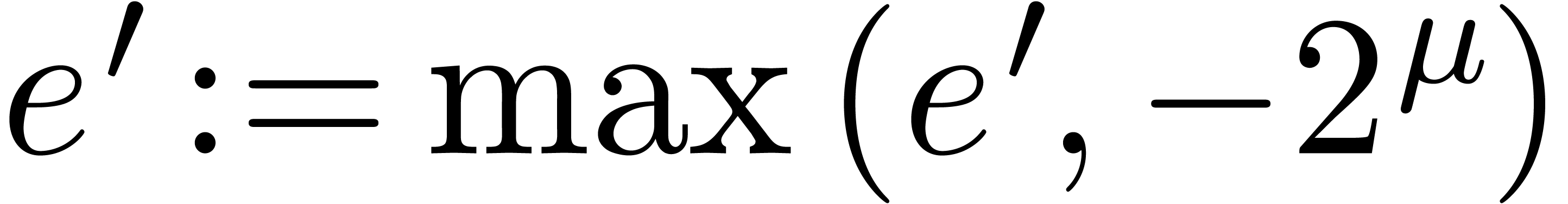
return 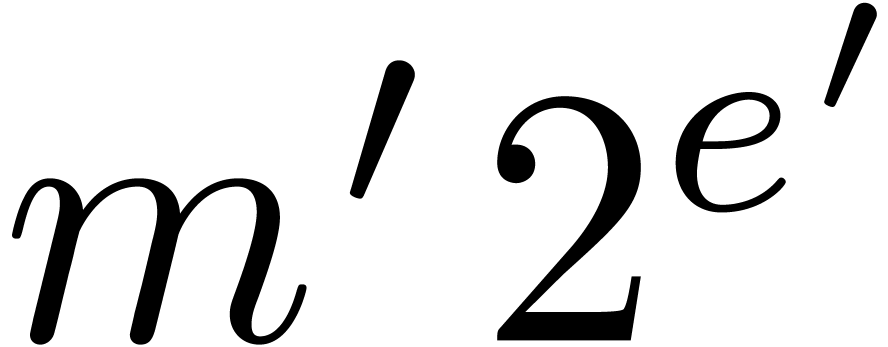
|
|
Proof. If  ,
then CarryNormalize returns
,
then CarryNormalize returns  and
it is easy to verify that the proposition holds. Assume therefore that
and
it is easy to verify that the proposition holds. Assume therefore that
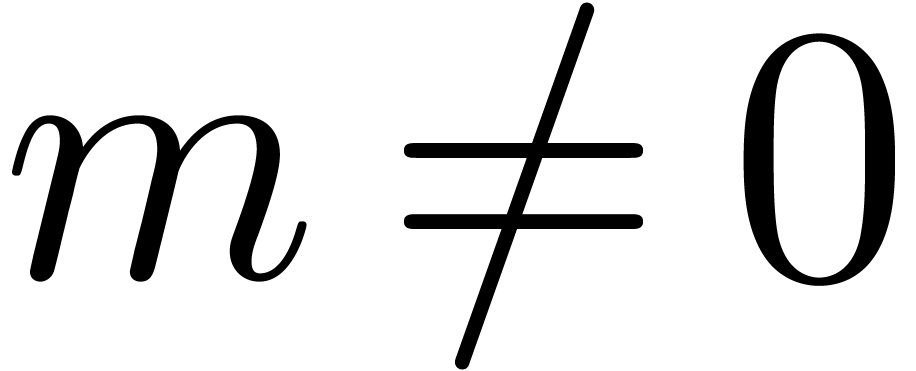 , so that
, so that 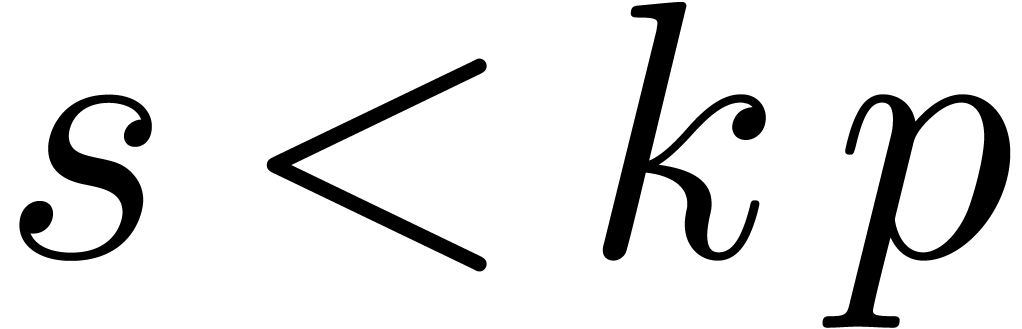 . By Proposition 4, we have
. By Proposition 4, we have 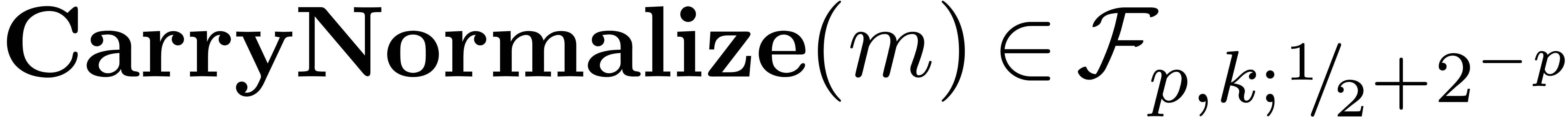 . Using Proposition 8,
it follows that
. Using Proposition 8,
it follows that 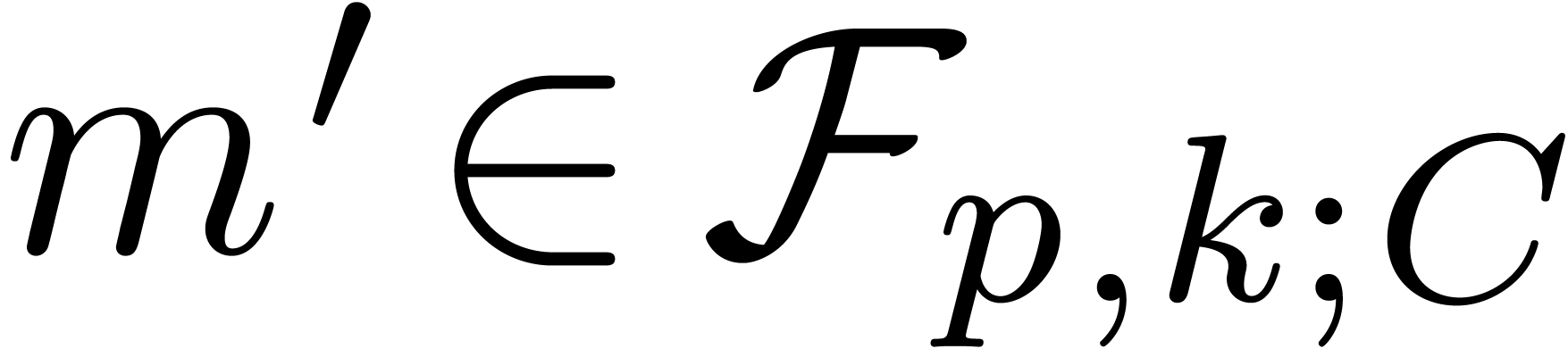 with
with  , whence
, whence  is carry normal. We
also have
is carry normal. We
also have 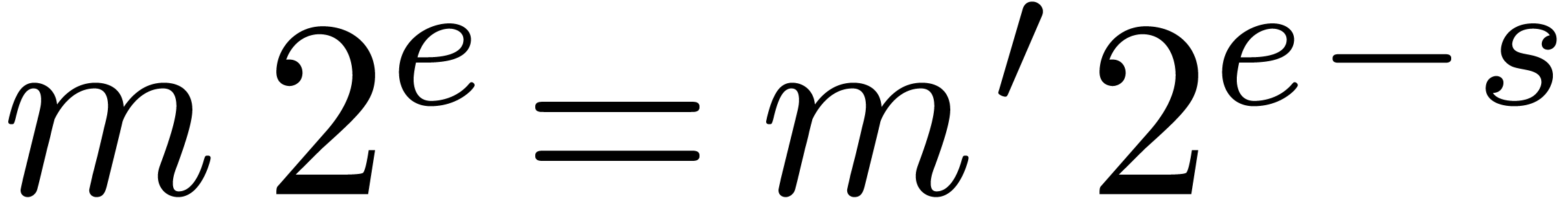 and
and 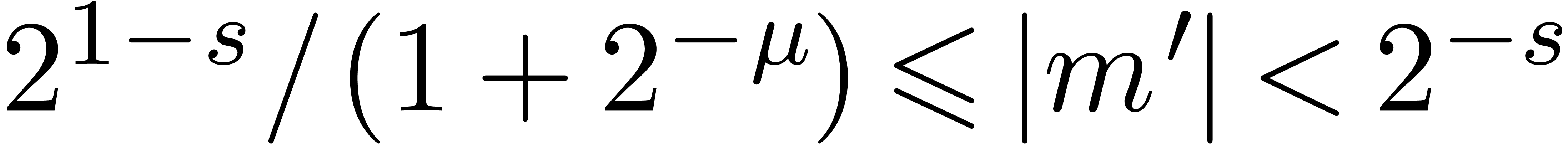 ,
whence
,
whence 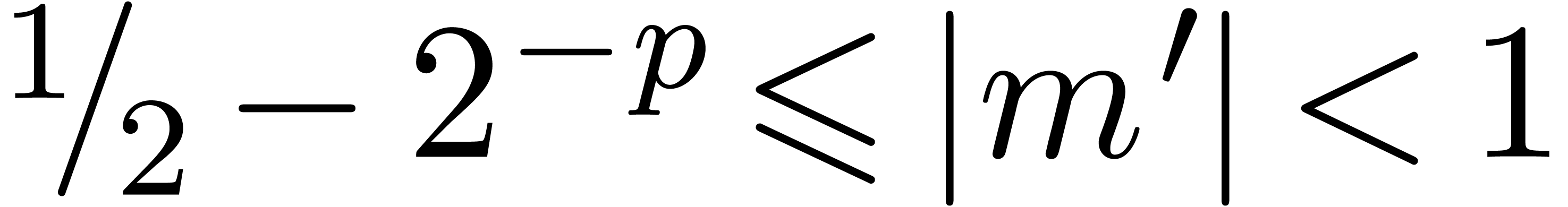 . This also implies
. This also implies
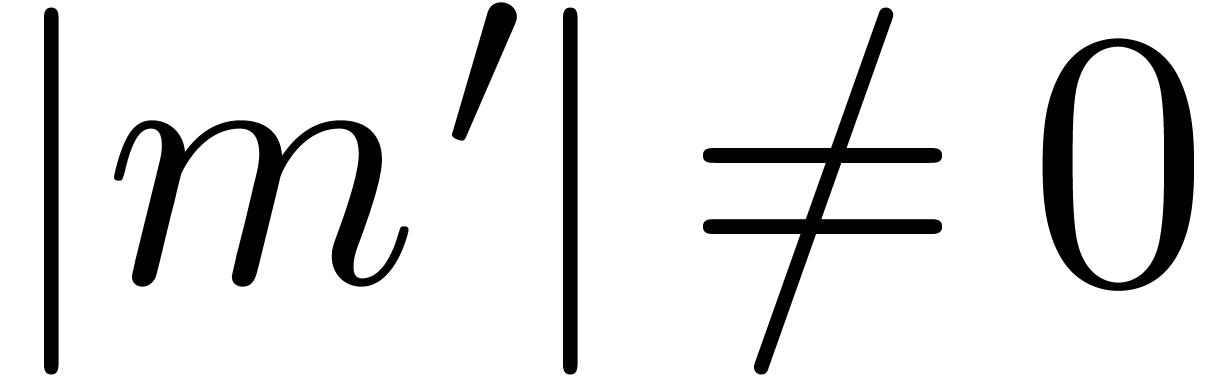 and
and 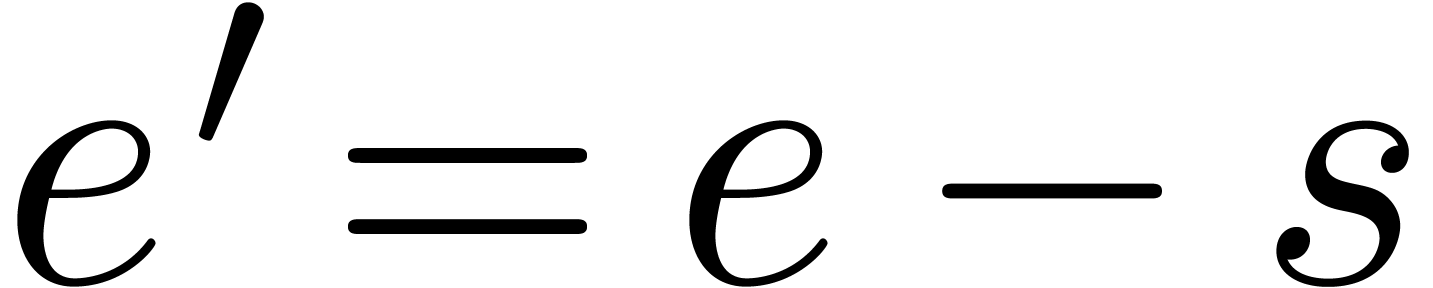 ,
since
,
since  . We conclude that
. We conclude that 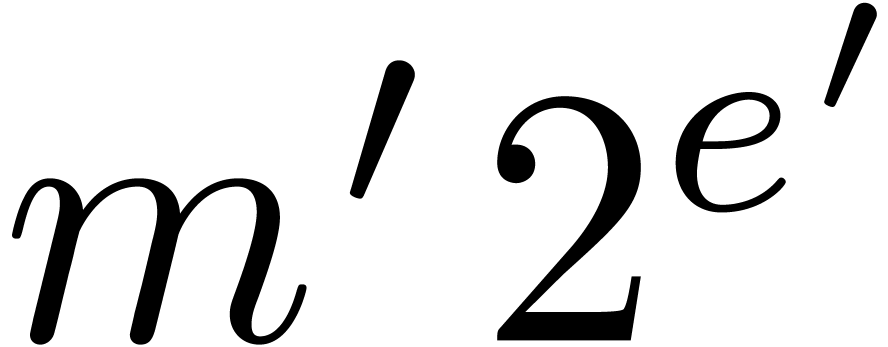 is dot normal and its value coincides with
is dot normal and its value coincides with 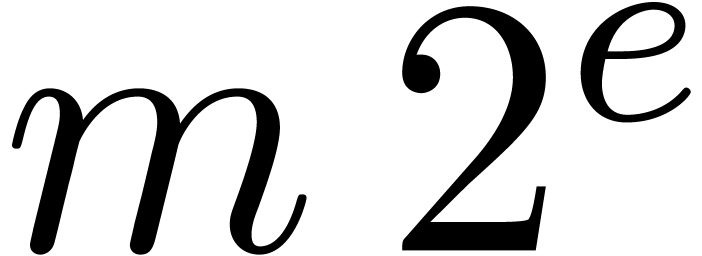 . If
. If  ,
then it can be checked that
,
then it can be checked that  still satisfies
still satisfies  and that
and that  .
From Proposition 8, it again follows that
.
From Proposition 8, it again follows that 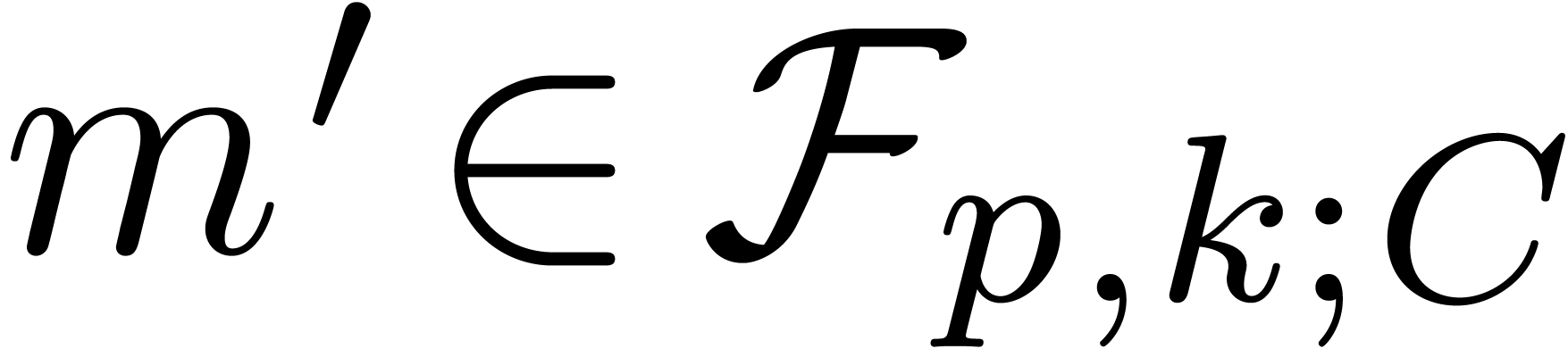 with
with  , whence
, whence  is carry normal. The remainder of the correctness of
QuickNormalize follows as before.□
is carry normal. The remainder of the correctness of
QuickNormalize follows as before.□
4.2.Arithmetic operations
Addition and subtraction of normalized floating-point numbers are
computed as usual, by putting the mantissa under a common exponent, by
adding or subtracting the shifted mantissas, and by normalizing the
result. By increasing the common exponent by two, we also make sure that
the most significant word of the addition or subtraction never provokes
a carry.
|
|
Algorithm Subtract( ) )
|
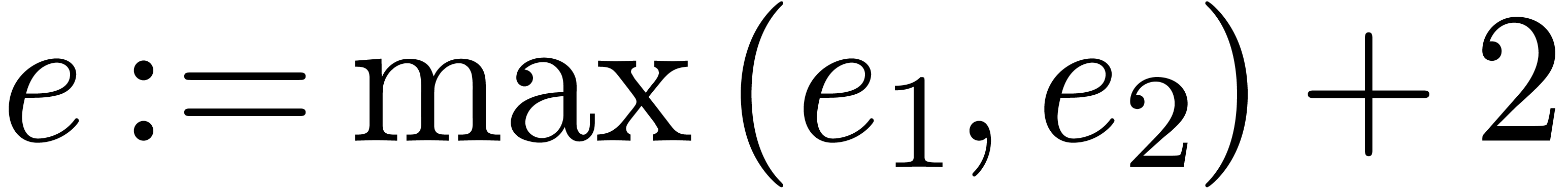
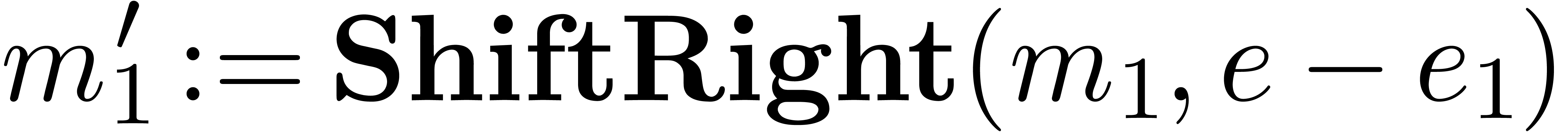
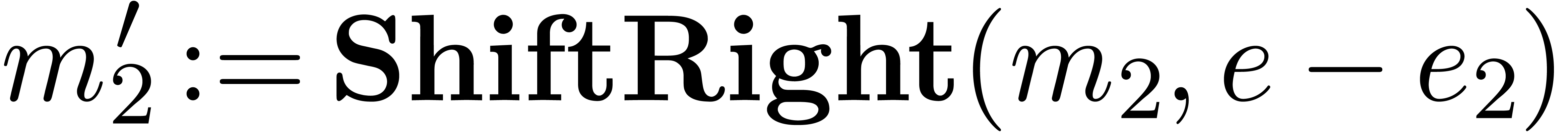

return 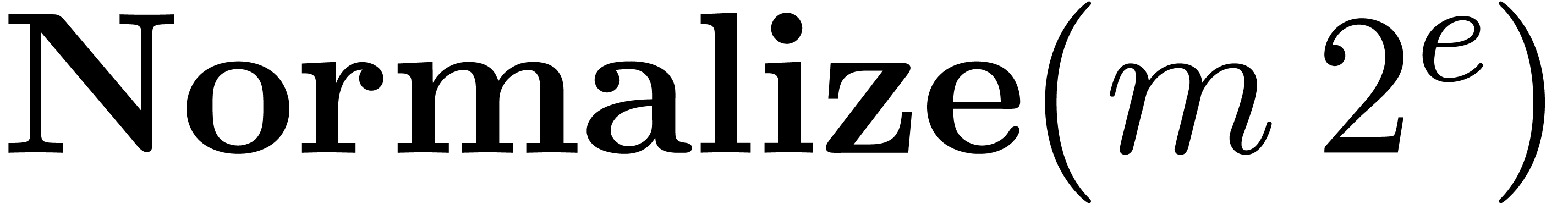
|
|
Floating-point multiplication is almost as efficient as its fixed-point
analogue, using the following straightforward:
Algorithm Multiply(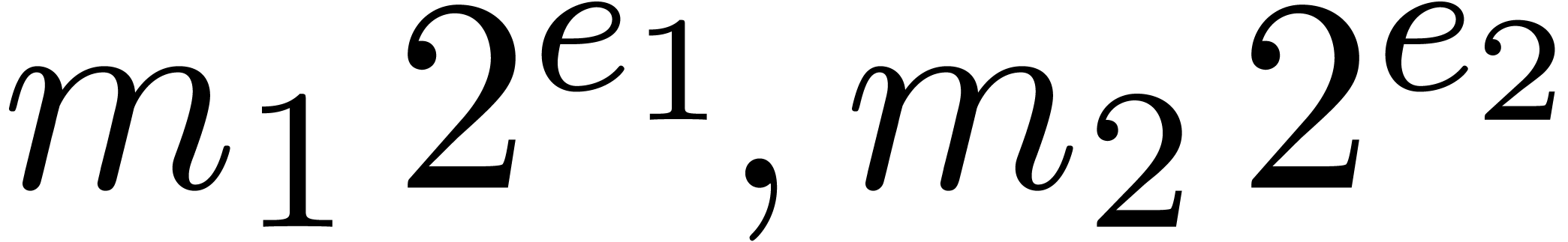 ) )
|

return 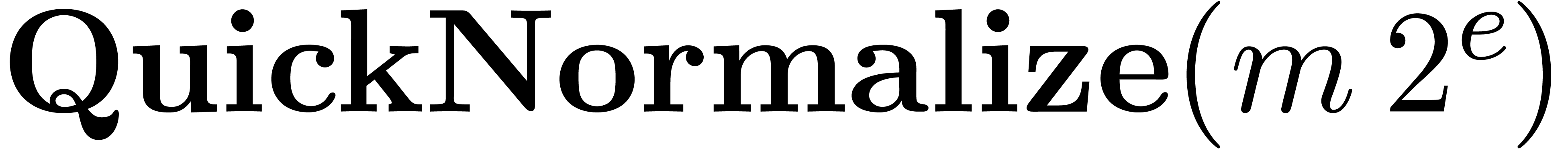
|
|
|
Remark 14. Strictly
speaking, for normal numbers 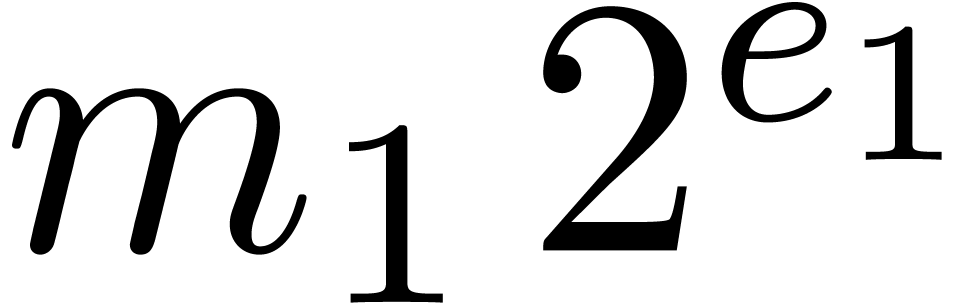 and
and 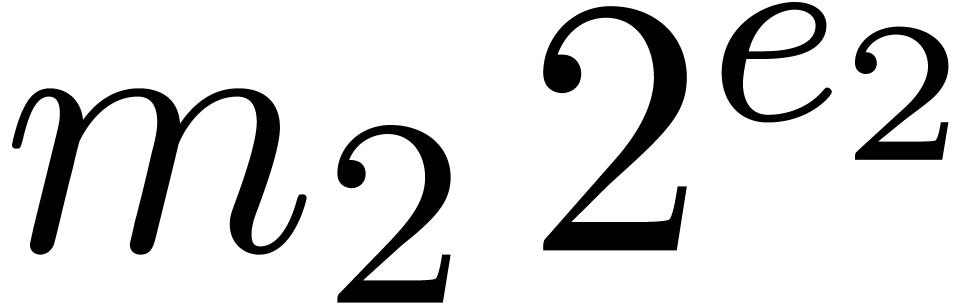 , it is still necessary to prove that
, it is still necessary to prove that 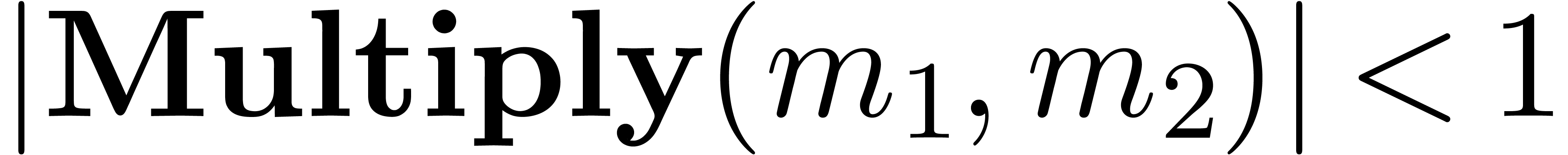 . This conclusion can only be
violated if
. This conclusion can only be
violated if 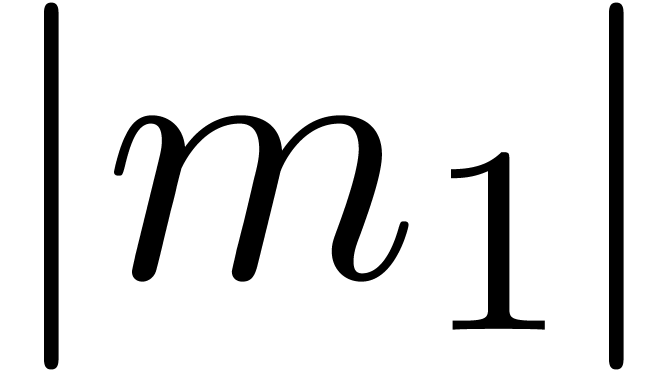 and
and 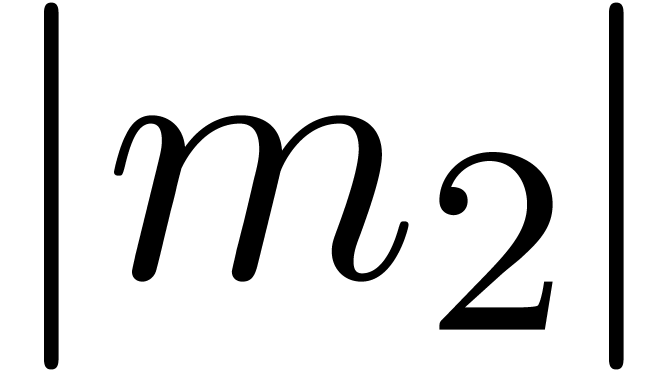 are very
close to one. Now it can be shown that a carry normal mantissa
are very
close to one. Now it can be shown that a carry normal mantissa 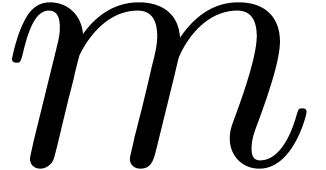 with
with 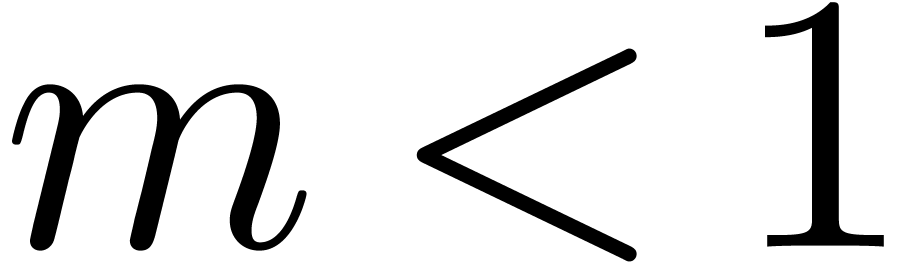 and
and 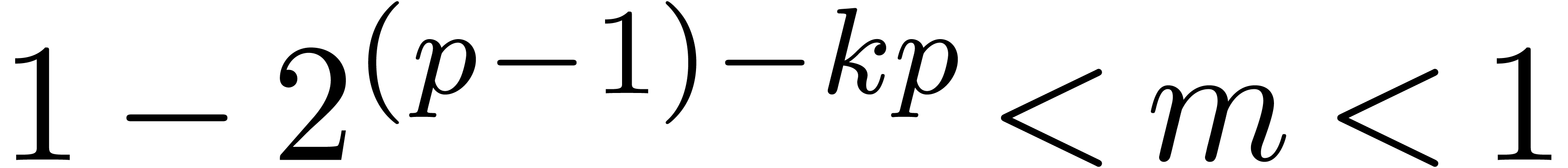 is necessarily of the form
is necessarily of the form 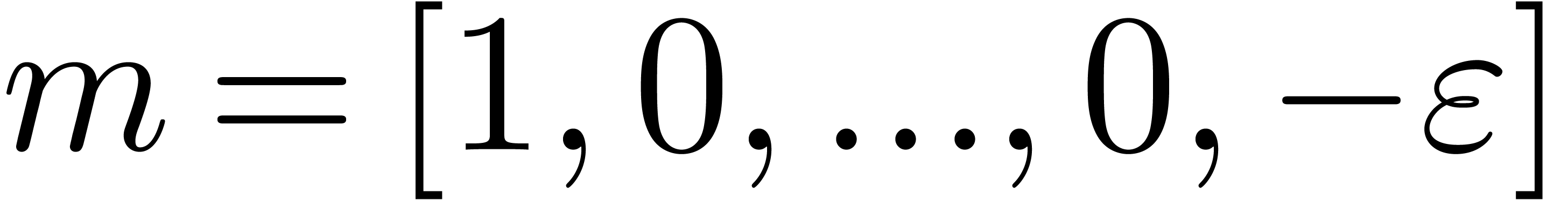 .
For numbers of this form, it is easy to check that
.
For numbers of this form, it is easy to check that 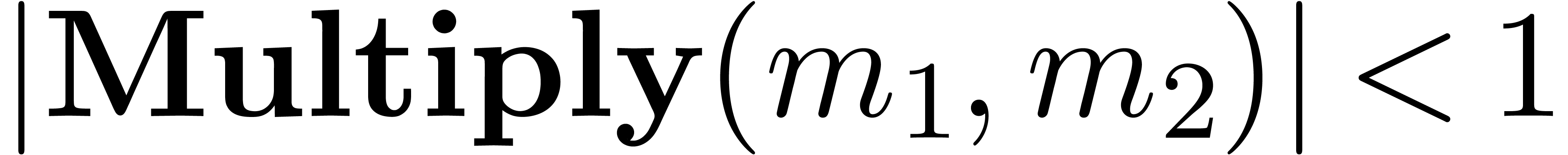 .
.
4.3.Shared exponents
If we are computing with an SIMD vector 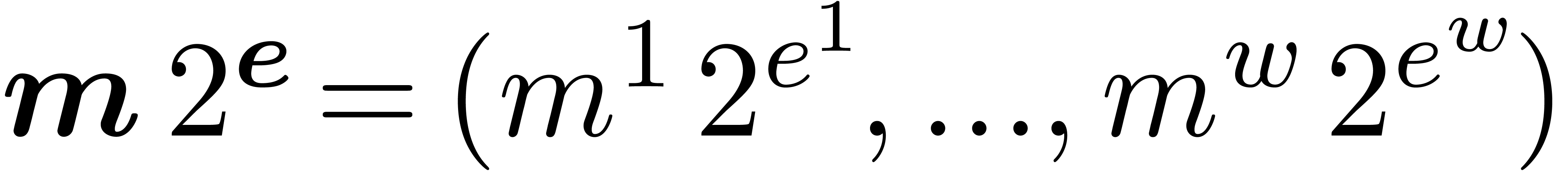 of
floating-point numbers, then another way to speed up shifting is to let
all entries share the same exponent
of
floating-point numbers, then another way to speed up shifting is to let
all entries share the same exponent 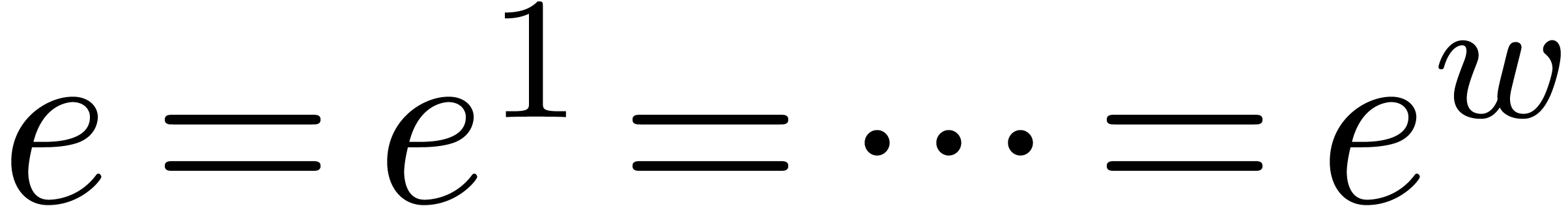 .
Of course, this strategy may compromise the accuracy of some of the
computations. Nevertheless, if all entries are of similar order of
magnitude, then the loss of accuracy is usually limited to a few bits.
Moreover, by counting the number of leading zeros of the mantissa of a
particular entry
.
Of course, this strategy may compromise the accuracy of some of the
computations. Nevertheless, if all entries are of similar order of
magnitude, then the loss of accuracy is usually limited to a few bits.
Moreover, by counting the number of leading zeros of the mantissa of a
particular entry 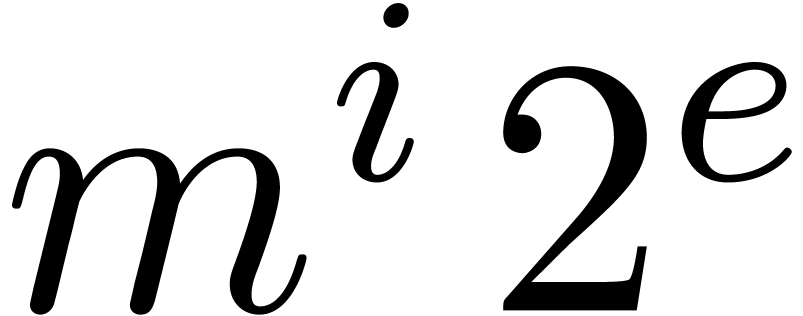 , it is
possible to monitor the loss of accuracy, and redo some of the
computations if necessary.
, it is
possible to monitor the loss of accuracy, and redo some of the
computations if necessary.
When sharing exponents, it becomes possible to use
UniformShiftLeft and UniformShiftRight
instead of LargeShiftLeft and
LargeShiftRight for multiple word shifts. The routine
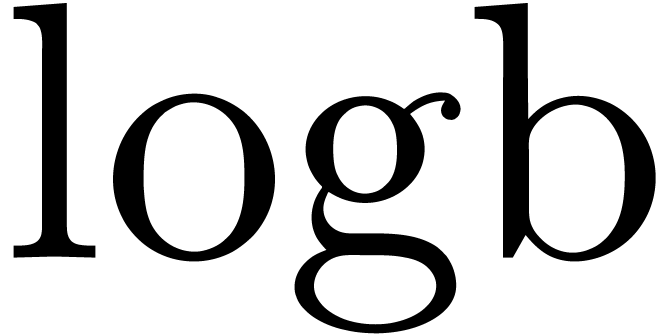 should also be adjusted: if the individual
exponents given by the vector
should also be adjusted: if the individual
exponents given by the vector 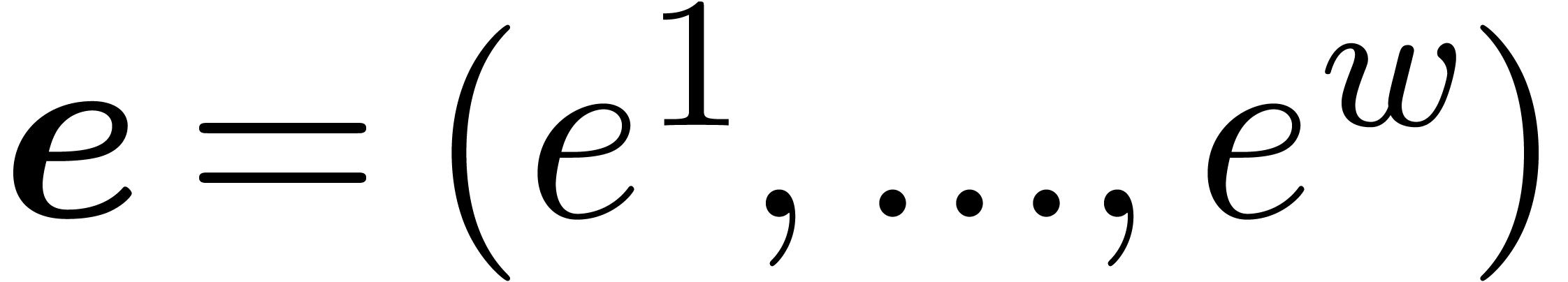 ,
then
,
then 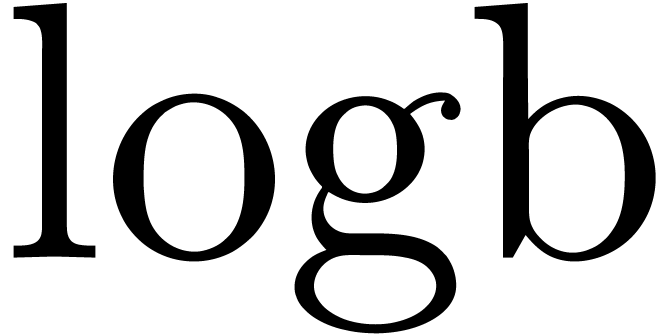 should now return the vector
should now return the vector  with
with 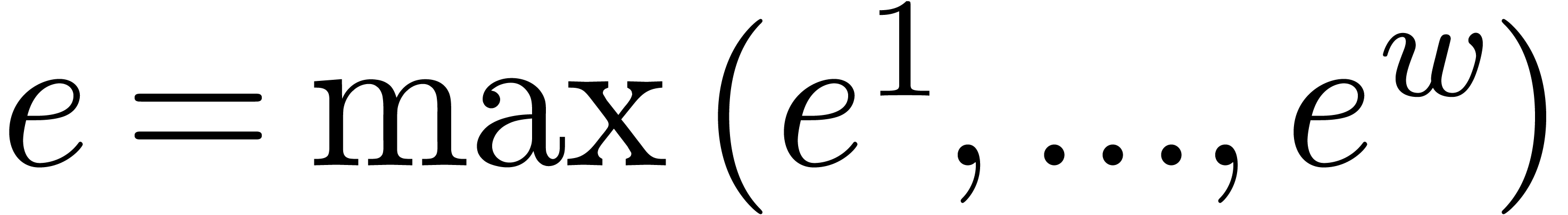 . Modulo
these changes, we may use the same routines as above for basic
floating-point arithmetic.
. Modulo
these changes, we may use the same routines as above for basic
floating-point arithmetic.
4.4.Operation counts
In Table 2, we give the operation counts for the various
variants of the basic arithmetic operations  ,
,  and
and  that we have discussed so far. For comparison, we have also shown the
operation count for the algorithm from [14] that is based
on floating-point expansions (notice that
that we have discussed so far. For comparison, we have also shown the
operation count for the algorithm from [14] that is based
on floating-point expansions (notice that 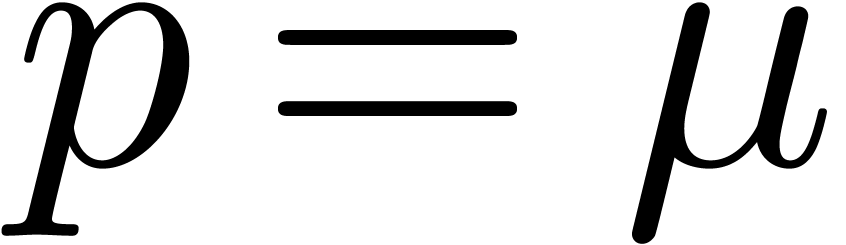 is
somewhat better for this algorithm, since our algorithms rather use
is
somewhat better for this algorithm, since our algorithms rather use
 ).
).
Due to the cost of shifting, we observe that additions and subtractions
are the most costly operations for small and medium precisions 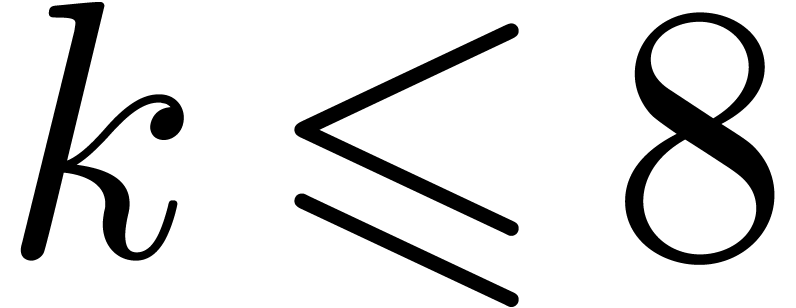 . For larger precisions
. For larger precisions 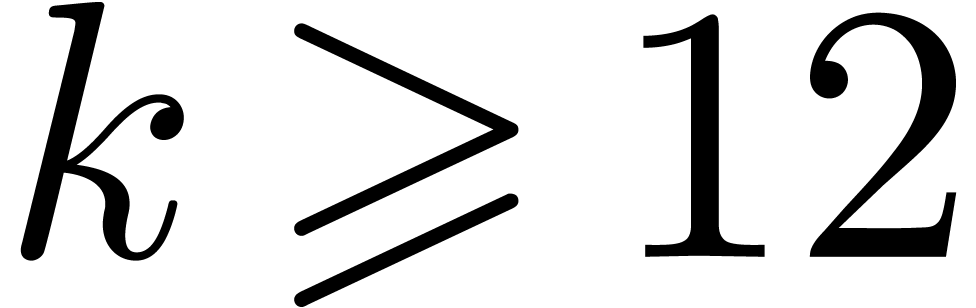 , multiplication becomes the main
bottleneck.
, multiplication becomes the main
bottleneck.
5.Floating-point arithmetic in base
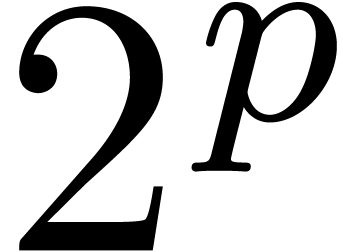
As we can see in Table 2, additions and subtractions are
quite expensive when working in base 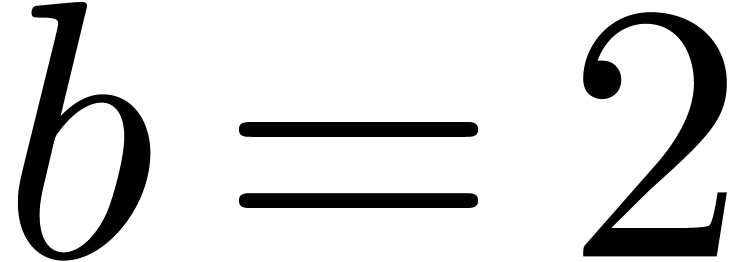 .
This is due to the facts that shifting is expensive with respect to this
base and that every addition involves three shifts. For this reason, we
will now examine floating-point arithmetic in the alternative base
.
This is due to the facts that shifting is expensive with respect to this
base and that every addition involves three shifts. For this reason, we
will now examine floating-point arithmetic in the alternative base 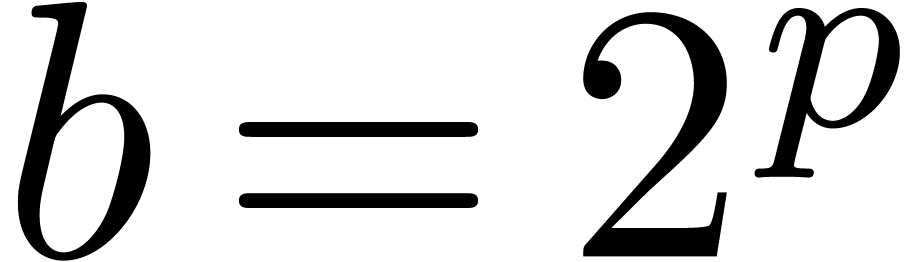 . One major disadvantage of this
base is that normalized non zero floating-point numbers may start with
as many as
. One major disadvantage of this
base is that normalized non zero floating-point numbers may start with
as many as  leading zero bits. This means that
leading zero bits. This means that
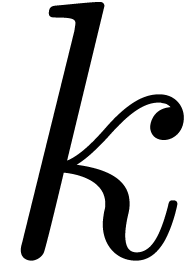 should be increased by one in order to achieve a
similar accuracy. We notice that the base
should be increased by one in order to achieve a
similar accuracy. We notice that the base 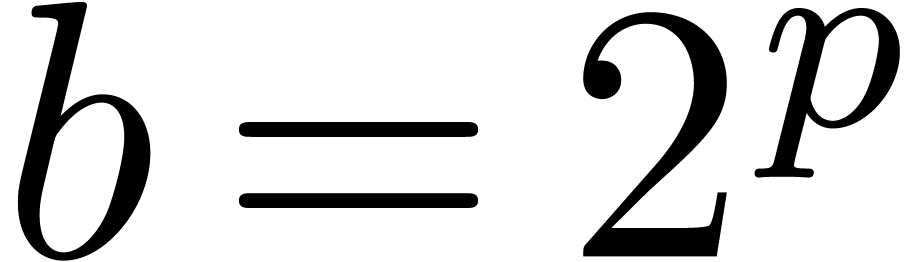 is
also used in the native mpf layer for floating-point
arithmetic in the Gmp library [7].
is
also used in the native mpf layer for floating-point
arithmetic in the Gmp library [7].
Carry normal forms are defined in the same way as in base 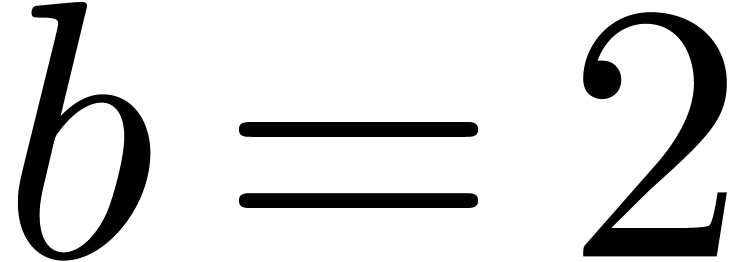 . We say that a floating-point number
. We say that a floating-point number 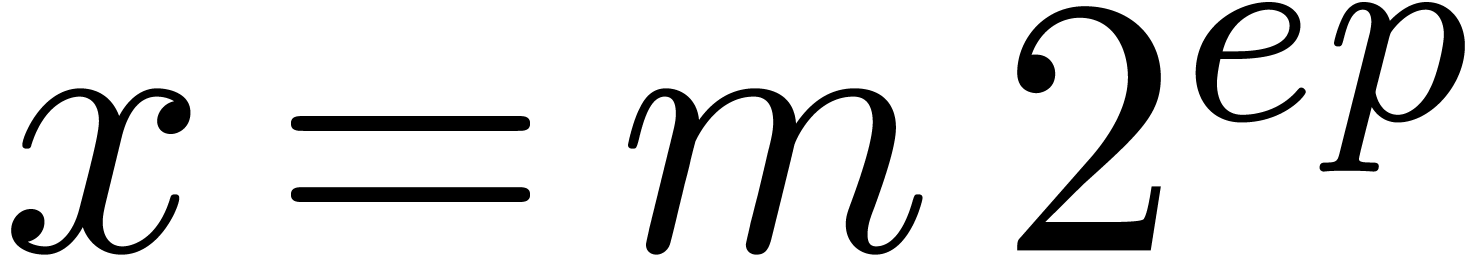 with
with  is in dot normal
form if
is in dot normal
form if 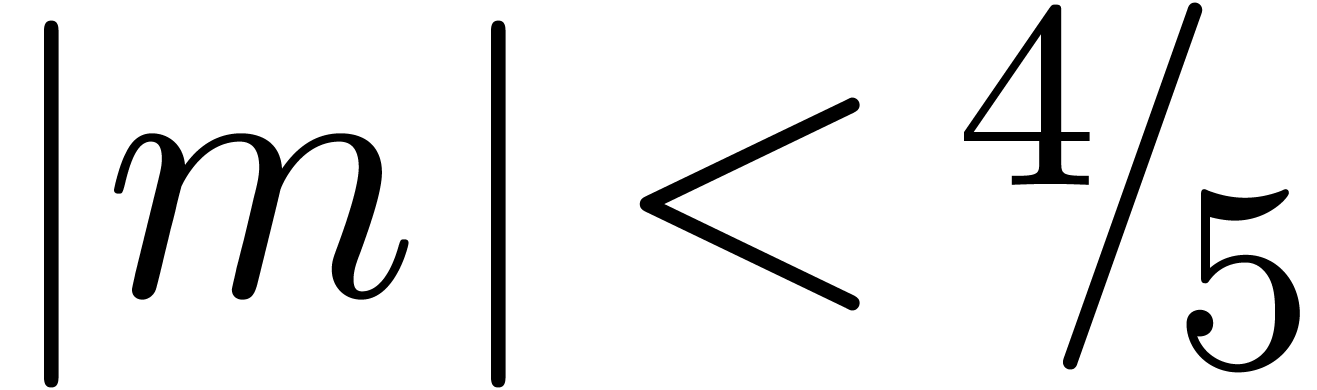 and either
and either 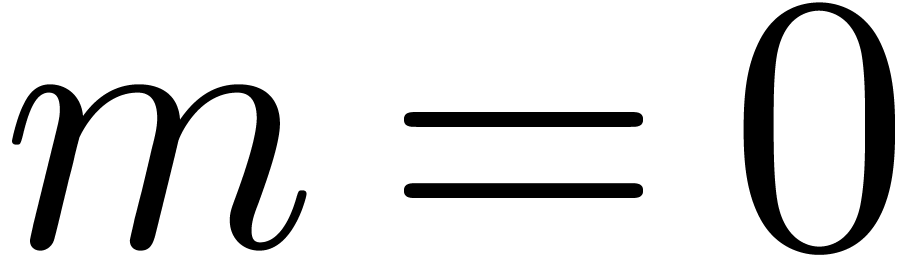 or
or 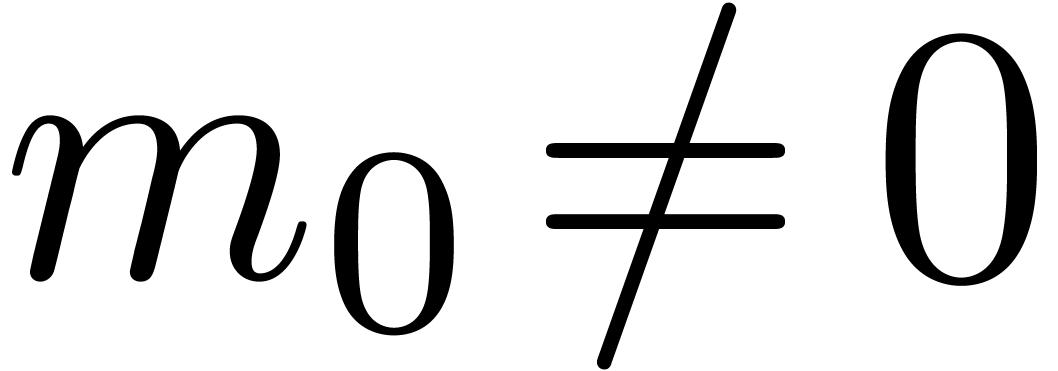 . We say that
. We say that  is in normal form if it is both in carry normal
form and in dot normal form.
is in normal form if it is both in carry normal
form and in dot normal form.
5.1.Addition and subtraction
In section 4.2, we increased the common exponent of the
summands of an addition by two in order to avoid carries. When working
in base 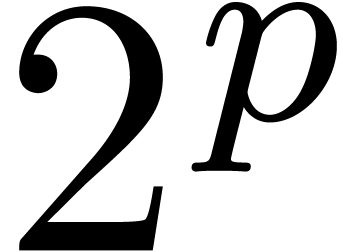 , a similar trick
would systematically shift out the least significant words of the
summands. Instead, it is better to allow for carries, but to adjust the
routine for normalization accordingly, by temporarily working with
mantissas of
, a similar trick
would systematically shift out the least significant words of the
summands. Instead, it is better to allow for carries, but to adjust the
routine for normalization accordingly, by temporarily working with
mantissas of  words instead of
words instead of  .
.
Algorithm Normalize(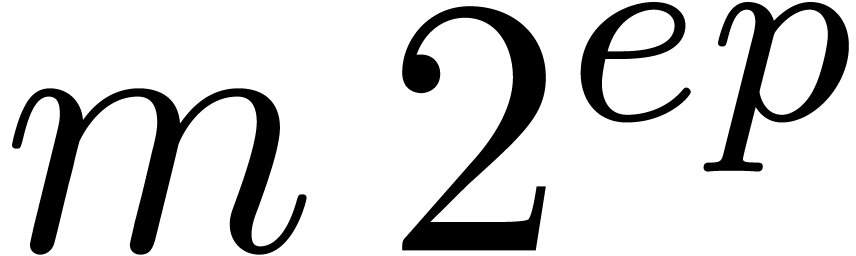 ) )
|
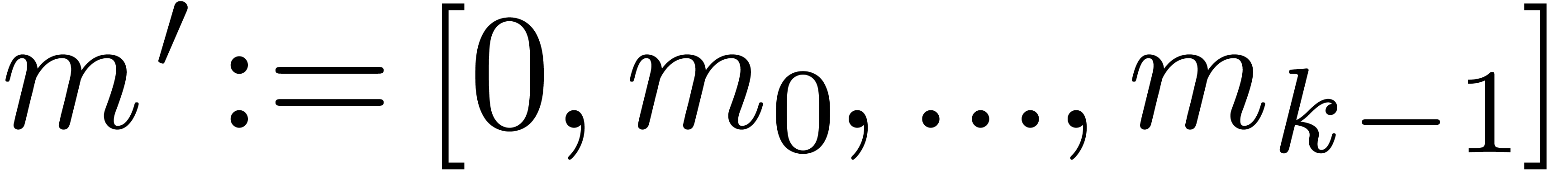

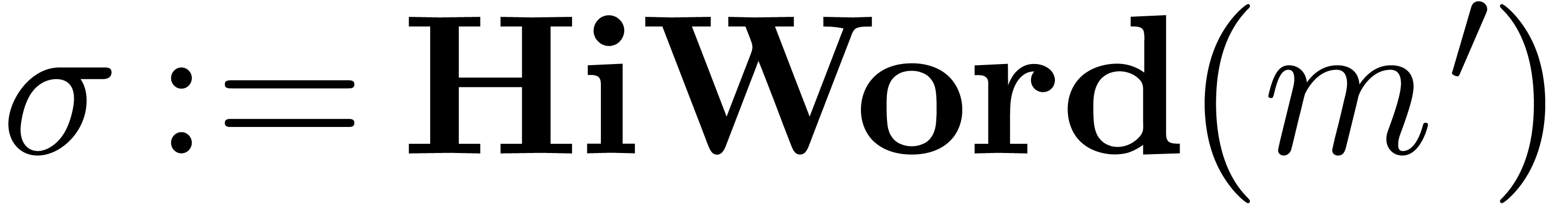

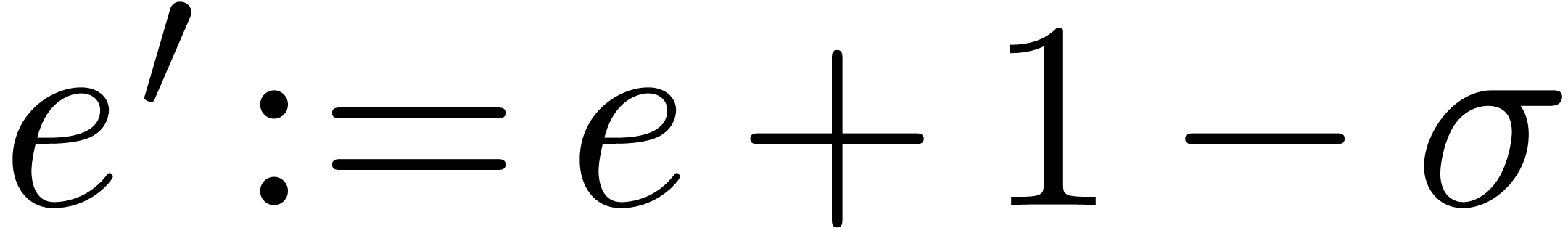
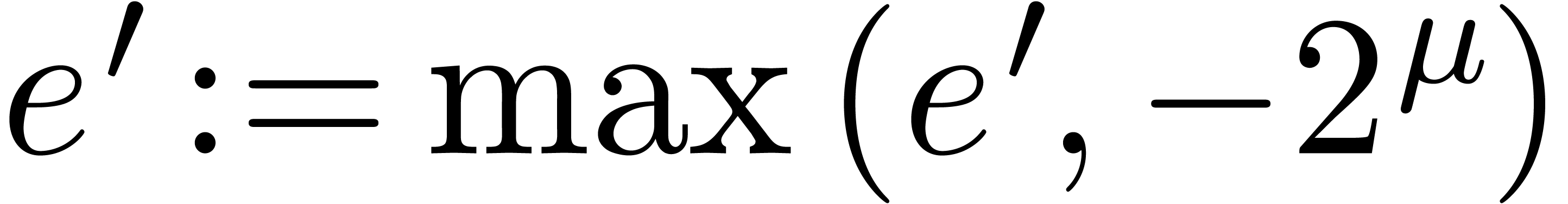

return 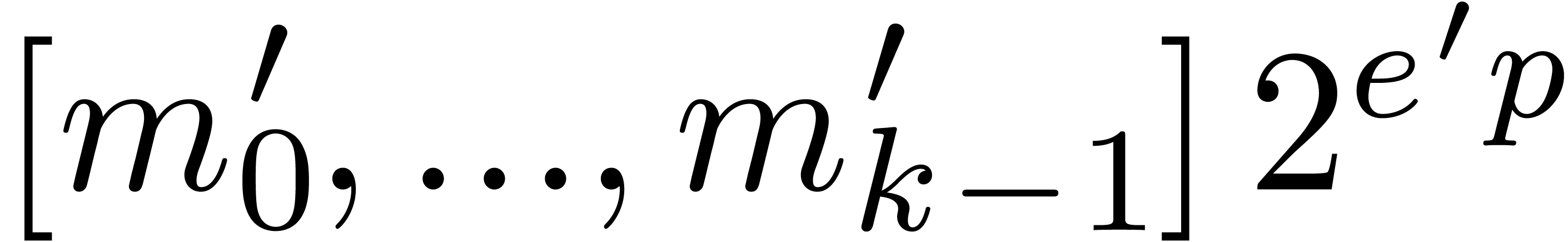
|
|
Modulo this change, the routines for addition and subtract are now as
follows:
|
|
Algorithm Subtract( ) )
|
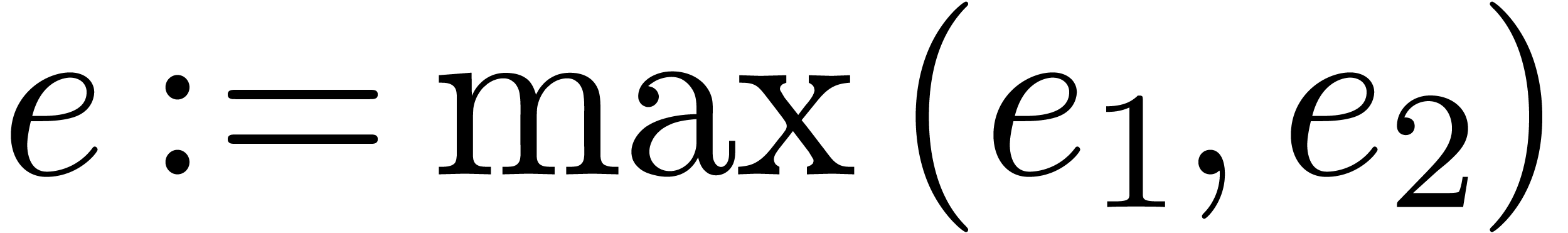
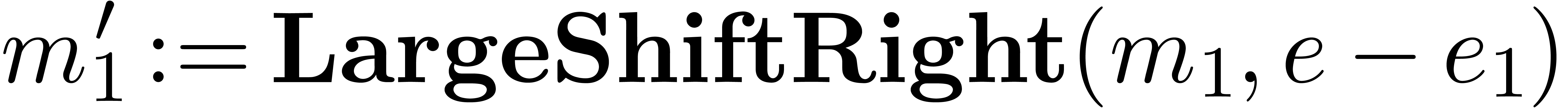
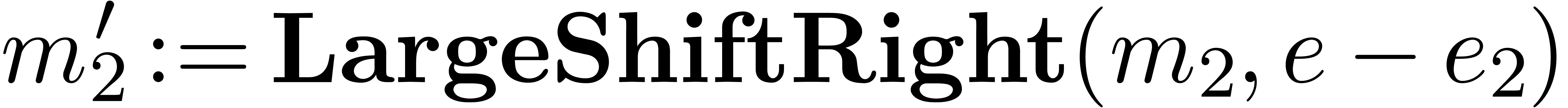

return 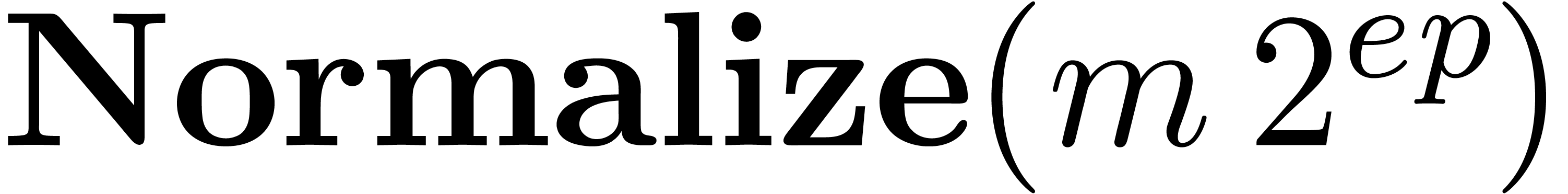
|
|
5.2.Multiplication
The dot normalization of a product becomes very particular when working
in base  since this can always be accomplished
using a large shift by either
since this can always be accomplished
using a large shift by either  or
or  or
or  bits. Let
bits. Let  be the variant of
be the variant of 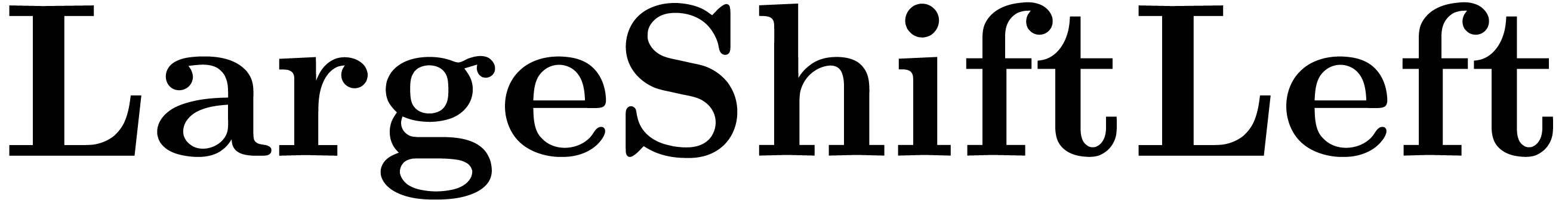 obtained by replacing the
condition
obtained by replacing the
condition  by
by 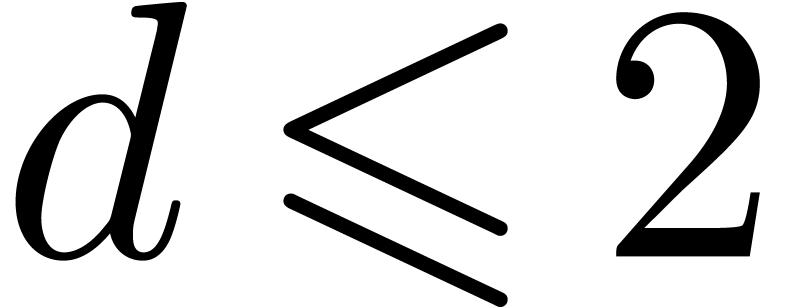 .
In order to achieve an accuracy of about
.
In order to achieve an accuracy of about 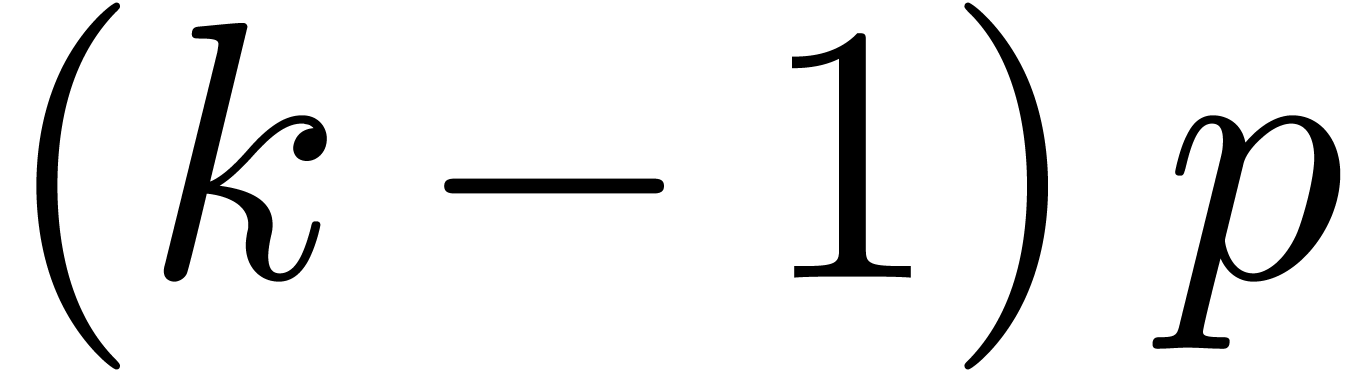 bits at
least, we extend the mantissas by one machine coefficient before
multiplying them. The routine QuickNormalize suppresses
the extra entry.
bits at
least, we extend the mantissas by one machine coefficient before
multiplying them. The routine QuickNormalize suppresses
the extra entry.
Algorithm QuickNormalize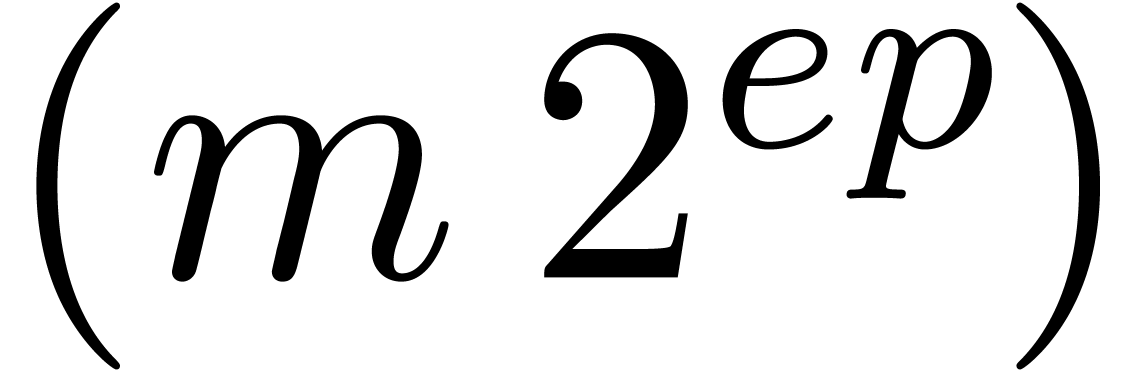
|

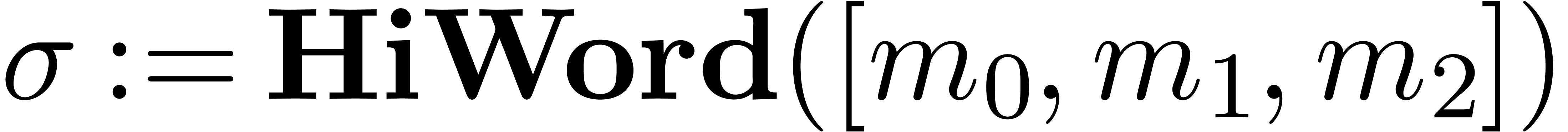

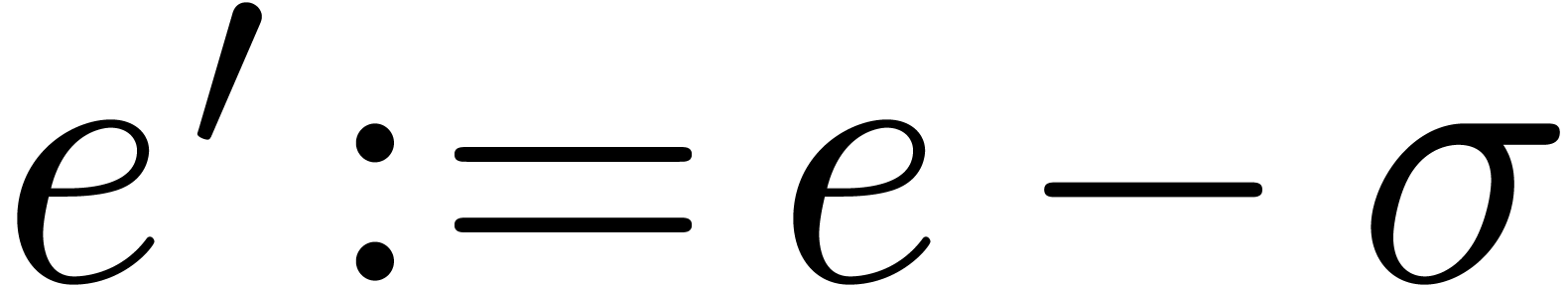
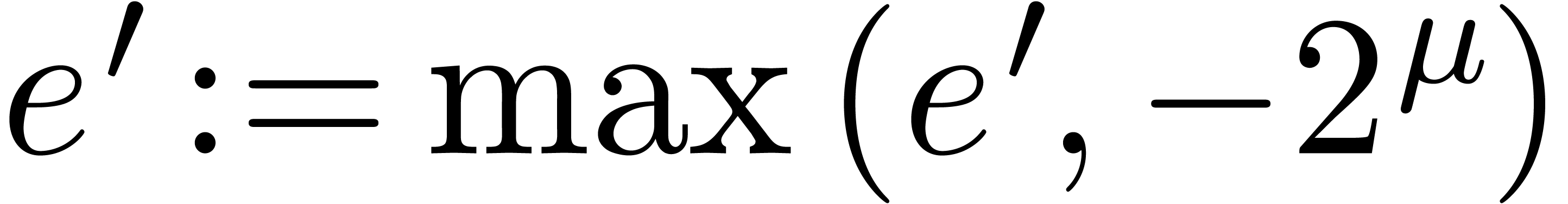
return 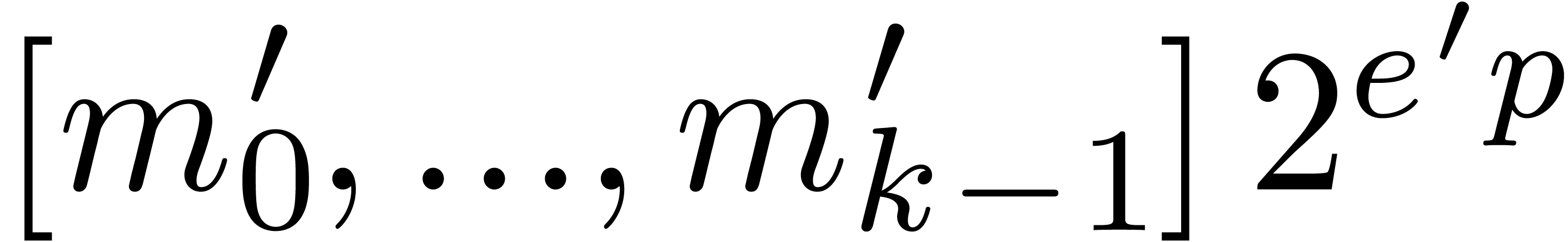
|
|
|
Algorithm Multiply(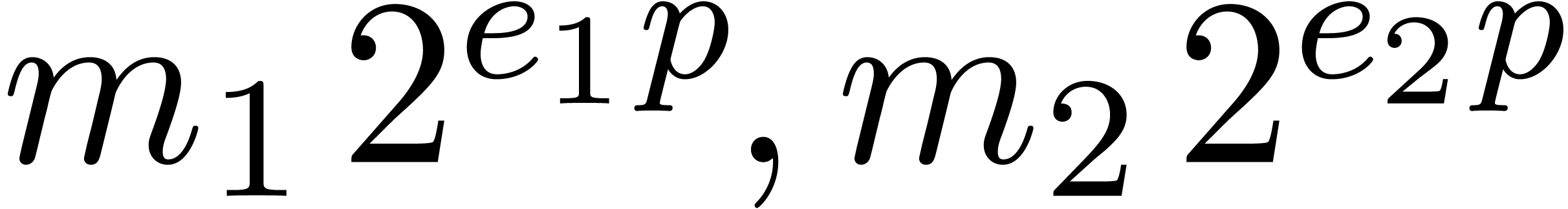 ) )
|
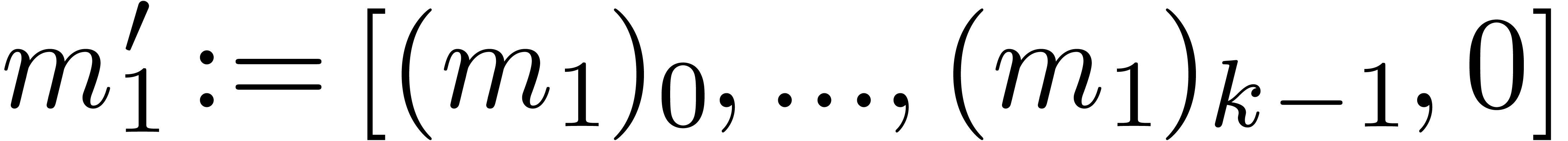
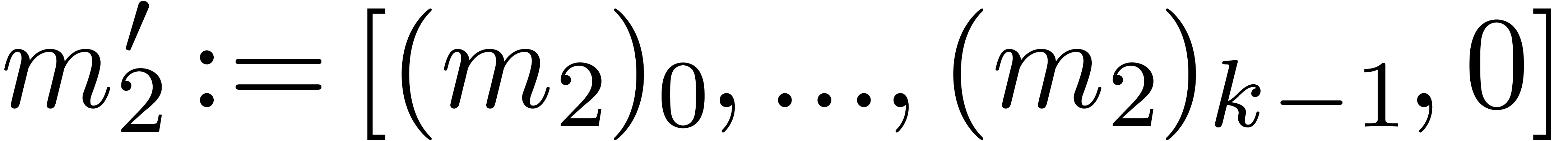

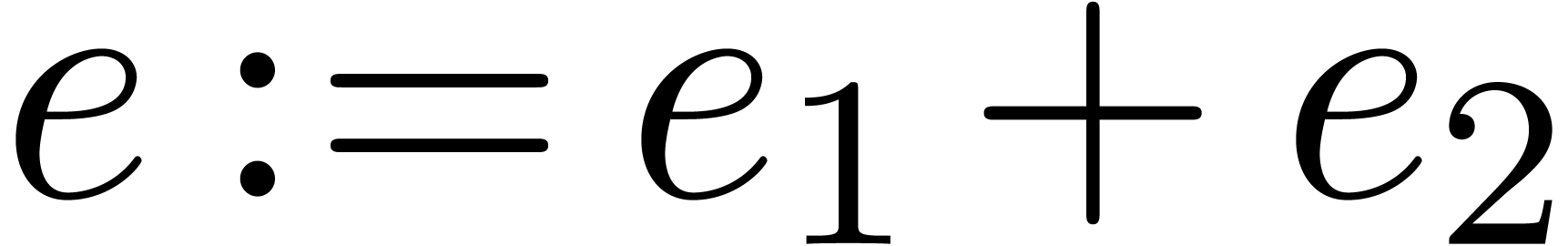
return 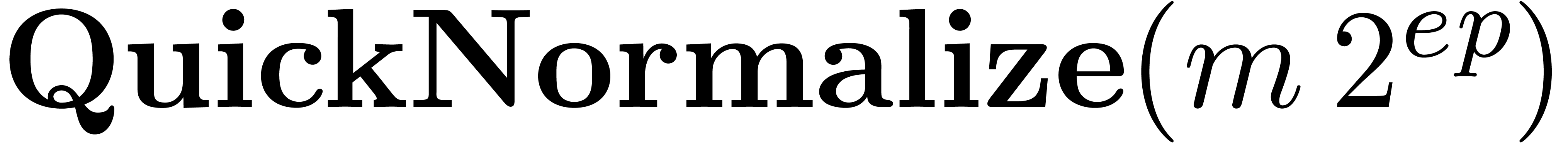
|
|
5.3.Operation counts
In Table 2, we give the operation counts for floating-point
addition, subtraction and multiplication in base 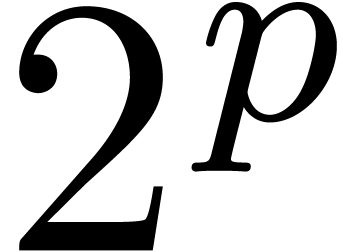 . In a similar way as in section 4.3,
it is possible to share exponents, and the table includes the operation
counts for this strategy. This time, additions and subtractions are
always cheaper than multiplications.
. In a similar way as in section 4.3,
it is possible to share exponents, and the table includes the operation
counts for this strategy. This time, additions and subtractions are
always cheaper than multiplications.
Bibliography
-
[1]
-
D. H. Bailey, R. Barrio, and J. M. Borwein. High
precision computation: mathematical physics and dynamics.
Appl. Math. Comput., 218:10106–10121, 2012.
-
[2]
-
R. P. Brent. A Fortran multiple-precision arithmetic
package. ACM Trans. Math. Software, 4:57–70, 1978.
-
[3]
-
R. P. Brent and P. Zimmermann. Modern Computer
Arithmetic. Cambridge University Press, 2010.
-
[4]
-
T. J. Dekker. A floating-point technique for
extending the available precision. Numer. Math.,
18(3):224–242, 1971.
-
[5]
-
N. Emmart, J. Luitjens, C. C. Weems, and C. Woolley.
Optimizing modular multiplication for nvidia's maxwell gpus. In
Paolo Montuschi, Michael Schulte, Javier Hormigo, Stuart
Oberman, and Nathalie Revol, editors, 23nd IEEE Symposium on
Computer Arithmetic, ARITH 2016, Silicon Valley, CA, USA, July
10-13, 2016, pages 47–54. IEEE, 2016.
-
[6]
-
L. Fousse, G. Hanrot, V. Lefèvre, P.
Pélissier, and P. Zimmermann. MPFR: a multiple-precision
binary floating-point library with correct rounding. ACM
Trans. Math. Software, 33(2), 2007. Software available at http://www.mpfr.org.
-
[7]
-
T. Granlund et al. GMP, the GNU multiple precision
arithmetic library. http://gmplib.org,
from 1991.
-
[8]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Even
faster integer multiplication. Journal of Complexity,
36:1–30, 2016.
-
[9]
-
Yozo Hida, Xiaoye S. Li, and D. H. Bailey. Algorithms
for quad-double precision floating-point arithmetic. In Proc.
15th IEEE Symposium on Computer Arithmetic, pages
155–162. IEEE, 2001.
-
[10]
-
J. van der Hoeven and G. Lecerf. Faster FFTs in
medium precision. In 22nd Symposium on Computer Arithmetic
(ARITH), pages 75–82, June 2015.
-
[11]
-
A. Karatsuba and J. Ofman. Multiplication of
multidigit numbers on automata. Soviet Physics Doklady,
7:595–596, 1963.
-
[12]
-
C. Lauter. Basic building blocks for a triple-double
intermediate format. Technical Report RR2005-38, LIP, ENS Lyon,
2005.
-
[13]
-
J.-M. Muller, N. Brisebarre, F. de Dinechin, C.-P.
Jeannerod, V. Lefèvre, G. Melquiond, N. Revol, D.
Stehlé, and S. Torres. Handbook of Floating-Point
Arithmetic. Birkhäuser Boston, 2010.
-
[14]
-
Jean-Michel Muller, Valentina Popescu, and Ping Tak
Peter Tang. A new multiplication algorithm for extended
precision using floating-point expansions. In Paolo Montuschi,
Michael Schulte, Javier Hormigo, Stuart Oberman, and Nathalie
Revol, editors, 23nd IEEE Symposium on Computer Arithmetic,
ARITH 2016, Silicon Valley, CA, USA, July 10-13, 2016, pages
39–46, 2016.
-
[15]
-
T. Nagai, H. Yoshida, H. Kuroda, and Y. Kanada. Fast
quadruple precision arithmetic library on parallel computer
SR11000/J2. In Computational Science - ICCS 2008, 8th
International Conference, Kraków, Poland, June 23-25,
2008, Proceedings, Part I, pages 446–455, 2008.
-
[16]
-
J.M. Pollard. The fast Fourier transform in a finite
field. Mathematics of Computation, 25(114):365–374,
1971.
-
[17]
-
D. M. Priest. Algorithms for arbitrary precision
floating-point arithmetic. In Proc. 10th Symposium on
Computer Arithmetic, pages 132–145. IEEE, 1991.
-
[18]
-
A. Schönhage and V. Strassen. Schnelle
Multiplikation großer Zahlen. Computing,
7:281–292, 1971.
-
[19]
-
D. Takahashi. Implementation of multiple-precision
floating-point arithmetic on Intel Xeon Phi coprocessors. In
Computational Science and Its Applications – ICCSA
2016: 16th International Conference, Beijing, China, July 4-7,
2016, Proceedings, Part II, pages 60–70, Cham, 2016.
Springer International Publishing.
 where
where  and
and  have no “overlapping bits”
(e.g.
have no “overlapping bits”
(e.g. 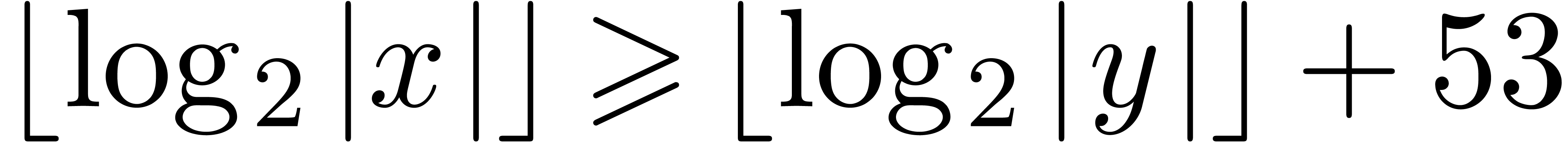 or
or 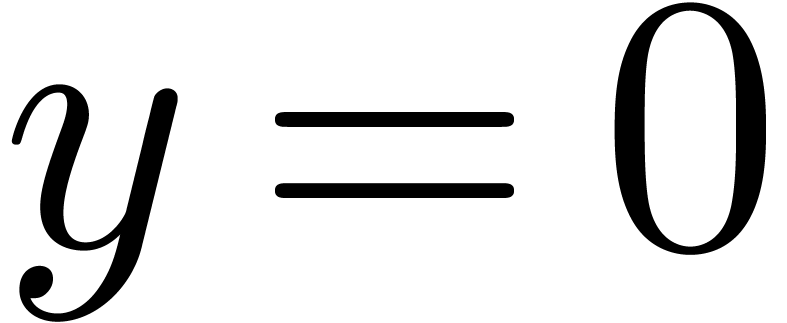 ). The TwoProduct operation can be
implemented using only two instructions when hardware offers the
fused-multiply-add (FMA) and fused-multiply-subtract
(FMS) instructions, as is for instance the case for AVX2 enabled
processors. The TwoSum operation could be done using
only two instructions as well if we had similar fused-add-add and
fused-add-subtract instructions. Unfortunately, this is not the case for
current hardware.
). The TwoProduct operation can be
implemented using only two instructions when hardware offers the
fused-multiply-add (FMA) and fused-multiply-subtract
(FMS) instructions, as is for instance the case for AVX2 enabled
processors. The TwoSum operation could be done using
only two instructions as well if we had similar fused-add-add and
fused-add-subtract instructions. Unfortunately, this is not the case for
current hardware.
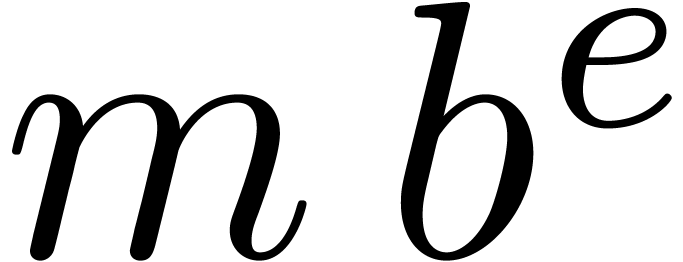 ,
,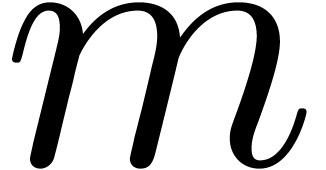 is a fixed-point mantissa,
is a fixed-point mantissa,  an
exponent, and
an
exponent, and 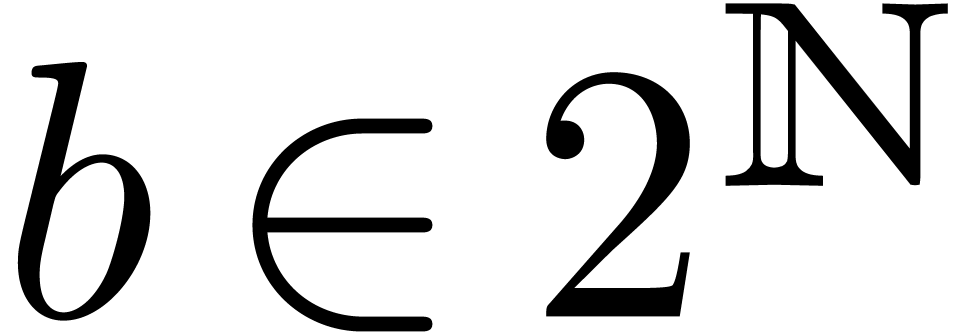 the base. This representation is
used in most of the existing multi-precision libraries such as
the base. This representation is
used in most of the existing multi-precision libraries such as  .
. be the bit precision of our machine floating-point numbers minus one (so
that
be the bit precision of our machine floating-point numbers minus one (so
that  for IEEE-754 double precision numbers).
Throughout this paper, we represent fixed-point numbers in base
for IEEE-754 double precision numbers).
Throughout this paper, we represent fixed-point numbers in base  by
by 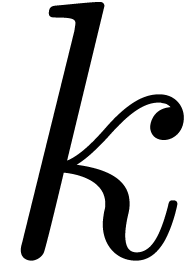 -tuplets
-tuplets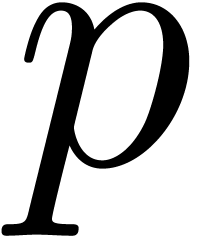 is
slightly smaller than
is
slightly smaller than 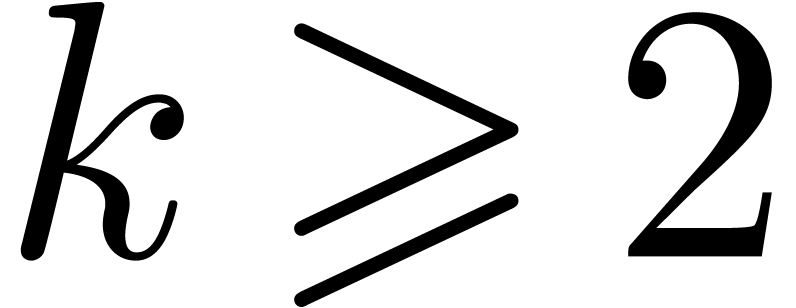 .
.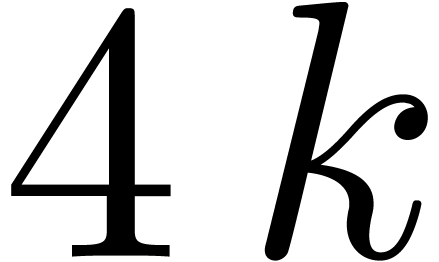 operations, whereas arbitrary
shifts require approximately
operations, whereas arbitrary
shifts require approximately 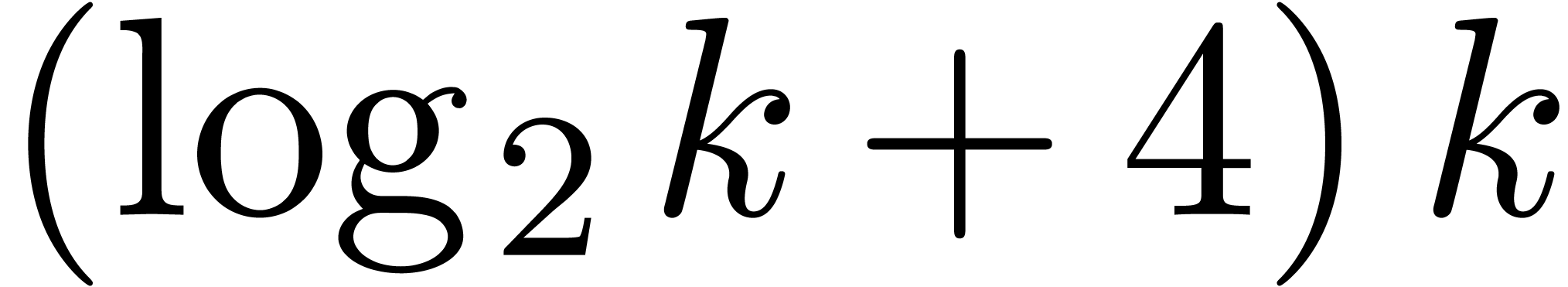 operations.
operations.
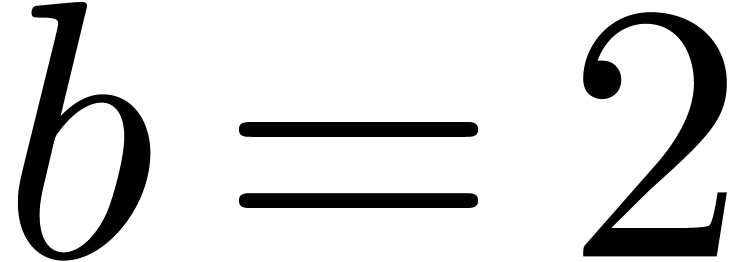 .
.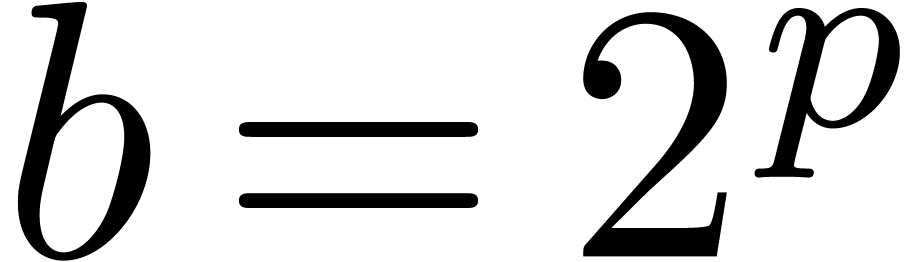 .
.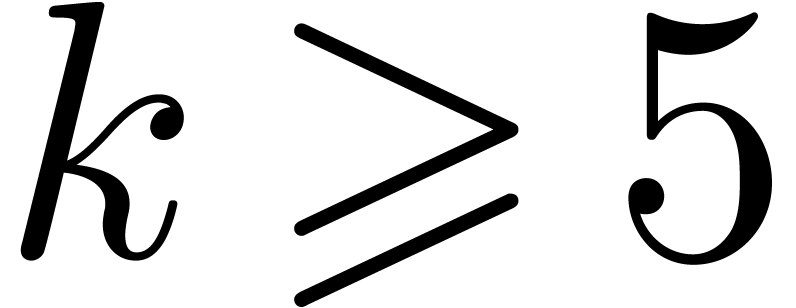 and maybe even for
and maybe even for 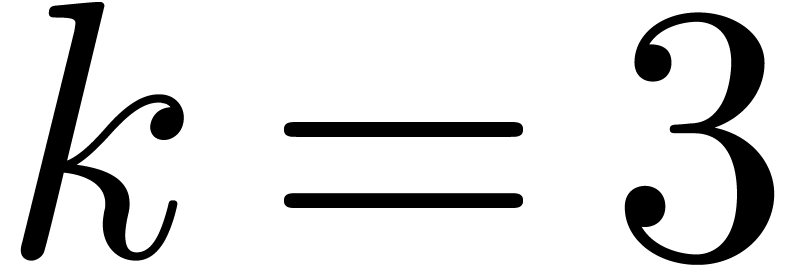 and
and 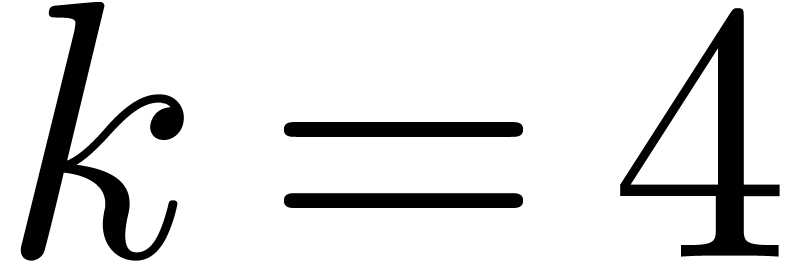 .
. the set of machine
floating-point numbers. We let
the set of machine
floating-point numbers. We let  be the machine
precision minus one (which corresponds to the number of fractional bits
of the mantissa) and let
be the machine
precision minus one (which corresponds to the number of fractional bits
of the mantissa) and let 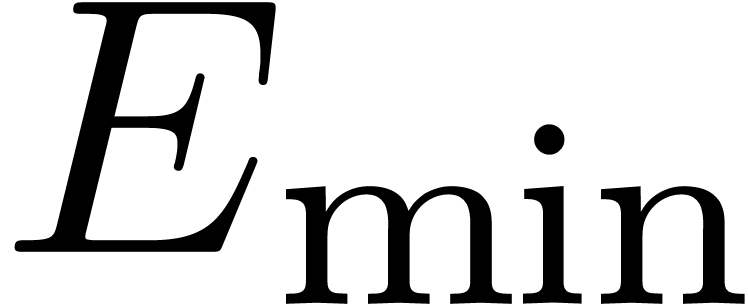 and
and 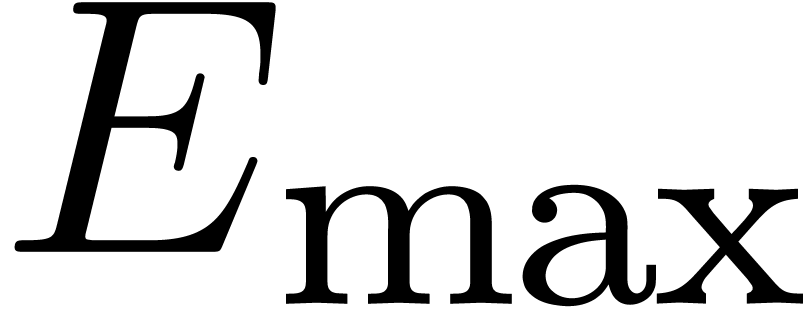 be the minimal and maximal exponents of machine floating-point numbers.
For IEEE double precision numbers, this means that
be the minimal and maximal exponents of machine floating-point numbers.
For IEEE double precision numbers, this means that 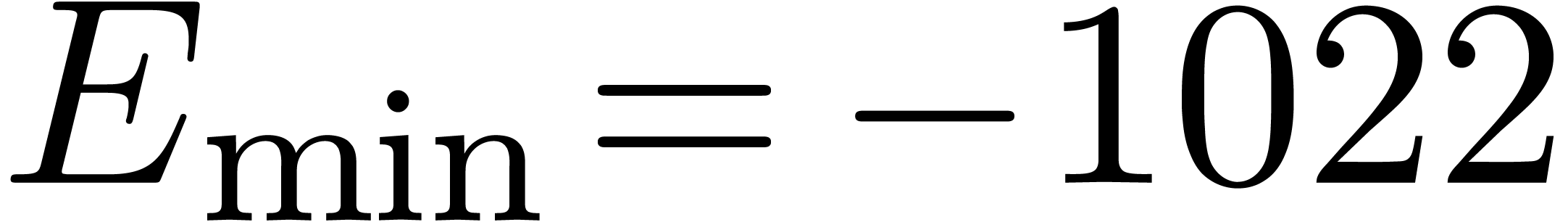 and
and 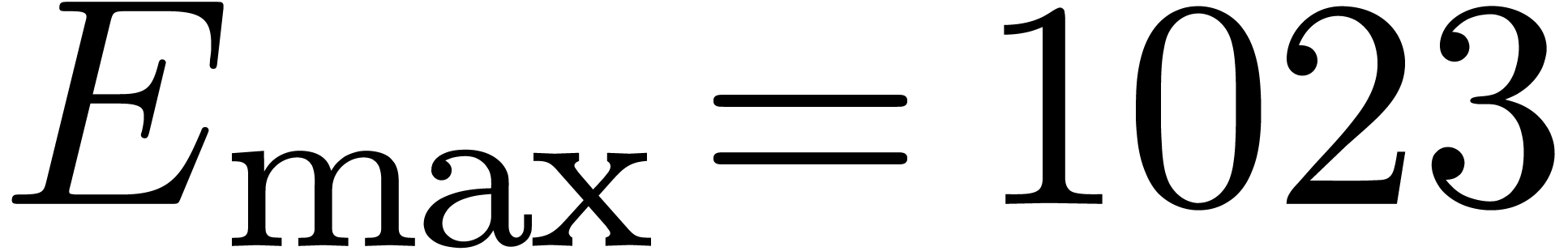 .
.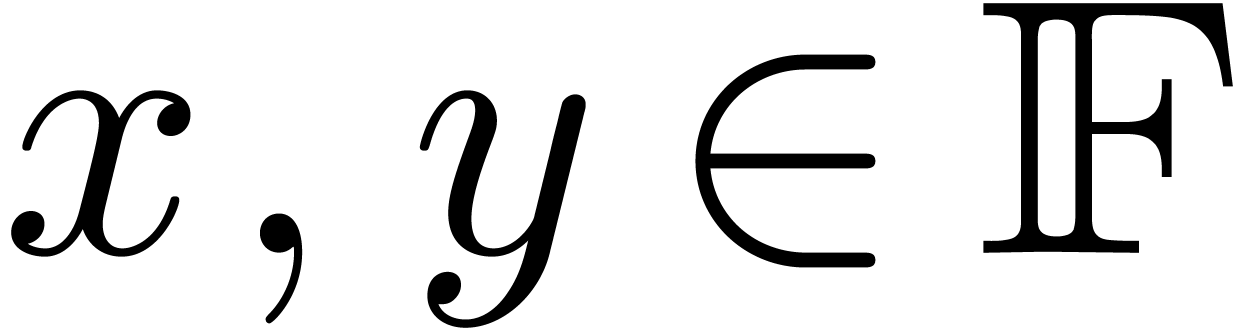 and
and  ,
,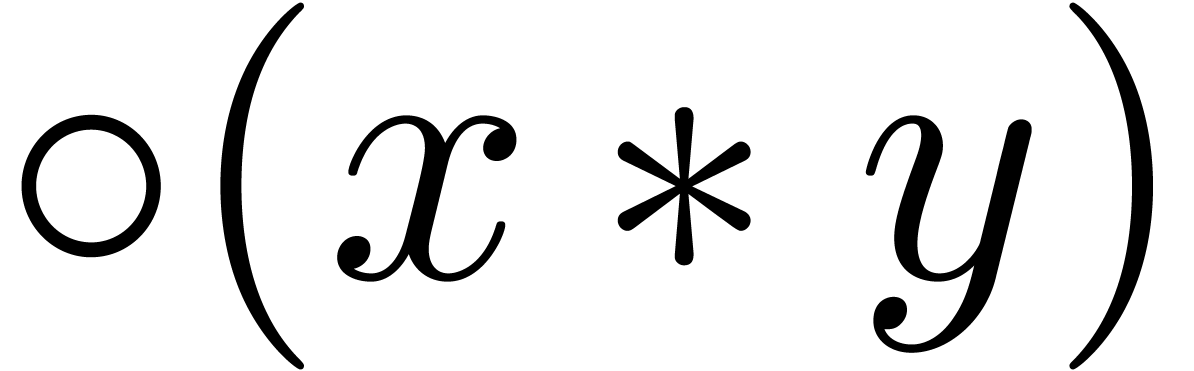 the rounding of
the rounding of  to
the nearest. For convenience of the reader, we denote
to
the nearest. For convenience of the reader, we denote 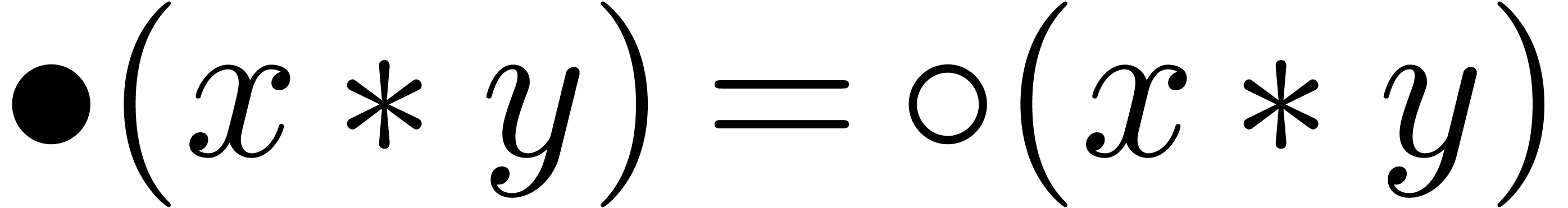 whenever the result
whenever the result 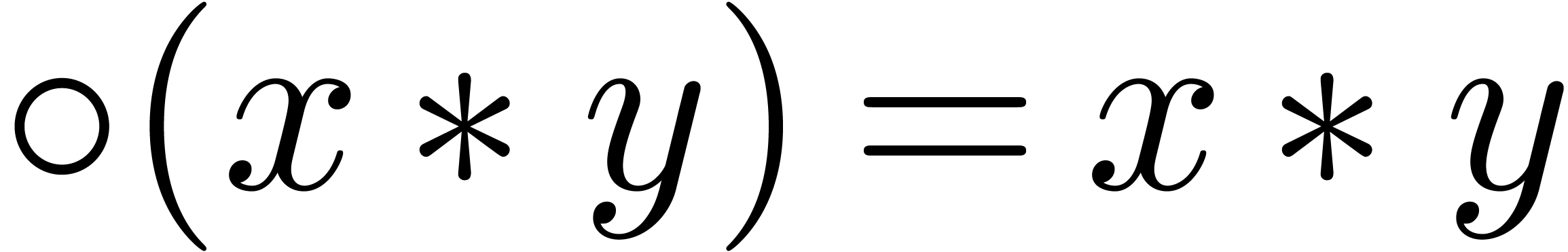 is provably exact in the
given context. If
is provably exact in the
given context. If  (i.e. in absence
of overflow and underflow), then we notice that
(i.e. in absence
of overflow and underflow), then we notice that 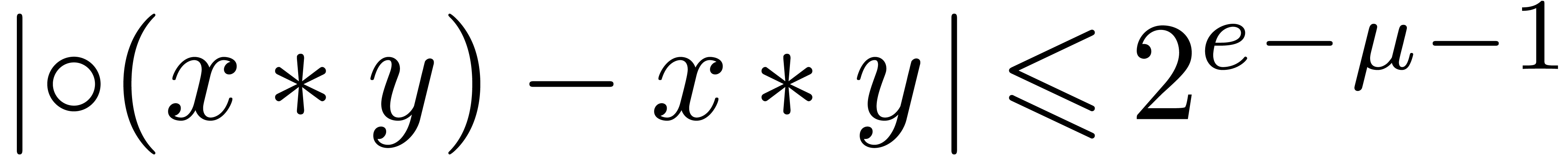 .
. and
and  the roundings of
the roundings of  and
and
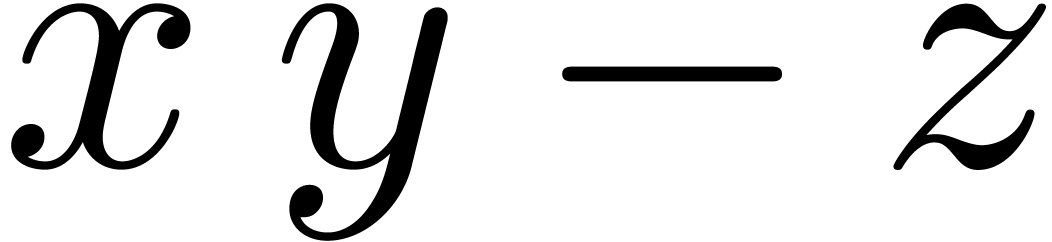 to the nearest.
to the nearest.
 and
and 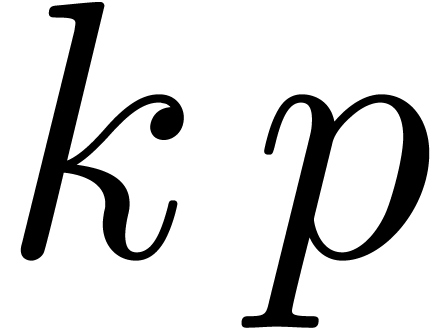 .
. .
.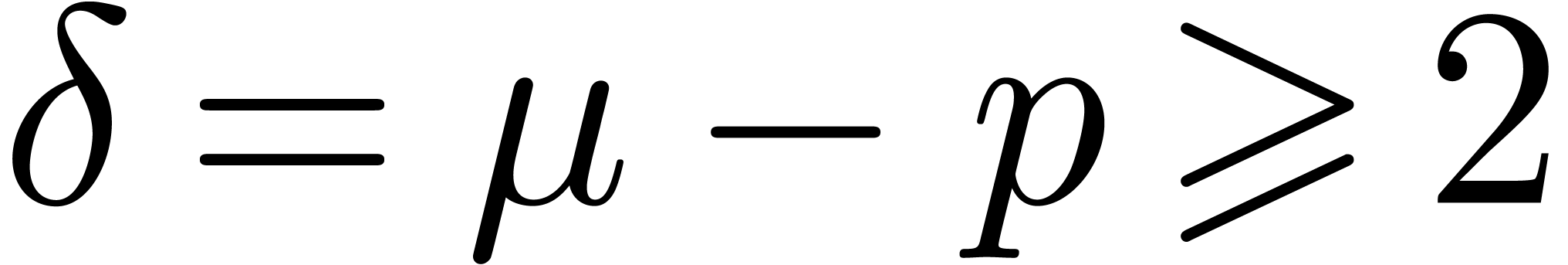 the number of extra carry bits
(these bits are sometimes called “nails”, following GMP [
the number of extra carry bits
(these bits are sometimes called “nails”, following GMP [ and an integer
and an integer 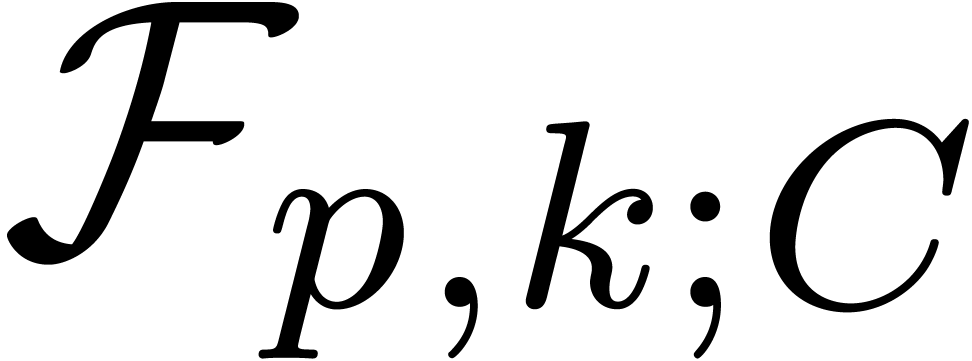 the set of
numbers of the form
the set of
numbers of the form
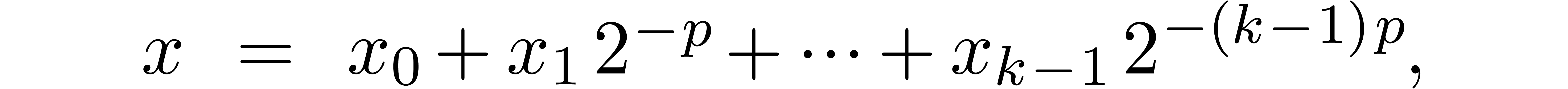
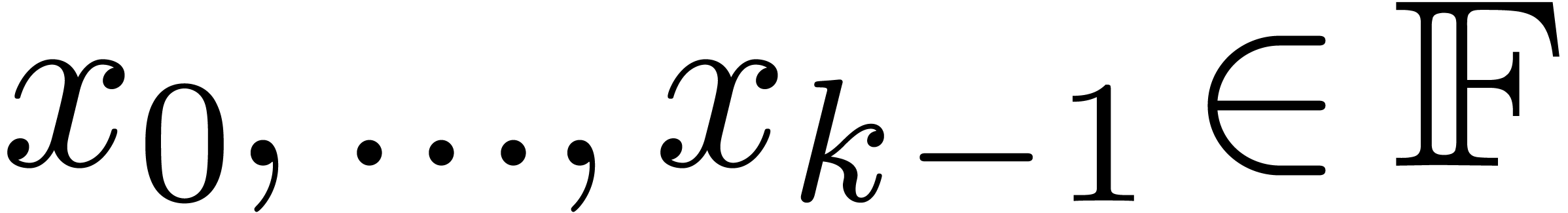 are such that
are such that
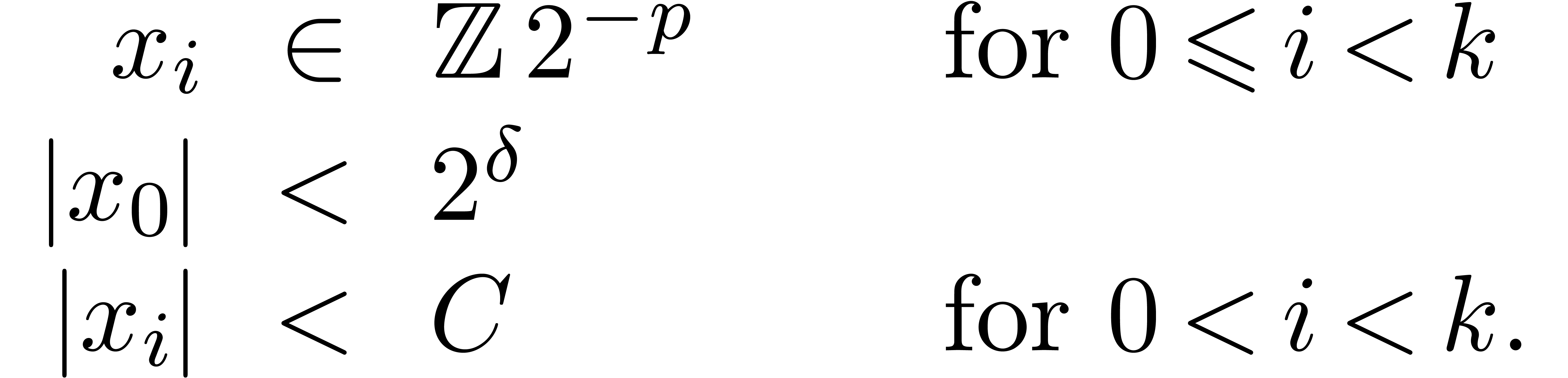
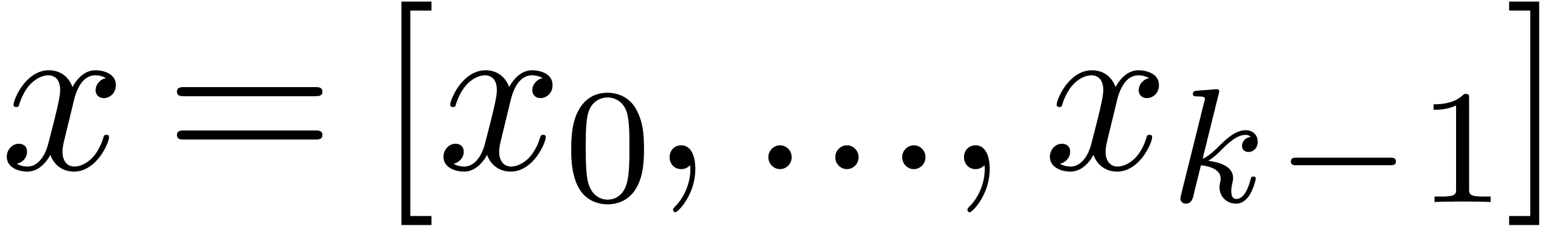 for numbers of the above form and
abbreviate
for numbers of the above form and
abbreviate 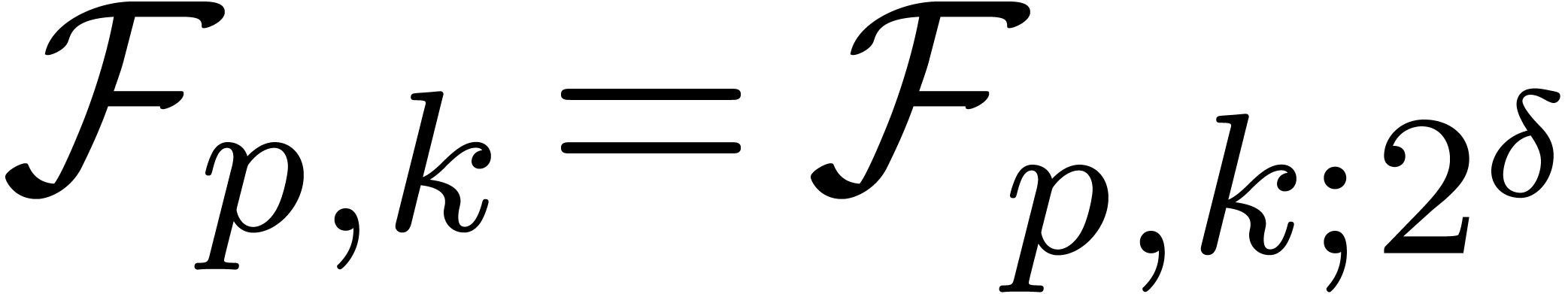 .
.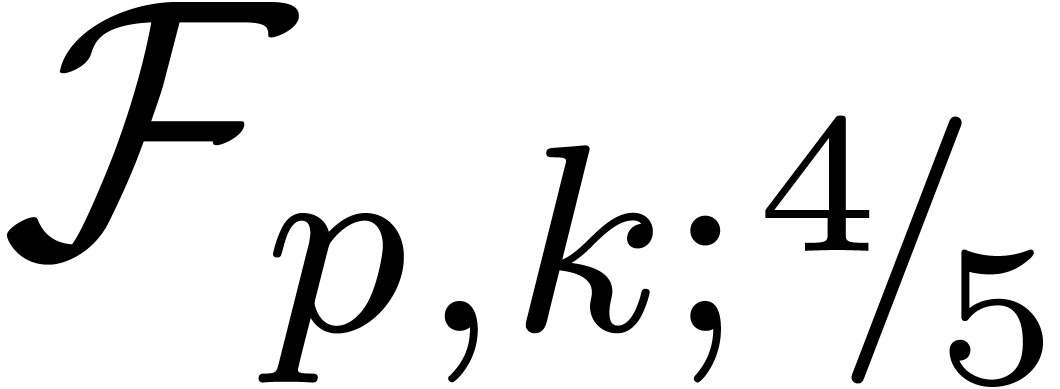 are said to be in carry normal form.
are said to be in carry normal form.
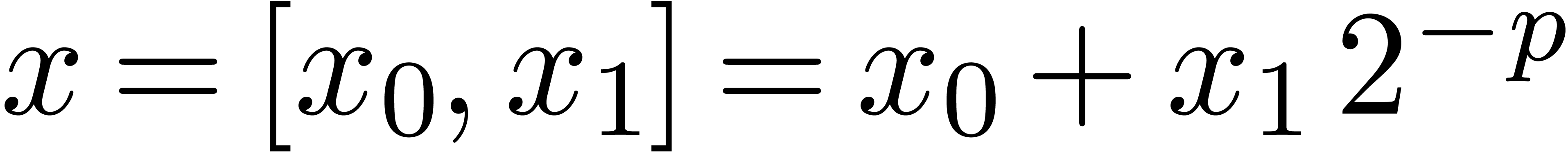 ,
,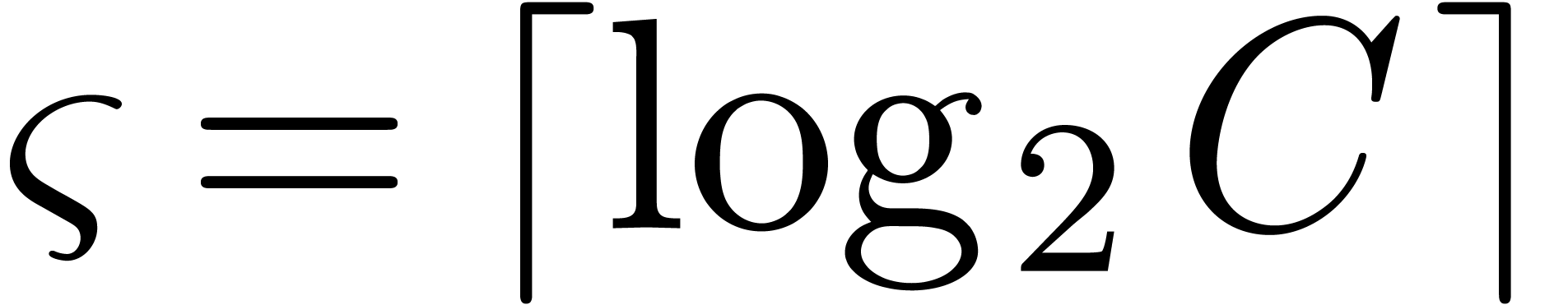 .
. with
with 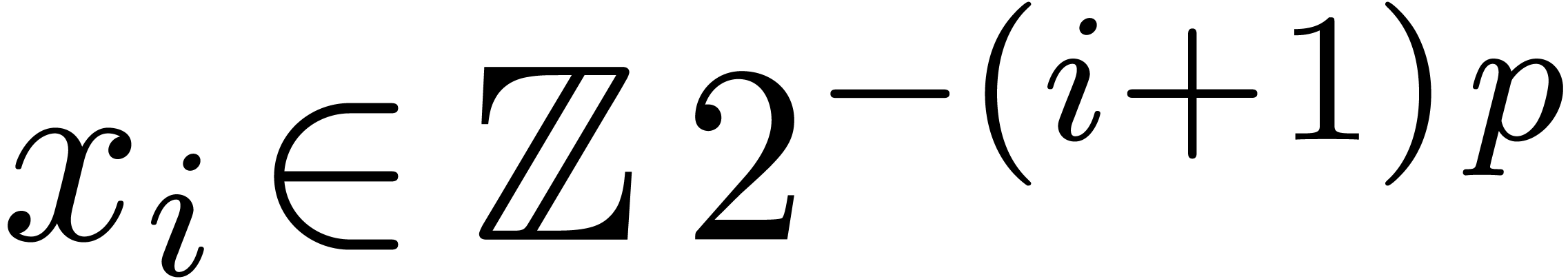 and
and 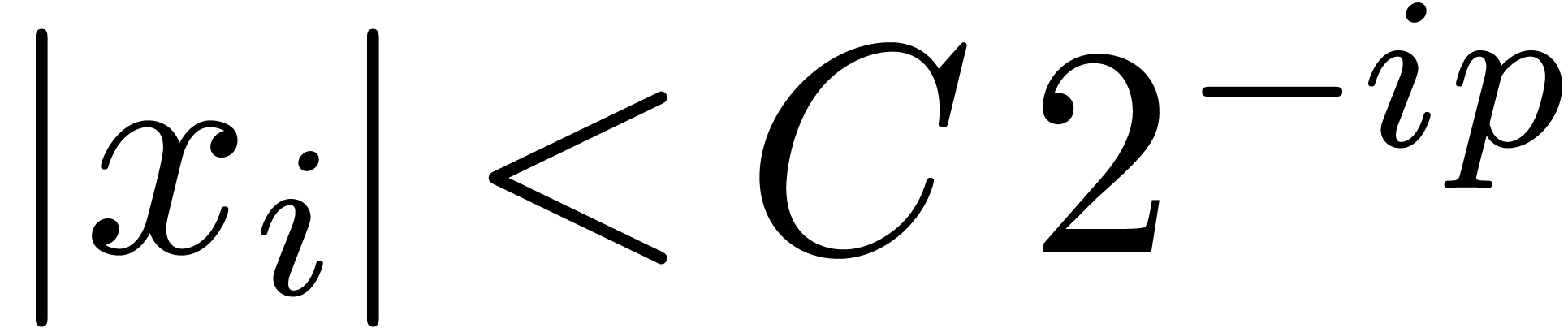 .
.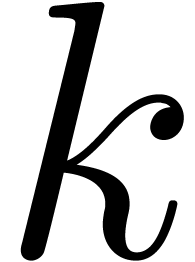 ,
,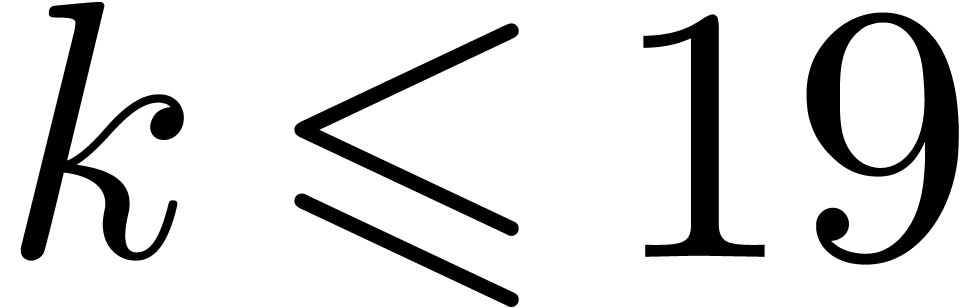 ),
),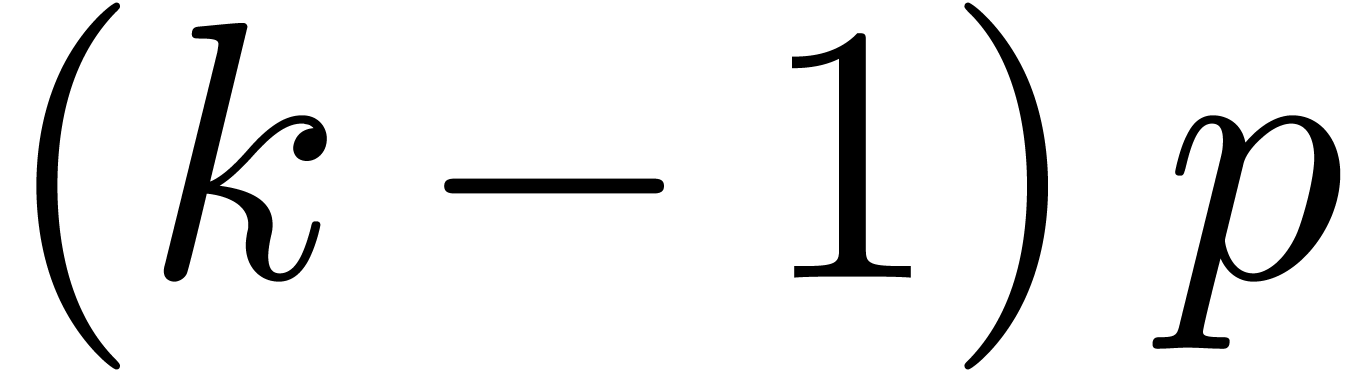 must required to be smaller than
must required to be smaller than  .
. to hold for the last index
to hold for the last index  .
.
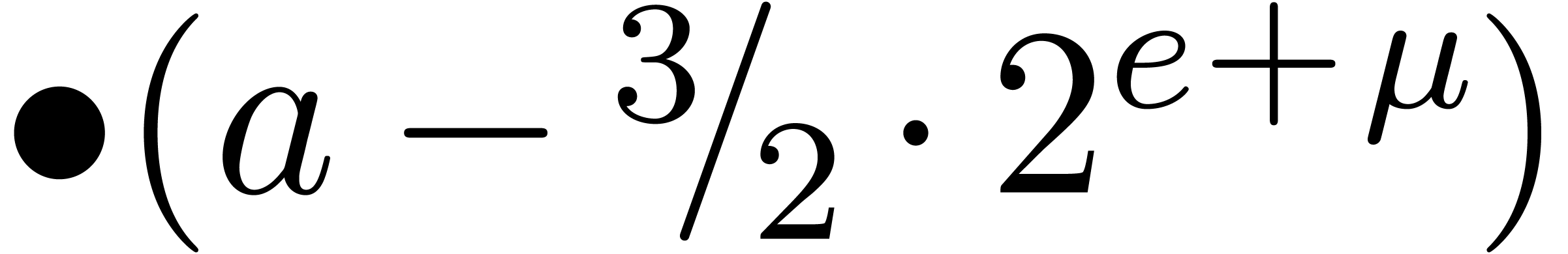
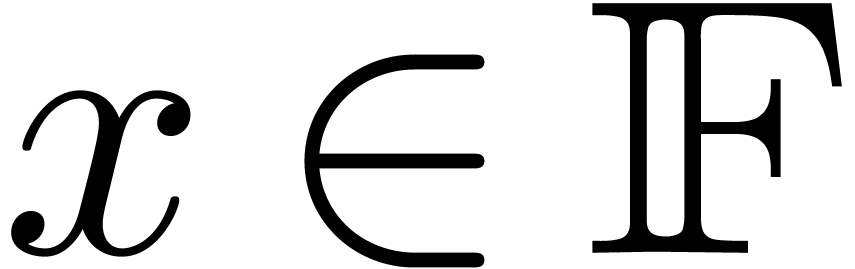 and
and  such that
such that 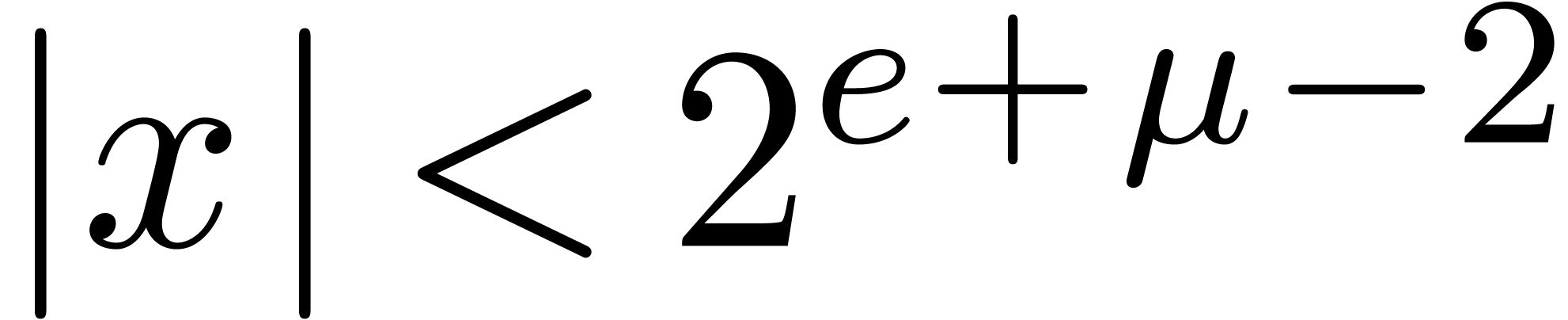 ,
, computes a number
computes a number 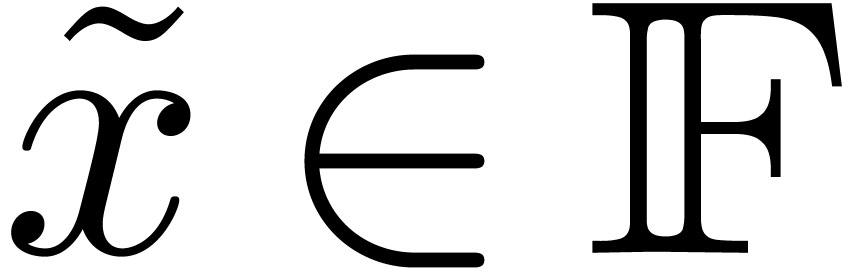 with
with  and
and 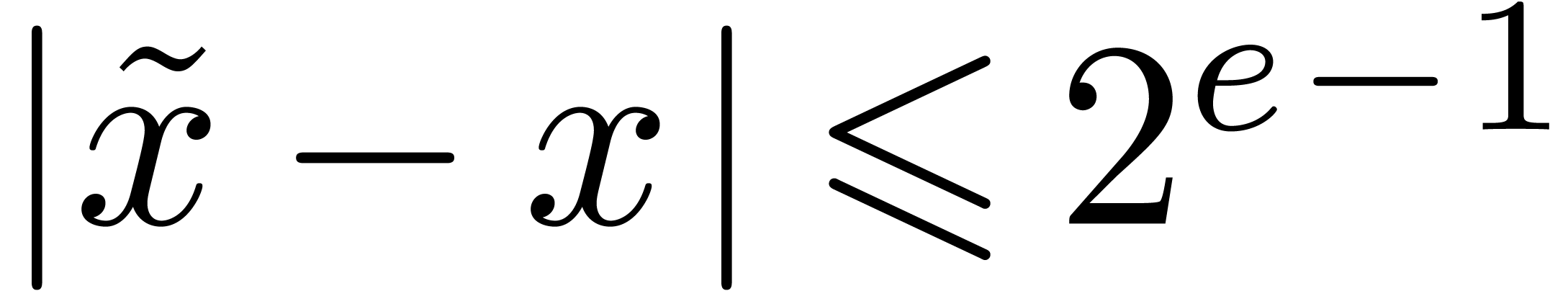 .
.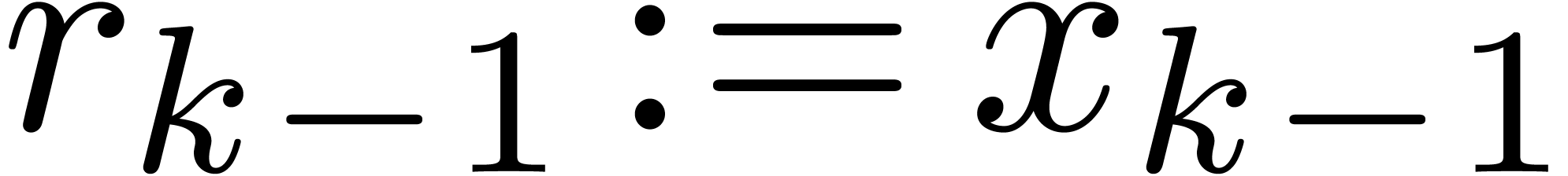
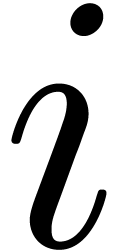 from
from
 down to
down to  do
do
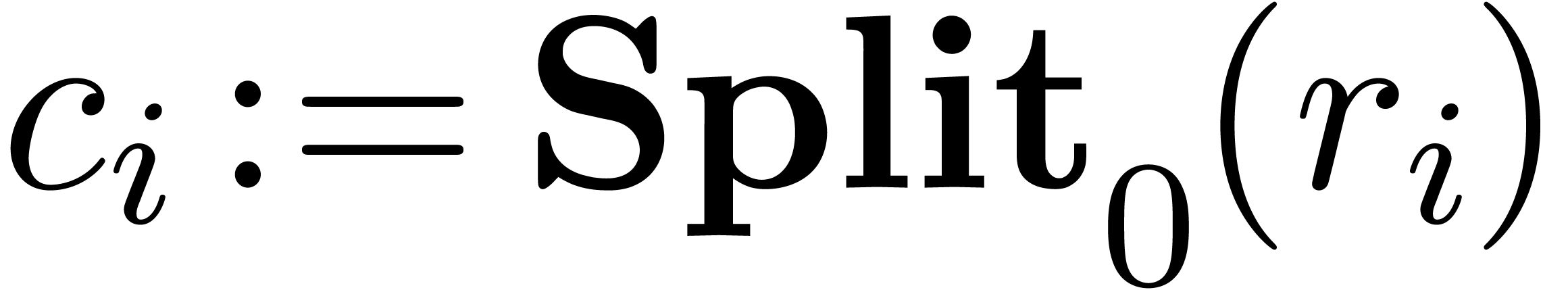
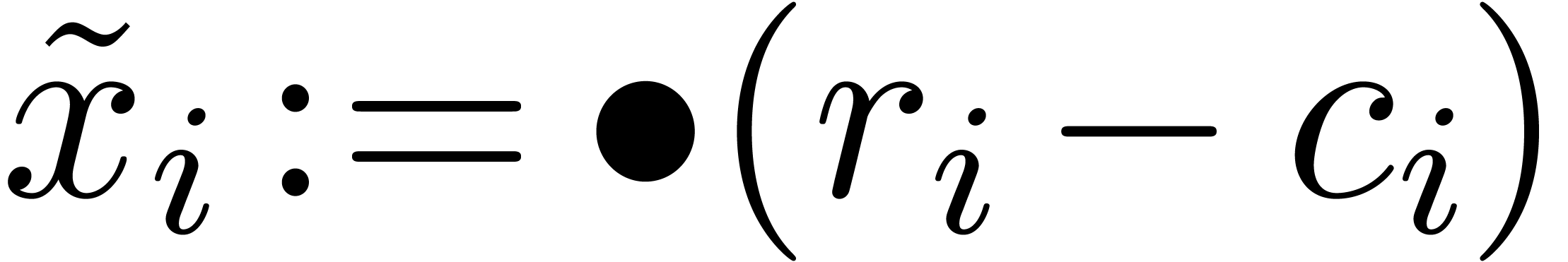
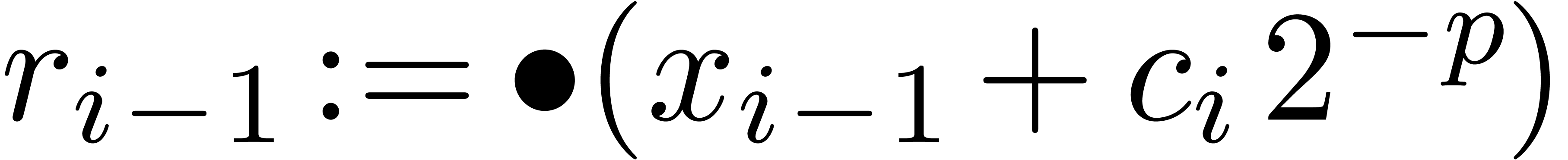
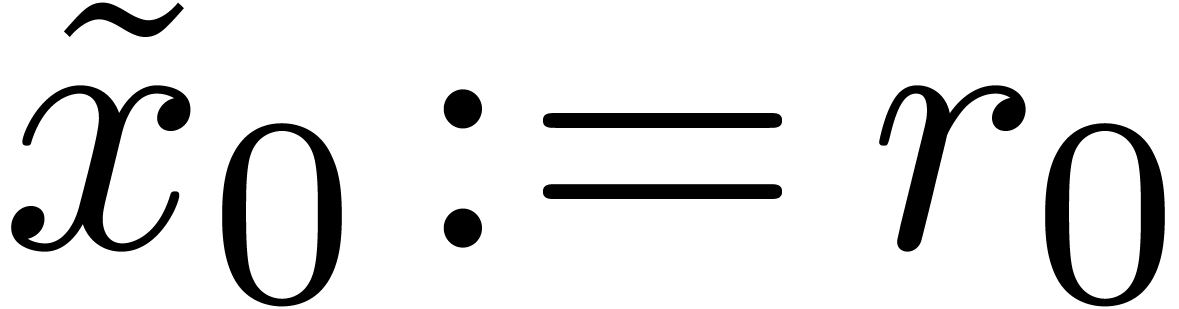
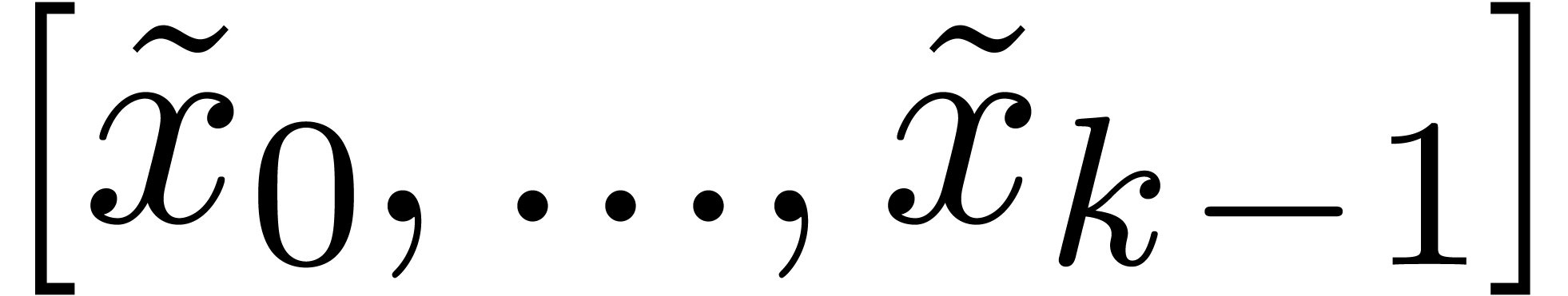
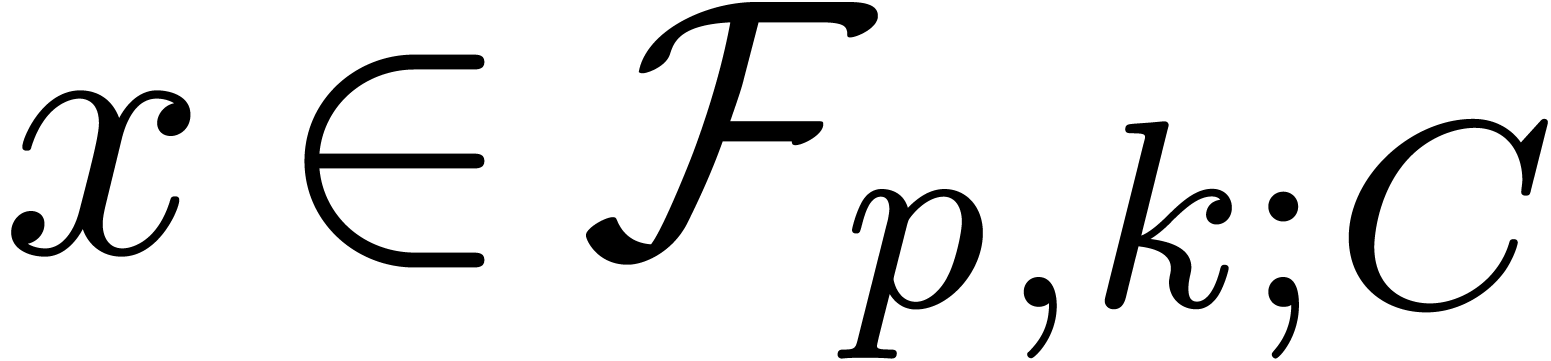 with
with  and
and  ,
, returns
returns 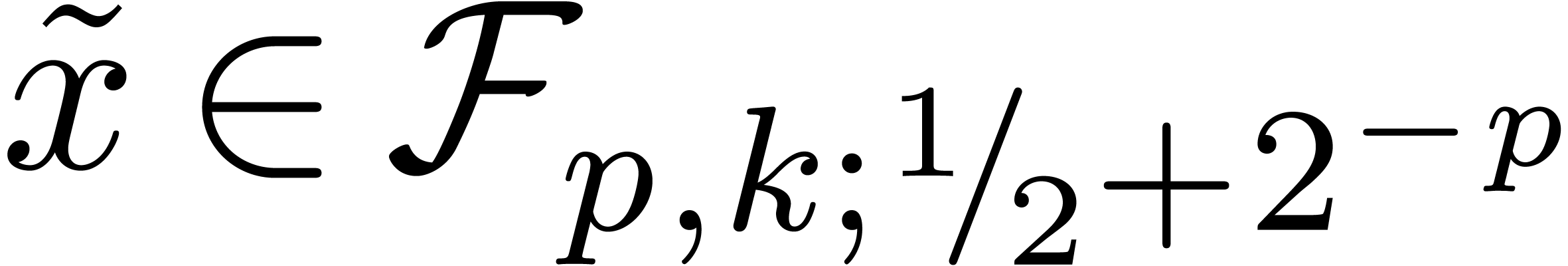 with
with  .
.
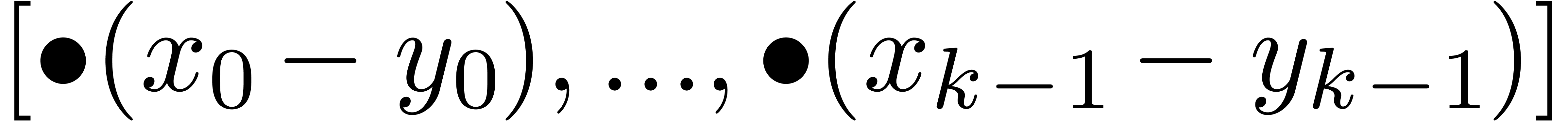
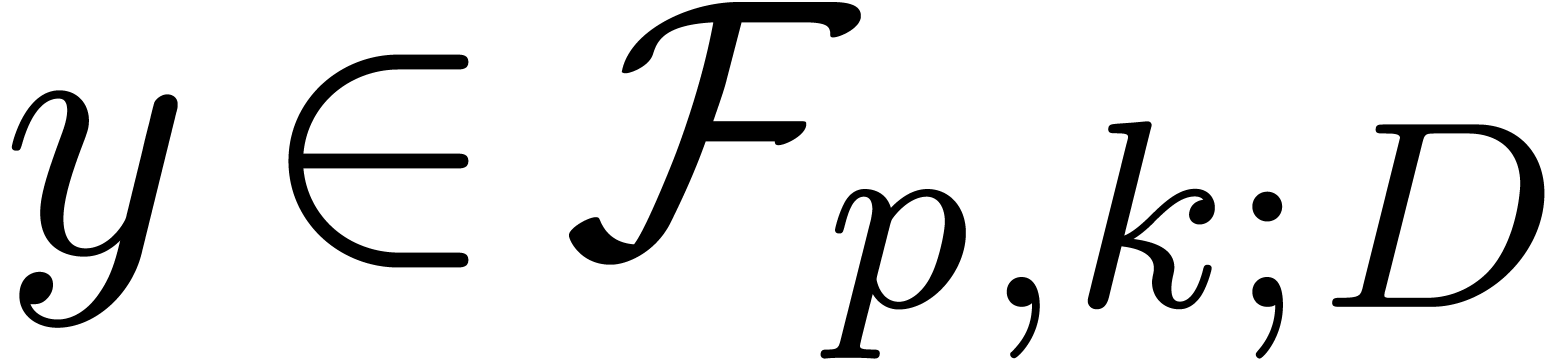 with
with 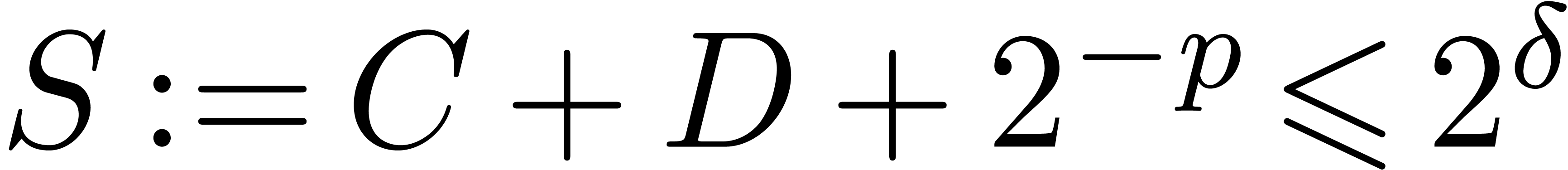 .
.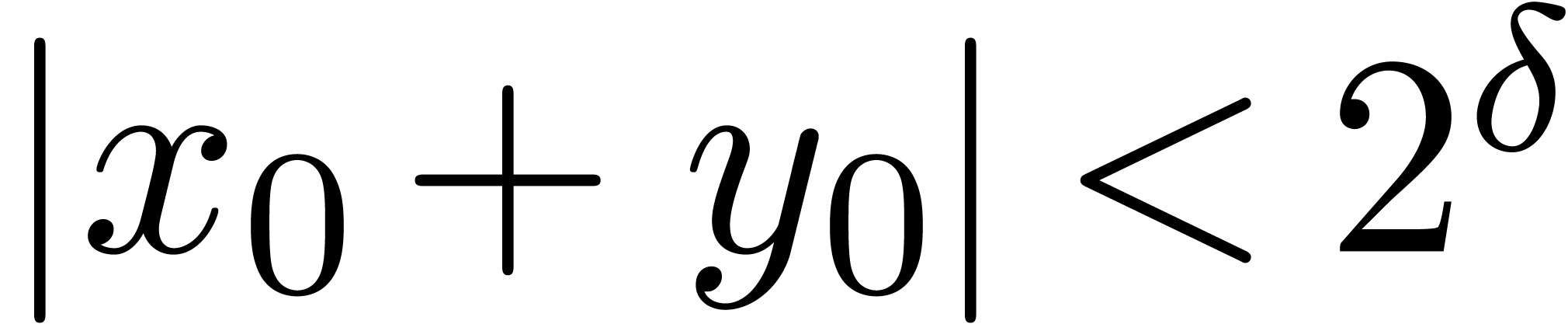 ,
,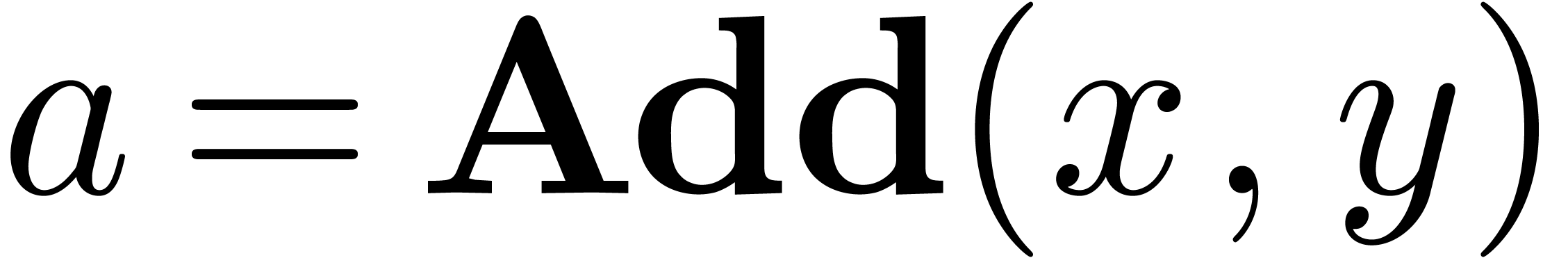 satisfies
satisfies
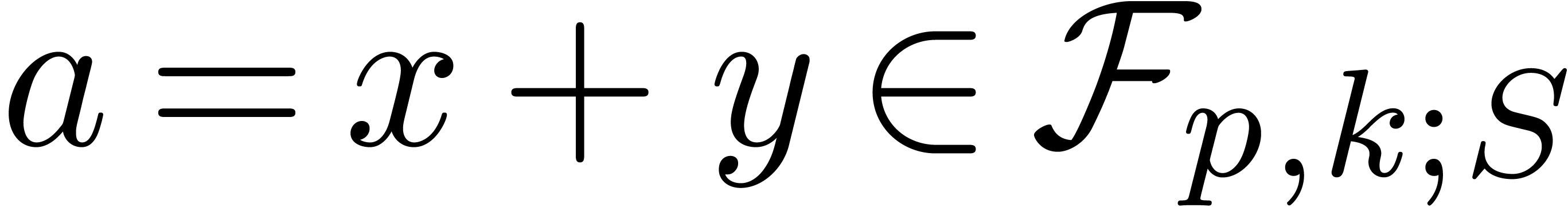 .
. ,
, satisfies
satisfies 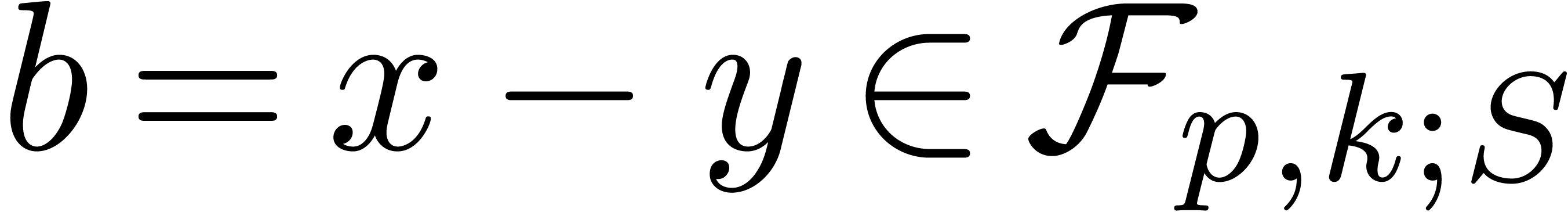 .
.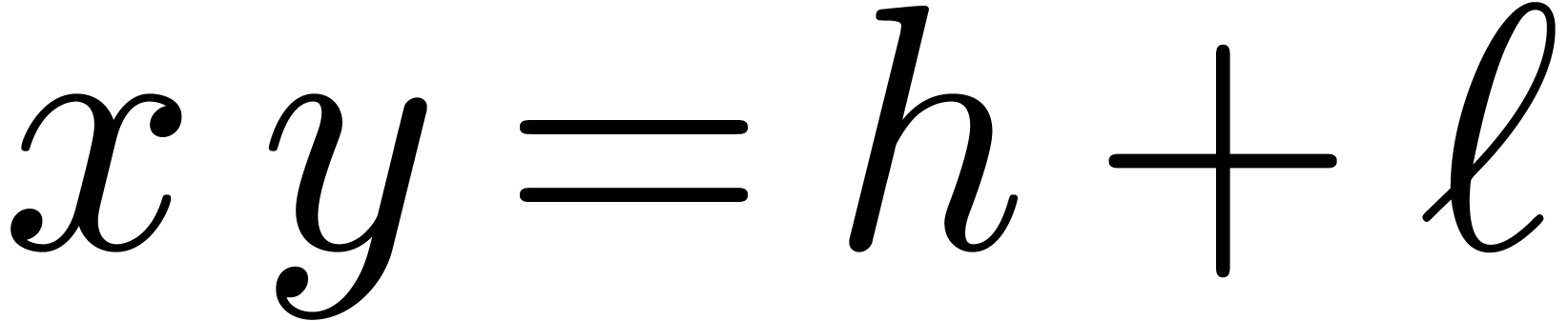 ,
,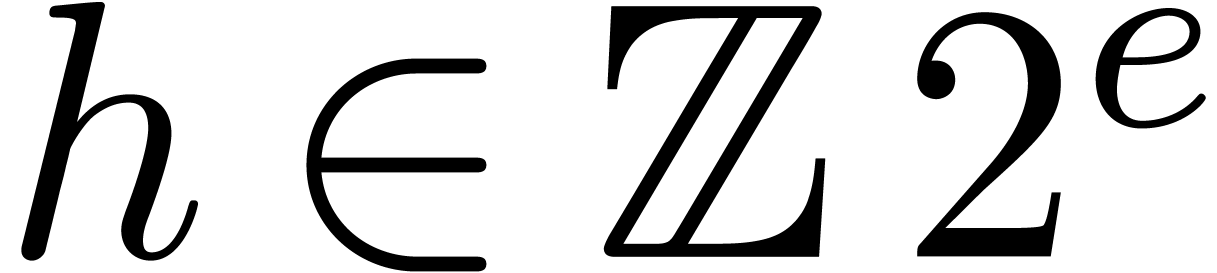 .
. and
and  can be
computed using the well known “Two Product” algorithm:
can be
computed using the well known “Two Product” algorithm: 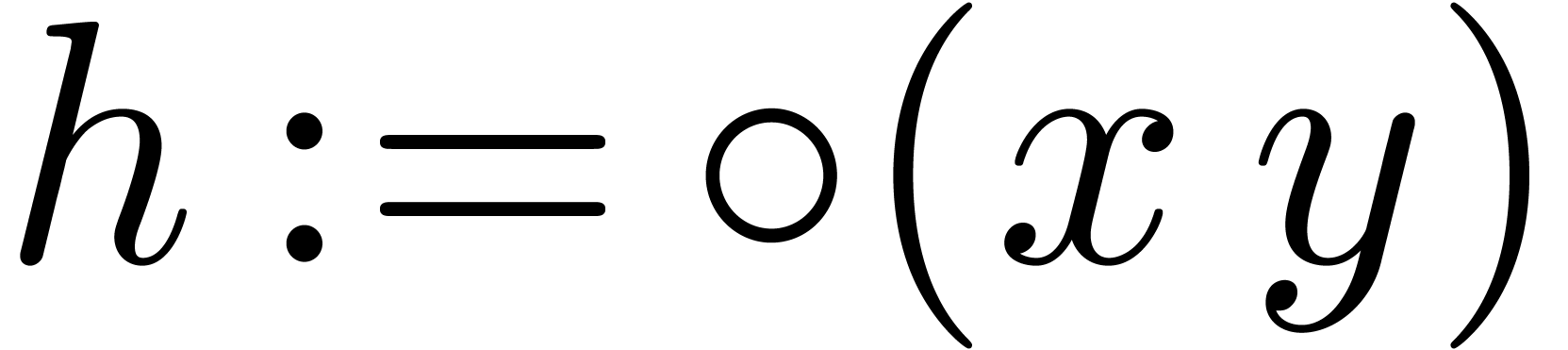 ,
,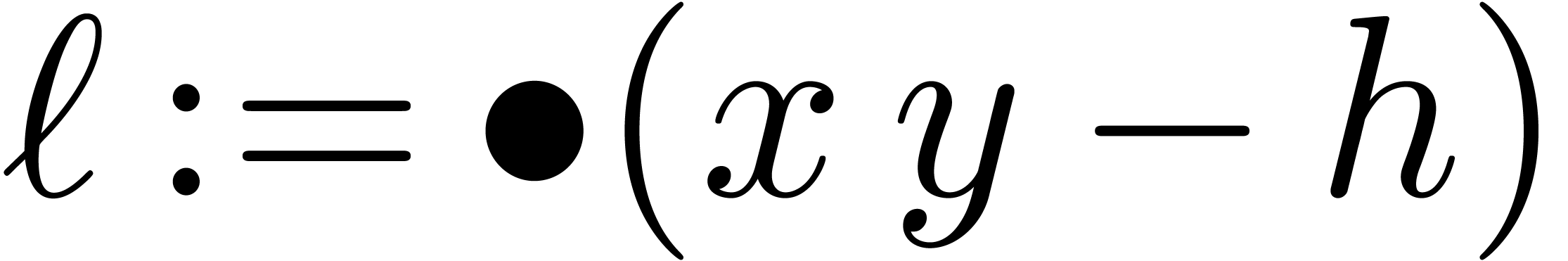 .
.
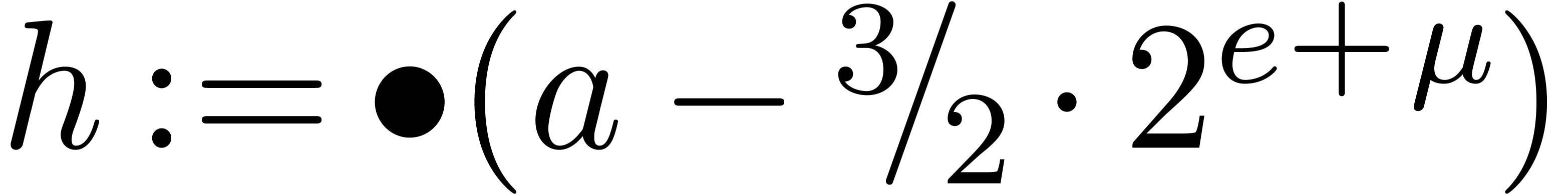
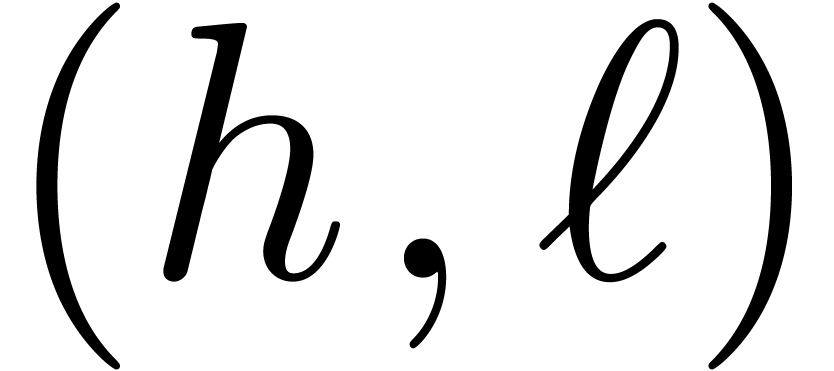
 and
and 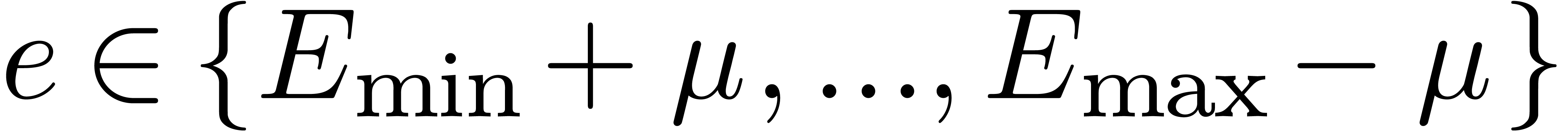 be such that
be such that 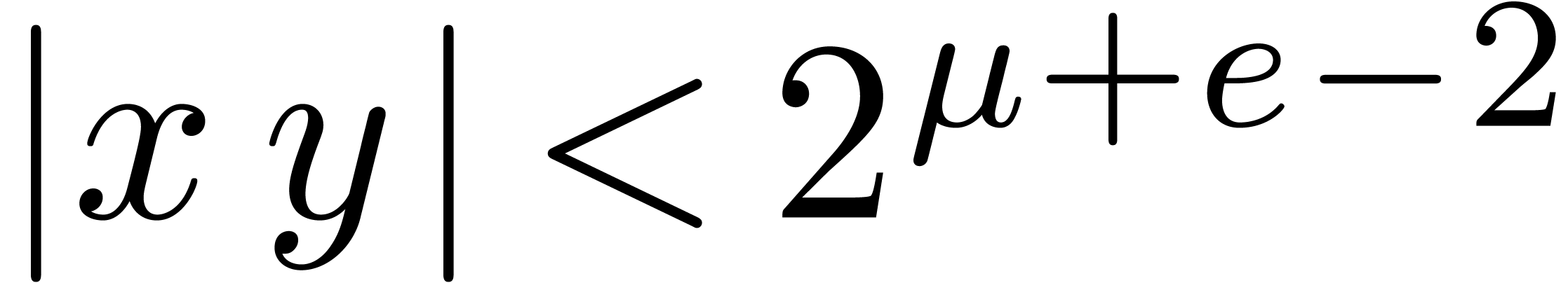 and
and  .
.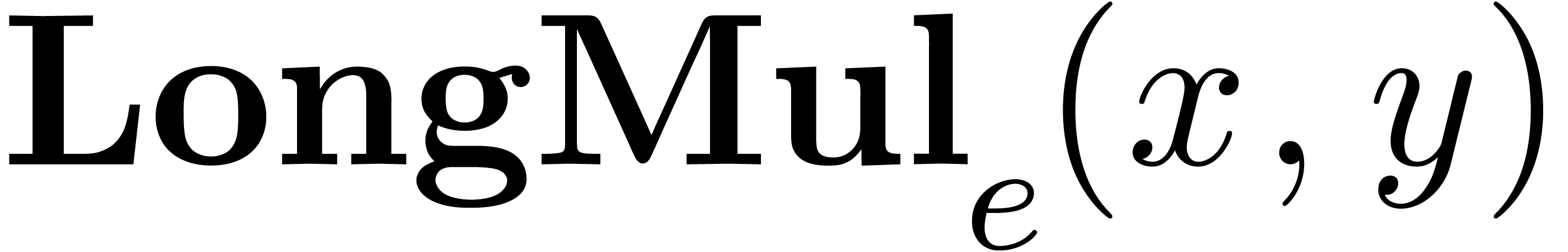 computes a pair
computes a pair 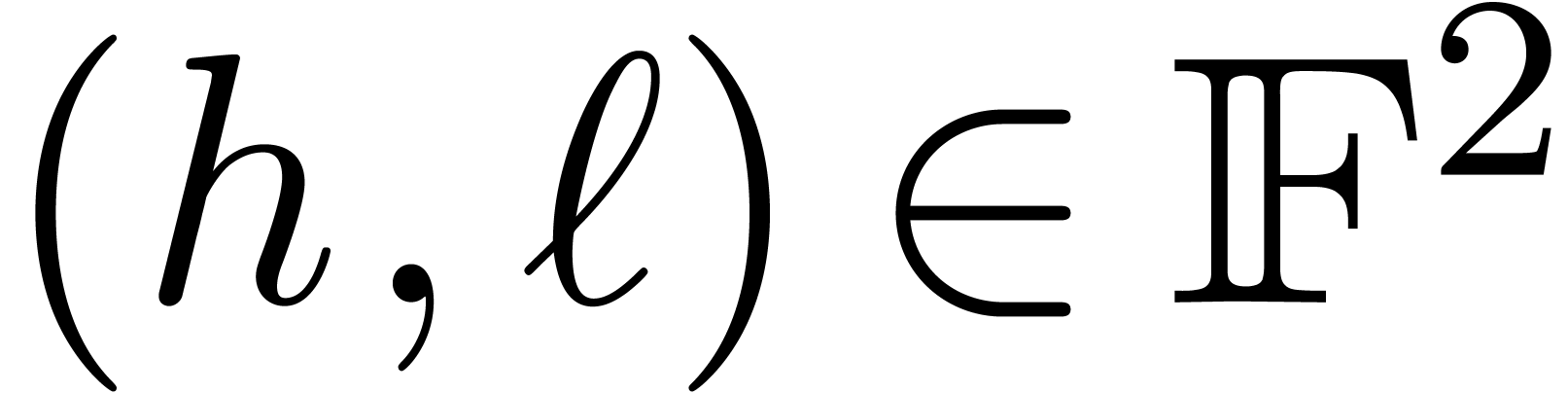 with
with 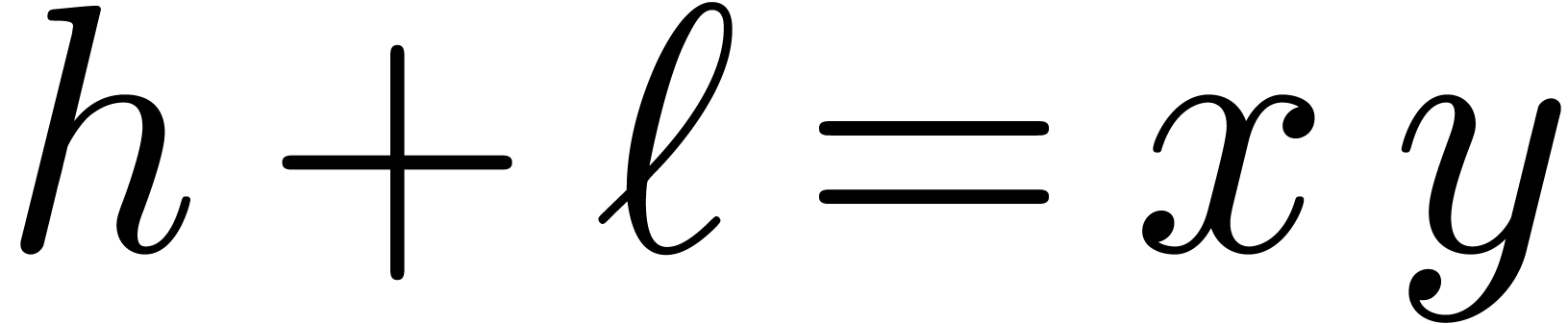 ,
,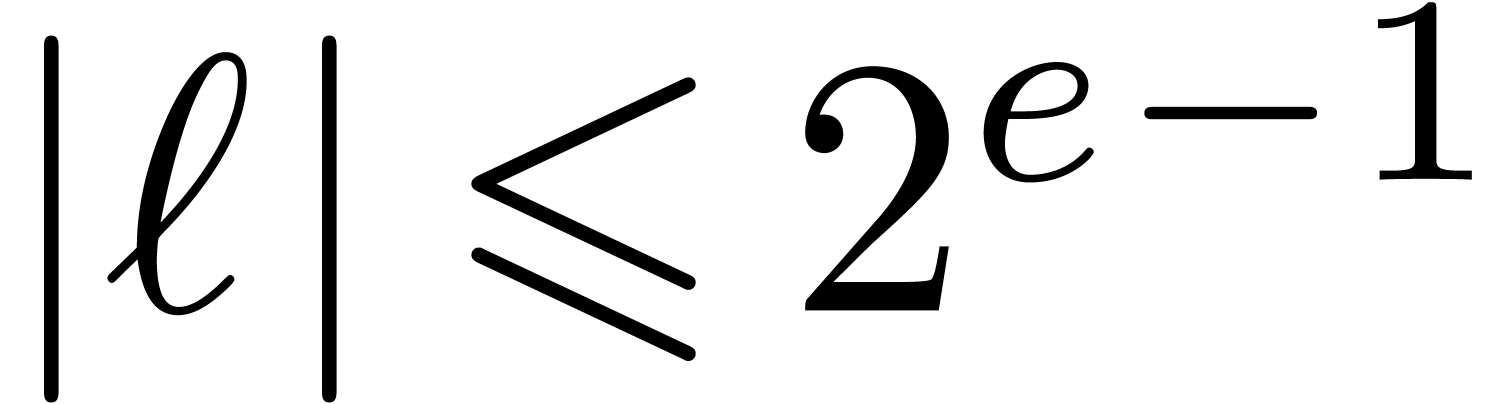 .
. large enough as a function of
large enough as a function of  )
)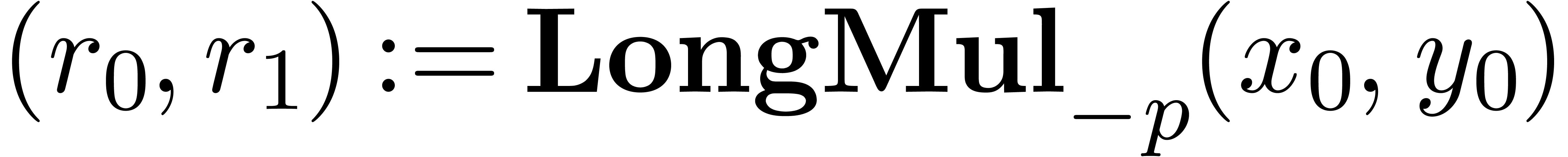
 do
do
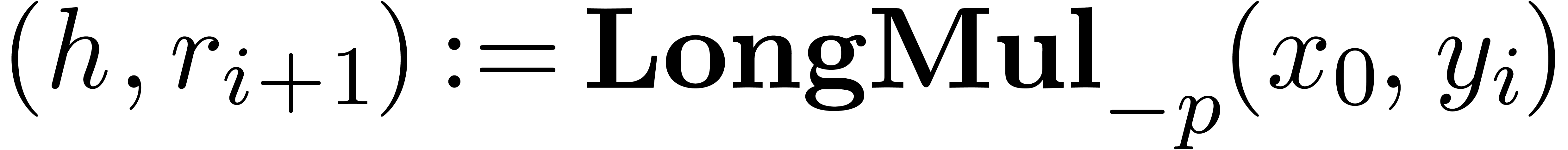
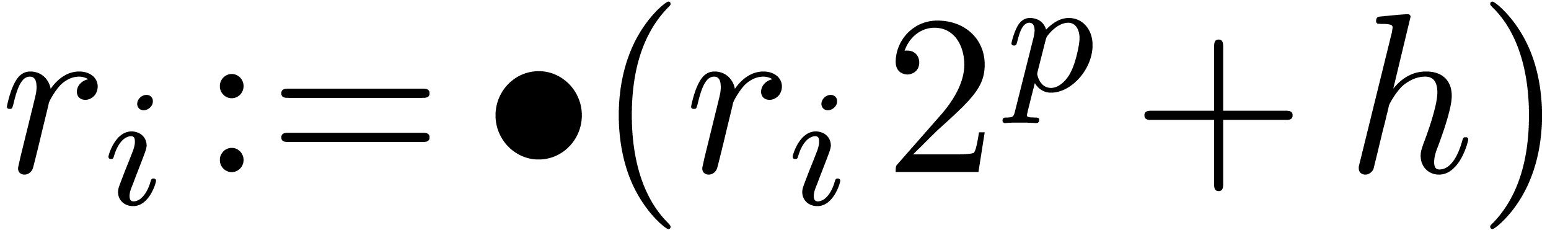
 from
from  to
to  do
do
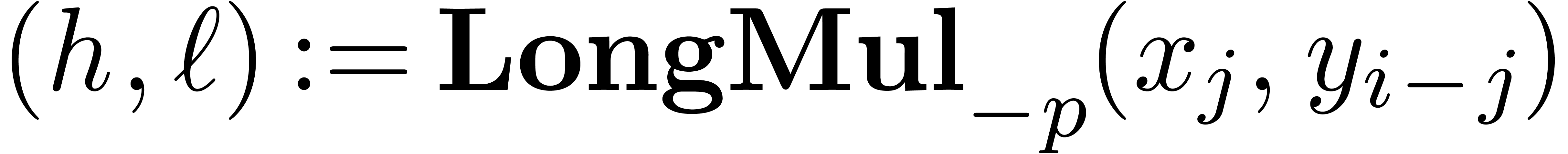
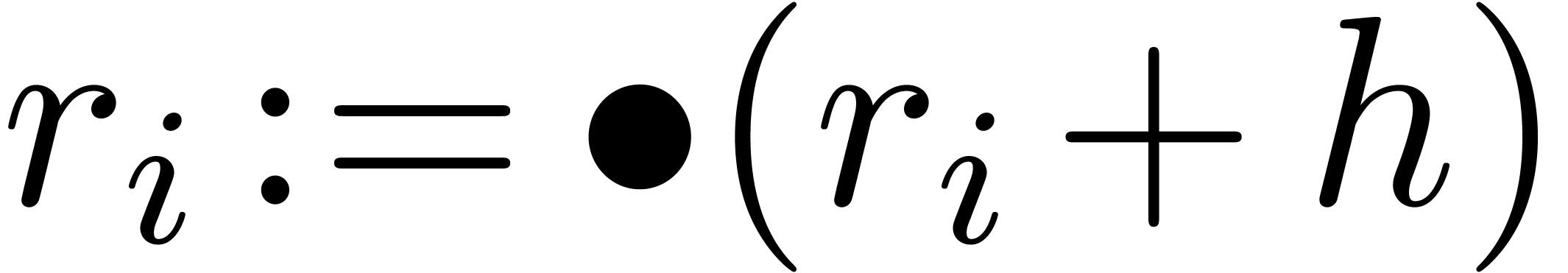
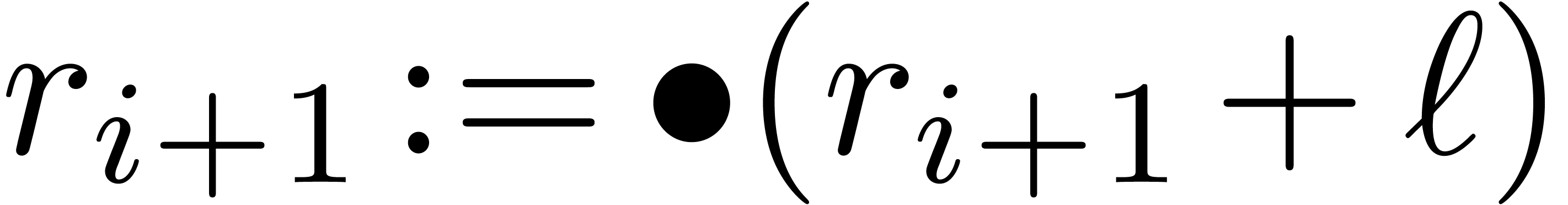
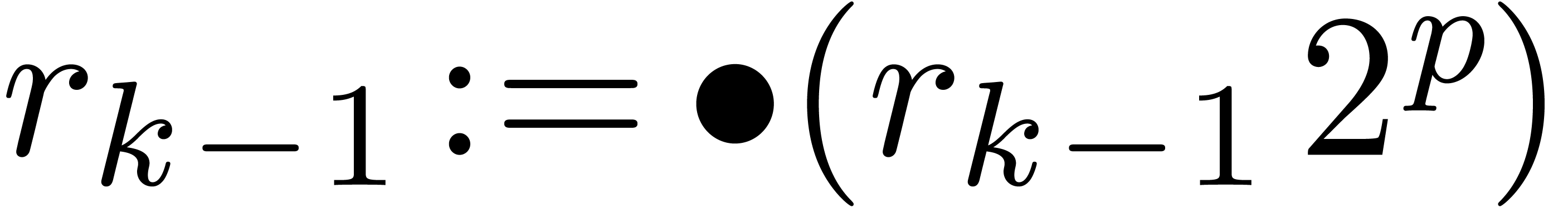
 to
to 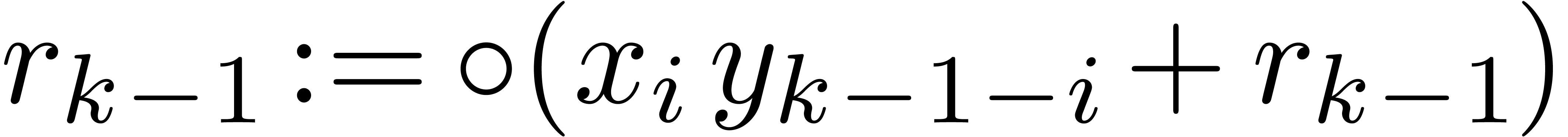

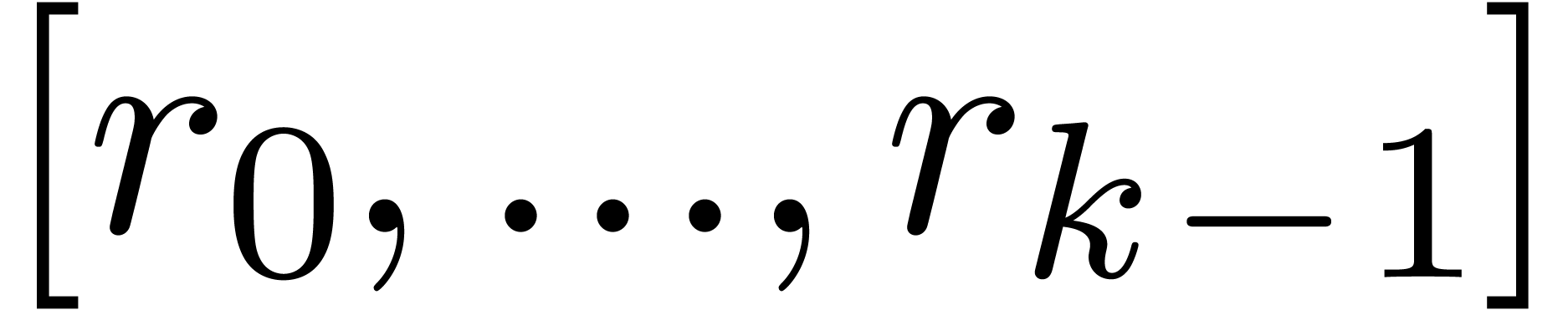
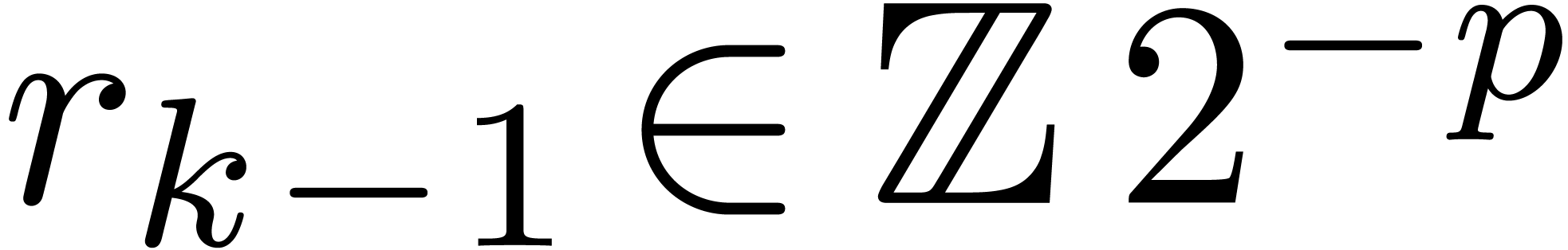 .
. ,
,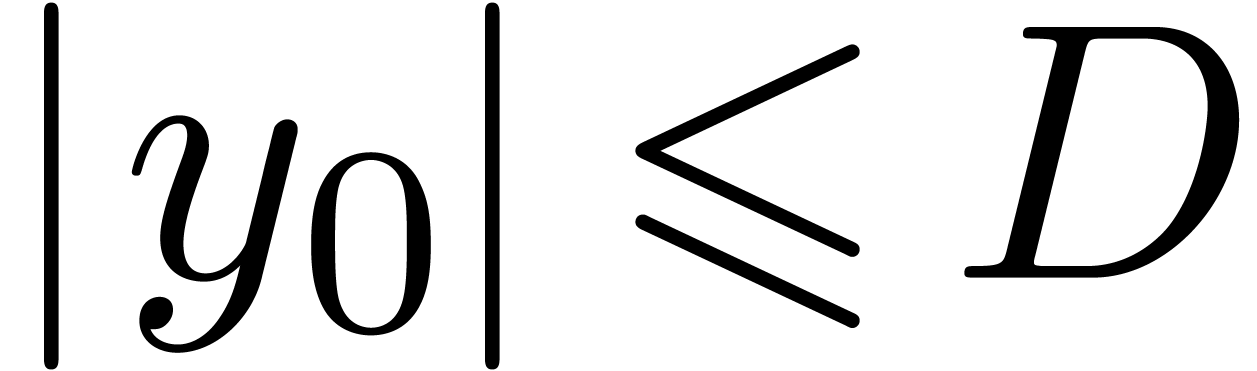 ,
,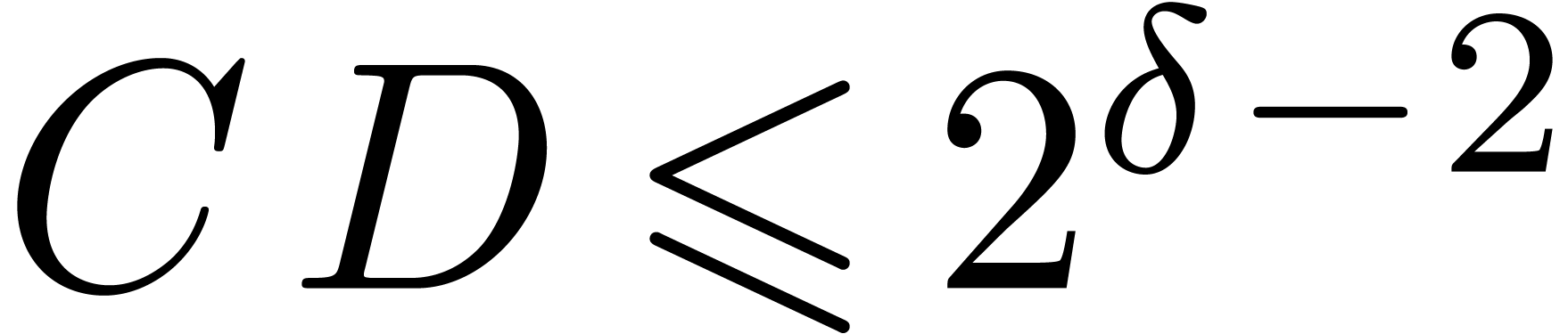 ,
,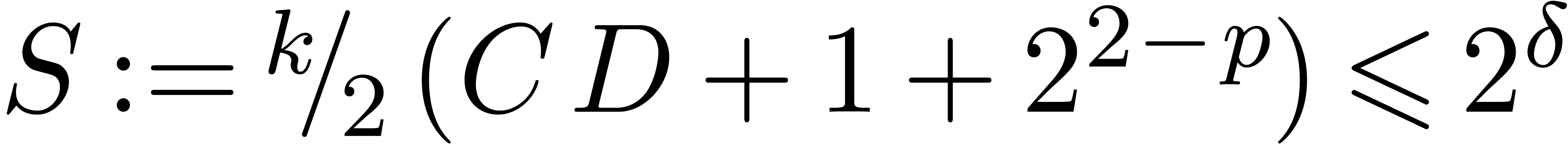 .
.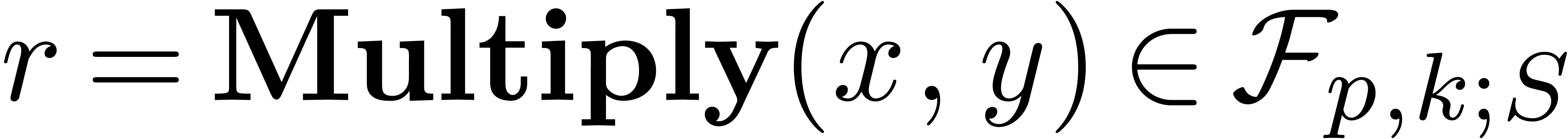 with
with  .
.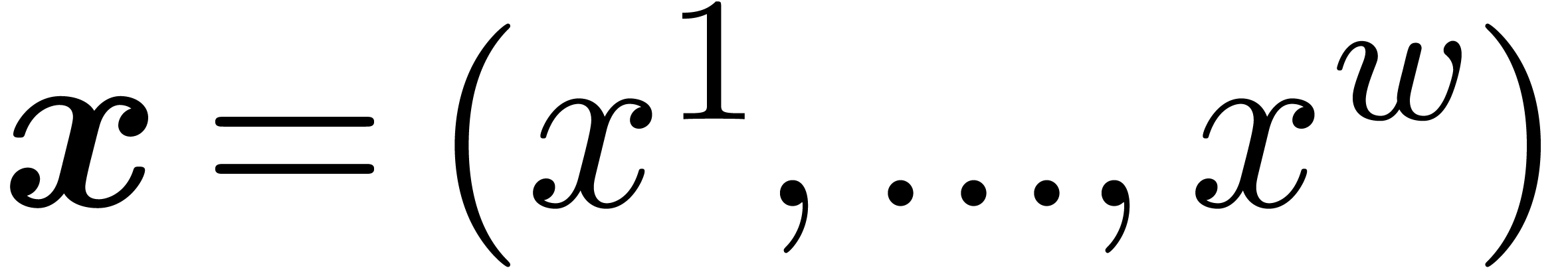 of fixed-point numbers
of fixed-point numbers 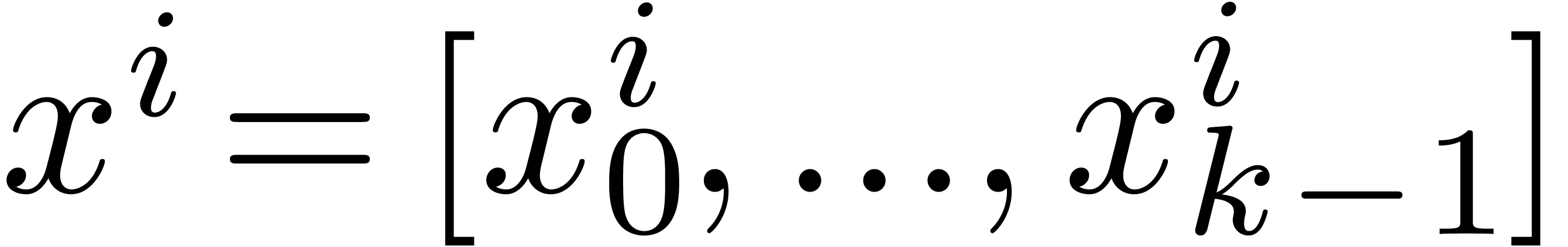 .
.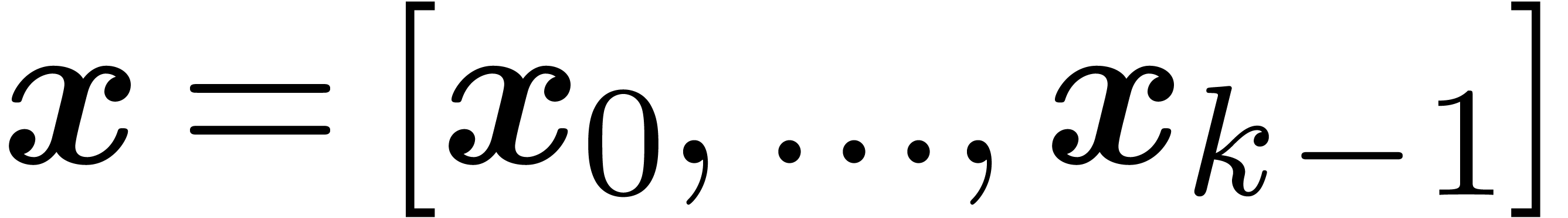 whose “coefficients” are machine SIMD vectors
whose “coefficients” are machine SIMD vectors 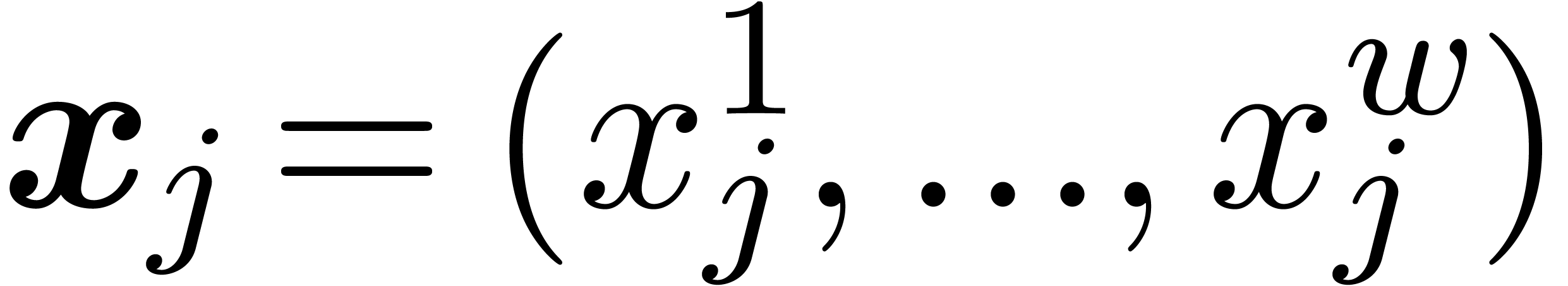 .
.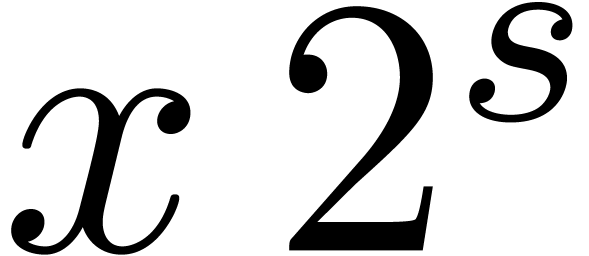 and right shifts
and right shifts 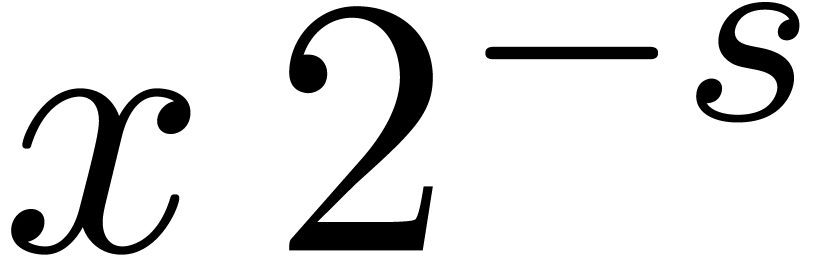 of
of  can be computed by cutting
the shifted coefficients
can be computed by cutting
the shifted coefficients 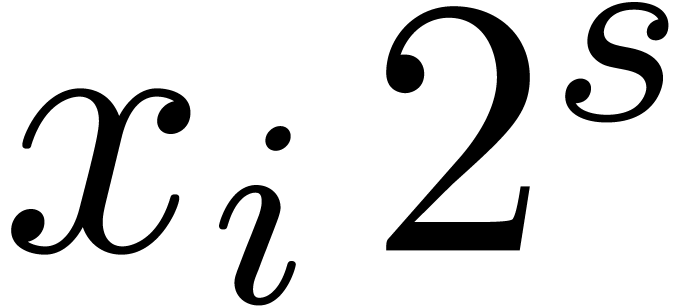 resp.
resp. 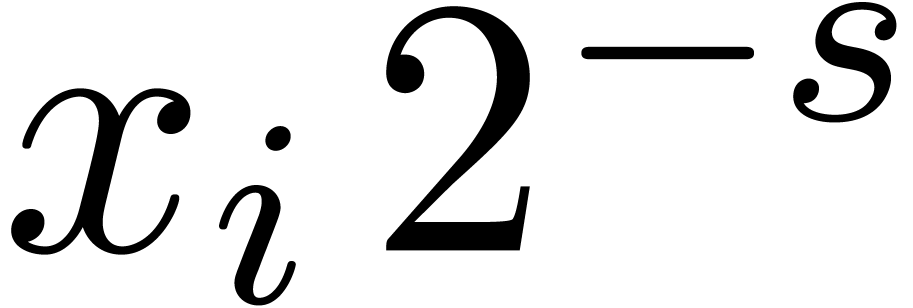 using the routine
using the routine  and
reassembling the pieces. The shift routines behave very much like
generalizations of the routine for carry normalization.
and
reassembling the pieces. The shift routines behave very much like
generalizations of the routine for carry normalization.
 )
)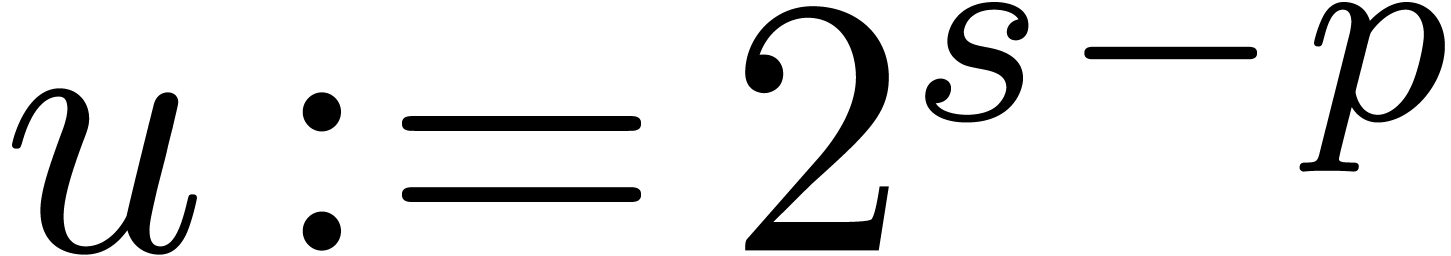

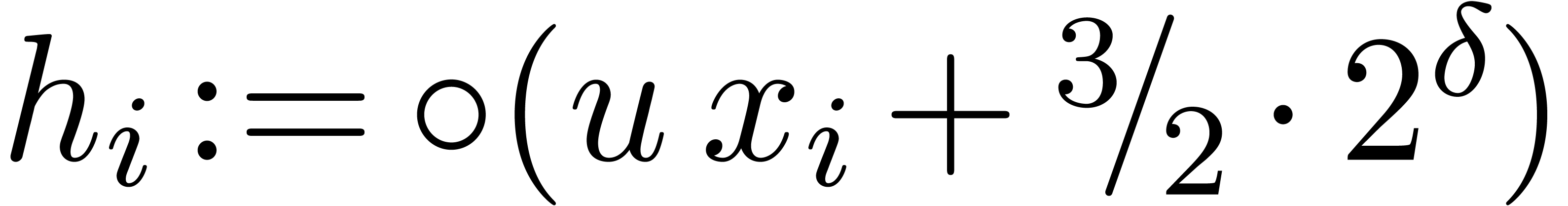
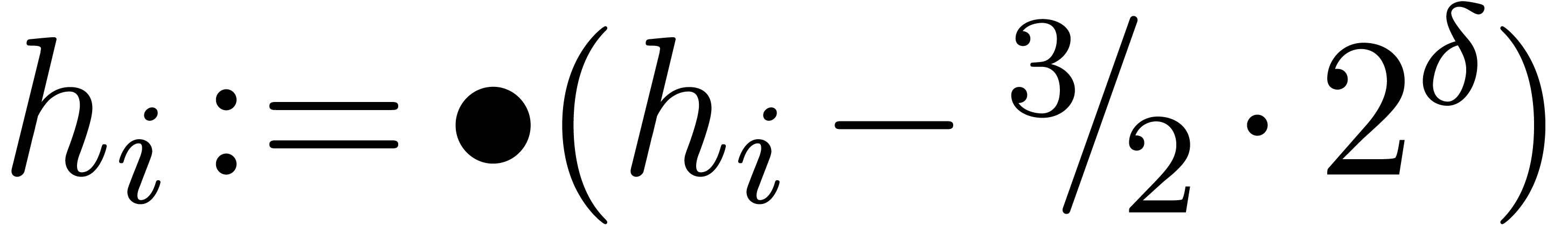
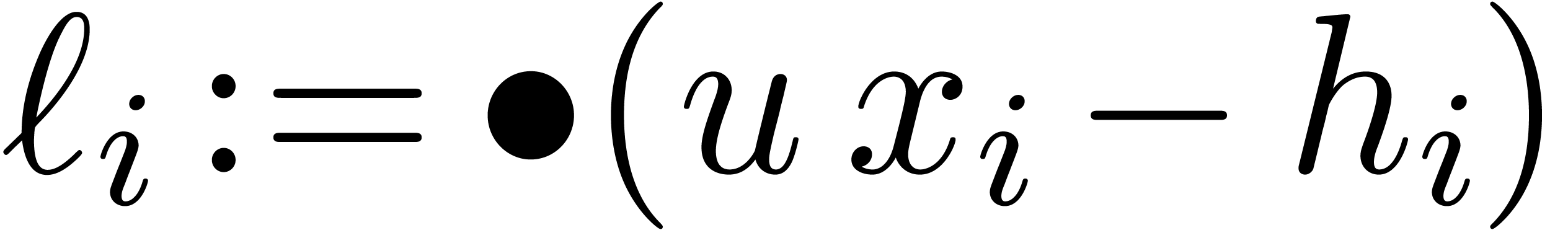
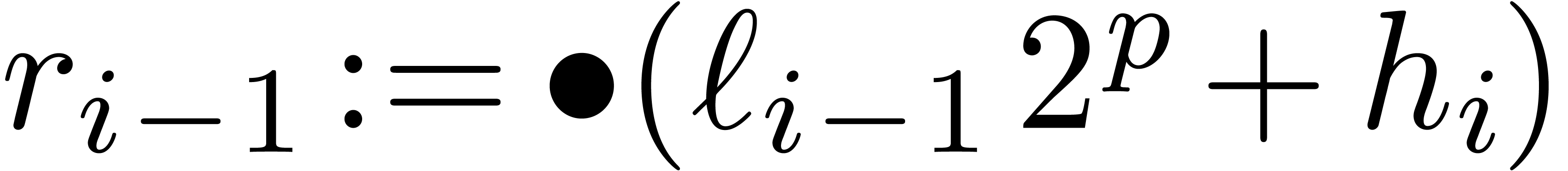

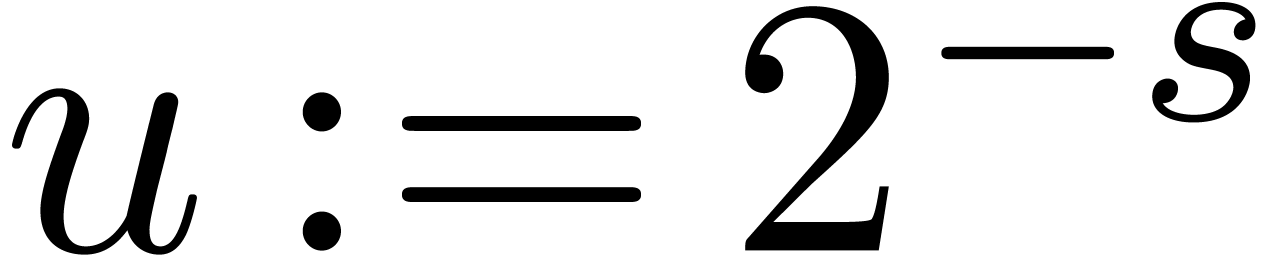
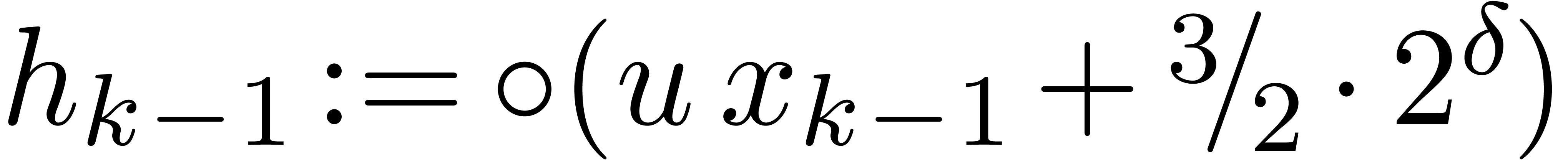
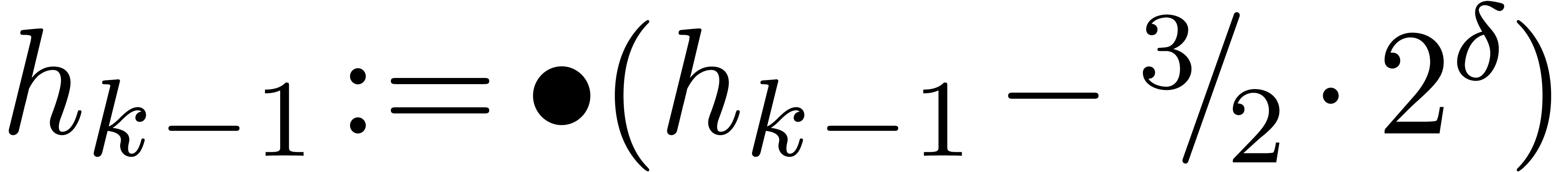
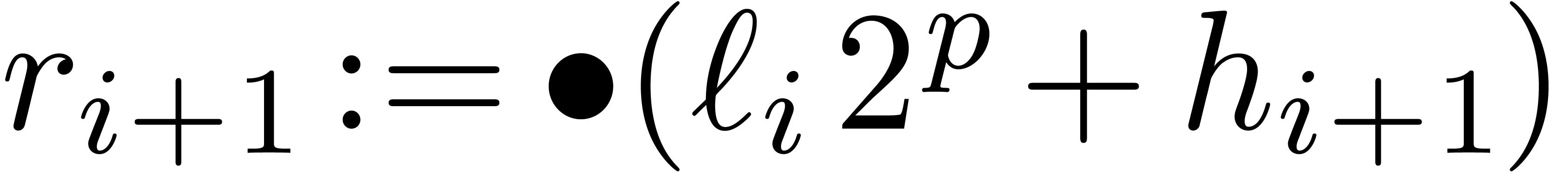

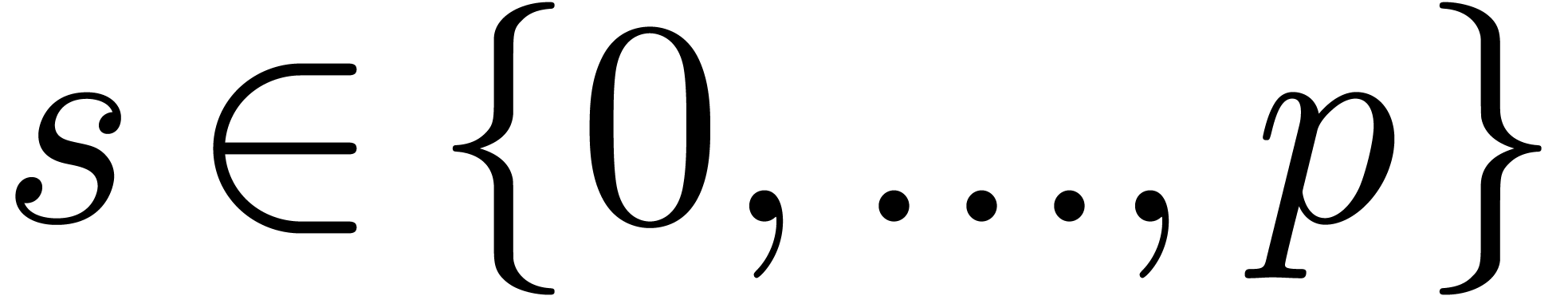 .
.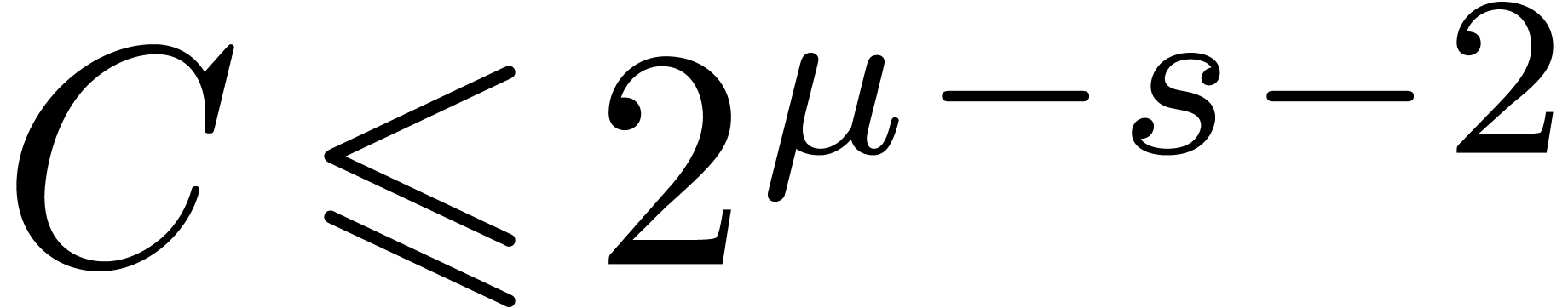 and
and 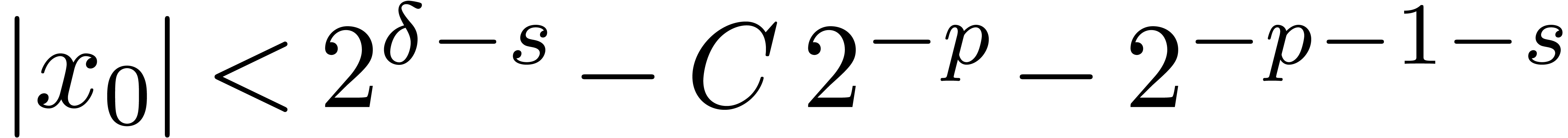 ,
, returns
returns 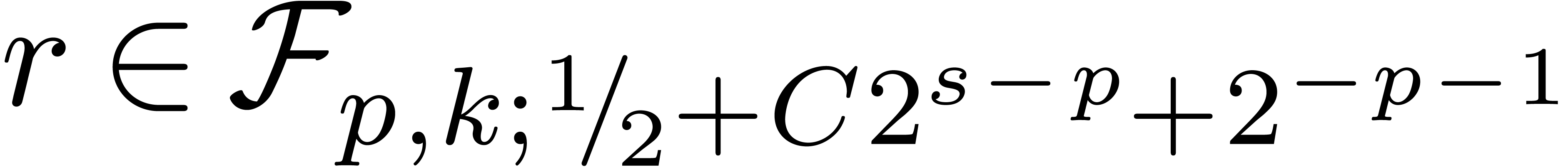 with
with
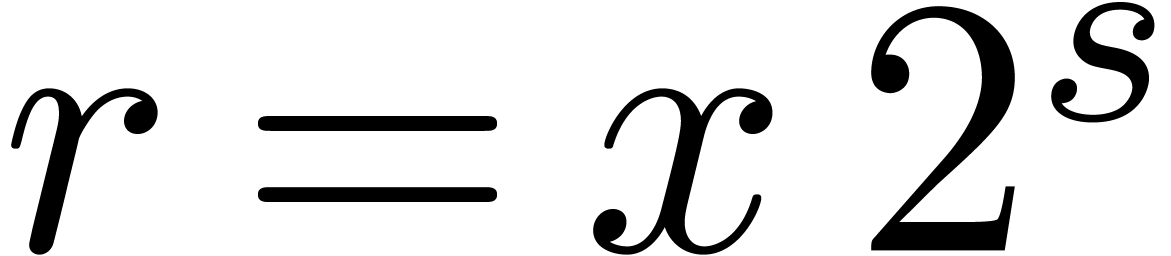 .
. and
and 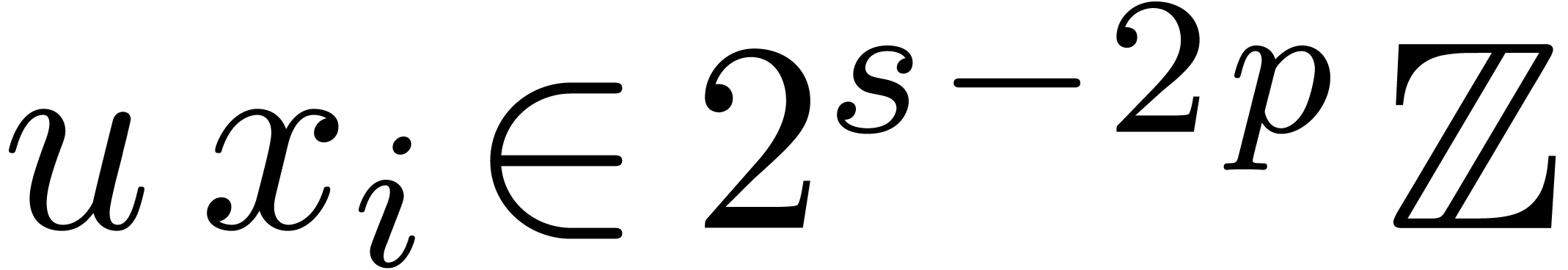 .
. and
and 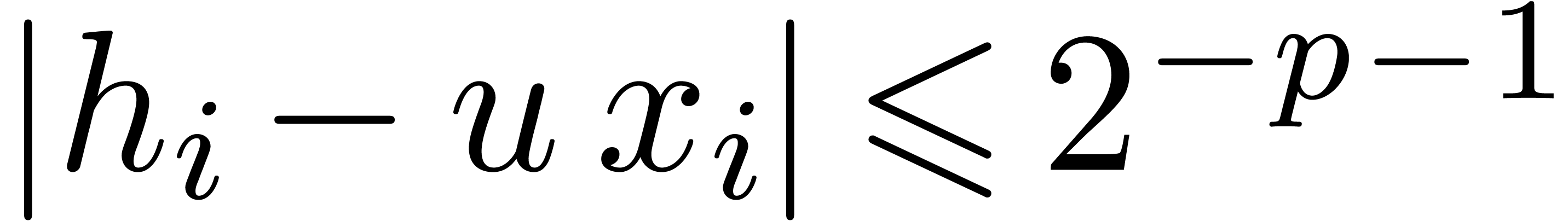 .
.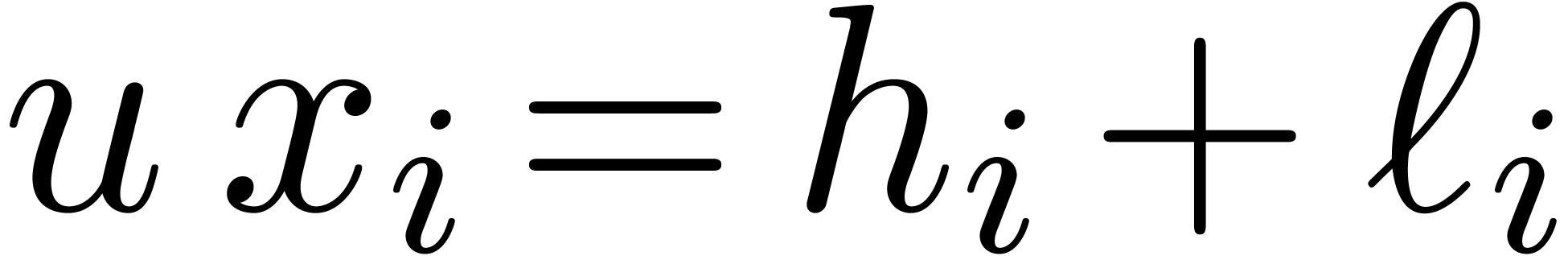 ,
, ,
,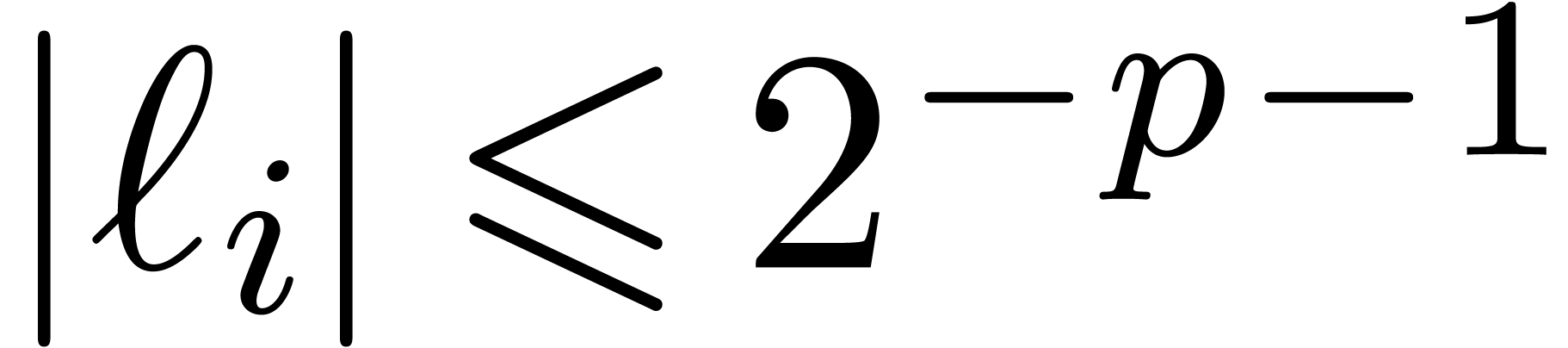 .
.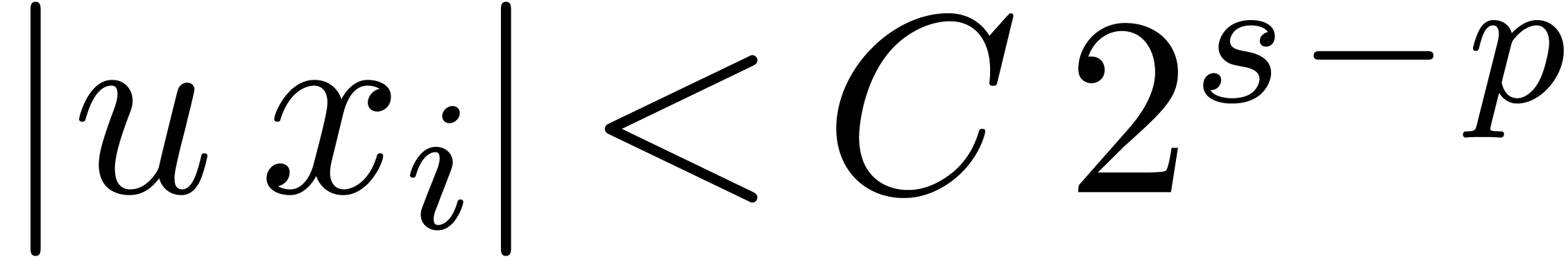 ,
,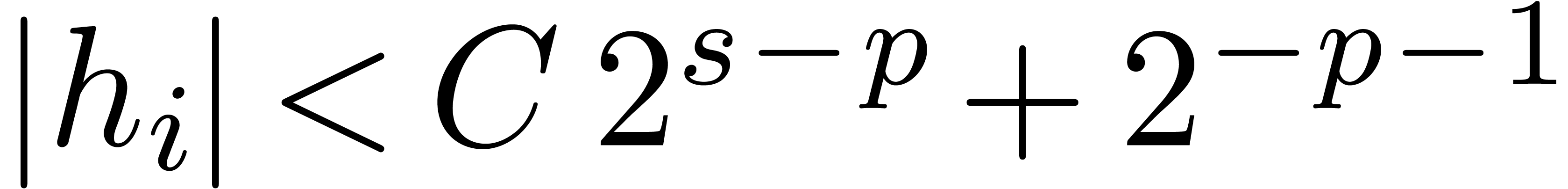 .
.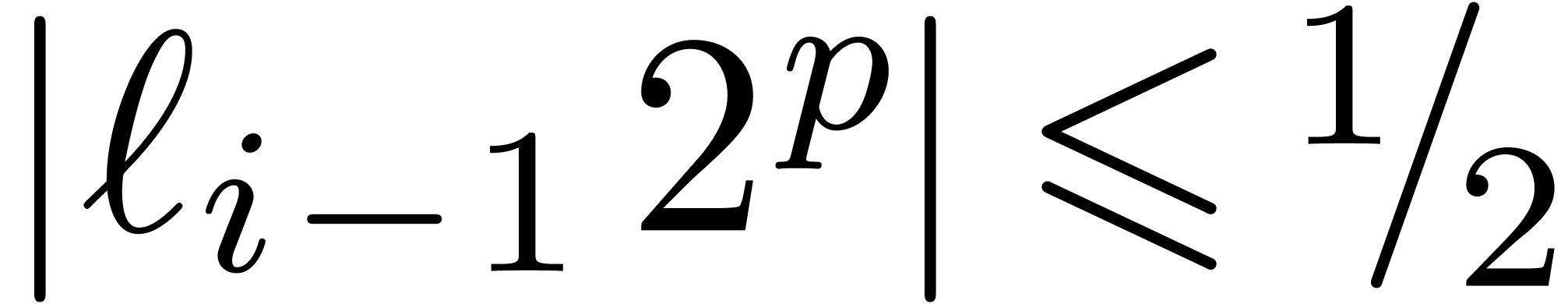 if
if
 and
and 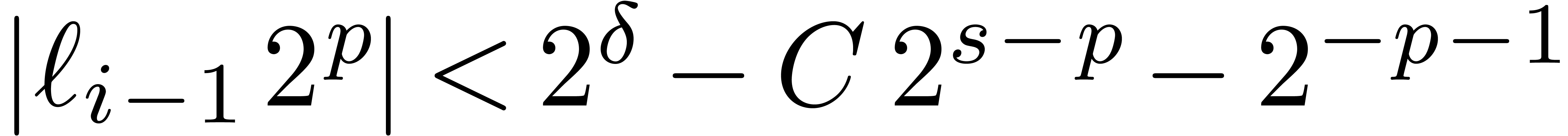 if
if  .
.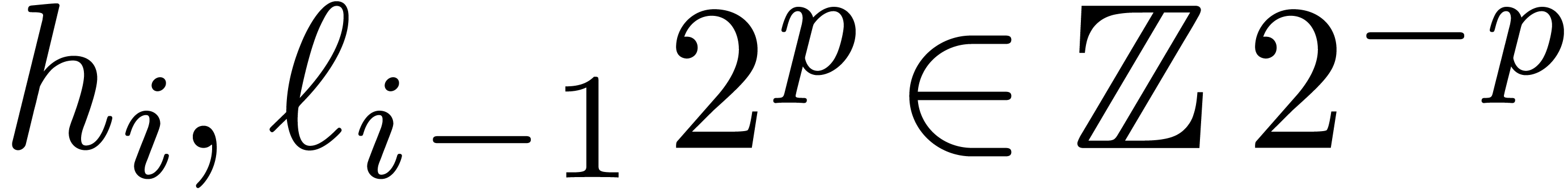 ,
,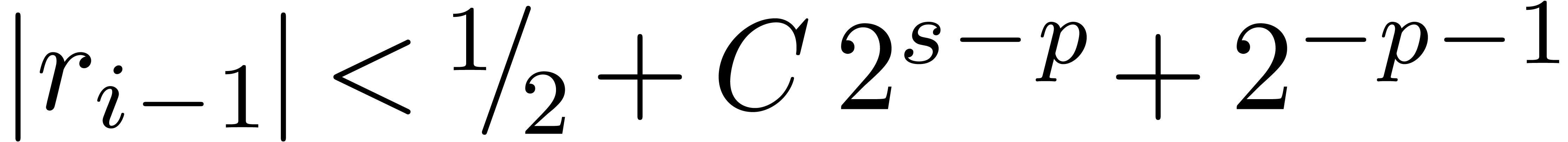 if
if 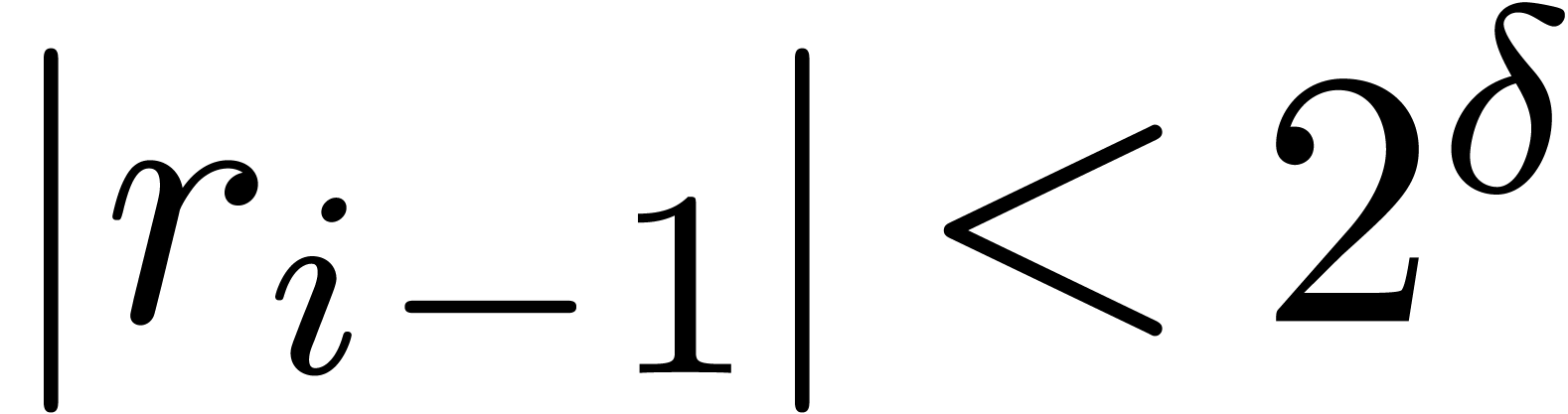 if
if
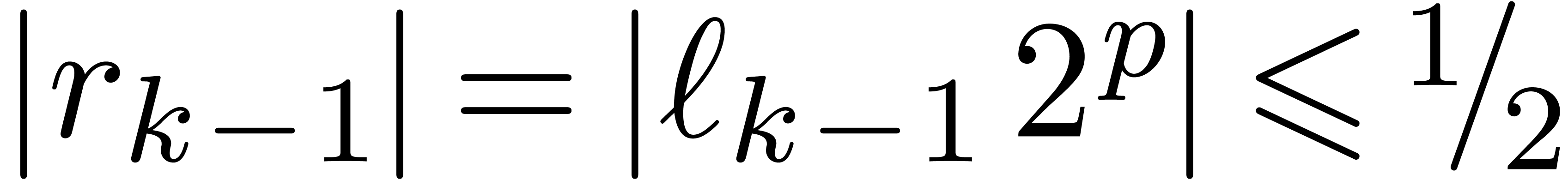 .
.
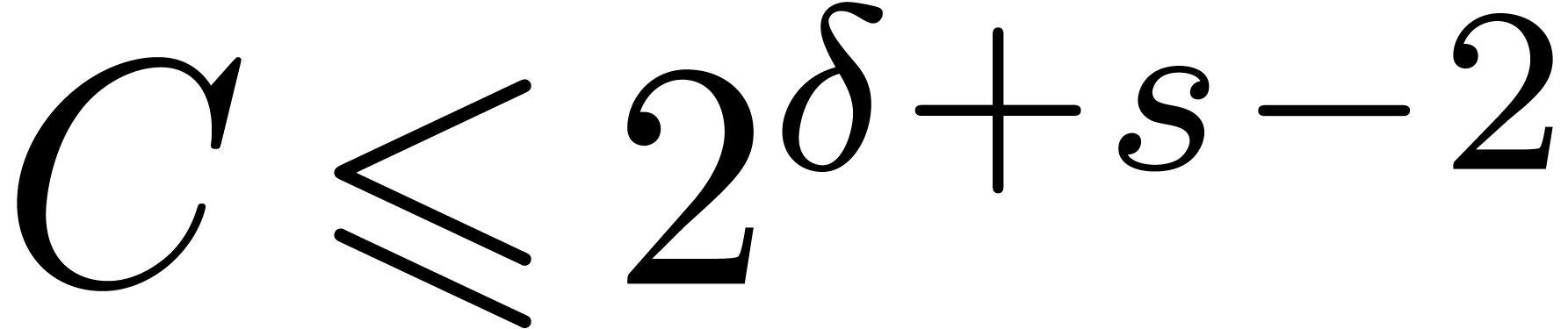 and
and  ,
, returns
returns  with
with
 .
.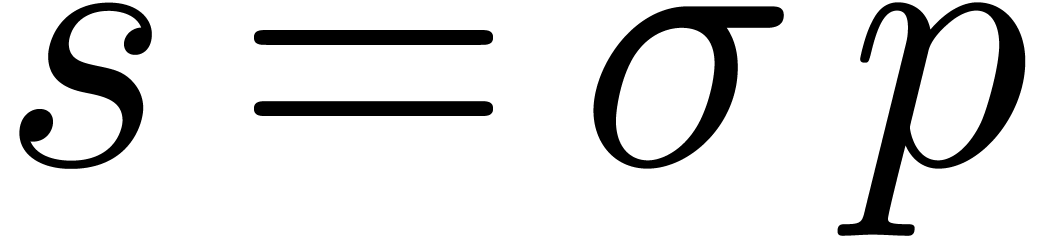 bits with
bits with  ,
,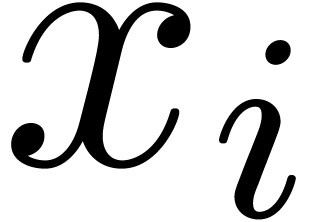 of the operand. Let
of the operand. Let 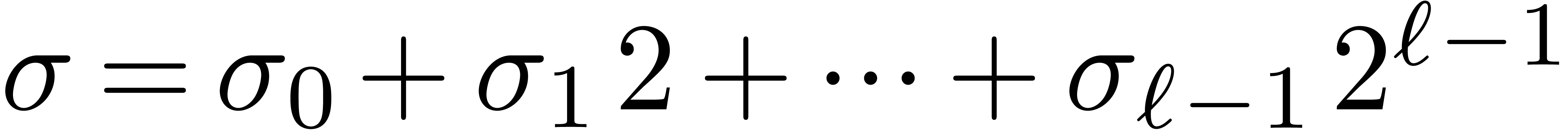 be the binary
representation of
be the binary
representation of  with
with 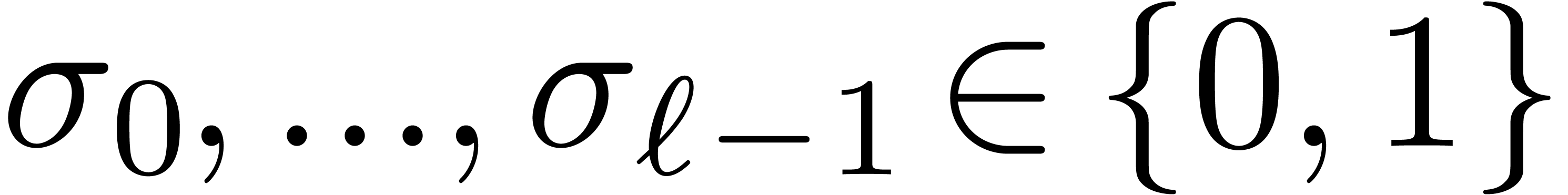 .
. bits as the composition of
bits as the composition of  bits for
bits for  ,
, or
or  .
. )
)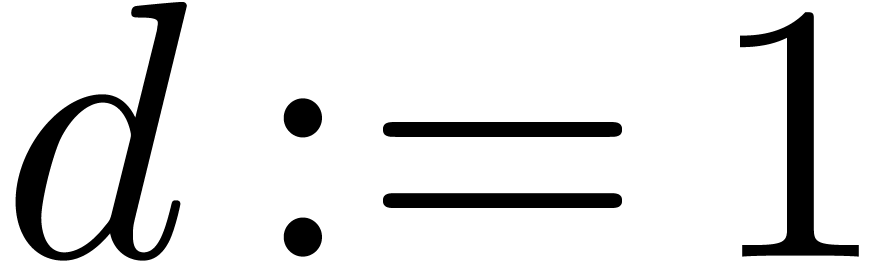
 do
do

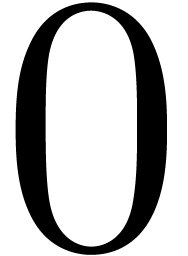 to
to 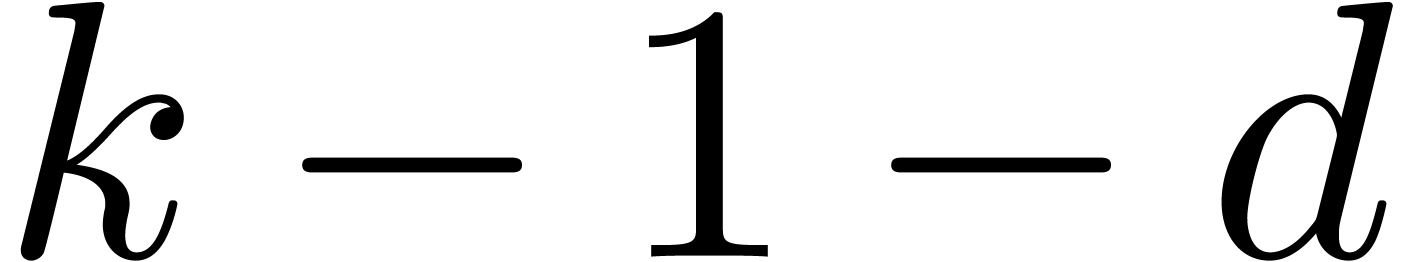 do
do

 to
to  do
do

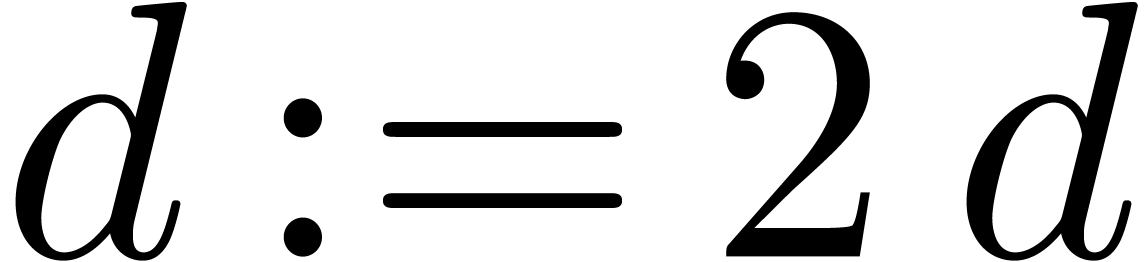
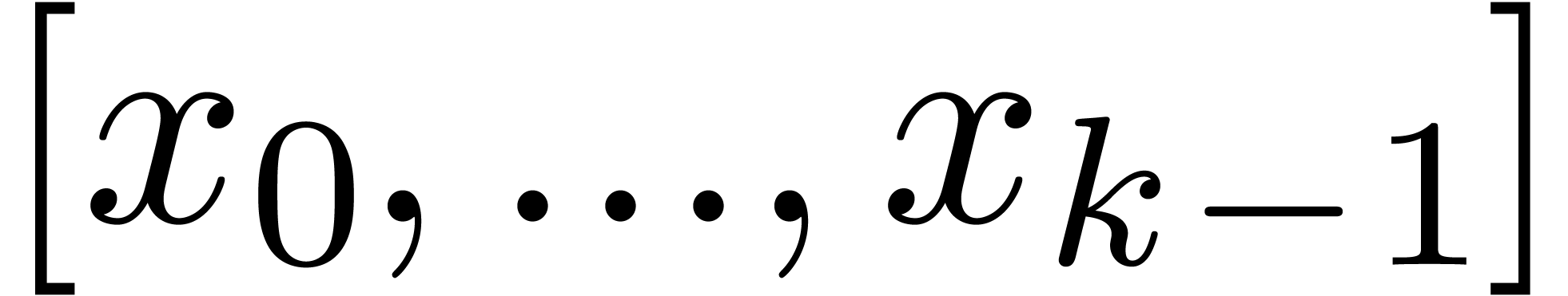
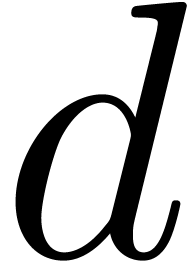 do
do

 down
to
down
to  .
.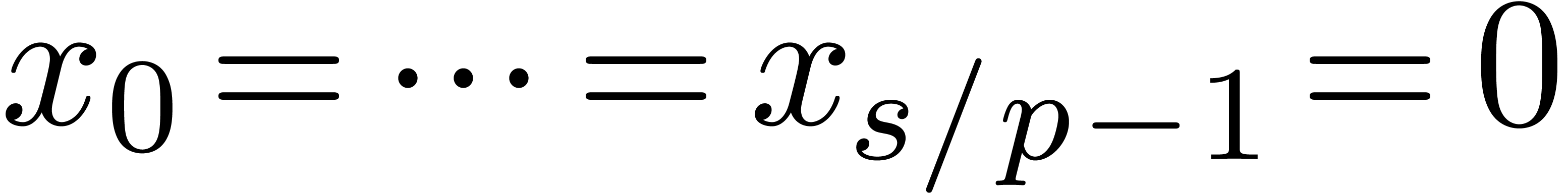 ,
, returns
returns 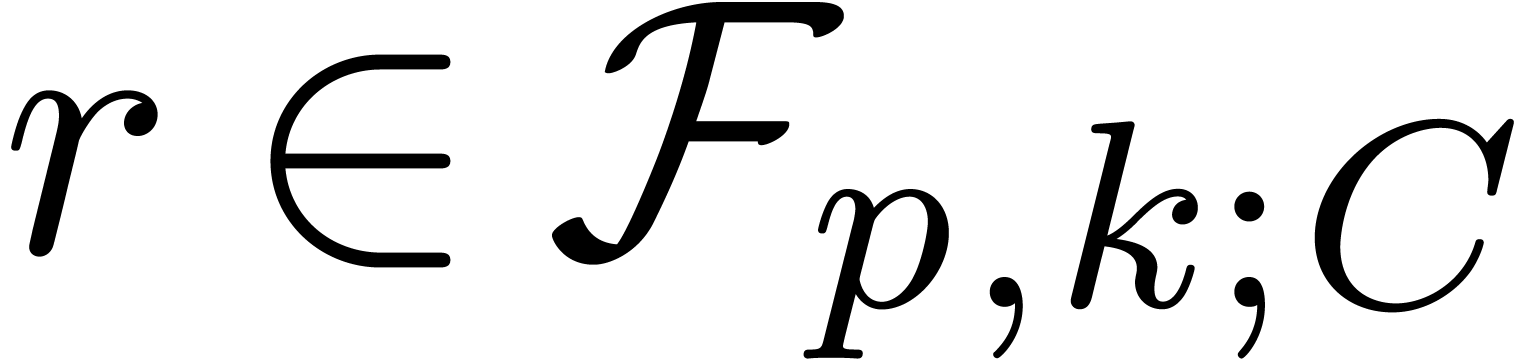 with
with  returns
returns 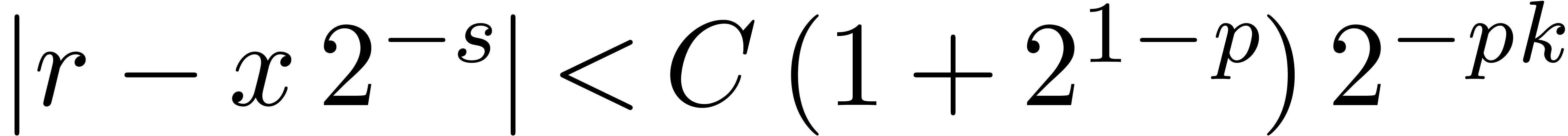 .
.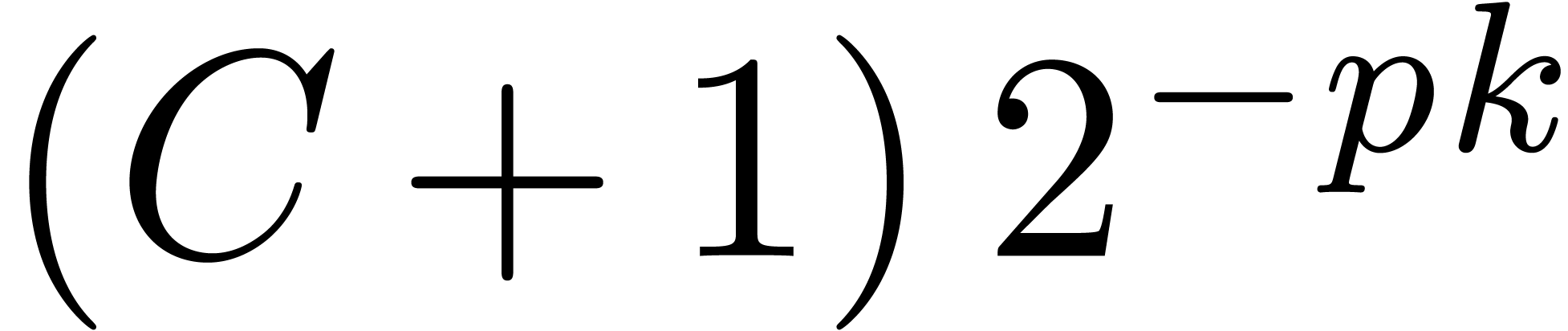 .
.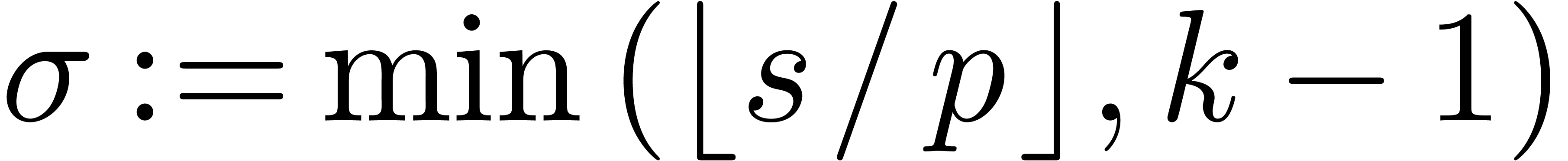
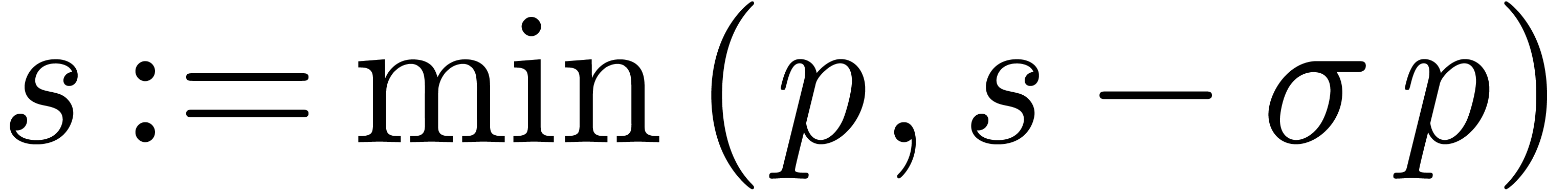




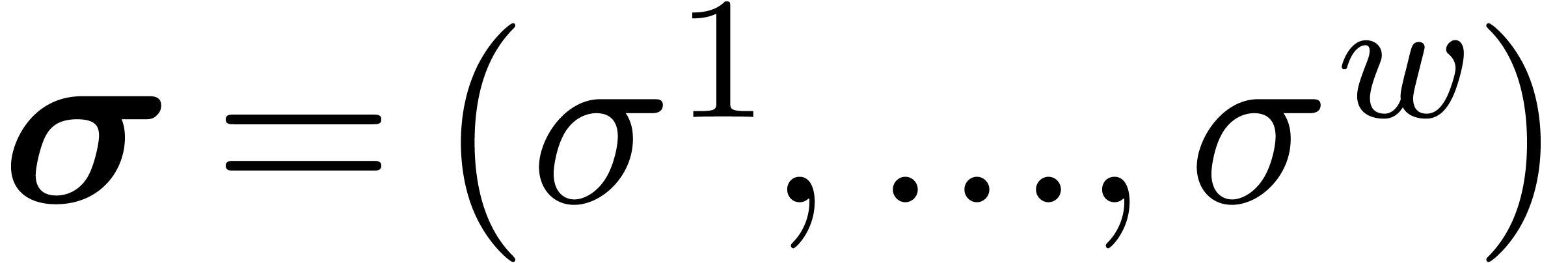 .
.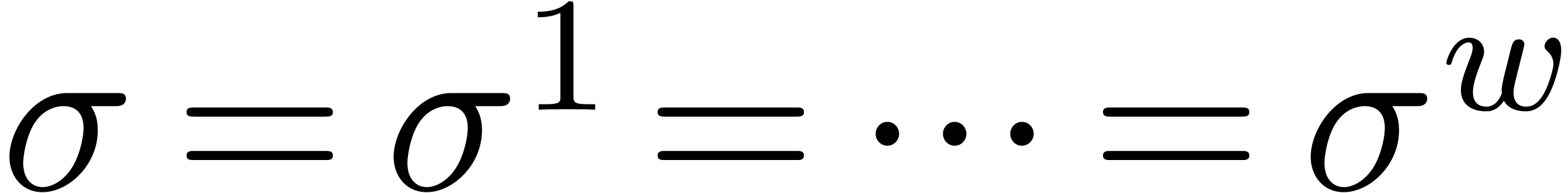 for all entries, then we may
use the following routines instead:
for all entries, then we may
use the following routines instead:
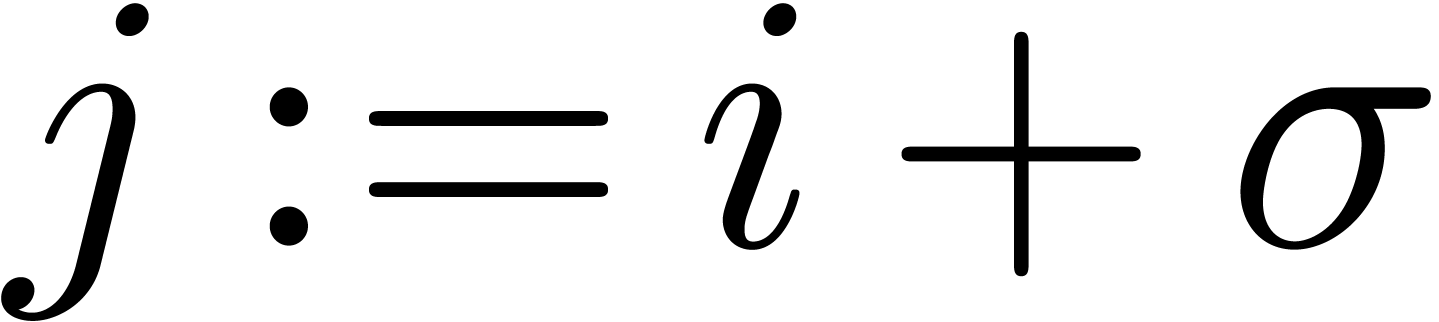

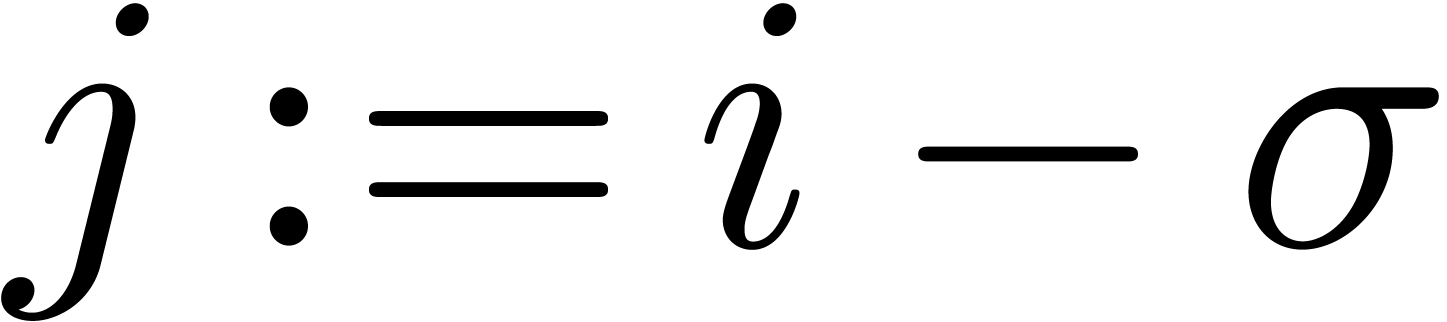

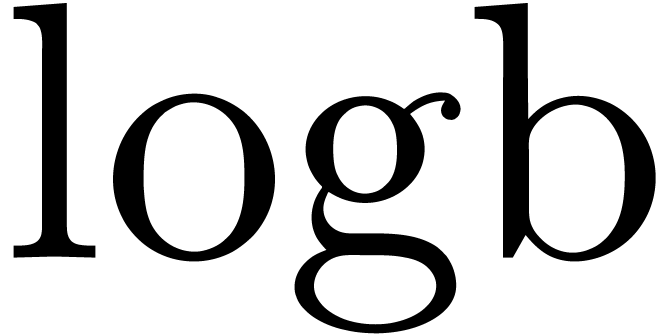 for
retrieving the exponent
for
retrieving the exponent 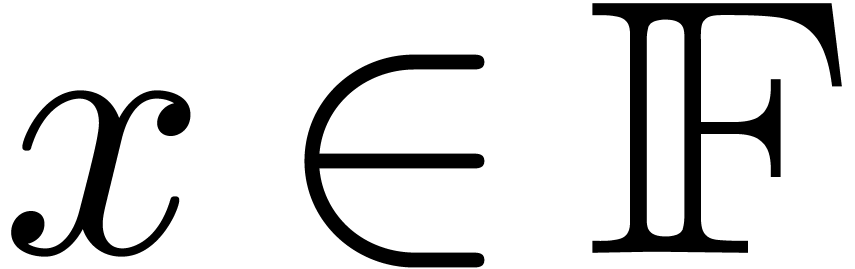 :
: ,
,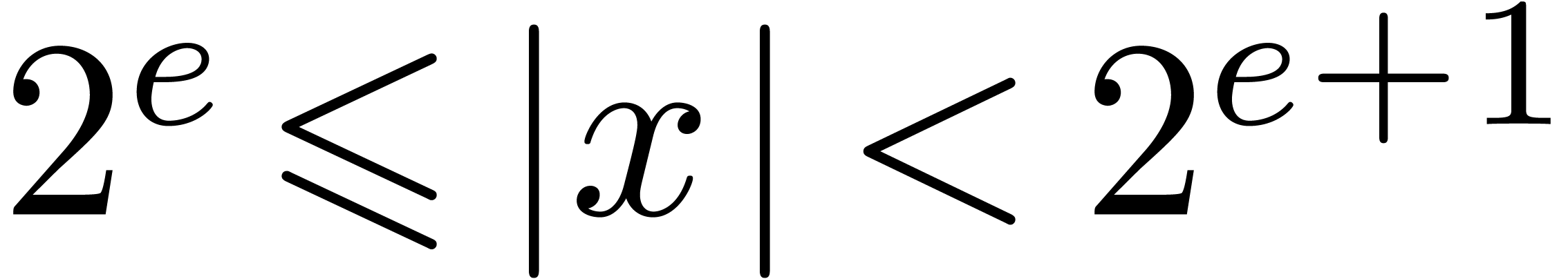 .
. ,
,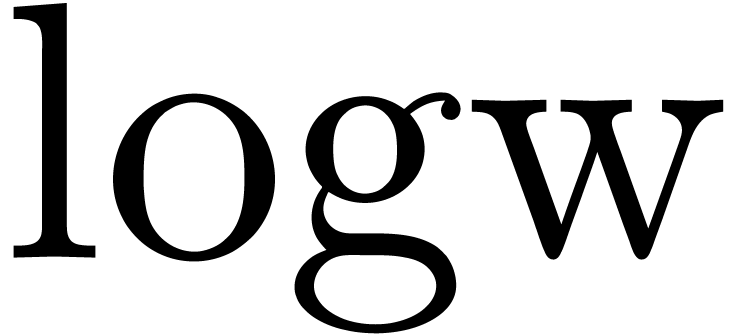 in base
in base 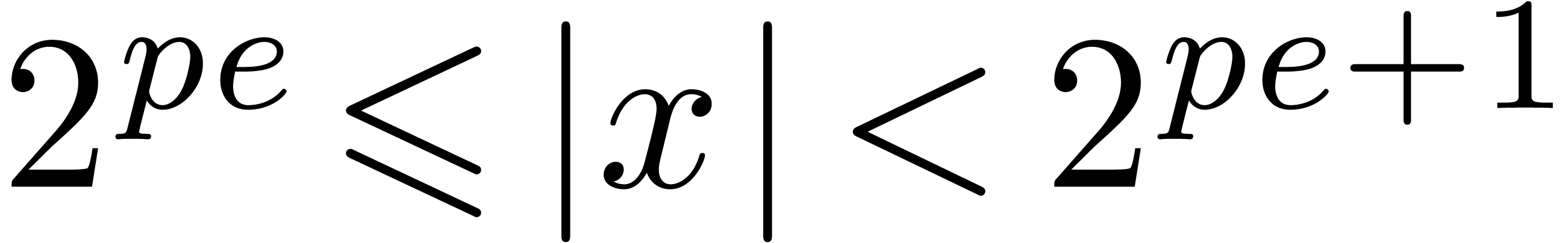 for every
for every 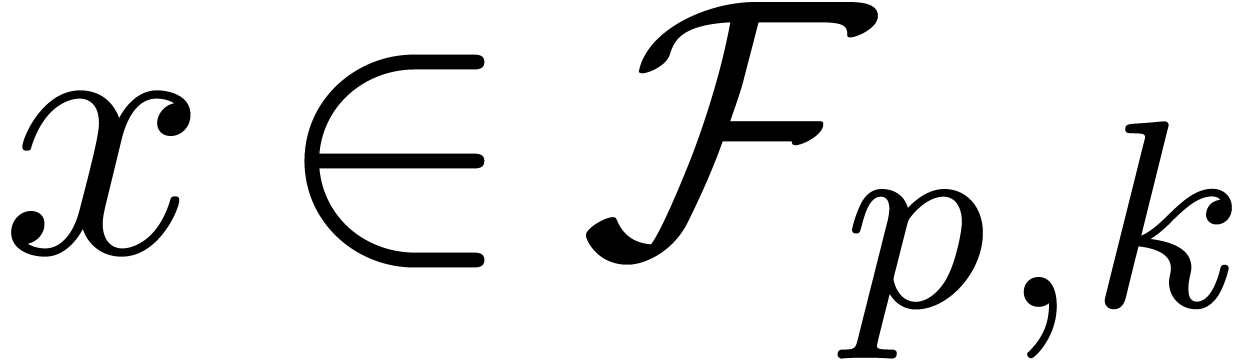 with
with 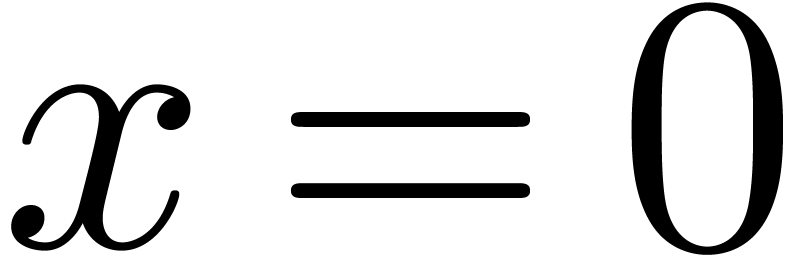 ,
,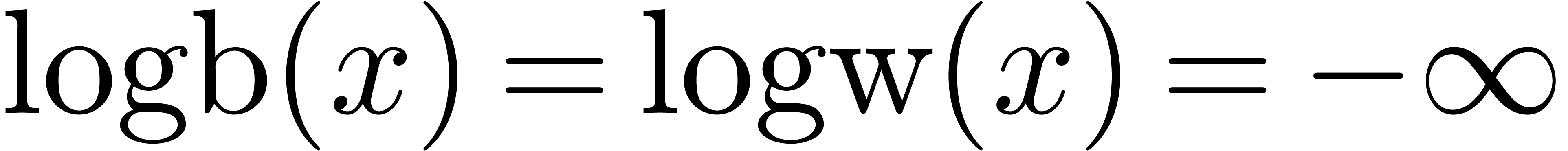 .
.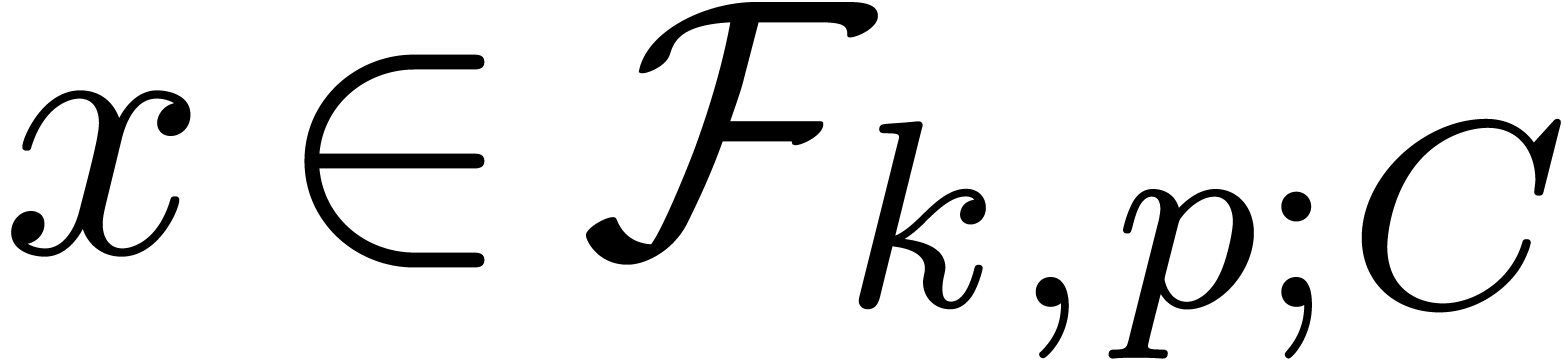 in carry normal form with
in carry normal form with  ,
,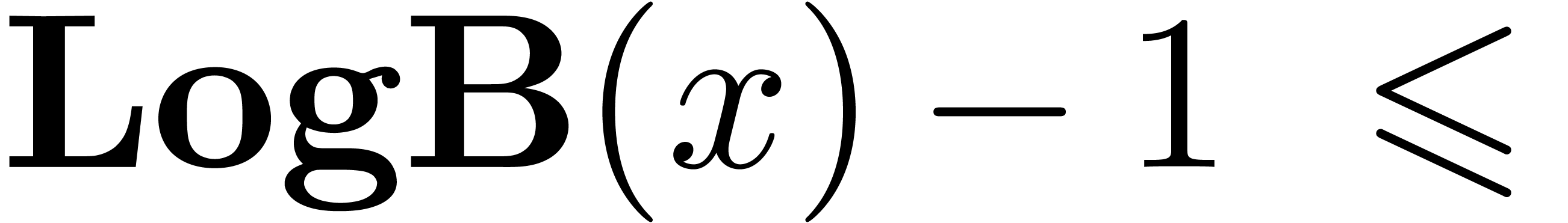
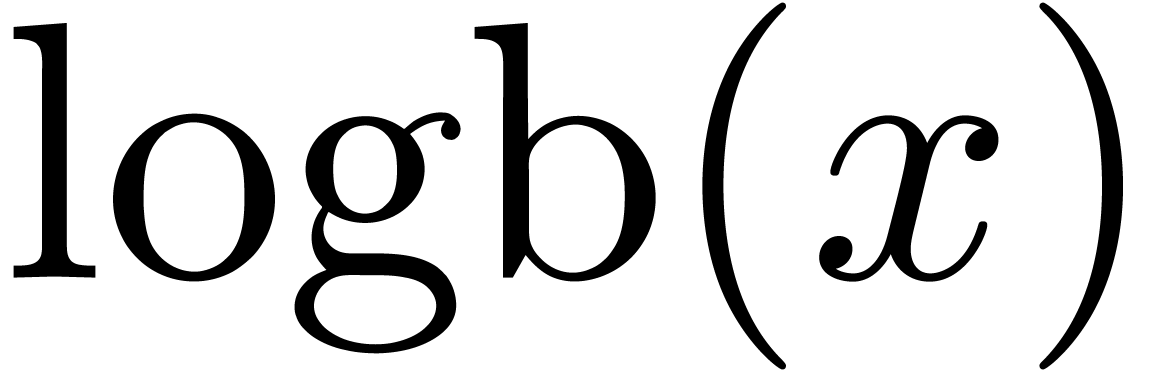
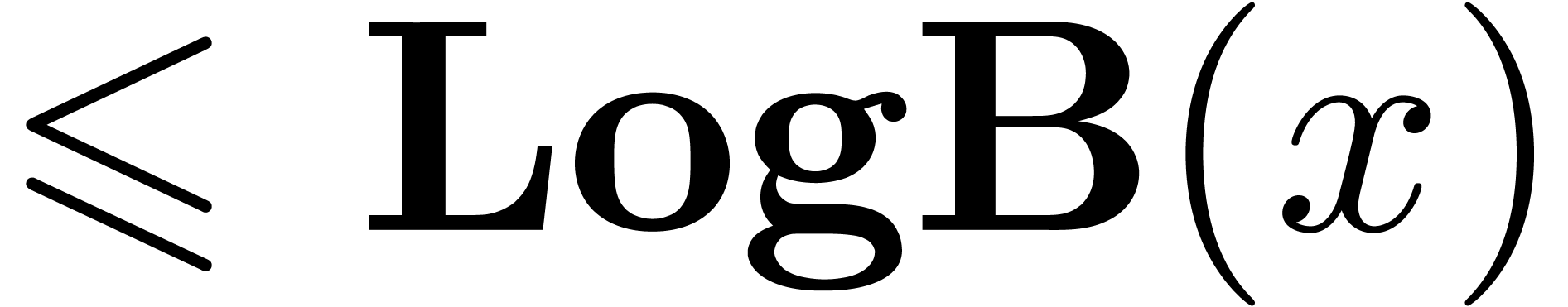
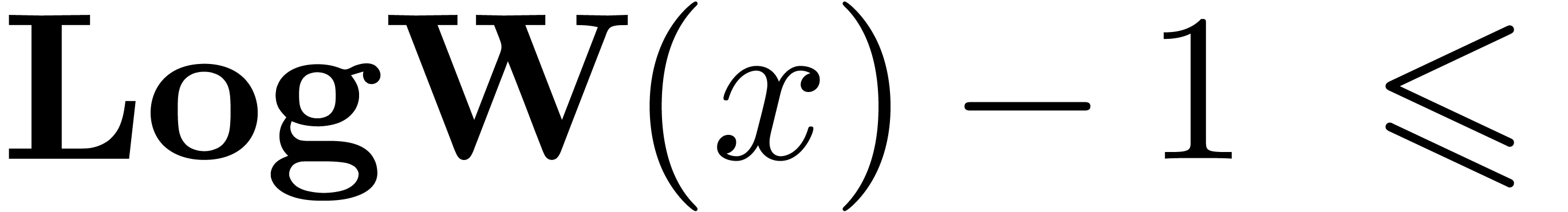
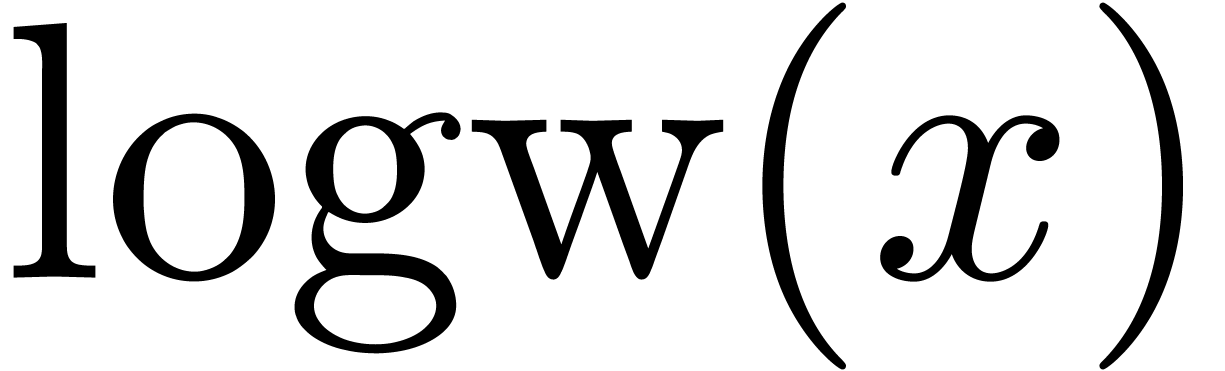
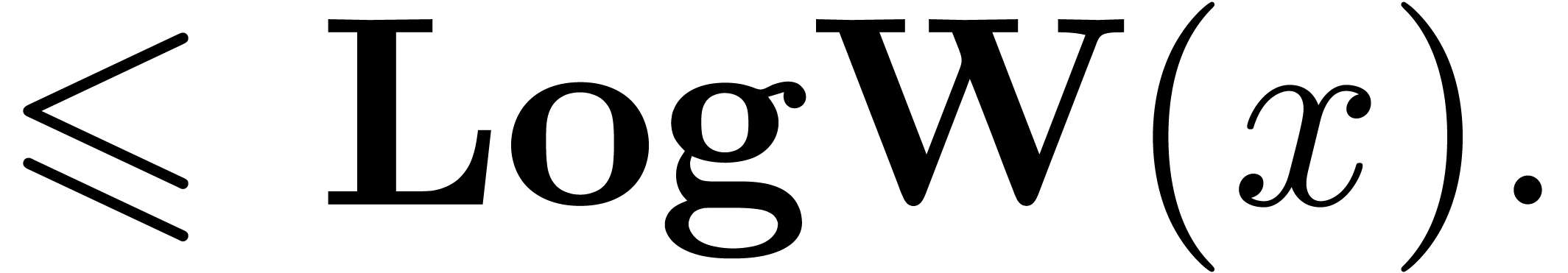
 with
with  that only works
under the assumption that
that only works
under the assumption that  .
. machine numbers. The routine LogW relies on a routine
HiWord that determines the smallest index
machine numbers. The routine LogW relies on a routine
HiWord that determines the smallest index  .
.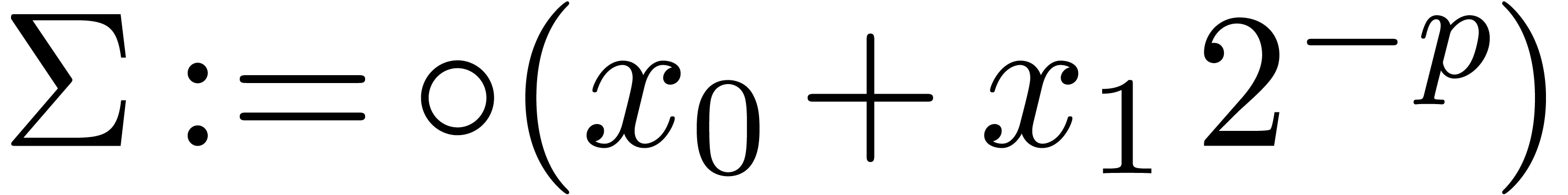
 to
to 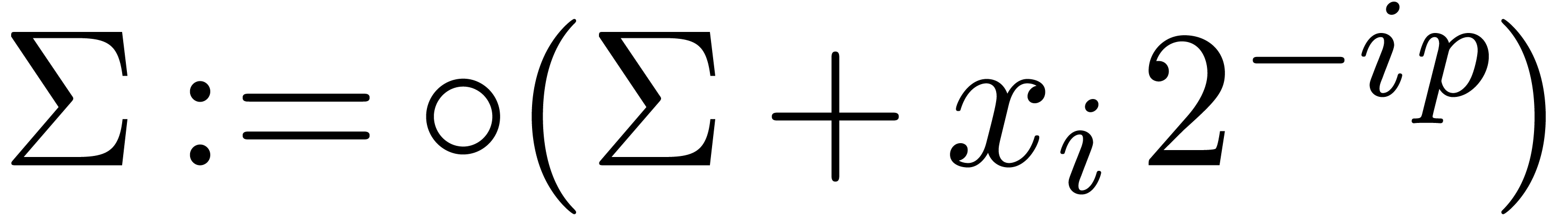

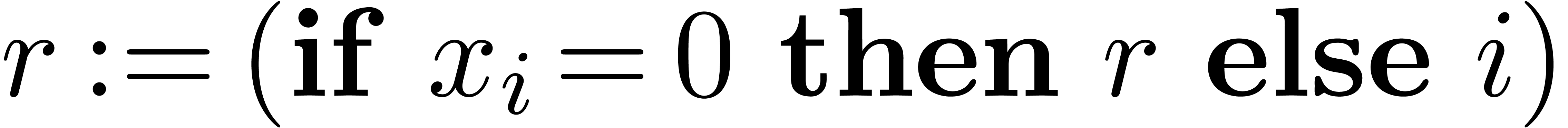

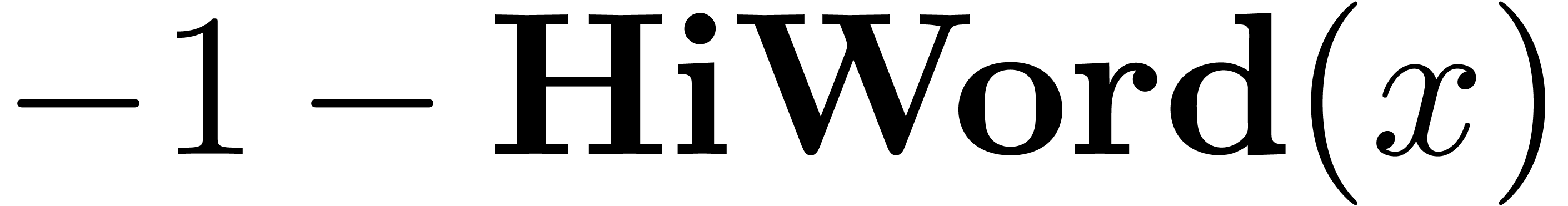
 be the value of
be the value of  after adding
after adding
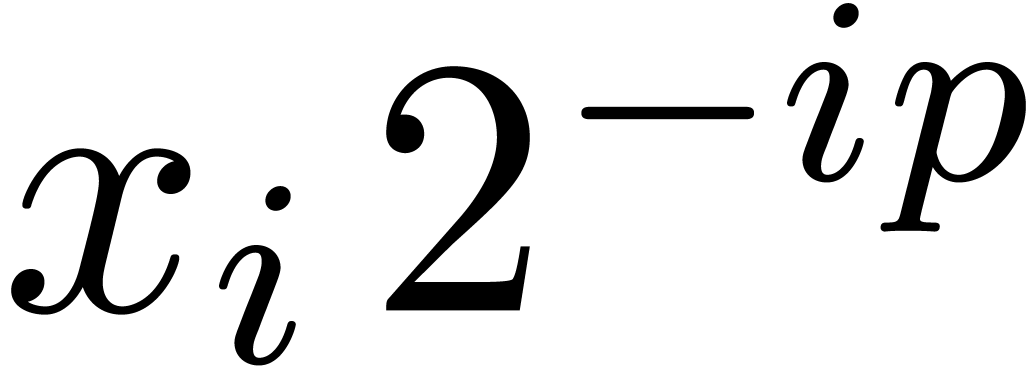 and notice that
and notice that 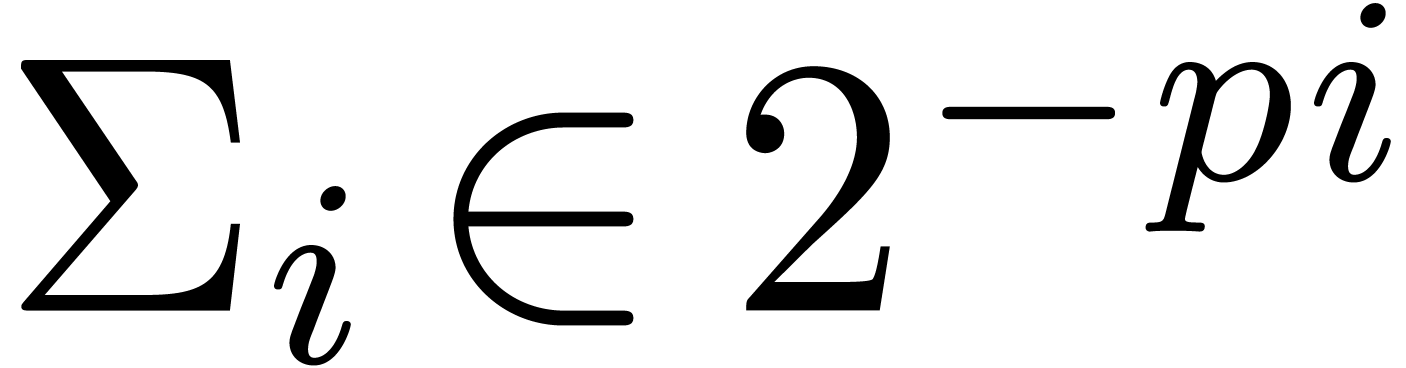 for all
for all
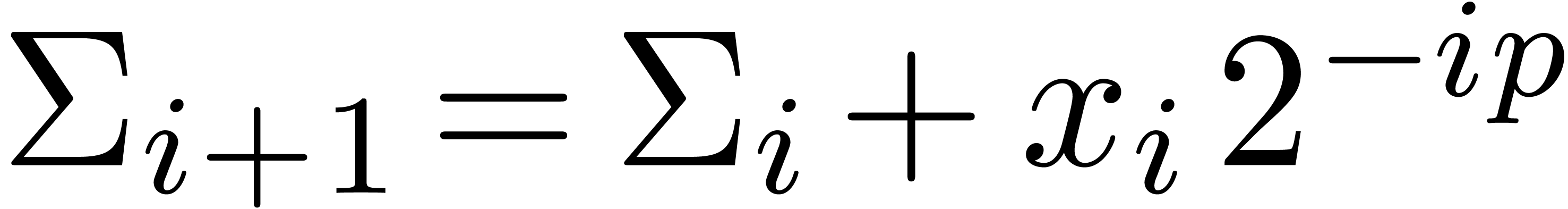 for all
for all 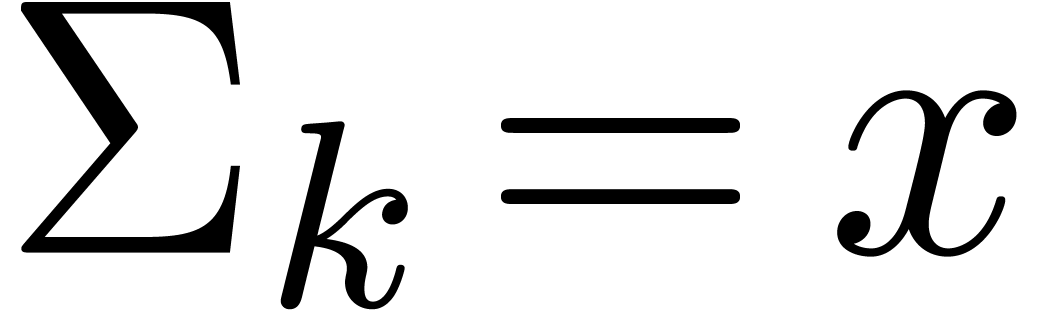 and Compress returns an exact result.
Otherwise, let
and Compress returns an exact result.
Otherwise, let 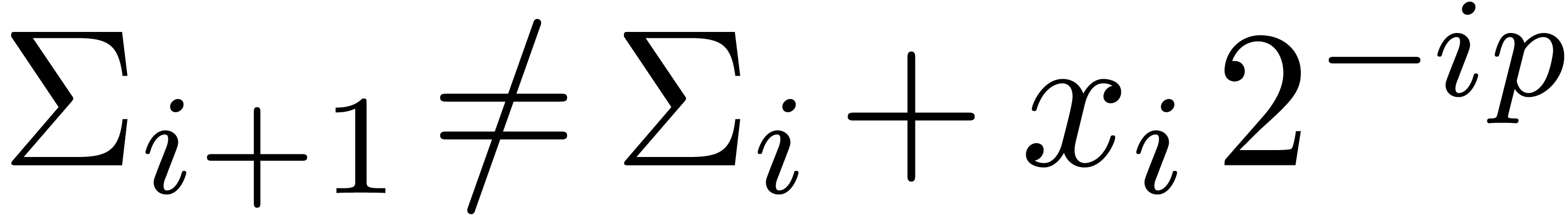 .
.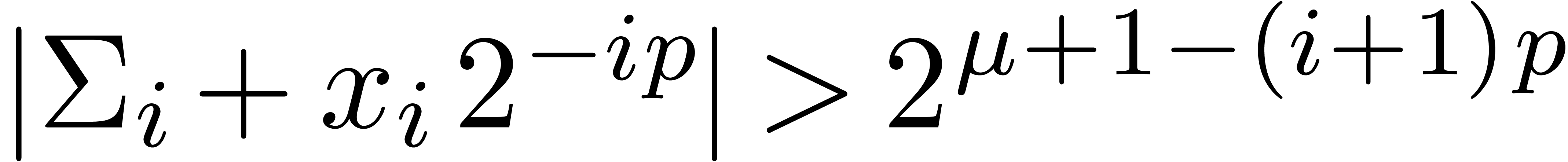 and
and 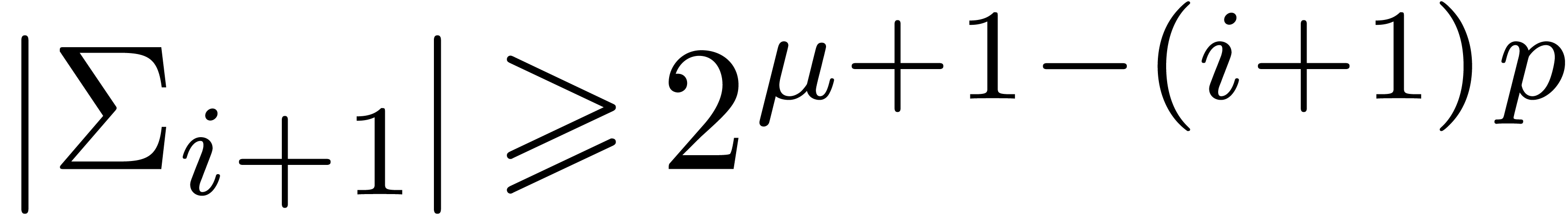 ,
,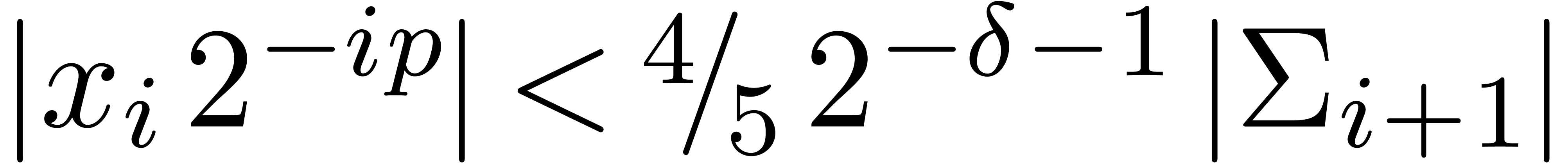 and
and 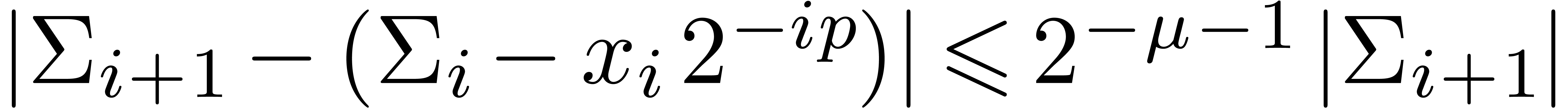 .
. of
of 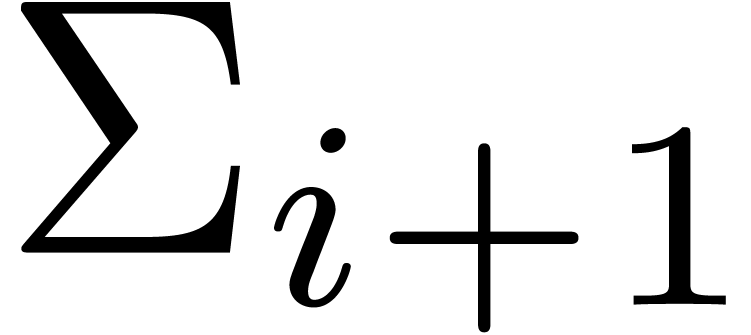 is at least
is at least 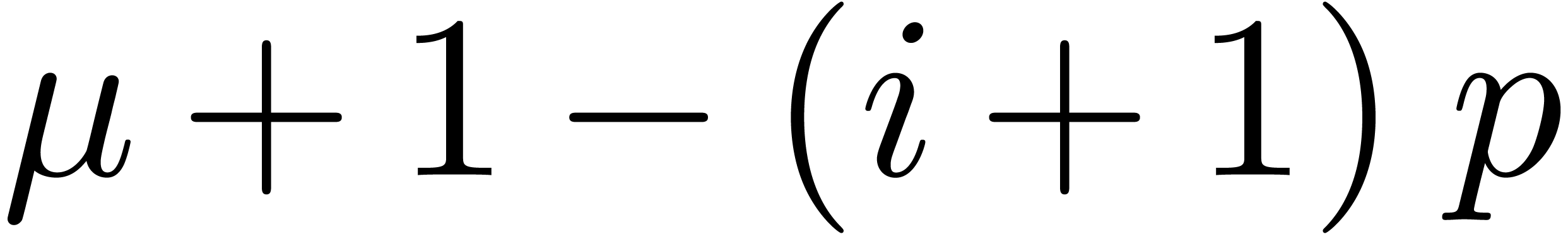 .
. ,
,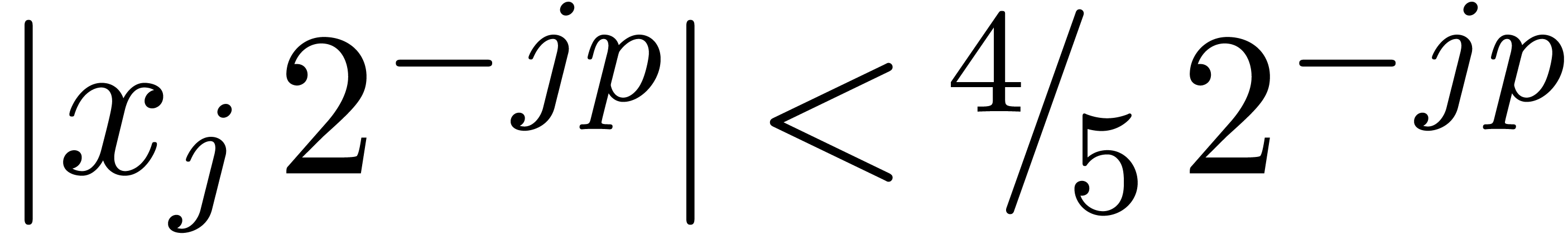 ,
, of
of 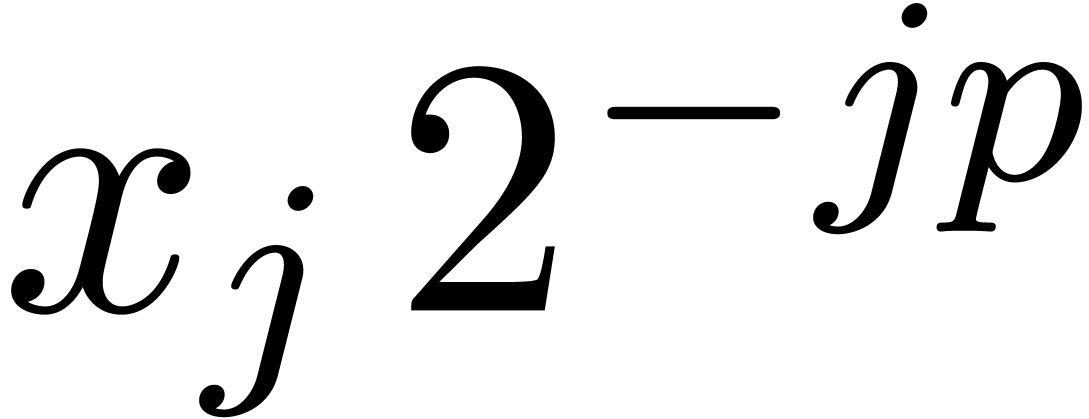 is at most
is at most  .
.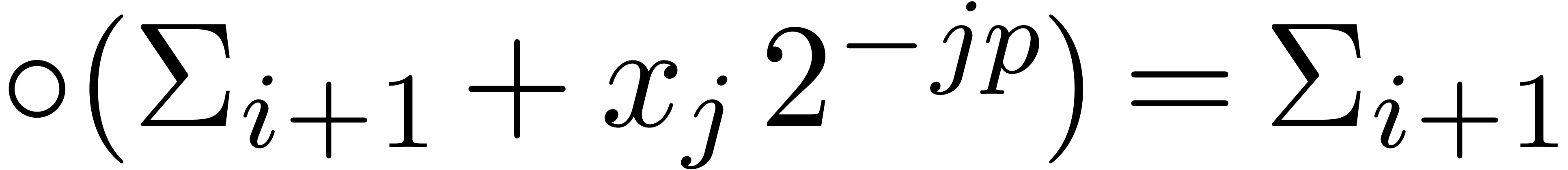 ,
,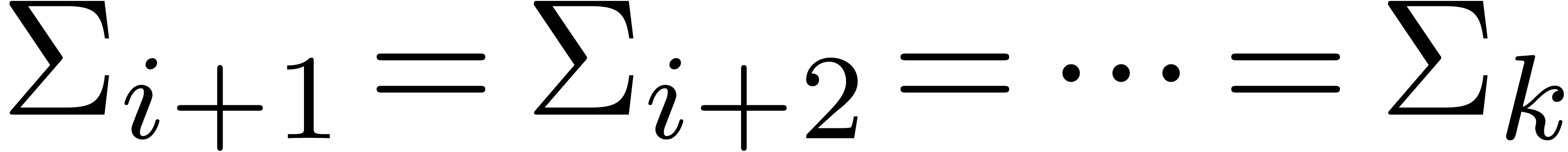 and
and  .
. and let
and let 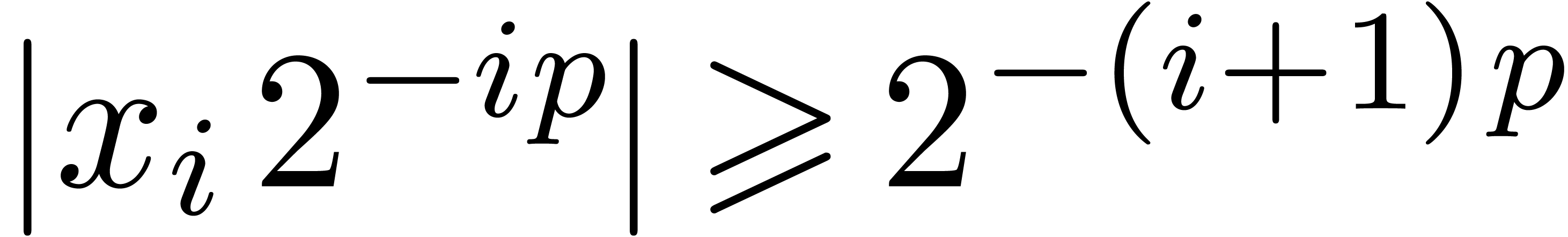 ,
,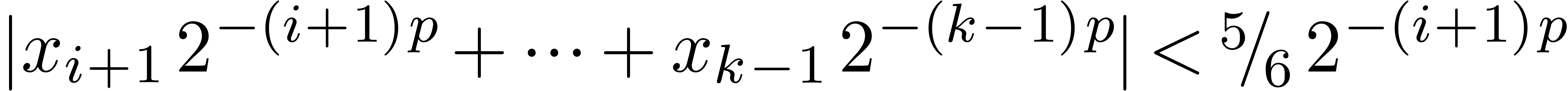 ,
,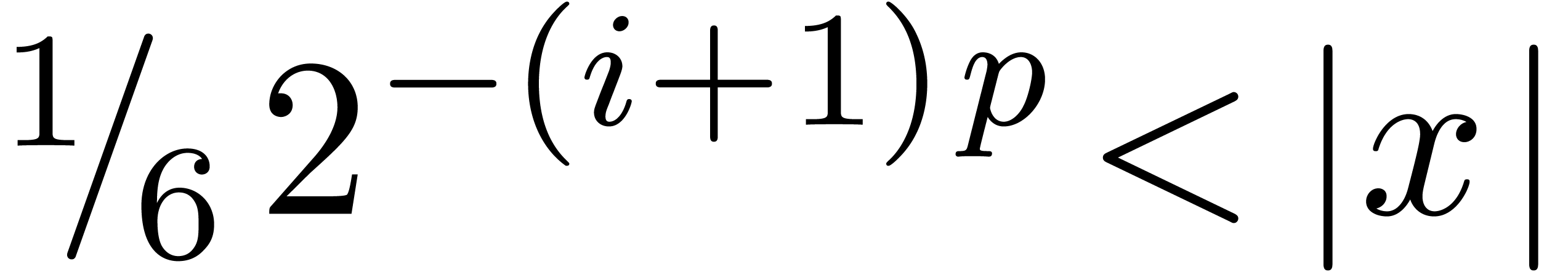 .
. ,
, ,
,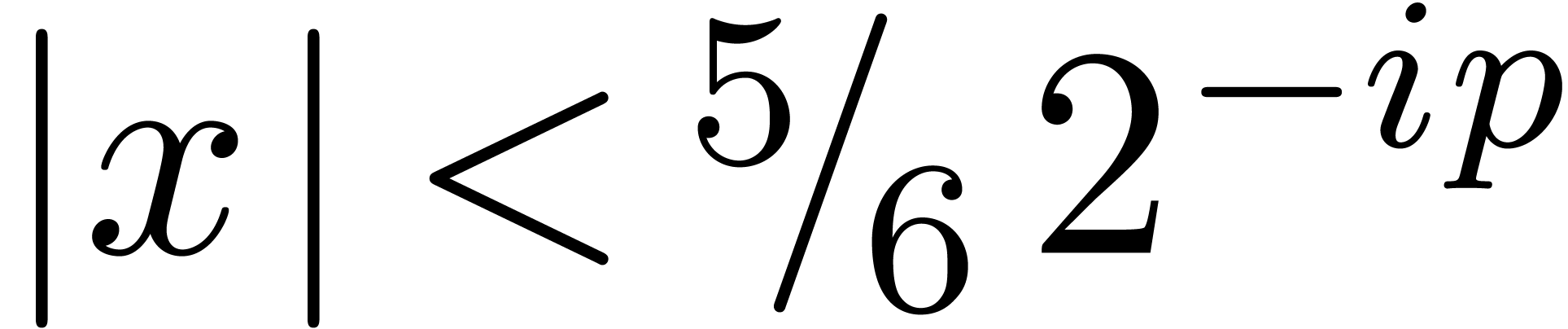 .
. ,
, as a single instruction.
as a single instruction.
 be as in section
be as in section 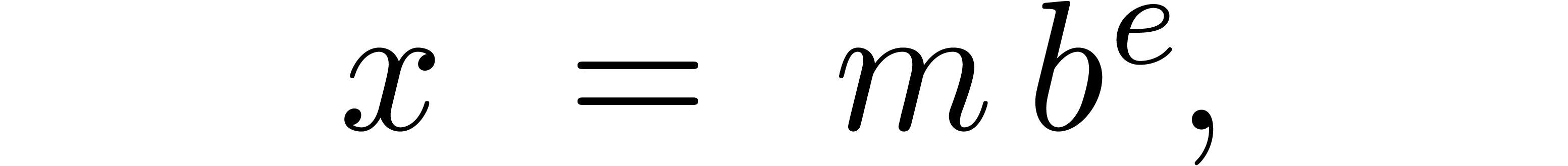
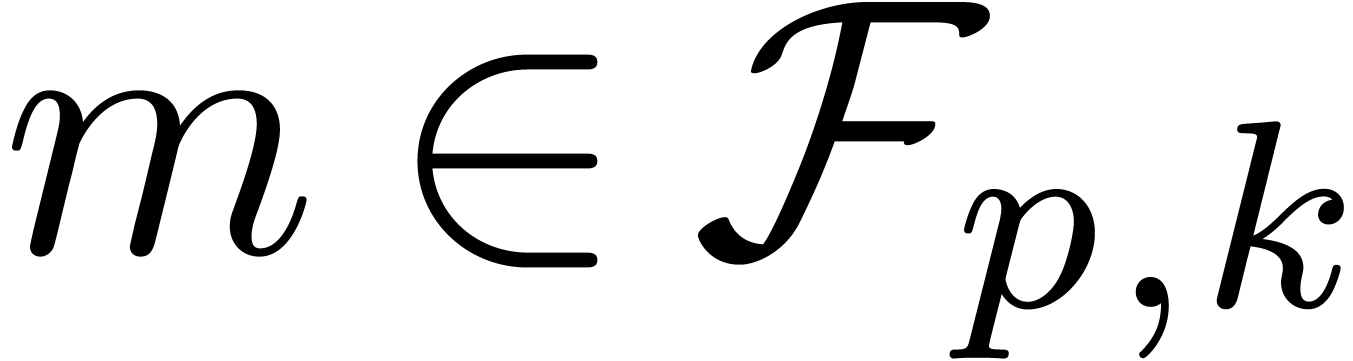 is the mantissa of
is the mantissa of 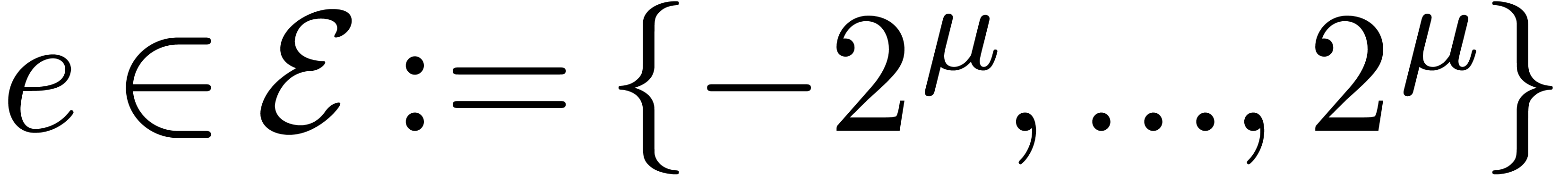 its exponent in base
its exponent in base
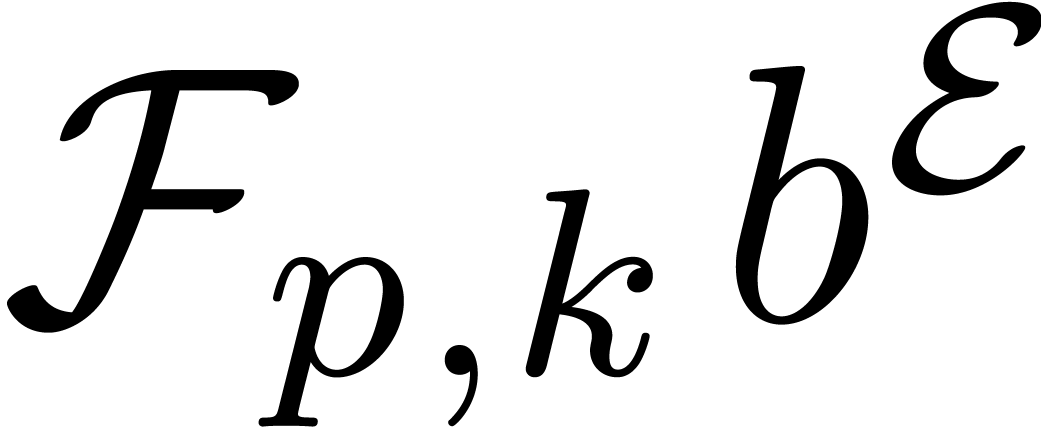 the set of all such floating-point numbers. We assume that
the exponents in
the set of all such floating-point numbers. We assume that
the exponents in  can be represented exactly, by
machine integers or numbers in
can be represented exactly, by
machine integers or numbers in  .
. are again said to be in carry normal form and the routine
CarryNormalize extends to
are again said to be in carry normal form and the routine
CarryNormalize extends to 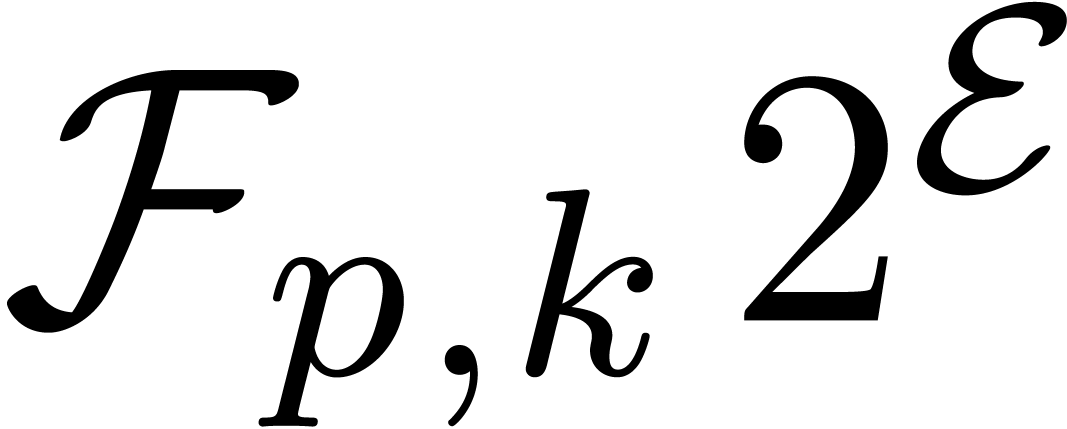 by
applying it to the mantissa. We say that a floating-point number
by
applying it to the mantissa. We say that a floating-point number 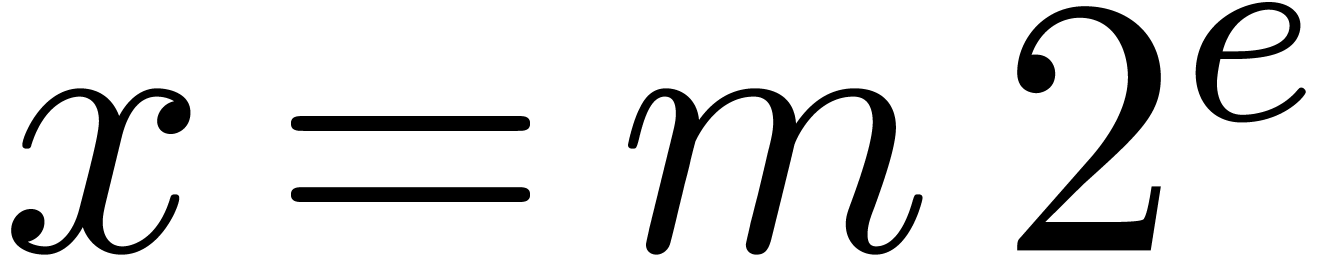 with
with 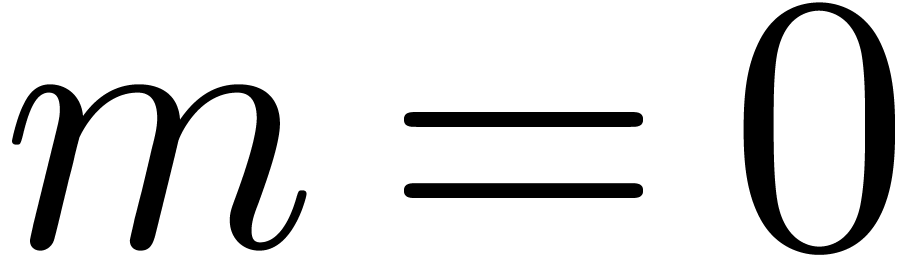 or
or  .
.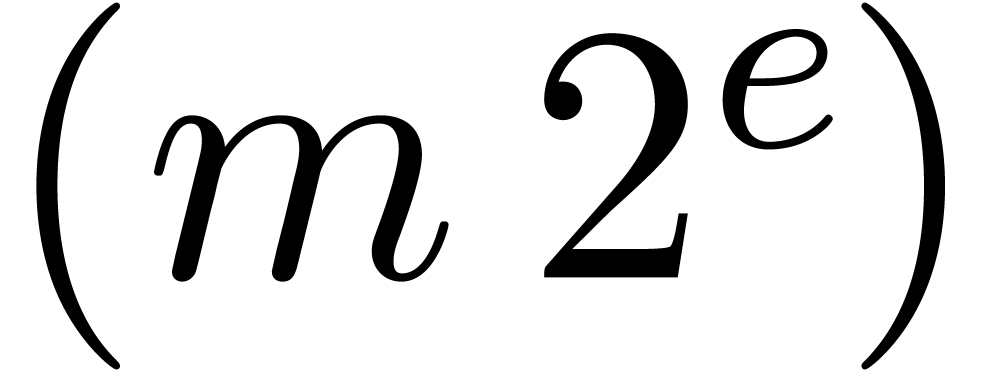

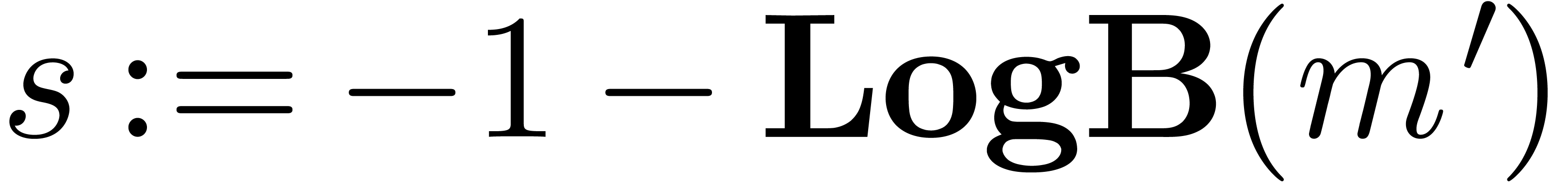
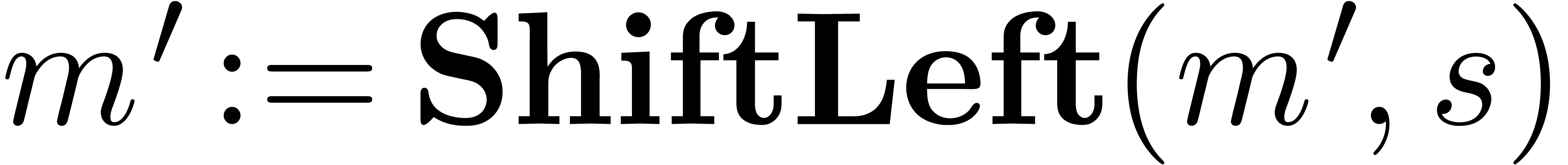
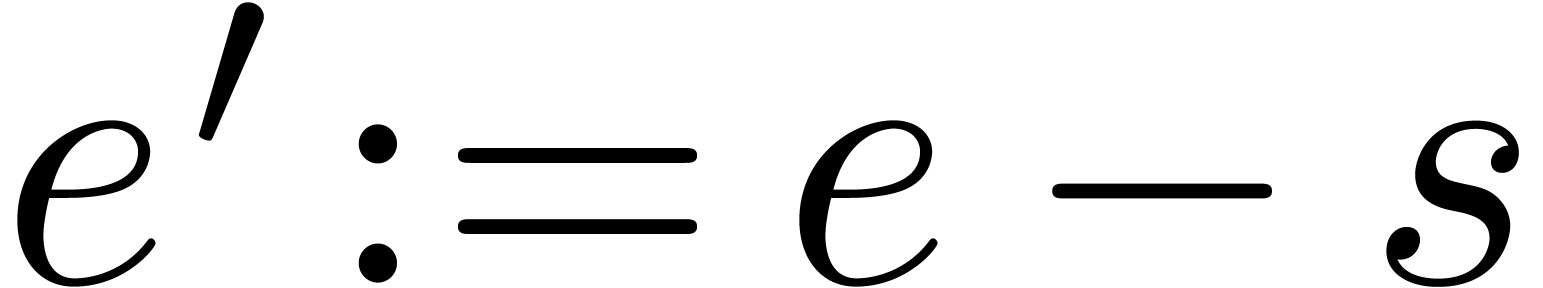
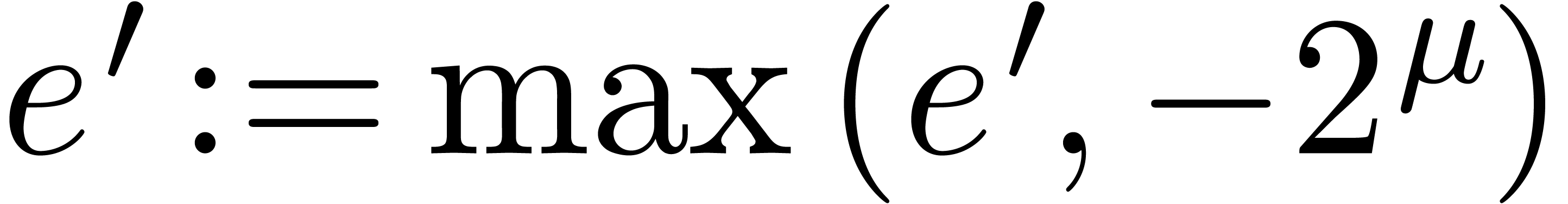


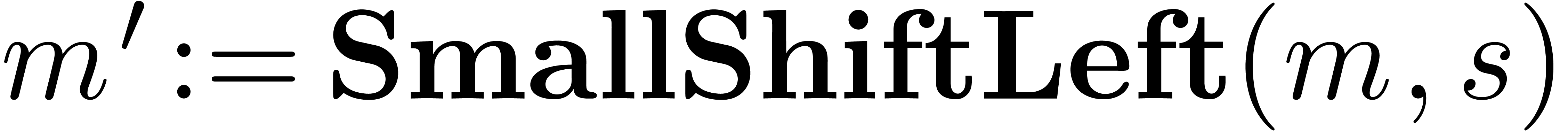
 with
with  and
and 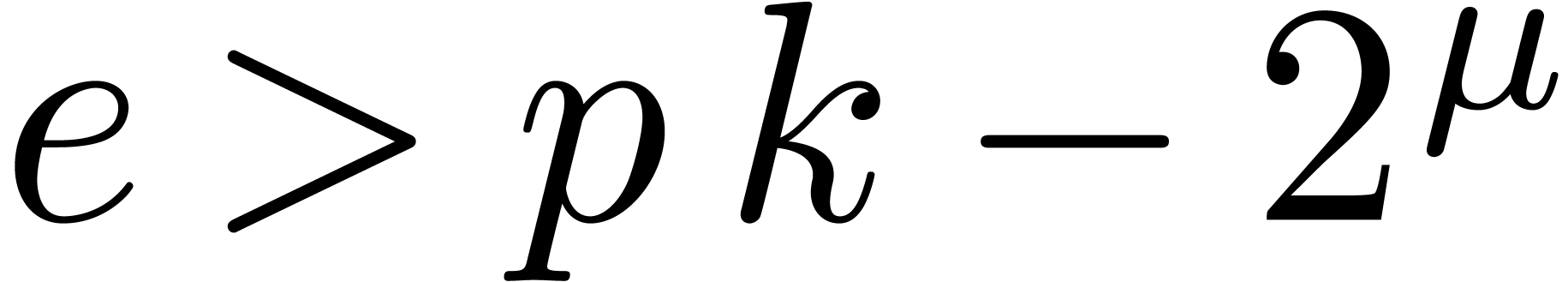 ,
,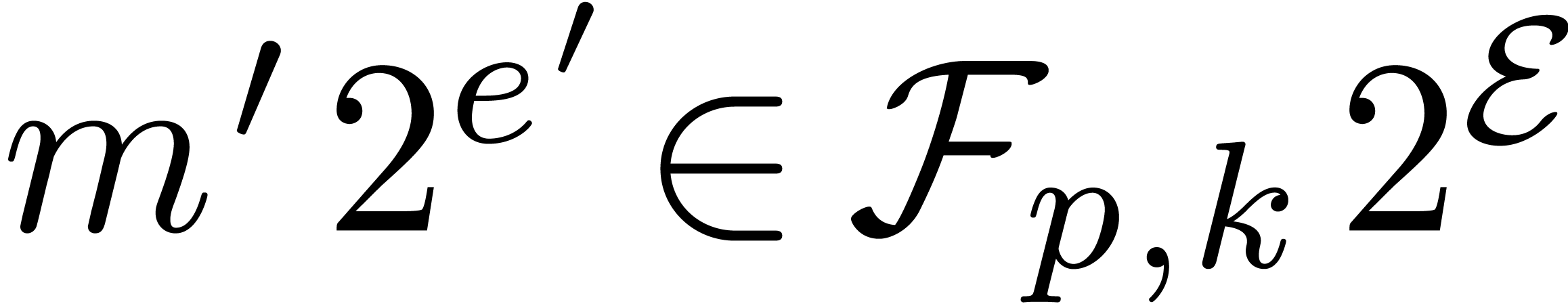 with
with 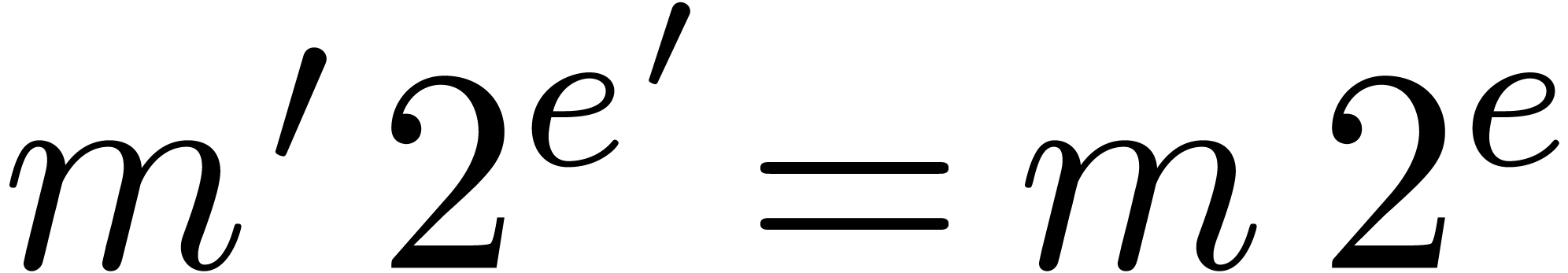 .
.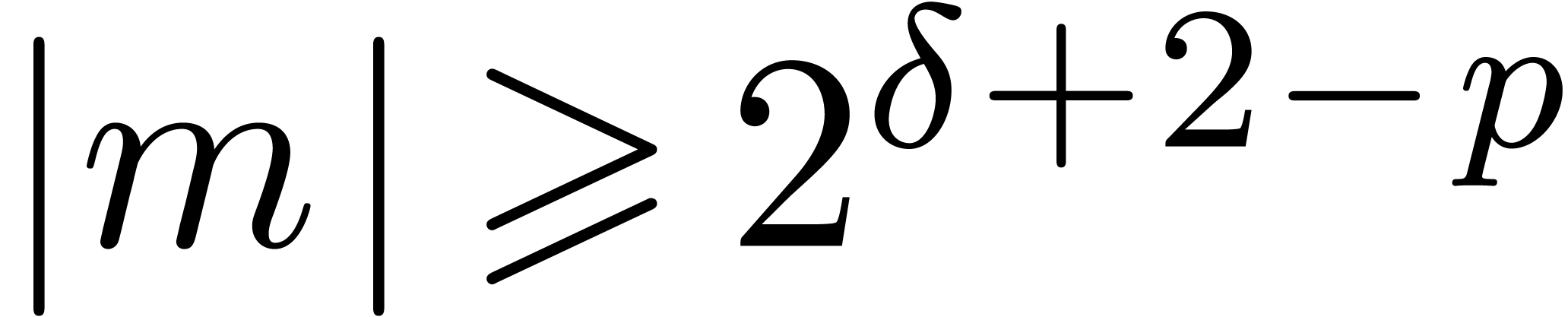 ,
,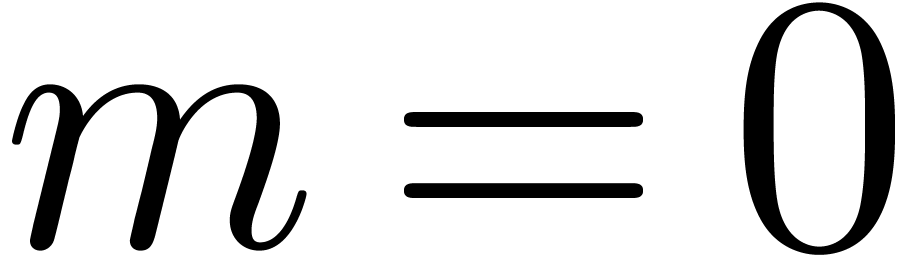 ,
, and
it is easy to verify that the proposition holds. Assume therefore that
and
it is easy to verify that the proposition holds. Assume therefore that
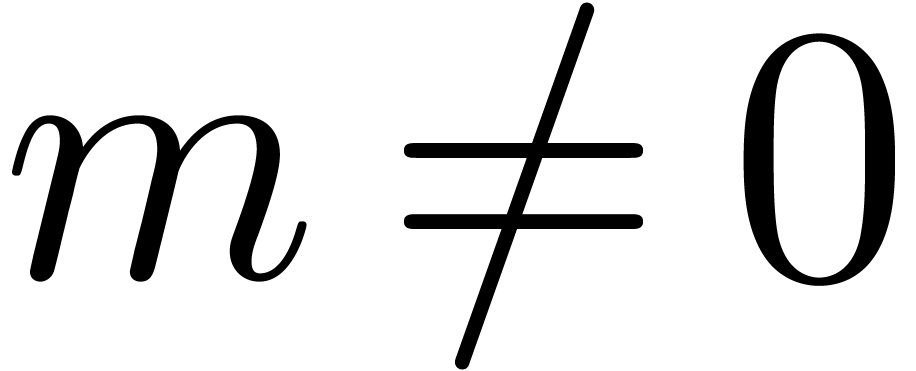 ,
,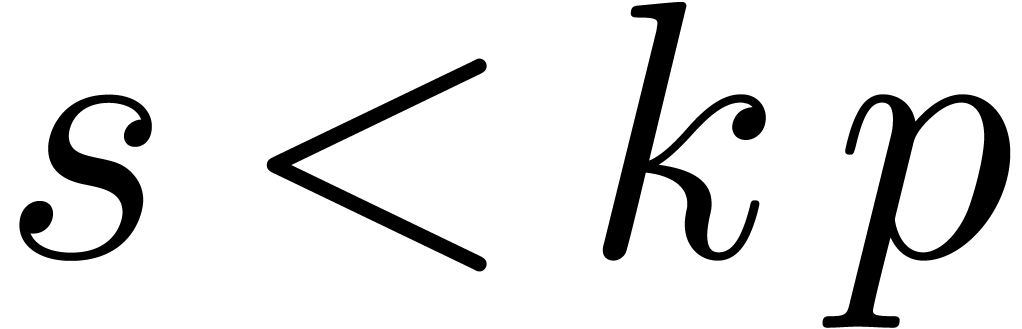 .
.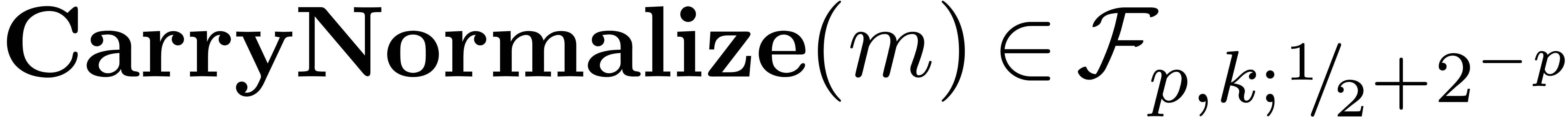 .
.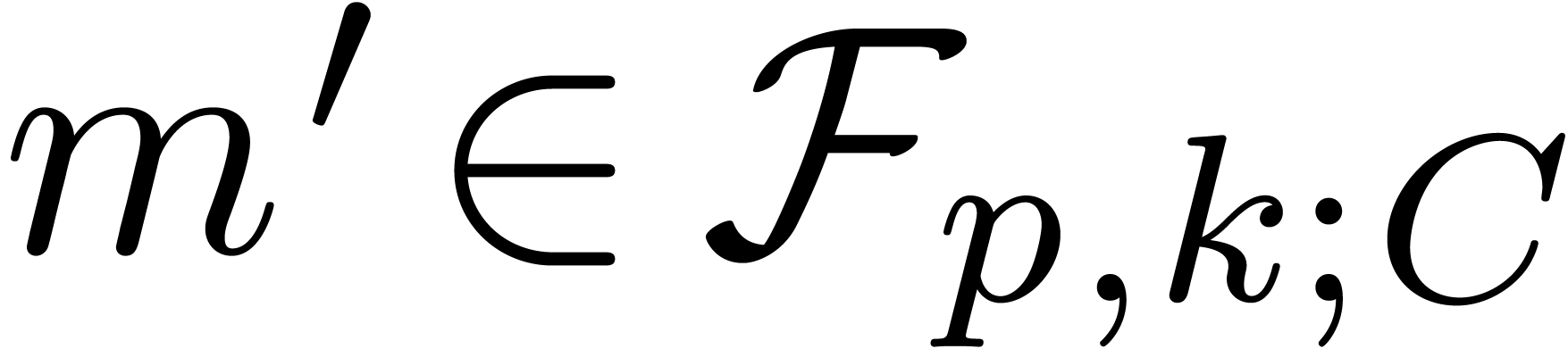 with
with  ,
, is carry normal. We
also have
is carry normal. We
also have 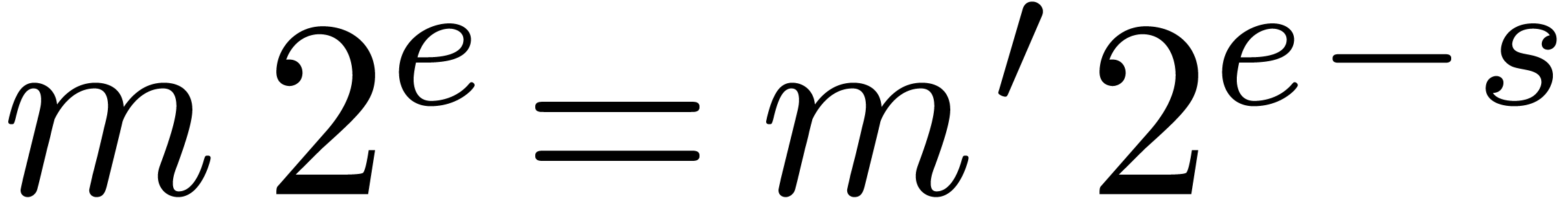 and
and 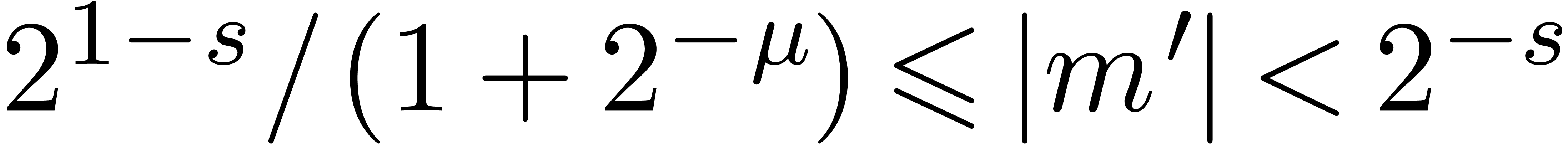 ,
,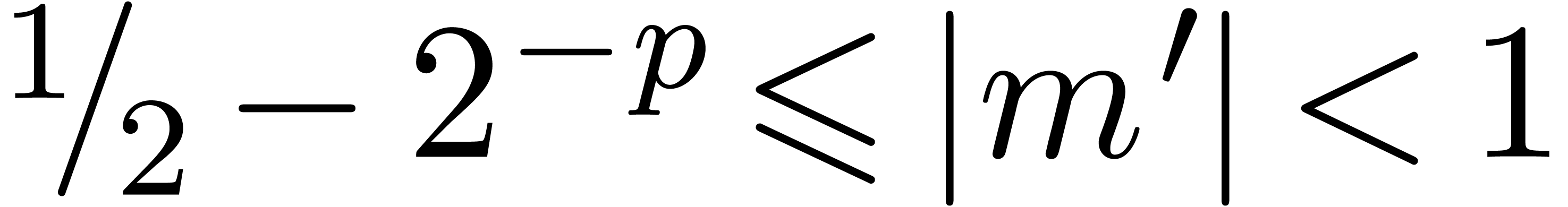 .
.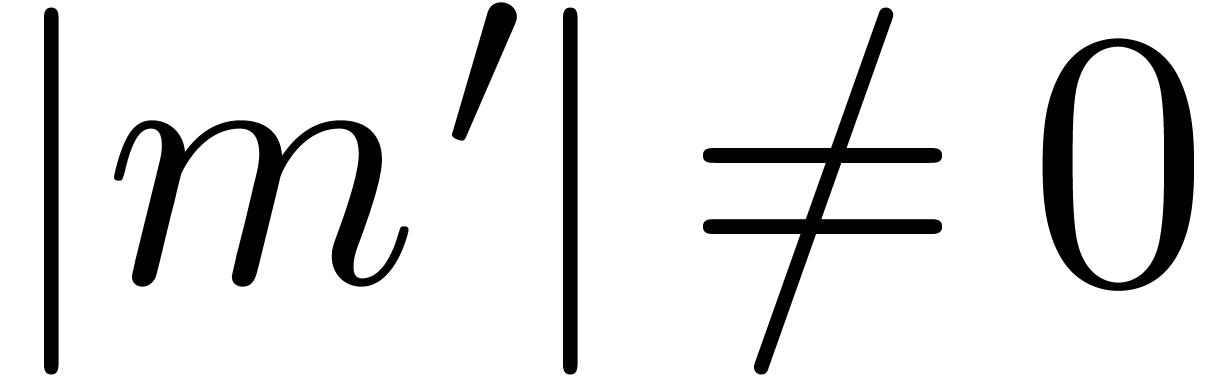 and
and 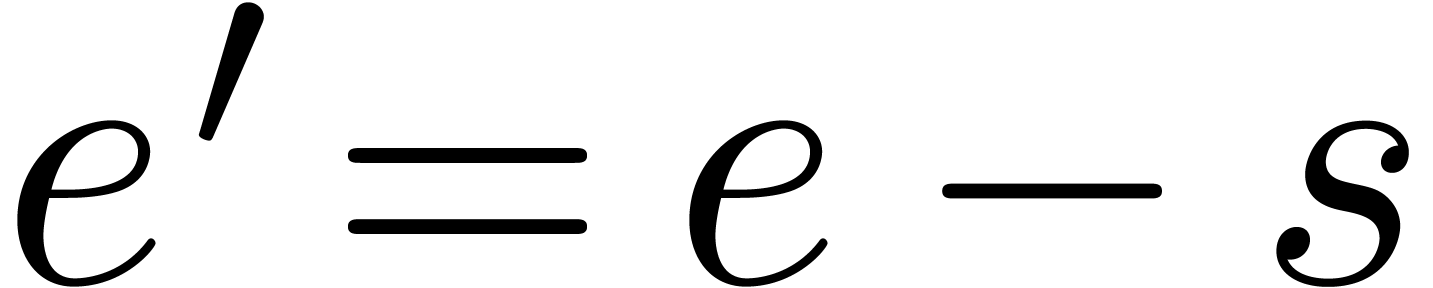 ,
,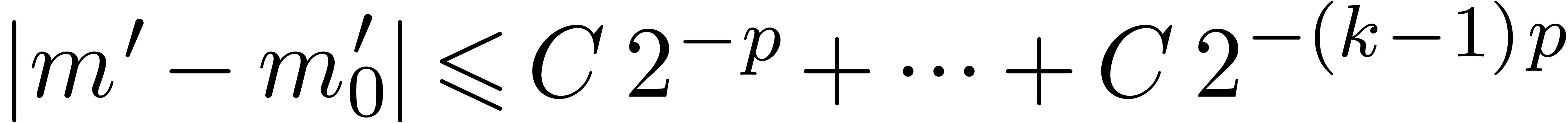 .
.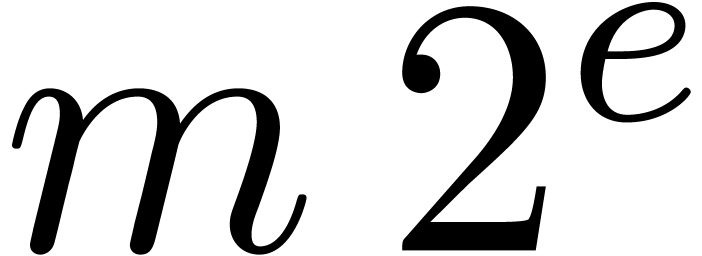 .
. still satisfies
still satisfies  and that
and that  .
. ,
,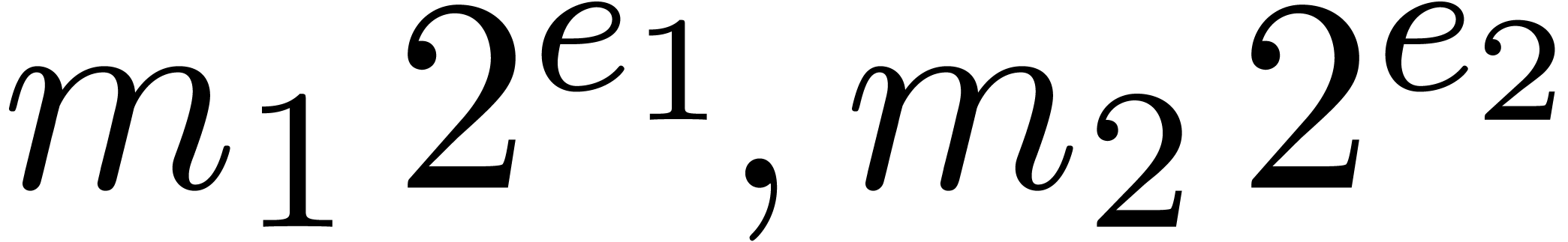 )
)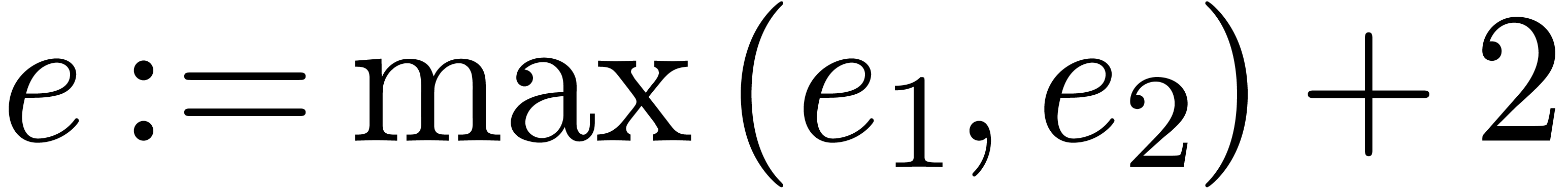
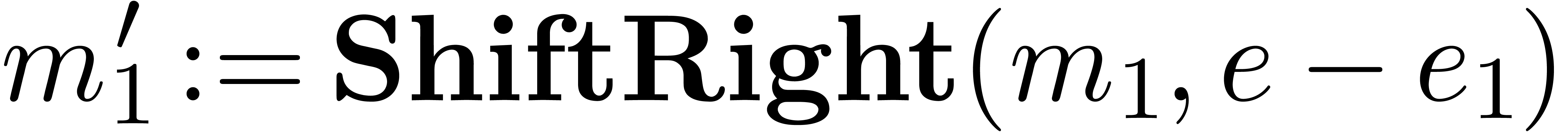
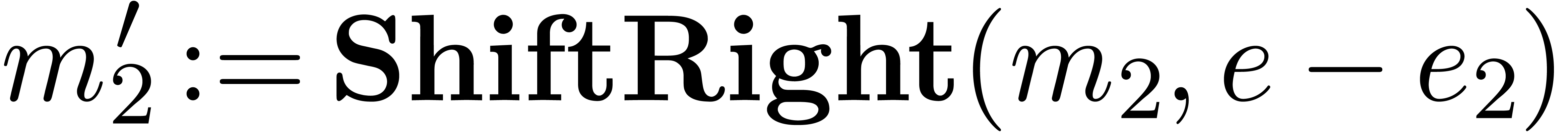
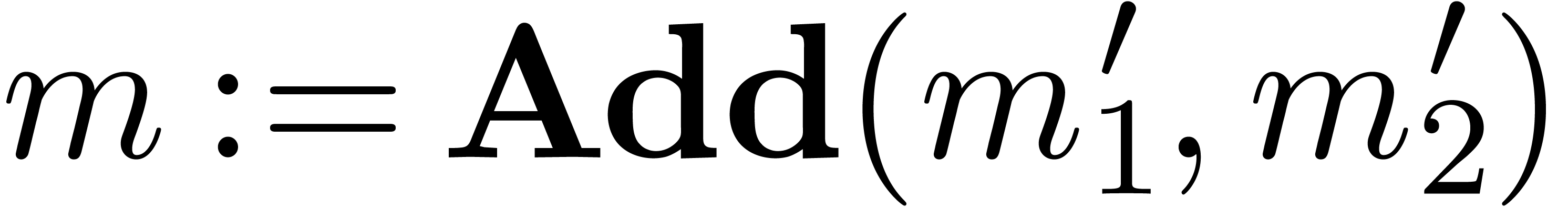
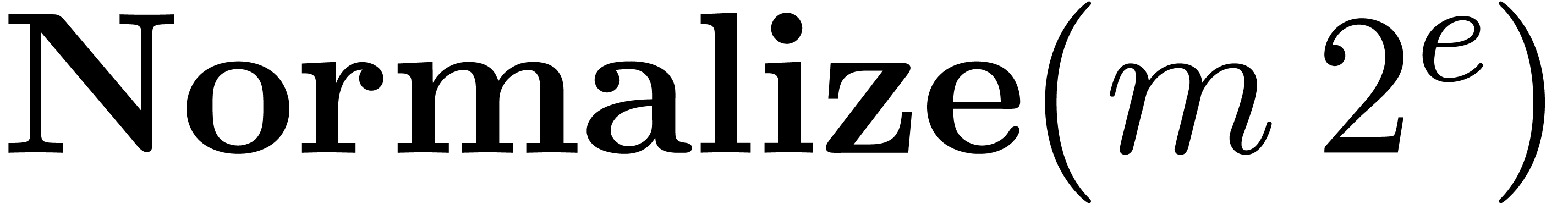


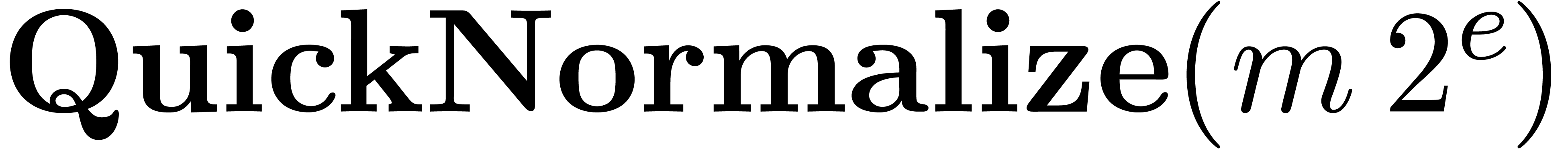
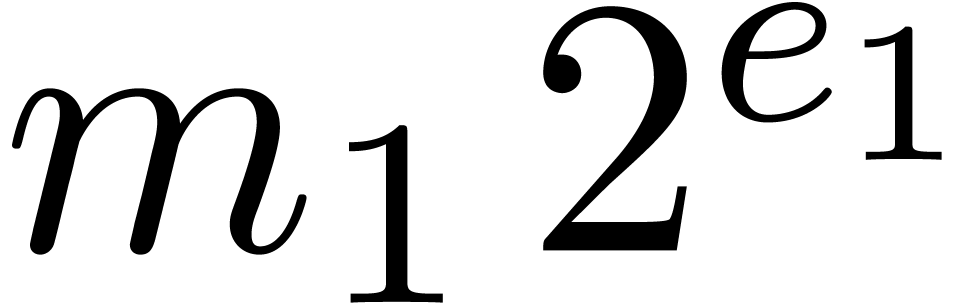 and
and 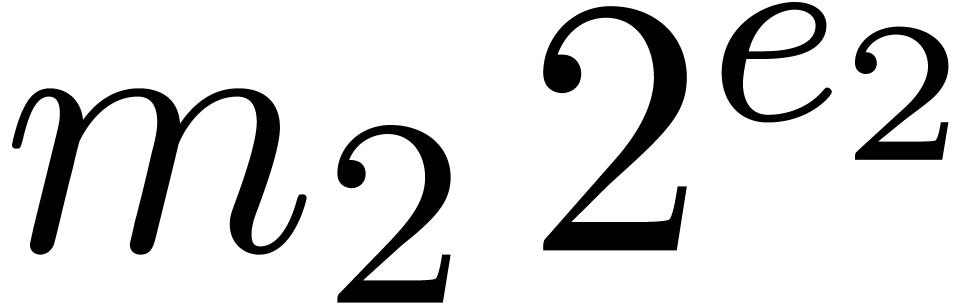 ,
,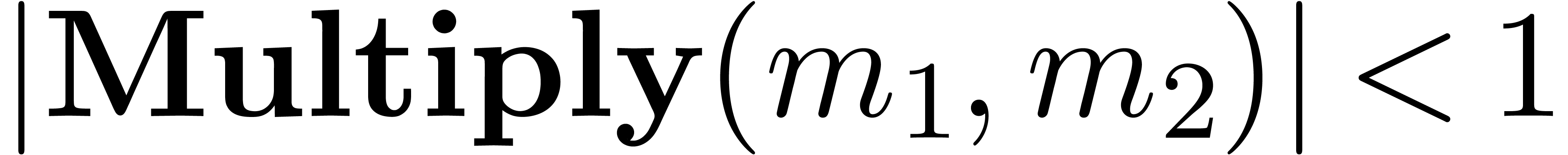 .
.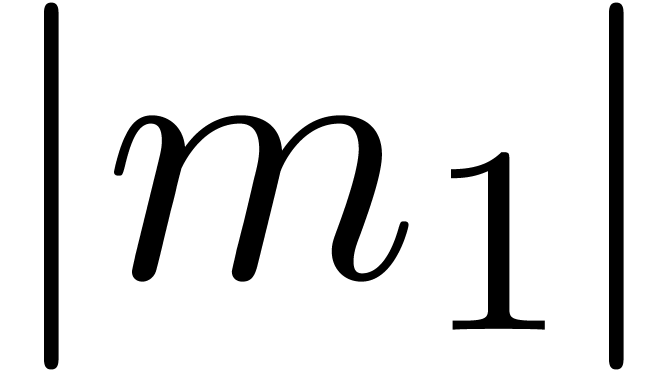 and
and 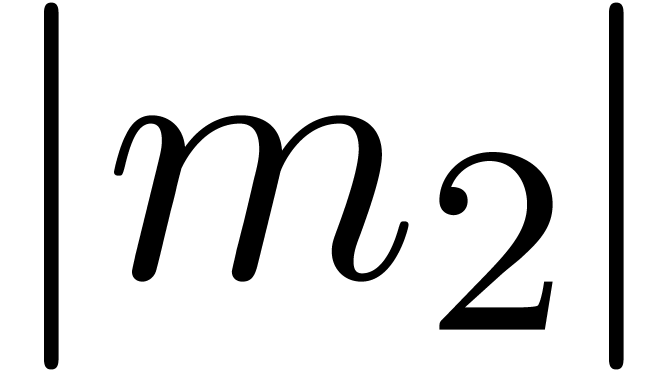 are very
close to one. Now it can be shown that a carry normal mantissa
are very
close to one. Now it can be shown that a carry normal mantissa 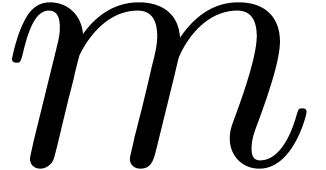 with
with  and
and 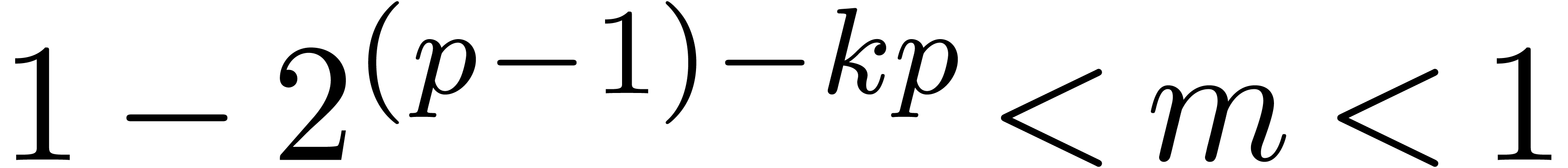 is necessarily of the form
is necessarily of the form 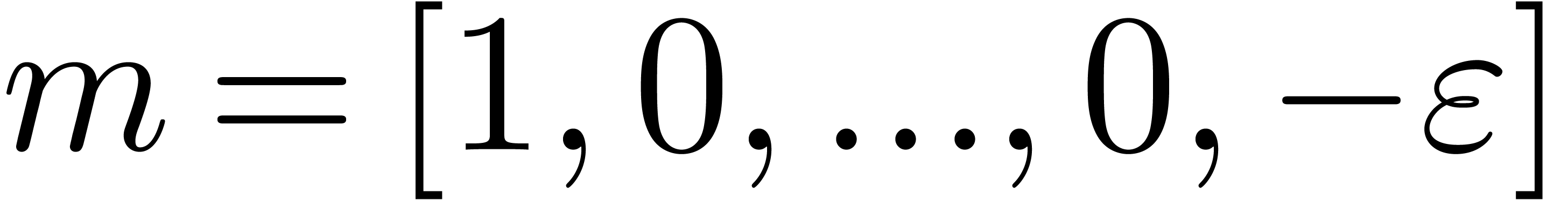 .
.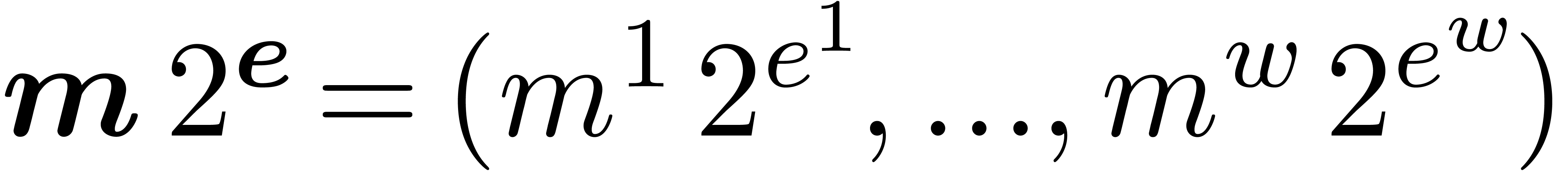 of
floating-point numbers, then another way to speed up shifting is to let
all entries share the same exponent
of
floating-point numbers, then another way to speed up shifting is to let
all entries share the same exponent 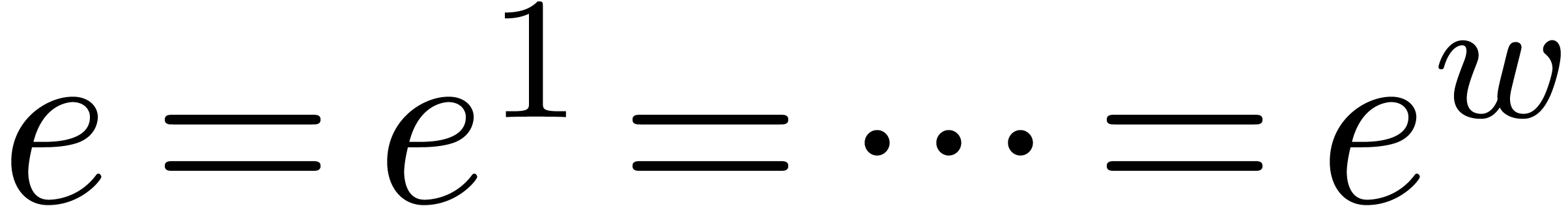 .
.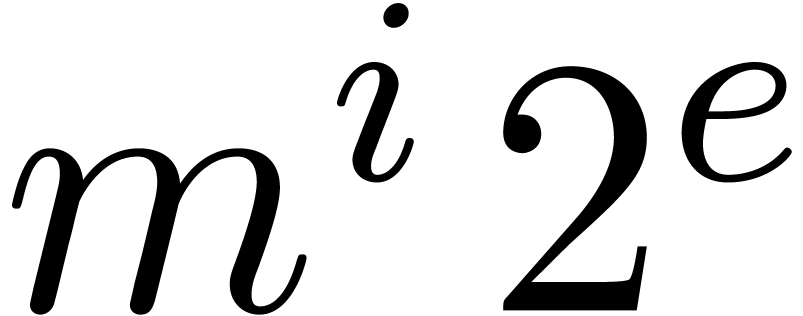 ,
,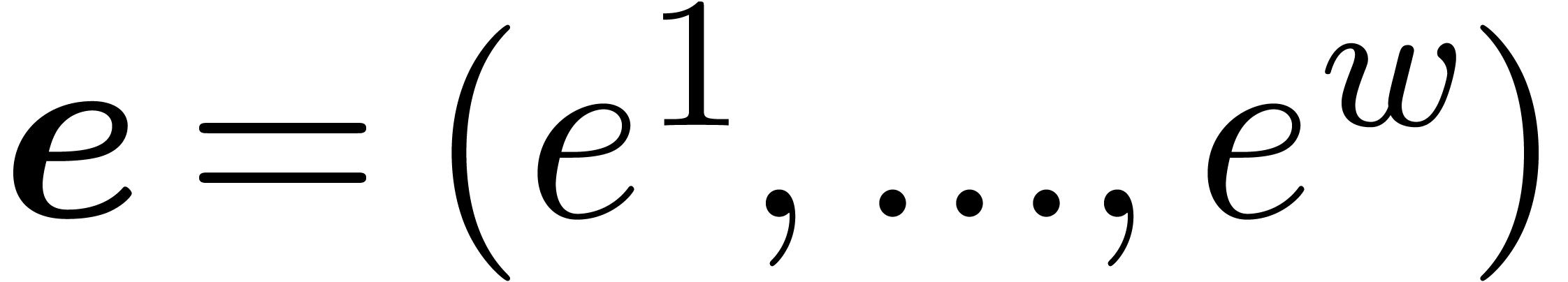 ,
, with
with 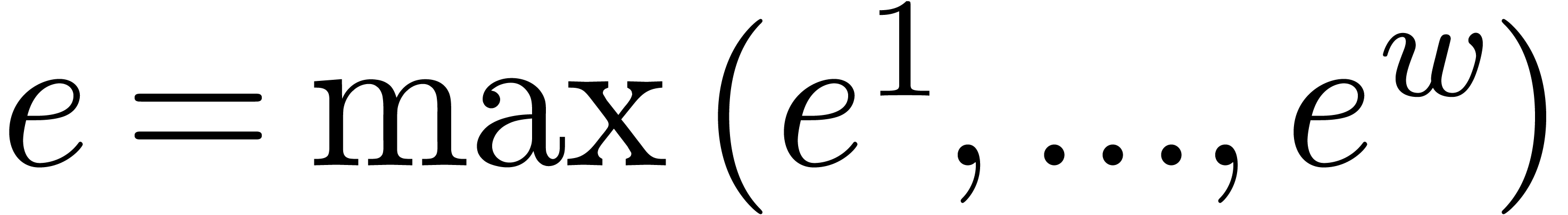 .
. ,
, and
and  that we have discussed so far. For comparison, we have also shown the
operation count for the algorithm from [
that we have discussed so far. For comparison, we have also shown the
operation count for the algorithm from [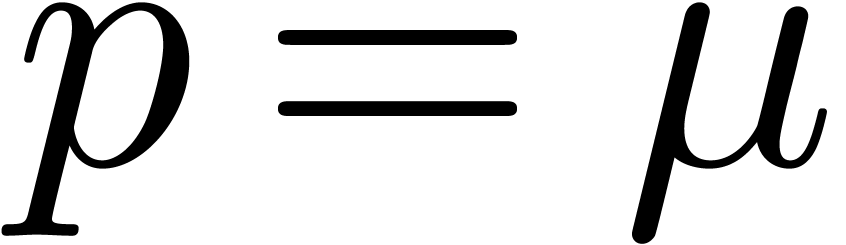 is
somewhat better for this algorithm, since our algorithms rather use
is
somewhat better for this algorithm, since our algorithms rather use
 ).
).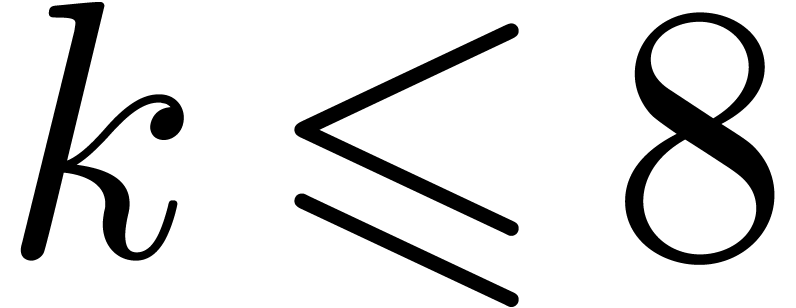 .
. ,
,
 .
. leading zero bits. This means that
leading zero bits. This means that
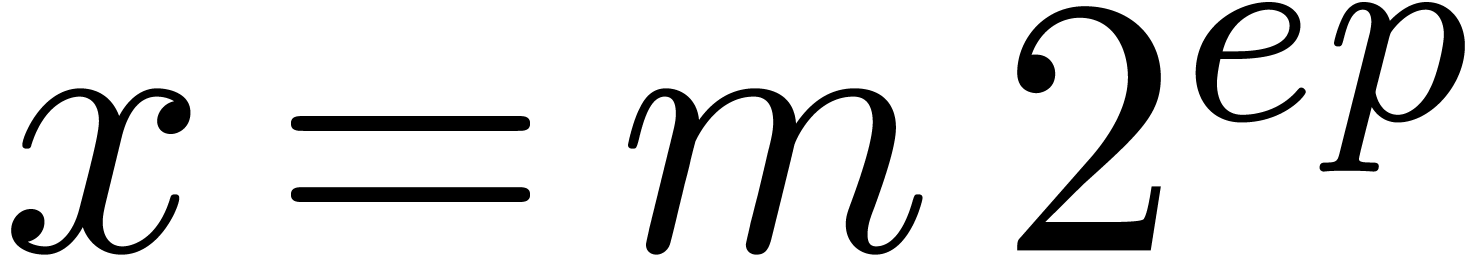 with
with  and either
and either 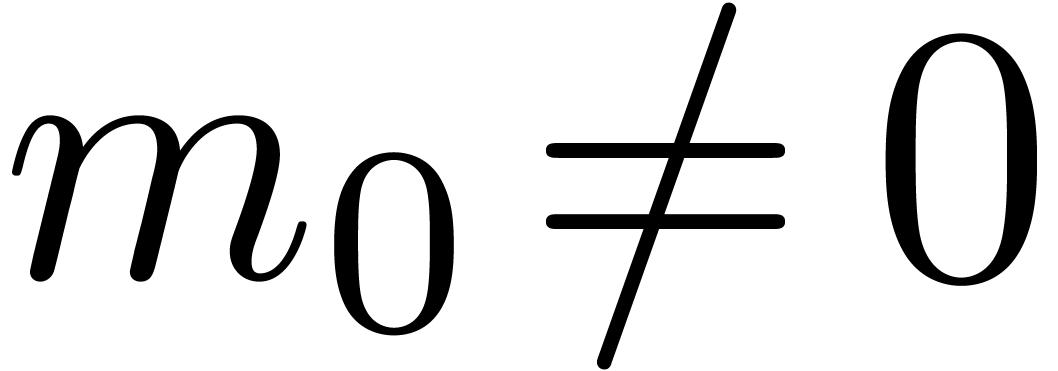 .
. words instead of
words instead of 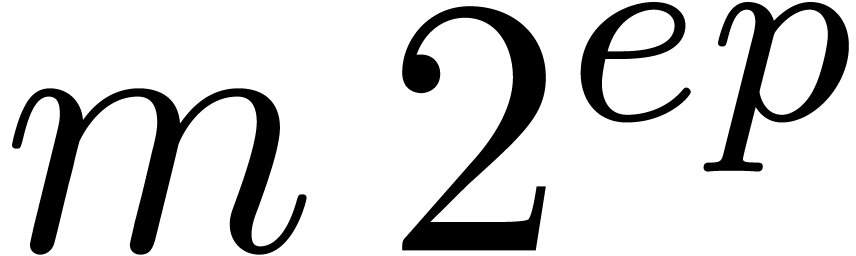 )
)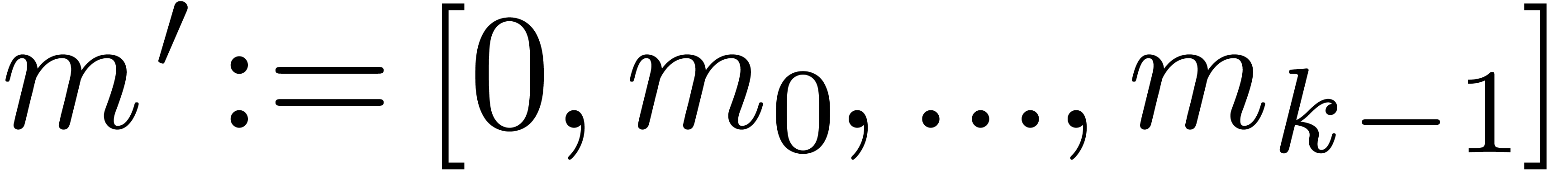

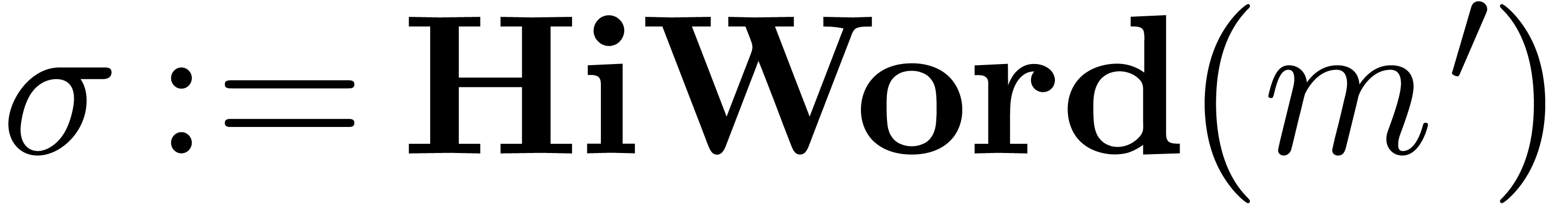

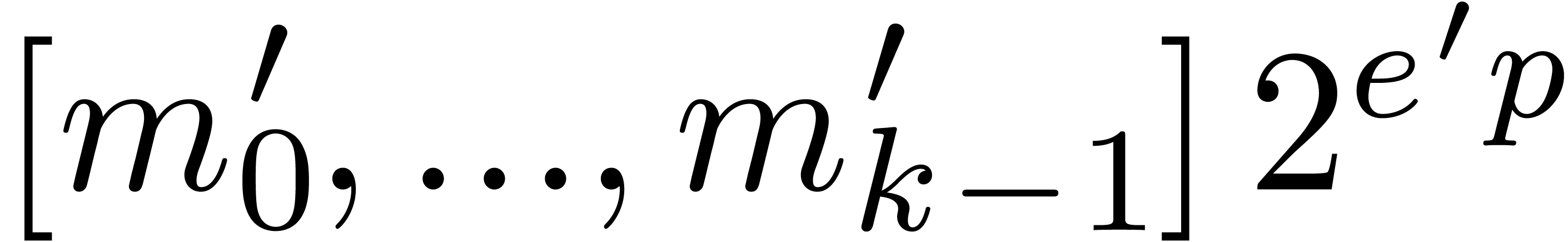
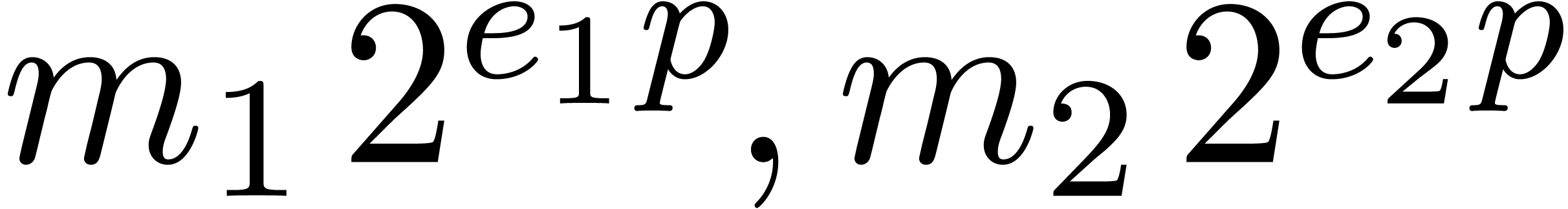 )
)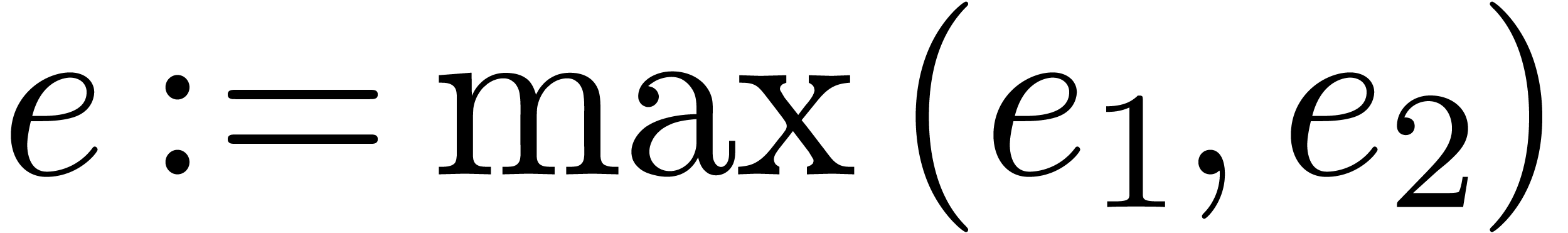
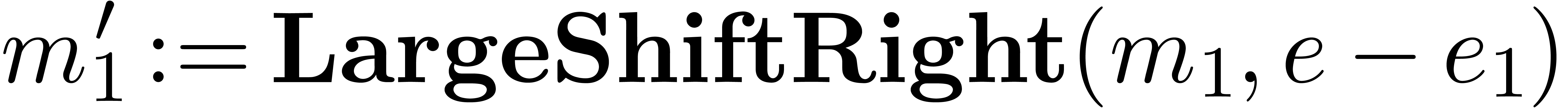
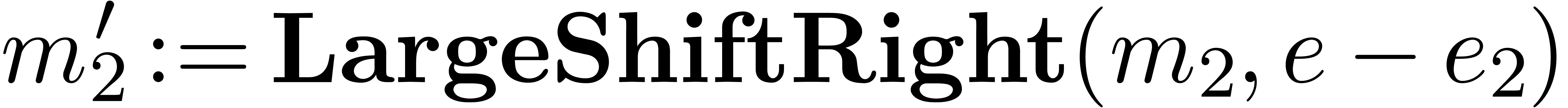
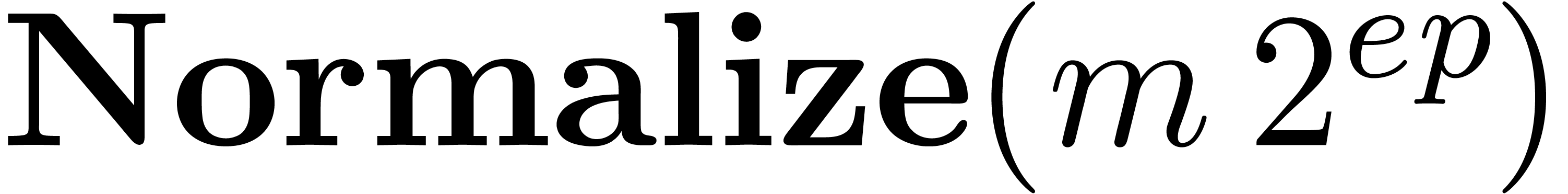
 bits. Let
bits. Let  be the variant of
be the variant of  obtained by replacing the
condition
obtained by replacing the
condition  .
.