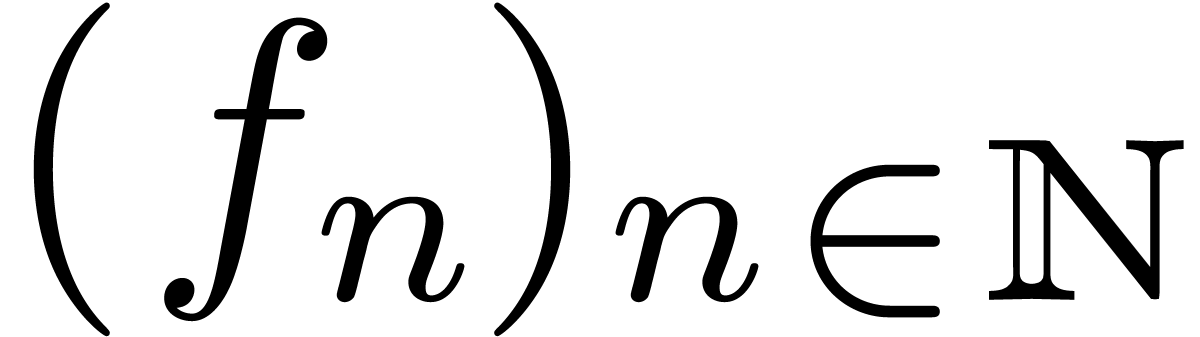 :
how to compute their asymptotics for large
:
how to compute their asymptotics for large 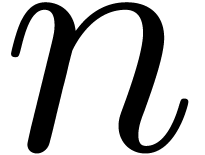 ?
How to evaluate
?
How to evaluate 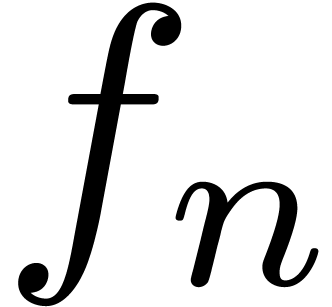 efficiently
for large
efficiently
for large 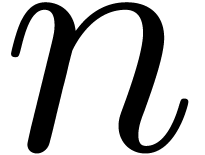 and/or large
precisions
and/or large
precisions 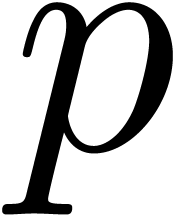 ? How to decide
whether
? How to decide
whether 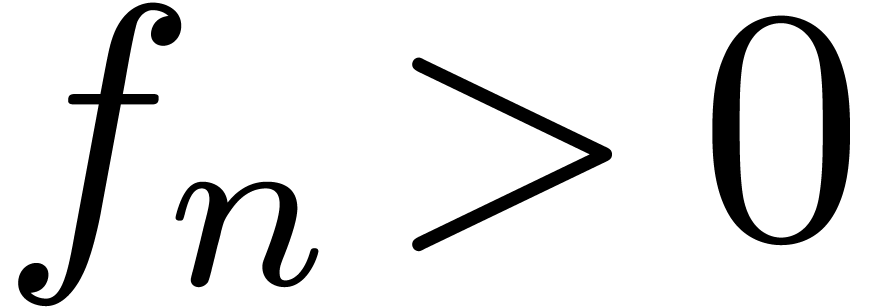 for all
for all 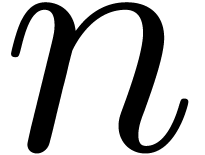 ?
?
| HomepagePublicationsTalksTeXmacsMathemagix |
Many sequences that arise in combinatorics and the analysis of
algorithms turn out to be holonomic (note that some authors prefer the
terminology D-finite). In this paper, we study various basic algorithmic
problems for such sequences 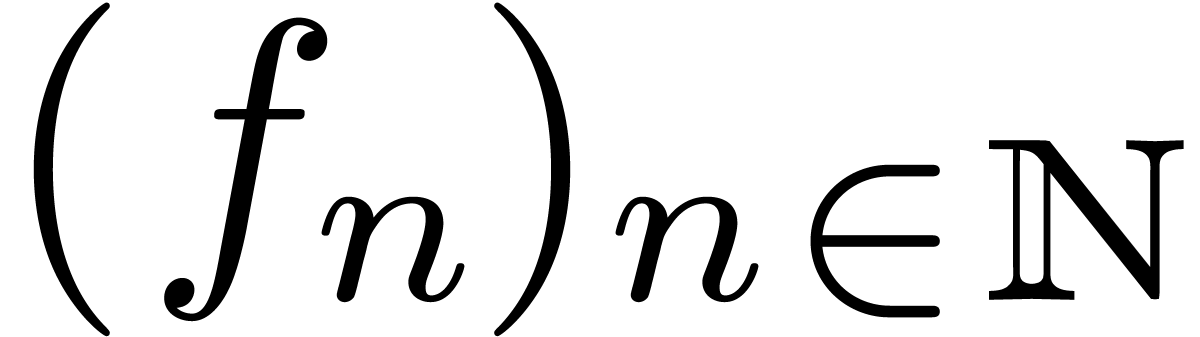 :
how to compute their asymptotics for large
:
how to compute their asymptotics for large 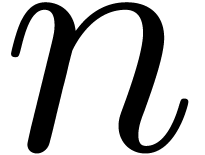 ?
How to evaluate
?
How to evaluate 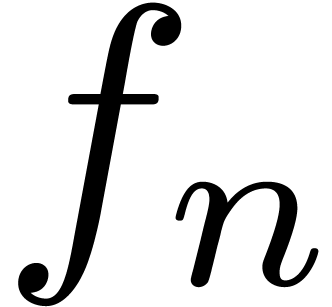 efficiently
for large
efficiently
for large 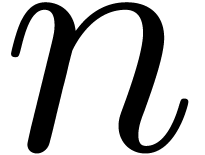 and/or large
precisions
and/or large
precisions 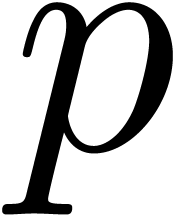 ? How to decide
whether
? How to decide
whether 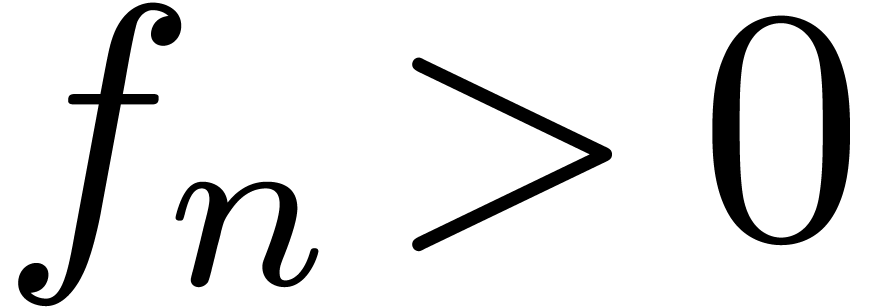 for all
for all 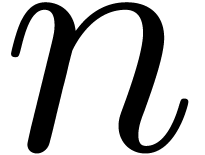 ?
?
We restrict our study to the case when the generating function 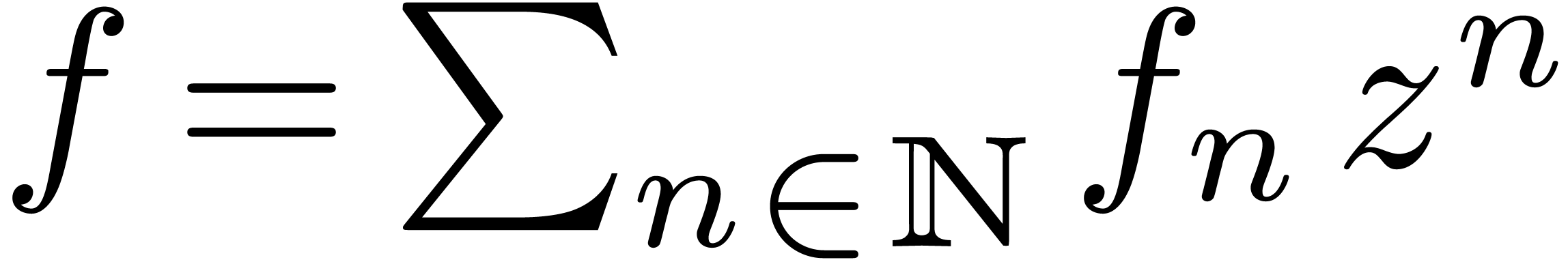 satisfies a Fuchsian differential
equation (often it suffices that the dominant singularities of
satisfies a Fuchsian differential
equation (often it suffices that the dominant singularities of 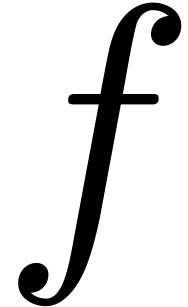 be Fuchsian). Even in this special
case, some of the above questions are related to long-standing problems
in number theory. We will present algorithms that work in many cases and
we carefully analyze what kind of oracles or conjectures are needed to
tackle the more difficult cases.
be Fuchsian). Even in this special
case, some of the above questions are related to long-standing problems
in number theory. We will present algorithms that work in many cases and
we carefully analyze what kind of oracles or conjectures are needed to
tackle the more difficult cases.
Authors: