|
 . Cet article est une traduction
libre de [15].
. Cet article est une traduction
libre de [15].
 . Ce document a été
rédigé avec GNU TeXmacs [16].
. Ce document a été
rédigé avec GNU TeXmacs [16].
CNRS, LIX (UMR 7161)
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau, France
Multiplier des entiers en temps
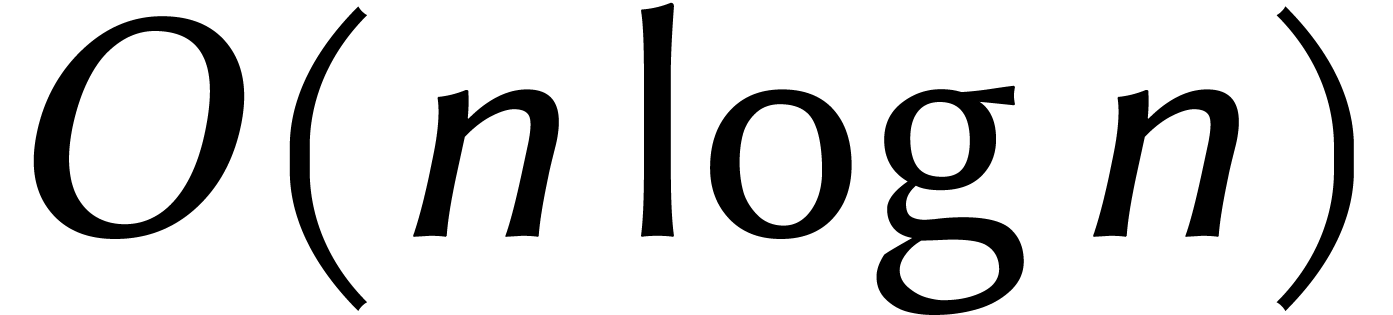


Mars 2021
 . Cet article est une traduction
libre de [15].
. Cet article est une traduction
libre de [15].
 . Ce document a été
rédigé avec GNU TeXmacs [16].
. Ce document a été
rédigé avec GNU TeXmacs [16].
Il a été démontré récemment que deux
entiers de 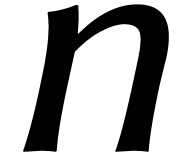 chiffres peuvent être
multipliés en temps
chiffres peuvent être
multipliés en temps 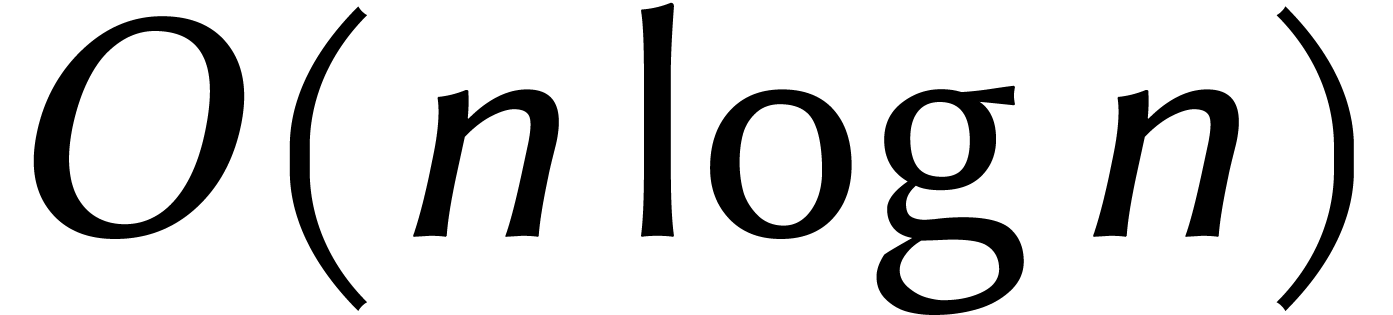 [12].
L'existence d'un tel algorithme fut conjecturé en 1971 par
Schönhage et Strassen [23]. Ils émettaient
également leurs doutes sur l'existence d'une méthode
encore plus rapide, ce que l'on ignore toujours.
[12].
L'existence d'un tel algorithme fut conjecturé en 1971 par
Schönhage et Strassen [23]. Ils émettaient
également leurs doutes sur l'existence d'une méthode
encore plus rapide, ce que l'on ignore toujours.
Dans cet article, je présenterai brièvement une longue histoire et je poursuivrai avec un aperçu du nouvel algorithme.
Quelle est la meilleure façon de multiplier deux entiers ? Cette question, simple en apparence, est peut-être le plus ancien problème mathématique non résolu. Ainsi, ce problème est au moins dix fois plus ancien que la conjecture de Fermat, alias « théorème de Wiles ».
Il faut bien sûr préciser ce que nous entendons par «
meilleur ». Pour cela, il a fallu attendre l'invention de la
machine de Turing : équipée d'un modèle de calcul
précis, on peut définir le nombre 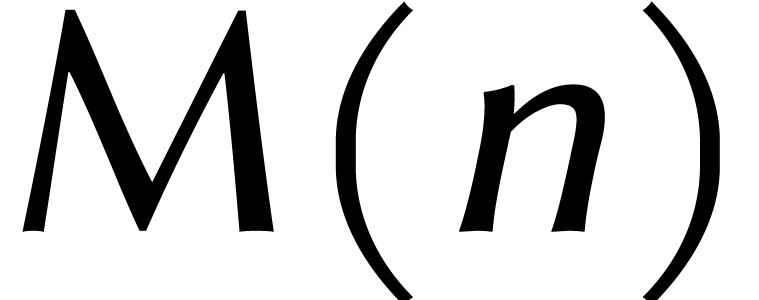 d'étapes nécessaires pour multiplier deux nombres de
d'étapes nécessaires pour multiplier deux nombres de 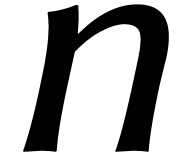 chiffres. La meilleure méthode est alors celle
pour laquelle
chiffres. La meilleure méthode est alors celle
pour laquelle 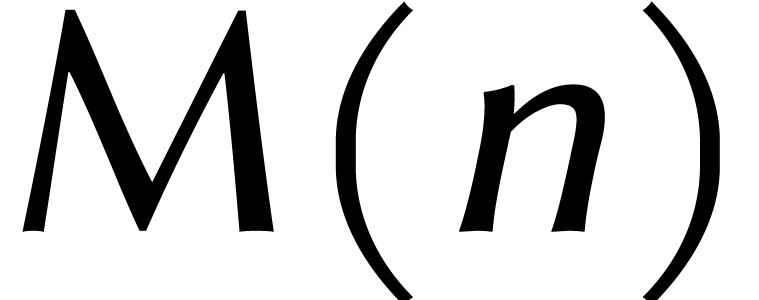 augmente aussi lentement que
possible en fonction de
augmente aussi lentement que
possible en fonction de 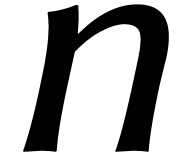 .
.
Prenons par exemple la méthode de l'école primaire, qui
consiste à multiplier chaque chiffre du premier nombre par chaque
chiffre du deuxième nombre, en ajoutant les résultats de
manière appropriée. Cela donne 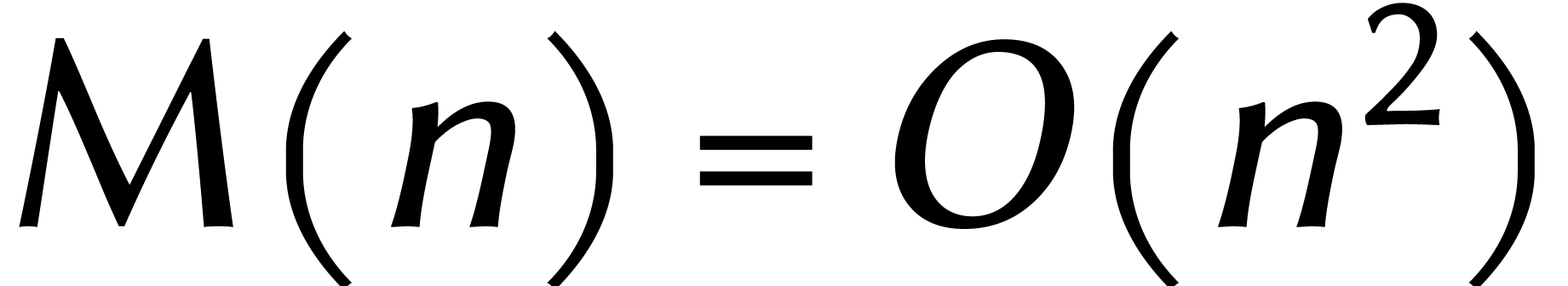 :
il existe une constante
:
il existe une constante 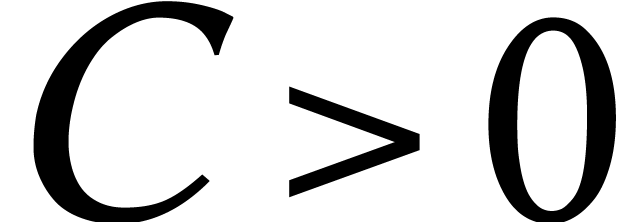 avec
avec 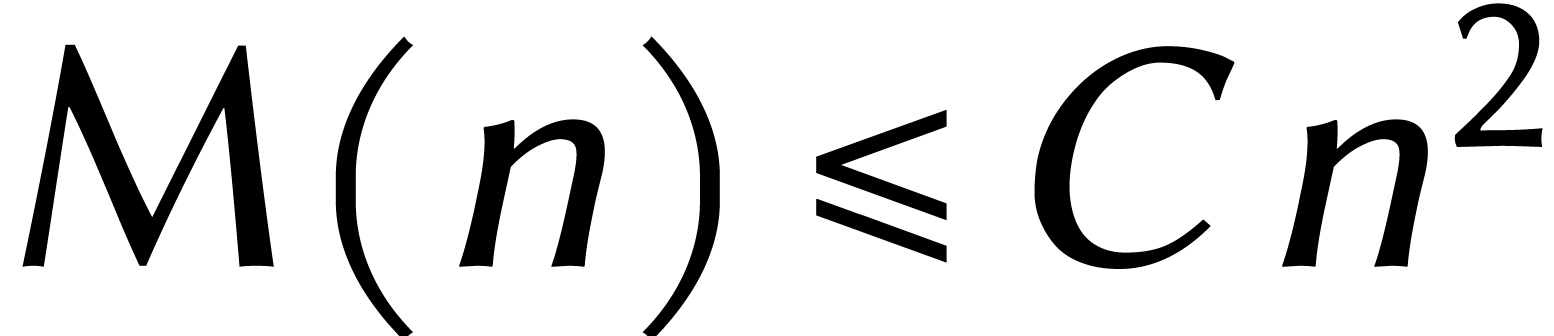 pour tout
pour tout 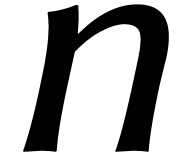 .
.
Afin de rendre notre question principale indépendante de la
machine de Turing en cher et en os sur laquelle nous faisons notre
calcul, nous nous intéressons uniquement au temps de calcul
à un facteur constant près. Une méthode 100 fois
plus rapide n'est donc pas une amélioration significative, mais
un algorithme 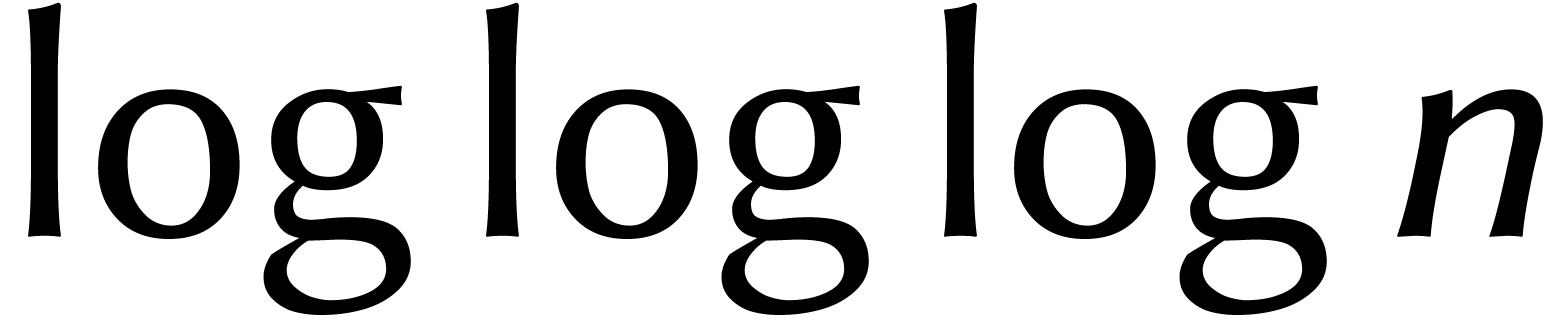 fois plus rapide est un
énorme pas en avant.
fois plus rapide est un
énorme pas en avant.
C'est probablement Kolmogorov
qui a été le premier à formuler notre problème ainsi, dans un séminaire célèbre à Moscou. Emporté par son enthousiasme, il avait également conjecturé que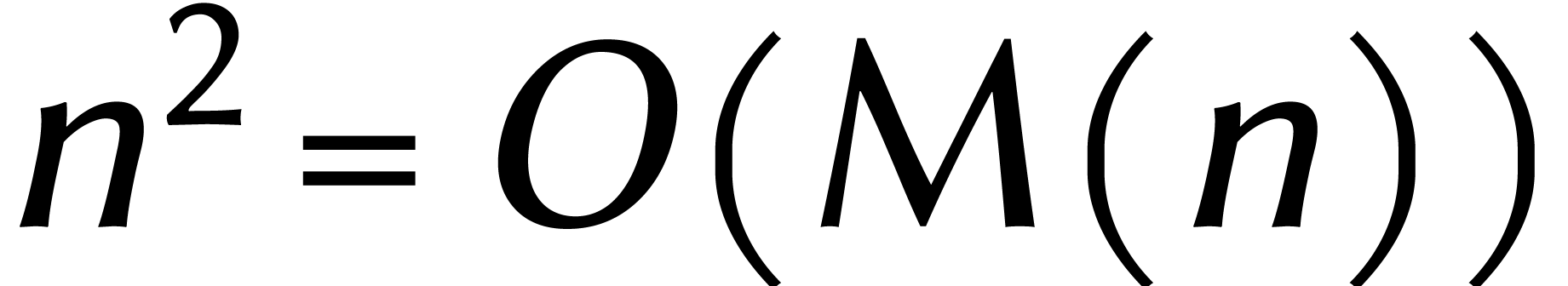 .
Car, raisonna-t-il, s'il y avait une meilleure méthode que celle
de l'école, on l'aurait bien trouvé depuis six mille ans.
.
Car, raisonna-t-il, s'il y avait une meilleure méthode que celle
de l'école, on l'aurait bien trouvé depuis six mille ans.
La formulation précise d'un problème facilite la recherche
de solutions. Mais l'absence d'une telle formulation n'exclut pas
d'éventuels progrès. Les Babyloniens ont
déjà calculé 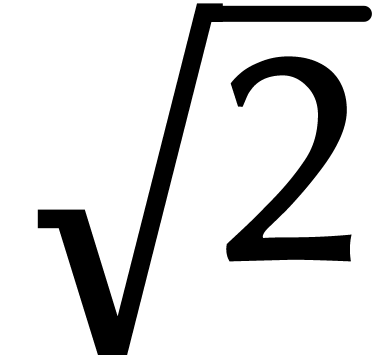 jusqu'à
seize chiffres derrière la virgule. Un jour, on trouvera
peut-être une tablette d'argile avec des méthodes
inédites de multiplication à grande vitesse. Les amateurs
du nombre π, comme mon compatriote Ludolph van Ceulen, auraient pu en
tirer profit (voir la figure 1).
jusqu'à
seize chiffres derrière la virgule. Un jour, on trouvera
peut-être une tablette d'argile avec des méthodes
inédites de multiplication à grande vitesse. Les amateurs
du nombre π, comme mon compatriote Ludolph van Ceulen, auraient pu en
tirer profit (voir la figure 1).
La conjecture de Kolmogorov ne fit pas long feu. Après trois
semaines, il a été surpris par un jeune
élève avec une méthode de multiplication en 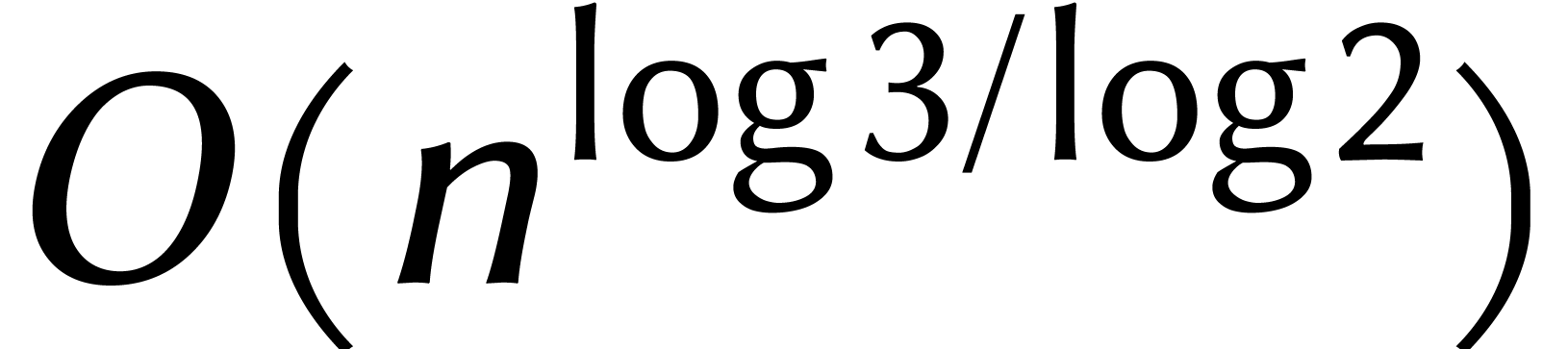 étapes. Kolmogorov rédigea
immédiatement cette nouvelle trouvaille, la publia sous le nom de
son créateur, Karatsuba, et la regroupa avec un autre article qui
n'avait rien à voir [18, 17].
étapes. Kolmogorov rédigea
immédiatement cette nouvelle trouvaille, la publia sous le nom de
son créateur, Karatsuba, et la regroupa avec un autre article qui
n'avait rien à voir [18, 17].
Expliquons l'idée de Karatsuba avec un exemple :
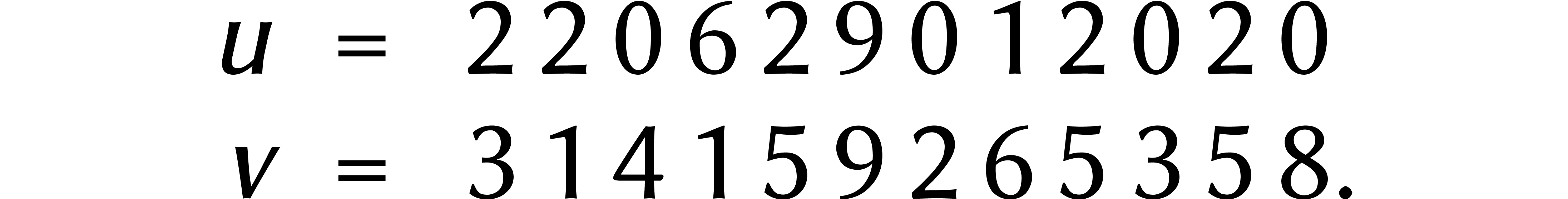
Nous commençons par couper les deux nombres en deux :
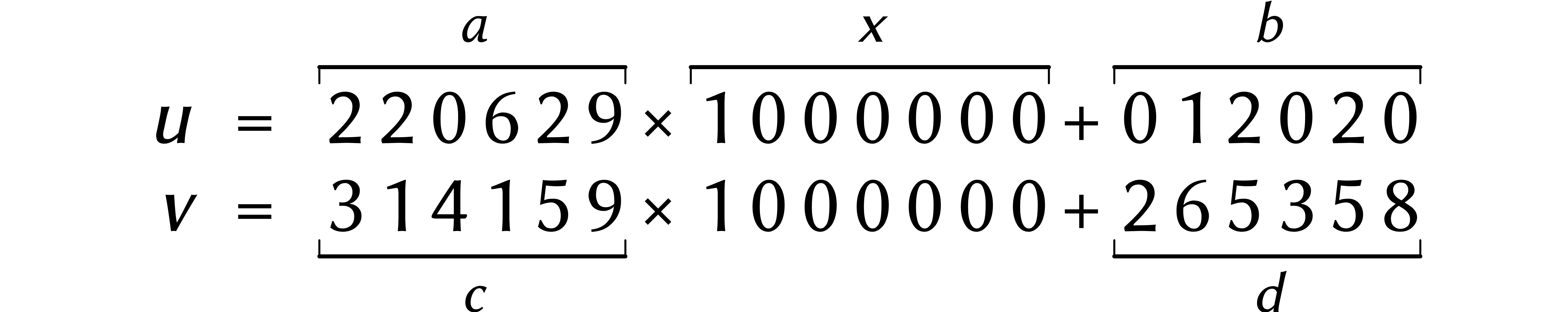
Ensuite, nous faisons deux additions et trois multiplications :
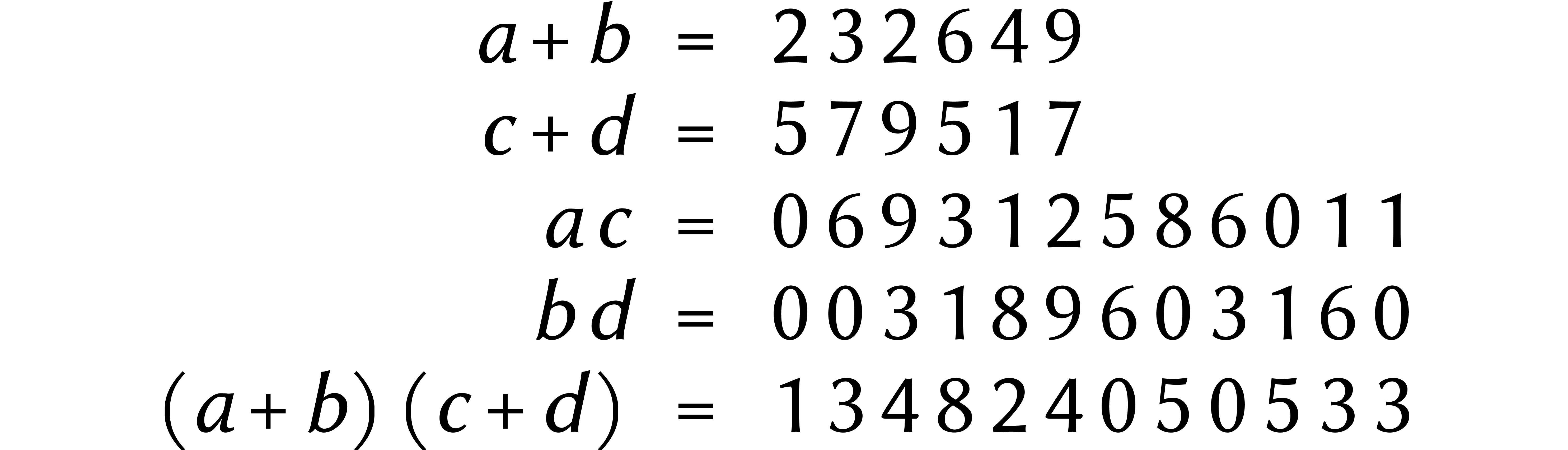
Maintenant, nous remarquons qu'il suffit de deux soustractions pour trouver
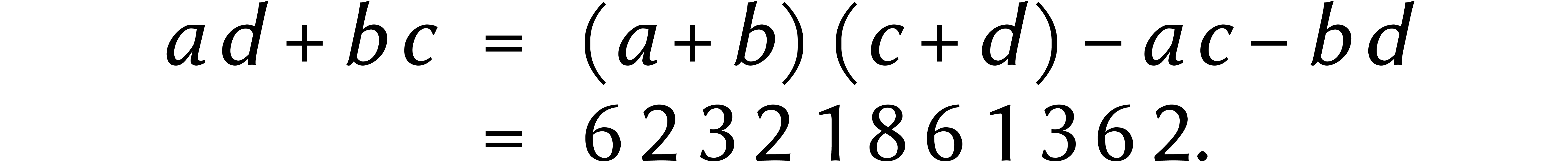
Enfin, on a
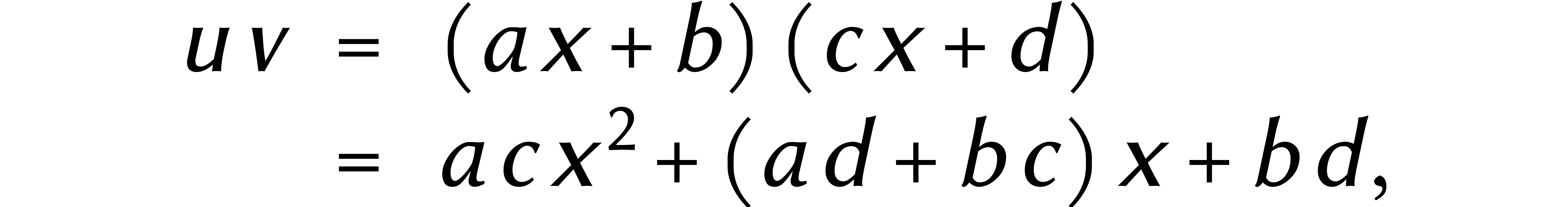
et on termine avec une dernière addition :
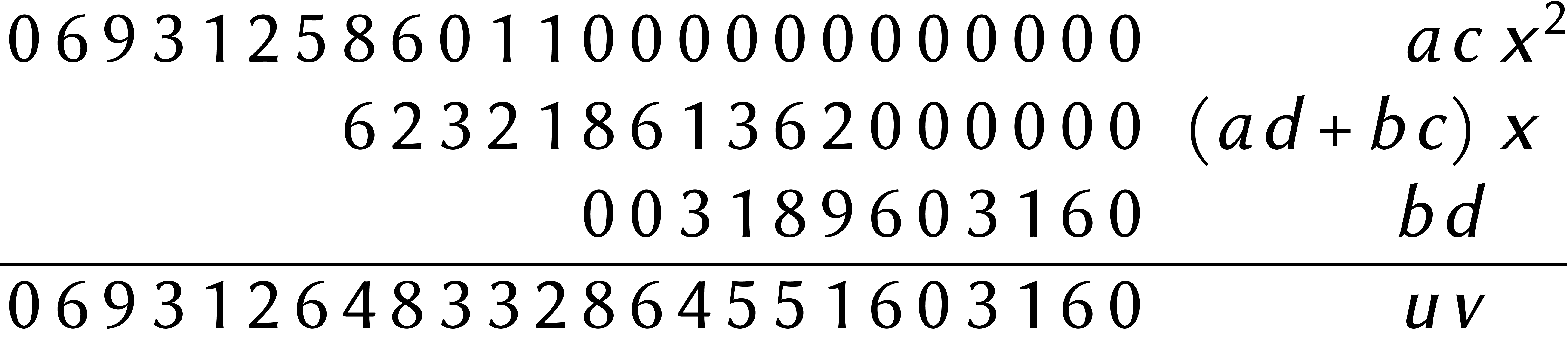
Au final, nous avons réduit une multiplication à 12 chiffres à trois multiplications à 6 chiffres et quelques additions et soustractions.
En général, multiplier des nombres deux fois plus longs prend environ trois fois plus de temps. Plus précisément, on a l'« inégalité récurrente » suivante :
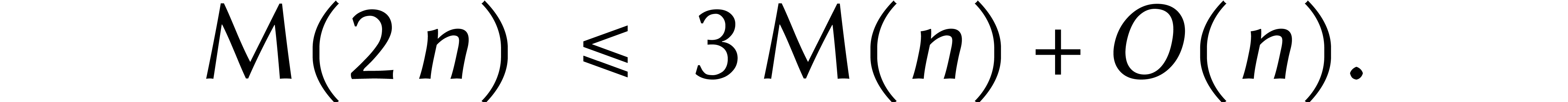
Pour une certaine constante  et pour
et pour 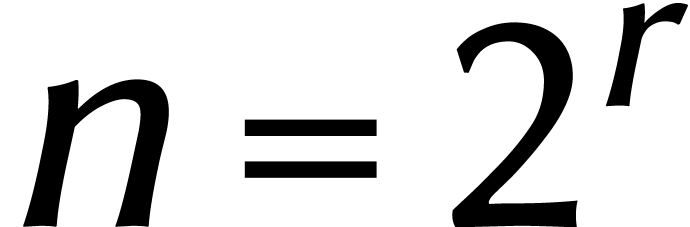 , nous avons donc
, nous avons donc
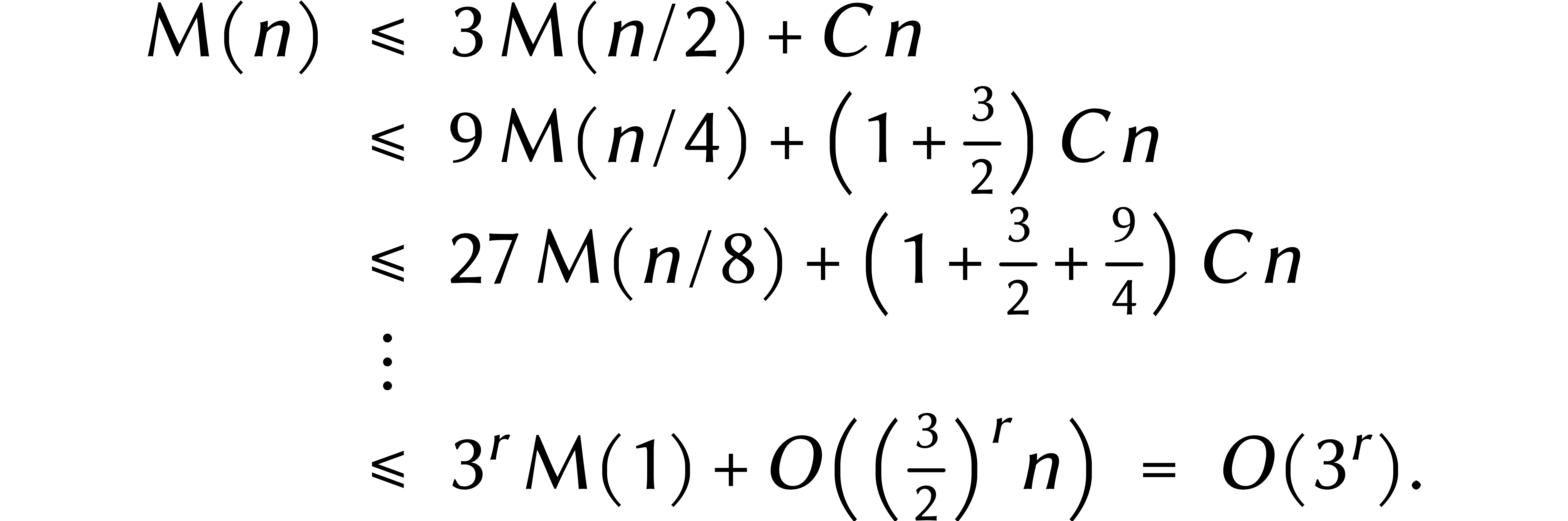
Or nous pouvons toujours rajouter des zéros à gauche d'un nombre afin que son nombre de chiffres devienne une puissance de deux. En fin de compte, ceci prouve
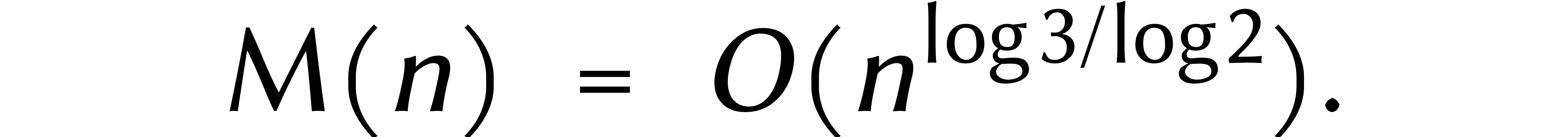
L'un des ingrédients de la méthode de Karatsuba est de
couper les nombres en deux morceaux. Cela permet de voir  et
et  comme des polynômes
comme des polynômes 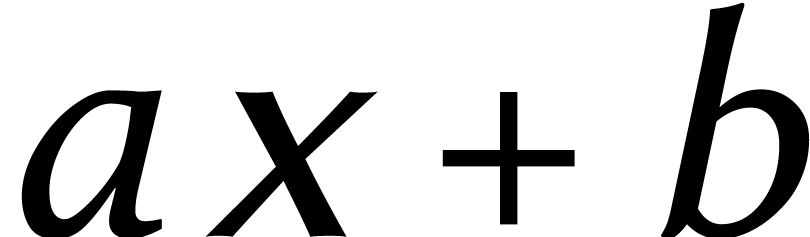 et
et 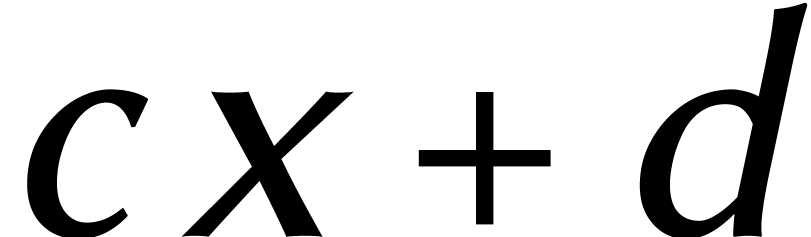 de degré <2. En
fait, cela revient simplement à travailler en base x = 1000000 au
lieu de 10.
de degré <2. En
fait, cela revient simplement à travailler en base x = 1000000 au
lieu de 10.
L'idée de remplacer l'arithmétique entière par
l'arithmétique polynomiale a déjà été
suggérée par Kronecker au 19ème
siècle. Par exemple, nous pouvons couper un nombre de 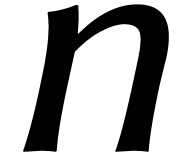 chiffres en
chiffres en  morceaux de
morceaux de 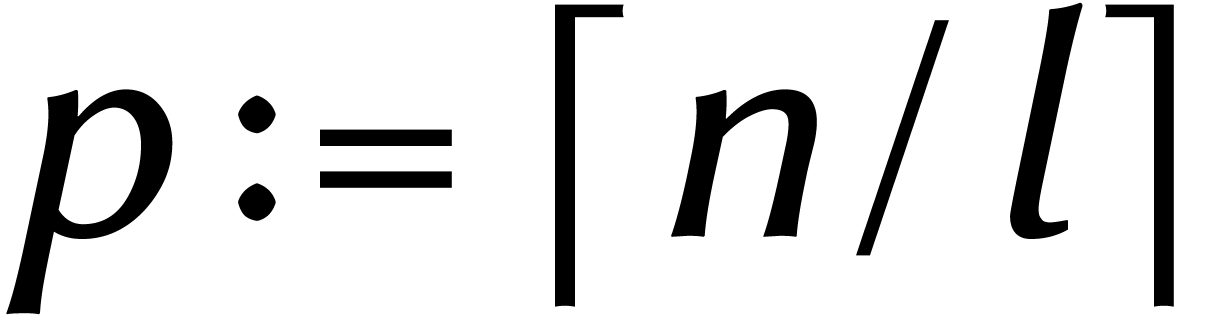 chiffres et réinterpréter le
résultat comme un polynôme.
chiffres et réinterpréter le
résultat comme un polynôme.
Dans les années 1960, on a développé une
série d'améliorations de la méthode de Karatsuba,
en prenant le nombre de morceaux
 supérieur à deux [
24
,
22
,
19
] ; voir le tableau
1
pour un aperçu historique.
supérieur à deux [
24
,
22
,
19
] ; voir le tableau
1
pour un aperçu historique.
|
||||||||||||||||||||||||||||||||||||||||
Sans entrer dans les détails, chacune de ces améliorations
est basée sur une généralisation de l'astuce de
Karatsuba. La multiplication de deux polynômes de degré
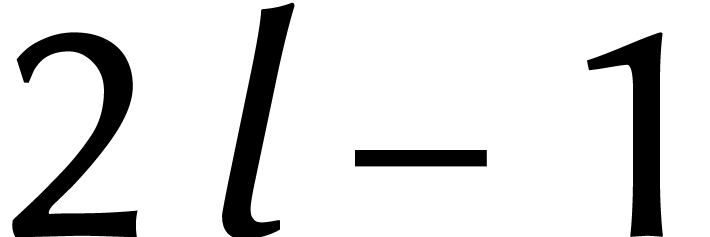 se réduit alors à
se réduit alors à 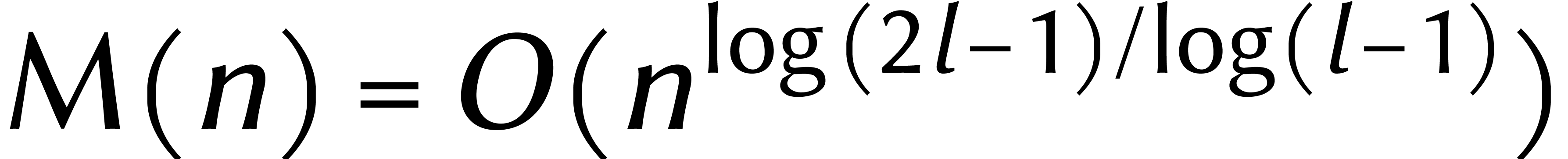 multiplications de coefficients, après quoi
multiplications de coefficients, après quoi 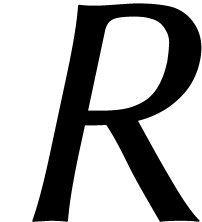 .
.
Désormais, nous nous focaliserons principalement sur la
multiplication de polynômes et il est utile de travailler avec des
coefficients dans un anneau général 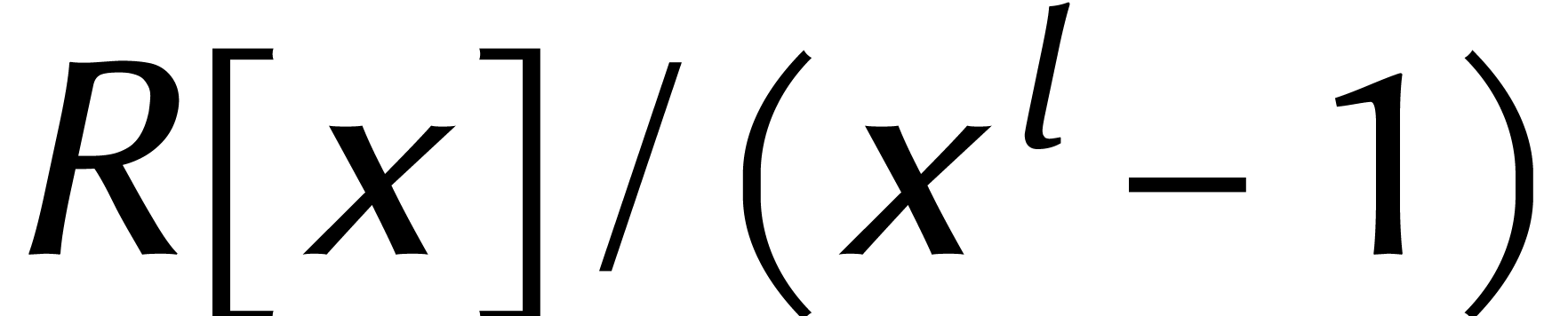 . Nous laissons de côté le choix
précis de
. Nous laissons de côté le choix
précis de 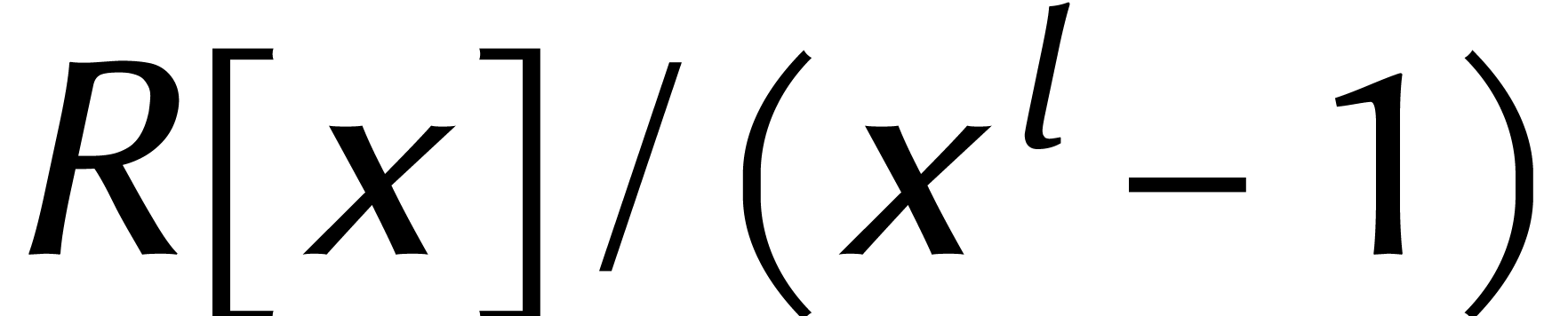 , pour
l'instant.
, pour
l'instant.
Pour la suite, il est également utile de travailler avec des
« cyclonômes » au lieu de polynômes. Un
cyclonôme de degré  est un
élément de
est un
élément de 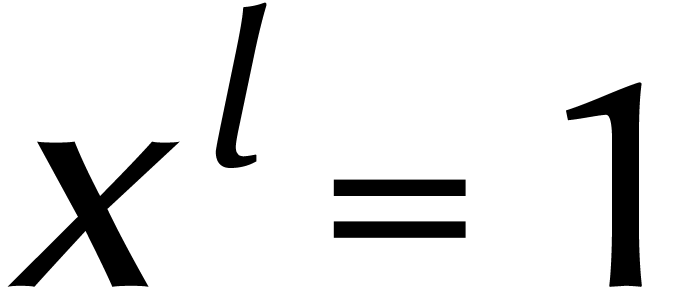 .
.
La relation 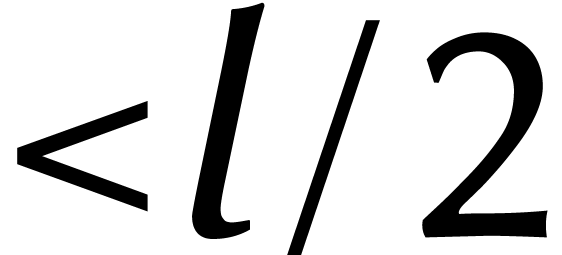 n'entre en action que lorsque le
degré d'un polynôme excède
n'entre en action que lorsque le
degré d'un polynôme excède  . Le produit de deux polynômes de degré
. Le produit de deux polynômes de degré
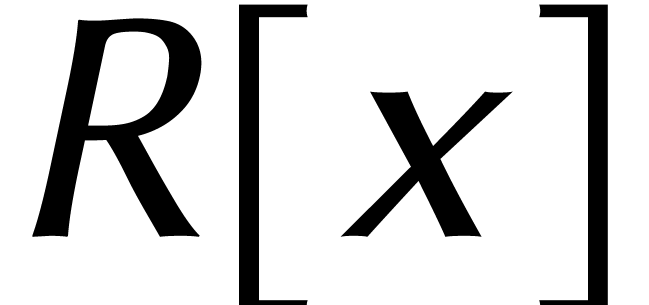 dans
dans 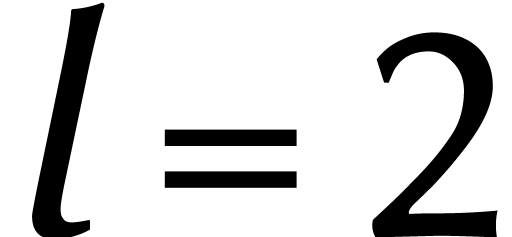 peut ainsi tout
aussi bien se calculer dans
peut ainsi tout
aussi bien se calculer dans 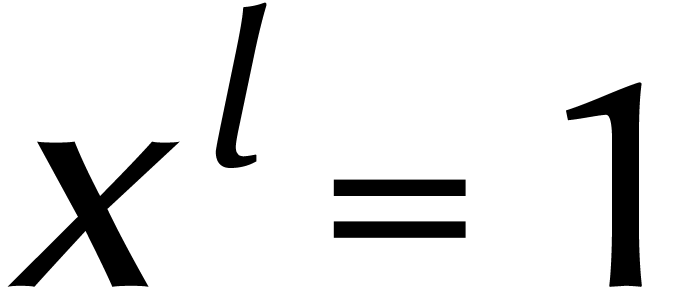 .
.
L'avantage des cyclonômes est que nous avons de nouvelles astuces
de calcul à notre disposition. Par exemple, supposons que 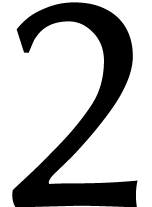 et que
et que 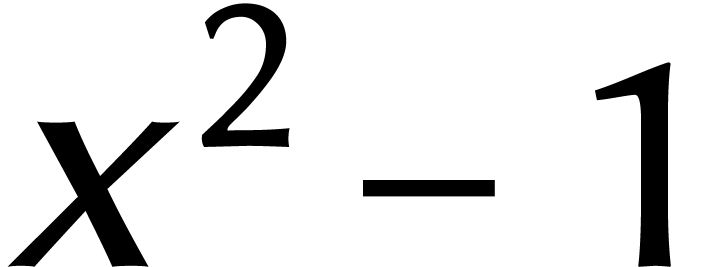 soit inversible dans
soit inversible dans
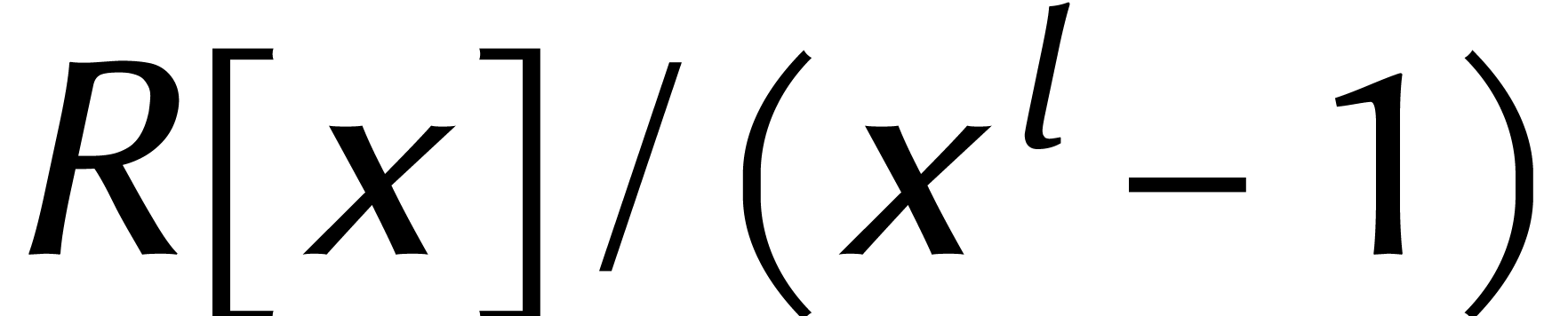 . Alors il devient possible
d'optimiser la méthode de Karatsuba : modulo
. Alors il devient possible
d'optimiser la méthode de Karatsuba : modulo 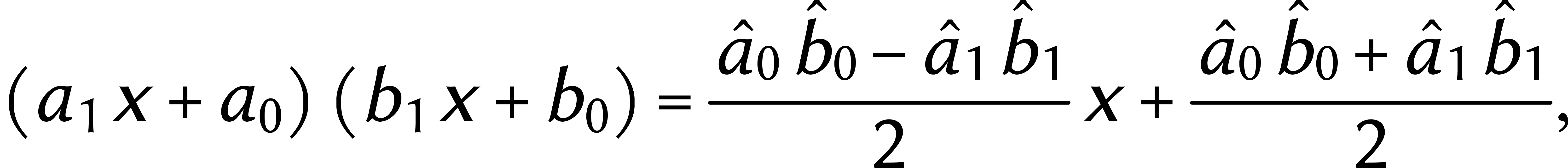 on a
on a
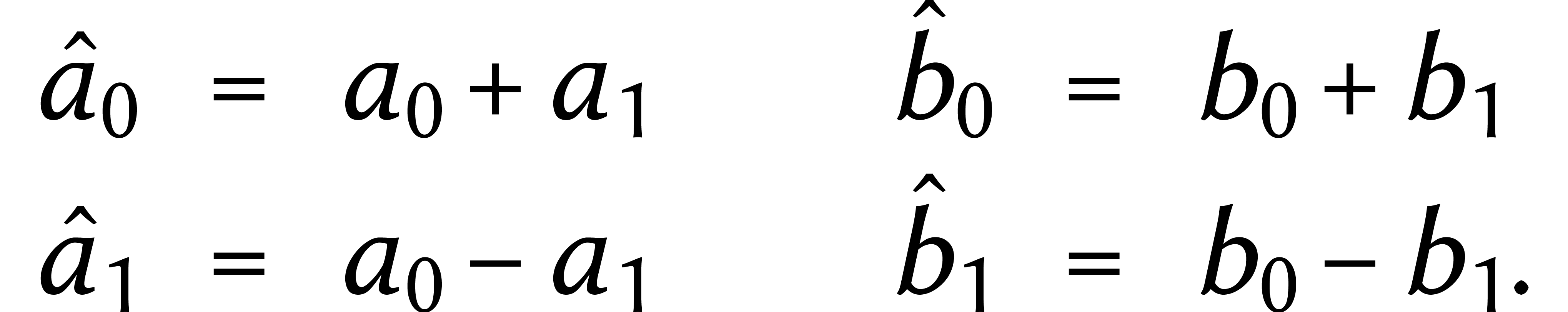
où
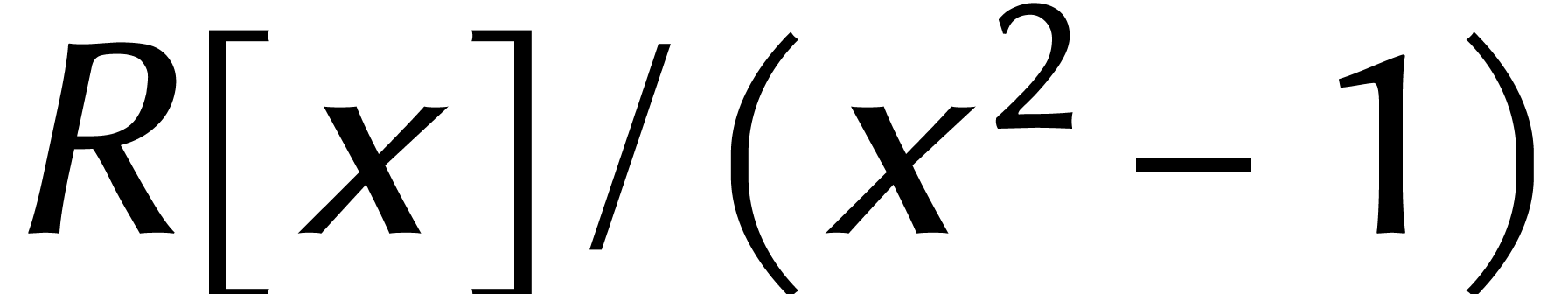
Dans 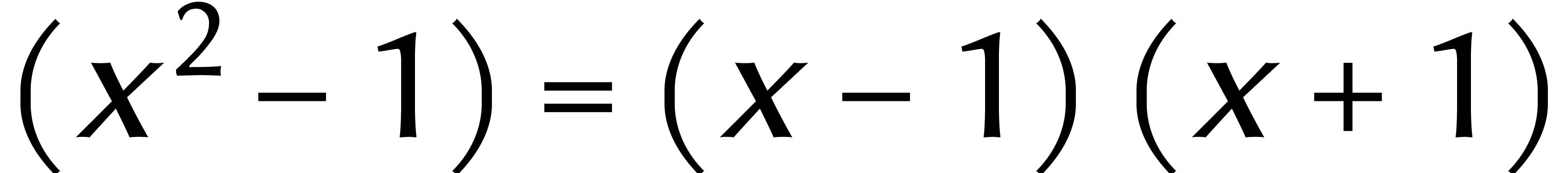 , le calcul d'un produit
ne nécessite donc que deux multiplications dans
, le calcul d'un produit
ne nécessite donc que deux multiplications dans 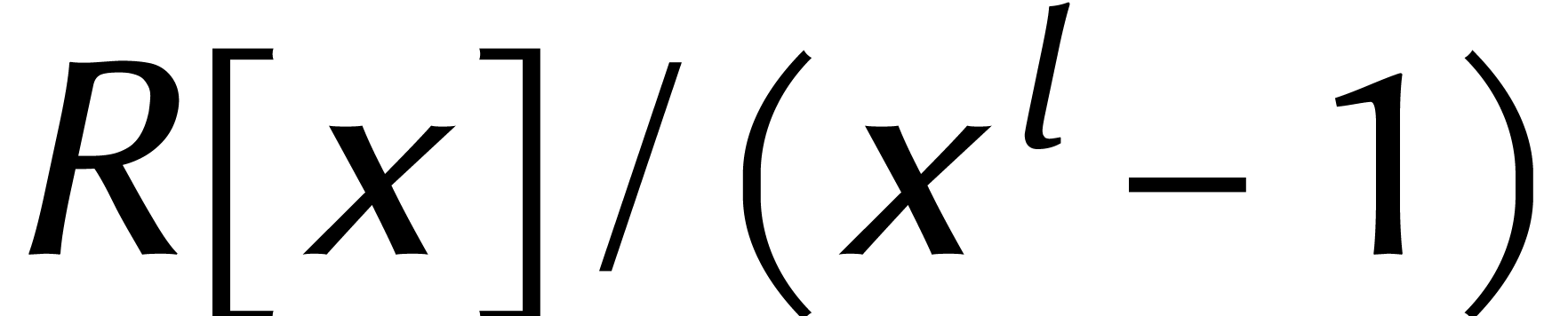 . Il y a aussi un certain nombre d'additions,
de soustractions et de divisions par deux.
. Il y a aussi un certain nombre d'additions,
de soustractions et de divisions par deux.
Les relations ci-dessus viennent de la factorisation
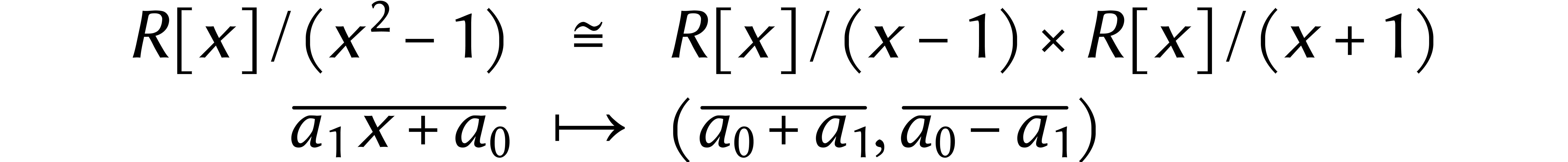 |
(1) |
et de l'application du théorème des restes chinois à celle-ci :
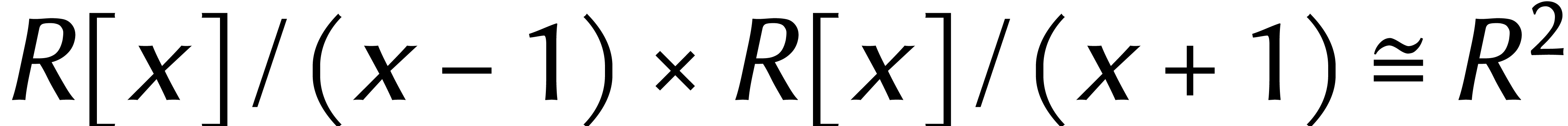
Cela permet de remplacer les calculs arbitraires dans 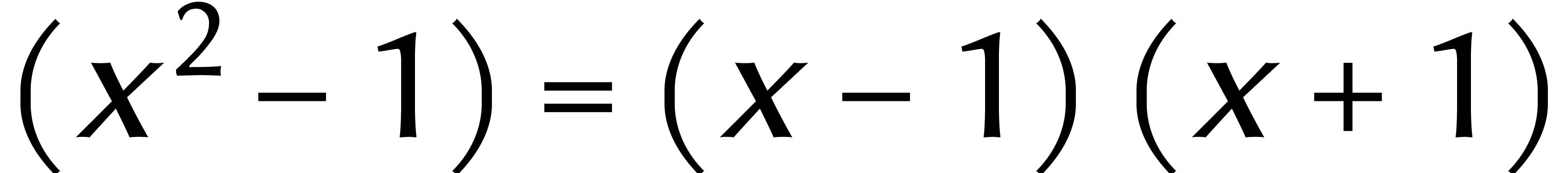 par des calculs dans
par des calculs dans 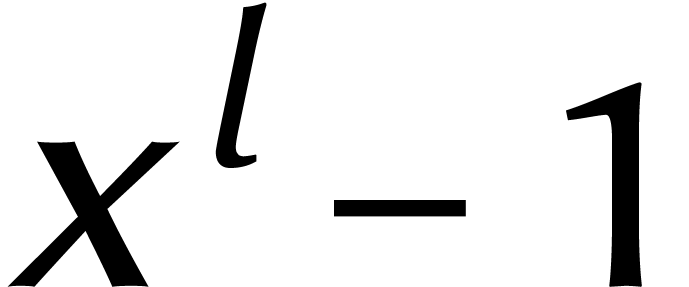 .
.
La factorisation (1) est valable pour chaque anneau 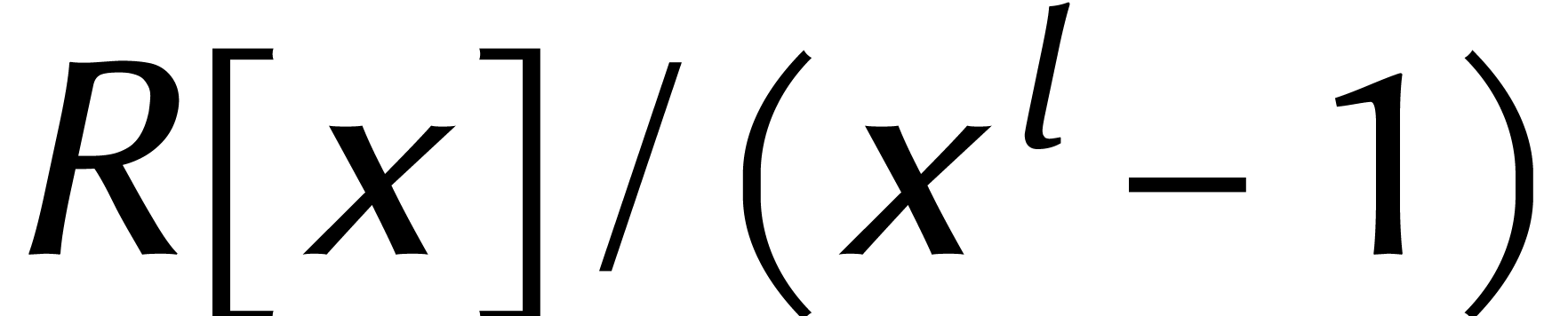 . Dans certains anneaux, le
polynôme
. Dans certains anneaux, le
polynôme 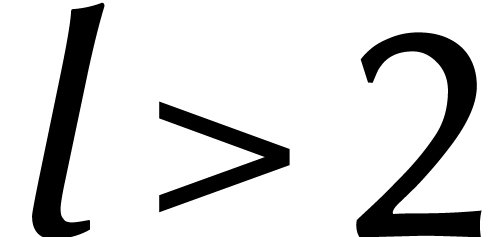 se scinde de la même
manière en facteurs linéaires pour certains
se scinde de la même
manière en facteurs linéaires pour certains 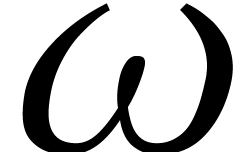 . Cela arrive dès que
. Cela arrive dès que 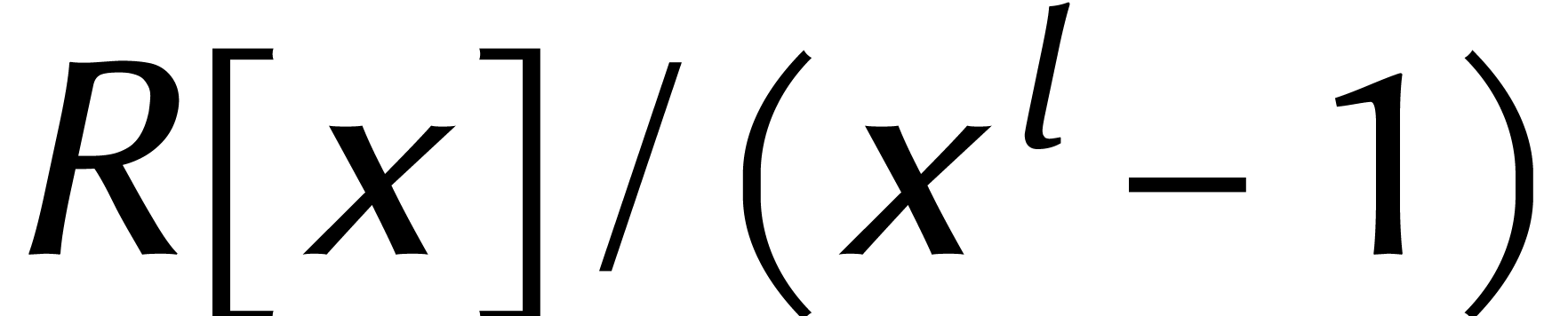 admet un élément
admet un élément 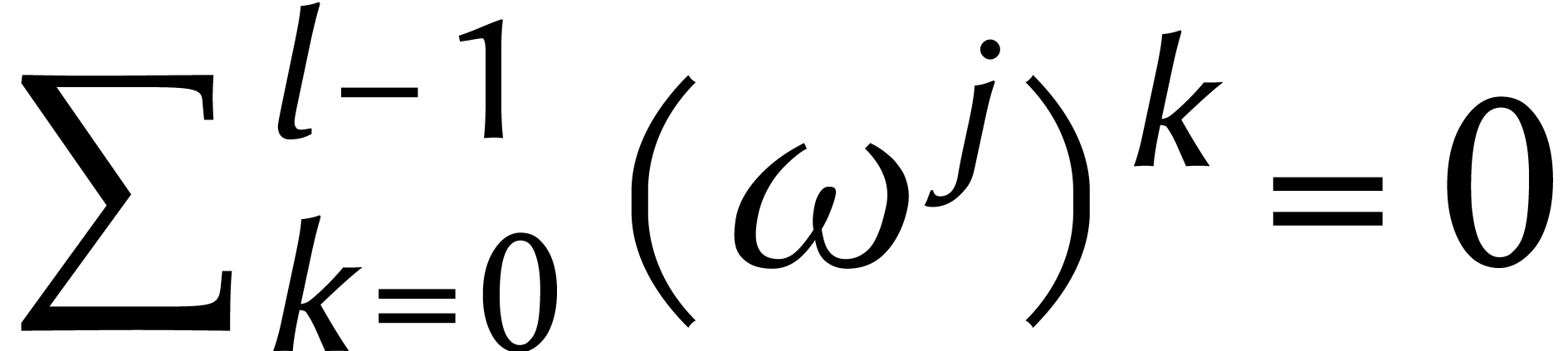 avec
avec  pour
pour 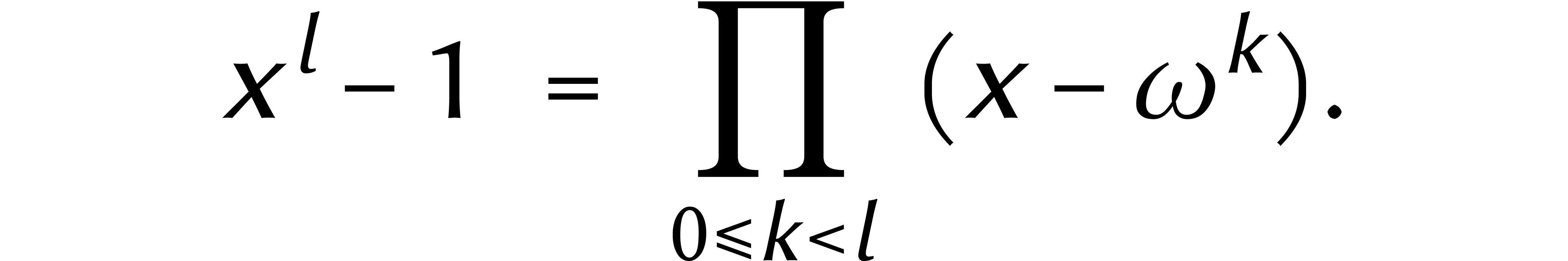 . Un tel
élément
. Un tel
élément 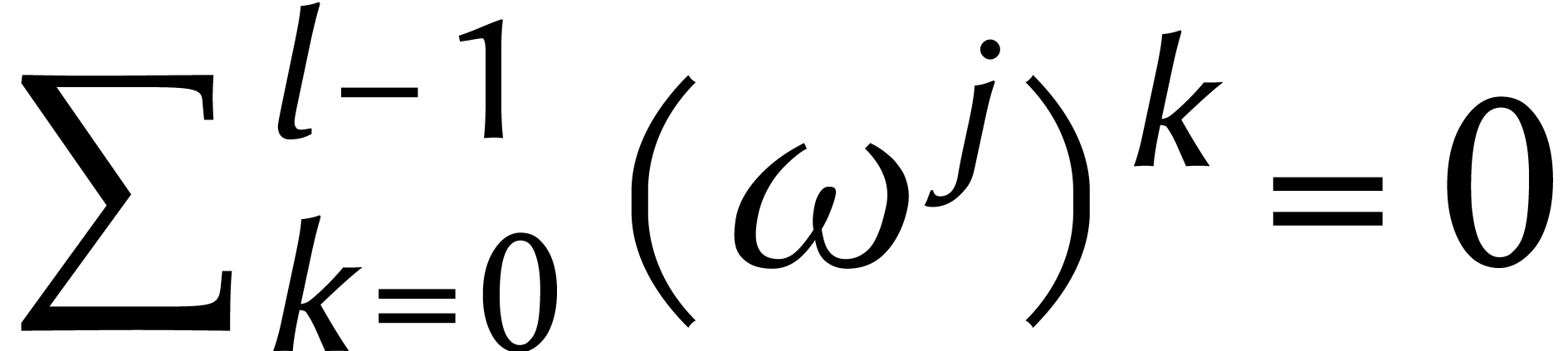 est appelé racine
principale d'unité d'ordre
est appelé racine
principale d'unité d'ordre  et conduit
à la factorisation
et conduit
à la factorisation
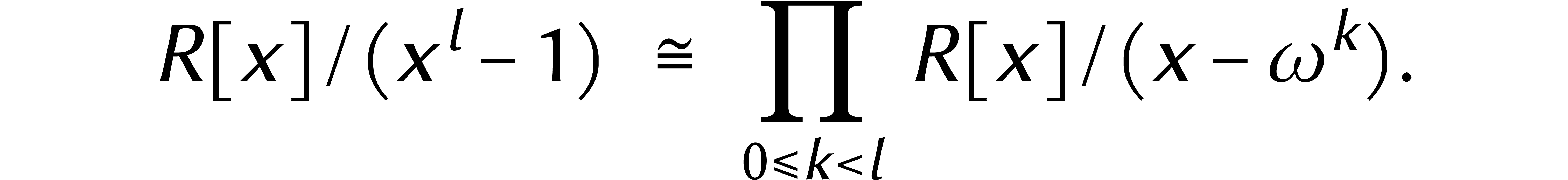
Si  est également inversible dans
est également inversible dans 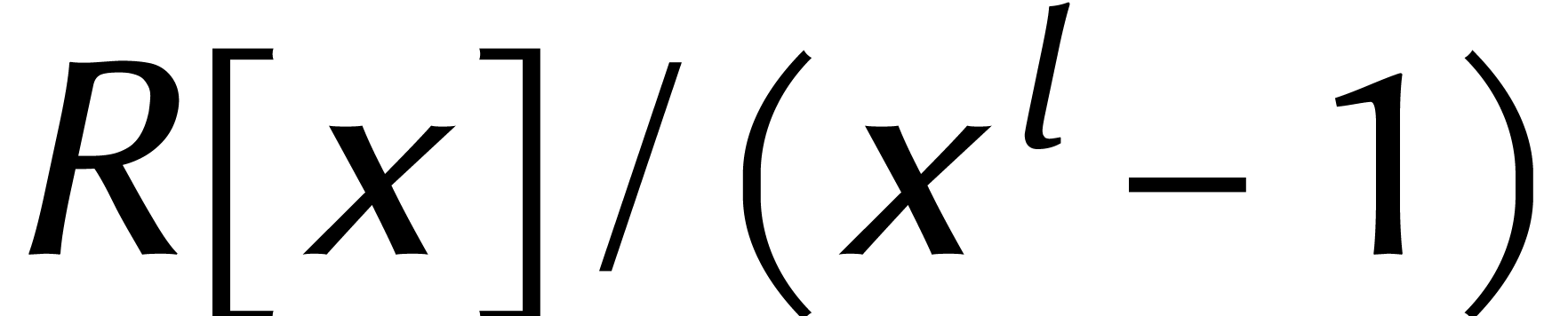 , alors le théorème
des restes chinois donne :
, alors le théorème
des restes chinois donne :

De gauche à droite, cet isomorphisme est appelé
transformée de Fourier discrète ou DFT. Pour tout
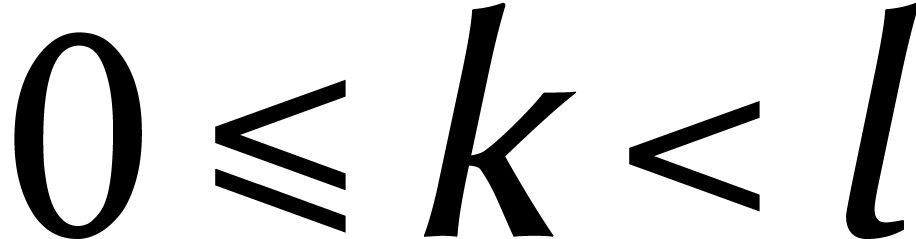 et
et 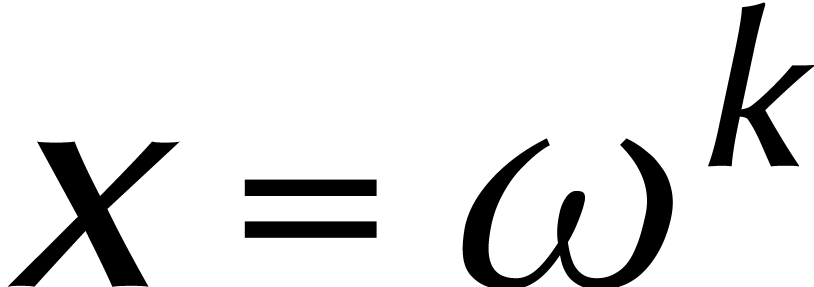 on a
on a 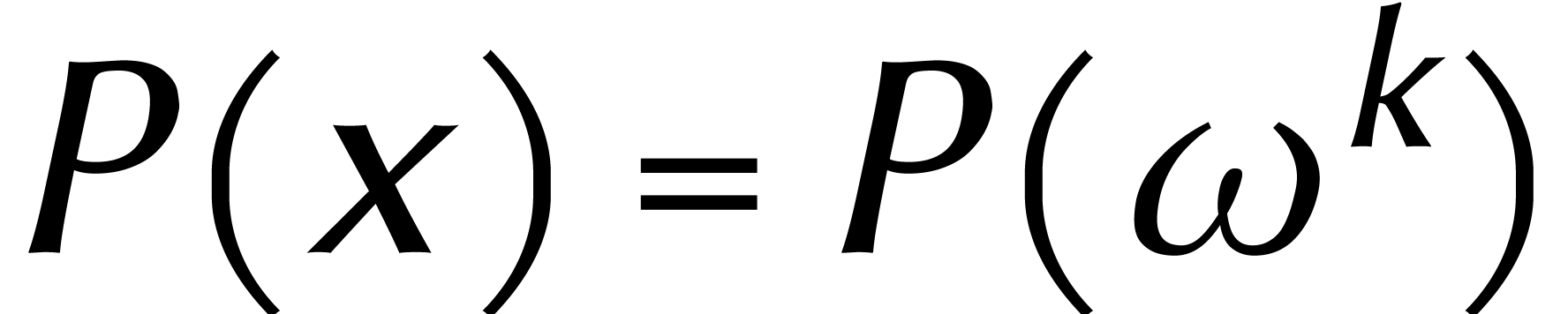 et
et 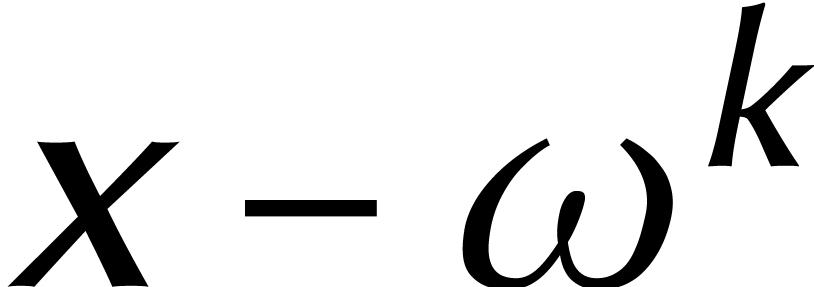 modulo
modulo 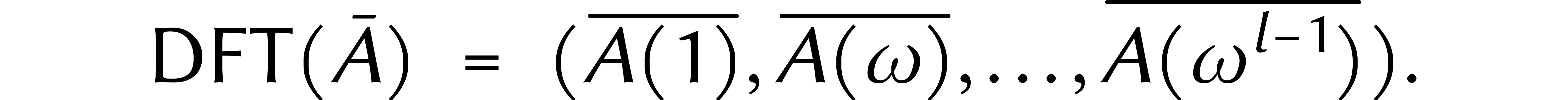 ,
donc
,
donc
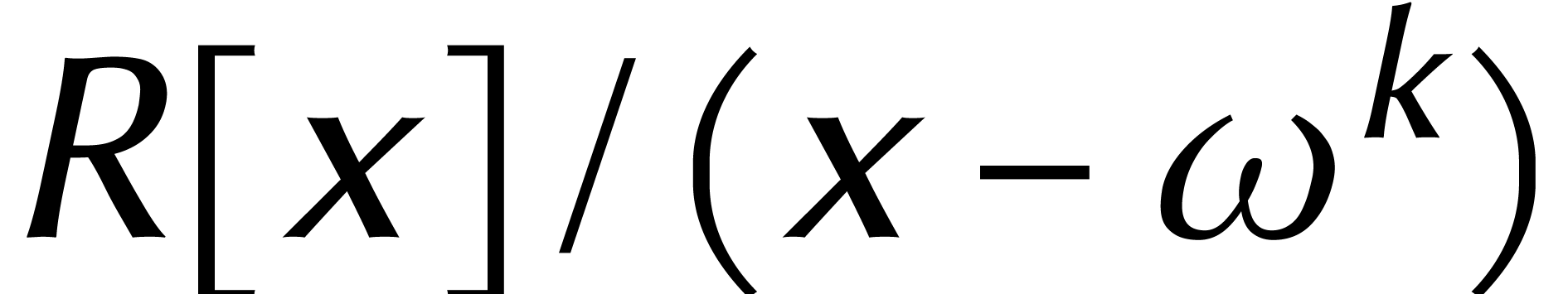
L'algèbre 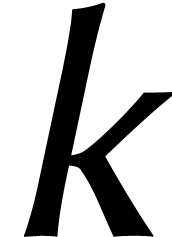 est à son tour isomorphe
à
est à son tour isomorphe
à 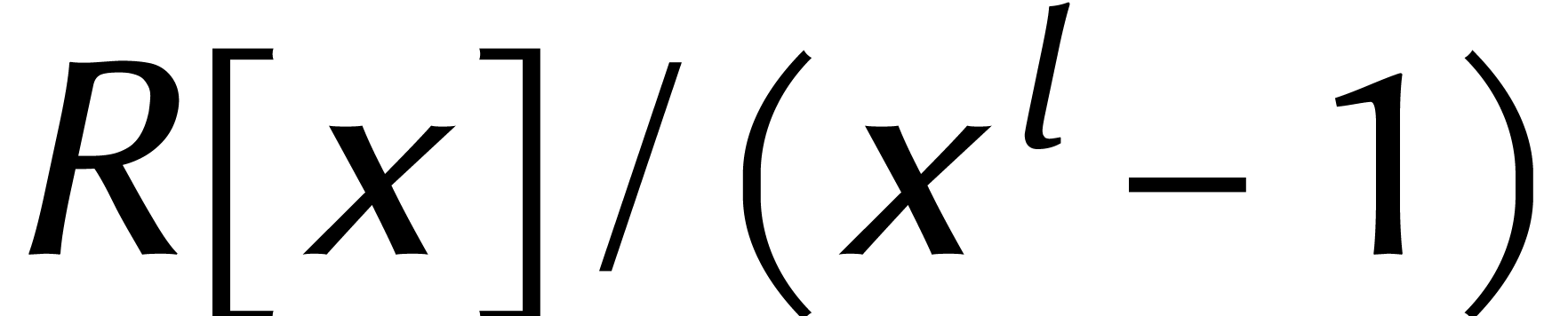 pour tout
pour tout 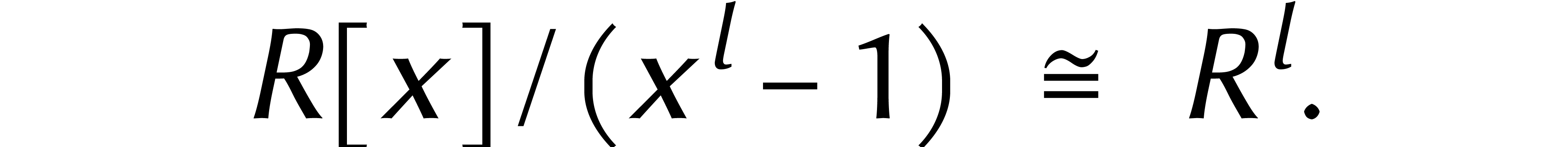 ,
d'où
,
d'où
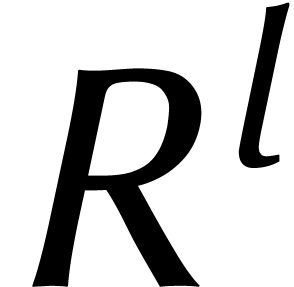
Or des calculs dans l'anneau  se font à
moindre frais : une multiplication dans
se font à
moindre frais : une multiplication dans  équivaut par exemple à
équivaut par exemple à  multiplications dans
multiplications dans 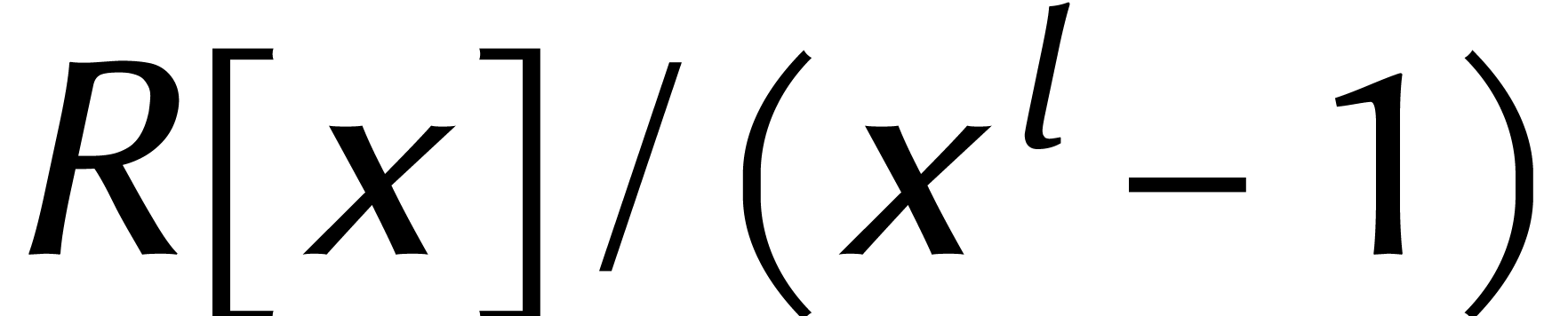 . Si
nous disposions d'algorithmes efficaces à la fois pour la
. Si
nous disposions d'algorithmes efficaces à la fois pour la  et son inverse
et son inverse 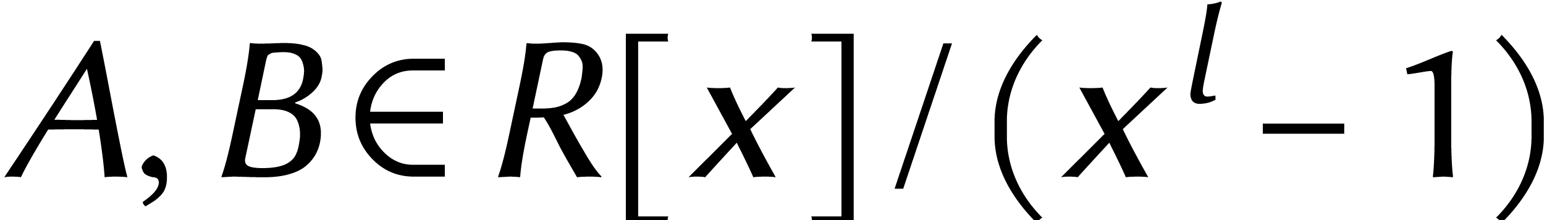 ,
alors cela donnerait une bonne méthode pour multiplier des
cyclonômes
,
alors cela donnerait une bonne méthode pour multiplier des
cyclonômes 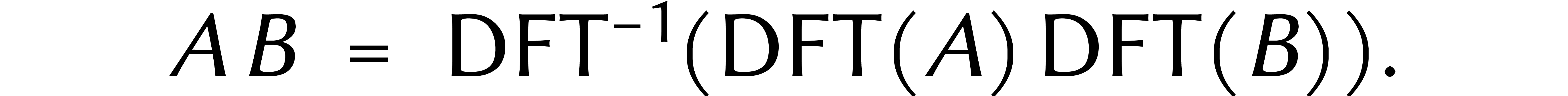 :
:
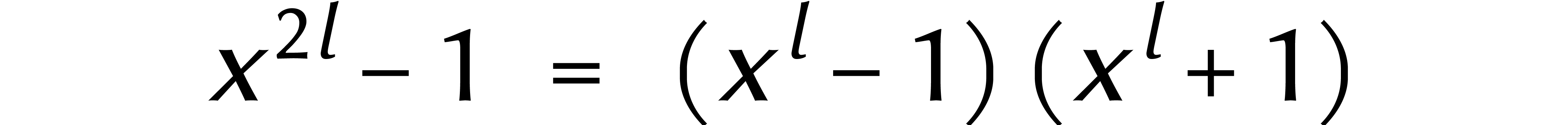
Cela s'appelle la multiplication FFT.
Mais comment calculer rapidement une telle DFT ? Nous avons
déjà étudié le cas 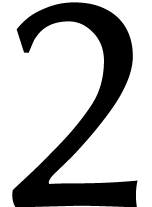 . Plus généralement, la factorisation
. Plus généralement, la factorisation
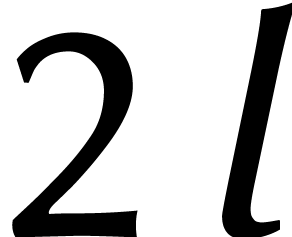
pour des degrés pairs 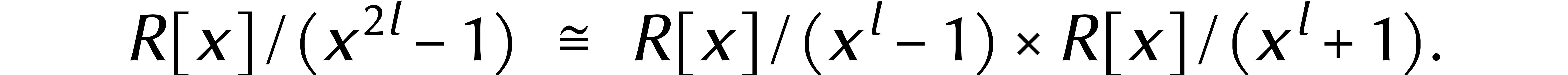 induit
l'isomorphisme
induit
l'isomorphisme

Si 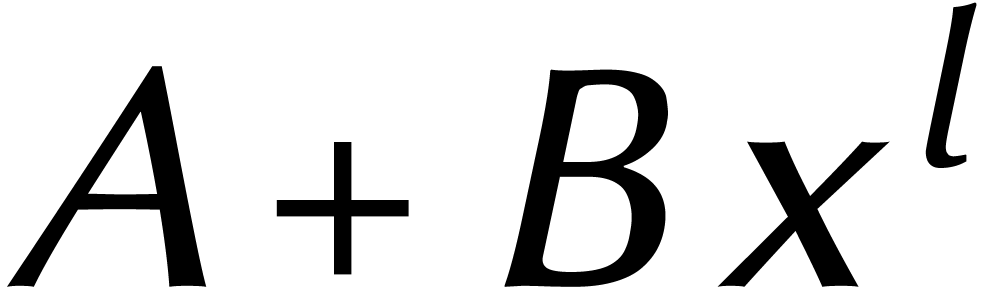 sont des polynômes de degré
sont des polynômes de degré
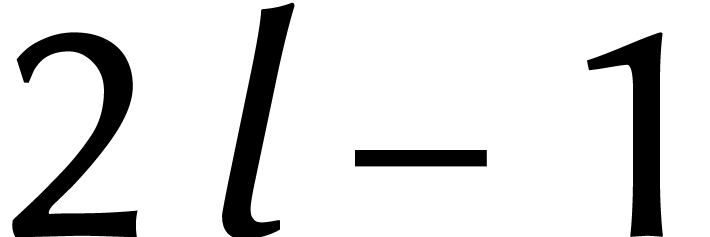 , alors cet isomorphisme
envoie
, alors cet isomorphisme
envoie 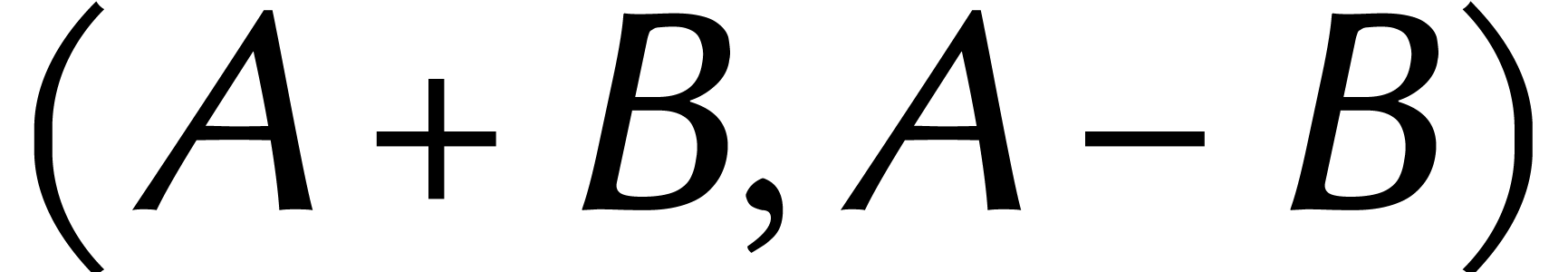 vers
vers  ; pour la
lisibilité, nous omettons désormais les barres des
modulos. Calculer
; pour la
lisibilité, nous omettons désormais les barres des
modulos. Calculer 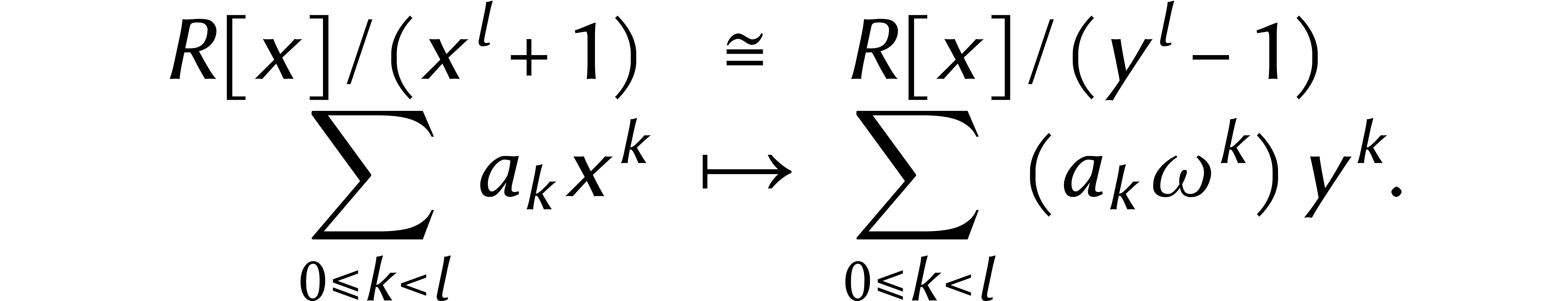 revient à additionner
et soustraire
revient à additionner
et soustraire  fois dans
fois dans 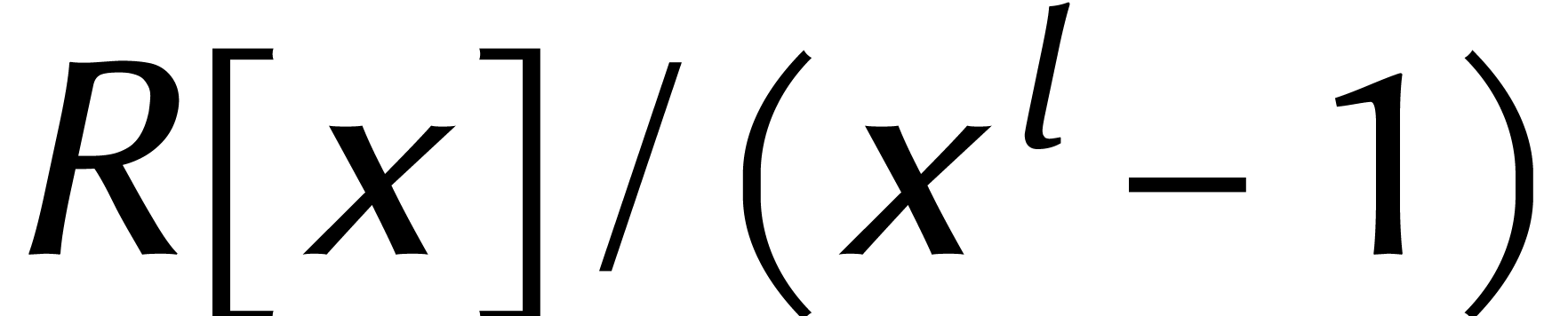 . Pour l'isomorphisme dans l'autre sens, il faut
rajouter
. Pour l'isomorphisme dans l'autre sens, il faut
rajouter 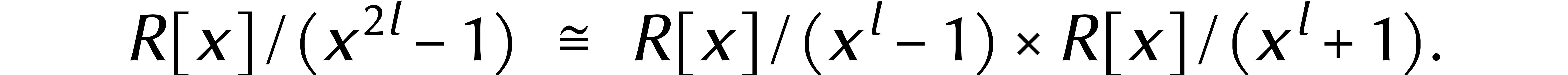 divisions par deux.
divisions par deux.
Si 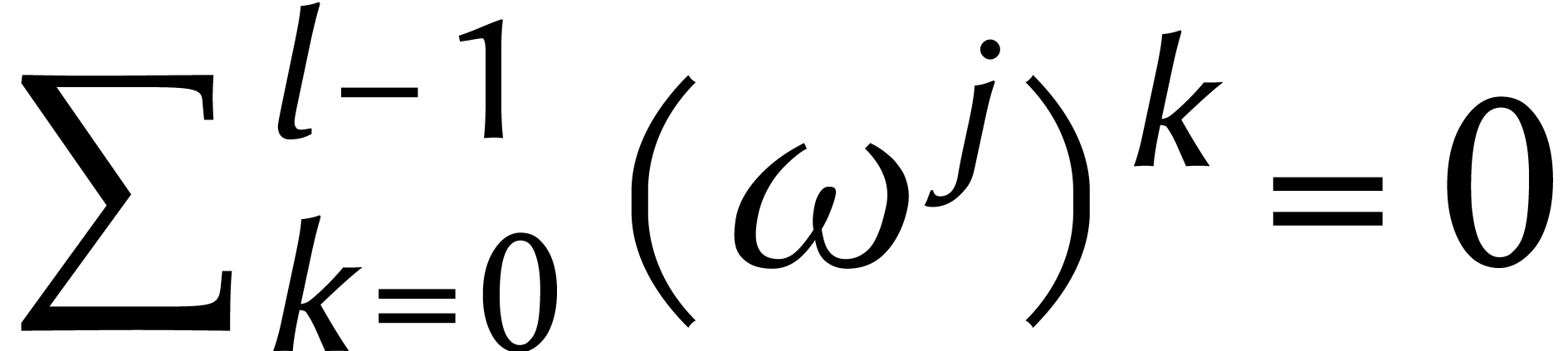 est une racine principale d'unité
d'ordre
est une racine principale d'unité
d'ordre 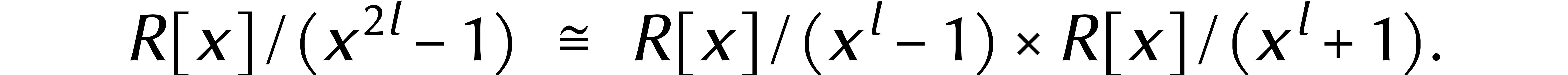 , on a en outre
l'isomorphisme suivant :
, on a en outre
l'isomorphisme suivant :
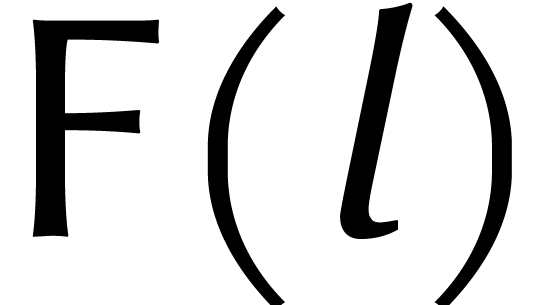
Le calcul de cet isomorphisme se réduit à  multiplications par des puissances de
multiplications par des puissances de 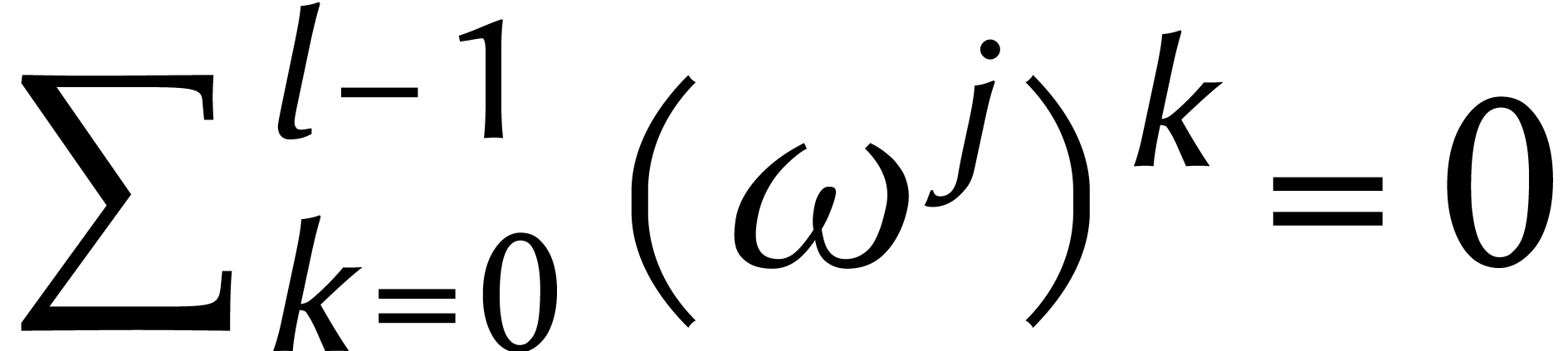 .
Ici, il est important de noter qu'une multiplication par une puissance
de
.
Ici, il est important de noter qu'une multiplication par une puissance
de 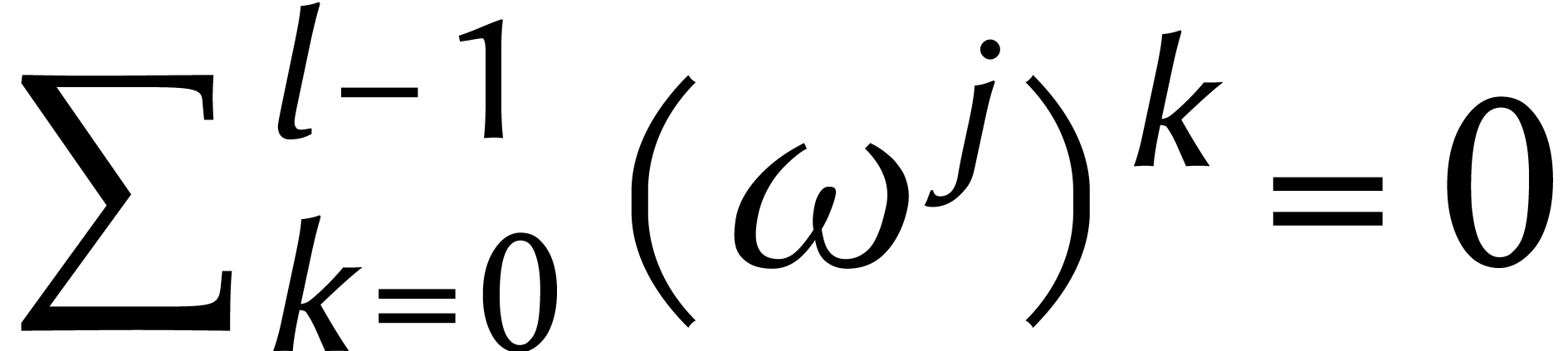 est parfois moins chère qu'une
multiplication arbitraire dans
est parfois moins chère qu'une
multiplication arbitraire dans 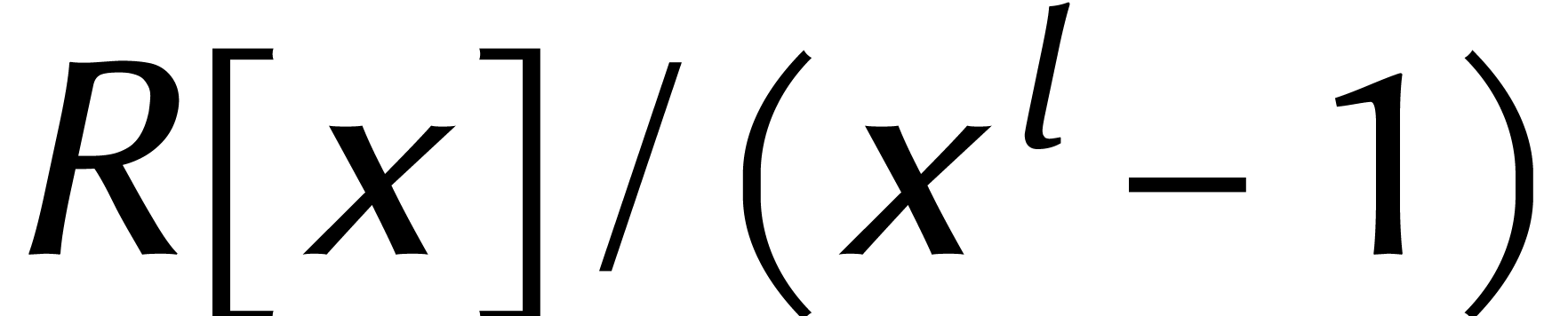 (voir plus bas).
(voir plus bas).
En résumé, cela montre comment une DFT de longueur 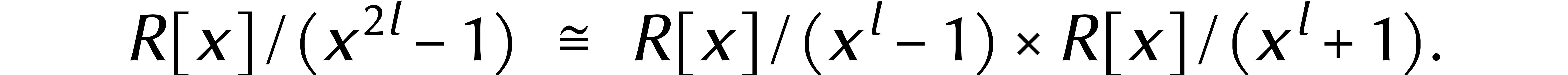 peut être réduite à deux DFTs de
longueur
peut être réduite à deux DFTs de
longueur  . Si on écrit
. Si on écrit
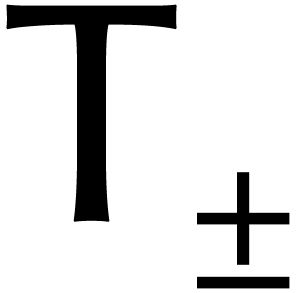 pour le temps qu'il faut pour calculer une DFT
de longueur
pour le temps qu'il faut pour calculer une DFT
de longueur  , puis
, puis  pour le temps d'une addition ou d'une soustraction dans R,
et
pour le temps d'une addition ou d'une soustraction dans R,
et 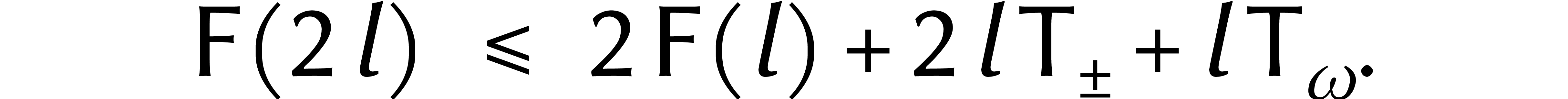 pour le temps d'une multiplication par une
puissance de
pour le temps d'une multiplication par une
puissance de 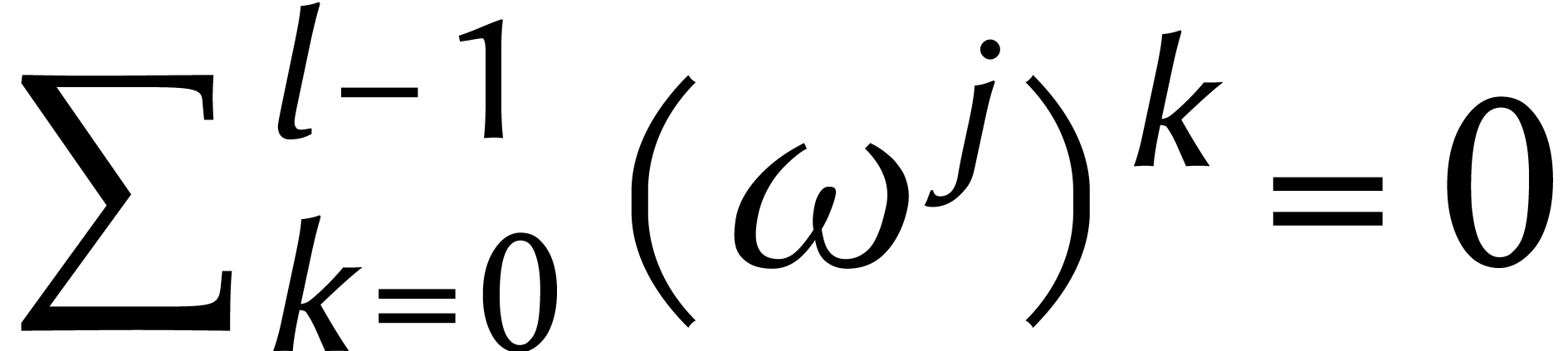 , alors nous
avons
, alors nous
avons
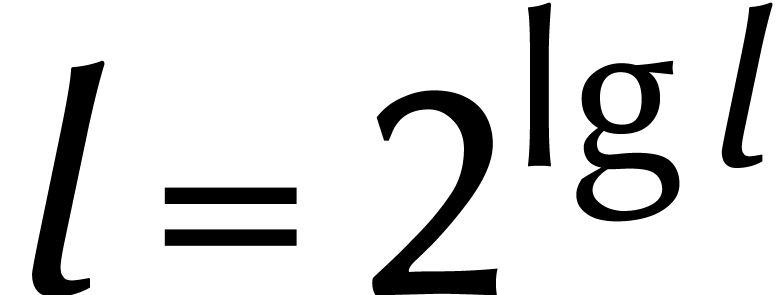
En appliquant cette formule récursivement dans le cas où
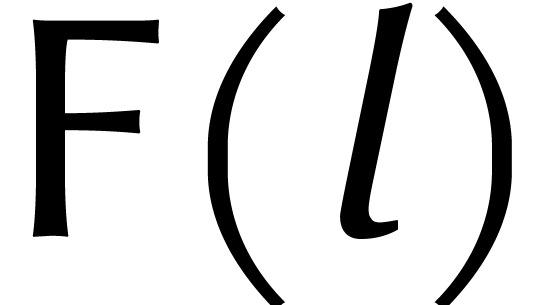 est une puissance de deux, nous obtenons
est une puissance de deux, nous obtenons
Pour la transformation inverse, il faut rajouter  divisions par
divisions par  .
.
Avant de continuer, c'est un bon moment pour quelques commentaires. La FFT a percé en 1965, après la publication de l'article de Cooley et Tukey [3]. Mais une méthode similaire avait déjà été décrite dans des travaux non publiés de Gauss [6, 14].
Par ailleurs, nous avons vu qu'une multiplication de cyclonômes
peut être réduite à deux DFT directes plus une DFT
inverse. En 1970, Bluestein a noté qu'une DFT de longueur  peut également être réduite
à un produit de cyclonômes de même degré
peut également être réduite
à un produit de cyclonômes de même degré  [2].
[2].
Pour expliquer cela, supposons pour simplifier que  est pair et que
est pair et que 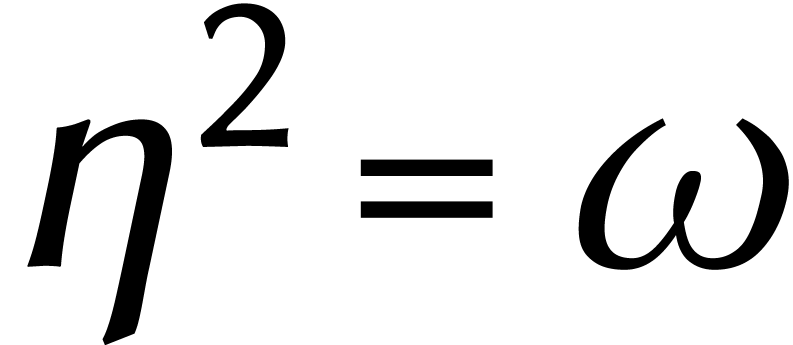 est une racine principale
d'unité d'ordre
est une racine principale
d'unité d'ordre 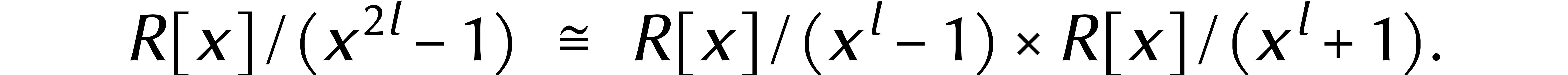 avec
avec 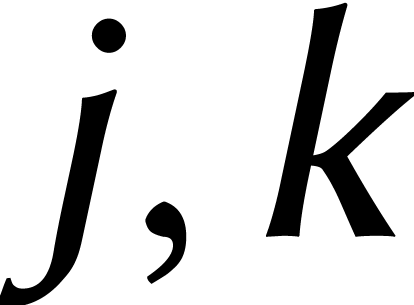 . Pour des entiers
. Pour des entiers 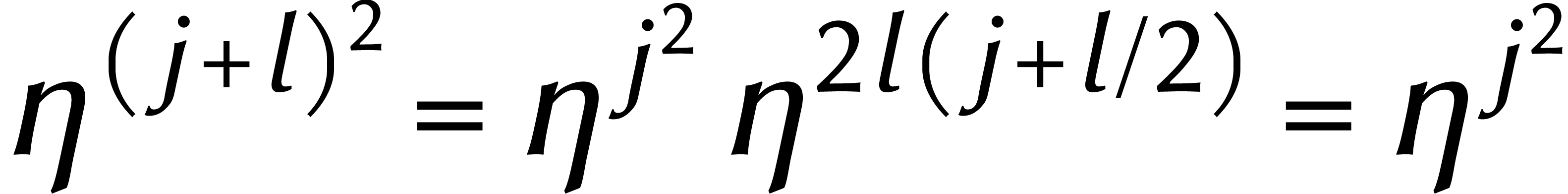 , on a alors
, on a alors

et
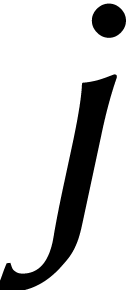
Le coefficient 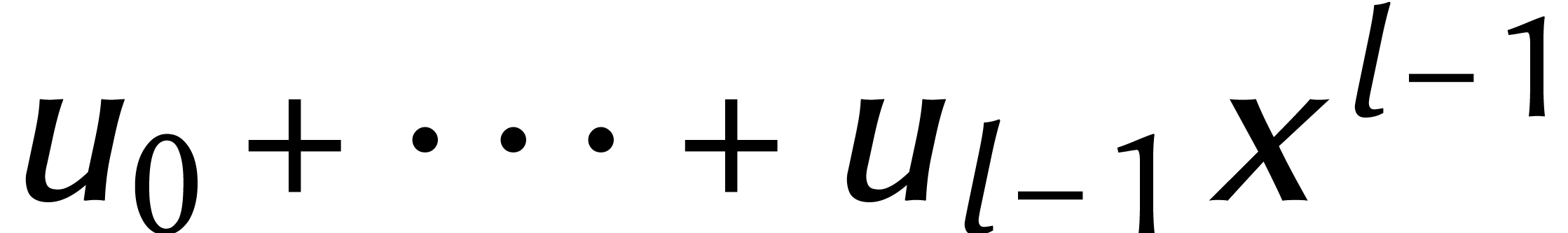 -ième
de la DFT d'un cyclonôme
-ième
de la DFT d'un cyclonôme 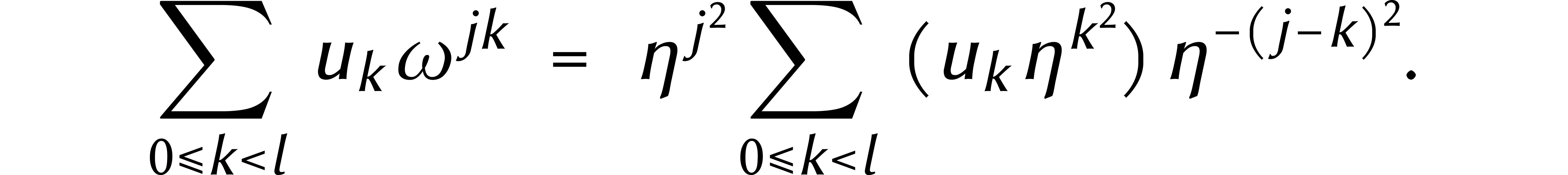 vaut donc
vaut donc
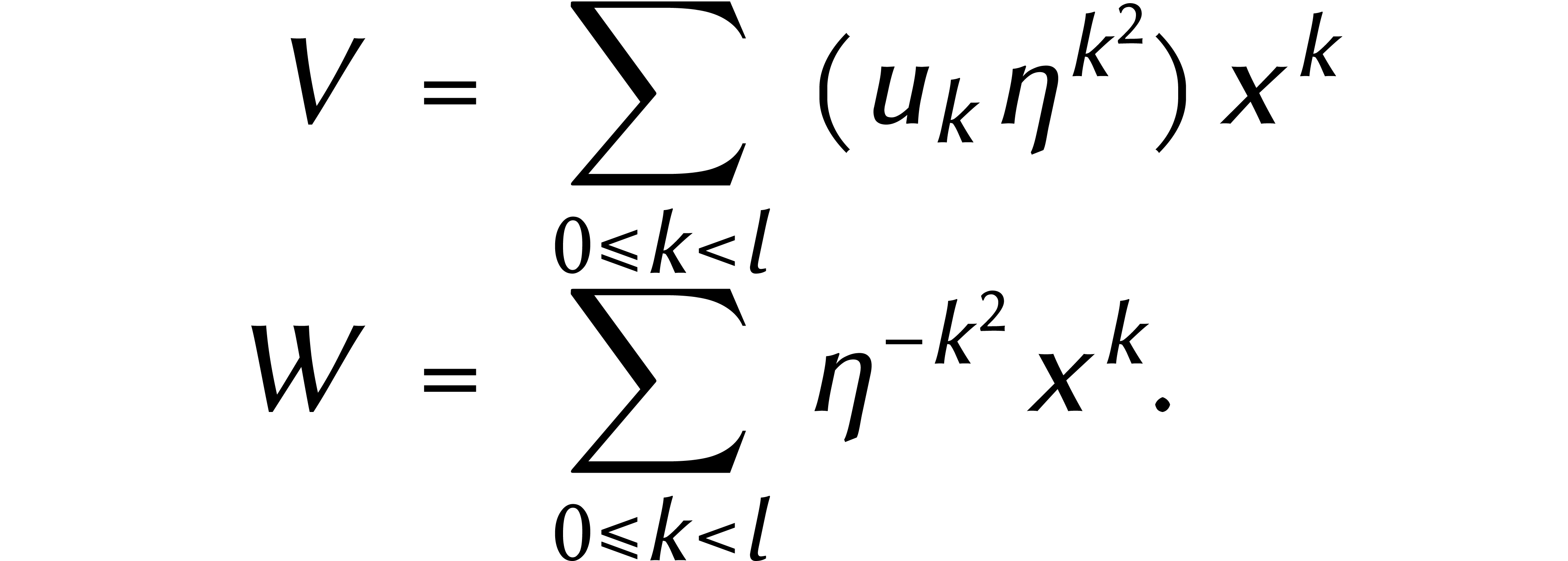
Dans la somme à droite nous reconnaissons maintenant le produit de deux cyclonômes :

En 1971, pas moins de trois méthodes apparurent pour appliquer la
FFT à la multiplication des nombres entiers [
21
,
23
]. Chacune de ces méthodes reposait sur un choix distinct de
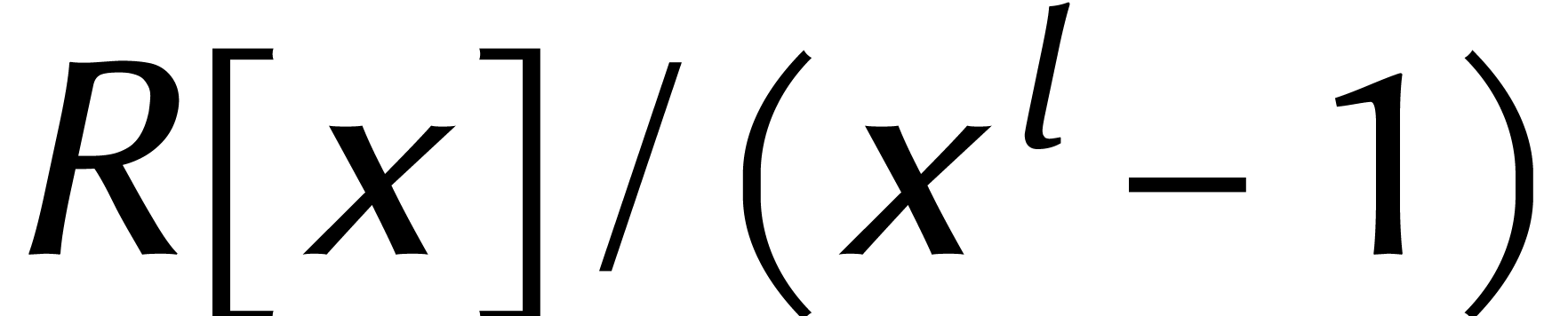 .
.
Le choix le plus naturel est de prendre 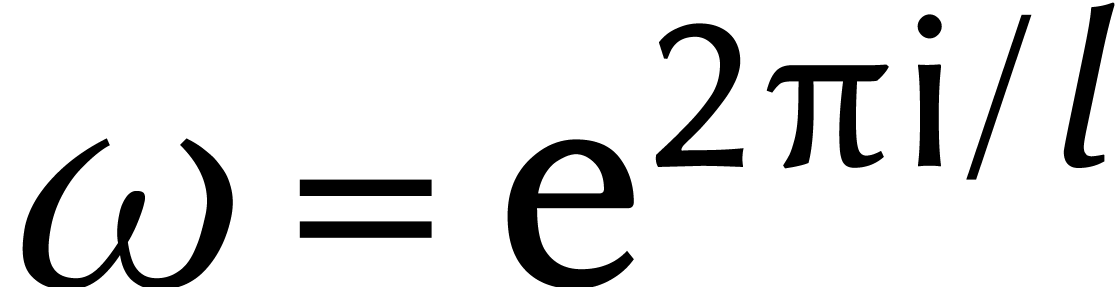 et
et 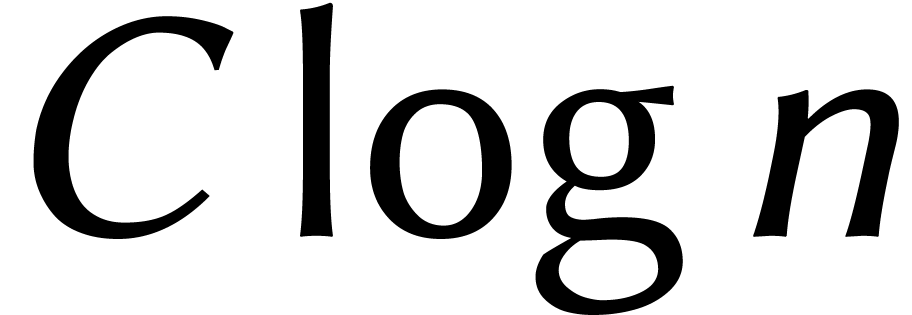 . Bien sûr, nous ne pouvons
travailler qu'avec des approximations de nombres complexes dans notre
cas. Pour multiplier des nombres de
. Bien sûr, nous ne pouvons
travailler qu'avec des approximations de nombres complexes dans notre
cas. Pour multiplier des nombres de 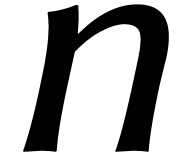 chiffres, on
peut prouver qu'il suffit de travailler avec une précision de
chiffres, on
peut prouver qu'il suffit de travailler avec une précision de
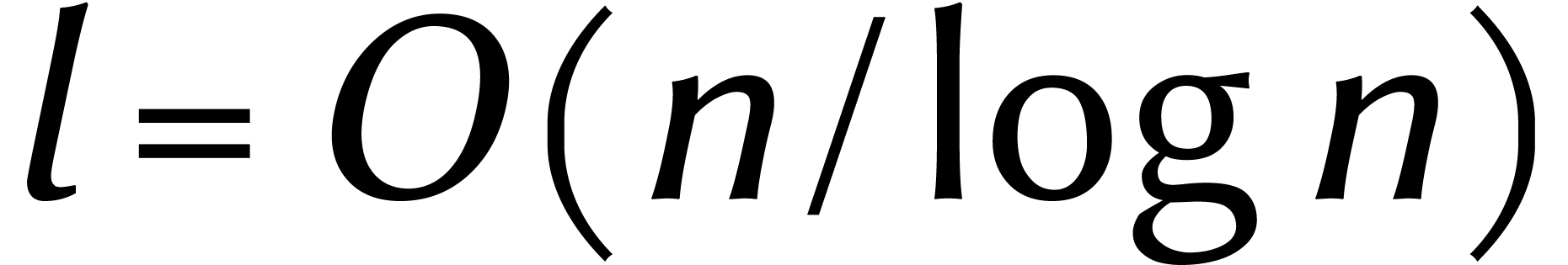 chiffres derrière la virgule pour une
certaine constante
chiffres derrière la virgule pour une
certaine constante  . Cela
signifie que nous pouvons travailler avec
. Cela
signifie que nous pouvons travailler avec 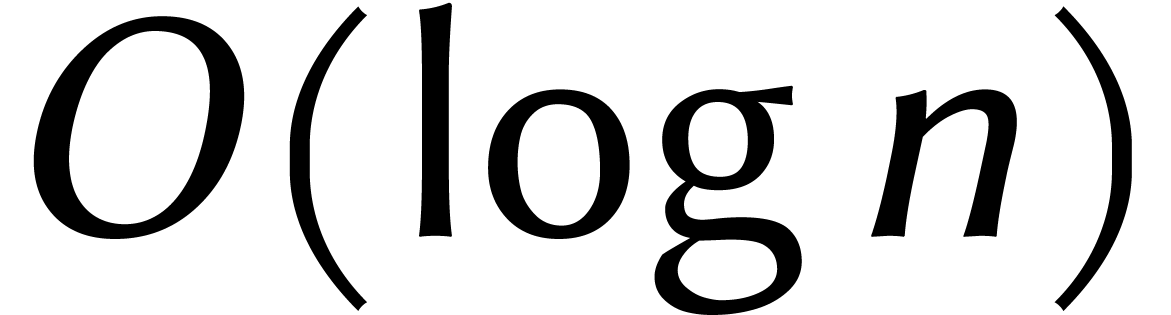 blocs
de
blocs
de 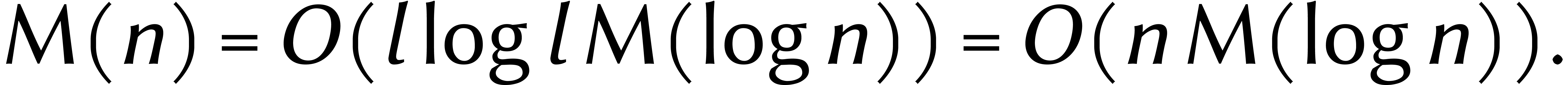 chiffres. En combinaison avec (2),
ceci donne
chiffres. En combinaison avec (2),
ceci donne
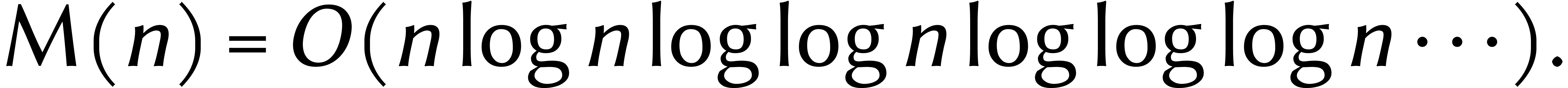
En appliquant cette formule de manière récursive, nous obtenons

Ceci donnait le «premier algorithme» de l'article de Schönhage–Strassen [23].
Cependant, l'algorithme zéro fut découvert légèrement plus tôt par Pollard [ 21 ].
Il proposa de prendre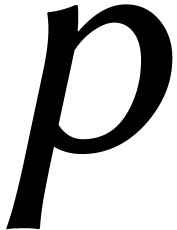 ,
où
,
où
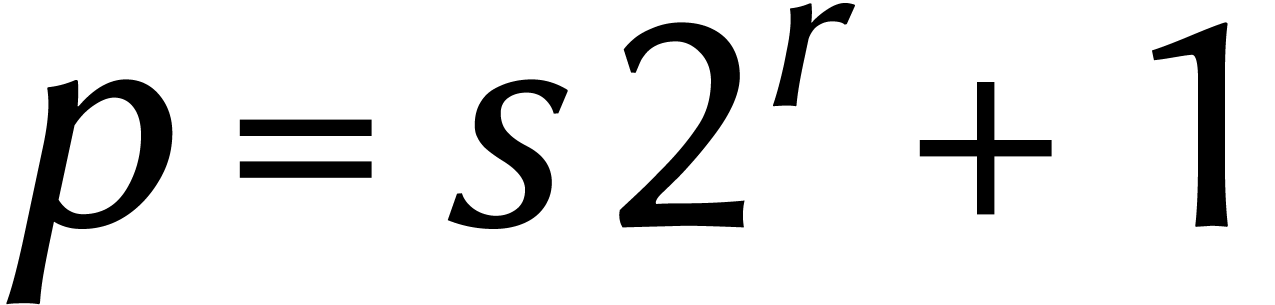 est un nombre premier de la forme
est un nombre premier de la forme
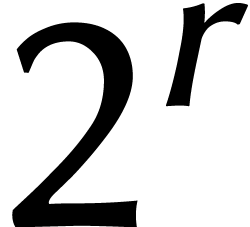 (plus que s soit petit, mieux que ça vaut). Pour de tels nombres
premiers
(plus que s soit petit, mieux que ça vaut). Pour de tels nombres
premiers
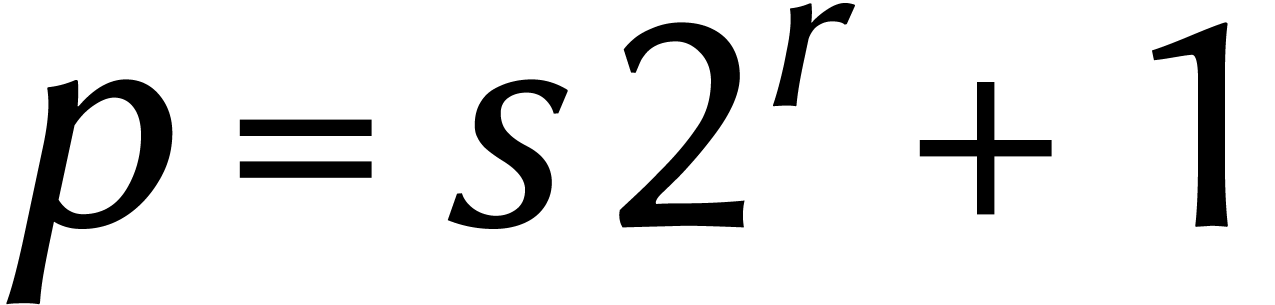 ,
nous savons qu'il existe des racines primitives d'unité d'ordre
,
nous savons qu'il existe des racines primitives d'unité d'ordre
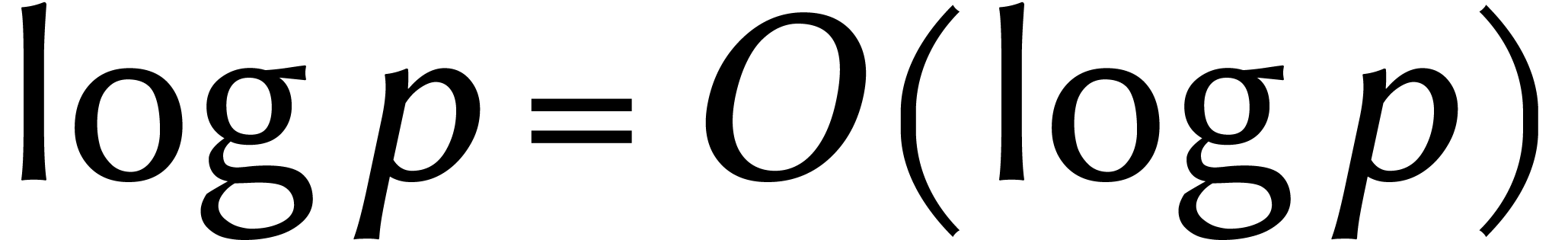 .
Cette fois-ci encore, cela permet de choisir
.
Cette fois-ci encore, cela permet de choisir
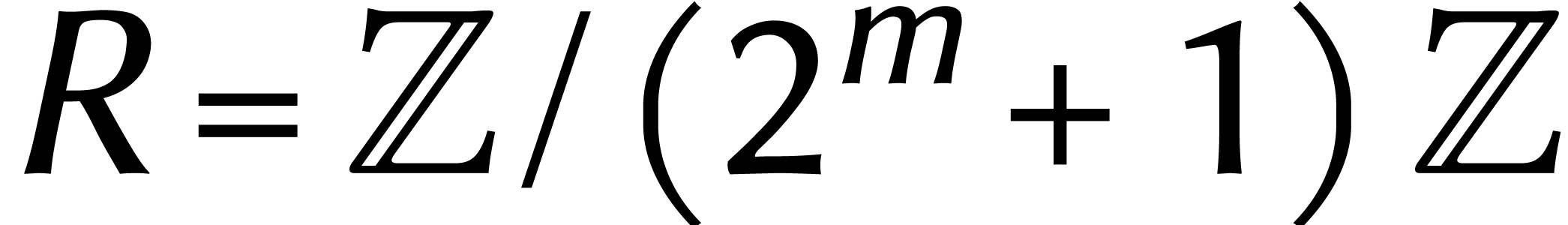 et
et
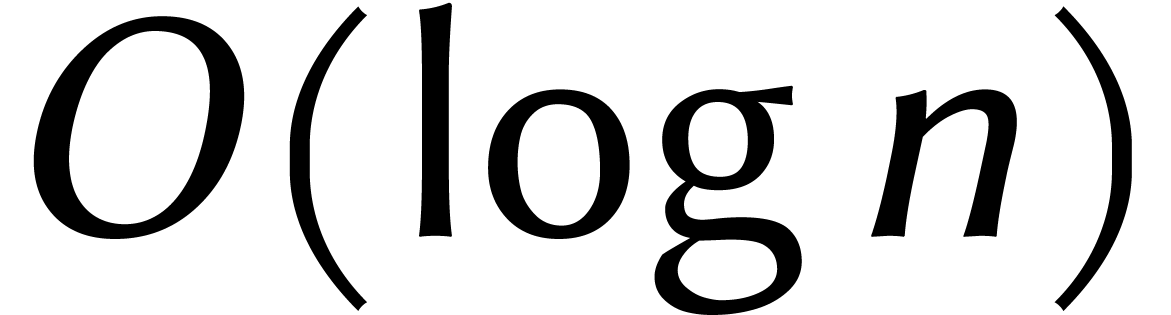 ,
ce qui conduit à la même borne de complexité pour
,
ce qui conduit à la même borne de complexité pour
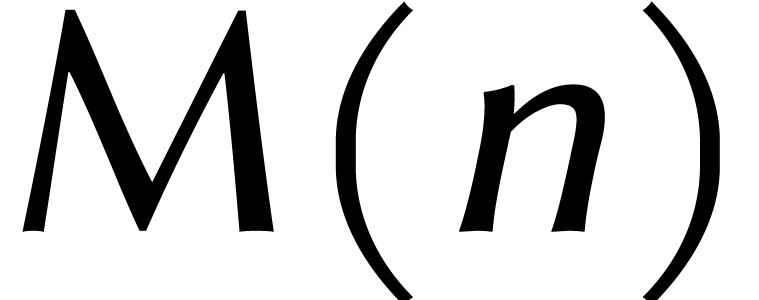 que ci-dessus. Pour être tout à fait correct, il faut
noter que cette borne de complexité ne figurait pas dans
l'article de Pollard. Il était plus intéressé par
un algorithme pratique et son article décrit plusieurs
optimisations en ce sens. Pour de très grands nombres, son
algorithme est toujours le meilleur sur les ordinateurs d'aujourd'hui [
8
].
que ci-dessus. Pour être tout à fait correct, il faut
noter que cette borne de complexité ne figurait pas dans
l'article de Pollard. Il était plus intéressé par
un algorithme pratique et son article décrit plusieurs
optimisations en ce sens. Pour de très grands nombres, son
algorithme est toujours le meilleur sur les ordinateurs d'aujourd'hui [
8
].
Pour le «deuxième algorithme» de
Schönhage–Strassen, nous passons au système binaire et
prenons 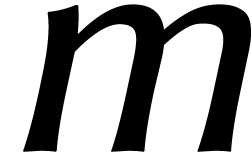 , où
, où 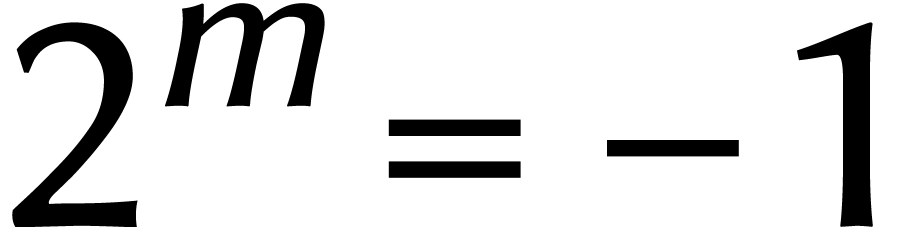 est une puissance de deux. Dans cet anneau, nous avons par
définition
est une puissance de deux. Dans cet anneau, nous avons par
définition 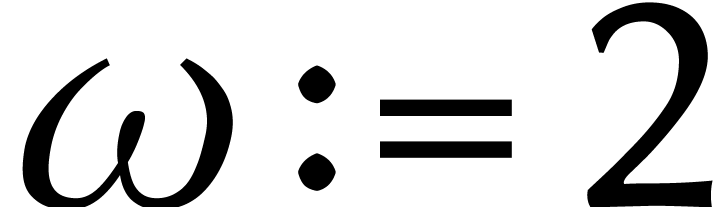 , de sorte
que
, de sorte
que 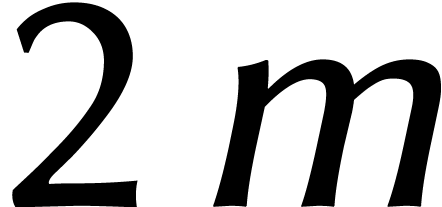 est une racine principale d'unité
d'ordre
est une racine principale d'unité
d'ordre 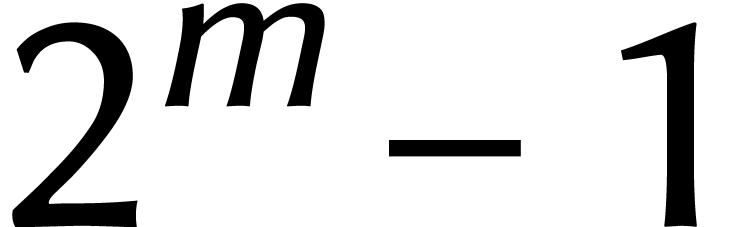 . Un autre avantage
est que
. Un autre avantage
est que 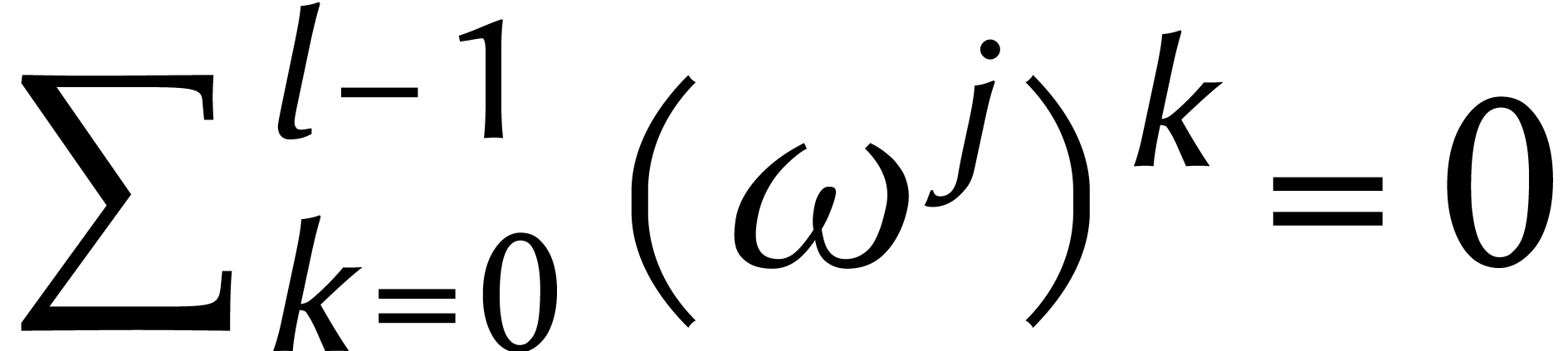 est une racine « rapide » de
l'unité. Nous entendons par là que nous pouvons rapidement
multiplier par des puissances de
est une racine « rapide » de
l'unité. Nous entendons par là que nous pouvons rapidement
multiplier par des puissances de 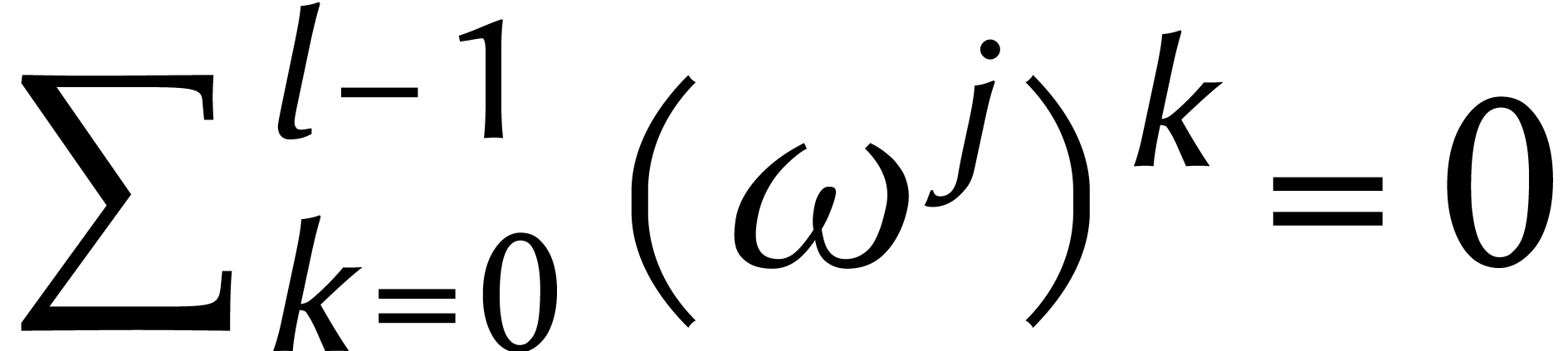 : il suffit de
décaler les bits du nombre en prenant soin d'utiliser la relation
: il suffit de
décaler les bits du nombre en prenant soin d'utiliser la relation
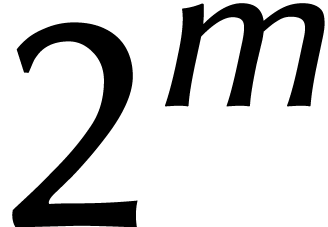 lorsque l'on dépasse
lorsque l'on dépasse 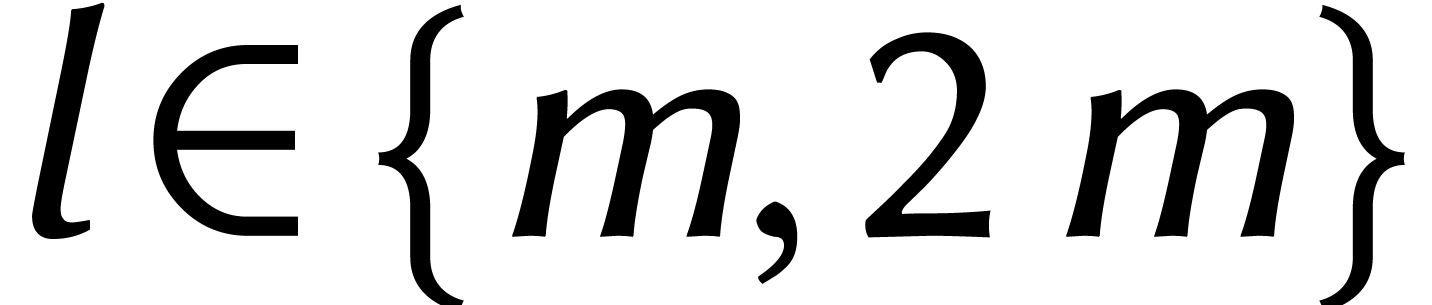 . Pour
. Pour 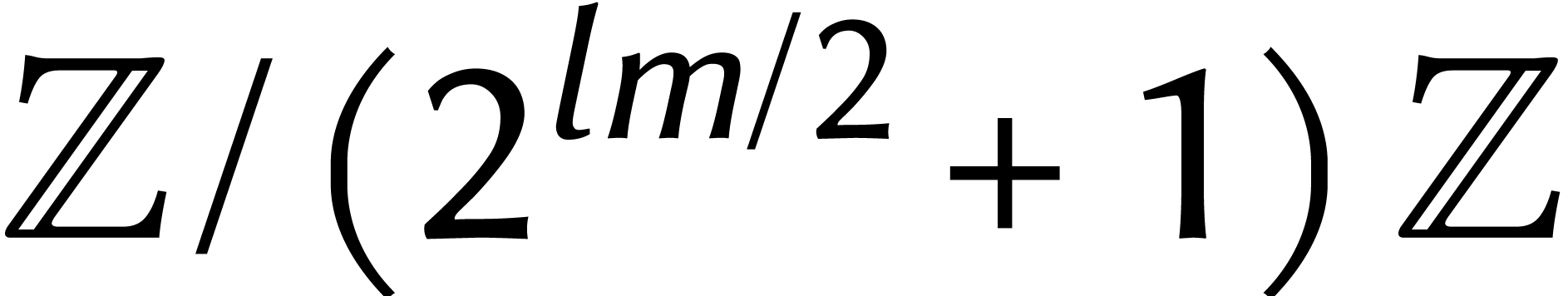 Schönhage
et Strassen montrent ensuite comment une multiplication dans
Schönhage
et Strassen montrent ensuite comment une multiplication dans 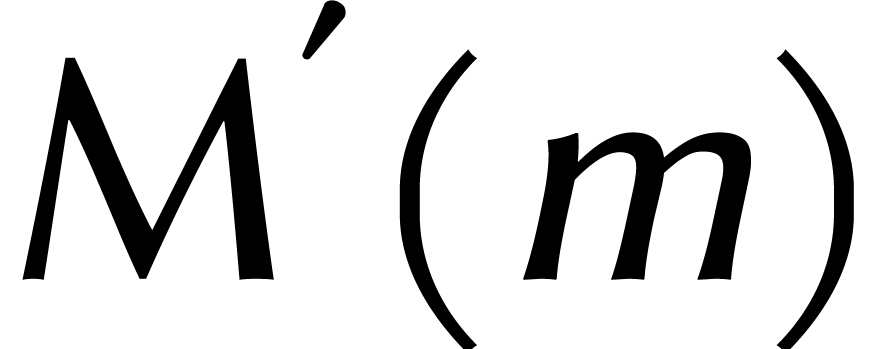 se réduit à
se réduit à  multiplications dans
multiplications dans 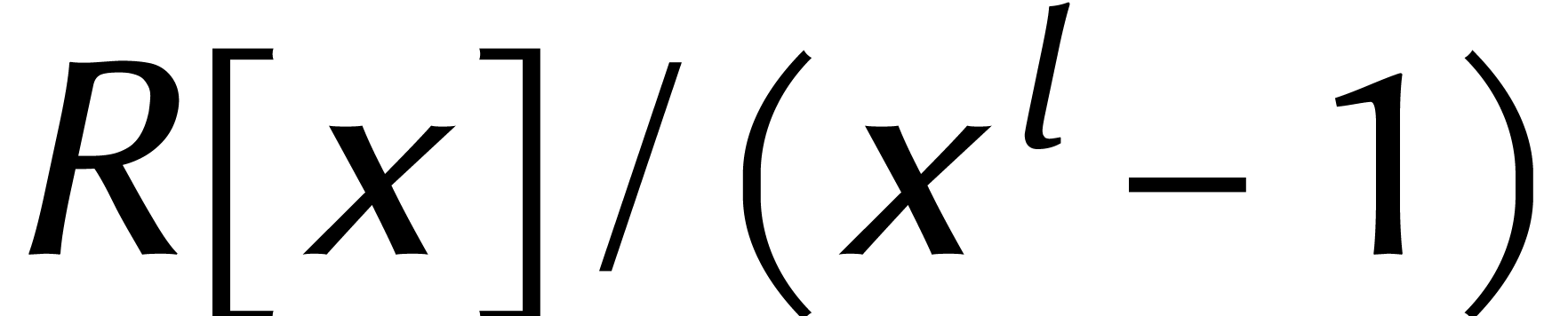 . En
écrivant
. En
écrivant 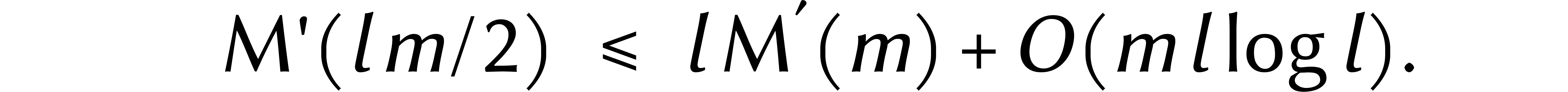 pour le coût d'une
multiplication dans
pour le coût d'une
multiplication dans 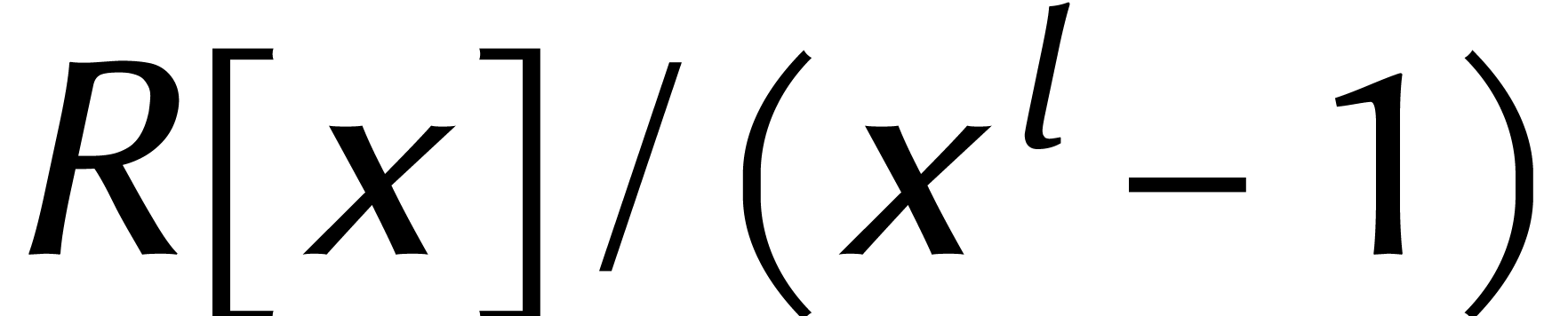 , cela
donne
, cela
donne
Le terme 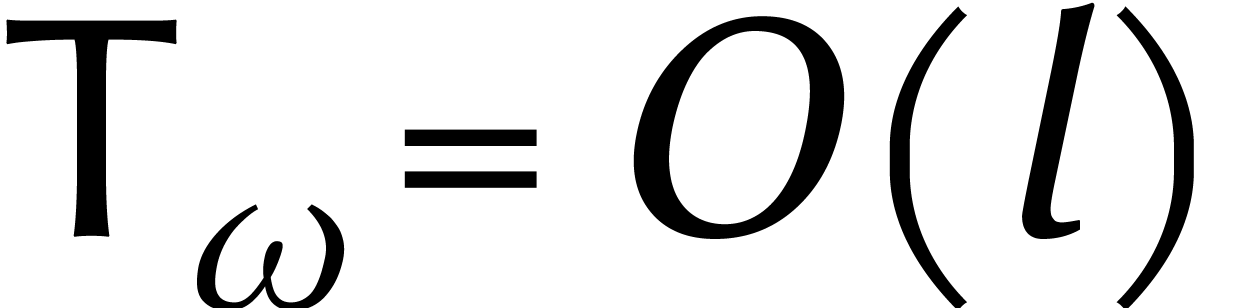 vient des DFTs, où on utilise le
fait que
vient des DFTs, où on utilise le
fait que 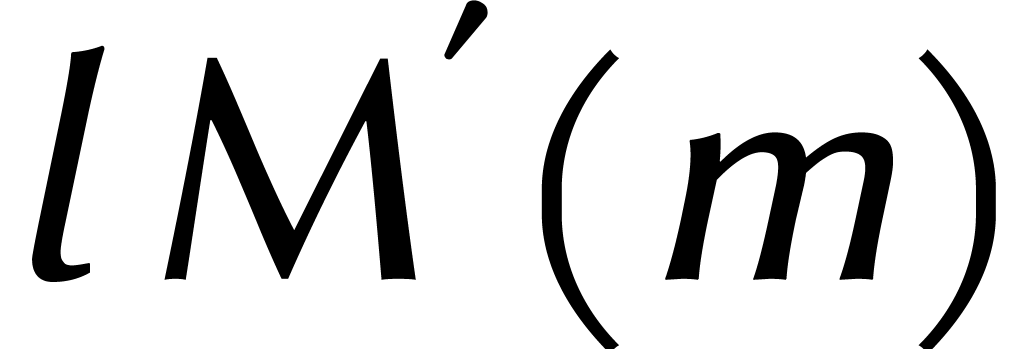 dans
dans 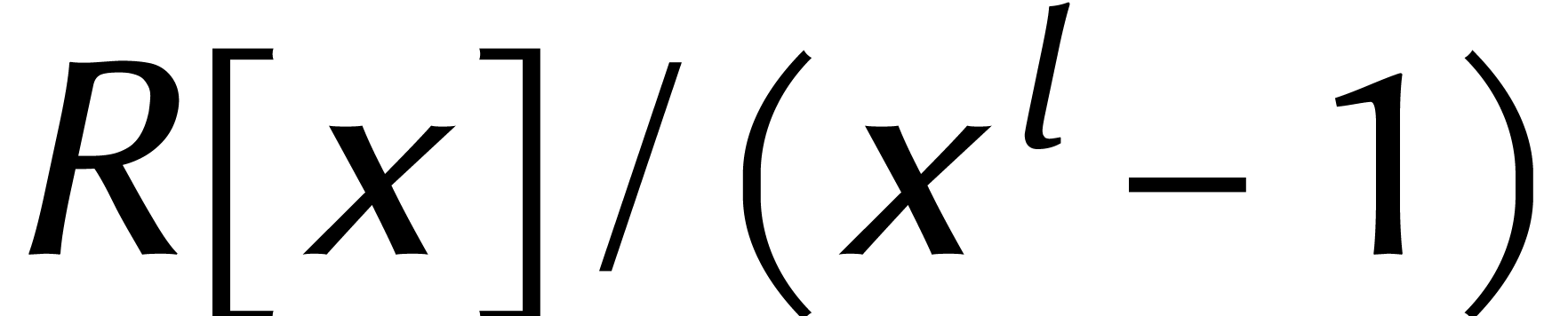 .
Le terme
.
Le terme 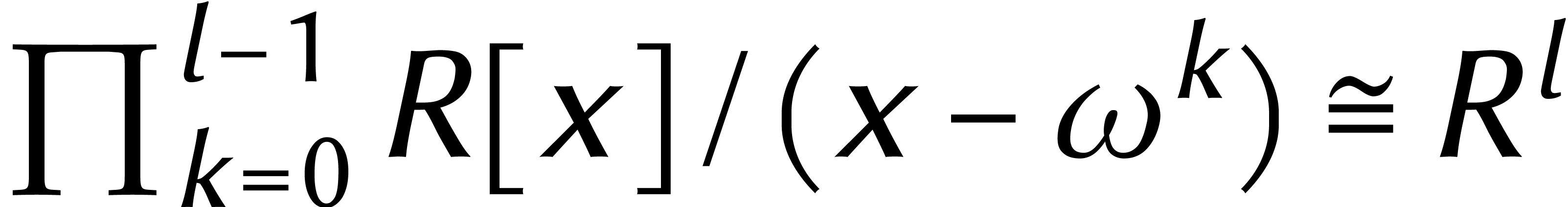 vient de la multiplication «
interne » dans
vient de la multiplication «
interne » dans 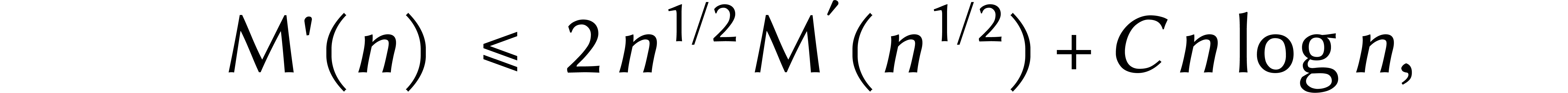 .
.
Réexprimé en fonction de 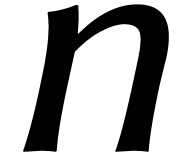 ,
l'inégalité (3) conduit grosso modo
à la relation
,
l'inégalité (3) conduit grosso modo
à la relation
pour une certaine constante  .
On peut ensuite « dérouler » cette formule :
.
On peut ensuite « dérouler » cette formule :
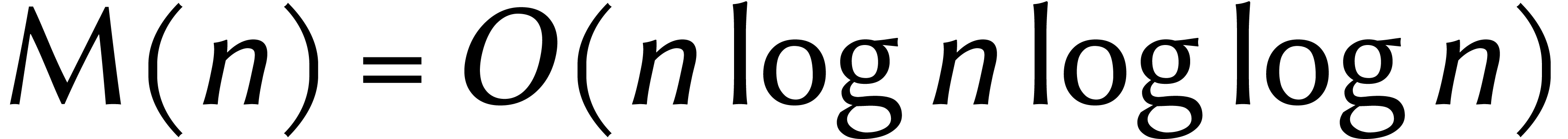
Cela prouve que 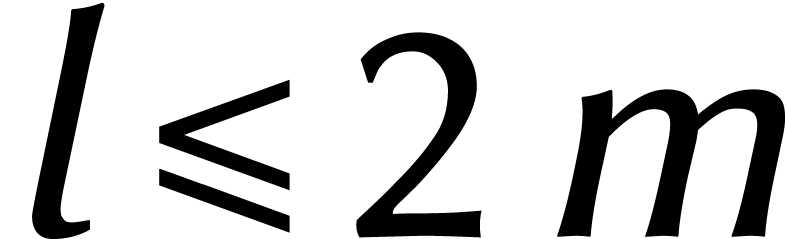 , et cette
borne a tenu pendant quarante-cinq ans.
, et cette
borne a tenu pendant quarante-cinq ans.
Parmi les trois méthodes de 1971 que l'on vient de rappeler, la
dernière présente un inconvénient majeur : puisque
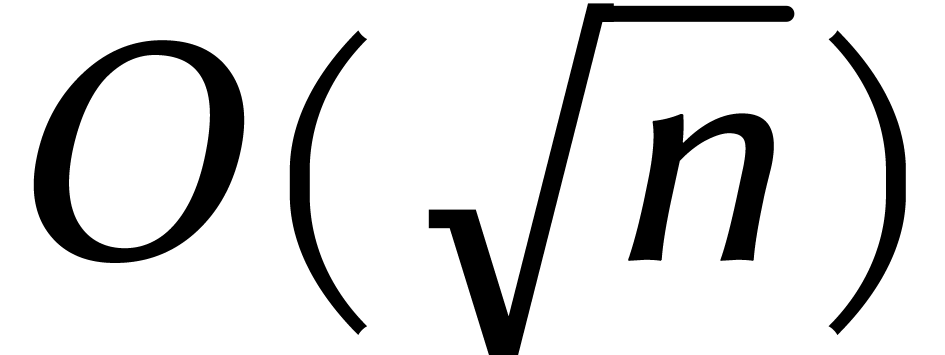 , une multiplication de
longueur
, une multiplication de
longueur 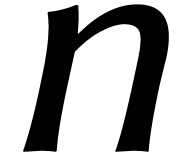 est « seulement »
réduite à des multiplications de longueur
est « seulement »
réduite à des multiplications de longueur  au lieu de
au lieu de 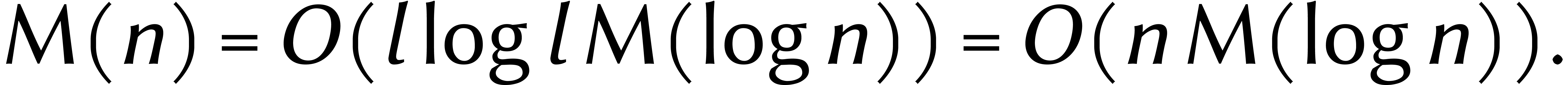 . En revanche,
contrairement aux deux autres méthodes, les DFTs ne coûtent
presque rien. Cela fournit deux pistes d'amélioration.
. En revanche,
contrairement aux deux autres méthodes, les DFTs ne coûtent
presque rien. Cela fournit deux pistes d'amélioration.
Une première option est de réduire les coûts des
DFTs à coefficients dans 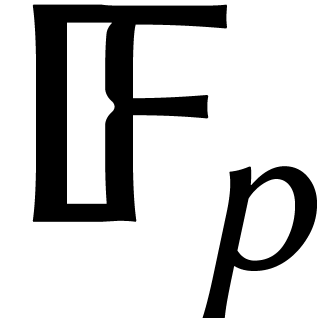 ou
ou 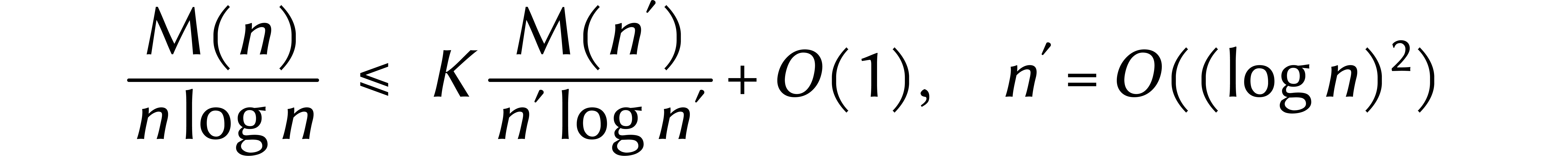 . En 2007, Fürer fut le premier a
appliquer cette stratégie avec succès [5]. Sa
méthode conduit à une inégalité de la forme
. En 2007, Fürer fut le premier a
appliquer cette stratégie avec succès [5]. Sa
méthode conduit à une inégalité de la forme
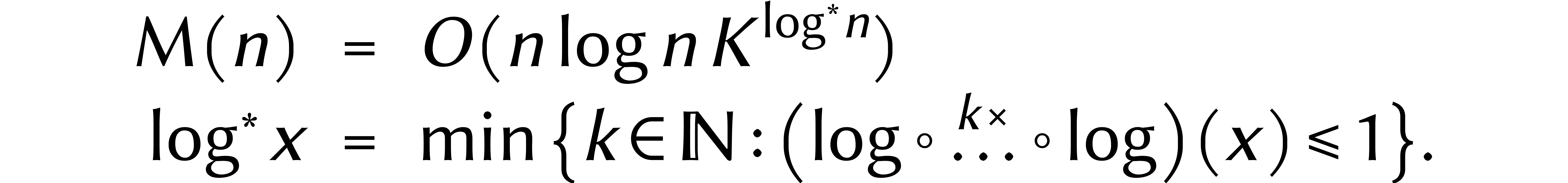
et la borne suivante pour 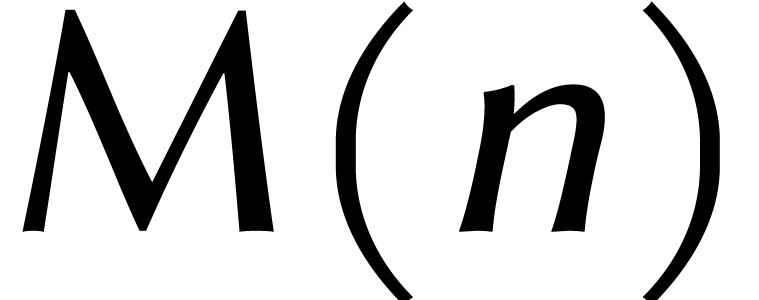 :
:
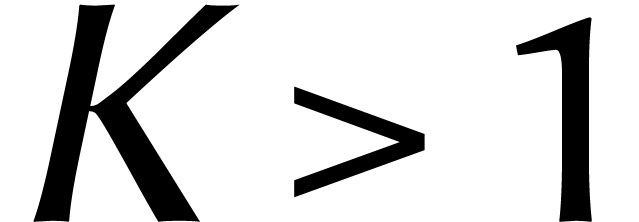
Fürer ne s'attarda pas sur le « facteur d'expansion »
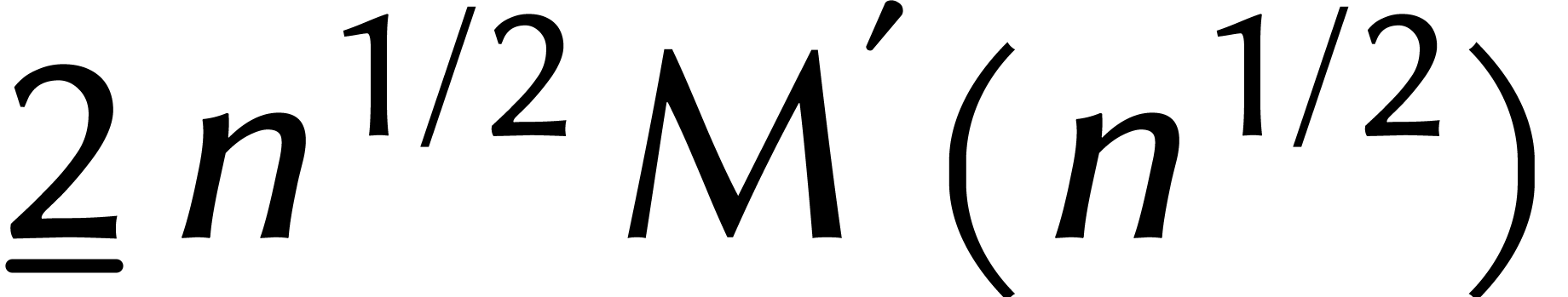 précis. Depuis 2014, David Harvey,
Grégoire Lecerf, et moi-même avons pu faire baisser ce
facteur de plus en plus [13, 9, 10,
11] ; voir le tableau 1.
précis. Depuis 2014, David Harvey,
Grégoire Lecerf, et moi-même avons pu faire baisser ce
facteur de plus en plus [13, 9, 10,
11] ; voir le tableau 1.
Notre deuxième option consiste à réexaminer
l'inégalité (4). Or le facteur 2 dans 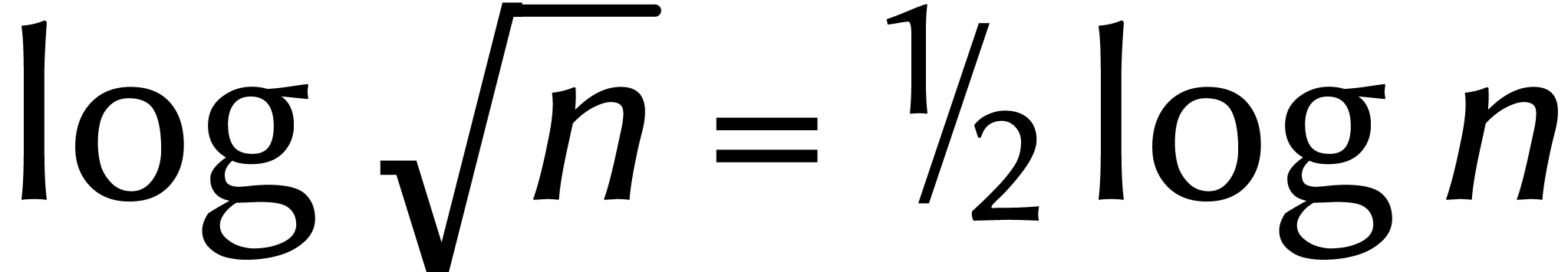 est très exactement compensé par le
fait que
est très exactement compensé par le
fait que 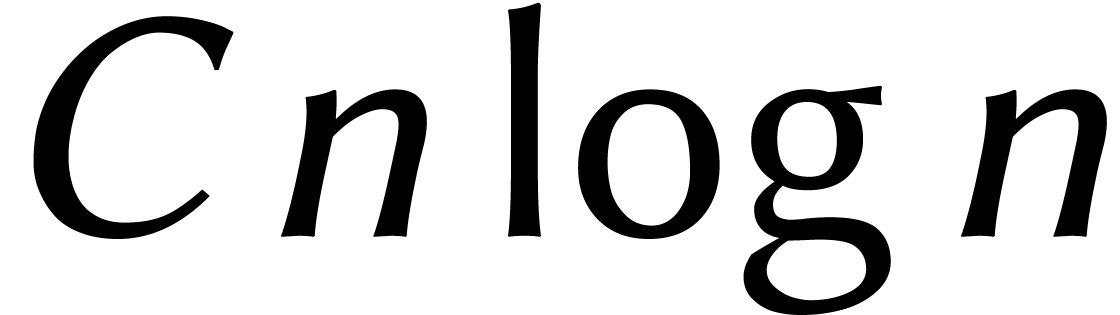 : en déroulant
l'inégalité, chaque itération nécessite
exactement
: en déroulant
l'inégalité, chaque itération nécessite
exactement 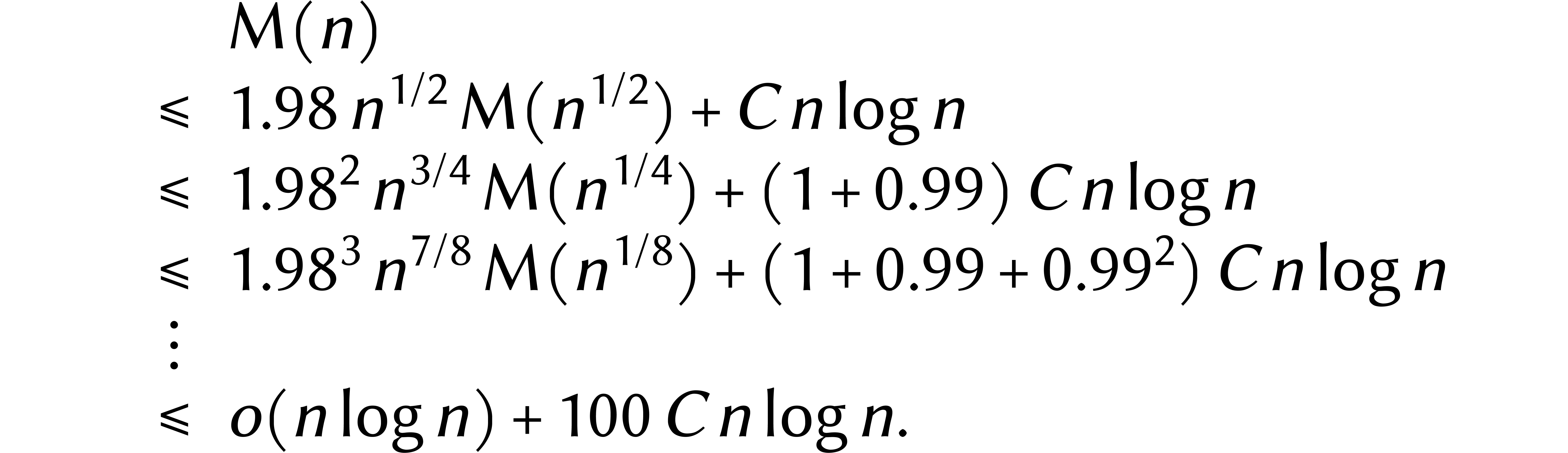 opérations
supplémentaires. Si nous pouvions améliorer ne serait-ce
que très légèrement ce facteur
opérations
supplémentaires. Si nous pouvions améliorer ne serait-ce
que très légèrement ce facteur 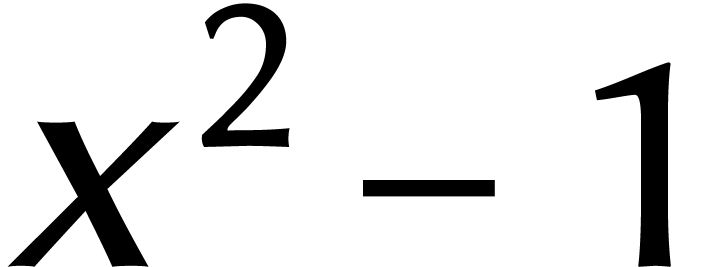 , le déroulement se ferait ainsi :
, le déroulement se ferait ainsi :
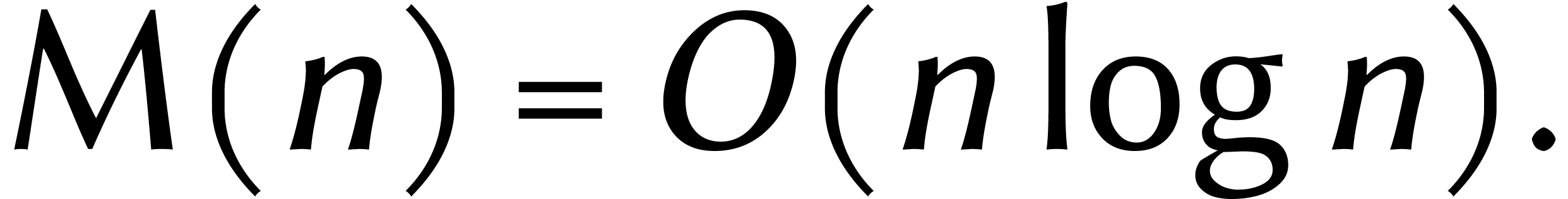
Halte ! Nous avons bien lu ?
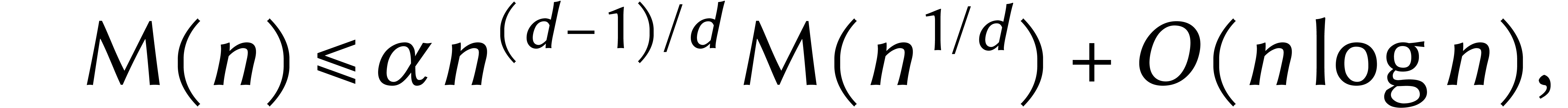
Avec cette nouvelle ligne de mire, nous allons pouvoir broder. Il suffit par exemple de prouver que
 |
(5) |
où 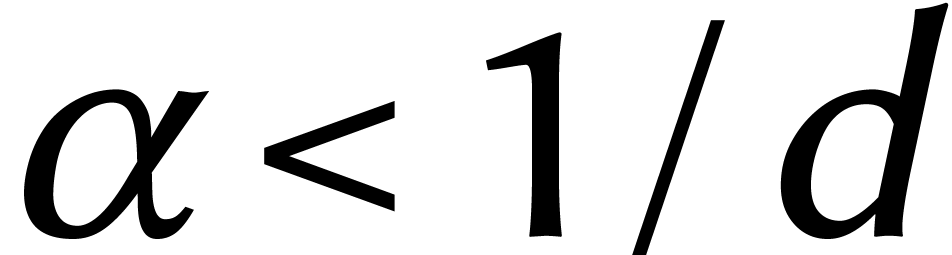 et
et 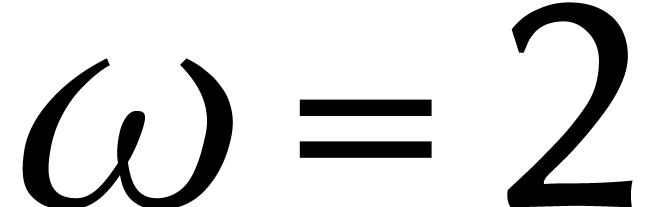 .
.
De fait, la méthode de Schönhage et Strassen présente
un aspect frustrant : la racine de l'unité  dans
dans 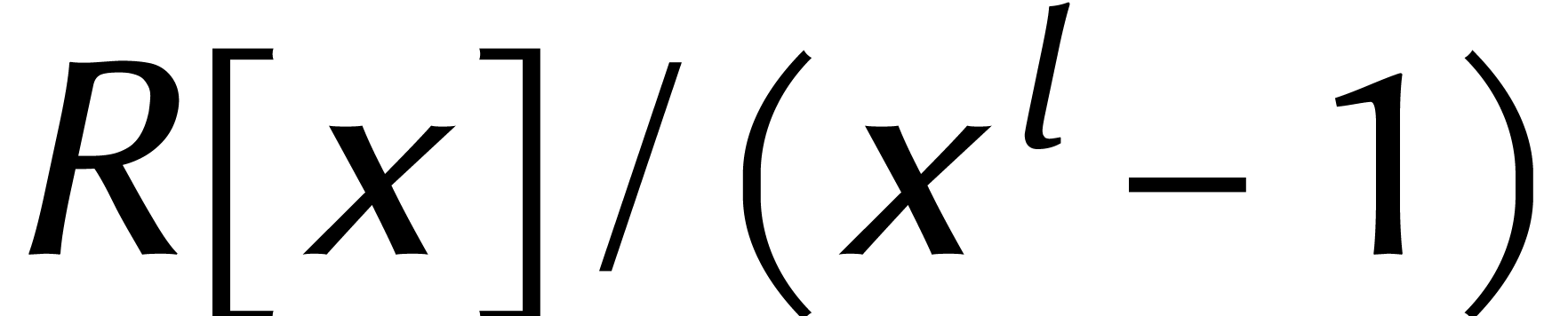 , que nous avons
créé artificiellement et à grand frais, est en
réalité terriblement « sous-utilisée ».
Pour cette raison, notre réduction de longueur
, que nous avons
créé artificiellement et à grand frais, est en
réalité terriblement « sous-utilisée ».
Pour cette raison, notre réduction de longueur  n'était que très modeste.
n'était que très modeste.
Or il existe aussi des DFTs qui fonctionnent dans plusieurs directions.
Supposons à nouveau que 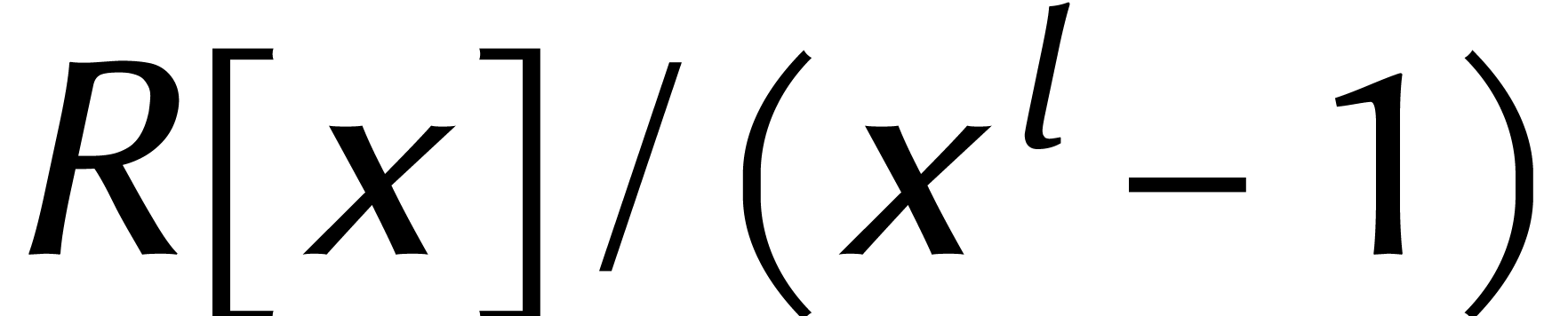 est un anneau
arbitraire avec une racine d'unité
est un anneau
arbitraire avec une racine d'unité 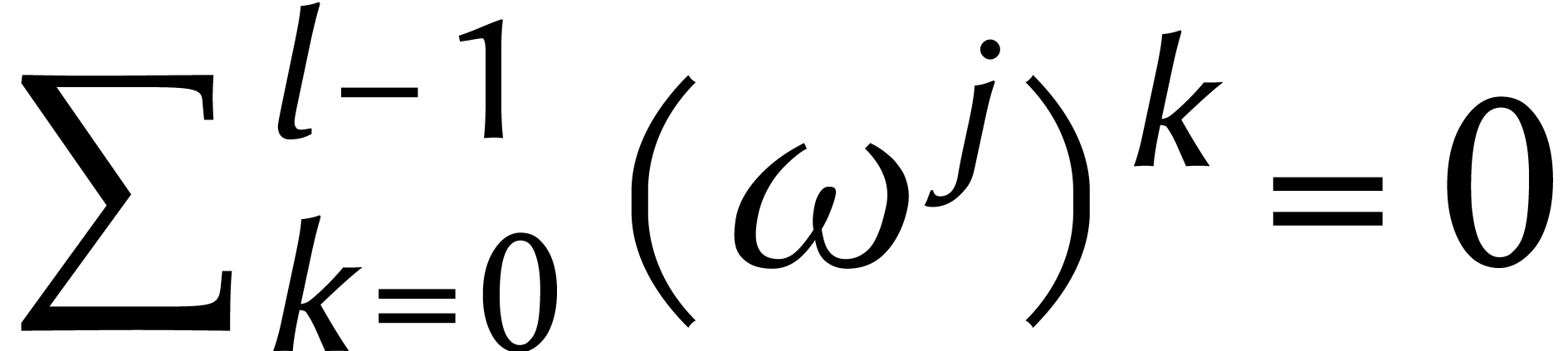 d'ordre
d'ordre  . Une DFT
. Une DFT 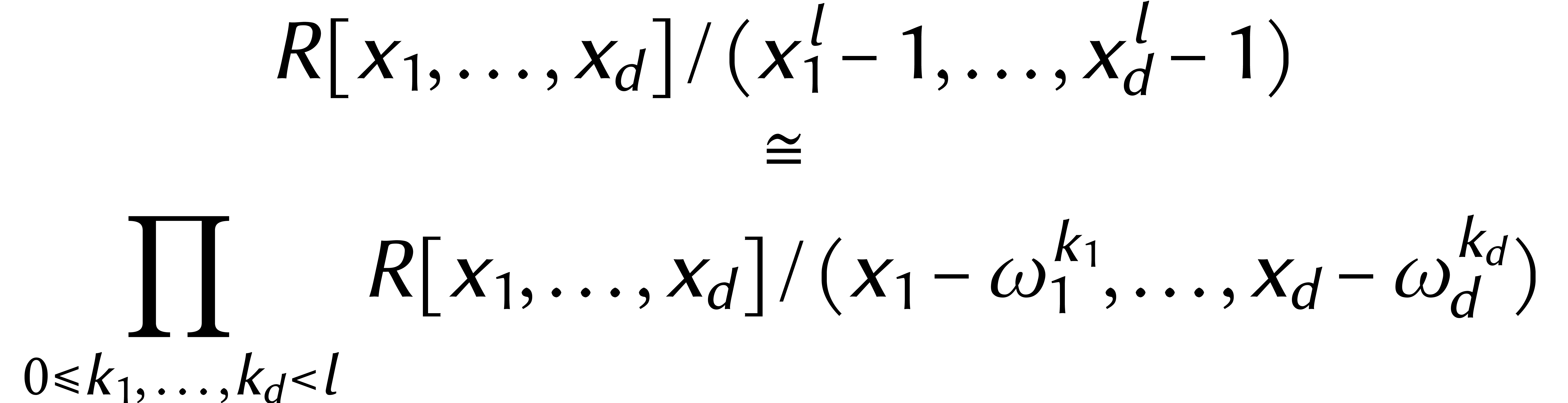 -dimensionnelle effectue
l'isomorphisme
-dimensionnelle effectue
l'isomorphisme

Si nous remplaçons maintenant les DFTs en 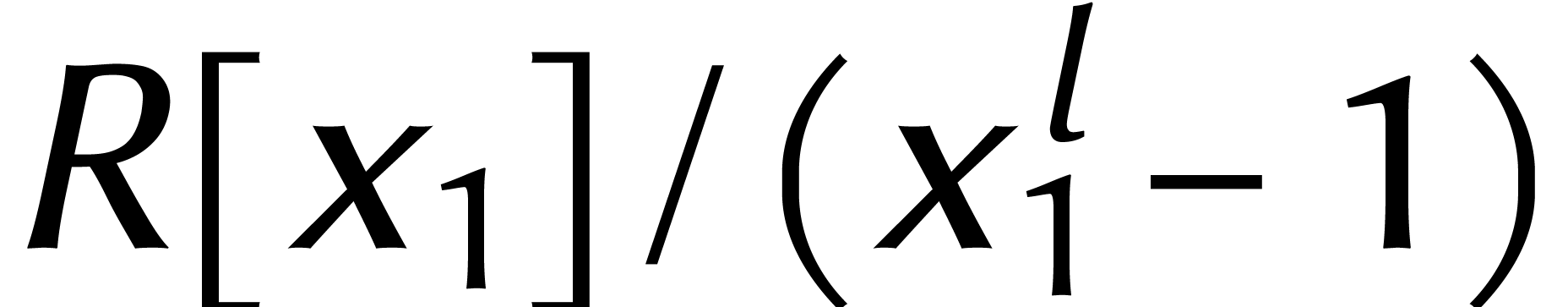 par des DFTs à coefficients dans l'anneau
par des DFTs à coefficients dans l'anneau 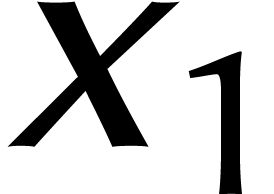 , ils coûteront beaucoup moins cher, puisque
, ils coûteront beaucoup moins cher, puisque
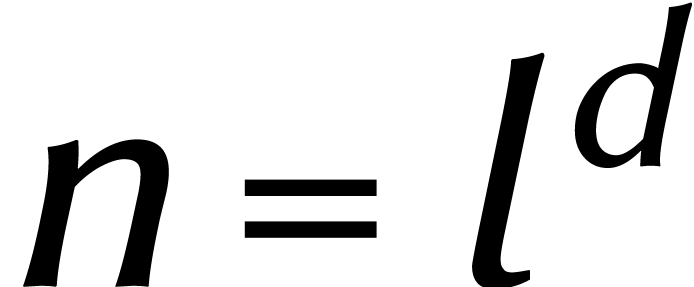 est une racine rapide de l'unité dans cet
anneau. L'utilisation systématique de ce type de DFTs a d'abord
été proposée par Nussbaumer et Quandalle [20].
est une racine rapide de l'unité dans cet
anneau. L'utilisation systématique de ce type de DFTs a d'abord
été proposée par Nussbaumer et Quandalle [20].
Cette idée nous permet de faire un grand pas en direction de (5). Si 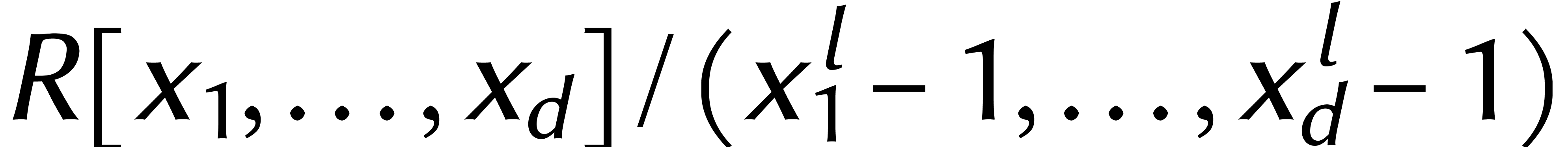 , alors une
multiplication dans
, alors une
multiplication dans 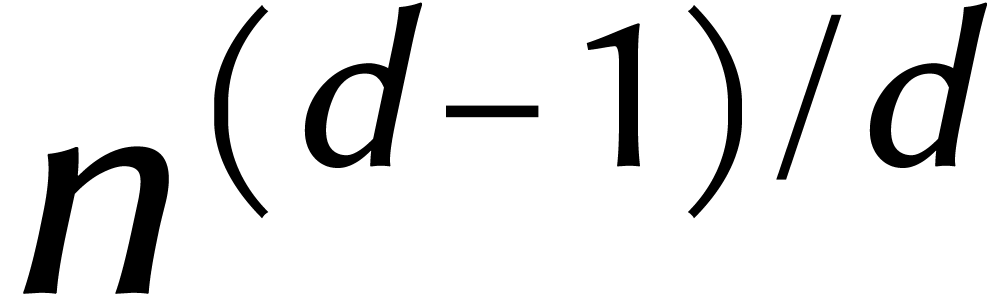 nécessite
nécessite 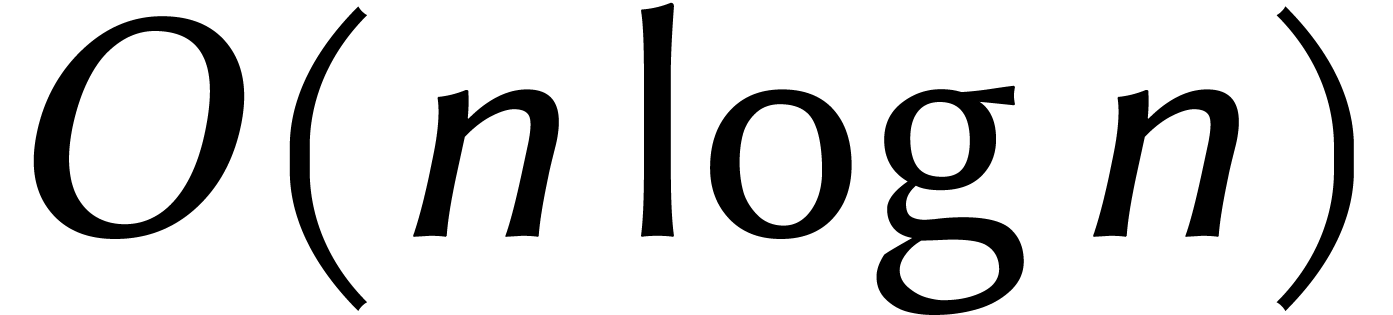 additions et soustractions dans
additions et soustractions dans 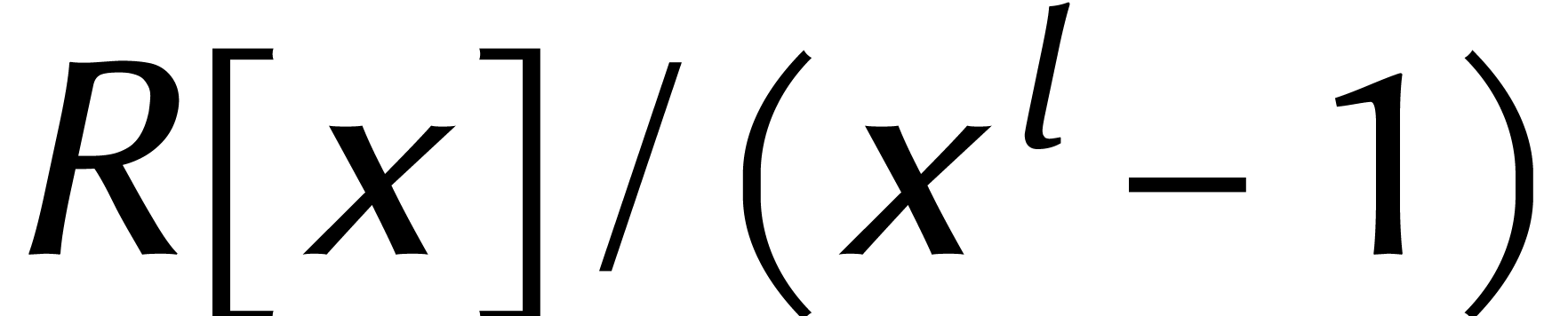 plus
plus 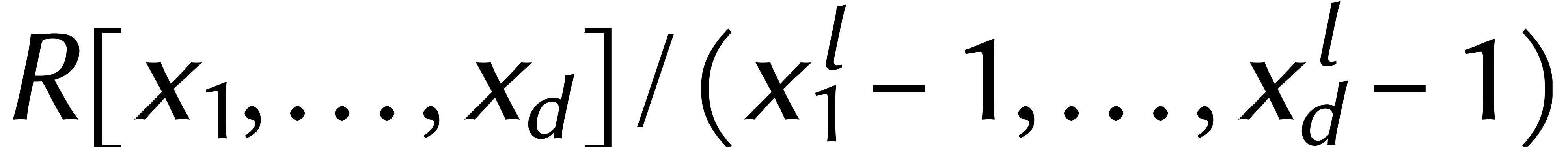 multiplications dans
multiplications dans 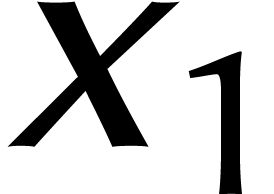 .
.
Il reste cependant un problème de taille : la multiplication
rapide dans 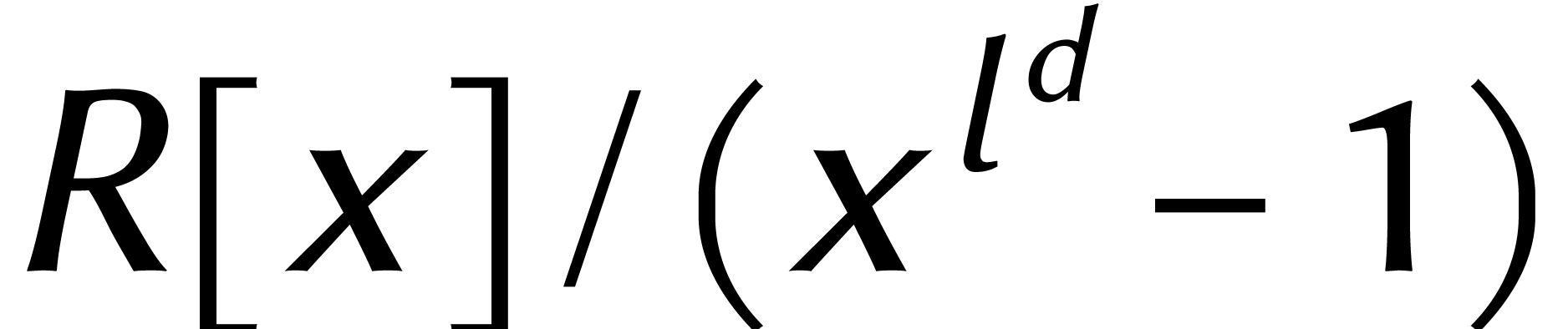 n'est pas la même chose que la
multiplication rapide dans
n'est pas la même chose que la
multiplication rapide dans  .
Nous avons donc besoin d'un moyen de transformer des cyclonômes en
une variable
.
Nous avons donc besoin d'un moyen de transformer des cyclonômes en
une variable  en cyclonômes en plusieurs
variables
en cyclonômes en plusieurs
variables  .
.
Dans certains cas, il est en effet possible de changer de dimension.
Supposons que 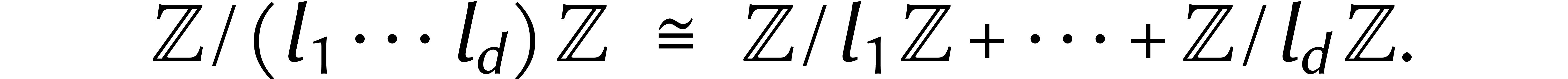 soient premiers entres eux. Selon
le théorème des restes chinois, nous avons
soient premiers entres eux. Selon
le théorème des restes chinois, nous avons
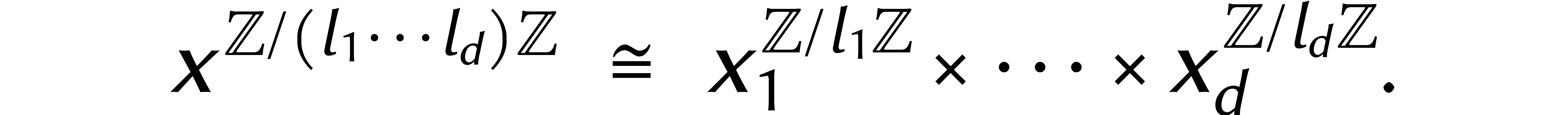
Formellement, ceci donne également
Considérant ensuite des combinaisons linéaires, ceci nous amène enfin à
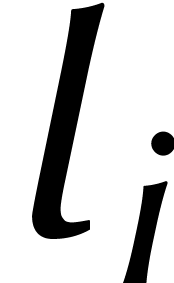
En relation avec les DFTs, ceci a été remarqué pour la première fois par Good [7]. Agarwal et Cooley ont ensuite utilisé cet isomorphisme pour calculer des convolutions [1].
Cependant, nous avons maintenant un nouveau problème : dans la
section précédente nous avions besoin d'un isomorphisme
pour lequel tous les  étaient
égaux. Mais notre isomorphisme ne marche que dans le cas
où
étaient
égaux. Mais notre isomorphisme ne marche que dans le cas
où 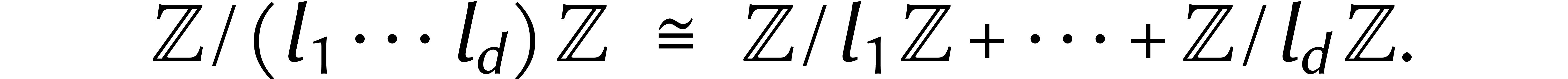 sont au contraire premiers entre
eux...
sont au contraire premiers entre
eux...
Le dernier ingrédient qui nous manque est un moyen de modifier
légèrement la longueur d'une DFT. Cela permettrait de
réduire une DFT 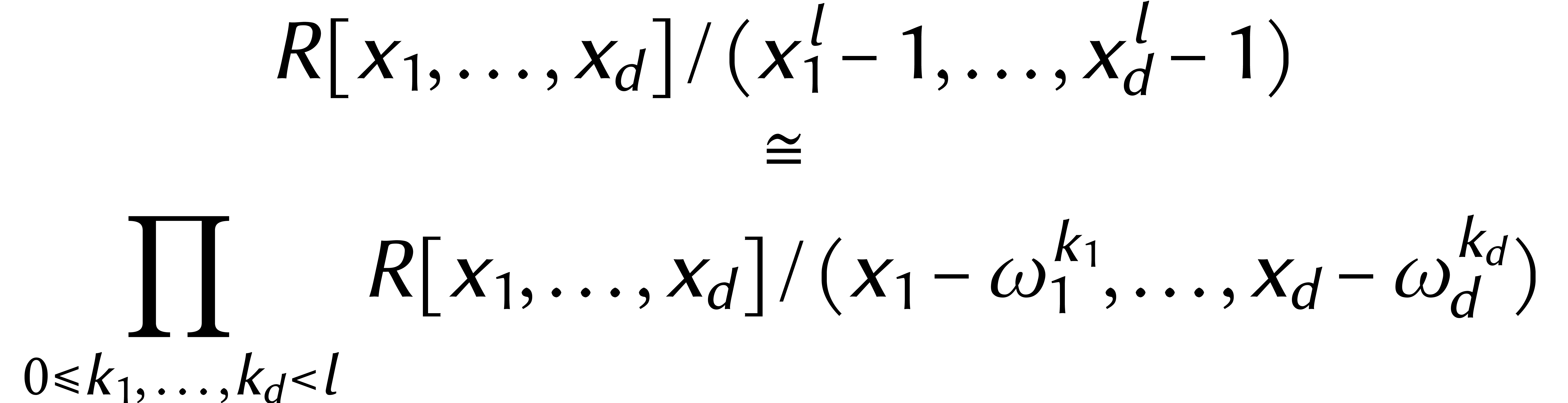 -dimensionnelle
de longueur
-dimensionnelle
de longueur  en une autre de longueur
en une autre de longueur  . En utilisant une version
. En utilisant une version 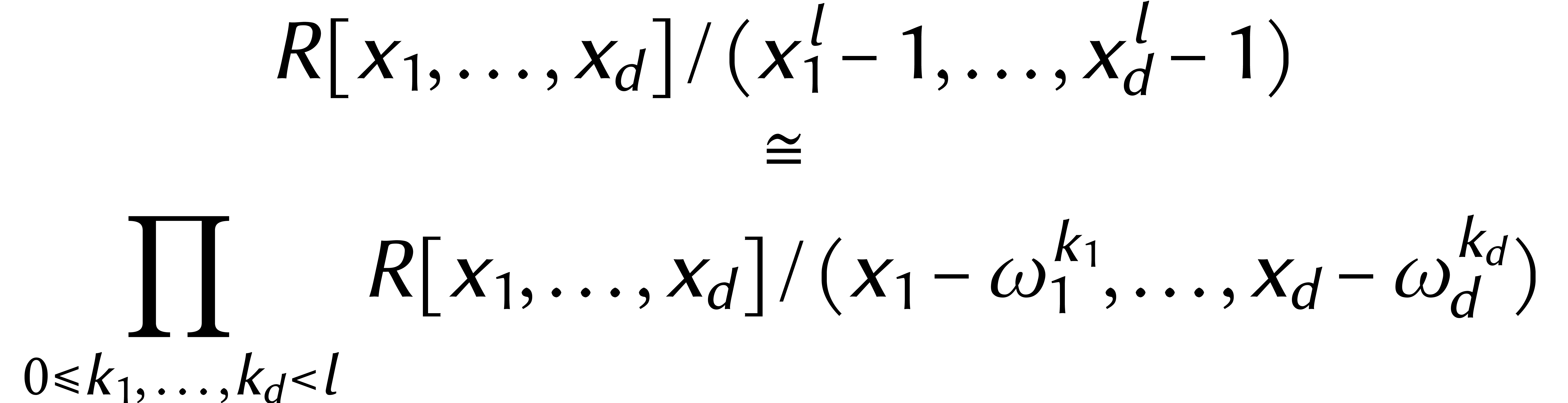 -dimensionnelle de l'algorithme de
Bluestein, une telle DFT se réduit ensuite à une
multiplication dans
-dimensionnelle de l'algorithme de
Bluestein, une telle DFT se réduit ensuite à une
multiplication dans 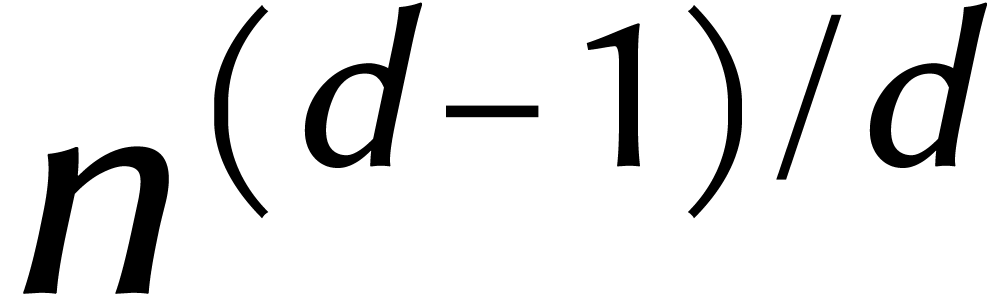 . Et cela
peut être fait efficacement à l'aide des racines rapides de
l'unité.
. Et cela
peut être fait efficacement à l'aide des racines rapides de
l'unité.
Comment remplacer une DFT de longueur  par une
DFT de longueur
par une
DFT de longueur 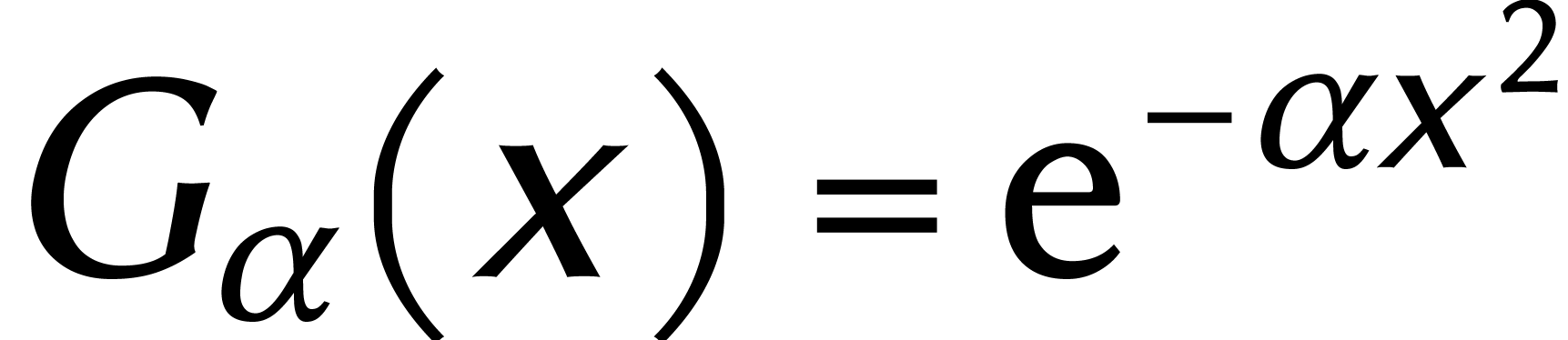 légèrement
supérieure ? Pour y parvenir, nous supposons à partir de
maintenant que
légèrement
supérieure ? Pour y parvenir, nous supposons à partir de
maintenant que 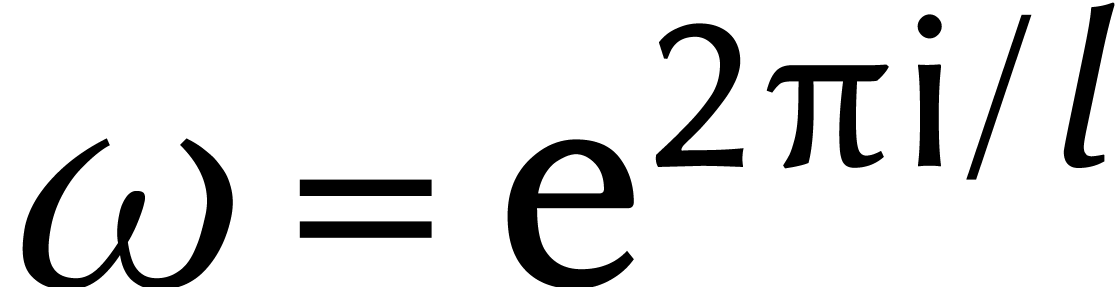 .
.
Considérons une DFT de longueur  .
Dans la théorie du signal, l'entrée est vue comme une
série d'échantillons d'un signal. La fréquence
d'échantillonnage est proportionnelle à
.
Dans la théorie du signal, l'entrée est vue comme une
série d'échantillons d'un signal. La fréquence
d'échantillonnage est proportionnelle à  . Est-il possible de reconstruire le signal
original à partir de notre ensemble d'échantillons ? Cela
permettrait de prendre un nouvel ensemble d'échantillons, avec
une fréquence différente.
. Est-il possible de reconstruire le signal
original à partir de notre ensemble d'échantillons ? Cela
permettrait de prendre un nouvel ensemble d'échantillons, avec
une fréquence différente.
La manière la plus évidente de rendre un signal
numérique analogique est par convolution avec une gaussienne
 . Plus
. Plus 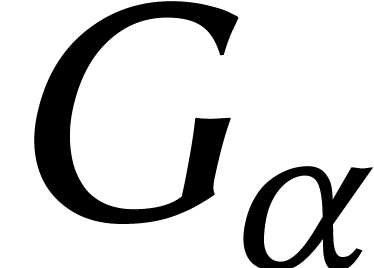 est petit, plus le signal analogique est lisse (mais moins net). Une
propriété utile est que la transformée de Fourier
de
est petit, plus le signal analogique est lisse (mais moins net). Une
propriété utile est que la transformée de Fourier
de 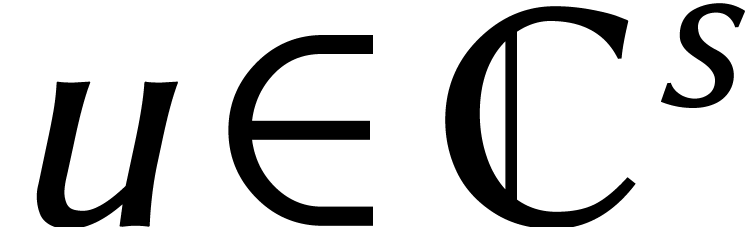 est à nouveau une gaussienne.
est à nouveau une gaussienne.
Traduisons ces idées en formules. Au lieu de cyclonômes de
degré  , nous
considérons maintenant leurs vecteurs associés
, nous
considérons maintenant leurs vecteurs associés 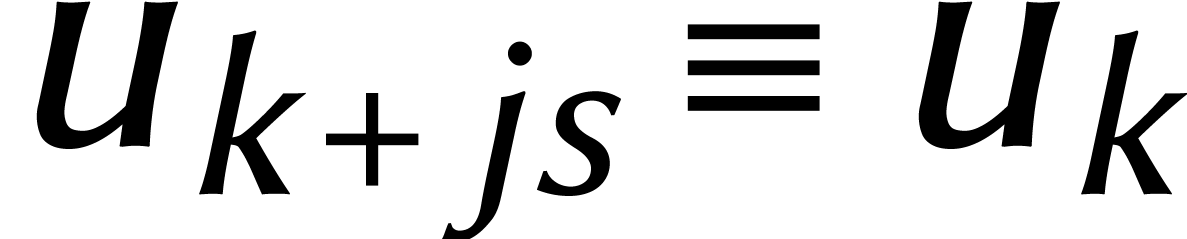 de coefficients. Nous convenons que
de coefficients. Nous convenons que 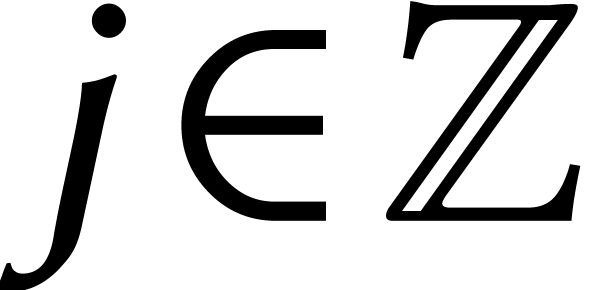 pour tout
pour tout 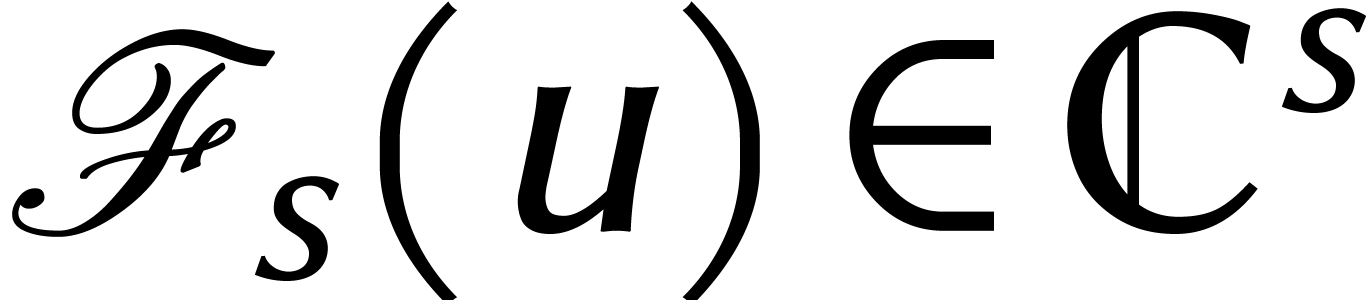 . Étant
donné
. Étant
donné 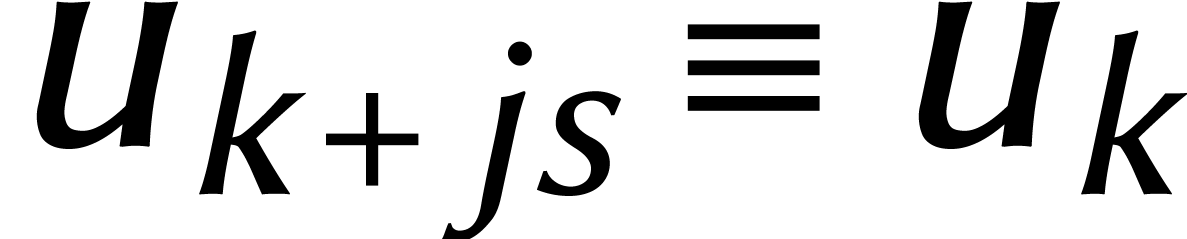 , on
définit
, on
définit 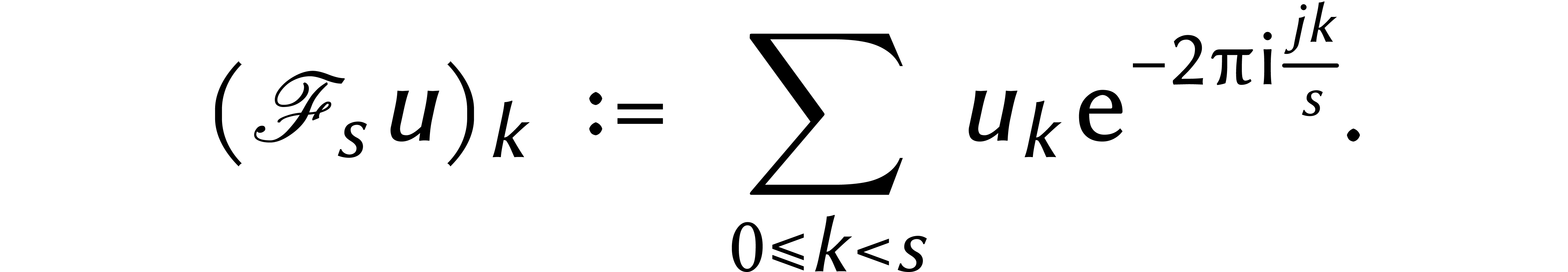 par
par
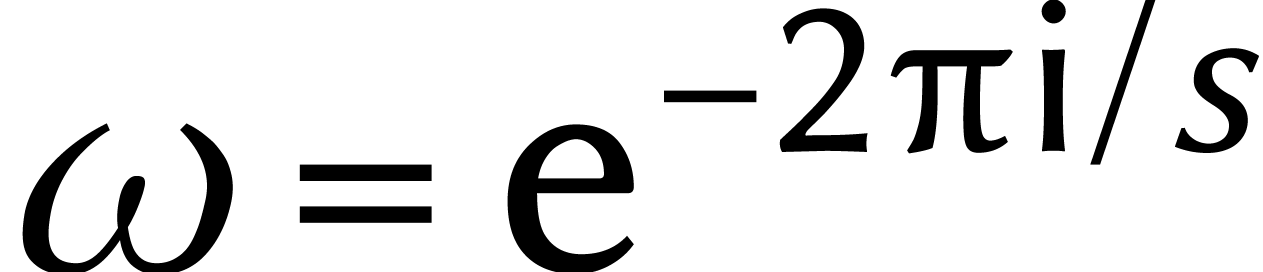
Ceci est une variante de notre définition
précédente d'une DFT (ici  ).
Puis on définit deux applications linéaires
).
Puis on définit deux applications linéaires 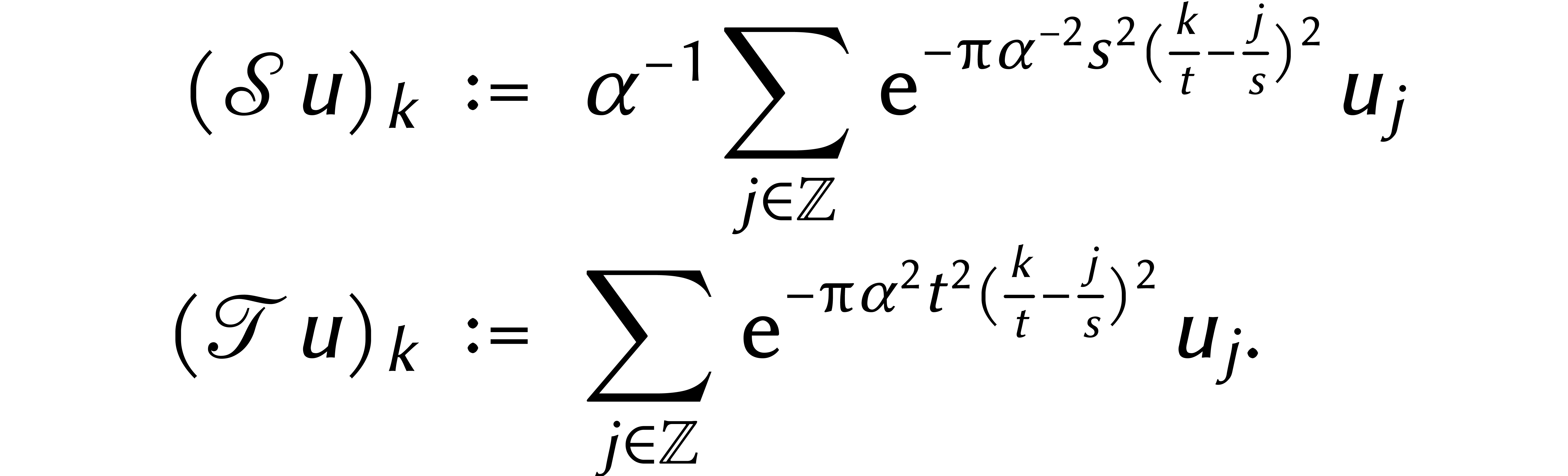 par
par
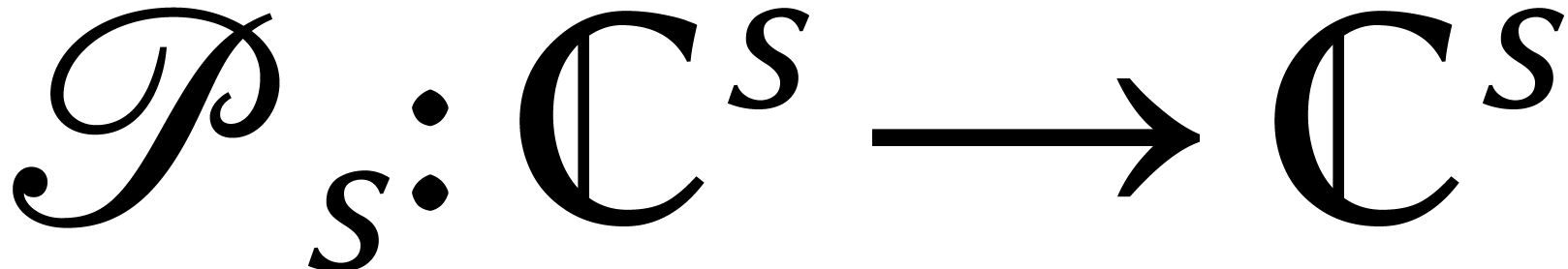
Enfin, nous introduisons deux permutations 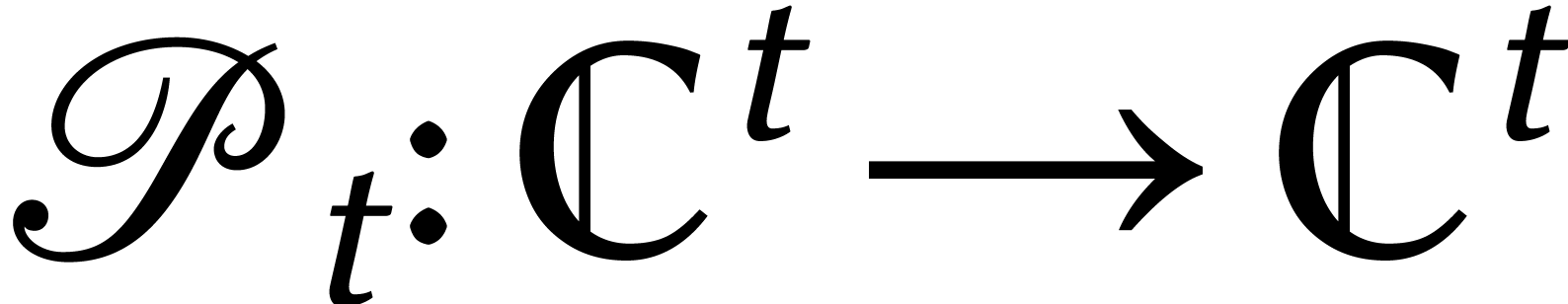 et
et
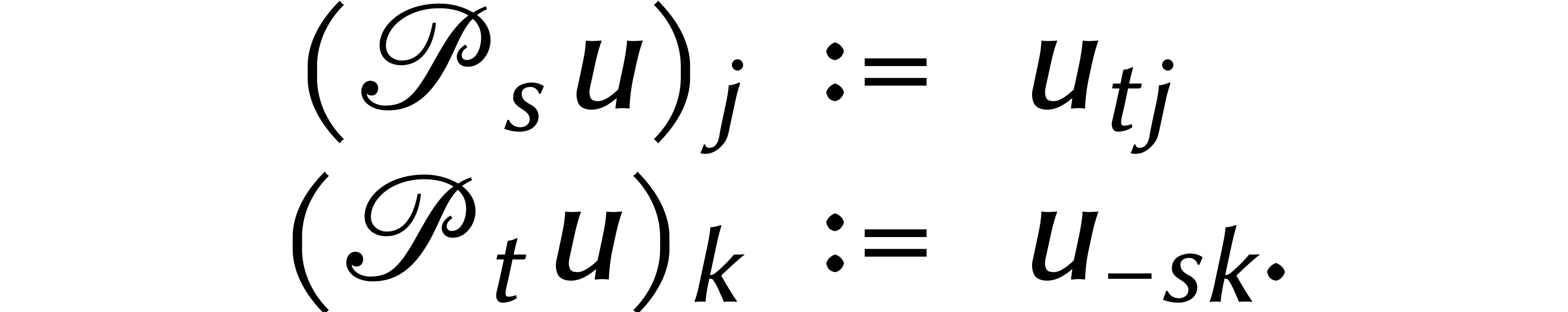 par
par
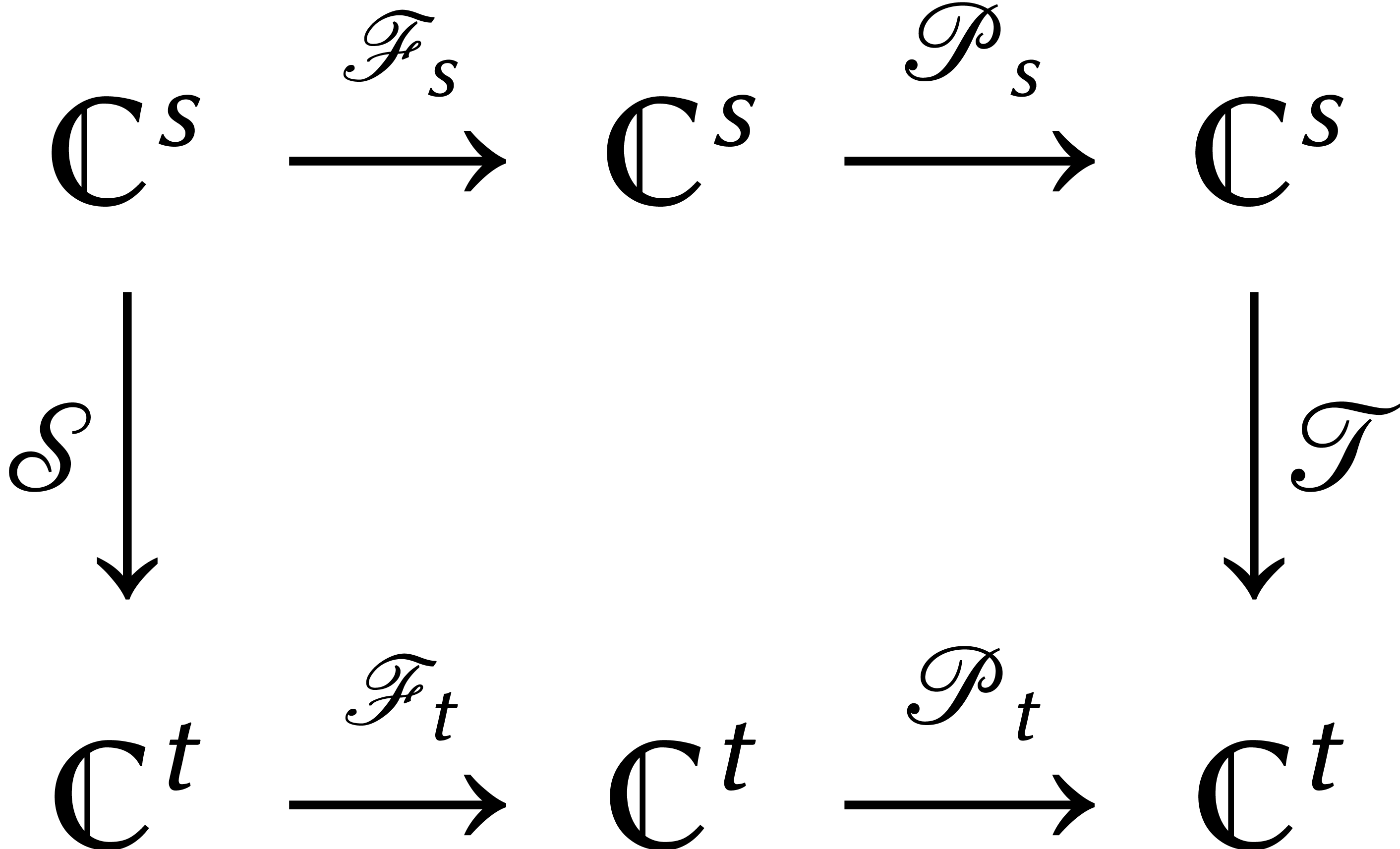
Dans [12, Theorem 4.2] nous montrons que le diagramme suivant commute :

C'est ce que nous utilisons pour réduire le calcul de  au calcul de
au calcul de  .
.
Puisque  , les matrices de
, les matrices de
 et
et 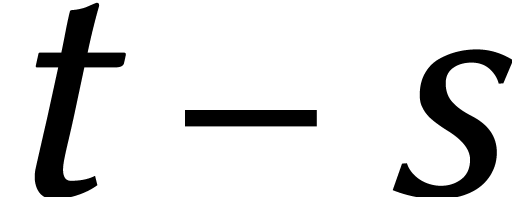 ne sont pas
carrées. Par construction, les éléments qui ne sont
pas sur la diagonale diminuent rapidement. En effet, les gaussiennes
déclinent à la vitesse de l'éclair loin du centre.
En supprimant
ne sont pas
carrées. Par construction, les éléments qui ne sont
pas sur la diagonale diminuent rapidement. En effet, les gaussiennes
déclinent à la vitesse de l'éclair loin du centre.
En supprimant  des lignes bien choisies de
des lignes bien choisies de 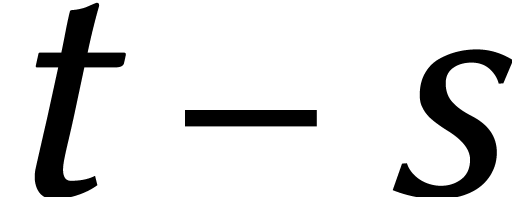 , il reste une matrice presque
diagonale. Ceci peut être utilisé pour calculer rapidement
, il reste une matrice presque
diagonale. Ceci peut être utilisé pour calculer rapidement
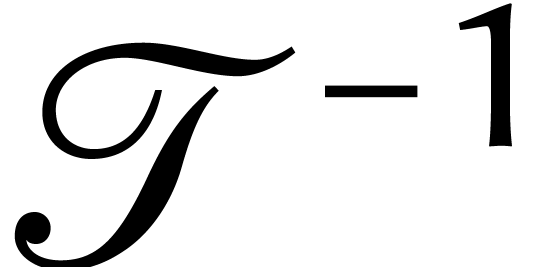 .
.
Si l'on choisit 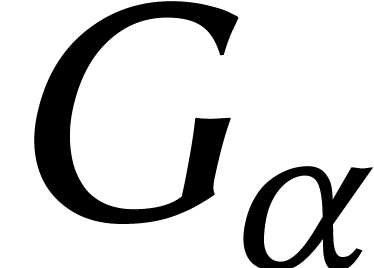 et la précision de calcul
avec précaution, on montre que
et la précision de calcul
avec précaution, on montre que  peut
être calculé ainsi avec presque autant de précision
que
peut
être calculé ainsi avec presque autant de précision
que  et que le temps de calcul de
et que le temps de calcul de  et de
et de 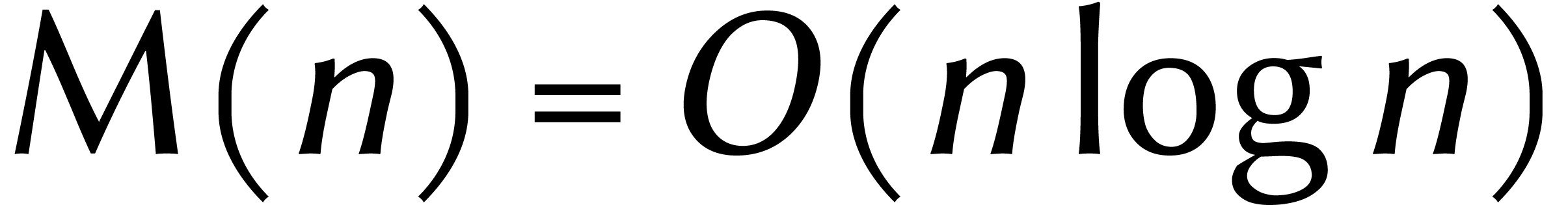 est négligeable par
rapport à celui de
est négligeable par
rapport à celui de  .
.
Ceci parachève notre méthode et la démonstration
que
 .
La figure
6
récapitule toutes les réductions que nous avons
utilisées.
.
La figure
6
récapitule toutes les réductions que nous avons
utilisées.
Une variante de notre méthode de rééchantillonnage
fut publiée pour la première fois par Dutt et Rokhlin [4]. Cette variante est plus générale et permet
de calculer des DFT quand échantillons des signaux sont
irréguliers. En revanche, leur méthode ne fonctionne que
pour  ; de ce fait, elle est juste un peu trop
lente pour notre application.
; de ce fait, elle est juste un peu trop
lente pour notre application.
D'un point de vue pratique, nous verrons... Mais la fonction 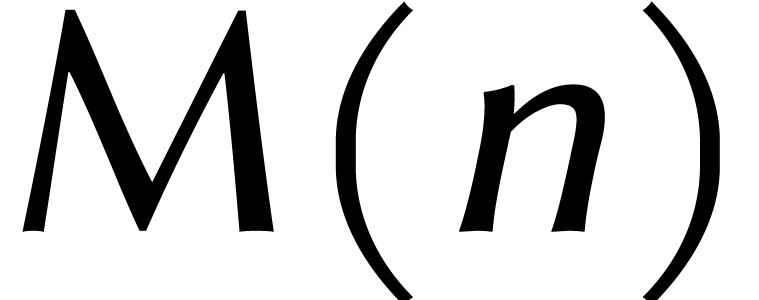 est importante pour la théorie, afin de décrire avec
précision les coûts de toutes sortes d'opérations
arithmétiques. Ainsi la division de deux entiers de
est importante pour la théorie, afin de décrire avec
précision les coûts de toutes sortes d'opérations
arithmétiques. Ainsi la division de deux entiers de 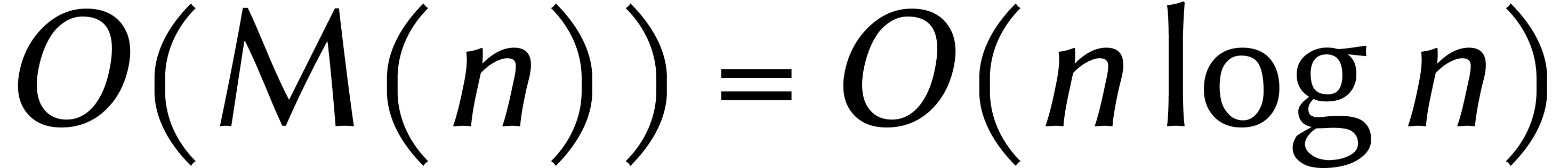 chiffres prend
chiffres prend 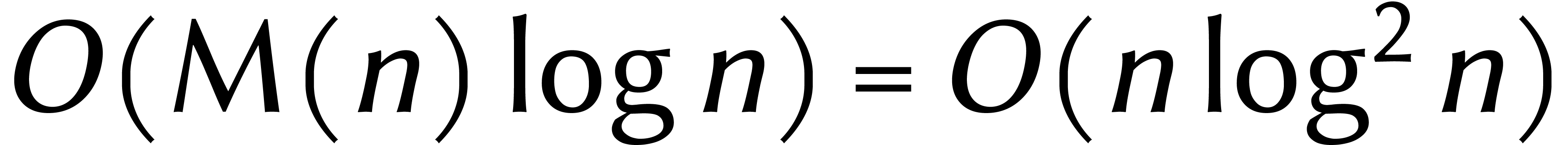 opérations
et le calcul d'un pgcd en prend
opérations
et le calcul d'un pgcd en prend  .
Désormais, on sait calculer
.
Désormais, on sait calculer 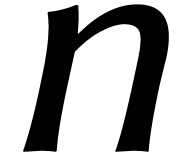 chiffres de
chiffres de
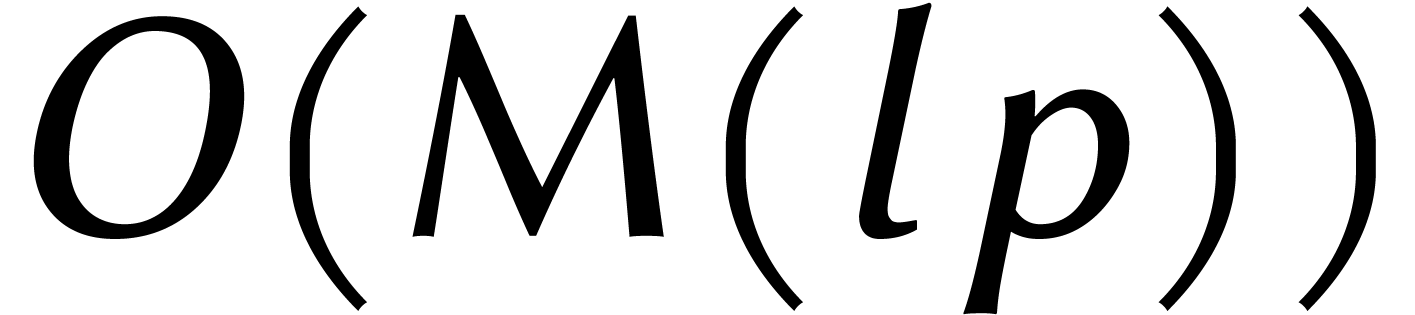 en temps
en temps  .
Une DFT complexe de longueur
.
Une DFT complexe de longueur  nécessite
nécessite
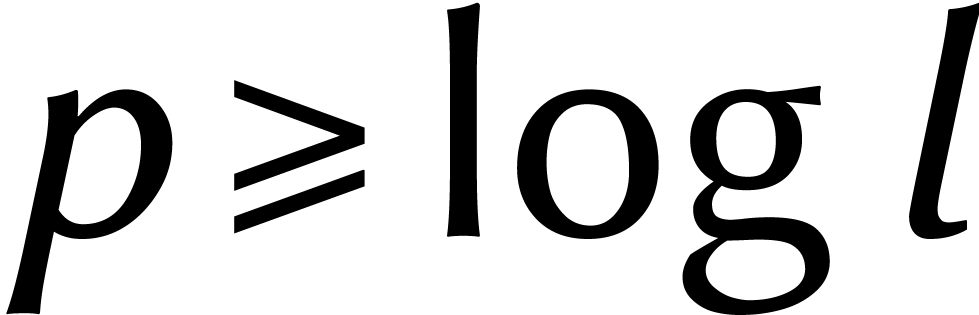 opérations, si on calcule avec
opérations, si on calcule avec  chiffres derrière la virgule [13].
Cela détermine également les émissions minimales de
CO2 pour des gros calculs sur le réchauffement
climatique. D'une certaine manière, la fonction
chiffres derrière la virgule [13].
Cela détermine également les émissions minimales de
CO2 pour des gros calculs sur le réchauffement
climatique. D'une certaine manière, la fonction 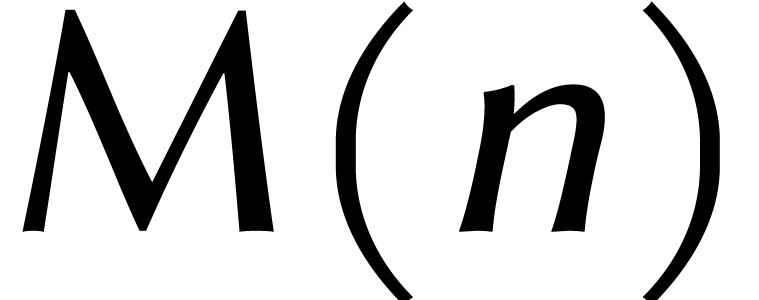 comme « vitesse de l'arithmétique élémentaire
» joue donc un rôle similaire à la vitesse de la
lumière
comme « vitesse de l'arithmétique élémentaire
» joue donc un rôle similaire à la vitesse de la
lumière 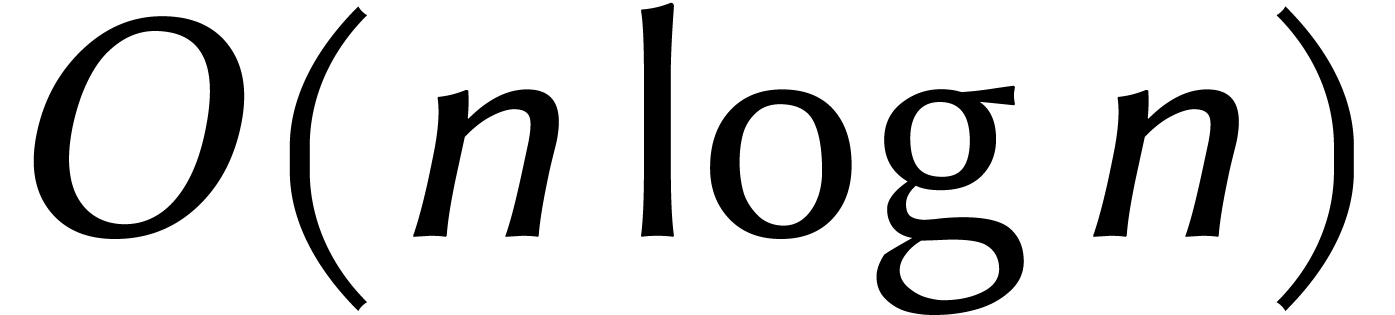 en physique.
en physique.
Nous l'ignorons !
R. Agarwal et J. Cooley. New algorithms for digital convolution. IEEE Transactions on Acoustics, Speech, and Signal Processing, 25(5):392–410, 1977.
Leo I. Bluestein. A linear filtering approach to the computation of discrete Fourier transform. IEEE Transactions on Audio and Electroacoustics, 18(4):451–455, 1970.
J. W. Cooley et J. W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
A. Dutt et V. Rokhlin. Fast Fourier transforms for nonequispaced data. SIAM J. Sci. Comput., 14(6):1368–1393, 1993.
M. Fürer. Faster integer multiplication. Dans Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing (STOC 2007), pages 57–66. San Diego, California, 2007.
C. F. Gauss. Nachlass: theoria interpolationis methodo nova tractata. Dans Werke, volume 3, pages 265–330. Königliche Gesellschaft der Wissenschaften, Göttingen, 1866.
I. J. Good. The interaction algorithm and practical Fourier analysis. Journal of the Royal Statistical Society, Series B. 20(2):361–372, 1958.
D. Harvey. Faster arithmetic for number-theoretic transforms. J. Symbolic Comput., 60:113–119, 2014.
D. Harvey. Faster truncated integer multiplication. https://arxiv.org/abs/1703.00640, 2017.
D. Harvey et J. van der Hoeven. Faster integer and polynomial multiplication using cyclotomic coefficient rings. Technical Report, ArXiv, 2017. http://arxiv.org/abs/1712.03693.
D. Harvey et J. van der Hoeven. Faster integer multiplication using short lattice vectors. Dans R. Scheidler et J. Sorenson, éditeurs, Proc. of the 13-th Algorithmic Number Theory Symposium, Open Book Series 2, pages 293–310. Mathematical Sciences Publishes, Berkeley, 2019.
D. Harvey et J. van der Hoeven. Integer
multiplication in time  .
Annals of Mathematics, 193(2):563–617, 2021.
.
Annals of Mathematics, 193(2):563–617, 2021.
D. Harvey, J. van der Hoeven, et G. Lecerf. Even faster integer multiplication. Journal of Complexity, 36:1–30, 2016.
M. T. Heideman, D. H. Johnson, et C. S. Burrus. Gauss and the history of the FFT. IEEE Acoustics, Speech and Signal Processing Magazine, 1:14–21, oct 1984.
J. van der Hoeven. Getallen vermenigvuldigen in  stappen. Nieuw Archief voor Wiskunde,
21(1):55–60, 2020. Vijfde serie.
stappen. Nieuw Archief voor Wiskunde,
21(1):55–60, 2020. Vijfde serie.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
A. A. Karatsuba. The complexity of computations. Proc. of the Steklov Inst. of Math., 211:169–183, 1995. English translation; Russian original at pages 186–202.
A. Karatsuba et J. Ofman. Multiplication of multidigit numbers on automata. Soviet Physics Doklady, 7:595–596, 1963.
D. E. Knuth. The Art of Computer Programming, volume 2: Seminumerical Algorithms. Addison-Wesley, 1969.
H. J. Nussbaumer et P. Quandalle. Computation of convolutions and discrete Fourier transforms by polynomial transforms. IBM J. Res. Develop., 22(2):134–144, 1978.
J. M. Pollard. The fast Fourier transform in a finite field. Mathematics of Computation, 25(114):365–374, 1971.
A. Schönhage. Multiplikation großer Zahlen. Computing, 1(3):182–196, 1966.
A. Schönhage et V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
A. L. Toom. The complexity of a scheme of functional elements realizing the multiplication of integers. Soviet Mathematics, 4(2):714–716, 1963.