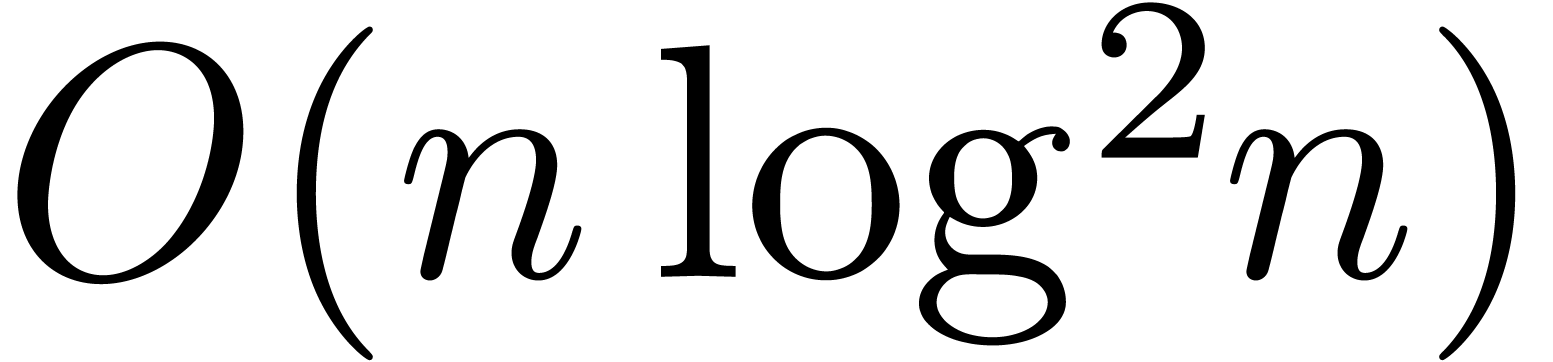For most fast algorithms to manipulate formal power series, a fast multiplication algorithm is essential. If one desires to compute all coefficients of a product of two power series up to a given order, then several efficient algorithms are available, such as fast Fourier multiplication. However, one often needs a lazy multiplication algorithm, for instance when the product computation is part of the computation of the coefficients of an implicitly defined power series. In this paper, we describe two lazy multiplication algorithms, which are faster than the naive method. In particular, we give an algorithm of time complexity .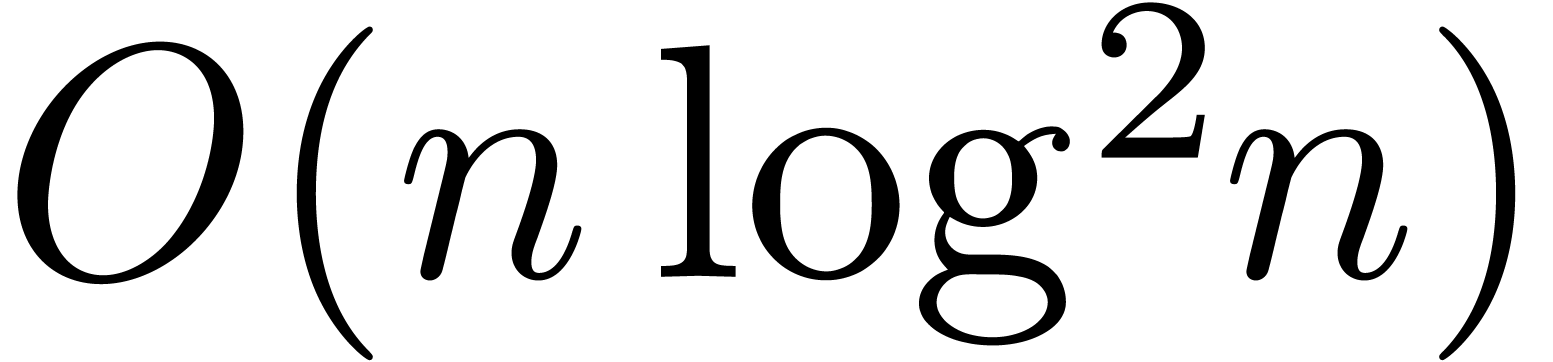

Keywords: power series, multiplication, algorithm

View: Pdf, BibTeX