Abstract
It is well known that the operation of integration may lead to divergent
formal expansions like 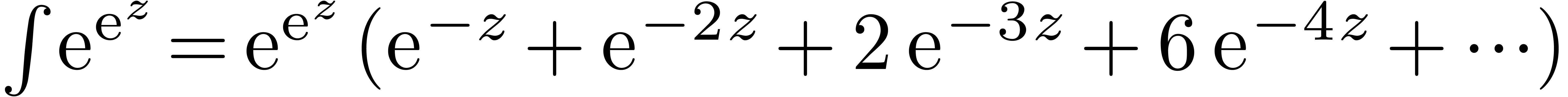 as
soon as one leaves the area of formal power series for the area of
formal transseries. On the other hand, from the analytic point of view,
the operation of integration is usually “regularizing”, in
the sense that it improves convergence rather than destroying it. For
this reason, it is natural to consider so called “integral
transseries” which are similar to usual transseries except that we
are allowed to recursively keep integrals in the expansions. Integral
transseries come with a natural notion of “combinatorial
convergence”, which is preserved under the usual operations on
transseries, as well as integration. In this paper, we lay the formal
foundations for this calculus.
as
soon as one leaves the area of formal power series for the area of
formal transseries. On the other hand, from the analytic point of view,
the operation of integration is usually “regularizing”, in
the sense that it improves convergence rather than destroying it. For
this reason, it is natural to consider so called “integral
transseries” which are similar to usual transseries except that we
are allowed to recursively keep integrals in the expansions. Integral
transseries come with a natural notion of “combinatorial
convergence”, which is preserved under the usual operations on
transseries, as well as integration. In this paper, we lay the formal
foundations for this calculus.
View: Html, TeXmacs, Pdf,
BibTeX
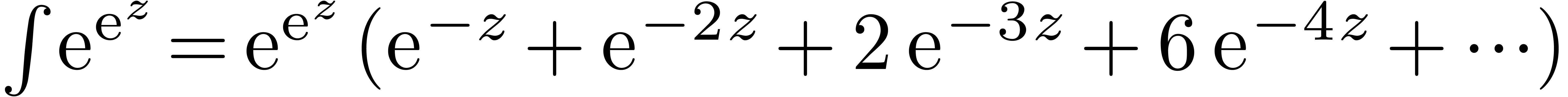 as
soon as one leaves the area of formal power series for the area of
formal transseries. On the other hand, from the analytic point of view,
the operation of integration is usually “regularizing”, in
the sense that it improves convergence rather than destroying it. For
this reason, it is natural to consider so called “integral
transseries” which are similar to usual transseries except that we
are allowed to recursively keep integrals in the expansions. Integral
transseries come with a natural notion of “combinatorial
convergence”, which is preserved under the usual operations on
transseries, as well as integration. In this paper, we lay the formal
foundations for this calculus.
as
soon as one leaves the area of formal power series for the area of
formal transseries. On the other hand, from the analytic point of view,
the operation of integration is usually “regularizing”, in
the sense that it improves convergence rather than destroying it. For
this reason, it is natural to consider so called “integral
transseries” which are similar to usual transseries except that we
are allowed to recursively keep integrals in the expansions. Integral
transseries come with a natural notion of “combinatorial
convergence”, which is preserved under the usual operations on
transseries, as well as integration. In this paper, we lay the formal
foundations for this calculus.