| A differential intermediate value
theorem |
|
Dépt. de Mathématiques
(Bât. 425)
Université Paris-Sud
91405 Orsay Cedex
France
|
|
|
1Introduction
1.1Statement of the results
Let  be a totally ordered exp-log field. In
chapter 2 of [vdH97], we introduced the field
be a totally ordered exp-log field. In
chapter 2 of [vdH97], we introduced the field 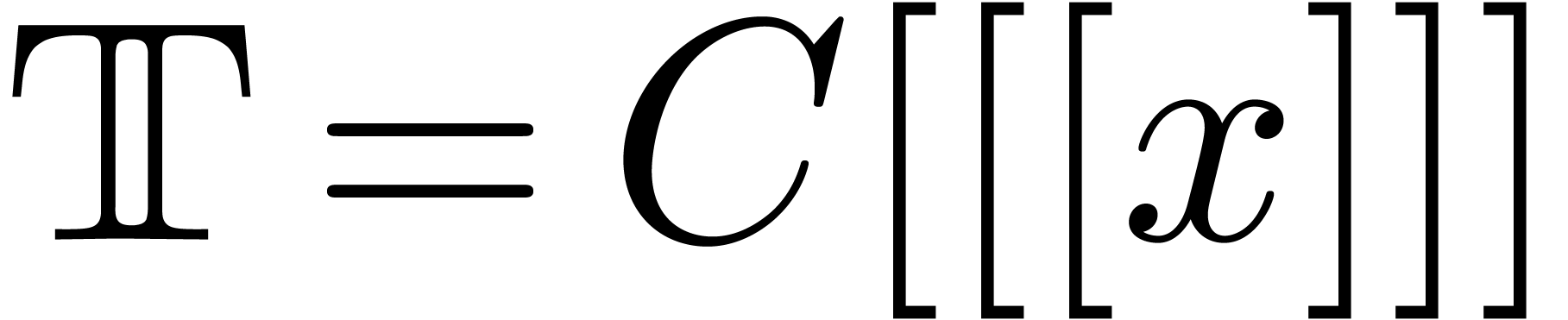 of transseries in
of transseries in  of finite
logarithmic and exponential depths. In chapter 5, we then gave an (at
least theoretical) algorithm to solve algebraic differential equations
with coefficients in
of finite
logarithmic and exponential depths. In chapter 5, we then gave an (at
least theoretical) algorithm to solve algebraic differential equations
with coefficients in  . By
that time, the following theorem was already known to us (and stated in
the conclusion), but due to lack of time, we had not been able to
include the proof.
. By
that time, the following theorem was already known to us (and stated in
the conclusion), but due to lack of time, we had not been able to
include the proof.
Theorem 1. Let  be a differential polynomial with coefficients in
be a differential polynomial with coefficients in
 . Given
. Given 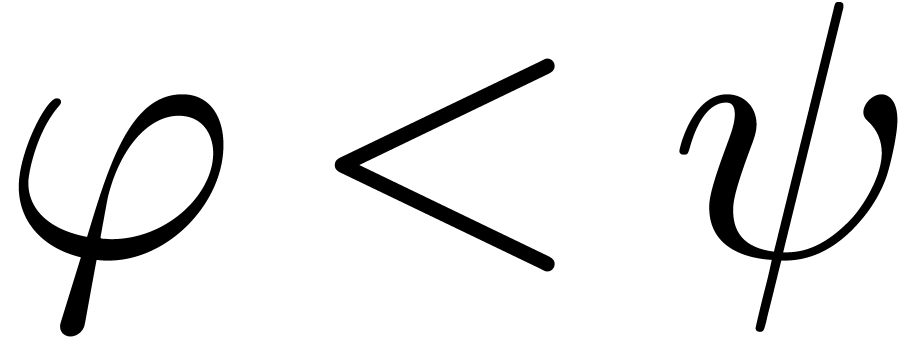 in
in  , such that
, such that 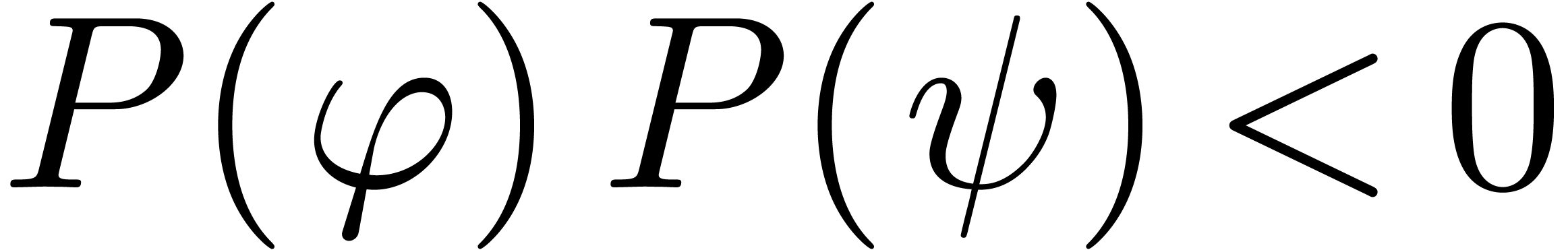 , there exists an
, there exists an  with
with
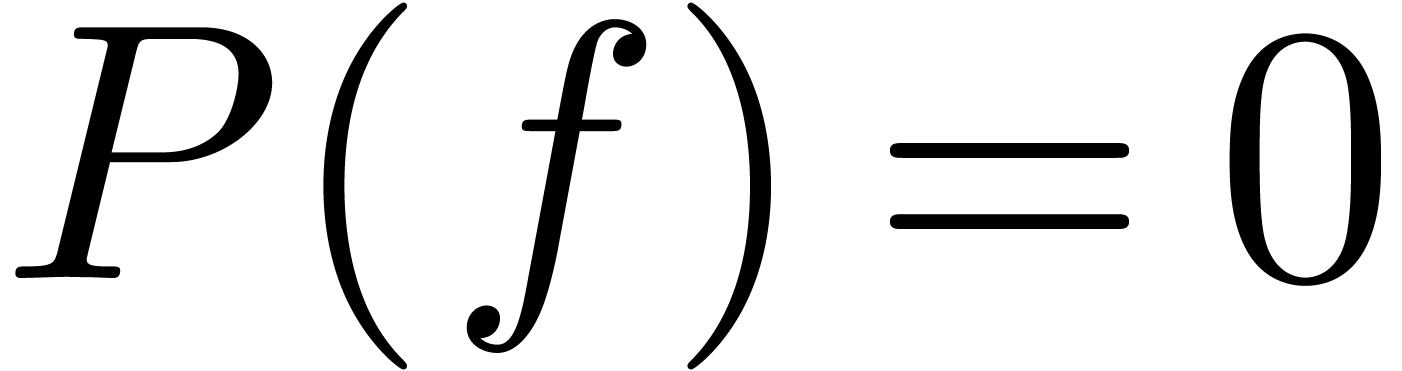 .
.
In the theorem, 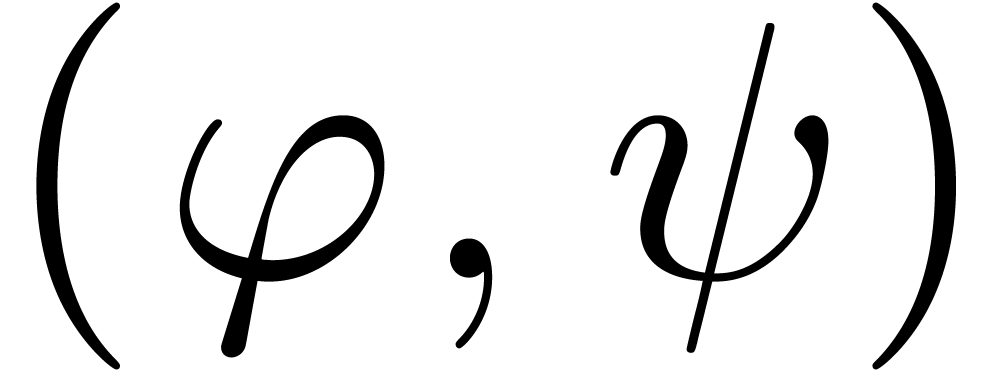 stands for the open interval
between
stands for the open interval
between  and
and 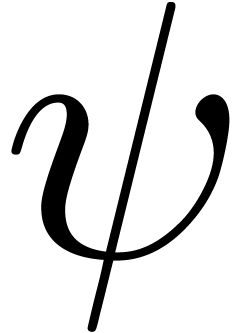 .
The proof that we will present in this note will be based on the
differential Newton polygon method as described in chapter 5 of [vdH97]. We will freely use any results from there. We recall
(and renew) some notations in section 2.
.
The proof that we will present in this note will be based on the
differential Newton polygon method as described in chapter 5 of [vdH97]. We will freely use any results from there. We recall
(and renew) some notations in section 2.
In chapter 1 of [vdH97], we also introduced the field of
grid-based  transseries in
transseries in  . In chapter 12, we have shown that our algorithm
for solving algebraic differential equations preserves the grid-based
property. Therefore, it is easily checked that theorem 1
also holds for
. In chapter 12, we have shown that our algorithm
for solving algebraic differential equations preserves the grid-based
property. Therefore, it is easily checked that theorem 1
also holds for 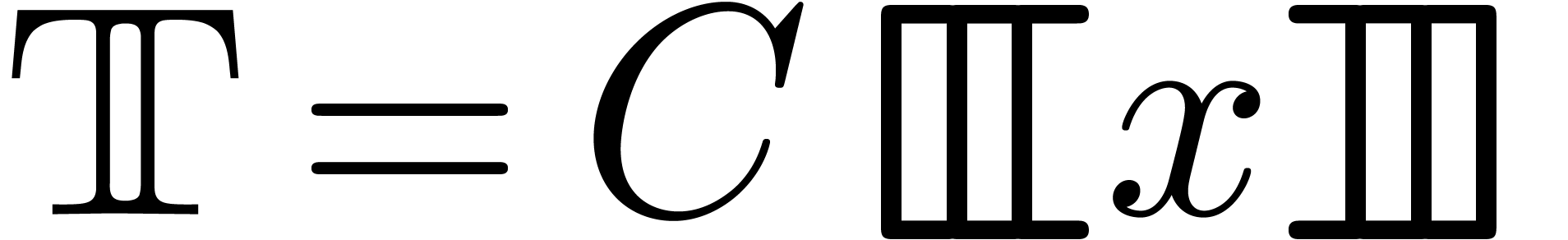 . Similarly,
it may be checked that the theorem holds if we take for
. Similarly,
it may be checked that the theorem holds if we take for  the field of transseries of finite logarithmic depths (and possibly
countable exponential depths).
the field of transseries of finite logarithmic depths (and possibly
countable exponential depths).
1.2Proof strategy
Assume that 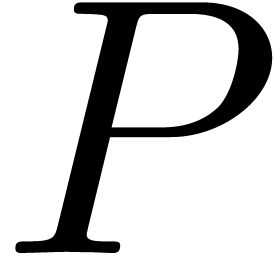 is a differential polynomial with
coefficients in
is a differential polynomial with
coefficients in  , which
admits a sign change on a non empty interval
, which
admits a sign change on a non empty interval 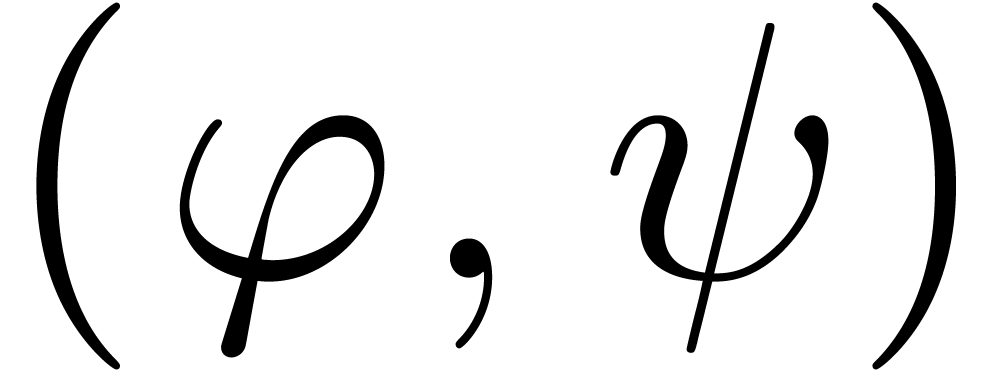 of
transseries. The idea behind the proof of theorem 1 is very
simple: using the differential Newton polygon method, we shrink the
interval
of
transseries. The idea behind the proof of theorem 1 is very
simple: using the differential Newton polygon method, we shrink the
interval 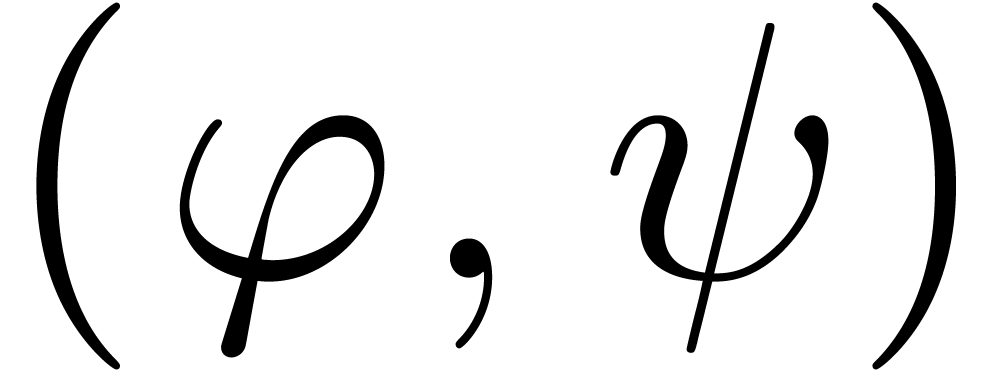 further and further while preserving
the sign change property. Ultimately, we end up with an interval which
is reduced to a point, which will then be seen to be a zero of
further and further while preserving
the sign change property. Ultimately, we end up with an interval which
is reduced to a point, which will then be seen to be a zero of 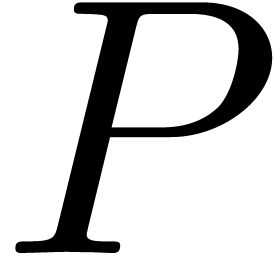 .
.
However, in order to apply the above idea, we will need to allow non
standard intervals 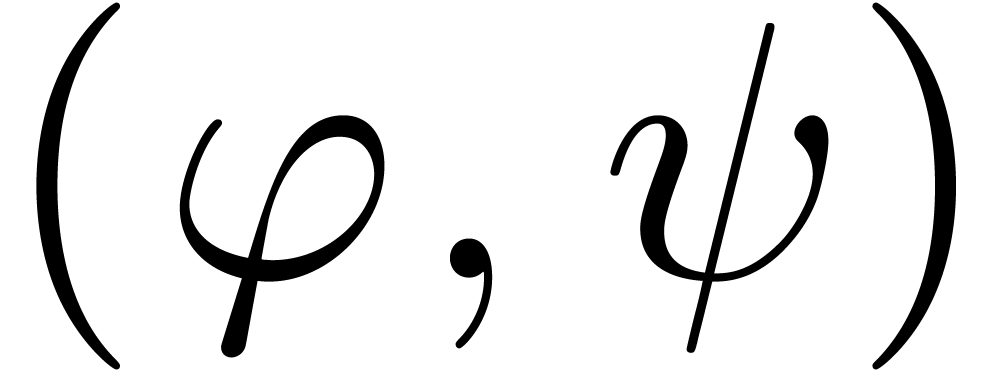 in the proof. More precisely,
in the proof. More precisely,
 and
and  may generally be
taken in the compactification of
may generally be
taken in the compactification of  ,
as constructed in section 2.6 of [vdH97]. In this paper we
will consider non standard
,
as constructed in section 2.6 of [vdH97]. In this paper we
will consider non standard  (resp.
(resp.  ) of the following forms:
) of the following forms:
Here  and
and  respectively
designate the infinitely small and large constants
respectively
designate the infinitely small and large constants  and
and  in the compactification of
in the compactification of  . Similarly,
. Similarly, 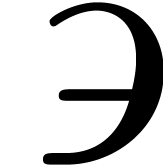 and
and 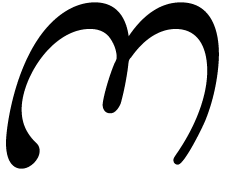 designate the infinitely small and large constants
designate the infinitely small and large constants
 and
and  in the
compactification of
in the
compactification of  . We may
then interpret
. We may
then interpret  as a cut of the transline
as a cut of the transline  into two pieces
into two pieces  .
Notice that
.
Notice that
Remark 2. Actually, the notations
 ,
,  , and so on are redundant. Indeed,
, and so on are redundant. Indeed,  does not depend on
does not depend on  , we have
, we have
 whenever
whenever 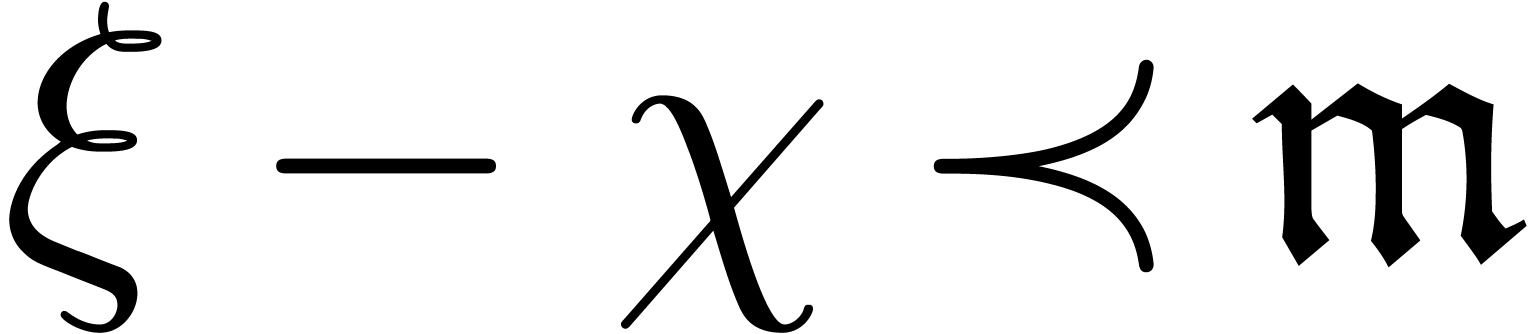 ,
etc.
,
etc.
Now consider a generalized interval  ,
where
,
where  and
and 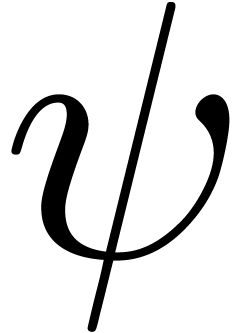 may be as
above. We have to give a precise meaning to the statement that
may be as
above. We have to give a precise meaning to the statement that 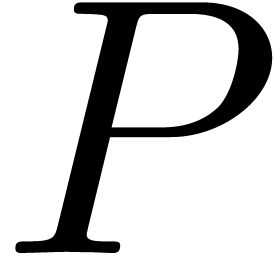 admits a sign change on
admits a sign change on 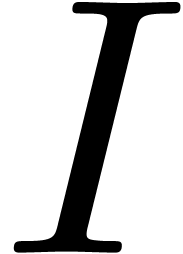 .
This will be the main object of sections 3 and 4.
We will show there that, given a cut
.
This will be the main object of sections 3 and 4.
We will show there that, given a cut  of the
above type, the function
of the
above type, the function 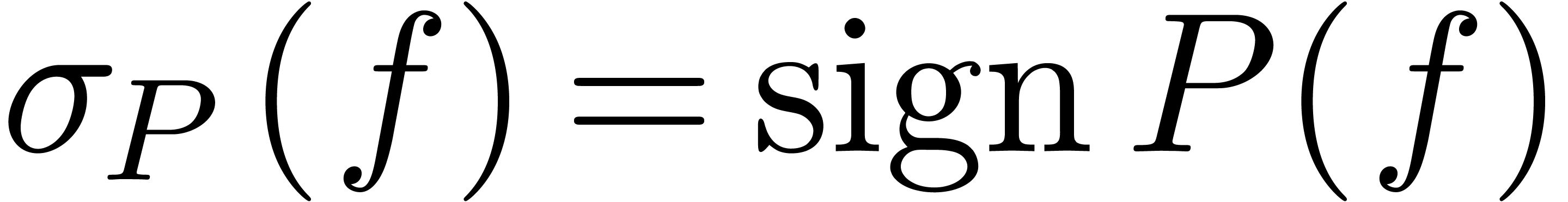 may be prolongated by
continuity into
may be prolongated by
continuity into  from at least one direction:
from at least one direction:
(In the cases  ,
, 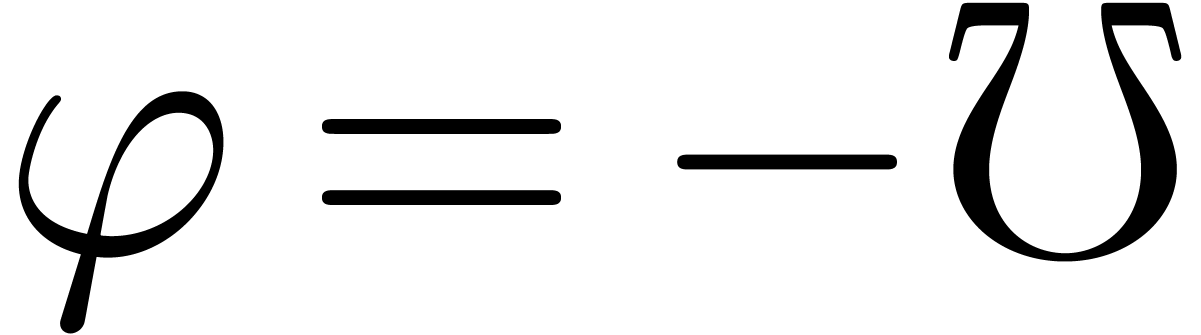 and so on, one has to interchange left and right
continuity in the above list.) Now we understand that
and so on, one has to interchange left and right
continuity in the above list.) Now we understand that 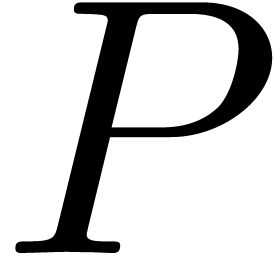 admits a sign change on a generalized interval
admits a sign change on a generalized interval 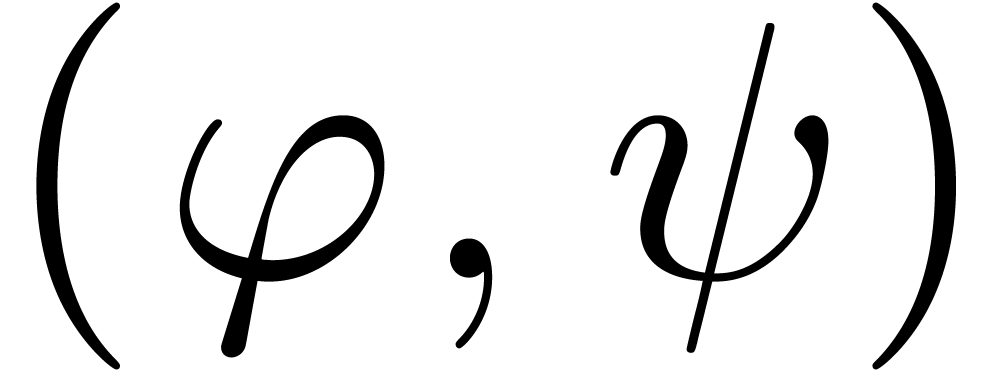 if
if 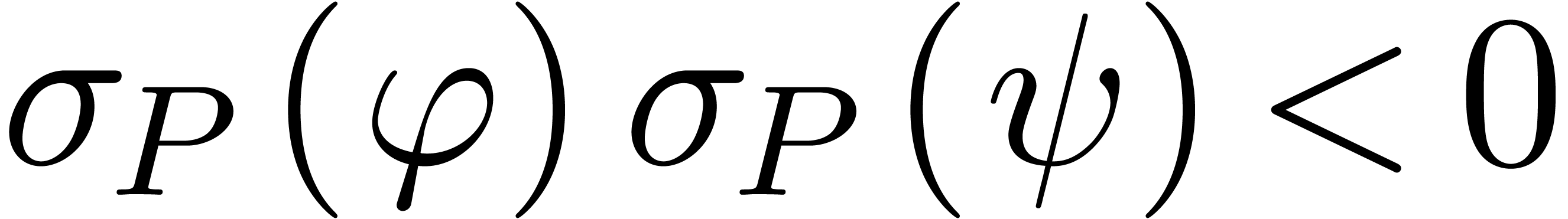 .
.
2List of notations
Asymptotic relations.
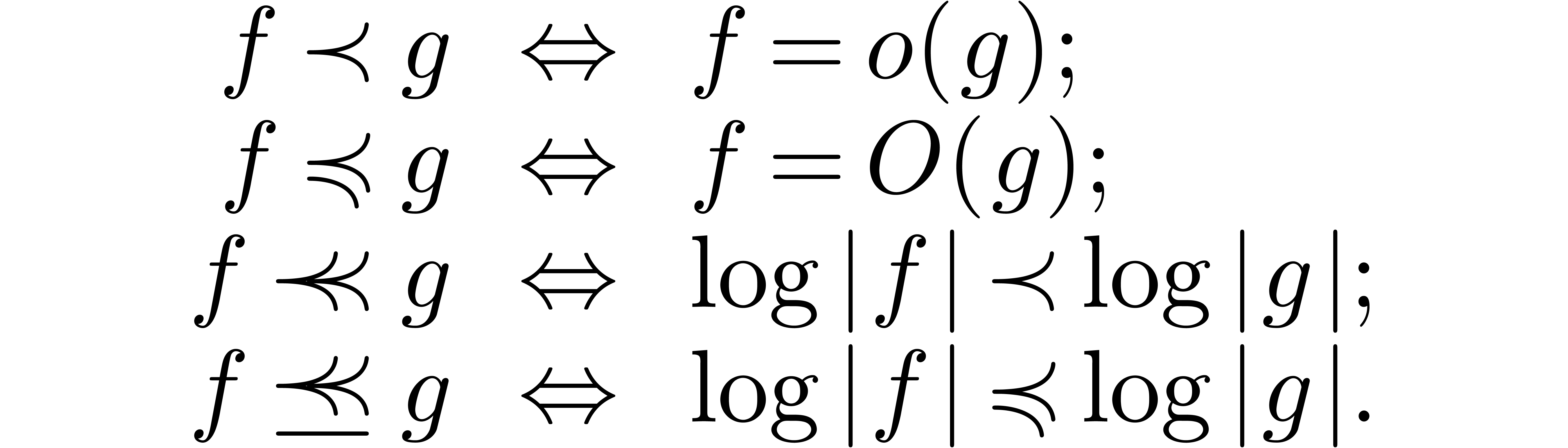
Logarithmic derivatives.
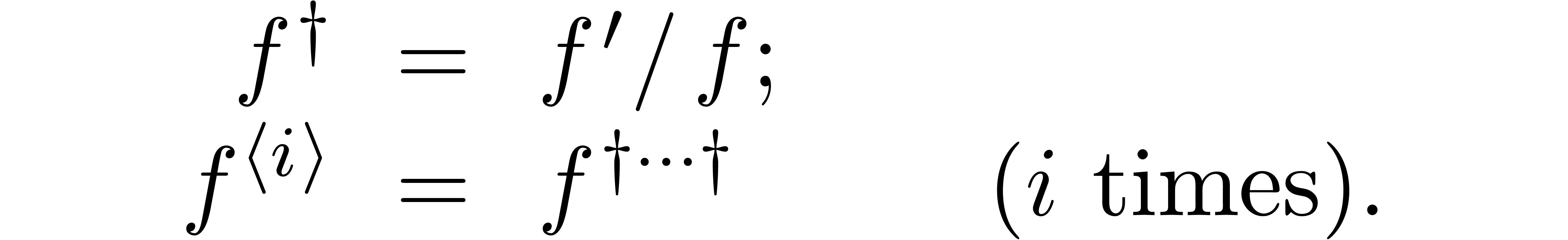
Natural decomposition of  .
.
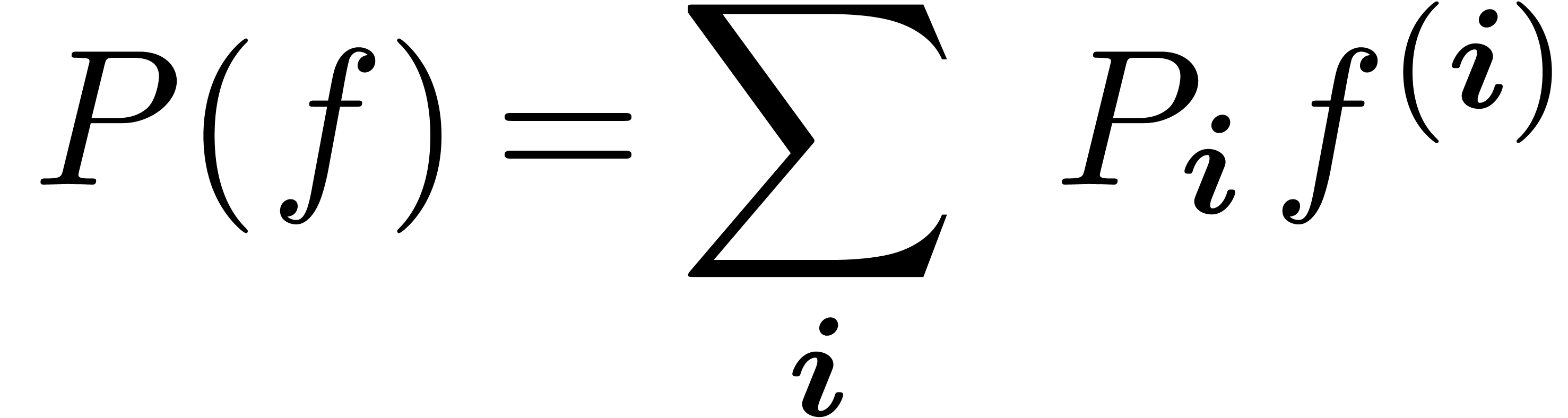 |
(1) |
Here we use vector notation for tuples 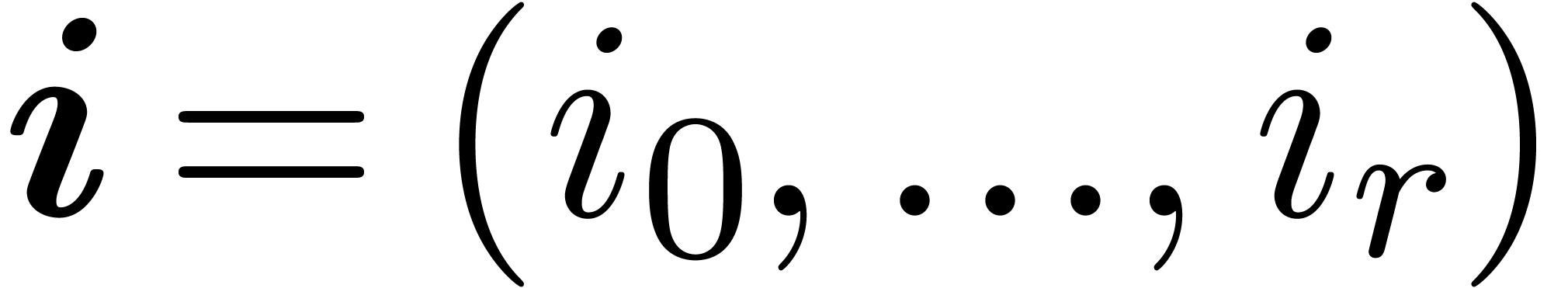 and
and 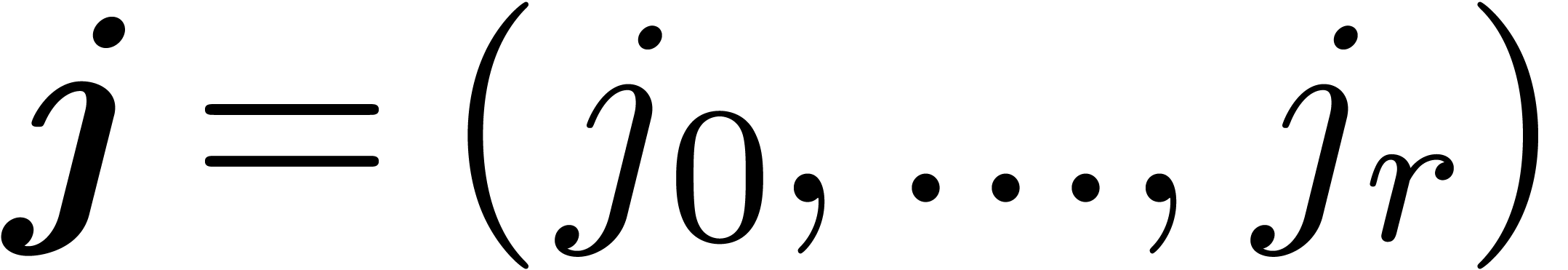 of integers:
of integers:
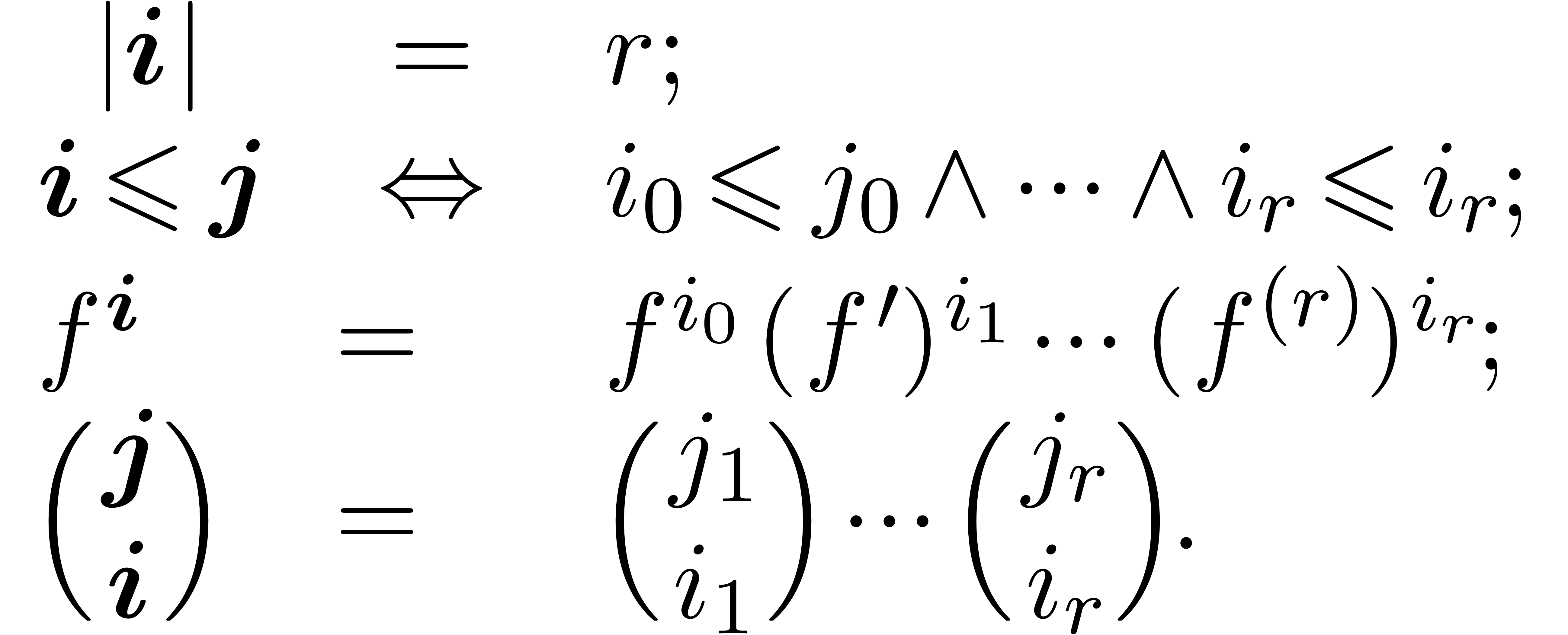
Decomposition of  along orders.
along orders.
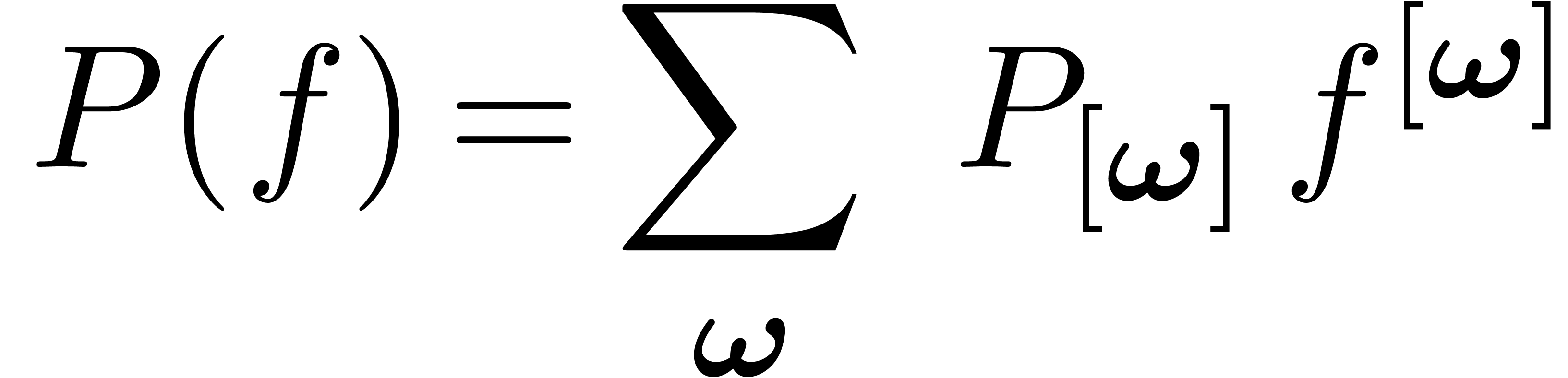 |
(2) |
In this notation,  runs through tuples
runs through tuples 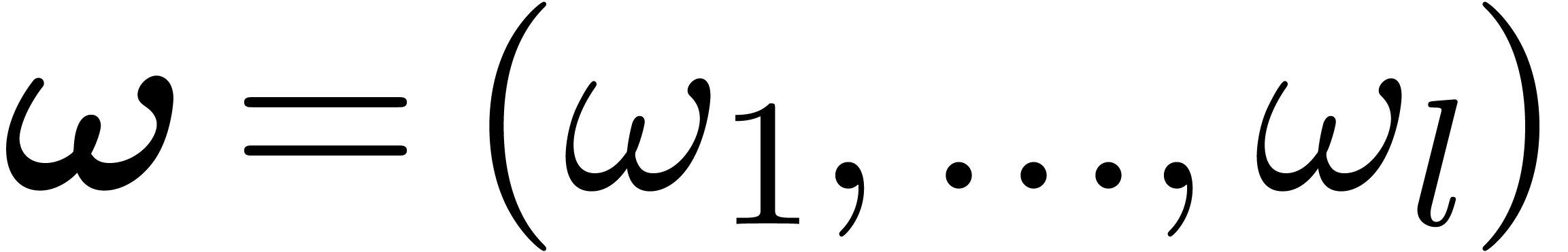 of integers in
of integers in  of length
of length 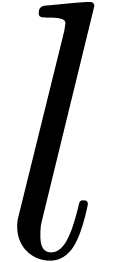 at most
at most 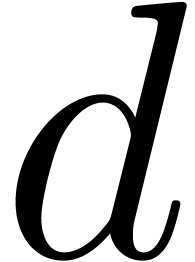 , and
, and
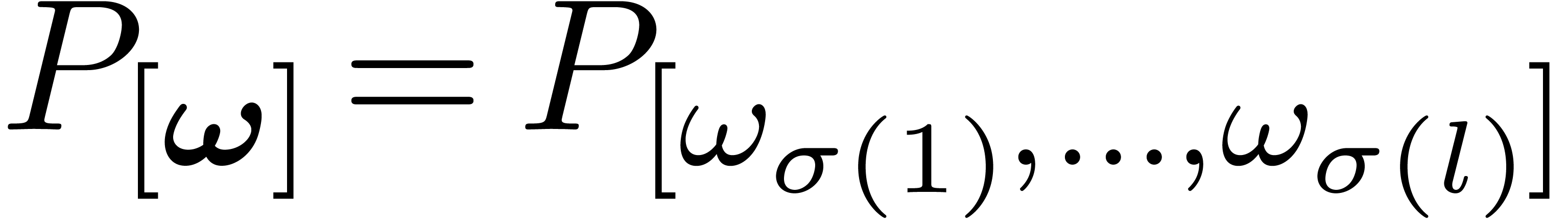 for all permutations of integers. We again use
vector notation for such tuples
for all permutations of integers. We again use
vector notation for such tuples
We call  || the weight
of
|| the weight
of  and
and
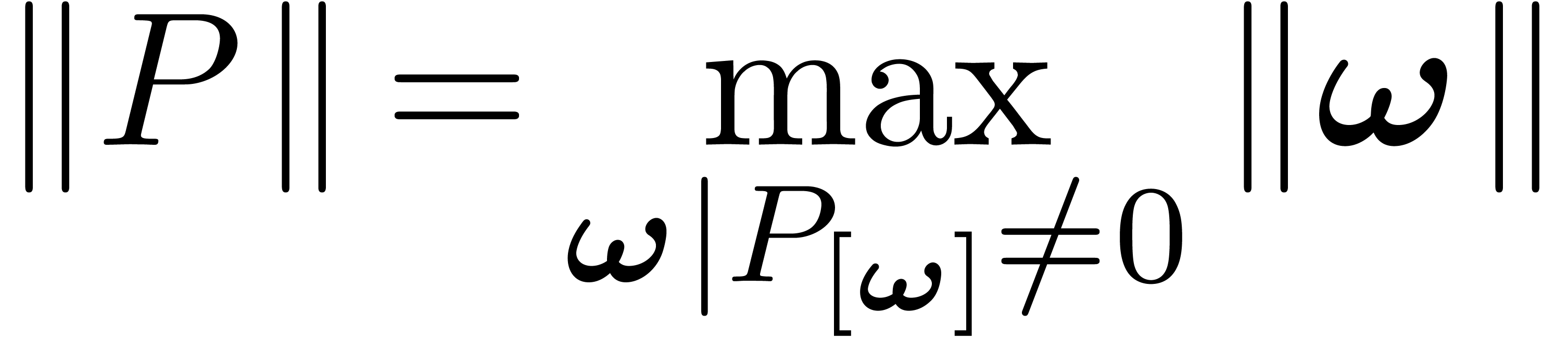
the weight of  .
.
Additive, multiplicative and compositional conjugations or upward
shifting.
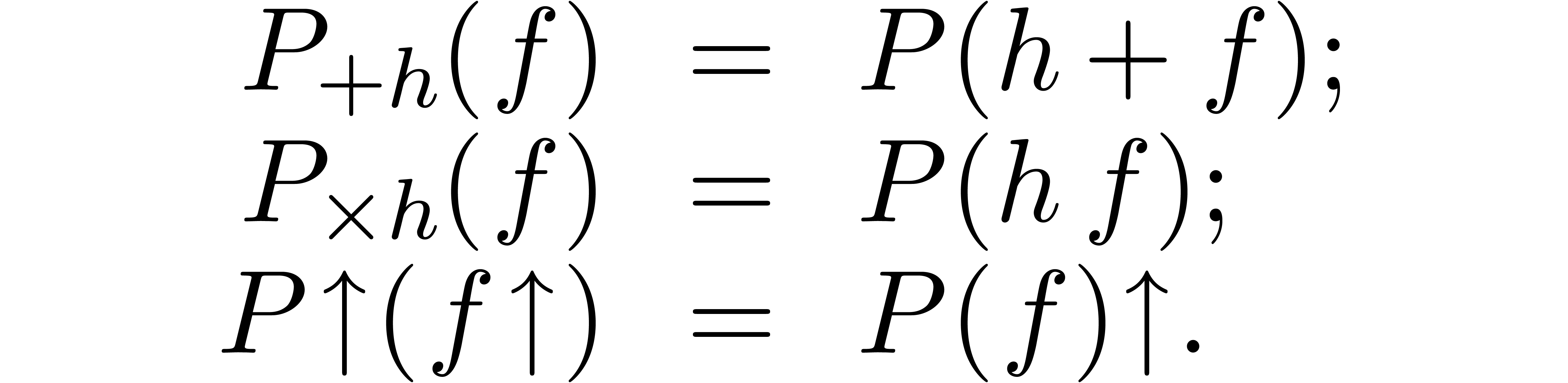
Additive conjugation:
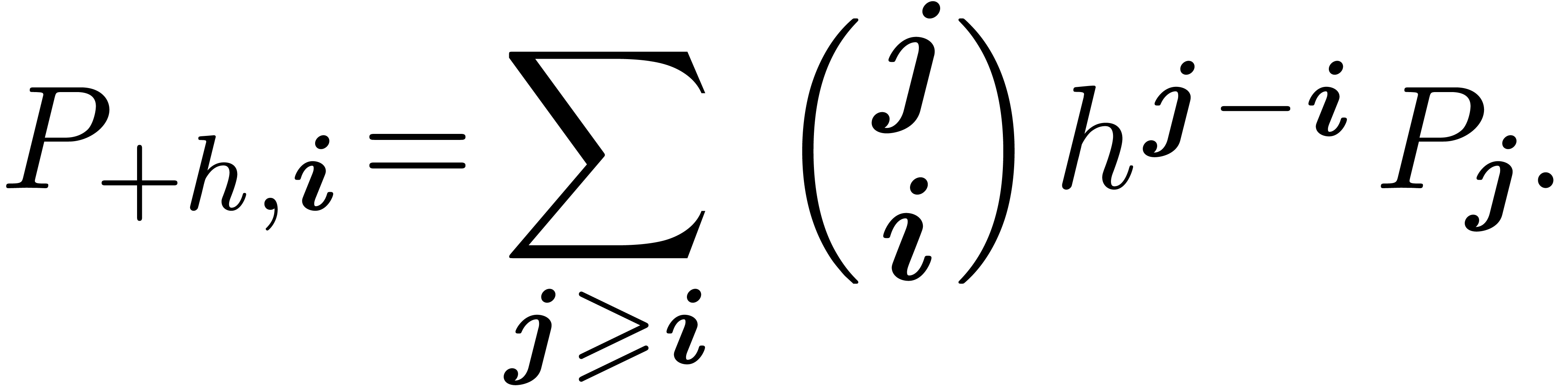 |
(3) |
Multiplicative conjugation:
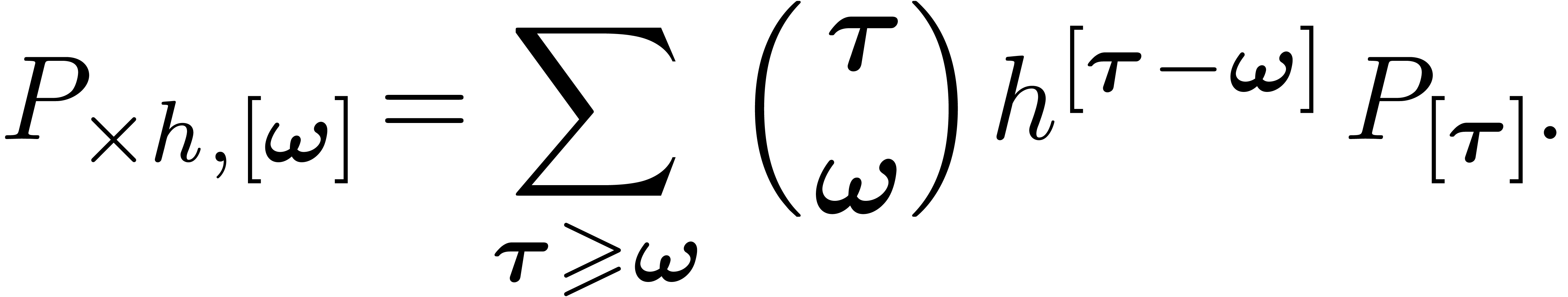 |
(4) |
Upward shifting (compositional conjugation):
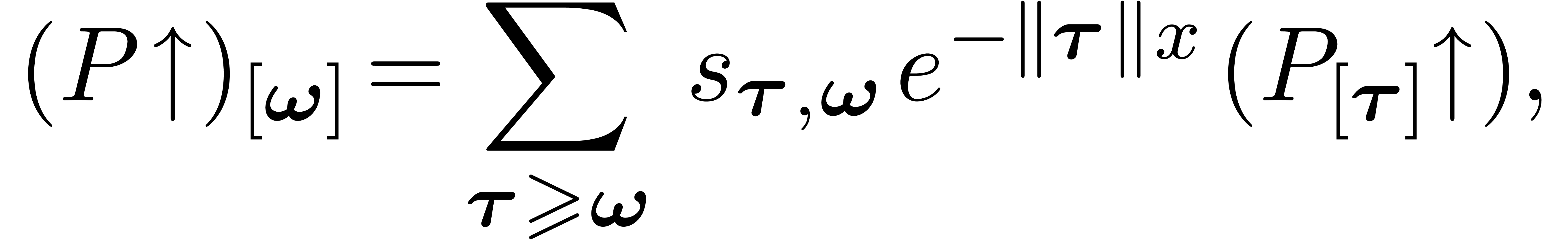 |
(5) |
where the 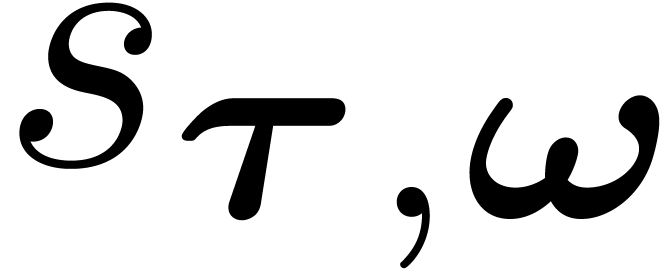 are generalized Stirling numbers of
the first kind:
are generalized Stirling numbers of
the first kind:
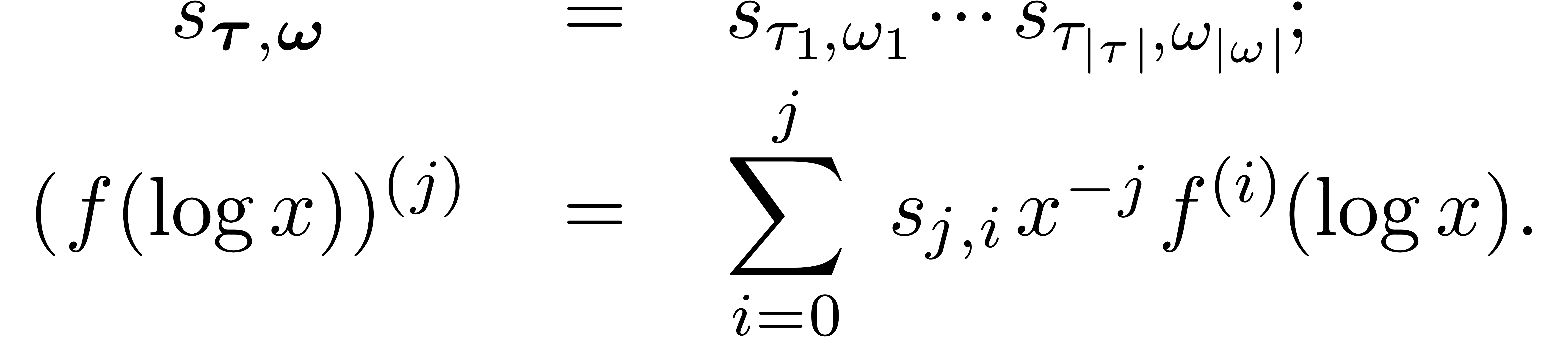
3Behaviour of  near zero and infinity
near zero and infinity
3.1Behaviour of 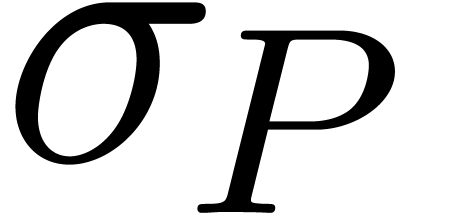 near
infinity
near
infinity
Lemma 3. Let  be a differential polynomial with coefficients in
be a differential polynomial with coefficients in
 . Then
. Then 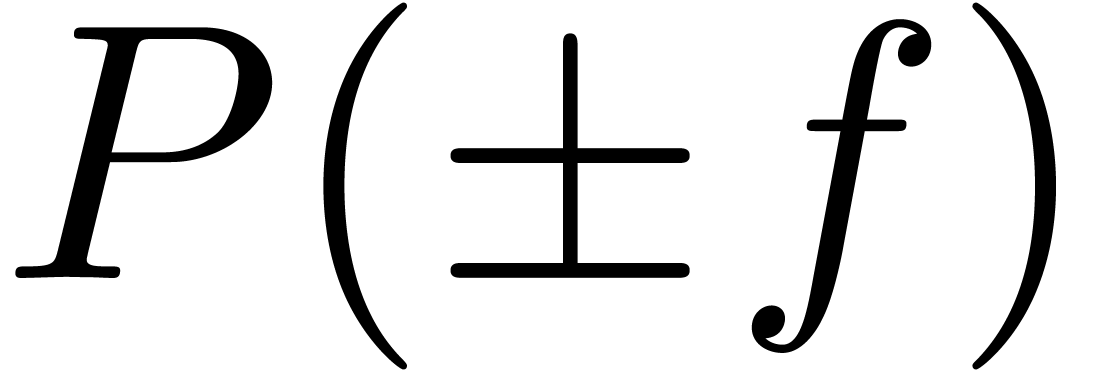 has constant sign for all sufficiently large
has constant sign for all sufficiently large 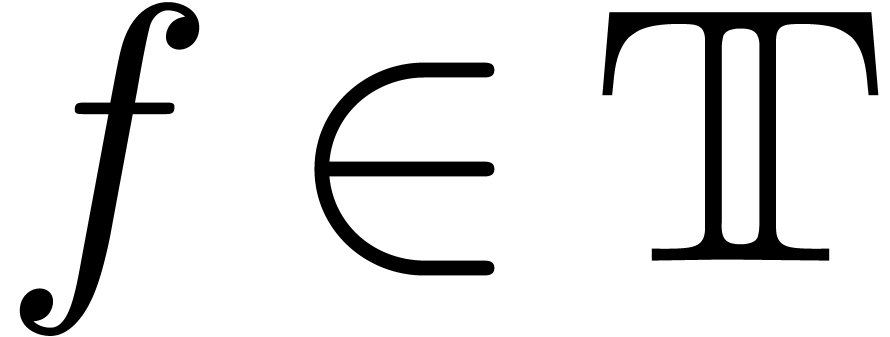 .
.
Proof. If 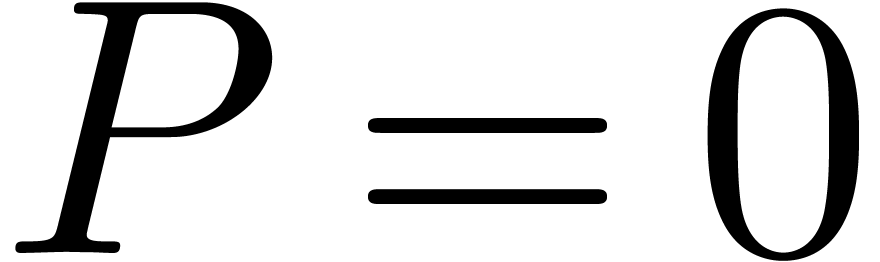 ,
then the lemma is clear, so assume that
,
then the lemma is clear, so assume that 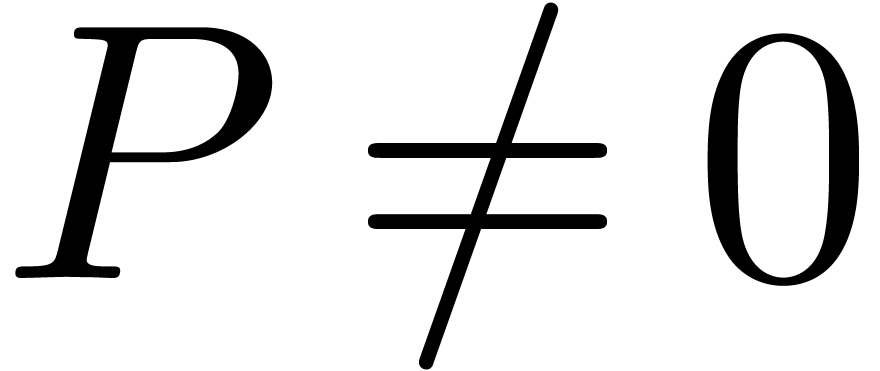 .
Using the rules
.
Using the rules
we may rewrite 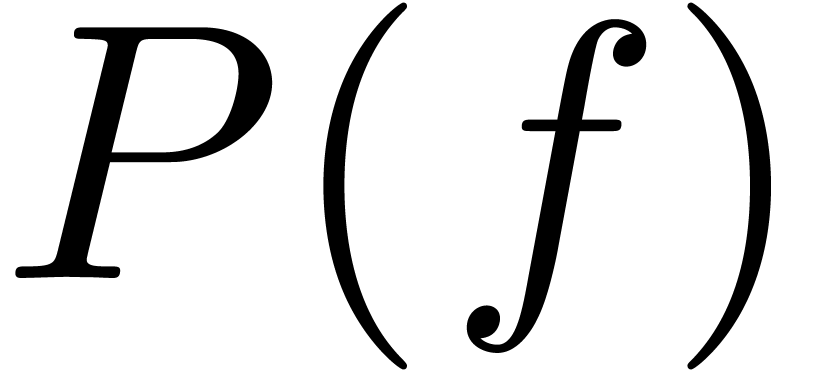 as an expression of the form
as an expression of the form
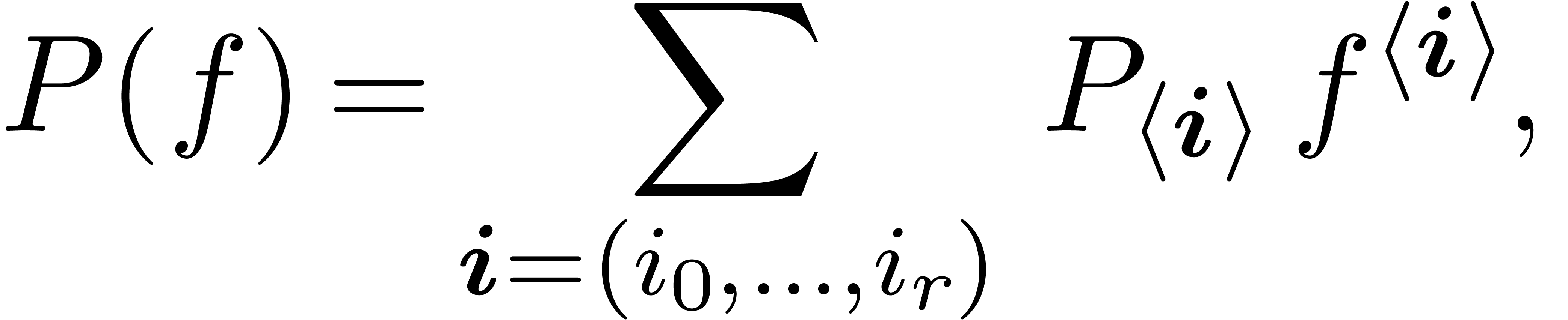 |
(6) |
where 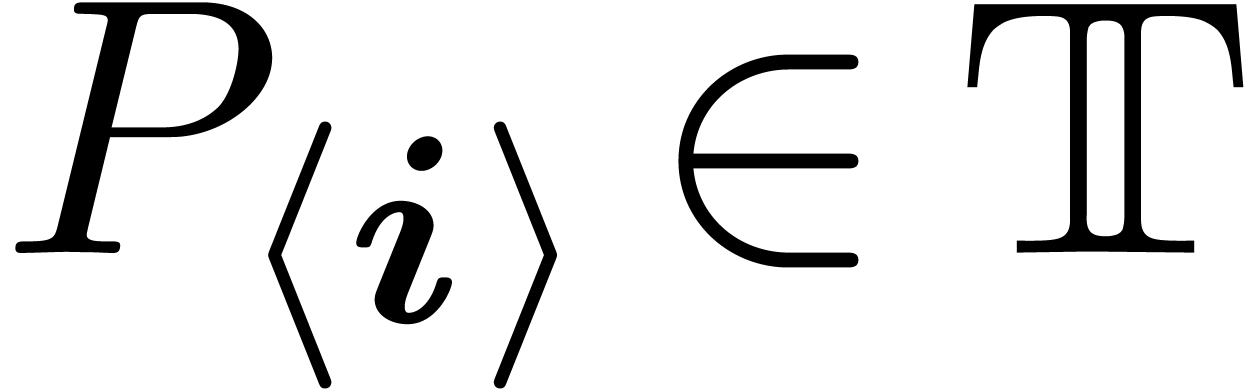 and
and 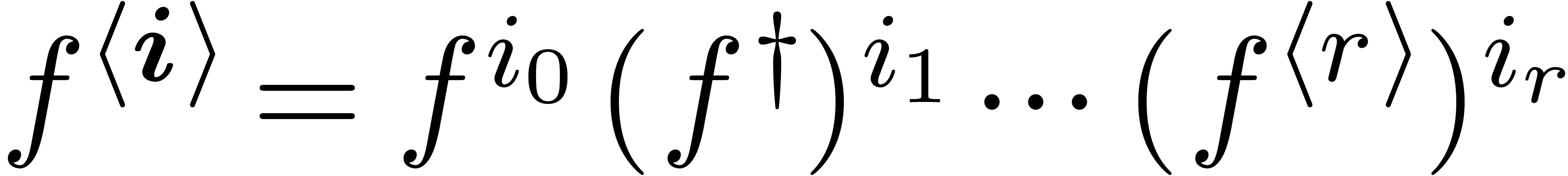 for each
for each  . Now consider the lexicographical
ordering
. Now consider the lexicographical
ordering 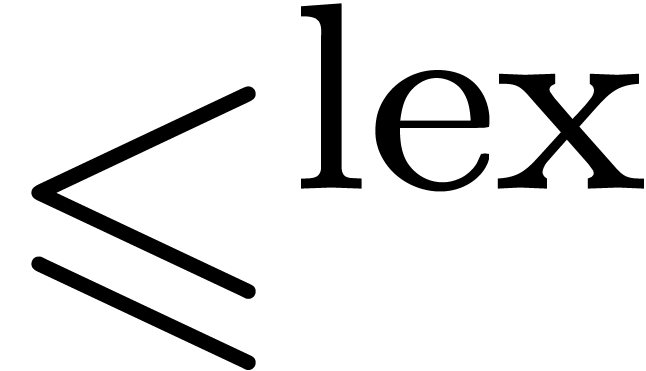 on
on 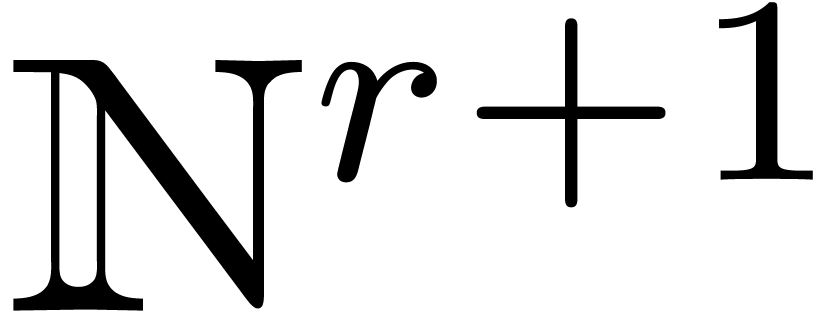 ,
defined by
,
defined by
This ordering is total, so there exists a maximal 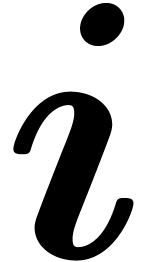 for
for 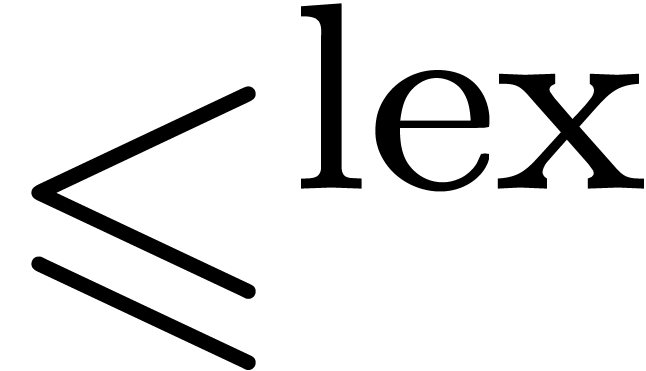 , such that
, such that 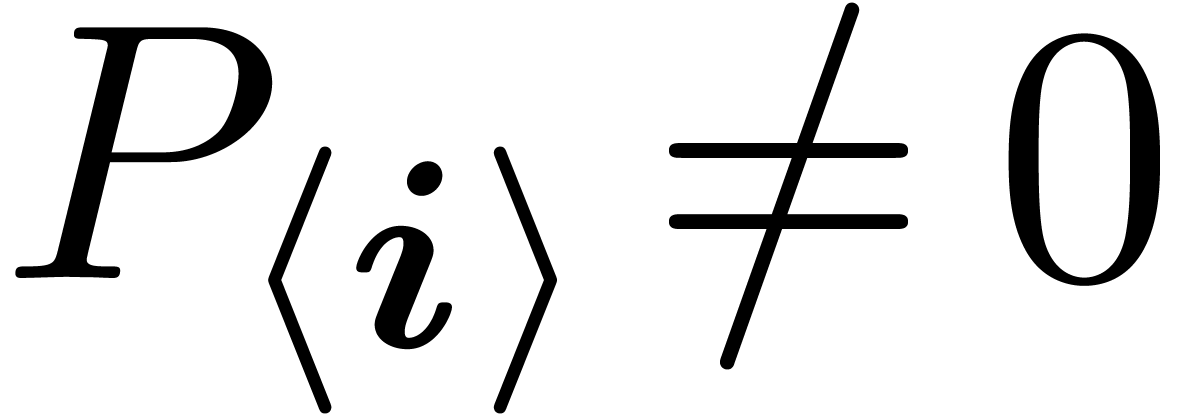 . Now let
. Now let 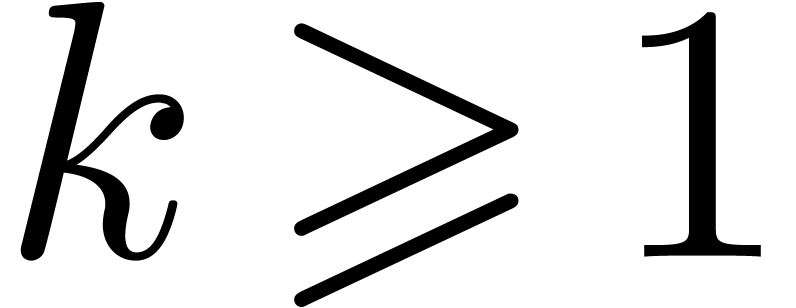 be
sufficiently large such that
be
sufficiently large such that  for all
for all  . Then
. Then
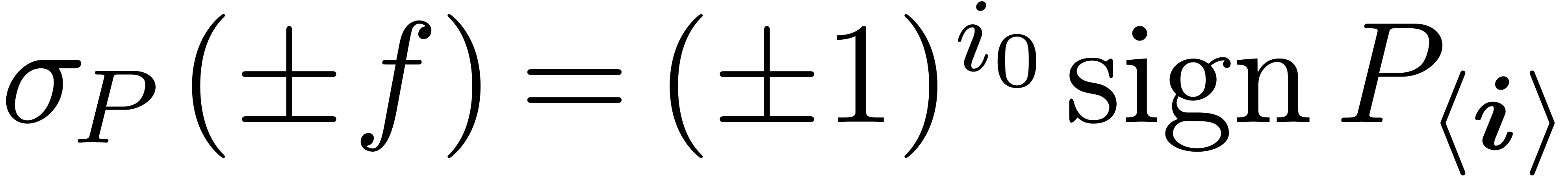 |
(7) |
for all postive, infinitely large 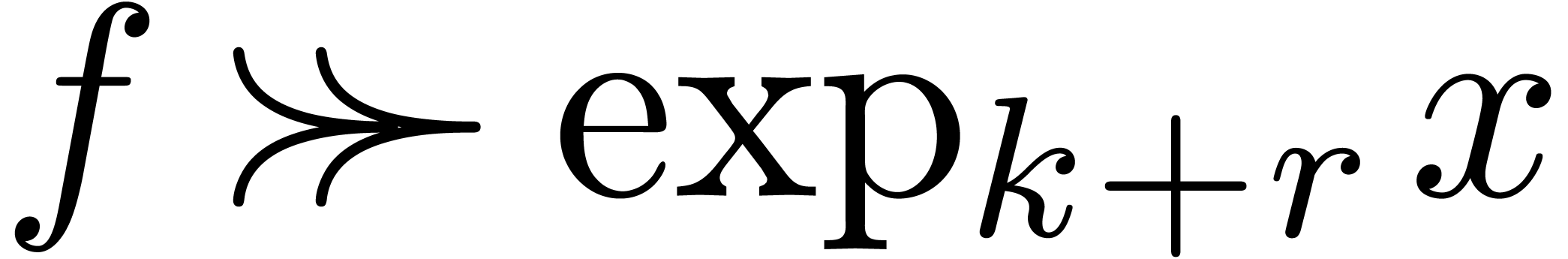 ,
since
,
since  for all such
for all such 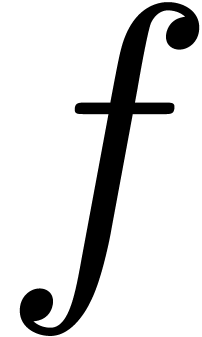 .
.
3.2Behaviour of  near
zero
near
zero
Lemma 4. Let  be a differential polynomial with coefficients in
be a differential polynomial with coefficients in
 . Then
. Then  has constant sign for all sufficiently small
has constant sign for all sufficiently small  .
.
Proof. If 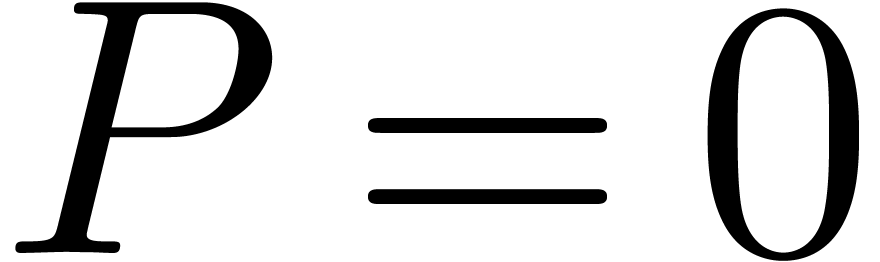 ,
then the lemma is clear. Assume that
,
then the lemma is clear. Assume that 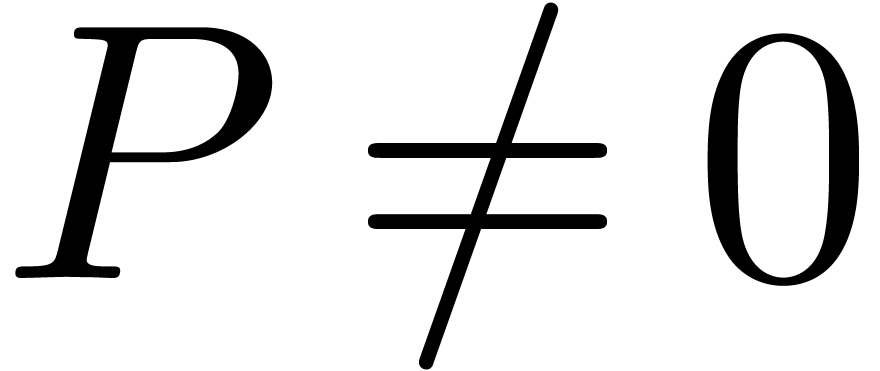 and rewrite
and rewrite
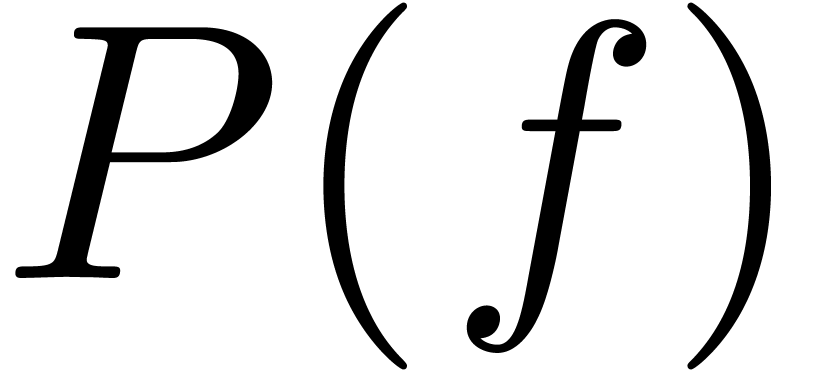 as in (6). Now consider the twisted
lexicographical ordering
as in (6). Now consider the twisted
lexicographical ordering 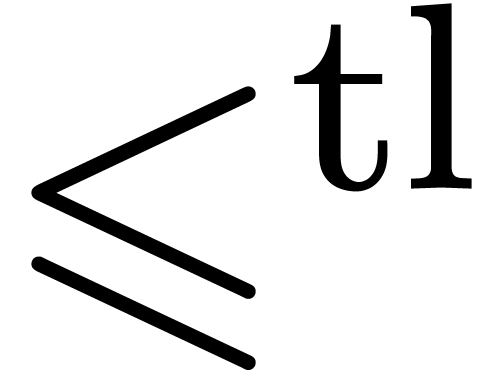 on
on 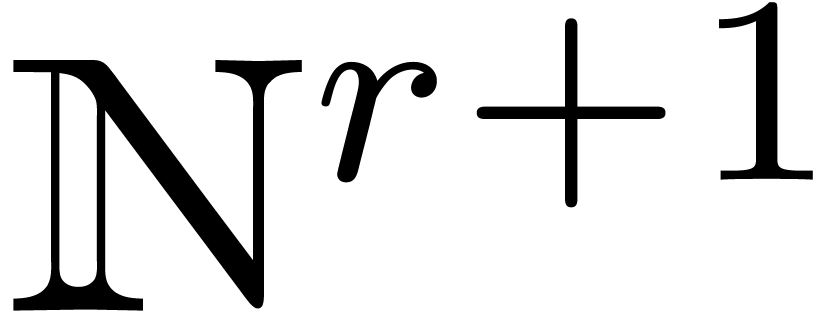 , defined by
, defined by
This ordering is total, so there exists a maximal  for
for 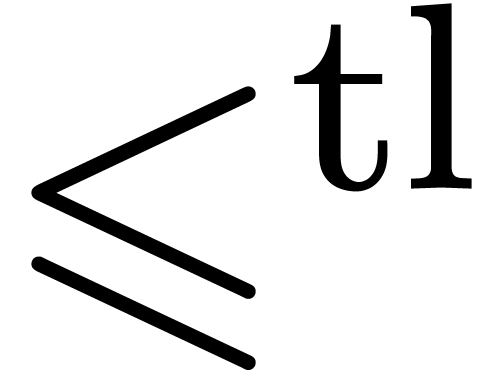 , such that
, such that 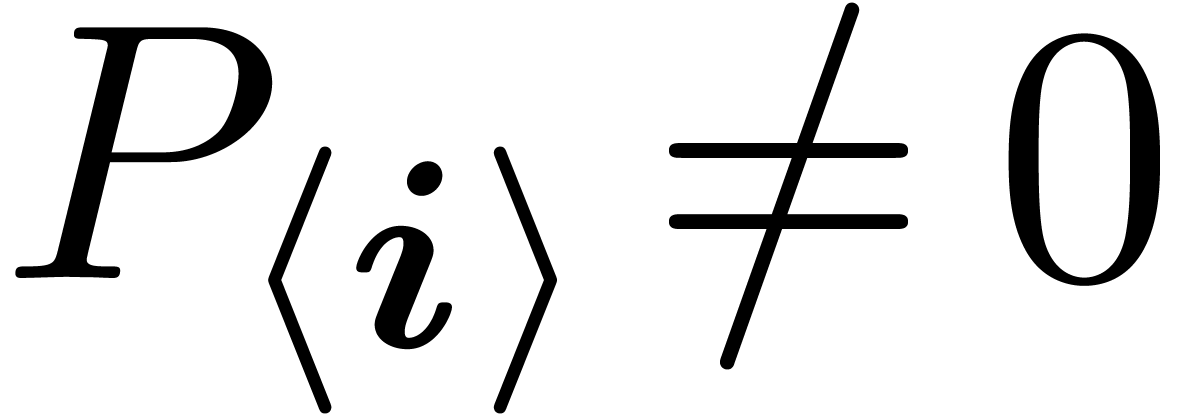 . If
. If 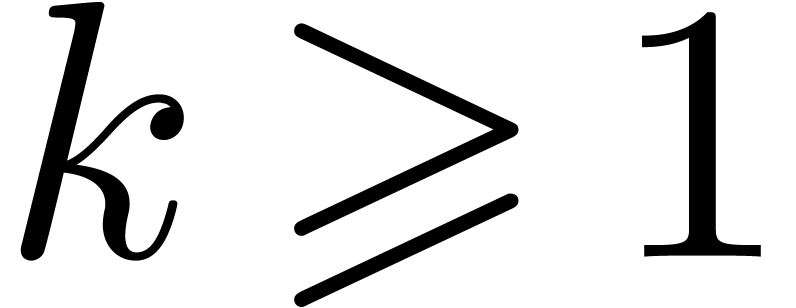 is sufficiently
large such that
is sufficiently
large such that  for all
for all 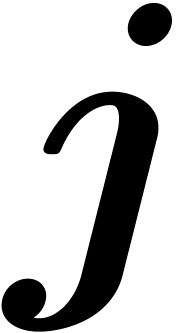 , then
, then
 |
(8) |
for all postive infinitesimal 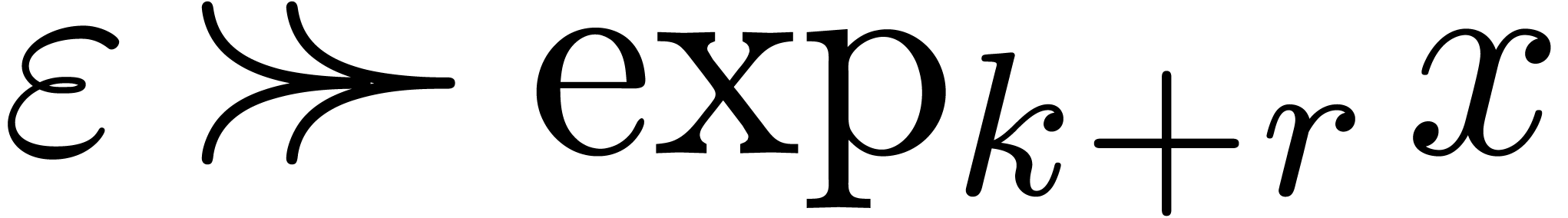 .
.
3.3Canonical form of differential Newton
polynomials
Assume that 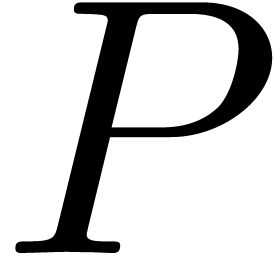 has purely exponential coefficients.
In what follows, we will denote by
has purely exponential coefficients.
In what follows, we will denote by 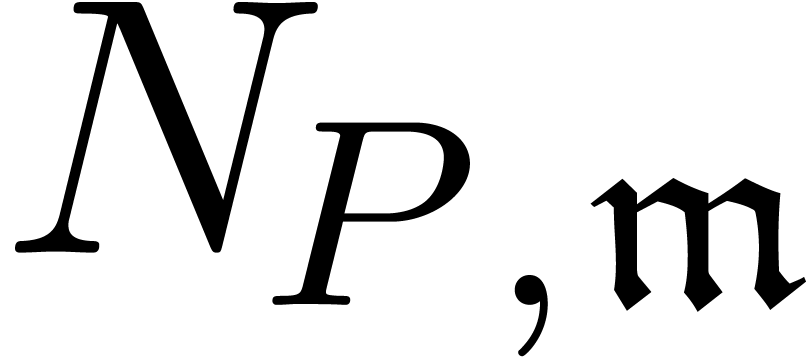 the purely
exponential differential Newton polynomial associated to a monomial
the purely
exponential differential Newton polynomial associated to a monomial
 , i.e.
, i.e.
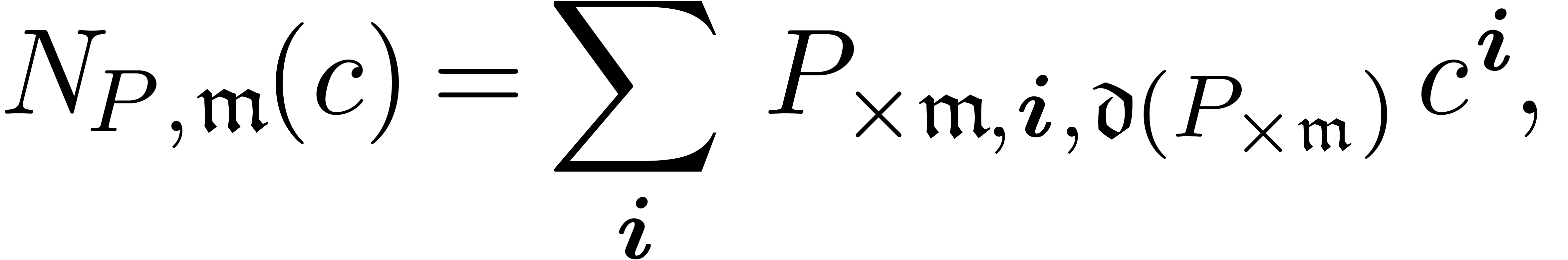 |
(9) |
where
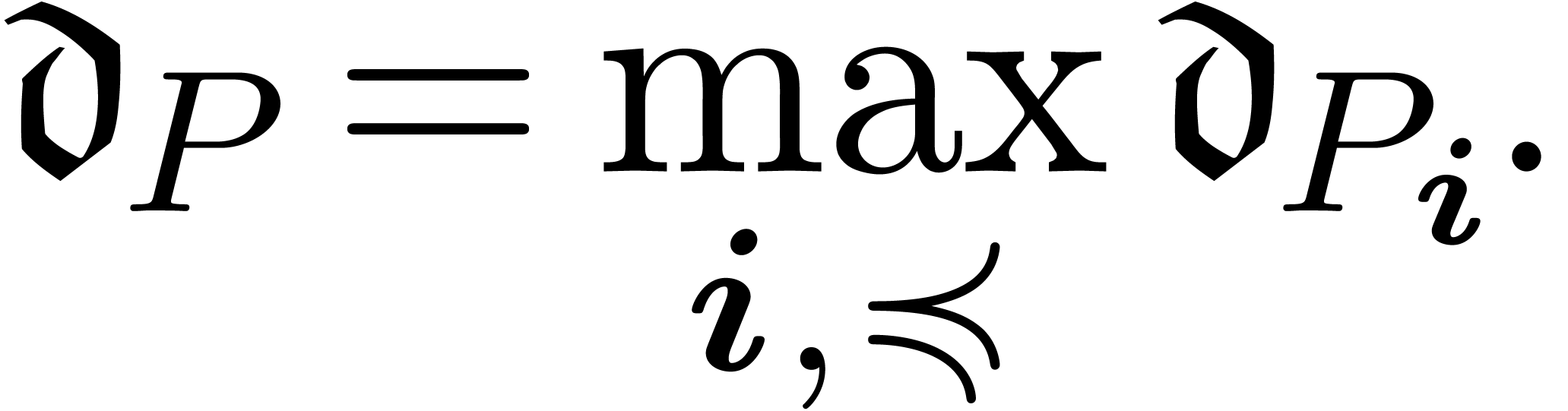 |
(10) |
The following theorem shows how 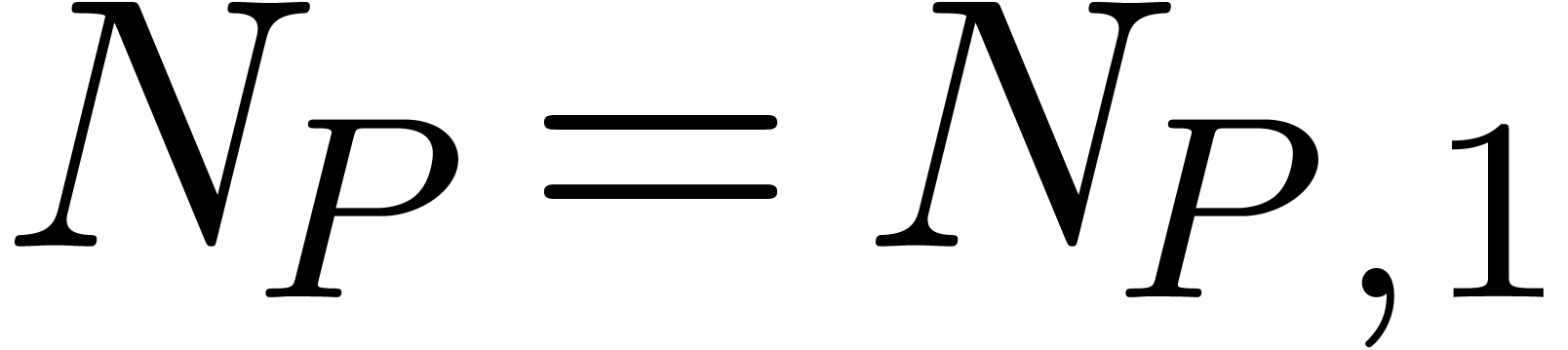 looks like after
sufficiently many upward shiftings:
looks like after
sufficiently many upward shiftings:
Theorem 5. Let  be a differential polynomial with purely exponential
coefficients. Then there exists a polynomial
be a differential polynomial with purely exponential
coefficients. Then there exists a polynomial 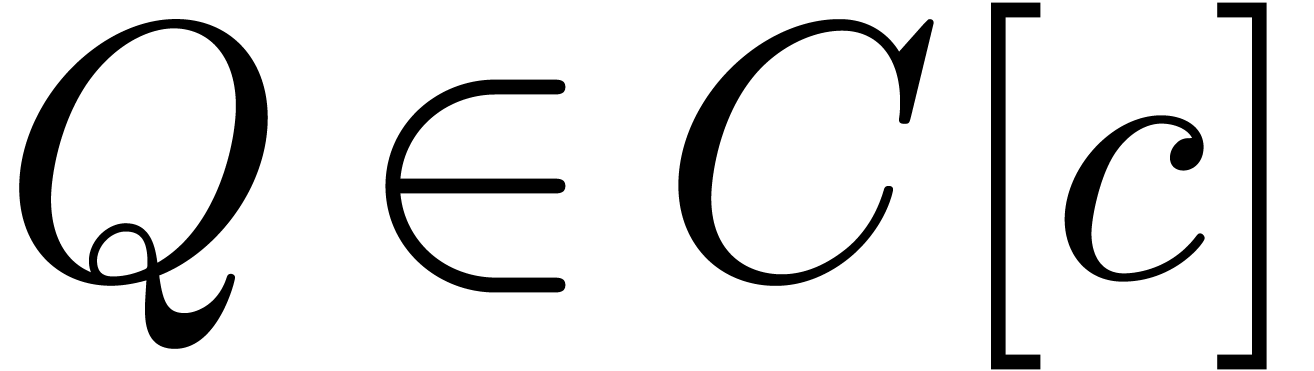 and
an integer
and
an integer 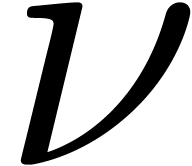 , such that for
all
, such that for
all 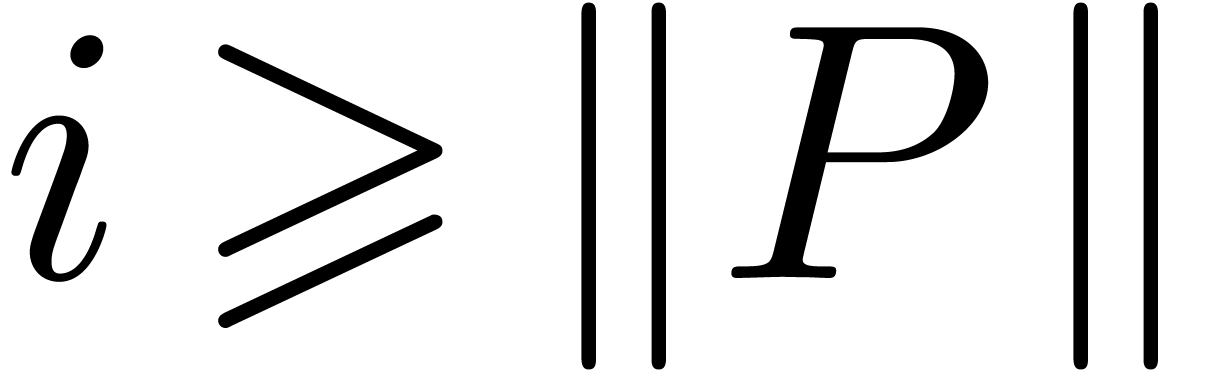 , we have
, we have 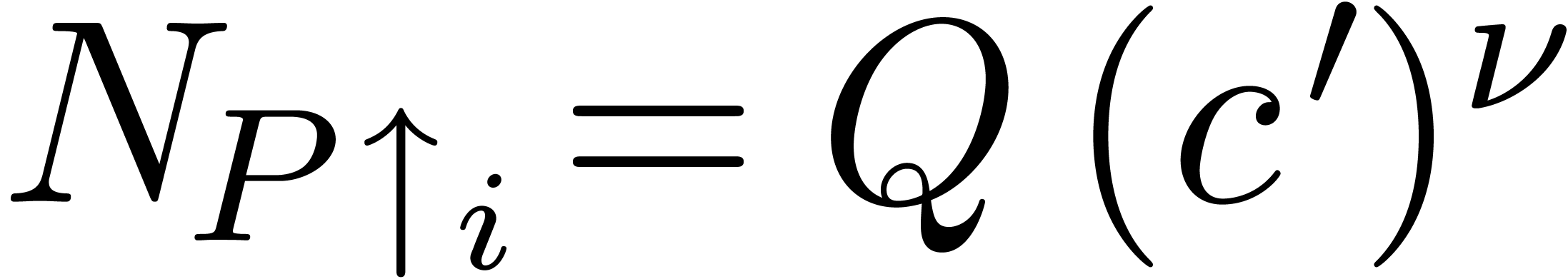 .
.
Proof. Let 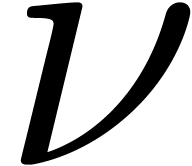 be minimal, such
that there exists an
be minimal, such
that there exists an  with
with 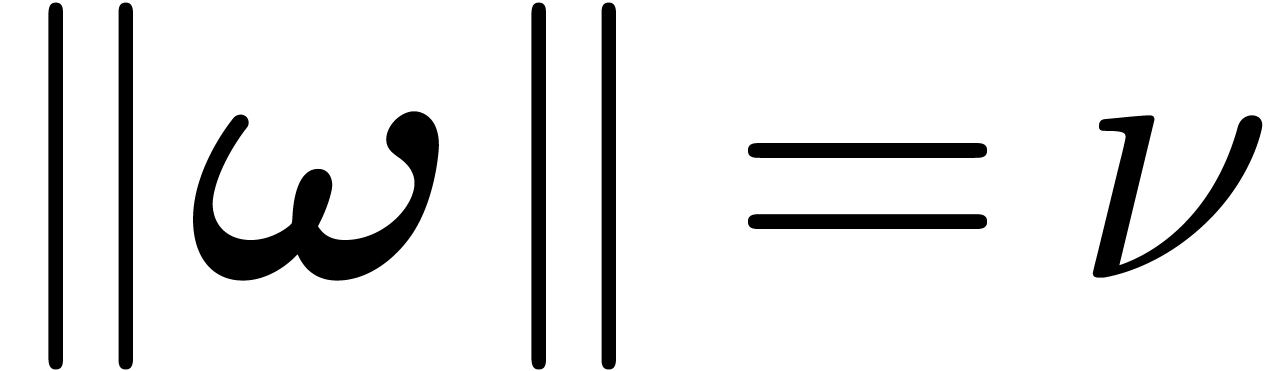 and
and 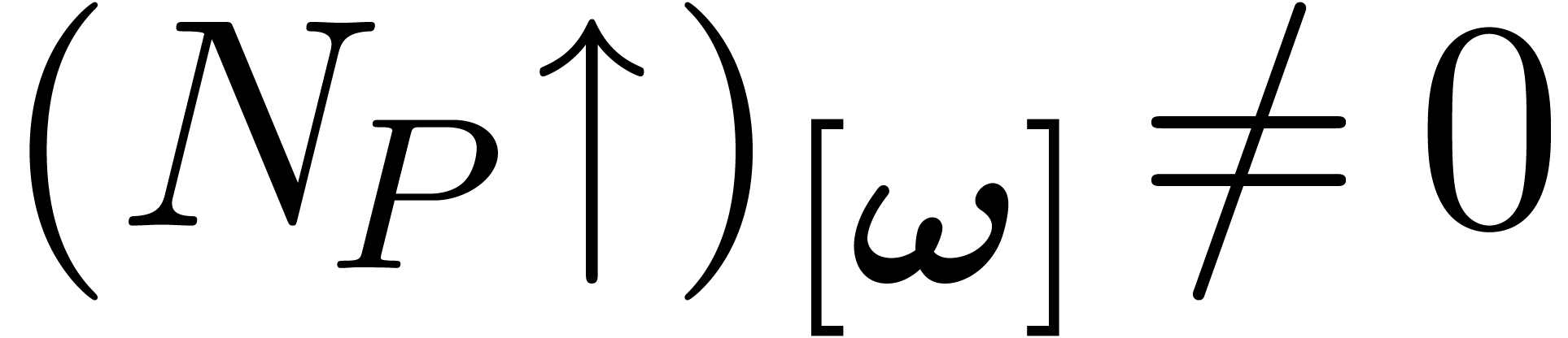 . Then we have
. Then we have  and
and
 |
(11) |
by formula (5). Since 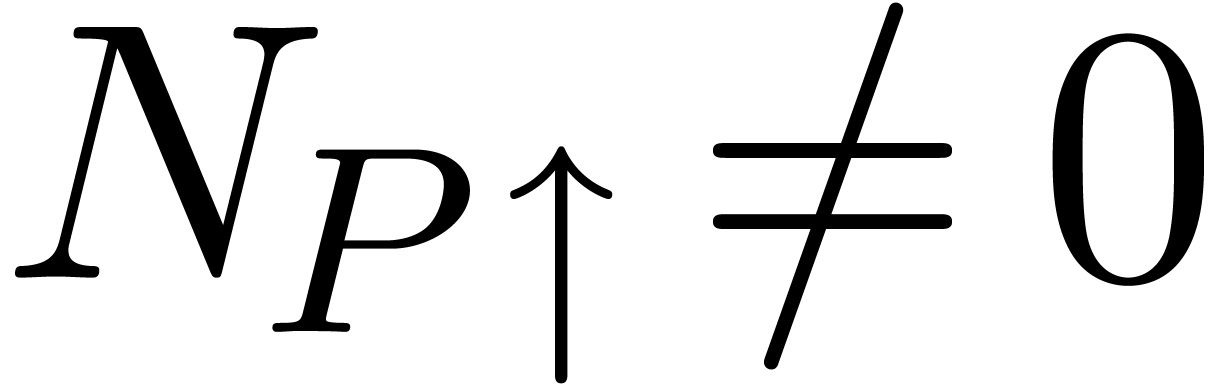 ,
we must have
,
we must have 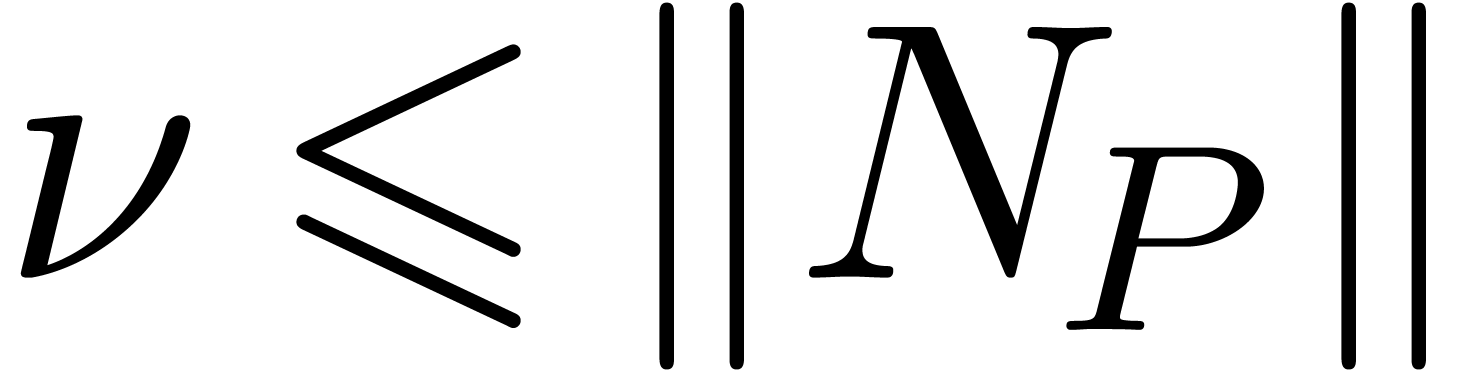 . Consequently,
. Consequently,
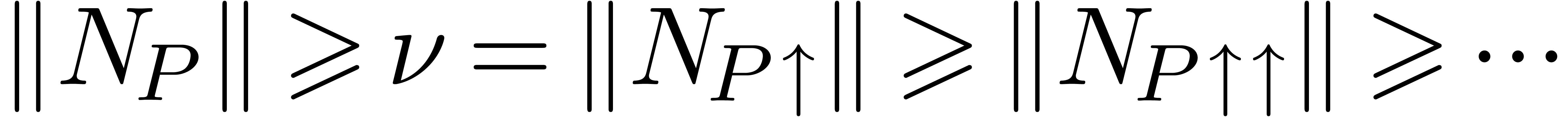 . Hence, for some
. Hence, for some 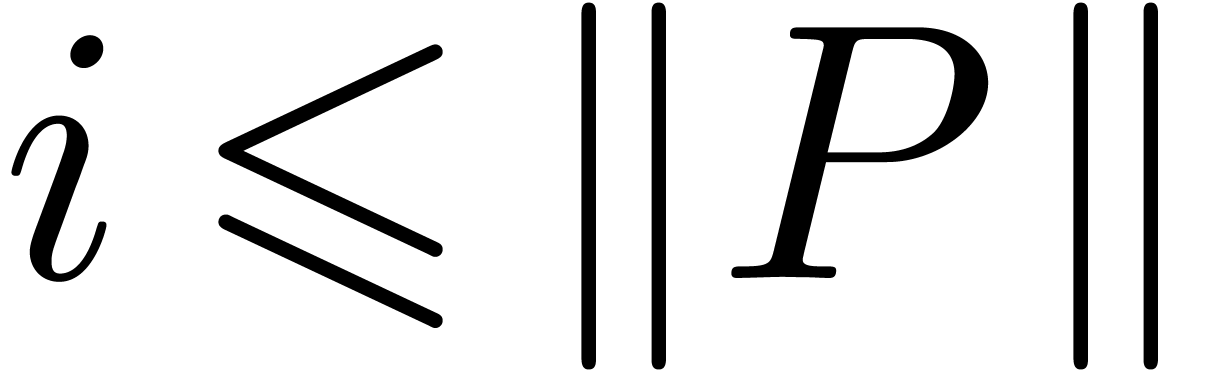 , we have
, we have 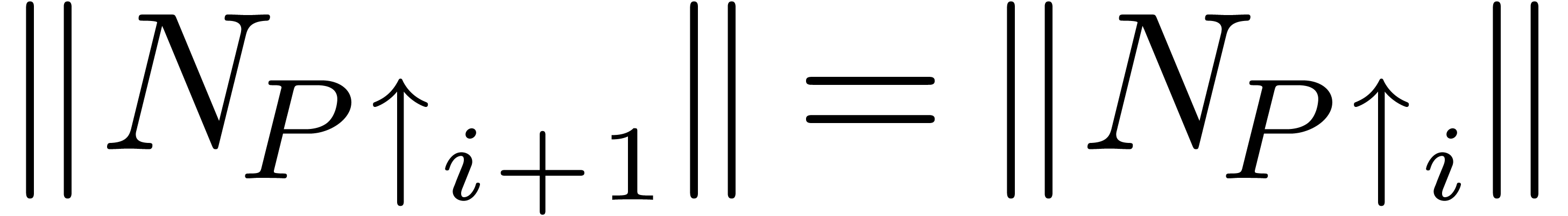 . But then (11) applied on
. But then (11) applied on 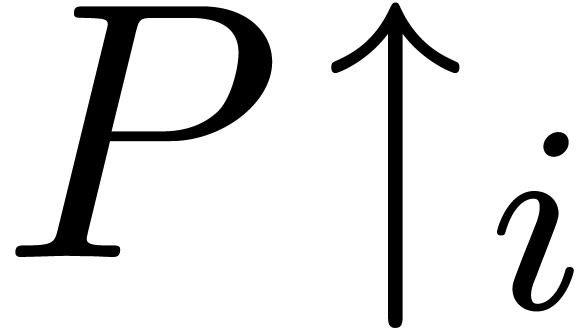 instead of
instead of  yields
yields 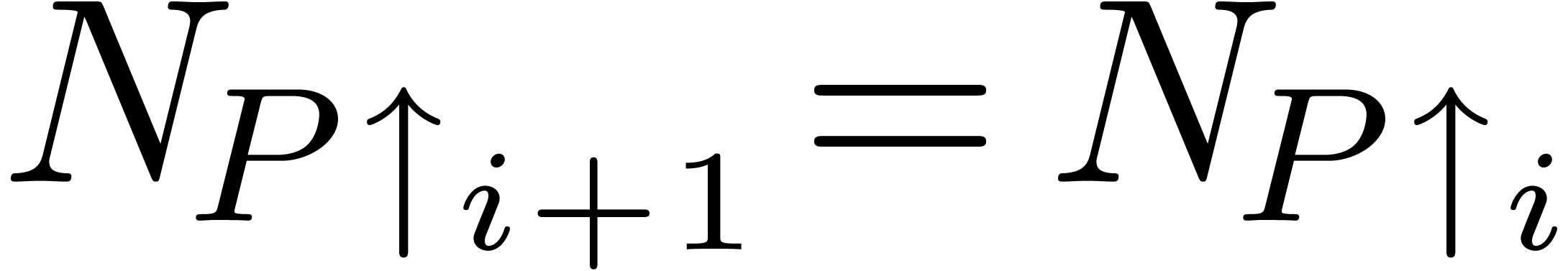 . This shows that
. This shows that 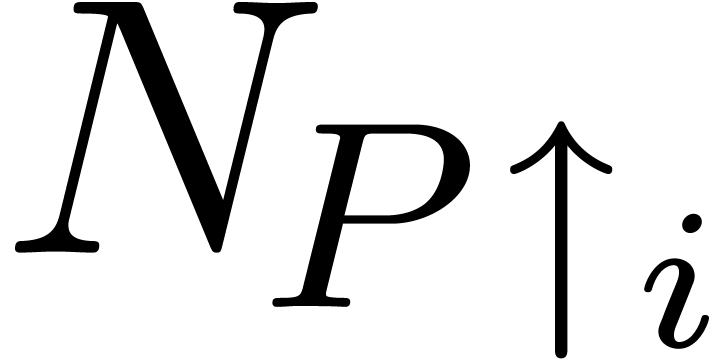 is
independent of
is
independent of 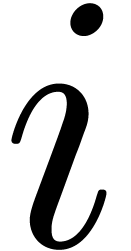 , for
, for 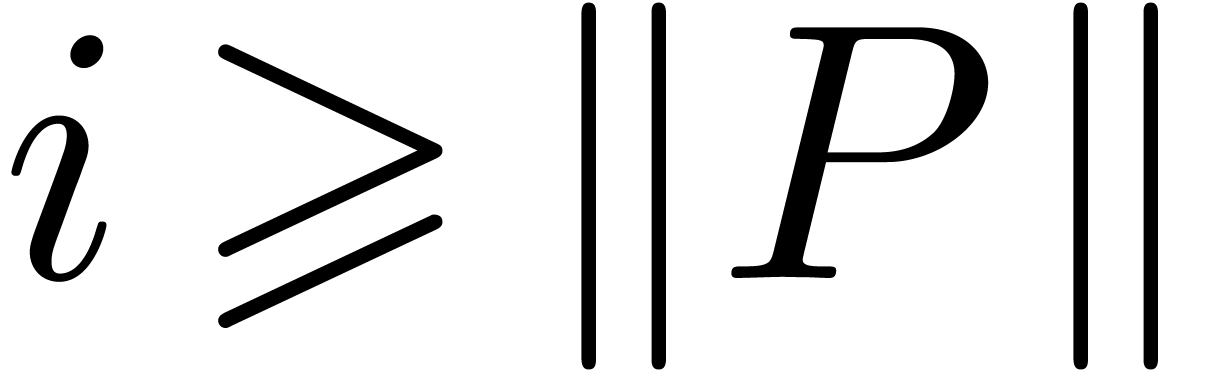 .
.
In order to prove the theorem, it now suffices to show that  implies
implies  for some polynomial
for some polynomial 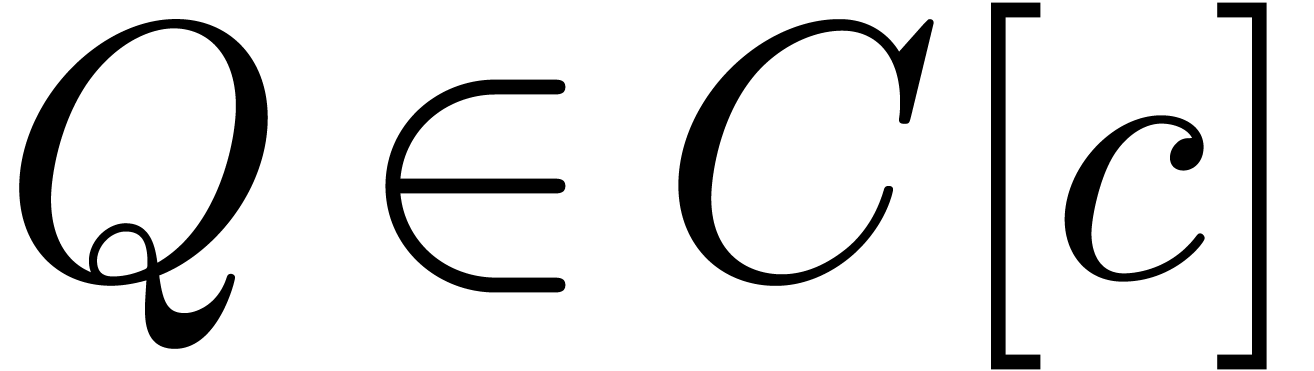 . For all differential polynomials
. For all differential polynomials
 of homogeneous weight
of homogeneous weight  , let
, let
 |
(12) |
Since 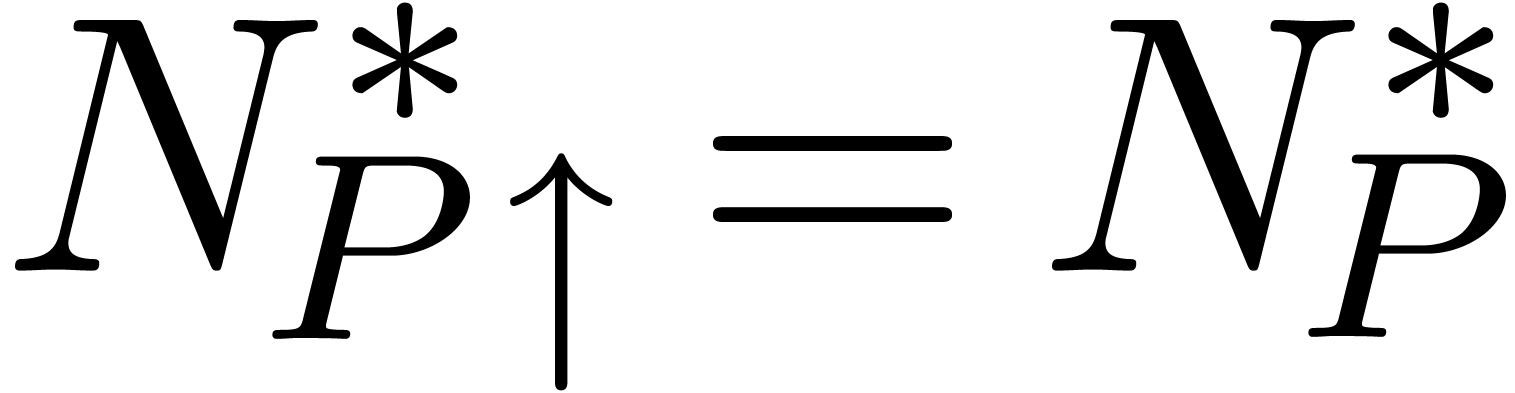 , it suffices to show
that
, it suffices to show
that 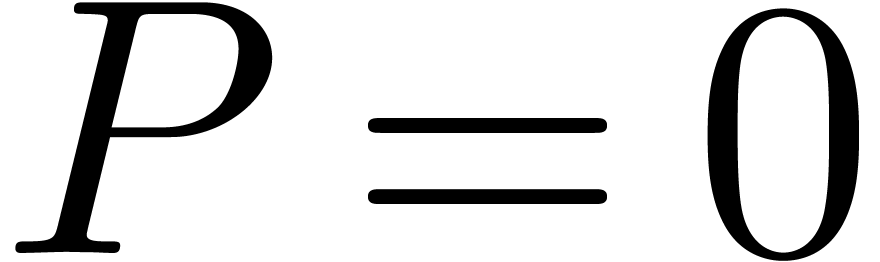 whenever
whenever 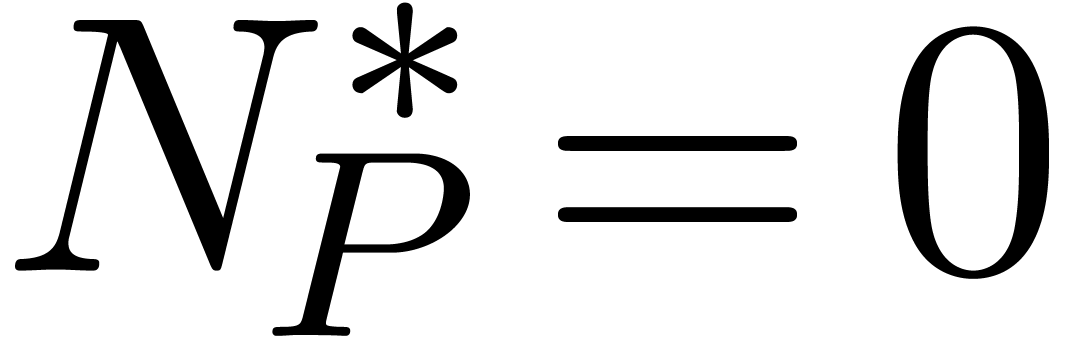 .
Now
.
Now 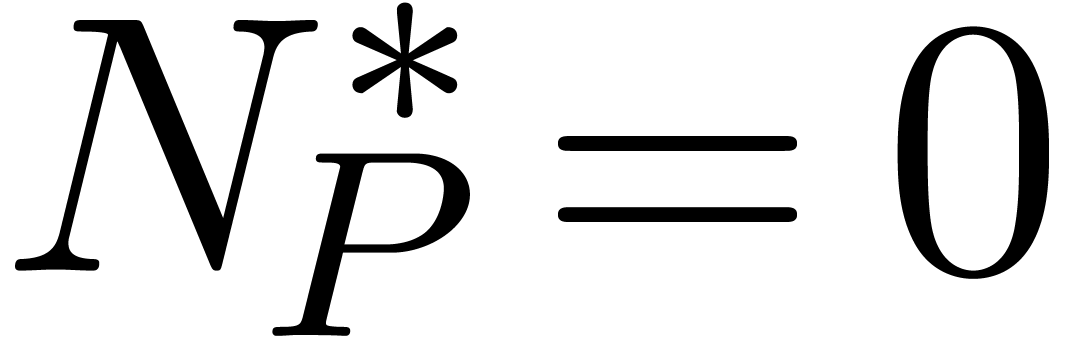 implies that
implies that 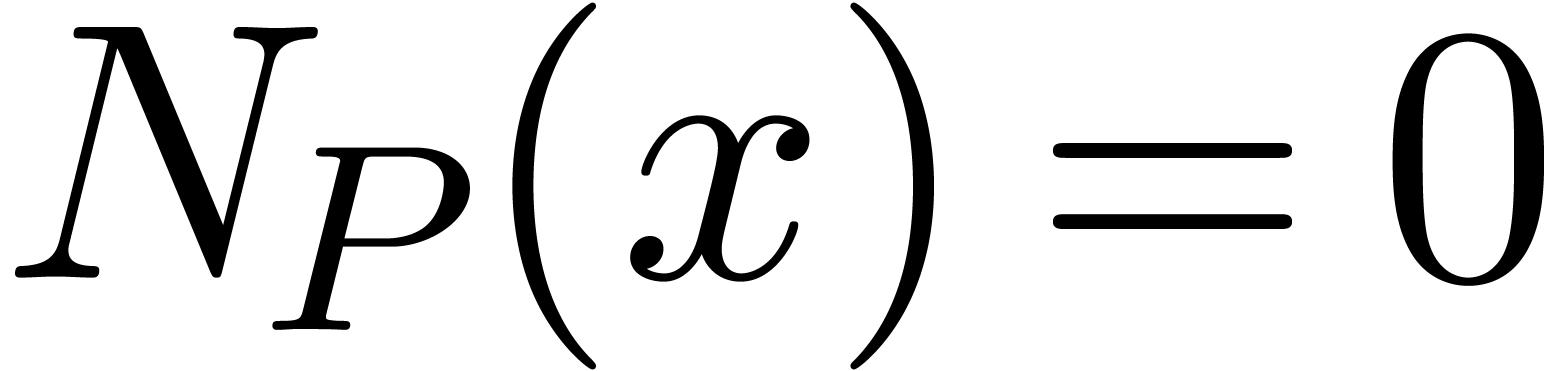 .
Furthermore, (5) yields
.
Furthermore, (5) yields
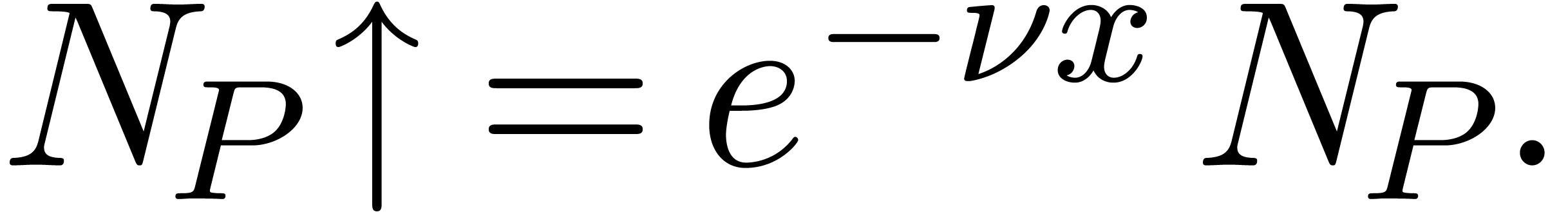 |
(13) |
Consequently, we also have 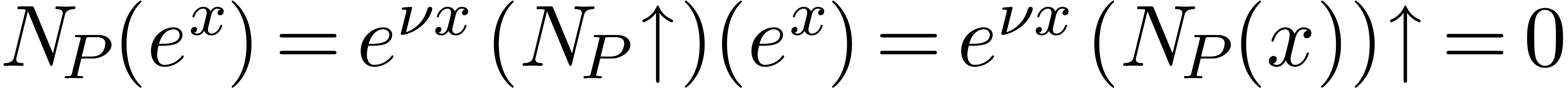 .
By induction, it follows that
.
By induction, it follows that 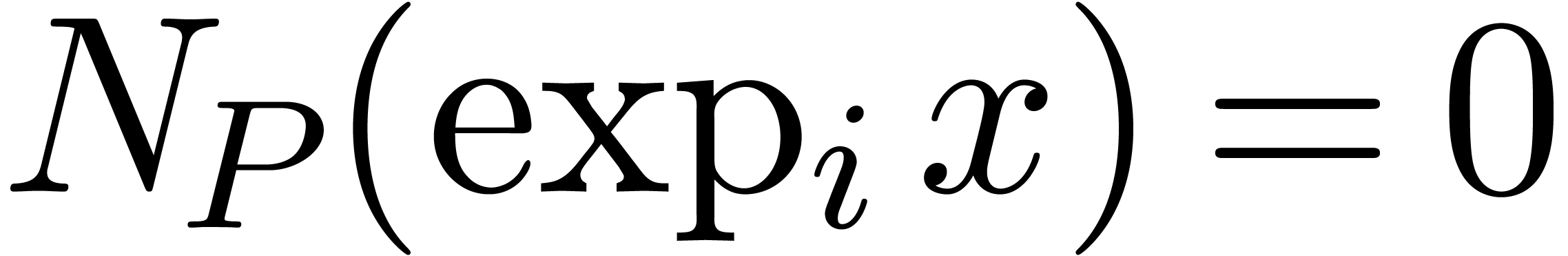 for any iterated
exponential of
for any iterated
exponential of  . We conclude
that
. We conclude
that 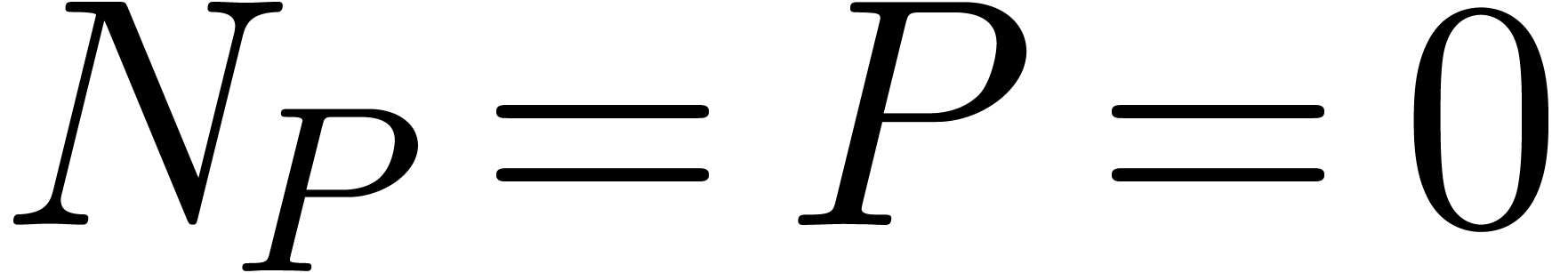 , by the lemma 3.
, by the lemma 3.
Remark 6. Given any differential
polynomial  with coefficients in
with coefficients in  , this polynomial becomes purely exponential
after sufficiently many upward shiftings. After at most
, this polynomial becomes purely exponential
after sufficiently many upward shiftings. After at most 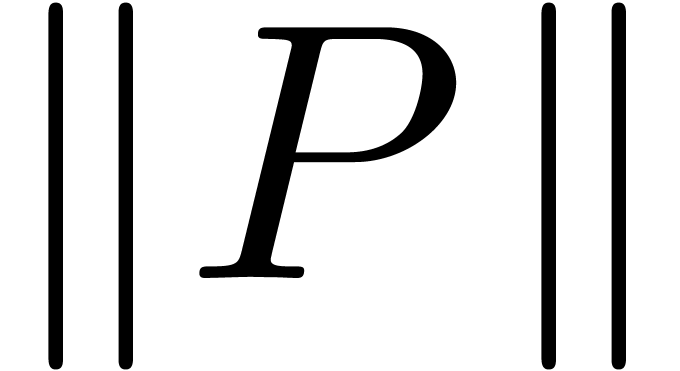 more upward shiftings, the purely exponential Newton polynomial
stabilizes. The resulting purely exponential differential Newton
polynomial, which is in
more upward shiftings, the purely exponential Newton polynomial
stabilizes. The resulting purely exponential differential Newton
polynomial, which is in 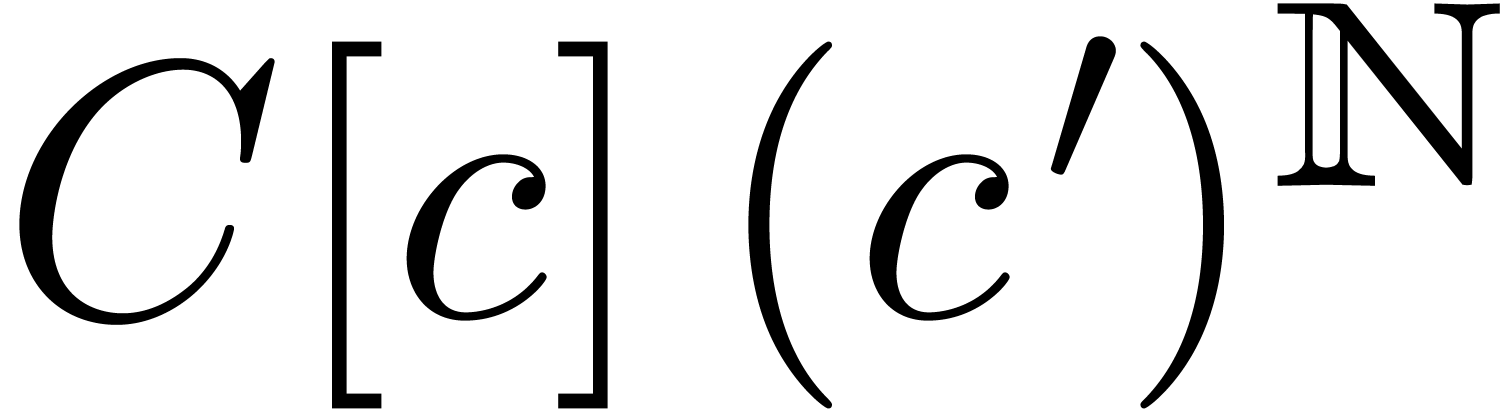 , is
called the differential Newton polynomial of
, is
called the differential Newton polynomial of  .
.
4Behaviour of 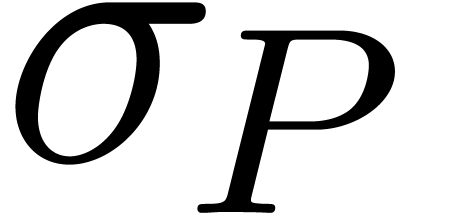 near constants
near constants
In the previous section, we have seen how to compute 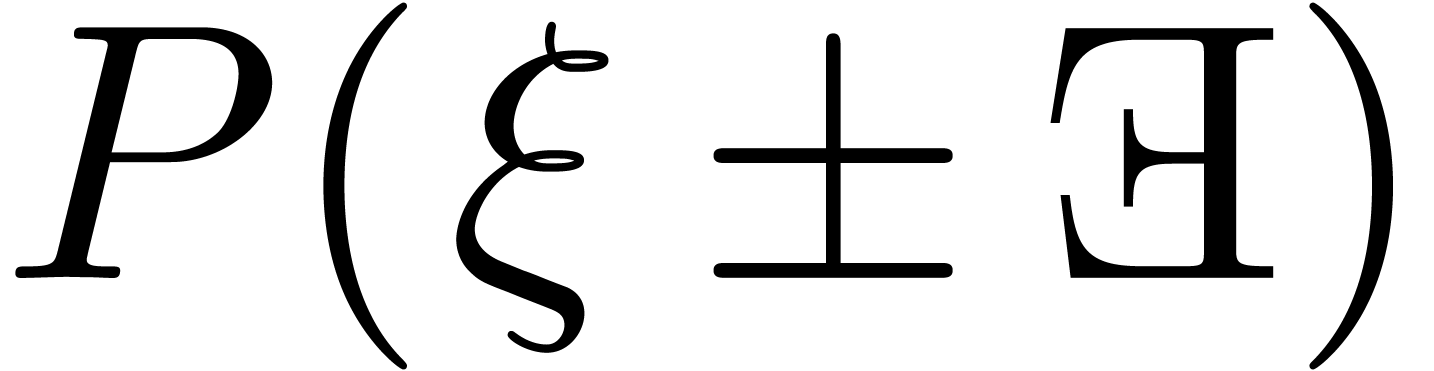 and
and 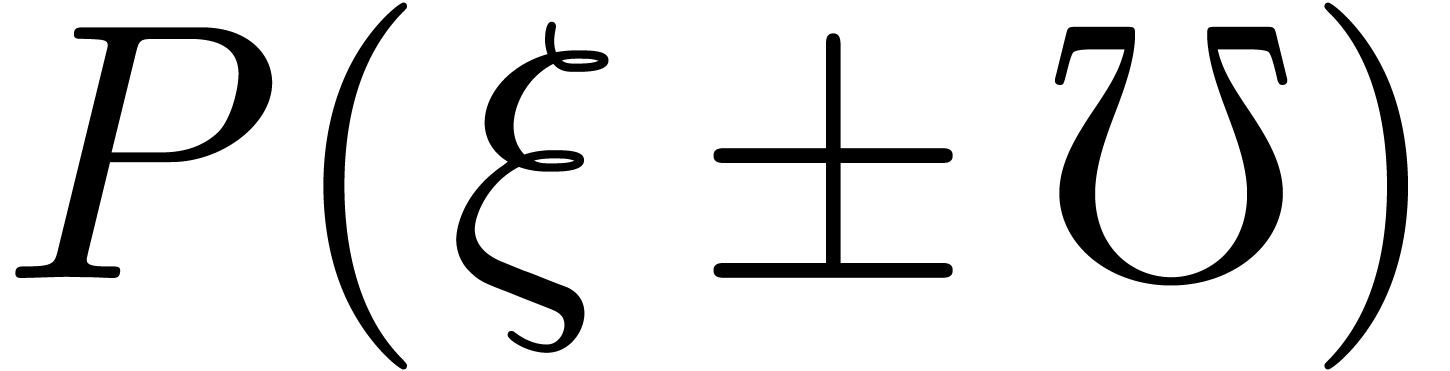 for all
for all 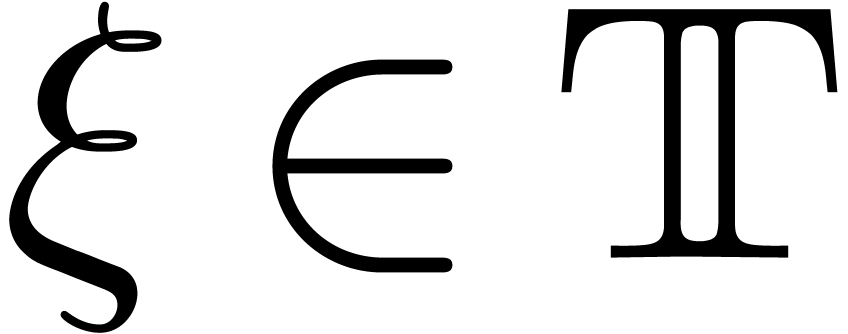 .
In this section, we show how to compute
.
In this section, we show how to compute 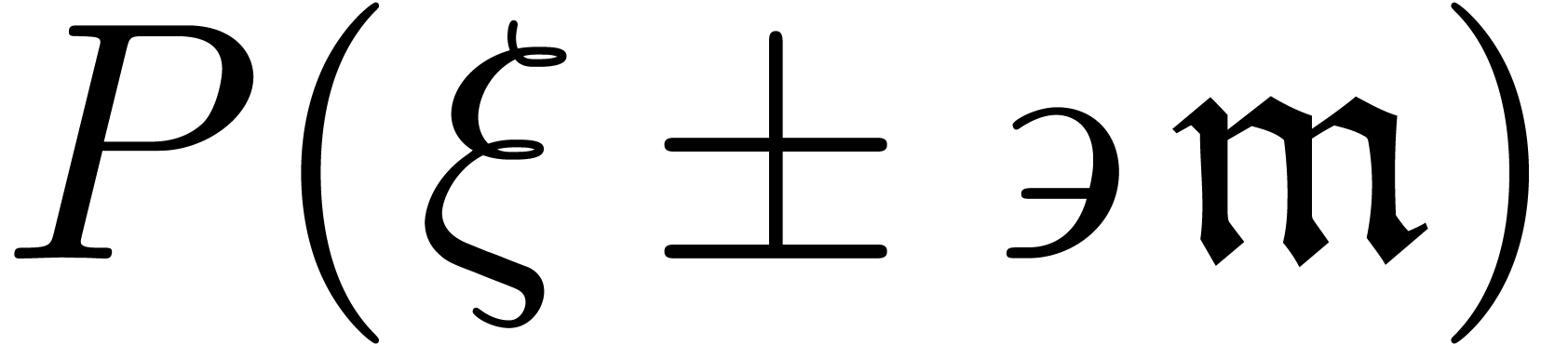 and
and 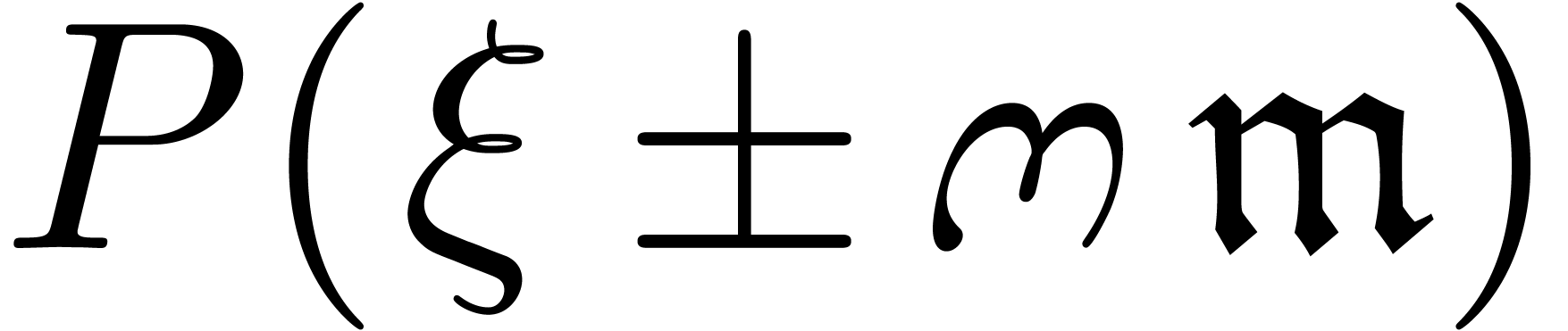 for all
for all 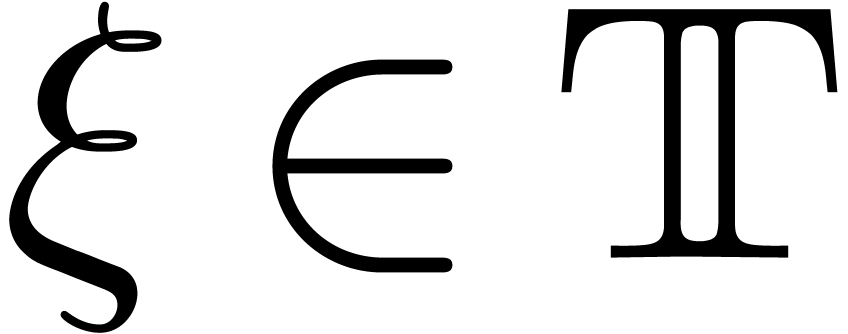 and all
transmonomials
and all
transmonomials 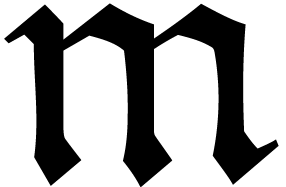 . Modulo an
additive and a multiplicative conjugation with
. Modulo an
additive and a multiplicative conjugation with  resp.
resp. 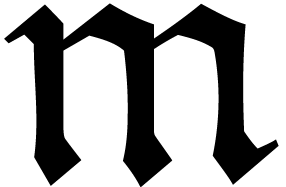 , we may assume without
loss of generality that
, we may assume without
loss of generality that 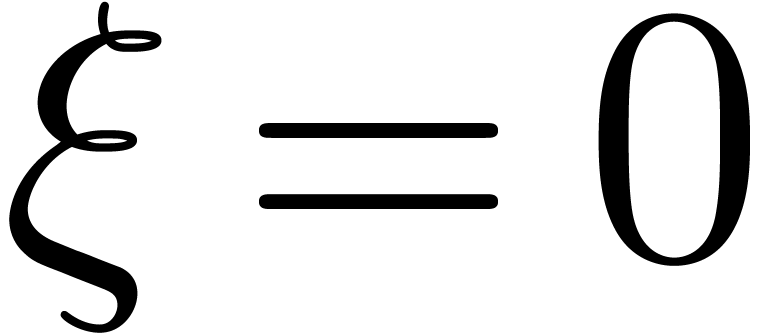 and
and 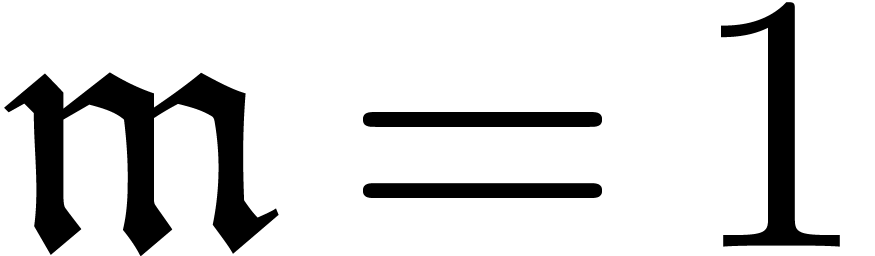 . Hence it will suffice to study the behaviour
of
. Hence it will suffice to study the behaviour
of 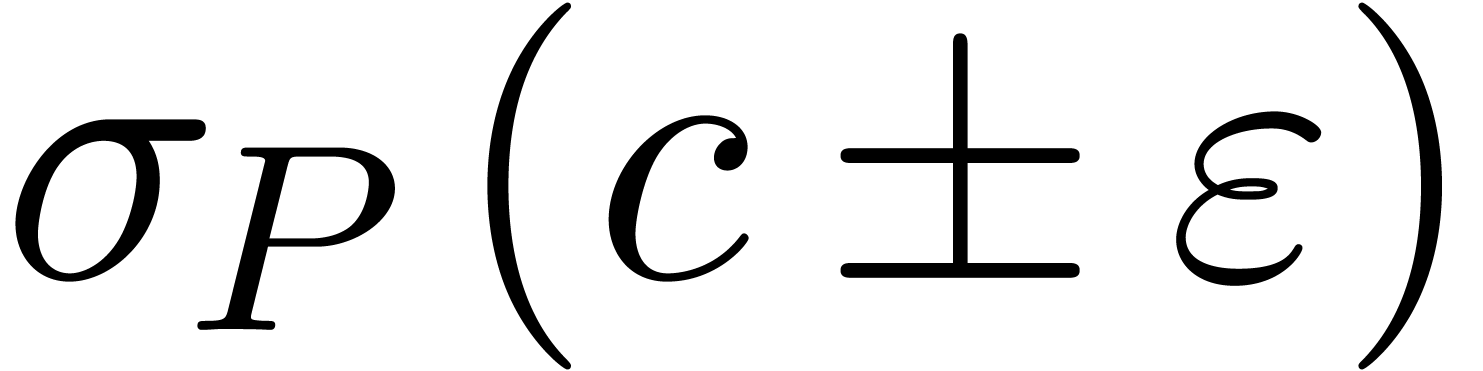 for
for  and positive
infinitesimal (but sufficiently large)
and positive
infinitesimal (but sufficiently large)  ,
as well as the behaviour of
,
as well as the behaviour of 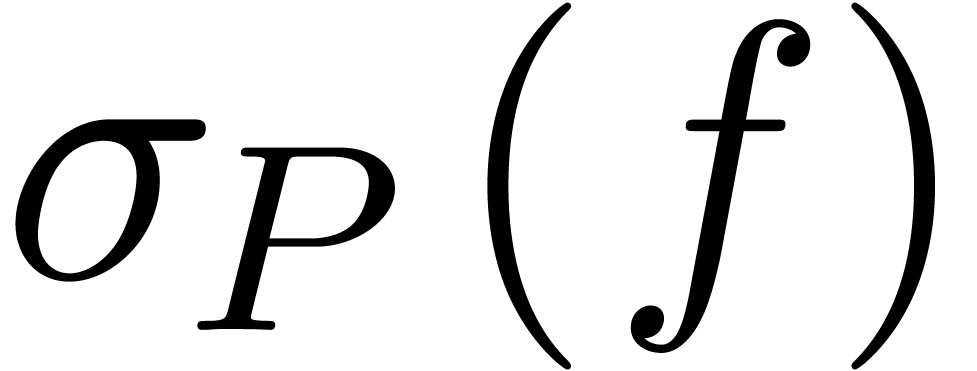 for positive
infinitely large (but sufficiently small)
for positive
infinitely large (but sufficiently small) 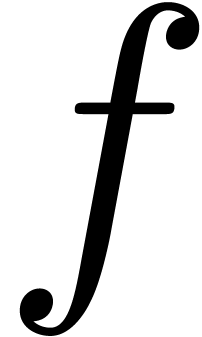 .
.
Modulo suffiently upward shiftings (we have  and
and
 ), we may assume that
), we may assume that 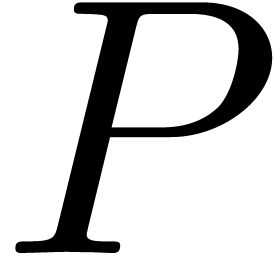 has purely exponential coefficients. By theorem 5 and modulo at most
has purely exponential coefficients. By theorem 5 and modulo at most 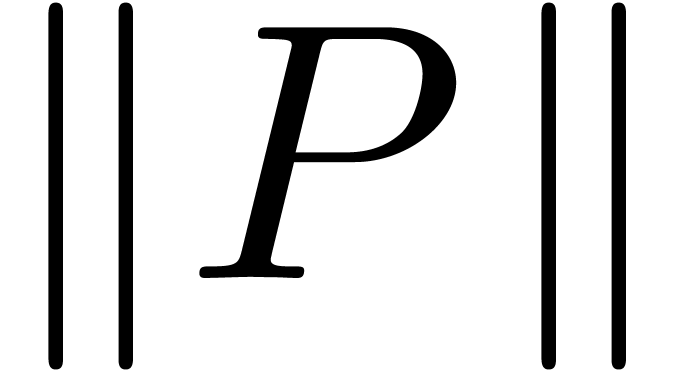 more upward
shiftings, we may also assume that
more upward
shiftings, we may also assume that
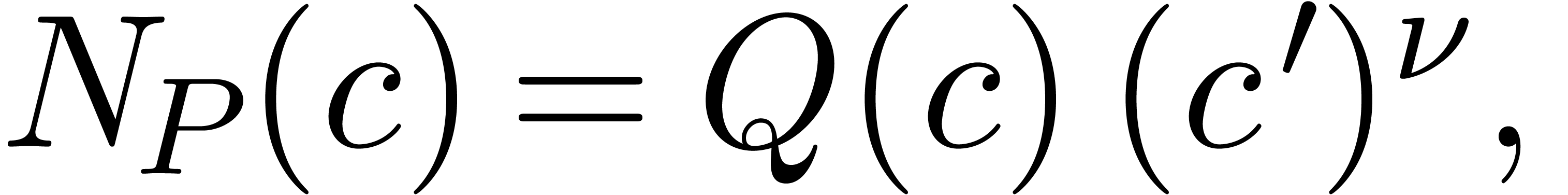 |
(14) |
for some polynomial 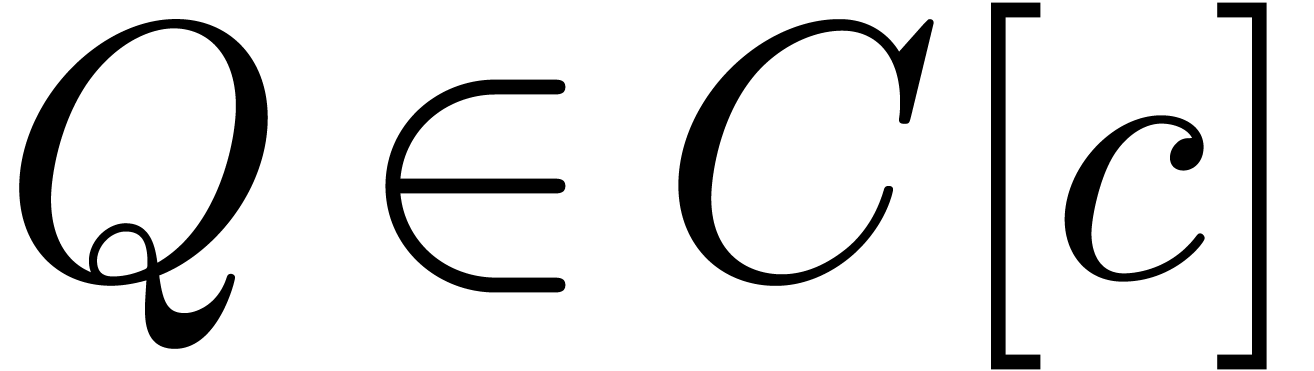 and
and 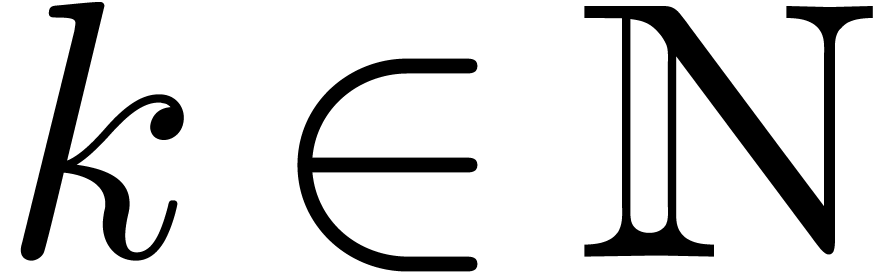 . We will denote by
. We will denote by 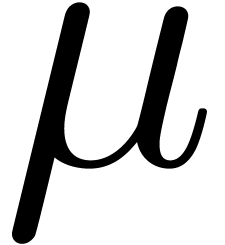 the
multiplicity of
the
multiplicity of  as a root of
as a root of  . Finally, modulo division of
. Finally, modulo division of 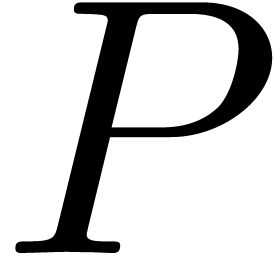 by its dominant monomial (this does not alter
by its dominant monomial (this does not alter 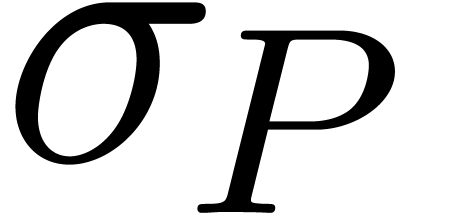 ), we may assume without loss of generality that
), we may assume without loss of generality that
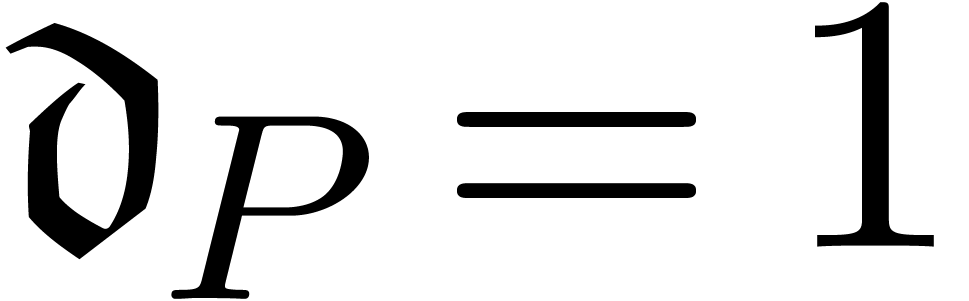 .
.
4.1Behaviour of 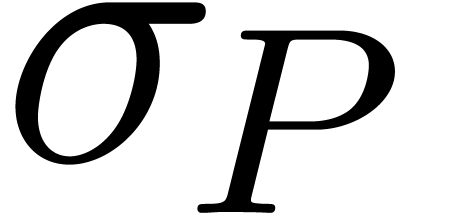 in
between constants
in
between constants
Lemma 7. For all
 with
with  ,
the signs of
,
the signs of 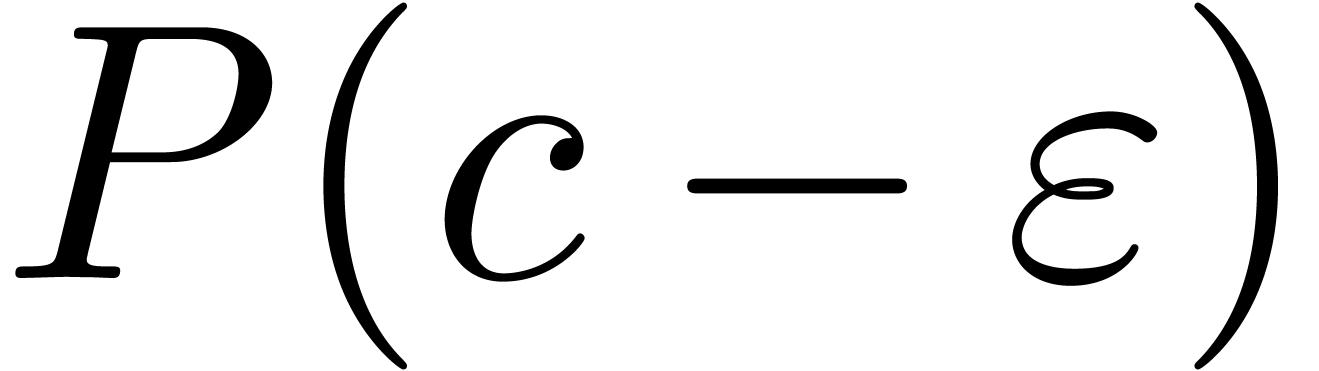 and
and 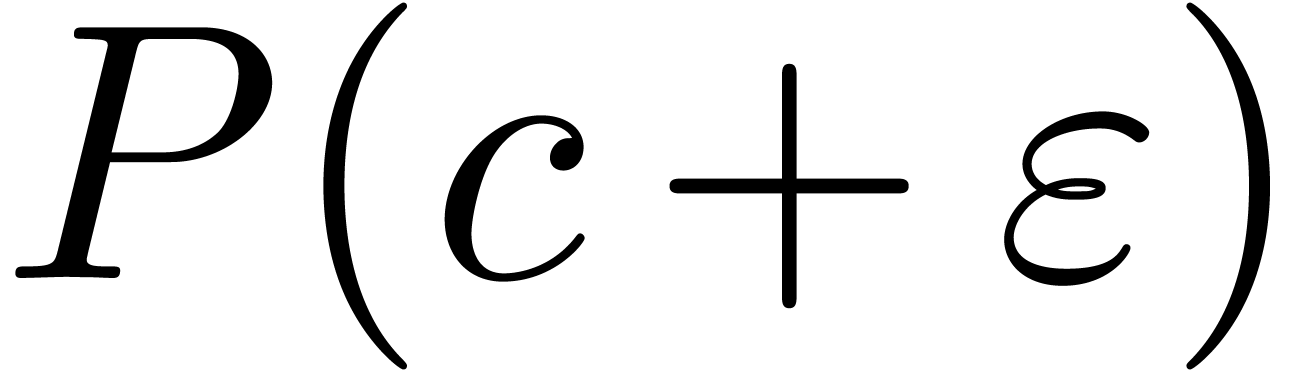 are
independent of
are
independent of  and given by
and given by
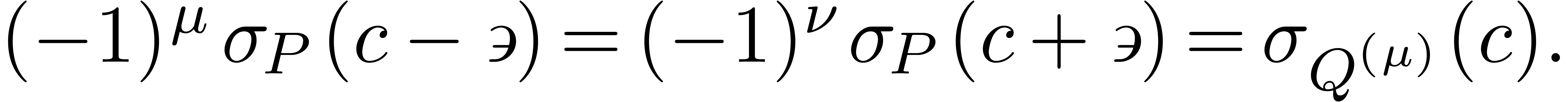 |
(15) |
Proof. Since  is purely
exponential and
is purely
exponential and 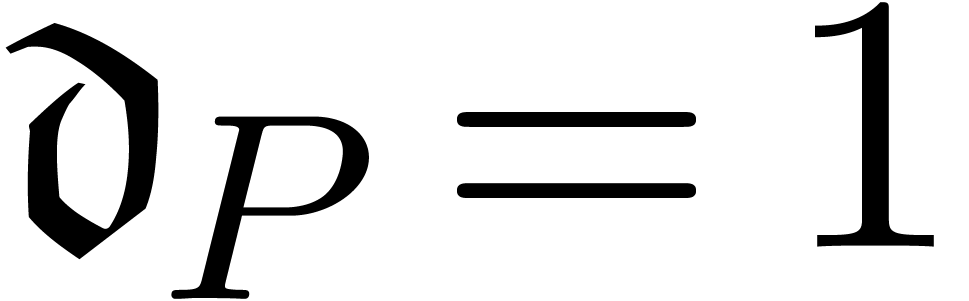 , there
exists an
, there
exists an  such that
such that
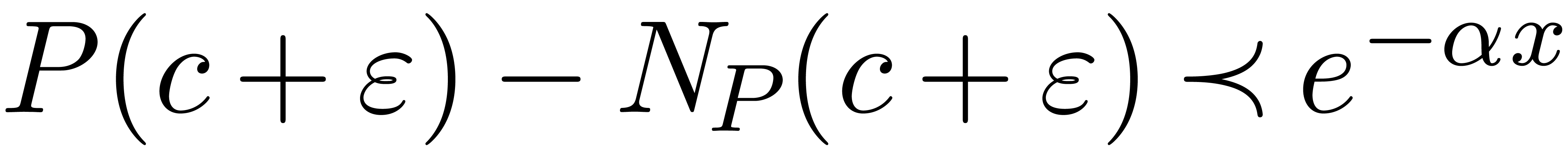 |
(16) |
for all  . Let
. Let  be such that
be such that  ,
where
,
where 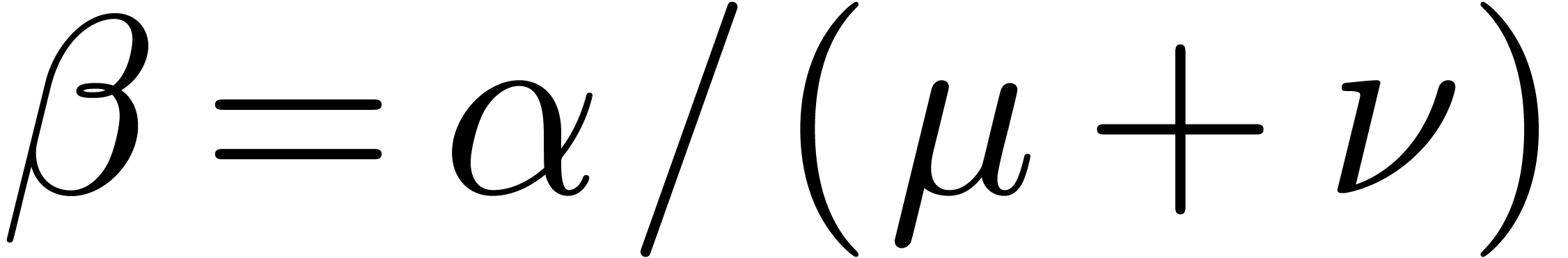 . Then
. Then 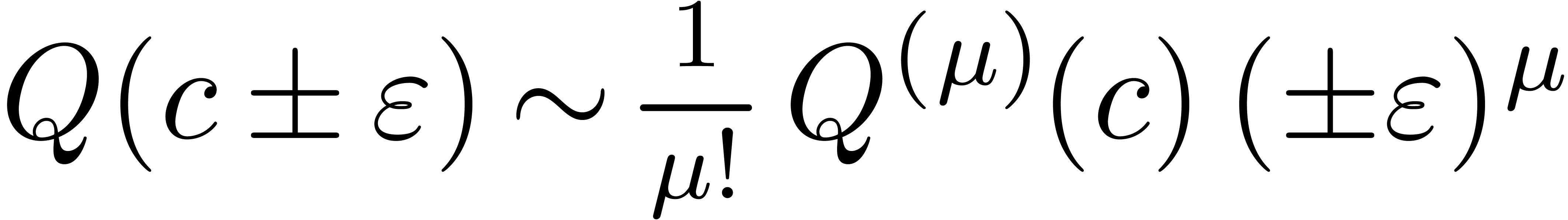 , whence
, whence
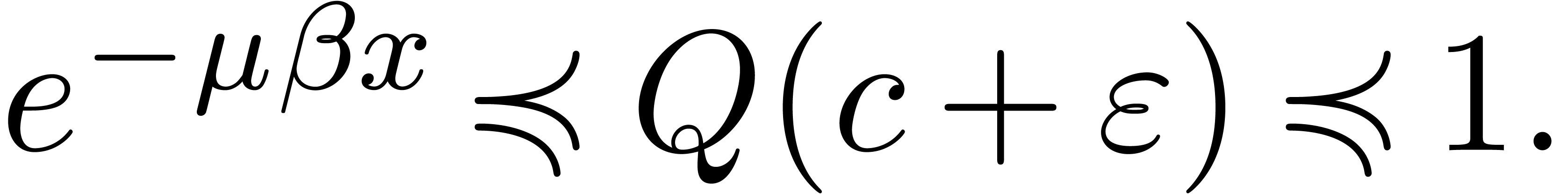 |
(17) |
Furthermore, 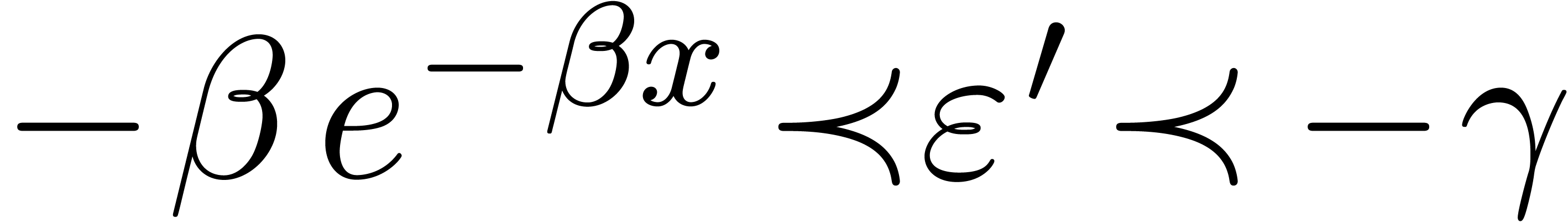 , whence
, whence
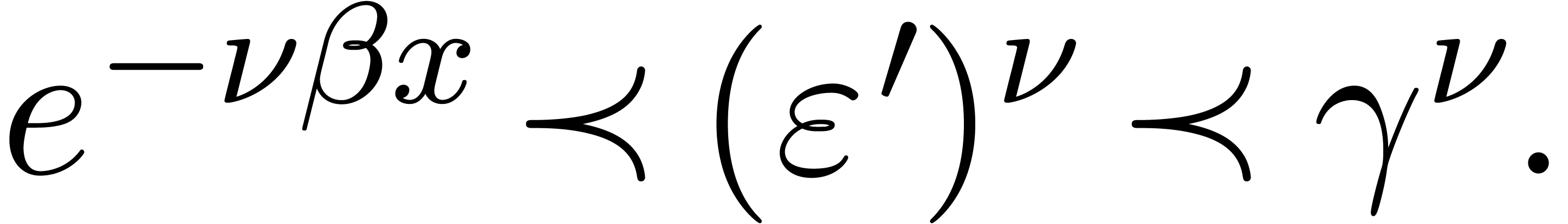 |
(18) |
Put together, (17) and (18) imply that 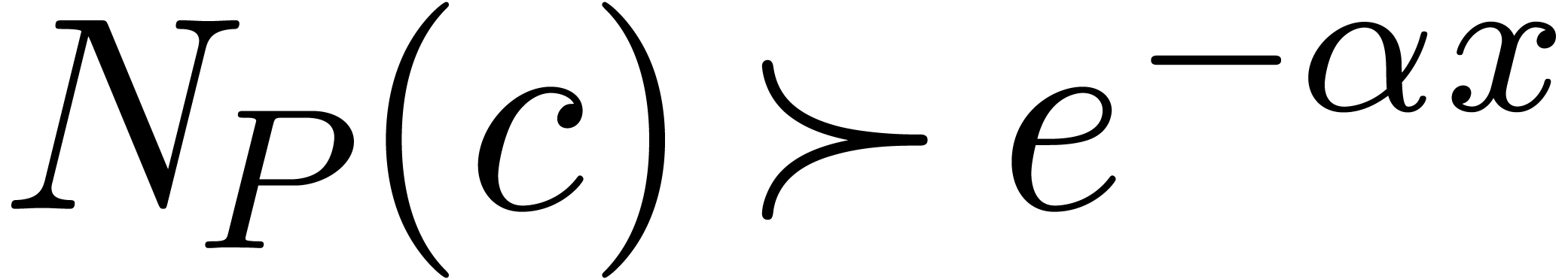 . Hence
. Hence 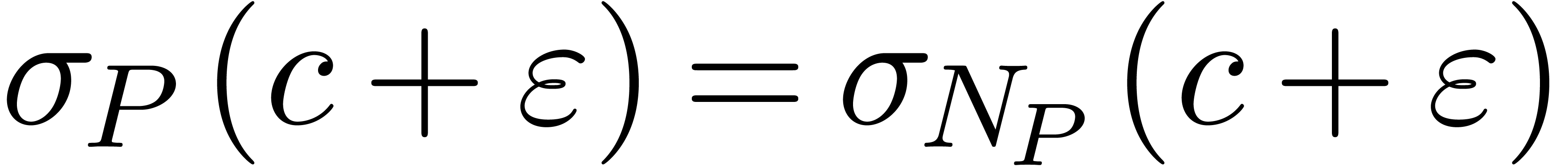 , by (16). Now
, by (16). Now
 |
(19) |
since 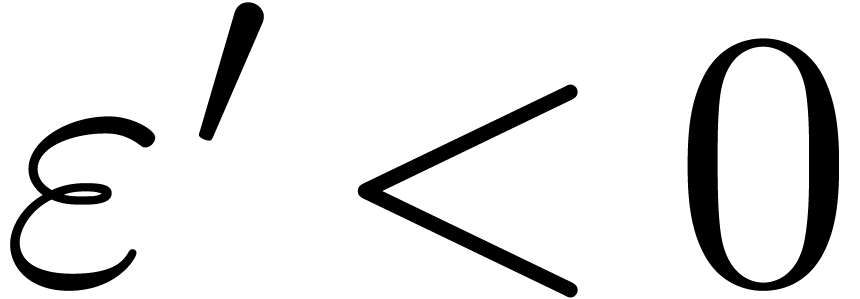 for all positive infinitesimal
for all positive infinitesimal  .
.
Corollary 8. If  is homogeneous of degree
is homogeneous of degree  ,
then
,
then
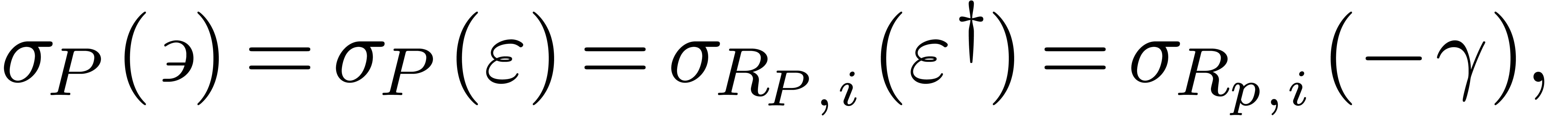 |
(20) |
for all  with
with  .
.
Corollary 9. Let
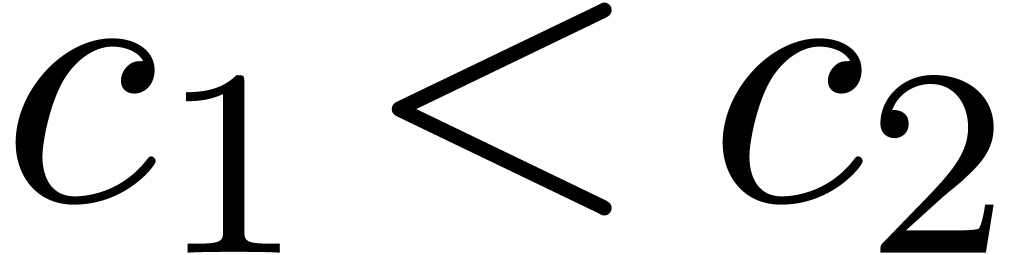 be constants such that
be constants such that 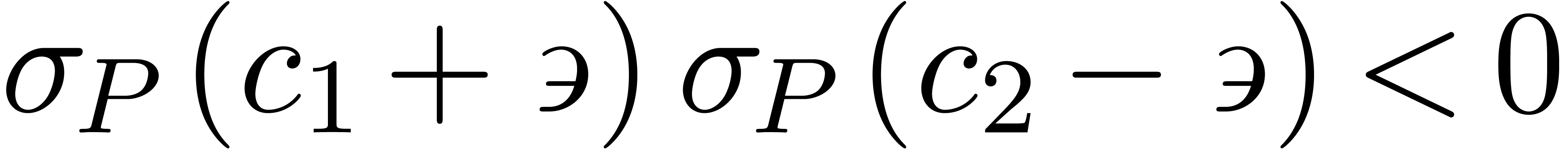 . Then there exists a constant
. Then there exists a constant 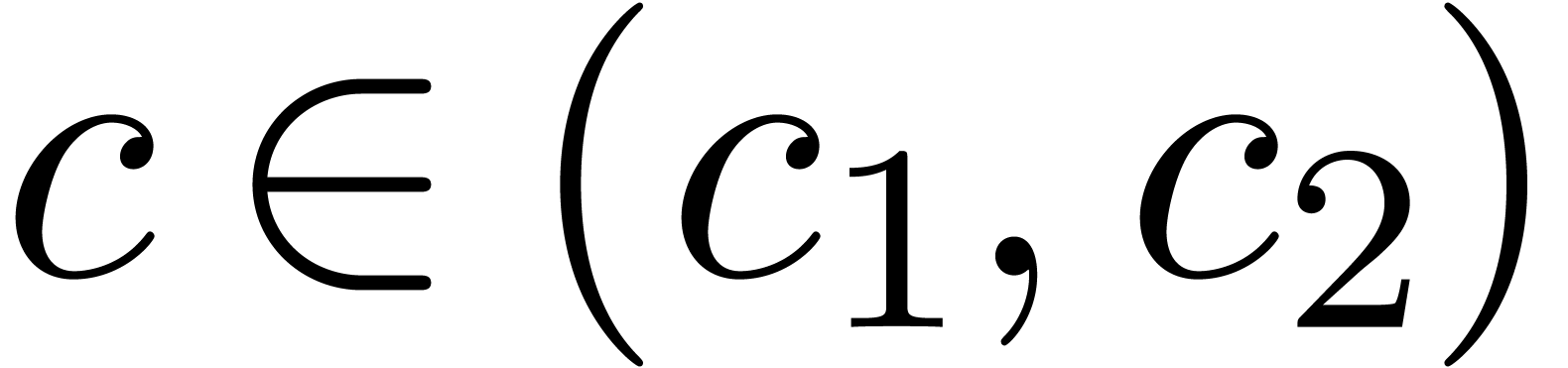 with
with 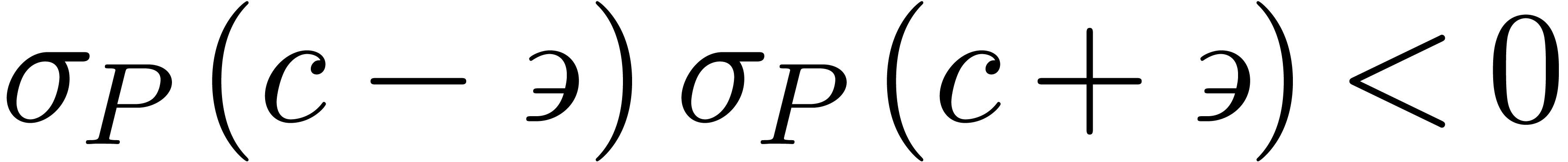 .
.
Proof. In the case when  is odd,
then
is odd,
then 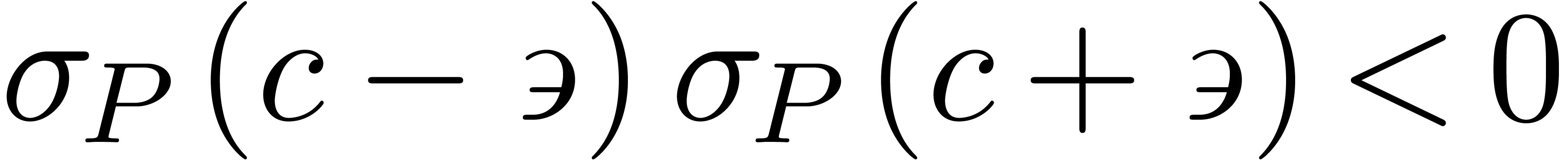 holds for any
holds for any 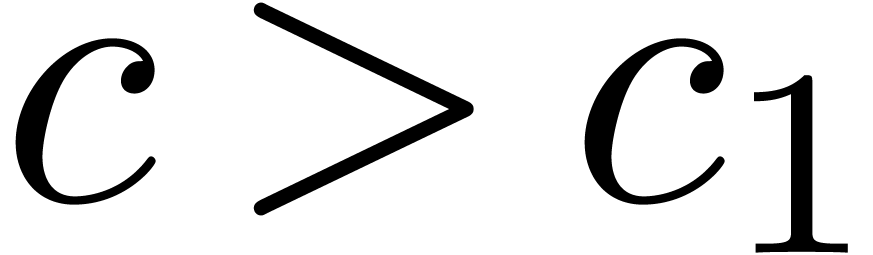 with
with
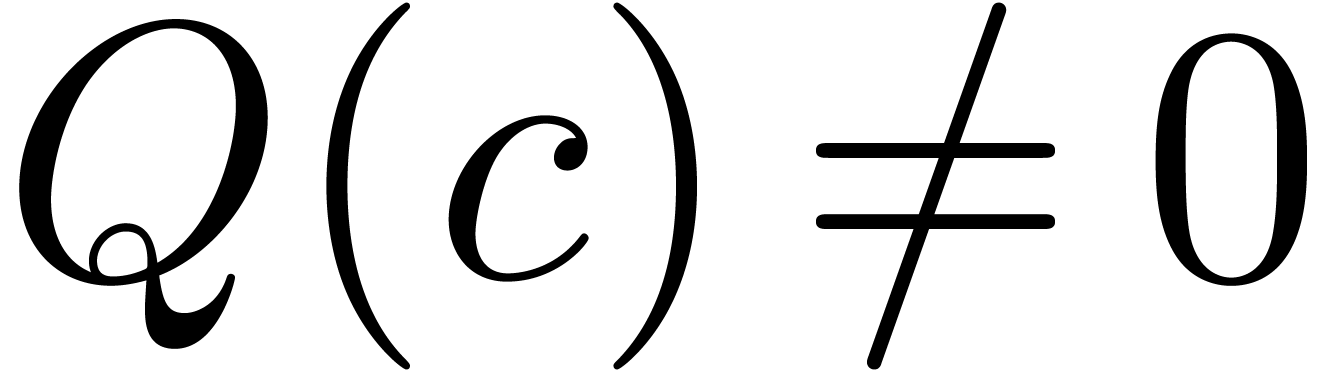 , by (15).
Assume therefore that
, by (15).
Assume therefore that  is even and let
is even and let 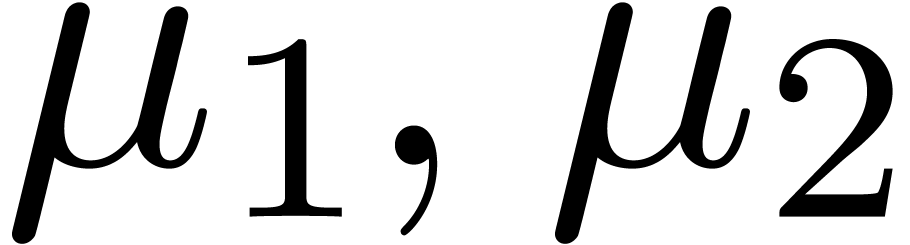 denote the multiplicities of
denote the multiplicities of 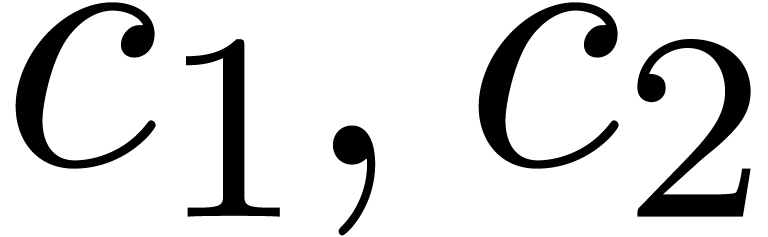 as
roots of
as
roots of  . From (15)
we deduce that
. From (15)
we deduce that
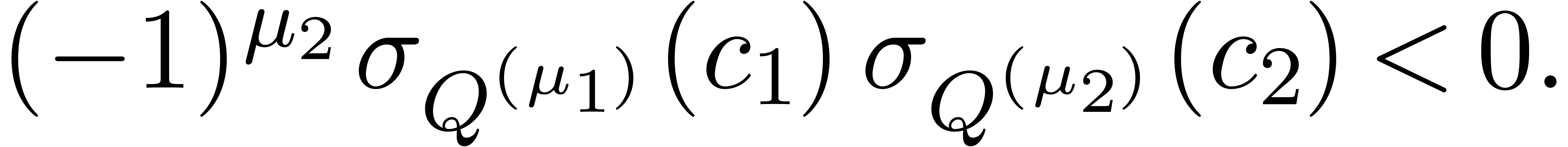 |
(21) |
In other words, the signs of  for
for  and
and  are different. Hence, there
exists a root
are different. Hence, there
exists a root  of
of  between
between
 and
and  which has odd
multiplicity
which has odd
multiplicity  . For this root
. For this root
 , (15) again
implies that
, (15) again
implies that  .
.
4.2Behaviour of  before
and after the constants
before
and after the constants
Lemma 10. For all
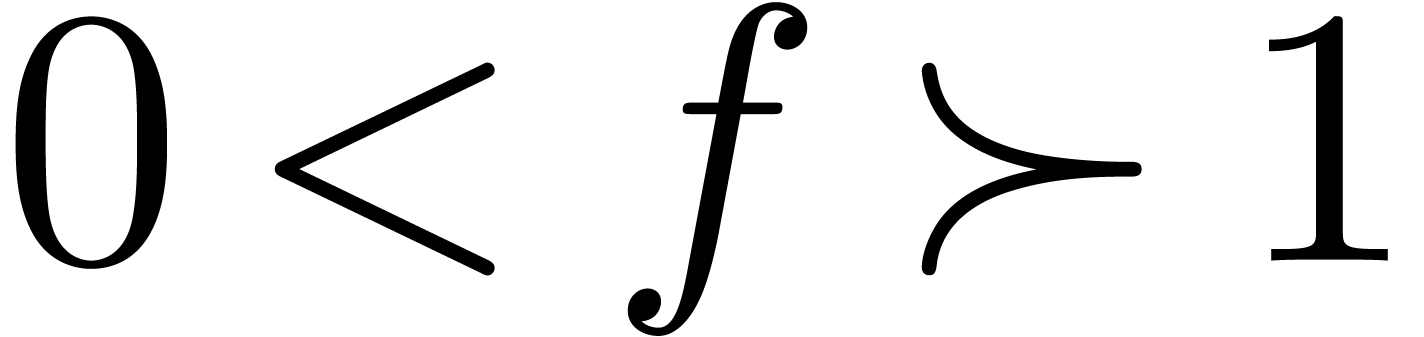 with
with  ,
the signs of
,
the signs of 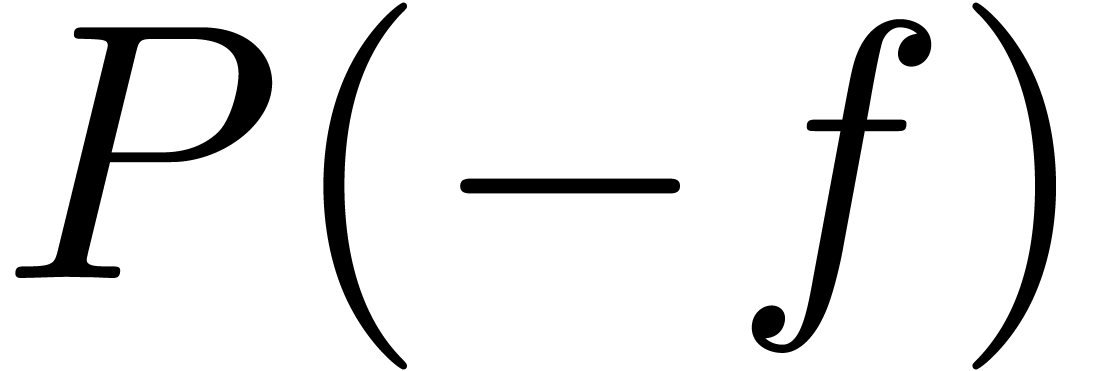 and
and 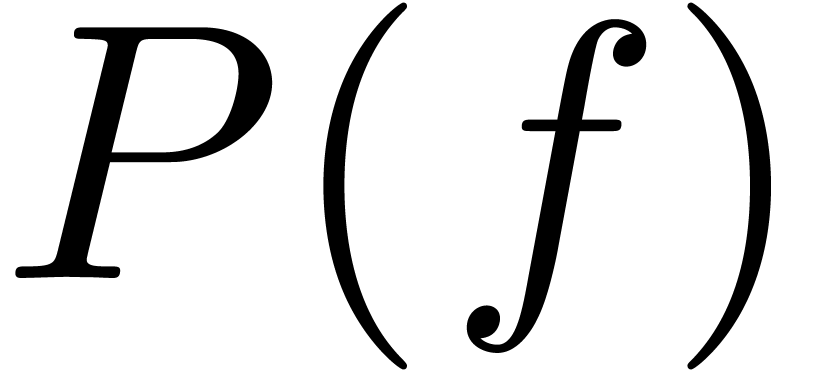 are
independent of
are
independent of  and given by
and given by
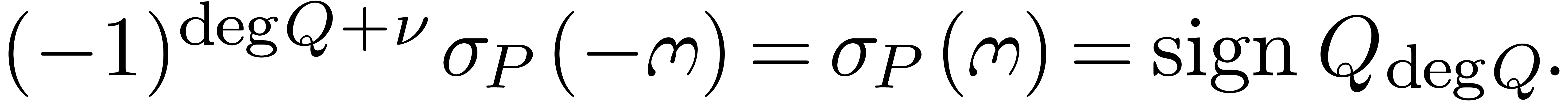 |
(22) |
Proof. Since  is purely
exponential and
is purely
exponential and 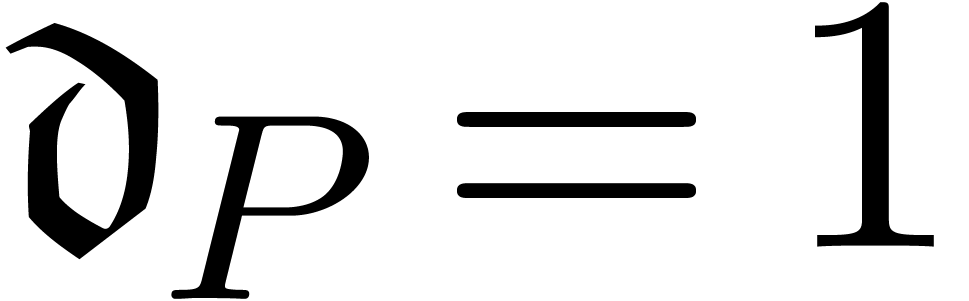 , there
exists an
, there
exists an  such that
such that
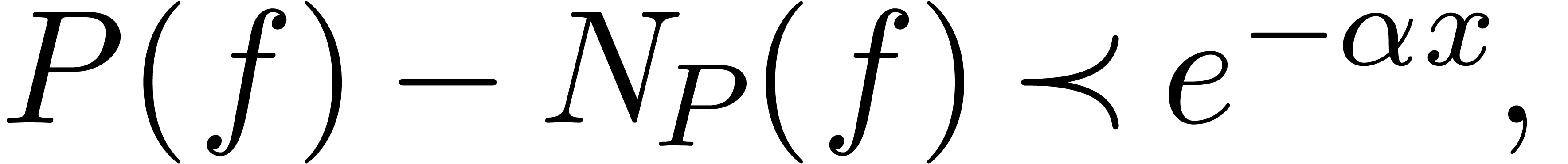 |
(23) |
since 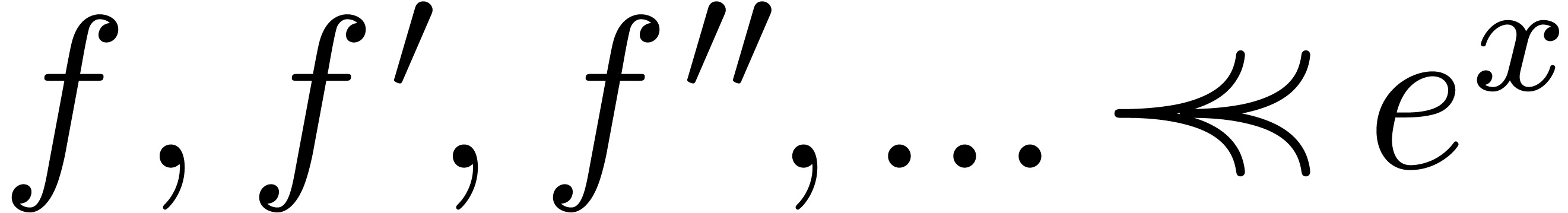 . Furthermore
. Furthermore 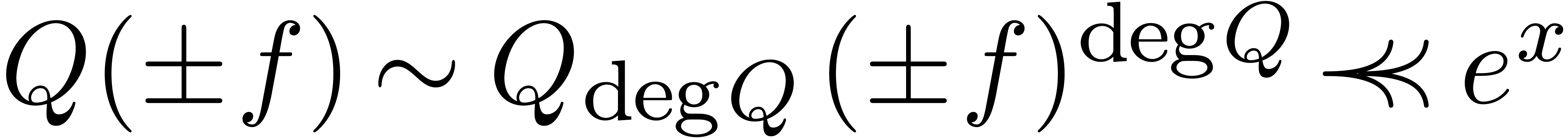 and
and 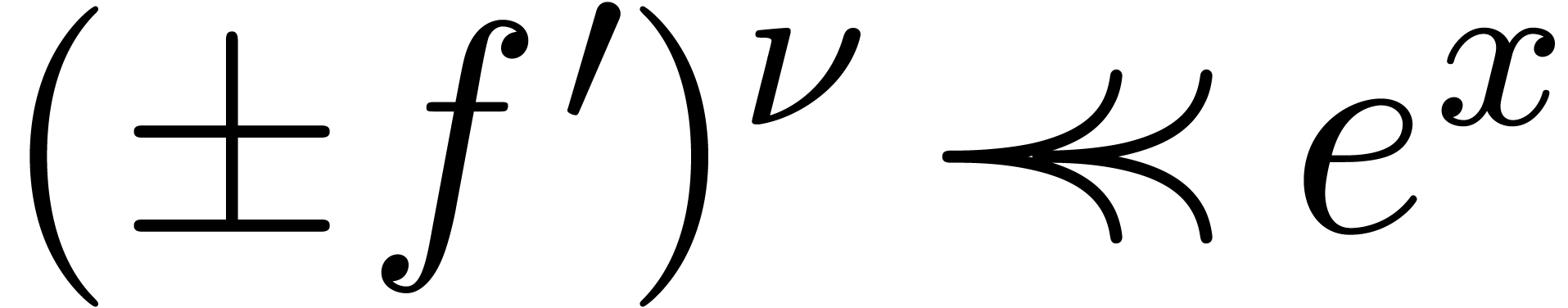 , whence
, whence
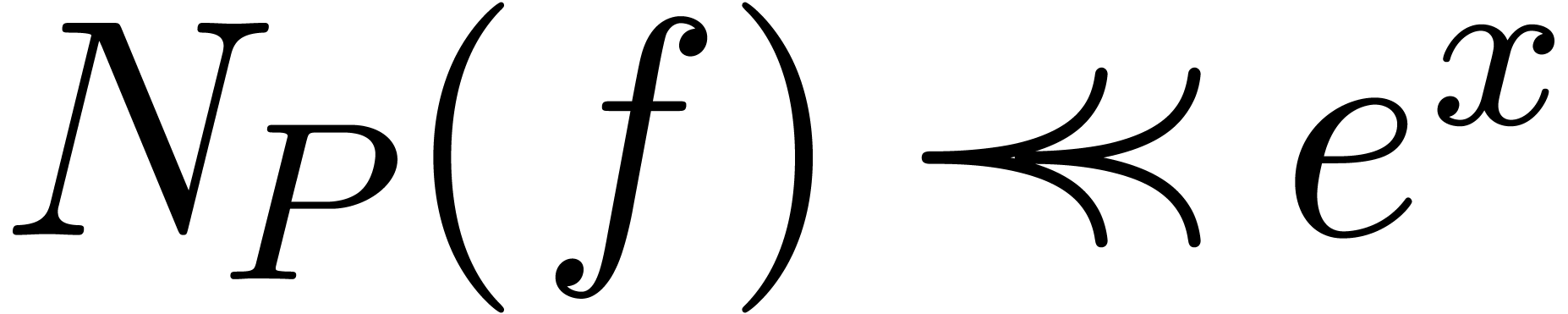 . In particular,
. In particular, 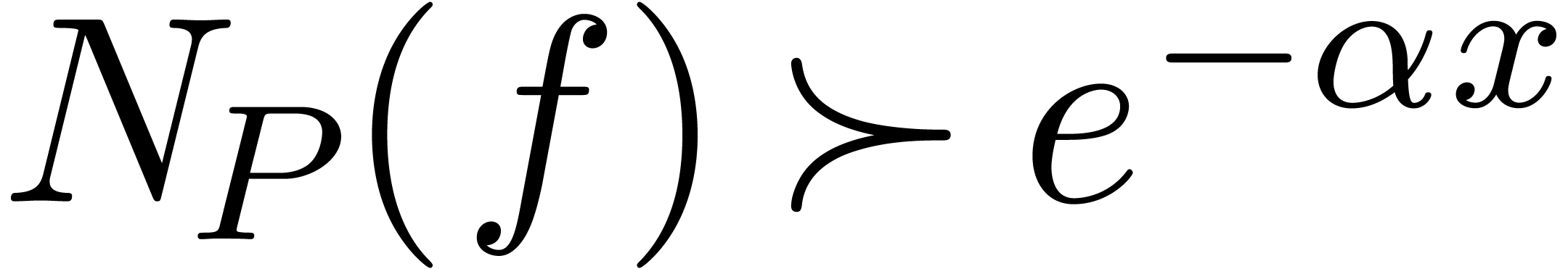 , so that
, so that 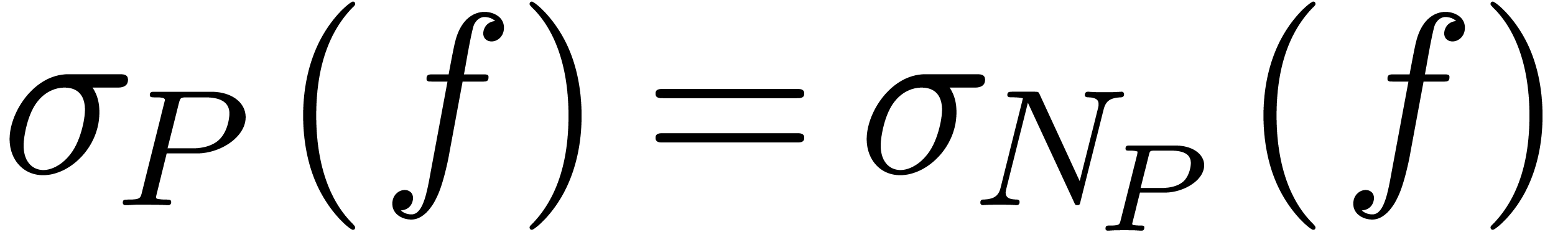 ,
by (23). Now
,
by (23). Now
 |
(24) |
since 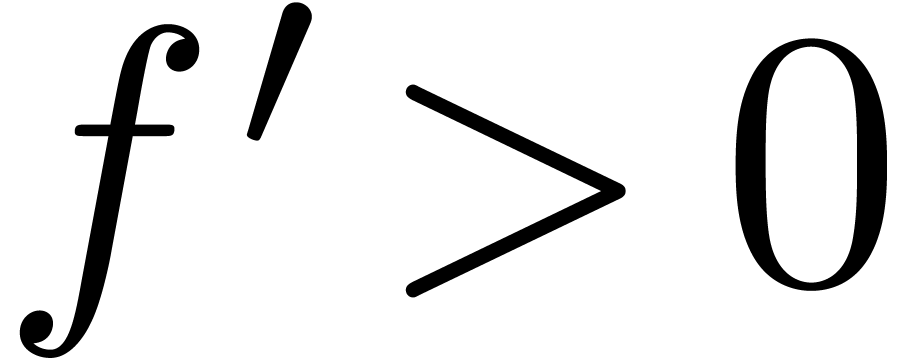 for positive infinitely large
for positive infinitely large  .
.
Corollary 11. If  is homogeneous of degree
is homogeneous of degree  ,
then
,
then
 |
(25) |
for all  with
with  .
.
Corollary 12. Let
 be a constant such that
be a constant such that 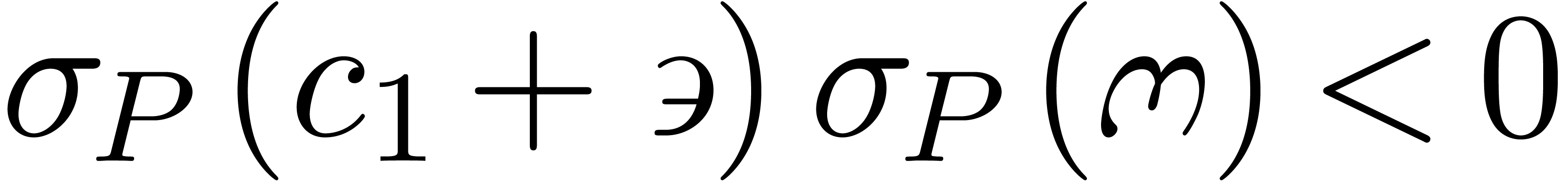 . Then there exists a constant
. Then there exists a constant  with
with 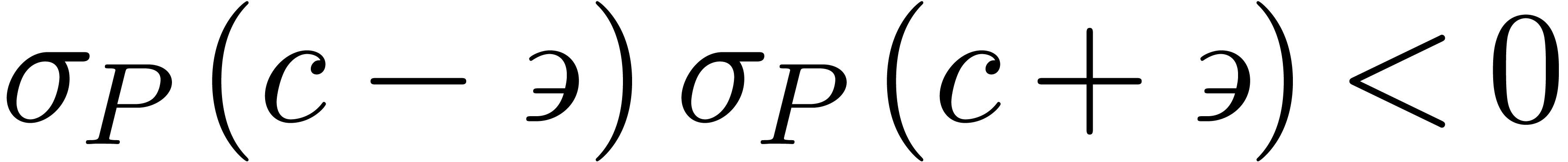 .
.
Proof. In the case when  is odd,
then
is odd,
then 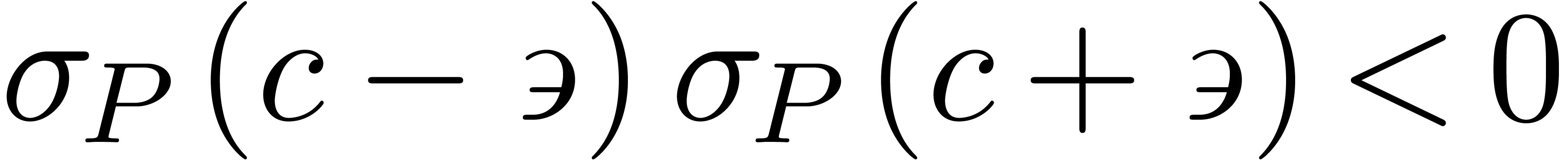 holds for any
holds for any  with
with
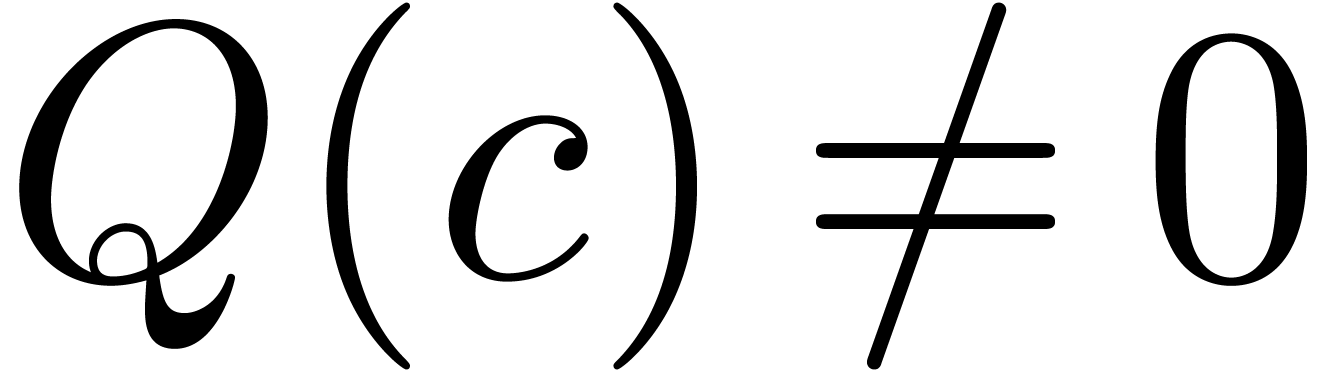 , by (15).
Assume therefore that
, by (15).
Assume therefore that  is even and let
is even and let  be the multiplicity of
be the multiplicity of  as a root
of
as a root
of  . From (15)
and (22) we deduce that
. From (15)
and (22) we deduce that
 |
(26) |
In other words, the signs of  for
for  and
and  are different. Hence, there
exists a root
are different. Hence, there
exists a root  of
of  which
has odd multiplicity
which
has odd multiplicity 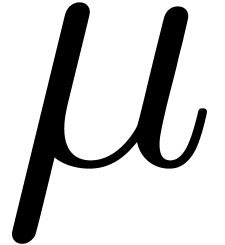 . For
this root
. For
this root  , (15)
implies that
, (15)
implies that  .
.
5Proof of the intermediate value theorem
It is convenient to prove the following generalizations of theorem 1.
Theorem 13. Let
 and
and  be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in  .
Assume that
.
Assume that  changes sign on an open interval
changes sign on an open interval
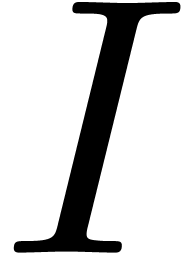 of one of the following forms:
of one of the following forms:
-
 , for some
, for some 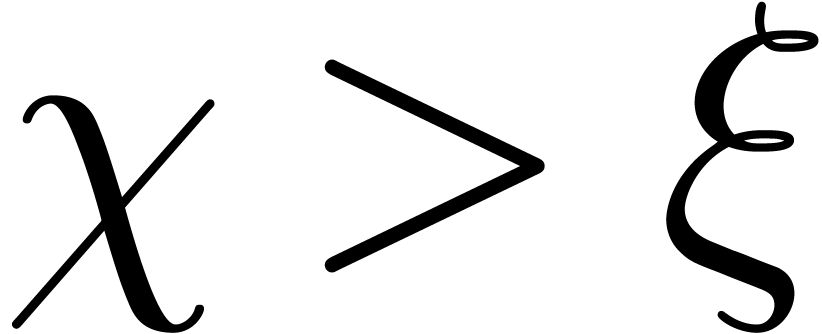 with
with 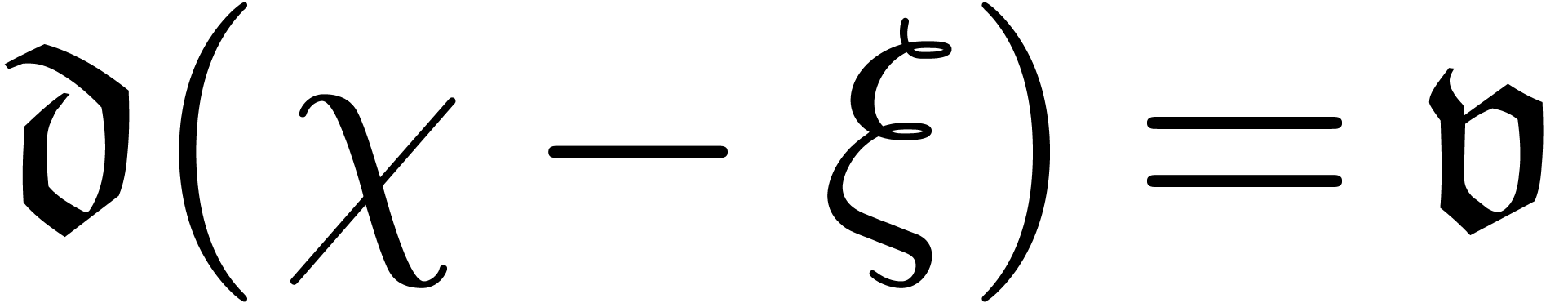 .
.
-
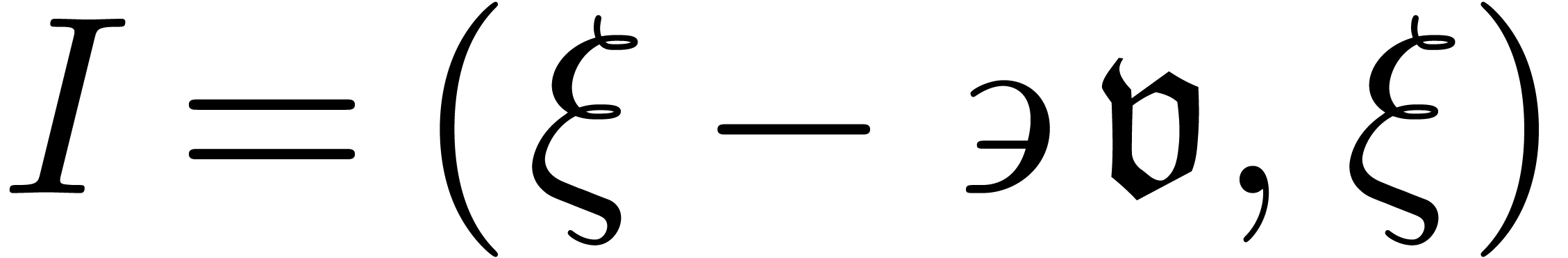 .
.
-
 .
.
-
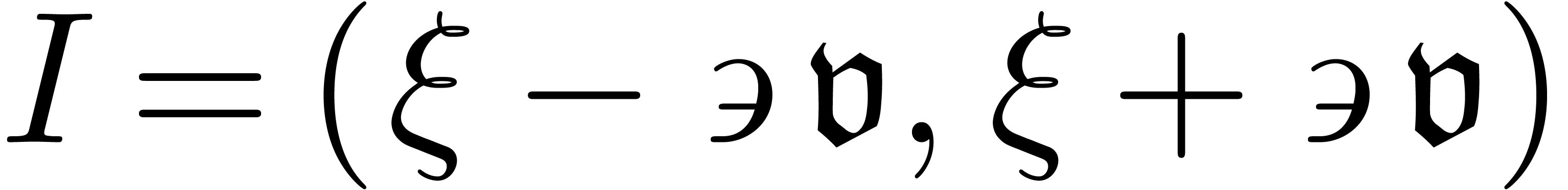 .
.
Then  changes sign at some
changes sign at some  .
.
Theorem 14. Let
 and
and  be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in  .
Assume that
.
Assume that  changes sign on an open interval
changes sign on an open interval
 of one of the following forms:
of one of the following forms:
-
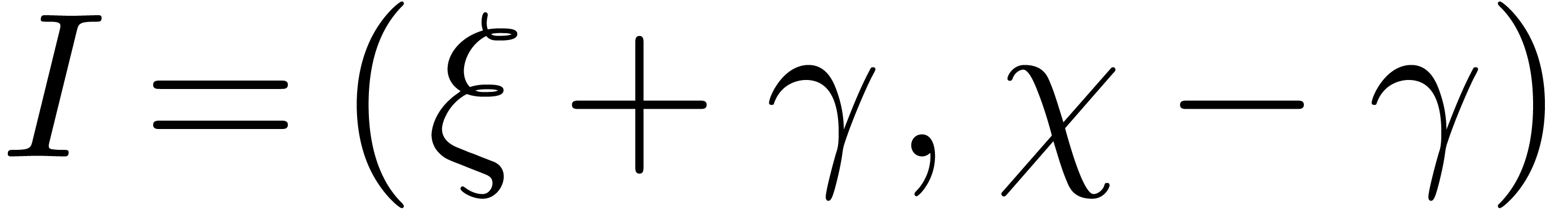 , for some
, for some  with
with 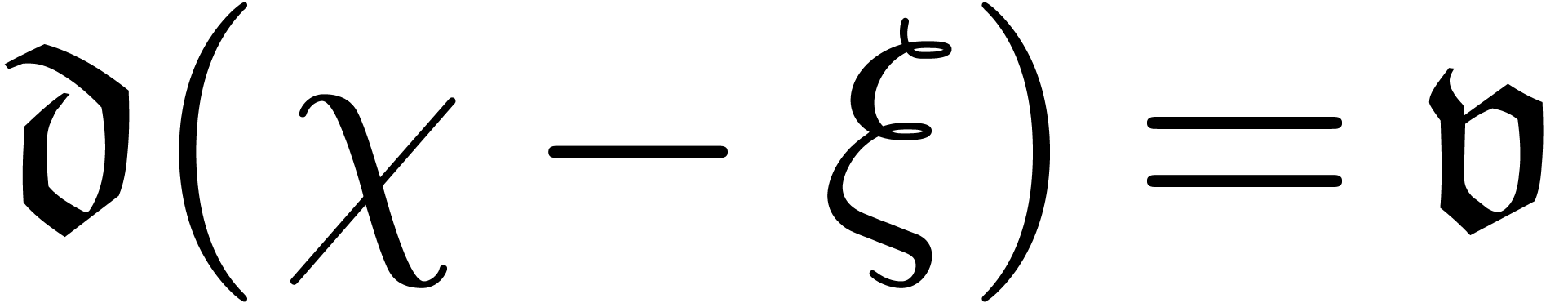 .
.
-
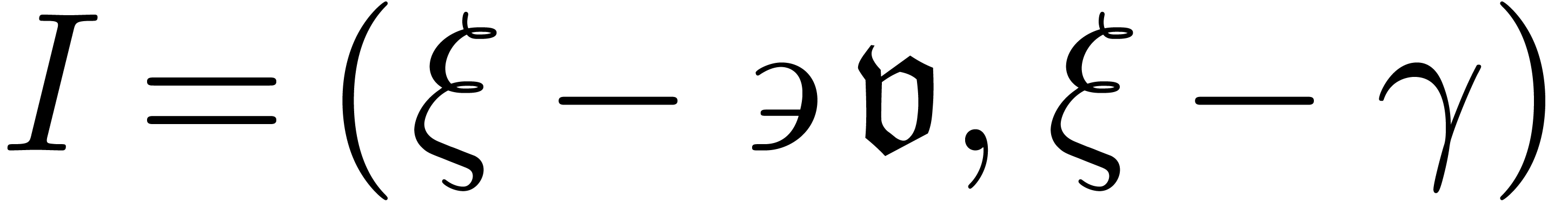 .
.
-
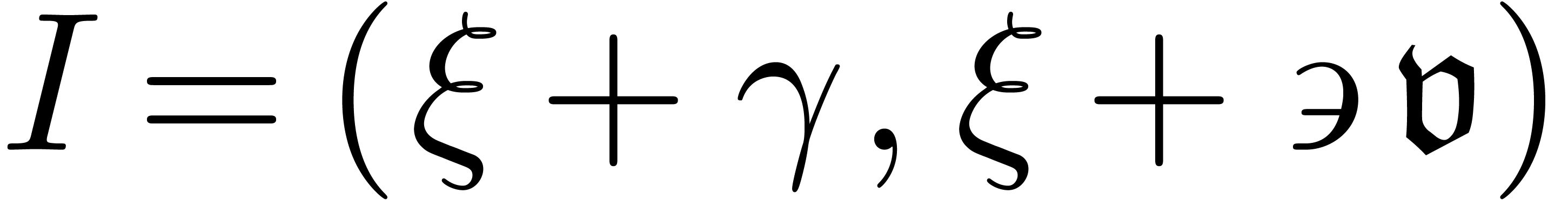 .
.
-
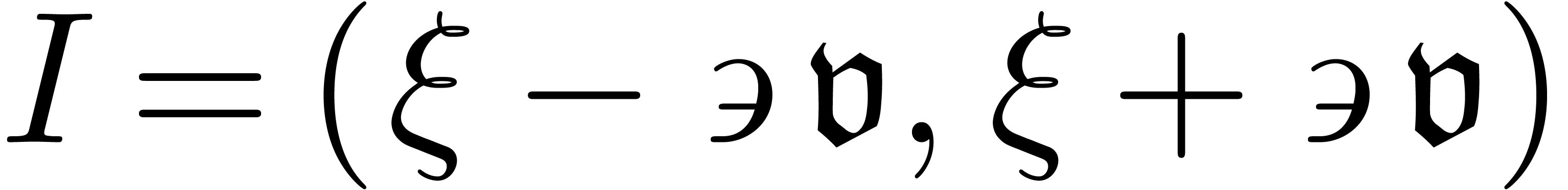 .
.
Then  changes sign on
changes sign on 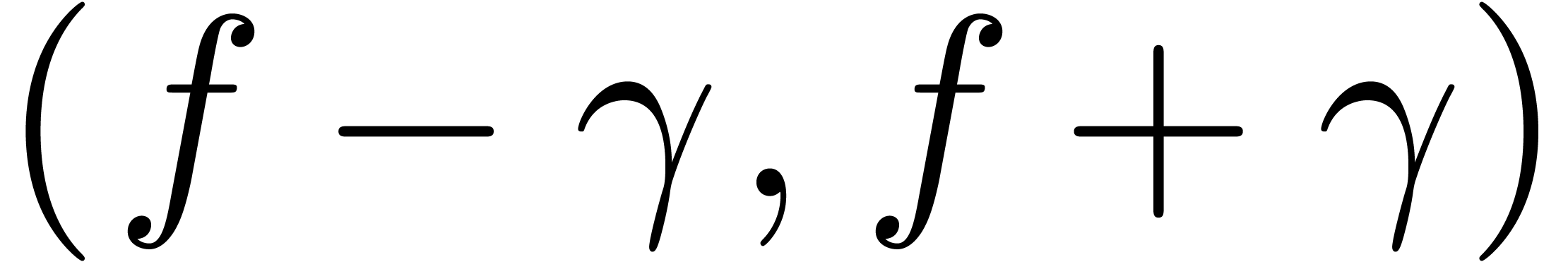 for some
for some  with
with 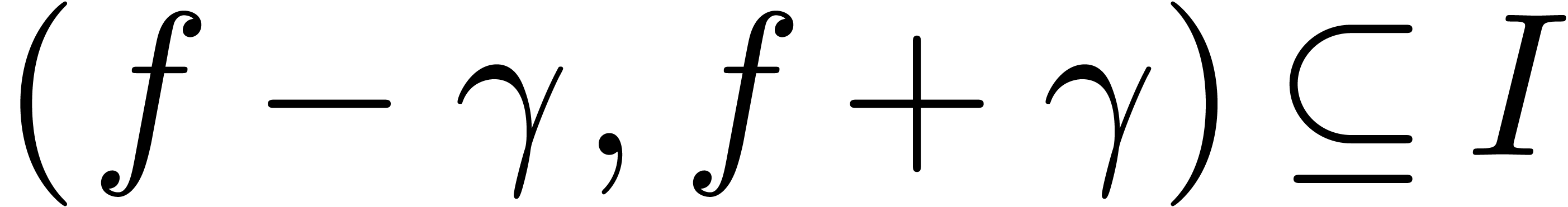 .
.
Proof. Let us first show that cases a, b
and d may all be reduced to case c. We will show this in
the case of theorem 13; the proof is similar in the case of
theorem 14. Let us first show that case a may be
reduced to cases b, c and d. Indeed, if  changes sign on
changes sign on 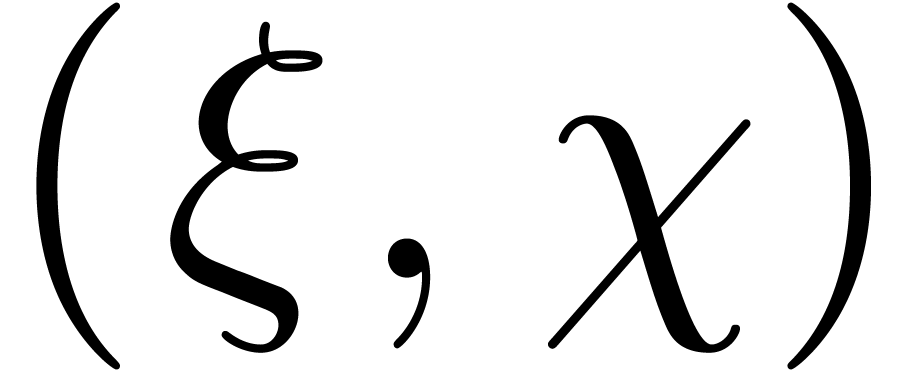 ,
then
,
then  changes sign on
changes sign on 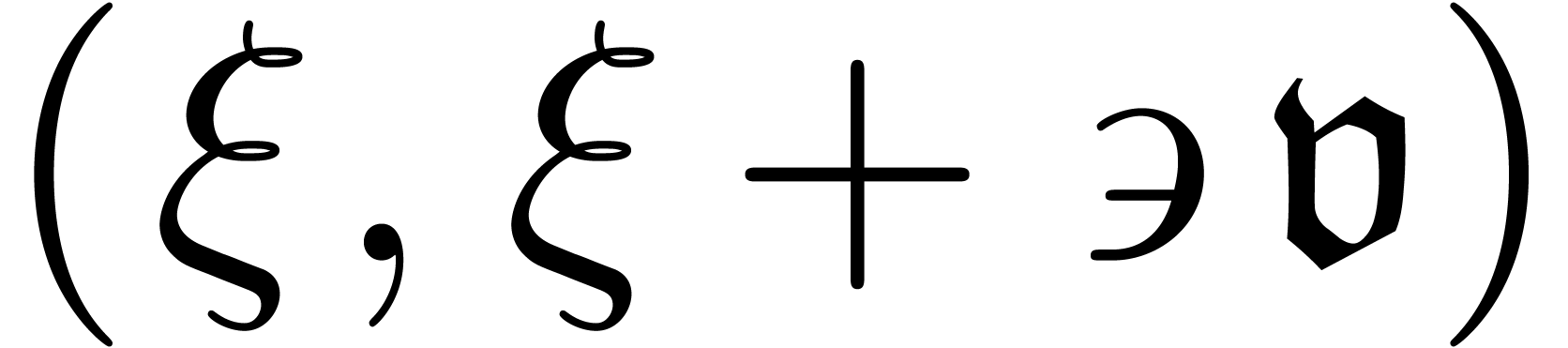 ,
, 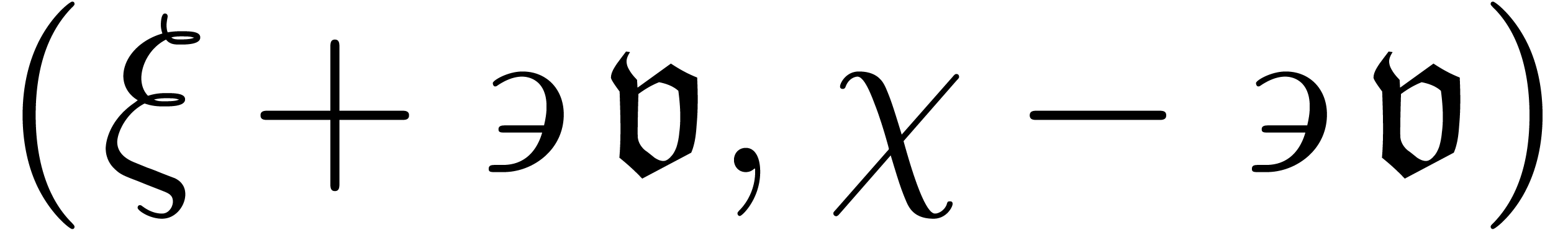 or
or 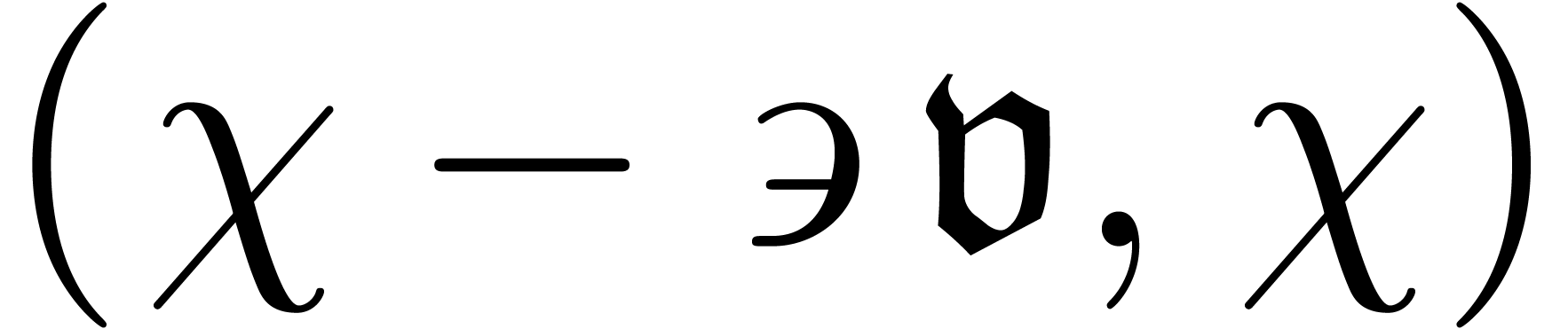 . In the second case, modulo a multiplicative
conjugation and upward shifting, corollary 9 implies that
there exists a
. In the second case, modulo a multiplicative
conjugation and upward shifting, corollary 9 implies that
there exists a 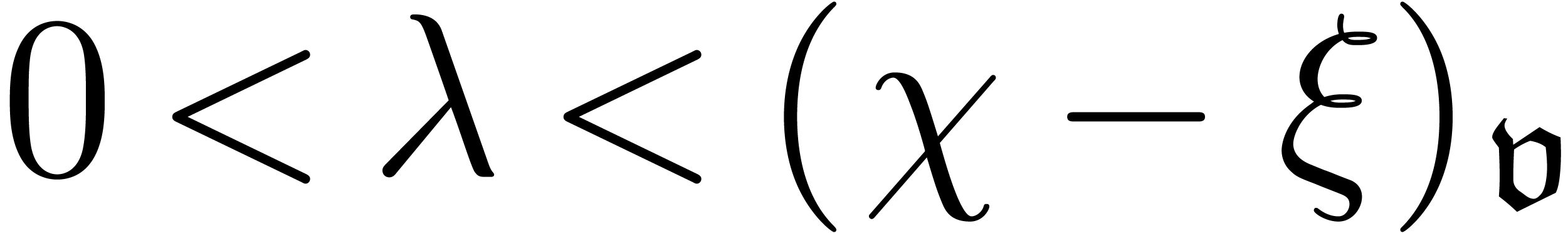 such that
such that  admits a sign change on
admits a sign change on 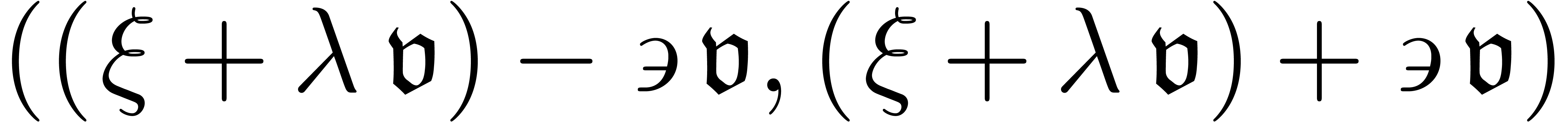 .
Similarly, case d may be reduced to cases b and c
by splitting the interval in two parts. Finally, cases b and
c are symmetric when replacing
.
Similarly, case d may be reduced to cases b and c
by splitting the interval in two parts. Finally, cases b and
c are symmetric when replacing  by
by 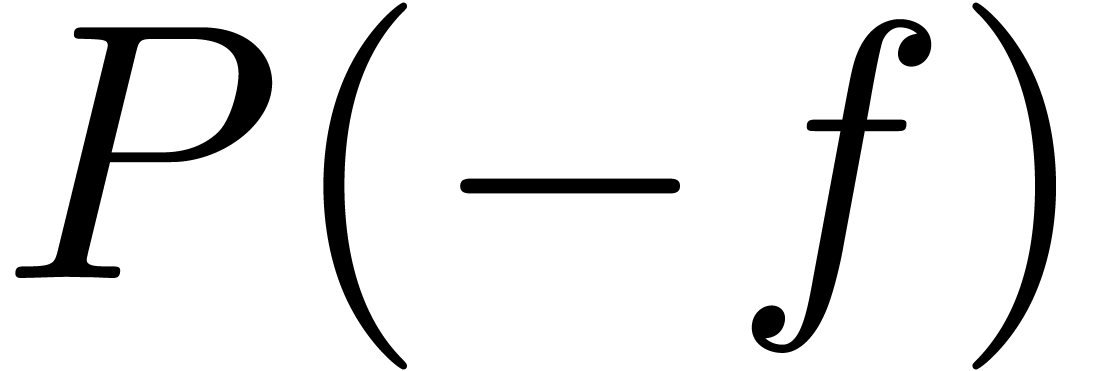 .
.
Without loss of generality we may assume that 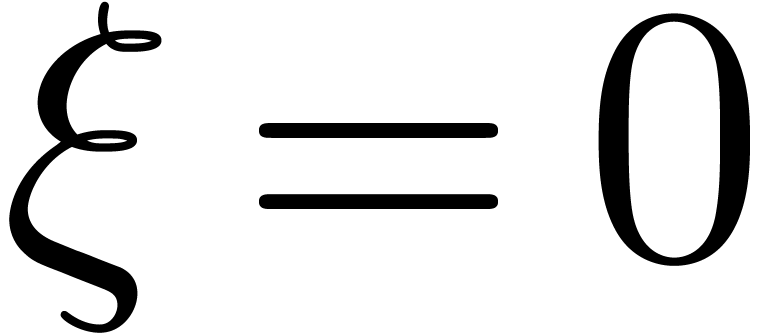 , modulo an additive conjugation of
, modulo an additive conjugation of  by
by  . We prove the theorem by
a triple induction over the order
. We prove the theorem by
a triple induction over the order 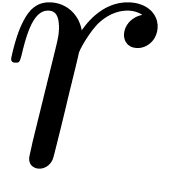 of
of  , the Newton degree
, the Newton degree  of the asymptotic algebraic differential equation
of the asymptotic algebraic differential equation
 |
(27) |
and the maximal length 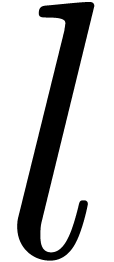 of a sequence of
privileged refinements of Newton degree
of a sequence of
privileged refinements of Newton degree 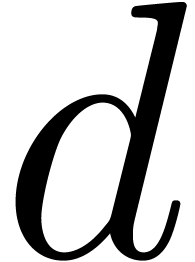 (we have
(we have
 , by proposition 5.12 in [vdH97]).
, by proposition 5.12 in [vdH97]).
Let us show that, modulo upward shiftings, we may assume without loss of
generality that  and
and  are
purely exponential and that
are
purely exponential and that  .
In the case of theorem 13, we indeed have
.
In the case of theorem 13, we indeed have 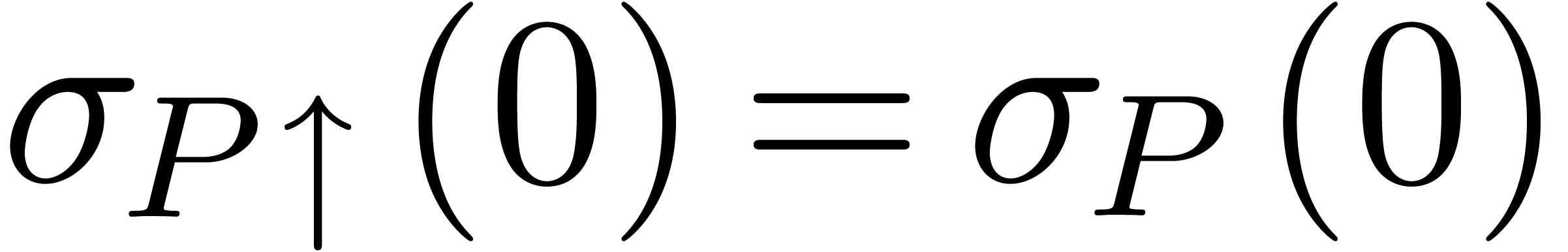 and
and 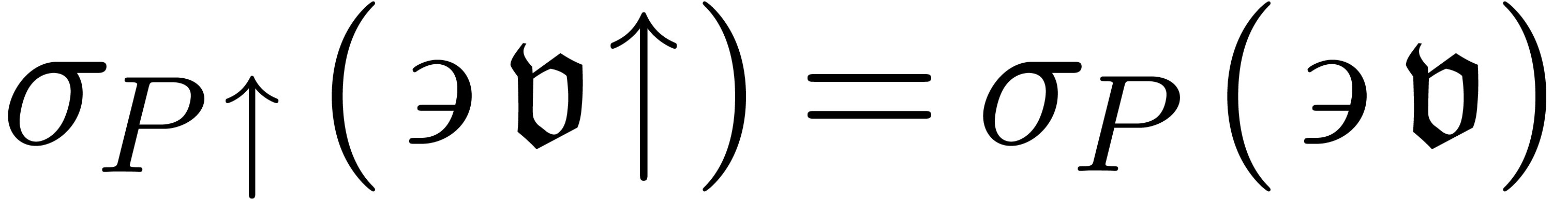 . In the case of theorem
14, we also have
. In the case of theorem
14, we also have  .
Furthermore, if
.
Furthermore, if  is such that
is such that  changes sign on
changes sign on 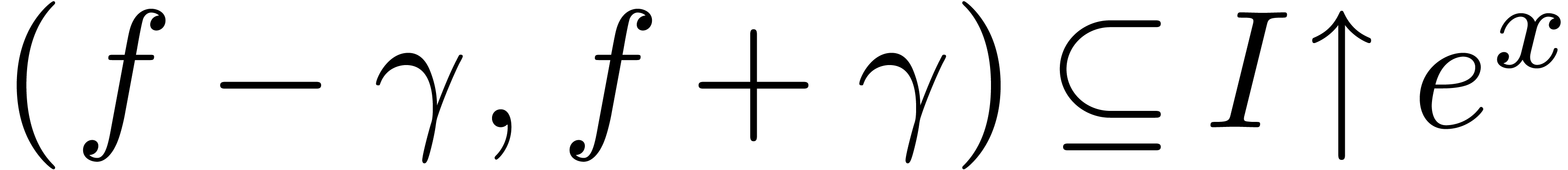 , then
, then 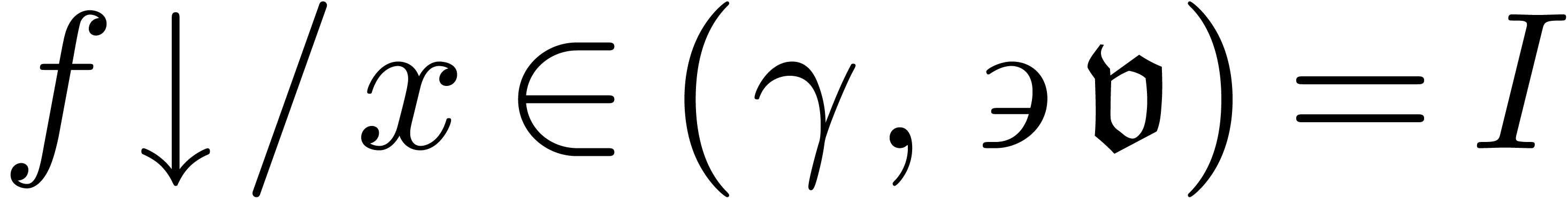 is such that
is such that  changes sign on
changes sign on
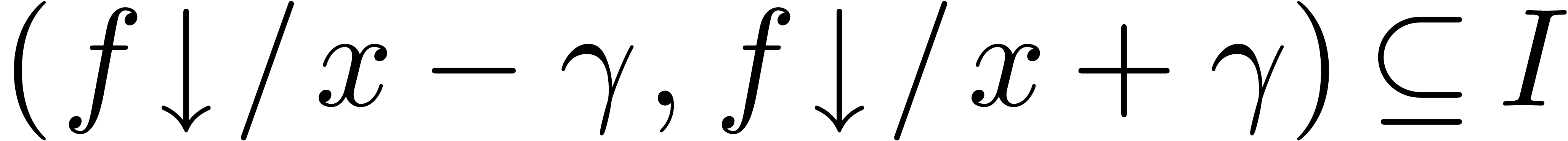 .
.
Case 1: (27) is quasi-linear. Let  be the potential dominant monomial relative to (27). We may
assume without loss of generality that
be the potential dominant monomial relative to (27). We may
assume without loss of generality that  ,
modulo a multiplicative conjugation with
,
modulo a multiplicative conjugation with  .
Since By
.
Since By 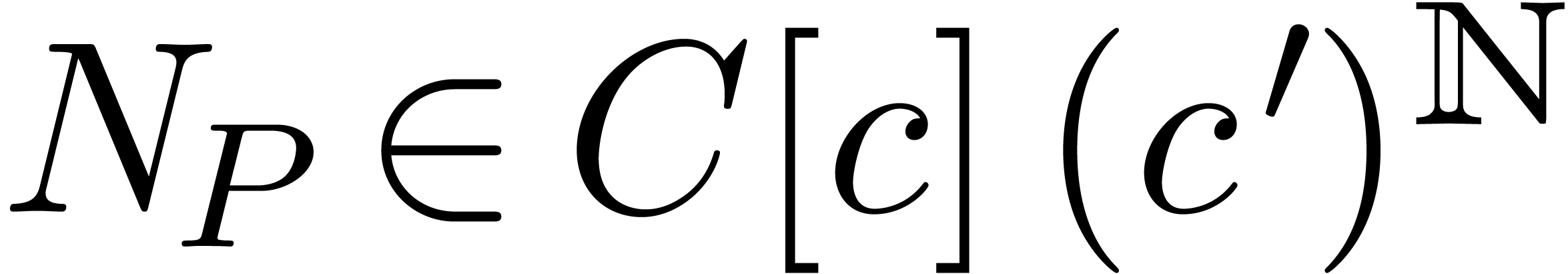 , we have
, we have  or
or 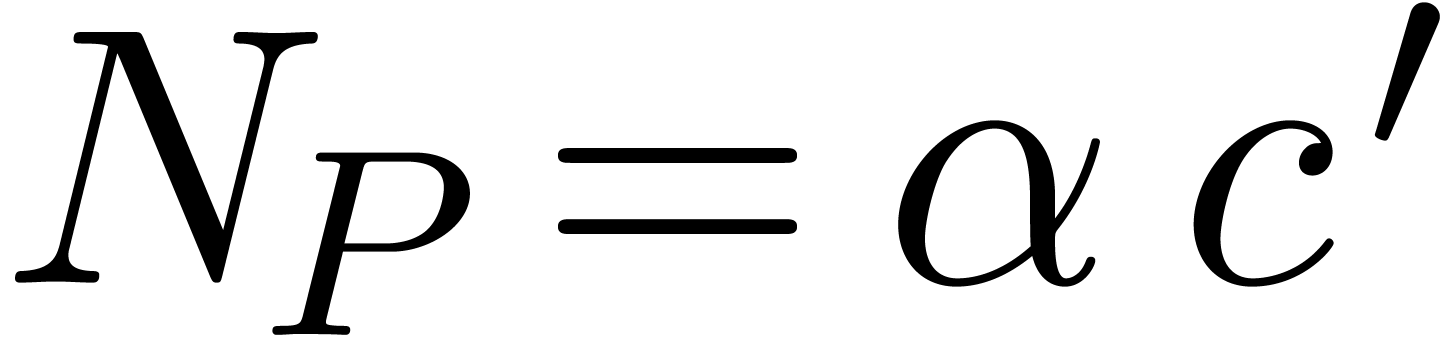 for certain constants
for certain constants 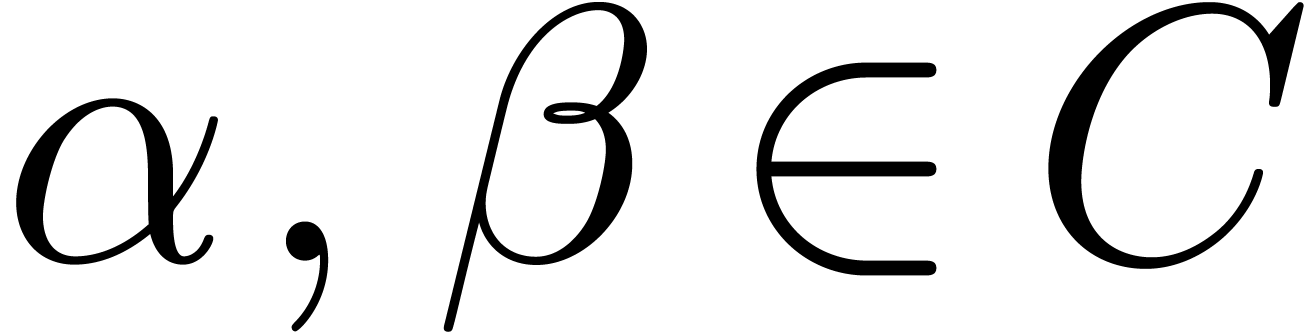 .
.
In the case when  , there
exists a solution to (27) with
, there
exists a solution to (27) with 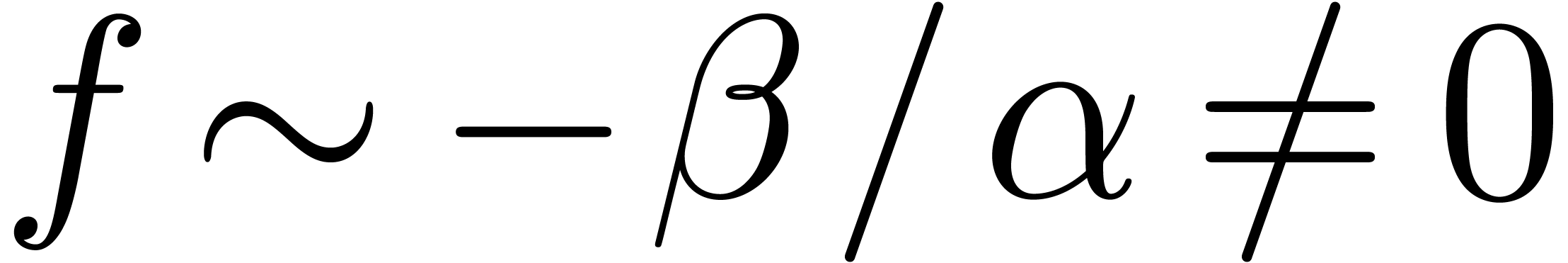 . Now
. Now 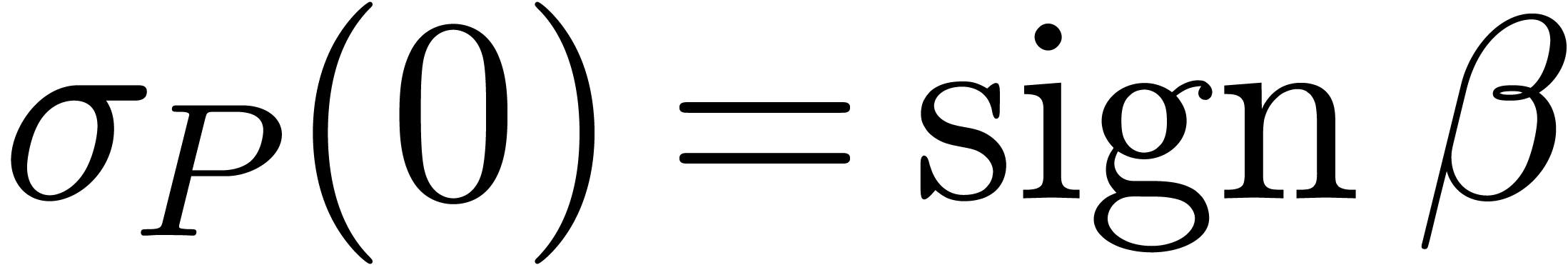 and
and 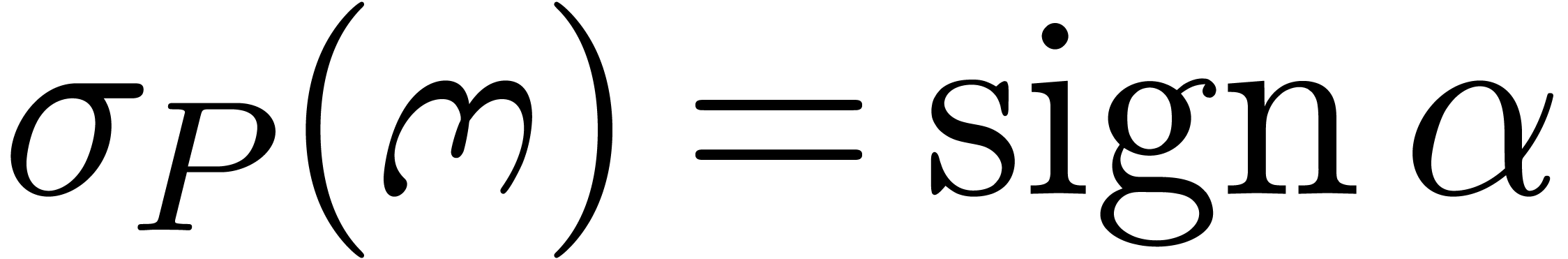 . We claim that
. We claim that 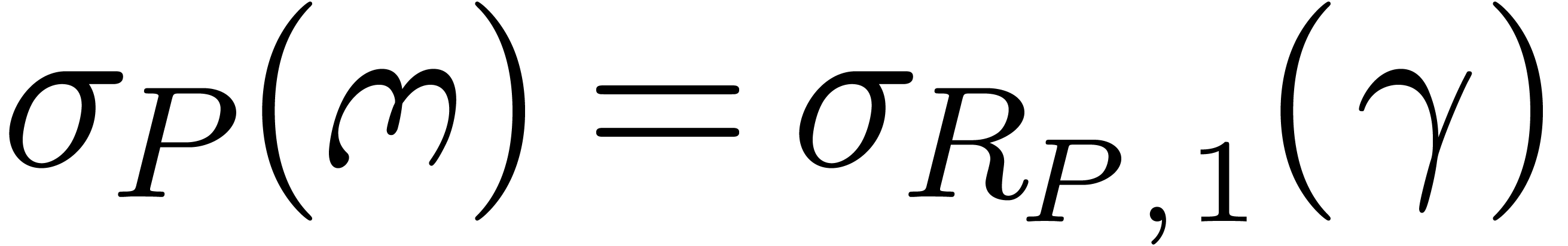 and
and
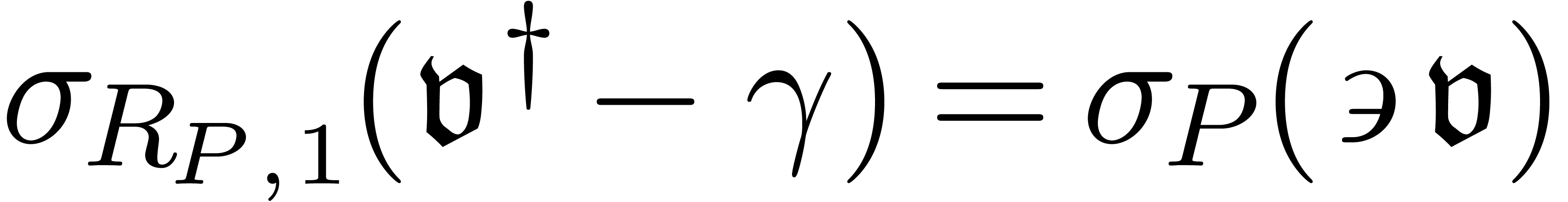 must be equal. Otherwise
must be equal. Otherwise 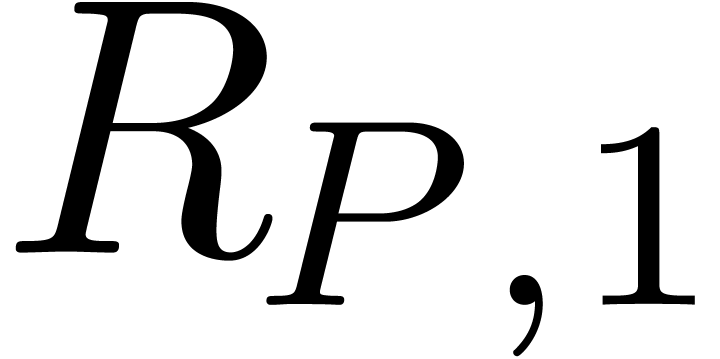 would admit a solution between
would admit a solution between 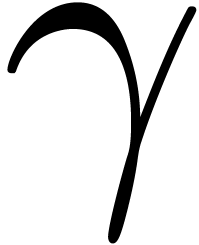 and
and 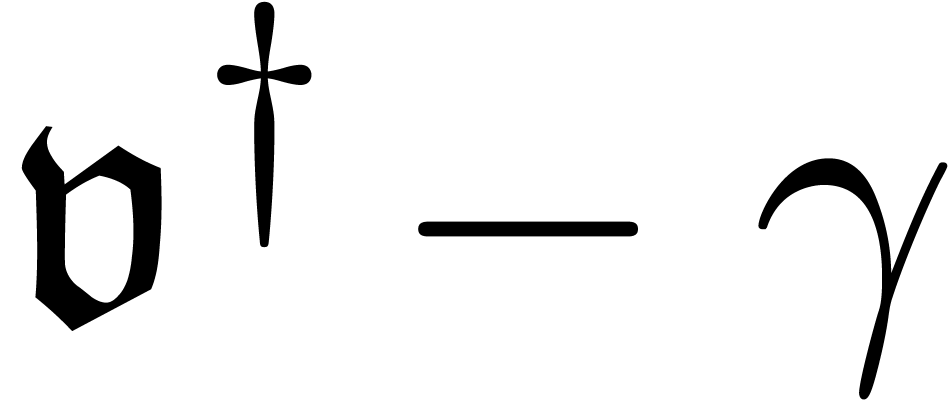 , by the induction hypothesis. But then the
potential dominant monomial relative to (27) should have
been
, by the induction hypothesis. But then the
potential dominant monomial relative to (27) should have
been  , if
, if  is the largest such solution. Our claim implies that
is the largest such solution. Our claim implies that 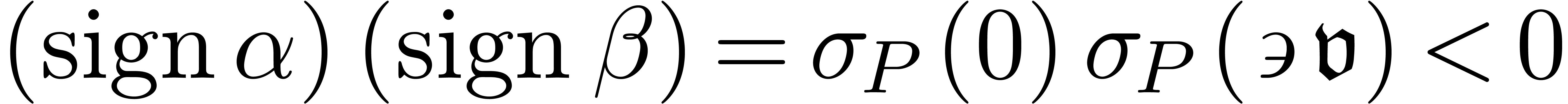 , so that
, so that  .
Finally, lemma 4 implies that
.
Finally, lemma 4 implies that  admits a sign-change at
admits a sign-change at  .
Lemma 7 also shows that
.
Lemma 7 also shows that 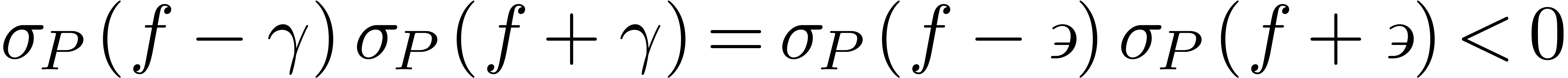 .
.
In the case when 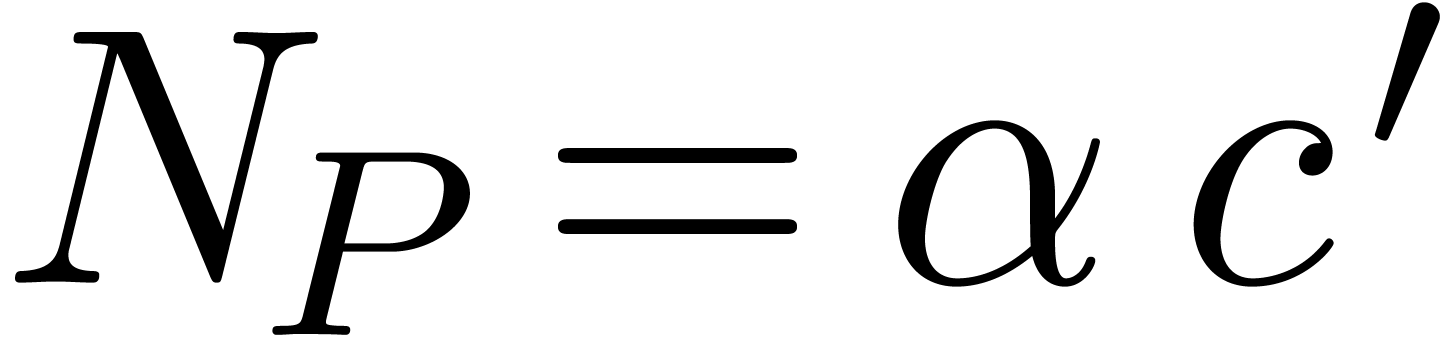 , then any
constant
, then any
constant 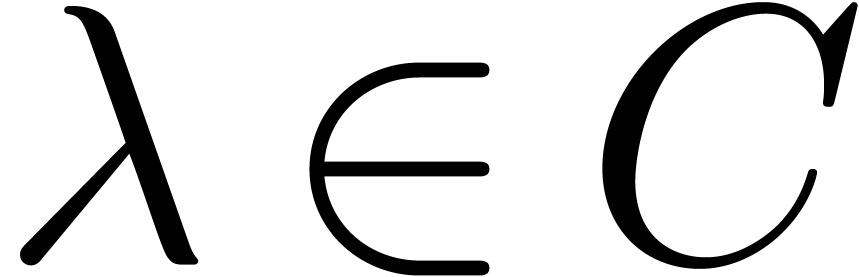 is a root of
is a root of  . Hence, for each
. Hence, for each  ,
there exists a solution
,
there exists a solution  to (27)
with
to (27)
with  . Again by lemmas 4 and 7, it follows that
. Again by lemmas 4 and 7, it follows that  admits a sign change at
admits a sign change at  and on
and on  .
.
Case 2:  . Let
. Let  be the largest classical potential dominant monomial
relative to (27). Since
be the largest classical potential dominant monomial
relative to (27). Since  (resp.
(resp.
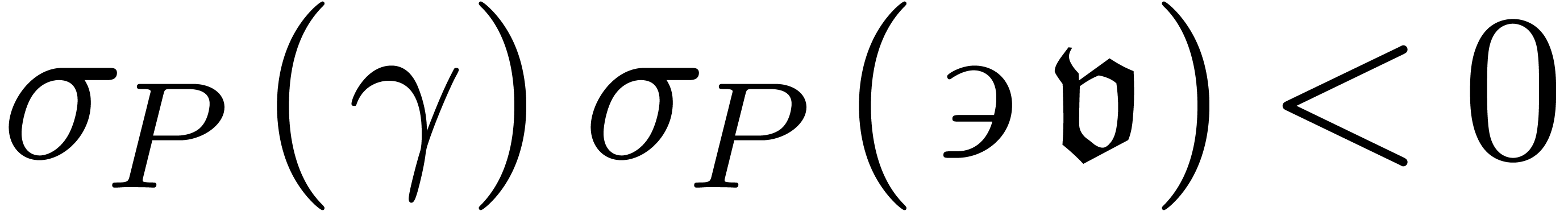 ), one of the following
always holds:
), one of the following
always holds:
-
Case 2a
-
We have 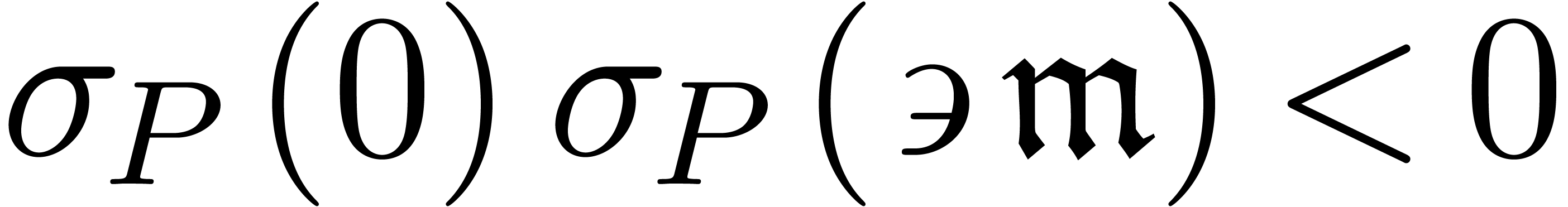 (resp.
(resp. 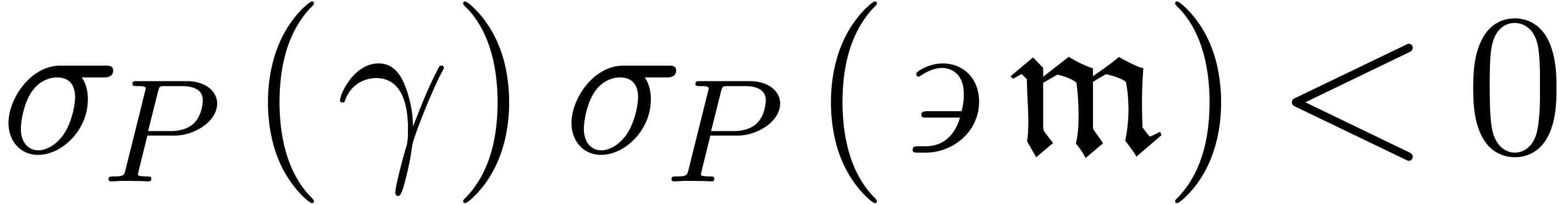 ).
).
-
Case 2b
-
We have 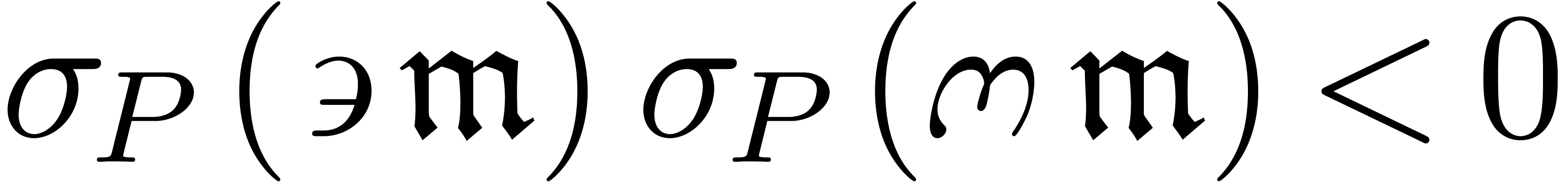 .
.
-
Case 2c
-
We have 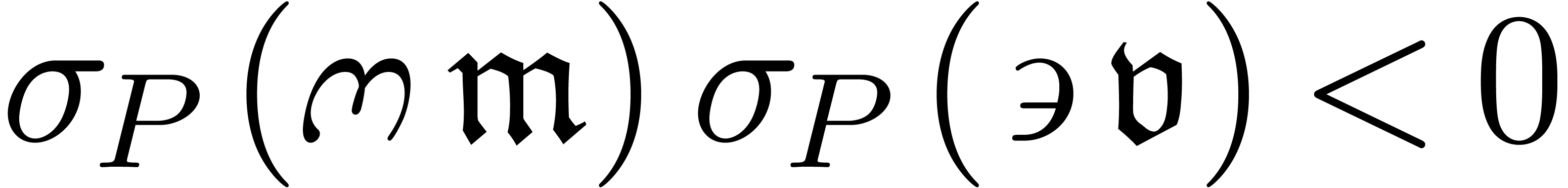 .
.
For the proof of theorem 14, we also assume that  in the above three cases and distinguish a last case
2d in which
in the above three cases and distinguish a last case
2d in which  .
.
Case 2a. We are directly done by the induction hypothesis, since
the equation
 |
(28) |
has a strictly smaller Newton degree than (27).
Case 2b. Modulo multiplicative conjugation with  , we may assume without loss of generality that
, we may assume without loss of generality that
 . By corollary 12,
there exists a
. By corollary 12,
there exists a  such that
such that 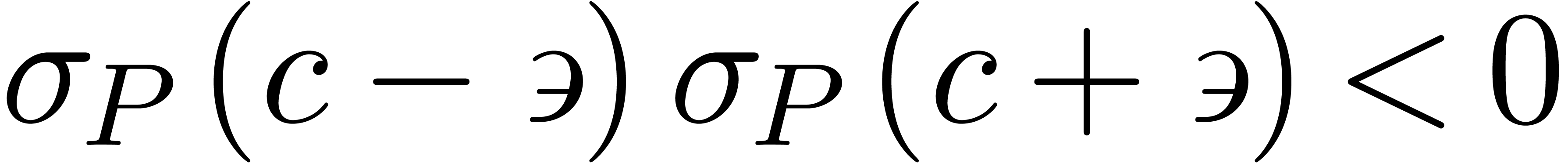 . Actually, for any transseries
. Actually, for any transseries  we then have
we then have 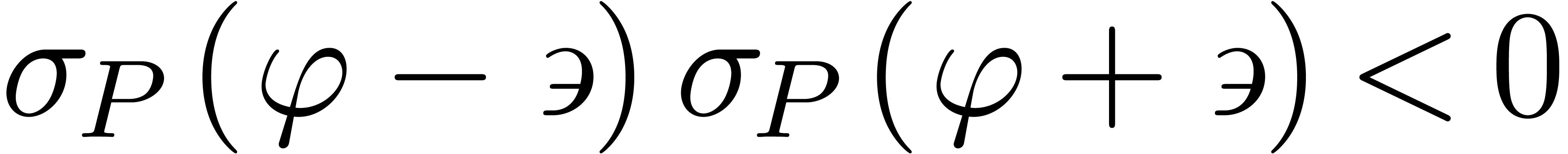 . Take
. Take  such that
such that
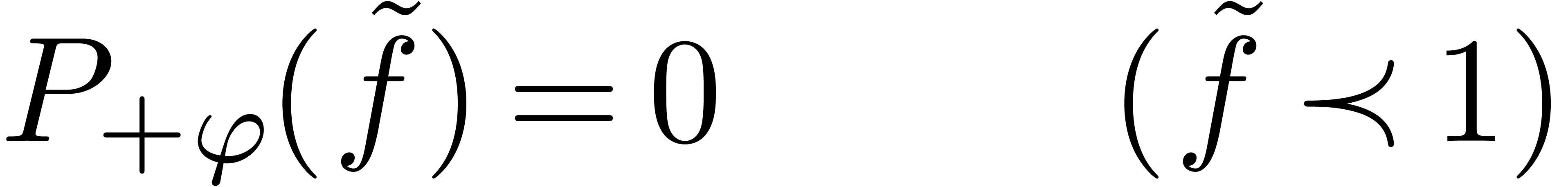 |
(29) |
is a privileged refinement of (27). Then either the Newton
degree of (29) is strictly less than 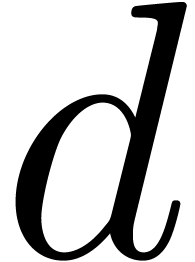 , or the longest chain of refinements of (29)
of Newton degree
, or the longest chain of refinements of (29)
of Newton degree 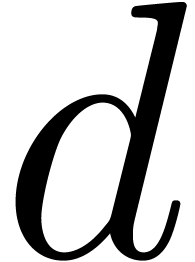 is strictly less than
is strictly less than 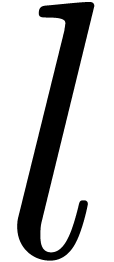 . We conclude by the induction
hypothesis.
. We conclude by the induction
hypothesis.
Case 2c. Since 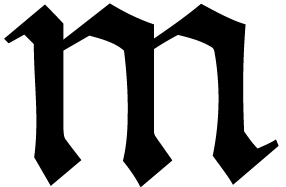 is the largest classical
dominant monomial relative to (27), the degree of the
Newton polynomial associated to any monomial between
is the largest classical
dominant monomial relative to (27), the degree of the
Newton polynomial associated to any monomial between 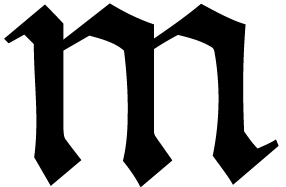 and
and  must be
must be 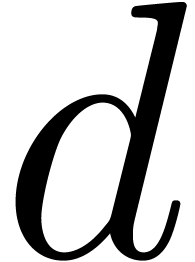 .
Consequently,
.
Consequently,
 |
(30) |
By the induction hypothesis, there exists a monomial  with
with  and
and
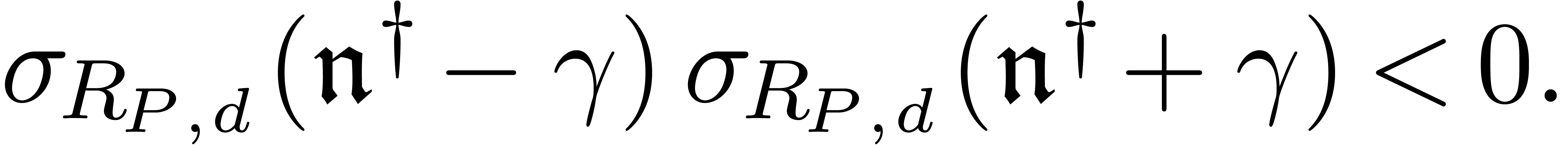 |
(31) |
In other words,  is a dominant monomial, such
that
is a dominant monomial, such
that  and
and
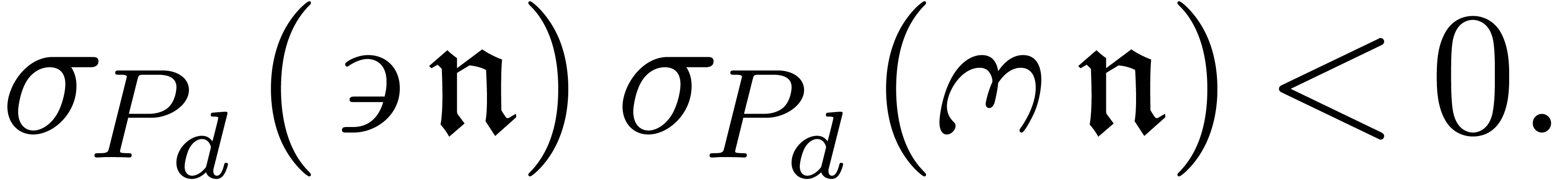 |
(32) |
We conclude by the same argument as in case 2b, where we let  play the role of
play the role of 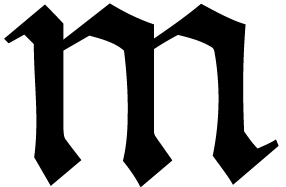 .
.
Case 2d. Since  is the largest classical
dominant monomial relative to (27), the degree of the
Newton polynomial associated to any monomial between
is the largest classical
dominant monomial relative to (27), the degree of the
Newton polynomial associated to any monomial between 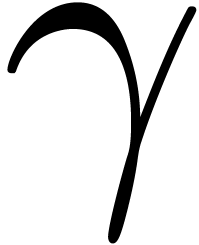 and
and  must be
must be  .
Consequently,
.
Consequently,
 |
(33) |
By the induction hypothesis, there exists a monomial  with
with  and
and
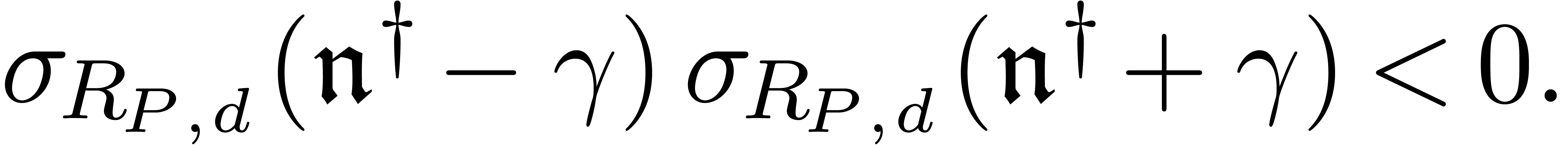 |
(34) |
In other words,  is a dominant monomial, such
that
is a dominant monomial, such
that  and
and
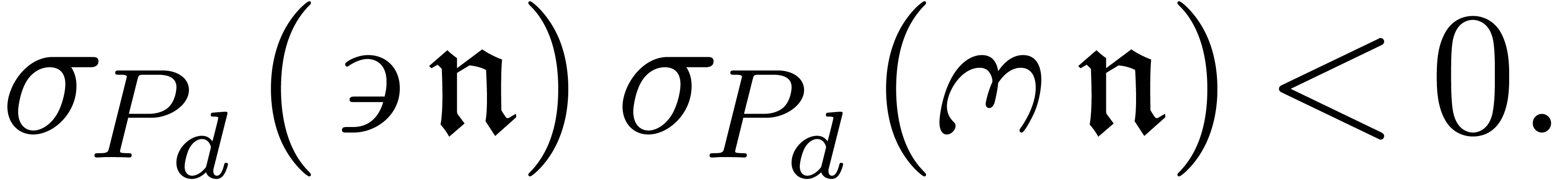 |
(35) |
We again conclude by the same argument as in case 2b.
Corollary 15. Any differential
polynomial of odd degree and with coefficients in  admits a root in
admits a root in  .
.
Proof. Let  be a polynomial of
odd degree with coefficients in
be a polynomial of
odd degree with coefficients in  .
Then formula (7) shows that for sufficiently large
.
Then formula (7) shows that for sufficiently large 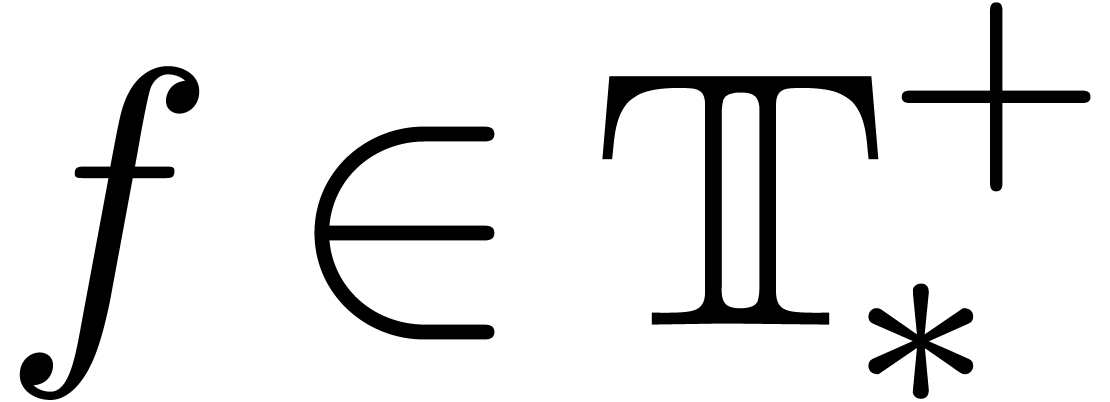 we have
we have 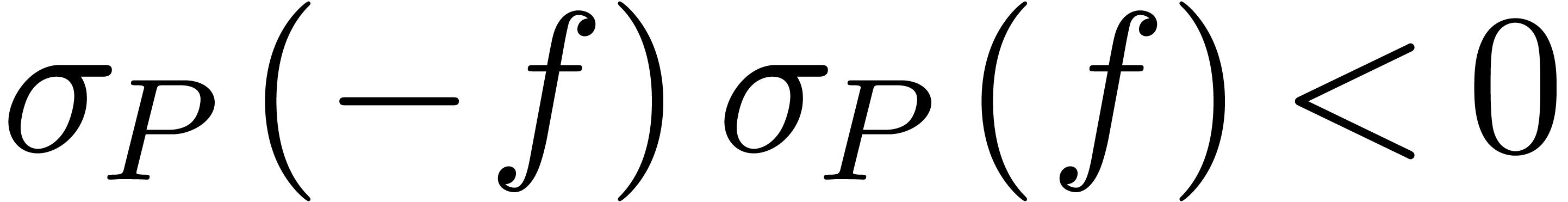 ,
since
,
since 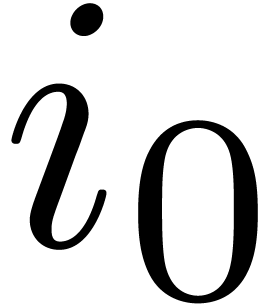 is odd in this formula. We now apply the
intermediate value theorem between
is odd in this formula. We now apply the
intermediate value theorem between 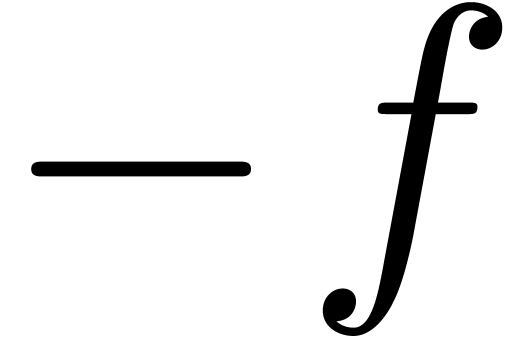 and
and 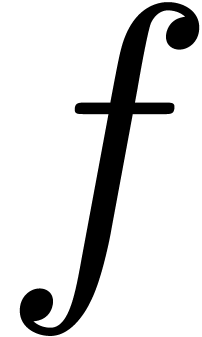 .
.
Bibliography
-
[vdH97]
-
J. van der Hoeven. Automatic asymptotics. PhD
thesis, École polytechnique, France, 1997.
 be the field of grid-based
transseries or the field of transseries with finite logarithmic
depths. In our PhD. we announced that given a differential polynomial
be the field of grid-based
transseries or the field of transseries with finite logarithmic
depths. In our PhD. we announced that given a differential polynomial
 with coefficients in
with coefficients in  and transseries
and transseries  with
with 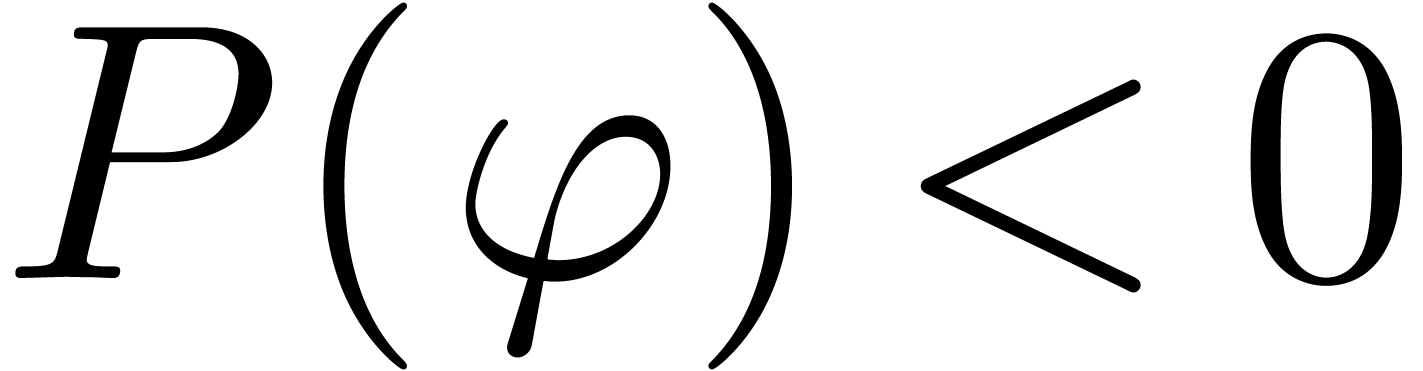 and
and 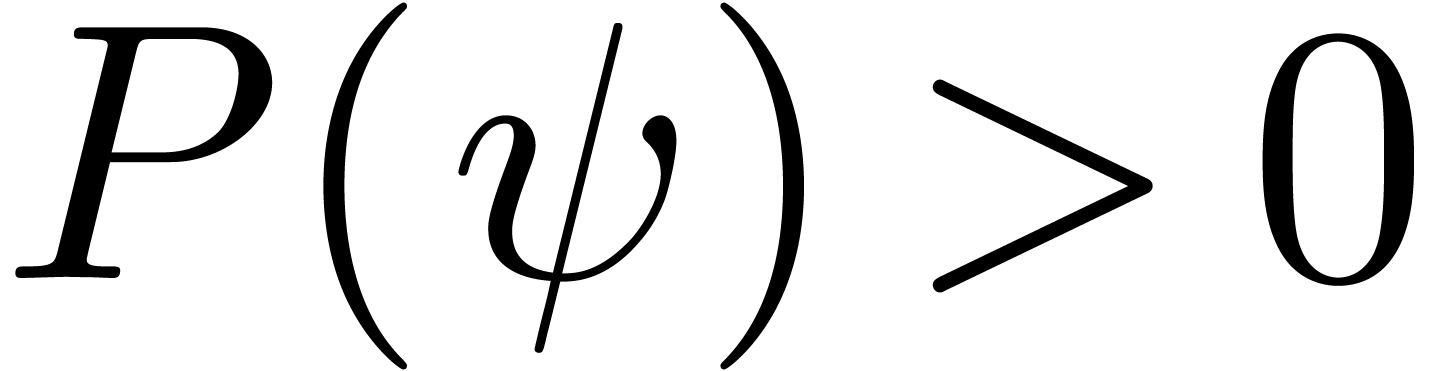 , there exists an
, there exists an  , such that
, such that 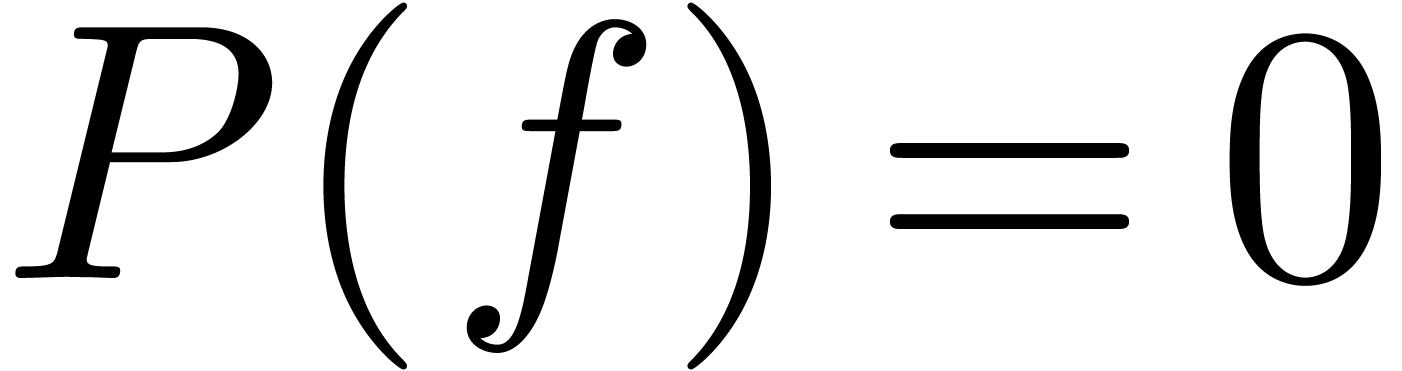 . In this note, we will prove this
theorem.
. In this note, we will prove this
theorem.
 be a totally ordered exp-log field. In
chapter 2 of [
be a totally ordered exp-log field. In
chapter 2 of [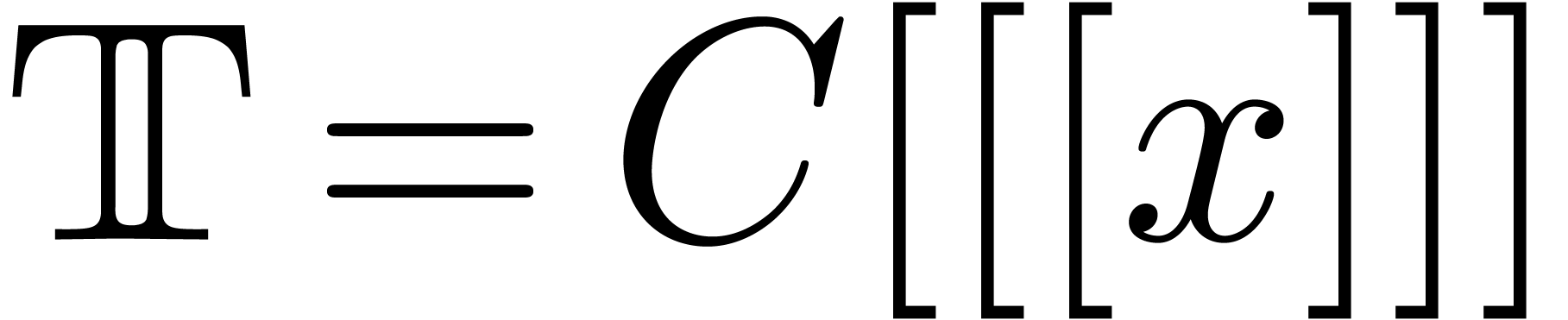 of transseries in
of transseries in  of finite
logarithmic and exponential depths. In chapter 5, we then gave an (at
least theoretical) algorithm to solve algebraic differential equations
with coefficients in
of finite
logarithmic and exponential depths. In chapter 5, we then gave an (at
least theoretical) algorithm to solve algebraic differential equations
with coefficients in  .
.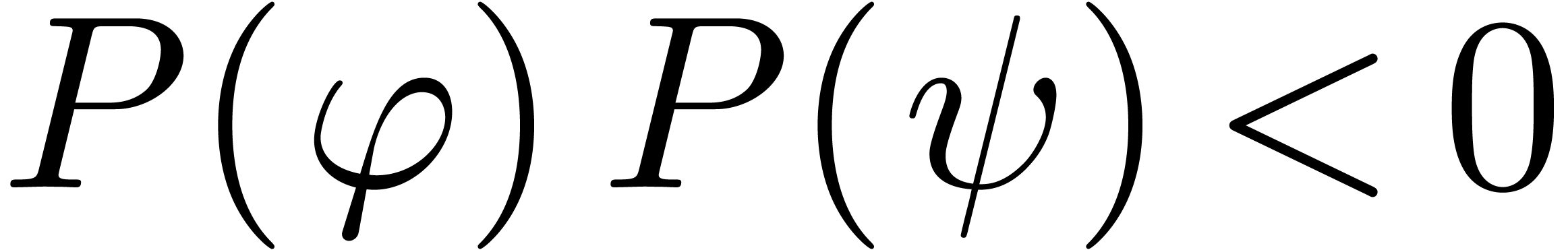 ,
,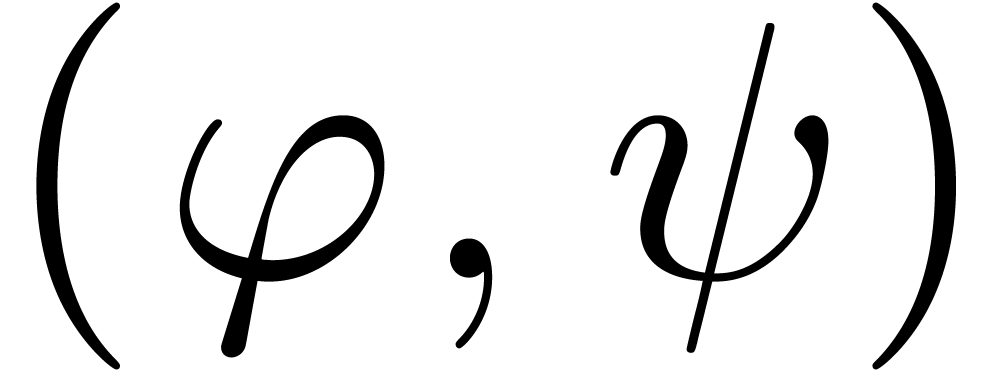 stands for the open interval
between
stands for the open interval
between  and
and  .
. transseries in
transseries in 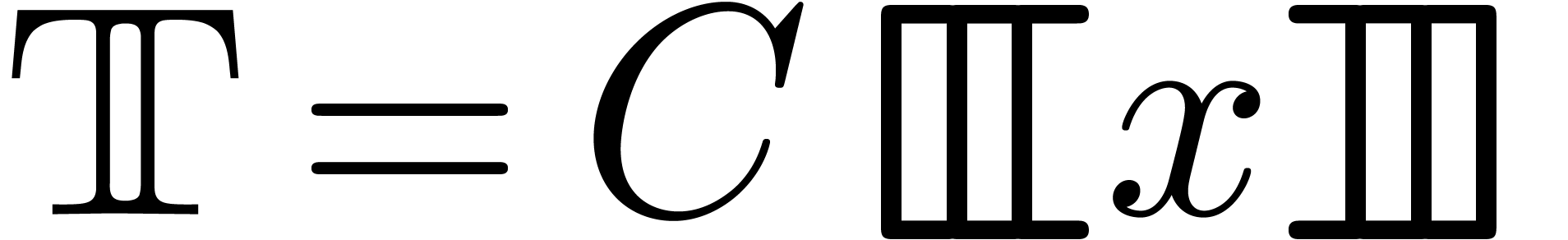 .
.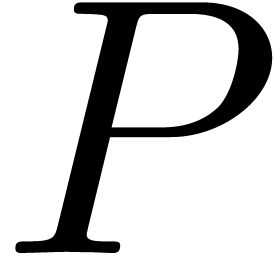 is a differential polynomial with
coefficients in
is a differential polynomial with
coefficients in  ,
,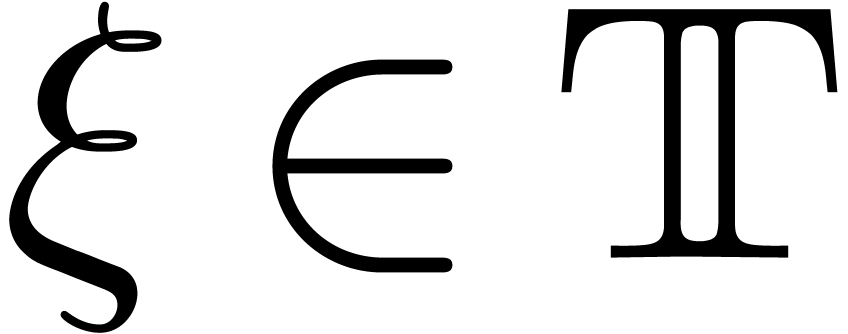 ;
; ,
, ,
, is a transmonomial.
is a transmonomial.
 ,
, ,
, .
. and
and  respectively
designate the infinitely small and large constants
respectively
designate the infinitely small and large constants 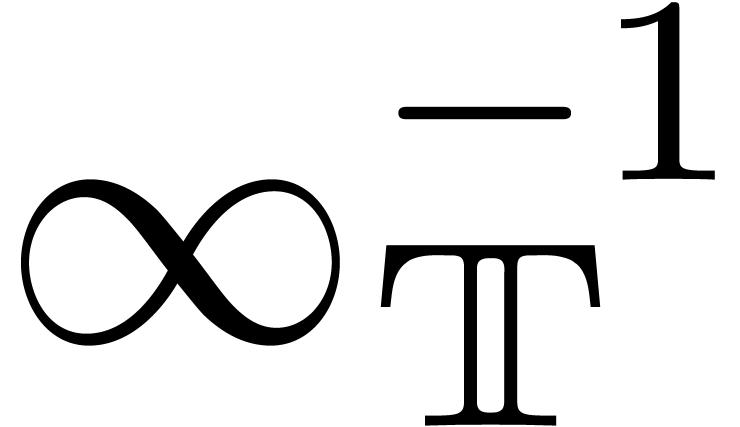 and
and  in the compactification of
in the compactification of 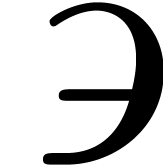 and
and 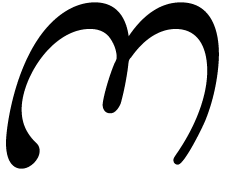 designate the infinitely small and large constants
designate the infinitely small and large constants
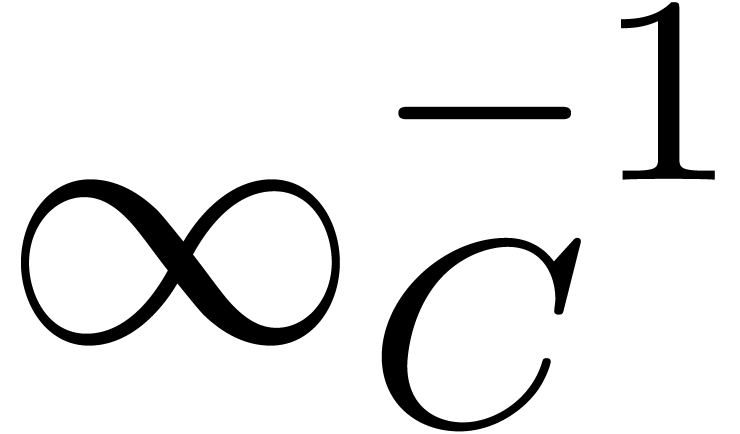 and
and  in the
compactification of
in the
compactification of  .
.
 ,
, ,
, ,
, whenever
whenever  ,
, ,
, .
. may be prolongated by
continuity into
may be prolongated by
continuity into  ,
, is constant on
is constant on 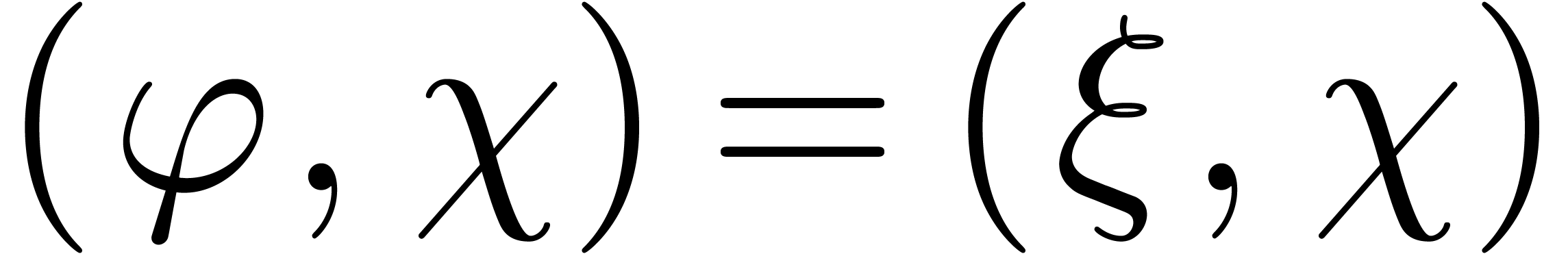 for some
for some 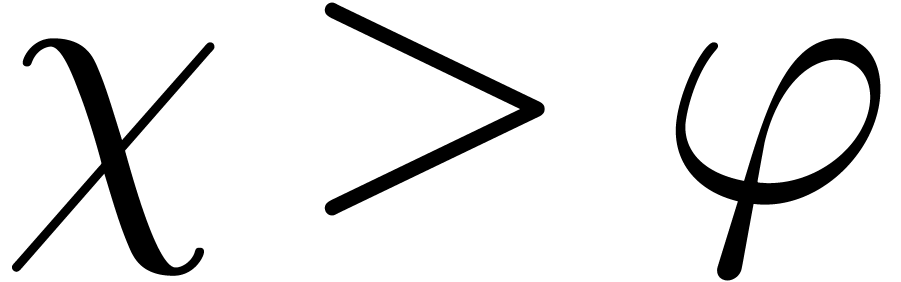 .
. ,
,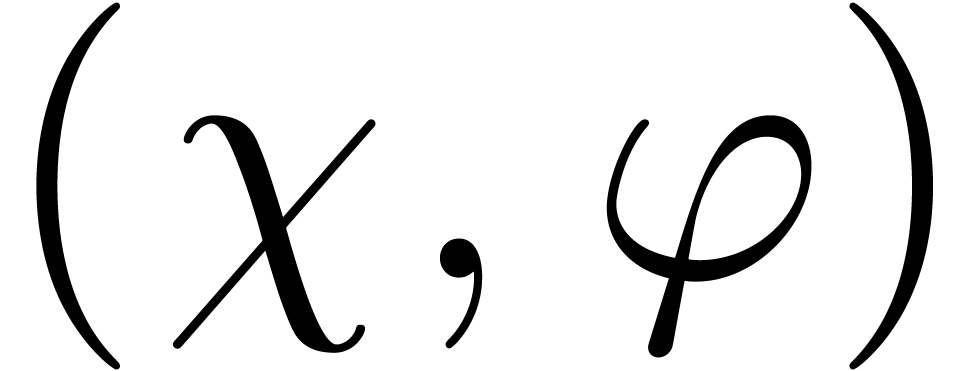 for some
for some 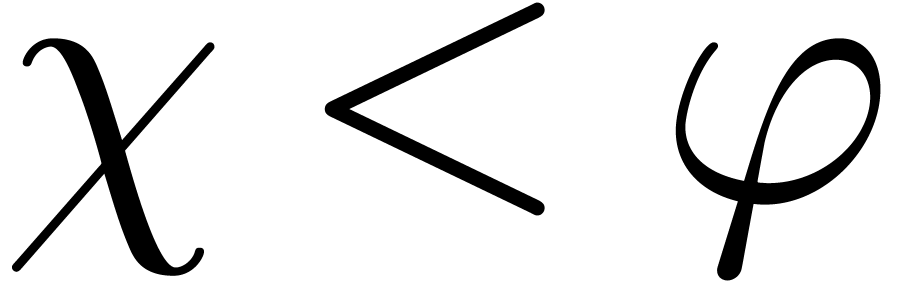 .
.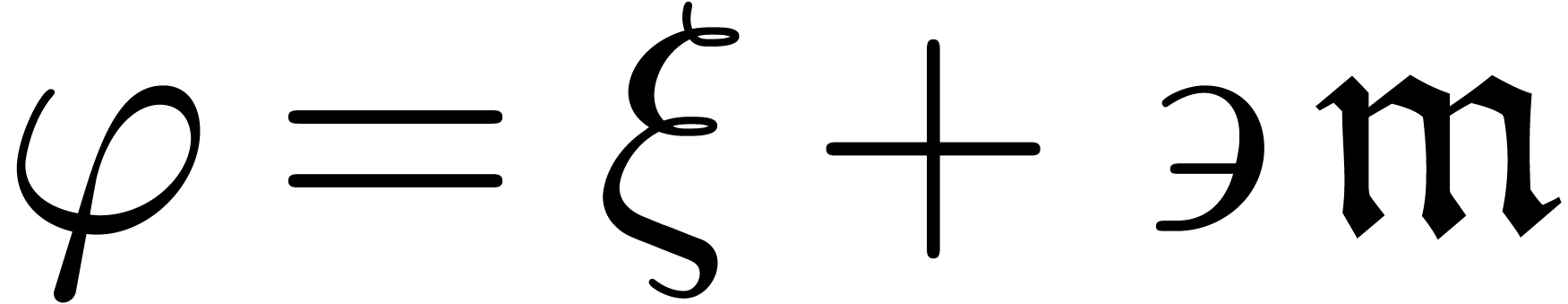 ,
,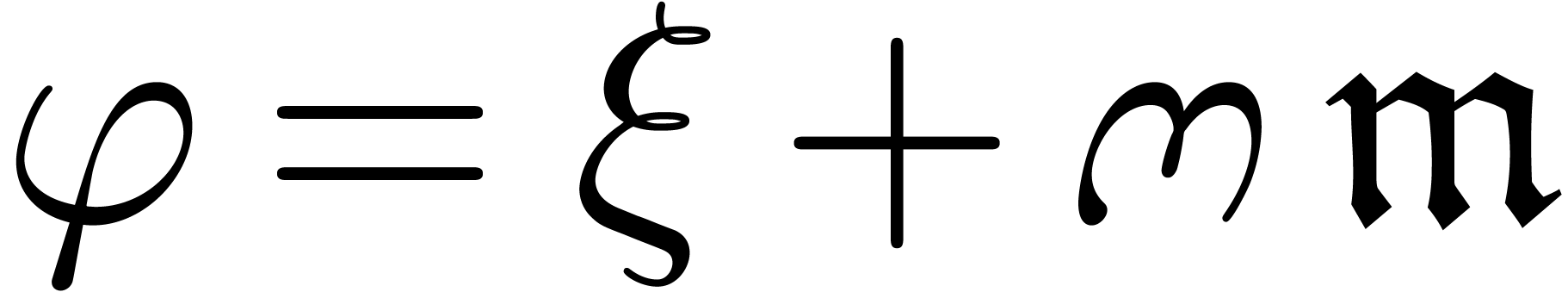 ,
,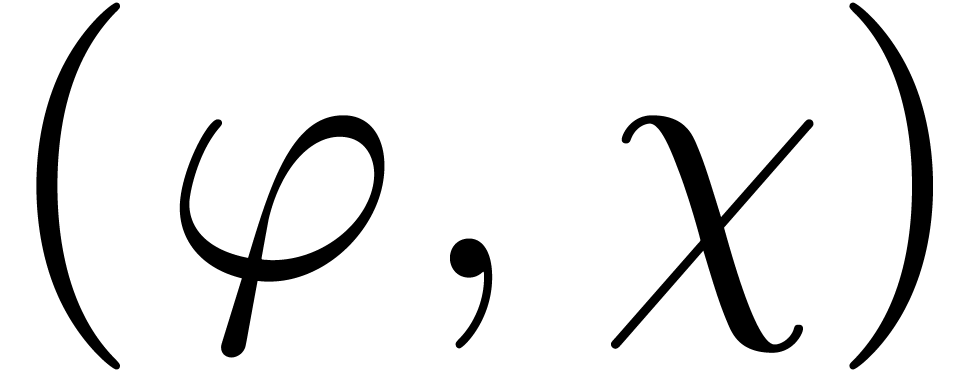 for some
for some  ,
, ,
,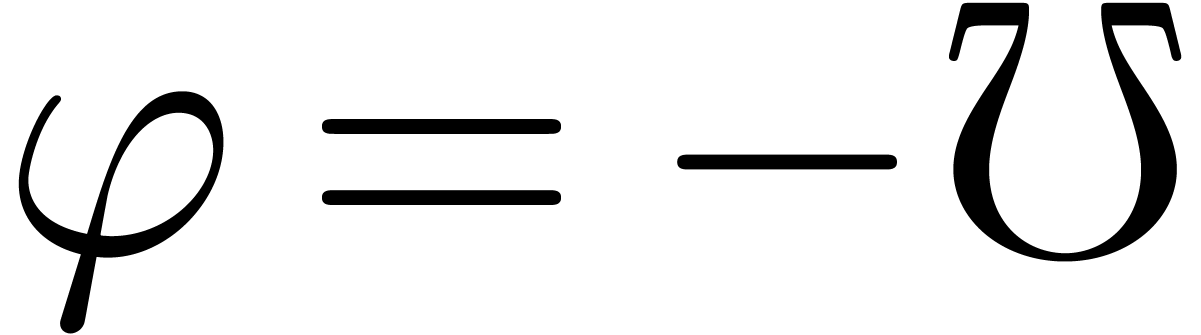 and so on, one has to interchange left and right
continuity in the above list.) Now we understand that
and so on, one has to interchange left and right
continuity in the above list.) Now we understand that 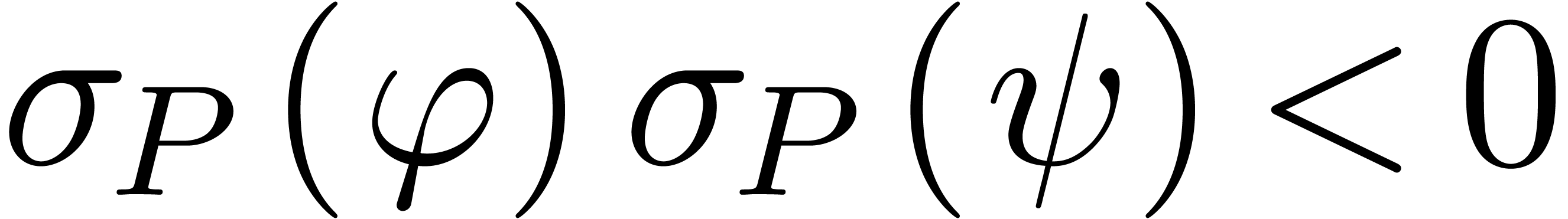 .
.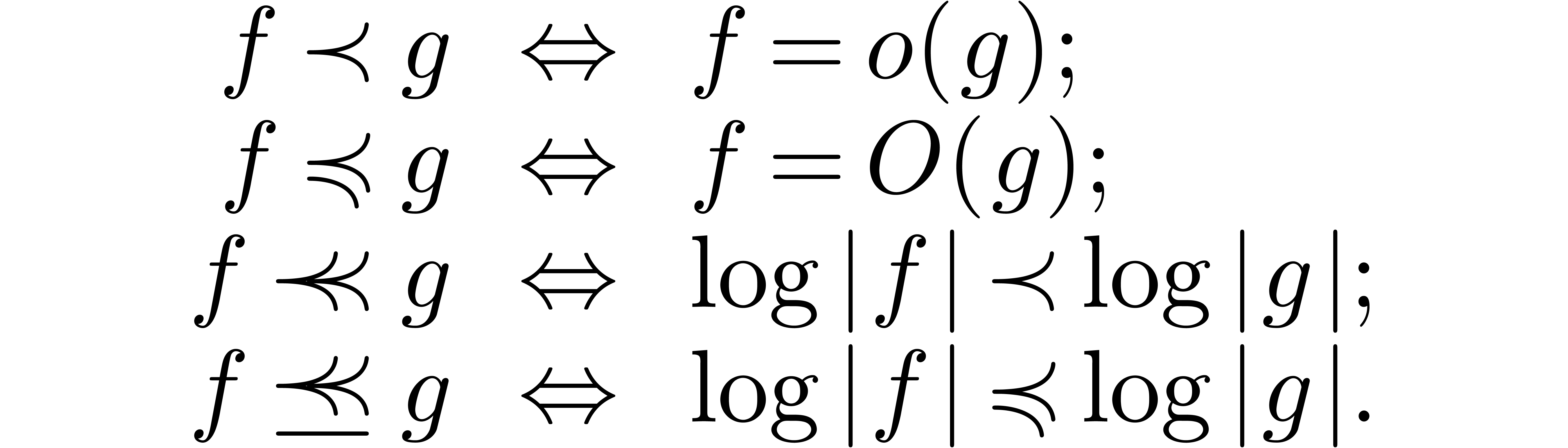
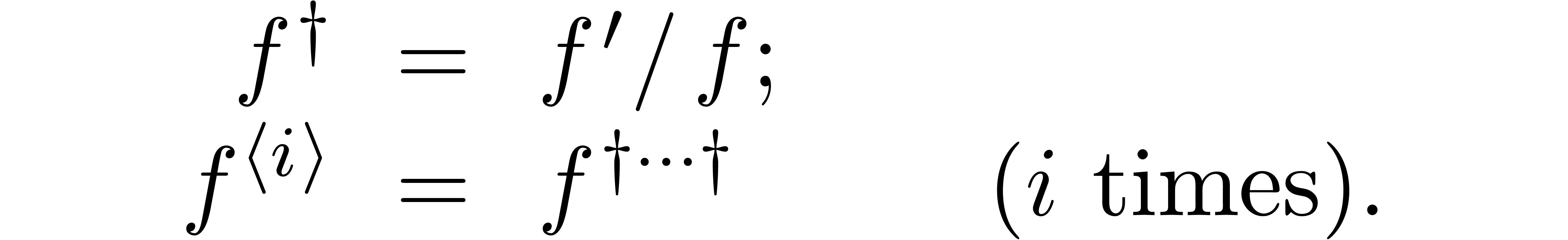
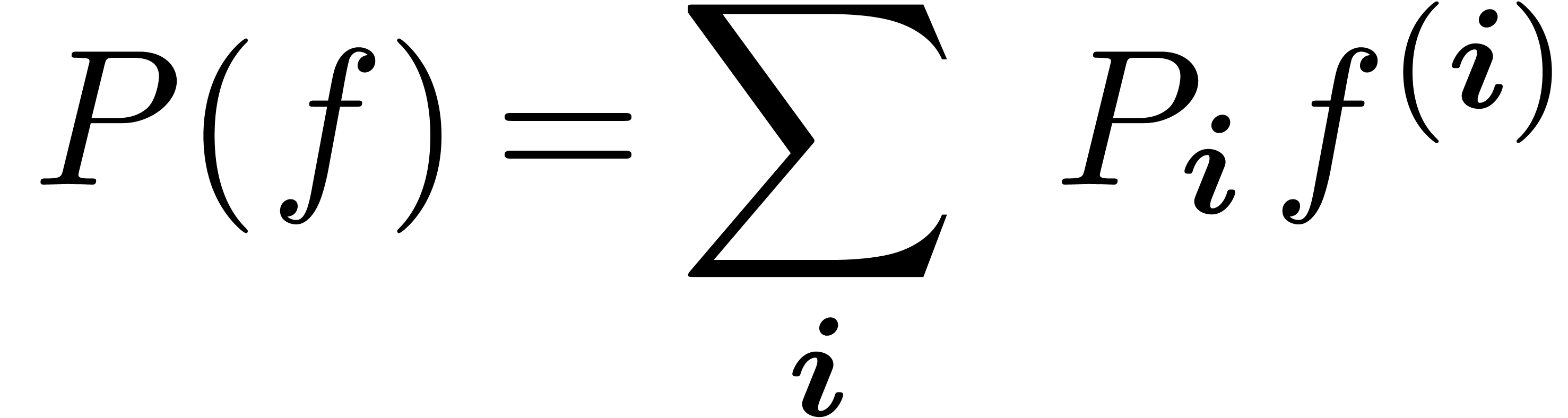
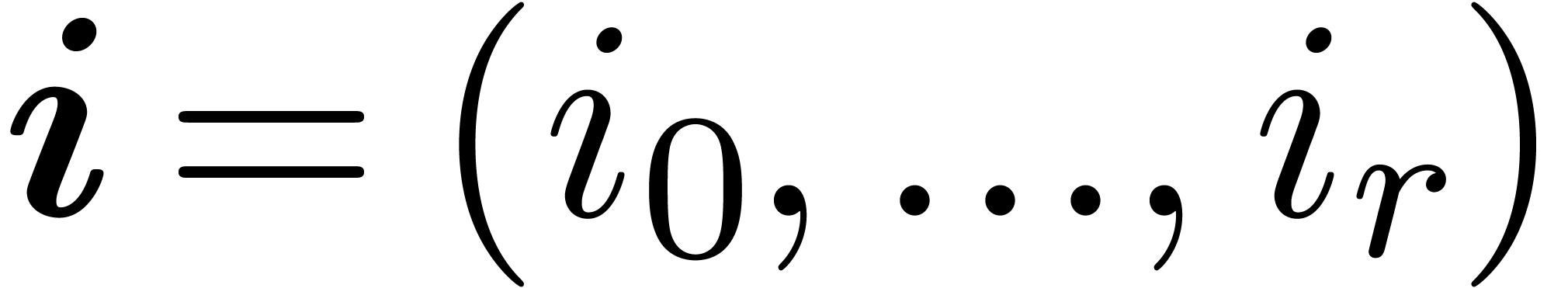 and
and 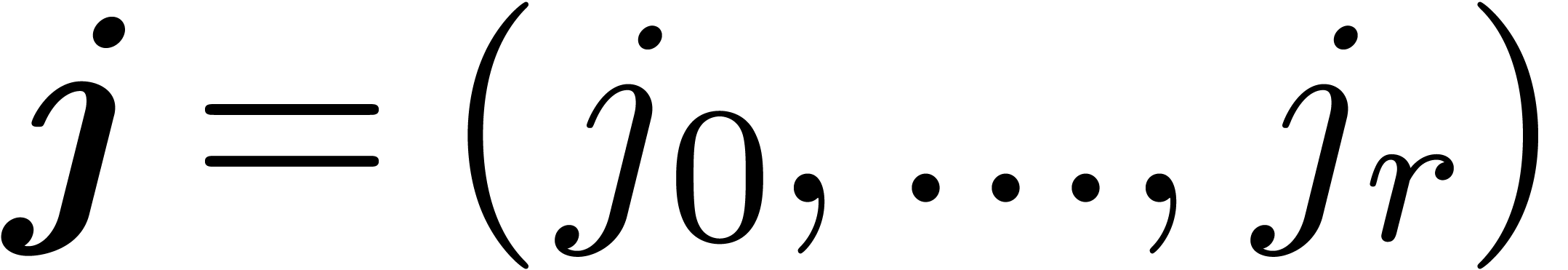 of integers:
of integers:
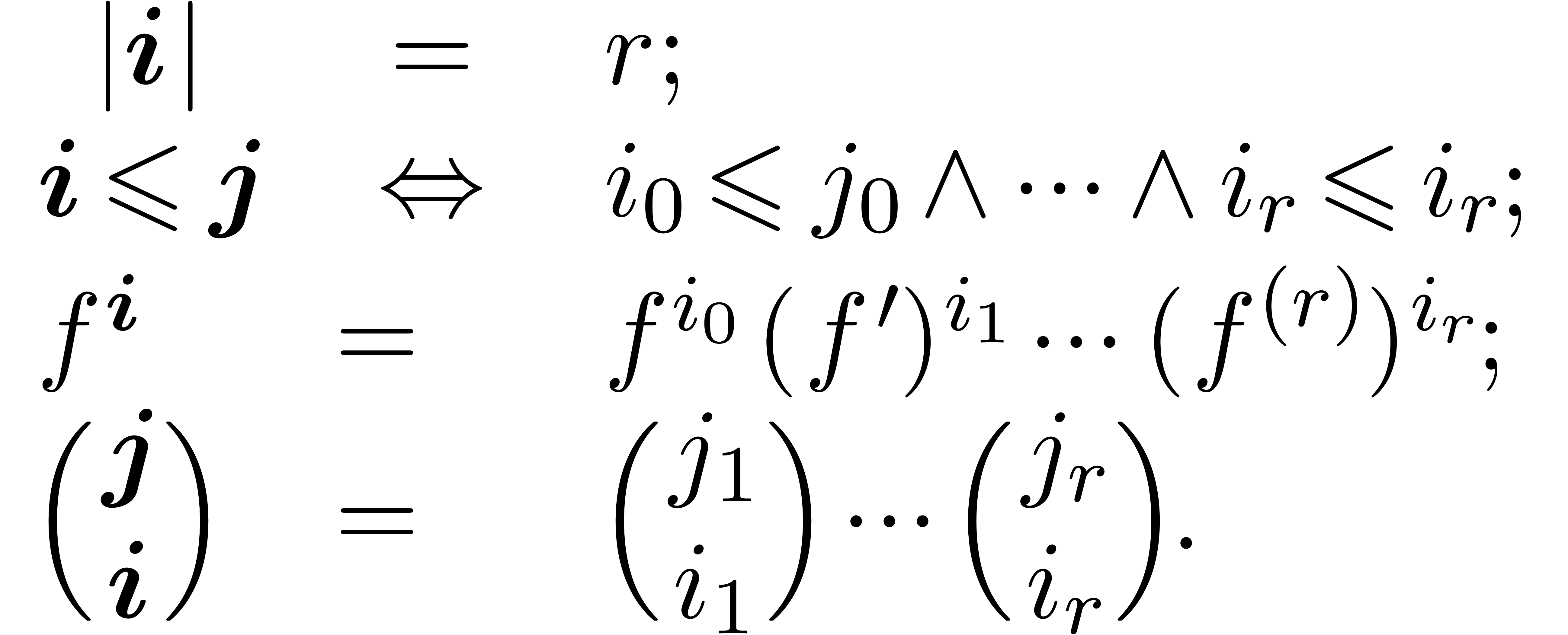
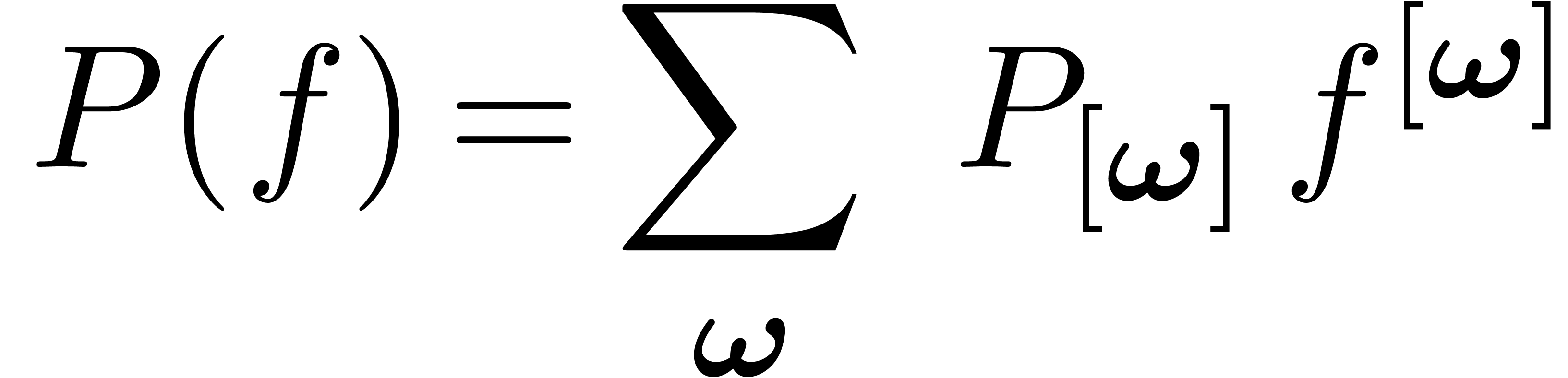
 runs through tuples
runs through tuples 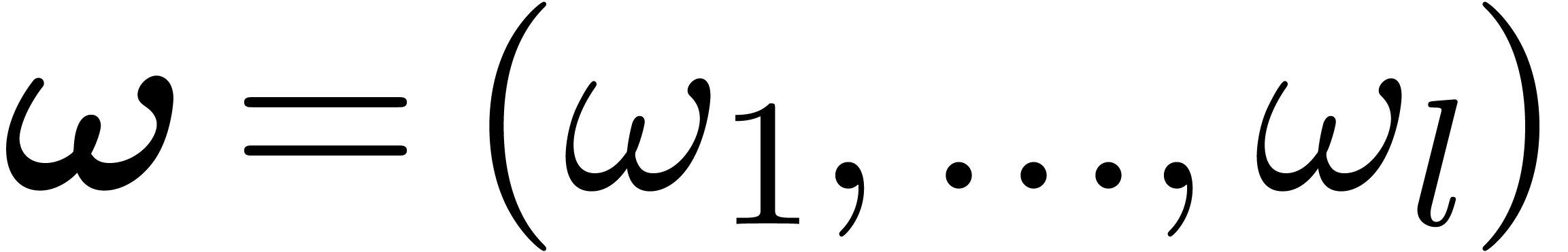 of integers in
of integers in  of length
of length 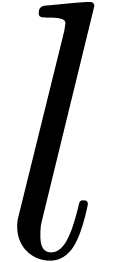 at most
at most  ,
, for all permutations of integers. We again use
vector notation for such tuples
for all permutations of integers. We again use
vector notation for such tuples
 ||
||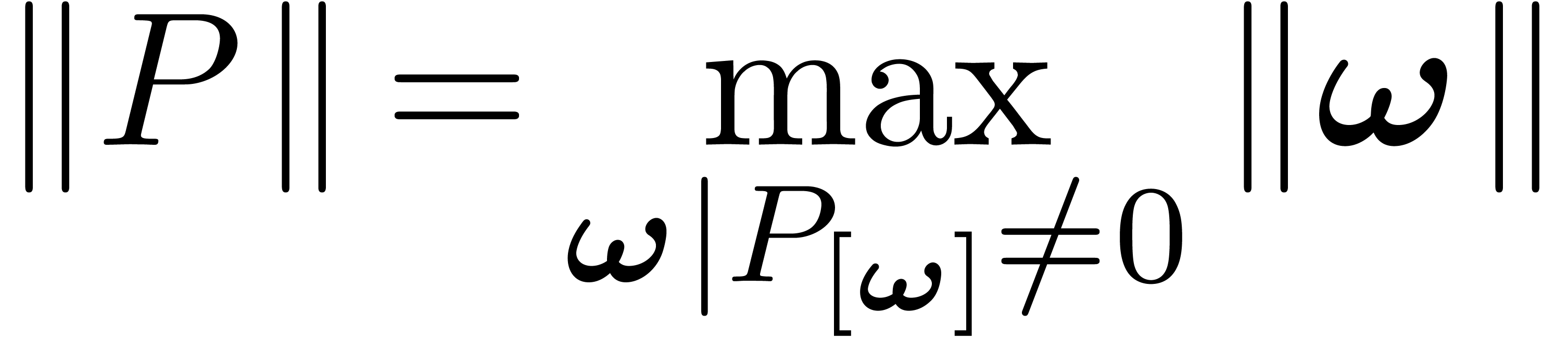
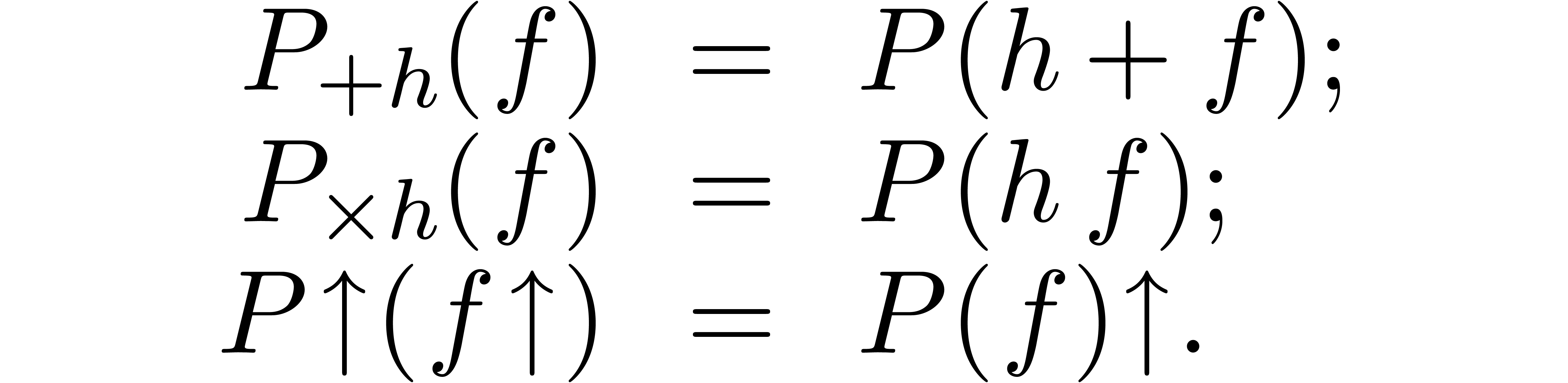
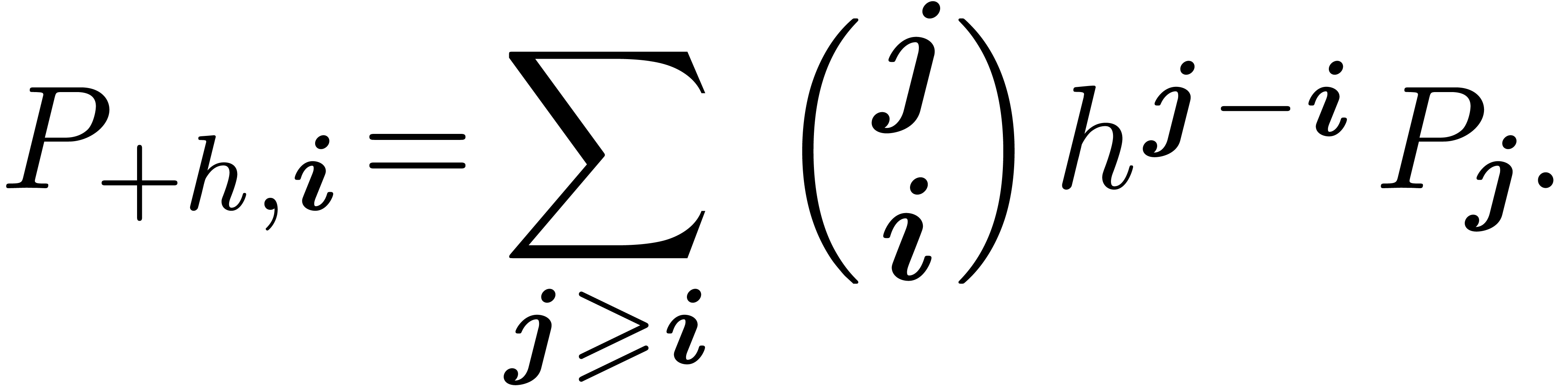
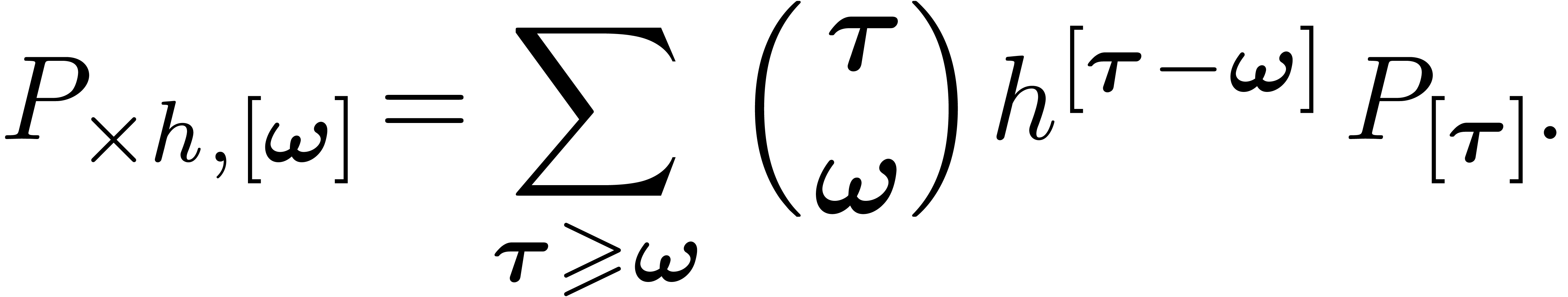
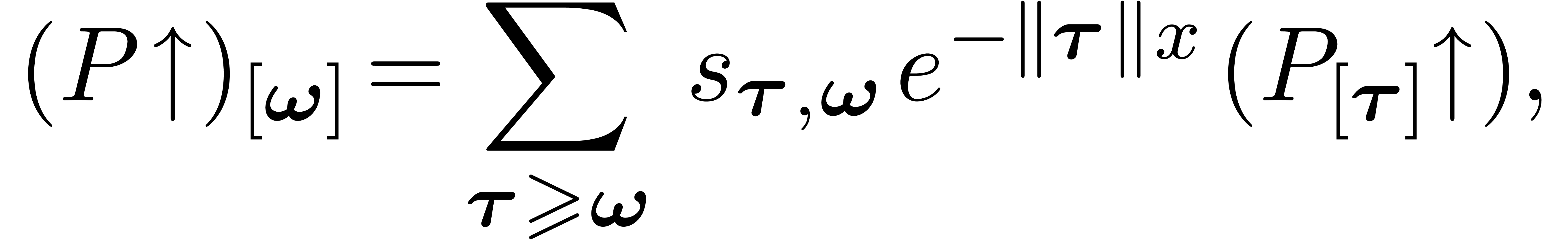
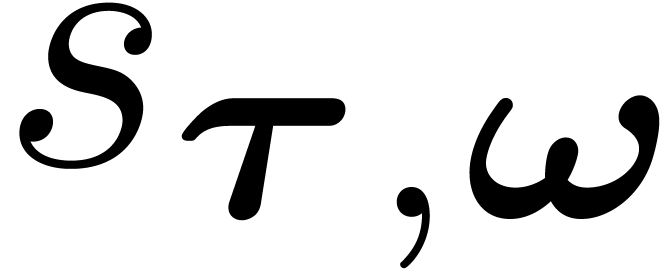 are generalized Stirling numbers of
the first kind:
are generalized Stirling numbers of
the first kind:
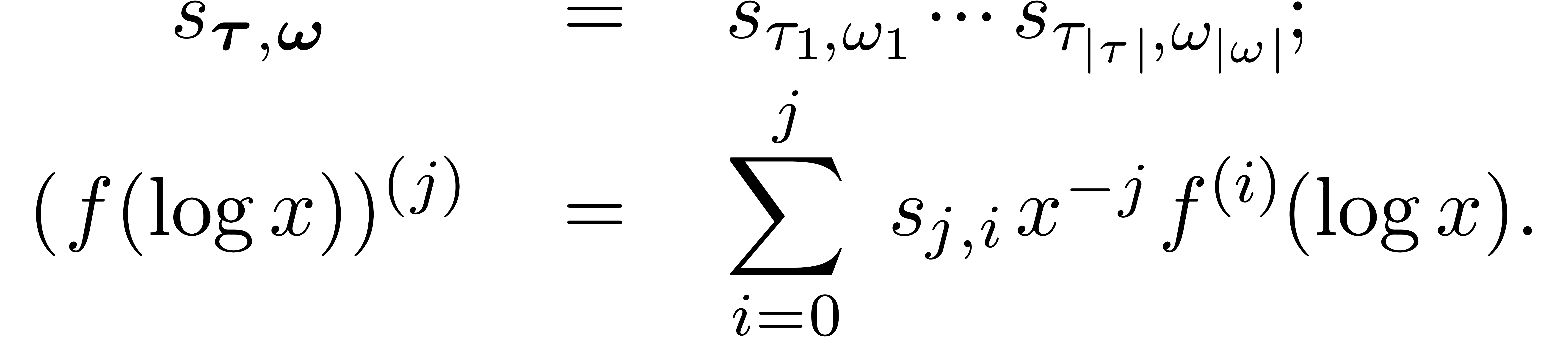
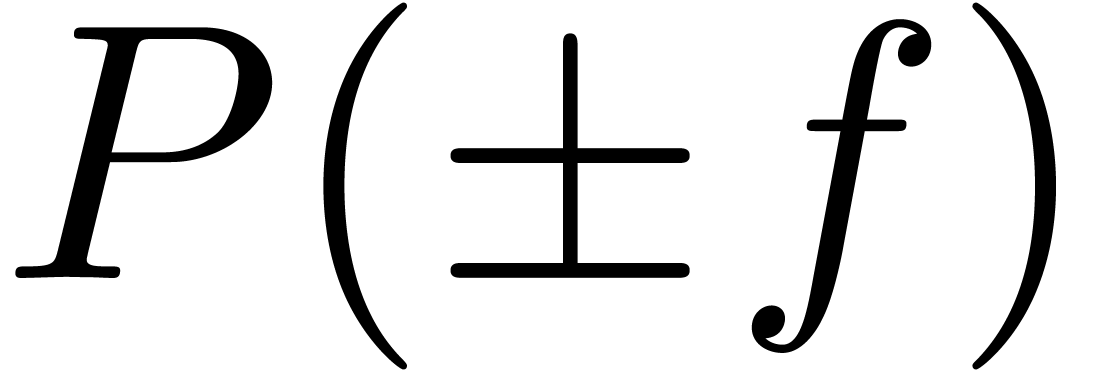 has constant sign for all sufficiently large
has constant sign for all sufficiently large 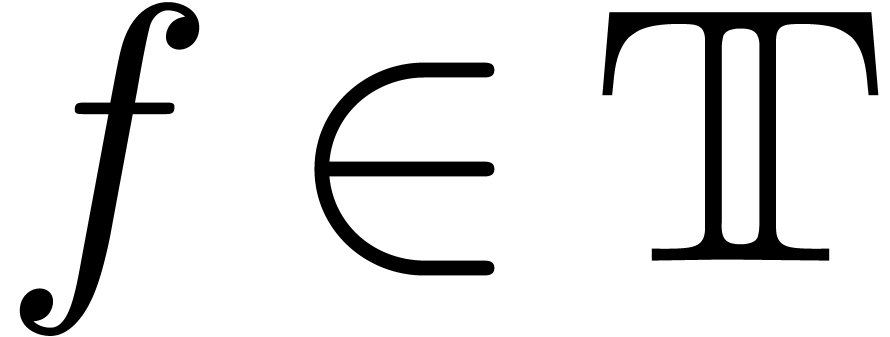 .
.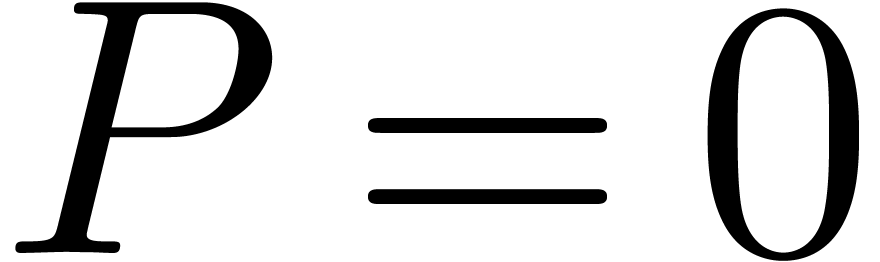 ,
,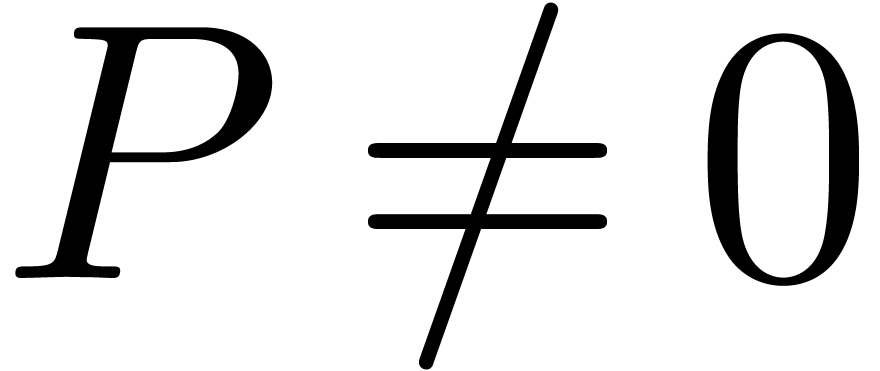 .
.
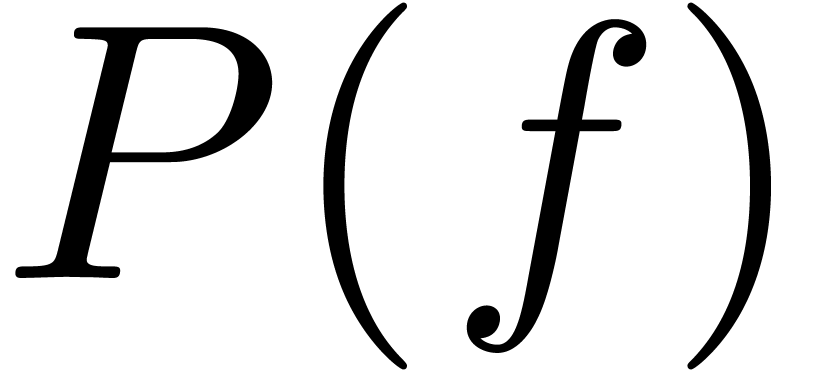 as an expression of the form
as an expression of the form
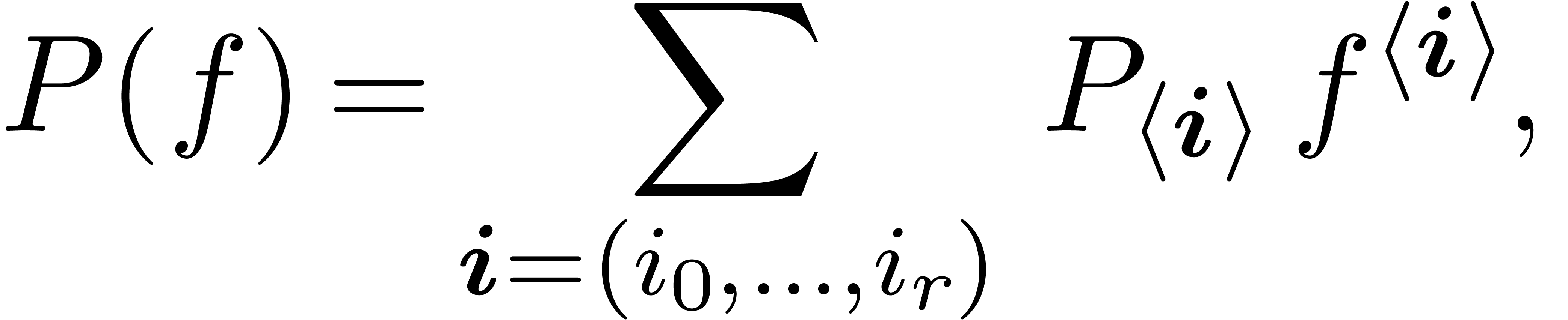
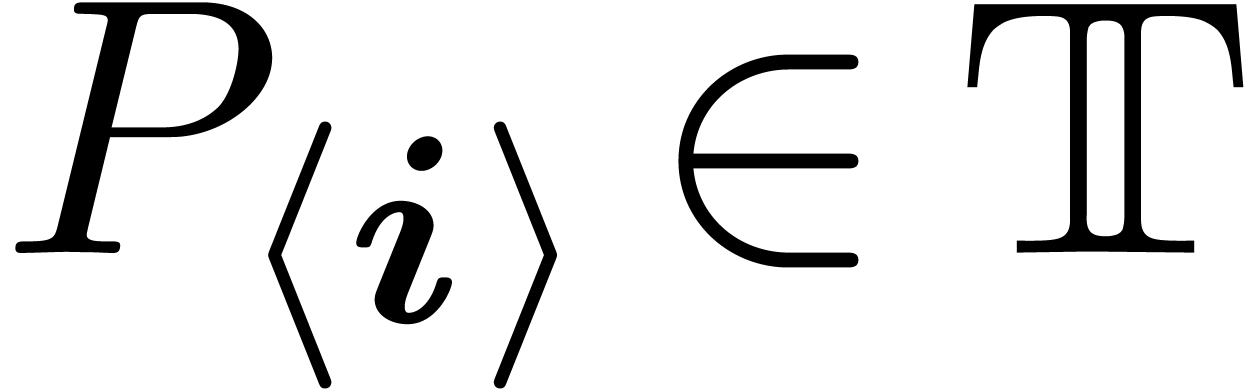 and
and 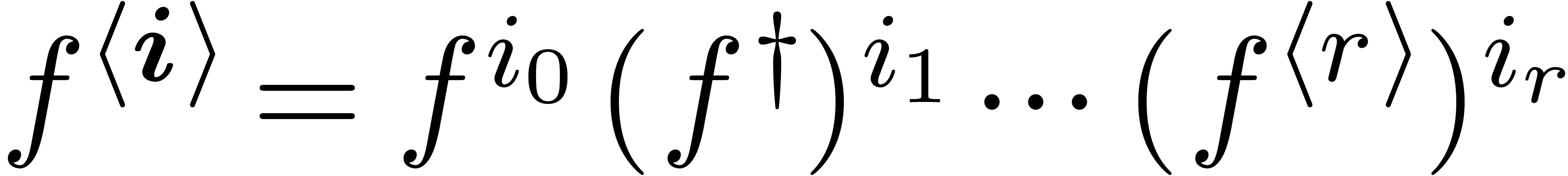 for each
for each 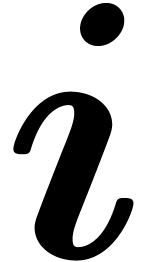 .
.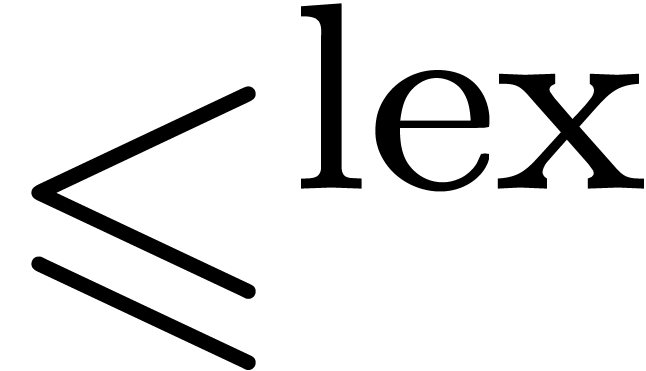 on
on 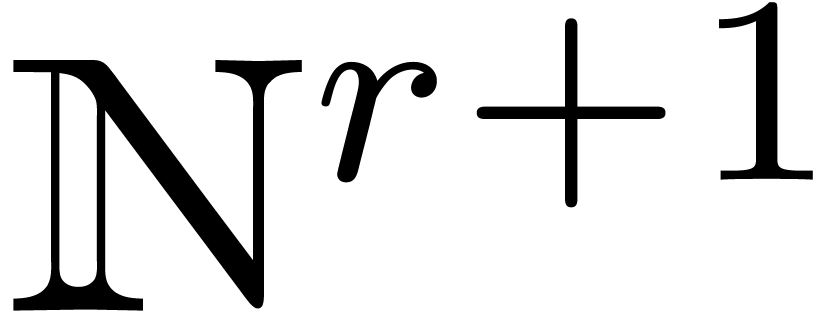 ,
,
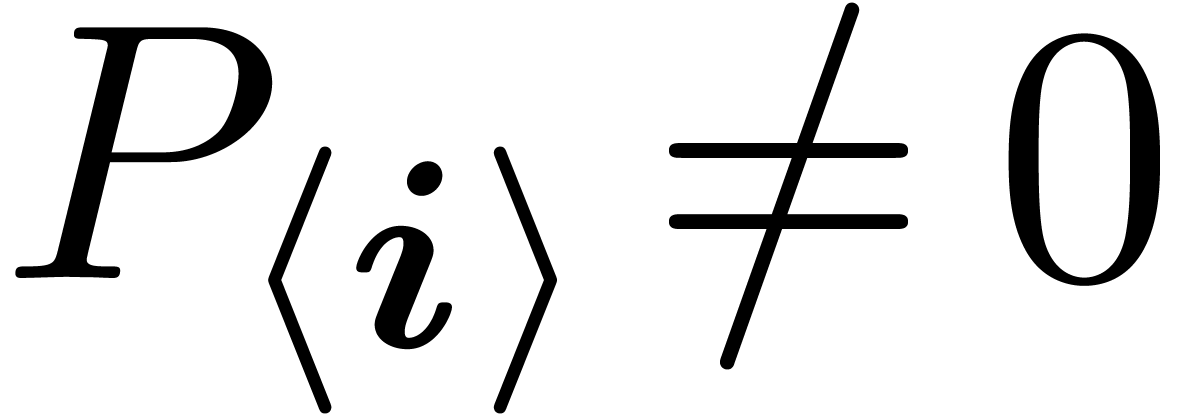 .
.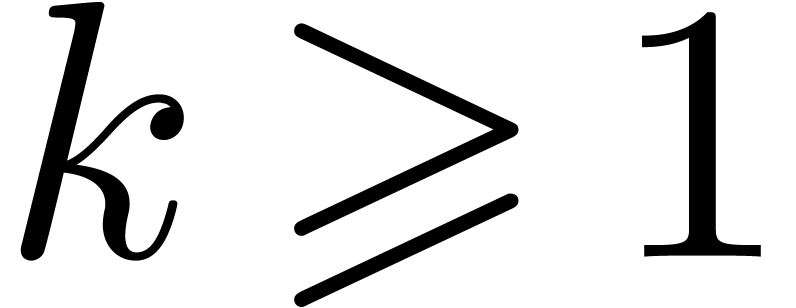 be
sufficiently large such that
be
sufficiently large such that  for all
for all  .
.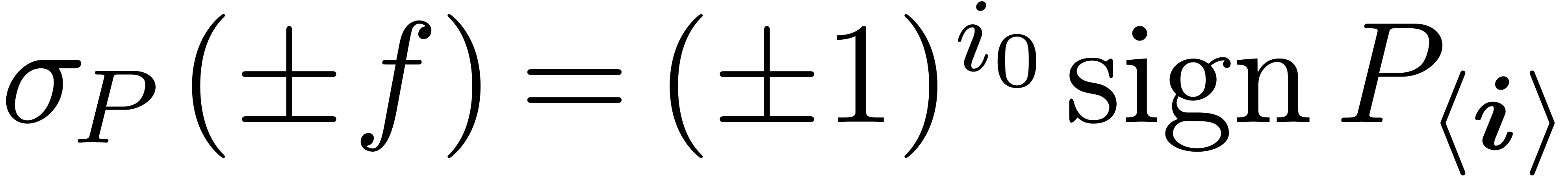
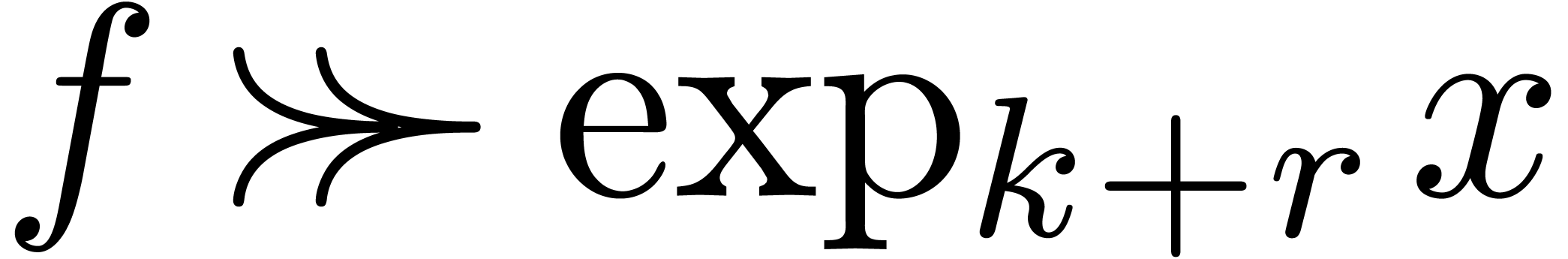 ,
, for all such
for all such  .
.
 has constant sign for all sufficiently small
has constant sign for all sufficiently small 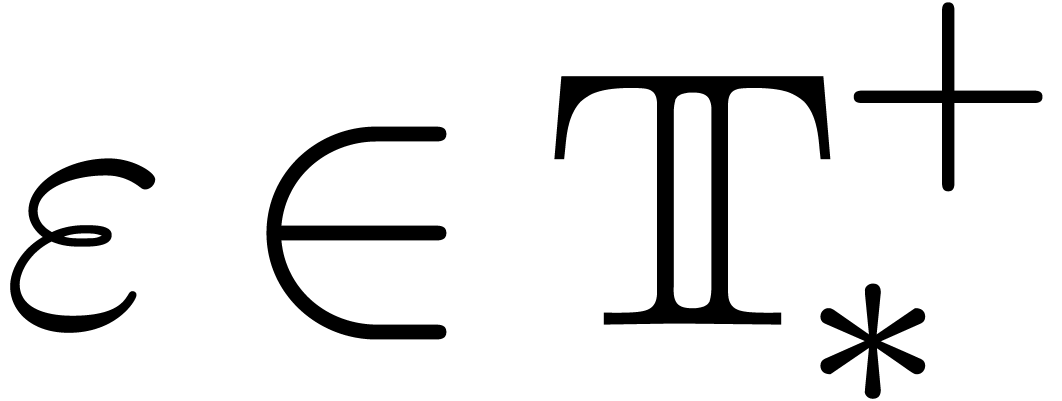 .
.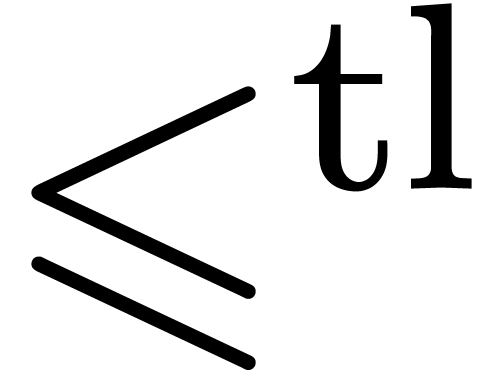 on
on 

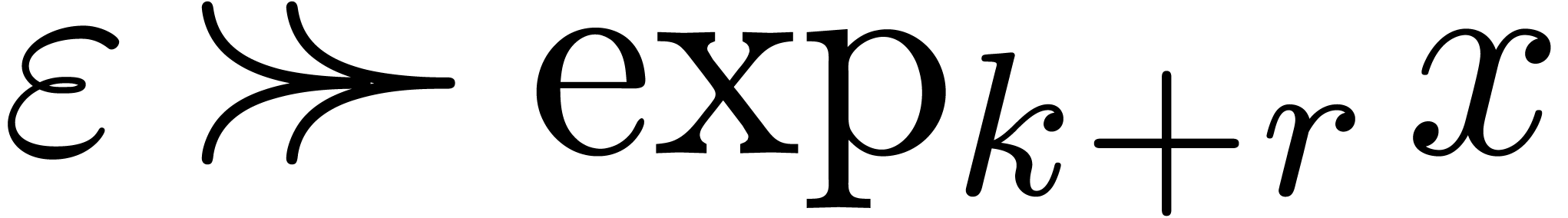 .
. the purely
exponential differential Newton polynomial associated to a monomial
the purely
exponential differential Newton polynomial associated to a monomial
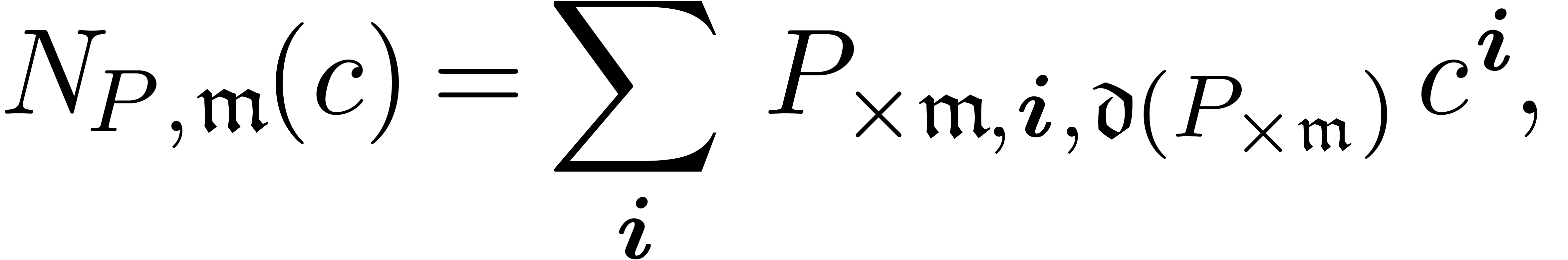
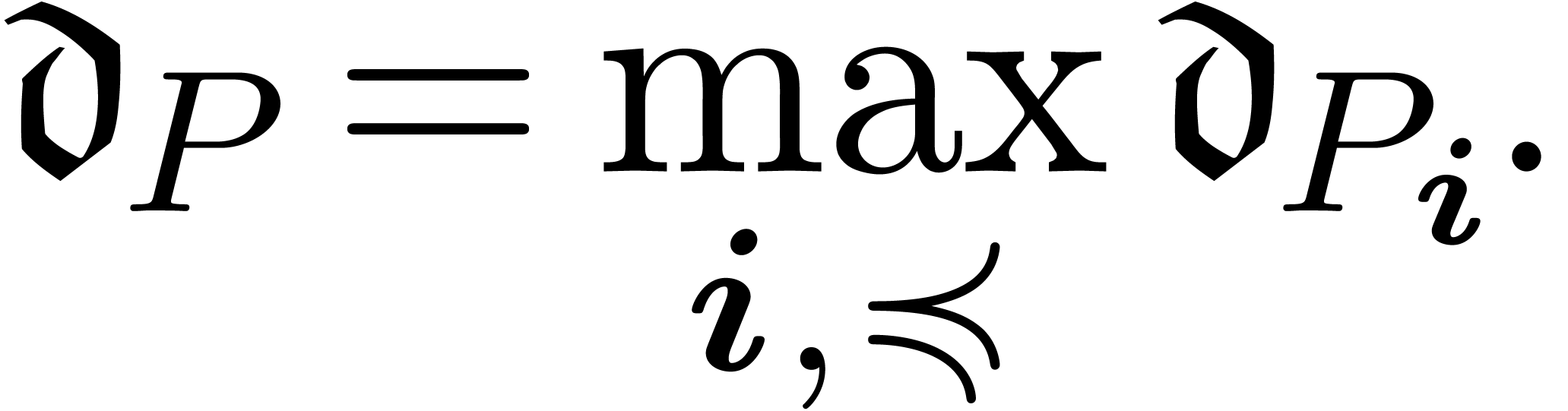
 looks like after
sufficiently many upward shiftings:
looks like after
sufficiently many upward shiftings:
 and
an integer
and
an integer  ,
,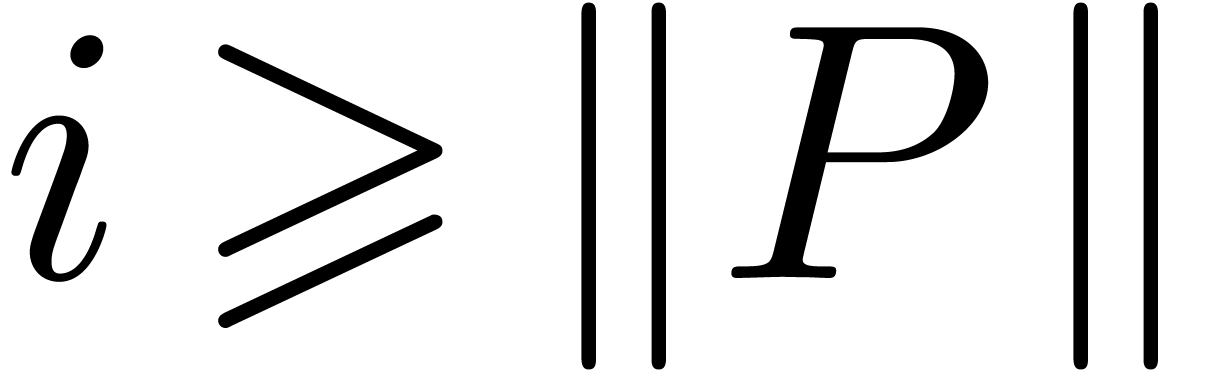 ,
,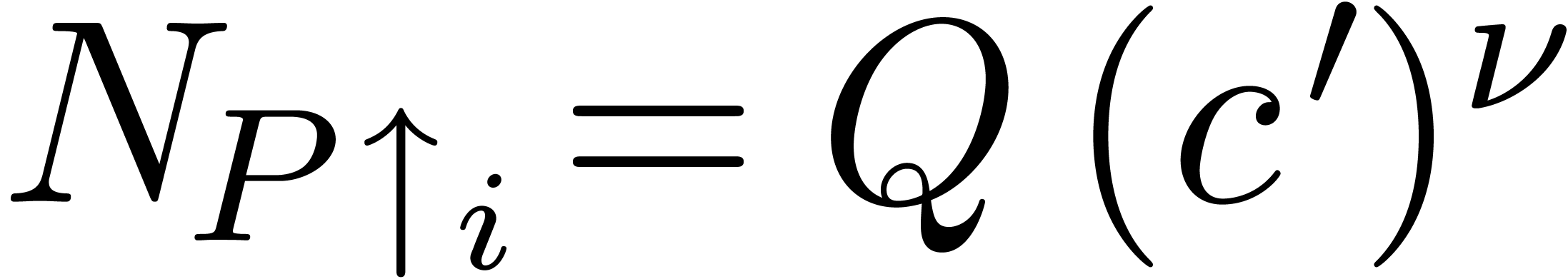 .
. with
with 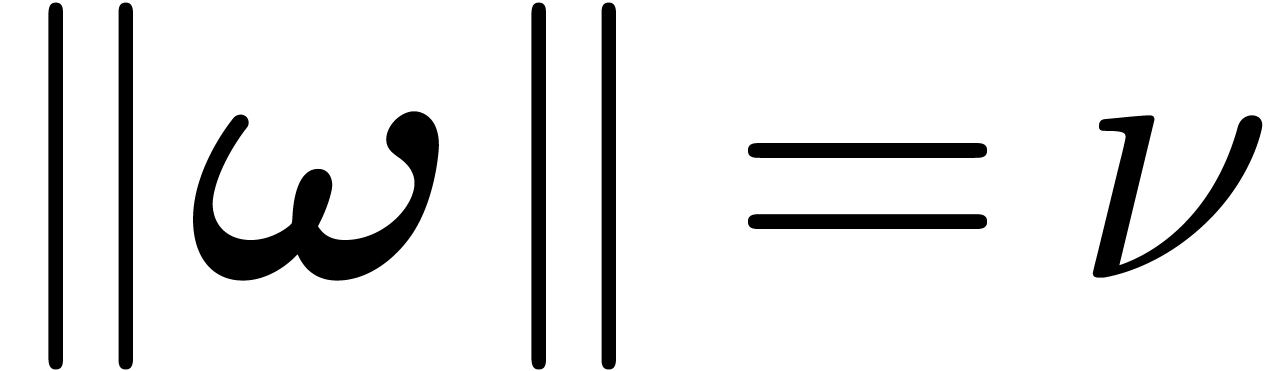 and
and 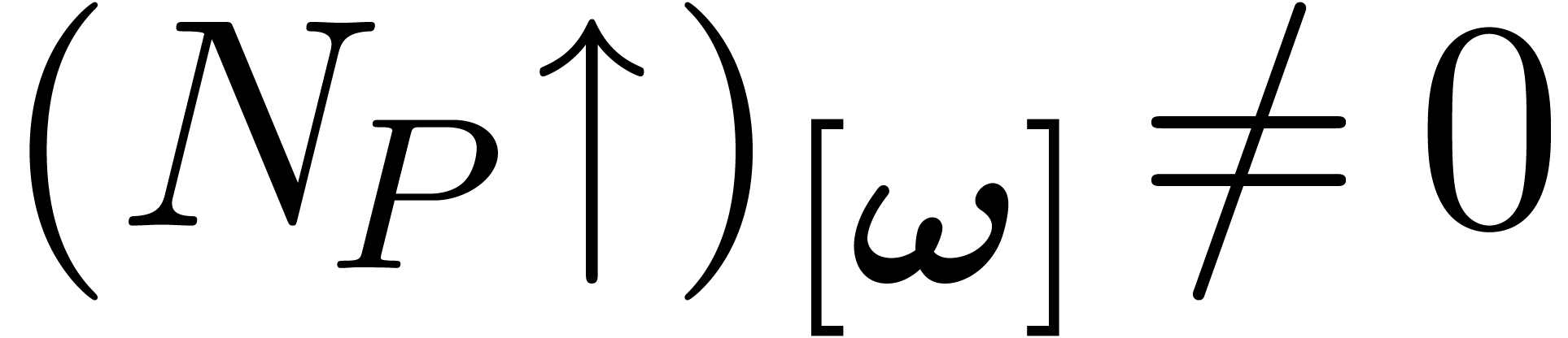 .
.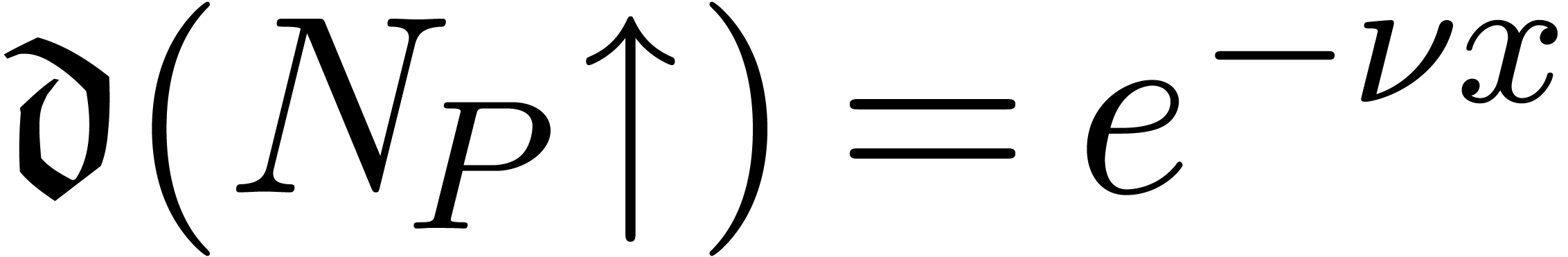 and
and
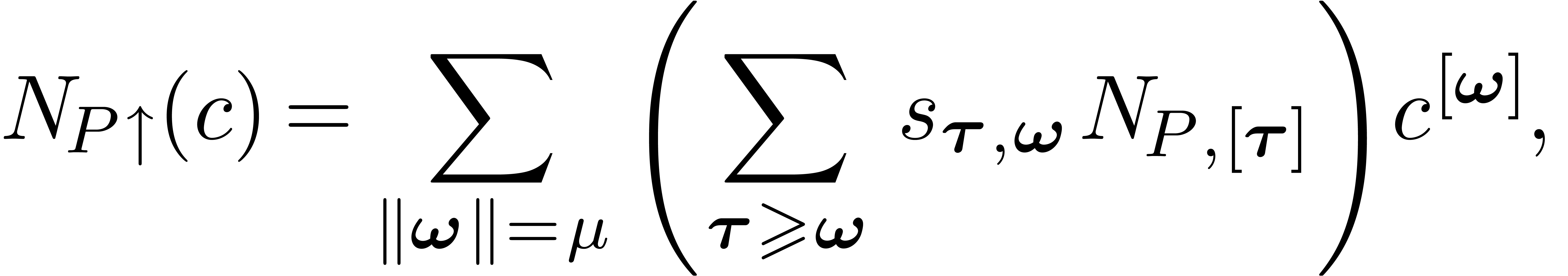
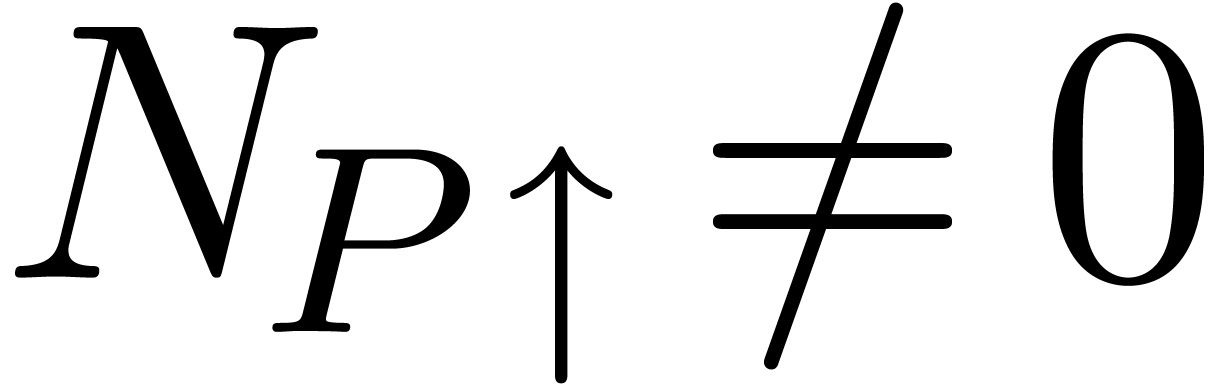 ,
,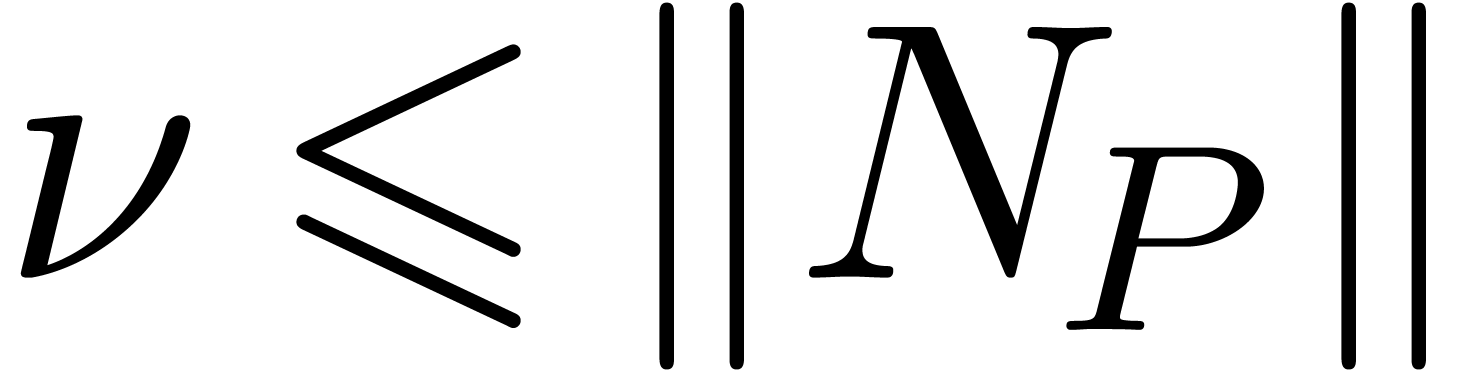 .
.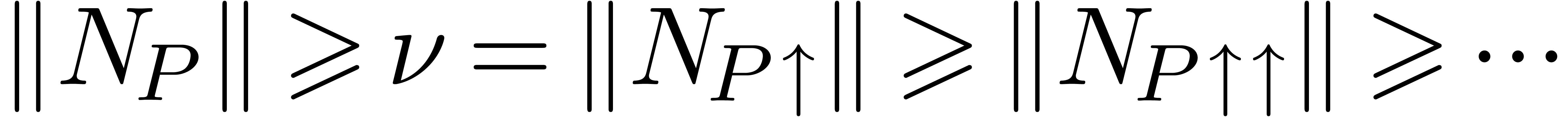 .
.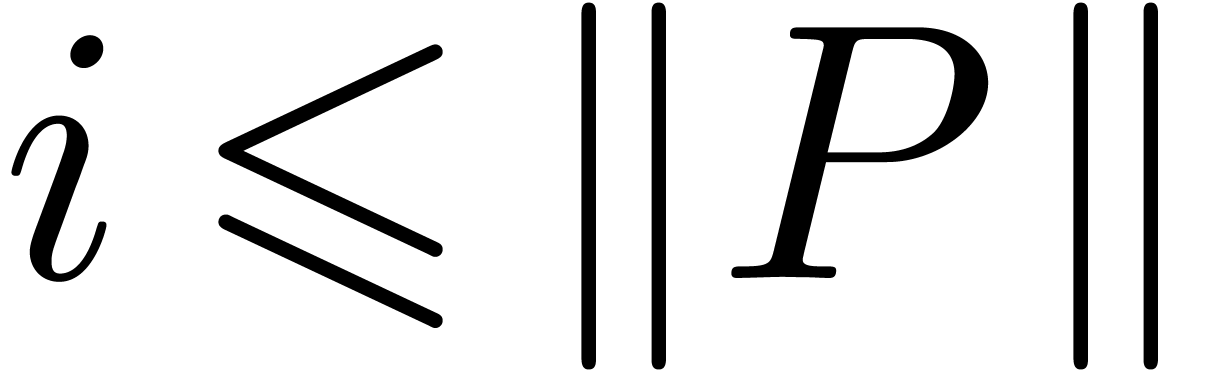 ,
,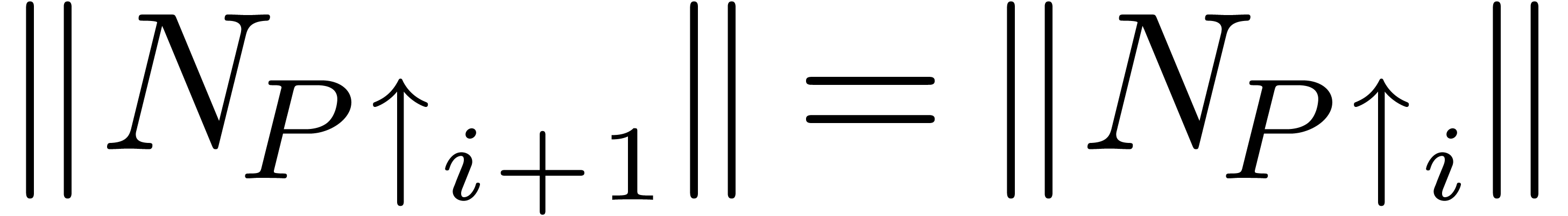 .
. instead of
instead of 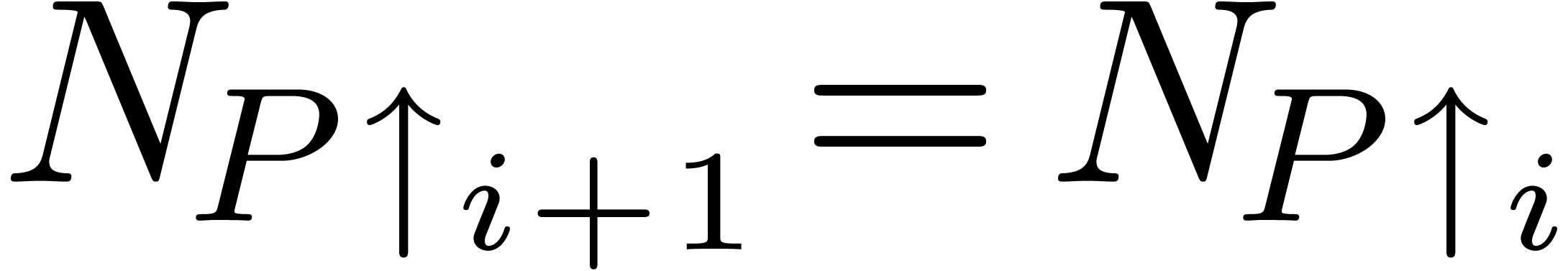 .
.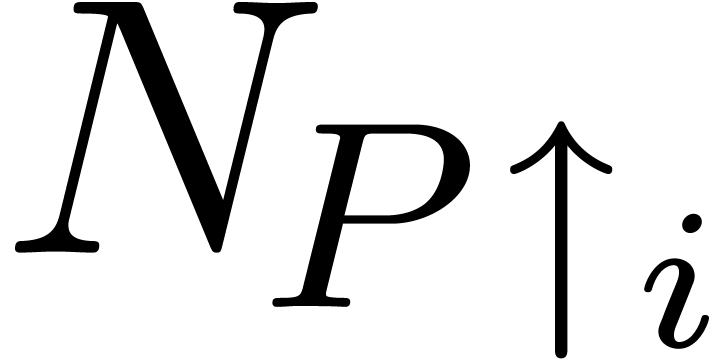 is
independent of
is
independent of 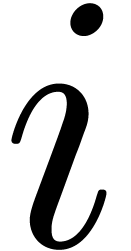 ,
,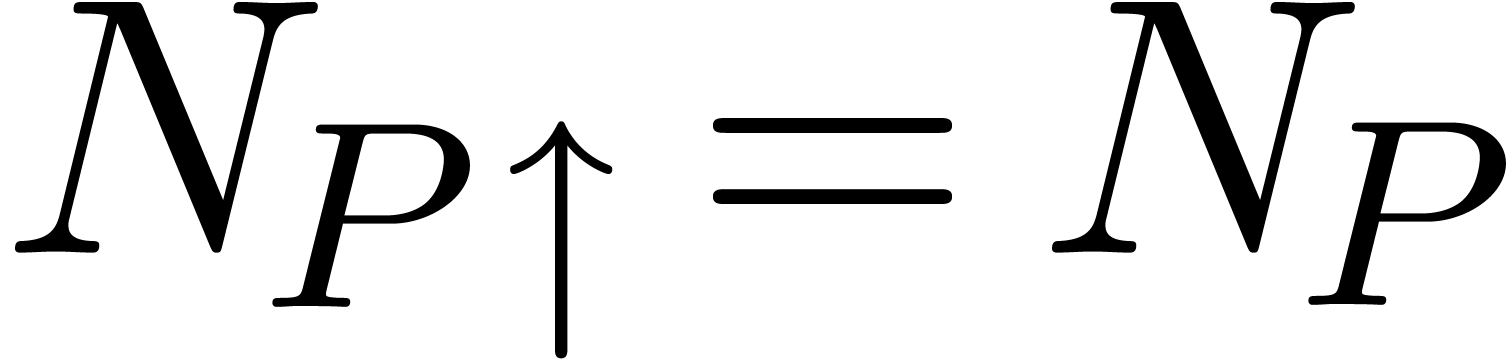 implies
implies 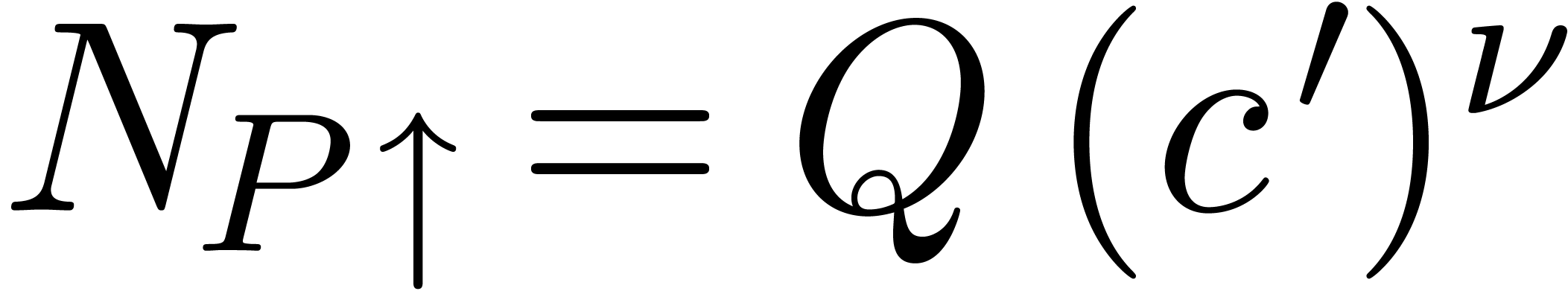 for some polynomial
for some polynomial 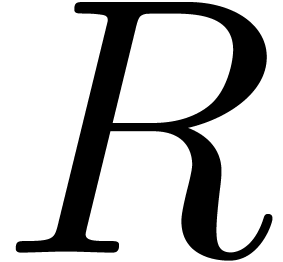 of homogeneous weight
of homogeneous weight 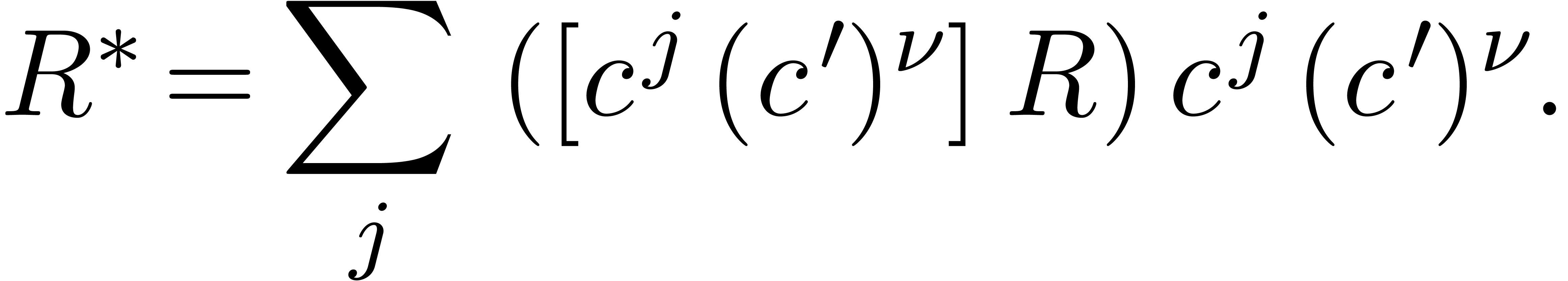
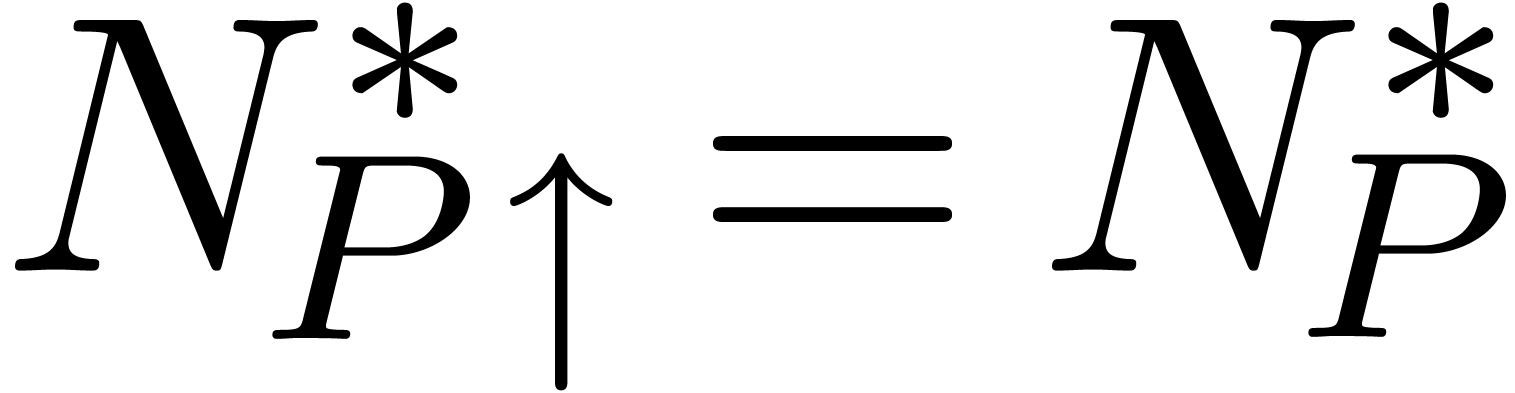 ,
,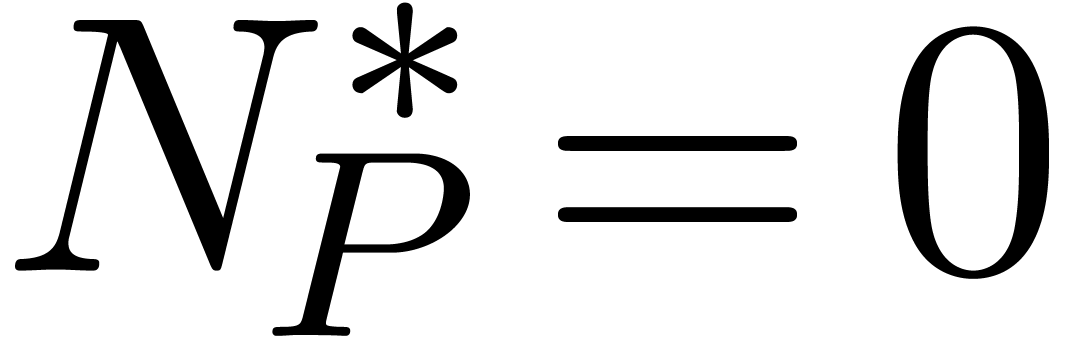 .
.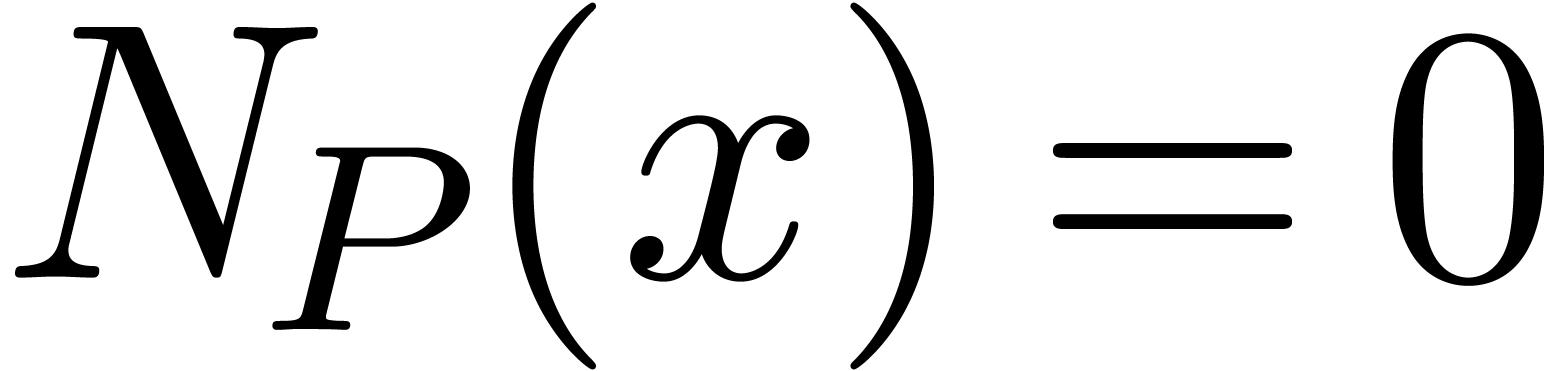 .
.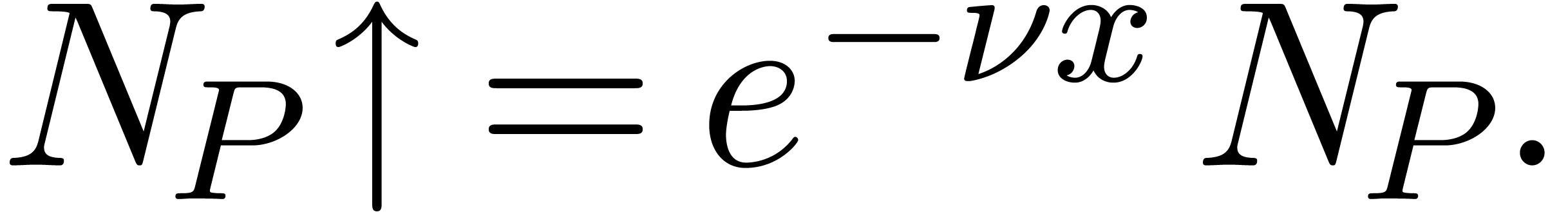
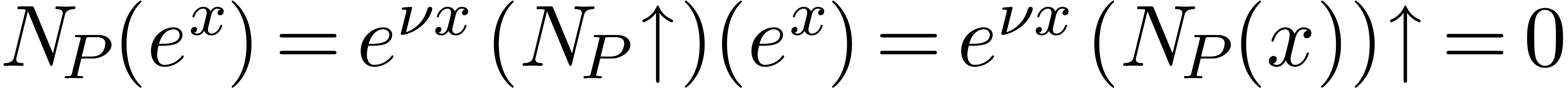 .
.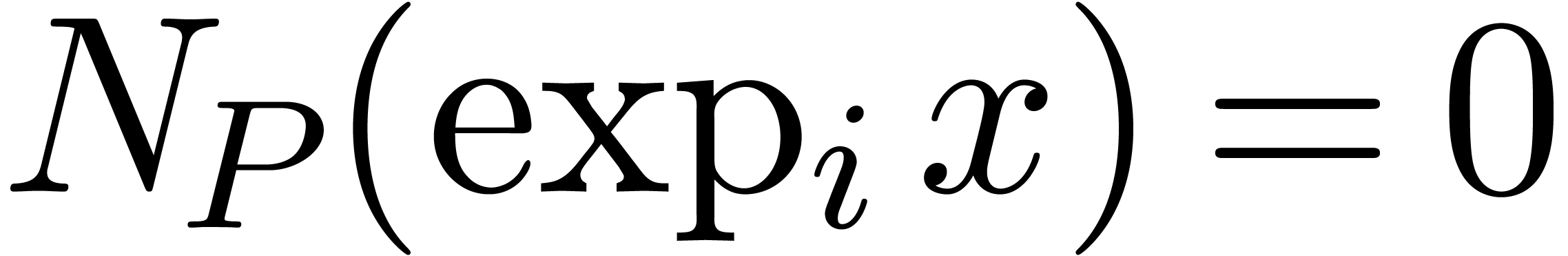 for any iterated
exponential of
for any iterated
exponential of  .
.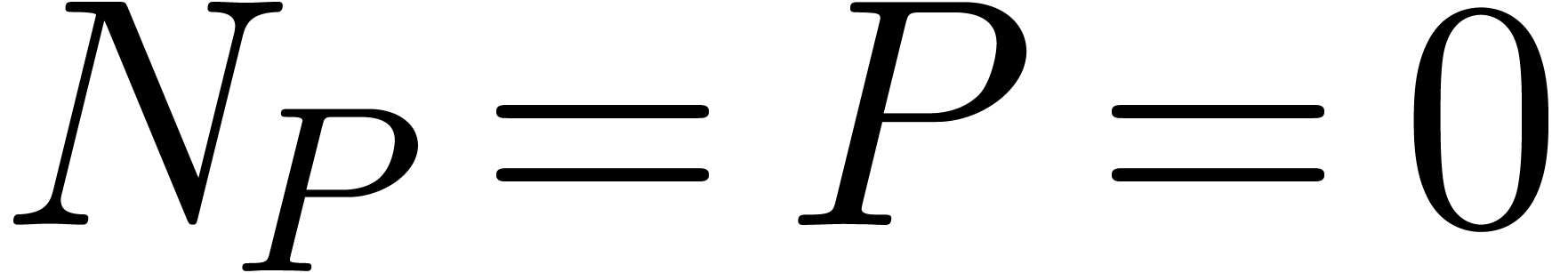 ,
,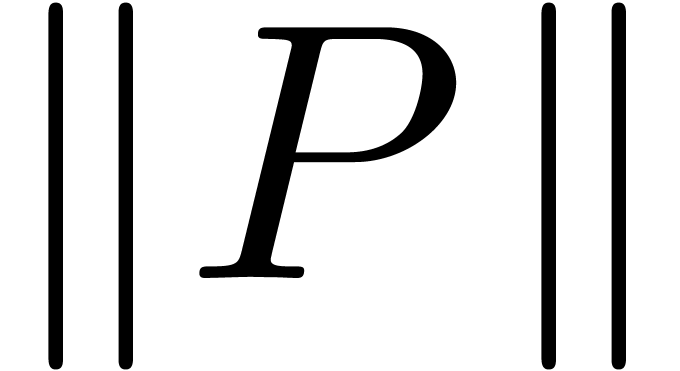 more upward shiftings, the purely exponential Newton polynomial
stabilizes. The resulting purely exponential differential Newton
polynomial, which is in
more upward shiftings, the purely exponential Newton polynomial
stabilizes. The resulting purely exponential differential Newton
polynomial, which is in 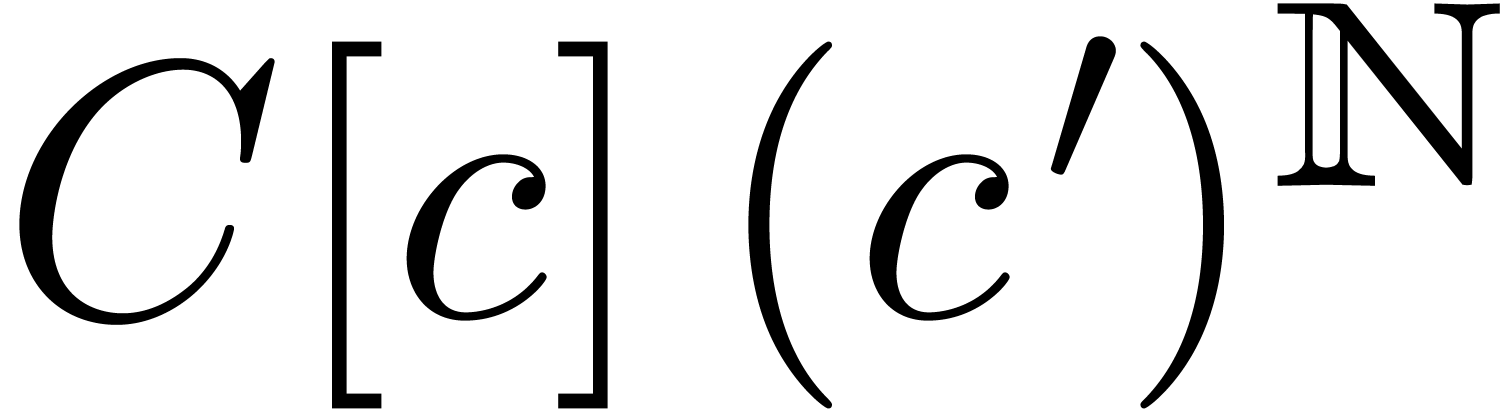 ,
,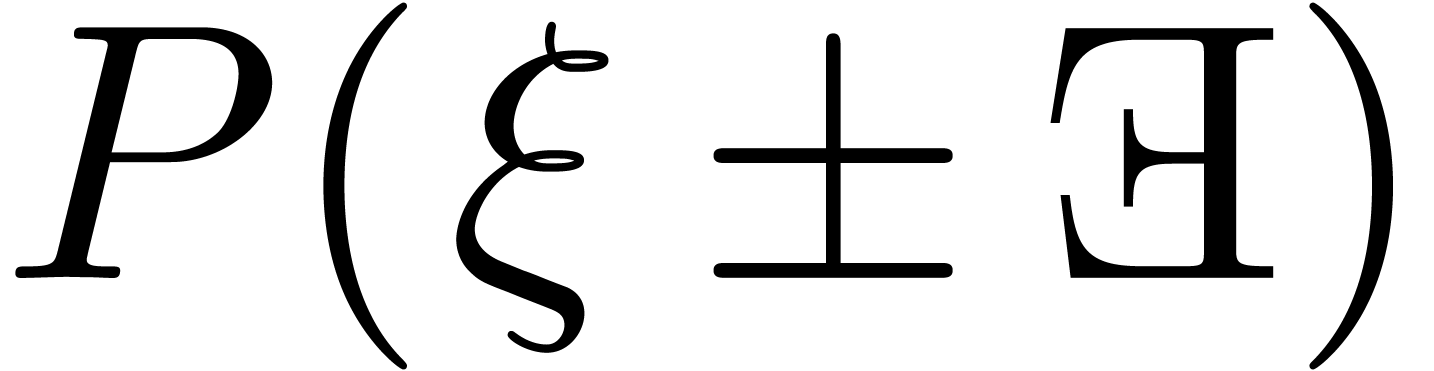 and
and 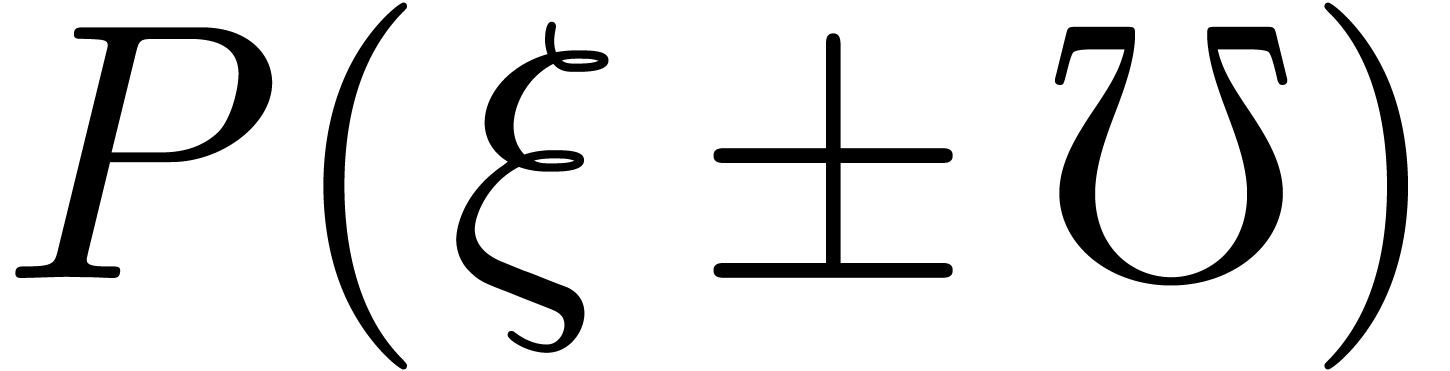 for all
for all  and
and 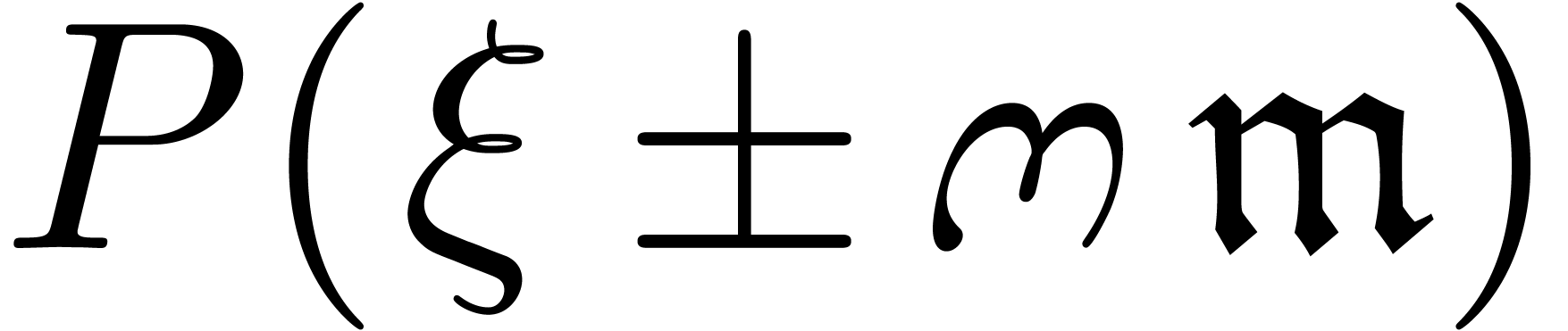 for all
for all  resp.
resp. 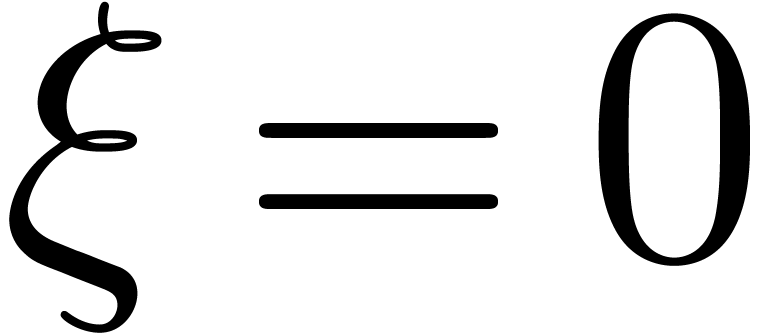 and
and 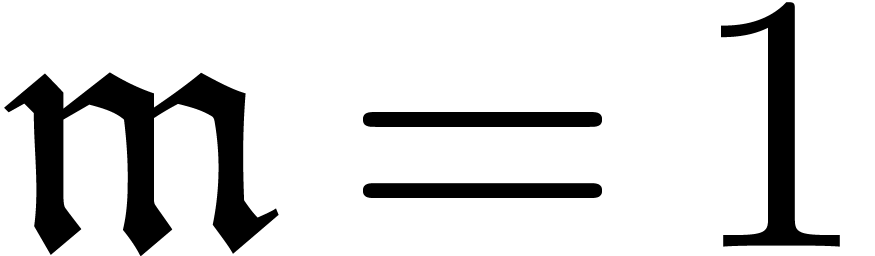 .
.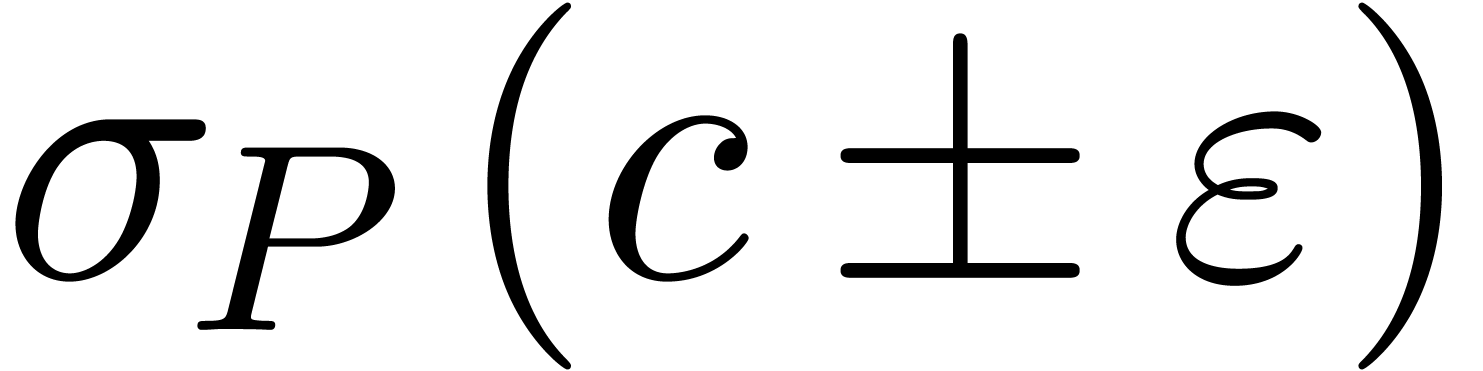 for
for 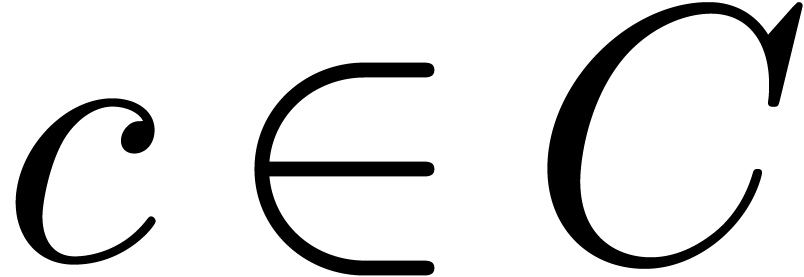 and positive
infinitesimal (but sufficiently large)
and positive
infinitesimal (but sufficiently large)  ,
,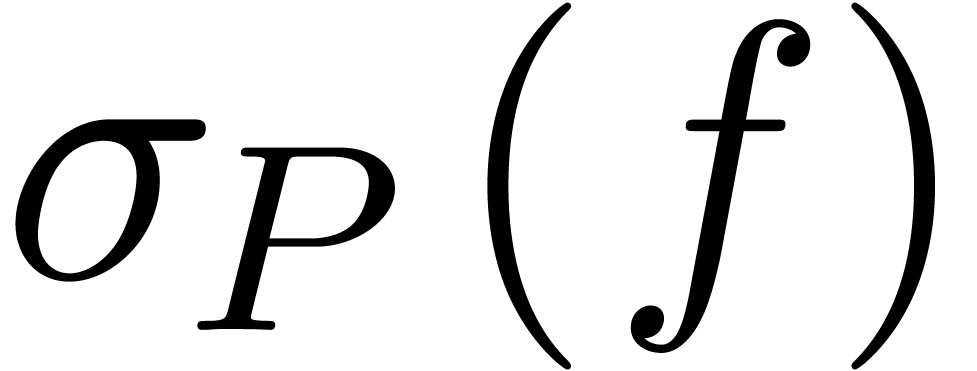 for positive
infinitely large (but sufficiently small)
for positive
infinitely large (but sufficiently small) 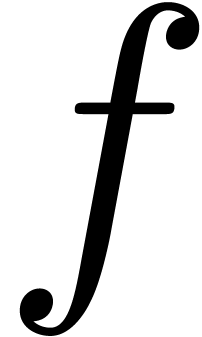 .
.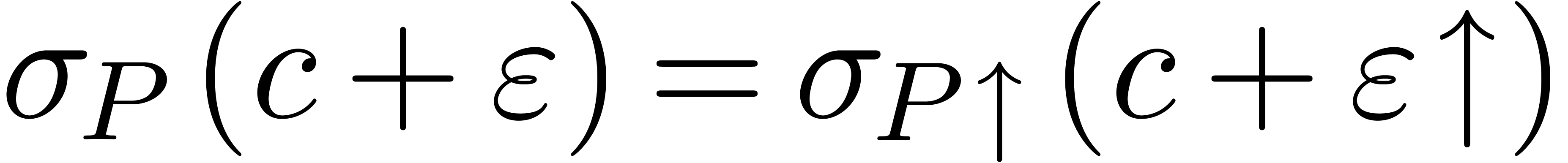 and
and
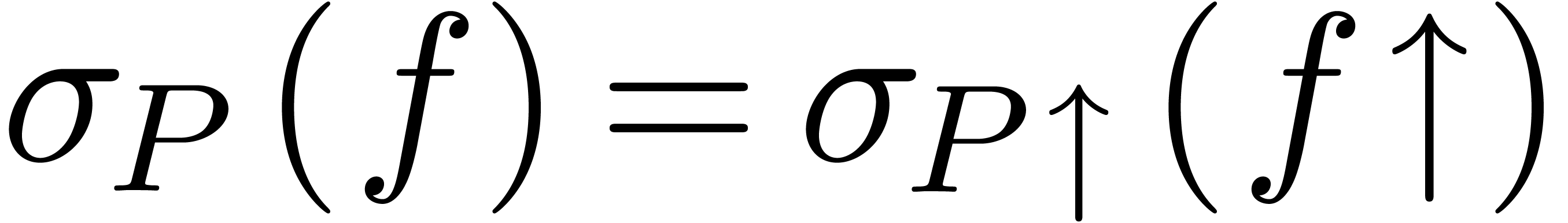 ),
),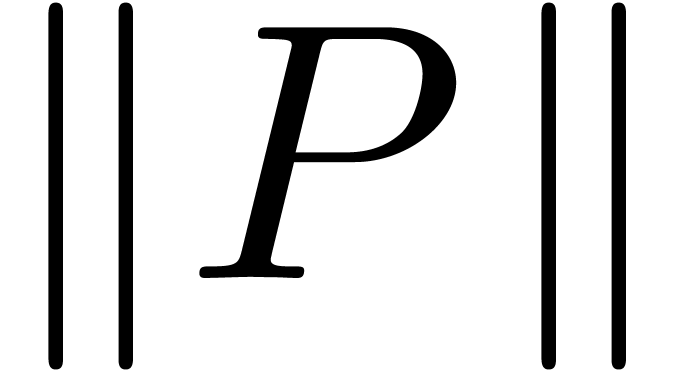 more upward
shiftings, we may also assume that
more upward
shiftings, we may also assume that
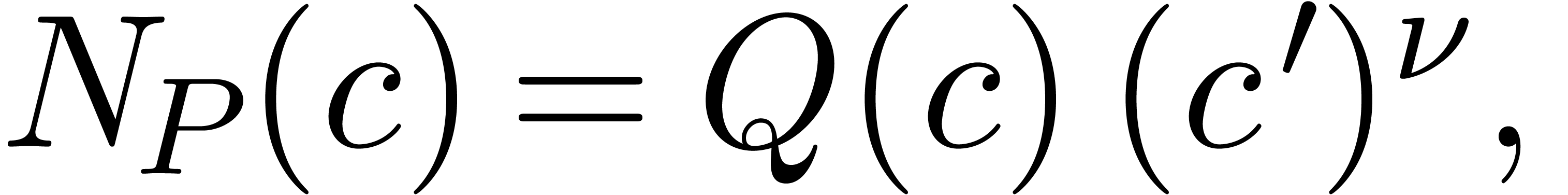
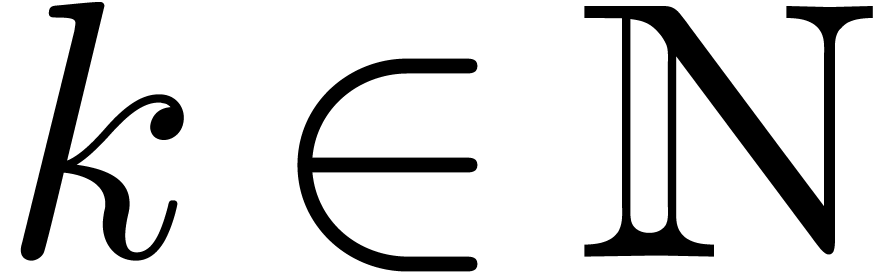 .
.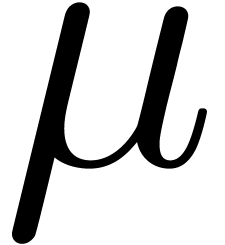 the
multiplicity of
the
multiplicity of  as a root of
as a root of  .
.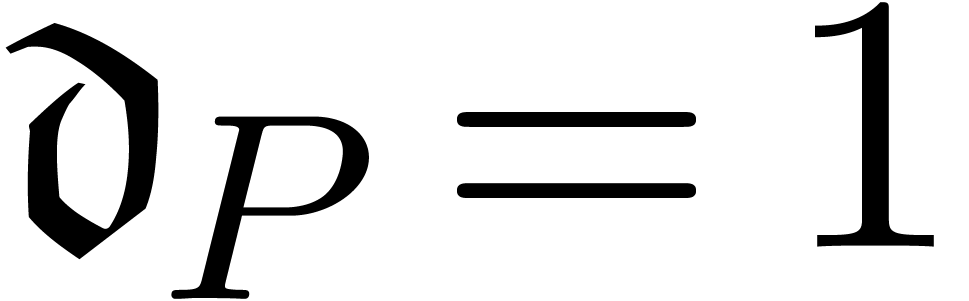 .
. with
with  ,
,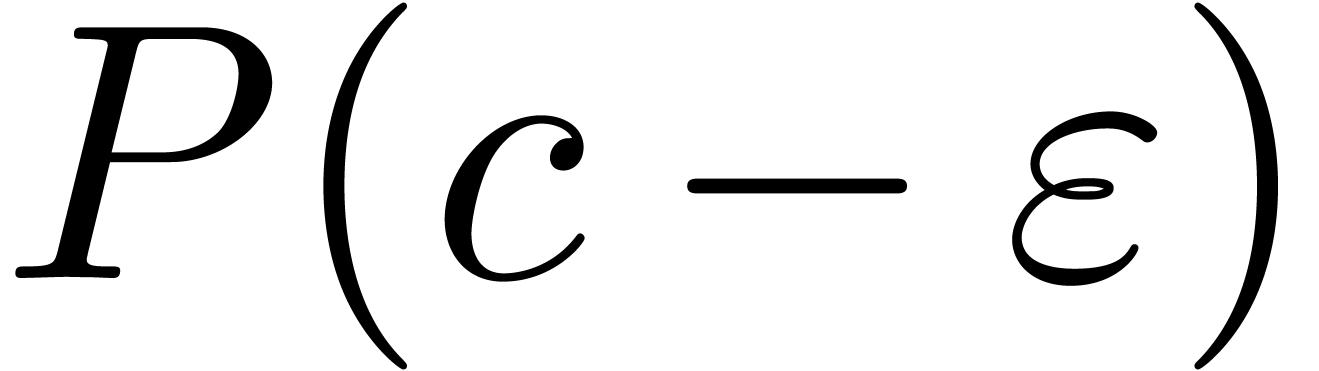 and
and 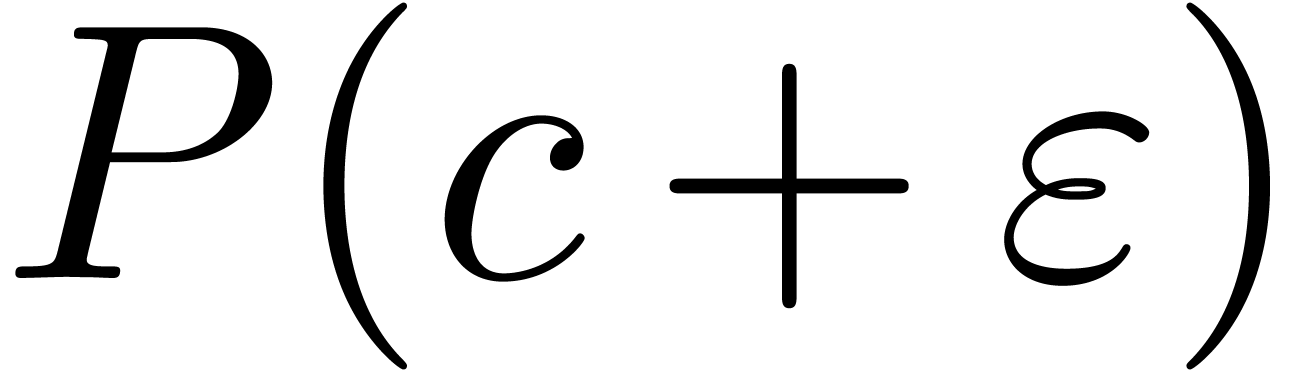 are
independent of
are
independent of  and given by
and given by
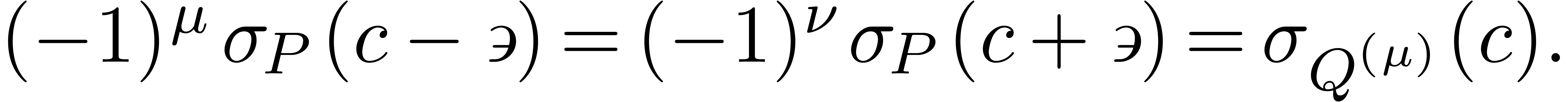
 such that
such that
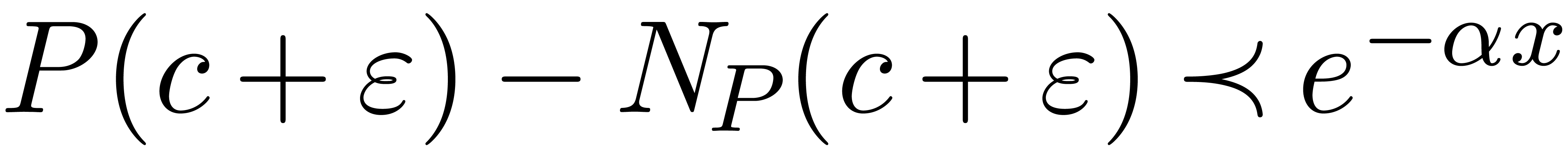
 .
. be such that
be such that  ,
,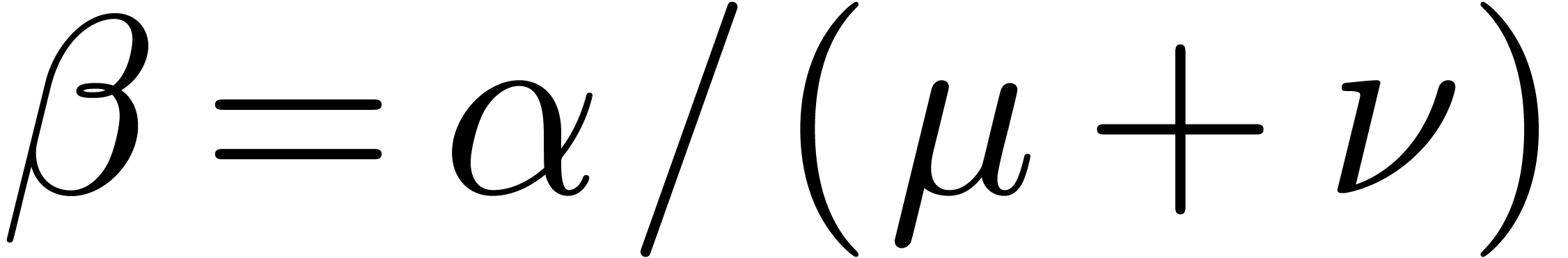 .
.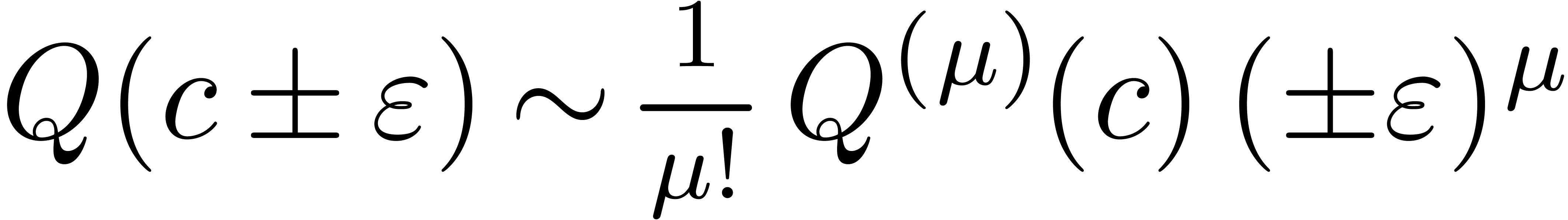 ,
,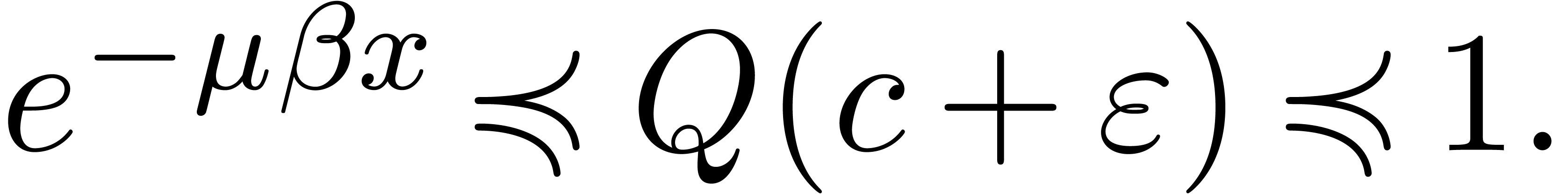
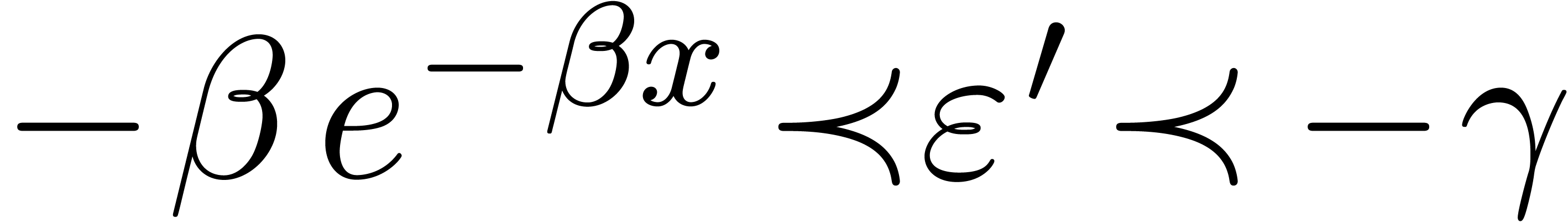 ,
,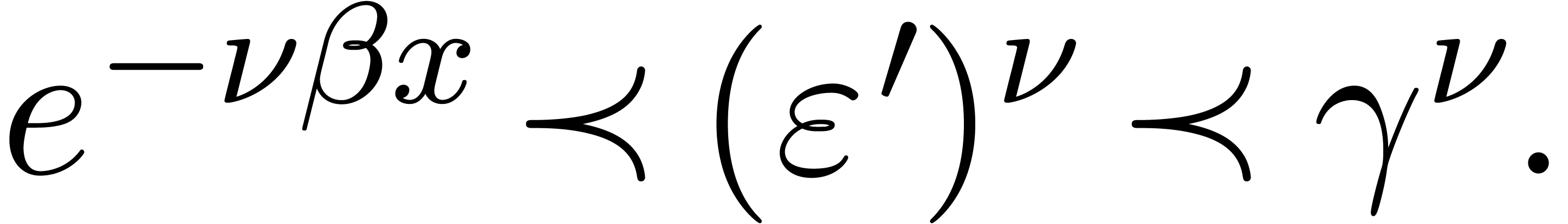
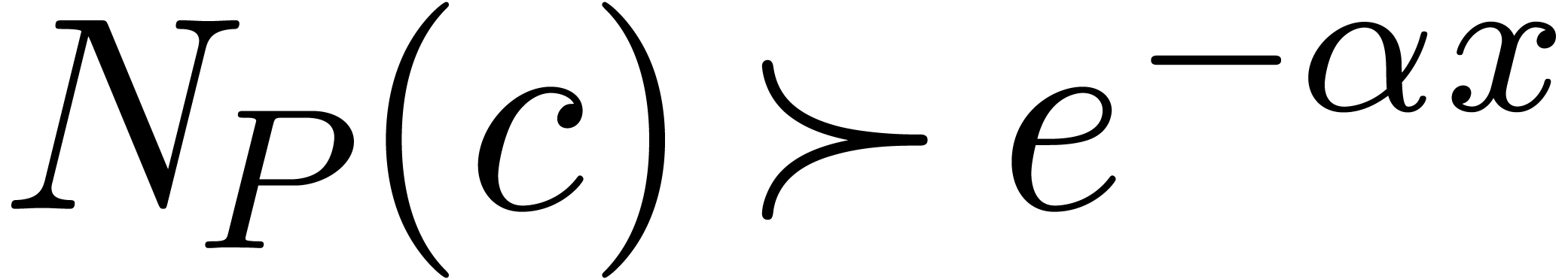 .
.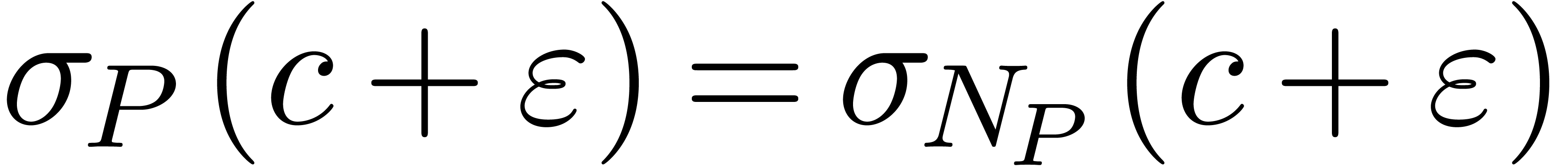 ,
,
 for all positive infinitesimal
for all positive infinitesimal 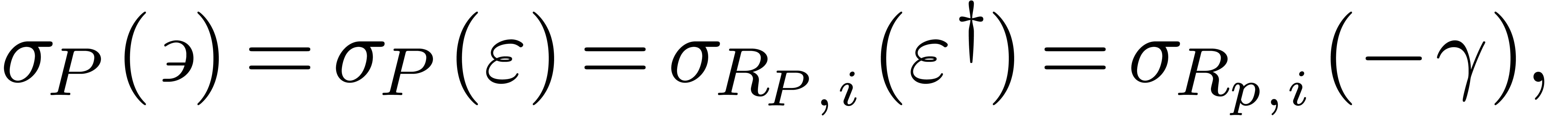
 be constants such that
be constants such that 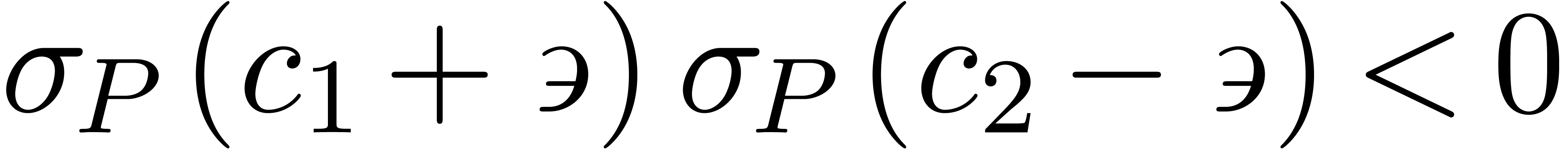 .
.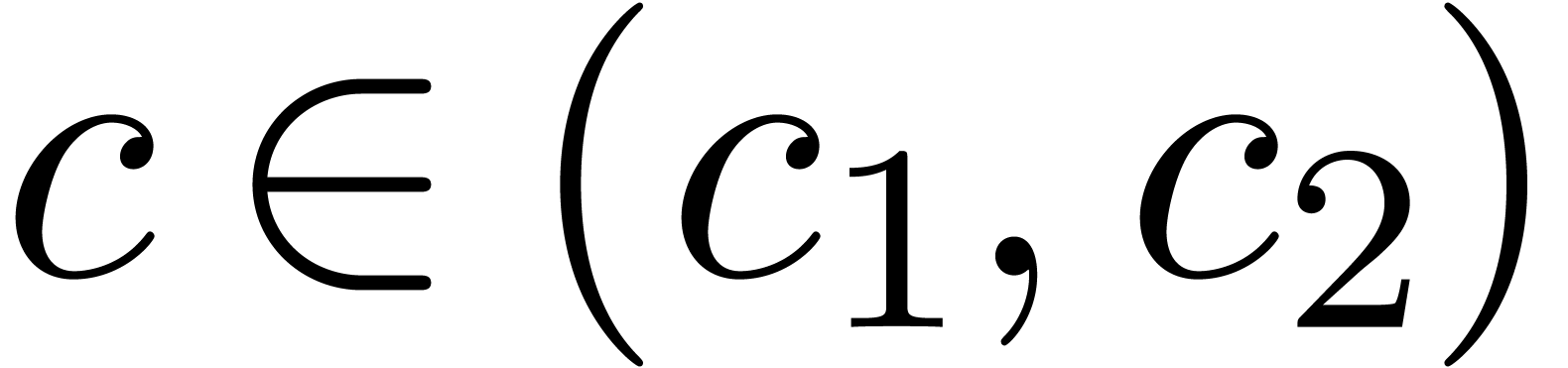 with
with 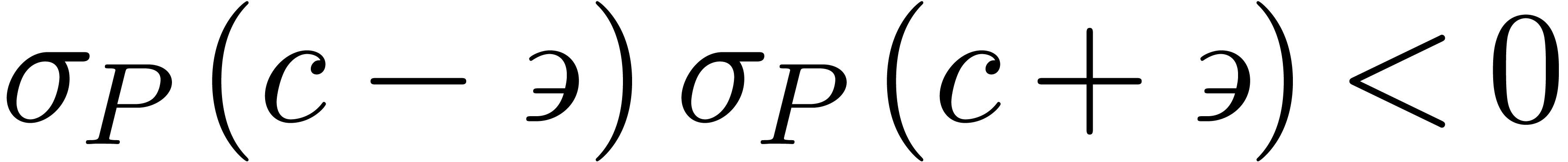 .
.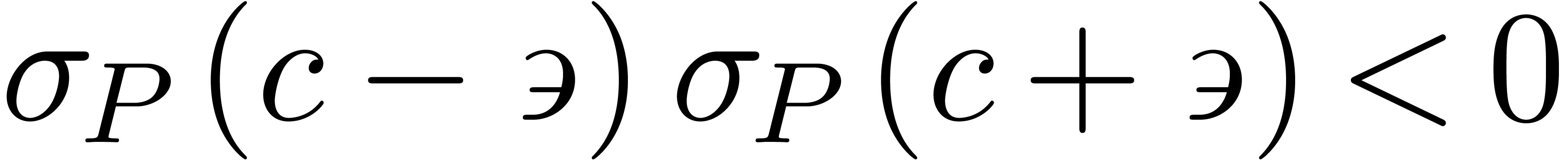 holds for any
holds for any  with
with
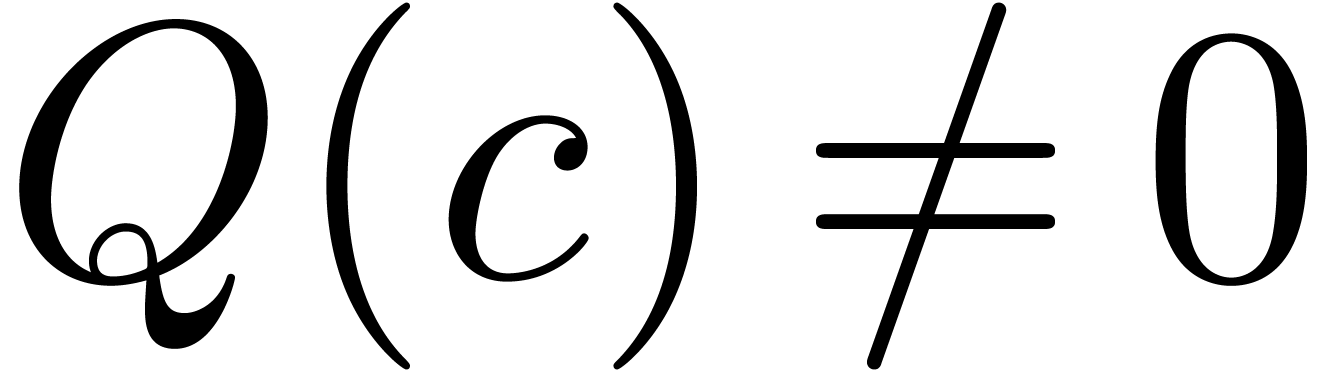 ,
,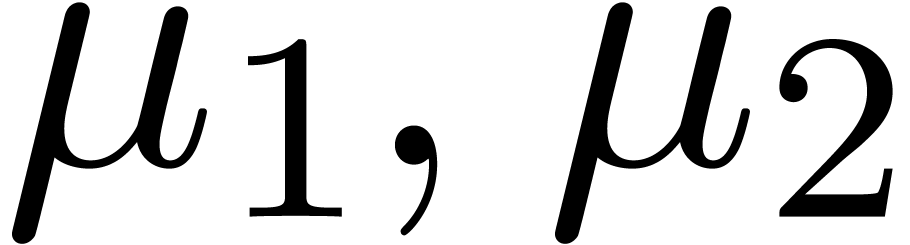 denote the multiplicities of
denote the multiplicities of  as
roots of
as
roots of  .
.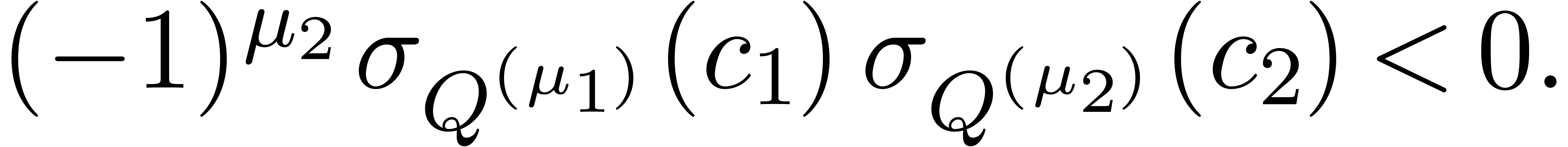
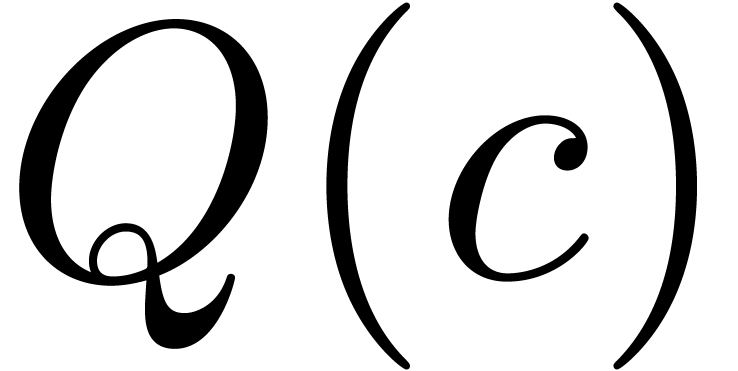 for
for  and
and  are different. Hence, there
exists a root
are different. Hence, there
exists a root  of
of 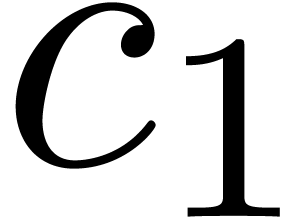 and
and 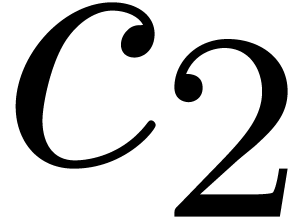 which has odd
multiplicity
which has odd
multiplicity  .
. with
with  ,
, and
and 
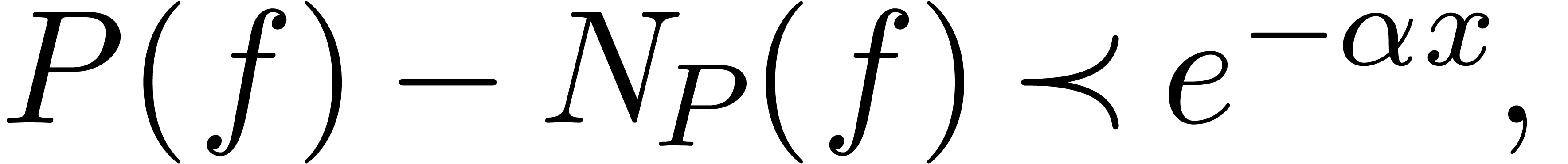
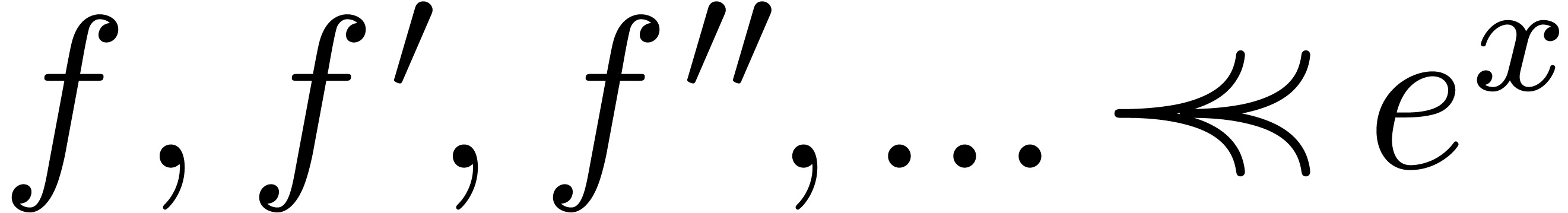 .
.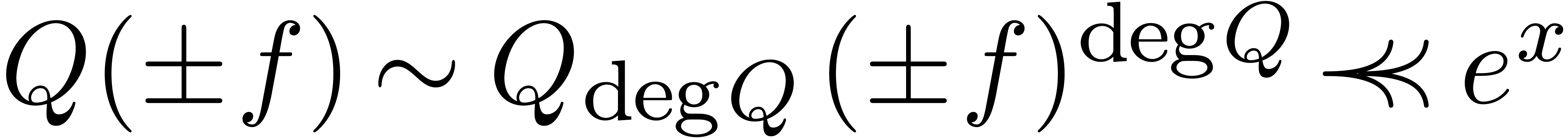 and
and 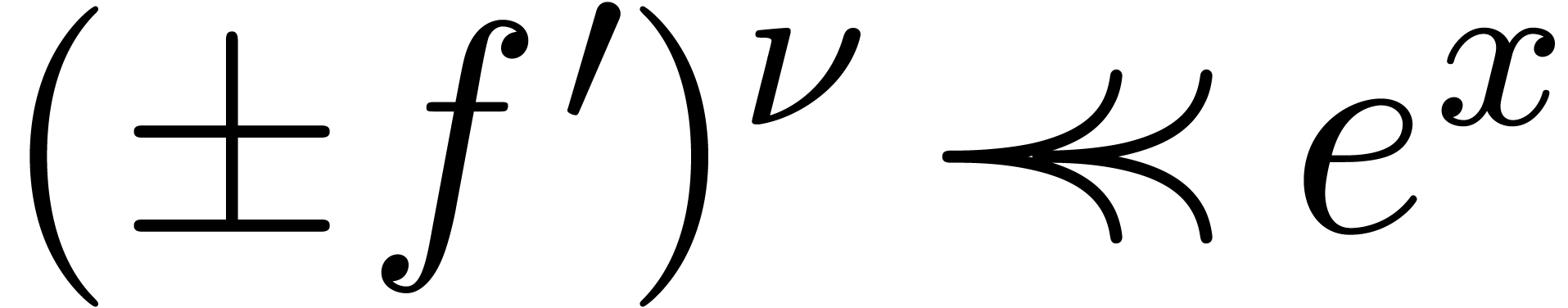 ,
,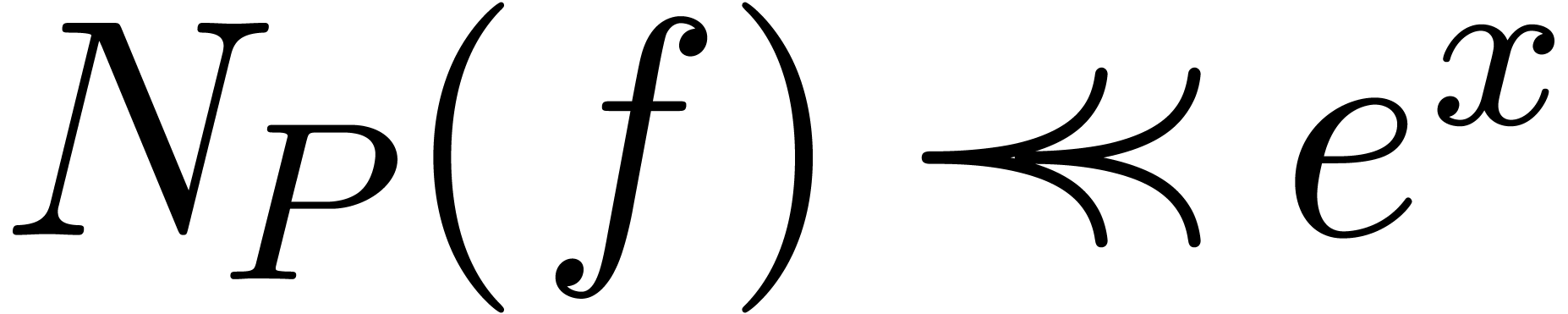 .
.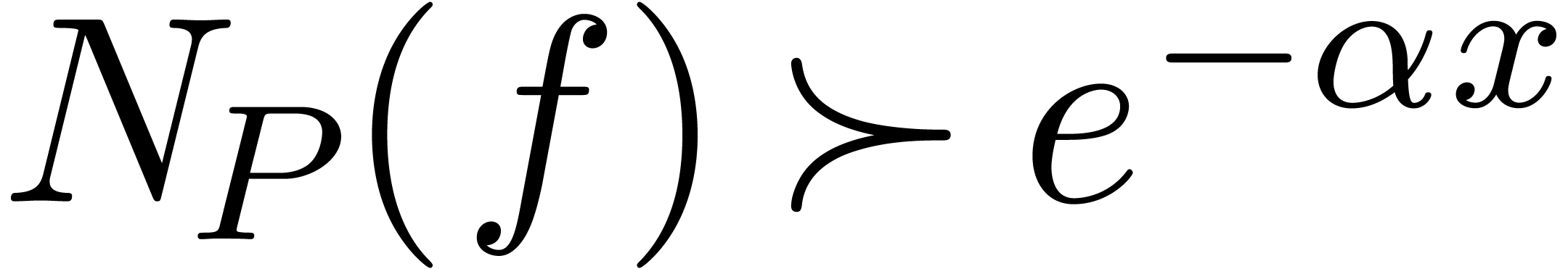 ,
,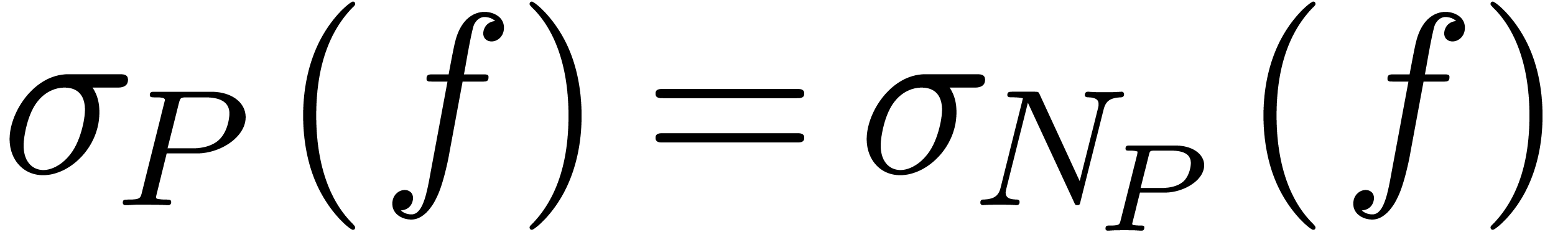 ,
,
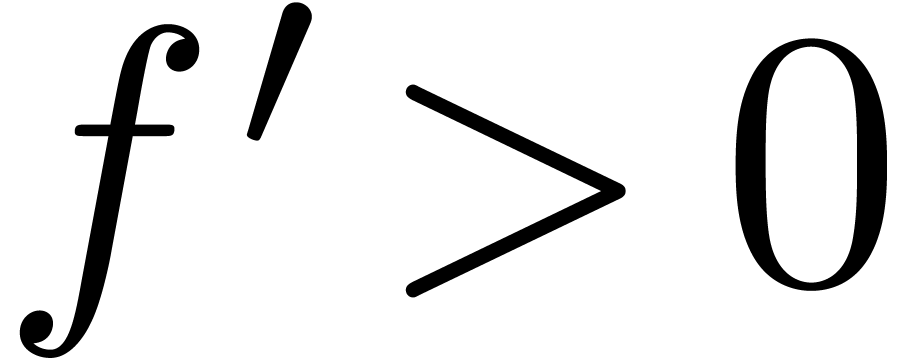 for positive infinitely large
for positive infinitely large 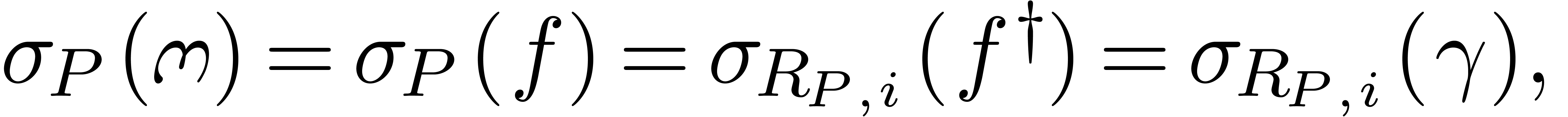
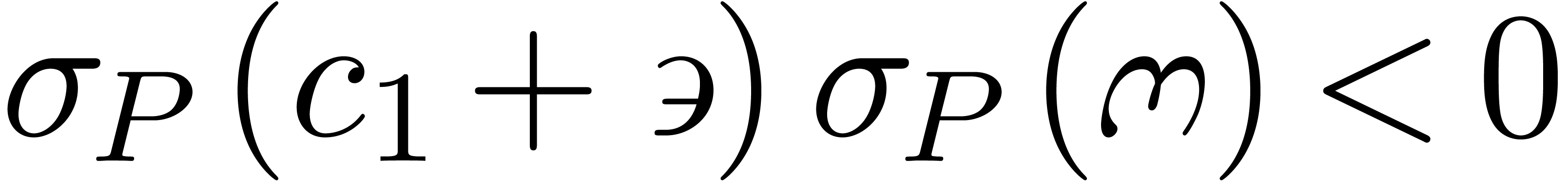 .
.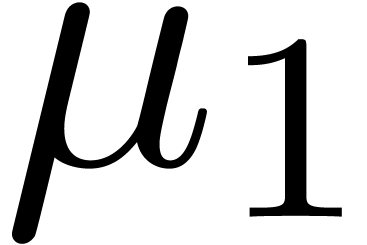 be the multiplicity of
be the multiplicity of 
 are different. Hence, there
exists a root
are different. Hence, there
exists a root  be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in 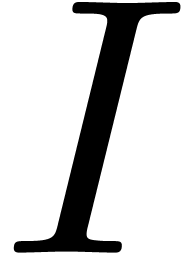 of one of the following forms:
of one of the following forms:
 ,
, with
with 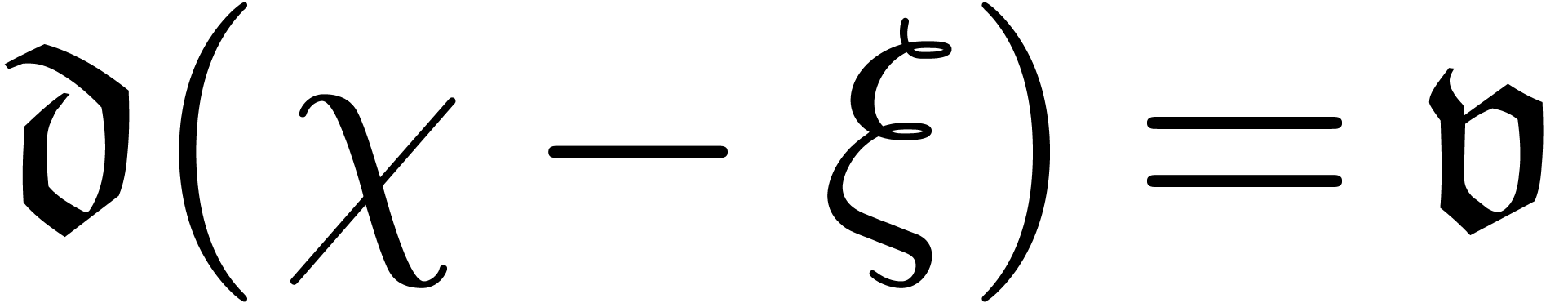 .
.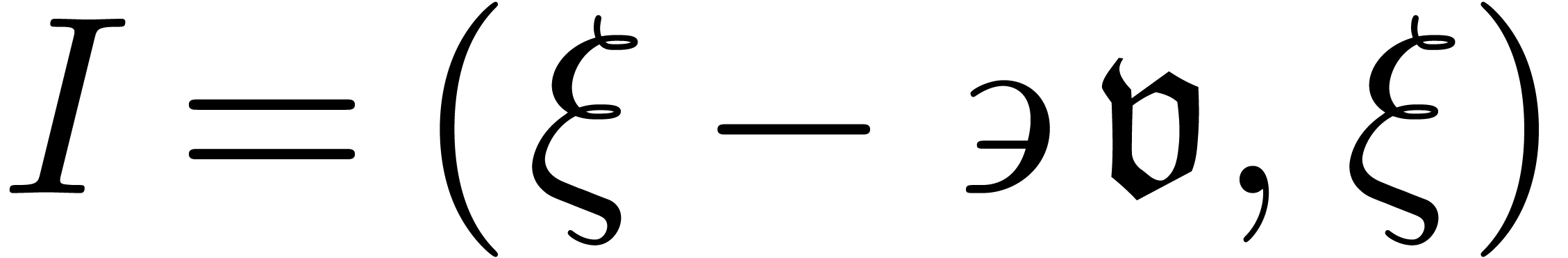 .
. .
.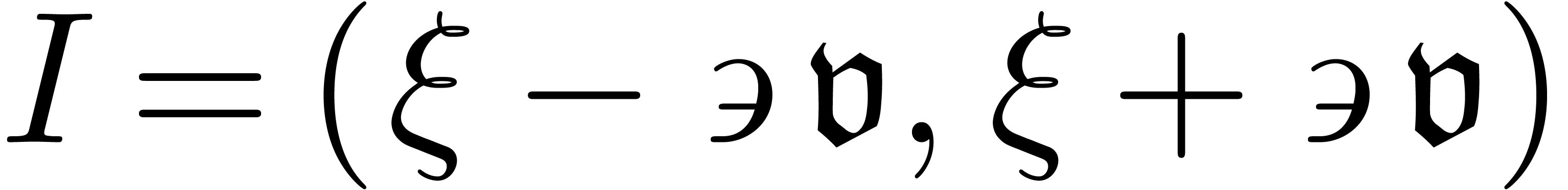 .
. .
. be a transseries
resp. a transmonomial in
be a transseries
resp. a transmonomial in 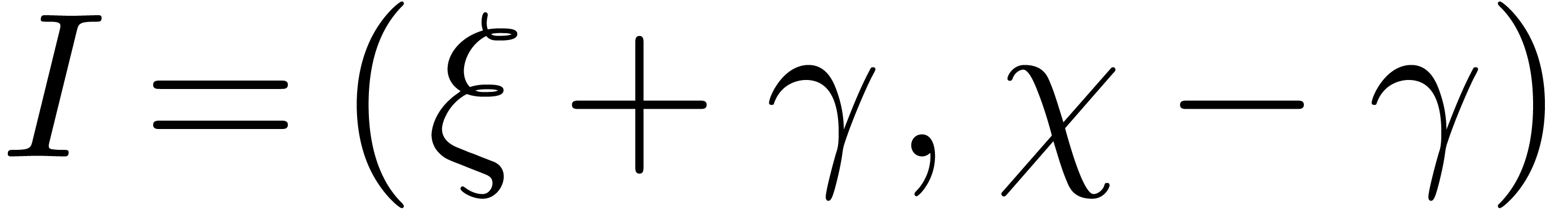 ,
,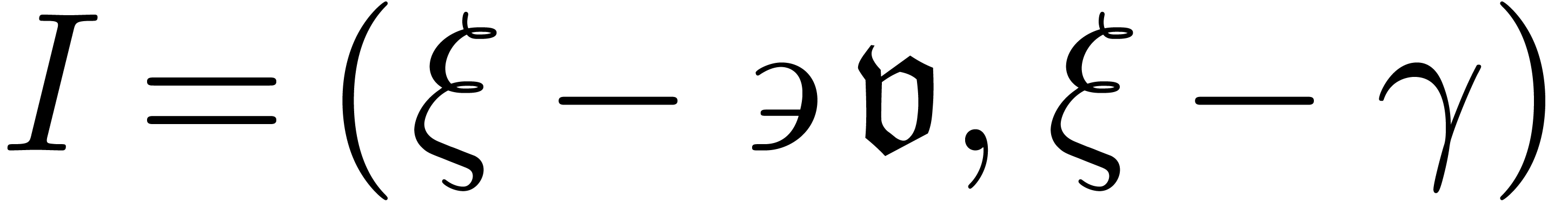 .
.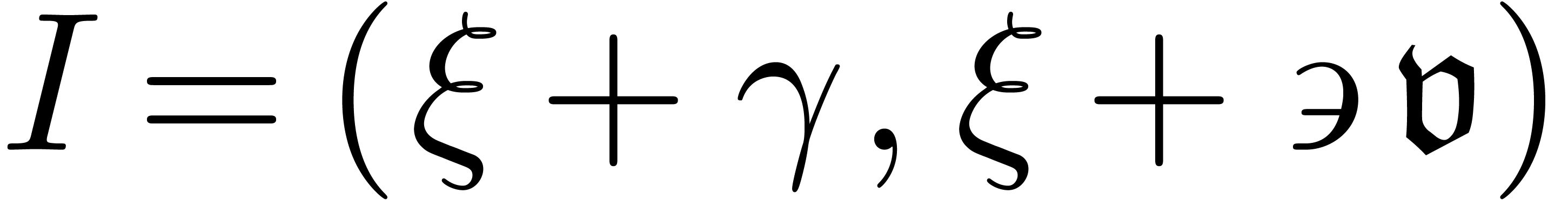 .
.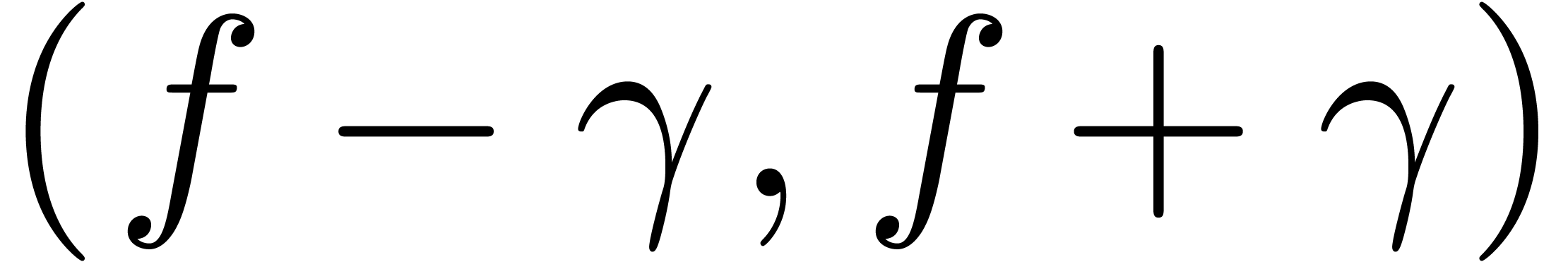 for some
for some 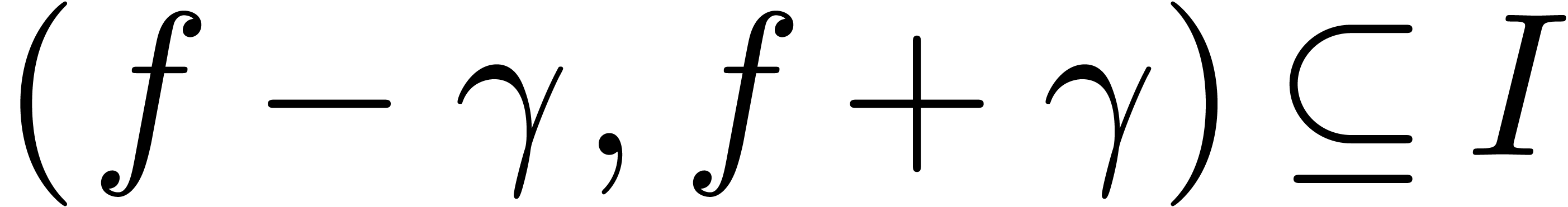 .
.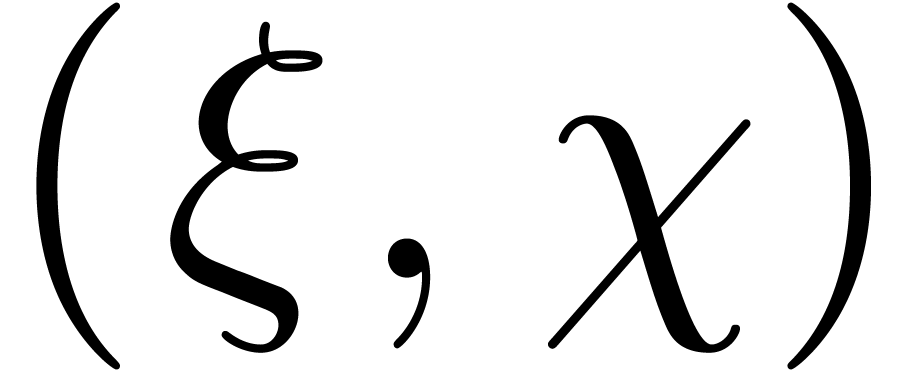 ,
,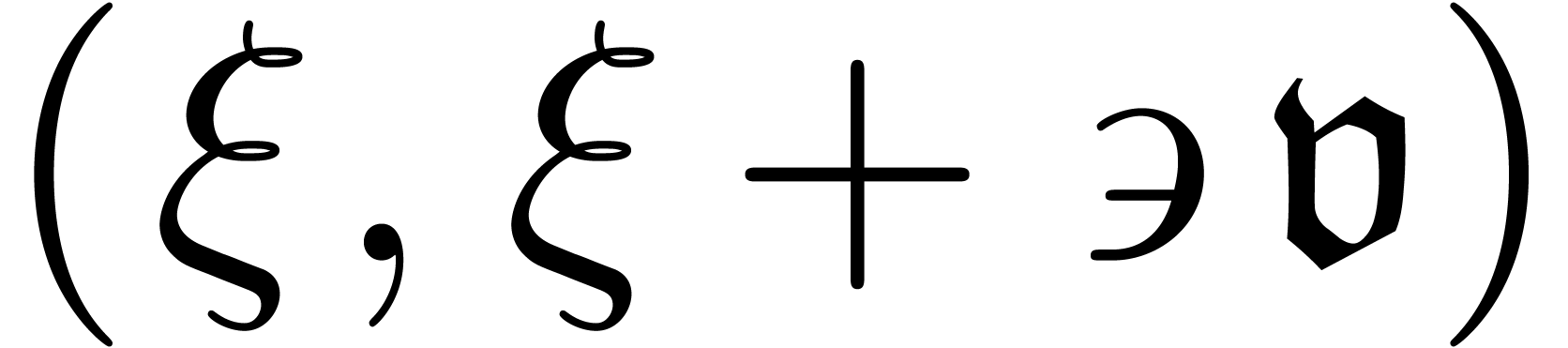 ,
,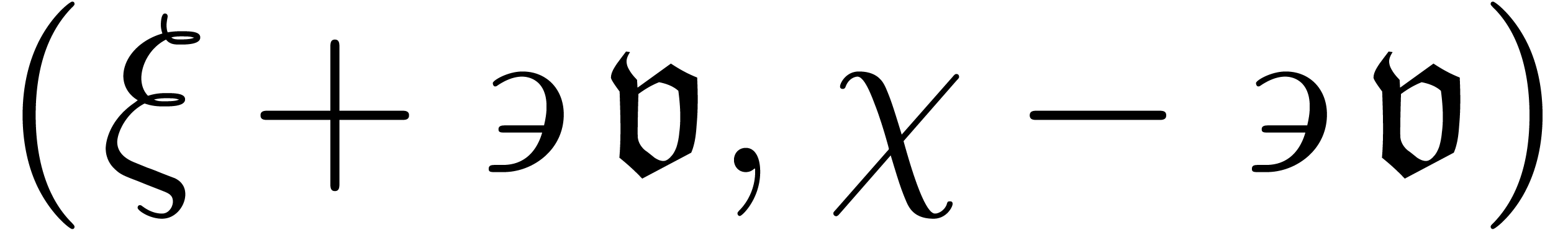 or
or 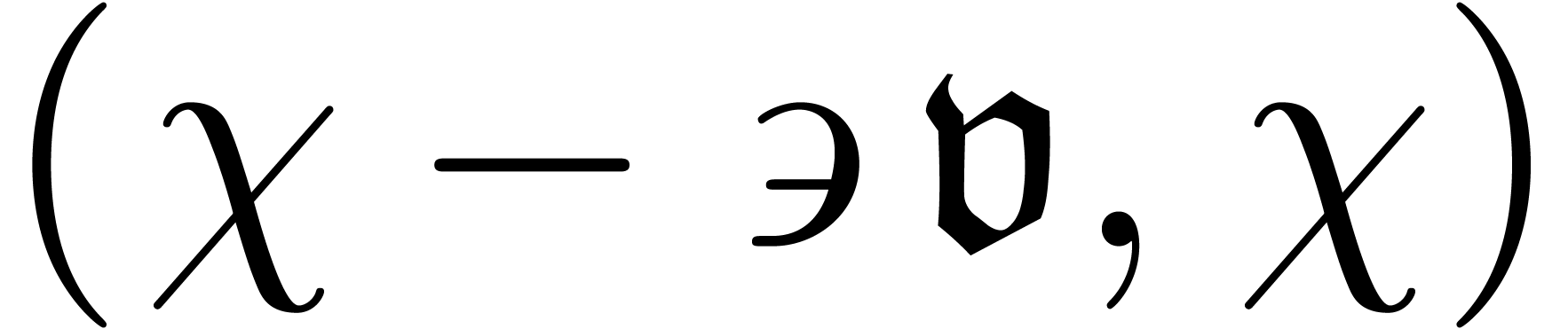 .
.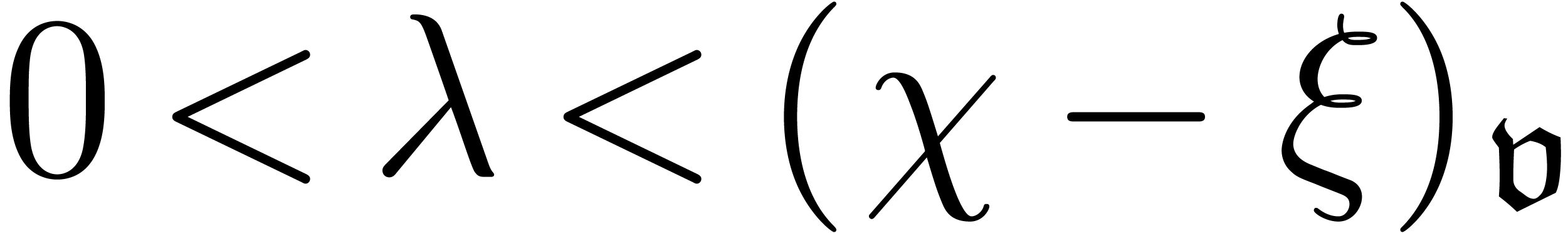 such that
such that 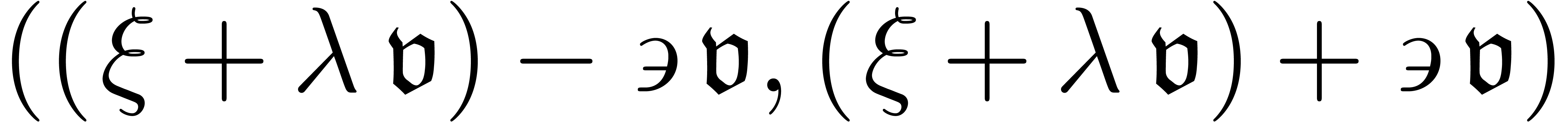 .
.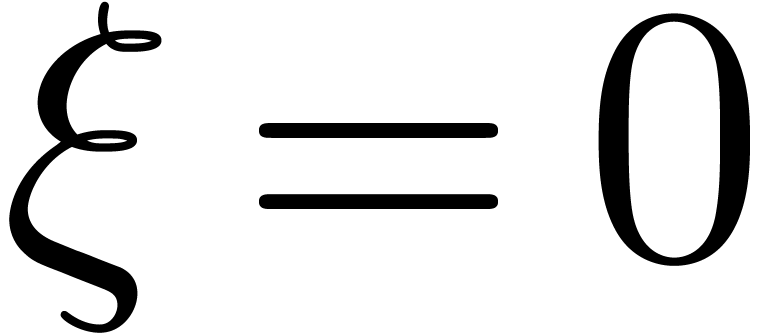 ,
,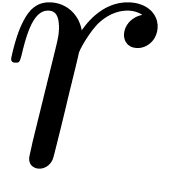 of
of 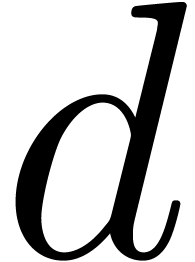 of the asymptotic algebraic differential equation
of the asymptotic algebraic differential equation

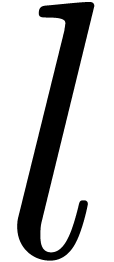 of a sequence of
privileged refinements of Newton degree
of a sequence of
privileged refinements of Newton degree 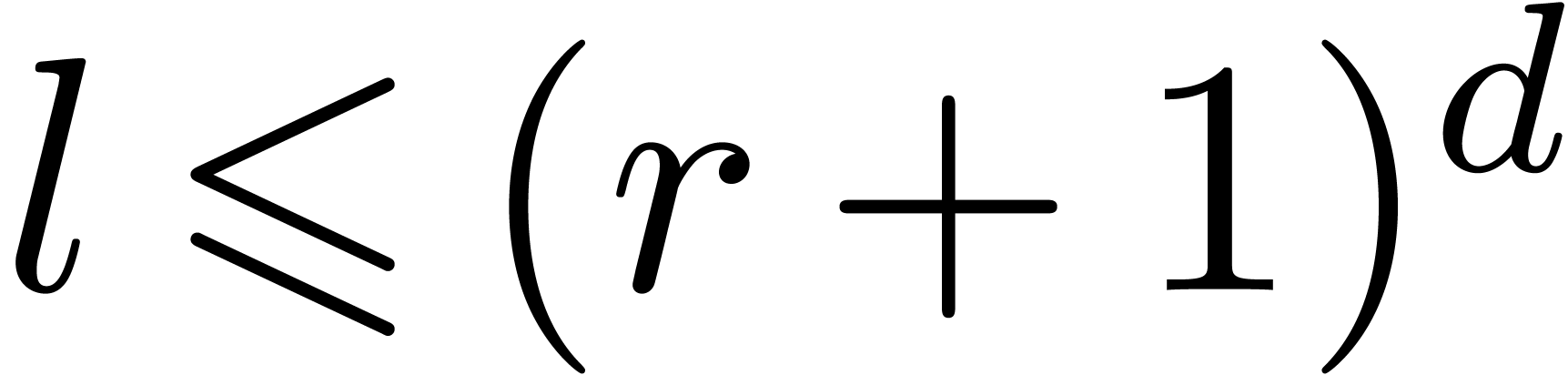 ,
,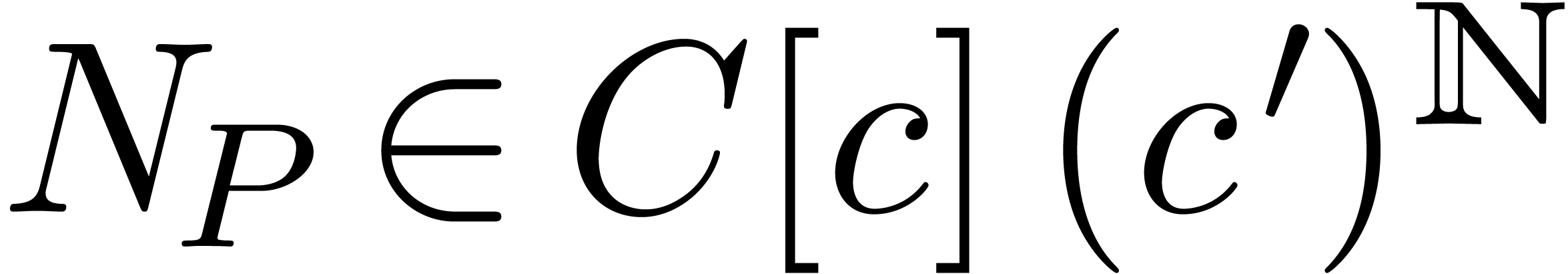 .
. and
and  .
. .
. is such that
is such that  changes sign on
changes sign on  ,
,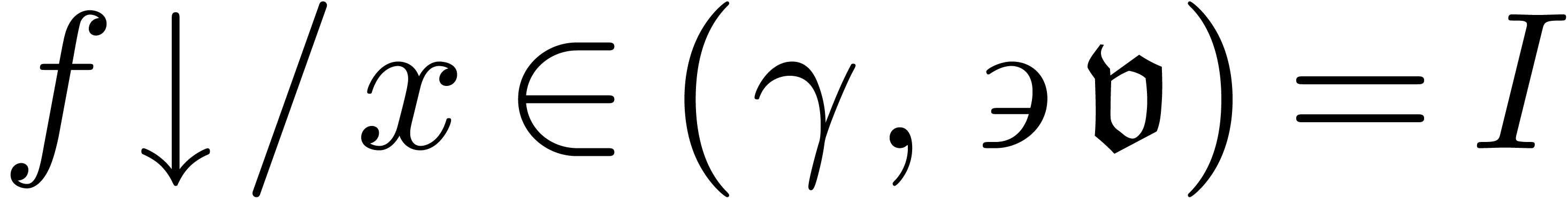 is such that
is such that 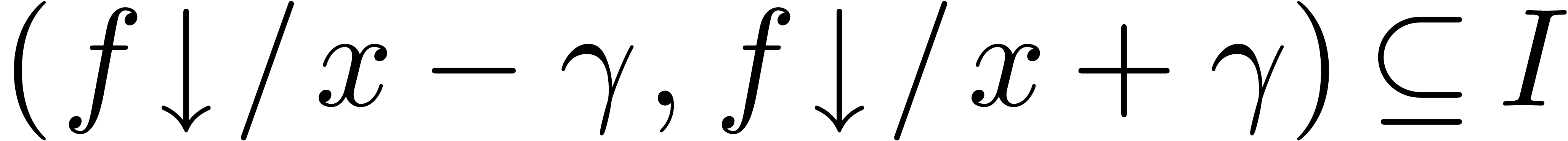 .
. be the potential dominant monomial relative to (
be the potential dominant monomial relative to (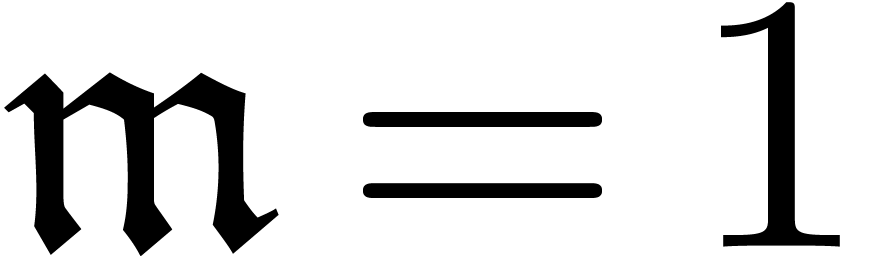 ,
, or
or 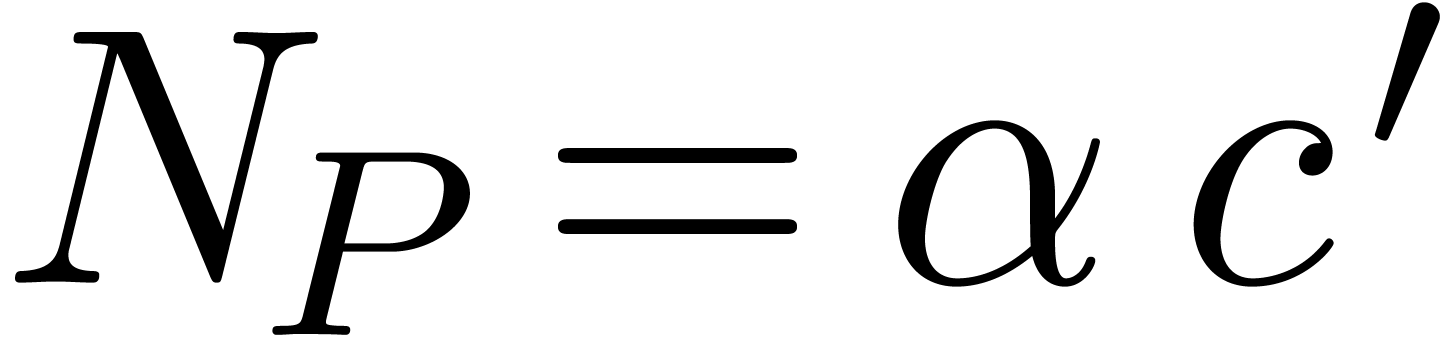 for certain constants
for certain constants 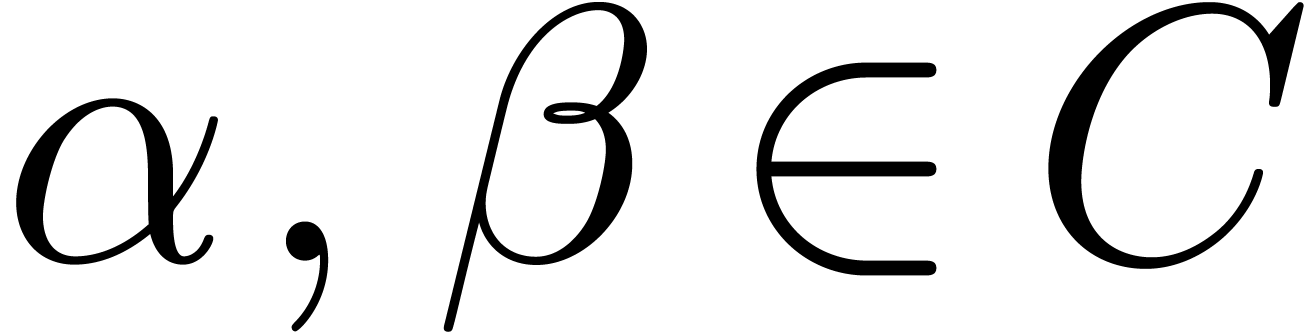 .
.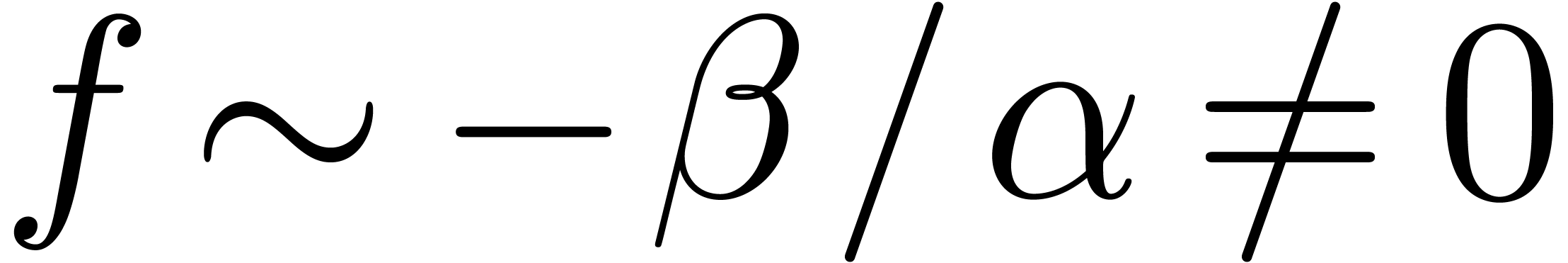 .
.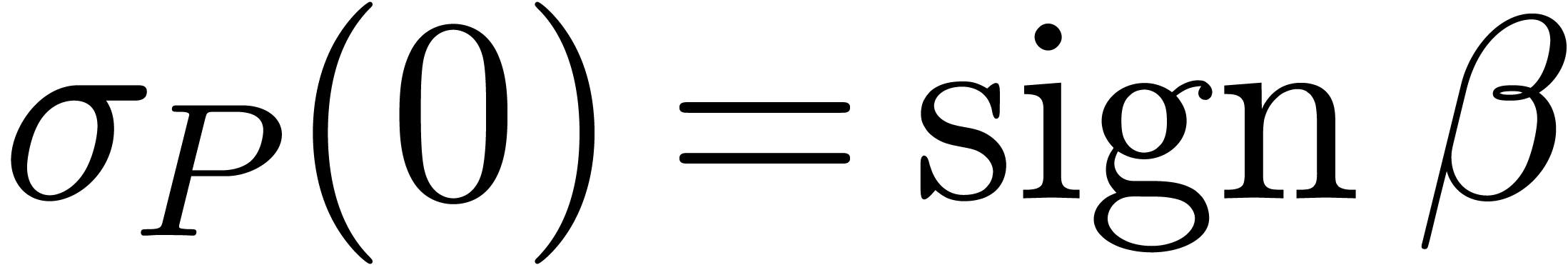 and
and 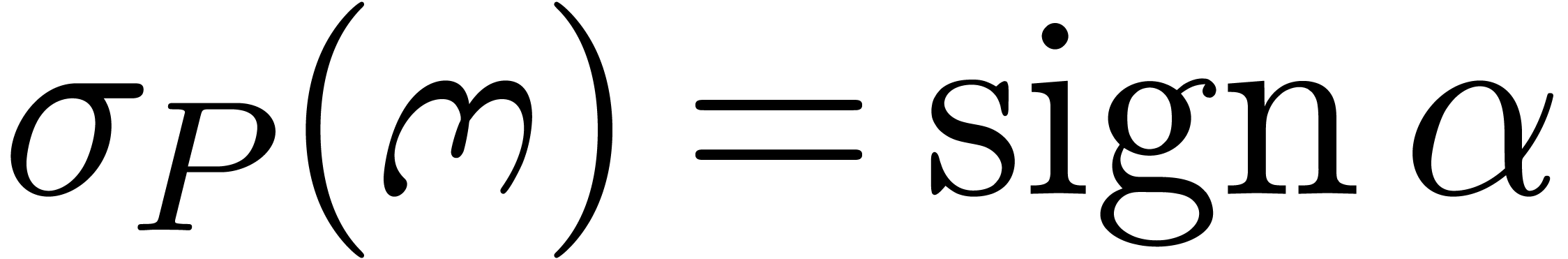 .
.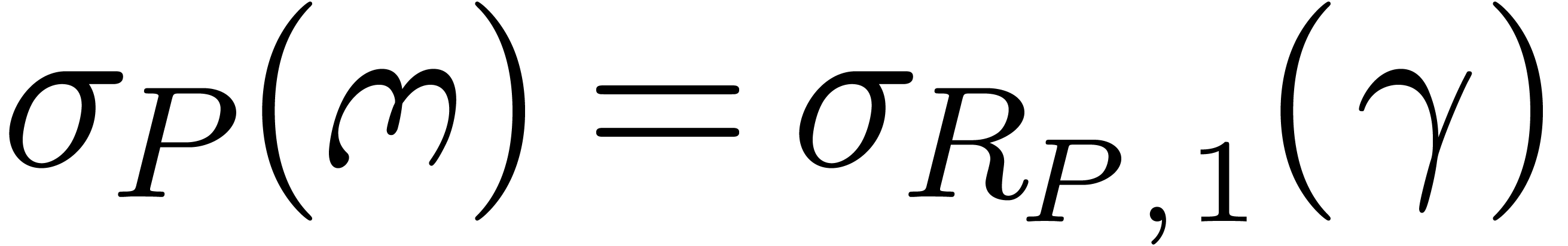 and
and
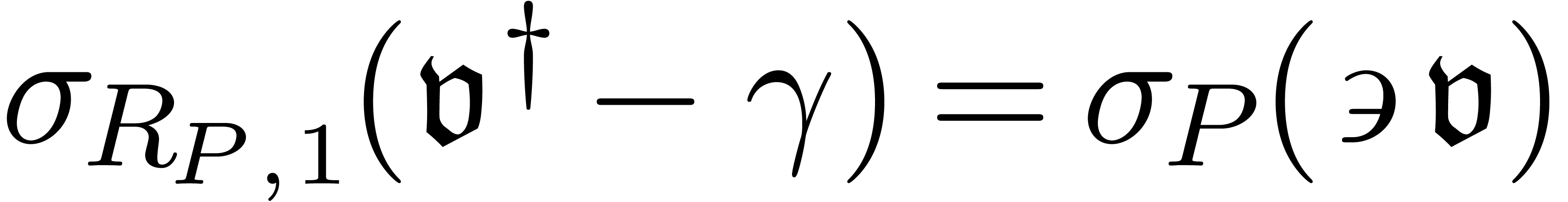 must be equal. Otherwise
must be equal. Otherwise  would admit a solution between
would admit a solution between 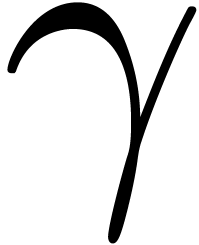 and
and 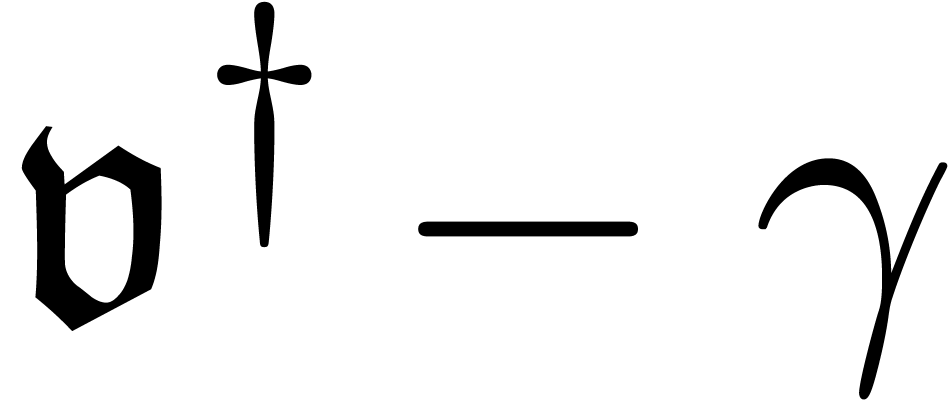 ,
,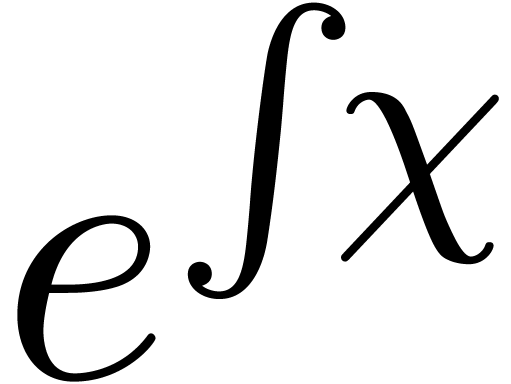 ,
,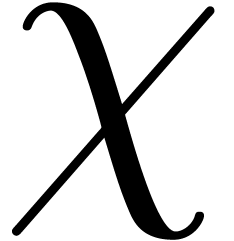 is the largest such solution. Our claim implies that
is the largest such solution. Our claim implies that 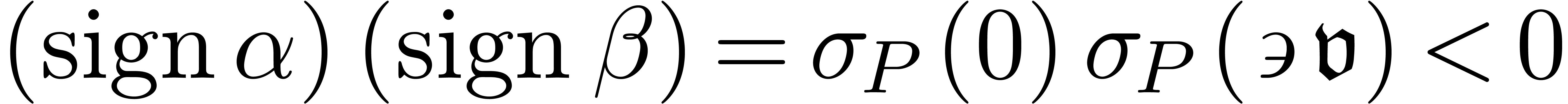 ,
, .
.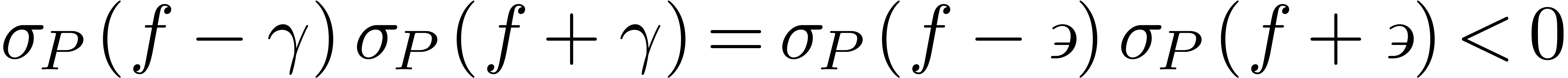 .
.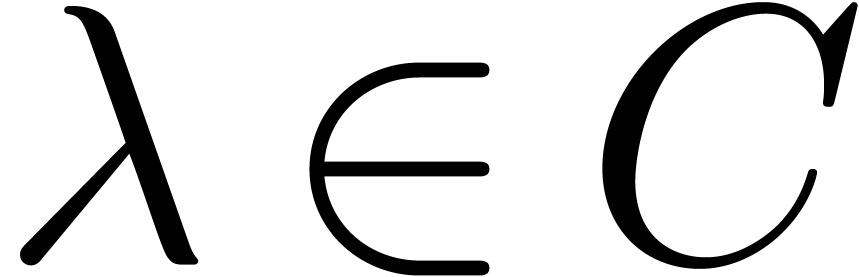 is a root of
is a root of  .
. ,
, .
. .
.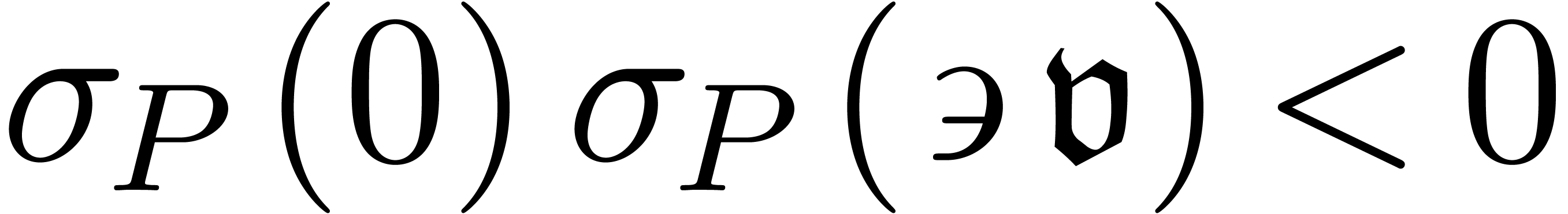 (resp.
(resp.
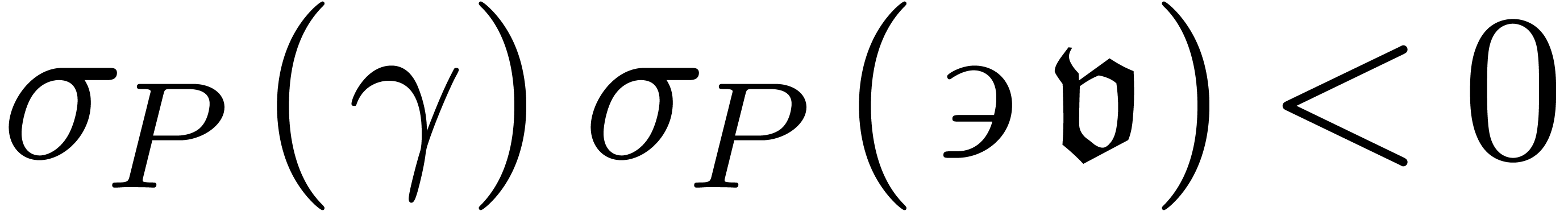 ),
),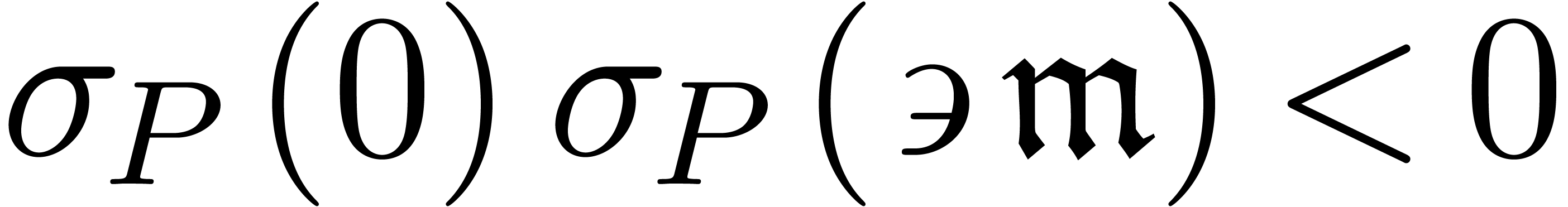 (resp.
(resp. 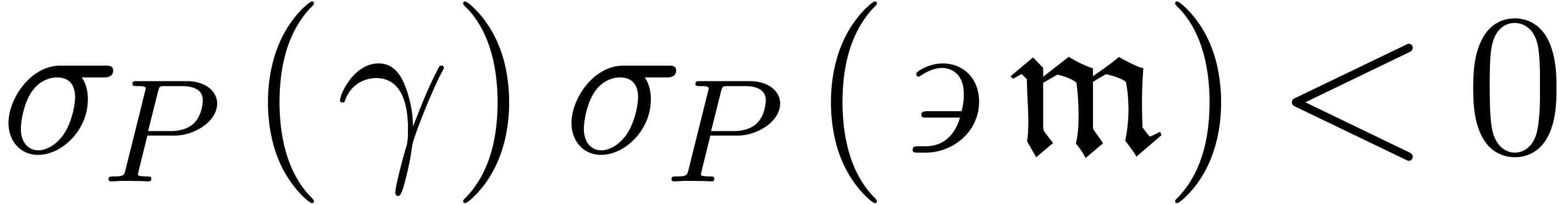 ).
).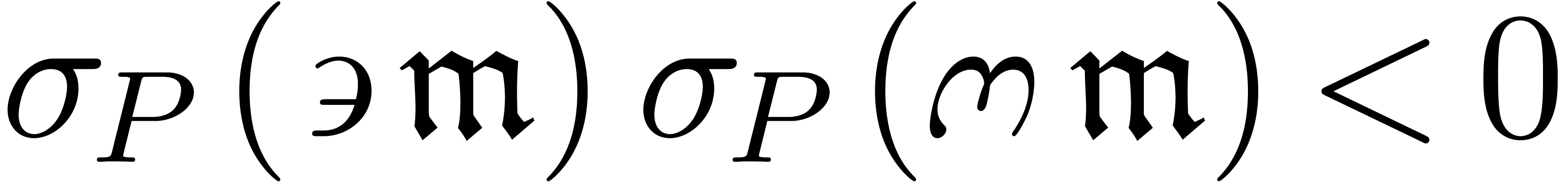 .
.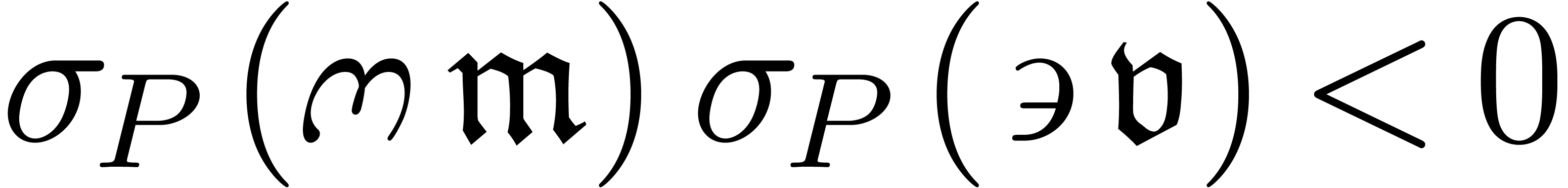 .
. in the above three cases and distinguish a last case
2d in which
in the above three cases and distinguish a last case
2d in which  .
.
 such that
such that 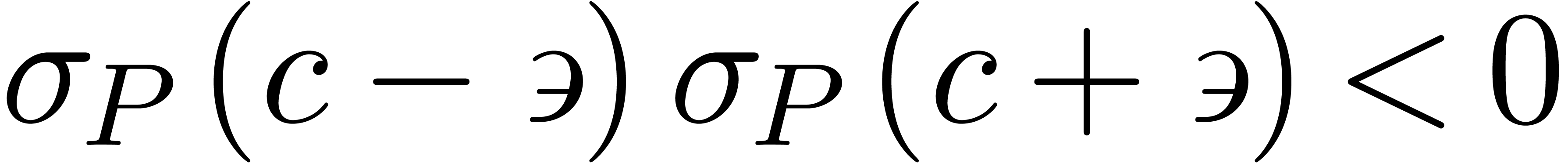 .
. we then have
we then have 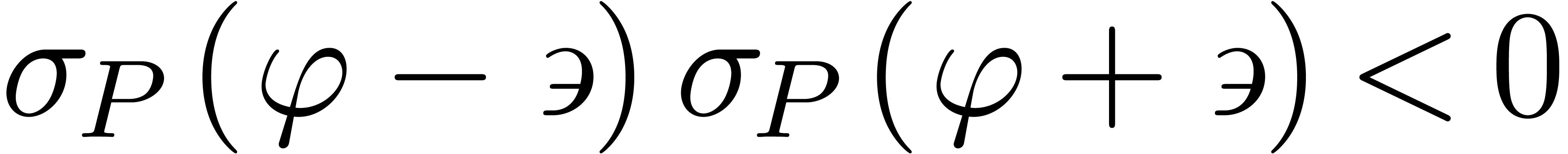 .
. such that
such that
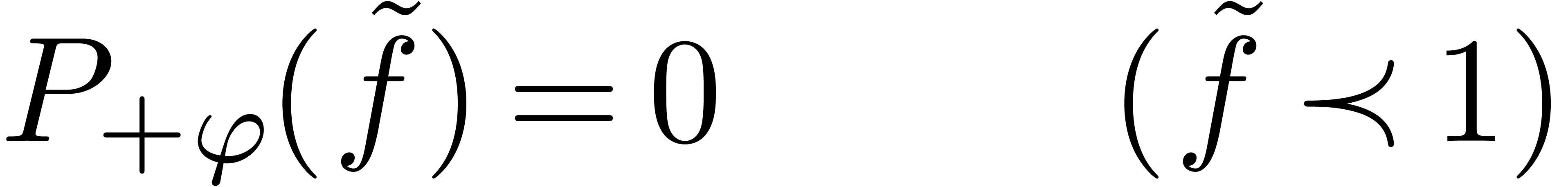
 with
with  and
and
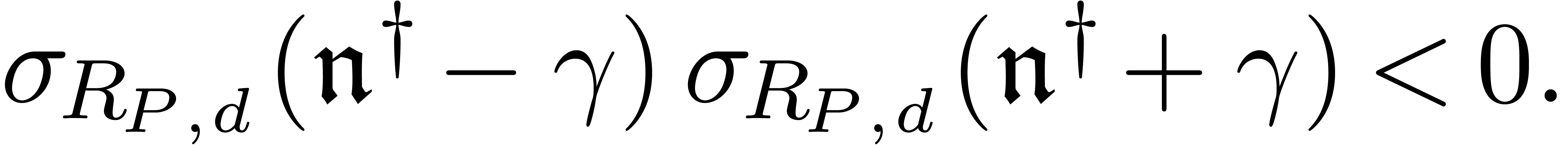
 and
and
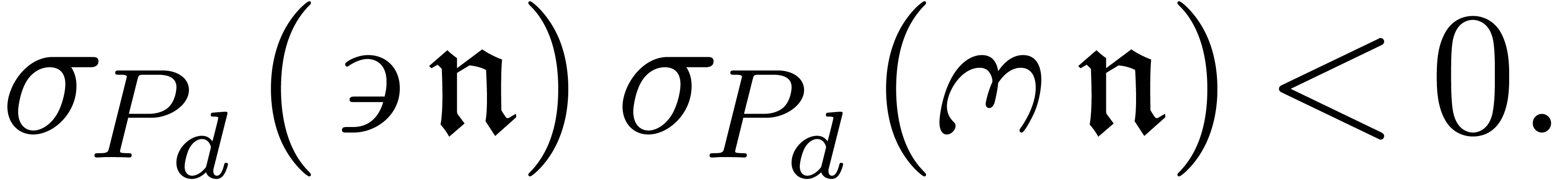
 and
and
 and
and
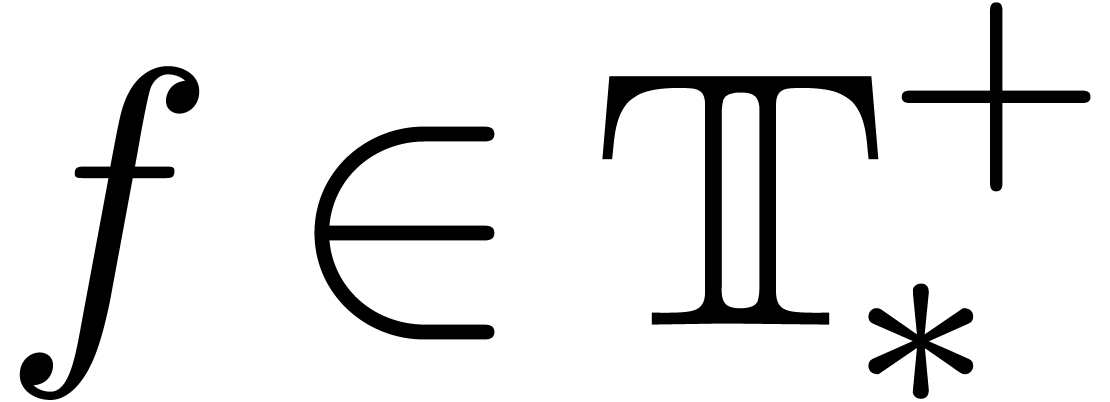 we have
we have 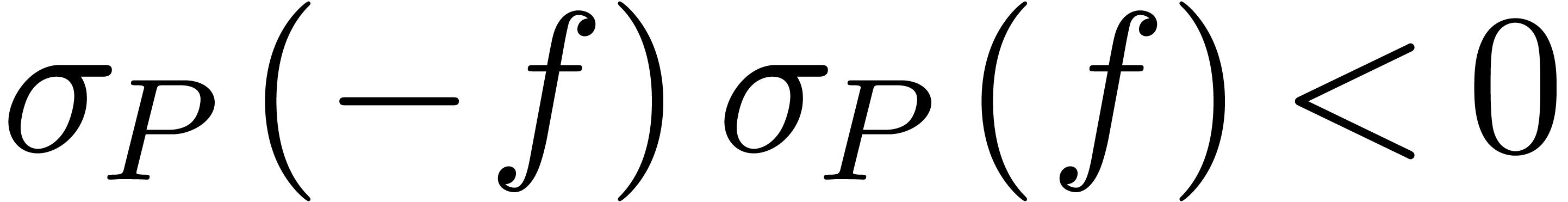 ,
, is odd in this formula. We now apply the
intermediate value theorem between
is odd in this formula. We now apply the
intermediate value theorem between  and
and