Meta-expansion of transseries |
|
| January 31, 2008 |
|
 . This work has
partially been supported by the ANR Gecko project.
. This work has
partially been supported by the ANR Gecko project.
The asymptotic behaviour of many univariate functions can only be expressed in generalized asymptotic scales, which are not merely formed of powers of a single variable. The computation of asymptotic expansions of functions in such generalized scales may lead to infinite cancellations, which complicate the design and implementation of practical algorithms. In this paper, we introduce a new heuristic technique of “meta-expansions”, which is both simple and efficient in practice, even though the answers are not guaranteed to be correct in general.
|
The asymptotic behaviour of many univariate functions can only be expressed in generalized asymptotic scales, which are not merely formed of powers of a single variable.
It was already noticed by Hardy [Har10, Har11]
that many interesting functions arising in combinatorics, number theory
or physics can be expanded w.r.t. scales formed by so
called exp-log functions or L-functions. An exp-log function is
constructed from an indeterminate  and the real
numbers using the field operations, exponentiation and logarithm. An
L-function is defined similarly, by adding algebraic functions
to our set of building blocks.
and the real
numbers using the field operations, exponentiation and logarithm. An
L-function is defined similarly, by adding algebraic functions
to our set of building blocks.
However, the class of functions which can be expanded with respect to a scale formed by exp-log functions (or L-functions) is not stable under several simple operations such as integration or functional inversion [Sha93, vdH97, MMvdD97]. More recently, exp-log functions have been generalized so as to allow for expressions with infinite sums, giving rise to the notion of transseries [DG86, É92]. In section 2, we briefly recall some of the most important definitions and properties. For more details, we refer to [vdH06c].
Given an explicit expression (such as an exp-log function), or the
solution to an implicit equation, an interesting question is how to find
its asymptotic expansion automatically. When working with respect to a
generalized asymptotic scale, such as 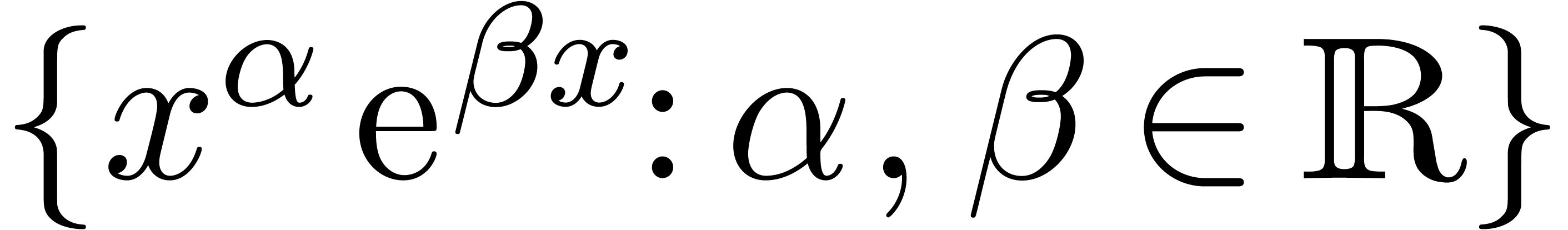 at
infinity (
at
infinity ( ), even simple
expressions can lead to infinite cancellations:
), even simple
expressions can lead to infinite cancellations:
In many cases, the detection of infinite cancellations can be reduced to the zero-test problem in a suitable class of functions [Sha90, GG92, RSSvdH96, Sal91, vdH97].
However, zero-test problems are often very hard. In the case of exp-log functions, a complete zero-test is only known if Schanuel's conjecture holds [Ric97, vdH98, vdHS06, Ric07]. If we want to expand more general expressions or more general solutions to differential or functional equations, the corresponding zero-test problem tends to get even harder. Consequently, the zero-testing tends to complicate the design of mathematically correct algorithms for more general asymptotic expansions. From the practical point of view, the implementation of robust zero-tests also requires a lot of work. Moreover, mathematically correct zero-tests tend to monopolize the execution time.
In this paper, we will investigate an alternative, more heuristic approach for the computation of asymptotic expansions. We will adopt a similar point of view as a numerical analyst who conceives a real number as the limit of a sequence of better and better approximations. In our case, the asymptotic expansion will be the limit of more and more precise polynomial approximations, where the monomials are taken in the asymptotic scale. As is often the case in numerical analysis, our approach will only be justified by informal arguments and the fact that it seems to work very well in practice.
Besides the analogy with numerical analysis there are a few additional
interesting points which deserve to be mentioned. First of all, a finite
sequence 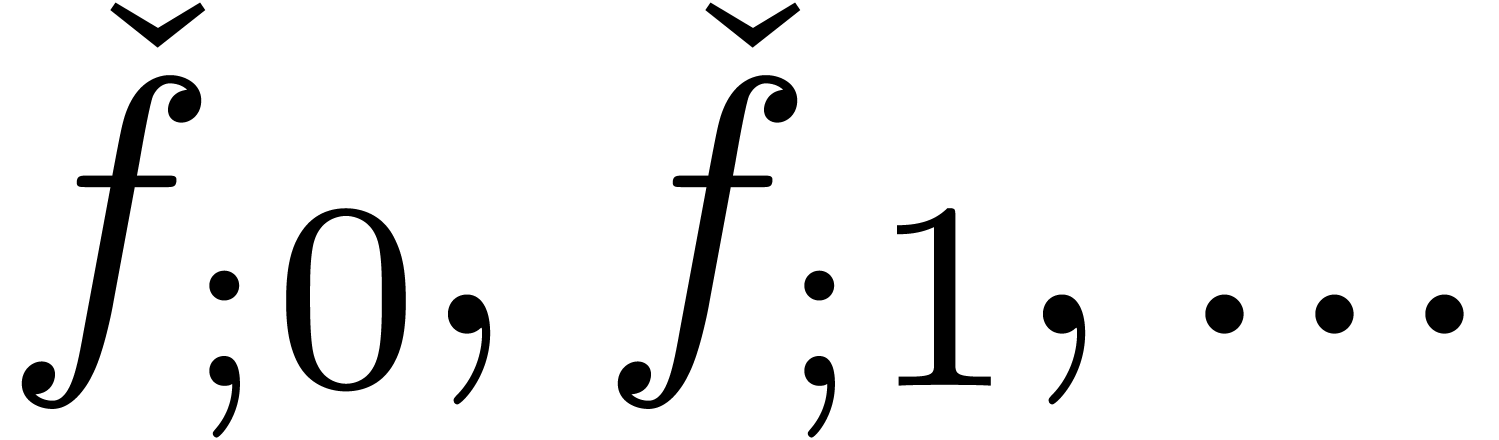 of better and better approximations
gives rise to a second sequence
of better and better approximations
gives rise to a second sequence 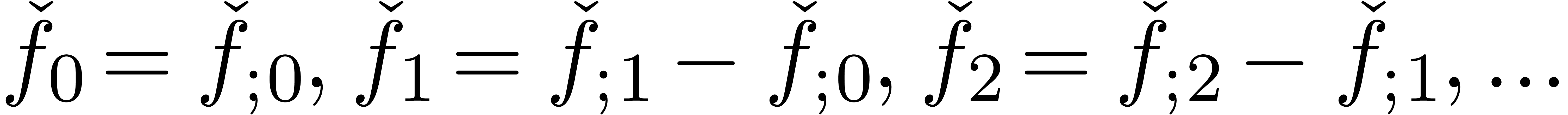 ,
which can itself be encoded by a generating series
,
which can itself be encoded by a generating series
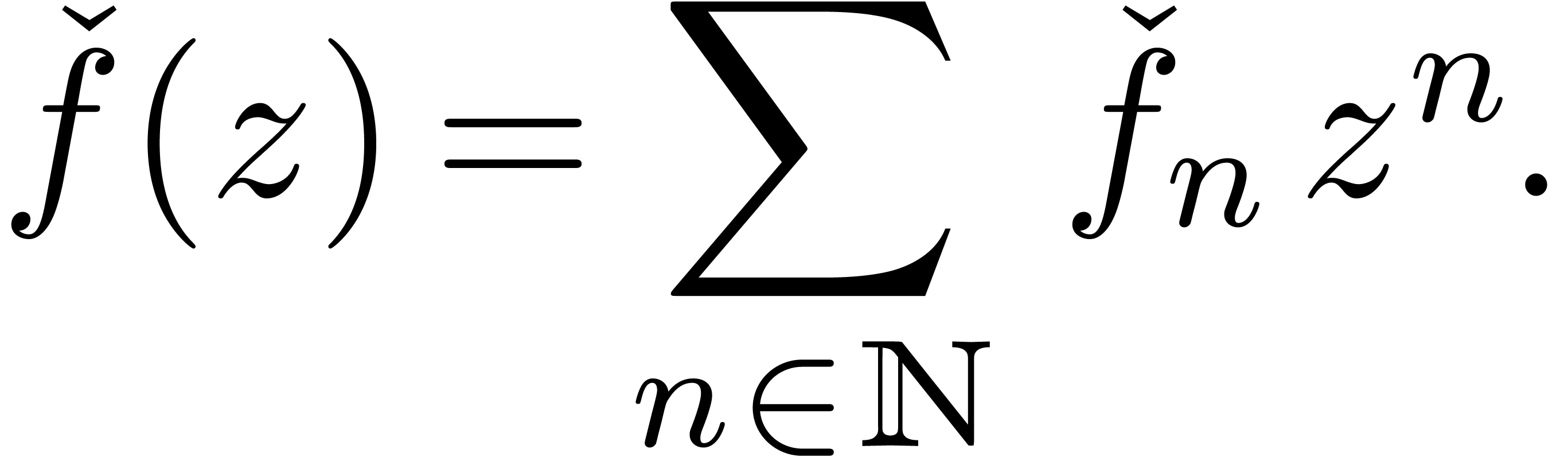
The computation of the expansion of 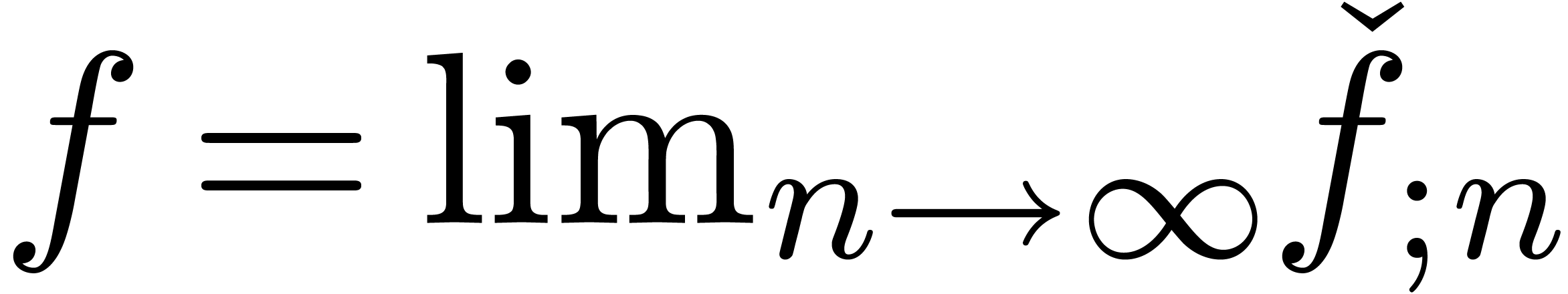 can thus be
re-interpreted as the computation of the expansion of
can thus be
re-interpreted as the computation of the expansion of 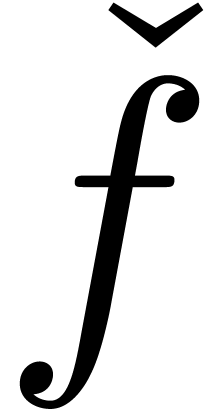 , which we therefore regard as the
“meta-expansion” of
, which we therefore regard as the
“meta-expansion” of  .
This technique will be detailed in section 3. Additional
complications arise in the context of transseries, because the elements
of the asymptotic scale are themselves exponentials of other
transseries. The computation of meta-expansions for transseries will be
detailed in sections 4 and 5.
.
This technique will be detailed in section 3. Additional
complications arise in the context of transseries, because the elements
of the asymptotic scale are themselves exponentials of other
transseries. The computation of meta-expansions for transseries will be
detailed in sections 4 and 5.
A second interesting aspect of meta-expansions is that we may operate on
the meta-expansion without changing the underlying expansion. In a
complex computation involving lots of auxiliary series, this provides
some meta-control to the user. For instance, some subexpressions can be
computed with more accuracy (or less accuracy) and one can focus on a
specific range of terms. Techniques for the acceleration of convergence
play a similar role in numerical analysis [PTVF07, Section
5.3]. Another operation, called “stabilization”, removes
those terms in the expansions 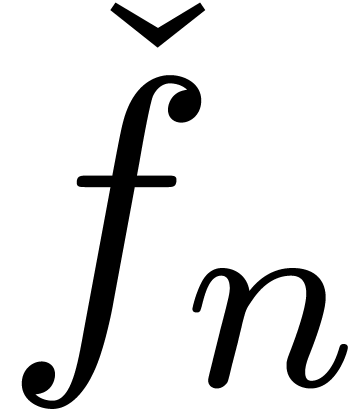 which change at
every few steps. After stabilization, we tend to compute only terms
which occur in the final expansion of
which change at
every few steps. After stabilization, we tend to compute only terms
which occur in the final expansion of  ,
even though they usually appear in a different order. In particular,
stabilization gives rise to a heuristic zero-test. Meta-operations on
meta-expansions will be discussed in section 6.
,
even though they usually appear in a different order. In particular,
stabilization gives rise to a heuristic zero-test. Meta-operations on
meta-expansions will be discussed in section 6.
One motivation behind the present paper was its application to the
asymptotic extrapolation of sequences by transseries [vdH06a].
This application requires the computation of discrete sums and products
of transseries. In section 7, we have included a small
demonstration of our current implementation in the
For the purpose of this application, we have mainly considered univariate transseries expansions so far. Of course, the approach of our paper generalizes to expansions in several variables. A natural next step for future developments would be to implement the Newton polygon method for rather general functional equations. Another interesting question is how to re-incorporate theoretically correct zero-tests in our mechanism and how much we really sacrifice when using our heuristic substitute. A few ideas in these directions will be given in section 8, some of which actually go back to [vdH94].
In this section, we briefly survey some basic properties of transseries. For more details, we refer to [vdH06c, vdH97, É92, MMvdD97, MMvdD99].
Let  be a ring and
be a ring and  a
commutative monomial monoid which is partially ordered by an
asymptotic dominance relation
a
commutative monomial monoid which is partially ordered by an
asymptotic dominance relation  .
A subset
.
A subset 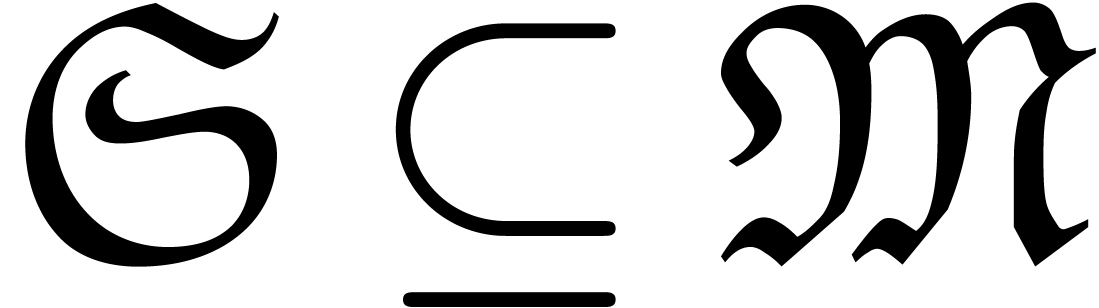 is said to be well-based if it
well-quasi-ordered [Pou85, Mil85] for the
opposite ordering of
is said to be well-based if it
well-quasi-ordered [Pou85, Mil85] for the
opposite ordering of  and grid-based if
it satisfies a bound of the form
and grid-based if
it satisfies a bound of the form
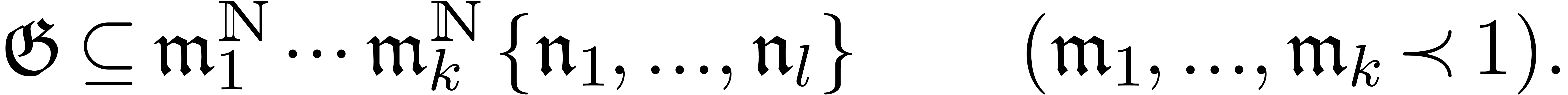 |
(1) |
A well-based power series is a formal sum 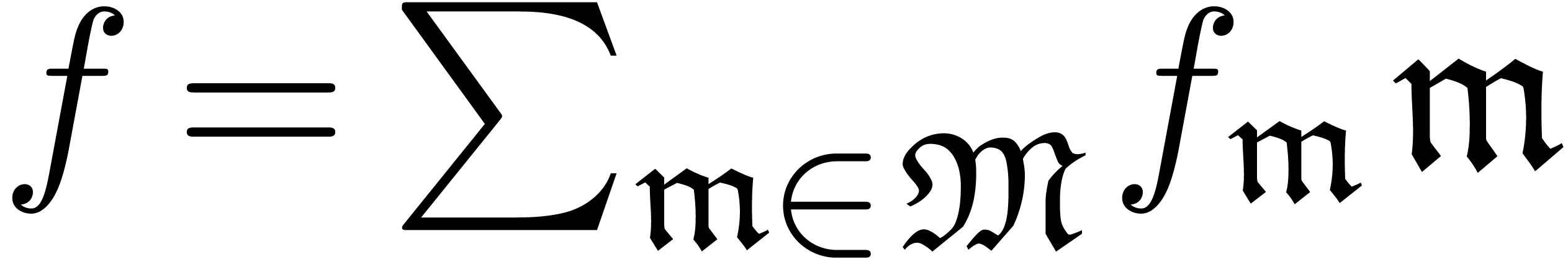 , whose support
, whose support 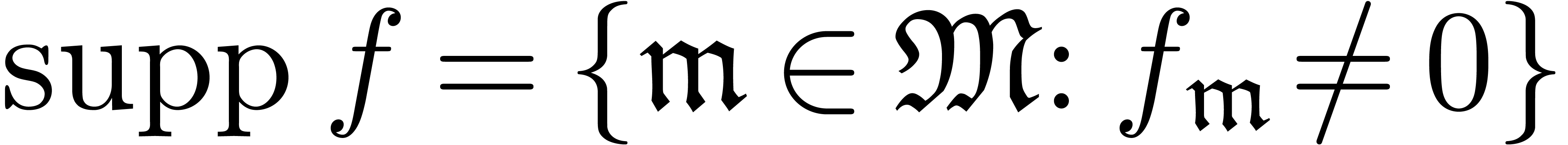 is
well-based. It is classical [Hah07, Hig52]
that the set
is
well-based. It is classical [Hah07, Hig52]
that the set 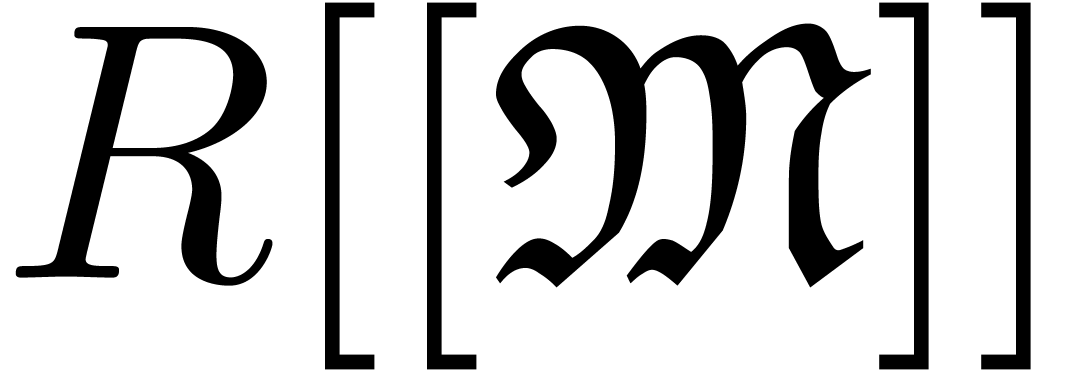 of well-based power series forms a
ring. The subset
of well-based power series forms a
ring. The subset 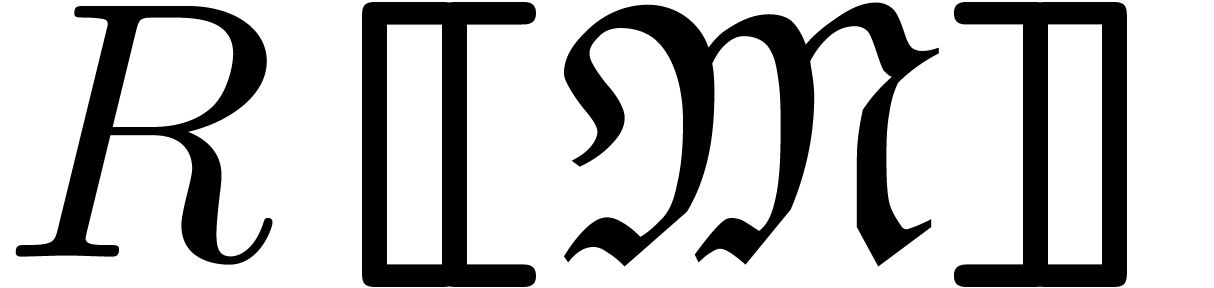 of grid-based power series
(i.e. with grid-based support) forms a subring of
of grid-based power series
(i.e. with grid-based support) forms a subring of 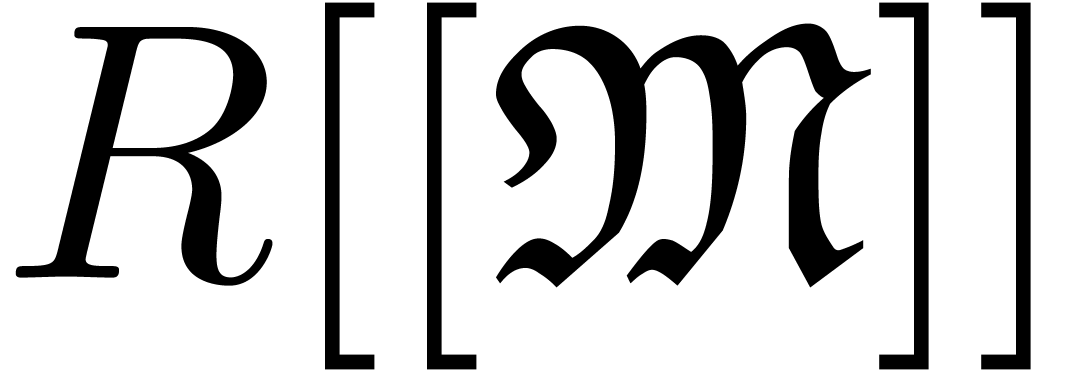 .
.
Example
with 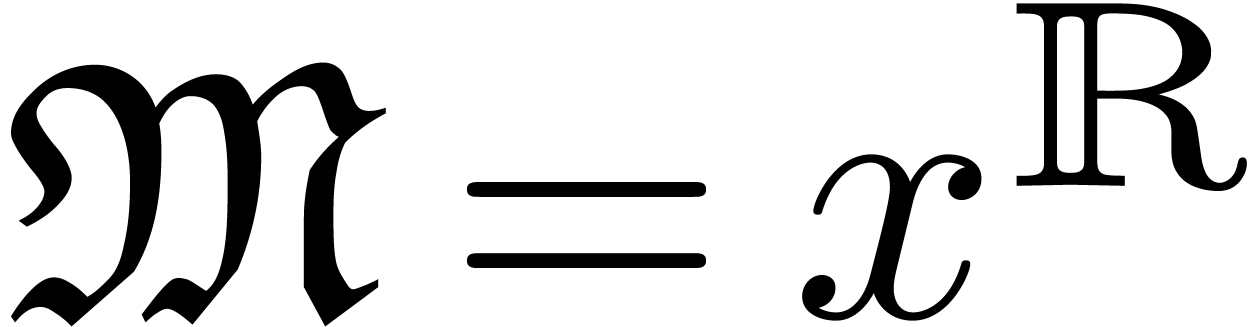 for
for  (i.e.
(i.e. 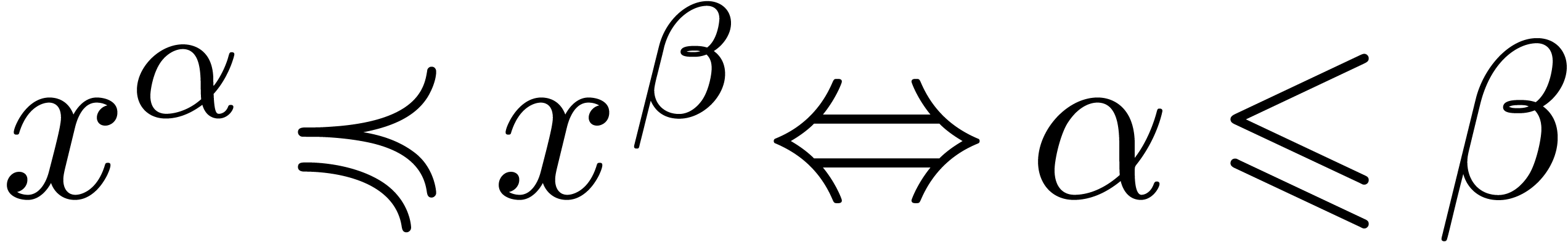 ). Then
the first series is grid-based and the second one only well-based.
). Then
the first series is grid-based and the second one only well-based.
A family 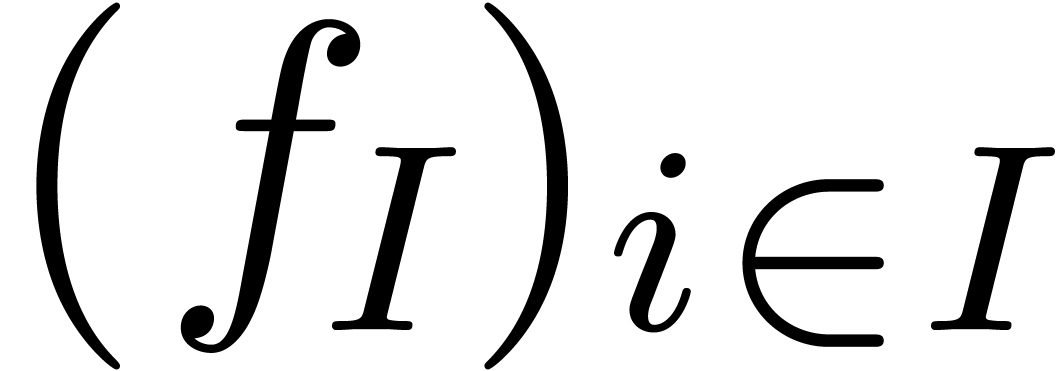 of series in
of series in 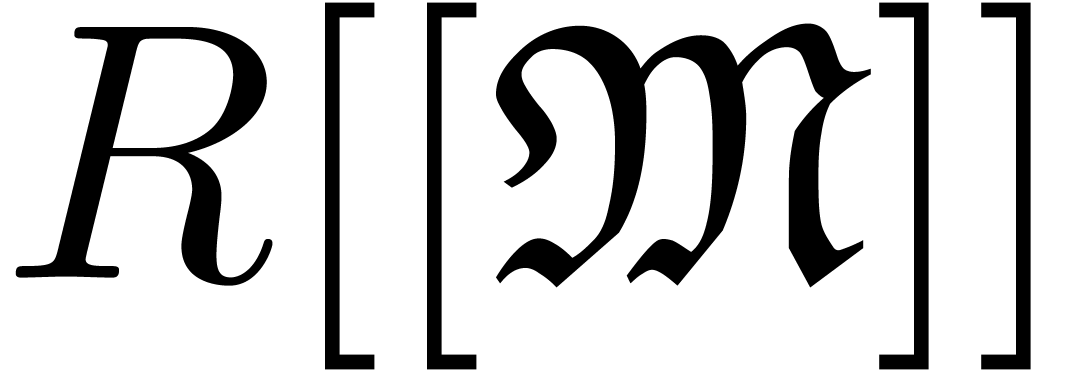 is
said to be well-based if
is
said to be well-based if 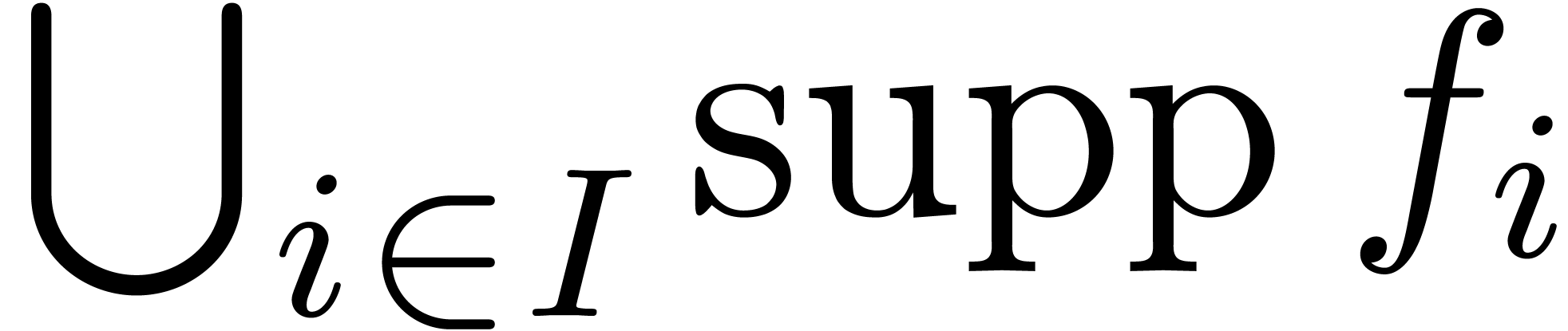 is well-based
and
is well-based
and 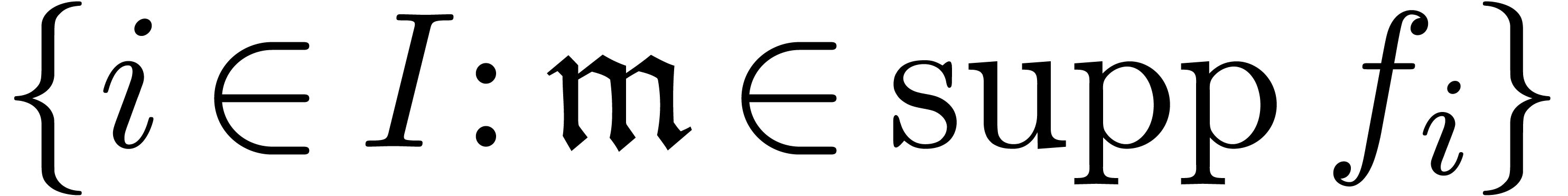 is finite for every
is finite for every 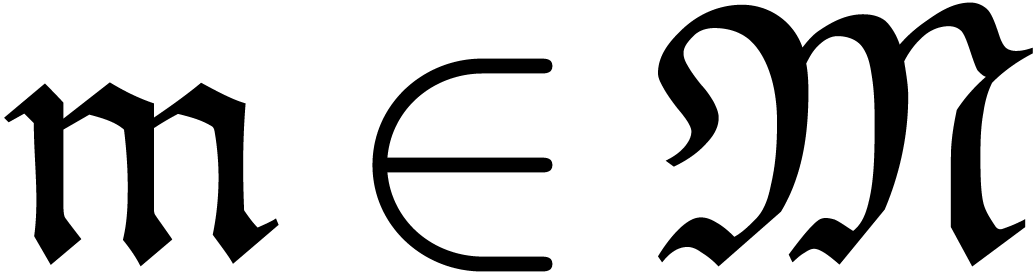 . In that case, the sum
. In that case, the sum 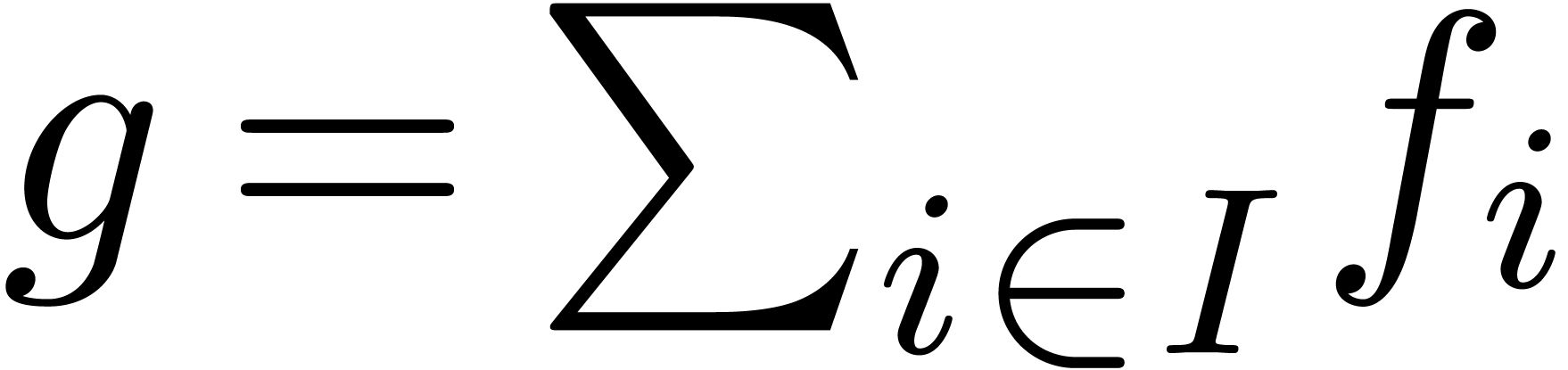 with
with
 is again in
is again in 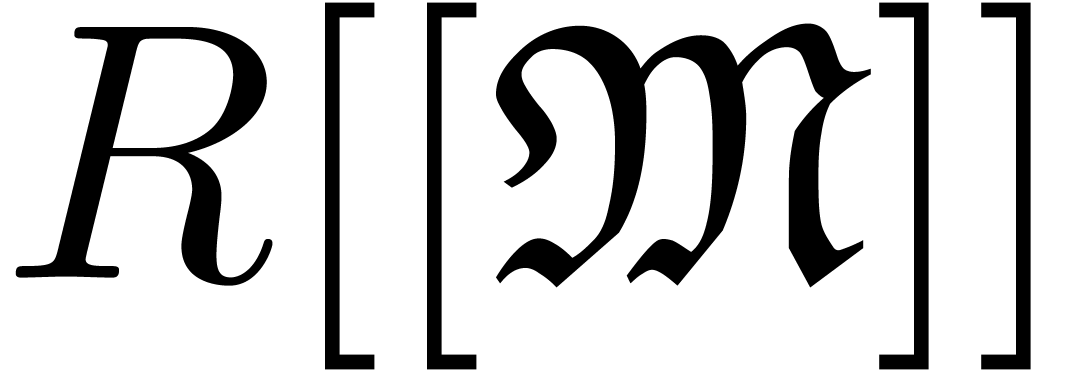 .
A linear mapping
.
A linear mapping 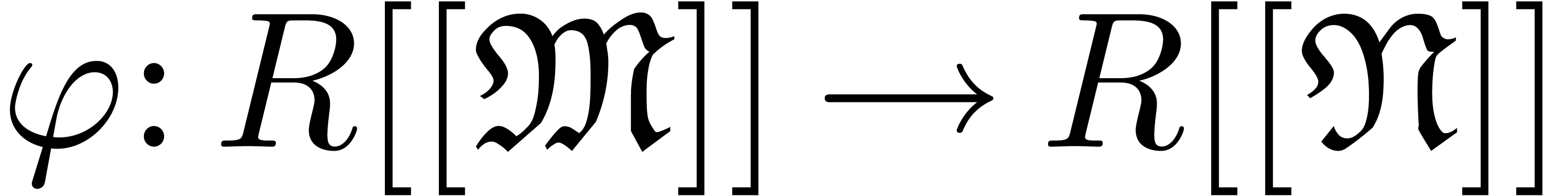 is said to be strong
it preserves well-based summation. Grid-based families and the
corresponding notion of strong linearity are defined similarly.
is said to be strong
it preserves well-based summation. Grid-based families and the
corresponding notion of strong linearity are defined similarly.
In the case when  is a field and
is a field and  is totally ordered, then
is totally ordered, then 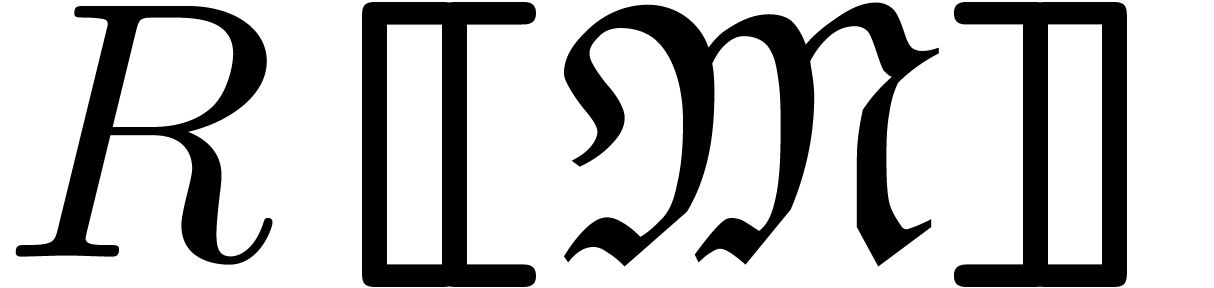 and
and 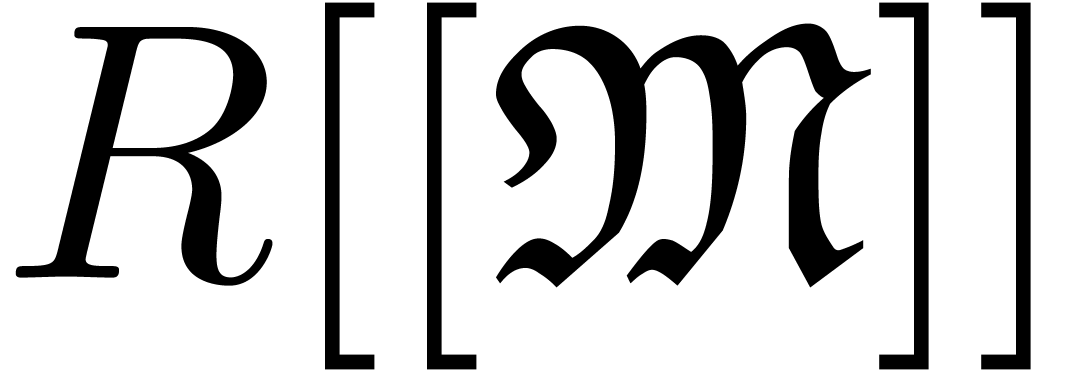 are also fields. Furthermore, any non-zero
are also fields. Furthermore, any non-zero 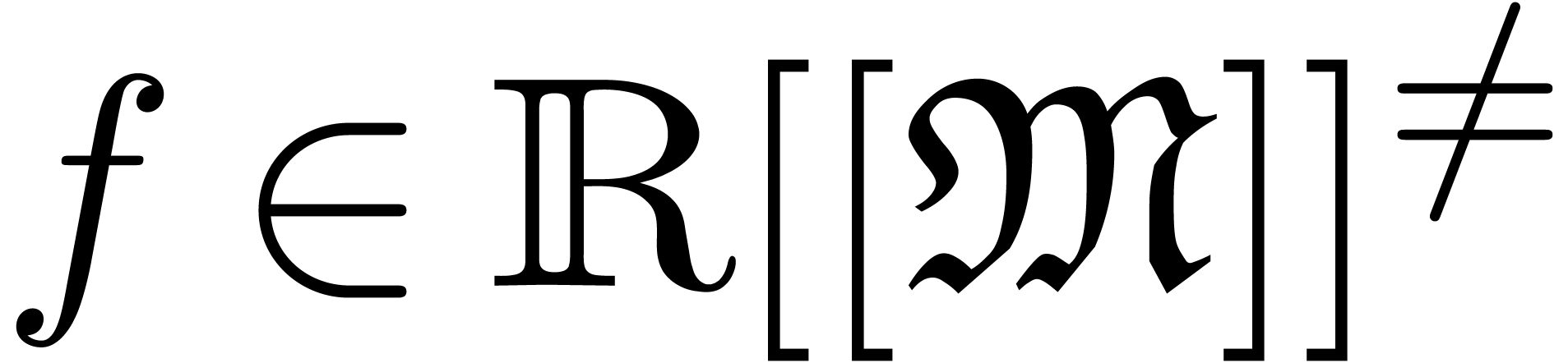 admits a unique dominant monomial
admits a unique dominant monomial 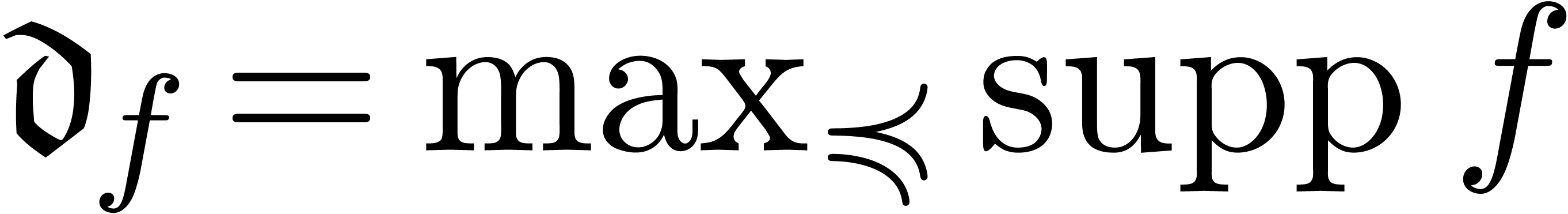 with
corresponding dominant coefficient
with
corresponding dominant coefficient 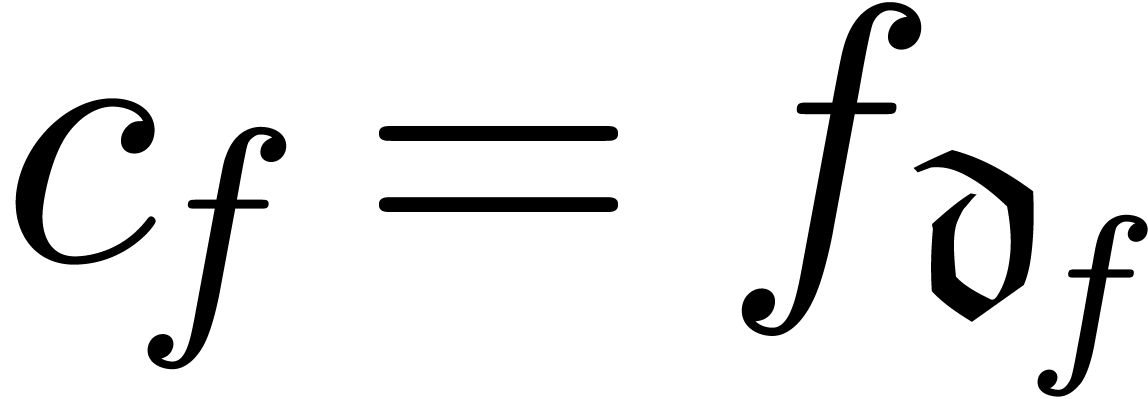 and relative remainder
and relative remainder 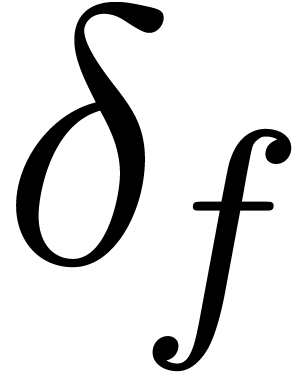 such that
such that 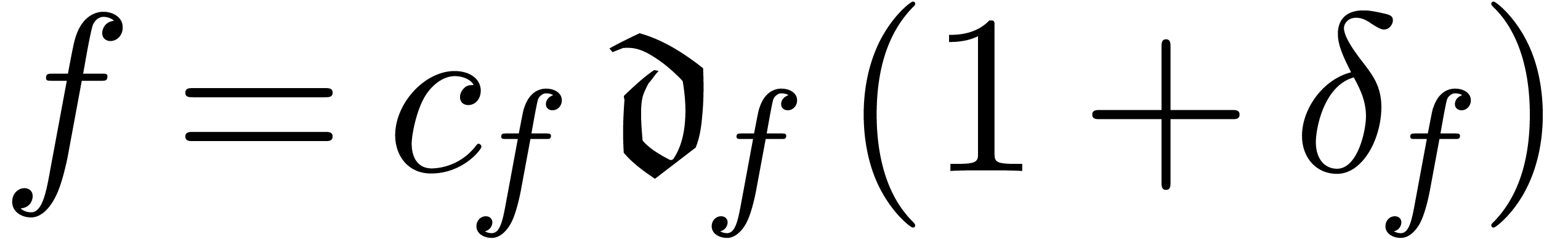 . We call
. We call 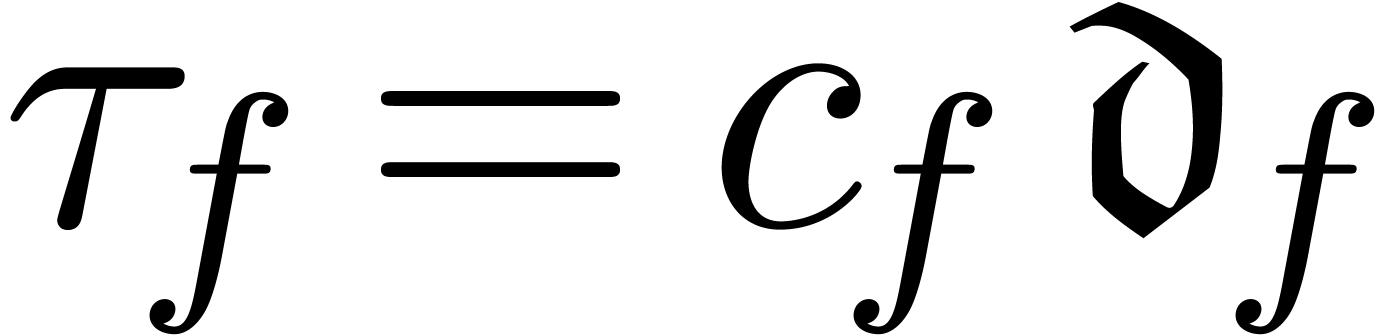 the dominant term of
the dominant term of  and define
and define 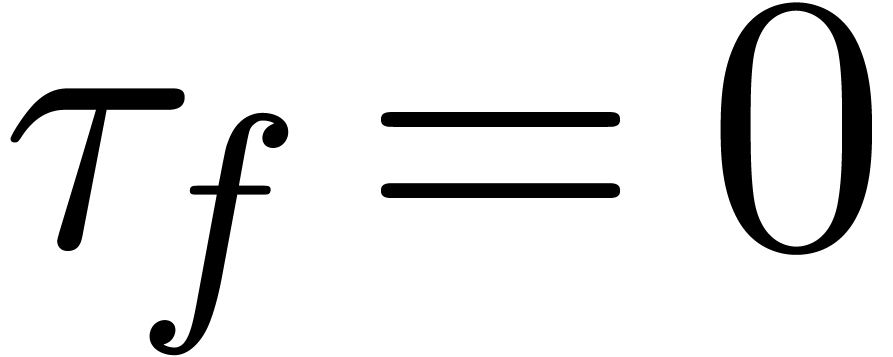 in the case when
in the case when 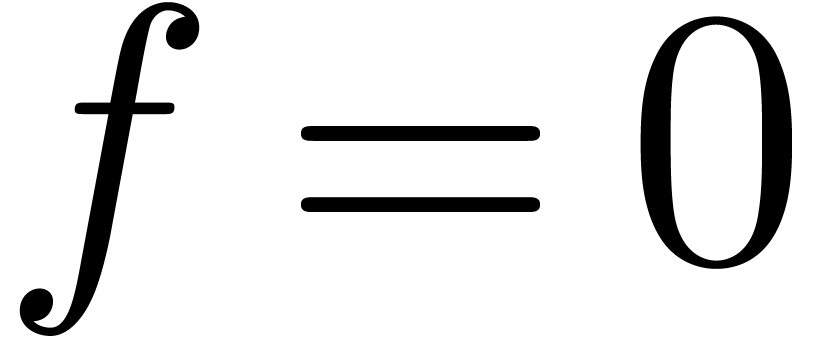 .
The series
.
The series  also admits a canonical
decomposition
also admits a canonical
decomposition
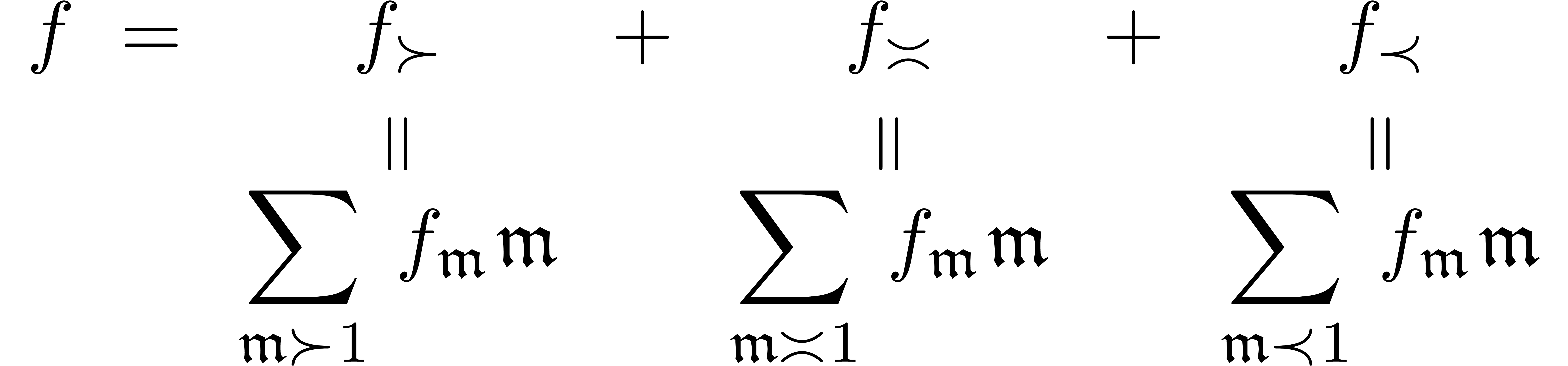
Here  just means that
just means that 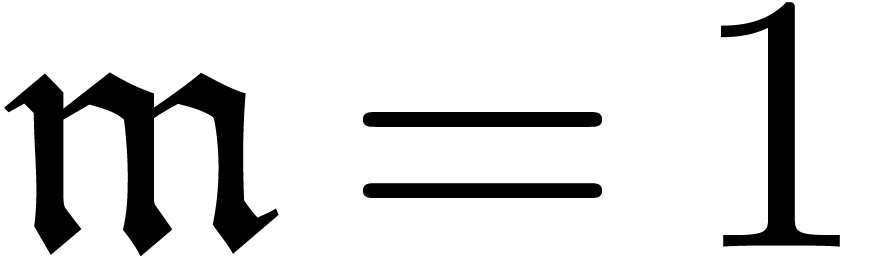 ; more generally,
; more generally,  .
If
.
If  is grid-based, then so are
is grid-based, then so are 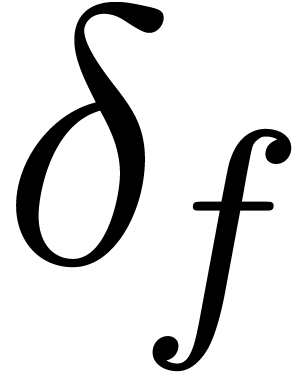 ,
,  and
and  . If
. If  is actually an
ordered field, then so are
is actually an
ordered field, then so are 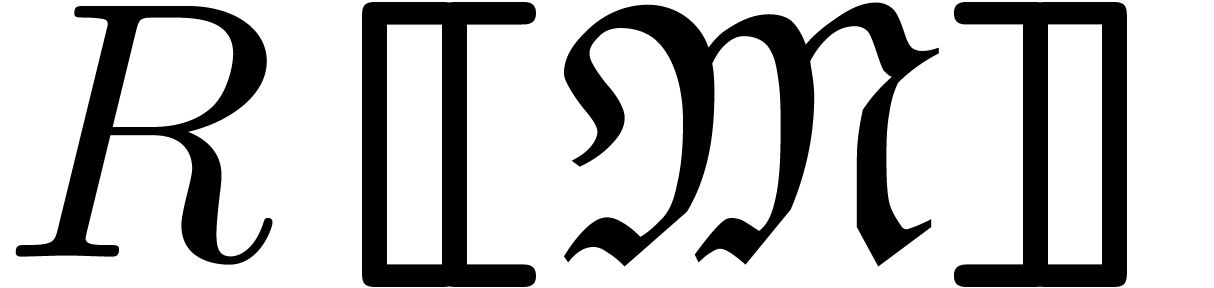 and
and 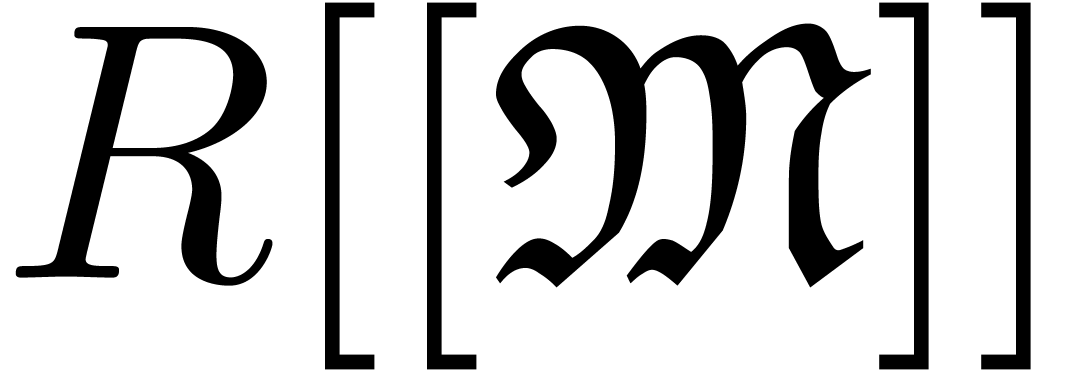 , by taking
, by taking  for all
for all
 .
.
The field  of grid-based transseries is a field
of the form
of grid-based transseries is a field
of the form  with additional operators
with additional operators 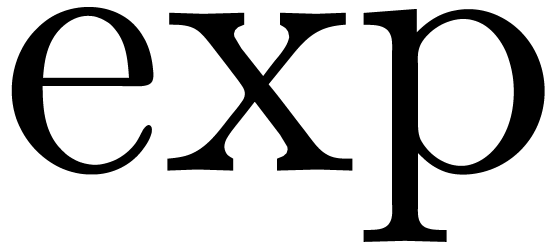 and
and 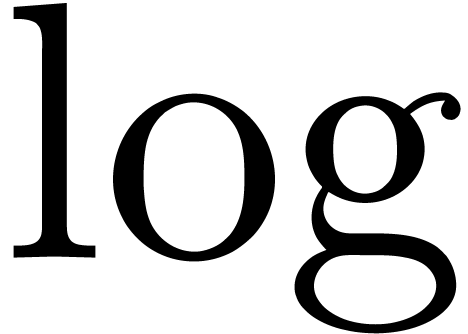 . The set
of transmonomials
. The set
of transmonomials  coincides with the
set
coincides with the
set 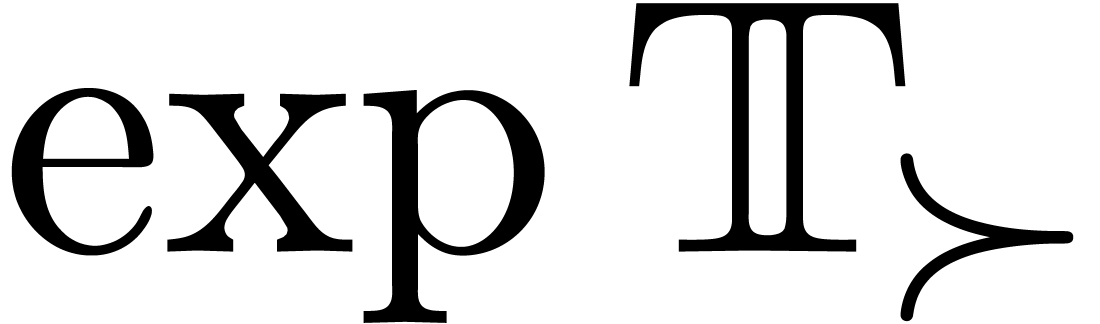 of exponentials of transseries
of exponentials of transseries  with
with 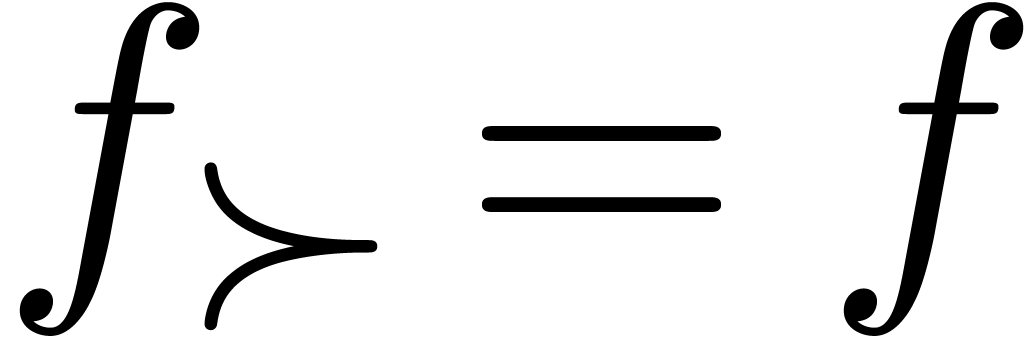 . More
generally, we have
. More
generally, we have
for any 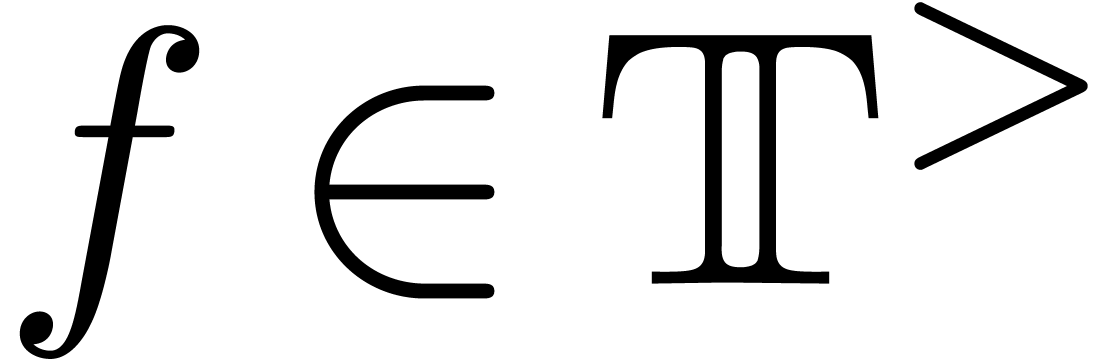 (i.e.
(i.e.  ) and
) and
The construction of  is detailed in [vdH06c,
Chapter 4]. The construction of fields of well-based transseries is a
bit more delicate [DG86, vdH97, Sch01],
because one cannot simultaneously ensure stability under exponentiation
and infinite summation. However, there is a smallest such field
is detailed in [vdH06c,
Chapter 4]. The construction of fields of well-based transseries is a
bit more delicate [DG86, vdH97, Sch01],
because one cannot simultaneously ensure stability under exponentiation
and infinite summation. However, there is a smallest such field 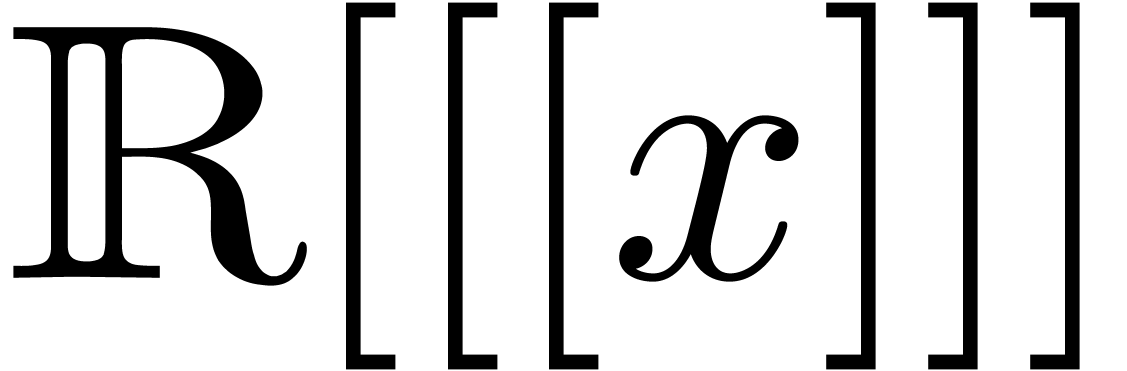 , if we exclude transseries with
arbitrarily nested logarithms or exponentials, such as
, if we exclude transseries with
arbitrarily nested logarithms or exponentials, such as 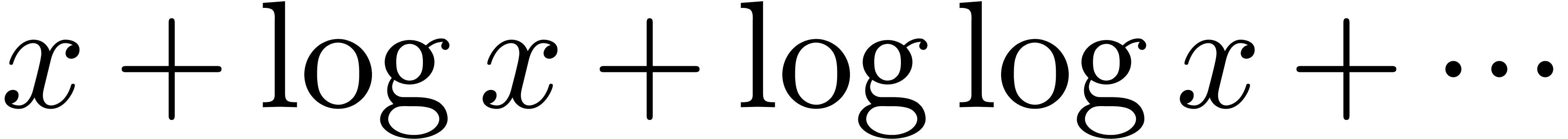 .
.
Let  be one of the fields
be one of the fields  or
or 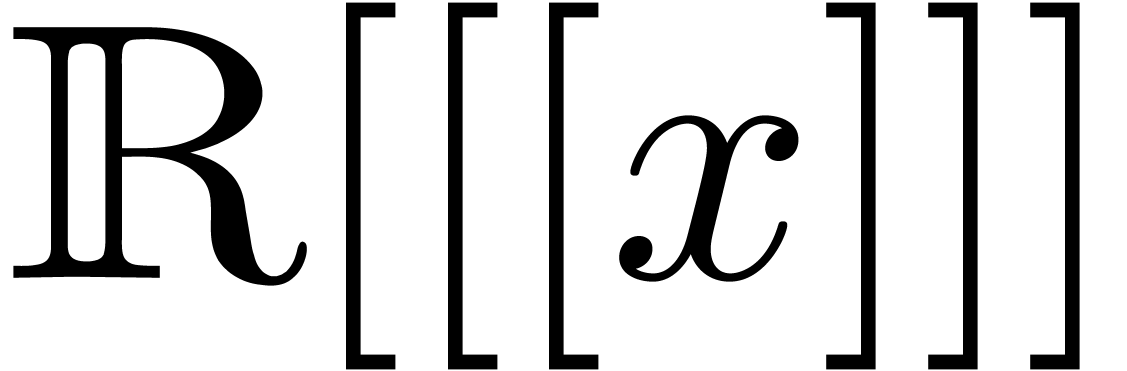 . Then
. Then  admits a lot of additional structure:
admits a lot of additional structure:
There exists a unique strong derivation  with
with
 ,
, 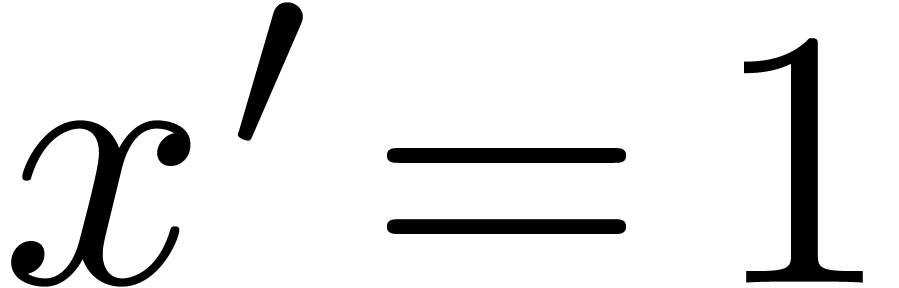 and
and 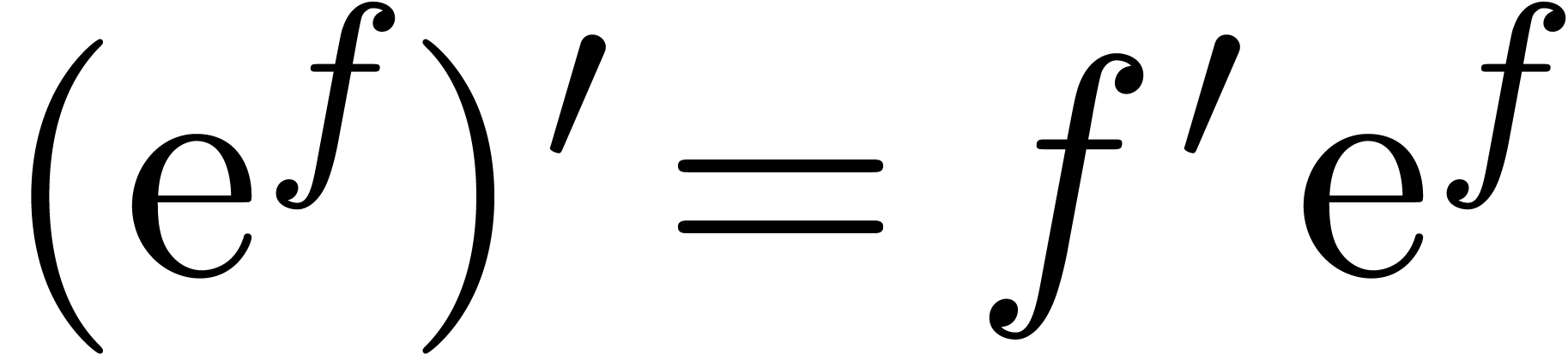 for all
for all 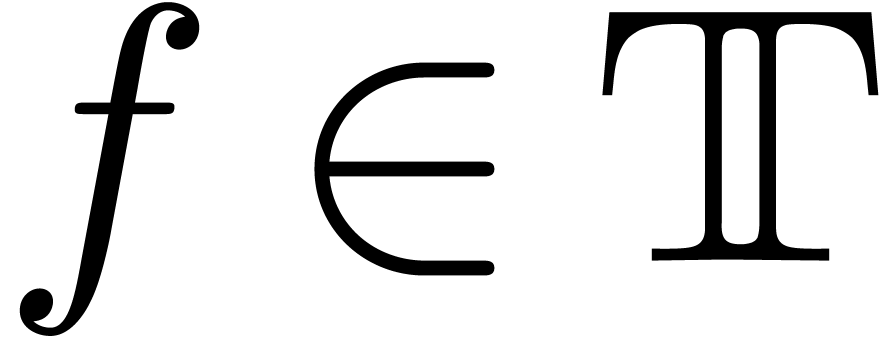 .
.
There exists a unique strong integration 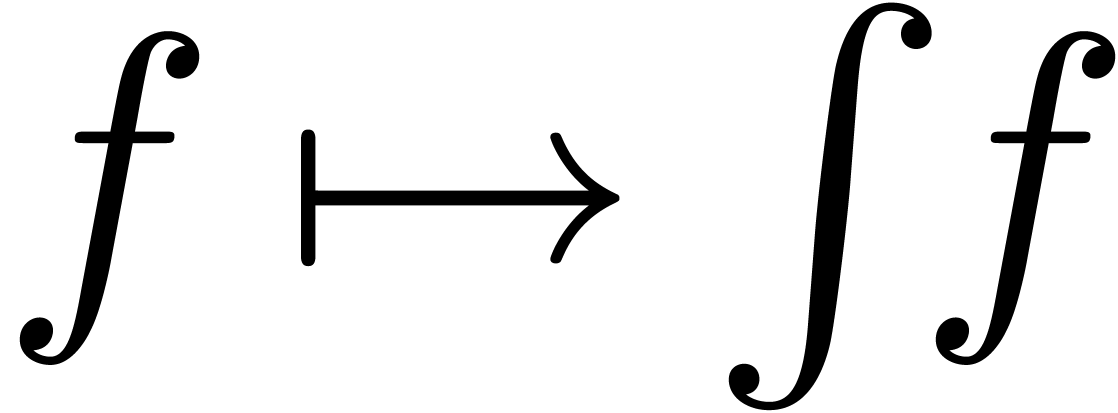 with
with 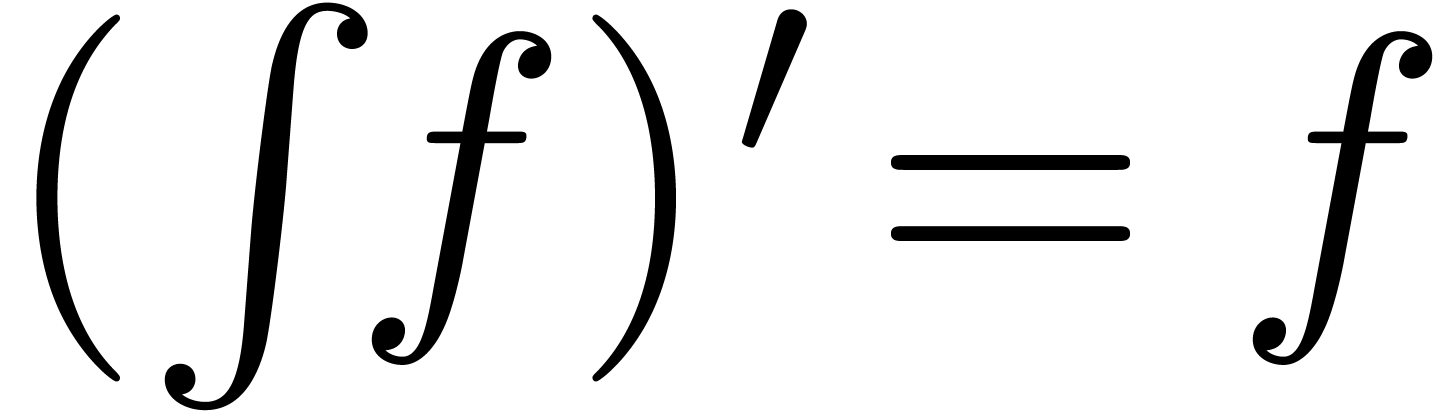 and
and  for all
for all
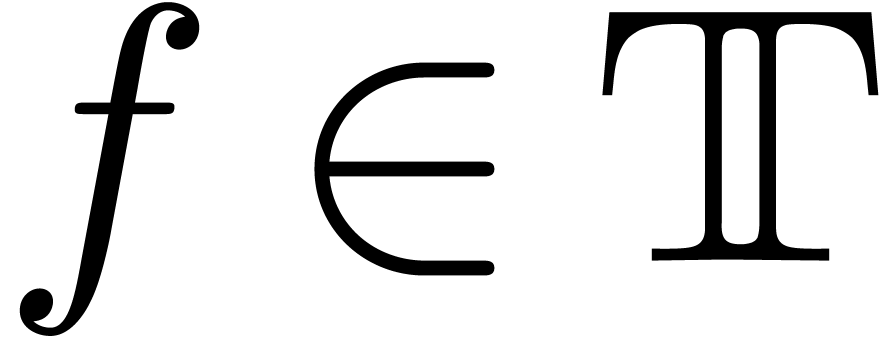 .
.
For any positive, infinitely large transseries  , there exists a unique strongly linear
right composition
, there exists a unique strongly linear
right composition 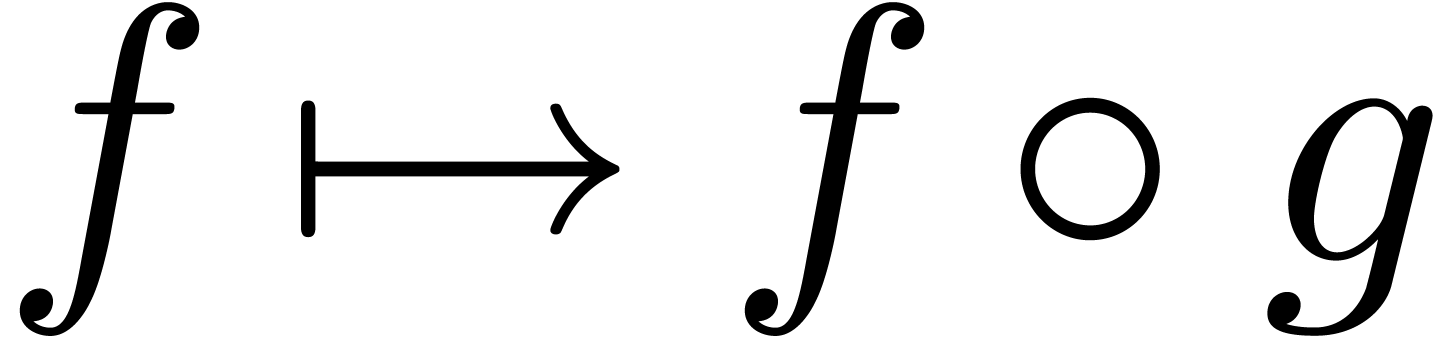 , with
, with
 (
( ),
),
 and
and 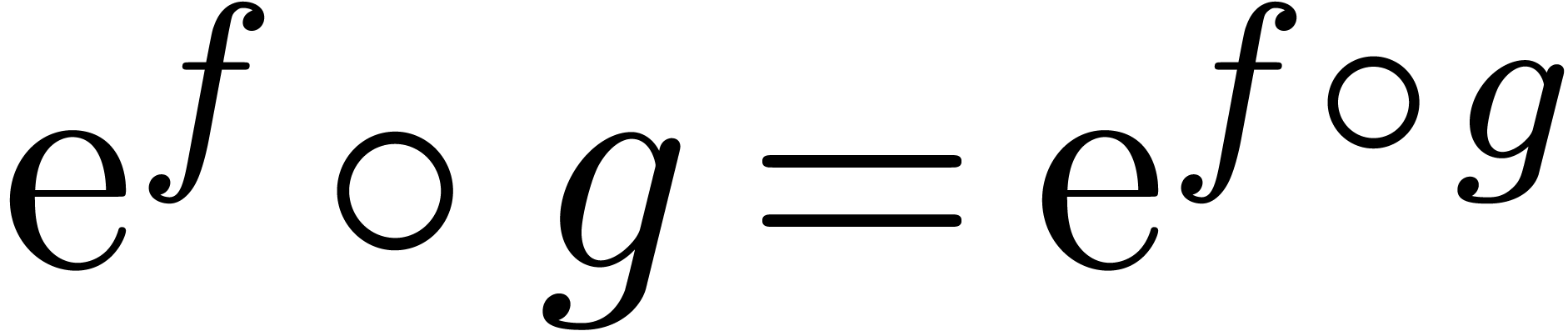 .
.
Each  admits a unique functional inverse
admits a unique functional inverse
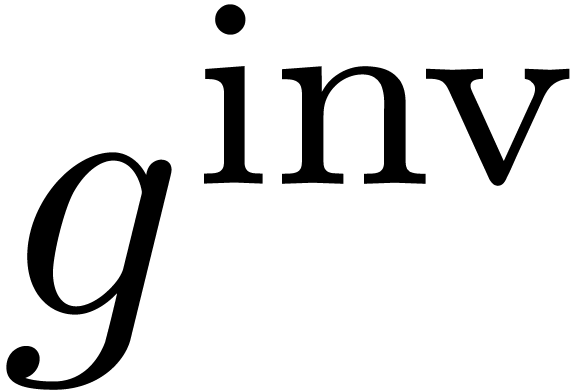 .
.
 is real closed. Even better: given a
differential polynomial
is real closed. Even better: given a
differential polynomial 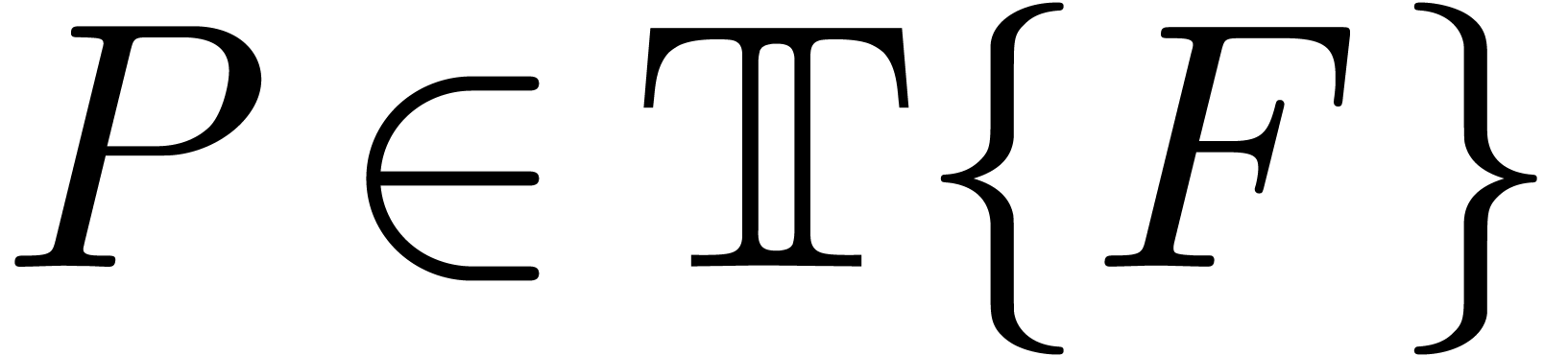 and
and 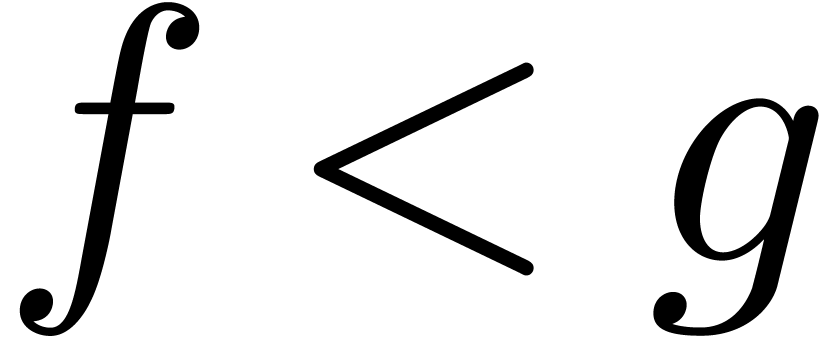 in
in  with
with 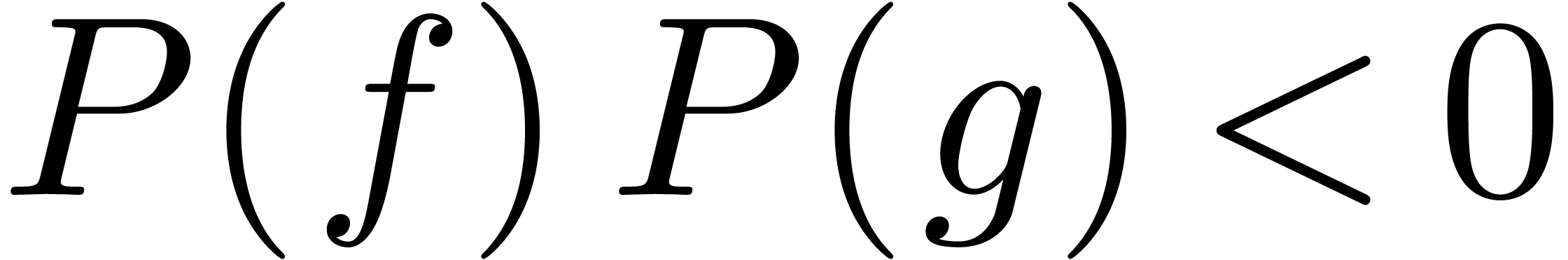 ,
there exists an
,
there exists an 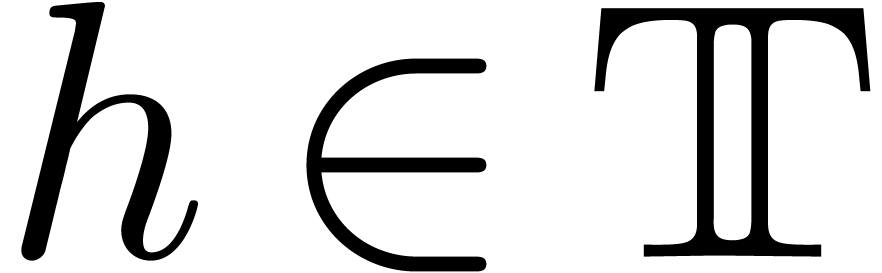 with
with 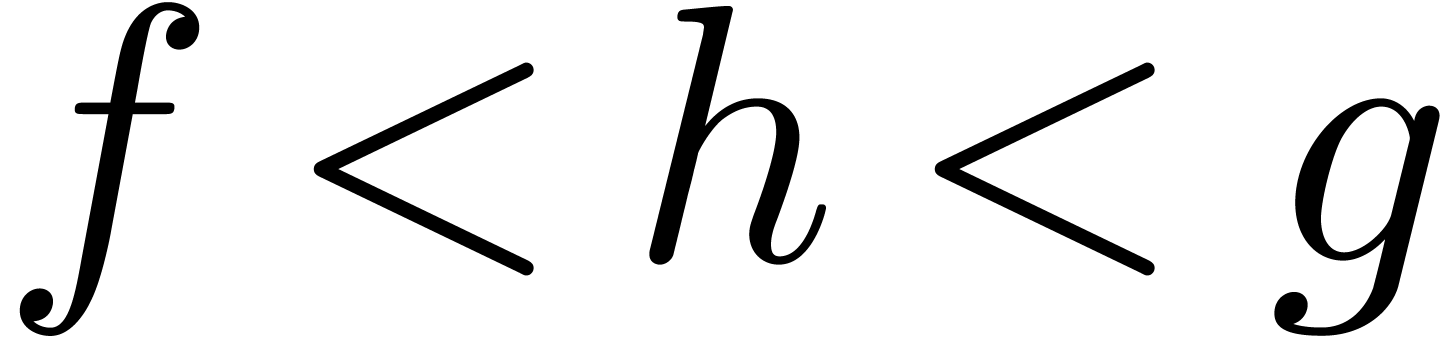 and
and 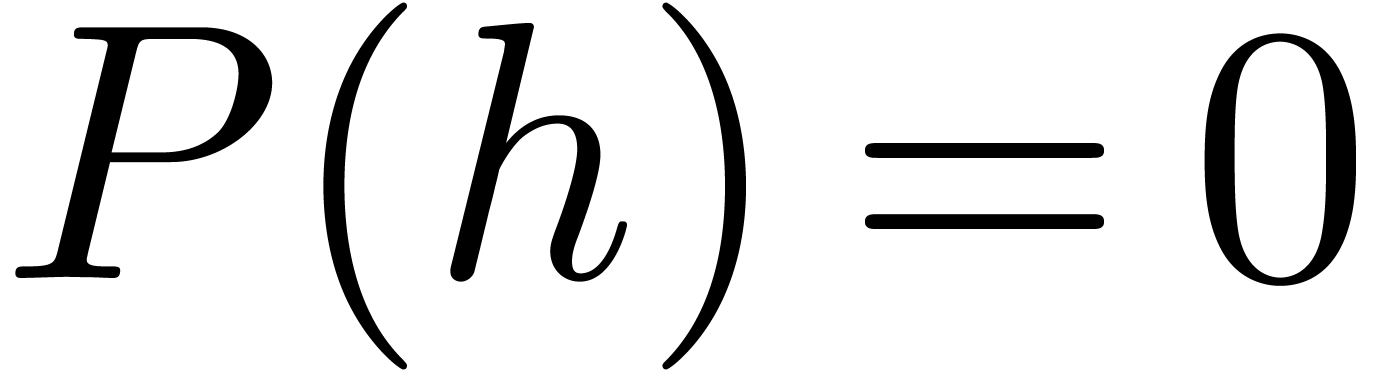 .
.
Furthermore, there exist very general implicit function theorems [vdH01, vdH06c], which can be used in order to solve functional equations, when put in a suitable normal form.
The field  is highly non-Archimedean. For what
follows it will be introduce the asymptotic flatness relation
is highly non-Archimedean. For what
follows it will be introduce the asymptotic flatness relation
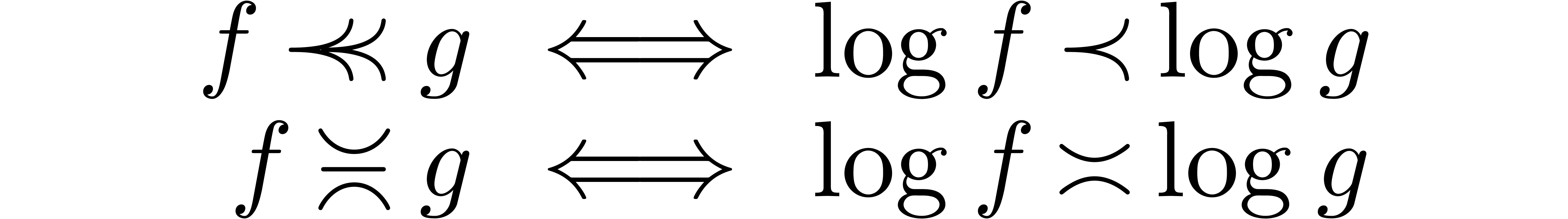
For  , one has
, one has  if and only if
if and only if  for all
for all 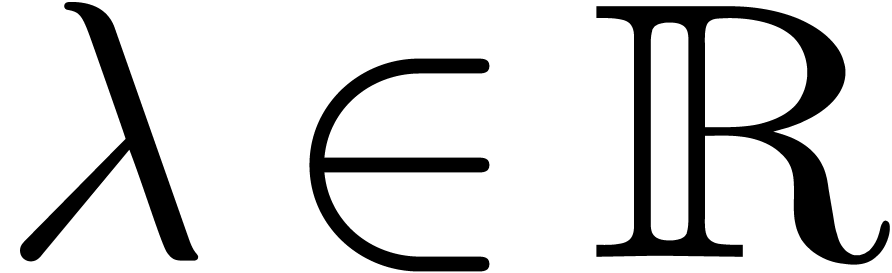 .
.
The intuitive idea behind meta-expansion is that, from the computational point of view, series usually arise as a sequence of successive approximations of an interesting object. We will make this simple idea operational by taking the approximations to be polynomials. In order to avoid repetitions, we will systematically work in the well-based setting; it is easy to adapt the definitions to the grid-based case.
Let 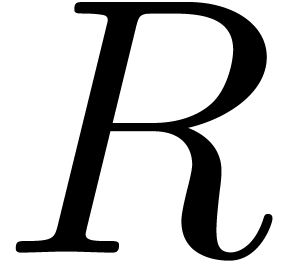 be an effective ring and
be an effective ring and  an effective monomial monoid. Recall that
an effective monomial monoid. Recall that 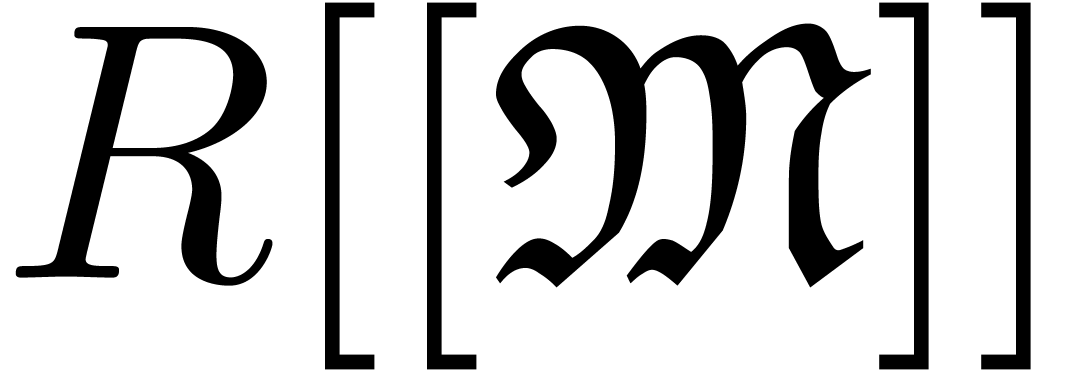 stands
for the ring of well-based generalized power series and let
stands
for the ring of well-based generalized power series and let 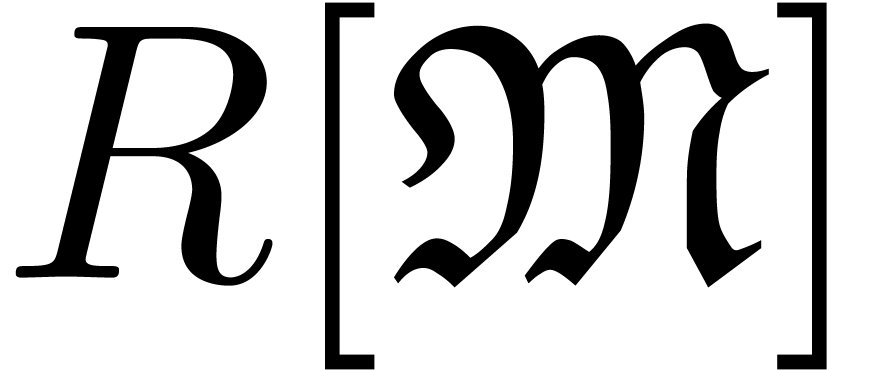 be the corresponding set of polynomials (i.e.
series with finite support). We define an expander to be a
computable well-based sequence
be the corresponding set of polynomials (i.e.
series with finite support). We define an expander to be a
computable well-based sequence 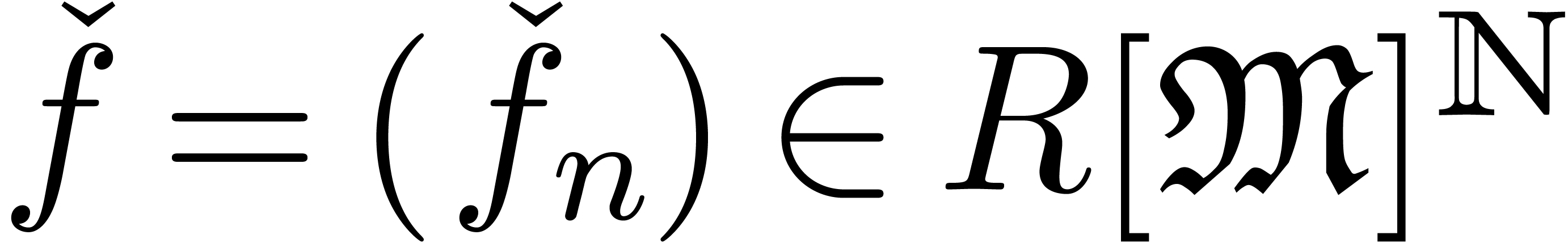 of polynomials.
Its sum
of polynomials.
Its sum  will be called the result of
the expander and we say that
will be called the result of
the expander and we say that  is an expander
for
is an expander
for  . We also define
an approximator to be a computable sequence
. We also define
an approximator to be a computable sequence 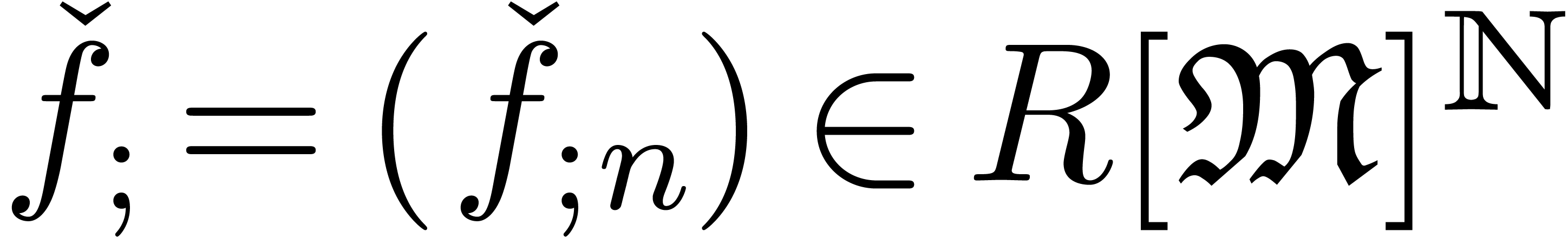 , such that
, such that 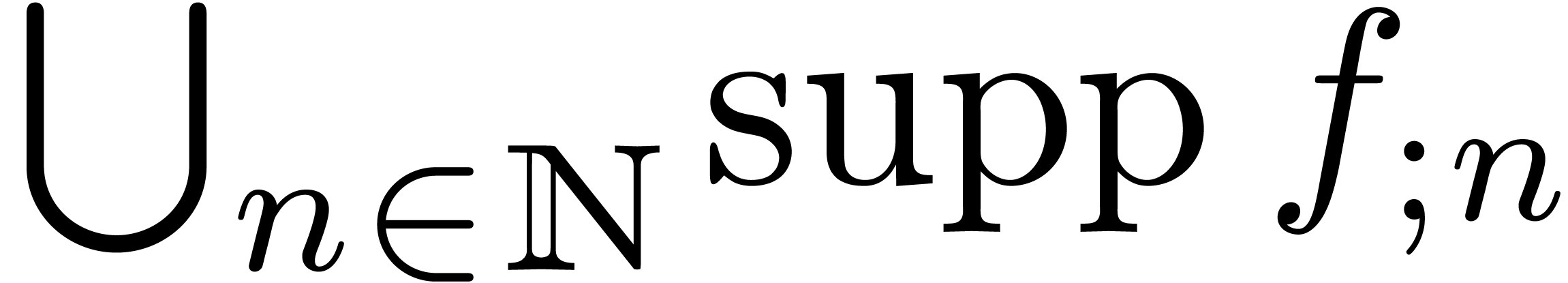 is
well-based and such that for each
is
well-based and such that for each 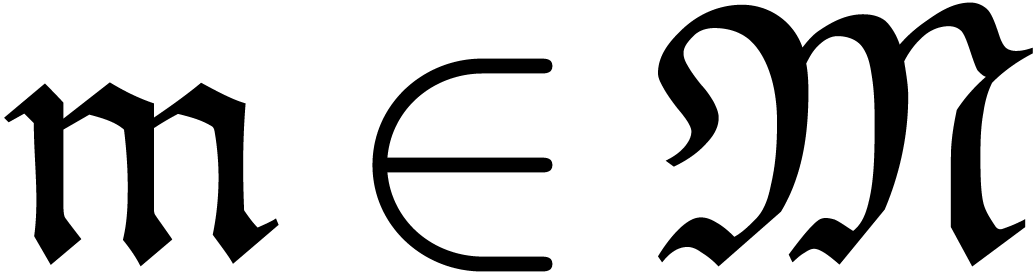 ,
there exists an
,
there exists an  for which
for which 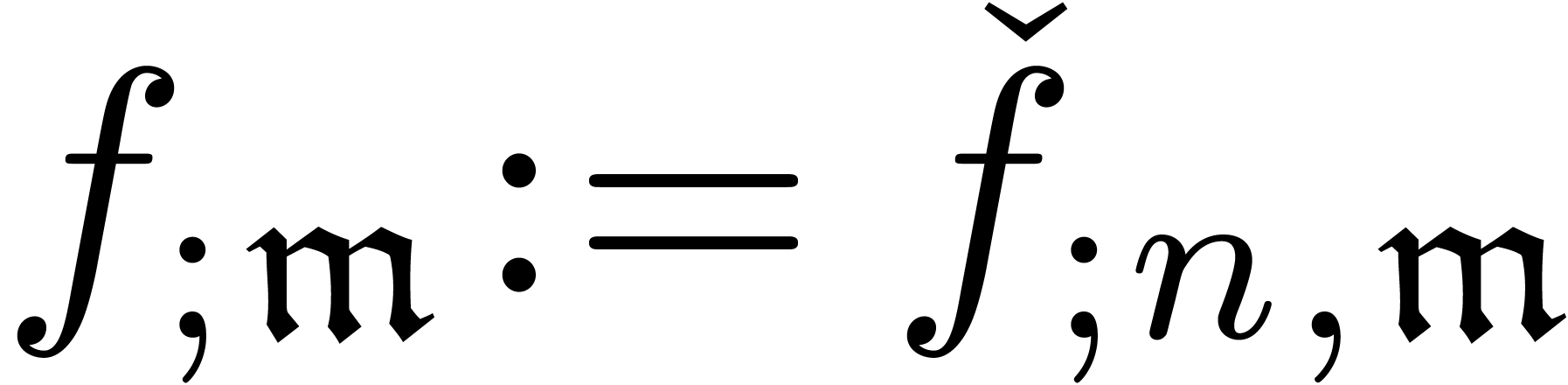 is constant for
is constant for 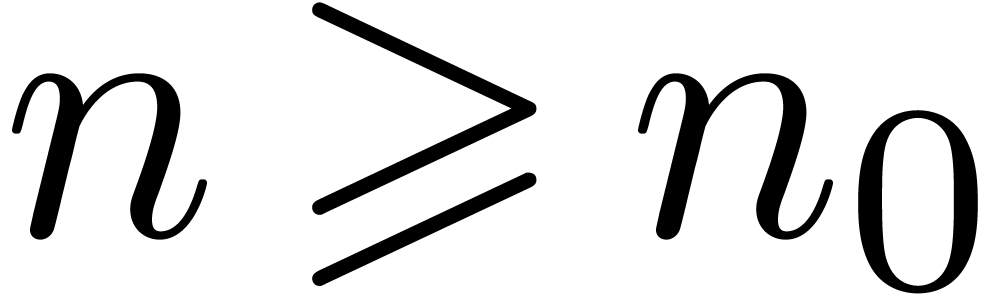 . In that
case, the limit
. In that
case, the limit 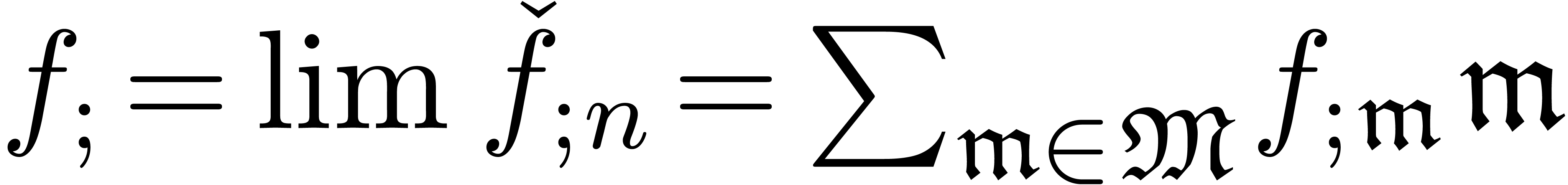 is called the result of
the approximator.
is called the result of
the approximator.
Clearly, the notions of expander and approximator are variants of
another: if 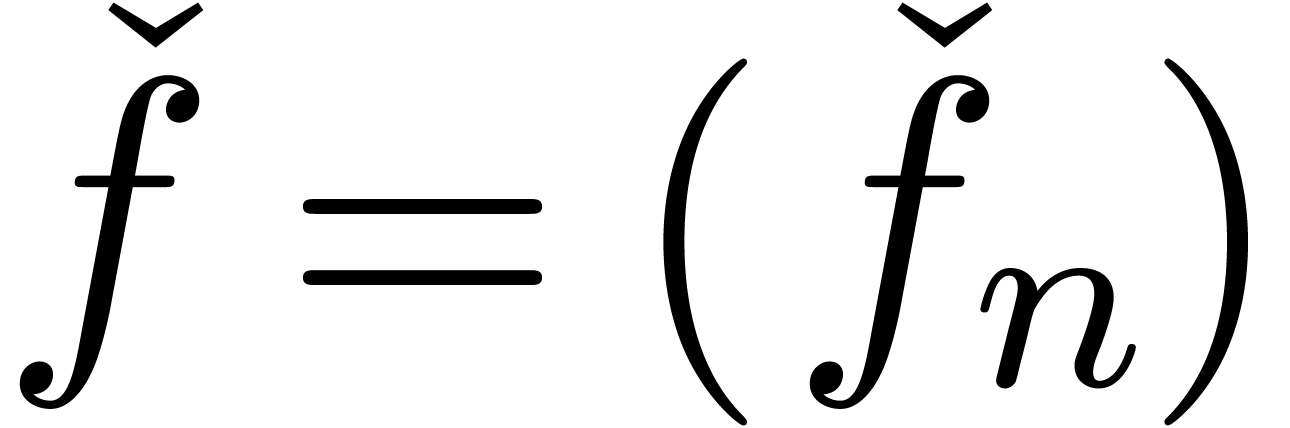 is an expander, then
is an expander, then 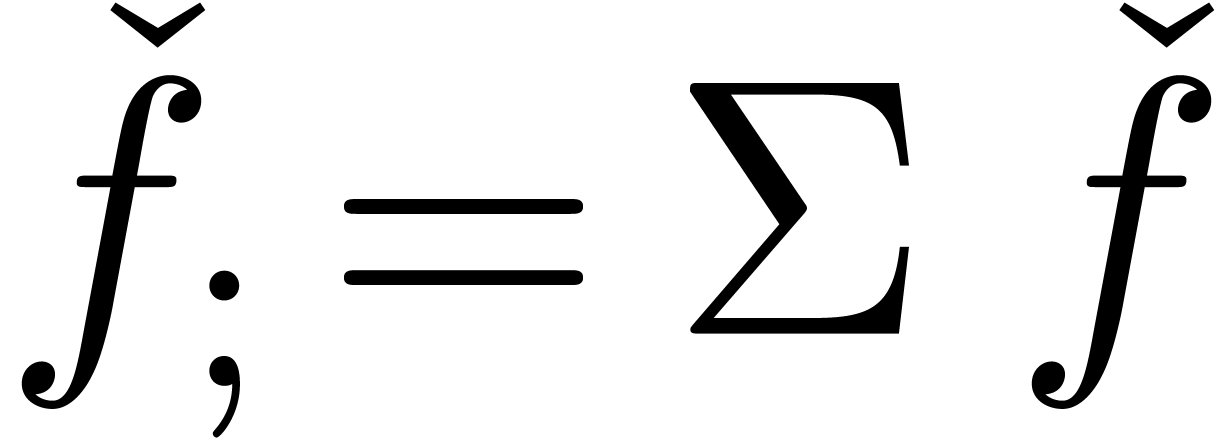 with
with 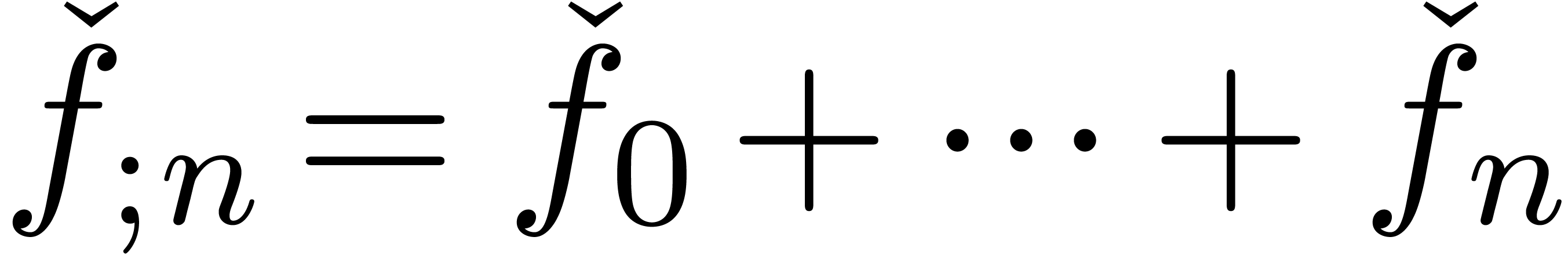 defines an approximator with
the same result. Similarly, if
defines an approximator with
the same result. Similarly, if 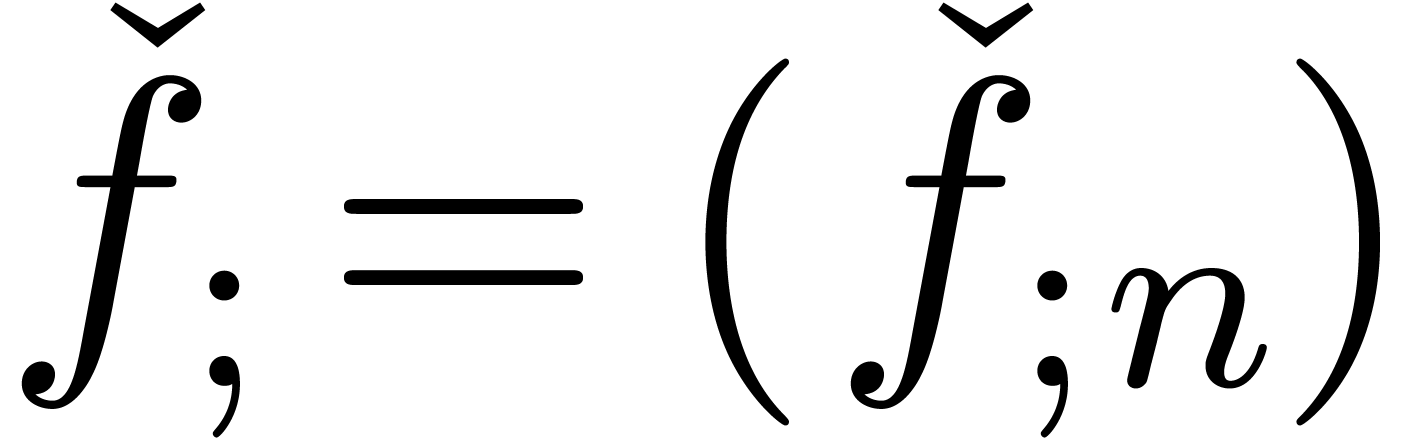 is an
approximator, then
is an
approximator, then 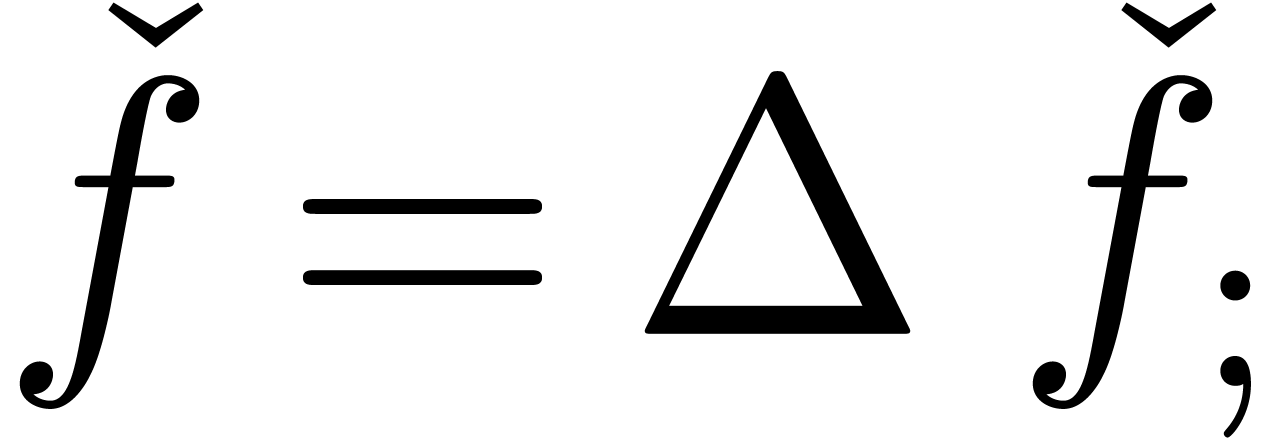 with
with 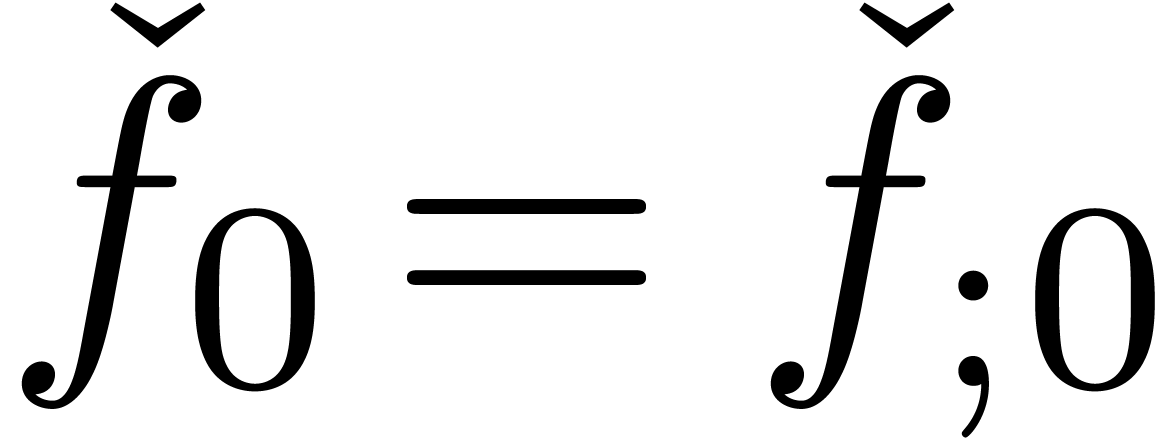 ,
, 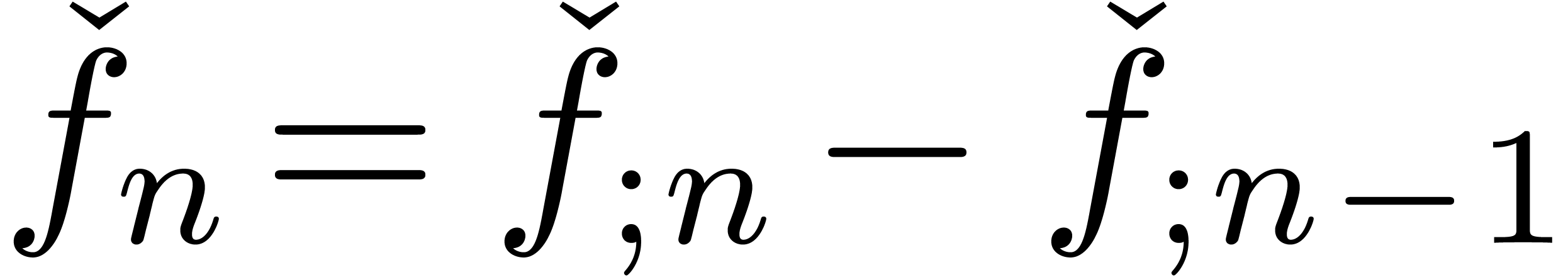 (
( ) defines an expander with the same result. However,
for certain purposes, expanders are more suitable, because an expander
) defines an expander with the same result. However,
for certain purposes, expanders are more suitable, because an expander
 can be manipulated via its generating
series
can be manipulated via its generating
series
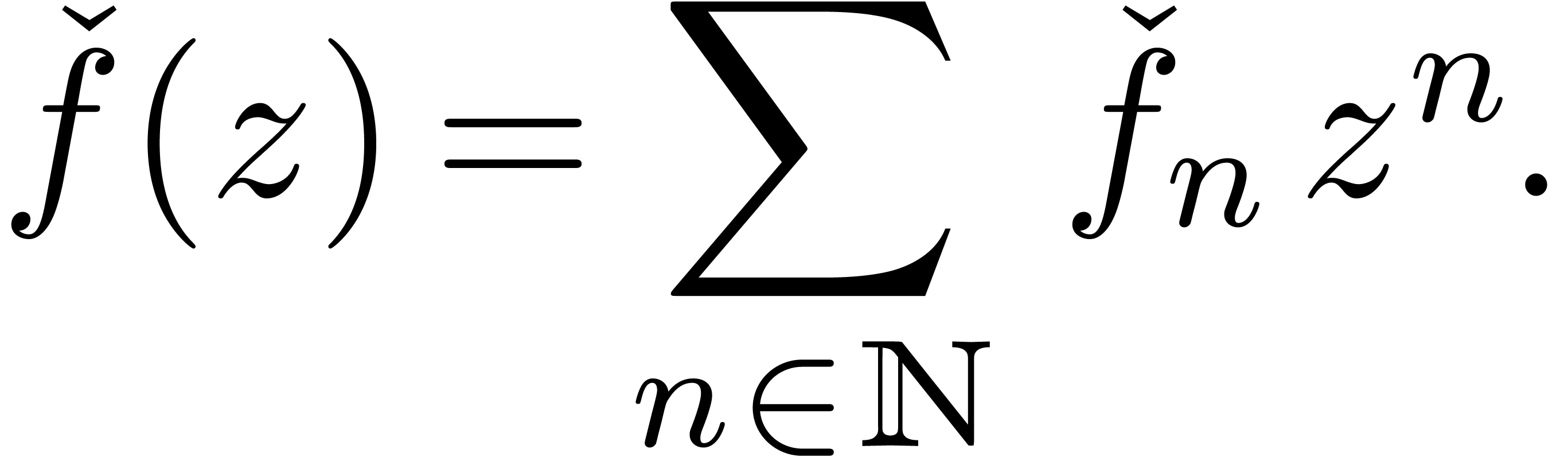
For other purposes though, approximators are the more natural choice. As
far as notations are concerned, it is convenient to pass from expanders
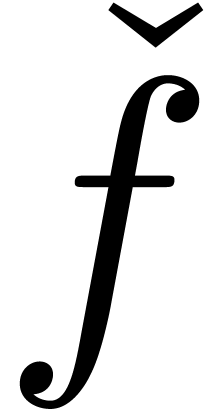 to approximators
to approximators 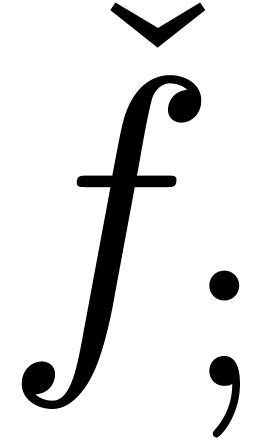 (and
vice versa) by prefixing the index by a semicolon
(resp. removing the semicolon).
(and
vice versa) by prefixing the index by a semicolon
(resp. removing the semicolon).
We will denote by 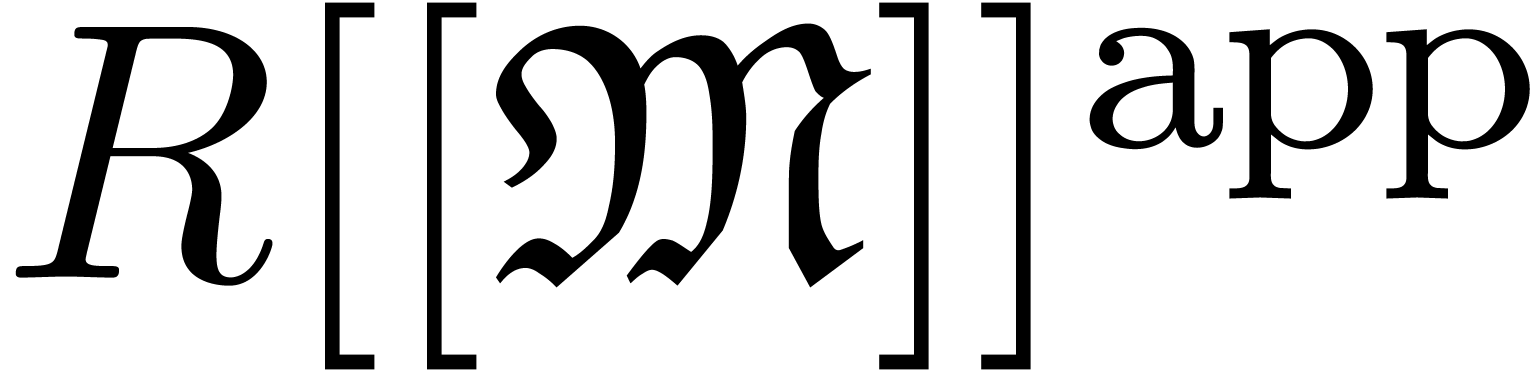 the set of approximable
series in
the set of approximable
series in 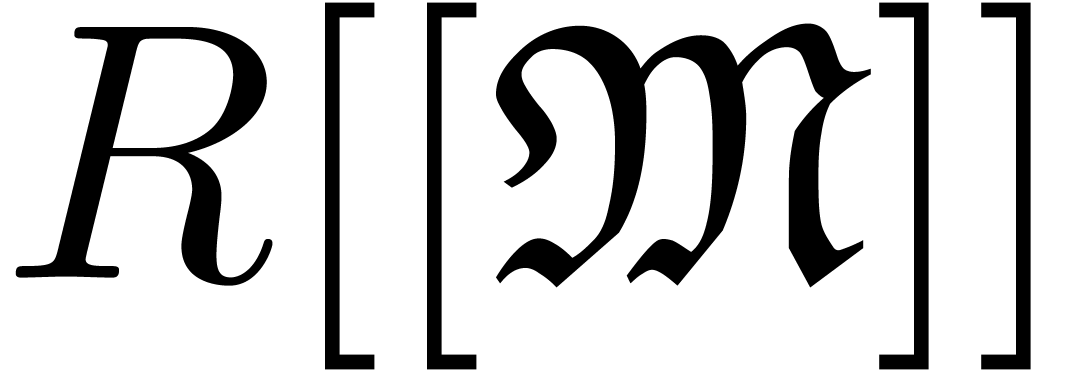 which admit an expander (or
approximator). The corresponding set of expanders will be denoted by
which admit an expander (or
approximator). The corresponding set of expanders will be denoted by
 . Given
. Given 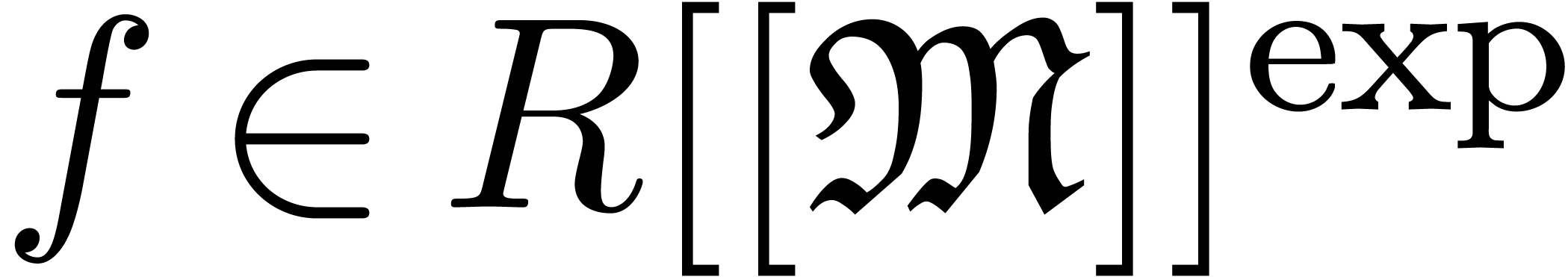 , we use the notation
, we use the notation  to indicate that
to indicate that  represents
represents  . Given
. Given 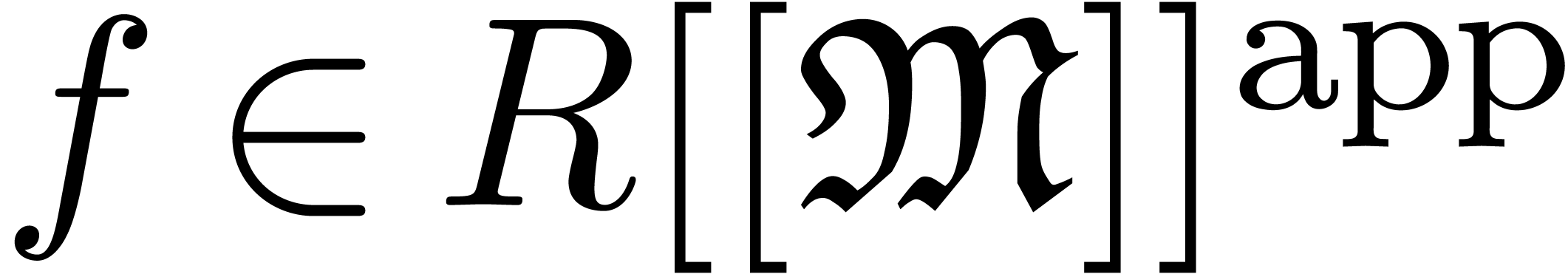 ,
we will also use the notation
,
we will also use the notation  to indicate that
to indicate that
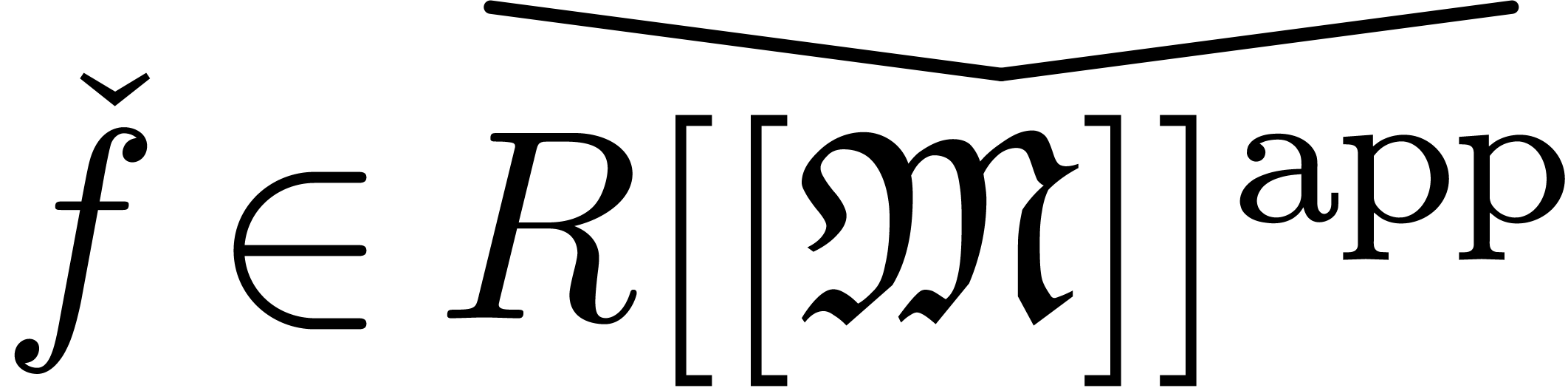 is a representation for
is a representation for  . For more details on this convention, see [vdH07,
Section 2.1].
. For more details on this convention, see [vdH07,
Section 2.1].
In practice, expanders and approximators are usually implemented by
pointers to an abstract class with a method to compute its coefficients.
For more details on how to do this, we refer to [vdH02a].
Let us now show how to implement expanders and approximators for basic
operations in  .
.
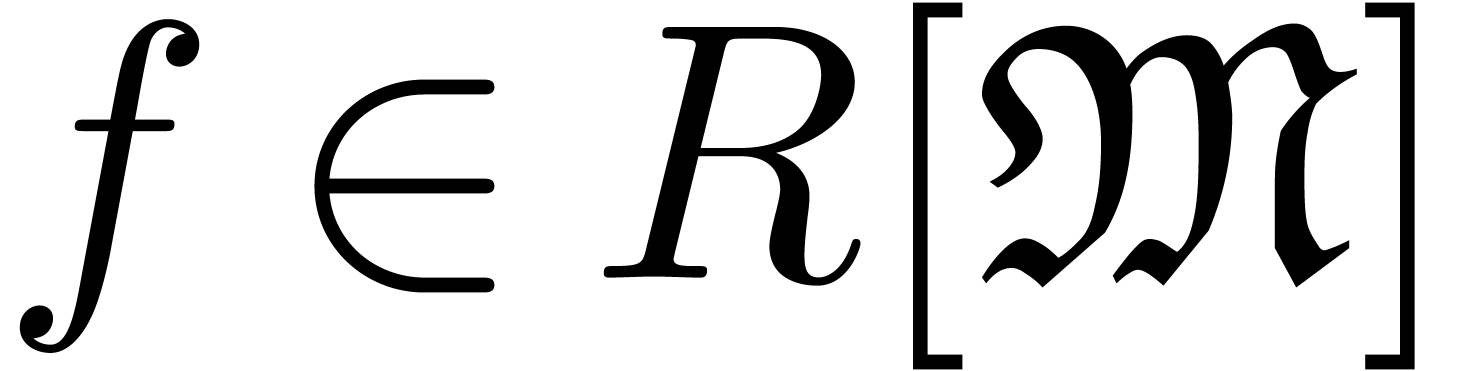 , an
expander and approximator for
, an
expander and approximator for  are given by
are given by
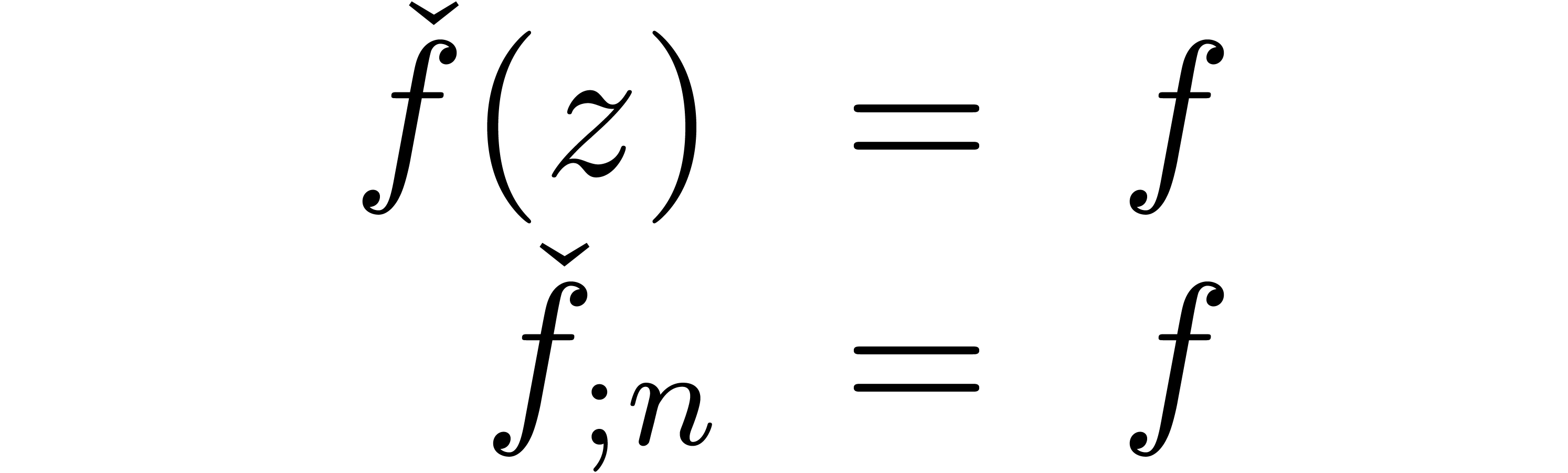
It will be convenient to simply regard 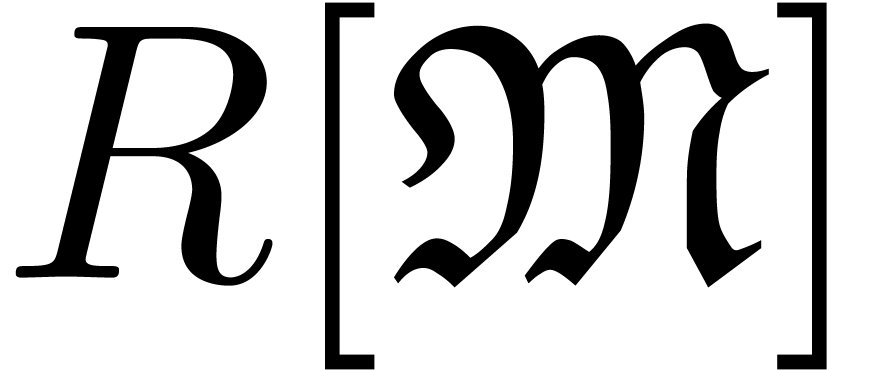 as a
subset of
as a
subset of  .
.
 , we may compute an
expander and an approximator for
, we may compute an
expander and an approximator for  by
by
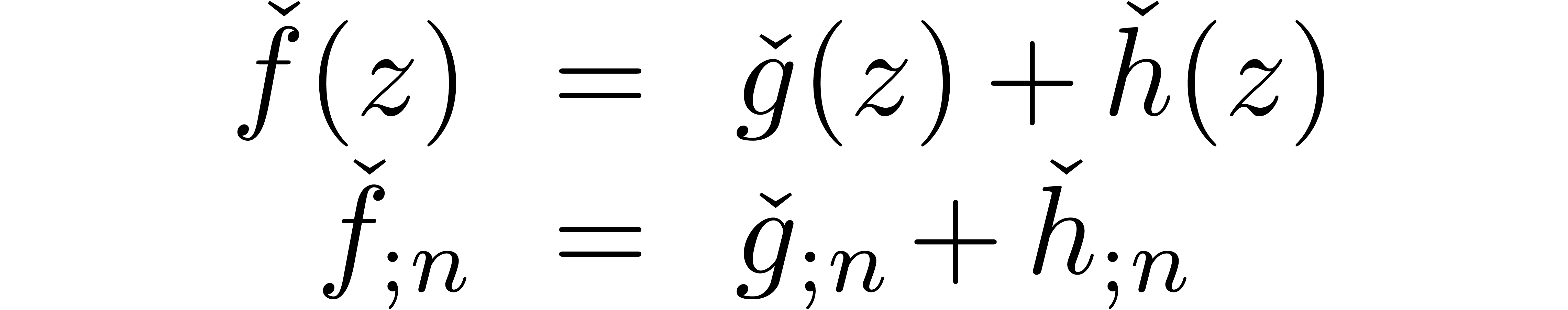
Subtraction is treated in a similar way.
However, a subtlety occurs here. Consider for instance the case when
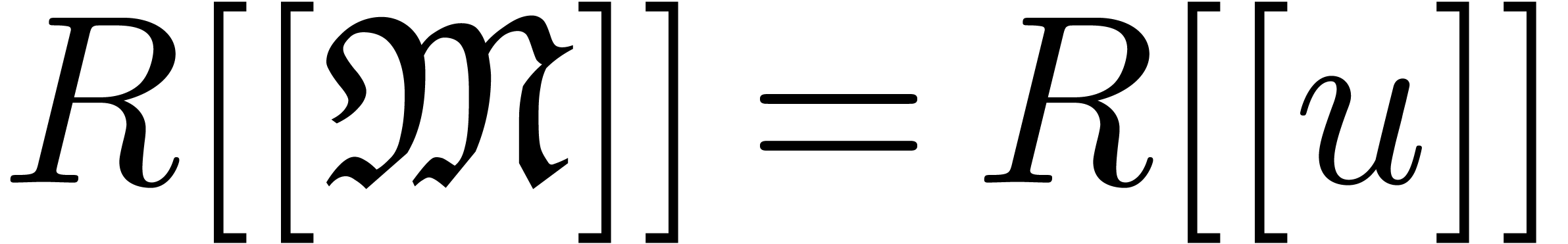 and
and 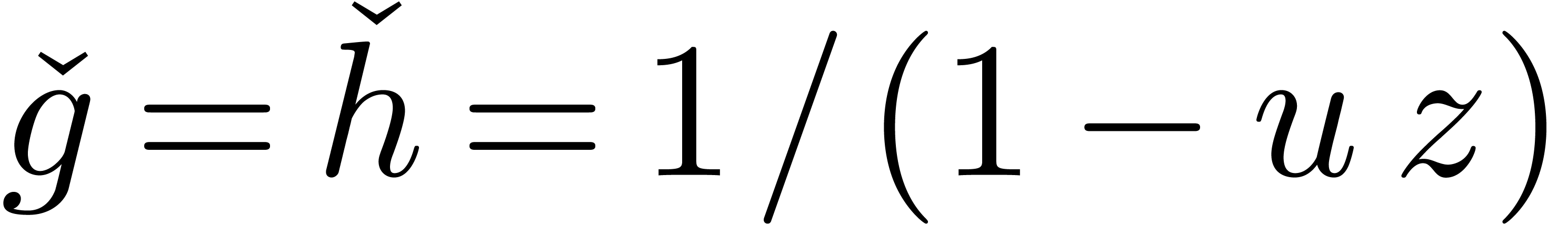 ,
so that
,
so that 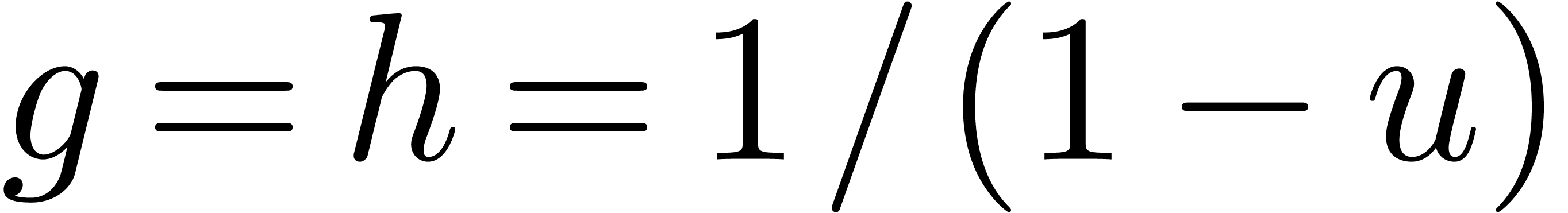 and
and 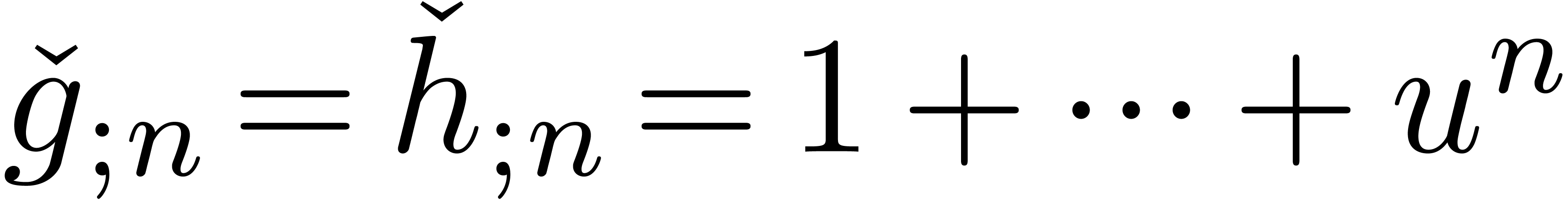 .
Contrary to what happened in the case of addition, the definitions (6) and (7) do not coincide in the sense that
.
Contrary to what happened in the case of addition, the definitions (6) and (7) do not coincide in the sense that
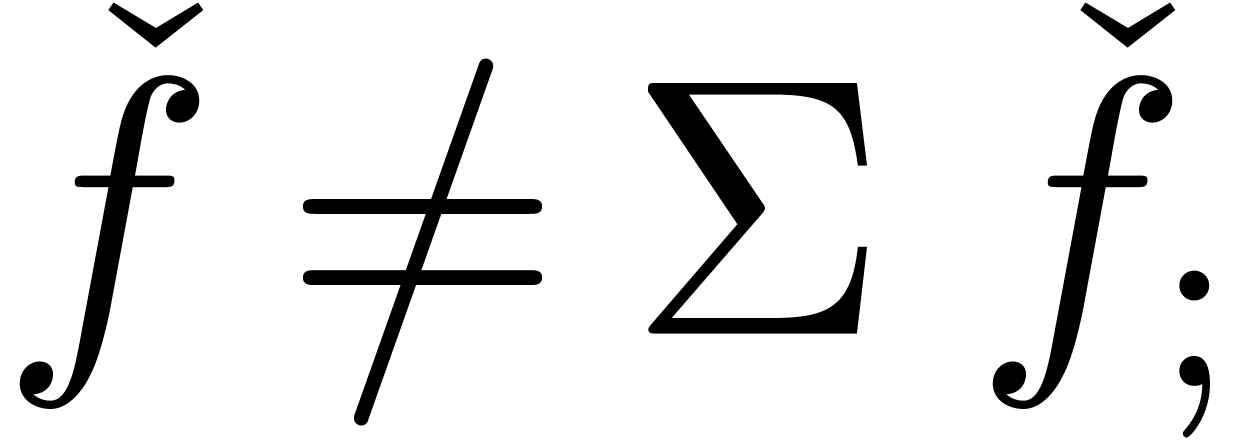 . Indeed, we respectively
find
. Indeed, we respectively
find
As a general rule, the manipulation of expanders tends to be a bit more economic from the computational point of view, its coefficients being smaller in size.
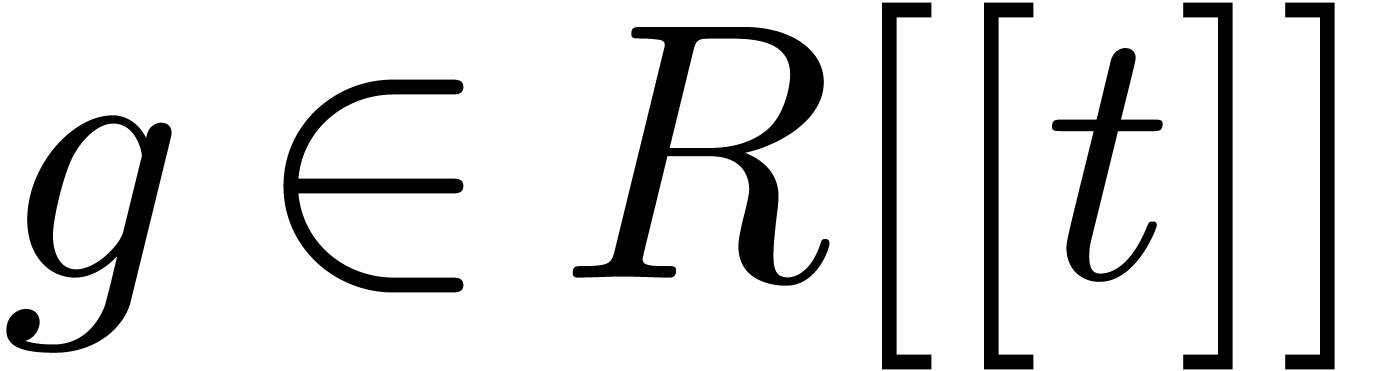 be a computable formal power series and
let
be a computable formal power series and
let  be infinitesimal. Then we may compute an
expander for
be infinitesimal. Then we may compute an
expander for 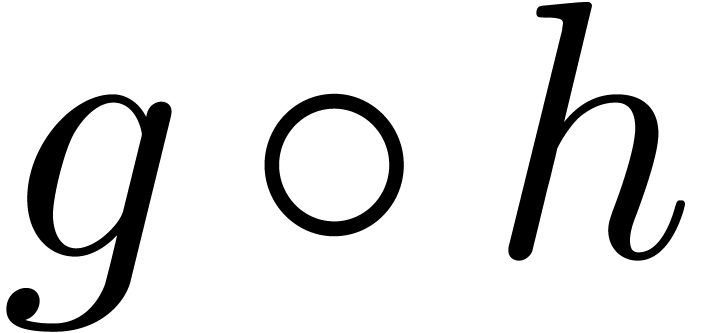 using
using
Notice that the individual coefficients of 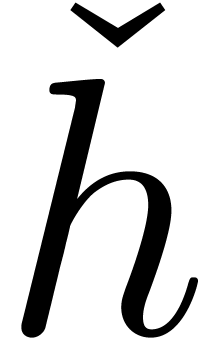 need
not be infinitesimal. Besides, the composition
need
not be infinitesimal. Besides, the composition  is usually not a polynomial. Therefore, we have forced
is usually not a polynomial. Therefore, we have forced 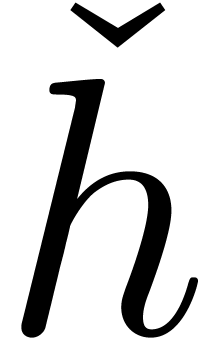 to become infinitesimal using a multiplication by
to become infinitesimal using a multiplication by  . This is justified by the fact that
. This is justified by the fact that
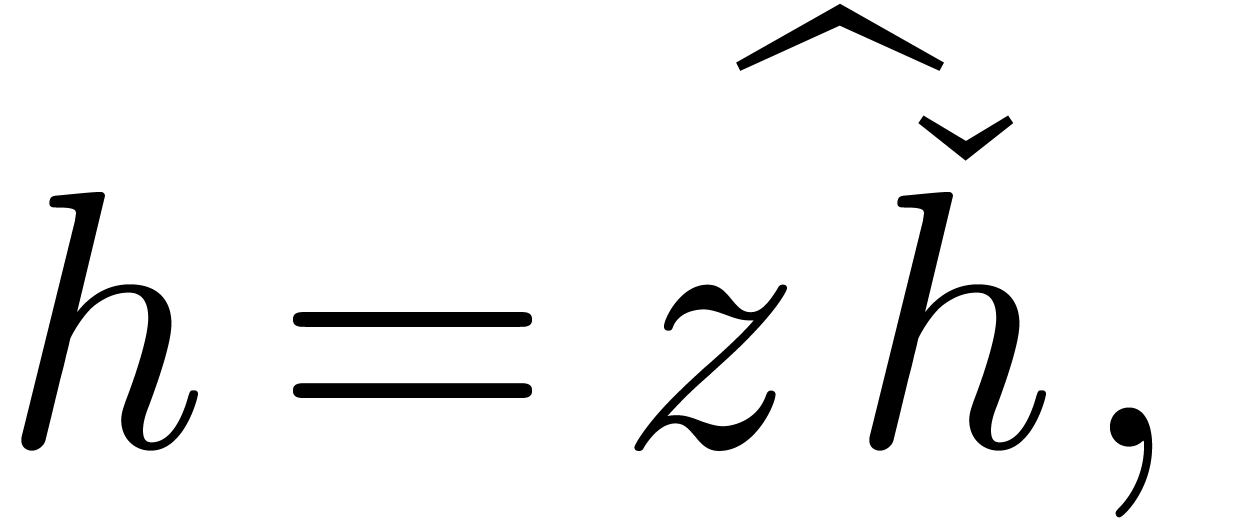
Multiplication of 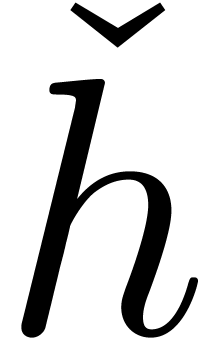 by
by  corresponds to delaying the approximation process of
corresponds to delaying the approximation process of 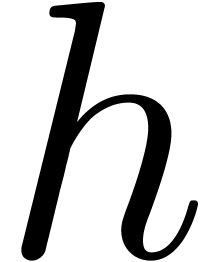 .
.
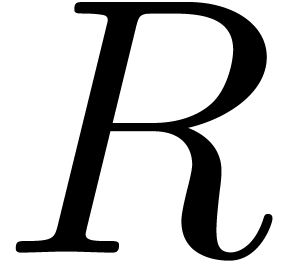 is a field and
is a field and  a totally ordered group. The inverse of a series
a totally ordered group. The inverse of a series 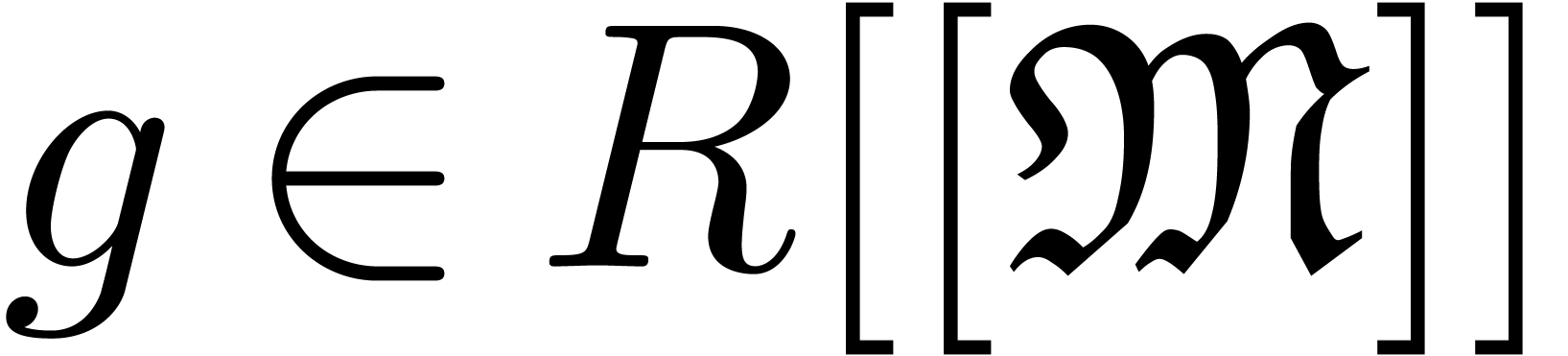 may be computed using left composition with power
series:
may be computed using left composition with power
series:
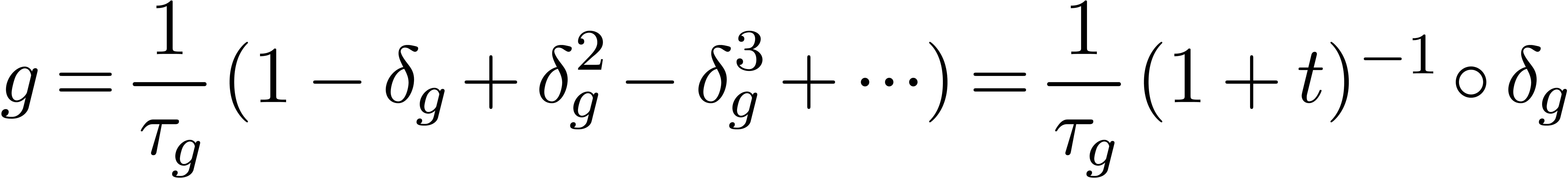 |
(9) |
Unfortunately, there exists no general algorithm for the computation of
the dominant term 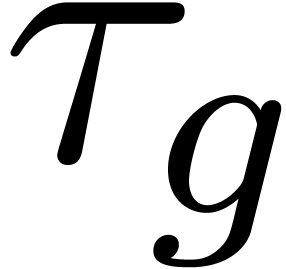 . We will
therefore assume the existence of an oracle for this purpose. In section
6, we will present a heuristic algorithm which can be used
in practice.
. We will
therefore assume the existence of an oracle for this purpose. In section
6, we will present a heuristic algorithm which can be used
in practice.
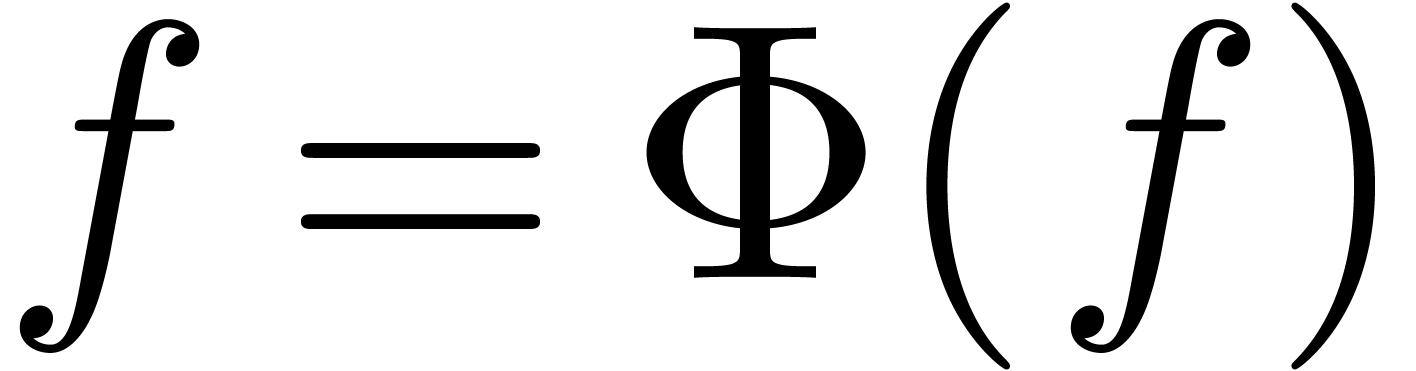
and apply a fixed-point theorem. In our case, this requires a well-based
operator  for which we can prove that
for which we can prove that  admits a well-based limit in
admits a well-based limit in 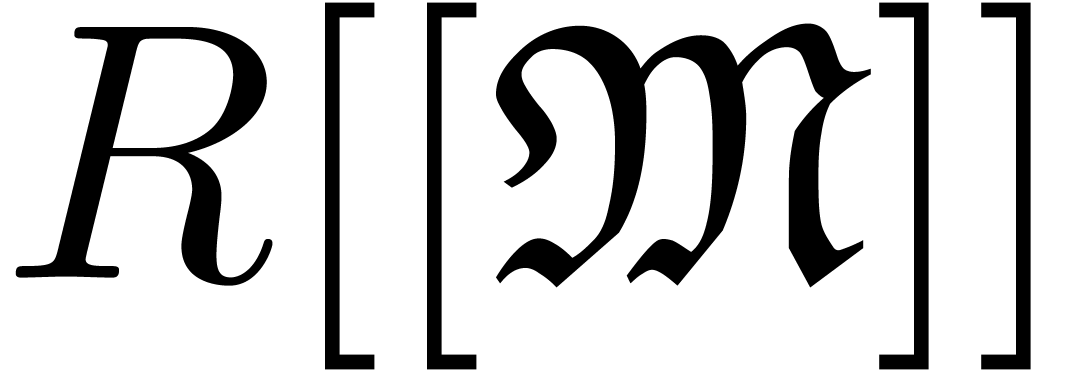 .
The obvious expander for
.
The obvious expander for  is given by
is given by
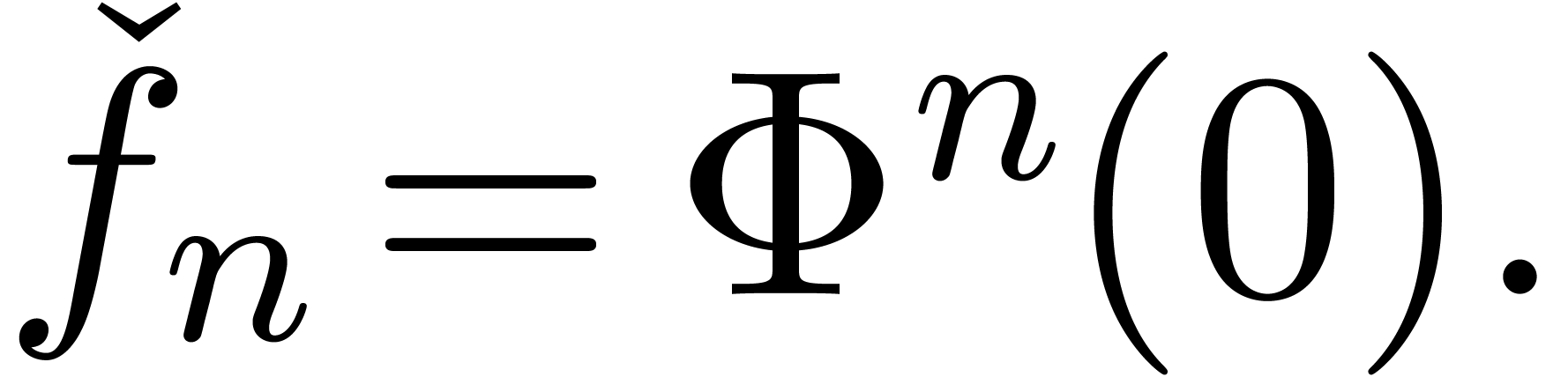
For some general fixed-point theorems for sequences 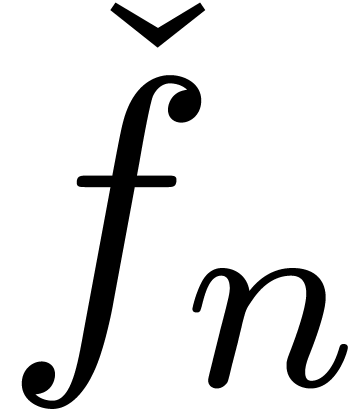 of this kind, we refer to [vdH01] and [vdH06c,
Chapter 6].
of this kind, we refer to [vdH01] and [vdH06c,
Chapter 6].
In order to compute with well-based transseries in  , we take our coefficients in an effective
subfield
, we take our coefficients in an effective
subfield 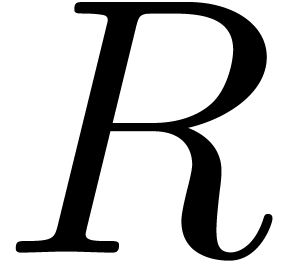 of
of  and our
monomials in an effective subgroup
and our
monomials in an effective subgroup  of
of  . Moreover, the monomials in
. Moreover, the monomials in  which are not iterated logarithms are themselves
exponentials of approximable transseries.
which are not iterated logarithms are themselves
exponentials of approximable transseries.
More precisely, elements in  are represented by
monomials
are represented by
monomials 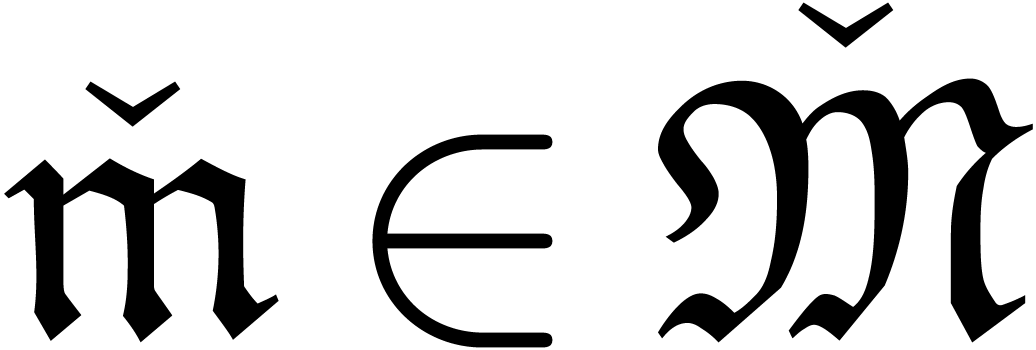 which are of one of the following
forms:
which are of one of the following
forms:
either 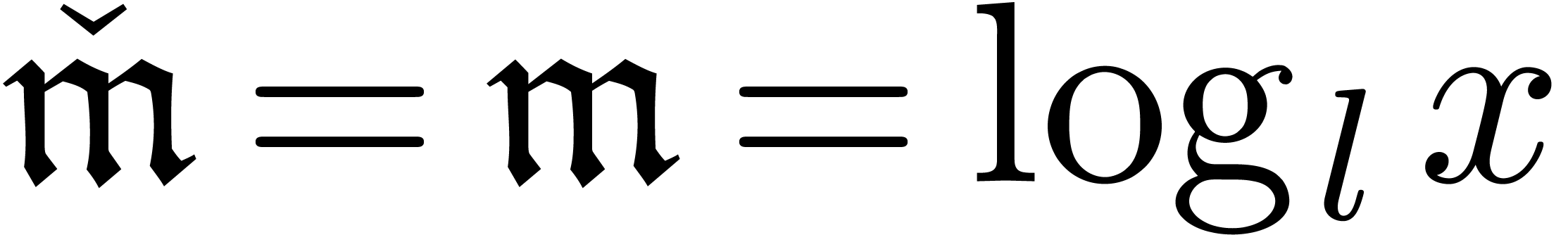 for some
for some 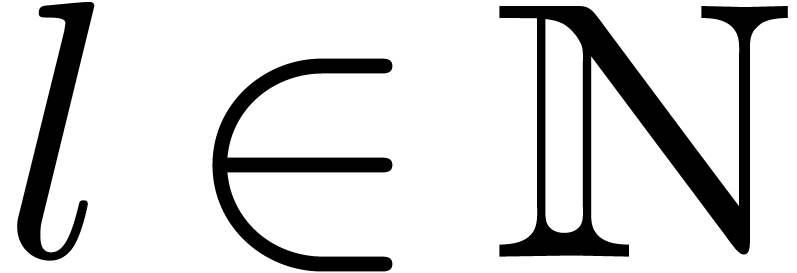 ;
;
or 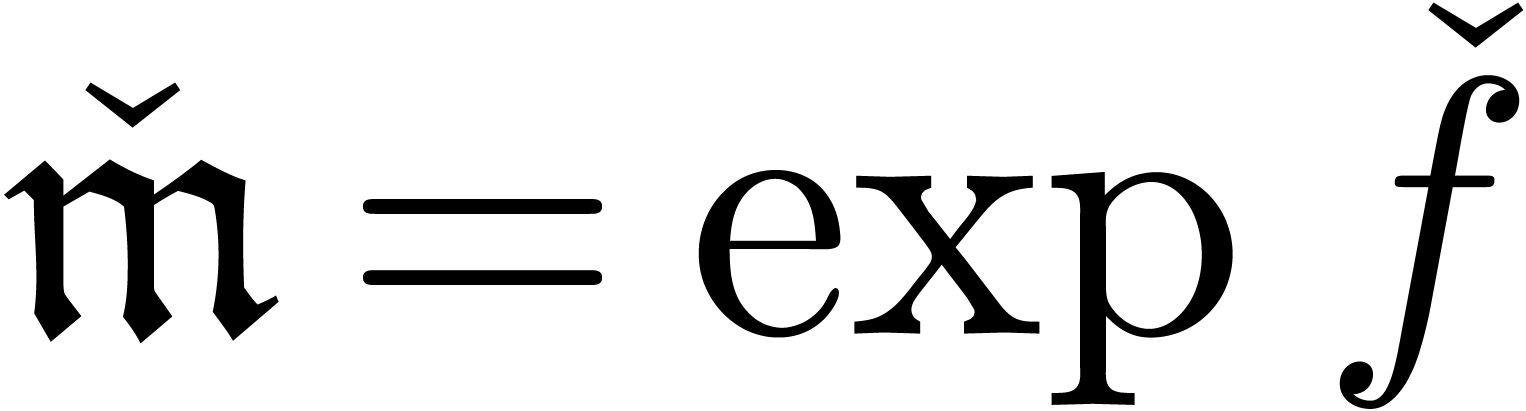 , with
, with  .
.
In the first case, the exponential height 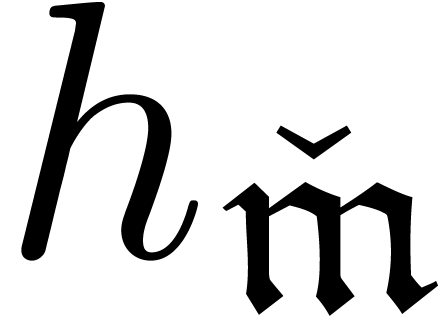 of
of
 is defined to be zero and in the second case, we
set
is defined to be zero and in the second case, we
set 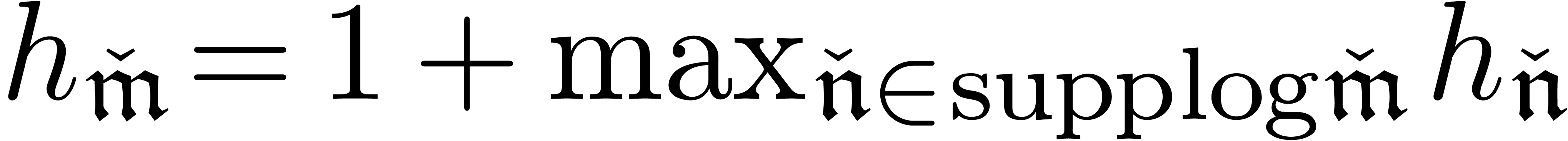 .
.
Elements  are multiplied using
are multiplied using 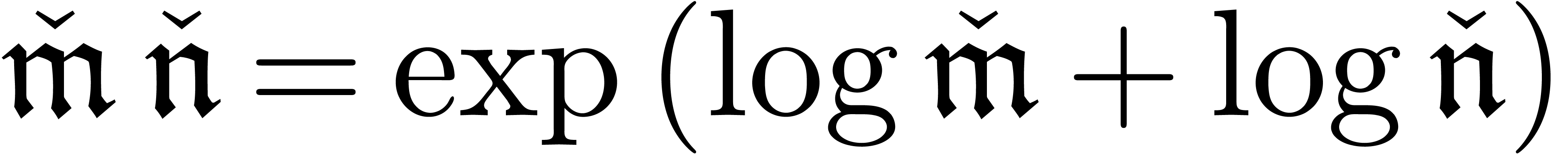 and inverted using
and inverted using 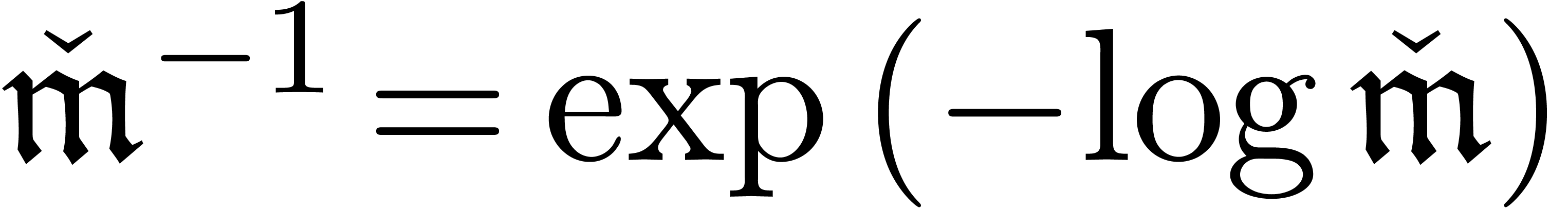 . Here
. Here
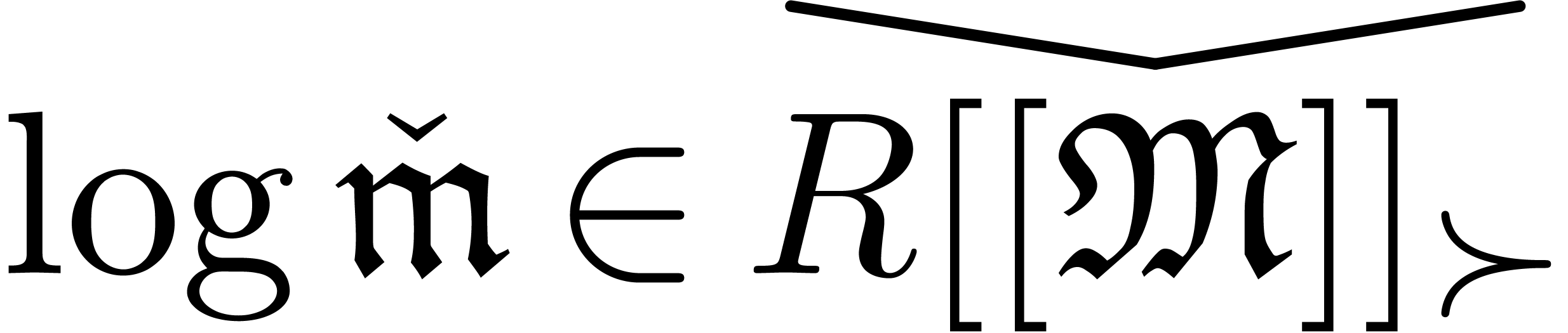 : if
: if  , then
, then 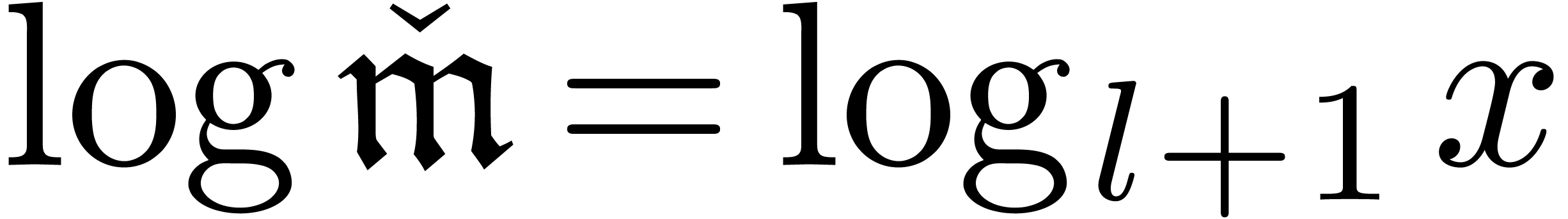 ;
if
;
if 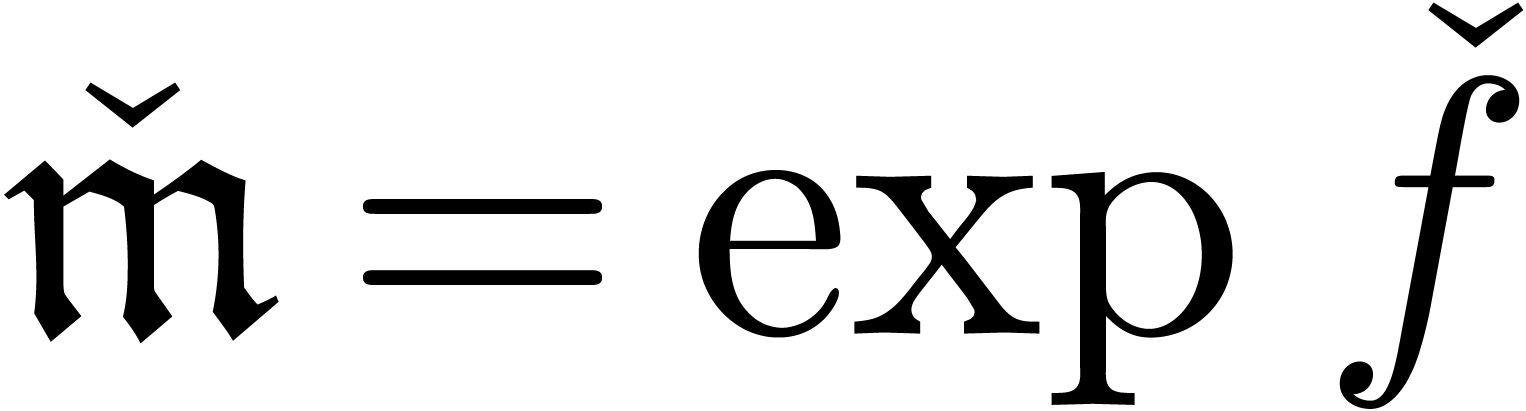 , then
, then 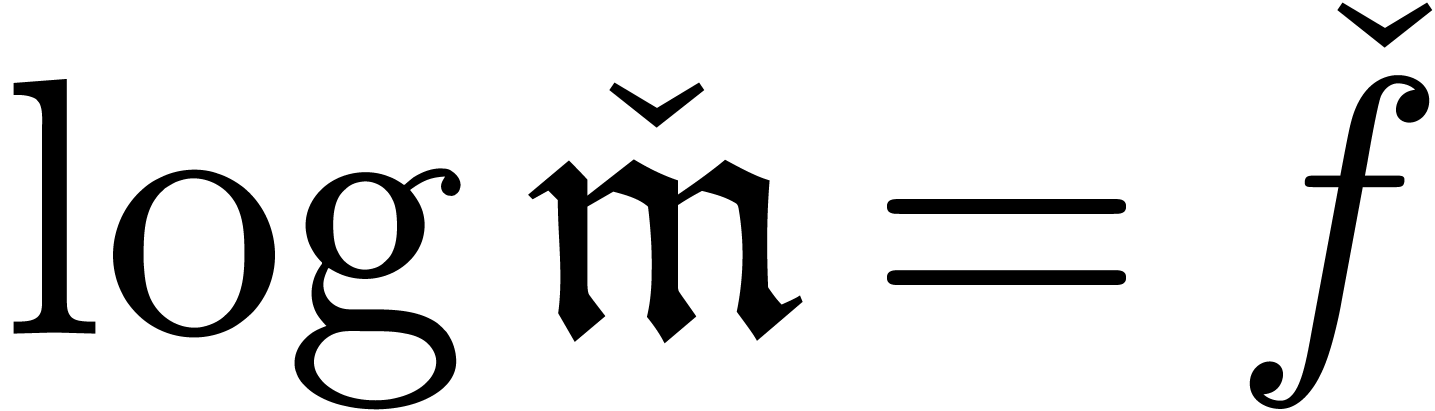 . The asymptotic ordering
. The asymptotic ordering  on
on  is implemented using
is implemented using
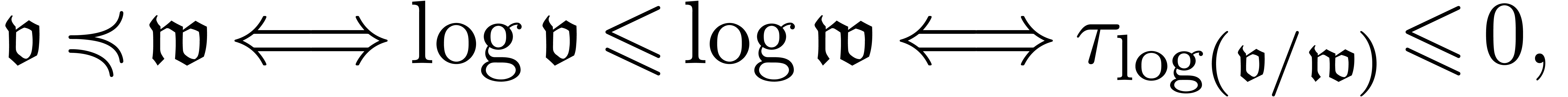
and therefore relies on an oracle for the computation of 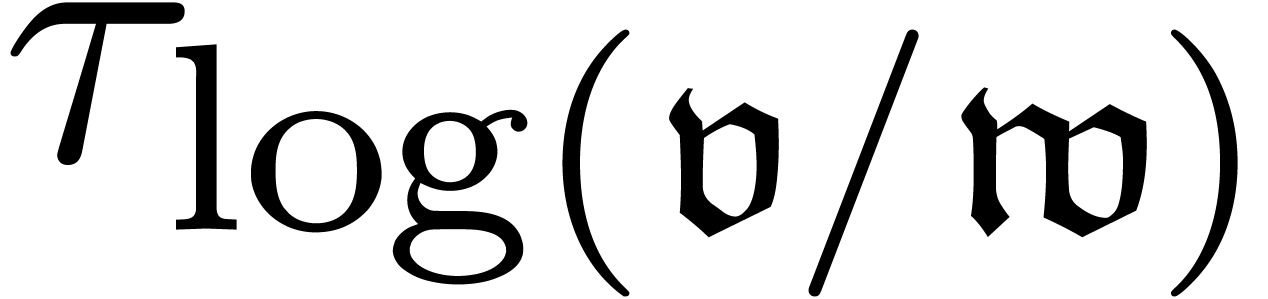 . Setting
. Setting 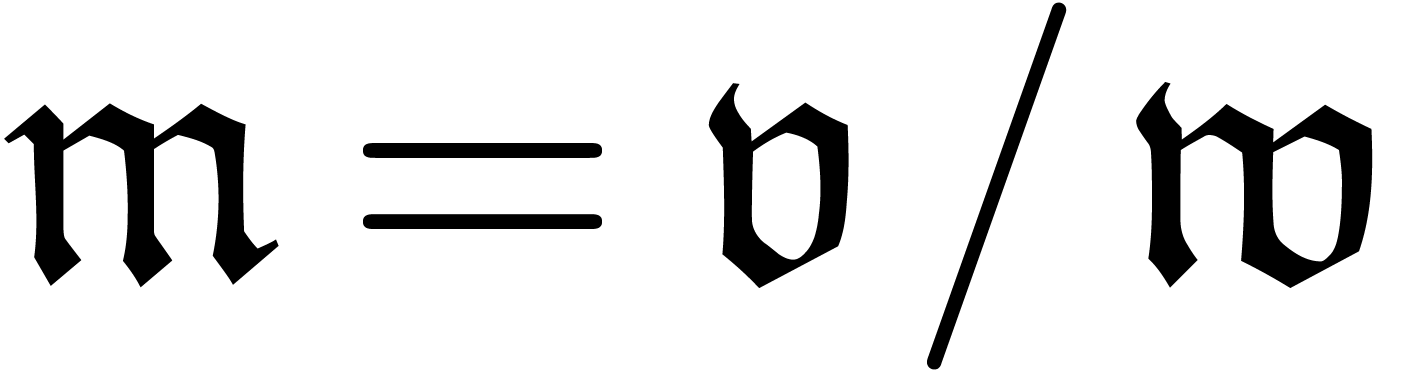 ,
we notice that heuristic algorithms for the computation of this dominant
term recursively need to compare elements
,
we notice that heuristic algorithms for the computation of this dominant
term recursively need to compare elements  in
in
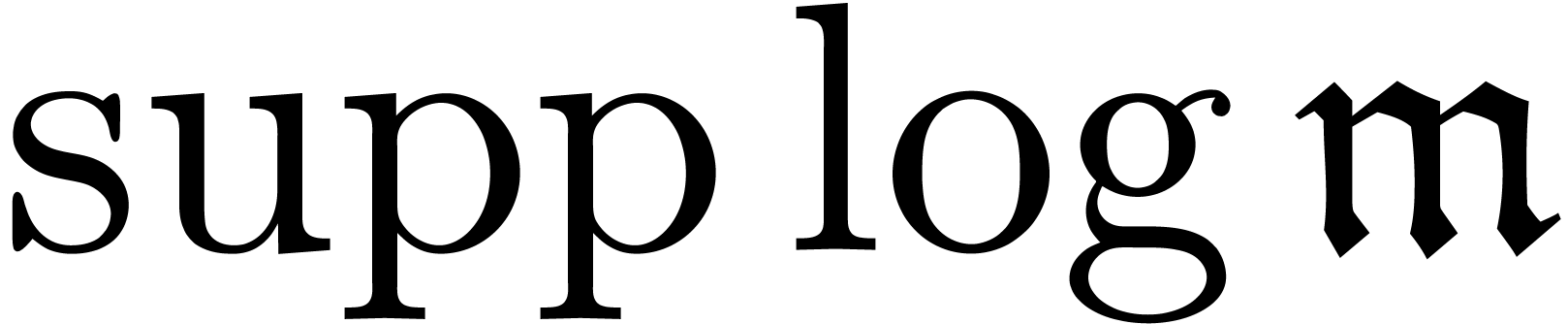 with respect to
with respect to  .
The termination of the recursion is based on the fact that
.
The termination of the recursion is based on the fact that 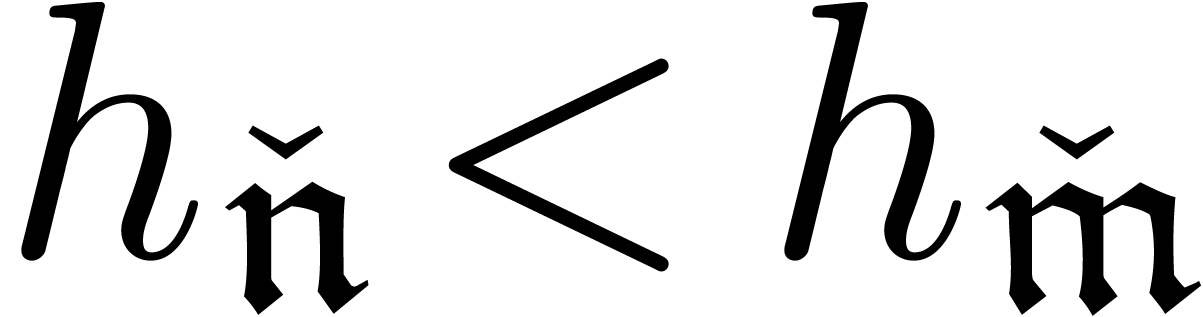 .
.
The main additional operations for the manipulation of transseries are exponentiation and logarithm. Since exponentiation relies on canonical decompositions, we start with the general operation of restriction of support.
 , we define the
restriction of
, we define the
restriction of 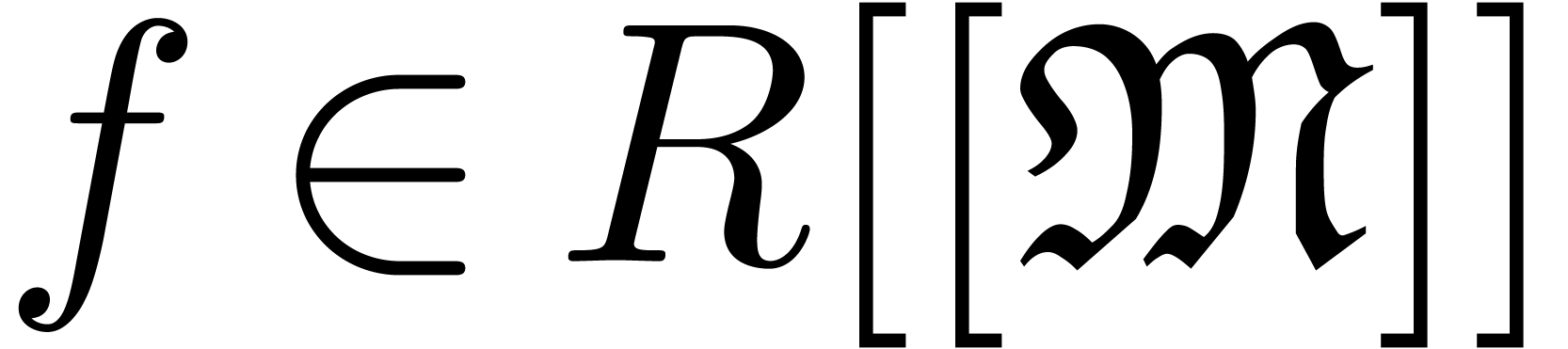 to
to  by
by
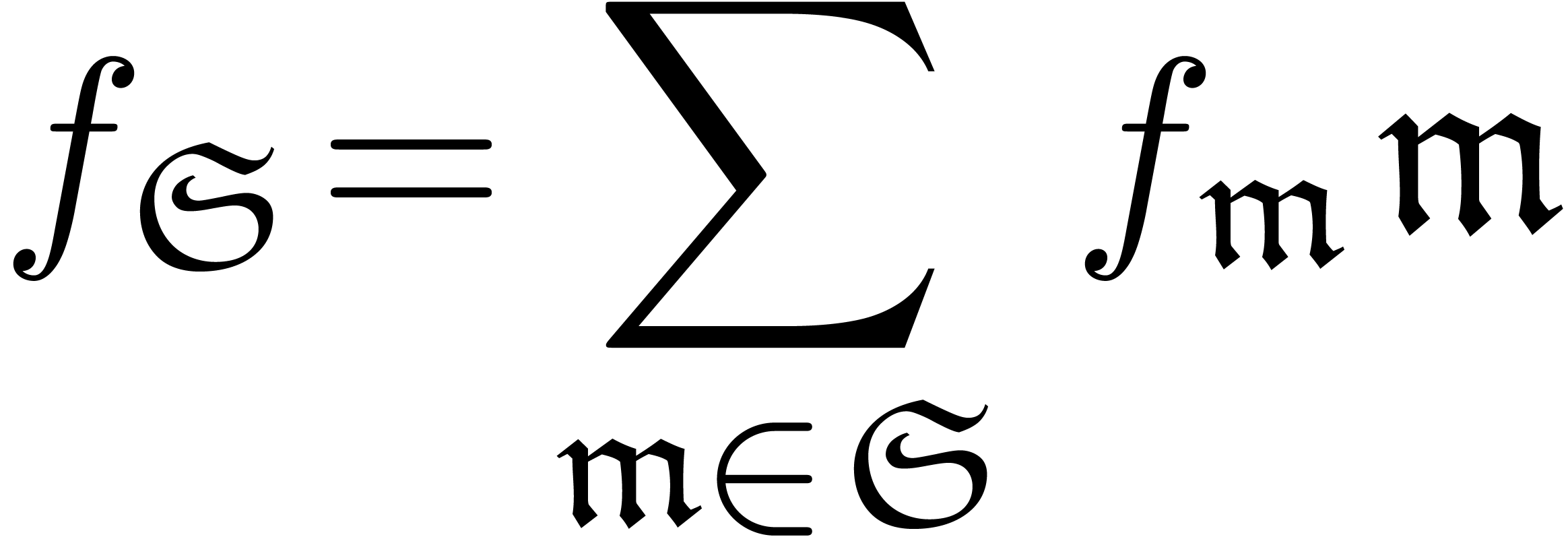
If the subset  is a computable, i.e.
is a computable, i.e.
 admits a computable membership test, then the
mapping
admits a computable membership test, then the
mapping 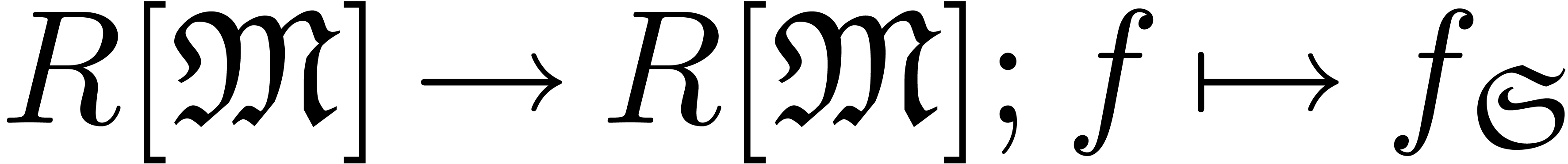 is computable. In particular, given
is computable. In particular, given
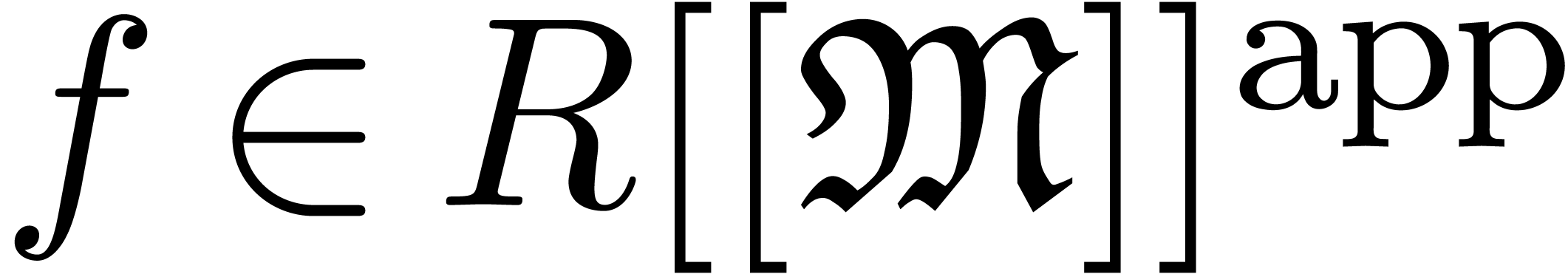 , we may compute
, we may compute  using
using
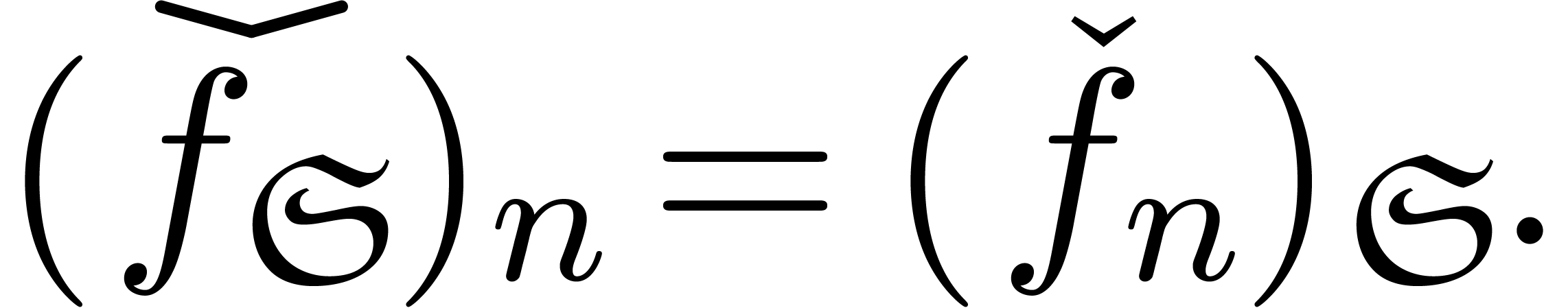
Now making continued use of our oracle for the computation of dominant
terms, the sets  ,
,  and
and 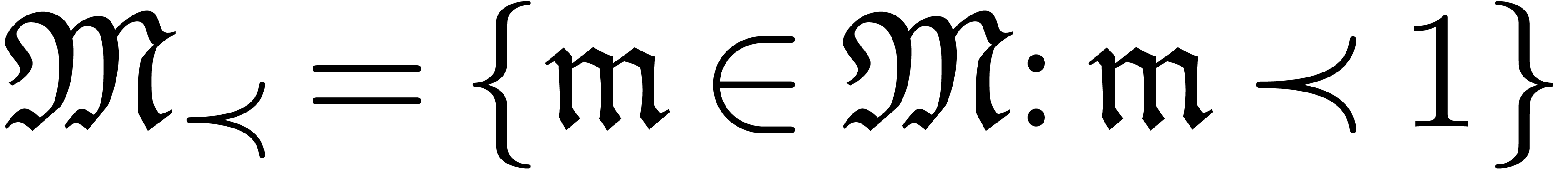 are computable. Consequently,
we have algorithms to compute
are computable. Consequently,
we have algorithms to compute 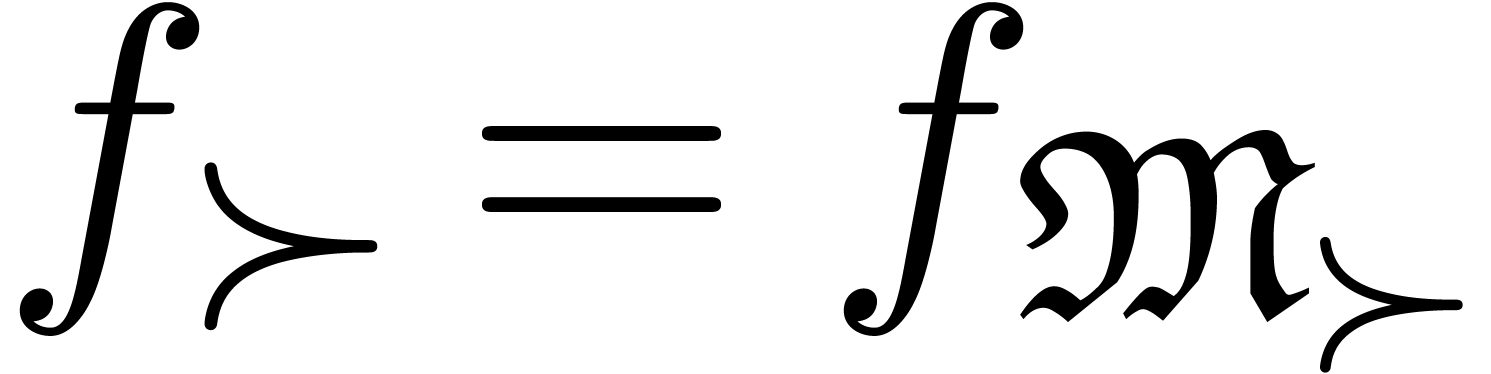 ,
,
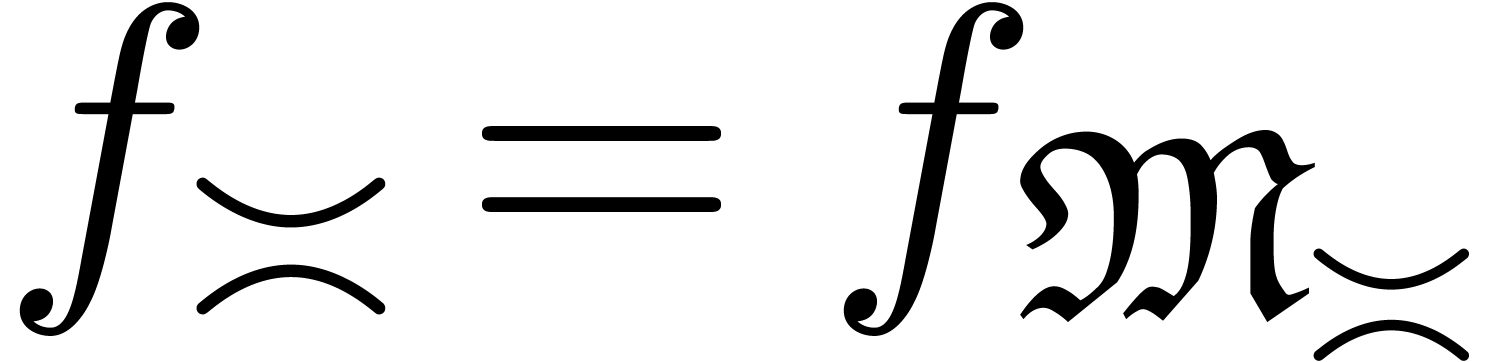 and
and 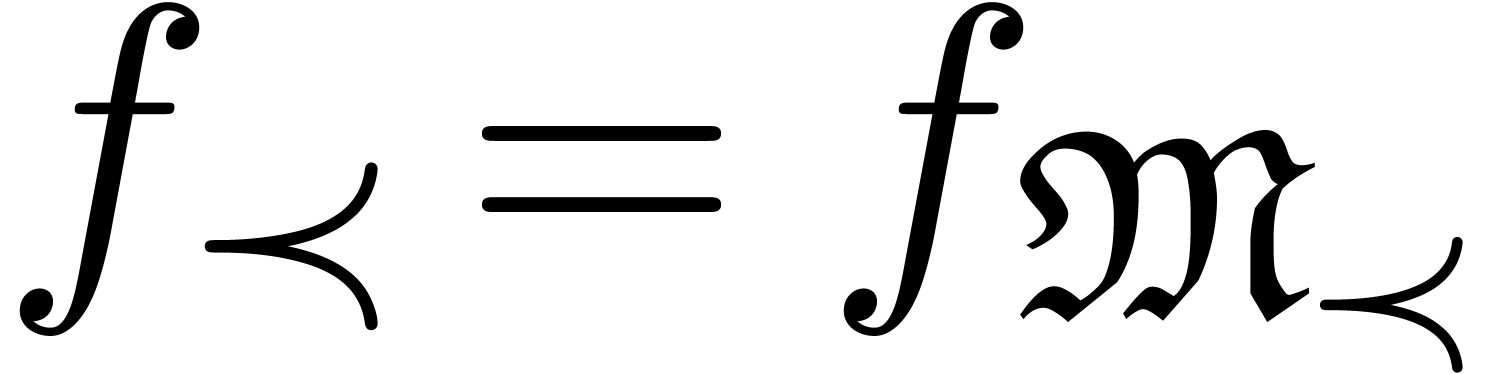 .
.
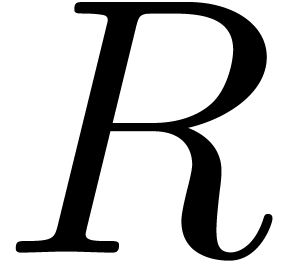 is closed under logarithm (for
positive elements) and exponentiation. Then the formulas (2–5) and our algorithms for canonical decomposition and left
composition with power series yield a way to compute logarithms and
exponentials of elements in
is closed under logarithm (for
positive elements) and exponentiation. Then the formulas (2–5) and our algorithms for canonical decomposition and left
composition with power series yield a way to compute logarithms and
exponentials of elements in 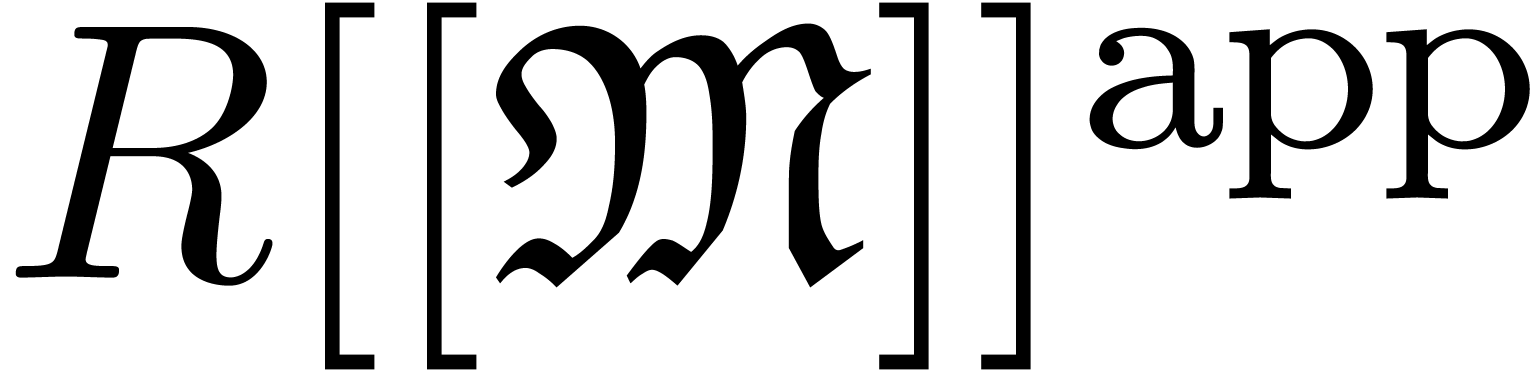 .
The smallest subfield
.
The smallest subfield 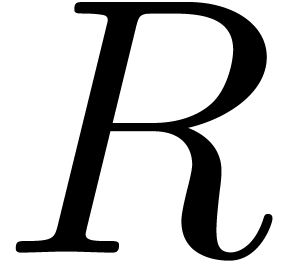 of
of  which is stable under exponentiation and logarithm is called the field
of exp-log constants. There exists a zero-test for this field
which relies on Schanuel's conjecture for its termination [Ric97].
which is stable under exponentiation and logarithm is called the field
of exp-log constants. There exists a zero-test for this field
which relies on Schanuel's conjecture for its termination [Ric97].
Example
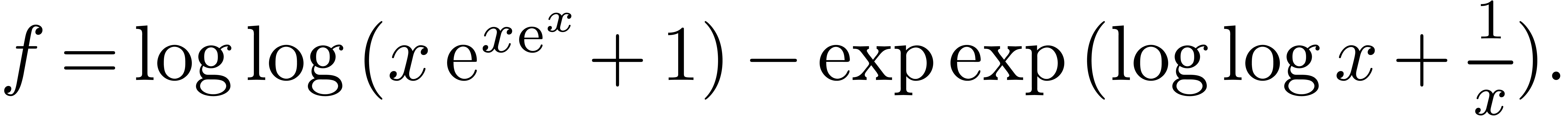
When computing an expander  with the routines
presented so far, we obtain
with the routines
presented so far, we obtain

Remark 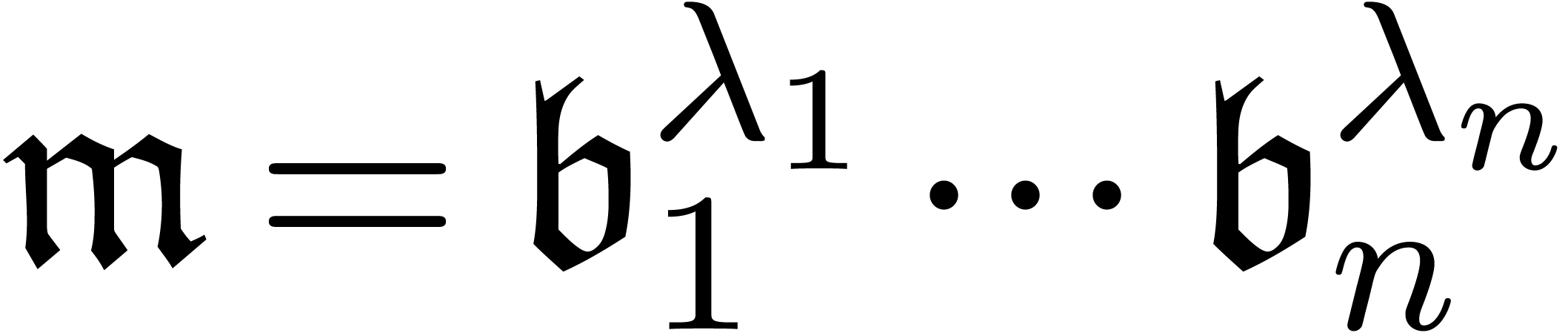 with respect to a transbasis
with respect to a transbasis
 which is constructed incrementally during the
computations. In our well-based setting, we merely require that the
which is constructed incrementally during the
computations. In our well-based setting, we merely require that the 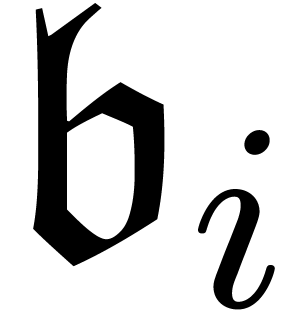 satisfy the hypotheses
satisfy the hypotheses
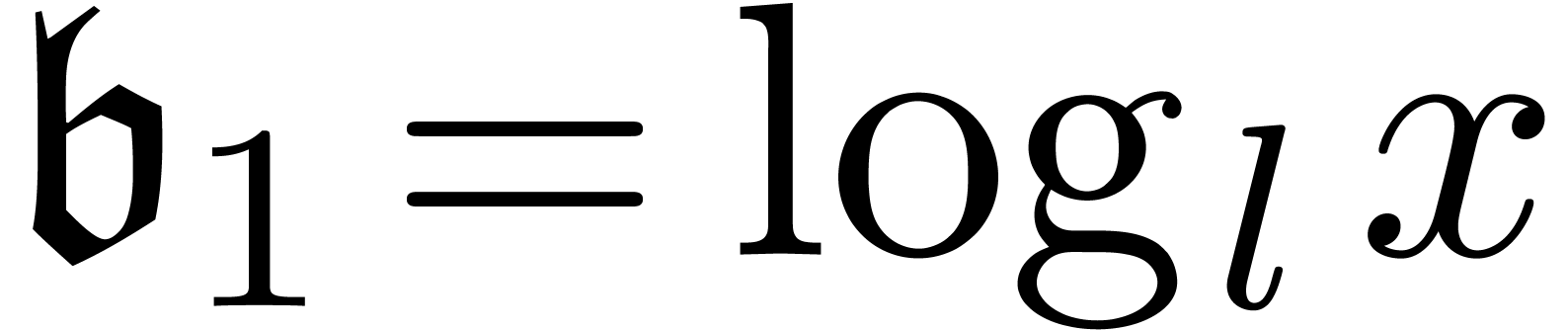 for some
for some 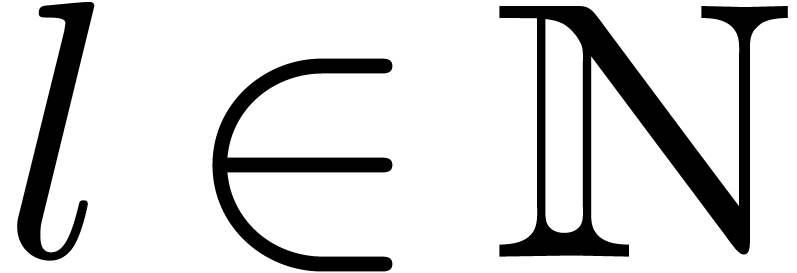 .
.
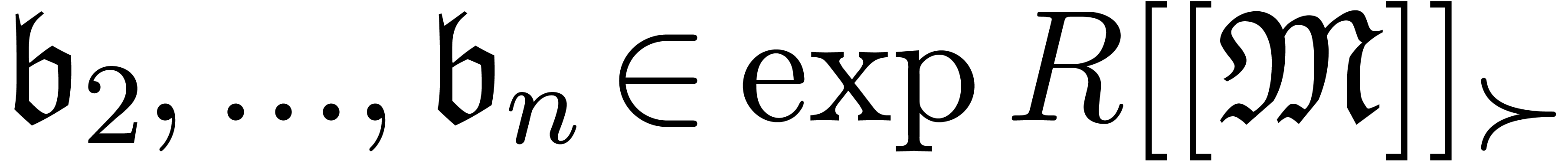 .
.
 .
.
In the grid-based setting TB2 may be replaced by the
stronger requirement that 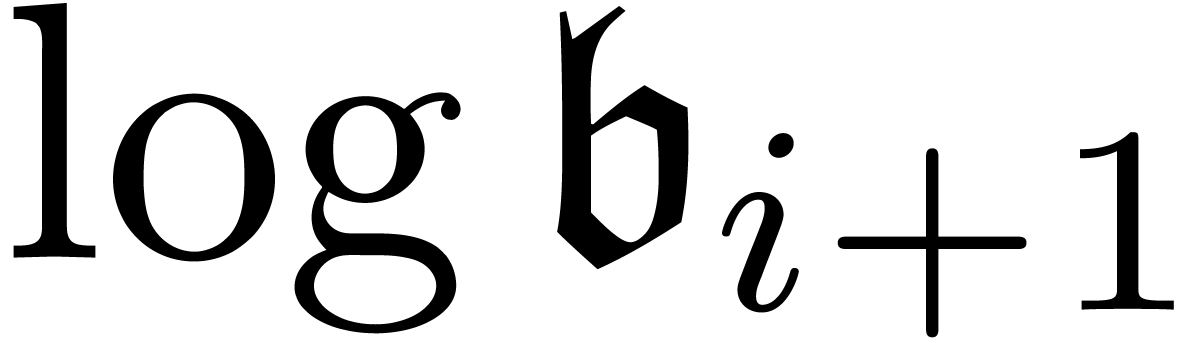 can be expanded
w.r.t.
can be expanded
w.r.t.  for all
for all  .
.
Let us now come to the more interesting operations on transseries. Differentiation and composition rely on the general principle of extension by strong linearity.
 be a map such that each well-based subset
be a map such that each well-based subset
 of
of  is mapped into a
well-based family
is mapped into a
well-based family 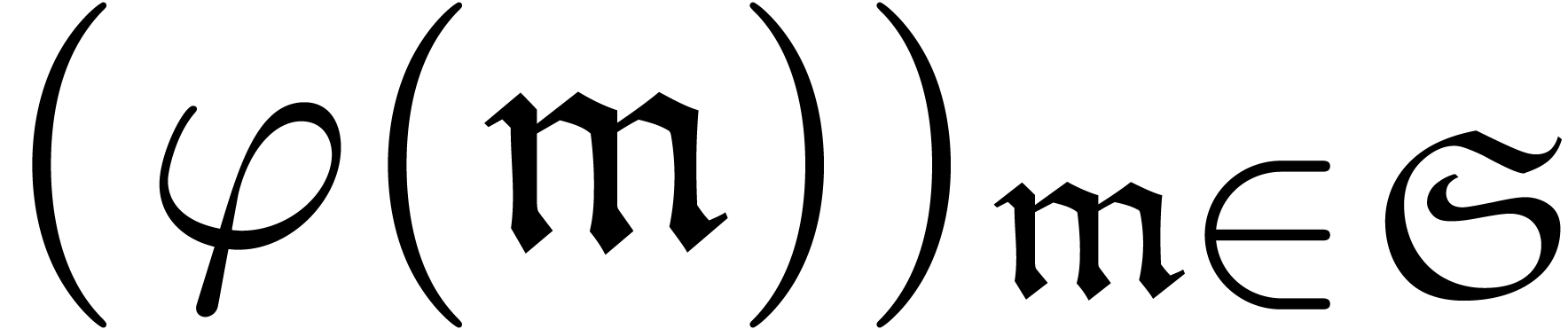 . Then
there exists a unique strongly linear extension
. Then
there exists a unique strongly linear extension 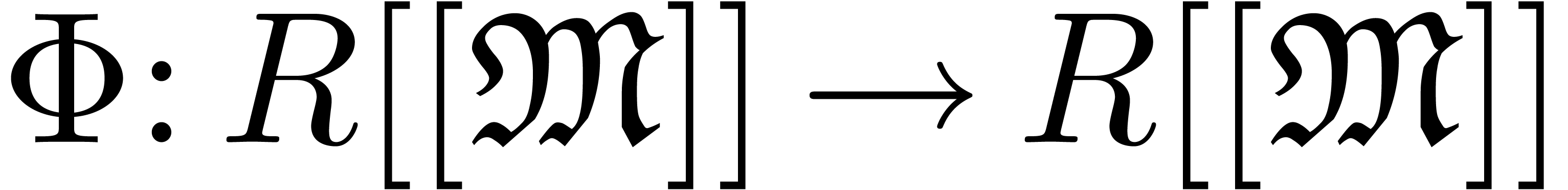 of
of  . If
. If 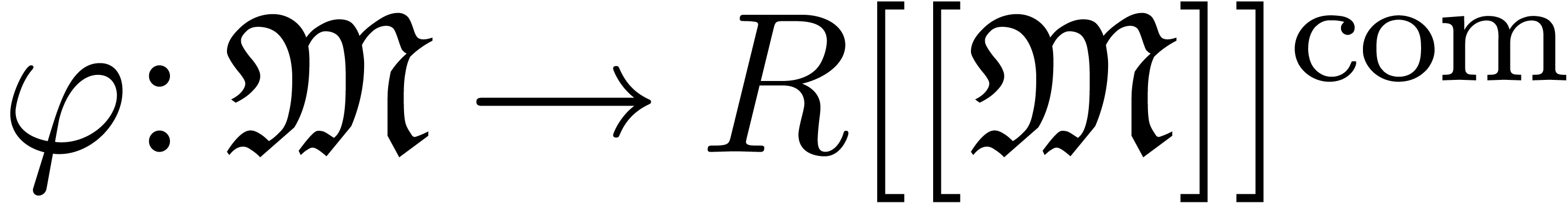 is computable, then we may compute the restriction of
is computable, then we may compute the restriction of  to
to 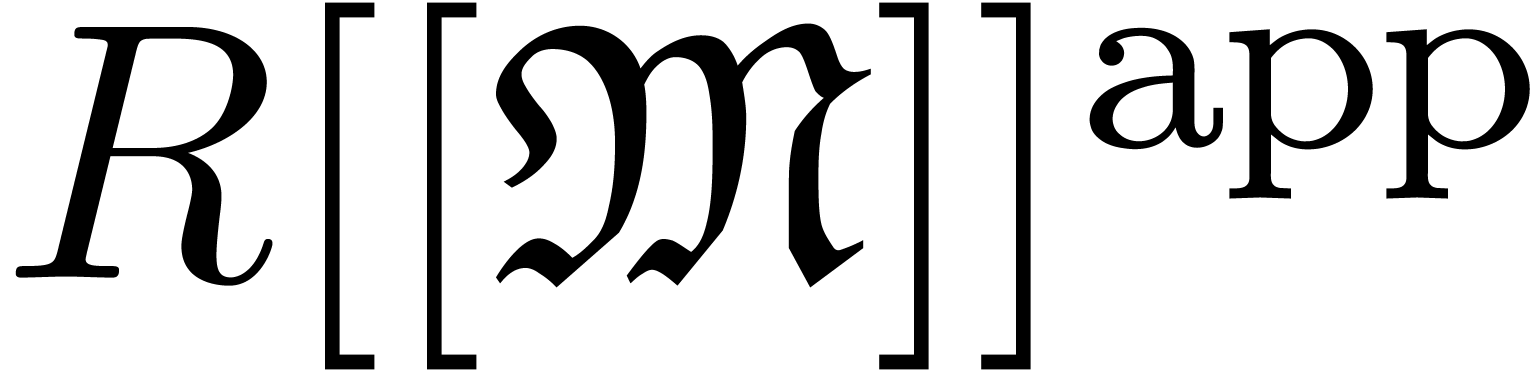 by
by
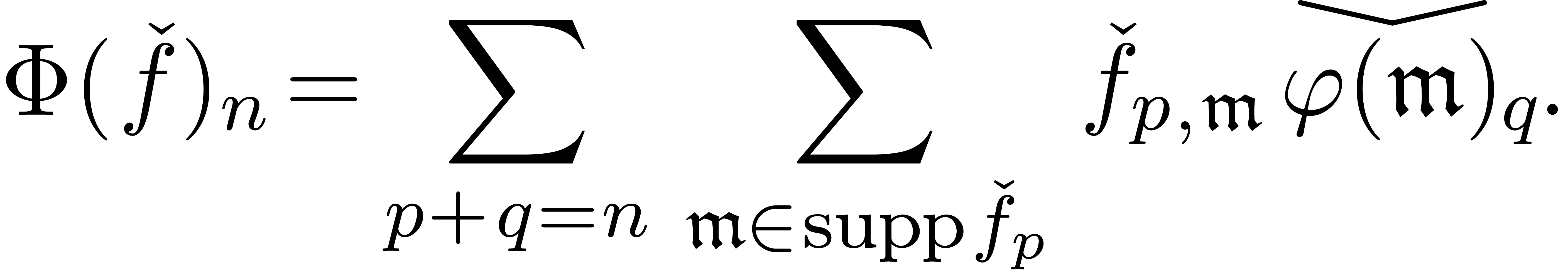
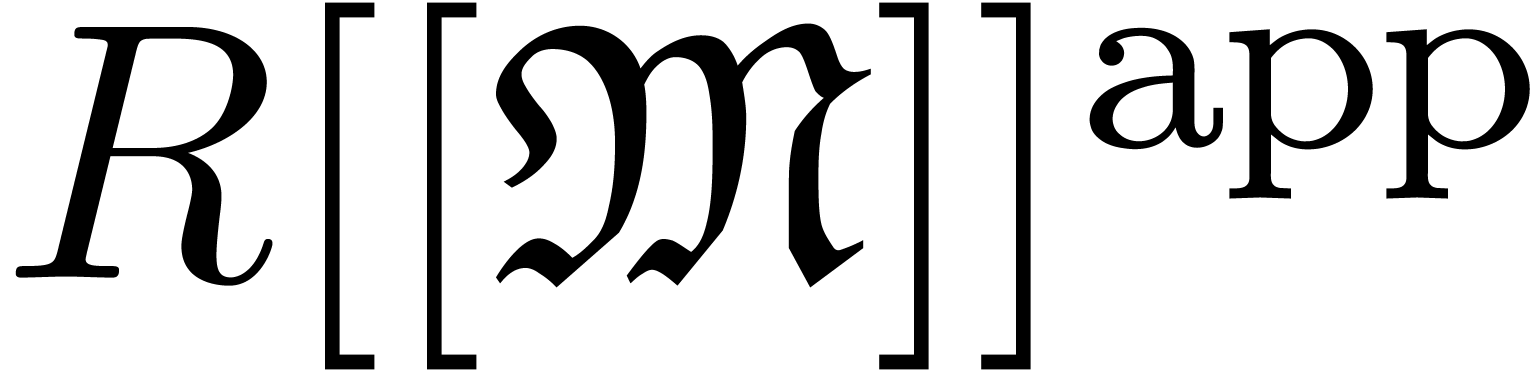 is computed using extension by strong linearity. The derivative of a
transmonomial is computed recursively:
is computed using extension by strong linearity. The derivative of a
transmonomial is computed recursively: 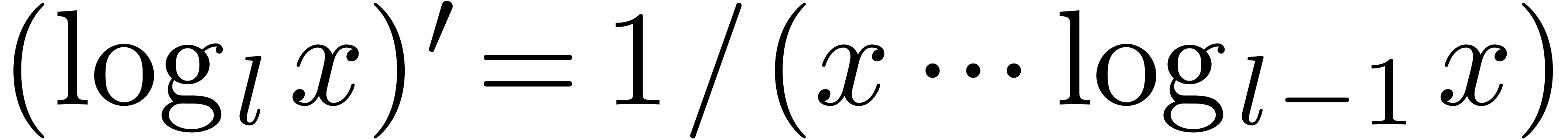 and
and
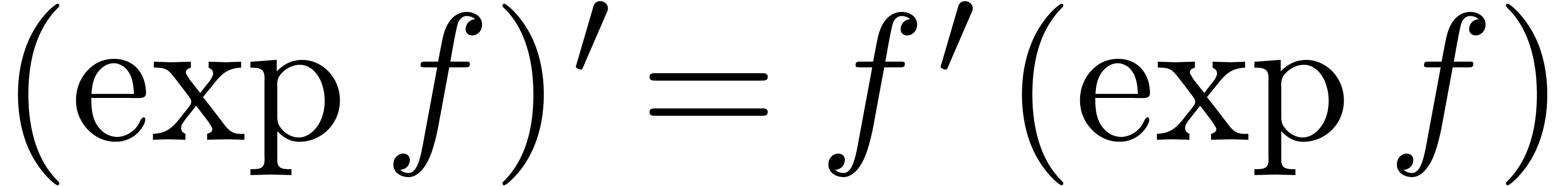 .
.
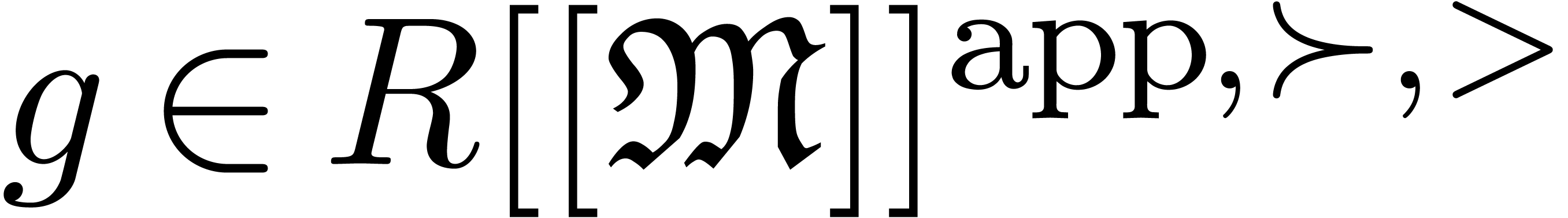 is done
similarly. For arbitrary transseries in
is done
similarly. For arbitrary transseries in 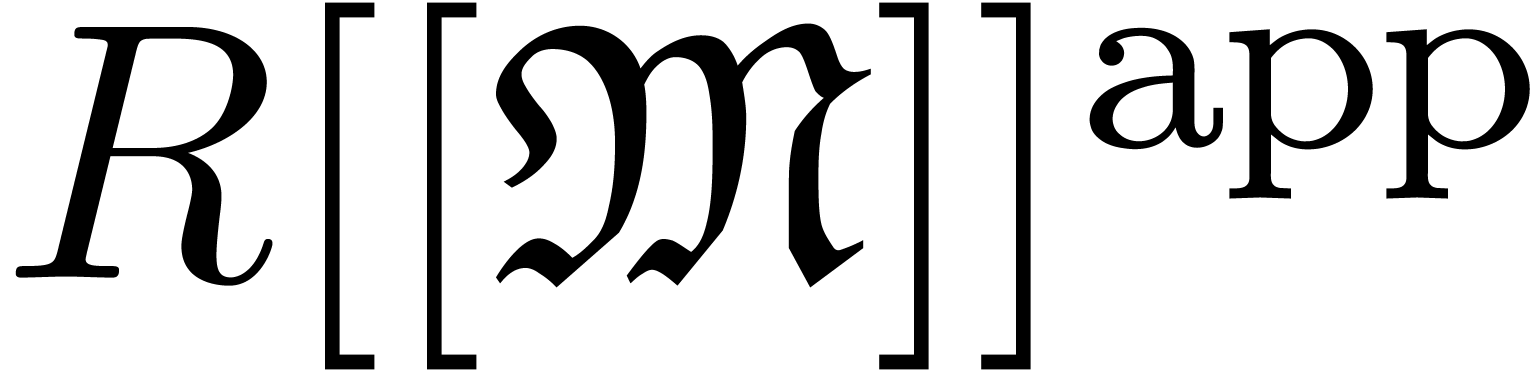 ,
we use extension by strong linearity. Transmonomials are handled
recursively:
,
we use extension by strong linearity. Transmonomials are handled
recursively: 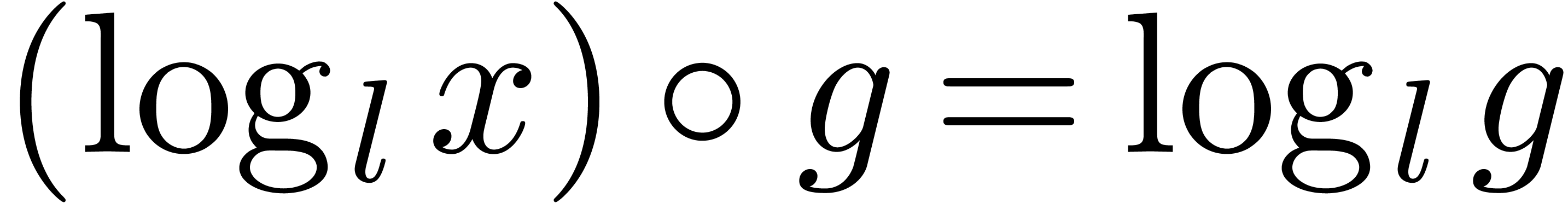 and
and 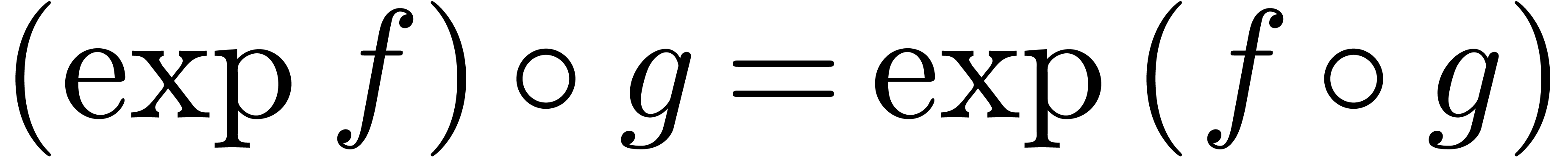 .
.
It can be shown [vdH06c, vdH97] that the
derivation w.r.t.  admits a unique
strongly linear right inverse
admits a unique
strongly linear right inverse 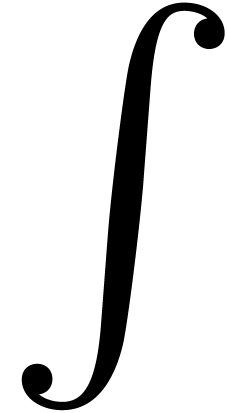 with the
“distinguished property” that
with the
“distinguished property” that  for
all
for
all  . One way to construct
. One way to construct
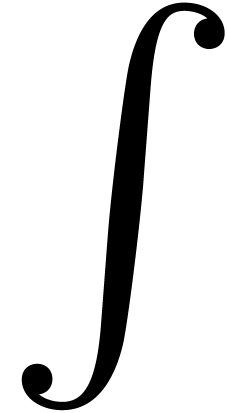 is to first compute its “trace”
is to first compute its “trace” 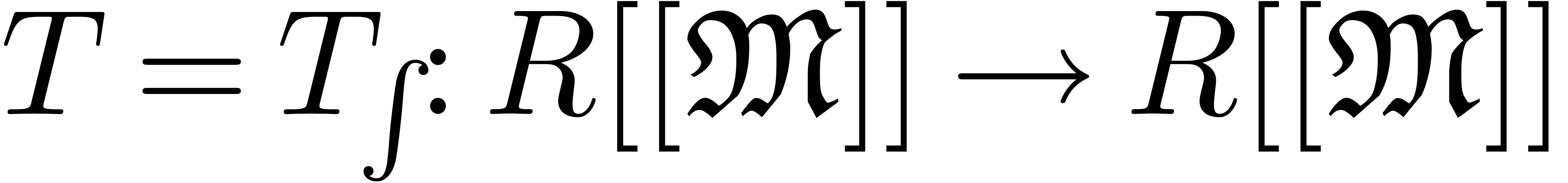 which is the unique strongly linear operator with
which is the unique strongly linear operator with
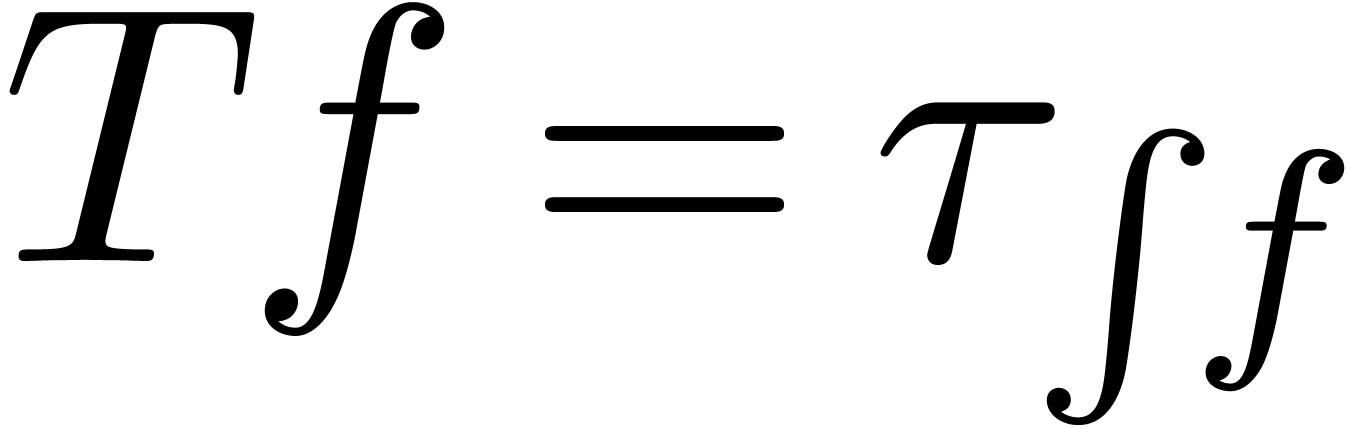 on
on  .
We then compute
.
We then compute 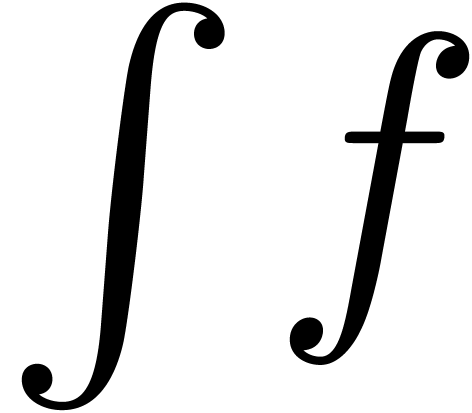 by solving the implicit equation
by solving the implicit equation
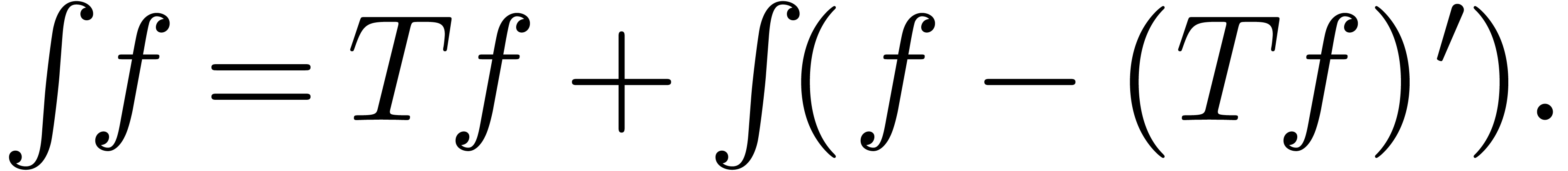 |
(10) |
One may either apply (10) for monomials and extend by
strong linearity, or apply it directly for arbitrary transseries  .
.
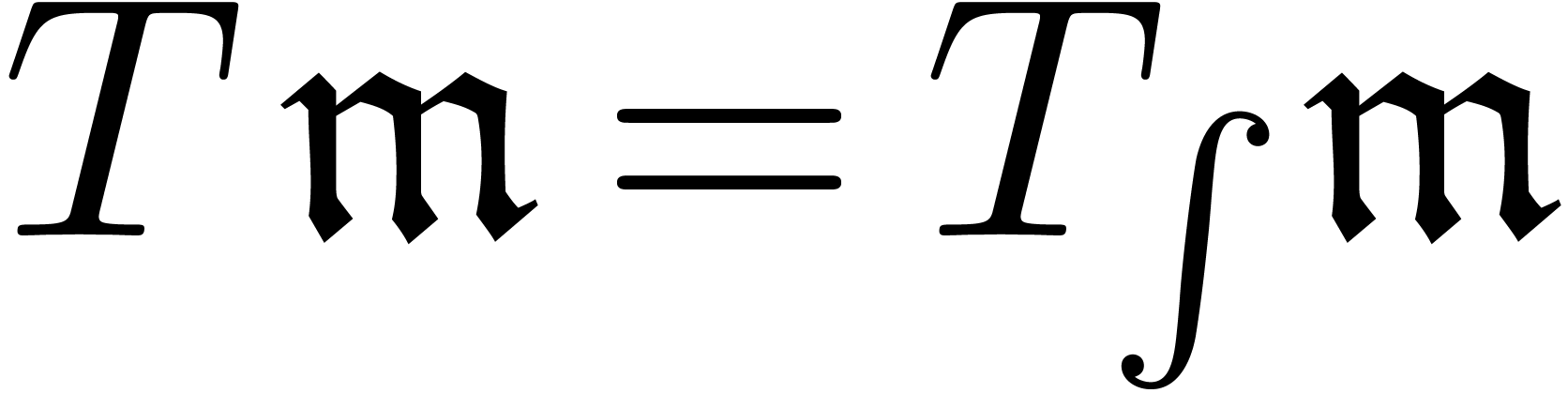 of a transmonomial is computed using
the formula
of a transmonomial is computed using
the formula
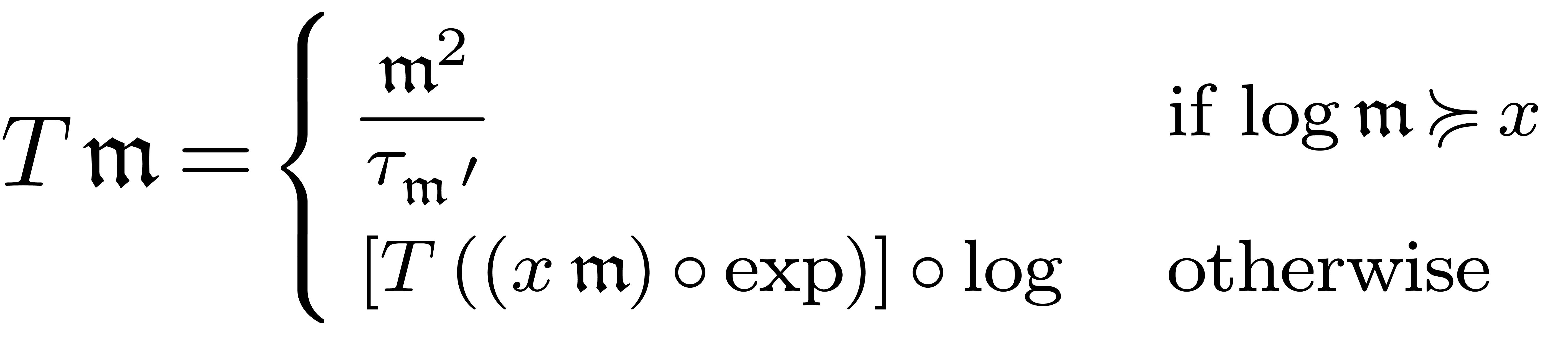
We next extend by strong linearity.
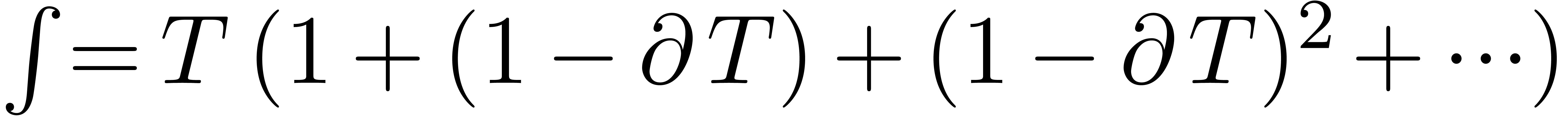
and define an expander for this operator:
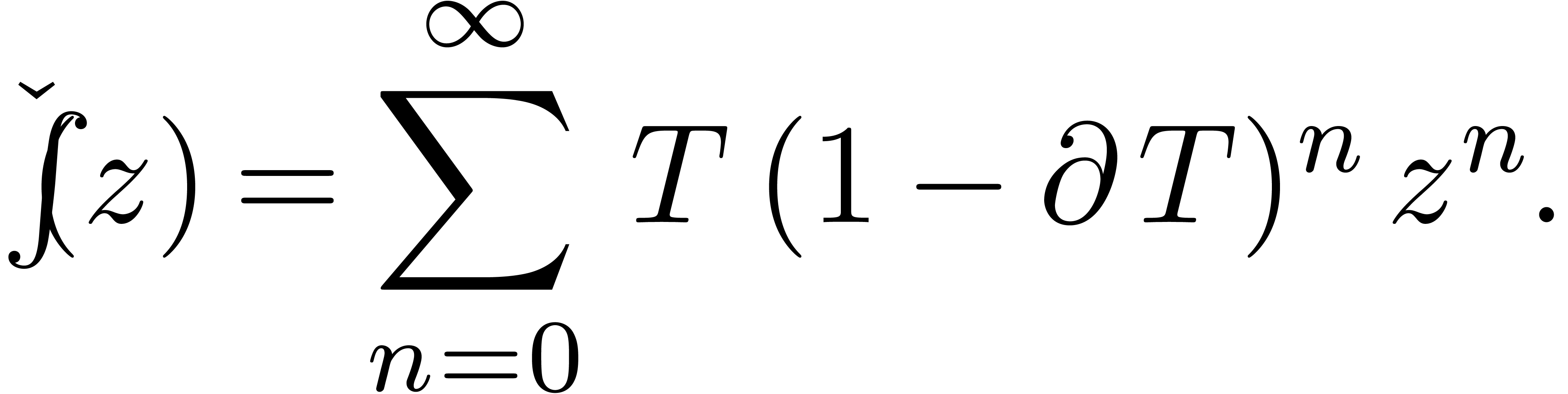
Then distinguished integration can be regarded as the application of
this operator expander to another expander 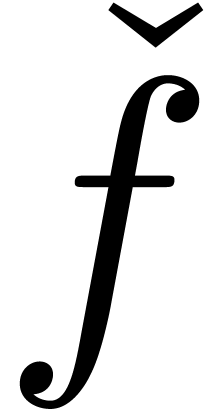 :
:
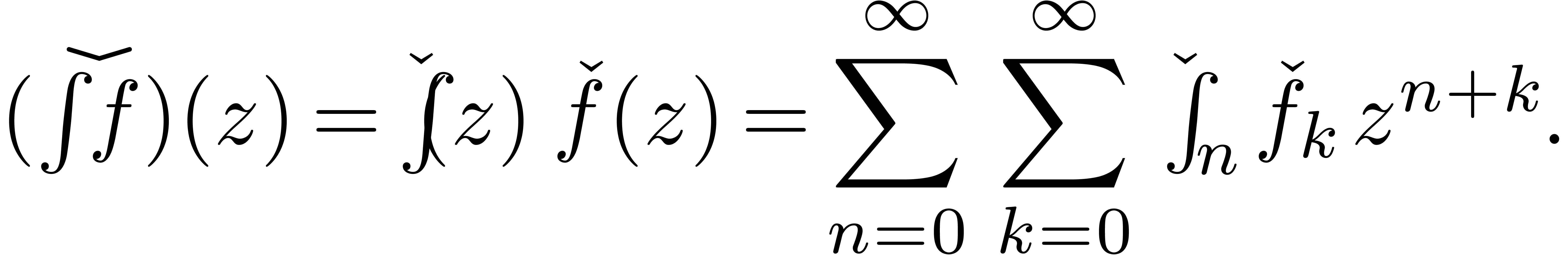
We also notice that  is a fixed-point of the
operator
is a fixed-point of the
operator
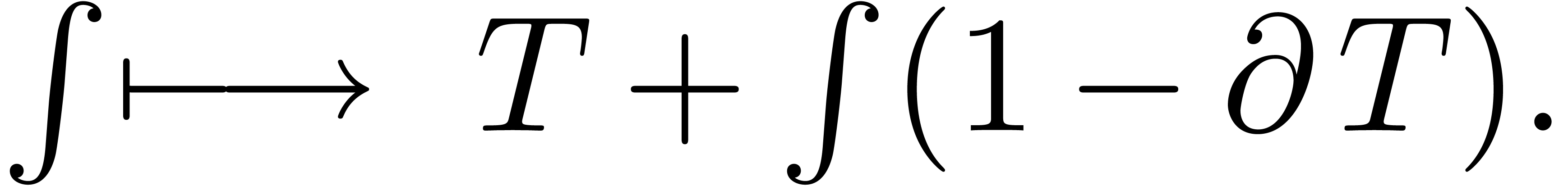
Adapting our general mechanism for the computation of fixed points for
operators instead of series, we find 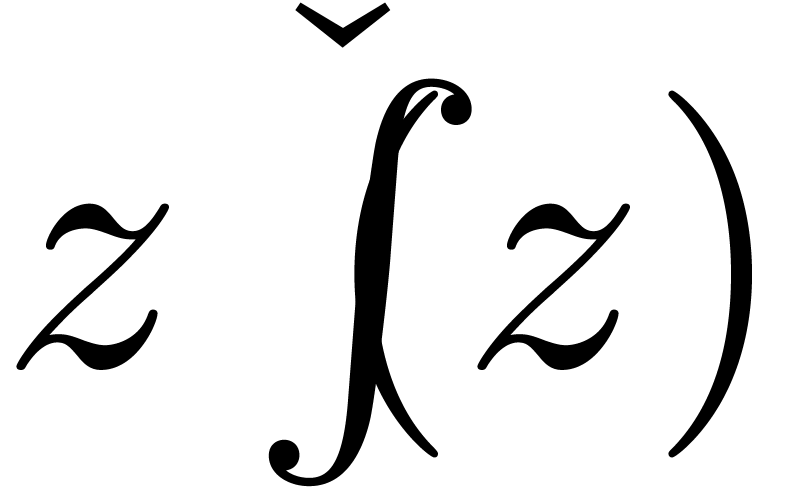 as the
natural expander of
as the
natural expander of  .
.
Functional inversion of transseries can be done using formulas in [vdH06c, Section 5.4] and we will not detail this operation here. Two other interesting operations are finite differences and discrete summation:

We implemented these operations because they are critically needed in an
algorithm for the asymptotic extrapolation of sequences [vdH06a].
Modulo compositions with  and
and 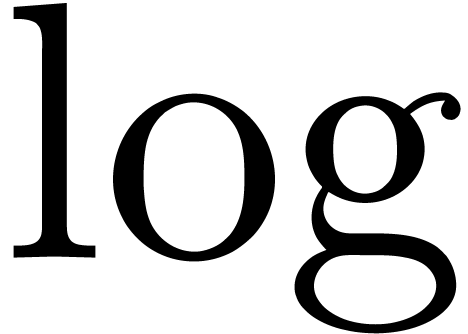 , they are related to finite quotients
and discrete products:
, they are related to finite quotients
and discrete products:
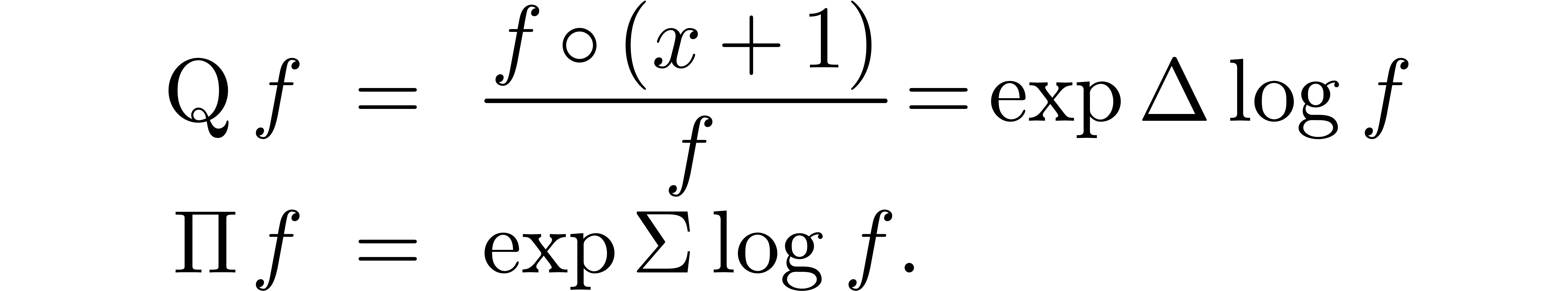
Our algorithm for right-composition clearly yields a way to compute  for
for  . The
distinguished summation
. The
distinguished summation  is the unique
distinguished strongly linear right-inverse of
is the unique
distinguished strongly linear right-inverse of  , i.e.
, i.e. 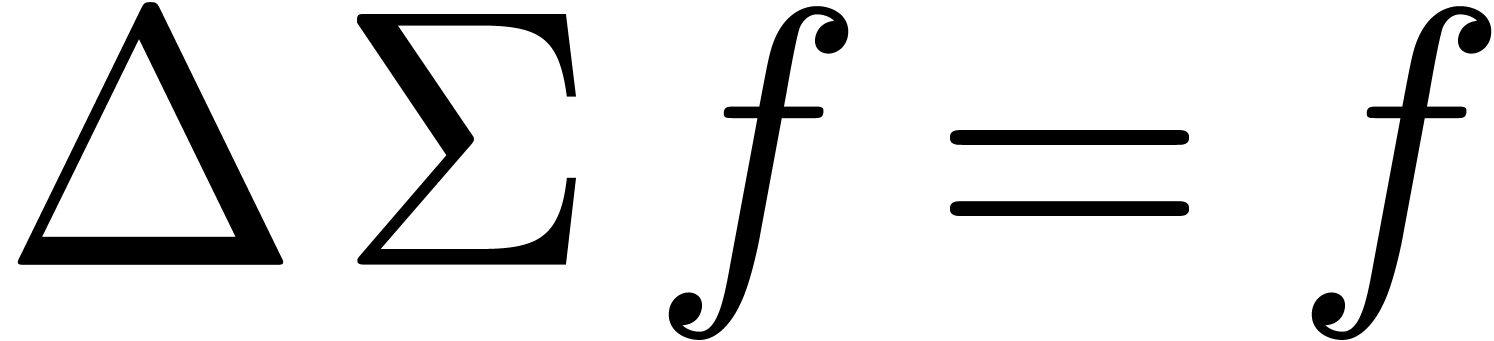 and
and  for all
for all  .
It therefore suffices to show how to compute
.
It therefore suffices to show how to compute  for
monomials
for
monomials 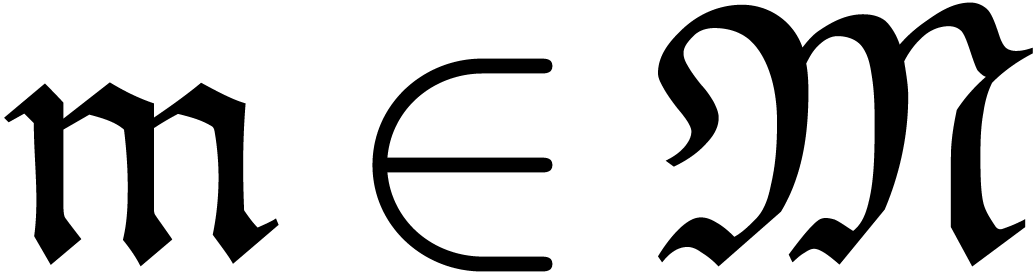 . Three different
cases need to be distinguished :
. Three different
cases need to be distinguished :
 (i.e.
(i.e.  ), we compute
), we compute  by
solving the equation
by
solving the equation
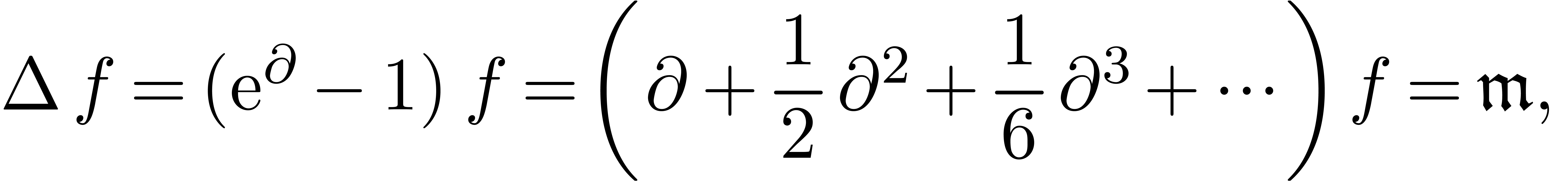
which yields a solution
The application of the operator
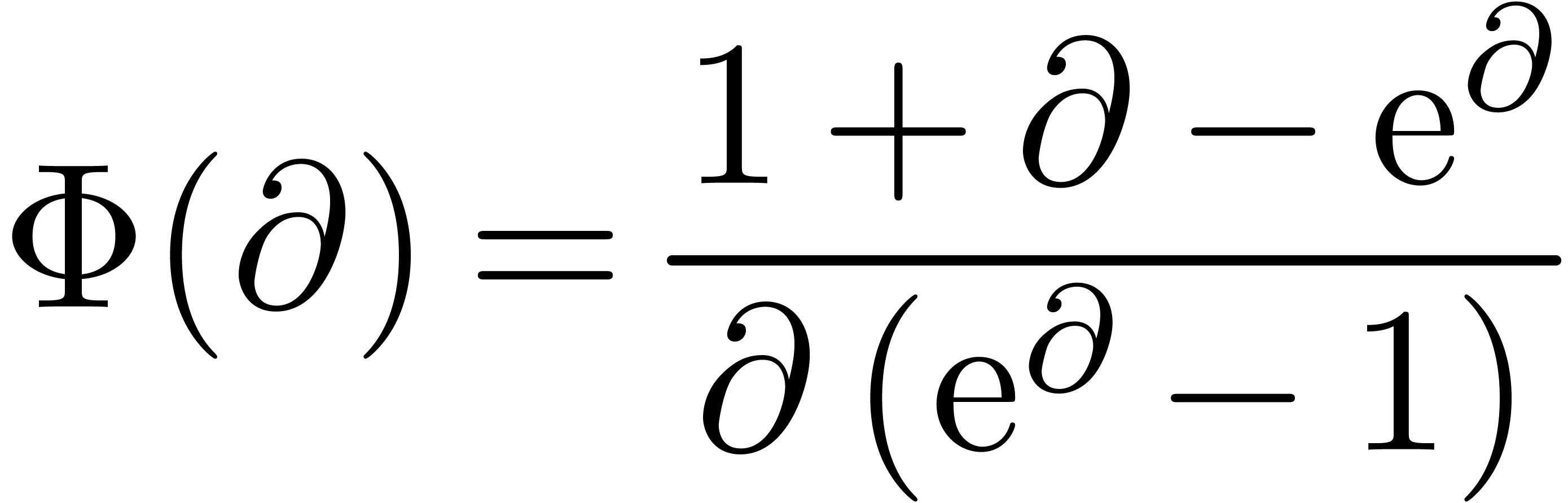
to  is computed in a similar way as in the case
of distinguished integration. In fact, the expander
is computed in a similar way as in the case
of distinguished integration. In fact, the expander 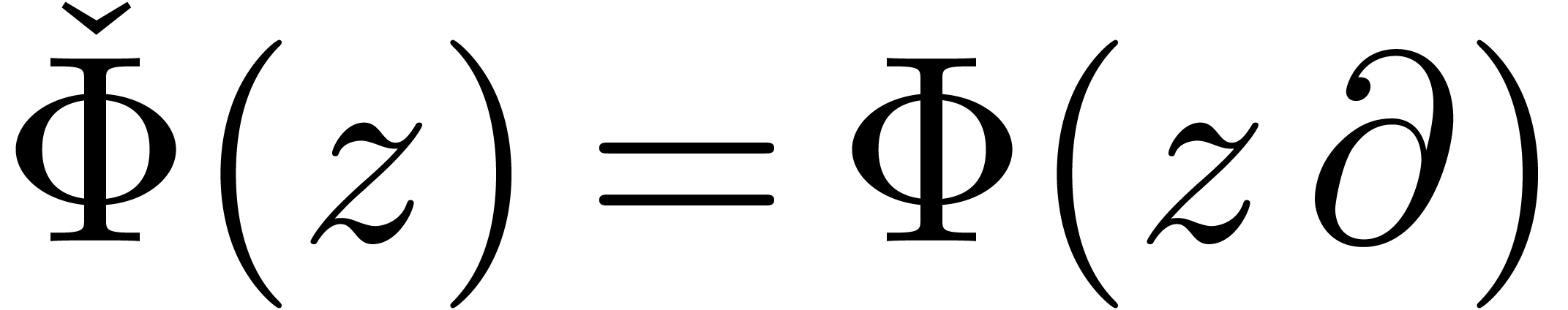 can directly be applied to expanders
can directly be applied to expanders  with
with  for all
for all  .
Moreover, this application preserves grid-basedness.
.
Moreover, this application preserves grid-basedness.
 (i.e.
(i.e.  ), let
), let 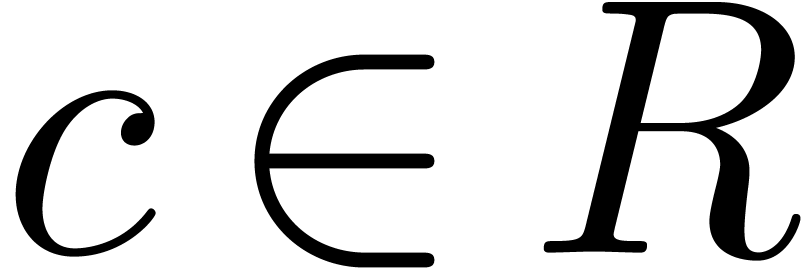 be
such that
be
such that  with
with  .
We now search for a solution to
.
We now search for a solution to 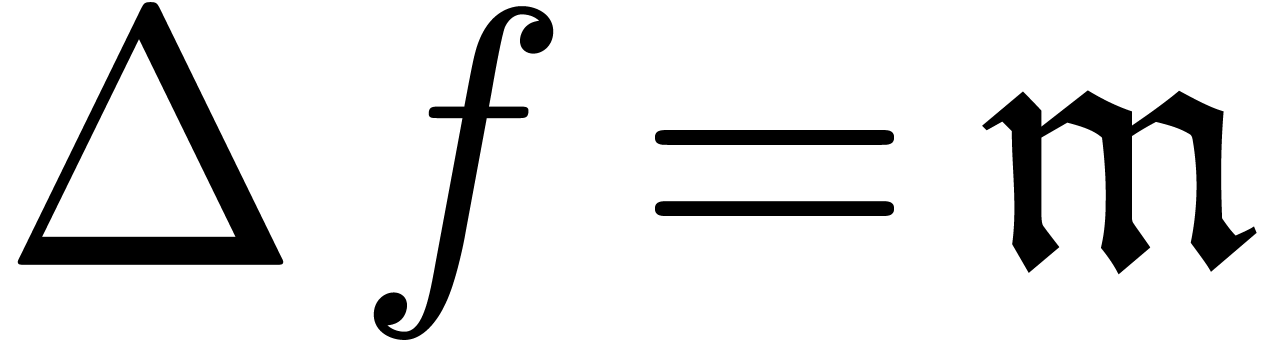 of the form
of the form
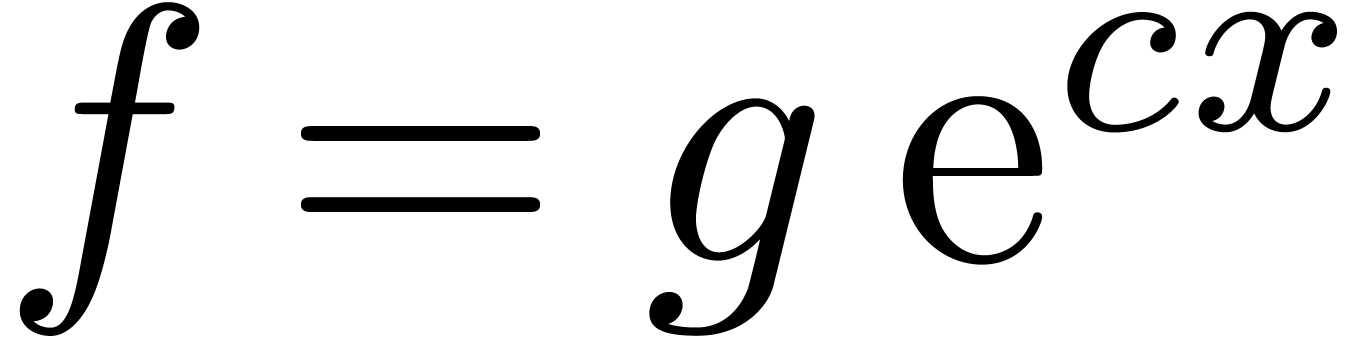 , which leads to the
equation
, which leads to the
equation
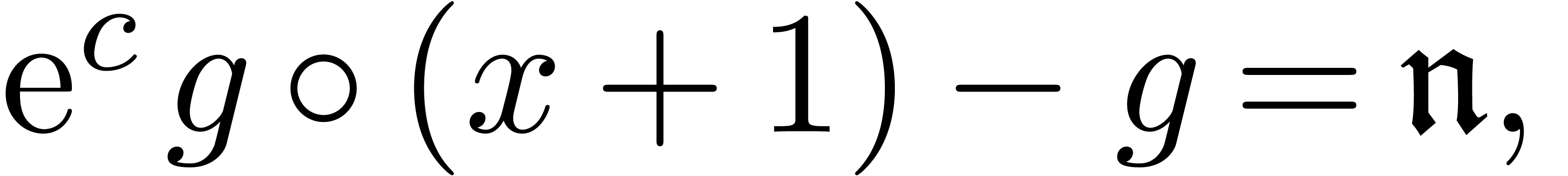 |
(11) |
We rewrite this equation in operator form
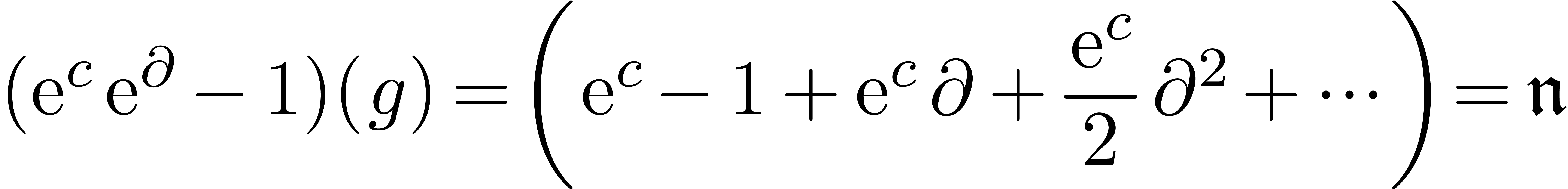
and we invert the operator 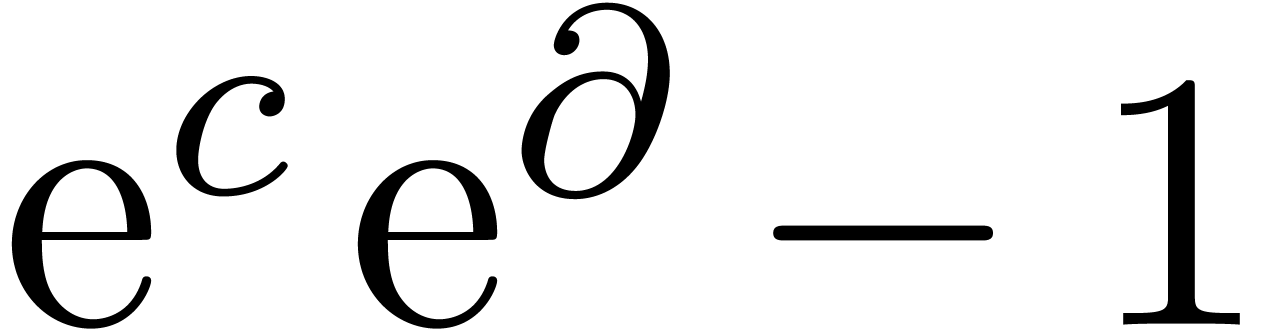 as in the flat case.
No integration is needed this time, since
as in the flat case.
No integration is needed this time, since 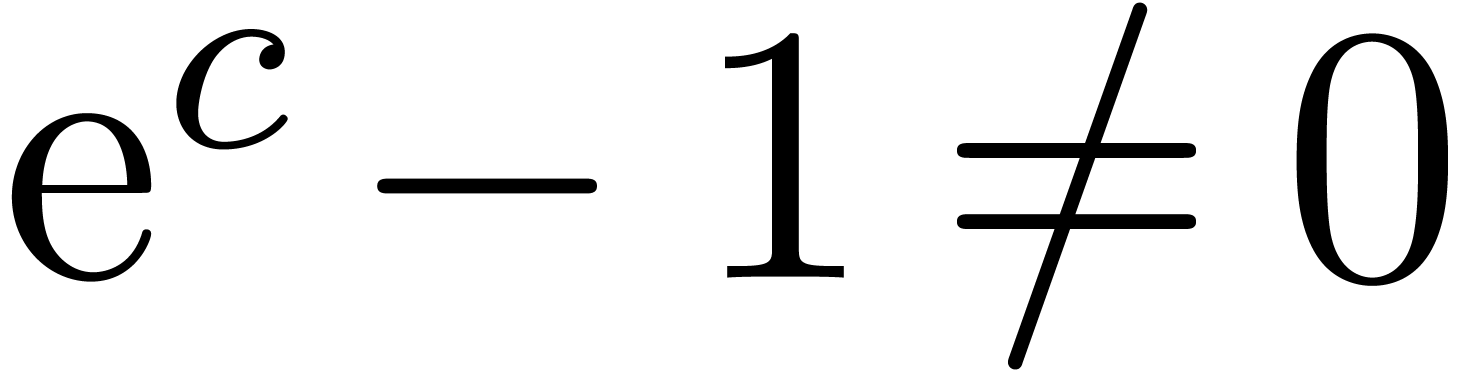 .
Again, the grid-based property is preserved by moderate discrete
summation.
.
Again, the grid-based property is preserved by moderate discrete
summation.
 (i.e.
(i.e.  ), we have to solve the equation
), we have to solve the equation
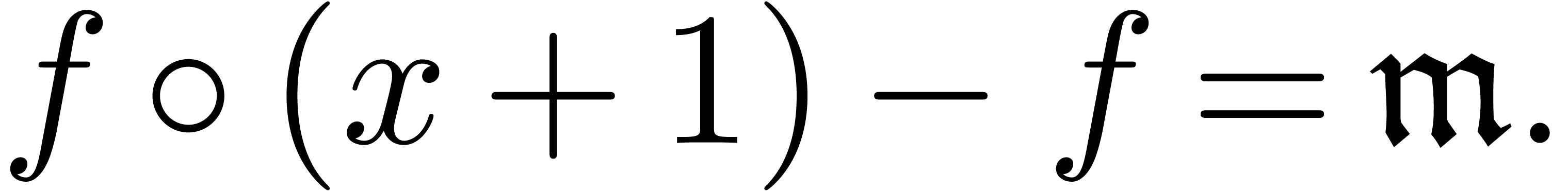
If  , then this is done by
computing a fixed point for the operator
, then this is done by
computing a fixed point for the operator
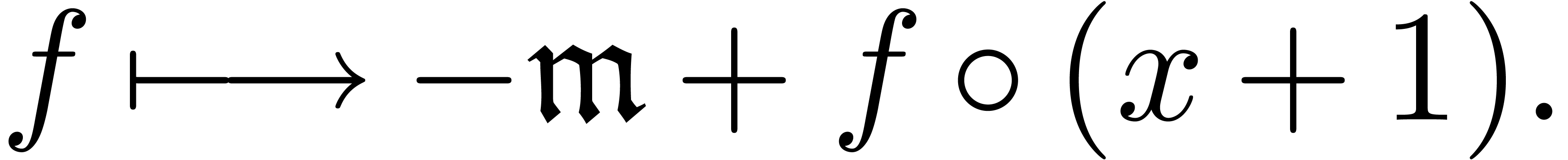
If  , then we compute a fixed
point for the operator
, then we compute a fixed
point for the operator
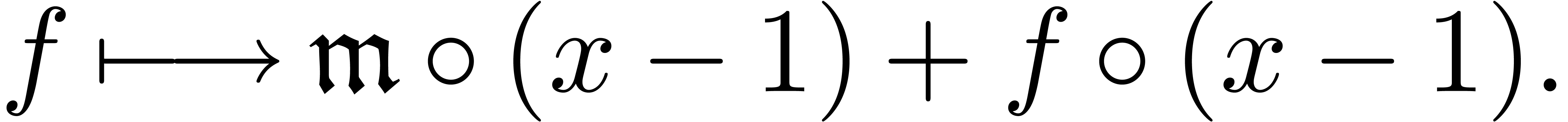
It can be shown that  is grid-based if
is grid-based if  is grid-based and there exists a
is grid-based and there exists a 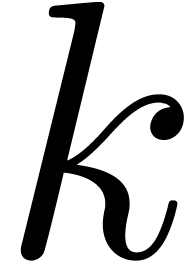 such that
such that  for all
for all  .
.
So far, we have not really exploited the extra level of abstraction provided by expanders. In this section, we will describe several “meta-operations” on expanders. These operations do not affect the series being represented, but rather concern qualitative aspects of the approximation process: they guide the rate of convergence, the terms which appear first, etc. Based on the process of “stabilization”, we will also describe a heuristic zero-test and a heuristic method for the computation of dominant terms.
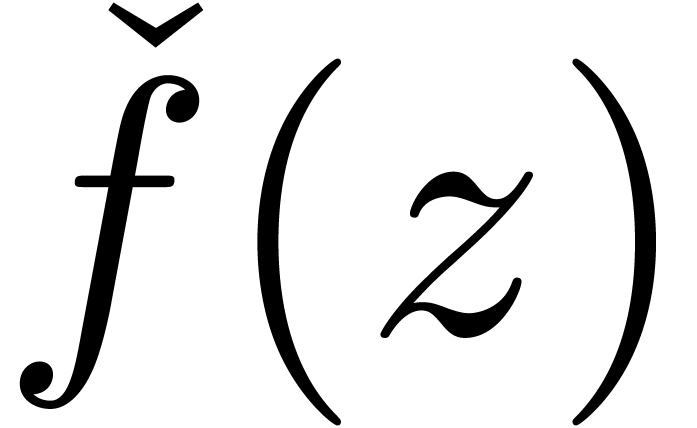 and
and
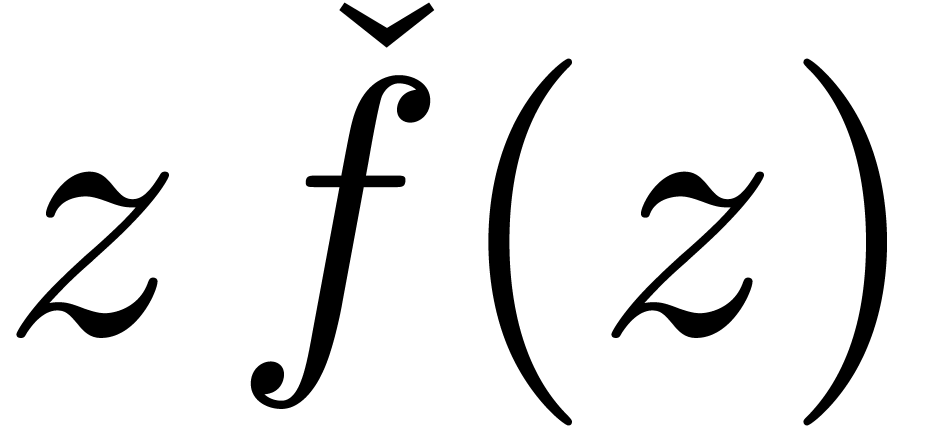 represent the same series. More generally,
given a computable function
represent the same series. More generally,
given a computable function 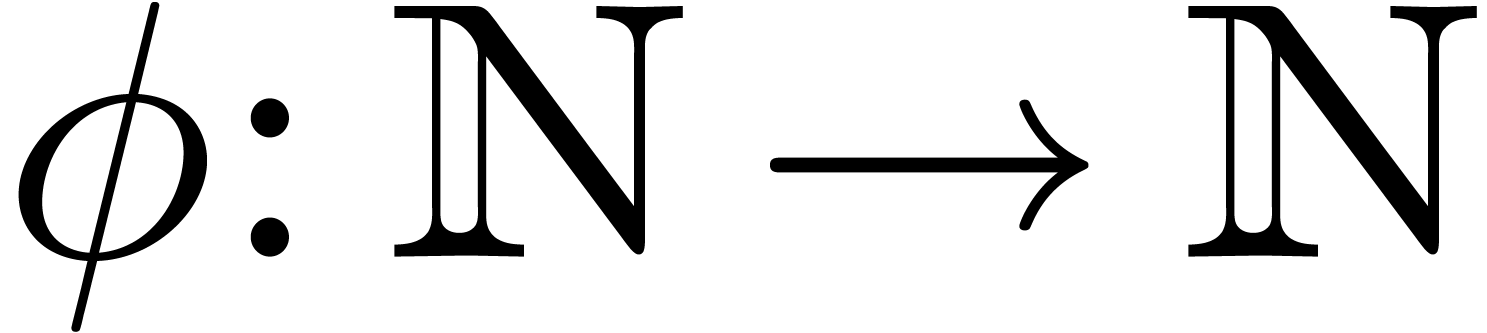 with
with 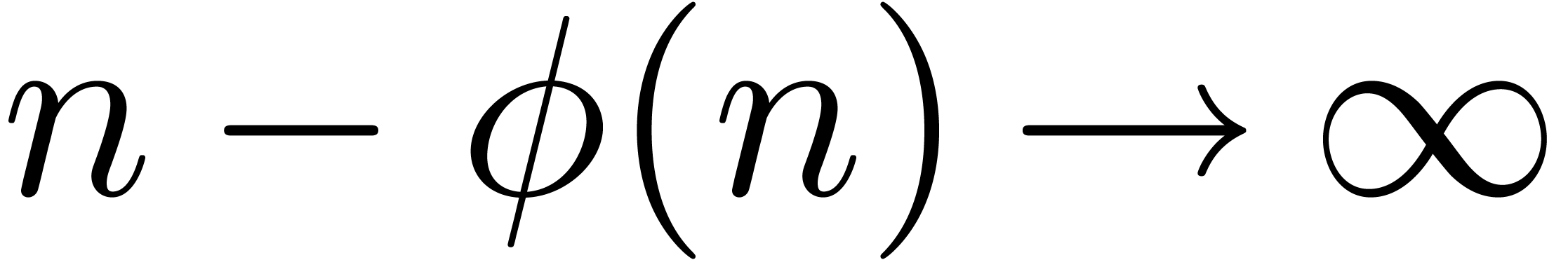 , we define the shortening operator
, we define the shortening operator
 by
by
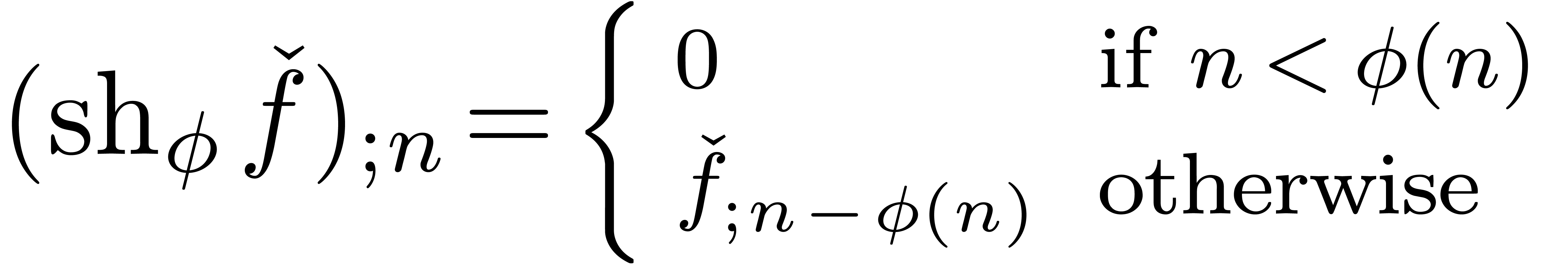
In the case when  is a constant function, we have
is a constant function, we have
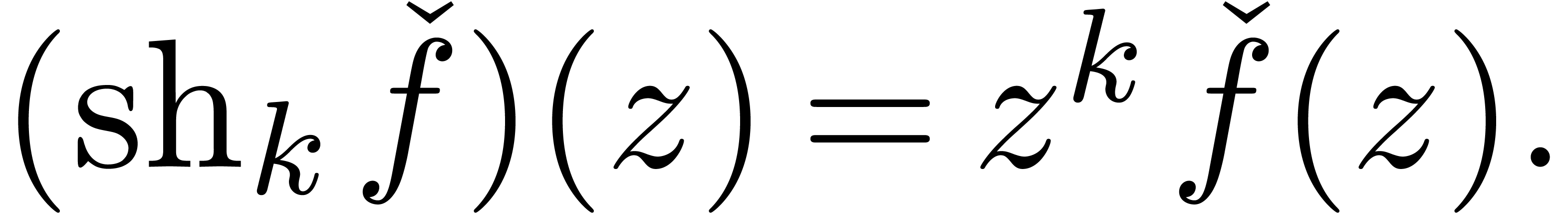
The shortening operator is typically used for the expansion of
expressions which involve an expander 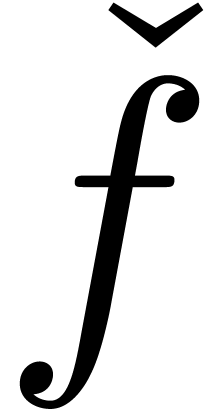 ,
such that the expression size of
,
such that the expression size of 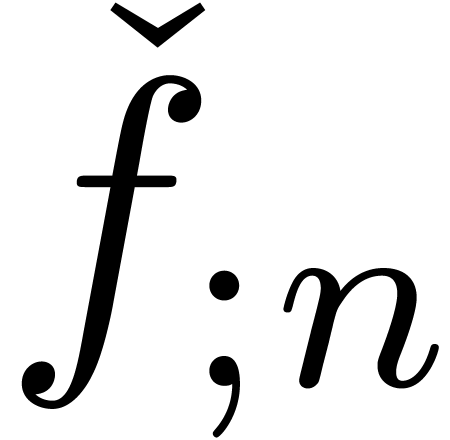 tends to grow
very rapidly with
tends to grow
very rapidly with 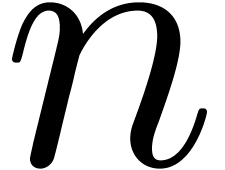 . For
instance, we may prefer to compute a sum
. For
instance, we may prefer to compute a sum  using
the expander
using
the expander 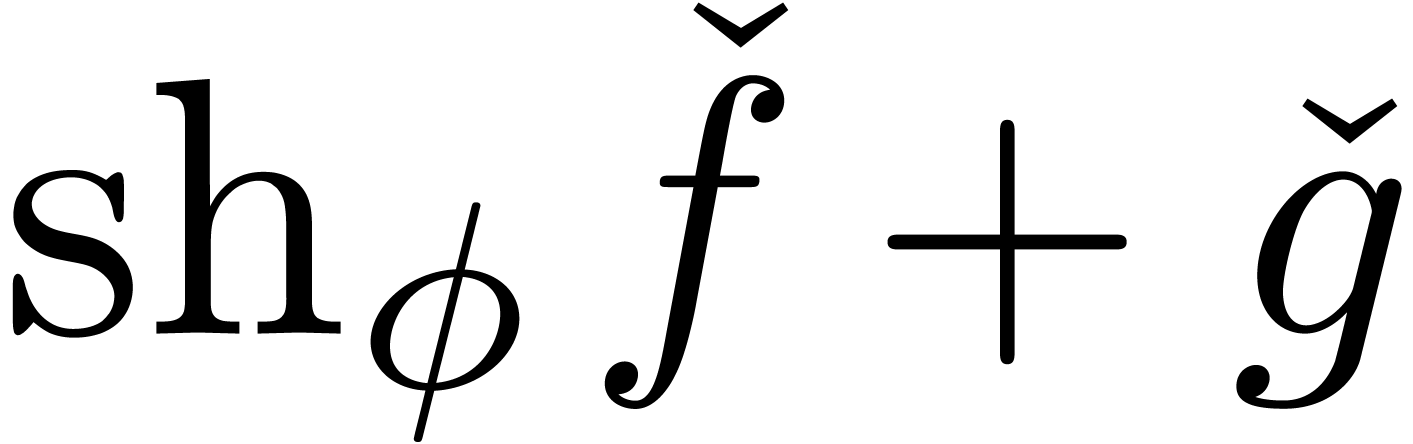 instead of
instead of  .
.
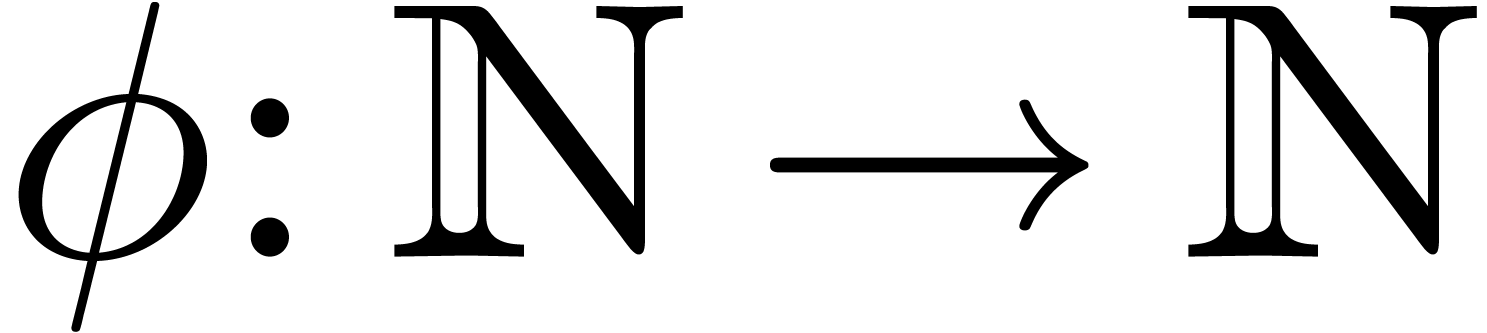 ,
the lengthening operator
,
the lengthening operator 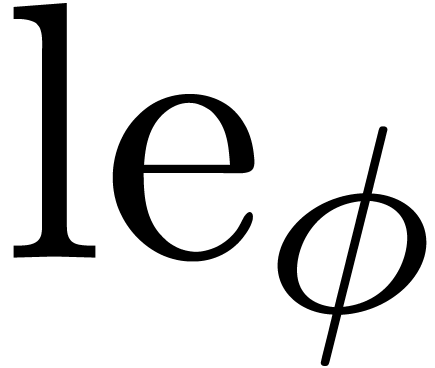 is defined
by
is defined
by
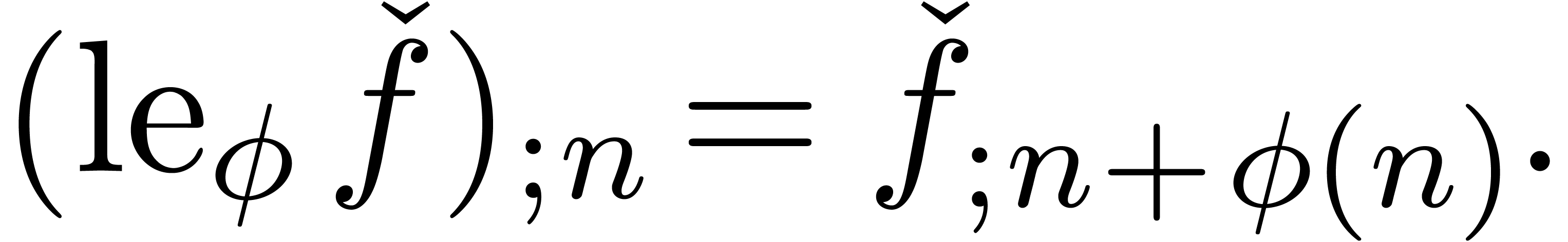
In the case when  is a constant function, we have
is a constant function, we have
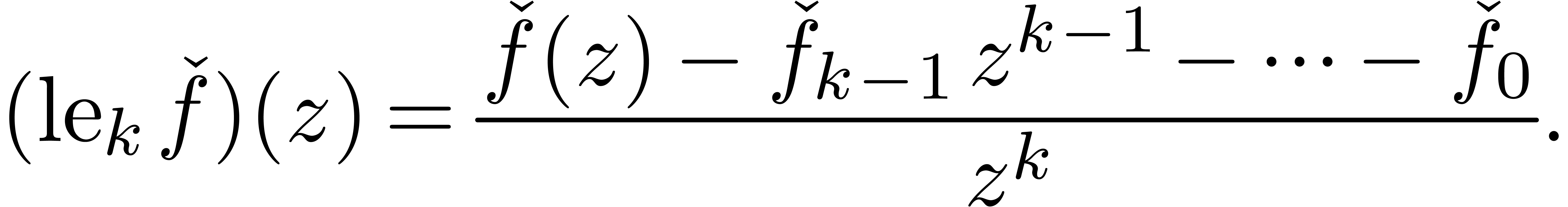
During the expansion of an expression, the lengthening operator may for
instance be used in order to boost the precision of a subexpression. We
may also use it as a substitute for the order parameter of a typical
expansion command. E.g., we would simply display 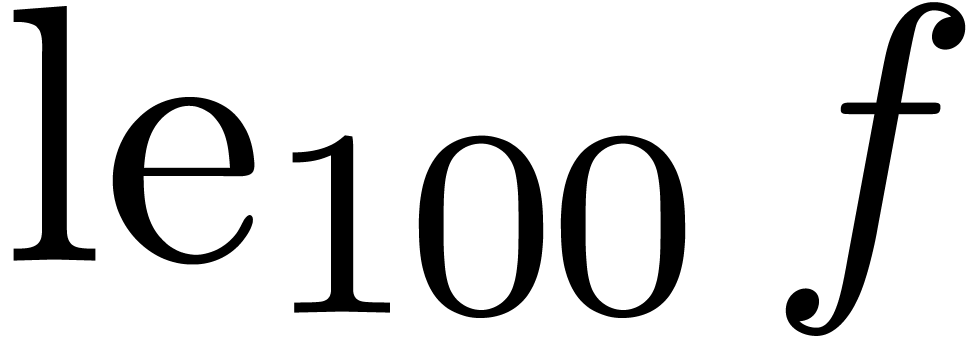 in order to show an additional
in order to show an additional 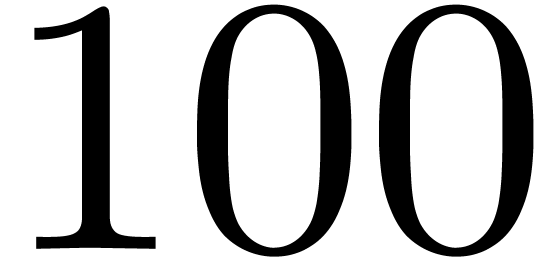 terms of
terms of  .
.
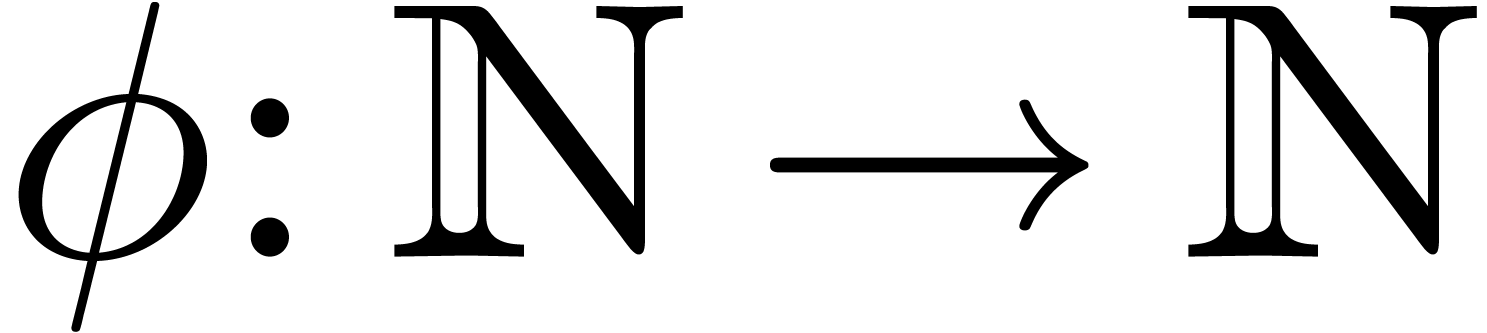 ,
we define it by
,
we define it by
The stabilization operator removes all terms from the expansion 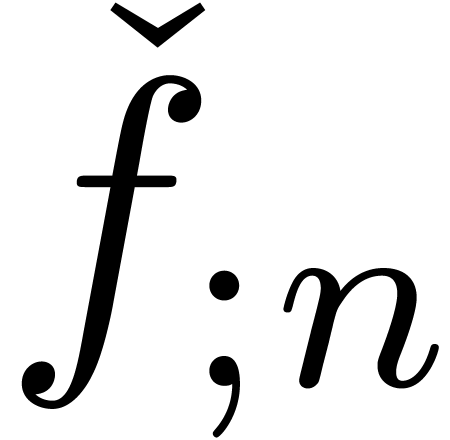 which are still subject to changes during the next
which are still subject to changes during the next
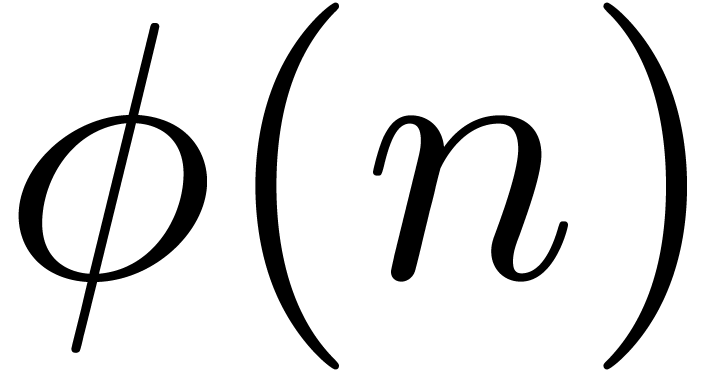 approximations. Even for small values of
approximations. Even for small values of 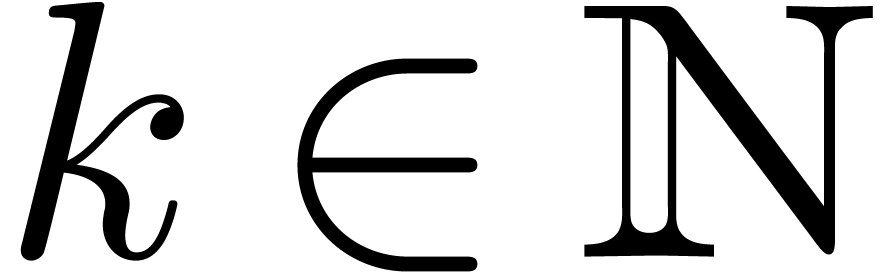 , such as
, such as 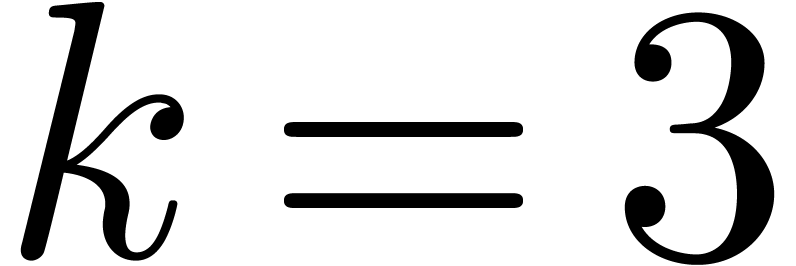 , we usually have
, we usually have
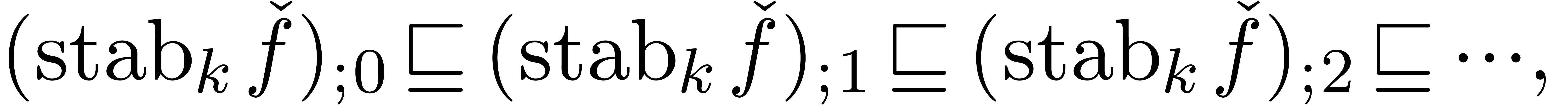 |
(12) |
where
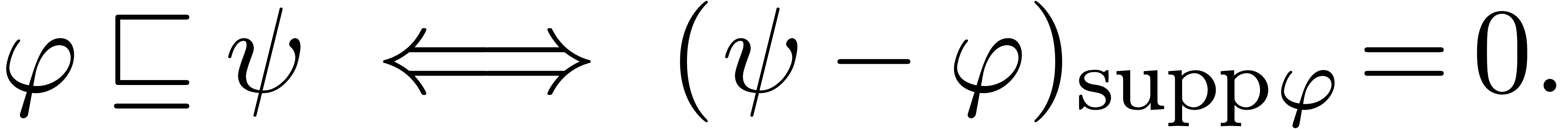
In particular, the successive approximations 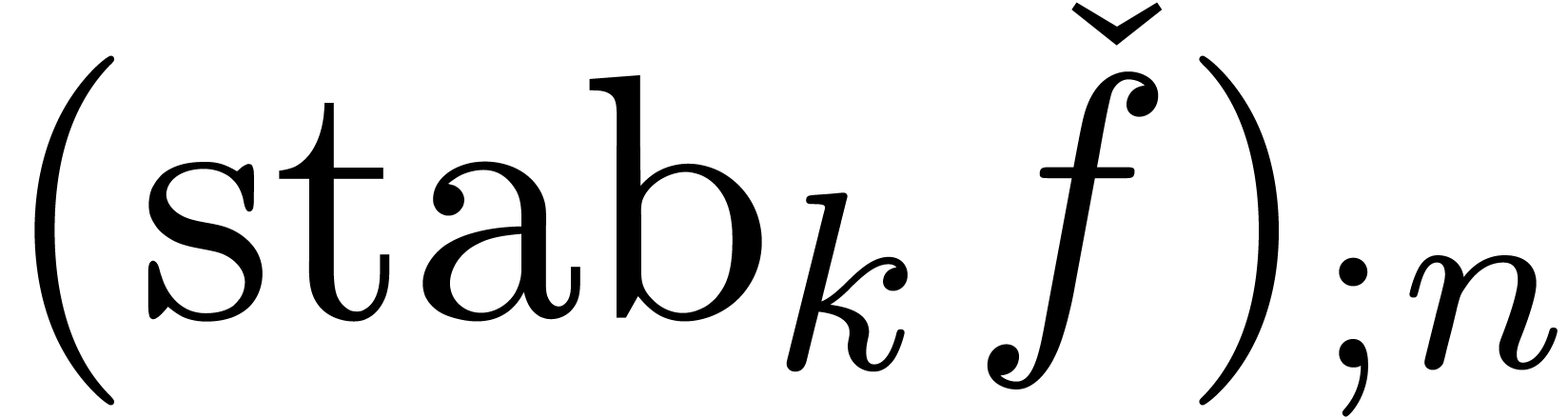 usually only contain terms which occur in the final result
usually only contain terms which occur in the final result  .
.
Example 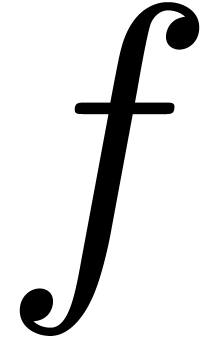 from example 2.
When approximating
from example 2.
When approximating 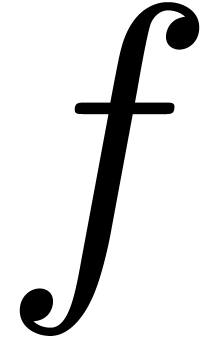 using
using  instead of
instead of 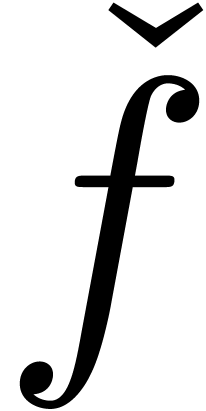 , we get:
, we get:
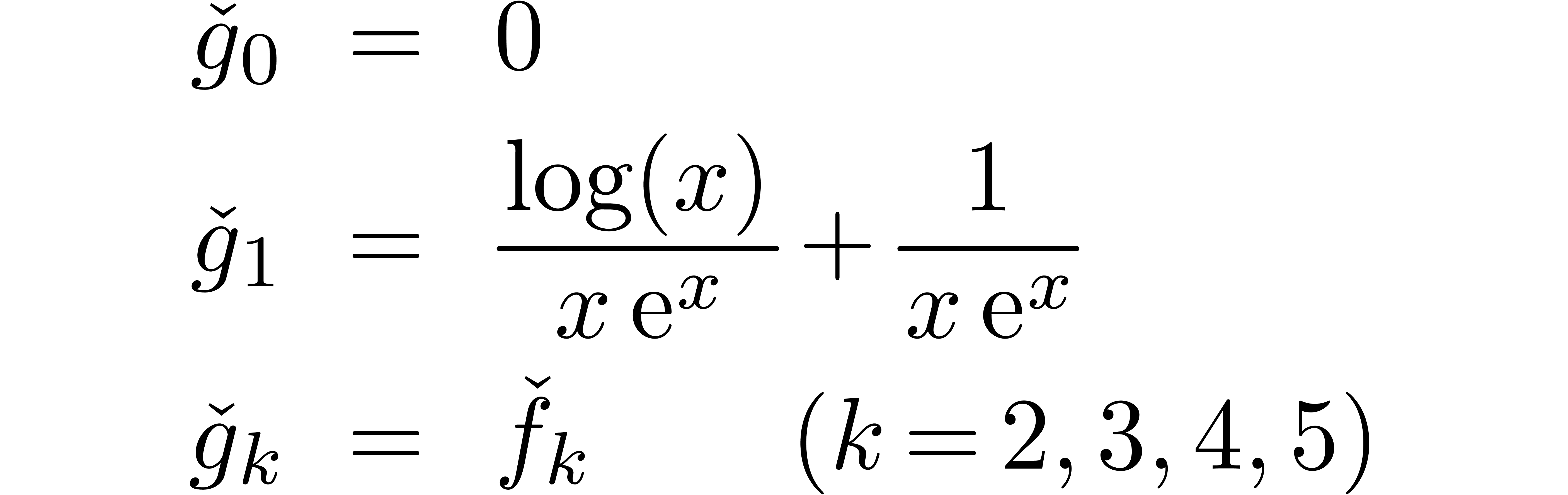
Example  is the expander
is the expander
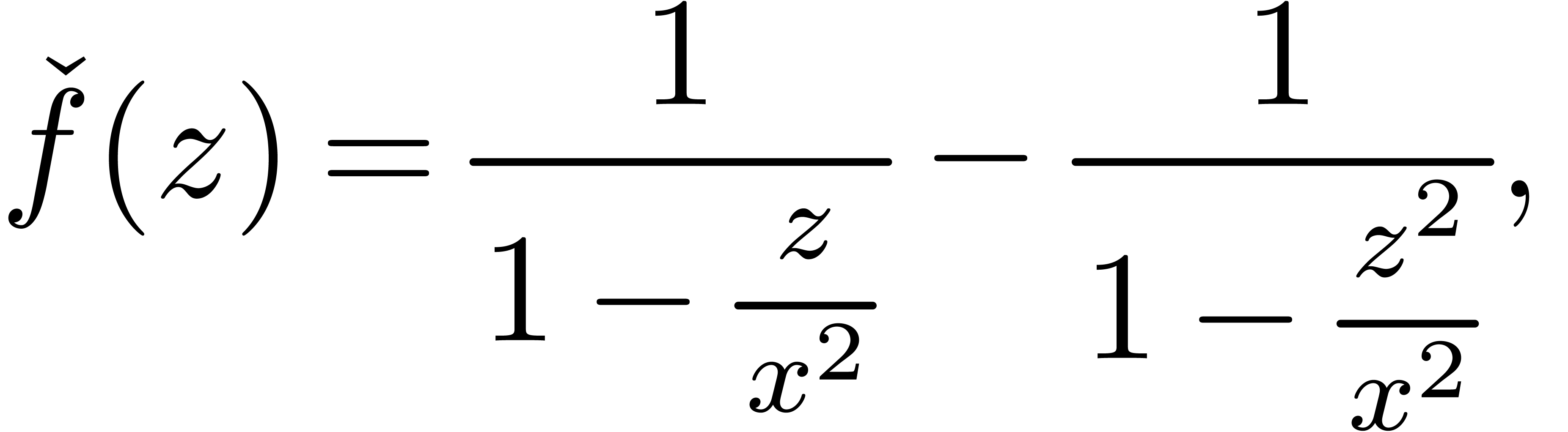
which arises during the computation of
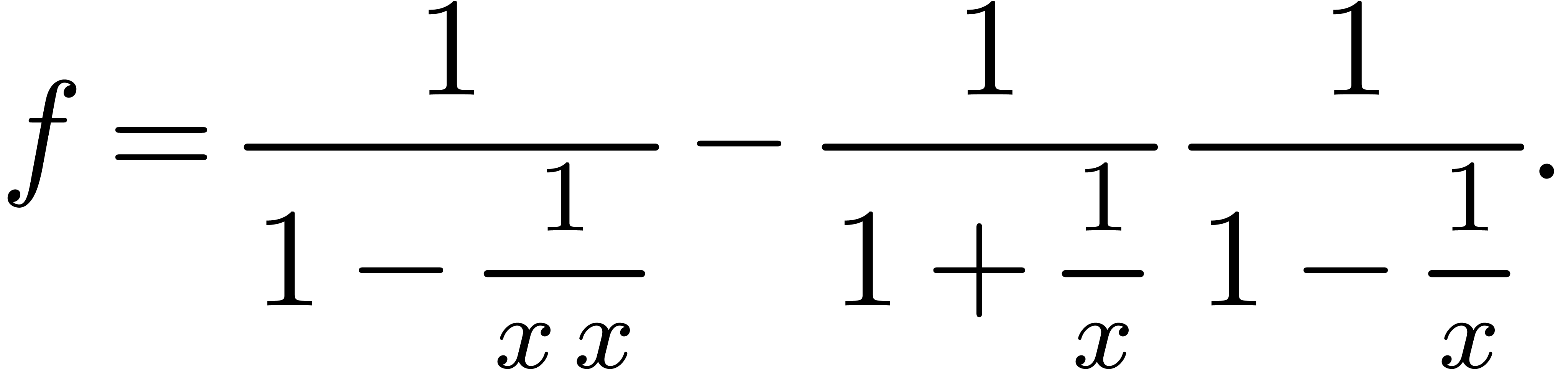
Indeed, the first terms of  are given by
are given by
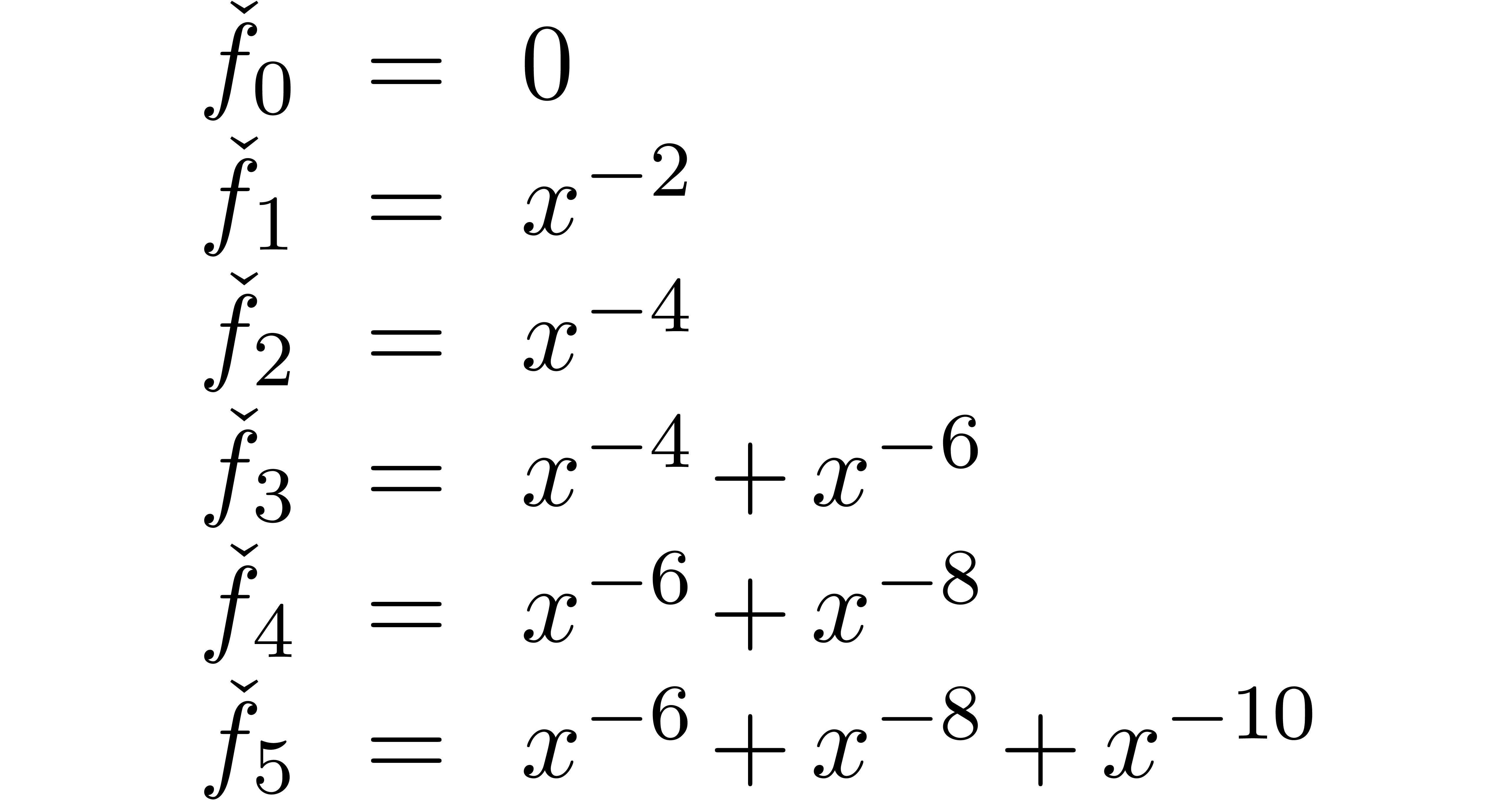
In this kind of situations, it may be necessary to consider more
powerful stabilizations of the form 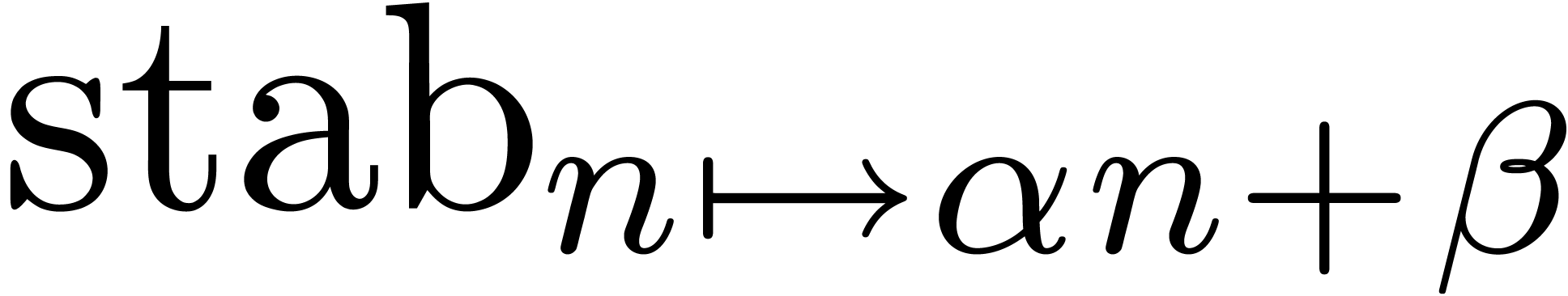 .
.
 |
(13) |
for a sufficiently large value of 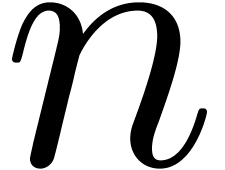 .
When taking
.
When taking 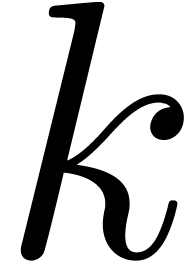 and
and 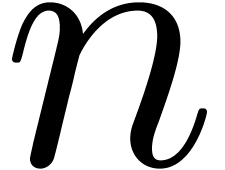 fixed,
the formula (13) also provides us with a reasonable
heuristic for the computation of
fixed,
the formula (13) also provides us with a reasonable
heuristic for the computation of 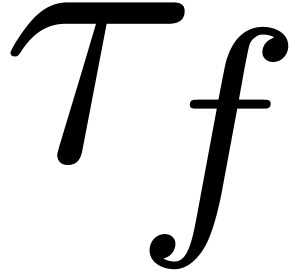 (which implies
a zero-test for
(which implies
a zero-test for  ). Of course,
the values
). Of course,
the values 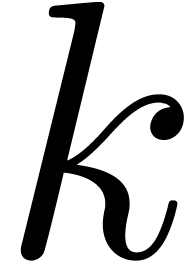 and
and 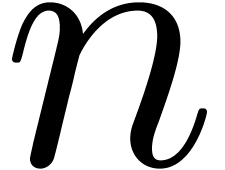 should
not be taken too small, so as to provide sufficient robustness. On the
other hand, large values of
should
not be taken too small, so as to provide sufficient robustness. On the
other hand, large values of 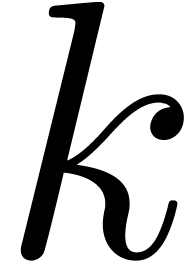 and
and 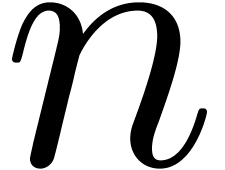 may lead to unacceptable computation times. Our current compromise
may lead to unacceptable computation times. Our current compromise 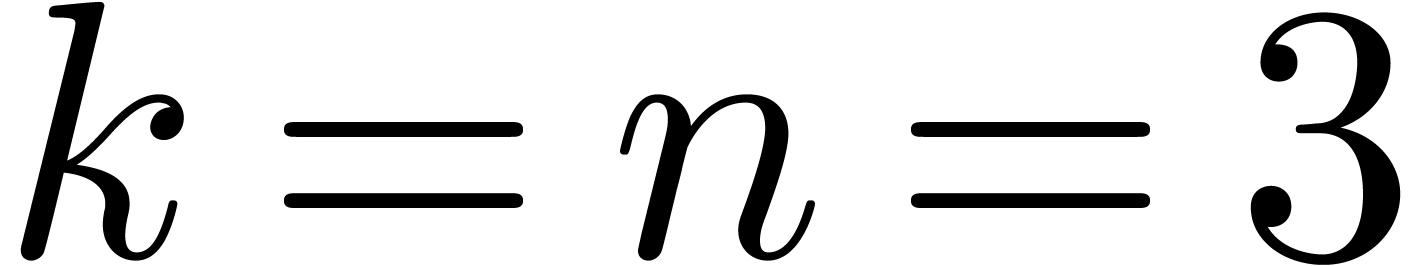 has worked for all practical examples we have tried
so far.
has worked for all practical examples we have tried
so far.
Remark 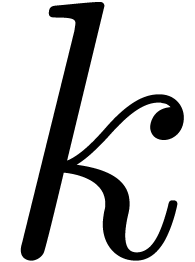 and
and 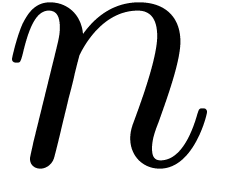 provide sufficient robustness may seem very surprising at first sight
and is indeed the remarkable feature which make meta-expansions
so useful in our opinion. The intuitive justification lies in the fact
that we expand in a really massive way all our operations and all our
parameters. On the one hand, canceling terms usually change after every
step before they vanish, and are thereby “stabilized out”.
On the other hand, deeper combinations of parameters which lead to a
genuine non-canceling contribution can usually be detected after a few
steps. In particular, small power series expressions with large
valuations [vdH06b] tend to be less harmful in our context.
provide sufficient robustness may seem very surprising at first sight
and is indeed the remarkable feature which make meta-expansions
so useful in our opinion. The intuitive justification lies in the fact
that we expand in a really massive way all our operations and all our
parameters. On the one hand, canceling terms usually change after every
step before they vanish, and are thereby “stabilized out”.
On the other hand, deeper combinations of parameters which lead to a
genuine non-canceling contribution can usually be detected after a few
steps. In particular, small power series expressions with large
valuations [vdH06b] tend to be less harmful in our context.
Remark 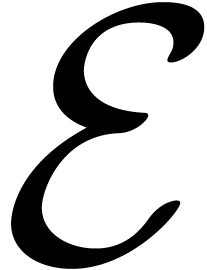 be the class of expanders which are obtained by applying
our expansion algorithms to exp-log expressions. From a theoretical
point of view, it might be interesting to investigate the existence of a
simple computable function
be the class of expanders which are obtained by applying
our expansion algorithms to exp-log expressions. From a theoretical
point of view, it might be interesting to investigate the existence of a
simple computable function 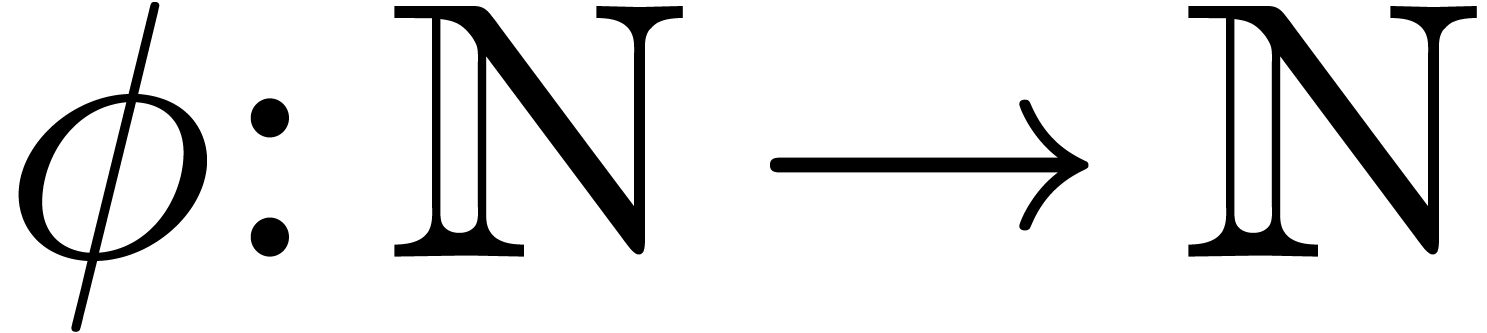 such that, for any
such that, for any
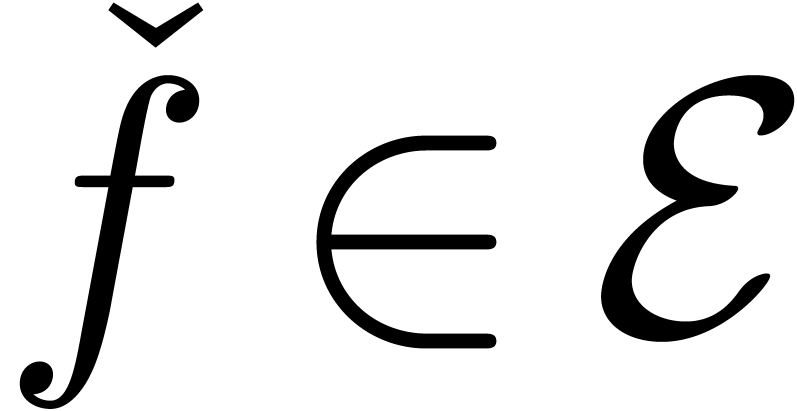 , there exists a
, there exists a 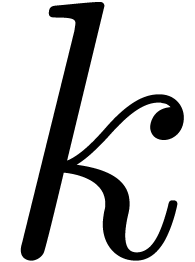 with
with
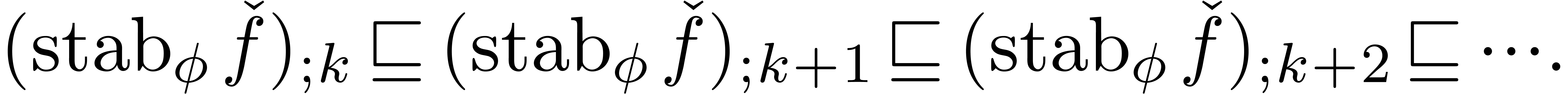
Generalizing example 5, we see that we must take 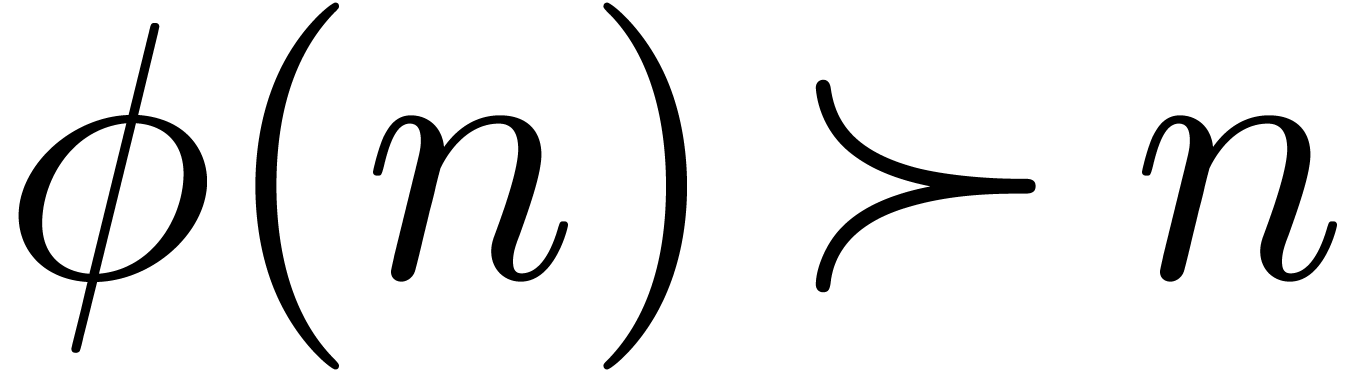 . Would
. Would 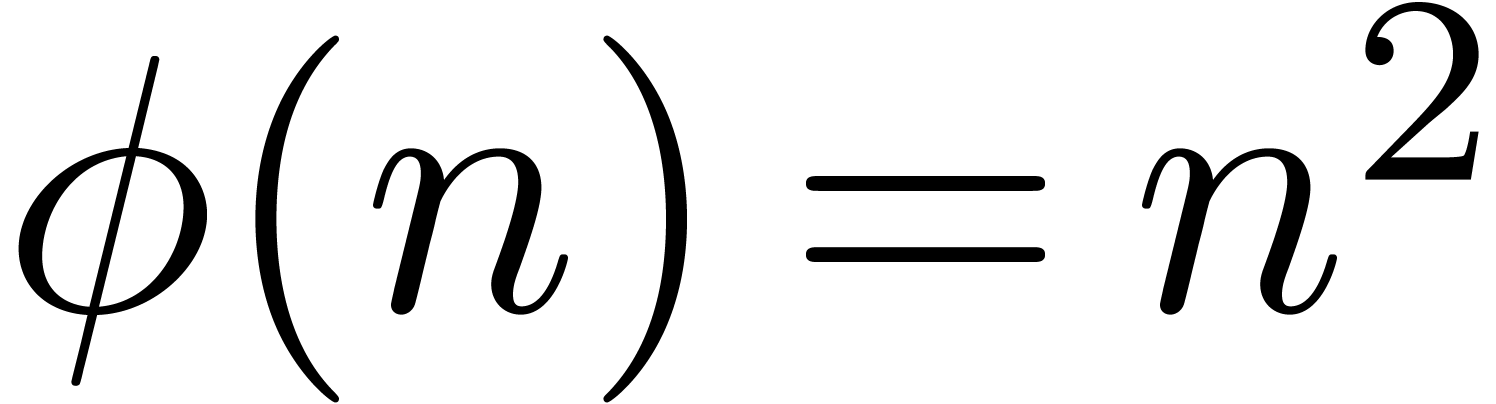 be
sufficient?
be
sufficient?
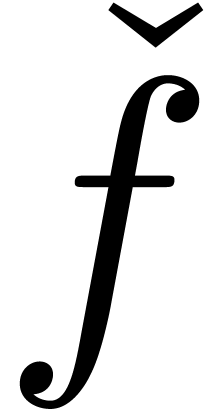 might
for instance be to print
might
for instance be to print 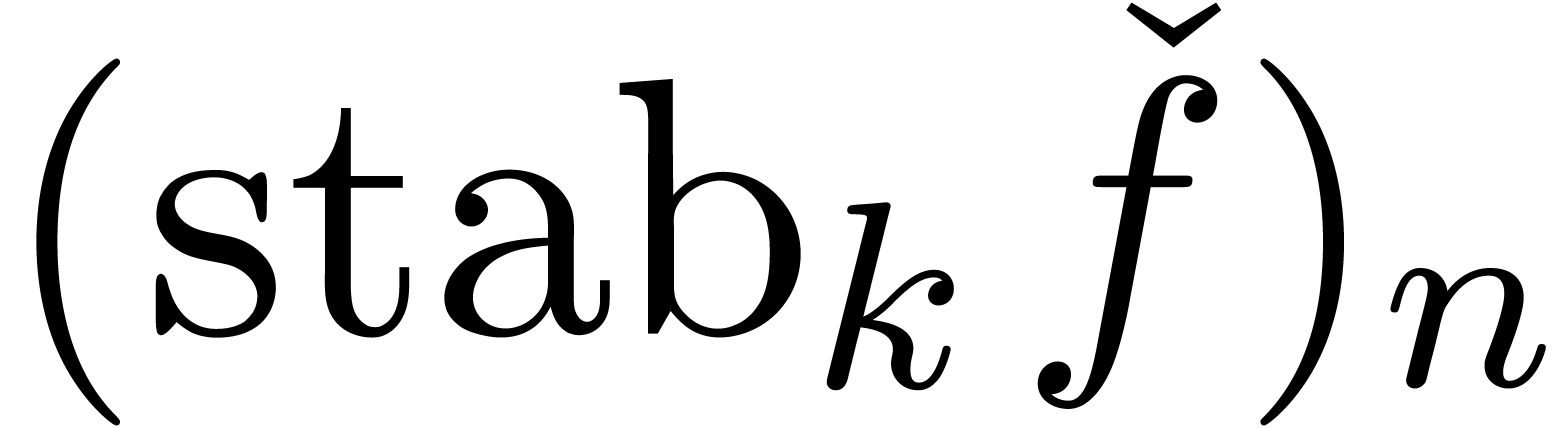 for suitable values
of
for suitable values
of 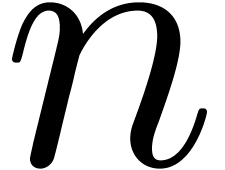 and
and 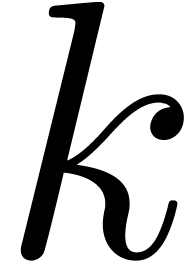 (e.g.
(e.g. 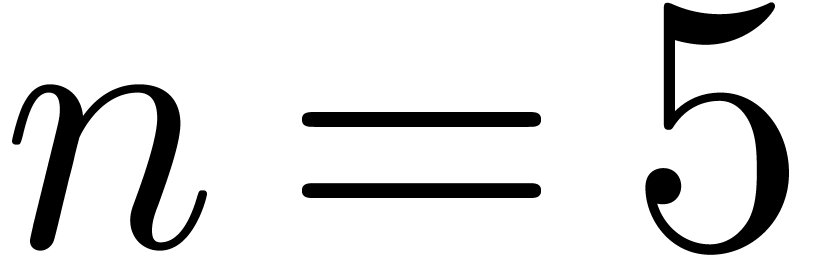 and
and 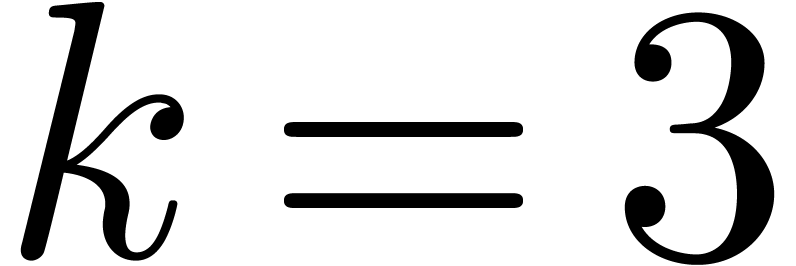 ). This method can be further improved as follows:
first compute
). This method can be further improved as follows:
first compute 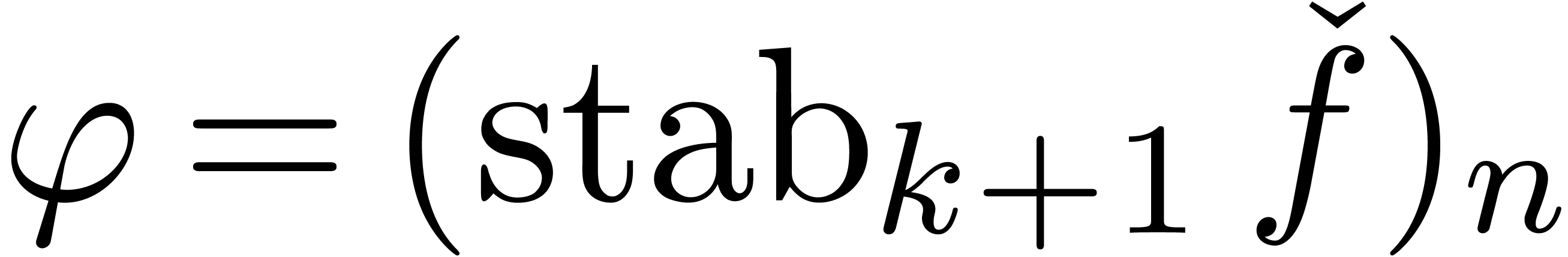 and
and 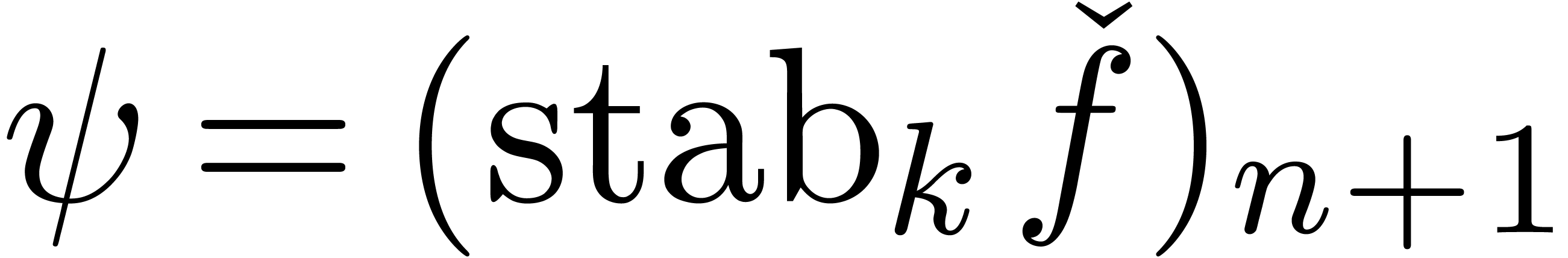 with
with
 . When considering the
successive terms of
. When considering the
successive terms of  in decreasing order for
in decreasing order for
 , we may decompose the
expansion
, we may decompose the
expansion  in blocks
in blocks
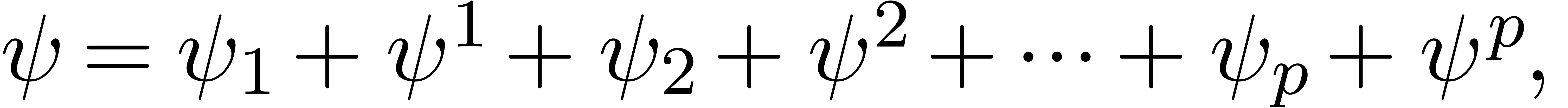 |
(14) |
with 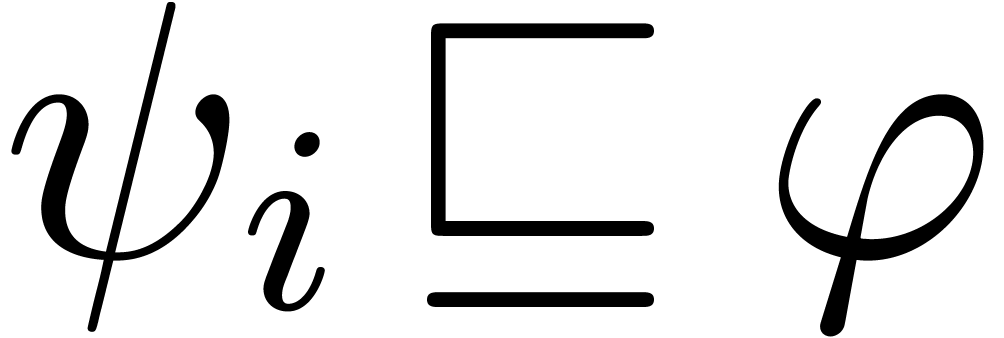 ,
, 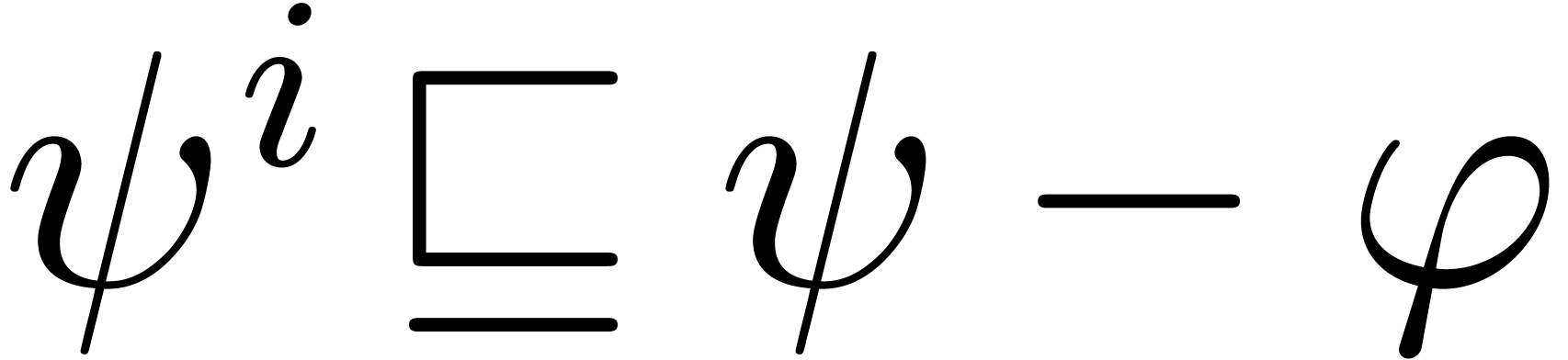 ,
,  and
and 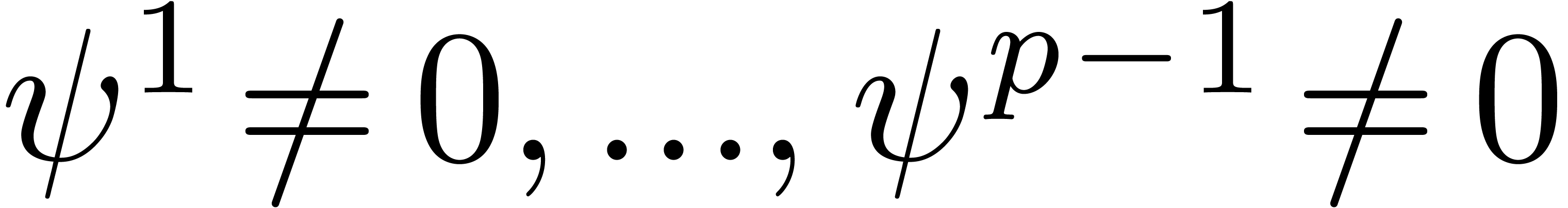 . In (14), we now replace each non-zero
. In (14), we now replace each non-zero
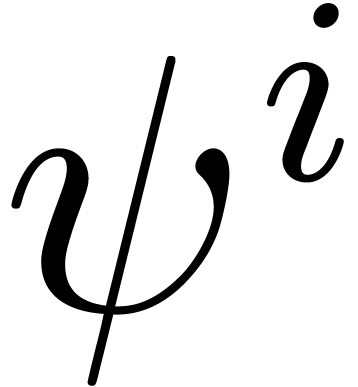 by the expression
by the expression 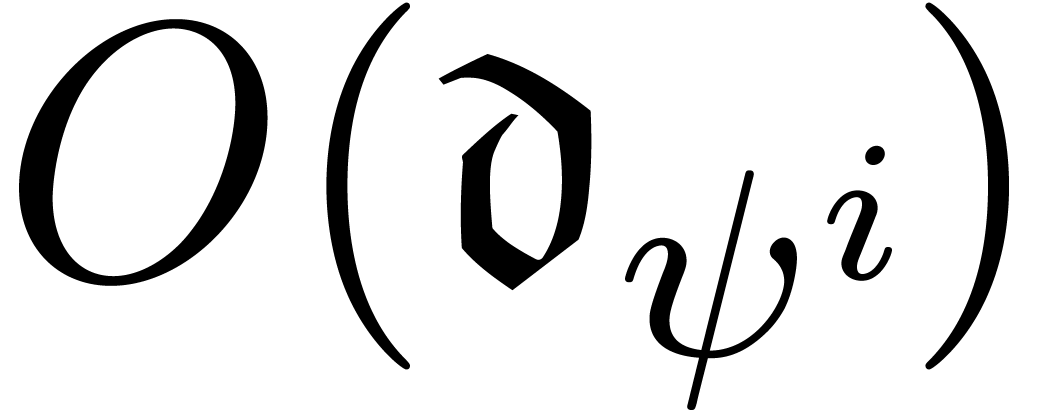 ,
and print the result. For instance, if
,
and print the result. For instance, if
then we print
An interesting feature of this way of printing is that it allows us to
see some of the remaining terms after the first  leading terms. In certain cases, such as
leading terms. In certain cases, such as
one might prefer to suppress some of these extra terms. One criterion
for suppression could be the following: given the last term  of some
of some 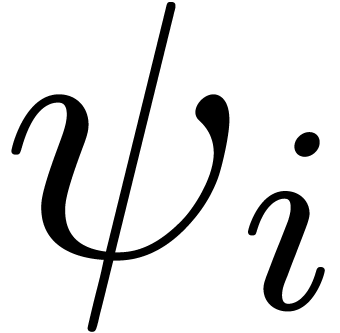 and any term
and any term 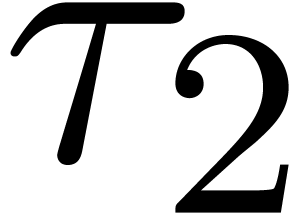 of
of 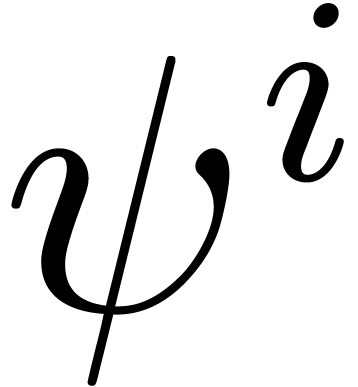 , suppress
all terms
, suppress
all terms  with
with 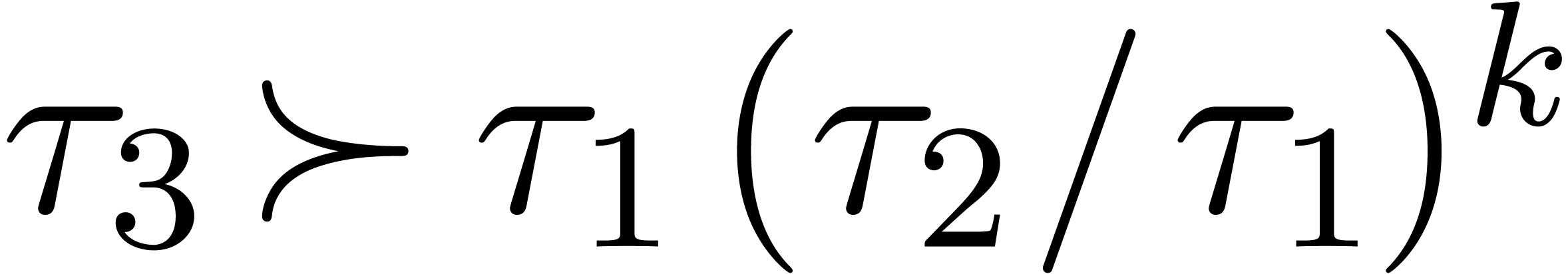 for some
for some
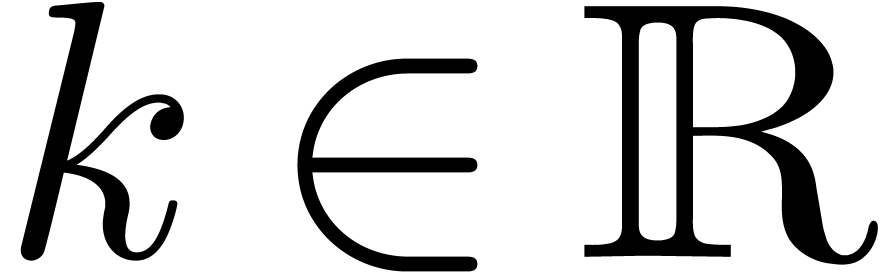 .
.
 terms of an expansion, then you may want to give early terms a higher
priority during the computations. Given an expander
terms of an expansion, then you may want to give early terms a higher
priority during the computations. Given an expander  , let
, let 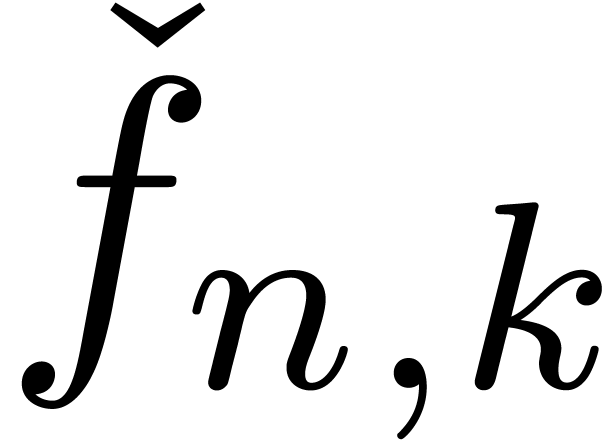 denote the
denote the
 -th term in the polynomial
-th term in the polynomial
 (in decreasing order for
(in decreasing order for  ). If
). If 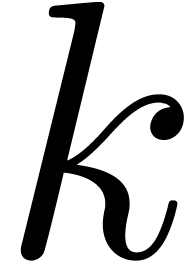 is larger than
the number of terms of
is larger than
the number of terms of 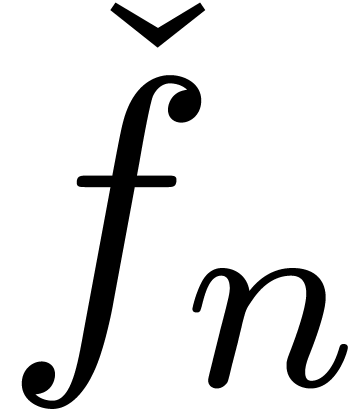 ,
then we set
,
then we set 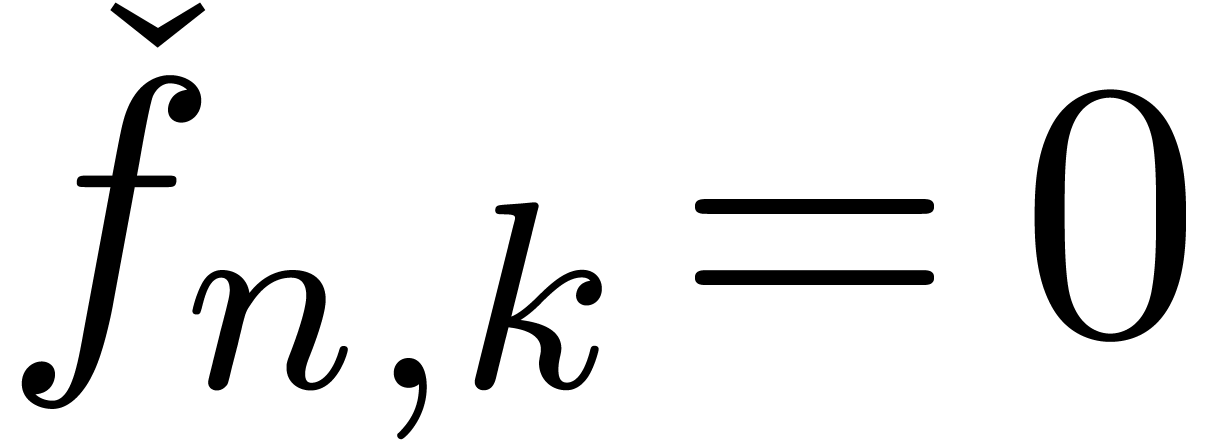 . Now for each
computable increasing function
. Now for each
computable increasing function  ,
we define
,
we define
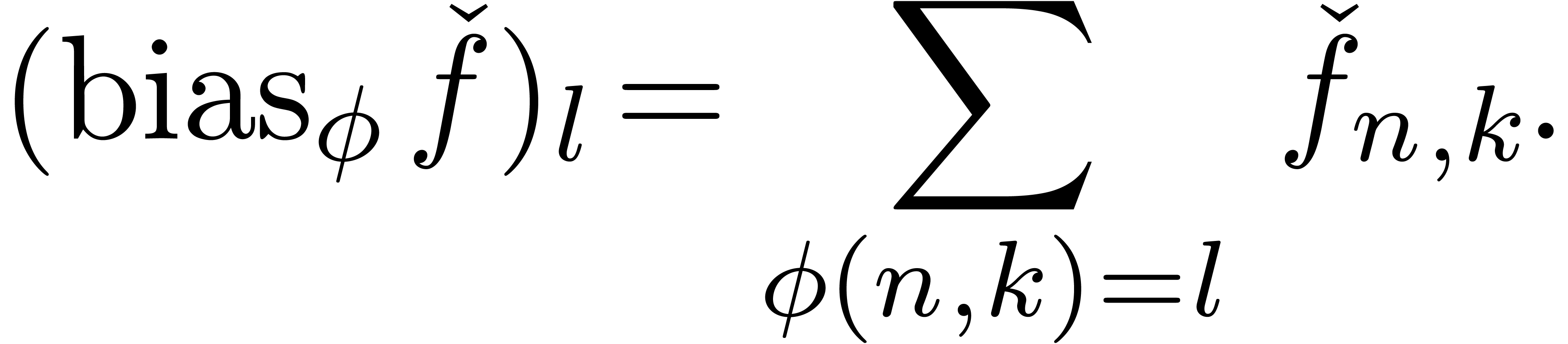
In the case when 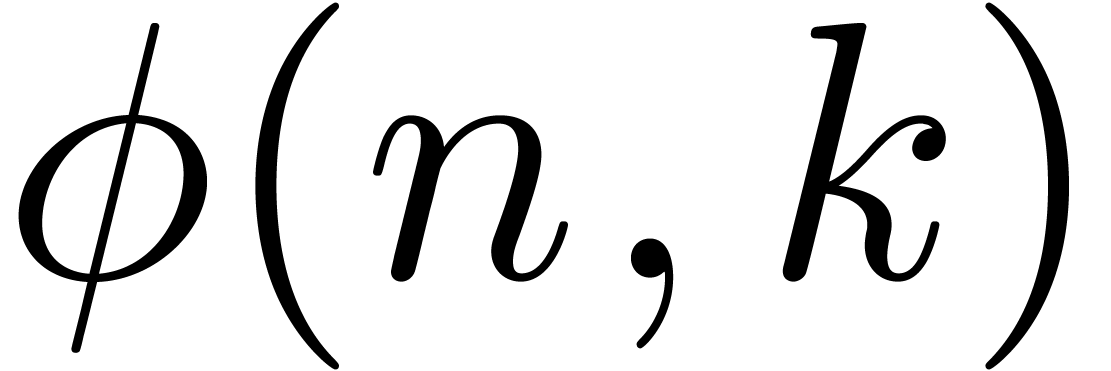 , then we
have
, then we
have
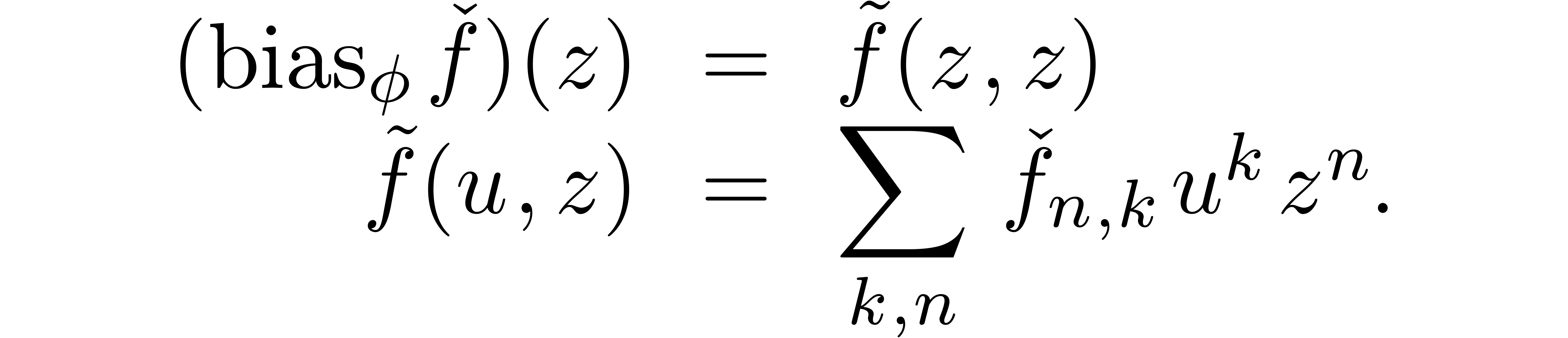
We call  a dominant bias operator. We
may typically apply it on auxiliary series
a dominant bias operator. We
may typically apply it on auxiliary series 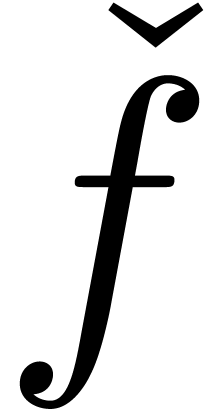 with
a sharp increase of the number of terms of
with
a sharp increase of the number of terms of 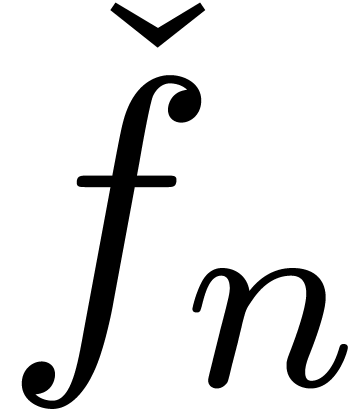 with
with
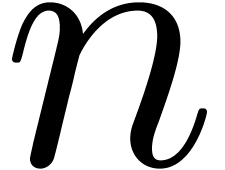 . More generally, it is
possible to define operators which favour terms at the tail, in the
middle, or close to a specified monomial. However, these generalization
do not seem to have any practical applications, at first sight.
. More generally, it is
possible to define operators which favour terms at the tail, in the
middle, or close to a specified monomial. However, these generalization
do not seem to have any practical applications, at first sight.
Most of the algorithms described in this paper have been implemented
inside the
| Mmx] | use "numerix"; use "algebramix"; use "multimix"; use "symbolix"; |
| Mmx] |
x == infinity ('x); |
| Mmx] | 1 / (x + 1) |
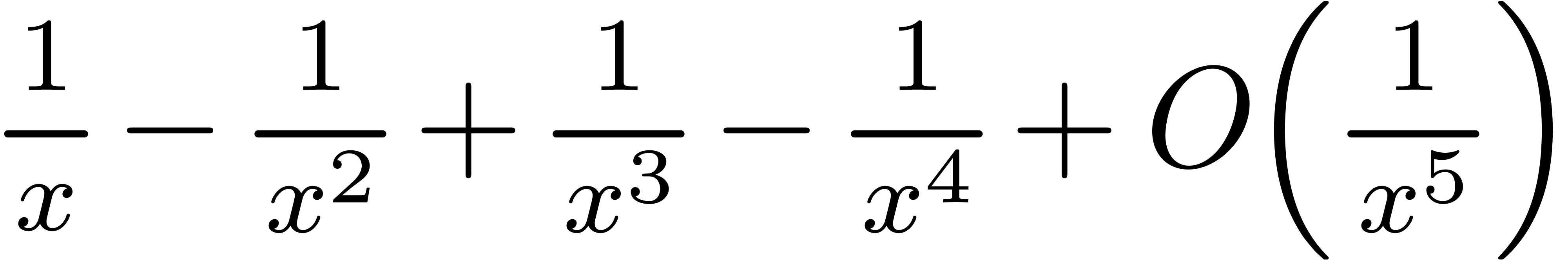
| Mmx] | 1 / (x + log x + log log x) |
| Mmx] | 1 / (1 + 1/x + 1/exp x) |
| Mmx] | 1 / (1 + 1/x + 1/exp x) - 1 / (1 + 1/x) |
| Mmx] | exp (x + exp (-exp x)) - exp (x) |
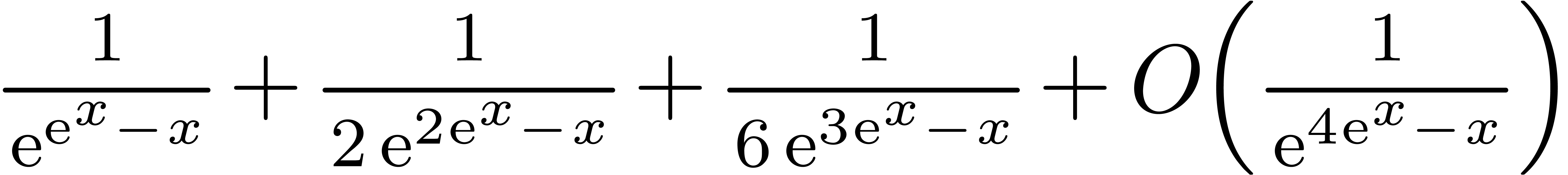
| Mmx] | exp (exp (x) / (x + 1)) |
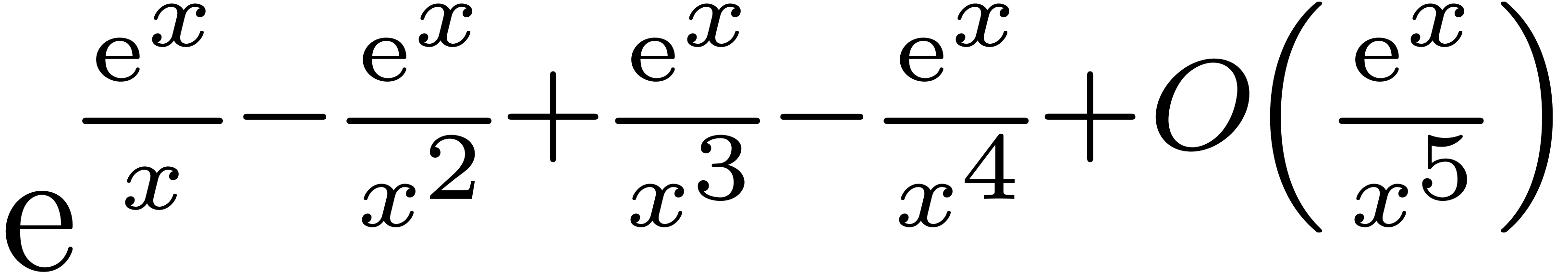
| Mmx] | derive (exp (exp (x) / (x + 1)), x) |
| Mmx] | integrate (exp (x^2), x) |
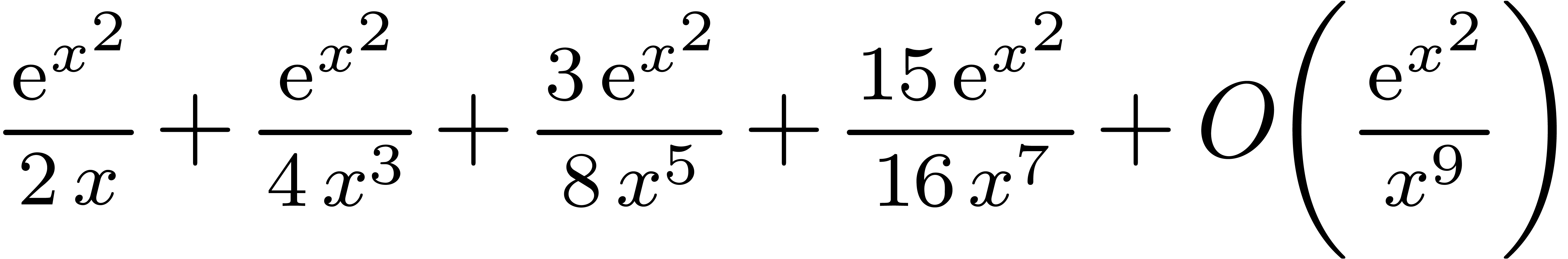
| Mmx] | integrate (x^x, x) |
| Mmx] | sum (x^4, x) |
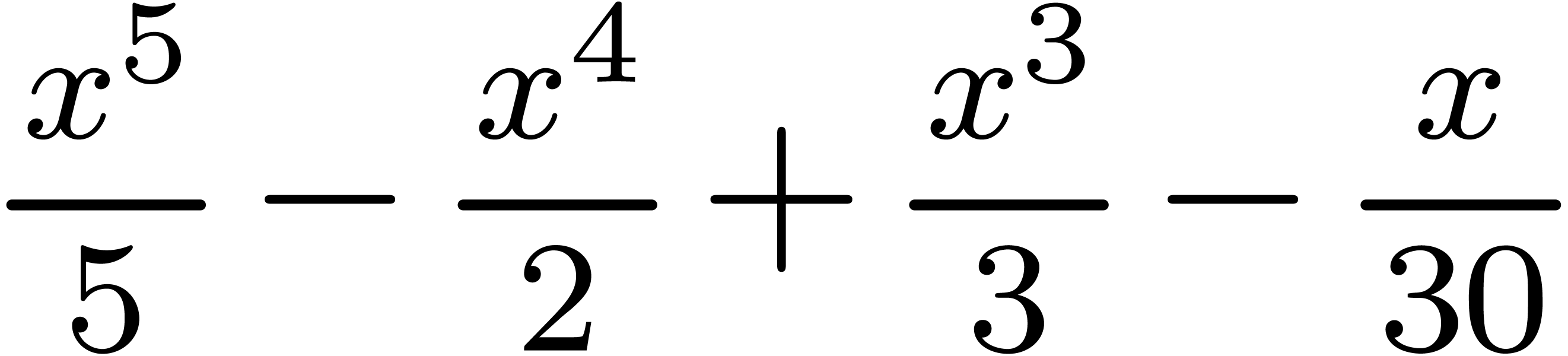
| Mmx] | product (x, x) |
| Mmx] | lengthen (product (x, x), 8) |
| Mmx] | product (log x, x) |
| Mmx] | fixed_point (f :-> log x + f @ (log x)) |
| Mmx] | la == derive (fixed_point (f :-> log x + f @ (log x)), x) |
| Mmx] | mu == la * la + 2 * derive (la, x) |
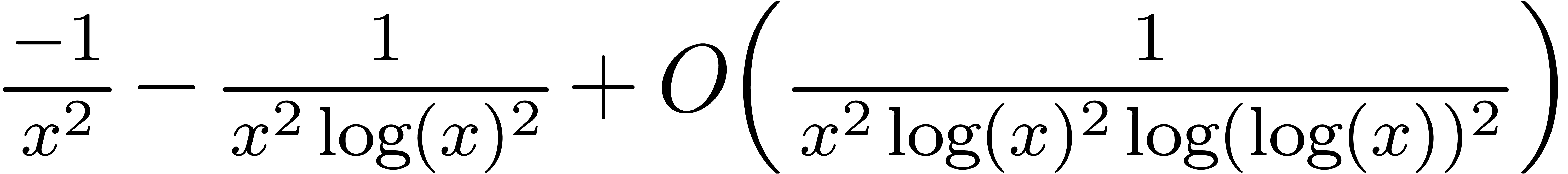
| Mmx] | fixed_point (f :-> 1/x + f @ (x^2) + f @ (x^x)) |
Even though the expansion algorithms developed so far are usually
sufficient for applications, they lack robustness in several ways. First
of all, we have used heuristic algorithms for zero-testing and the
computation of dominant terms. Some of our algorithms crucially depend
on the correctness of these heuristic algorithms. For instance, our
algorithm for the computation of an inverse 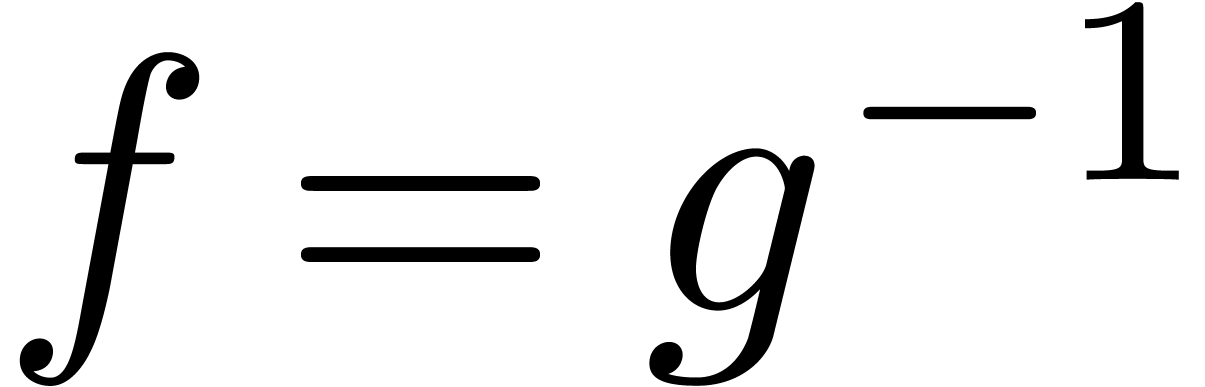 yields an erroneous result if
yields an erroneous result if 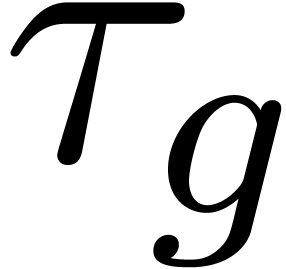 is computed
incorrectly. Finally, expanders
is computed
incorrectly. Finally, expanders 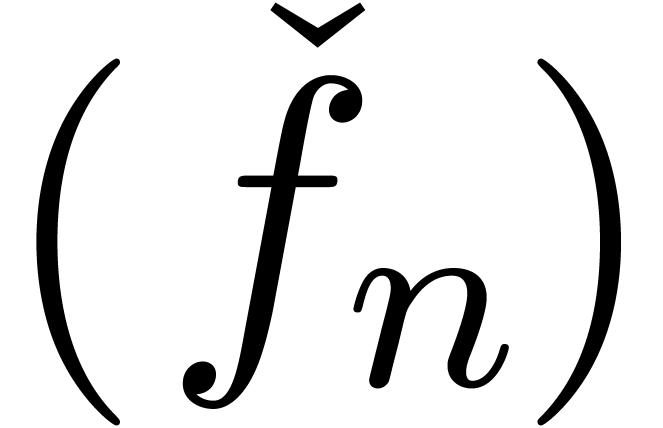 only
asymptotically tend to
only
asymptotically tend to  . Even
if we know that a given monomial
. Even
if we know that a given monomial 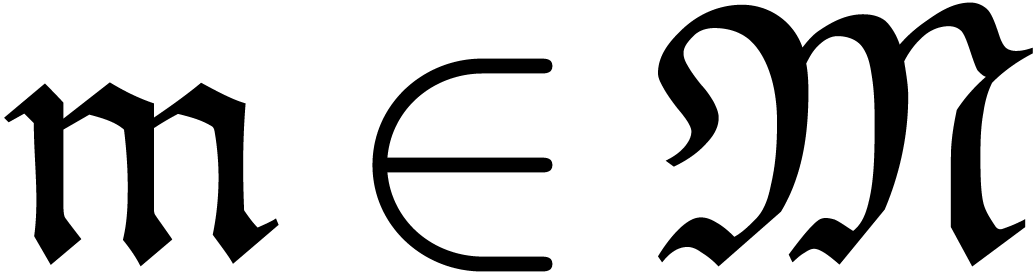 is in the
support of
is in the
support of  , we do not know
how large
, we do not know
how large 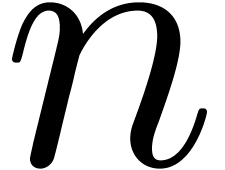 should be in order to guarantee that
should be in order to guarantee that
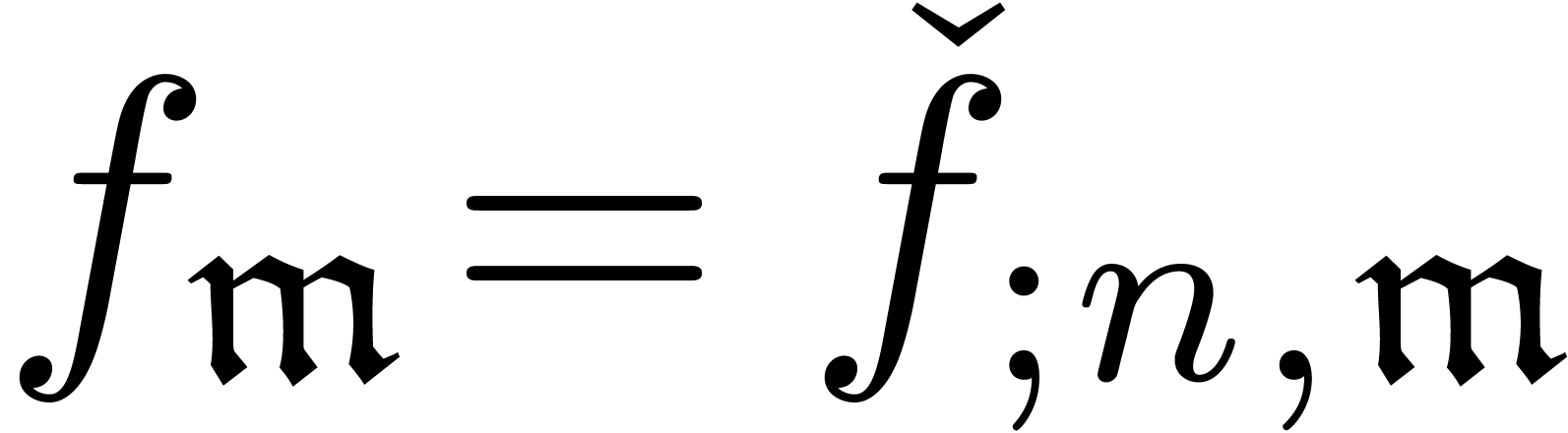 . In this section, we
describe a few ideas which may be used to increase the robustness of our
algorithms.
. In this section, we
describe a few ideas which may be used to increase the robustness of our
algorithms.
 ,
we started with the computation of
,
we started with the computation of 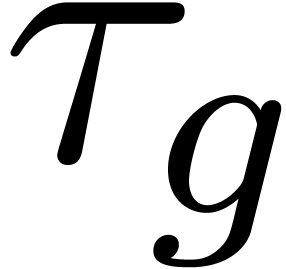 .
Instead, we might imagine that the expander of
.
Instead, we might imagine that the expander of 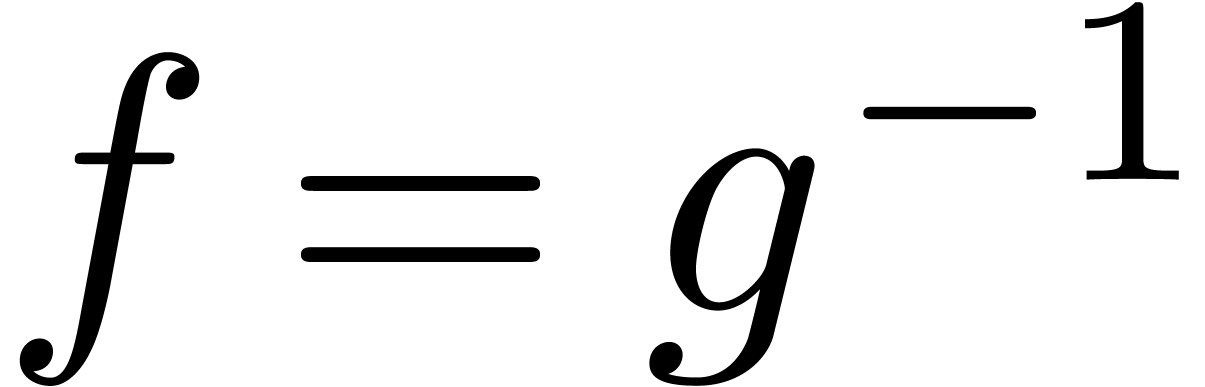 is allowed to adjust its initial value of
is allowed to adjust its initial value of 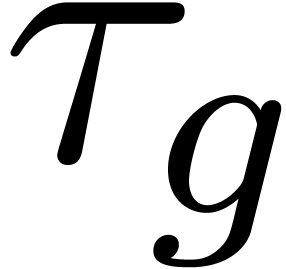 at
later stages of the approximation. More precisely, for
at
later stages of the approximation. More precisely, for  and a suitable
and a suitable 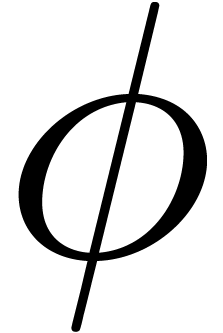 ,
let
,
let 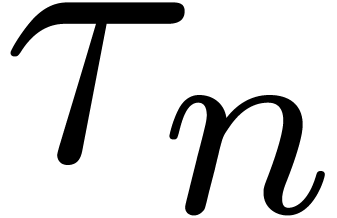 be the dominant term of
be the dominant term of  and consider the expander
and consider the expander
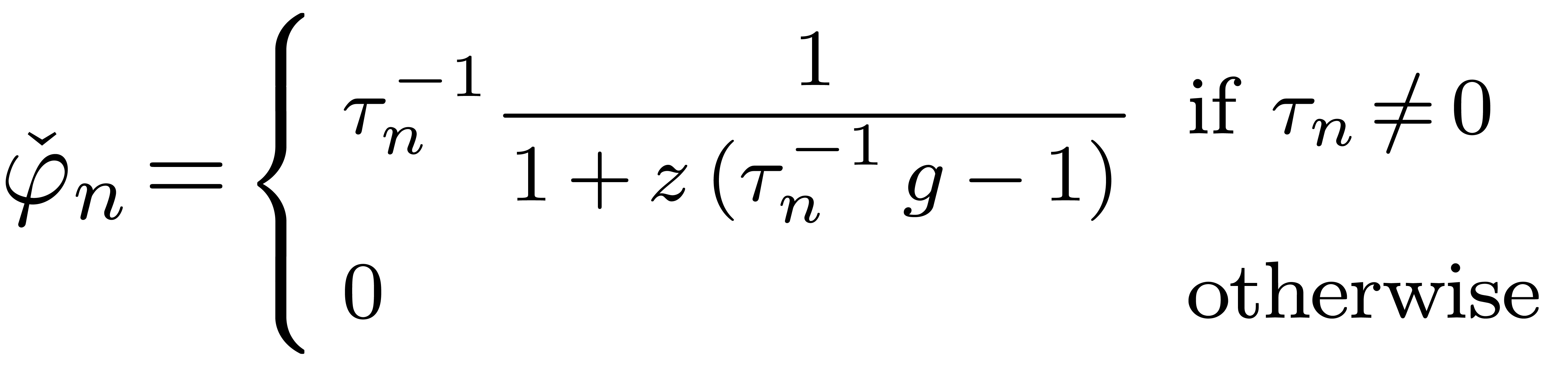
Then we may define a new expander 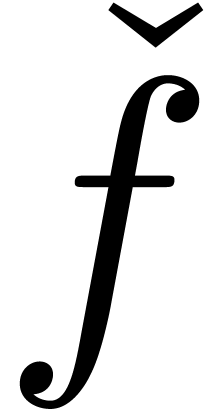 by taking the
diagonal
by taking the
diagonal
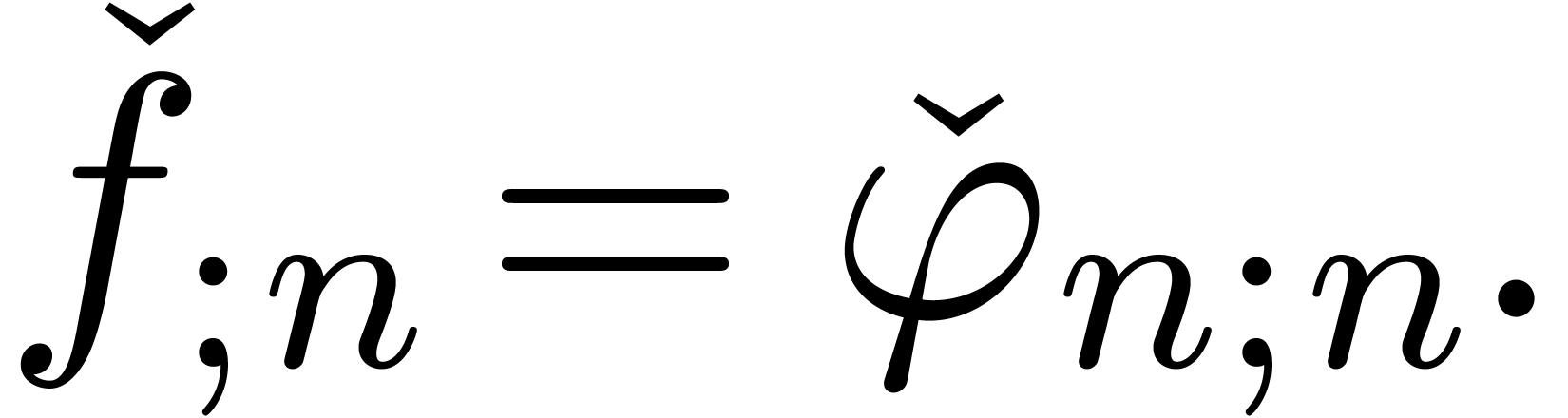
In order to have 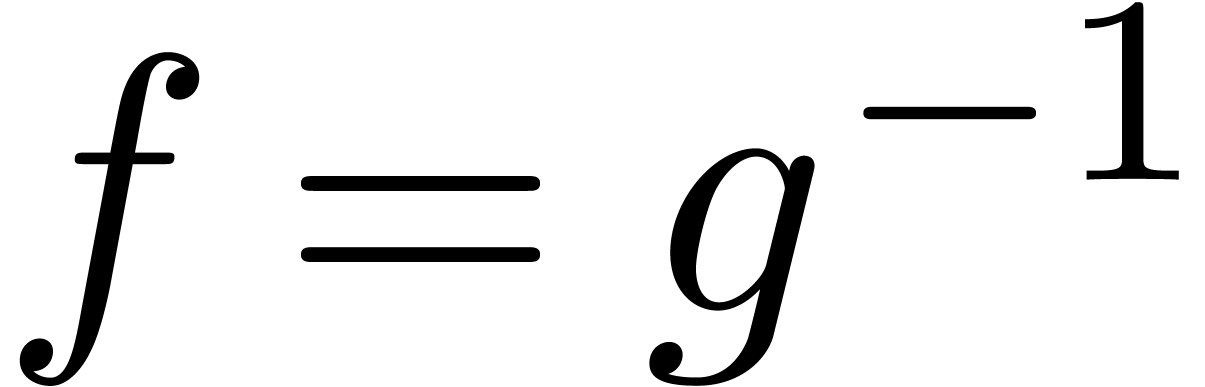 , it now
suffices to have
, it now
suffices to have 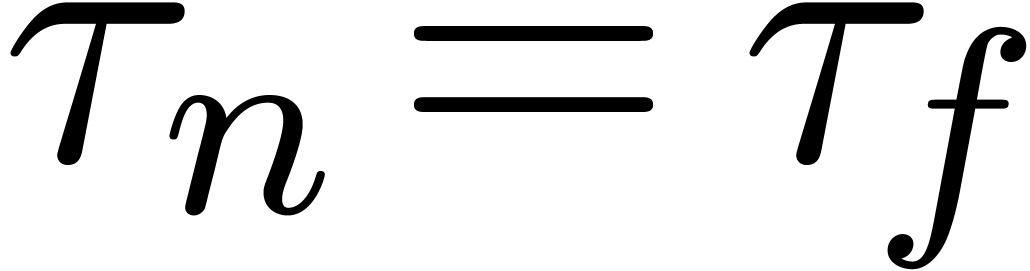 (
( ),
instead of
),
instead of 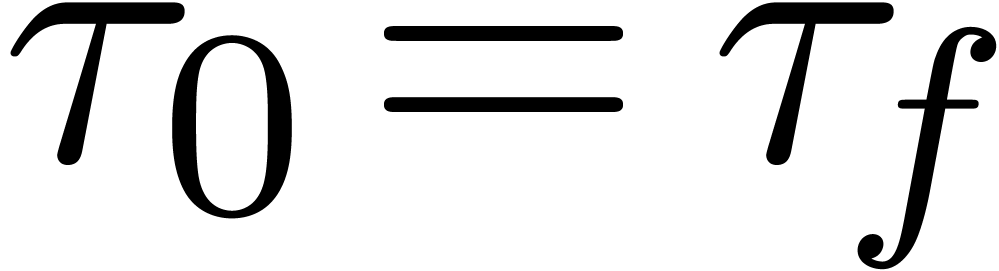 . Of course, in
nasty cases, it might still happen that
. Of course, in
nasty cases, it might still happen that 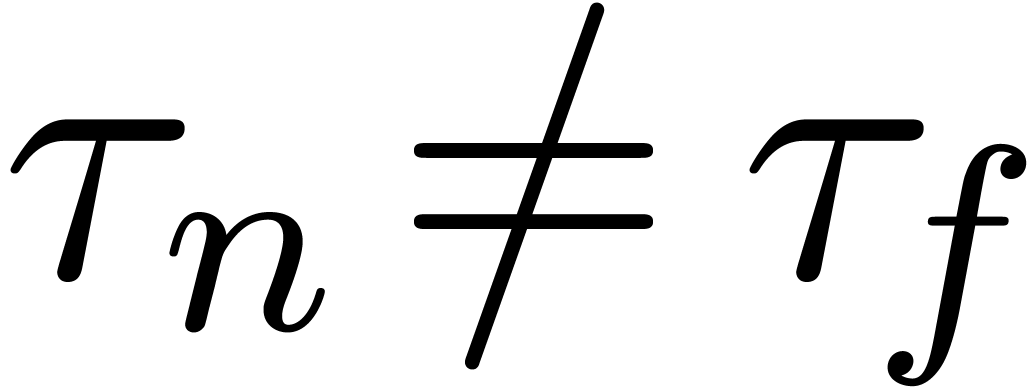 for all
for all
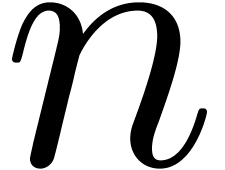 . In other words, the
strategy of auto-correction produces no miracles and does not substitute
for a genuine zero-test. Even in the case when the stabilization
operator
. In other words, the
strategy of auto-correction produces no miracles and does not substitute
for a genuine zero-test. Even in the case when the stabilization
operator 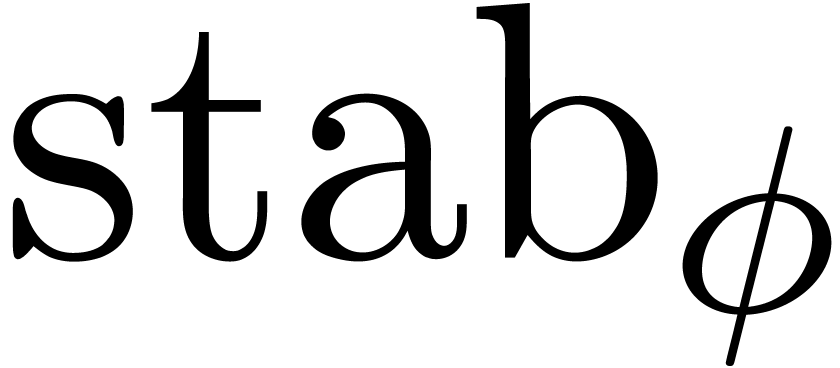 is sufficiently powerful to guarantee
is sufficiently powerful to guarantee
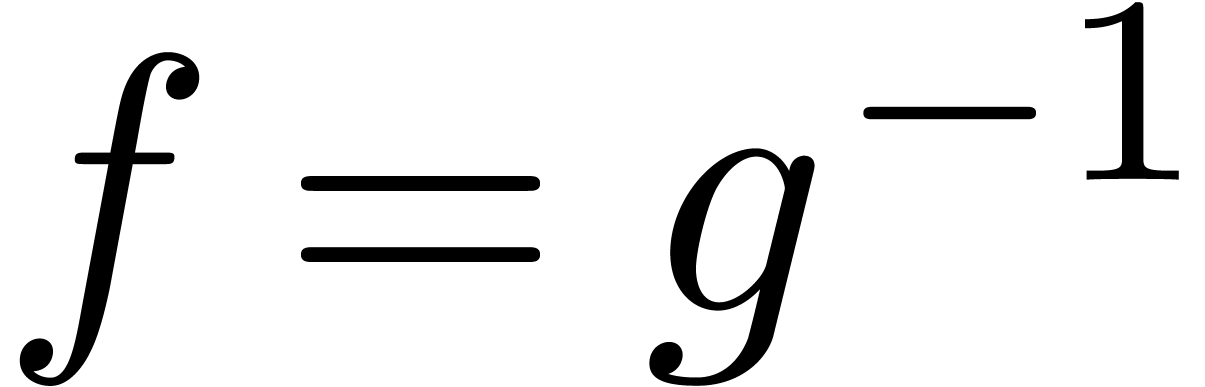 for a certain class of expanders, one should
keep in mind that the result only becomes correct at the limit; we still
don't know how many terms need to be computed.
for a certain class of expanders, one should
keep in mind that the result only becomes correct at the limit; we still
don't know how many terms need to be computed.
From a practical point, the strategy of auto-correction is easy to
implement on the series level from section 3: in our
example of inversion, the expander 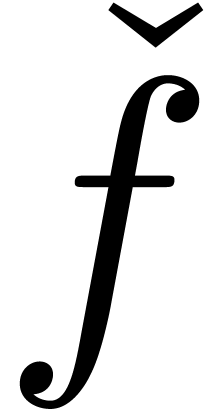 may simply
keep
may simply
keep 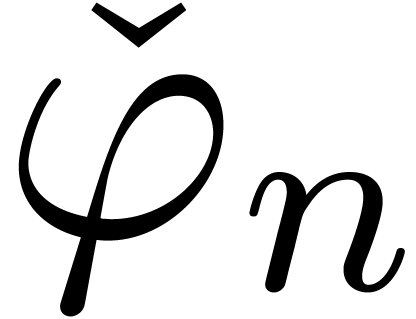 in memory for the largest
in memory for the largest 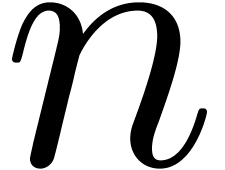 considered so far and only update its value when
considered so far and only update its value when 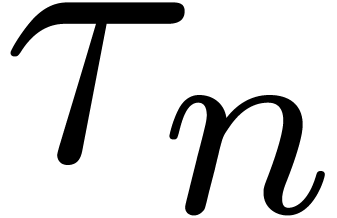 changes. Implementations become more involved when considering recursive
transseries expansions, as in section 4. Indeed, in this
more general setting, we also need to correct erroneous outcomes for the
asymptotic ordering
changes. Implementations become more involved when considering recursive
transseries expansions, as in section 4. Indeed, in this
more general setting, we also need to correct erroneous outcomes for the
asymptotic ordering  , which
recursively relies on the orderings
, which
recursively relies on the orderings 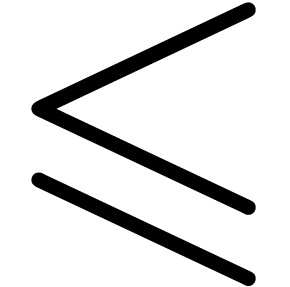 and
and  for expanders of lower exponential height. In order
to generalize the idea, one thus has to define sequences of
approximations
for expanders of lower exponential height. In order
to generalize the idea, one thus has to define sequences of
approximations 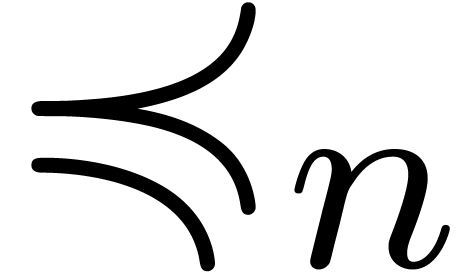 and
and 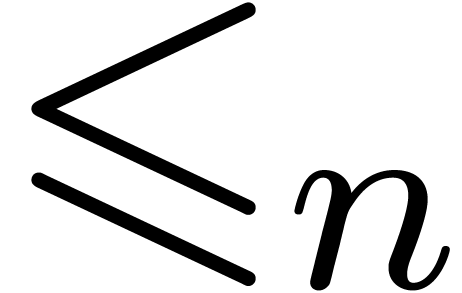 for
for
 and
and  ,
and systematically work with the relations
,
and systematically work with the relations 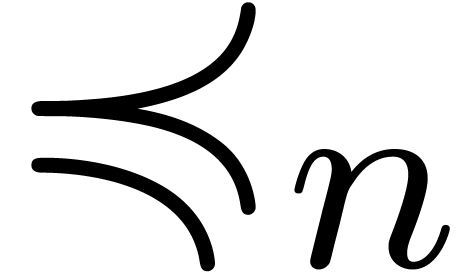 and
and
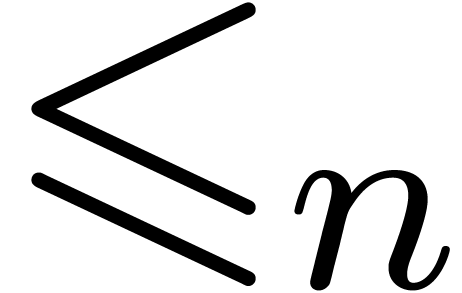 when making decisions for expansions at stage
when making decisions for expansions at stage
 .
.
 , it sometimes
happens that
, it sometimes
happens that  admits a zero-test. For instance,
if
admits a zero-test. For instance,
if  is the class of exp-log functions, then a
zero-test can be given whose correctness relies on Schanuel's
conjecture [vdH98, Ric97].
is the class of exp-log functions, then a
zero-test can be given whose correctness relies on Schanuel's
conjecture [vdH98, Ric97].
An interesting question is whether we can use a zero-test in  in order to design a non-heuristic algorithm for the
computation of dominant terms. In order to make this work, we have to be
able to detect infinite cancellations of terms which occur in
expressions such as
in order to design a non-heuristic algorithm for the
computation of dominant terms. In order to make this work, we have to be
able to detect infinite cancellations of terms which occur in
expressions such as  . A
general mechanism for doing this is to refine the mechanism of expanders
by indexing over a suitable well-based set.
. A
general mechanism for doing this is to refine the mechanism of expanders
by indexing over a suitable well-based set.
More precisely, given an abstract well-based set  (i.e. a set
(i.e. a set  which is
well-quasi-ordered for the opposite ordering of
which is
well-quasi-ordered for the opposite ordering of  ), we define a sequence
), we define a sequence  of
finite subsets of
of
finite subsets of  by
by  . In general, the sequence
. In general, the sequence  is transfinite, but if we have
is transfinite, but if we have 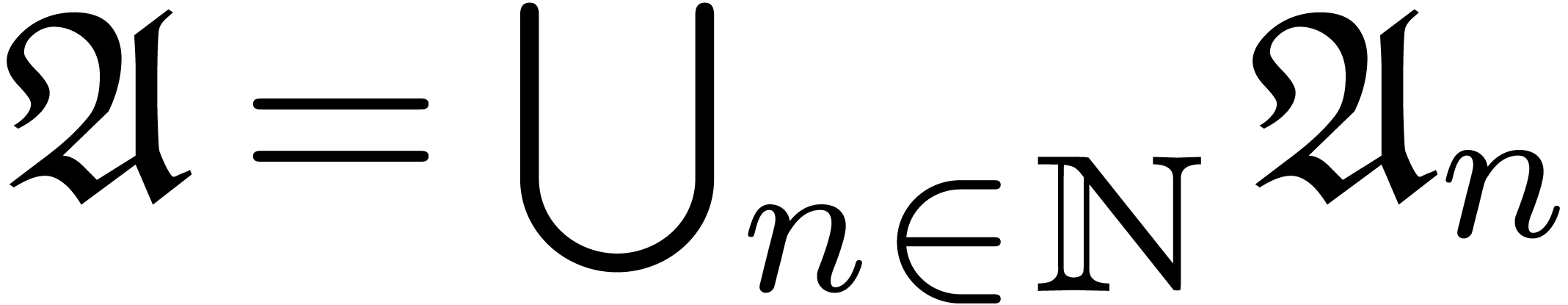 ,
then we say that
,
then we say that  is accessible. We say
that
is accessible. We say
that  is computable, if for any finite
subset
is computable, if for any finite
subset  , we can compute
, we can compute 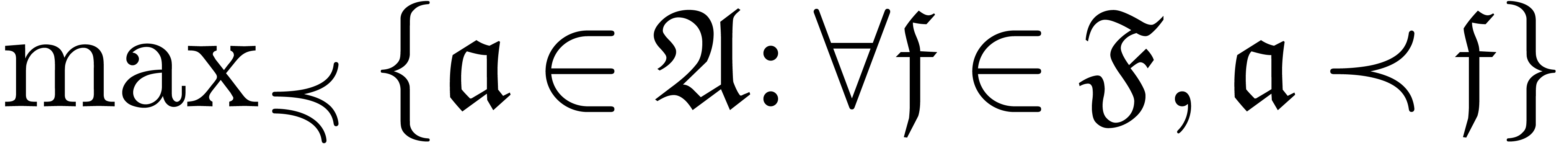 . In particular, this implies the
sequence
. In particular, this implies the
sequence  to be computable.
to be computable.
A well-based expander is a computable well-based family  , indexed by a computable
accessible well-based set
, indexed by a computable
accessible well-based set  . A
well-based expander is the natural refinement of an expander
. A
well-based expander is the natural refinement of an expander 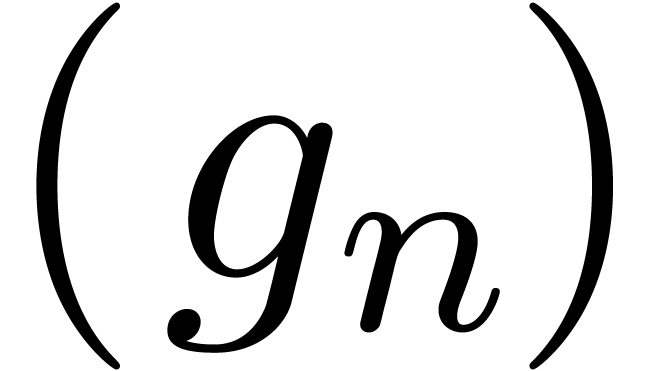 in the usual sense, by regrouping terms
in the usual sense, by regrouping terms 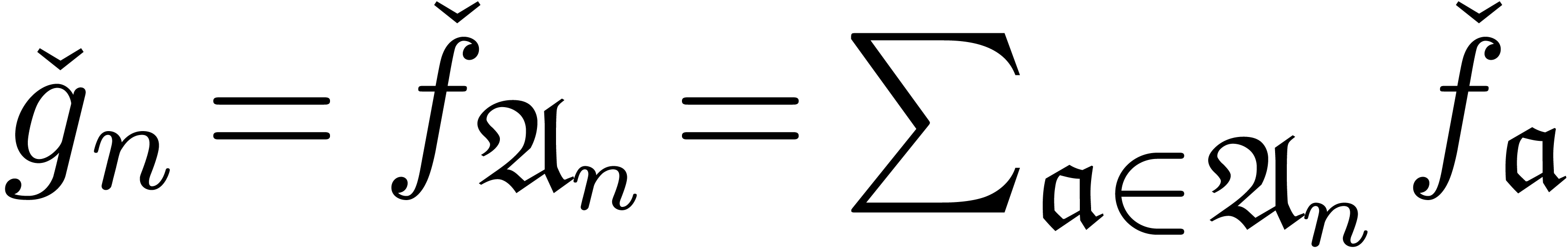 . We say that
. We say that 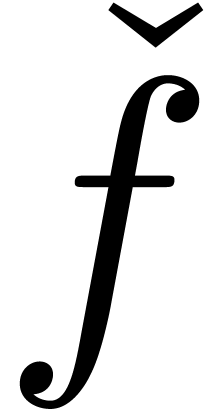 is a
termwise well-based expander if each
is a
termwise well-based expander if each 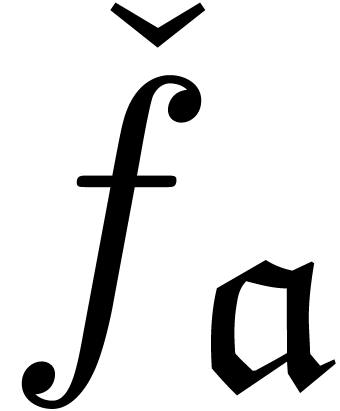 is
of the form
is
of the form  and the mapping
and the mapping 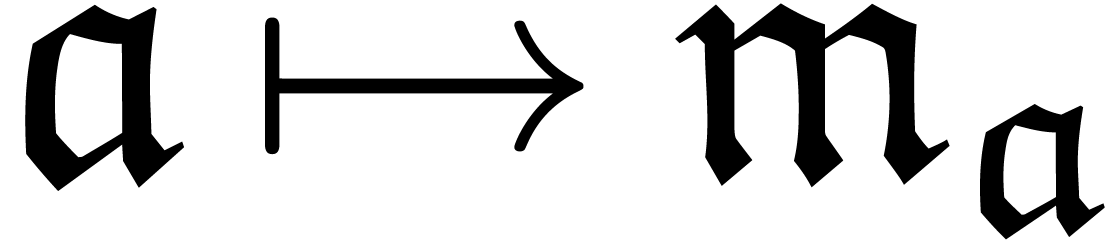 is increasing. Notice that
is increasing. Notice that 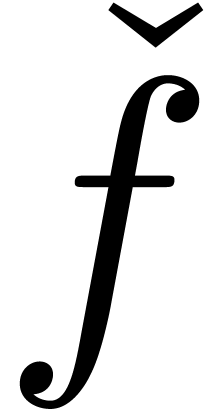 is automatically
well-based if
is automatically
well-based if  is increasing.
is increasing.
Recall that the initial segment generated by a finite subset
 is defined by
is defined by  .
Now consider a termwise well-based expander
.
Now consider a termwise well-based expander 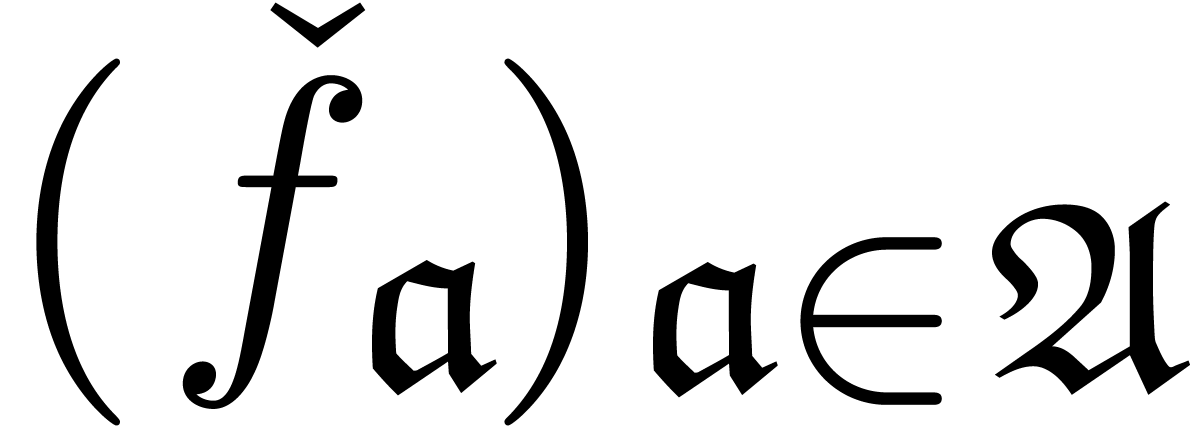 such
that
such
that 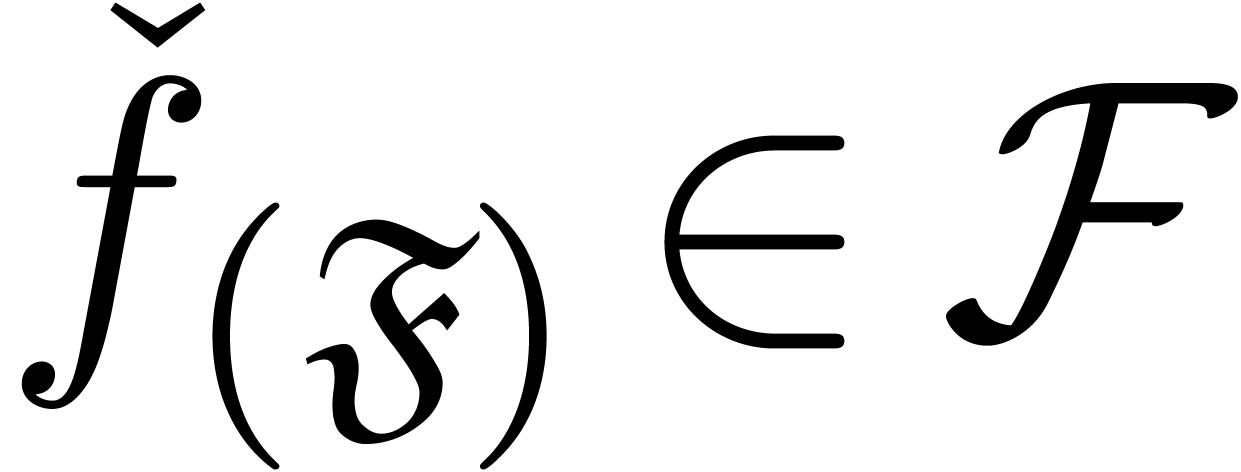 for any finite subset
for any finite subset  . If the mapping
. If the mapping 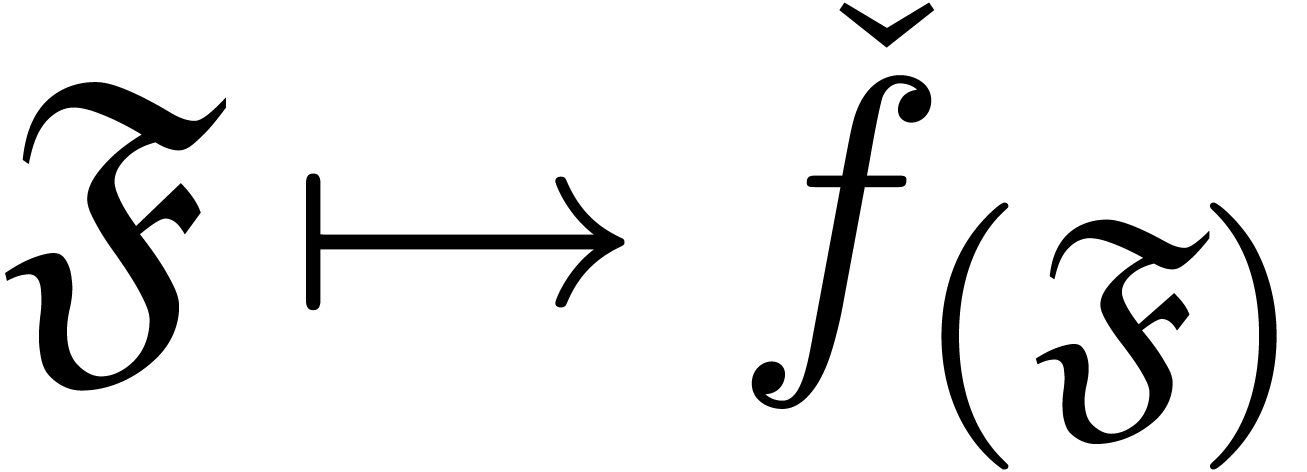 is
effective, then we call
is
effective, then we call  an expander over
an expander over
 . For the operations we have considered in
this paper, it should be possible to replace the usual notion of
expander by expanders of
. For the operations we have considered in
this paper, it should be possible to replace the usual notion of
expander by expanders of  (assuming that
(assuming that  is stable under the operation). This was already
shown in [vdH94] for the basic operations from section 3 and still waits to be worked out for the other ones.
is stable under the operation). This was already
shown in [vdH94] for the basic operations from section 3 and still waits to be worked out for the other ones.
Given an expander 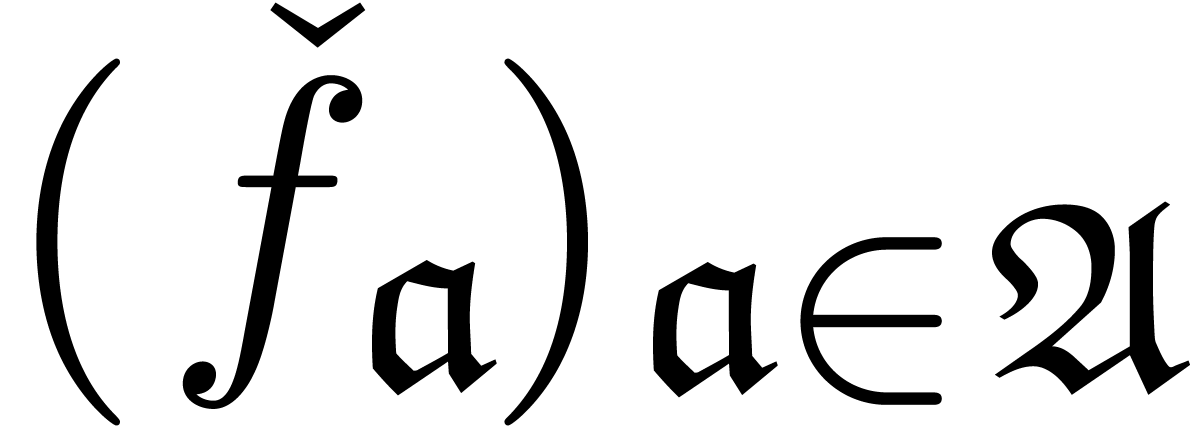 over
over  , the zero-test in
, the zero-test in  may now
be used in order to compute the set
may now
be used in order to compute the set 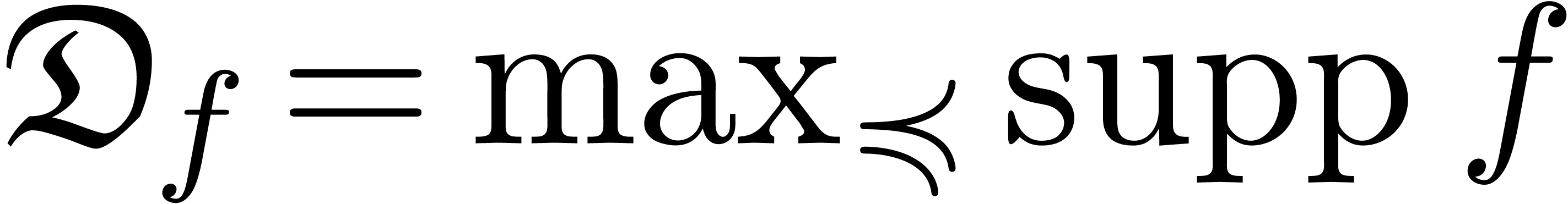 of dominant
monomials of
of dominant
monomials of  . The algorithm
again goes back to [vdH94]:
. The algorithm
again goes back to [vdH94]:
Let 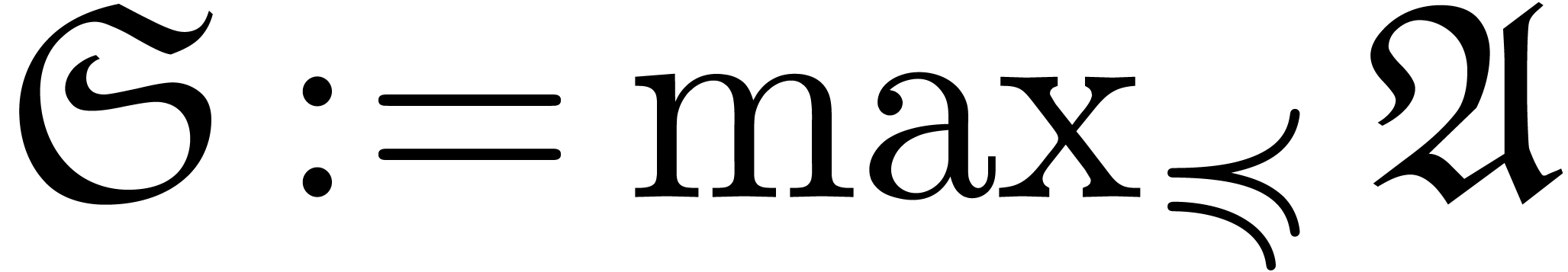 .
.
Replace  by a minimal subset
by a minimal subset  with
with 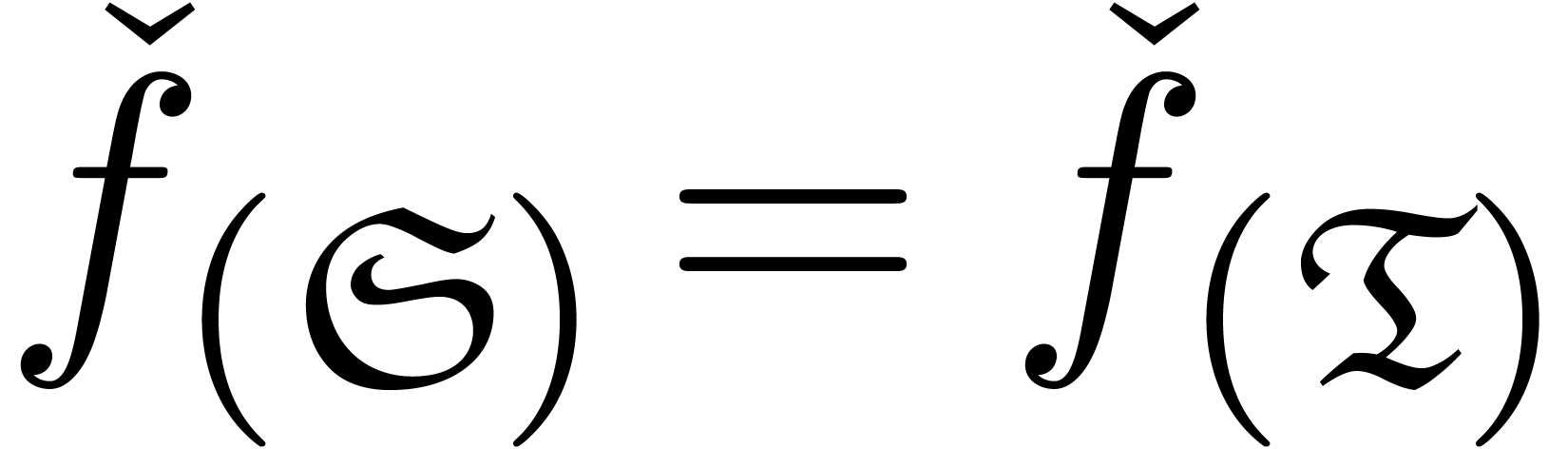 .
.
Let 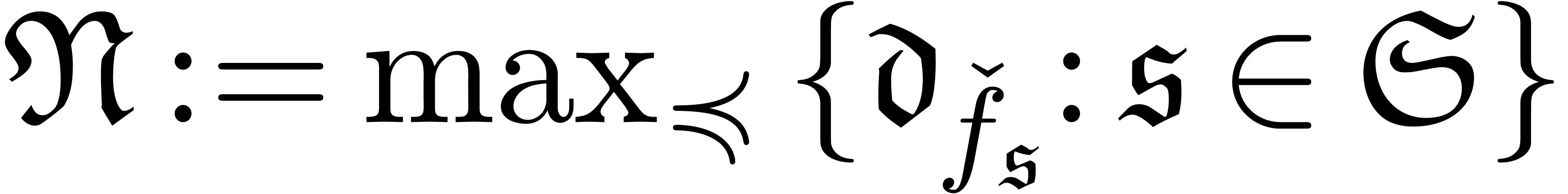 and
and 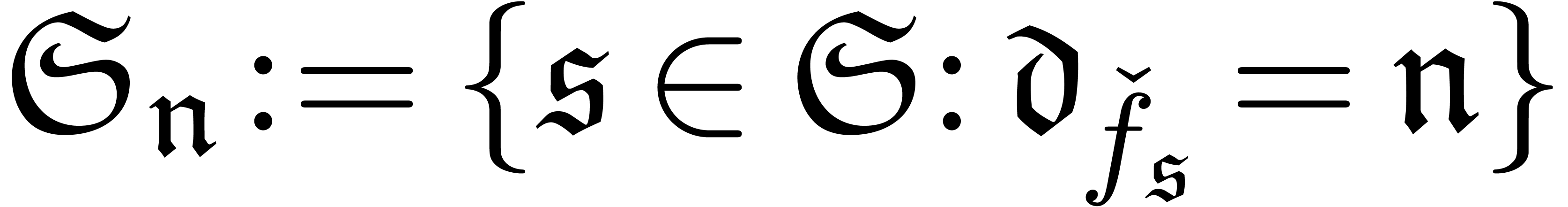 for each
for each
 .
.
If there exists an 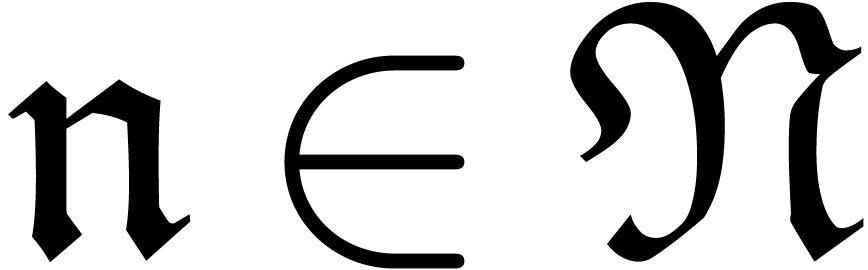 with
with 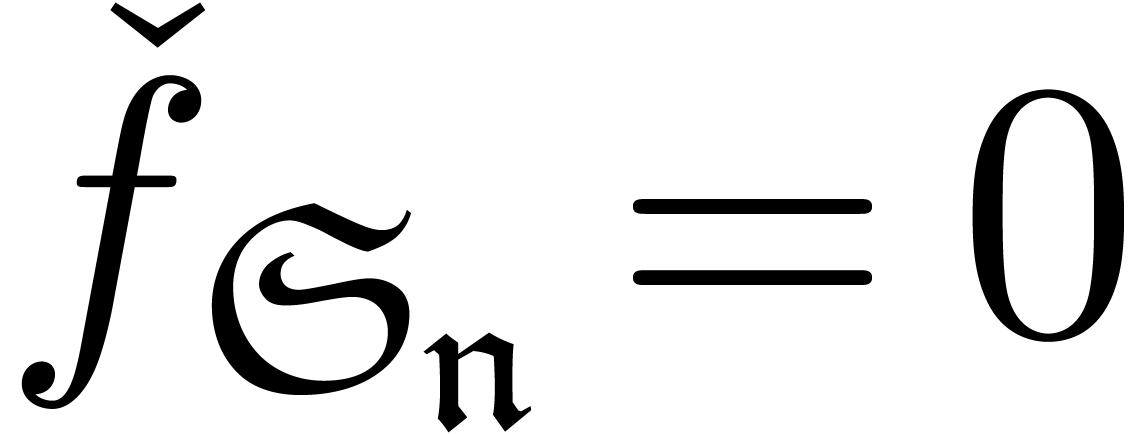 , then set
, then set
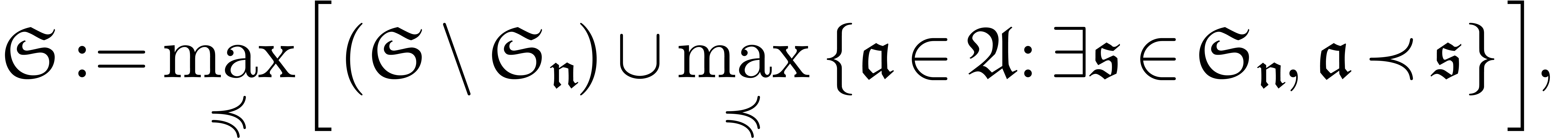
and go to step 2.
Return  .
.
 is said to be approximable if there
exists a computable sequence
is said to be approximable if there
exists a computable sequence 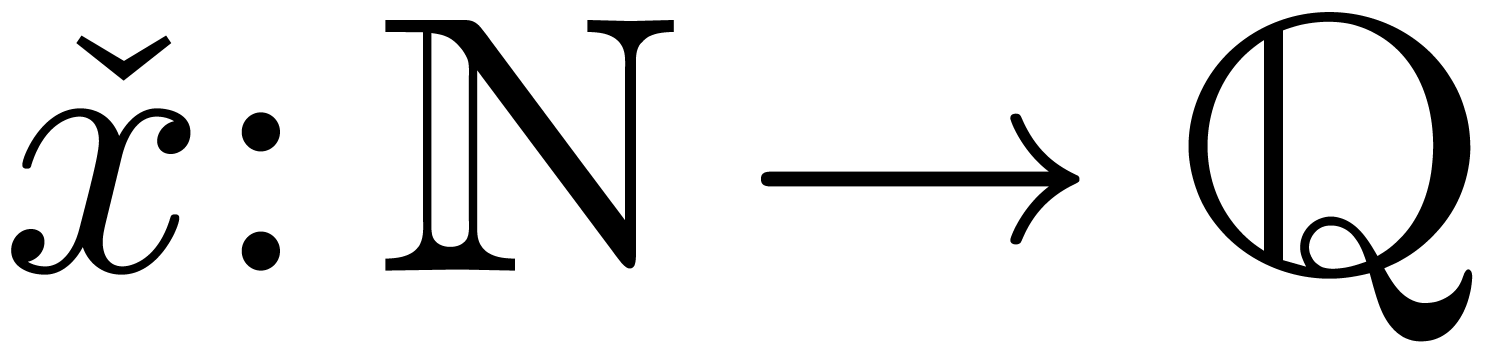 ,
which converges to
,
which converges to  . A
stronger and more robust notion is the one of computable real numbers:
we say that
. A
stronger and more robust notion is the one of computable real numbers:
we say that 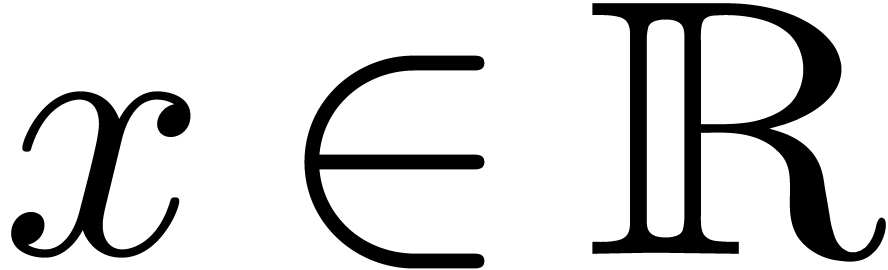 is computable, if there
exists a computable function
is computable, if there
exists a computable function 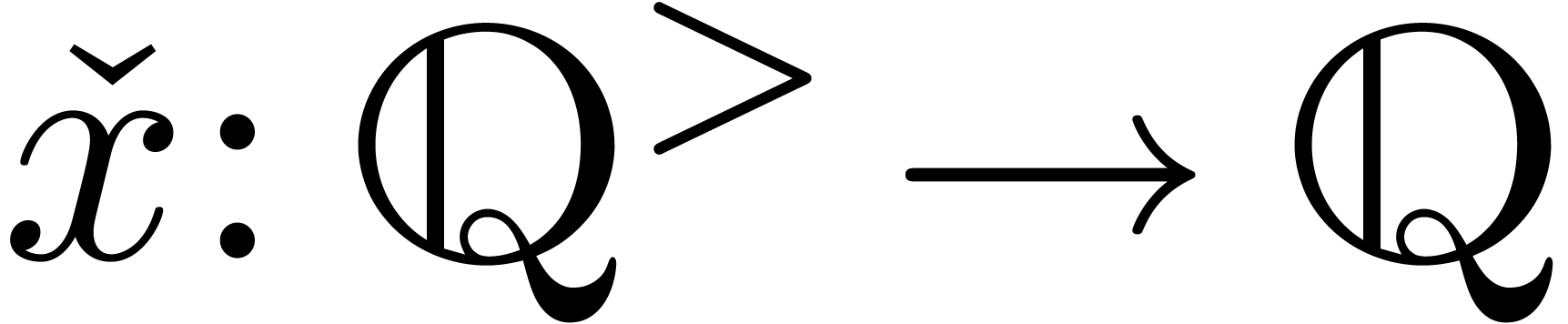 which takes
which takes 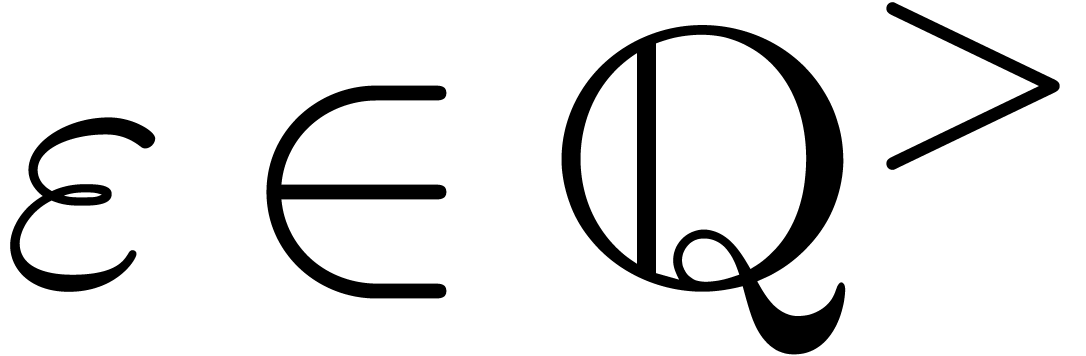 on input and produces an approximation
on input and produces an approximation 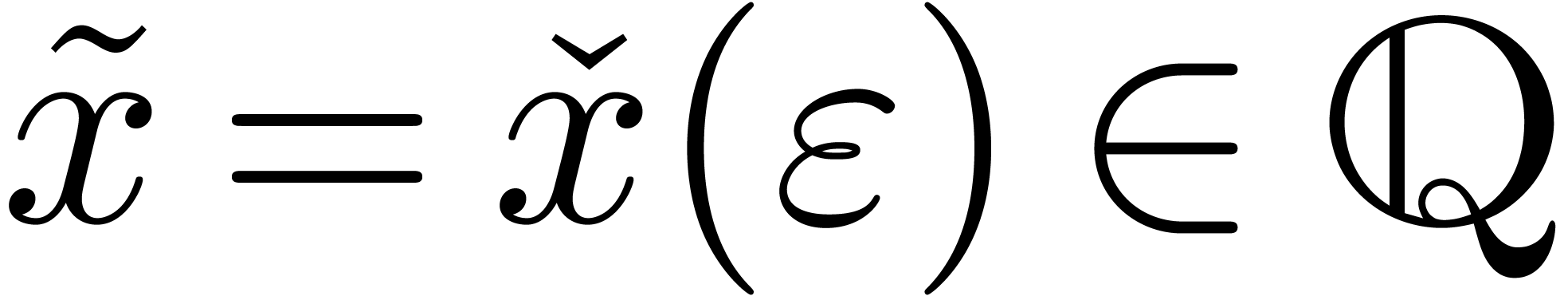 with
with 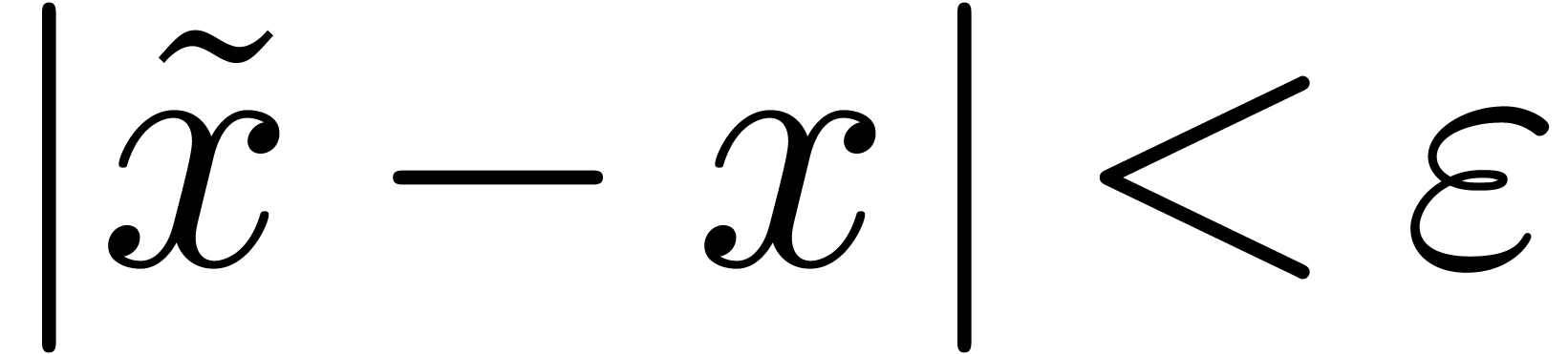 . It is
natural to search for an analogue notion of computable well-based
series.
. It is
natural to search for an analogue notion of computable well-based
series.
There are really two aspects to a computable well-based series  . On the one hand, we should be
able to compute its coefficient
. On the one hand, we should be
able to compute its coefficient  for any monomial
for any monomial
 . On the other hand, its
support should be sufficiently effective. In the case of ordinary power
series
. On the other hand, its
support should be sufficiently effective. In the case of ordinary power
series 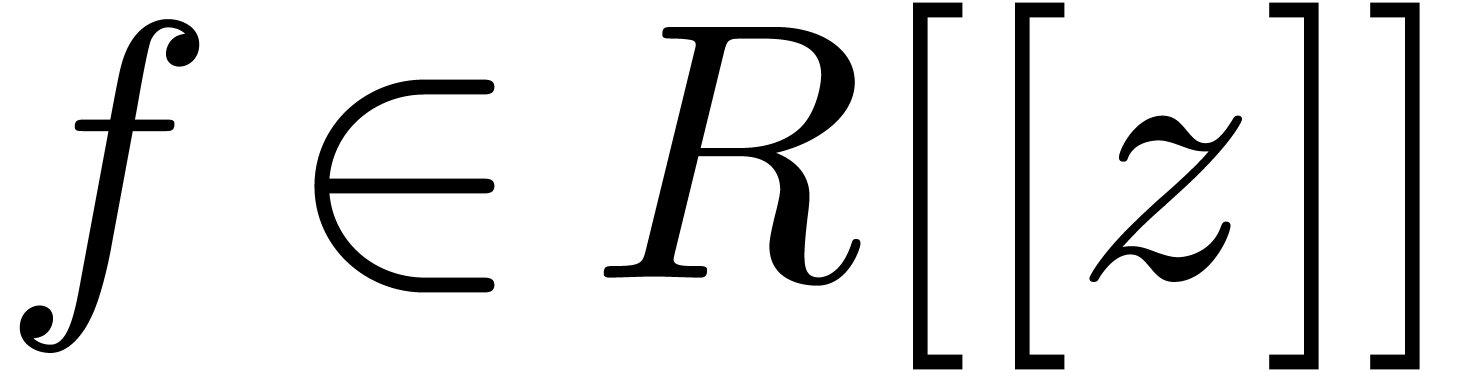 , the second issue
does not really arise, because the support is necessarily included in
the well-based set
, the second issue
does not really arise, because the support is necessarily included in
the well-based set  . In
general, one might require that
. In
general, one might require that  is given by a
termwise well-based expander, which yields quite a lot of information
about
is given by a
termwise well-based expander, which yields quite a lot of information
about 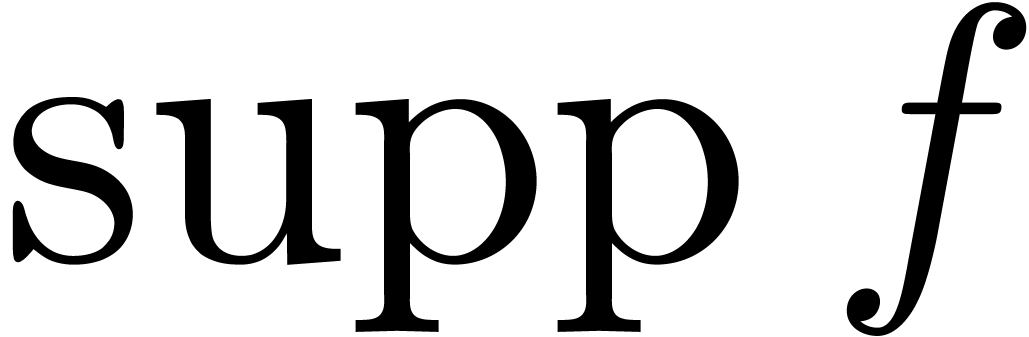 .
.
As to the computation of coefficients 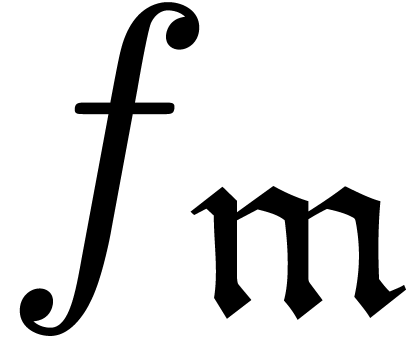 ,
consider the case of a product
,
consider the case of a product  ,
where
,
where  is totally ordered and
is totally ordered and  and
and  are given by
are given by 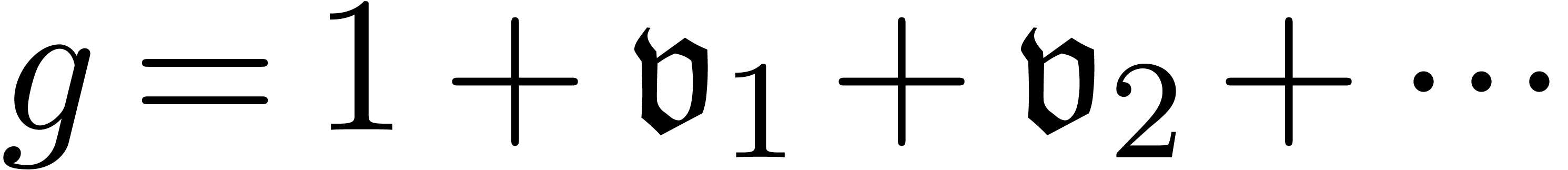 and
and
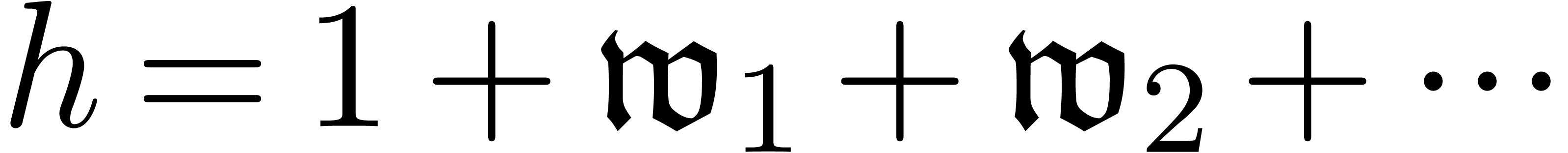 with
with  and
and 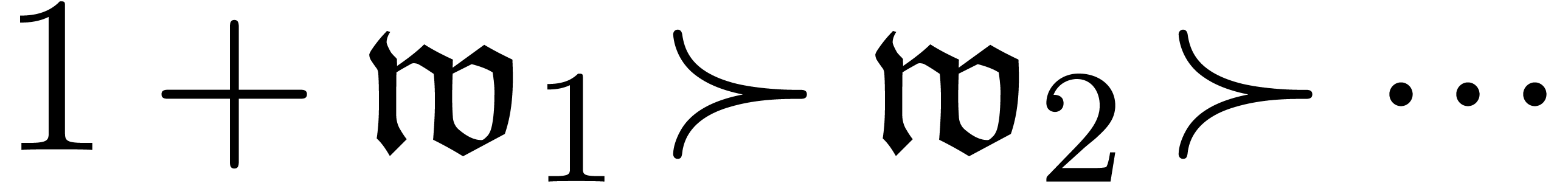 . Given
. Given  ,
we hit the problem that we don't have any a priori information
on the asymptotic behaviour of the
,
we hit the problem that we don't have any a priori information
on the asymptotic behaviour of the 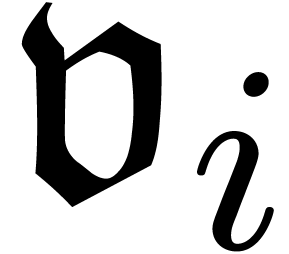 and the
and the 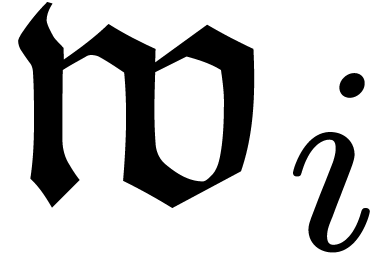 . In order to design an algorithm
for the computation of
. In order to design an algorithm
for the computation of  , we
need more control over this asymptotic behaviour.
, we
need more control over this asymptotic behaviour.
In the grid-based setting, we are really computing with multivariate
power series, and no real difficulties arise. In the well-based setting,
things get more involved. When we restrict our attention to transseries,
there are ways to represent and compute with monomial cuts [vdH06c, Chapter 9]. A monomial cut is the analogue of a
Dedekind cut for the set of transmonomials instead of  . Given a termwise well-based expander
. Given a termwise well-based expander 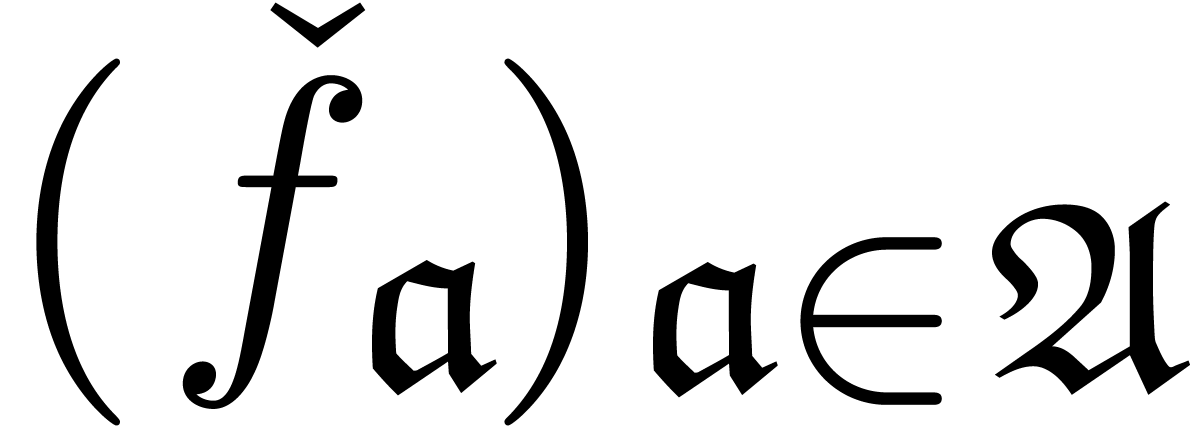 , any initial segment
, any initial segment  naturally induces a transseries
naturally induces a transseries 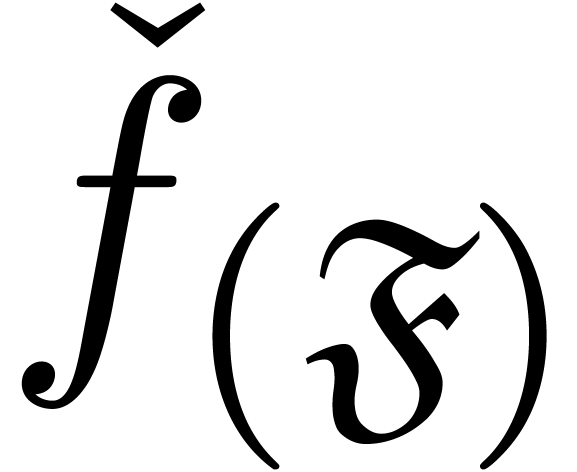 and a monomial cut, called the width of
and a monomial cut, called the width of 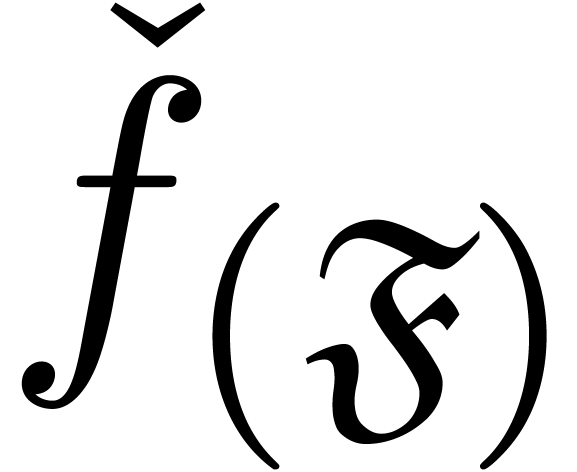 .
For a fully satisfactory definition of computable well-based series, one
should be able to compute these widths. However, we have not
investigated this matter in detail yet.
.
For a fully satisfactory definition of computable well-based series, one
should be able to compute these widths. However, we have not
investigated this matter in detail yet.
B. I. Dahn and P. Göring. Notes on exponential-logarithmic terms. Fundamenta Mathematicae, 127:45–50, 1986.
J. Écalle. Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, collection: Actualités mathématiques, 1992.
G.H. Gonnet and D. Gruntz. Limit computation in computer algebra. Technical Report 187, ETH, Zürich, 1992.
H. Hahn. Über die nichtarchimedischen Größensysteme. Sitz. Akad. Wiss. Wien, 116:601–655, 1907.
G.H. Hardy. Orders of infinity. Cambridge Univ. Press, 1910.
G.H. Hardy. Properties of logarithmico-exponential functions. Proceedings of the London Mathematical Society, 10(2):54–90, 1911.
G. Higman. Ordering by divisibility in abstract algebras. Proc. London Math. Soc., 2:326–336, 1952.
E. C. Milner. Basic wqo- and bqo- theory. In Rival, editor, Graphs and orders, pages 487–502. D. Reidel Publ. Comp., 1985.
A. Macintyre, D. Marker, and L. van den Dries. Logarithmic-exponential power series. Journal of the London Math. Soc., 56(2):417–434, 1997.
A. Macintyre, D. Marker, and L. van den Dries. Logarithmic exponential series. Annals of Pure and Applied Logic, 1999. To appear.
M. Pouzet. Applications of well quasi-ordering and better quasi-ordering. In Rival, editor, Graphs and orders, pages 503–519. D. Reidel Publ. Comp., 1985.
W.H. Press, S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery. Numerical recipes, the art of scientific computing. Cambridge University Press, 3rd edition, 2007.
D. Richardson. How to recognise zero. JSC, 24:627–645, 1997.
D. Richardson. Zero tests for constants in simple scientific computation. MCS, 1(1):21–37, 2007.
D. Richardson, B. Salvy, J. Shackell, and J. van der Hoeven. Expansions of exp-log functions. In Y.N. Lakhsman, editor, Proc. ISSAC '96, pages 309–313, Zürich, Switzerland, July 1996.
B. Salvy. Asymptotique automatique et fonctions génératrices. PhD thesis, École Polytechnique, France, 1991.
M.C. Schmeling. Corps de transséries. PhD thesis, Université Paris-VII, 2001.
J. Shackell. Growth estimates for exp-log functions. Journal of Symbolic Computation, 10:611–632, 1990.
J. Shackell. Inverses of Hardy L-functions. Bull. of the London Math. Soc., 25:150–156, 1993.
J. van der Hoeven. Outils effectifs en asymptotique et applications. Technical Report LIX/RR/94/09, LIX, École polytechnique, France, 1994.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1997.
J. van der Hoeven. Generic asymptotic expansions. AAECC, 9(1):25–44, 1998.
J. van der Hoeven. Operators on generalized power series. Journal of the Univ. of Illinois, 45(4):1161–1190, 2001.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven et al. Mathemagix, 2002. http://www.mathemagix.org.
J. van der Hoeven. Algorithms for asymptotic interpolation. Technical Report 2006-12, Univ. Paris-Sud, 2006. Submitted to JSC.
J. van der Hoeven. Counterexamples to witness conjectures. JSC, 41:959–963, 2006.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
J. van der Hoeven. On effective analytic continuation. MCS, 1(1):111–175, 2007.
J. van der Hoeven and J.R. Shackell. Complexity bounds for zero-test algorithms. JSC, 41:1004–1020, 2006.