Interfacing Mathemagix
with C++ |
|
|
Laboratoire d'Informatique
UMR 7161 CNRS
Campus de l'École polytechnique
91128 Palaiseau Cedex
France
|
|
Email:
vdhoeven@lix.polytechnique.fr
|
|
|
|
Laboratoire d'Informatique
UMR 7161 CNRS
Campus de l'École polytechnique
91128 Palaiseau Cedex
France
|
|
Email:
gregoire.lecerf@math.cnrs.fr
|
|
|
| Preliminary version of November 3, 2023 |
|
Abstract
In this paper, we give a detailed description of the interface between
the Mathemagix language and C++. In particular, we
describe the mechanism which allows us to import a C++ template library
(which only permits static instantiation) as a fully generic Mathemagix template library.
Keywords: Mathemagix, C++, generic programming,
template library
A.M.S. subject classification: 68W30
1Introduction
1.1Motivation behind Mathemagix
Until the mid nineties, the development of computer algebra systems
tended to exploit advances in the area of programming languages, and
sometimes even influenced the design of new languages. The Formac
system [2] was developed shortly after the introduction of
Fortran. Symbolic algebra was an important branch
of the artificial intelligence project at Mit
during the sixties. During a while, the Macsyma
system [21, 23, 25] was the
largest program written in Lisp, and motivated the
development of better Lisp compilers.
The Scratchpad system [11, 16]
was at the origin of yet another interesting family of computer algebra
systems, especially after the introduction of domains and categories as
function values and dependent types in Modlisp and
Scratchpad II [17, 19,
27]. These developments were at the forefront of language
design and type theory [9, 22, 24].
Scratchpad later evolved into the Axiom
system [1, 18]. In the A#
project [29, 30], later renamed into Aldor, the language and compiler were redesigned from
scratch and further purified.
After this initial period, computer algebra systems have been less keen
on exploiting new ideas in language design. One important reason is that
a good language for computer algebra is more important for developers
than for end users. Indeed, typical end users tend to use computer
algebra systems as enhanced pocket calculators, and rarely write
programs of substantial complexity themselves. Another reason is
specific to the family of systems that grew out of Scratchpad:
after IBM's decision to no longer support the development, there has
been a long period of uncertainty for developers and users on how the
system would evolve. This has discouraged many of the programmers who
did care about the novel programming language concepts in these systems.
In our opinion, this has led to an unpleasant current situation in
computer algebra: there is a dramatic lack of a modern, sound and fast
general purpose programming language. The major systems Mathematicatm
[31] and Mapletm [20]
are both interpreted, weakly typed, besides being proprietary and
expensive. The Sage system [26]
relies on Python and merely contents itself to
glue together various existing libraries and other software components.
The absence of modern languages for computer algebra is even more
critical whenever performance is required. Nowadays, many important
computer algebra libraries (such as Gmp [10],
Mpfr [6], Flint
[12], FGb [5], etc.) are
directly written in C or C++. Performance issues are also important
whenever computer algebra is used in combination with numerical
algorithms. We would like to emphasize that high level ideas can be
important even for traditionally low level applications. For instance,
in a suitable high level language it should be easy to operate on
SIMD vectors of, say, 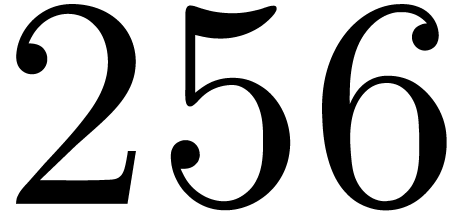 bit
floating point numbers. Unfortunately, Mpfr would
have to be completely redesigned in order to make such a thing possible.
bit
floating point numbers. Unfortunately, Mpfr would
have to be completely redesigned in order to make such a thing possible.
For these reasons, we have started the design of a new software, Mathemagix [14, 15], based on a
compiled and strongly typed language, featuring signatures, dependent
types, and overloading. Mathemagix is intended as
a general purpose language, which supports both functional and
imperative programming styles. Although the design has greatly been
influenced by Scratchpad II and its successors
Axiom and Aldor, the type
system of Mathemagix contains several novel
aspects, as described in [13]. Mathemagix
is also a free software, which can be downloaded from http://www.mathemagix.org.
1.2Interfacing Mathemagix
with C++
One major design goal of the Mathemagix compiler
is to admit a good compatibility with existing programming languages.
For the moment, we have focussed on C and C++. Indeed, on the one hand,
in parallel with the development of the compiler, we have written
several high performance C++ template libraries for various basic
mathematical structures (polynomials, matrices, series, etc.). On the
other hand, the compiler currently generates C++ code.
We already stated that Mathemagix was inspired by
Axiom and Aldor in many
respects. Some early work on interfacing with C++ was done in the
context of Aldor [4, 7].
There are two major differences between C++ and Aldor
which are important in this context.
On the one hand, Aldor provides support for
genuine generic functional programming: not only functions, but also
data types can be passed as function arguments. For instance, one may
write a routine which takes a ring 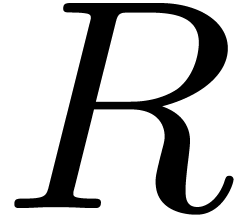 and an
integer
and an
integer 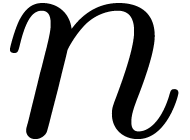 on input and which returns the ring
on input and which returns the ring
 . The language also provides
support for dependent types: a function may very well take a ring
. The language also provides
support for dependent types: a function may very well take a ring 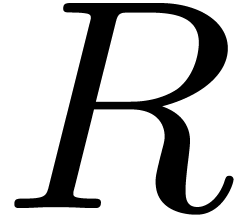 together with an instance
together with an instance 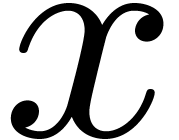 of
of
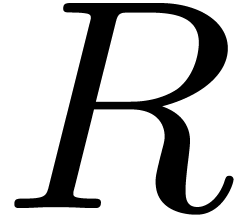 as its arguments or return value.
as its arguments or return value.
On the other hand, C++ provides support for
templates. We may write a routine cube which takes an
instance x of an arbitrary type R on
input and returns x*x*x. However, and even though there
is some work in this direction [8], it is currently not
possible to add the requirement that R must be a ring
when declaring the template cube. Hence, the correctness
of the template body x*x*x can only be checked at the
moment when the template is instantiated for a particular type R. Furthermore, only a finite number of these instantiations
can occur in a program or library, and template parameters cannot be
passed to functions as objects.
In Aldor, there is no direct equivalent of
templates. Nevertheless, it is possible to implement a function cube which takes a ring R and an instance
x of R on input, and which returns x*x*x. It thus makes sense to consider the importation of
C++ template libraries into Aldor. Although [4, 7] contain a precise strategy for realizing
such interfacing, part of the interface still had to be written by hand.
Mathemagix features two main novelties with
respect to the previous work which was done in the context of Axiom and Aldor. First of all, the
language itself admits full support for templates with typed parameters;
see our paper [13] on the type system for more details.
Secondly, C++ template libraries can be imported into Mathemagix
in a straightforward way, without the need to write any non trivial
parts of the interface by hand.
The ability to transform a C++ template library which only permits
static instantiation into a fully generic template library is somewhat
surprising. Part of the magic occurs in the specification of the
interface itself. Indeed, the interface should in particular provide the
missing type information about the parameters of the C++ templates. In
this paper, we will describe in more details how this mechanism works.
We think that similar techniques can be applied for the generic
importation of C++ templates into other languages such as Aldor
or OCaml. It might also be useful for future
extensions of C++ itself.
The paper is organized as follows. In Section 2, we
describe how to import and export non templated classes and functions
from and to C++. In Section 3, we
briefly recall how genericity works in Mathemagix,
and we describe what kind of C++ code is generated by the compiler for
generic classes and functions. The core of the paper is Section 4,
where we explain how C++ templates are imported into Mathemagix.
In Section 5 we summarize the main C++ libraries that have
been interfaced to Mathemagix, and Section 6 contains a conclusion and several ideas for future
extensions.
2Basic interface principles to
C++
2.1Preparing imports from C++
Different programming languages have different conventions for compiling
programs, organizing projects into libraries, and mechanisms for
separate compilation.
C++ is particularly complex, since the language does not provide any
direct support for the management of big projects. Instead, this task is
delegated to separate configuration and Makefile systems, which are
responsible for the detection and specification of external and internal
dependencies, and the determination of the correct compilation flags.
Although these tasks may be facilitated up to a certain extent when
using integrated development environments such as Eclipsetm
(trademark of Eclipse Foundation, Inc.), Xcodetm (trademark of Apple
Inc.), or C++ Buildertm (trademark of
Embarcadero Technologies, Inc.), they usually remain non trivial for
projects of a certain size.
Mathemagix uses a different philosophy for
managing big projects. Roughly speaking, any source file contains all
information which is necessary for building the corresponding binary.
Consequently, there is no need for external configuration or Makefile
systems.
Whenever we import functionality from C++ into Mathemagix,
our design philosophy implies that we have to specify the necessary
instructions for compiling and/or linking the imported code. To this
effect, Mathemagix provides special primitives cpp_flags, cpp_libs and cpp_include
for specifying the compilation and linking flags, and C++ header files
to be included.
For instance, the numerix library of Mathemagix
contains implementation for various numerical types. In particular, it
contains wrappers for the Gmp and Mpfr
libraries [6, 10] with implementations of
arbitrary precision integers, rational numbers and floating point
numbers. The Mathemagix interface for importing
the wrapper for arbitrary precision integers starts as follows:
foreign cpp import {
cpp_flags "`numerix-config --cppflags`";
cpp_libs "`numerix-config --libs`";
cpp_include "numerix/integer.hpp";
…
} |
On installation of the numerix library, a special script
numerix-config is installed in the user's path. In the
above example, we use this script in order to retrieve the compilation
and linking flags. Notice also that numerix/integer.hpp
is the C++ header file for basic arbitrary precision integer arithmetic.
2.2Importing simple classes and
functions
Ideally speaking, the bulk of an interface between Mathemagix
and a foreign language is simply a dictionary which specifies how
concepts in one system should be mapped into the other one. For ordinary
classes, functions and constants, there is a direct correspondence
between Mathemagix and C++, so the interface is
very simple in this case.
Assume for instance that we want to map the C++ class integer
from integer.hpp into the Mathemagix
class Integer, and import the basic constructors and
arithmetic operations on integers. This is done by completing the
previous example into:
foreign cpp import {
cpp_flags "`numerix-config --cppflags`";
cpp_libs "`numerix-config --libs`";
cpp_include "numerix/integer.hpp";
class Integer == integer;
literal_integer: Literal -> Integer ==
make_literal_integer;
prefix -: Integer -> Integer == prefix -;
infix +: (Integer, Integer) -> Integer == infix +;
infix -: (Integer, Integer) -> Integer == infix -;
infix *: (Integer, Integer) -> Integer == infix *;
…
} |
The special constructor literal_integer allows us to
write literal integer constants such as 12345678987654321
using the traditional notation. This literal constructor corresponds to
the C++ routine
integer make_literal_integer (const literal&); |
where literal is a special C++ class for string symbols.
2.3Syntactic sugar
The syntax of C++ is quite rigid and often directly related to
implementation details. For instance, in C++ the notation p.x
necessarily presupposes the definition of a class or structure with a
field x. In Mathemagix, the
operator postfix .x can be defined anywhere. More
generally, the language provides a lot of syntactic sugar which allows
for a flexible mapping of C++ functionality to Mathemagix.
Another example is type inheritance. In C++, type inheritance can only
be done at the level of class definitions. Furthermore, type inheritance
induces a specific low level representation in memory for the
corresponding class instances. In Mathemagix, we
may declare any type T to inherit from a type U
by defining an operator downgrade: T -> U. This
operator really acts as a converter with the special property that for
any second converter X -> T, Mathemagix
automatically generates the converter X -> U. This
allows for a more high level view of type inheritance.
Mathemagix also provides a few built-in type
constructors: Alias T provides a direct equivalent for
the C++ reference types, the type Tuple T can be used
for writing functions with an arbitrary number of arguments of the same
type T, and Generator T corresponds to a
stream of coefficients of type T. The built-in types Alias T, Tuple T and Generator
T are automatically mapped to the C++ types T&,
mmx::vector<T> and mmx::iterator<T>
in definitions of foreign interfaces. The containers mmx::vector<T>
and mmx::iterator<T> are defined in the C++
support library basix for Mathemagix,
where mmx represents the Mathemagix
namespace.
2.4Compulsory functions
When importing a C++ class T into Mathemagix,
we finally notice that the user should implement a few compulsory
operators on T. These operators have fixed named in C++
and in Mathemagix, so it is not necessary to
explicitly specify them in foreign interfaces.
The first compulsory operator is flatten: T ->
Syntactic, which converts instances of type T into
syntactic expression trees which can then be printed in several formats
(ASCII, Lisp, TeXmacs, etc.). The other compulsory
operators are three types of equality (and inequality) tests and the
corresponding hash functions. Indeed, Mathemagix
distinguishes between “semantic” equality, exact
“syntactic” equality and “hard” pointer
equality. Finally, any C++ type should provide a default constructor
with no arguments.
2.5Exporting basic functionality to C++
Simple Mathemagix classes and functions can be
exported to C++ in a similar way as C++ classes and functions are
imported. Assume for instance that we wrote a Mathemagix
class Point with a constructor, accessors, and a few
operations on points. Then we may export this functionality to C++ as follows:
foreign cpp export {
class Point == point;
point: (Double, Double) -> Point ==
keyword constructor;
postfix .x: Point -> Double == get_x;
postfix .y: Point -> Double == get_y;
middle: (Point, Point) -> Point == middle;
} |
3Categories and genericity in
Mathemagix
Before we discuss the importation of C++ template libraries into Mathemagix, let us first describe how to define generic
classes and functions in Mathemagix, and how such
generic declarations are reflected on the C++ side.
Mathemagix provides the forall
construct for the declaration of generic functions. For instance, a
simple generic function for the computation of a cube is the following:
forall (M: Monoid) cube (x: M): M == x*x*x; |
This function can be applied to any element x whose type
M is a monoid. For instance, we may write
The parameters of generic functions are necessarily typed. In our
example, the parameter M is a type itself and the type
of M a category. The category Monoid
specifies the requirements which are made upon the type M,
and a typical declaration would be the following:
category Monoid == {
infix *: (This, This) -> This;
} |
Hence, a type M is considered to have the structure of a
Monoid in a given context, as soon as the function infix *: (M, M) -> M is defined in this context. Notice
that the compiler does not provide any means for checking mathematical
axioms that are usually satisfied, such as associativity.
Already on this simple example, we notice several important differences
with the C++ “counterpart” of the declaration of cube:
template<typename M> M
cube (const M& x) { return x*x*x; } |
First of all, C++ does not provide a means for checking that M
admits the structure of a monoid. Consequently, the correctness of the
body return x*x*x can only be checked for actual
instantiations of the template. In particular, it is not possible to
compile a truly generic version of cube.
By default, Mathemagix always compiles functions
such as cube in a generic way. Let us briefly describe
how this is implemented. First of all (and similarly to [4,
7]), the definition of the category Monoid
gives rise to a corresponding abstract base class on the C++ side:
class Monoid_rep: public rep_struct {
inline Monoid_rep ();
virtual inline ~Monoid_rep ();
virtual generic mul (const generic&,
const generic&) const = 0;
…
}; |
A concrete monoid is a “managed pointer” (i.e.
the objects to which they point are reference counted) to a derived
class of Monoid_rep with an actual implementation of the
multiplication mul. Instances of the Mathemagix
type generic correspond to managed pointers to objects
of arbitrary types. The declaration of cube gives rise
to the following code on the C++ side:
generic
cube (const Monoid& M, const generic& x) {
// x is assumed to contain an object "of type M"
return M->mul (x, M->mul (x, x));
} |
The declaration c: Int == cube 3; gives rise to the
automatic generation of a class Int_Monoid_rep which
corresponds to the class Int with the structure of a Monoid:
struct Int_Ring_rep: public Ring_rep {
…
generic
mul (const generic& x, const generic& y) const {
return as_generic<int> (from_generic<int> (x) *
from_generic<int> (y));
}
…
}; |
The declaration itself corresponds to the following C++ code:
Monoid Int_Ring= new Int_Ring_rep ();
int c= from_generic<int>
(cube (Int_Ring, as_generic<int> (3))); |
Notice that we did not generate any specific instantiation of cube
for the Int type. This may lead to significantly smaller
executables with respect to C++ when the function cube
is applied to objects of many different types. Indeed, in the case of
C++, a separate instantiation of the function needs to be generated for
each of these types. In particular, the function can only be applied to
a finite number of types in the course of a program.
Remark 1. Of course, for very low
level types such as Int, the use of generic functions
does imply a non trivial overhead. Nevertheless, since the type generic is essentially a void*, the overhead
is kept as small as possible. In particular, the overhead is guaranteed
to be bounded by a fixed constant. We also notice that Mathemagix
provides an experimental keyword specialize which allows
for the explicit instantiation of a generic function.
Remark 2. Although generic
functions such as cube are not instantiated by default,
our example shows that we do have to generate special code for
converting the type parameter Int to a Monoid.
Although this code is essentially trivial, it may become quite
voluminous when there are many different types and categories. We are
still investigating how to reduce this size as much as possible while
keeping the performance overhead small.
Mathemagix also allows for the declaration of
generic container classes; the user simply has to specify the typed
parameters when declaring the class:
class Complex (R: Ring) == {
re: R;
im: R;
constructor complex (r: R, i: R) == {
re == r;
im == i;
}
} |
Again, only the generic version of this class is compiled by default. In
particular, the internal representation of the corresponding C++ class
is simply a class with two fields re and im
of type generic.
Regarding functions and templates, there are a few other important
differences between C++ and Mathemagix:
-
Dependencies are allowed between function and template parameters
and return values, as in the following example:
forall (R: Ring, M: Module R)
infix * (c: R, v: Vector M): Vector M ==
[ c * x | x: M in v ]; |
-
Template parameters can be arbitrary types or (not necessarily
constant) instances. For instance, one may define a container Vec (R: Ring, n: Int) for vectors with a fixed size.
-
Functions can be used as arguments and as values:
compose (f: Int -> Int, g: Int -> Int)
(x: Int): Int ==
f g x; |
Notice that Axiom and Aldor
admit the same advantages with respect to C++.
4Importing C++ containers and
templates
One of the most interesting aspects of our interface between Mathemagix and C++ is its ability to import C++ template
classes and functions. This makes it possible to provide a fully generic
Mathemagix interface on top of an existing C++
template library. We notice that the interface between Aldor
and C++ [4, 7] also provided a strategy for
the importation of templates. However, the bulk of the actual work still
had to be done by hand.
4.1Example of a generic C++ import
Before coming to the technical details, let us first give a small
example of how to import part of the univariate polynomial arithmetic
from the C++ template library algebramix, which is
shipped with Mathemagix:
foreign cpp import {
…
class Pol (R: Ring) == polynomial R;
forall (R: Ring) {
pol: Tuple R -> Pol R == keyword constructor;
upgrade: R -> Pol R == keyword constructor;
deg: Pol R -> Int == deg;
postfix []: (Pol R, Int) -> R == postfix [];
prefix -: Pol R -> Pol R == prefix -;
infix +: (Pol R, Pol R) -> Pol R == infix +;
infix -: (Pol R, Pol R) -> Pol R == infix -;
infix *: (Pol R, Pol R) -> Pol R == infix *;
…
}
} |
As is clear from this example, the actual syntax for template imports is
a straightforward extension of the syntax of usual imports and the
syntax of generic declarations on the Mathemagix
side.
Actually, the above code is still incomplete: in order to make it work,
we also have to specify how the ring operations on R
should be interpreted on the C++ side. This is done by
exporting the category Ring to C++:
foreign cpp export
category Ring == {
convert: Int -> This == keyword constructor;
prefix -: This -> This == prefix -;
infix +: (This, This) -> This == infix +;
infix -: (This, This) -> This == infix -;
infix *: (This, This) -> This == infix *;
} |
This means that the ring operations in C++ are the constructor from int and the usual operators +, -
and *. The programmer should make sure that the C++
implementations of the imported templates only rely on these ring
operations.
4.2Generation of generic instance classes
The first thing the compiler does with the above C++ export of Ring is the creation of a C++ class capable of representing
generic instances of arbitrary ring types. Any mechanism for doing this
has two components: we should not only store the actual ring elements,
but also the rings themselves to which they belong. This can actually be
done in two ways.
The most straightforward idea is to represent an instance of a generic
ring by a pair 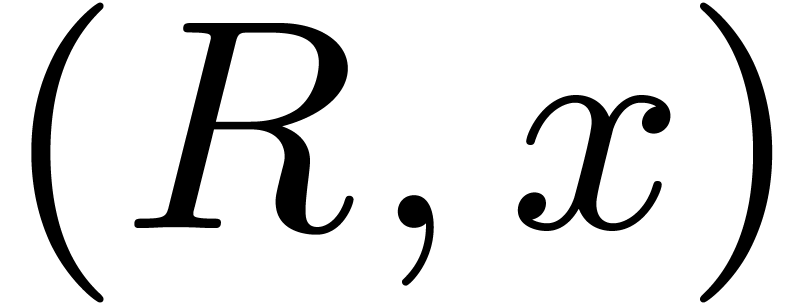 , where
, where 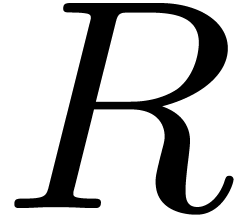 is the actual ring (similar to the example of the C++
counterpart of a monoid in Section 3) and
is the actual ring (similar to the example of the C++
counterpart of a monoid in Section 3) and 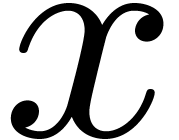 an actual element of
an actual element of 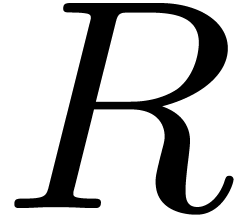 . This
approach has the advantage of being purely functional, but it requires
non trivial modifications on the C++ side.
. This
approach has the advantage of being purely functional, but it requires
non trivial modifications on the C++ side.
Indeed, whenever a function returns a ring object, we should be able to
determine the underlying ring 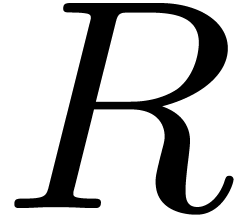 from the input
arguments. In the case of a function such as postfix []: (Pol
R, Int) -> R, this means that R has to be read
off from the coefficients of the input polynomial. But the most
straightforward implementation of the zero polynomial does not have any
coefficients! In principle, it is possible to tweak all C++ containers
so as to guarantee the ability to determine the underlying generic
parameters from actual instances. We have actually implemented this
idea, but it required a lot of work, and it violates the principle that
writing a Mathemagix interface for a C++ template
library should essentially be trivial.
from the input
arguments. In the case of a function such as postfix []: (Pol
R, Int) -> R, this means that R has to be read
off from the coefficients of the input polynomial. But the most
straightforward implementation of the zero polynomial does not have any
coefficients! In principle, it is possible to tweak all C++ containers
so as to guarantee the ability to determine the underlying generic
parameters from actual instances. We have actually implemented this
idea, but it required a lot of work, and it violates the principle that
writing a Mathemagix interface for a C++ template
library should essentially be trivial.
The second approach is to store the ring 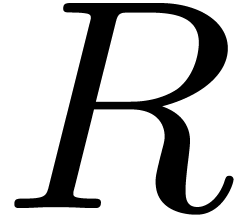 in a
global variable, whose value will frequently be changed in the course of
actual computations. In fact, certain templates might carry more than
one parameter of type Ring, in which case we need more
than one global ring. For this reason, we chose to implement a container
instance<Cat,Nr> for generic instances of a type
of category Cat, with an additional integer parameter
Nr for distinguishing between various parameters of the
same category Cat. The container instance<Cat,Nr>
is really a wrapper for generic:
in a
global variable, whose value will frequently be changed in the course of
actual computations. In fact, certain templates might carry more than
one parameter of type Ring, in which case we need more
than one global ring. For this reason, we chose to implement a container
instance<Cat,Nr> for generic instances of a type
of category Cat, with an additional integer parameter
Nr for distinguishing between various parameters of the
same category Cat. The container instance<Cat,Nr>
is really a wrapper for generic:
template<typename Cat, int Nr>
class instance {
public:
generic rep;
static Cat Cur;
inline instance (const instance& prg2):
rep (prg2.rep) {}
inline instance (const generic& prg):
rep (prg) {}
instance ();
template<typename C1> instance (const C1& c1);
…
}; |
For instance, objects of type instance<Ring,2> are
instances of the second generic Ring parameter of
templates. The corresponding underlying ring is stored in the global
static variable instance<Ring,2>::Cur.
When exporting the Ring category to C++, the Mathemagix compiler automatically generates generic C++
counterparts for the ring operations. For instance, the following
multiplication is generated for instance<Ring,Nr>:
template<int Nr> inline instance<Ring,Nr>
operator * (const instance<Ring,Nr> &a1,
const instance<Ring,Nr> &a2) {
typedef instance<Ring,Nr> Inst;
return Inst (Inst::Cur->mul (a1.rep, a2.rep));
} |
Since all C++ compilers do not allow us to directly specialize
constructors of instance<Cat,Nr>, we provide a
general default constructor of instance<Cat,Nr>
from an arbitrary type T, which relies on the in place
routine
void set_as (instance<Ring,Nr>&, const T&); |
This routine can be specialized for particular categories. For instance,
the converter convert: Int -> This from Ring
gives rise to following routine, which induces a constructor for instance<Ring,Nr> from int:
template<int Nr> inline void
set_as (instance<Ring,Nr> &ret, const int &a1) {
typedef instance<Ring,Nr> Inst;
ret = Inst (Inst::Cur->cast (a1));
} |
In this example, Inst::Cur->cast represents the
function that sends an int into an element of the
current ring.
4.3Importing C++ templates
Now that we have a way to represent arbitrary Mathemagix
classes R with the structure of a Ring
by a C++ type instance<Ring,Nr>, we are in a
position to import arbitrary C++ templates with Ring
parameters. This mechanism is best explained on an example. Consider the
importation of the routine
forall (R: Ring)
infix *: (Pol R, Pol R) -> Pol R; |
The compiler essentially generates the following C++ code for this
import:
polynomial<generic>
mul (const Ring &R,
const polynomial<generic> &p1,
const polynomial<generic> &p2)
{
typedef instance<Ring,1> Inst;
Ring old_R= Inst::Cur;
Inst::Cur= R;
polynomial<Inst> P1= as<polynomial<Inst> > (p1);
polynomial<Inst> P2= as<polynomial<Inst> > (p2);
polynomial<Inst> R = P1 * P2;
polynomial<generic> r=
as<polynomial<generic> > (R);
Inst::Cur= old_R;
return r;
} |
There are two things to be observed in this code. First of all, for the
computation of the actual product P1 * P2, we have made
sure that Inst::Cur contains the ring R
corresponding to the coefficients of the generic coefficients of the
inputs p1 and p2. Moreover, the old
value of Inst::Cur is restored on exit. Secondly, we
notice that polynomial<Inst> and polynomial<generic>
have exactly the same internal representation. The template as
simply casts between these two representations. In the actual code
generated by the compiler, these casts are done without any cost,
directly on pointers.
The above mechanism provides us with a fully generic way to import C++
templates. However, as long as the template parameters are themselves
types which were imported from C++, it is usually more efficient to
shortcut the above mechanism and directly specialize the templates on
the C++ side. For instance, the Mathemagix program
p: Pol Integer == …;
q: Pol Integer == p * p; |
is compiled into the following C++ code:
polynomial<integer> p= …;
polynomial<integer> q= p * p; |
5Currently interfaced C++
libraries
Currently, most of the mathematical features available in Mathemagix
are imported from C++ libraries, either of our own or external [15].
In this section, we briefly describe what these libraries provide, and
the main issues we encountered.
5.1Mathemagix
libraries
C++ libraries of the Mathemagix project provide
the user with usual data types and mathematical objects. We have already
mentioned the basix library which is devoted to vectors,
iterators, lists, hash tables, generic objects, parsers, pretty
printers, system commands, and the TeXmacs interface. The numerix
library is dedicated to numerical types including integers, modular
integers, rational numbers, floating point numbers, complex numbers,
intervals, and balls. Univariate polynomials, power series, fraction
fields, algebraic numbers, and matrices are provided by the algebramix
library, completed by analyziz for when working with
numerical coefficient types. Multivariate polynomials, jets, and power
series and gathered in the multimix library. Finally continewz implements analytic functions and numerical
homotopy continuation for polynomial system solving.
The Mathemagix compiler is itself written in
Mathemagix on the top of the basix
library. In order to produce a first binary for this compiler, we
designed a mechanism for producing standalone C++ sources from its
Mathemagix sources (namely the mmcompileregg
package). This mechanism is made available to the user via the option
–keep-cpp of the mmc compiler
command.
In the following example we illustrate simple calculations with analytic
functions. We use the notation ==> for macro
definitions. We first construct the polynomial indeterminate 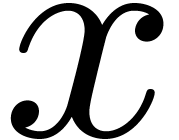 of
of 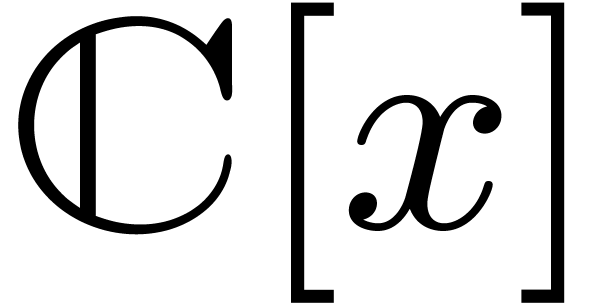 , and
convert it into the analytic function indeterminate
, and
convert it into the analytic function indeterminate  . We display
. We display 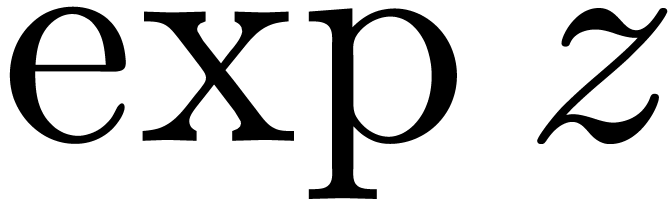 ,
,
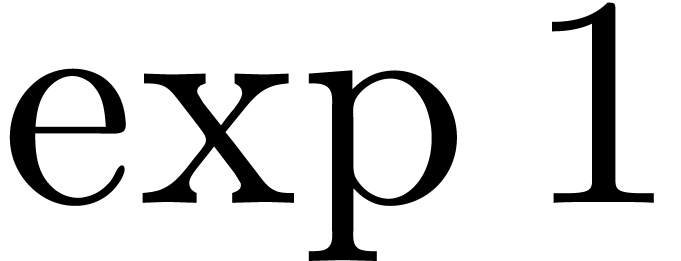 , and
, and 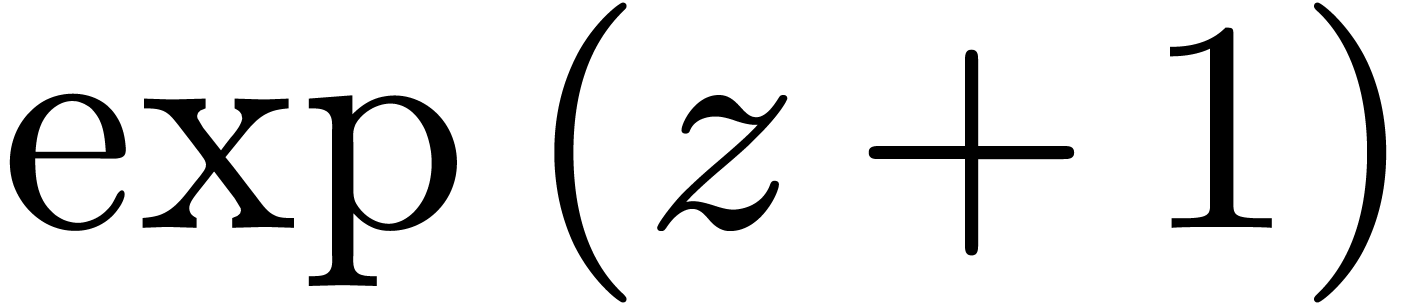 on the standard output mmout. Internal computations are
performed up to
on the standard output mmout. Internal computations are
performed up to 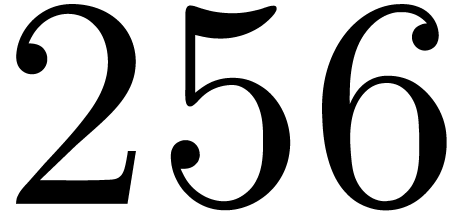 bits of precision, but printing
is restricted to
bits of precision, but printing
is restricted to  decimal digits. Analytic
functions are displayed as their underlying power series at the origin,
for which we set the output order to
decimal digits. Analytic
functions are displayed as their underlying power series at the origin,
for which we set the output order to  .
.
include "basix/fundamental.mmx";
include "numerix/floating.mmx";
include "numerix/complex.mmx";
include "continewz/analytic.mmx";
R ==> Floating;
C ==> Complex R;
Pol ==> Polynomial C;
Afun ==> Analytic (R, C);
bit_precision := 256;
x: Pol == polynomial (complex (0.0 :> R),
complex (1.0 :> R));
z: Afun == x :> Pol;
f: Afun == exp z;
significant_digits := 5;
set_output_order (x :> (Series C), 5);
mmout << "f= " << f << lf;
mmout << "f (1)= " << f (1.0 :> C) << lf;
mmout << "f (1 + z)= " << move (f, 1.0 :> C) << lf; |
Compiling and running this program in a textual terminal yields:
f= 1.0000 + 1.0000 * z + 0.50000 * z^2
+ 0.16667 * z^3 + 0.041667 * z^4 + O (z^5)
f (1)= 2.7183
f (1 + z)= 2.7183 + 2.7183 * z + 1.3591 * z^2
+ 0.45305 * z^3 + 0.11326 * z^4 + O (z^5)
5.2External libraries
Importing a library that is completely external to the Mathemagix
project involves several issues. First of all, as mentioned in Section
2.4, all the data types to be imported should satisfy mild
conditions in order to be properly usable from Mathemagix.
Usually, these conditions can easily be satisfied by writing a C++
wrapper whenever necessary.
However, when introducing new types and functions, one usually wants
them to interact naturally with other librairies. For instance, if
several libraries have their own arbitrarily long integer type,
straightforward interfaces introduce several Mathemagix
types of such integers, leaving to the user the responsibility of the
conversions in order to use functions of different librairies within a
single program.
For C and C++ libraries involving only a finite number of types, we
prefer to design lower level interfaces to the C++ libraries of Mathemagix. In this way, we focus on writing efficient
converters between external and C++ Mathemagix
objects, and then on interfacing new functions at the Mathemagix
language level. This is the way we did for instance with lattice
reduction of the Fplll library [3],
where we mainly had to write converters for integer matrices. Similarly
the interface with FGb [5] mainly
consists in converters between different representations of multivariate
polynomials.
When libraries contain many data types, functions, and have their own
memory management, the interface quickly becomes tedious. This situation
happened with the Pari library [28].
We first created a C++ wrapper of generic Pari
objects, so that wrapped objects are reference counted and have memory
space allocated by Mathemagix. Before calling a
Pari function, the arguments are copied onto the
Pari stack. Once the function has terminated, the
result from the stack is wrapped into a Mathemagix
object. Of course converters for the different representations of
integers, rationals, polynomials and matrices were needed. The following
example calls the Pari function nfbasis
to compute an integral basis of the number field defined by 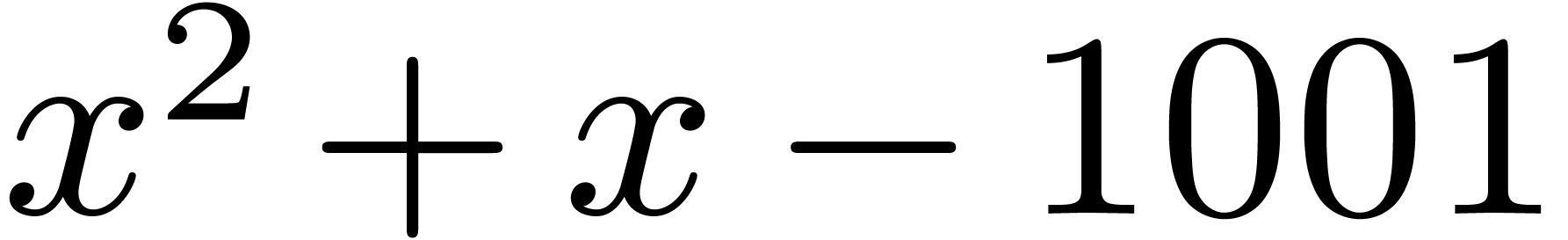 :
:
include "basix/fundamental.mmx";
include "mpari/pari.mmx";
Pol ==> Polynomial Integer;
x: Pol == polynomial (0 :> Integer, 1 :> Integer);
p: Pol == x^2 + x - 1001;
mmout << pari_nf_basis p << lf; |
[1, 1 / 3 * x - 1 / 3]
6Conclusion and future
extensions
The current mechanism for importing C++ template libraries has been
tested for the standard mathematical libraries which are shipped with
Mathemagix. For this purpose, it has turned out to
be very user friendly, flexible and robust. We think that other
languages may develop facilities for the importation of C++ template
libraries along similar lines. In the future, our approach may even be
useful for adding more genericity to C++ itself. A few points deserve to
be developed further:
Exporting Mathemagix containers and
templates
So far, we have focussed on the importation of C++ containers and
templates, and Mathemagix only allows for the
exportation of simple, non generic functions and non parameterized
classes. Nevertheless, it should not be hard to add support for the
more general exportation of generic functions and parameterized
classes. Of course, the types of the template parameters would be lost
in this process and the resulting templates will only allow for static
instantiation.
Multi-threading
The main disadvantage of relying on global variables for storing the
current values of template parameters is that this strategy is not
thread-safe. In order to allow generic code to be run simultaneously
by several threads, the global variables have to be replaced by fast
lookup tables which determine the current values of template
parameters as a function of the current thread.
Non class parameters
The current interface only allows for the importation of C++ templates
with type parameters. This is not a big limitation, because templates
with value parameters are only supported for built-in types and they
can only be instantiated for constant values. Nevertheless, it is
possible to define auxiliary classes for storing mutable static
variables, and use these instead as our template parameters; notice
that this is exactly the purpose of the instance<Cat,Nr>
template. In Mathemagix, we also use this
mechanism for the implementation of modular arithmetic, with a modulus
that can be changed during the execution. After fixing a standard
convention for the creation of auxiliary classes, our implementation
could be extended to the importation of C++ with “value
parameters” of this kind.
Interfacing more libraries
Interfacing libraries often involves portability issues, and also
create dependencies that have a risk to be broken in case the library
stops being maintained. In the Mathemagix
project we considered that functionalities imported from an external
library should be implemented even naively directly in Mathemagix
(excepted for Gmp and Mpfr).
This represents a certain amount of work (for lattice reduction,
Gröbner basis, finite fields, etc), but this eases testing the
interfaces and allows the whole software to run on platforms where
some libraries are not available.
Acknowledgments
We would like to thank Jean-Charles Faugère for helping us in the
interface with FGb, and also Karim Belabas and
Bill Allombert for their precious advices in the design of our interface
with the Pari library.
Bibliography
-
[1]
-
Axiom computer algebra system. Software available
from http://wiki.axiom-developer.org.
-
[2]
-
E. Bond, M. Auslander, S. Grisoff, R. Kenney, M.
Myszewski, J. Sammet, R. Tobey, and S. Zilles. FORMAC an
experimental formula manipulation compiler. In Proceedings of
the 1964 19th ACM national conference, ACM '64, pages
112.101–112.1019, New York, NY, USA, 1964. ACM.
-
[3]
-
D. Cade, X. Pujol, and D. Stehlé. Fplll,
library for LLL-reduction of Euclidean lattices. Software
available from http://perso.ens-lyon.fr/damien.stehle/fplll,
1998.
-
[4]
-
Y. Chicha, F. Defaix, and S. M. Watt. Automation of
the Aldor/C++ interface: User's guide. Technical Report Research
Report D2.2.2c, FRISCO Consoritum, 1999. Available from http://www.csd.uwo.ca/~watt/pub/reprints/1999-frisco-aldorcpp-ug.pdf.
-
[5]
-
J.-C. Faugère. FGb: A Library for Computing
Gröbner Bases. In K. Fukuda, J. van der Hoeven, M. Joswig,
and N. Takayama, editors, Mathematical Software - ICMS 2010,
Third International Congress on Mathematical Software, Kobe,
Japan, September 13-17, 2010, volume 6327 of Lecture
Notes in Computer Science, pages 84–87. Springer
Berlin / Heidelberg, 2010.
-
[6]
-
L. Fousse, G. Hanrot, V. Lefèvre, P.
Pélissier, and P. Zimmermann. MPFR: A multiple-precision
binary floating-point library with correct rounding. ACM
Transactions on Mathematical Software, 33(2), 2007. Software
available from http://www.mpfr.org.
-
[7]
-
M. Gaëtano and S. M. Watt. An object model
correspondence for Aldor and C++. Technical Report Research
Report D2.2.1, FRISCO Consortium, 1997. Available from http://www.csd.uwo.ca/~watt/pub/reprints/1997-frisco-aldorcppobs.pdf.
-
[8]
-
R. Garcia, J. Järvi, A. Lumsdaine, J. G. Siek,
and J. Willcock. A comparative study of language support for
generic programming. In Proceedings of the 2003 ACM SIGPLAN
conference on Object-oriented programming, systems, languages,
and applications (OOPSLA'03), October 2003.
-
[9]
-
J. Y. Girard. Une extension de
l'interprétation de Gödel à l'analyse, et son
application à l'élimination de coupures dans
l'analyse et la théorie des types. In J. E. Fenstad,
editor, Proceedings of the Second Scandinavian Logic
Symposium, pages 63–92. North-Holland Publishing Co.,
1971.
-
[10]
-
T. Granlund and the GMP development team. GNU MP: The
GNU Multiple Precision Arithmetic Library. Software available
from http://gmplib.org, 1991.
-
[11]
-
J. H. Griesmer, R. D. Jenks, and D. Y. Y. Yun.
SCRATCHPAD User's Manual. Computer Science Department
monograph series. IBM Research Division, 1975.
-
[12]
-
W. Hart. An introduction to Flint. In K. Fukuda, J.
van der Hoeven, M. Joswig, and N. Takayama, editors,
Mathematical Software - ICMS 2010, Third International
Congress on Mathematical Software, Kobe, Japan, September 13-17,
2010, volume 6327 of Lecture Notes in Computer
Science, pages 88–91. Springer Berlin / Heidelberg,
2010.
-
[13]
-
J. van der Hoeven. Overview of the Mathemagix type
system. In Electronic proc. ASCM '12, Beijing, China,
October 2012. Available from http://hal.archives-ouvertes.fr/hal-00702634.
-
[14]
-
J. van der Hoeven, G. Lecerf, B. Mourrain, et al.
Mathemagix, 2002. Software available from http://www.mathemagix.org.
-
[15]
-
J. van der Hoeven, G. Lecerf, B. Mourrain, Ph.
Trébuchet, J. Berthomieu, D. Diatta, and A. Manzaflaris.
Mathemagix, the quest of modularity and efficiency for symbolic
and certified numeric computation. ACM Commun. Comput.
Algebra, 45(3/4):186–188, 2012.
-
[16]
-
R. D. Jenks. The SCRATCHPAD language. SIGPLAN
Not., 9(4):101–111, 1974.
-
[17]
-
R. D. Jenks. MODLISP – an introduction
(invited). In Proceedings of the International Symposium on
Symbolic and Algebraic Computation, EUROSAM '79, pages
466–480, London, UK, UK, 1979. Springer-Verlag.
-
[18]
-
R. D. Jenks and R. Sutor. AXIOM: the scientific
computation system. Springer-Verlag, New York, NY, USA,
1992.
-
[19]
-
R. D. Jenks and B. M. Trager. A language for
computational algebra. SIGPLAN Not., 16(11):22–29,
1981.
-
[20]
-
Maple user manual. Toronto: Maplesoft, a division of
Waterloo Maple Inc., 2005–2012. Maple is a trademark of
Waterloo Maple Inc. http://www.maplesoft.com/products/maple.
-
[21]
-
W. A. Martin and R. J. Fateman. The MACSYMA system.
In Proceedings of the second ACM symposium on symbolic and
algebraic manipulation, SYMSAC '71, pages 59–75, New
York, NY, USA, 1971. ACM.
-
[22]
-
P. Martin-Löf. Constructive mathematics and
computer programming. Logic, Methodology and Philosophy of
Science VI, pages 153–175, 1979.
-
[23]
-
Maxima, a computer algebra system (free version).
Software available from http://maxima.sourceforge.net,
2011.
-
[24]
-
R. Milner. A theory of type polymorphism in
programming. Journal of Computer and System Sciences,
17:348–375, 1978.
-
[25]
-
J. Moses. Macsyma: A personal history. Journal of
Symbolic Computation, 47(2):123–130, 2012.
-
[26]
-
W. A. Stein et al. Sage Mathematics Software.
The Sage Development Team, 2004. Software available from http://www.sagemath.org.
-
[27]
-
R. S. Sutor and R. D. Jenks. The type inference and
coercion facilities in the Scratchpad II interpreter. SIGPLAN
Not., 22(7):56–63, 1987.
-
[28]
-
The PARI Group, Bordeaux. PARI/GP, 2012.
Software available from http://pari.math.u-bordeaux.fr.
-
[29]
-
S. Watt, P. A. Broadbery, S. S. Dooley, P. Iglio, S.
C. Morrison, J. M. Steinbach, and R. S. Sutor. A first report on
the A# compiler. In Proceedings of the international
symposium on symbolic and algebraic computation, ISSAC '94,
pages 25–31, New York, NY, USA, 1994. ACM.
-
[30]
-
S. Watt et al. Aldor programming language. Software
available from http://www.aldor.org, 1994.
-
[31]
-
S. Wolfram. Mathematica: A System for Doing
Mathematics by Computer. Addison-Wesley, second edition,
1991. Mathematica is a trademark of Wolfram Research, Inc. http://www.wolfram.com/mathematica.

 . This work has
been partly supported by the
. This work has
been partly supported by the  bit
floating point numbers. Unfortunately,
bit
floating point numbers. Unfortunately, 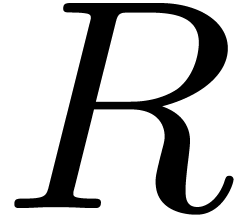 and an
integer
and an
integer 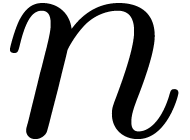 on input and which returns the ring
on input and which returns the ring
 .
.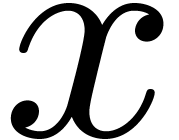 of
of
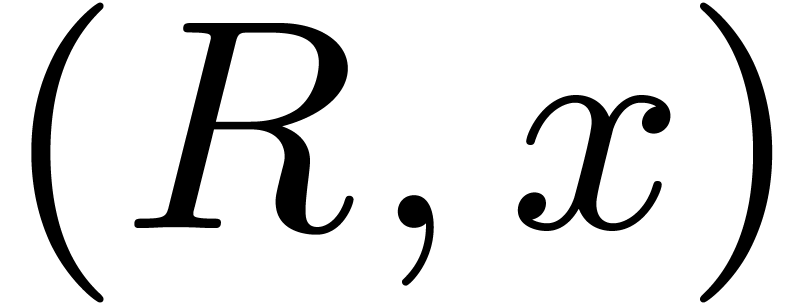 ,
,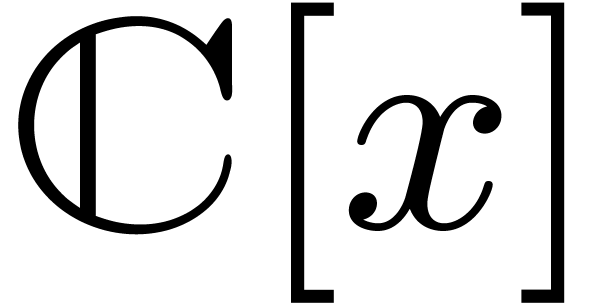 ,
, .
.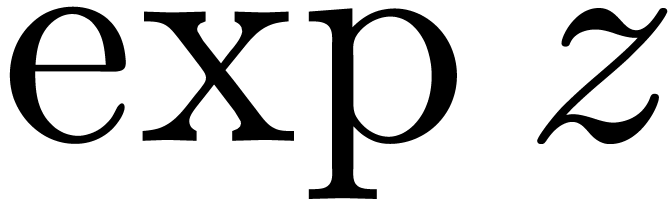 ,
,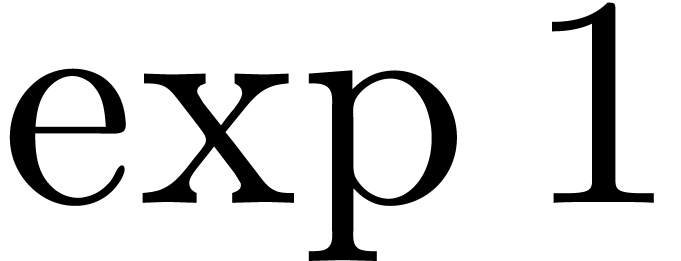 ,
,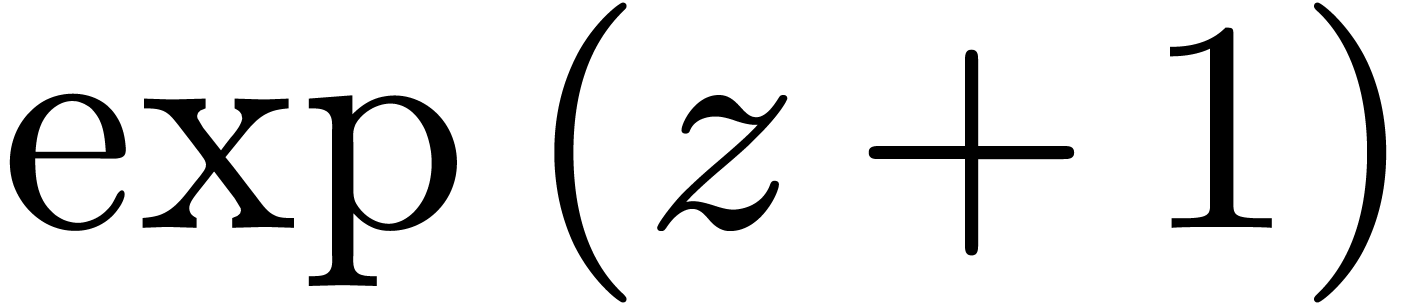 on the standard output mmout. Internal computations are
performed up to
on the standard output mmout. Internal computations are
performed up to  decimal digits. Analytic
functions are displayed as their underlying power series at the origin,
for which we set the output order to
decimal digits. Analytic
functions are displayed as their underlying power series at the origin,
for which we set the output order to 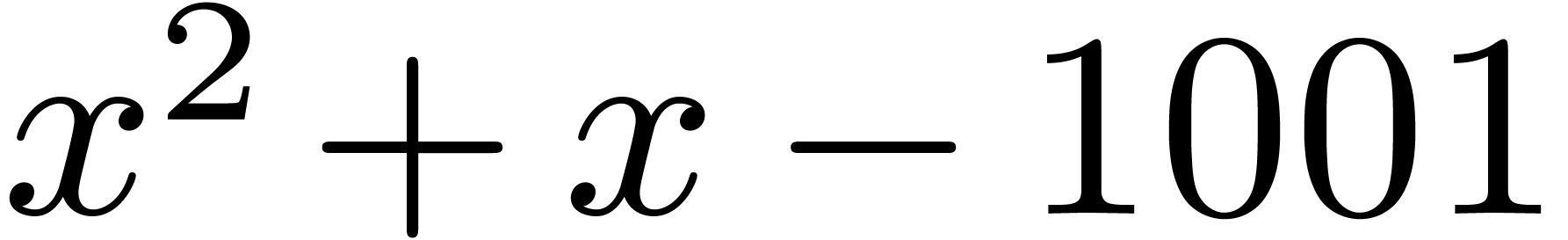 :
: