Overview of the Mathemagix type
system |
|
LIX, CNRS
École polytechnique
91128 Palaiseau Cedex
France
|
|
vdhoeven@lix.polytechnique.fr
|
|
http://lix.polytechnique.fr/~vdhoeven
|
|
|
Abstract
The goal of the Mathemagix project is to develop a
new and free software for computer algebra and computer analysis, based
on a strongly typed and compiled language. In this paper, we focus on
the underlying type system of this language, which allows for heavy
overloading, including parameterized overloading with parameters in so
called “categories”. The exposition is informal and aims at
giving the reader an overview of the main concepts, ideas and
differences with existing languages. In a forthcoming paper, we intend
to describe the formal semantics of the type system in more details.
Keywords
Mathemagix, type system, overloading, parametric polymorphism, language
design, computer algebra
1.Introduction
Motivation for a new language
Until the mid nineties, the development of computer algebra systems
tended to exploit advances in the area of programming languages, and
sometimes even influenced the design of new languages. The Formac
system [3] was developed shortly after the introduction of
Fortran. Symbolic algebra was an important branch
of the artificial intelligence project at Mit
during the sixties. During a while, the Macsyma
system [27, 23, 26] was the
largest program written in Lisp, and motivated the
development of better Lisp compilers.
The Scratchpad system [18, 12]
was at the origin of yet another interesting family of computer algebra
systems, especially after the introduction of domains and categories as
function values and dependent types in Scratchpad
II [20, 33, 19]. These
developments were at the forefront of language design and type theory
[9, 25, 24]. Scratchpad
later evolved into the Axiom system [1,
21]. In the A# project [36,
35], later renamed into Aldor, the
language and compiler were redesigned from scratch and further purified.
After this initial period, computer algebra systems have been less keen
on exploiting new ideas in language design. One important reason is that
a good language for computer algebra is more important for developers
than for end users. Indeed, typical end users tend to use computer
algebra systems as enhanced pocket calculators, and rarely write
programs of substantial complexity themselves. Another reason is
specific to the family of systems that grew out of Scratchpad:
after IBM's decision to no longer support the development, there has
been a long period of uncertainty for developers and users on how the
system would evolve. This has discouraged many of the programmers who
did care about the novel programming language concepts in these systems.
In our opinion, this has lead to an unpleasant current situation in
computer algebra: there is a dramatic lack of a modern, sound and fast
programming language. The major systems Mathematica
[37] and Maple [8] are
both interpreted, weakly typed (even the classical concept of a closure
has been introduced only recently in Maple!),
besides being proprietary and very expensive. The Sage
system [32] relies on Python and
merely contents itself to glue together various existing libraries and
other software components.
The absence of modern languages for computer algebra is even more
critical whenever performance is required. Nowadays, many important
computer algebra libraries (such as Gmp [10],
Mpfr [13], Flint
[14], FGb [7], etc.) are
directly written in C or C++. Performance issues are also important
whenever computer algebra is used in combination with numerical
algorithms. We would like to emphasize that high level ideas can be
important even for traditionally low level applications. For instance,
in a suitable high level language it should be easy to operate on
SIMD vectors of, say, 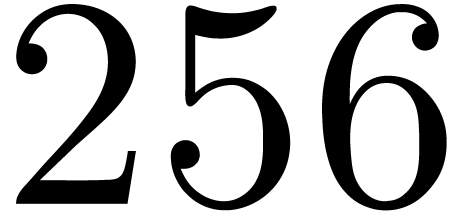 bit
floating point numbers. Unfortunately, Mpfr would
have to be completely redesigned in order to make such a thing possible.
bit
floating point numbers. Unfortunately, Mpfr would
have to be completely redesigned in order to make such a thing possible.
For these reasons, we have started the design of a new and free
software, Mathemagix [15, 16],
based on a compiled and strongly typed language, featuring signatures,
dependent types, and overloading. Although the design has greatly been
influenced by Scratchpad II and its successors
Axiom and Aldor, there are
several important differences, as we will see.
In this paper, we will focus on the underlying type system. We present
an informal overview of this system and highlight in which respect it
differs from existing systems. We plan to provide a more detailed formal
description of the type system in a future paper.
Main philosophy behind the type system
The central idea behind the design of the Mathemagix
language is that the declaration of a function is analogous to the
statement of a mathematical theorem, whereas the implementation of the
function is analogous to giving a proof. Of course, this idea is also
central in the area of automated proof assistants, such as Coq
[5, 4] or Isabelle/Hol
[28]. However, Mathemagix only
insists on very detailed declarations, whereas the actual
implementations do need not to be formally proven.
One consequence of this design philosophy is that program interfaces
admit very detailed specifications: although the actual implementations
are not formally proven, the combination of various components is sound
as long as each of the components fulfills its specification. By
contrast, Maple, Mathematica
or Sage functions can only be specified in quite
vague manners, thereby introducing a big risk of errors when combining
several libraries.
Another consequence of the Mathemagix design is
that it allows for massively overloaded notations. This point is crucial
for computer algebra and also the main reason why mainstream strongly
typed functional programming languages, such as Haskell
[29, 17] or OCaml [22], are not fully suitable for our applications. To go short,
we insist on very detailed and unambiguous function declarations, but
provide a lot of flexibility at the level of function applications. On
the contrary, languages such as Ocaml require
unambiguous function applications, but excel at assigning types to
function declarations in which no types are specified for the arguments.
The Mathemagix type system also allows for a very
flat design of large libraries: every function comes with the hypotheses
under which it is correct, and can almost be regarded as a module on its
own. This is a major difference with respect to Axiom
and Aldor, where functionality is usually part of
a class or a module. In such more hierarchical systems, it is not always
clear where to put a given function. For instance, should a converter
between lists and vectors be part of the list or the vector class?
Overview of this paper
In order to make the above discussion about the main design philosophy
more concrete, we will consider the very simple example of computing the
square of an element  in a monoid. In section 2, we will show how such a function would typically be written
in various existing languages, and compare with what we would do in
Mathemagix.
in a monoid. In section 2, we will show how such a function would typically be written
in various existing languages, and compare with what we would do in
Mathemagix.
In section 3, we will continue with a more complete
description of the primitives of the type system which have currently
been implemented in the compiler. We will also discuss various
difficulties that we have encountered and some plans for extensions.
As stated before, we have chosen to remain quite informal in this paper.
Nevertheless, in section 4, we will outline the formal
semantics of the type system. The main difficulty is to carefully
explain what are the possible meanings of expressions based on heavily
overloaded notations, and to design a compiler which can determine these
meanings automatically.
Given the declarative power of the language, it should be noticed that
the compiler will not always be able to find all possible meanings of a
program. However, this is not necessarily a problem as long as the
compiler never assigns a wrong meaning to an expression. Indeed, given
an expression whose meanings are particularly hard to detect, it is not
absurd to raise an error, or even to loop forever. Indeed, in such
cases, it will always be possible to make the expression easier to
understand by adding some explicit casts. Fortunately, most natural
mathematical notations also have a semantics which is usually easy to
determine: otherwise, mathematicians would have a hard job to understand
each other at the first place!
2.Comparison on an example
We will consider a very simple example in order to illustrate the most
essential differences between Mathemagix and
various existing programming languages: the computation of the square of
an element  of a monoid. Here we recall that a
monoid is simply a set
of a monoid. Here we recall that a
monoid is simply a set  together with an
associative multiplication
together with an
associative multiplication  .
.
2.1Mathemagix
In Mathemagix, we would start by a formal
declaration of the concept of a monoid. As in the case of Aldor,
this is done by introducing the monoid category:
category Monoid == {
infix *: (This, This) -> This;
} |
We may now define the square of an element  of a
monoid by
of a
monoid by
forall (M: Monoid)
square (x: M): M == x * x; |
Given an instance x of any type T with a
multiplication infix *: (T, T) -> T, we may then
compute the square of x using square x.
In our definition of a monoid, we notice that we did not
specify the multiplication to be associative. Nothing withholds the user
from replacing the definition by
category Monoid == {
infix *: (This, This) -> This;
associative: This -> Void;
} |
This allows the user to indicate that the multiplication on a
type T is associative, by implementing the
“dummy” function associative for T.
At this point, the type system provides no means for specifying the
mathematical semantics of associativity: if we would like to take
advantage out of this kind of semantics, then we should also be able to
automatically prove associativity during type conversions. This
is really an issue for automatic theorem provers which is beyond the
current design goals of Mathemagix. Notice
nevertheless that it would be quite natural to extend the language in
this direction in the further future.
2.2Aldor
As stated in the introduction, a lot of the inspiration for Mathemagix comes from the Aldor
system and its predecessors. In Aldor, the
category Monoid would be defined using
define Monoid: Category == with {
*: (%, %) -> %;
} |
However, the forall primitive inside Mathemagix
for the definition of templates does not have an analogue inside Aldor. In Aldor, one would rather
define a parameterized class which exports the template. For instance:
Squarer (M: Monoid): with {
square: M -> M;
} == add {
square (x: M): M == x * x;
} |
In order to use the template for a particular class, say Integer,
one has to explicitly import the instantiation of the template for that
particular class:
import from Squarer (Integer); |
The necessity to encapsulate templates inside classes makes the class
hierarchy in Aldor rather rigid. It also forces
the user to think more than necessary about where to put various
functions and templates. This is in particular the case for routines
which involve various types in a natural way. For instance, where should
we put a converter from vectors to lists? Together with other routines
on vectors? With other routines on lists? Or in an entirely separate
module?
2.3C++
The C++ language [34] does provide support for the
definition of templates:
template<typename M>
square (const M& x) {
return x * x;
} |
However, as we see on this example, the current language does not
provide a means for requiring M to be a monoid. Several
C++ extensions with “signatures” [2] or
“concepts” [30] have been proposed in order to
add such requirements. C++ also imposes a lot of
restrictions on how templates can be used. Most importantly, the
template arguments should be known statically, at compile time. Also,
instances of user defined types cannot be used as template arguments.
In the above piece of code, we also notice that the argument x
is of type const M& instead of M.
This kind of interference of low level details with the type system is
at the source of many problems when writing large computer algebras
libraries in C++. Although Mathemagix
also gives access to various low level details, we decided to follow a
quite different strategy in order to achieve this goal. However, these
considerations fall outside the main scope of this paper.
2.4Ocaml
Mainstream strongly typed functional programming languages, such as
Ocaml and Haskell, do not
provide direct support for operator overloading. Let us first examine
the consequences of this point of our view in the case of Ocaml.
First of all, multiplication does not carry the same name for different
numeric types. For instance:
# let square x = x * x;;
val square: int -> int = <fun>
# let float_square x = x *. x;;
val float_square: float -> float = <fun> |
At any rate, this means that we somehow have to specify the monoid in
which we want to take a square when applying the square function of our
example. Nevertheless, modulo acceptance of this additional
disambiguation constraint, it is possible to define the analogue of the
Monoid category and the routine square:
# module type Monoid =
sig
type t
val mul : t -> t -> t
end;;
# module Squarer =
functor (El: Monoid) ->
struct
let square x = El.mul x x
end;; |
As in the case of Aldor, we need to encapsulate
the square function in a special module Squarer.
Moreover, additional efforts are required in order to instantiate this
module for a specific type, such as int:
# module int_Monoid =
struct
type t = int
let mul x y = x * y
end;;
# module int_Squarer = Squarer (int_Monoid);;
# int_Squarer.square 11111;;
- : int = 123454321 |
2.5Haskell
Haskell is similar in spirit to Ocaml,
but Haskell type classes allow for a more compact
formulation. The square function would be defined as follows:
class Monoid a where
(*) :: a -> a -> a
square x = x * x |
In order to enable the square function for a particular type, one has to
create an instance of the monoid for this particular type. For instance,
we may endow String with the structure of a monoid by
using concatenation as our multiplication:
instance Monoid [Char] a where
x * y :: x ++ y |
After this instantiation, we may square the string "hello"
using square "hello". In order to run this
example in practice, we notice that there are a few minor problems: the
operator * is already reserved for standard
multiplication of numbers, and one has to use the -XFlexibleInstances
option in order to allow for the instantiation of the string type.
The nice thing of the above mechanism is that we may instantiate other
types as monoids as well and share the name * of the
multiplication operator among all these instantiations. Haskell
style polymorphism thereby comes very close to operator overloading.
However, there are some important differences. First of all, it is not
allowed to use the same name * inside another type
class, such as Ring, except when the other type class is
explicitly derived from Monoid. Secondly, the user still
has to explicitly instantiate the type classes for specific types: in
Mathemagix, the type String can
automatically be regarded as a Monoid as soon as the
operator * is defined on strings.
2.6Coq
Although the automated proof assistant Coq is not
really a programming language, it implements an interesting facility for
implicit conversions [31]. This facility is not present in
Ocaml, on which Coq is
based. Besides elementary implicit conversions, such as the inclusion of
 in
in  ,
it is also possible to define parametric implicit conversions, such as
the inclusion of
,
it is also possible to define parametric implicit conversions, such as
the inclusion of  in
in  . Moreover, implicit conversions can be composed
into chains of implicit conversions.
. Moreover, implicit conversions can be composed
into chains of implicit conversions.
One major problem with implicit conversions is that they quickly tend to
become ambiguous (and this explains why they were entirely removed from
Aldor and Mathemagix; see
section 3.6 below). For example, the implicit conversion
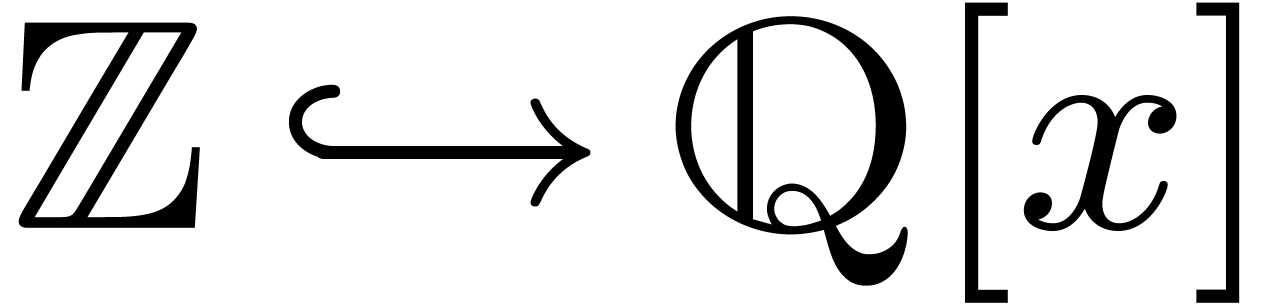 may typically be achieved in two different ways
as the succession of two implicit conversions; namely, as
may typically be achieved in two different ways
as the succession of two implicit conversions; namely, as 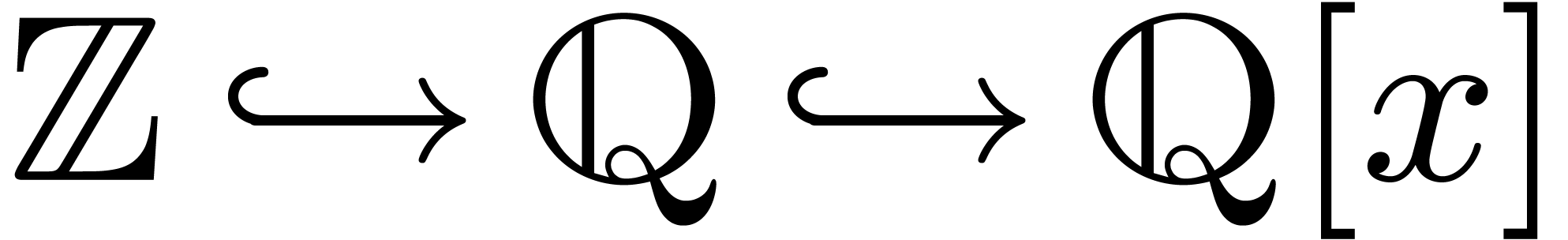 or as
or as 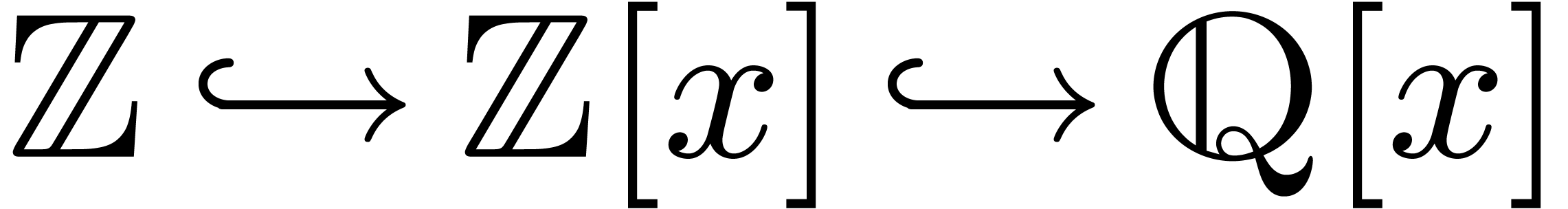 .
.
In Coq, such ambiguities are resolved by
privileging the implicit conversions which are declared first. It is
interesting to notice that this makes sense in an automated proof
assistant: the correctness of the final proof does not really
depend on the way how we performed implicit conversions. However, such
ambiguities are more problematic for general purpose programming
languages: the conversion 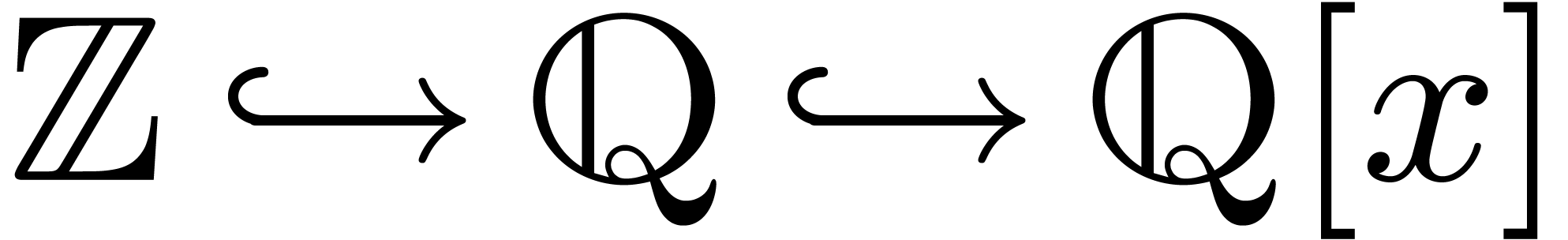 is usually more
efficient than
is usually more
efficient than 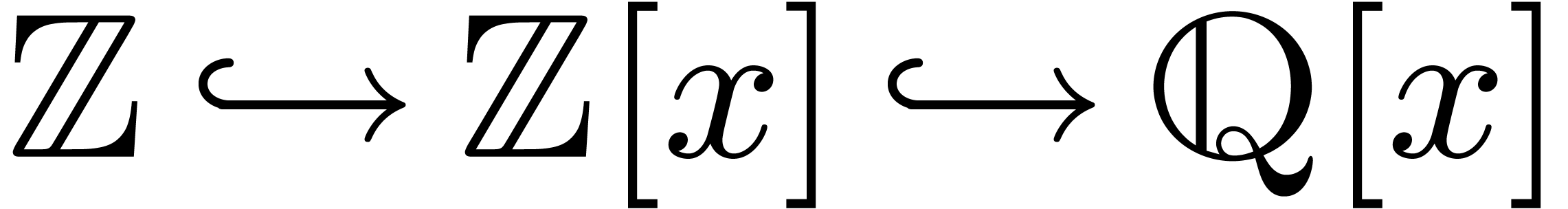 , so
we really want to enforce the most efficient solution. Currently, Coq does not provide genuine support for overloading. If
such support existed, then a similar discussion would probably apply.
, so
we really want to enforce the most efficient solution. Currently, Coq does not provide genuine support for overloading. If
such support existed, then a similar discussion would probably apply.
2.7Discussion
Essentially, the difference between Mathemagix and
classical strongly typed functional languages such as Ocaml
and Haskell is explained by the following
observation: if we want to be able to declare the square function simply
by writing
and without specifying the type of x, then the
symbol * should not be too heavily overloaded in order
to allow the type system to determine the type of square.
In other words, no sound strongly typed system can be designed which
allows both for highly ambiguous function declarations and
highly ambiguous function applications.
Whether the user prefers a type system which allows for more freedom at
the level of function declarations or function applications is a matter
of personal taste. We may regard Ocaml and Haskell as prominent members of the family of strongly
typed languages which accomodate a large amount of flexibility at the
declaration side. But if we are rather looking for high expressiveness
at the function application side, and insist on the possibility to
heavily overload notations, then we hope that the Mathemagix
type system will be a convenient choice.
We finally notice that signatures are now implemented under various
names in a variety of languages. For instance, in Java,
one may use the concept of an interface. Nevertheless, to the best of
our knowledge, the current section describes the main lines along which
signatures are conceived in current languages.
3.Overview of the language
3.1Ordinary variables and functions
There are three main kinds of objects inside the Mathemagix
type system: ordinary variables (including functions), classes and
categories. Ordinary variables are defined using the following syntax:
test?: Boolean == pred? x; // constant
flag?: Boolean := false; // mutable |
In this example, test? is a constant, whereas flag?
is a mutable variable which can be given new values using the assignment
operator :=. The actual type of the mutable variable flag? is Alias Boolean. Functions can be
declared using a similar syntax:
foo (x: Int): Int == x * x; |
Mathemagix is a fully functional language, so that
functions can both be used as arguments and as return values:
shift (x: Int) (y: Int): Int == x + y;
iterate (foo: Int -> Int, n: Int)
(x: Int): Int ==
if n = 0 then x
else iterate (foo, n-1) (foo x); |
The return type and the types of part of the function arguments are
allowed to depend on the arguments themselves. For instance:
square (x: M, M: Monoid): M == x * x; |
Mathemagix does not allow for mutually dependent
arguments, but dependent arguments can be specified in an arbitrary
order.
3.2Classes
New classes are defined using the class primitive, as in
the following example:
class Point == {
mutable {
x: Double;
y: Double;
}
constructor point (x2: Int, y2: Int) == {
x == x2;
y == y2;
}
} |
We usually use similar names for constructors as for the class itself,
but the user is free to pick other names. The mutable
keyword specifies that we have both read and read-write accessors postfix .x and postfix .y for the fields x and y. Contrary to C++, new accessors can
be defined outside the class itself:
postfix .length (p: Point): Double ==
sqrt (p.x * p.x + p.y * p.y); |
As in the case of functions, classes are allowed to depend on
parameters, which may be either type parameters or ordinary values.
Again, there may be dependencies among the parameters. One simple
example of a class definition with parameters is:
class Num_Vec (n: Int) == {
mutable v: Vector Double;
constructor num_vec (c: Double) == {
v == [ c | i: Int in 0..n ];
}
} |
3.3Categories
Categories are the central concept for achieving genericity. We have
already seen an example of the definition of a category in section 2.1. Again, categories may take parameters, with possible
dependencies among them. For instance:
category Module (R: Ring) == {
This: Abelian_Group;
infix *: (R, This) -> This;
} |
As in Ocaml or Haskell, the
This type can occur in the category fields in many ways.
In the above example, the line This: Abelian_Group means
that Module R in particular includes all fields of Abelian_Group. More generally, This can be
part of function argument types, of return types, or part of the
declaration of an ordinary variable. For instance, the category To T below formalizes the concept of a type with an implicit
converter to T.
category Type {}
category To (T: Type) == {
convert: This -> T;
} |
Given an ordinary type T, we write x: T
if x is an instance of T. In the case of
a category Cat, we write  if a
type T satisfies the category, that is, if all
category fields are defined in the current context, when replacing This by T. Contrary to Ocaml
or Haskell, it follows that Mathemagix
is very name sensitive: if we want a type T to be a
monoid, then we need a multiplication on T with the
exact name infix *. Of course, wrappers can easily be
defined if we want different names, but one of the design goals of
Mathemagix is that it should be particularly easy
to consistently use standard names.
if a
type T satisfies the category, that is, if all
category fields are defined in the current context, when replacing This by T. Contrary to Ocaml
or Haskell, it follows that Mathemagix
is very name sensitive: if we want a type T to be a
monoid, then we need a multiplication on T with the
exact name infix *. Of course, wrappers can easily be
defined if we want different names, but one of the design goals of
Mathemagix is that it should be particularly easy
to consistently use standard names.
3.4Discrete overloading
The main strength of the Mathemagix type system is
that it allows for heavy though fully type safe overloading. Similarly
as in C++ or Aldor, discrete
overloading of a symbol is achieved by declaring it several times with
different types:
infix * (c: Double, p: Point): Point ==
point (c * p.x, c * p.y);
infix * (p: Point, c: Double): Point ==
point (p.x * c, p.y * c); |
Contrary to C++, non function variables and return
values of functions can also be overloaded:
bar: Int == 11111;
bar: String == "Hello";
mmout << bar * bar << lf;
mmout << bar >< " John!" << lf; |
Internally, the Mathemagix type system associates
a special intersection type And (Int, String)
to the overloaded variable bar. During function
applications, Mathemagix consistently takes into
account all possible meanings of the arguments and returns a possibly
overloaded value which corresponds to all possible meanings of the
function application. For instance, consider the overloaded function
foo (x: Int): Int == x + x;
foo (s: String): String == reverse s; |
Then the expression foo bar will be assigned the type
And (Int, String). An example of a truly ambiguous
expression would be bar = bar, since it is unclear
whether we want to compare the integers 11111 or the
strings "Hello". True ambiguities will provoke
compile time errors.
3.5Parametric overloading
The second kind of parametric overloading relies on the forall
keyword. The syntax is similar to template declarations in C++,
with the difference that all template parameters should be rigourously
typed:
forall (M: Monoid)
fourth_power (x: M): M == x * x * x * x; |
Internally, the Mathemagix type system associates
a special universally quantified type Forall (M:
Monoid, M -> M) to the overloaded function fourth_power.
In a similar way, values themselves can be parametrically overloaded.
The main challenge for the Mathemagix type system
is to compute consistently with intersection types and universally
quantified types. For instance, we may define the notation [
1, 2, 3 ] for vectors using
forall (T: Type)
operator [] (t: Tuple T): Vector T == vector t; |
This notation in particular defines the empty vector []
which admits the universally quantified type Forall (T: Type,
Vector T). In particular, and contrary to what would have been the
case in C++, it is not necessary to make the type
of [] explicit as soon as we perform the template
instantiation. Thus, writing
v: Vector Int == [];
w: Vector Int == [] >< []; // concatenation |
would typically be all right. On the other hand, the expression #[] (size of the empty vector) is an example of a genuine
and parametric ambiguity.
In comparison with C++, it should be noticed in
addition that parametric overloading is fully dynamic and that there are
no restrictions on the use of ordinary variables as template parameters.
Again, there may be dependencies between template arguments. Mathemagix also implements the mechanism of partial
specialization. For instance, if we have a fast routine square
for double precision numbers, then we may define
fourth_power (x: Double): Double ==
square square x; |
Contrary to C++, partial specialization of a
function takes into account both the argument types and the
return type. This make it more natural to use the partial specialization
mechanism for functions for which not all template parameters occur in
the argument types:
forall (R: Number_Type) pi (): R == …;
pi (): Double == …; |
3.6Implicit conversions
One major difference between Aldor and Axiom is that Aldor does
not contain any mechanism for implicit conversions. Indeed, in
Axiom, the mechanism of implicit conversions [33] partially depends on heuristics, which makes its behaviour
quite unpredictable in non trivial situations. We have done a lot of
experimentation with the introduction of implicit conversions in the
Mathemagix type system, and decided to ban them
from the core language. Indeed, systematic implicit conversions
introduce too many kinds of ambiguities, which are sometimes of a very
subtle nature.
Nevertheless, the parametric overloading facility makes it easy to
emulate implicit conversions, with the additional benefit that
it can be made precise when exactly implicit conversions are permitted.
Indeed, we have already introduced the To T category,
defined by
category To (T: Type) == {
convert: This -> T;
} |
Here convert is the standard operator for type
conversions in Mathemagix. Using this category, we
may define scalar multiplication for vectors by
forall (M: Monoid, C: To M)
infix * (c: C, v: Vector M): Vector M ==
[ (c :> M) * x | x: M in v ]; |
Here c :> M stands for the application of convert
to c and retaining only the results of type M
(recall that c might have several meanings due to
overloading). This kind of emulated “implicit” conversions
are so common that Mathemagix defines a special
notation for them:
forall (M: Monoid)
infix * (c :> M, v: Vector M): Vector M ==
[ c * x | x: M in v ]; |
In particular, this mechanism can be used in order to define converters
with various kinds of transitivity:
convert (x :> Integer): Rational == x / 1;
convert (cp: Colored_Point) :> Point == cp.p; |
The first example is also called an upgrader and provides a
simple way for the construction of instances of more complex types from
instances of simpler types. The second example is called a
downgrader and can be used in order to customize type
inheritance, in a way which is unrelated to the actual representation
types in memory.
The elimination of genuine implicit converters also allows for several
optimizations in the compiler. Indeed, certain operations such as
multiplication can be overloaded hundreds of times in non trivial
applications. In the above example of scalar multiplication, the Mathemagix compiler takes advantage of the fact that at
least one of the two arguments must really be a vector. This is done
using a special table lookup mechanism for retaining only those few
overloaded values which really have a chance of succeeding when applying
a function to concrete arguments.
3.7Syntactic sugar
Functions with several arguments use a classical tuple notation. It
would have been possible to follow the Ocaml and
Haskell conventions, which rely on currying, and
rather regard a binary function 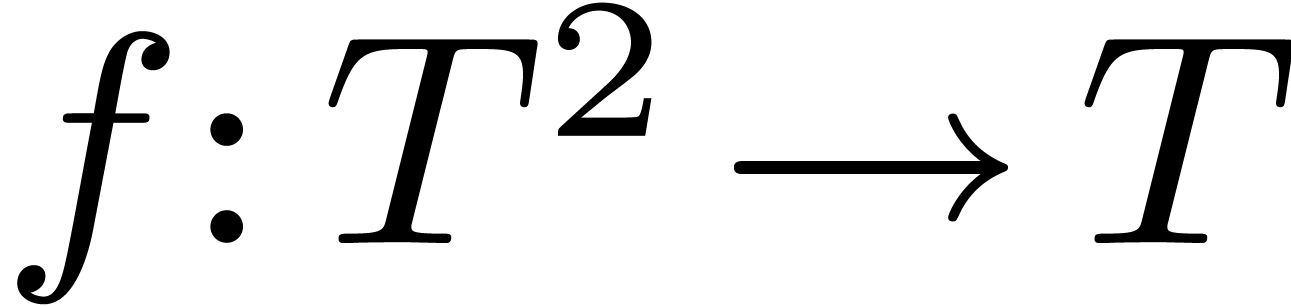 as a function of
type
as a function of
type 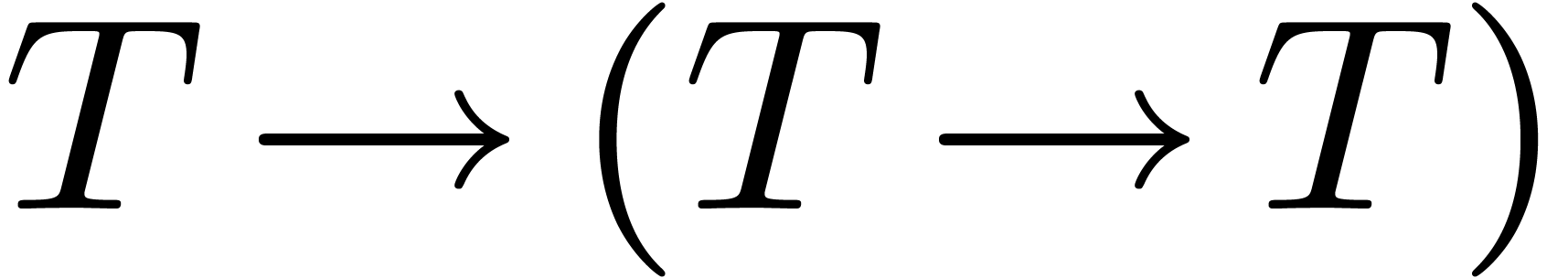 . Although this
convention is more systematic and eases the implementation of a
compiler, it is also non standard in mainstream mathematics; in Mathemagix, we have chosen to keep syntax as close as
possible to classical mathematics. Furthermore, currying may be a source
of ambiguities in combination with overloading. For instance, the
expression - 1 might be interpreted as the unary
negation applied to
. Although this
convention is more systematic and eases the implementation of a
compiler, it is also non standard in mainstream mathematics; in Mathemagix, we have chosen to keep syntax as close as
possible to classical mathematics. Furthermore, currying may be a source
of ambiguities in combination with overloading. For instance, the
expression - 1 might be interpreted as the unary
negation applied to 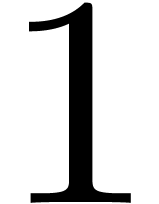 , or as
the operator
, or as
the operator  .
.
In order to accomodate for functions with an arbitrary number of
arguments and lazy streams of arguments, Mathemagix
uses a limited amount of syntactic sugar. Given a type T,
the type Tuple T stands for an arbitrary tuple of
arguments of type T, and Generator T
stands for a lazy stream of arguments of type T. For
instance, (1, 2) would be a typical tuple of type Tuple Int and 0..10 a typical generator of
type Generator Int. For instance, the prototype of a
function which evaluates a multivariate polynomial at a tuple of points
might be
forall (R: Ring)
eval (P: MVPol R, p: Tuple R): R == …; |
The syntactic sugar takes care of the necessary conversions between
tuples and generators. For instance, given a polynomial P:
MVPol Int, the following would be valid evaluations:
eval (P, 1, 2..8, (9, 10), 11..20);
eval (P, (i^2 | i: Int in 0..100)); |
Notice that the notation of function application (or evaluation) can be
overloaded itself:
postfix .() (fs: Vector (Int -> Int),
x: Int): Vector Int ==
[ f x | f: Int -> Int in fs ]; |
3.8Future extensions
There are various natural and planned extensions of the current type
system.
One of the most annoying problems that we are currently working on
concerns literal integers: the expression 1 can
naturally be interpreted as a machine Int or as a long
Integer. Consequently, it is natural to consider 1 to be of type And (Int, Integer). For
efficiency reasons, it is also natural to implement each of the
following operations:
infix =: (Int, Int) -> Boolean;
infix =: (Integer, Integer) -> Boolean;
infix =: (Int, Integer) -> Boolean;
infix =: (Integer, Int) -> Boolean; |
This makes an expression such as 1 = 1 highly ambiguous.
Our current solution permits the user to prefer certain operations or
types over others. For instance, we would typically prefer the type Integer over Int, since Int
arithmetic might overflow. However, we still might prefer infix
=: (Int, Int) -> Boolean over infix =: (Int, Integer)
-> Boolean. Indeed, given i: Int, we would like
the test i = 0 to be executed fast.
One rather straightforward extension of the type system is to consider
other “logical types”. Logical implication is already
implemented using the assume primitive:
forall (R: Ring) {
…
assume (R: Ordered)
sign (P: Polynomial R): Int ==
if P = 0 then 0 else sign P[deg P];
…
} |
The implementation of existentially quantified types will allow
us to write routines such as
forall (K: Field)
exists (L: Algebraic_Extension K)
roots (p: Polynomial K): Vector L == …; |
Similarly, we plan the implementation of union types and abstract data
types, together with various pattern matching utilities similar to those
found in Ocaml and Haskell.
We also plan to extend the syntactic sugar. For instance, given two
aliases i, j: Alias Int, we would like to be able to
write (i, j) := (j, i) or (i, j) += (1,
1). A macro facility should also be included, comparable to the one
that can be found in Scheme. Some further
syntactic features might be added for specific areas. For instance, in
the Macaulay2 system [11, 6],
one may use the declaration
for the simultaneous introduction of the polynomial ring 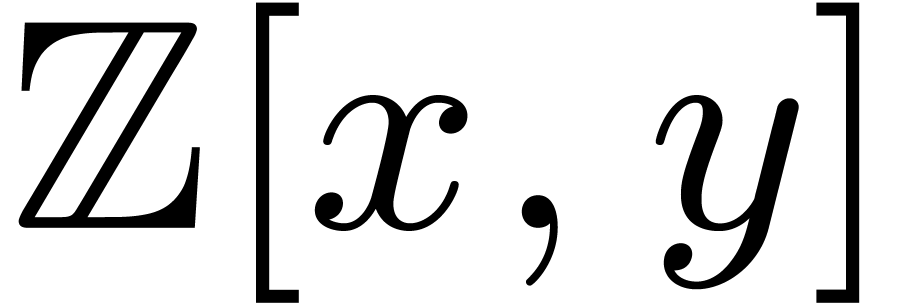 and the two coordinate functions
and the two coordinate functions 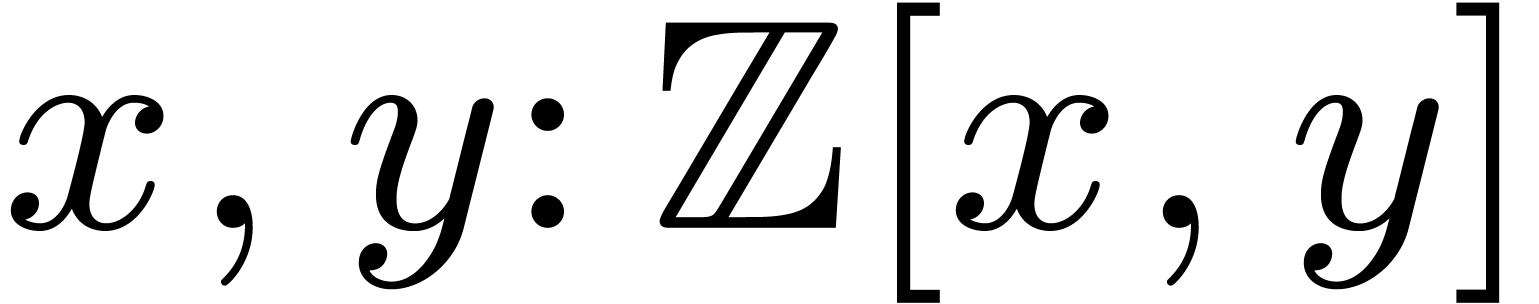 .
.
In the longer future, we would like to be able to formally describe
mathematical properties of categories and algorithms, and provide
suitable language constructs for supplying partial or complete
correctness proofs.
4.Semantics and compilation
4.1Source language
In order to specify the semantics of the Mathemagix
language, it is useful to forget about all syntactic sugar and
schematize the language by remaining as close as possible to more
conventional typed  -calculus.
Source programs can be represented in a suitable variant of typed
-calculus.
Source programs can be represented in a suitable variant of typed  -calculus, extended with special
notations for categories and overloading.
-calculus, extended with special
notations for categories and overloading.
We will use a few notational conventions. For the sake of brevity, we
will now use superscripts for specifying types. For instance, 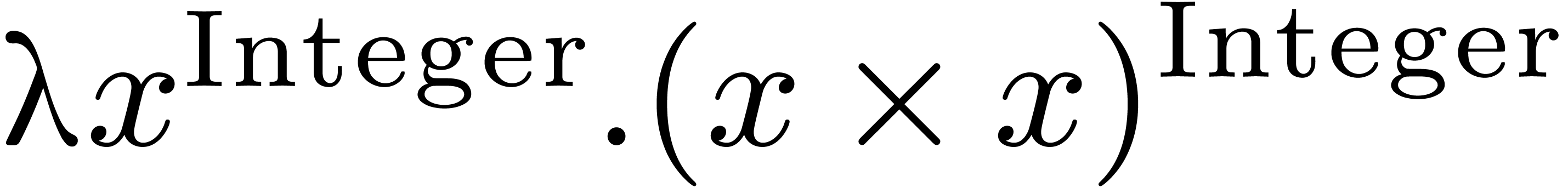 denotes the function
denotes the function  .
.
For the sake of readability, we will also denote types  ,
,  ,
etc. using capitalized identifiers and categories
,
etc. using capitalized identifiers and categories  ,
, 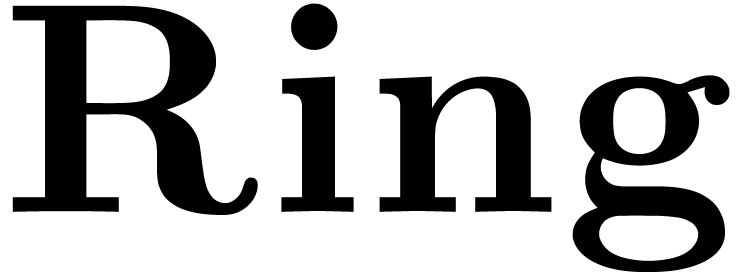 ,
etc. using bold capitalized identifiers. Similarly, we will
use the terms “type expressions” and “category
expressions” whenever an expression should be considered as a type
or category. Notice however that this terminology is not formally
enforced by the language itself.
,
etc. using bold capitalized identifiers. Similarly, we will
use the terms “type expressions” and “category
expressions” whenever an expression should be considered as a type
or category. Notice however that this terminology is not formally
enforced by the language itself.
The source language contains three main components:
Typed lambda expressions.
The first component consists of ordinary typed
 -expressions,
-expressions, and notations for their types:
-
Given expressions 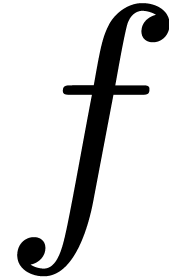 and
and  , we denote function application by
, we denote function application by 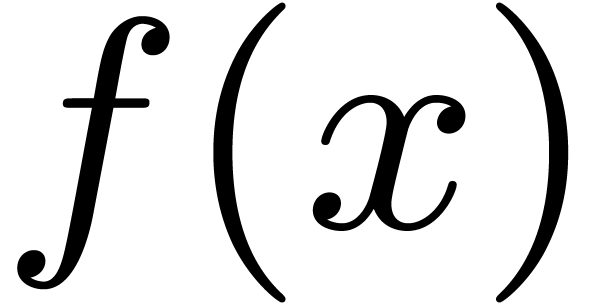 ,
, 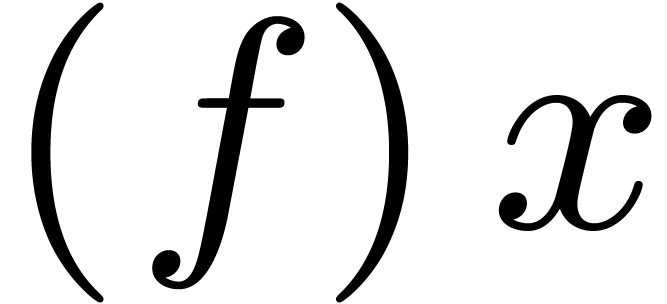 ,
or
,
or 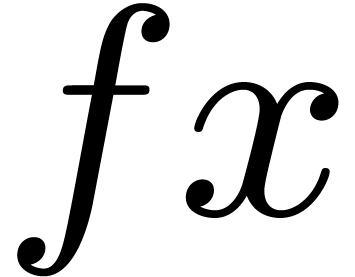 .
.
-
Given a variable  , an
expression
, an
expression  and type expressions
and type expressions  and
and  , we
denote by
, we
denote by 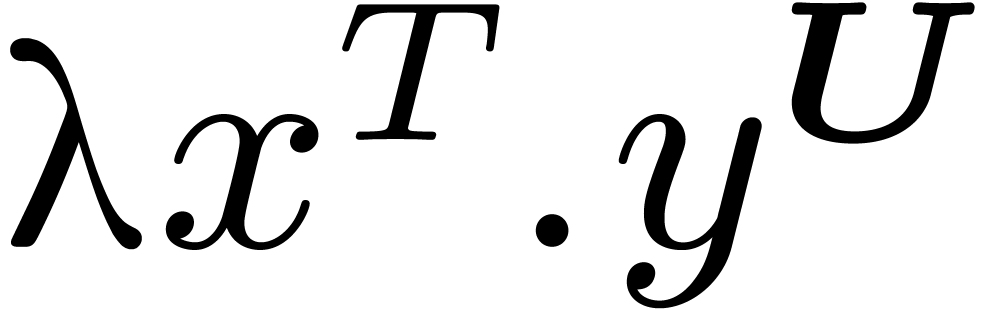 the lambda expression which sends
the lambda expression which sends
 of type
of type  to
to  of type
of type  .
.
-
We will denote by  the type of the above
the type of the above
 -expression. In the case
when
-expression. In the case
when  depends on
depends on  , we will rather write
, we will rather write 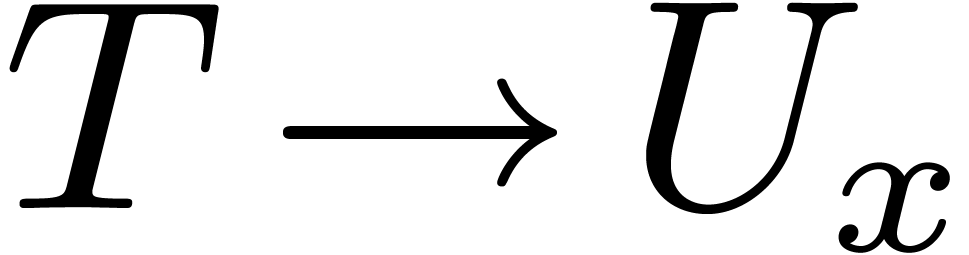 for this type.
for this type.
Hence, all lambda expressions are typed and there are no syntactic
constraints on the types  and
and  . However, “badly typed”
expressions such as
. However, “badly typed”
expressions such as 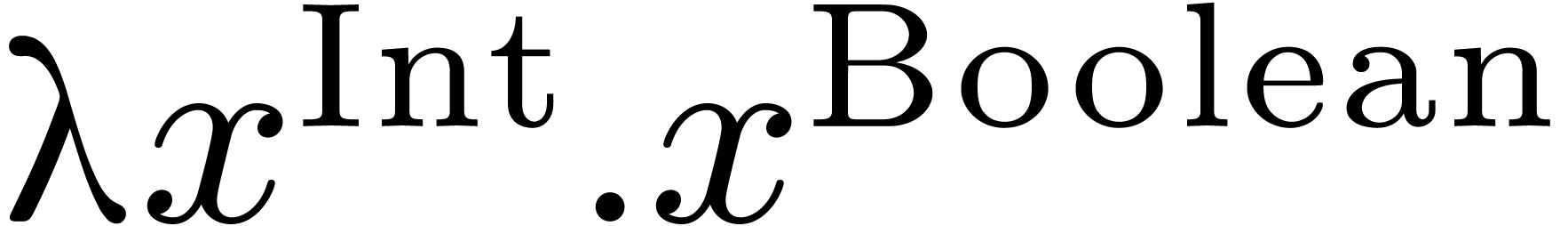 will have no correct
interpretation in the section below.
will have no correct
interpretation in the section below.
Declarations.
The second part of the language concerns declarations of recursive
functions, classes and categories.
-
Given variables  , type
expressions
, type
expressions  and expressions
and expressions  , we may form the expression
, we may form the expression 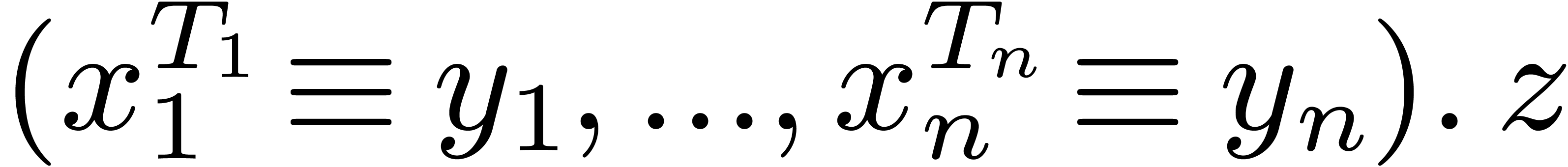 . The informal meaning is: the expression
. The informal meaning is: the expression
 , with mutually recursive
bindings
, with mutually recursive
bindings  .
.
-
Given variables  and type expressions
and type expressions  , we may form the data type
, we may form the data type
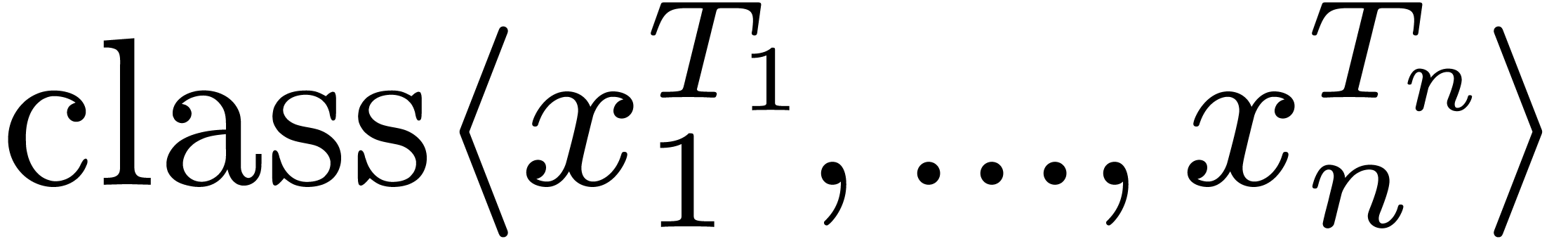 . For instance, a list of
integers might be declared using
. For instance, a list of
integers might be declared using  .
We also introduce a special variable
.
We also introduce a special variable  which
will be the type of
which
will be the type of 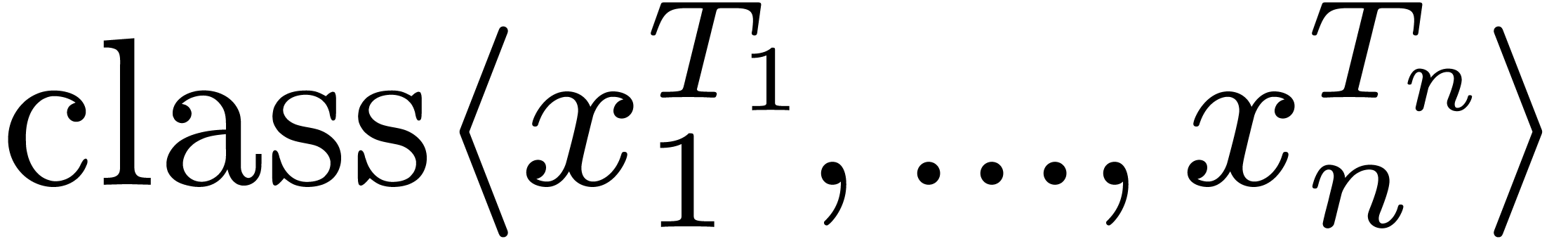 .
.
-
Given variables  and type expressions
and type expressions 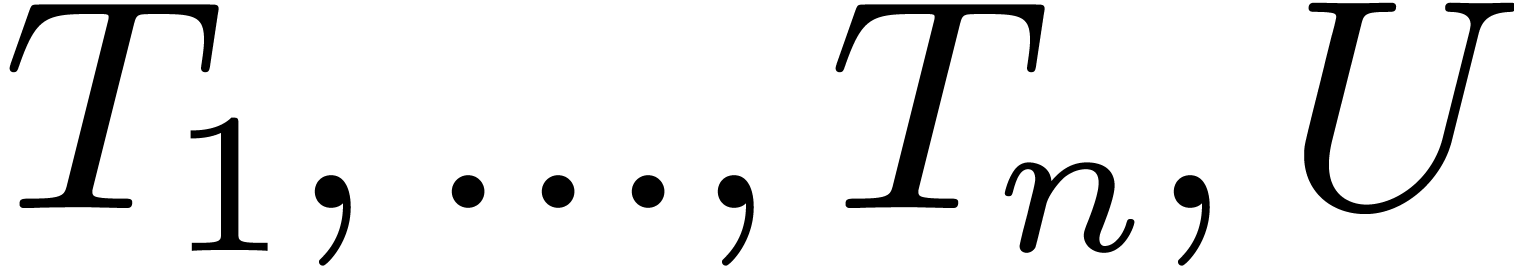 , we may form the category
, we may form the category
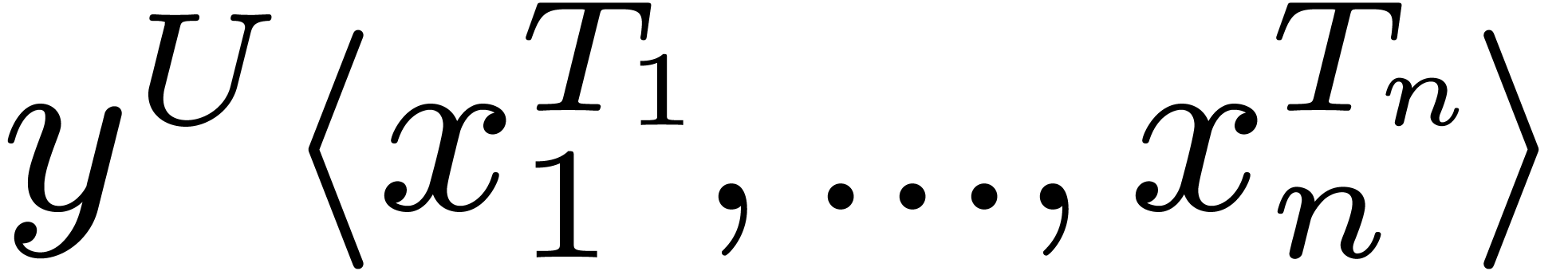 . For instance, we might
introduce the
. For instance, we might
introduce the  category using
category using 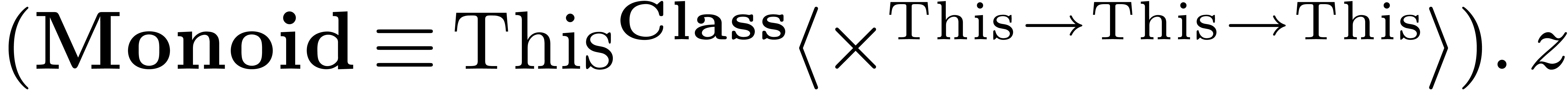 .
.
Overloaded expressions.
The last part of the language includes explicit constructs for
overloaded expressions and their types:
-
Given two expressions  and
and  , we may form the overloaded expression
, we may form the overloaded expression
 .
.
-
Given type expressions  and
and  , we may form the intersection type
, we may form the intersection type  .
.
-
Given a variable  , a type
expression
, a type
expression  and an expression
and an expression  , we may form the parametrically overloaded
expression
, we may form the parametrically overloaded
expression 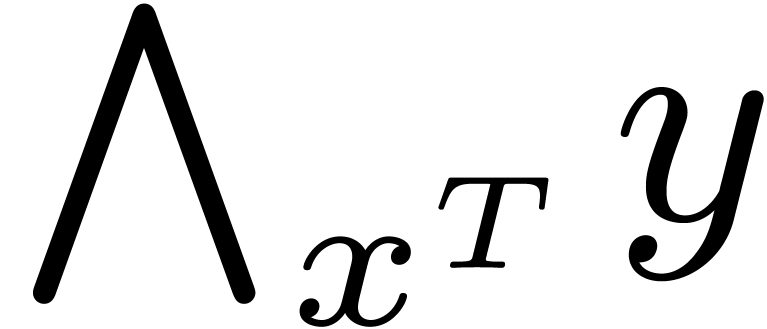 .
.
-
Given a variable  , a type
expression
, a type
expression  and a type expression
and a type expression  , we may form the universally
quantified type expression
, we may form the universally
quantified type expression 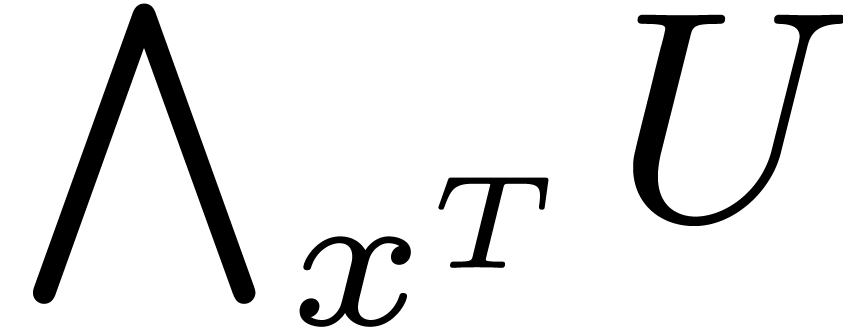 .
.
In the last two cases, the variable  is often
(but not necessarily) a type variable
is often
(but not necessarily) a type variable  and its
type
and its
type  a category
a category  .
.
4.2Target language
The source language allows us to define an overloaded function such as
In a context where 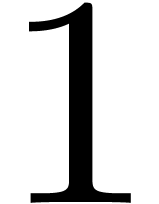 is of type
is of type 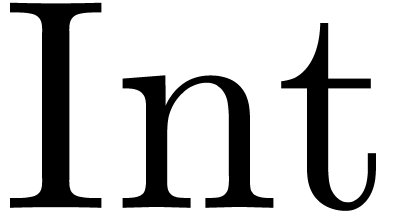 , it is the job of the compiler to recognize
that
, it is the job of the compiler to recognize
that 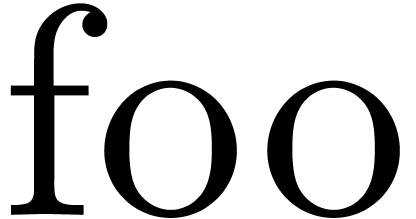 should be interpreted as a function of type
should be interpreted as a function of type
 in the expression
in the expression 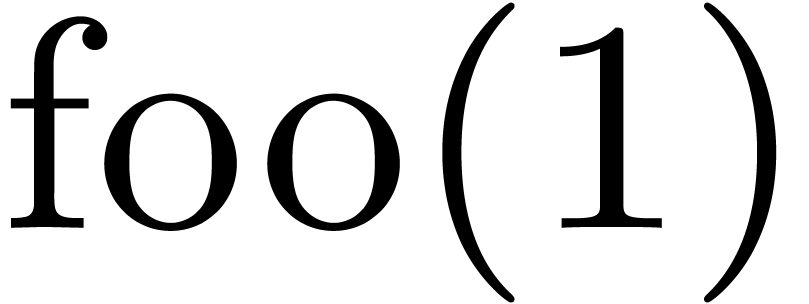 .
.
In order to do so, we first extend the source language with a few
additional constructs in order to disambiguate overloaded expressions.
The extended language will be called the target language. In a
given context  , we next
specify when a source expression
, we next
specify when a source expression  can be
interpreted as a non ambiguous expression
can be
interpreted as a non ambiguous expression 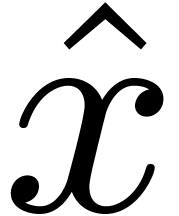 in the
target language. In that case, we will write
in the
target language. In that case, we will write 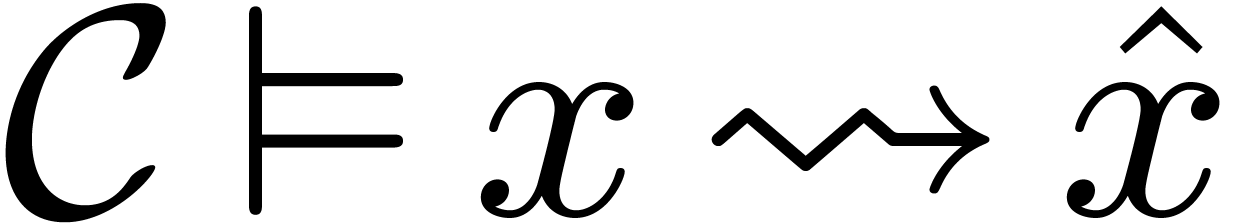 and
the expression
and
the expression 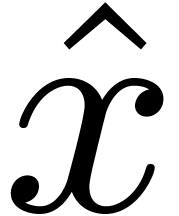 will always admit a unique type.
will always admit a unique type.
For instance, for 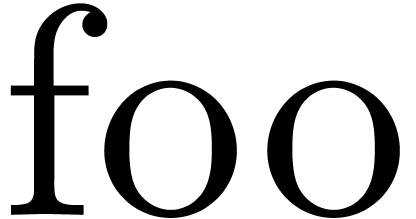 as above, we introduce
operators
as above, we introduce
operators 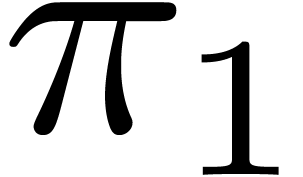 and
and 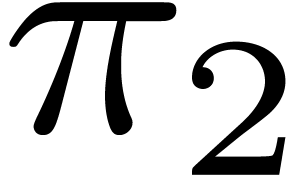 for
accessing the two possible meanings, so that
for
accessing the two possible meanings, so that

For increased clarity, we will freely annotate target expressions by
their types when appropriate. For instance, we might have written 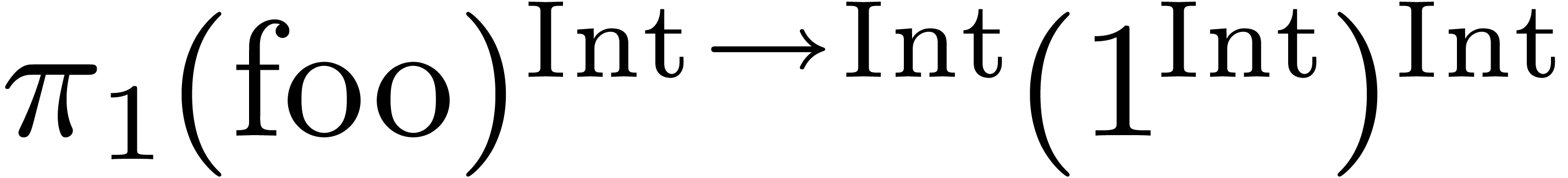 instead of
instead of 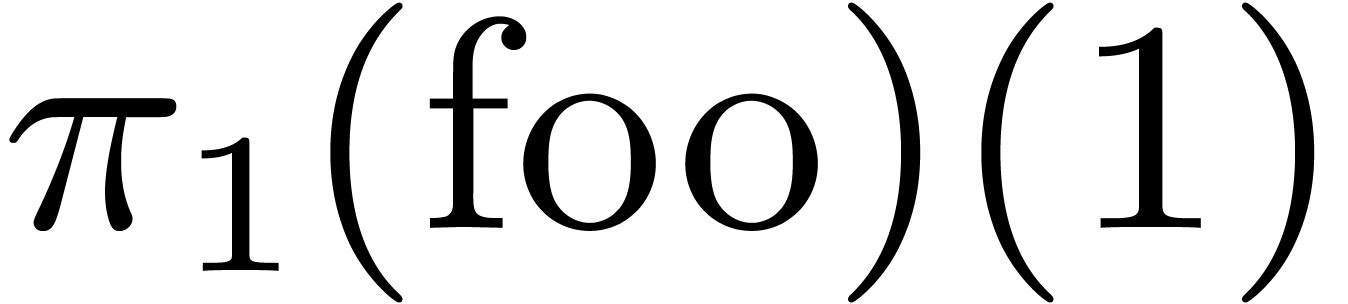 .
.
Disambiguation operators.
In the target language, the following notations will be used for
disambiguating overloaded expressions:
-
Given an expression  , we
may form the expressions
, we
may form the expressions 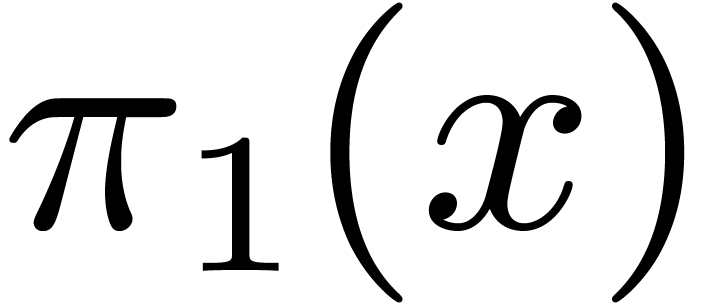 and
and 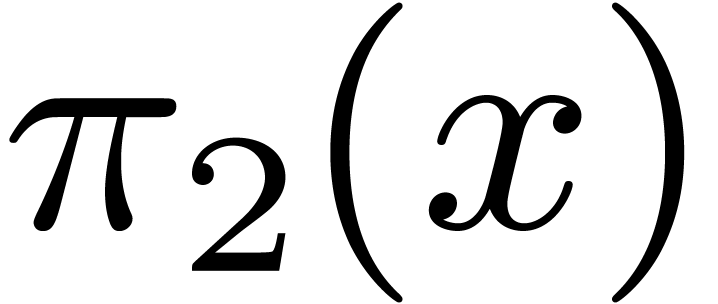 .
.
-
Given expressions  and
and 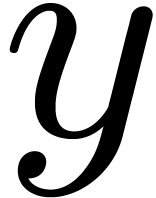 , we may form the expression
, we may form the expression 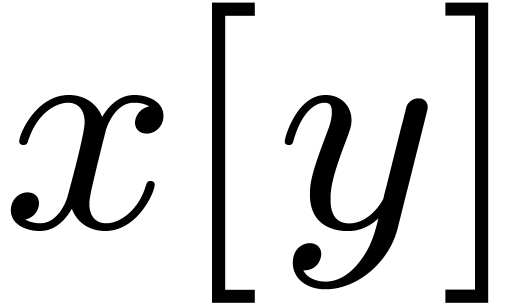 . Here
. Here  should be
regarded as a template and
should be
regarded as a template and 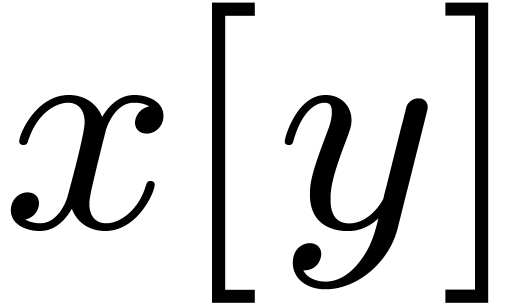 as its
specialization at
as its
specialization at 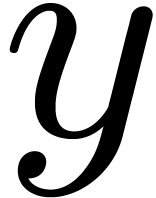 .
.
There are many rules for specifying how to interpret expressions. We
list a few of them:
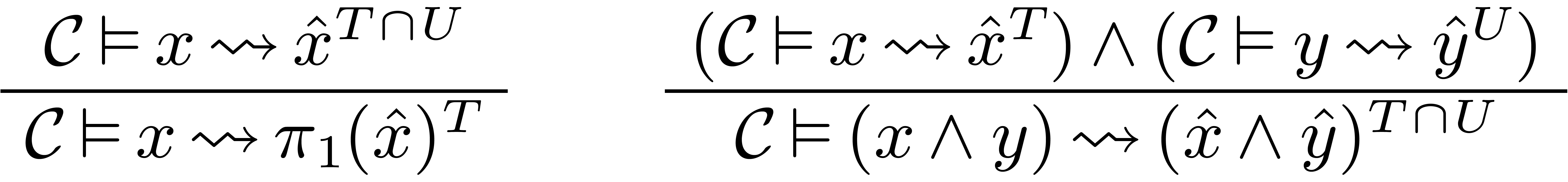
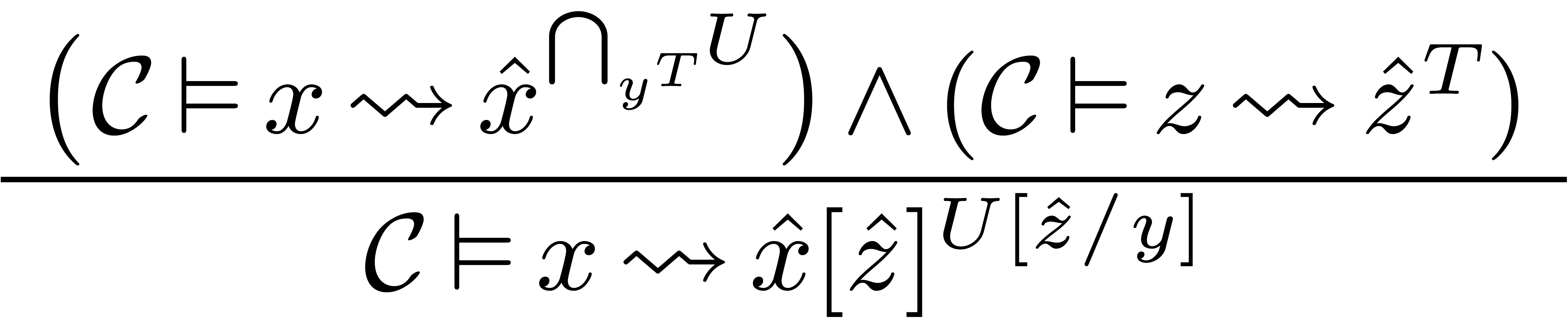
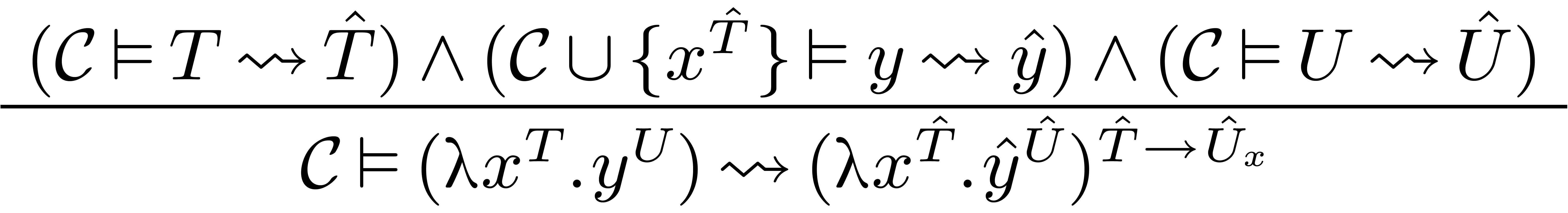
Here 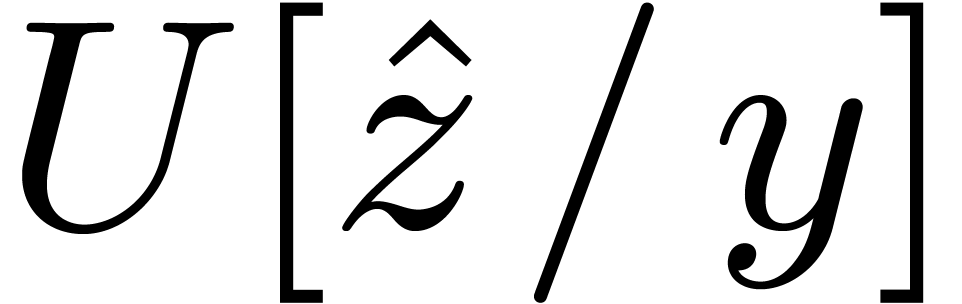 stands for the substitution of
stands for the substitution of  for
for  in
in  .
.
Category matching.
The second kind of extensions in the target language concern notations
for specifying how types match categories:
-
Given expressions  ,
,  and
and  ,
we may form the expression
,
we may form the expression  .
The informal meaning of this expression is “the type
.
The informal meaning of this expression is “the type  considered as an instance of
considered as an instance of  , through specification of the structure
, through specification of the structure  ”.
”.
-
Given an expression  , we
may form
, we
may form  , meaning
“forget the category of
, meaning
“forget the category of  ”.
”.
-
Given expressions  and
and  , we may form the expression
, we may form the expression 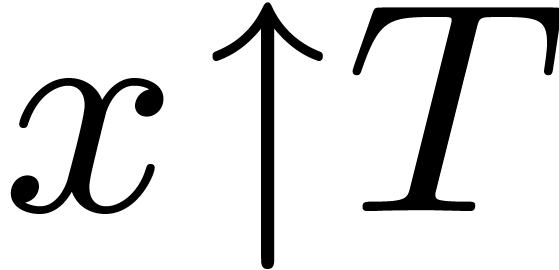 , which allows us to cast to a type
, which allows us to cast to a type  of the form
of the form 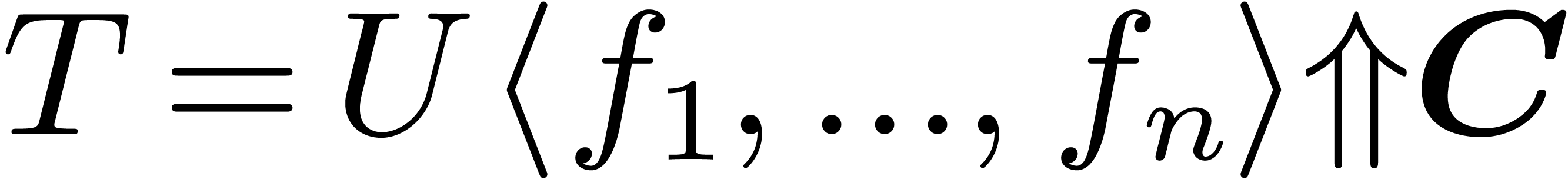 .
.
-
Given an expression  , we
may form
, we
may form 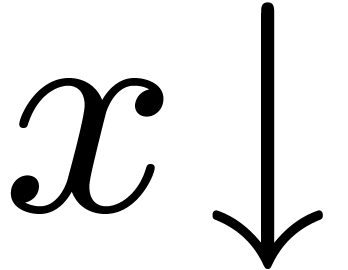 .
.
In order to cast a given type 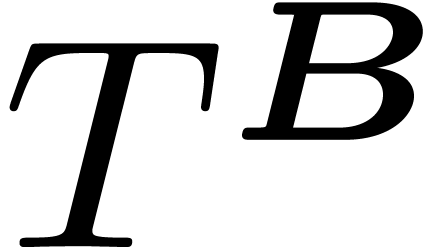 to a given
category
to a given
category 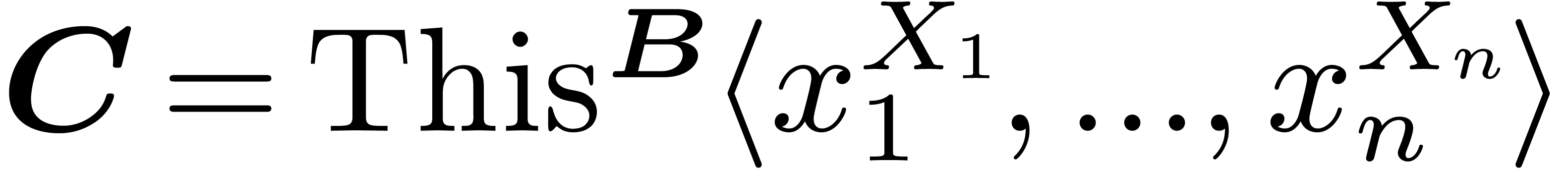 , all fields of the
category should admit an interpretation in the current context:
, all fields of the
category should admit an interpretation in the current context:
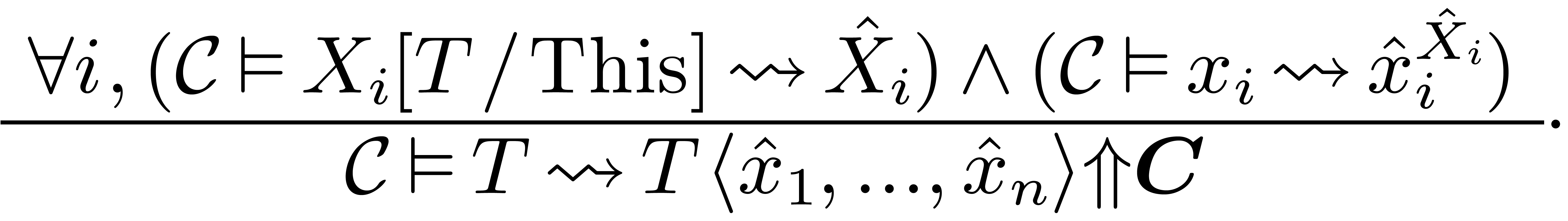
Assuming in addition that 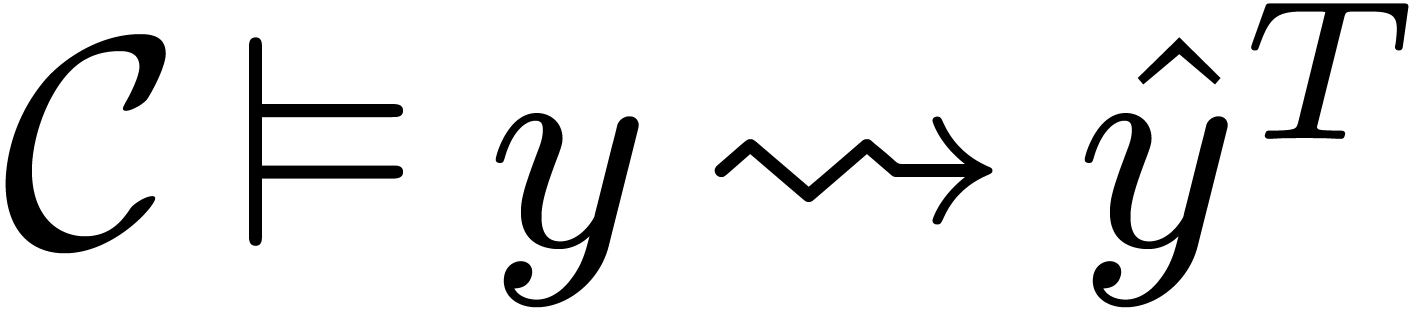 ,
we also have
,
we also have 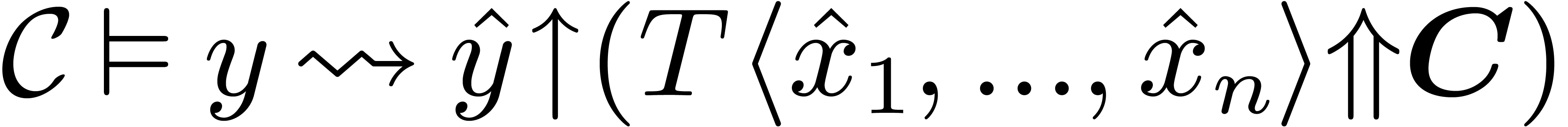 . There are
further rules for casting down.
. There are
further rules for casting down.
4.3Compilation
4.3.1Schematic behaviour
A target expression 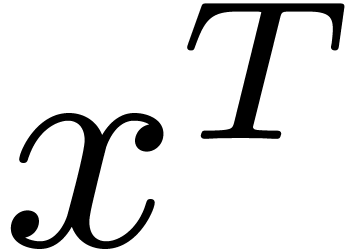 is said to be reduced if its
type
is said to be reduced if its
type  is not of the form
is not of the form  ,
,  , or
, or
 or
or  .
The task of the compiler is to recursively determine all reduced
interpretations of all subexpressions of a source program. Since each
subexpression
.
The task of the compiler is to recursively determine all reduced
interpretations of all subexpressions of a source program. Since each
subexpression  may have several interpretations,
we systematically try to represent the set of all possible reduced
interpretations by a conjunction
may have several interpretations,
we systematically try to represent the set of all possible reduced
interpretations by a conjunction  of universally
quantified expressions. In case of success, this target expression
of universally
quantified expressions. In case of success, this target expression 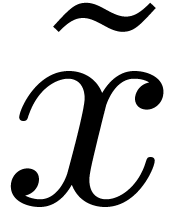 will be the result of the compilation in the relevant
context
will be the result of the compilation in the relevant
context  , and we will write
, and we will write
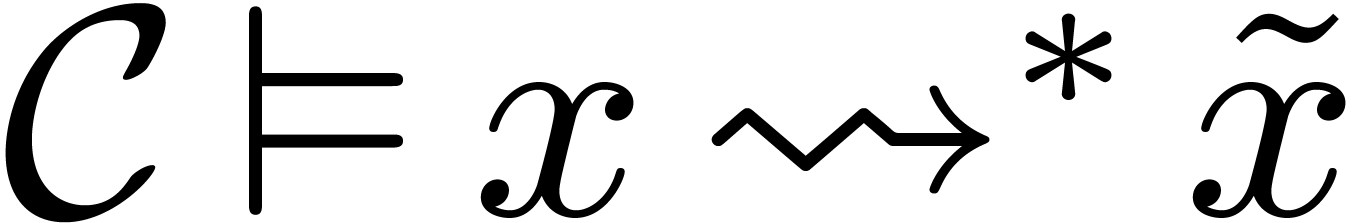 .
.
Let us illustrate this idea on two examples. With 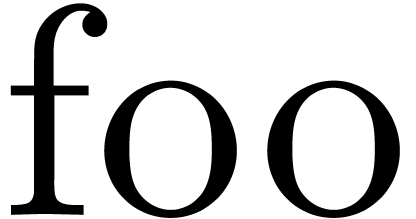 as in (1) and
as in (1) and 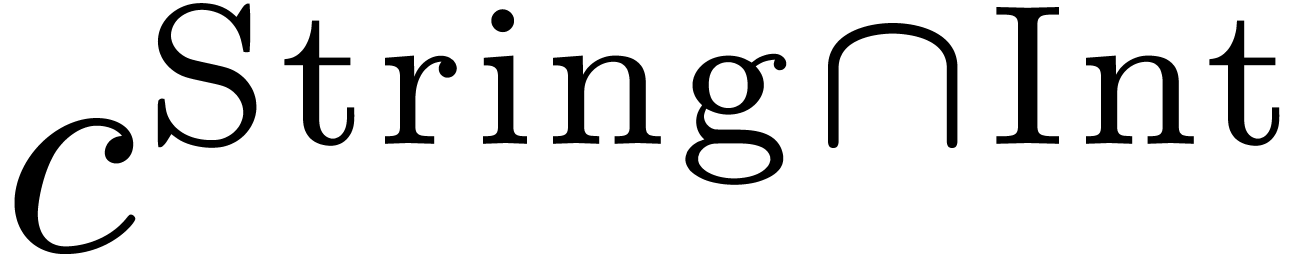 ,
there are two reduced interpretations of
,
there are two reduced interpretations of 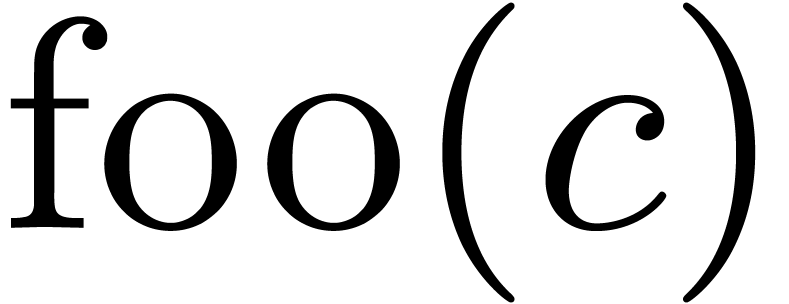 :
:
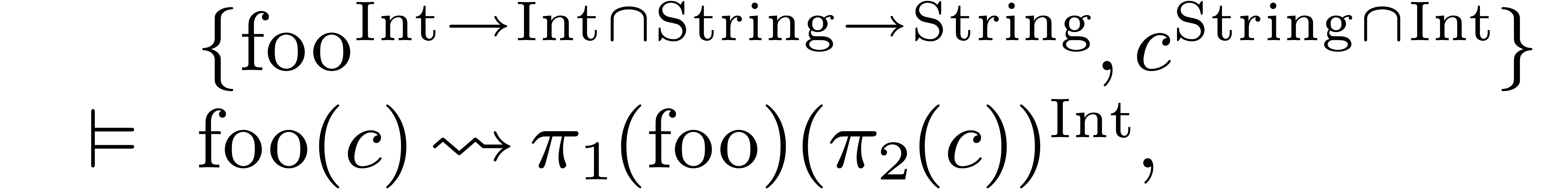
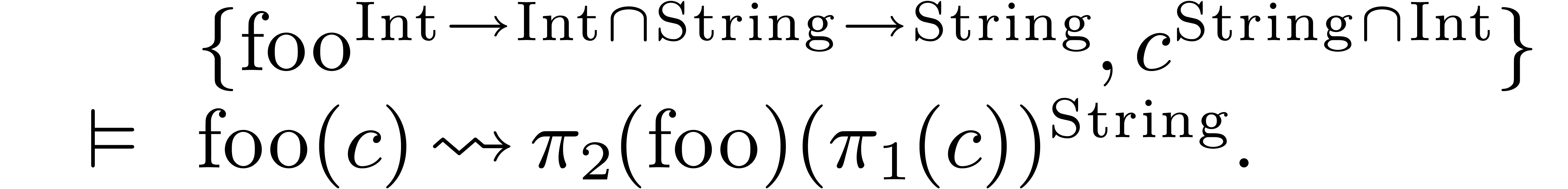
Hence, the result of the compilation of 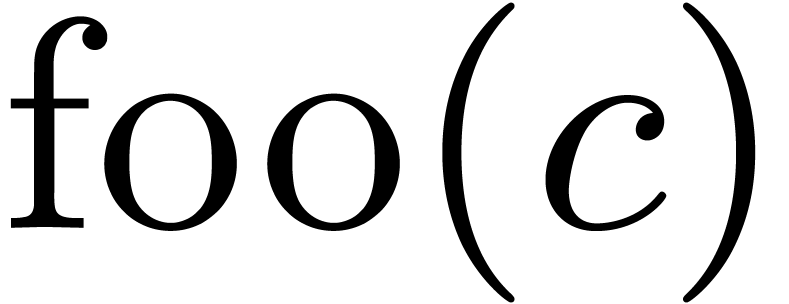 is given
by
is given
by
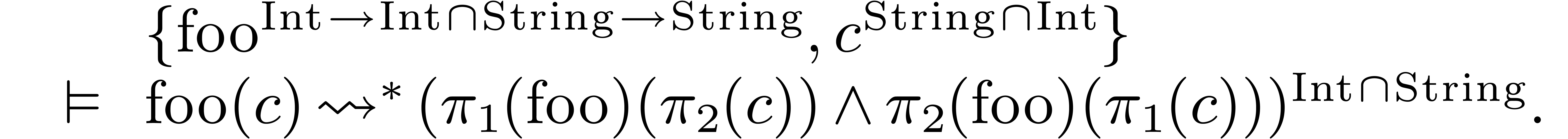
In a similar way, the result of compilation may be a parametrically
overloaded expression:
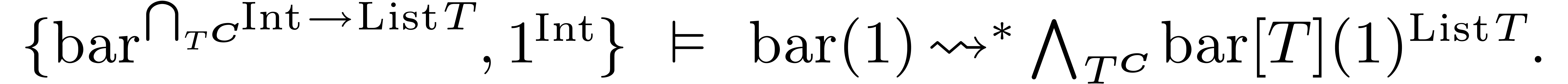
4.3.2Resolution of ambiguities
Sometimes, the result 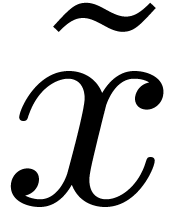 of the compilation of
of the compilation of  is a conjunction which contains at least two
expressions of the same type. In that case,
is a conjunction which contains at least two
expressions of the same type. In that case,  is
truly ambiguous, so the compiler should return an error message, unless
we can somehow resolve the ambiguity. In order to do this, the idea is
to define a partial preference relation
is
truly ambiguous, so the compiler should return an error message, unless
we can somehow resolve the ambiguity. In order to do this, the idea is
to define a partial preference relation  on
target expressions and to keep only those expressions in the conjunction
on
target expressions and to keep only those expressions in the conjunction
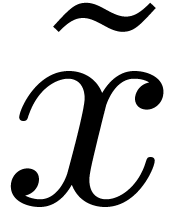 which are maximal for this relation.
which are maximal for this relation.
For instance, assume that we have a function  of
type
of
type 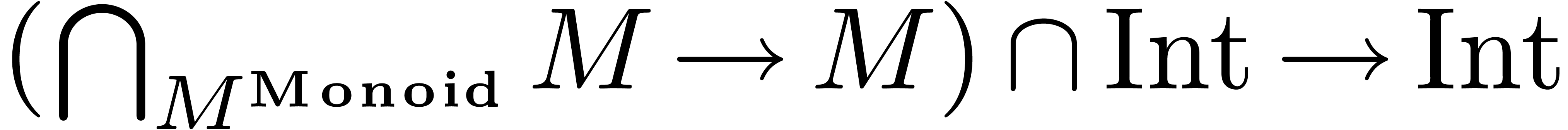 and the constant
and the constant  of
type
of
type 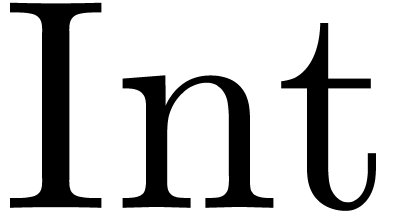 . In section 3.5,
we have seen that Mathemagix supports partial
specialization. Now
. In section 3.5,
we have seen that Mathemagix supports partial
specialization. Now 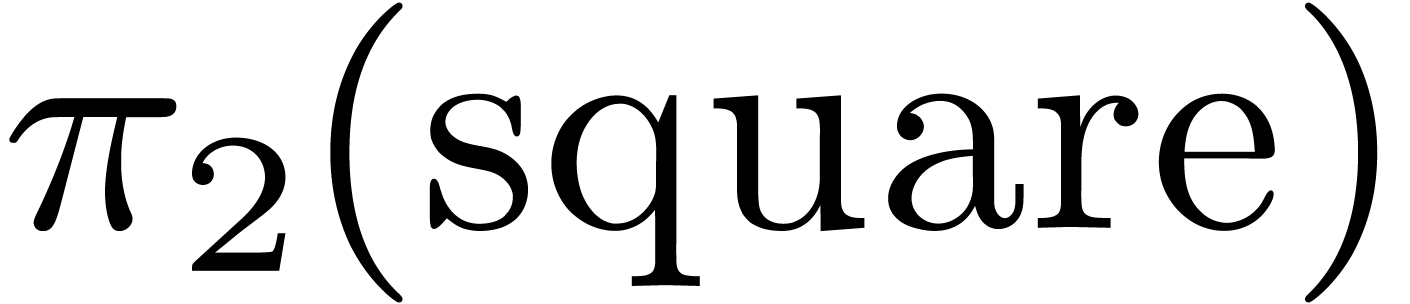 is a partial specialization
of
is a partial specialization
of 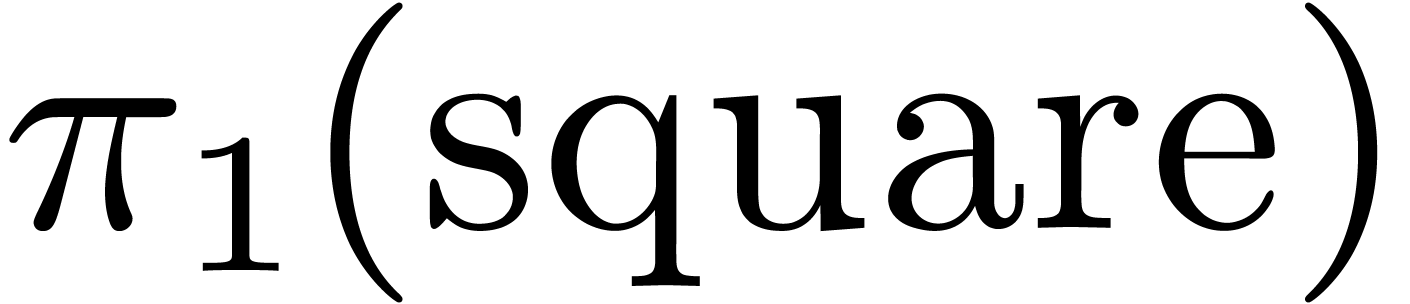 , but not the inverse.
Consequently, we should strictly prefer
, but not the inverse.
Consequently, we should strictly prefer 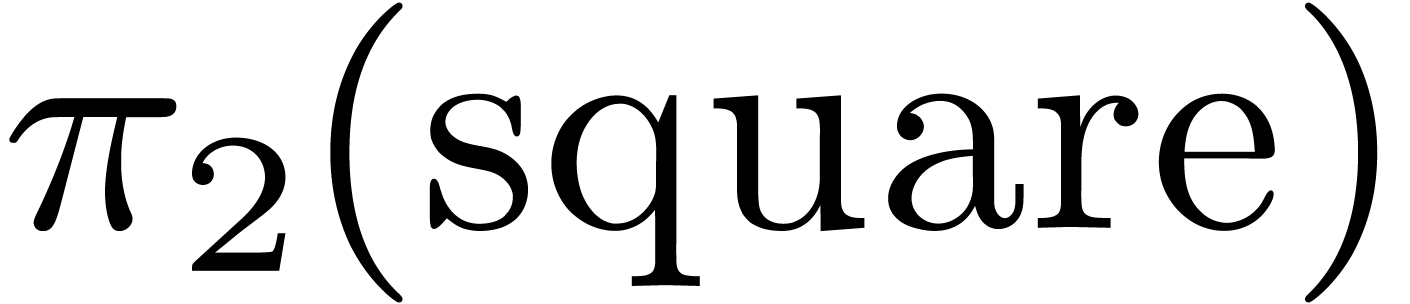 over
over
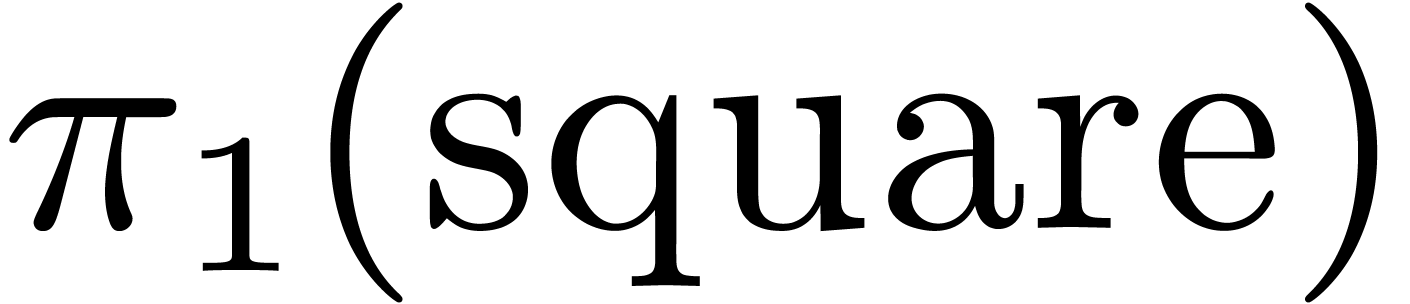 , and
, and 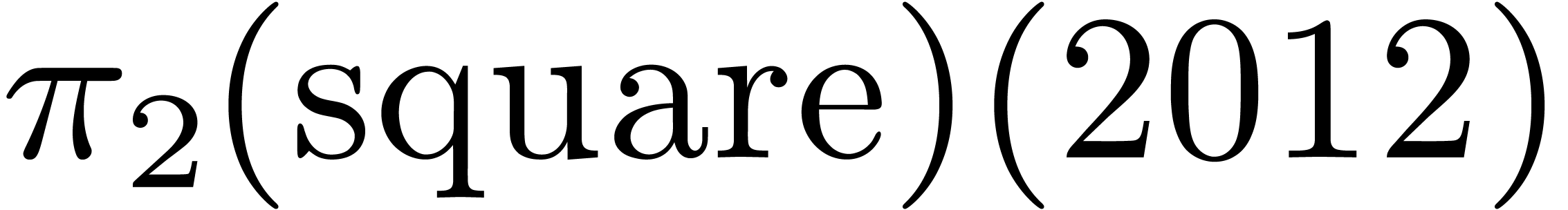 over
over 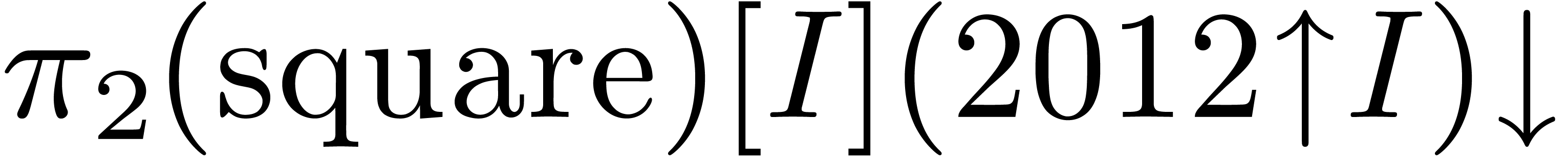 , where
, where 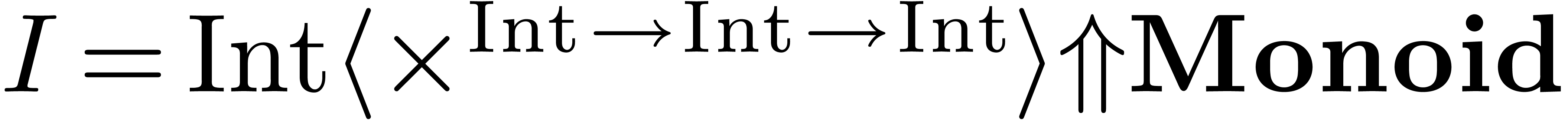 .
.
As indicated in section 3.8, we are currently investigating
further extensions of the preference relation  via user provided preference rules.
via user provided preference rules.
4.3.3Implementation issues
In absence of universal quantification, the search process for all
reduced interpretations can in principle be designed to be finite and
complete. The most important implementation challenge for Mathemagix
compilers therefore concerns universal quantification.
The main idea behind the current implementation is that all pattern
matching is done in two stages: at the first stage, we propose possible
matches for free variables introduced during unification of quantified
expressions. At a second stage, we verify that the proposed matches
satisfy the necessary categorical constraints, and we rerun the pattern
matching routines for the actual matches. When proceeding this way, it
is guaranteed that casts of a type to a category never involve free
variables.
Let us illustrate the idea on the simple example of computing a square.
So assume that we have the function 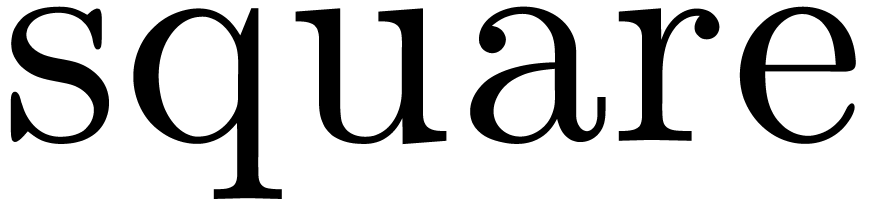 of type
of type 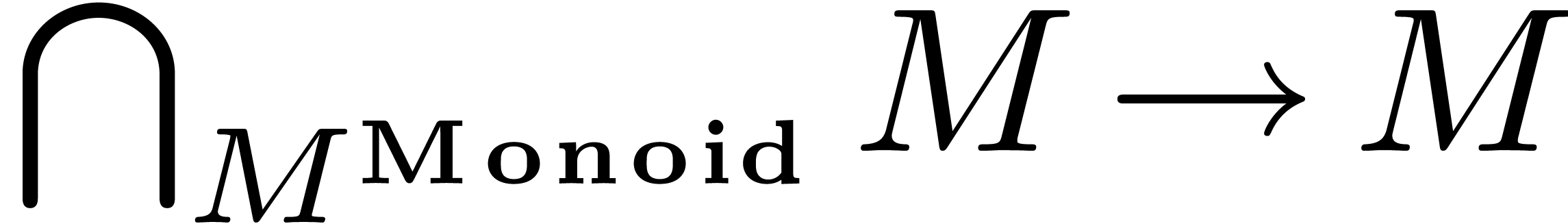 in our context, as well as a multiplication
in our context, as well as a multiplication  . In order to compile the
expression
. In order to compile the
expression 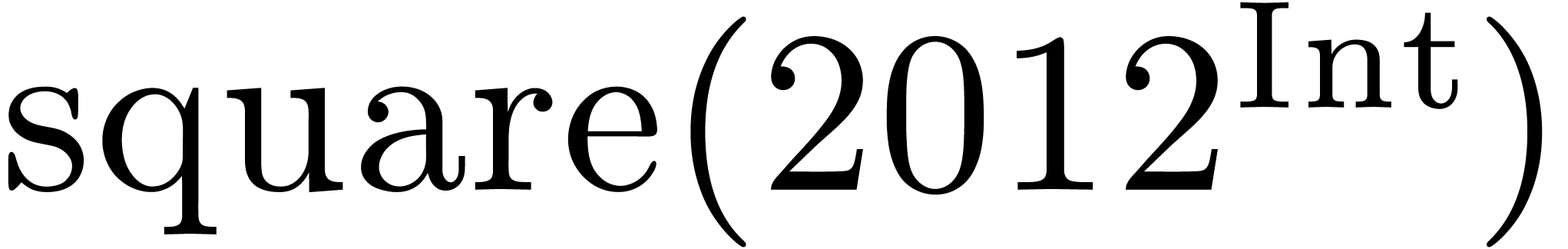 , the algorithm
will attempt to match
, the algorithm
will attempt to match 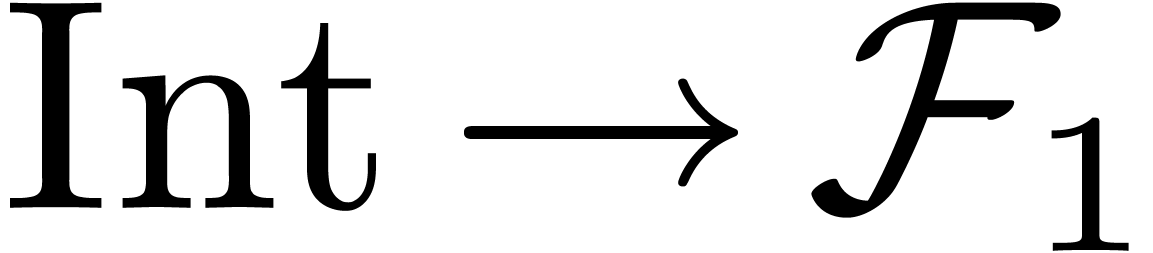 with
with 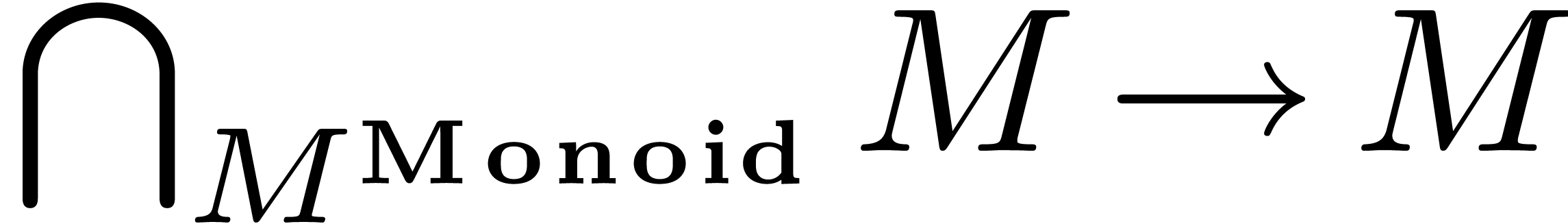 for some free variable
for some free variable 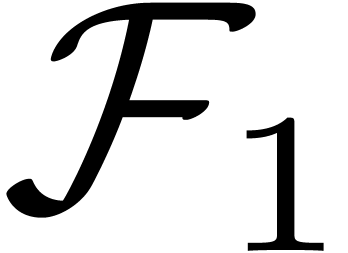 . At a
first stage, we introduce a new free variable
. At a
first stage, we introduce a new free variable 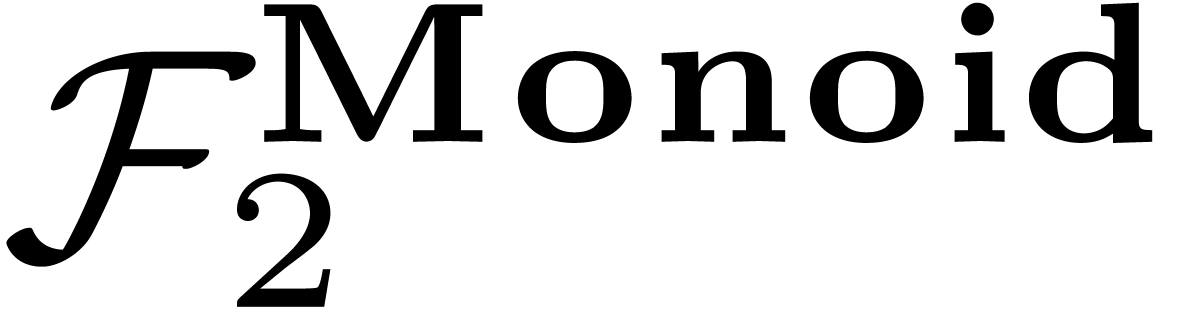 and match
and match  against
against 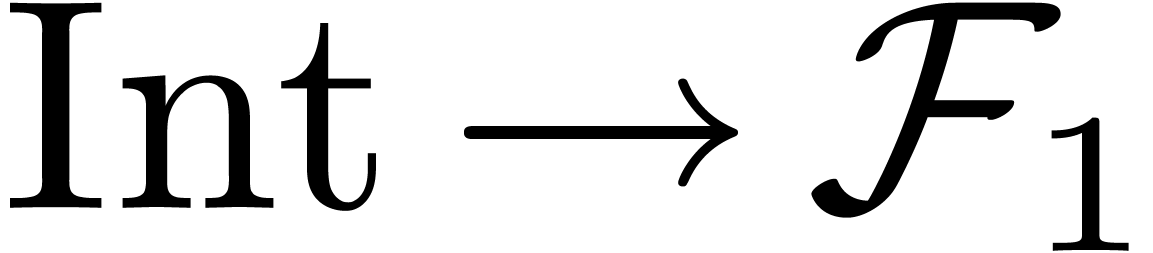 .
This check succeeds with the bindings
.
This check succeeds with the bindings 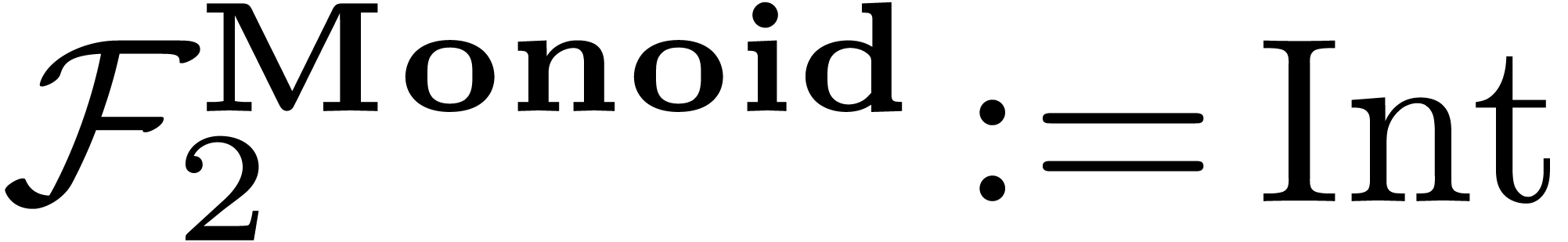 and
and 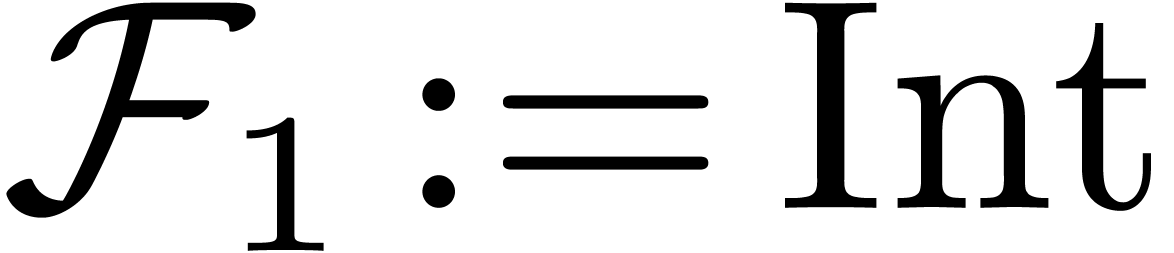 , but without performing any type
checking for these bindings. At a second stage, we have to resolve the
innermost binding
, but without performing any type
checking for these bindings. At a second stage, we have to resolve the
innermost binding 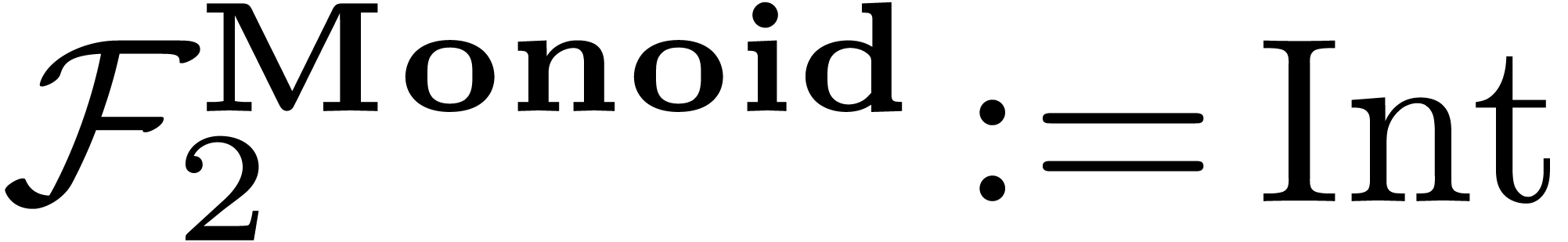 and cast
and cast 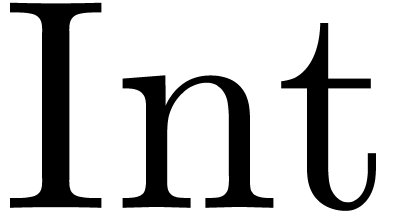 to
to  . This results in the
correct proposal
. This results in the
correct proposal  for the free variable, where
for the free variable, where
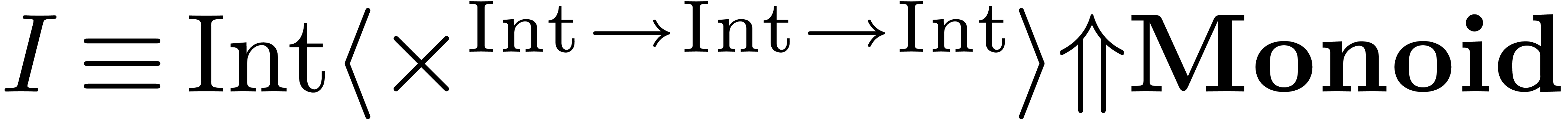 . We finally rematch
. We finally rematch 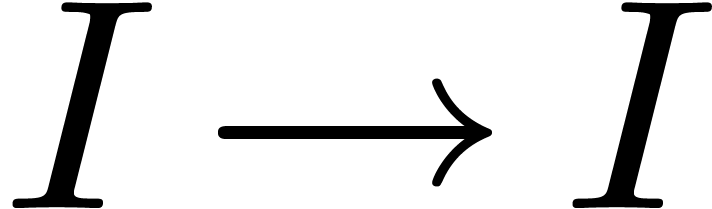 with
with  and find the return type
and find the return type
 .
.
In practice the above idea works very well. Apart from more pathological
theoretical problems that will be discussed below, the only practically
important problem that we do not treat currently, is finding a
“smallest common supertype” with respect to type conversions
(see also [33]).
For instance, let 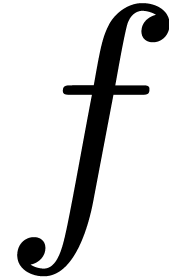 be a function of type
be a function of type  . What should be the type of
. What should be the type of 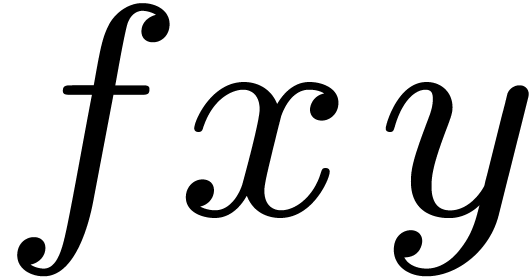 , where
, where  and
and
 are such that
are such that 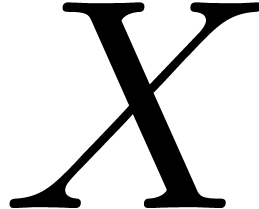 and
and  are different? Theoretically speaking, this should be
the type
are different? Theoretically speaking, this should be
the type 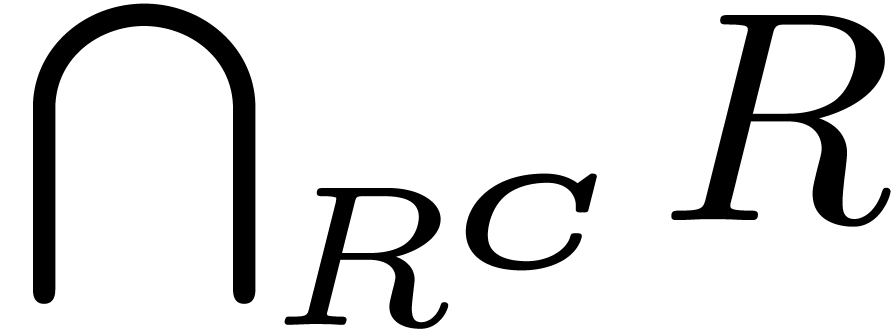 , where
, where  is the category
is the category 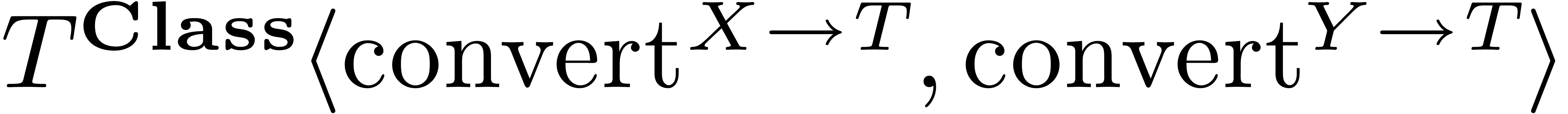 .
However, the current pattern matching mechanism in the Mathemagix
compiler will not find this type.
.
However, the current pattern matching mechanism in the Mathemagix
compiler will not find this type.
4.3.4Theoretical problems
It is easy to write programs which make the compiler fail or loop
forever. For instance, given a context with the category 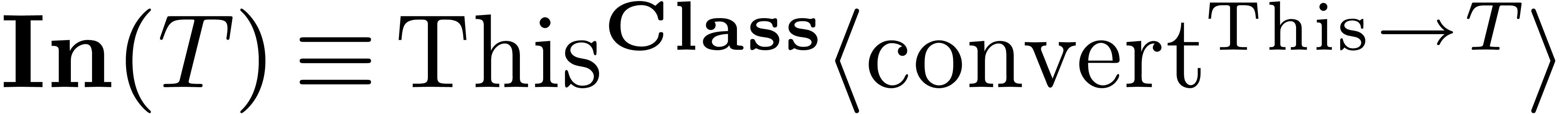 and functions
and functions  and
and  of types
of types 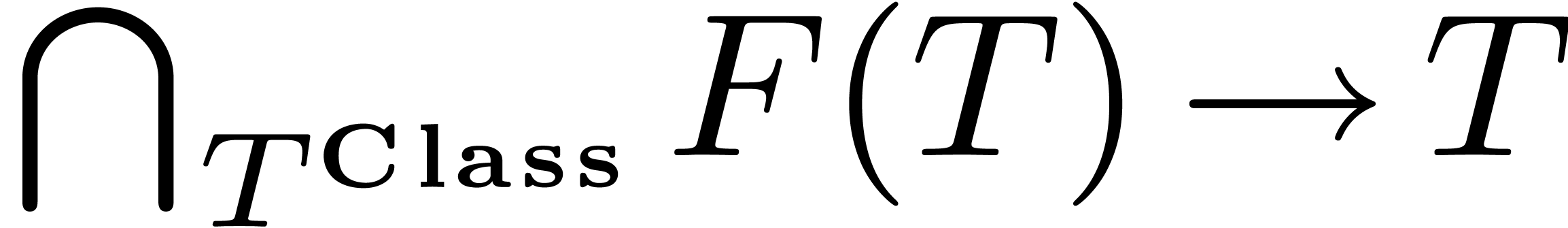 and
and 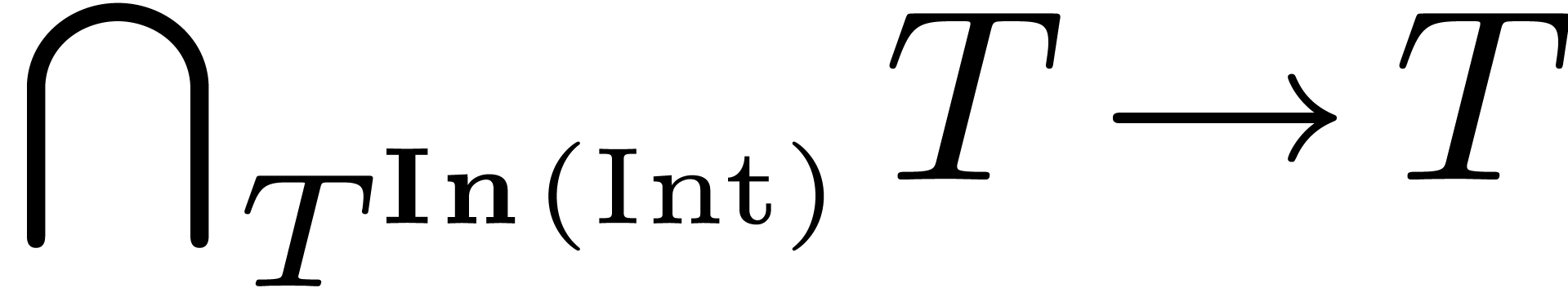 ,
the compilation of
,
the compilation of 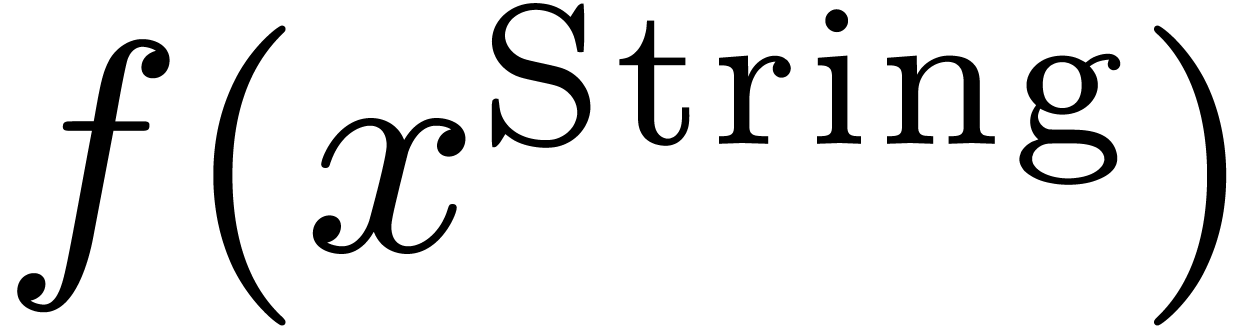 will loop. Indeed, the
compiler will successively search for converters
will loop. Indeed, the
compiler will successively search for converters  ,
, 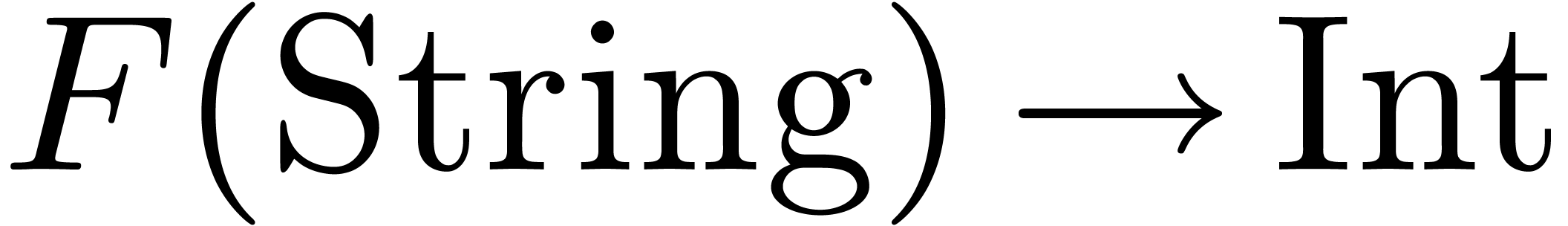 ,
, 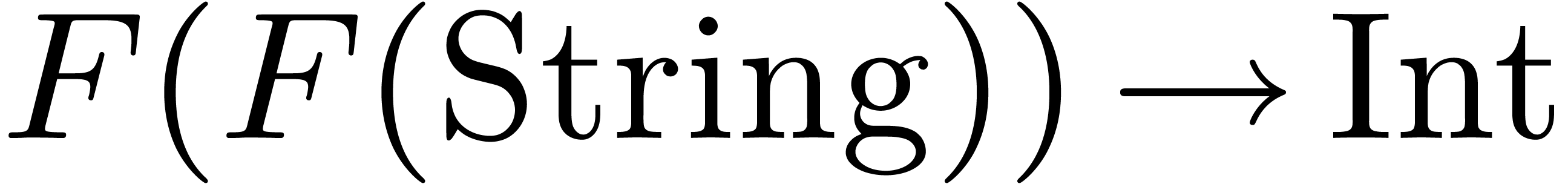 , etc. Currently, some safeguards
have been integrated which will make the compiler abort with an error
message when entering this kind of loops.
, etc. Currently, some safeguards
have been integrated which will make the compiler abort with an error
message when entering this kind of loops.
The expressiveness of the type system actually makes it possible to
encode any first order theory directly in the system. For instance,
given a binary predicate 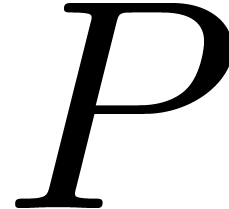 and function symbols
and function symbols
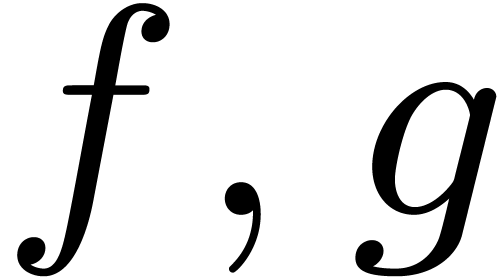 , the statement
, the statement  might be encoded by the declaration of a function
might be encoded by the declaration of a function 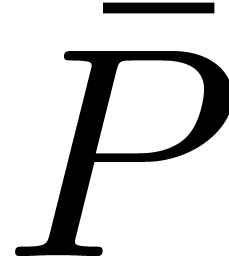 of type
of type 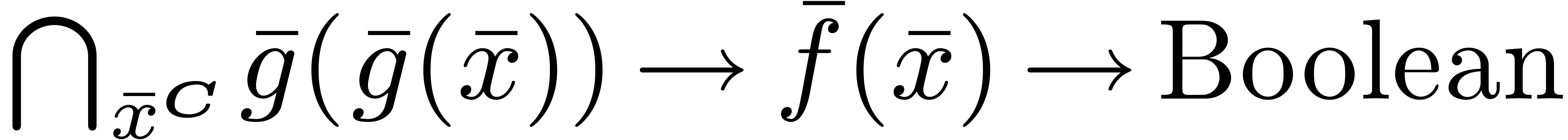 ,
where
,
where 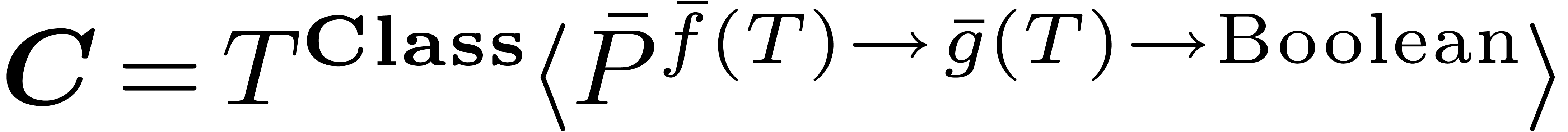 .
.
These negative remarks are counterbalanced by the fact that the type
system is not intended to prove mathematical theorems, but rather to
make sense out of commonly used overloaded mathematical notations. It
relies upon the shoulders of the user to use the type system in order to
define such common notations and not misuse it in order to prove general
first order statements. Since notations are intended to be easily
understandable at the first place, they can usually be given a sense by
following simple formal procedures. We believe that our type system is
powerful enough to cover most standard notations in this sense.
The above discussion shows that we do not aim completeness for the
Mathemagix system. So what about soundness? The
rules for interpretation are designed in such a way that all
interpretations are necessarily correct. The only possible problems
which can therefore occur are that the compiler loops forever or that it
is not powerful enough to automatically find certain non trivial
interpretations.
We also notice that failure of the compiler to find the intended meaning
does not necessarily mean that we will get an error message or that the
compiler does not terminate. Indeed, theoretically speaking, we might
obtain a correct interpretation, even though the intended interpretation
should be preferred. In particular, it is important to use the
overloading facility in such a way that all possible interpretations are
always correct, even though some of them may be preferred.
4.4Execution
Given an expression  on which the compilation
process succeeds, we finally have to show what it means to evaluate
on which the compilation
process succeeds, we finally have to show what it means to evaluate
 . So let
. So let  with
with 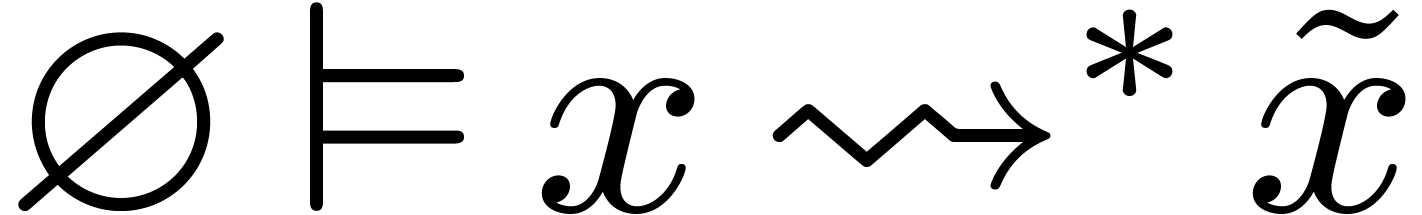 be the expression in the target language
which is produced by the compiler. The target language has the property
that it is quite easy to “downgrade”
be the expression in the target language
which is produced by the compiler. The target language has the property
that it is quite easy to “downgrade”  into an expression of classical untyped
into an expression of classical untyped  -calculus.
This reduces the evaluation semantics of Mathemagix
to the one of this calculus.
-calculus.
This reduces the evaluation semantics of Mathemagix
to the one of this calculus.
Some of the most prominent rules for rewriting 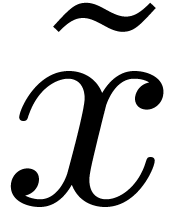 into a term of classical untyped
into a term of classical untyped  -calculus
are the following:
-calculus
are the following:
-
Overloaded expressions  are rewritten as
pairs
are rewritten as
pairs 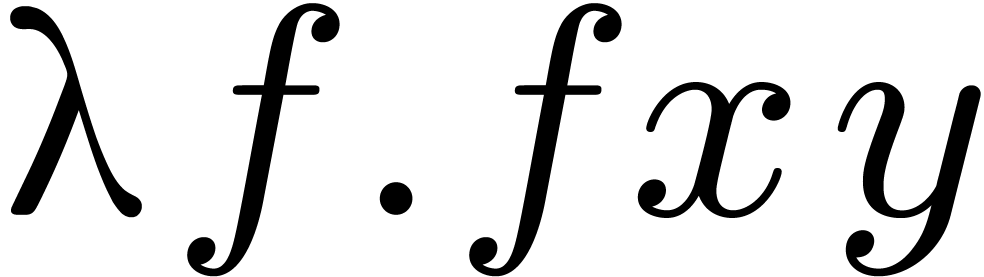 .
.
-
The projections 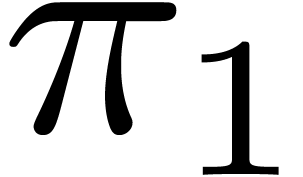 and
and 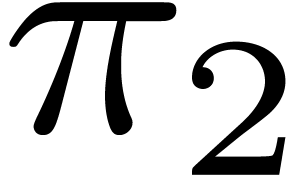 are simply
are simply 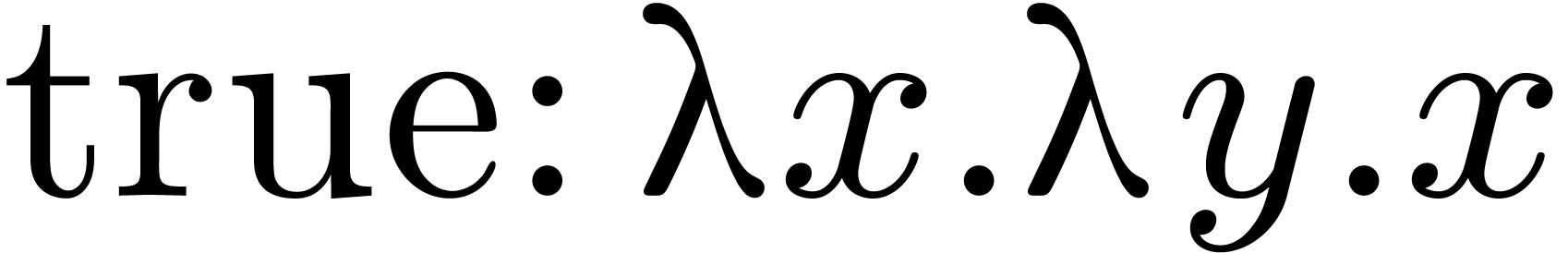 and
and 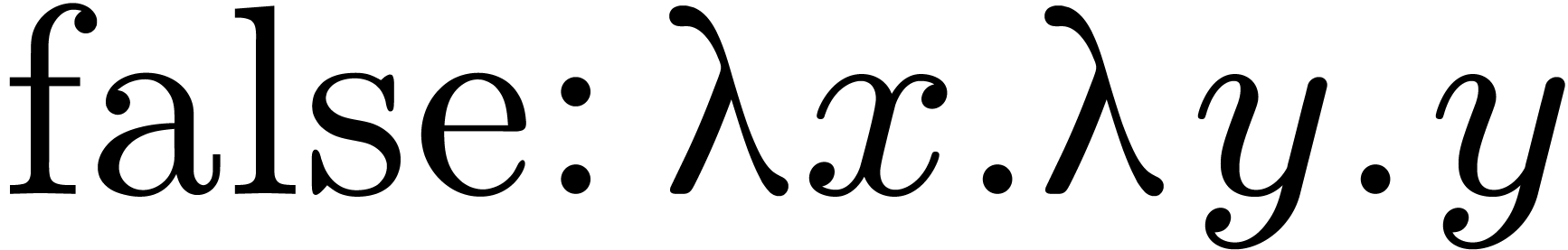 .
.
-
Template expressions 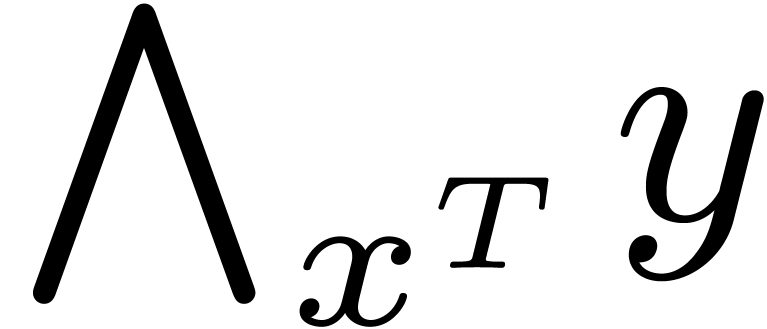 are rewritten as
are rewritten as  -expressions
-expressions 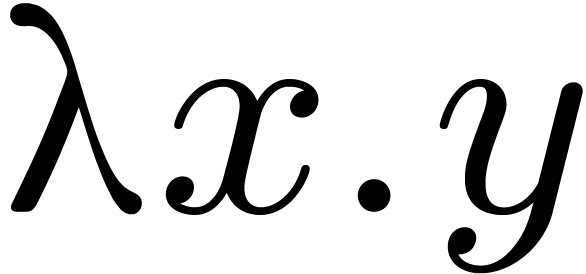 .
.
-
Template instantiation 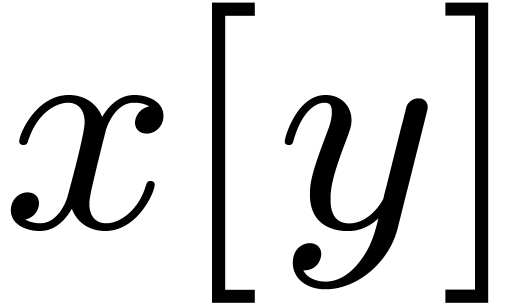 is rewritten into
function application
is rewritten into
function application 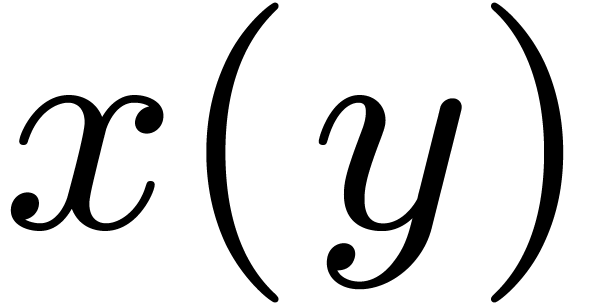 .
.
-
Instances 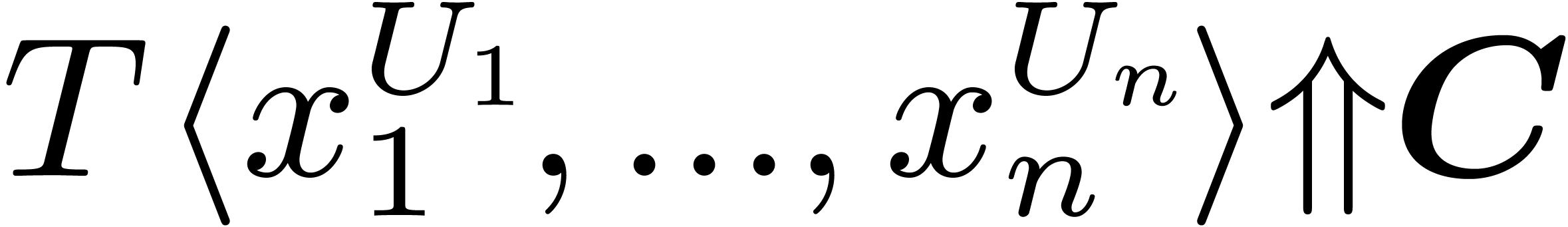 of categories are implemented as
of categories are implemented as
 -tuples
-tuples 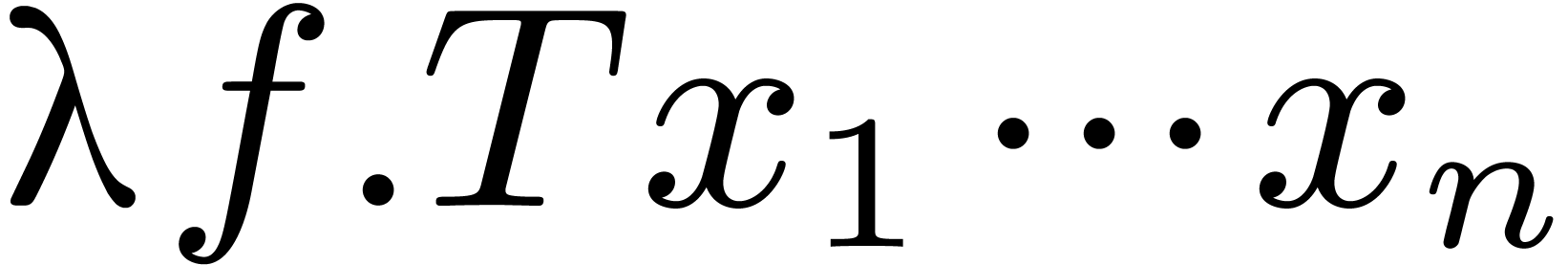 .
.
For instance, consider the template 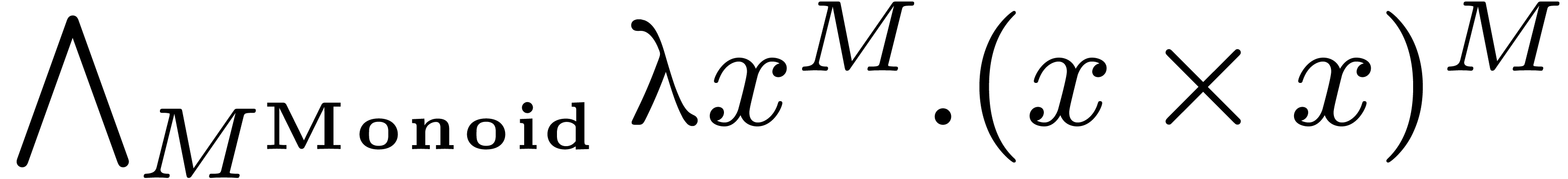 .
After compilation, this template is transformed into the expression
.
After compilation, this template is transformed into the expression
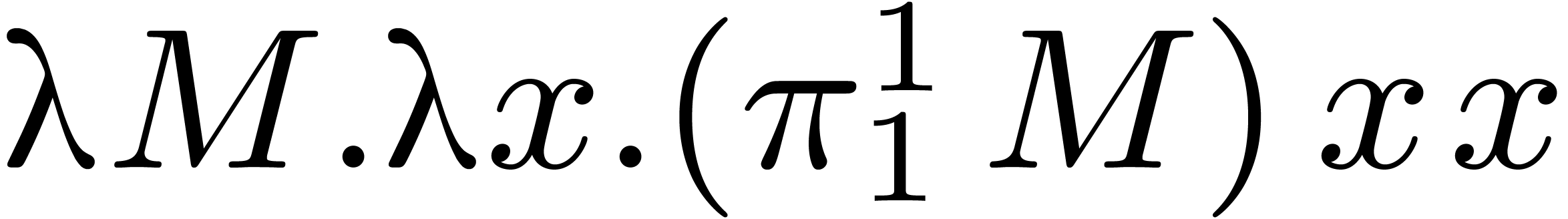 , where
, where  .
.
One of the aims of the actual Mathemagix compiler
is to be compatible with existing C libraries and
C++ template libraries. For this reason, the
backend of Mathematics really transforms
expressions in the target language into C++
programs instead of terms of untyped  -calculus.
-calculus.
5.References
-
[1]
-
The Axiom computer algebra system.
http://wiki.axiom-developer.org/FrontPage
.
-
[2]
-
G. Baumgartner and V.F. Russo. Implementing
signatures for C++. ACM Trans. Program. Lang. Syst.,
19(1):153–187, 1997.
-
[3]
-
E. Bond, M. Auslander, S. Grisoff, R. Kenney, M.
Myszewski, J. Sammet, R. Tobey and S. Zilles. FORMAC an
experimental formula manipulation compiler. In Proceedings
of the 1964 19th ACM national conference, ACM '64, pages
112–101. New York, NY, USA, 1964. ACM.
-
[4]
-
T. Coquand and G. Huet. The calculus of
constructions. Inf. Comput., 76(2-3):95–120,
1988.
-
[5]
-
T. Coquand et al. The Coq proof assistant.
http://coq.inria.fr/
, 1984.
-
[6]
-
D. Eisenbud, D.R. Grayson, M.E. Stillman and B.
Sturmfels, editors. Computations in algebraic geometry with
Macaulay 2. Springer-Verlag, London, UK, UK, 2002.
-
[7]
-
J.-C. Faugère. FGb: A Library for Computing
Gröbner Bases. In Komei Fukuda, Joris Hoeven, Michael
Joswig and Nobuki Takayama, editors, Mathematical Software
- ICMS 2010, volume 6327 of Lecture Notes in Computer
Science, pages 84–87. Berlin, Heidelberg, September
2010. Springer Berlin / Heidelberg.
-
[8]
-
K. Geddes, G. Gonnet and Maplesoft. Maple.
http://www.maplesoft.com/products/maple/
, 1980.
-
[9]
-
J. Y. Girard. Une extension de
l'interprétation de Gödel à l'analyse, et
son application à l'élimination de coupures dans
l'analyse et la théorie des types. In J. E. Fenstad,
editor, Proceedings of the Second Scandinavian Logic
Symposium, pages 63–92. North-Holland Publishing
Co., 1971.
-
[10]
-
T. Granlund et al. GMP, the GNU multiple precision
arithmetic library.
http://www.swox.com/gmp
, 1991.
-
[11]
-
D.R. Grayson and M.E. Stillman. Macaulay2, a
software system for research in algebraic geometry. Available
at http://www.math.uiuc.edu/Macaulay2/.
-
[12]
-
J.H. Griesmer, R.D. Jenks and D.Y.Y. Yun.
SCRATCHPAD User's Manual. Computer Science Department
monograph series. IBM Research Division, 1975.
-
[13]
-
G. Hanrot, V. Lefèvre, K. Ryde and P.
Zimmermann. MPFR, a C library for multiple-precision
floating-point computations with exact rounding.
http://www.mpfr.org
, 2000.
-
[14]
-
W. Hart. An introduction to Flint. In K. Fukuda, J.
van der Hoeven, M. Joswig and N. Takayama, editors,
Mathematical Software - ICMS 2010, Third International
Congress on Mathematical Software, Kobe, Japan, September
13-17, 2010, volume 6327 of Lecture Notes in Computer
Science, pages 88–91. Springer, 2010.
-
[15]
-
J. van der Hoeven, G. Lecerf, B. Mourain et al.
Mathemagix. 2002.
http://www.mathemagix.org
.
-
[16]
-
J. van der Hoeven, G. Lecerf, B. Mourrain, P.
Trébuchet, J. Berthomieu, D. Diatta and A. Manzaflaris.
Mathemagix, the quest of modularity and efficiency for
symbolic and certified numeric computation. ACM Commun.
Comput. Algebra, 45(3/4):186–188, 2012.
-
[17]
-
P. Hudak, J. Hughes, S. Peyton Jones and P. Wadler.
A history of haskell: being lazy with class. In Proceedings
of the third ACM SIGPLAN conference on History of programming
languages, HOPL III, pages 12–1. New York, NY, USA,
2007. ACM.
-
[18]
-
R. D. Jenks. The SCRATCHPAD language. SIGPLAN
Not., 9(4):101–111, mar 1974.
-
[19]
-
R.D. Jenks. Modlisp – an introduction
(invited). In Proceedings of the International Symposiumon
on Symbolic and Algebraic Computation, EUROSAM '79, pages
466–480. London, UK, UK, 1979. Springer-Verlag.
-
[20]
-
R.D. Jenks and B.M. Trager. A language for
computational algebra. SIGPLAN Not.,
16(11):22–29, 1981.
-
[21]
-
R.D. Jenks and R. Sutor. AXIOM: the scientific
computation system. Springer-Verlag, New York, NY, USA,
1992.
-
[22]
-
X. Leroy et al. OCaml.
http://caml.inria.fr/ocaml/
, 1996.
-
[23]
-
W. A. Martin and R. J. Fateman. The MACSYMA system.
In Proceedings of the second ACM symposium on Symbolic and
algebraic manipulation, SYMSAC '71, pages 59–75. New
York, NY, USA, 1971. ACM.
-
[24]
-
P. Martin-Löf. Constructive mathematics and
computer programming. Logic, Methodology and Philosophy of
Science VI, :153–175, 1979.
-
[25]
-
R. Milner. A theory of type polymorphism in
programming. Journal of Computer and System Sciences,
17:348–375, 1978.
-
[26]
-
J. Moses. Macsyma: A personal history. Journal
of Symbolic Computation, 47(2):123–130, 2012.
-
[27]
-
The Maxima computer algebra system (free version).
http://maxima.sourceforge.net/
, 1998.
-
[28]
-
T. Nipkow, L. Paulson and M. Wenzel. Isabelle/Hol.
http://www.cl.cam.ac.uk/research/hvg/Isabelle/
, 1993.
-
[29]
-
S. Peyton Jones et al. The Haskell 98 language and
libraries: the revised report. Journal of Functional
Programming, 13(1):0–255, Jan 2003. Http://www.haskell.org/definition/.
-
[30]
-
G. Dos Reis and B. Stroustrup. Specifying C++
concepts. SIGPLAN Not., 41(1):295–308, 2006.
-
[31]
-
A. Sabi. Typing algorithm in type theory with
inheritance. In Proceedings of the 24th ACM SIGPLAN-SIGACT
symposium on Principles of programming languages, POPL
'97, pages 292–301. ACM, 1997.
-
[32]
-
W.A. Stein et al. Sage Mathematics Software.
The Sage Development Team, 2004.
http://www.sagemath.org
.
-
[33]
-
R. S. Sutor and R. D. Jenks. The type inference and
coercion facilities in the scratchpad ii interpreter.
SIGPLAN Not., 22(7):56–63, 1987.
-
[34]
-
B. Stroustrup. The C++ programming language.
Addison-Wesley, 2-nd edition, 1995.
-
[35]
-
S. Watt, P.A. Broadbery, S.S. Dooley, P. Iglio,
S.C. Morrison, J.M. Steinbach and R.S. Sutor. A first report
on the A# compiler. In Proceedings of the international
symposium on Symbolic and algebraic computation, ISSAC
'94, pages 25–31. New York, NY, USA, 1994. ACM.
-
[36]
-
S. Watt et al. Aldor programming language.
http://www.aldor.org/
, 1994.
-
[37]
-
Wolfram Research. Mathematica.
http://www.wolfram.com/mathematica/
, 1988.

 . This work has
been supported by the ANR-09-JCJC-0098-01
. This work has
been supported by the ANR-09-JCJC-0098-01  bit
floating point numbers. Unfortunately,
bit
floating point numbers. Unfortunately,  in a monoid. In section
in a monoid. In section 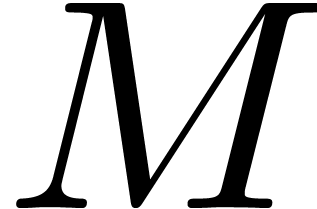 together with an
associative multiplication
together with an
associative multiplication 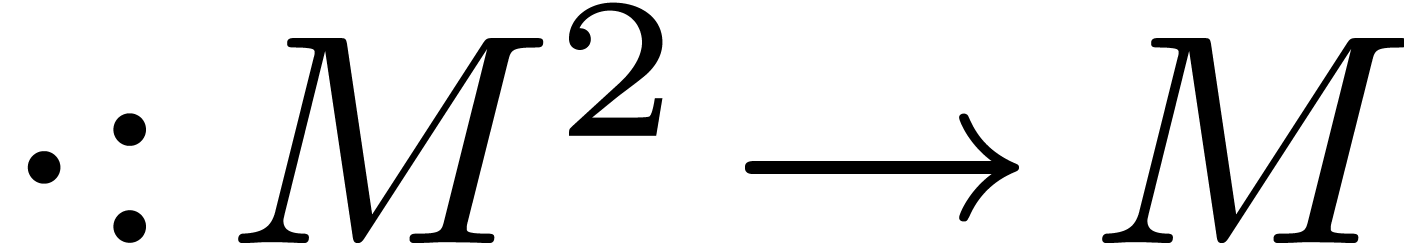 .
. in
in  ,
, in
in  .
. may typically be achieved in two different ways
as the succession of two implicit conversions; namely, as
may typically be achieved in two different ways
as the succession of two implicit conversions; namely, as  or as
or as 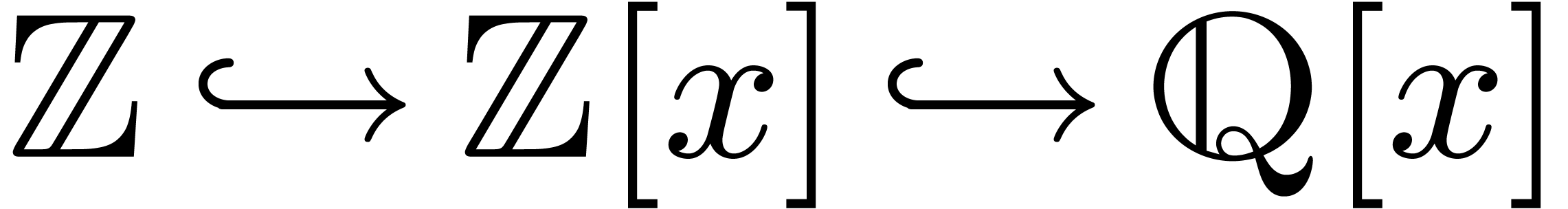 .
. if a
type T satisfies the category, that is, if all
category fields are defined in the current context, when replacing This by T. Contrary to
if a
type T satisfies the category, that is, if all
category fields are defined in the current context, when replacing This by T. Contrary to 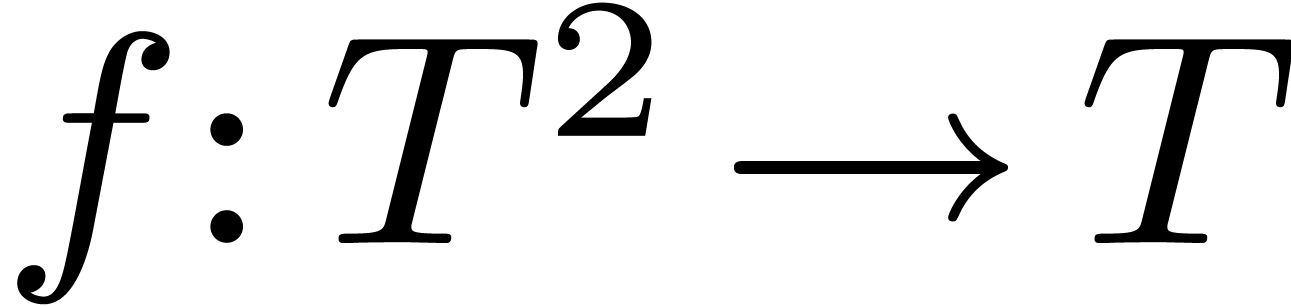 as a function of
type
as a function of
type 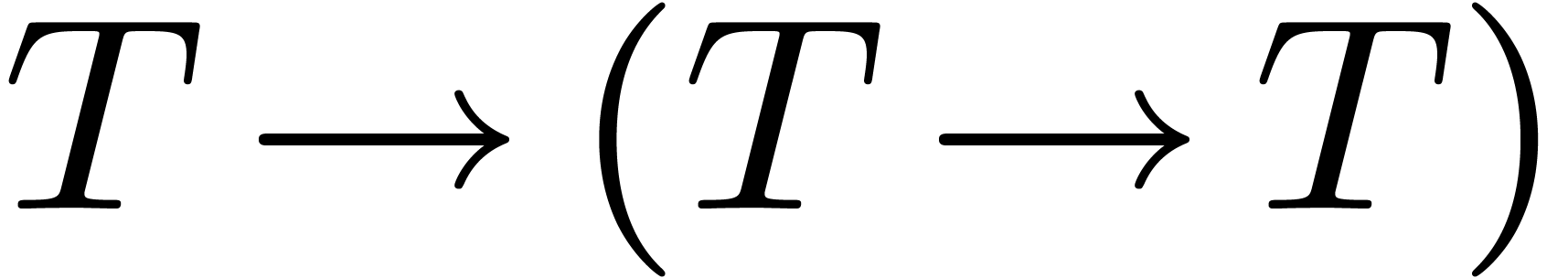 .
. ,
, .
.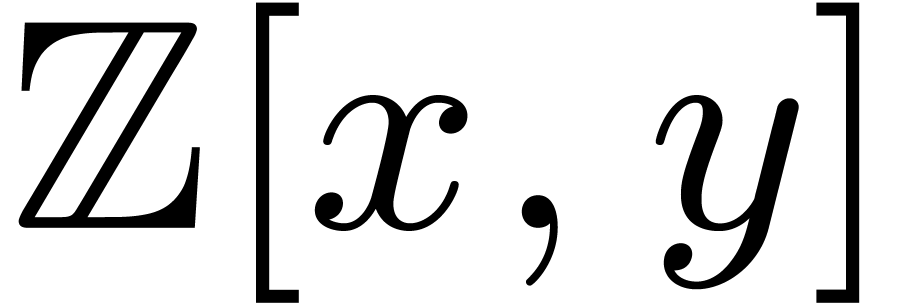 and the two coordinate functions
and the two coordinate functions 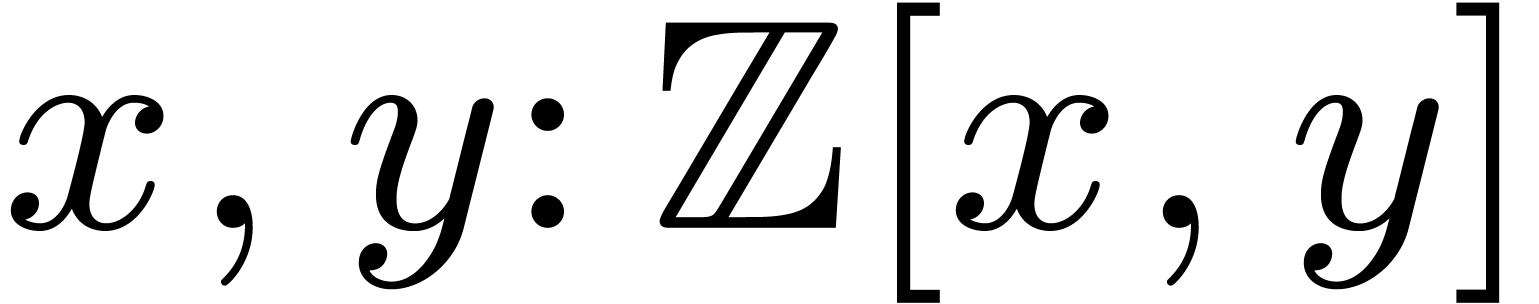 .
. -calculus.
-calculus.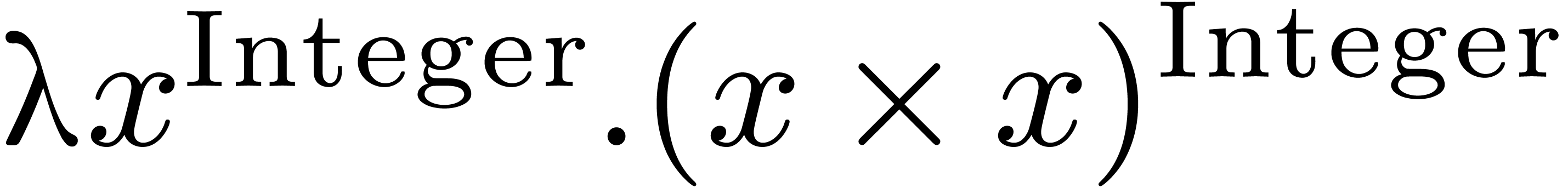 denotes the function
denotes the function  .
. ,
, ,
, ,
, ,
,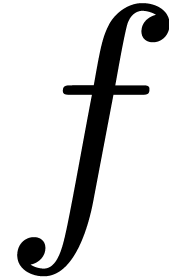 and
and 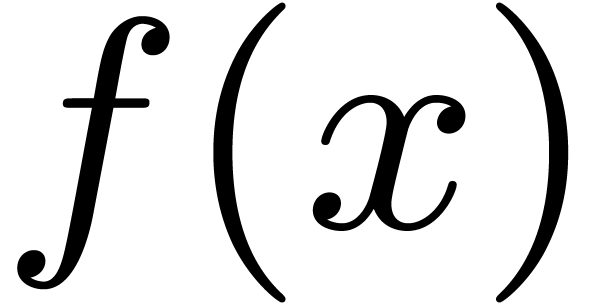 ,
,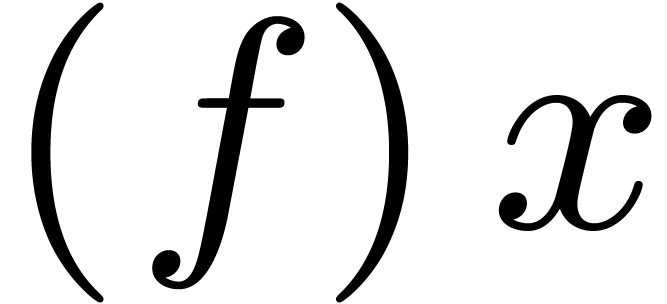 ,
,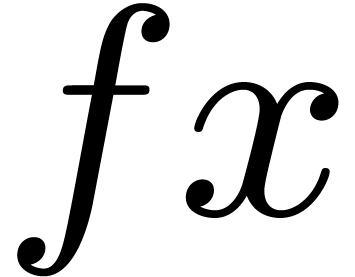 .
. and type expressions
and type expressions  ,
,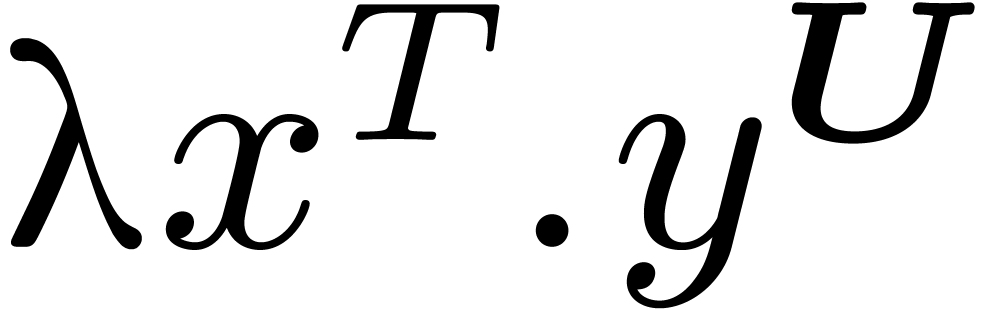 the lambda expression which sends
the lambda expression which sends
 the type of the above
the type of the above
 for this type.
for this type.
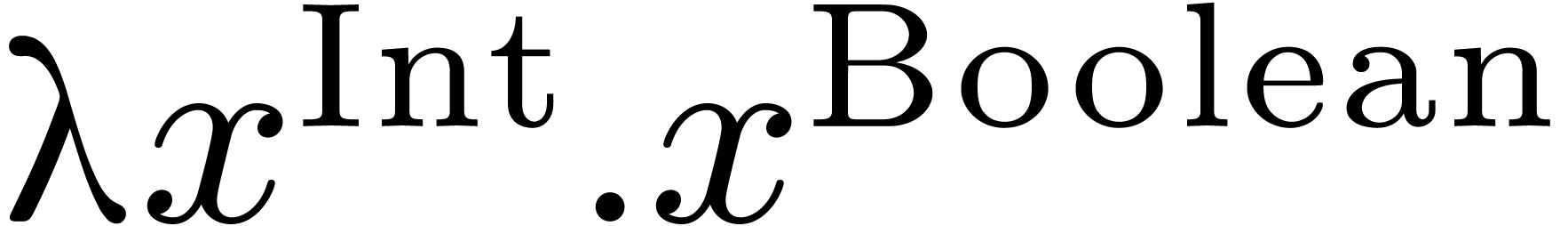 will have no correct
interpretation in the section below.
will have no correct
interpretation in the section below.
 ,
, and expressions
and expressions  ,
,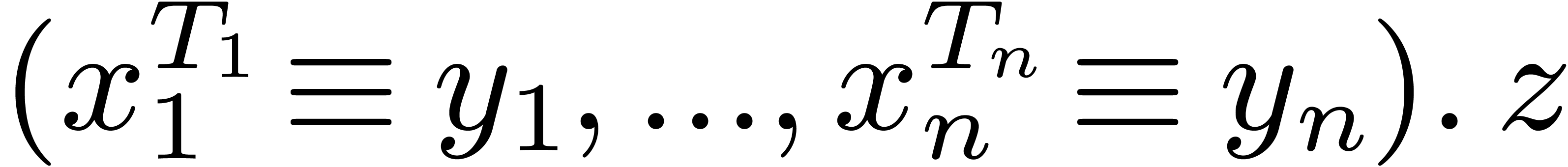 .
. ,
, .
.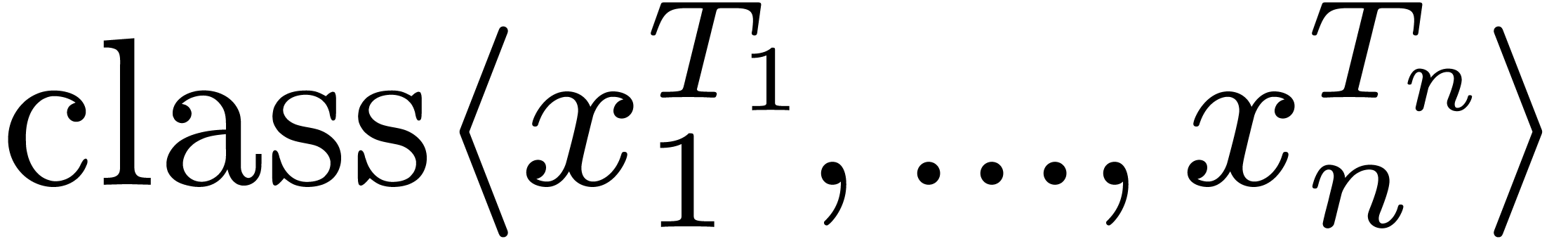 .
. .
. which
will be the type of
which
will be the type of  and type expressions
and type expressions 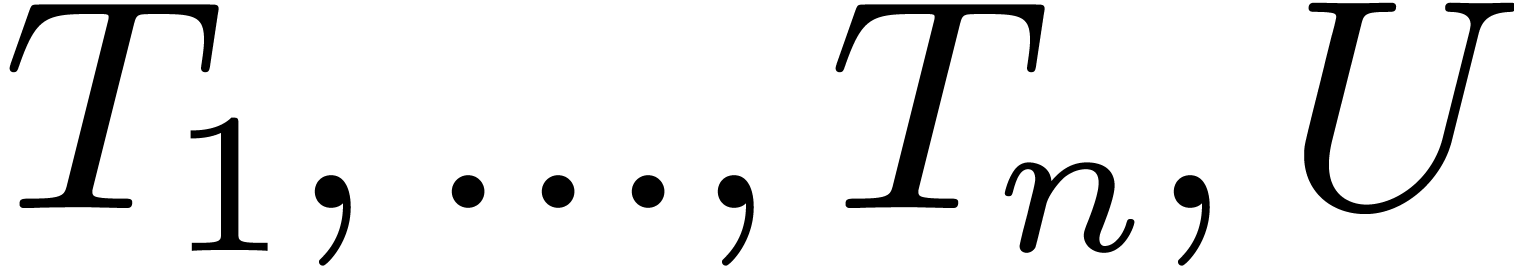 ,
,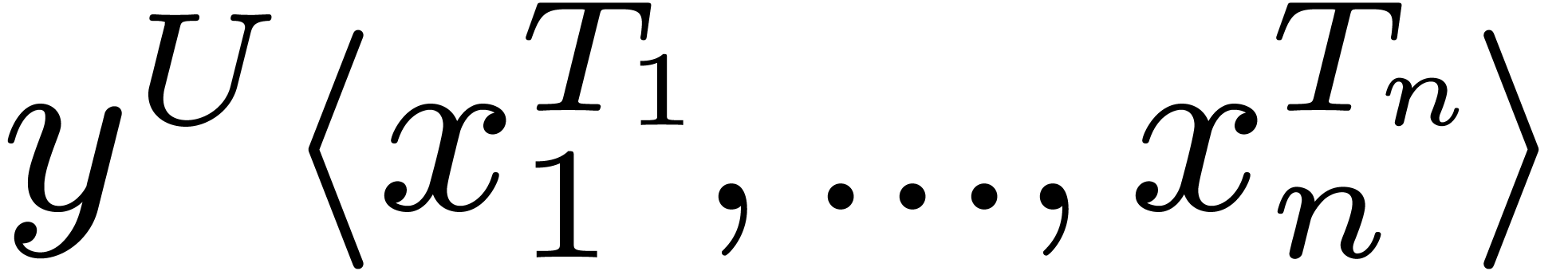 .
. category using
category using 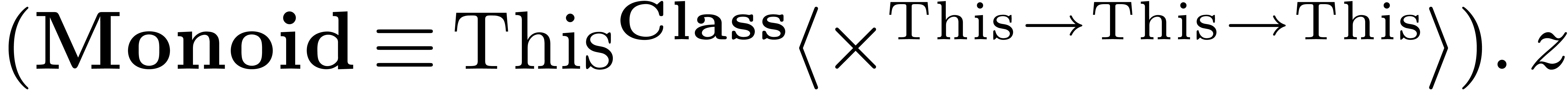 .
. .
. .
.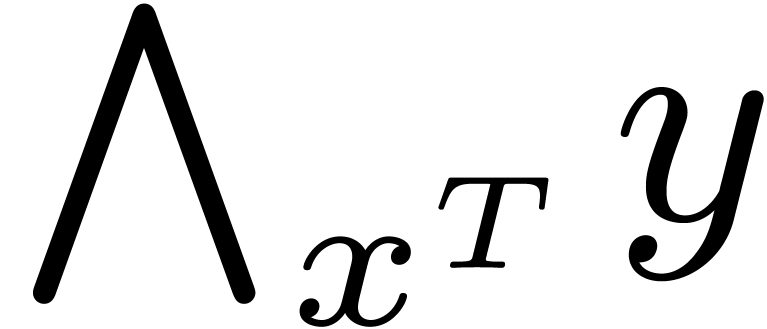 .
.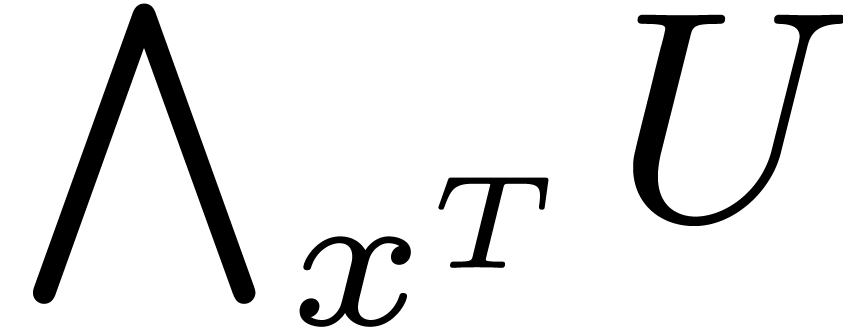 .
. and its
type
and its
type 
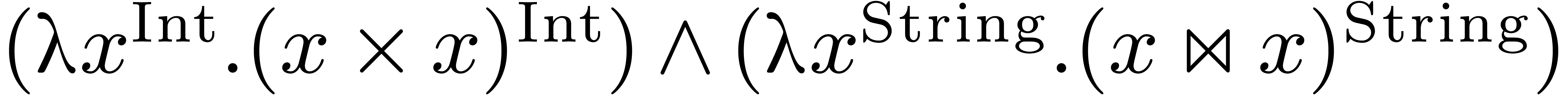
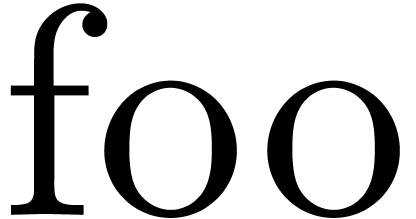 should be interpreted as a function of type
should be interpreted as a function of type
 in the expression
in the expression 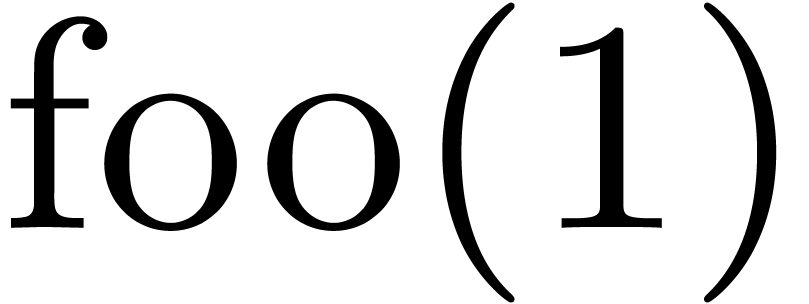 .
. ,
, in the
target language. In that case, we will write
in the
target language. In that case, we will write 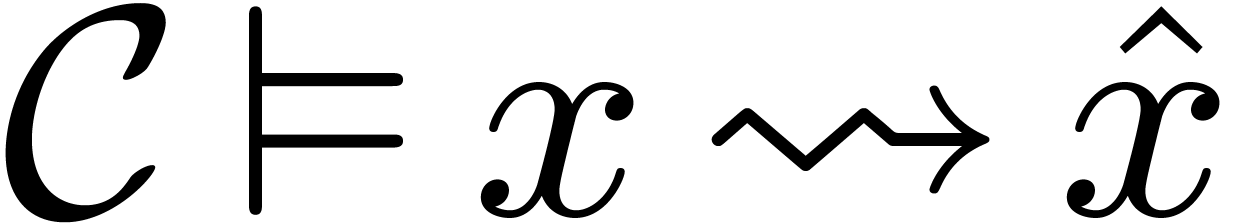 and
the expression
and
the expression 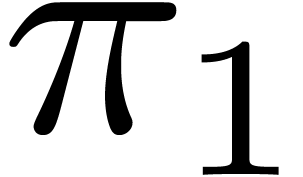 and
and 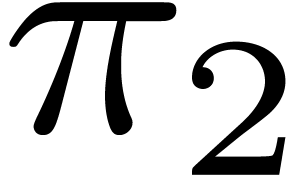 for
accessing the two possible meanings, so that
for
accessing the two possible meanings, so that

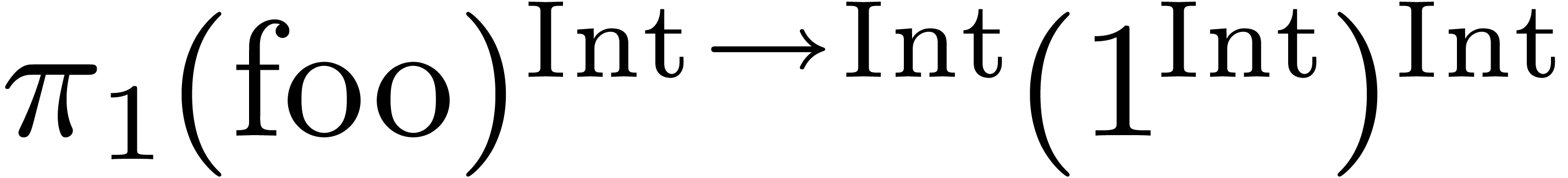 instead of
instead of 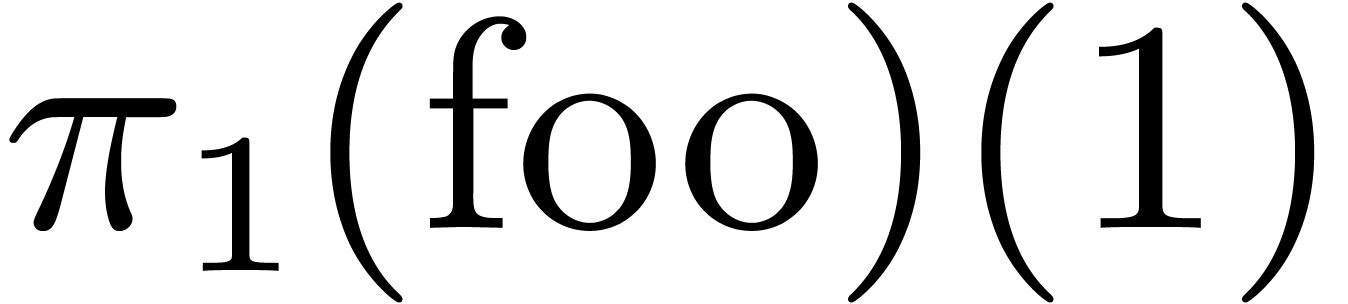 .
.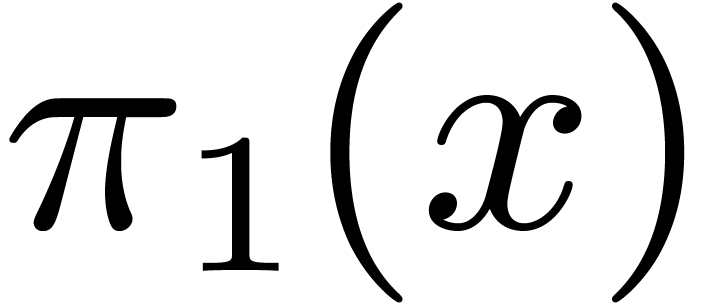 and
and 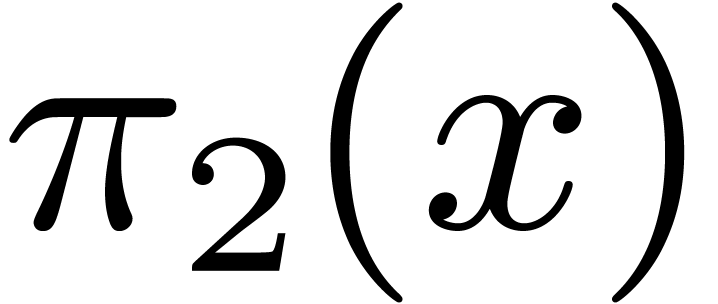 .
. .
.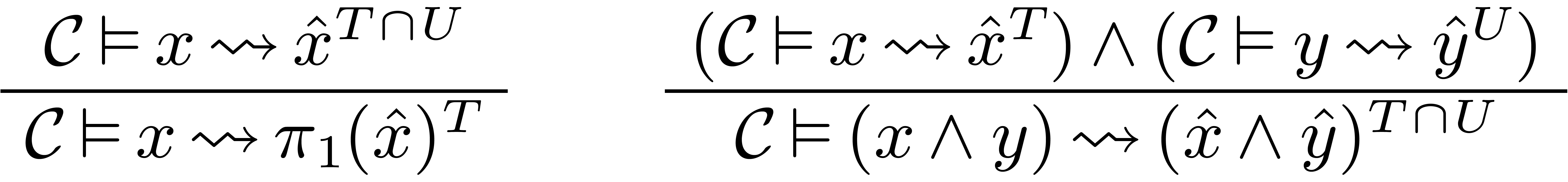
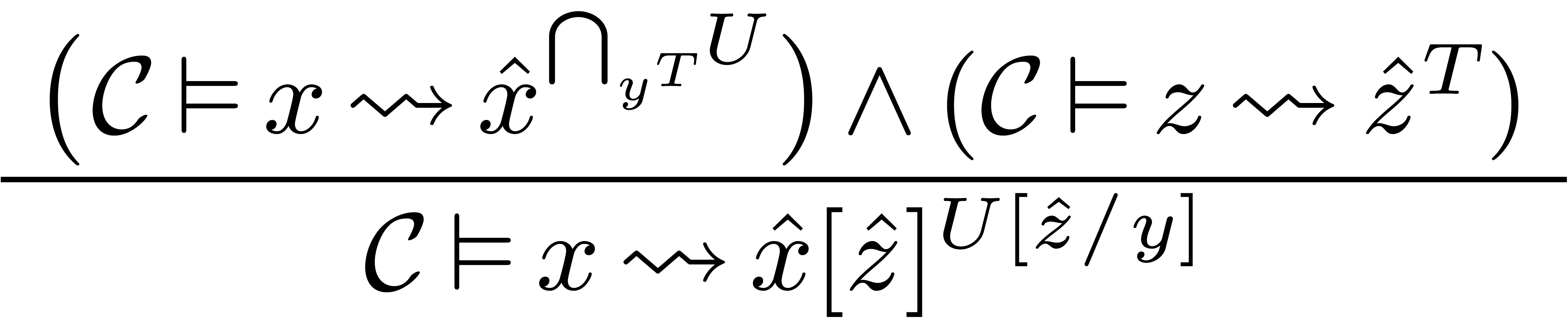
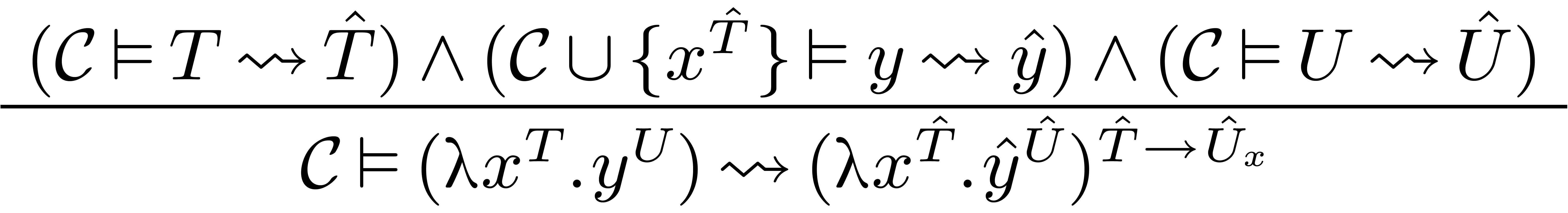
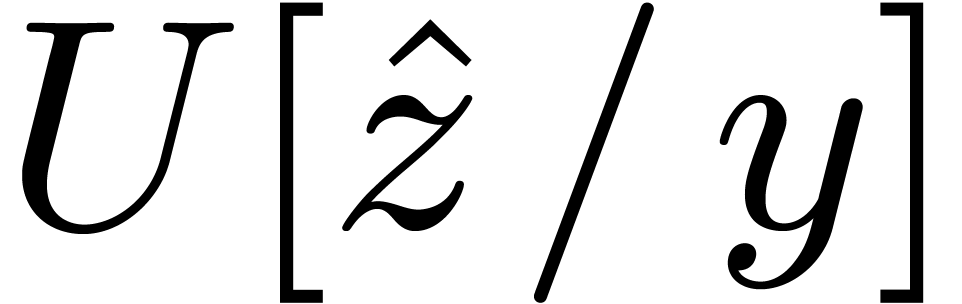 stands for the substitution of
stands for the substitution of  for
for  and
and  .
. considered as an instance of
considered as an instance of  ,
,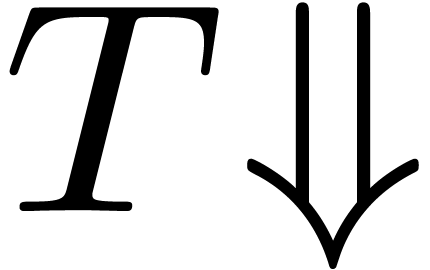 ,
, ,
,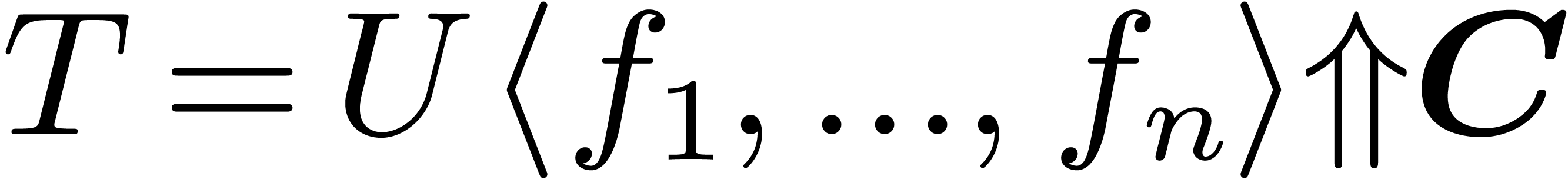 .
. .
.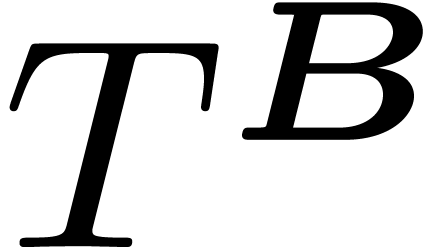 to a given
category
to a given
category 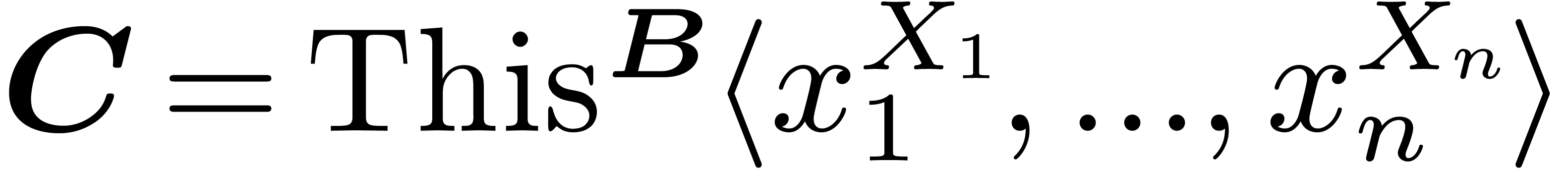 ,
,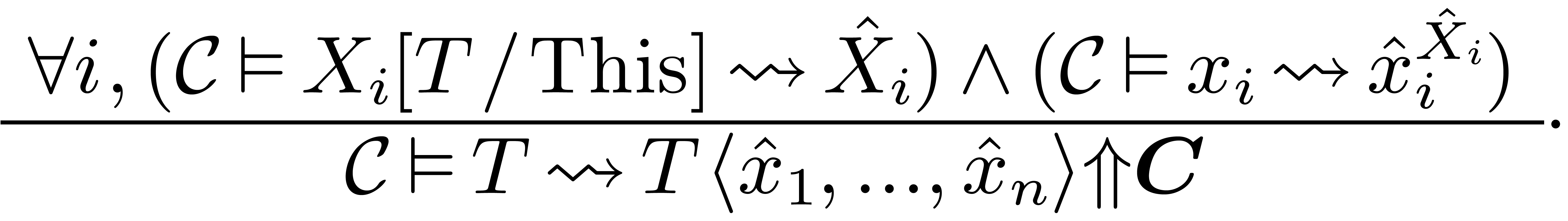
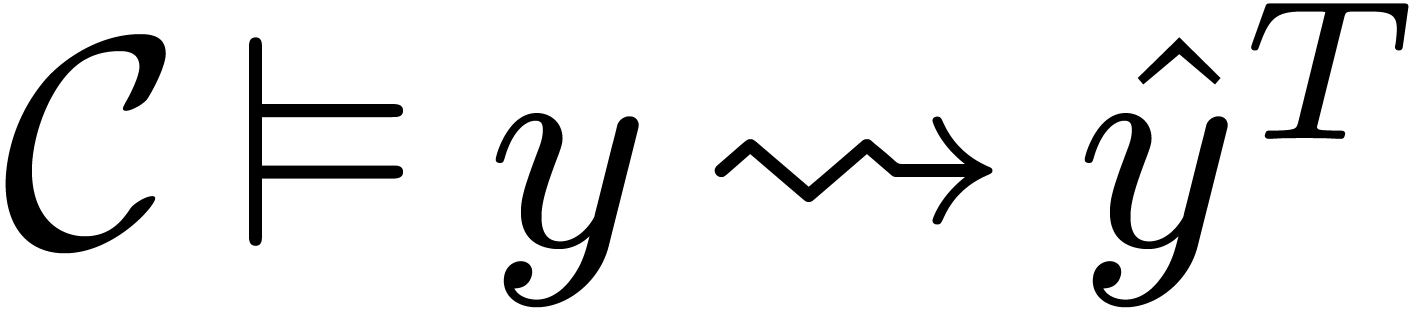 ,
,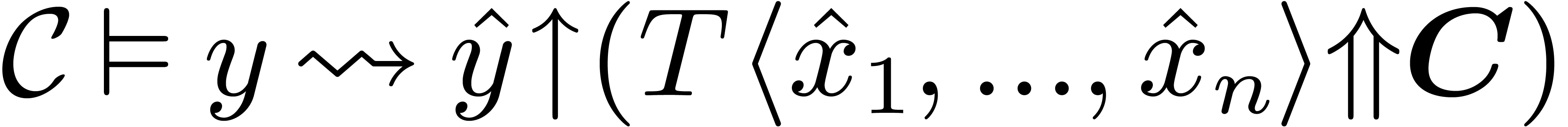 .
.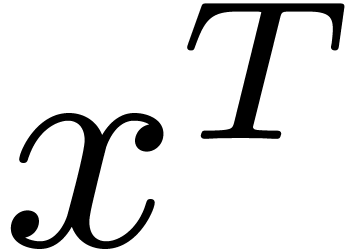 is said to be reduced if its
type
is said to be reduced if its
type  ,
, ,
, or
or  .
. of universally
quantified expressions. In case of success, this target expression
of universally
quantified expressions. In case of success, this target expression 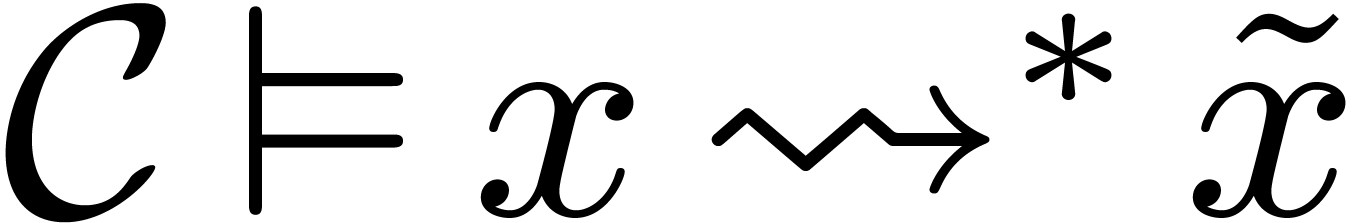 .
.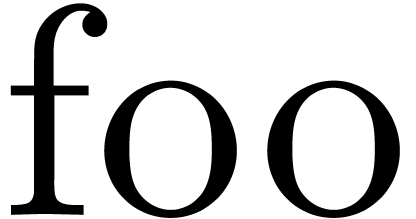 as in (
as in (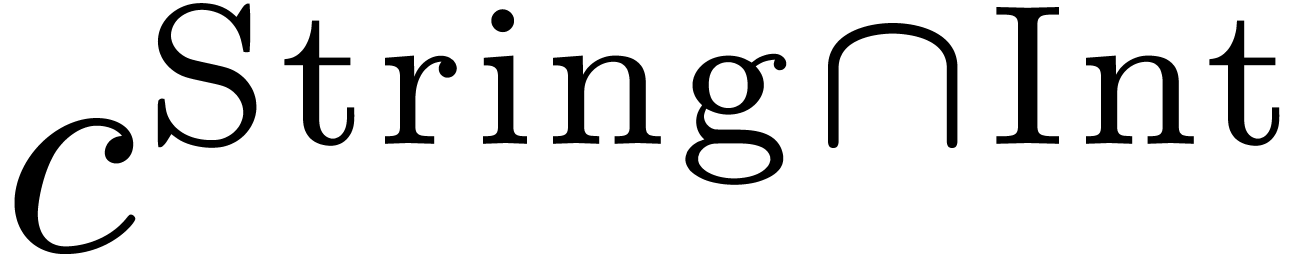 ,
,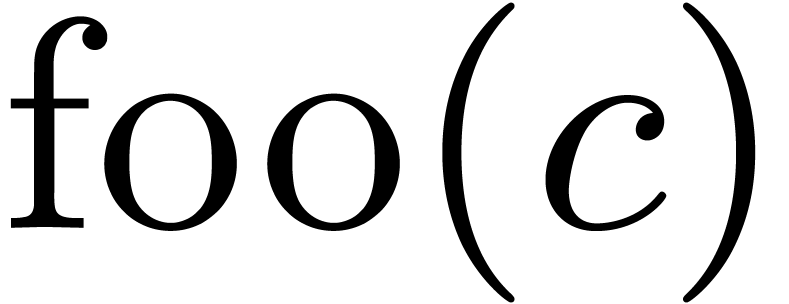 :
: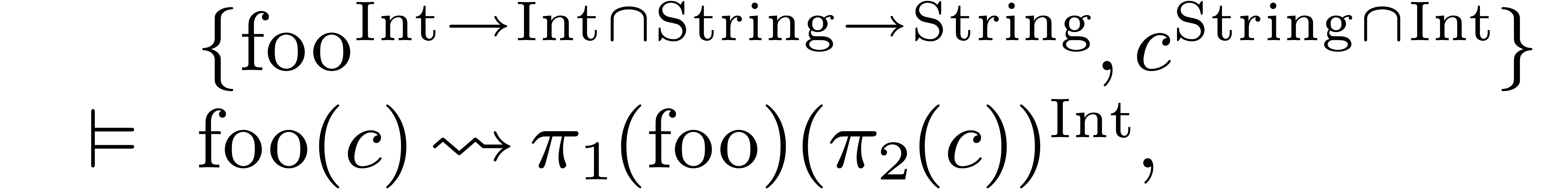
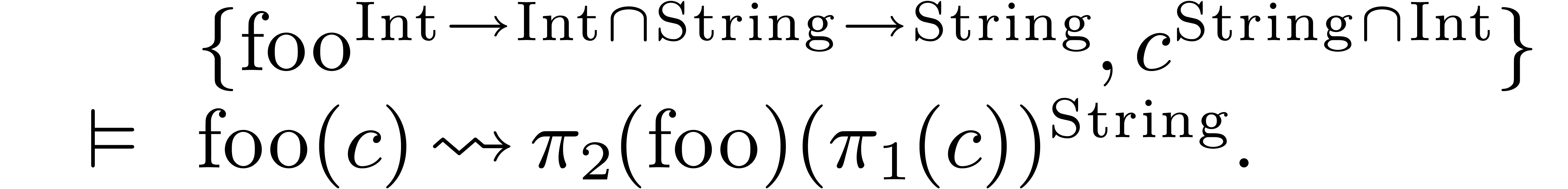
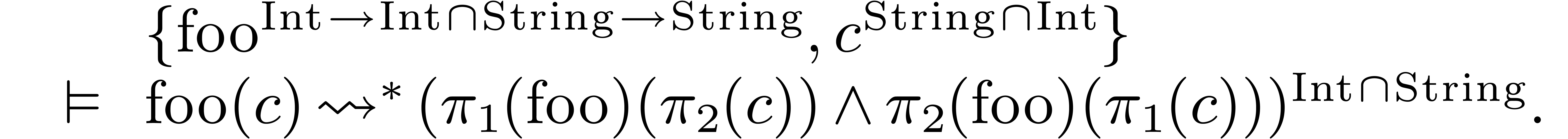
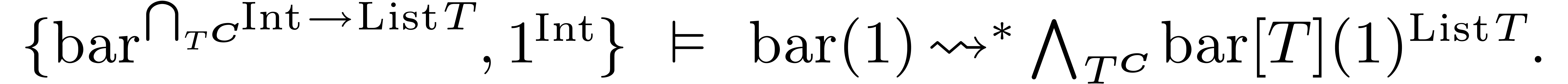
 on
target expressions and to keep only those expressions in the conjunction
on
target expressions and to keep only those expressions in the conjunction
 of
type
of
type 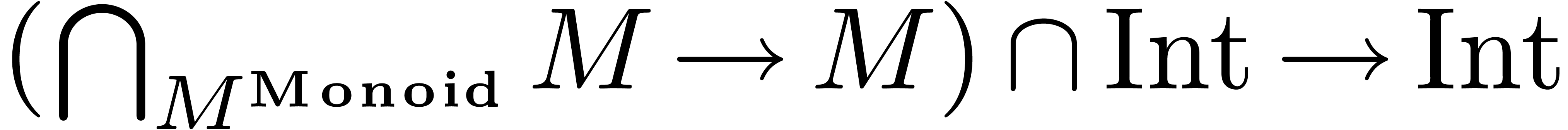 and the constant
and the constant  of
type
of
type  is a partial specialization
of
is a partial specialization
of 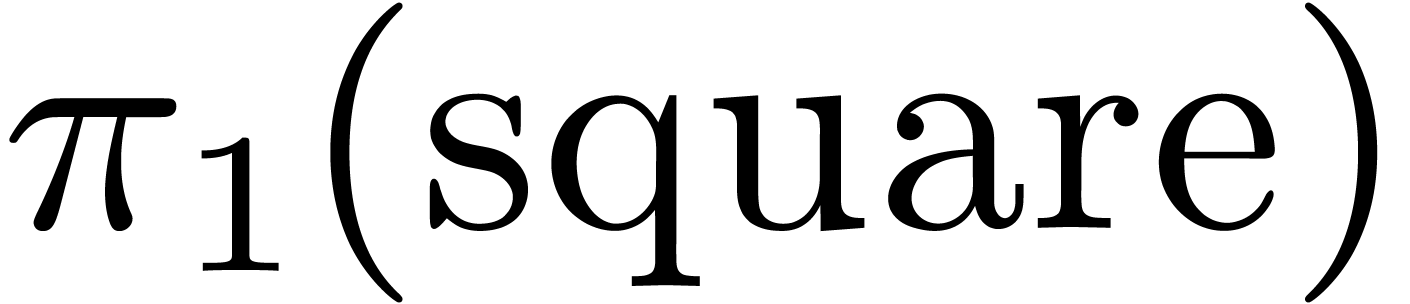 ,
,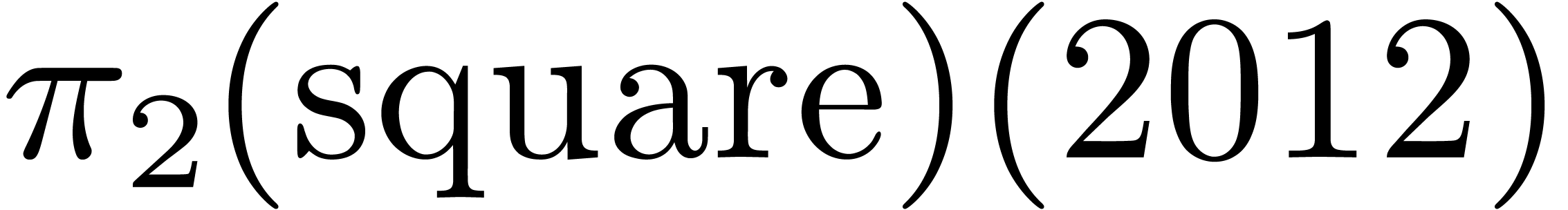 over
over 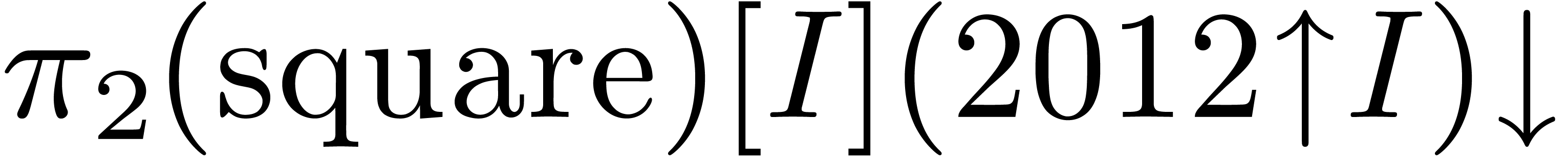 ,
,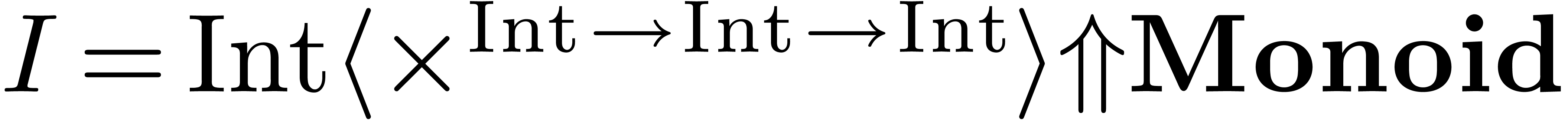 .
.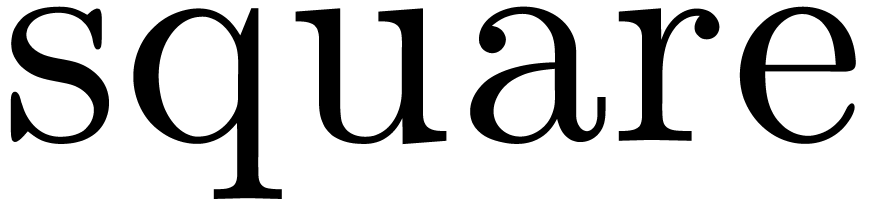 of type
of type 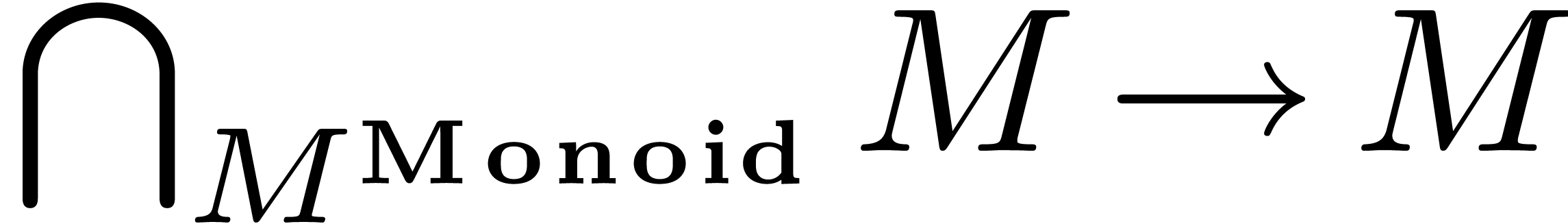 in our context, as well as a multiplication
in our context, as well as a multiplication  .
.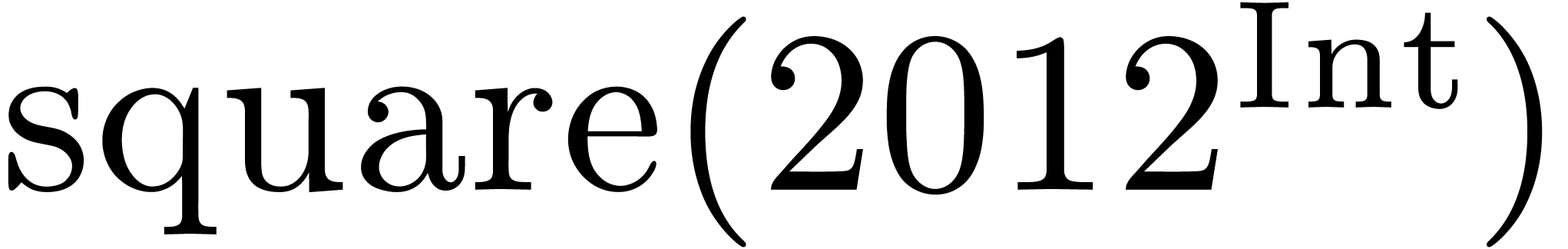 ,
,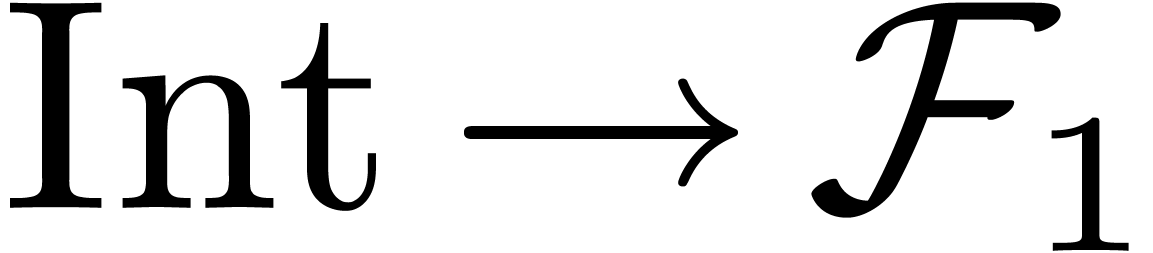 with
with 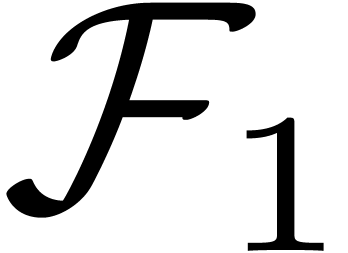 .
.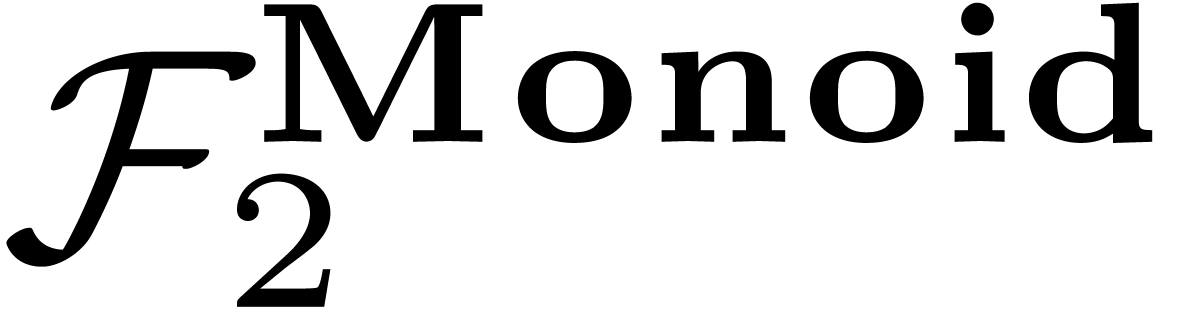 and match
and match  against
against 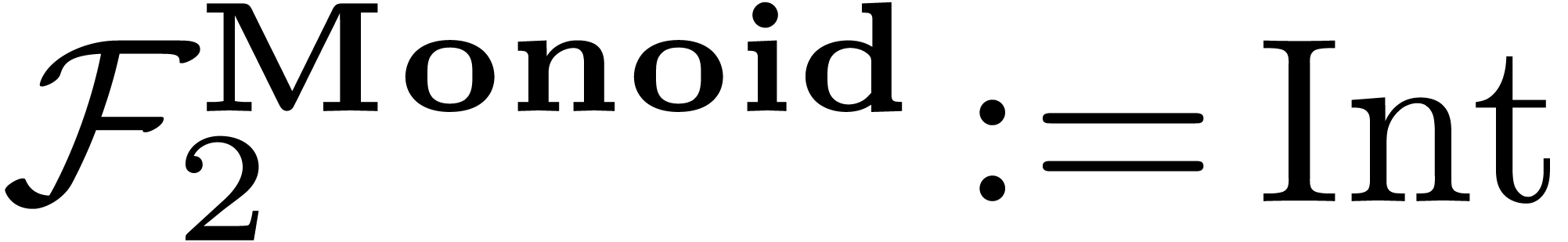 and
and 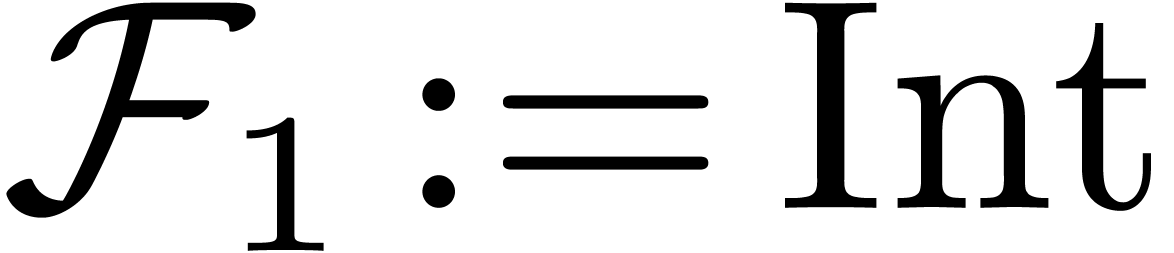 ,
, for the free variable, where
for the free variable, where
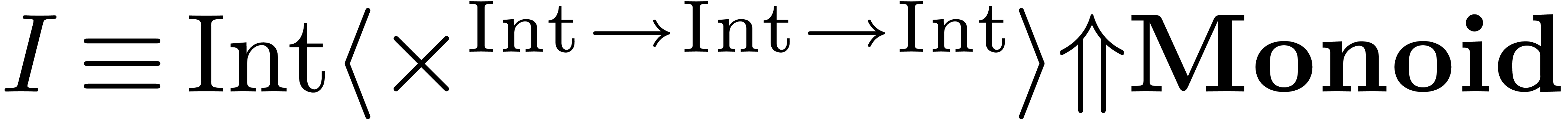 .
.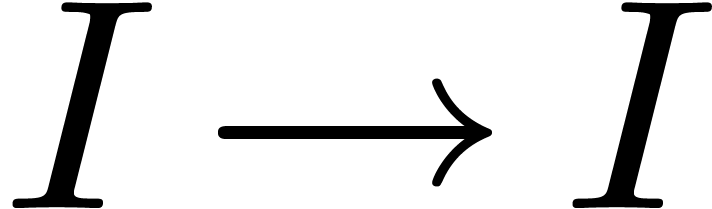 with
with 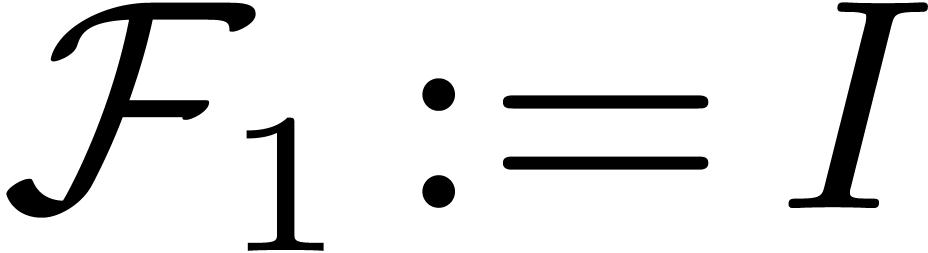 .
. .
.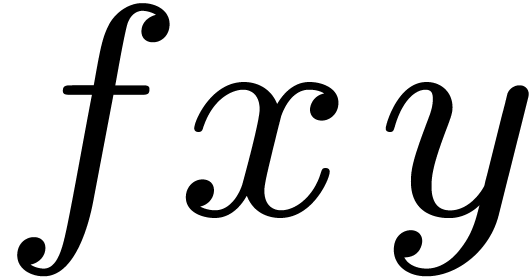 ,
, and
and
 are such that
are such that  and
and  are different? Theoretically speaking, this should be
the type
are different? Theoretically speaking, this should be
the type 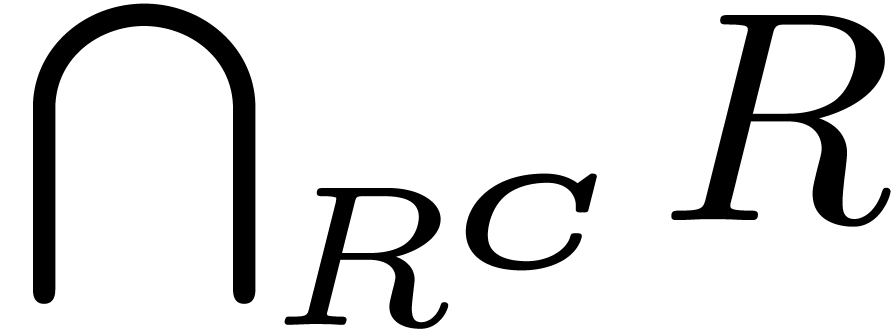 ,
,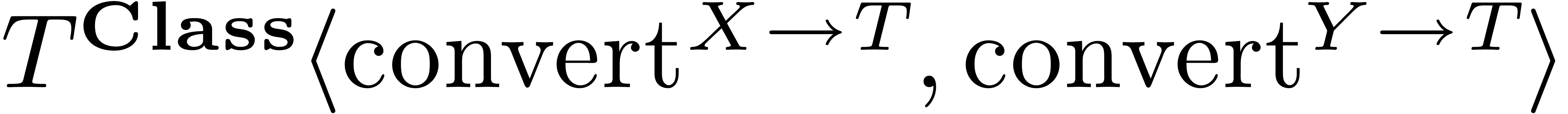 .
.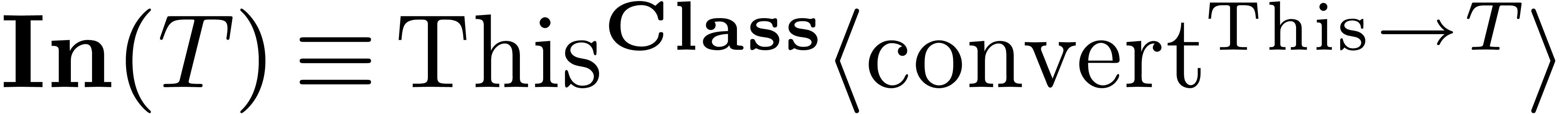 and functions
and functions  and
and  of types
of types 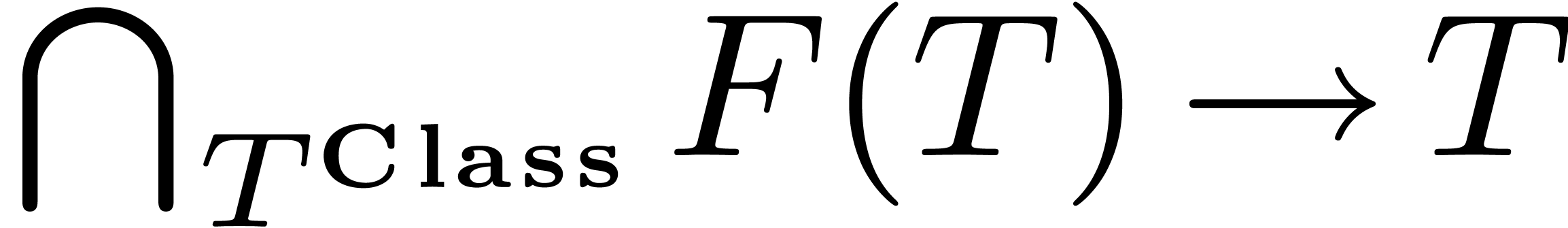 and
and 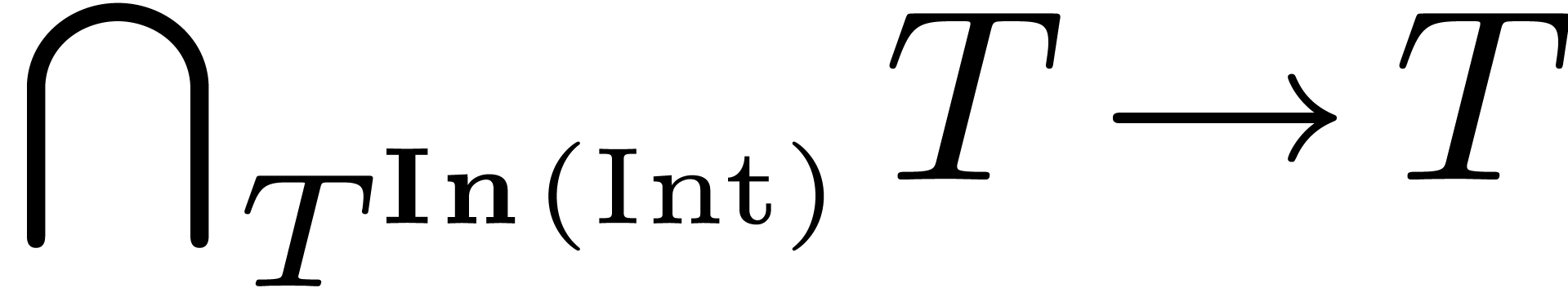 ,
,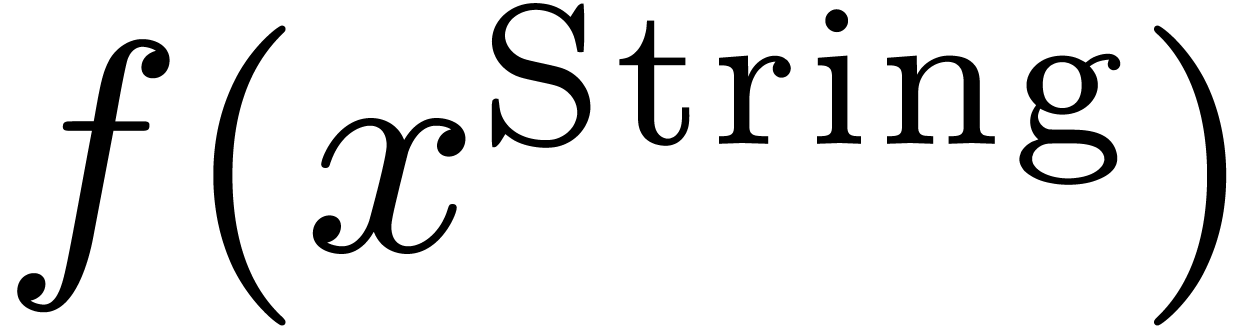 will loop. Indeed, the
compiler will successively search for converters
will loop. Indeed, the
compiler will successively search for converters 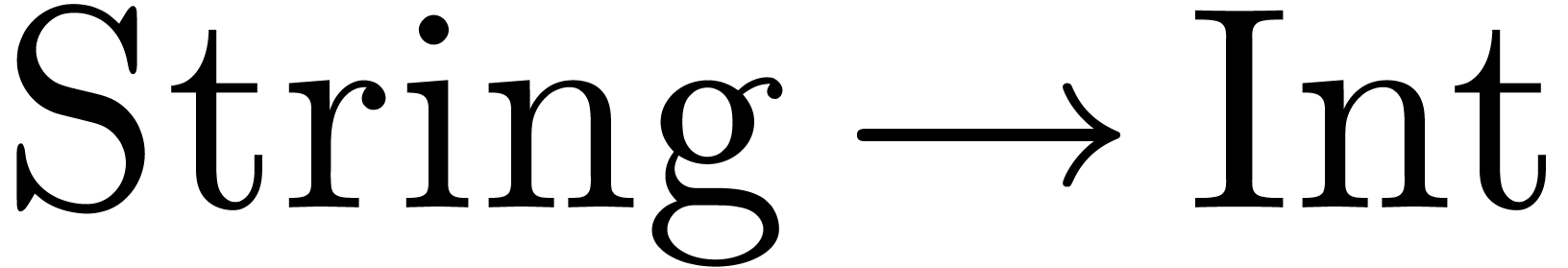 ,
,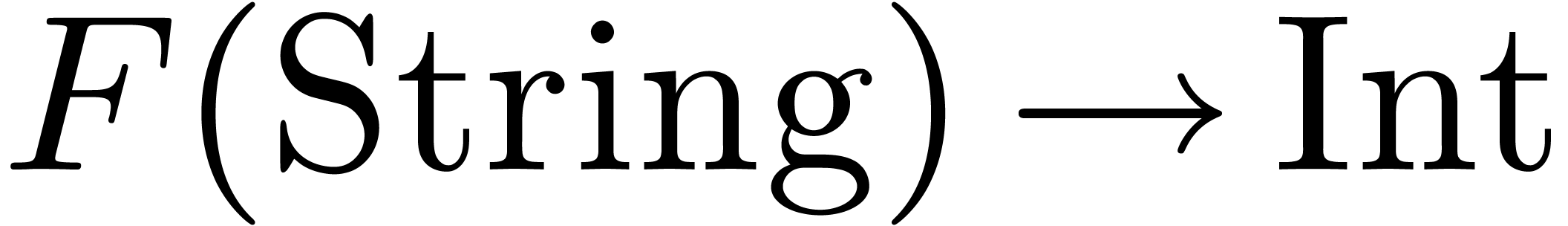 ,
,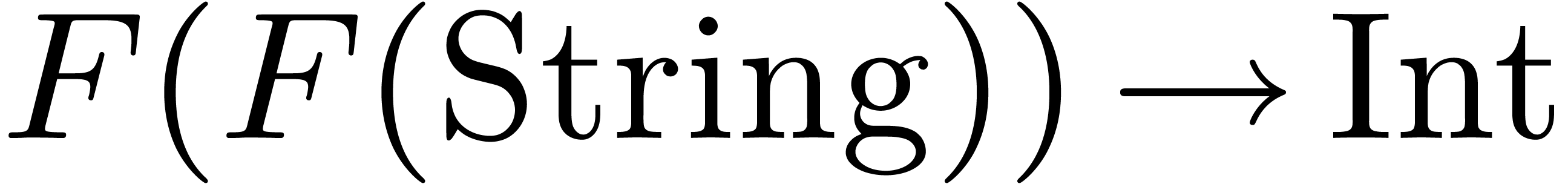 ,
, and function symbols
and function symbols
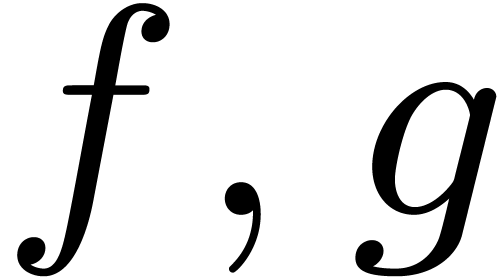 ,
, might be encoded by the declaration of a function
might be encoded by the declaration of a function 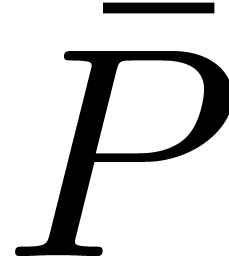 of type
of type 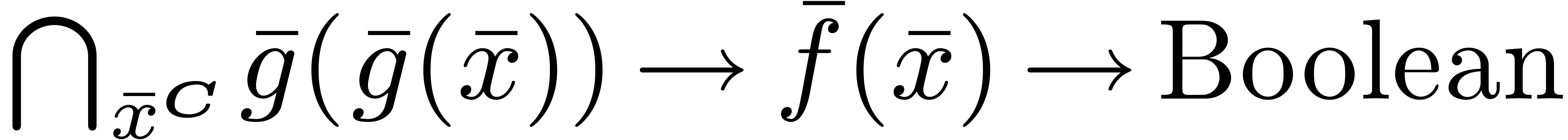 ,
,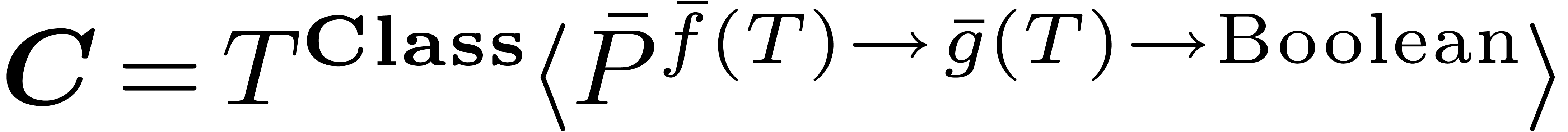 .
.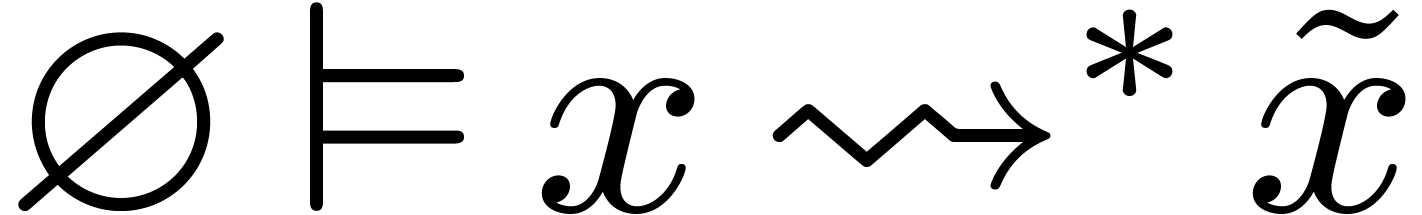 be the expression in the target language
which is produced by the compiler. The target language has the property
that it is quite easy to “downgrade”
be the expression in the target language
which is produced by the compiler. The target language has the property
that it is quite easy to “downgrade”  .
. and
and  .
.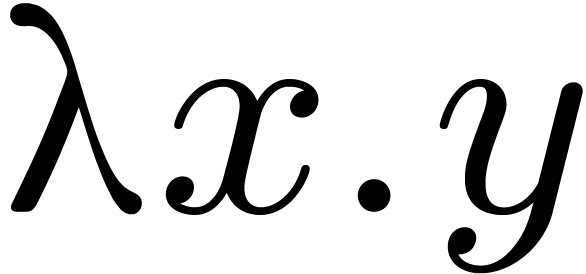 .
.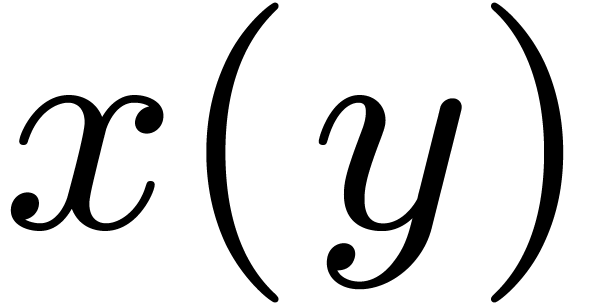 .
.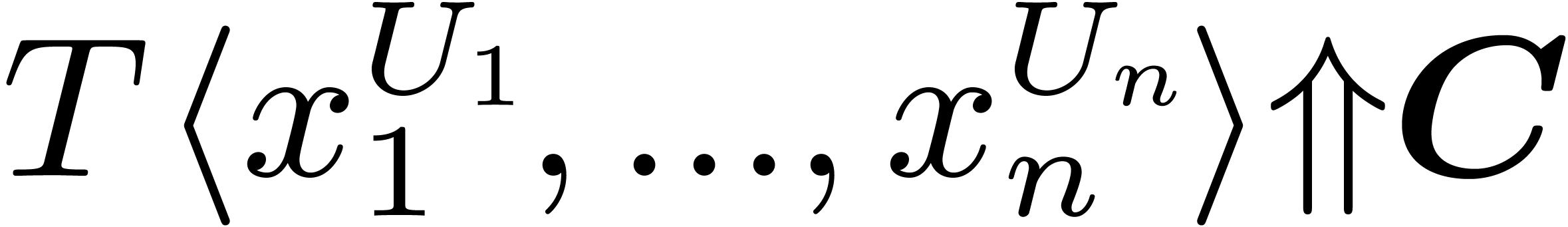 of categories are implemented as
of categories are implemented as
 -tuples
-tuples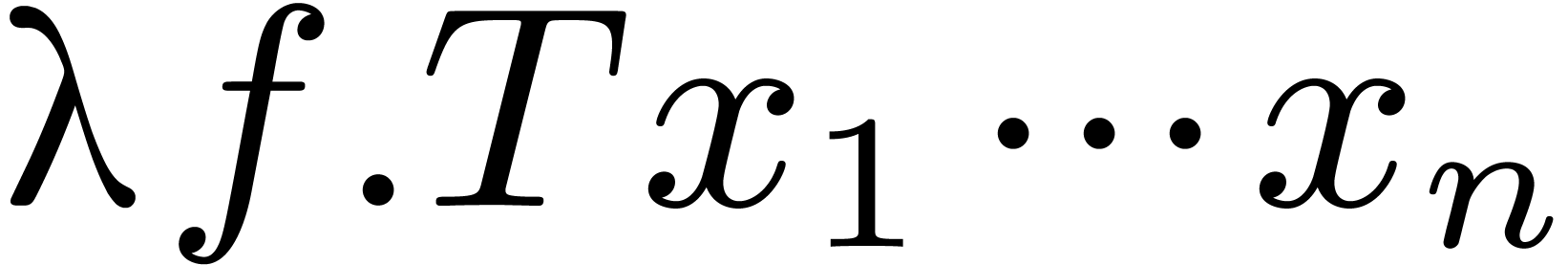 .
.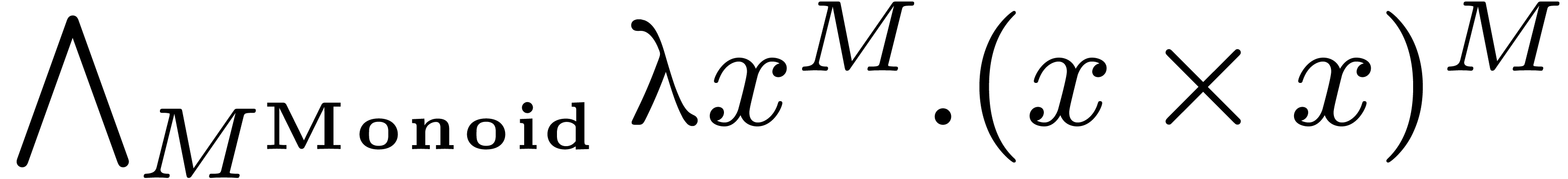 .
.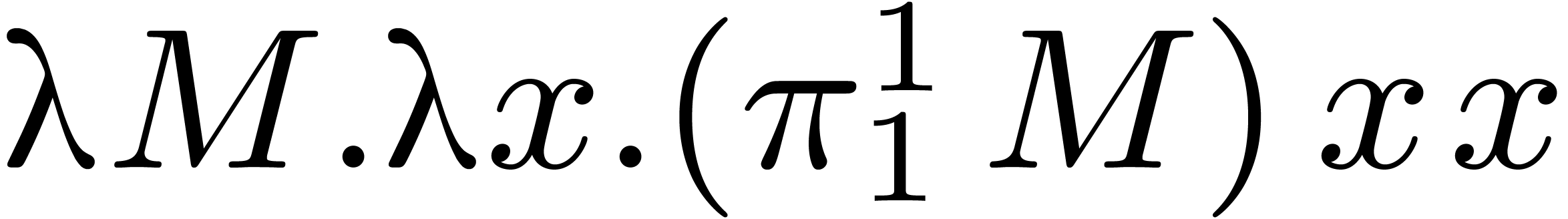 ,
, .
.