|
CNRS (UMI 3069, PIMS)
Department of Mathematics
Simon Fraser University
8888 University Drive
Burnaby, British Columbia
V5A 1S6, Canada
Getallen vermenigvuldigen in
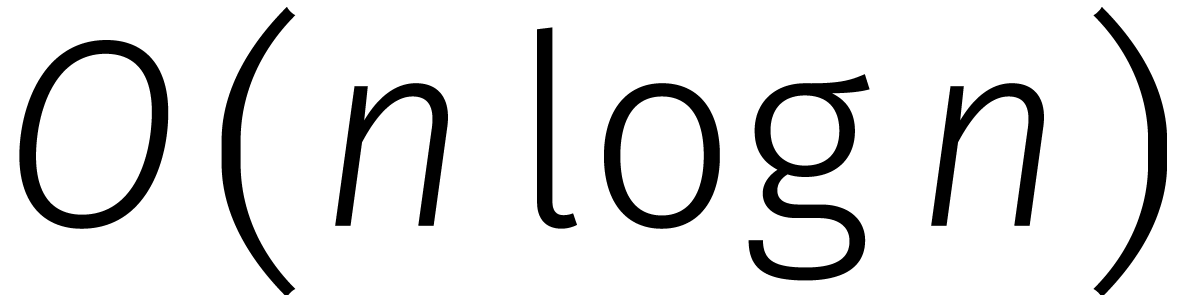 stappen
stappen
Onlangs werd bewezen dat twee getallen van 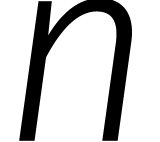 cijfers kunnen worden vermenigvuldigd in
cijfers kunnen worden vermenigvuldigd in 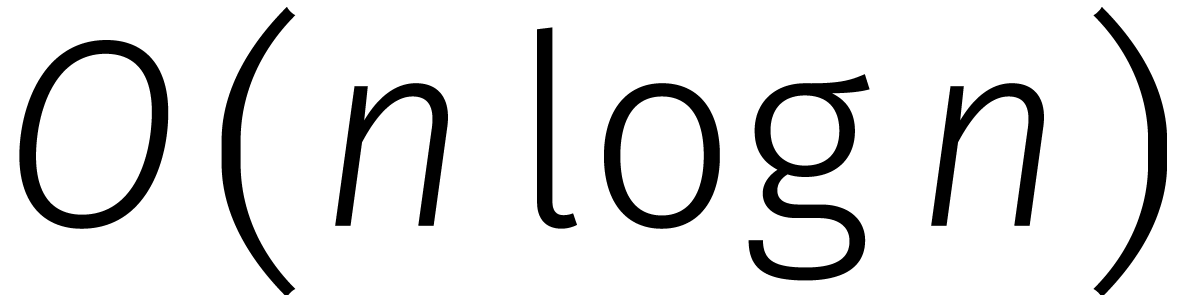 stappen
[12]. In 1971 werd het bestaan van zo'n methode door
Schönhage en Strassen geuit als vermoeden [21]. Ook
verwachtten zij dat het sneller niet gaat, iets dat we nog steeds niet
weten.
stappen
[12]. In 1971 werd het bestaan van zo'n methode door
Schönhage en Strassen geuit als vermoeden [21]. Ook
verwachtten zij dat het sneller niet gaat, iets dat we nog steeds niet
weten.
In dit artikel proberen we eerst een lange geschiedenis kort te houden et dan wat inzicht te geven in het nieuwe bewijs.
Wat is de beste manier om twee gehele getallen met elkaar te vermenigvuldigen? Deze ogenschijnlijk eenvoudige vraag is misschien wel het oudste onopgeloste wiskundeprobleem. Zo is het zeker tien maal ouder dan het vermoeden van Fermat, dat inmiddels de stelling van Wiles heet.
Wél moet hier natuurlijk duidelijk worden gemaakt wat we met
„beste” bedoelen. Dit werd eigenlijk pas mogelijk na de
uitvinding van de Turing machine: uitgerust met een precies rekenmodel
kunnen we spreken over het aantal stappen 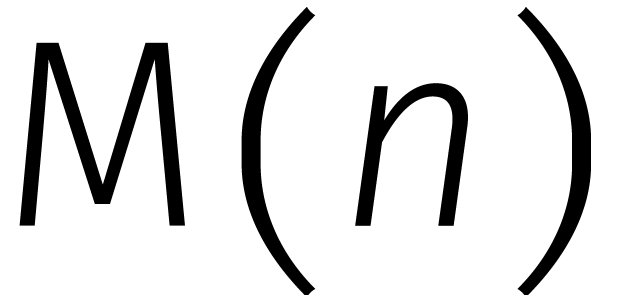 dat
nodig is om twee getallen van
dat
nodig is om twee getallen van 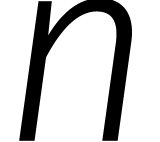 cijfers met elkaar
te vermenigvuldigen. De beste methode is dan diegene waarvoor
cijfers met elkaar
te vermenigvuldigen. De beste methode is dan diegene waarvoor 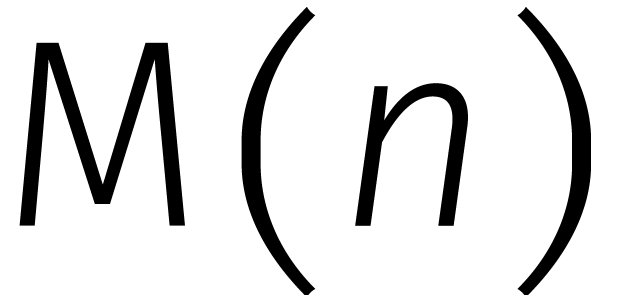 zo langzaam mogelijk stijgt als
zo langzaam mogelijk stijgt als 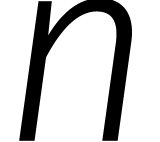 groter wordt.
groter wordt.
Neem bijvoorbeeld de methode van de lagere school. Dan vermenigvuldigen
we elk cijfer van het eerste getal met elk cijfer van het tweede getal
terwijl we de resultaten op de juiste posities bij elkaar optellen. Dat
geeft 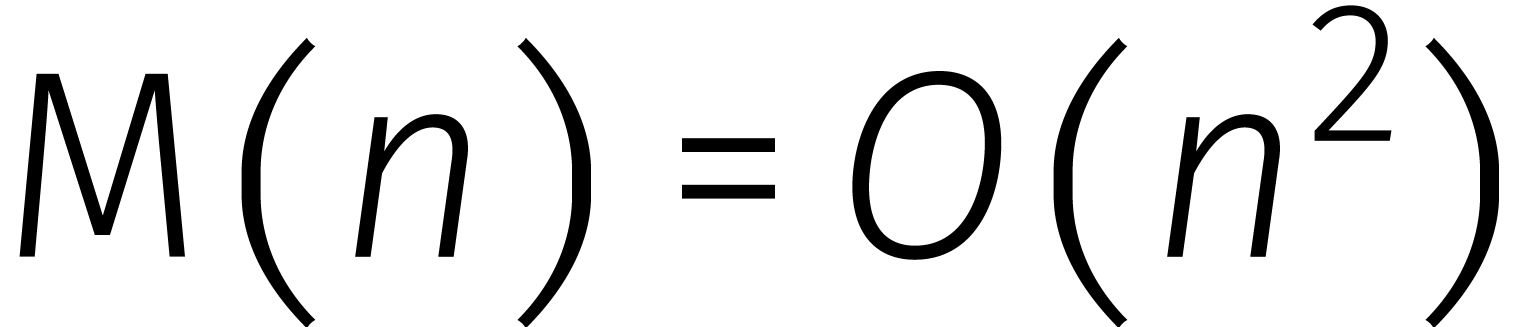 : er bestaat een
constante
: er bestaat een
constante  met
met 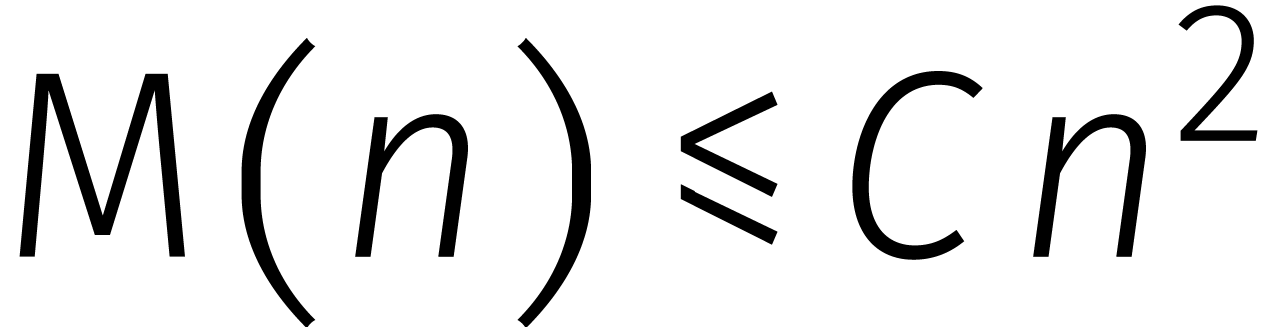 voor
iedere
voor
iedere 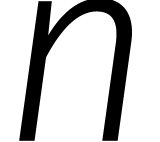 .
.
Om onze hoofdvraag onafhankelijk te maken van de daadwerkelijke Turing
machine waarop we onze berekening doen, zijn we enkel
geïnteresseerd in rekentijd op een constante factor na. Een honderd
maal snellere methode is dus geen wezenlijke verbetering, maar een  maal sneller algoritme is een enorme stap voorwaarts.
maal sneller algoritme is een enorme stap voorwaarts.
Waarschijnlijk formuleerde Kolmogorov
de vraag voor het eerst op deze manier, tijdens een beroemd seminarium in Moskou. In zijn enthousiasme lanceerde hij ook meteen het vermoeden dat .
Want, zo redeneerde hij, als er betere methode bestond dan die van
school, dan zou die sinds zesduizend jaar toch wel zijn uitgevonden.
.
Want, zo redeneerde hij, als er betere methode bestond dan die van
school, dan zou die sinds zesduizend jaar toch wel zijn uitgevonden.
De nauwkeurige formulering van een probleem maakt het zoeken naar
oplossingen makkelijker. Maar het ontbreken daarvan sluit het zoeken
naar oplossingen nou ook weer niet uit. De Babyloniërs berekenden
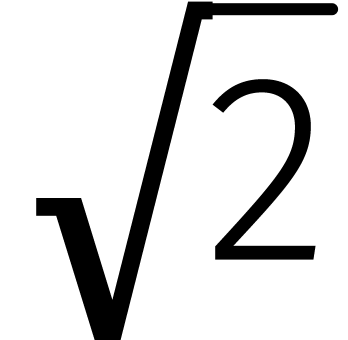 al tot op zestien decimalen achter de komma.
Wellicht vinden we ooit een kleitablet waarop
hogesnelheidsvermenigvuldigingsmethodes staan uitgelegd. Liefhebbers van
het getal
al tot op zestien decimalen achter de komma.
Wellicht vinden we ooit een kleitablet waarop
hogesnelheidsvermenigvuldigingsmethodes staan uitgelegd. Liefhebbers van
het getal  , zoals de bij ons
bekende Ludolph van Ceulen, zouden daar vast wel wat aan kunnen hebben
gehad (zie Figuur 1).
, zoals de bij ons
bekende Ludolph van Ceulen, zouden daar vast wel wat aan kunnen hebben
gehad (zie Figuur 1).
Kolmogorov's vermoeden hield niet lang stand. Na drie weken werd hij
verrast dooreen jonge student met een vermenigvuldigingsmethode in 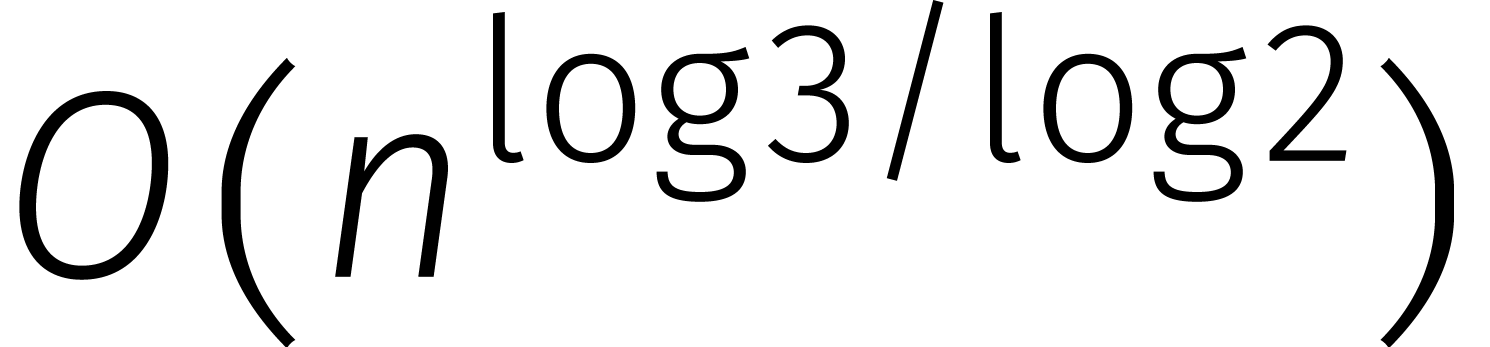 stappen. Meteen schreef hij het nieuwe algoritme op
en publiceerde het onder de naam van de bedenker, Karatsuba, samen met
een ander artikel dat er niets mee te maken had [16, 15].
stappen. Meteen schreef hij het nieuwe algoritme op
en publiceerde het onder de naam van de bedenker, Karatsuba, samen met
een ander artikel dat er niets mee te maken had [16, 15].
Laten we Karatsuba's idee uitleggen met een voorbeeld:
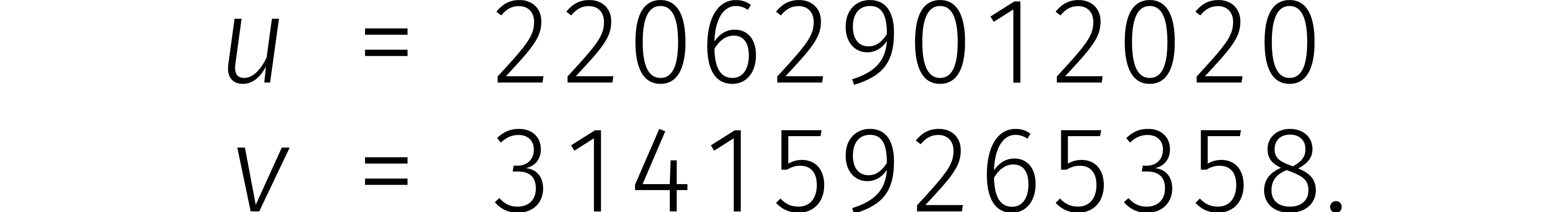
Eerst splitsen we beide getallen in tweeën:
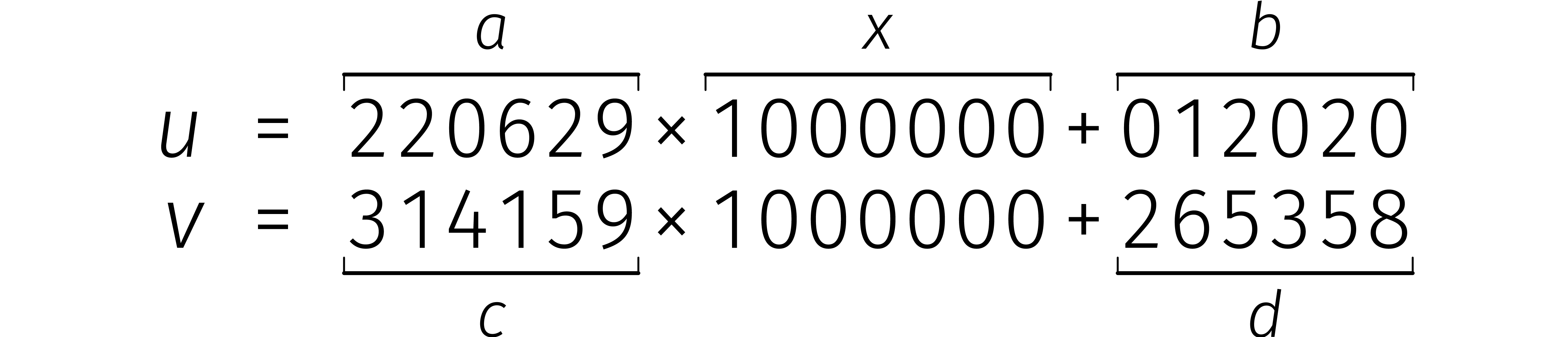
Daarna doen we twee optellingen en drie vermenigvuldigingen:
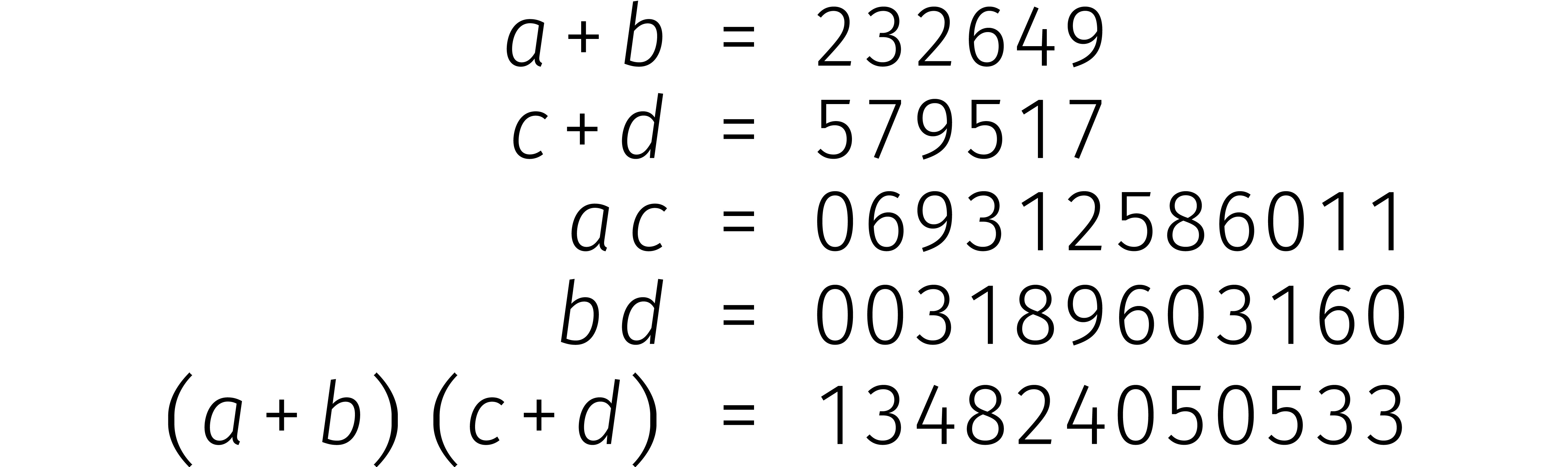
Nu merken we op dat het slechts twee keer aftrekken vergt om
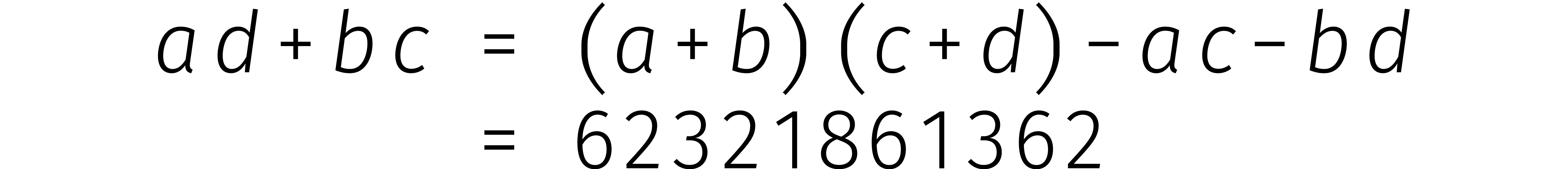
te bepalen. Tot slot geldt
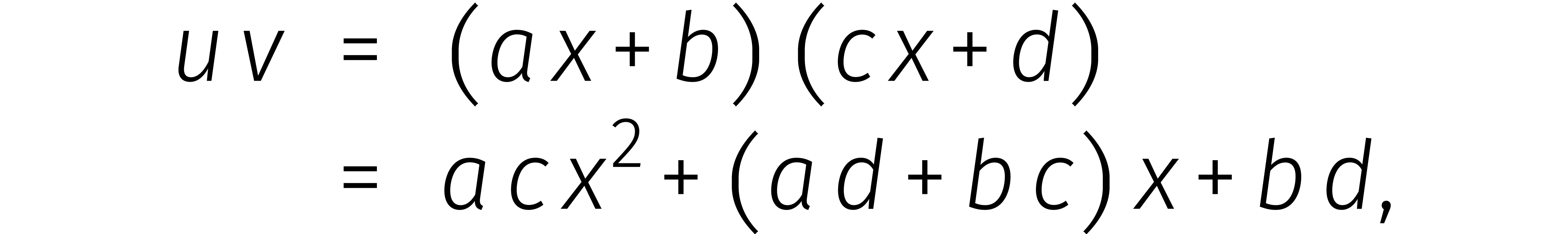
zodat we klaar zijn na een laatste optelsom

Al met al hebben we een vermenigvuldiging van 12 cijfers teruggevoerd tot drie vermenigvuldigingen van 6 cijfers en een stel optel- en aftreksommen.
In het algemeen kost het vermenigvuldigen van twee maal zo lange getallen ongeveer drie maal zoveel tijd. Dit kan goed worden samengevat in een recurrente ongelijkheid:
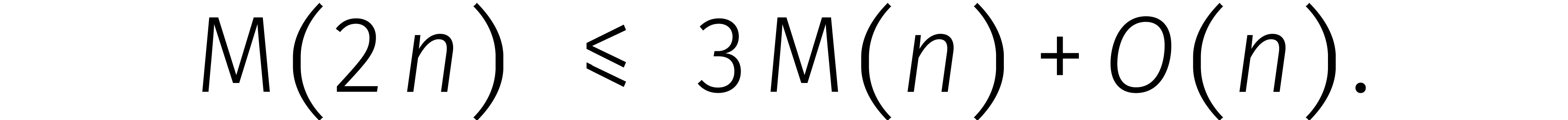
Voor een zekere constante  en
en 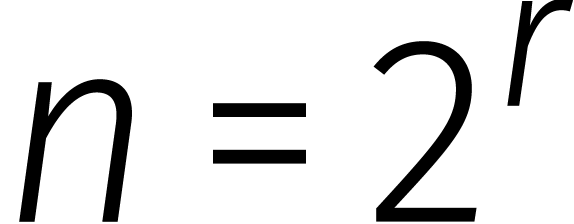 hebben we dus
hebben we dus
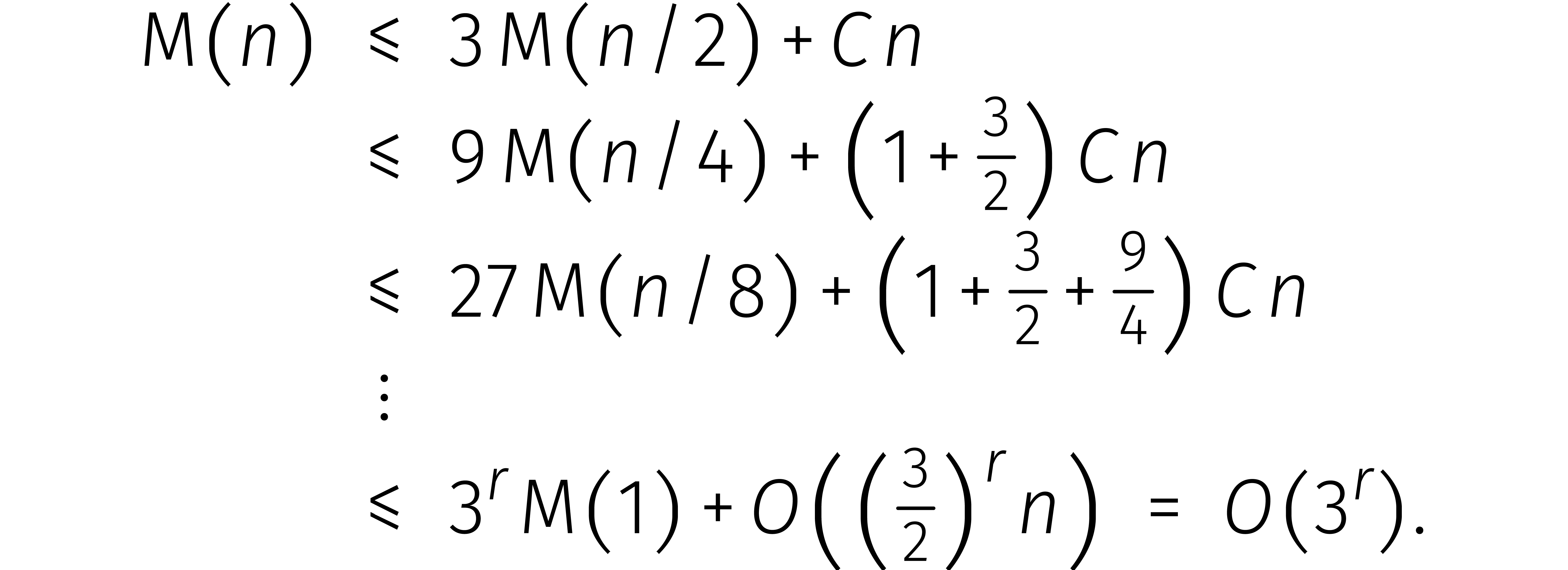
Nu kunnen we links altijd extra nullen aan een getal toevoegen zodat het aantal cijfers een tweemacht wordt. Uiteindelijk bewijzen we zo dat
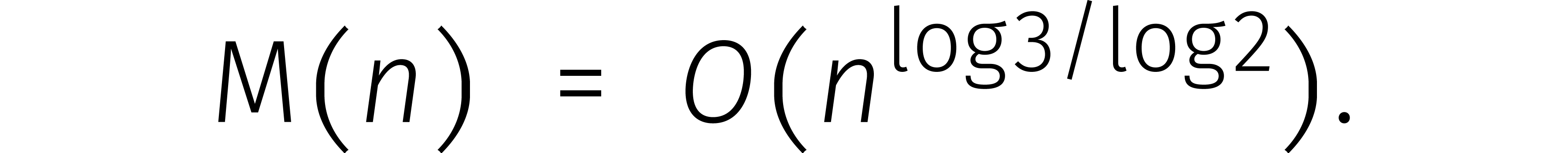
Één van de ingrediënten van Karatsuba's methode is
het opsplitsen van getallen in twee delen. Dit maakte het mogelijk om
 en
en 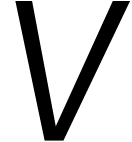 te zien als
veeltermen
te zien als
veeltermen 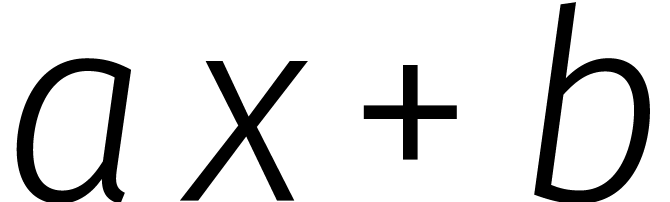 en
en 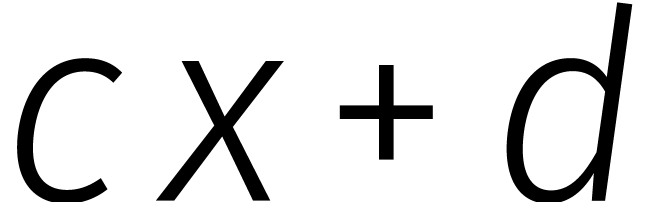 van graad
van graad
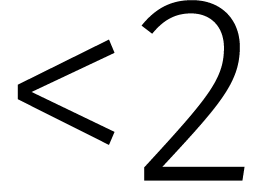 . In feite kwam dat simpelweg
neer op het werken in een talstelsel met grondtal
. In feite kwam dat simpelweg
neer op het werken in een talstelsel met grondtal 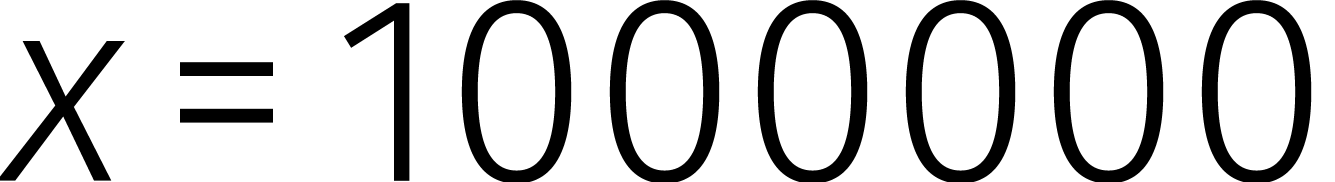 in plaats van
in plaats van 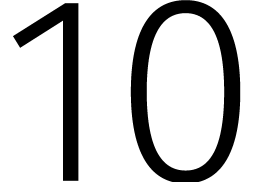 .
.
Dit idee om het rekenen met gehele getallen te vervangen door het
rekenen met veeltermen werd in the 19de eeuw reeds geopperd
door Kronecker. Zo kunnen we een getal van 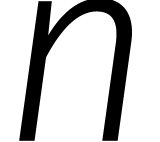 cijfers opsplitsen in
cijfers opsplitsen in 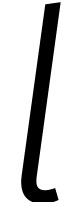 brokken van
brokken van 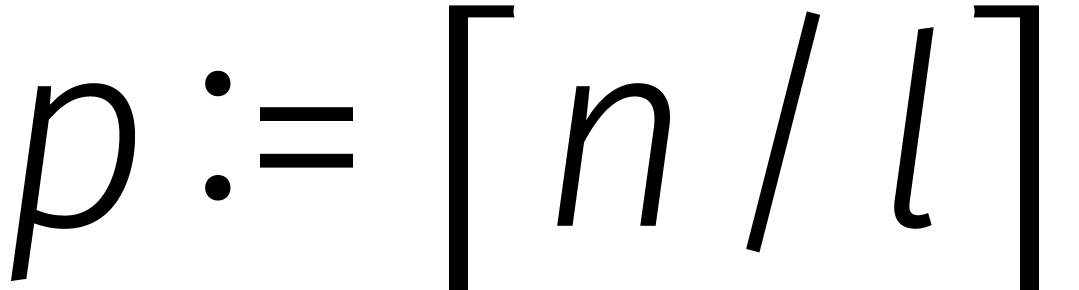 cijfers en daar weer een veelterm van maken.
cijfers en daar weer een veelterm van maken.
Door het aantal brokken
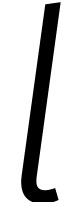 groter dan twee te kiezen, werden er in de zestiger jaren een reeks
snellere varianten van Karatsuba's methode ontwikkeld [
22
,
20
,
17
]; zie Tabel
1
voor een historisch overzicht.
groter dan twee te kiezen, werden er in de zestiger jaren een reeks
snellere varianten van Karatsuba's methode ontwikkeld [
22
,
20
,
17
]; zie Tabel
1
voor een historisch overzicht.
|
||||||||||||||||||||||||||||||||||||||||
Zonder al te ver op details in te gaan, is elk van deze varianten
gebaseerd op een veralgemening van Karatsuba's rekentruc. In dit geval
wordt de vermenigvuldiging van twee veeltermen van graad 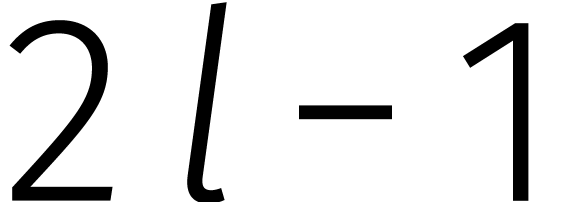 gereduceerd tot
gereduceerd tot 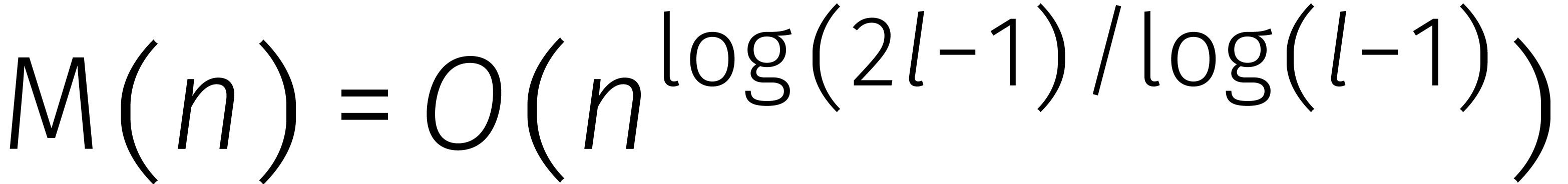 vermenigvuldigingen van coëfficiënten, waarna
vermenigvuldigingen van coëfficiënten, waarna 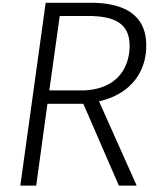 .
.
Vanaf nu gaan we we het vooral hebben over het vermenigvuldigen van
veeltermen en is het handig om te werken met coëfficiënten in
een algemene ring 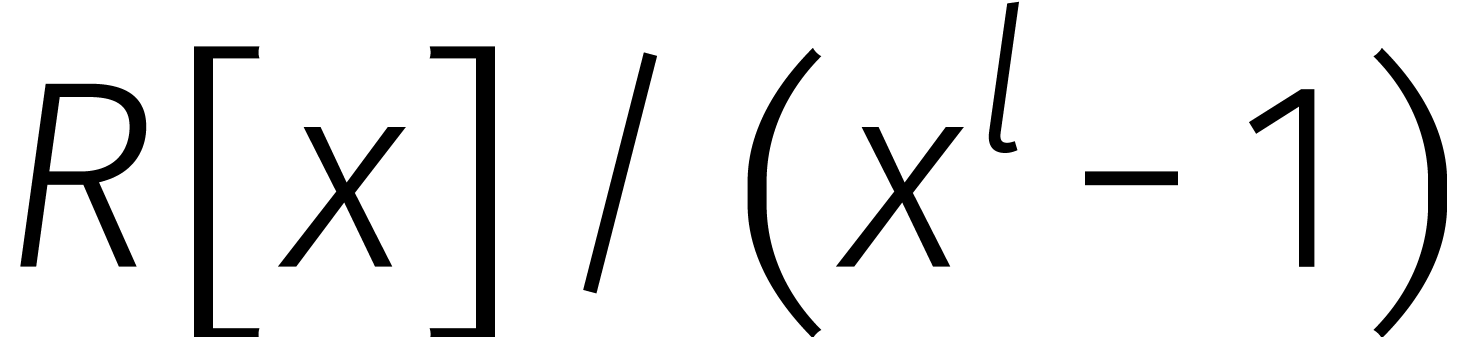 . De
precieze keus van
. De
precieze keus van 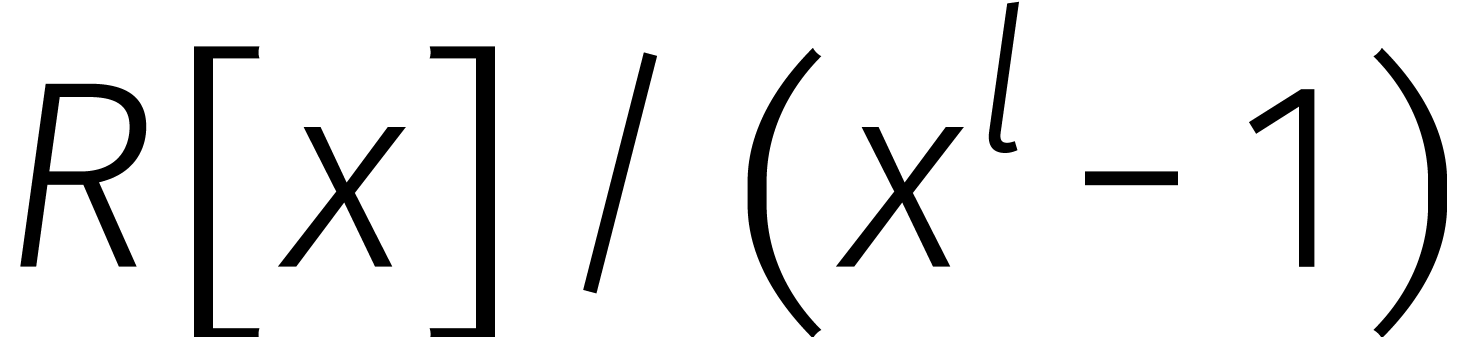 laten we voorlopig in het
midden.
laten we voorlopig in het
midden.
Voor wat komen gaat, is het ook handig om met zogenaamde
„kringtermen” in plaats van veeltermen te werken. Een
kringterm van lengte 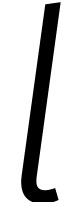 is een element van
is een element van
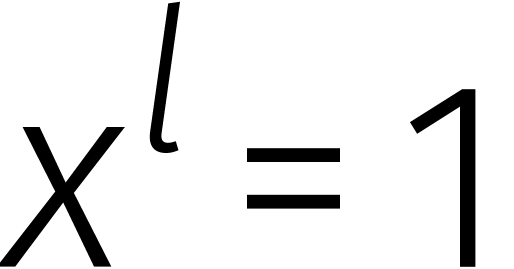 .
.
De relatie 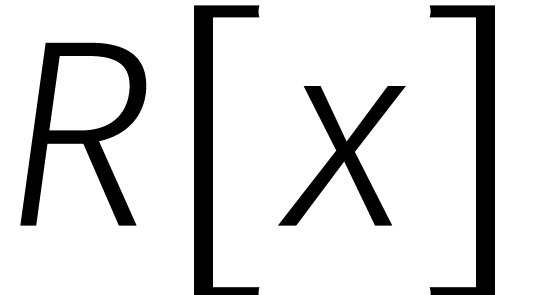 treedt pas in actie zodra de graad
van een veelterm over de
treedt pas in actie zodra de graad
van een veelterm over de 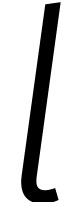 gaat. Het uitrekenen
van een product van twee veeltermen in
gaat. Het uitrekenen
van een product van twee veeltermen in 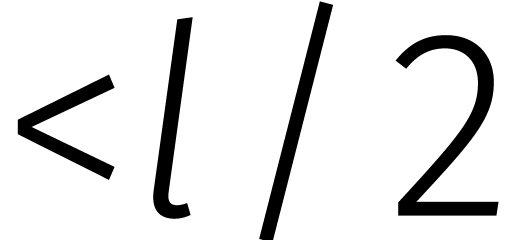 van graad
van graad
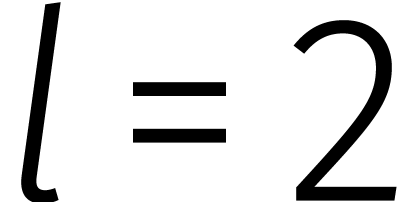 kunnen we dus net zo goed in
kunnen we dus net zo goed in 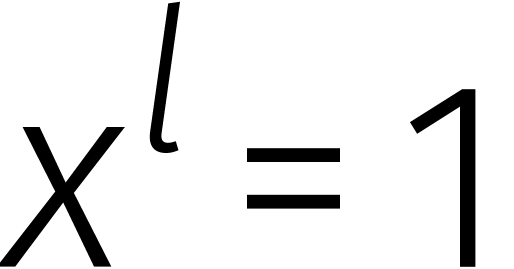 doen.
doen.
Het voordeel van kringtermen is dat we een aantal nieuwe rekentrucs
rijker worden. Veronderstel bijvoorbeeld dat 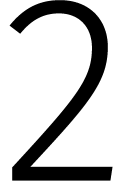 en
dat
en
dat 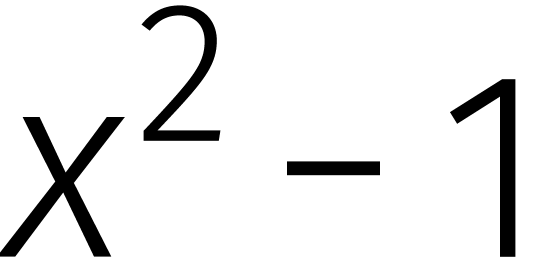 omkeerbaar is in
omkeerbaar is in 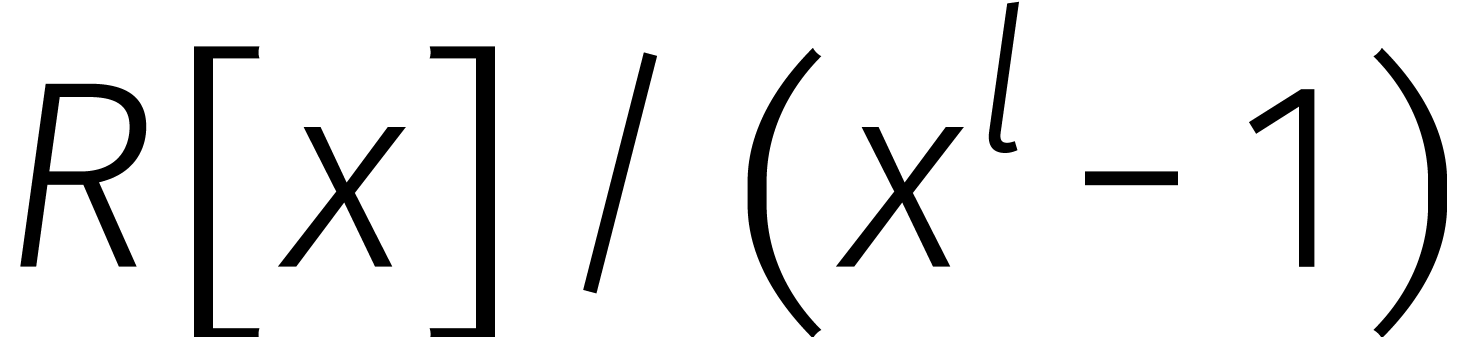 . Dan is het mogelijk om Karatsuba's methode verder
te verbeteren: modulo
. Dan is het mogelijk om Karatsuba's methode verder
te verbeteren: modulo 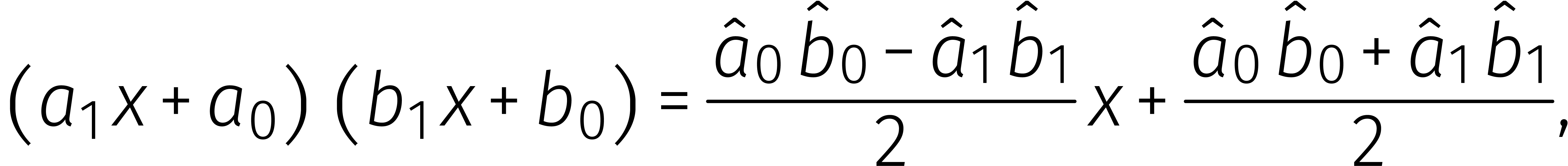 geldt
geldt
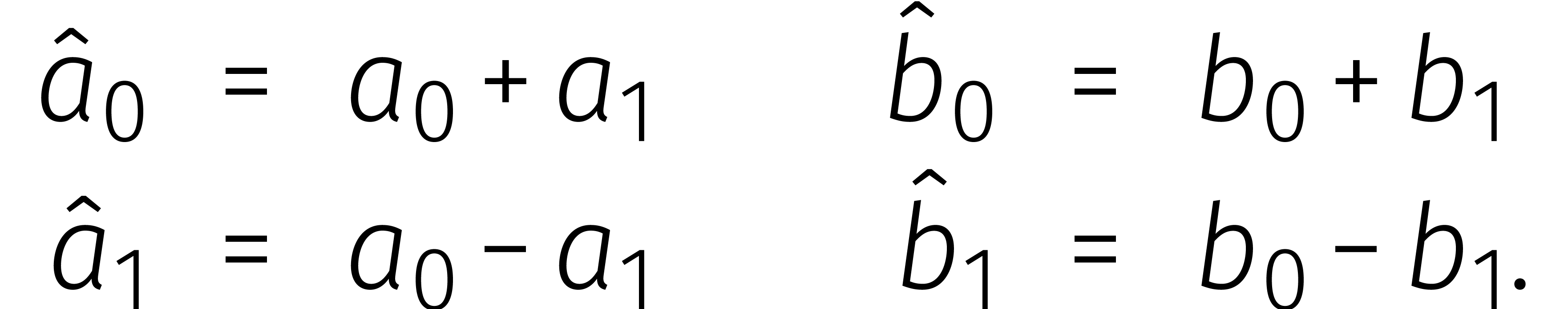
waar
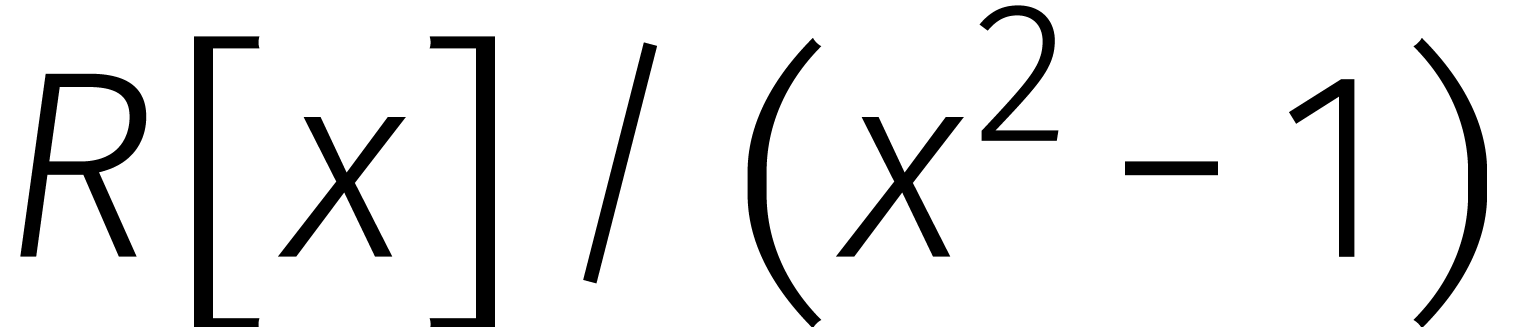
In 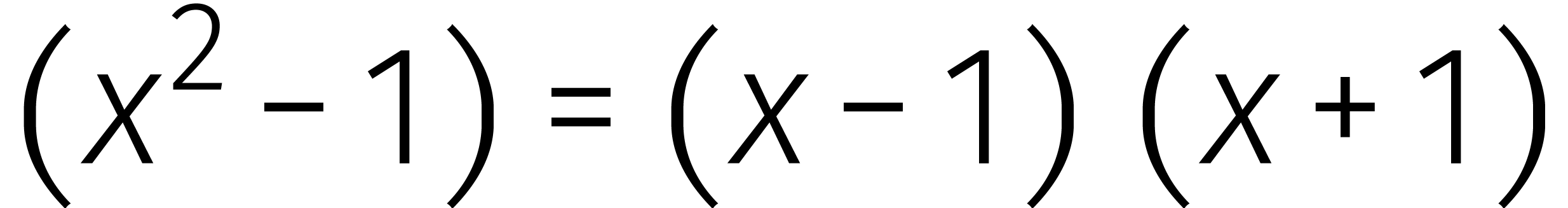 vergt het uitrekenen van een product dus
slechts twee vermenigvuldigingen in
vergt het uitrekenen van een product dus
slechts twee vermenigvuldigingen in 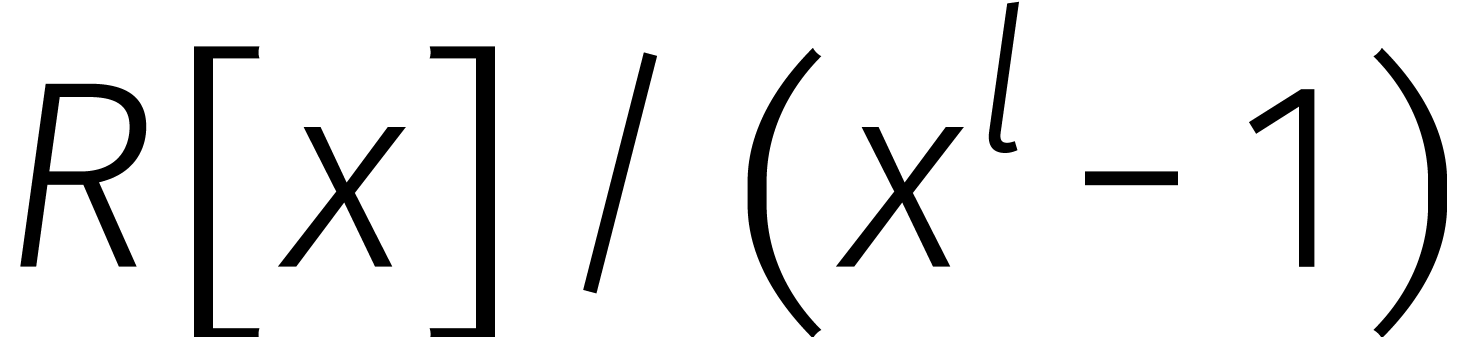 .
Ook zijn er een aantal optellingen, aftrekkingen, en delingen door twee
nodig.
.
Ook zijn er een aantal optellingen, aftrekkingen, en delingen door twee
nodig.
Bovenstaande relaties zijn het gevolg van
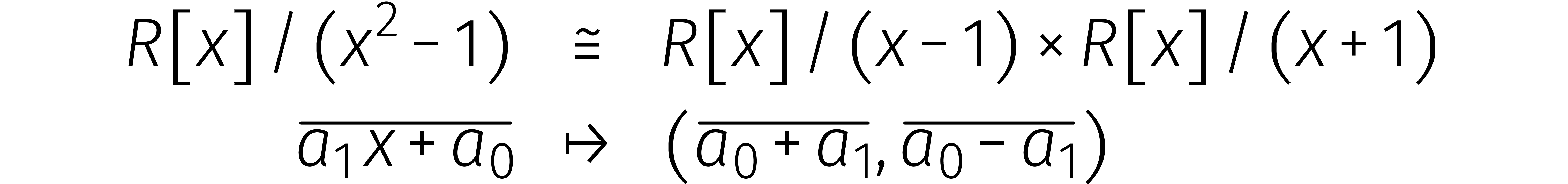 |
(1) |
en toepassing van de Chinese reststelling op deze ontbinding:
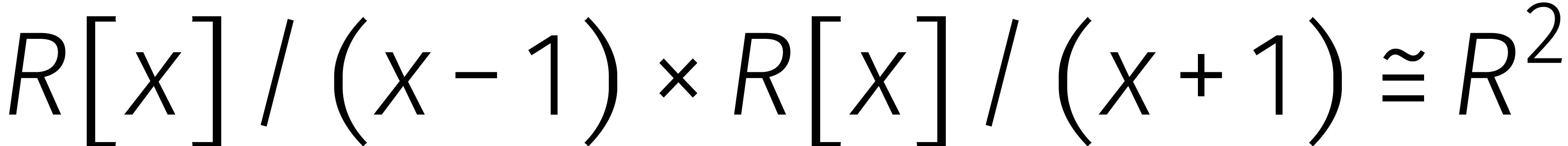
Dit maakt het mogelijk willekeurige berekeningen in 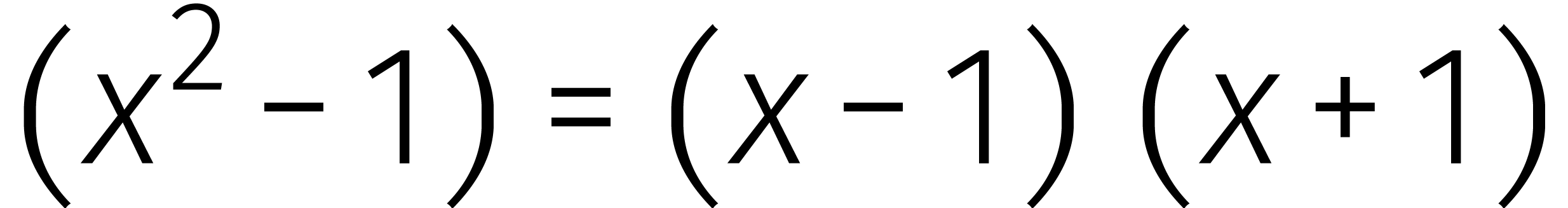 te vervangen door berekeningen in
te vervangen door berekeningen in 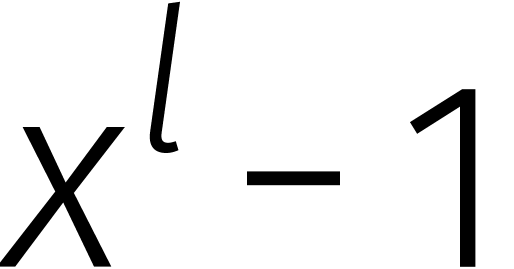 .
.
De ontbinding (1) geldt voor elke ring 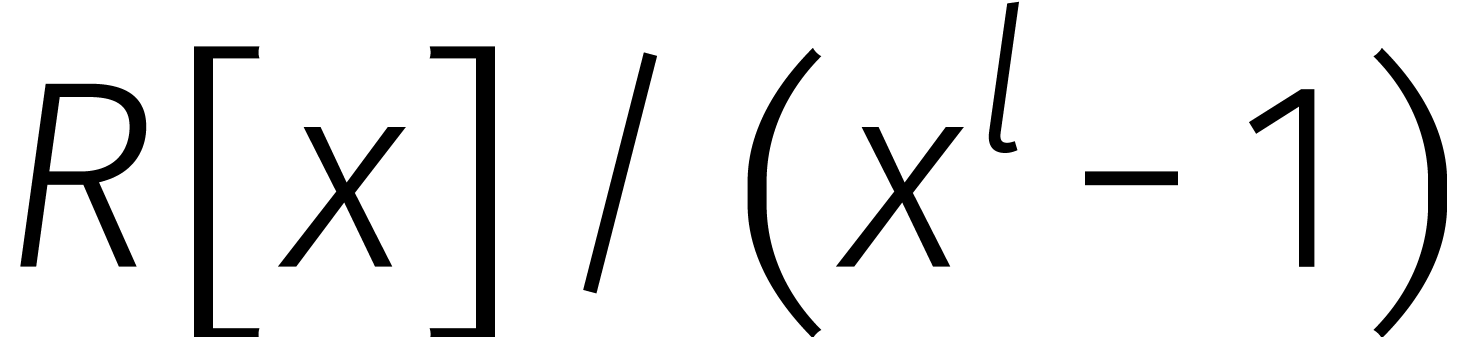 . In sommige ringen kan ook
. In sommige ringen kan ook 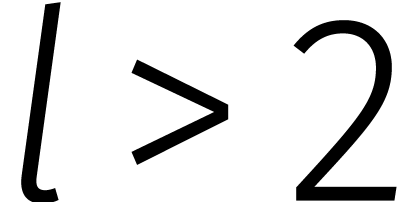 op soortgelijke wijze ontbonden worden voor
op soortgelijke wijze ontbonden worden voor 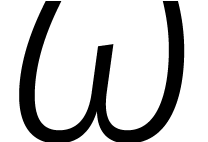 . Dat is het geval zodra
. Dat is het geval zodra 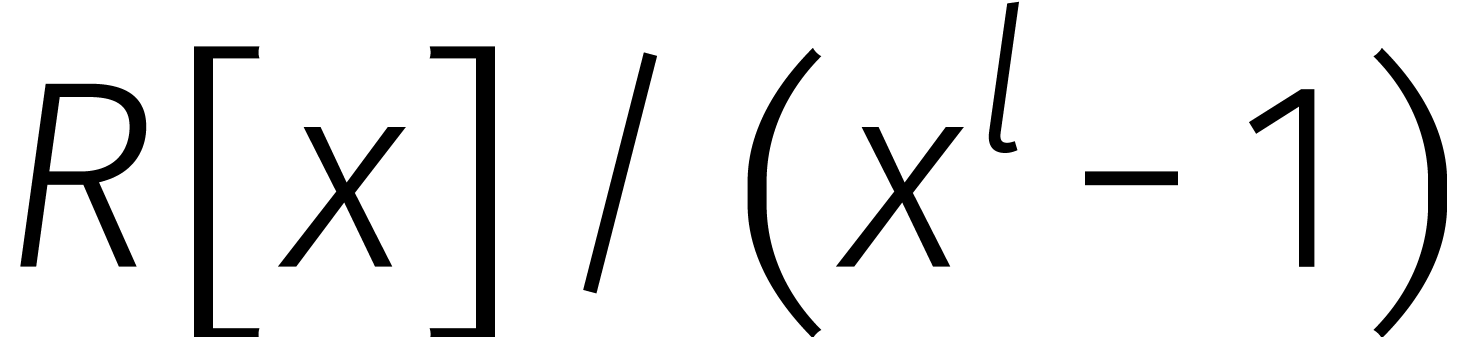 een
element
een
element 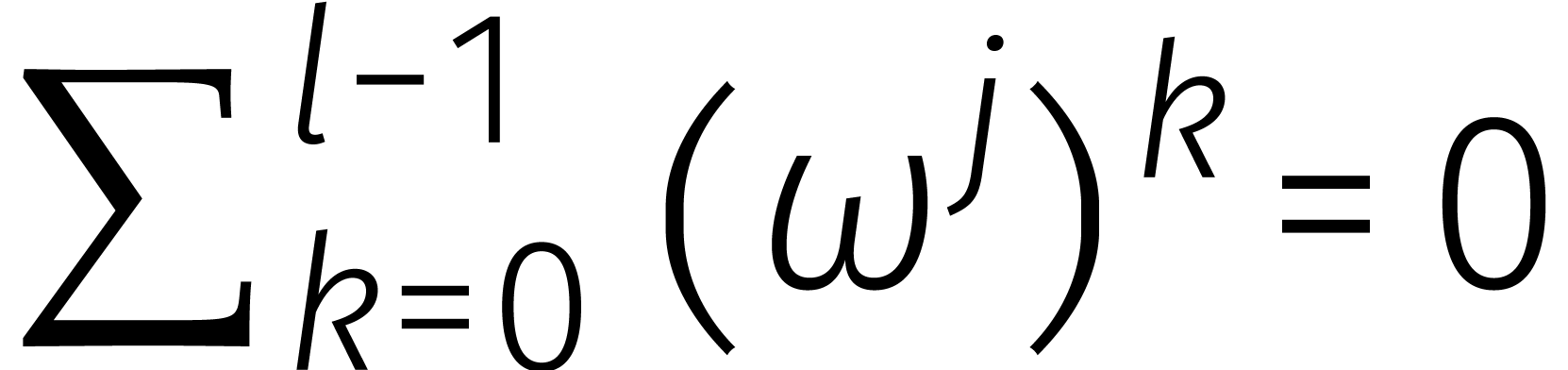 bezit met
bezit met  voor
voor
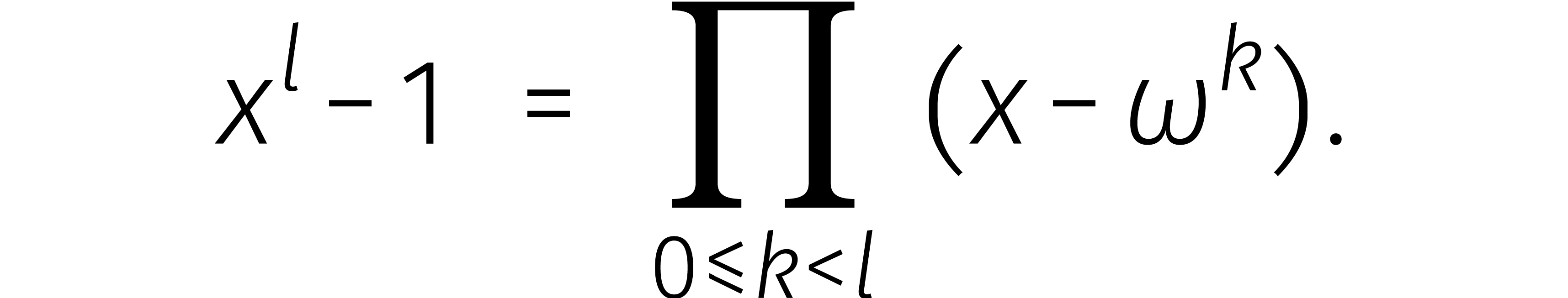 . Zo'n element
. Zo'n element 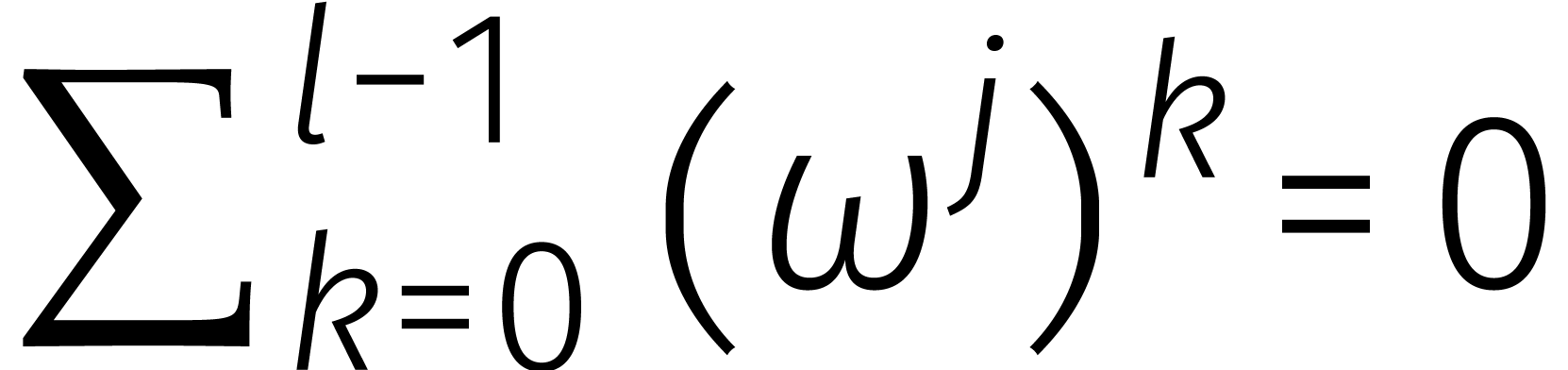 heet een principiële eenheidswortel van orde
heet een principiële eenheidswortel van orde
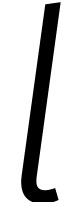 en leidt tot de ontbinding
en leidt tot de ontbinding

Is 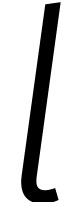 ook nog eens omkeerbaar in
ook nog eens omkeerbaar in 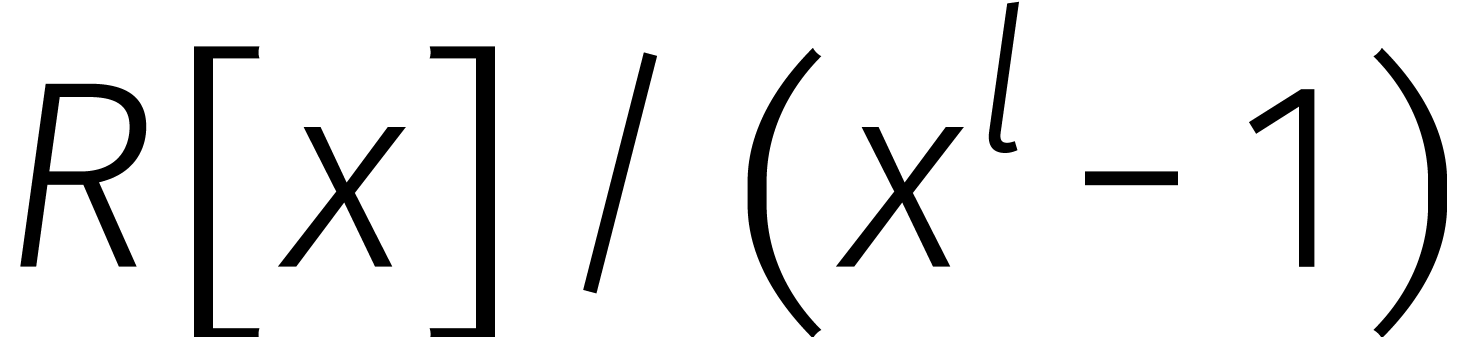 , dan kan bovendien de Chinese reststelling
worden toegepast op deze ontbinding:
, dan kan bovendien de Chinese reststelling
worden toegepast op deze ontbinding:

Van links naar rechts heet dit isomorfisme de discrete
fouriertransformatie of 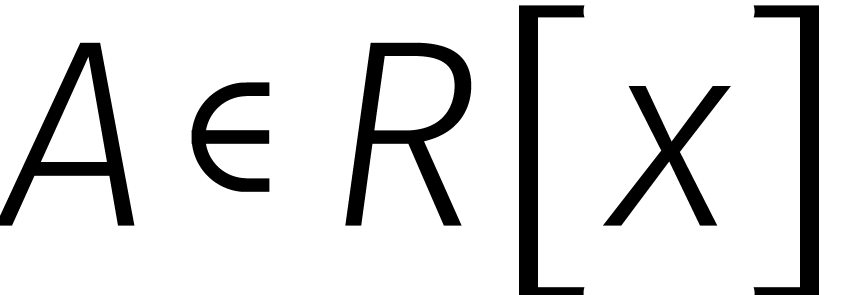 .
Voor alle
.
Voor alle 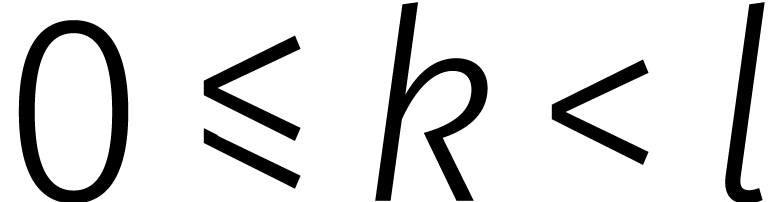 en
en 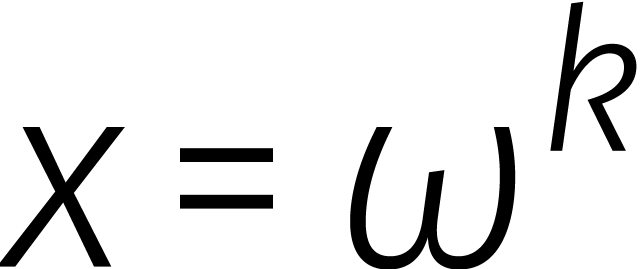 hebben we
hebben we
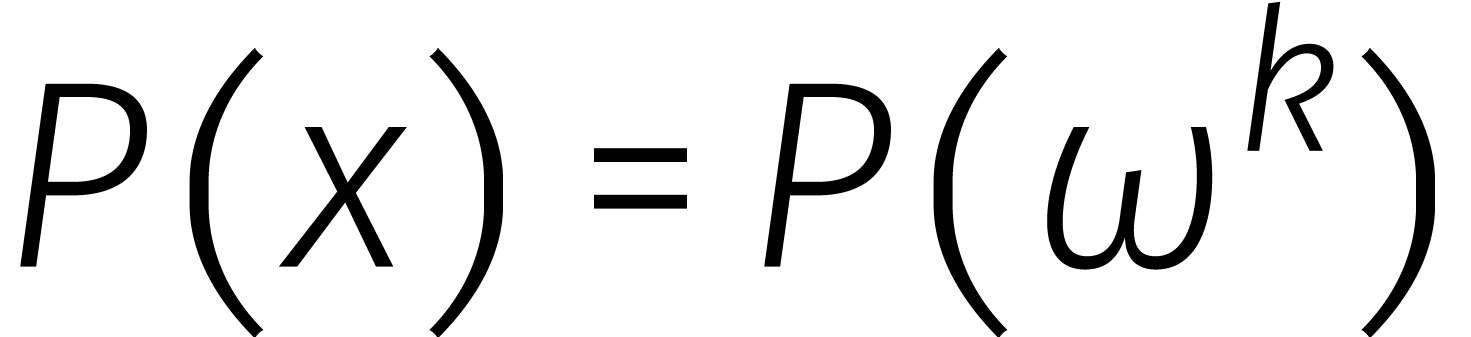 en
en 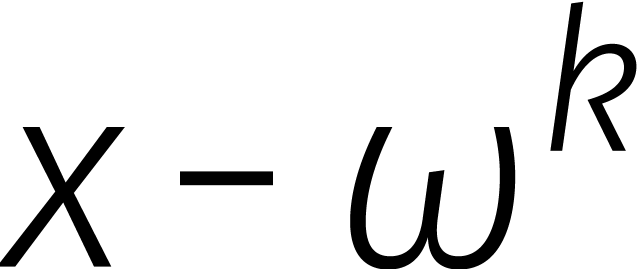 modulo
modulo 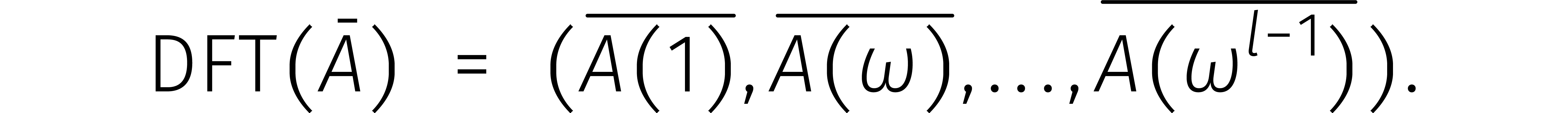 , zodat
, zodat
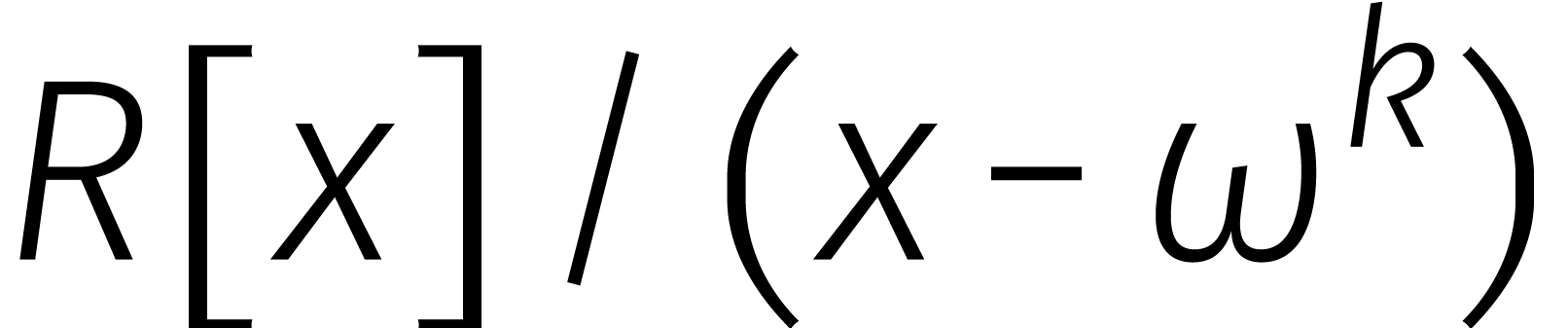
De algebra 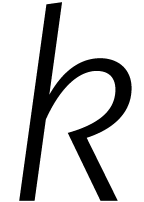 is op zijn beurt weer isomorf met
is op zijn beurt weer isomorf met
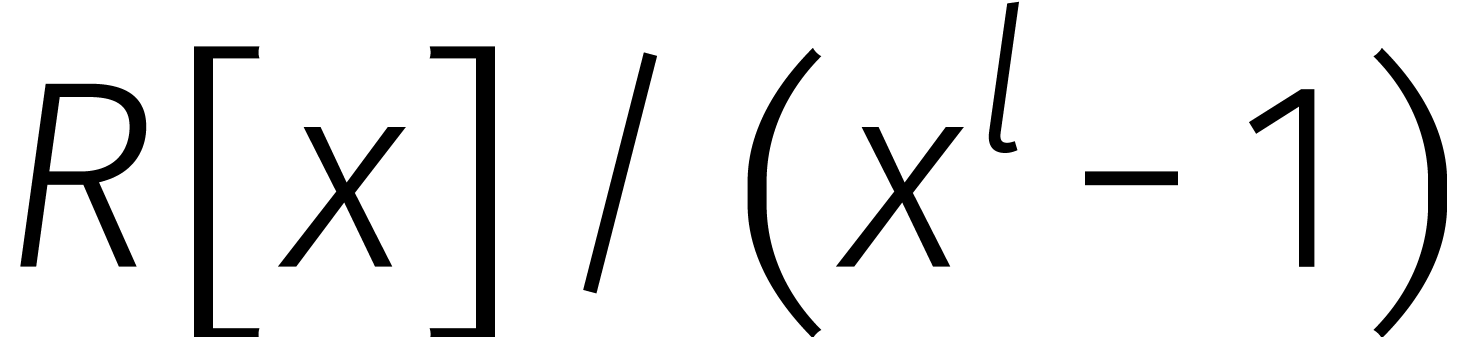 voor elke
voor elke 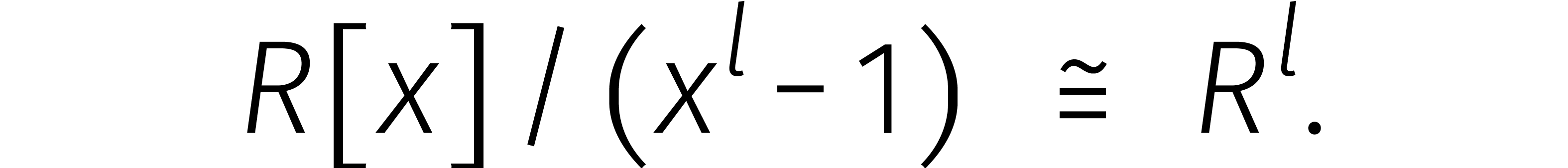 ,
zodat
,
zodat
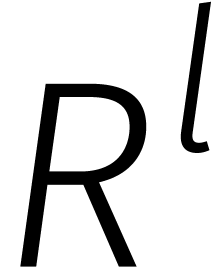
Nu is rekenen aan de rechterkant goedkoop: één
vermenigvuldiging in  komt bijvoorbeeld neer op
komt bijvoorbeeld neer op
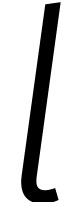 vermenigvuldigingen in
vermenigvuldigingen in 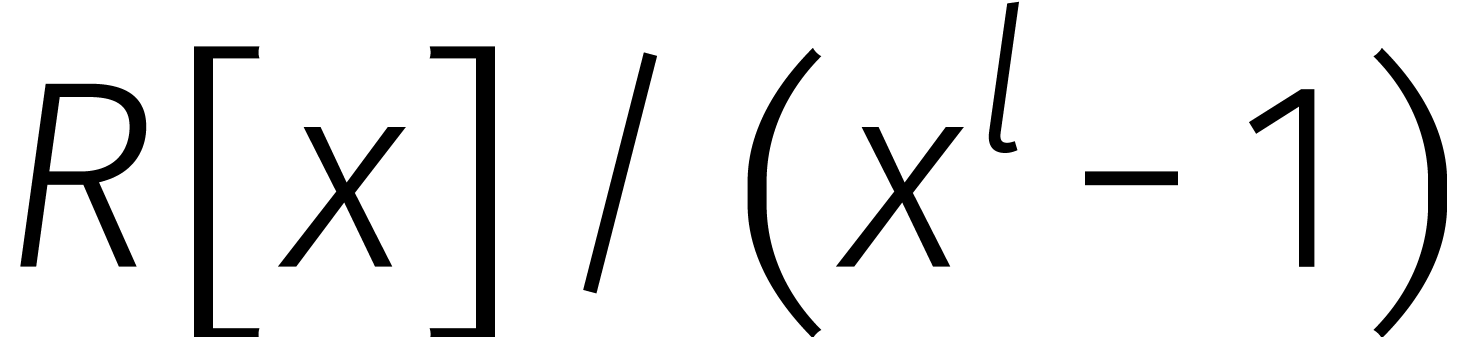 . Als we zowel de
. Als we zowel de 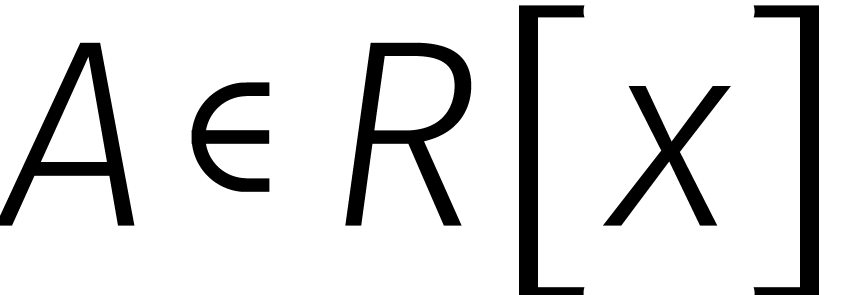 en de
inverse
en de
inverse 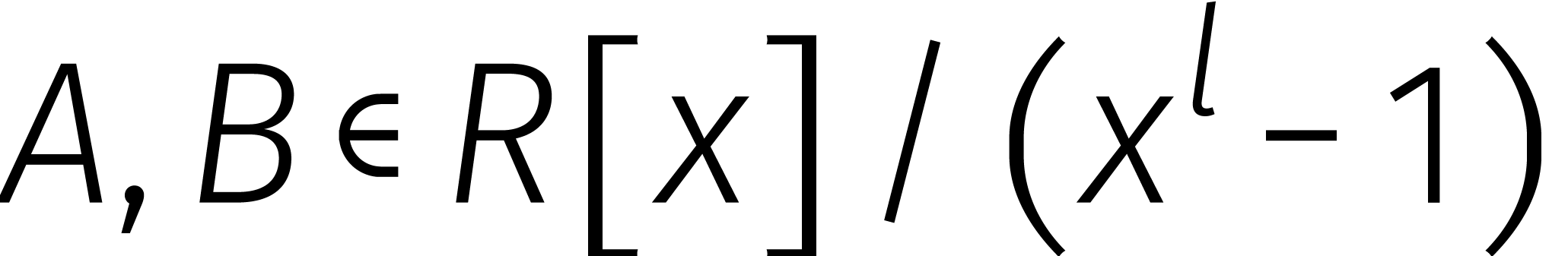 snel uit kunnen rekenen, dan hebben we
dus een goede methode om kringtermen
snel uit kunnen rekenen, dan hebben we
dus een goede methode om kringtermen 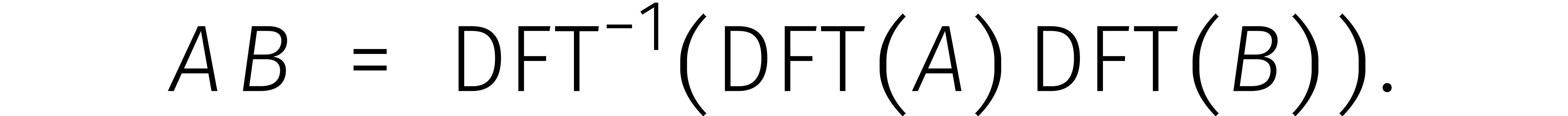 te
vermenigvuldigen:
te
vermenigvuldigen:
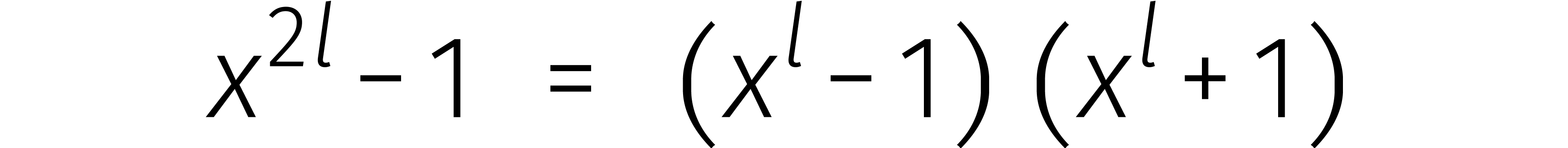
Dit heet FFT-vermenigvuldigen.
Maar hoe rekenen we zo'n DFT snel uit? Het geval 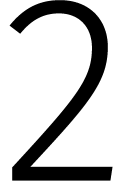 bestudeerden we al eerder. Meer in het algemeen leidt de ontbinding
bestudeerden we al eerder. Meer in het algemeen leidt de ontbinding
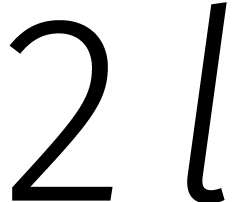
voor even lengtes 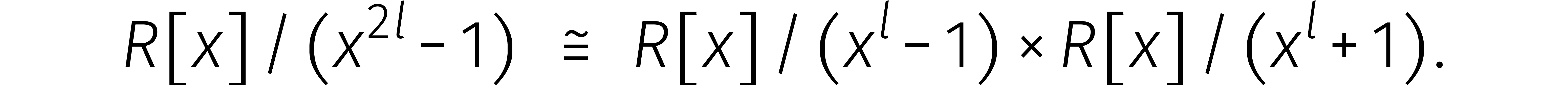 tot een isomorfisme
tot een isomorfisme
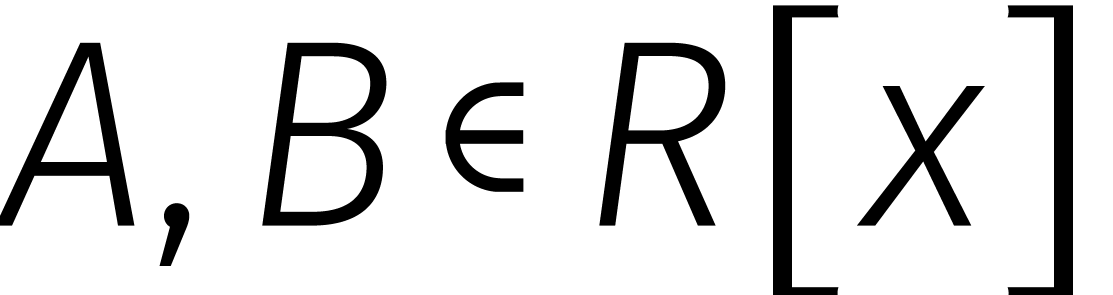
Als 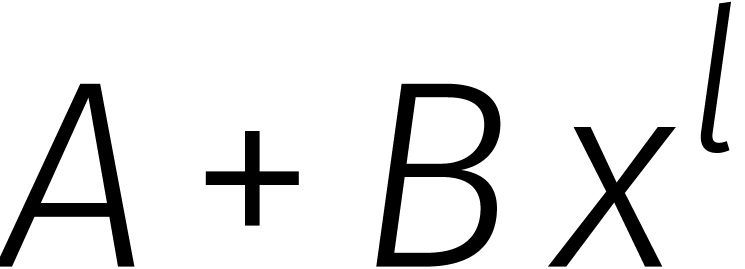 veeltermen van graad
veeltermen van graad 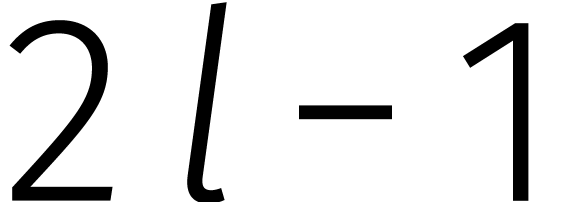 zijn, dan zendt dit isomorfisme
zijn, dan zendt dit isomorfisme 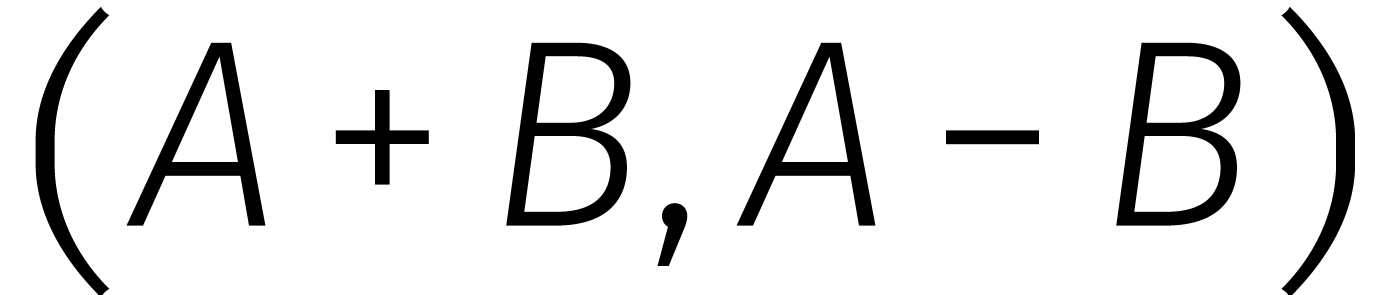 naar
naar 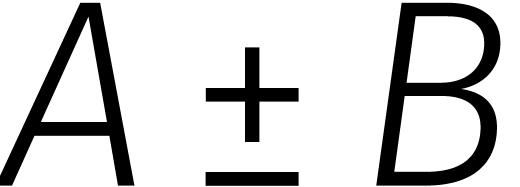 , waar we voor het gemak de hebben
weggelaten. Het uitrekenen van
, waar we voor het gemak de hebben
weggelaten. Het uitrekenen van 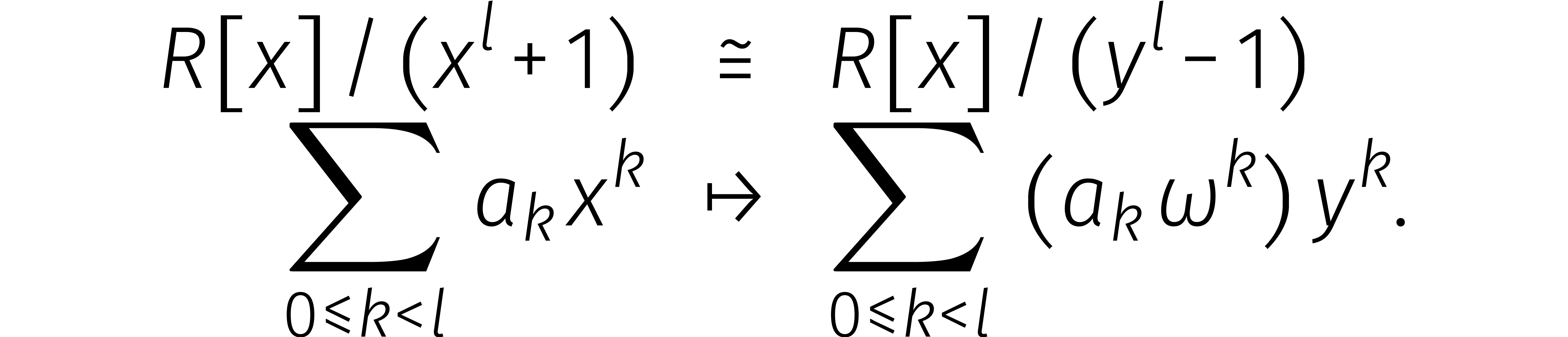 komt neer op
komt neer op 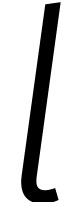 maal optellen en aftrekken in
maal optellen en aftrekken in 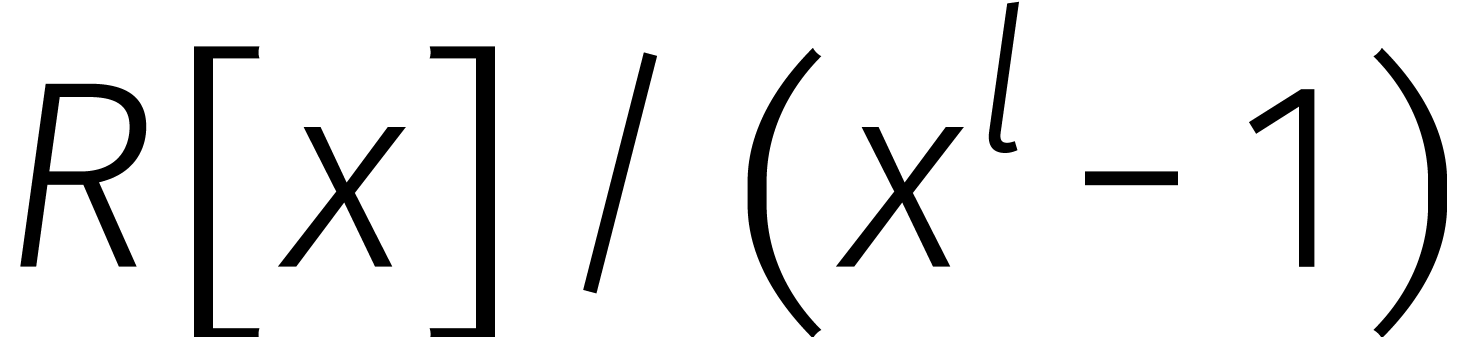 . Voor het isomorfisme in de andere richting komen
daar
. Voor het isomorfisme in de andere richting komen
daar 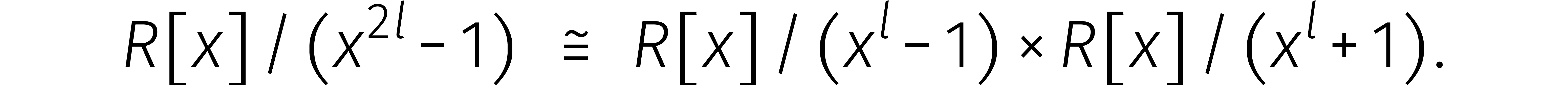 delingen door twee bij.
delingen door twee bij.
Als 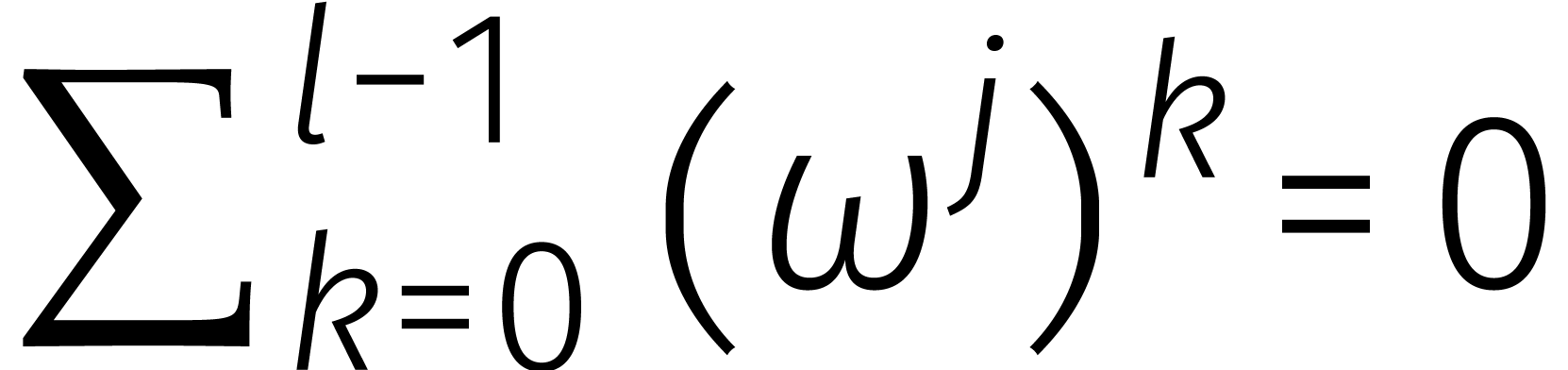 een principiële eenheidswortel van orde
een principiële eenheidswortel van orde
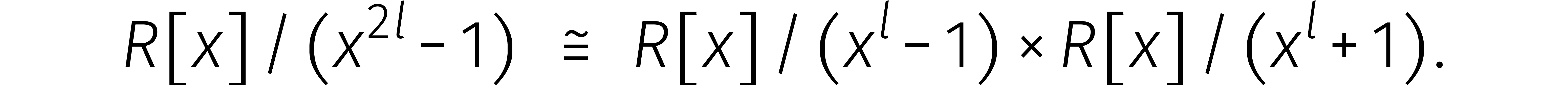 is, dan hebben we bovendien het volgende
isomorfisme:
is, dan hebben we bovendien het volgende
isomorfisme:
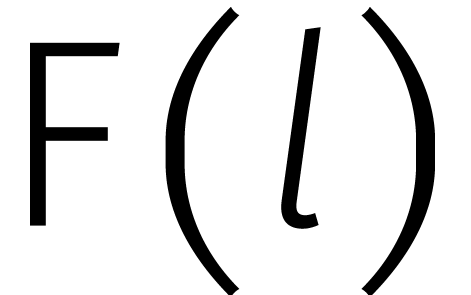
Het uitrekenen van dit isomorfisme komt neer op 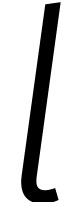 vermenigvuldigingen met machten van
vermenigvuldigingen met machten van 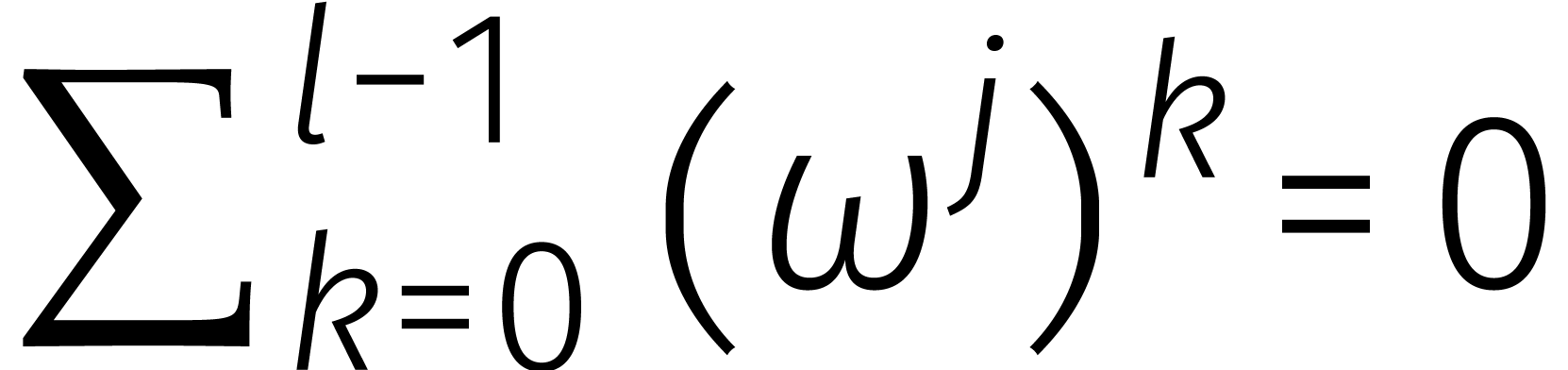 .
Hier is het belangrijk om op te merken dat een vermenigvuldiging met een
macht van
.
Hier is het belangrijk om op te merken dat een vermenigvuldiging met een
macht van 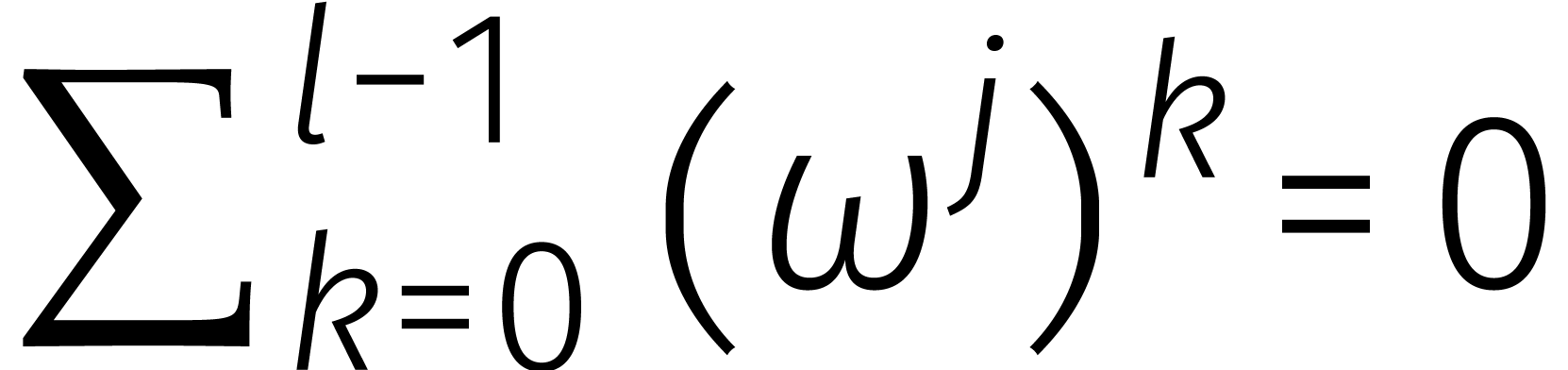 soms goedkoper is dan een willekeurige
vermenigvuldiging in
soms goedkoper is dan een willekeurige
vermenigvuldiging in 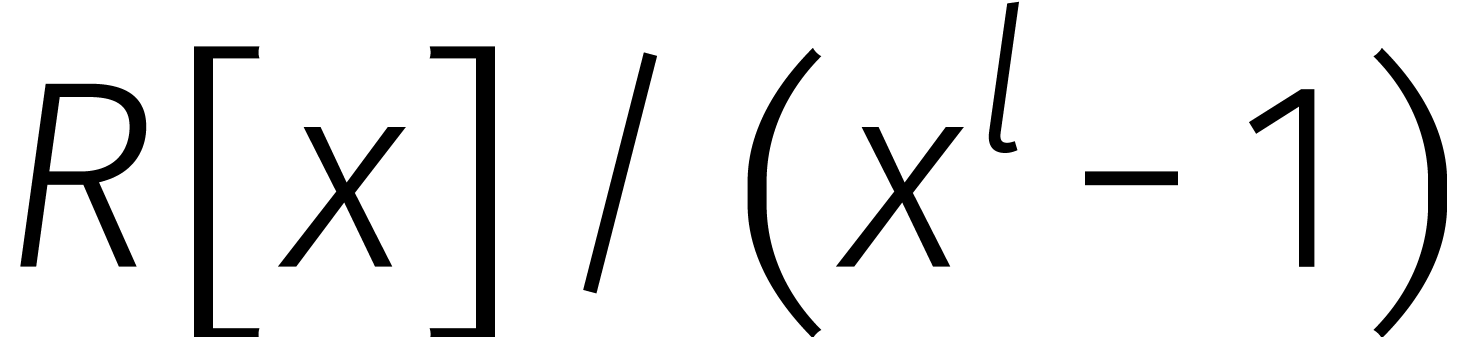 .
.
Al met al laat dit zien hoe een DFT van lengte 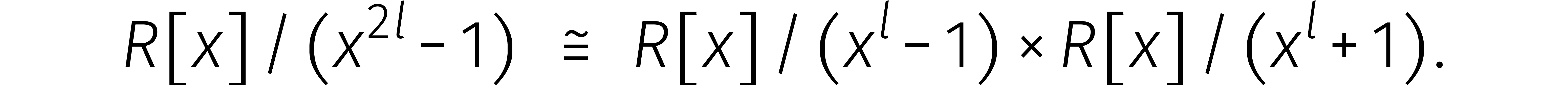 kan worden gereduceerd tot twee DFTs van lengte
kan worden gereduceerd tot twee DFTs van lengte 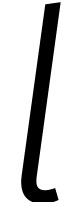 . Schrijven we
. Schrijven we 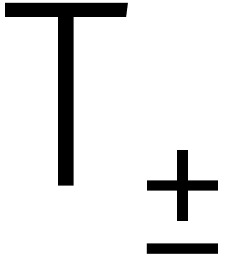 voor de tijd
die het kost om een DFT van lengte
voor de tijd
die het kost om een DFT van lengte 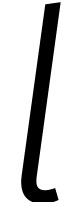 uit te
rekenen,
uit te
rekenen, 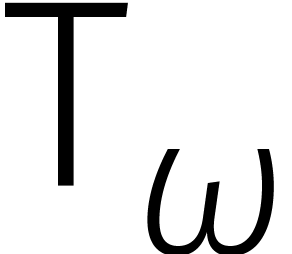 voor de tijd van een optelling of
aftrekking in
voor de tijd van een optelling of
aftrekking in 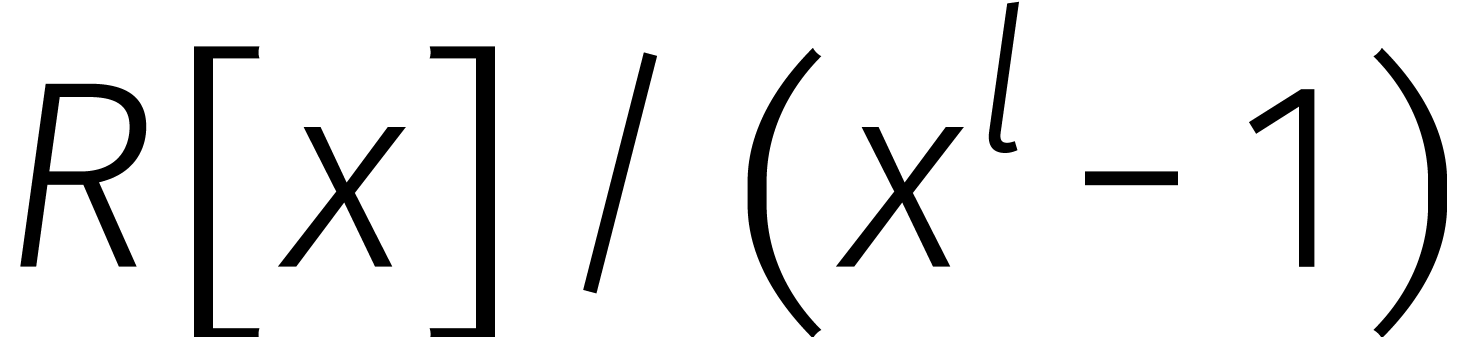 , en
, en 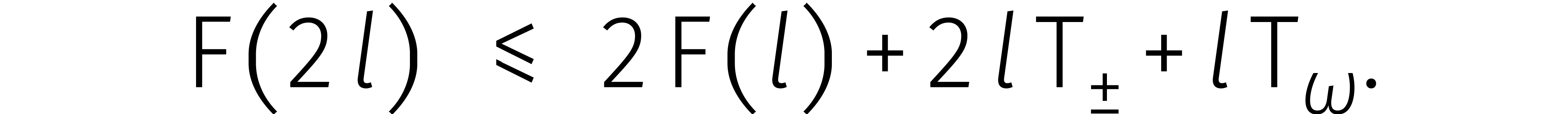 voor de tijd van een vermenigvuldiging met een macht van
voor de tijd van een vermenigvuldiging met een macht van
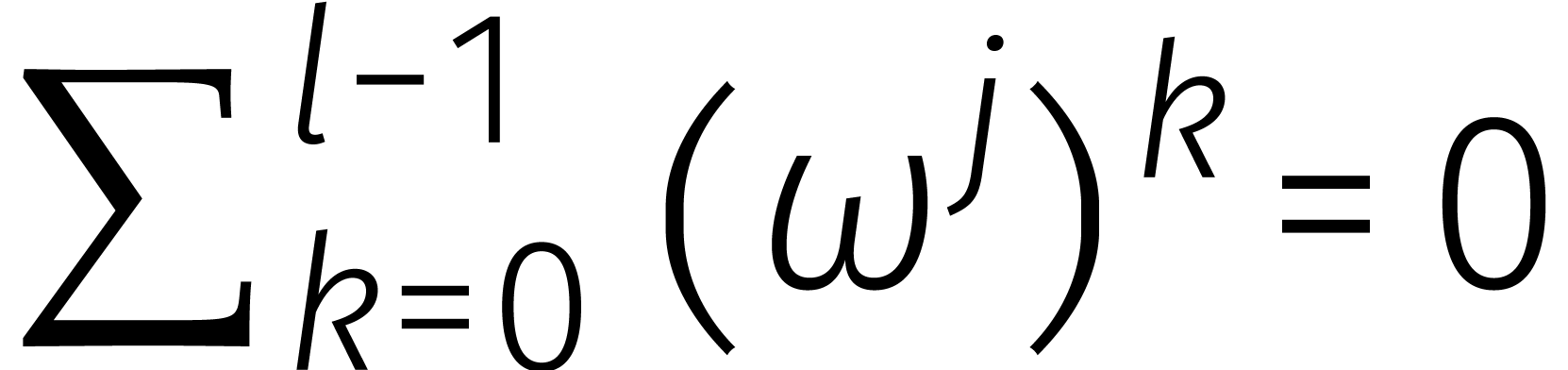 , dan hebben we
, dan hebben we
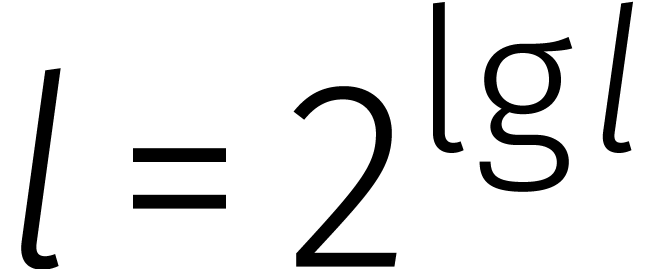
Passen we deze formule recursief toe in het geval dat 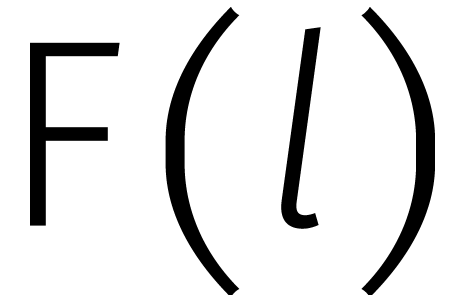 een tweemacht is, dan vinden we
een tweemacht is, dan vinden we
Voor de inverse transformatie komen daar ook nog 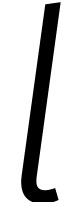 delingen door
delingen door 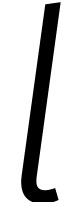 bij.
bij.
Voordat we verder gaan, is het een mooi moment voor wat opmerkingen. De FFT brak door in 1965, na de publicatie van Cooley en Tukey's artikel [3]. Maar een soortgelijke methode werd eerder beschreven in ongepubliceerd werk van Gauss [6, 14].
Daarnaast hebben we gezien dat een vermenigvuldiging van kringtermen kan
worden gereduceerd tot twee directe plus één inverse DFT.
In 1970 merkte Bluestein op dat een DFT van lengte 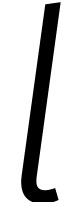 ook kan worden gereduceerd tot een kringproduct van dezelfde lengte
ook kan worden gereduceerd tot een kringproduct van dezelfde lengte 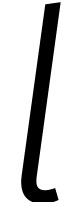 [2].
[2].
Laten we, om dit uit te leggen, voor het gemak veronderstellen dat 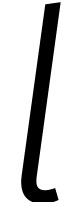 even is en
even is en 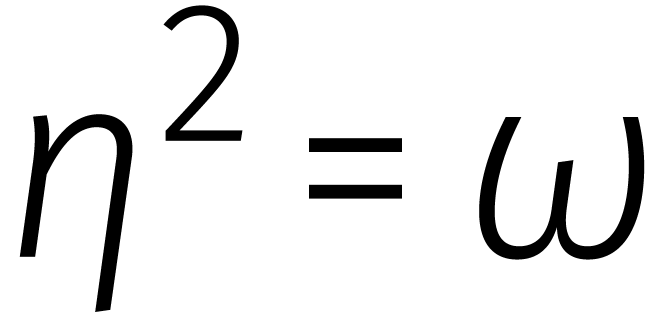 een
principiële eenheidswortel van orde
een
principiële eenheidswortel van orde 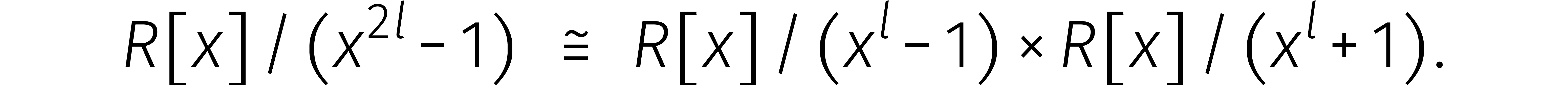 met
met
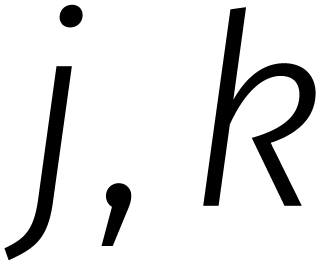 . Voor gehele
. Voor gehele 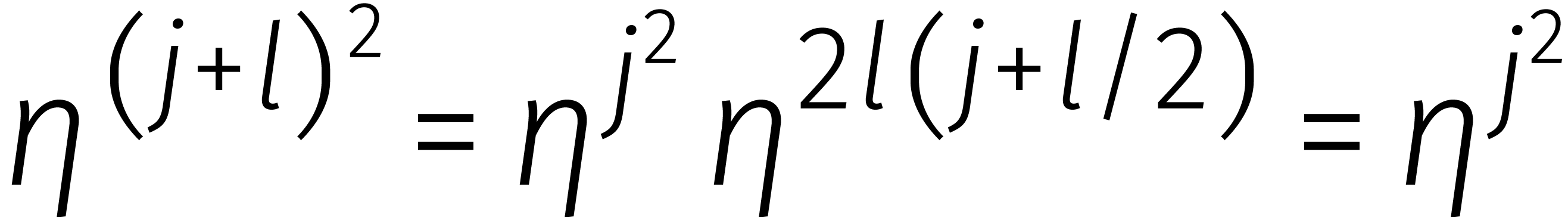 geldt dan
geldt dan
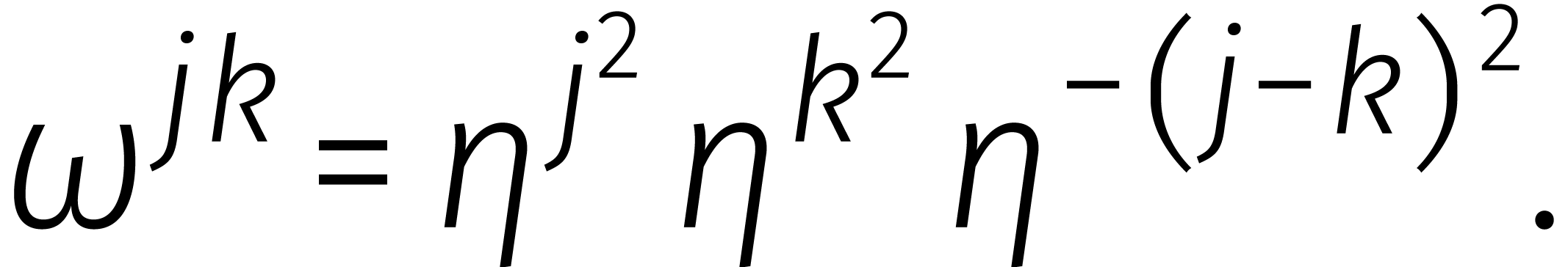
en
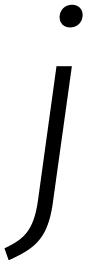
De 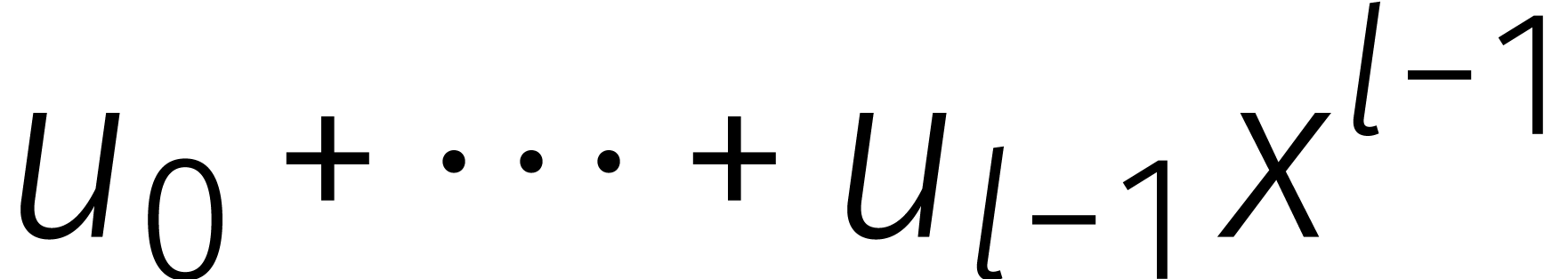 -de coëfficiënt
van de DFT van een kringterm
-de coëfficiënt
van de DFT van een kringterm 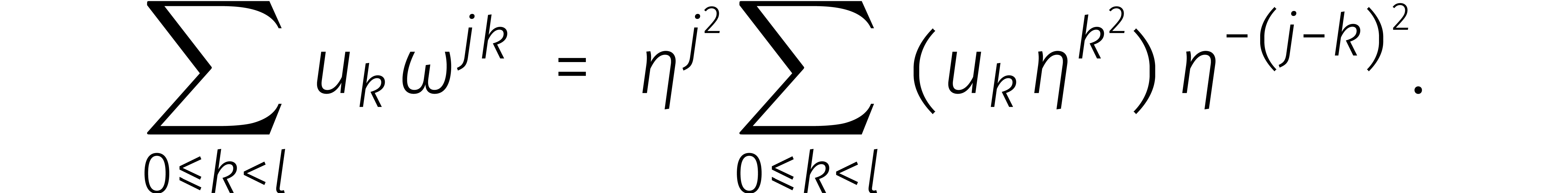 is dus gelijk aan
is dus gelijk aan
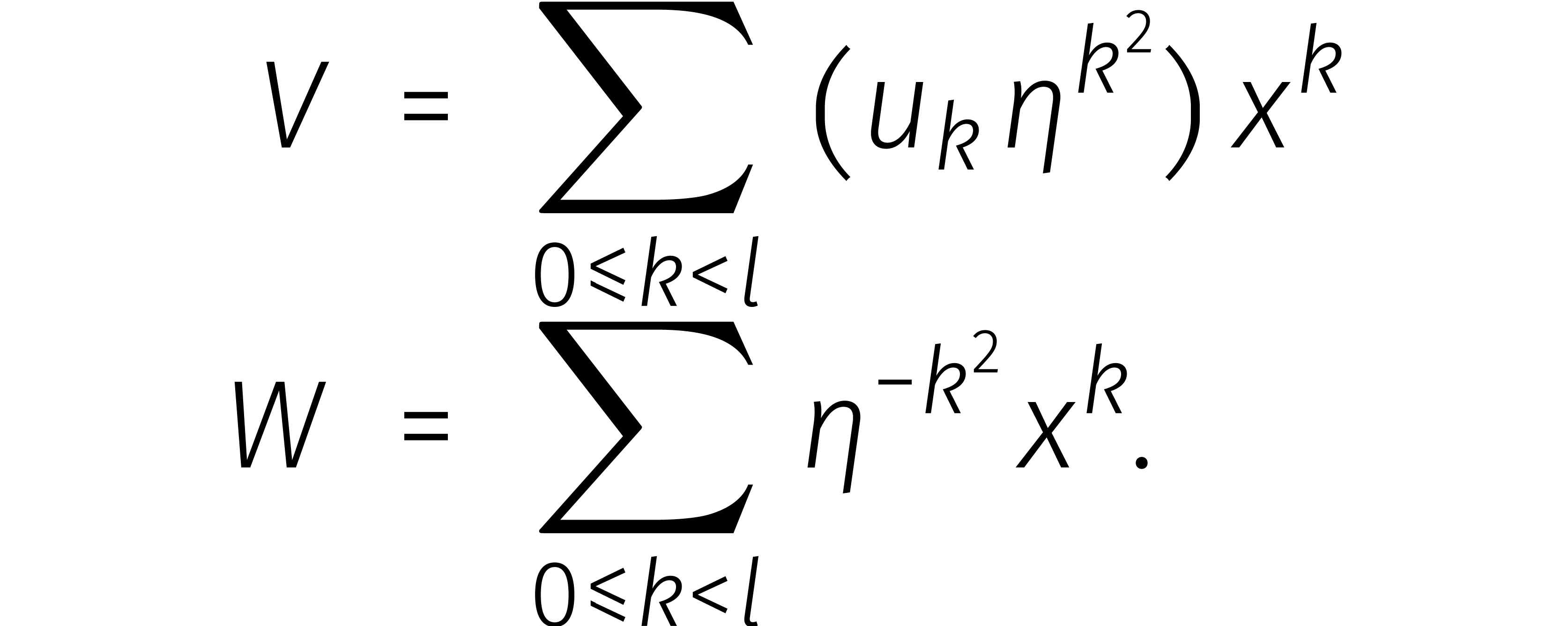
De rechtersom herkennen we nu als de 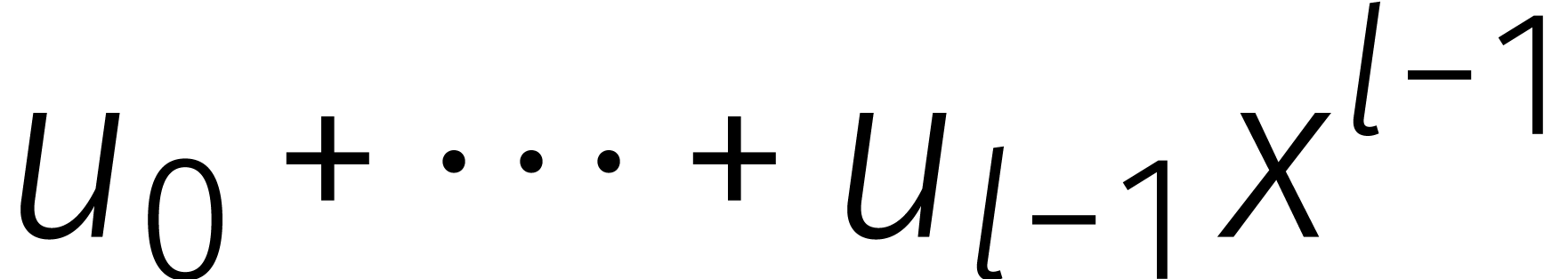 -de
coëfficiënt van het product van de volgende twee kringtermen:
-de
coëfficiënt van het product van de volgende twee kringtermen:

In mijn geboortejaar 1971 verschenen er maar liefst drie methodes om de
FFT toe te passen op het vermenigvuldigen van gehele getallen [
19
,
21
]. Elk van deze methodes was gebaseerd op een aparte keuze van
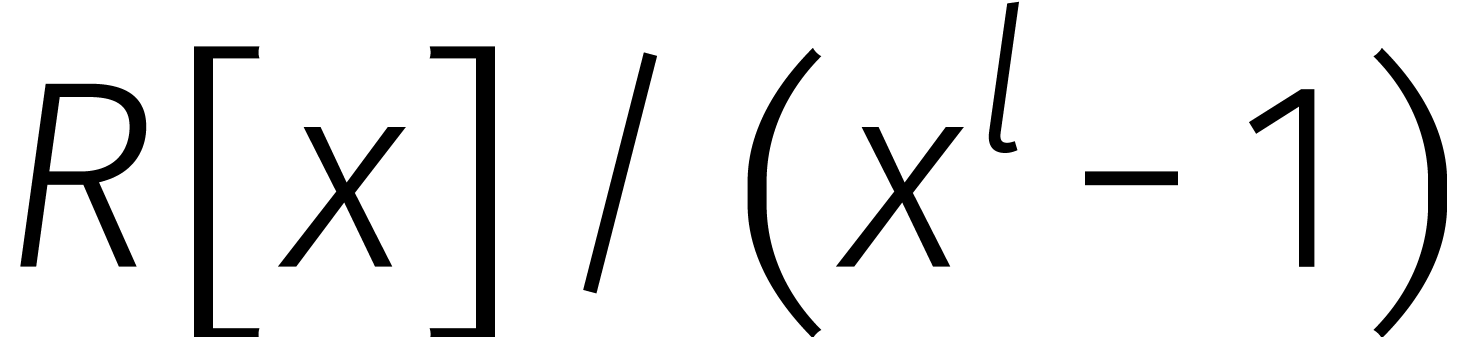 .
.
Het meest voor de hand ligt het om 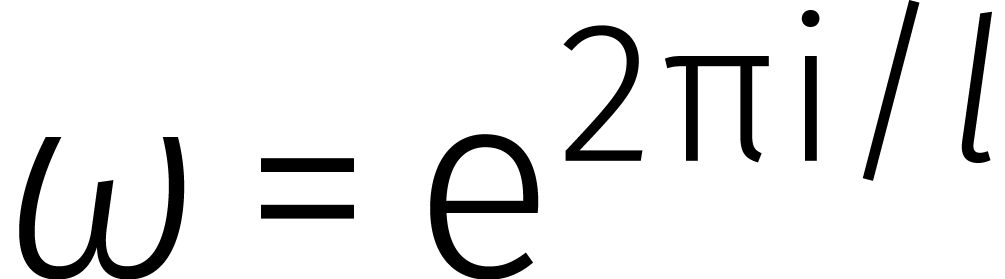 en
en 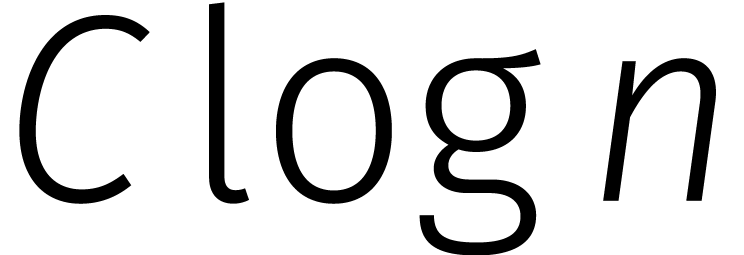 te nemen. In ons geval kunnen we natuurlijk alleen maar
met benaderingen van complexe getallen werken. Voor het vermenigvuldigen
van getallen van
te nemen. In ons geval kunnen we natuurlijk alleen maar
met benaderingen van complexe getallen werken. Voor het vermenigvuldigen
van getallen van 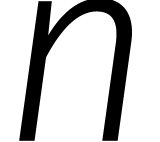 cijfers kan worden bewezen dat
benaderingen tot op
cijfers kan worden bewezen dat
benaderingen tot op 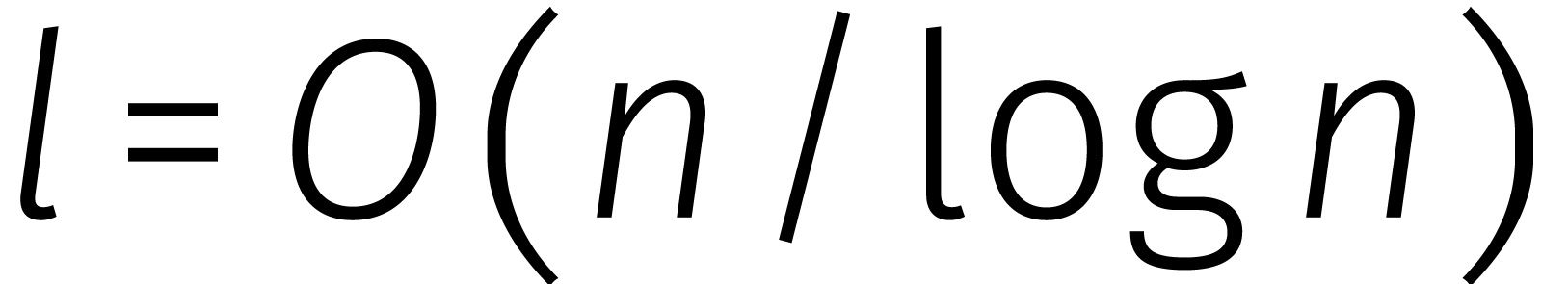 cijfers achter de komma
voldoende zijn voor een zekere constante
cijfers achter de komma
voldoende zijn voor een zekere constante  .
Dat betekent dat we kunnen werken met
.
Dat betekent dat we kunnen werken met 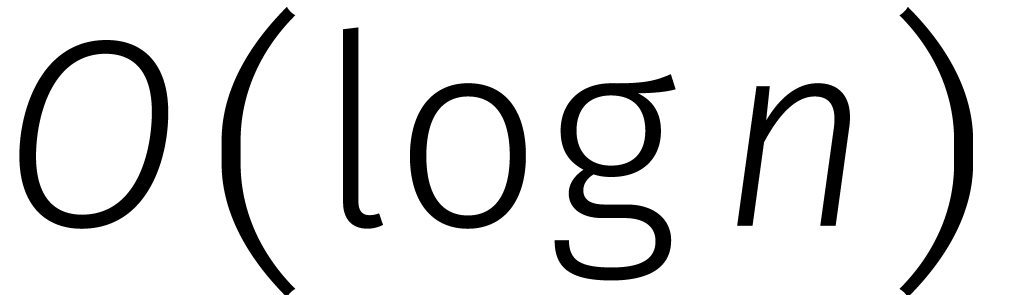 brokken
van
brokken
van 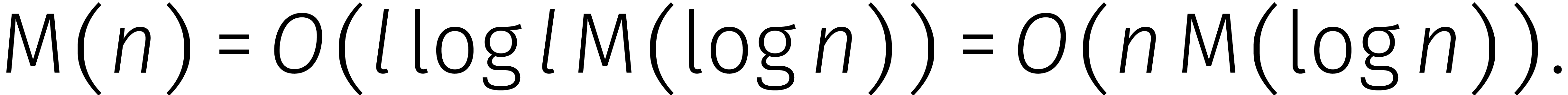 cijfers. In combinatie met (2)
vinden we dan
cijfers. In combinatie met (2)
vinden we dan
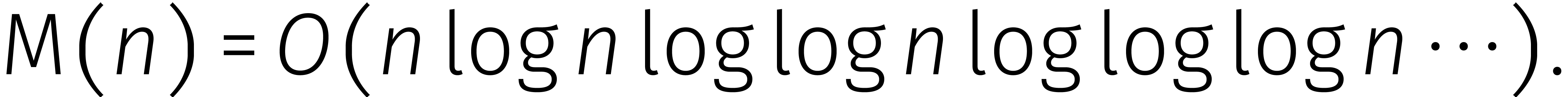
Laten we deze formule recursief op zichzelf los, dan vinden we

Dit was het „eerste algoritme” in het artikel van Schönhage–Strassen [21].
Het nulde algoritme werd echter al iets eerder door Pollard ontdekt [ 19 ].
Híj stelde voor om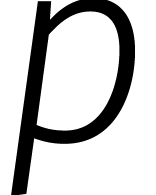 te nemen, waar
te nemen, waar
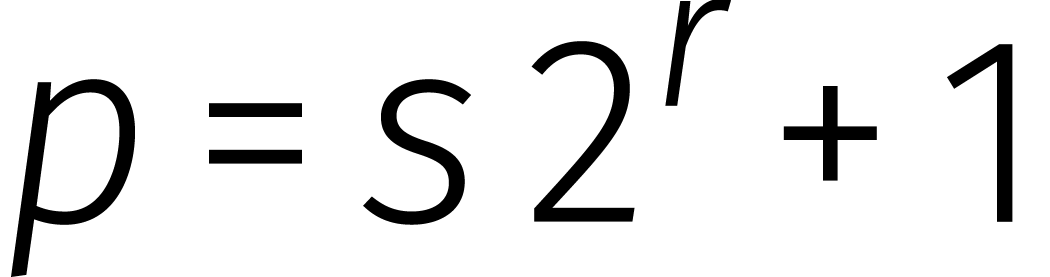 een priemgetal is van de vorm
een priemgetal is van de vorm
 ;
hoe kleiner
;
hoe kleiner
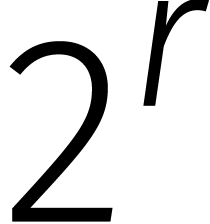 ,
hoe beter. Voor zulke priemgetallen
,
hoe beter. Voor zulke priemgetallen
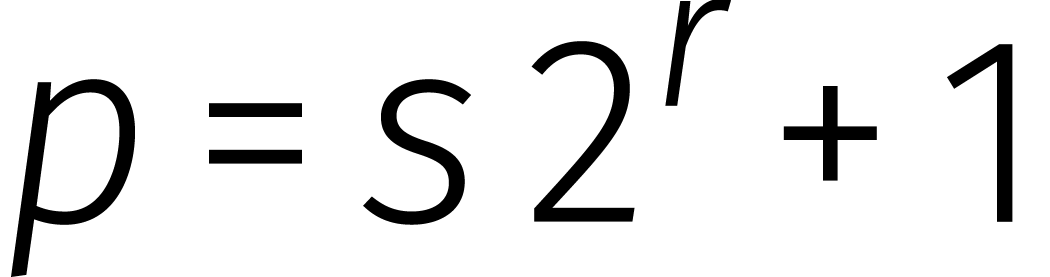 weten we dat er primitieve eenheidswortels van orde
weten we dat er primitieve eenheidswortels van orde
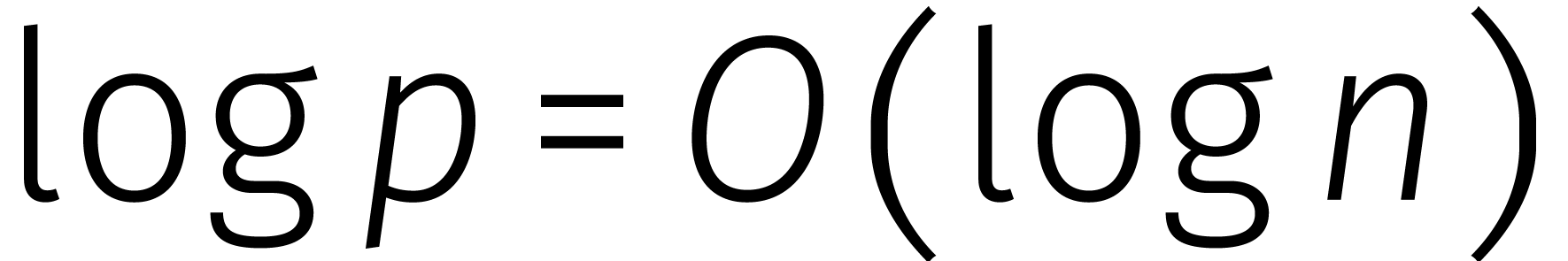 bestaan. Opnieuw is het dan mogelijk om
bestaan. Opnieuw is het dan mogelijk om
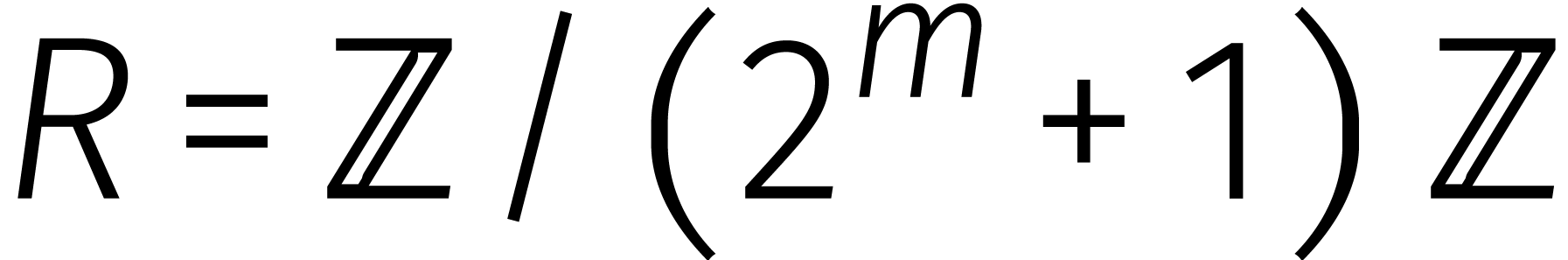 en
en
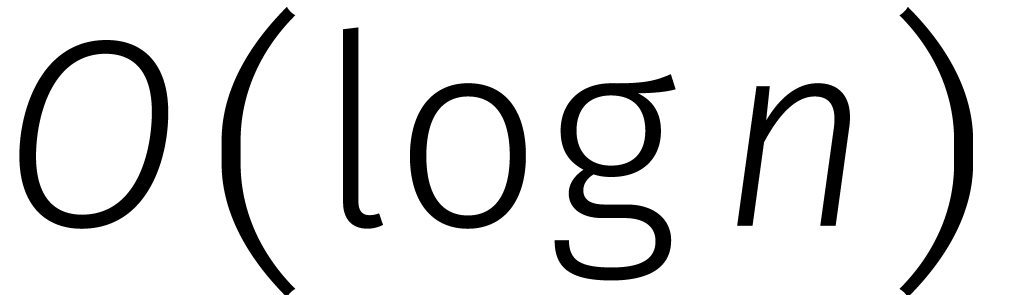 te kiezen, en we vinden een soortgelijke bovengrens voor
te kiezen, en we vinden een soortgelijke bovengrens voor
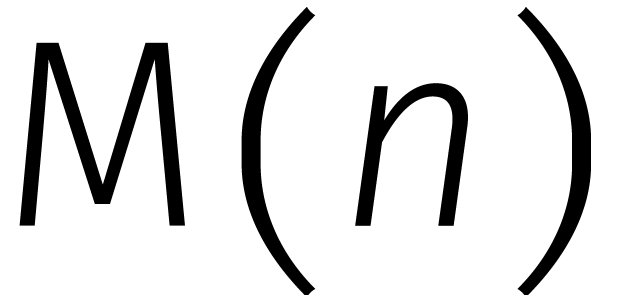 als net. Eerlijkheidshalve moet er wel worden bijgezegd dat dit laatste
níet in Pollard's artikel stond. Hij was meer uit op een
praktisch algoritme en beschreef verschillende optimalisaties. Voor zeer
grote getallen is zijn algoritme op hedendaagse computers het beste [
8
].
als net. Eerlijkheidshalve moet er wel worden bijgezegd dat dit laatste
níet in Pollard's artikel stond. Hij was meer uit op een
praktisch algoritme en beschreef verschillende optimalisaties. Voor zeer
grote getallen is zijn algoritme op hedendaagse computers het beste [
8
].
Voor het „tweede algoritme” van
Schönhage–Strassen schakelen we over naar het binaire stelsel
en nemen we 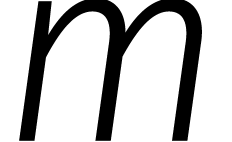 , waar
, waar 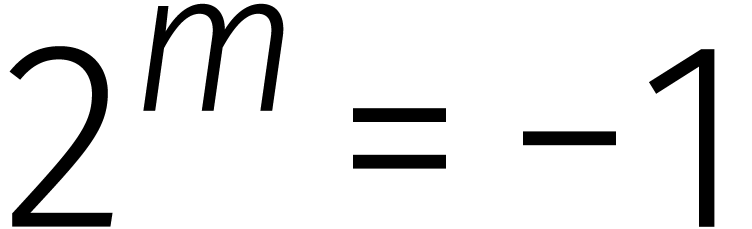 een tweemacht is. In deze ring hebben we per definitie
een tweemacht is. In deze ring hebben we per definitie
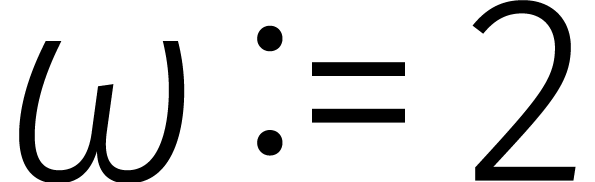 , zodat
, zodat 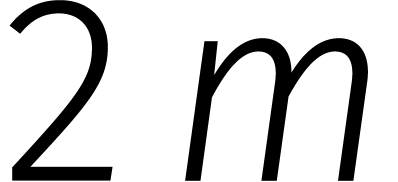 een principiële eenheidswortel van orde
een principiële eenheidswortel van orde 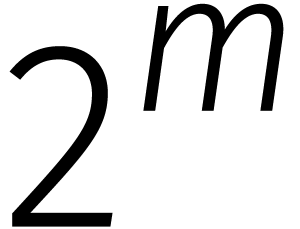 is.
Een ander voordeel is dat
is.
Een ander voordeel is dat 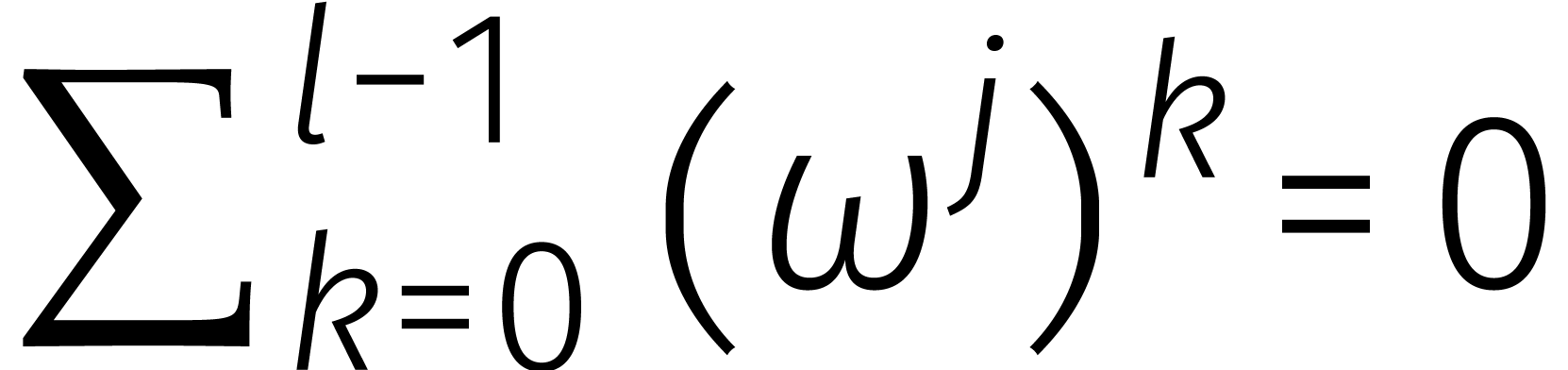 een snelle
eenheidswortel is. Daarmee bedoelen we dat we snel kunnen
vermenigvuldigen met machten van
een snelle
eenheidswortel is. Daarmee bedoelen we dat we snel kunnen
vermenigvuldigen met machten van 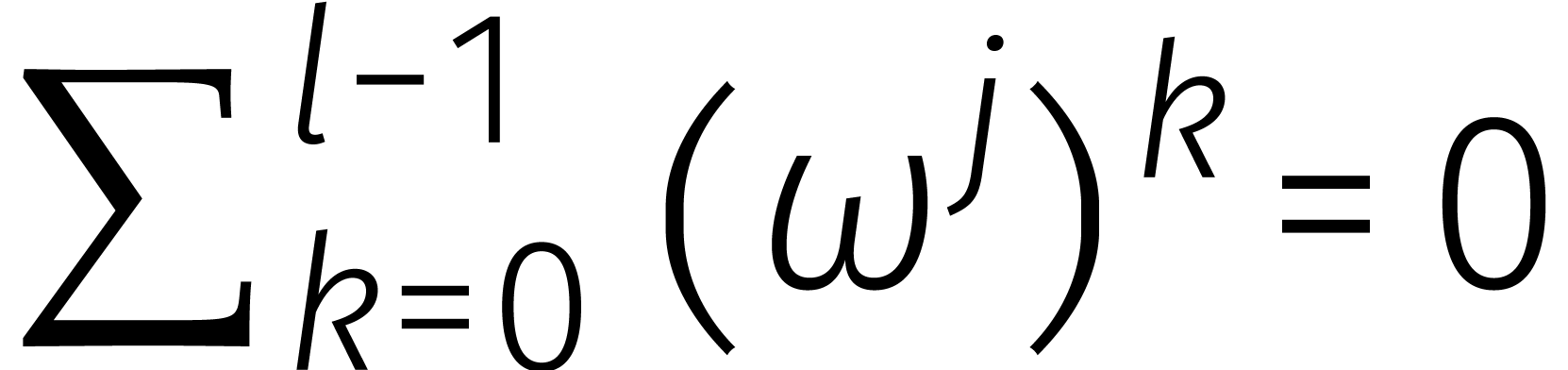 :
we schuiven gewoon de bits van het getal op terwijl we de relatie
:
we schuiven gewoon de bits van het getal op terwijl we de relatie 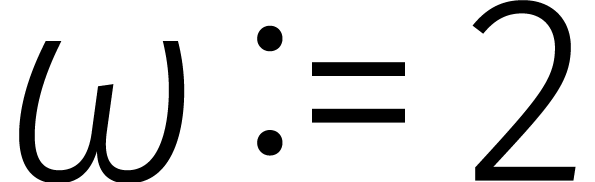 gebruiken zodra we de
gebruiken zodra we de 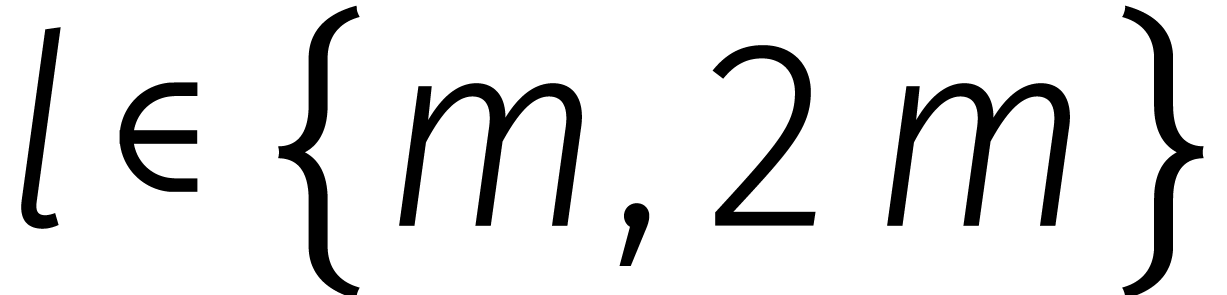 passeren. Voor
passeren. Voor 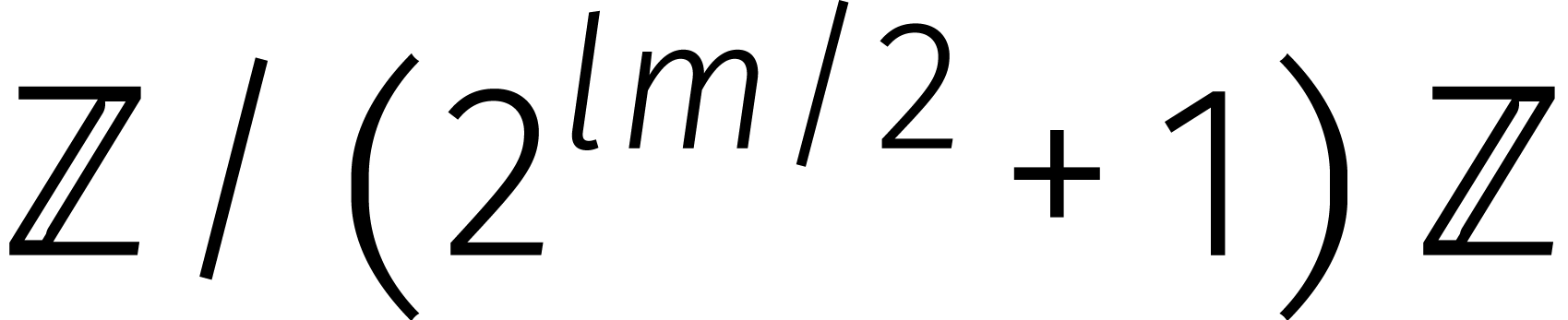 laten Schönhage en Strassen
vervolgens zien hoe een vermenigvuldiging in
laten Schönhage en Strassen
vervolgens zien hoe een vermenigvuldiging in 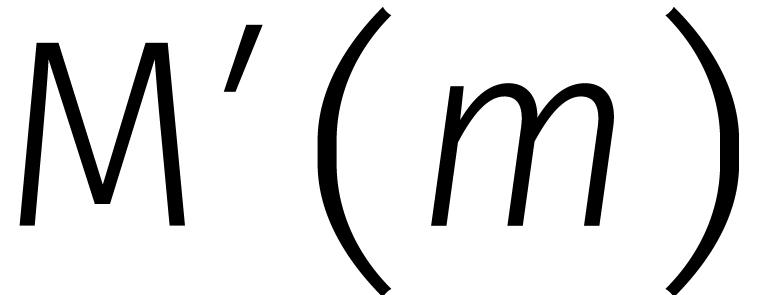 kan
worden gereduceerd tot
kan
worden gereduceerd tot 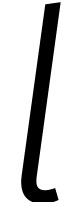 vermenigvuldigingen in
vermenigvuldigingen in
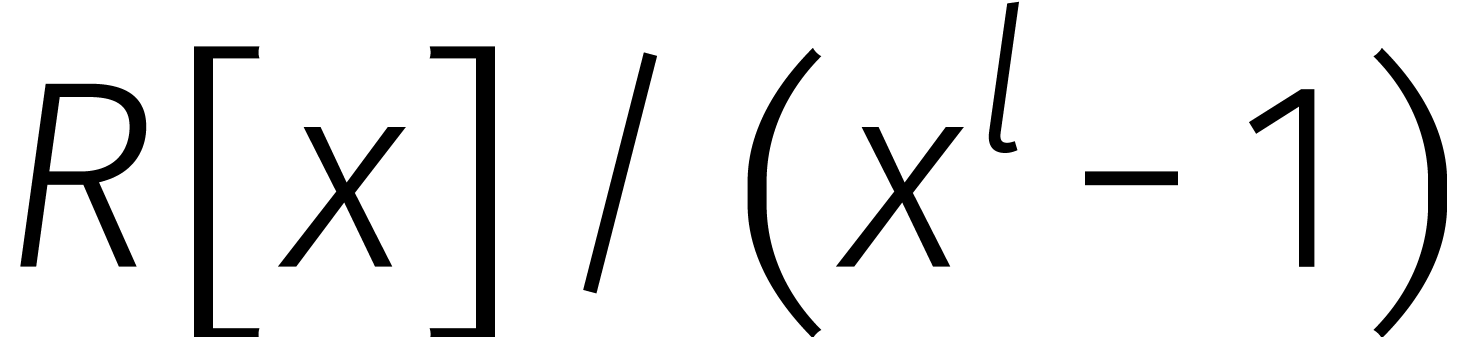 . Schrijven we
. Schrijven we 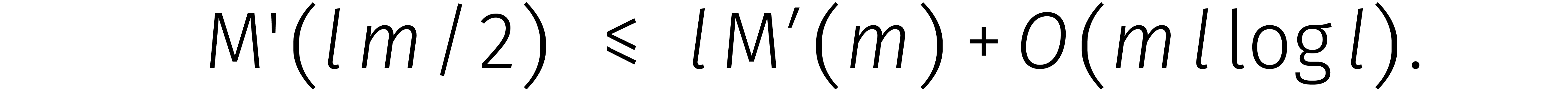 voor de kosten van één vermenigvuldiging in
voor de kosten van één vermenigvuldiging in
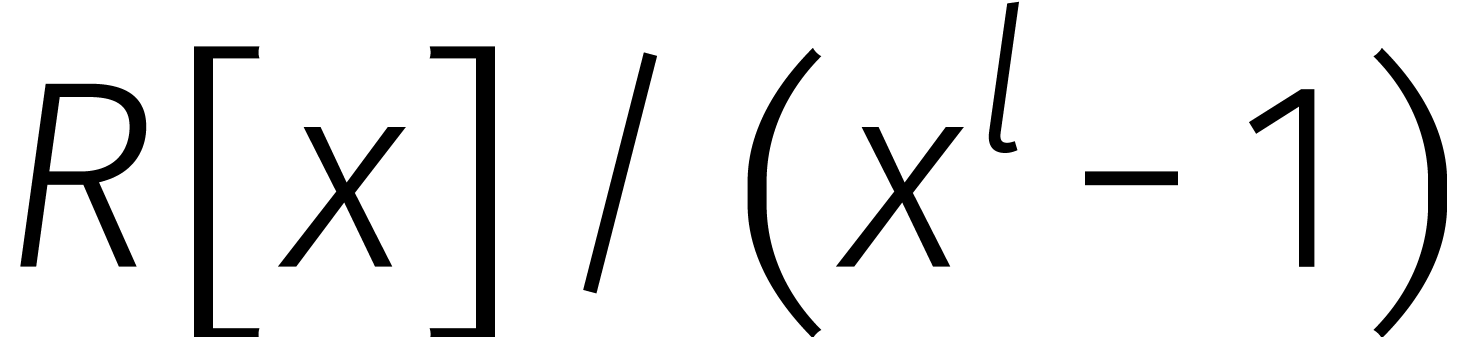 , dan geeft dit
, dan geeft dit
De term 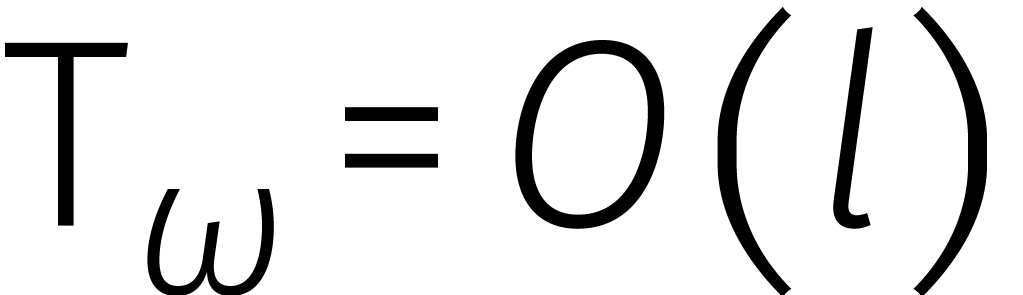 komt van de DFTs, waar we gebruik maken
van het feit dat
komt van de DFTs, waar we gebruik maken
van het feit dat 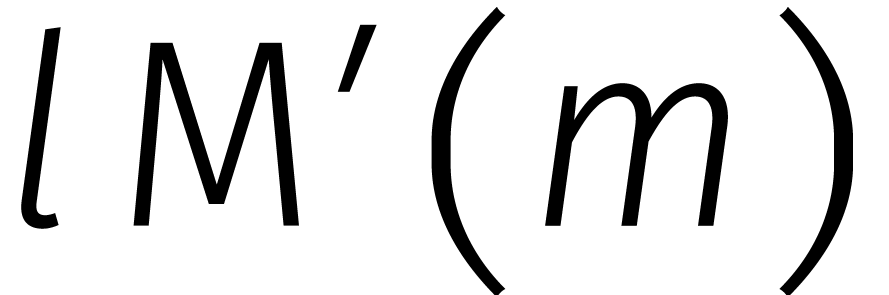 in
in 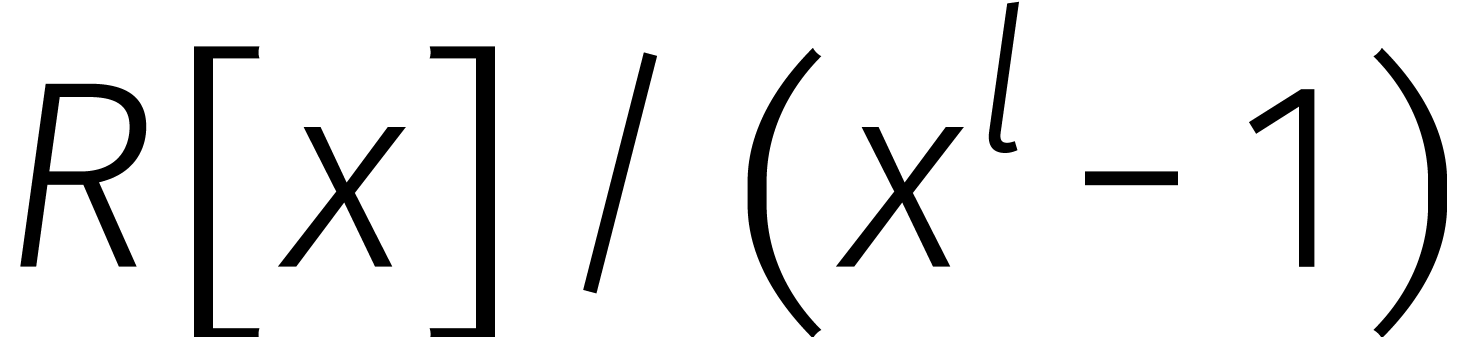 . De term
. De term 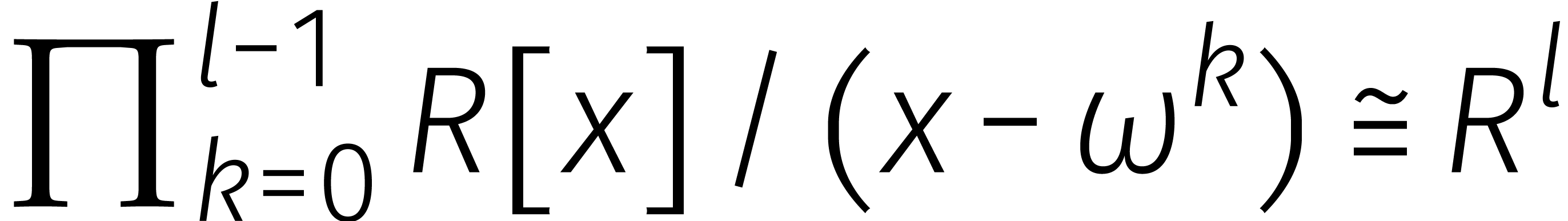 komt van de
„interne” vermenigvuldiging in
komt van de
„interne” vermenigvuldiging in 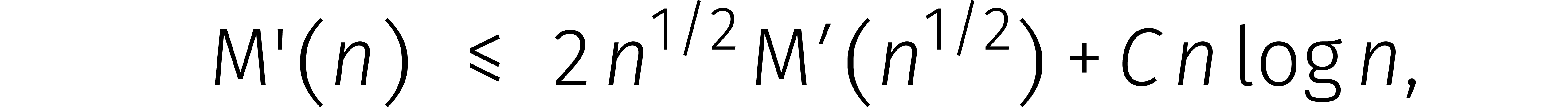 .
.
Omgerekend ten opzichte van 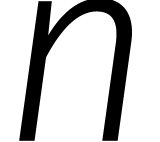 leidt (3)
grofweg tot de ongelijkheid
leidt (3)
grofweg tot de ongelijkheid
voor een zekere constante  .
Deze formule kunnen we vervolgens „uitrollen”:
.
Deze formule kunnen we vervolgens „uitrollen”:
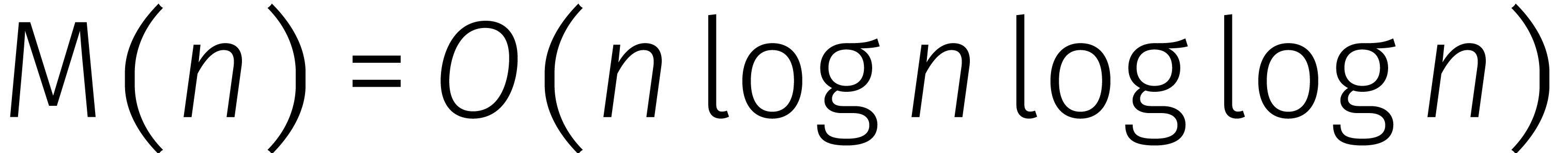
Dit bewijst dat 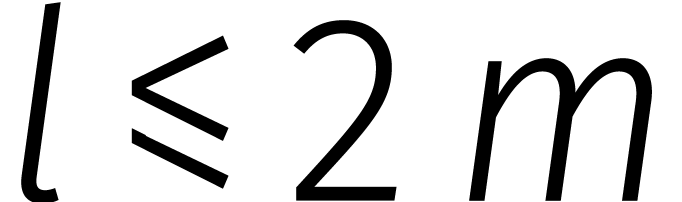 , een
bovengrens die vijfenveertig jaar stand hield.
, een
bovengrens die vijfenveertig jaar stand hield.
Van de drie op de FFT gebaseerde methodes uit 1971 heeft de laatste
methode één groot nadeel: omdat 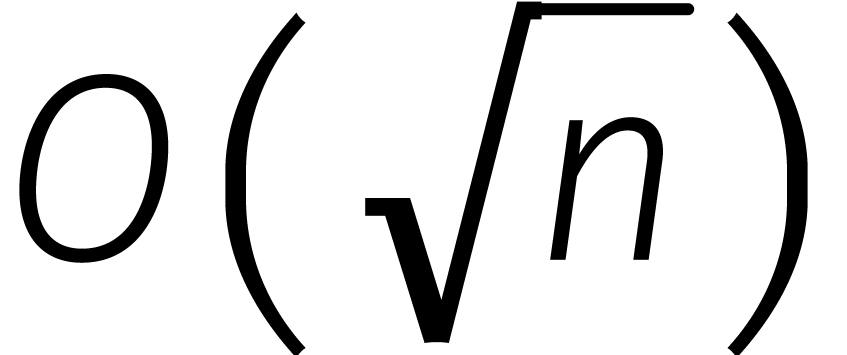 wordt een vermenigvuldiging van lengte
wordt een vermenigvuldiging van lengte 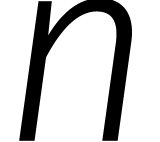 „slechts” gereduceerd tot vermenigvuldigingen van lengte
„slechts” gereduceerd tot vermenigvuldigingen van lengte
 in plaats van
in plaats van 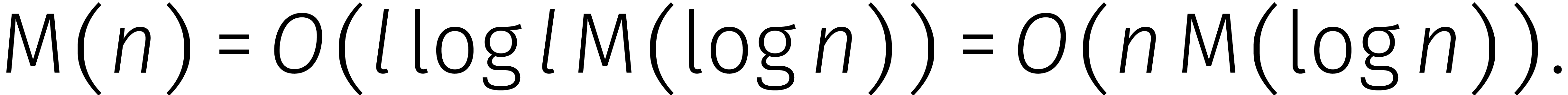 .
In tegenstelling tot de twee andere methodes kosten de DFTs daarentegen
bijna niets. Dit levert twee sporen op voor verdere verbeteringen.
.
In tegenstelling tot de twee andere methodes kosten de DFTs daarentegen
bijna niets. Dit levert twee sporen op voor verdere verbeteringen.
Een eerste mogelijkheid is om de kosten van DFTs over 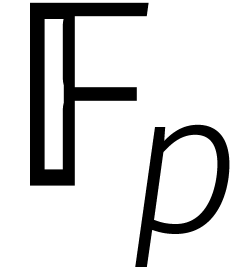 en/of
en/of 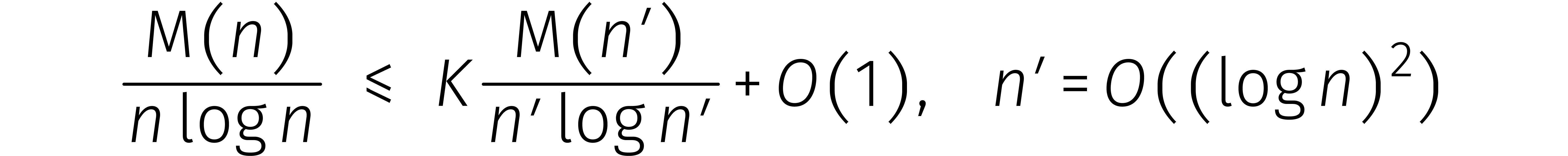 te drukken. In 2007 lukte Fürer dit
voor het eerst [5]. Zijn methode leidt tot een ongelijkheid
van de vorm
te drukken. In 2007 lukte Fürer dit
voor het eerst [5]. Zijn methode leidt tot een ongelijkheid
van de vorm
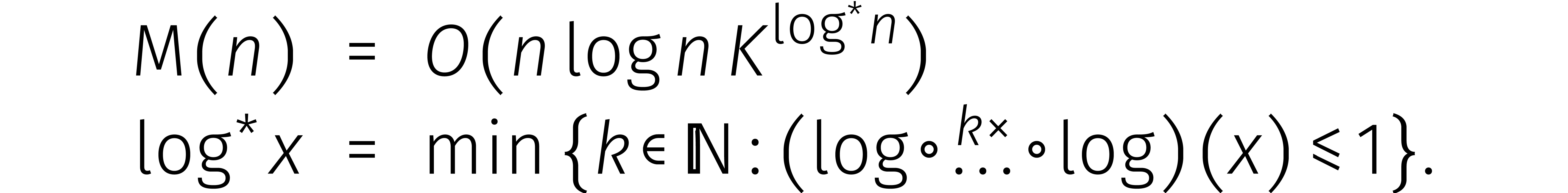
en de verbeterde bovengrens
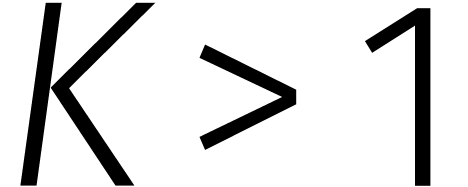
Fürer besteedde geen aandacht aan de precieze
„uitdijingsfactor” 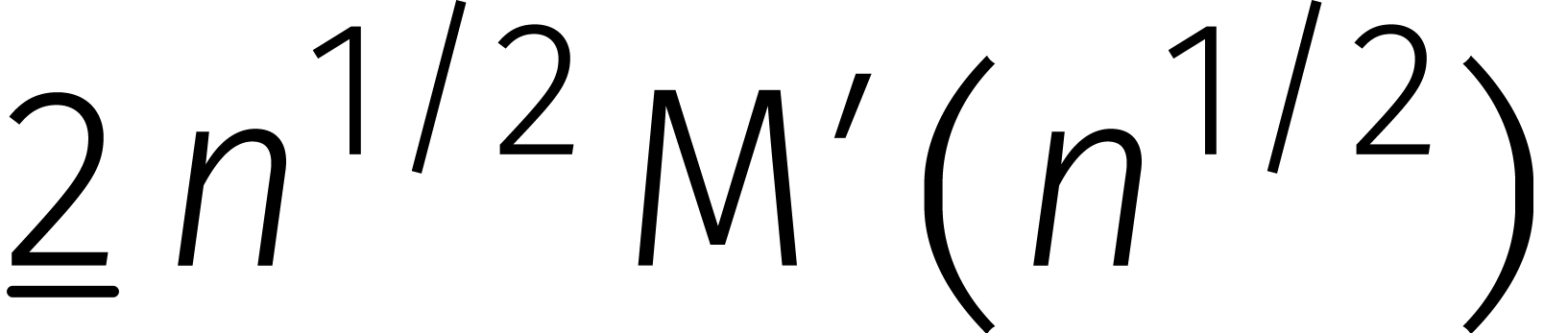 .
Vanaf 2014 lukte het David Harvey, Grégoire Lecerf, en mijzelf om
deze factor steeds verder naar beneden te jagen [13, 9, 10, 11]; zie Tabel 1.
.
Vanaf 2014 lukte het David Harvey, Grégoire Lecerf, en mijzelf om
deze factor steeds verder naar beneden te jagen [13, 9, 10, 11]; zie Tabel 1.
Onze tweede optie is een verscherping van de ongelijkheid (4).
Hier merken we op dat de factor 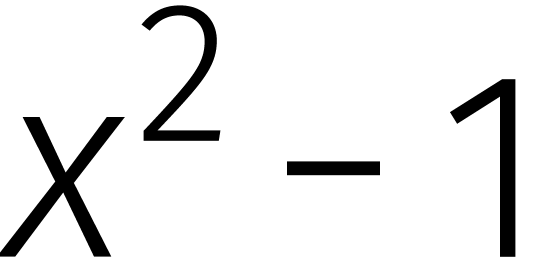 in
in 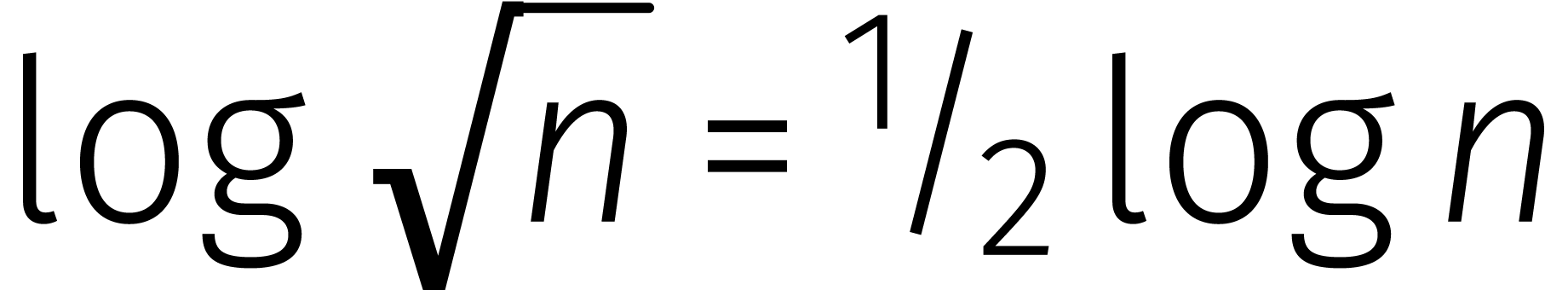 precies wordt gecompenseerd door het feit dat
precies wordt gecompenseerd door het feit dat 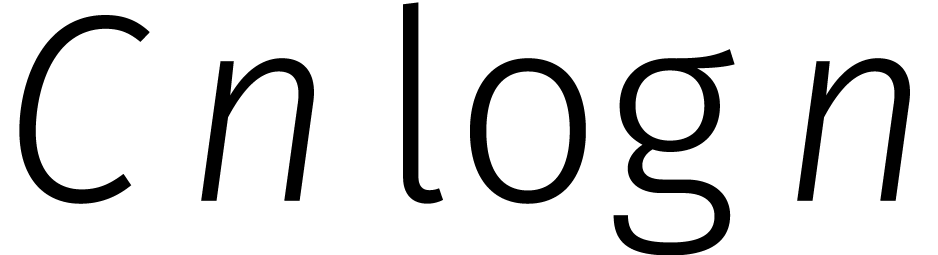 : bij het uitrollen kost elke iteratie precies
: bij het uitrollen kost elke iteratie precies
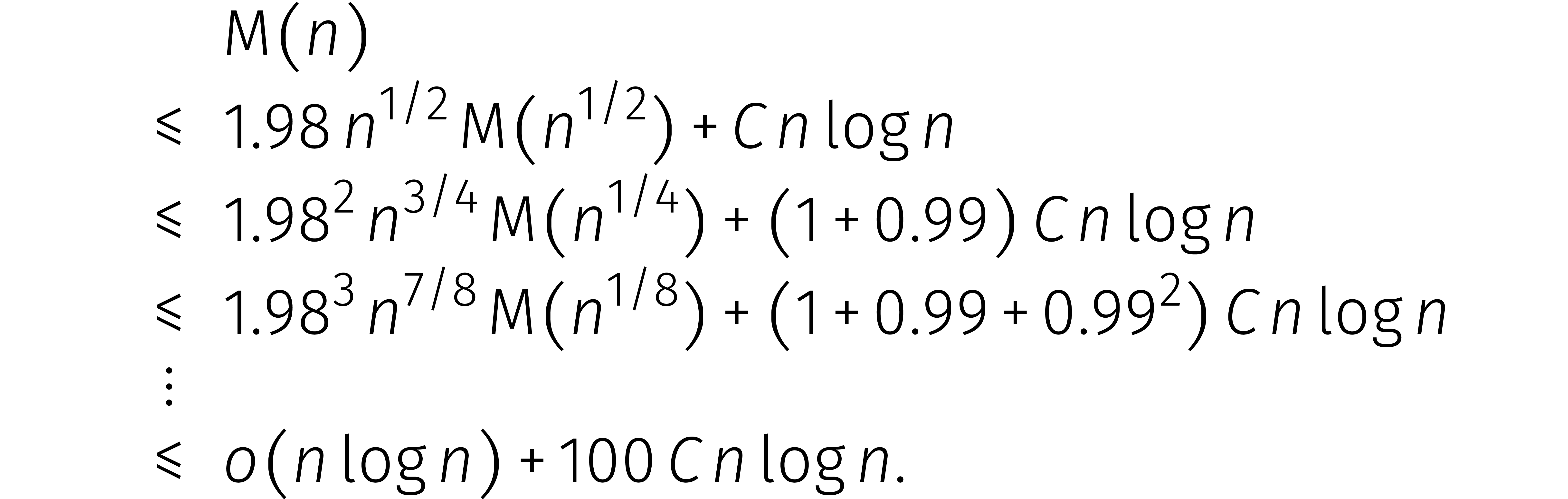 stappen extra. Kunnen we deze factor
stappen extra. Kunnen we deze factor 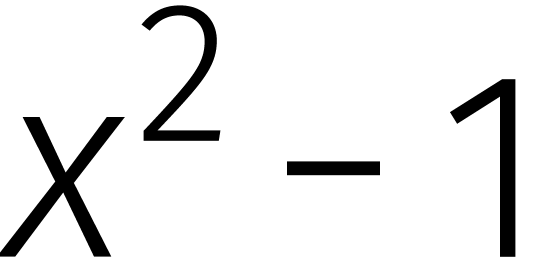 maar een fractie verbeteren, dan verloopt het uitrollen
zich als volgt:
maar een fractie verbeteren, dan verloopt het uitrollen
zich als volgt:
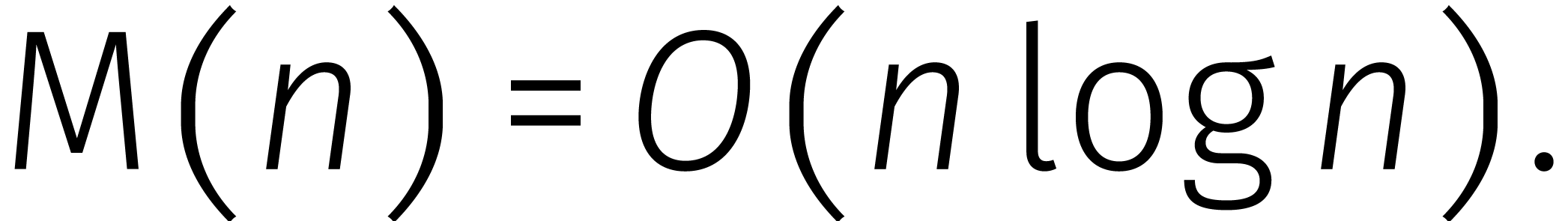
Ho! Lezen we dat goed?
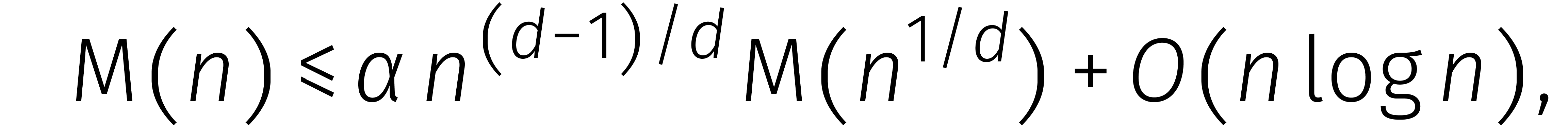
Op deze wens kunnen we voortborduren. Zo is het ook genoeg om te bewijzen dat
 |
(5) |
waar 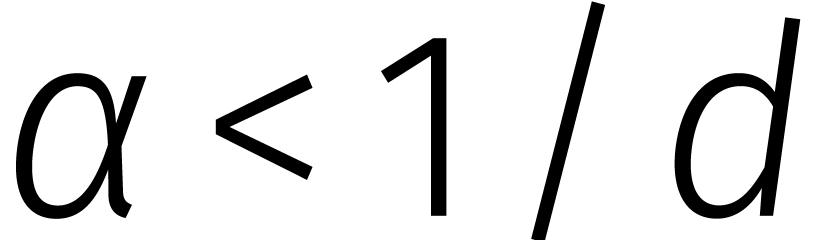 en
en 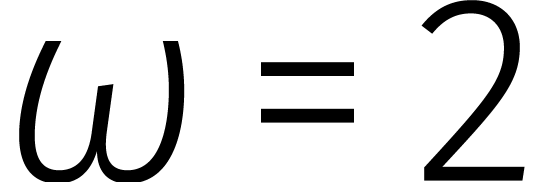 .
.
Nu heeft de methode van Schönhage en Strassen inderdaad een
frustrerend aspect: de kunstmatig aangemaakte eenheidswortel 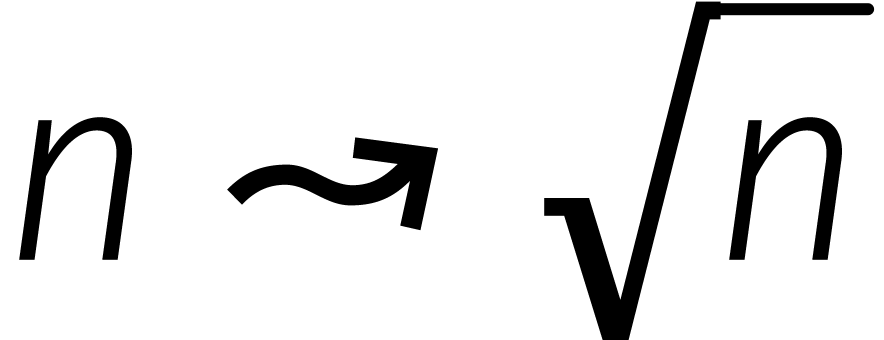 in
in 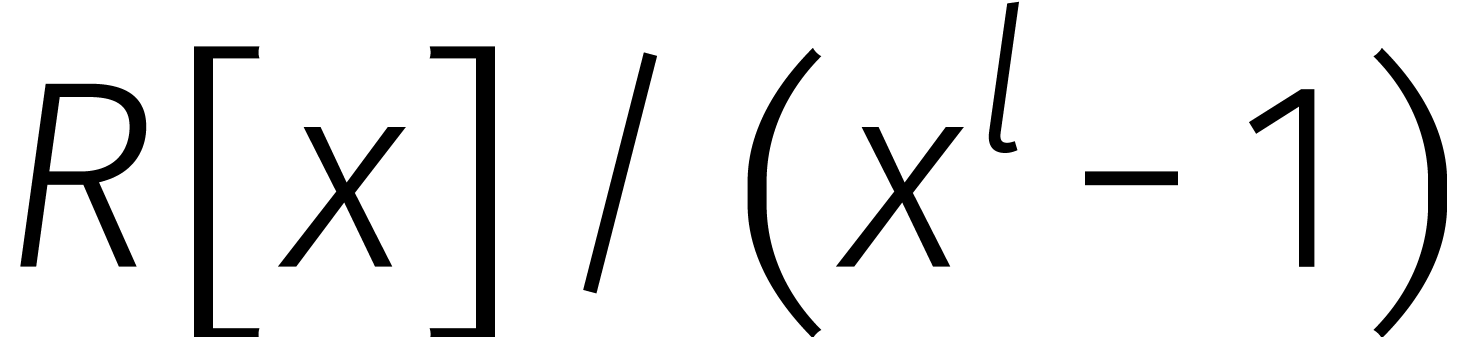 wordt eigenlijk reuze
„ondergebruikt”. Om die reden is onze lengtereductie
wordt eigenlijk reuze
„ondergebruikt”. Om die reden is onze lengtereductie 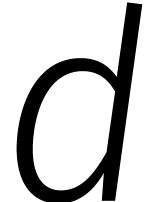 zeer bescheiden.
zeer bescheiden.
Nu zijn er ook DFTs die in meer dan één richting werken.
Stel opnieuw dat 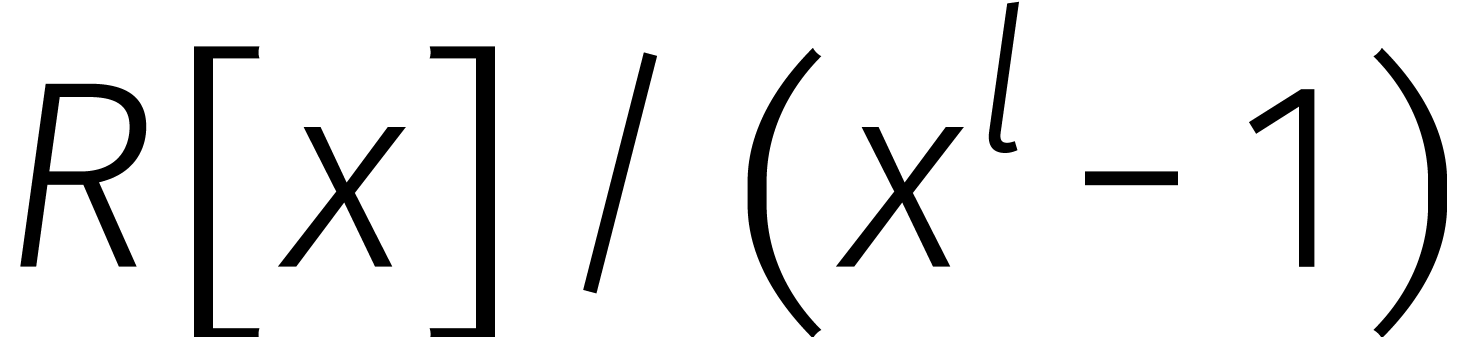 een willekeurige ring is met
een principiële eenheidswortel
een willekeurige ring is met
een principiële eenheidswortel 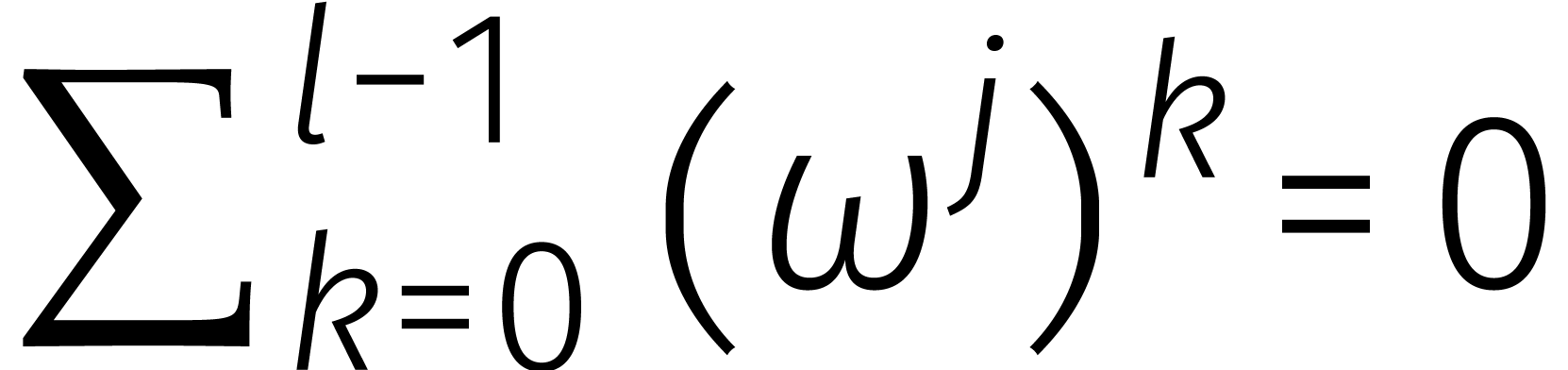 van orde
van orde
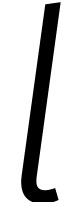 . Een
. Een 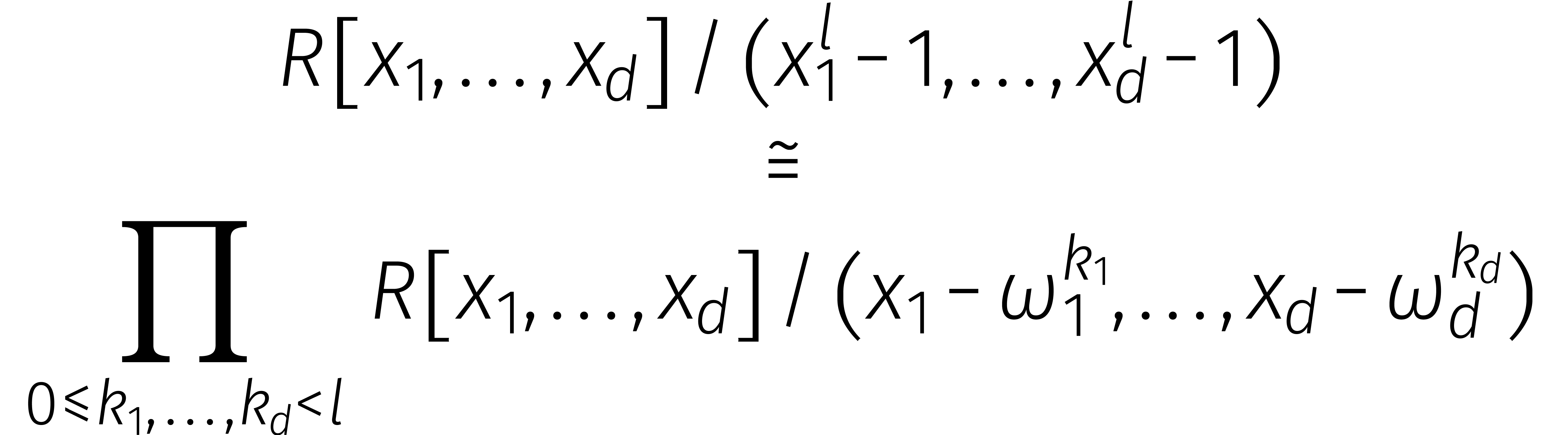 -dimensionale DFT bewerkstelligt dan het isomorfisme
-dimensionale DFT bewerkstelligt dan het isomorfisme

Als we de DFTs in 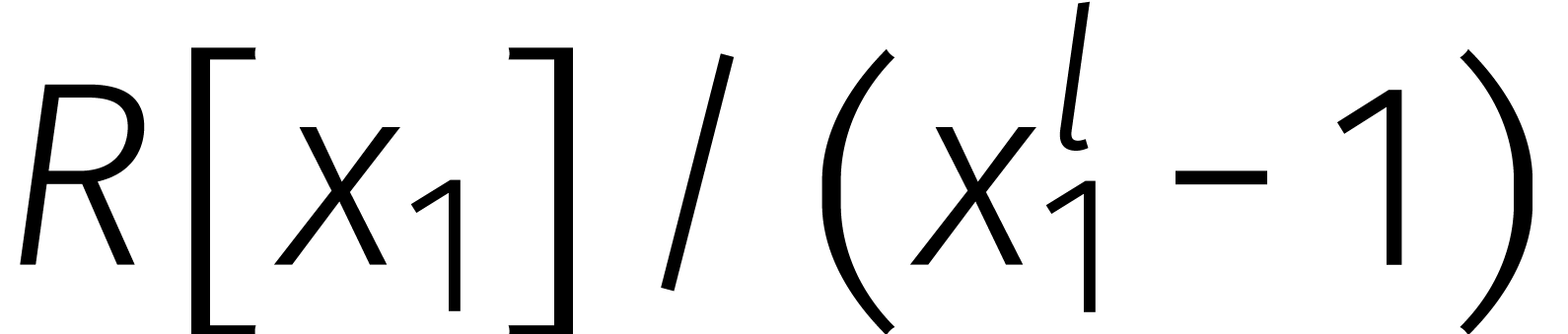 nu vervangen door DFTs over de
ring
nu vervangen door DFTs over de
ring 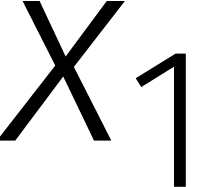 , dan kosten ze veel
minder, want
, dan kosten ze veel
minder, want 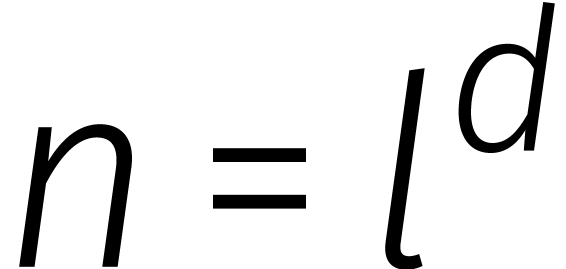 is een snelle eenheidswortel in
deze ring. Het systematische gebruik van dit soort DFTs werd voor het
eerst voorgesteld door Nussbaumer en Quandalle [18].
is een snelle eenheidswortel in
deze ring. Het systematische gebruik van dit soort DFTs werd voor het
eerst voorgesteld door Nussbaumer en Quandalle [18].
Met dat idee maken we meteen al een grote stap in de richting van (5). Als 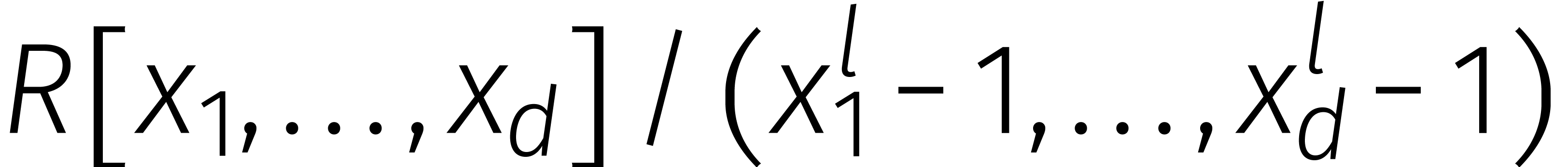 , dan vergt
een vermenigvulding in
, dan vergt
een vermenigvulding in 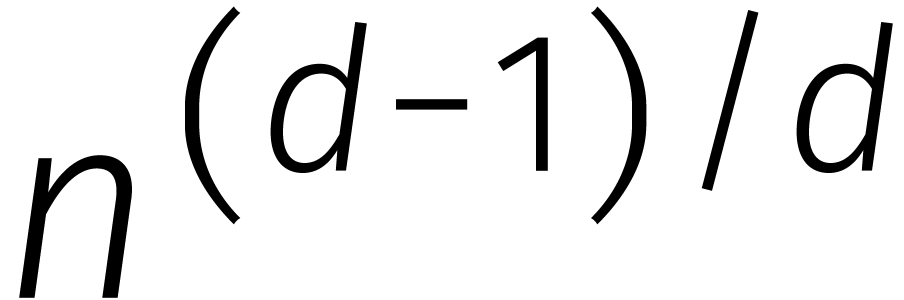 namelijk
namelijk 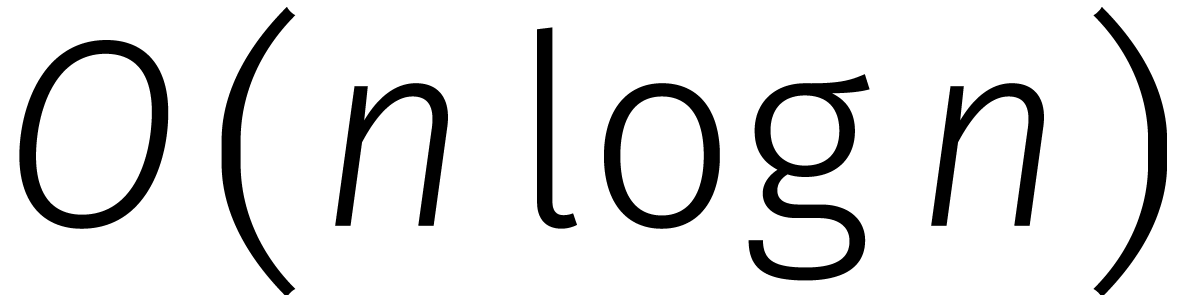 optelleningen en aftrekkingen in
optelleningen en aftrekkingen in 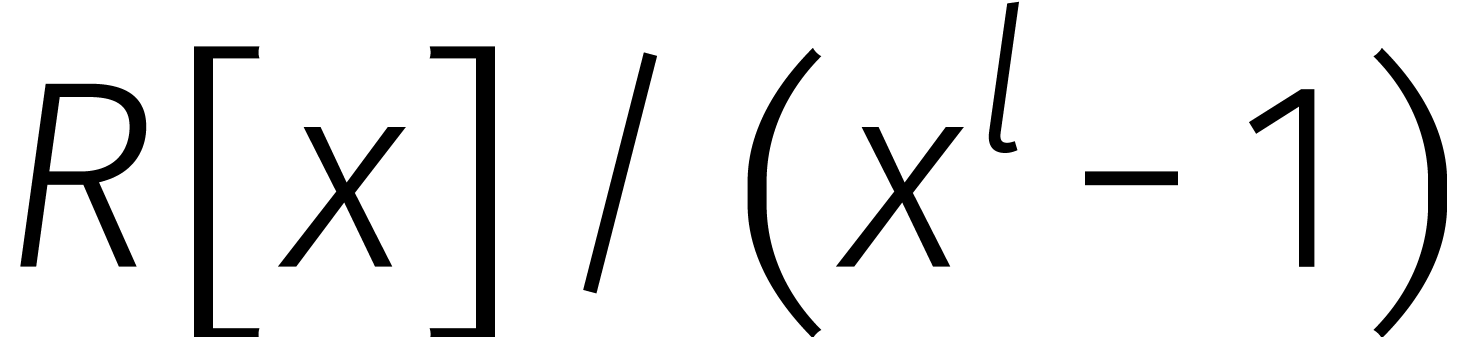 plus
plus 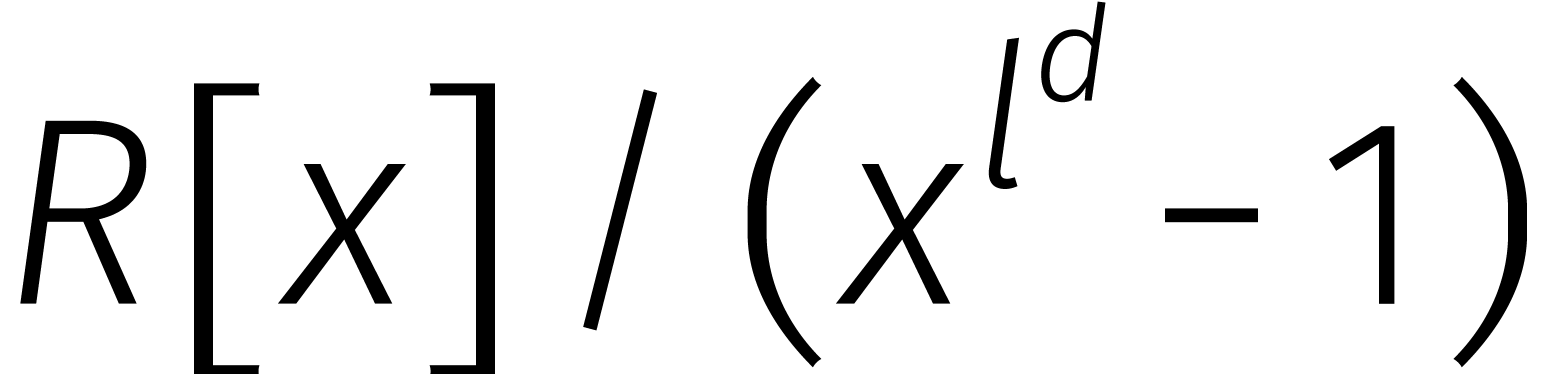 vermenigvuldigingen in
vermenigvuldigingen in 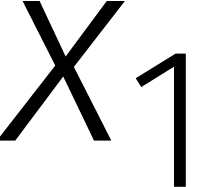 .
.
Er is echter één probleem: snel vermenigvuldigen in 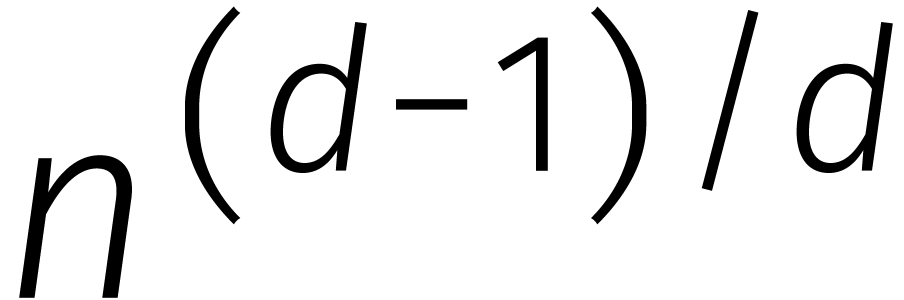 is niet hetzelfde als snel vermenigvuldigen in
is niet hetzelfde als snel vermenigvuldigen in  . We hebben dus een manier nodig om
kringtermen in één variabele
. We hebben dus een manier nodig om
kringtermen in één variabele  om te
smeden tot kringtermen in
om te
smeden tot kringtermen in 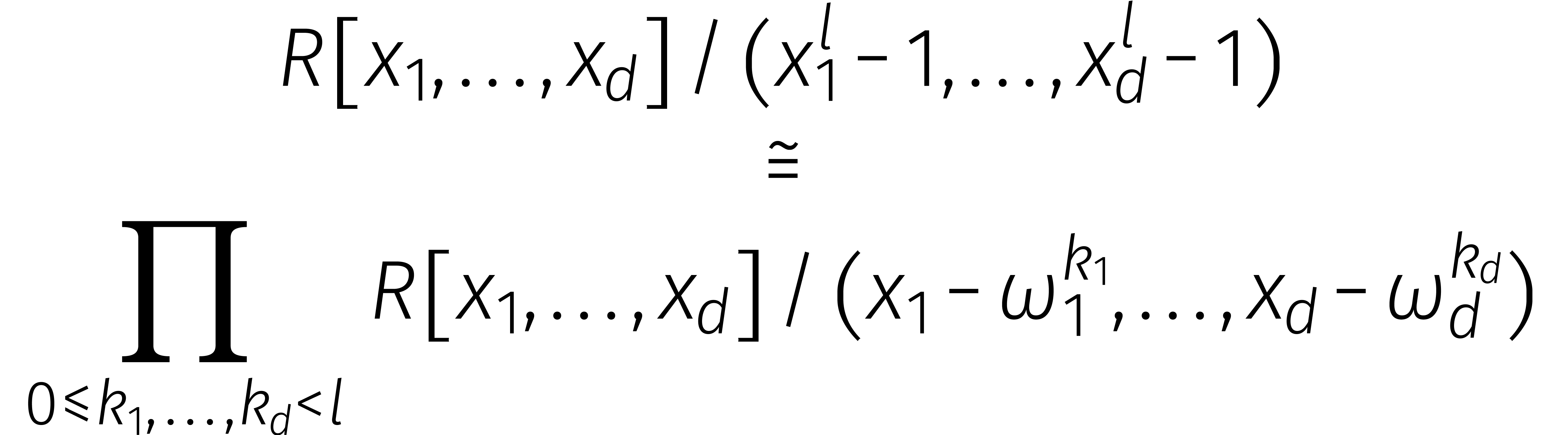 variabelen
variabelen  .
.
Nu is het in bepaalde gevallen inderdaad mogelijk om van dimensie te
veranderen. Stel dat 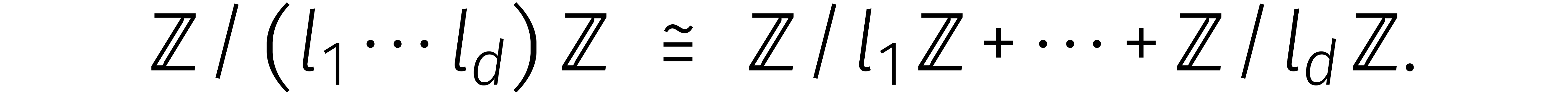 onderling ondeelbaar zijn.
Volgens de Chinese reststelling hebben we dan
onderling ondeelbaar zijn.
Volgens de Chinese reststelling hebben we dan
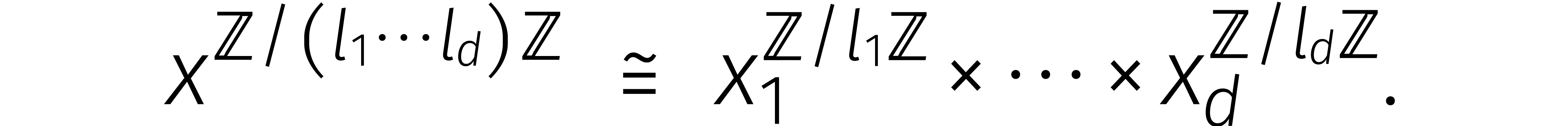
Formeel gesproken hebben we dus ook
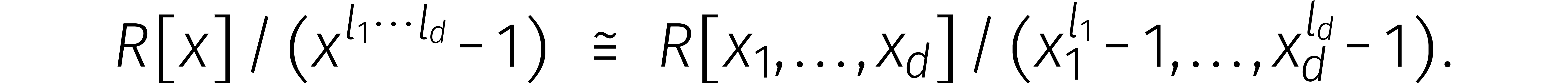
Nemen we vervolgens lineaire combinaties, dan zien we uiteindelijk dat
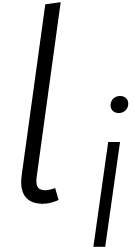
In verband met DFTs werd dit voor het eerst opgemerkt door Good [7]. Agarwal en Cooley gebruikten dit isomorfisme daarna voor het uitrekenen van convoluties [1].
Wel zitten we nu weer met een nieuw probleem: in de vorige paragraaf
vroegen we om een isomorfisme waarvoor alle  gelijk zijn. Maar ons isomorfisme werkt juist alleen in het geval
wanneer
gelijk zijn. Maar ons isomorfisme werkt juist alleen in het geval
wanneer 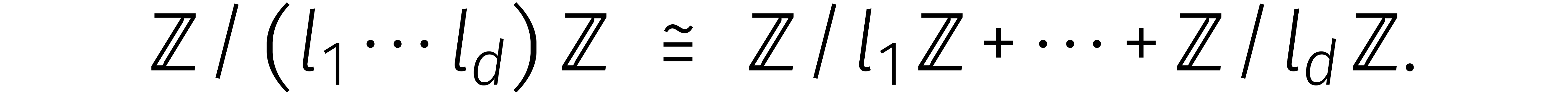 onderling ondeelbaar zijn.
onderling ondeelbaar zijn.
Wat er tot slot nog ontbreekt is een manier om de lengte van een DFT
iets te veranderen. Dit zou het mogelijk maken om een 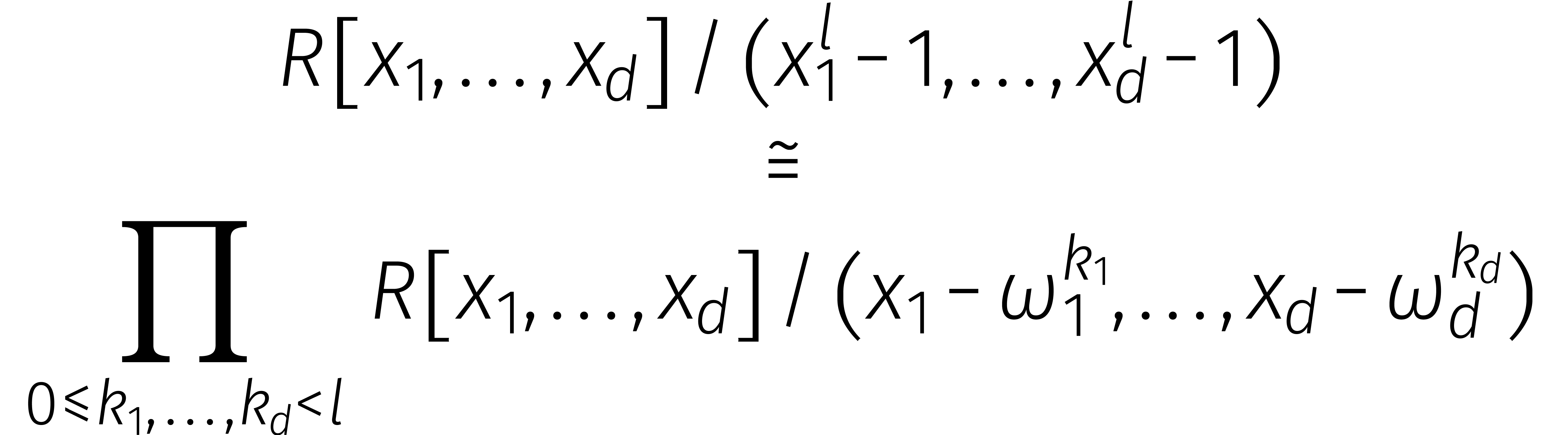 -dimensionale DFT van lengte
-dimensionale DFT van lengte  om te smeden tot eentje van lengte
om te smeden tot eentje van lengte  .
Met behulp van een
.
Met behulp van een 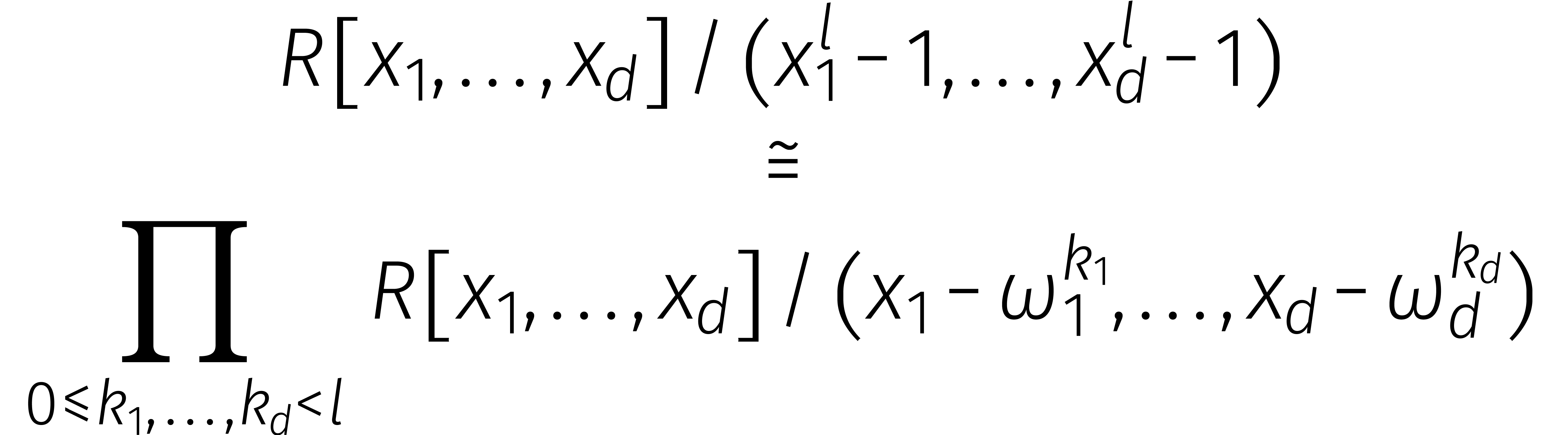 -dimensionale
versie van Bluestein's algoritme kan zo'n DFT vervolgens worden
gereduceerd tot een vermenigvuldiging in
-dimensionale
versie van Bluestein's algoritme kan zo'n DFT vervolgens worden
gereduceerd tot een vermenigvuldiging in 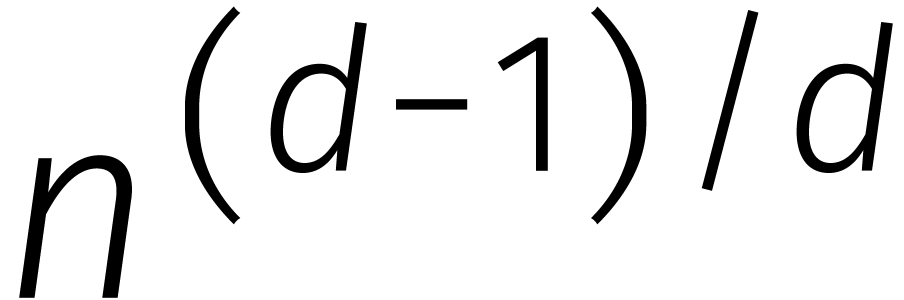 .
En dat kan uiteindelijk weer efficiënt worden gedaan met behulp van
snelle eenheidswortels.
.
En dat kan uiteindelijk weer efficiënt worden gedaan met behulp van
snelle eenheidswortels.
Hoe kunnen we een DFT van lengte 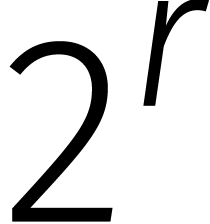 vervangen door
een DFT van een iets grotere lengte
vervangen door
een DFT van een iets grotere lengte 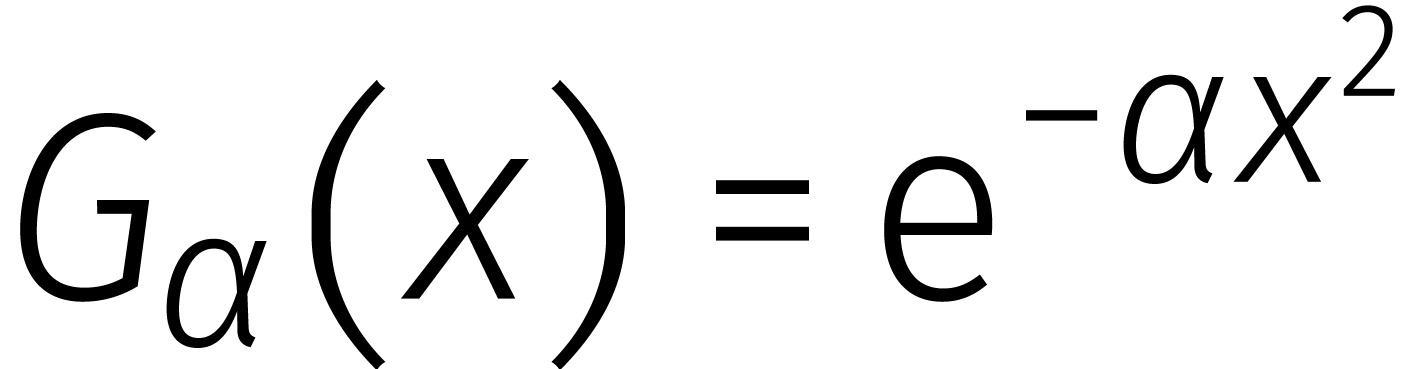 ?
Om dit te bereiken veronderstellen we vanaf hier dat
?
Om dit te bereiken veronderstellen we vanaf hier dat 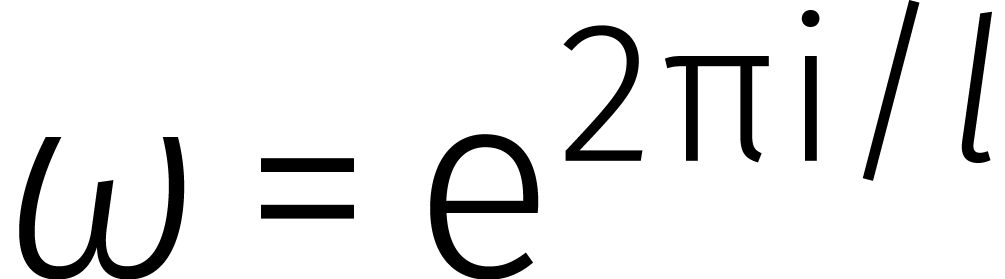 .
.
Neem een DFT van lengte 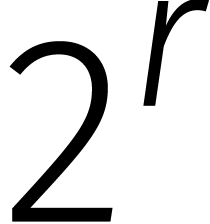 . In
de signaaltheorie wordt de invoer gezien als een reeks monsters van een
signaal. De frequentie van de monstername is hierbij evenredig aan
. In
de signaaltheorie wordt de invoer gezien als een reeks monsters van een
signaal. De frequentie van de monstername is hierbij evenredig aan 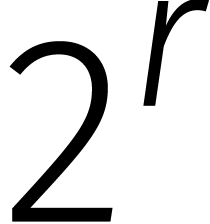 . Is het mogelijk het
oorspronkelijke signaal uit onze reeks monsters te reconstrueren? Dan
zouden we daarna een nieuwe reeks monsters kunnen nemen, met een andere
frequentie.
. Is het mogelijk het
oorspronkelijke signaal uit onze reeks monsters te reconstrueren? Dan
zouden we daarna een nieuwe reeks monsters kunnen nemen, met een andere
frequentie.
De meest voor de hand liggende manier om een digitaal signaal analoog te
maken is via convolutie met een Gaussiaan 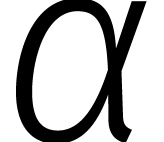 .
Hoe kleiner
.
Hoe kleiner 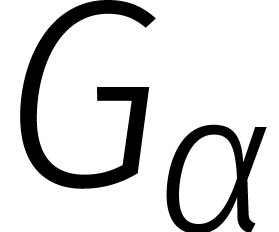 , hoe gladder
(en minder scherp) het analoge signaal. Een andere prettige eigenschap
is dat de fouriertransformatie van
, hoe gladder
(en minder scherp) het analoge signaal. Een andere prettige eigenschap
is dat de fouriertransformatie van  opnieuw een
Gaussiaan is.
opnieuw een
Gaussiaan is.
Laten we deze ideeën in formules . In plaats van kringtermen van
lengte 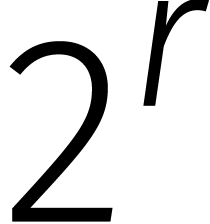 beschouwen we nu de bijbehorende vectoren
van coëfficiënten
beschouwen we nu de bijbehorende vectoren
van coëfficiënten 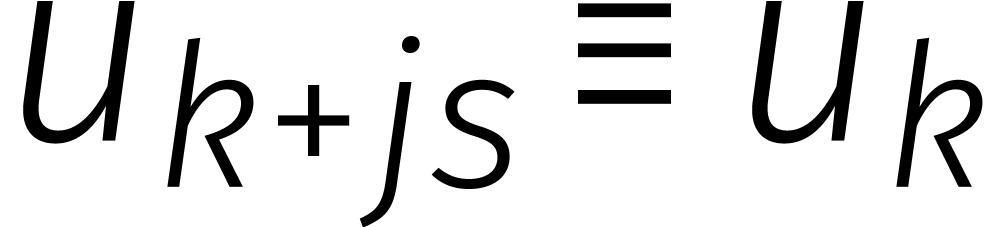 .
Wel spreken we af dat
.
Wel spreken we af dat 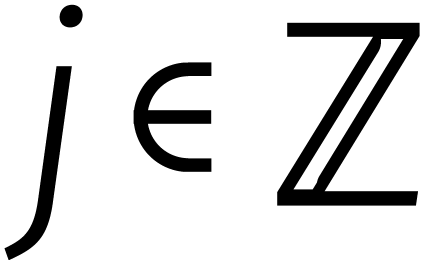 voor alle
voor alle 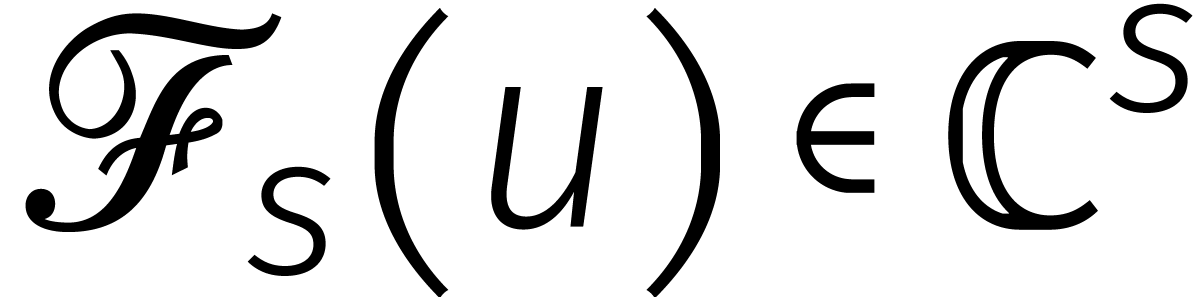 . Gegeven
. Gegeven 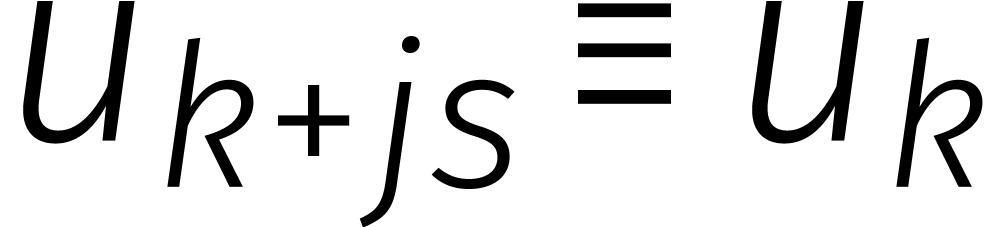 definiëren we
definiëren we 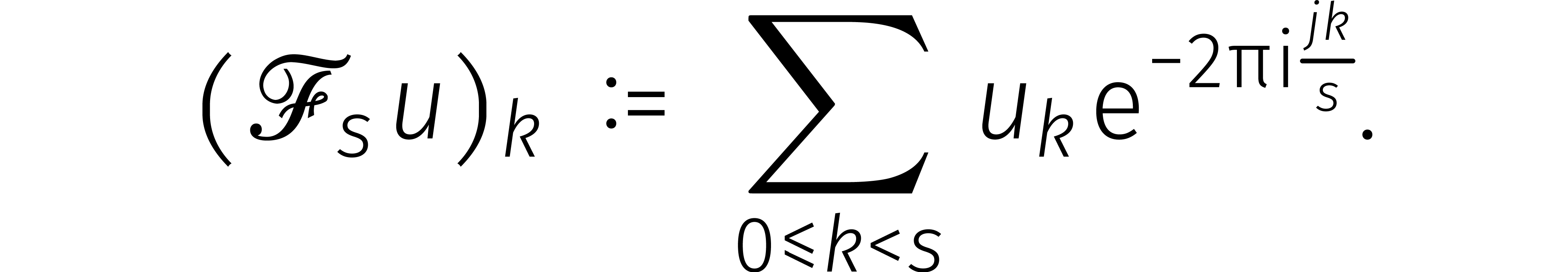 door
door
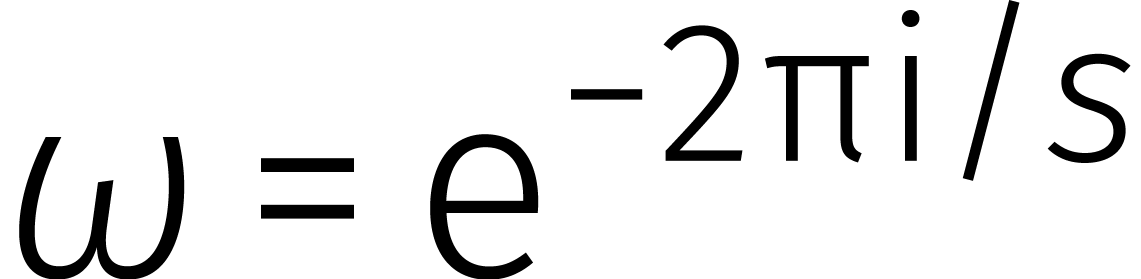
Dit is een variant op onze eerdere definitie van een DFT (nu nemen we
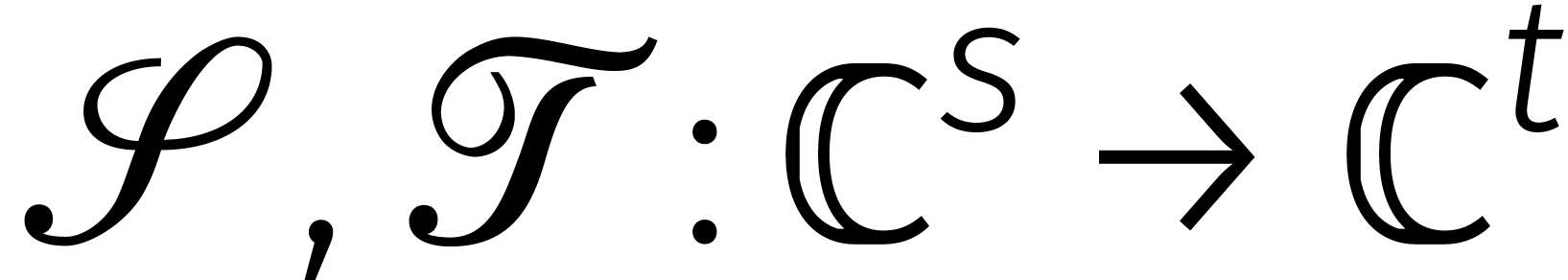 ). Vervolgens definiëren
we twee lineaire afbeeldingen
). Vervolgens definiëren
we twee lineaire afbeeldingen 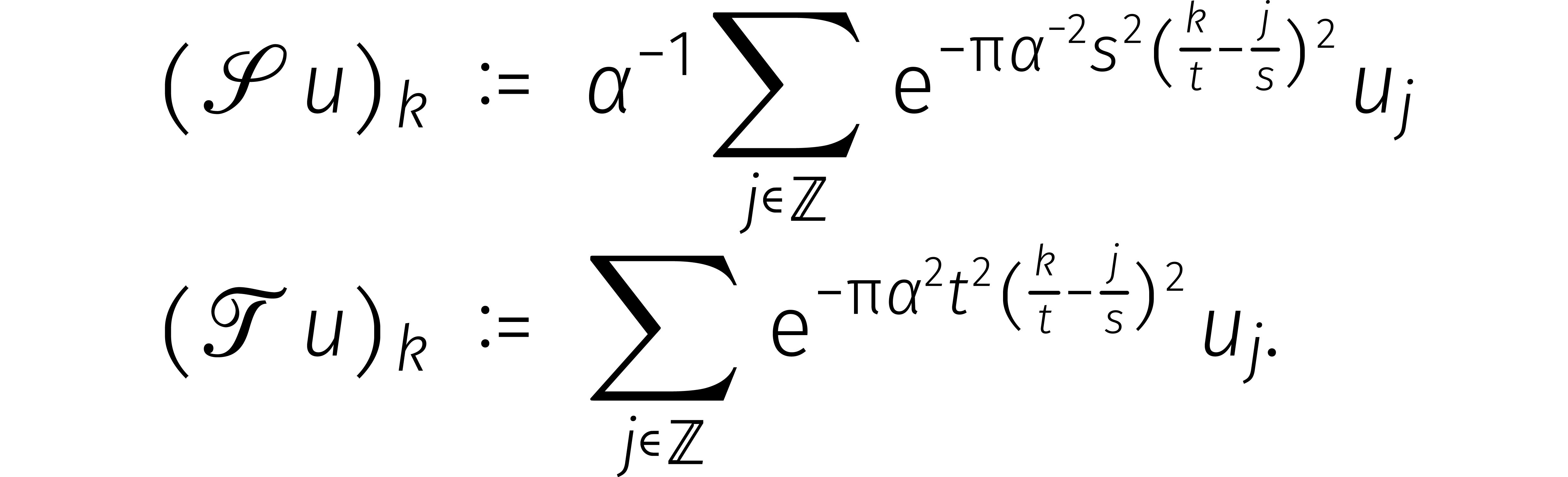 door
door
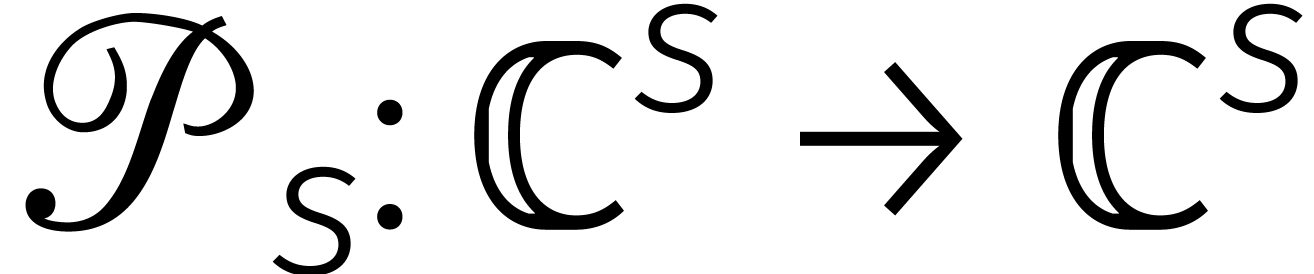
Tot slot definiëren we twee permutaties 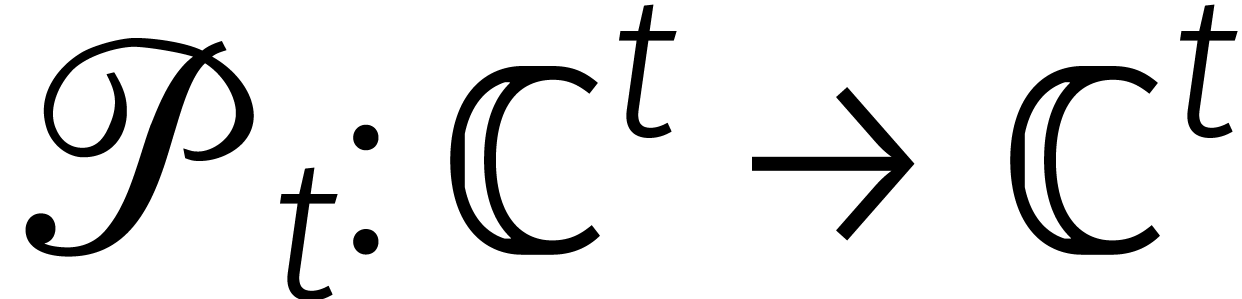 en
en
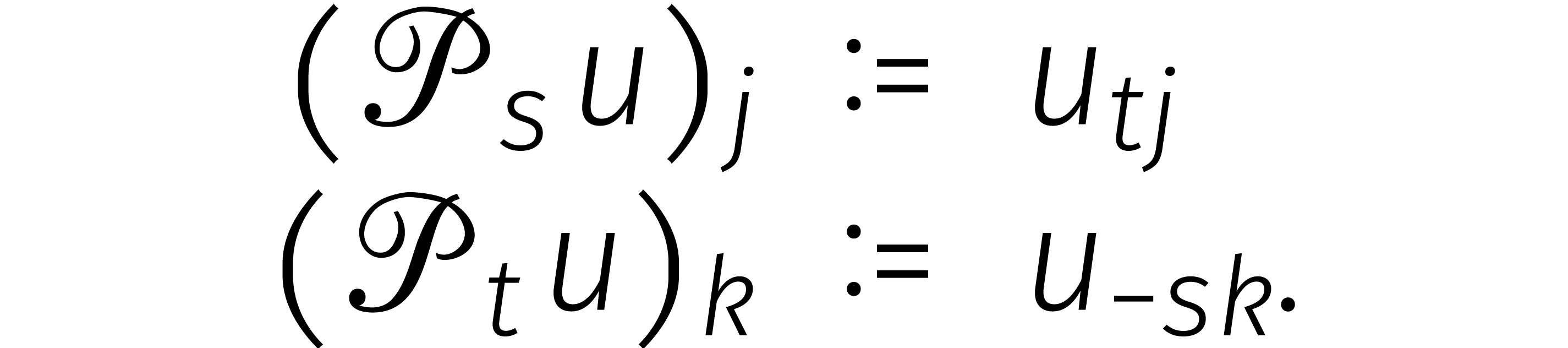 door
door
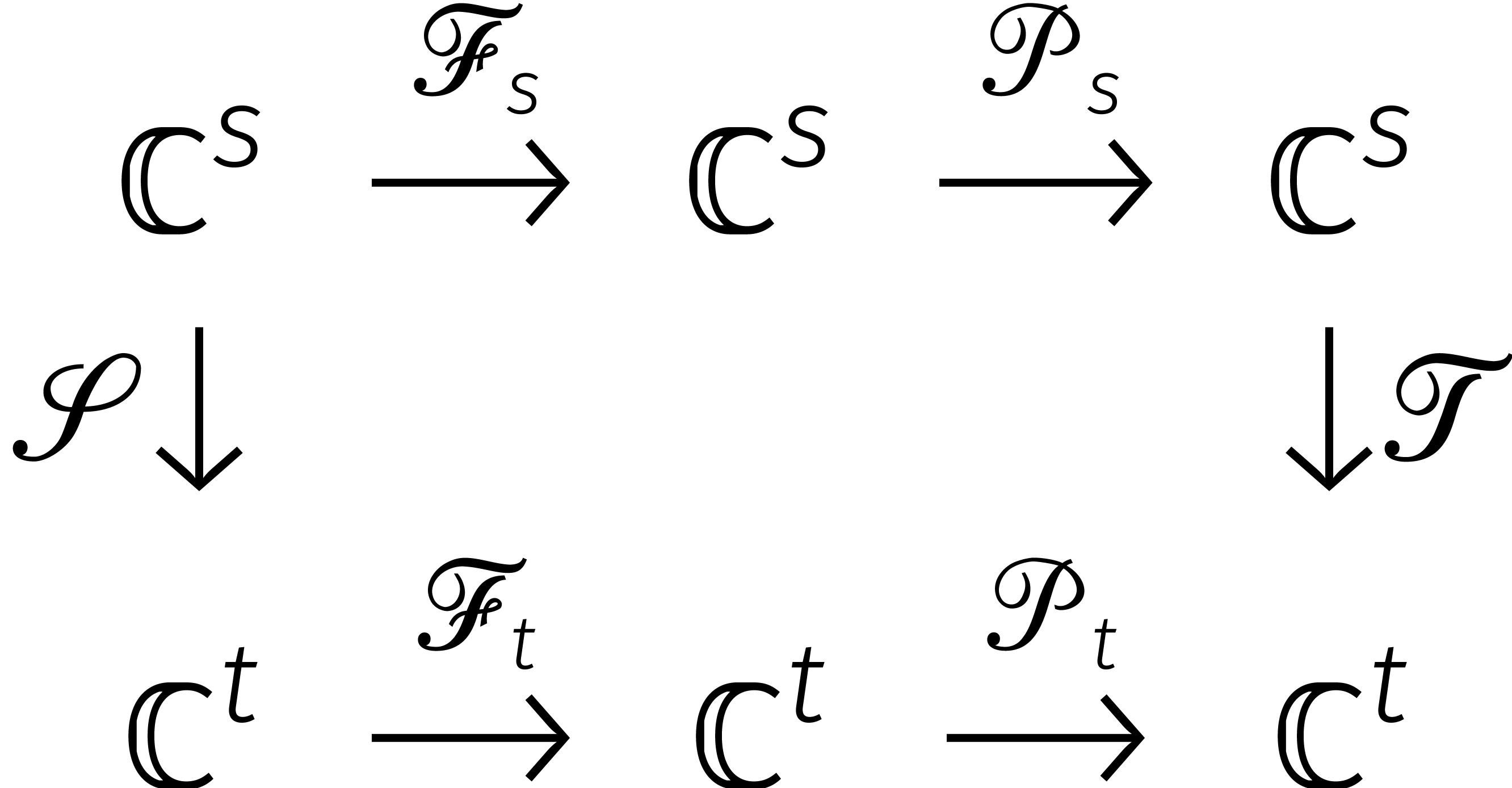
In [12, Theorem 4.2] bewijzen we dan dat het volgende diagram commuteert:

Dit is wat we gebruiken om het berekenen van  terug te voeren op het berekenen van
terug te voeren op het berekenen van 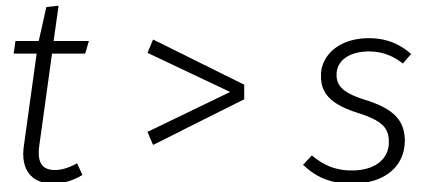 .
.
Omdat 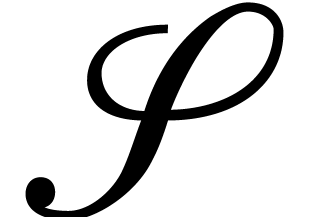 , zijn de matrices voor
, zijn de matrices voor
 en
en 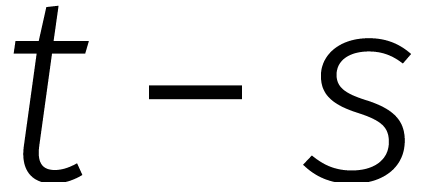 niet vierkant.
Wél is het zo dat de elementen die niet op de diagonaal liggen
razendsnel afnemen. Dat komt doordat Gaussianen uit het centrum ook
razendsnel afnemen. Door
niet vierkant.
Wél is het zo dat de elementen die niet op de diagonaal liggen
razendsnel afnemen. Dat komt doordat Gaussianen uit het centrum ook
razendsnel afnemen. Door 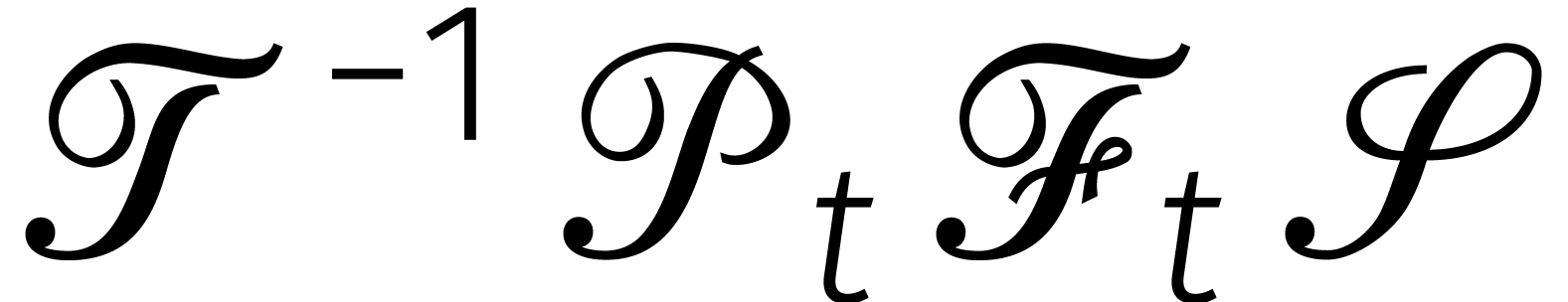 goed gekozen rijen uit
goed gekozen rijen uit
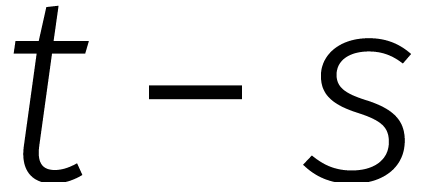 weg te nemen blijft er om die reden een bijna
diagonale matrix over. Dit kan worden benut om
weg te nemen blijft er om die reden een bijna
diagonale matrix over. Dit kan worden benut om  snel uit te rekenen.
snel uit te rekenen.
Kiezen we 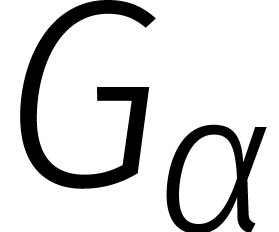 en de precisie met beleid, dan kunnen
we bewijzen dat
en de precisie met beleid, dan kunnen
we bewijzen dat  op deze manier met bijna
evenveel precisie als
op deze manier met bijna
evenveel precisie als 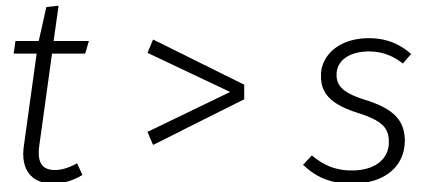 kan worden berekend en dat
de rekentijd van
kan worden berekend en dat
de rekentijd van  and
and 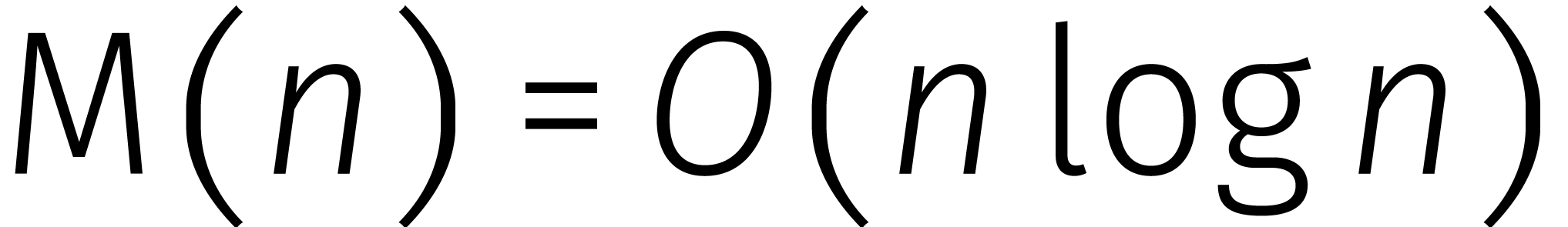 verwaarloosbaar is ten opzichte van die van
verwaarloosbaar is ten opzichte van die van 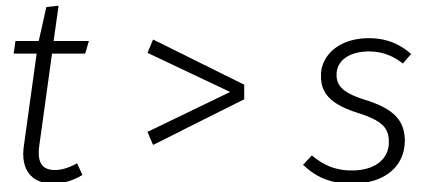 .
.
Daarmee is de kous af en hebben we bewezen dat
 .
In Figuur
6
worden alle benodigde reducties nog eens samengevat.
.
In Figuur
6
worden alle benodigde reducties nog eens samengevat.
Een variant van onze overmonsteringsmethode werd voor het eerst
gepubliceerd door Dutt en Rokhlin [4]. Deze variant is
algemener en maakt het mogelijk DFTs te berekenen van onregelmatig
gemonsterde signalen. Daarentegen werkt hun methode alleen voor 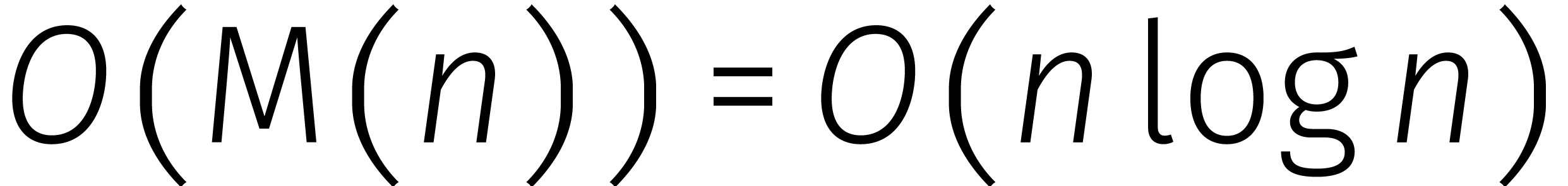 en is daarom net iets te traag voor ons uiteindelijke
doel.
en is daarom net iets te traag voor ons uiteindelijke
doel.
Praktisch gezien moeten we dat afwachten. Voor theoretische doeleinden
is de functie 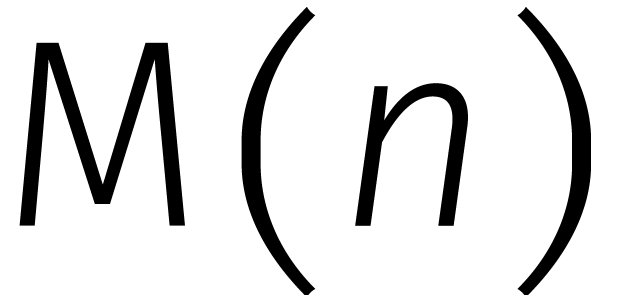 van belang om de kosten van
allerlei rekenkundige operaties nauwkeurig te beschrijven. Zo kost het
delen van getallen van
van belang om de kosten van
allerlei rekenkundige operaties nauwkeurig te beschrijven. Zo kost het
delen van getallen van 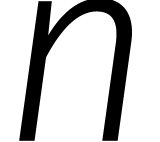 cijfers
cijfers 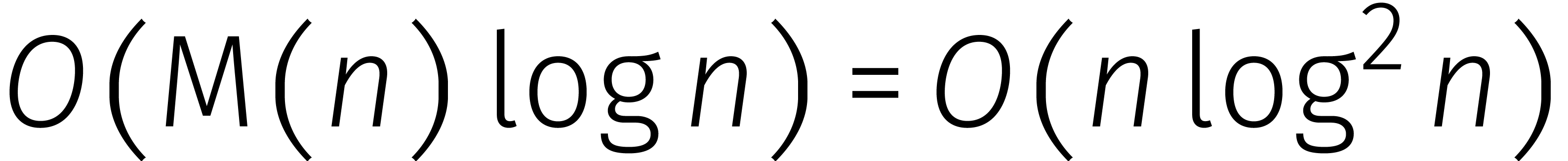 en het uitrekenen van een grootste gemene deler
en het uitrekenen van een grootste gemene deler 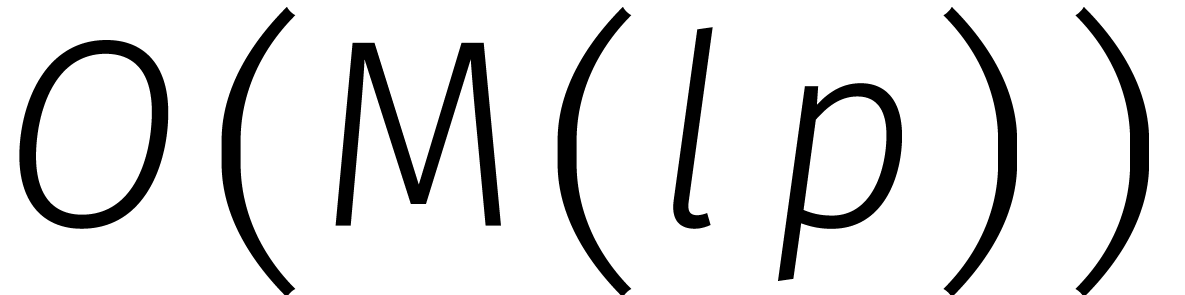 . Ook
. Ook 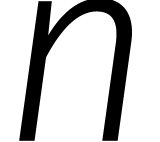 decimalen van
decimalen van  kunnen nu in
kunnen nu in 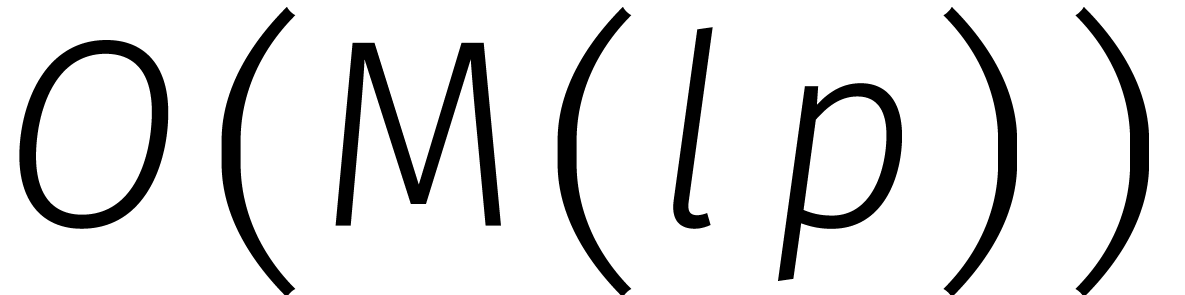 stappen worden
berekend. Een DFT van lengte
stappen worden
berekend. Een DFT van lengte 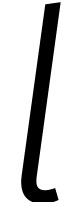 over de complexe
getallen kost
over de complexe
getallen kost 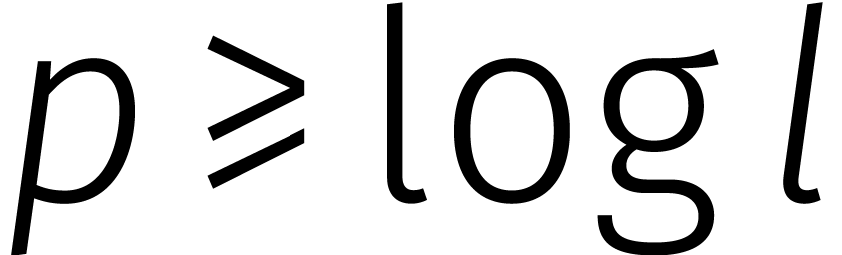 als we rekenen met een precisie
van
als we rekenen met een precisie
van  cijfers [13]. Dat bepaalt ook
de minimale CO2 uitstoot die men kan verwachten bij grote
berekeningen aan het weer. Al met al speelt
cijfers [13]. Dat bepaalt ook
de minimale CO2 uitstoot die men kan verwachten bij grote
berekeningen aan het weer. Al met al speelt 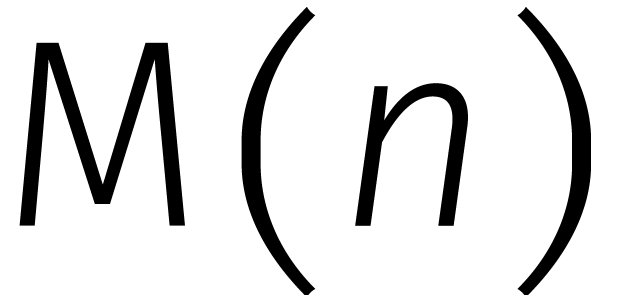 als
elementaire „rekensnelheid” dus een zelfde soort rol als de
lichtsnelheid
als
elementaire „rekensnelheid” dus een zelfde soort rol als de
lichtsnelheid 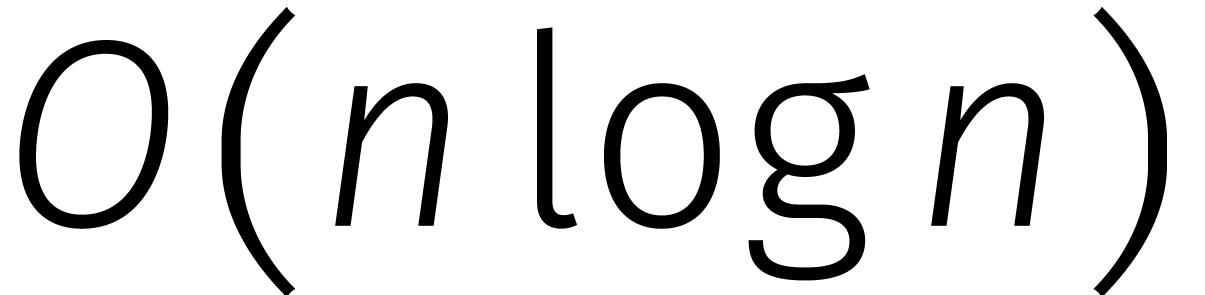 in de natuurkunde.
in de natuurkunde.
Dat weten we niet!
R. Agarwal en J. Cooley. New algorithms for digital convolution. IEEE Transactions on Acoustics, Speech, and Signal Processing, 25(5):392–410, 1977.
Leo I. Bluestein. A linear filtering approach to the computation of discrete Fourier transform. IEEE Transactions on Audio and Electroacoustics, 18(4):451–455, 1970.
J. W. Cooley en J. W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
A. Dutt en V. Rokhlin. Fast Fourier transforms for nonequispaced data. SIAM J. Sci. Comput., 14(6):1368–1393, 1993.
M. Fürer. Faster integer multiplication. In Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing (STOC 2007), pagina's 57–66. San Diego, California, 2007.
C. F. Gauss. Nachlass: theoria interpolationis methodo nova tractata. In Werke, volume 3, pagina's 265–330. Königliche Gesellschaft der Wissenschaften, Göttingen, 1866.
I. J. Good. The interaction algorithm and practical Fourier analysis. Journal of the Royal Statistical Society, Series B. 20(2):361–372, 1958.
D. Harvey. Faster arithmetic for number-theoretic transforms. J. Symbolic Comput., 60:113–119, 2014.
D. Harvey. Faster truncated integer multiplication. https://arxiv.org/abs/1703.00640, 2017.
D. Harvey en J. van der Hoeven. Faster integer and polynomial multiplication using cyclotomic coefficient rings. Technical Report, ArXiv, 2017. http://arxiv.org/abs/1712.03693.
D. Harvey en J. van der Hoeven. Faster integer multiplication using short lattice vectors. In R. Scheidler en J. Sorenson, editors, Proc. of the 13-th Algorithmic Number Theory Symposium, Open Book Series 2, pagina's 293–310. Mathematical Sciences Publishes, Berkeley, 2019.
D. Harvey en J. van der Hoeven. Integer
multiplication in time  .
Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070778.
.
Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070778.
D. Harvey, J. van der Hoeven, en G. Lecerf. Even faster integer multiplication. J. Complexity, 36:1–30, 2016.
M. T. Heideman, D. H. Johnson, en C. S. Burrus. Gauss and the history of the FFT. IEEE Acoustics, Speech and Signal Processing Magazine, 1:14–21, oct 1984.
A. A. Karatsuba. The complexity of computations. Proc. of the Steklov Inst. of Math., 211:169–183, 1995. English translation; Russian original at pages 186–202.
A. Karatsuba en J. Ofman. Multiplication of multidigit numbers on automata. Soviet Physics Doklady, 7:595–596, 1963.
D. E. Knuth. The Art of Computer Programming, volume 2: Seminumerical Algorithms. Addison-Wesley, 1969.
H. J. Nussbaumer en P. Quandalle. Computation of convolutions and discrete Fourier transforms by polynomial transforms. IBM J. Res. Develop., 22(2):134–144, 1978.
J. M. Pollard. The fast Fourier transform in a finite field. Mathematics of Computation, 25(114):365–374, 1971.
A. Schönhage. Multiplikation großer Zahlen. Computing, 1(3):182–196, 1966.
A. Schönhage en V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
A. L. Toom. The complexity of a scheme of functional elements realizing the multiplication of integers. Soviet Mathematics, 4(2):714–716, 1963.