Abstract
The technique of relaxed power series expansion provides an efficient
way to solve so called recursive equations of the form 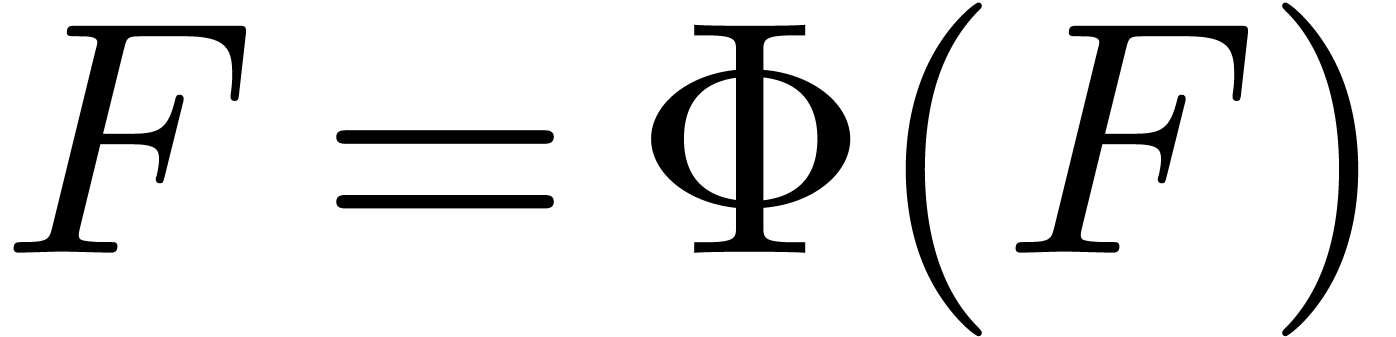 , where the unknown
, where the unknown  is a vector of power series, and where the solution
can be obtained as the limit of the sequence
is a vector of power series, and where the solution
can be obtained as the limit of the sequence 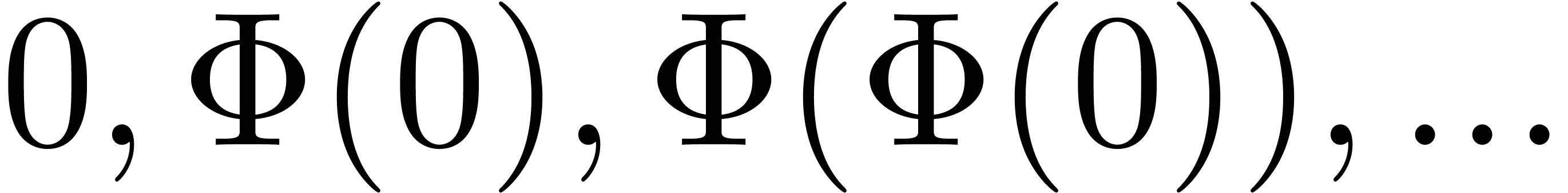 . With respect to other techniques, such as Newton's
method, two major advantages are its generality and the fact that it
takes advantage of possible sparseness of
. With respect to other techniques, such as Newton's
method, two major advantages are its generality and the fact that it
takes advantage of possible sparseness of  .
In this paper, we consider more general implicit equations of the form
.
In this paper, we consider more general implicit equations of the form
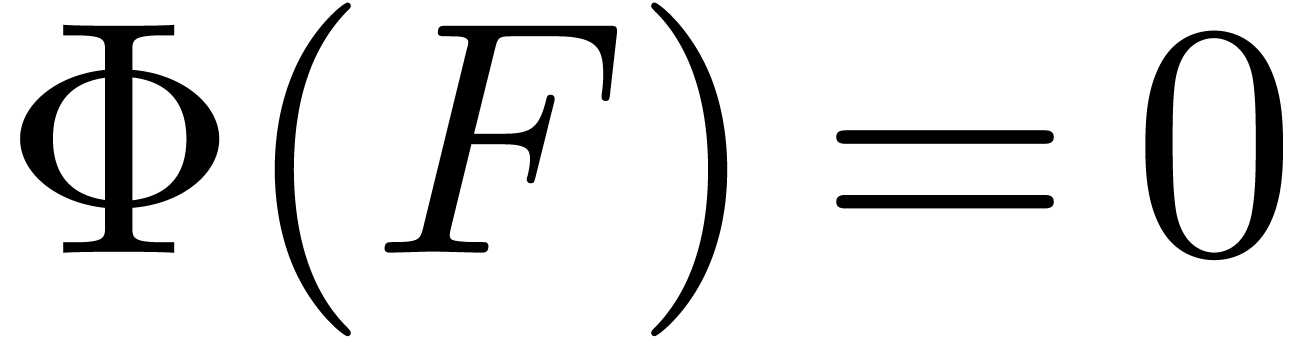 . Under mild assumptions on
such an equation, we will show that it can be rewritten as a recursive
equation. Preprint version only: If we are actually computing
with analytic functions, then recursive equations also provide a
systematic device for the computation of verified error bounds. We will
show how to apply our results in this context.
. Under mild assumptions on
such an equation, we will show that it can be rewritten as a recursive
equation. Preprint version only: If we are actually computing
with analytic functions, then recursive equations also provide a
systematic device for the computation of verified error bounds. We will
show how to apply our results in this context.
Author: Joris van der Hoeven
Keywords: implicit equation, relaxed power series,
algorithm
A.M.S. subject classification: 68W25, 42-04, 68W30,
65G20, 30B10
View: Html, TeXmacs, Pdf,
BibTeX
Revisited AAECC Version: Html, TeXmacs,
Pdf, BibTeX
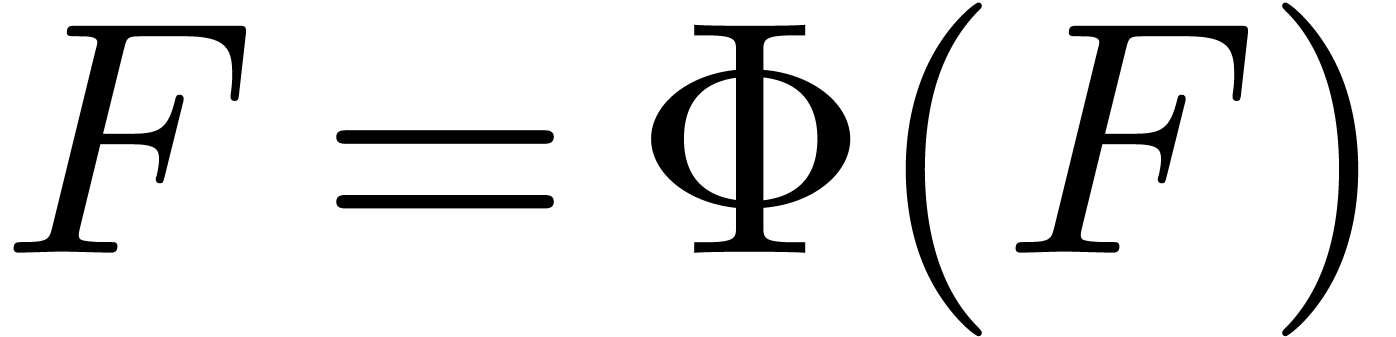 , where the unknown
, where the unknown  is a vector of power series, and where the solution
can be obtained as the limit of the sequence
is a vector of power series, and where the solution
can be obtained as the limit of the sequence 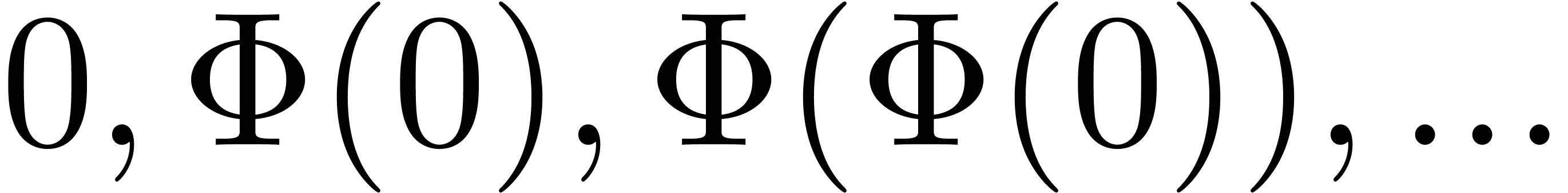 . With respect to other techniques, such as Newton's
method, two major advantages are its generality and the fact that it
takes advantage of possible sparseness of
. With respect to other techniques, such as Newton's
method, two major advantages are its generality and the fact that it
takes advantage of possible sparseness of  .
In this paper, we consider more general implicit equations of the form
.
In this paper, we consider more general implicit equations of the form
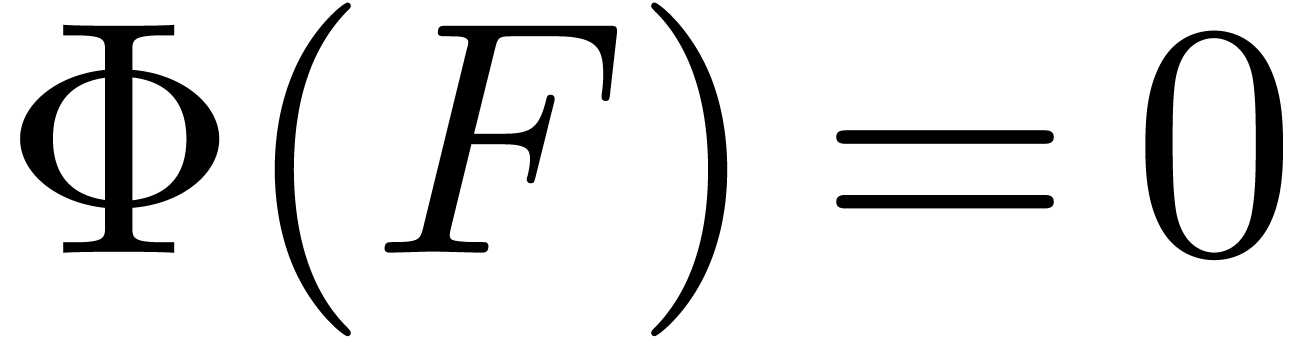 . Under mild assumptions on
such an equation, we will show that it can be rewritten as a recursive
equation. Preprint version only: If we are actually computing
with analytic functions, then recursive equations also provide a
systematic device for the computation of verified error bounds. We will
show how to apply our results in this context.
. Under mild assumptions on
such an equation, we will show that it can be rewritten as a recursive
equation. Preprint version only: If we are actually computing
with analytic functions, then recursive equations also provide a
systematic device for the computation of verified error bounds. We will
show how to apply our results in this context.