| New algorithms for relaxed
multiplication |
|
Dépt. de Mathématiques
(Bât. 425)
CNRS, Université Paris-Sud
91405 Orsay Cedex
France
Email: joris@texmacs.org
|
|
|
In previous work, we have introduced the technique of relaxed
power series computations. With this technique, it is possible to
solve implicit equations almost as quickly as doing the operations
which occur in the implicit equation. Here “almost as
quickly” means that we need to pay a logarithmic overhead.
In this paper, we will show how to reduce this logarithmic factor
in the case when the constant ring has sufficiently many  -th roots of unity. -th roots of unity.
Keywords: power series, multiplication,
algorithm, FFT, computer algebra
A.M.S. subject classification: 68W25,
42-04, 68W30, 30B10, 33F05, 11Y55
|
1.Introduction
Let  be an effective ring and consider two power
series
be an effective ring and consider two power
series 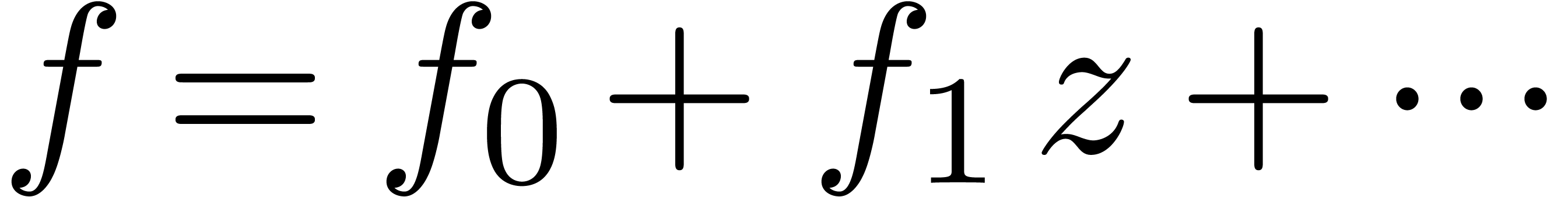 and
and 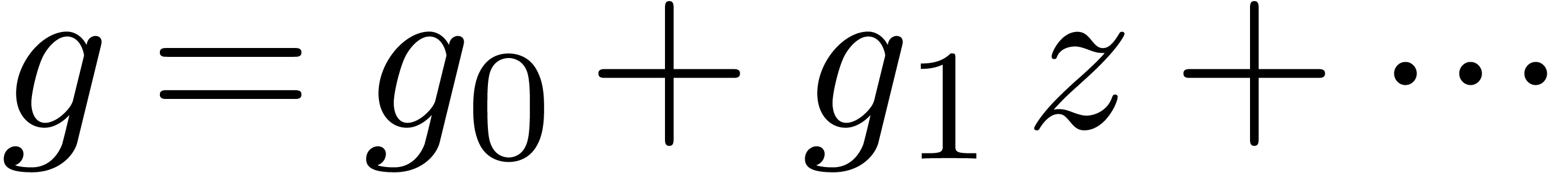 in
in 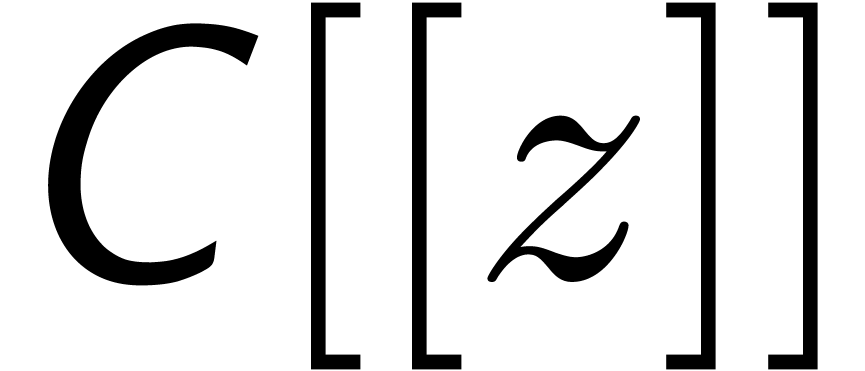 . In this paper we will be
concerned with the efficient computation of the first
. In this paper we will be
concerned with the efficient computation of the first 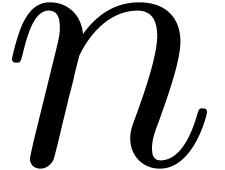 coefficients of the product
coefficients of the product 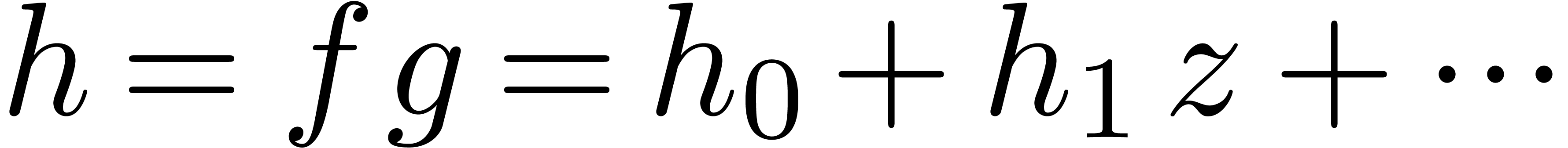 .
.
If the first 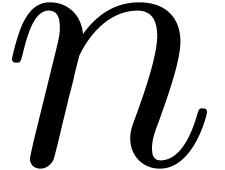 coefficients of
coefficients of  and
and  are known beforehand, then we may use any
fast multiplication for polynomials in order to achieve this goal, such
as divide and conquer multiplication [KO63, Knu97],
which has a time complexity
are known beforehand, then we may use any
fast multiplication for polynomials in order to achieve this goal, such
as divide and conquer multiplication [KO63, Knu97],
which has a time complexity 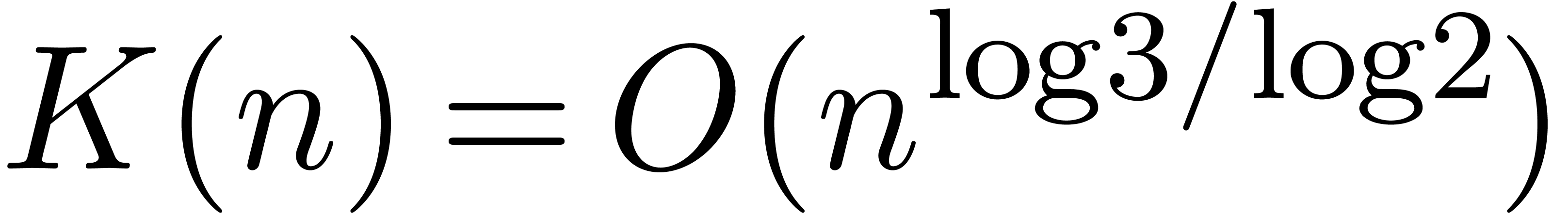 ,
or F.F.T. multiplication [CT65, SS71,
CK91, vdH02a], which has a time complexity
,
or F.F.T. multiplication [CT65, SS71,
CK91, vdH02a], which has a time complexity
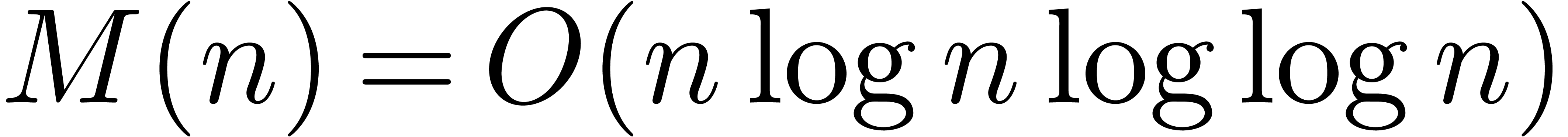 .
.
For certain computations, and most importantly the resolution of
implicit equations, it is interesting to use so called “relaxed
algorithms” which output the first  coefficients of
coefficients of 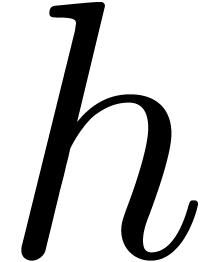 as soon as the first
as soon as the first 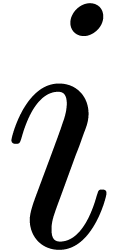 coefficients of
coefficients of 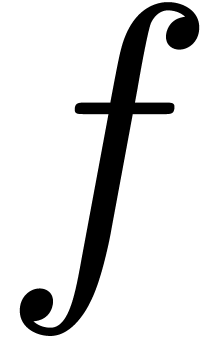 and
and  are known for each
are known for each 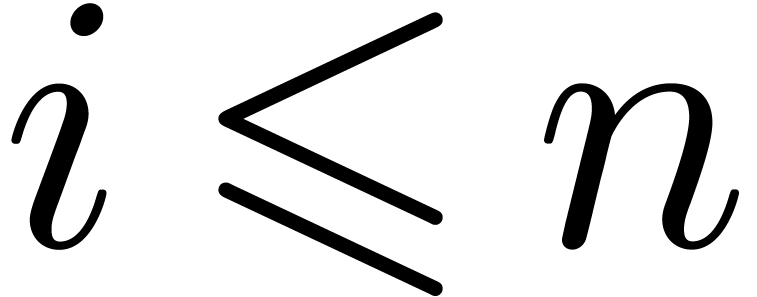 .
This allows for instance the computation of the exponential
.
This allows for instance the computation of the exponential 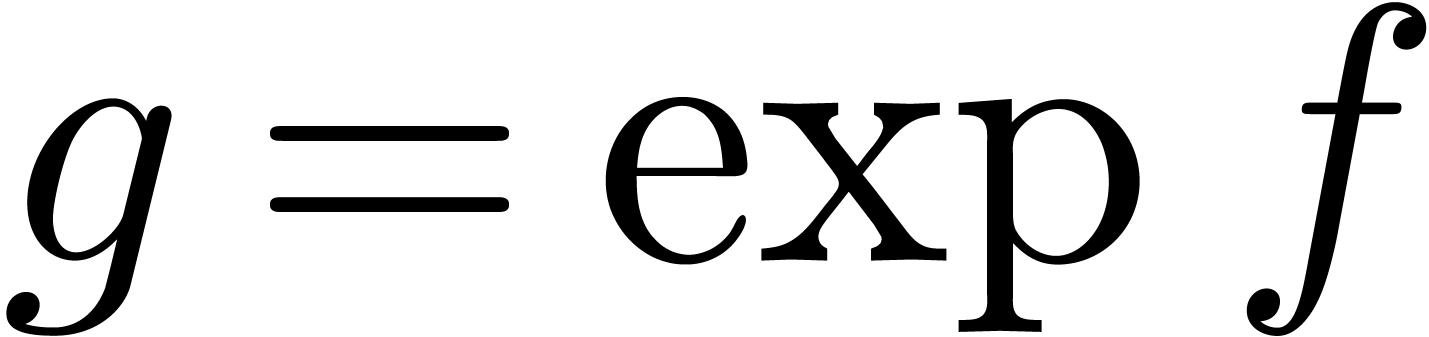 of a series
of a series 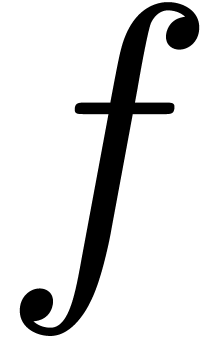 with
with 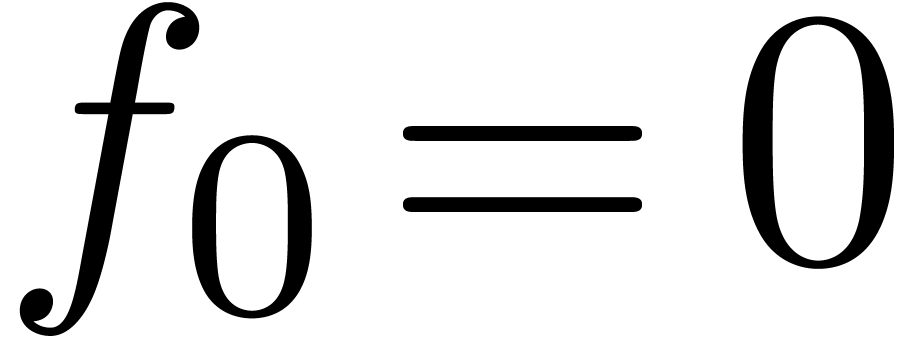 using the formula
using the formula
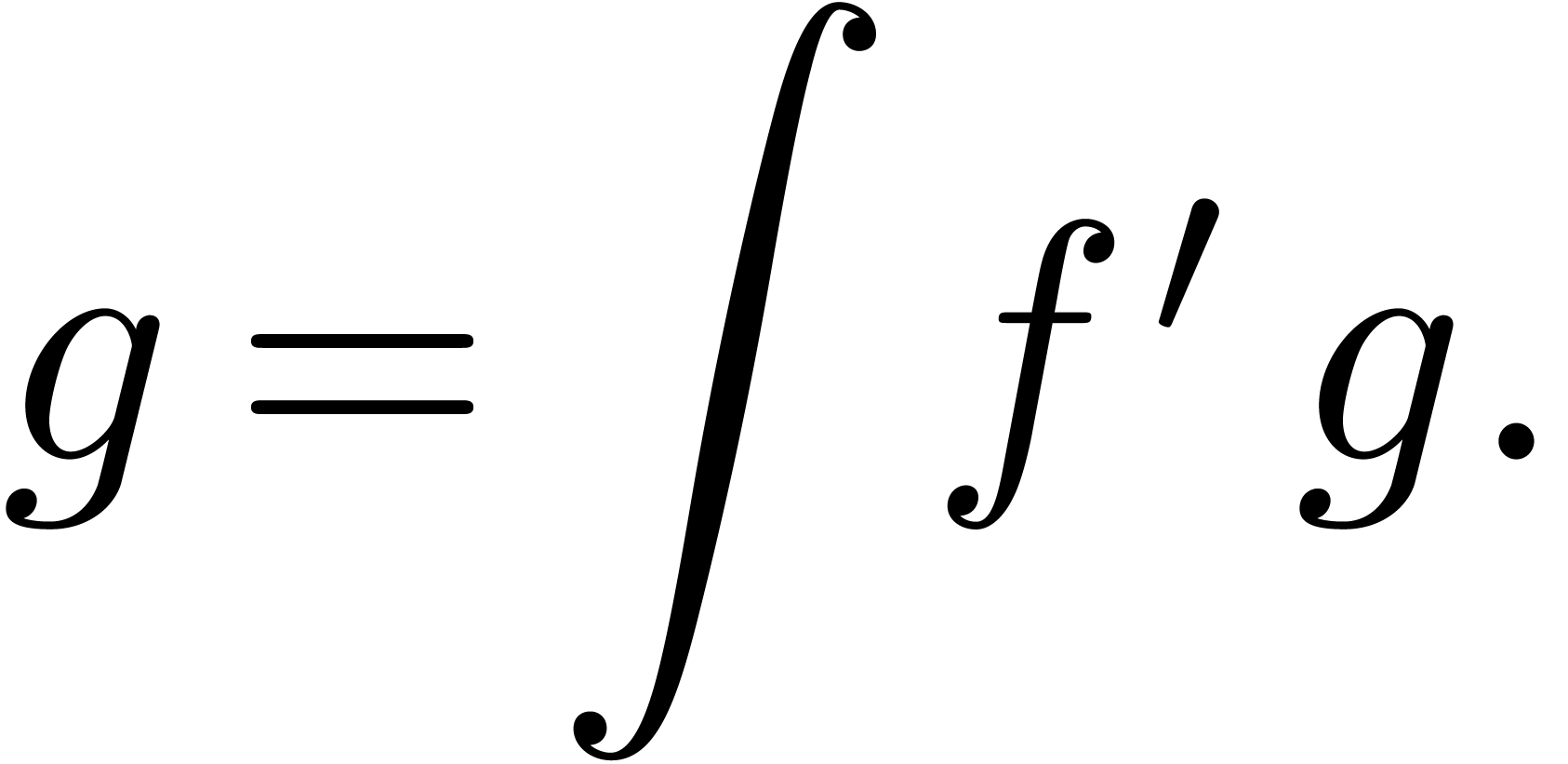 |
(1) |
More precisely, this formula shows that the computation of 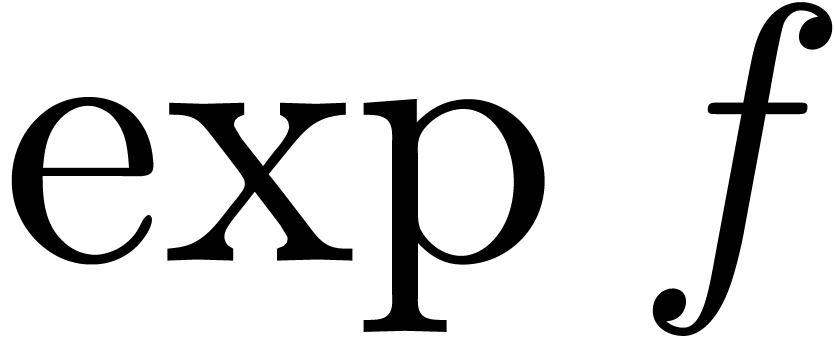 reduces to one differentiation, one relaxed product and
one relaxed integration. Differentiation and relaxed integration being
linear in time, it follows that
reduces to one differentiation, one relaxed product and
one relaxed integration. Differentiation and relaxed integration being
linear in time, it follows that 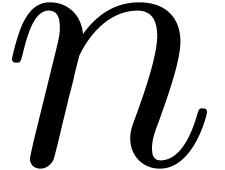 terms of
terms of 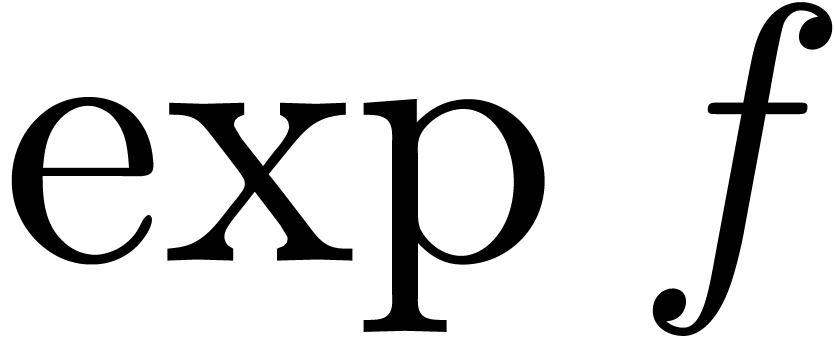 can be computed in time
can be computed in time  ,
where
,
where 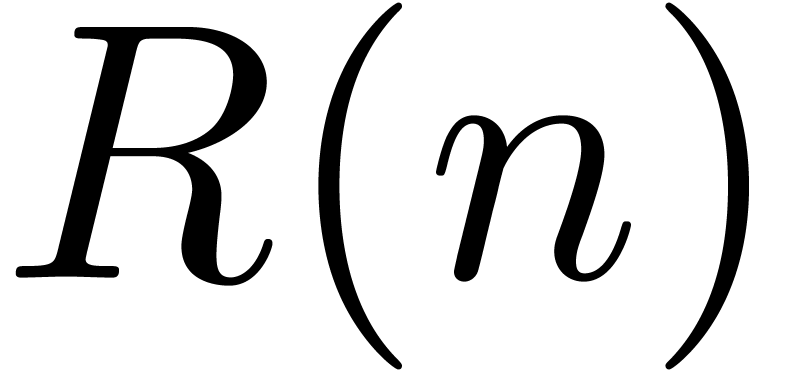 denotes the time complexity of relaxed
multiplication. In [vdH97, vdH02a], we proved
the following theorem:
denotes the time complexity of relaxed
multiplication. In [vdH97, vdH02a], we proved
the following theorem:
Theorem 1. There exists a relaxed multiplication algorithm of time
complexity
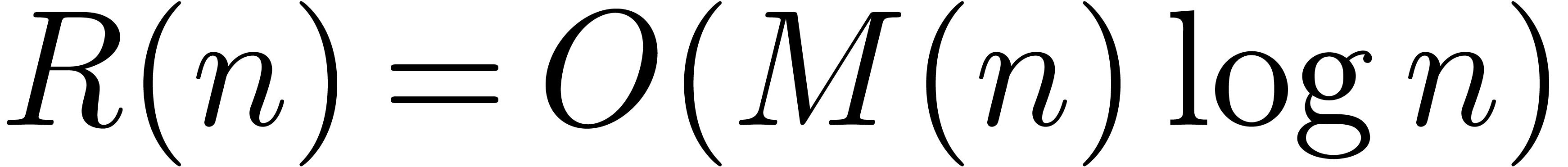
and space complexity 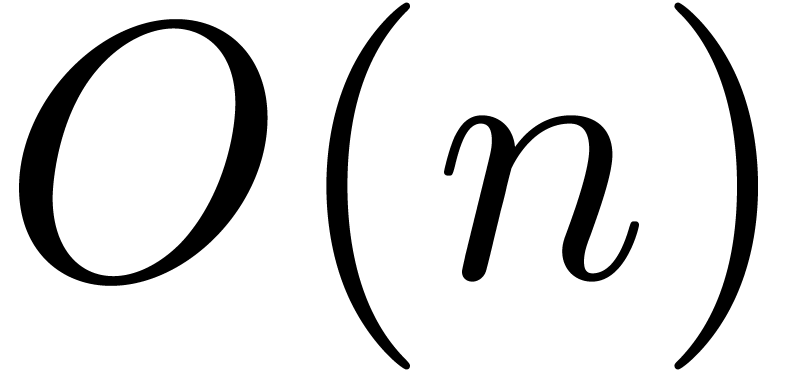 .
.
In this paper, we will improve the time complexity bound in this theorem
in the case when  admits
admits 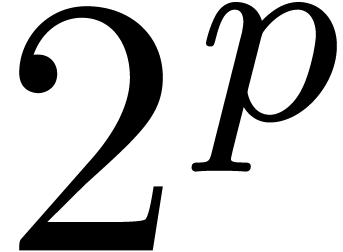 -th roots of unity for any
-th roots of unity for any 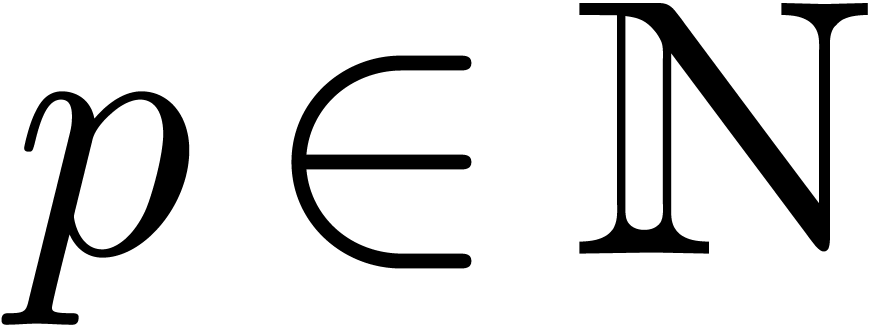 . In section 2, we first reduce this
problem to the case of “semi-relaxed multiplication”, when
one of the arguments is fixed and the other one relaxed. More precisely,
let
. In section 2, we first reduce this
problem to the case of “semi-relaxed multiplication”, when
one of the arguments is fixed and the other one relaxed. More precisely,
let 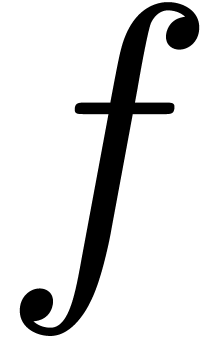 and
and  be power series,
such that
be power series,
such that  is known up to order
is known up to order 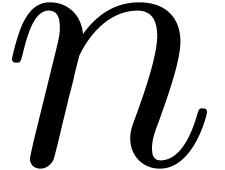 . Then a semi-relaxed multiplication algorithm
computes the product
. Then a semi-relaxed multiplication algorithm
computes the product  up to order
up to order 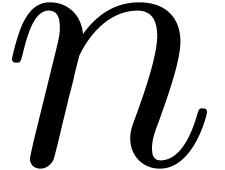 and outputs
and outputs 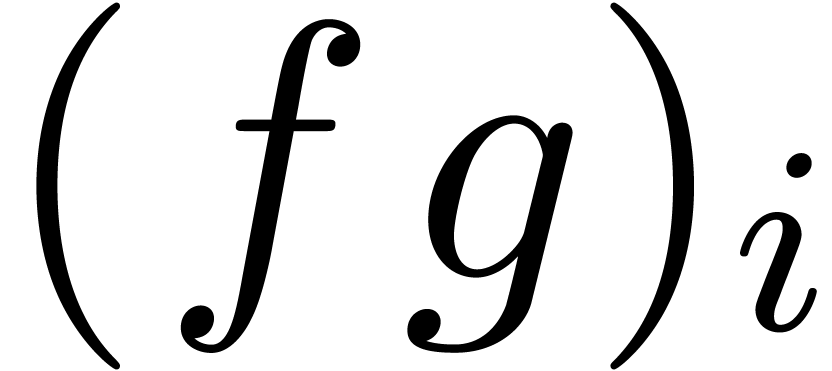 as soon as
as soon as  are known, for all
are known, for all 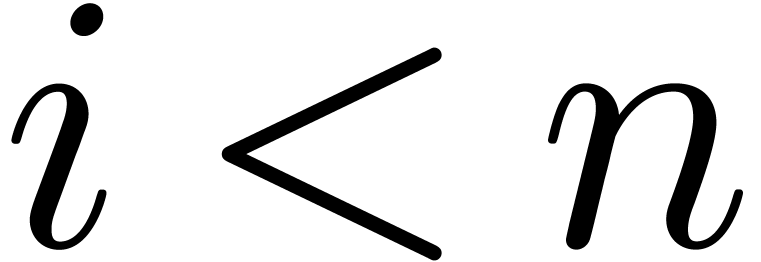 .
In section 3, we show that the
.
In section 3, we show that the 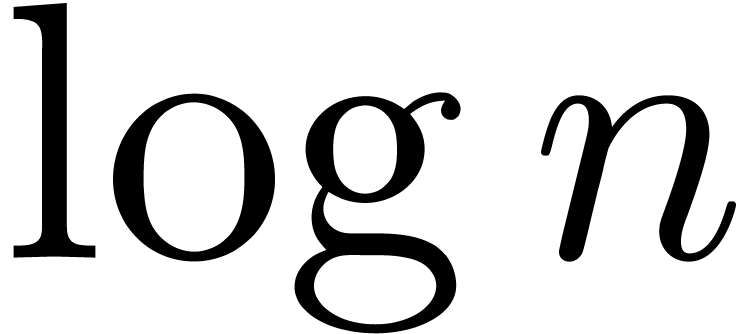 overhead in theorem 1 can be reduced to
overhead in theorem 1 can be reduced to 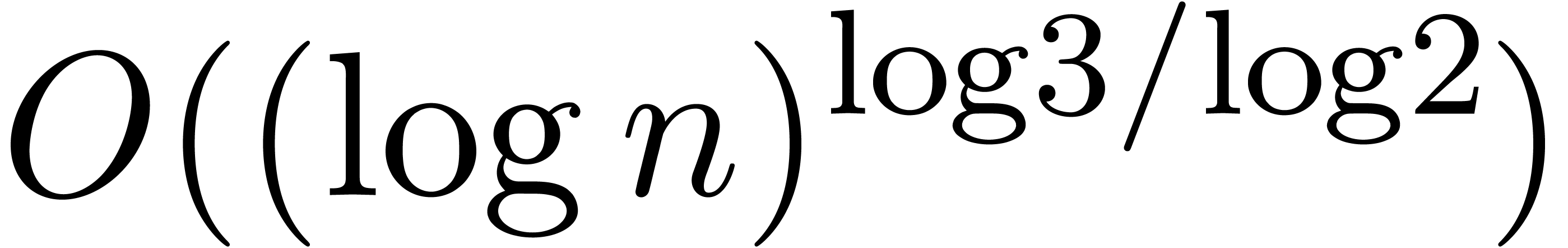 . In section 4, the technique of
section 3 is further improved so as to yield an
. In section 4, the technique of
section 3 is further improved so as to yield an 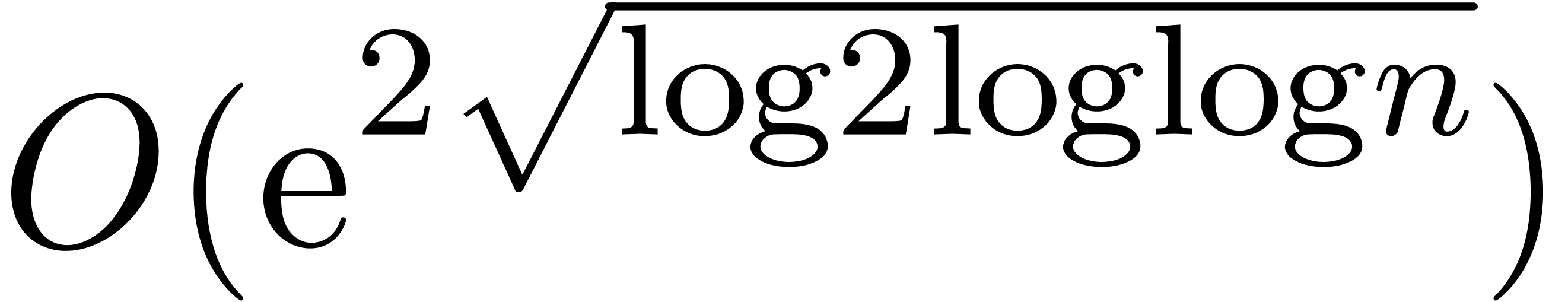 overhead.
overhead.
In the sequel, we will use the following notations from [vdH02a]:
we denote by 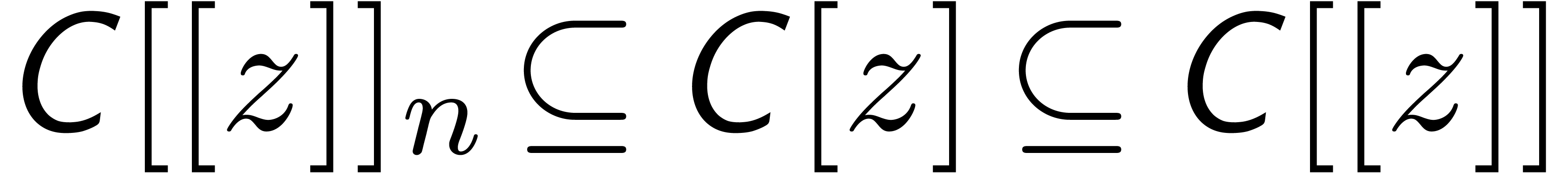 the set of truncated power series
of order
the set of truncated power series
of order 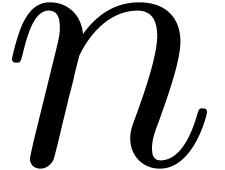 , like
, like 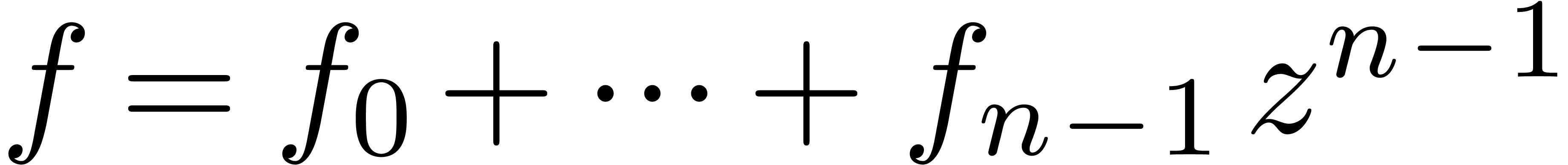 . Given
. Given 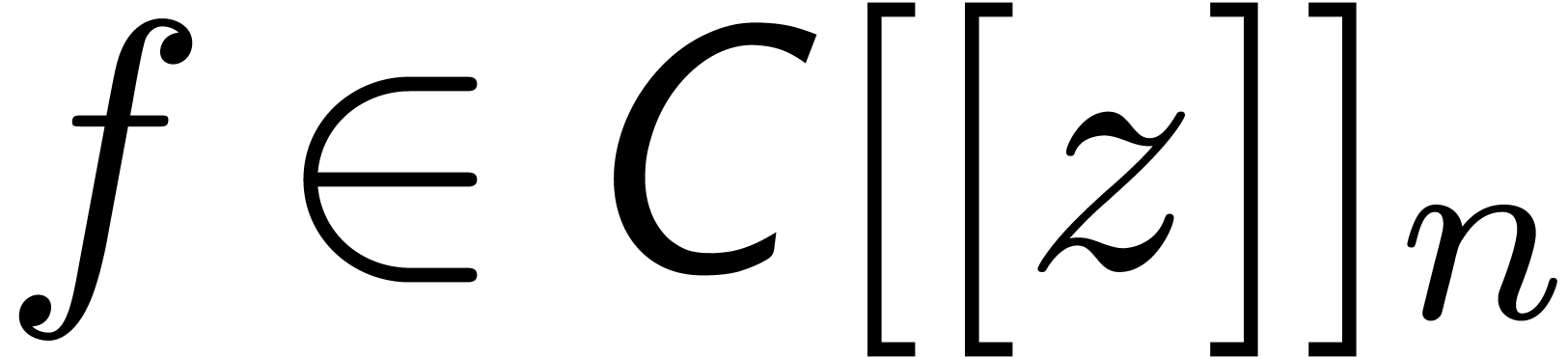 and
and  , we will denote
, we will denote 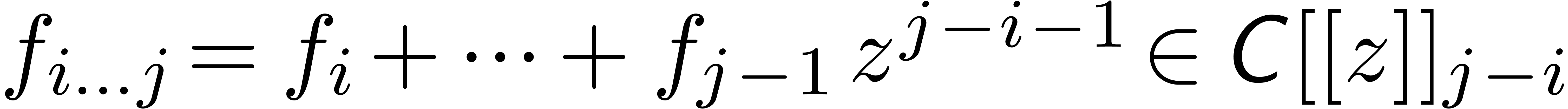 .
.
Remark 2. An preprint of
the present paper was published a few years ago [vdH03a].
The current version includes a new section 5 with
implementation details, benchmarks and a few notes on how to apply
similar ideas in the Karatsuba and Toom-Cook models. Another algorithm
for semi-relaxed multiplication, based on the middle product [HQZ04],
was also published before [vdH03b].
Remark 3. The exotic form
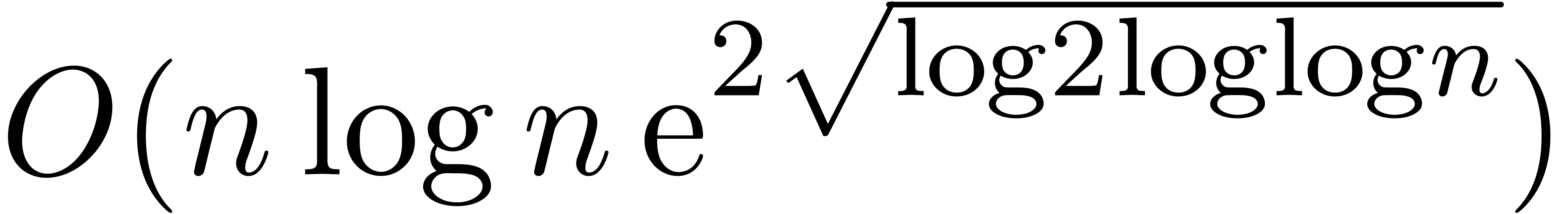 of the new complexity for relaxed multiplication
might surprise the reader. It should be noticed that the time complexity
of Toom-Cook's algorithm for polynomial multiplication [Too63,
Coo66] has a similar complexity
of the new complexity for relaxed multiplication
might surprise the reader. It should be noticed that the time complexity
of Toom-Cook's algorithm for polynomial multiplication [Too63,
Coo66] has a similar complexity 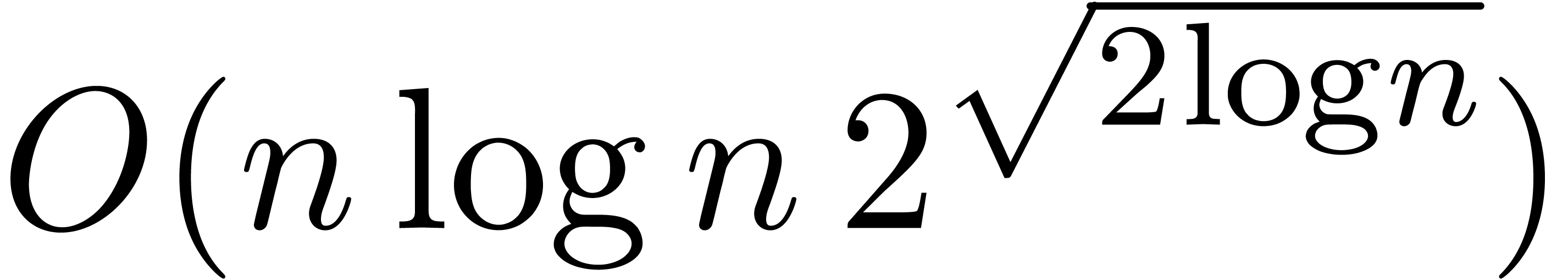 [Knu97, Section 4.3, p. 286 and exercise 5, p. 300]. Indeed,
whereas our algorithm from section 3 has a Karatsuba-like
flavour, the algorithm from section 4 uses a generalized
subdivision which is similar to the one used by Toom and Cook.
[Knu97, Section 4.3, p. 286 and exercise 5, p. 300]. Indeed,
whereas our algorithm from section 3 has a Karatsuba-like
flavour, the algorithm from section 4 uses a generalized
subdivision which is similar to the one used by Toom and Cook.
An interesting question is whether even better time complexities can be
obtained (in analogy with FFT-multiplication). However, we have not
managed so far to reduce the cost of relaxed multiplication to 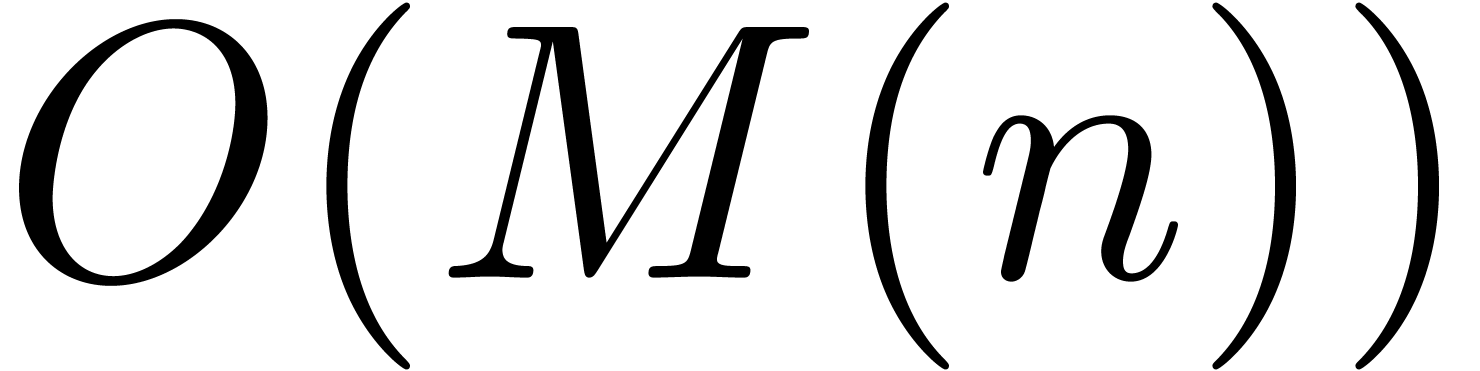 or
or 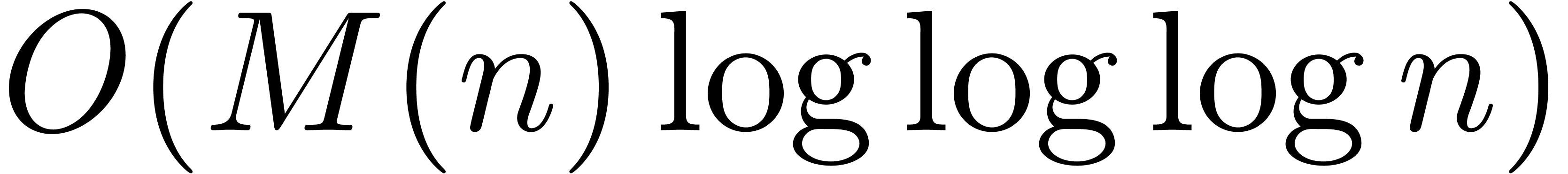 .
Nevertheless, it should be noticed that the function
.
Nevertheless, it should be noticed that the function 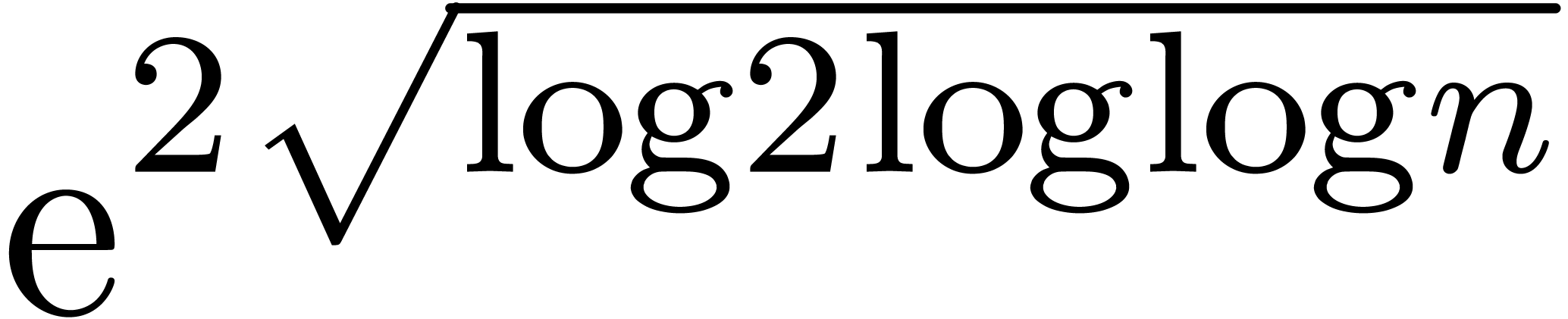 grows very slowly; in practice, it very much behaves like as a constant
(see section 5).
grows very slowly; in practice, it very much behaves like as a constant
(see section 5).
Remark 4. The reader may
wonder whether further improvements in the complexity of relaxed
multiplication are really useful, since the algorithms from [vdH97,
vdH02a] are already optimal up to a factor 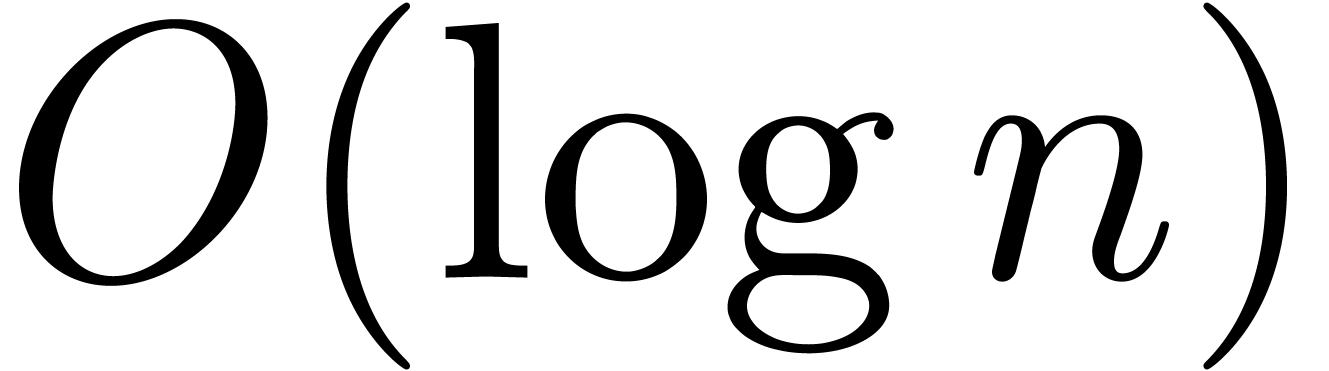 . In fact, we expect fast algorithms for formal
power series to be one of the building bricks for effective analysis [vdH06b]. Therefore, even small improvements in the complexity
of relaxed multiplication should lead to global speed-ups for this kind
of software.
. In fact, we expect fast algorithms for formal
power series to be one of the building bricks for effective analysis [vdH06b]. Therefore, even small improvements in the complexity
of relaxed multiplication should lead to global speed-ups for this kind
of software.
2.Full and semi-relaxed multiplication
In [vdH97, vdH02a], we have stated
several fast algorithms for relaxed multiplication. Let us briefly
recall some of the main concepts and ideas. For details, we refer to [vdH02a]. Throughout this section, 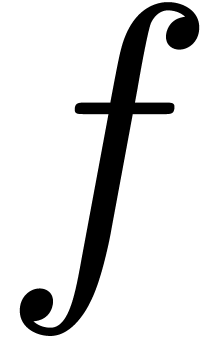 and
and
 are two power series in
are two power series in 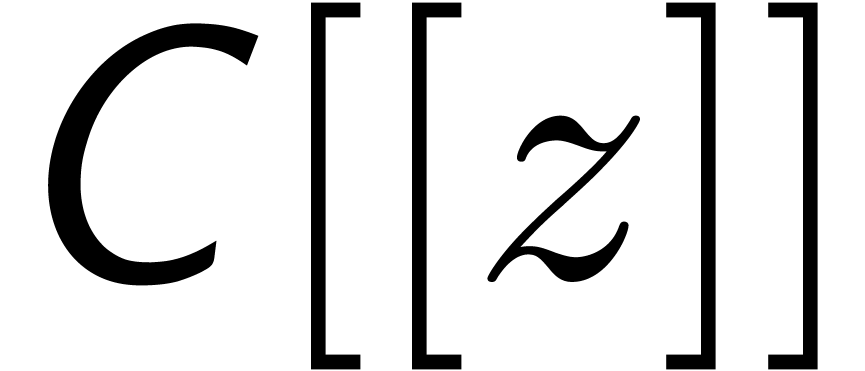 .
.
We will denote by  ,
,  and
and 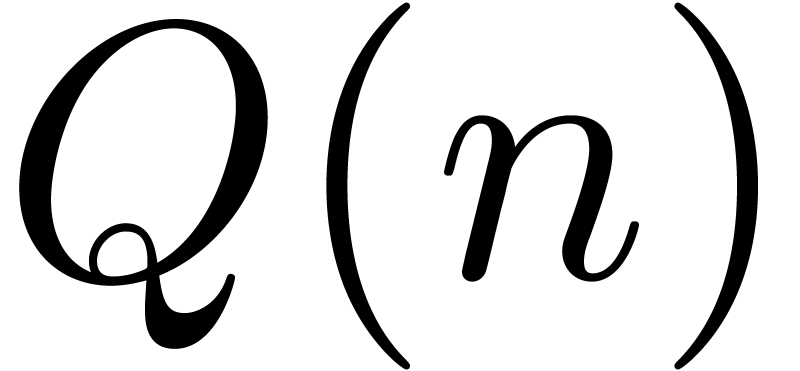 the time complexities of full
zealous, relaxed and semi-relaxed multiplication at order
the time complexities of full
zealous, relaxed and semi-relaxed multiplication at order 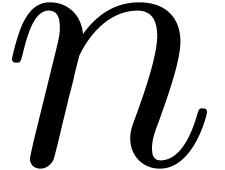 , where it is understood that the ring
operations in
, where it is understood that the ring
operations in  can be performed in time
can be performed in time 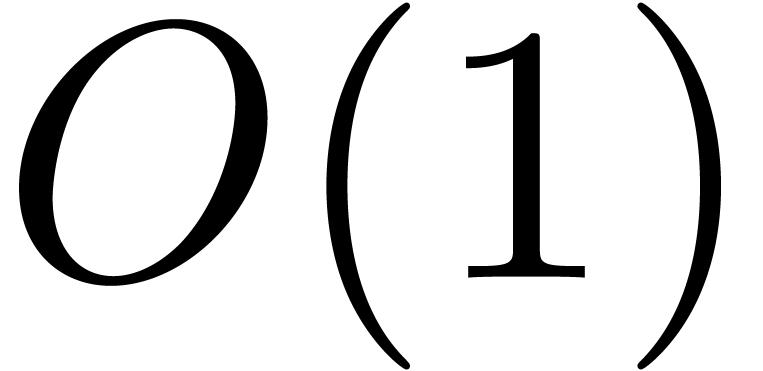 . We notice that full zealous
multiplication is equivalent to polynomial multiplication. Hence,
classical fast multiplication algorithms can be applied in this case [KO63, Too63, Coo66, CT65,
SS71, CK91, vdH02a].
. We notice that full zealous
multiplication is equivalent to polynomial multiplication. Hence,
classical fast multiplication algorithms can be applied in this case [KO63, Too63, Coo66, CT65,
SS71, CK91, vdH02a].
The main idea behind efficient algorithms for relaxed multiplication is
to anticipate on future computations. More precisely, the computation of
a full product (2) can be represented by an  square with entries
square with entries 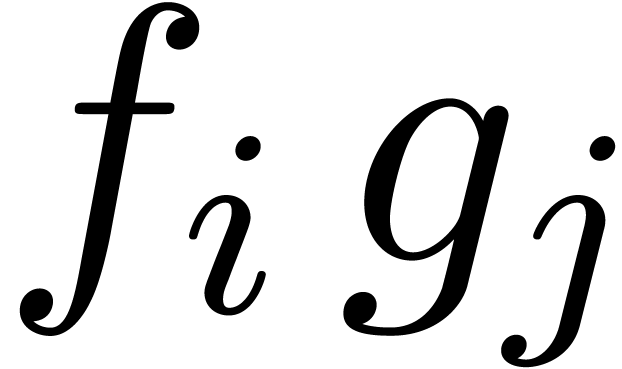 ,
,
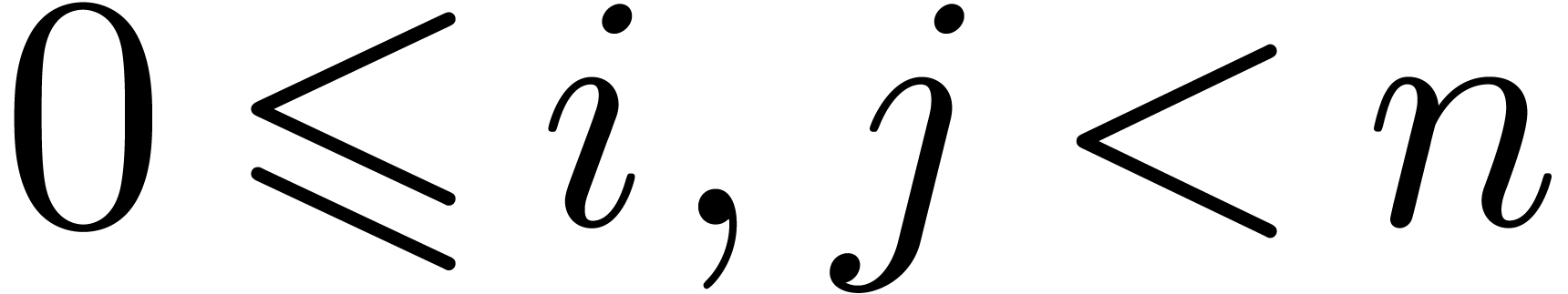 . As soon as
. As soon as  and
and  are known, it becomes possible to compute
the contributions of the products
are known, it becomes possible to compute
the contributions of the products 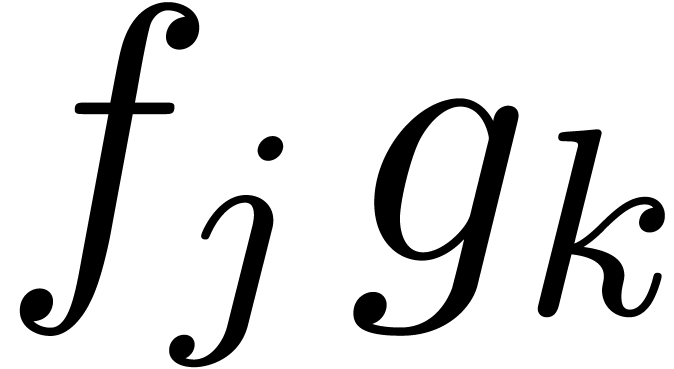 with
with 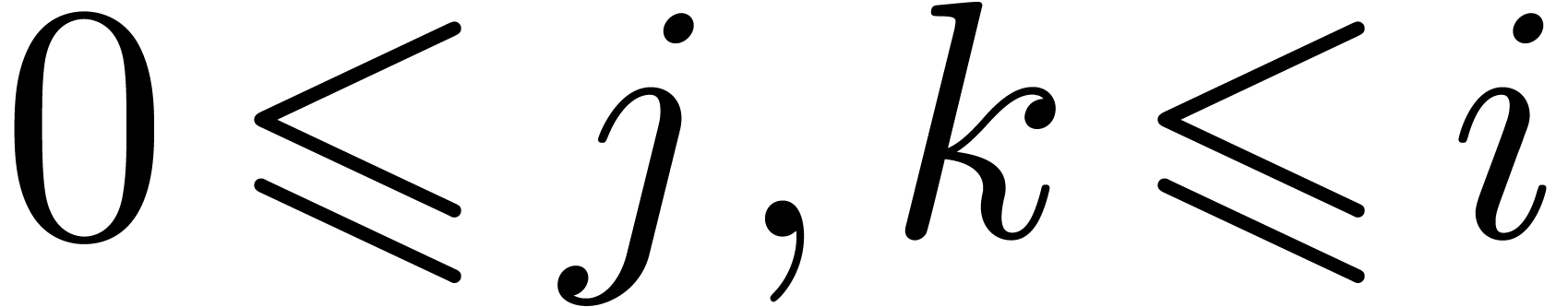 to
to  , even
though the contributions of
, even
though the contributions of 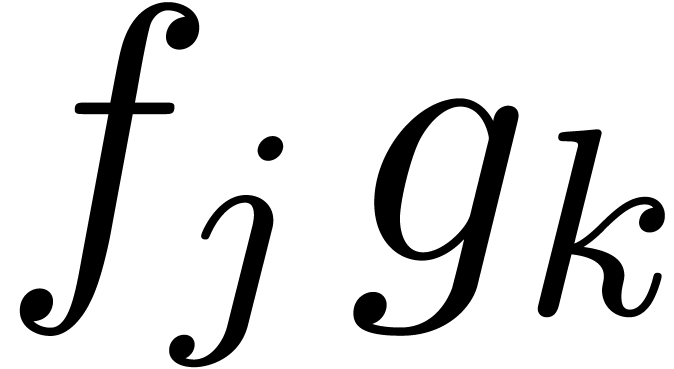 with
with  are not yet needed. The next idea is to subdivide the
are not yet needed. The next idea is to subdivide the  square into smaller squares, in such a way that the
contribution of each small square to
square into smaller squares, in such a way that the
contribution of each small square to  can be
computed using a zealous algorithm. Now the contribution of such a small
square is of the form
can be
computed using a zealous algorithm. Now the contribution of such a small
square is of the form  .
Therefore, the requirement
.
Therefore, the requirement 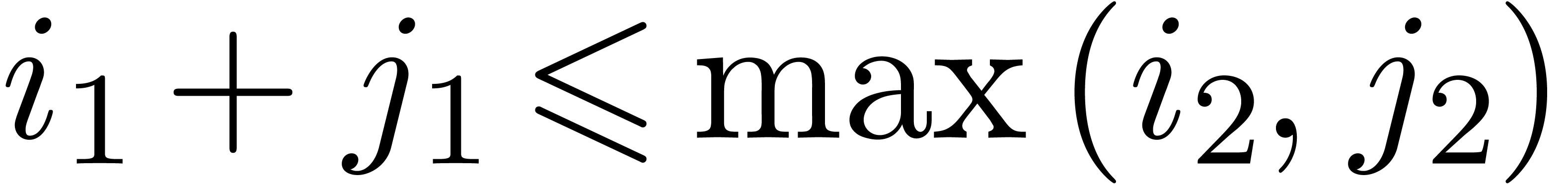 suffices to ensure
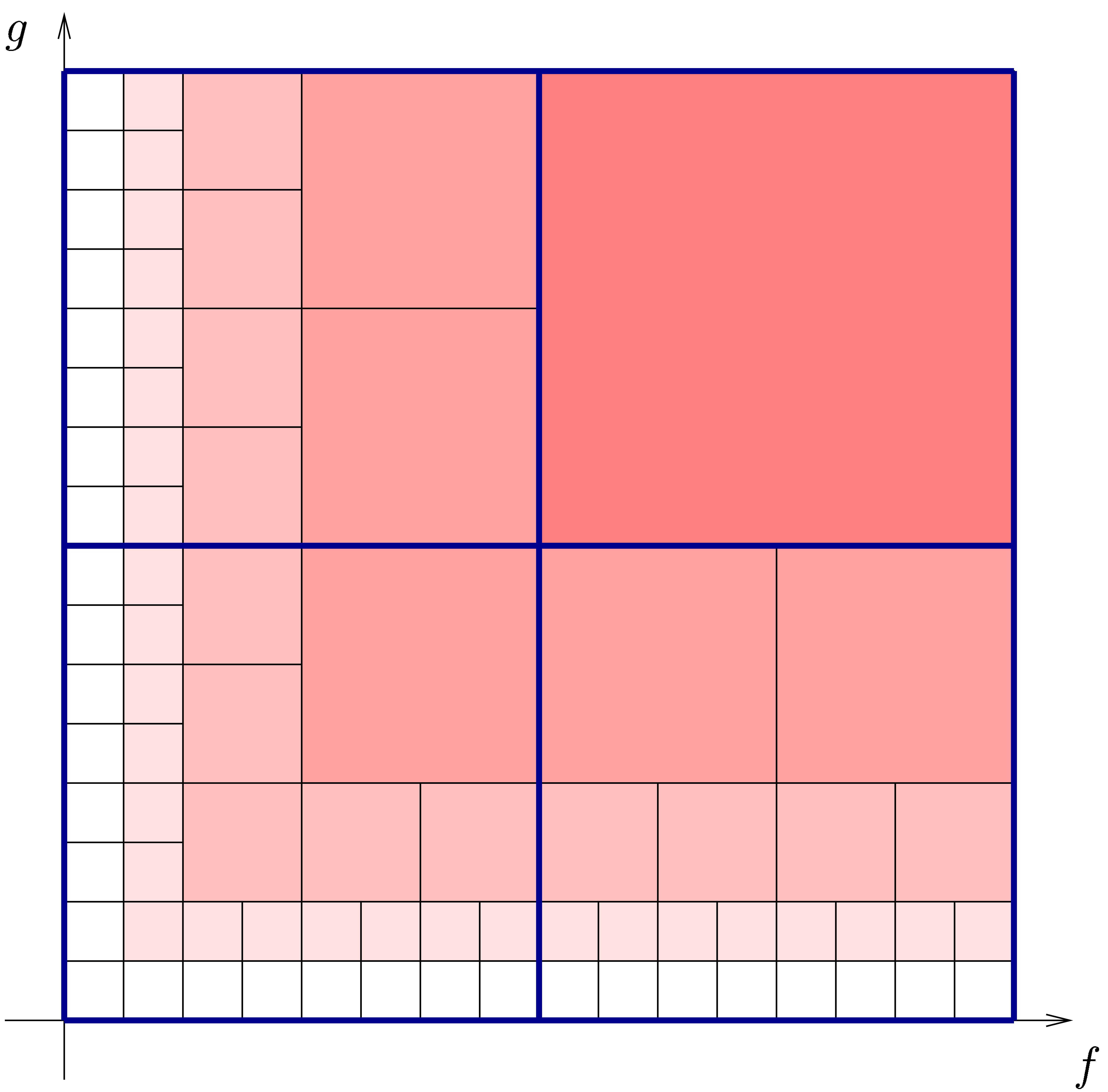
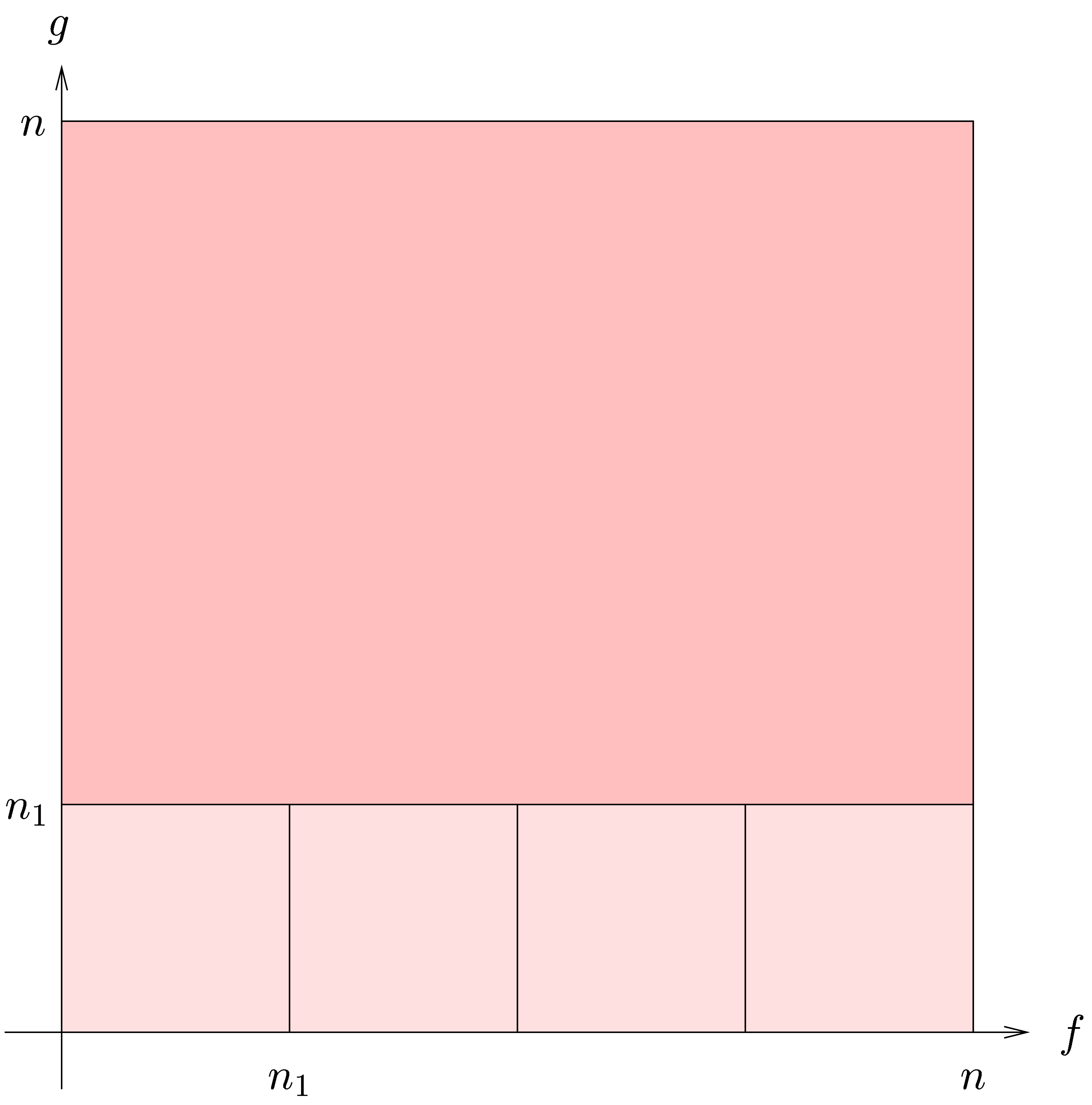
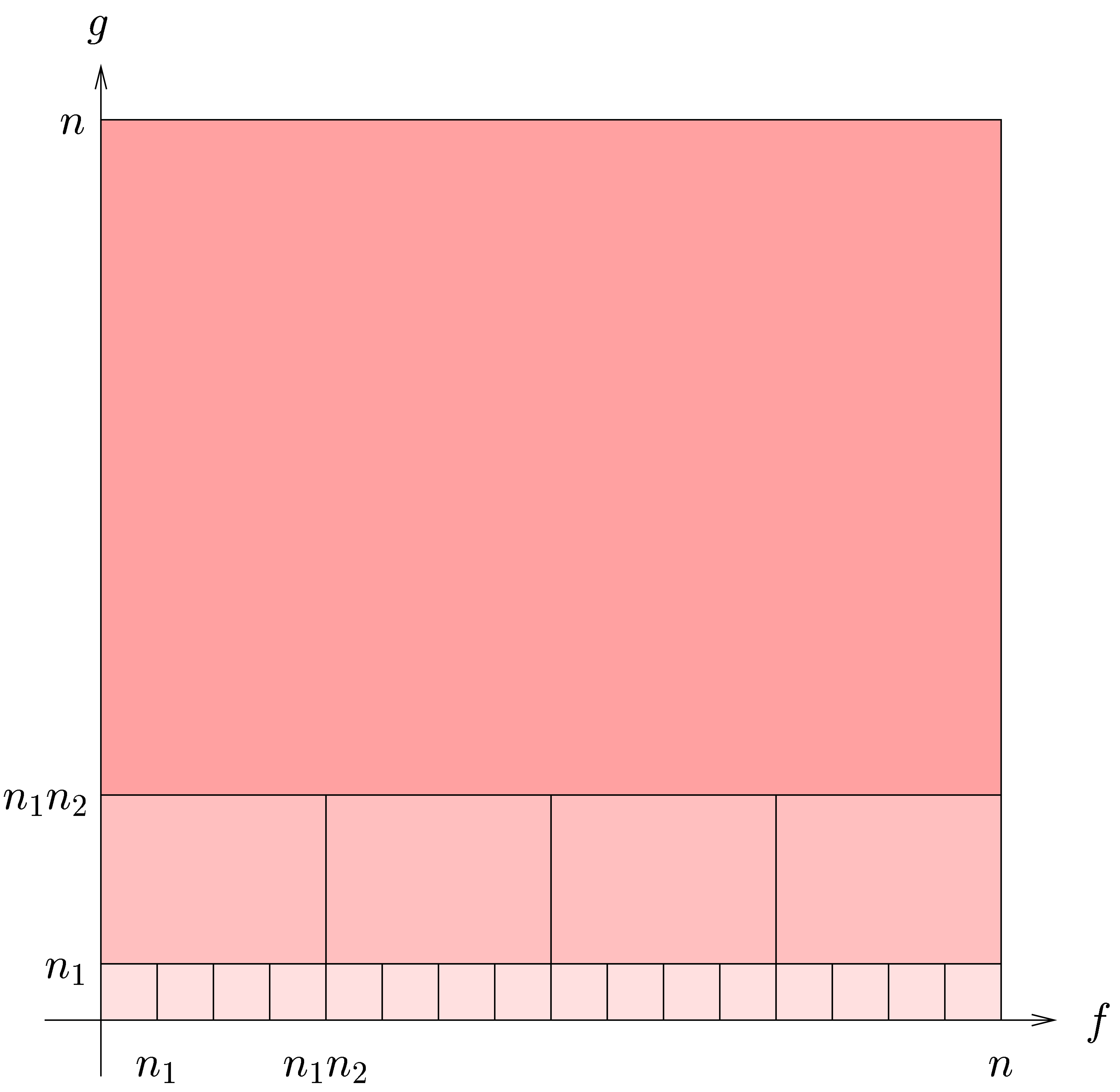
that the resulting algorithm will be relaxed. In the left hand image of
figure 1, we have shown the subdivision from the main
algorithm of [vdH97, vdH02a], which has time
complexity
suffices to ensure
that the resulting algorithm will be relaxed. In the left hand image of
figure 1, we have shown the subdivision from the main
algorithm of [vdH97, vdH02a], which has time
complexity 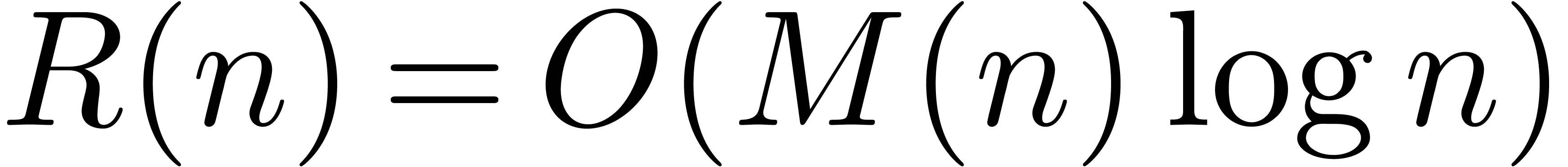 .
.
There is an alternative interpretation of the left hand image in figure
1: when interpreting the big square as a  multiplication
multiplication
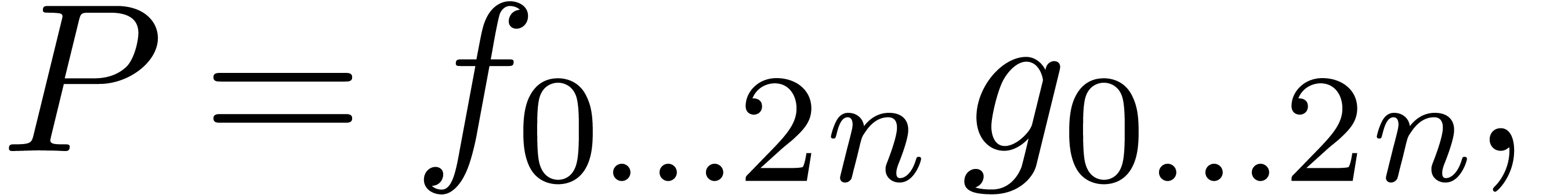
we may regard it as the sum
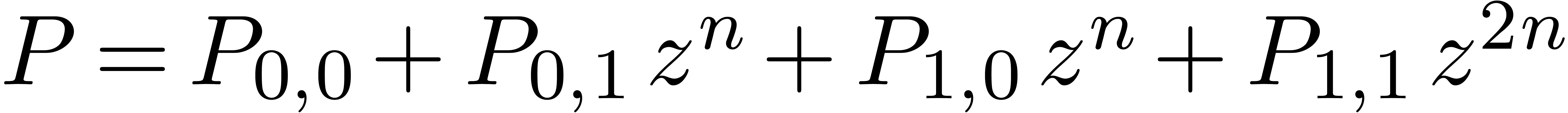
of four  multiplications
multiplications
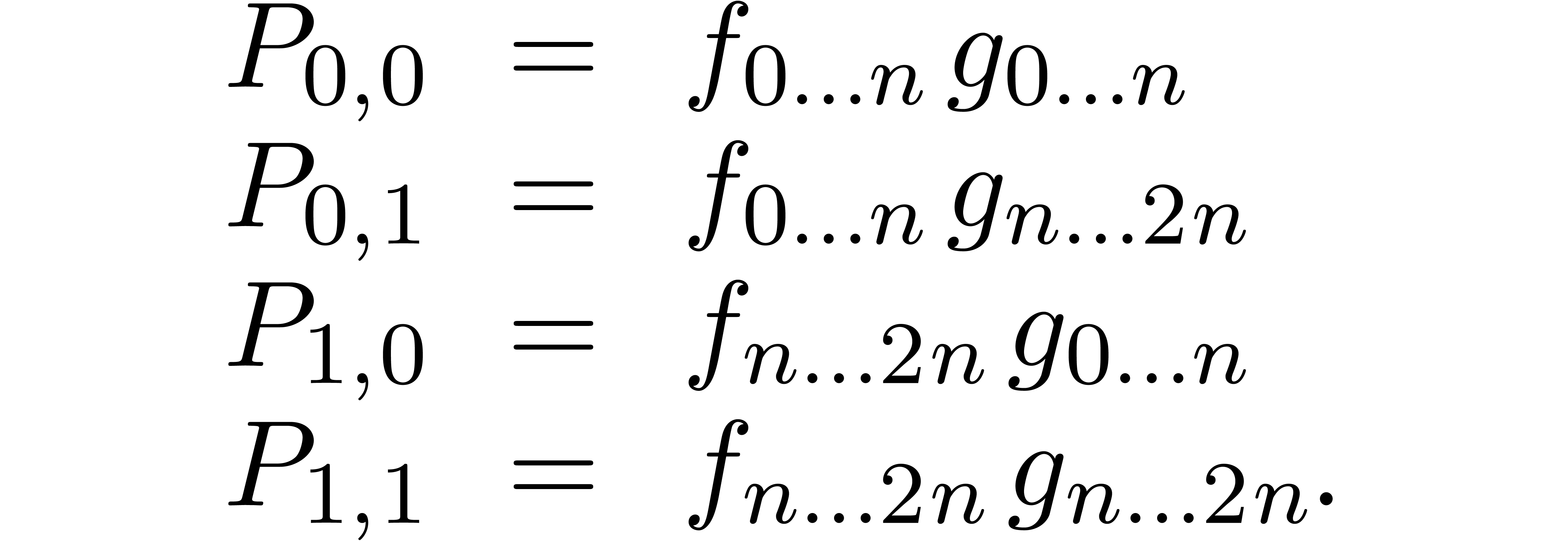
Now 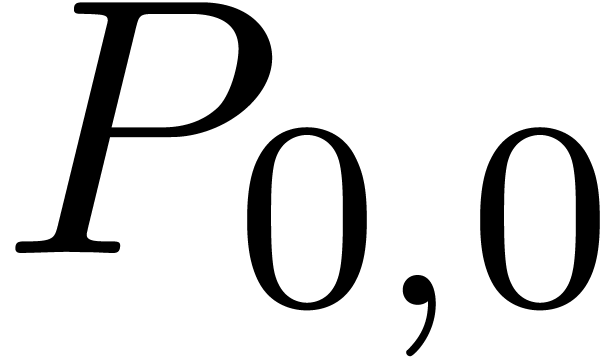 is a relaxed multiplication at order
is a relaxed multiplication at order 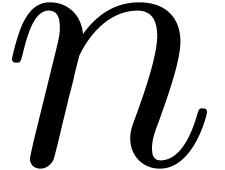 , but
, but 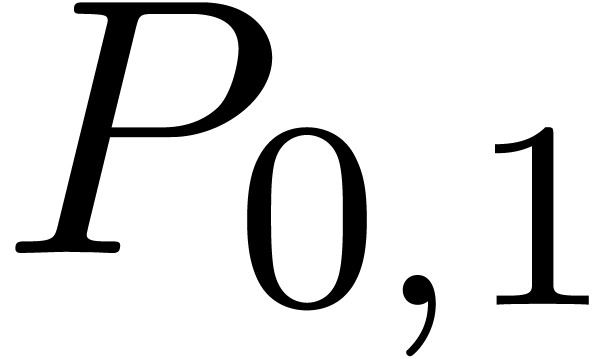 is
even semi-relaxed, since
is
even semi-relaxed, since  are already known by
the time that we need
are already known by
the time that we need 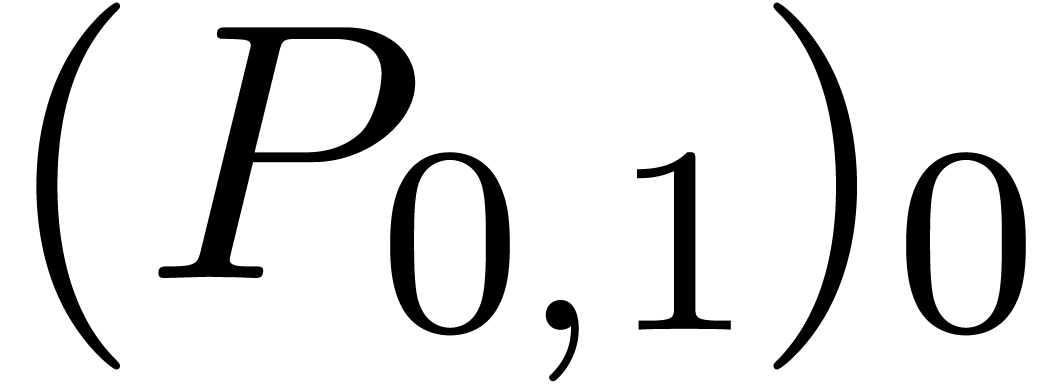 .
Similarly,
.
Similarly, 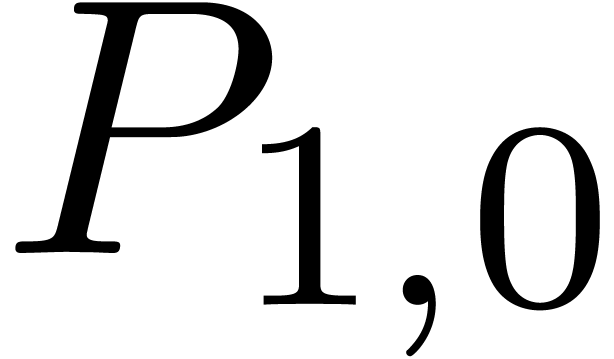 corresponds to a semi-relaxed product
and
corresponds to a semi-relaxed product
and 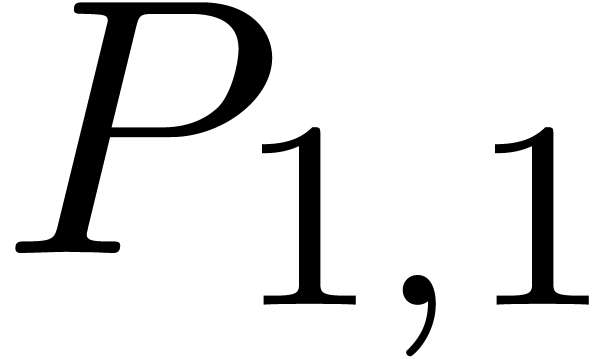 to a zealous product. This shows that
to a zealous product. This shows that
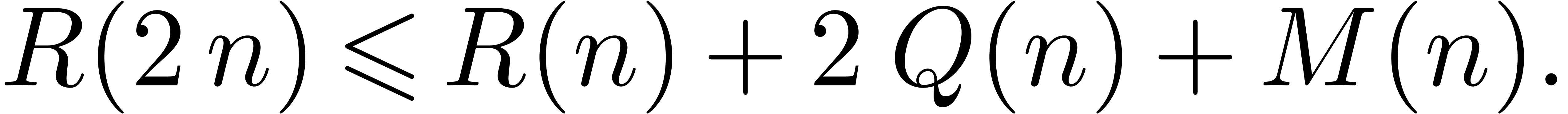
Similarly, we have
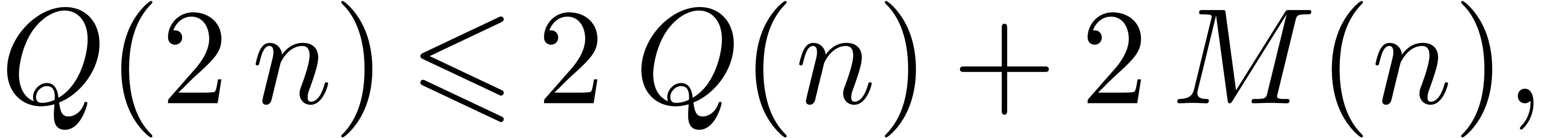
as illustrated in the right-hand image of figure 1. Under
suitable regularity hypotheses for 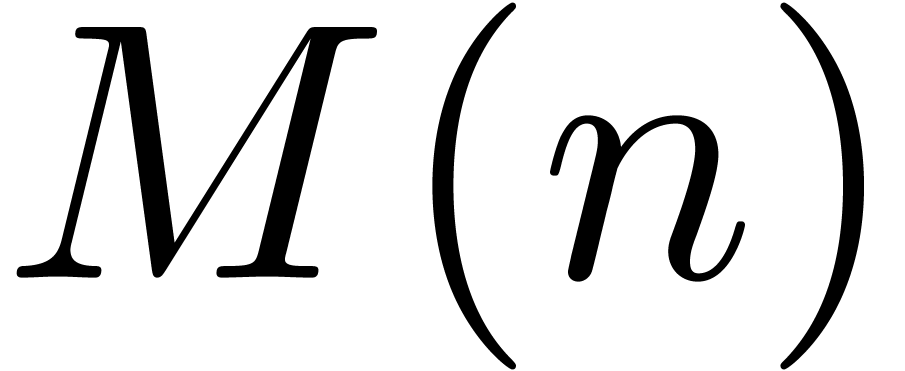 and
and 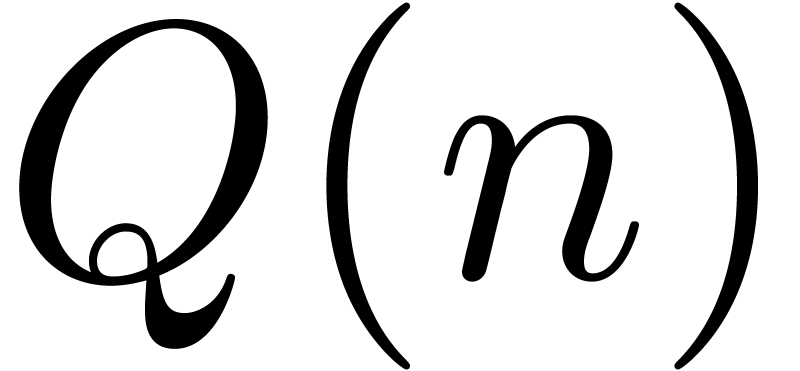 , the above relations imply:
, the above relations imply:
A consequence of part (b) of the theorem is that it suffices to
design fast algorithms for semi-relaxed multiplication in order to
obtain fast algorithms for relaxed multiplication. This fact may be
reinterpreted by observing that the fast relaxed multiplication
algorithm actually applies Newton's method in a hidden way. Indeed,
since Brent and Kung [BK78], it is well known that Newton's
method can also be used in the context of formal power series in order
to solve differential or functional equations. One step of Newton's
method at order 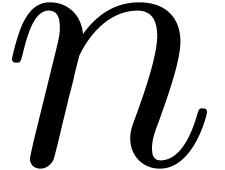 involves the recursive
application of the method at order
involves the recursive
application of the method at order 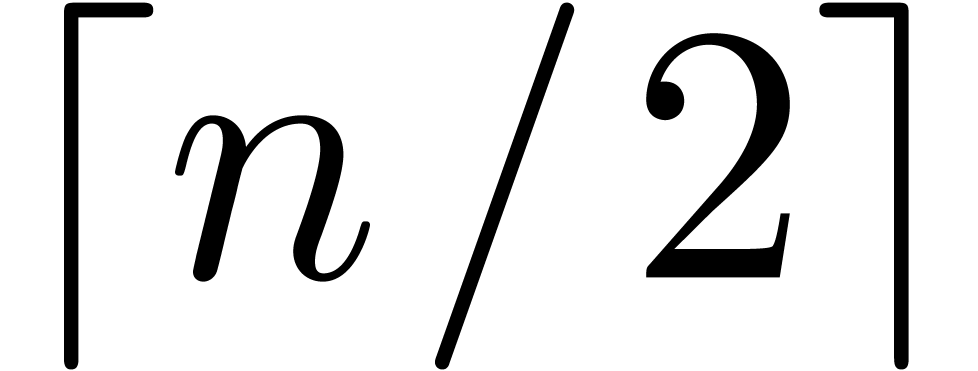 and the
resolution of a linear equation at order
and the
resolution of a linear equation at order 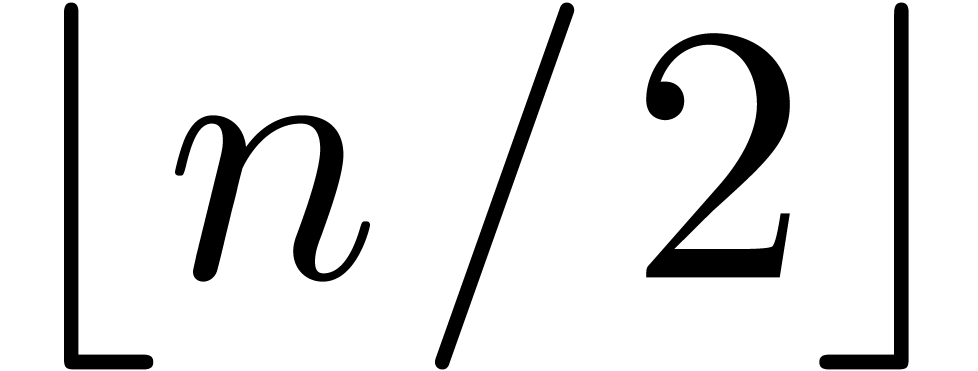 .
The resolution of the linear equation corresponds to the computation of
the two semi-relaxed products.
.
The resolution of the linear equation corresponds to the computation of
the two semi-relaxed products.
3.A new algorithm for fast relaxed
multiplication
Assume from now on that  admits an
admits an
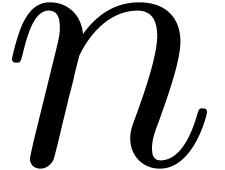 -th root of unity
-th root of unity 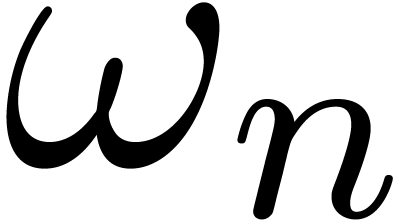 for every power of two
for every power of two 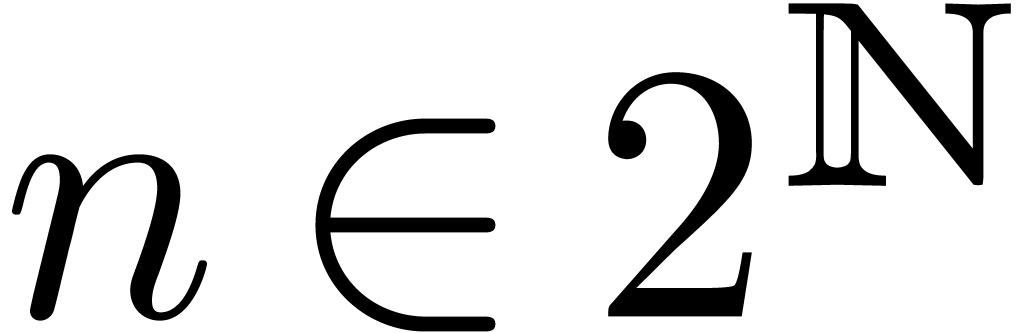 .
Given an element
.
Given an element 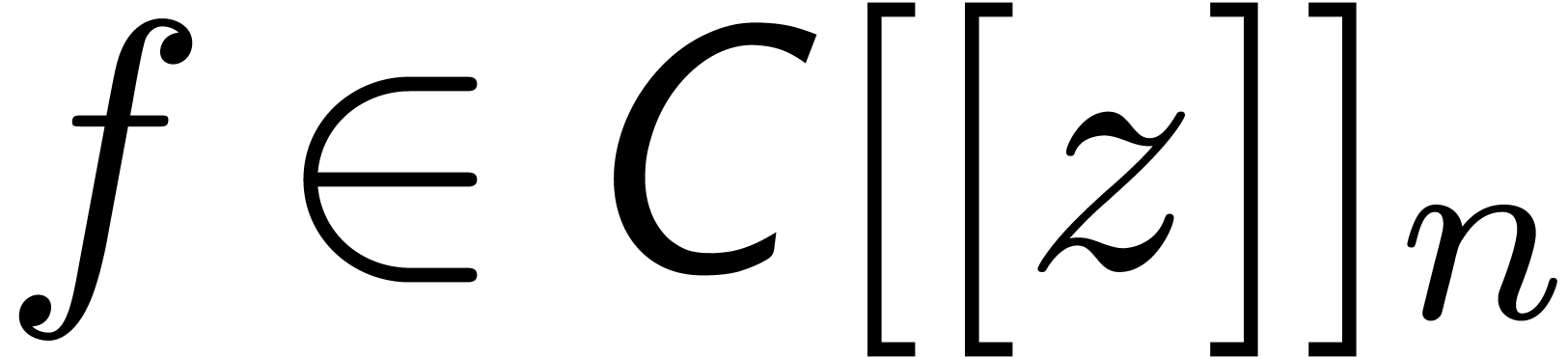 , let
, let 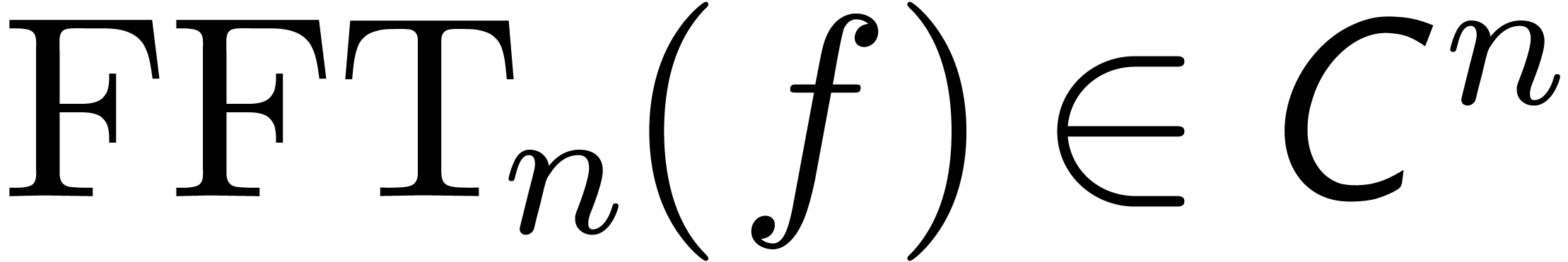 denote its Fourier transform
denote its Fourier transform
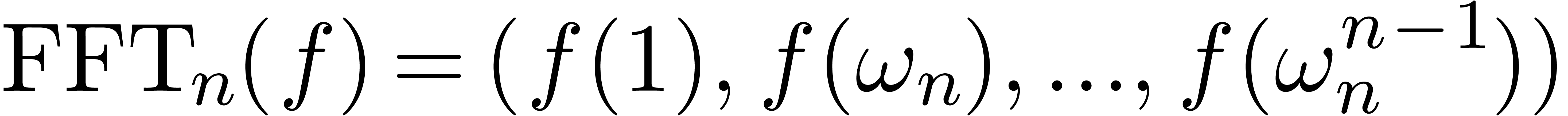
and let 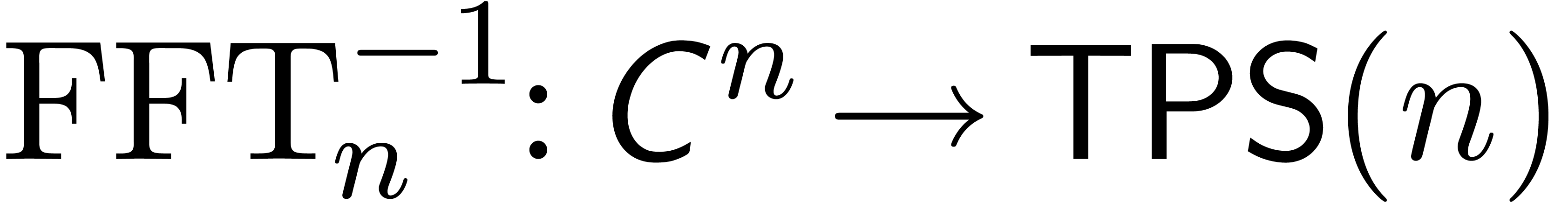 be the inverse mapping of
be the inverse mapping of  . It is well known that both
. It is well known that both  and
and 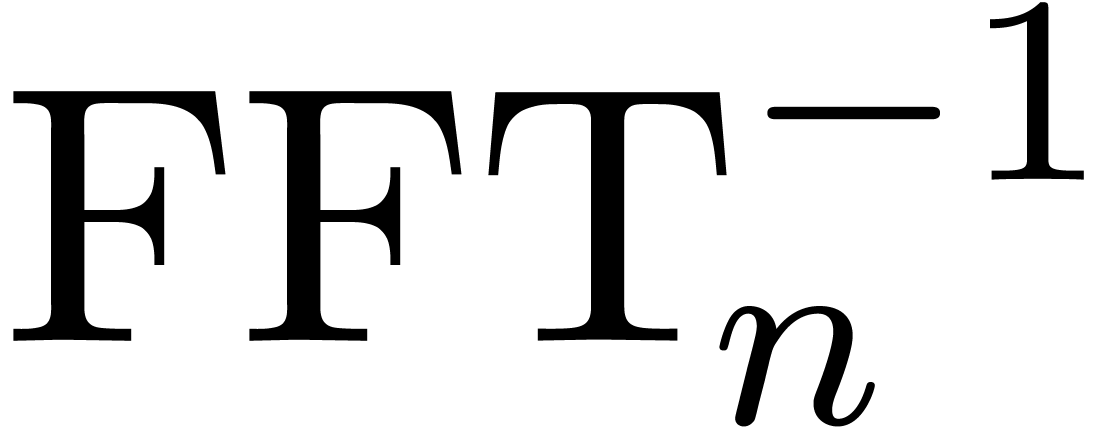 can be computed in time
can be computed in time 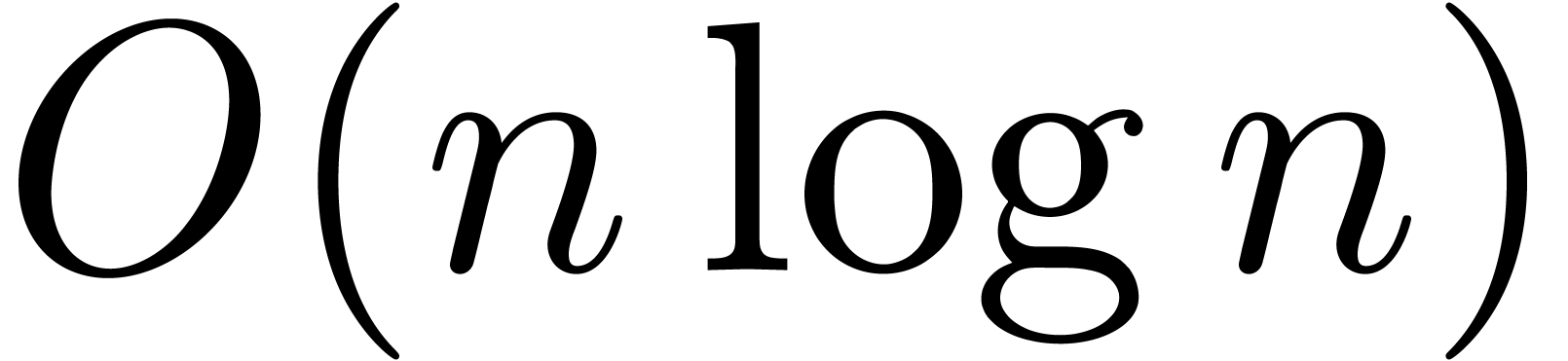 . Furthermore, if
. Furthermore, if 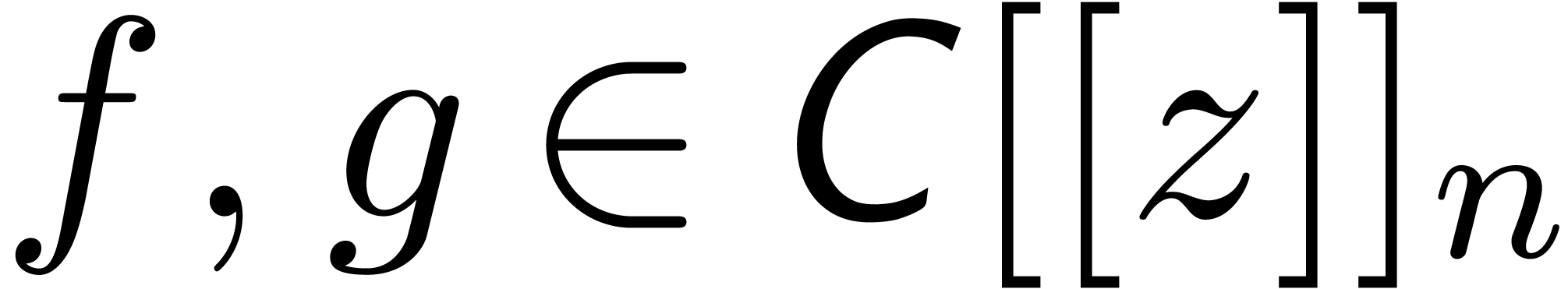 are
such that
are
such that  , then
, then
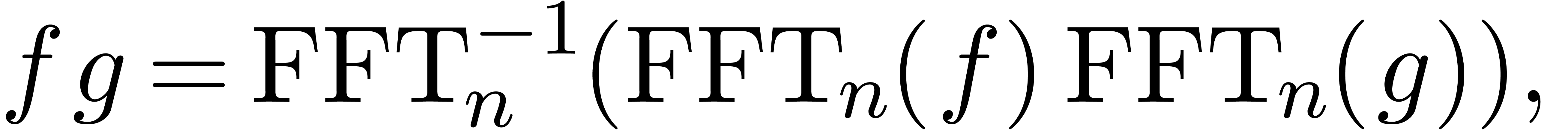
where the product in  is scalar multiplication
is scalar multiplication
 .
.
Now consider a decomposition  with
with 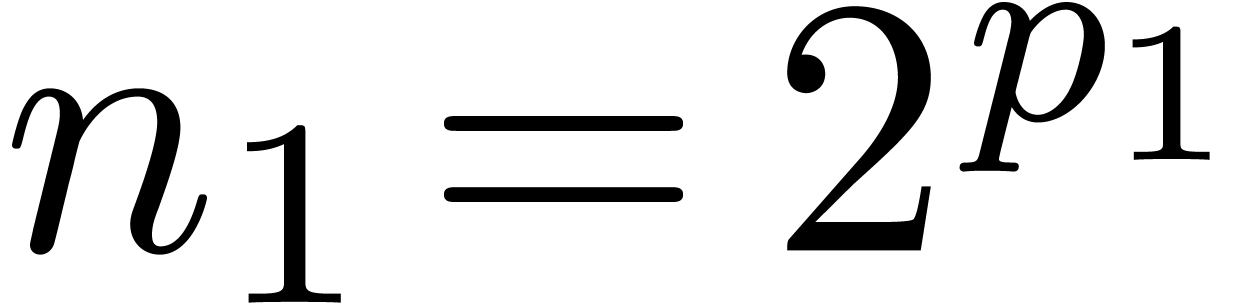 and
and 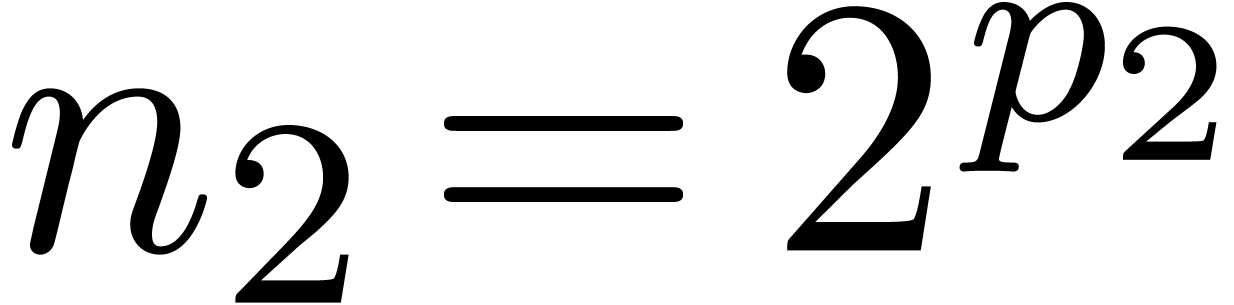 . Then a
truncated power series
. Then a
truncated power series  can be rewritten as a
series
can be rewritten as a
series
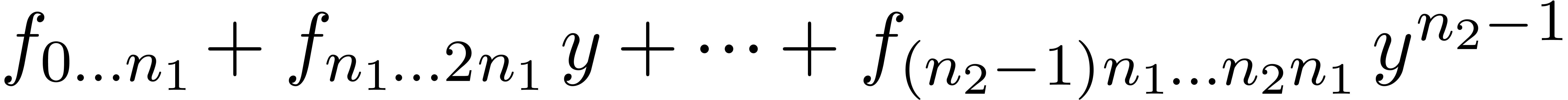
in 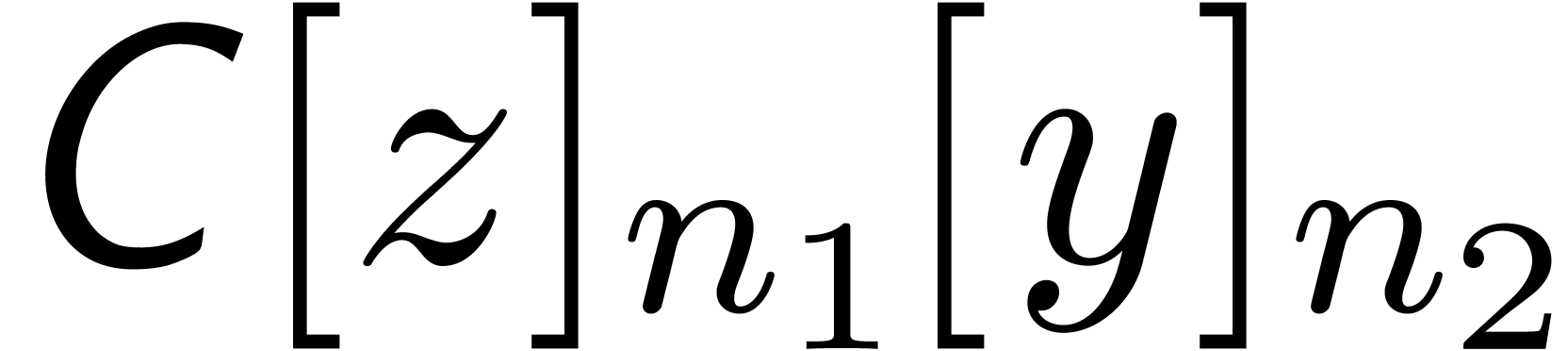 , where
, where 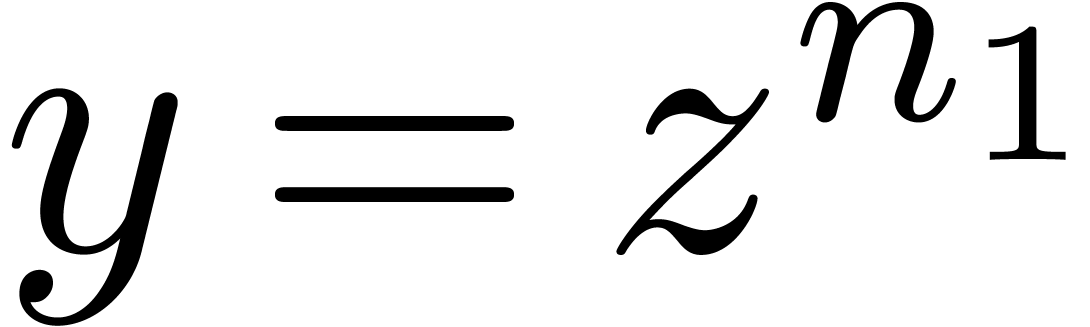 . This series may again be reinterpreted as a
series
. This series may again be reinterpreted as a
series 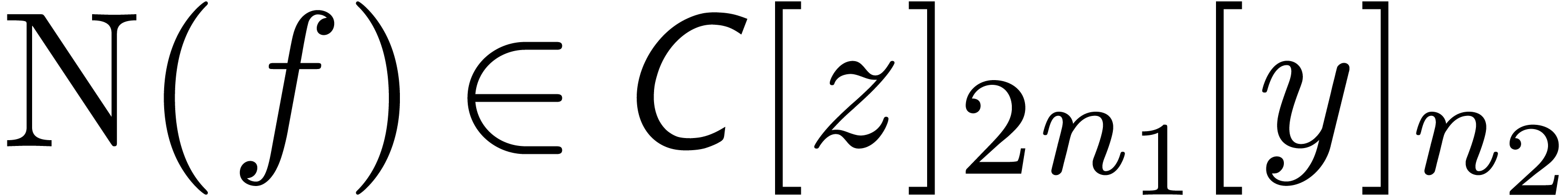 , and we have
, and we have
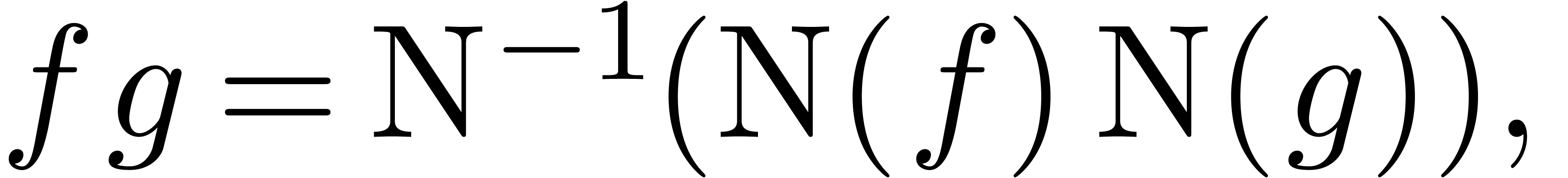
where 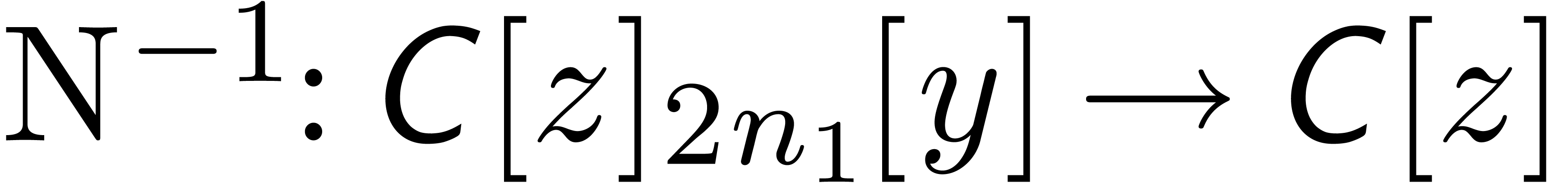 is the mapping which substitutes
is the mapping which substitutes  for
for  . Also, the
FFT-transform
. Also, the
FFT-transform 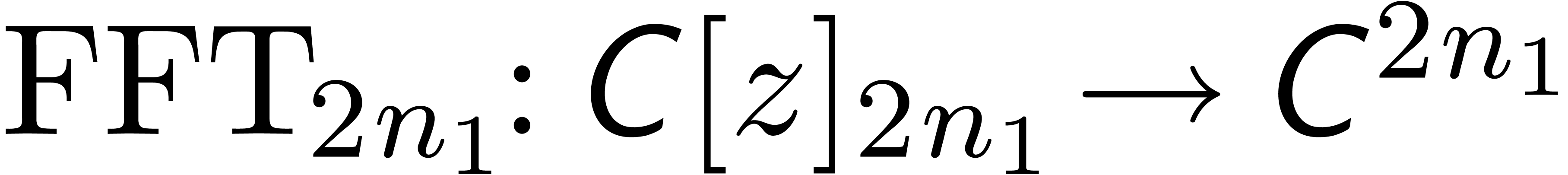 may be extended to a mapping
may be extended to a mapping
for each  , and similarly for
its inverse
, and similarly for
its inverse 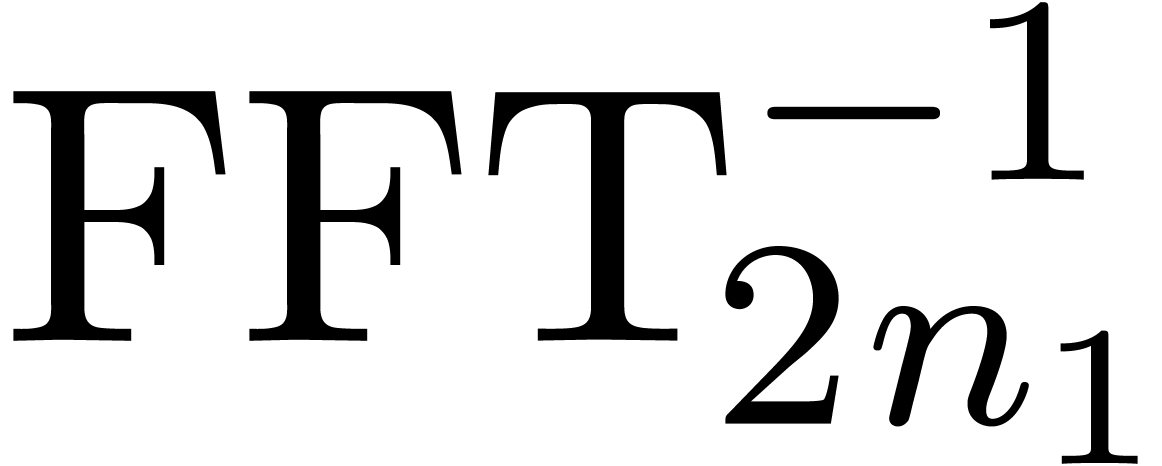 . Now the formula
. Now the formula
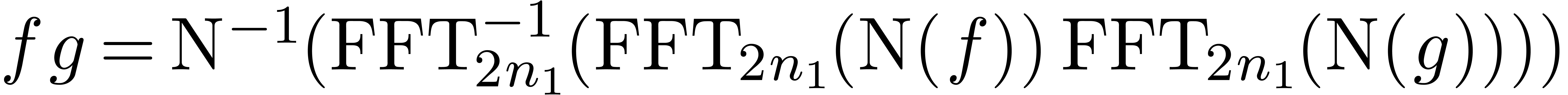
yields a way to compute 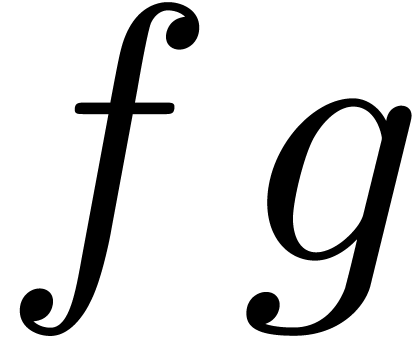 by reusing the Fourier
transforms of the “bunches of coefficients”
by reusing the Fourier
transforms of the “bunches of coefficients” 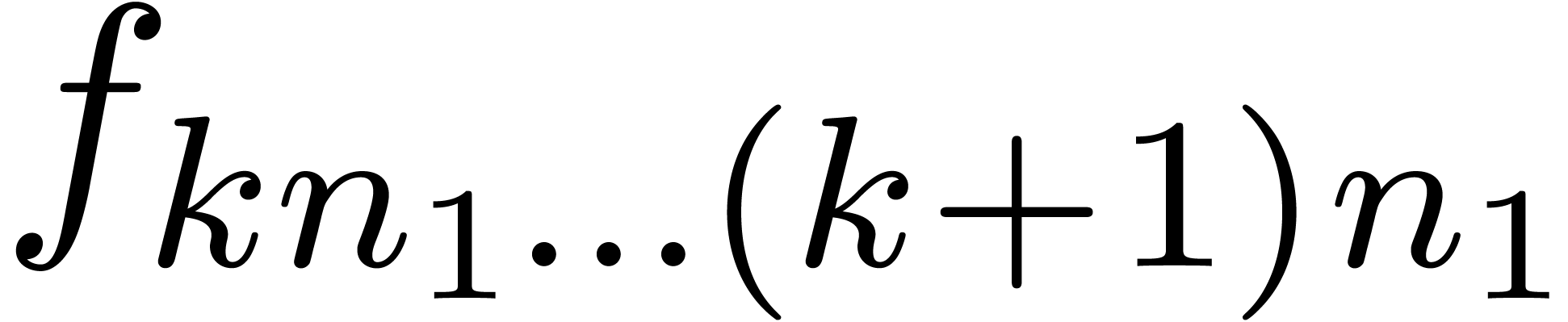 and
and 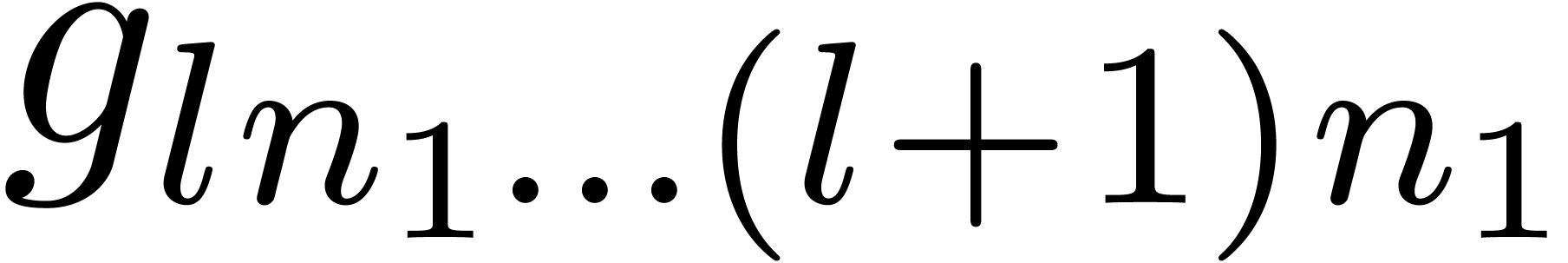 many times.
many times.
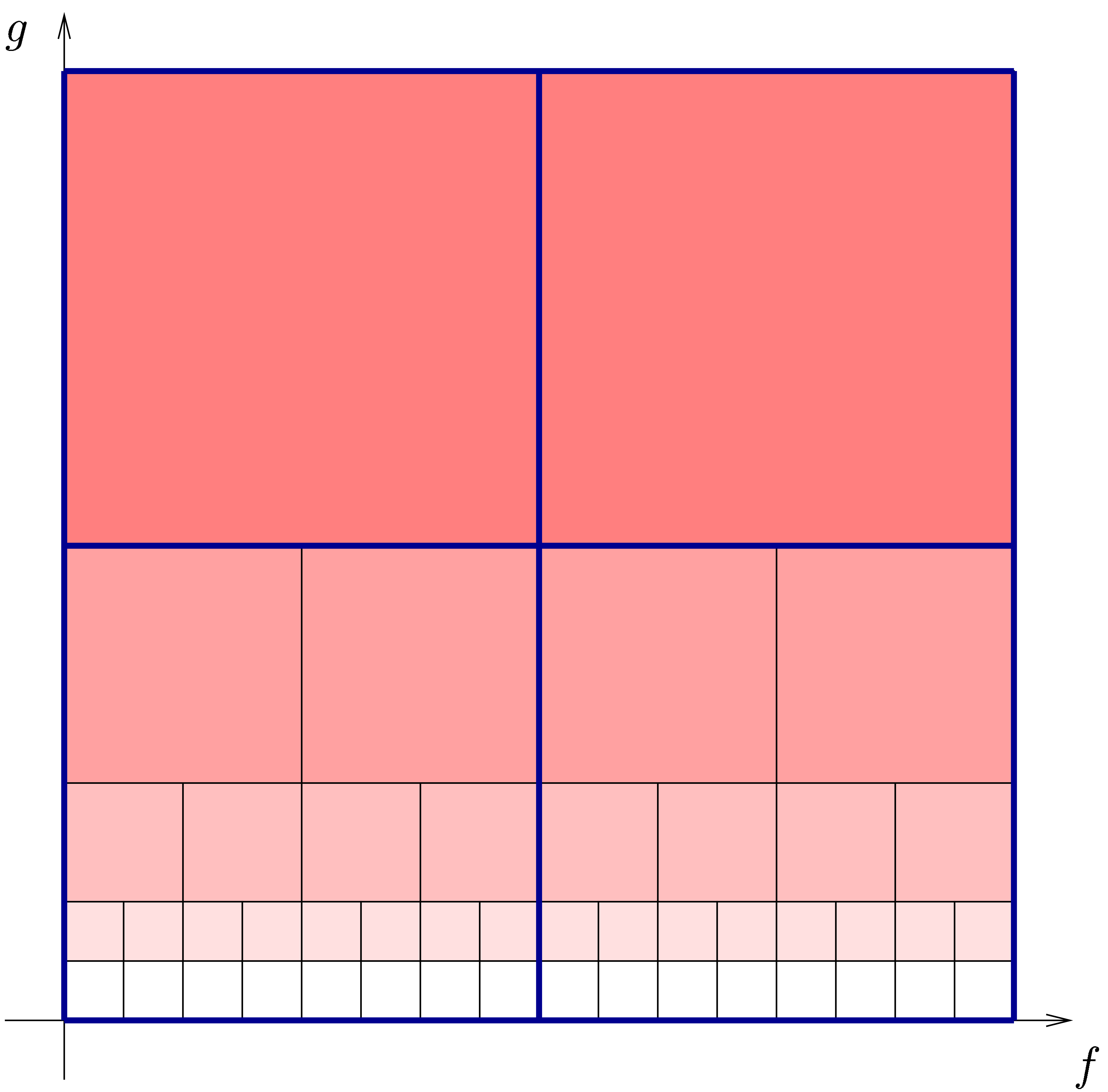
In the context of a semi-relaxed multiplication 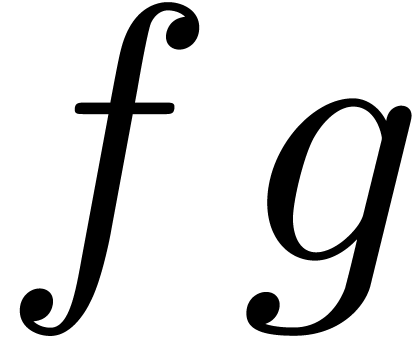 with fixed argument
with fixed argument  , the
above scheme almost reduces the computation of an
, the
above scheme almost reduces the computation of an  product with coefficients in
product with coefficients in  to the computation
of an
to the computation
of an  product with coefficients in
product with coefficients in 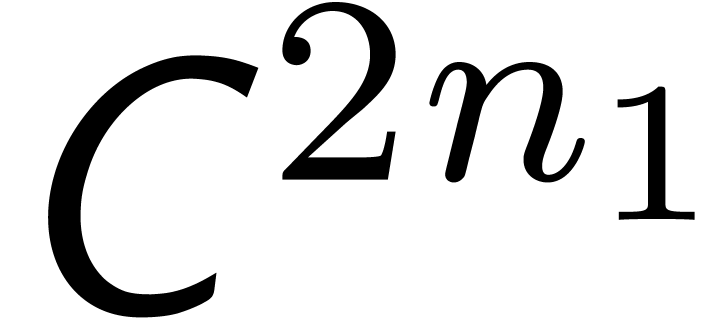 . The only problem which remains is that we can
only compute
. The only problem which remains is that we can
only compute 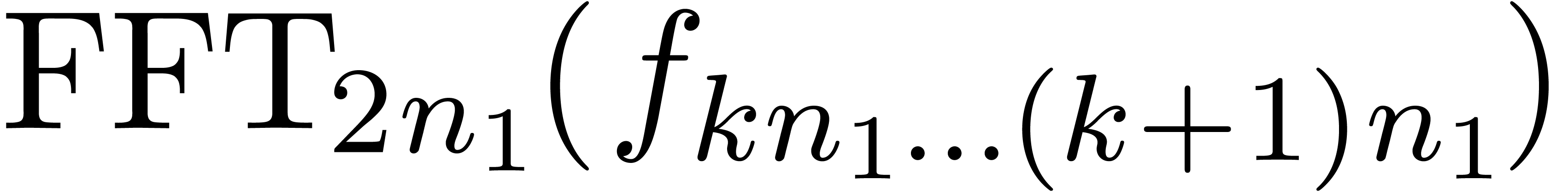 when
when 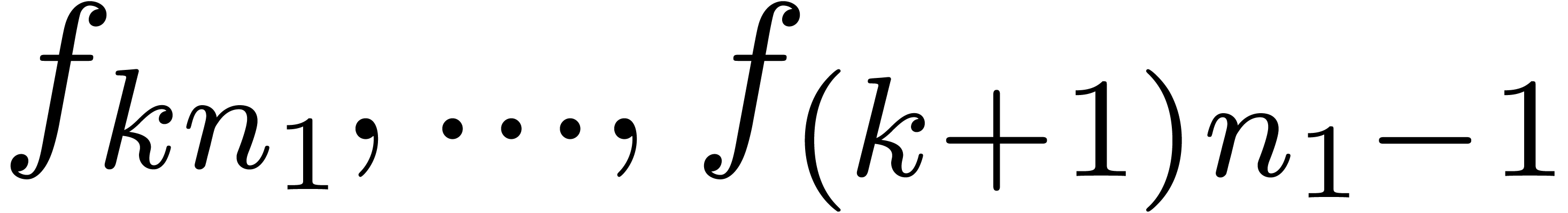 are
all known. Consequently, the products
are
all known. Consequently, the products 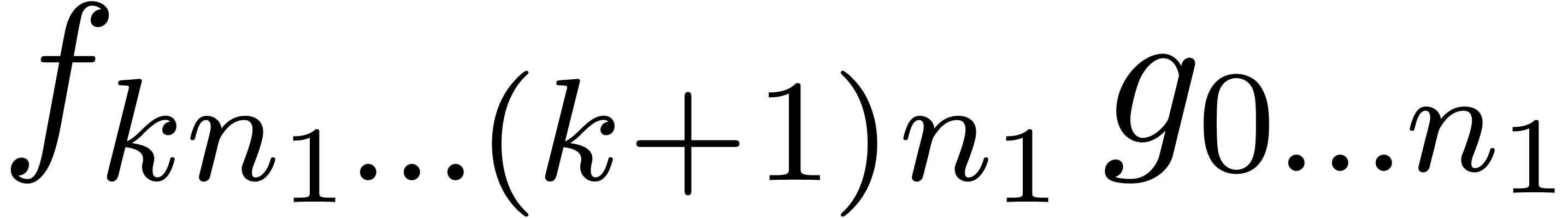 should be
computed apart, using a traditional semi-relaxed multiplication. In
other words, we have reduced the computation of a semi-relaxed
should be
computed apart, using a traditional semi-relaxed multiplication. In
other words, we have reduced the computation of a semi-relaxed  product with coefficients in
product with coefficients in  to
the computation of
to
the computation of  semi-relaxed
semi-relaxed  products with coefficients in
products with coefficients in  ,
one semi-relaxed
,
one semi-relaxed 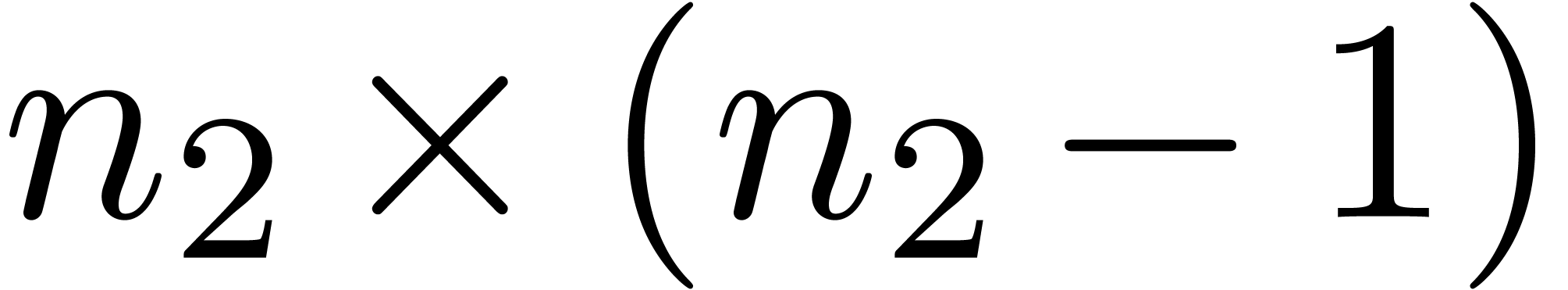 product with coefficients in
product with coefficients in
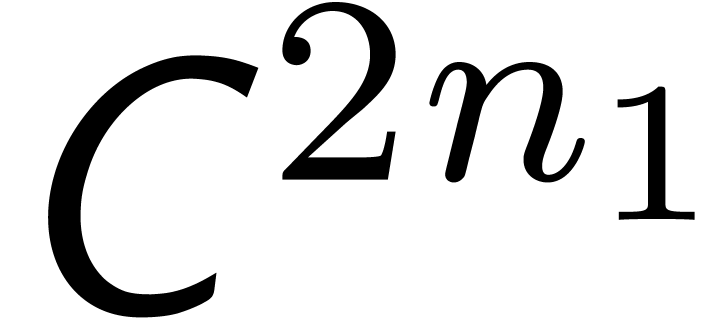 and
and 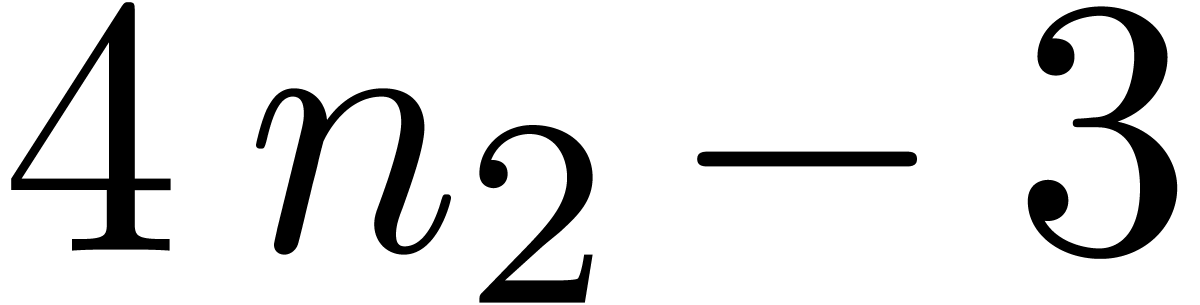 FFT-transforms of
length
FFT-transforms of
length 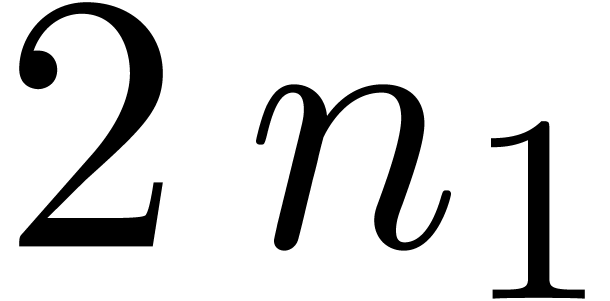 . This has been
illustrated in figure 2.
. This has been
illustrated in figure 2.
In order to obtain an efficient algorithm, we may choose 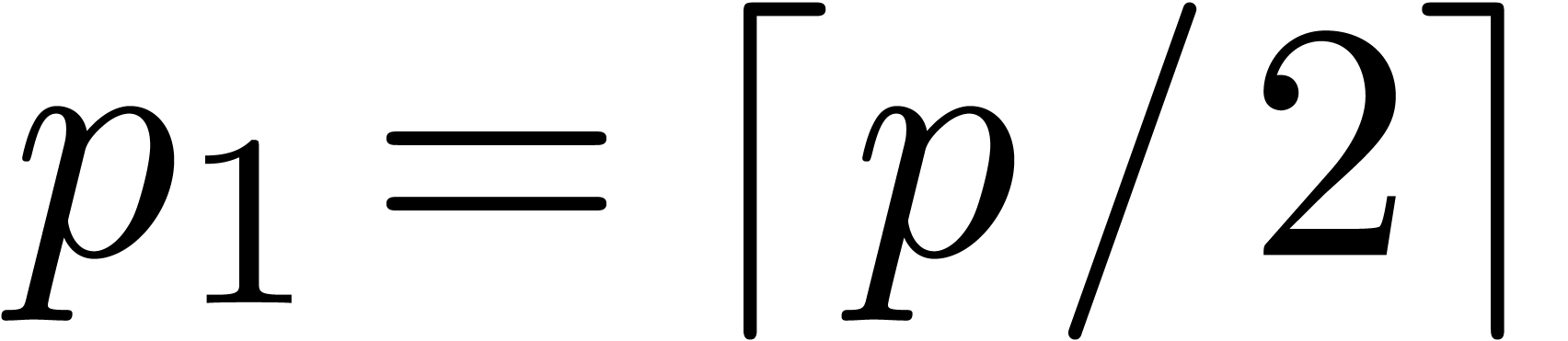 and
and 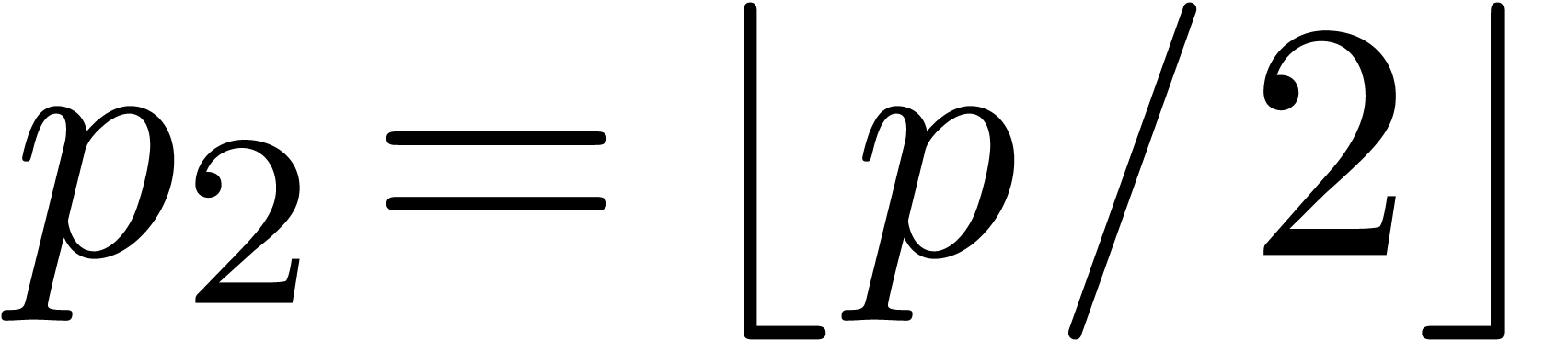 :
:
Proof. In view of section 2, it
suffices to consider the case of a semi-relaxed product. Let 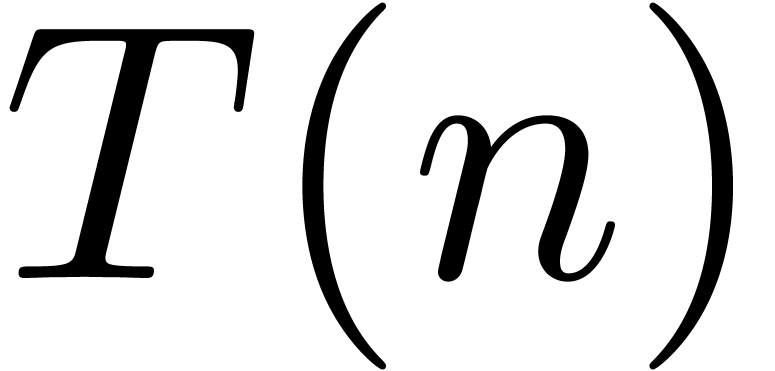 denote the time complexity of the above method. Then we
observe that
denote the time complexity of the above method. Then we
observe that
Taking 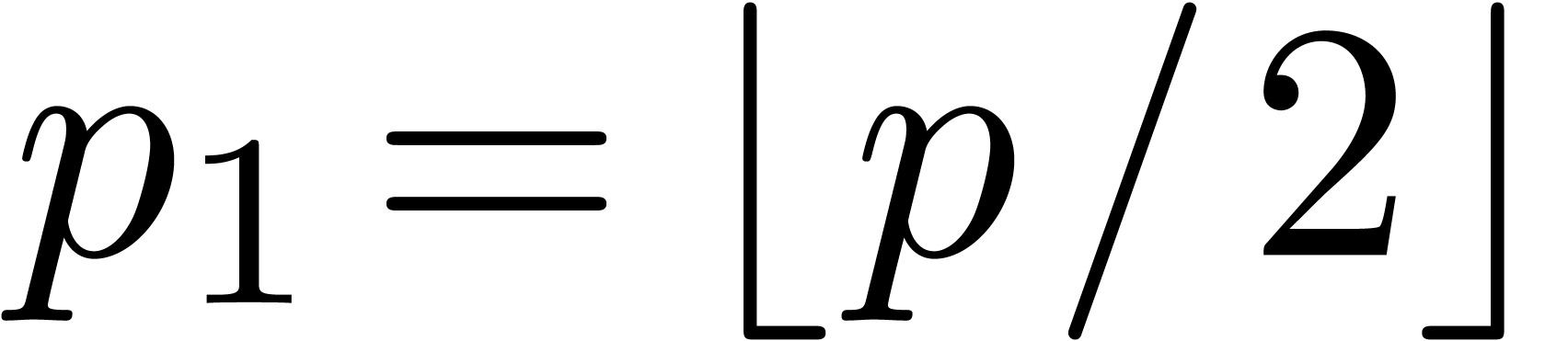 ,
, 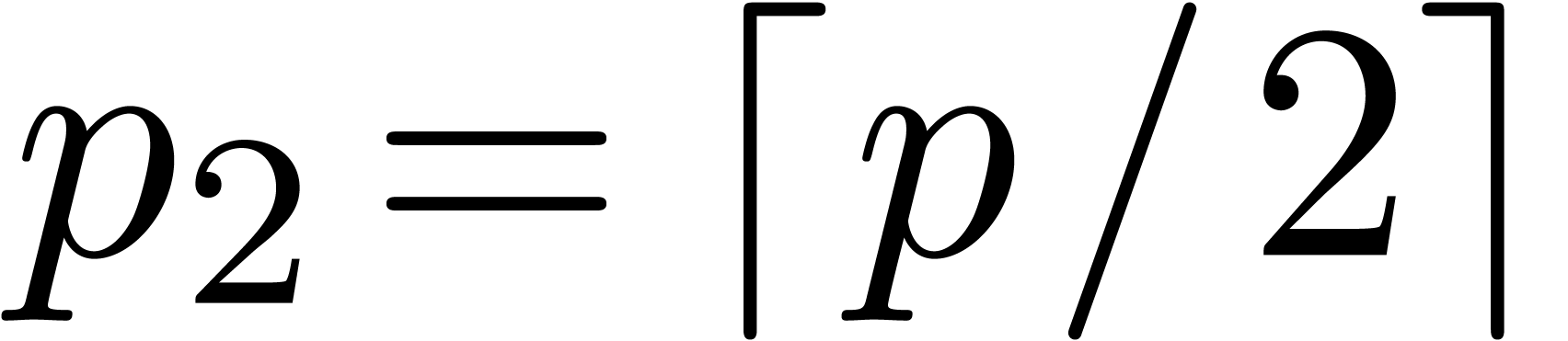 and
and 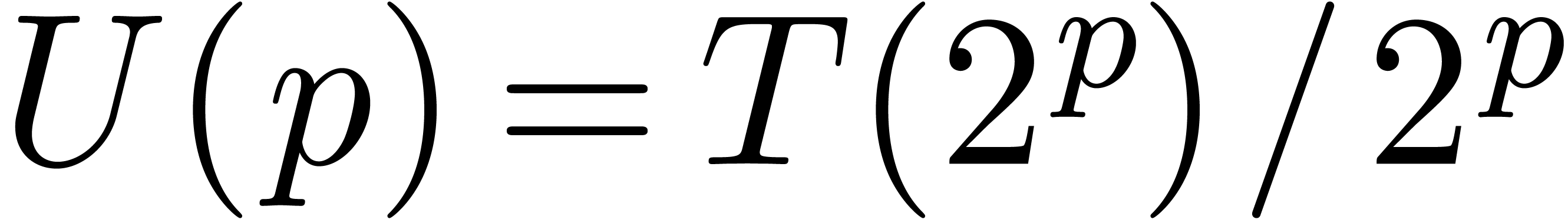 , we obtain
, we obtain
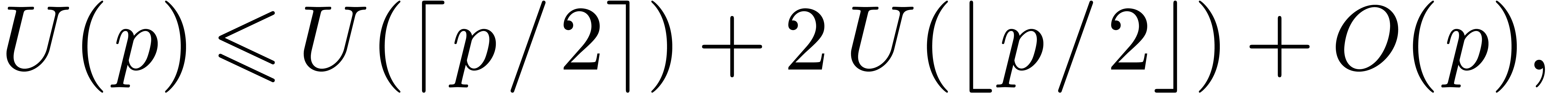
from which we deduce that 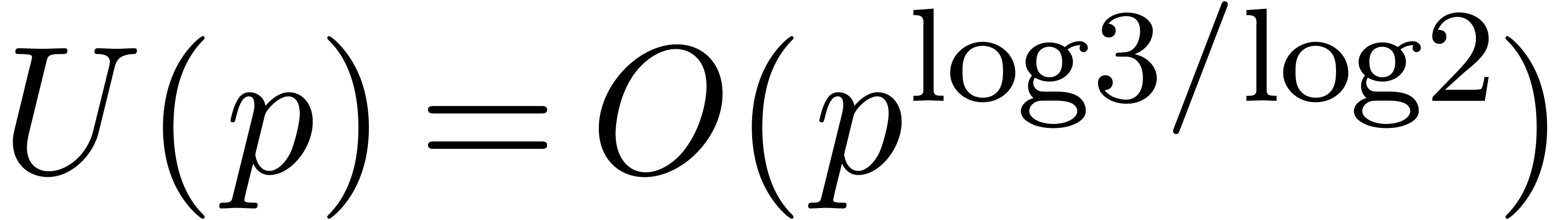 and
and 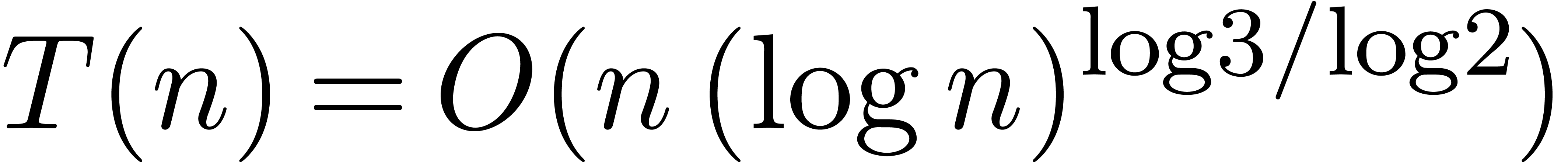 . Similarly, the space complexity
. Similarly, the space complexity 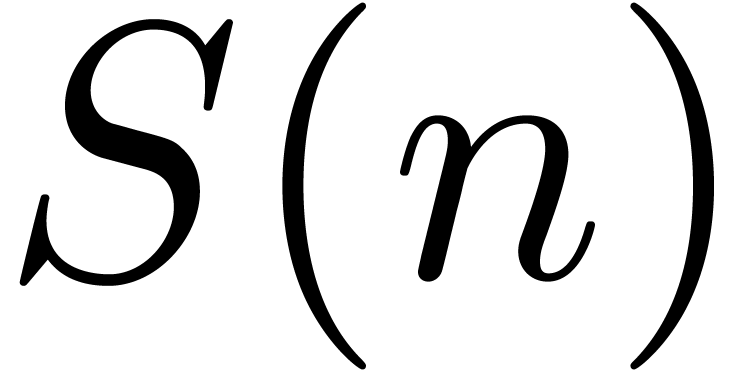 satisfies the bound
satisfies the bound
Setting 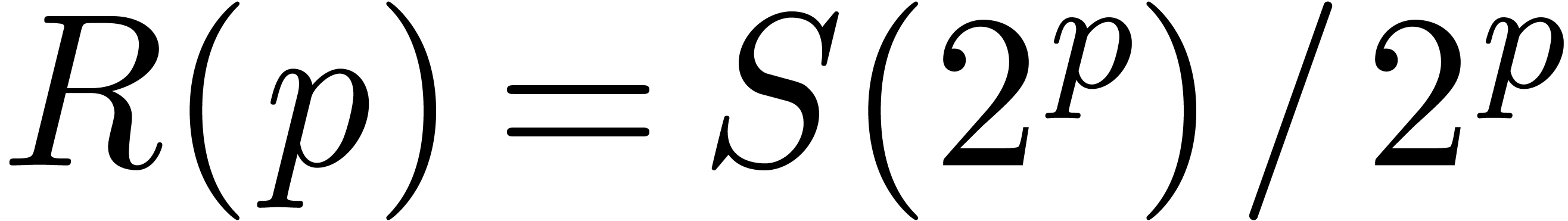 , it follows that
, it follows that
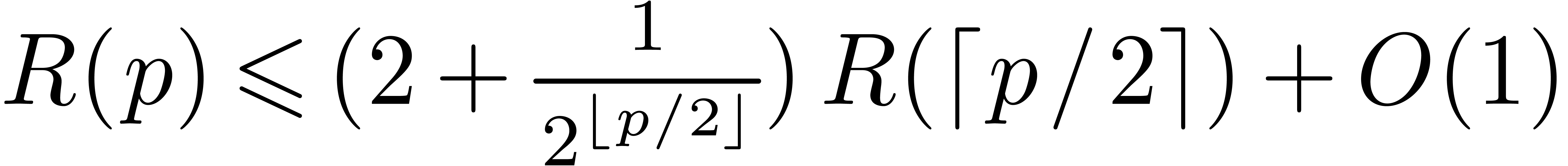
Consequently, 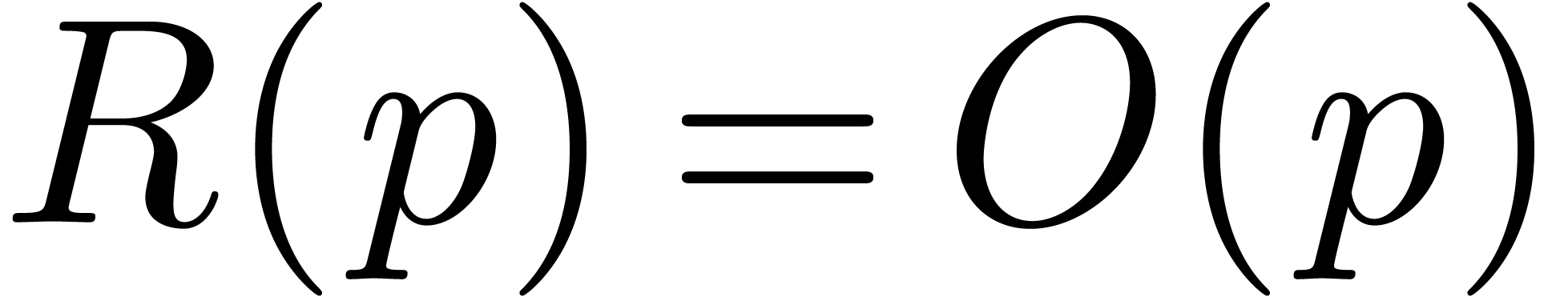 and
and 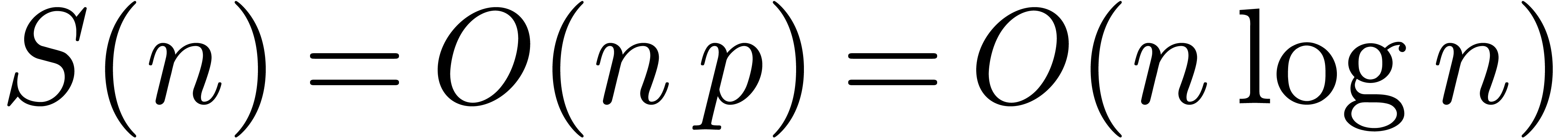 .
.
4.Further improvements of the algorithm
More generally, if 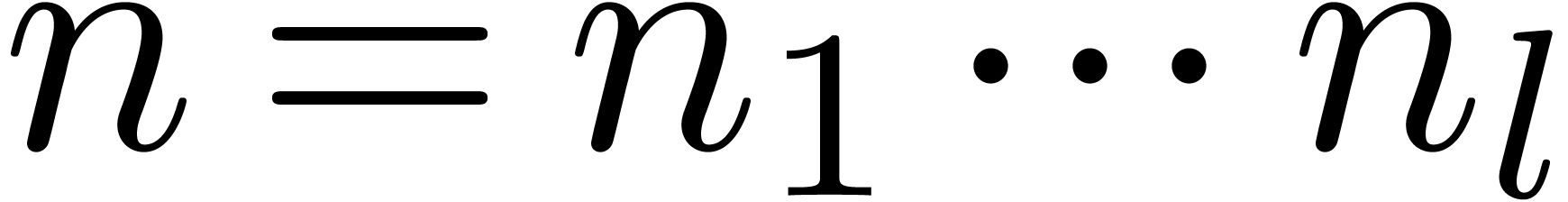 with
with  , then we may reduce the computation of a
semi-relaxed
, then we may reduce the computation of a
semi-relaxed  product with coefficients in
product with coefficients in  into the computation of
into the computation of
This computation is illustrated in 3. From the complexity
point of view, it leads to the following theorem:
Proof. In view of theorem 10(b),
it suffices to consider the case of a semi-relaxed product. Denoting by
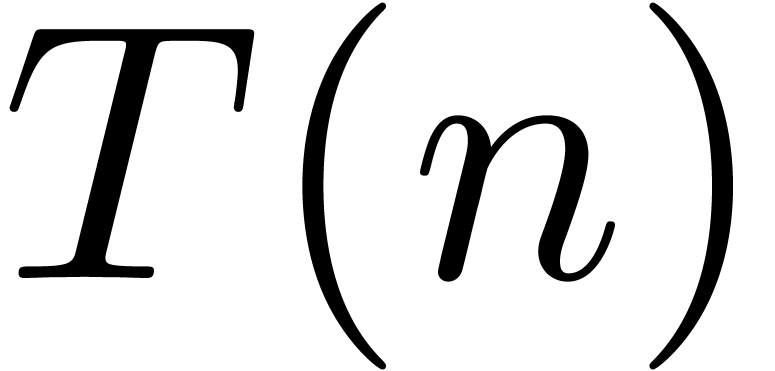 the time complexity of the above method, we have
the time complexity of the above method, we have
 |
(4) |
Let
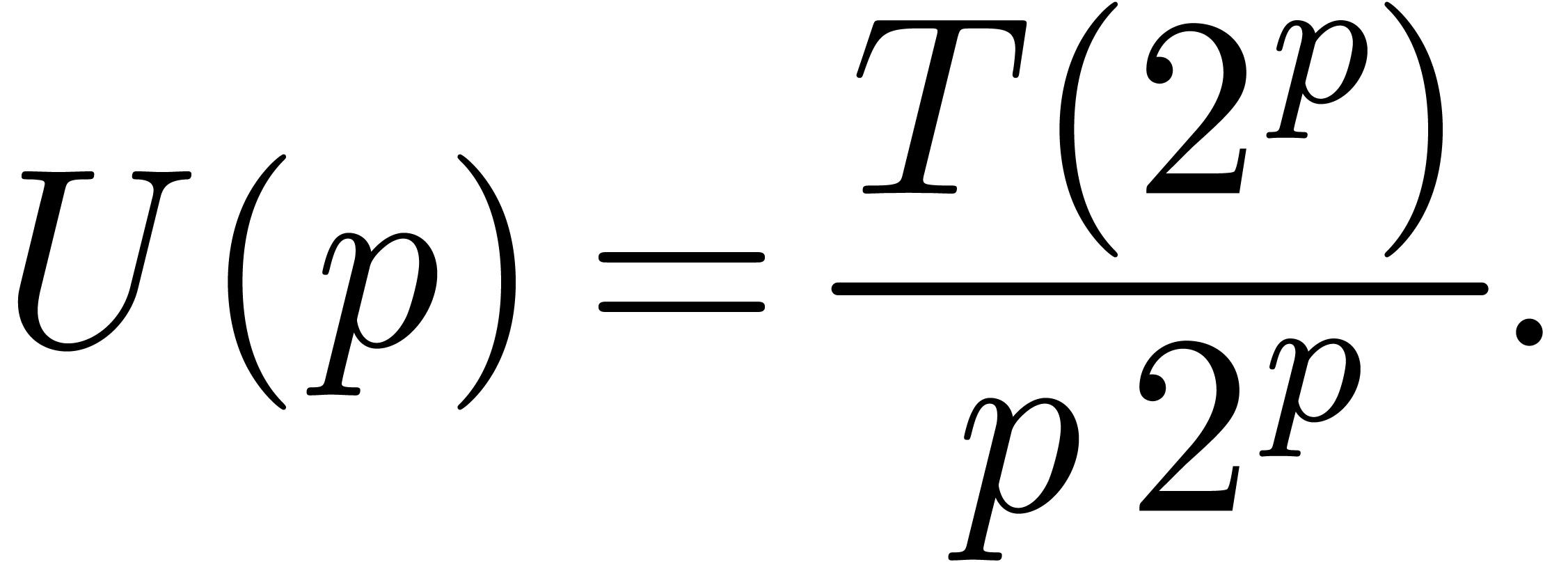
Taking 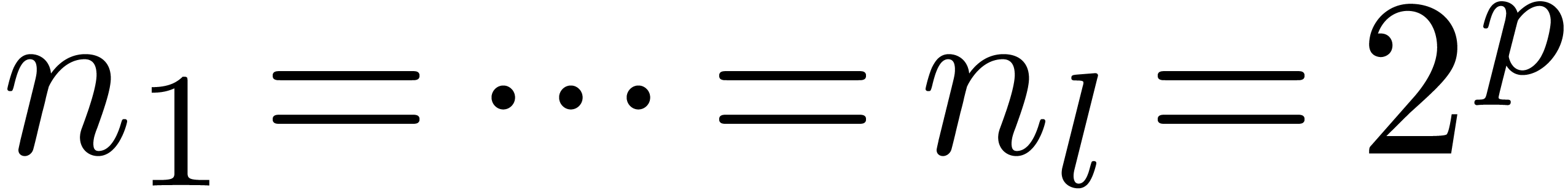 in (4), it follows for any
in (4), it follows for any
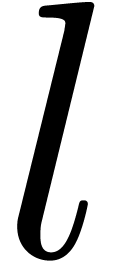 that
that
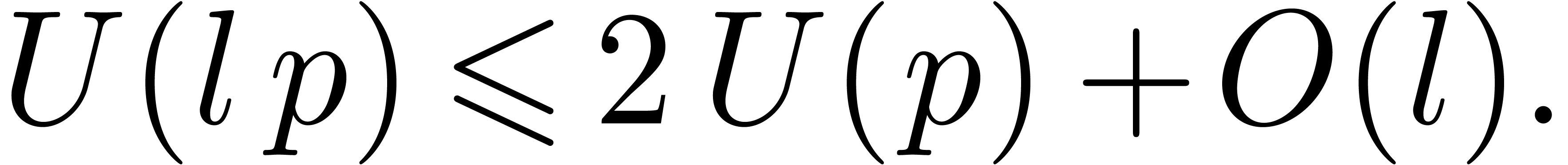 |
(5) |
Applying this relation 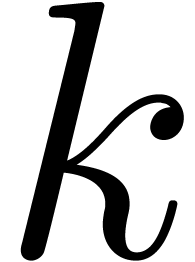 times, we obtain
times, we obtain
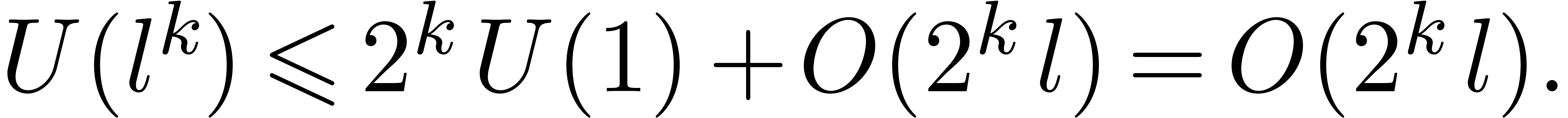 |
(6) |
For a fixed 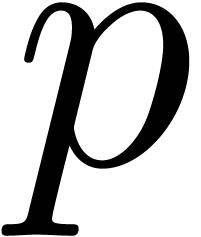 such that
such that 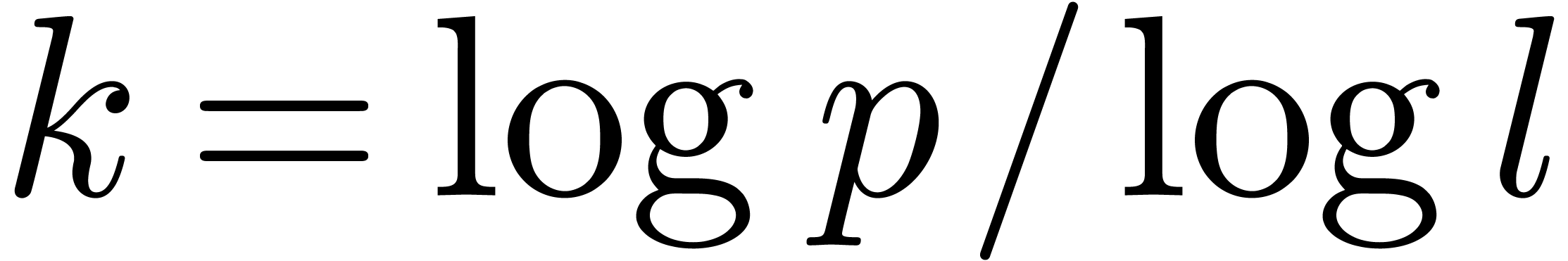 is
an integer, we obtain
is
an integer, we obtain
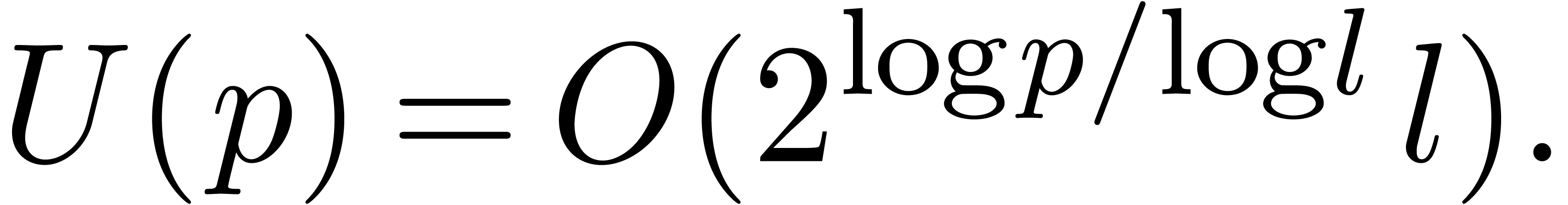 |
(7) |
The minimum of 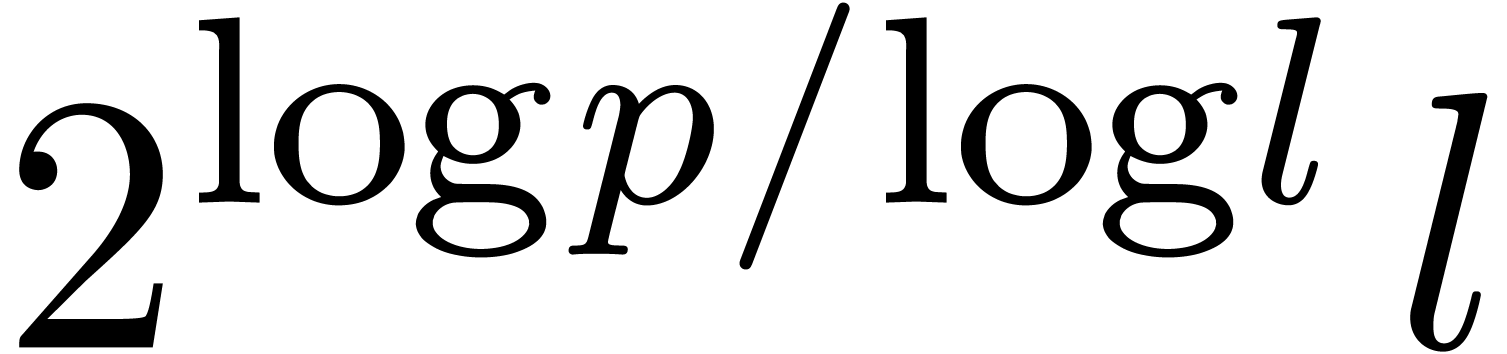 is reached when its derivative
w.r.t.
is reached when its derivative
w.r.t. 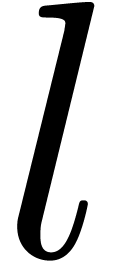 cancels. This happens for
cancels. This happens for
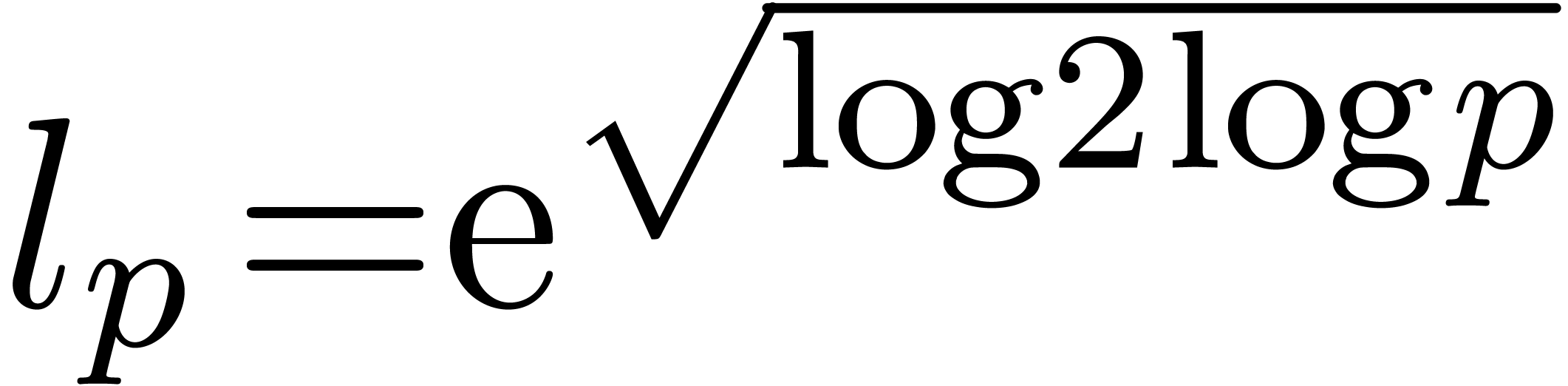
Plugging this value into (7), we obtain
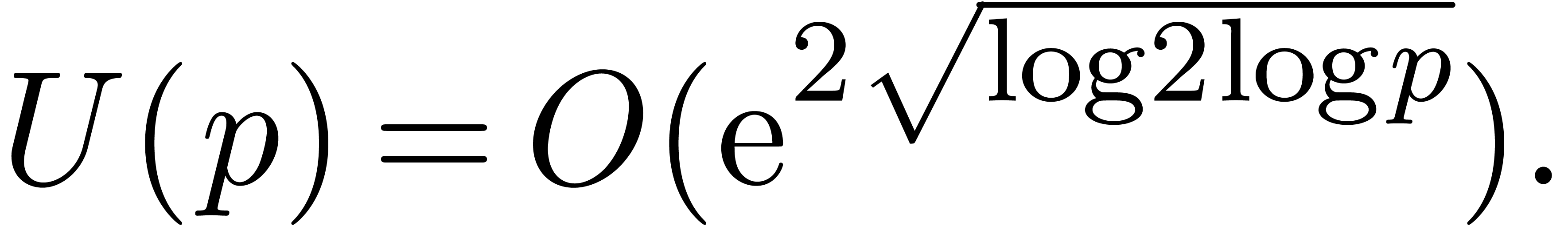
Substitution of 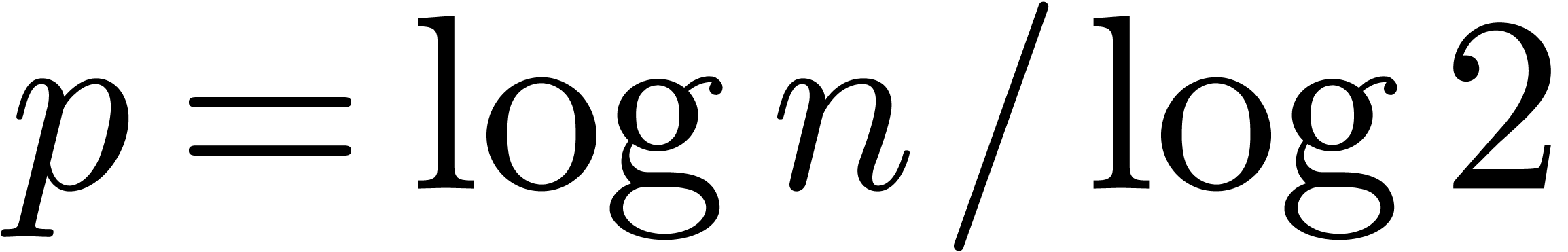 finally gives the desired
estimate
finally gives the desired
estimate
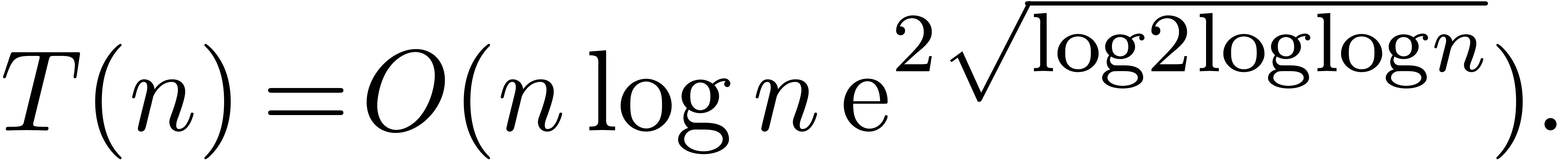 |
(8) |
In order to be painstakingly correct, we notice that we really proved
(7) for  of the form
of the form 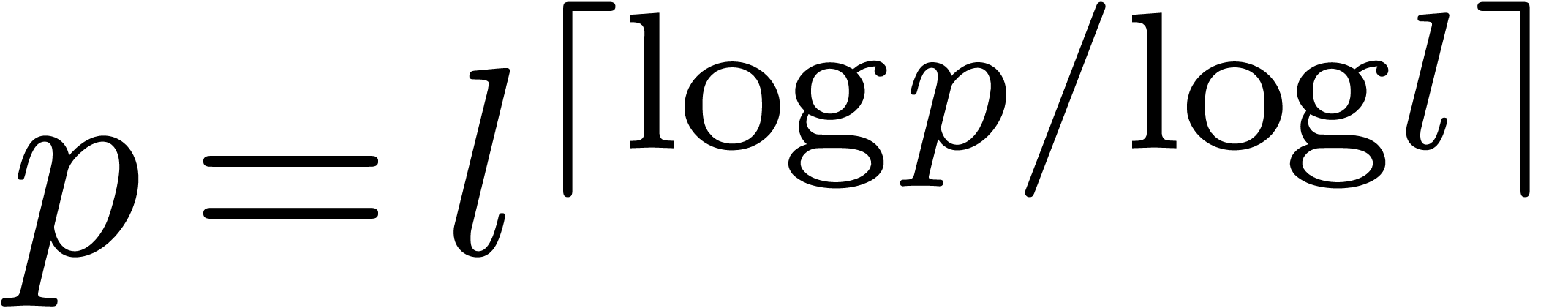 and (8) for
and (8) for 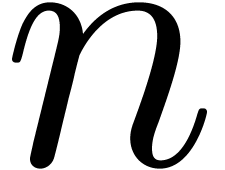 of the
form
of the
form 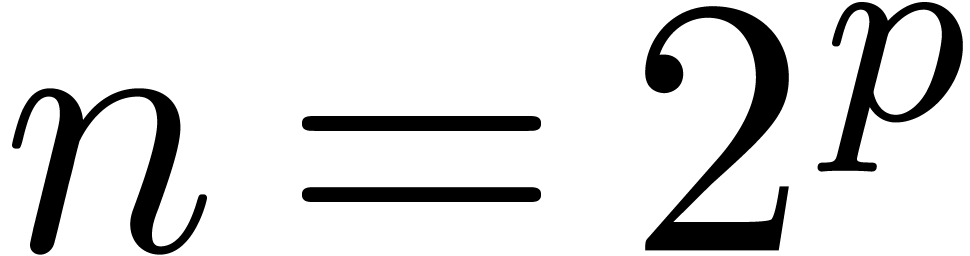 . Of course, we may
always replace
. Of course, we may
always replace 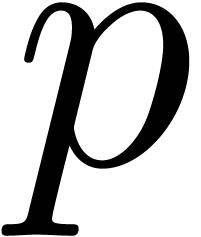 and
and 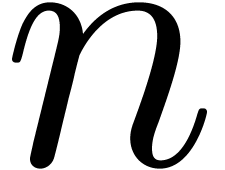 by
larger values which do have this form. Since these replacements only
introduce additional constant factors in the complexity bounds, the
bound (8) holds for general
by
larger values which do have this form. Since these replacements only
introduce additional constant factors in the complexity bounds, the
bound (8) holds for general 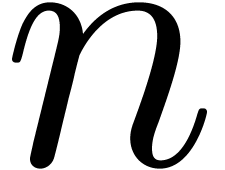 .
.
As to the space complexity 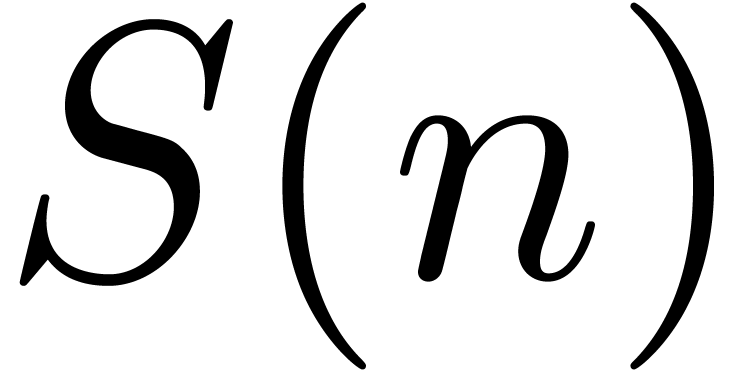 ,
we have
,
we have

Let
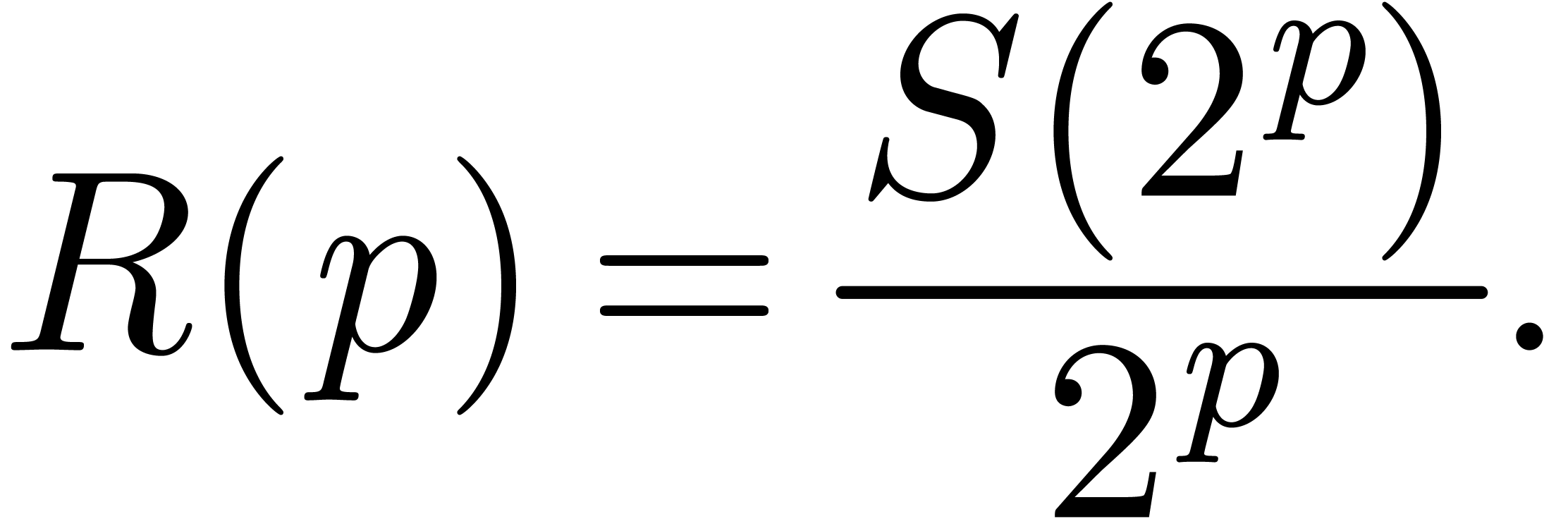
Taking  , it follows for any
, it follows for any
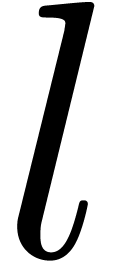 that
that
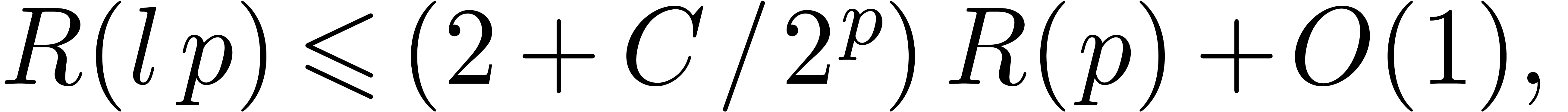
for some fixed constant  .
Applying this bound
.
Applying this bound 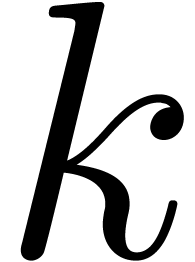 times, we obtain
times, we obtain
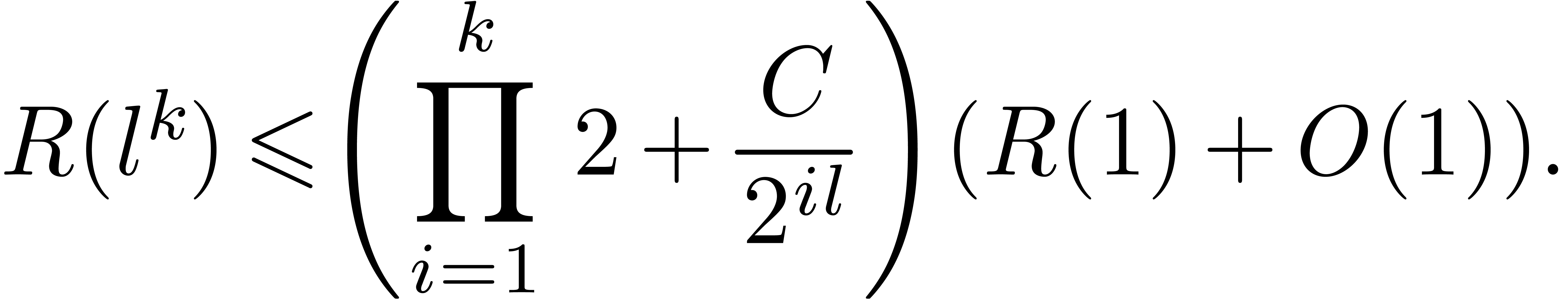
For  , this bound simplifies
to
, this bound simplifies
to
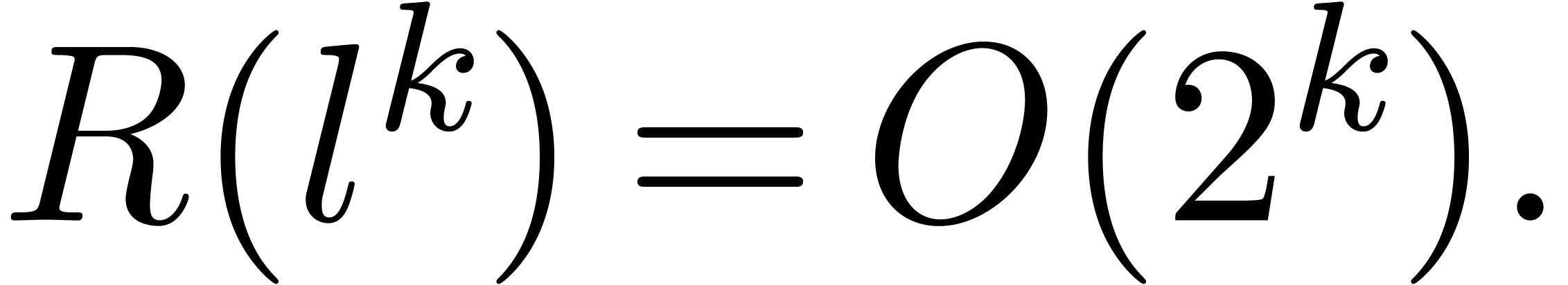
Taking 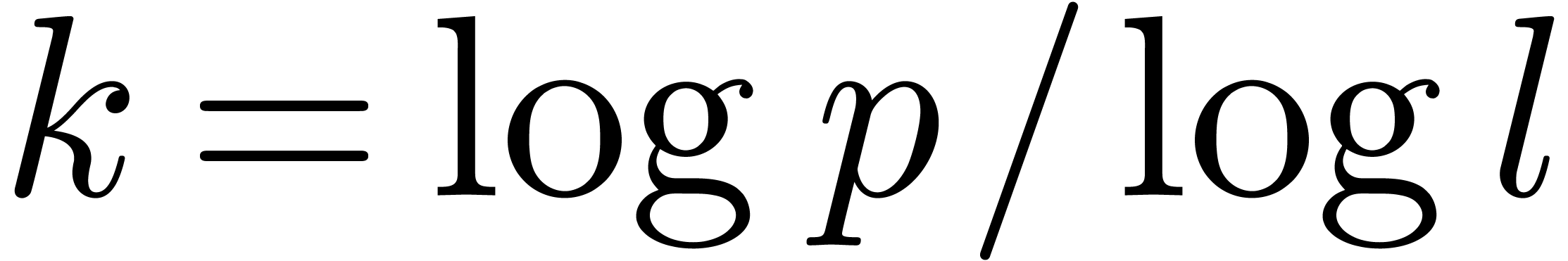 and
and 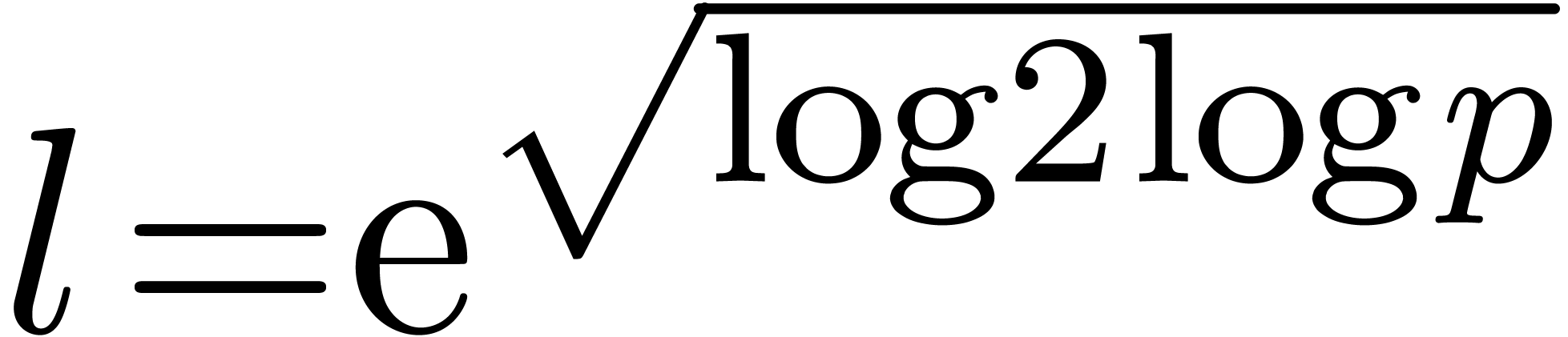 as above, it
follows that
as above, it
follows that
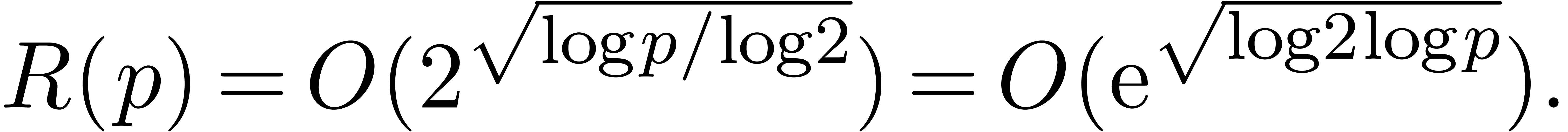
Substitution of 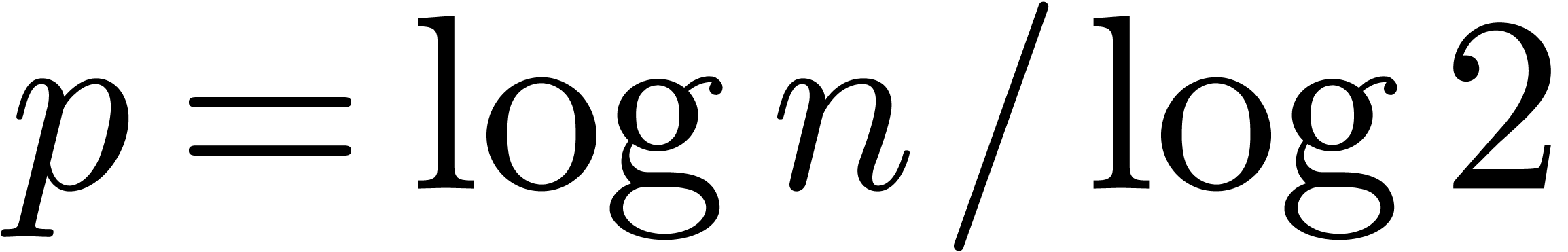 finally gives us the desired
estimate
finally gives us the desired
estimate
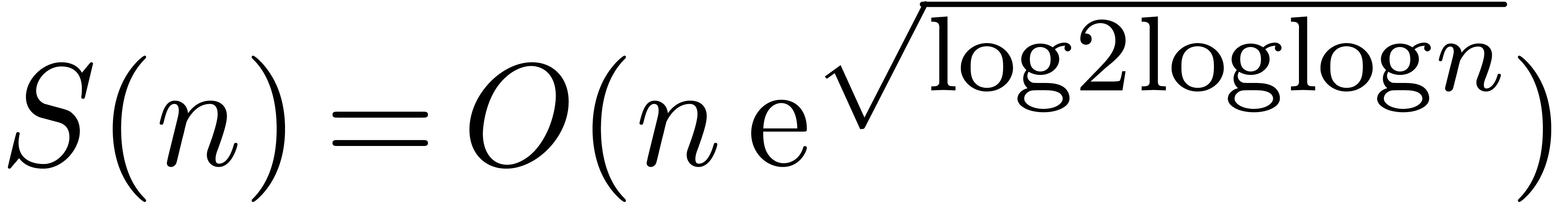
for the space complexity. For similar reasons as above, the bound holds
for general 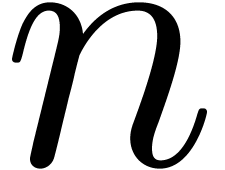 .
.
5.Implementation details and benchmarks
We implemented the algorithm from section 3 in
the C++ library Mmxlib [vdH02b]. Instead of taking  ,
we took
,
we took 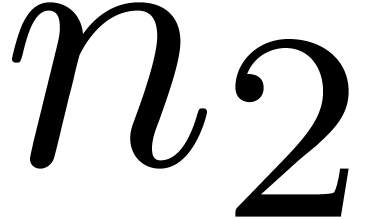 small (with
small (with 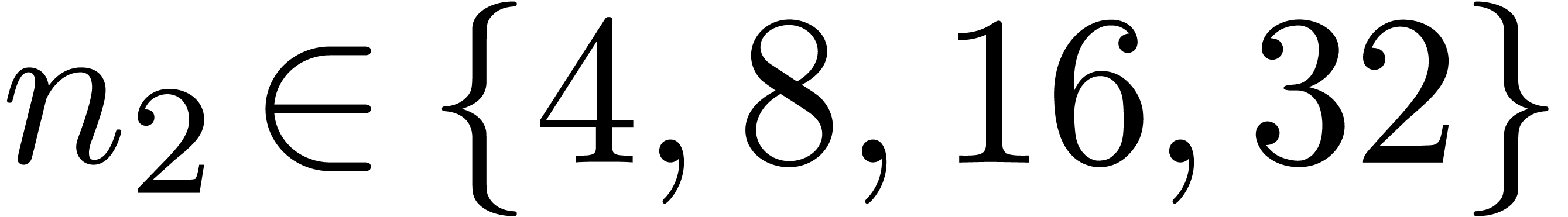 in
the FFT range up to
in
the FFT range up to 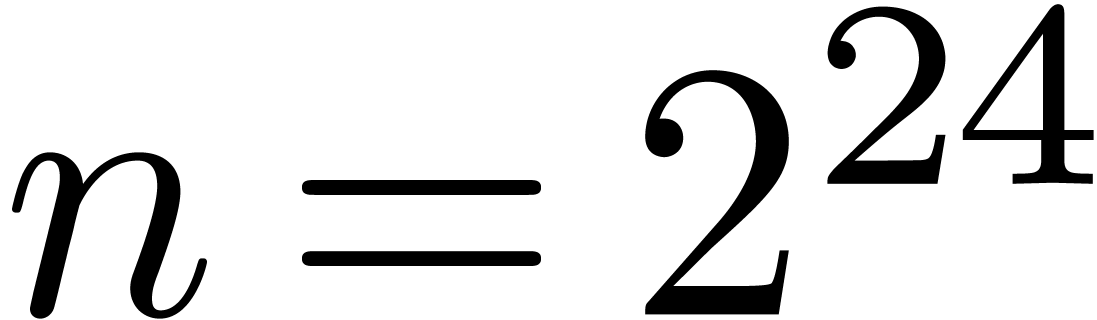 ), and
used a naive multiplication algorithm on the FFT-ed blocks. The reason
behind this change is that
), and
used a naive multiplication algorithm on the FFT-ed blocks. The reason
behind this change is that 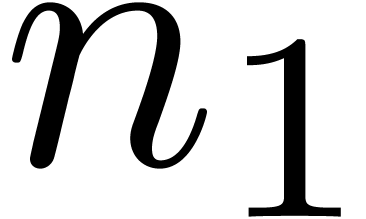 needs to be
reasonably large in order to profit from the better asymptotic
complexity of relaxed multiplication. In practice, the optimal choice of
needs to be
reasonably large in order to profit from the better asymptotic
complexity of relaxed multiplication. In practice, the optimal choice of
 is obtained by taking
is obtained by taking 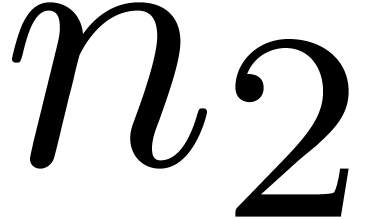 quite small.
quite small.
Moreover, our implementation uses a truncated version of relaxed
multiplication [vdH02a, Section 4.4.2]. In particular, the
use of naive multiplication on the FFT-ed blocks allows us to gain a
factor 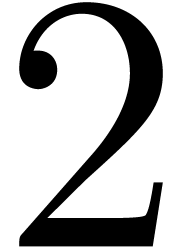 at the top-level. For small values of
at the top-level. For small values of
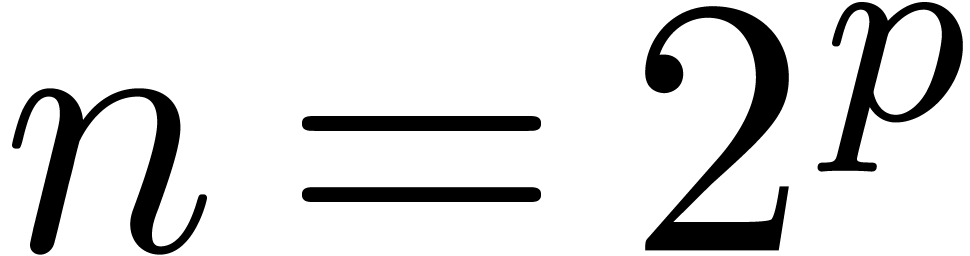 , we also replaced FFT
transforms by “Karatsuba transforms”: given a polynomial
, we also replaced FFT
transforms by “Karatsuba transforms”: given a polynomial
 , we may form a polynomial
, we may form a polynomial
 in
in  variables with
coefficients
variables with
coefficients 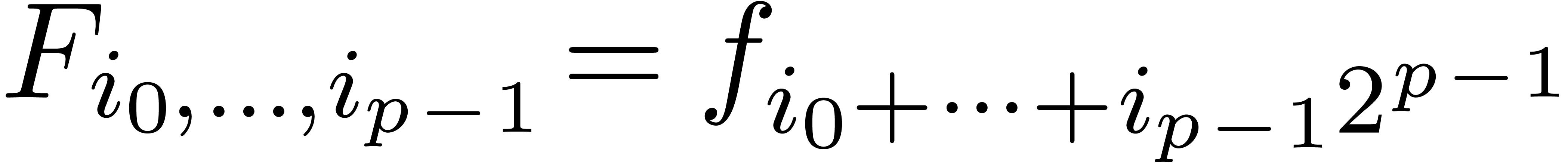 for
for 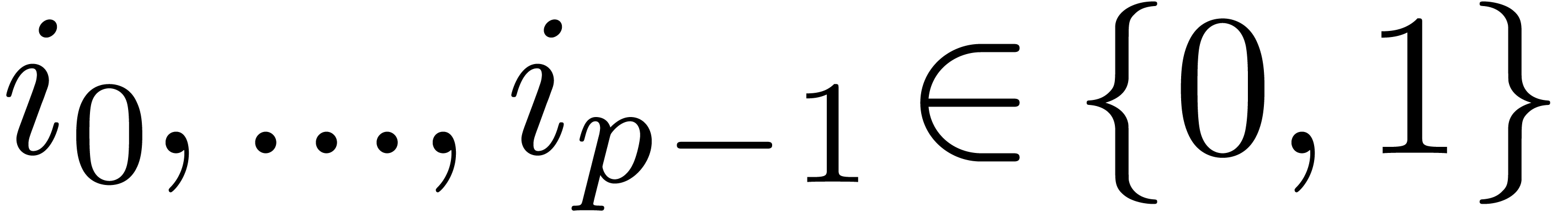 .
Then the Karatsuba transform of
.
Then the Karatsuba transform of 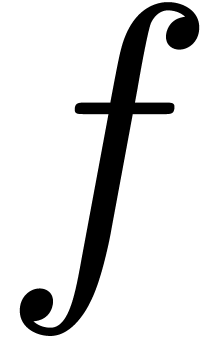 is the vector
is the vector
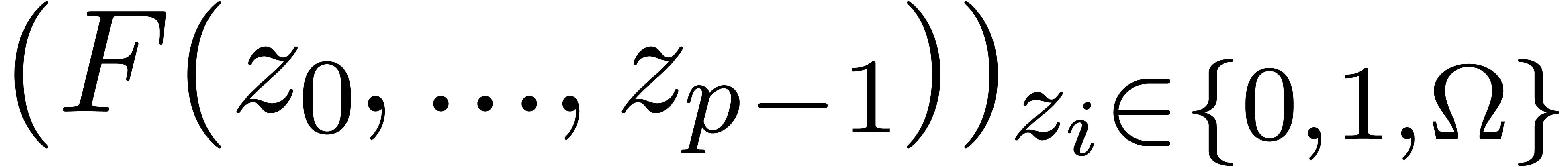 of size
of size 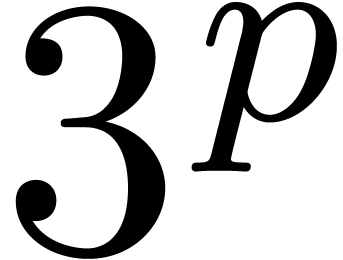 ,
where
,
where 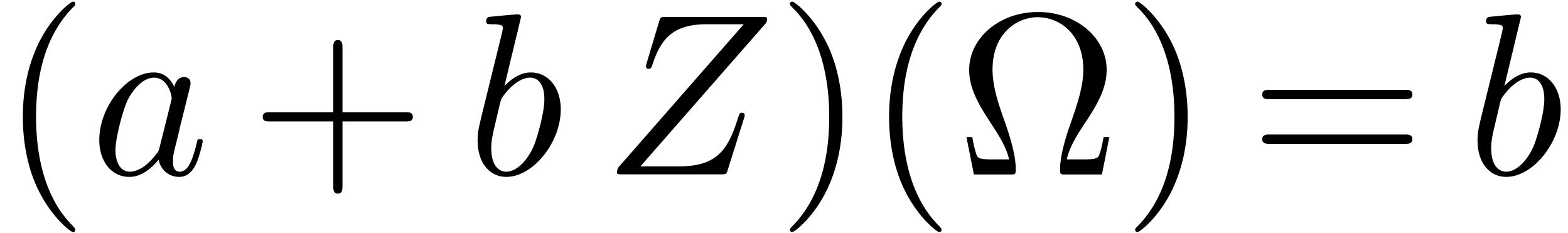 .
.
We have both tested (truncated) relaxed and semi-relaxed multiplication
for different types of coefficients on an Intel Xeon processor at  with
with  of memory. The results
of our benchmarks can be found in tables 1 and 2
below. Our benchmarks start at the order
of memory. The results
of our benchmarks can be found in tables 1 and 2
below. Our benchmarks start at the order 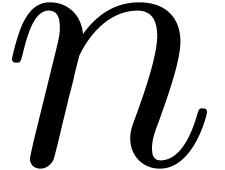 where
FFT multiplication becomes useful. Notice that working with orders in
where
FFT multiplication becomes useful. Notice that working with orders in
 does not give us any significant advantage,
because the top-level product on FFT-ed blocks is naive. In table 1, the choice of
does not give us any significant advantage,
because the top-level product on FFT-ed blocks is naive. In table 1, the choice of 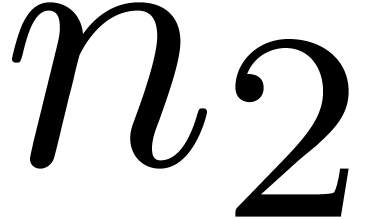 as a function of
as a function of 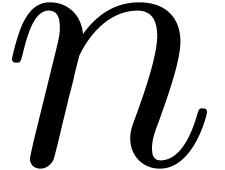 has been optimized for complex double coefficients.
No particular optimization effort was made for the coefficient types in
table 2, and it might be possible to gain about
has been optimized for complex double coefficients.
No particular optimization effort was made for the coefficient types in
table 2, and it might be possible to gain about  on our timings.
on our timings.
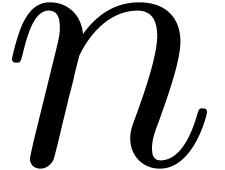 |
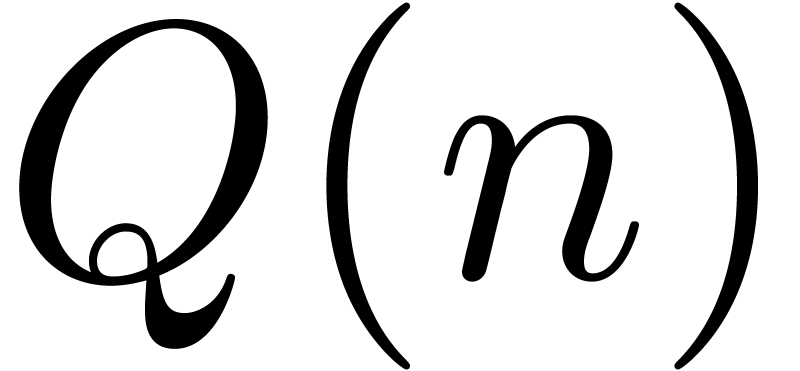 |
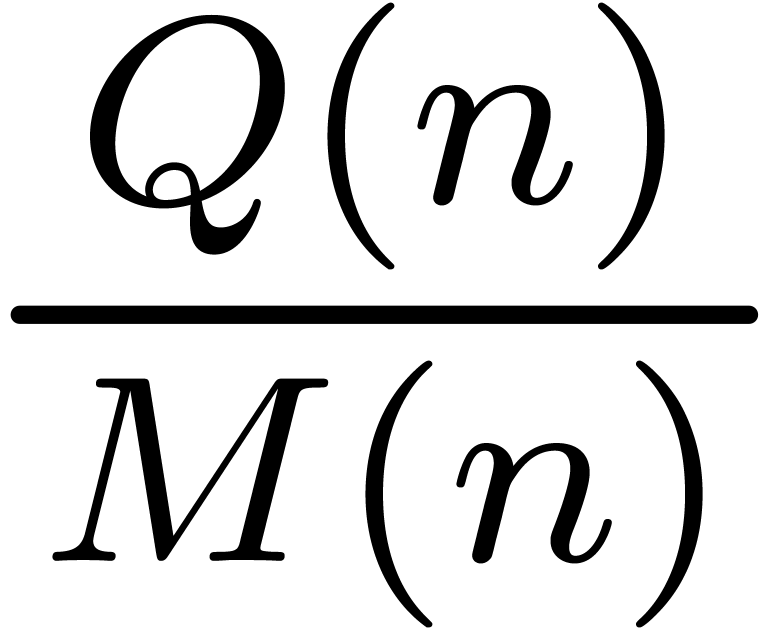 |
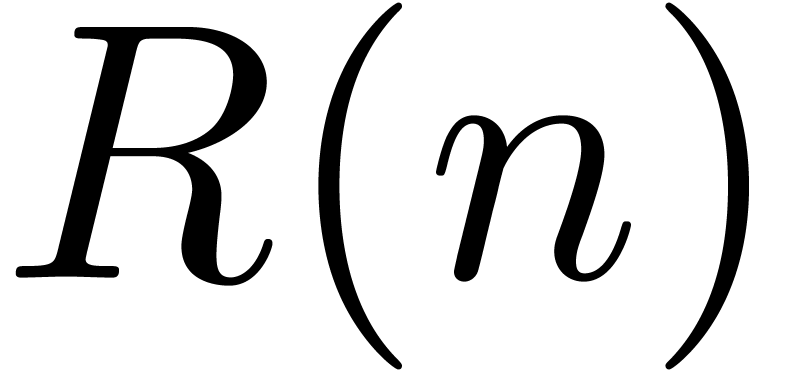 |
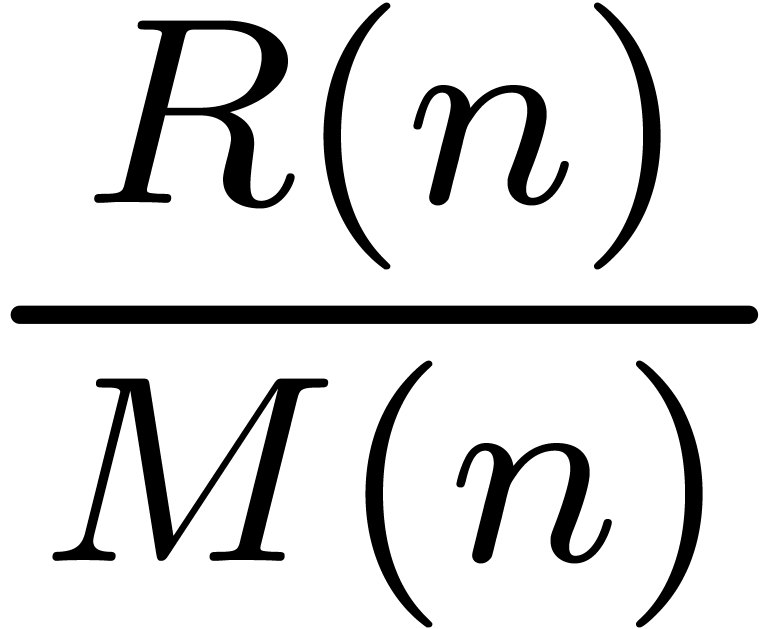 |
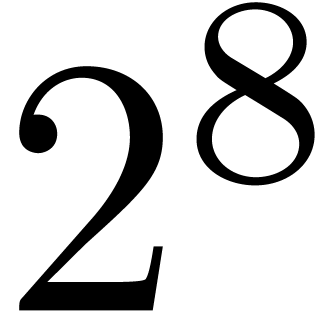 |
0.001 |
1.844 |
0.001 |
1.923 |
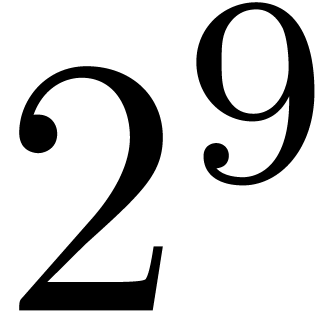 |
0.003 |
2.266 |
0.003 |
2.633 |
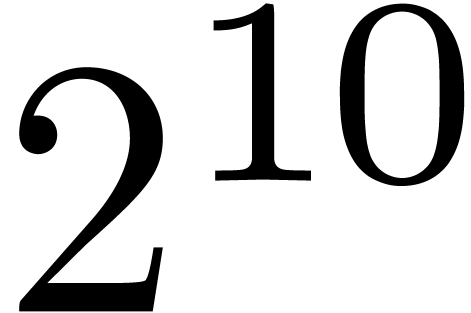 |
0.007 |
2.426 |
0.008 |
2.879 |
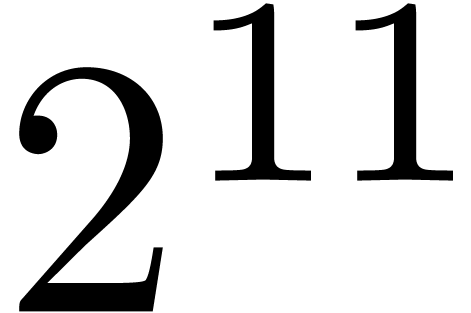 |
0.014 |
2.377 |
0.017 |
2.878 |
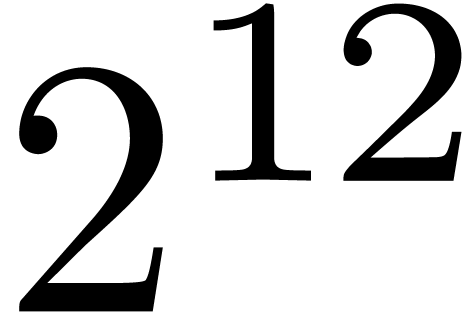 |
0.031 |
2.537 |
0.037 |
3.037 |
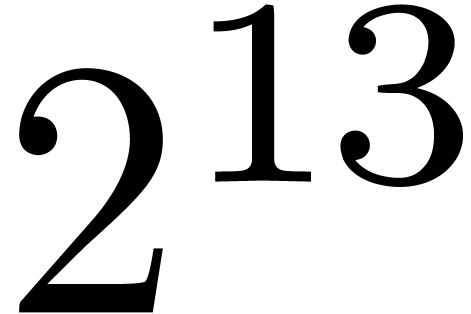 |
0.068 |
2.659 |
0.088 |
3.385 |
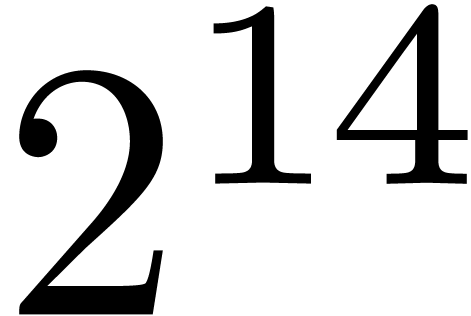 |
0.158 |
2.844 |
0.190 |
3.420 |
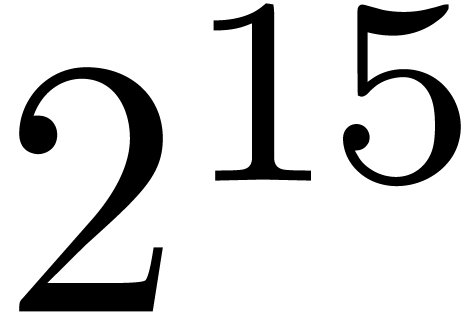 |
0.341 |
2.893 |
0.437 |
3.701 |
 |
0.767 |
3.038 |
1.018 |
4.032 |
 |
1.703 |
3.151 |
2.195 |
4.061 |
 |
3.618 |
2.968 |
4.618 |
3.770 |
 |
8.097 |
3.001 |
10.319 |
3.820 |
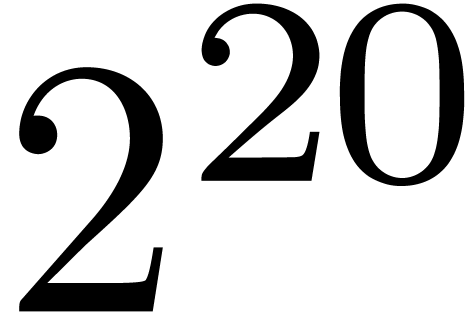 |
17.307 |
2.921 |
22.149 |
3.723 |
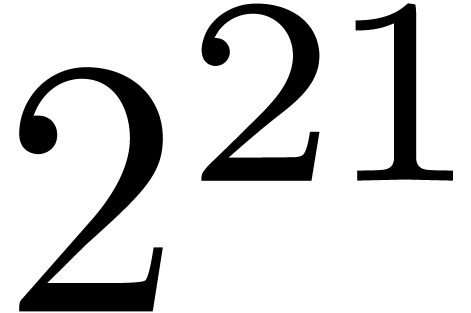 |
37.804 |
2.916 |
49.347 |
3.856 |
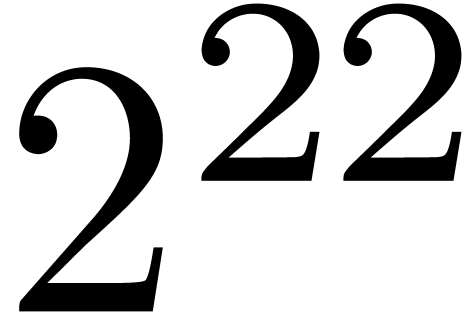 |
80.298 |
2.881 |
104.159 |
3.746 |
|
|
|
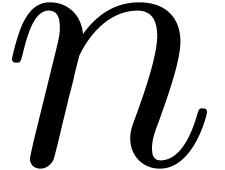 |
semi,  |
both,  |
semi,  |
both,  |
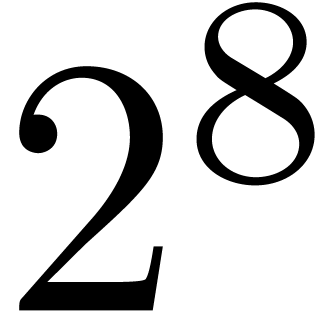 |
2.552 |
2.793 |
1.481 |
1.627 |
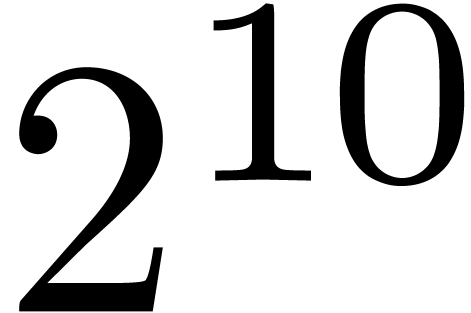 |
2.794 |
3.423 |
1.851 |
2.168 |
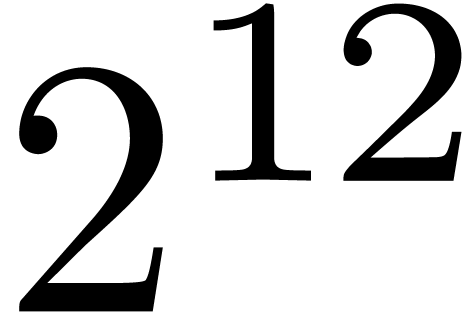 |
3.486 |
4.250 |
2.484 |
2.987 |
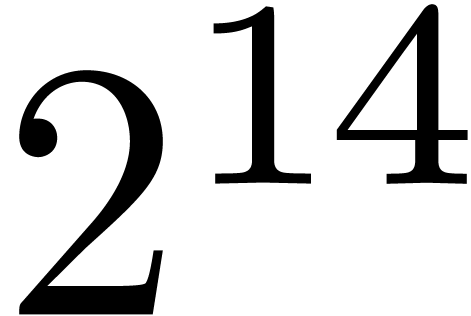 |
3.576 |
4.584 |
2.757 |
3.683 |
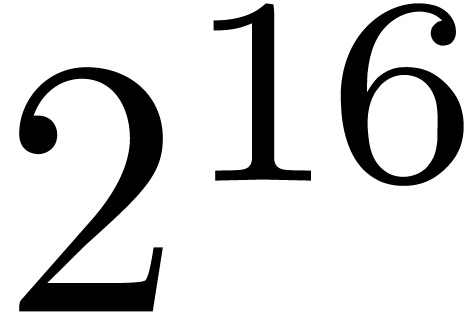 |
3.940 |
5.135 |
3.429 |
4.604 |
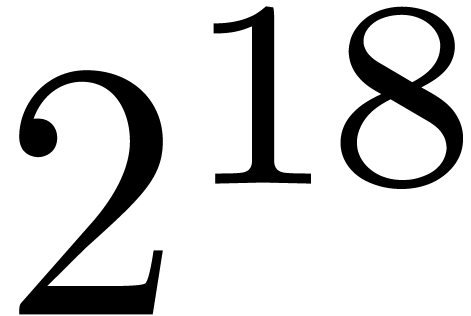 |
4.293 |
5.490 |
3.842 |
5.418 |
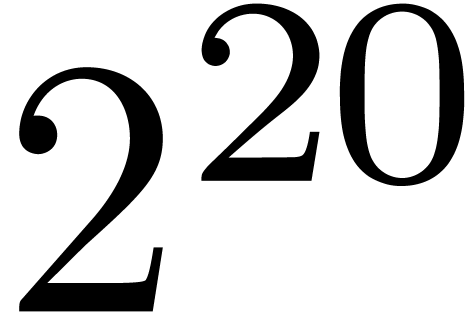 |
4.329 |
5.839 |
|
|
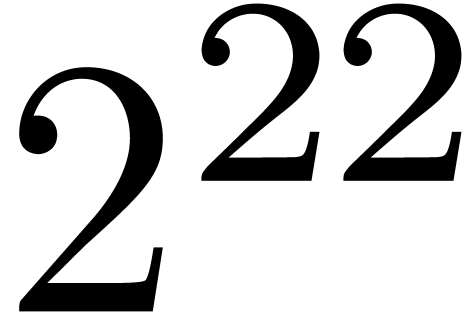 |
4.509 |
6.006 |
|
|
|
|
|
Remark 13. It is
instructive to compare the efficiencies of relaxed evaluation and
Newton's method. For instance, the exponentiation algorithm from [BK78] has a time complexity 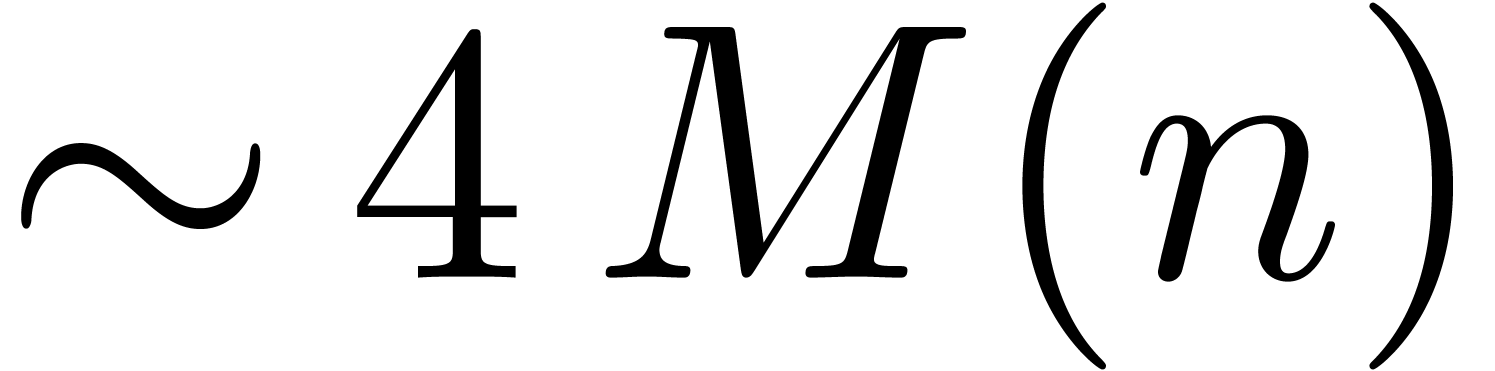 .
Although this is better from an asymptotic point of view, the ratio
.
Although this is better from an asymptotic point of view, the ratio 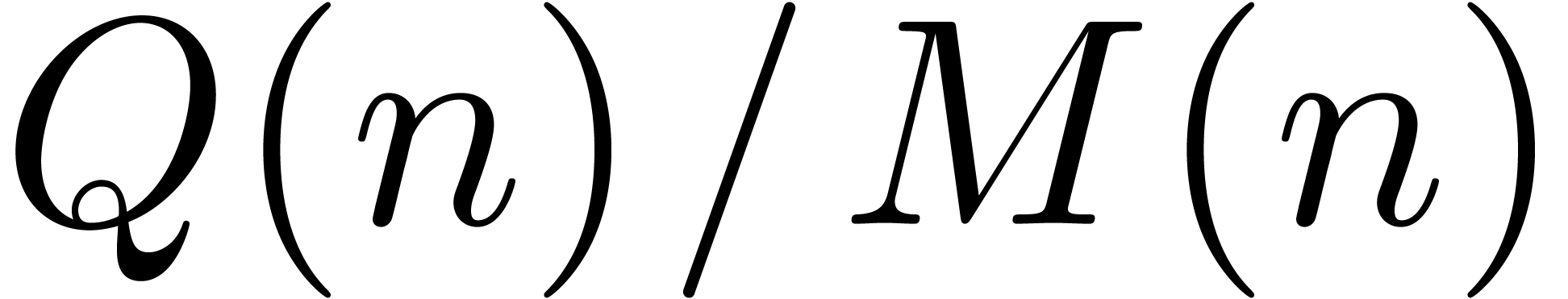 rarely reaches
rarely reaches  in our tables.
Consequently, relaxed algorithms are often better. A similar phenomenon
was already observed in [vdH02a, Tables 4 and 5]. It would
be interesting to pursue the comparisons in view of some recent advances
concerning Newton's method [BCO+06, vdH06a];
see also [Sed01, Section 5.2.1].
in our tables.
Consequently, relaxed algorithms are often better. A similar phenomenon
was already observed in [vdH02a, Tables 4 and 5]. It would
be interesting to pursue the comparisons in view of some recent advances
concerning Newton's method [BCO+06, vdH06a];
see also [Sed01, Section 5.2.1].
Remark 14. Although the
emphasis of this paper is on asymptotic complexity, the idea behind the
new algorithms also applies in the Karatsuba and Toom-Cook models. In
the latter case, we take 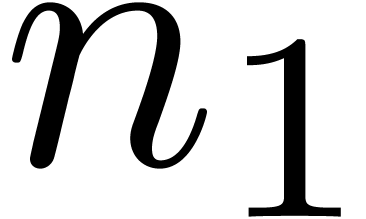 small (typically
small (typically 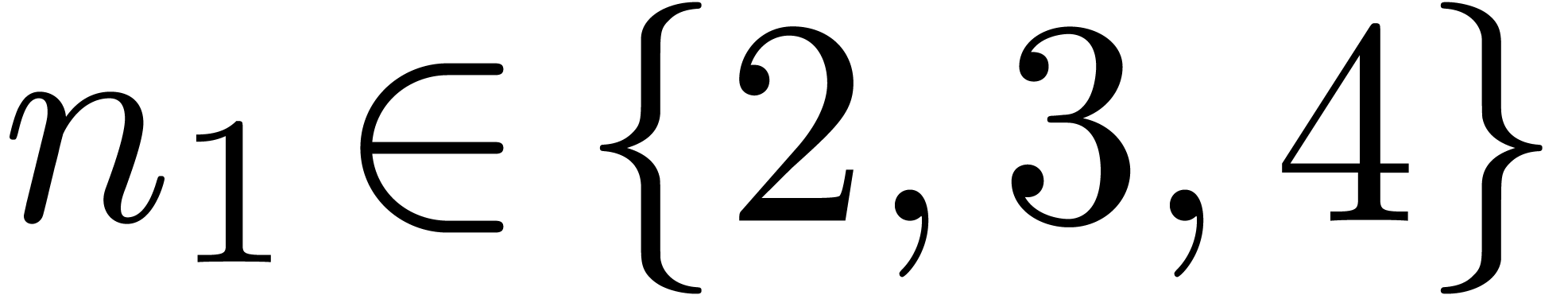 ) and use evaluation
(interpolation) for polynomials of degree
) and use evaluation
(interpolation) for polynomials of degree 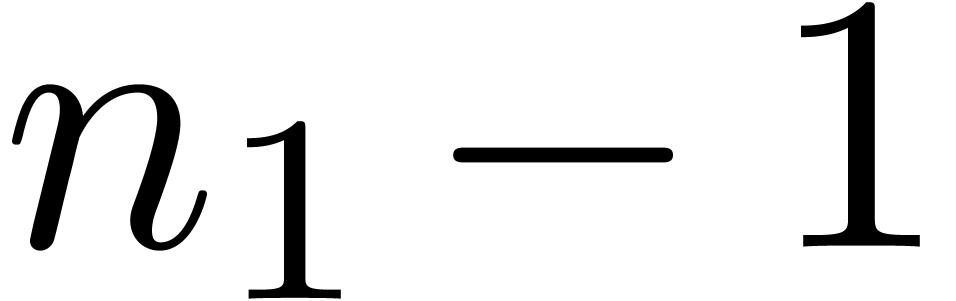 (
(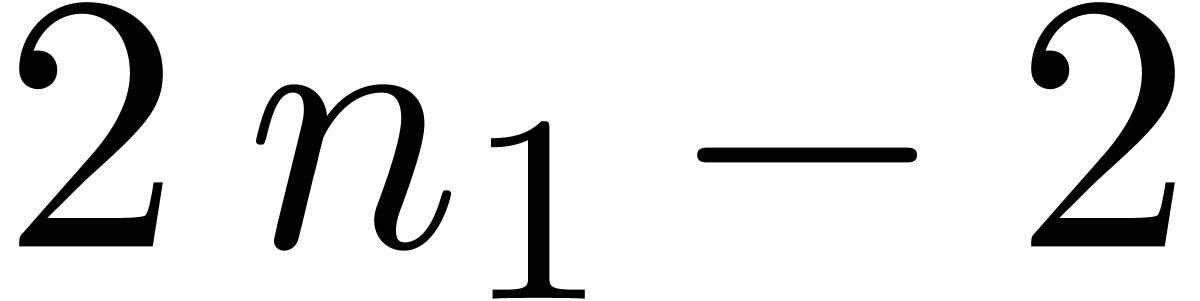 ) at
) at 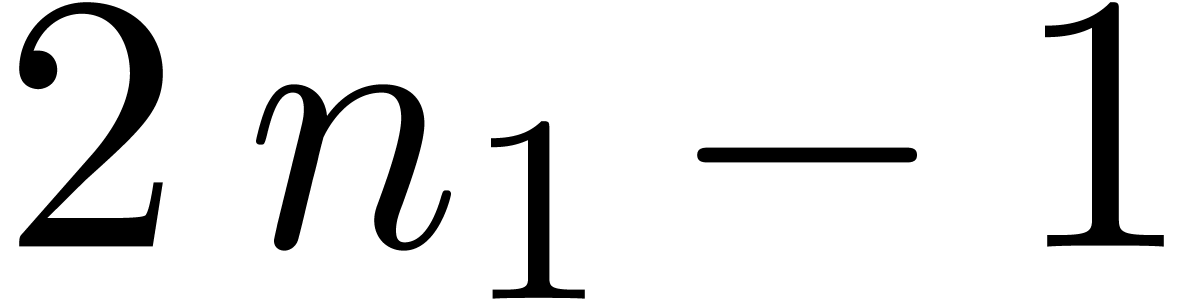 points. From an asymptotic point of view, this yields
points. From an asymptotic point of view, this yields 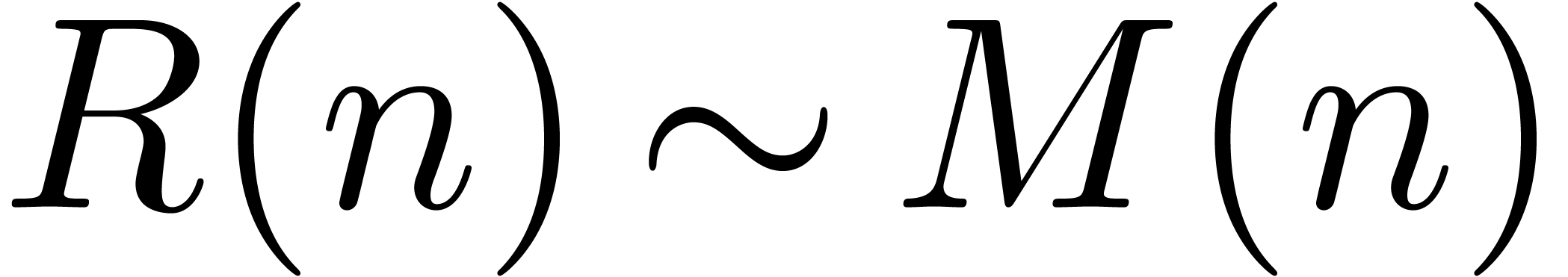 for relaxed multiplication. Moreover, the approach naturally combines
with the generalization of pair/odd decompositions [HZ02],
which also yields an optimal bound for truncated multiplications. In
fact, we notice that truncated pair/odd Karatsuba multiplication is
“essentially relaxed” [vdH02a, Section 4.2].
for relaxed multiplication. Moreover, the approach naturally combines
with the generalization of pair/odd decompositions [HZ02],
which also yields an optimal bound for truncated multiplications. In
fact, we notice that truncated pair/odd Karatsuba multiplication is
“essentially relaxed” [vdH02a, Section 4.2].
On the negative side, these theoretically fast algorithms have bad space
complexities and they are difficult to implement. In order to obtain
good timings, it seems to be necessary to use dedicated code generation
at different (ranges of) orders 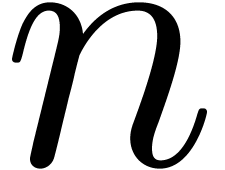 ,
which can be done using the C++ template
mechanism. The current implementation in Mmxlib
does not achieve the theoretical time complexity by far, because the
recursive function calls suffer from too much overhead.
,
which can be done using the C++ template
mechanism. The current implementation in Mmxlib
does not achieve the theoretical time complexity by far, because the
recursive function calls suffer from too much overhead.
6.Conclusion
We have shown how to improve the complexity of relaxed multiplication in
the case when the coefficient ring admits sufficiently many 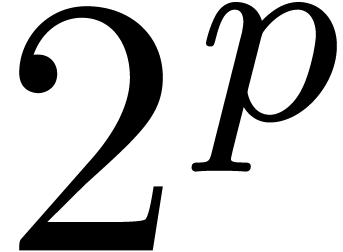 -th roots of unity. The improvement is based on
reusing FFT-transforms of pieces of the multiplicands at different
levels of the underlying binary splitting algorithm. The new approach
has proved to be efficient in practice (see tables 1 and 2).
-th roots of unity. The improvement is based on
reusing FFT-transforms of pieces of the multiplicands at different
levels of the underlying binary splitting algorithm. The new approach
has proved to be efficient in practice (see tables 1 and 2).
For further studies, it would be interesting to study the price of
artificially adding 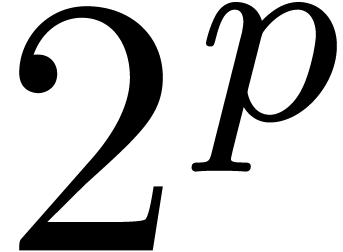 -th roots
of unity, like in Schönhage-Strassen's algorithm. In practice, we
notice that it is often possible, and better, to “cut the
coefficients into pieces” and to replace them by polynomials over
the complexified doubles
-th roots
of unity, like in Schönhage-Strassen's algorithm. In practice, we
notice that it is often possible, and better, to “cut the
coefficients into pieces” and to replace them by polynomials over
the complexified doubles 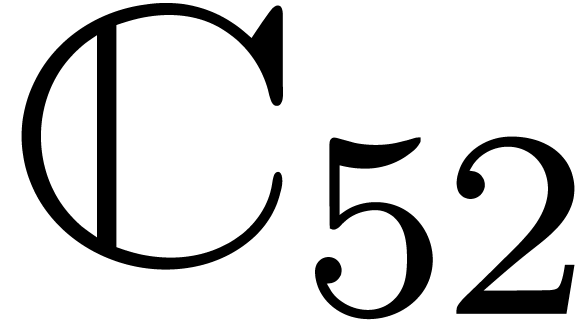 or
or  with
with 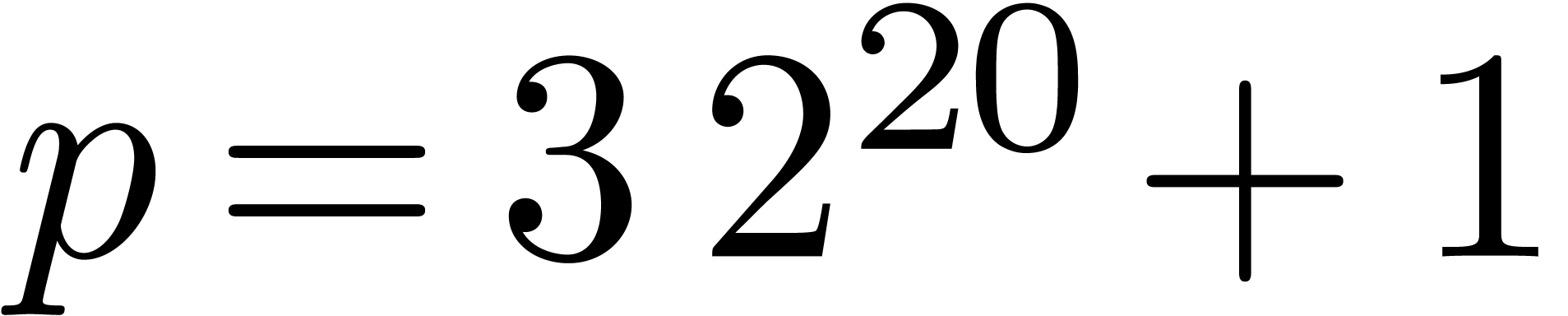 . However, this approach
requires more implementation effort.
. However, this approach
requires more implementation effort.
Acknowledgement
We would like to thank the third referee for his detailed comments on
the proof of theorem
12, which also resulted in slightly
sharper bounds.
Bibliography
-
[BCO+06]
-
A. Bostan, F. Chyzak, F. Ollivier, B. Salvy,
É. Schost, and A. Sedoglavic. Fast computation of power
series solutions of systems of differential equation. preprint,
april 2006. submitted, 13 pages.
-
[BK78]
-
R.P. Brent and H.T. Kung. Fast algorithms for
manipulating formal power series. Journal of the ACM,
25:581–595, 1978.
-
[CK91]
-
D.G. Cantor and E. Kaltofen. On fast multiplication
of polynomials over arbitrary algebras. Acta Informatica,
28:693–701, 1991.
-
[Coo66]
-
S.A. Cook. On the minimum computation time of
functions. PhD thesis, Harvard University, 1966.
-
[CT65]
-
J.W. Cooley and J.W. Tukey. An algorithm for the
machine calculation of complex Fourier series. Math.
Computat., 19:297–301, 1965.
-
[HQZ04]
-
Guillaume Hanrot, Michel Quercia, and Paul
Zimmermann. The middle product algorithm I. speeding up the
division and square root of power series. AAECC,
14(6):415–438, 2004.
-
[HZ02]
-
Guillaume Hanrot and Paul Zimmermann. A long note on
Mulders' short product. Research Report 4654, INRIA, December
2002. Available from http://www.loria.fr/
hanrot/Papers/mulders.ps.
-
[Knu97]
-
D.E. Knuth. The Art of Computer Programming,
volume 2: Seminumerical Algorithms. Addison-Wesley, 3-rd
edition, 1997.
-
[KO63]
-
A. Karatsuba and J. Ofman. Multiplication of
multidigit numbers on automata. Soviet Physics Doklady,
7:595–596, 1963.
-
[Sed01]
-
Alexandre Sedoglavic. Méthodes
seminumériques en algèbre différentielle ;
applications à l'étude des
propriétés structurelles de systèmes
différentiels algébriques en automatique. PhD
thesis, École polytechnique, 2001.
-
[SS71]
-
A. Schönhage and V. Strassen. Schnelle
Multiplikation grosser Zahlen. Computing 7,
7:281–292, 1971.
-
[Too63]
-
A.L. Toom. The complexity of a scheme of functional
elements realizing the multiplication of integers. Soviet
Mathematics, 4(2):714–716, 1963.
-
[vdH97]
-
J. van der Hoeven. Lazy multiplication of formal
power series. In W. W. Küchlin, editor, Proc. ISSAC
'97, pages 17–20, Maui, Hawaii, July 1997.
-
[vdH02a]
-
J. van der Hoeven. Relax, but don't be too lazy.
JSC, 34:479–542, 2002.
-
[vdH02b]
-
J. van der Hoeven et al. Mmxlib: the standard library
for Mathemagix, 2002.
http://www.mathemagix.org/mml.html.
-
[vdH03a]
-
J. van der Hoeven. New algorithms for relaxed
multiplication. Technical Report 2003-44, Université
Paris-Sud, Orsay, France, 2003.
-
[vdH03b]
-
J. van der Hoeven. Relaxed multiplication using the
middle product. In Manuel Bronstein, editor, Proc. ISSAC
'03, pages 143–147, Philadelphia, USA, August 2003.
-
[vdH06a]
-
J. van der Hoeven. Newton's method and FFT trading.
Technical Report 2006-17, Univ. Paris-Sud, 2006. Submitted to
JSC.
-
[vdH06b]
-
J. van der Hoeven. On effective analytic
continuation. Technical Report 2006-15, Univ. Paris-Sud, 2006.
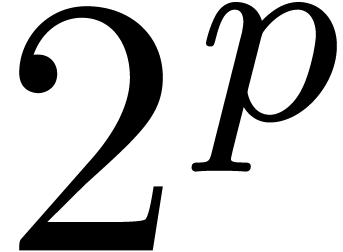 -th
-th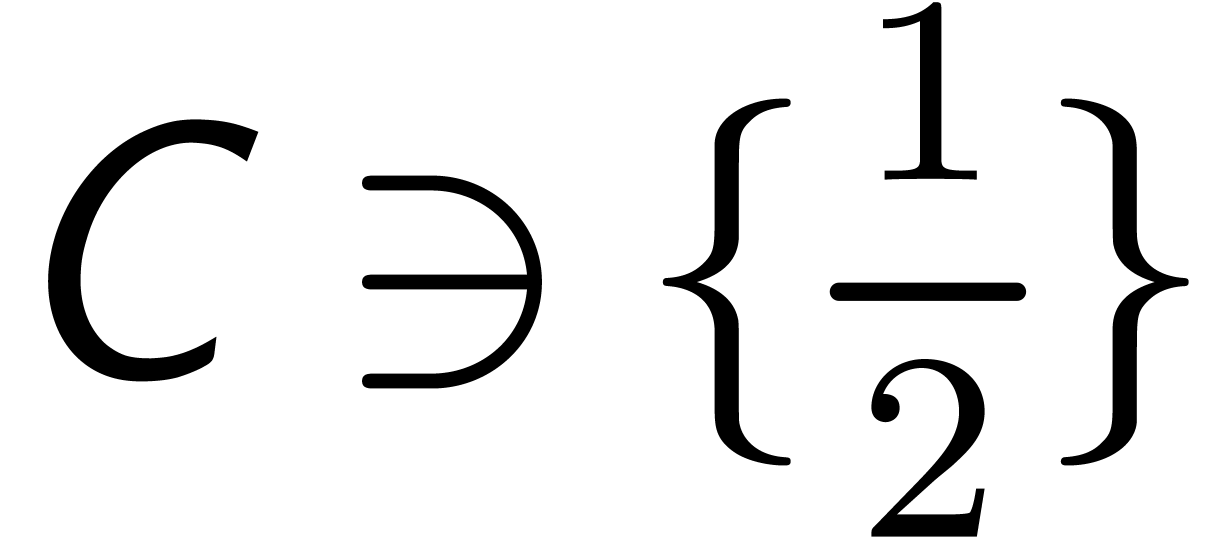 be an effective ring and consider two power
series
be an effective ring and consider two power
series 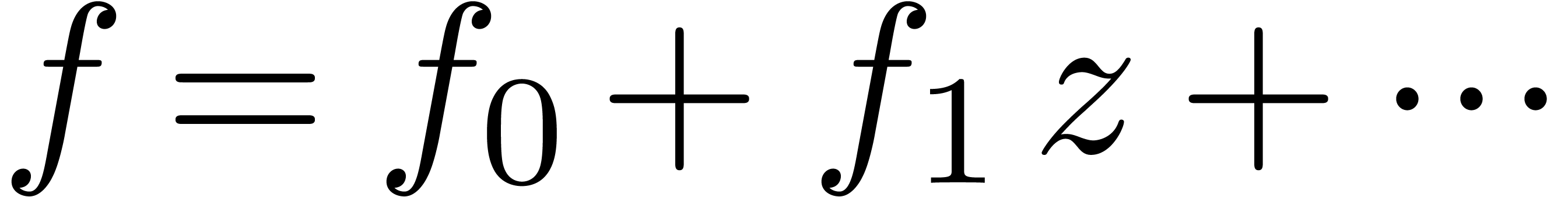 and
and 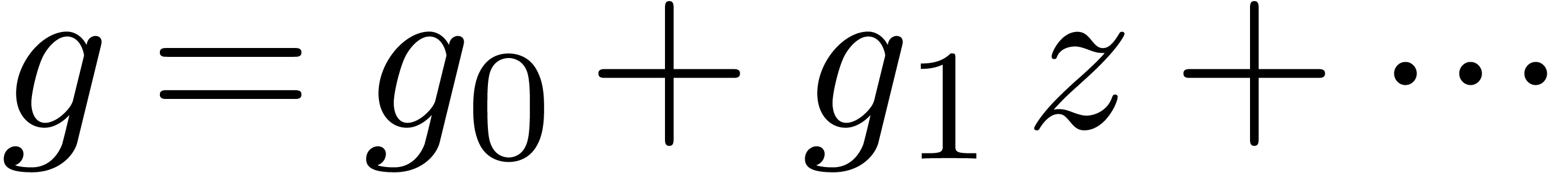 in
in 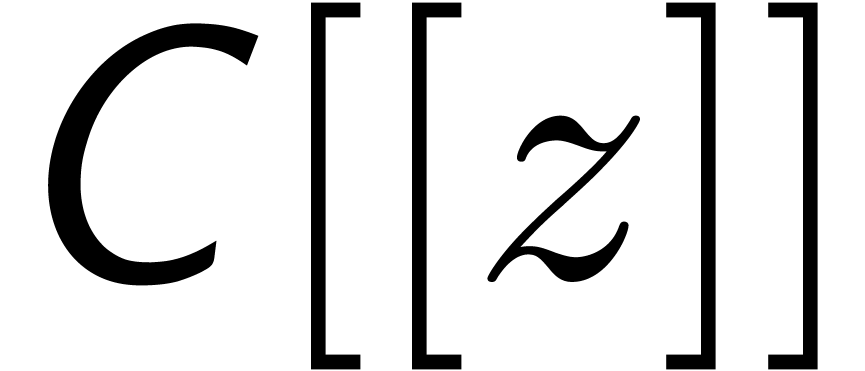 .
.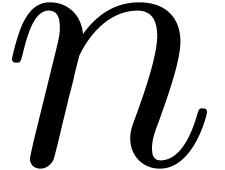 coefficients of the product
coefficients of the product 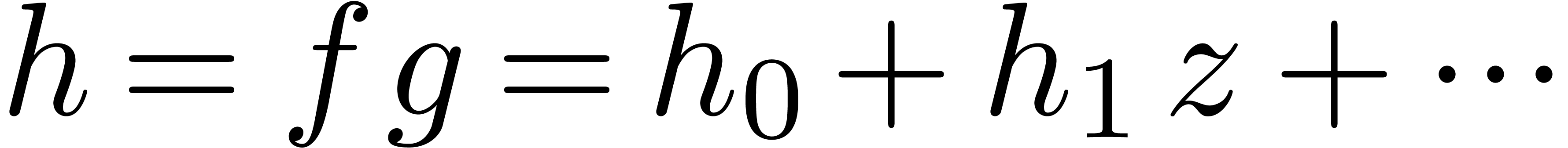 .
. and
and  are known beforehand, then we may use any
fast multiplication for polynomials in order to achieve this goal, such
as divide and conquer multiplication [
are known beforehand, then we may use any
fast multiplication for polynomials in order to achieve this goal, such
as divide and conquer multiplication [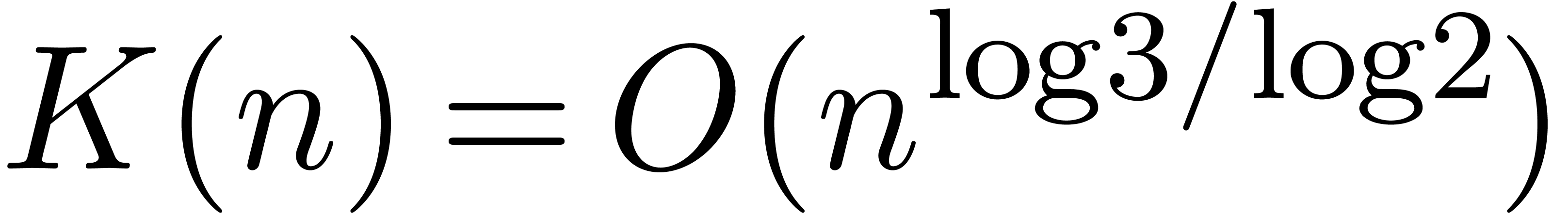 ,
,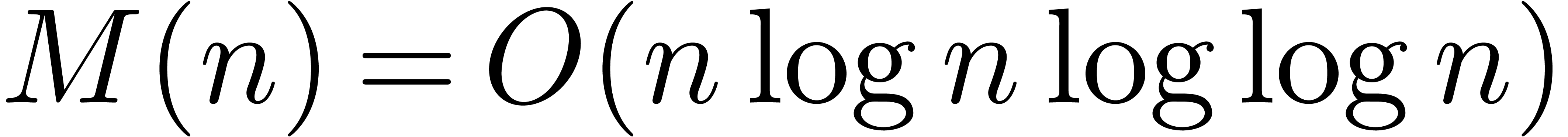 .
.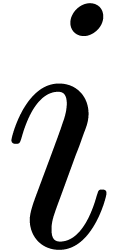 coefficients of
coefficients of 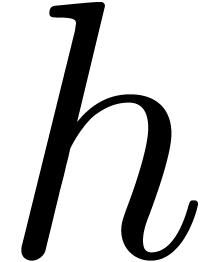 as soon as the first
as soon as the first  .
.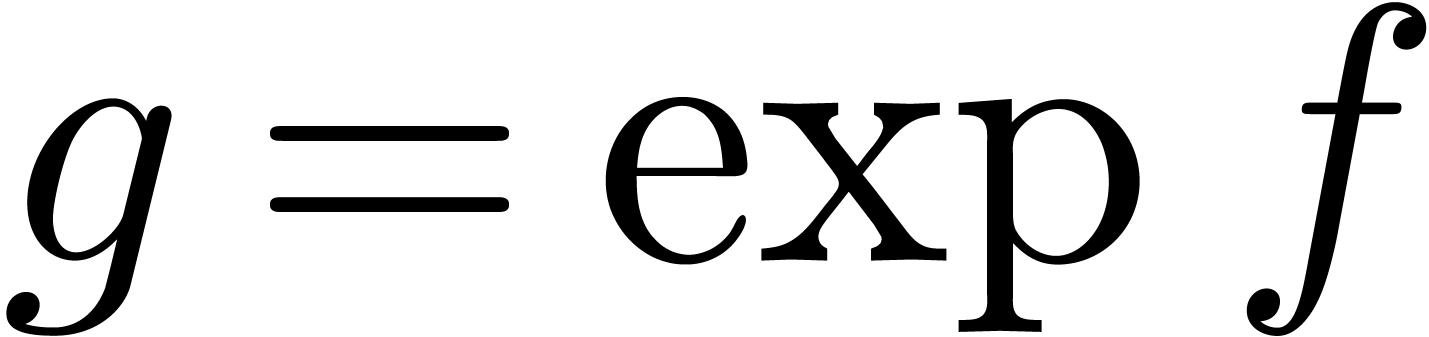 of a series
of a series 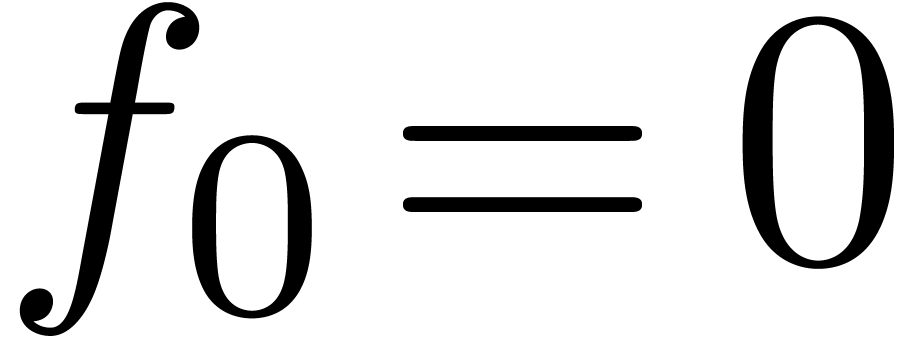 using the formula
using the formula
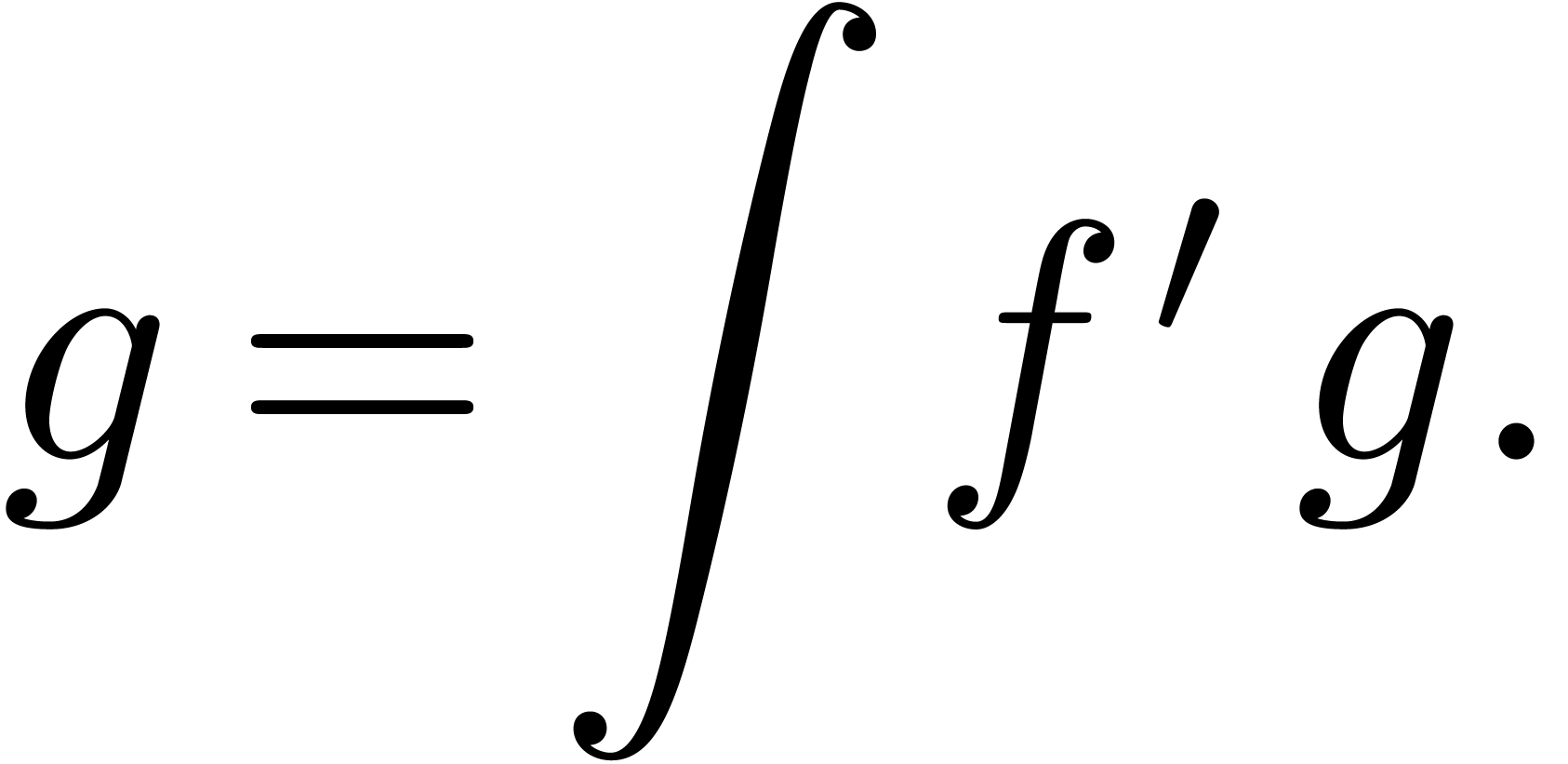
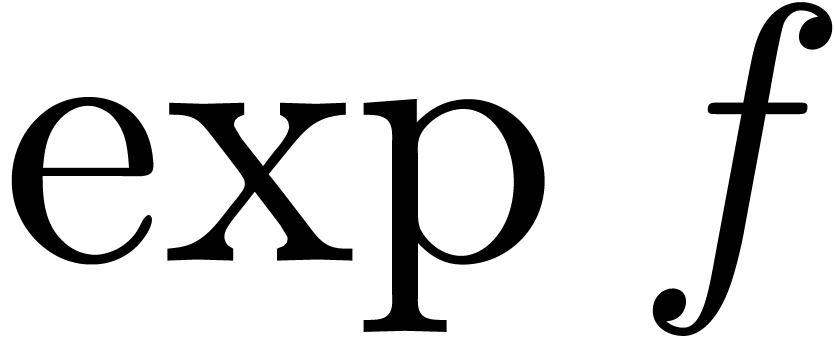 reduces to one differentiation, one relaxed product and
one relaxed integration. Differentiation and relaxed integration being
linear in time, it follows that
reduces to one differentiation, one relaxed product and
one relaxed integration. Differentiation and relaxed integration being
linear in time, it follows that  ,
,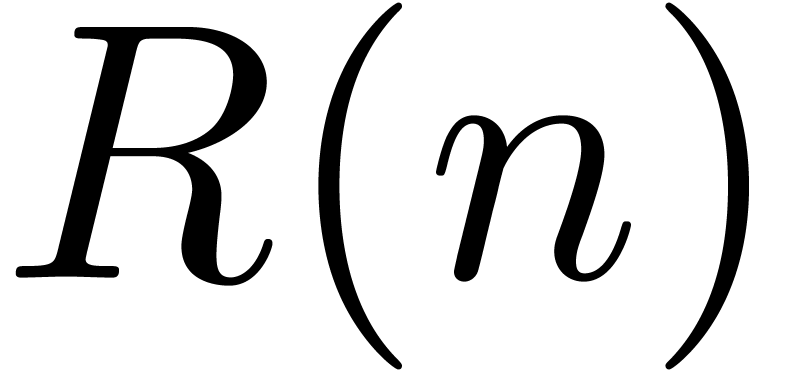 denotes the time complexity of relaxed
multiplication. In [
denotes the time complexity of relaxed
multiplication. In [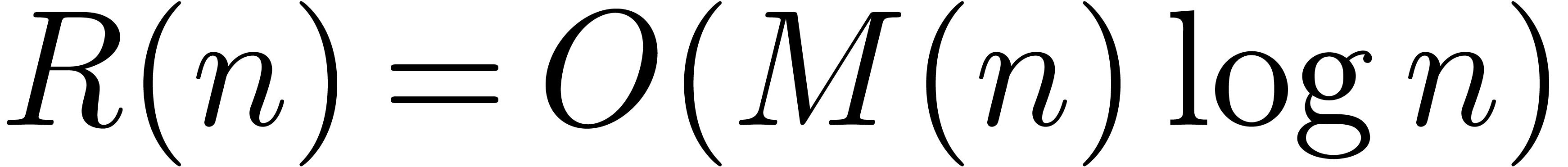
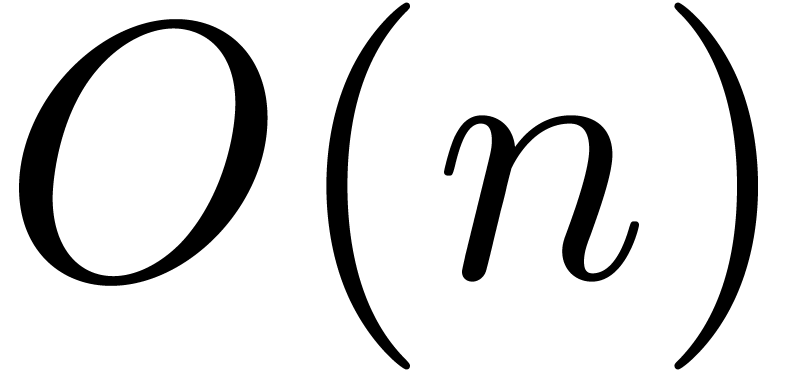 .
. admits
admits 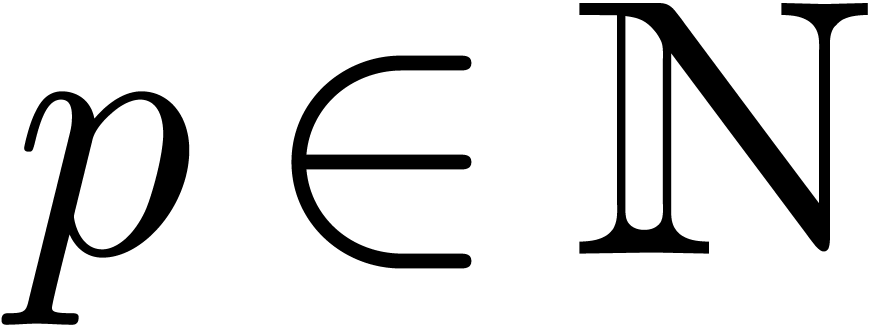 .
. up to order
up to order  as soon as
as soon as  are known, for all
are known, for all 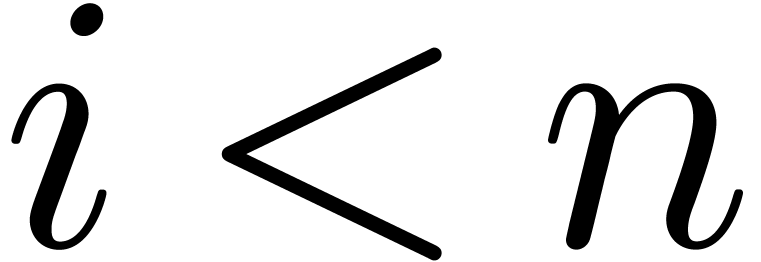 .
.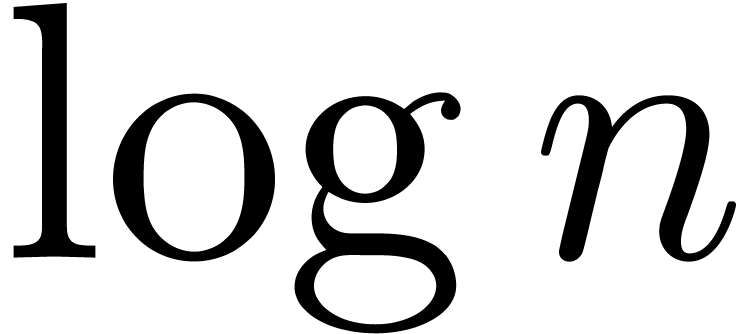 overhead in theorem
overhead in theorem 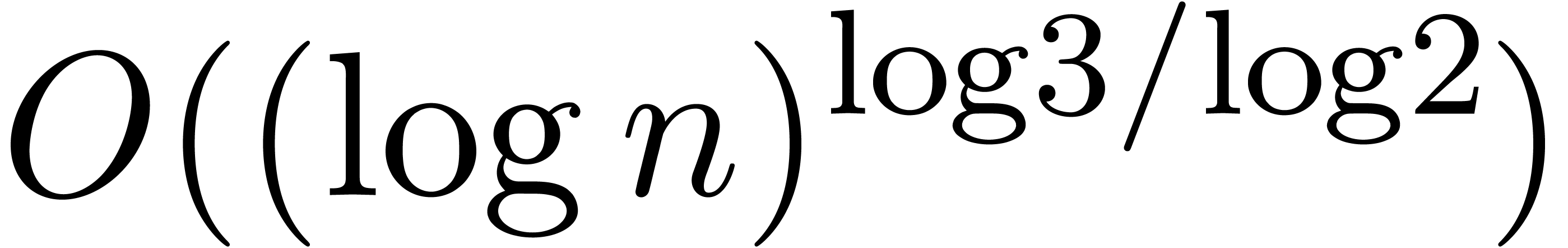 .
.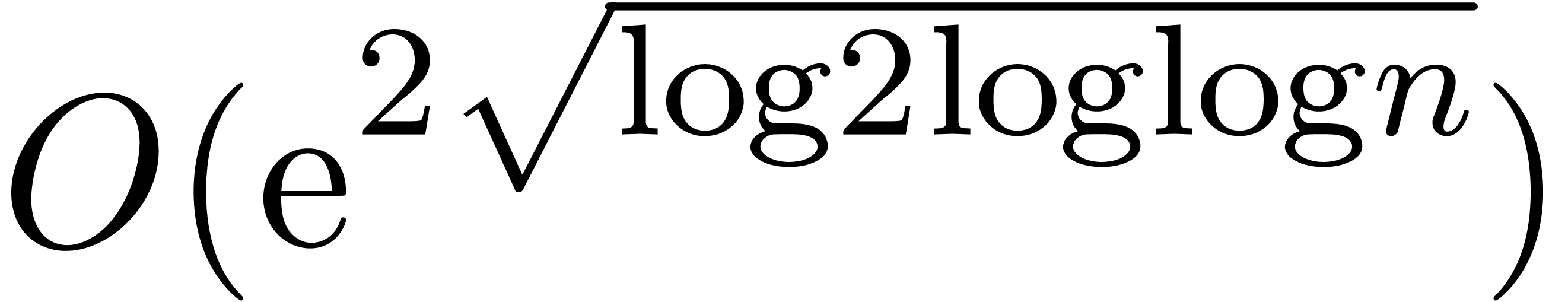 overhead.
overhead.
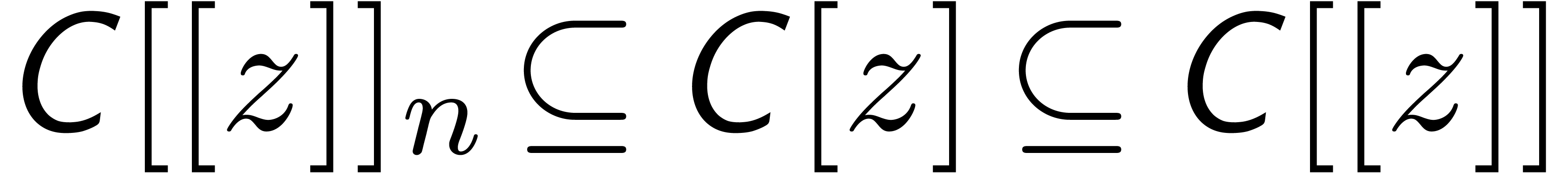 the set of truncated power series
of order
the set of truncated power series
of order 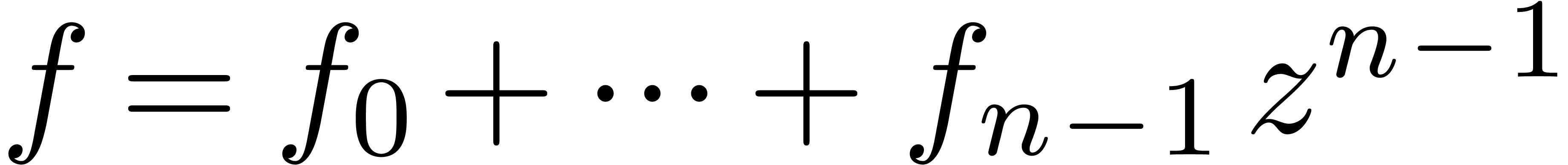 .
.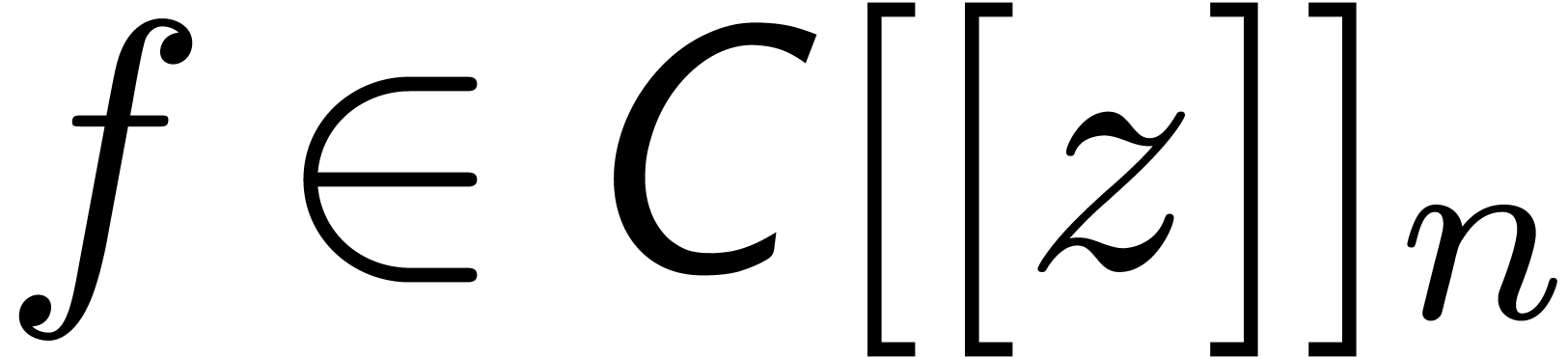 and
and  ,
,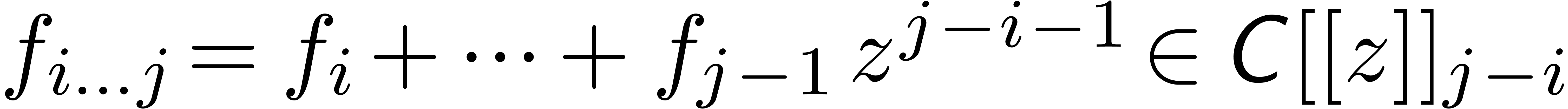 .
.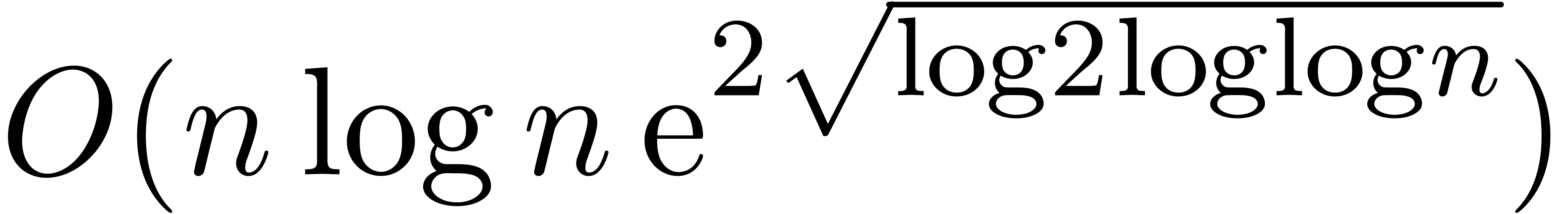 of the new complexity for relaxed multiplication
might surprise the reader. It should be noticed that the time complexity
of Toom-Cook's algorithm for polynomial multiplication [
of the new complexity for relaxed multiplication
might surprise the reader. It should be noticed that the time complexity
of Toom-Cook's algorithm for polynomial multiplication [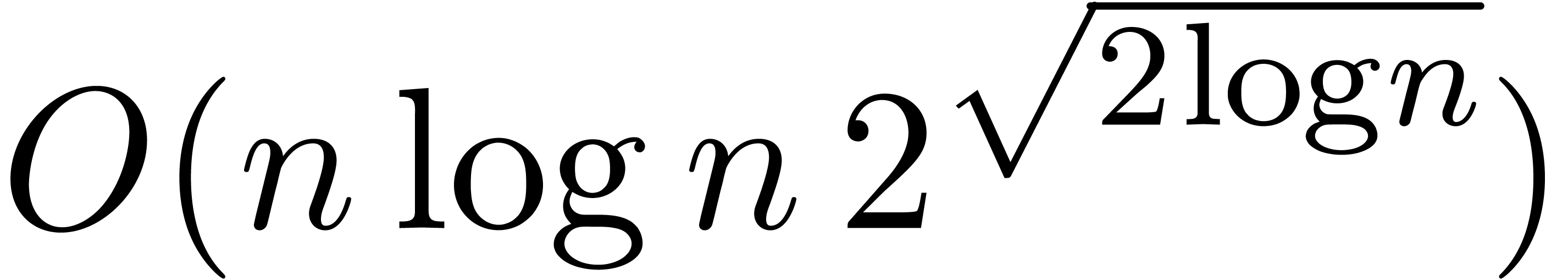 [
[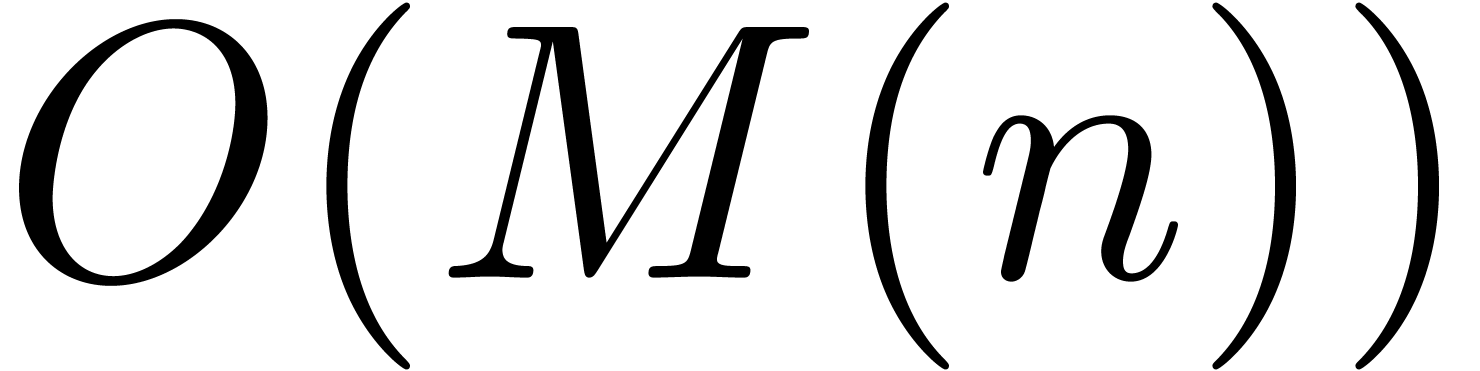 or
or 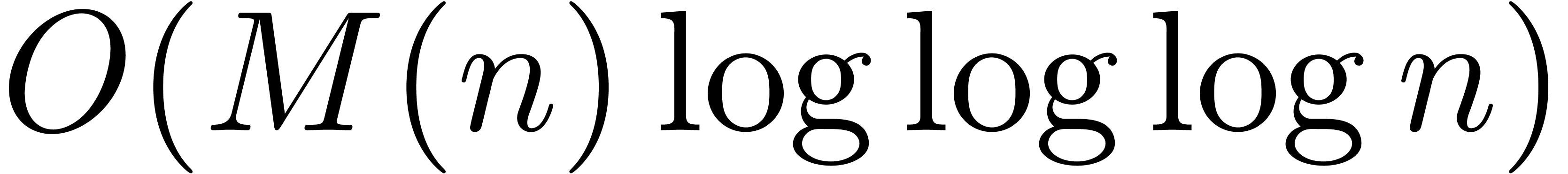 .
.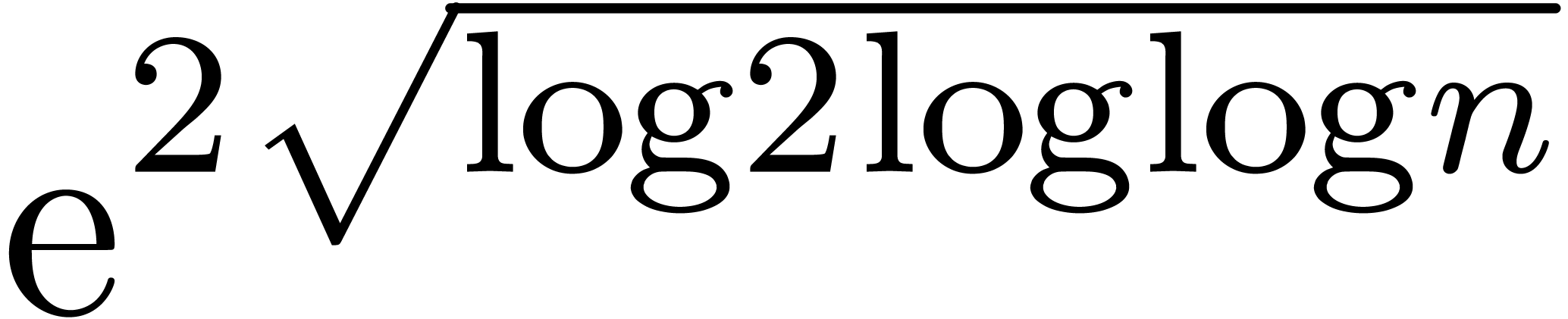 grows very slowly; in practice, it very much behaves like as a constant
(see section
grows very slowly; in practice, it very much behaves like as a constant
(see section 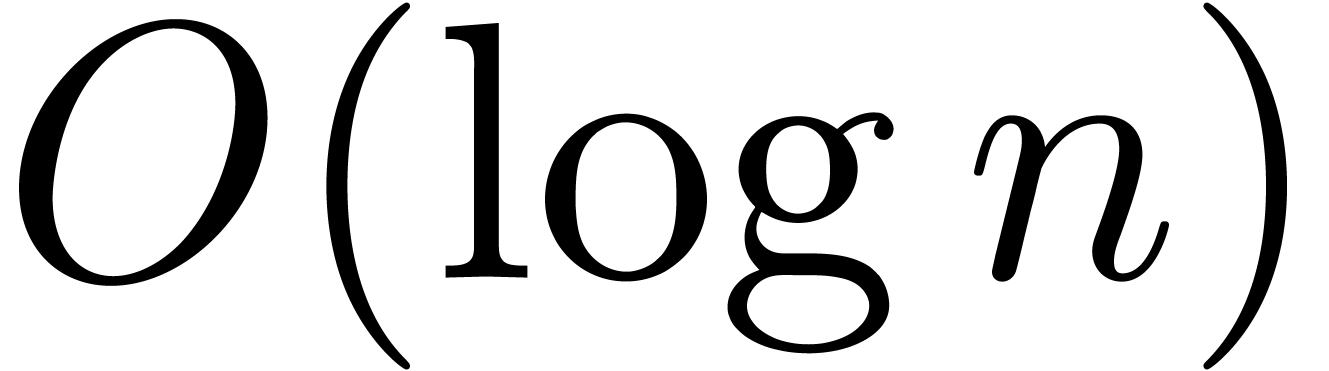 .
.
 and
and  at order
at order 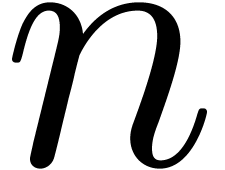 .
.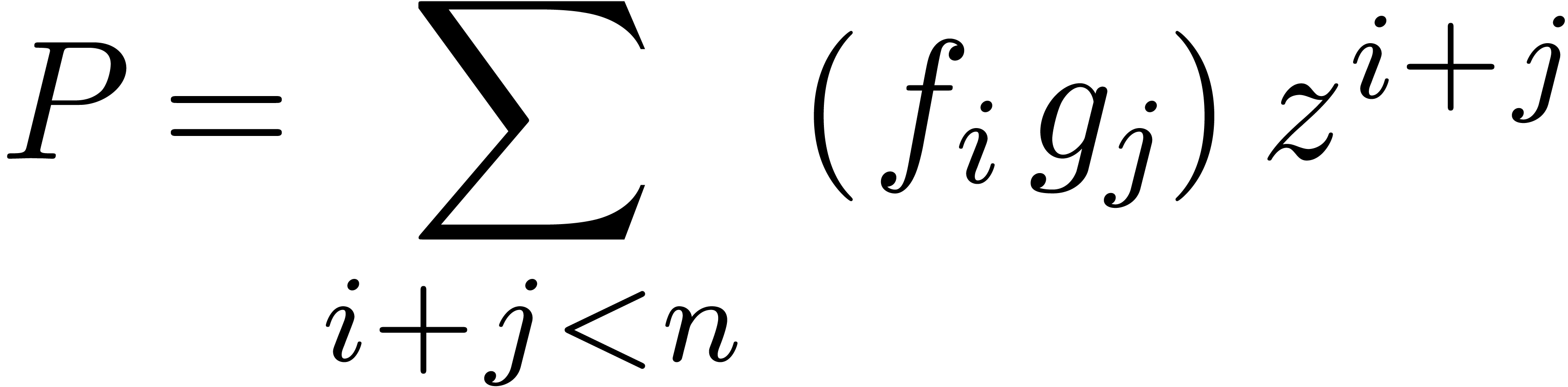
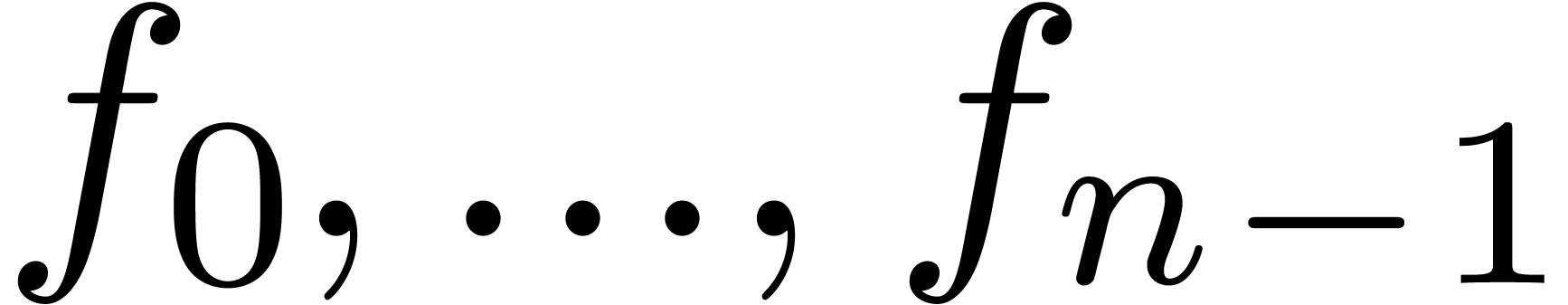 and
and  on input and
computes
on input and
computes 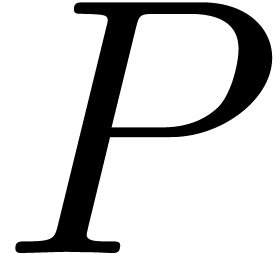 as in (
as in (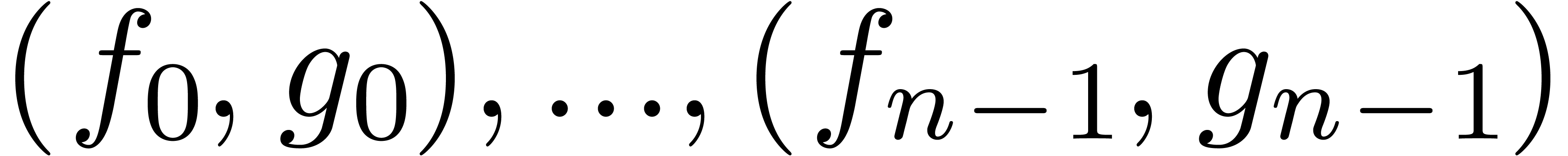 on input and
successively computes
on input and
successively computes  (resp.
(resp.  ).
). is output as soon as
is output as soon as  are
known.
are
known.
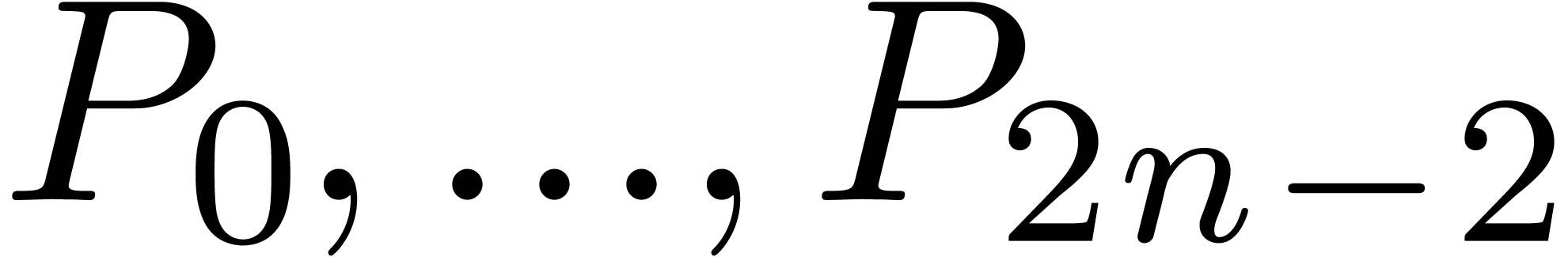 (resp.
(resp.  are
known.
are
known.
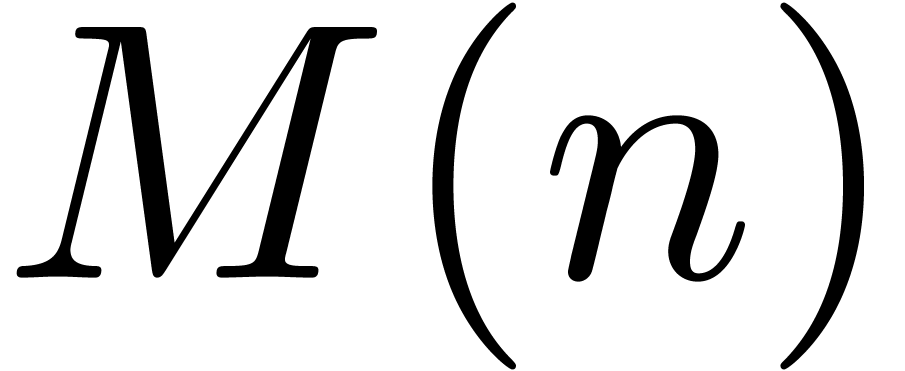 ,
,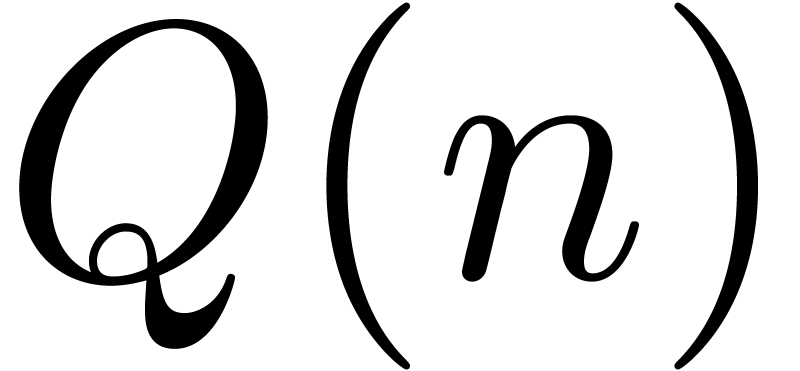 the time complexities of full
zealous, relaxed and semi-relaxed multiplication at order
the time complexities of full
zealous, relaxed and semi-relaxed multiplication at order 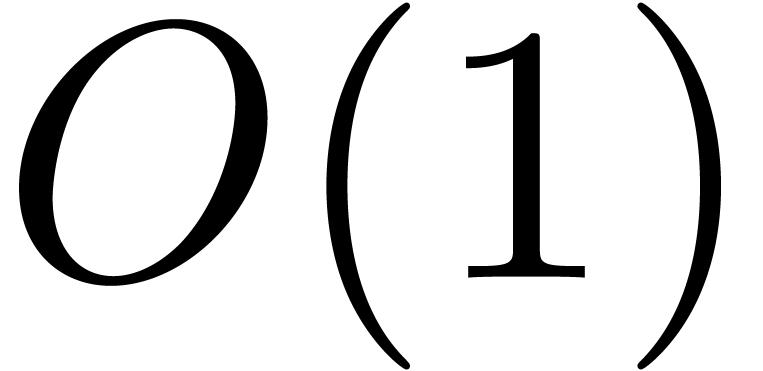 .
. square with entries
square with entries 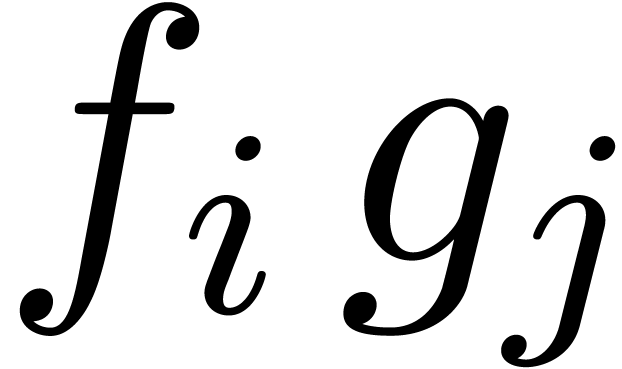 ,
,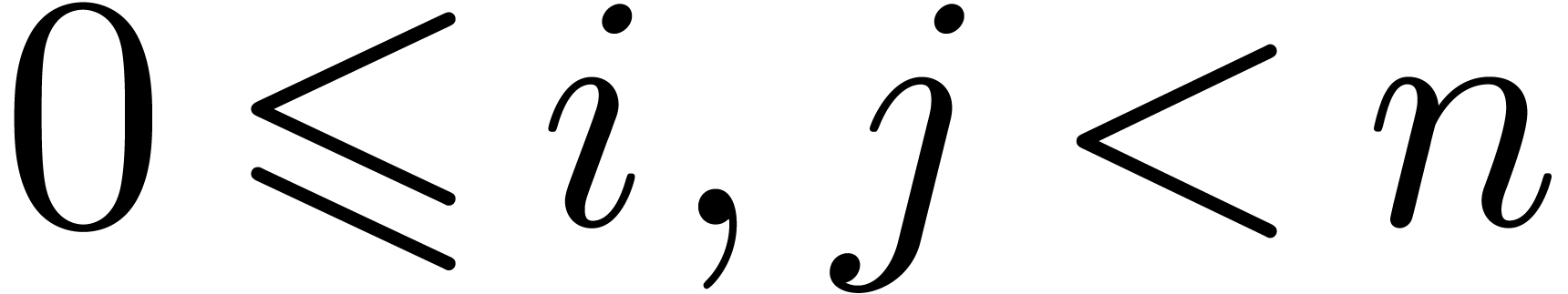 .
. are known, it becomes possible to compute
the contributions of the products
are known, it becomes possible to compute
the contributions of the products 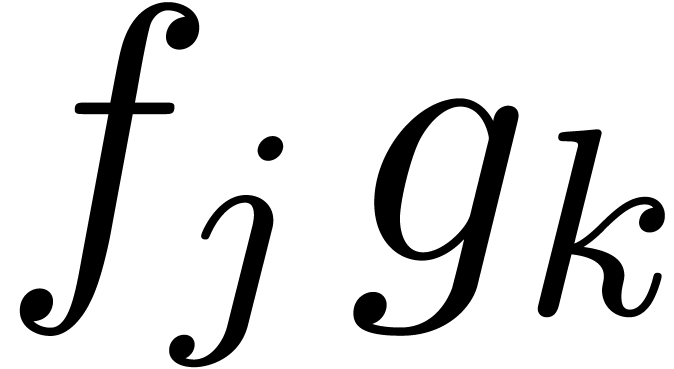 with
with 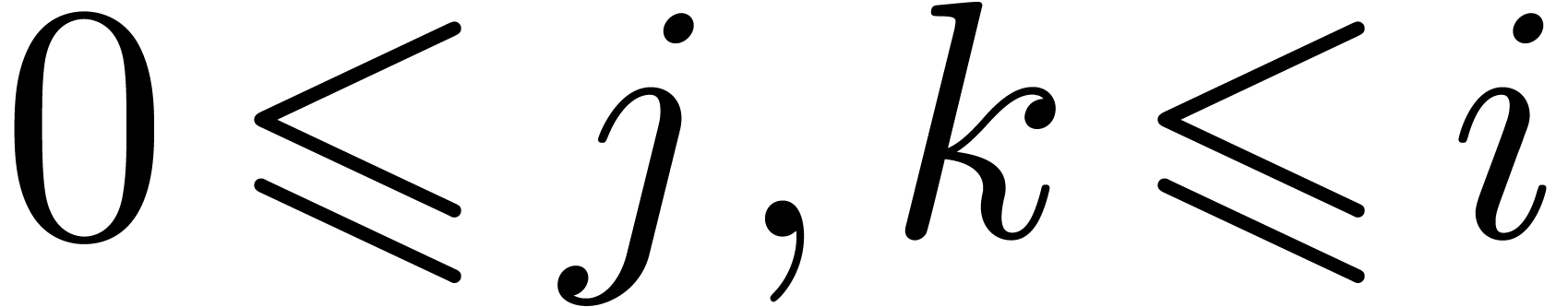 to
to 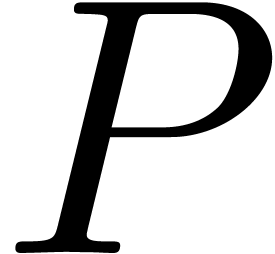 ,
,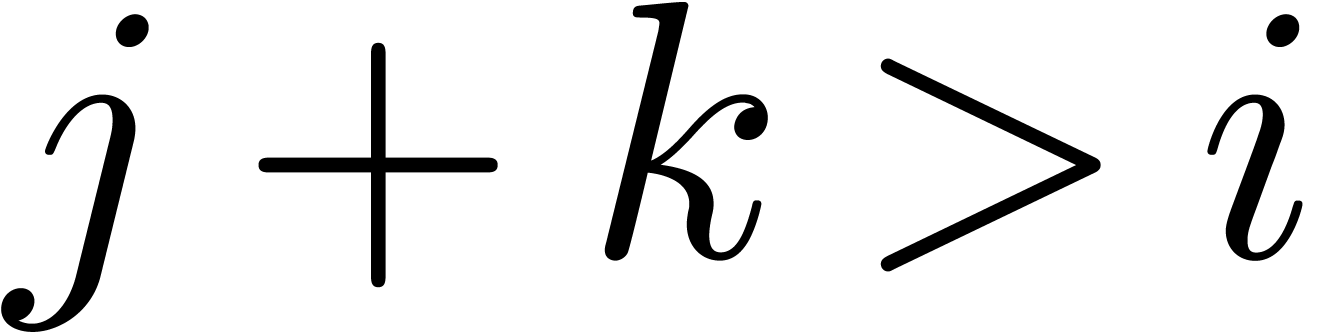 are not yet needed. The next idea is to subdivide the
are not yet needed. The next idea is to subdivide the  .
. suffices to ensure
that the resulting algorithm will be relaxed. In the left hand image of
figure
suffices to ensure
that the resulting algorithm will be relaxed. In the left hand image of
figure 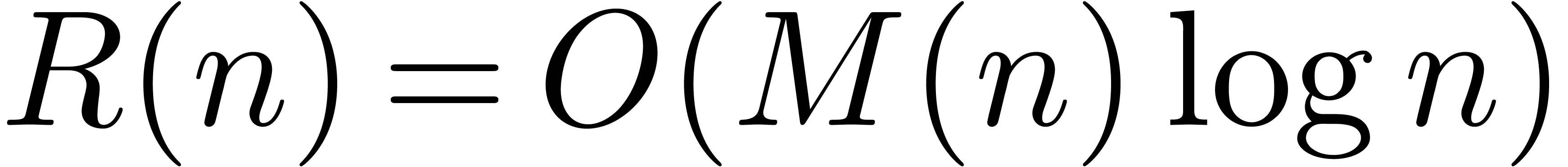 .
.
 multiplication
reduces to one full relaxed
multiplication
reduces to one full relaxed  multiplication, two semi-relaxed
multiplication, two semi-relaxed  multiplication
multiplication
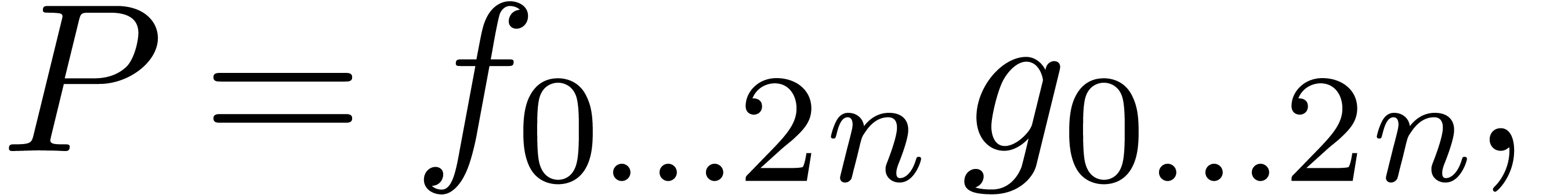
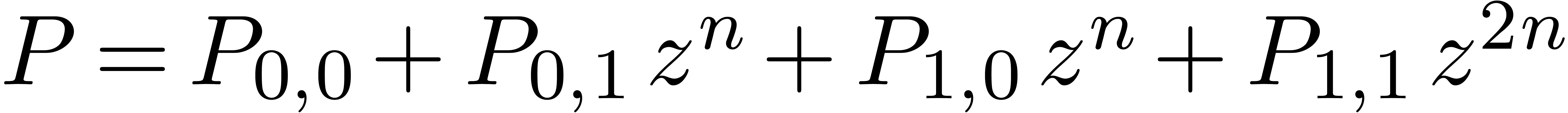
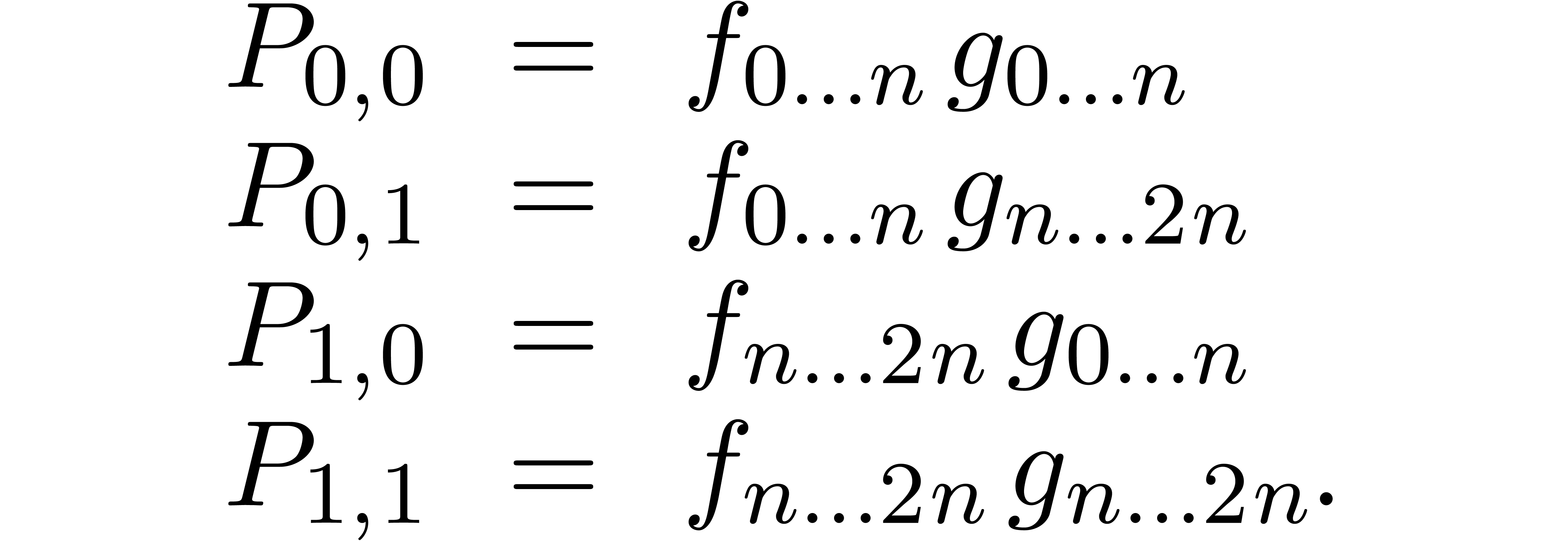
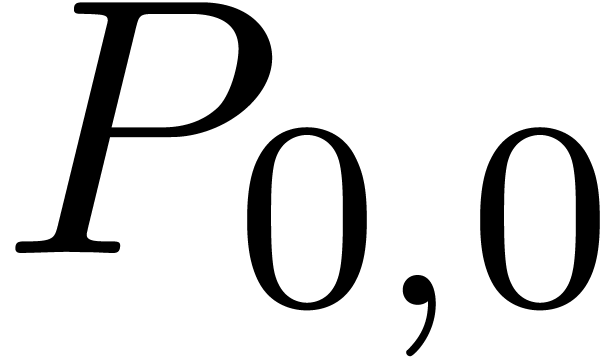 is a relaxed multiplication at order
is a relaxed multiplication at order 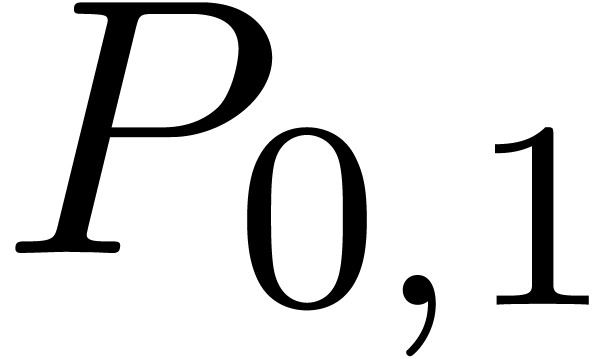 is
even semi-relaxed, since
is
even semi-relaxed, since  are already known by
the time that we need
are already known by
the time that we need 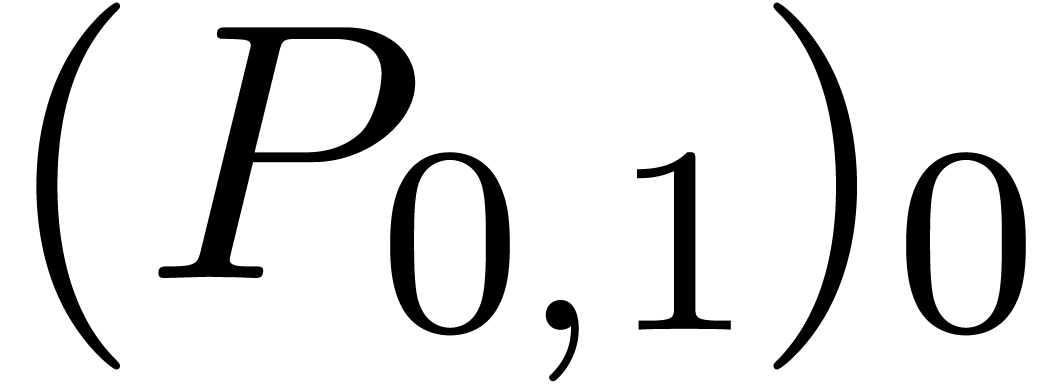 .
.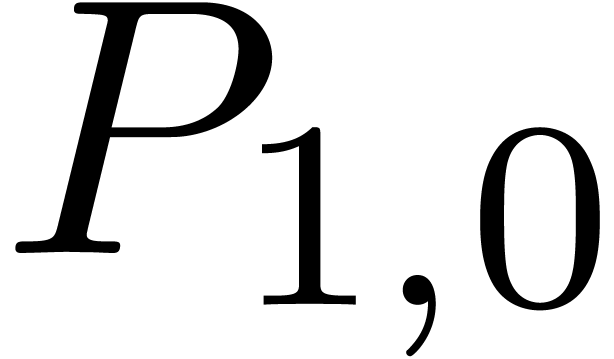 corresponds to a semi-relaxed product
and
corresponds to a semi-relaxed product
and 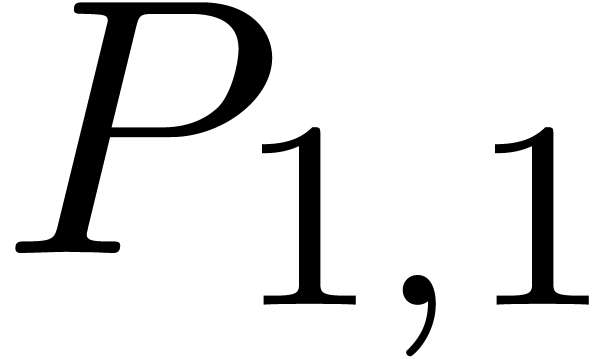 to a zealous product. This shows that
to a zealous product. This shows that
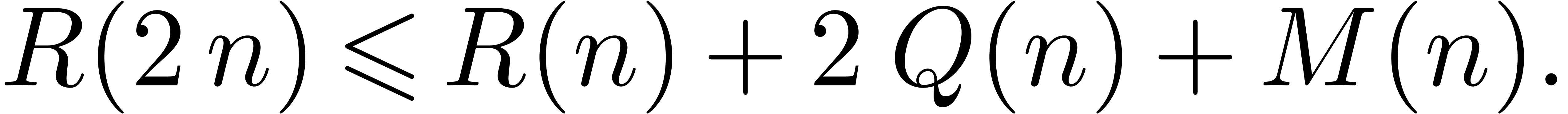
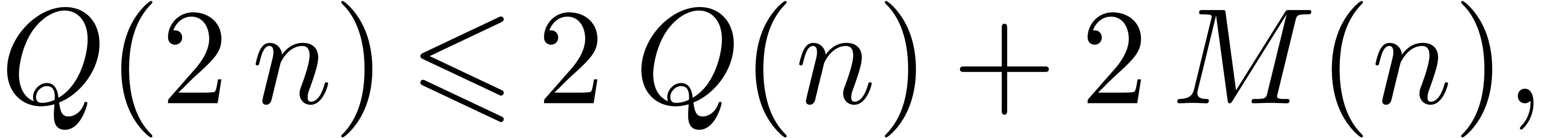
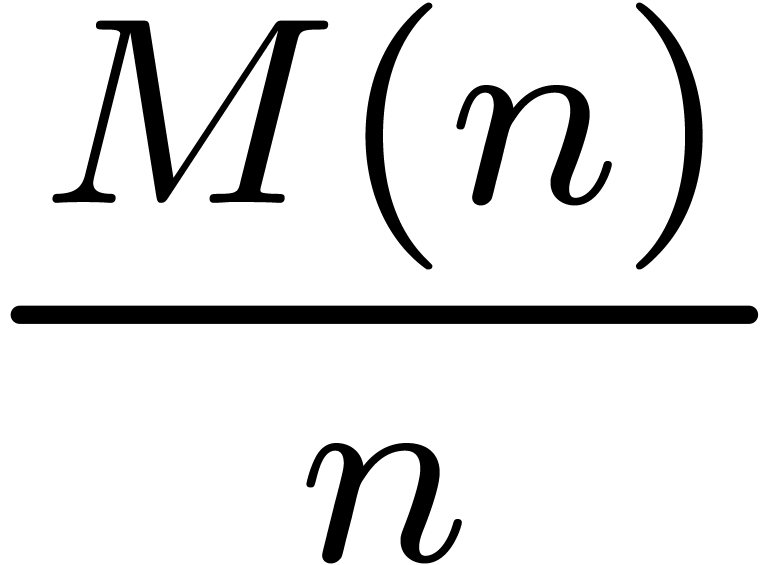 is increasing, then
is increasing, then 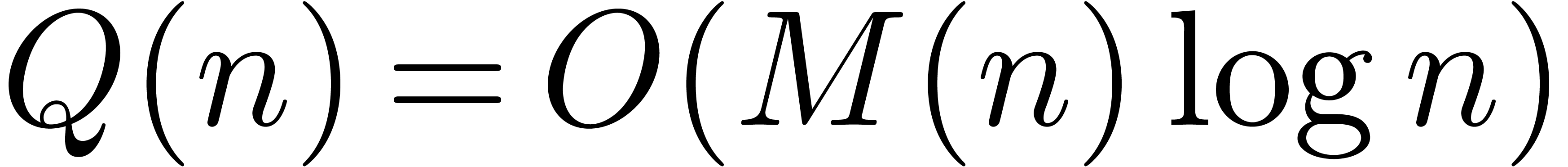 .
.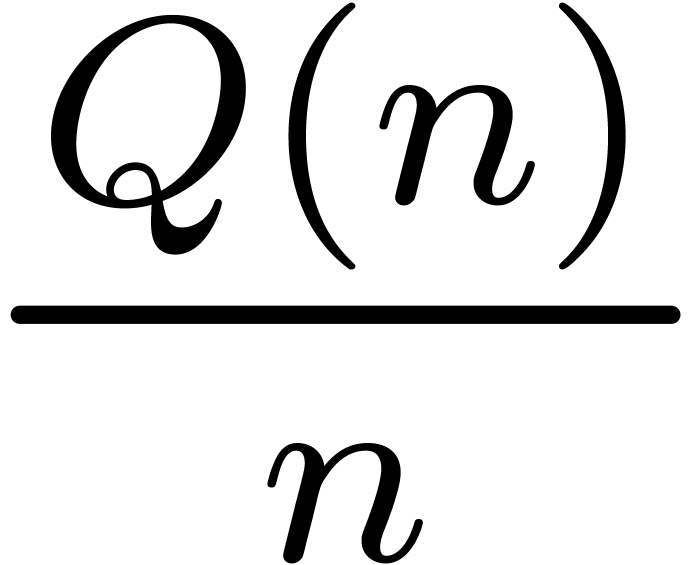 is increasing, then
is increasing, then 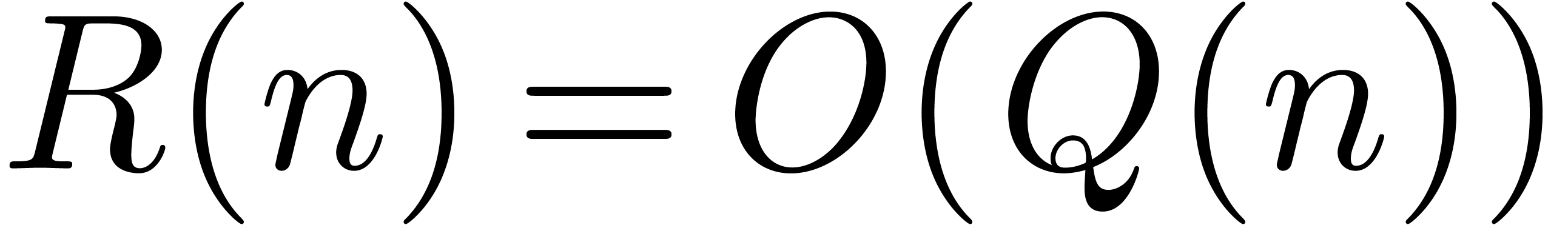 .
.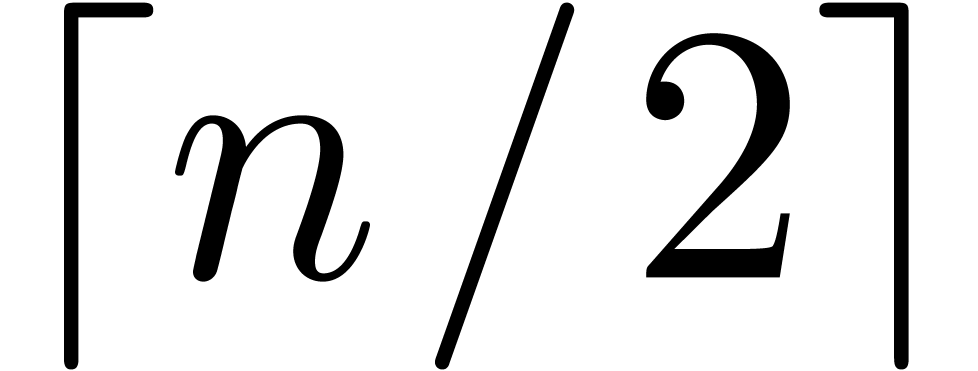 and the
resolution of a linear equation at order
and the
resolution of a linear equation at order 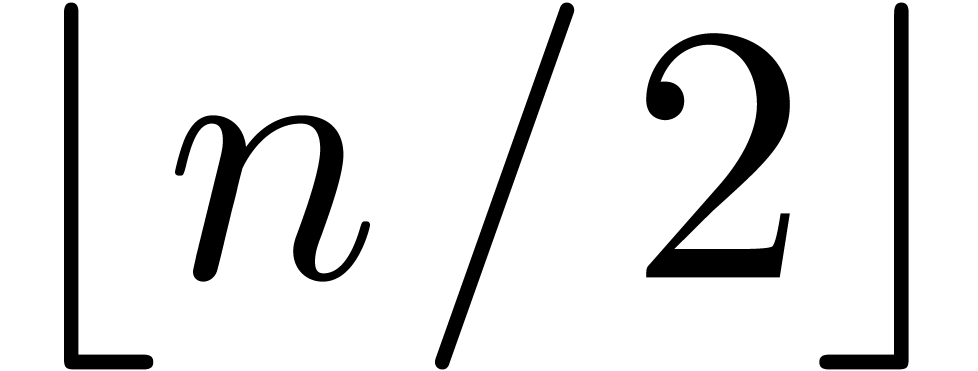 .
. for every power of two
for every power of two 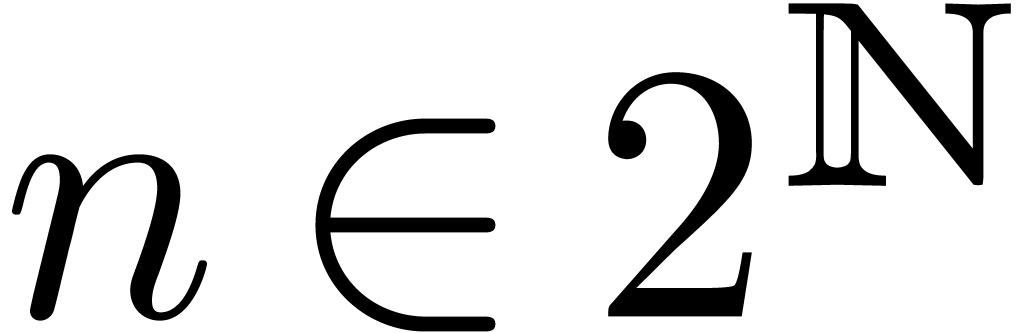 .
.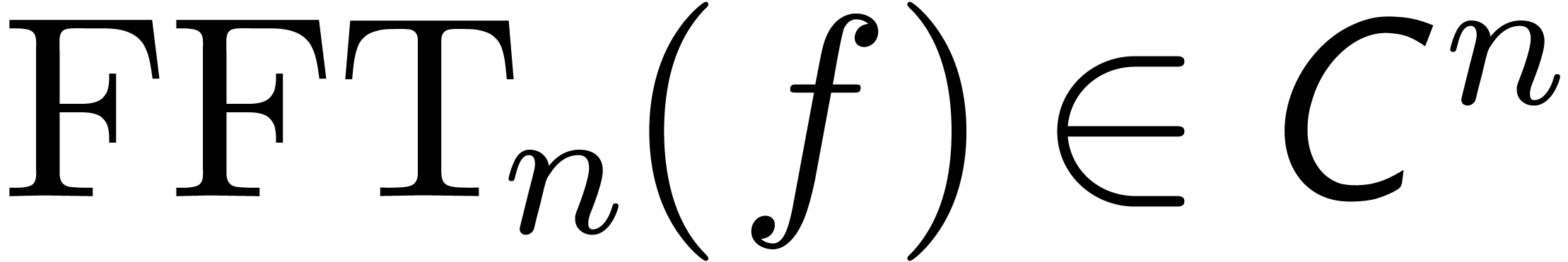 denote its Fourier transform
denote its Fourier transform
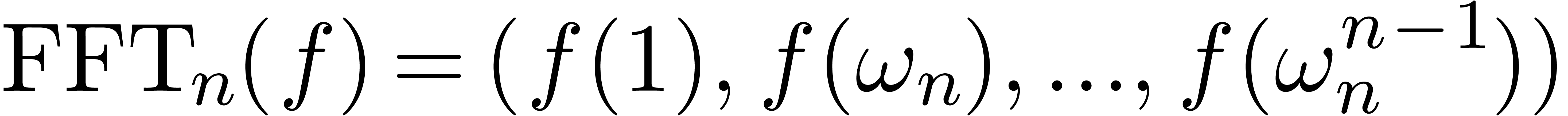
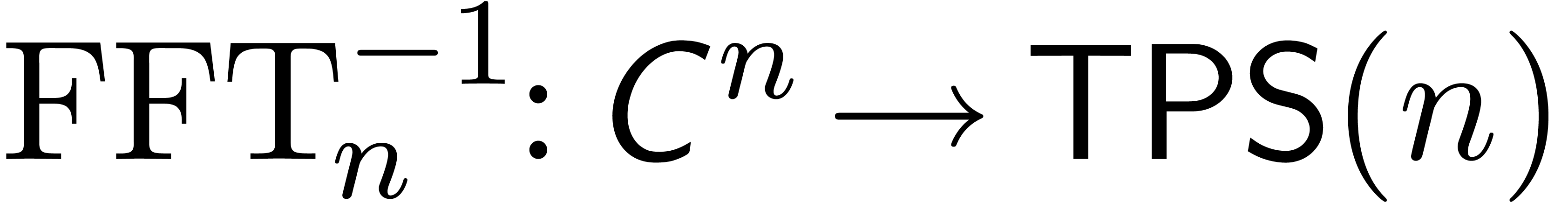 be the inverse mapping of
be the inverse mapping of  .
.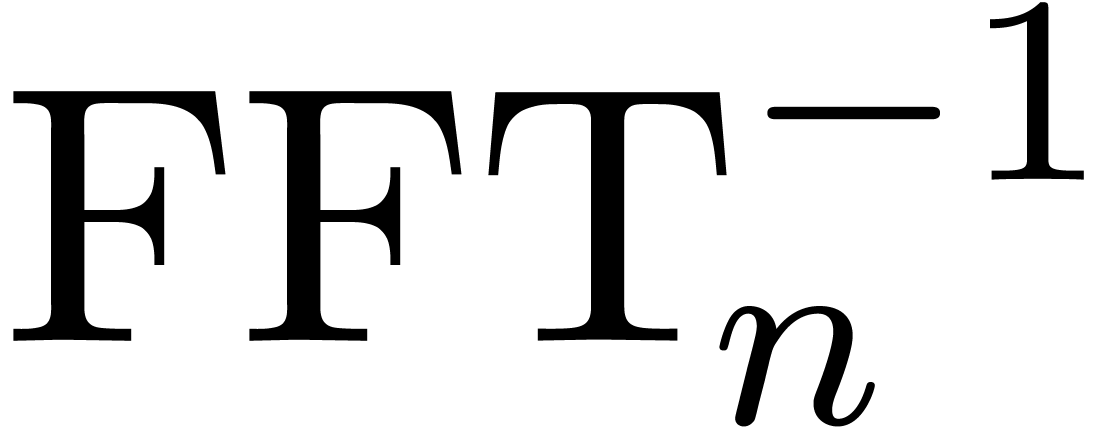 can be computed in time
can be computed in time 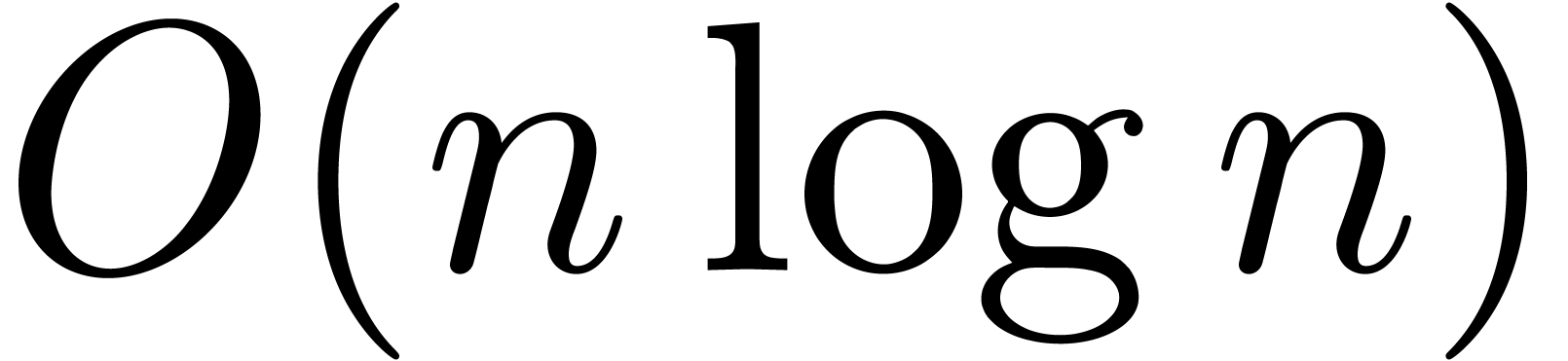 .
.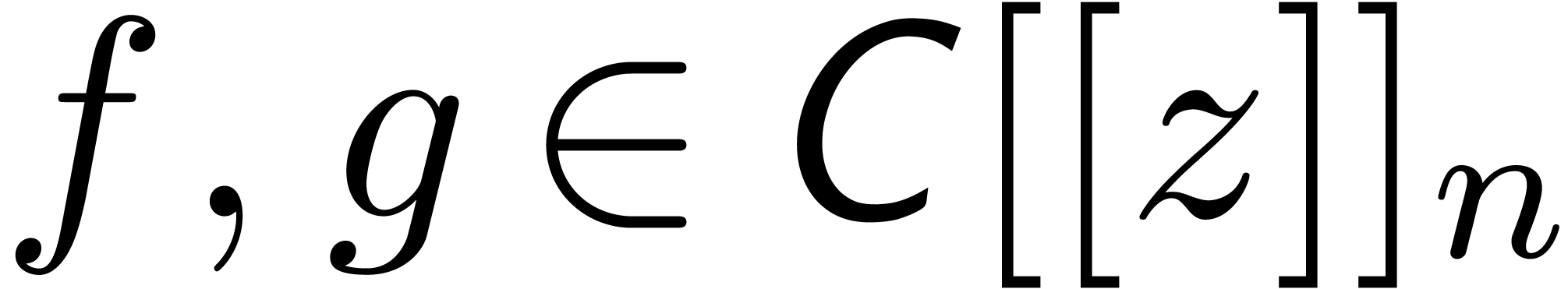 are
such that
are
such that  ,
,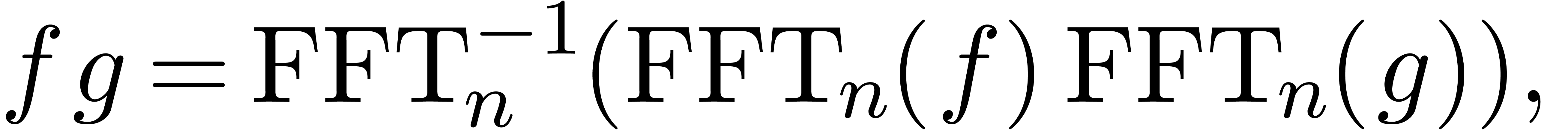
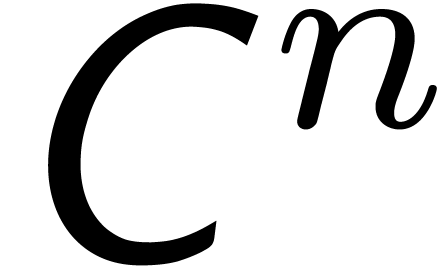 is scalar multiplication
is scalar multiplication
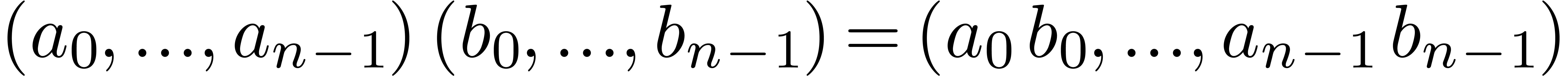 .
.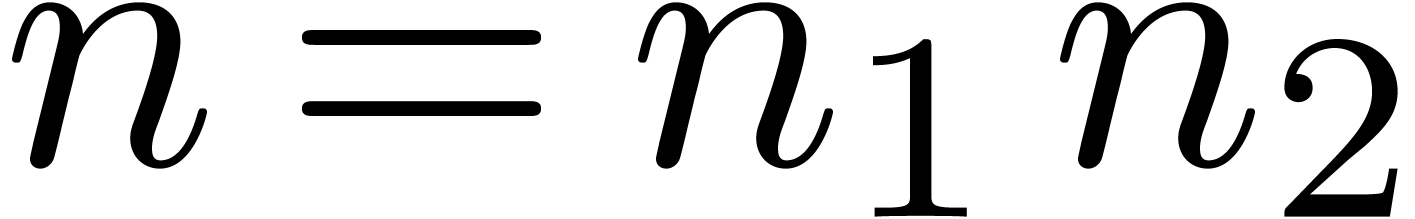 with
with 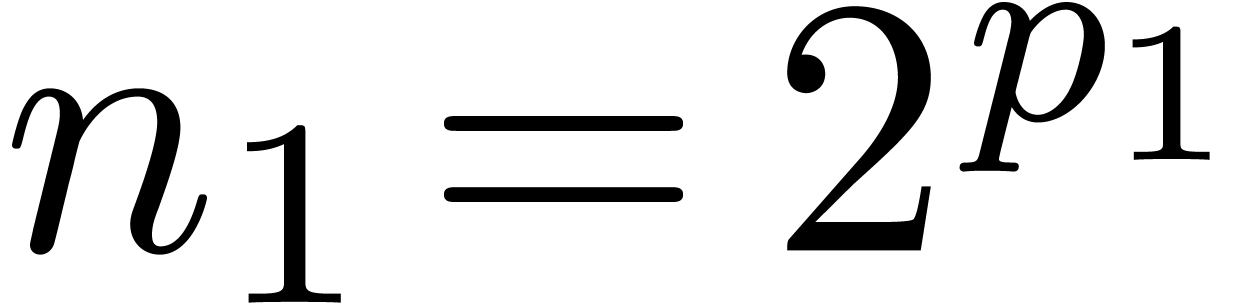 and
and 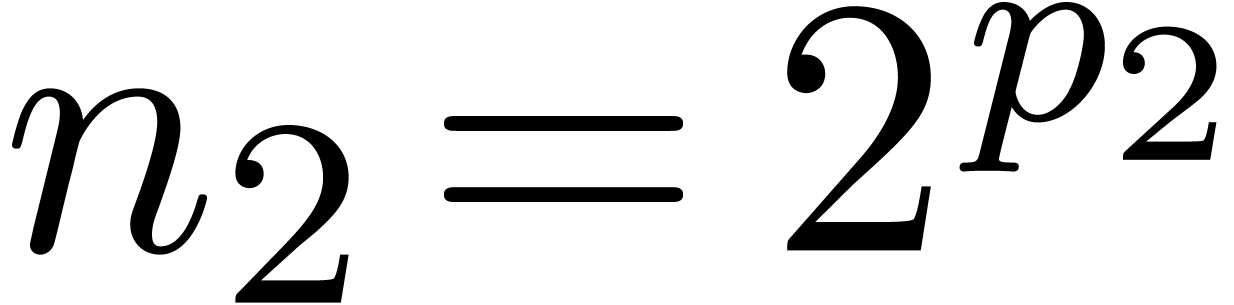 .
. can be rewritten as a
series
can be rewritten as a
series
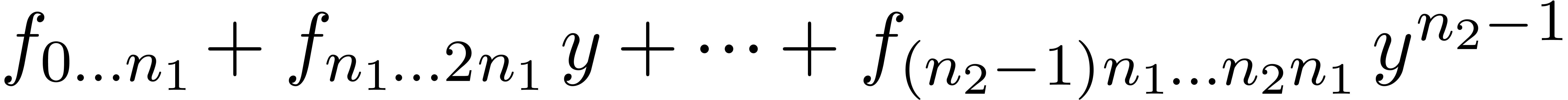
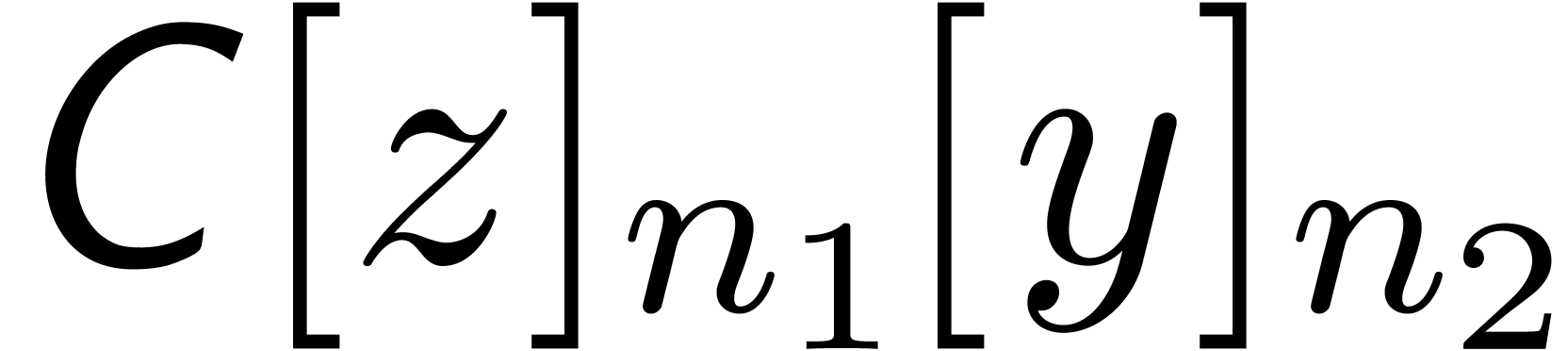 ,
,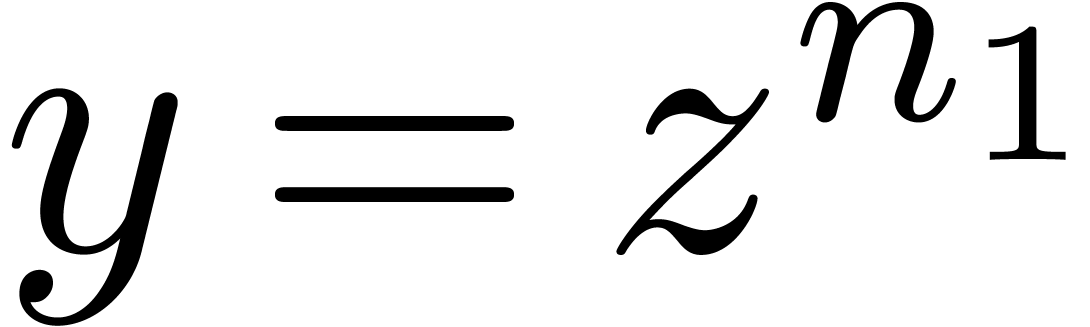 .
.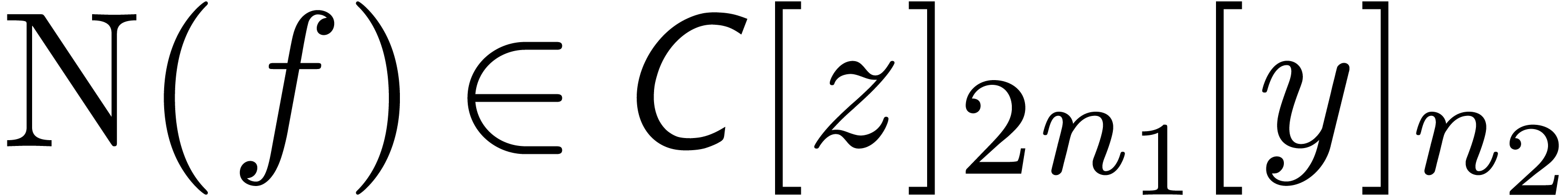 ,
,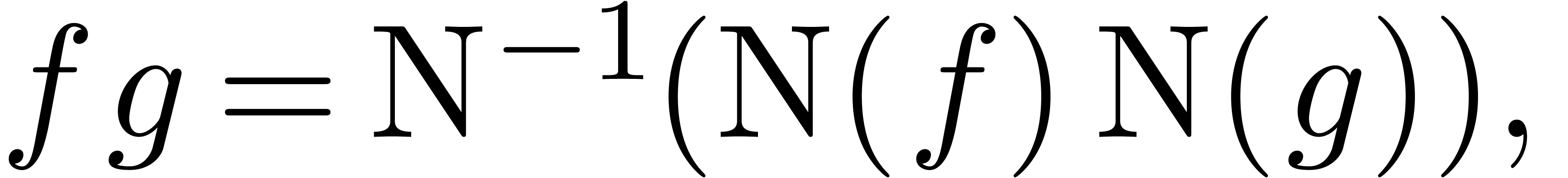
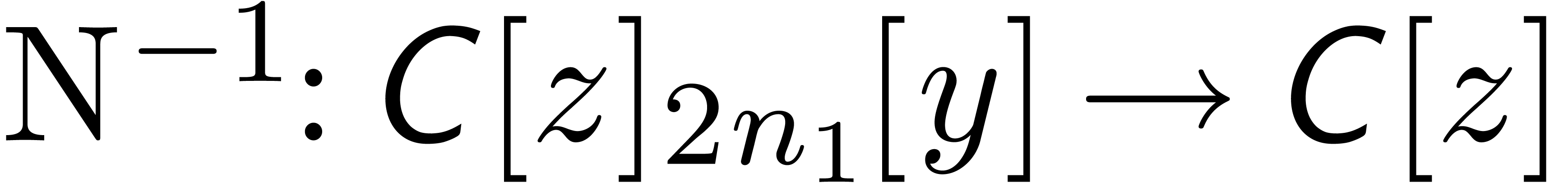 is the mapping which substitutes
is the mapping which substitutes 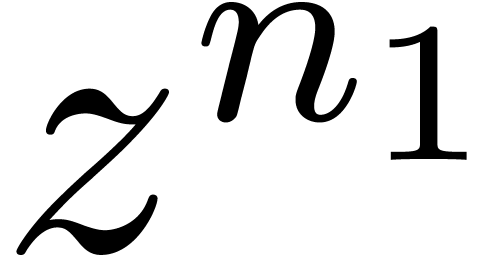 for
for  .
.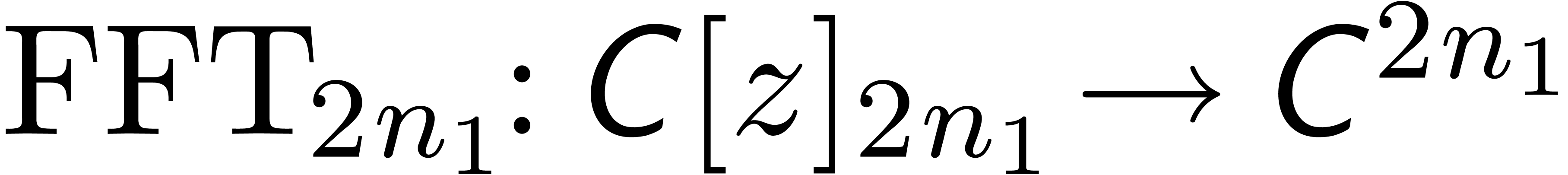 may be extended to a mapping
may be extended to a mapping
 ,
,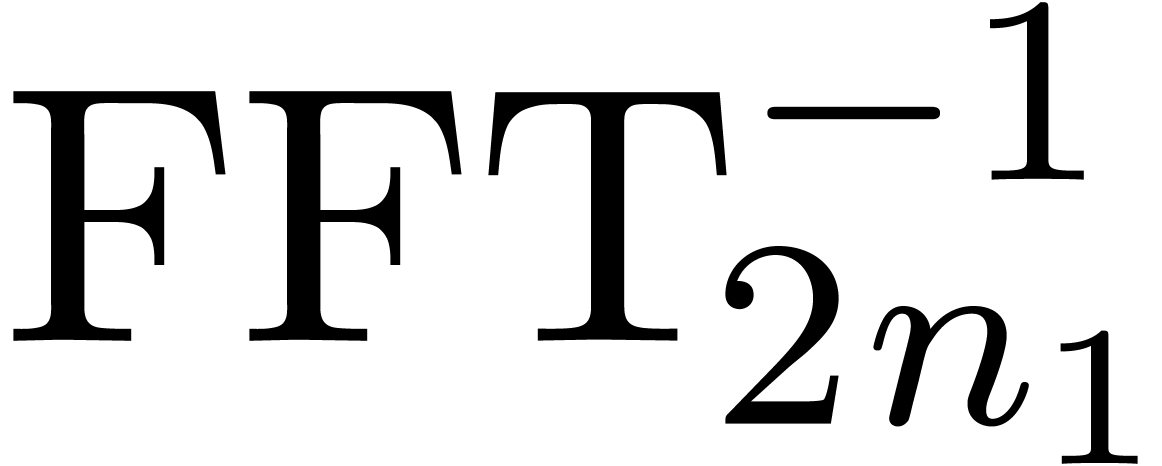 .
.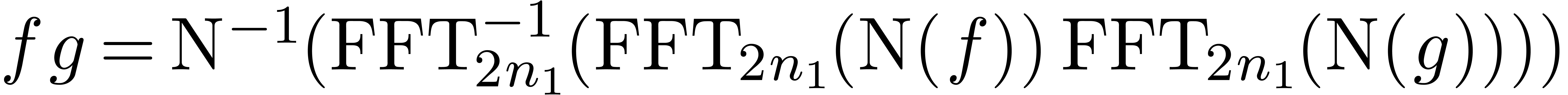
 by reusing the Fourier
transforms of the “bunches of coefficients”
by reusing the Fourier
transforms of the “bunches of coefficients”  and
and 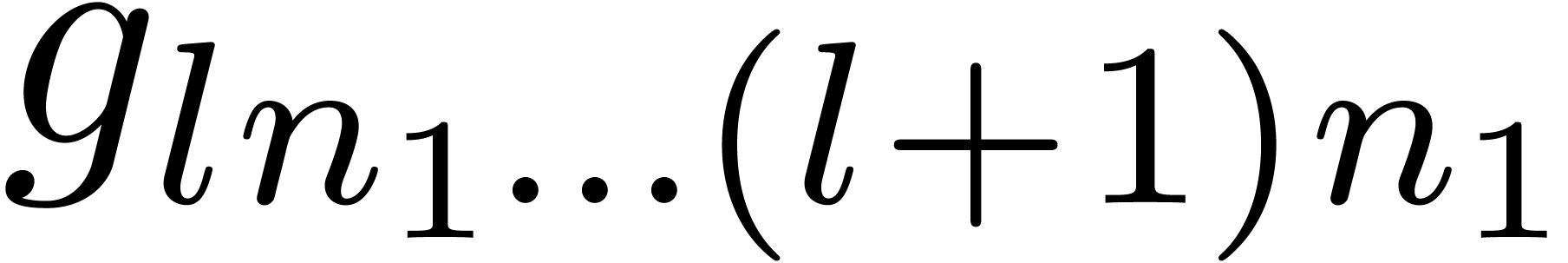 many times.
many times.
 product with coefficients in
product with coefficients in 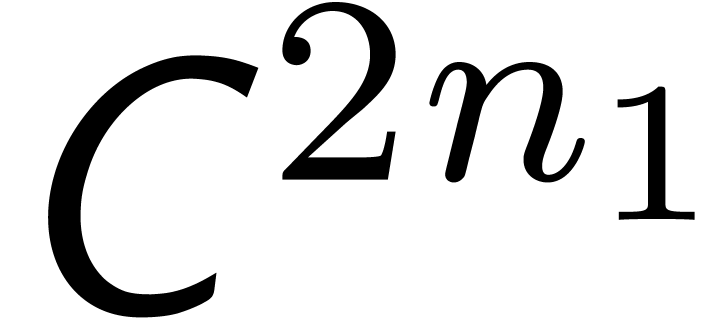 .
.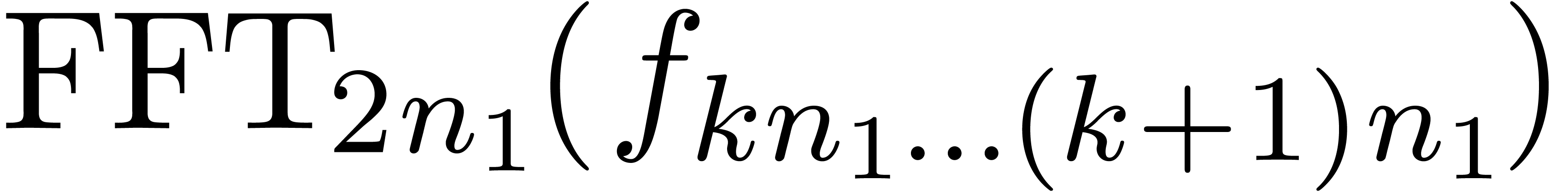 when
when 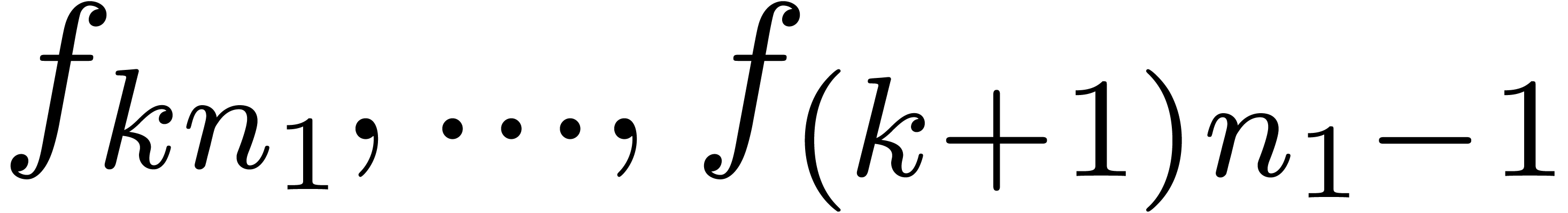 are
all known. Consequently, the products
are
all known. Consequently, the products 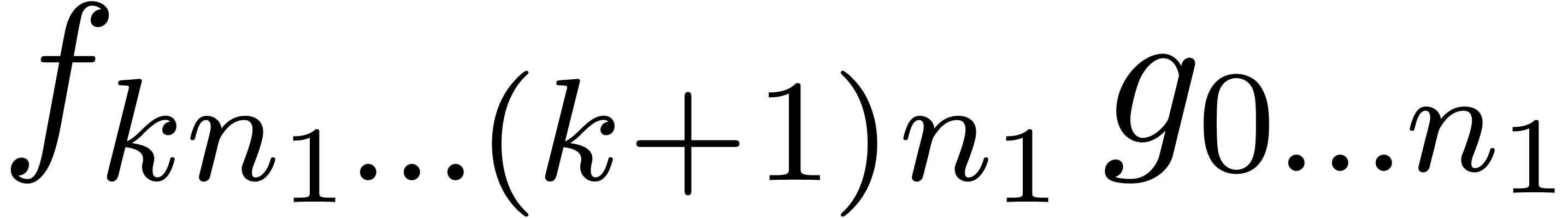 should be
computed apart, using a traditional semi-relaxed multiplication. In
other words, we have reduced the computation of a semi-relaxed
should be
computed apart, using a traditional semi-relaxed multiplication. In
other words, we have reduced the computation of a semi-relaxed 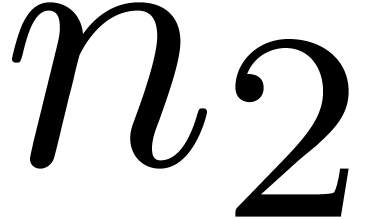 semi-relaxed
semi-relaxed  products with coefficients in
products with coefficients in 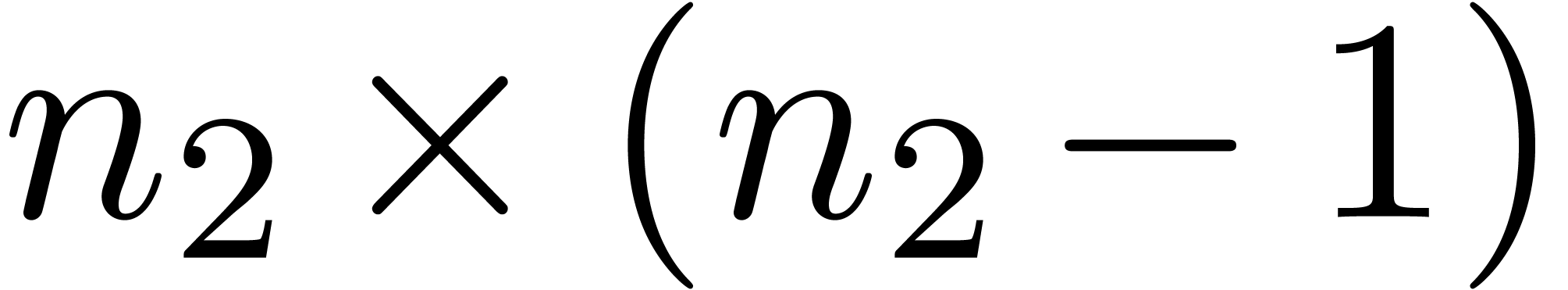 product with coefficients in
product with coefficients in
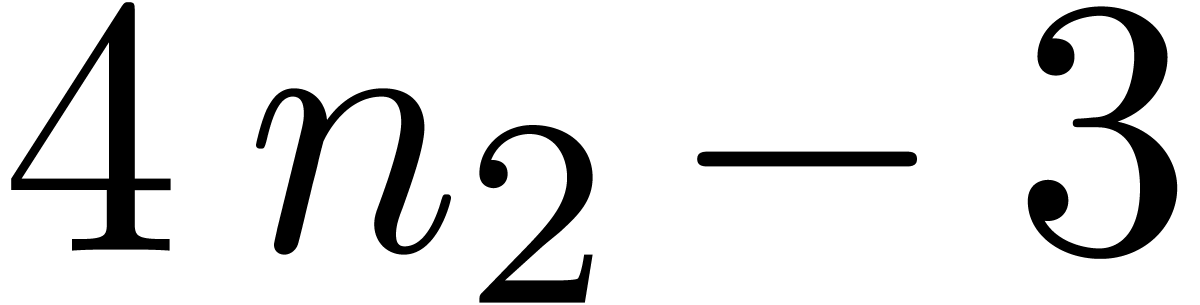 FFT-transforms of
length
FFT-transforms of
length 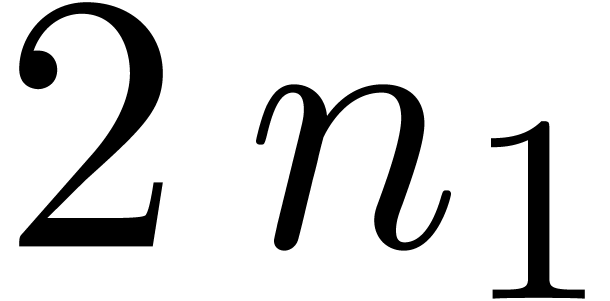 .
.
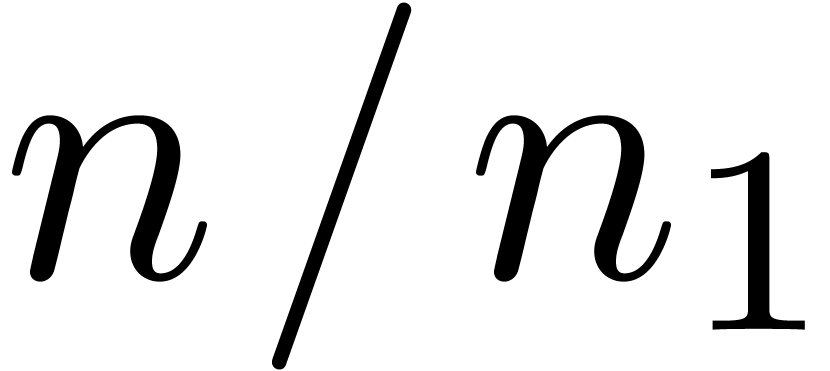 semi-relaxed
semi-relaxed 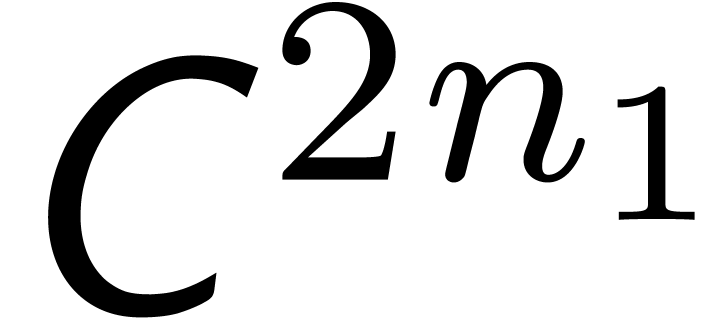 .
.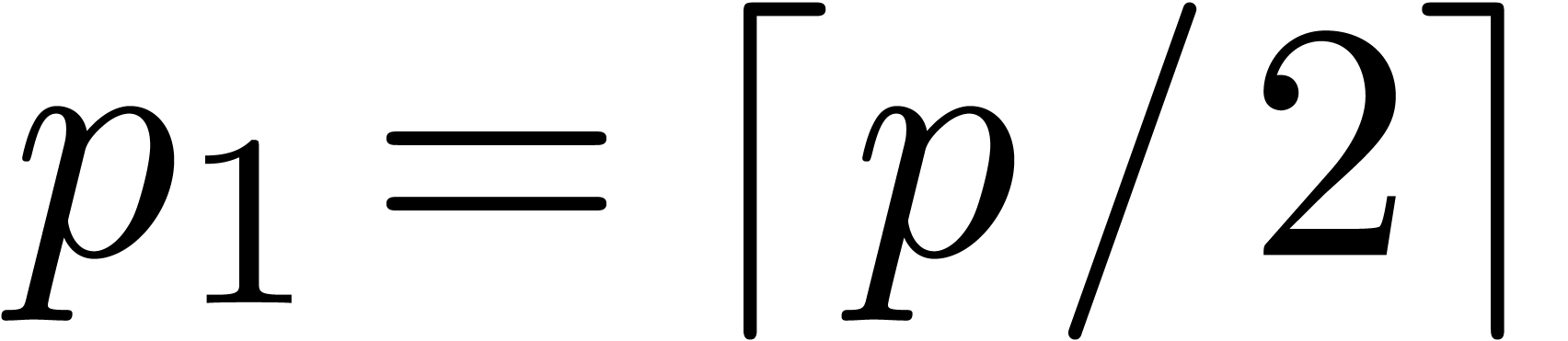 and
and 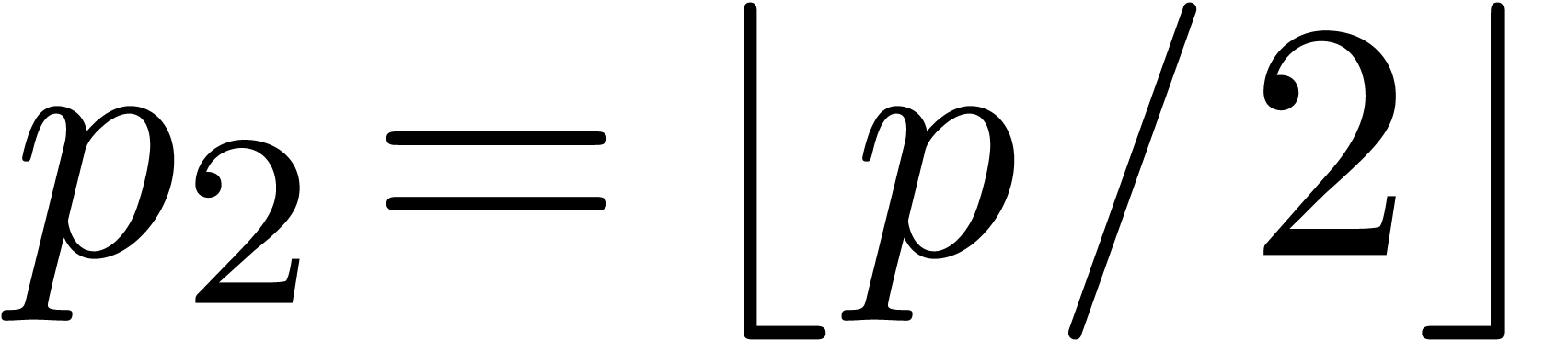 :
:
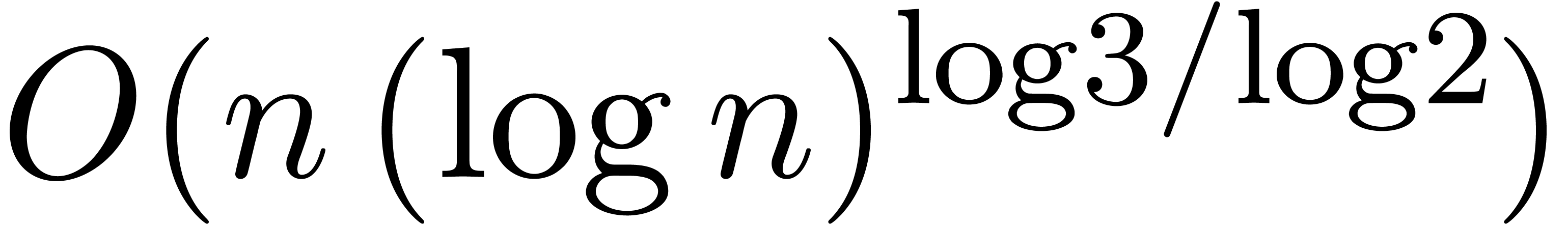 and space complexity
and space complexity 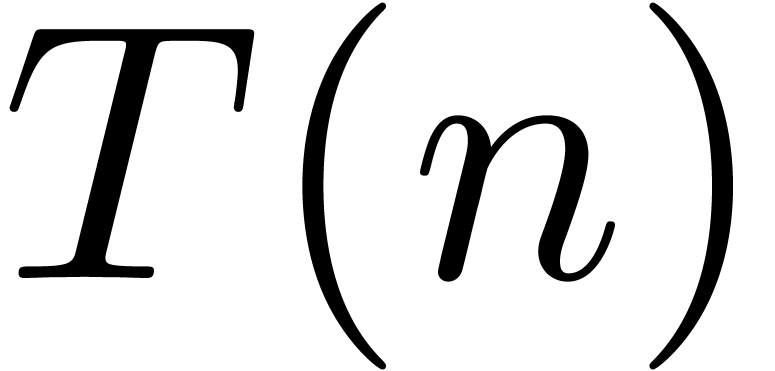 denote the time complexity of the above method. Then we
observe that
denote the time complexity of the above method. Then we
observe that
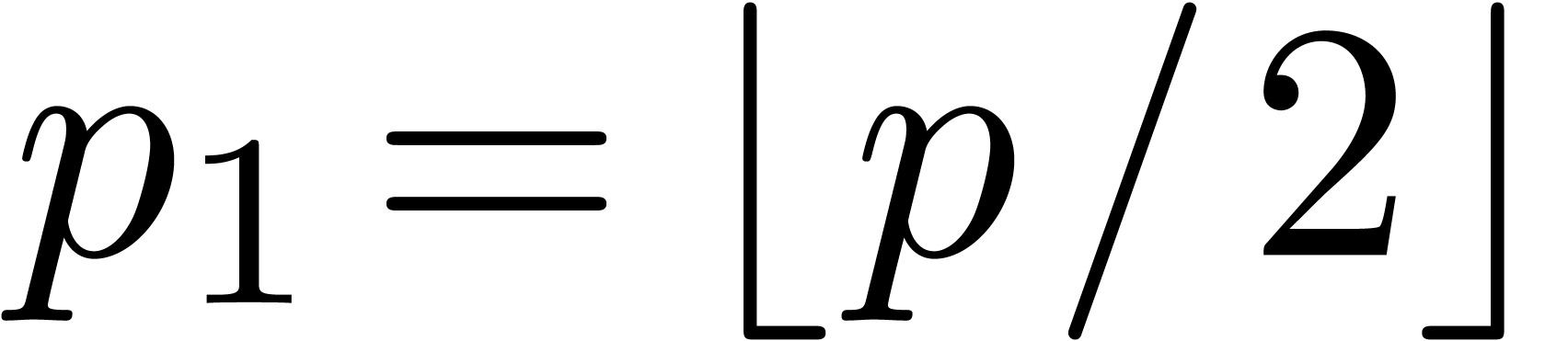 ,
,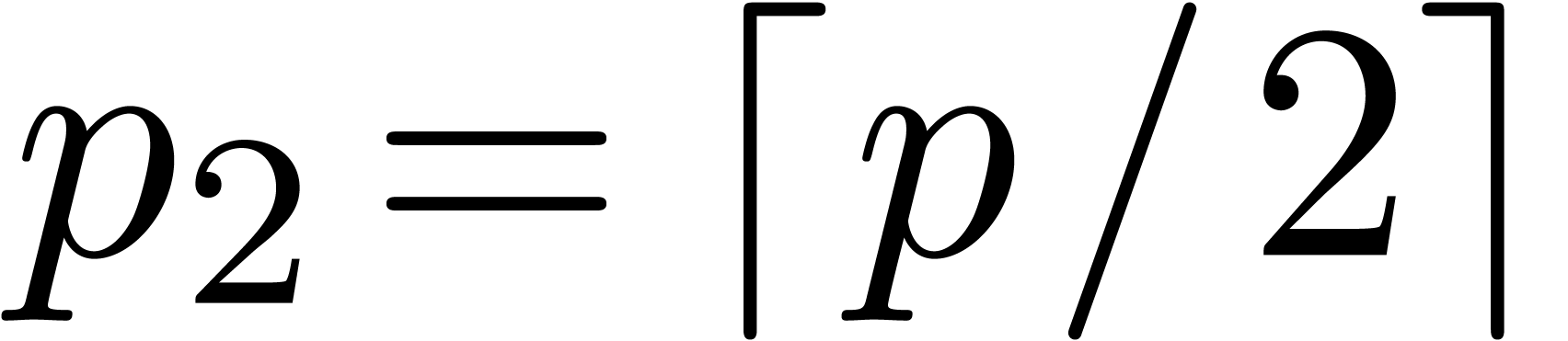 and
and 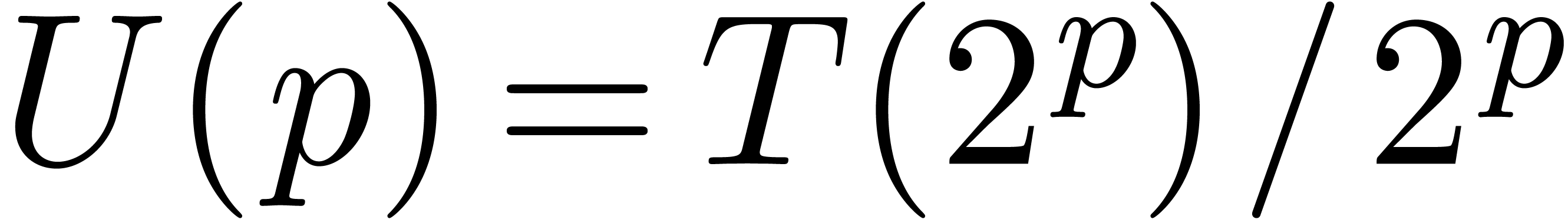 ,
,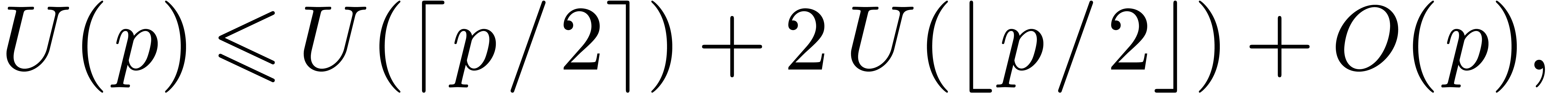
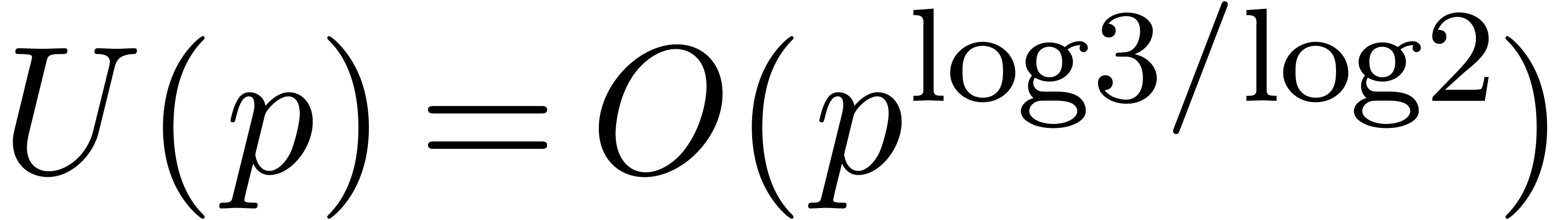 and
and 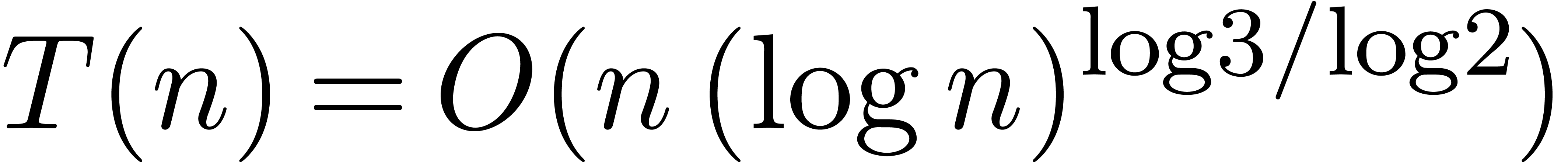 .
. satisfies the bound
satisfies the bound
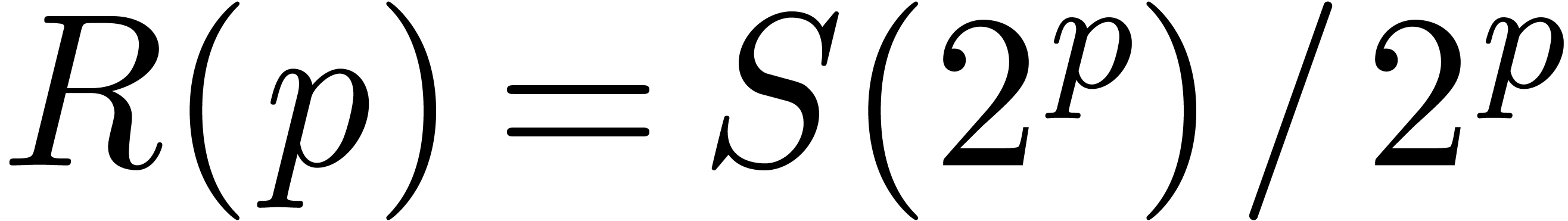 ,
,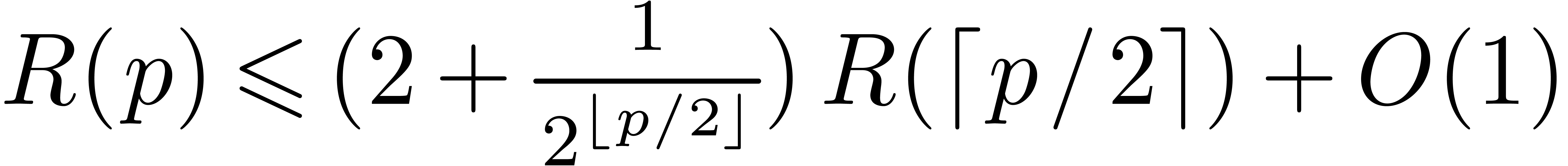
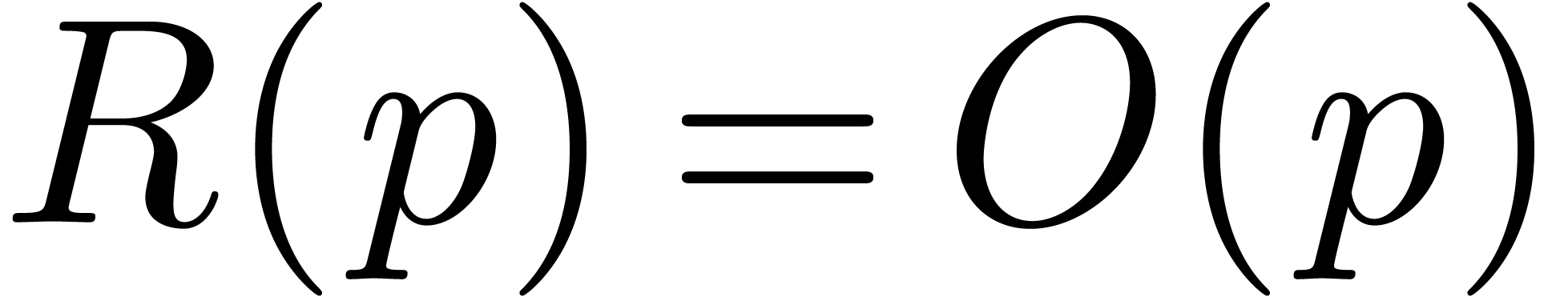 and
and 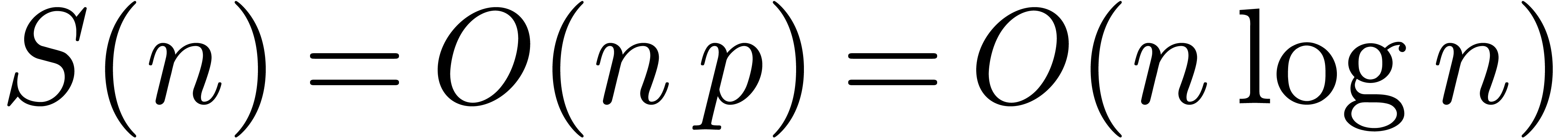 .
.
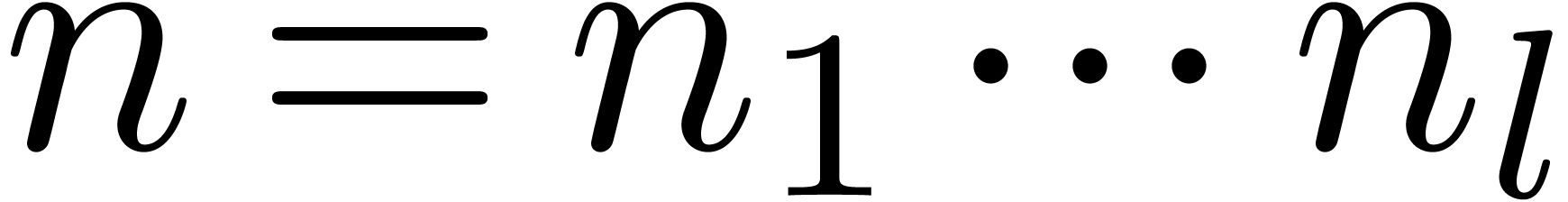 with
with  ,
,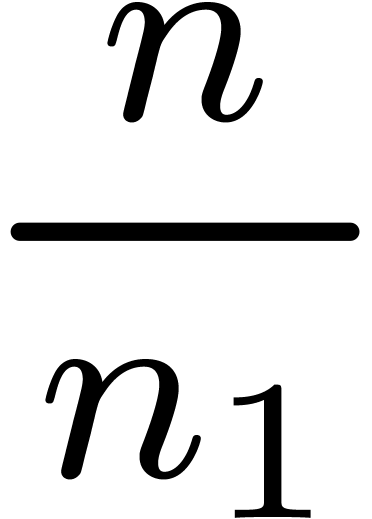 semi-relaxed
semi-relaxed 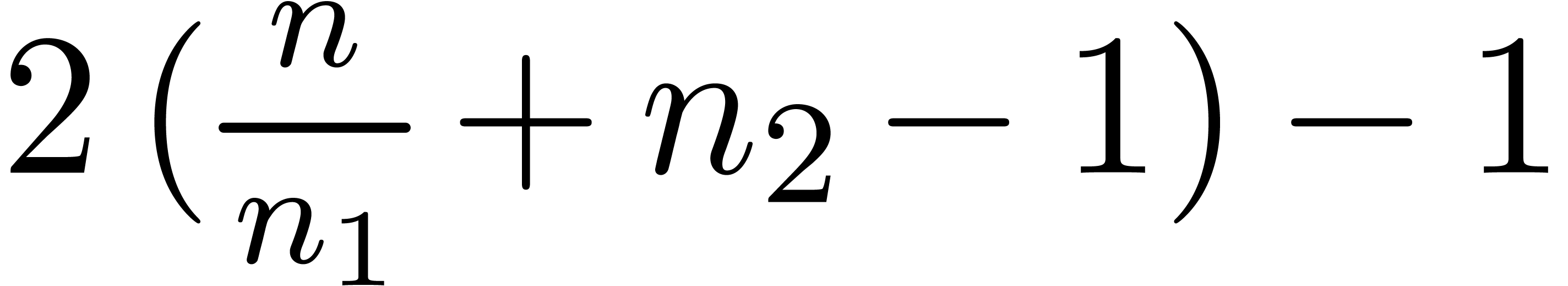 FFT-transforms of length
FFT-transforms of length 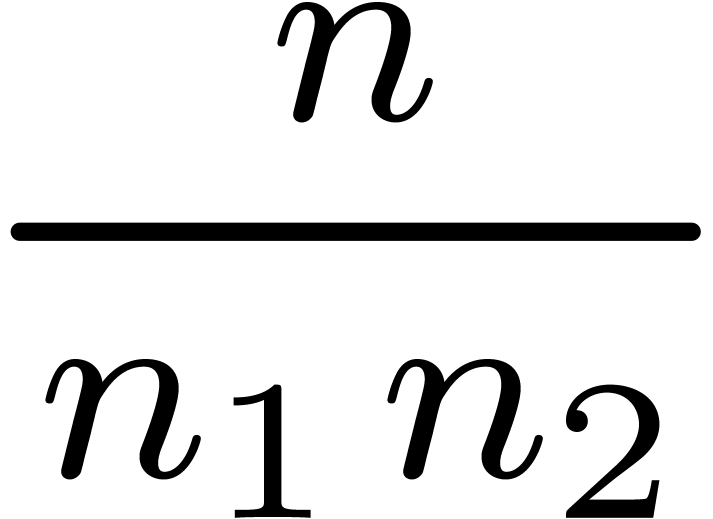 semi-relaxed
semi-relaxed 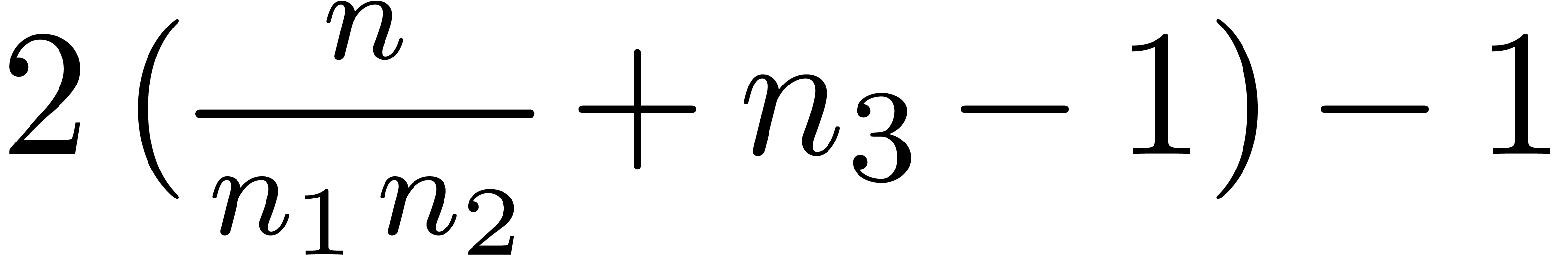 FFT-transforms of length
FFT-transforms of length 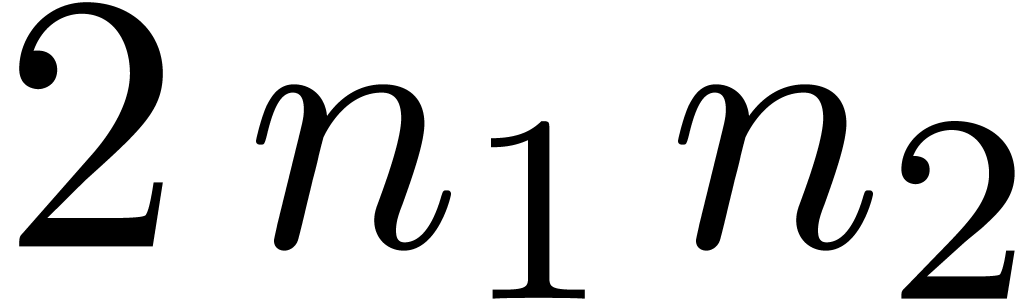 ;
;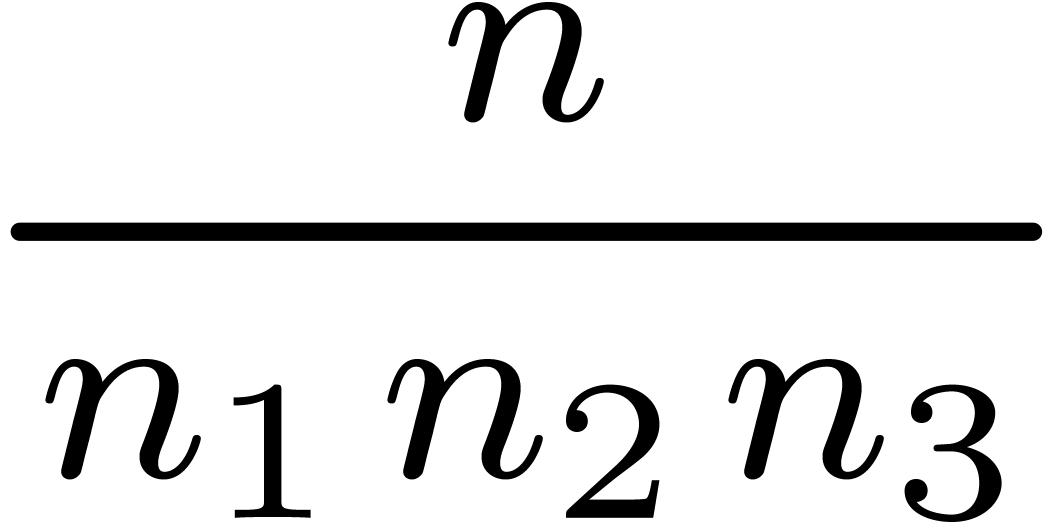 semi-relaxed
semi-relaxed 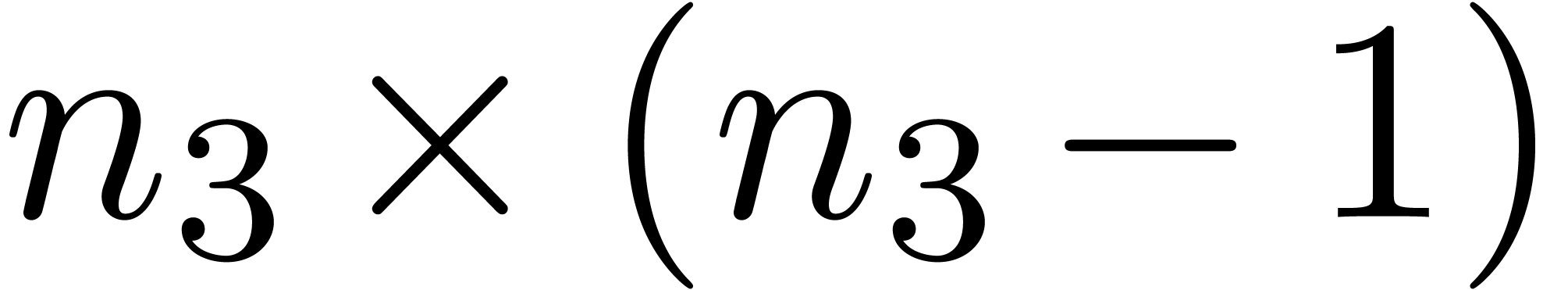 products over
products over 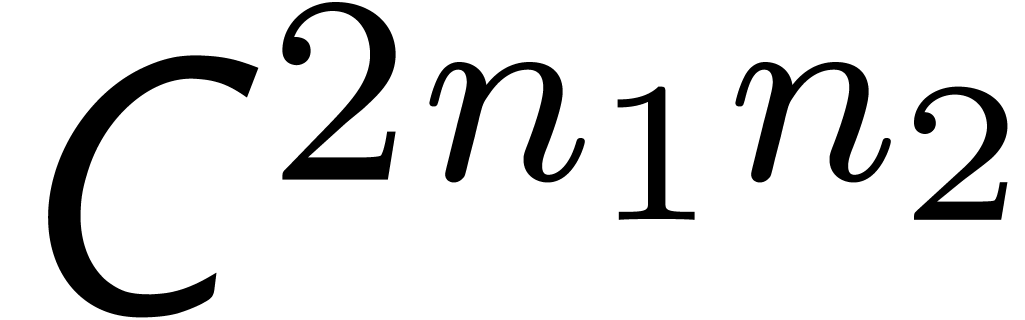 ;
;
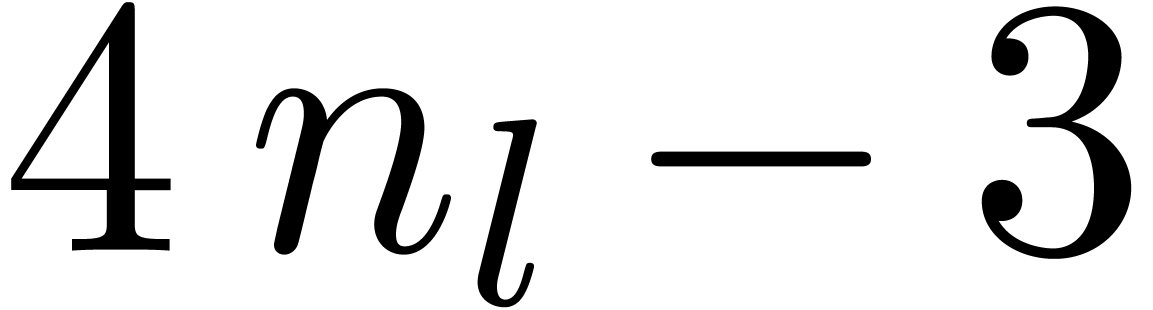 FFT-transforms of length
FFT-transforms of length 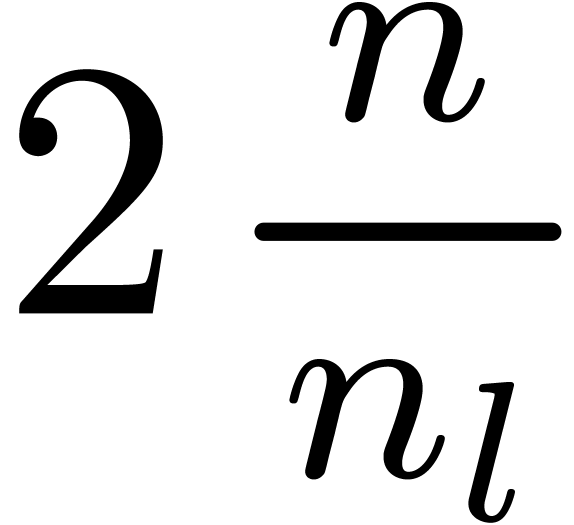 ;
;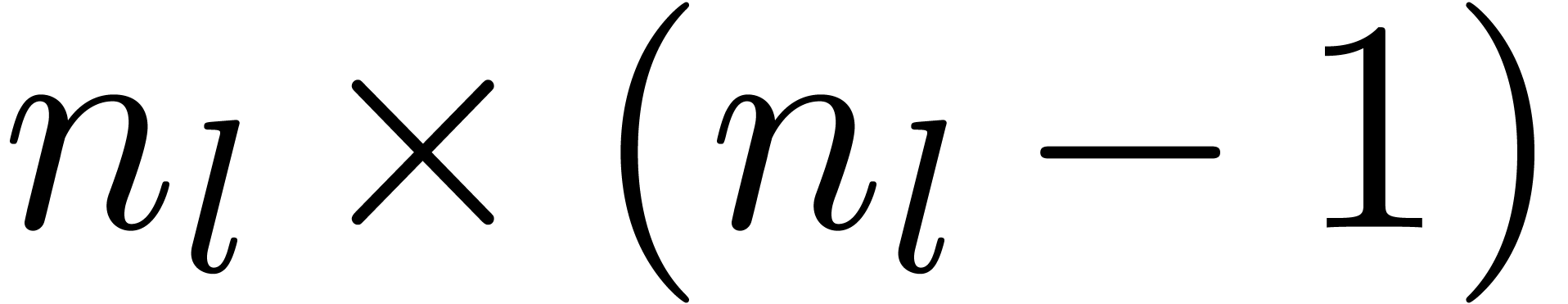 product over
product over 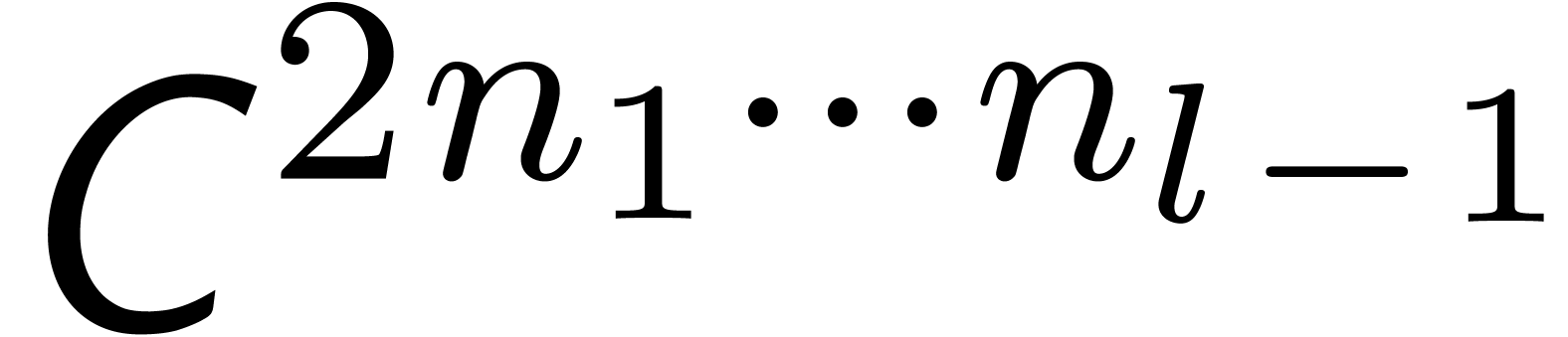 .
.
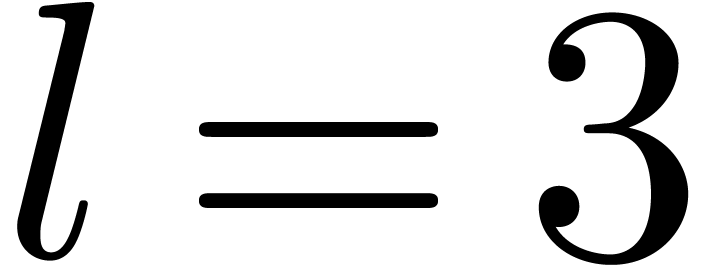 layers.
layers.
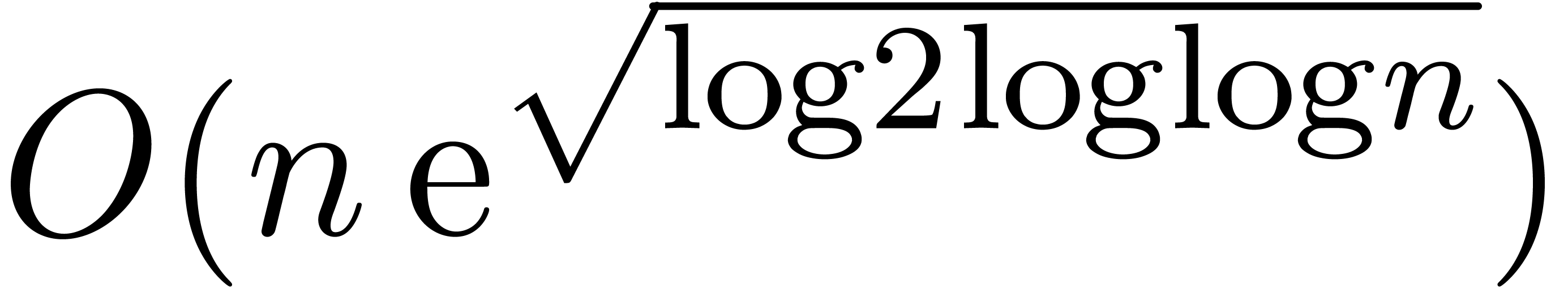 .
.
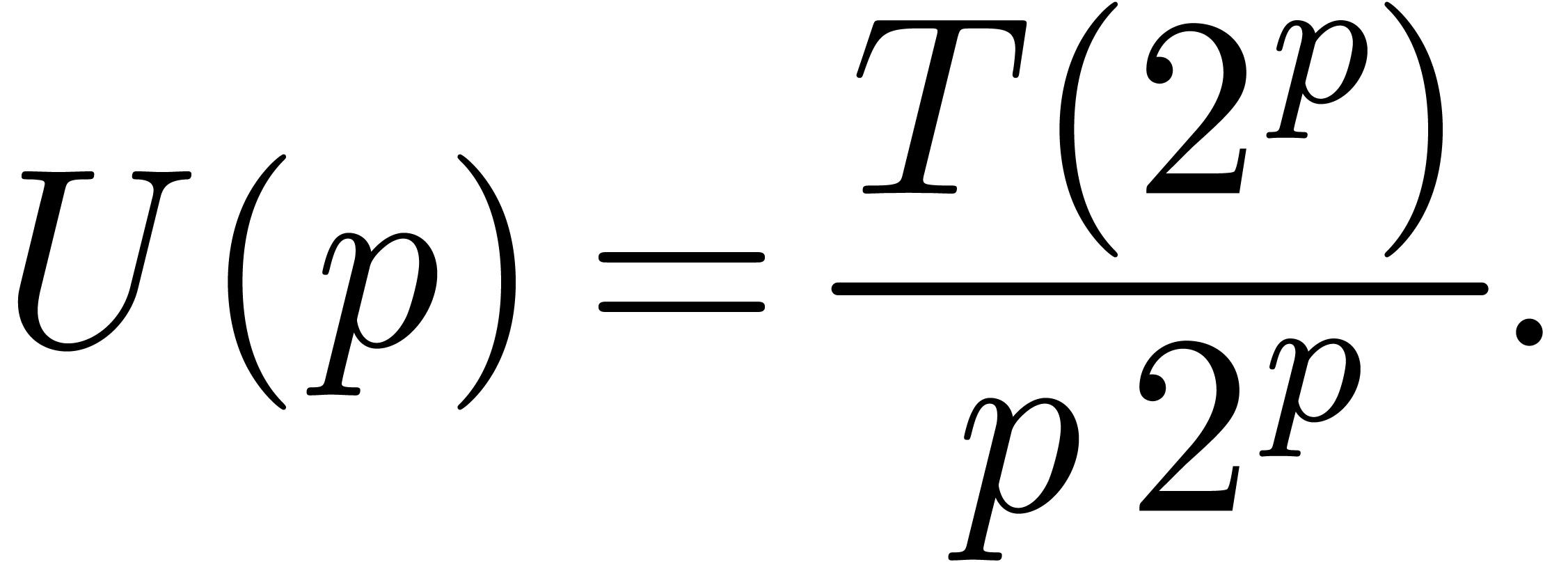
 in (
in (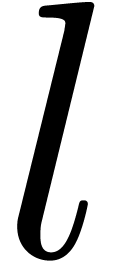 that
that
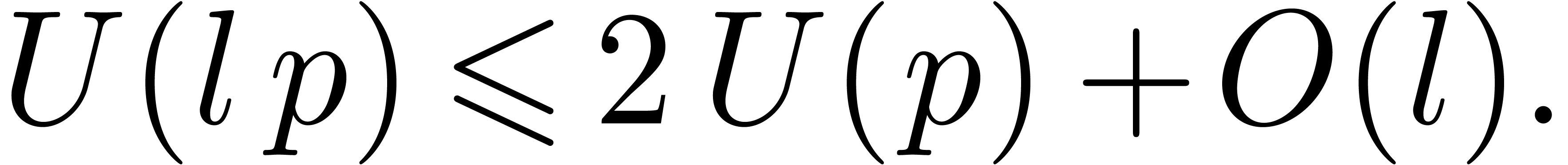
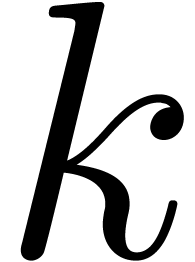 times, we obtain
times, we obtain
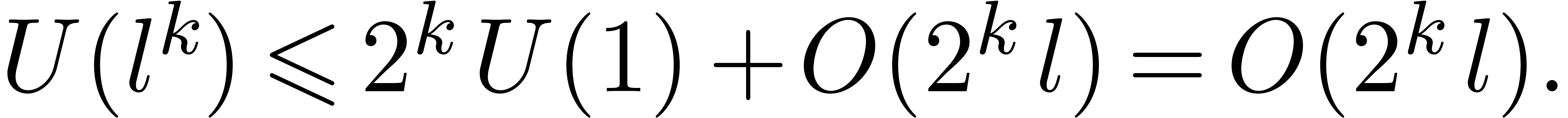
 such that
such that 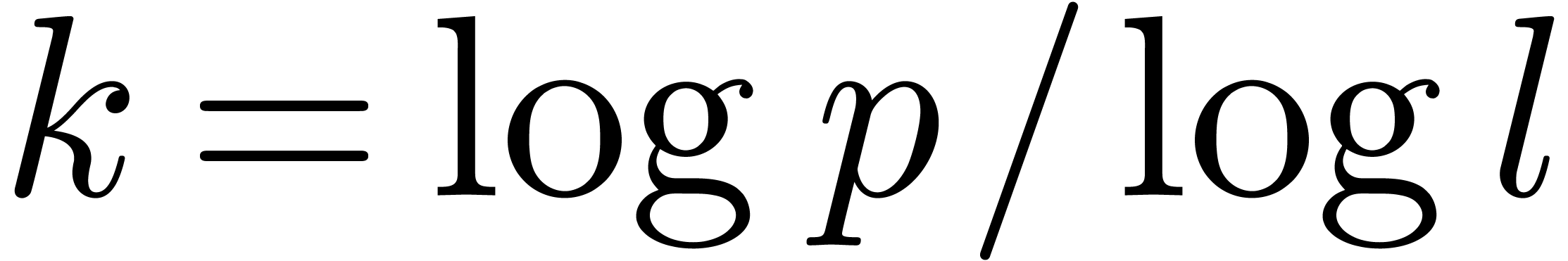 is
an integer, we obtain
is
an integer, we obtain
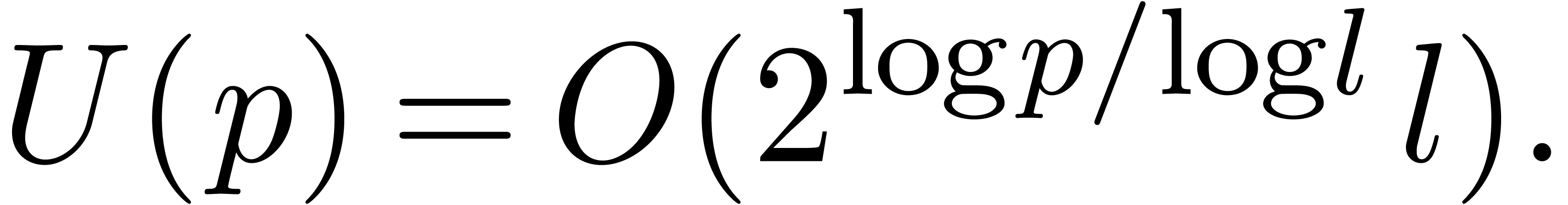
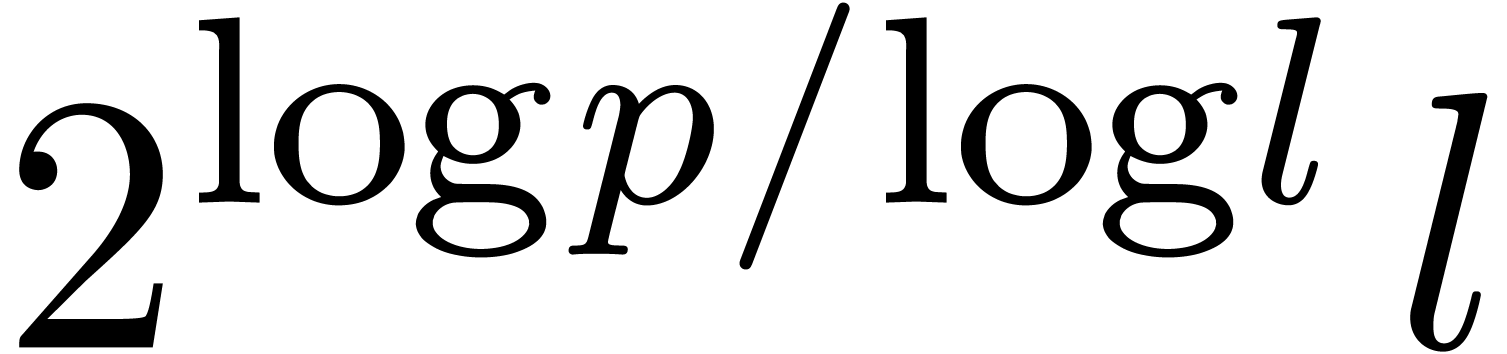 is reached when its derivative
w.r.t.
is reached when its derivative
w.r.t. 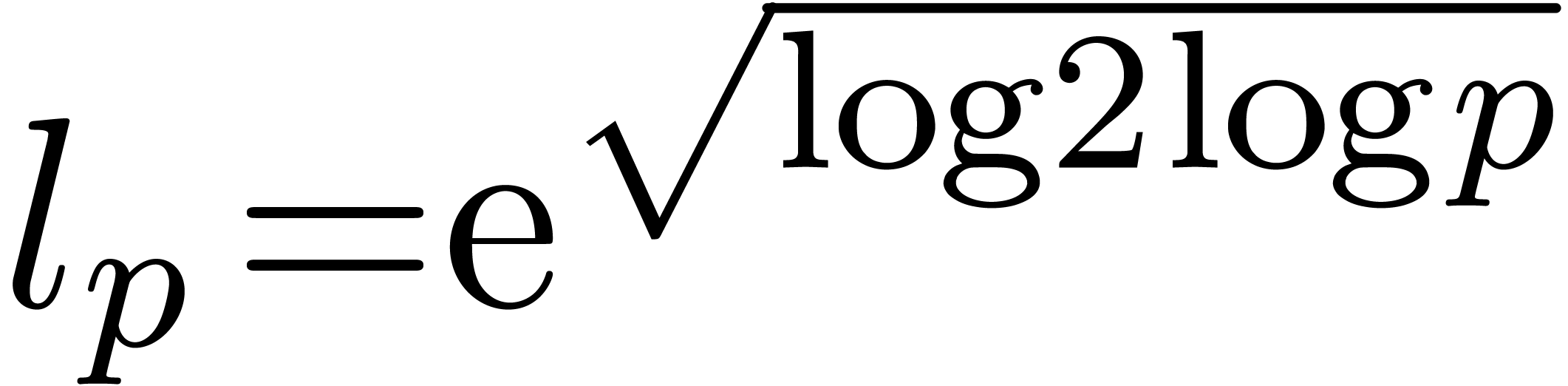
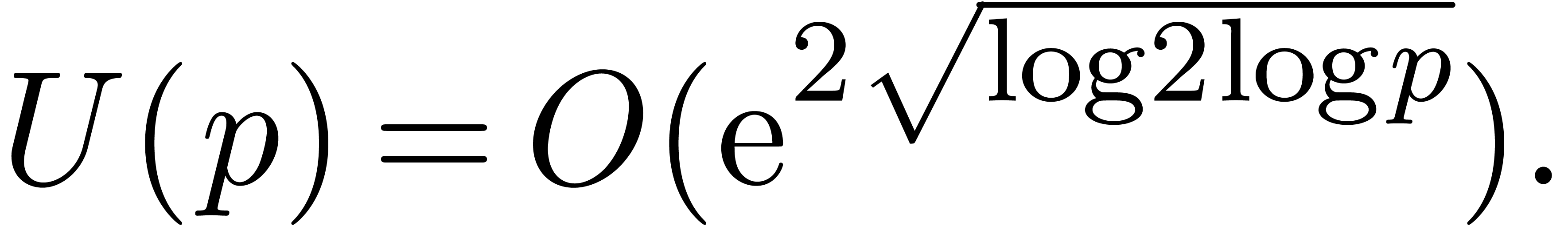
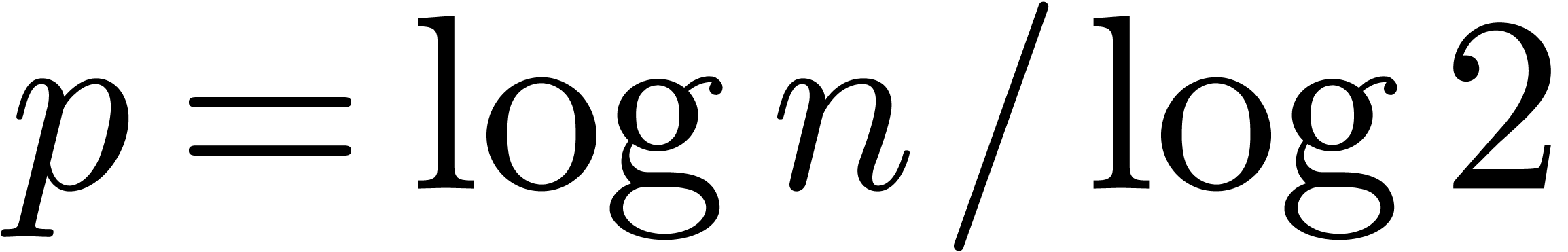 finally gives the desired
estimate
finally gives the desired
estimate
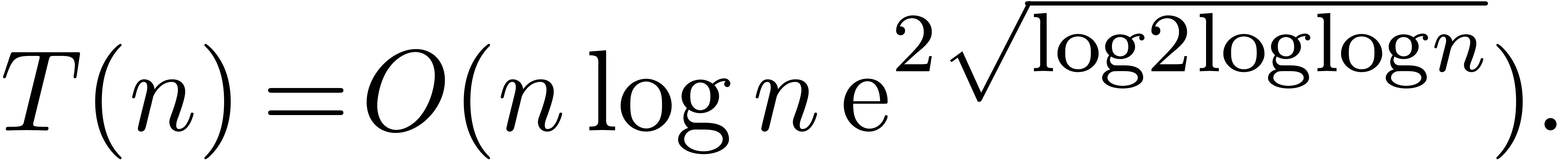
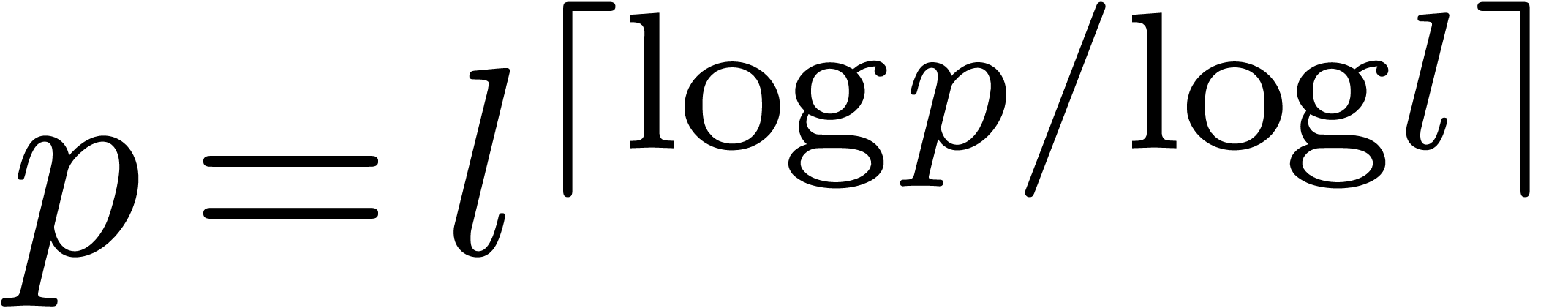 and (
and (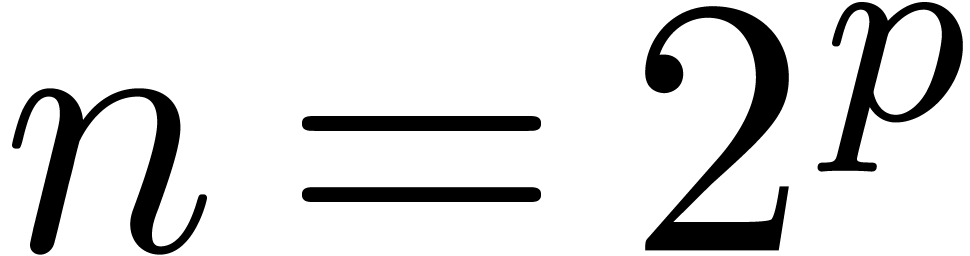 .
.
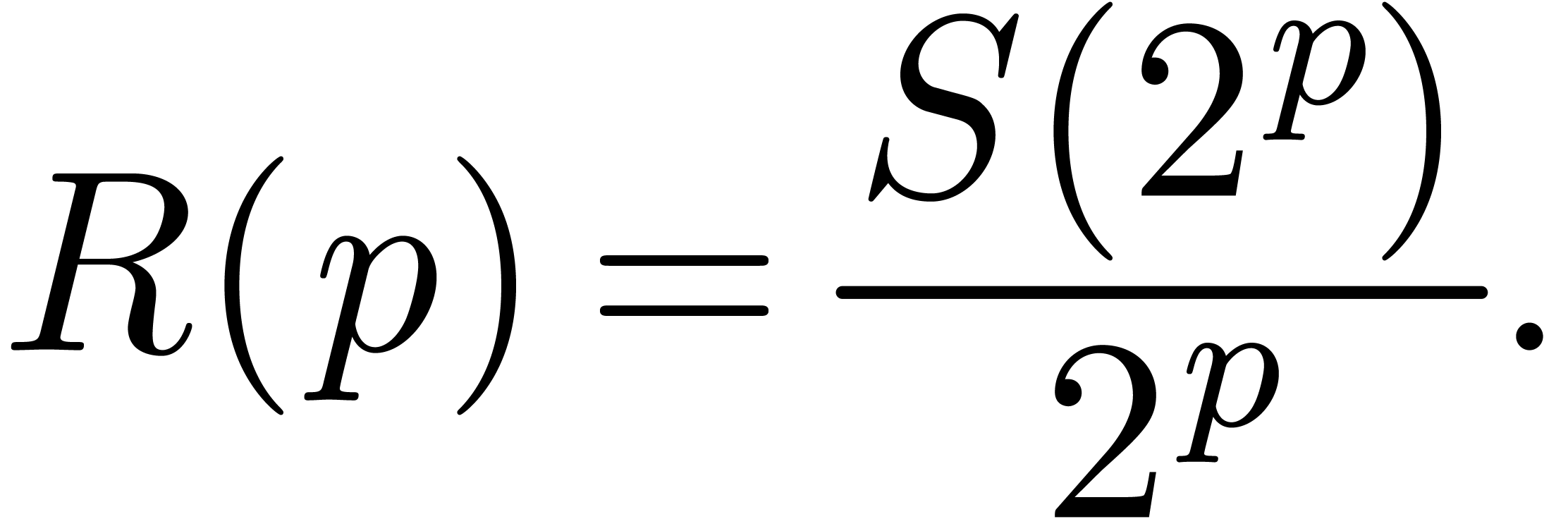
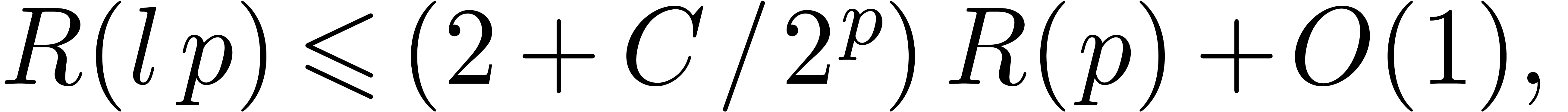
 .
.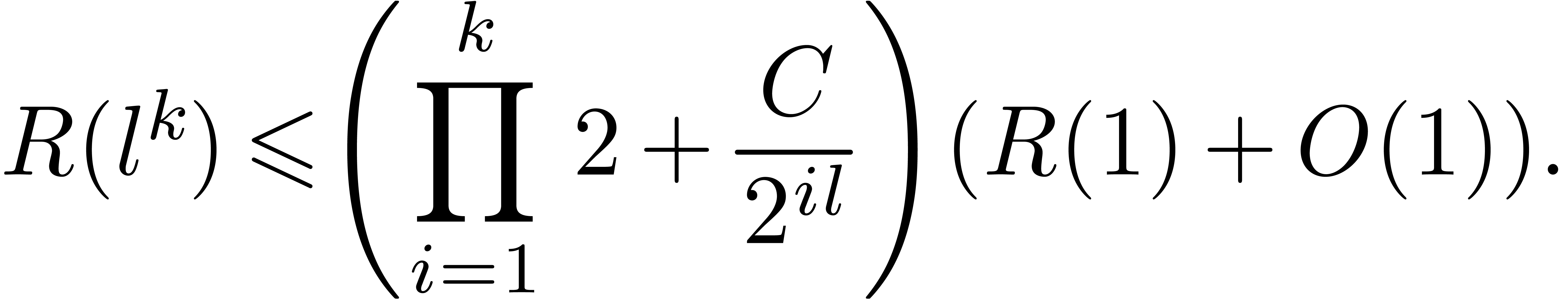
 ,
,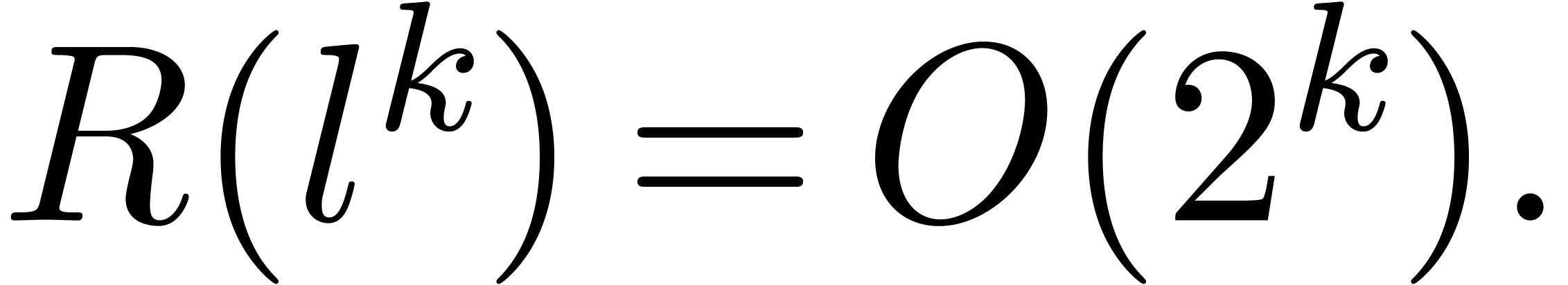
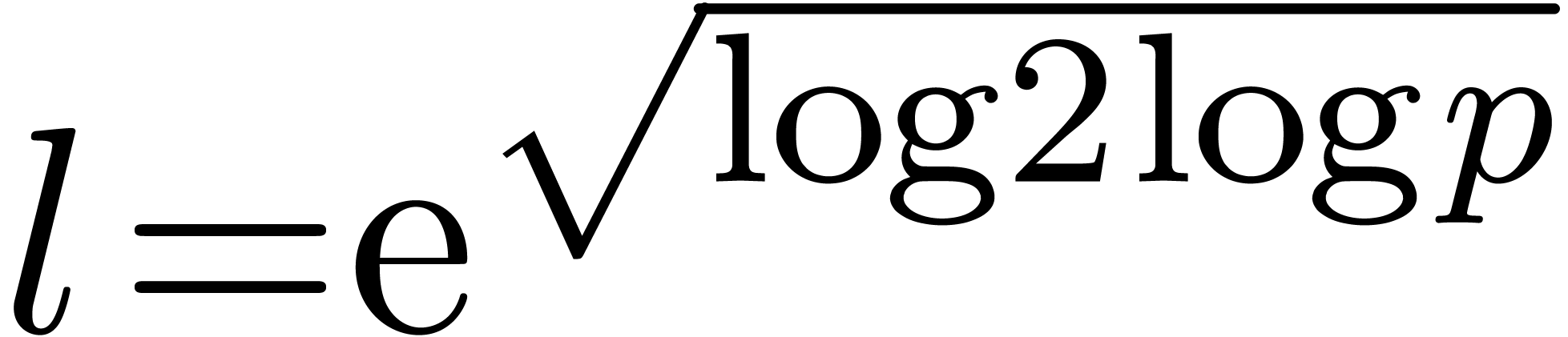 as above, it
follows that
as above, it
follows that
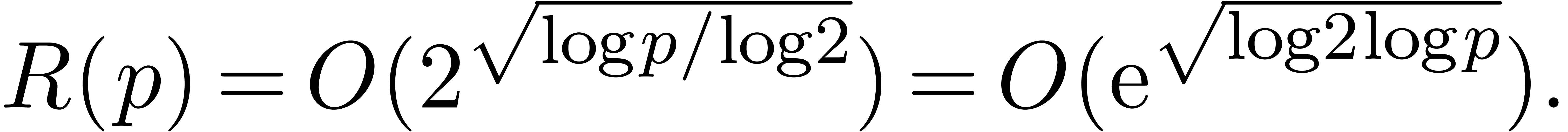
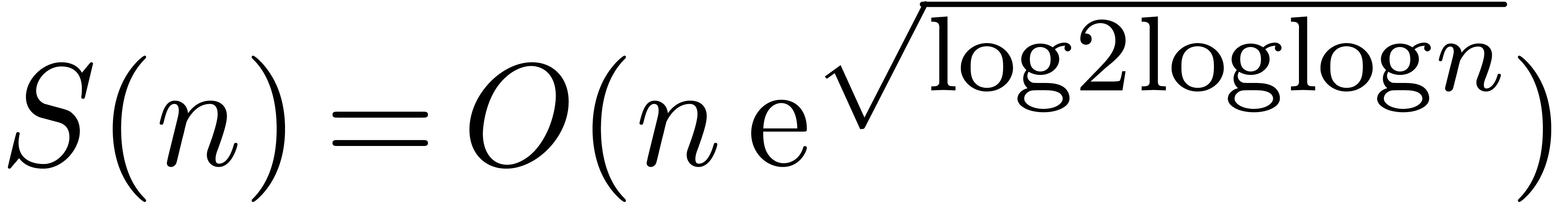
 ,
,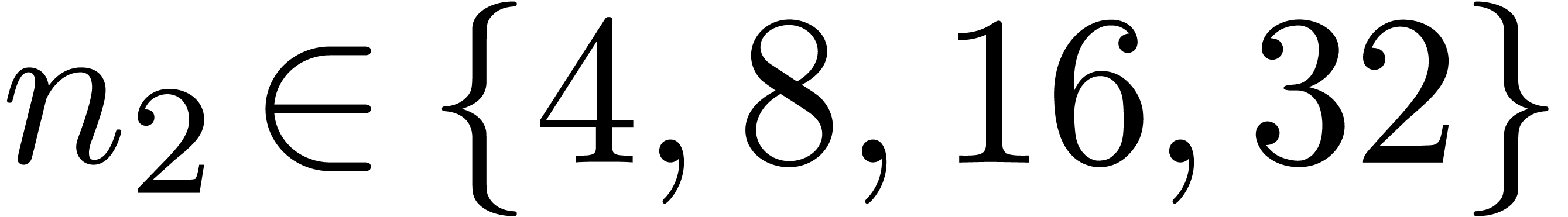 in
the FFT range up to
in
the FFT range up to 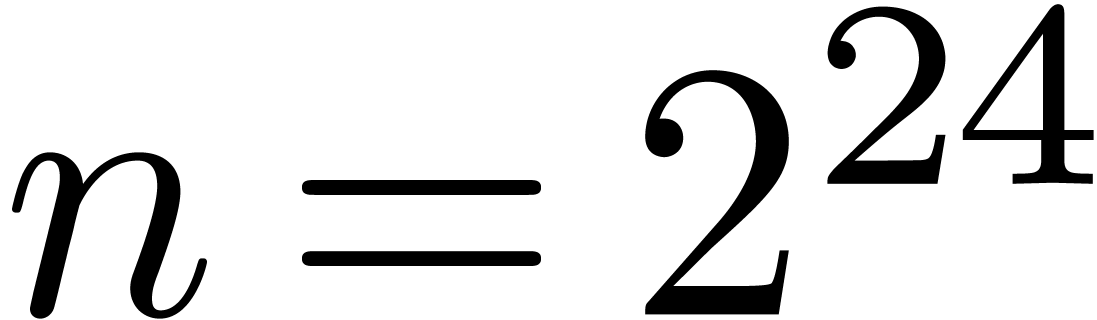 ),
), needs to be
reasonably large in order to profit from the better asymptotic
complexity of relaxed multiplication. In practice, the optimal choice of
needs to be
reasonably large in order to profit from the better asymptotic
complexity of relaxed multiplication. In practice, the optimal choice of
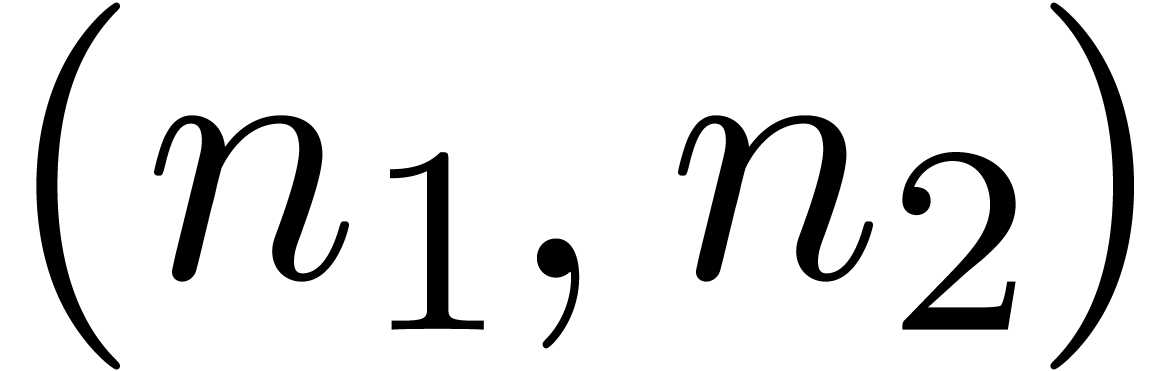 is obtained by taking
is obtained by taking 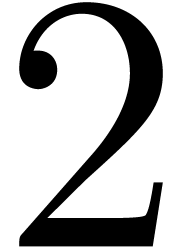 at the top-level. For small values of
at the top-level. For small values of
 ,
, in
in 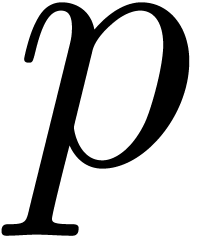 variables with
coefficients
variables with
coefficients 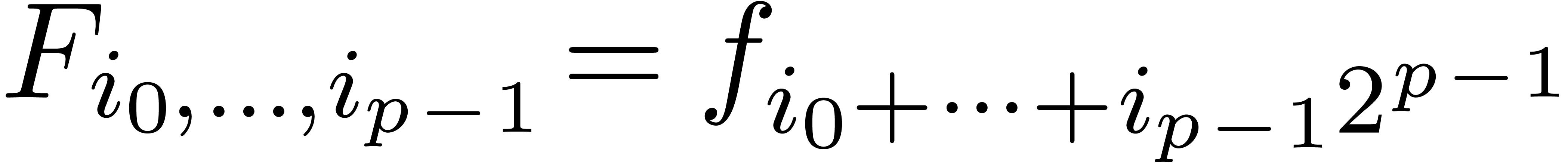 for
for 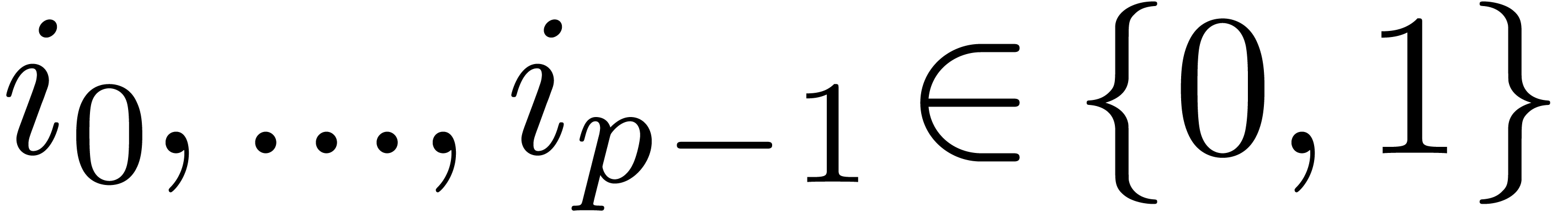 .
.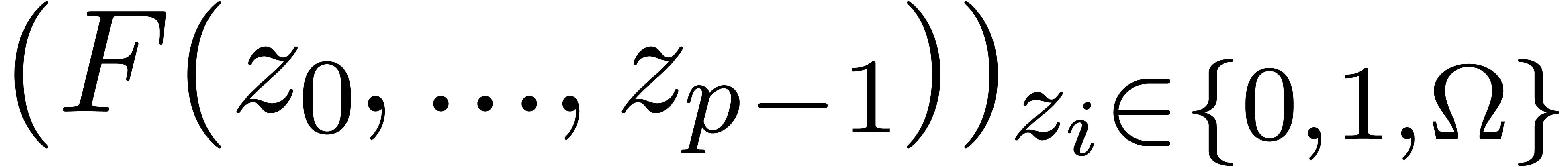 of size
of size 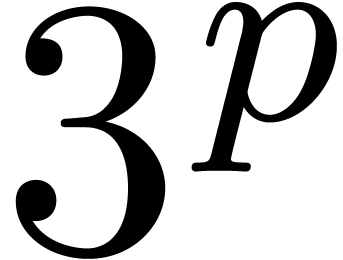 ,
,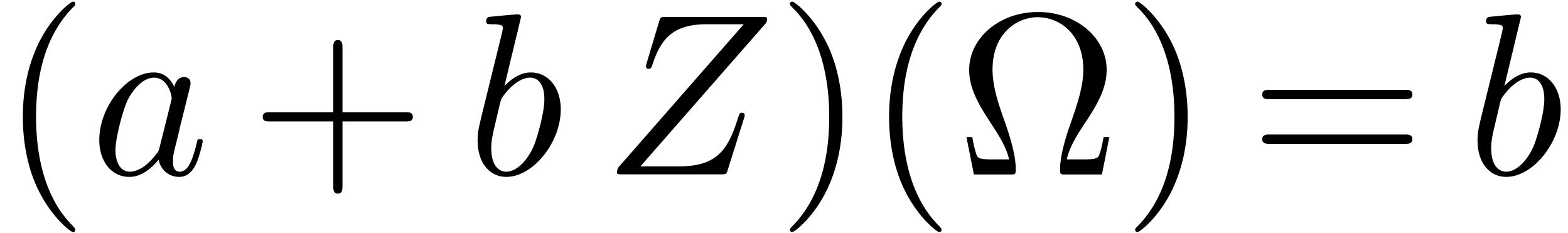 .
. with
with  of memory. The results
of our benchmarks can be found in tables
of memory. The results
of our benchmarks can be found in tables  does not give us any significant advantage,
because the top-level product on FFT-ed blocks is naive. In table
does not give us any significant advantage,
because the top-level product on FFT-ed blocks is naive. In table  on our timings.
on our timings.
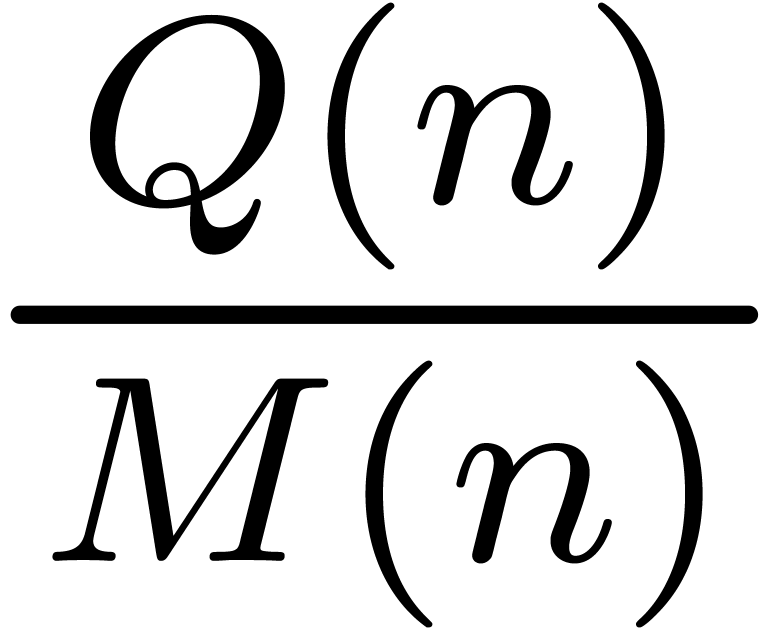
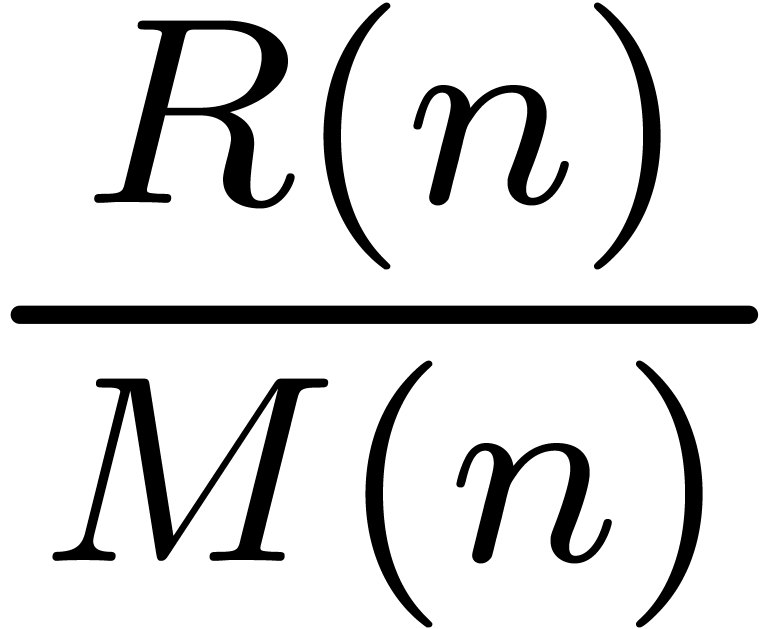
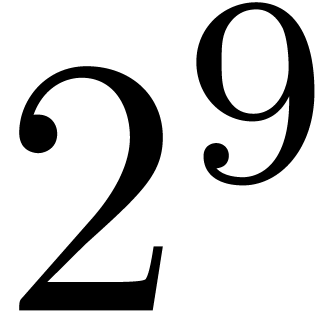
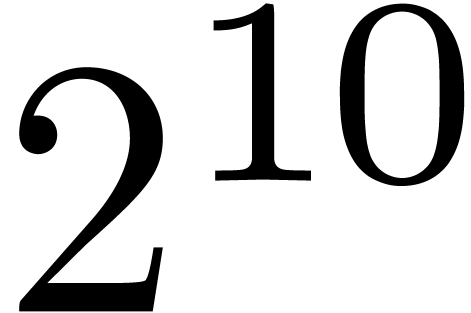
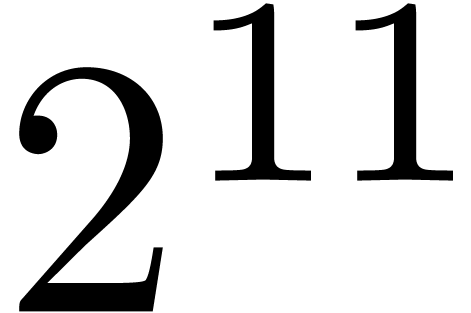
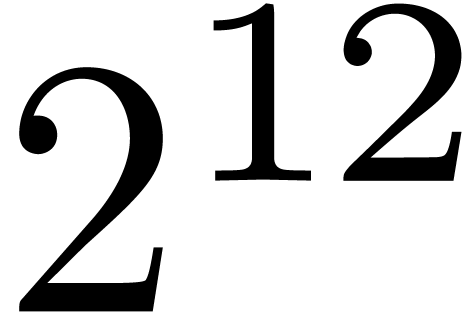
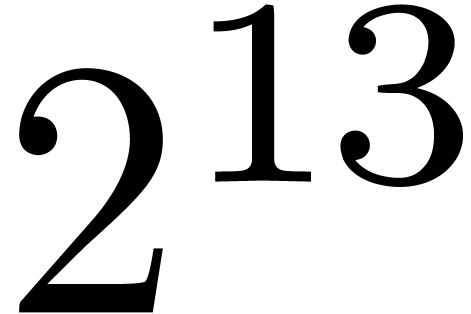
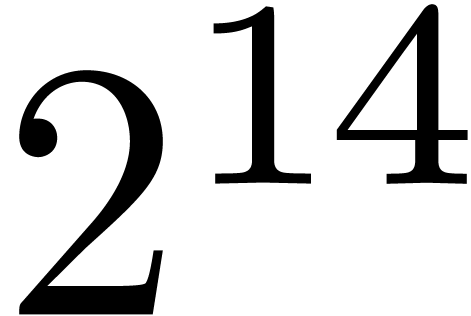
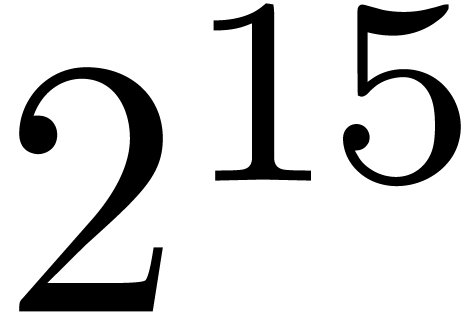
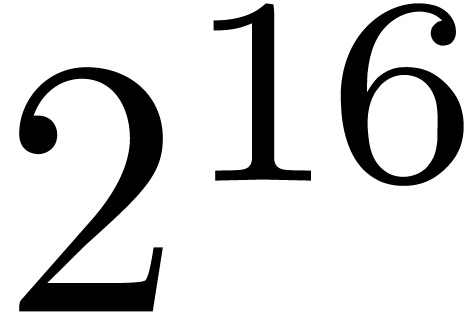
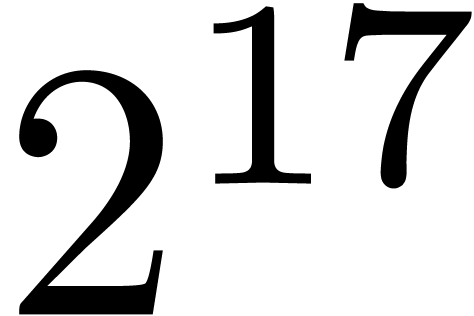
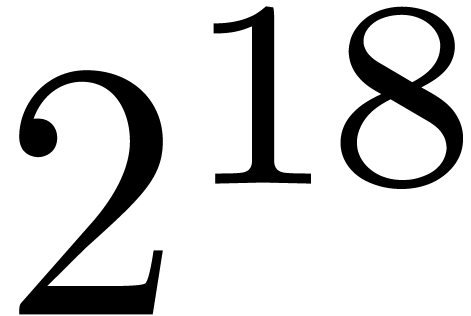
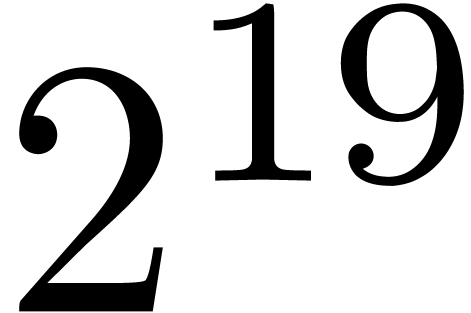
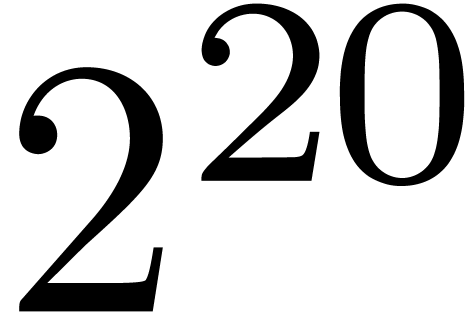
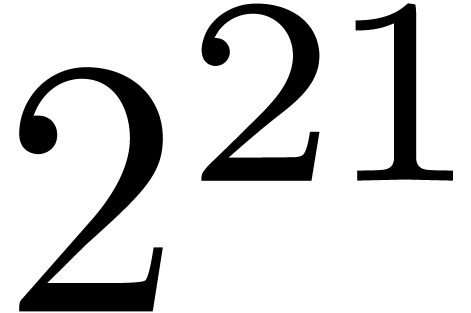
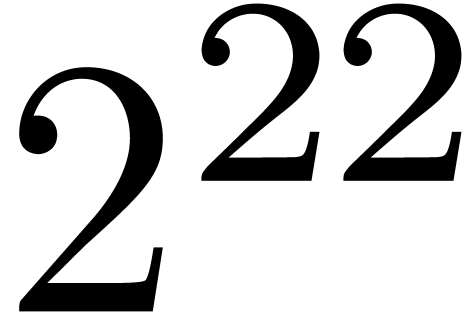
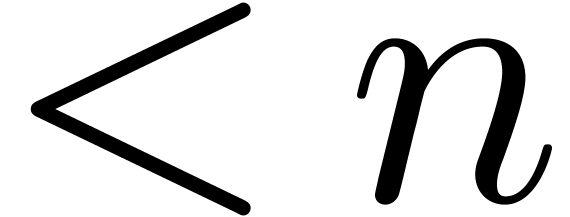 .
.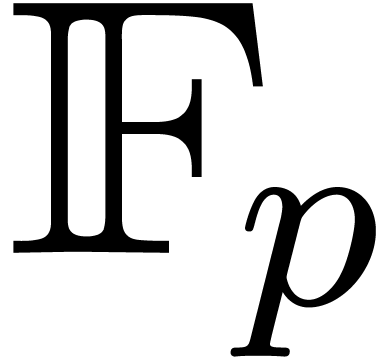
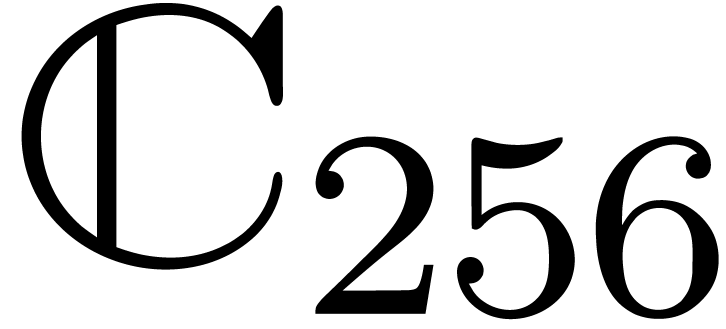
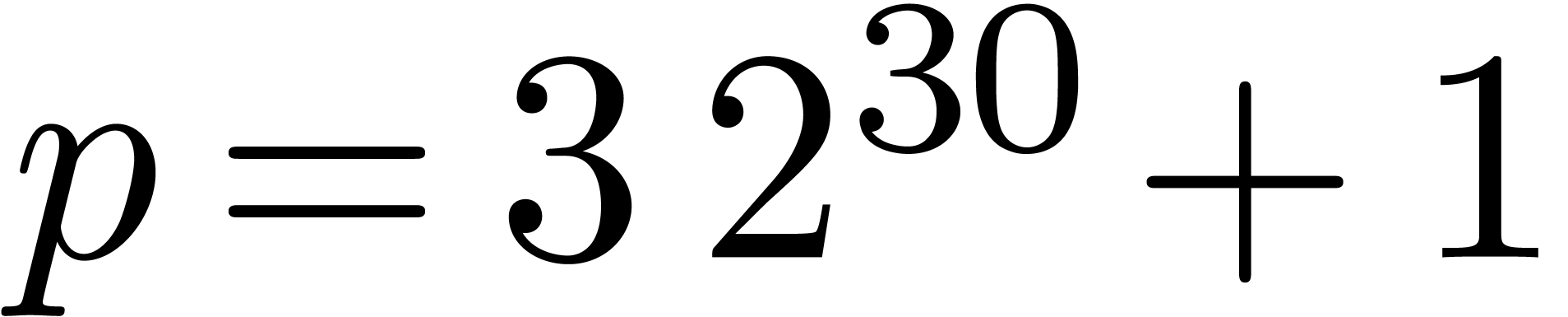 .
.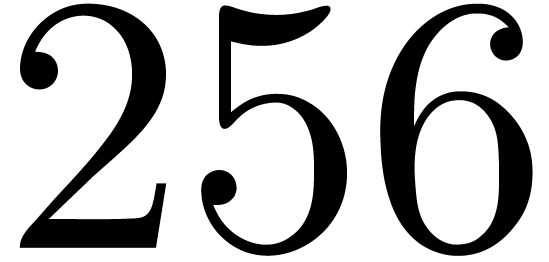 bit complex
floats from the
bit complex
floats from the 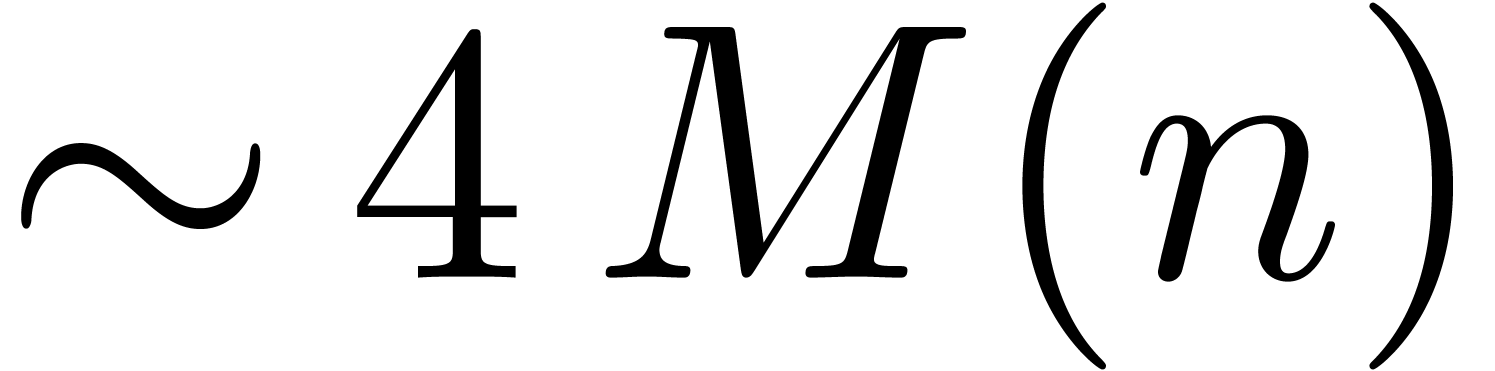 .
.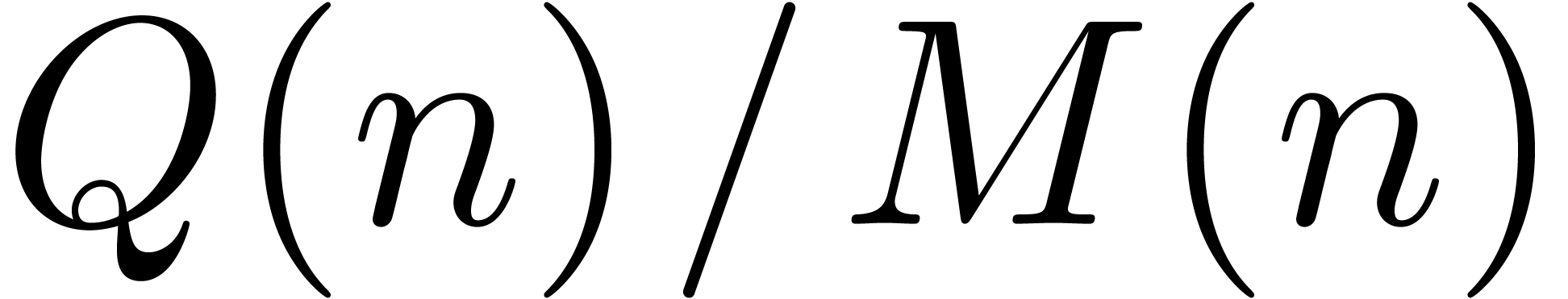 rarely reaches
rarely reaches  in our tables.
Consequently, relaxed algorithms are often better. A similar phenomenon
was already observed in [
in our tables.
Consequently, relaxed algorithms are often better. A similar phenomenon
was already observed in [ )
) (
( )
)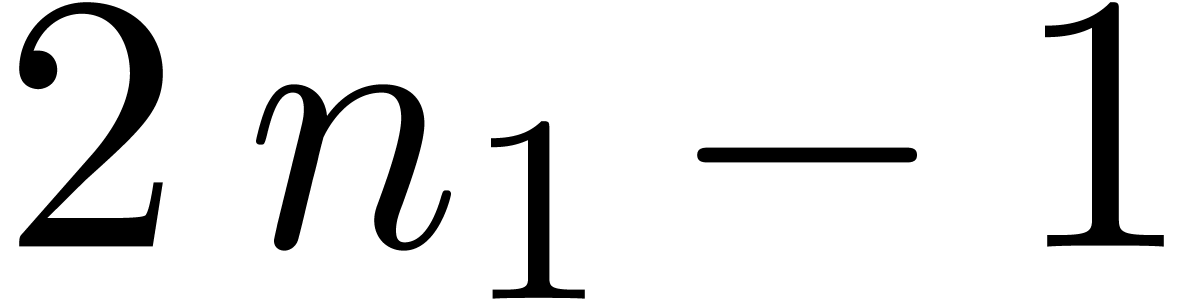 points. From an asymptotic point of view, this yields
points. From an asymptotic point of view, this yields 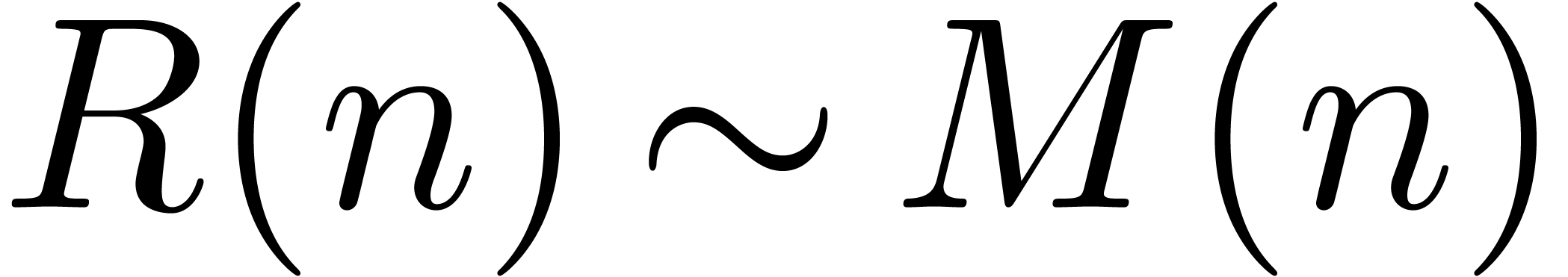 for relaxed multiplication. Moreover, the approach naturally combines
with the generalization of pair/odd decompositions [
for relaxed multiplication. Moreover, the approach naturally combines
with the generalization of pair/odd decompositions [ or
or 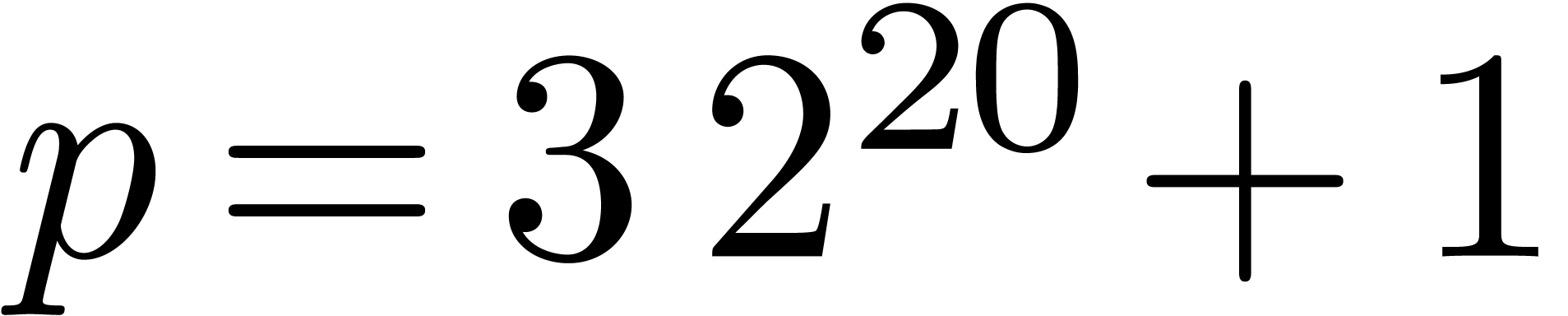 .
.