Effective power series
computations |
|
| Final version of June 15, 2019 |
|
 . This work has
been supported by the ANR-10-BLAN 0109 LEDA project.
. This work has
been supported by the ANR-10-BLAN 0109 LEDA project.
Abstract
Let  be an effective field of
characteristic zero. An effective tribe is a subset of
be an effective field of
characteristic zero. An effective tribe is a subset of  that is effectively stable under the
that is effectively stable under the  -algebra operations, restricted division,
composition, the implicit function theorem, as well as restricted
monomial transformations with arbitrary rational exponents. Given an
effective tribe with an effective zero test, we will prove that an
effective version of the Weierstrass division theorem holds inside the
tribe, and that this can be used for the computation of standard
bases.
-algebra operations, restricted division,
composition, the implicit function theorem, as well as restricted
monomial transformations with arbitrary rational exponents. Given an
effective tribe with an effective zero test, we will prove that an
effective version of the Weierstrass division theorem holds inside the
tribe, and that this can be used for the computation of standard
bases.
Keywords: Power series, algorithm, Weierstrass preparation, standard basis, d-algebraic power series, tribe
There are two main aspects about effective computations with formal power series. On the one hand, we need fast algorithms for the computation of coefficients. There is an important literature on this subject and the asymptotically fastest methods either rely on Newton's method [4] or on relaxed power series evaluation [12].
On the other hand, there is the problem of deciding whether a given power series is zero. This problem is undecidable in general, since we need to check the cancellation of an infinite number of coefficients. Therefore, a related subject is the isolation of sufficiently large classes of power series such that most of the common operations on power series can be carried out inside the class, but such that the class remains sufficiently restricted such that we can design effective zero tests.
The abstract description of a suitable framework for power series
computations is the subject of section 2. We first recall
the most common operations on formal power series over a field  of characteristic zero: the
of characteristic zero: the  -algebra
operations, restricted division, composition, the resolution of implicit
equations, and so called restricted monomial transformations with
arbitrary rational exponents. A subset
-algebra
operations, restricted division, composition, the resolution of implicit
equations, and so called restricted monomial transformations with
arbitrary rational exponents. A subset  of
of  that is stable under each of these operations will be
called a tribe. We will also specify effective counterparts of these
notions.
that is stable under each of these operations will be
called a tribe. We will also specify effective counterparts of these
notions.
The main results of this paper are as follows. Given an effective tribe with an effective zero test, we show in section 4 that the tribe also satisfies an effective version of the Weierstrass preparation theorem [23], and we give an algorithm for performing Weierstrass division with remainder. In section 5, we also introduce “Weierstrass bases” and a recursive version of Weierstrass division that works for ideals. For Archimedean monomial orderings, this can in turn be used for the computation of standard bases of ideals generated by series in the tribe in the sense of Hironaka [10].
Our results can for instance be applied to the tribe of algebraic power series. In that particular case, various alternative algorithms have been developed. An algorithm for Weierstrass division was given in [2]. This algorithm has recently been extended to the computation of reduced standard bases of ideals that satisfy a suitable condition [1] (namely Hironaka's box condition). In the case that the ideals are generated by polynomials instead of power series, one may compute (non-reduced) standard bases using Mora's tangent cone algorithm [20] or Lazard's homogenization technique [17].
The main other example that motivated our work is the tribe of d-algebraic power series (see also [7, 8, 15]). The fact that the collection of all d-algebraic power series satisfies the Weierstrass preparation theorem was first proved in a more ad hoc way by van den Dries [9]. The notion of a tribe also shares some common properties with the notion of a Weierstrass system, as introduced by Denef and Lipshitz [6] and used in [9]. Our approach can be regarded as a simpler, effective and more systematic way to prove that certain types of power series form Weierstrass systems. Moreover, we show how to compute more general standard bases in this context.
The idea behind our main algorithm for the computation of Weierstrass
polynomials is very simple: given a series 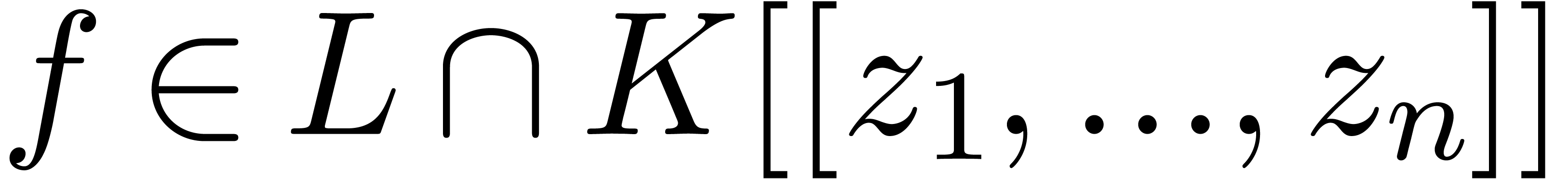 of
Weierstrass degree
of
Weierstrass degree 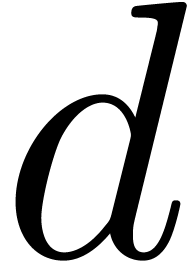 in
in 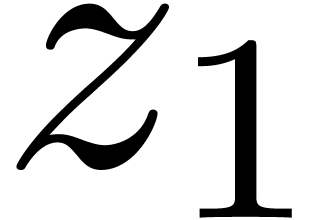 , we just compute the solutions
, we just compute the solutions  of the equation
of the equation 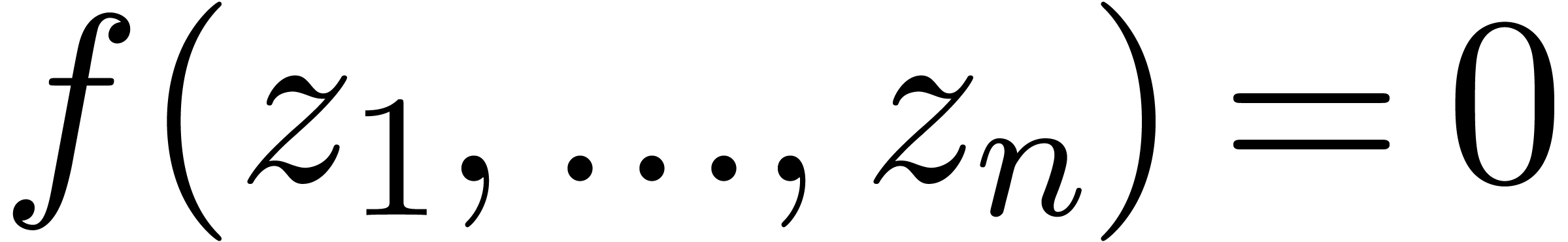 in
in 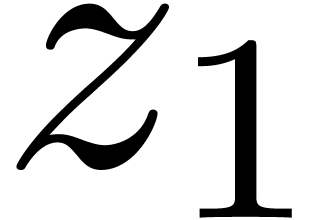 inside a sufficiently large field of grid-based power series. This
allows us to compute the polynomial
inside a sufficiently large field of grid-based power series. This
allows us to compute the polynomial 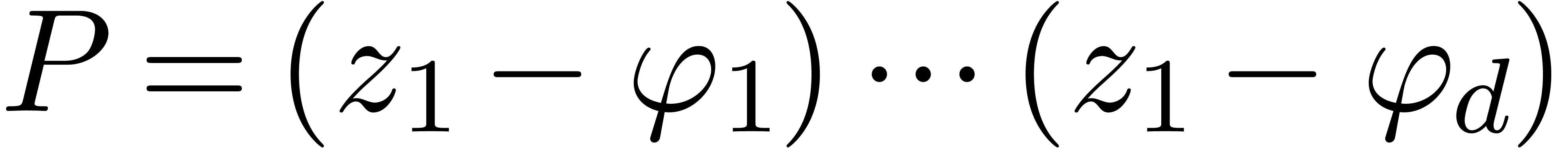 which we
know to be the Weierstrass polynomial associated to
which we
know to be the Weierstrass polynomial associated to  . Using the stability of the tribe
under restricted monomial transformations, we will be able to compute
. Using the stability of the tribe
under restricted monomial transformations, we will be able to compute
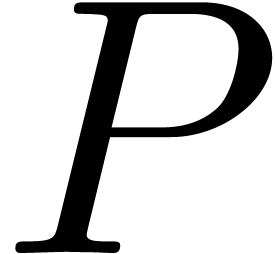 as an element of
as an element of  .
.
The algorithms rely on our ability to compute with the auxiliary
grid-based power series  . For
this reason, we briefly recall some basic facts about grid-based power
series in section 3, as well as the basic techniques that
are needed in order to compute with them.
. For
this reason, we briefly recall some basic facts about grid-based power
series in section 3, as well as the basic techniques that
are needed in order to compute with them.
Weierstrass division is a precursor of the more general notion of
Hironaka division in the particular case of a principal ideal in general
position. For arbitrary ideals in general position (or, more precisely,
in “Weierstrass position”), we introduce a recursive version
of Weierstrass division in section 5. Assuming that such an
ideal  is finitely generated by elements in the
tribe
is finitely generated by elements in the
tribe  , this allows us to
compute a “Weierstrass basis” for
, this allows us to
compute a “Weierstrass basis” for  and to decide ideal membership for other elements of
and to decide ideal membership for other elements of  . Another application is the computation of the
Hilbert function of
. Another application is the computation of the
Hilbert function of  . The
main ingredients in section 5 are the possibility to put
ideals in Weierstrass position modulo a suitable linear change of
variables and ordinary Weierstrass division in the principal ideal case.
For tribes in which we have alternative algorithms for the Weierstrass
preparation theorem, the techniques of section 5 can use
these algorithms instead of the ones from section 4.
. The
main ingredients in section 5 are the possibility to put
ideals in Weierstrass position modulo a suitable linear change of
variables and ordinary Weierstrass division in the principal ideal case.
For tribes in which we have alternative algorithms for the Weierstrass
preparation theorem, the techniques of section 5 can use
these algorithms instead of the ones from section 4.
In the last section 6, we show how to compute more
traditional standard bases of ideals  that are
finitely generated by elements of
that are
finitely generated by elements of  .
The main difficulty with standard bases in the power series setting (in
contrast to Gröbner bases in the polynomial setting) is
termination. This difficulty is overcome by using the fact that we may
compute the Hilbert function of the ideal using the techniques from
section 5. During the construction of a standard basis,
this essentially allows us to decide whether the S-series of two basis
elements reduces to zero or whether it reduces to a series of high
valuation. In general, our algorithm does not compute a reduced standard
basis: it is actually known that such a reduced standard basis does not
necessarily exist. An interesting open question is under which
conditions our algorithm still does compute one. In the algebraic
setting, we already mentioned above that [1] furnishes a
conditional algorithm for the computation of reduced standard bases.
.
The main difficulty with standard bases in the power series setting (in
contrast to Gröbner bases in the polynomial setting) is
termination. This difficulty is overcome by using the fact that we may
compute the Hilbert function of the ideal using the techniques from
section 5. During the construction of a standard basis,
this essentially allows us to decide whether the S-series of two basis
elements reduces to zero or whether it reduces to a series of high
valuation. In general, our algorithm does not compute a reduced standard
basis: it is actually known that such a reduced standard basis does not
necessarily exist. An interesting open question is under which
conditions our algorithm still does compute one. In the algebraic
setting, we already mentioned above that [1] furnishes a
conditional algorithm for the computation of reduced standard bases.
Our paper uses several notations from the theory of grid-based power series [13] that are uncommon in the area of standard bases. For instance, admissible orderings are replaced by monomial orderings, initial monomials by dominant monomials, and Weierstrass position is reminiscent of Hironaka's box condition that is essential in [1]. The general motivation behind our notations is their natural asymptotic meaning. They have been very useful for the development of asymptotic differential algebra and we refer the reader to [3] for a more extensive background and dictionary.
Acknowledgments. The author wishes to express his gratitude to the two referees for their careful reading and helpful comments, as well as to Alin Bostan and Lou van den Dries for historical references.
Let  be a field of characteristic zero and denote
be a field of characteristic zero and denote
where we understand that  is naturally included
in
is naturally included
in  for each
for each 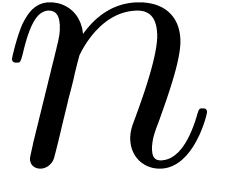 .
So each element
.
So each element 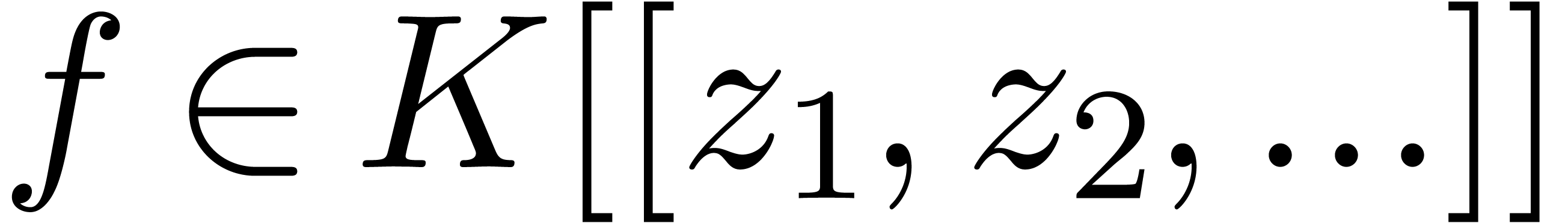 is a power series in a finite
number of variables.
is a power series in a finite
number of variables.
We say that  is effective if its
elements can be represented by concrete data structures and if all field
operations can be carried out by algorithms. We say that
is effective if its
elements can be represented by concrete data structures and if all field
operations can be carried out by algorithms. We say that  admits an effective zero test if we also have an
algorithm that takes
admits an effective zero test if we also have an
algorithm that takes 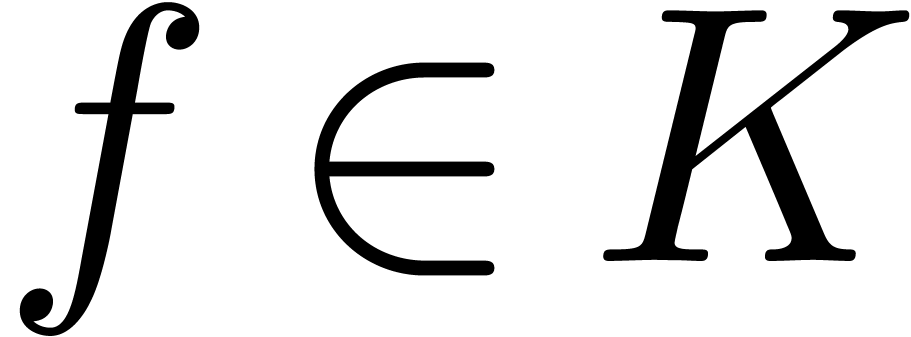 as input and that returns
true if
as input and that returns
true if 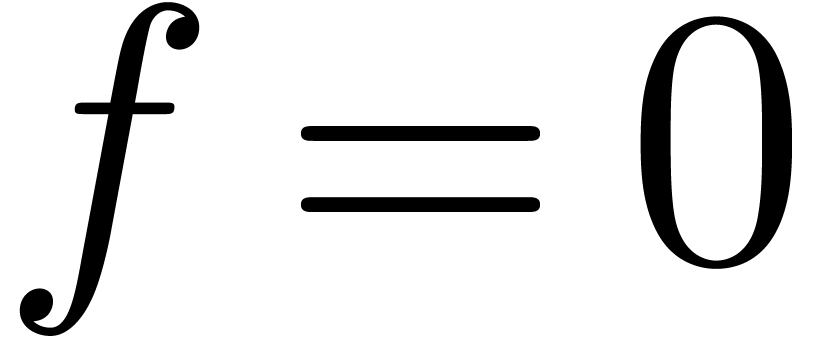 and
false otherwise.
and
false otherwise.
If  is effective, then a power series
is effective, then a power series 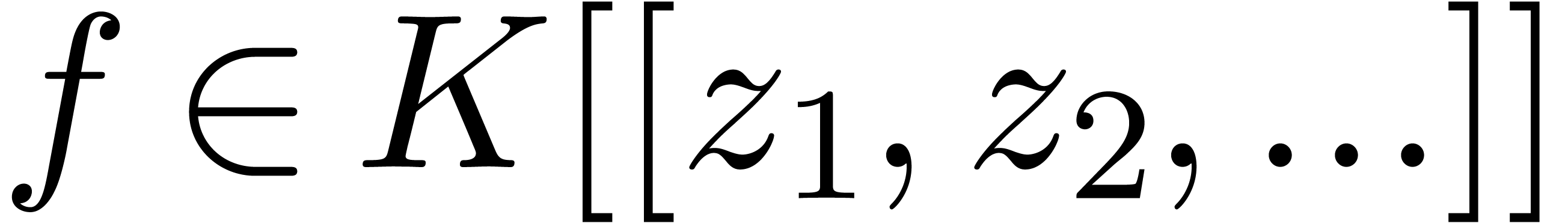 is said to be computable if we have an effective
bound
is said to be computable if we have an effective
bound 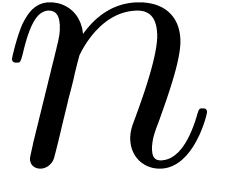 for its dimension (so that
for its dimension (so that 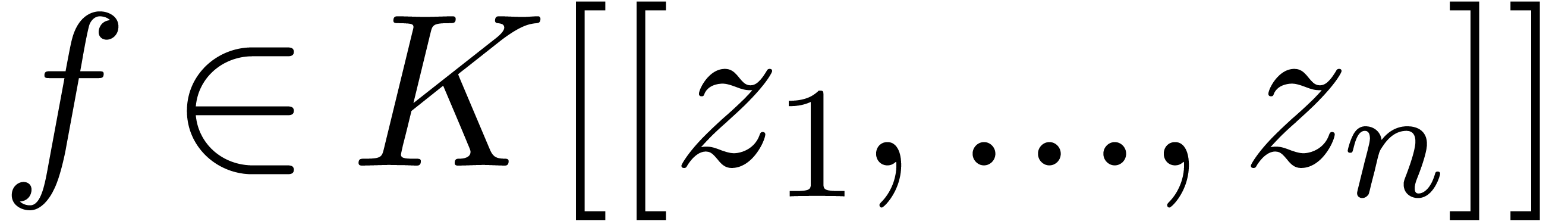 ), together with an algorithm that takes
), together with an algorithm that takes 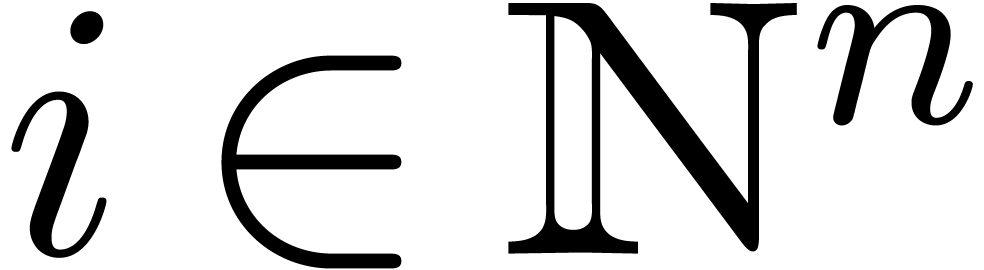 as input and produces the coefficient
as input and produces the coefficient  of
of 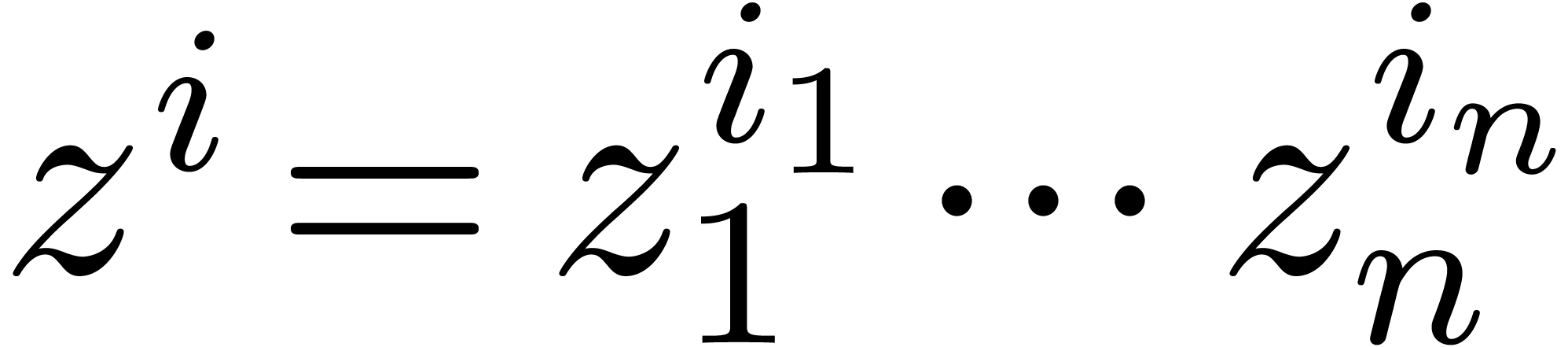 on output. We will denote the
set of computable power series by
on output. We will denote the
set of computable power series by 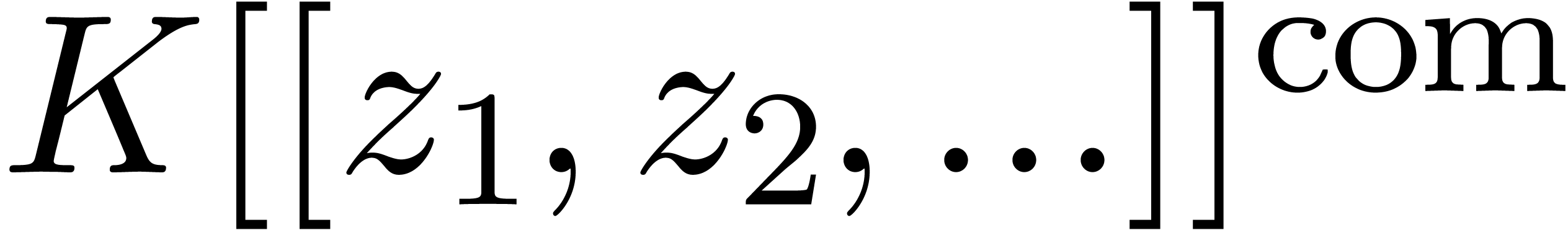 .
.
Let  be a subset of
be a subset of 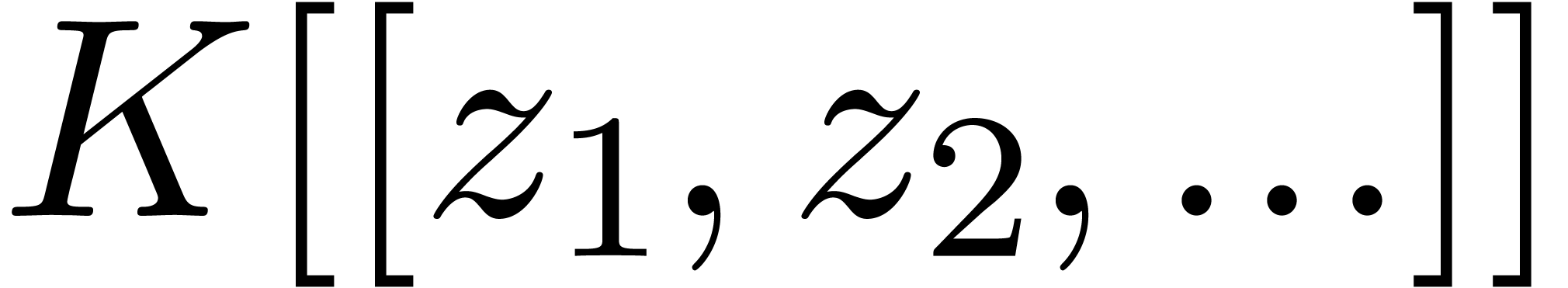 .
We will denote
.
We will denote 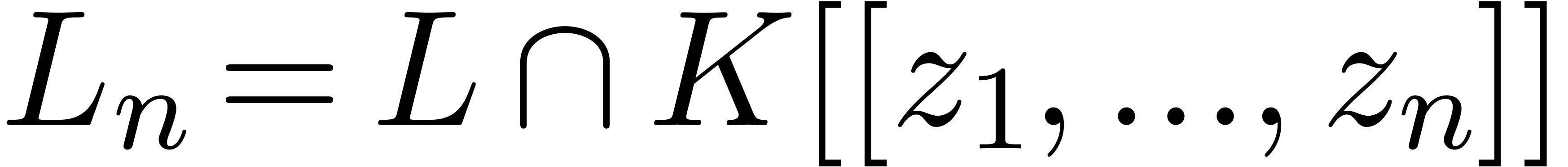 for each
for each  and say that
and say that  is effective if
is effective if  . In this section, we will give
definitions of several operations on power series and the corresponding
closure properties that
. In this section, we will give
definitions of several operations on power series and the corresponding
closure properties that  may satisfy. We say that
may satisfy. We say that
 is a power series algebra if
is a power series algebra if  is a
is a  -algebra.
From now on, we will always assume that this is the case. It is also
useful to assume that
-algebra.
From now on, we will always assume that this is the case. It is also
useful to assume that  is inhabited in
the sense that
is inhabited in
the sense that  for all
for all 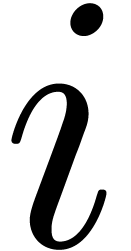 . For each
. For each 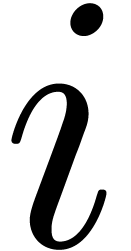 ,
we will denote
,
we will denote 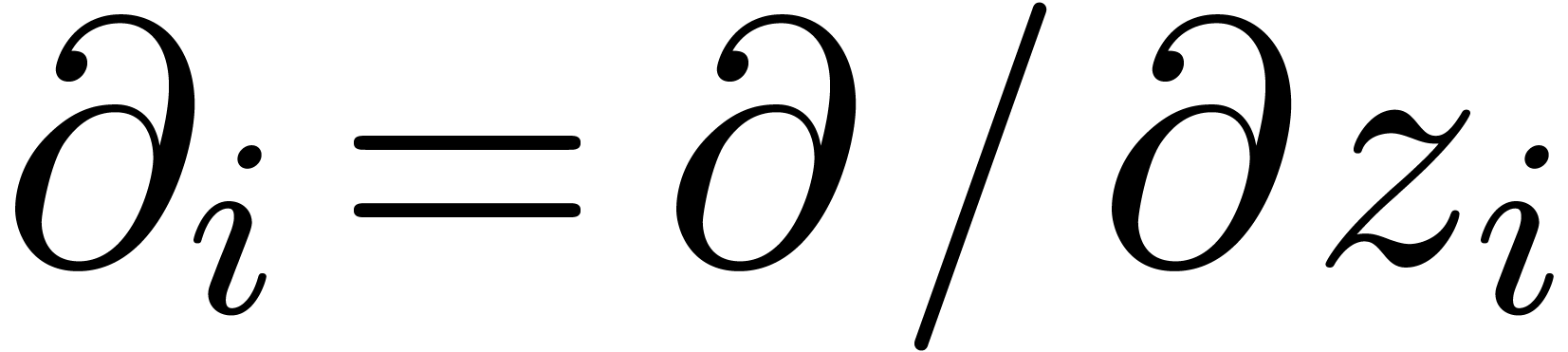 and
and 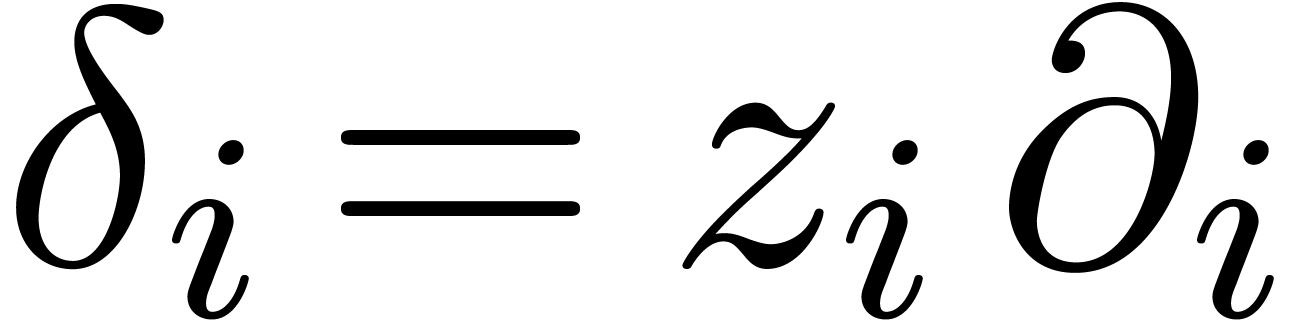 .
We say that
.
We say that  is stable under
differentiation if
is stable under
differentiation if  for all
for all  (whence
(whence 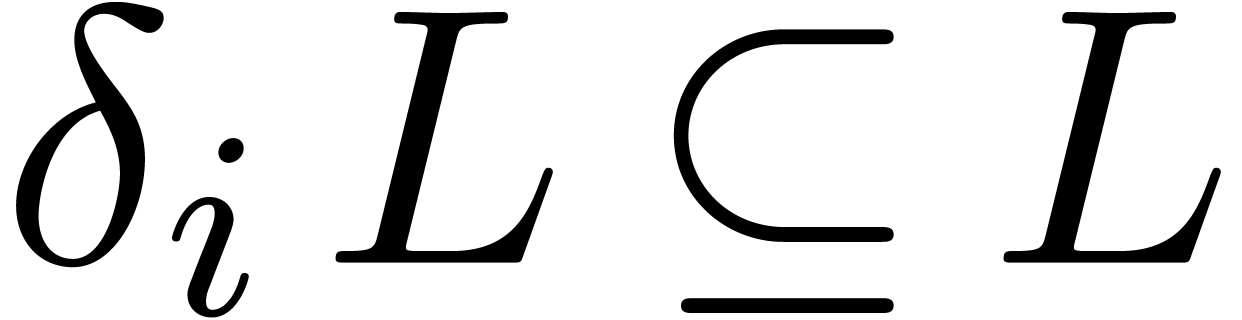 ).
).
The above closure properties admit natural effective analogues. We say
that  is an effective power series
algebra if
is an effective power series
algebra if  is an effective field, if the
elements of
is an effective field, if the
elements of  can be represented by concrete data
structures and the
can be represented by concrete data
structures and the  -algebra
operations can be carried out by algorithms. We say that
-algebra
operations can be carried out by algorithms. We say that  is effectively inhabited if there is an algorithm
that takes
is effectively inhabited if there is an algorithm
that takes 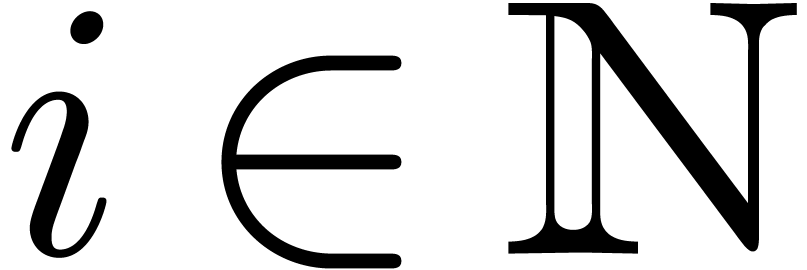 as input and that computes
as input and that computes  . We say that
. We say that  is effectively stable under differentiation if there exists an
algorithm that takes
is effectively stable under differentiation if there exists an
algorithm that takes  and
and 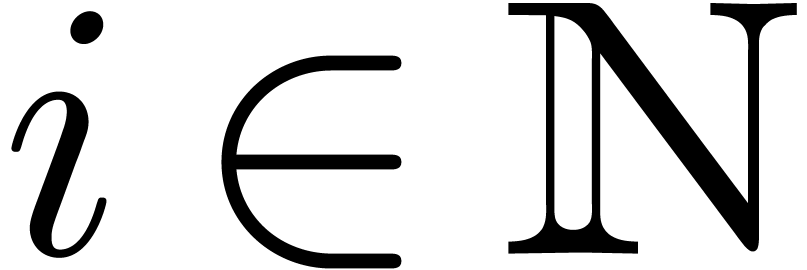 as input and that computes
as input and that computes 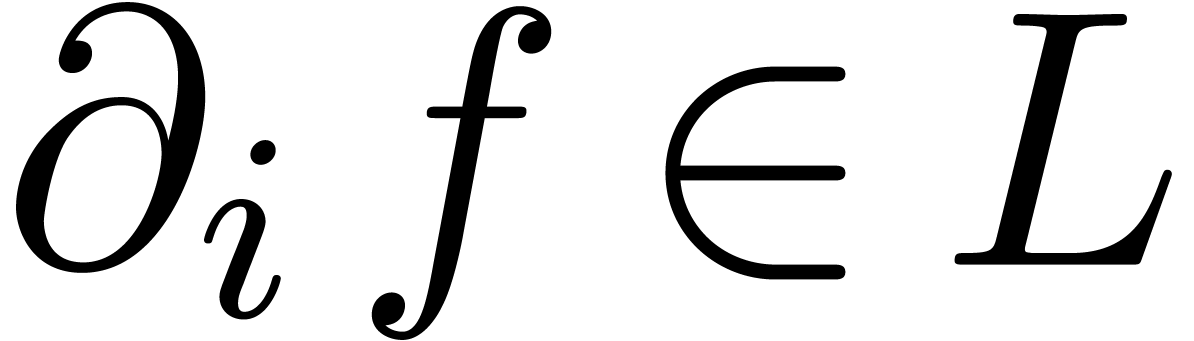 .
.
For any ring  , let
, let 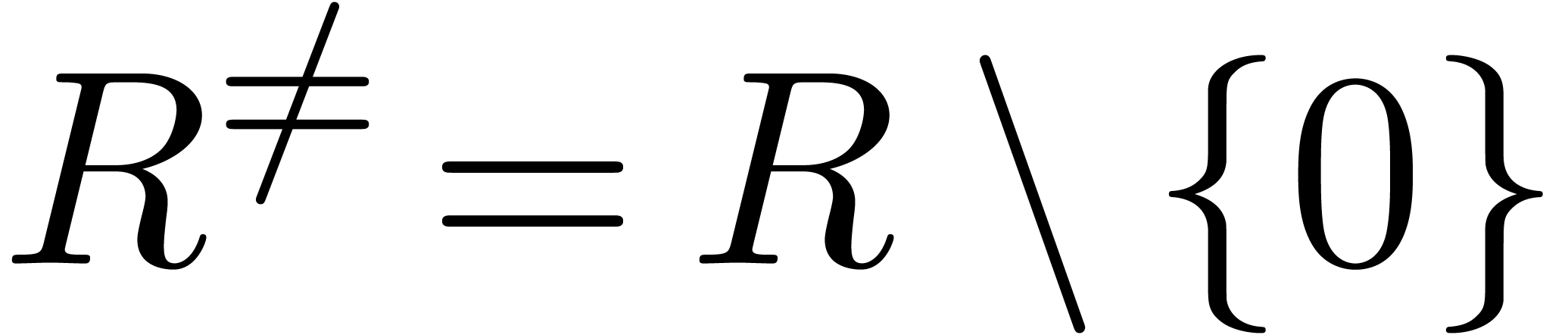 . We say that
. We say that  is stable under restricted division if
is stable under restricted division if 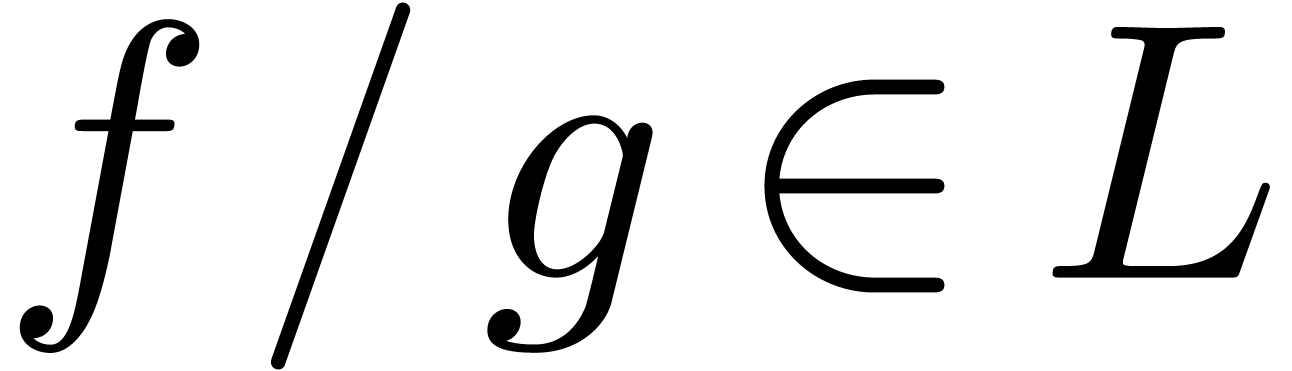 whenever
whenever  and
and 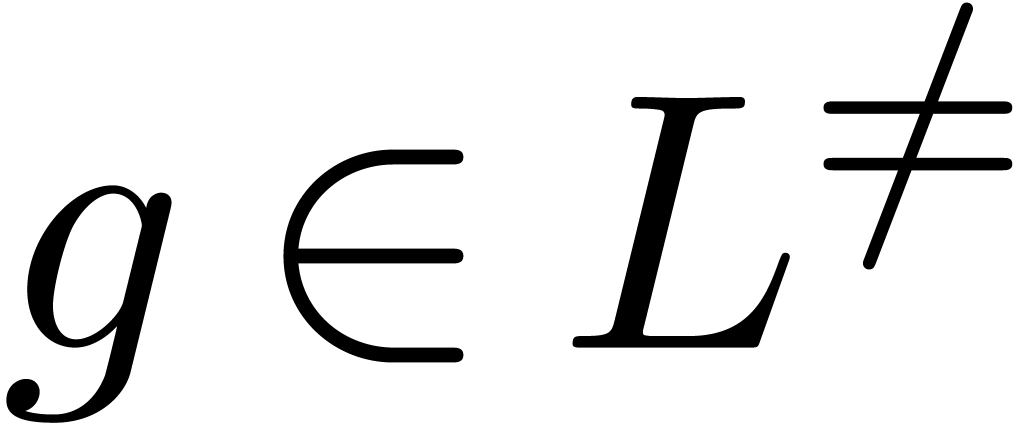 are such
that
are such
that 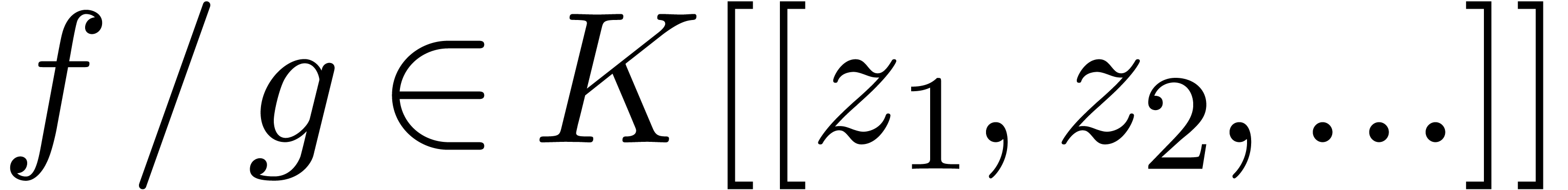 . If
. If  is effective, then we say that
is effective, then we say that  is
effectively stable under restricted division if we also have an
algorithm that computes
is
effectively stable under restricted division if we also have an
algorithm that computes 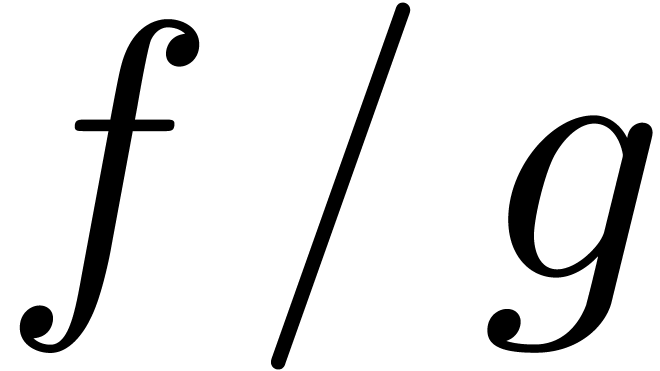 as a function of
as a function of 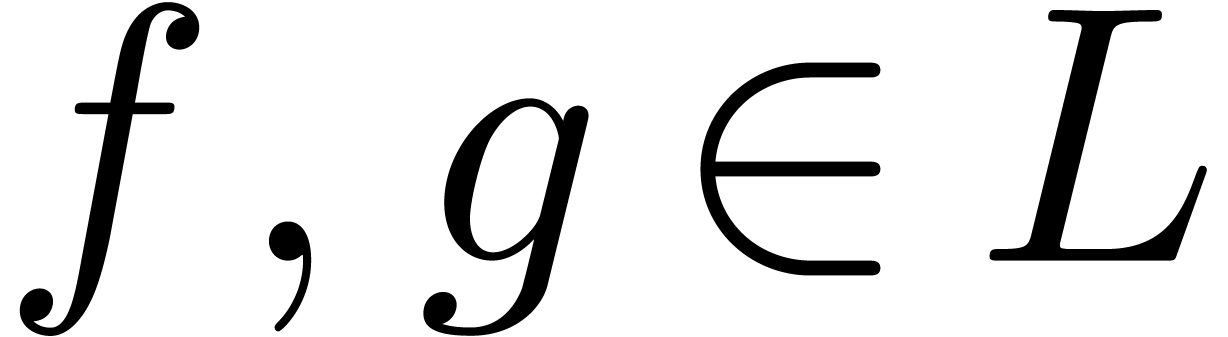 , whenever
, whenever 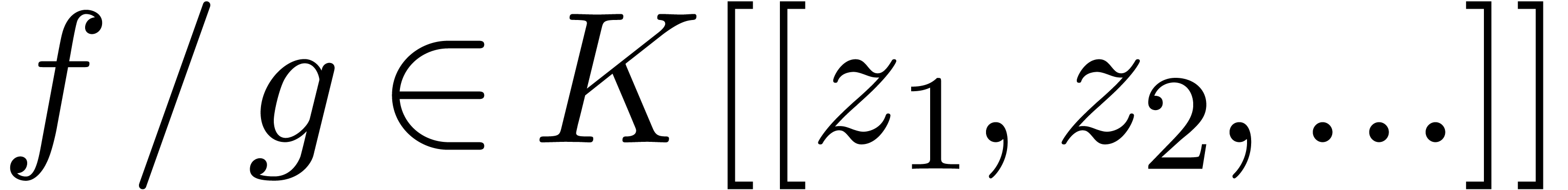 . Here we do not assume the existence of a
test whether
. Here we do not assume the existence of a
test whether 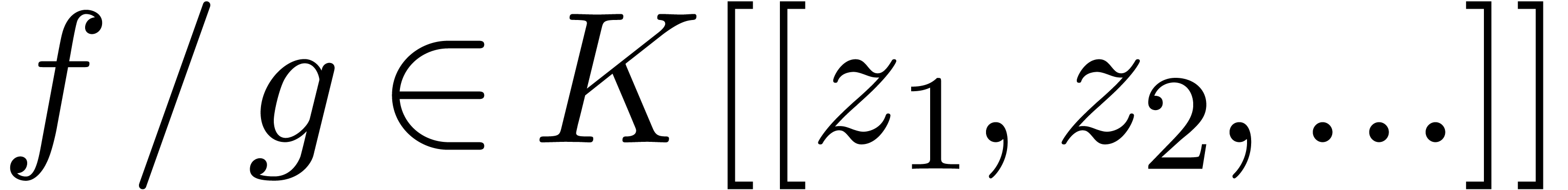 (the behaviour of the algorithm
being unspecified if
(the behaviour of the algorithm
being unspecified if 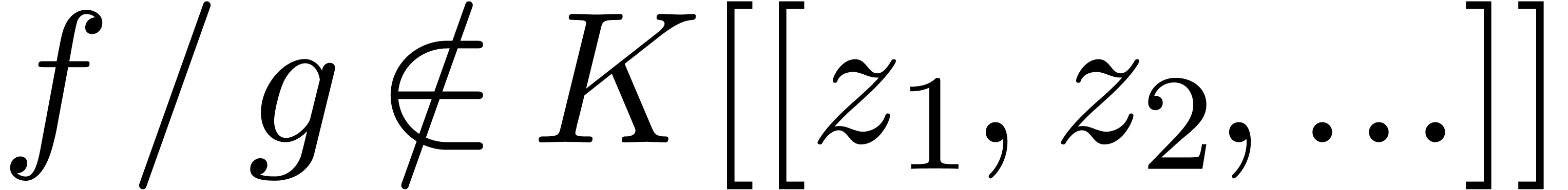 ). More
generally, given
). More
generally, given 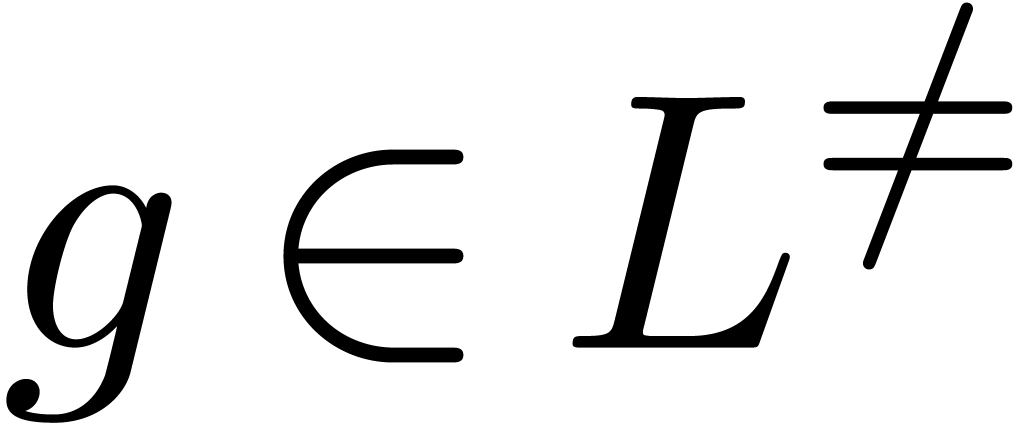 , we say
that
, we say
that  is stable under restricted division by
is stable under restricted division by
 if
if 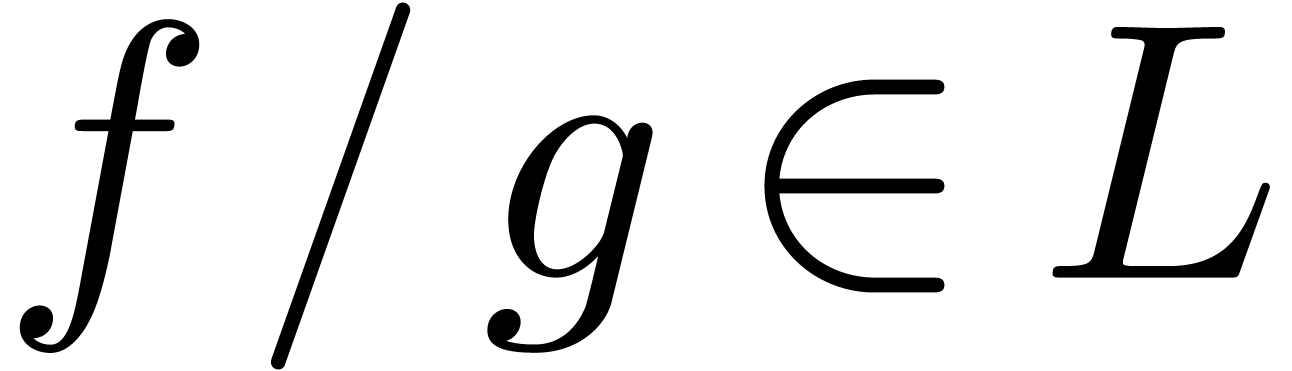 whenever
whenever 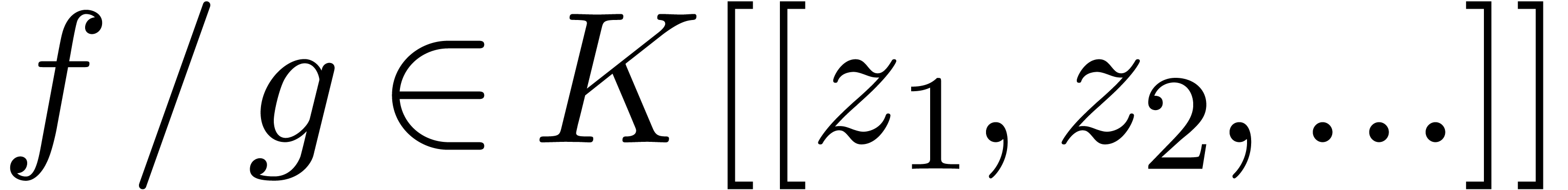 , and that
, and that  is effectively stable under restricted division by
is effectively stable under restricted division by  if this division can be carried out by an algorithm.
if this division can be carried out by an algorithm.
Given 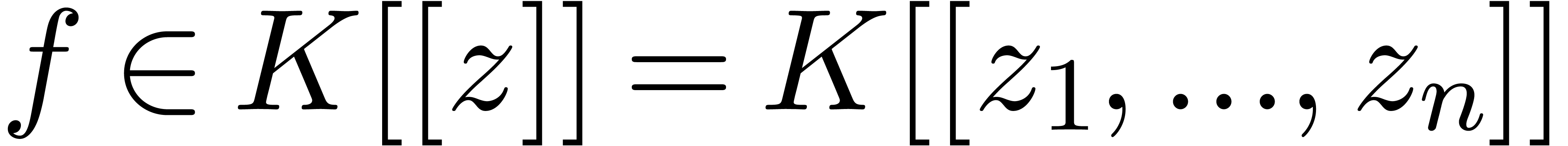 , we let
, we let  denote the evaluation of
denote the evaluation of  at
at 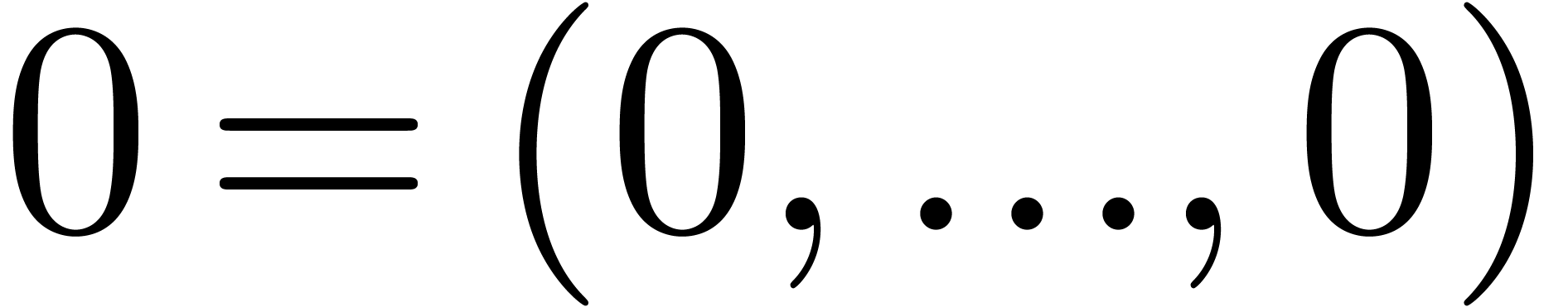 . Given
. Given 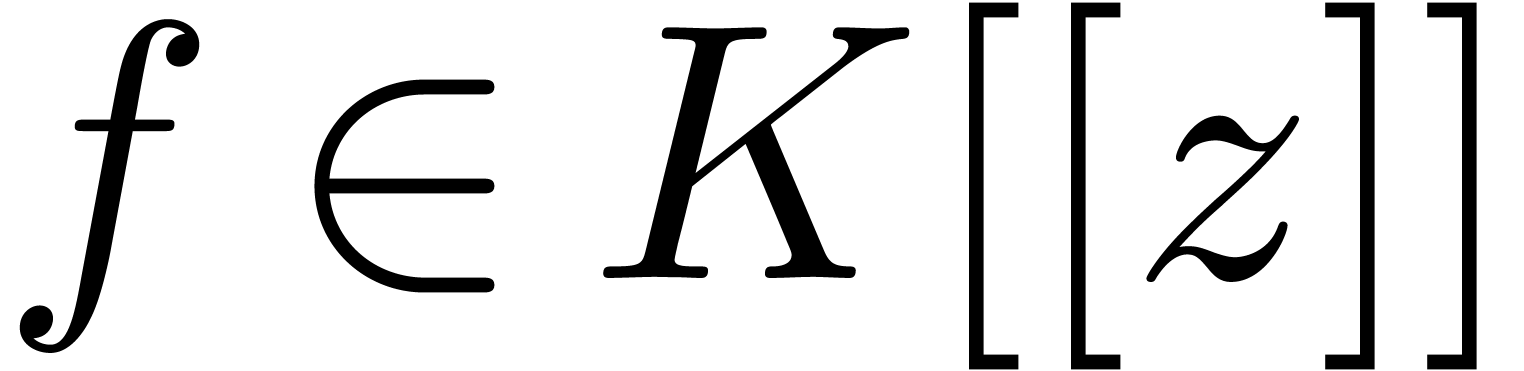 and
and
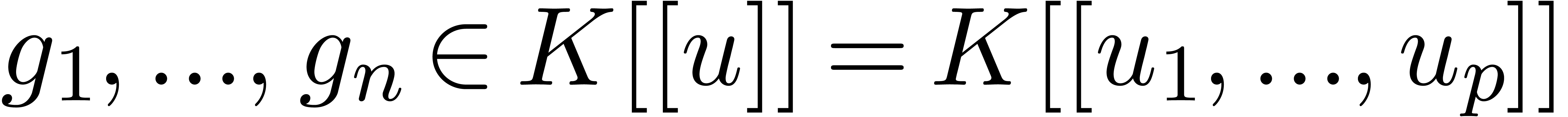 with
with  ,
we define the composition
,
we define the composition  of
of  and
and  to be the unique power series
to be the unique power series  with
with
We say that a power series domain  is stable
under composition if
is stable
under composition if  for any
for any 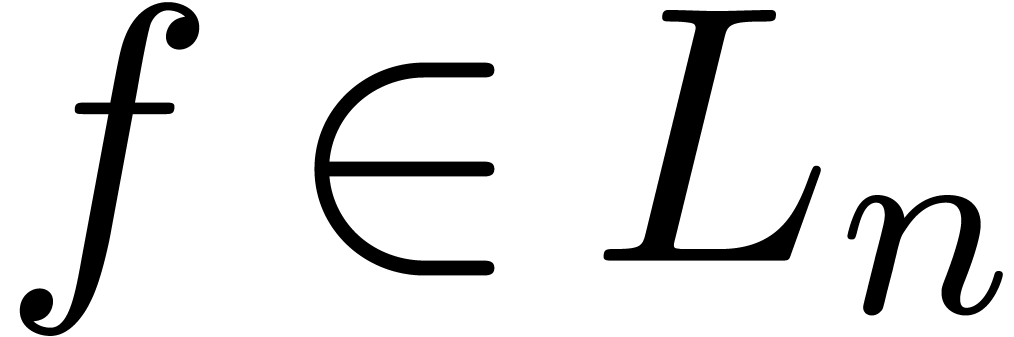 and
and 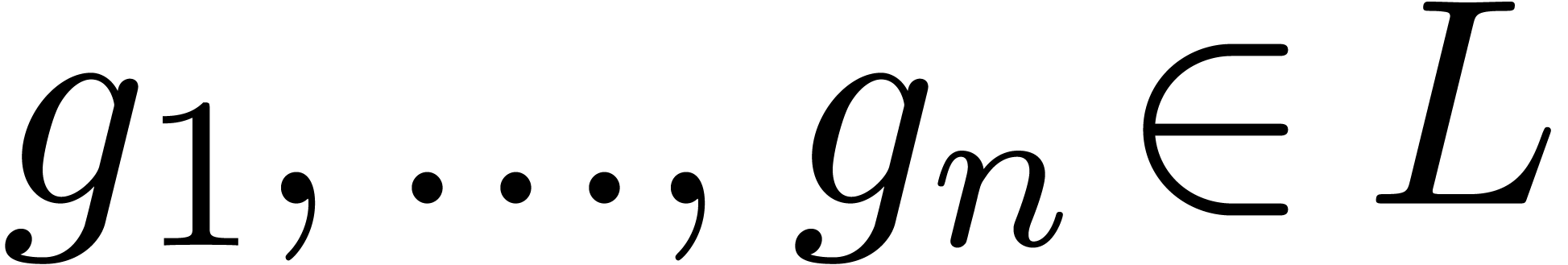 with
with 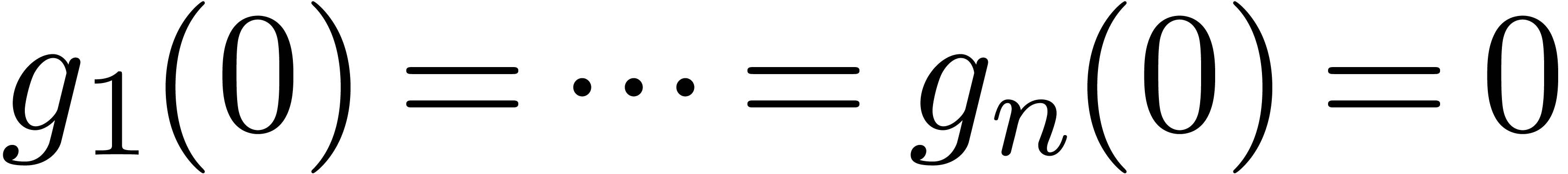 . If we also have an algorithm for the computation
of
. If we also have an algorithm for the computation
of 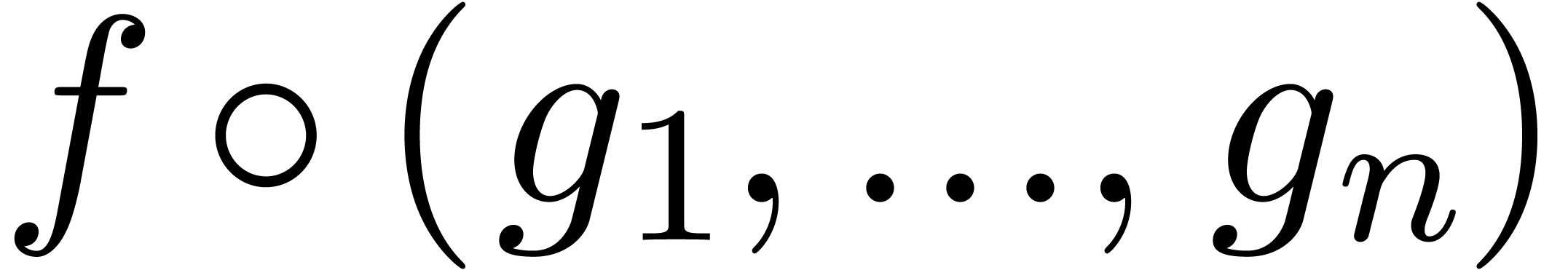 , then we say that
, then we say that  is effectively stable under composition.
is effectively stable under composition.
We notice that stability under composition implies stability under
permutations of the 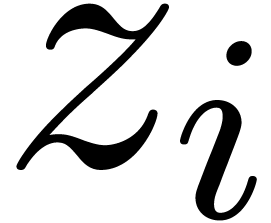 . In
particular, it suffices that
. In
particular, it suffices that  for
for  to be inhabited. Stability under composition also implies
stability under the projections
to be inhabited. Stability under composition also implies
stability under the projections 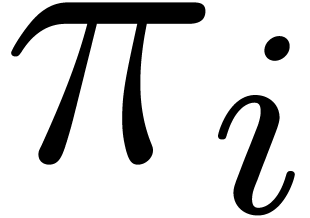 with
with
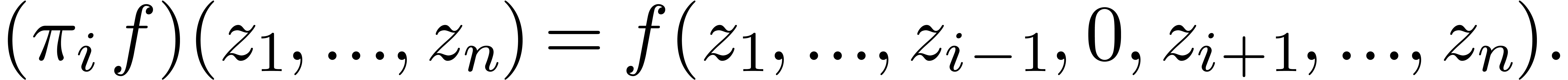
If  is also stable under restricted division by
is also stable under restricted division by
 (whence under restricted division by any
(whence under restricted division by any  ), then this means that we may
compute the coefficients
), then this means that we may
compute the coefficients  of the power series
expansion of
of the power series
expansion of  with respect to
with respect to  by induction over
by induction over  :
:
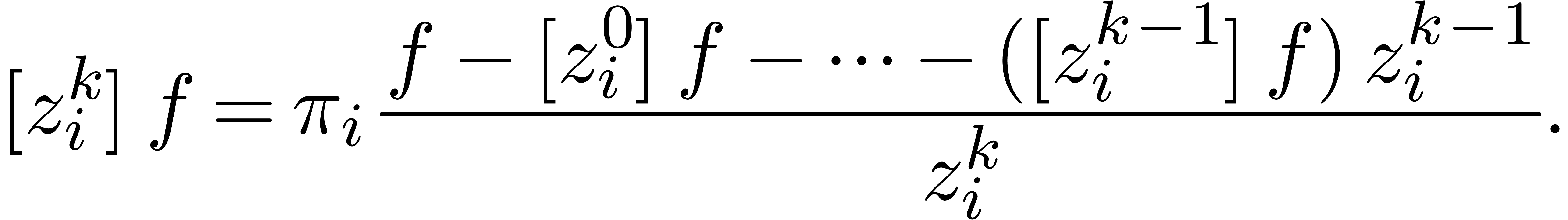
Similarly, we obtain stability under the differentiation: for any 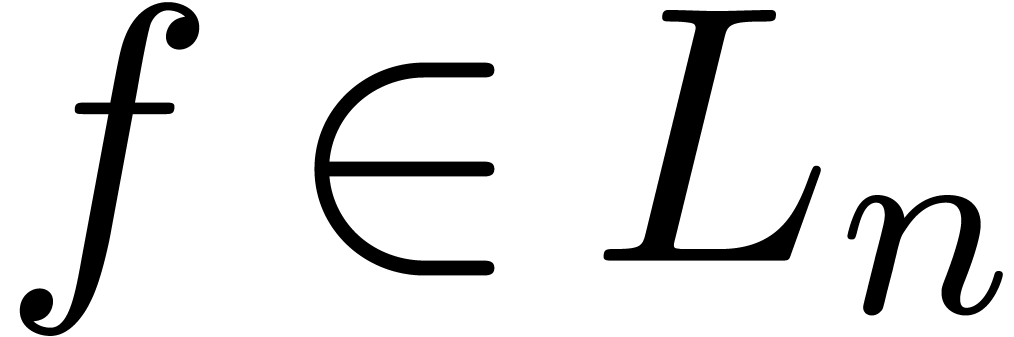 and
and 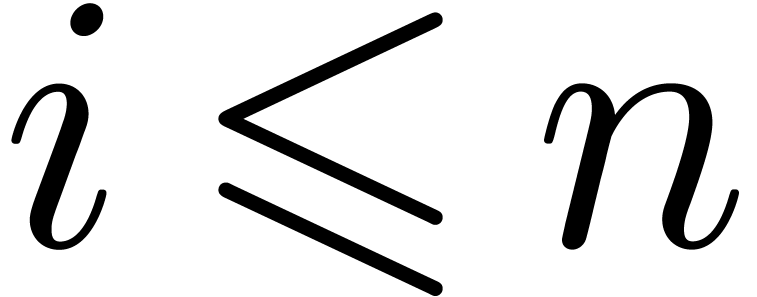 , we
have
, we
have
Let 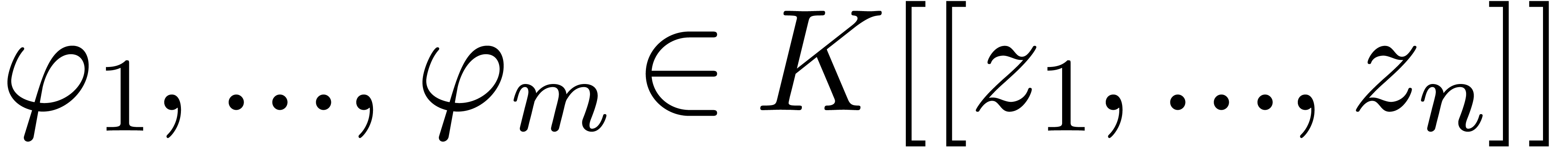 with
with 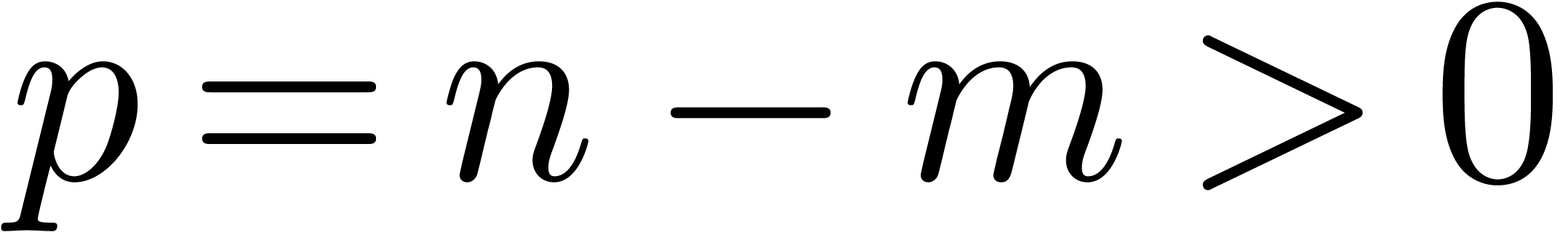 and
and 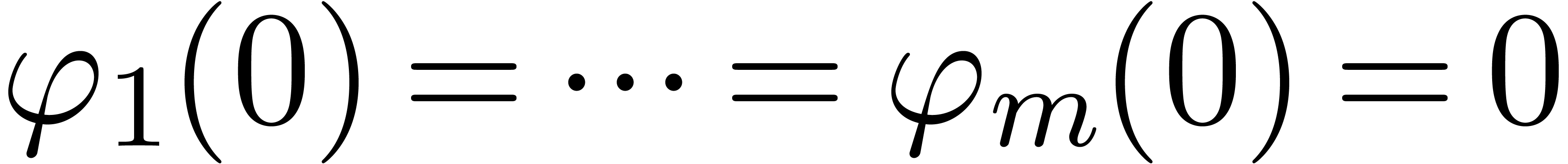 . Assume that the matrix formed by
the first
. Assume that the matrix formed by
the first 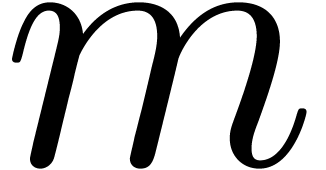 columns of the scalar matrix
columns of the scalar matrix
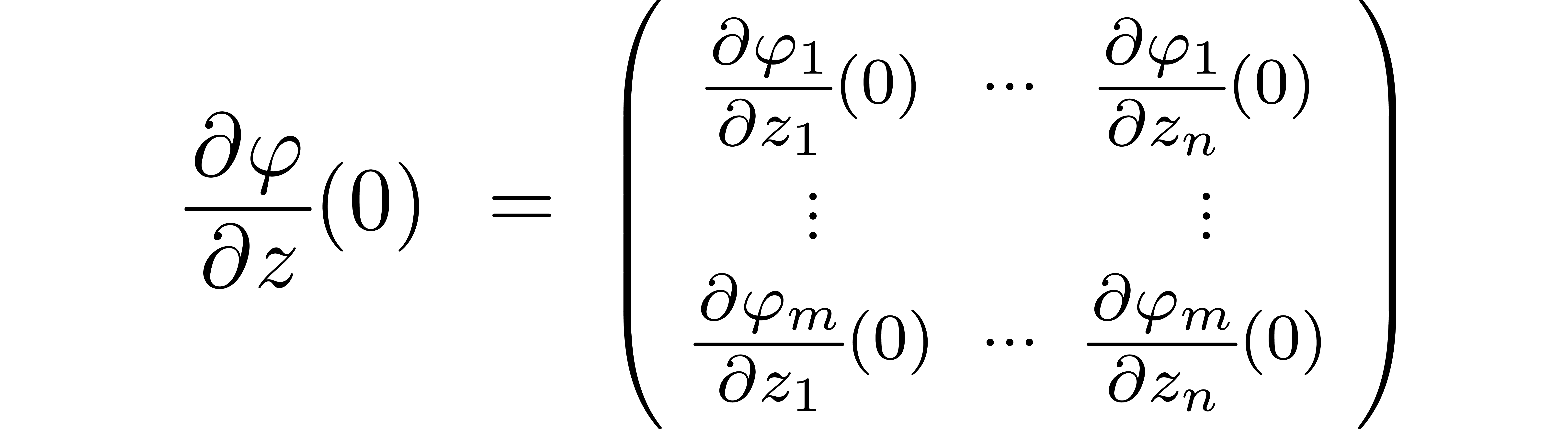
is invertible. Then the implicit function theorem implies that there
exist unique power series 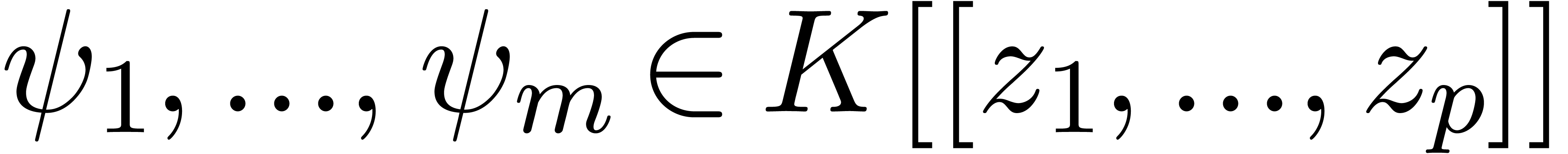 ,
such that the completed vector
,
such that the completed vector 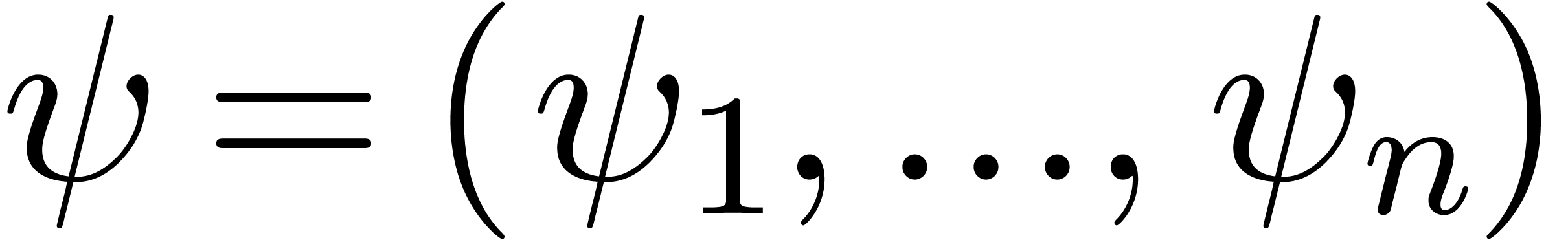 with
with 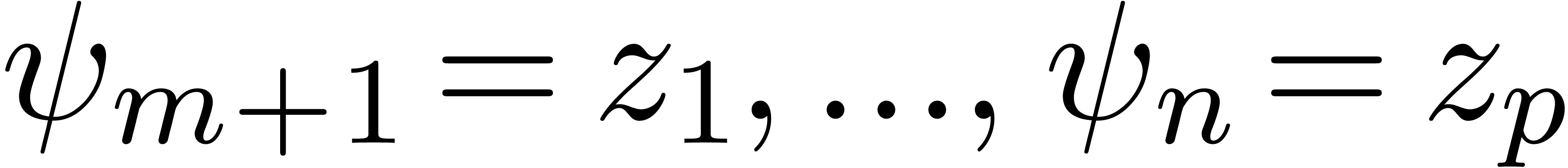 satisfies
satisfies 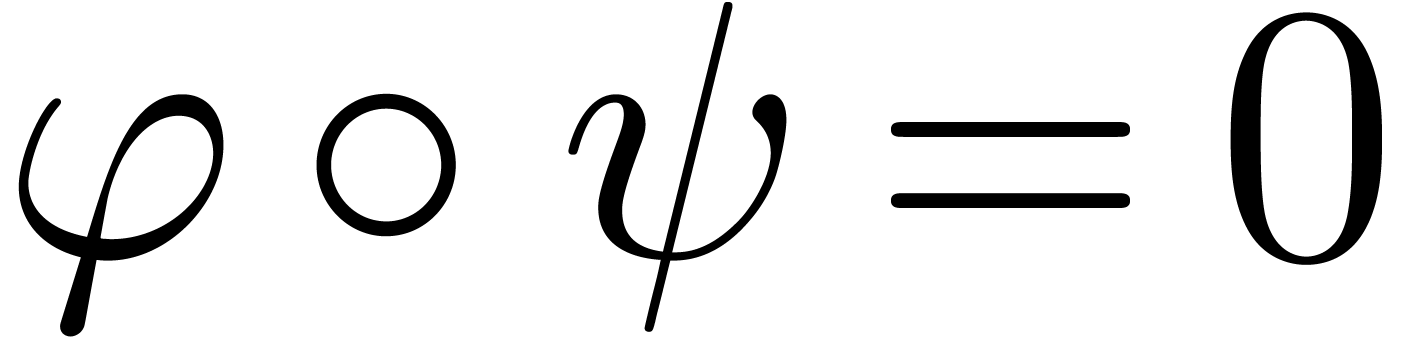 . We
say that a power series domain
. We
say that a power series domain 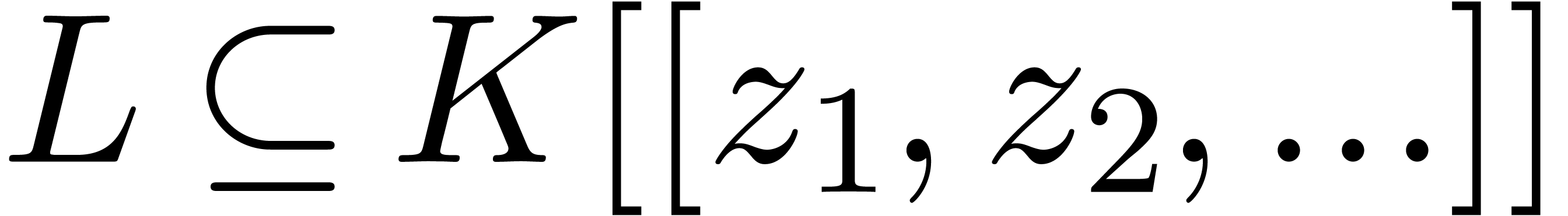 satisfies the
implicit function theorem (for
satisfies the
implicit function theorem (for  implicit
functions) if
implicit
functions) if 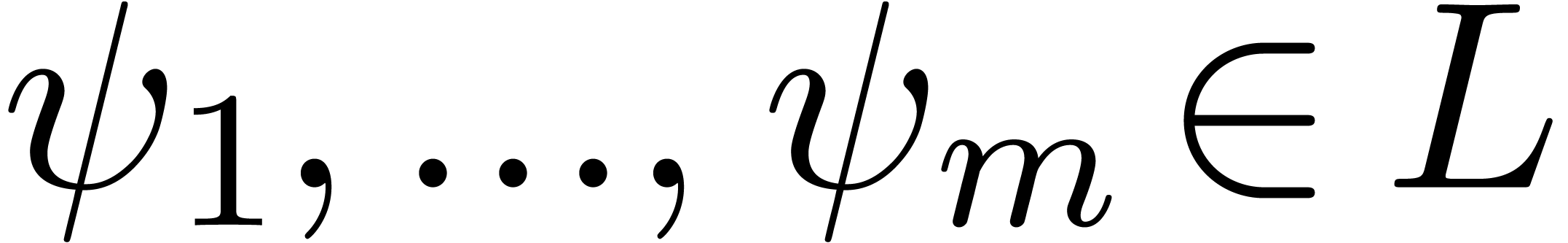 for the above solution of
for the above solution of 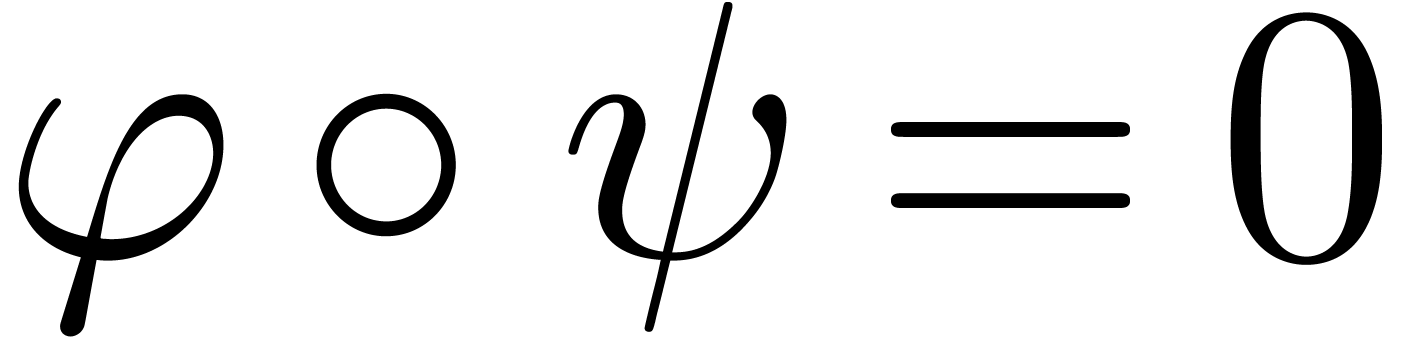 , whenever
, whenever 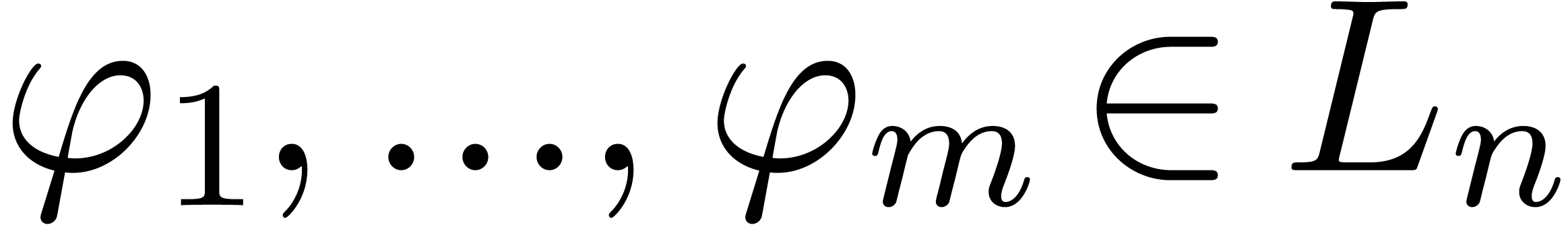 . We say that
. We say that  effectively satisfies the implicit function theorem if we also
have an algorithm to compute
effectively satisfies the implicit function theorem if we also
have an algorithm to compute  as a function of
as a function of
 .
.
We claim that  satisfies the implicit function
theorem for
satisfies the implicit function
theorem for  implicit functions as soon as
implicit functions as soon as  satisfies the implicit function theorem for one
implicit function and
satisfies the implicit function theorem for one
implicit function and  is stable under restricted
division and composition. We prove this by induction over
is stable under restricted
division and composition. We prove this by induction over  . For
. For 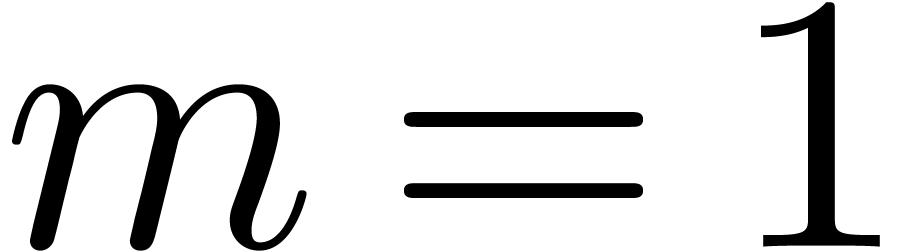 the statement is
clear, so assume that
the statement is
clear, so assume that 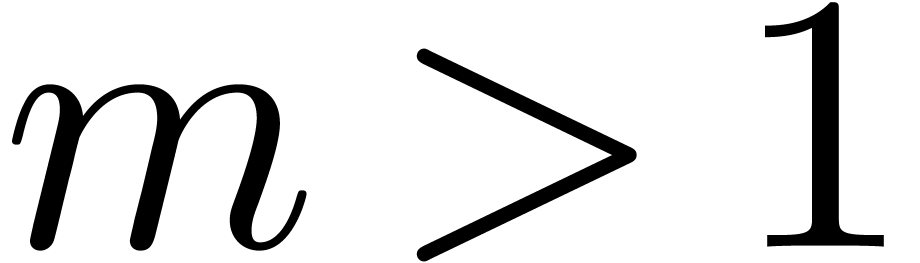 . Since
the matrix formed by the first
. Since
the matrix formed by the first 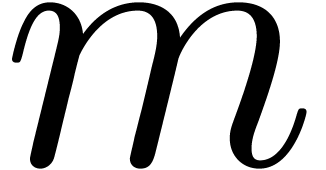 columns of
columns of  is invertible, at least one of the
is invertible, at least one of the 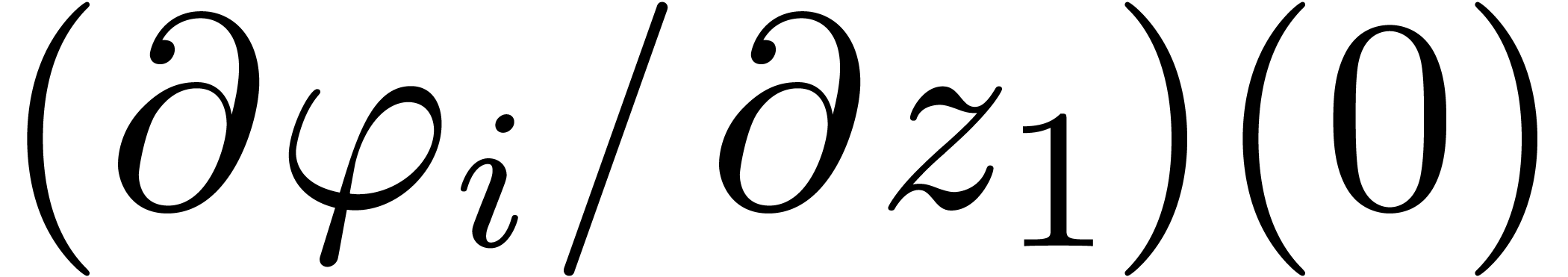 must be non-zero. Modulo a permutation of rows we may assume that
must be non-zero. Modulo a permutation of rows we may assume that 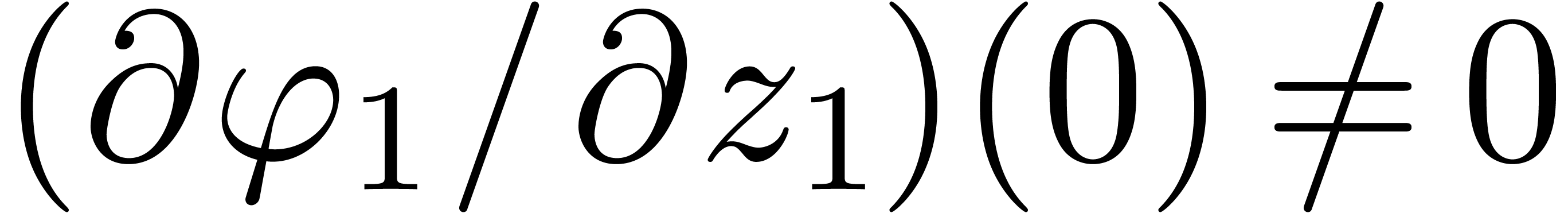 . Applying the implicit function
theorem to
. Applying the implicit function
theorem to 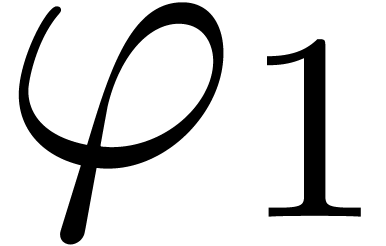 only, we obtain a function
only, we obtain a function 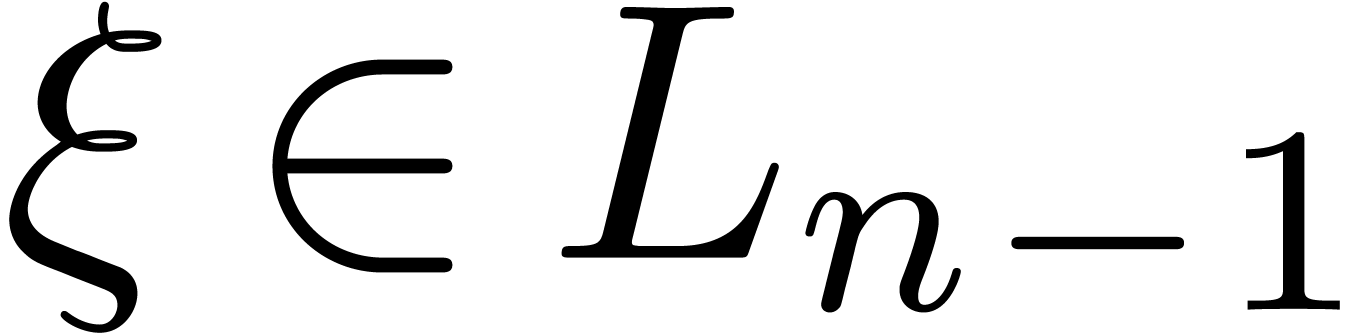 with
with  .
Differentiating this relation, we also obtain
.
Differentiating this relation, we also obtain
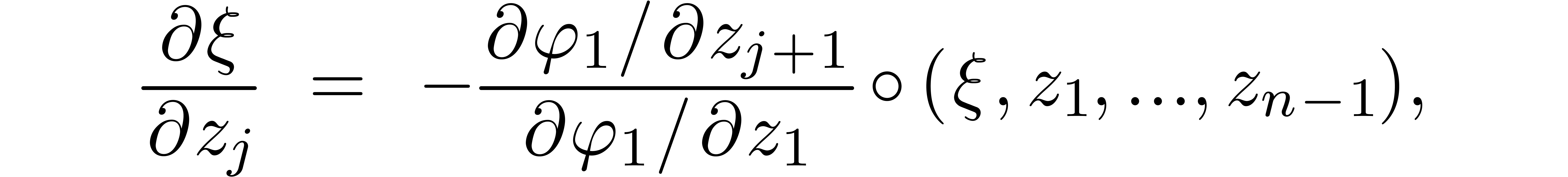
for each  . Setting
. Setting 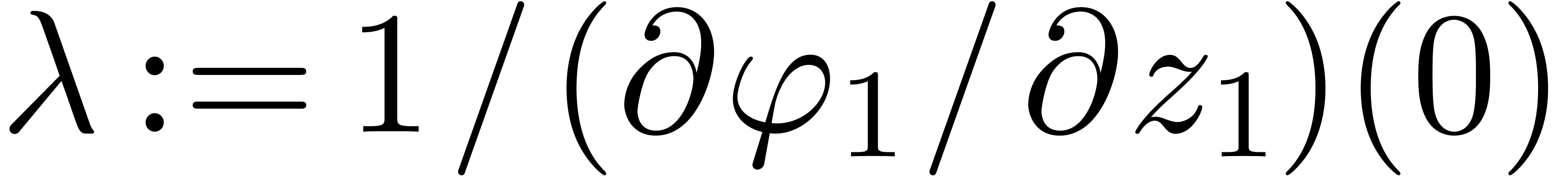 , this yields in particular
, this yields in particular
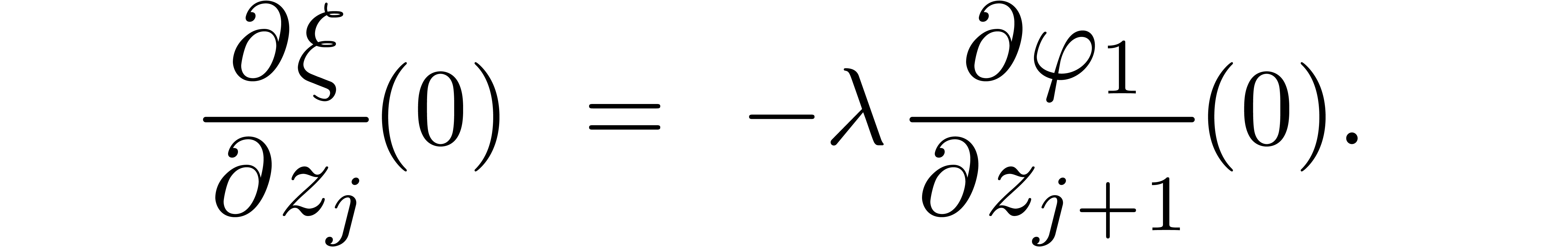
Now consider the series 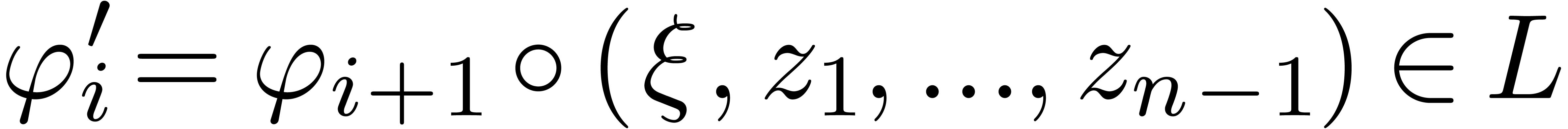 . For
each
. For
each 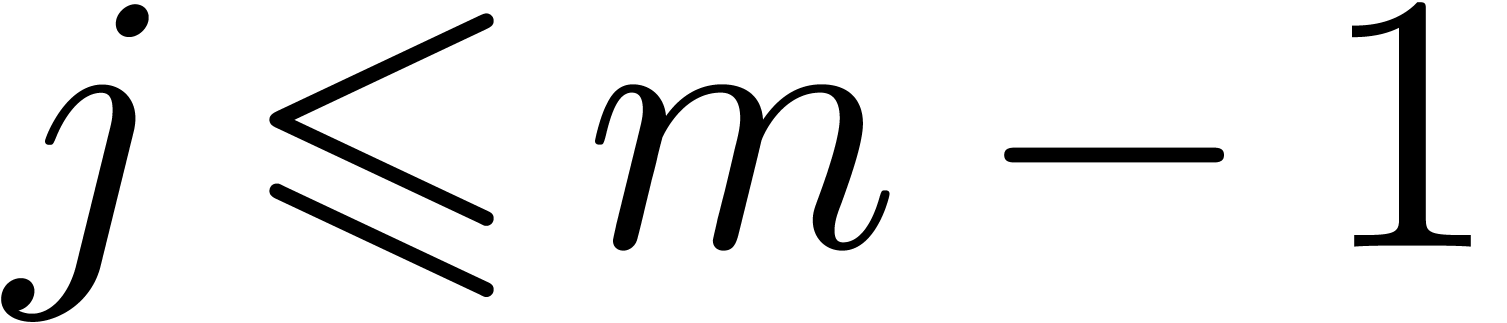 , we have
, we have
In particular,
By the induction hypothesis, we may thus compute series 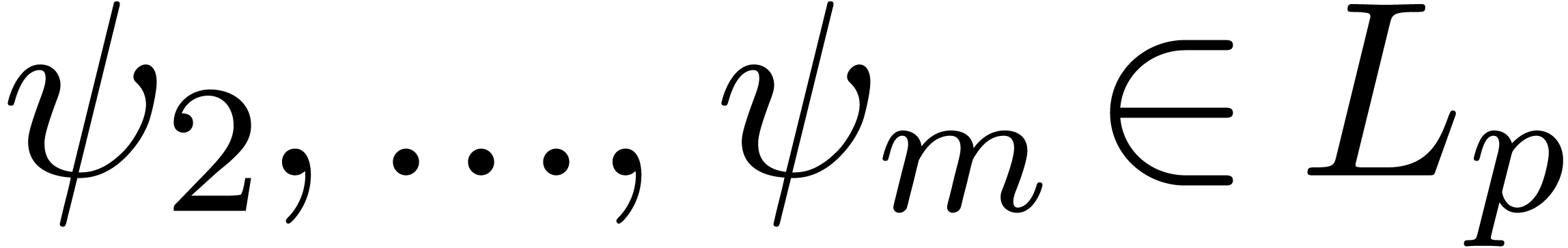 such that
such that  for all
for all  .
Setting
.
Setting  , we conclude that
, we conclude that
 and
and
for all 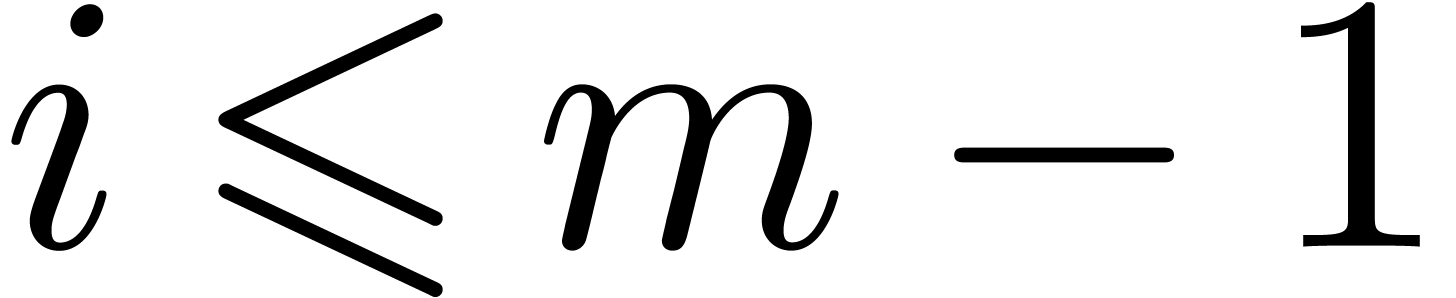 .
.
Consider an invertible  matrix
matrix 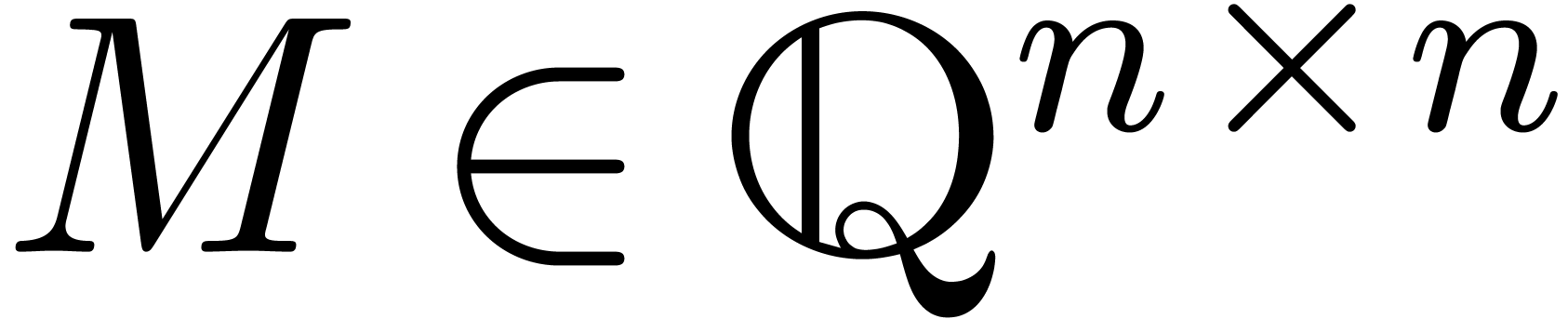 with rational coefficients. Then the transformation
with rational coefficients. Then the transformation
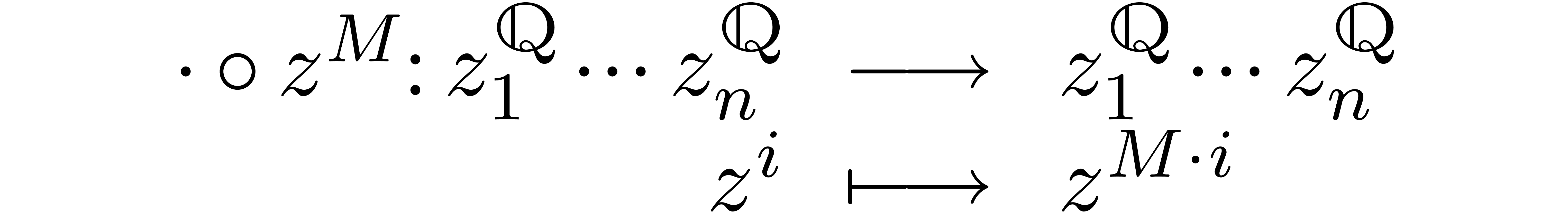
is called a monomial transformation, where 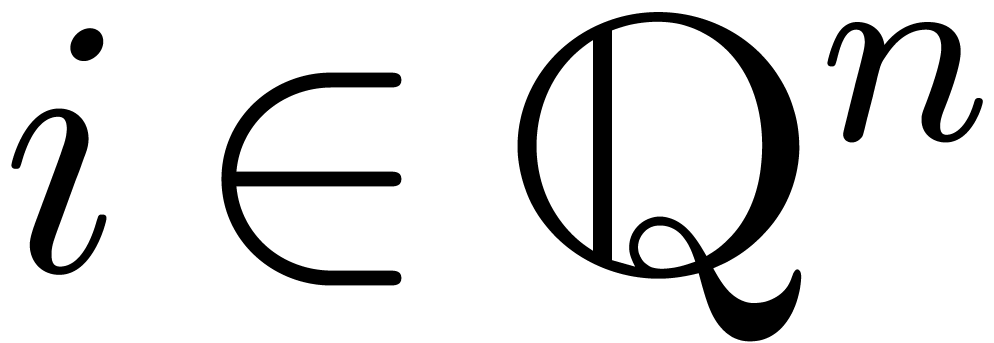 is
considered as a column vector. For a power series
is
considered as a column vector. For a power series 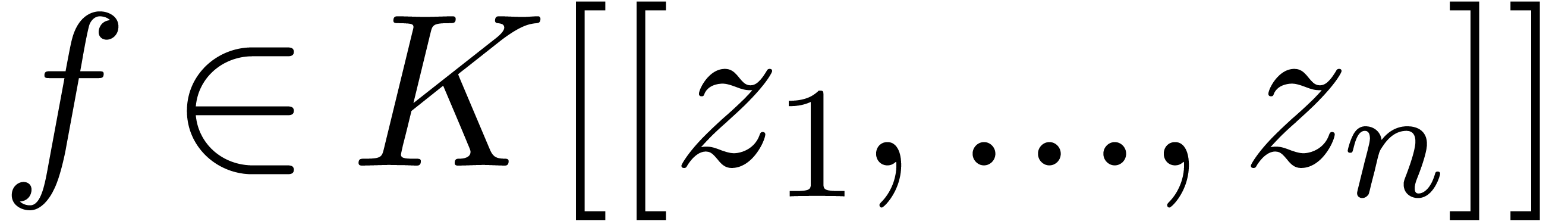 whose support
whose support  satisfies
satisfies 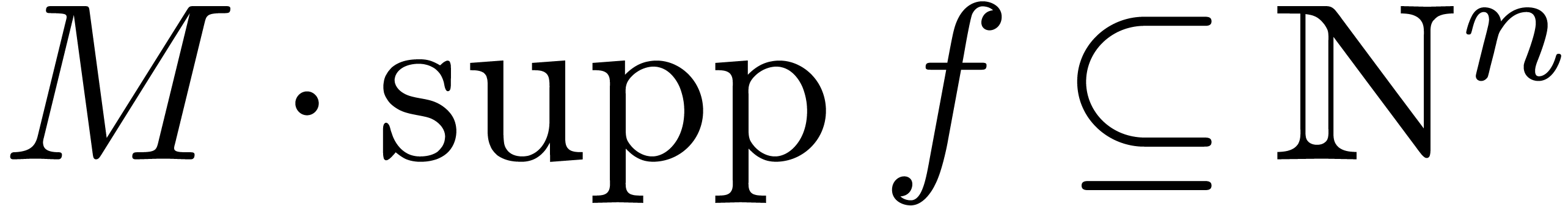 , we may apply the monomial transformation to
, we may apply the monomial transformation to  as well:
as well:
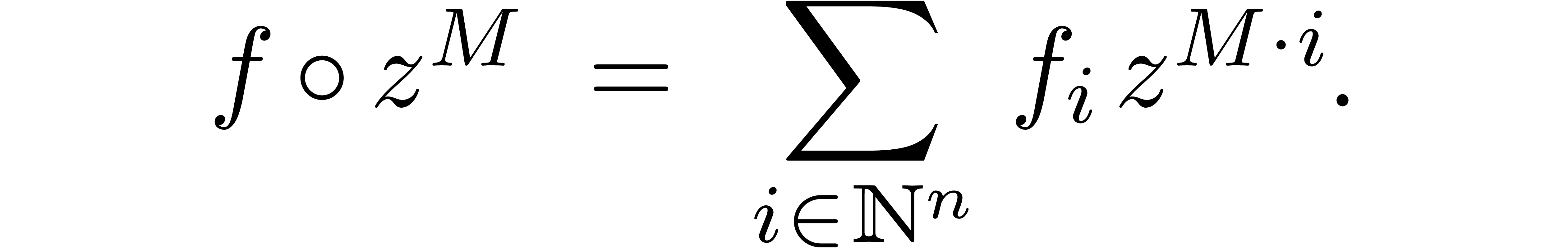
We say that  is stable under restricted
monomial transformations if for any
is stable under restricted
monomial transformations if for any 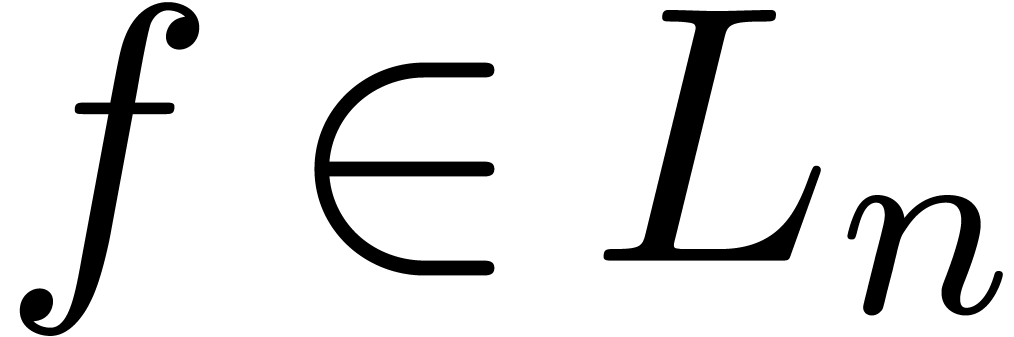 and
invertible matrix
and
invertible matrix  with
with 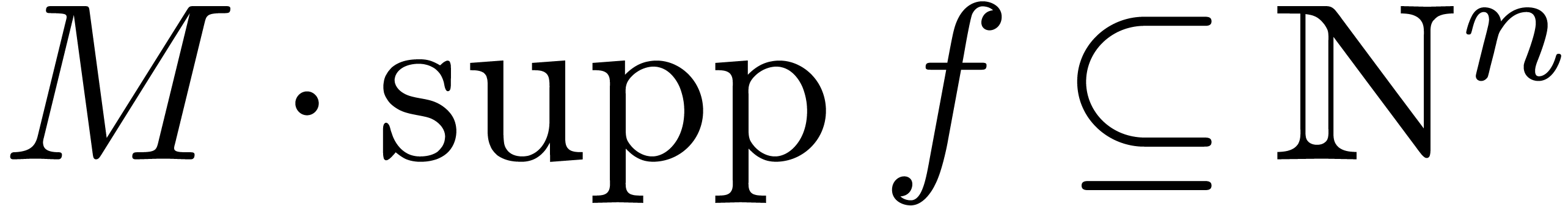 , we have
, we have 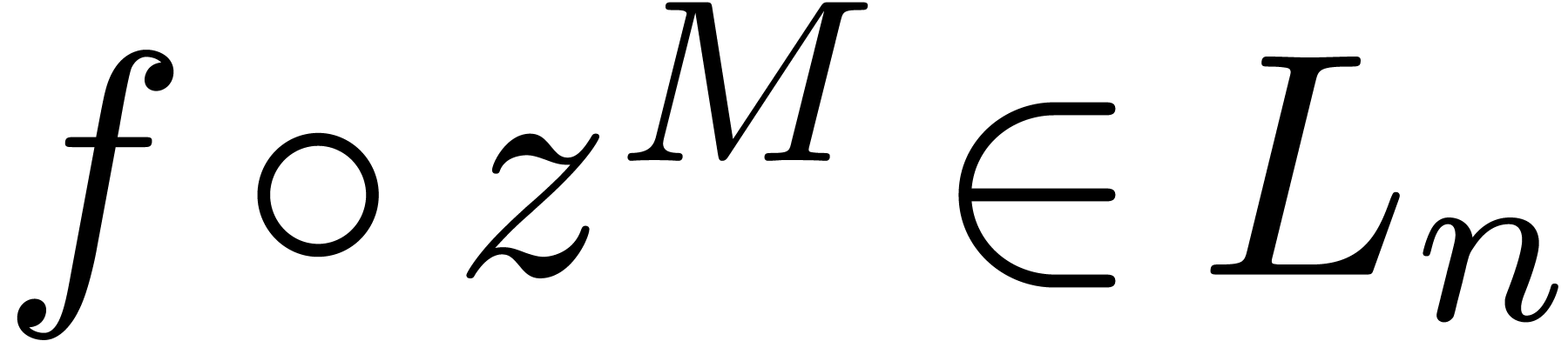 .
We say that
.
We say that  is effectively stable under
restricted monomial transformations if we also have an algorithm to
compute
is effectively stable under
restricted monomial transformations if we also have an algorithm to
compute 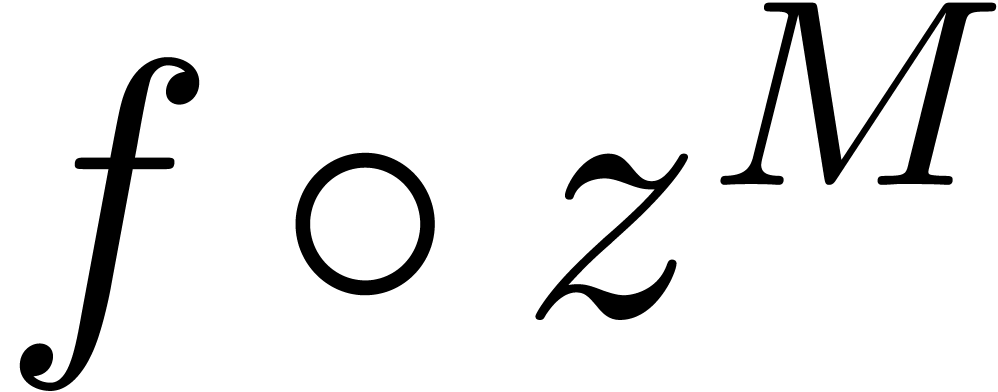 as a function of
as a function of  and
and  . Notice that we do
not require the existence of a test whether
. Notice that we do
not require the existence of a test whether 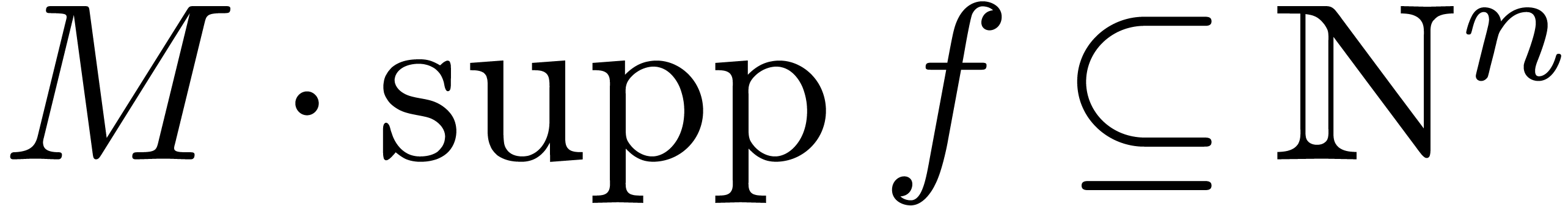 in this case (the behaviour of the algorithm being unspecified whenever
in this case (the behaviour of the algorithm being unspecified whenever
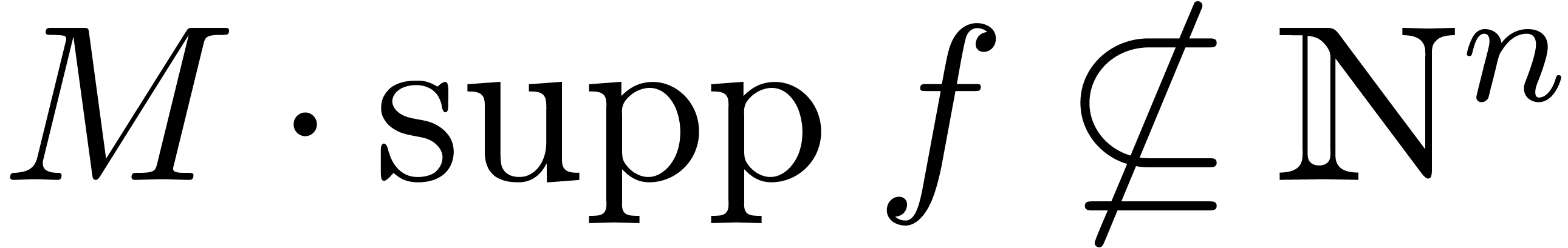 ).
).
If  has non-negative integer coefficients, then
we always have
has non-negative integer coefficients, then
we always have 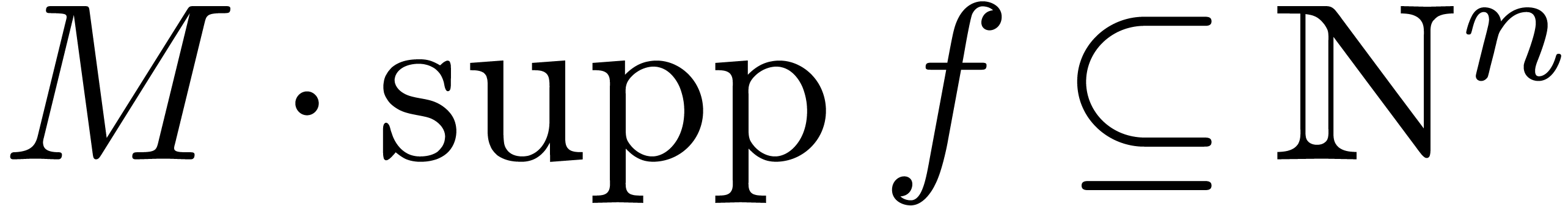 and
and  is
trivially stable under the monomial transformation
is
trivially stable under the monomial transformation 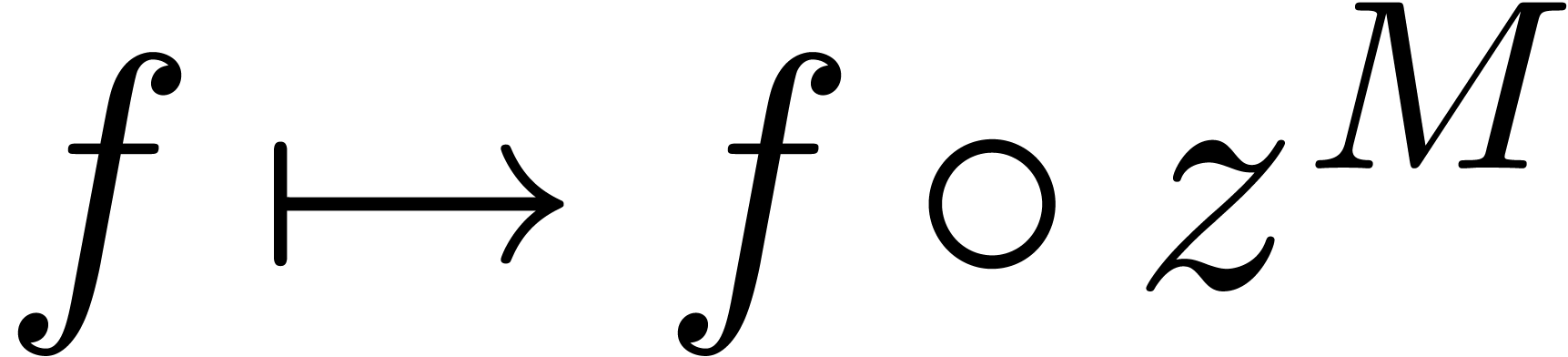 whenever
whenever  is stable under composition.
is stable under composition.
We say that the  -algebra
-algebra  with
with  is a local
community if
is a local
community if  is stable under composition,
the resolution of implicit equations, and restricted division by
is stable under composition,
the resolution of implicit equations, and restricted division by  . We say that
. We say that  is a tribe if
is a tribe if  is also stable under
restricted division and restricted monomial transformations. Effective
local communities and tribes are defined similarly.
is also stable under
restricted division and restricted monomial transformations. Effective
local communities and tribes are defined similarly.
A power series  is said to be algebraic
if it satisfies a non-trivial algebraic equation over the polynomial
ring
is said to be algebraic
if it satisfies a non-trivial algebraic equation over the polynomial
ring  . Setting
. Setting  , this is the case if and only if the module
, this is the case if and only if the module
 is an
is an  -vector
space of finite dimension. Using this criterion, one can prove that the
set
-vector
space of finite dimension. Using this criterion, one can prove that the
set 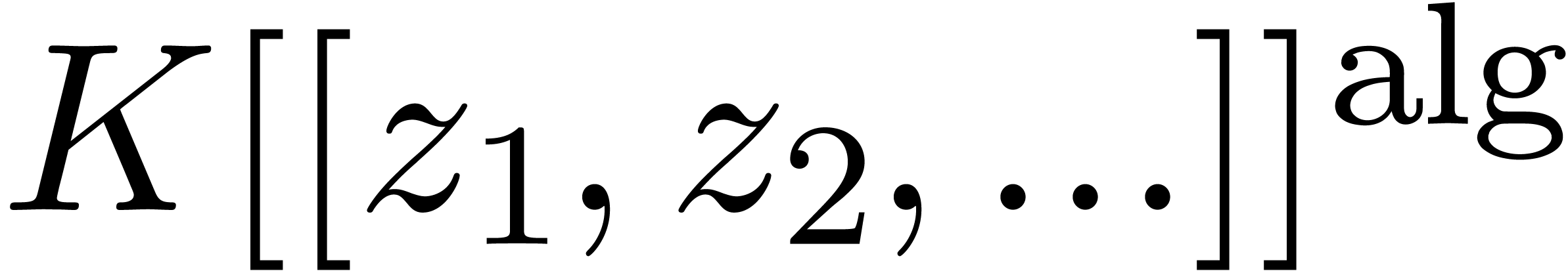 of algebraic power series is a tribe (and
actually the smallest tribe for inclusion). For convenience of the
reader, let us state and prove an effective version of this result.
Assume that
of algebraic power series is a tribe (and
actually the smallest tribe for inclusion). For convenience of the
reader, let us state and prove an effective version of this result.
Assume that  is an effective field. Then an
effective algebraic power series
is an effective field. Then an
effective algebraic power series 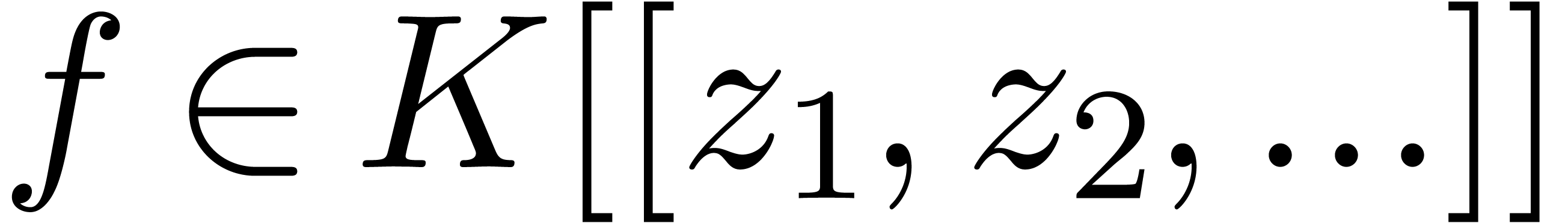 can be
effectively represented as an effective power series together with an
annihilator
can be
effectively represented as an effective power series together with an
annihilator 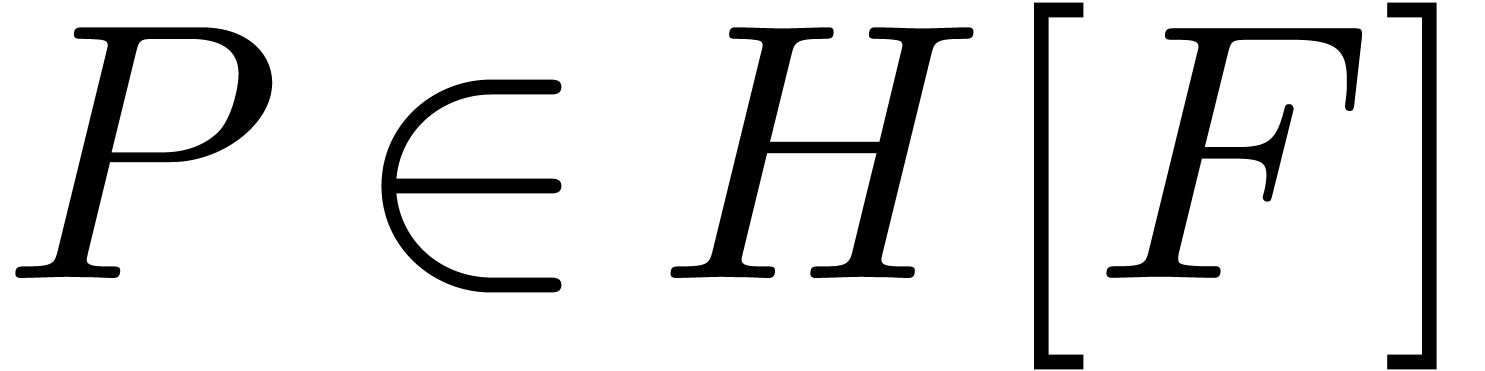 . We claim that
. We claim that
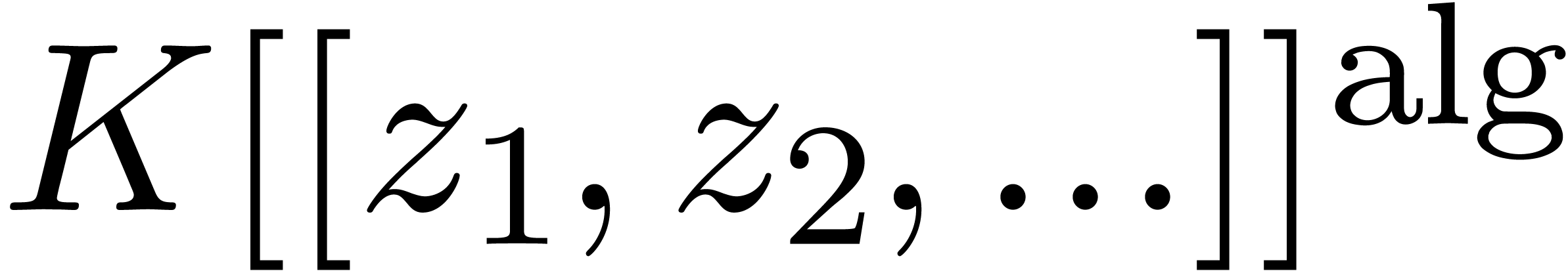 is an effective tribe for this representation.
is an effective tribe for this representation.
Proposition  -algebra
-algebra 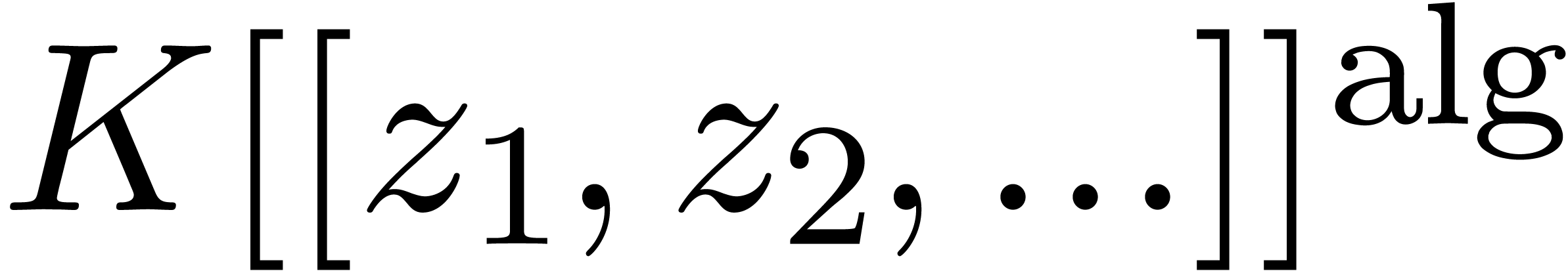 forms an effective tribe.
forms an effective tribe.
Proof. Let 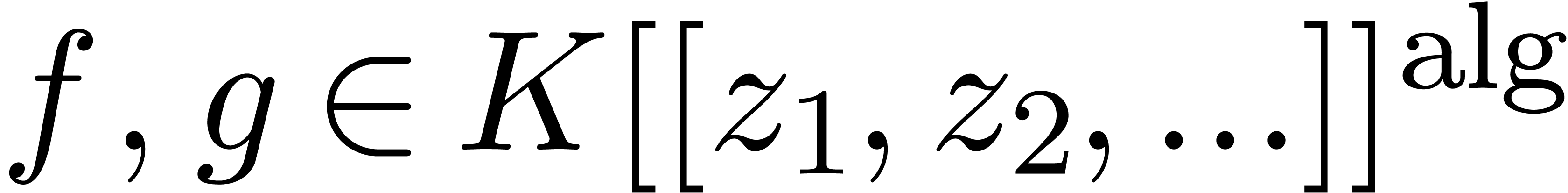 ,
so that
,
so that 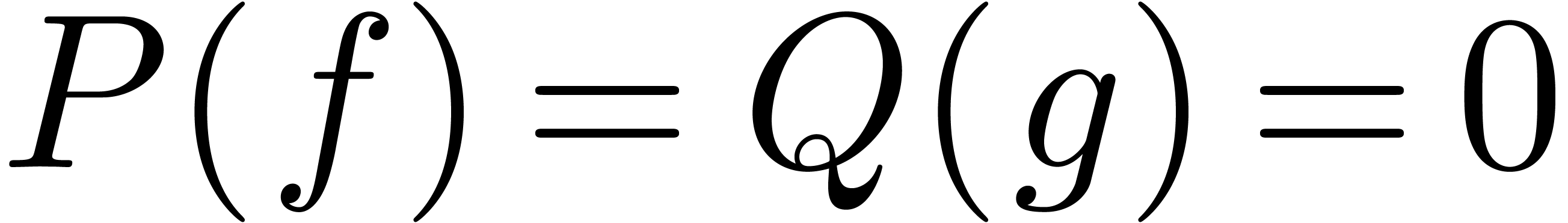 for certain monic polynomials
for certain monic polynomials 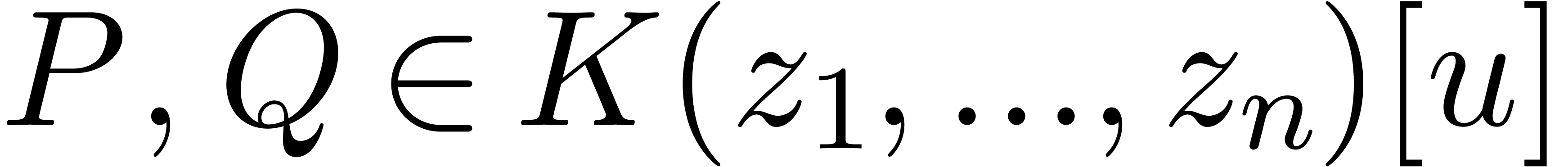 of degrees
of degrees 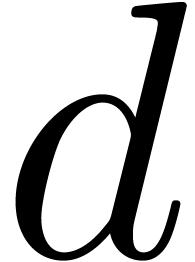 and
and  in
in  . For
. For  , these relations allow us to rewrite both
, these relations allow us to rewrite both  and
and 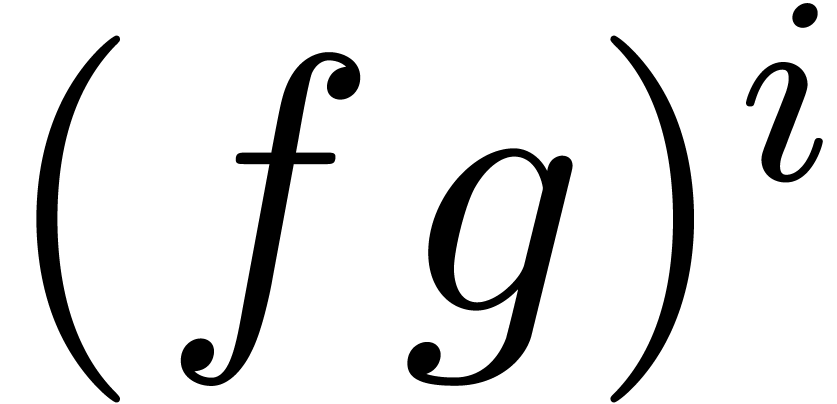 as
as  -linear combinations of
-linear combinations of 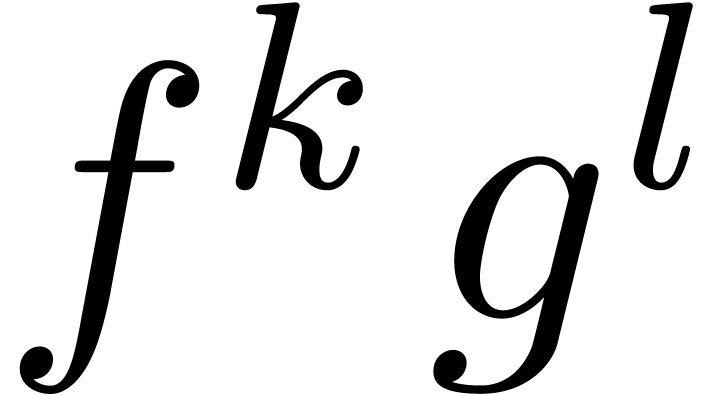 with
with
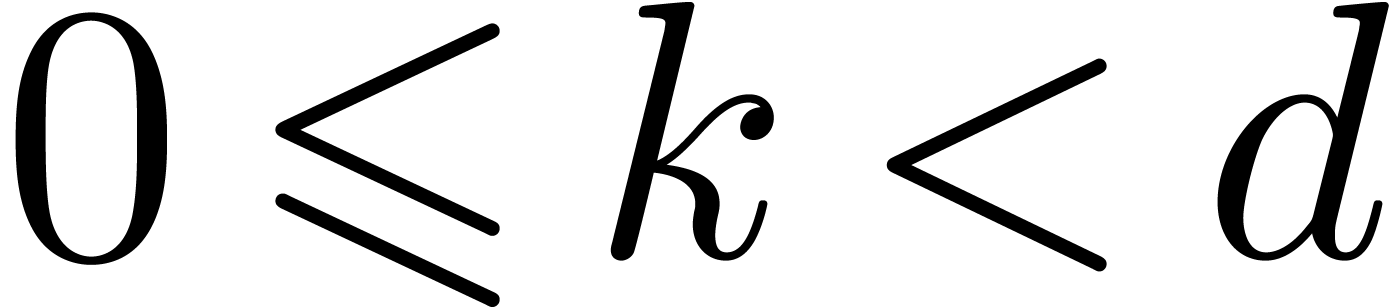 and
and 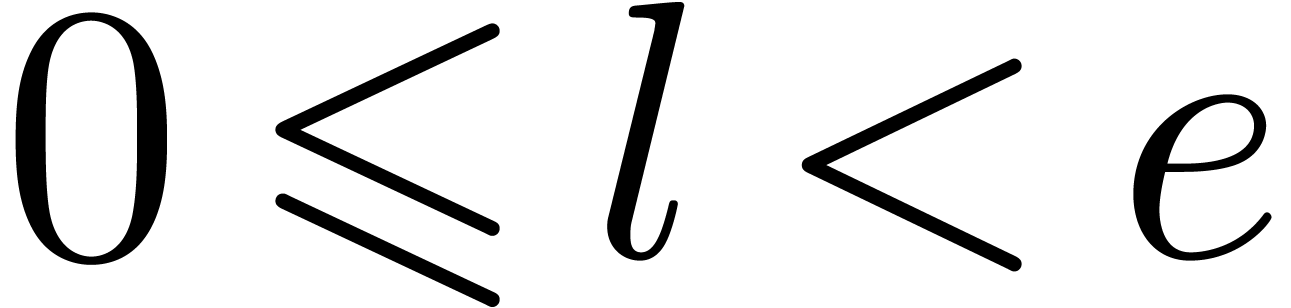 .
Since these
.
Since these 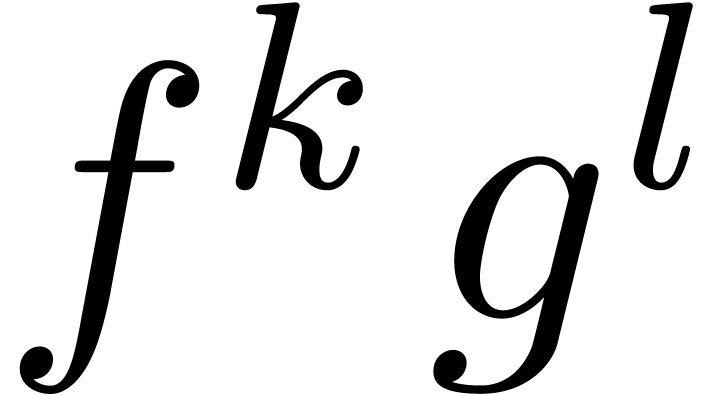 span a vector space of dimension at
most
span a vector space of dimension at
most  , this means that there
exist monic polynomials
, this means that there
exist monic polynomials  of degree
of degree  with
with 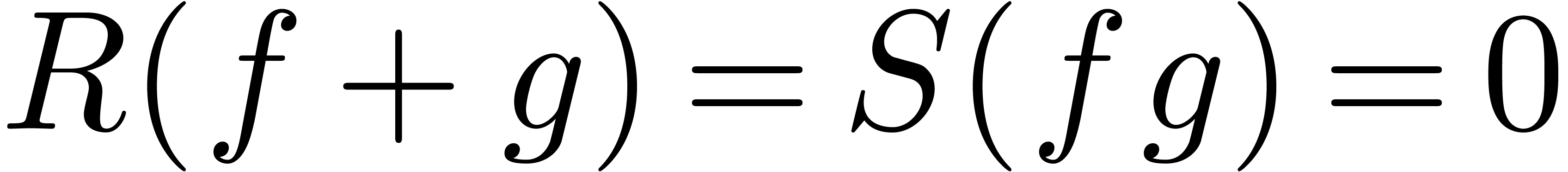 , and we
may compute
, and we
may compute  and
and  using
linear algebra. This shows that
using
linear algebra. This shows that 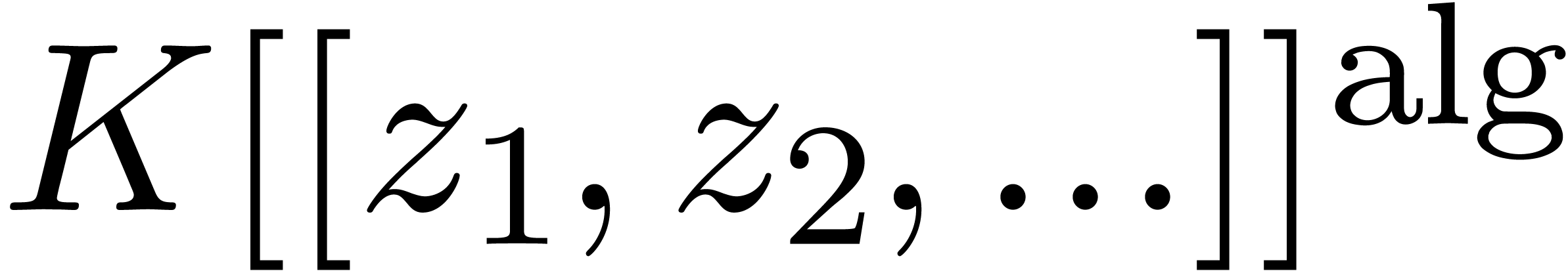 forms an
effective power series algebra that is clearly inhabited.
forms an
effective power series algebra that is clearly inhabited.
With the above notations, let  and assume that
and assume that
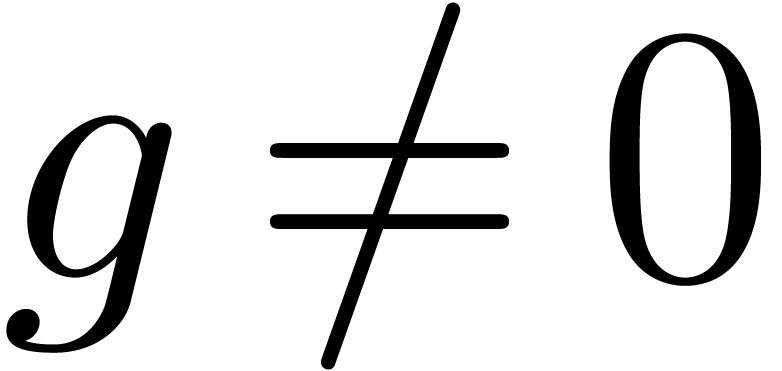 . Then we notice that
. Then we notice that 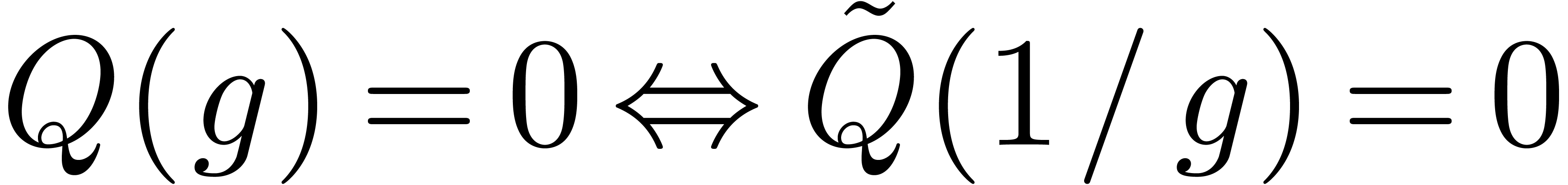 , so we can compute a polynomial
, so we can compute a polynomial
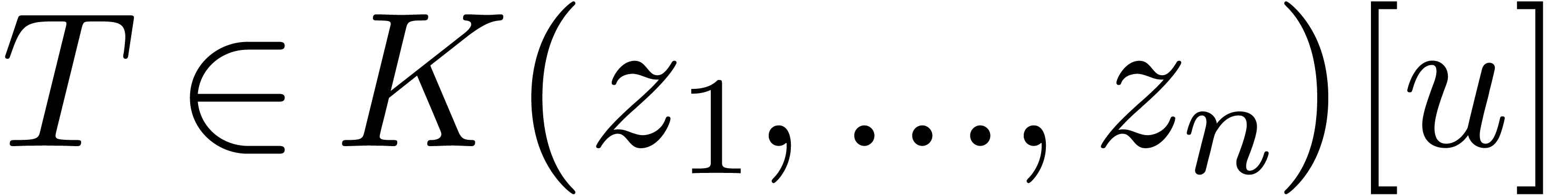 with
with 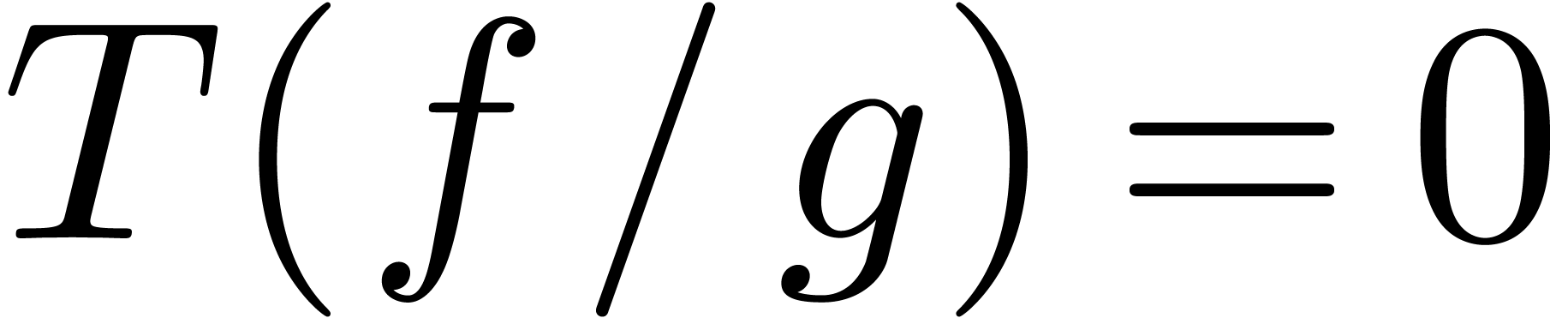 in a similar way as
above. This shows that
in a similar way as
above. This shows that 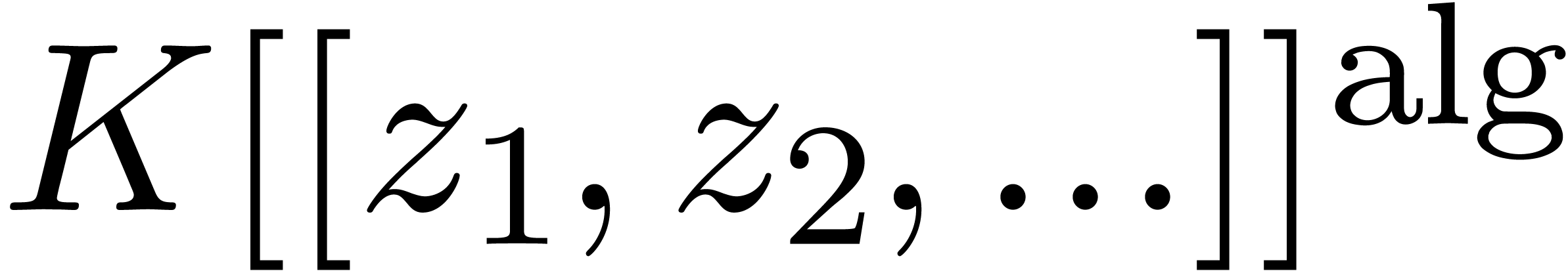 is effectively stable
under restricted division by
is effectively stable
under restricted division by  .
.
Assume now that 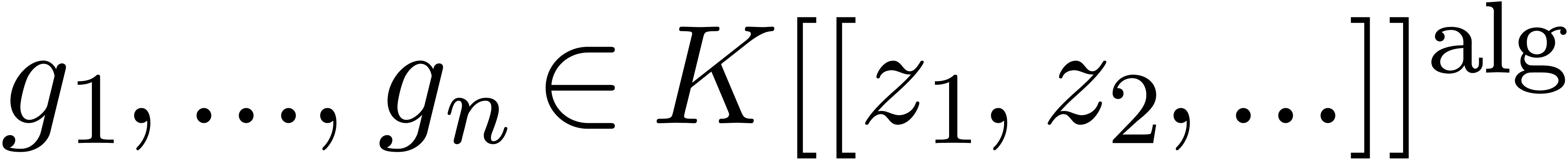 with
with  and
let
and
let  be a monic annihilator of
be a monic annihilator of 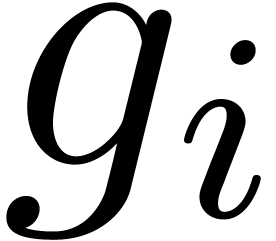 of degree
of degree 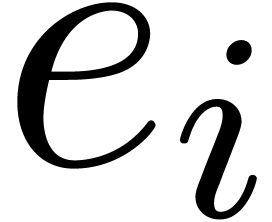 for
for  .
Assume first that the annihilator
.
Assume first that the annihilator  of
of  belongs to
belongs to  .
Given any
.
Given any  , we may then
rewrite
, we may then
rewrite  as a linear combination of
as a linear combination of 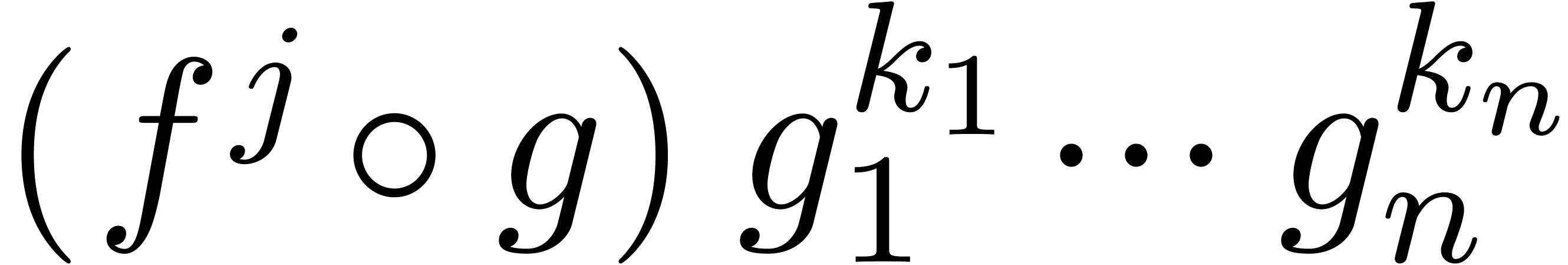 with
with 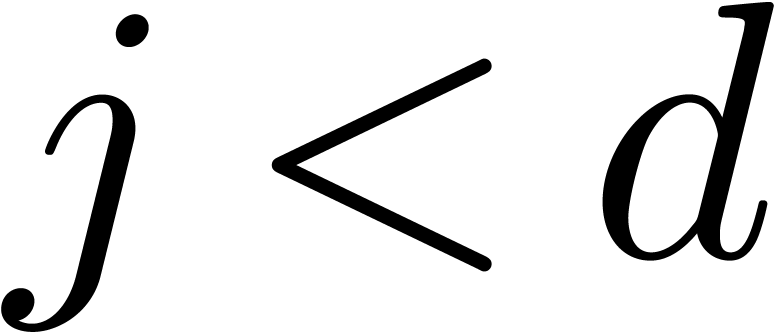 ,
,  . In a similar way as above, this
allows us to compute a non trivial annihilator of degree
. In a similar way as above, this
allows us to compute a non trivial annihilator of degree 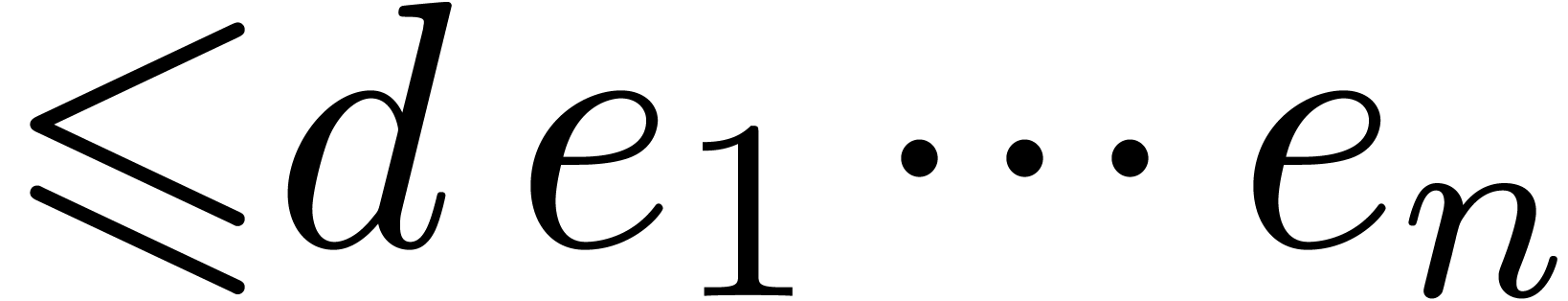 of
of  . In
general, the annihilator of
. In
general, the annihilator of  belongs to
belongs to 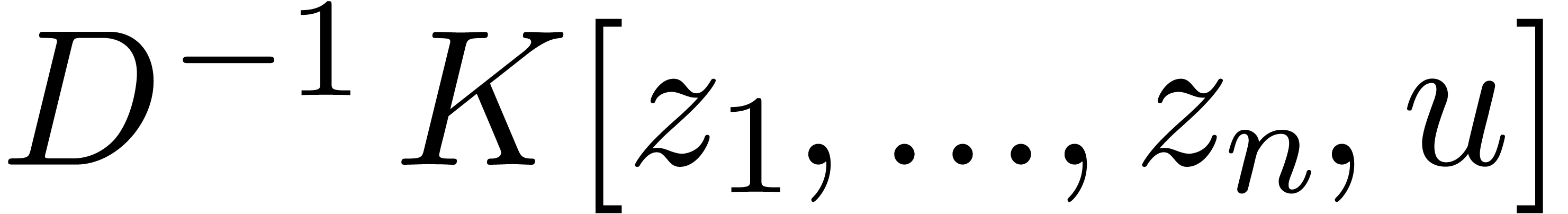 for some denominator
for some denominator 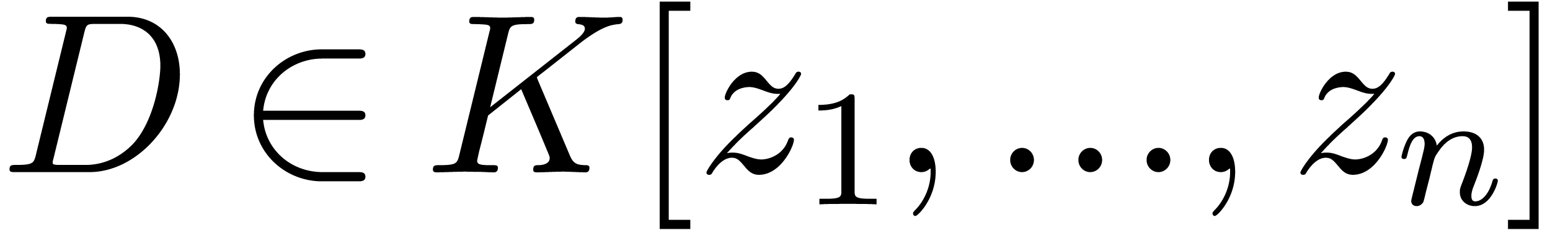 .
In that case, the annihilator of
.
In that case, the annihilator of  belongs to
belongs to
 , whence
, whence 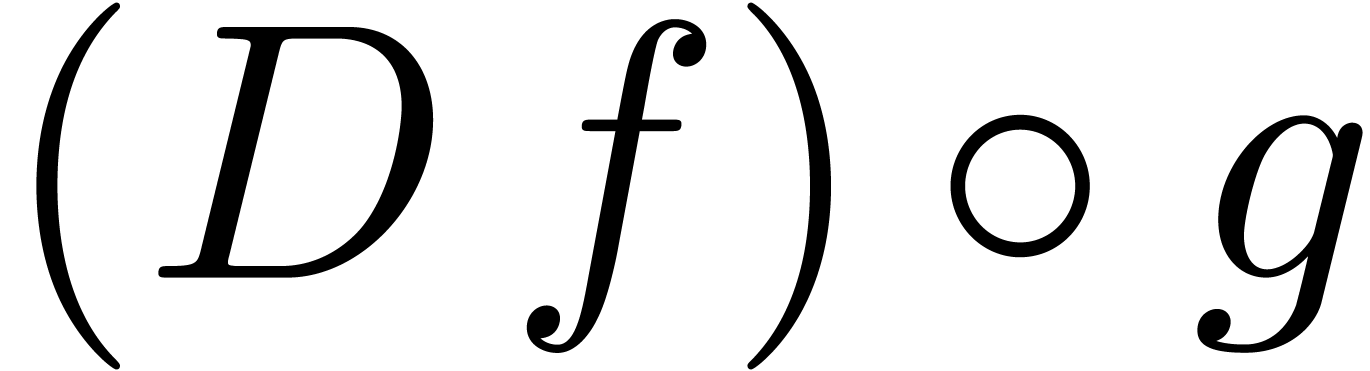 is algebraic, and so is
is algebraic, and so is 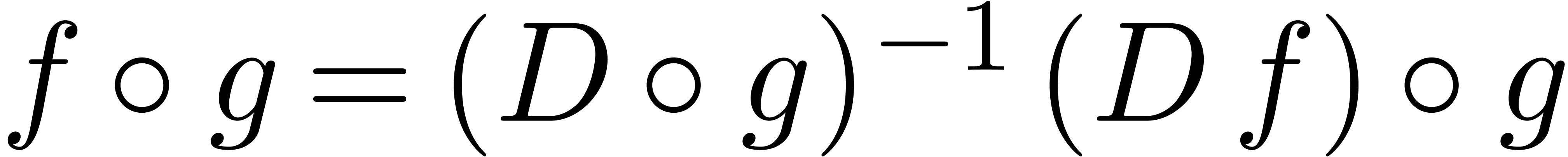 . In
other words,
. In
other words, 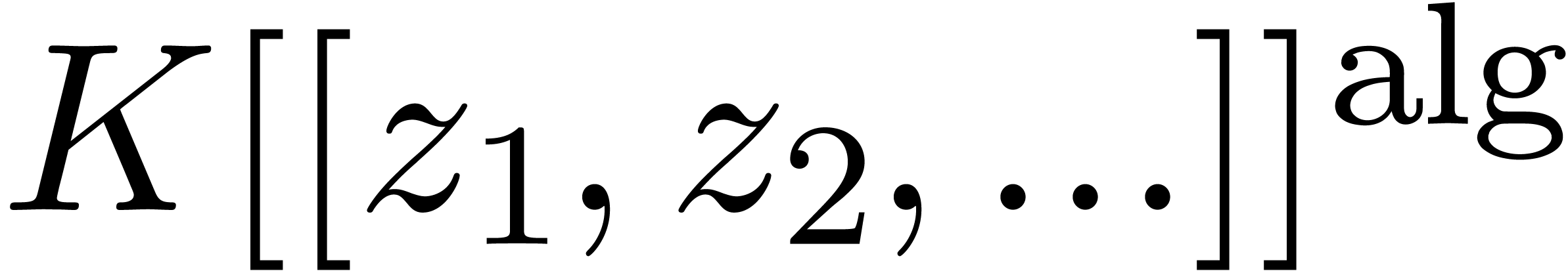 is effectively stable under
composition. A similar argument shows the effective stability under
restricted monomial transformations.
is effectively stable under
composition. A similar argument shows the effective stability under
restricted monomial transformations.
Let us finally assume that 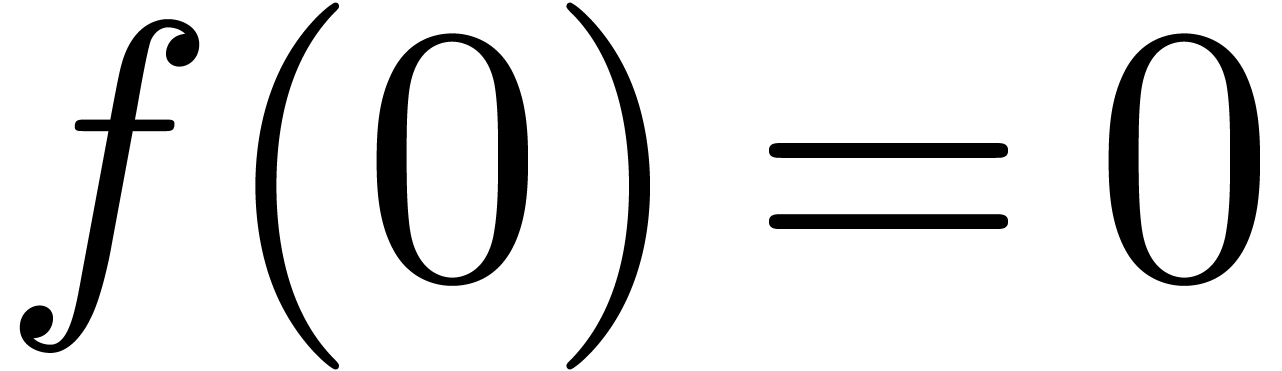 ,
but
,
but 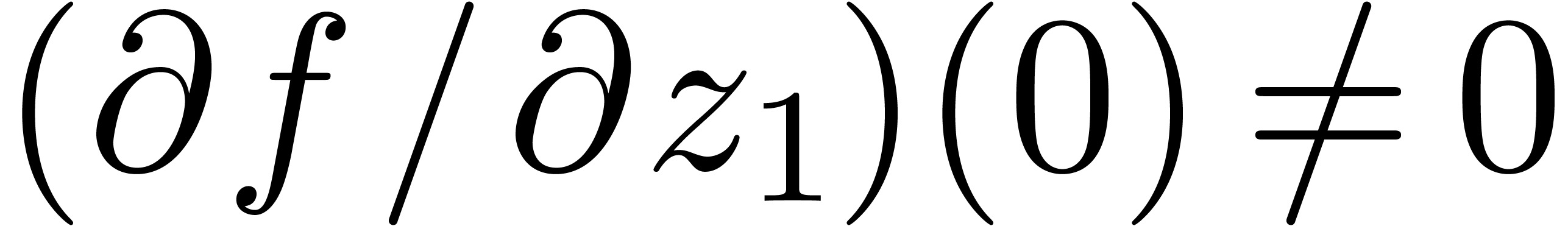 , and let
, and let 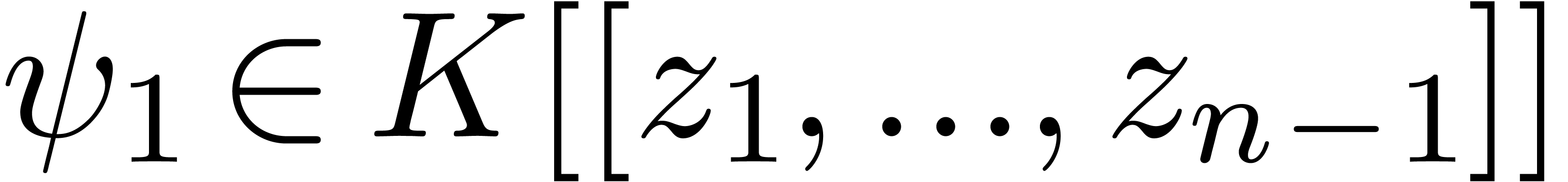 and
and 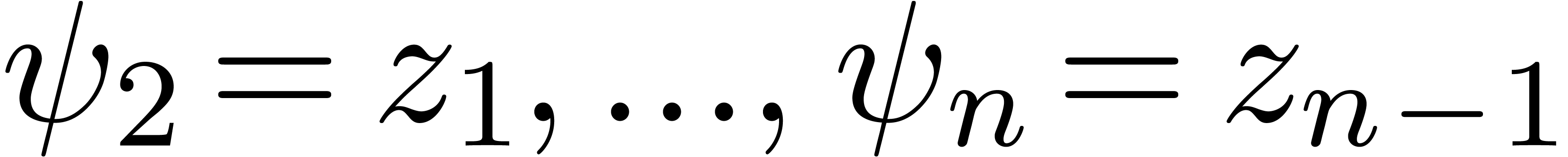 be such that
be such that 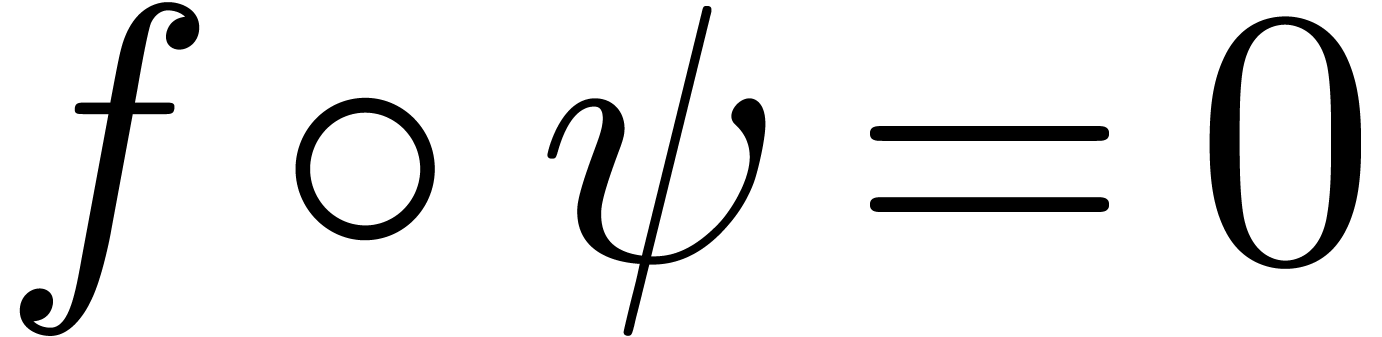 . Let
. Let  still be the
annihilator of
still be the
annihilator of 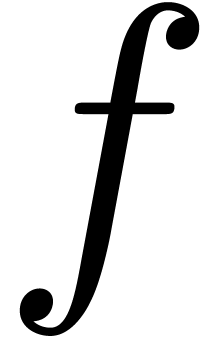 . Then
. Then  yields a non trivial annihilator for
yields a non trivial annihilator for 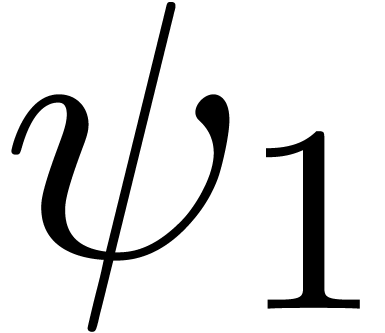 . This shows that
. This shows that 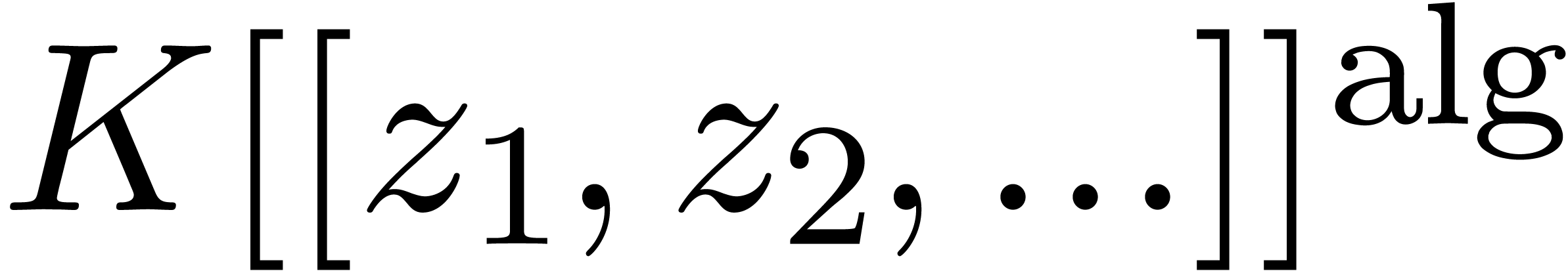 is
effectively stable under the implicit function theorem.
is
effectively stable under the implicit function theorem.
In order to conclude, we still need to prove the existence of an
effective zero test for 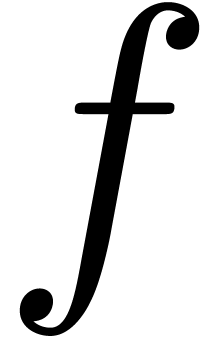 (given by its
annihilator
(given by its
annihilator 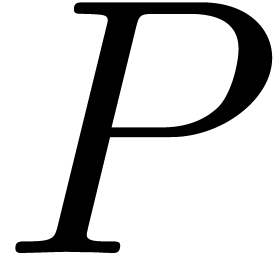 and an algorithm to compute its
coefficients). Now the polynomial equation
and an algorithm to compute its
coefficients). Now the polynomial equation 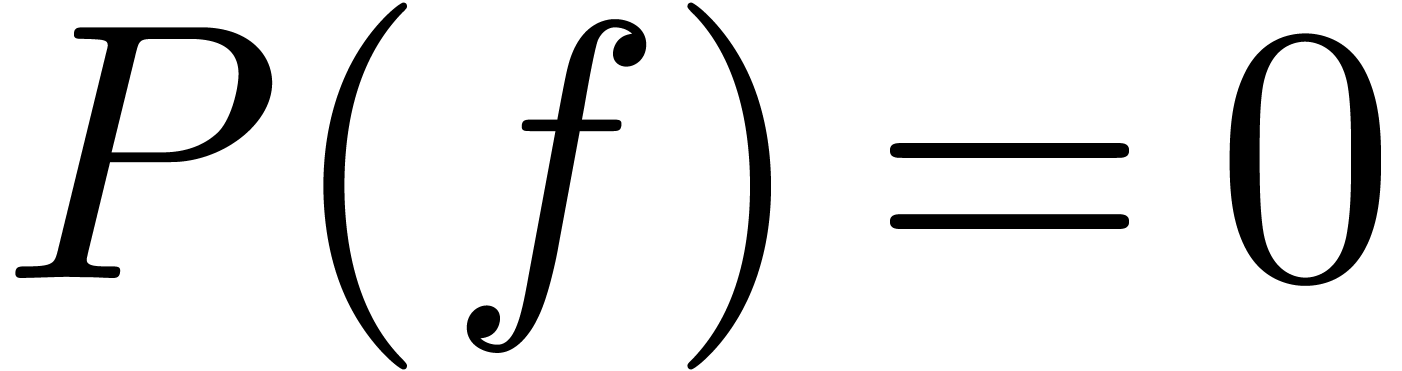 admits at most
admits at most 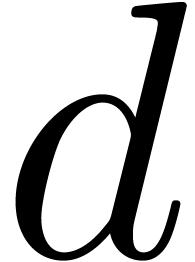 solutions. Using the Newton
polygon method for a suitable valuation, it is possible to derive a
bound for the maximal valuation of
solutions. Using the Newton
polygon method for a suitable valuation, it is possible to derive a
bound for the maximal valuation of 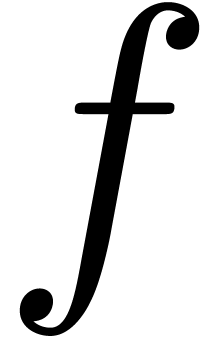 in the case
when
in the case
when 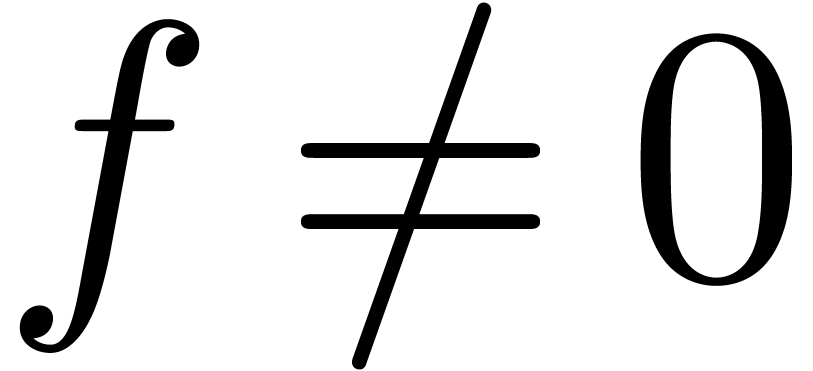 . It then suffices to
compute the coefficients of
. It then suffices to
compute the coefficients of 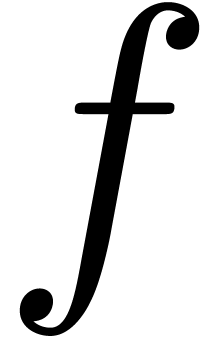 up to this valuation
bound. For more details, we refer to [15], where we proved
a stronger result in a more general setting.
up to this valuation
bound. For more details, we refer to [15], where we proved
a stronger result in a more general setting.
A power series 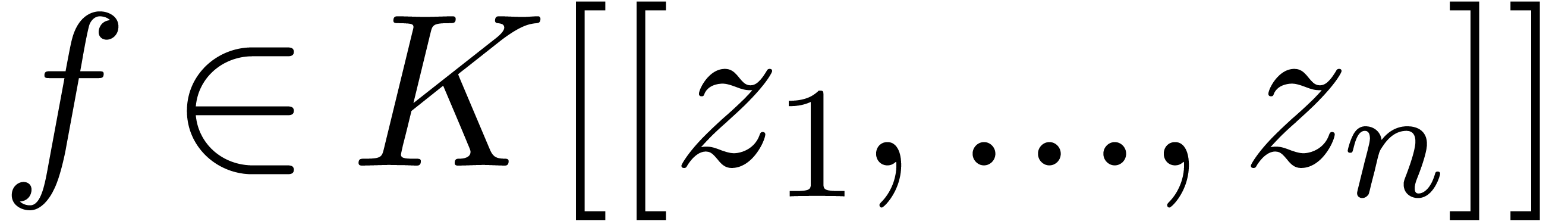 is said to be
d-algebraic if it satisfies an algebraic differential equation
is said to be
d-algebraic if it satisfies an algebraic differential equation
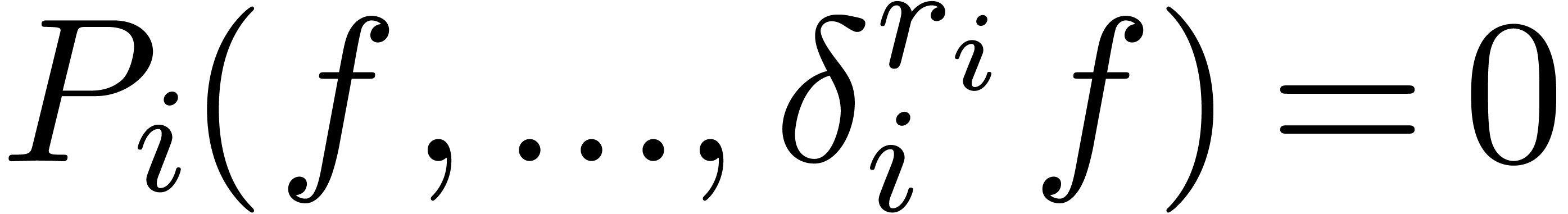 for each
for each 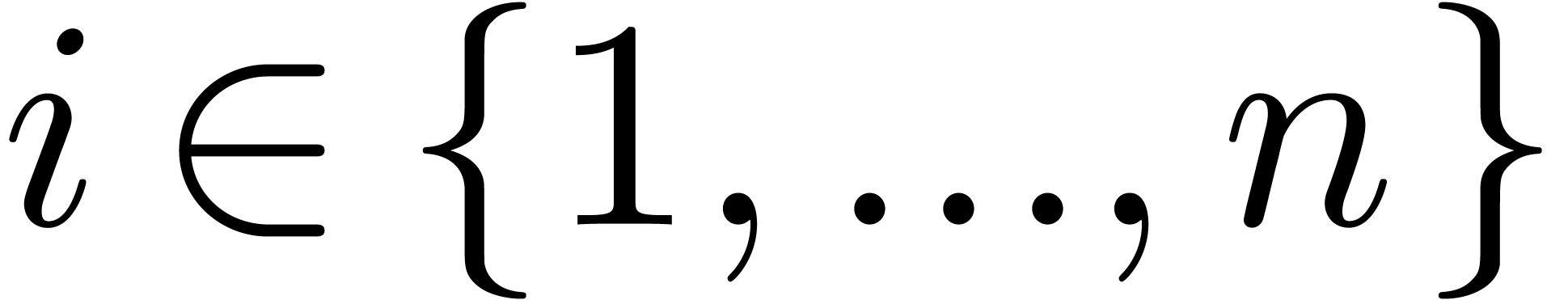 ,
where
,
where 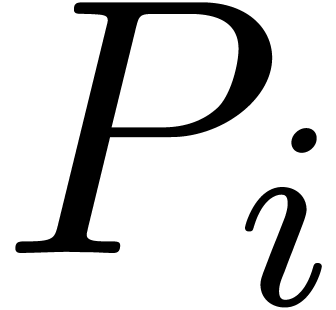 is a non-zero polynomial in
is a non-zero polynomial in 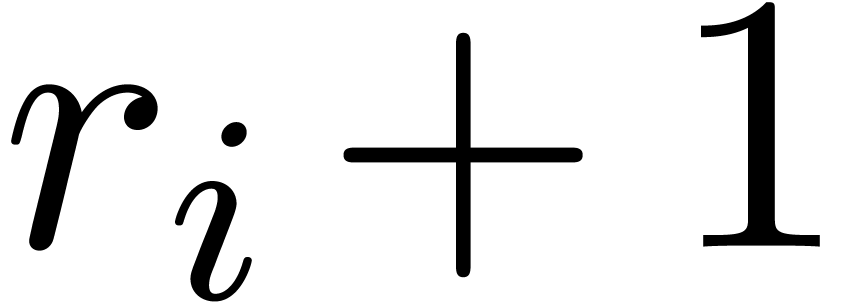 variables with coefficients in
variables with coefficients in  . This is the case if and only if the differential
field
. This is the case if and only if the differential
field 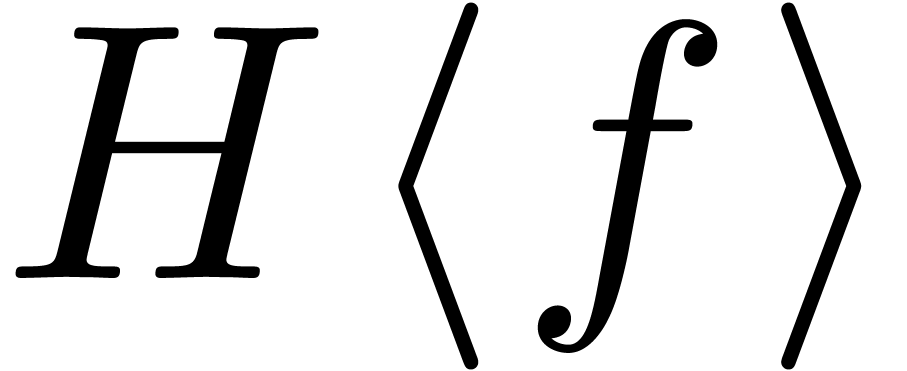 generated by
generated by  over
over
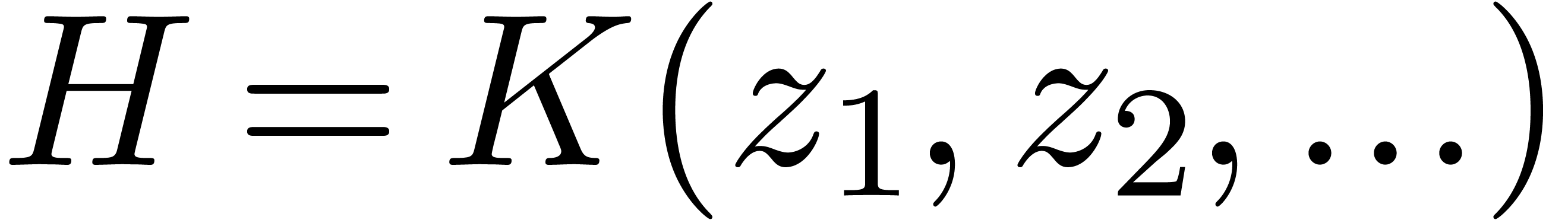 admits a finite transcendence degree. We denote
by
admits a finite transcendence degree. We denote
by 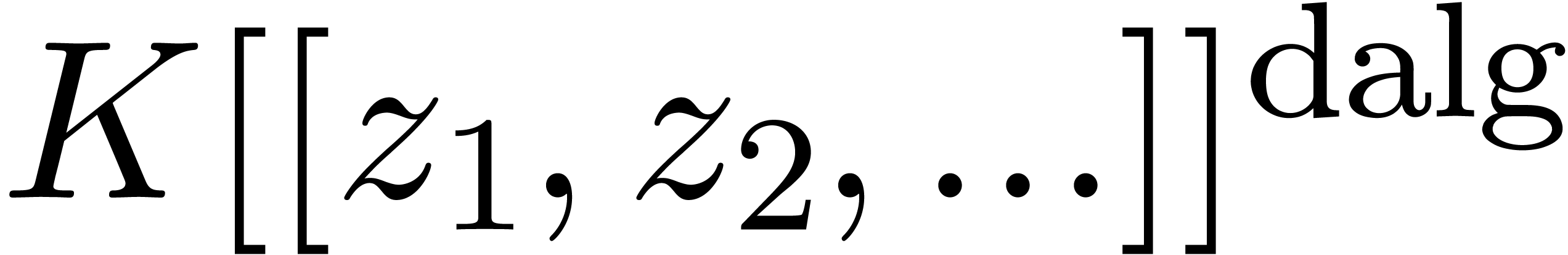 the set of d-algebraic power series. Using
the finite transcendence degree criterion, and similar techniques as in
the proof of Proposition 1, it can be shown that
the set of d-algebraic power series. Using
the finite transcendence degree criterion, and similar techniques as in
the proof of Proposition 1, it can be shown that 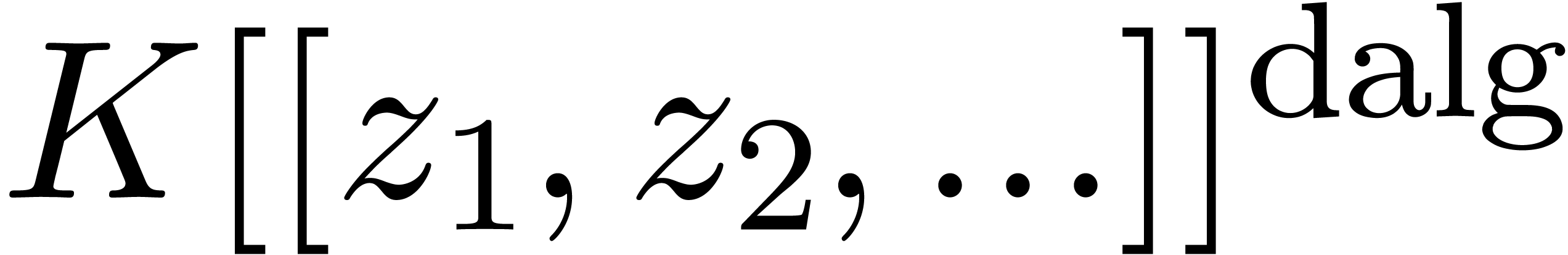 forms a tribe.
forms a tribe.
If  is an effective field, then effective
d-algebraic power series may again be represented through an effective
power series and differential annihilators
is an effective field, then effective
d-algebraic power series may again be represented through an effective
power series and differential annihilators 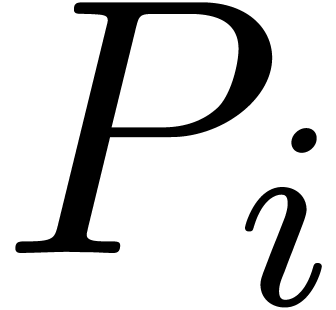 of
the above form. In [15], one may find more information on
how to compute with d-algebraic power series, and a full proof of the
fact that
of
the above form. In [15], one may find more information on
how to compute with d-algebraic power series, and a full proof of the
fact that 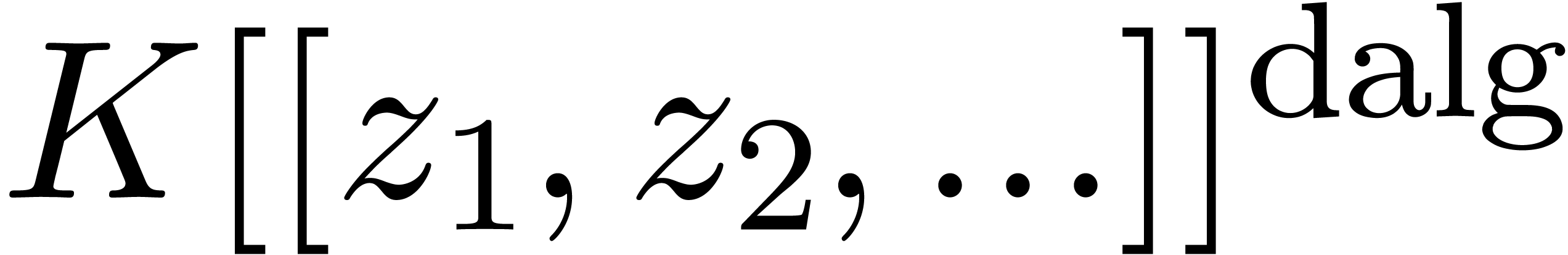 is actually an effective tribe (the
proof being based on earlier techniques from [7, 8]).
Notice that the most intricate part of this kind of computations is zero
testing.
is actually an effective tribe (the
proof being based on earlier techniques from [7, 8]).
Notice that the most intricate part of this kind of computations is zero
testing.
In what follows, we will only consider commutative monoids. A
monomial monoid is a multiplicative monoid  with a partial ordering
with a partial ordering  that is compatible with
the multiplication (i.e.
that is compatible with
the multiplication (i.e. 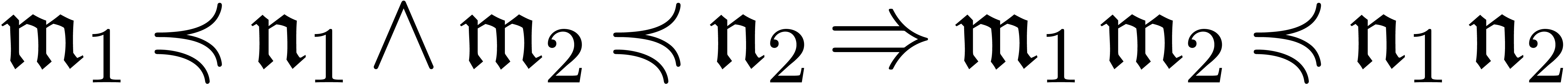 and
and  ). The notation
). The notation  generalizes Hardy's notation from asymptotic analysis, so we call
generalizes Hardy's notation from asymptotic analysis, so we call  an asymptotic ordering. We denote by
an asymptotic ordering. We denote by 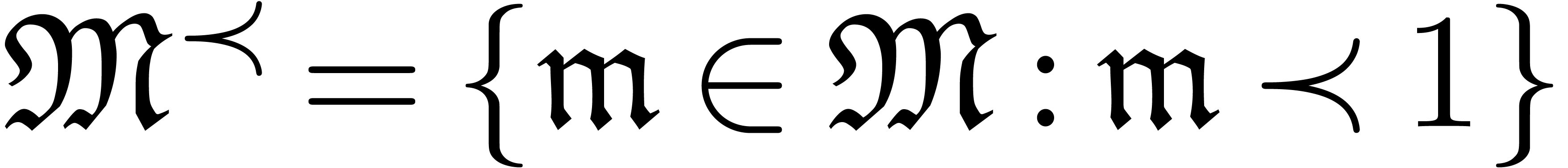 the set of infinitesimal elements in
the set of infinitesimal elements in  and by
and by  the set of
bounded elements in
the set of
bounded elements in  .
We say that
.
We say that  has
has  -powers
if we also have a powering operation
-powers
if we also have a powering operation 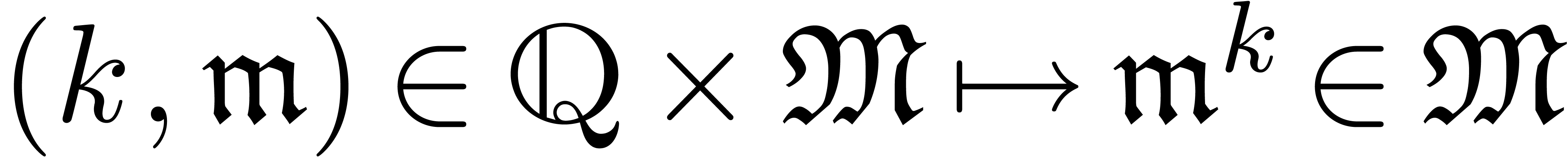 such that
such that
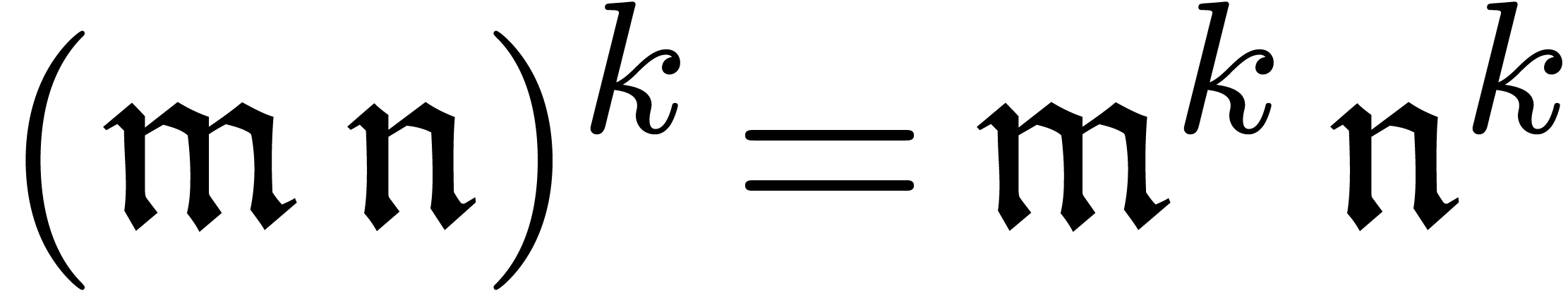 and
and 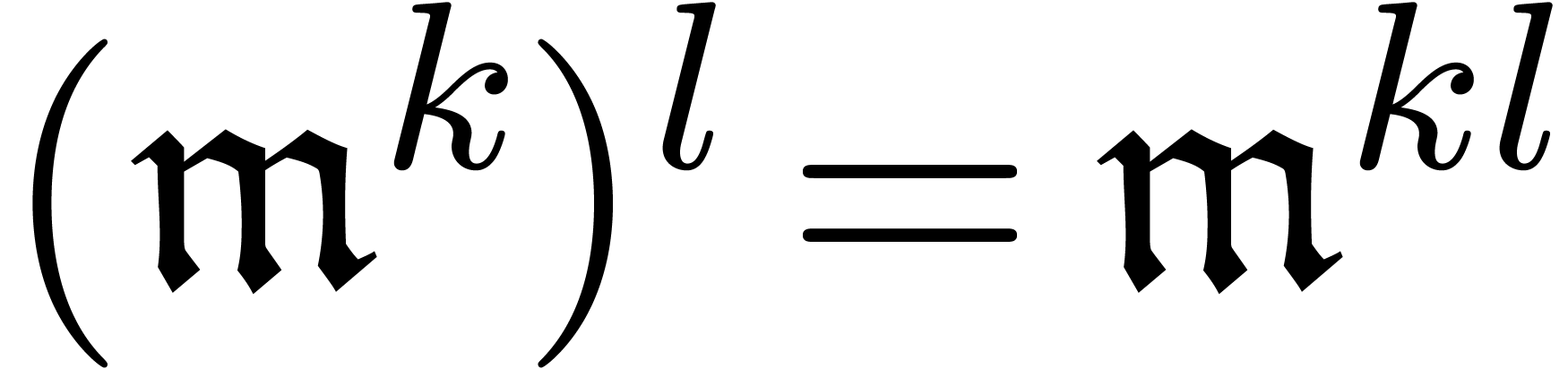 for all
for all 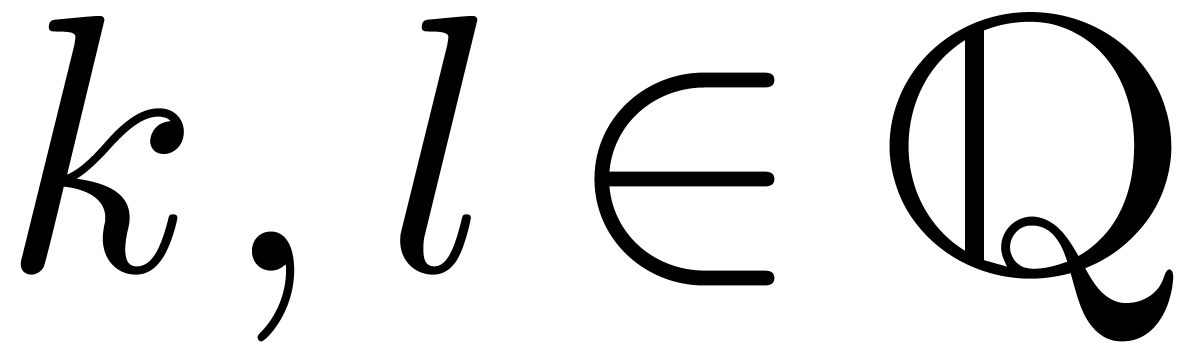 and
and 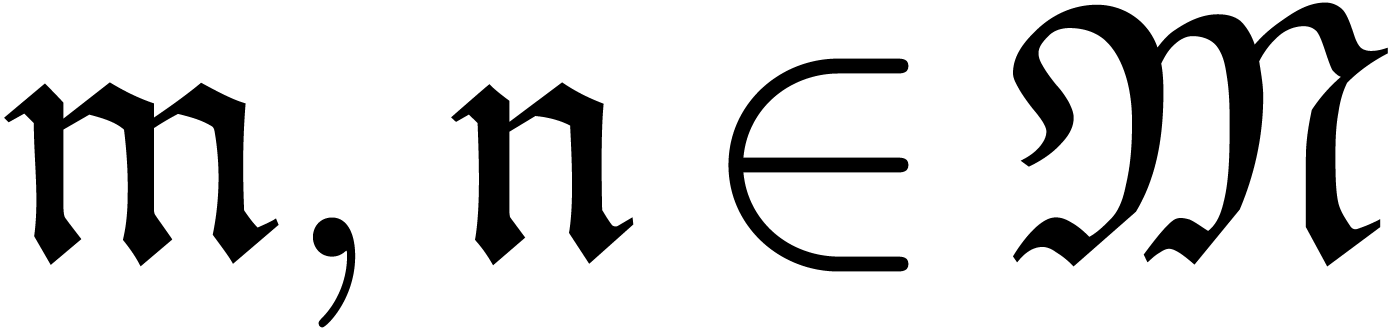 .
.
A monomial monoid  is said to be
effective if its elements can be represented by effective data
structures and if we have algorithms for the multiplication and the
asymptotic ordering
is said to be
effective if its elements can be represented by effective data
structures and if we have algorithms for the multiplication and the
asymptotic ordering  . Since
. Since
 this implies the existence of an effective
equality test. A monomial group
this implies the existence of an effective
equality test. A monomial group  is said to be
effective if it is an effective monomial monoid with an
algorithm for the group inverse. We say that
is said to be
effective if it is an effective monomial monoid with an
algorithm for the group inverse. We say that  is
an effective monomial group with
is
an effective monomial group with  -powers
if we also have a computable powering operation.
-powers
if we also have a computable powering operation.
A subset 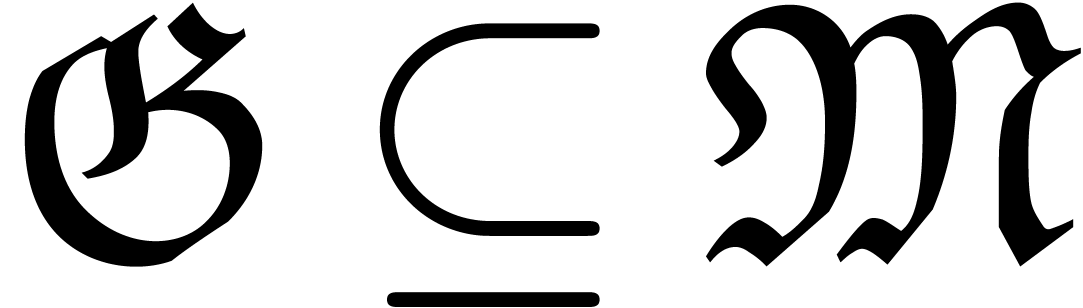 is said to be grid-based if
there exist finite sets
is said to be grid-based if
there exist finite sets 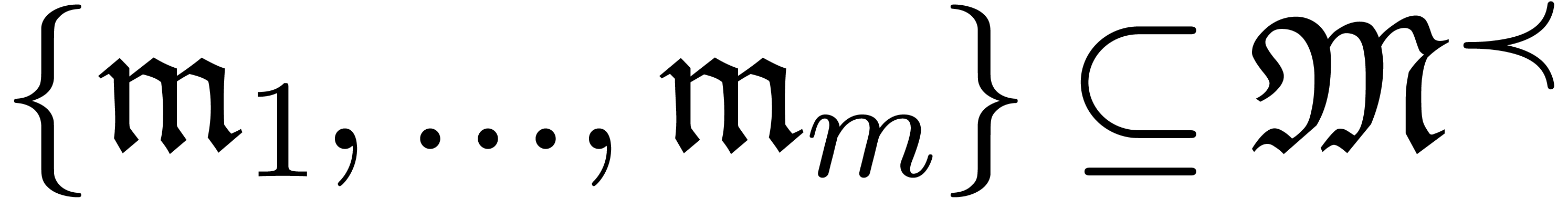 and
and 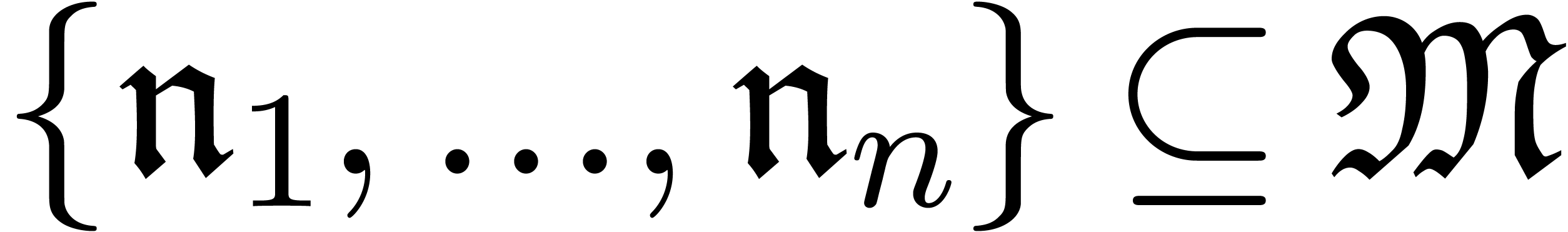 such that
such that
If  is actually a monomial group that is
generated (as a group) by its infinitesimal elements, then we may always
take
is actually a monomial group that is
generated (as a group) by its infinitesimal elements, then we may always
take 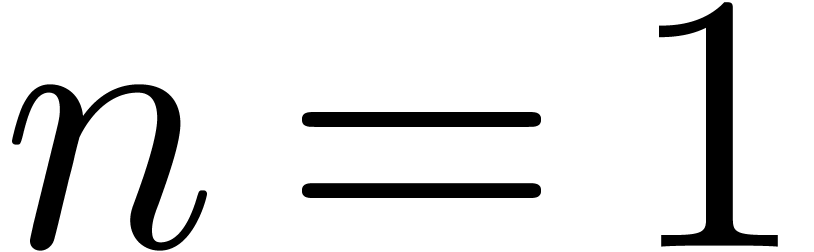 .
.
If  is an effective monomial monoid, then a
grid-based subset
is an effective monomial monoid, then a
grid-based subset 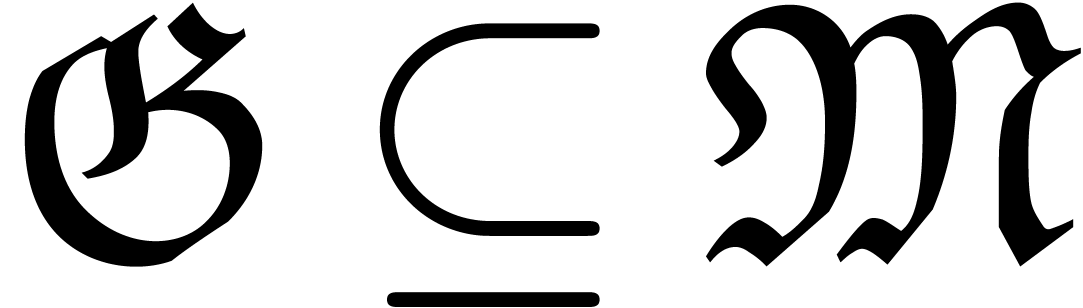 is said to be
effective if the predicate
is said to be
effective if the predicate  is
computable and if finite sets
is
computable and if finite sets 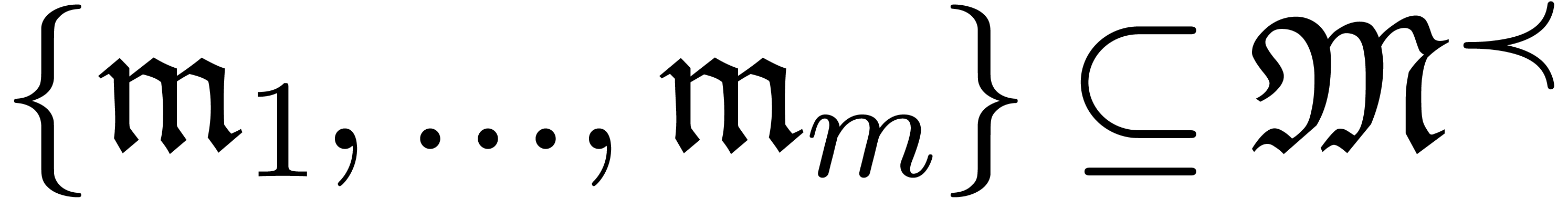 and
and 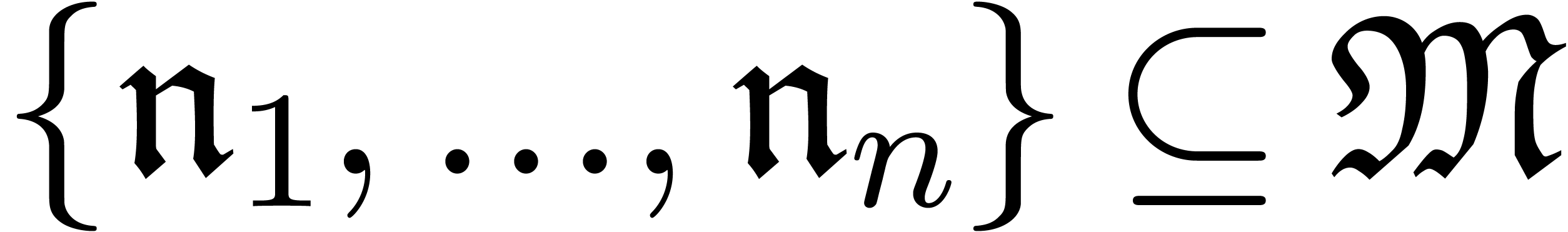 with (1) are explicitly given.
with (1) are explicitly given.
Let  be a field of characteristic zero. Given a
formal series
be a field of characteristic zero. Given a
formal series 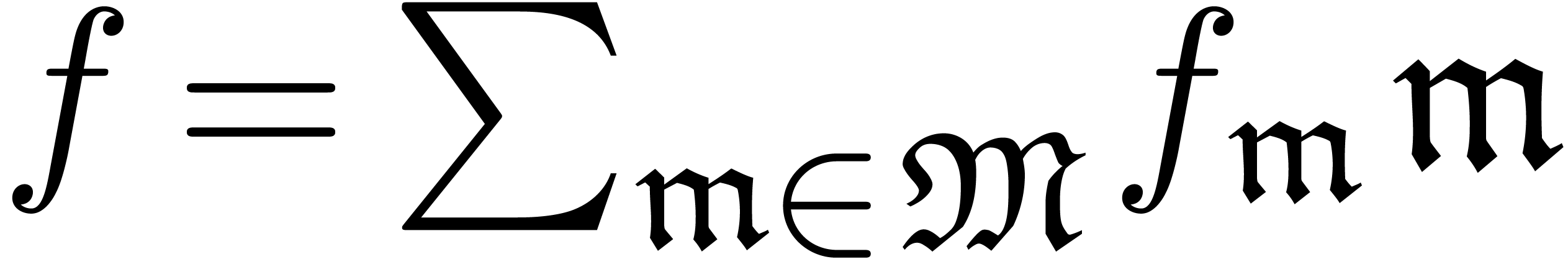 with
with 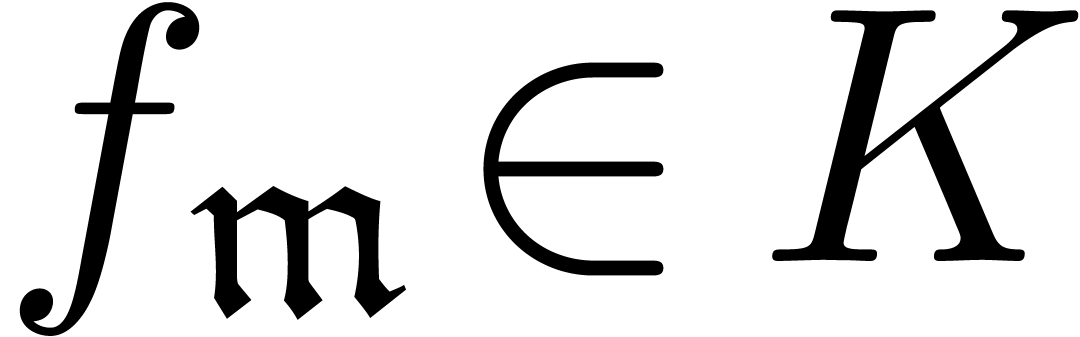 ,
the set
,
the set 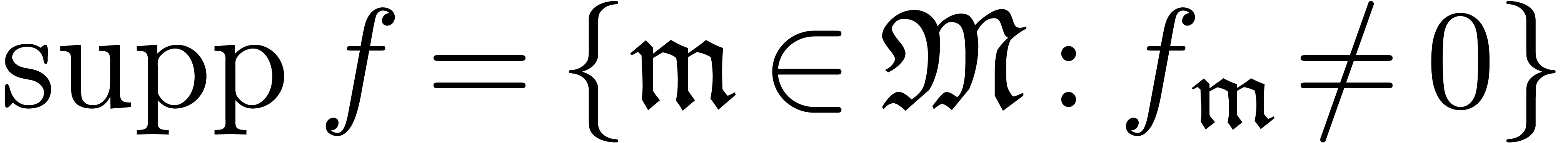 will be called the support of
will be called the support of
 . We say that the formal
series
. We say that the formal
series  is grid-based if its support is
grid-based and we denote by
is grid-based if its support is
grid-based and we denote by 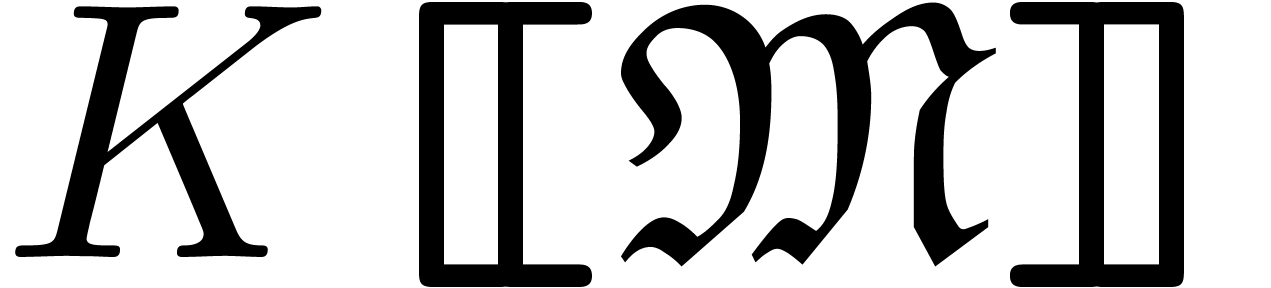 the set of such
series. A grid-based series
the set of such
series. A grid-based series 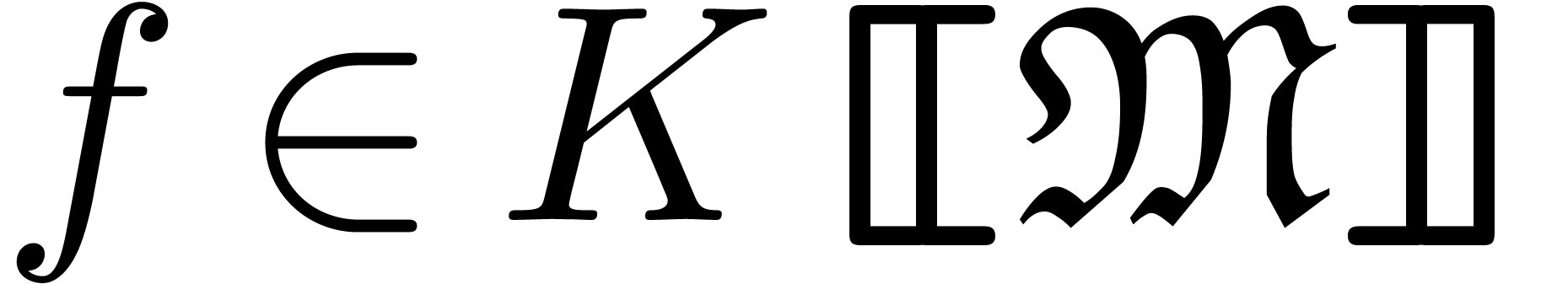 is said to be
infinitesimal or bounded if
is said to be
infinitesimal or bounded if 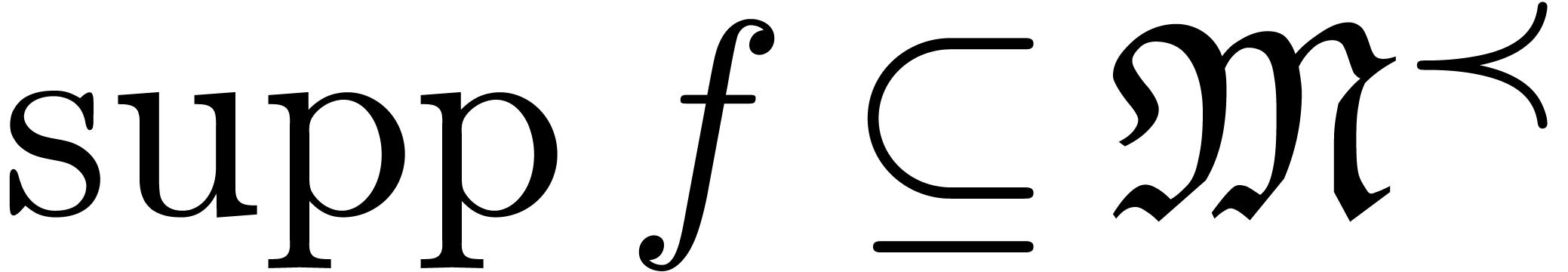 resp.
resp. 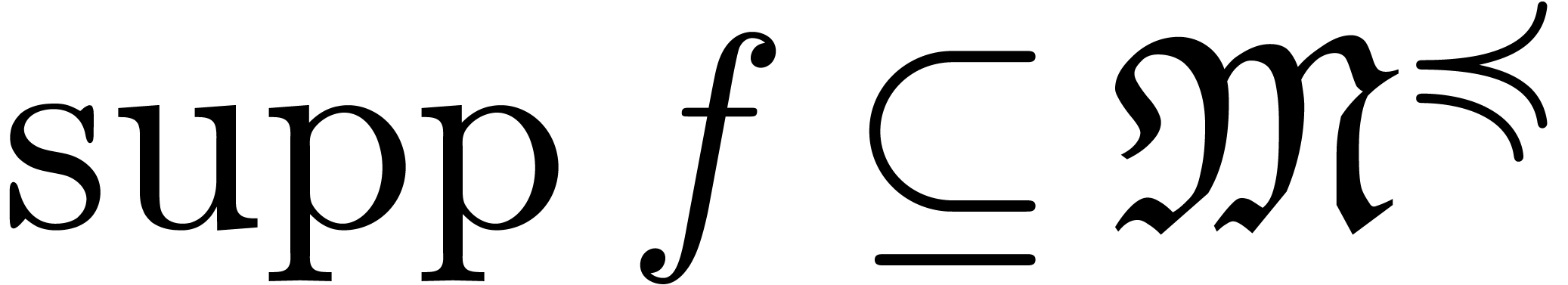 , and we
denote by
, and we
denote by  resp.
resp.  the sets of such series.
the sets of such series.
In [13, Chapter 2] elementary properties of grid-based
series are studied at length. We prove there that 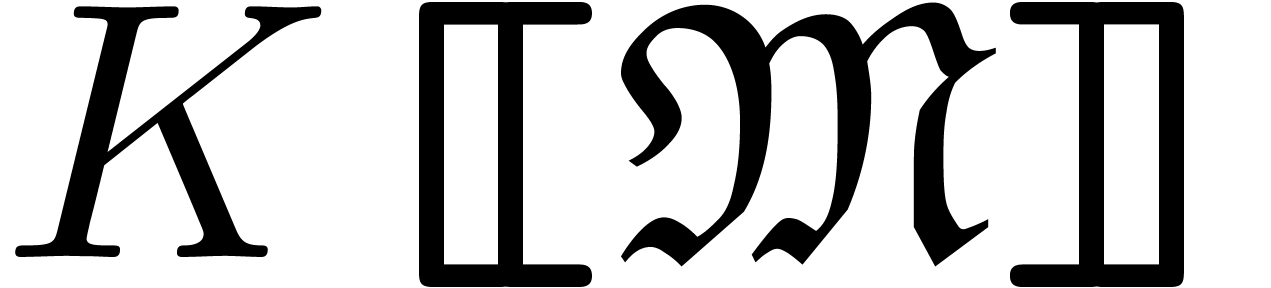 forms a ring in which all series
forms a ring in which all series  with
with 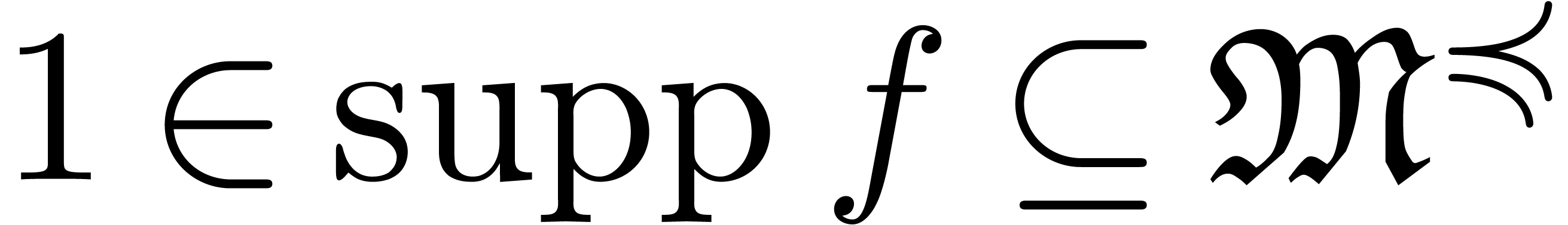 are invertible. In particular, if
are invertible. In particular, if  is a totally ordered group, then
is a totally ordered group, then 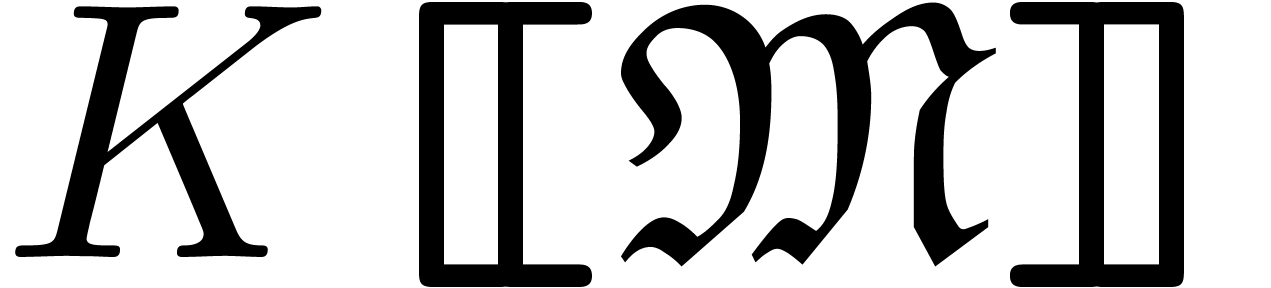 forms a field.
Given a power series
forms a field.
Given a power series 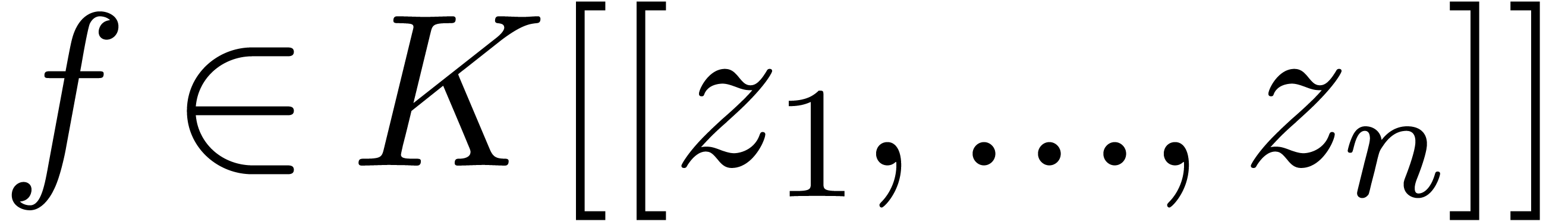 and grid-based series
and grid-based series 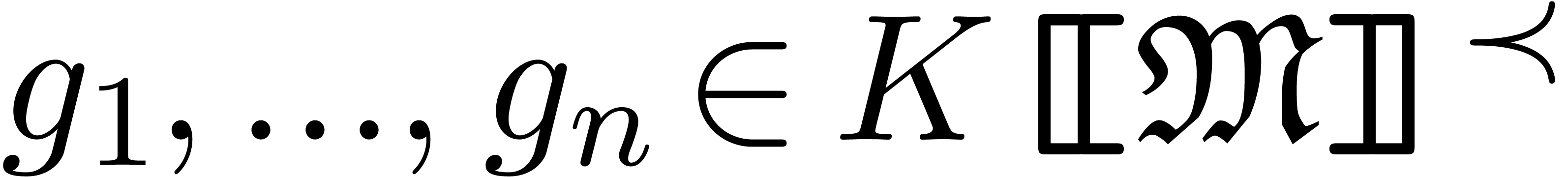 , there is also a natural
definition for the composition
, there is also a natural
definition for the composition  .
.
Given a grid-based series 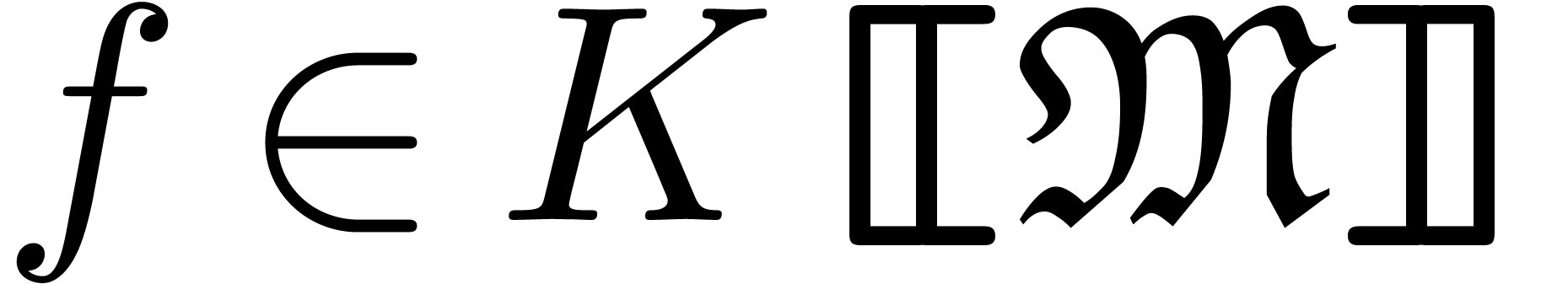 the maximal elements
of
the maximal elements
of 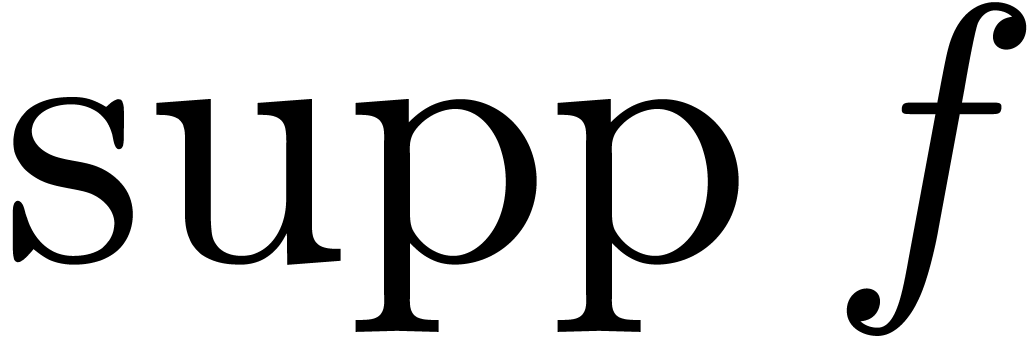 for
for  are called
dominant monomials for
are called
dominant monomials for  .
If
.
If  has a unique dominant monomial, then we say
that
has a unique dominant monomial, then we say
that  is regular, we write
is regular, we write 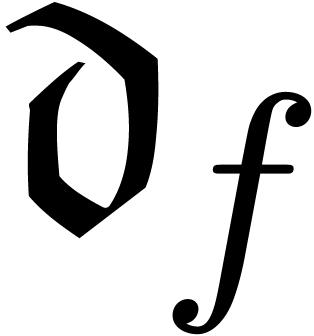 for the dominant monomial of
for the dominant monomial of  ,
and call
,
and call  the dominant coefficient of
the dominant coefficient of
 . If
. If  is totally ordered, then any non-zero grid-based series in
is totally ordered, then any non-zero grid-based series in  is regular. Given
is regular. Given 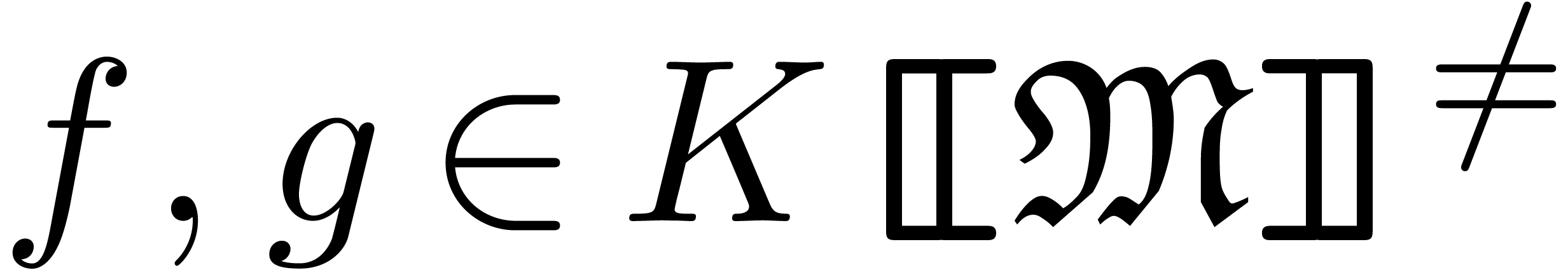 ,
this allows us to extend the relations
,
this allows us to extend the relations  and
and  by defining
by defining  and
and  . By convention, we also define
. By convention, we also define  and
and  for all
for all 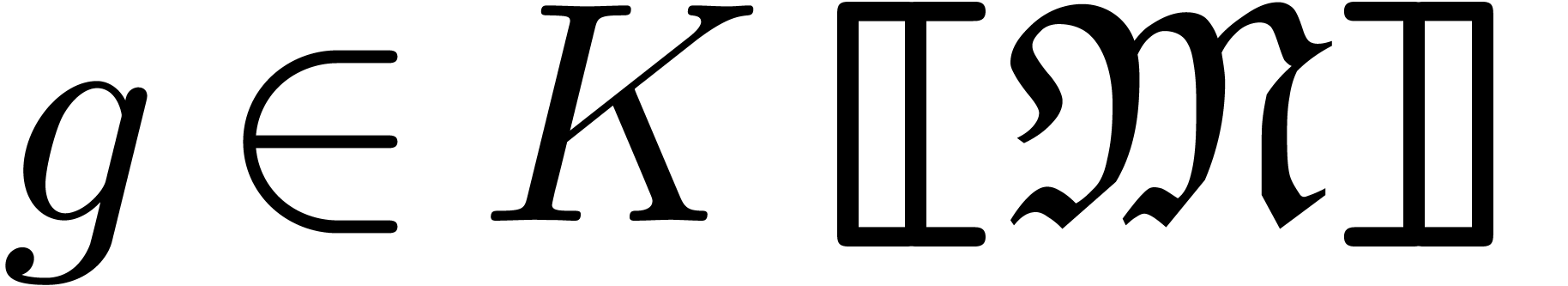 .
.
Assume that  and
and  are
effective. Then a grid-based series
are
effective. Then a grid-based series 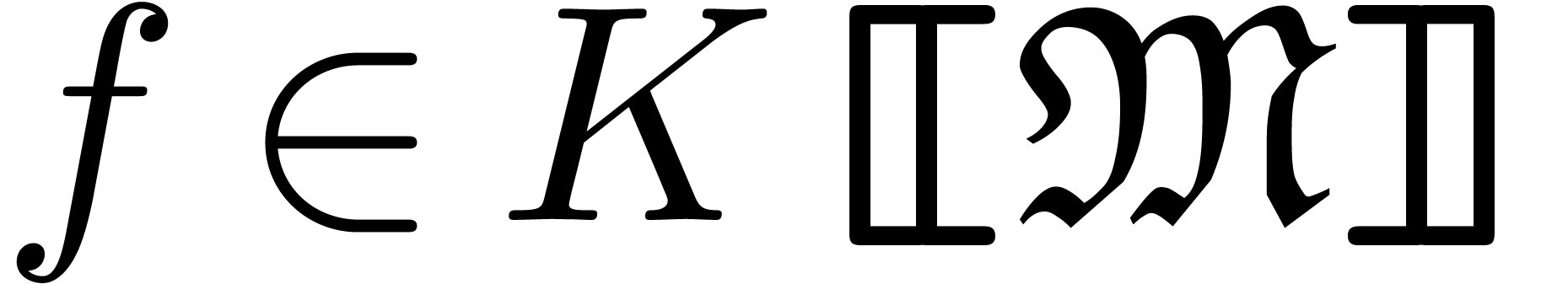 is said to
be effective if its support is effective and if the map
is said to
be effective if its support is effective and if the map  is computable. It can be shown that the set
is computable. It can be shown that the set 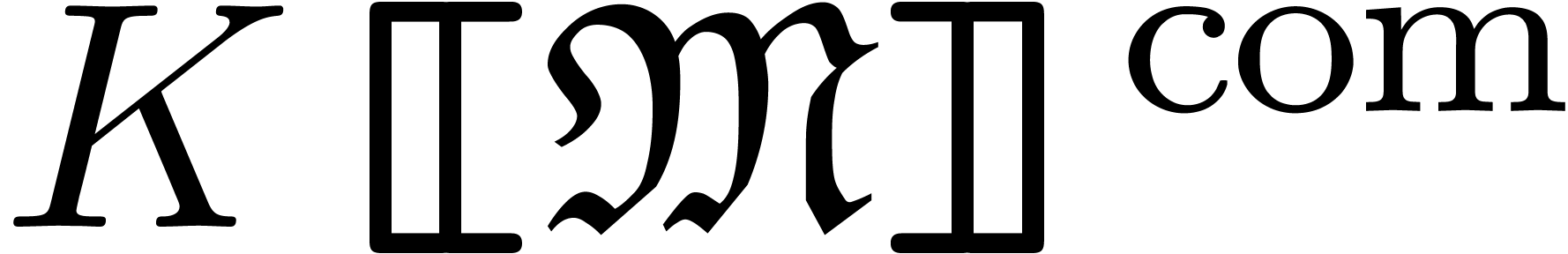 of computable grid-based series forms an effective
of computable grid-based series forms an effective  -algebra.
-algebra.
Given an “infinitesimal” indeterminate  , the set
, the set 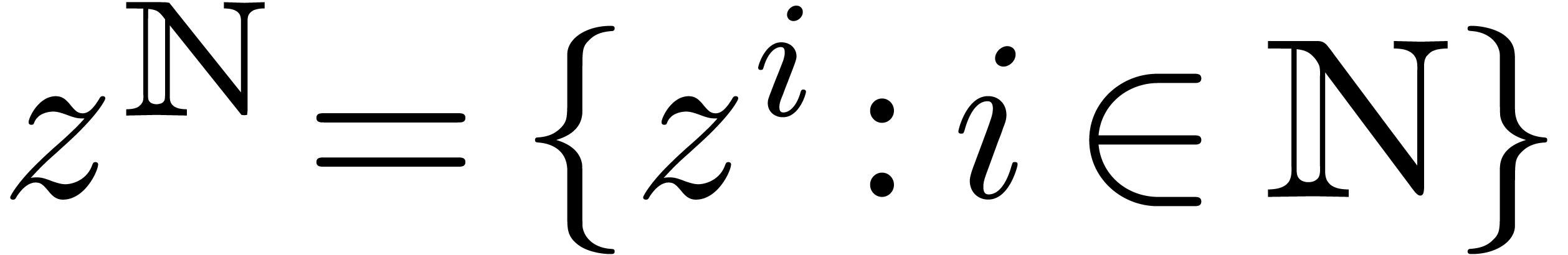 is a monomial
monoid for the asymptotic ordering
is a monomial
monoid for the asymptotic ordering 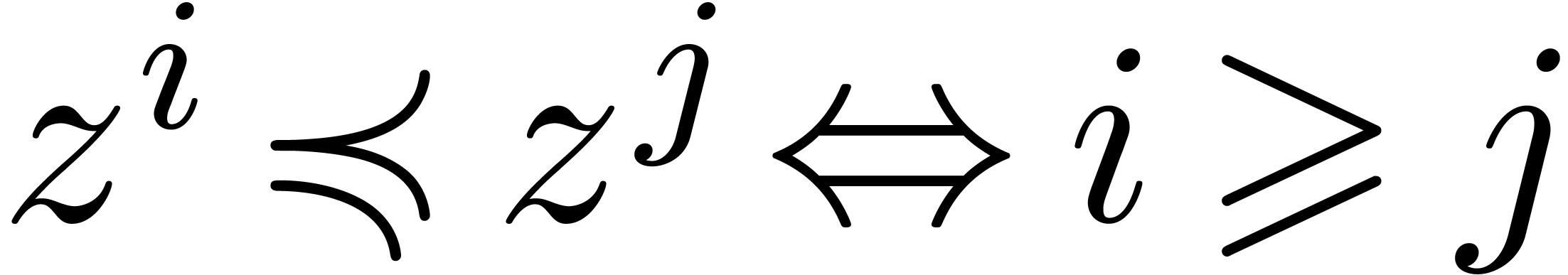 ,
and
,
and 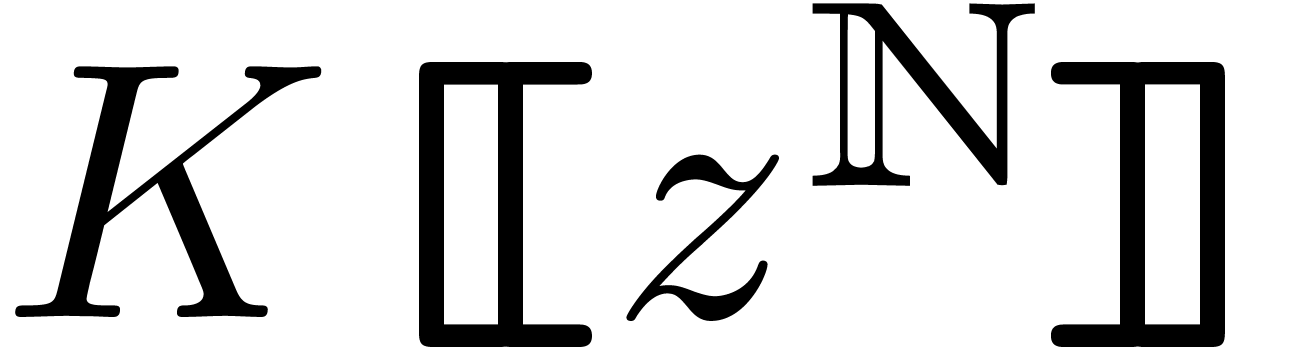 coincides with
coincides with 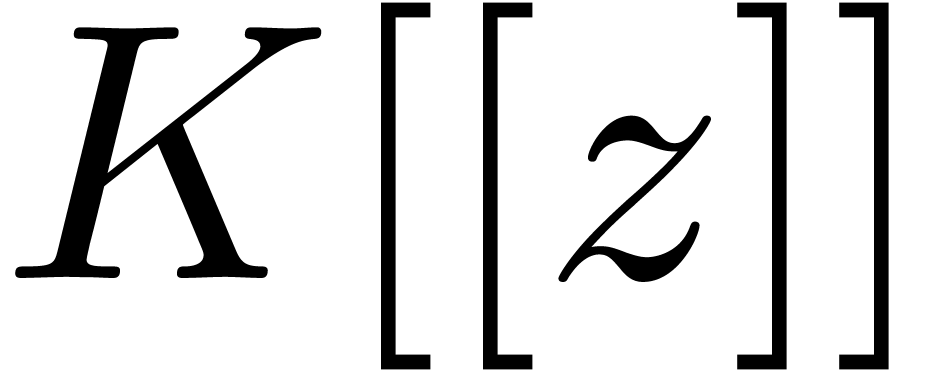 .
Similarly,
.
Similarly,  coincides with the field of Laurent
series
coincides with the field of Laurent
series 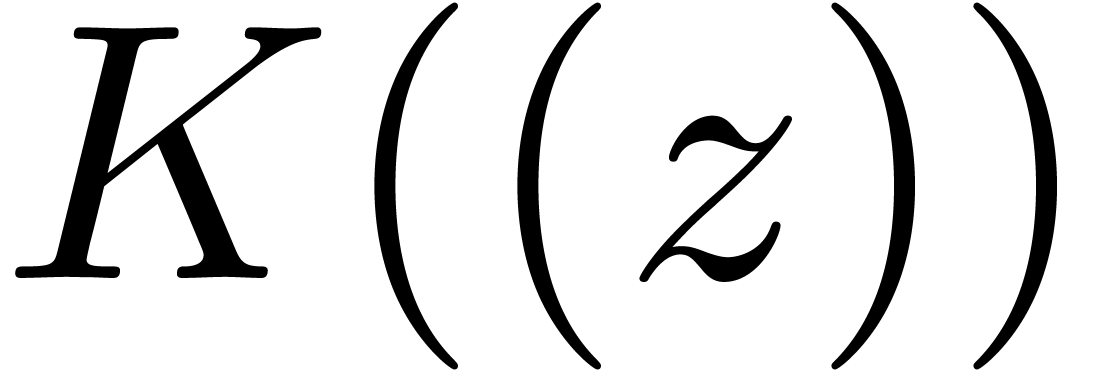 . Notice that
. Notice that 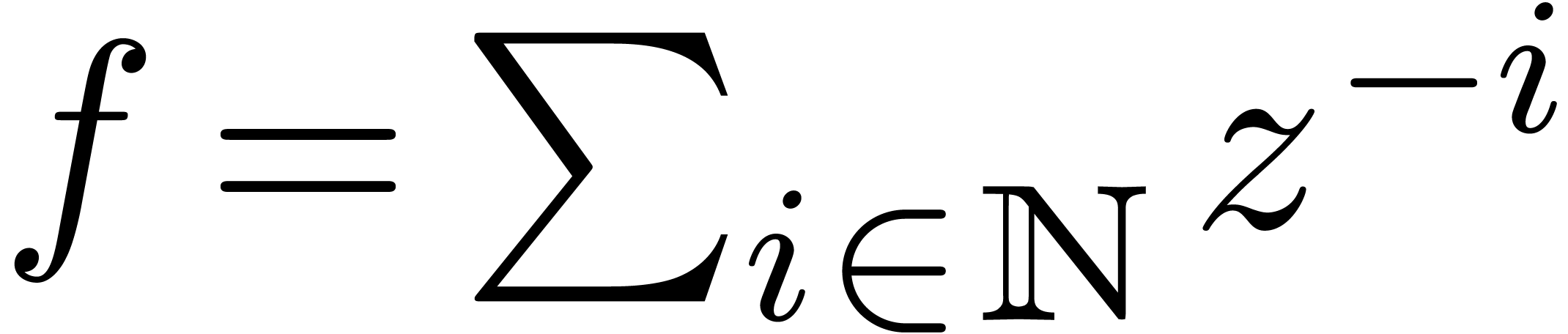 is not an element of
is not an element of  , since its support
, since its support 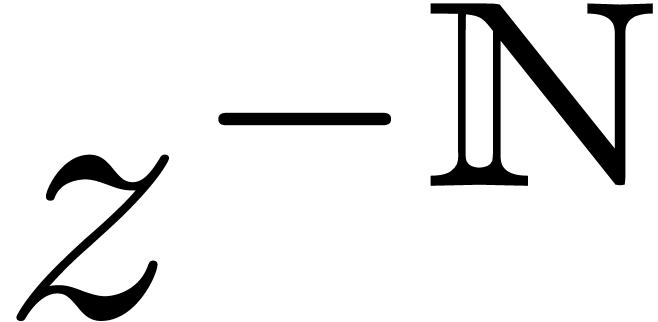 admits
no largest element for
admits
no largest element for  ,
whence it cannot be grid-based. Beyond Laurent series, it is easily
verified that
,
whence it cannot be grid-based. Beyond Laurent series, it is easily
verified that 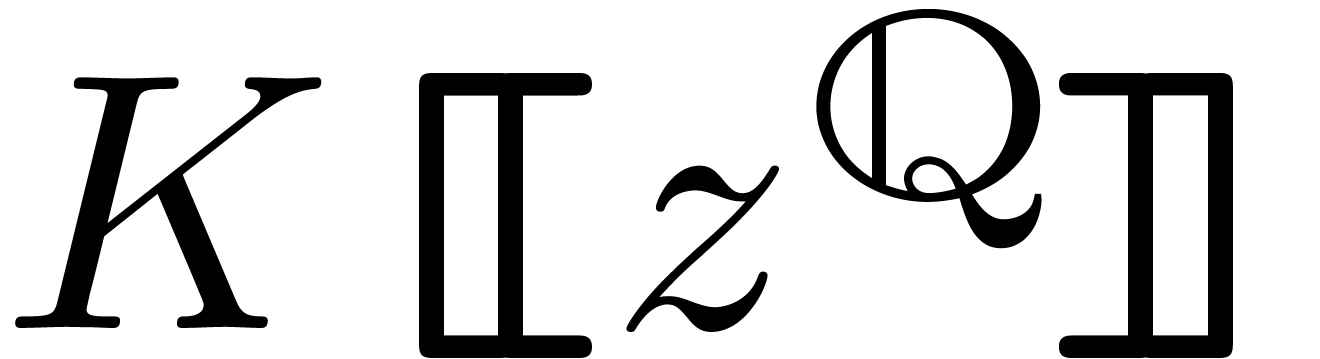 coincides with the field of
Puiseux series in
coincides with the field of
Puiseux series in  over
over  . If
. If  is algebraically
closed, then so is
is algebraically
closed, then so is 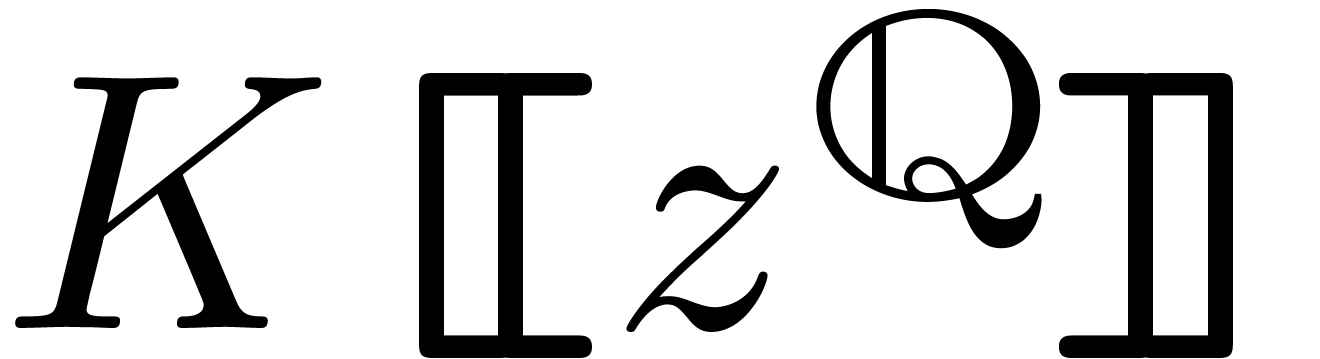 .
.
Given monomial monoids  , one
may form the product monomial monoid
, one
may form the product monomial monoid  with
with  for all
for all  .
Then
.
Then  coincides with the set of power series
coincides with the set of power series
 , whereas
, whereas  coincides with the set of Laurent series that we denote by
coincides with the set of Laurent series that we denote by  . If
. If 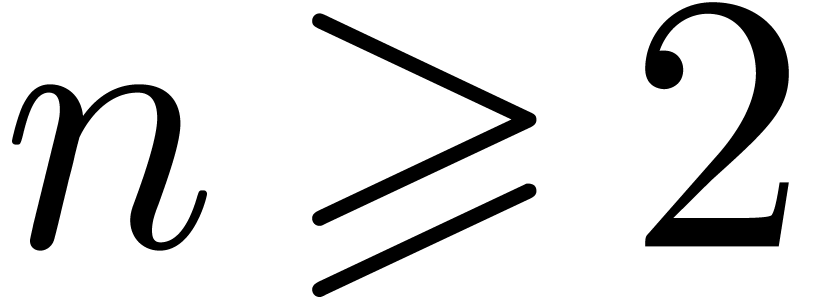 ,
then we notice that
,
then we notice that  is a strict subring of the
quotient field of
is a strict subring of the
quotient field of  .
.
Given monomial monoids  , one
may also form the set
, one
may also form the set  whose elements
whose elements  are ordered anti-lexicographically:
are ordered anti-lexicographically: 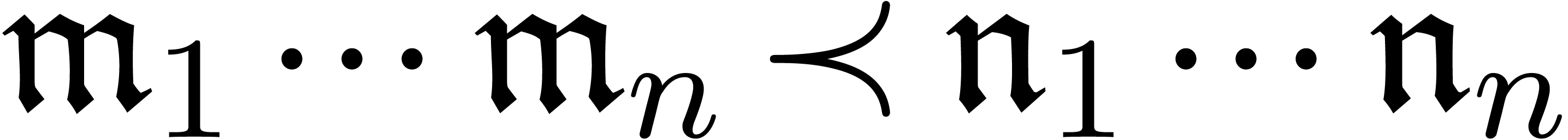 if there exists an
if there exists an 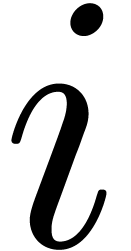 with
with  and
and  for all
for all  .
The set
.
The set  should naturally be interpreted as
should naturally be interpreted as  (which is isomorphic to
(which is isomorphic to  ).
The set
).
The set  is a field that contains
is a field that contains  , and this inclusion is strict if
, and this inclusion is strict if 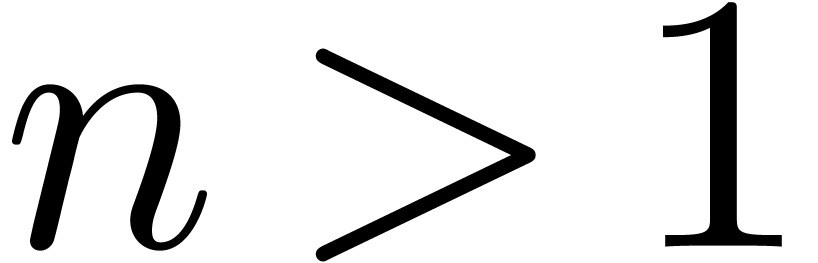 (notice also that
(notice also that 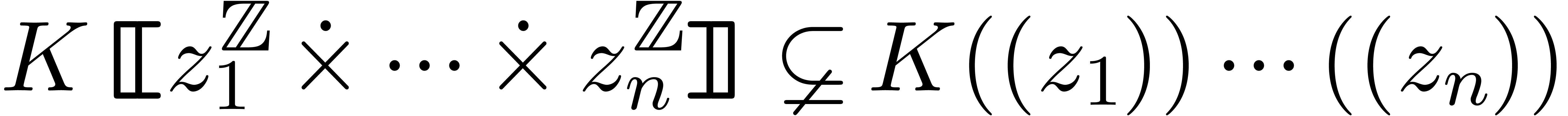 ).
If
).
If  is algebraically closed, then
is algebraically closed, then  is again an algebraically closed field (and again, we have
is again an algebraically closed field (and again, we have
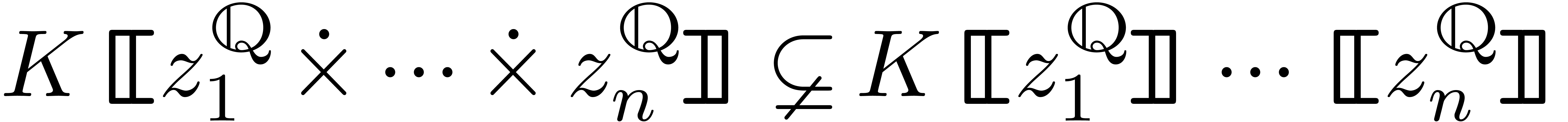 ).
).
Let  be a totally ordered group. Given
be a totally ordered group. Given 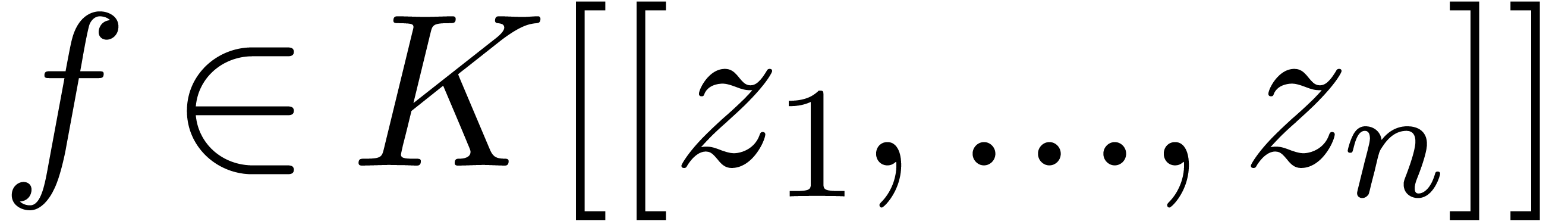 and
and 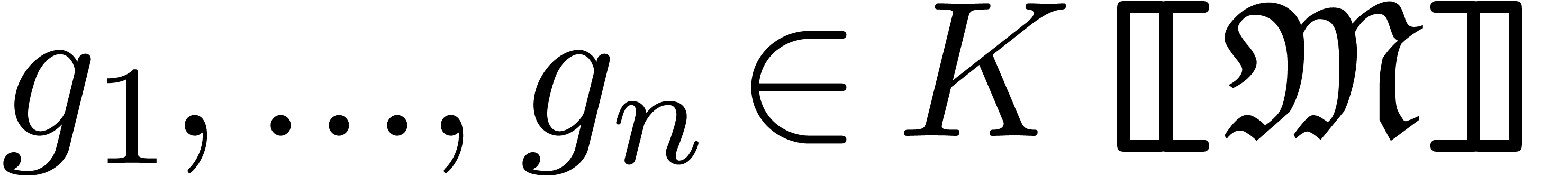 , we have
already observed that
, we have
already observed that 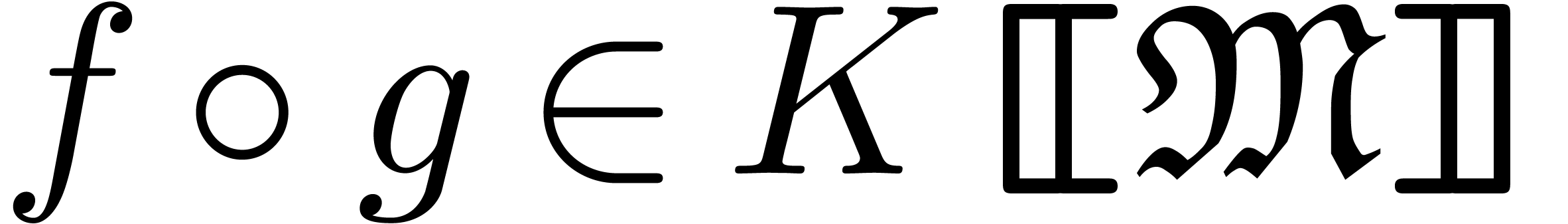 whenever
whenever  . This means that we may regard
. This means that we may regard  as a space of “local functions”
as a space of “local functions” 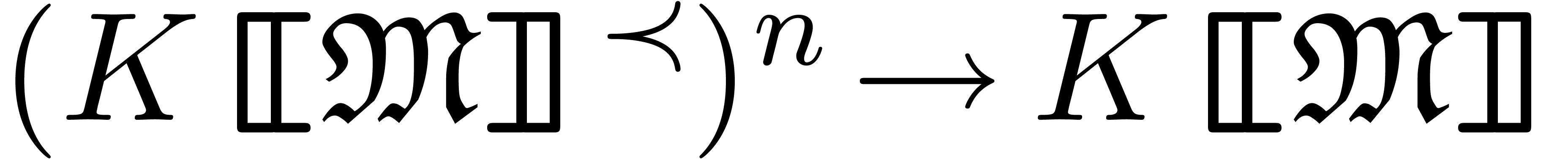 . Similarly,
. Similarly, 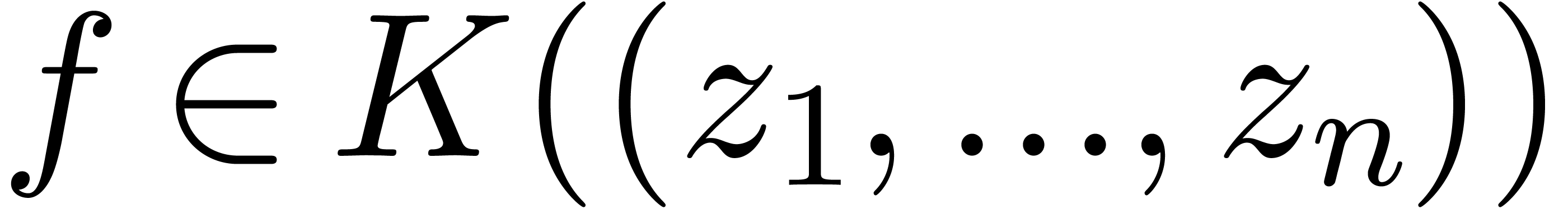 can be
regarded as a function
can be
regarded as a function  and
and 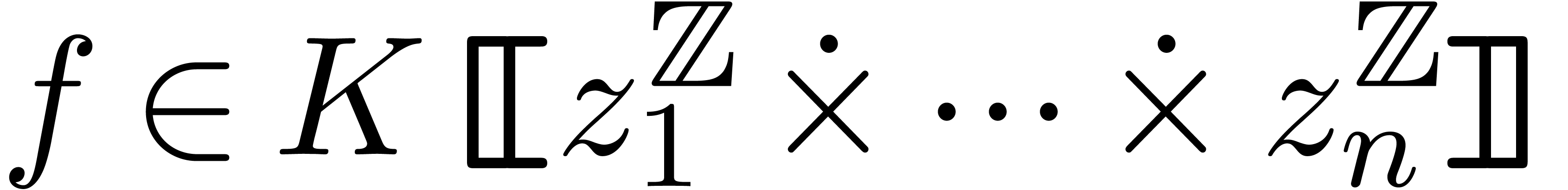 as a function
as a function 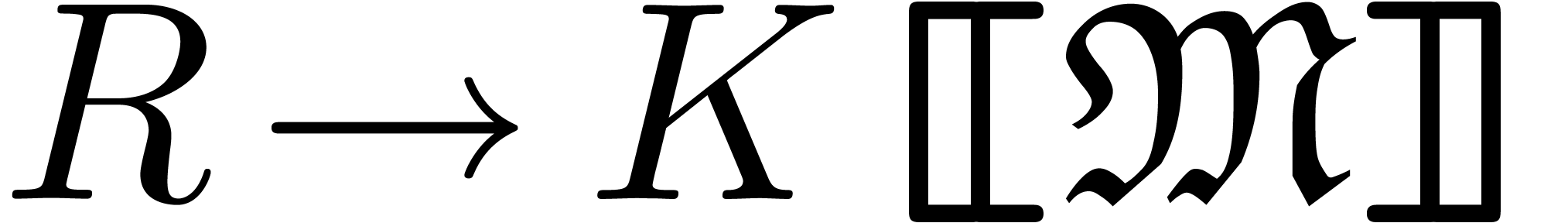 where
where  . More generally, for any monomial group
. More generally, for any monomial group  with underlying group
with underlying group  ,
the algebra
,
the algebra 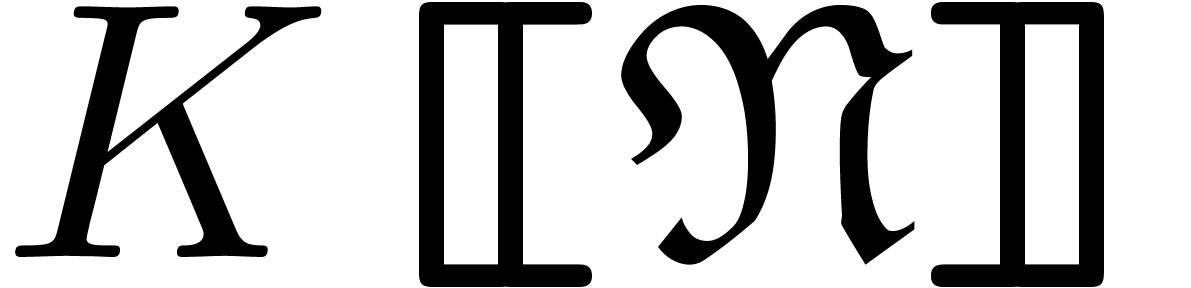 can be regarded as a local function
space on a subset of
can be regarded as a local function
space on a subset of  .
.
From now on, we will assume that  is a monomial
group that is generated as a group by its infinitesimal elements. Given
a series
is a monomial
group that is generated as a group by its infinitesimal elements. Given
a series 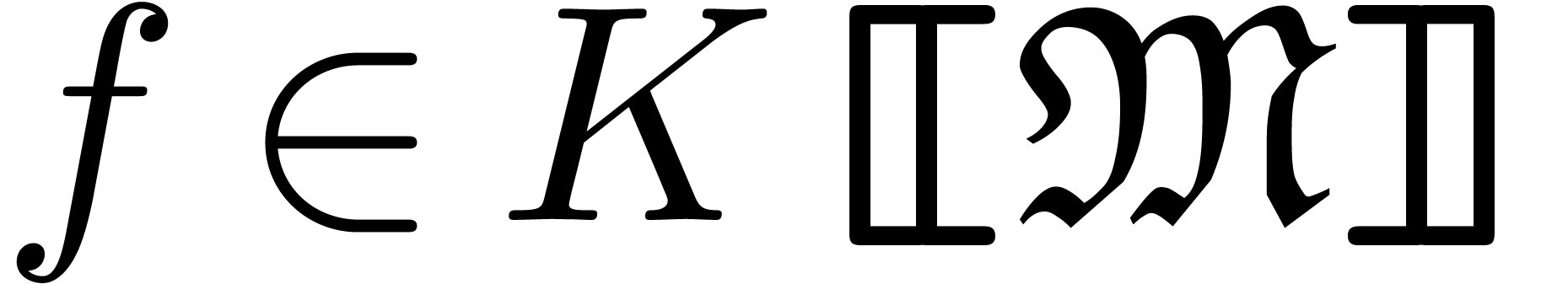 , a Cartesian
representation for
, a Cartesian
representation for  is a Laurent series
is a Laurent series 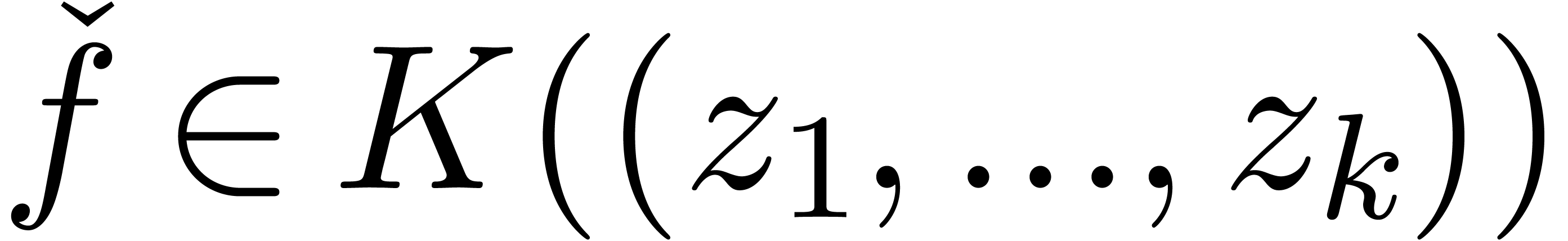 together with monomials
together with monomials 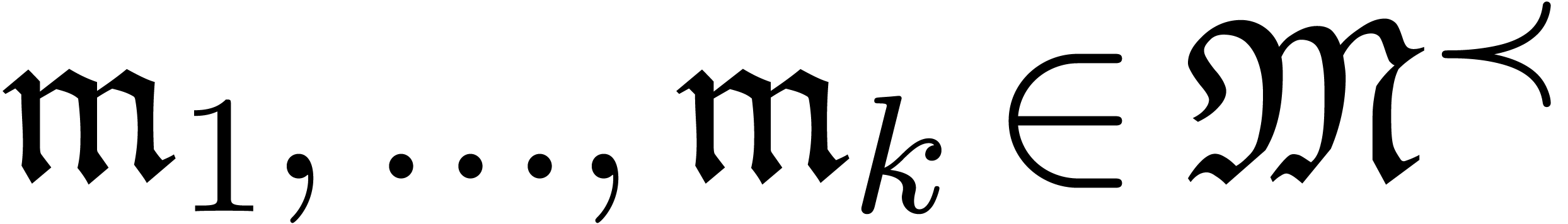 such
that
such
that 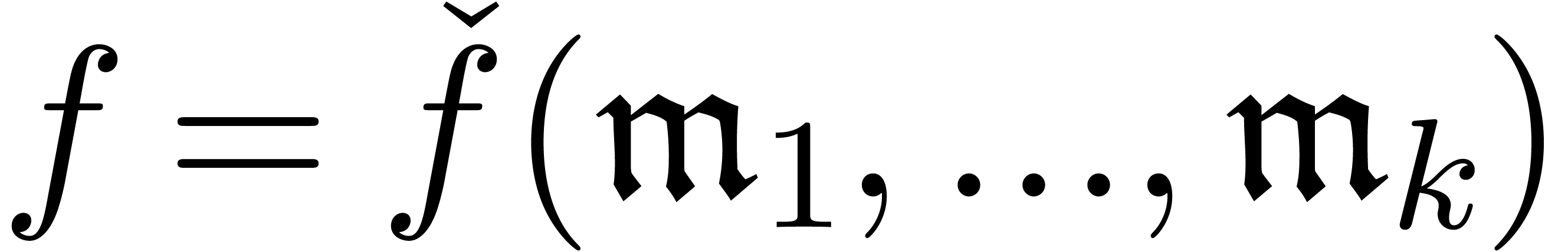 . Given several series
. Given several series
 , and Cartesian
representations for each of the
, and Cartesian
representations for each of the  ,
we say that these Cartesian representations are compatible if
they are of the form
,
we say that these Cartesian representations are compatible if
they are of the form 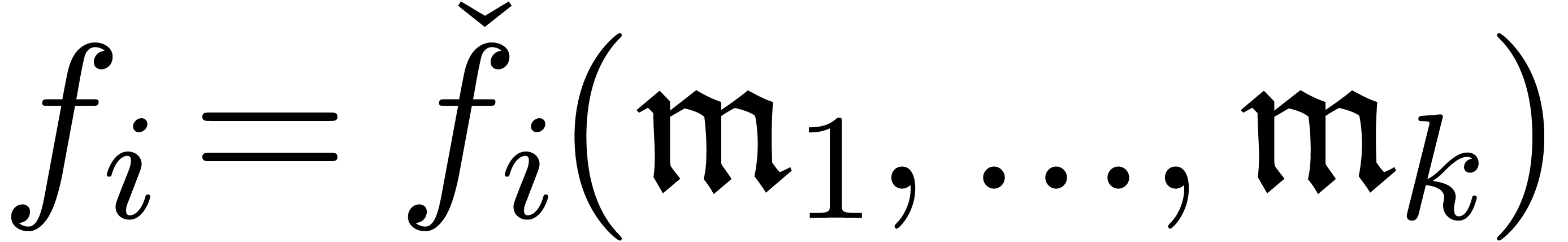 for
for 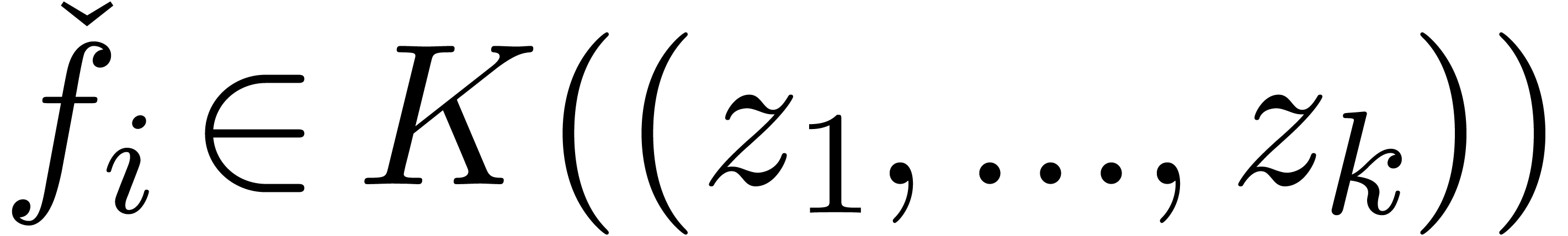 and
and 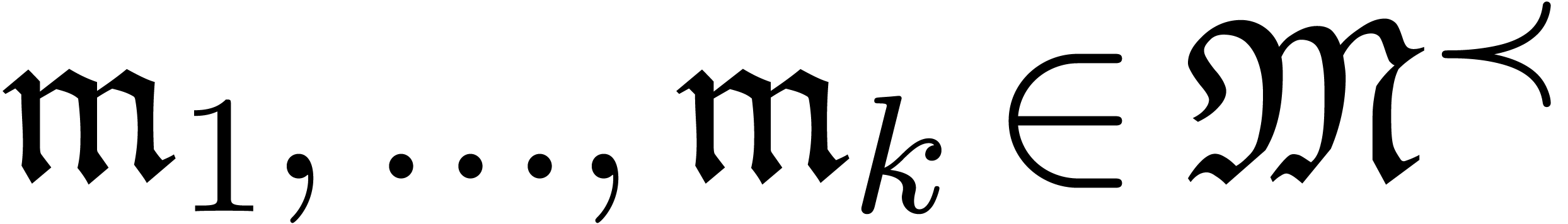 . In [13,
Proposition 3.12] we show that such compatible Cartesian representations
always exist.
. In [13,
Proposition 3.12] we show that such compatible Cartesian representations
always exist.
In [13, Chapter 3], we gave constructive proofs of several
basic facts about Cartesian representations and  -based series to be introduced below. These
constructive proofs can easily be transformed into algorithms, so we
will only state the effective counterparts of the main results. First of
all, in order to keep the number of variables
-based series to be introduced below. These
constructive proofs can easily be transformed into algorithms, so we
will only state the effective counterparts of the main results. First of
all, in order to keep the number of variables 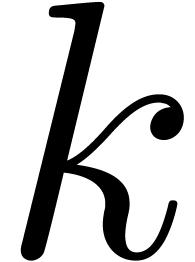 in
Cartesian representations as low as possible, we may use the following
effective variant of [13, Lemma 3.13]:
in
Cartesian representations as low as possible, we may use the following
effective variant of [13, Lemma 3.13]:
Lemma
 be infinitesimal elements of an
effective totally ordered monomial group
be infinitesimal elements of an
effective totally ordered monomial group  with
with
 -powers, such that we have
explicit expressions for
-powers, such that we have
explicit expressions for 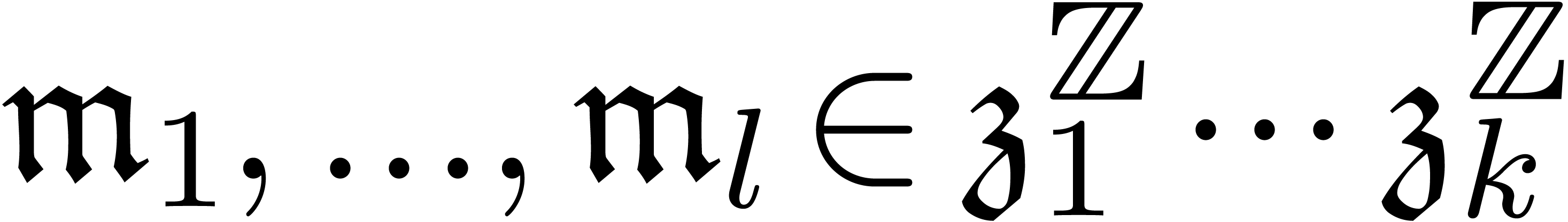 as power products.
Then we may effectively compute infinitesimal
as power products.
Then we may effectively compute infinitesimal 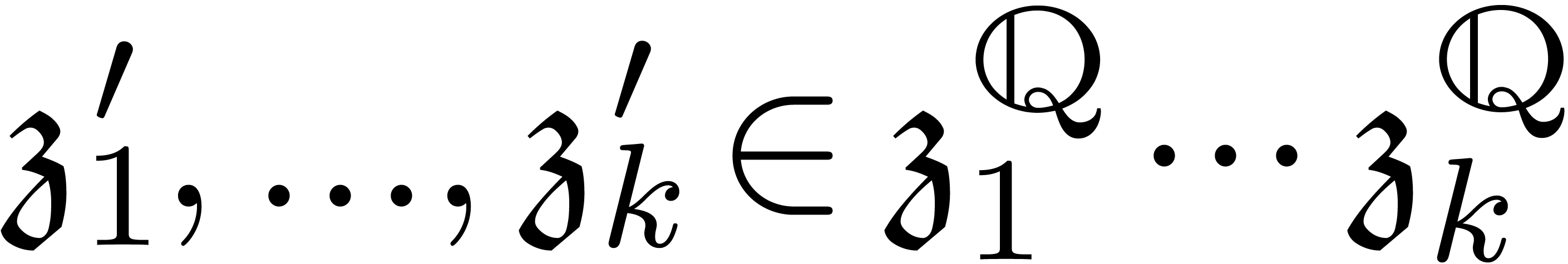 with
with 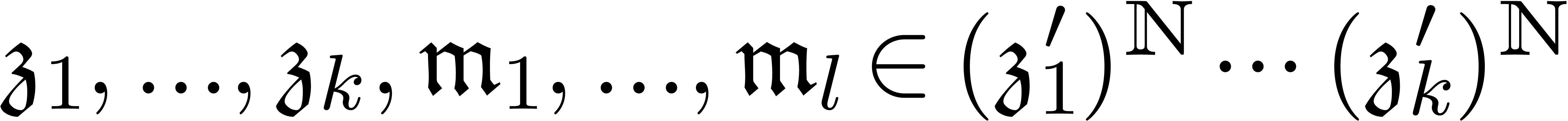 .
.

 -based power
series
-based power
series
Let  be a local community. We will say that
be a local community. We will say that 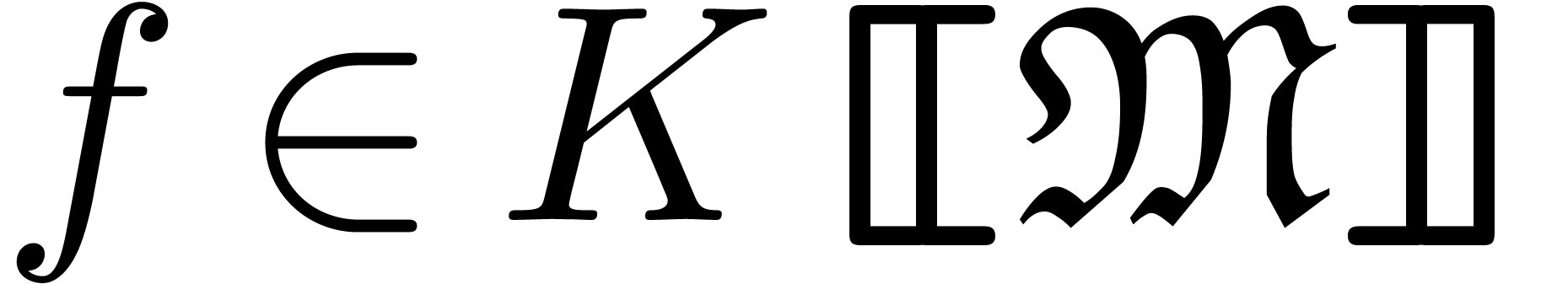 is L-based if
is L-based if  admits
a Cartesian representation of the form
admits
a Cartesian representation of the form 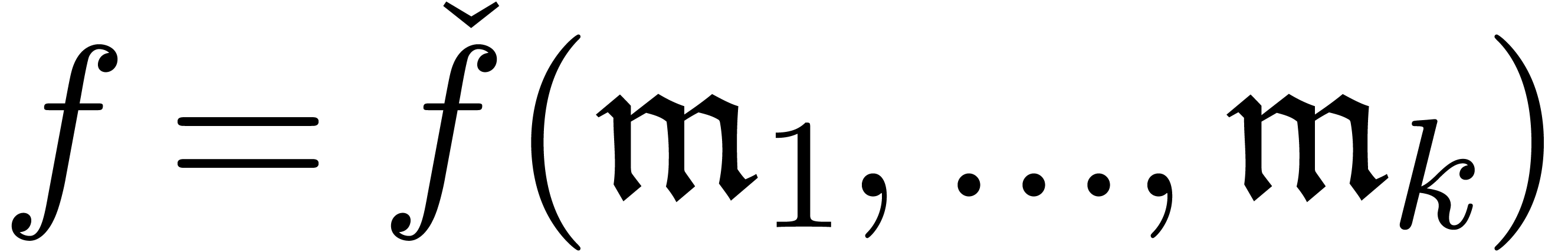 with
with
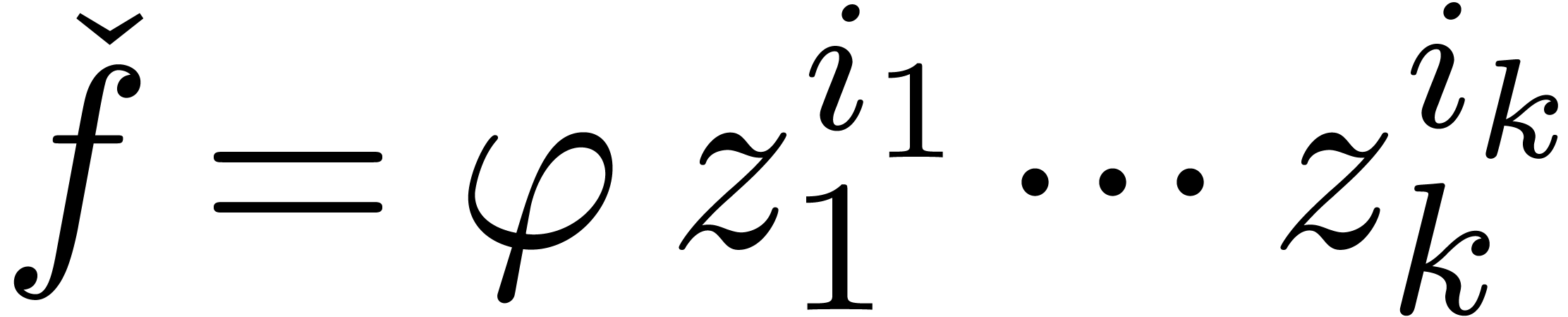 ,
, 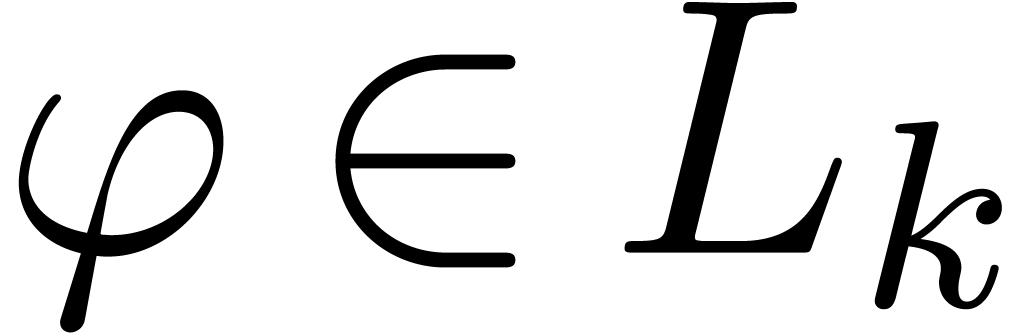 and
and
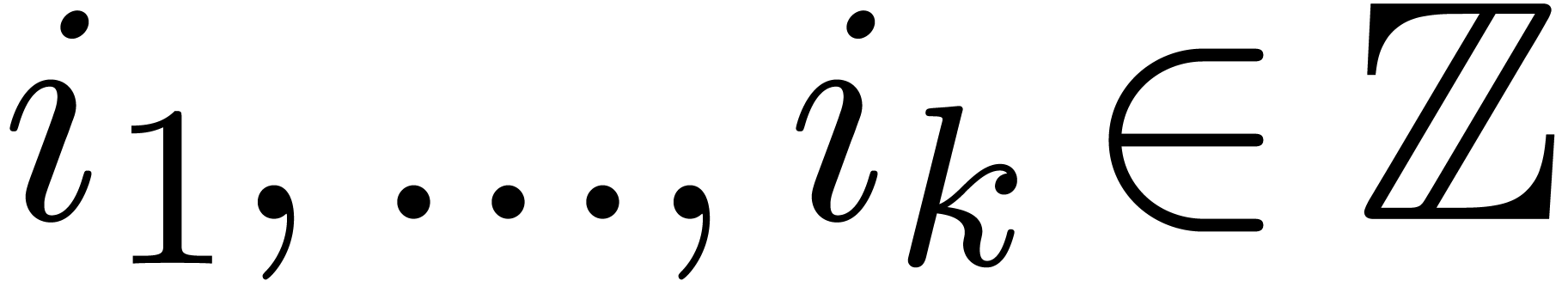 . The set
. The set  of all such series forms a
of all such series forms a  -algebra
[13, Proposition 3.14]. If
-algebra
[13, Proposition 3.14]. If  ,
,
 and
and  are effective, then
any grid-based series in
are effective, then
any grid-based series in  is computable.
Moreover, we may effectively represent series in
is computable.
Moreover, we may effectively represent series in  by Cartesian representations, and
by Cartesian representations, and  is an
effective
is an
effective  -algebra for this
representation.
-algebra for this
representation.
A Cartesian representation 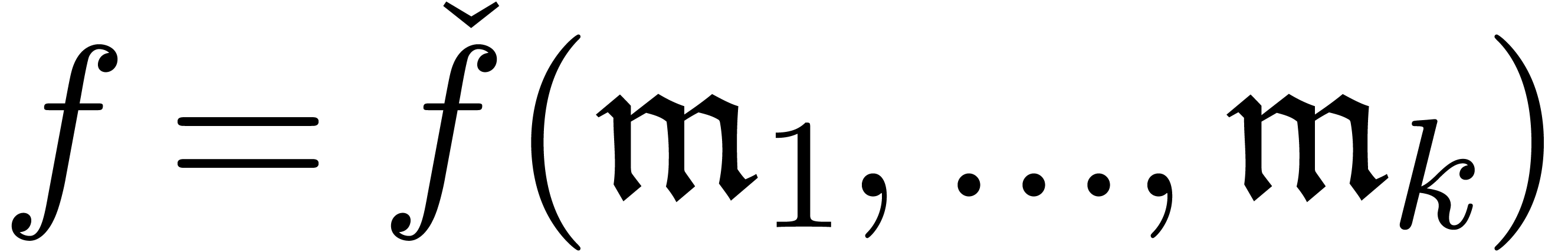 of
of 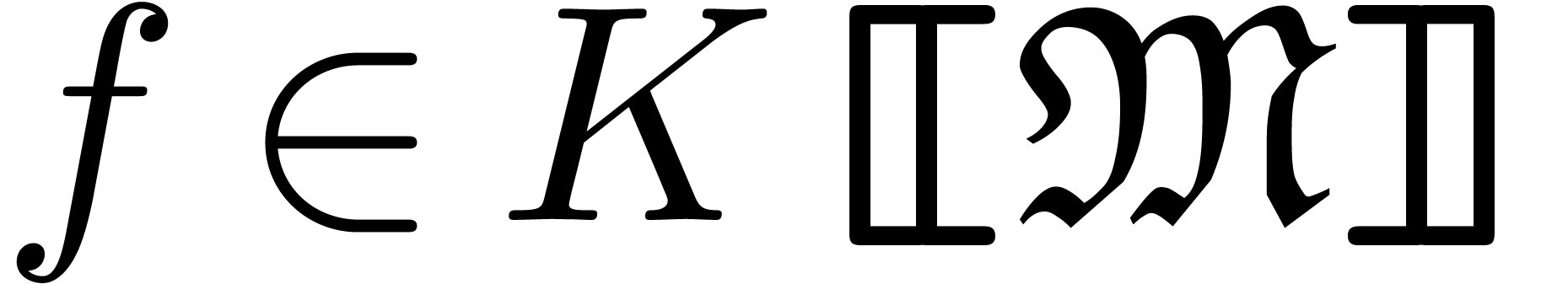 is said to be faithful if for each dominant monomial
is said to be faithful if for each dominant monomial 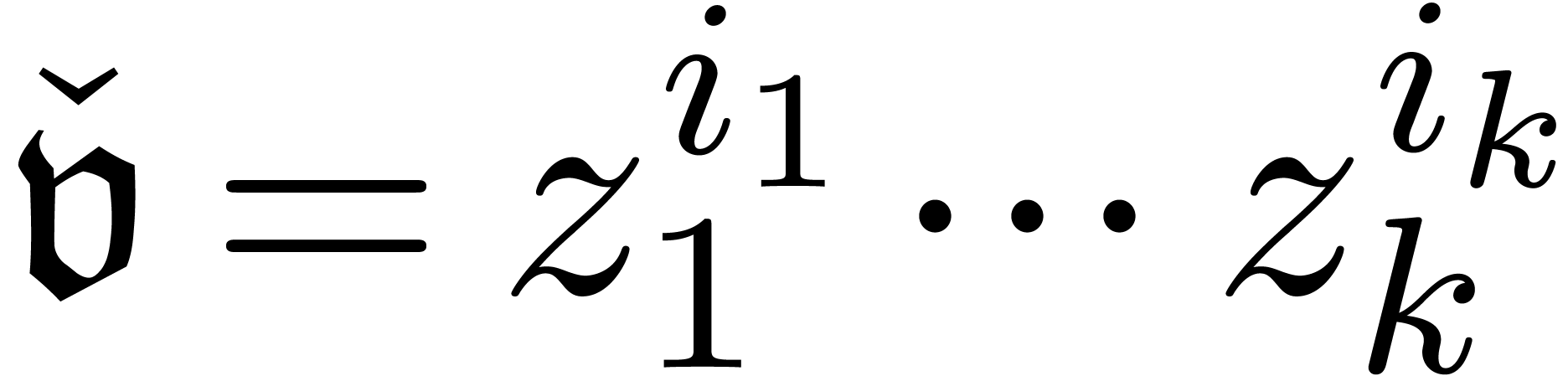 of
of  , there
exists a dominant monomial
, there
exists a dominant monomial  of
of  with
with 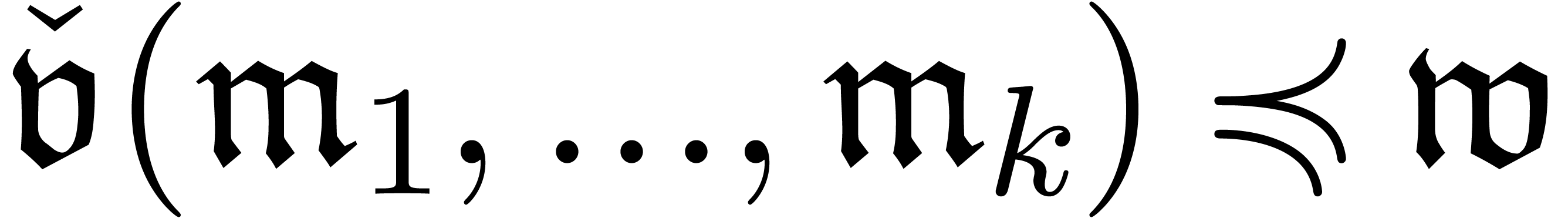 . We have the following
effective counterpart of [13, Proposition 3.19]:
. We have the following
effective counterpart of [13, Proposition 3.19]:
Proposition
 ,
,  and
and  are effective. Then there
exists an algorithm that takes a series in
are effective. Then there
exists an algorithm that takes a series in  as
input and computes a faithful Cartesian representation
as
input and computes a faithful Cartesian representation 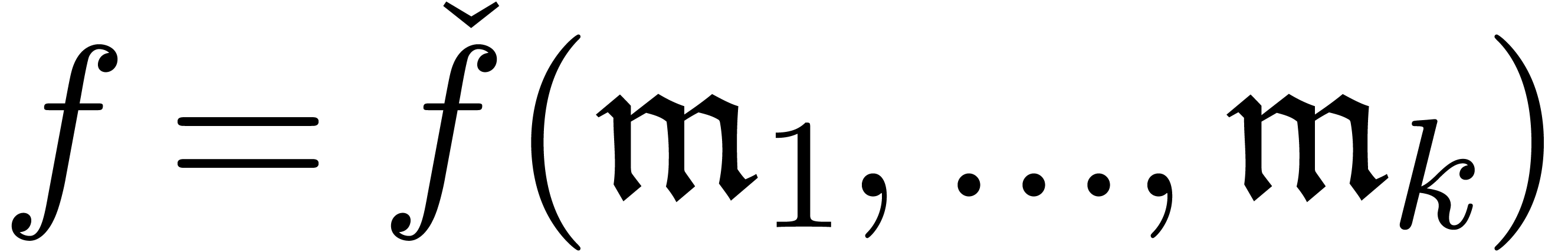 with
with 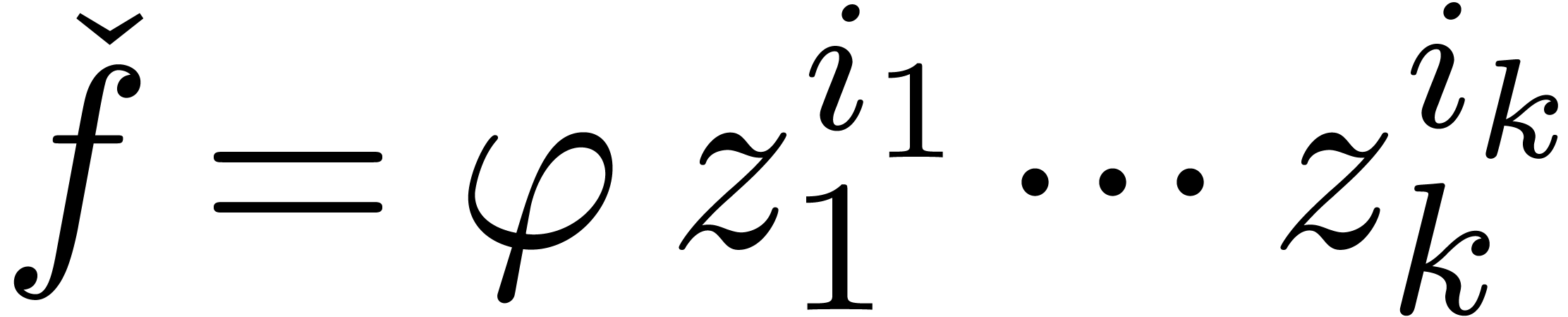 ,
, 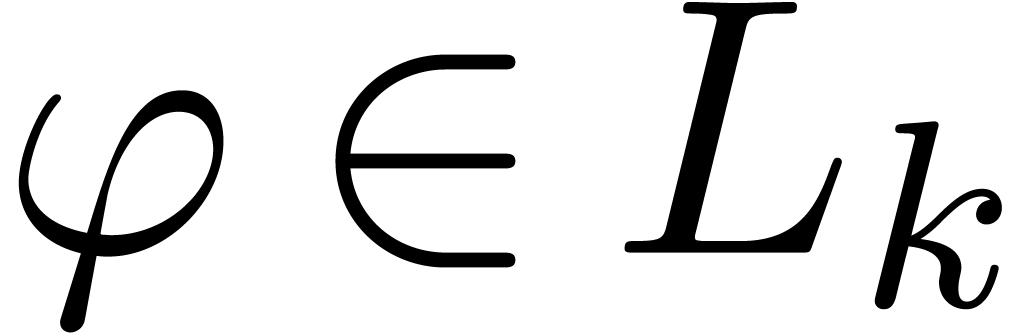 and
and 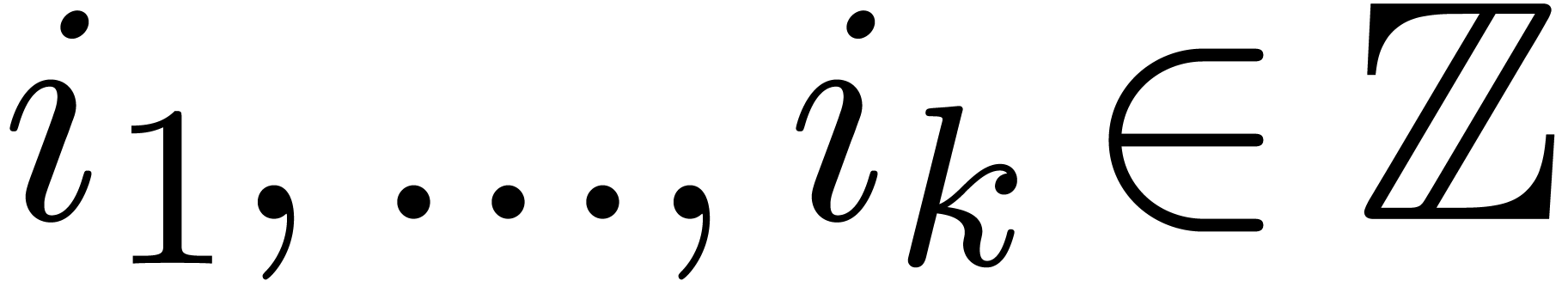 .
.

Faithful Cartesian representations are a useful technical tool for various computations. They occur for instance in the proof of the following effective counterpart of [13, Proposition 3.20]:
Proposition
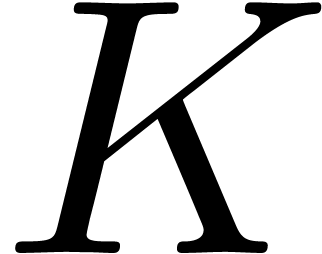 ,
,
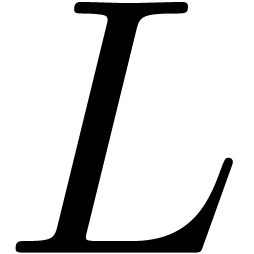 and
and  are effective.
There exists an algorithm that takes an infinitesimal (or bounded, or
regular) series
are effective.
There exists an algorithm that takes an infinitesimal (or bounded, or
regular) series 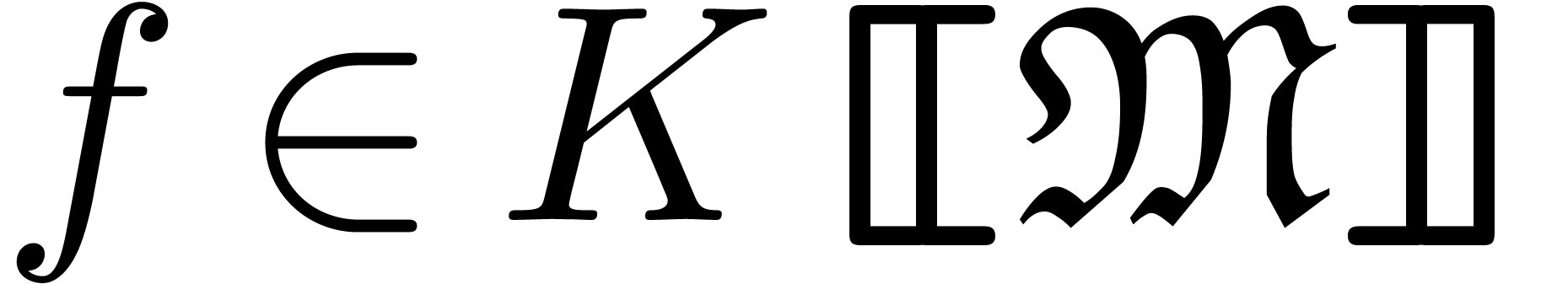 as input and that computes a
Cartesian representation
as input and that computes a
Cartesian representation 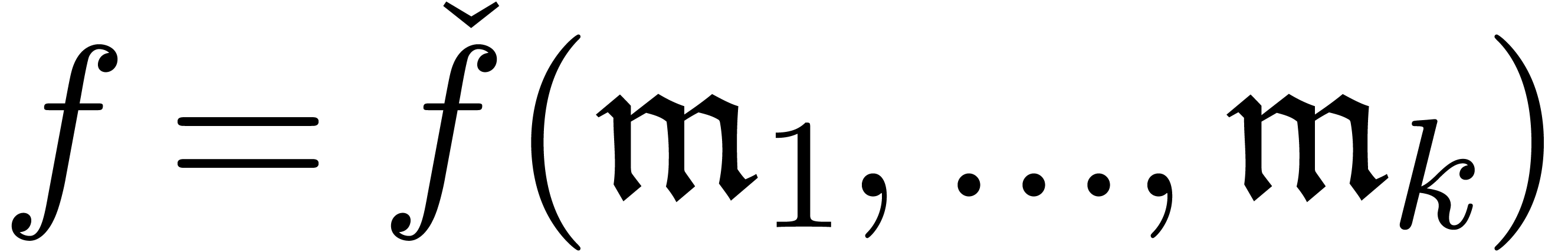 such that
such that  is again infinitesimal (or bounded, or regular,
respectively).
is again infinitesimal (or bounded, or regular,
respectively).

Solving power series equations
Assume now that  is an effective field with an
effective zero test and an algorithm for determining the roots in
is an effective field with an
effective zero test and an algorithm for determining the roots in  of polynomials in
of polynomials in 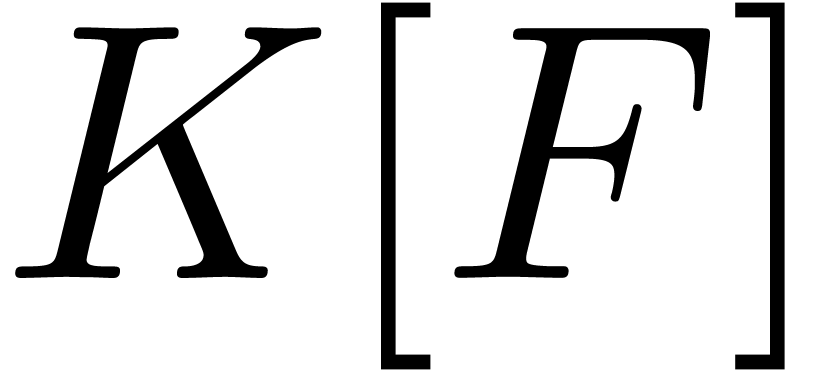 ,
where
,
where  is a new indeterminate. Let
is a new indeterminate. Let  be an effective local community over
be an effective local community over  and
and  an effective totally ordered monomial group.
We notice that a grid-based series in
an effective totally ordered monomial group.
We notice that a grid-based series in  can also
be regarded as an ordinary power series in
can also
be regarded as an ordinary power series in 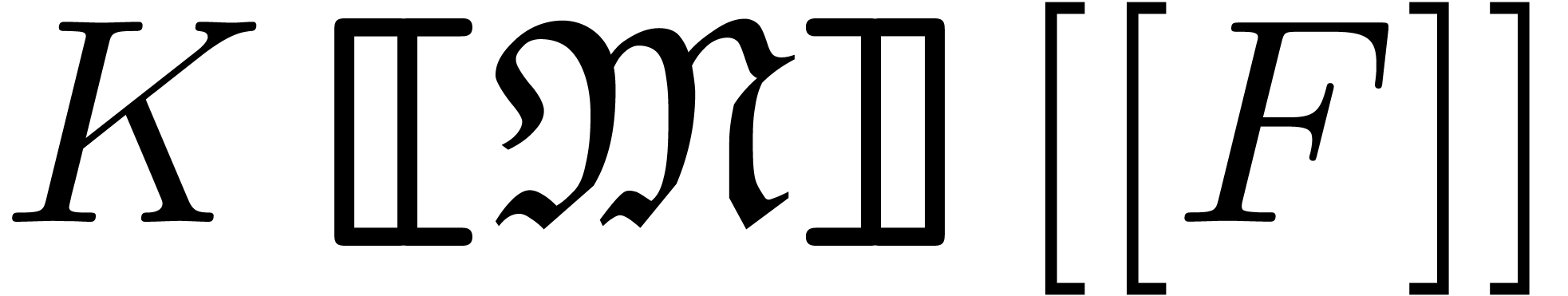 .
We are interested in finding all infinitesimal solutions of a power
series equation
.
We are interested in finding all infinitesimal solutions of a power
series equation
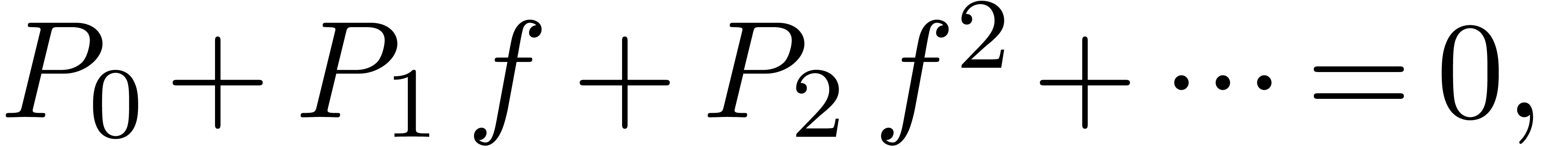
where 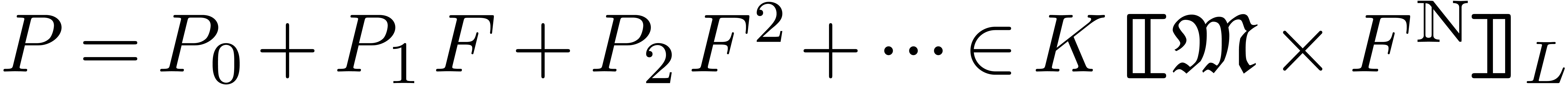 . The Newton polygon
method from [13, Chapter 3] can be generalized in a
straightforward way to power series equations instead of polynomial
equations and the effective counterpart of [13, Theorem
3.21] becomes:
. The Newton polygon
method from [13, Chapter 3] can be generalized in a
straightforward way to power series equations instead of polynomial
equations and the effective counterpart of [13, Theorem
3.21] becomes:
Theorem
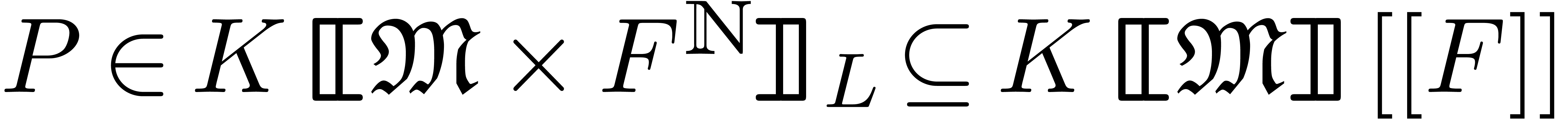 with
with 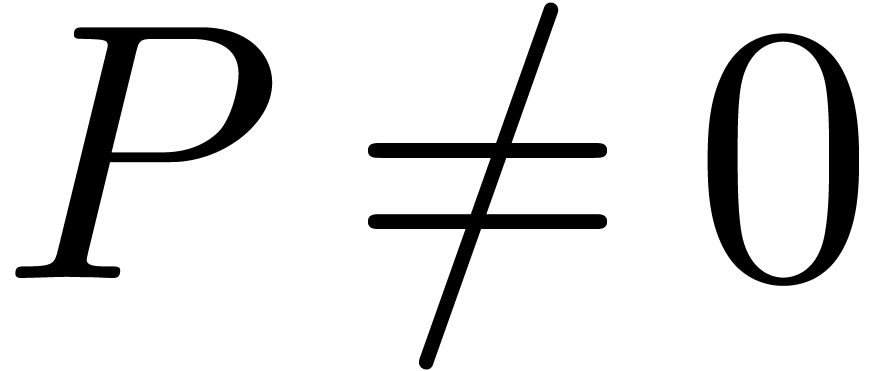 as input and that computes all solutions
of the equation
as input and that computes all solutions
of the equation 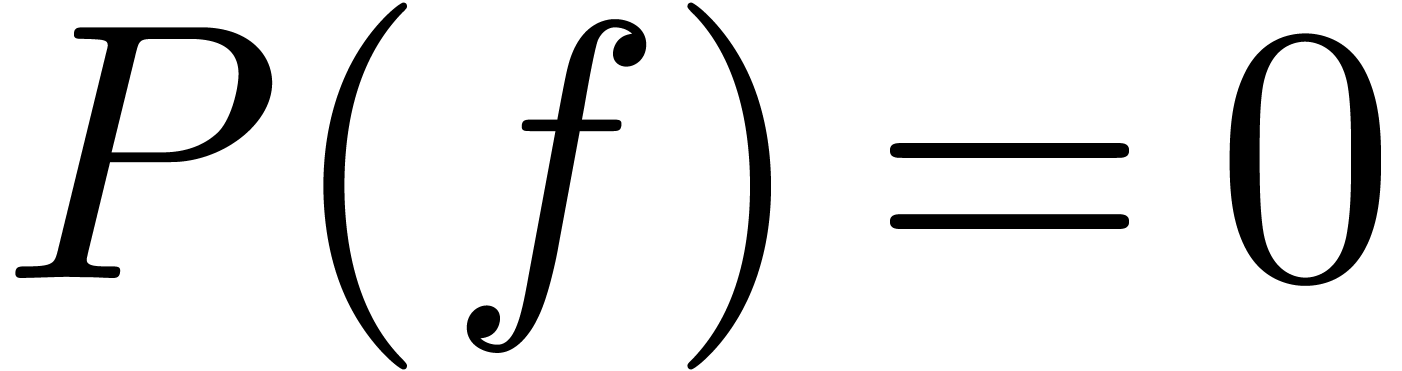 with
with 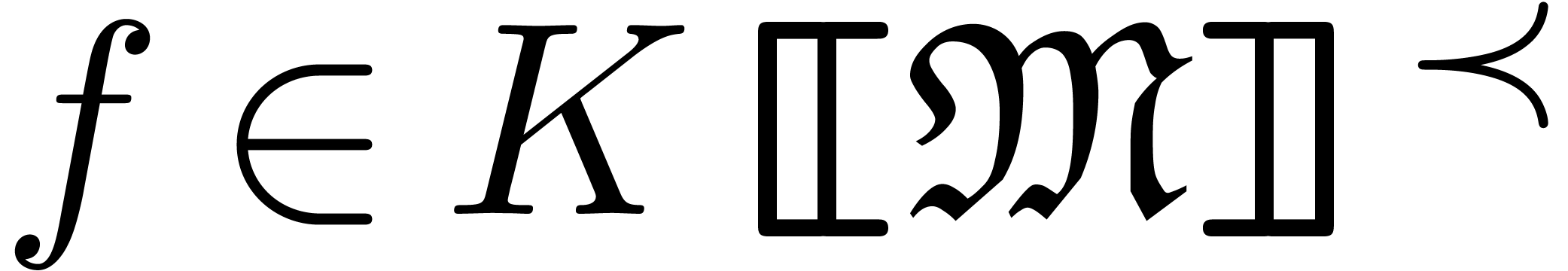 .
.

Given  with
with 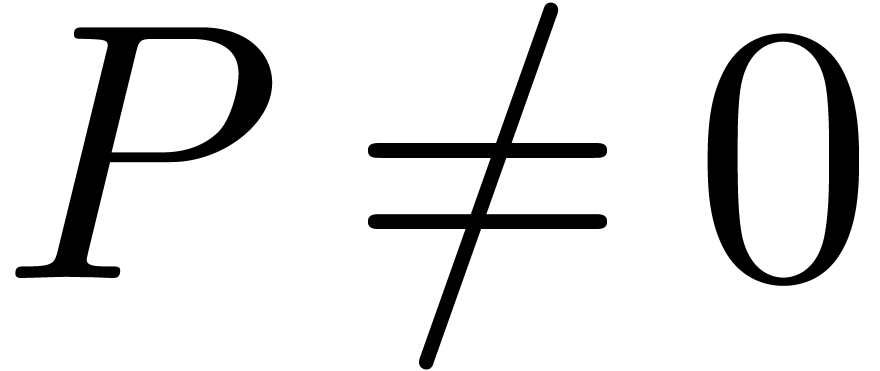 ,
we may also consider
,
we may also consider  as an element of
as an element of  . Let
. Let 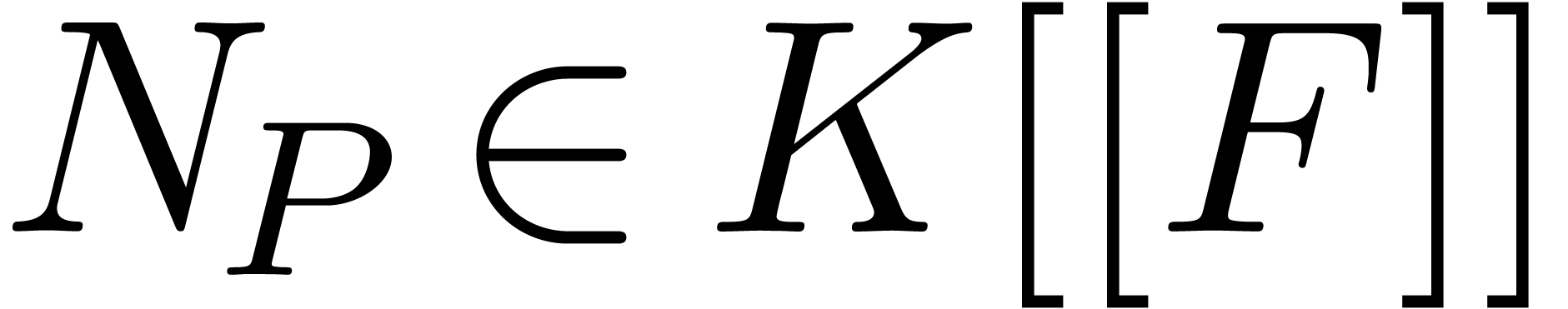 be
the dominant coefficient of
be
the dominant coefficient of  for this latter
representation. The valuation of
for this latter
representation. The valuation of  in
in  is called the Weierstrass degree of
is called the Weierstrass degree of  . If
. If  is algebraically
closed, then it can be shown that the number of solutions to the
equation in Theorem 5 coincides with the Weierstrass
degree, when counting with multiplicities.
is algebraically
closed, then it can be shown that the number of solutions to the
equation in Theorem 5 coincides with the Weierstrass
degree, when counting with multiplicities.
Scalar extensions
Let  be a tribe over
be a tribe over  and
let
and
let  be indeterminates. Then there exists a
smallest tribe over
be indeterminates. Then there exists a
smallest tribe over 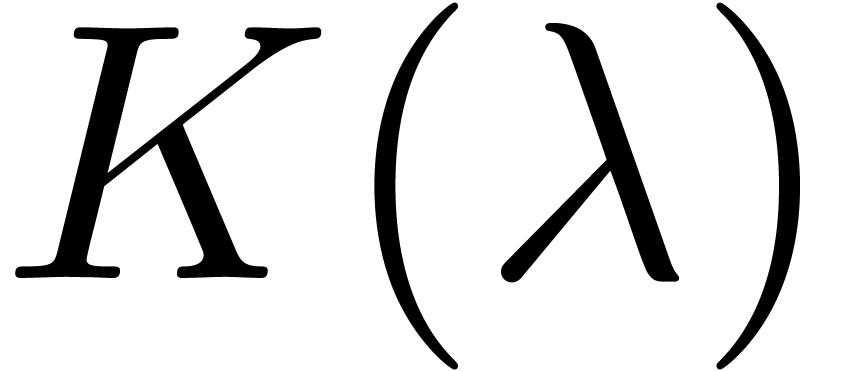 that extends
that extends  . We will denote this tribe by
. We will denote this tribe by 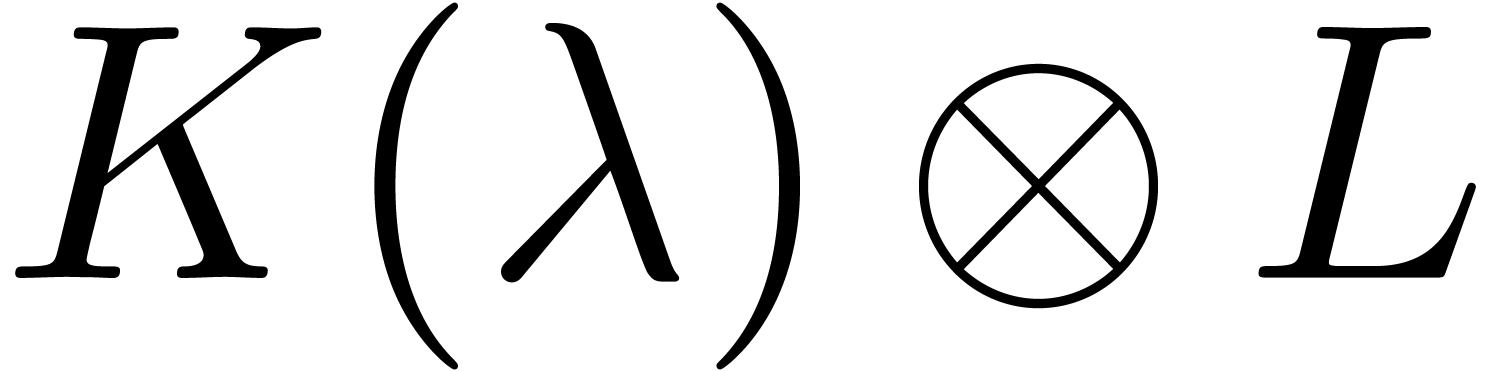 . Setting
. Setting
we notice that  and
and 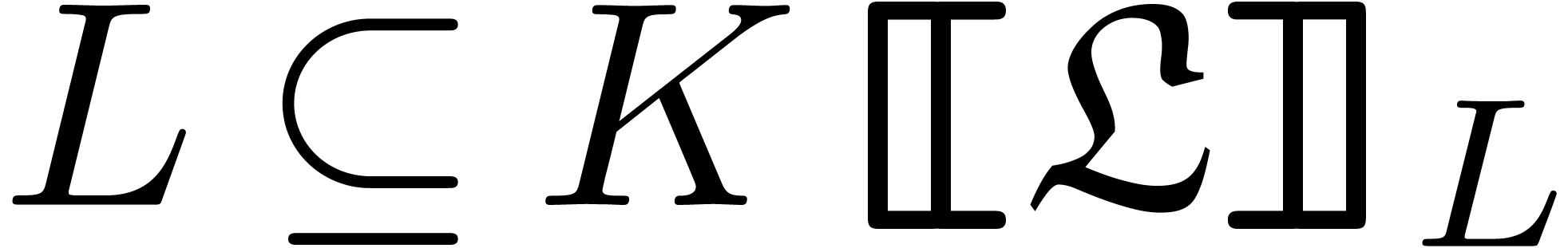 .
This shows that any element in
.
This shows that any element in 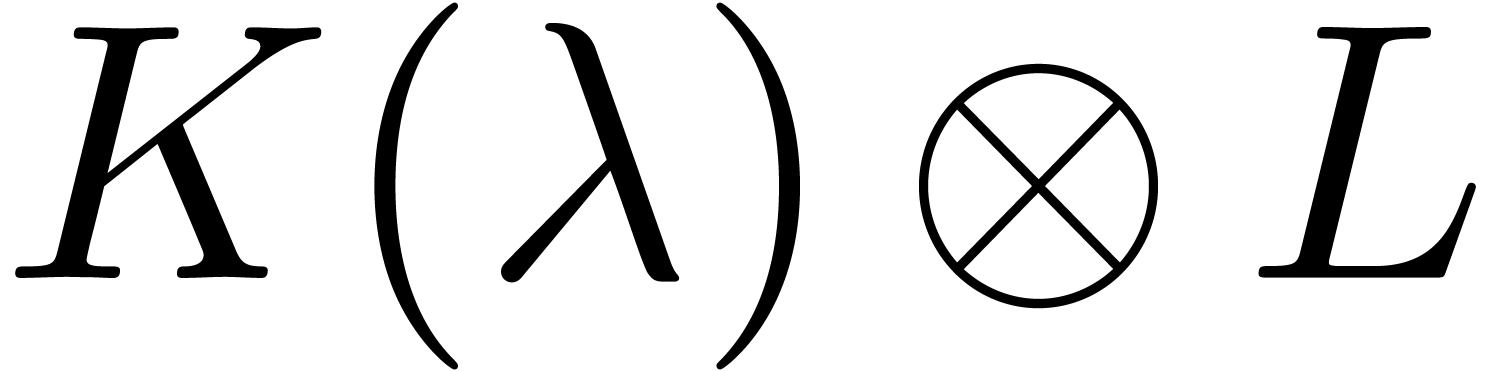 can be
represented by an element of
can be
represented by an element of  .
In particular, if
.
In particular, if  is effective, then so is
is effective, then so is 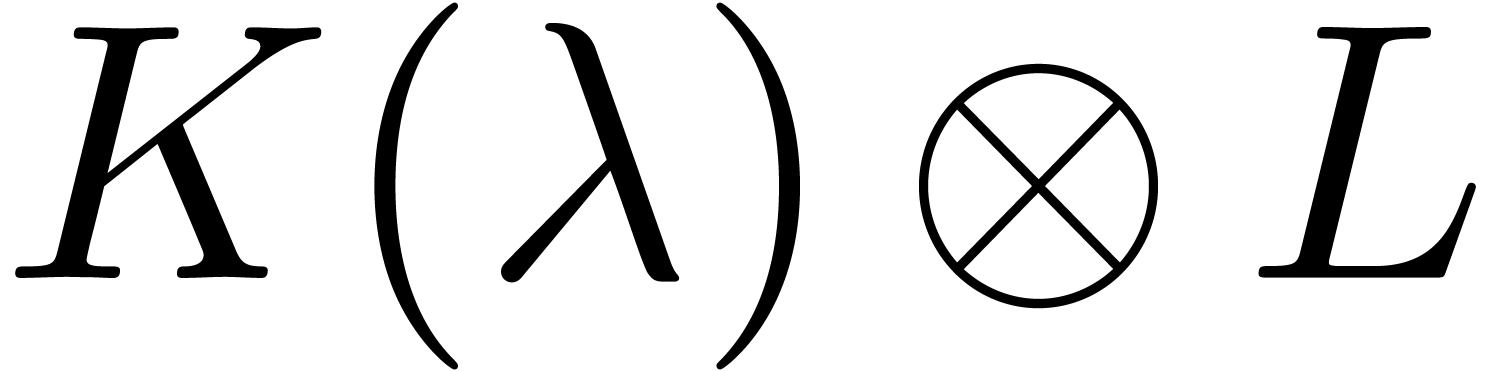 .
.
Let  be an effective field with an effective zero
test. We may consider its algebraic closure
be an effective field with an effective zero
test. We may consider its algebraic closure 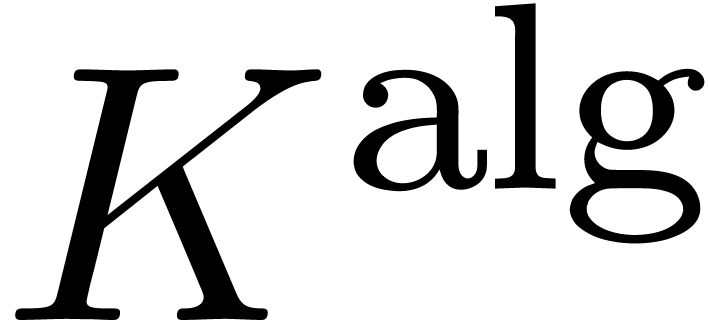 as
an effective field with an effective zero test, when computing
non-deterministically (we refer to [5] for more details
about this technique, which is also called dynamic evaluation).
as
an effective field with an effective zero test, when computing
non-deterministically (we refer to [5] for more details
about this technique, which is also called dynamic evaluation).
Let  be an effective tribe over
be an effective tribe over  with an effective zero test. It is convenient to represent elements of
with an effective zero test. It is convenient to represent elements of
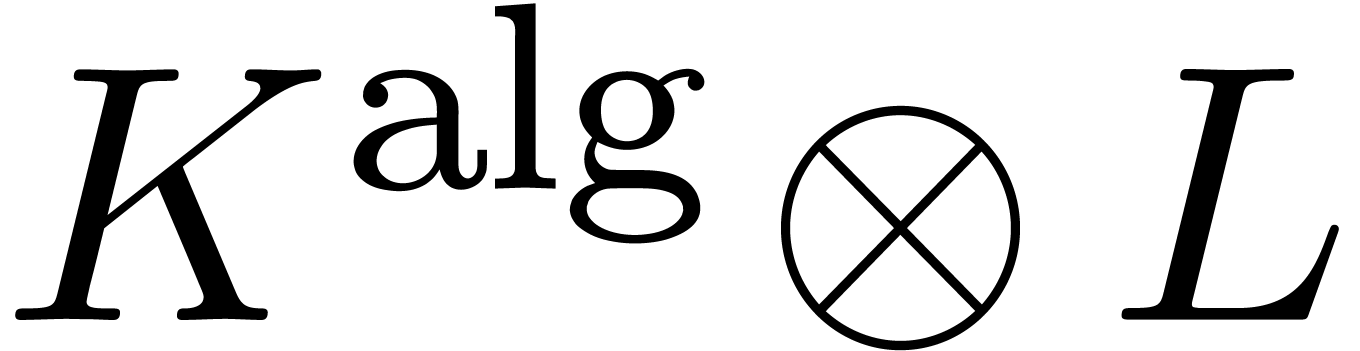 by evaluations of polynomials
by evaluations of polynomials 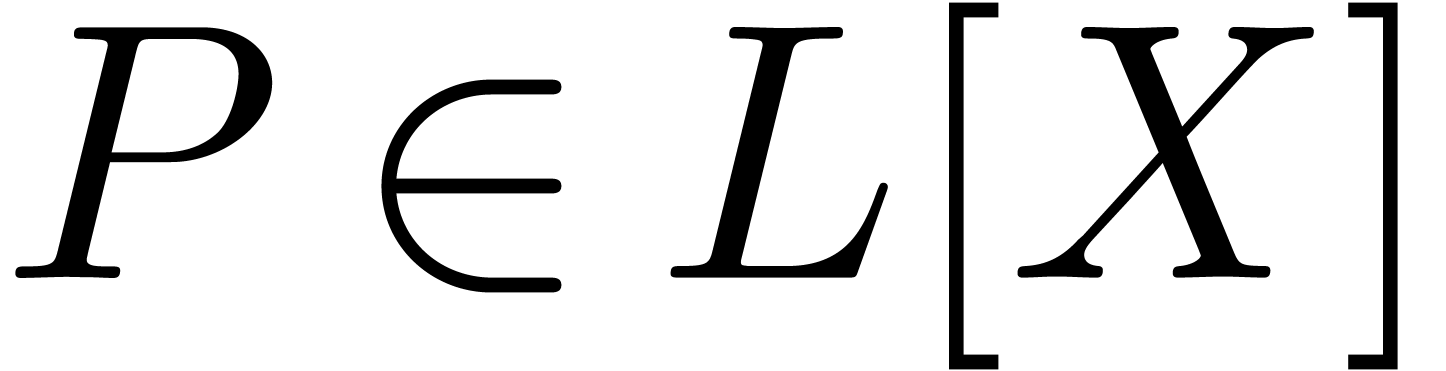 at
at 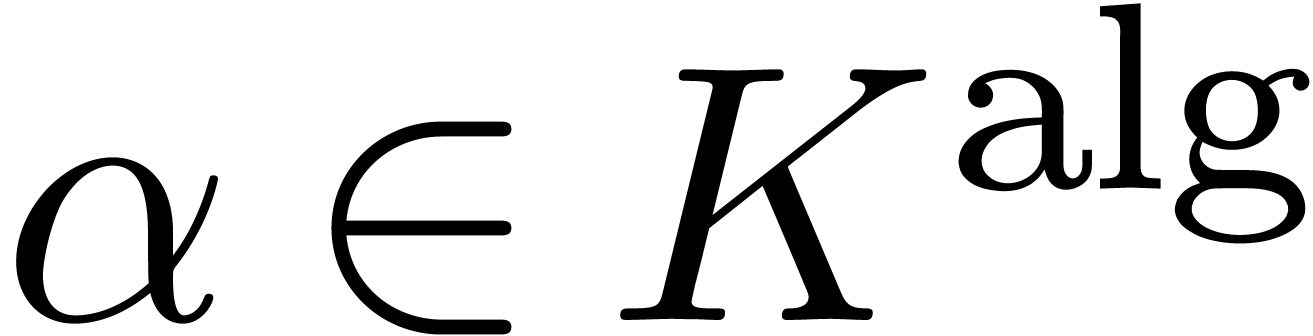 . The algebraic number
. The algebraic number
 is effectively represented using an annihilator
is effectively represented using an annihilator
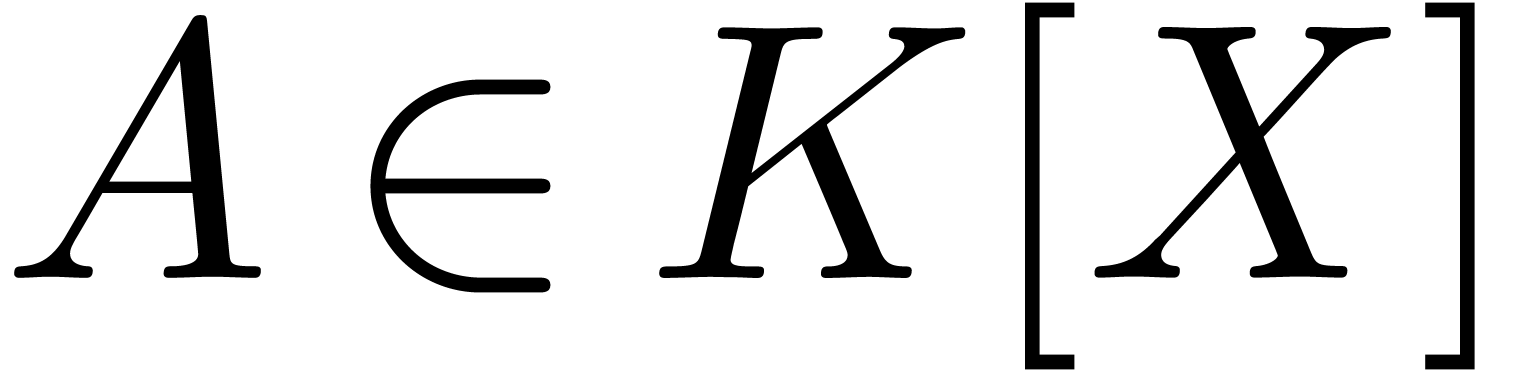 and we may always take
and we may always take  such that
such that  . We say that
. We say that  is algebraically stable if
is algebraically stable if 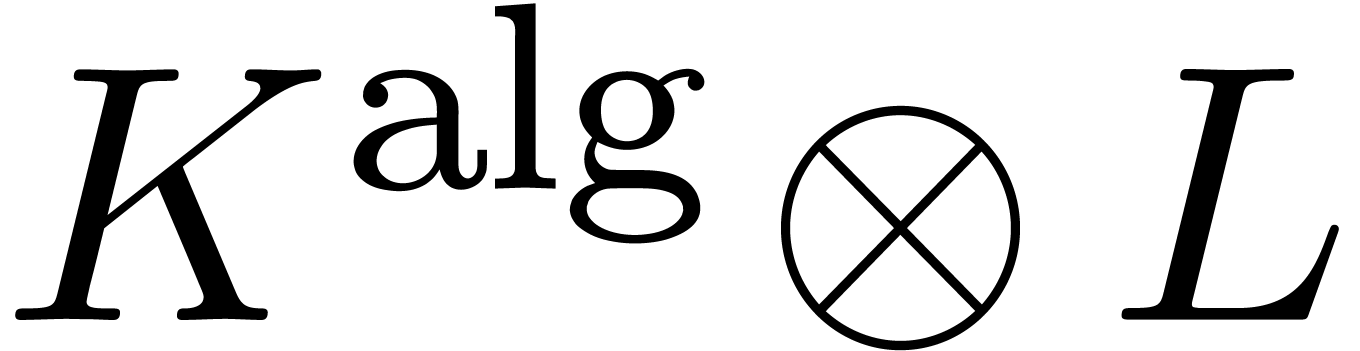 forms again an effective tribe for this representation. This is the case
for the tribes of algebraic and d-algebraic power series, but not for
arbitrary tribes: if
forms again an effective tribe for this representation. This is the case
for the tribes of algebraic and d-algebraic power series, but not for
arbitrary tribes: if 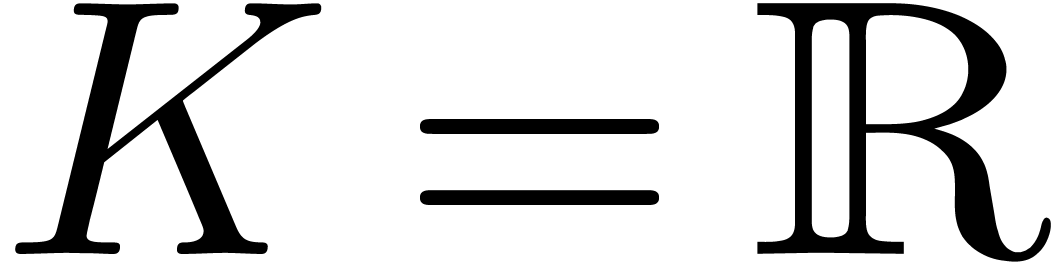 and
and  is the smallest tribe that contains the exponential power series
is the smallest tribe that contains the exponential power series  , then it follows from Wilkie's
theorem [18] that
, then it follows from Wilkie's
theorem [18] that  does not contain
does not contain
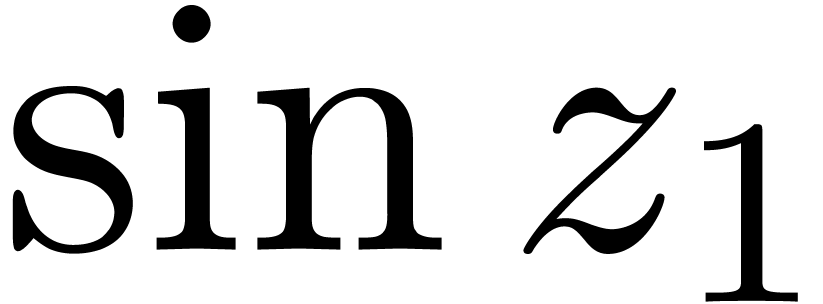 ; on the other hand, any
tribe that contains
; on the other hand, any
tribe that contains  must contain
must contain 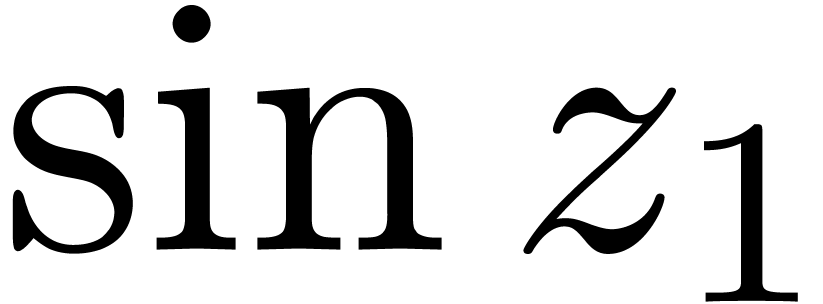 .
.
Assume that  is algebraically stable. Consider a
series
is algebraically stable. Consider a
series 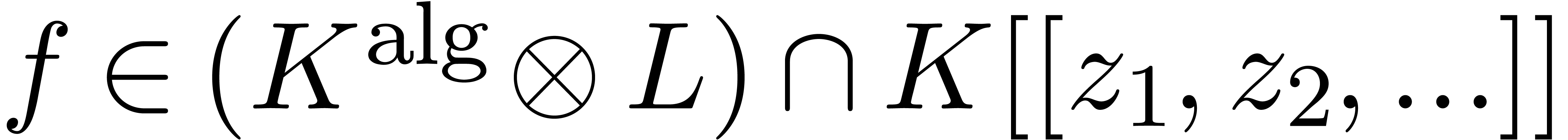 , represented as
, represented as 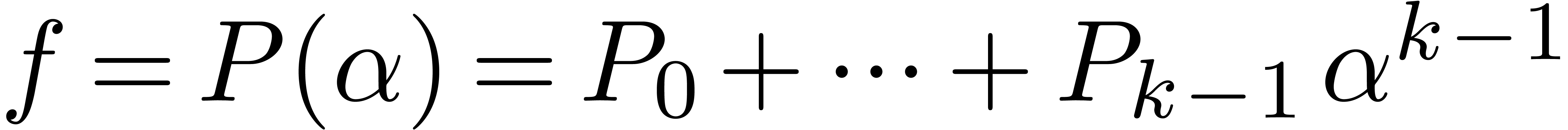 , where
, where 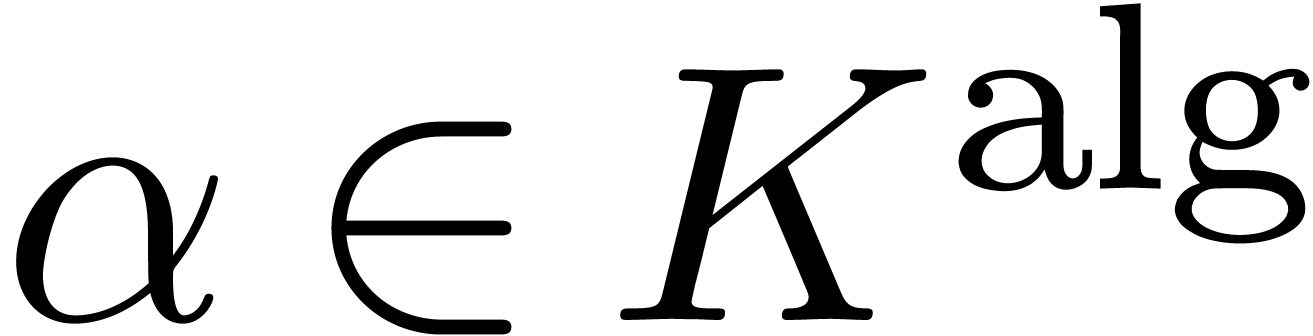 is
given by an annihilator of degree
is
given by an annihilator of degree  ,
and
,
and 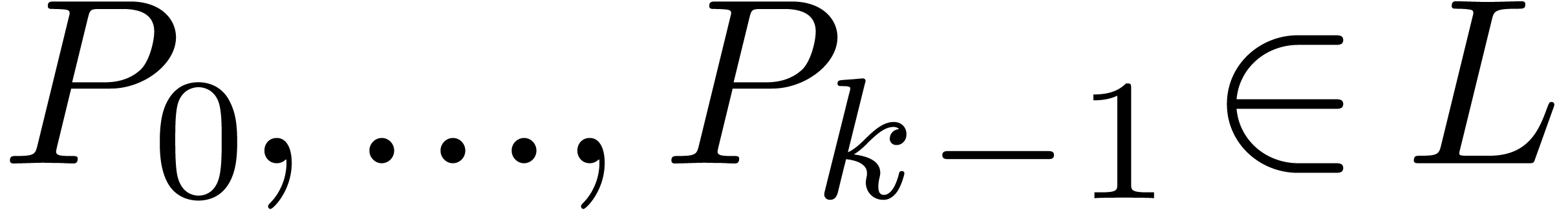 . Then we notice that we
can compute a representation for
. Then we notice that we
can compute a representation for  as a element of
as a element of
 . Indeed, whenever
. Indeed, whenever 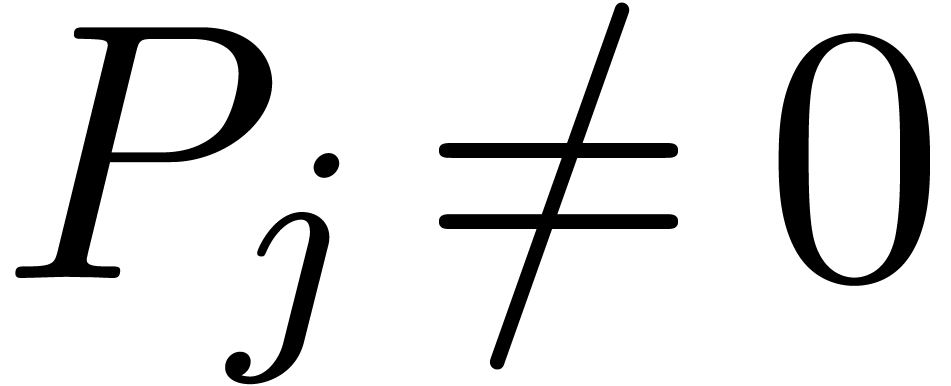 for some
for some  , then
this means that there exists a monomial
, then
this means that there exists a monomial 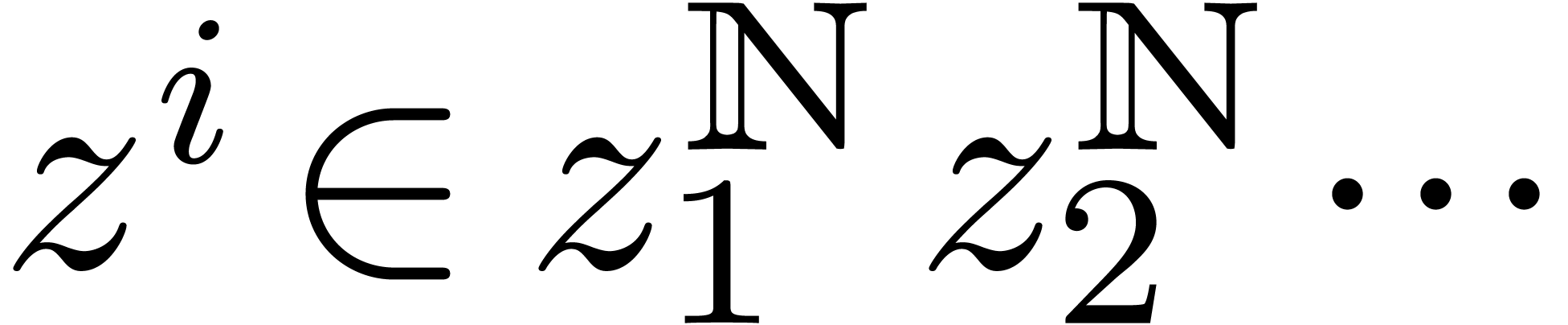 such
that the coefficient
such
that the coefficient  of
of 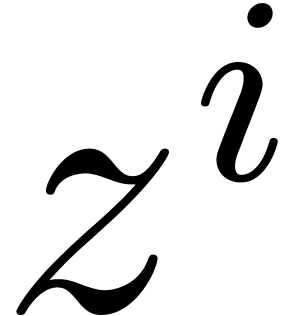 in
in  is a polynomial of non-zero degree in
is a polynomial of non-zero degree in  . On the other hand,
. On the other hand,  , which means that we can compute an
annihilator for
, which means that we can compute an
annihilator for  of degree
of degree  . Repeating this reduction a finite number of times,
we thus reach the situation in which
. Repeating this reduction a finite number of times,
we thus reach the situation in which 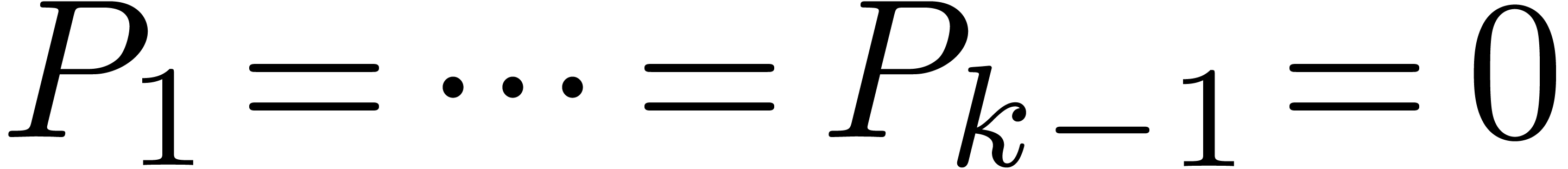 ,
so that
,
so that 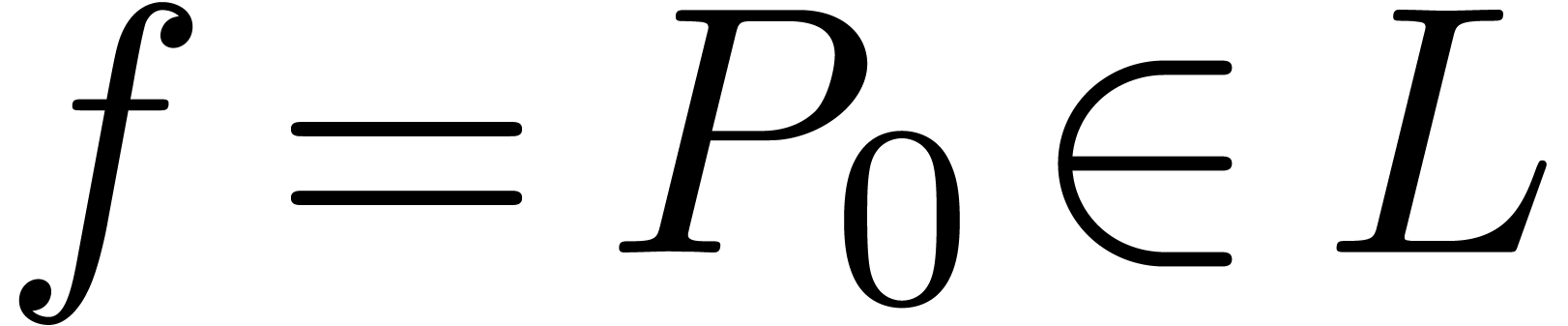 .
.
Let  still be an effective algebraically stable
tribe over
still be an effective algebraically stable
tribe over  with an effective zero test. Given
with an effective zero test. Given
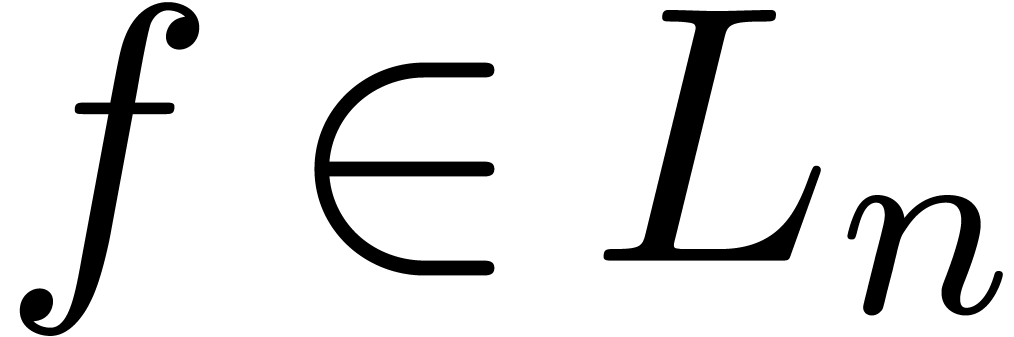 , we recall that
, we recall that  is said to have Weierstrass degree
is said to have Weierstrass degree 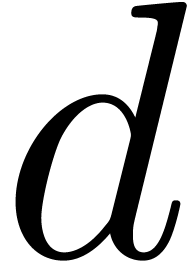 in
in 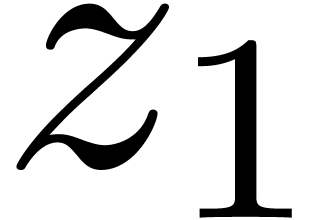 if
if 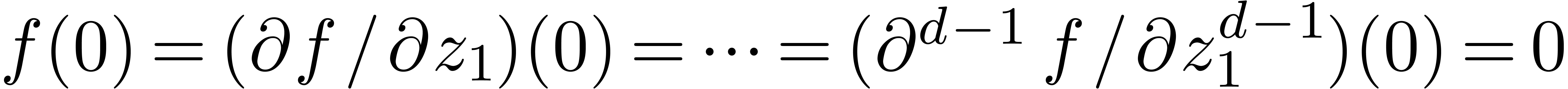 , but
, but 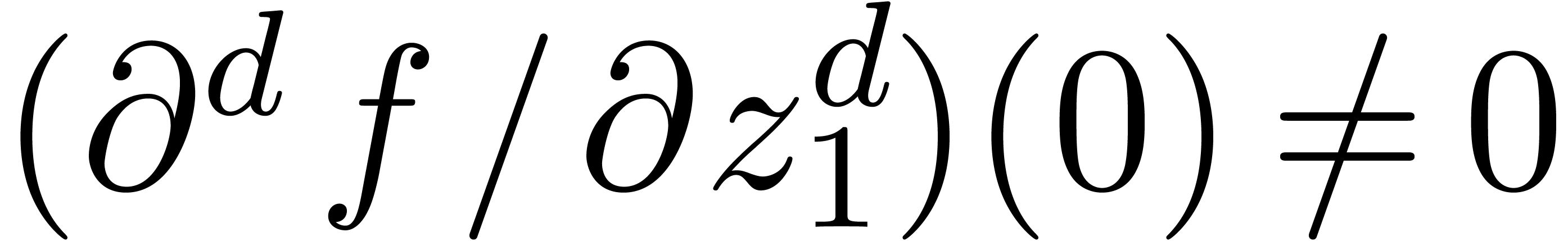 .
In that case, the Weierstrass preparation theorem states that there
exists a unit
.
In that case, the Weierstrass preparation theorem states that there
exists a unit 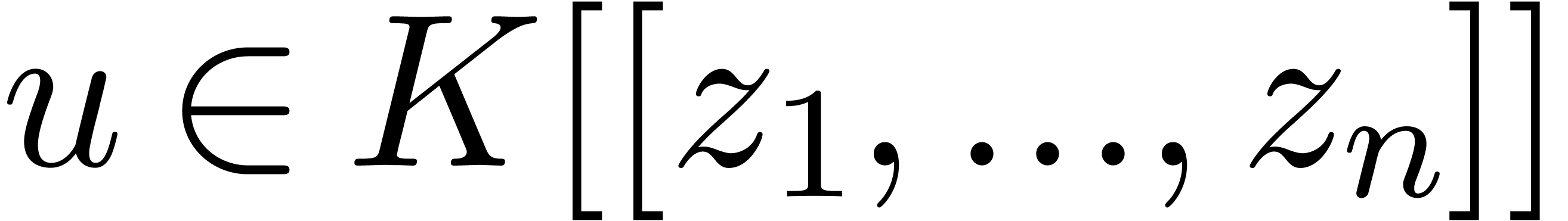 and a monic polynomial
and a monic polynomial 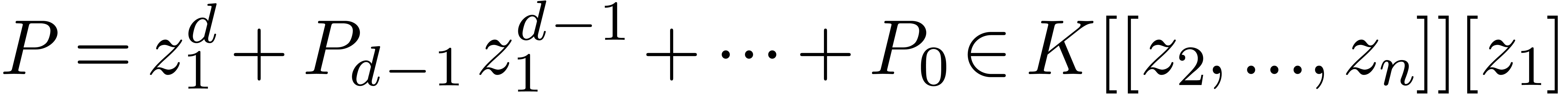 of degree
of degree 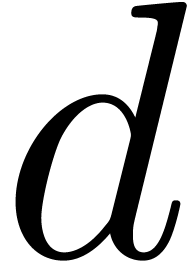 such that
such that 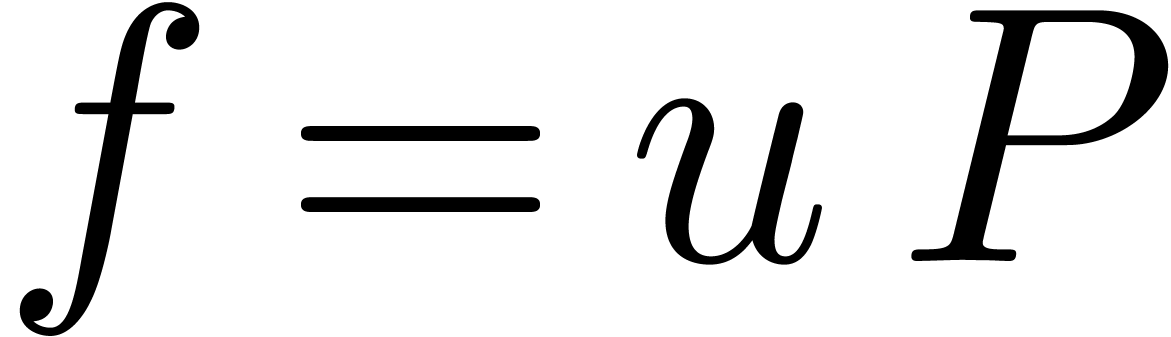 . The polynomial
. The polynomial 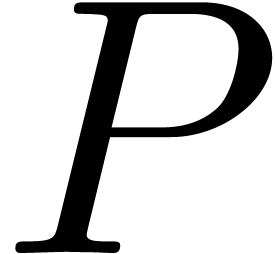 is
called the Weierstrass polynomial associated to
is
called the Weierstrass polynomial associated to  (with respect to
(with respect to 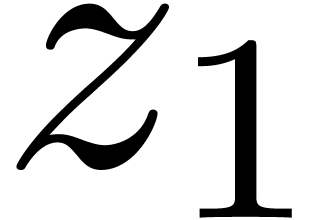 ).
We claim that
).
We claim that 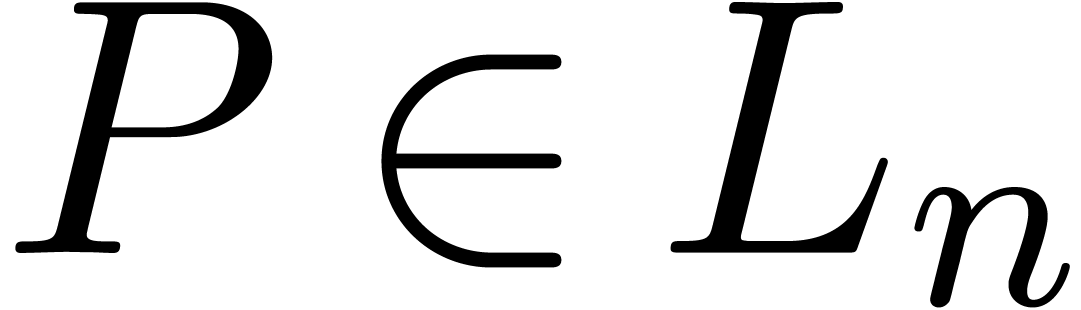 and that there exists an algorithm
to compute
and that there exists an algorithm
to compute 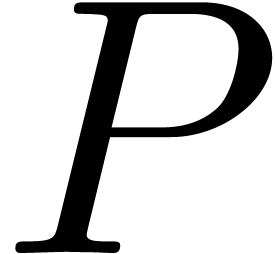 (and therefore the corresponding unit
(and therefore the corresponding unit
 , since
, since 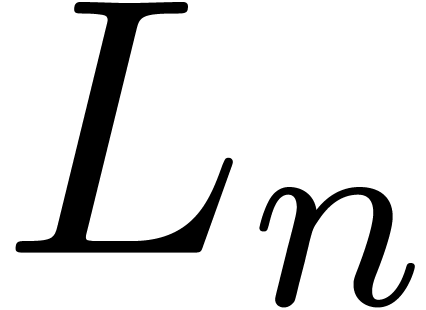 is effectively stable under restricted division):
is effectively stable under restricted division):
Theorem 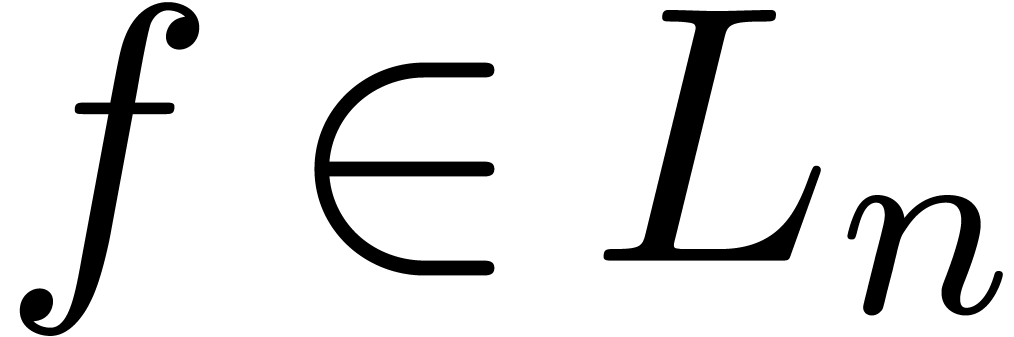 of
Weierstrass degree
of
Weierstrass degree 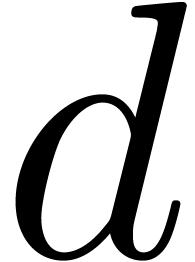 in
in  as
input and computes its Weierstrass polynomial
as
input and computes its Weierstrass polynomial  as
an element of
as
an element of  .
.
Proof. Consider the effective totally ordered monomial
group  with
with  -powers.
We have a natural inclusion
-powers.
We have a natural inclusion 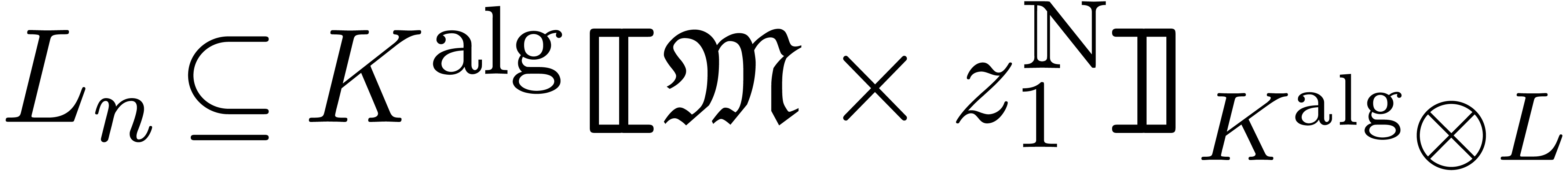 .
Now consider
.
Now consider 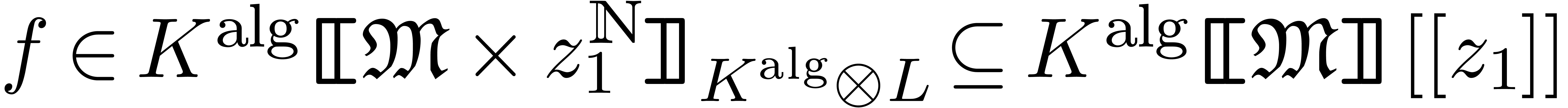 . By theorem 5, we may compute all infinitesimal solutions
. By theorem 5, we may compute all infinitesimal solutions 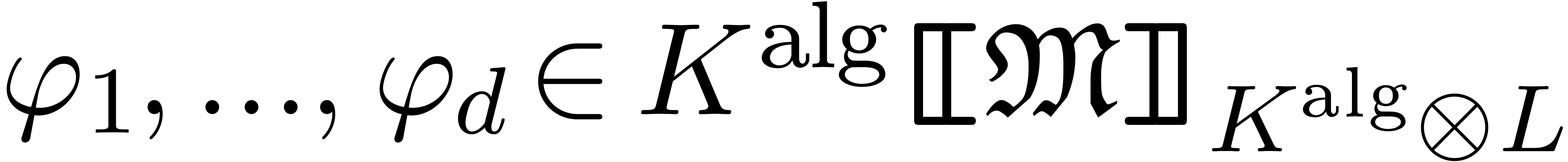 to the equation
to the equation 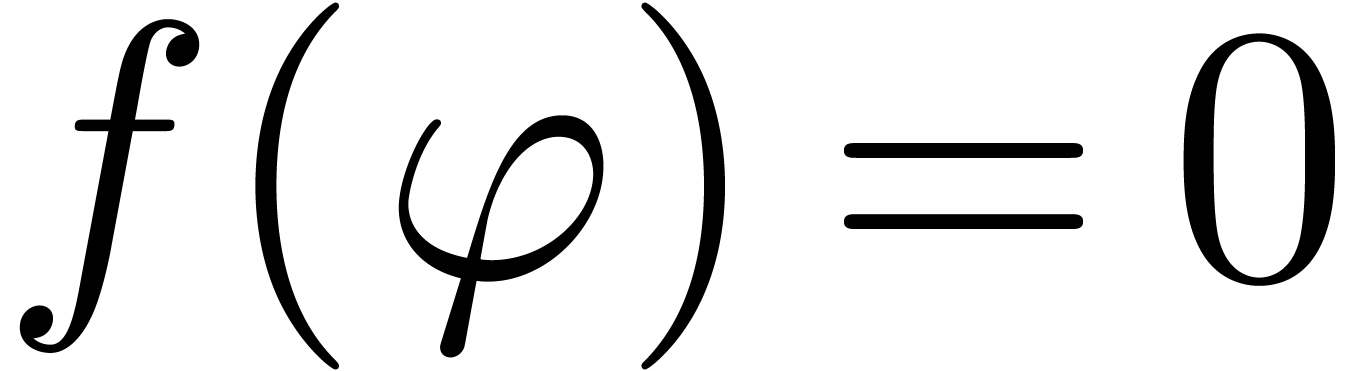 in
in 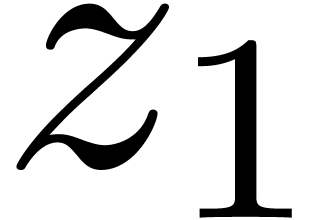 (we
recall that there are
(we
recall that there are 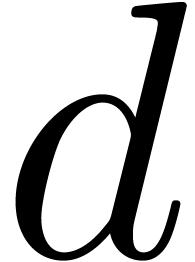 such solutions, when
counting with multiplicities, since
such solutions, when
counting with multiplicities, since  is
algebraically closed). Now consider
is
algebraically closed). Now consider
and let 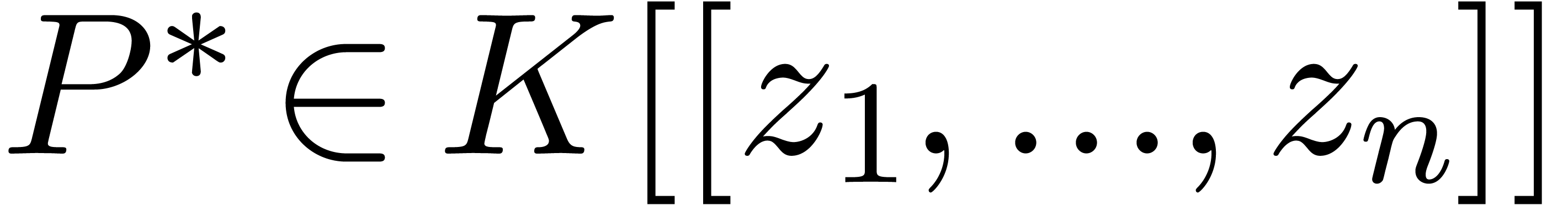 be the Weierstrass polynomial associated
to
be the Weierstrass polynomial associated
to  . Since
. Since 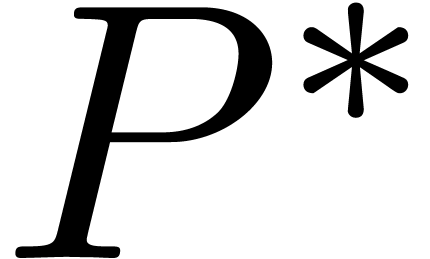 also admits the infinitesimal roots
also admits the infinitesimal roots  when
considered as an element of
when
considered as an element of 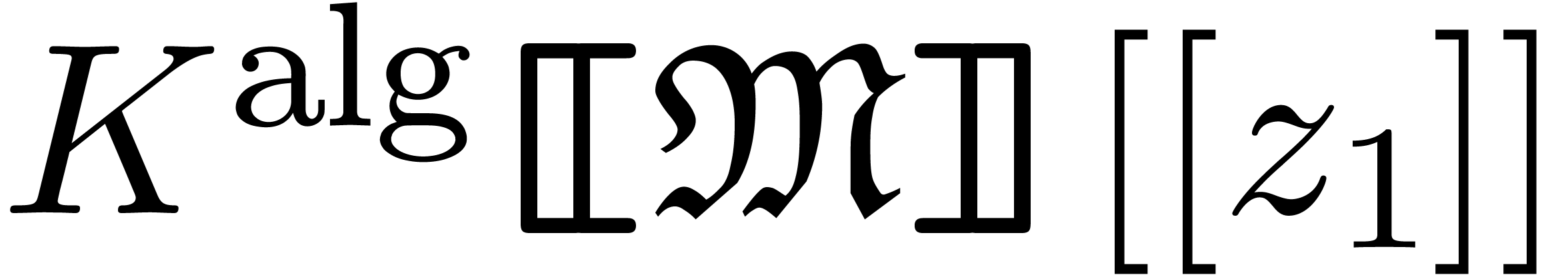 ,
we have
,
we have 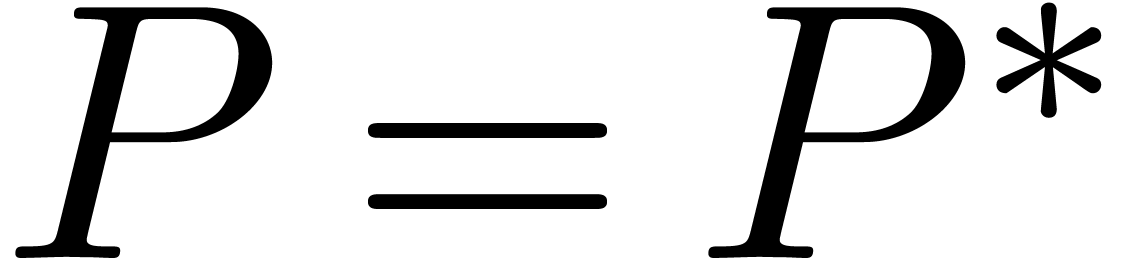 when considering
when considering 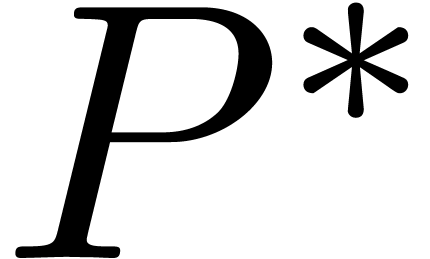 as an element of
as an element of  . It follows
that
. It follows
that
Now consider a Cartesian representation 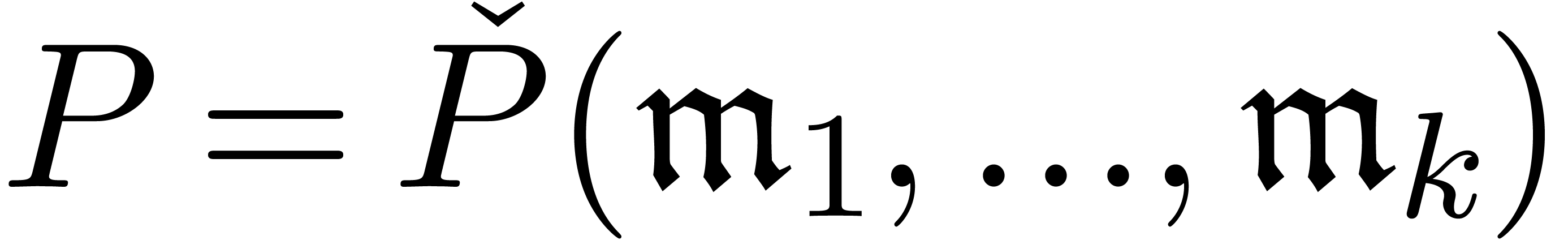 for
for  with
with  . By
Proposition 4, we may take
. By
Proposition 4, we may take 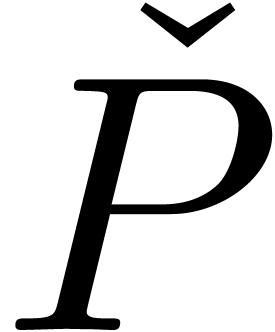 to be
infinitesimal. Since
to be
infinitesimal. Since  are infinitesimal and
are infinitesimal and 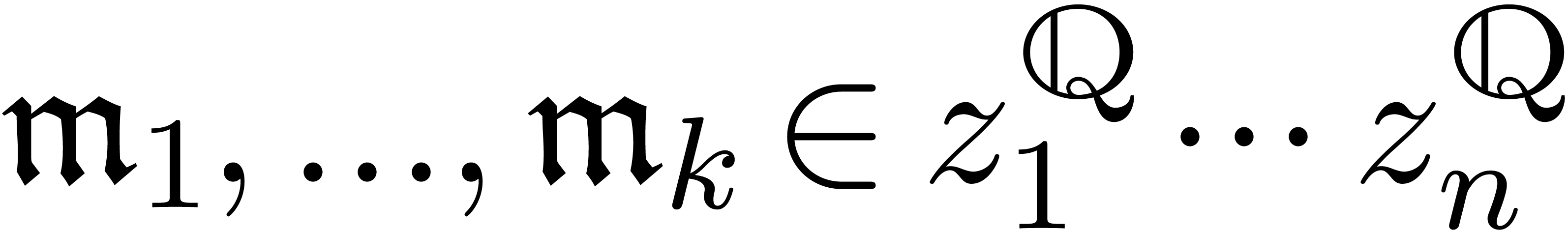 , Lemma 2 also shows
that we may assume without loss of generality that
, Lemma 2 also shows
that we may assume without loss of generality that 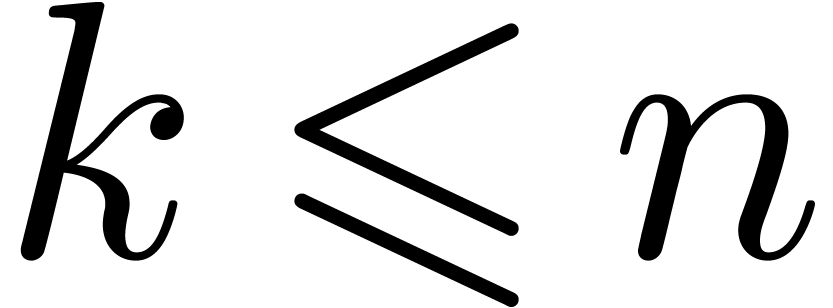 . Completing the
. Completing the  with
additional elements if necessary, this means that we may compute an
invertible matrix
with
additional elements if necessary, this means that we may compute an
invertible matrix  such that
such that 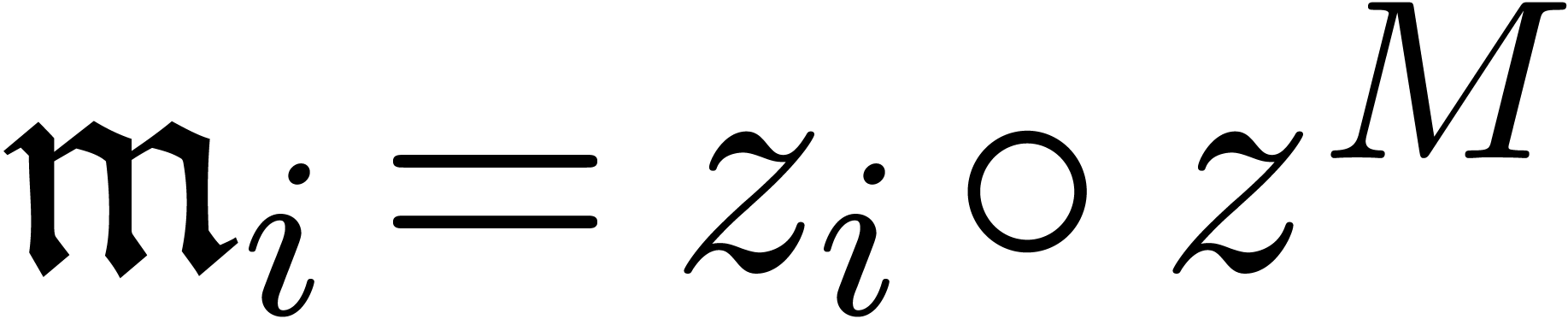 for all
for all 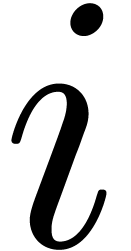 . In other words,
. In other words,
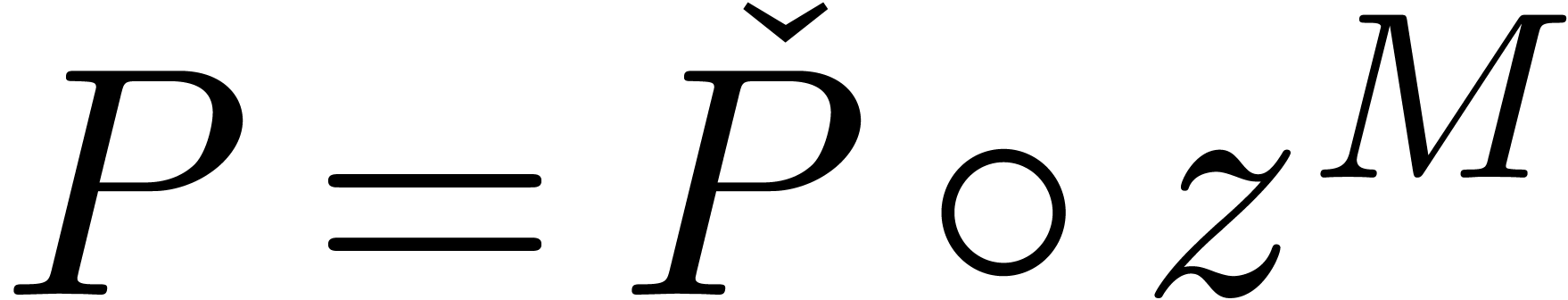 with
with 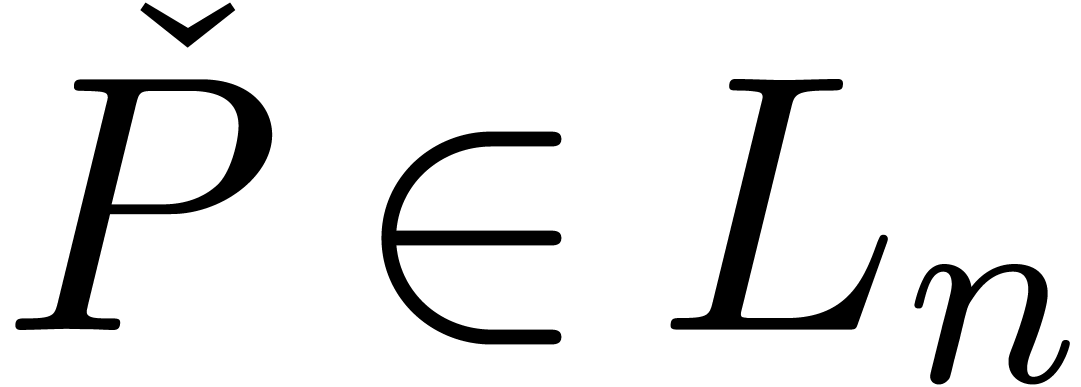 .
Since
.
Since 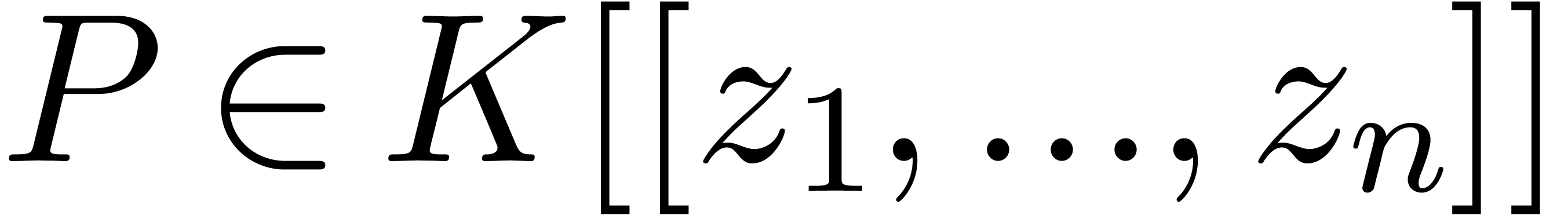 and
and  is effectively
closed under restricted monomial transformations, we conclude that
is effectively
closed under restricted monomial transformations, we conclude that 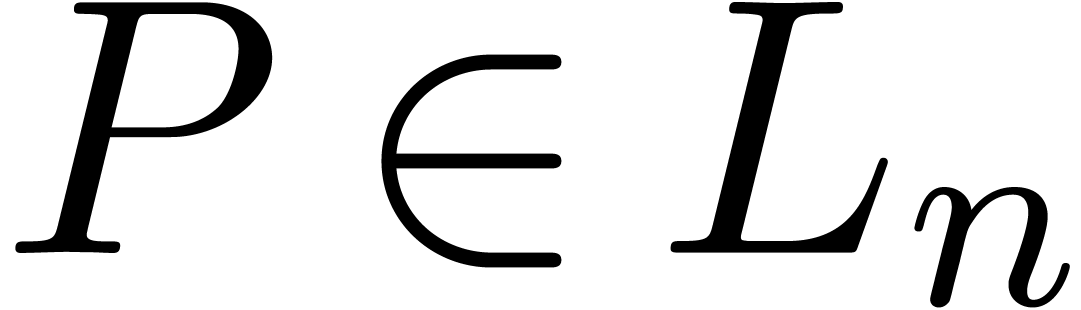 .
.
Recall that  is an effective algebraically stable
tribe over
is an effective algebraically stable
tribe over  with an effective zero test. Assume
that
with an effective zero test. Assume
that 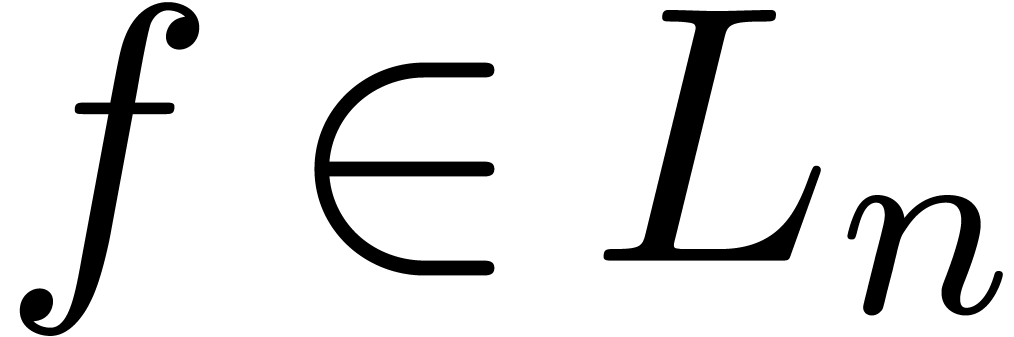 has Weierstrass degree
has Weierstrass degree  in
in  and let
and let 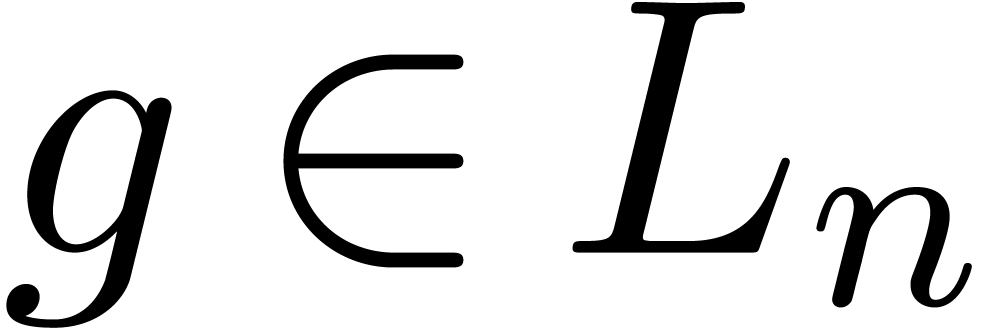 .
The Weierstrass division theorem states that there exist unique
.
The Weierstrass division theorem states that there exist unique 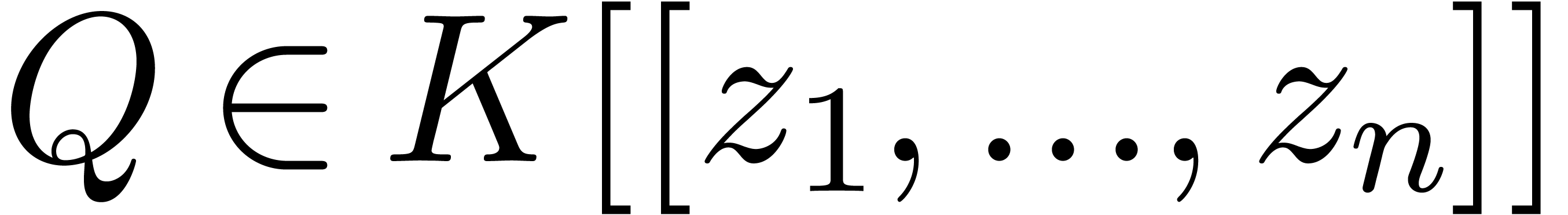 and
and 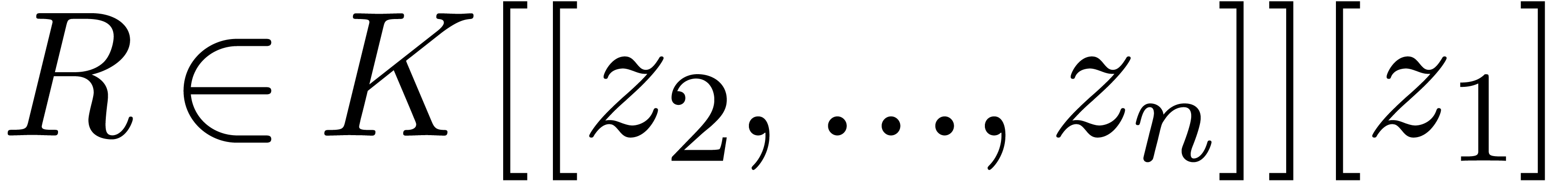 with
with

and 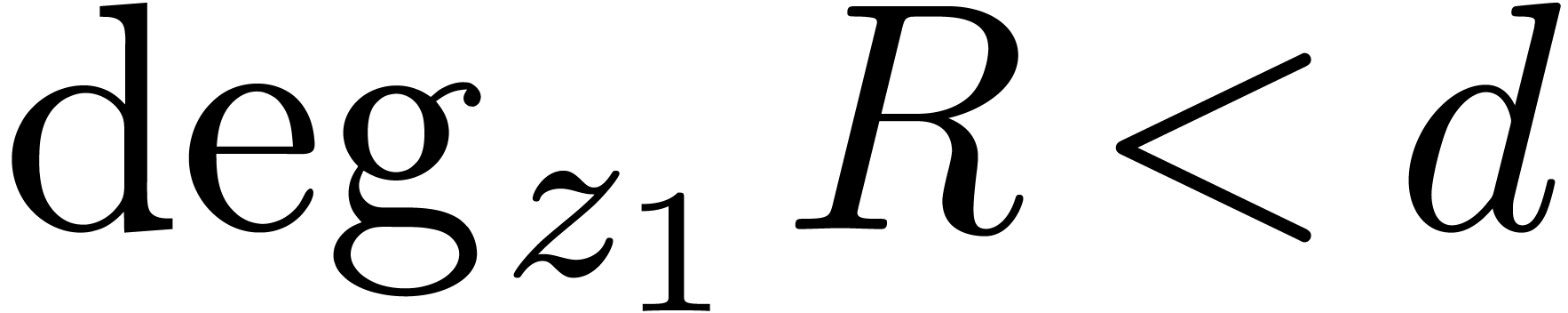 . We claim that the
quotient
. We claim that the
quotient  and remainder
and remainder 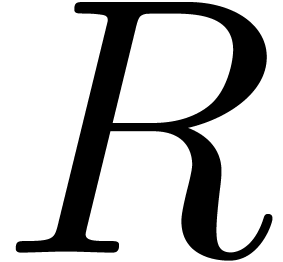 of this division once again belong to
of this division once again belong to 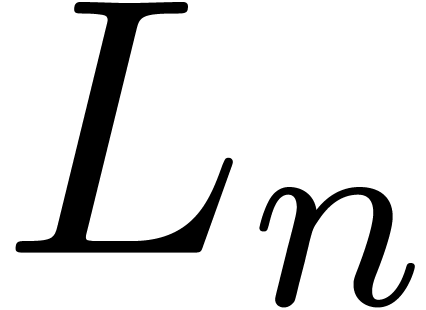 and that there exists an algorithm to compute them:
and that there exists an algorithm to compute them:
Theorem 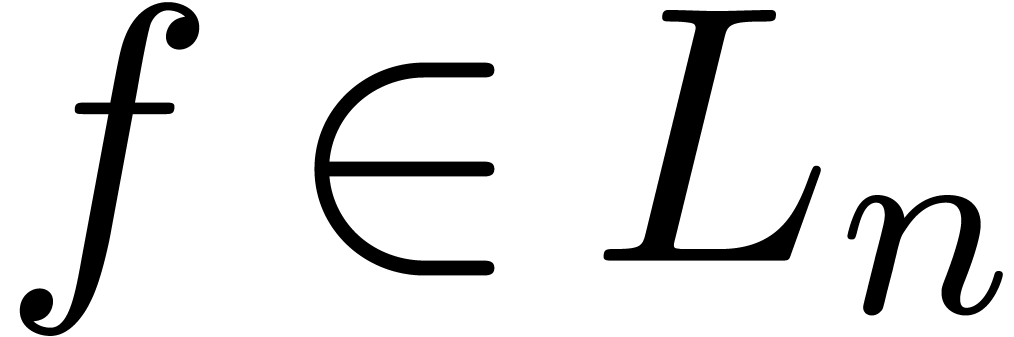 of
Weierstrass degree
of
Weierstrass degree 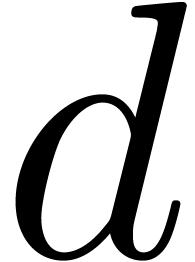 in
in 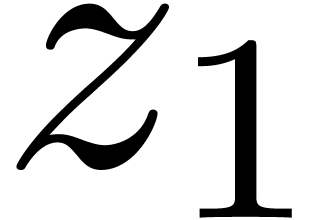 and
and 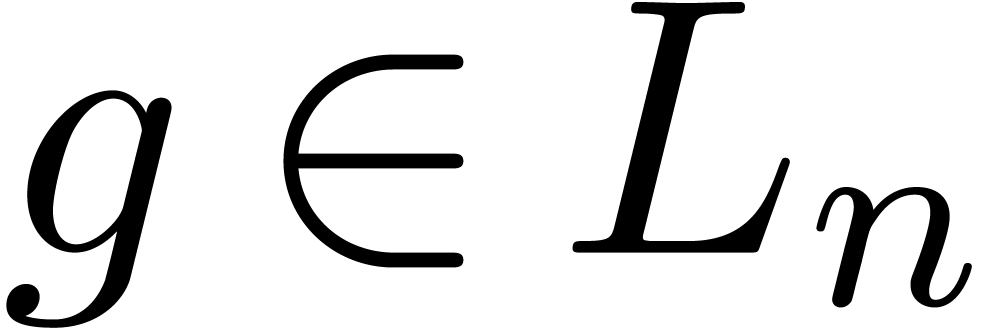 as input and computes the quotient and
remainder of the Weierstrass division of
as input and computes the quotient and
remainder of the Weierstrass division of  by
by 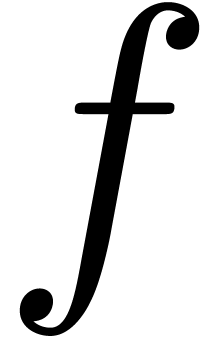 as elements of
as elements of 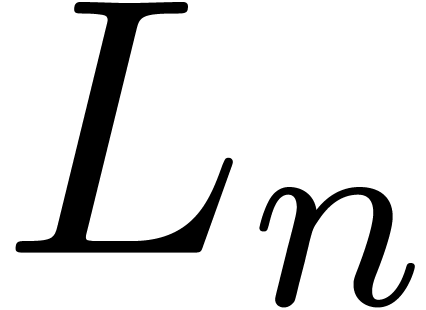 .
.
Proof. Let 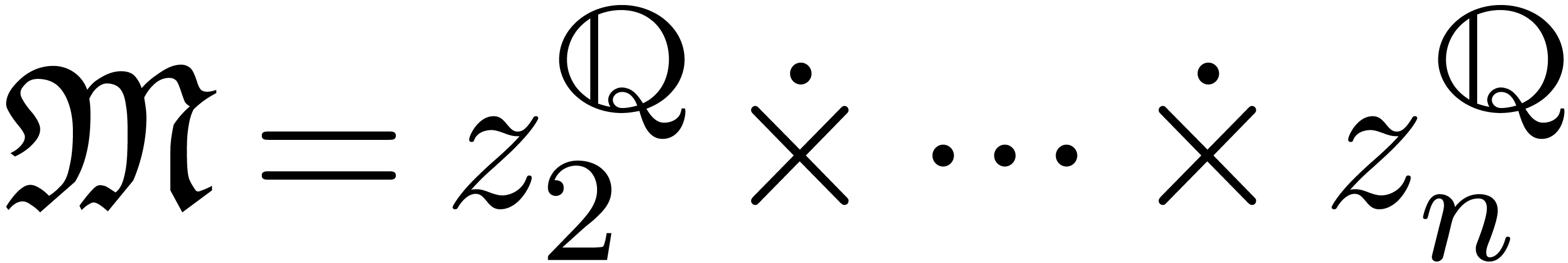 be as in the proof
of Theorem 6. Let
be as in the proof
of Theorem 6. Let  be the distinct
solutions of
be the distinct
solutions of  when considered as an equation in
when considered as an equation in
 , and let
, and let  be the multiplicity of each
be the multiplicity of each  ,
so that
,
so that 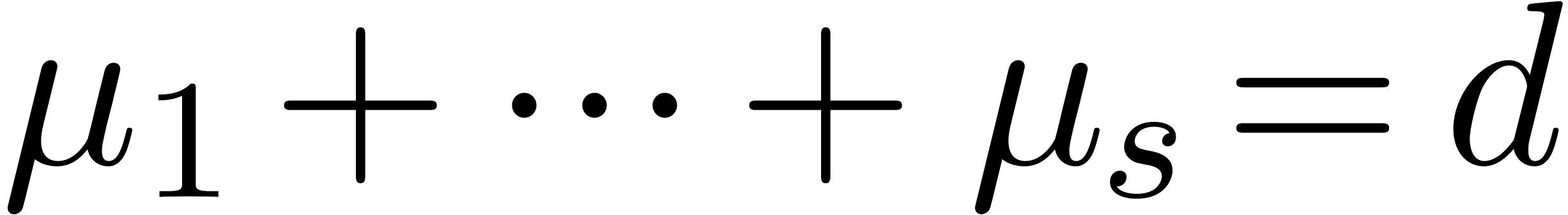 . For each
. For each  , we compute the multiplicity
, we compute the multiplicity  and the polynomials
and the polynomials
Using Chinese remaindering, we next compute the unique 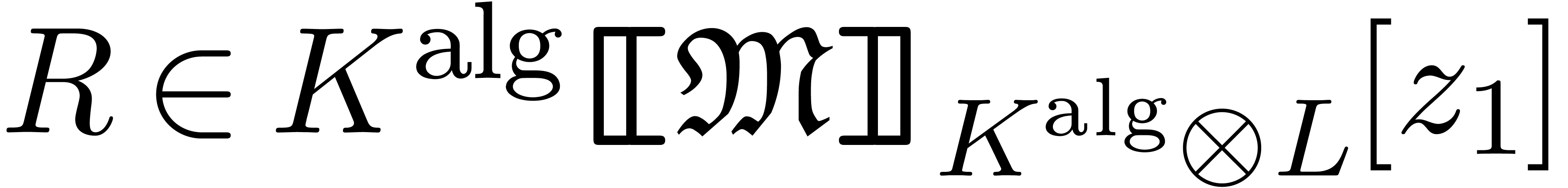 such that
such that 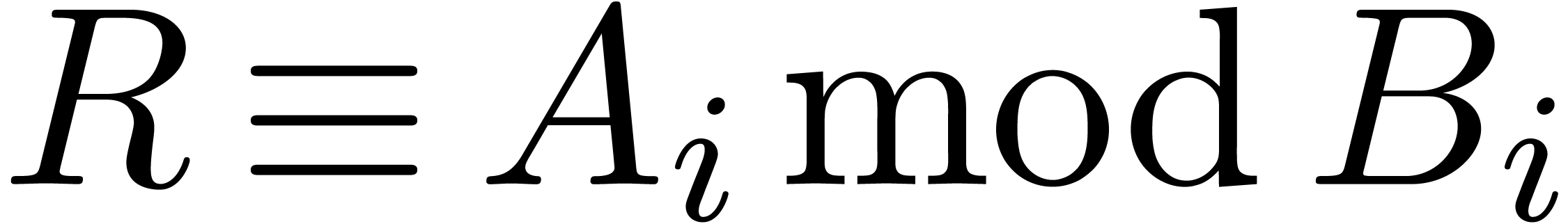 for each
for each 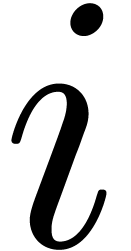 and
and
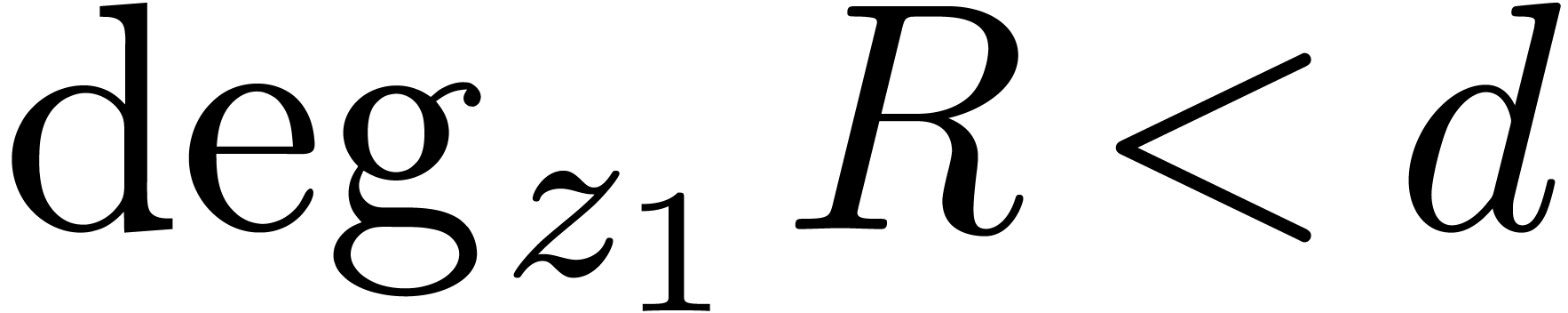 . It is easily verified that
. It is easily verified that
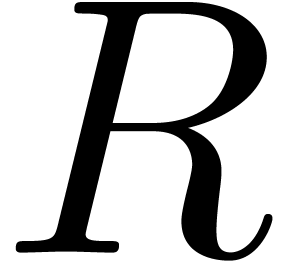 coincides with the remainder of the Weierstrass
division of
coincides with the remainder of the Weierstrass
division of  by
by 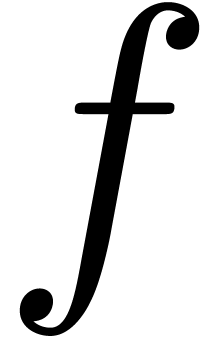 .
In particular,
.
In particular, 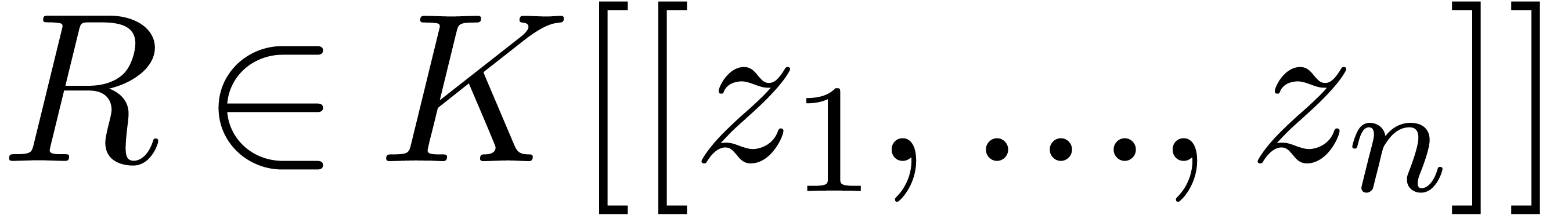 and we may obtain
and we may obtain 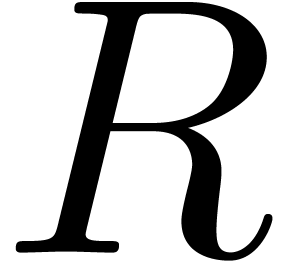 as an element of
as an element of 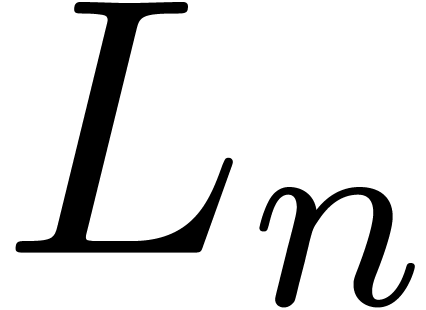 in the same way
as in the proof of Theorem 6. We obtain the quotient
in the same way
as in the proof of Theorem 6. We obtain the quotient  of the Weierstrass division by performing the
restricted division of
of the Weierstrass division by performing the
restricted division of  by
by  .
.
Often, it is possible to regard or represent elements of the tribe  as functions. For instance, we may regard
as functions. For instance, we may regard  as a function
as a function 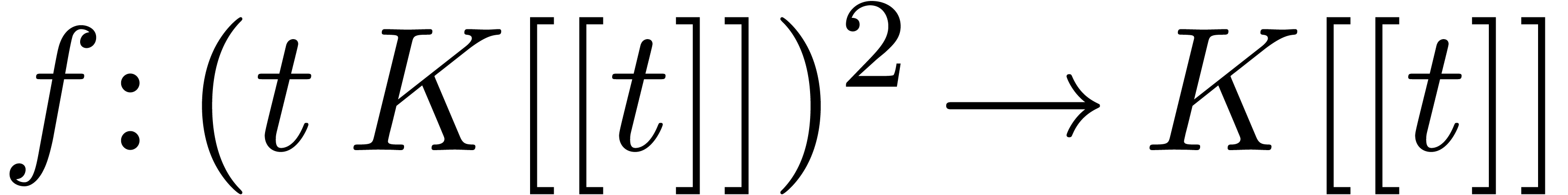 that sends
that sends 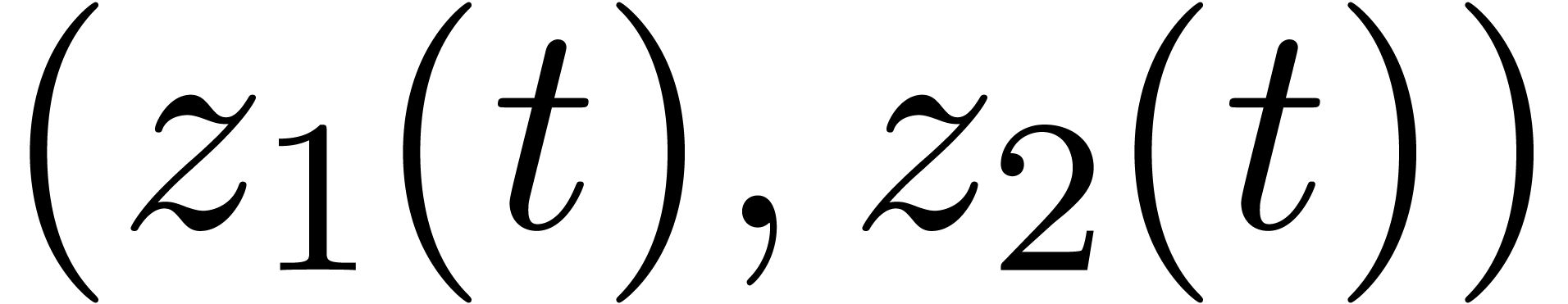 to
to 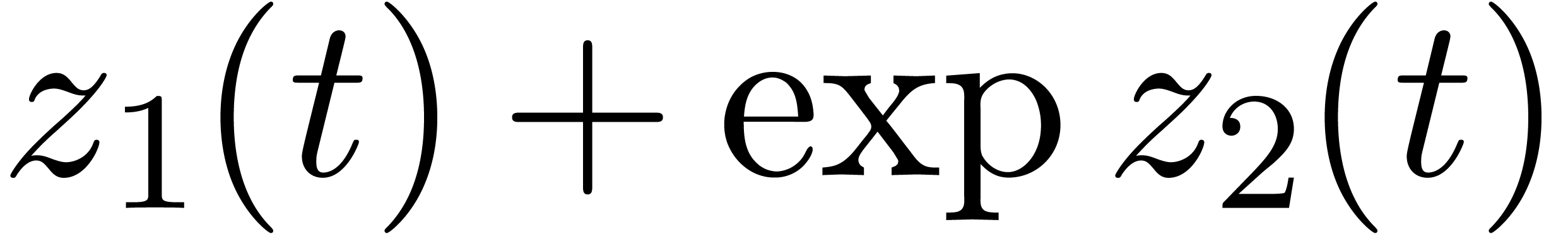 . This point
of view is very useful for heuristic zero testing: in order to test
whether
. This point
of view is very useful for heuristic zero testing: in order to test
whether 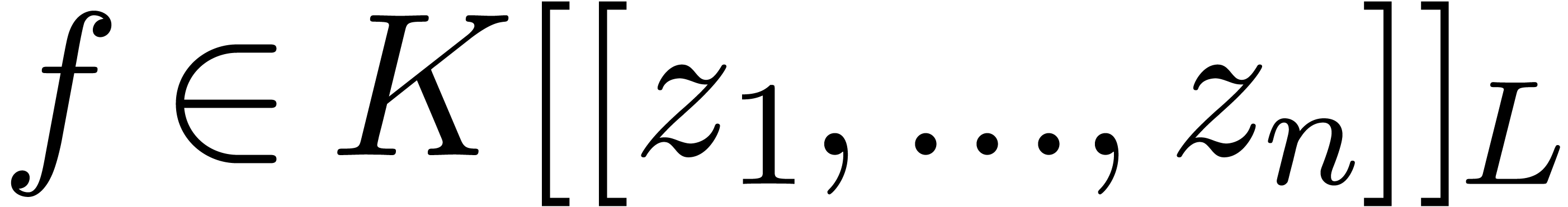 vanishes, just pick random infinitesimal
univariate series
vanishes, just pick random infinitesimal
univariate series 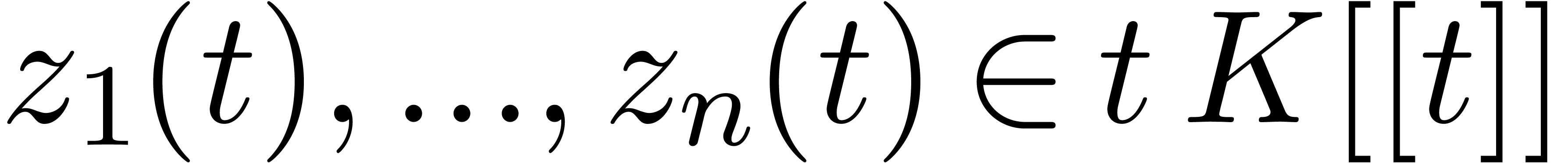 and check whether the first
and check whether the first
 terms of
terms of  vanish for some
suitable large number
vanish for some
suitable large number  .
.
In this evaluation approach, we notice that Weierstrass preparation
becomes far less expensive: instead of explicitly computing 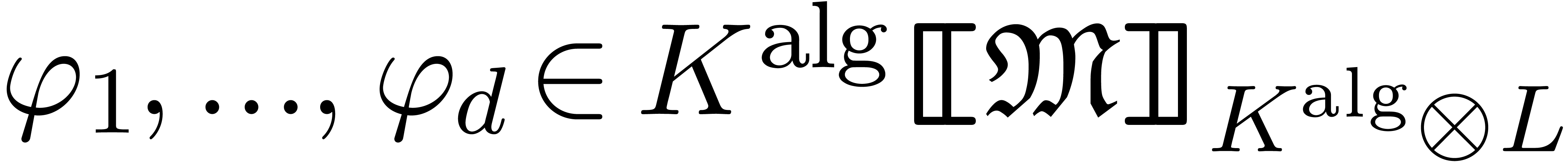 as above, it suffices to show how to evaluate
as above, it suffices to show how to evaluate
 (in terms of the evaluations of
(in terms of the evaluations of  ). For instance, if we evaluate
). For instance, if we evaluate  at infinitesimal ordinary power series in
at infinitesimal ordinary power series in 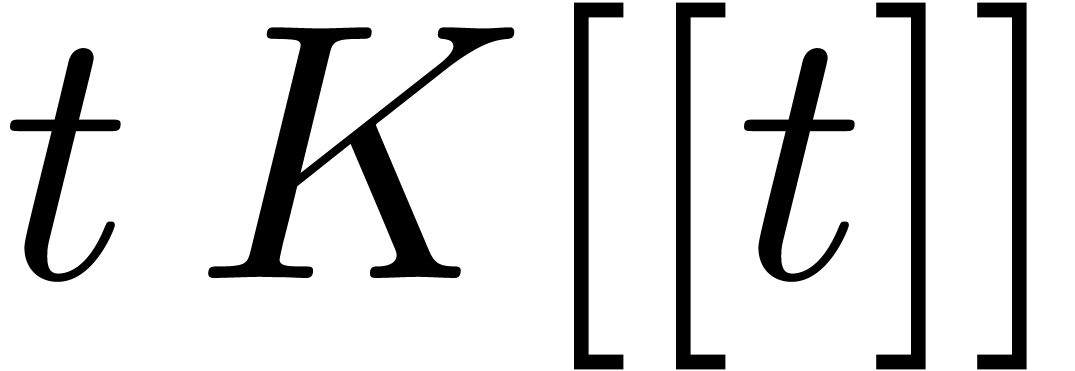 , then the evaluations of
, then the evaluations of  will be Puiseux series in
will be Puiseux series in  that can be computed
fast using the Newton polygon method.
that can be computed
fast using the Newton polygon method.
In the special case of algebraic power series, we recall from the
introduction that an alternative approach to Weierstrass division was
proposed in [2]. In this approach, algebraic functions are
represented in terms of unique power series solutions to certain systems
of polynomial equations. Given an algebraic series  of Weierstrass degree
of Weierstrass degree 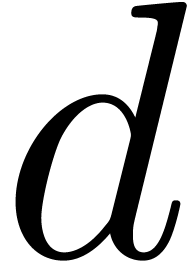 in
in 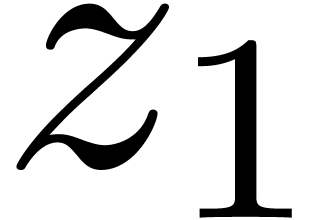 , the idea is then to represent the Weierstrass
polynomial
, the idea is then to represent the Weierstrass
polynomial 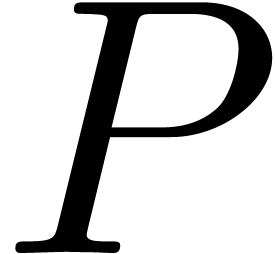 associated to
associated to  as
as 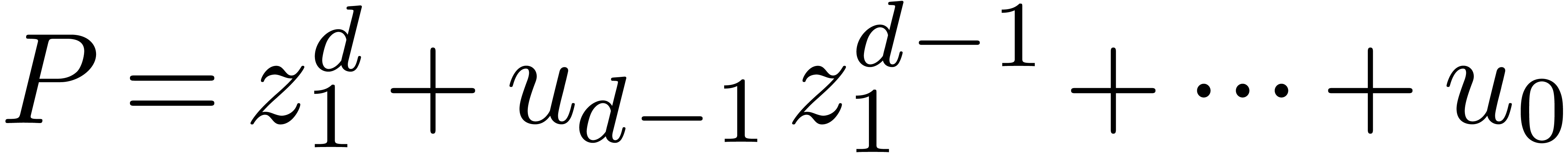 for certain undetermined coefficients. Next,
it suffices to form a new system of equations in
for certain undetermined coefficients. Next,
it suffices to form a new system of equations in  for which the unique solution yields the actual Weierstrass polynomial.
For instance, if
for which the unique solution yields the actual Weierstrass polynomial.
For instance, if  is a polynomial, then the
relation
is a polynomial, then the
relation 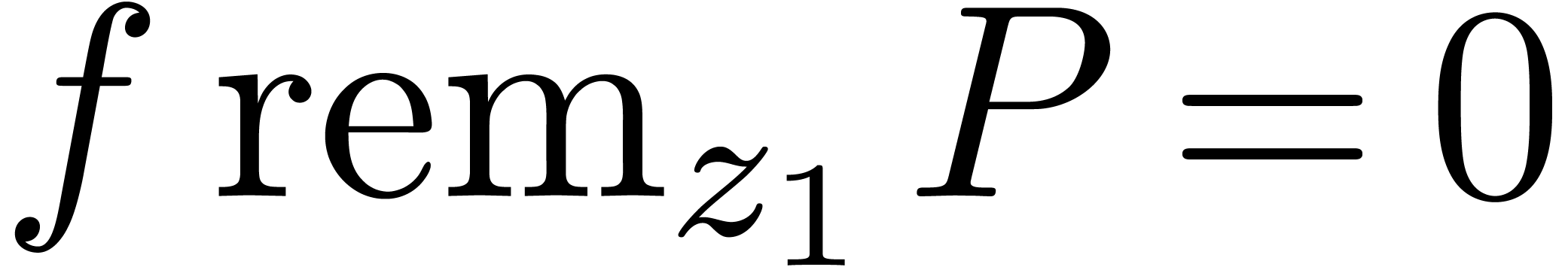 essentially provides us with such a
system, where
essentially provides us with such a
system, where 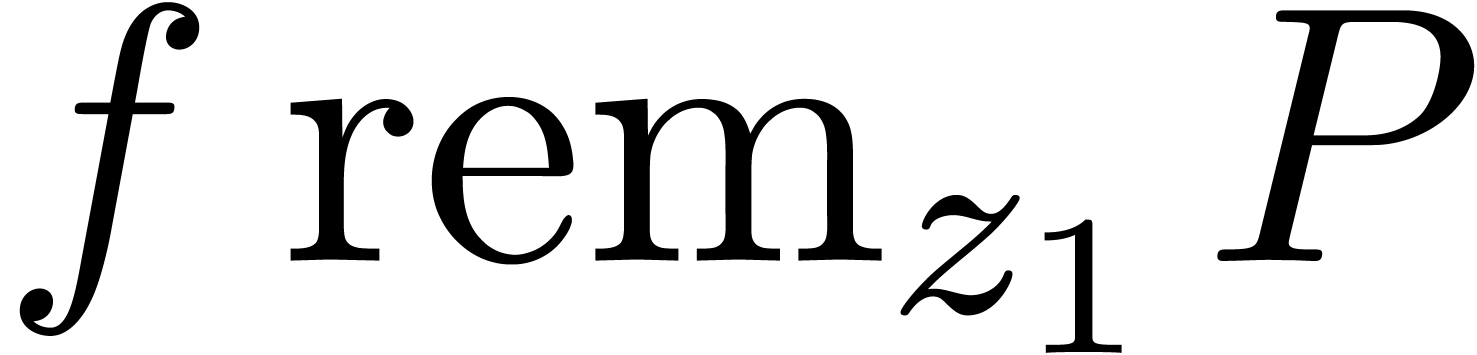 stands for the remainder of the
Euclidean division of
stands for the remainder of the
Euclidean division of  by
by 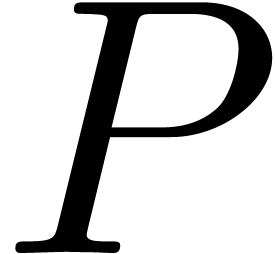 as polynomials in
as polynomials in 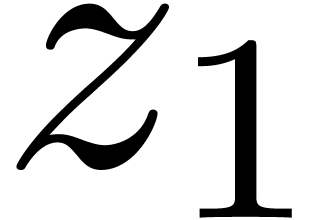 .
.
The efficiency of this approach from [2] highly depends on
the way how the systems of equations that are satisfied by algebraic
power series are represented. For instance, completely writing out the
remainder 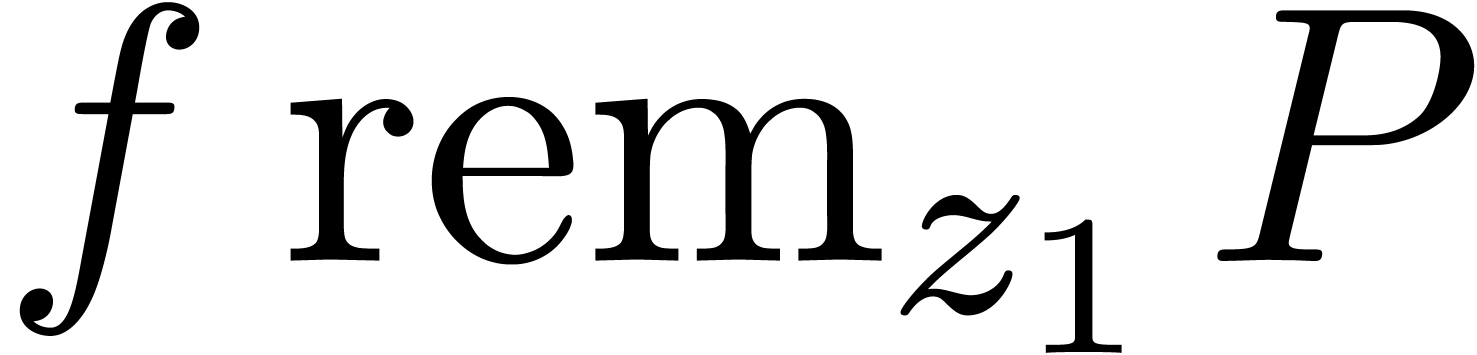 as a polynomial in
as a polynomial in 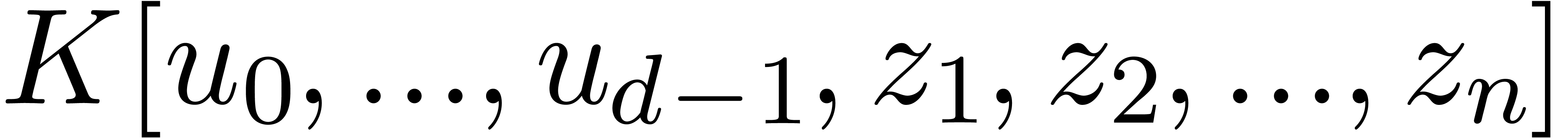 typically leads to very large expressions. On the other hand, we expect
the approach to be efficient in combination with the evaluation approach
mentioned above. If we replace the variables
typically leads to very large expressions. On the other hand, we expect
the approach to be efficient in combination with the evaluation approach
mentioned above. If we replace the variables  by
infinitesimal power series in
by
infinitesimal power series in 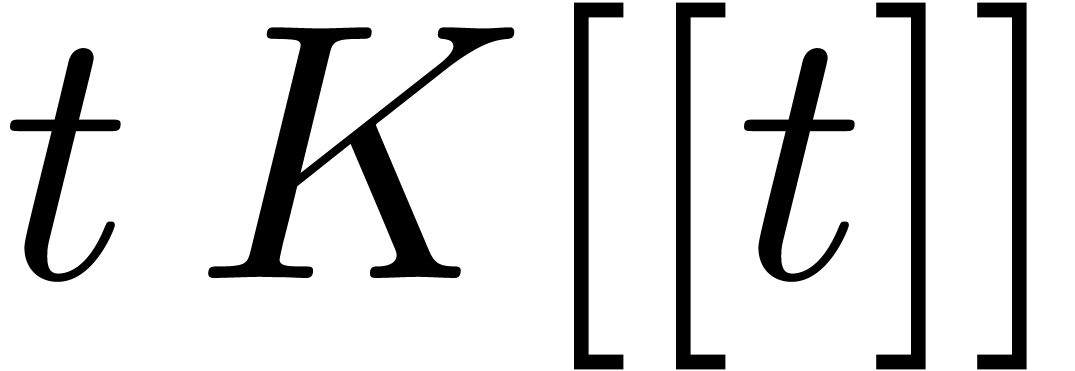 ,
then one may solve the evaluated system of equations in
,
then one may solve the evaluated system of equations in  using the relaxed technique from [14].
using the relaxed technique from [14].
One attractive way to represent d-algebraic power series in  is as elements of a suitable type of finitely generated
algebras
is as elements of a suitable type of finitely generated
algebras 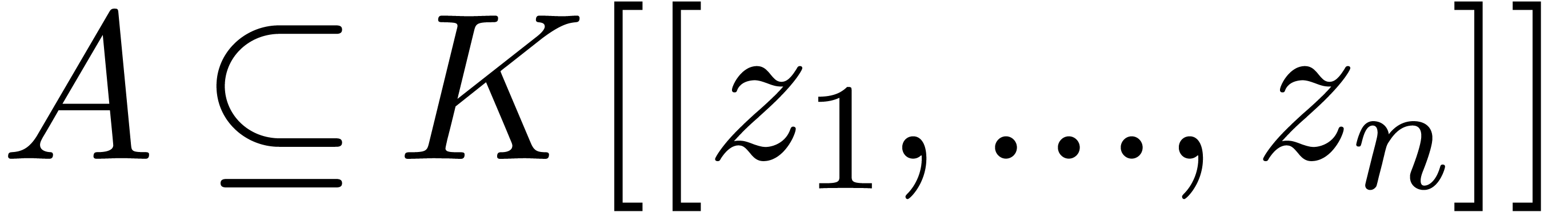 over
over  that are
stable under the derivations
that are
stable under the derivations  with respect to
with respect to
 . For instance, we might have
. For instance, we might have
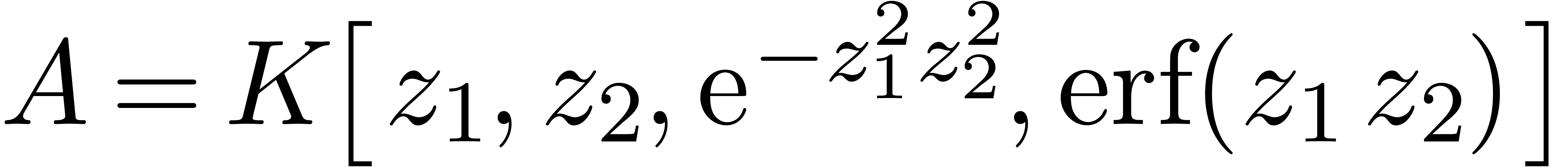 .
.
In order to compute with implicit functions, there are essentially two
approaches. The traditional one procedes by the elimination of one or
more coordinates, which may lead to expensive rewritings. An alternative
strategy is to represent restrictions of functions in  to subvarieties by the same functions in
to subvarieties by the same functions in  ,
and rather focus on the computation of the derivations that leave the
subvariety invariant. Consider for instance the sphere
,
and rather focus on the computation of the derivations that leave the
subvariety invariant. Consider for instance the sphere 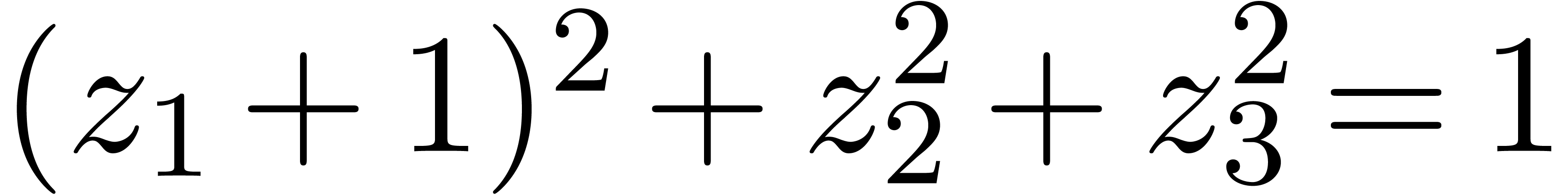 . We keep representing functions on the sphere
using all three coordinates
. We keep representing functions on the sphere
using all three coordinates 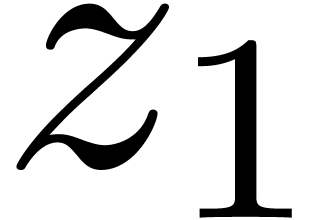 ,
,
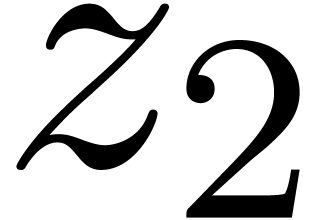 , and
, and 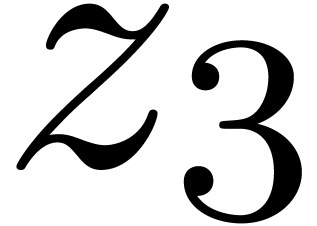 . On the other hand, for differential calculus, we
only work with derivations that annihilate the equation of the sphere.
In particular, the local coordinates
. On the other hand, for differential calculus, we
only work with derivations that annihilate the equation of the sphere.
In particular, the local coordinates  and
and  give rise to derivations
give rise to derivations 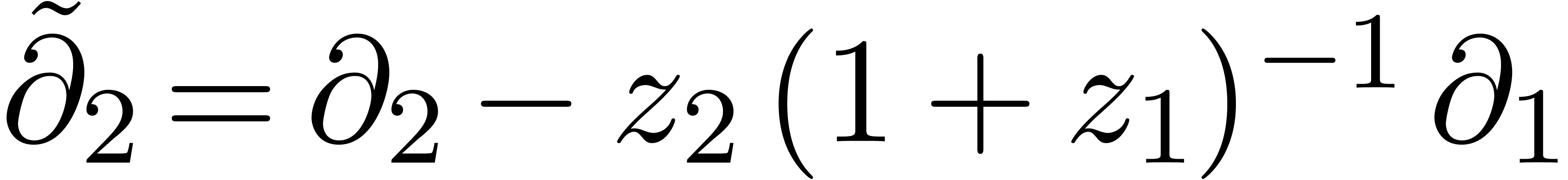 and
and
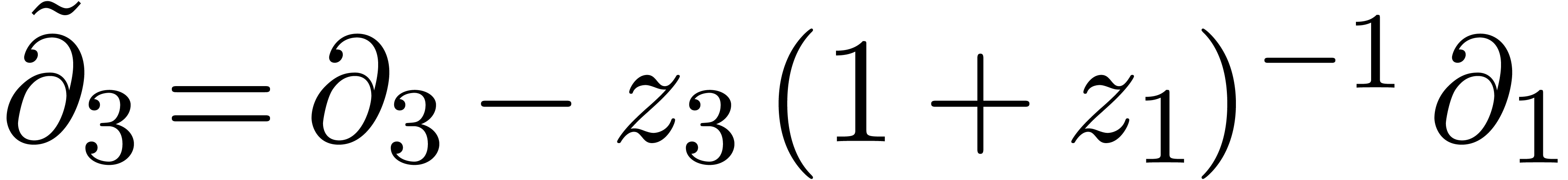 that do not commute. We refer to [15,
Section 5] for more details on how to compute with respect to such
curved coordinates and how to derive an implicit function theorem in
this way.
that do not commute. We refer to [15,
Section 5] for more details on how to compute with respect to such
curved coordinates and how to derive an implicit function theorem in
this way.
The second, more geometric approach can be generalized to Weierstrass
division, by regarding the implicit function theorem as division with
respect to a series of Weierstrass degree one. For a d-algebraic series
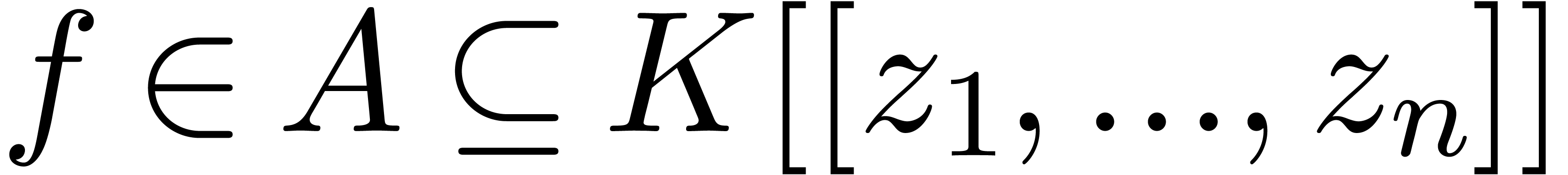 of higher Weierstrass degree
of higher Weierstrass degree 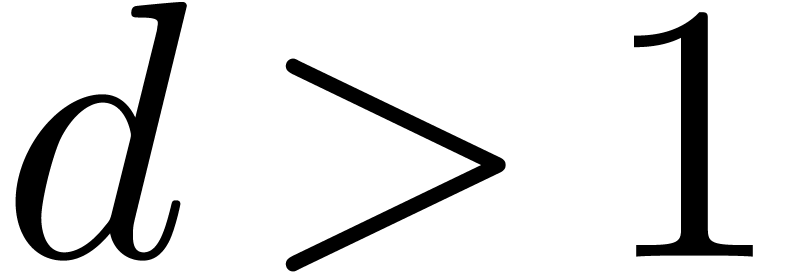 , we may again consider the restriction of the
ambient space to the zero-set of
, we may again consider the restriction of the
ambient space to the zero-set of  (recall that we
may regard
(recall that we
may regard  as a local function
as a local function 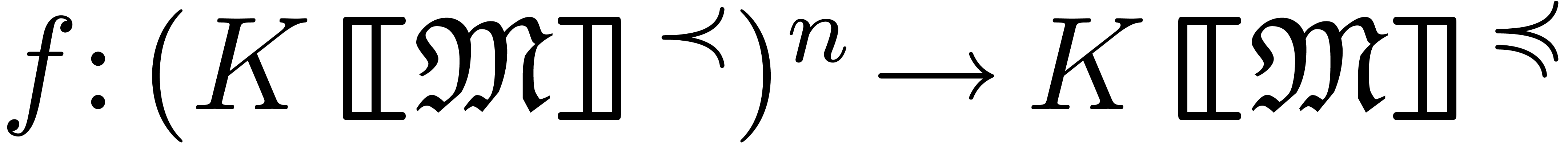 for any totally ordered monomial group
for any totally ordered monomial group  ).
Remainders of Weierstrass divisions by
).
Remainders of Weierstrass divisions by  then
correspond to functions on this zero-set. It is likely that an
alternative effective Weierstrass preparation theorem can be obtained by
pursuing this line of thought.
then
correspond to functions on this zero-set. It is likely that an
alternative effective Weierstrass preparation theorem can be obtained by
pursuing this line of thought.
Throughout this section, we assume that  is an
effective field with an effective zero test and that
is an
effective field with an effective zero test and that  is an effective algebraically stable tribe over
is an effective algebraically stable tribe over  with an effective zero test. We will write
with an effective zero test. We will write 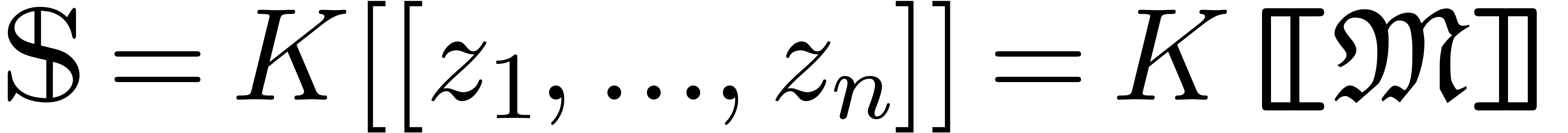 with
with
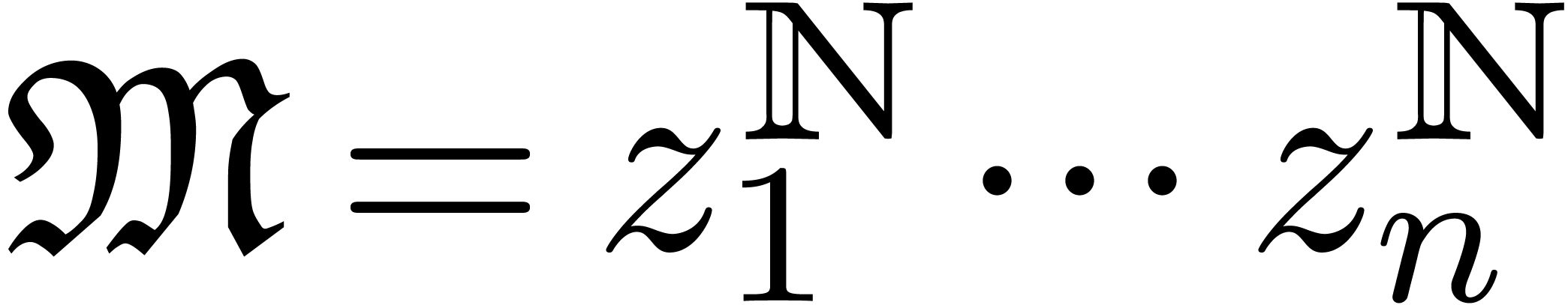 and assume that
and assume that  is
endowed with the asymptotic ordering
is
endowed with the asymptotic ordering  that
corresponds on the standard lexicographical ordering on the exponent
vectors:
that
corresponds on the standard lexicographical ordering on the exponent
vectors:

For each 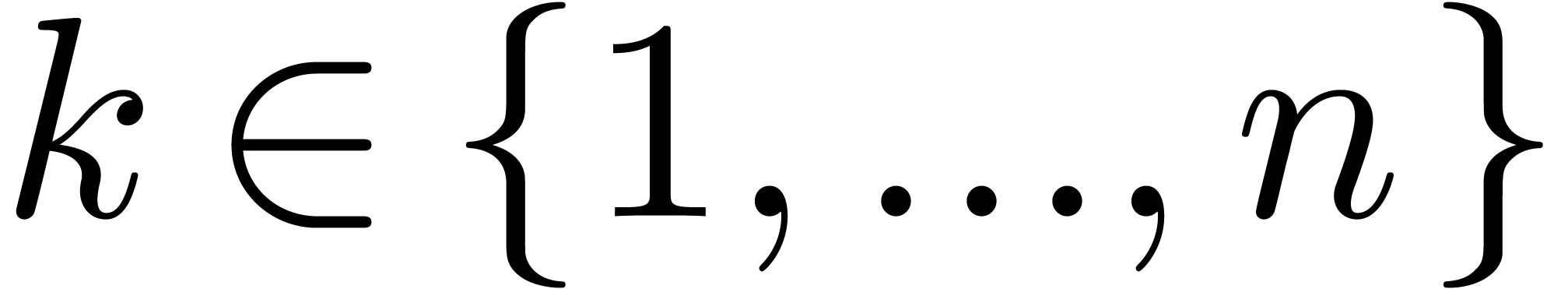 , we also define
, we also define
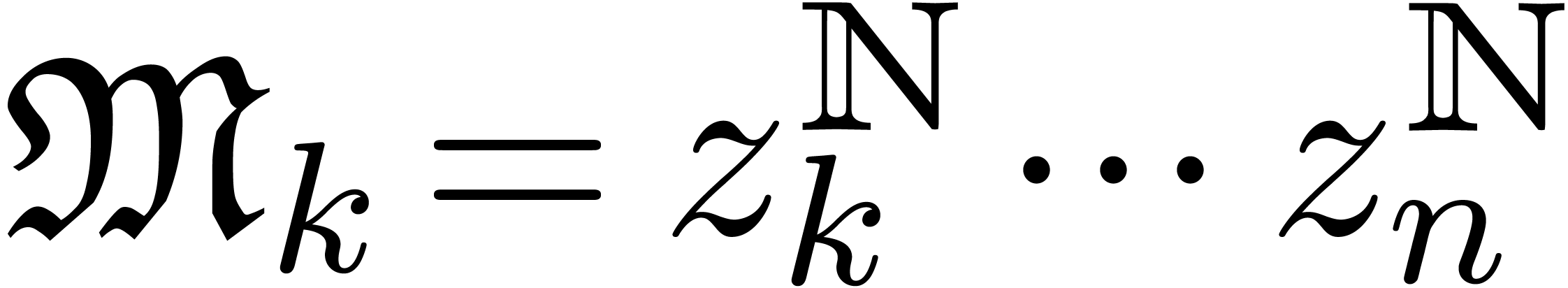 and
and 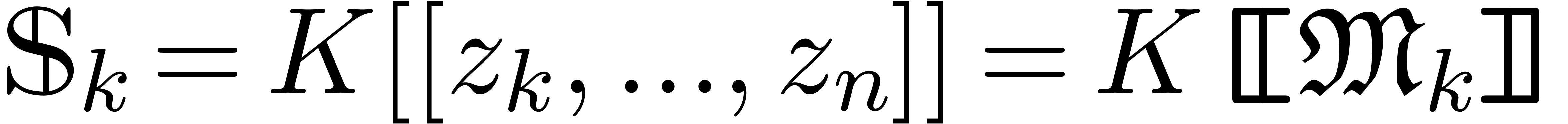 .
Given an arbitrary subset
.
Given an arbitrary subset  ,
we finally define
,
we finally define 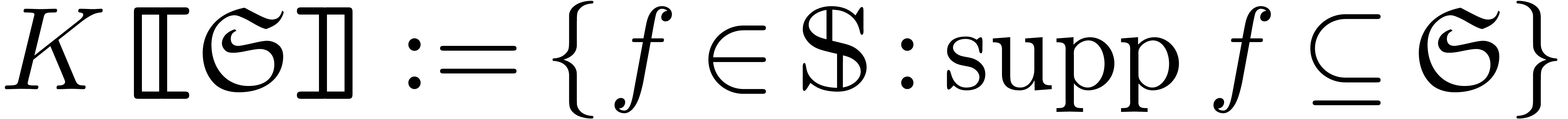 .
.
Consider a subset  together with a mapping
together with a mapping  with
with 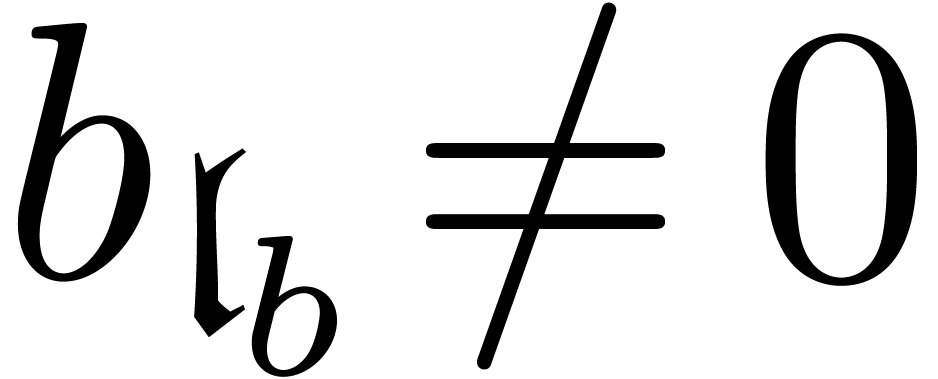 for each
for each  (intuitively speaking,
(intuitively speaking,  should be
interpreted as a “leading monomial” of
should be
interpreted as a “leading monomial” of  ; it will play a similar role as the
“dominant monomial”
; it will play a similar role as the
“dominant monomial”  of
of  from before). Setting
from before). Setting 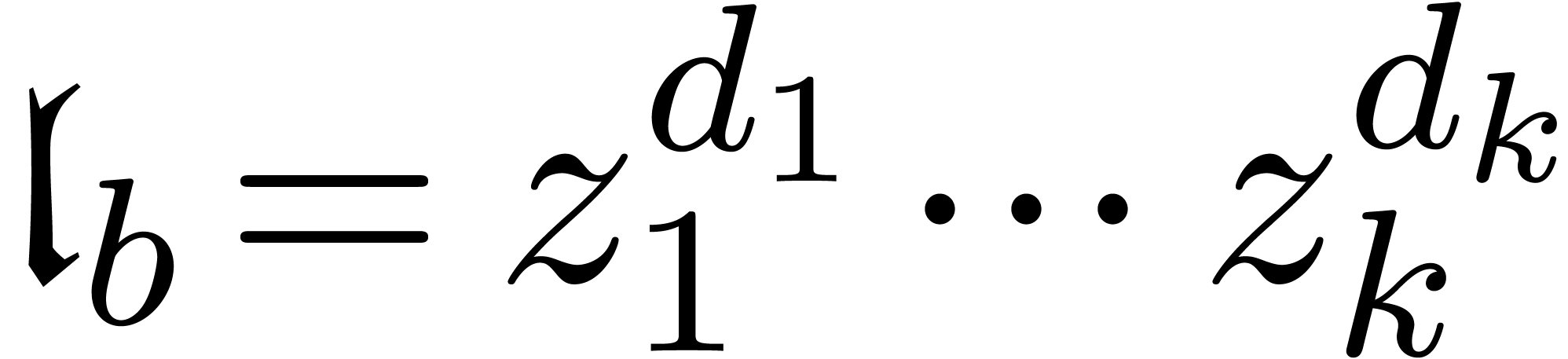 with
with 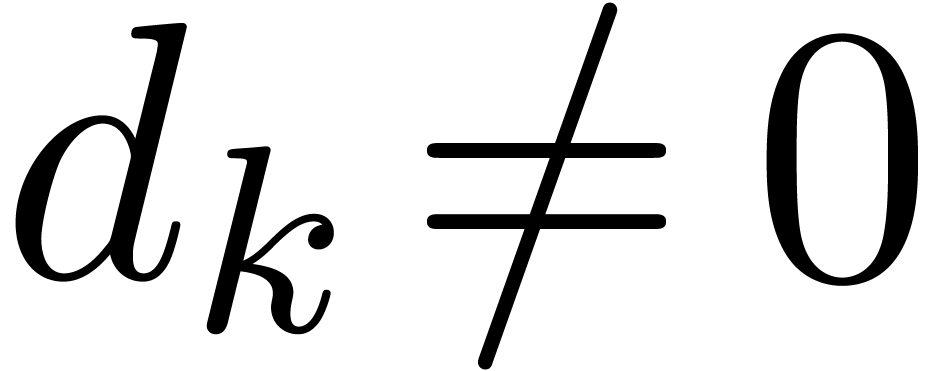 (or
(or 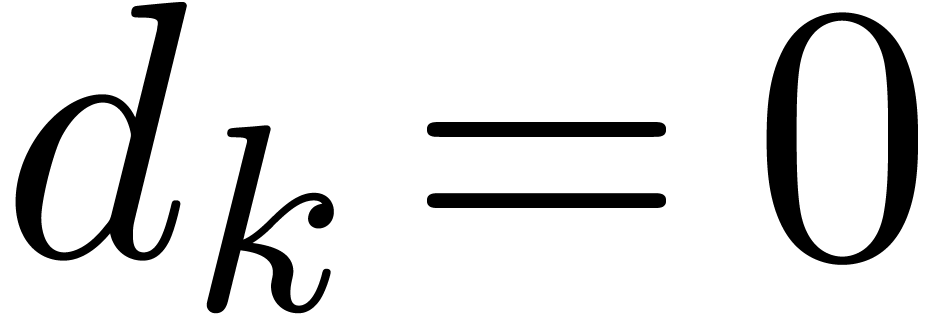 and
and 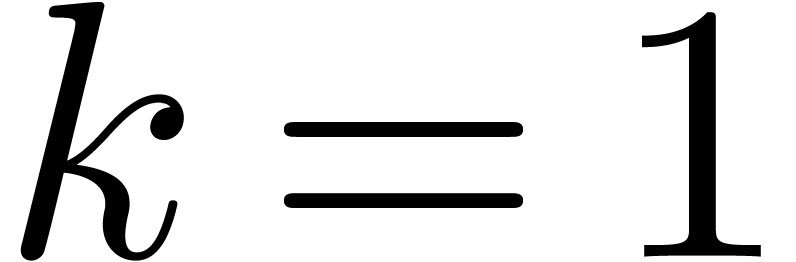 ), we call
), we call 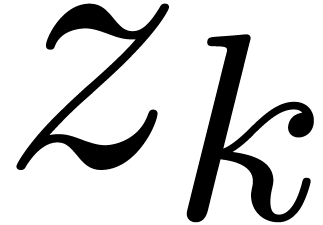 the
Weierstrass variable for
the
Weierstrass variable for 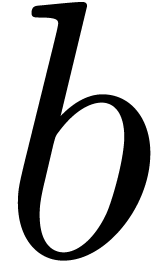 and
and 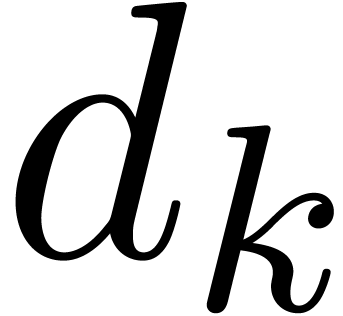 the corresponding Weierstrass degree. We also
denote
the corresponding Weierstrass degree. We also
denote 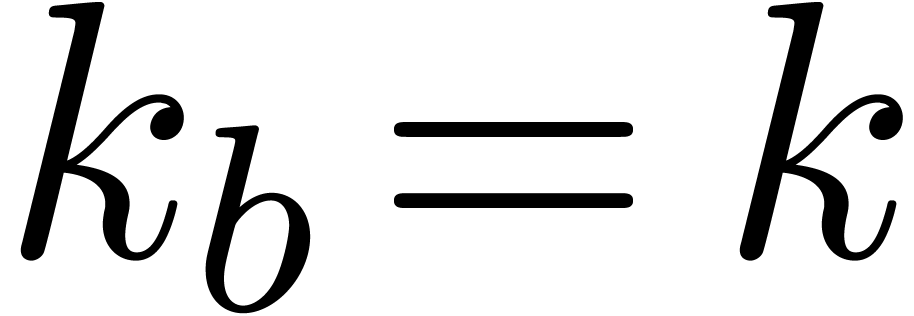 ,
, 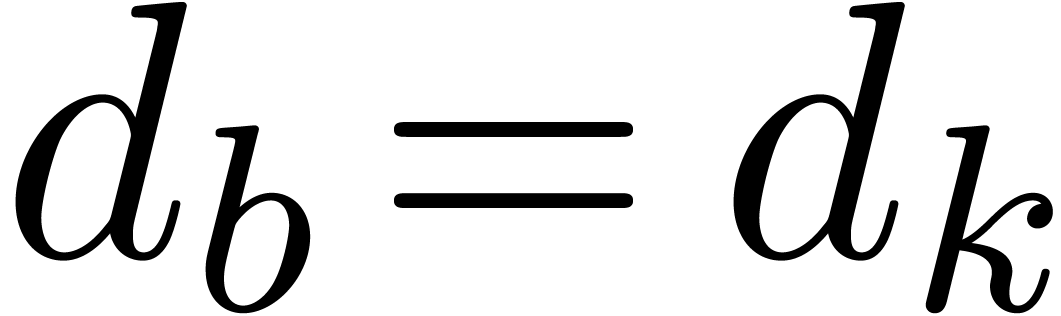 , and
, and
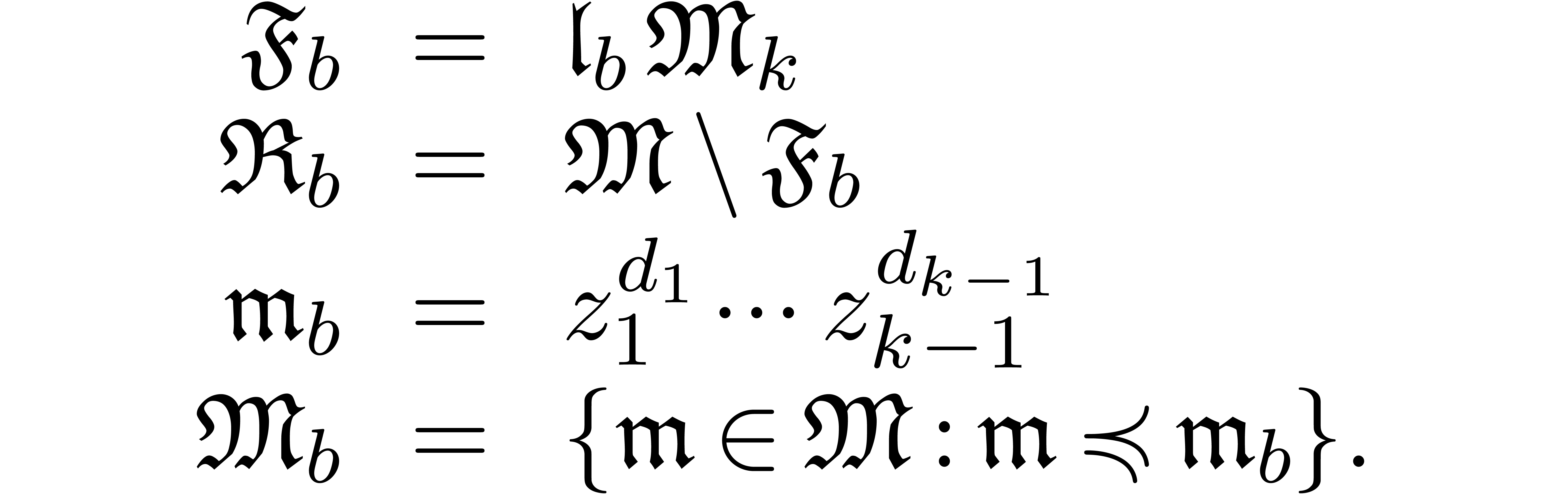
Given any  , we define
, we define
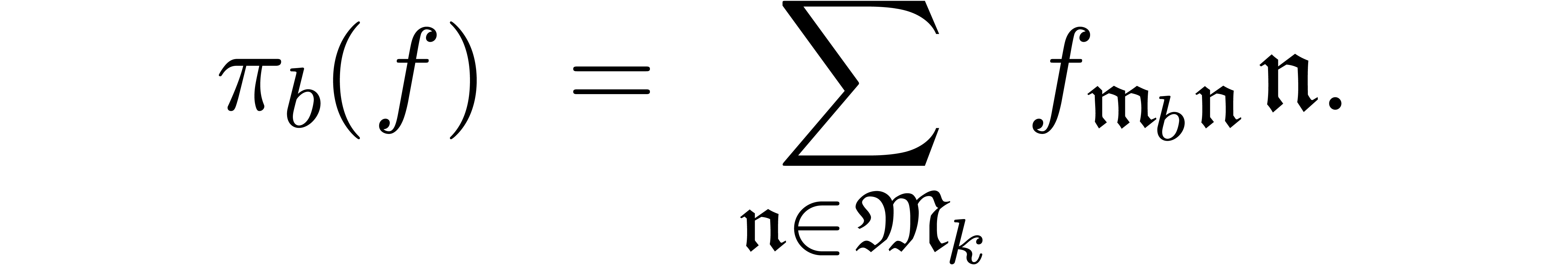
We say that  is a Weierstrass system if
is a Weierstrass system if
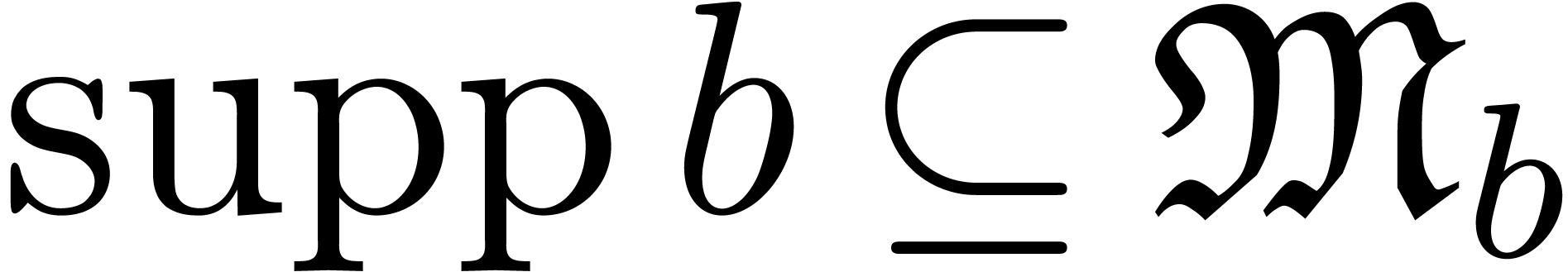 , if
, if 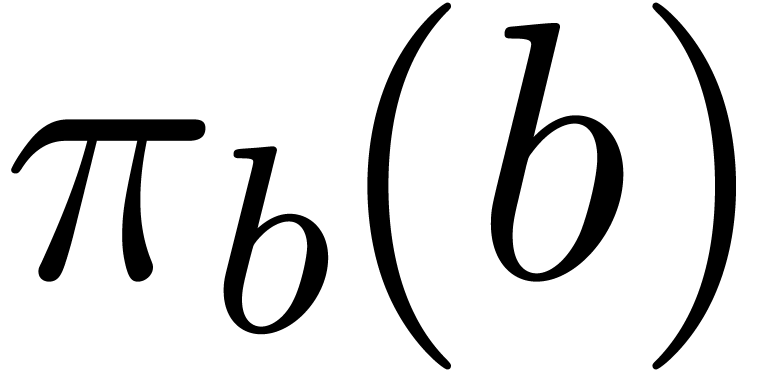 has valuation
has valuation 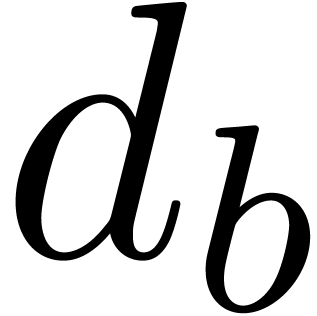 (w.r.t.
(w.r.t.  ) for each
) for each 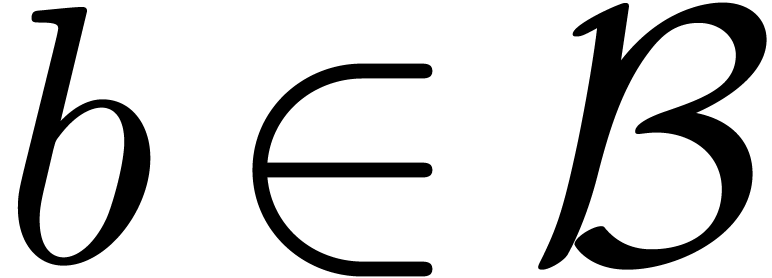 and if
and if  for all
for all 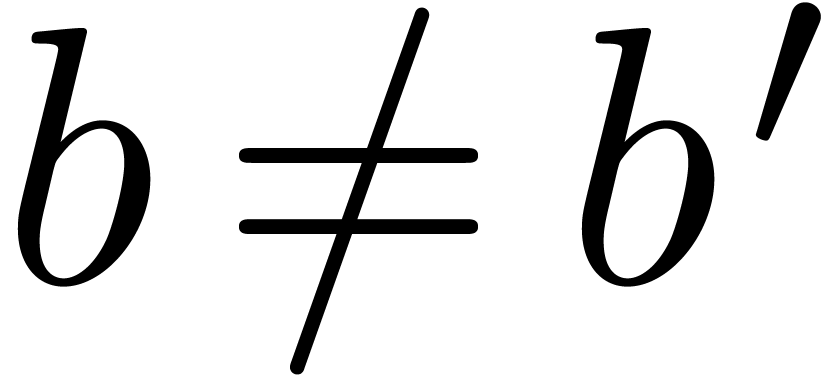 in
in  . In that case, the elements of
. In that case, the elements of  are totally ordered by
are totally ordered by 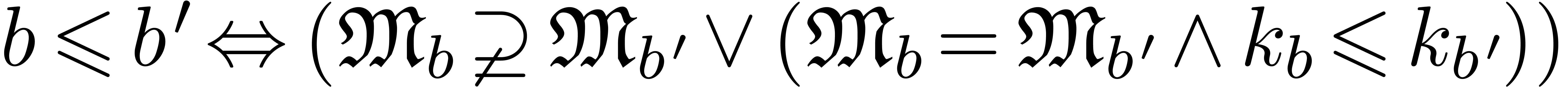 .
.
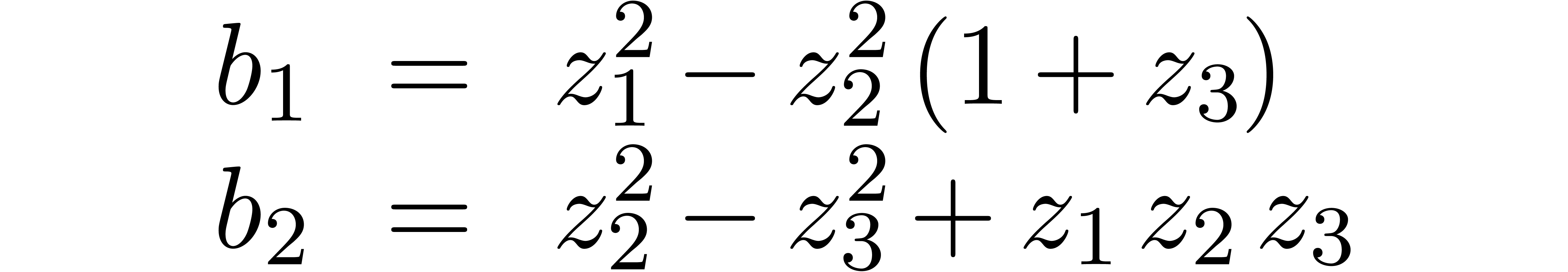
forms a Weierstrass system with  and
and
Let  be a Weierstrass system and
be a Weierstrass system and 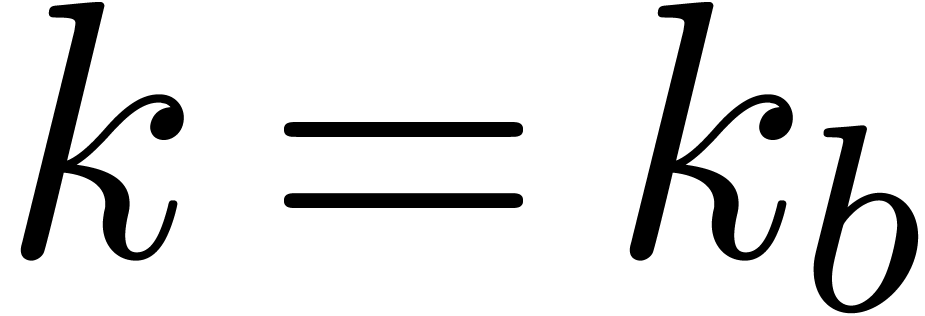 . Given
. Given  ,
Weierstrass division of
,
Weierstrass division of 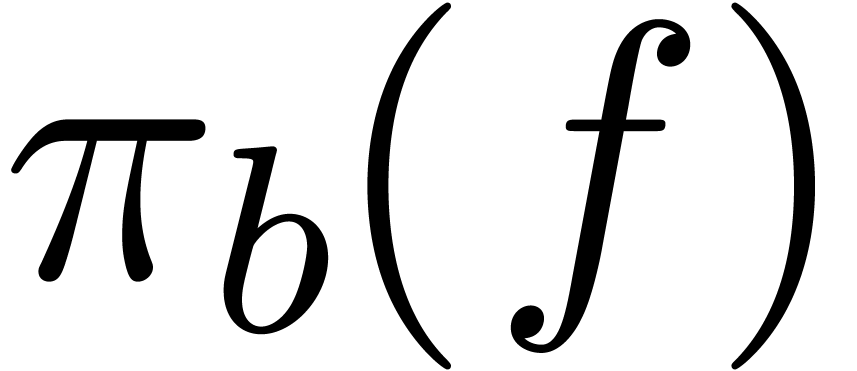 by
by 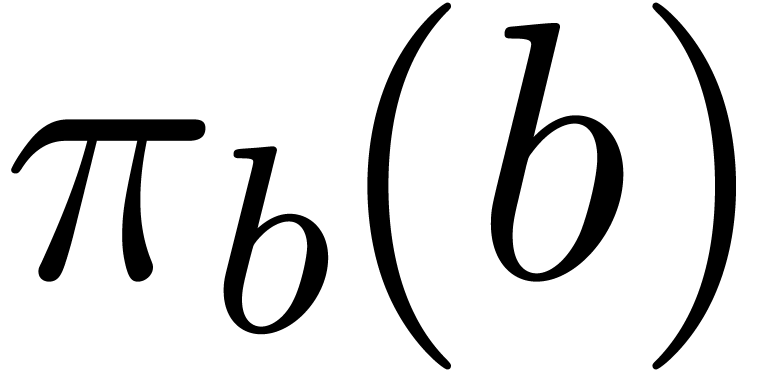 yields a unique series a unique
yields a unique series a unique 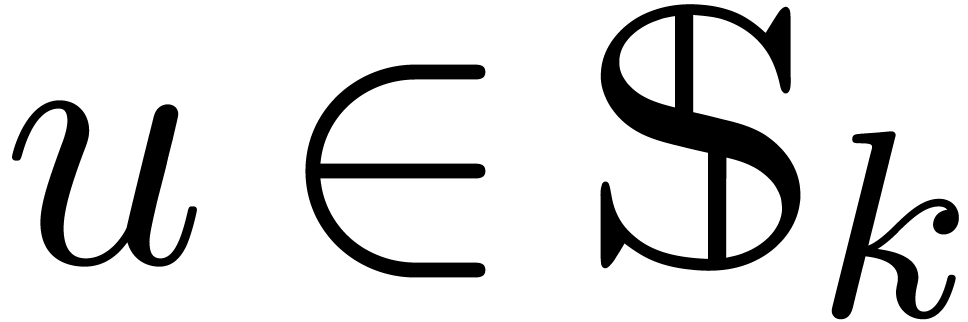 such that
such that
It follows that 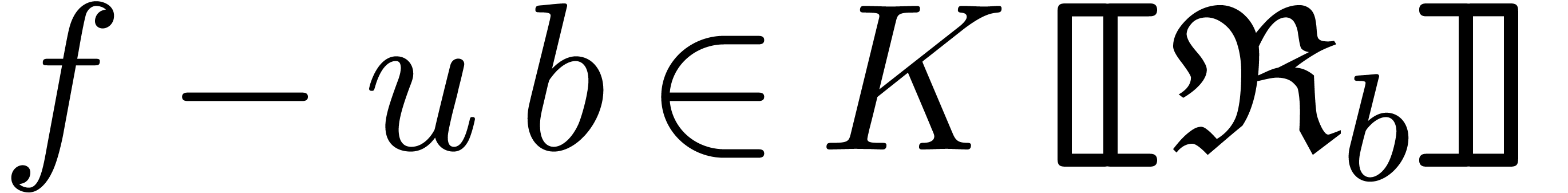 . Moreover,
if
. Moreover,
if 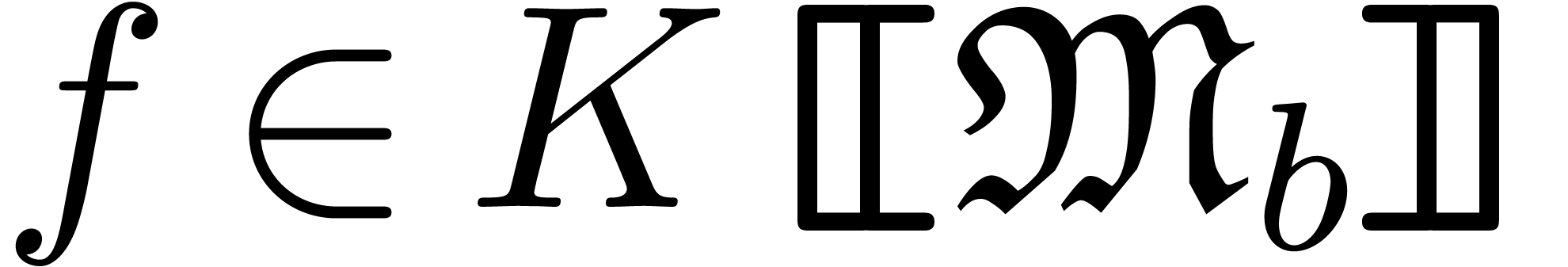 , then
, then 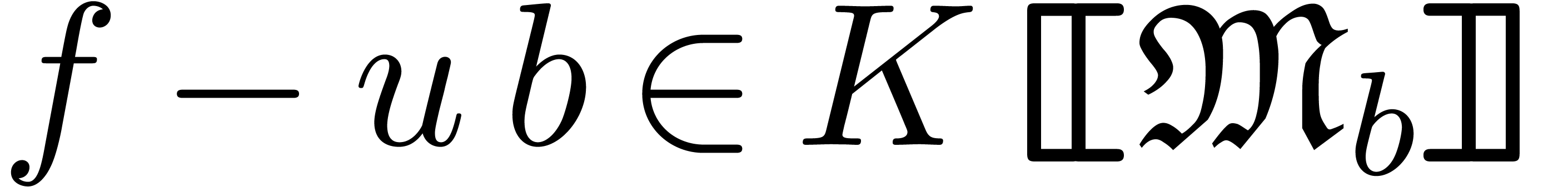 . We call
. We call 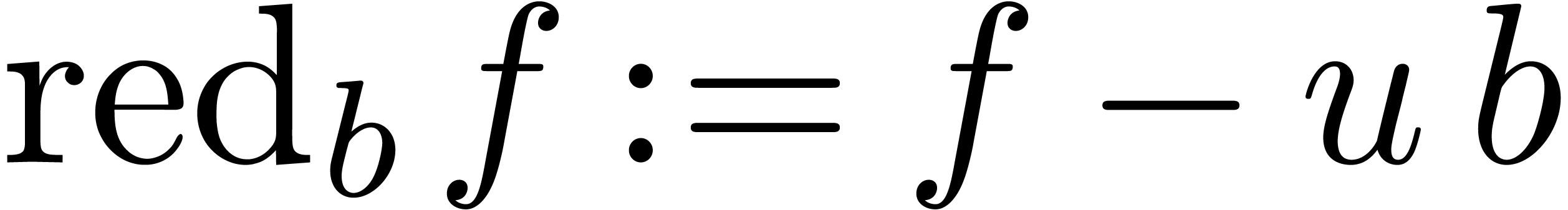 the
Weierstrass reduction of
the
Weierstrass reduction of  with respect
to
with respect
to  . If
. If 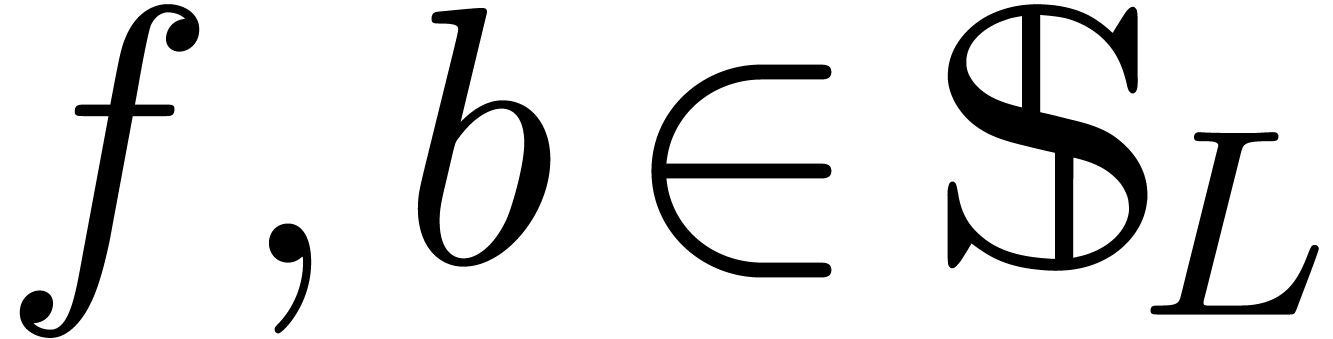 , then
, then 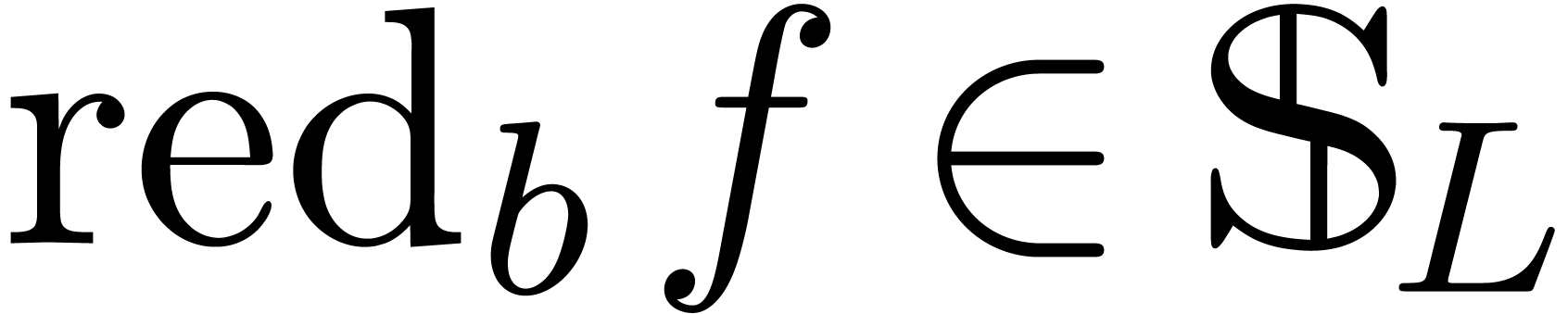 and we may
compute
and we may
compute 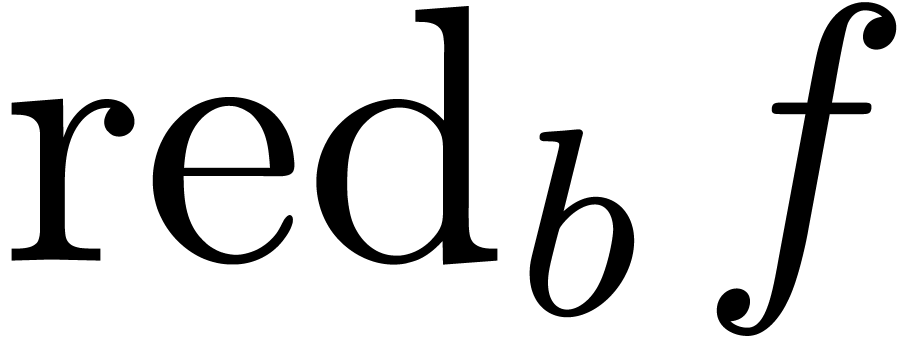 as described in Section 4.
as described in Section 4.
We notice that  is an
is an 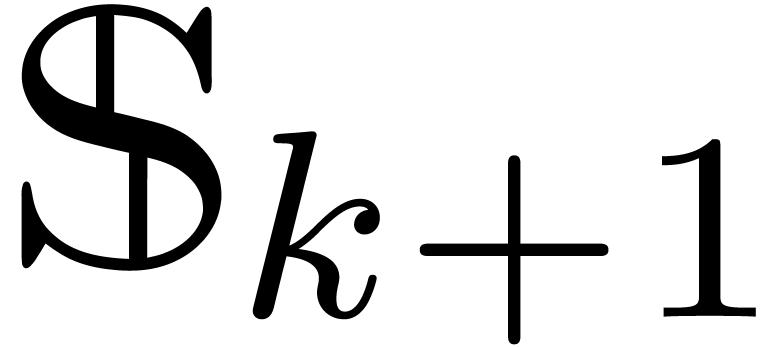 -linear mapping. The mapping actually preserves
infinite summation in the following sense: a family
-linear mapping. The mapping actually preserves
infinite summation in the following sense: a family 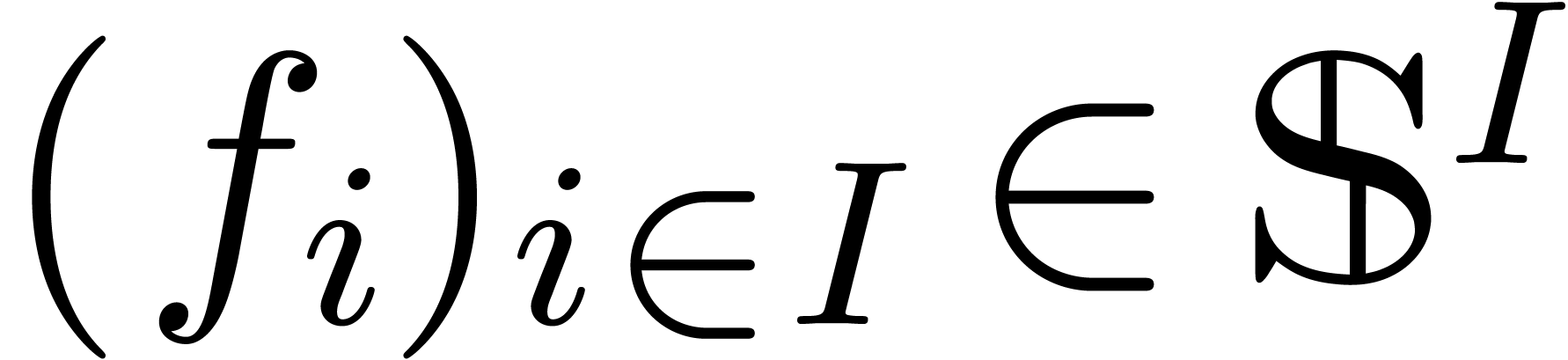 is said to be summable if the set
is said to be summable if the set 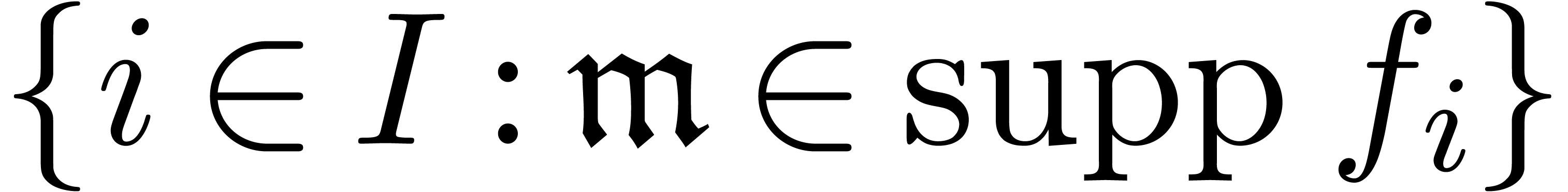 is finite for each
is finite for each  .
In that case, the sum
.
In that case, the sum 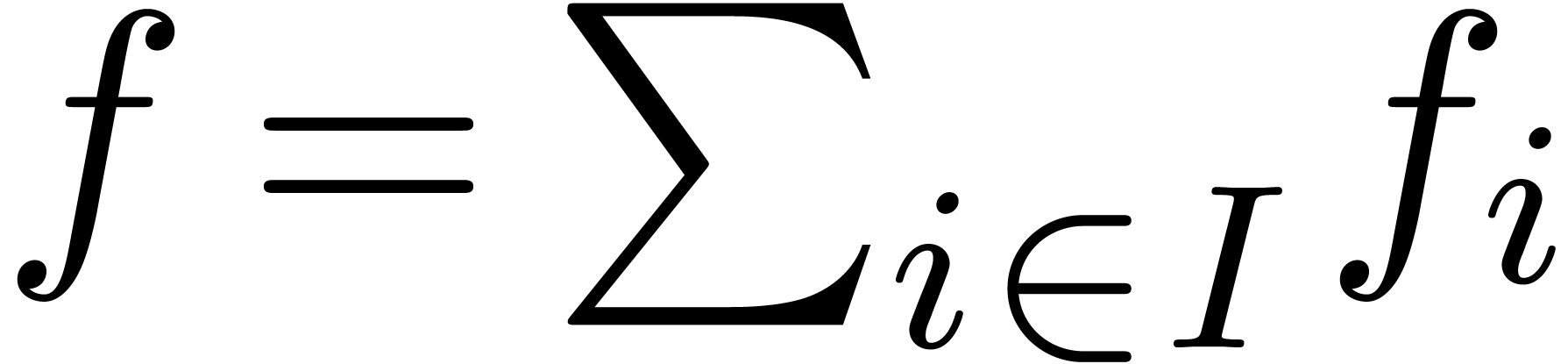 is well defined by taking
is well defined by taking
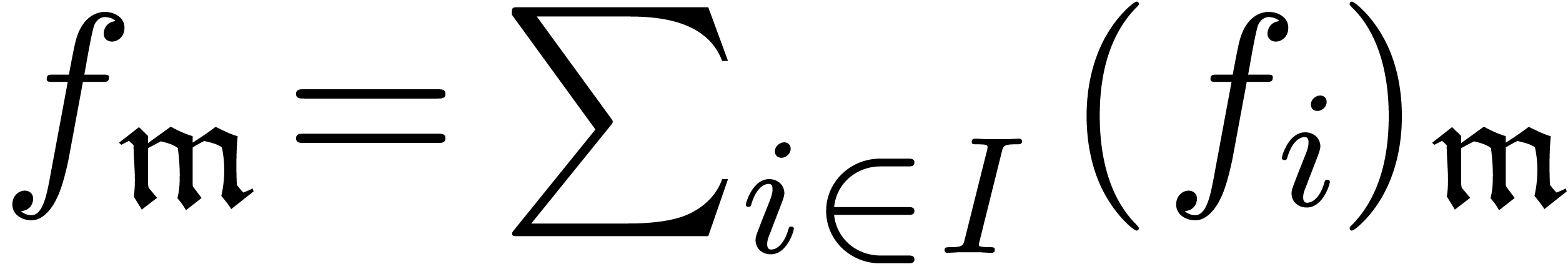 for each
for each  .
Linear mappings that preserve infinite summation are said to be
strongly linear.
.
Linear mappings that preserve infinite summation are said to be
strongly linear.
Now consider a Weierstrass system 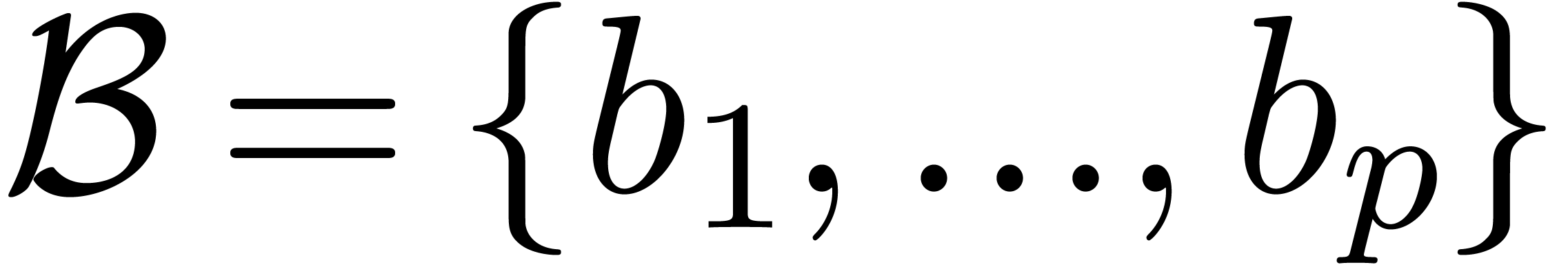 with
with  . Given
. Given  , we define its Weierstrass reduction with
respect to
, we define its Weierstrass reduction with
respect to  by
by
By induction over  , it can be
checked that
, it can be
checked that  is a strongly linear mapping, where
is a strongly linear mapping, where
 . If
. If 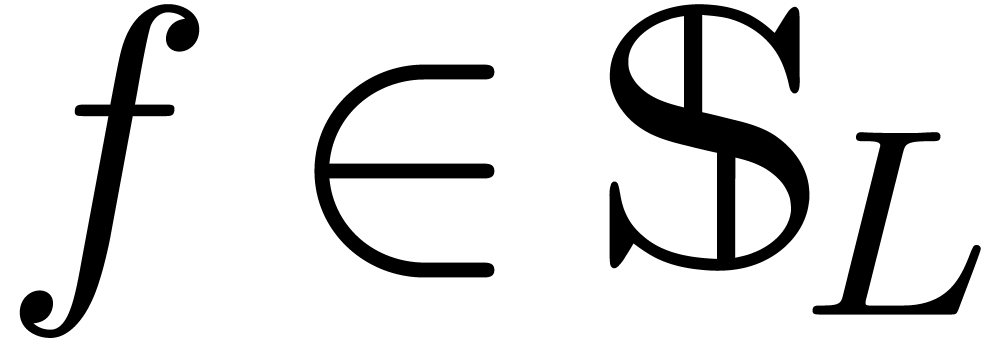 , then we also have
, then we also have 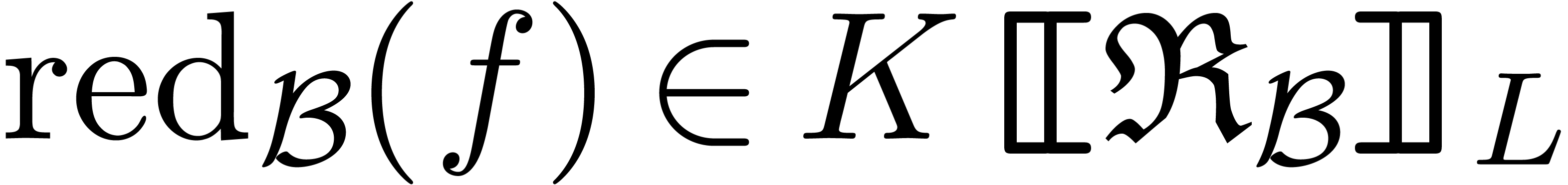 ,
and we may compute
,
and we may compute 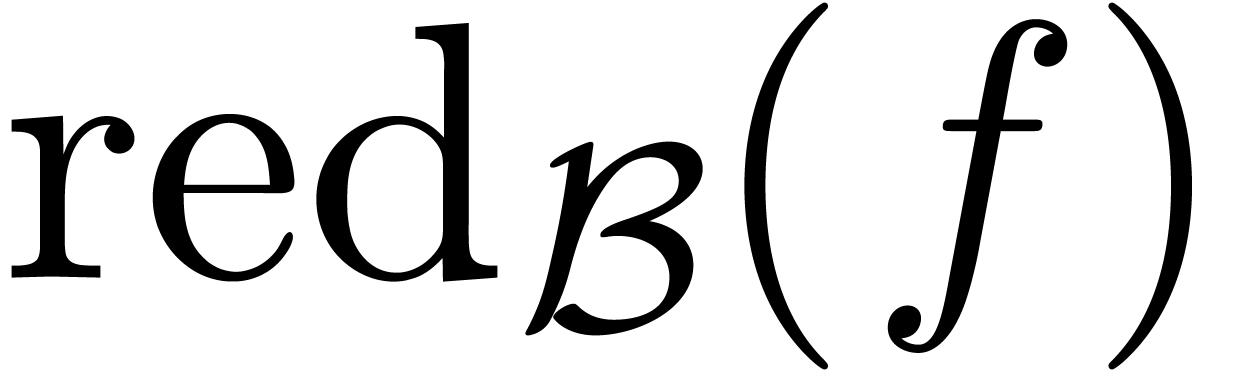 using (2).
using (2).
Example
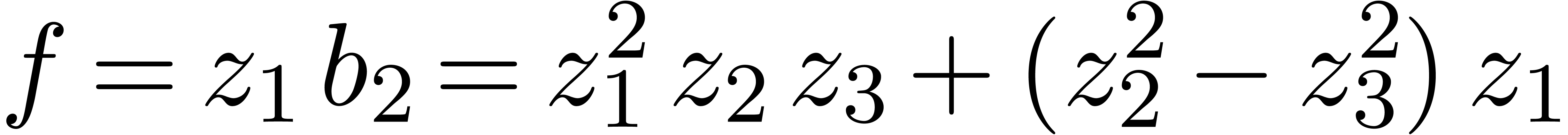
with respect to the Weierstrass system  from
Example 8. We start with the computation of
from
Example 8. We start with the computation of
Now 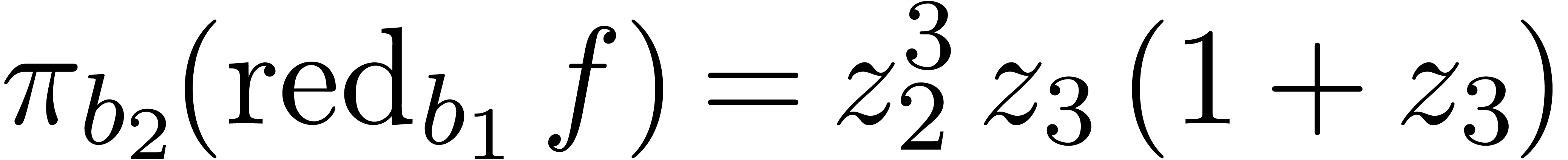 and
and 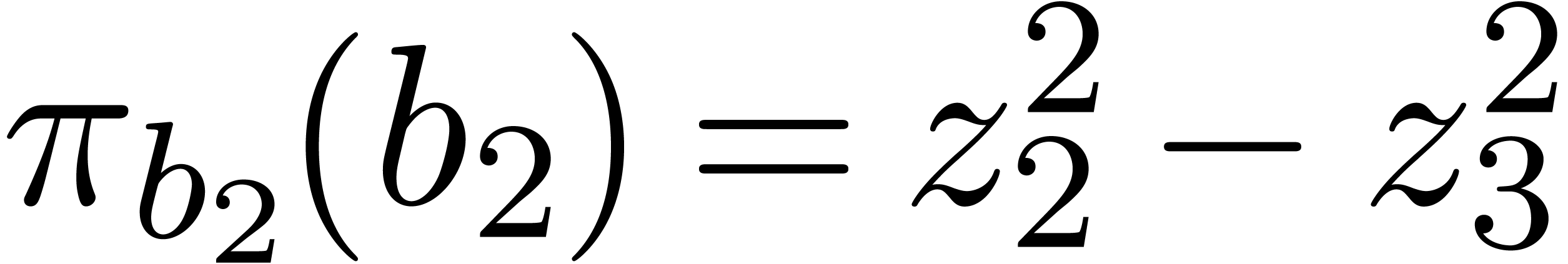 .
Abbreviating
.
Abbreviating 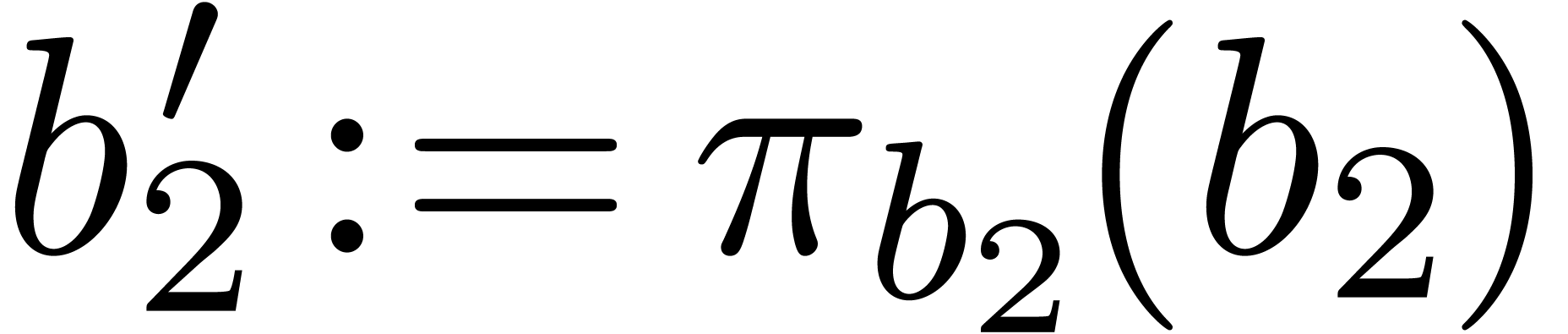 , it follows
that
, it follows
that 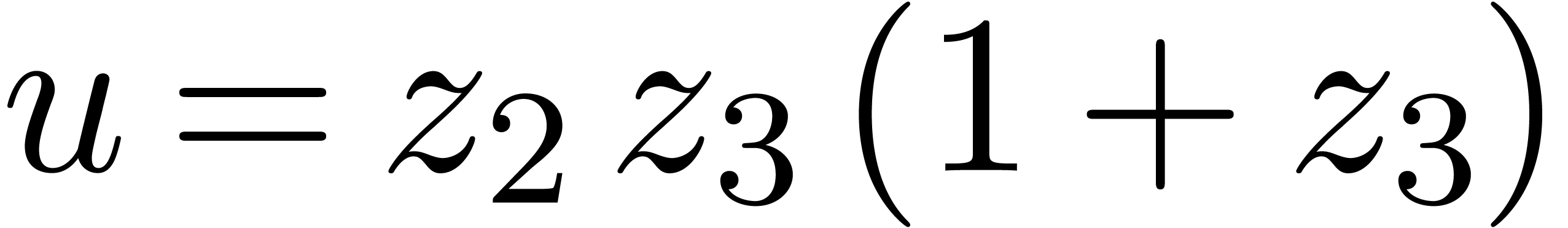 satisfies
satisfies 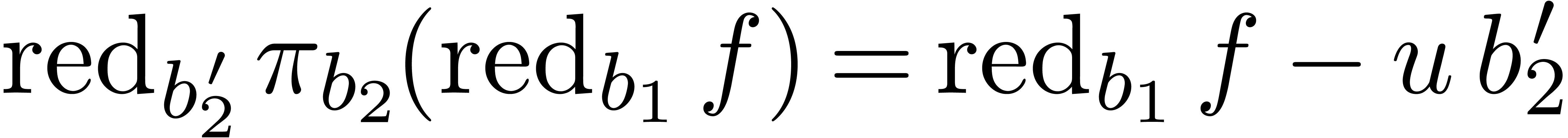 .
Consequently,
.
Consequently,
We indeed have 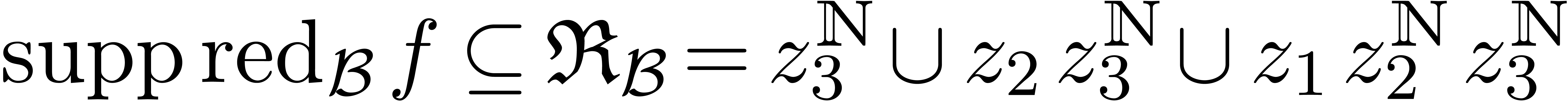 .
.
Remark  do not play a symmetric role. In particular, the notion of S-polynomials
has no direct counterpart in our context. Despite these differences,
Weierstrass reduction admits similar applications, such as the
computation of Hilbert functions, checking ideal membership, etc. The
set
do not play a symmetric role. In particular, the notion of S-polynomials
has no direct counterpart in our context. Despite these differences,
Weierstrass reduction admits similar applications, such as the
computation of Hilbert functions, checking ideal membership, etc. The
set  also plays a similar role as the set of
“boxes below a Gröbner staircase”.
also plays a similar role as the set of
“boxes below a Gröbner staircase”.
Remark  with
constant coefficients in
with
constant coefficients in 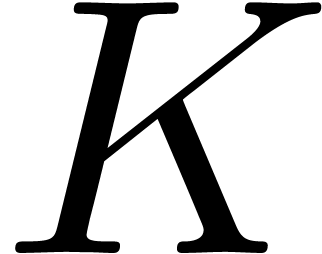 , in
which case we are really working with polynomials in
, in
which case we are really working with polynomials in  indeterminates
indeterminates  over
over 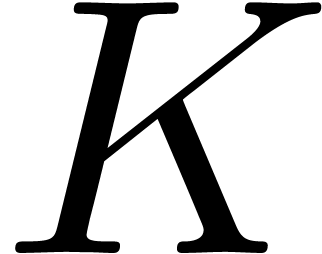 .
.
A Weierstrass system  is itself said to be
reduced if for each
is itself said to be
reduced if for each 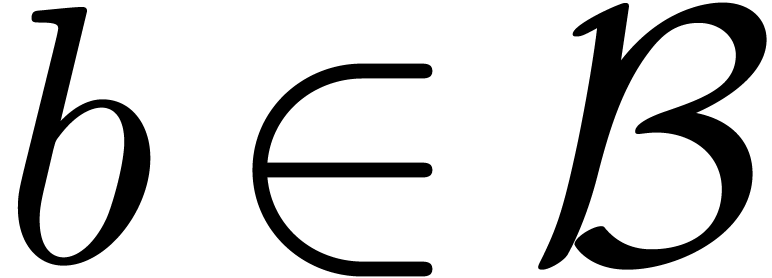 ,
we have
,
we have  . Two Weierstrass
systems
. Two Weierstrass
systems  and
and 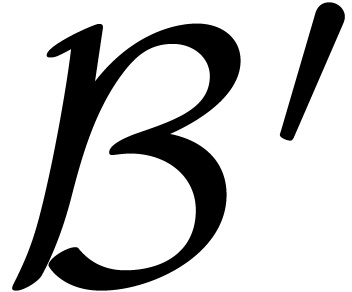 are said to
be equivalent if
are said to
be equivalent if  and
and  coincide.
coincide.
Let  be an arbitrary Weierstrass system and
consider
be an arbitrary Weierstrass system and
consider 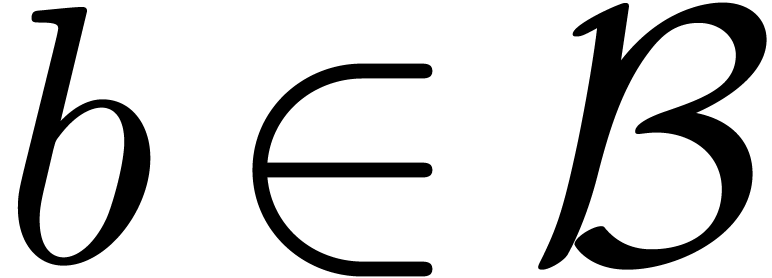 with
with 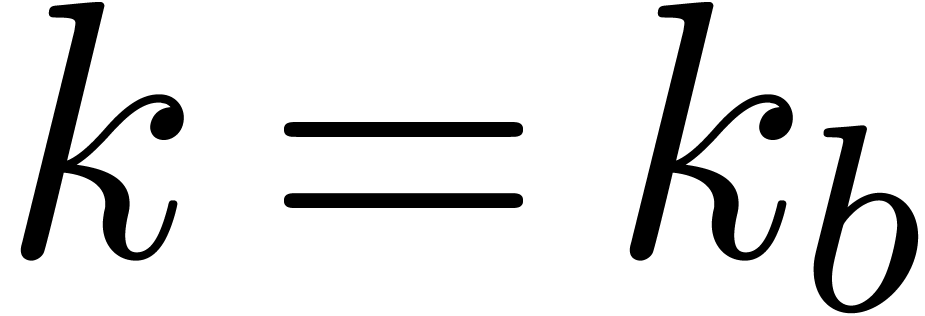 and
and 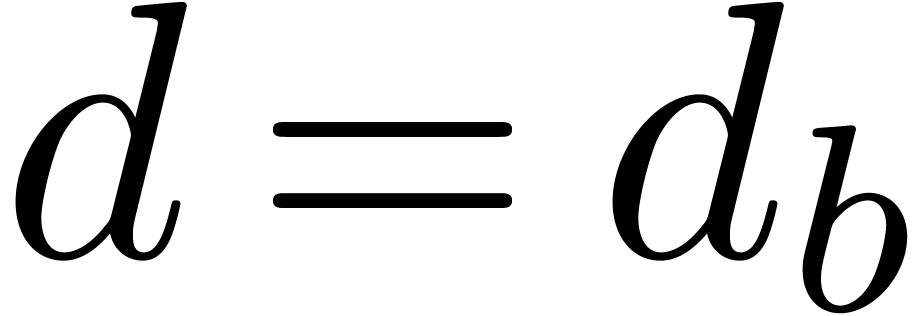 . We claim that there exists a
unique
. We claim that there exists a
unique 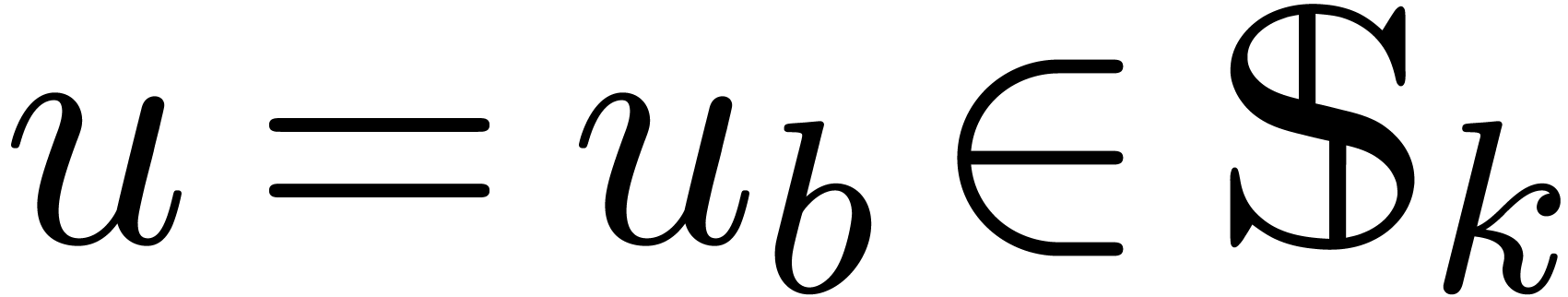 with
with 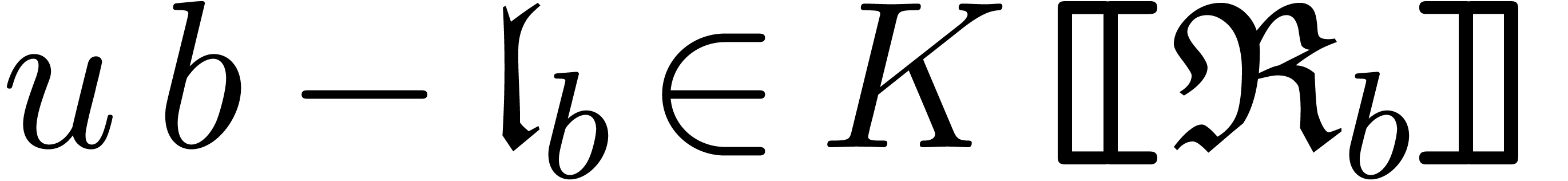 .
Indeed, the Weierstrass preparation theorem implies the existence of a
series
.
Indeed, the Weierstrass preparation theorem implies the existence of a
series 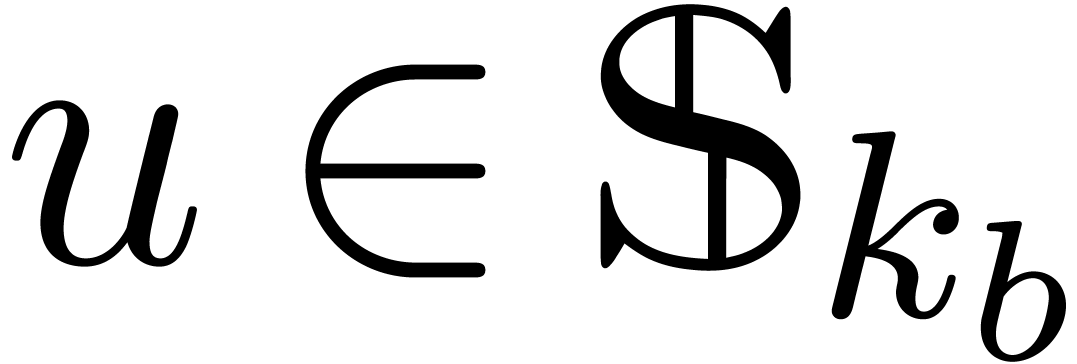 with
with 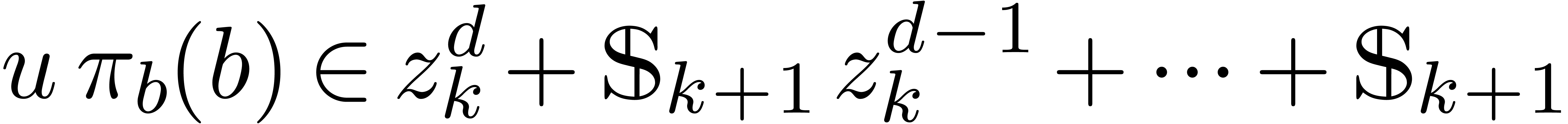 .
It follows that
.
It follows that 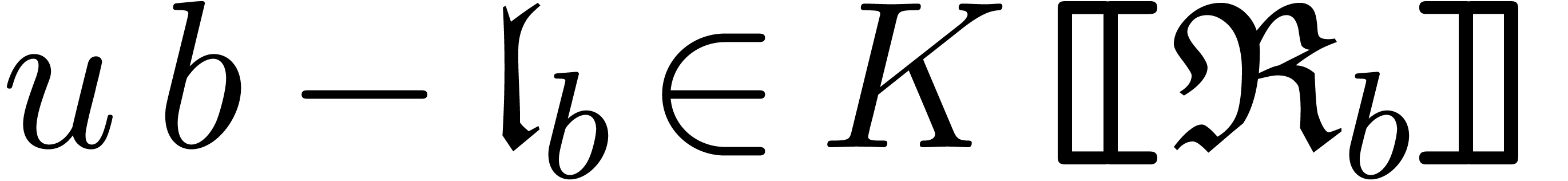 . If
. If 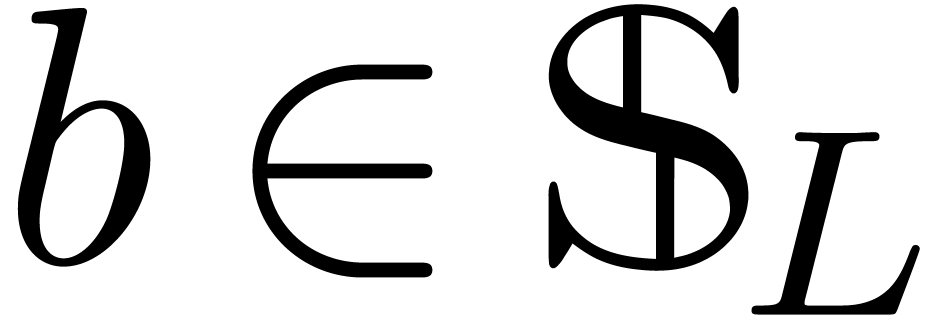 , then Theorem 6 shows
how to compute
, then Theorem 6 shows
how to compute  .
.
Replacing  by
by  for each
for each
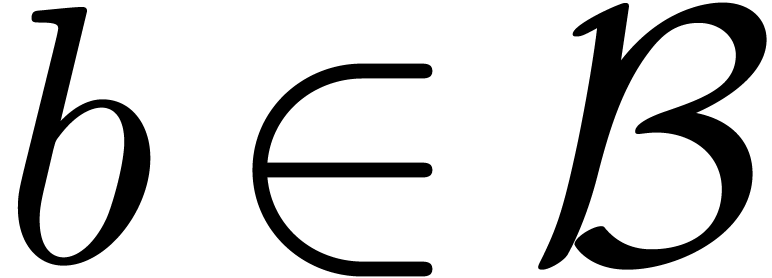 , we obtain an equivalent
Weierstrass system such that
, we obtain an equivalent
Weierstrass system such that 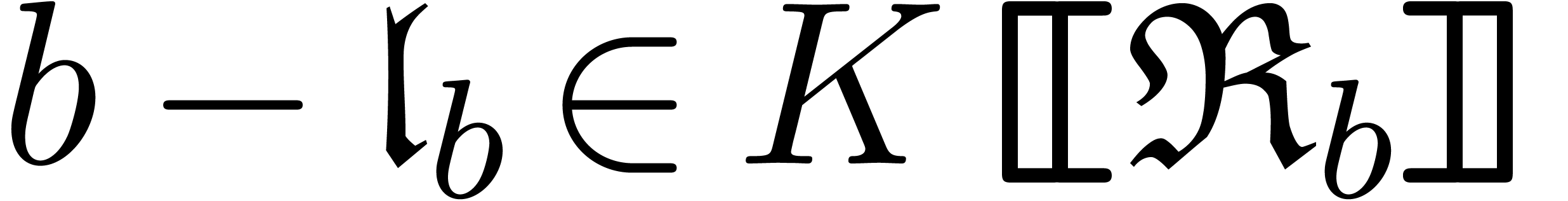 for each
for each 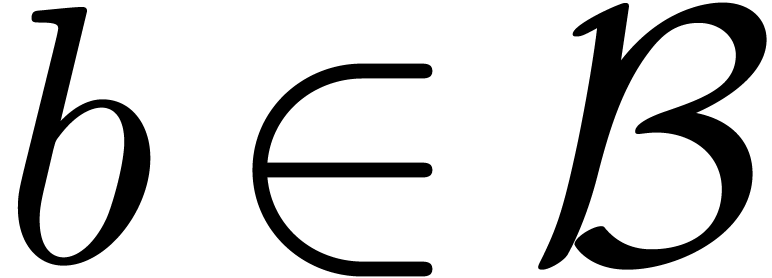 . Let
. Let 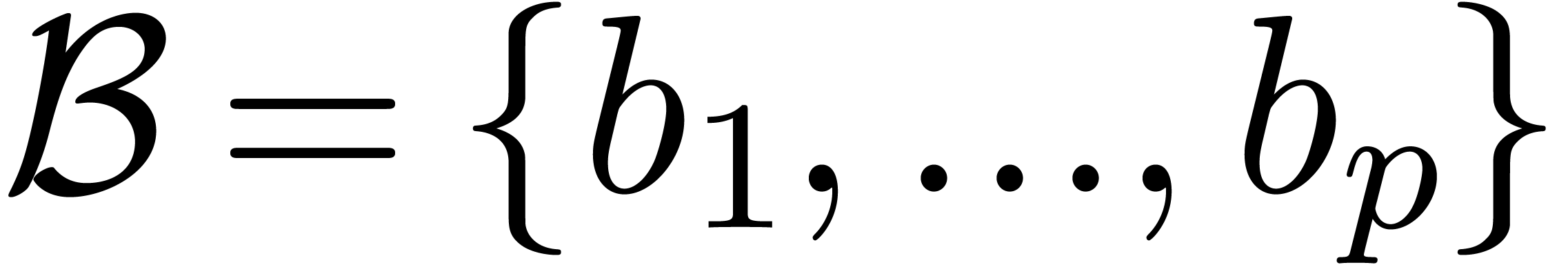 with
with
 . Replacing
. Replacing 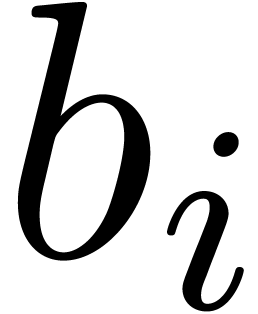 by
by 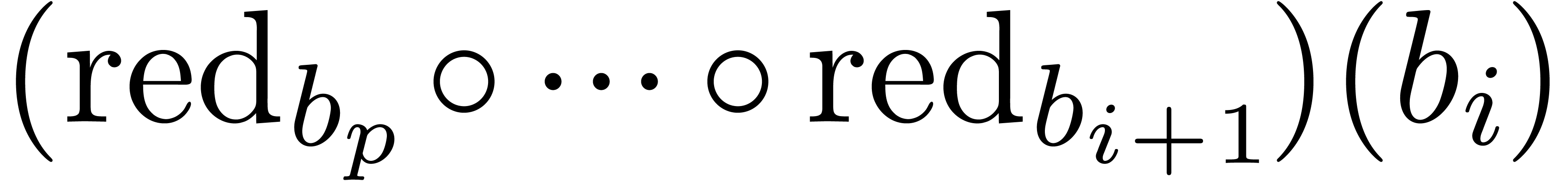 for
for 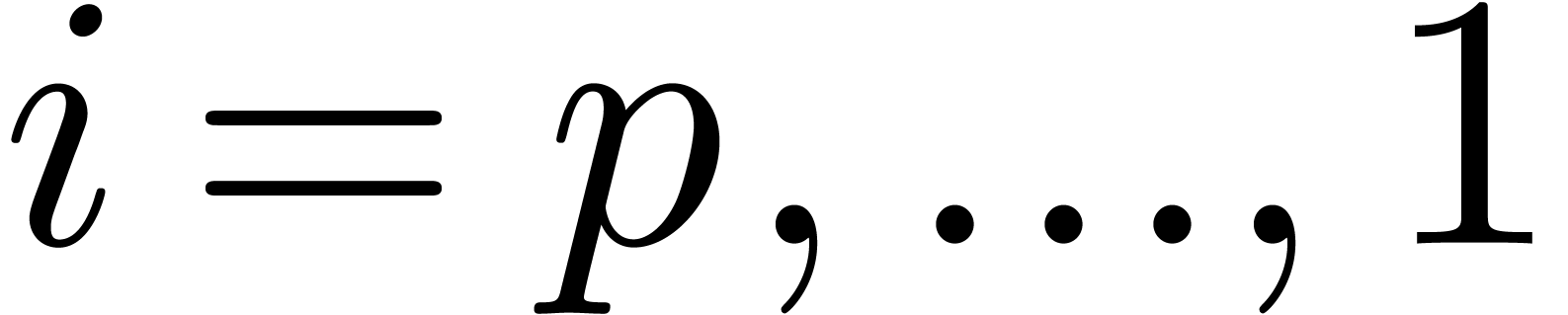 ,
we obtain an equivalent reduced Weierstrass system
,
we obtain an equivalent reduced Weierstrass system  . If
. If 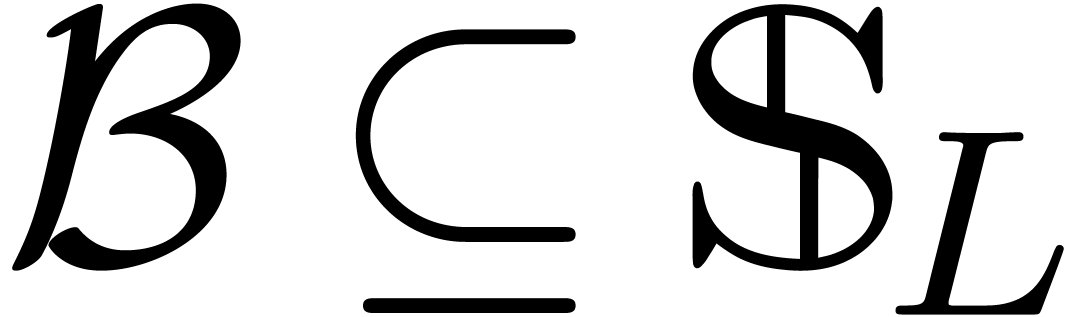 ,
then this procedure is completely effective, and
,
then this procedure is completely effective, and 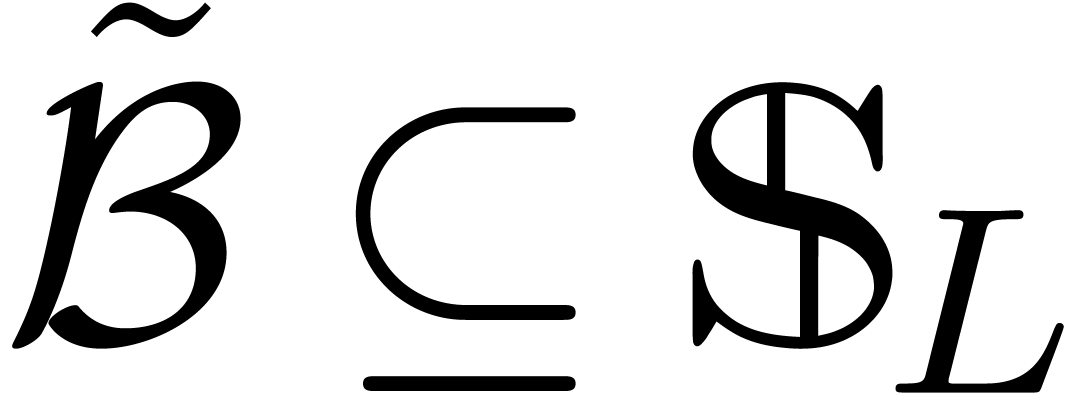 .
.
Let  be an ideal of
be an ideal of  .
In this subsection, we will define when
.
In this subsection, we will define when  is in
Weierstrass position. We proceed by induction over
is in
Weierstrass position. We proceed by induction over 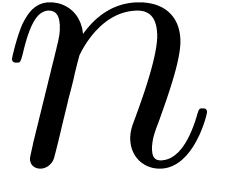 . The ideals
. The ideals 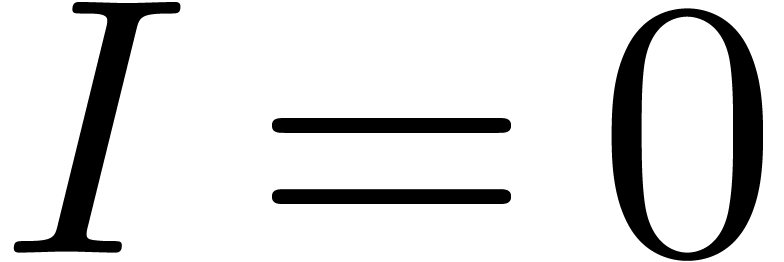 and
and 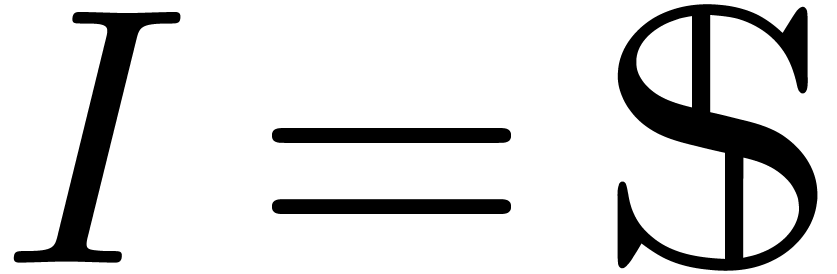 are always in Weierstrass position, which deals in
particular with the case when
are always in Weierstrass position, which deals in
particular with the case when 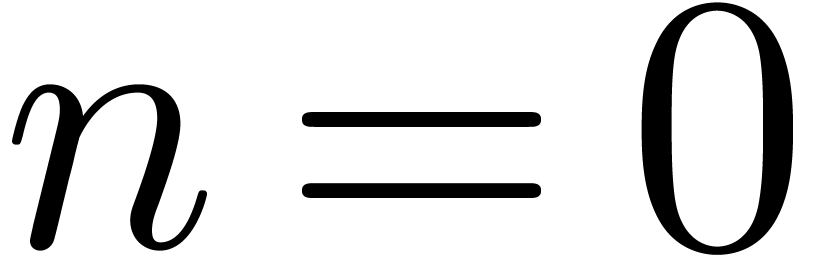 .
.
Assume that 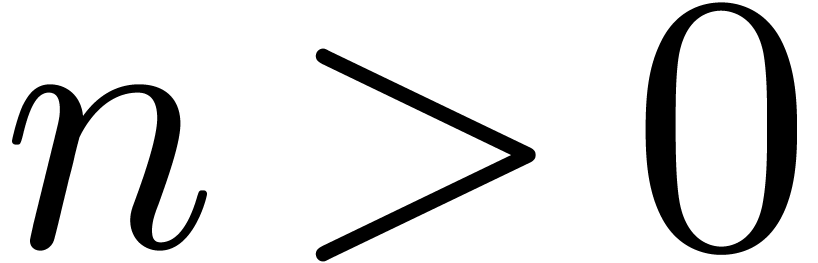 and
and 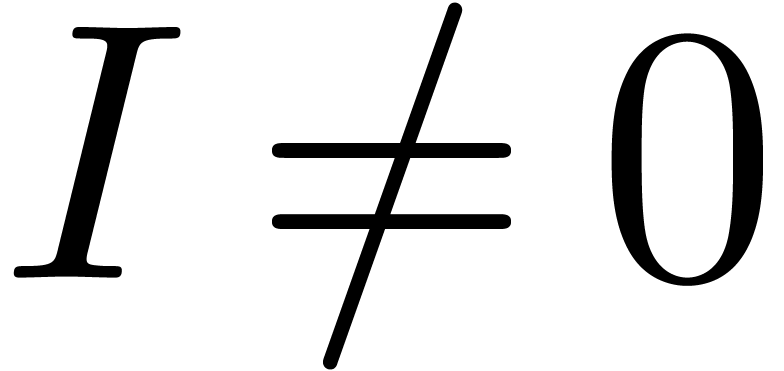 ,
and let
,
and let 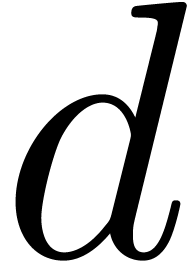 be the minimal valuation of a non-zero
element of
be the minimal valuation of a non-zero
element of  . Given a power
series
. Given a power
series  , let
, let 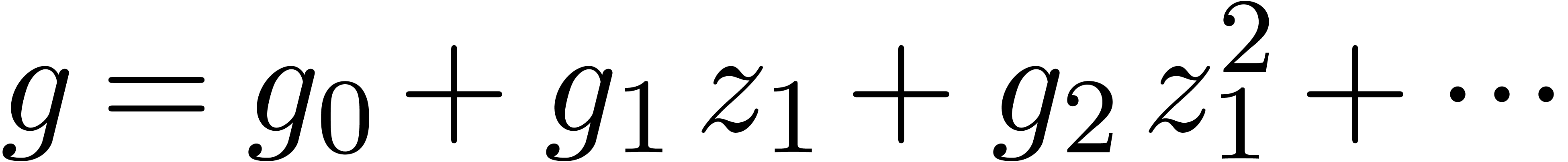 be its power series expansion with respect to
be its power series expansion with respect to 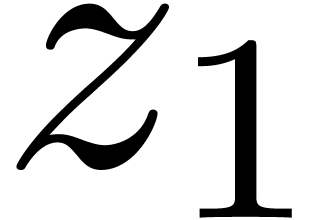 . For each
. For each 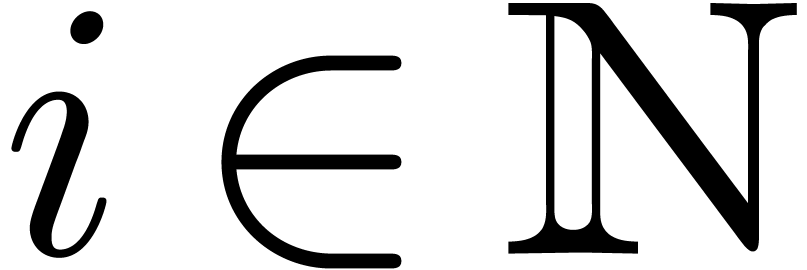 ,
the sets
,
the sets 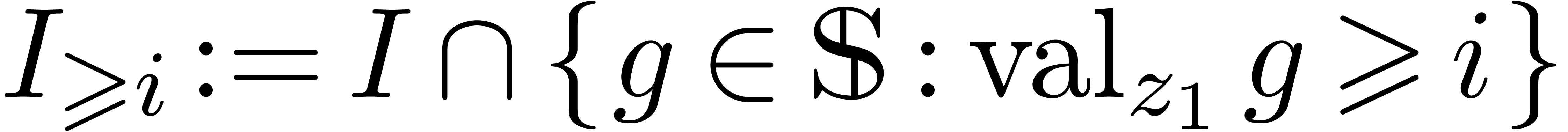 and
and 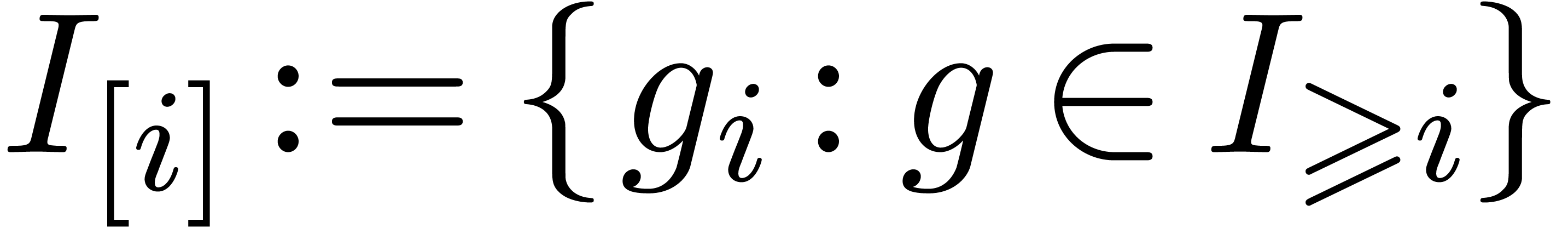 are ideals
of
are ideals
of  and
and  .
We say that
.
We say that  is in Weierstrass position if there
exists an element
is in Weierstrass position if there
exists an element  with
with 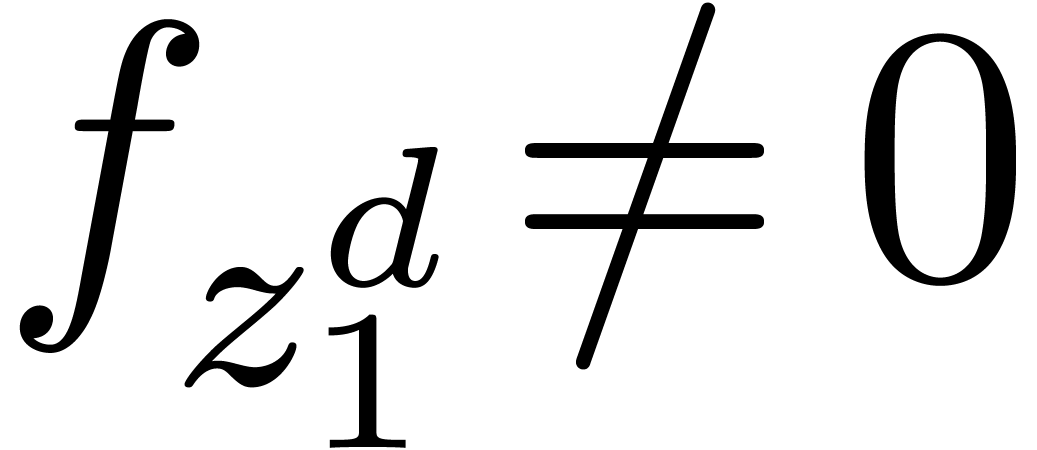 and such that the ideals
and such that the ideals 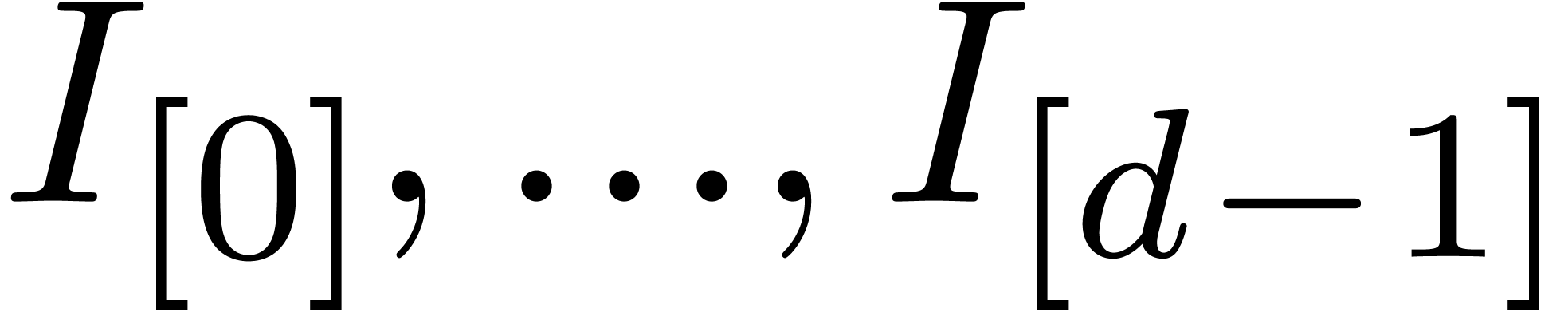 of
of  are in Weierstrass position.
are in Weierstrass position.
Since we assumed  to be of charactersitic zero,
it contains infinitely many elements. Given a finite number of ideals
to be of charactersitic zero,
it contains infinitely many elements. Given a finite number of ideals
 of
of  ,
let us show by induction over
,
let us show by induction over 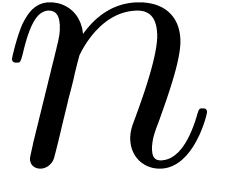 that there exists
a linear change of coordinates for which
that there exists
a linear change of coordinates for which  are
simultaneously in Weierstrass position. A linear change of coordinates
is a mapping
are
simultaneously in Weierstrass position. A linear change of coordinates
is a mapping 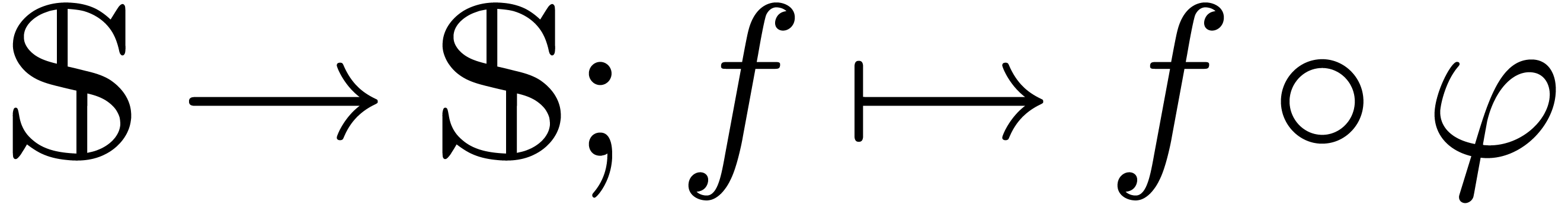 with
with 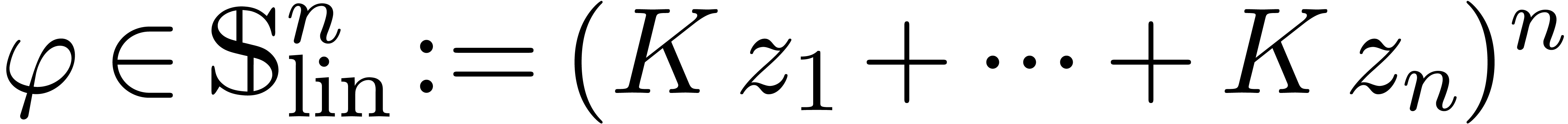
For 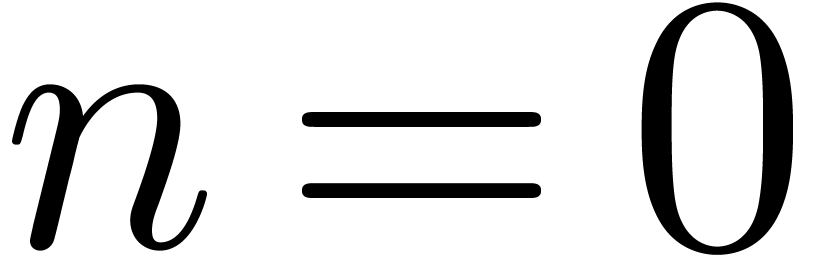 , we have nothing to do,
so assume that
, we have nothing to do,
so assume that  . For each
. For each
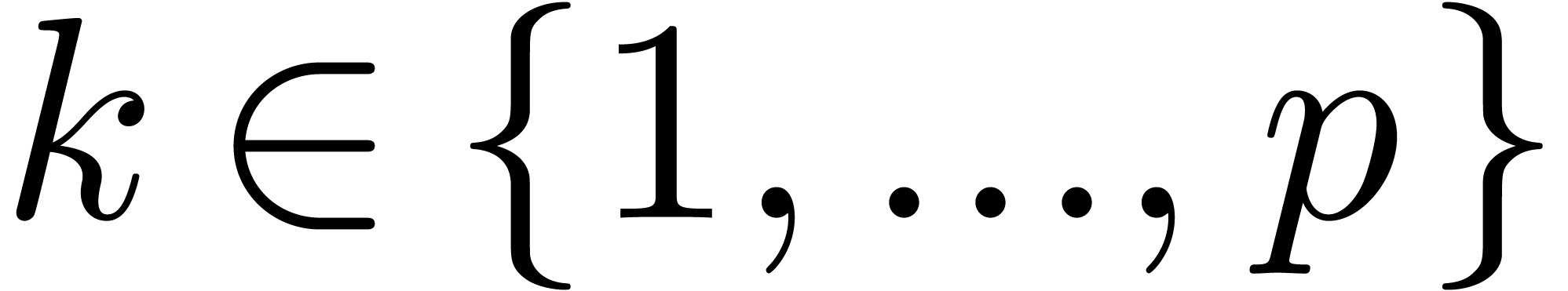 , let
, let  be a non-zero element of minimal valuation
be a non-zero element of minimal valuation 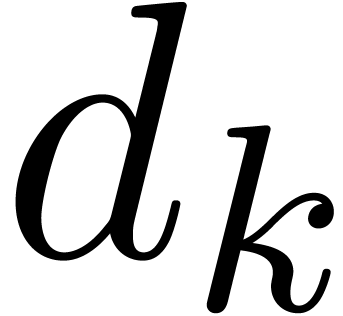 .
Since
.
Since  is infinite, there exist
is infinite, there exist 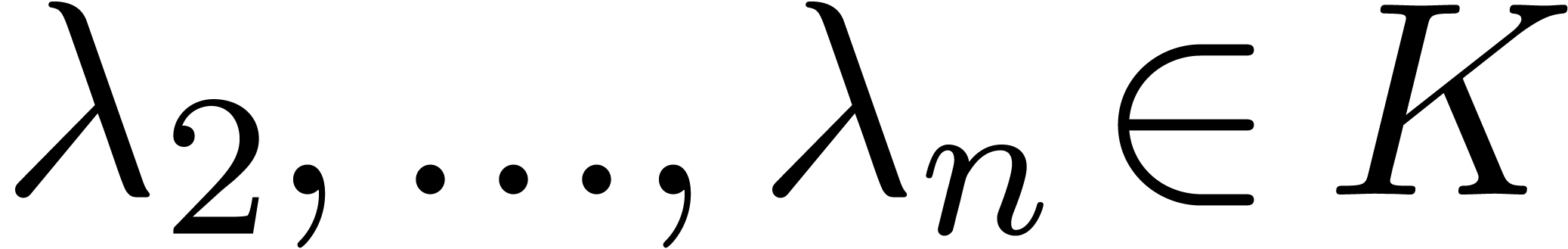 such that
such that 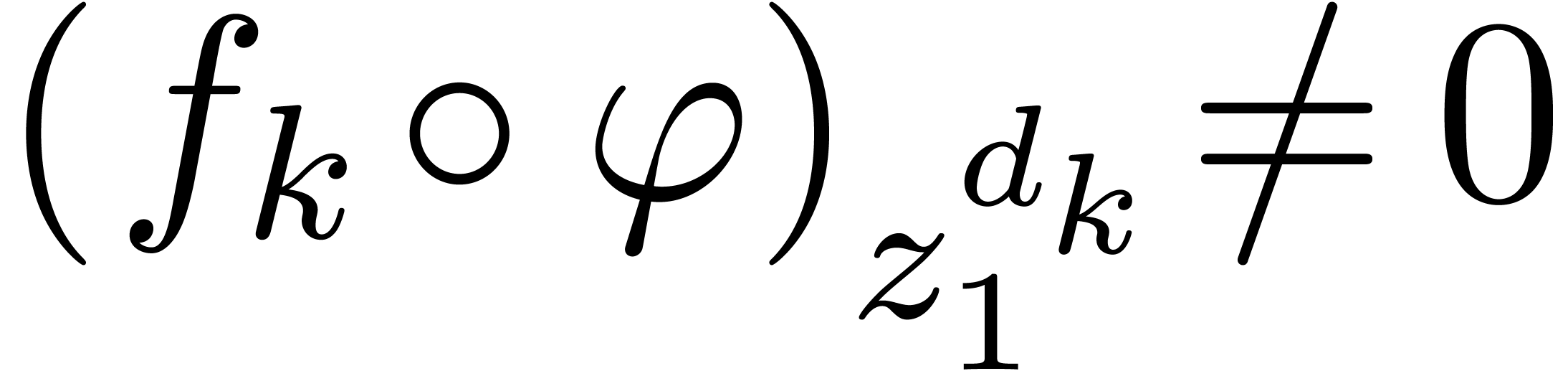 , where
, where 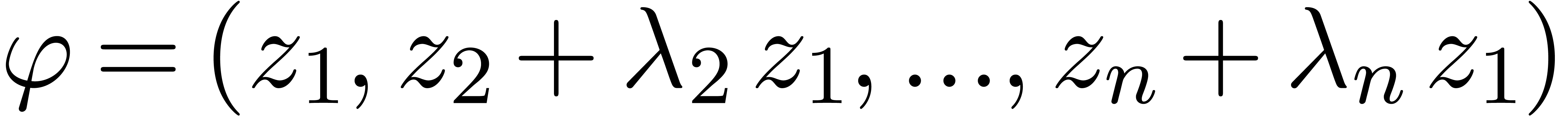 . By the induction hypothesis,
there exists a vector
. By the induction hypothesis,
there exists a vector 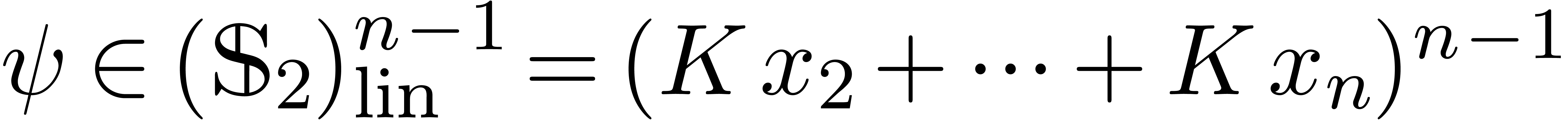 of linear series such that
of linear series such that
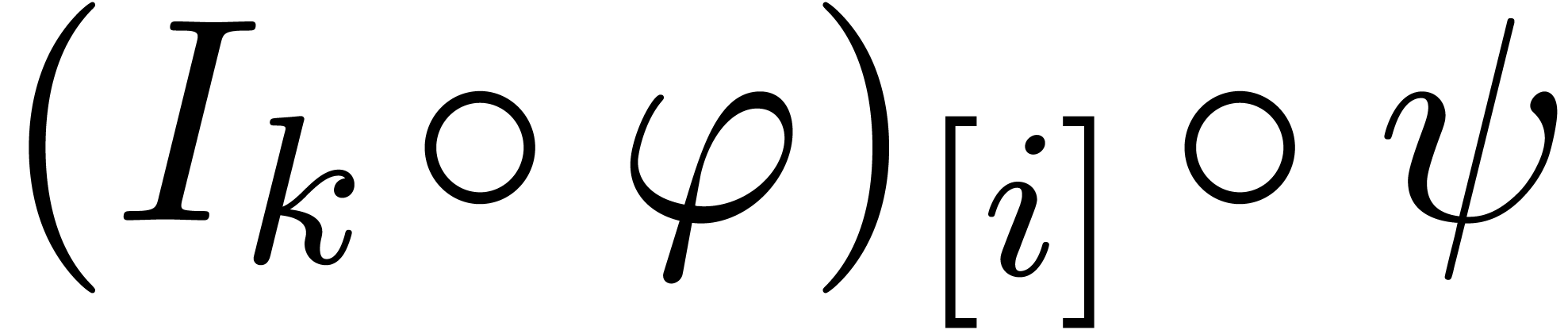 are simultaneously in Weierstrass position for
are simultaneously in Weierstrass position for
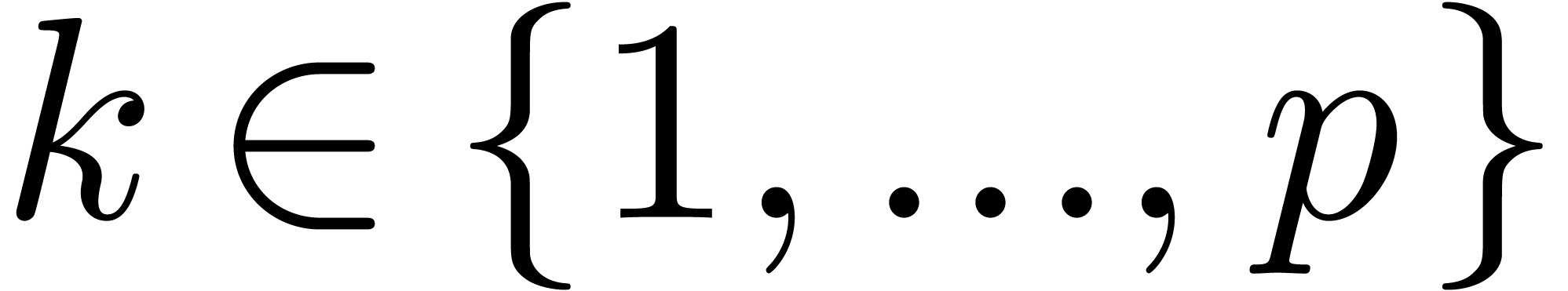 and
and 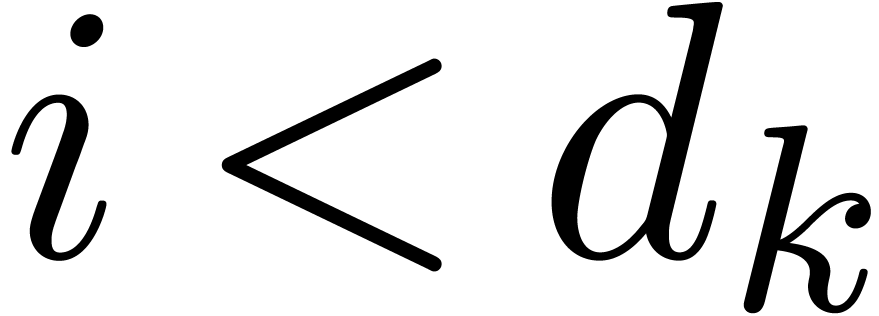 .
Setting
.
Setting  , we notice that
, we notice that 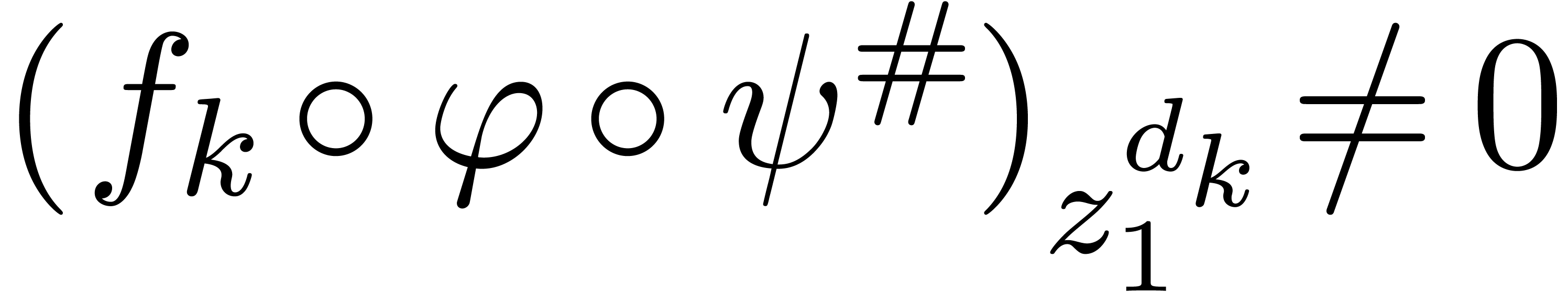 and
and 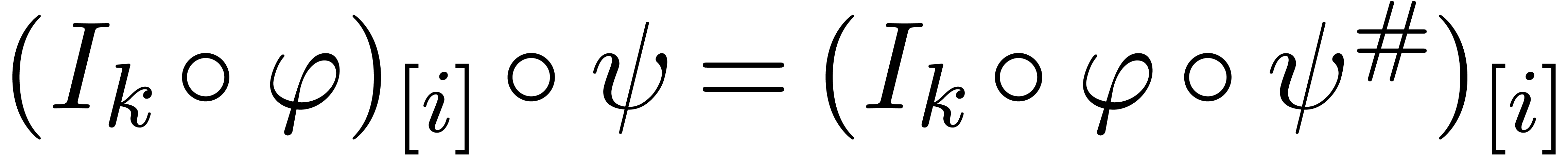 for all
for all 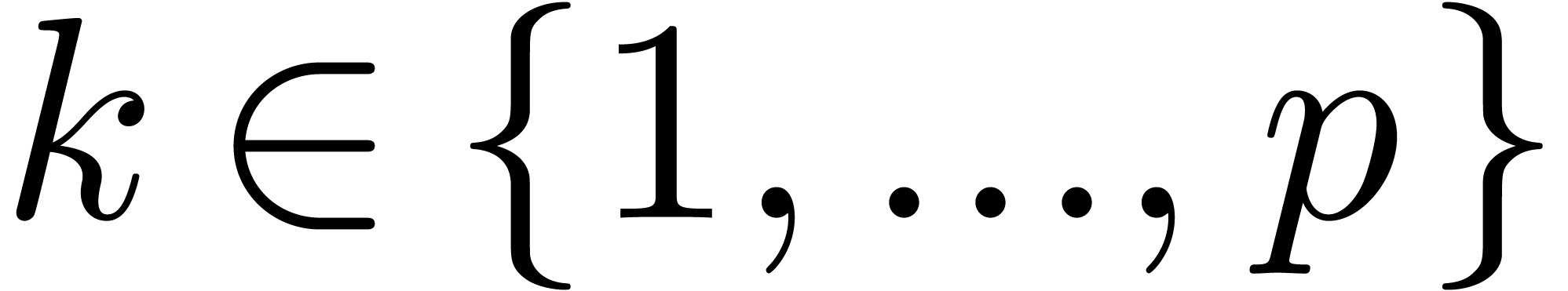 and
and 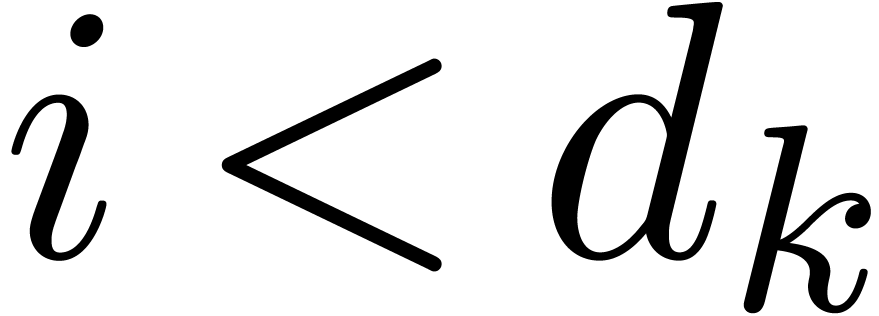 . Consequently, the
ideals
. Consequently, the
ideals 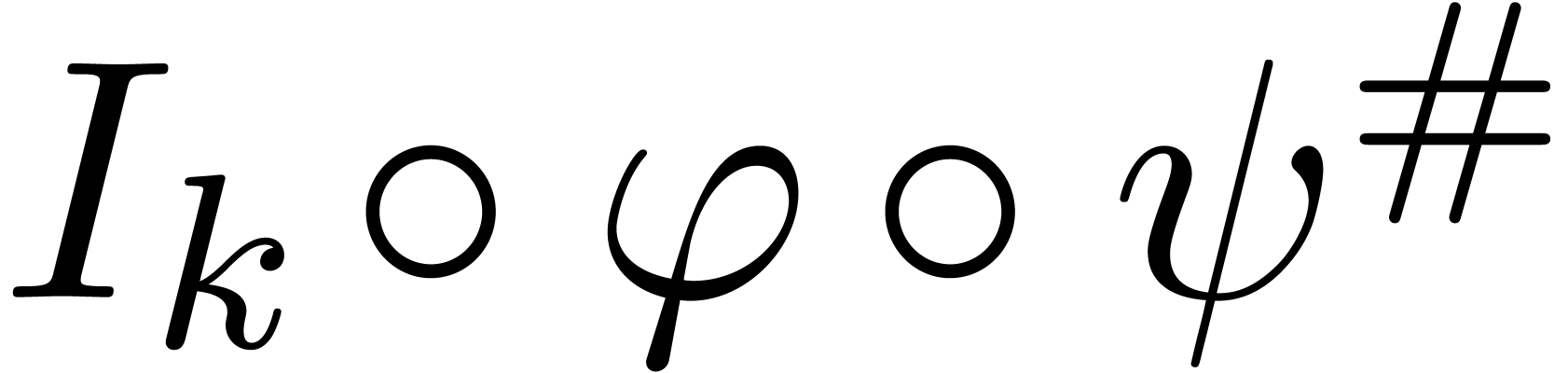 are all in Weierstrass position.
are all in Weierstrass position.
From a practical point of view, a random linear change of variables puts
an ideal into Weierstrass position with probability one. From a
theoretical standpoint, it suffices to extend  with
with  formal parameters and to perform a generic
triangular linear change of coordinates. The adjunction of new formal
parameters can be done effectively using the technique from the end of
Section 3.
formal parameters and to perform a generic
triangular linear change of coordinates. The adjunction of new formal
parameters can be done effectively using the technique from the end of
Section 3.
Let  be an ideal of
be an ideal of  .
A Weierstrass system
.
A Weierstrass system  is said to be a
Weierstrass basis for
is said to be a
Weierstrass basis for  if
if 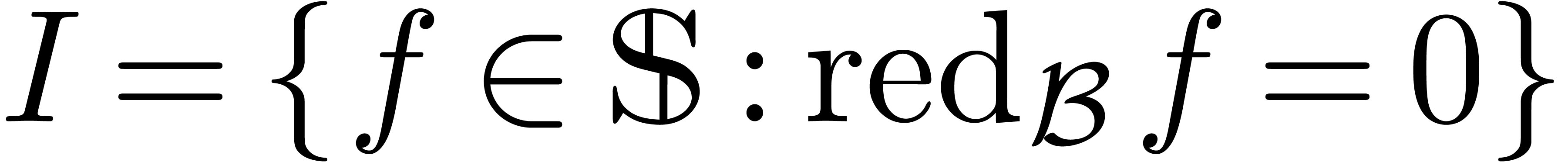 . Assuming that
. Assuming that  is in
Weierstrass position, an abstract way to construct a Weierstrass basis
goes as follows.
is in
Weierstrass position, an abstract way to construct a Weierstrass basis
goes as follows.
If 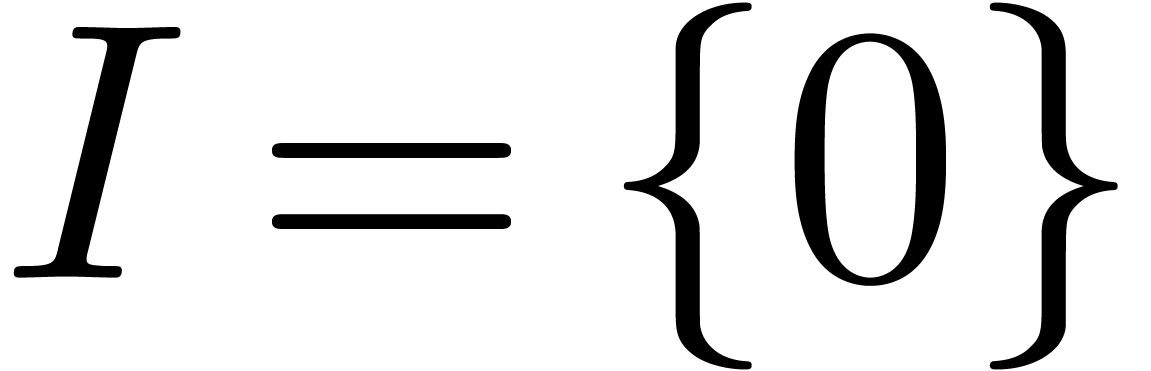 , then we take
, then we take 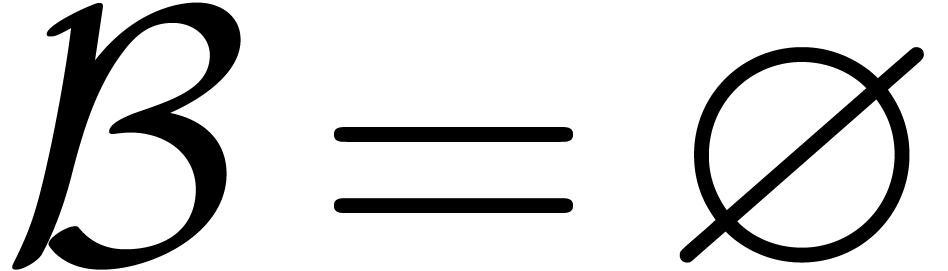 . Otherwise, let
. Otherwise, let  be an element of
be an element of  of minimal valuation
of minimal valuation 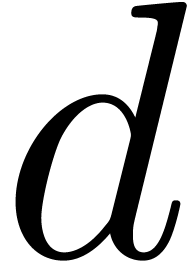 with
with 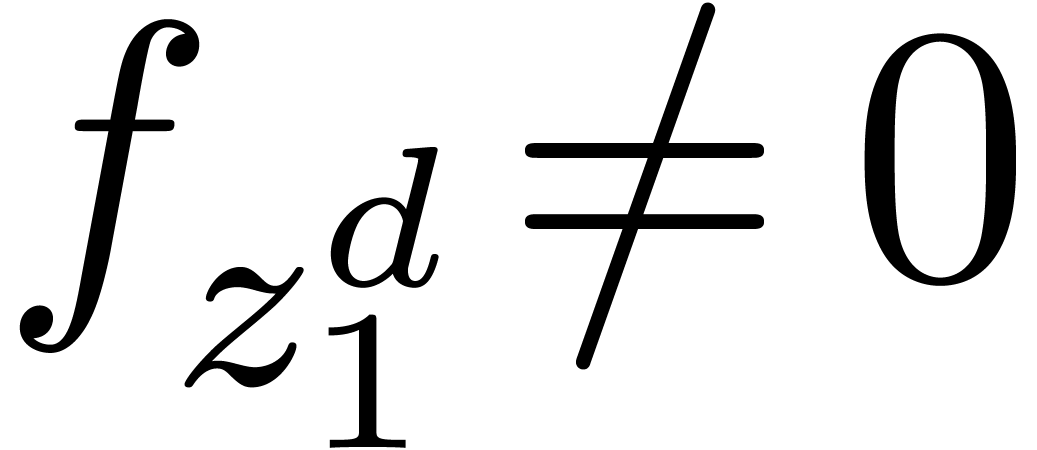 . For each
. For each
 , the induction hypothesis
yields a Weierstrass basis
, the induction hypothesis
yields a Weierstrass basis 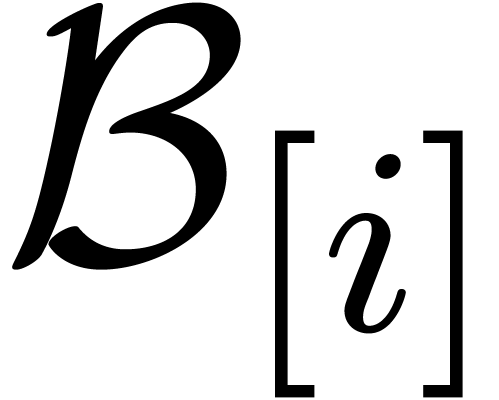 for the ideal
for the ideal 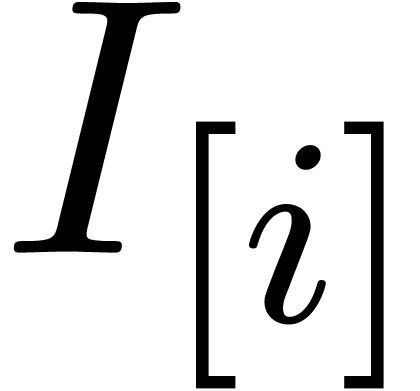 . For each
. For each 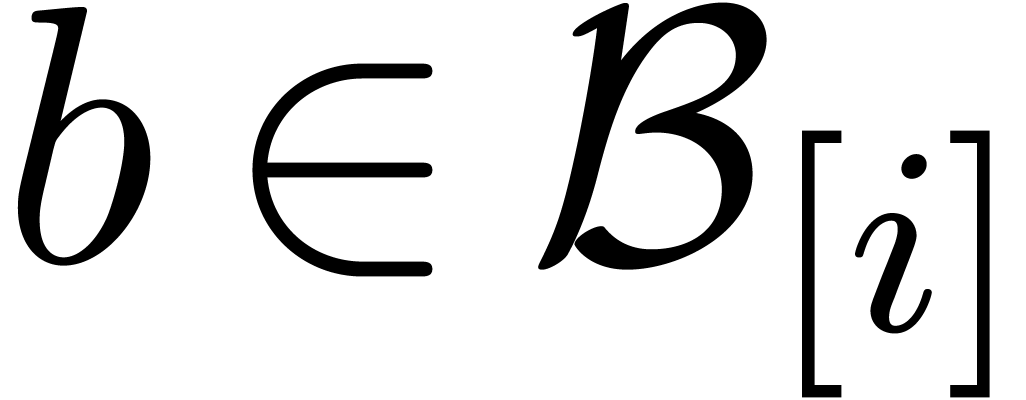 , there exists an element
, there exists an element 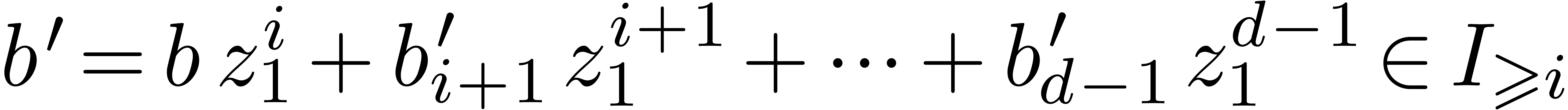 . Let
. Let 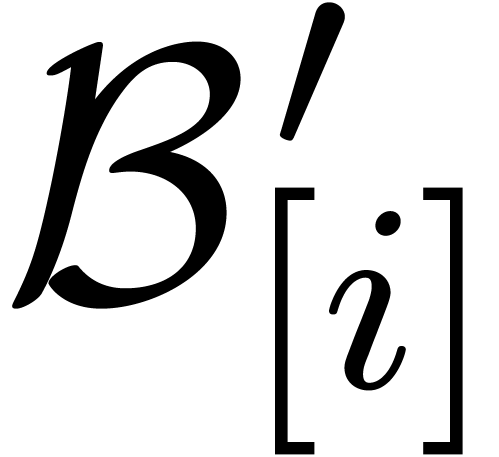 be the set of all such
elements
be the set of all such
elements 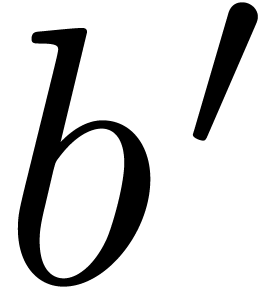 with
with 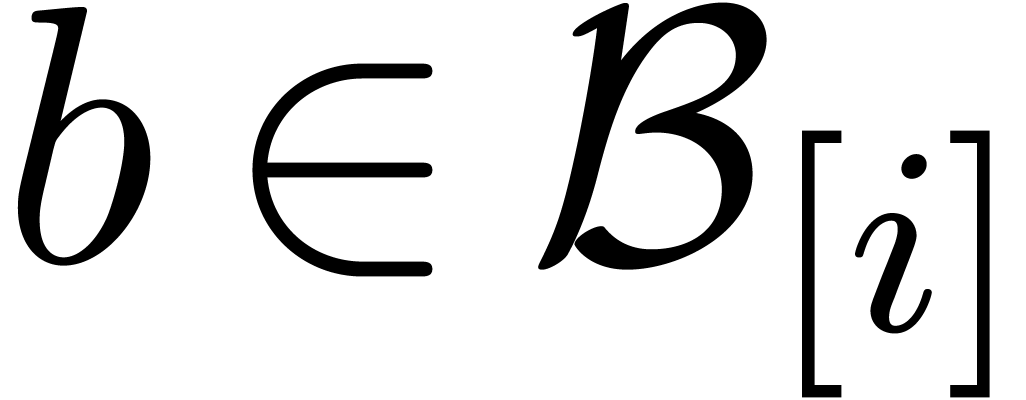 .
Then the disjoint union
.
Then the disjoint union 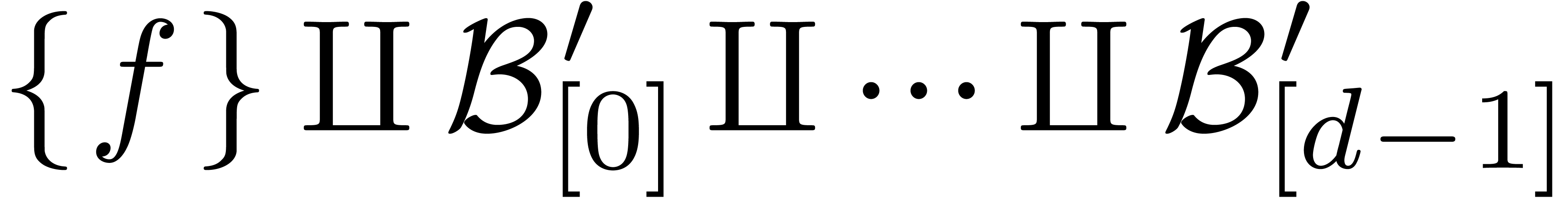 is a Weierstrass basis
for
is a Weierstrass basis
for  .
.
Our next aim is to provide a more effective criterion for checking
whether a reduced Weierstrass system  is in fact
a Weierstrass basis of an ideal. Given
is in fact
a Weierstrass basis of an ideal. Given 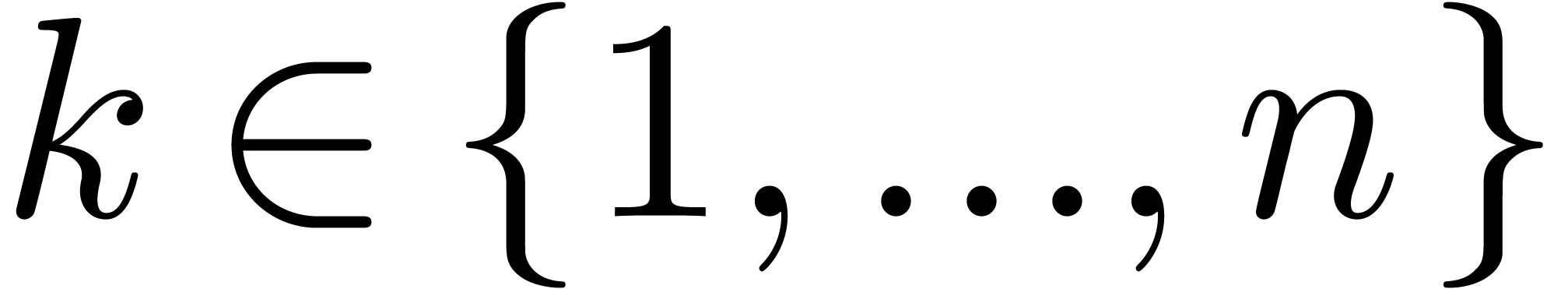 we will
denote
we will
denote
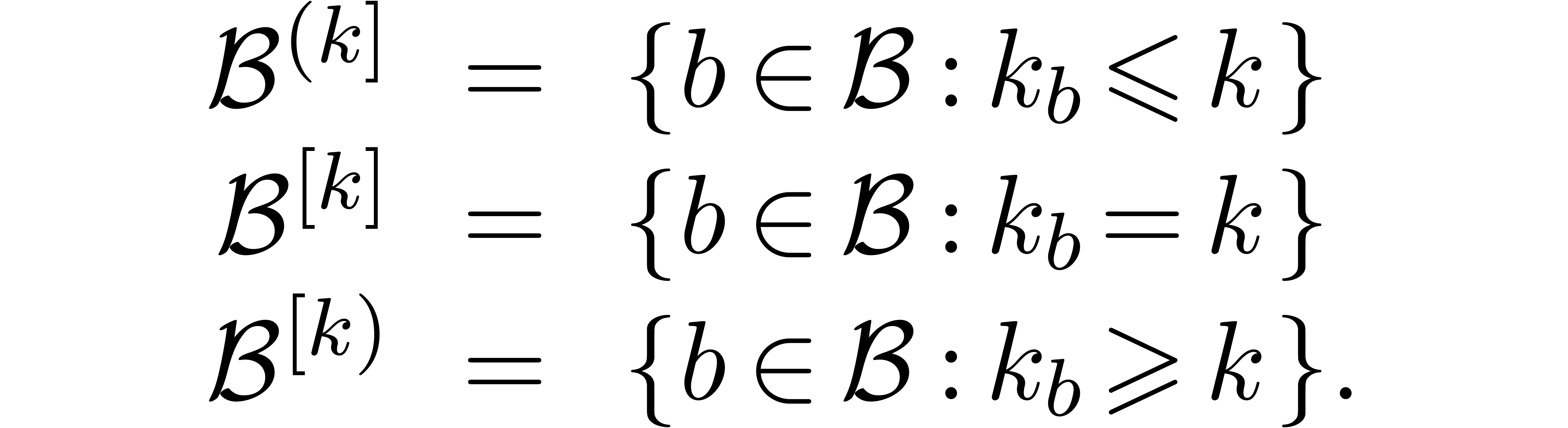
The Weierstrass system  is said to be
stable if for all
is said to be
stable if for all  and
and  , we have
, we have
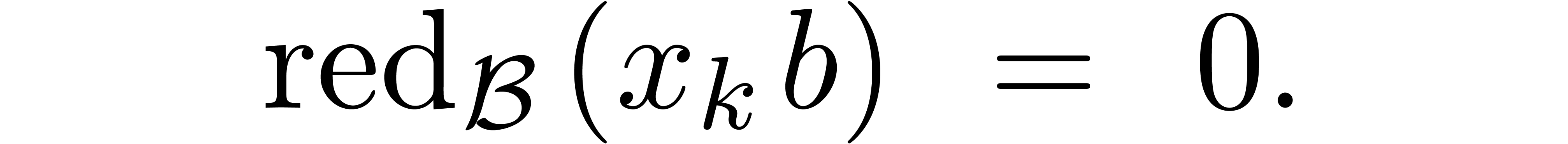
Notice that this relation automatically holds for 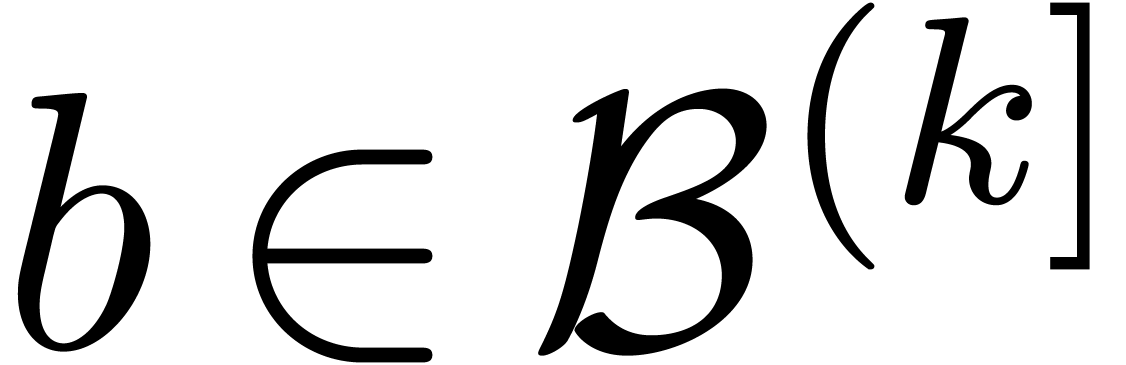 , so it suffices to prove the relation for all
, so it suffices to prove the relation for all  and
and  . The
main goal of this subsection is to prove the following theorem:
. The
main goal of this subsection is to prove the following theorem:
Theorem  is a
Weierstrass basis.
is a
Weierstrass basis.
Proof. Let  and notice that
and notice that 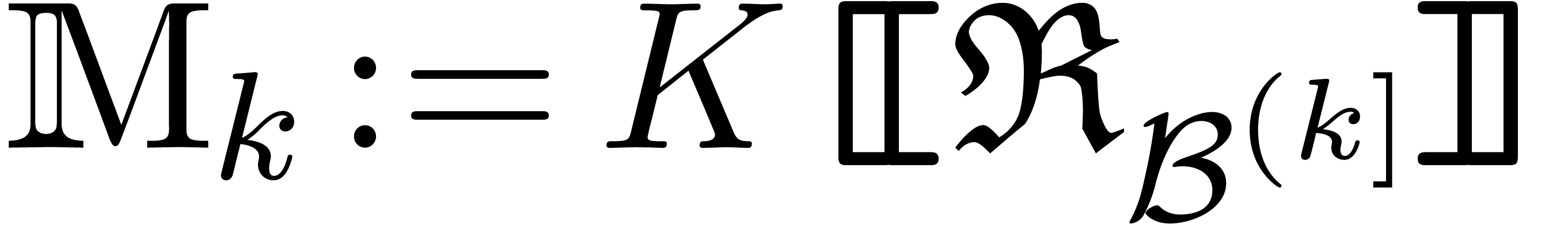 is an
is an  -module.
Now consider
-module.
Now consider
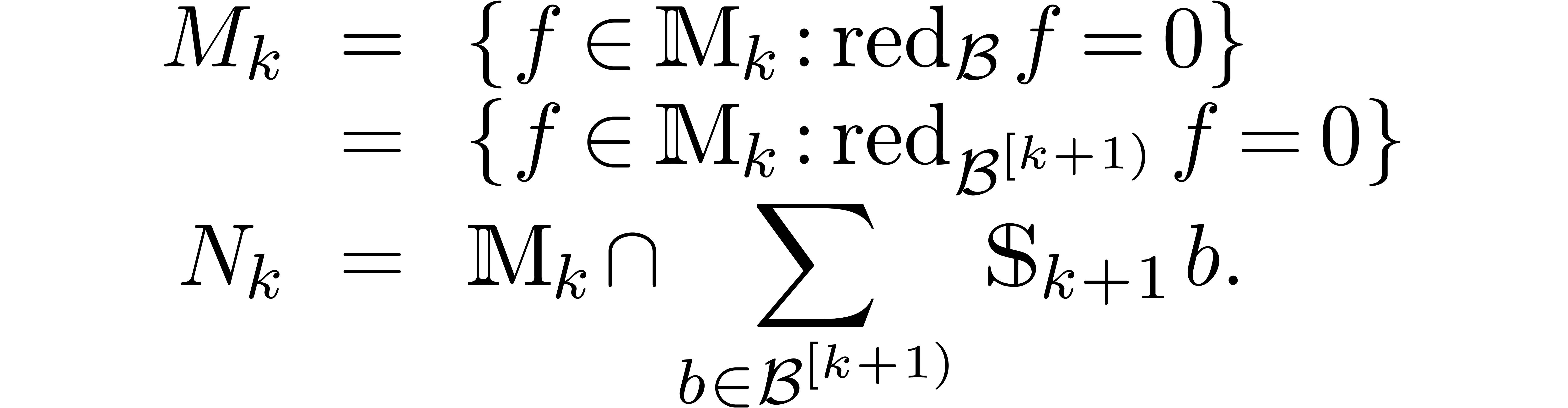
We claim that 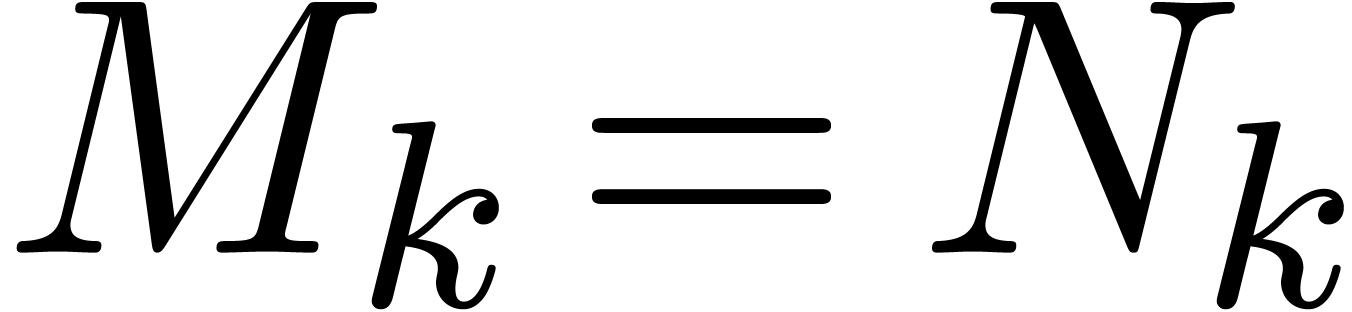 for all
for all  . We clearly have
. We clearly have 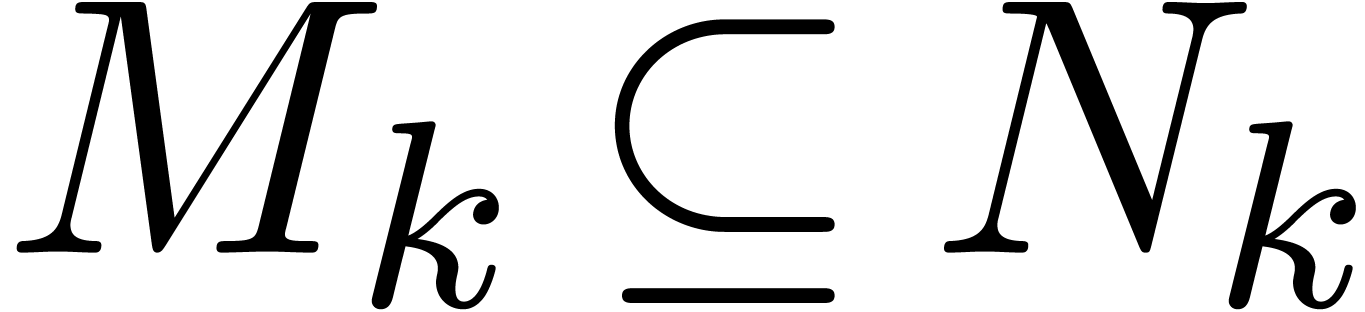 .
For the inverse inclusion, it suffices to show that
.
For the inverse inclusion, it suffices to show that 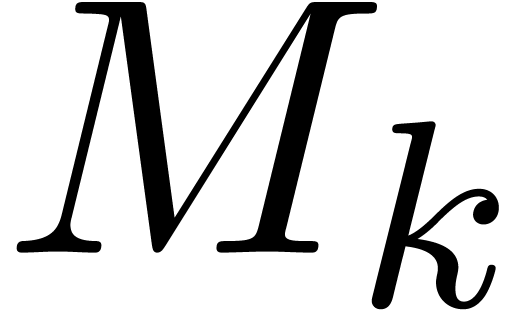 is an
is an 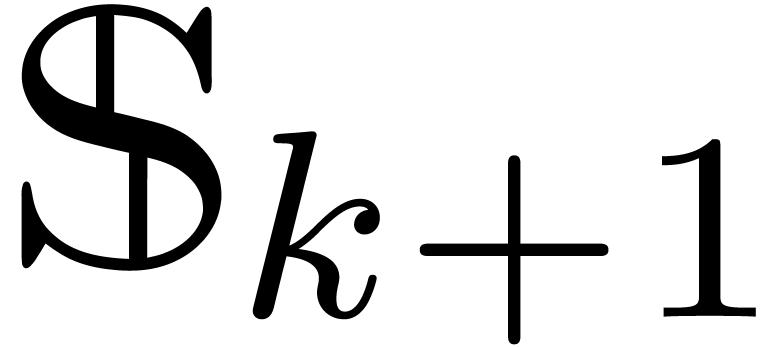 -module. We will use
induction over
-module. We will use
induction over  . For
. For  , we have
, we have  .
.
Assuming that 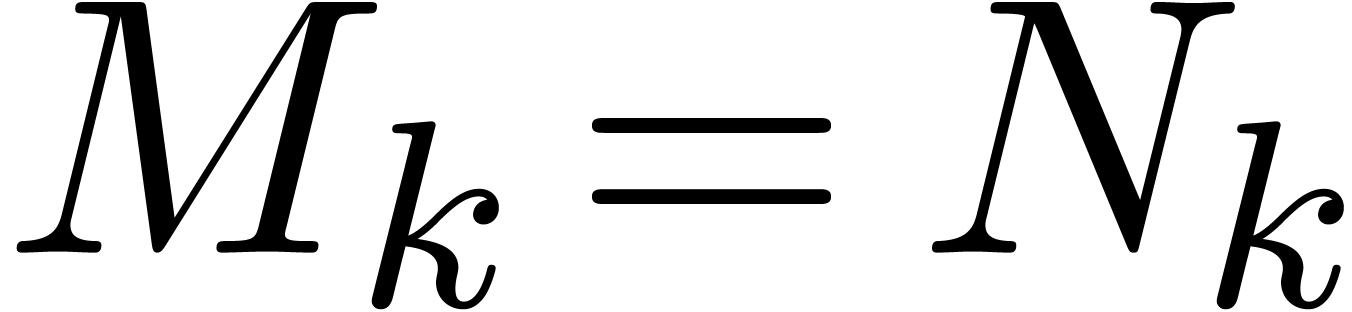 , let us now
show that
, let us now
show that 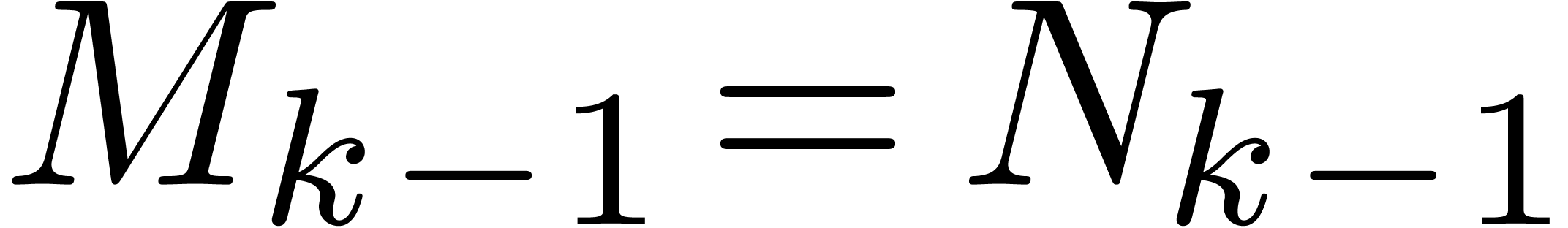 . Notice that
. Notice that
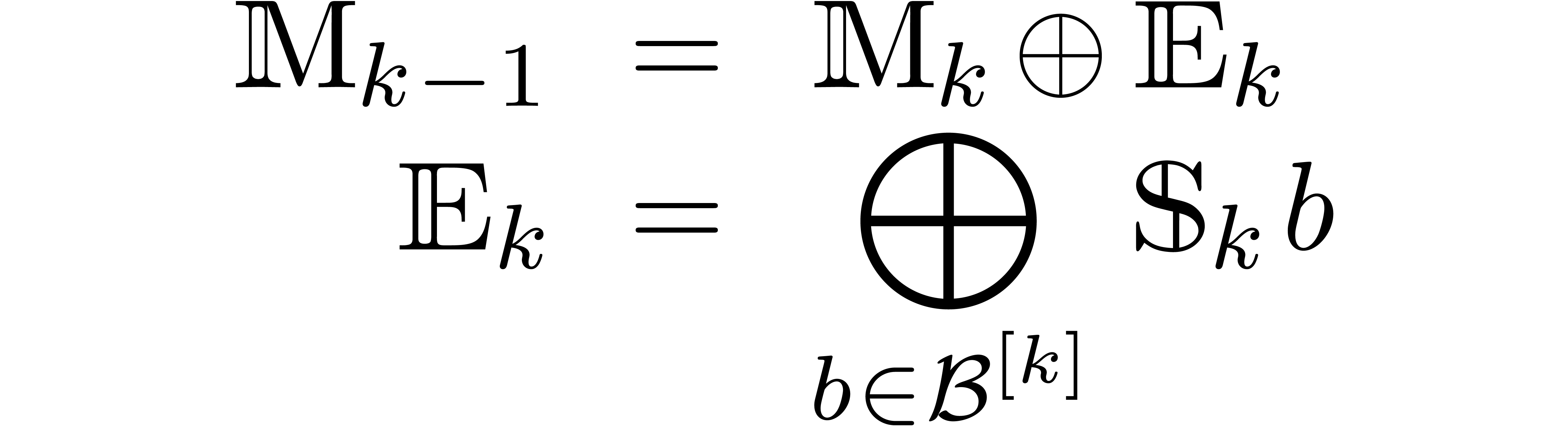
and 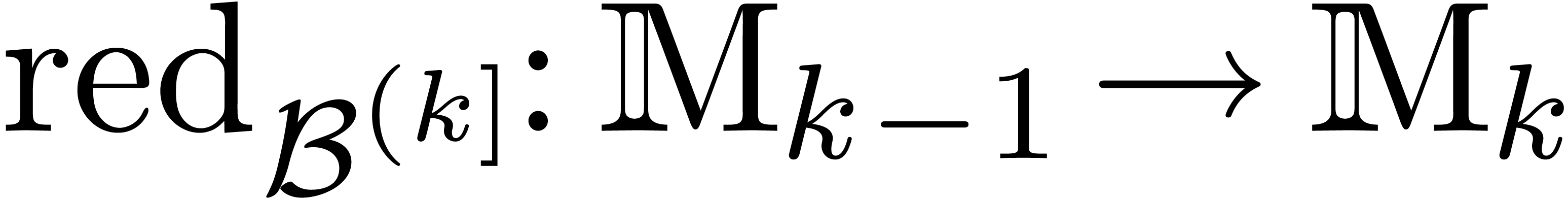 is an
is an 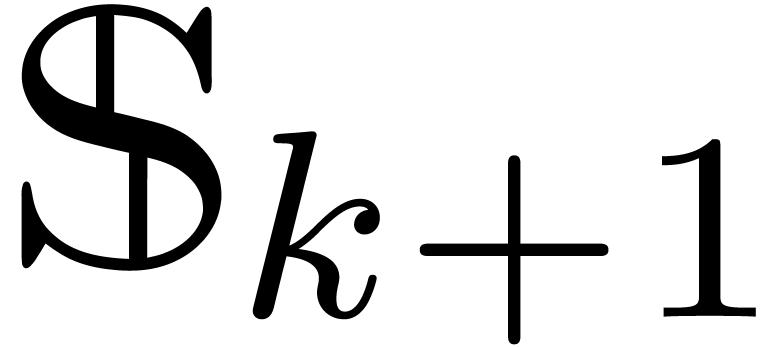 -linear
projection. Now
-linear
projection. Now  can be regarded as an
can be regarded as an 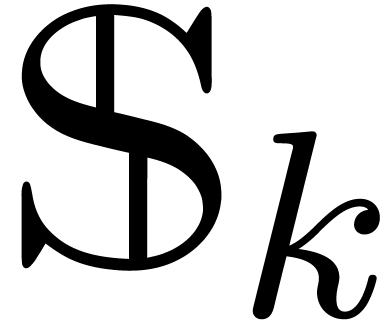 -module by letting multiplication
by
-module by letting multiplication
by  act as
act as
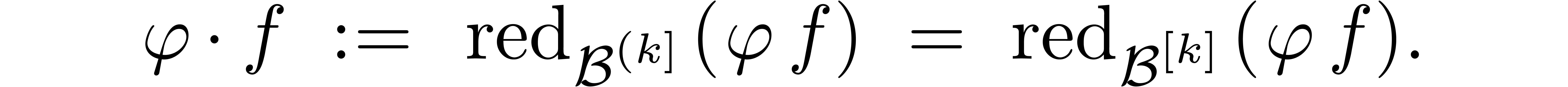
Since  is stable, we have
is stable, we have 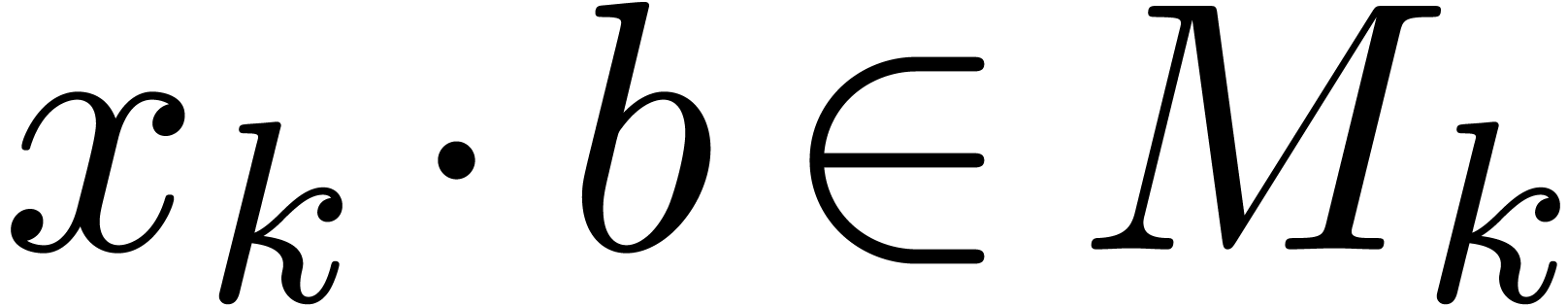 for all
for all  . Since
. Since  generates the
generates the 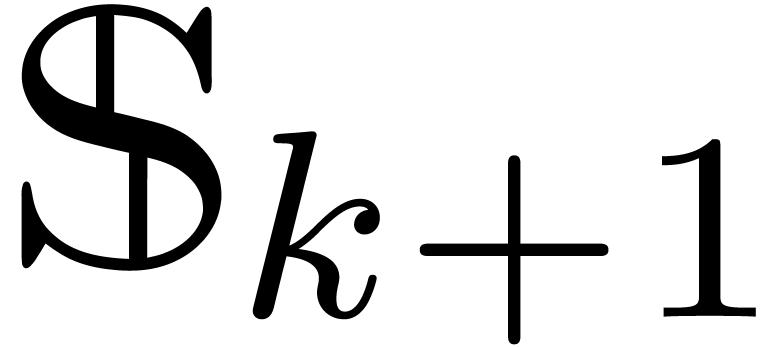 -module
-module
 , it follows that
, it follows that  is an
is an 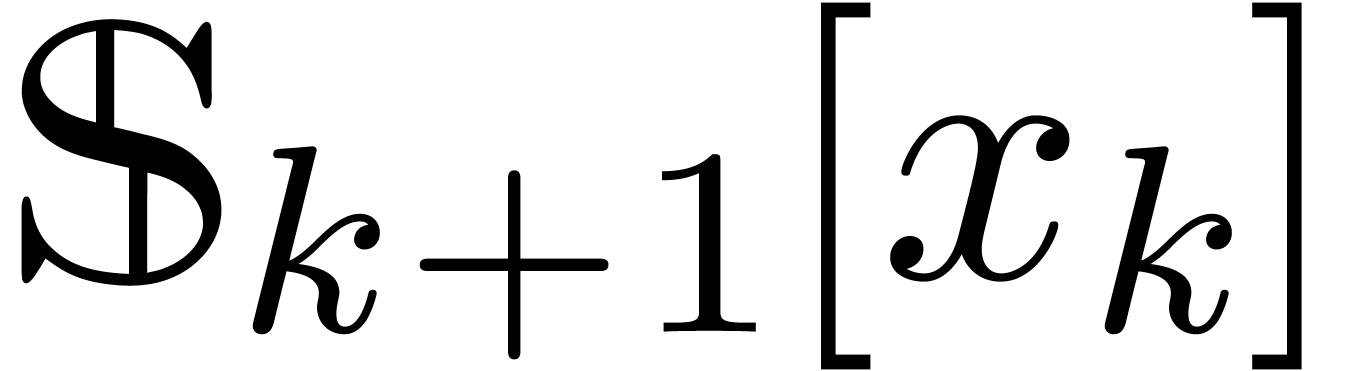 -submodule
of
-submodule
of  . Using the fact that
. Using the fact that  is strongly linear,
is strongly linear,  is
actually an
is
actually an  -submodule of
-submodule of
 . In other words,
. In other words, 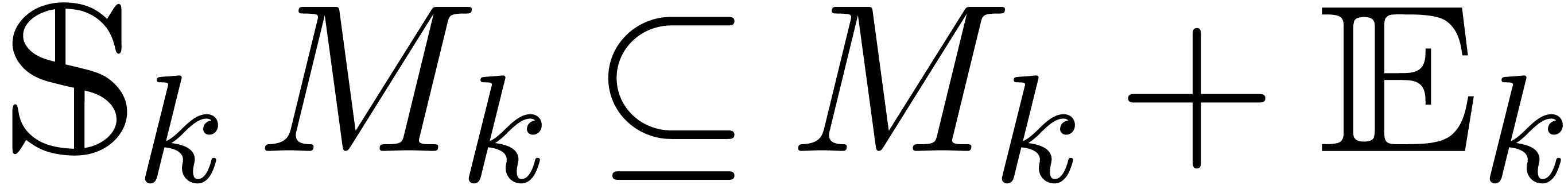 . Using that
. Using that 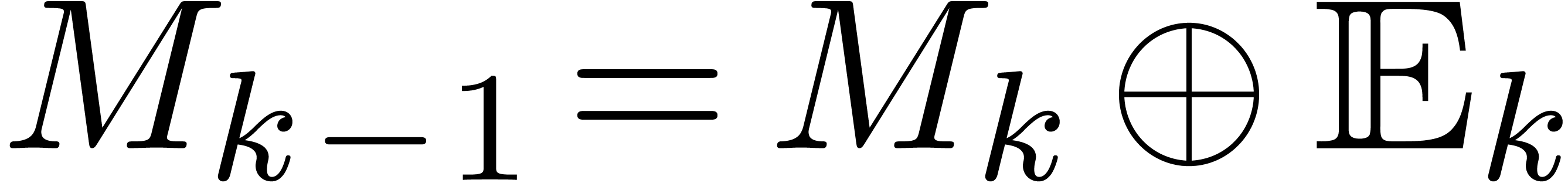 , we conclude that
, we conclude that 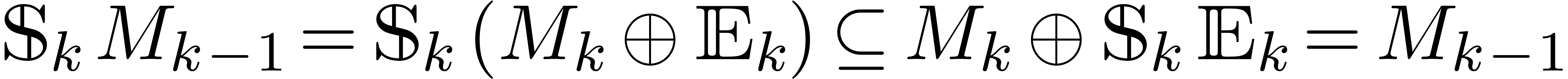 ,
whence
,
whence 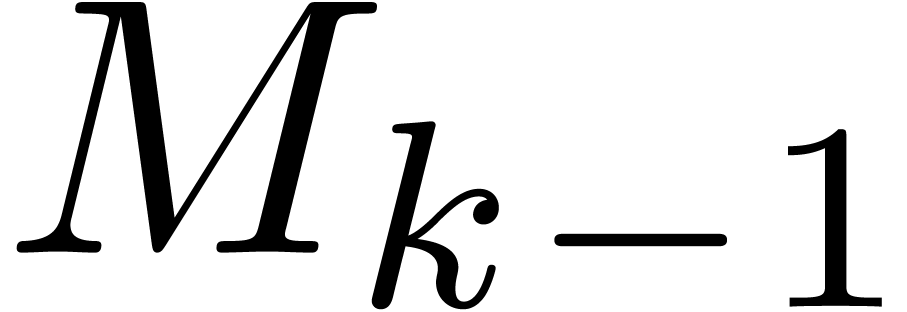 is an
is an  -module.
-module.
Having proved our claim, we finally observe that  is a Weierstrass basis for
is a Weierstrass basis for  .
.
Let  be a finite subset of
be a finite subset of  . Assuming “general position”, we will
show in this section how to compute a Weierstrass basis
. Assuming “general position”, we will
show in this section how to compute a Weierstrass basis  for the ideal
for the ideal  . The algorithm
will proceed by the repeated replacement of elements of
. The algorithm
will proceed by the repeated replacement of elements of  by linear combinations of elements in
by linear combinations of elements in  .
Consequently, along with the computations, we may calculate a matrix
.
Consequently, along with the computations, we may calculate a matrix
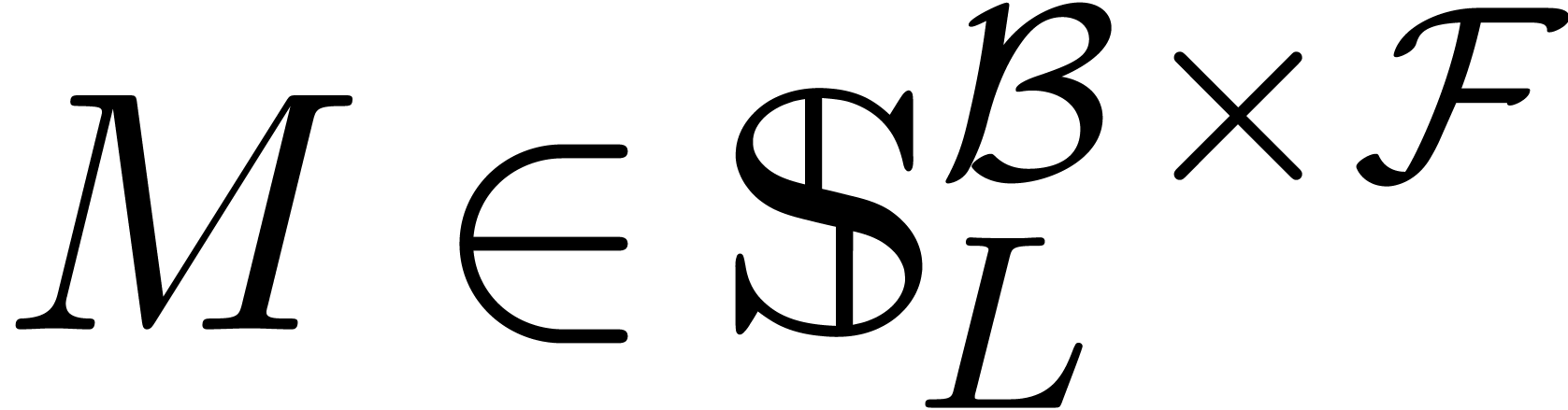 with
with 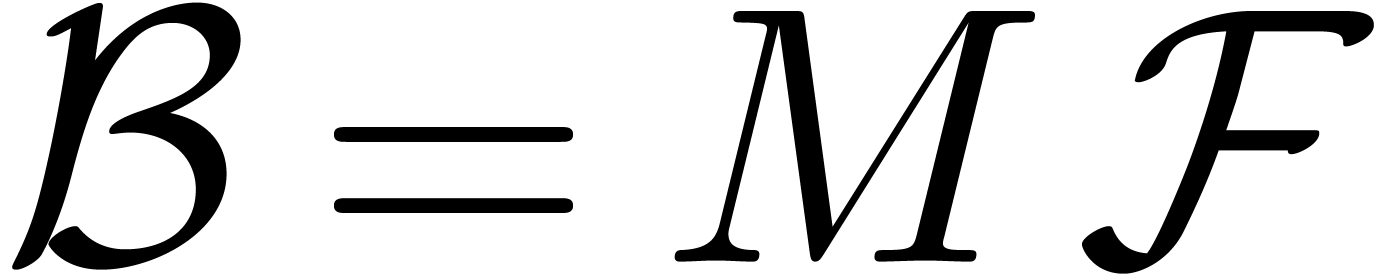 (in the sense that
(in the sense that
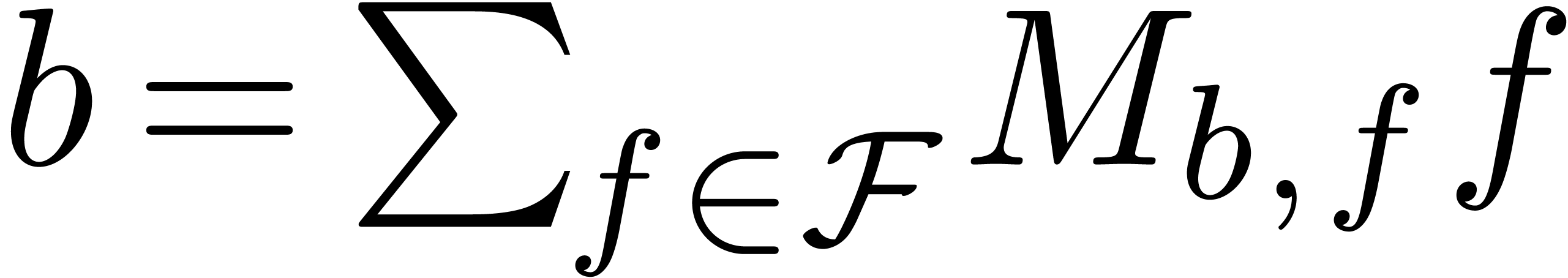 for all
for all  ).
The algorithm raises an error if the general position hypothesis is
violated.
).
The algorithm raises an error if the general position hypothesis is
violated.
As usual, we proceed by induction over 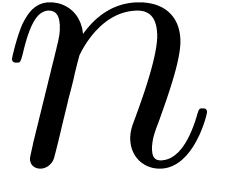 .
If
.
If 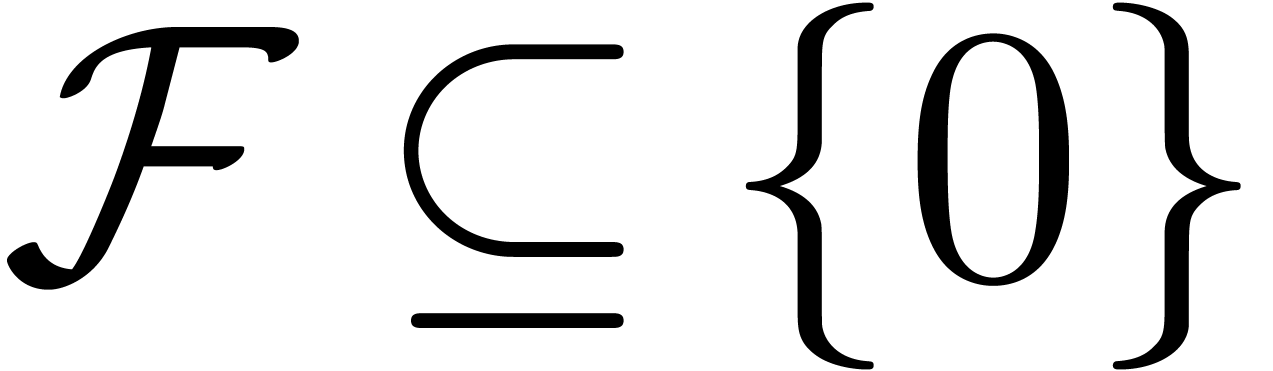 , then we may take
, then we may take  and we have nothing to do. Otherwise, let
and we have nothing to do. Otherwise, let 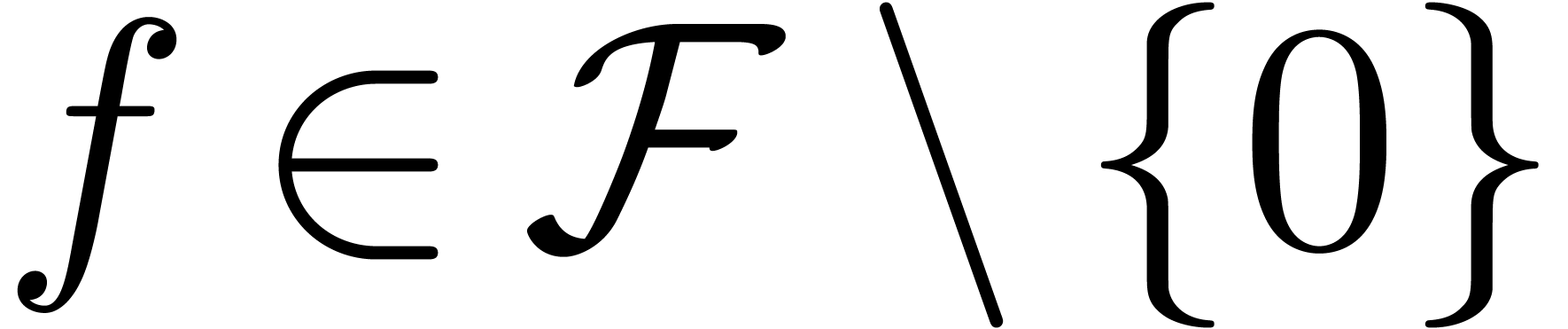 be of minimal valuation
be of minimal valuation 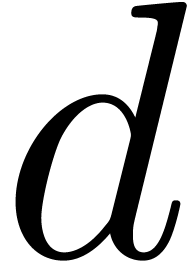 .
If
.
If 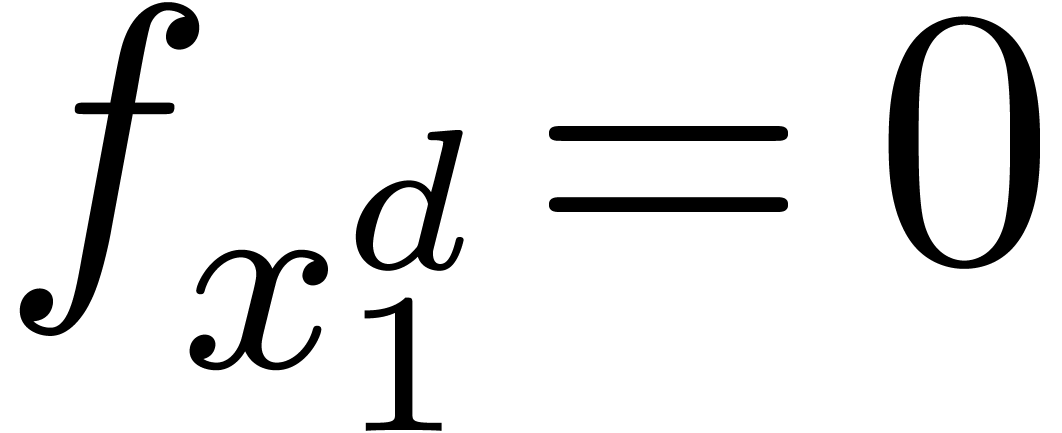 , then we raise an error.
Assuming that
, then we raise an error.
Assuming that 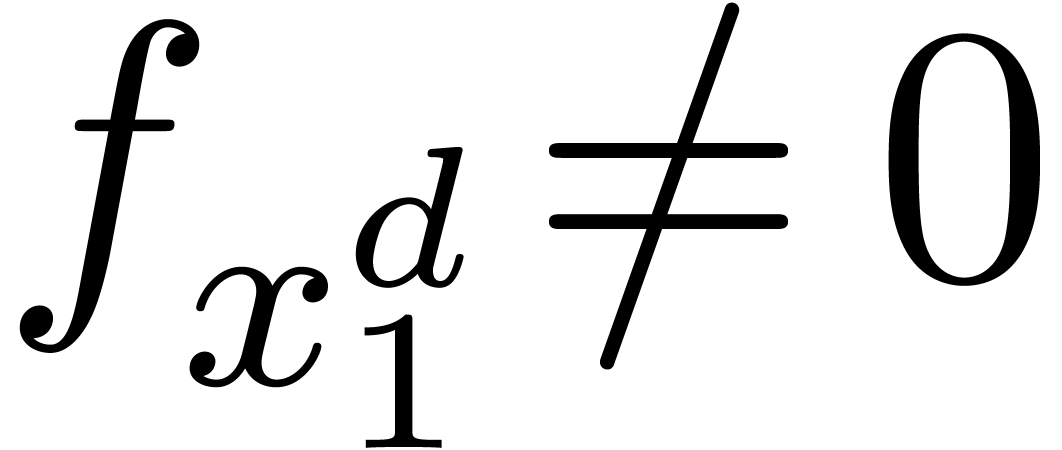 , we first
replace
, we first
replace  by
by 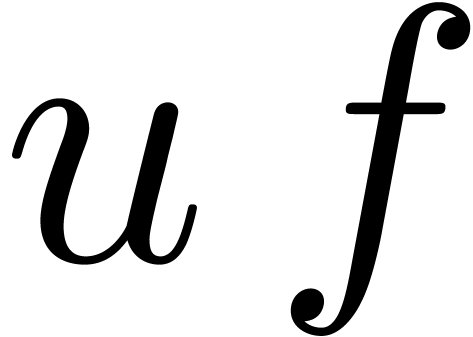 ,
where
,
where 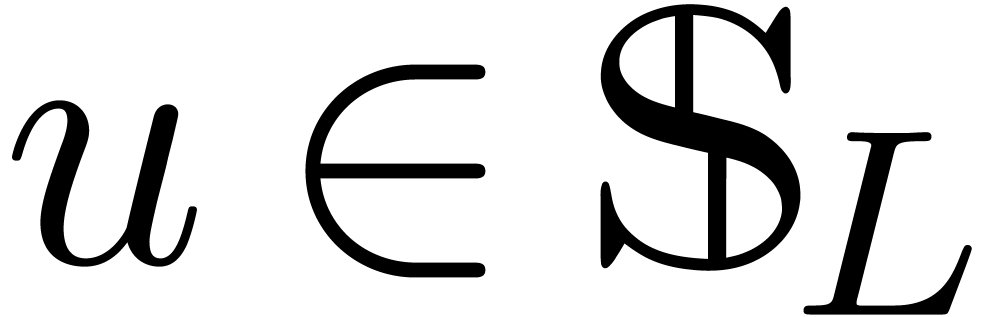 is such that
is such that 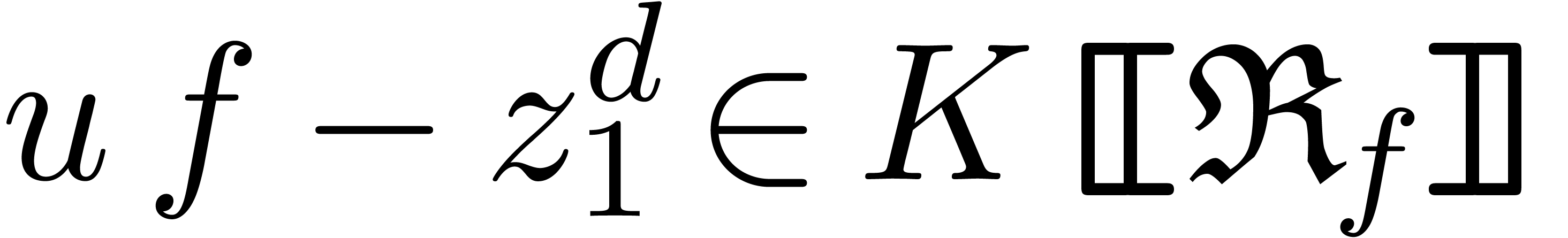 .
We next replace each other element
.
We next replace each other element  by
by  , so that
, so that 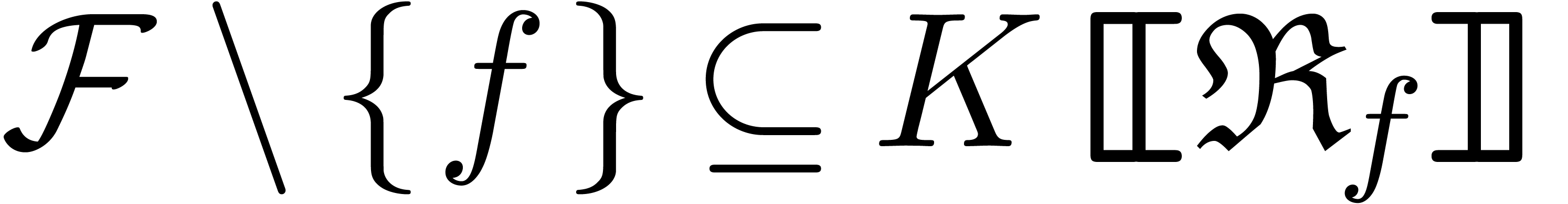 . For each
. For each  ,
let
,
let 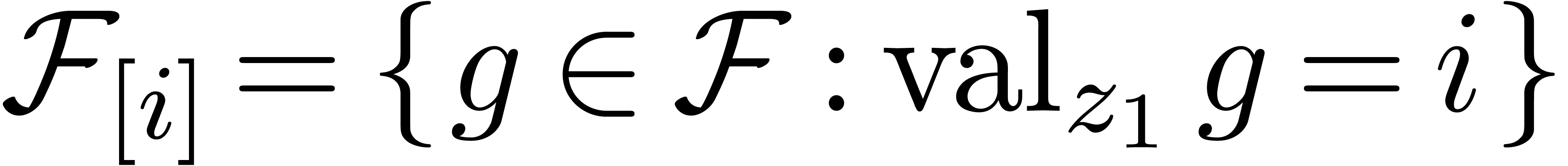 . The recursive
application of the algorithm to
. The recursive
application of the algorithm to 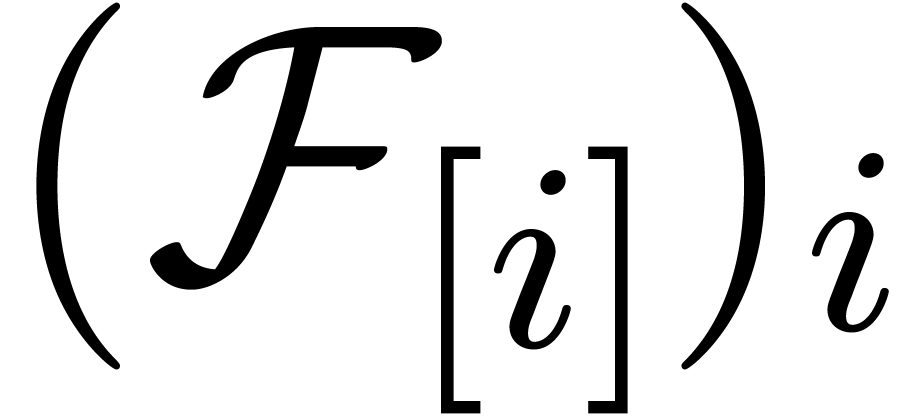 yields a matrix
yields a matrix
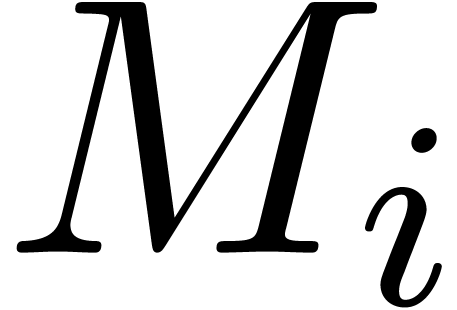 such that
such that 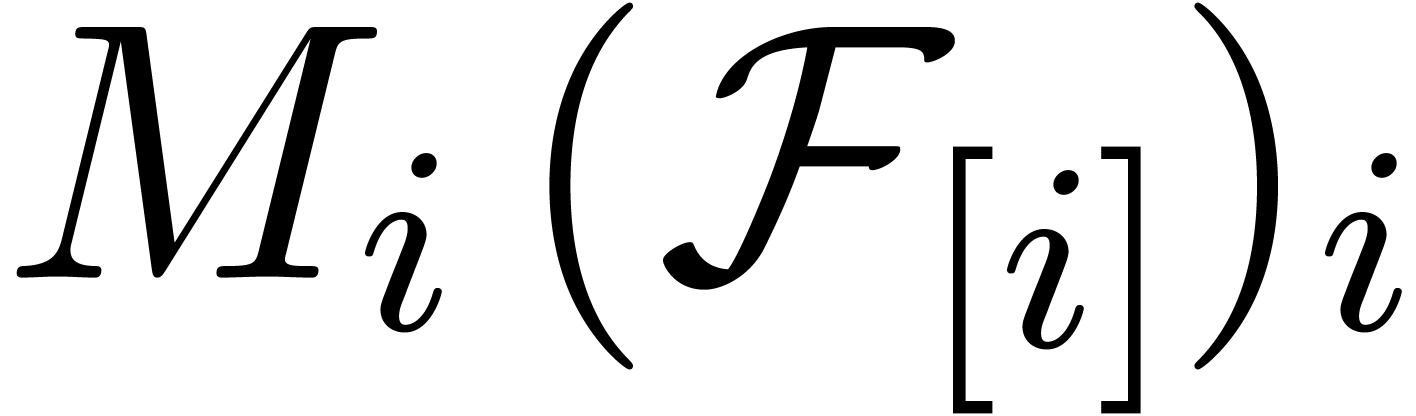 is a
Weierstrass basis of
is a
Weierstrass basis of 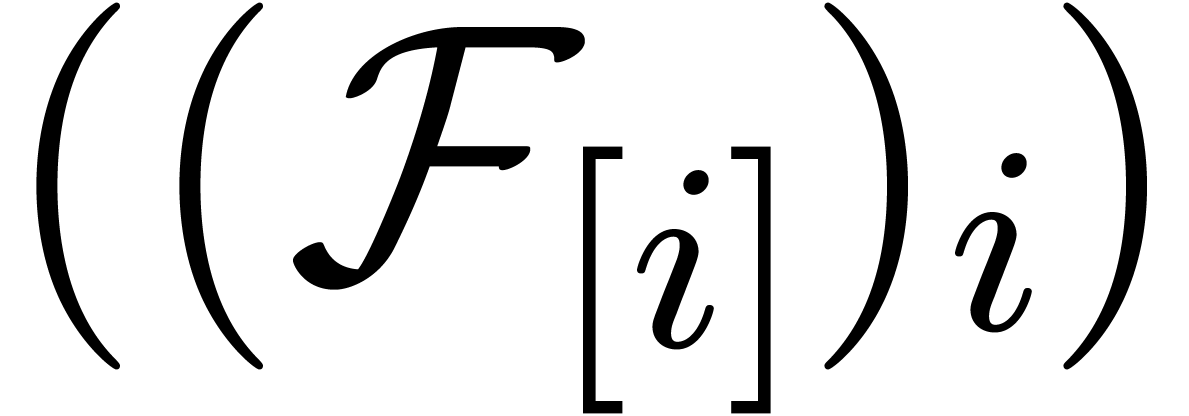 .
Consequently,
.
Consequently, 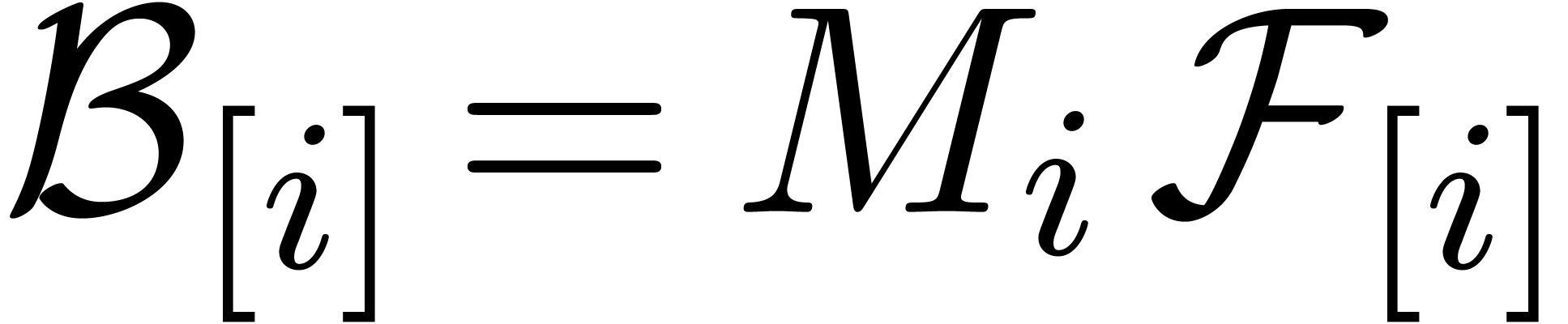 yields a Weierstrass system such
that
yields a Weierstrass system such
that 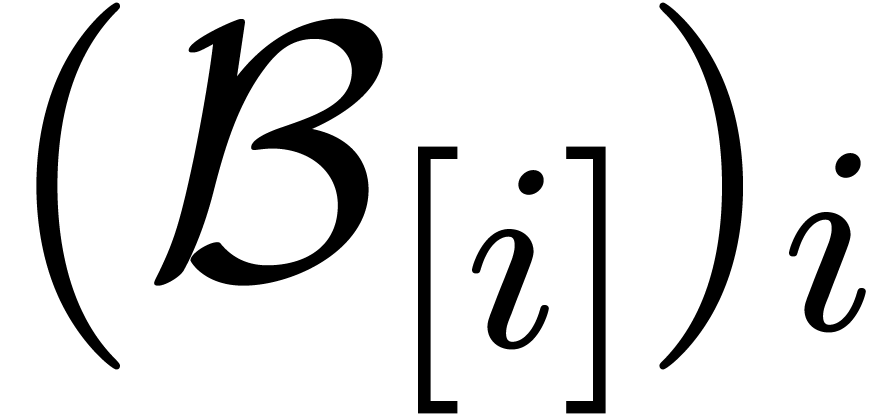 is a Weierstrass basis. The disjoint union
is a Weierstrass basis. The disjoint union
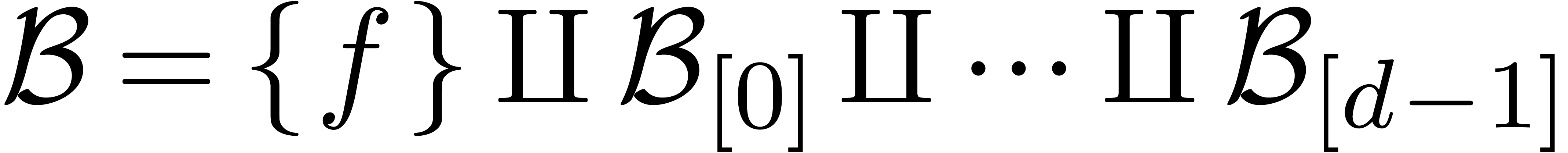 is also a Weierstrass system and we may reduce
it using the algorithm described above.
is also a Weierstrass system and we may reduce
it using the algorithm described above.
At this point, we have a reduced Weierstrass system with the property
that 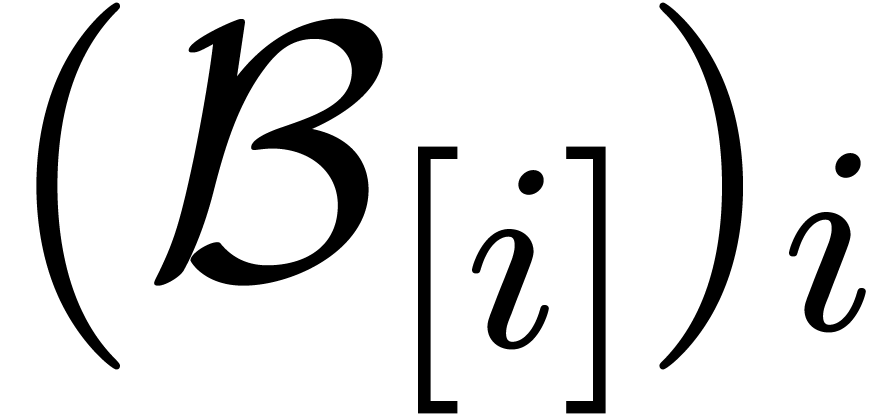 is a Weierstrass basis for each
is a Weierstrass basis for each  . We next compute
. We next compute 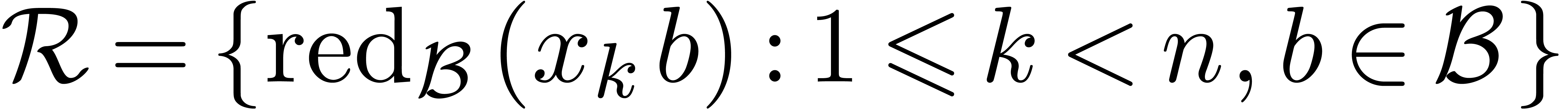 . If
. If 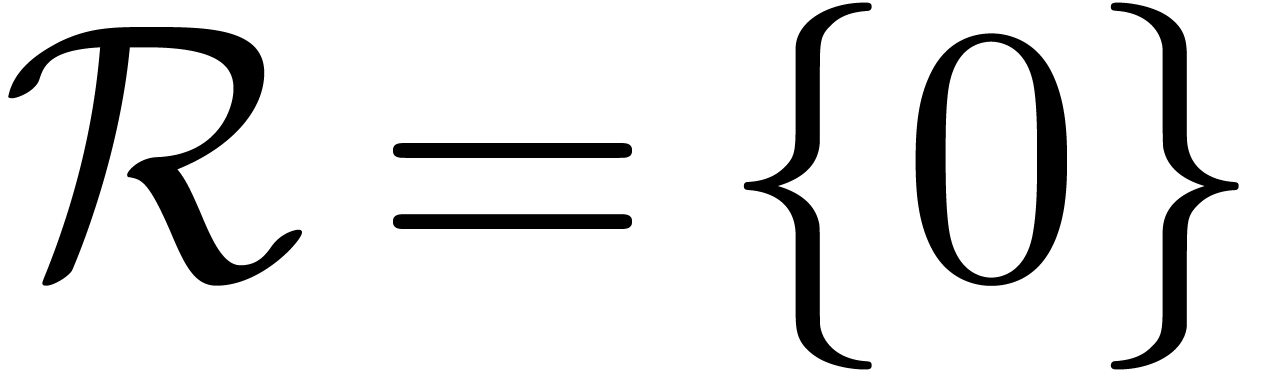 ,
then
,
then  is a Weierstrass basis by Theorem 12.
Otherwise, we replace
is a Weierstrass basis by Theorem 12.
Otherwise, we replace  by
by 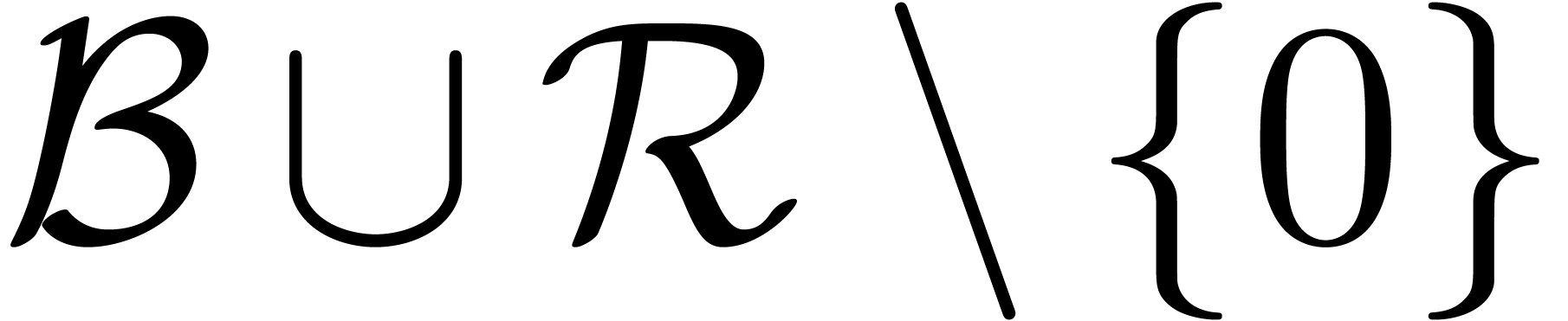 and recompute
and recompute  in the same way above, while
keeping the same
in the same way above, while
keeping the same  . During
each iteration of this loop, the ideals
. During
each iteration of this loop, the ideals 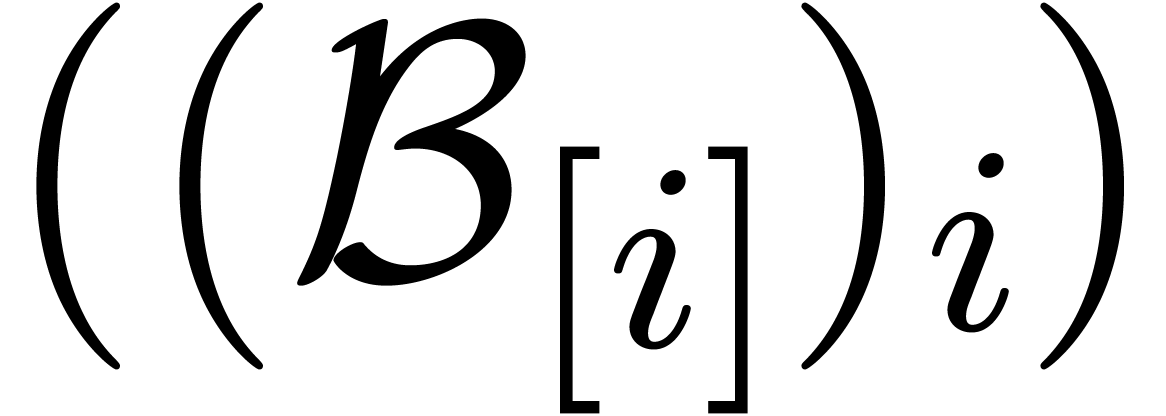 of
of  can only increase, and one of them must increase
strictly. Since
can only increase, and one of them must increase
strictly. Since  is Noetherian, the loop
therefore terminates.
is Noetherian, the loop
therefore terminates.
Sufficiently “general position” for avoiding any errors can
be forced in a similar way as described in the subsection about
Weierstrass position. In that case, we systematically work with
collections  such that each
such that each 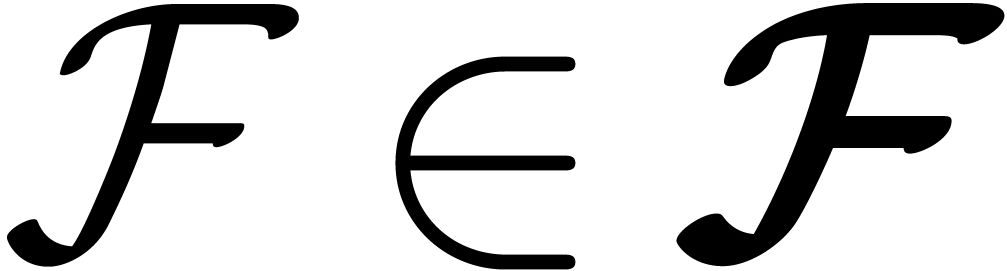 is a finite subset of
is a finite subset of  .
Modulo a common linear change of coordinates
.
Modulo a common linear change of coordinates  we
then compute a Weierstrass basis for each ideal
we
then compute a Weierstrass basis for each ideal  with
with  .
.
Let  be an ideal of
be an ideal of  .
For each
.
For each  , let
, let  be the ideal generated by all monomials
be the ideal generated by all monomials  with
with  . Setting
. Setting 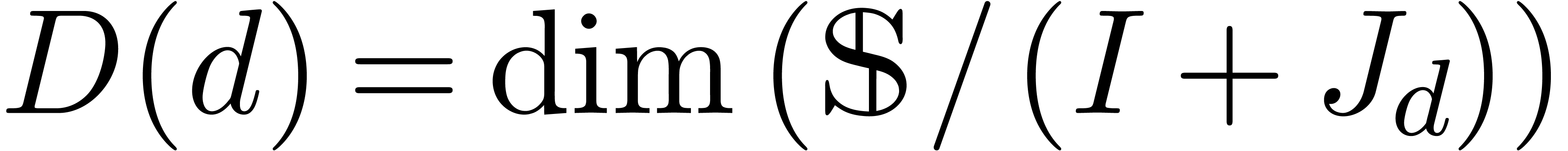 and
and 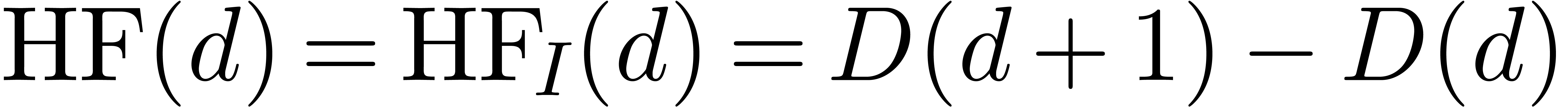 , the
function
, the
function  is called the Hilbert function
of
is called the Hilbert function
of  . It is well known that
there exists a degree
. It is well known that
there exists a degree  and a polynomial
and a polynomial 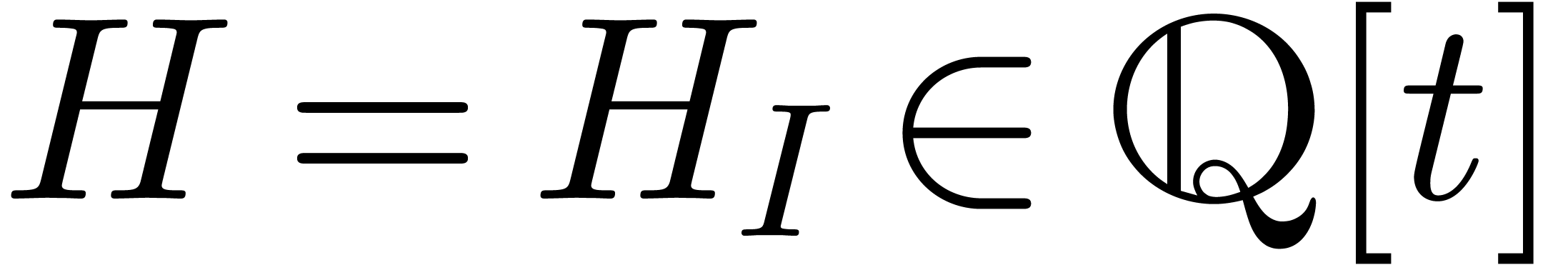 such that
such that 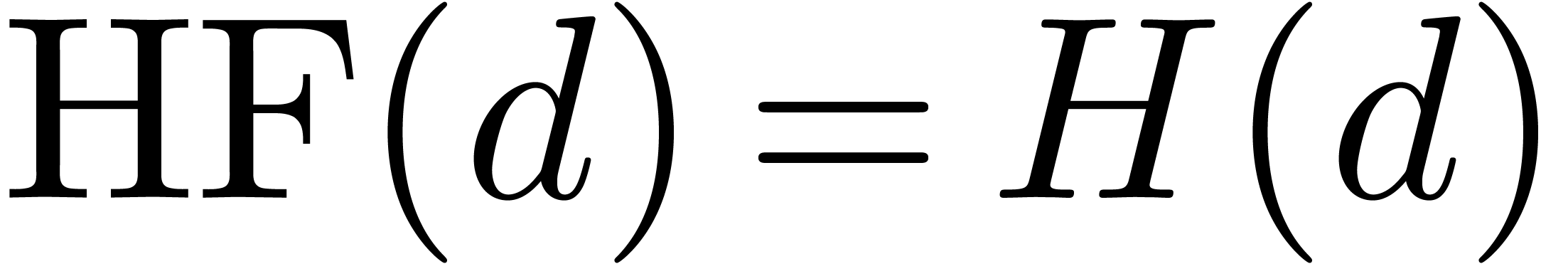 for all
for all  . This polynomial is called the Hilbert
polynomial of
. This polynomial is called the Hilbert
polynomial of  .
Moreover, the regularity
.
Moreover, the regularity  of
of  is the minimal
is the minimal  such that
such that 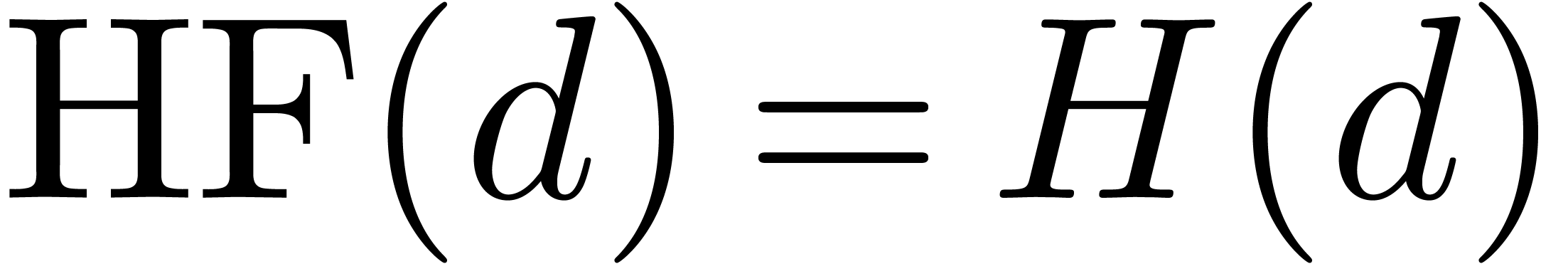 for all
for all 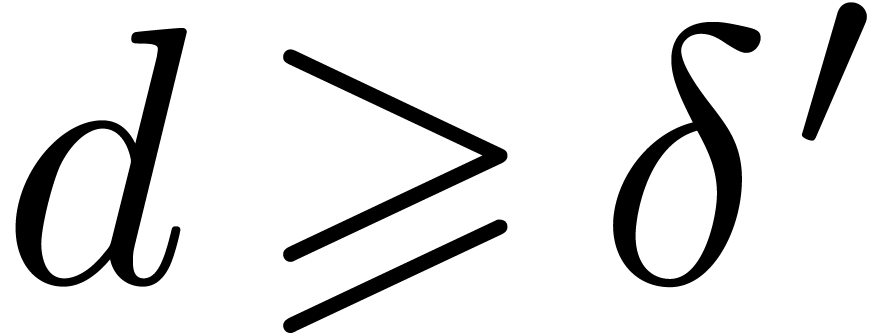 .
.
Now let  be a Weierstrass basis for
be a Weierstrass basis for  and denote
and denote
Given  , let
, let 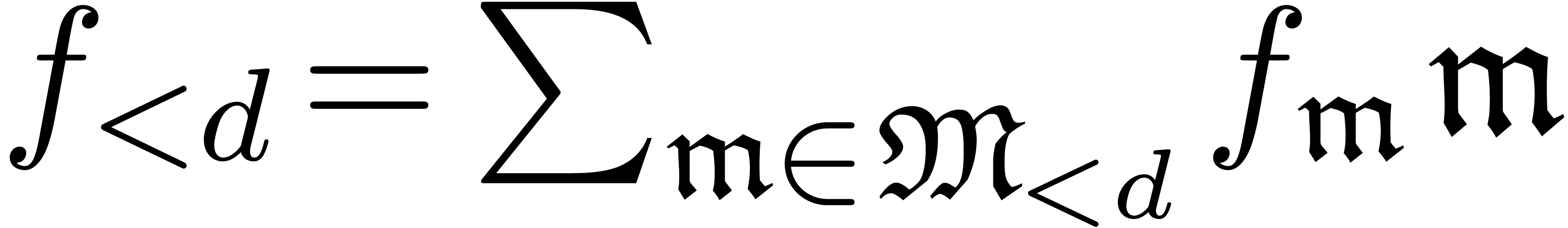 , so that
, so that 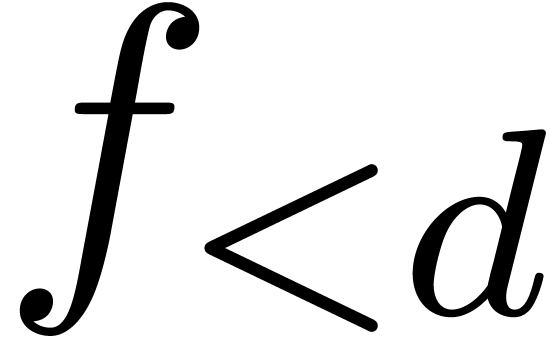 is a natural
representative of
is a natural
representative of  modulo
modulo  . For some
. For some 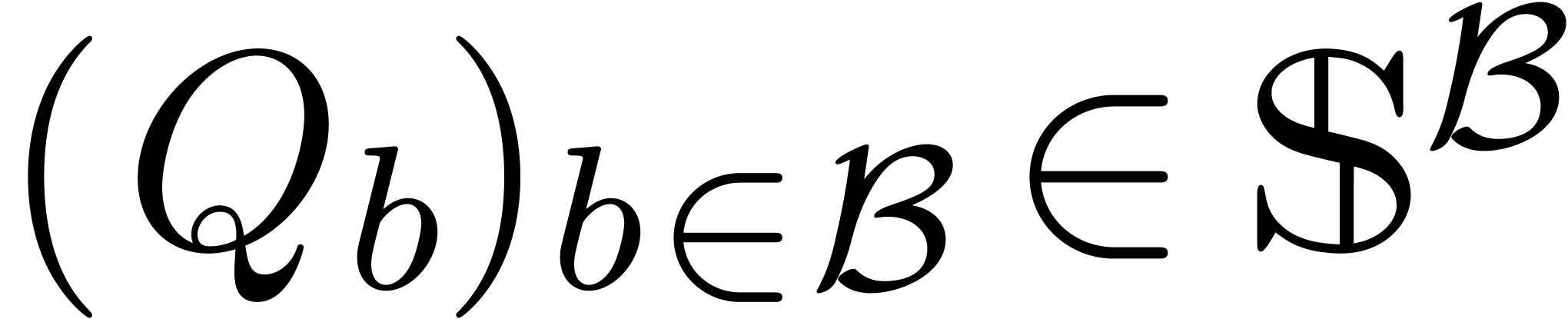 ,
we have
,
we have 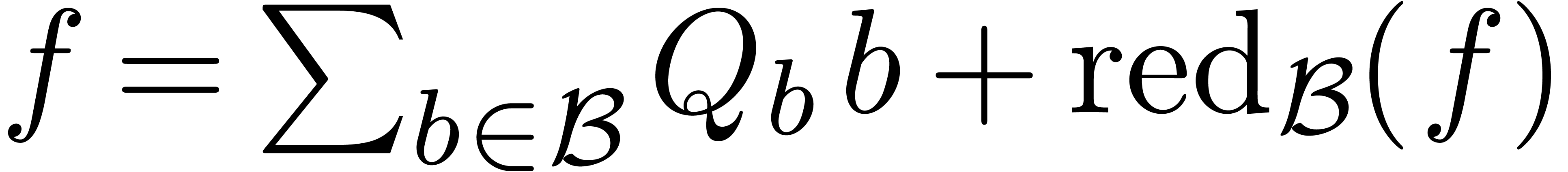 , whence
, whence 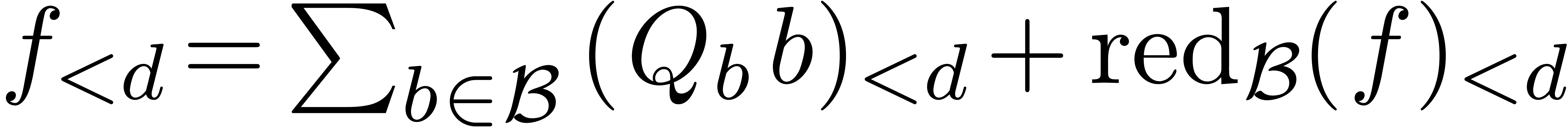 . It follows that
. It follows that  ,
whence
,
whence
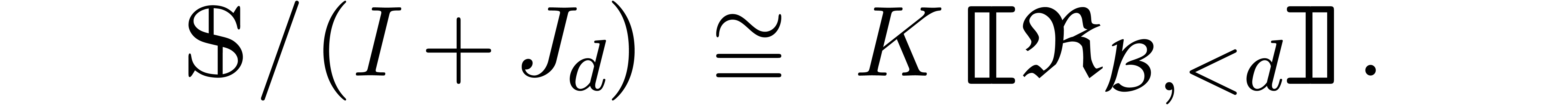
This simply means that
Now given  with
with 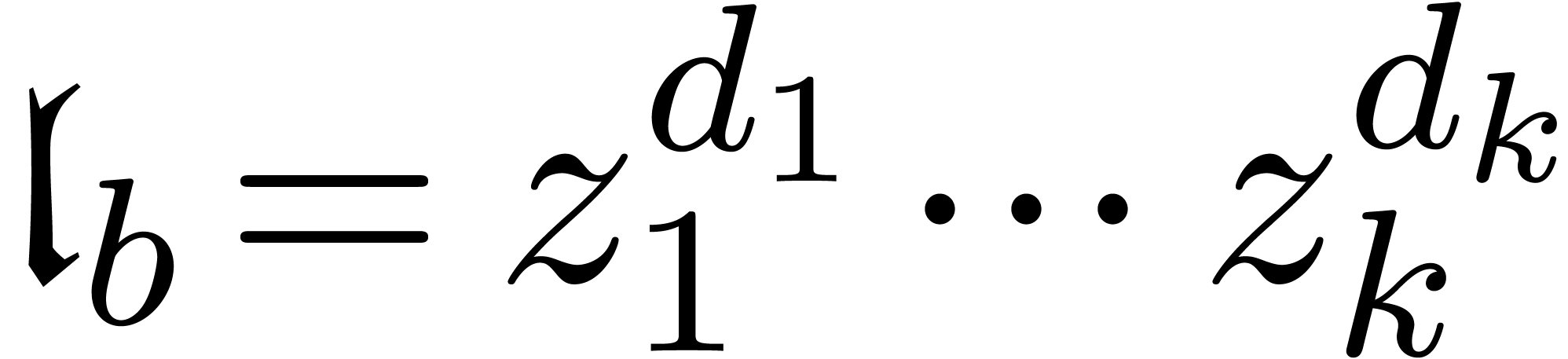 ,
we have
,
we have
for all 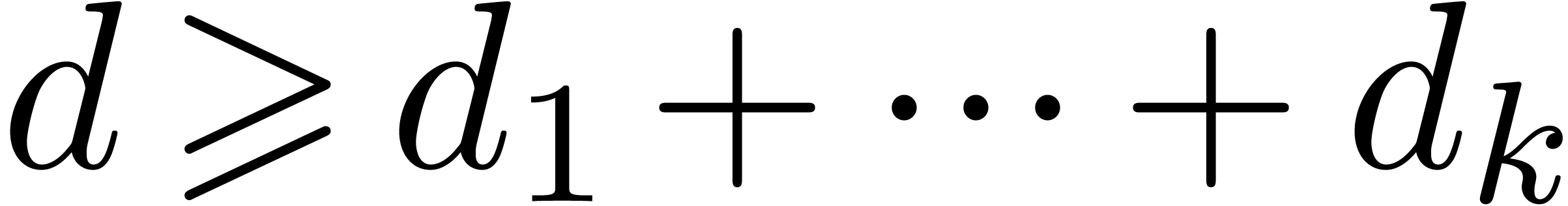 . These formulas
allow us to explicitly compute the Hilbert polynomial of
. These formulas
allow us to explicitly compute the Hilbert polynomial of  and the corresponding regularity.
and the corresponding regularity.
Using a fairly standard technique, let us briefly show how the results
of this section generalize to finitely generated  -modules instead of ideals.
-modules instead of ideals.
Let 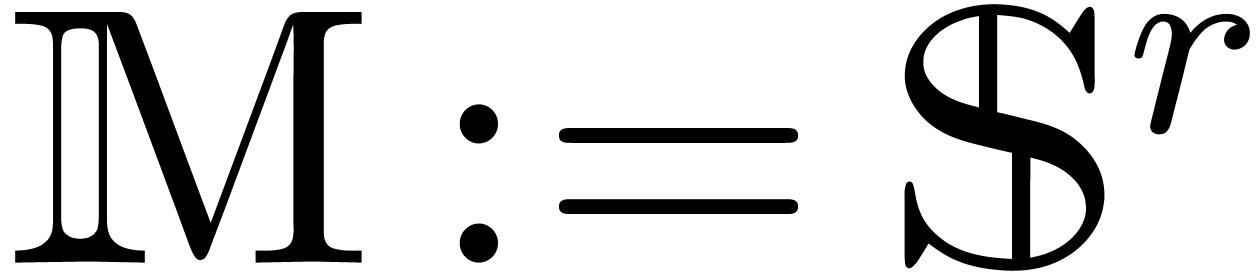 be the free
be the free  -module
with canonical basis
-module
with canonical basis  . We may
embed this module in the
. We may
embed this module in the  -submodule
-submodule
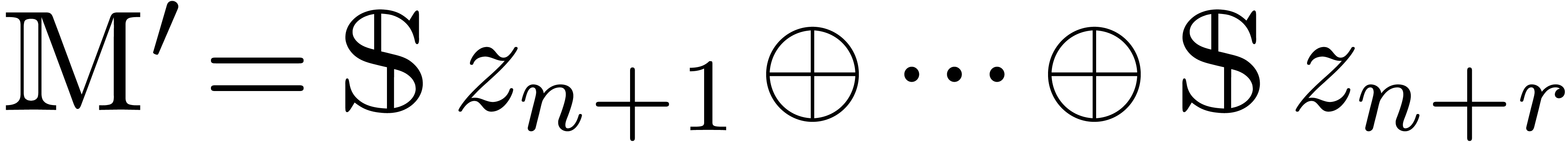 of
of 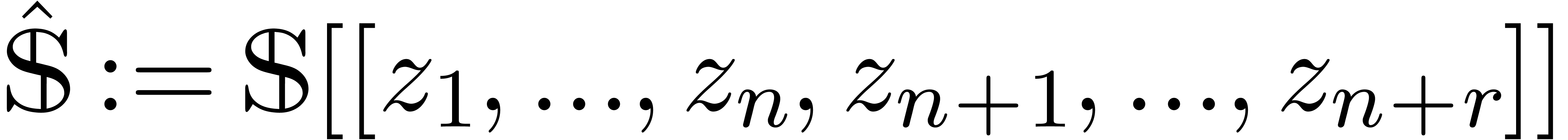 via the
mapping
via the
mapping 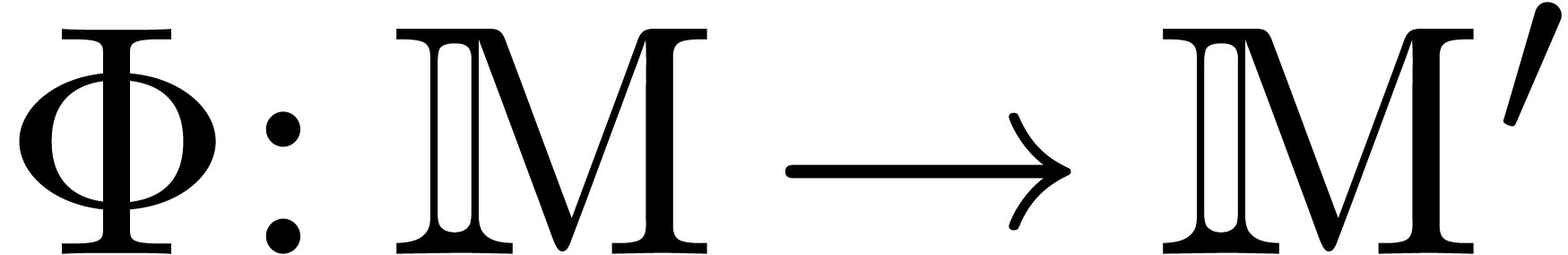 defined by
defined by
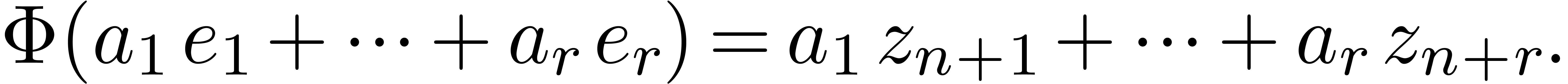
Now consider an  -submodule
-submodule
 of
of  and let
and let  be the ideal of
be the ideal of  generated by
generated by 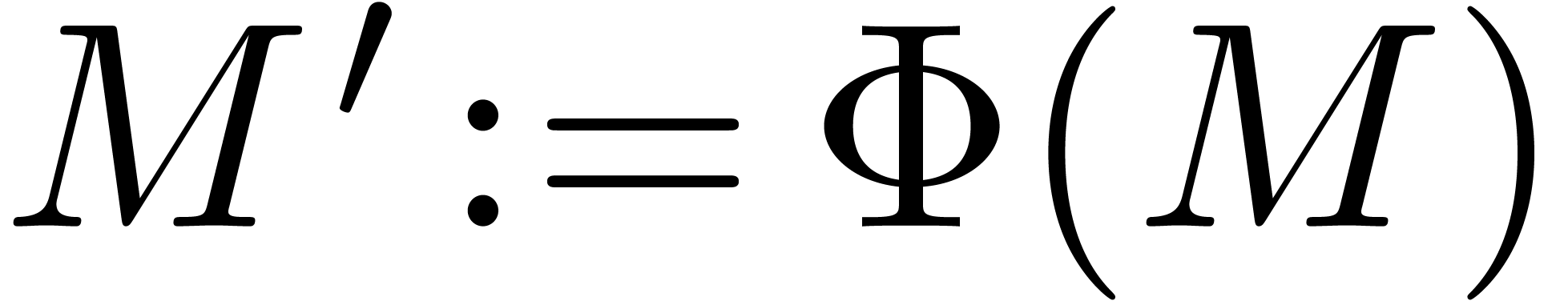 and
and  ,
where
,
where 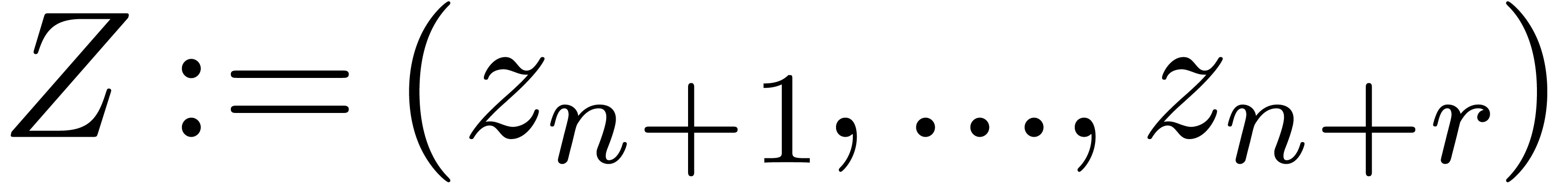 . Then
. Then
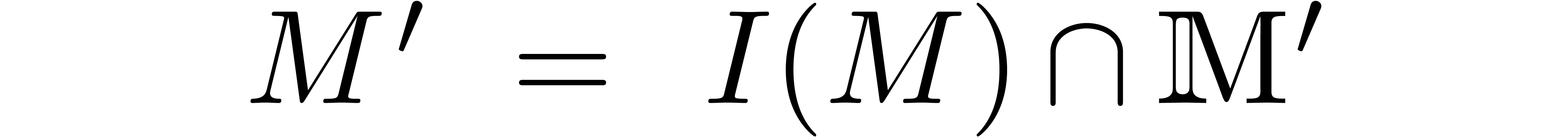
and we have a natural isomorphism of  -modules
-modules

This latter identity makes it possible to carry over the constructions
from this section to the case of  -modules.
In particular, one may define and compute the Hilbert function of
-modules.
In particular, one may define and compute the Hilbert function of  using the formula
using the formula
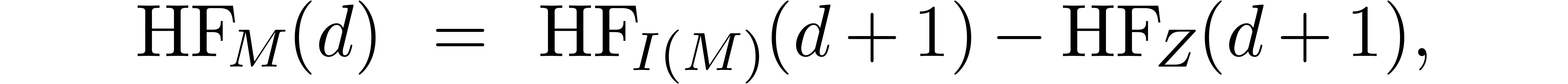
and it can be checked that 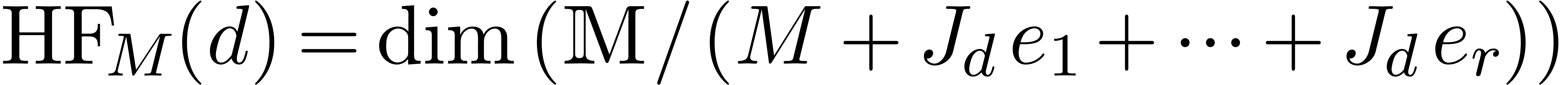 .
The corresponding Hilbert polynomial and Hilbert regularity satisfy
.
The corresponding Hilbert polynomial and Hilbert regularity satisfy
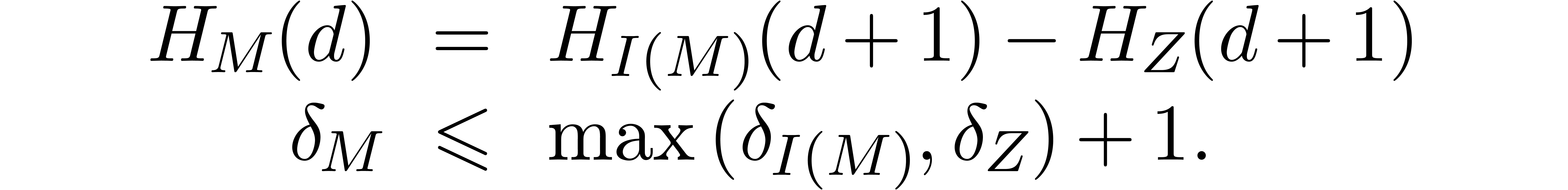
Let  ,
, 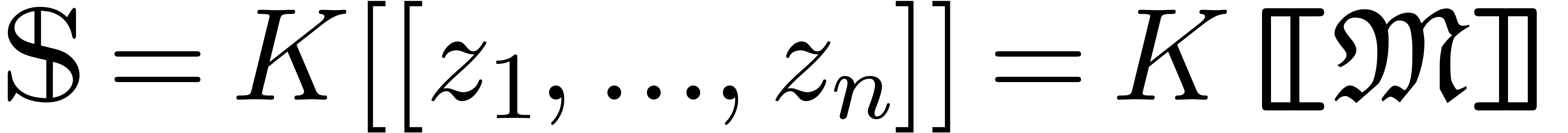 and
and  be as in the previous section, but the
reader may forget about the other notations defined there. Let
be as in the previous section, but the
reader may forget about the other notations defined there. Let  be an arbitrary total monomial ordering on
be an arbitrary total monomial ordering on  with
with  . Given a
series
. Given a
series  and a monomial
and a monomial  , we denote
, we denote  .
Given a subset
.
Given a subset  , we also
denote
, we also
denote 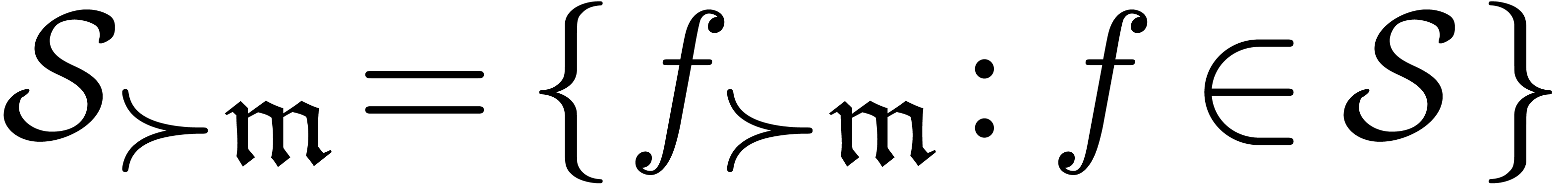 . The notations
. The notations  ,
,  ,
,
 , etc. are
defined likewise.
, etc. are
defined likewise.
In this section, we first very briefly recall the notions of Hironaka
reduction and standard bases; for more details, we refer to [10,
11]. Given a finite subset  of
of  , we next show how to compute a
(not necessarily reduced) standard base for
, we next show how to compute a
(not necessarily reduced) standard base for  , using the techniques from the previous section.
, using the techniques from the previous section.
Let  be a finite subset of
be a finite subset of  . We define
. We define
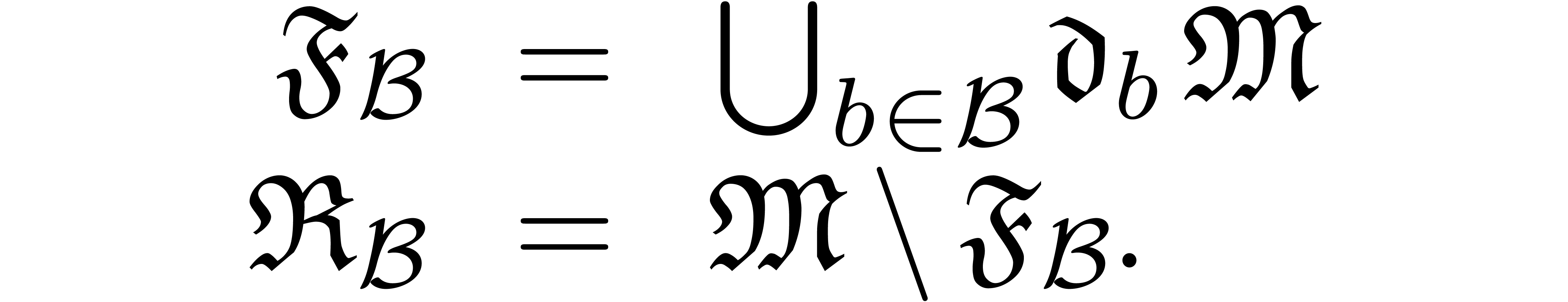
Given  , we say that
, we say that  is reduced with respect to
is reduced with respect to  if
if 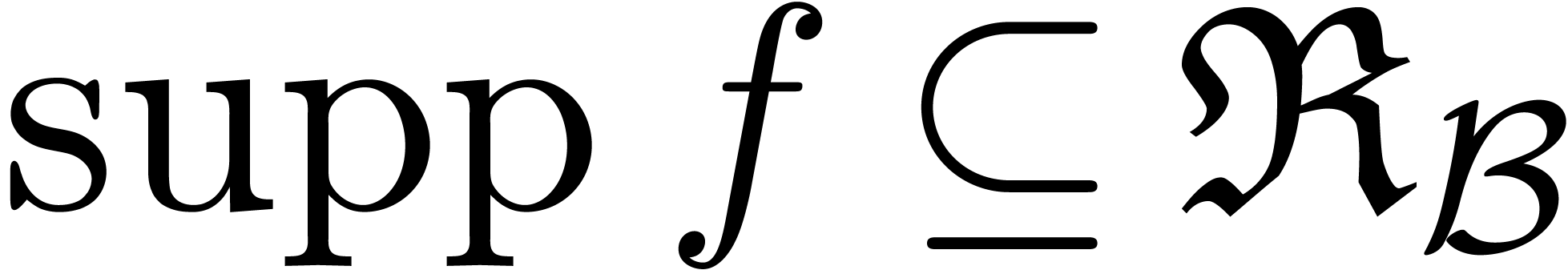 . There exists a
. There exists a 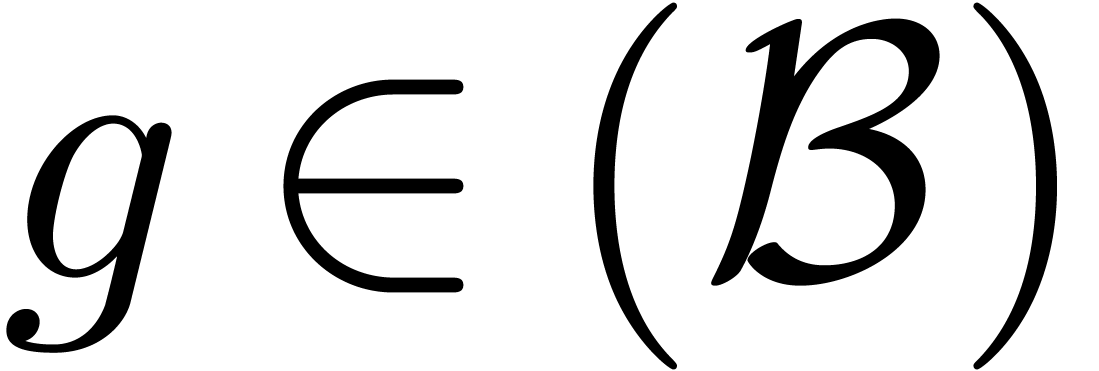 such that
such that 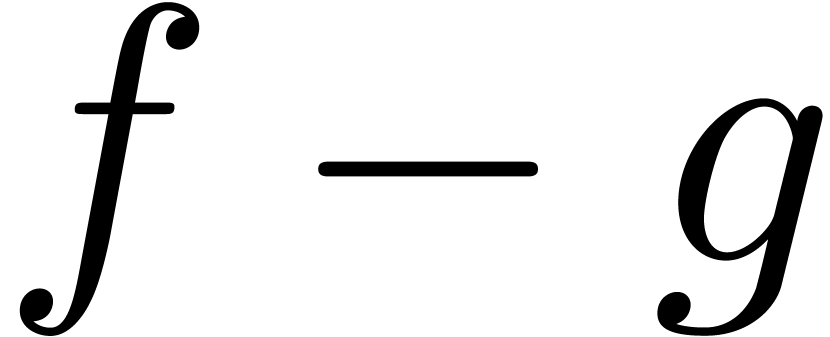 is reduced with respect
to
is reduced with respect
to  . Writing
. Writing 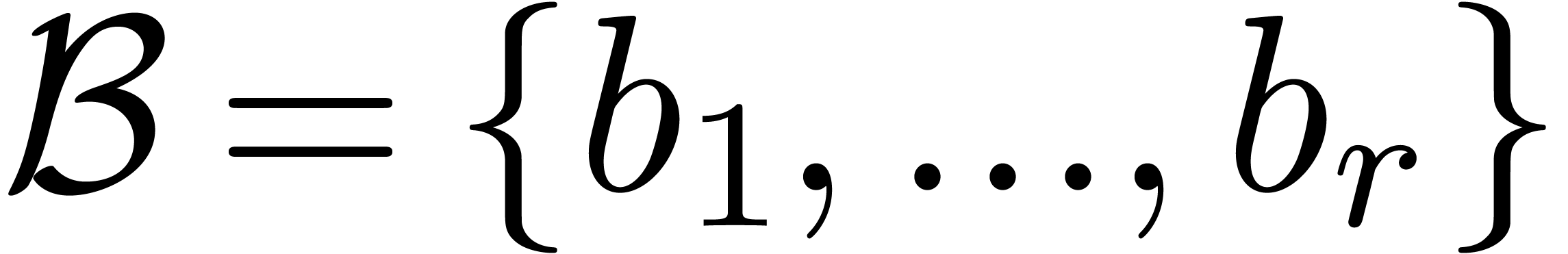 with
with  , there actually exist
unique
, there actually exist
unique  such that
such that 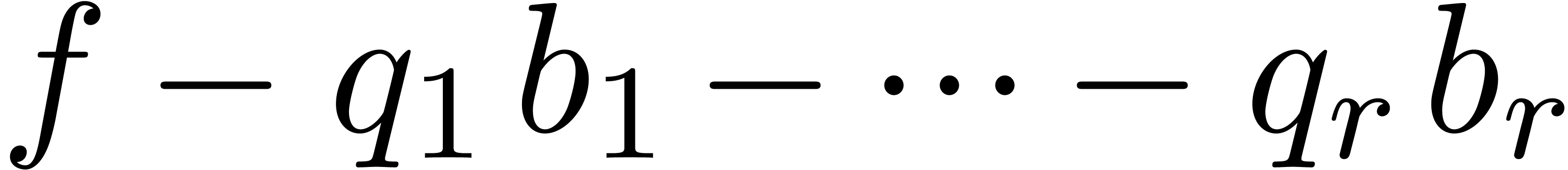 is
reduced with respect to
is
reduced with respect to  and
and 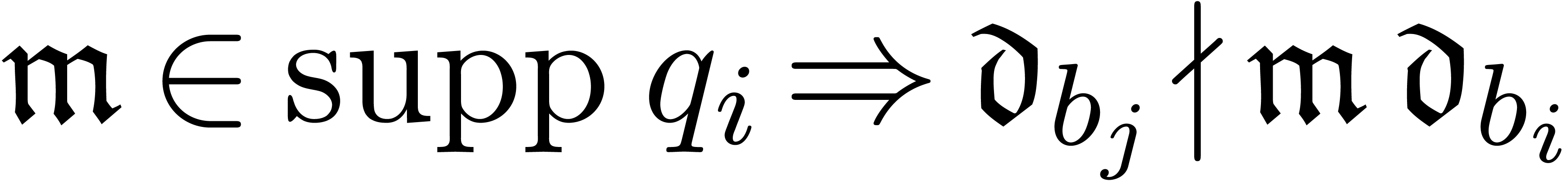 for all
for all  . We define
. We define 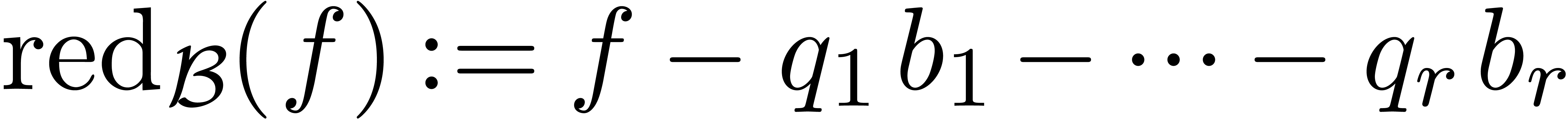 to be the Hironaka reduction of
to be the Hironaka reduction of  with respect to
with respect to  and simply write
and simply write  if
if  is a singleton. If
is a singleton. If 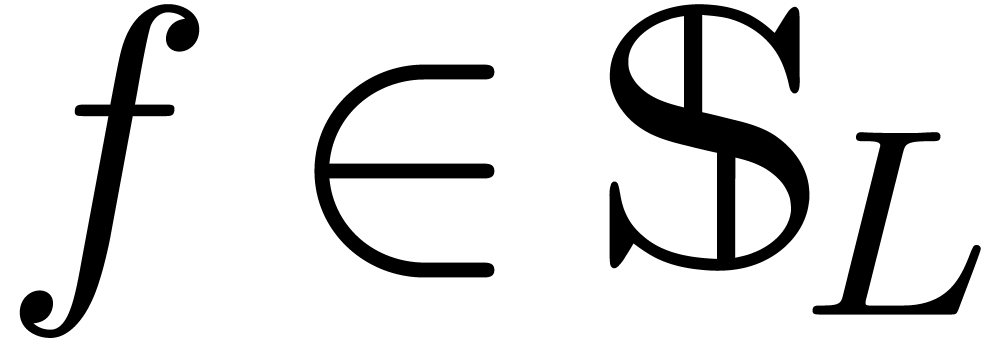 and
and 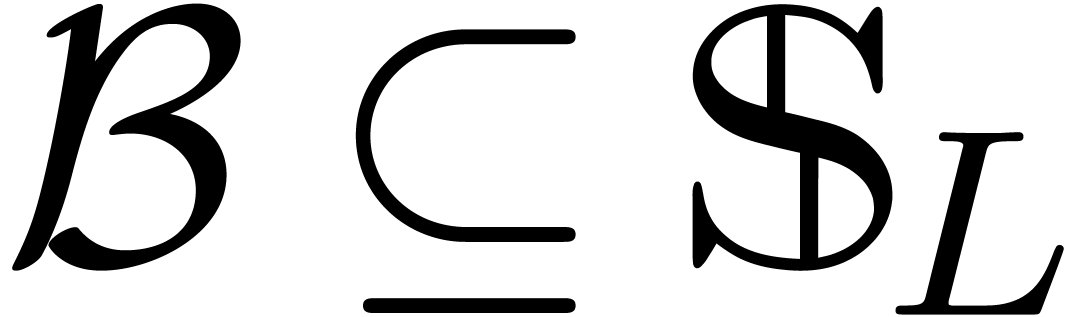 , then we
do not necessarily have
, then we
do not necessarily have 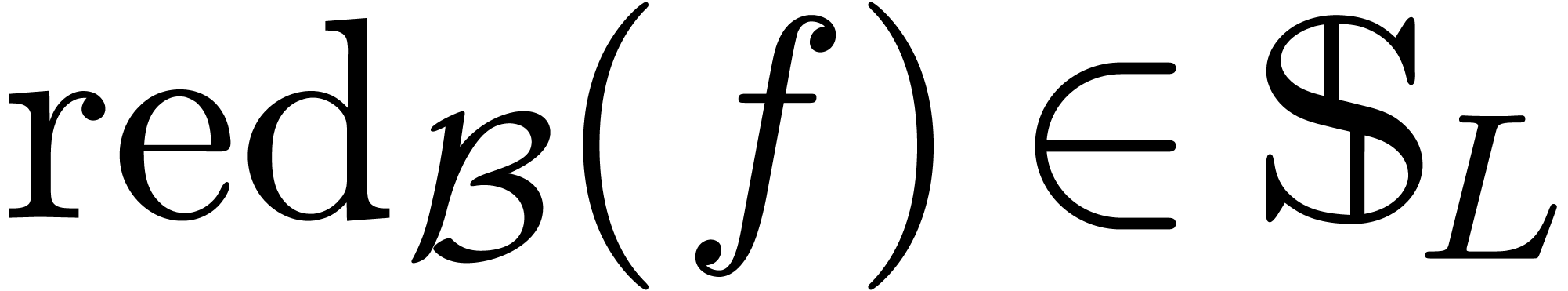 .
Nevertheless, for any
.
Nevertheless, for any  such that
such that  is finite, we may compute
is finite, we may compute  from
from  and
and  using a similar recursion (over
using a similar recursion (over  ) as in the case of Euclidean division. We say
that
) as in the case of Euclidean division. We say
that  is autoreduced if
is autoreduced if  is reduced with respect
is reduced with respect  for all
for all 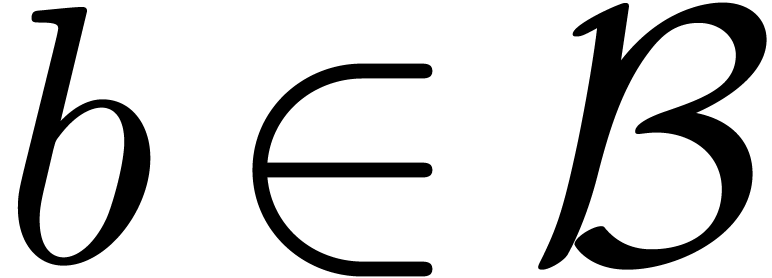 .
.
Example  be the tribe of algebraic power series. If
be the tribe of algebraic power series. If
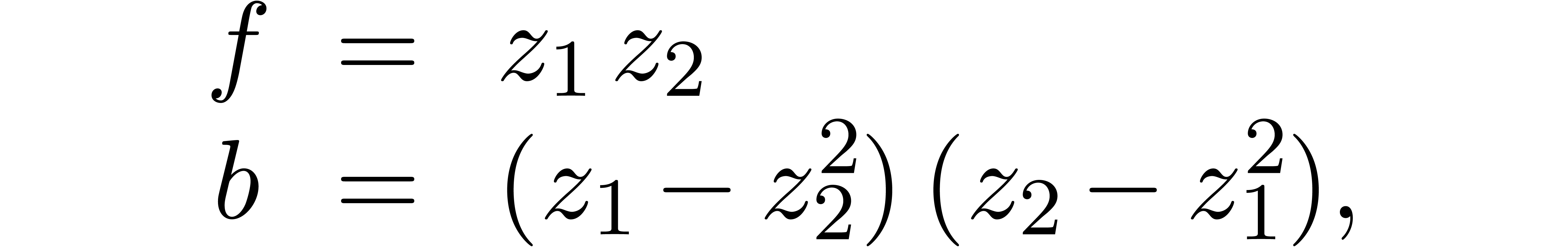
then it can be shown [11, p. 75] that
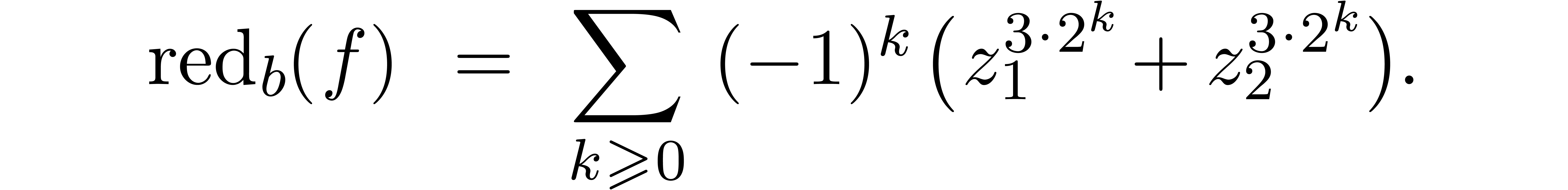
Since the power series 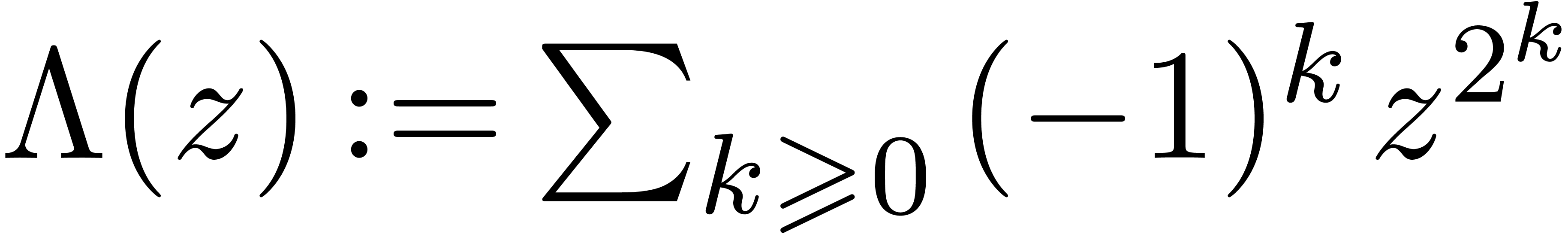 is lacunary, it cannot be
algebraic, whence
is lacunary, it cannot be
algebraic, whence 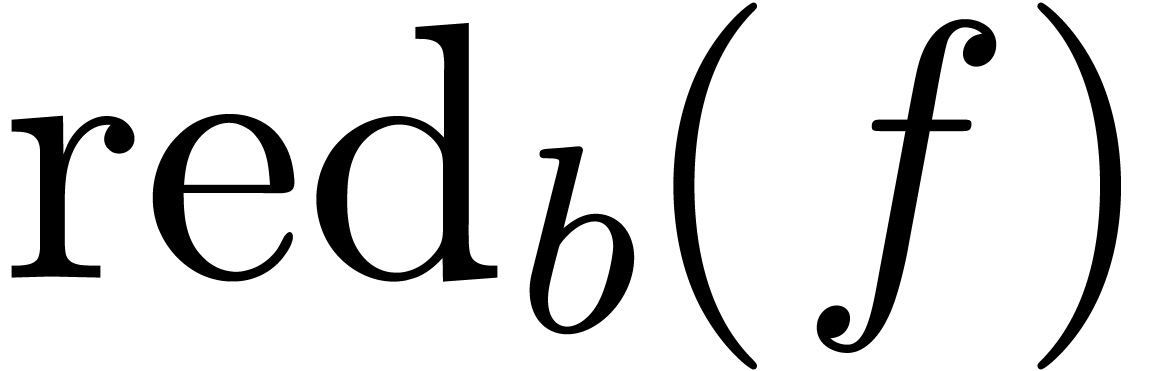 is transcendental. This means
that
is transcendental. This means
that  , but
, but 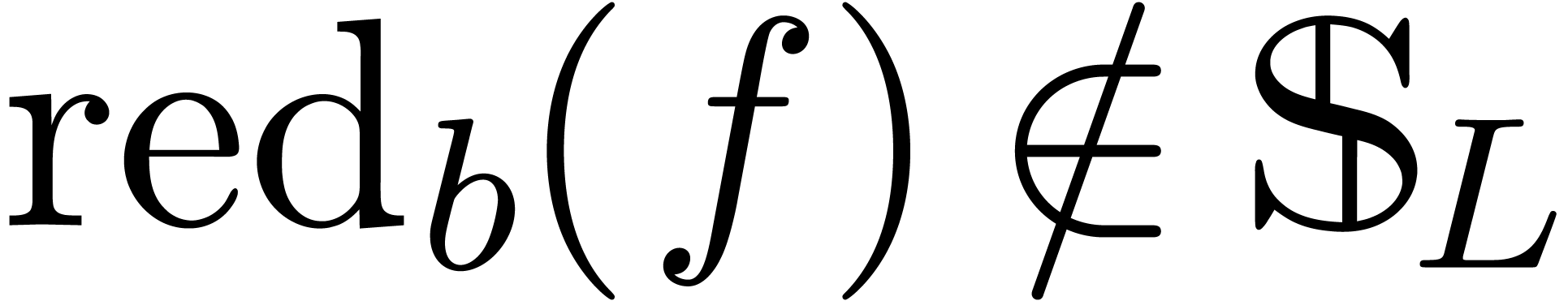 .
.
Example 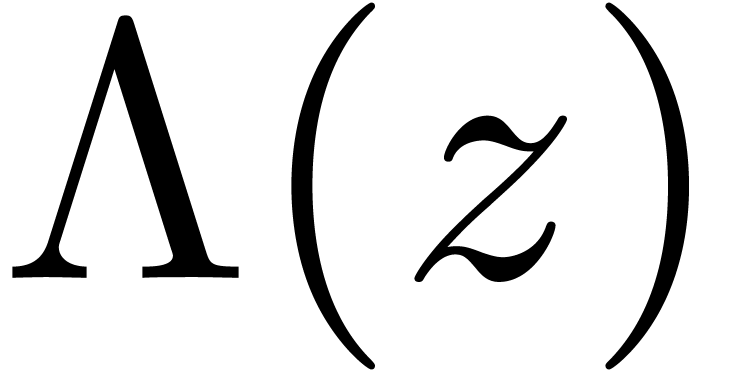 from the
previous example is even d-transcendental (this fact was first proved
using different techniques in [19]): assume the contrary
and consider a d-algebraic equation
from the
previous example is even d-transcendental (this fact was first proved
using different techniques in [19]): assume the contrary
and consider a d-algebraic equation  over
over  of minimal Ritt rank. We have
of minimal Ritt rank. We have 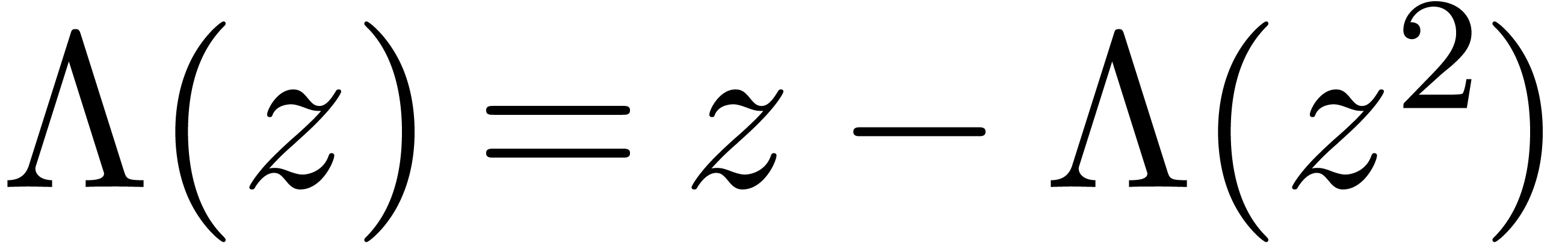 , so
, so  also yields an equation
of the same Ritt rank for
also yields an equation
of the same Ritt rank for 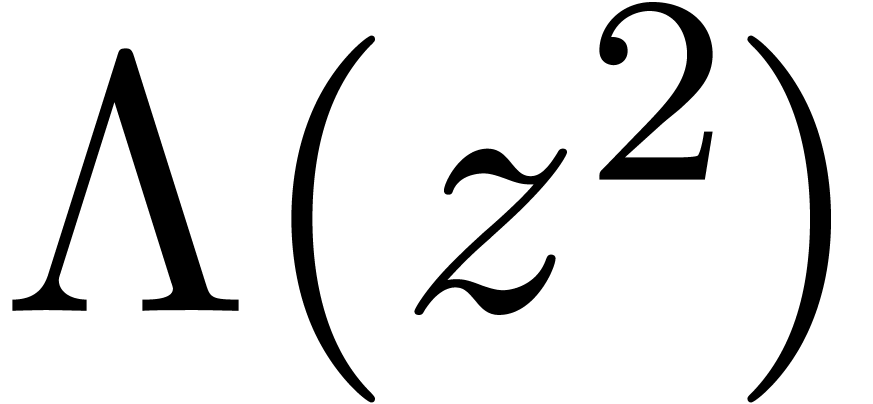 .
But the change of variables
.
But the change of variables 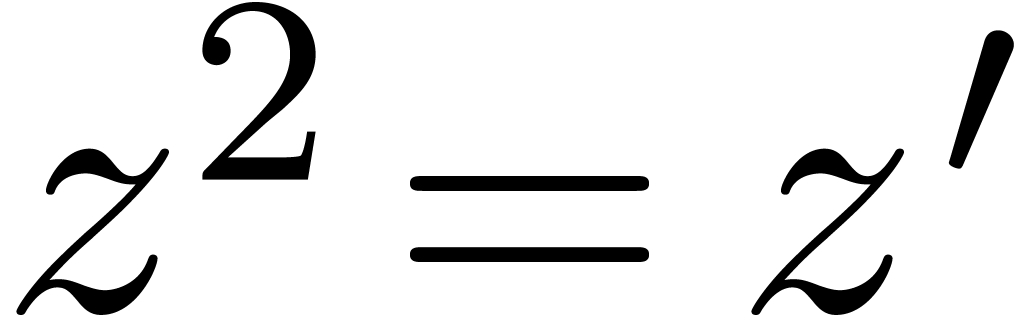 then gives a second,
different, d-algebraic equation for
then gives a second,
different, d-algebraic equation for 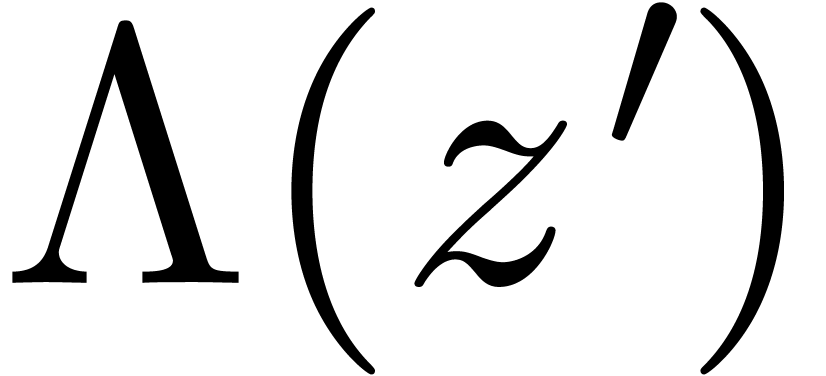 of the same
Ritt rank as
of the same
Ritt rank as  . Applying Ritt
reduction with respect to
. Applying Ritt
reduction with respect to 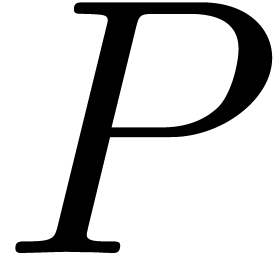 ,
this yields a new equation of smaller Ritt rank, which contradicts the
minimality hypothesis. In other words, if we replace
,
this yields a new equation of smaller Ritt rank, which contradicts the
minimality hypothesis. In other words, if we replace 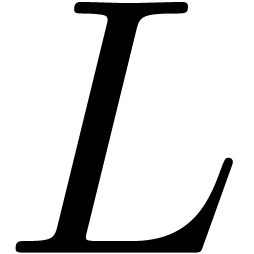 by the tribe of d-algebraic power series in the above example, then we
still have
by the tribe of d-algebraic power series in the above example, then we
still have 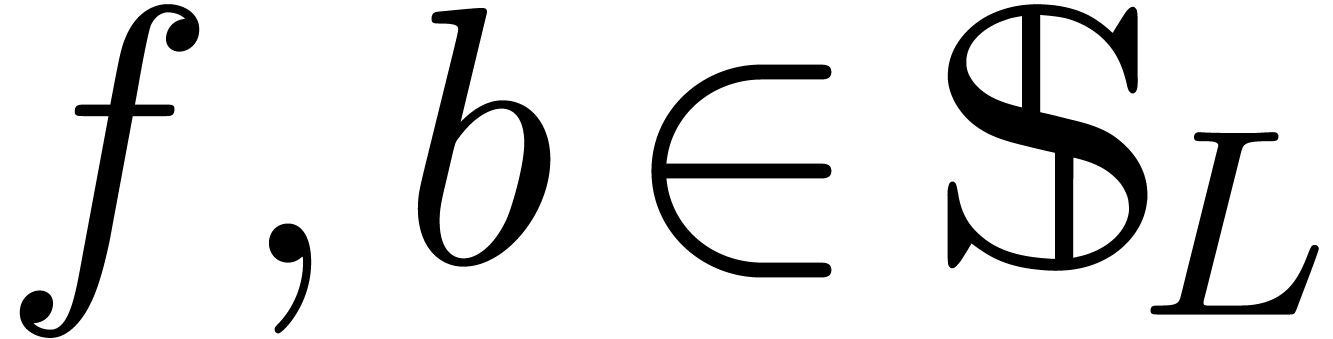 , but
, but 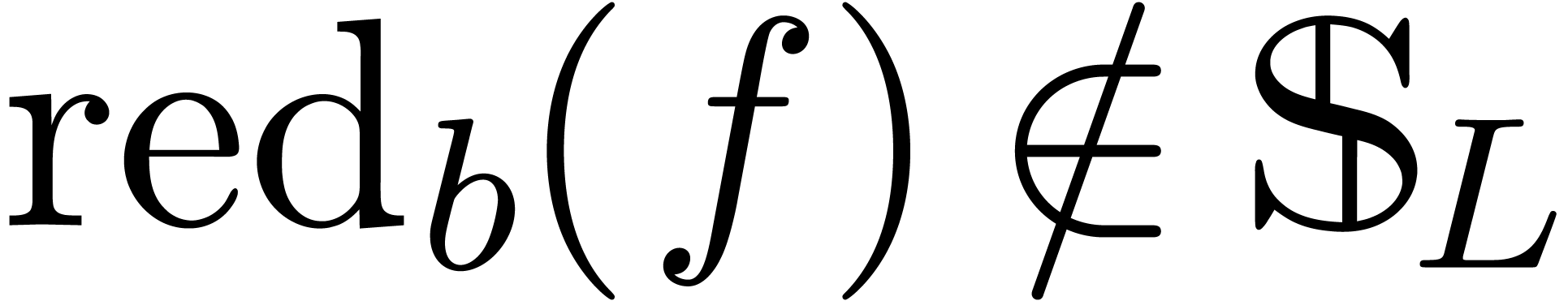 .
.
Given an ideal  , let
, let
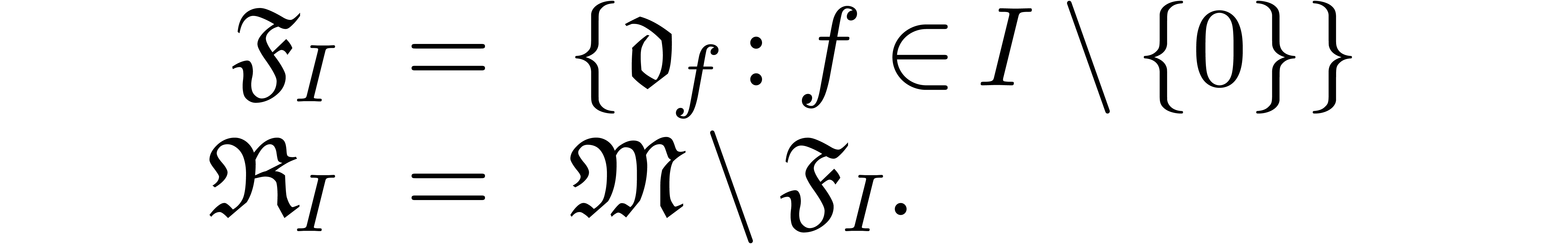
We say that a finite subset  of
of  is a standard basis for
is a standard basis for  if
if  is a set of generators of
is a set of generators of  .
We say that
.
We say that  is reduced if
is reduced if  is autoreduced and
is autoreduced and 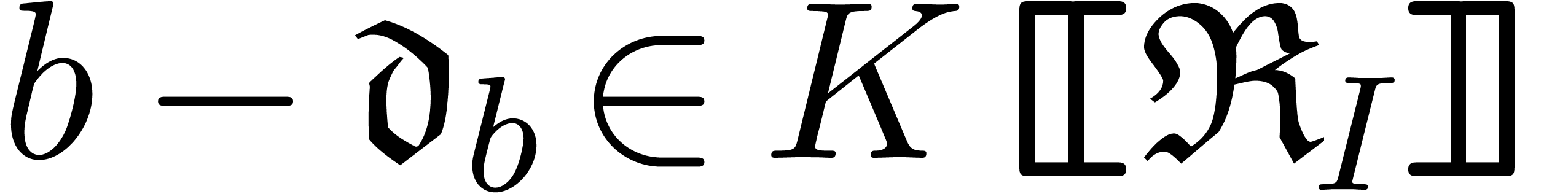 for all
for all 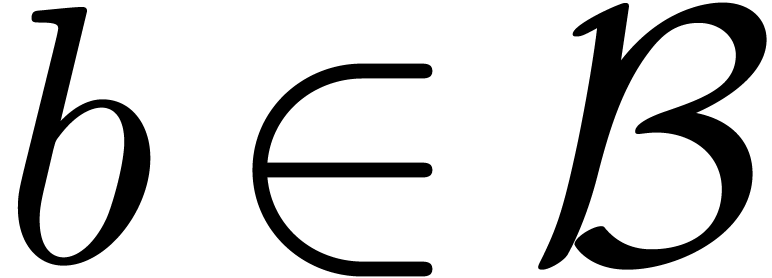 . Any ideal
. Any ideal  admits a unique reduced standard basis.
admits a unique reduced standard basis.
Let 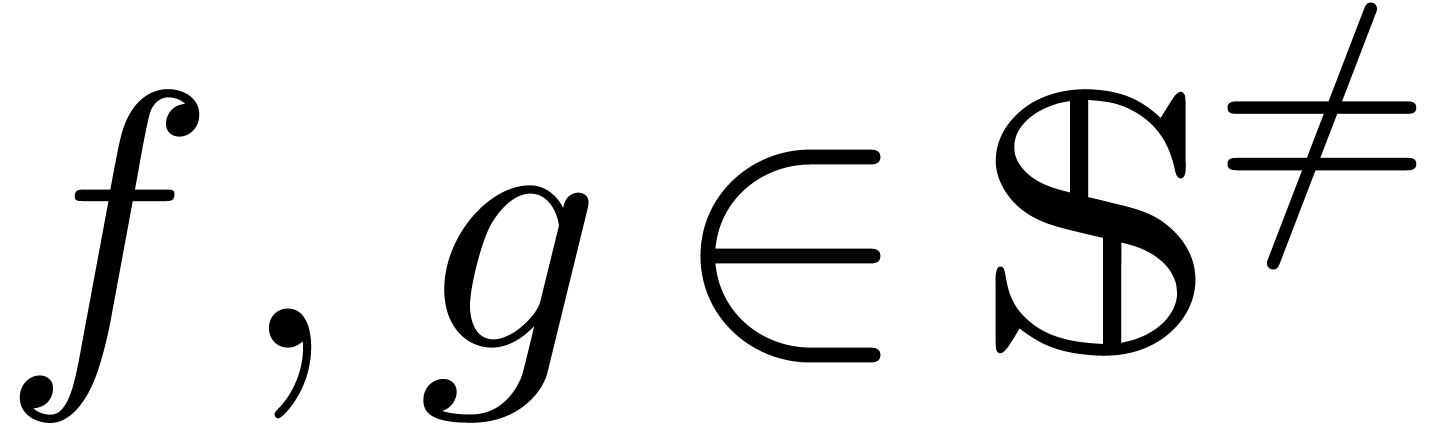 be such that
be such that 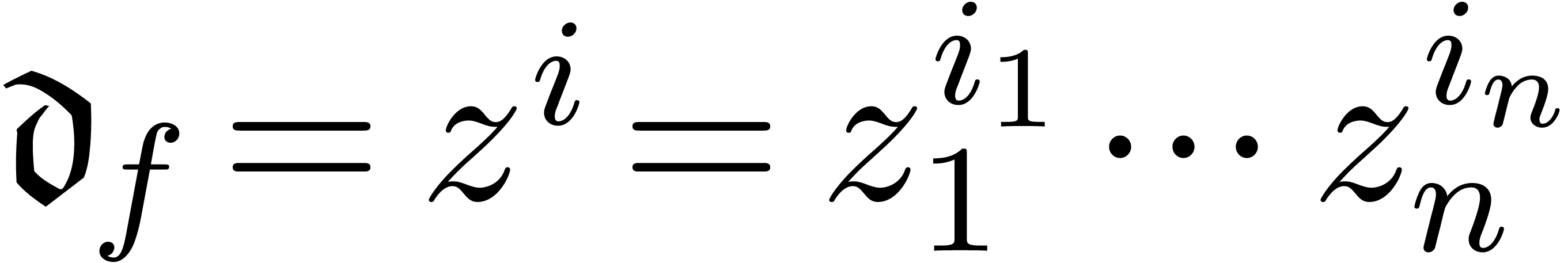 and
and
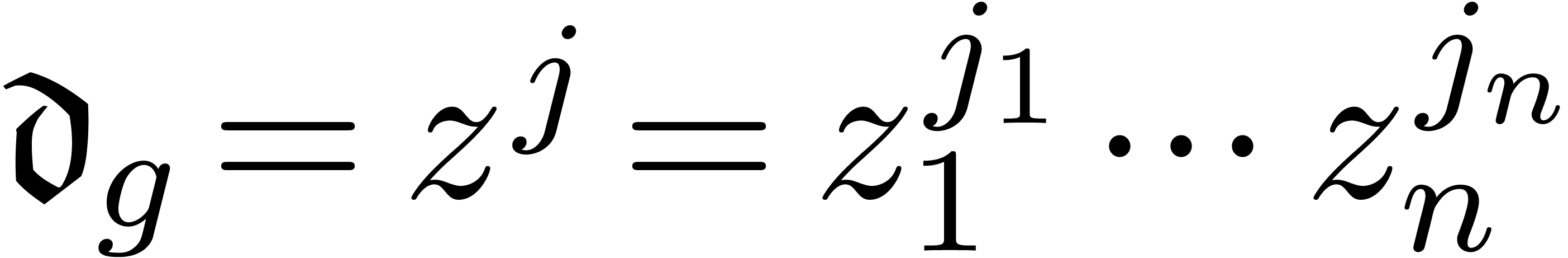 . Let
. Let 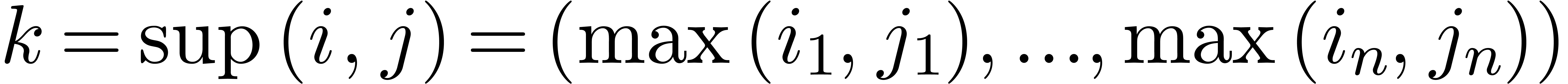 . We define the S-series
. We define the S-series 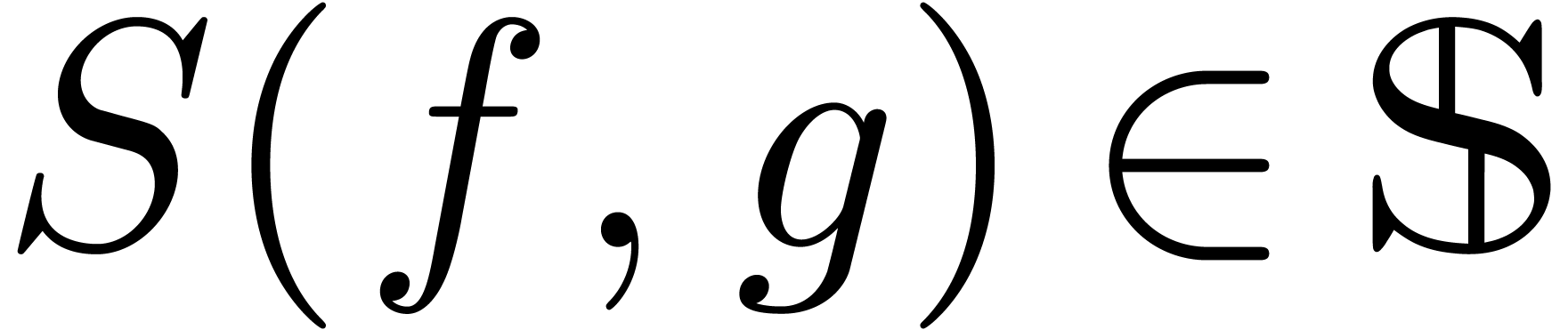 of
of
 and
and  to be
to be
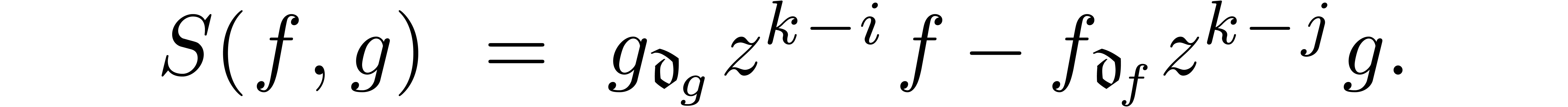
In a similar way as in the case of Gröbner bases, it can be shown
that a finite autoreduced subset  of
of  is a standard basis if and only if
is a standard basis if and only if 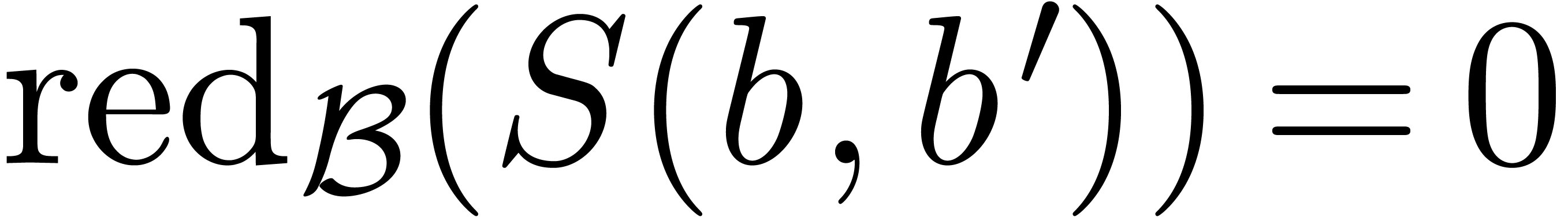 for all
for all 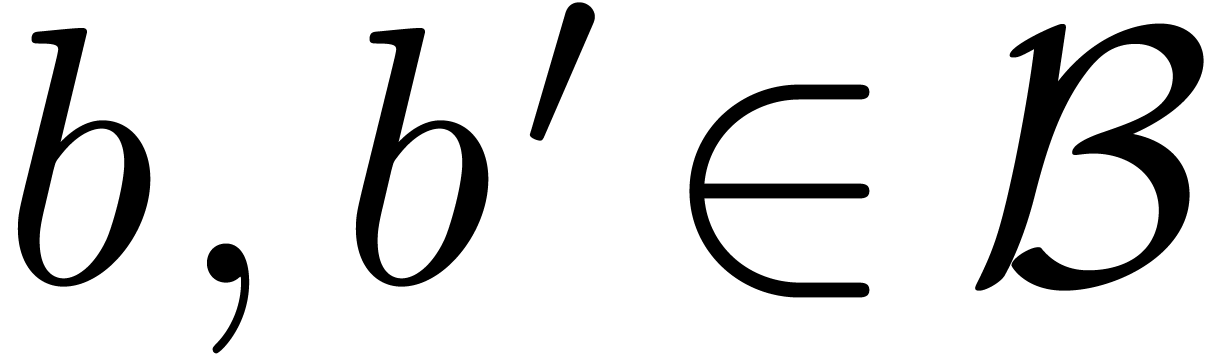 . For any pair
. For any pair 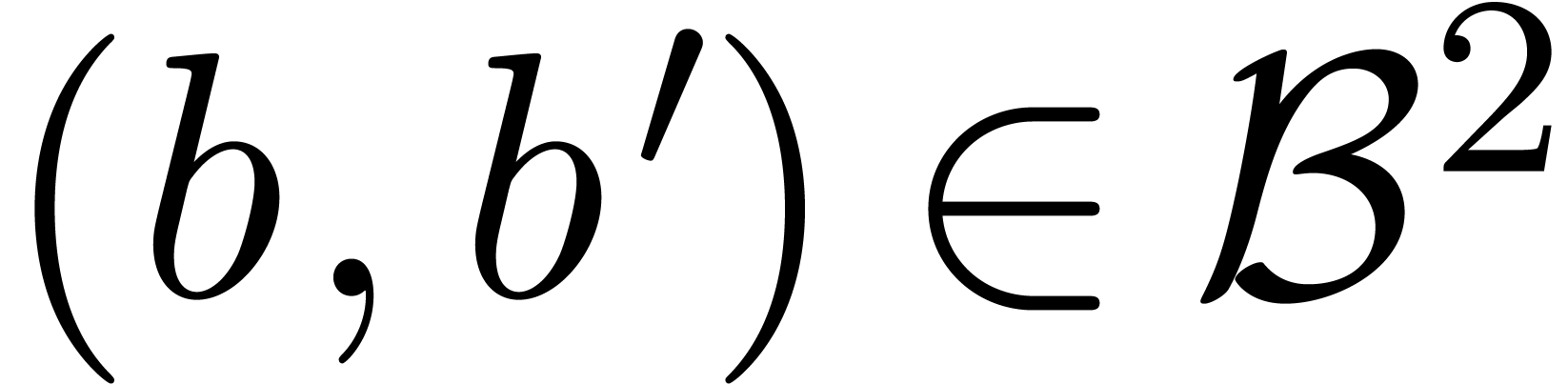 , the relation
, the relation 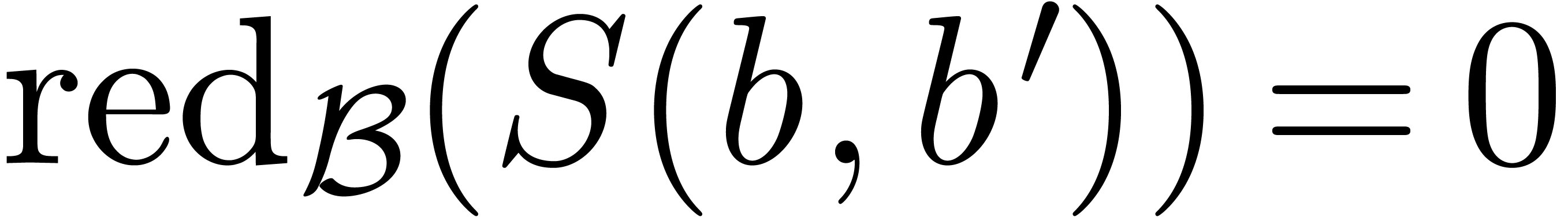 gives rise to an
gives rise to an  -linear
relation between the elements of
-linear
relation between the elements of  .
Using standard Gröbner basis techniques it can be shown that the
space of all
.
Using standard Gröbner basis techniques it can be shown that the
space of all  -linear
relations between elements of
-linear
relations between elements of  (the module of
syzygies) is generated by the relations of this special form.
(the module of
syzygies) is generated by the relations of this special form.
Given a finite set 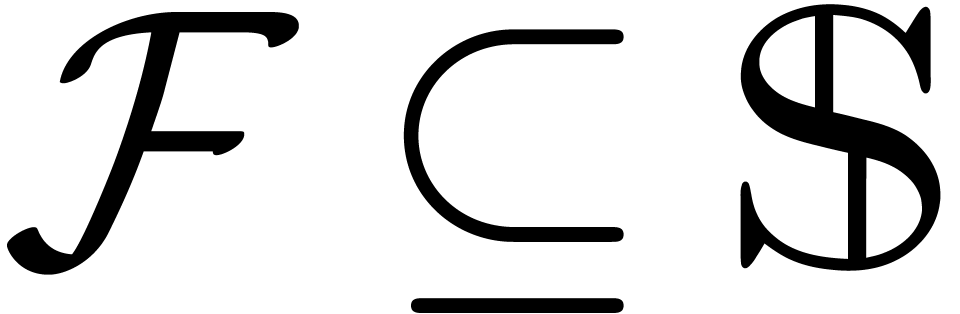 and
and 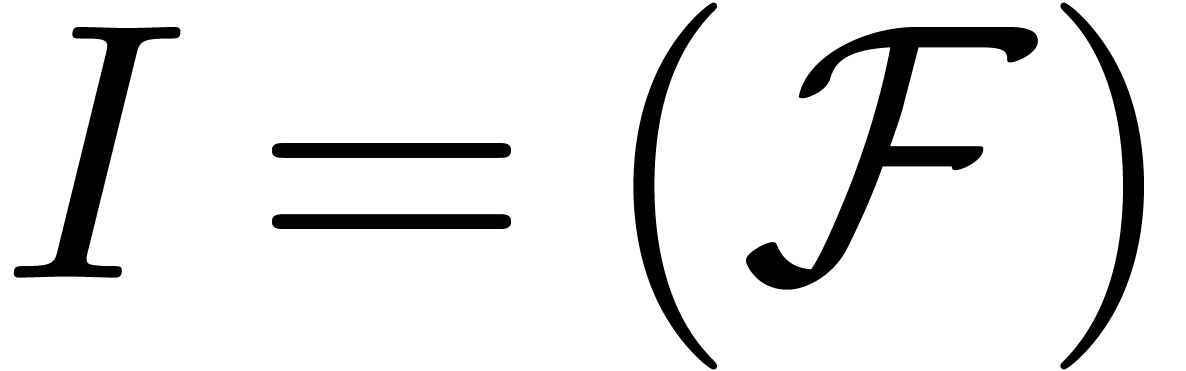 , this characterization theoretically allows us to
compute the reduced standard basis
, this characterization theoretically allows us to
compute the reduced standard basis  for
for  using a suitable local adaptation of Buchberger's
algorithm. However, such an “algorithm” relies on our
ability to compute reductions and Examples 13 and 14
show that we do not have any general algorithm for doing so.
Nevertheless, we will show next that it is still possible to compute
suitable truncations of
using a suitable local adaptation of Buchberger's
algorithm. However, such an “algorithm” relies on our
ability to compute reductions and Examples 13 and 14
show that we do not have any general algorithm for doing so.
Nevertheless, we will show next that it is still possible to compute
suitable truncations of  .
.
Given an ideal  and a monomial
and a monomial 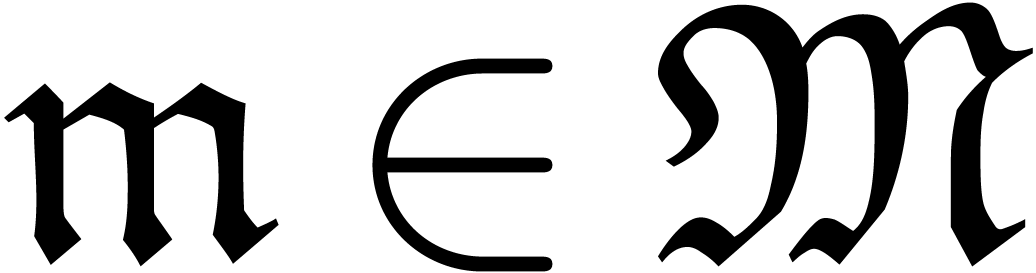 , we have
, we have 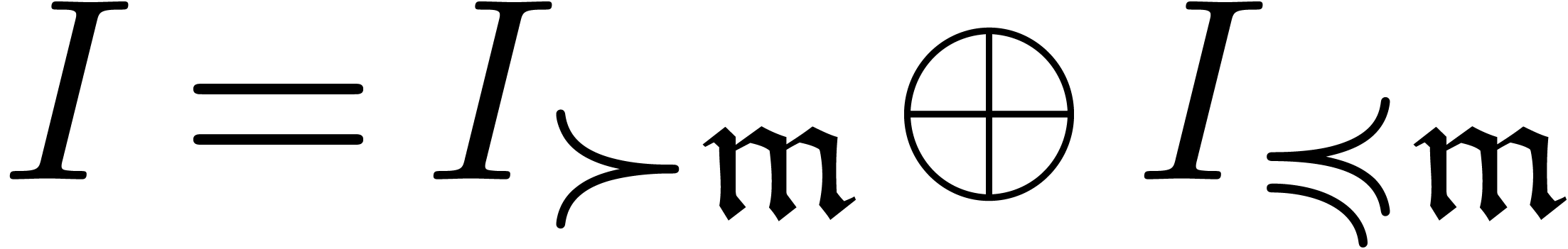 ,
where
,
where 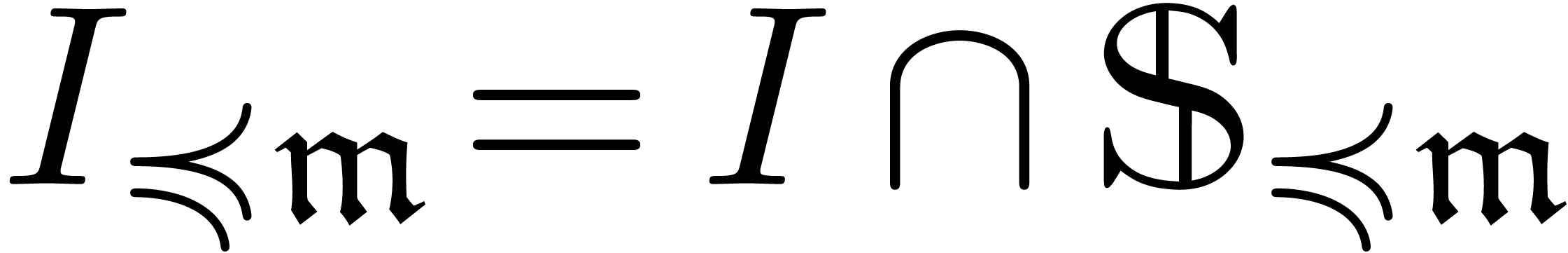 is again an ideal. Let
is again an ideal. Let  be the reduced standard basis for
be the reduced standard basis for  and assume
that
and assume
that  is generated by a finite subset
is generated by a finite subset  of
of  .
.
If  is finite, then for any
is finite, then for any 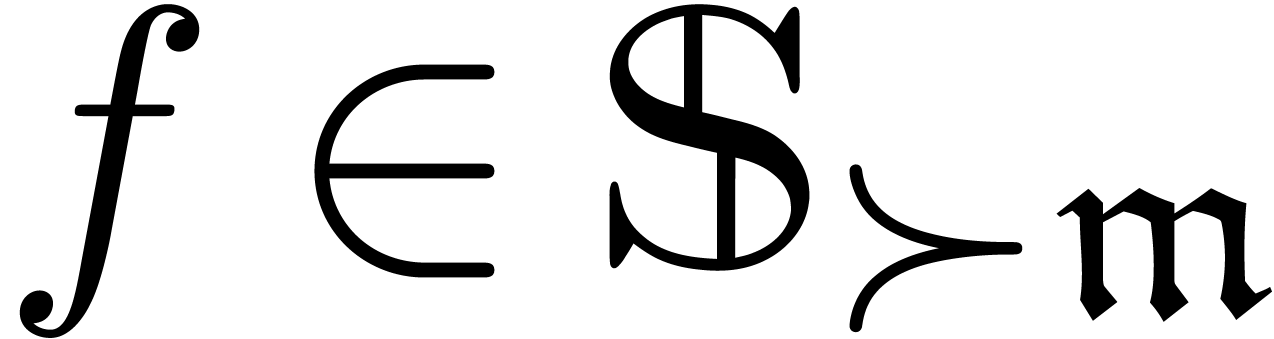 and
and 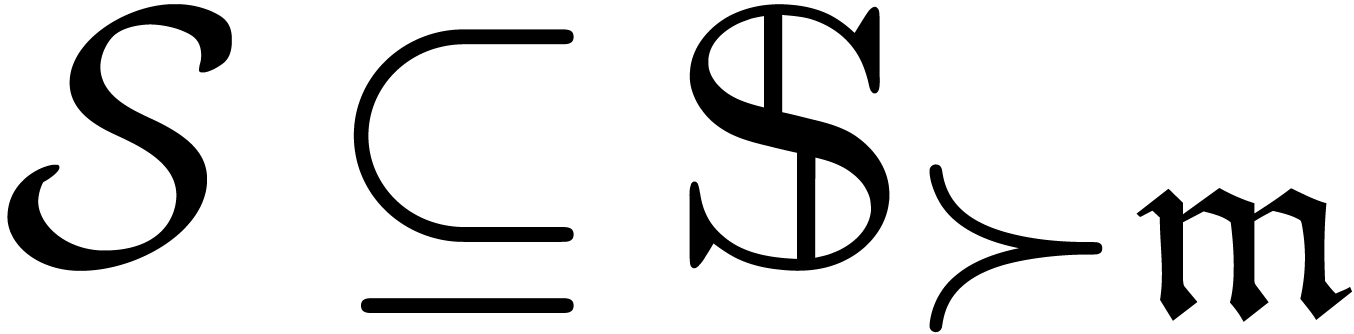 we have an algorithm to compute the
truncated reduction
we have an algorithm to compute the
truncated reduction  .
Similarly, for
.
Similarly, for  , we can
compute the truncated S-polynomial
, we can
compute the truncated S-polynomial  . When using these truncated variants of reduction
and S-polynomials, the local analogue of Buchberger's algorithm
terminates, since all computations take place in a finite dimensional
vector space. This provides us with an algorithm to compute
. When using these truncated variants of reduction
and S-polynomials, the local analogue of Buchberger's algorithm
terminates, since all computations take place in a finite dimensional
vector space. This provides us with an algorithm to compute  , together with a matrix
, together with a matrix 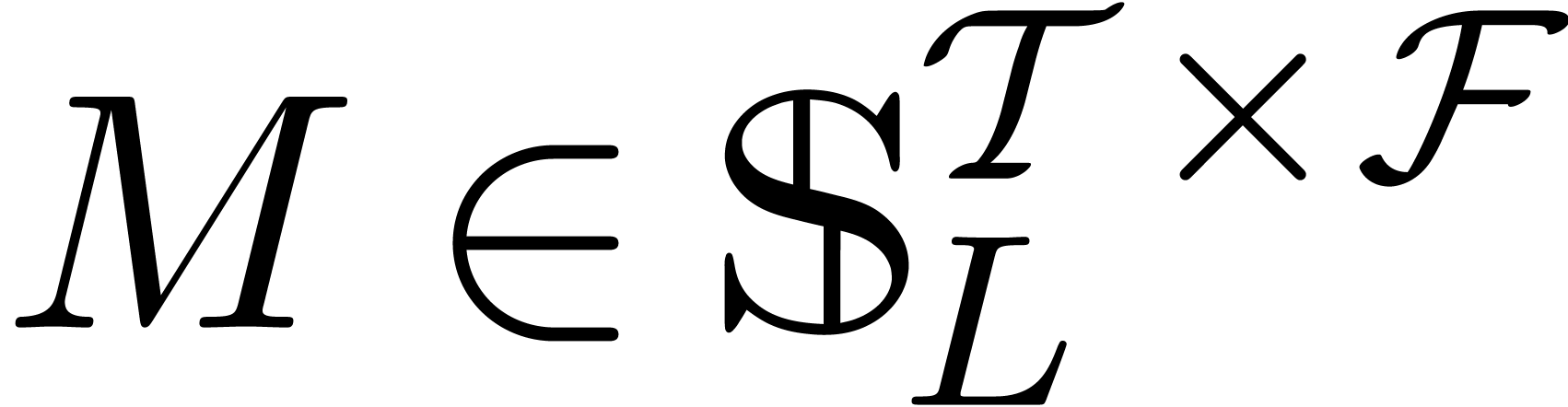 such that
such that 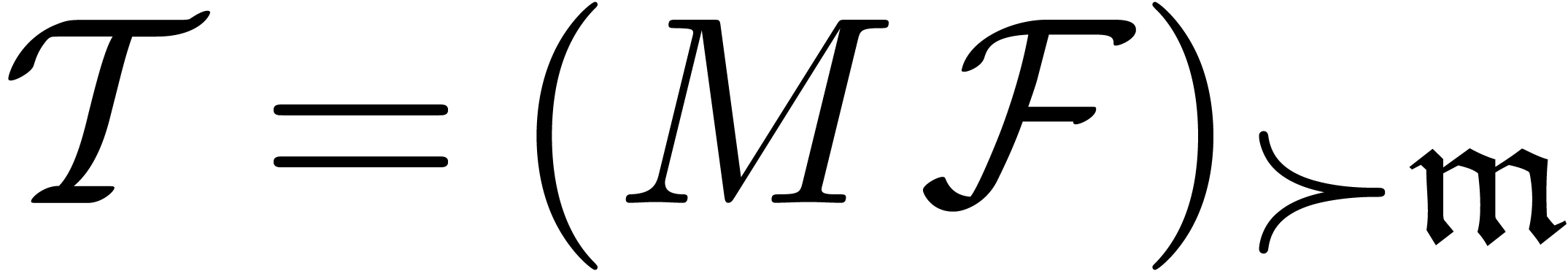 .
.
Let  be a standard basis of an ideal
be a standard basis of an ideal  of
of  , let
, let  , and let
, and let  be defined as in (3). In a similar way as at the end of
section 5, one can show that
be defined as in (3). In a similar way as at the end of
section 5, one can show that
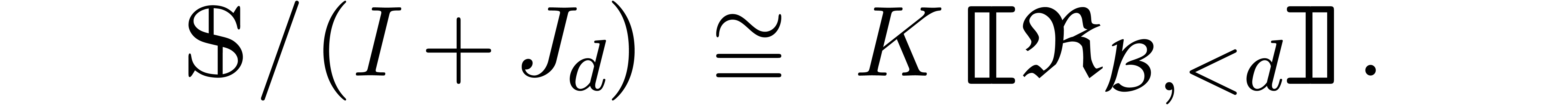
Moreover,  and the dimension of
and the dimension of 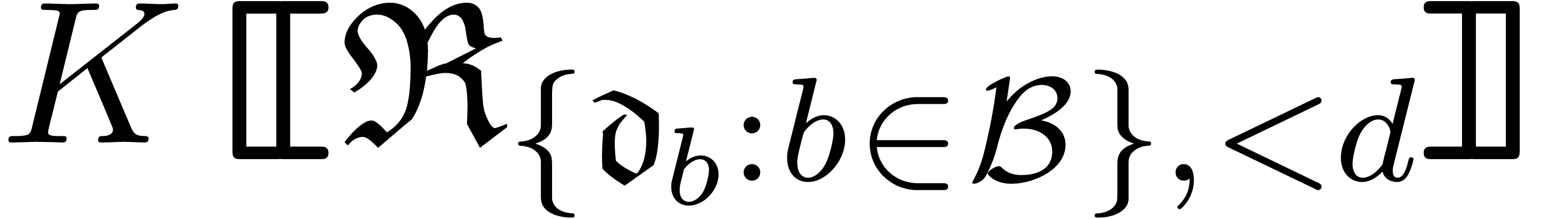 can be computed by the familiar technique of counting boxes below a
Gröbner staircase. In other words, if we know a standard basis
can be computed by the familiar technique of counting boxes below a
Gröbner staircase. In other words, if we know a standard basis 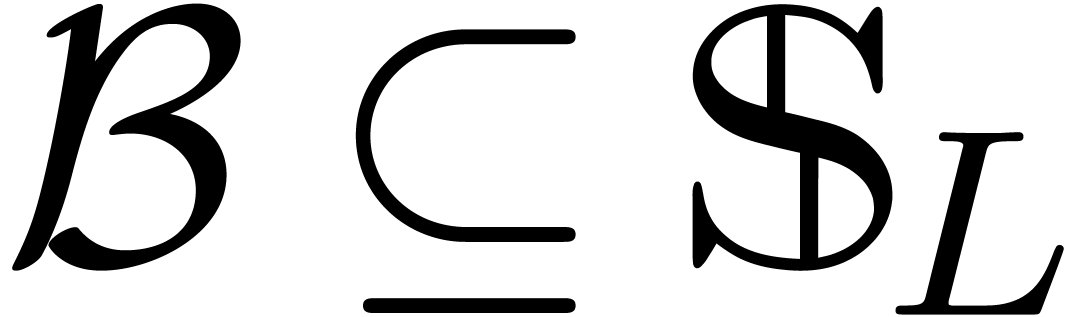 of an ideal
of an ideal  of
of  , then we can compute the Hilbert function of
, then we can compute the Hilbert function of
 .
.
In this subsection we show that the Hilbert function of  also provides us with information about the possible shapes of standard
bases for
also provides us with information about the possible shapes of standard
bases for  . We will assume
that the monomial ordering
. We will assume
that the monomial ordering  on
on  is Archimedean in the sense that for any
is Archimedean in the sense that for any  , there exists a
, there exists a  with
with  . In particular, the set
. In particular, the set  is finite for any
is finite for any  .
.
Theorem  be a finite subset of
be a finite subset of  and assume that the monomial ordering
and assume that the monomial ordering  on
on  is Archimedean. Then there exists an algorithm to
compute a standard basis
is Archimedean. Then there exists an algorithm to
compute a standard basis  for
for  , together with a matrix
, together with a matrix 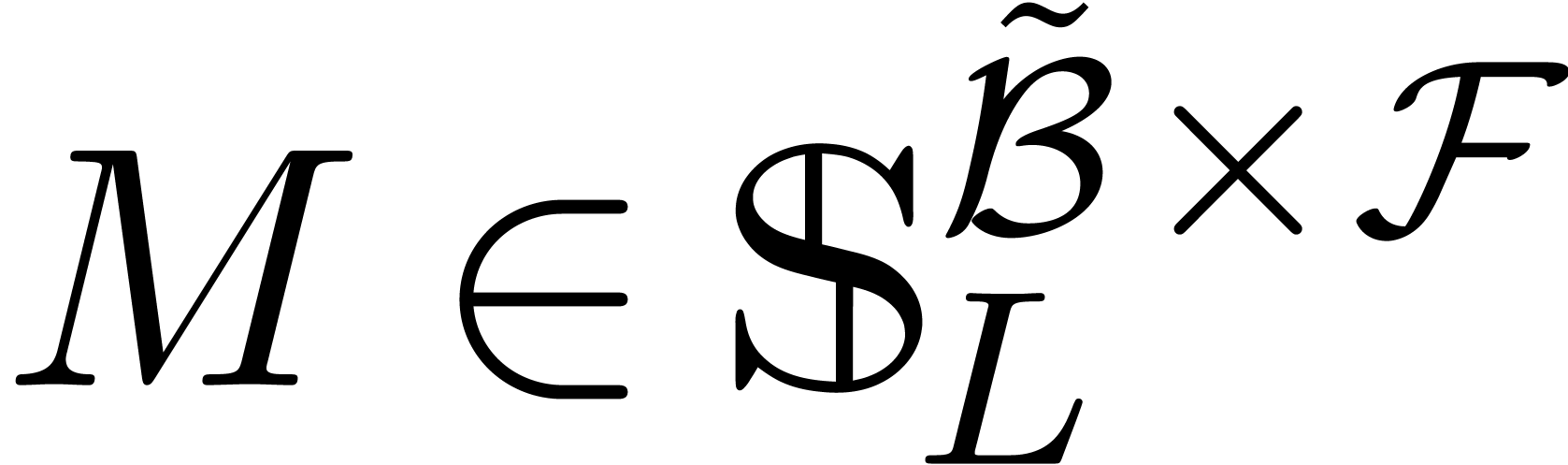 with
with 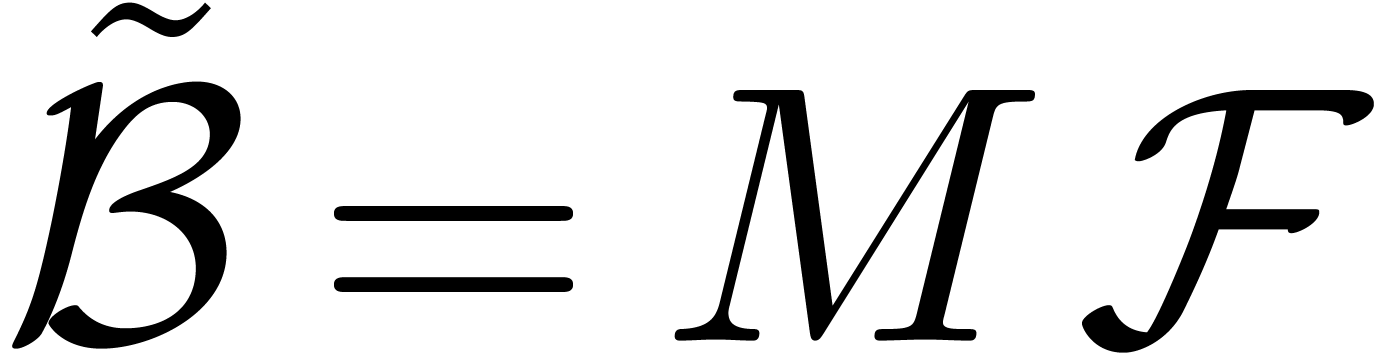 .
.
Proof. Using the techniques from Section 5,
we can compute the Hilbert function  of
of  . Let
. Let  be
the reduced standard basis of
be
the reduced standard basis of  and
and  . Since
. Since  is Archimedean,
the set
is Archimedean,
the set  is finite. We have shown above that this
allows us to compute
is finite. We have shown above that this
allows us to compute 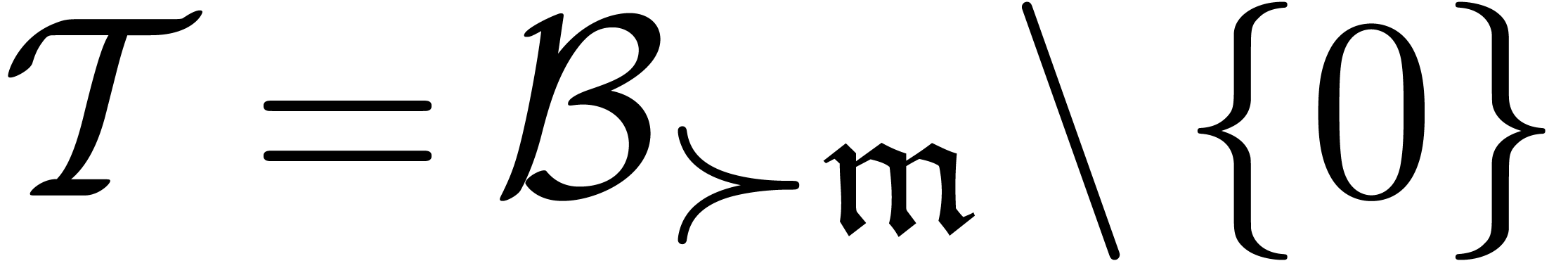 , as
well as a matrix
, as
well as a matrix 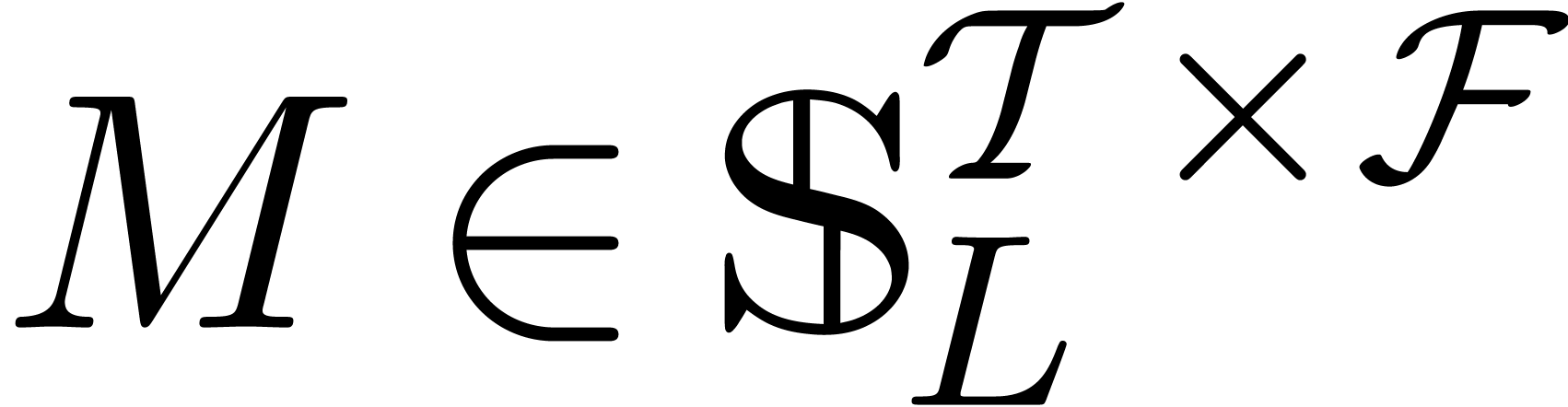 with
with 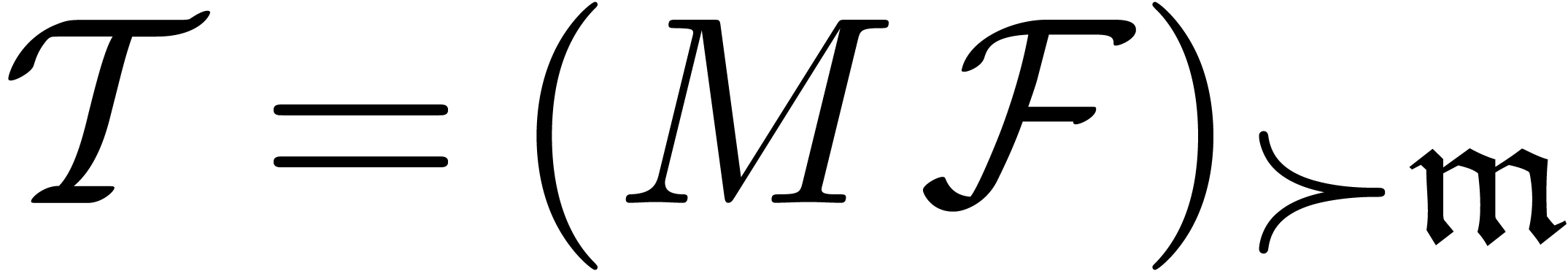 . Let
. Let 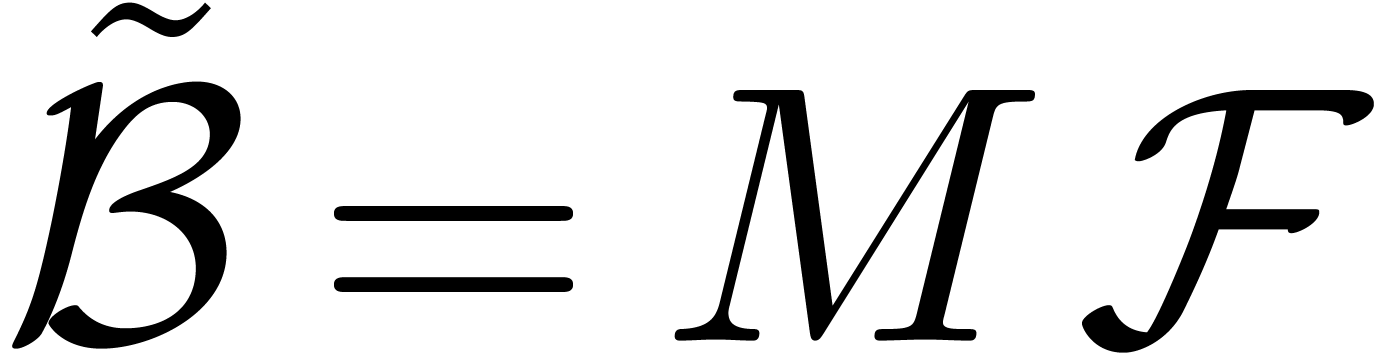 .
Given
.
Given  , there exists a
, there exists a  with
with  and
and  . Consequently,
. Consequently, 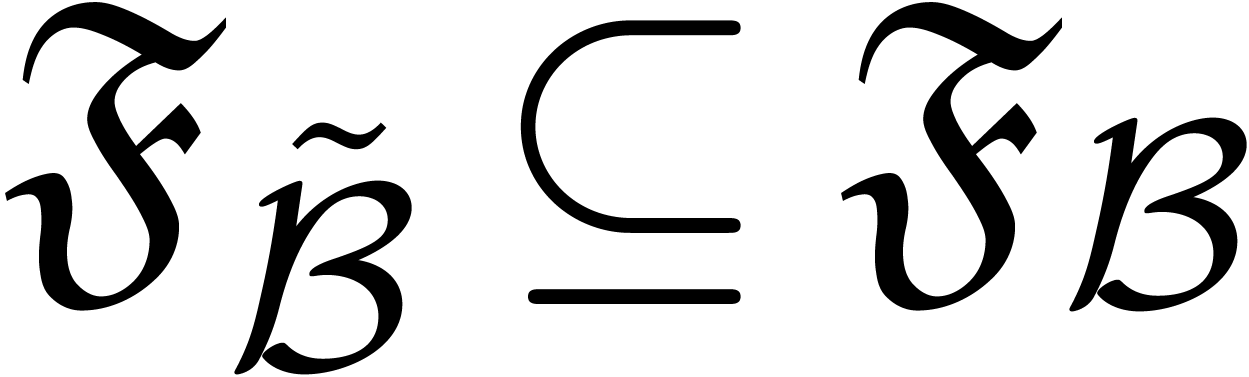 .
Now we may also compute the Hilbert function
.
Now we may also compute the Hilbert function  of
the ideal
of
the ideal 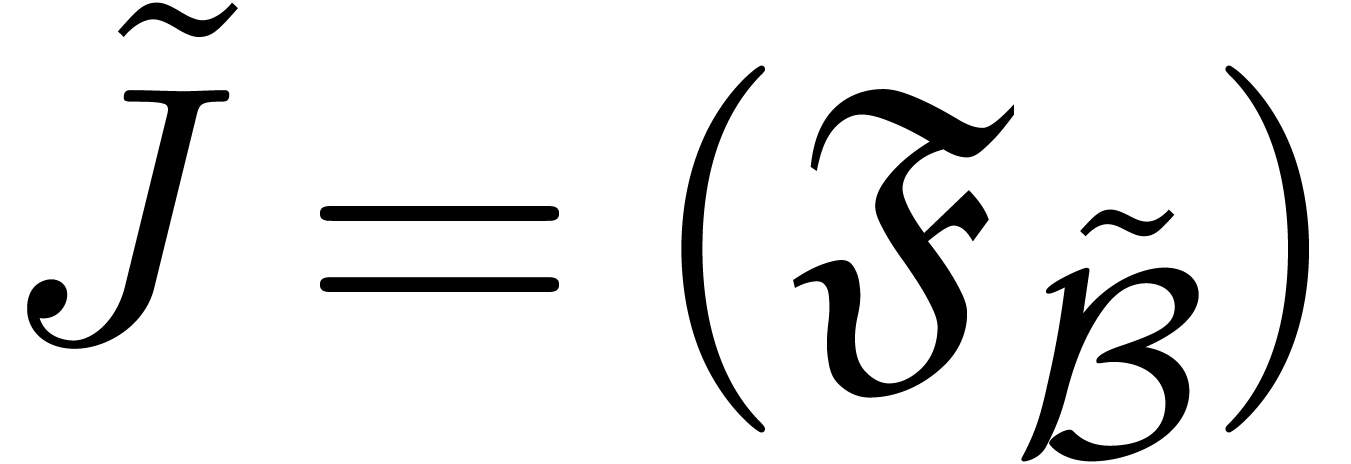 . We claim that
. We claim that
 is a standard basis for
is a standard basis for  if and only if
if and only if 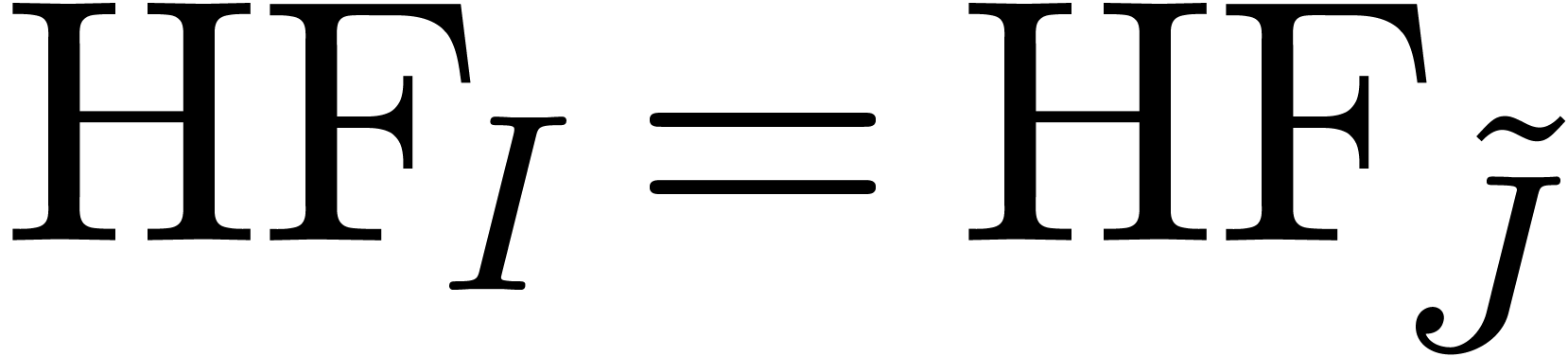 . Indeed, we
have
. Indeed, we
have 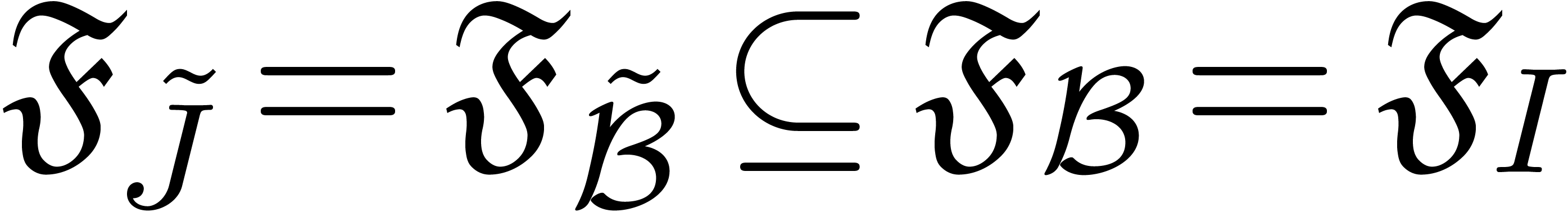 , so
, so 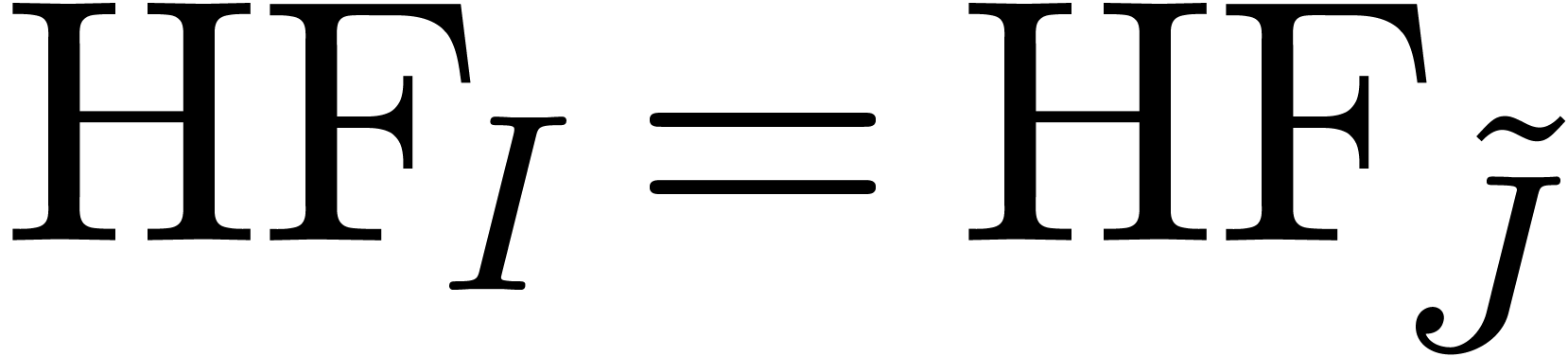 if and only if
if and only if 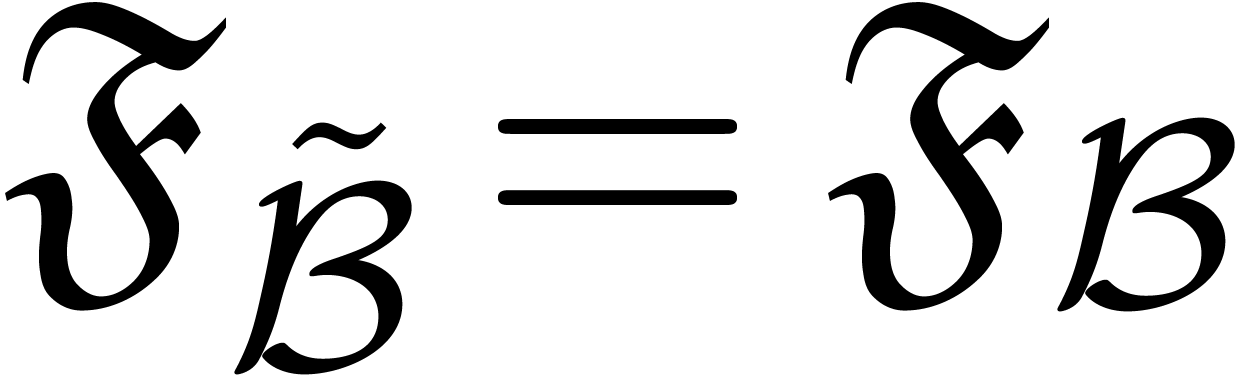 . By
definition, a subset
. By
definition, a subset 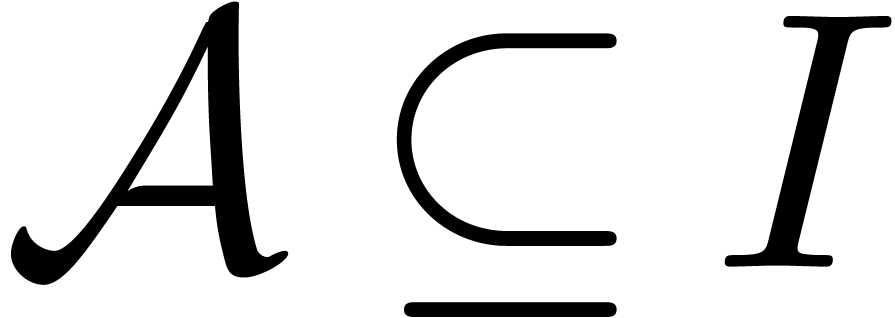 is a standard basis of
is a standard basis of  if and only
if and only  .
.
In order to compute a standard basis, we pick smaller and smaller
elements  for
for  ,
and perform the above computations until we have
,
and perform the above computations until we have  . Since
. Since  is Archimedean,
is Archimedean,  eventually becomes sufficiently small so that
eventually becomes sufficiently small so that  for all
for all 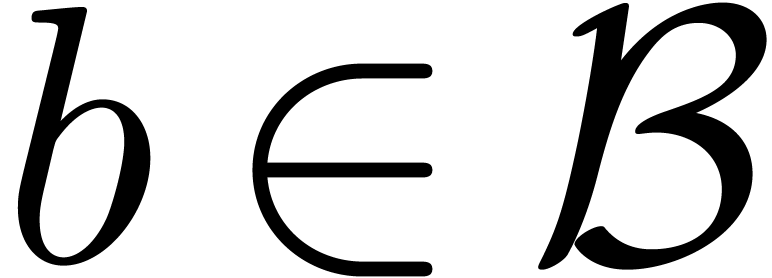 .
At that point, we necessarily have
.
At that point, we necessarily have 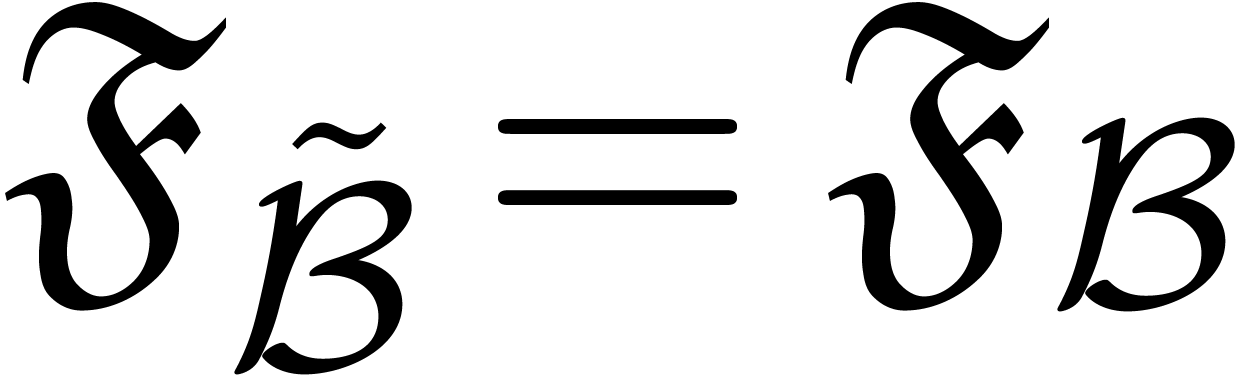 and
and 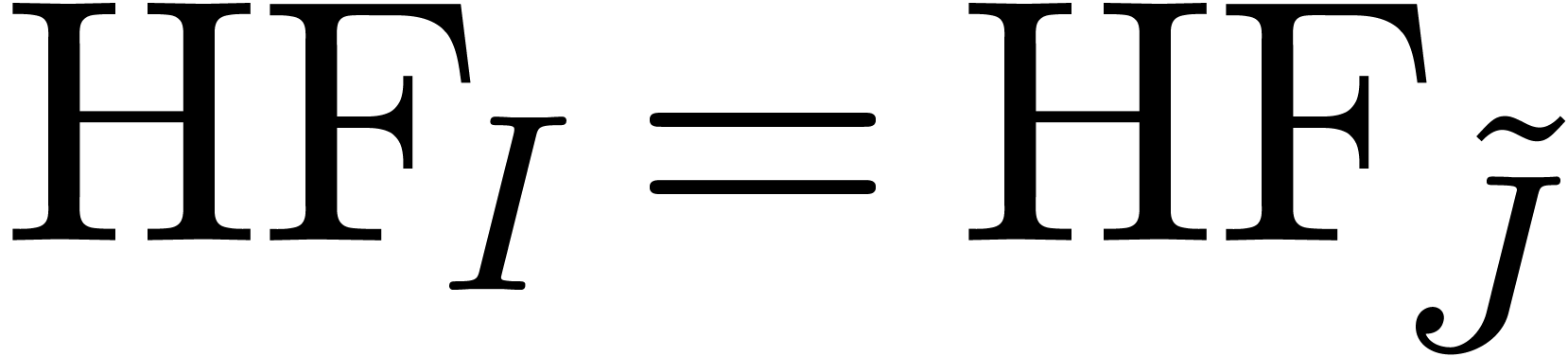 . This proves the termination of
our algorithm.
. This proves the termination of
our algorithm.
Let 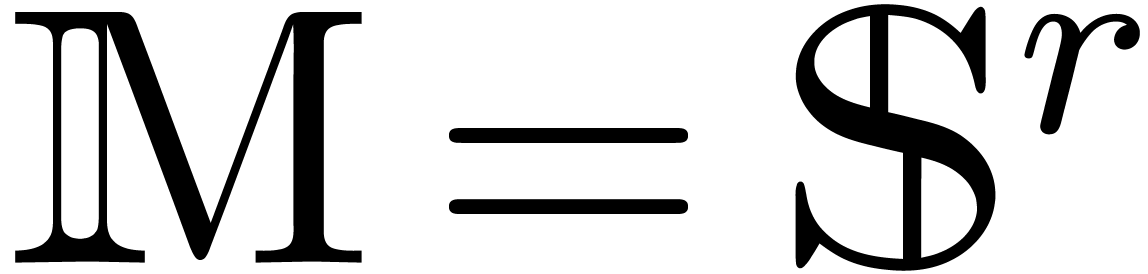 ,
, 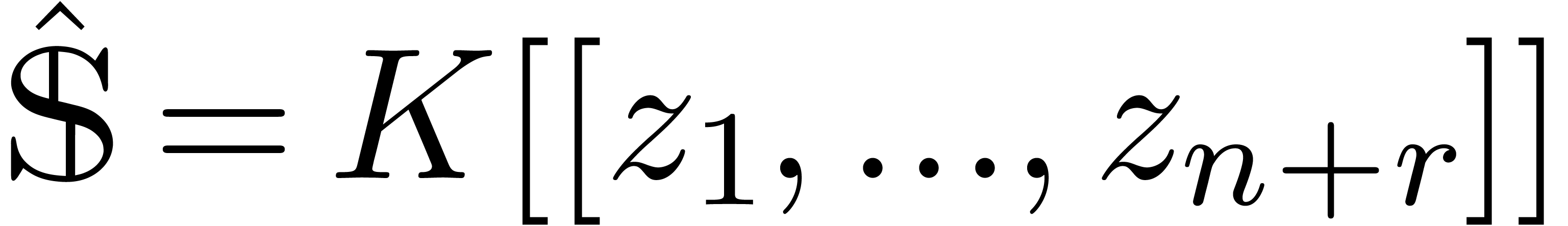 be as at the end of section 5, as well as the further
notations
be as at the end of section 5, as well as the further
notations  ,
,  and
and  . Assume also that the
monomial ordering on
. Assume also that the
monomial ordering on  has been extended to
has been extended to 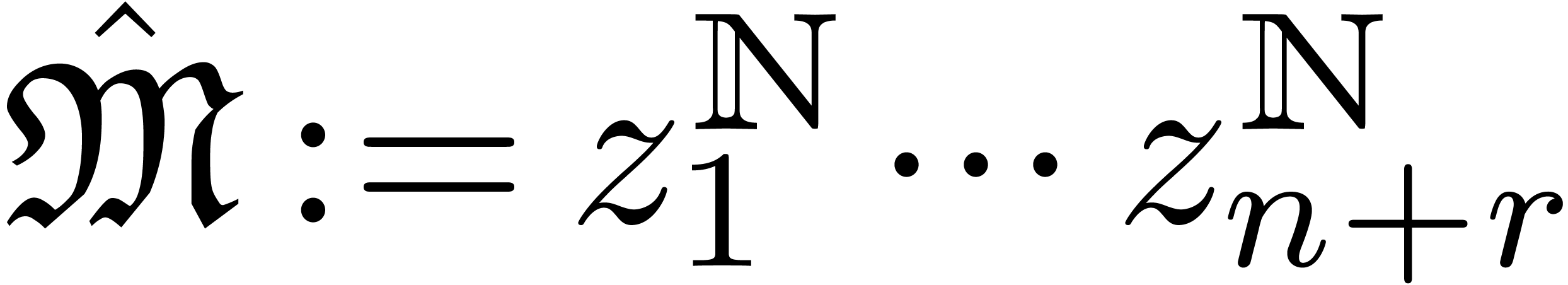 in such a way that
in such a way that  .
.
Given an  -submodule
-submodule  of
of  , a subset
, a subset
 of
of  is defined to be a
standard basis for
is defined to be a
standard basis for  if
if 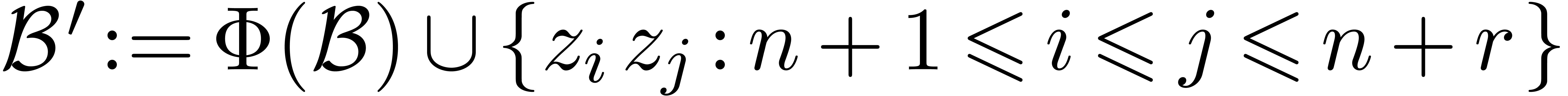 is a standard basis for the ideal
is a standard basis for the ideal  of
of  . Given such a standard basis, we
may compute the Hilbert function of
. Given such a standard basis, we
may compute the Hilbert function of  using
using 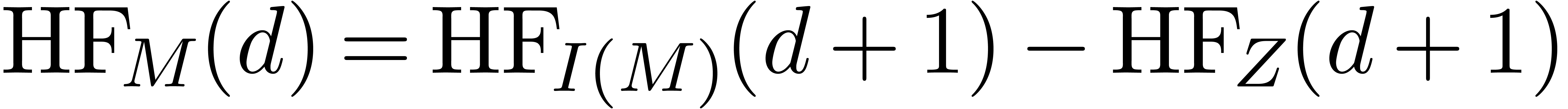 , by counting boxes below the
standard bases
, by counting boxes below the
standard bases  and
and  of
of
 and
and  .
.
Given a subset  and a monomial
and a monomial  , we denote
, we denote  ,
and we define
,
and we define  ,
etc. likewise. We again have
,
etc. likewise. We again have 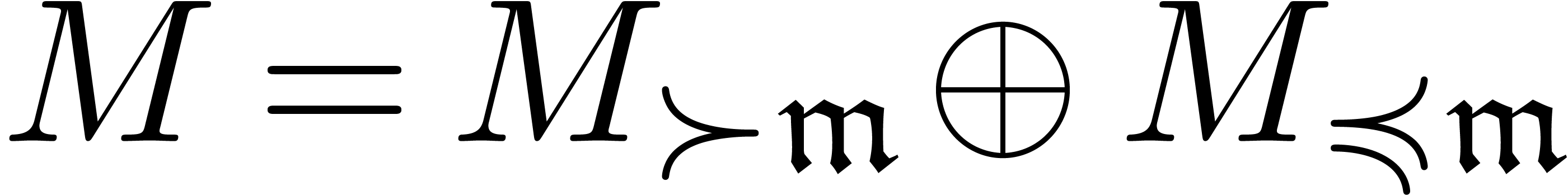 ,
where
,
where 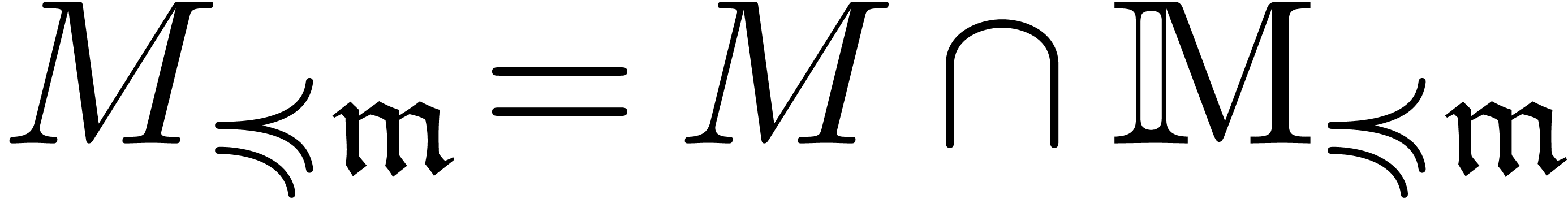 is an
is an  -module.
The notions of truncated reduction and truncated
S-“polynomials” readily generalize to modules (the
S-polynomial of
-module.
The notions of truncated reduction and truncated
S-“polynomials” readily generalize to modules (the
S-polynomial of  and
and  with
with
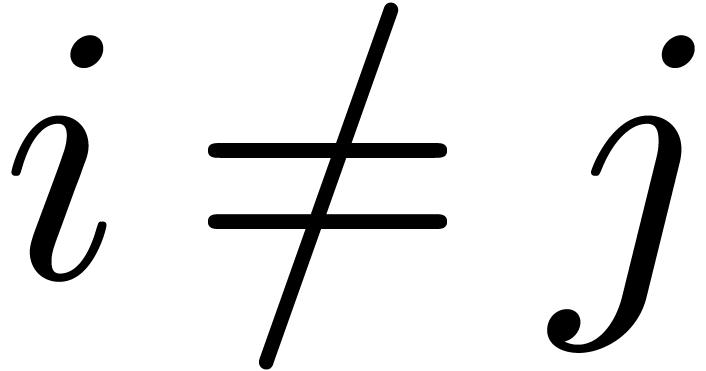 being zero, by definition) and it can be shown
that the same holds for Theorem 15. In fact, we are up to
proving something even better.
being zero, by definition) and it can be shown
that the same holds for Theorem 15. In fact, we are up to
proving something even better.
Modulo a permutation of variables, we may assume without loss of
generality that  . The
Archimedean rank of
. The
Archimedean rank of  is defined to be
the number of indices
is defined to be
the number of indices  such that
such that  or
or  and
and  for all
for all 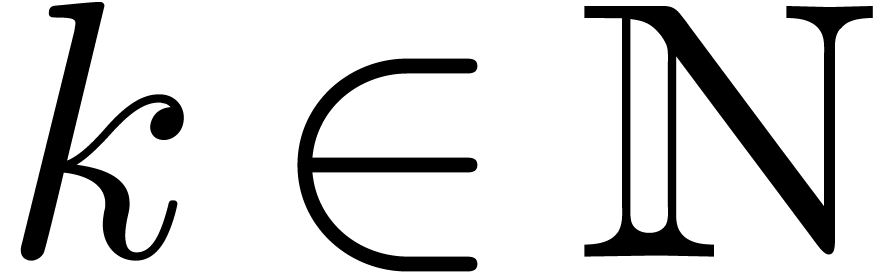 . Given a finite subset
. Given a finite subset  of
of 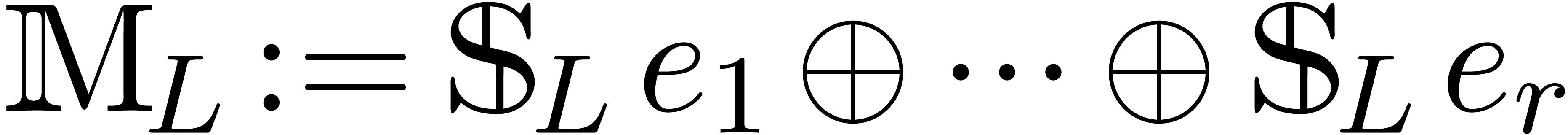 , we also
denote by
, we also
denote by  the
the  -module
generated by
-module
generated by  .
.
Theorem  be a finite subset of
be a finite subset of  . Then there exists an algorithm to compute a
standard basis
. Then there exists an algorithm to compute a
standard basis  for
for 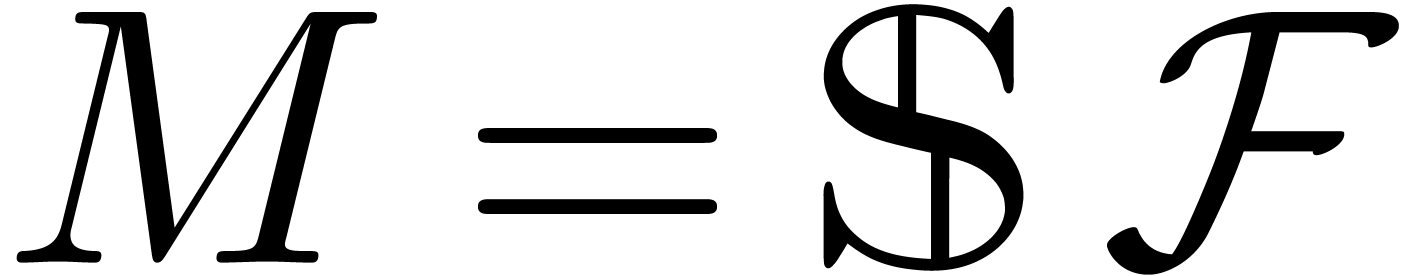 ,
together with a matrix
,
together with a matrix 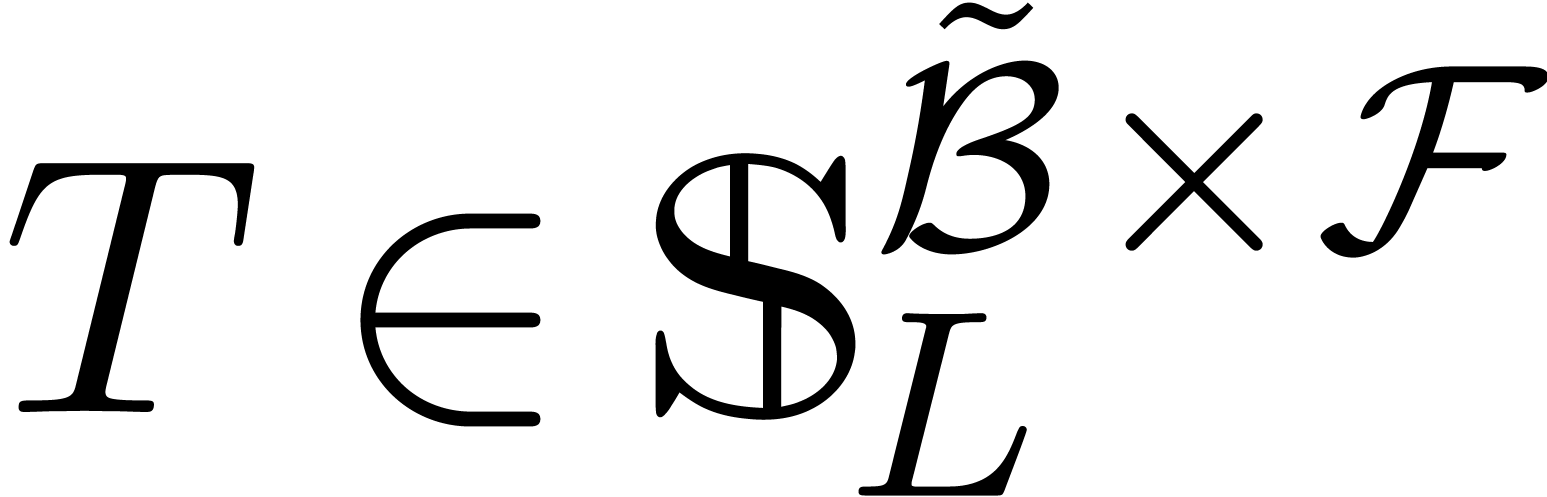 with
with 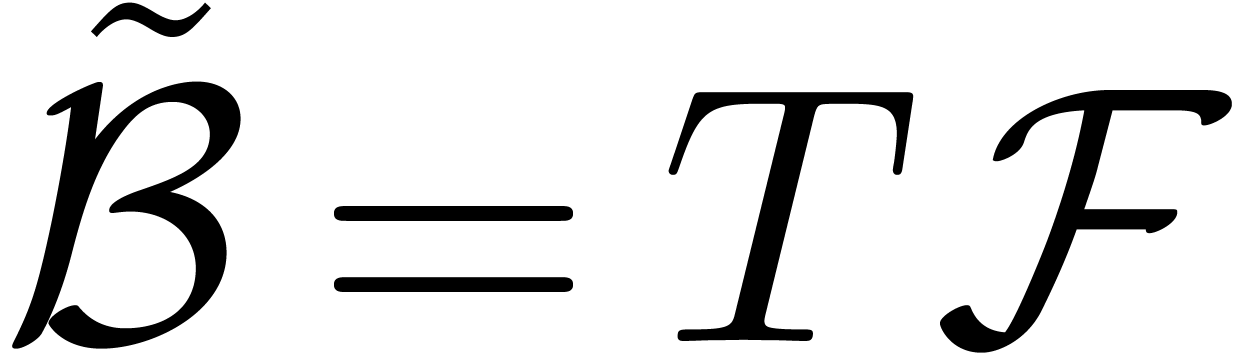 .
.
Proof. We proceed by induction over the Archimedean
rank  of
of  .
If
.
If 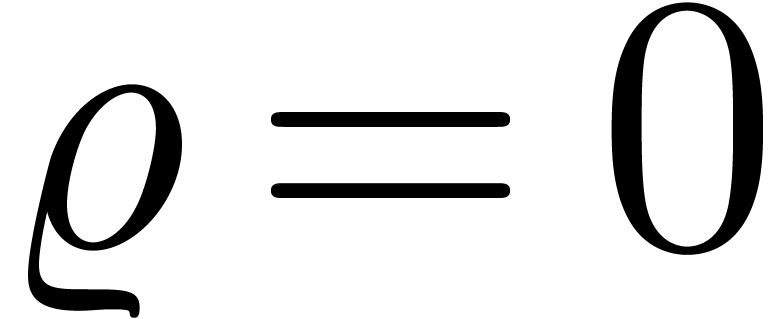 , then the result is
obvious. So assume that
, then the result is
obvious. So assume that  and let
and let 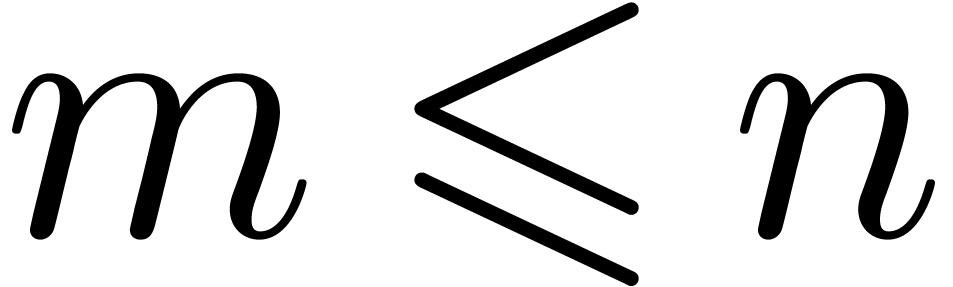 be maximal such that
be maximal such that 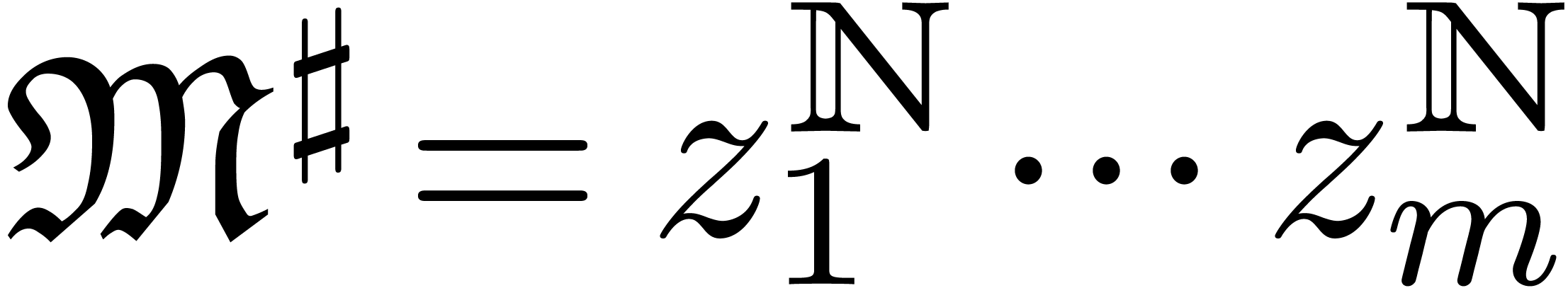 has Archimedean rank one.
We denote
has Archimedean rank one.
We denote 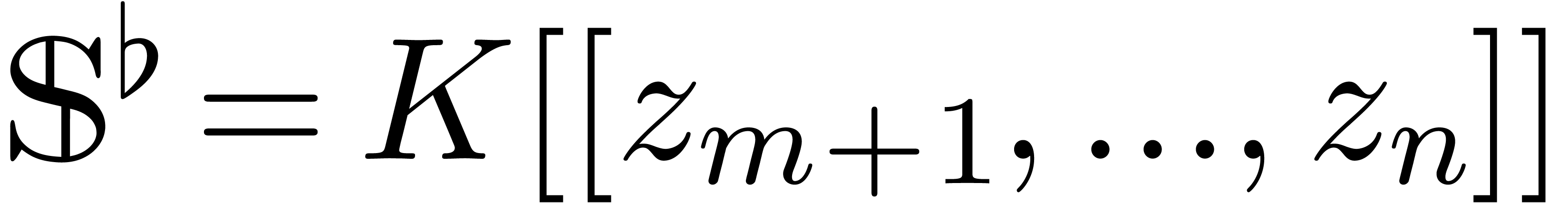 and notice that
and notice that 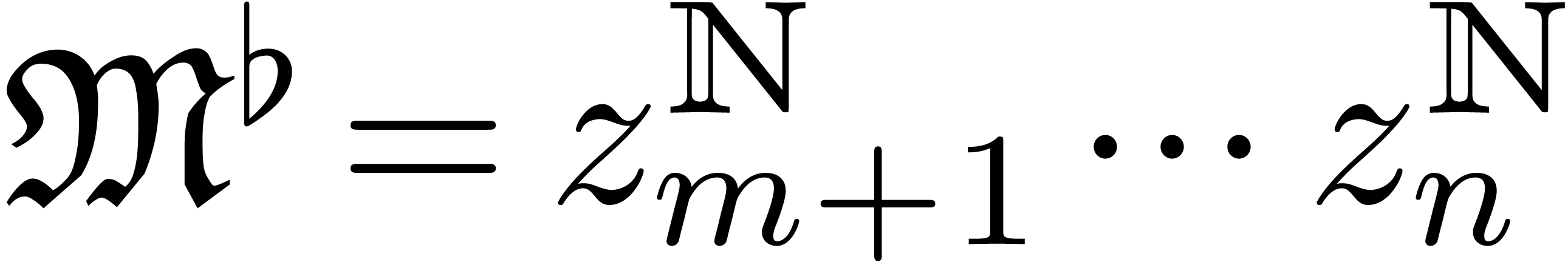 has Archimedean rank
has Archimedean rank  .
.
Given 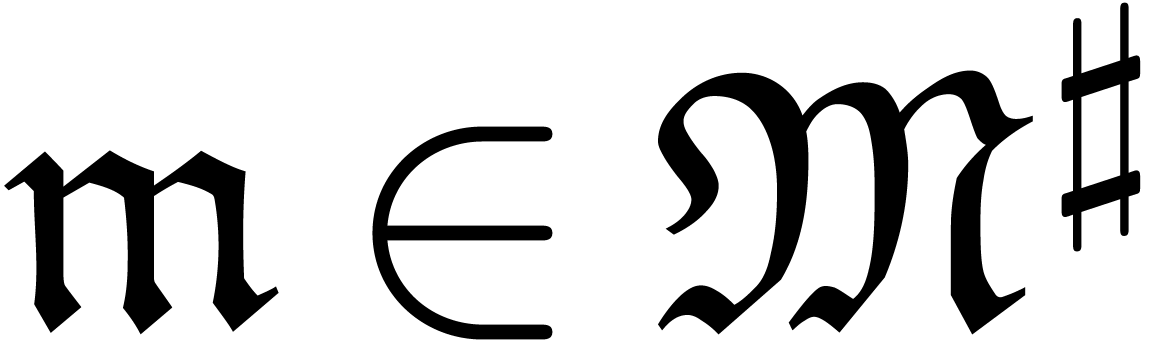 , we notice that the
truncation
, we notice that the
truncation  is a free finite dimensional
is a free finite dimensional  -module. By the induction
hypothesis, it follows that we can compute a standard basis for the
-module. By the induction
hypothesis, it follows that we can compute a standard basis for the
 -submodule generated by any
finite subset
-submodule generated by any
finite subset  of
of  .
Given
.
Given 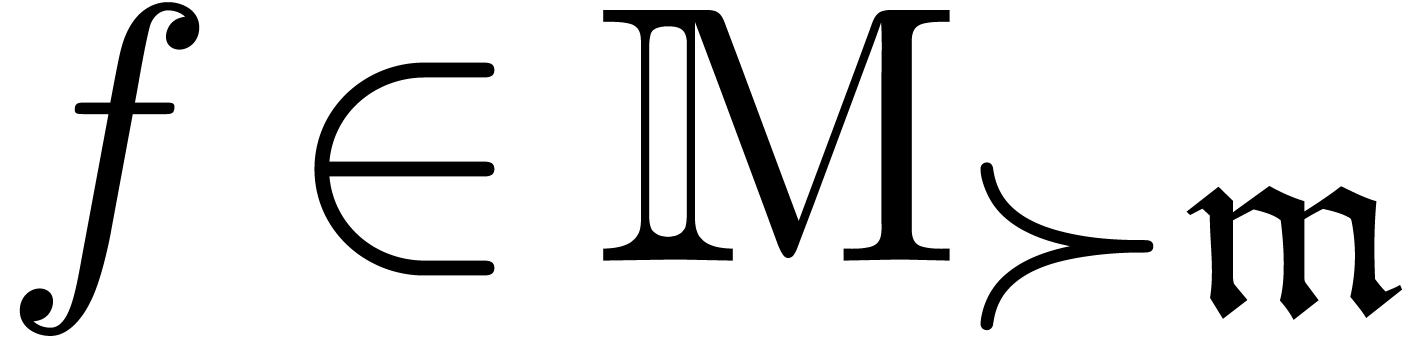 , we can also check
whether
, we can also check
whether 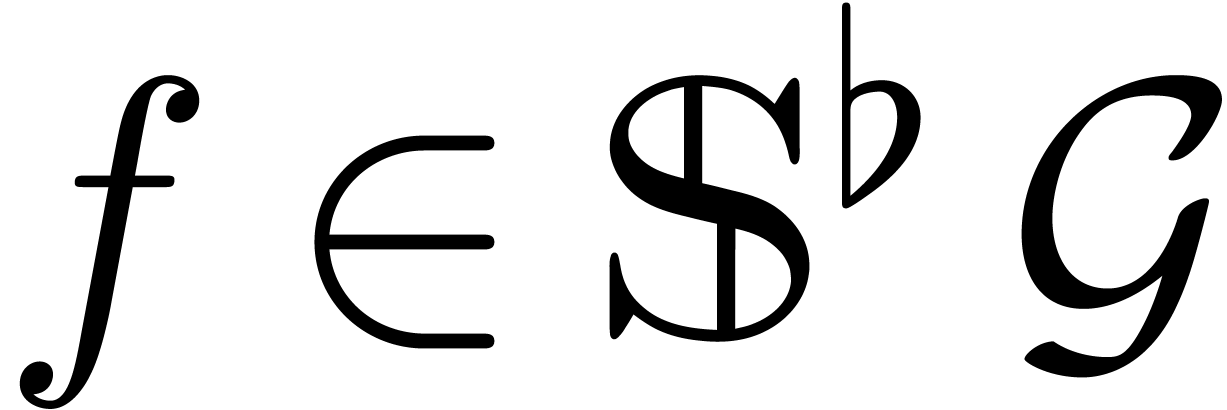 : it suffices to
decide whether the Hilbert functions of
: it suffices to
decide whether the Hilbert functions of  and
and 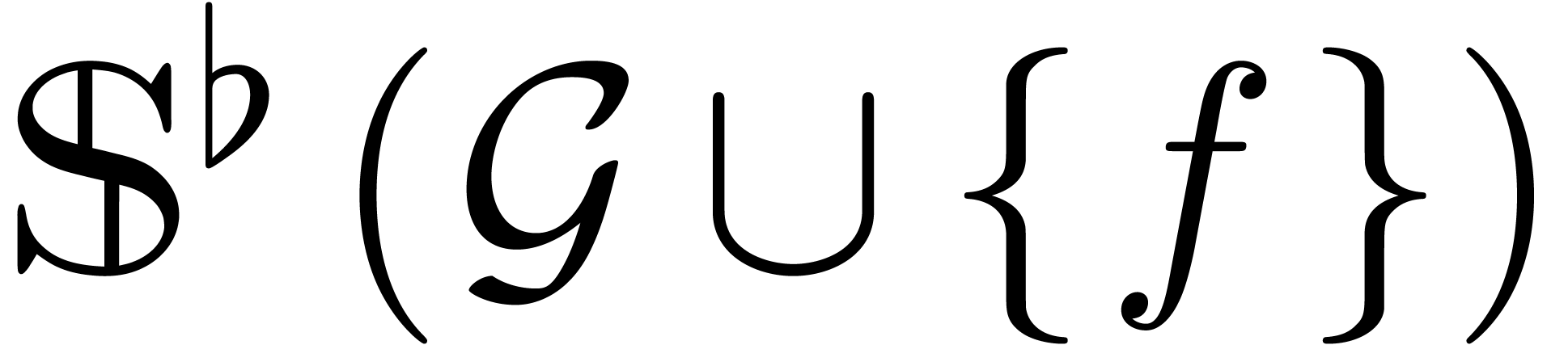 coincide.
coincide.
Given a finite subset  of
of  as above, we say that
as above, we say that  is stable if for
all
is stable if for
all 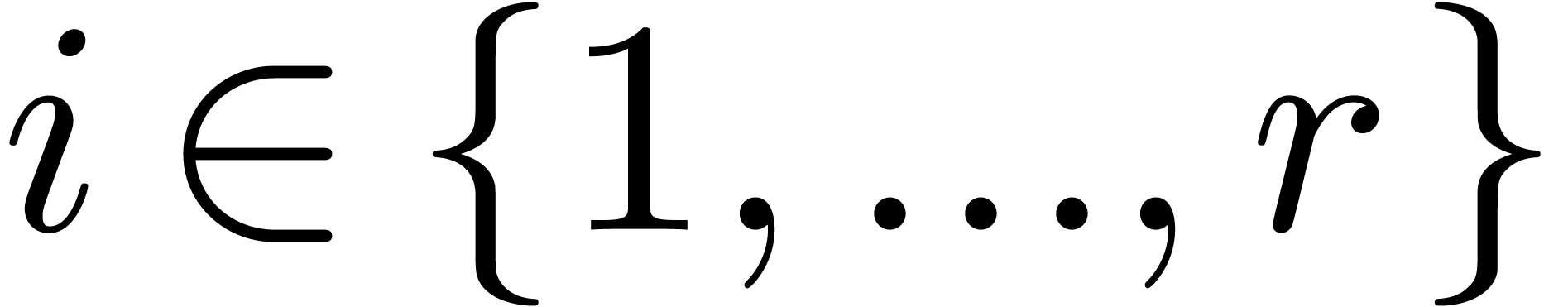 ,
, 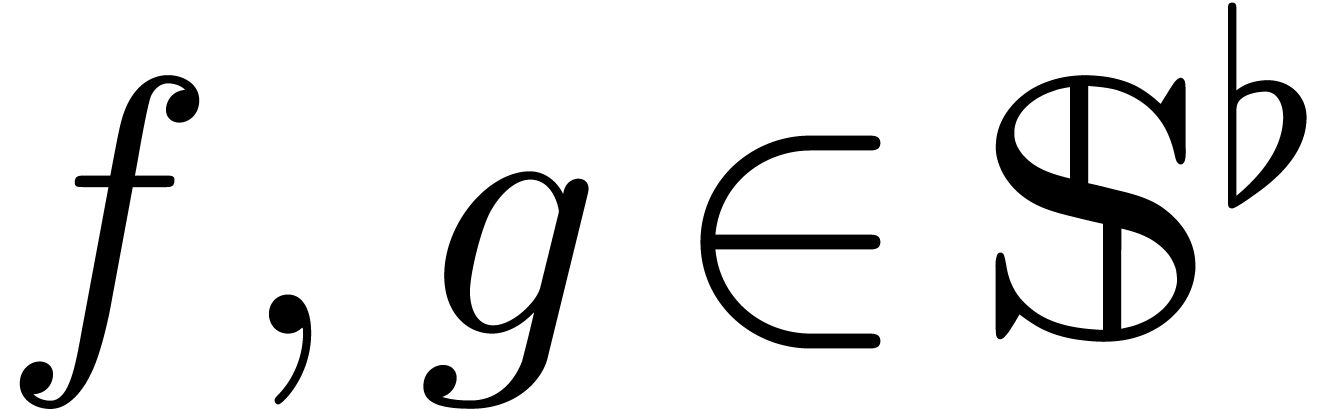 , and
, and 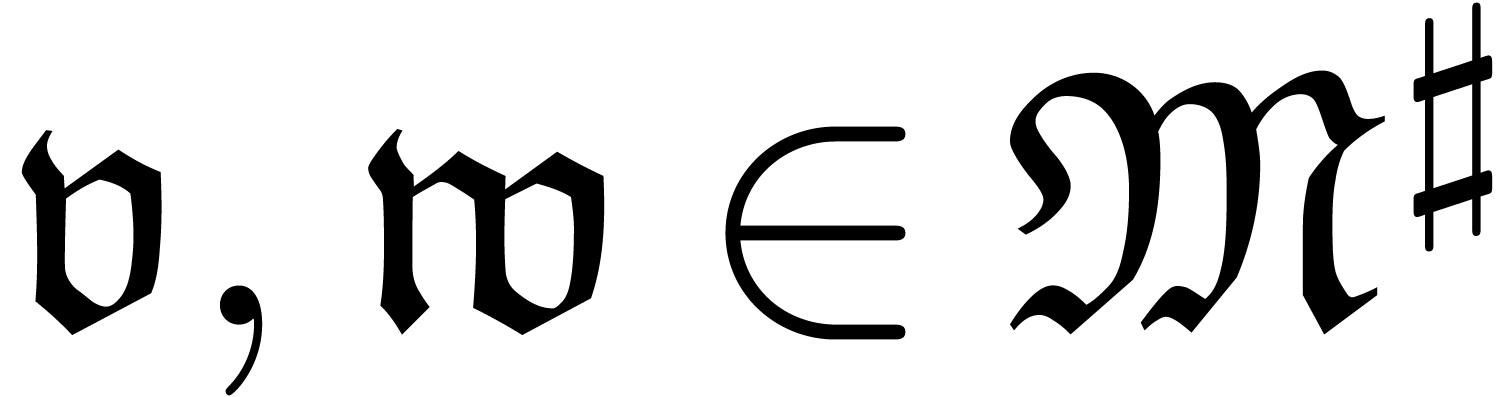 with
with  and
and  , we have
, we have
If 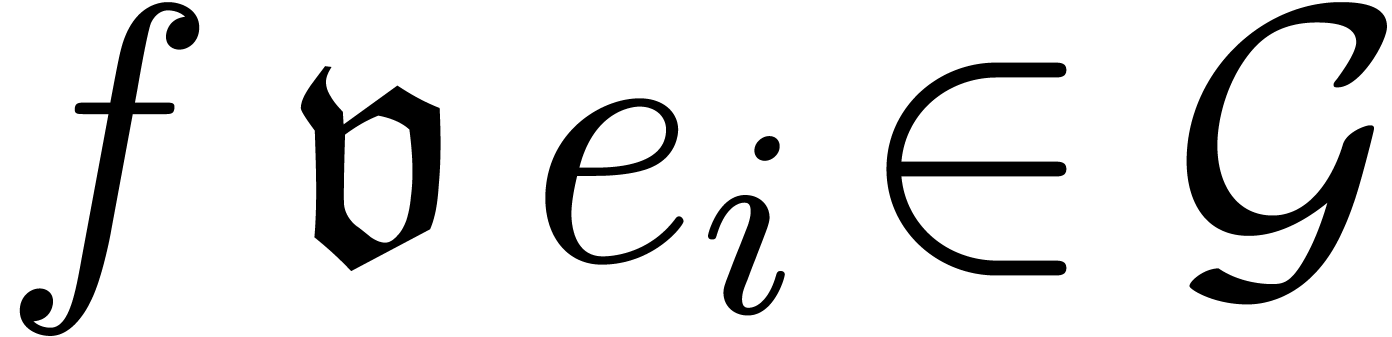 and
and 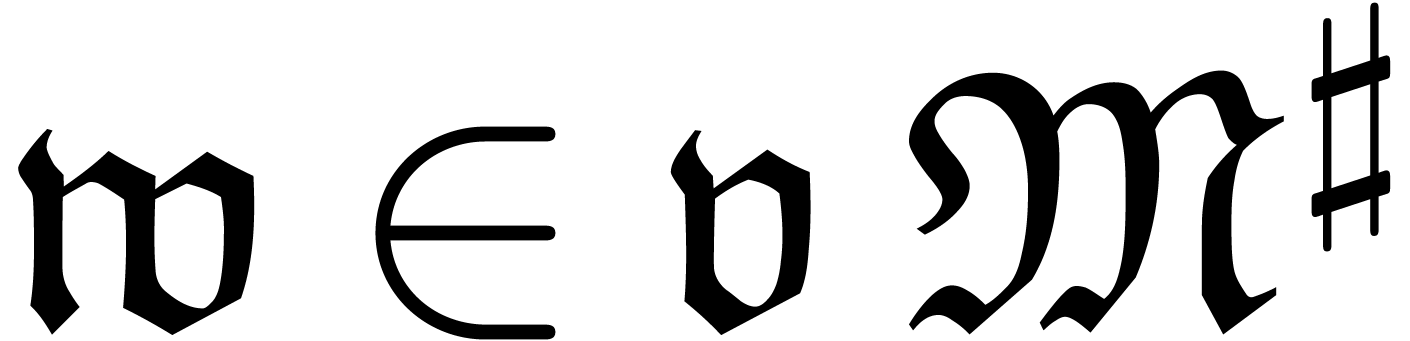 ,
then
,
then 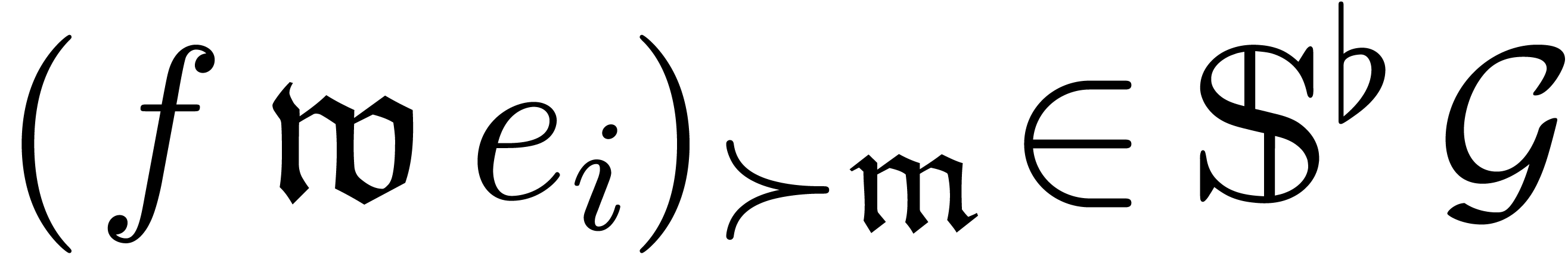 .
.
If 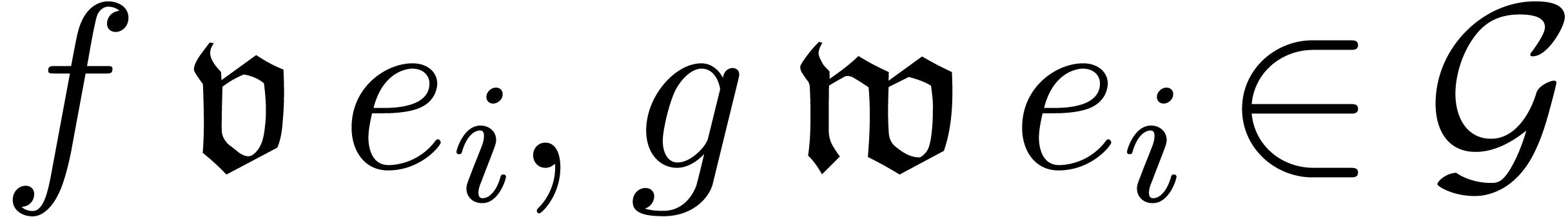 and
and 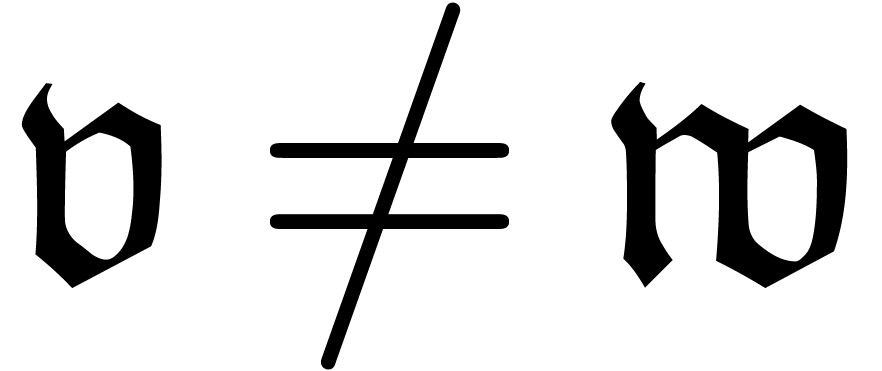 ,
then
,
then 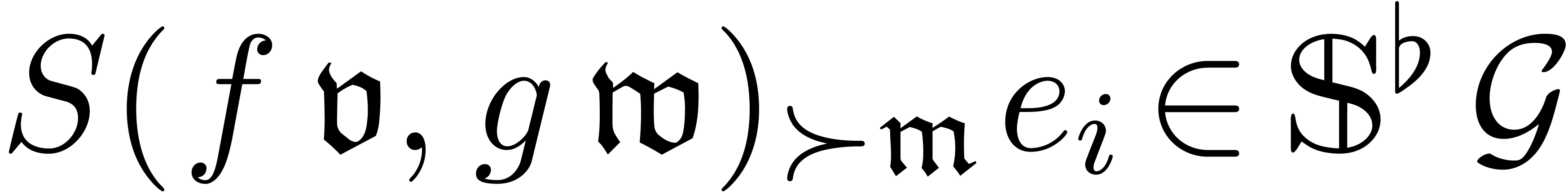 .
.
By what precedes, we have an algorithm to check whether  is stable. If not, then we may keep enlarging
is stable. If not, then we may keep enlarging  with elements of the form
with elements of the form 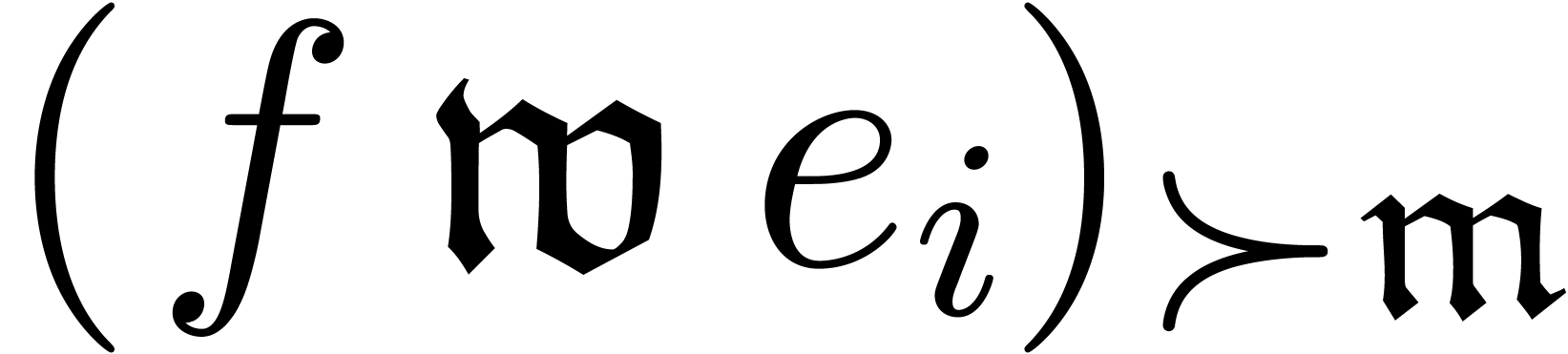 or
or 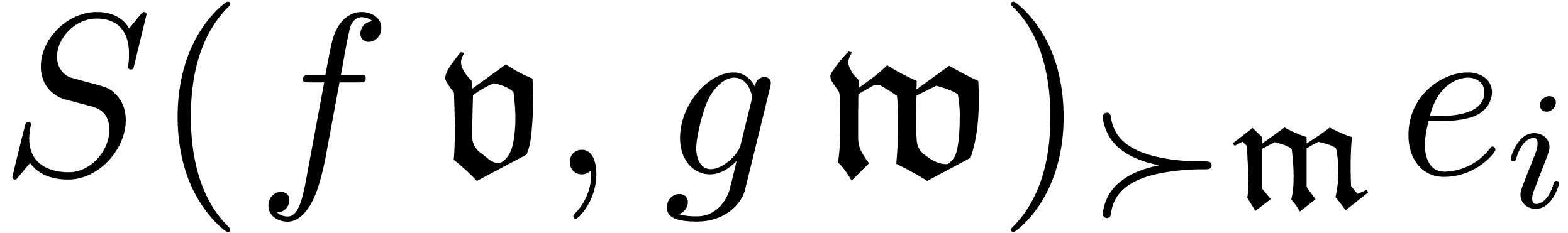 until stabilization takes place. Due to the Noetherianity of
until stabilization takes place. Due to the Noetherianity of  , this happens after a finite
number of steps.
, this happens after a finite
number of steps.
In other words, given 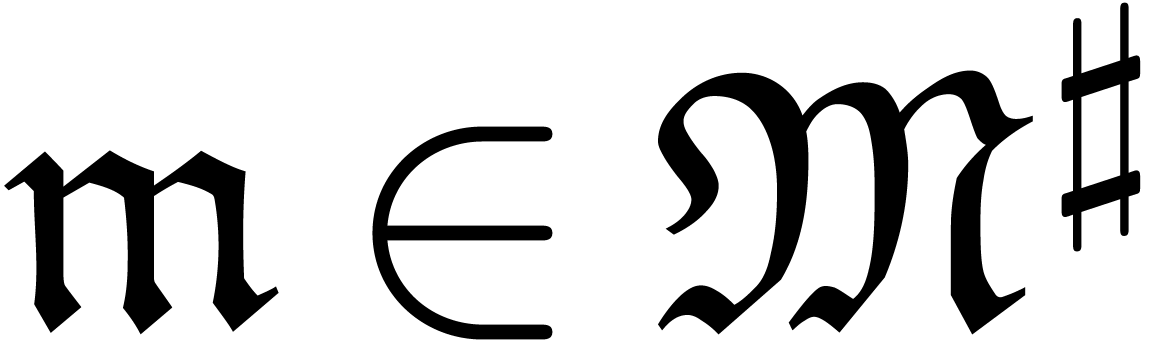 , the
above procedure allows us to compute a stable standard basis
, the
above procedure allows us to compute a stable standard basis  for the
for the  -module
-module
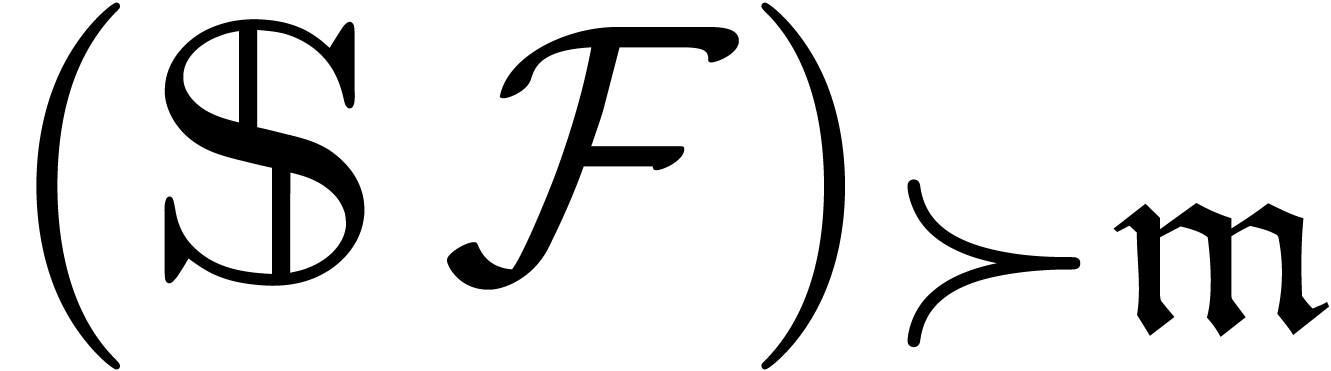 together with the matrix
together with the matrix 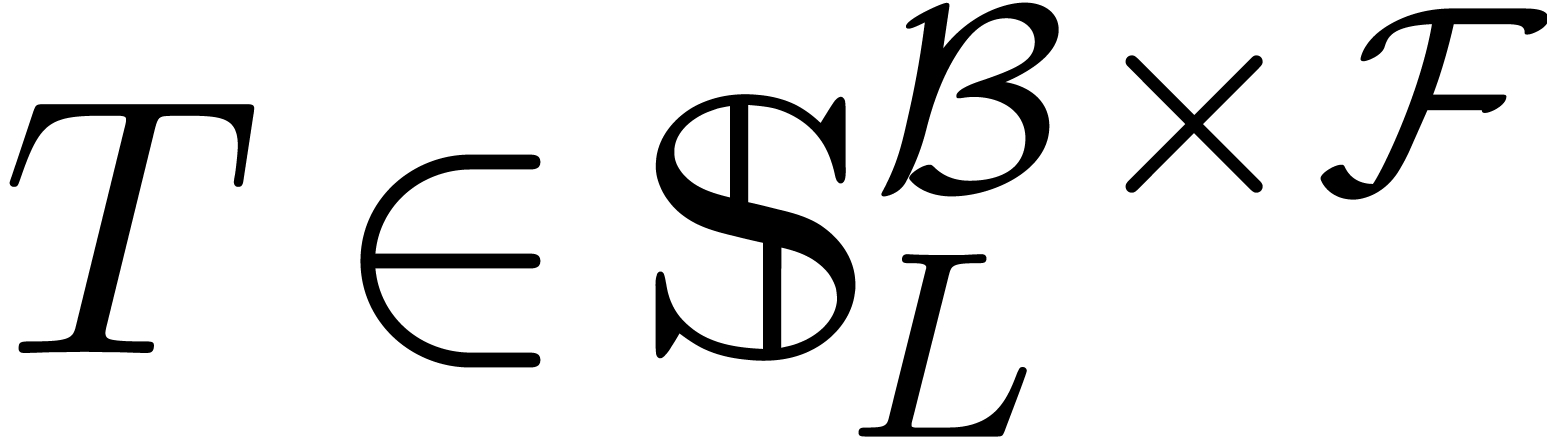 for which
for which 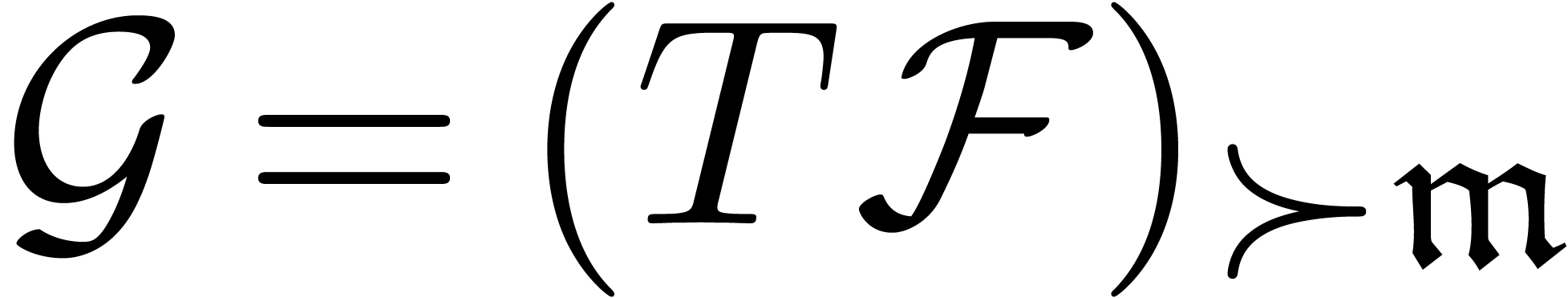 . Let
. Let 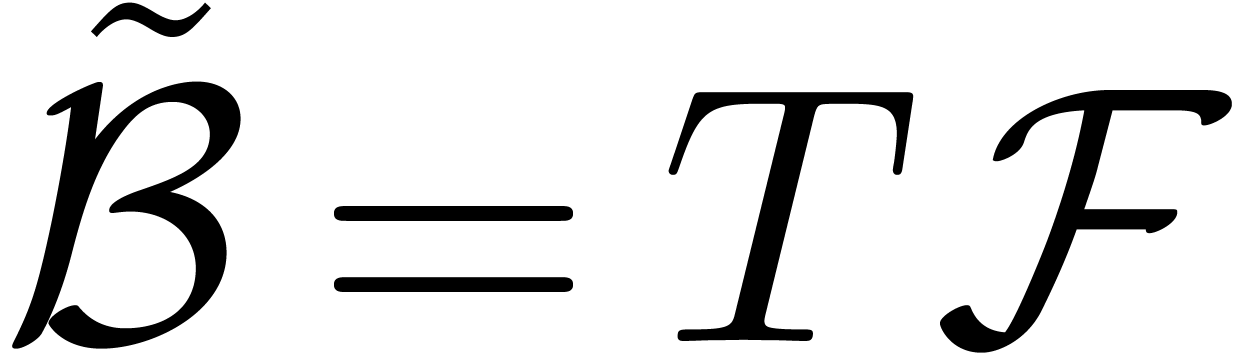 . Since
. Since  is Archimedean,
a similar reasoning as in the proof of Theorem 15 shows
that the Hilbert functions of
is Archimedean,
a similar reasoning as in the proof of Theorem 15 shows
that the Hilbert functions of  and
and  coincide for a sufficiently small
coincide for a sufficiently small  . At that point,
. At that point,  contains
the desired standard basis of
contains
the desired standard basis of  .
.
M. E. Alonso, F. J. Castro-Jiménez, and H. Hauser. Encoding algebraic power series. Technical report, ArXiv, 2014. http://arxiv.org/abs/1403.4104.
M. E. Alonso, T. Mora, and R. Raimondo. A computational model for algebraic power series. J. Pure and Appl. Alg., 77:1–38, 1992.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
R. P. Brent and H. T. Kung. Fast algorithms for manipulating formal power series. Journal of the ACM, 25:581–595, 1978.
J. Della Dora, C. Dicrescenzo, and D. Duval. A new method for computing in algebraic number fields. In G. Goos and J. Hartmanis, editors, Eurocal'85 (2), volume 174 of Lect. Notes in Comp. Science, pages 321–326. Springer, 1985.
J. Denef and L. Lipshitz. Ultraproducts and approximation in local rings. Math. Ann., 253:1–28, 1980.
J. Denef and L. Lipshitz. Power series solutions of algebraic differential equations. Math. Ann., 267:213–238, 1984.
J. Denef and L. Lipshitz. Decision problems for differential equations. The Journ. of Symb. Logic, 54(3):941–950, 1989.
L. van den Dries. On the elementary theory of restricted elementary functions. J. Symb. Logic, 53(3):796–808, 1988.
H. Hironaka. Resolution of singularities of an algebraic variety over a field of characteristic zero. Annals of Math., 79:109–326, 1964.
H. Hironaka. Idealistic exponents of singularity. In Algebraic geometry, The Johns Hopkins Centennial Lectures. John Hopkins University Press, 1975.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
J. van der Hoeven. From implicit to recursive equations. Technical report, HAL, 2011. http://hal.archives-ouvertes.fr/hal-00583125.
J. van der Hoeven. Computing with D-algebraic power series. Technical report, HAL, 2014. http://hal.archives-ouvertes.fr/hal-00979367.
M. Janet. Sur les systèmes d'équations aux dérivées partielles. PhD thesis, Faculté des sciences de Paris, 1920. Thèses françaises de l'entre-deux-guerres. Gauthiers-Villars.
D. Lazard. Gröbner bases, gaussian elimination and resolution of systems of algebraic equations. In J. A. van Hulzen, editor, Proc. EUROCAL'83, number 162 in Lect. Notes in Computer Sc., pages 146–156. Springer Berlin Heidelberg, 1983.
A. J. Macintyre and A. J. Wilkie. On the decidability of the real exponential field. Technical report, Oxford University, 1994.
K. Mahler. Arithmetische Eigenschaften einer Klasse transzendental-transzendenter Funktionen. Math. Z., 32:545–585, 1930.
F. Mora. An algorithm to compute the equations of tangent cones. In Proc. EUROCAM '82, number 144 in Lect. Notes in Computer Sc., pages 158–165. Springer Berlin Heidelberg, 1982.
J. F. Ritt. Differential algebra. Amer. Math. Soc., New York, 1950.
D. Robertz. Formal Algorithmic Elimination for PDEs, volume 2121 of Lecture Notres in Mathematics. Springer, Cham, 2014.
K. Weierstrass. Mathematische Werke II, Abhandlungen 2, pages 135–142. Mayer und Müller, 1895. Reprinted by Johnson, New York, 1967.