Let |
|
Let |
Let  be an effective field and consider an
algebra
be an effective field and consider an
algebra 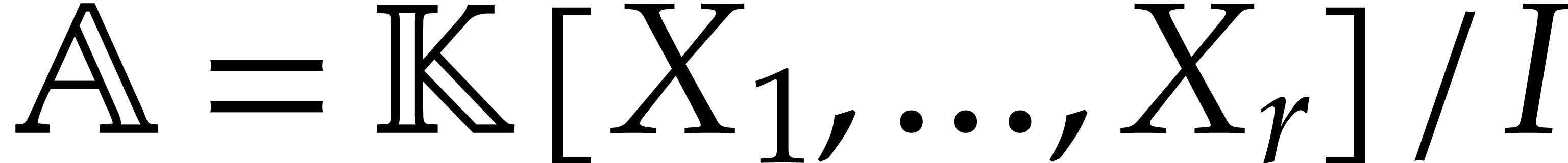 where
where 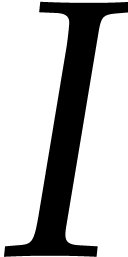 is a
finitely generated ideal. For actual computations in
is a
finitely generated ideal. For actual computations in  , we have three main tasks:
, we have three main tasks:
define a non-ambiguous representation for elements in  ;
;
design a multiplication algorithm for  ;
;
show how to convert between different representations for elements
in  .
.
Fast polynomial arithmetic based on FFT-multiplication allows for a quasi-optimal solution in the univariate case. However, reduction modulo an ideal of multivariate polynomials is non-trivial.
The most common approach for computations modulo ideals of polynomials is based on Gröbner bases. This immediately solves the first task, using the fact that any polynomial admits a unique normal form modulo a given Gröbner basis [4]. The second task is solved by reducing the product of two polynomials modulo the Gröbner basis. Finally, given a Gröbner basis with respect to a first term ordering, one may use the FGLM algorithm [9] to compute a reduced Gröbner basis with respect to a second term ordering; algorithms for the corresponding conversions are obtained as a by-product.
There is an abundant literature on efficient algorithms for the
computation of Gröbner bases; see for example [7, 8, 9] and references therein. Although the worst
case complexity is known to be very bad [23], polynomial
complexity bounds (for the number of operations in  in terms of the expected output size) exist for many important cases of
interest. For example, for fixed
in terms of the expected output size) exist for many important cases of
interest. For example, for fixed 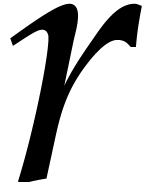 ,
and using naive linear algebra on Macaulay matrices, one may show [22, 14, 15] that a sufficiently
regular system of
,
and using naive linear algebra on Macaulay matrices, one may show [22, 14, 15] that a sufficiently
regular system of 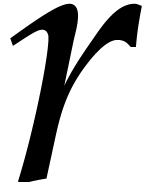 equations of degree
equations of degree  can be solved in time
can be solved in time 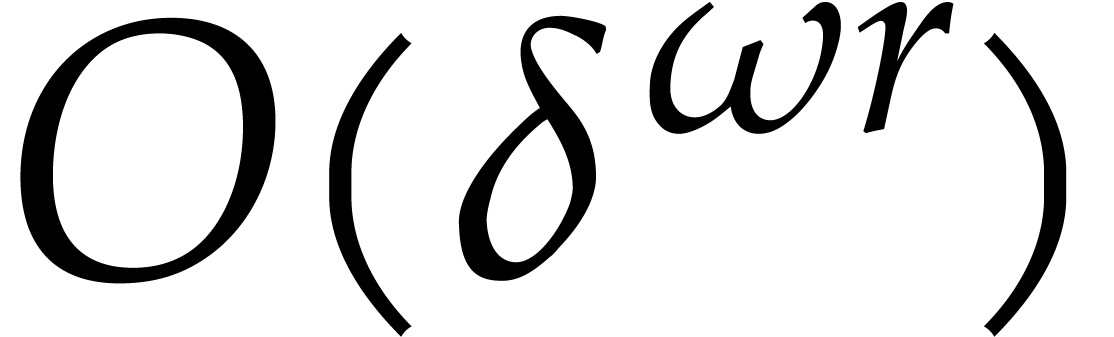 .
Here
.
Here  is the exponent of matrix multiplication
[11]. For such a system, the Bezout bound
is the exponent of matrix multiplication
[11]. For such a system, the Bezout bound 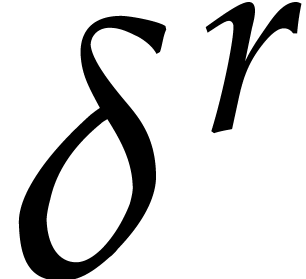 for the number
for the number 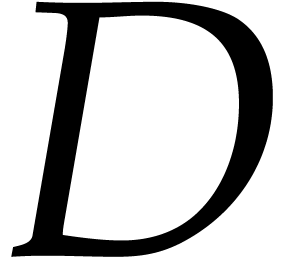 of solutions is reached, so the
running time
of solutions is reached, so the
running time 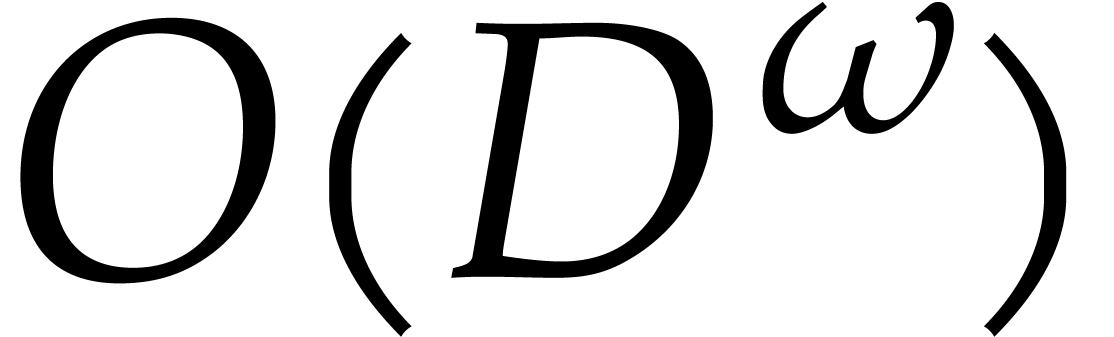 is polynomial in the expected
output size
is polynomial in the expected
output size  . The implicit
dependency of this bound on
. The implicit
dependency of this bound on  can be improved by
using the “matrix-F5” variant [2] of
Faugère's F5 algorithm [8].
can be improved by
using the “matrix-F5” variant [2] of
Faugère's F5 algorithm [8].
The F5 algorithm and all other currently known fast algorithms for
Gröbner basis computations rely on linear algebra. At this point,
one may wonder whether there is an intrinsic reason for this fact, or
whether fast FFT-based arithmetic might be used to accelerate
Gröbner basis computations. Instead of directly addressing this
difficult problem, one may investigate whether such accelerations are
possible for simpler problems in this area. One good candidate for such
a problem is the reduction of a polynomial  with
respect to a fixed reduced Gröbner basis
with
respect to a fixed reduced Gröbner basis 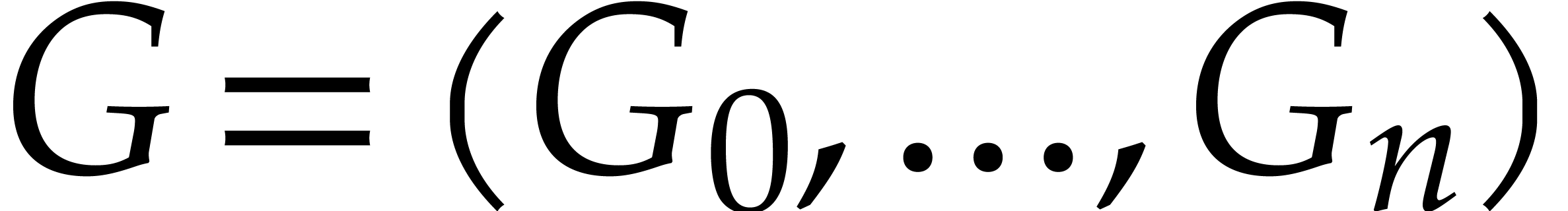 . In that case, the algebra
. In that case, the algebra  is given once and for all, so it becomes a matter of precomputation to
obtain
is given once and for all, so it becomes a matter of precomputation to
obtain  and any other data that could be useful
for efficient reductions modulo
and any other data that could be useful
for efficient reductions modulo  .
.
One step in this direction was made in [20]. Using relaxed
multiplication [19], it was shown that the reduction of
 with respect to
with respect to  can be
computed in quasi-linear time in terms of the size of the equation
can be
computed in quasi-linear time in terms of the size of the equation  . However, even in the case of
bivariate polynomials, this is not necessarily optimal. In order to see
the reason for this, consider
. However, even in the case of
bivariate polynomials, this is not necessarily optimal. In order to see
the reason for this, consider 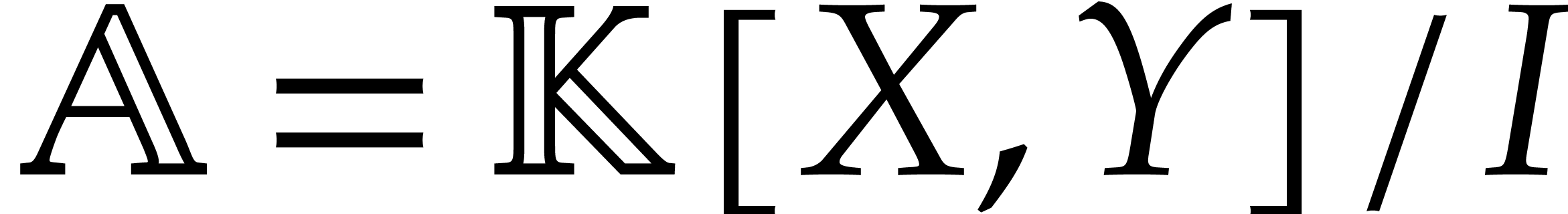 ,
where
,
where 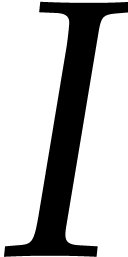 is the ideal generated by two generic
polynomials of total degree
is the ideal generated by two generic
polynomials of total degree  .
Then
.
Then 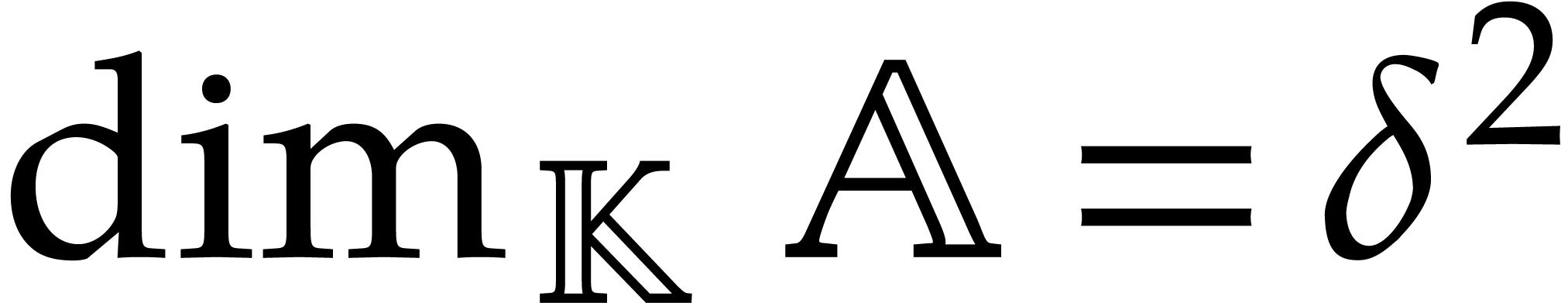 , but the Gröbner
basis for
, but the Gröbner
basis for 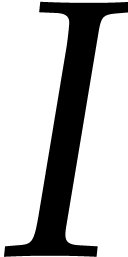 with respect the usual total degree
ordering contains
with respect the usual total degree
ordering contains  polynomials with
polynomials with 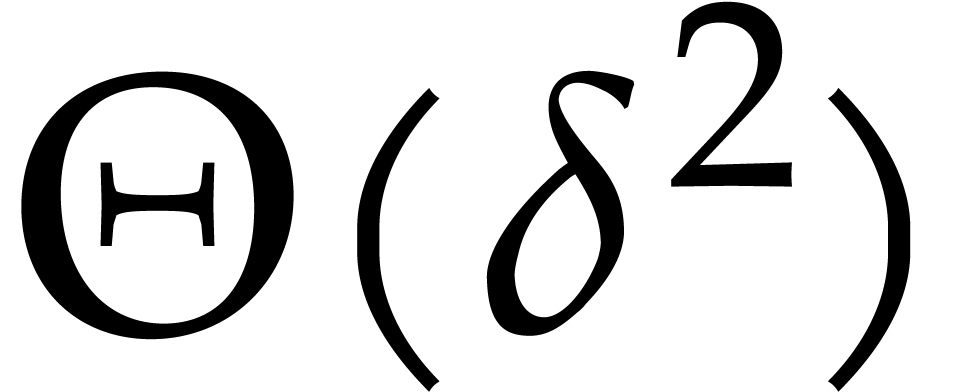 coefficients. This means that we need
coefficients. This means that we need 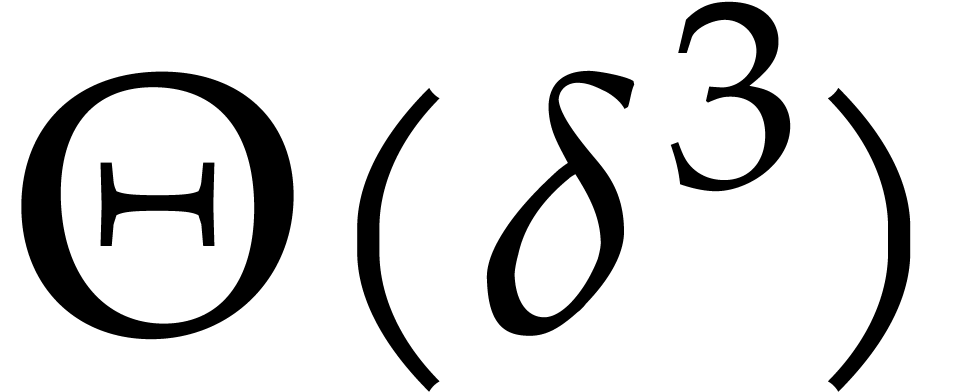 space, merely to write down
space, merely to write down  .
One crucial prerequisite for even faster algorithms is therefore to
design a terser representation for Gröbner bases.
.
One crucial prerequisite for even faster algorithms is therefore to
design a terser representation for Gröbner bases.
The main aim of this paper is to show that it is actually possible to perform polynomial reductions in quasi-linear time in some very specific cases. For simplicity, we will restrict our attention to bivariate polynomials and to ideals that satisfy suitable regularity conditions. Because of all these precautions, we do not expect our algorithms to be very useful for practical purposes, but rather regard our work as a “proof of concept” that quasi-linear complexities are not deemed impossible to achieve in this context.
More precisely, with 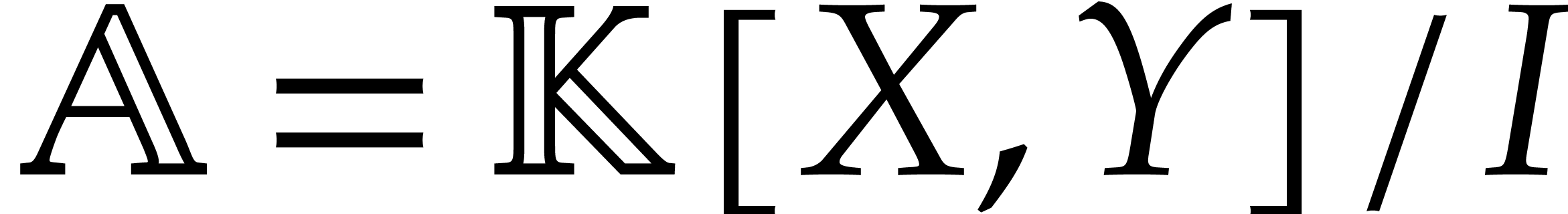 as above, our main results
are as follows. We first introduce the concept of a “vanilla
Gröbner basis” that captures the regularity assumptions that
are needed for our algorithms. Modulo potentially expensive
precomputations, we then present a more compact description of such a
Gröbner basis
as above, our main results
are as follows. We first introduce the concept of a “vanilla
Gröbner basis” that captures the regularity assumptions that
are needed for our algorithms. Modulo potentially expensive
precomputations, we then present a more compact description of such a
Gröbner basis  that holds all necessary
information in
that holds all necessary
information in 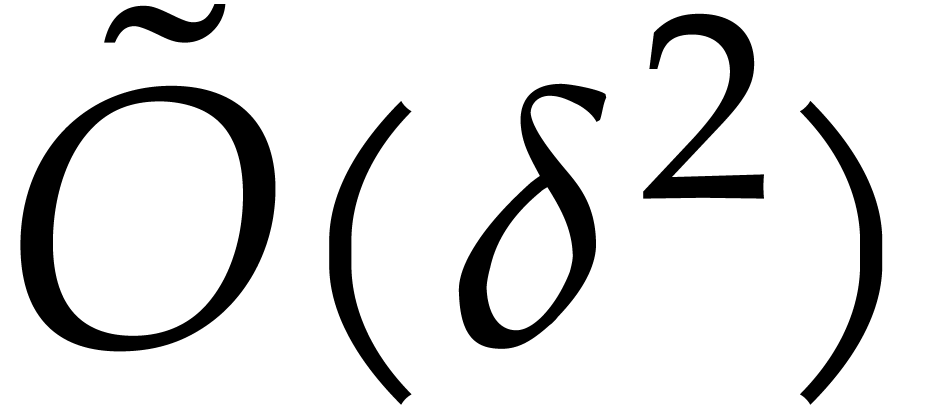 space. We next give an algorithm
for reducing a bivariate polynomial of total degree
space. We next give an algorithm
for reducing a bivariate polynomial of total degree  with respect to
with respect to  in quasi-linear time
in quasi-linear time 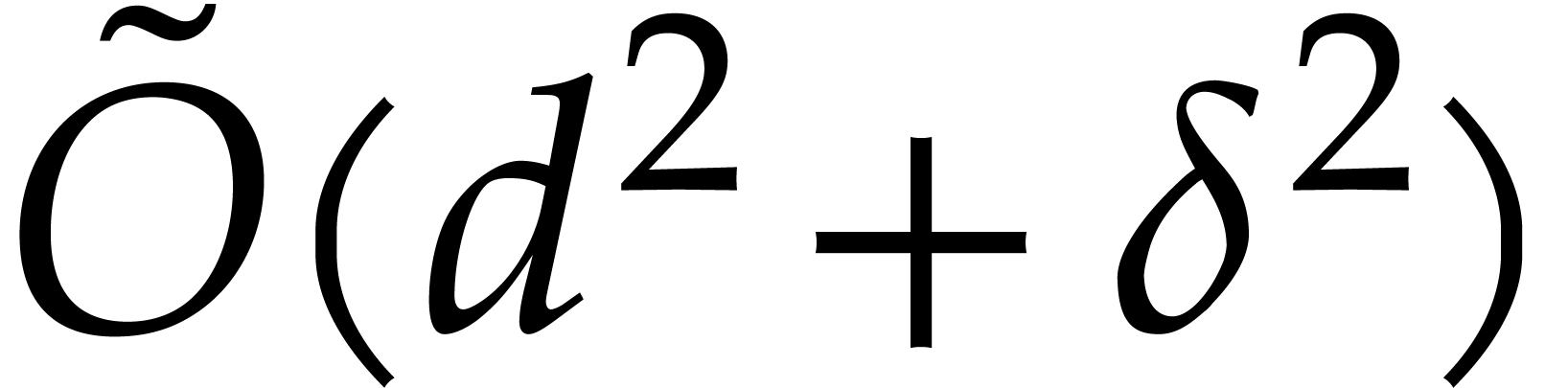 . In particular, multiplication in
. In particular, multiplication in
 can be done in time
can be done in time 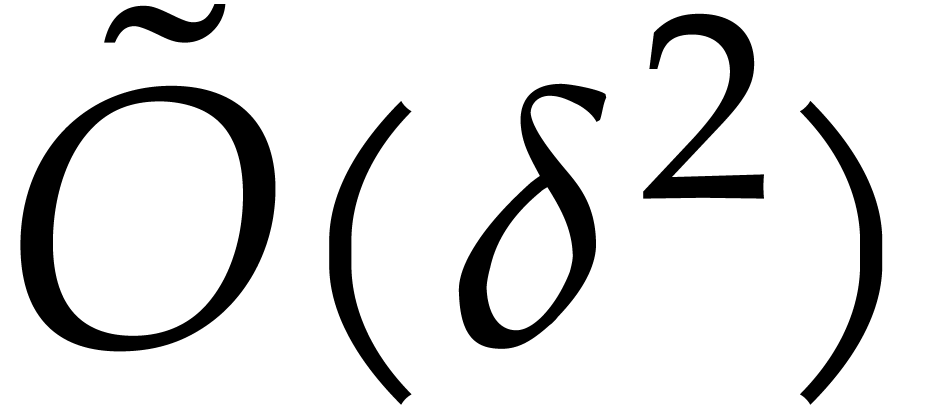 , which is intrinsically quasi-optimal. We also
present an algorithm to convert between normal forms with respect to
vanilla Gröbner bases for different monomial orderings. This
algorithm is based on a Gröbner walk [6] with at most
, which is intrinsically quasi-optimal. We also
present an algorithm to convert between normal forms with respect to
vanilla Gröbner bases for different monomial orderings. This
algorithm is based on a Gröbner walk [6] with at most
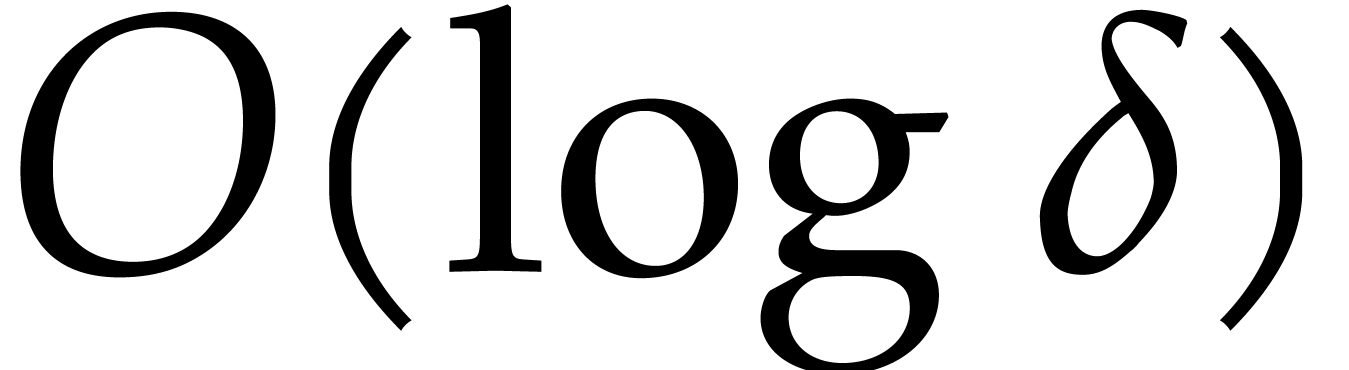 intermediate monomial orderings; its complexity
intermediate monomial orderings; its complexity
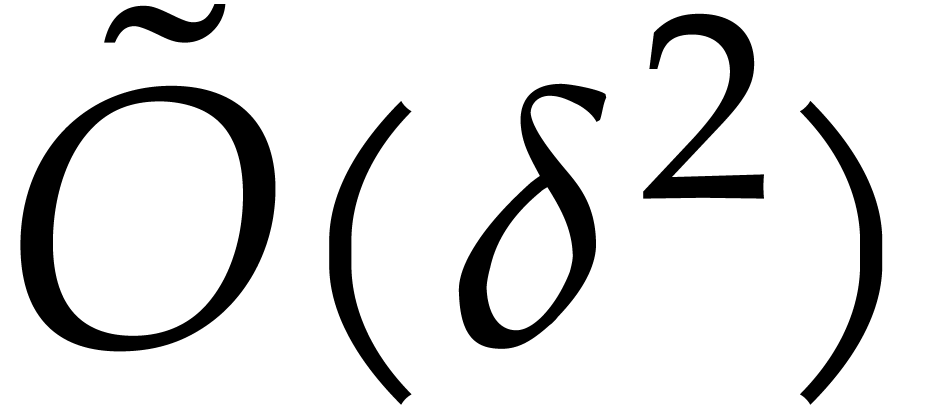 is again quasi-optimal.
is again quasi-optimal.
It is instructive to compare these complexity bounds with the
complexities of naive algorithms that are commonly implemented in
computer algebra systems. For multiplications in  , one may precompute the
, one may precompute the  matrix that allows us to obtain the reduction of a product of two normal
forms using a matrix-vector product of cost
matrix that allows us to obtain the reduction of a product of two normal
forms using a matrix-vector product of cost 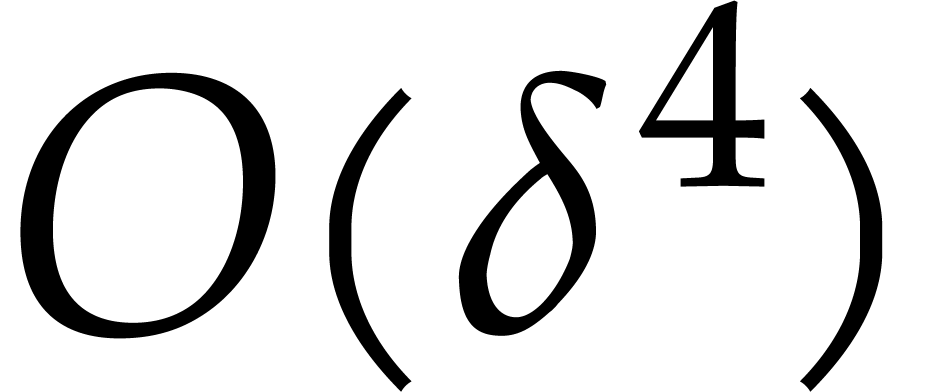 . Since the product of two normal forms can be
computed in quasi-linear time
. Since the product of two normal forms can be
computed in quasi-linear time 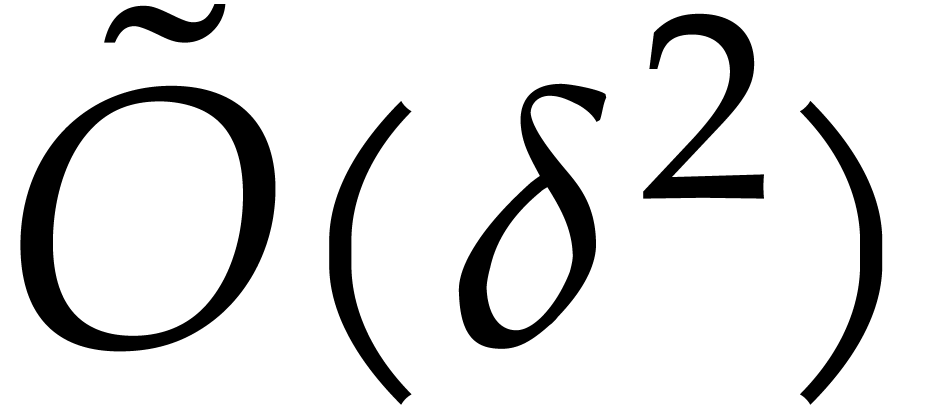 ,
it follows that multiplications in
,
it follows that multiplications in  take time
take time
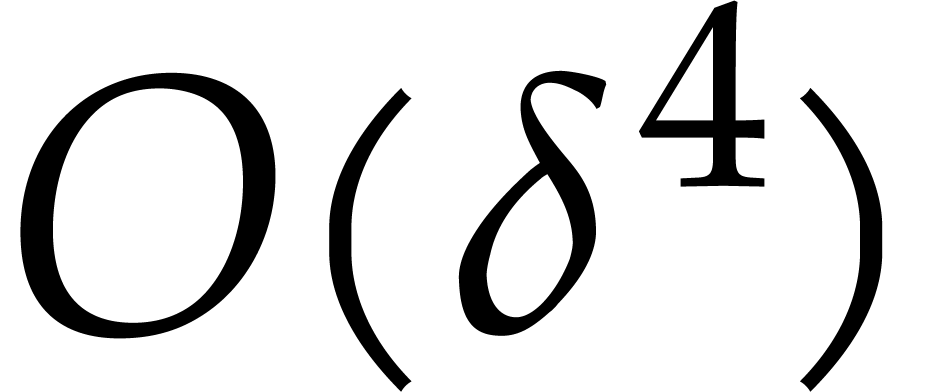 . Similarly, changes of
monomial orderings lead to
. Similarly, changes of
monomial orderings lead to  -matrices
for representing the corresponding base changes. Naive conversions can
then be performed in time
-matrices
for representing the corresponding base changes. Naive conversions can
then be performed in time 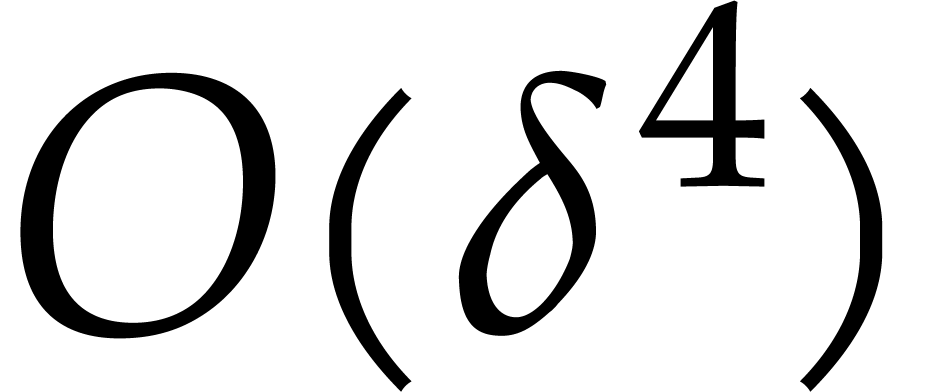 .
.
As a final remark, we notice that geometric methods provide an
alternative to Gröbner basis techniques for the resolution of
polynomial systems and computations in quotient algebras  . Examples include the Kronecker solver [16] and Rouillier's RUR [25]. Such algorithms are
often faster from a complexity point of view, but essentially only work
for bases that correspond to lexicographical orders in the Gröbner
basis setting. A similar remark applies to the elimination method by
Auzinger-Stetter [1]
. Examples include the Kronecker solver [16] and Rouillier's RUR [25]. Such algorithms are
often faster from a complexity point of view, but essentially only work
for bases that correspond to lexicographical orders in the Gröbner
basis setting. A similar remark applies to the elimination method by
Auzinger-Stetter [1]
Notations and terminology. We assume that the
reader is familiar with the theory of Gröbner basis and refer to
[12, 3] for basic expositions. We denote the
set of monomials in 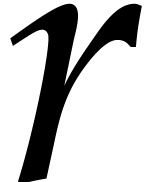 variables by
variables by 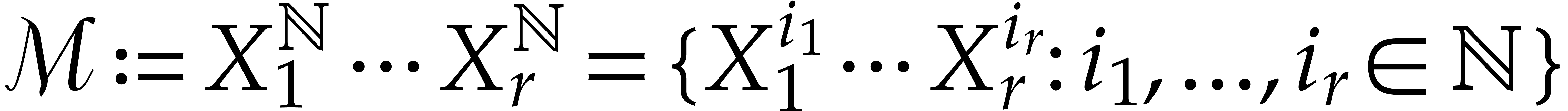 . A monomial ordering
. A monomial ordering  on
on 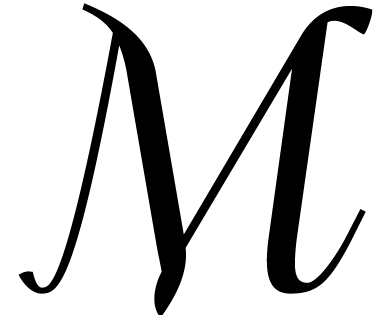 is a total ordering that
is compatible with multiplication. Given a polynomial in
is a total ordering that
is compatible with multiplication. Given a polynomial in 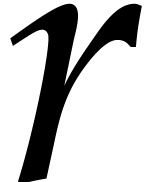 variables
variables 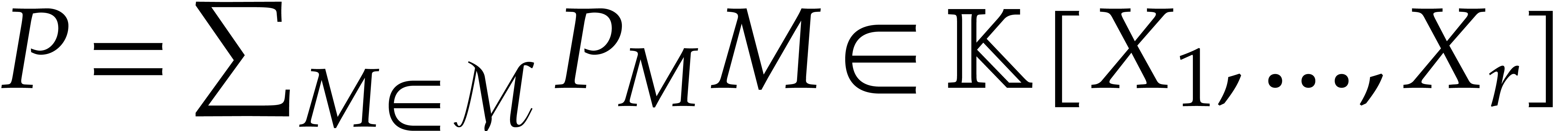 , its
support
, its
support  is the set of monomials
is the set of monomials  with
with 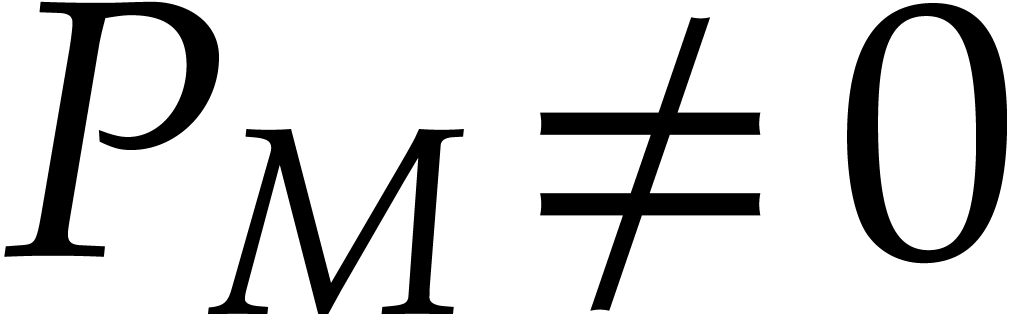 . If
. If
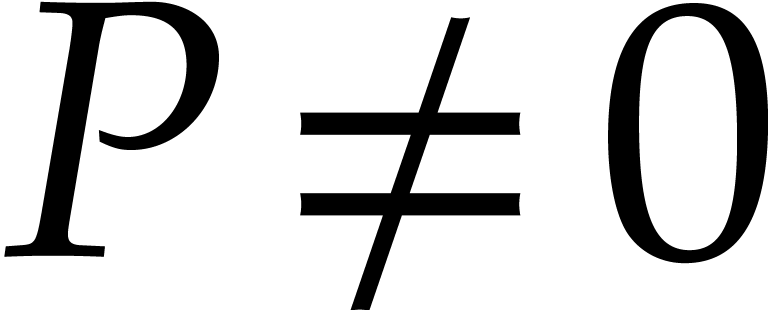 , then
, then  admits a maximal element for
admits a maximal element for  that is called its
leading monomial and that we denote by
that is called its
leading monomial and that we denote by 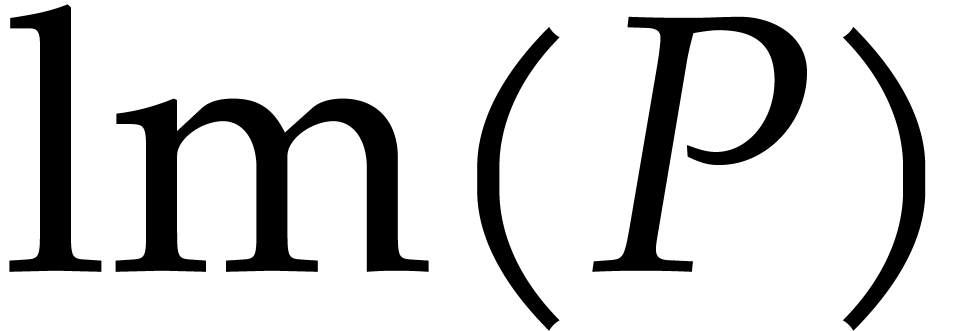 . If
. If  ,
then we say that
,
then we say that 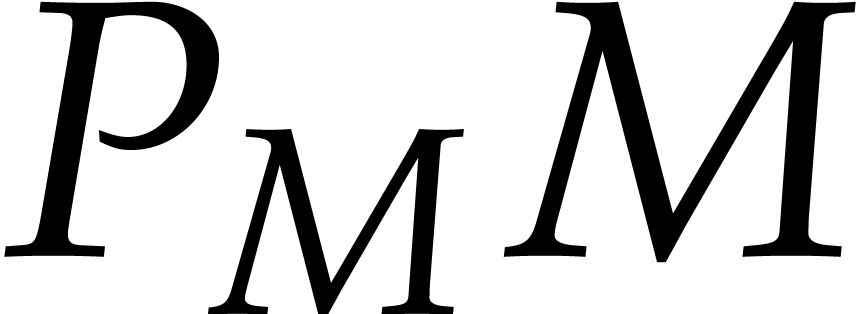 is a term in
is a term in  . Given a tuple
. Given a tuple 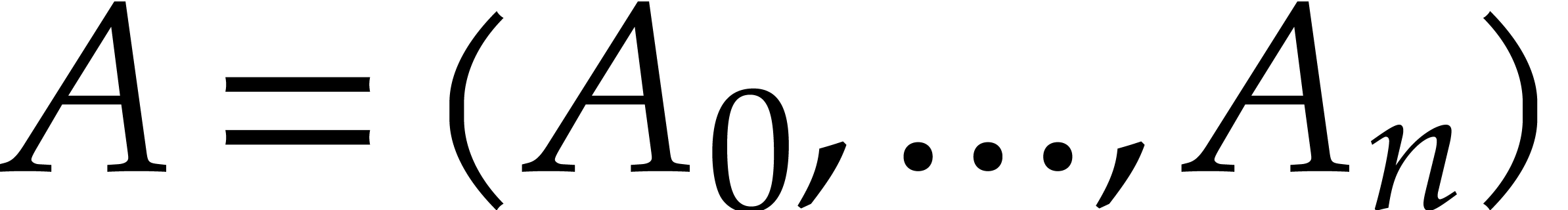 of polynomials in
of polynomials in 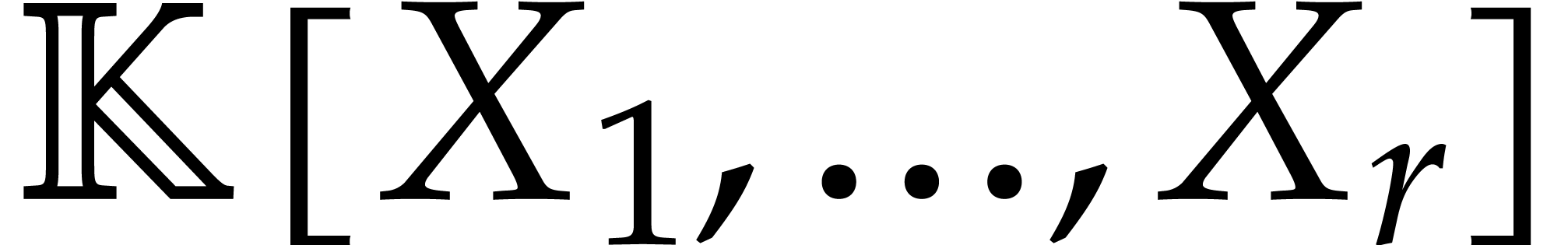 , we say
that
, we say
that 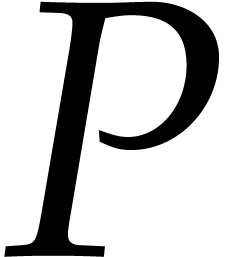 is reduced with respect to
is reduced with respect to  if
if  contains no monomial that
is a multiple of the leading monomial of one of the
contains no monomial that
is a multiple of the leading monomial of one of the 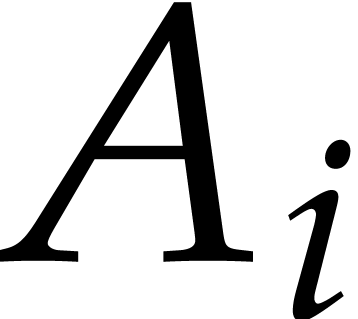 .
.
Unless stated otherwise, we will always work in the bivariate setting
when  , and use
, and use 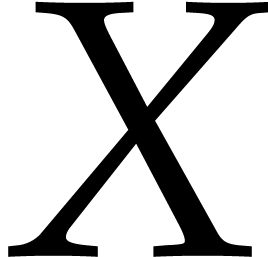 and
and 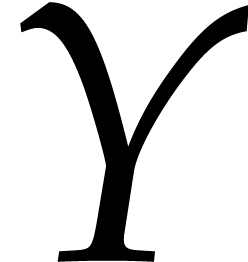 as our main indeterminates
instead of
as our main indeterminates
instead of 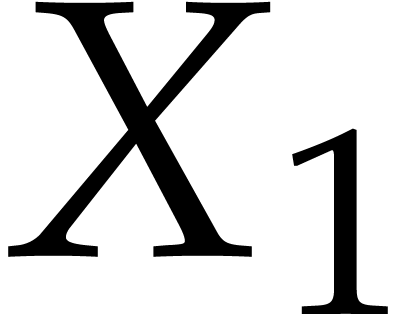 and
and 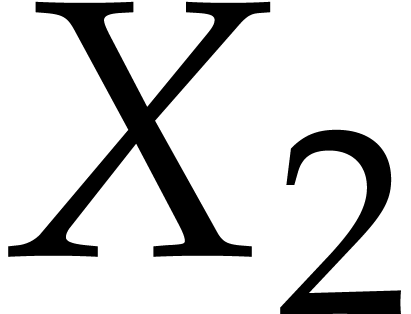 .
In particular,
.
In particular, 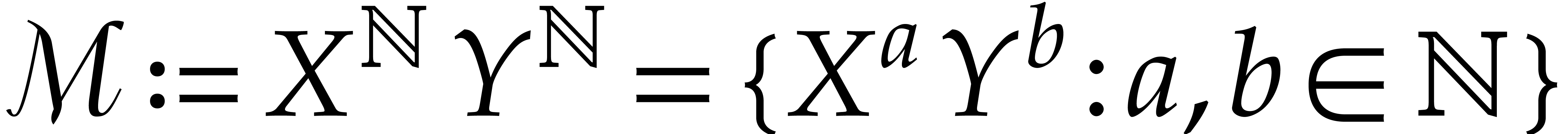 .
.
Acknowledgements. We thank the anonymous referees for their detailed comments and suggestions. We are aware that an example would be helpful for the intuition, unfortunately we were not able to give one because of the space constraints. Moreover, the reader should notice that a meaningful example cannot have a very small degree (say, at least 10), and that our setting requires non-structured dense polynomials, so that writing them down explicitly would hardly be readable.
Consider a zero-dimensional ideal 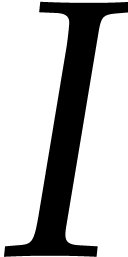 of
of 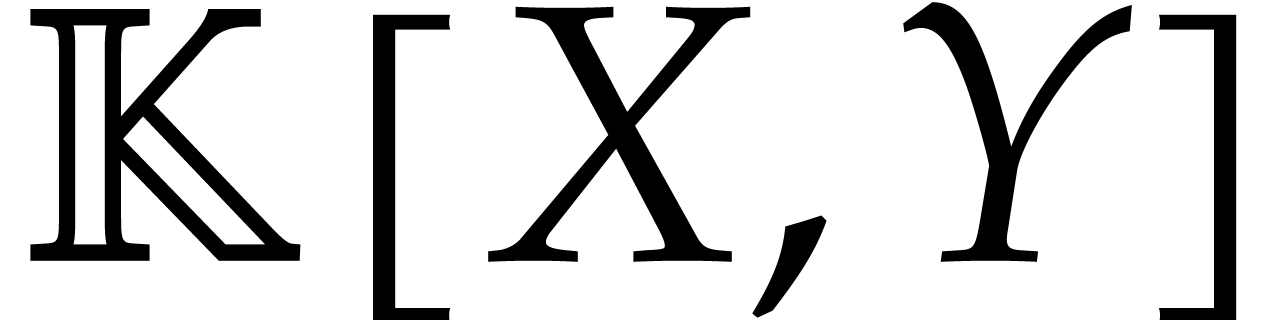 with Gröbner basis
with Gröbner basis  with
respect to a given monomial ordering
with
respect to a given monomial ordering  .
We define the degree
.
We define the degree 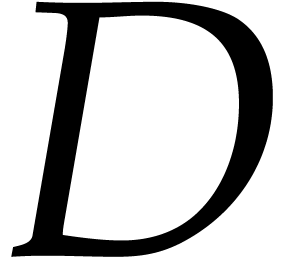 of
of 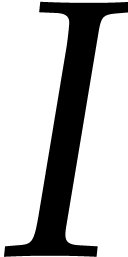 to be the dimension of the quotient
to be the dimension of the quotient 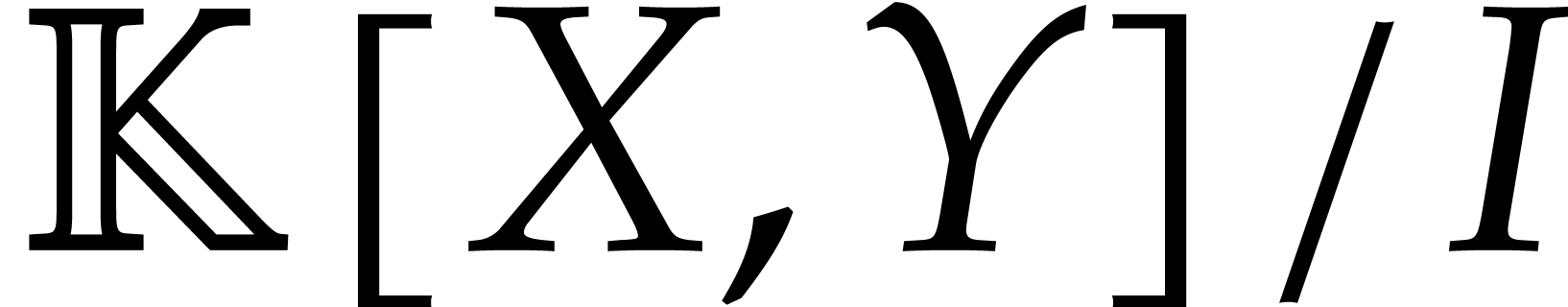 as a
as a  -vector space. Our
algorithms will only work for a special class of Gröbner bases with
suitable regularity properties. For a generic ideal in the space of all
zero-dimensional ideals with fixed degree
-vector space. Our
algorithms will only work for a special class of Gröbner bases with
suitable regularity properties. For a generic ideal in the space of all
zero-dimensional ideals with fixed degree 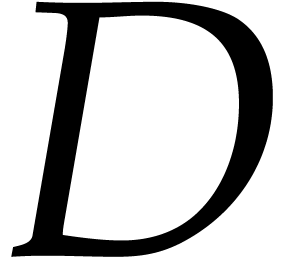 ,
we expect that these properties are always satisfied, although we have
not proved this yet. For the time being, we define a vanilla
Gröbner basis to be the Gröbner basis of an ideal of this
type.
,
we expect that these properties are always satisfied, although we have
not proved this yet. For the time being, we define a vanilla
Gröbner basis to be the Gröbner basis of an ideal of this
type.
General monomial orderings that are suitable for Gröbner basis computations have been classified in [24]. For the purpose of this paper, it is convenient to restrict our attention to a specific type of bivariate monomial ordering that will allow us to explicitly describe certain Gröbner stairs and to explicitly compute certain dimensions.
 . We define
the
. We define
the  -degree
of a monomial
-degree
of a monomial 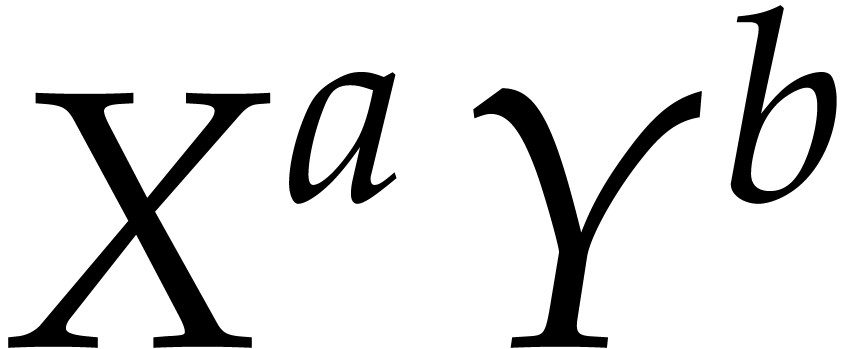 with
with  by
by
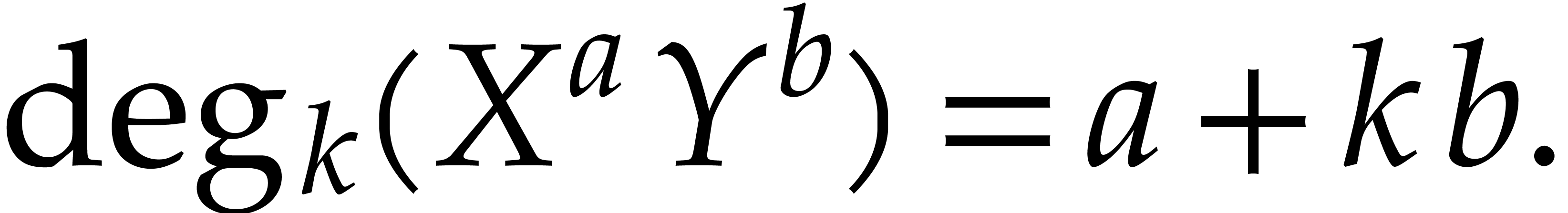
We define the  -order
to be the monomial order
-order
to be the monomial order  such that
such that

The  -order
-order  is also known as the weighed degree lexicographic order for the weight
vector
is also known as the weighed degree lexicographic order for the weight
vector 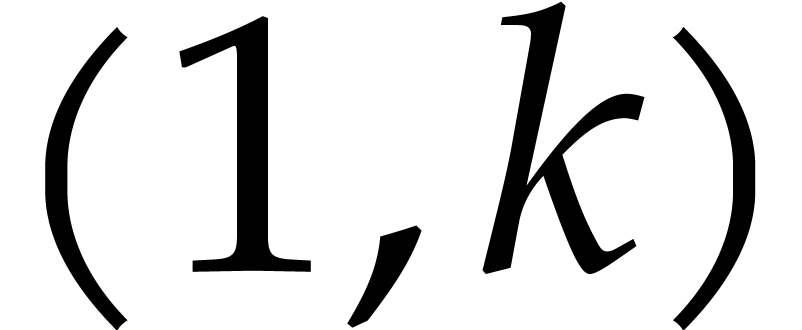 . Similarly,
. Similarly,  corresponds to the usual total degree order.
corresponds to the usual total degree order.
Consider a zero-dimensional ideal 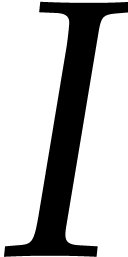 of
of 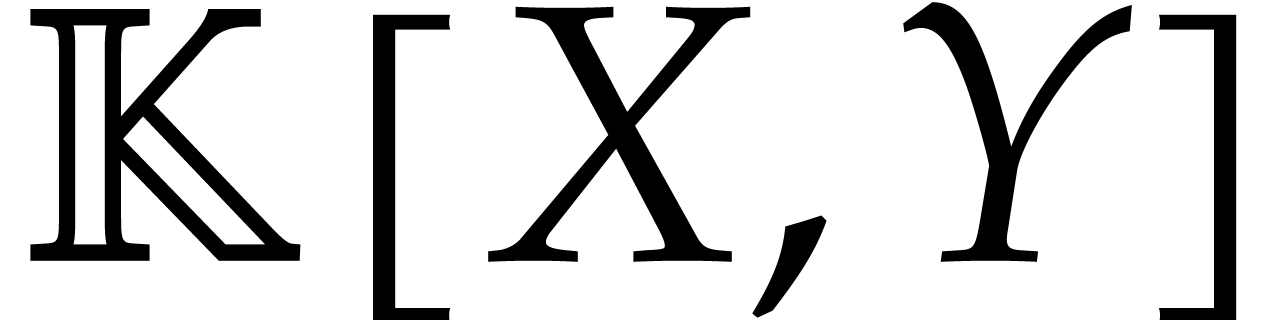 of degree
of degree 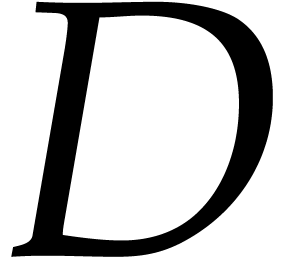 with Gröbner basis
with Gröbner basis
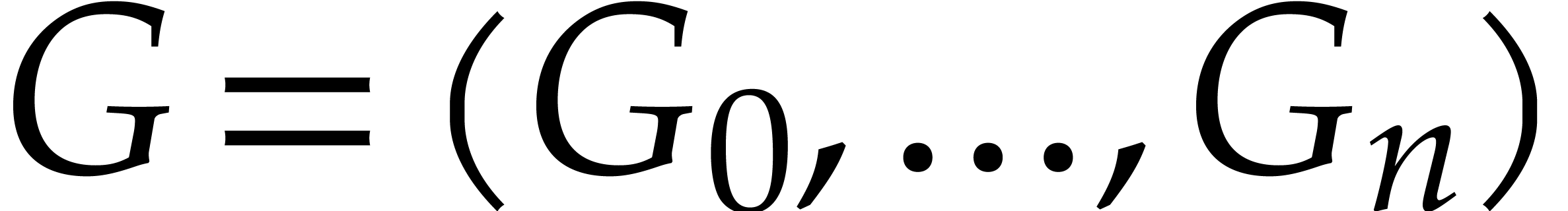 with respect to
with respect to  .
Let
.
Let 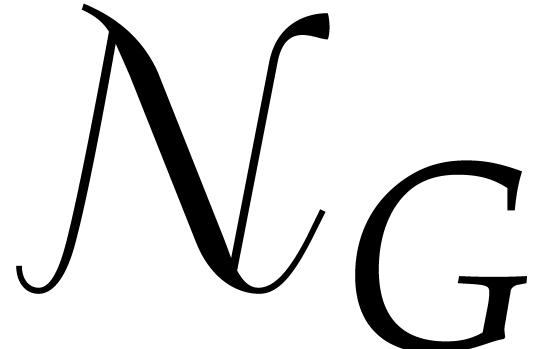 be the set of monomials
be the set of monomials 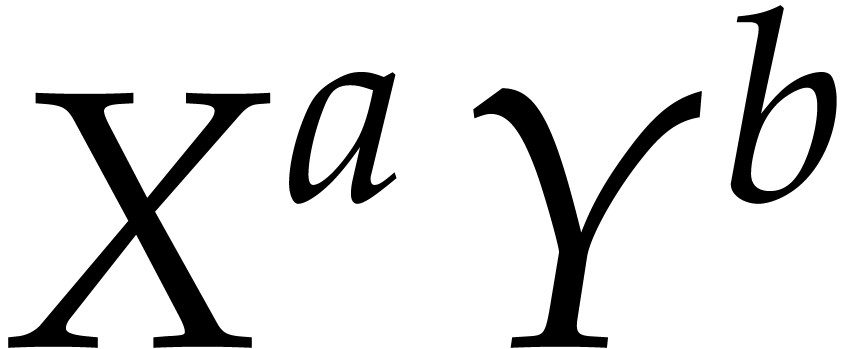 that are in normal form with respect to
that are in normal form with respect to  .
In other words,
.
In other words,  corresponds to the set of
corresponds to the set of  monomials “under the Gröbner
stairs”. For a sufficiently generic ideal of degree
monomials “under the Gröbner
stairs”. For a sufficiently generic ideal of degree  , we expect
, we expect  to consist
exactly of the smallest
to consist
exactly of the smallest  elements of
elements of  with respect to
with respect to  .
.
 form a
vanilla Gröbner stairs if
form a
vanilla Gröbner stairs if  coincides with the set
coincides with the set 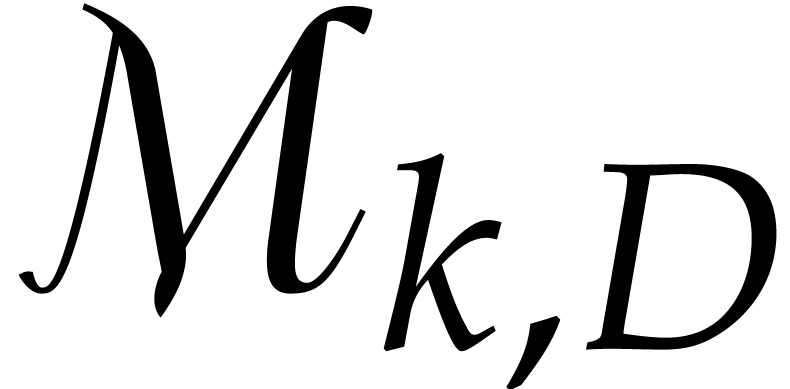 of the
of the 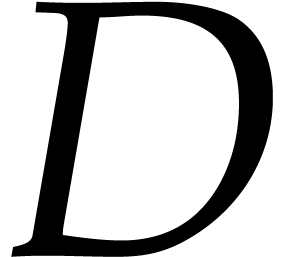 smallest elements of
smallest elements of 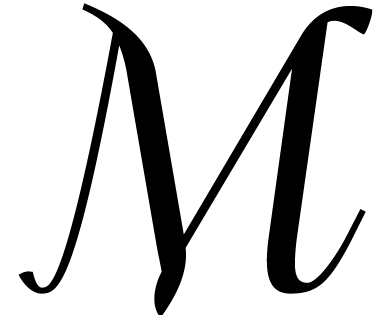 for
for  .
.
Figure
1
shows an example of a Gröbner basis whose leading monomials form a
vanilla Gröbner stairs. We observe that the stair admits almost
constant slope
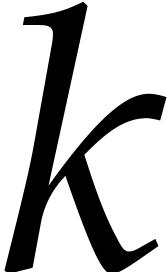 .
In fact, the set
.
In fact, the set
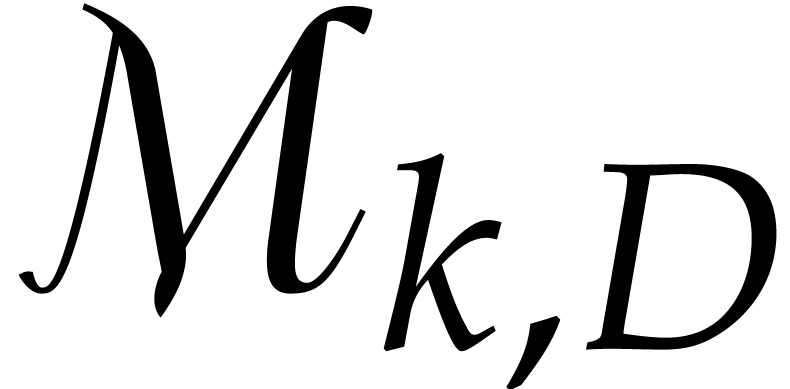 can be described explicitly:
can be described explicitly:
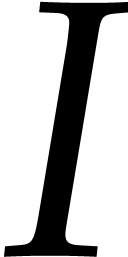 be an ideal of
degree
be an ideal of
degree 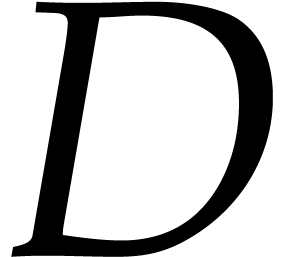 with Gröbner basis
with Gröbner basis  for
for  with
with 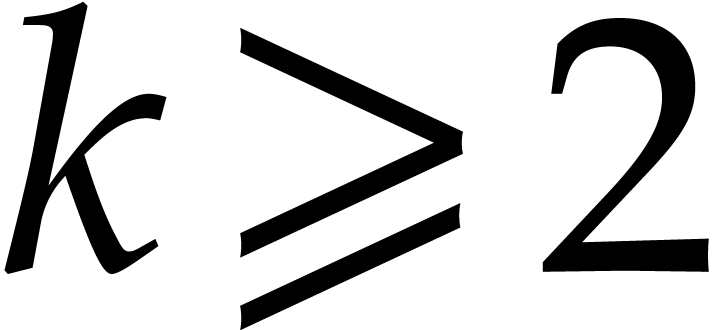 . Assume that the leading monomials of
. Assume that the leading monomials of  form a vanilla Gröbner stairs and define
form a vanilla Gröbner stairs and define
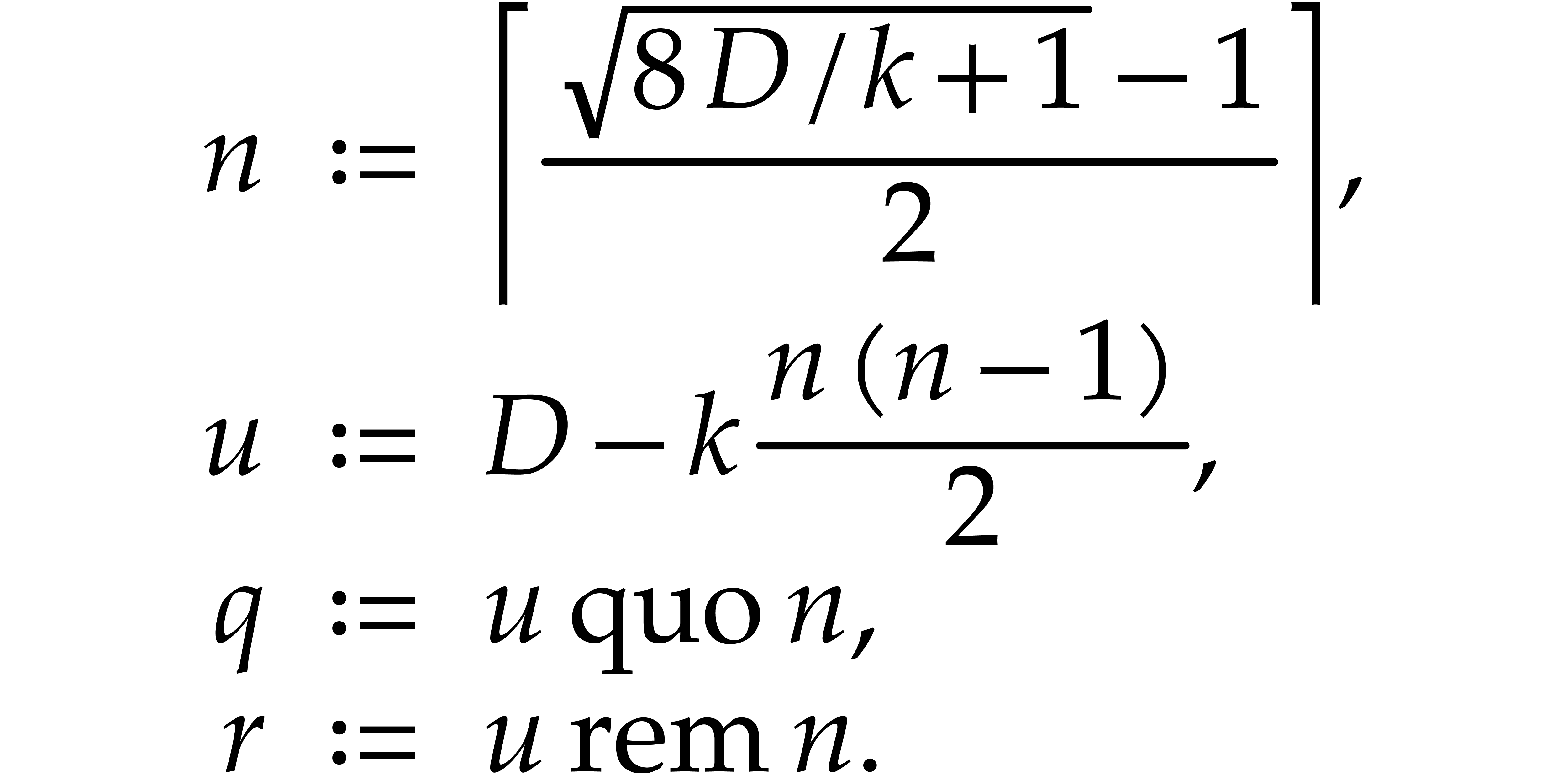
Then  has
has  elements
elements
 and for
and for 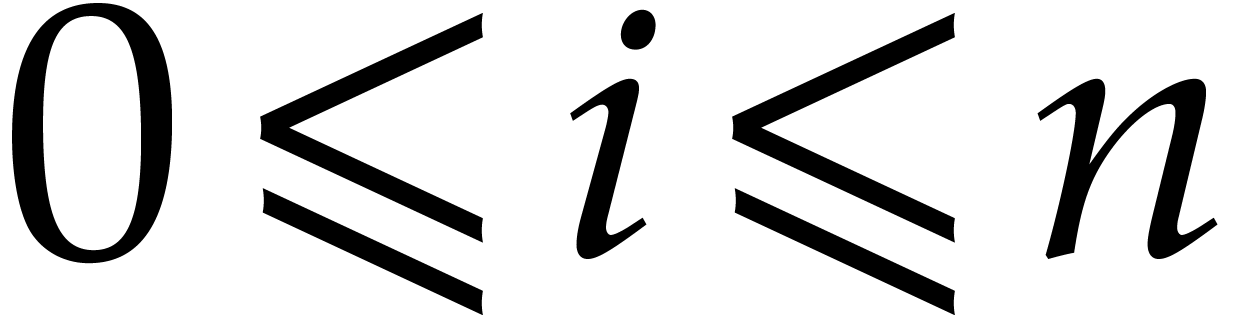 ,
the leading monomial of
,
the leading monomial of 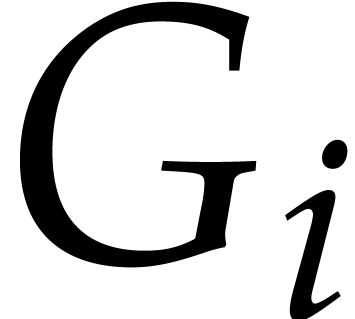 (denoted by
(denoted by 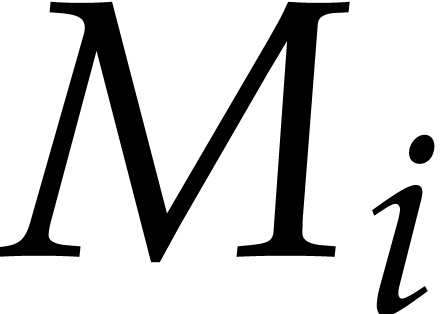 ) can be expressed in terms of
) can be expressed in terms of
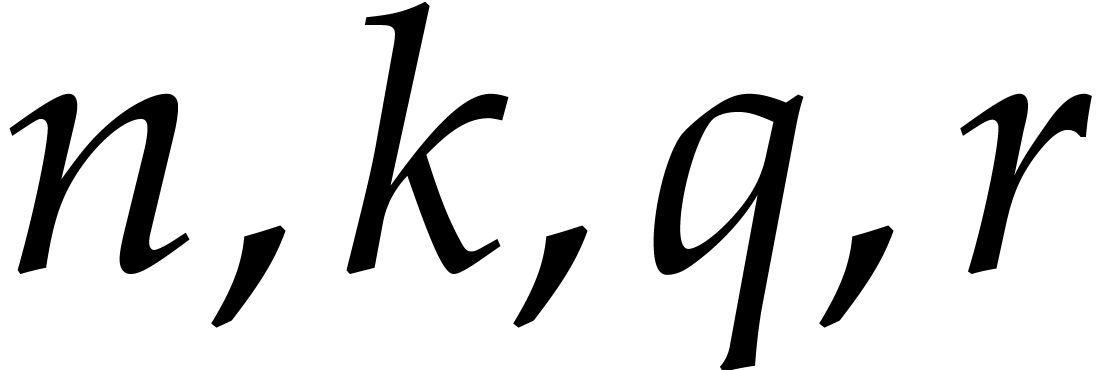 . Assuming the basis
elements are ordered such that the
. Assuming the basis
elements are ordered such that the 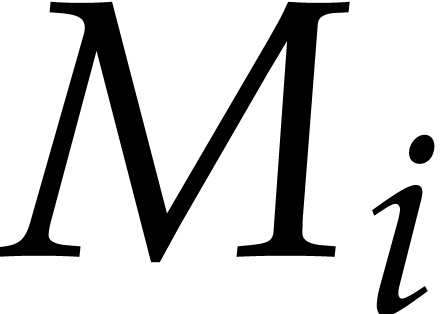 's
have increasing degree in the variable
's
have increasing degree in the variable 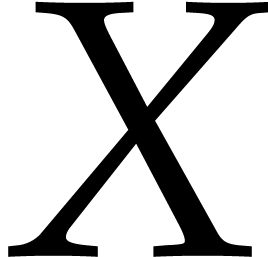 ,
we have:
,
we have:
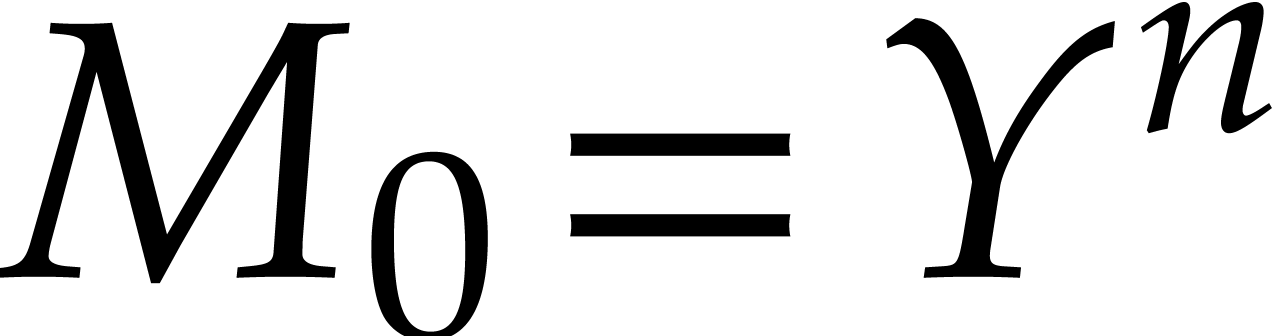 .
.
For all 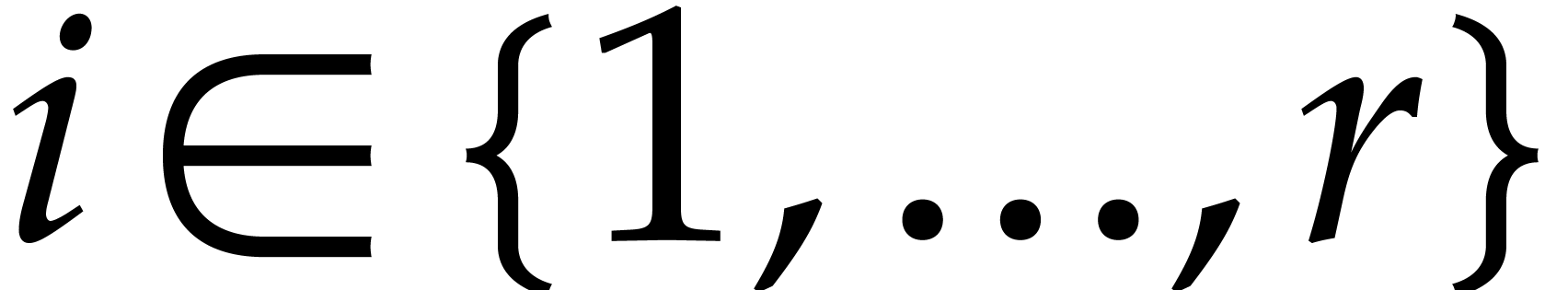 ,
, 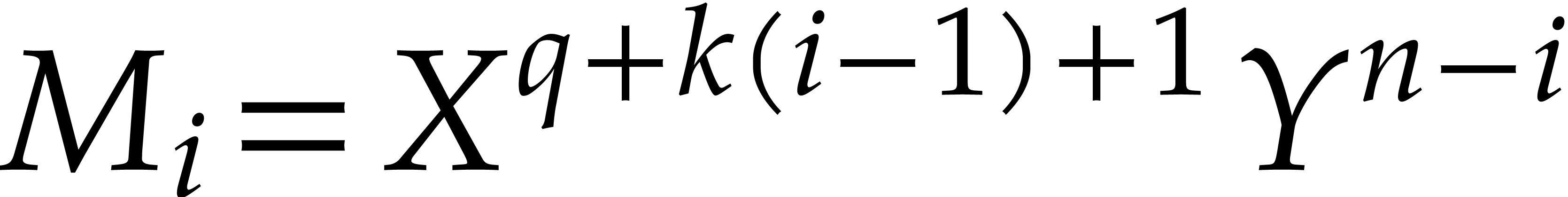 .
.
For all 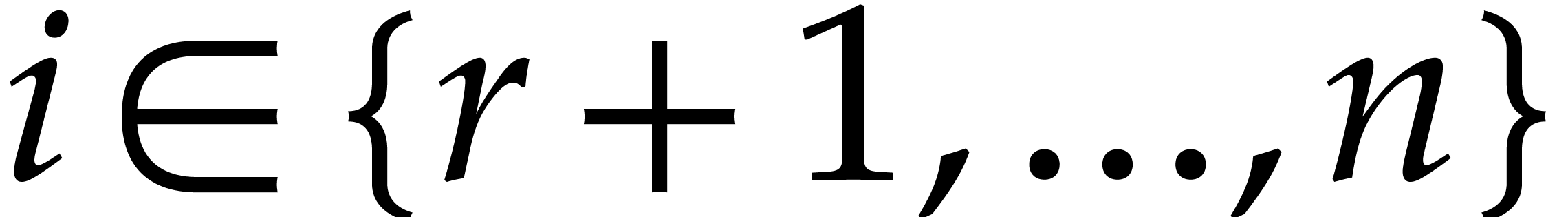 ,
, 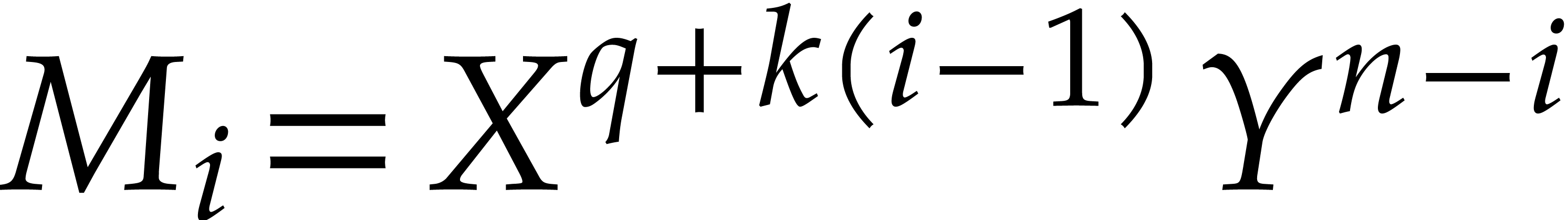 .
.
Proof. With this expression of 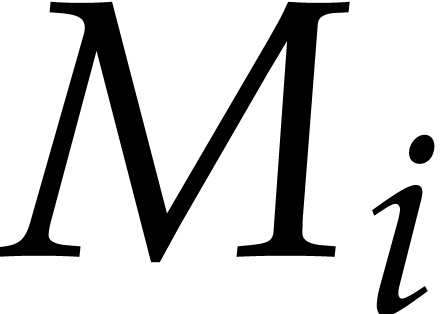 , we first notice that this sequence
, we first notice that this sequence  can indeed be the leading monomials for a reduced
Gröbner basis, that is
can indeed be the leading monomials for a reduced
Gröbner basis, that is 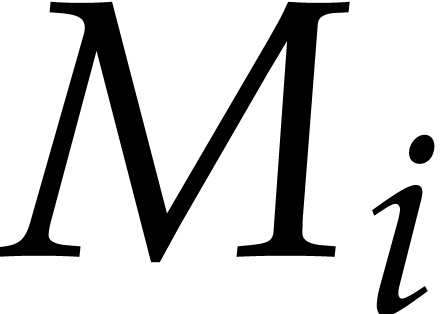 does not divide
does not divide 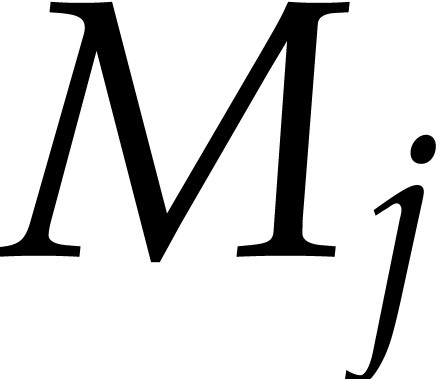 for any
for any 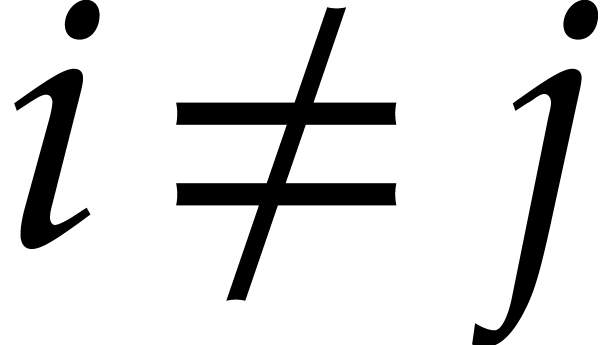 .
This is clear for
.
This is clear for 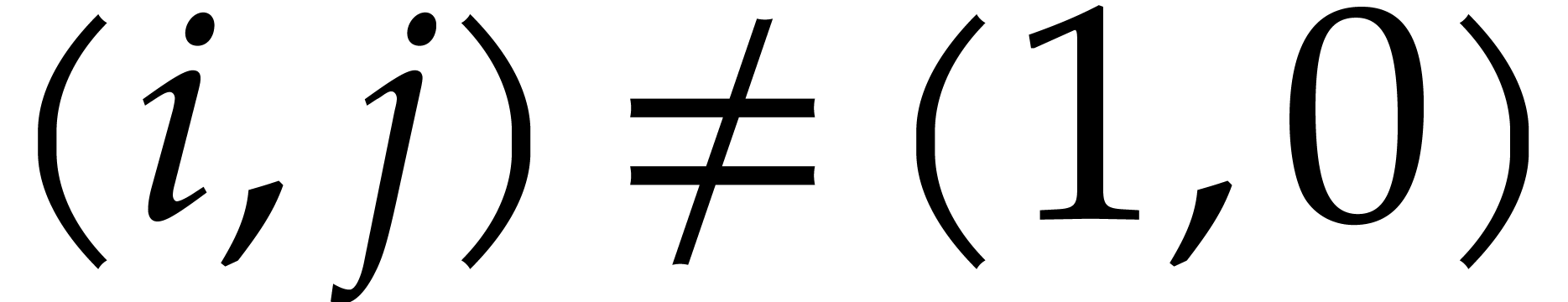 , so let us
prove that
, so let us
prove that  does not divide
does not divide  . We have
. We have 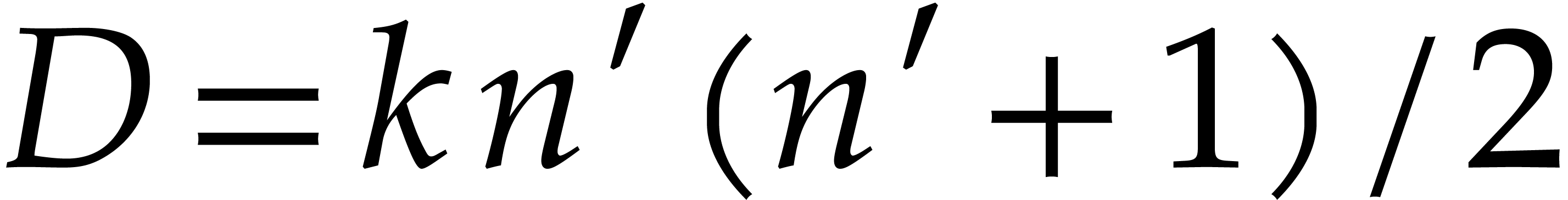 with
with 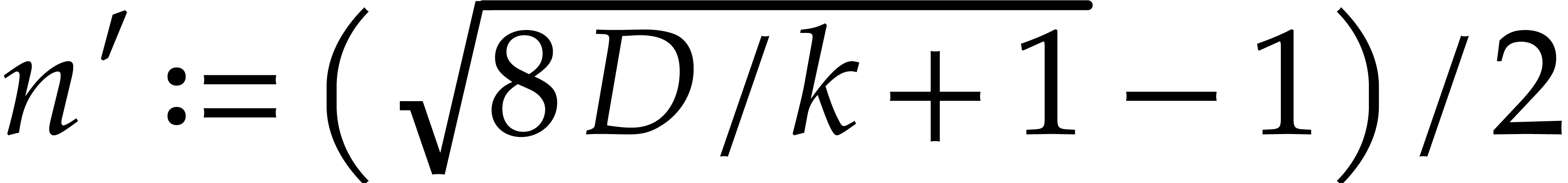 , so that
, so that
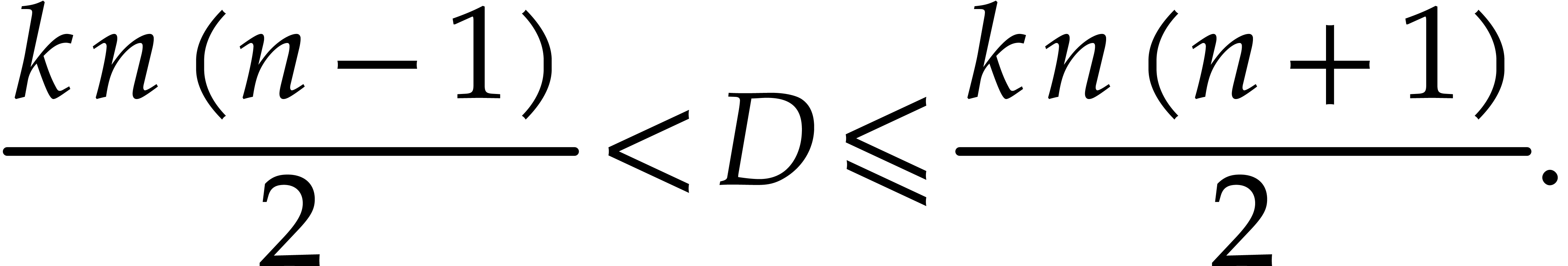
In particular, this implies  ,
whence
,
whence  or
or  .
Remains to prove that the sequence
.
Remains to prove that the sequence  form a
vanilla Gröbner stairs (for a degree
form a
vanilla Gröbner stairs (for a degree  ideal)
as claimed. Indeed, there are
ideal)
as claimed. Indeed, there are  monomials under
the stairs
monomials under
the stairs  (i.e. in normal form w.r.t.
(i.e. in normal form w.r.t.  ), and we notice that a monomial
), and we notice that a monomial
 is under the stairs if and only if
is under the stairs if and only if 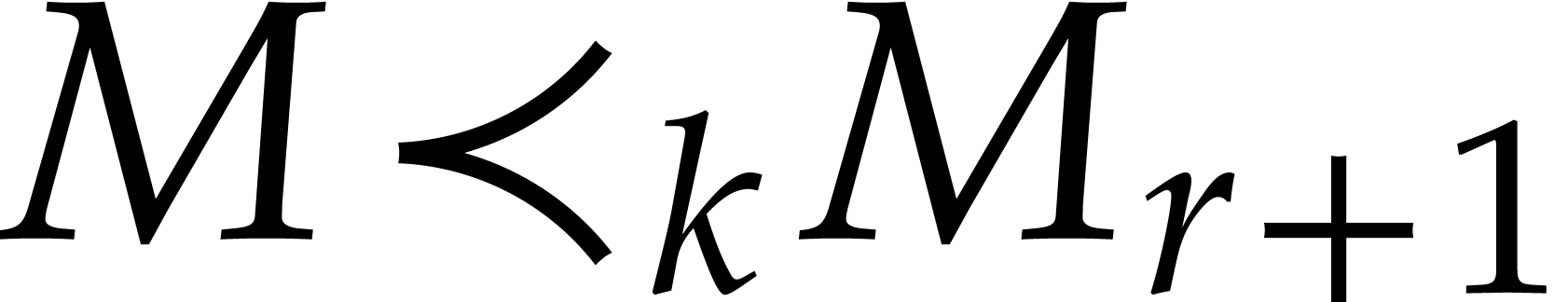 .
.
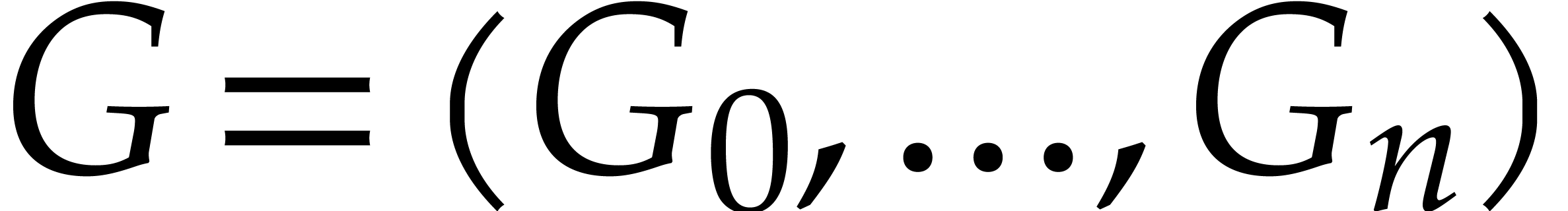 be as above, and let
be as above, and let 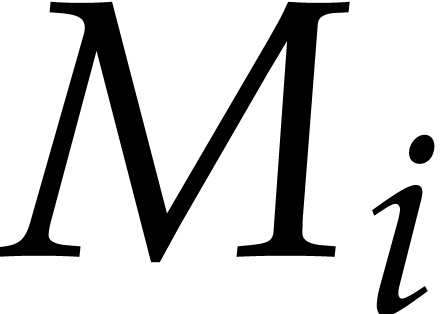 be the leading monomial of
be the leading monomial of 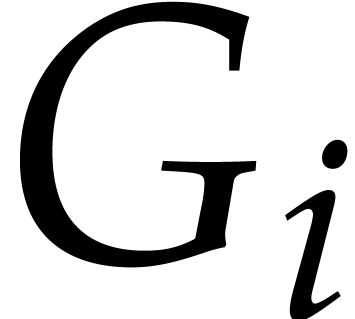 for
for
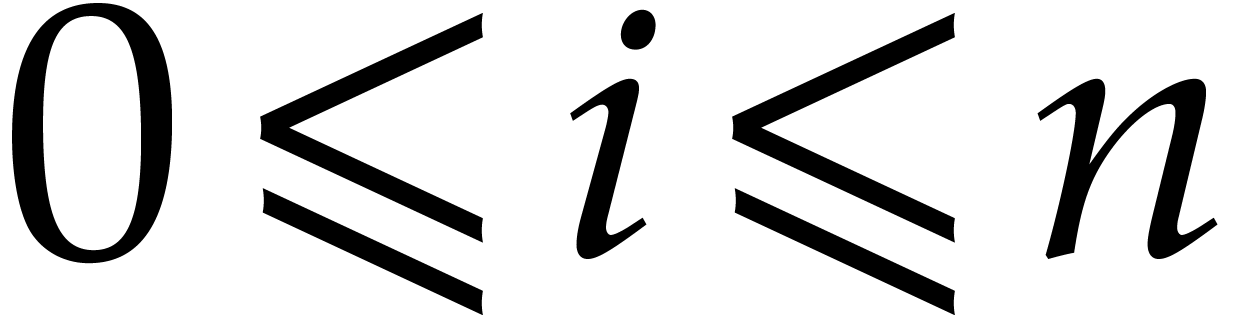 . With
. With 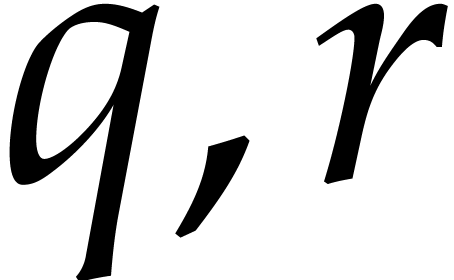 as in Proposition 3, the
as in Proposition 3, the  -degree
of
-degree
of  is given by
is given by
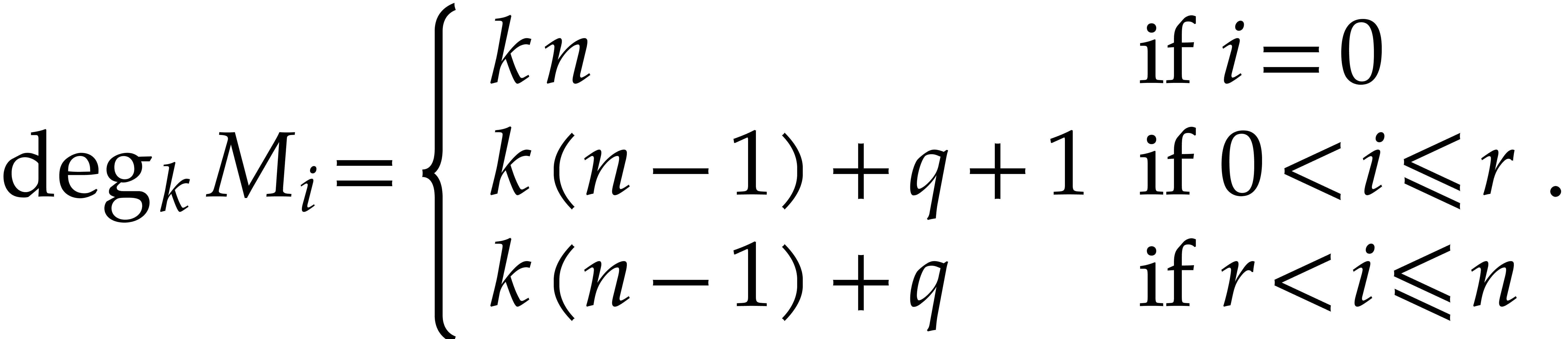
In particular, for all 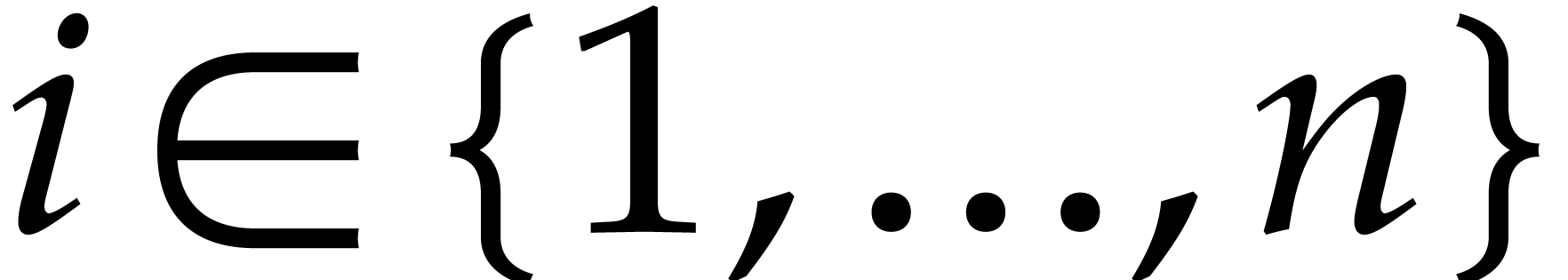 ,
we have
,
we have
Remark  with some precautions: if
with some precautions: if 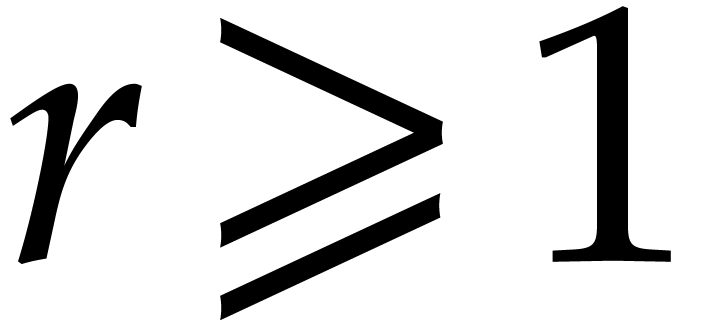 , one has to leave out
, one has to leave out 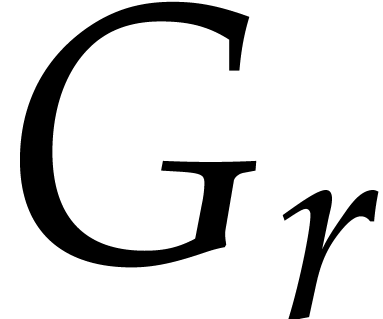 since
since
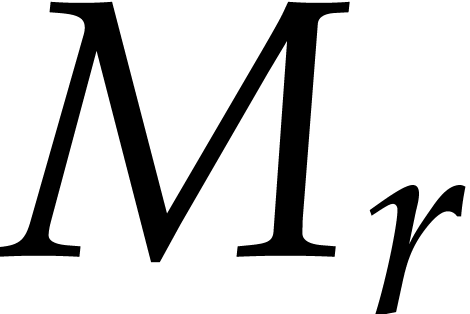 is divisible by
is divisible by 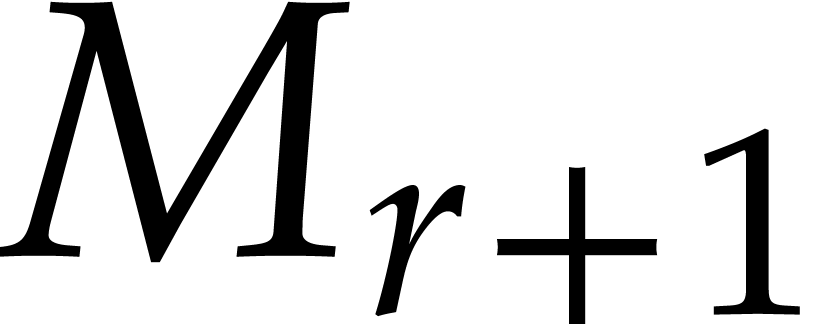 with the
given formulas. Then
with the
given formulas. Then  consists of
consists of 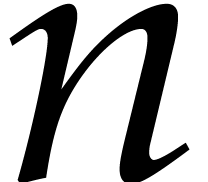 elements
elements 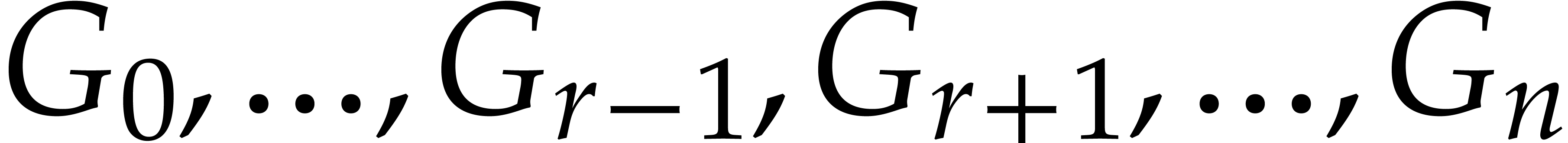 .
.
The main reduction algorithm in this paper relies on a rewriting
strategy that allows us to rewrite general linear combinations  of elements in the Gröbner basis as linear
combinations of fewer elements. In particular, it should be possible to
express each
of elements in the Gröbner basis as linear
combinations of fewer elements. In particular, it should be possible to
express each 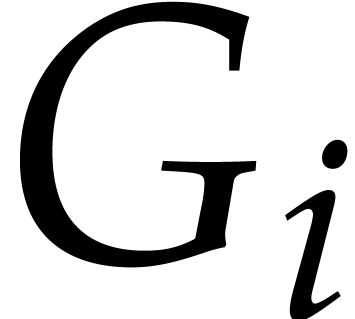 as a linear combination of elements
in a suitable subset
as a linear combination of elements
in a suitable subset  of
of  (this subset then generates the ideal
(this subset then generates the ideal  ),
with degrees that can be controlled.
),
with degrees that can be controlled.
It turns out that such a subset  may need to
contain three elements at least, but that
may need to
contain three elements at least, but that 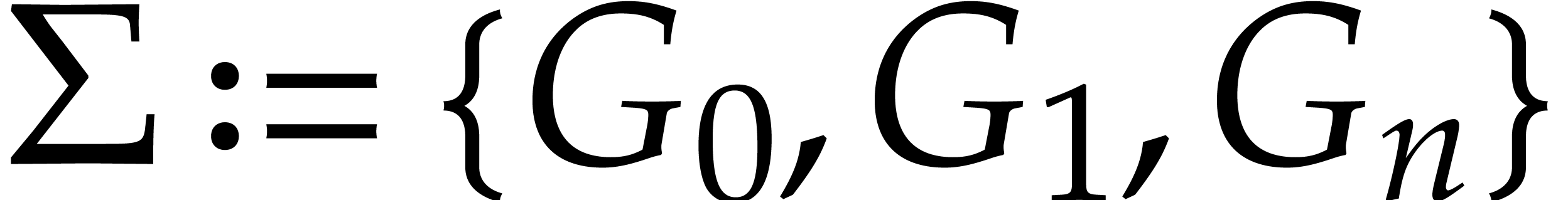 generically works. In order to control the degrees in the linear
combinations, we may also consider intermediate sets between
generically works. In order to control the degrees in the linear
combinations, we may also consider intermediate sets between 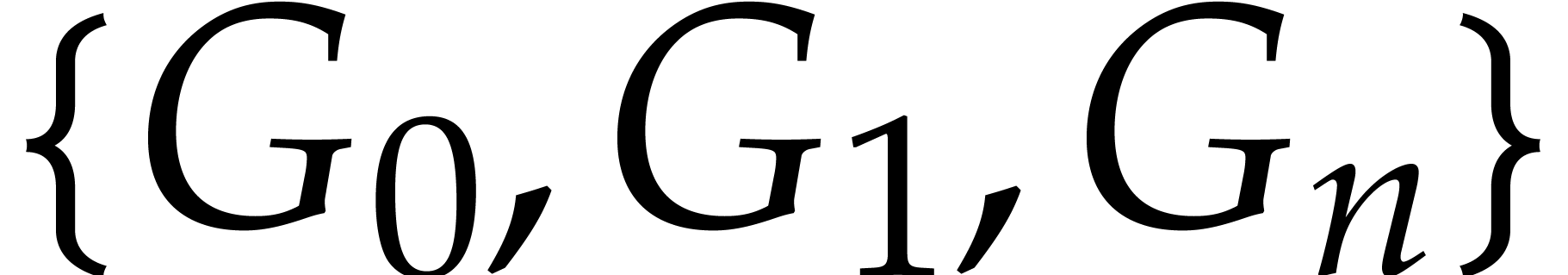 and the full set
and the full set  ,
such as
,
such as 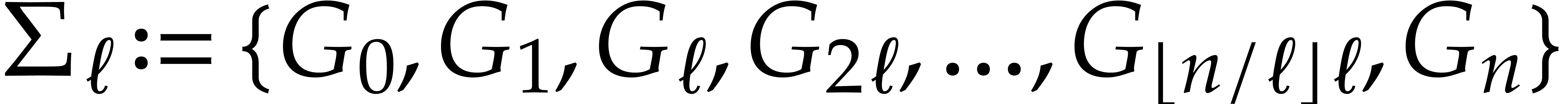 for various integer “step
lengths”
for various integer “step
lengths” 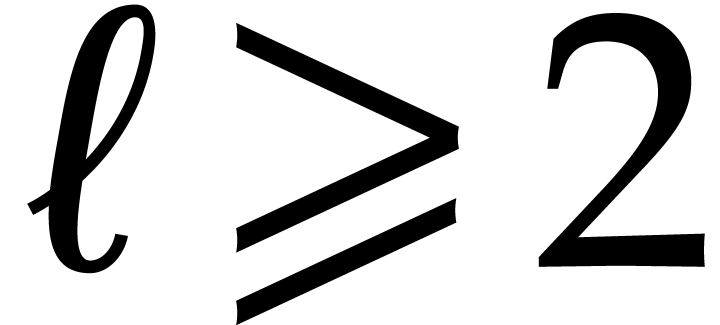 . This leads
us to the following definition:
. This leads
us to the following definition:
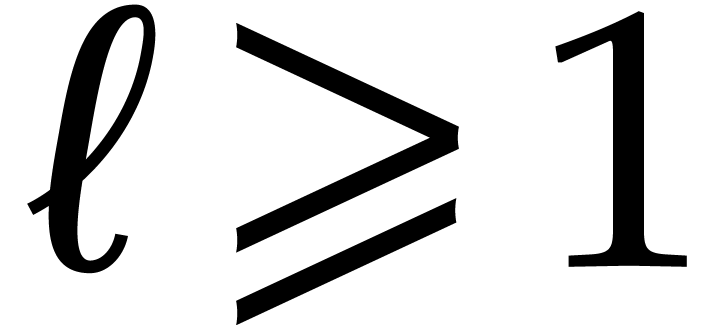 be an integer and consider the set
of indices
be an integer and consider the set
of indices
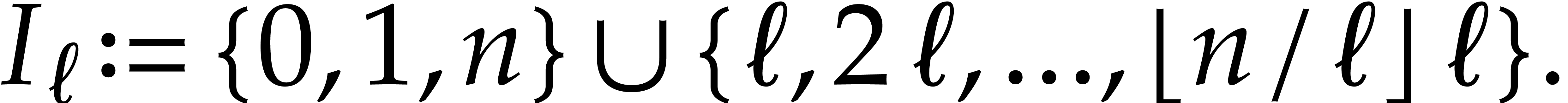 |
(1) |
We say that a family of polynomials 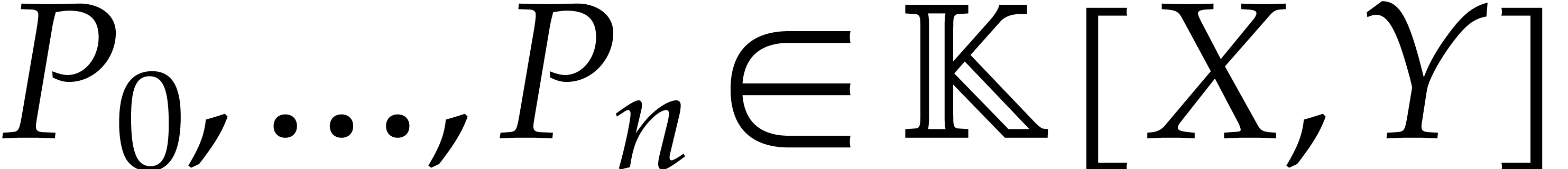 is
retractive for step length
is
retractive for step length 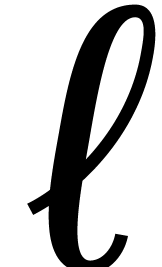 and
and  -degree
-degree  if for all
if for all 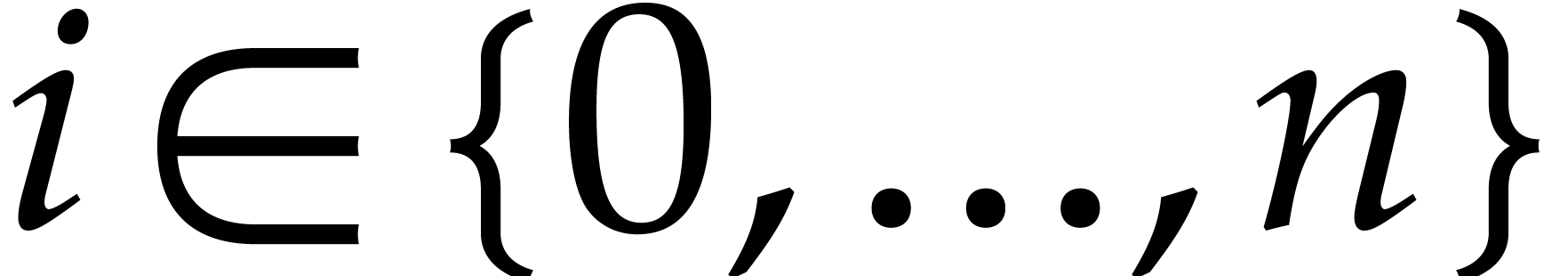 we can write
we can write
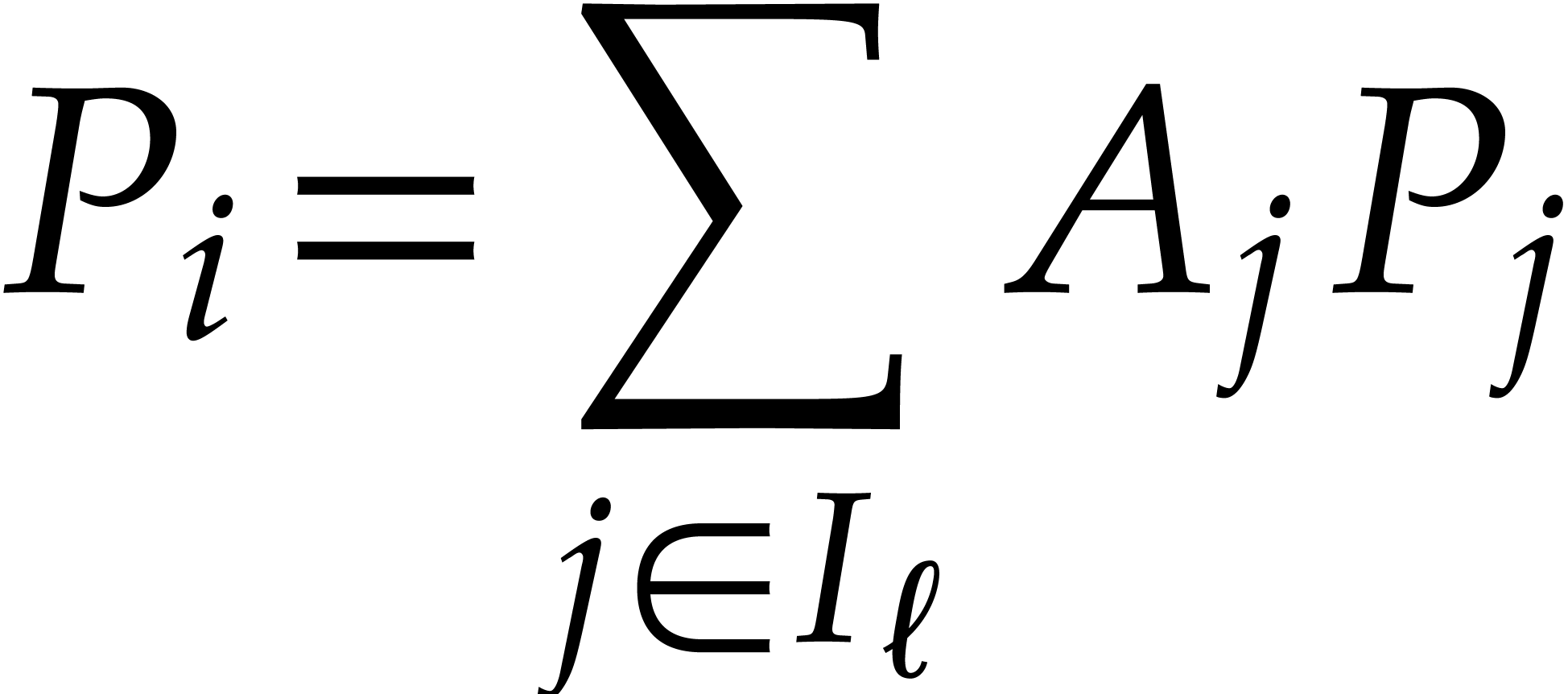
for some  with
with 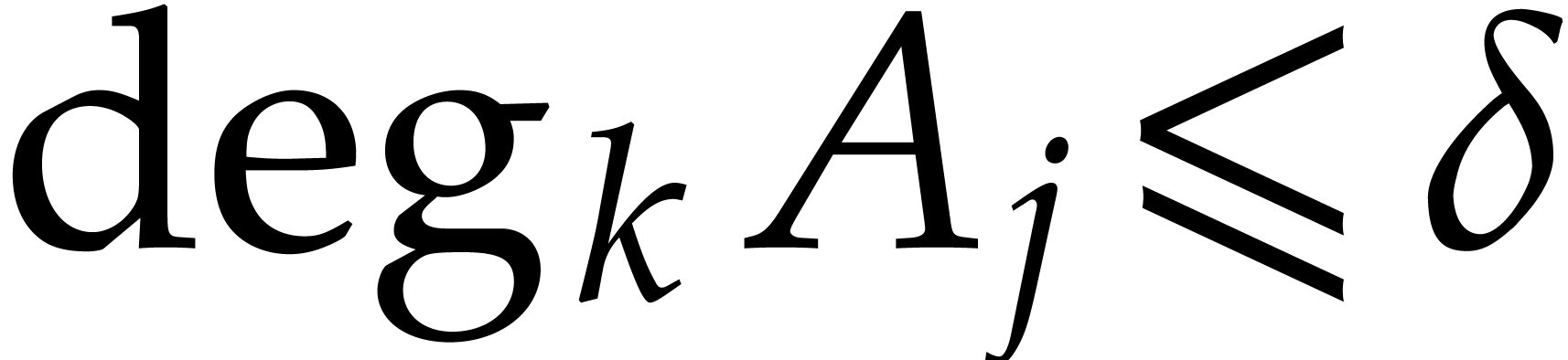 .
.
Consider a Gröbner basis  as in Proposition
3 and a linear combination
as in Proposition
3 and a linear combination 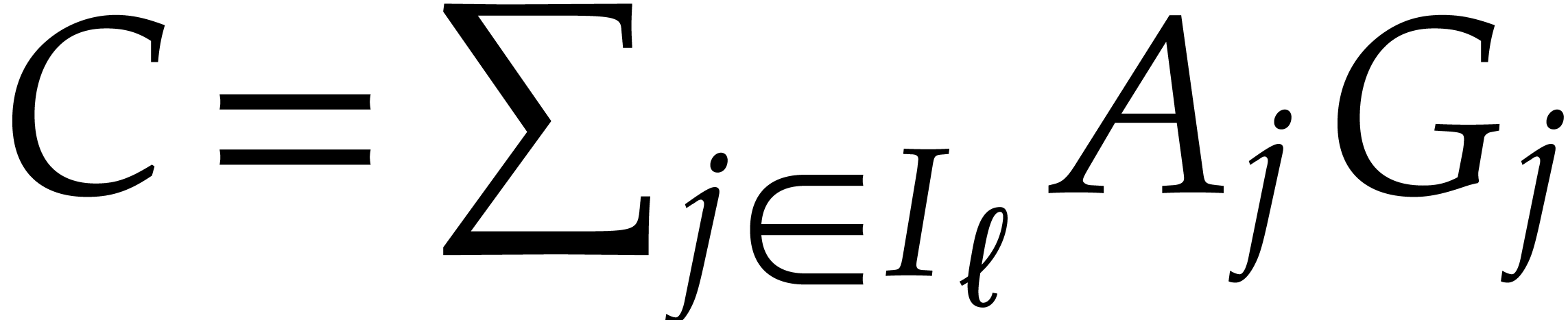 with
with
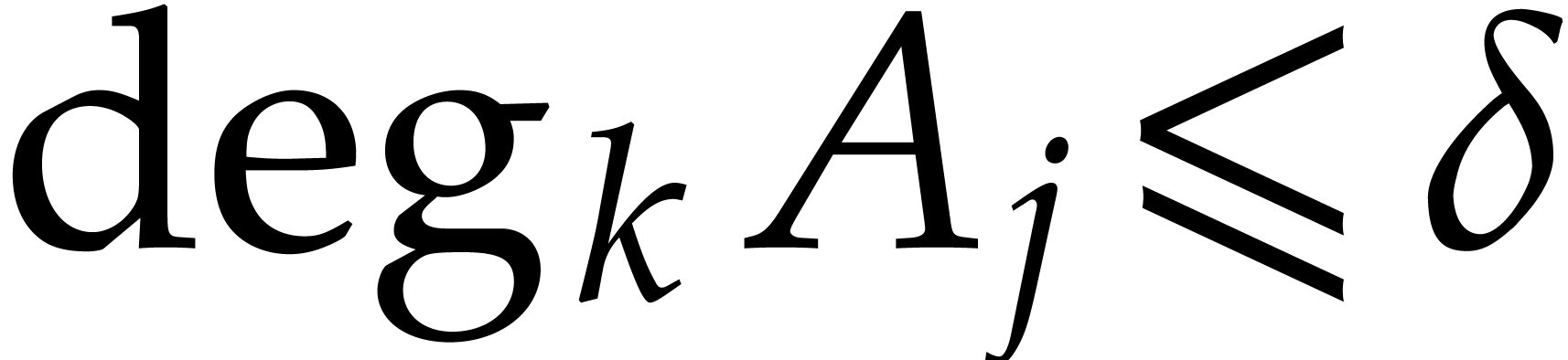 for all
for all  .
Making rough estimates, the number of monomials in
.
Making rough estimates, the number of monomials in  of
of 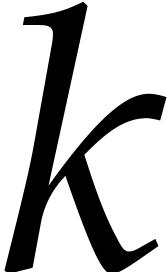 -degree
-degree 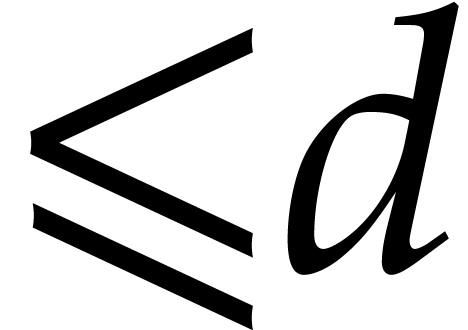 is
is 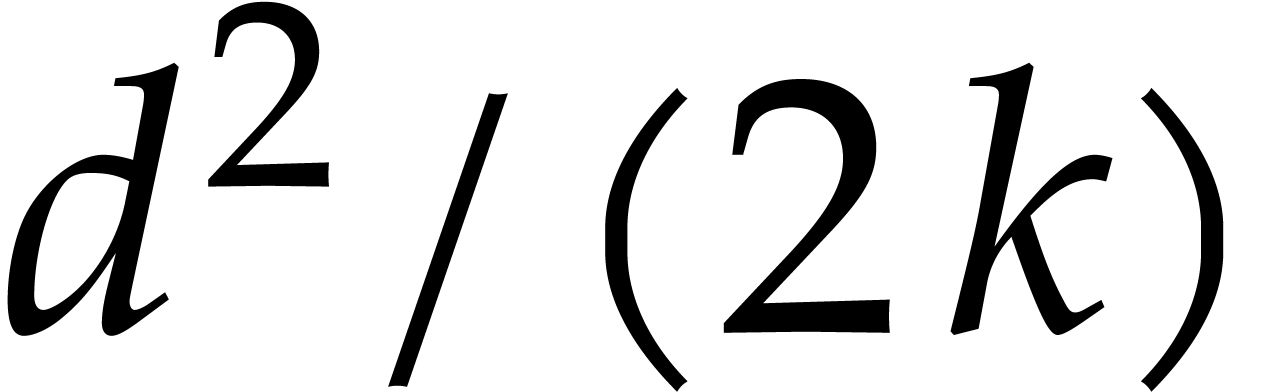 , whence the number of
monomials of
, whence the number of
monomials of 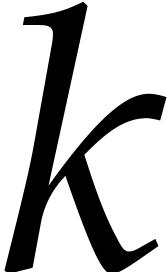 -degree between
-degree between
 and
and  is bounded by
is bounded by 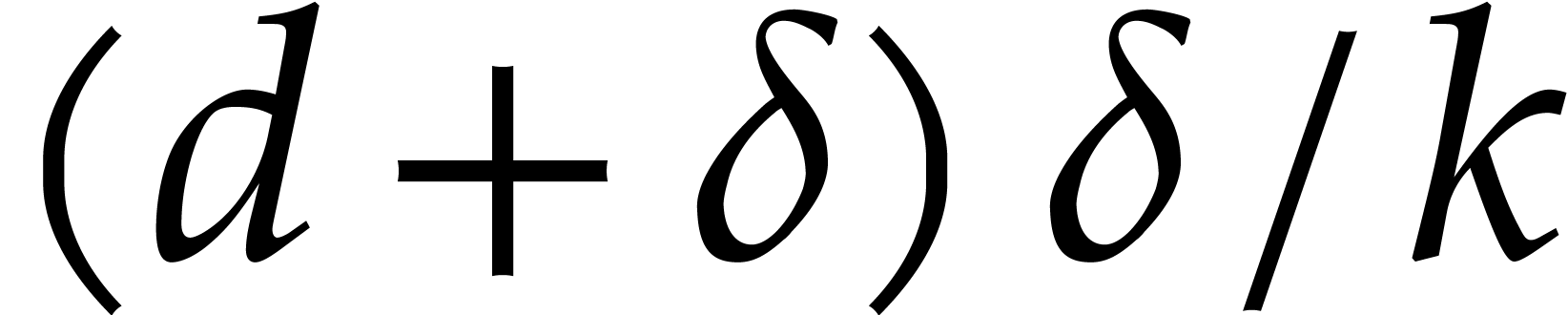 . The set
. The set 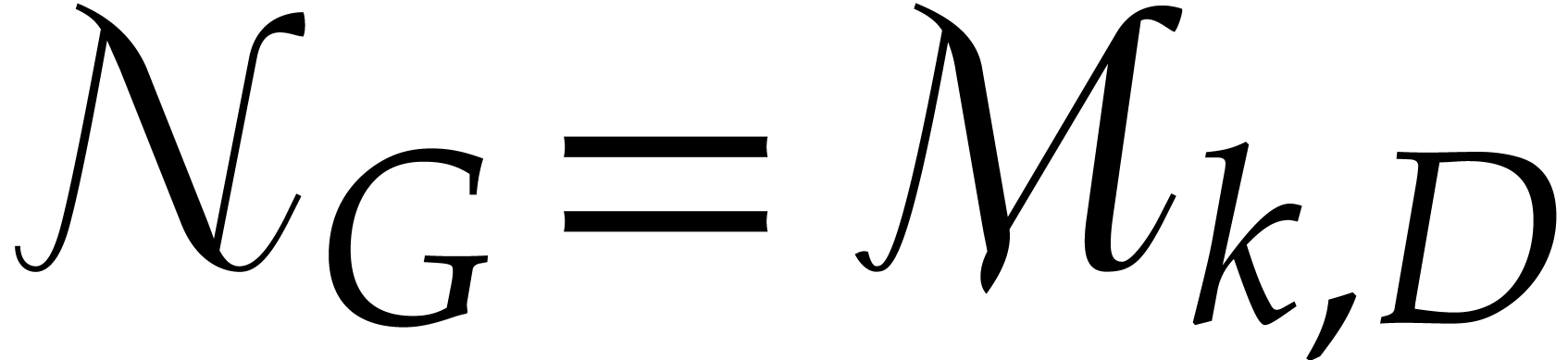 roughly corresponds to the set of monomials of
roughly corresponds to the set of monomials of 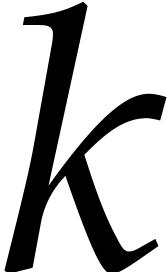 -degree
-degree  ,
whence the support of
,
whence the support of  contains at most
contains at most  monomials that are not in
monomials that are not in  . Notice that such a combination
. Notice that such a combination  is uniquely determined by its terms not in
is uniquely determined by its terms not in 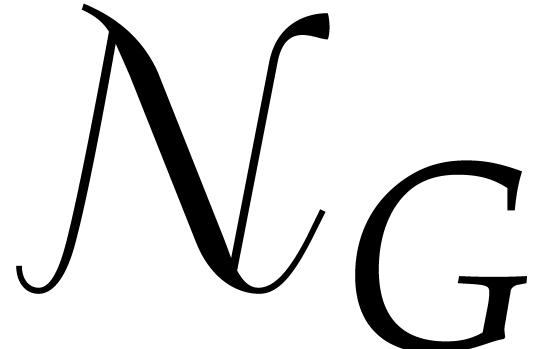 : if all the terms of
: if all the terms of 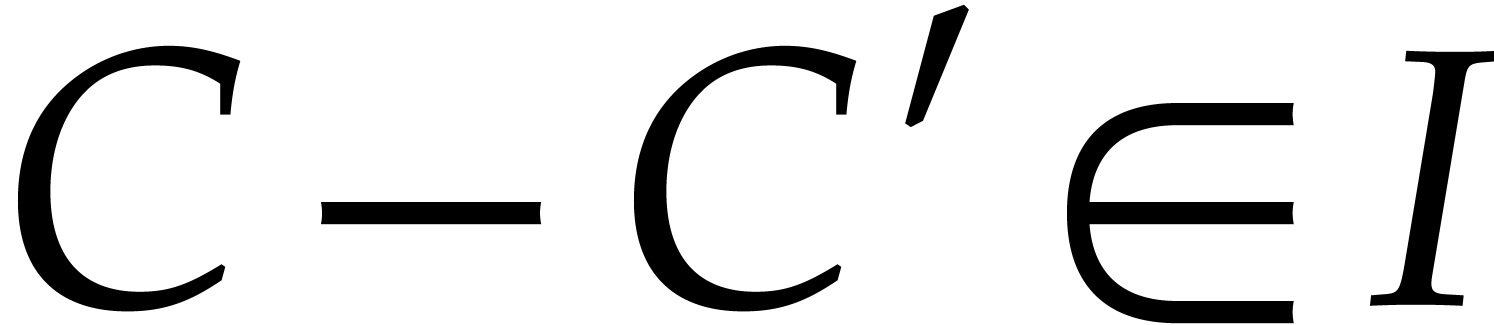 are in
are in 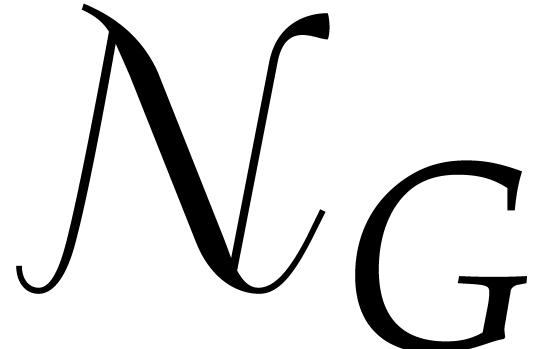 , then
, then 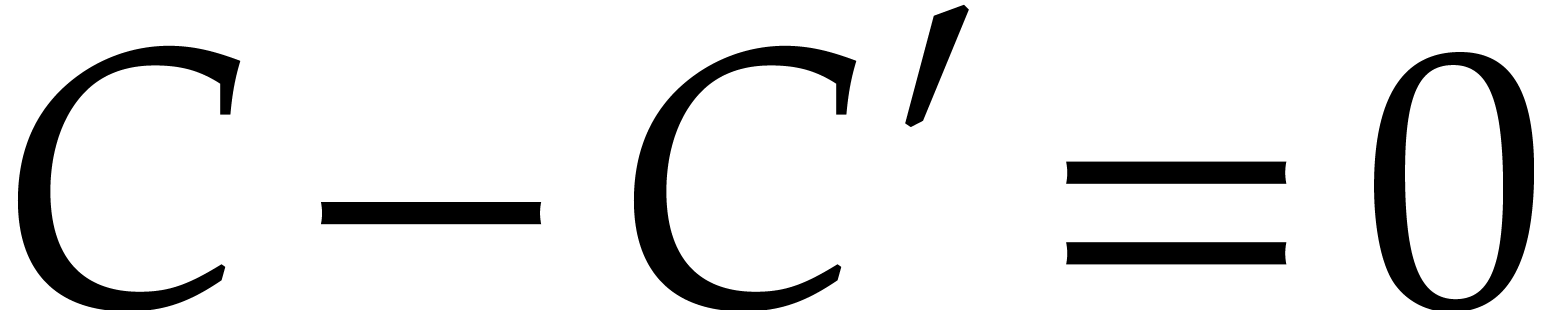 by definition of a Gröbner basis.
by definition of a Gröbner basis.
On the other hand the polynomials  with
with  are determined by approximately
are determined by approximately 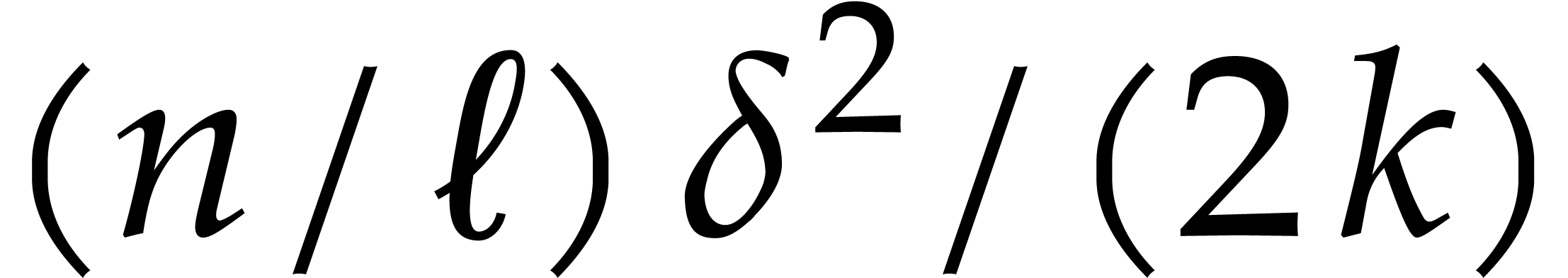 coefficients. As soon as
coefficients. As soon as 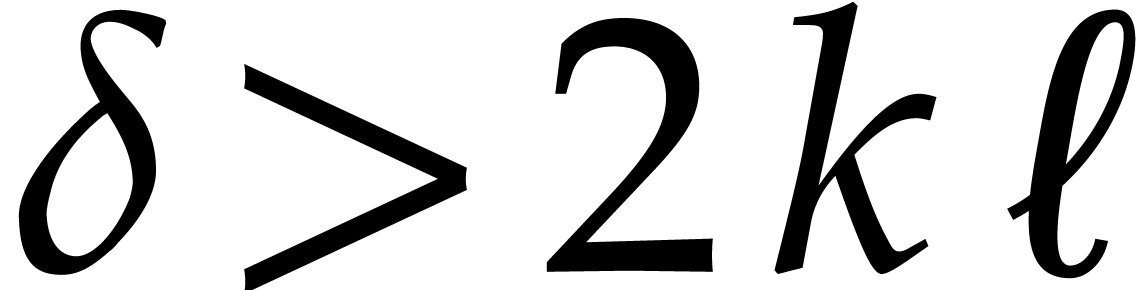 , it
follows that
, it
follows that
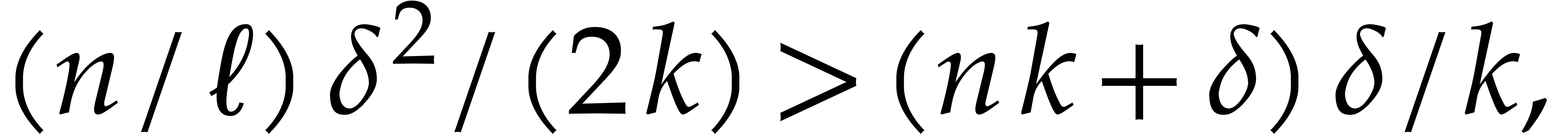
and it becomes likely that non-trivial relations of the type 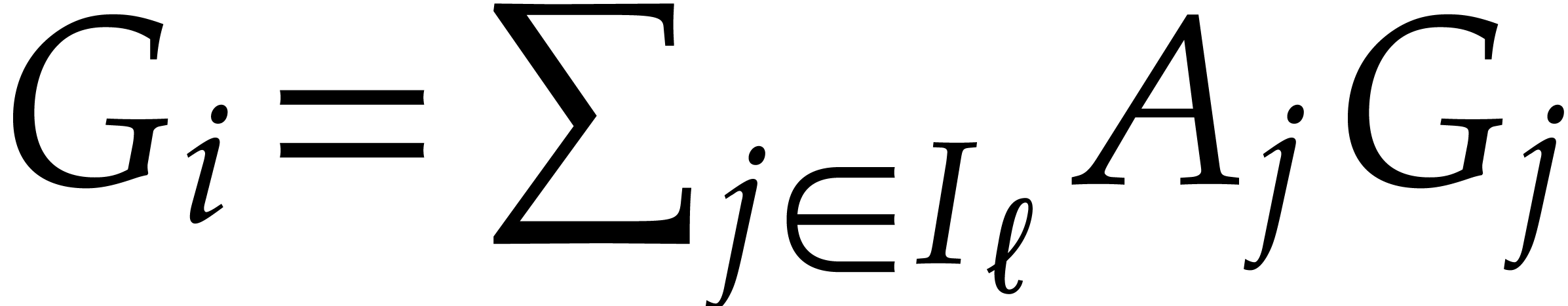 indeed exist. A refined analysis and practical experiments
show that the precise threshold is located at
indeed exist. A refined analysis and practical experiments
show that the precise threshold is located at 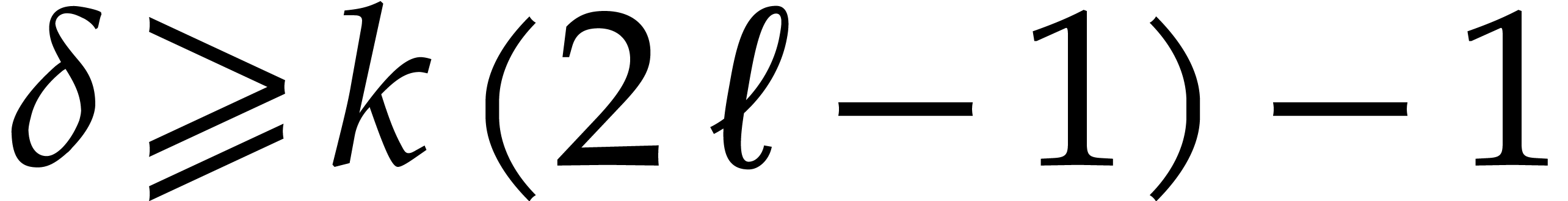 , although we have no formal proof of this empirical
fact.
, although we have no formal proof of this empirical
fact.
We are now in a position to describe the class of Gröbner bases with enough regularity for our fast reduction algorithm to work.
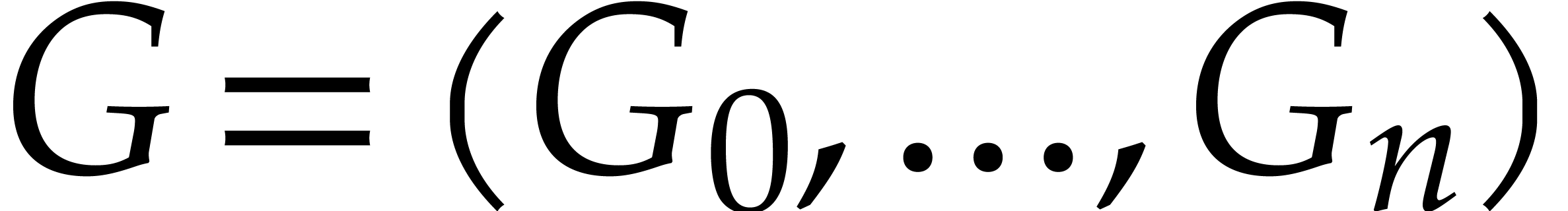 be the reduced Gröbner basis
for an ideal
be the reduced Gröbner basis
for an ideal 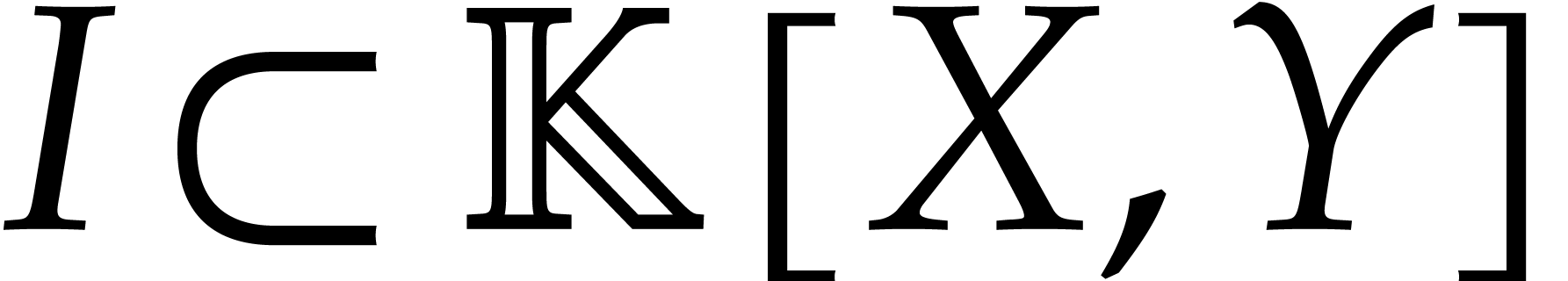 with respect to
with respect to  . We say that
. We say that  is a
vanilla Gröbner basis if
is a
vanilla Gröbner basis if
the leading monomials of  form a vanilla
Gröbner stairs;
form a vanilla
Gröbner stairs;
the family  is retractive for step length
is retractive for step length
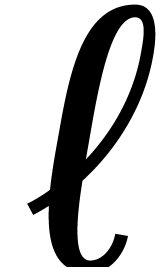 and
and 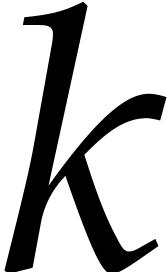 -degree
-degree
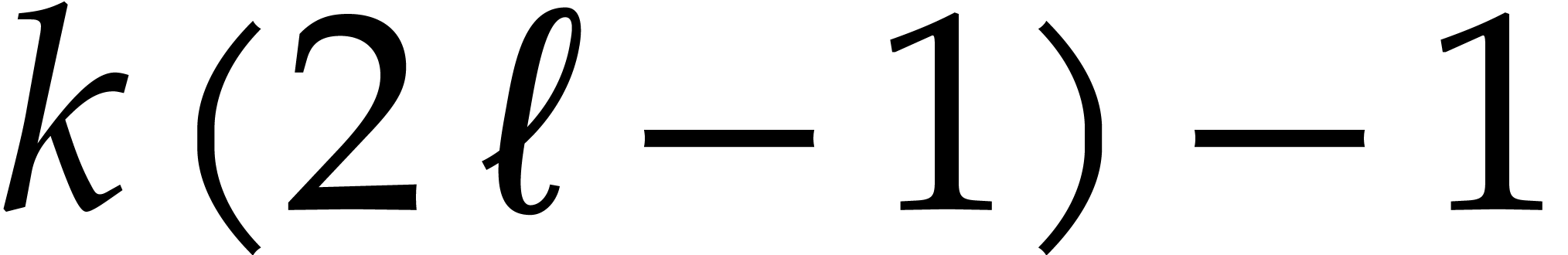 , for
, for  .
.
It appears that reduced Gröbner bases of sufficiently generic
ideals are always of vanilla type, although we have not been able to
prove this so far. We even do not know whether vanilla Gröbner
bases exist for arbitrary fields  (with
sufficiently many elements) and degrees
(with
sufficiently many elements) and degrees  .
Nevertheless, practical computer experiments suggest that sufficiently
random ideals of degree
.
Nevertheless, practical computer experiments suggest that sufficiently
random ideals of degree 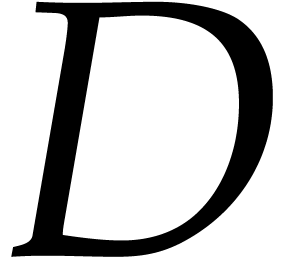 admit Gröbner bases
of this kind. More precisely, we have checked this (up to degrees in the
range of a few hundreds) for ideals that are generated as follows by two
random polynomials:
admit Gröbner bases
of this kind. More precisely, we have checked this (up to degrees in the
range of a few hundreds) for ideals that are generated as follows by two
random polynomials:
for 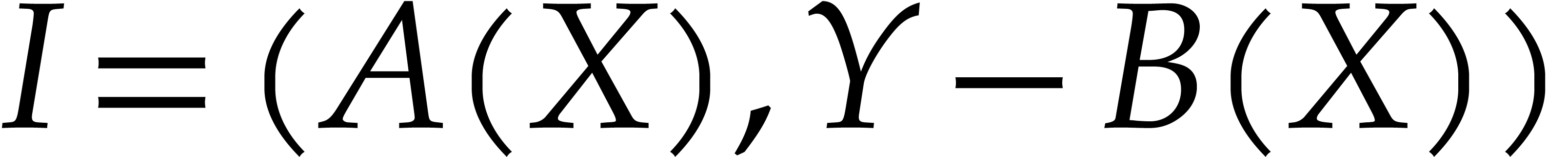 , where
, where  and
and 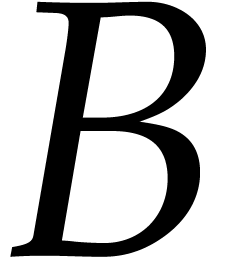 are random univariate
polynomials of degrees
are random univariate
polynomials of degrees 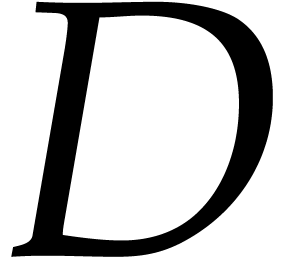 and
and 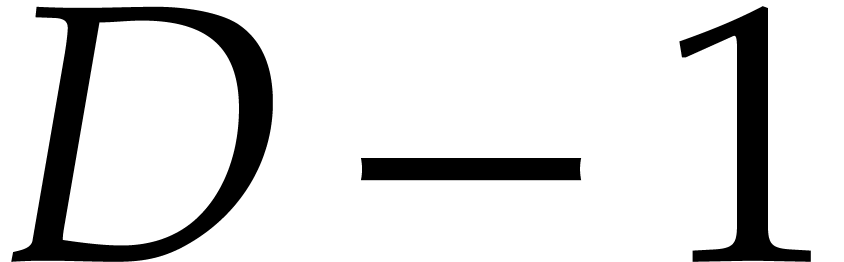 , and for any ordernig
, and for any ordernig  ;
;
for 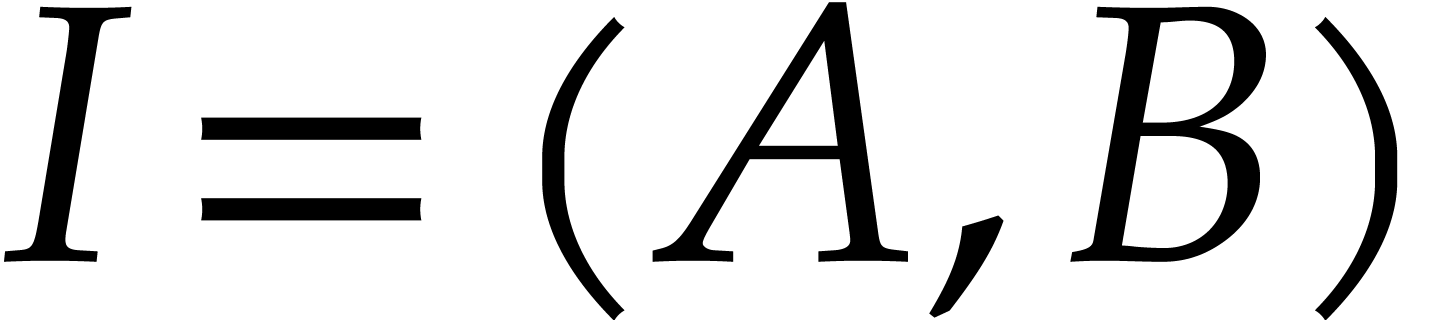 , where
, where  and
and 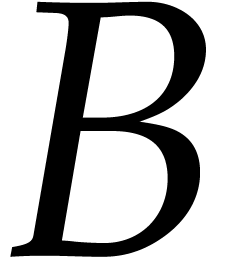 are random bivariate
polynomials of total degree
are random bivariate
polynomials of total degree  (in this case
the degree of the ideal is
(in this case
the degree of the ideal is 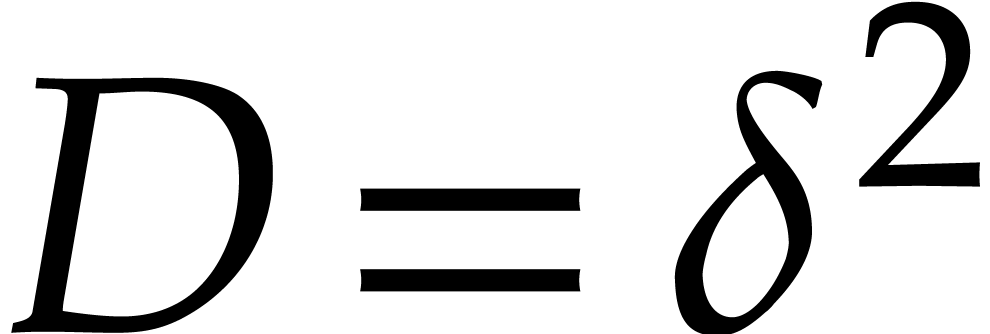 ),
and for any ordering
),
and for any ordering  with
with 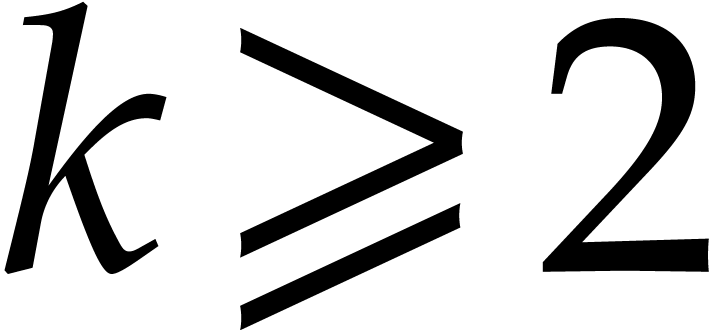 ;
;
for 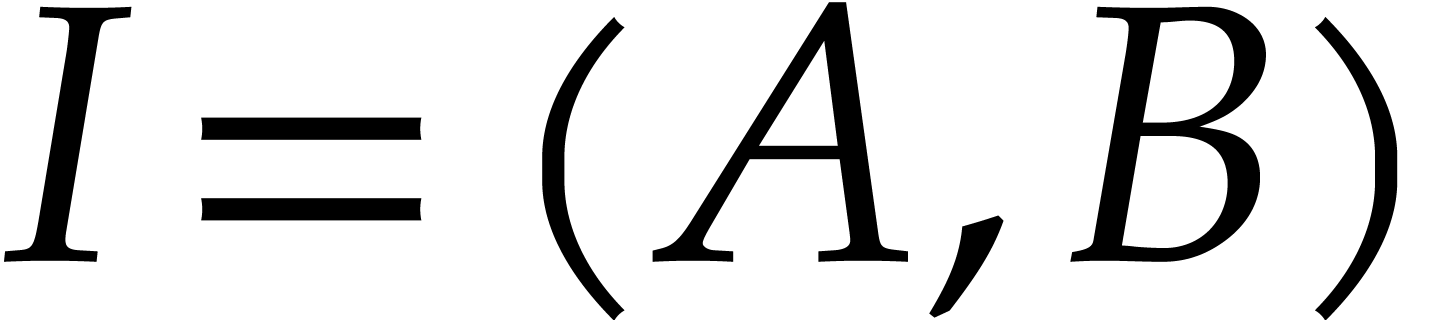 , where
, where  and
and 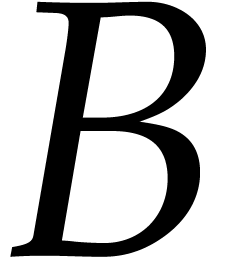 are random bivariate
polynomials of degree
are random bivariate
polynomials of degree  in both variables (in
this case the degree of the ideal is
in both variables (in
this case the degree of the ideal is 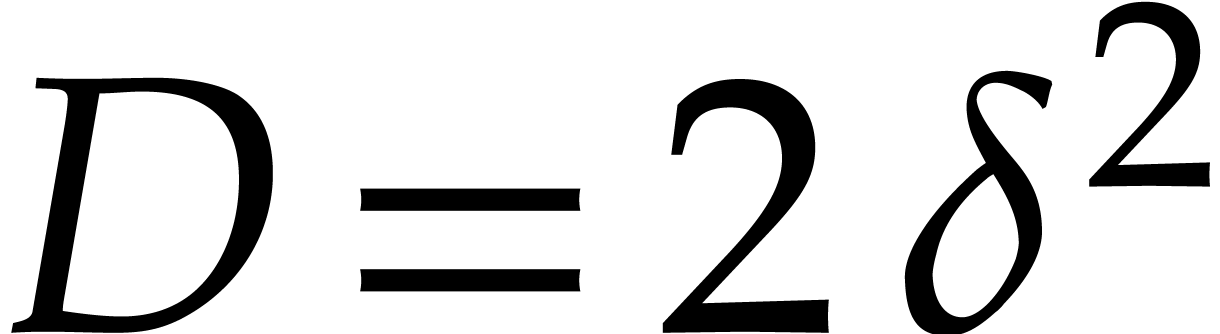 ),
and for any ordering
),
and for any ordering  with
with 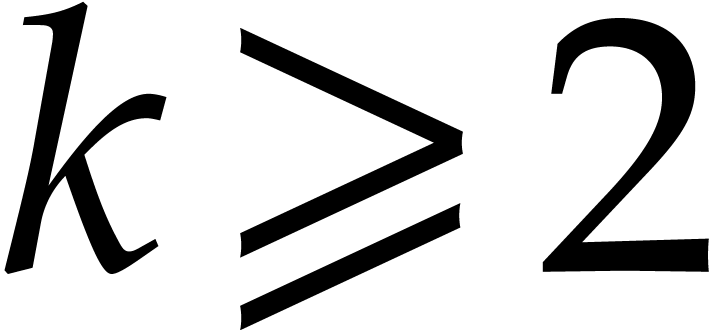 .
.
In each of these cases, the threshold 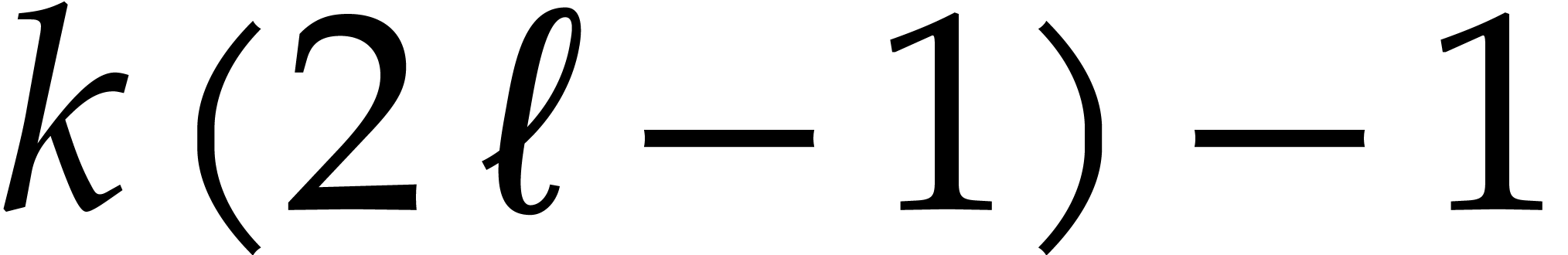 seems to
be sharp. Nevertheless, for our complexity bounds, a threshold of the
type
seems to
be sharp. Nevertheless, for our complexity bounds, a threshold of the
type  would suffice, for any constant
would suffice, for any constant 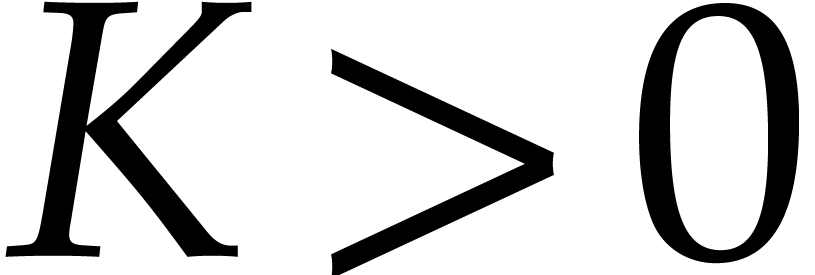 .
.
In this section, we quickly review some basic complexities for
fundamental operations on polynomials over a field  . Notice that results presented in this section
are not specific to the bivariate case. Running times will always be
measured in terms of the required number of field operations in
. Notice that results presented in this section
are not specific to the bivariate case. Running times will always be
measured in terms of the required number of field operations in  .
.
We denote by 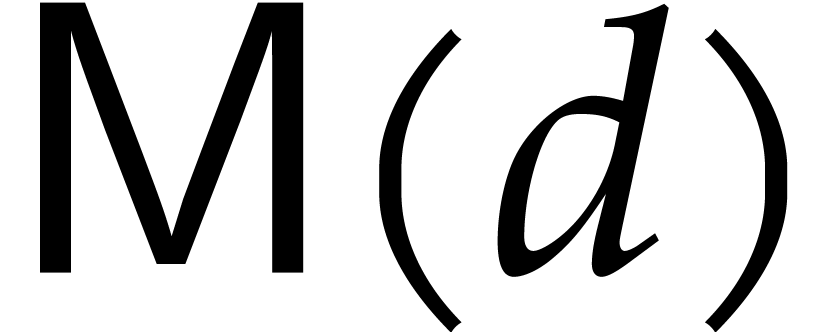 the cost of multiplying two dense
univariate polynomials of degree
the cost of multiplying two dense
univariate polynomials of degree  in
in 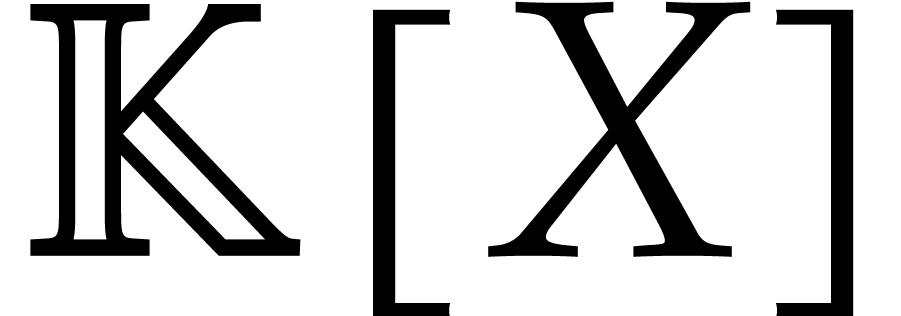 . Over general fields, one may take [27,
26, 5]
. Over general fields, one may take [27,
26, 5]
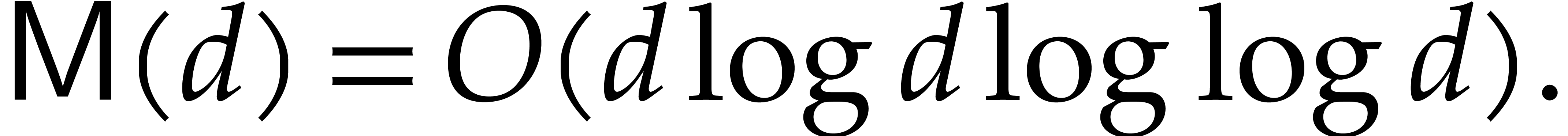
In the case of fields of positive characteristic, one may even take
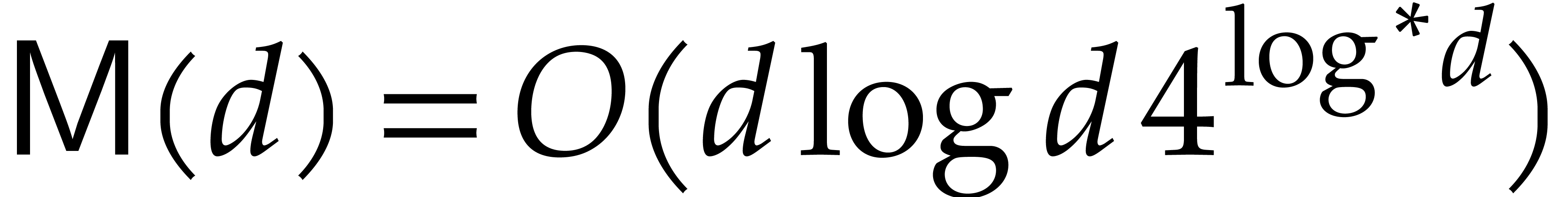 , where
, where  denotes the iterated logarithm [17, 18]. We
make the customary assumptions that
denotes the iterated logarithm [17, 18]. We
make the customary assumptions that 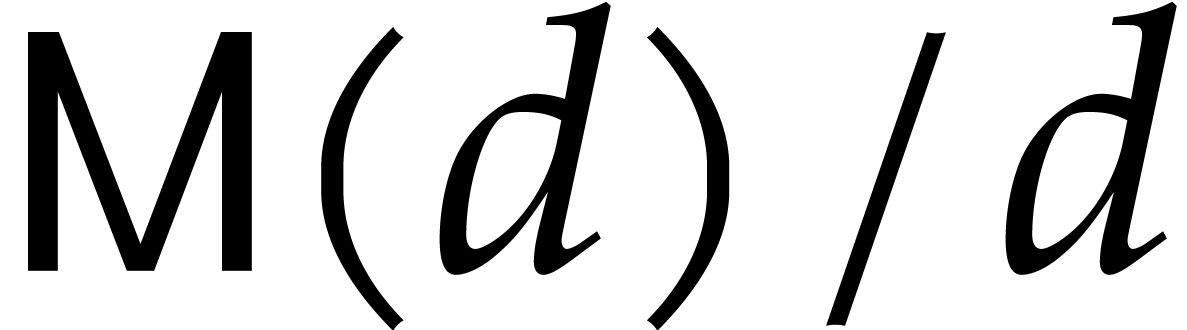 is
increasing and that
is
increasing and that 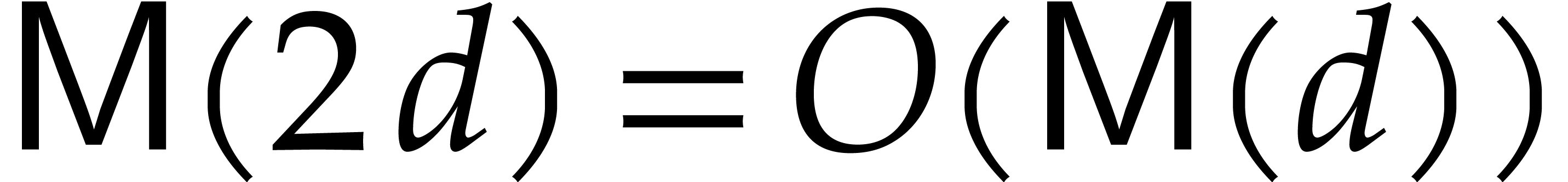 , with
the usual implications, such as
, with
the usual implications, such as 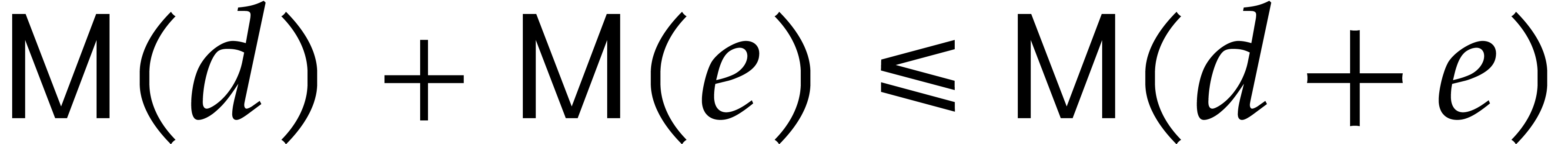 .
.
For multivariate polynomials, the cost of multiplication depends on the
geometry of the support. The multiplication of dense bivariate
“block” polynomials in 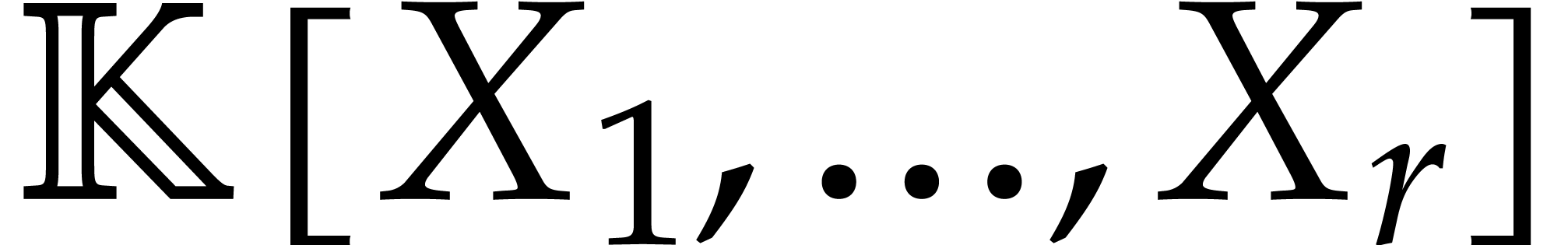 of degree
of degree
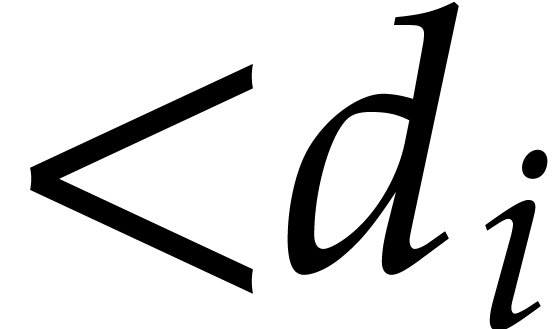 in each variable
in each variable 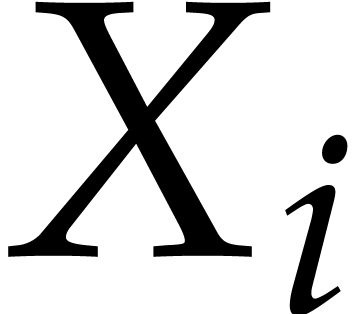 can be
reduced to multiplication of univariate polynomials of degree
can be
reduced to multiplication of univariate polynomials of degree 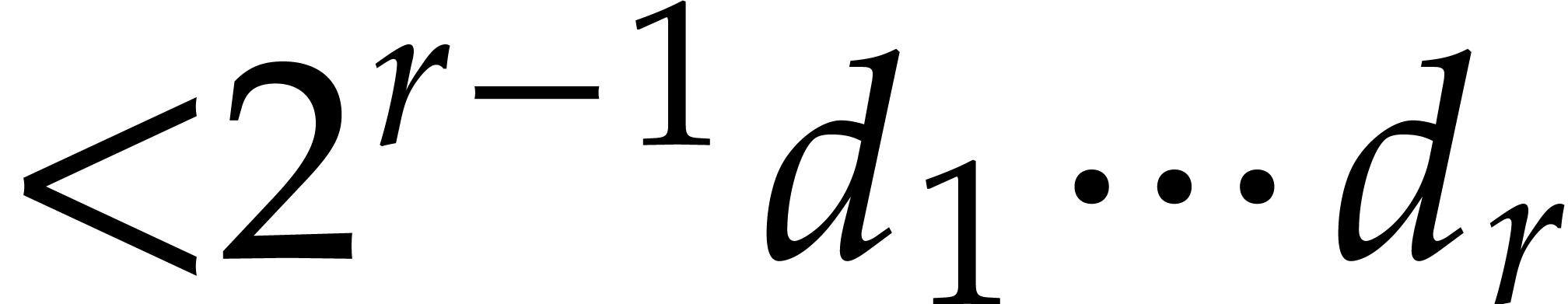 using the well known technique of Kronecker substitution
[12]. More generally, for polynomials such that the support
of the product is included in an initial segment with
using the well known technique of Kronecker substitution
[12]. More generally, for polynomials such that the support
of the product is included in an initial segment with  elements, it is possible to compute the product in time
elements, it is possible to compute the product in time 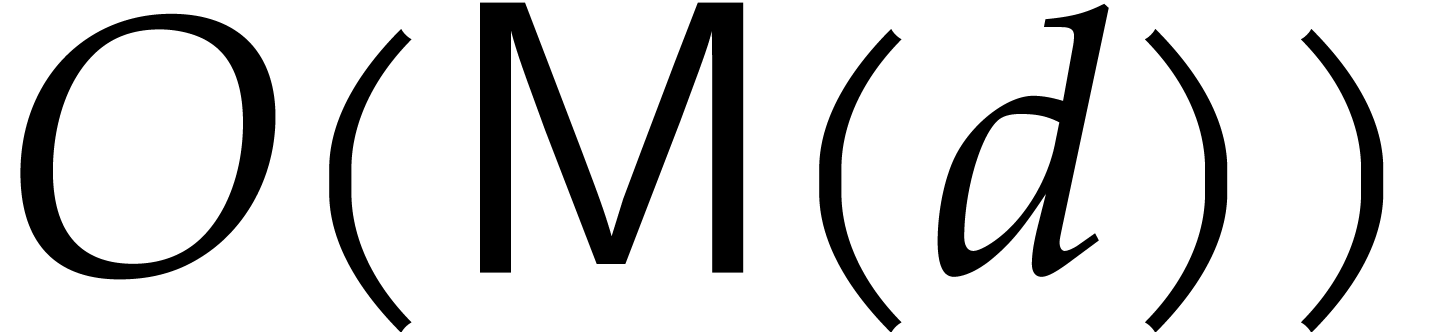 . Here an initial segment of
. Here an initial segment of  is a subset
is a subset  such that all divisors of any
monomial
such that all divisors of any
monomial  are again in
are again in  .
.
For the purpose of this paper, we need to consider dense polynomials
 in
in 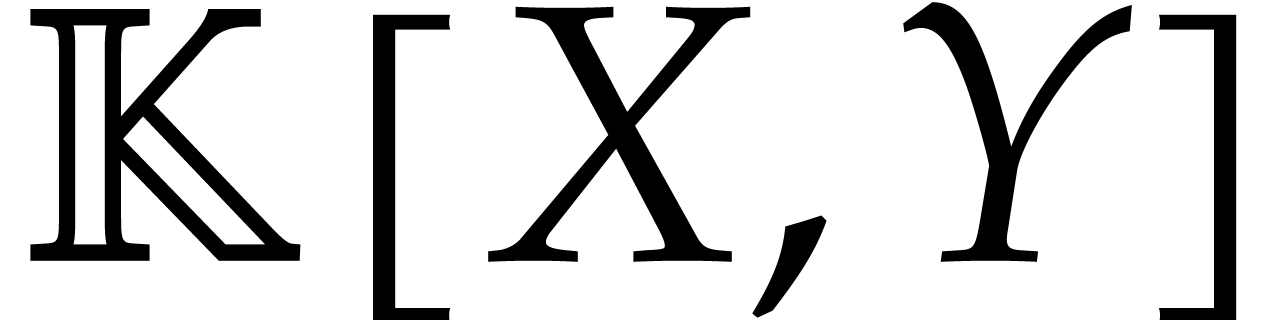 whose supports are
contained in sets of the form
whose supports are
contained in sets of the form  .
Modulo the change of variables
.
Modulo the change of variables 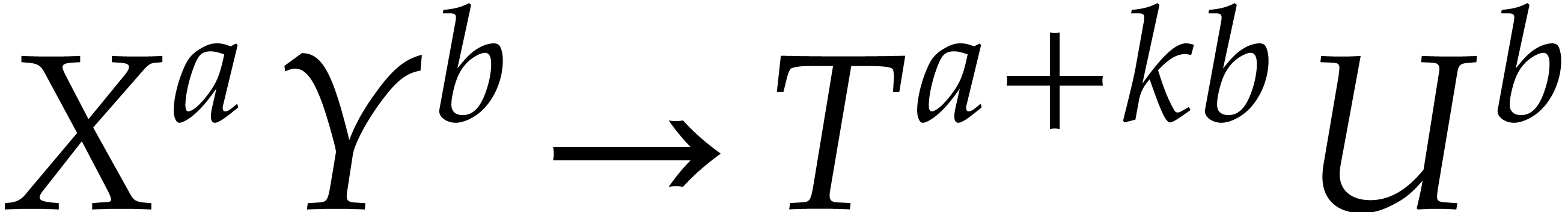 ,
such a polynomial can be rewritten as
,
such a polynomial can be rewritten as 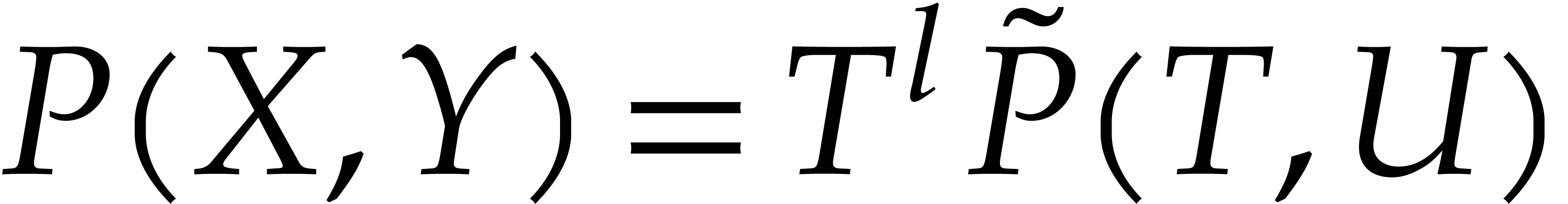 ,
where the support of
,
where the support of 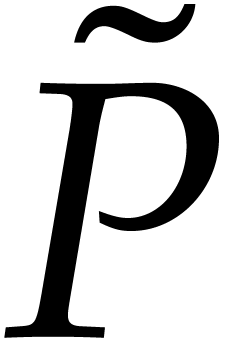 is an initial segment with
the same size as
is an initial segment with
the same size as 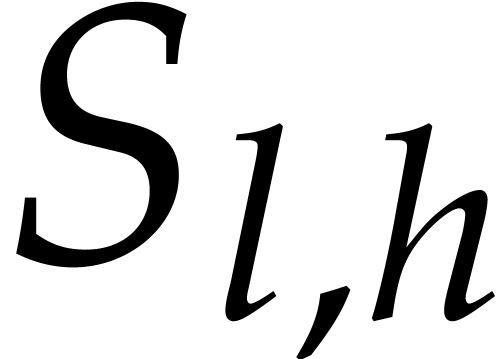 . For a
product of two polynomials of this type with a support of size
. For a
product of two polynomials of this type with a support of size  , this means that the product can
again be computed in time
, this means that the product can
again be computed in time 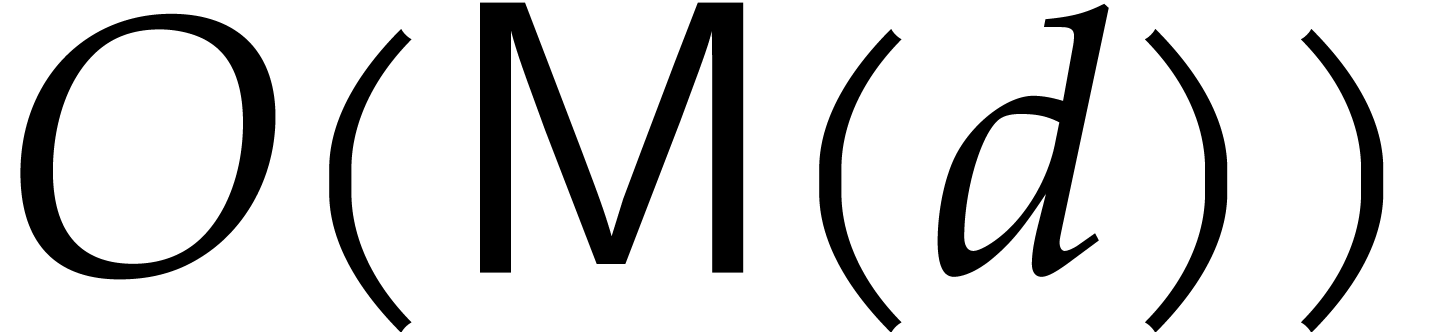 .
.
For the above polynomial multiplication algorithms, we assume that the
input polynomials are entirely given from the outset. In specific
settings, the input polynomials may be only partially known at some
point, and it can be interesting to anticipate the computation of the
partial output. This is particularly true when working with (truncated)
formal power series  instead of polynomials,
where it is common that the coefficients are given as a stream.
instead of polynomials,
where it is common that the coefficients are given as a stream.
In this so-called “relaxed (or online) computation model”,
the coefficient 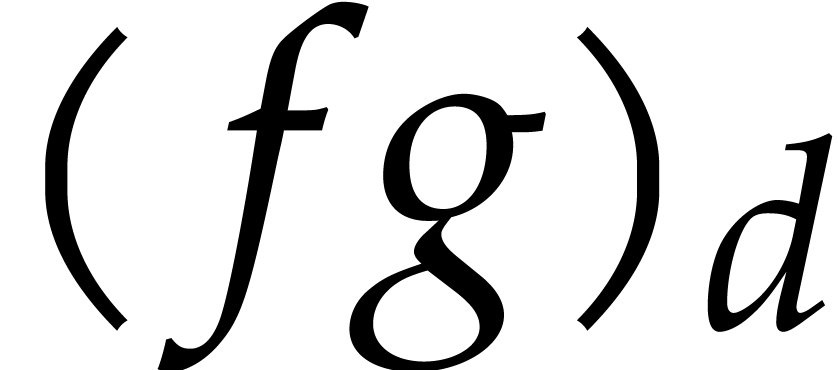 of a product of two series
of a product of two series 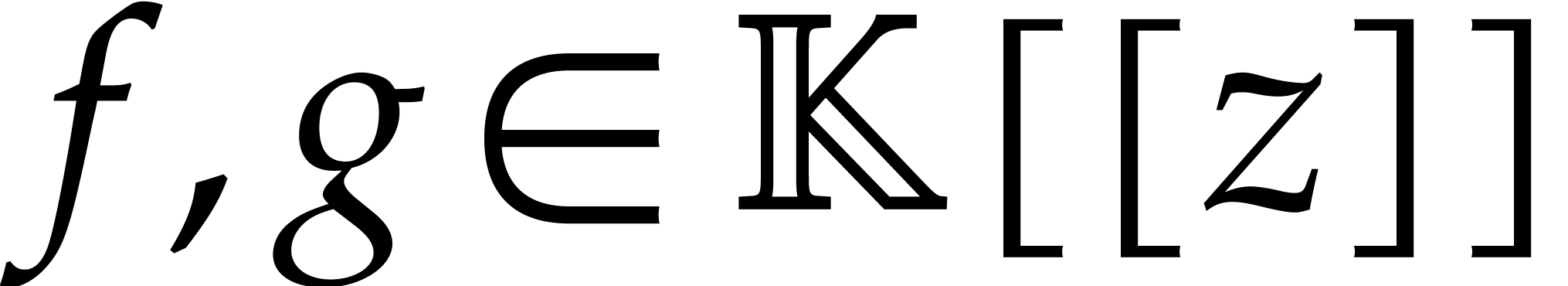 must be output as soon as
must be output as soon as  and
and
 are known. This model has the advantage that
subsequent coefficients
are known. This model has the advantage that
subsequent coefficients 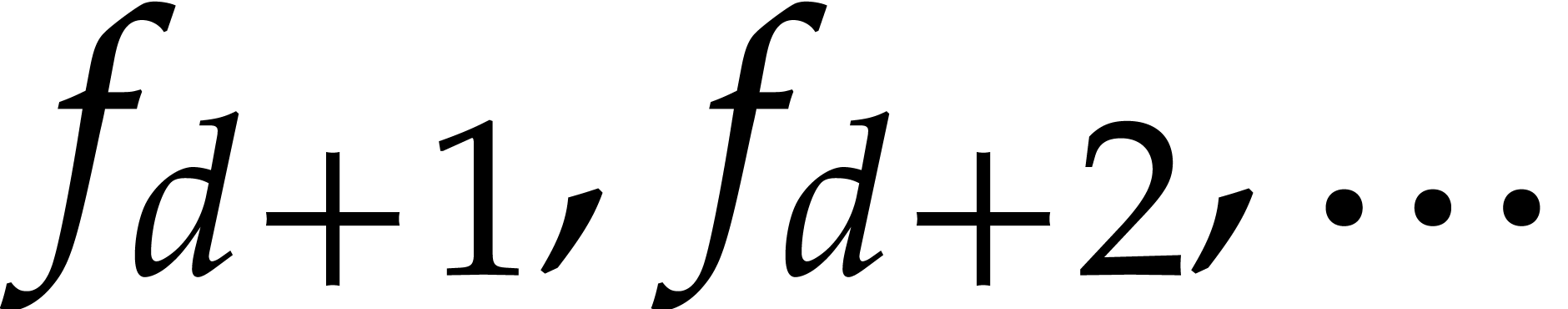 and
and 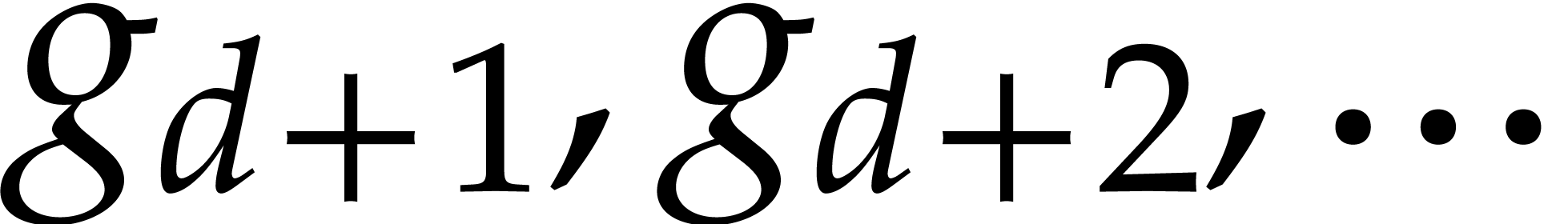 are allowed to depend on the result
are allowed to depend on the result 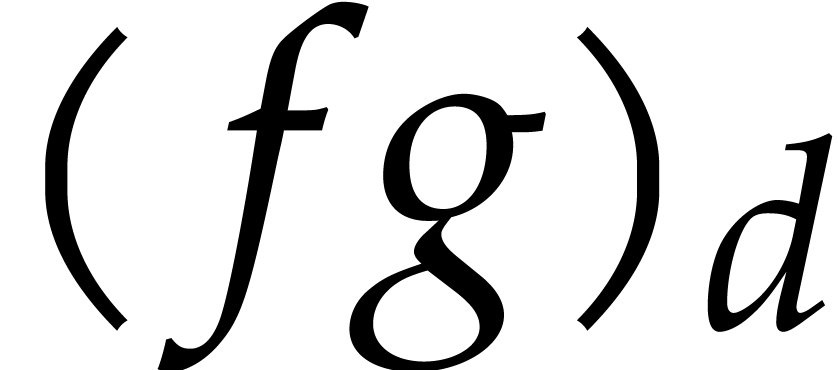 .
This often allows us to solve equations involving power series
.
This often allows us to solve equations involving power series 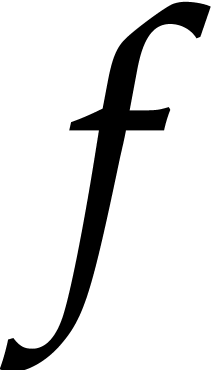 by rewriting them into recursive equations of the
form
by rewriting them into recursive equations of the
form  , with the property that
the coefficient
, with the property that
the coefficient 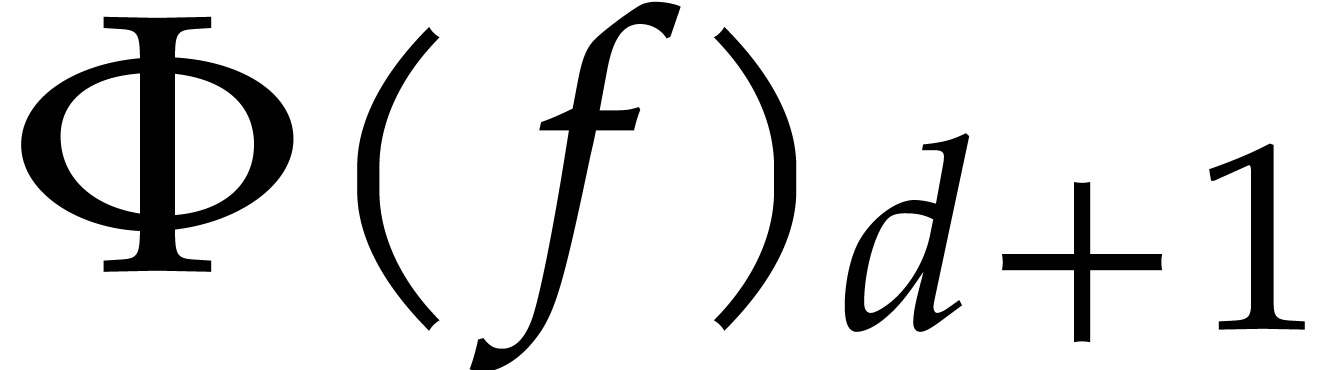 only depends on earlier
coefficients
only depends on earlier
coefficients  for all
for all  . For instance, in order to invert a power series of
the form
. For instance, in order to invert a power series of
the form 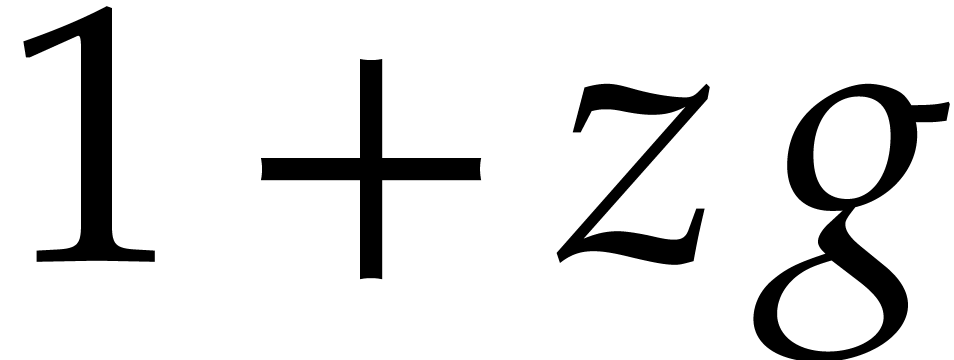 with
with 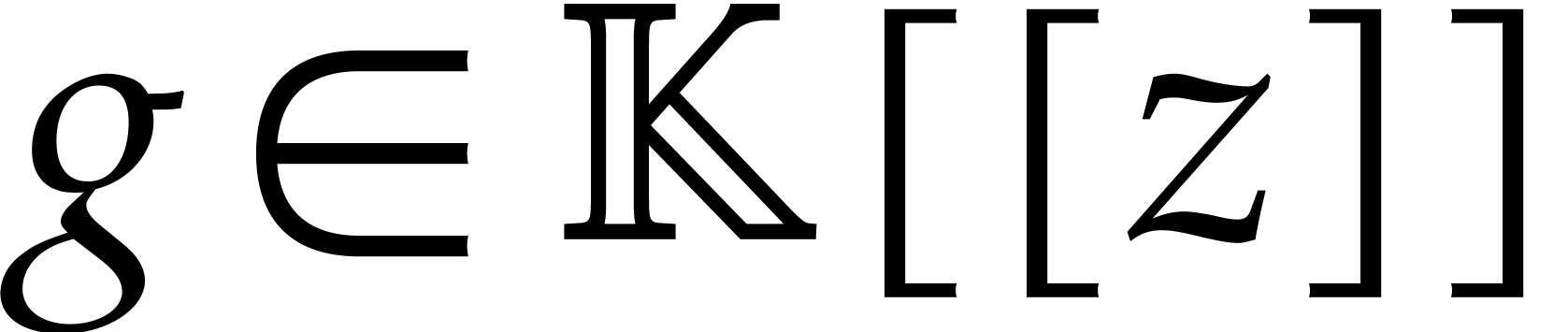 ,
we may take
,
we may take 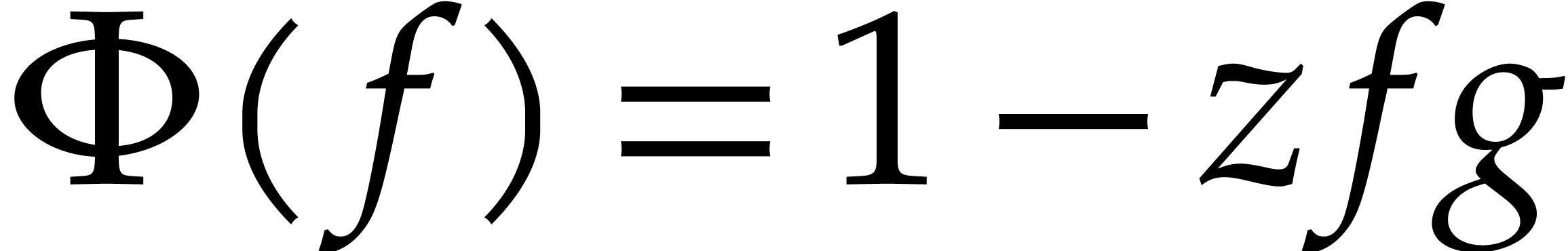 . Similarly, if
. Similarly, if
 has characteristic zero, then the exponential of
a power series
has characteristic zero, then the exponential of
a power series 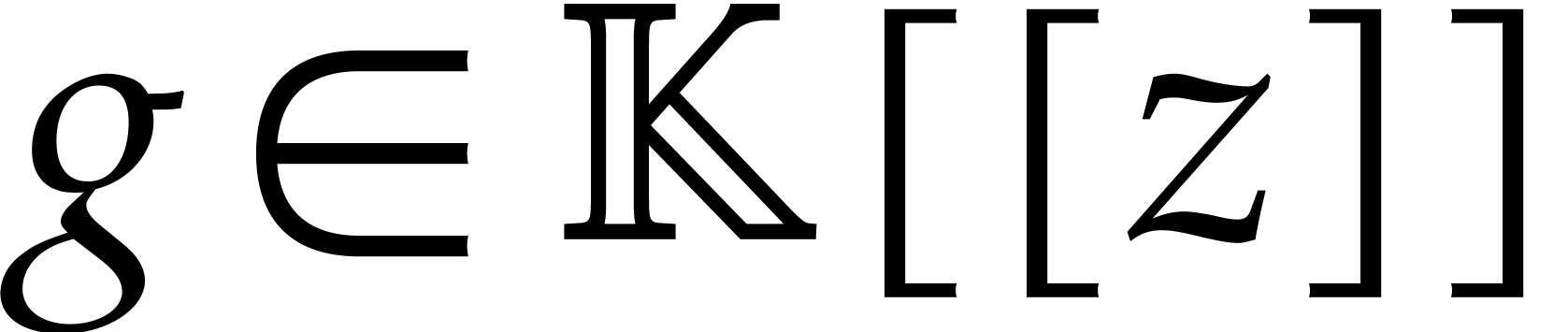 with
with 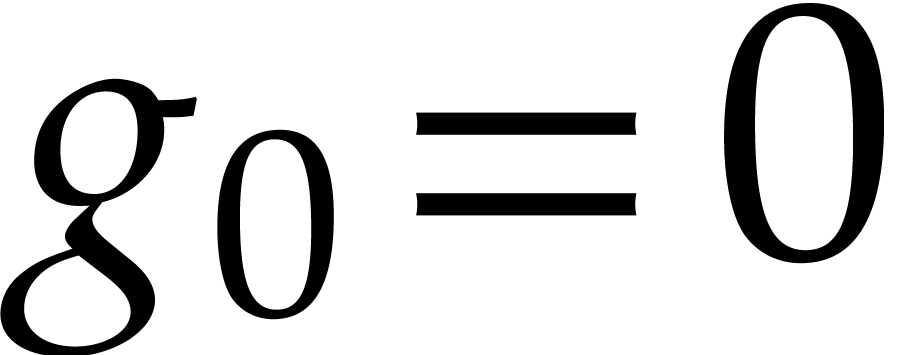 can
be computed by taking
can
be computed by taking 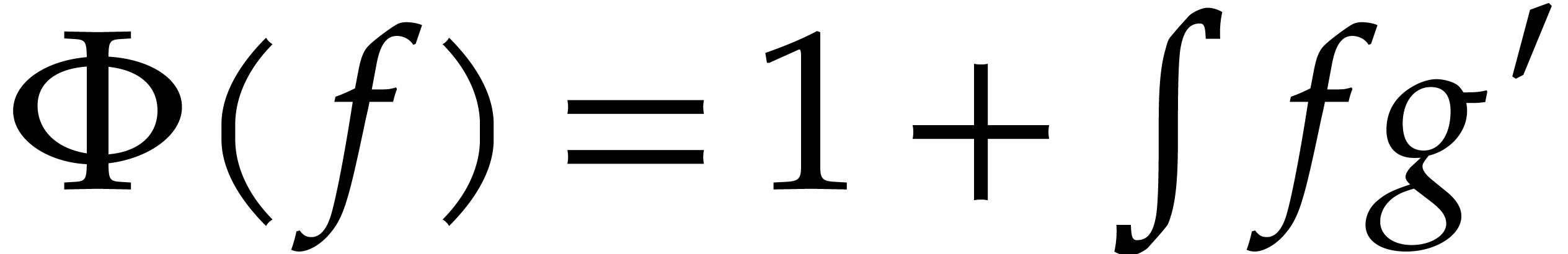 .
.
From a complexity point of view, let 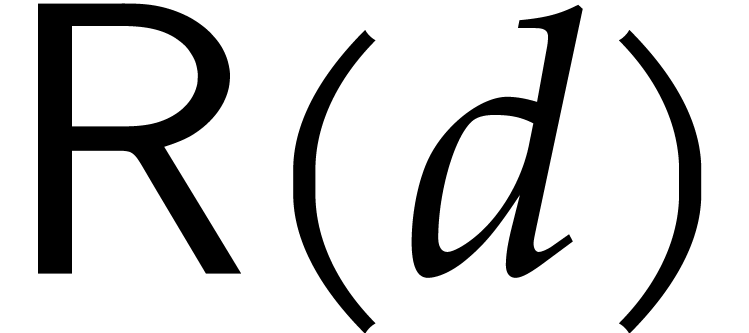 denote the
cost of the relaxed multiplication of two polynomials of degree
denote the
cost of the relaxed multiplication of two polynomials of degree 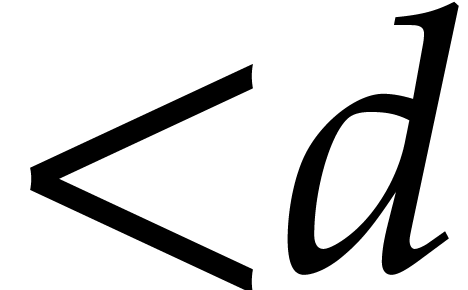 . The relaxed model prevents us
from directly using fast “zealous” multiplication algorithms
from the previous section that are typically based on
FFT-multiplication. Fortunately, it was shown in [19, 10] that
. The relaxed model prevents us
from directly using fast “zealous” multiplication algorithms
from the previous section that are typically based on
FFT-multiplication. Fortunately, it was shown in [19, 10] that
 |
(2) |
This relaxed multiplication algorithm admits the advantage that it may use any zealous multiplication as a black box. Through the direct use of FFT-based techniques, the following bound has also been established in [21]:
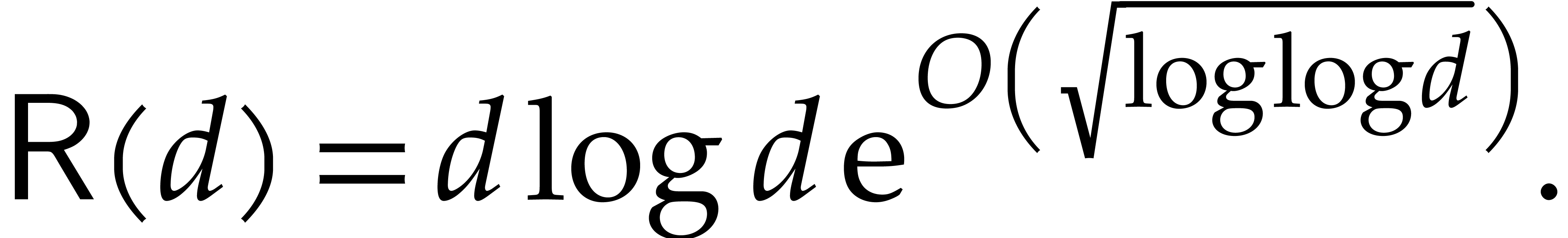
In the sequel, we will only use a suitable multivariate generalization
of the algorithm from [19, 10], so we will
always assume that 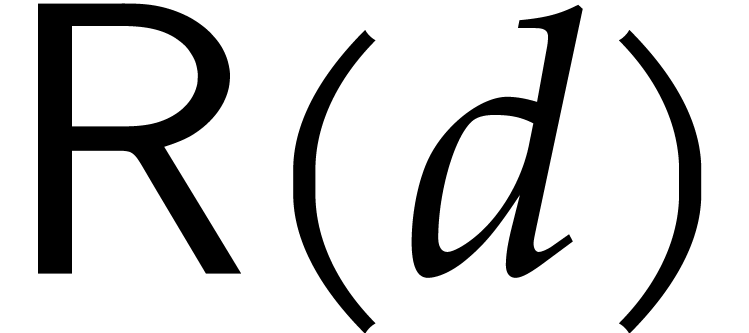 is of the form (2).
In particular, we have
is of the form (2).
In particular, we have 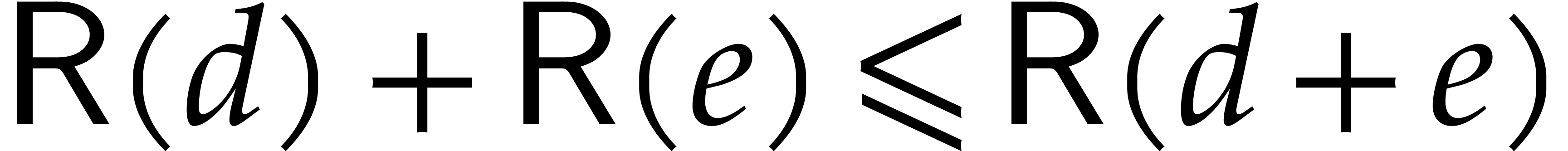 .
.
Let us now consider a Gröbner basis of an ideal in 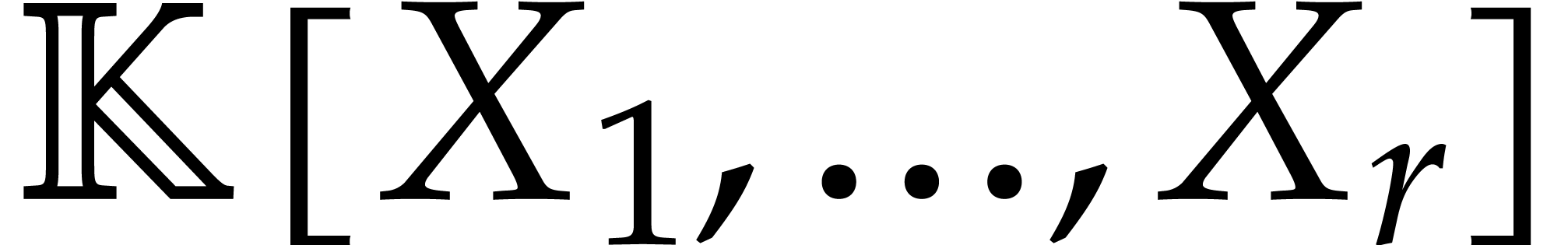 , or, more generally, an auto-reduced tuple
, or, more generally, an auto-reduced tuple
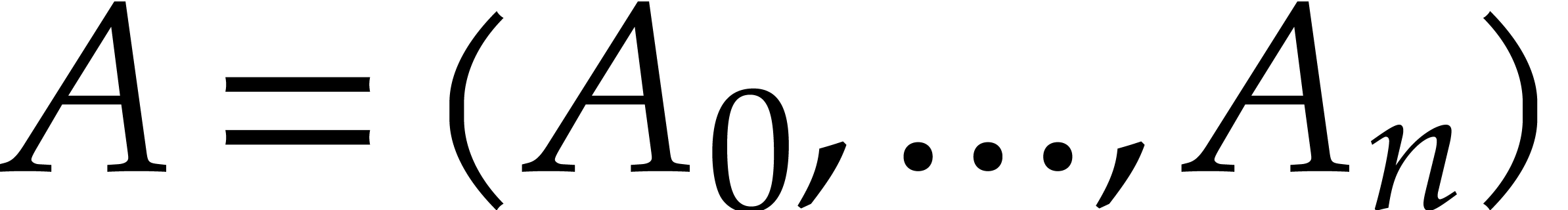 of polynomials in
of polynomials in 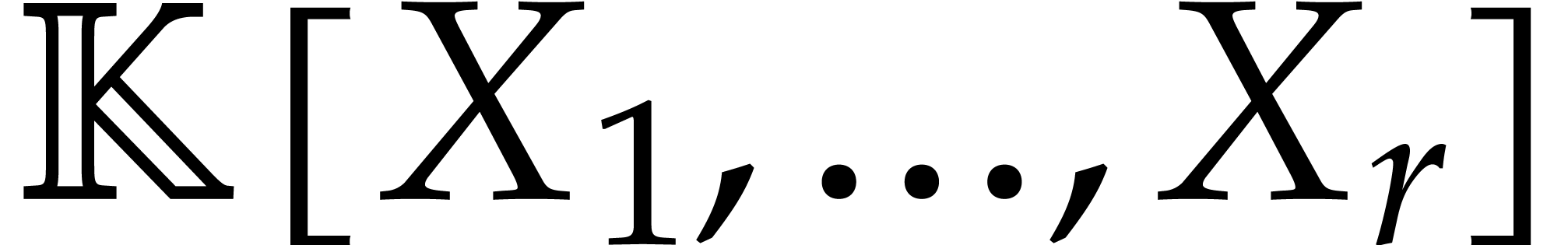 .
Then for any
.
Then for any 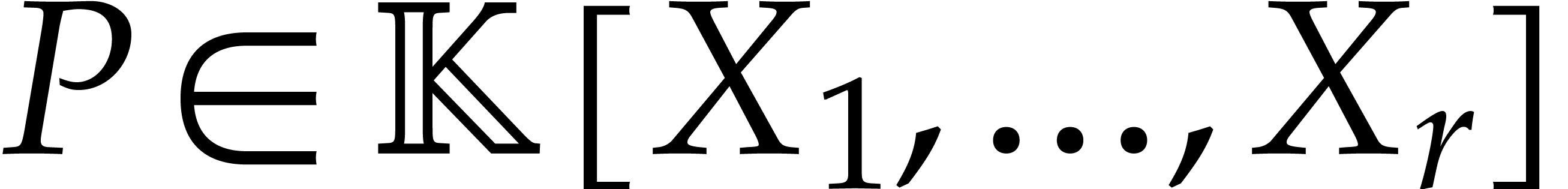 , we may compute
a relation
, we may compute
a relation

such that 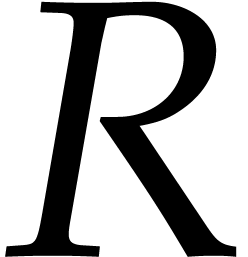 is reduced with respect to
is reduced with respect to  . We call
. We call 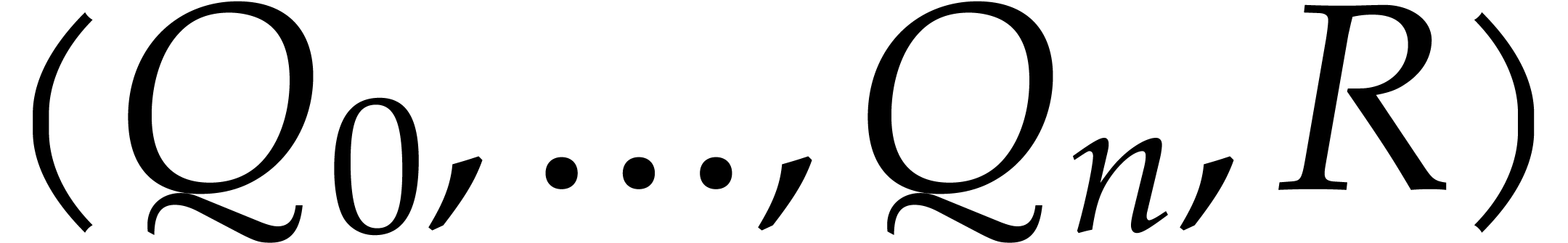 an extended reduction of
an extended reduction of 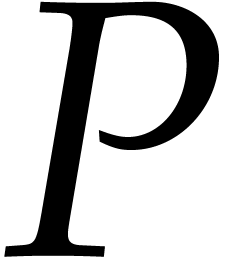 with respect
to
with respect
to  .
.
The computation of such an extended reduction is a good example of a
problem that can be solved efficiently using relaxed multiplication and
recursive equations. For a multivariate polynomial
 with dense support of any of the types discussed in section
3.1
, let
with dense support of any of the types discussed in section
3.1
, let
 denote a bound for the size of its support. With
denote a bound for the size of its support. With
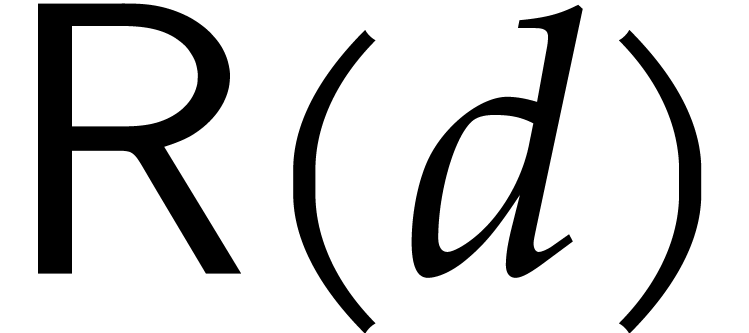 as in (
2
), it has been shown
as in (
2
), it has been shown
1. The results from [20] actually apply for more general types of supports, but this will not be needed in this paper.
 and the
remainder
and the
remainder
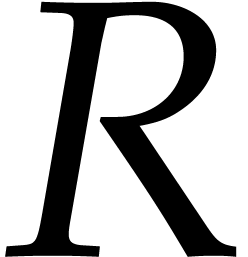 can be computed in time
can be computed in time
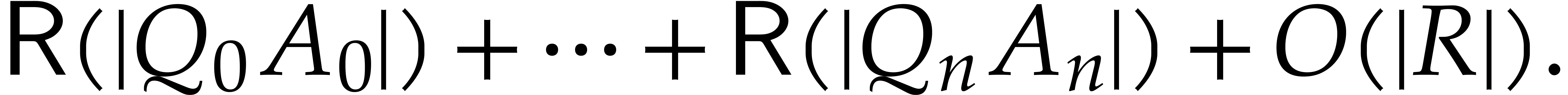 |
(3) |
This implies in particular that the extended reduction can be computed
in quasi-linear time in the size of the equation  . However, as pointed out in the introduction, this
equation is in general much larger than the input polynomial
. However, as pointed out in the introduction, this
equation is in general much larger than the input polynomial 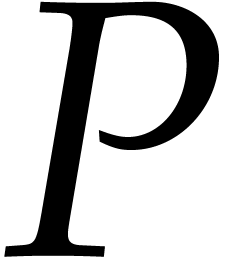 .
.
Extended reductions 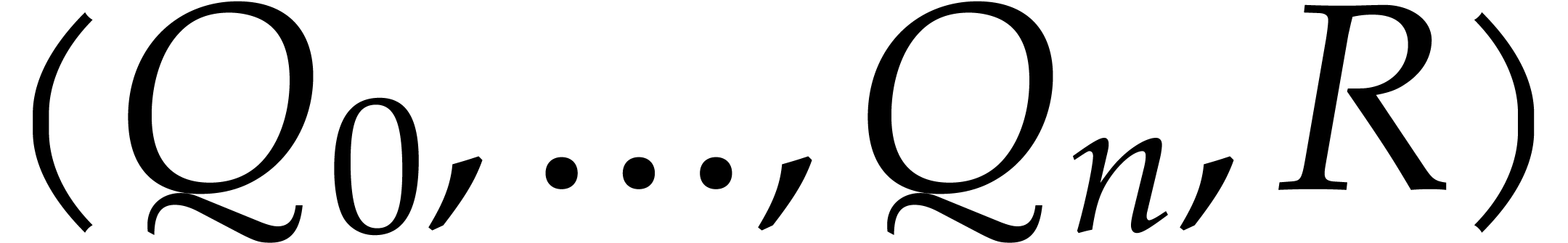 are far from being unique
(only
are far from being unique
(only 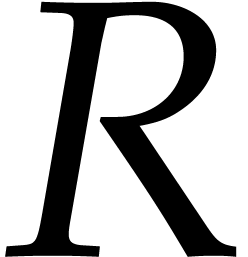 is unique, and only if
is unique, and only if  is a Gröbner basis). The algorithm from [20] for the
computation of an extended reduction relies on a selection
strategy that selects a particular index
is a Gröbner basis). The algorithm from [20] for the
computation of an extended reduction relies on a selection
strategy that selects a particular index 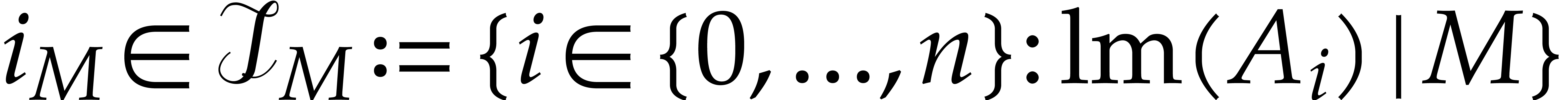 for every monomial
for every monomial  such that
such that 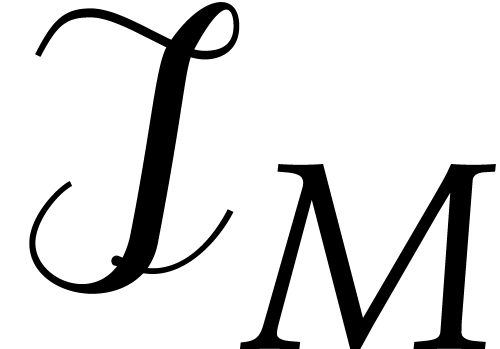 is non-empty. The initial formulation [20] used the
simplest such strategy by taking
is non-empty. The initial formulation [20] used the
simplest such strategy by taking  ,
but the complexity bound (3) holds for any selection
strategy. Now the total size of all quotients
,
but the complexity bound (3) holds for any selection
strategy. Now the total size of all quotients  may be much larger than the size of
may be much larger than the size of 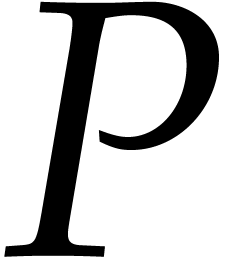 for a
general selection strategy. One of the key ingredients of the fast
reduction algorithm in this paper is the careful design of a
“dichotomic selection strategy” that enables us to control
the degrees of the quotients.
for a
general selection strategy. One of the key ingredients of the fast
reduction algorithm in this paper is the careful design of a
“dichotomic selection strategy” that enables us to control
the degrees of the quotients.
Remark
Let  be a vanilla Gröbner basis of some
ideal
be a vanilla Gröbner basis of some
ideal 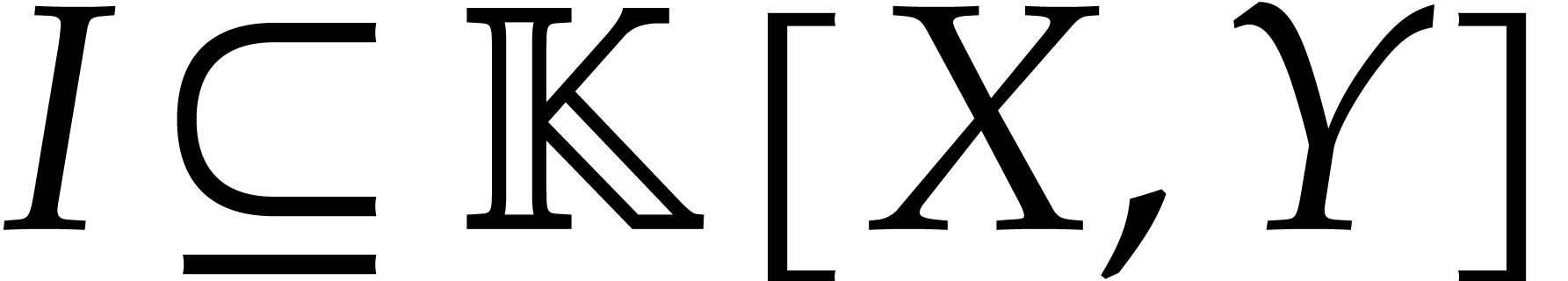 with respect to
with respect to  and assume the notations from Proposition 3. We recall from
the introduction that a major obstruction for the design of reduction
algorithms that run in quasi-linear time
and assume the notations from Proposition 3. We recall from
the introduction that a major obstruction for the design of reduction
algorithms that run in quasi-linear time 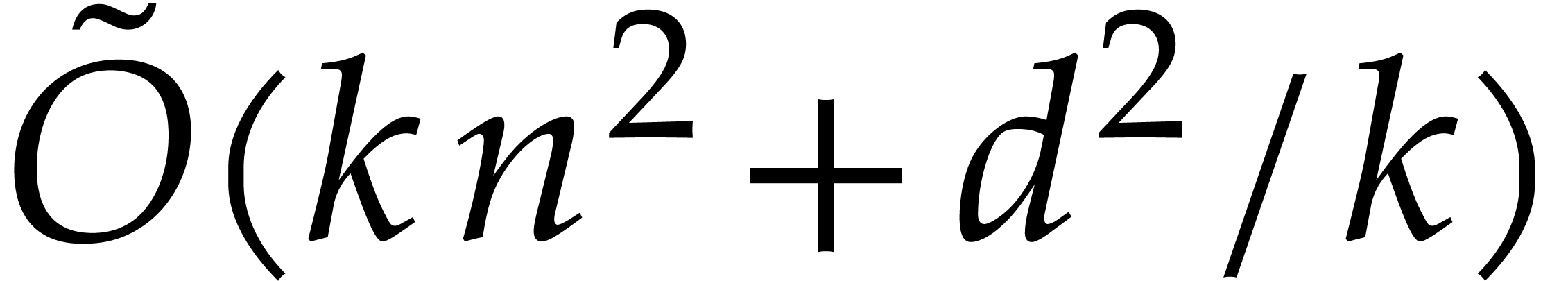 is that
it requires space
is that
it requires space 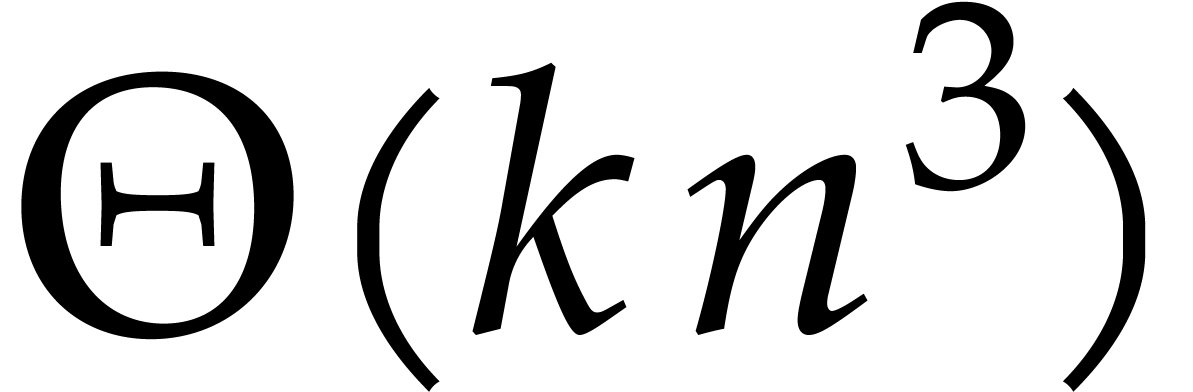 to explicitly write down the
full basis
to explicitly write down the
full basis  . The aim of this
section is to introduce a suitable “terse representation”
that can be stored in space
. The aim of this
section is to introduce a suitable “terse representation”
that can be stored in space 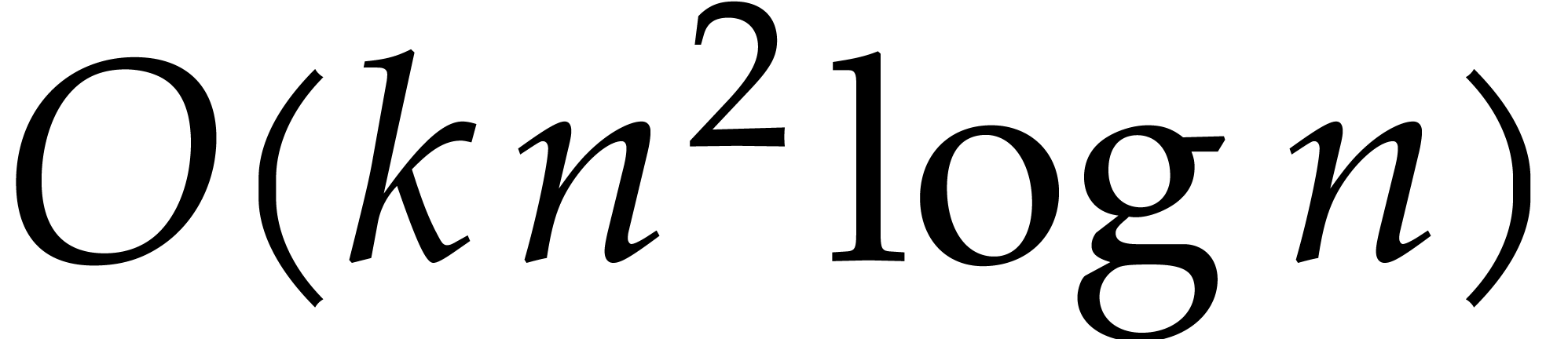 ,
but that still contains all necessary information for efficient
computations modulo
,
but that still contains all necessary information for efficient
computations modulo  .
.
For each 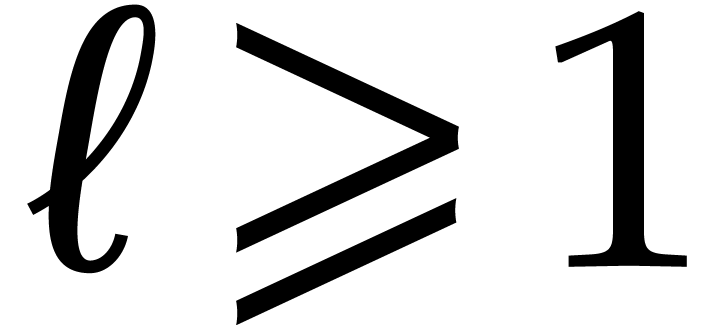 , let
, let 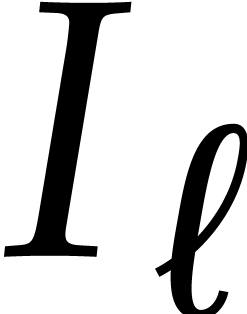 be as in (1). Also, for
be as in (1). Also, for 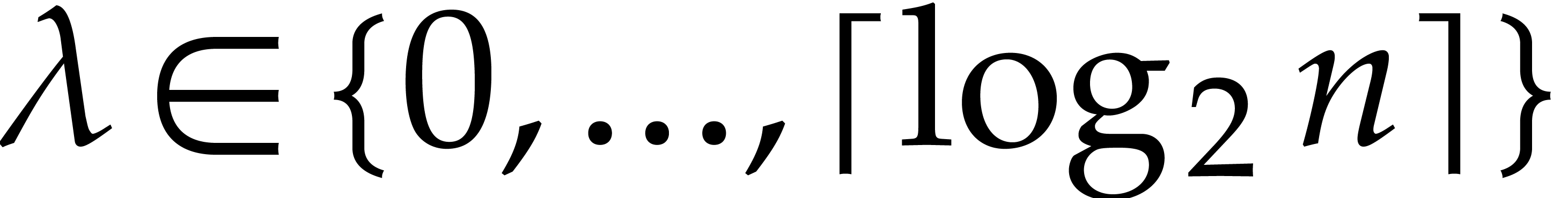 , let
, let 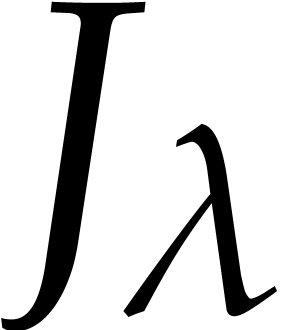 be a shorthand
for
be a shorthand
for 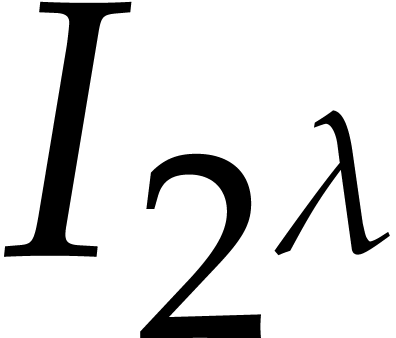 . Since
. Since 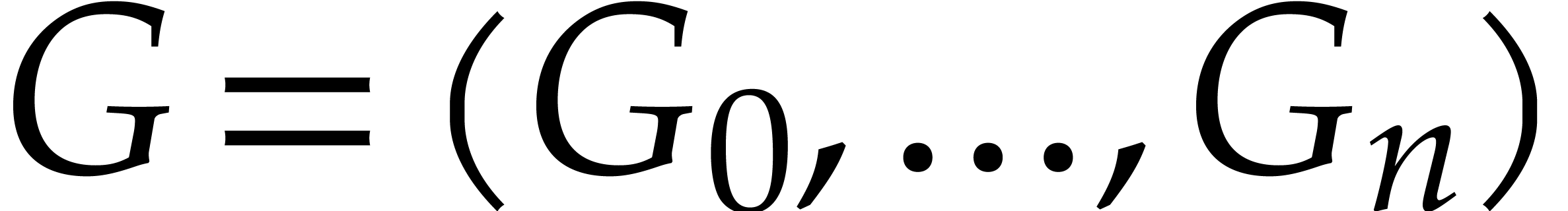 is a vanilla Gröbner basis, Definition 7 ensures in
particular the existence of coefficients
is a vanilla Gröbner basis, Definition 7 ensures in
particular the existence of coefficients 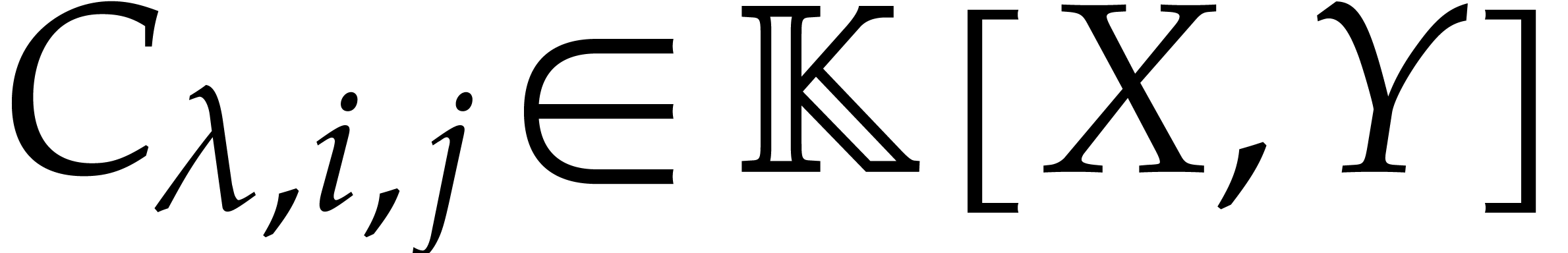 for
for
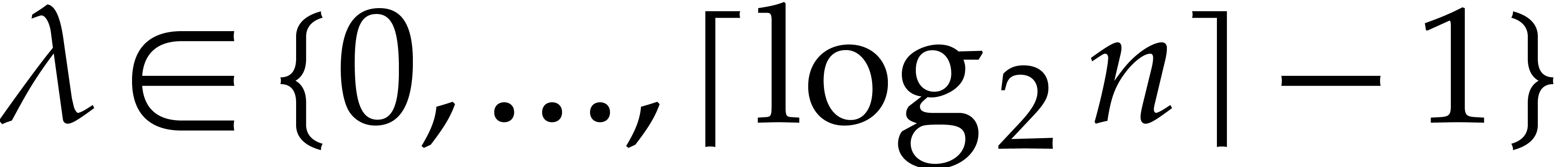 and
and 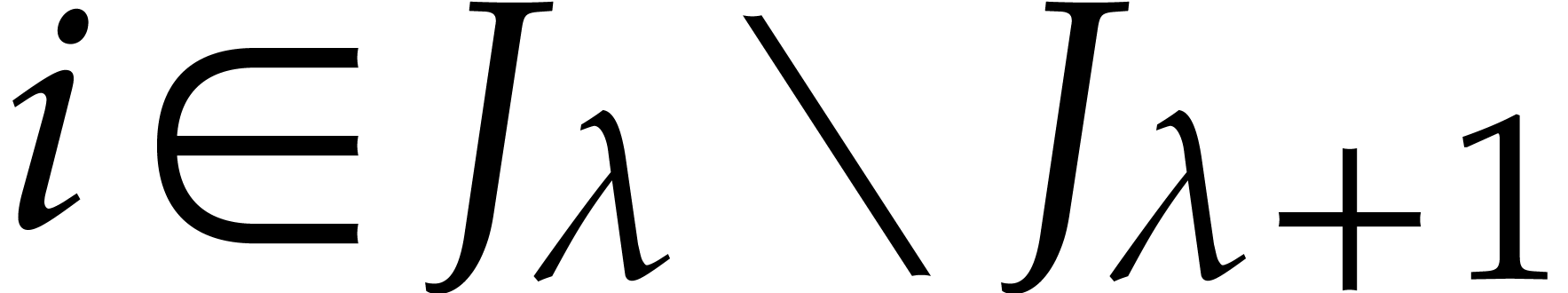 and
and 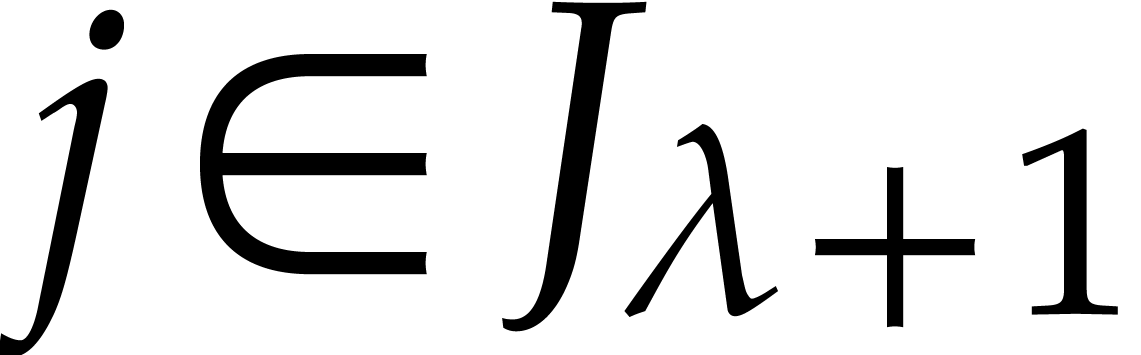 , such that
, such that
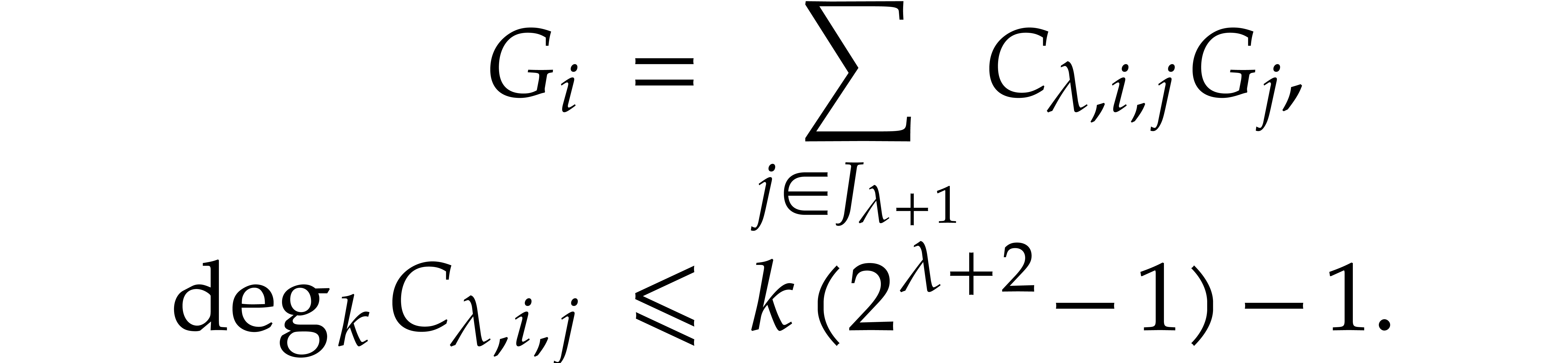
We call these 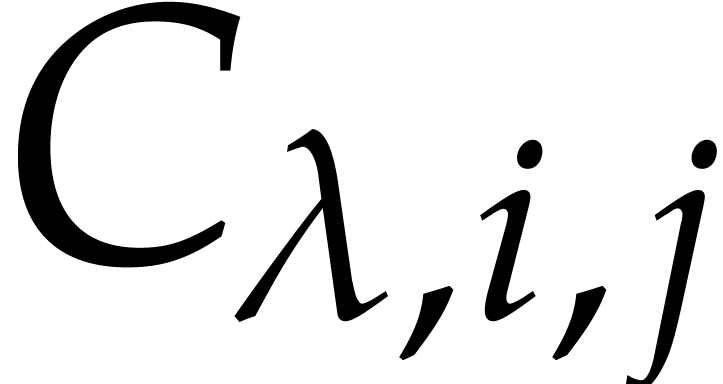 the retraction
coefficients for
the retraction
coefficients for  . For
each given
. For
each given 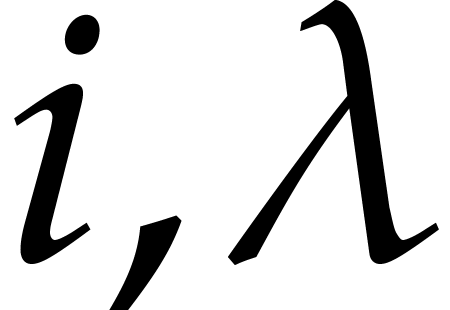 , the computation
of the retraction coefficients
, the computation
of the retraction coefficients 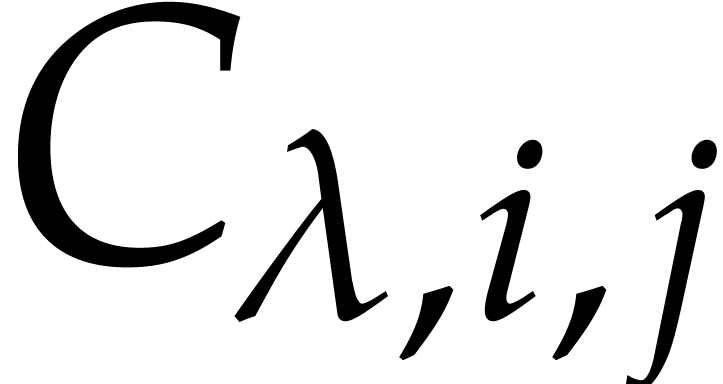 reduces to a
linear system of size
reduces to a
linear system of size  with
with  (for the image space, consider only the monomials that are
above the Gröbner stairs), which is easily solved by
Gaussian elimination. Notice that the space needed to write the
retraction coefficients is much smaller than the Gröbner basis:
(for the image space, consider only the monomials that are
above the Gröbner stairs), which is easily solved by
Gaussian elimination. Notice that the space needed to write the
retraction coefficients is much smaller than the Gröbner basis:
Proof. For every  ,
there are
,
there are 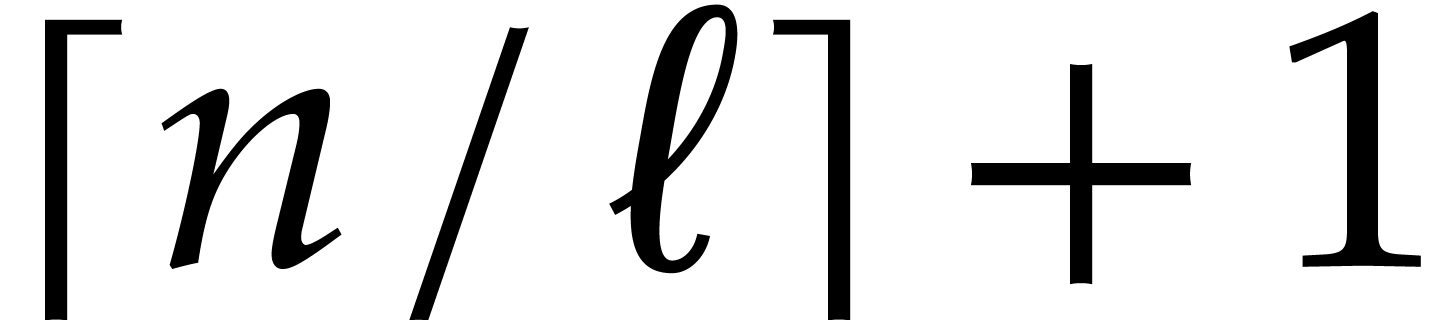 indices in
indices in 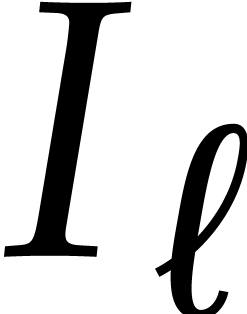 , and we notice that
, and we notice that  .
For any given
.
For any given 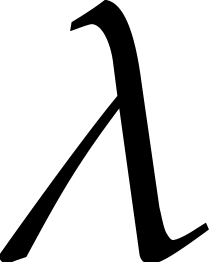 , the
retraction coefficients involve at most
, the
retraction coefficients involve at most 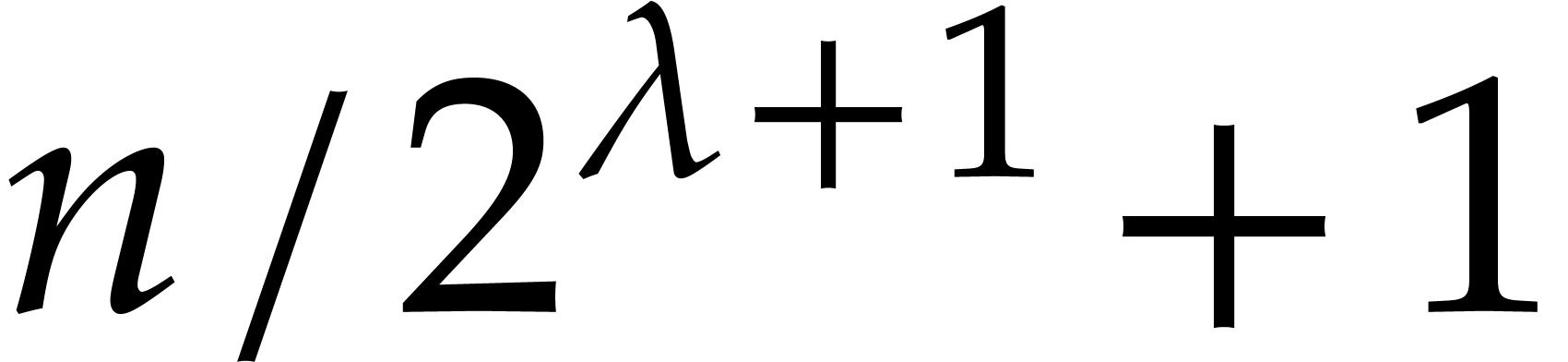 indices
indices
 and
and 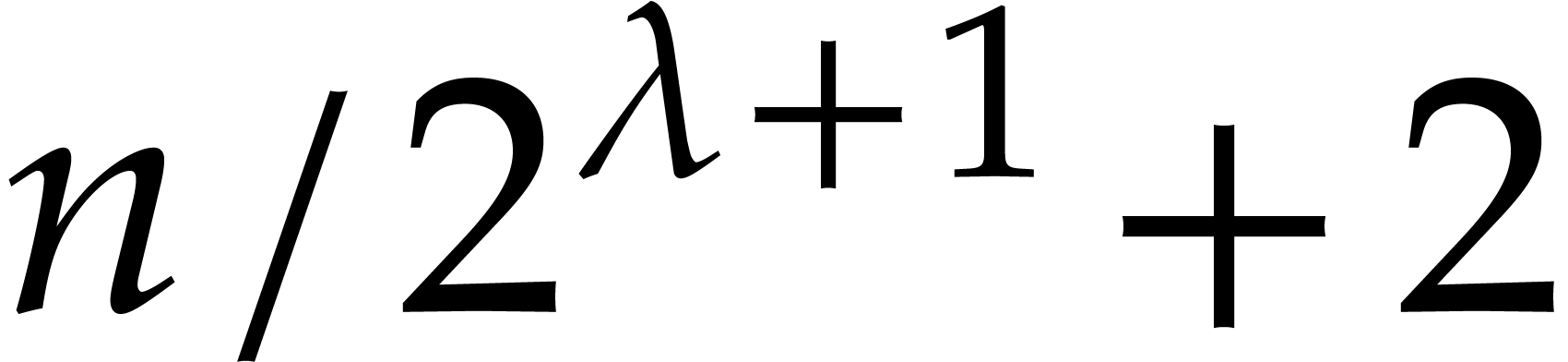 indices
indices  , whence at most
, whence at most 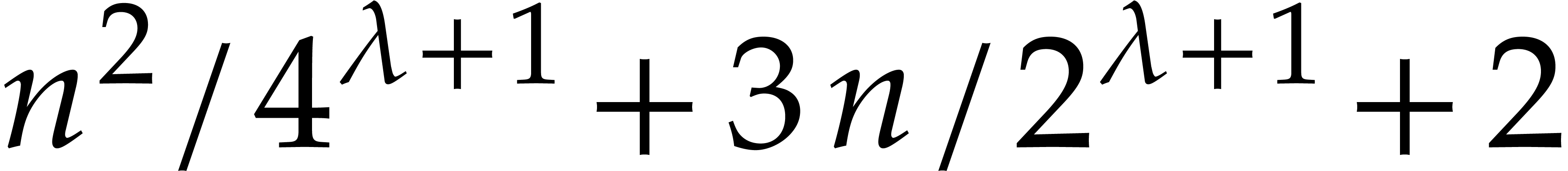 pairs
pairs
 . Since the support of
. Since the support of 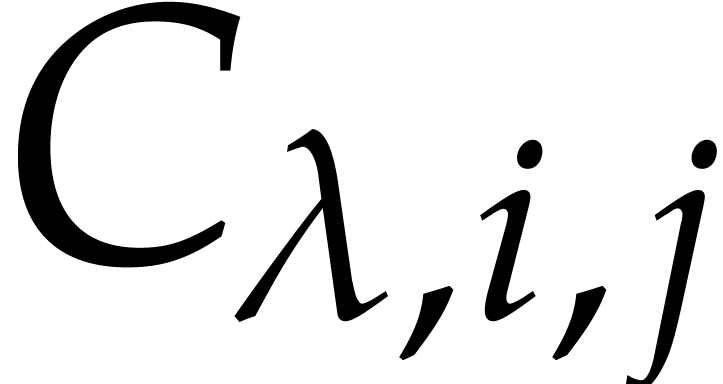 has size
has size 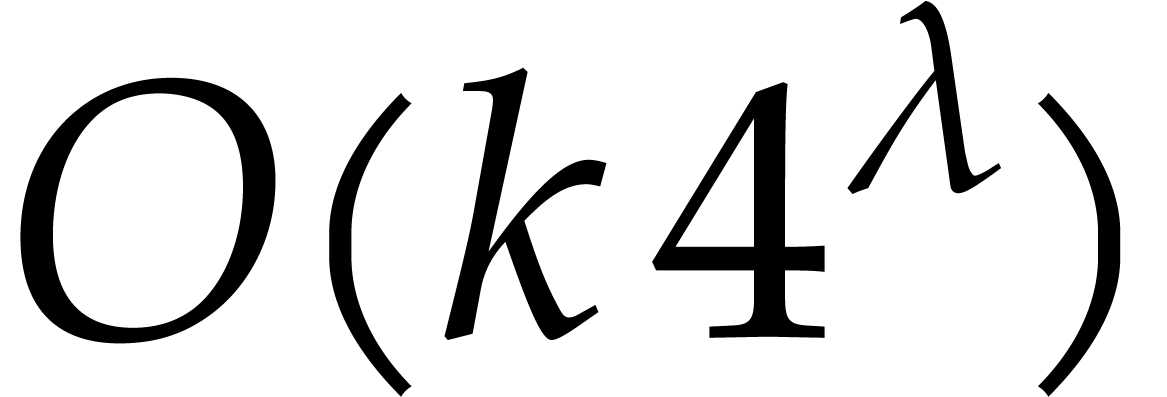 ,
it follows that all retraction coefficient together require space
,
it follows that all retraction coefficient together require space
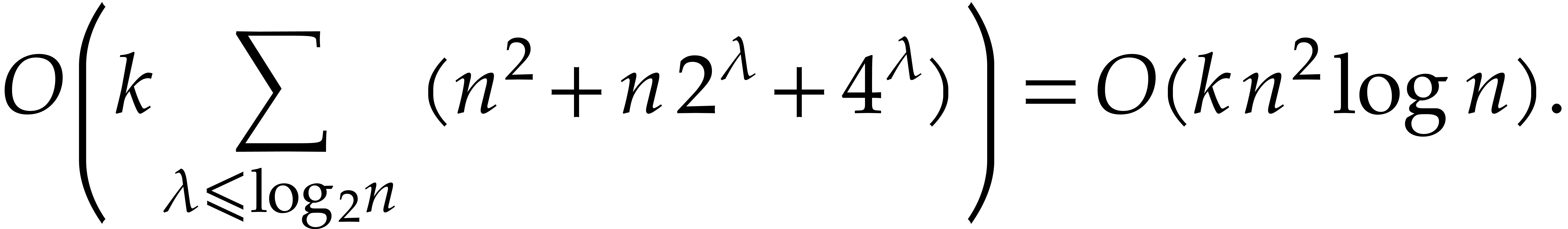

We observe that the space needed to write all relations is about the
same size as the dimension of the quotient algebra 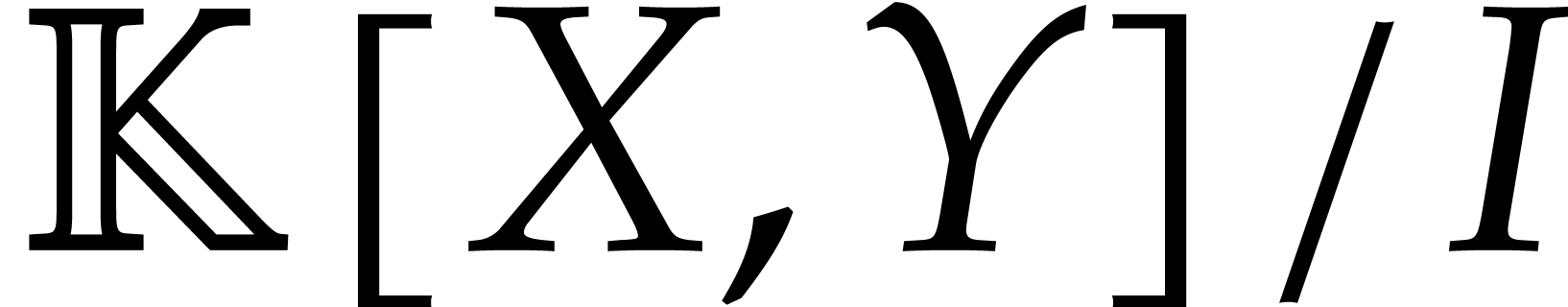 , up to a logarithmic factor.
, up to a logarithmic factor.
For vanilla Gröbner bases, it is a priori possible to
recover  from
from  using the
retraction coefficients: with
using the
retraction coefficients: with 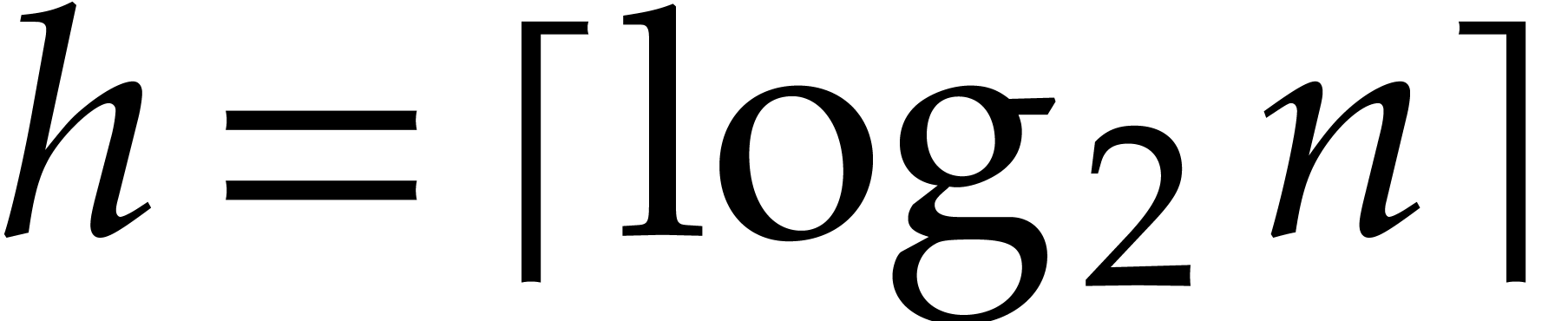 ,
first compute
,
first compute 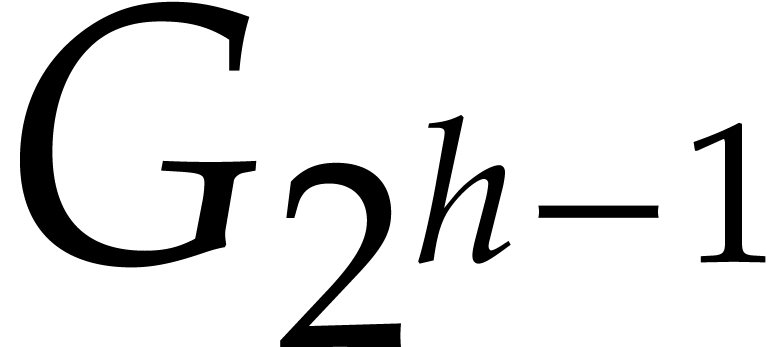 , next
, next 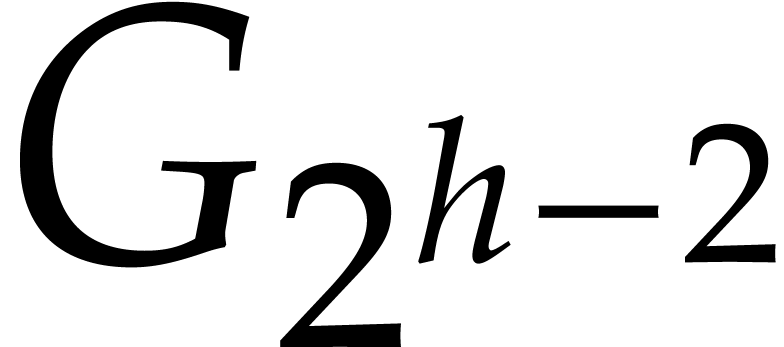 and
and 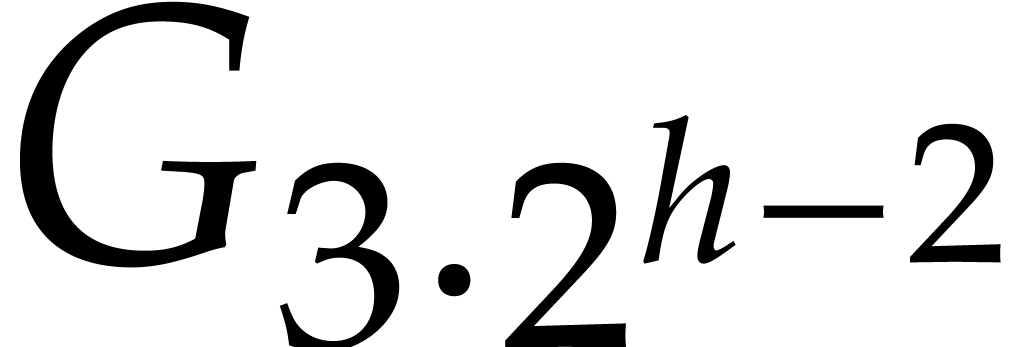 , and
so on. In order to compute reductions of the form
, and
so on. In order to compute reductions of the form  efficiently, we will need slightly more information. In particular, we
wish to access some of the head terms of the
efficiently, we will need slightly more information. In particular, we
wish to access some of the head terms of the 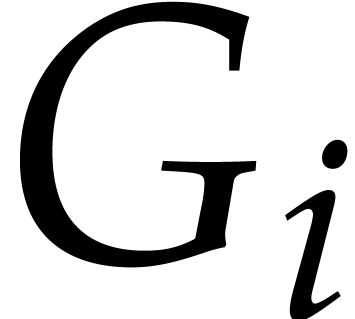 . More precisely, if the quotient
. More precisely, if the quotient 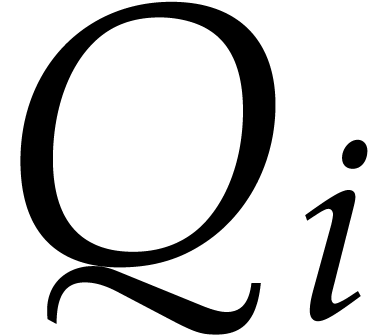 has degree
has degree  , then we need to
know the terms of
, then we need to
know the terms of 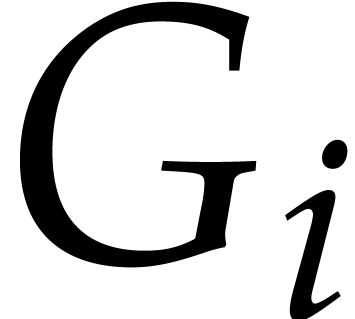 with degree at least
with degree at least 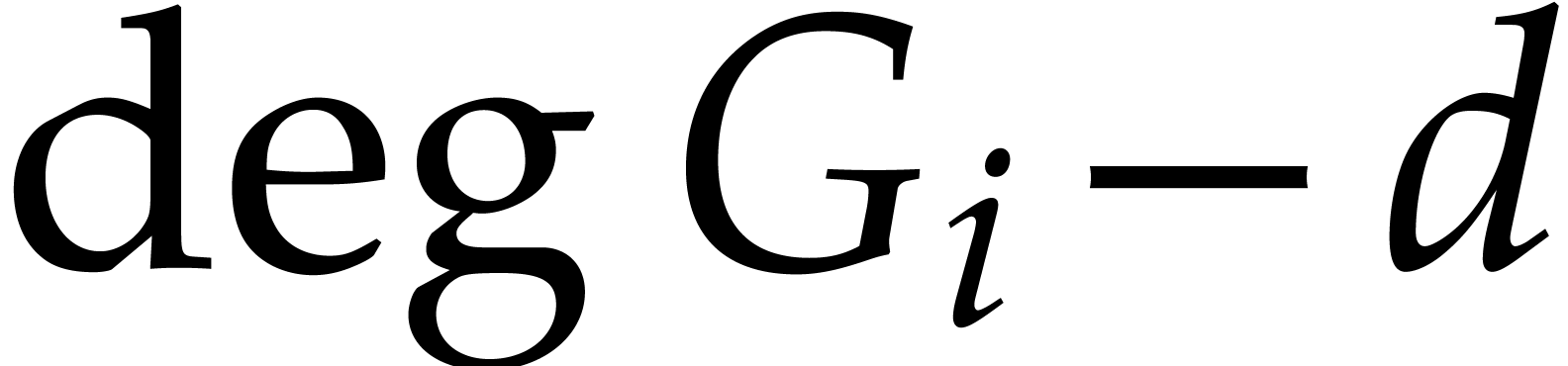 in order to compute the quotient
in order to compute the quotient  using a relaxed reduction algorithm.
using a relaxed reduction algorithm.
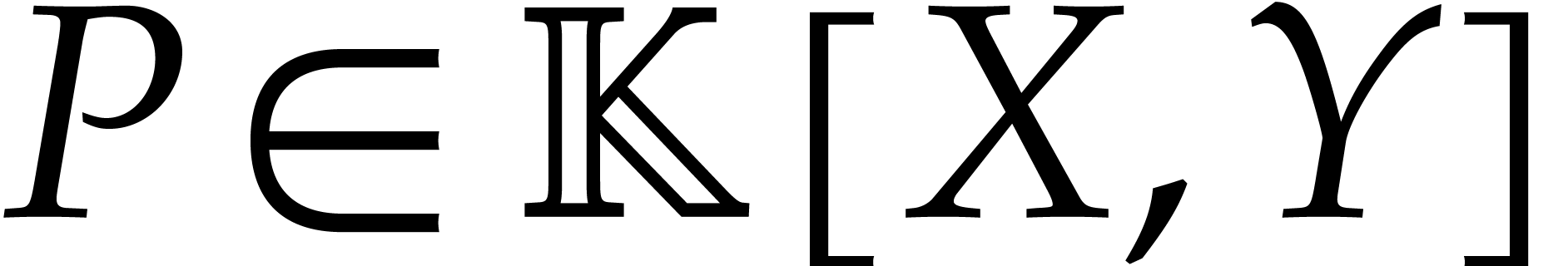 ,
we define its upper truncation with
,
we define its upper truncation with 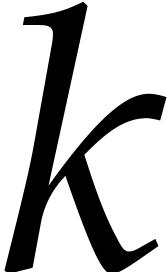 -precision
-precision 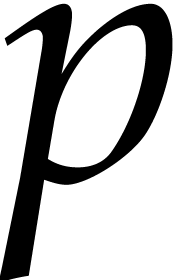 as the
polynomial
as the
polynomial  such that
such that
all terms of  of
of 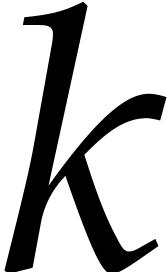 -degree less than
-degree less than 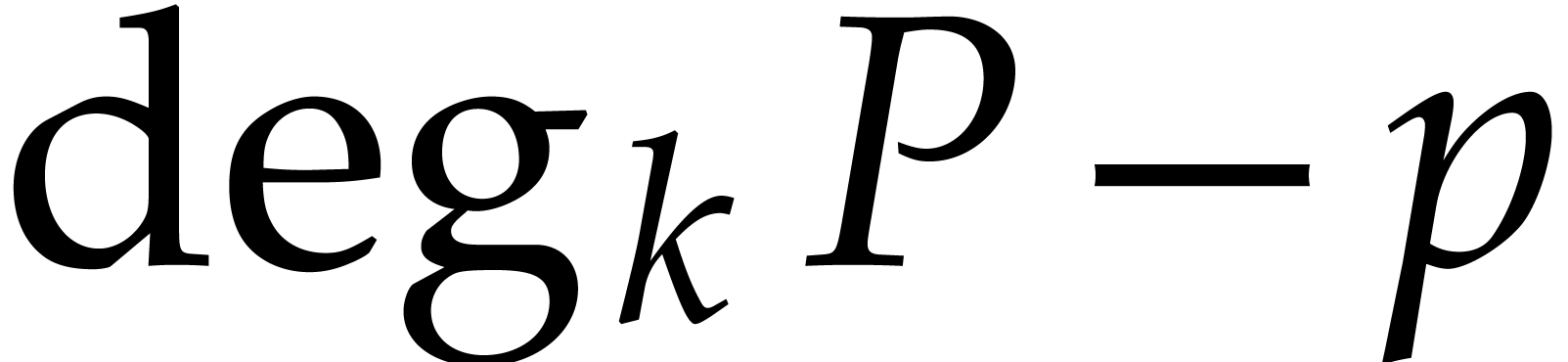 are zero;
are zero;
all terms of 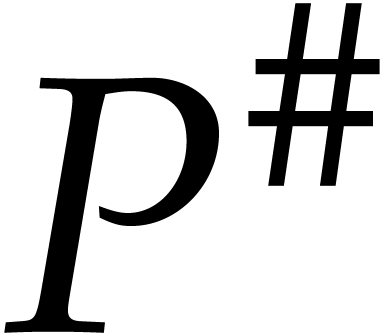 of
of 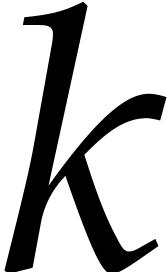 -degree at least
-degree at least 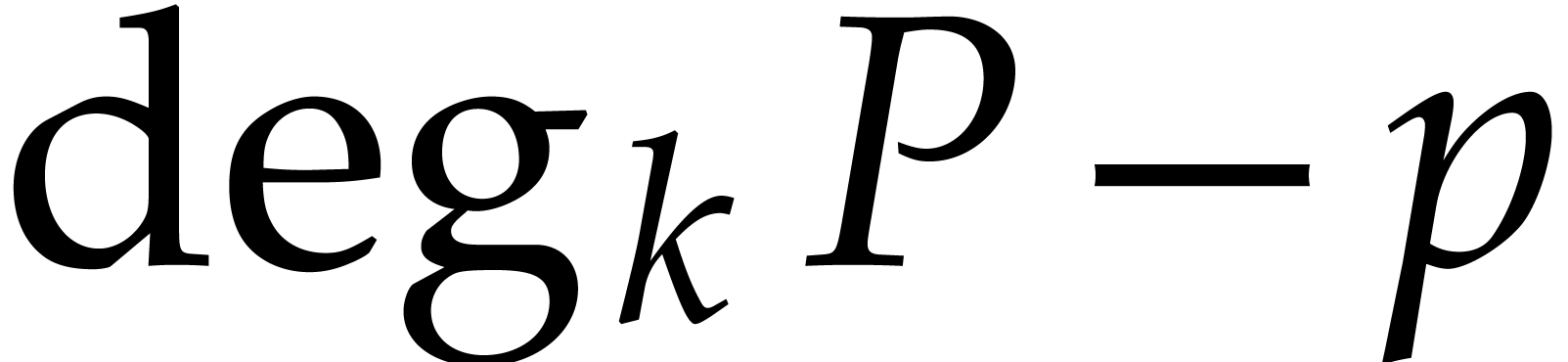 are
equal to the corresponding terms in
are
equal to the corresponding terms in 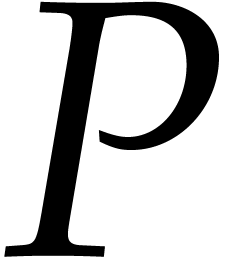 .
.
Notice that this upper truncation 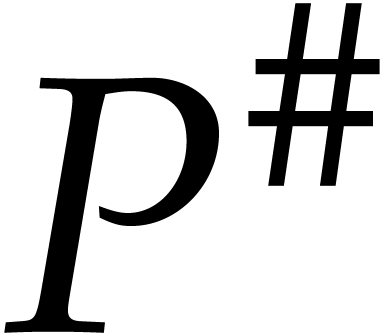 can be written
using space
can be written
using space 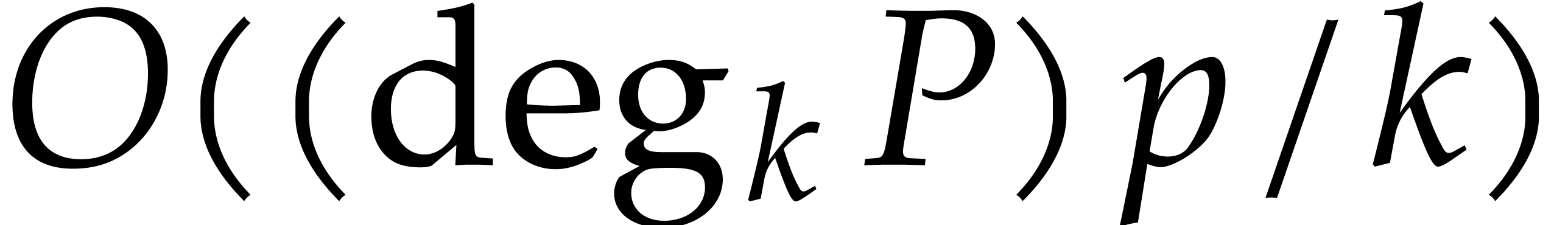 . For the
reduction strategy that we plan to use, we will have
. For the
reduction strategy that we plan to use, we will have
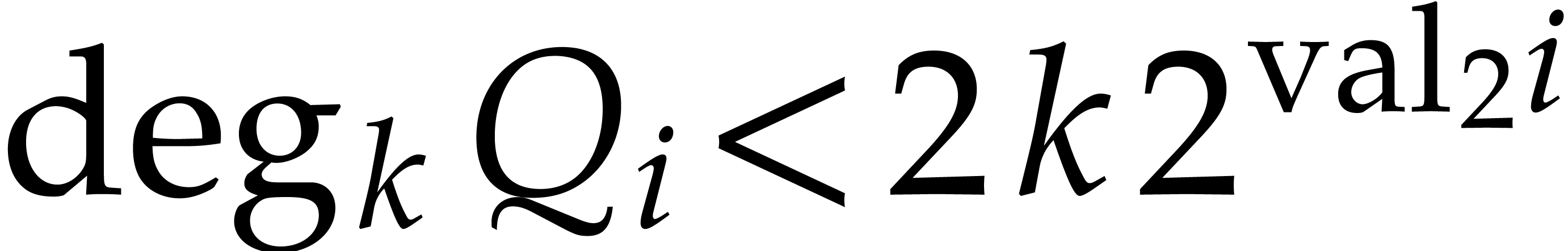 |
(4) |
for all  , where
, where 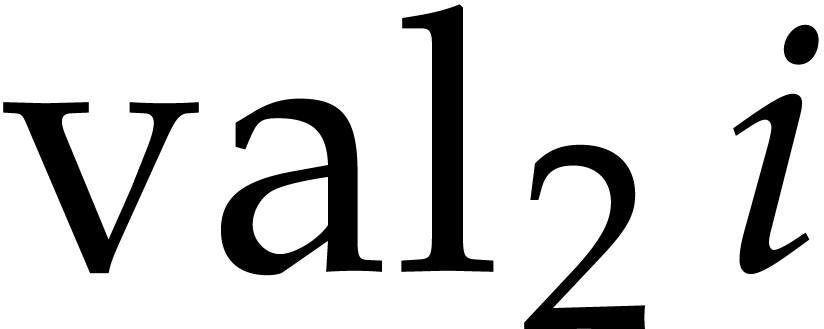 denotes the
denotes the  -adic
valuation of
-adic
valuation of  . This motivates
the following definition:
. This motivates
the following definition:
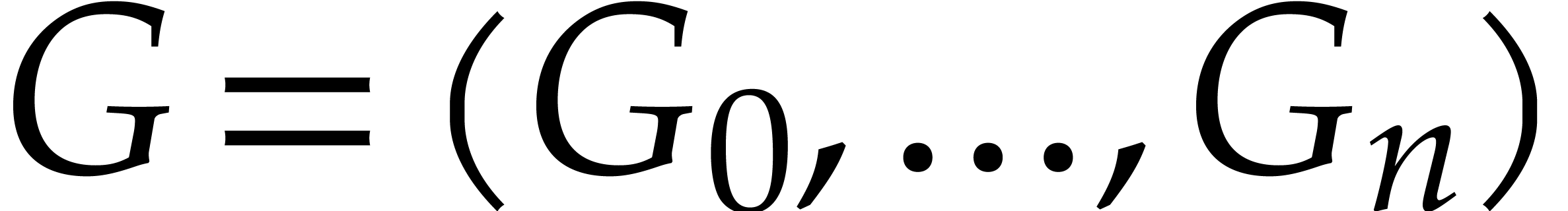 be a vanilla
Gröbner basis for an ideal
be a vanilla
Gröbner basis for an ideal 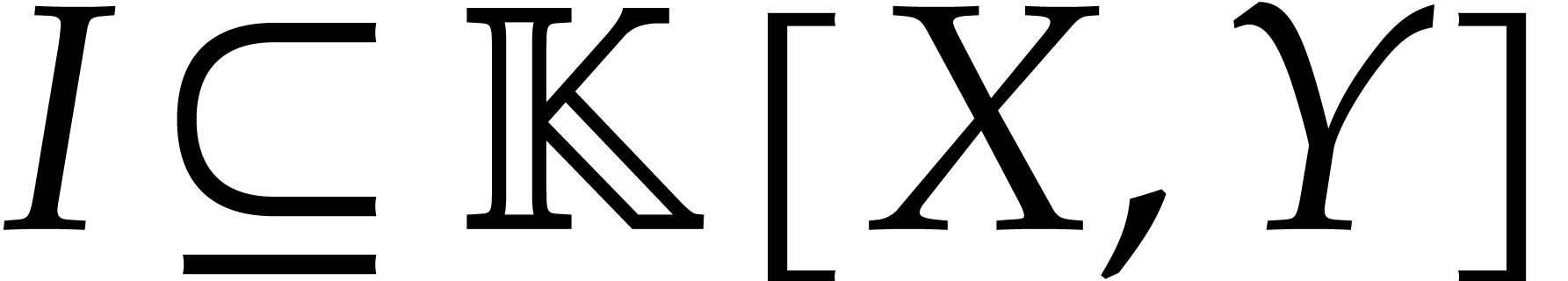 with respect
to
with respect
to  . The terse
representation of
. The terse
representation of  consists of the
following data:
consists of the
following data:
the sequence of truncated elements 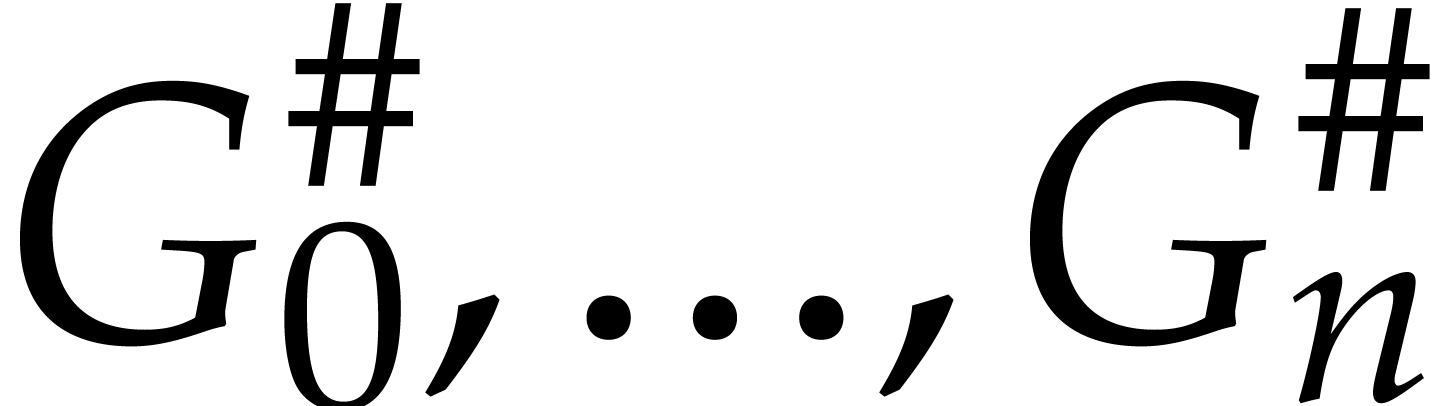 ,
where
,
where
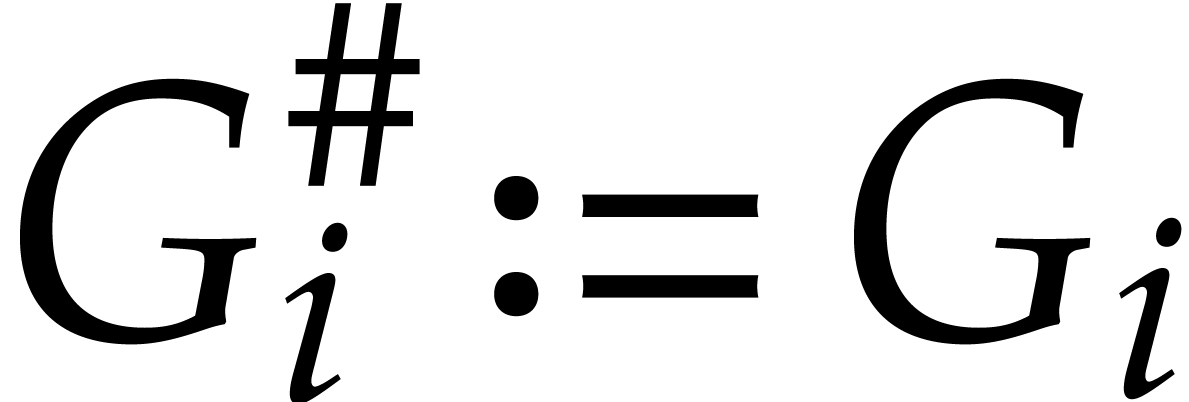 for
for 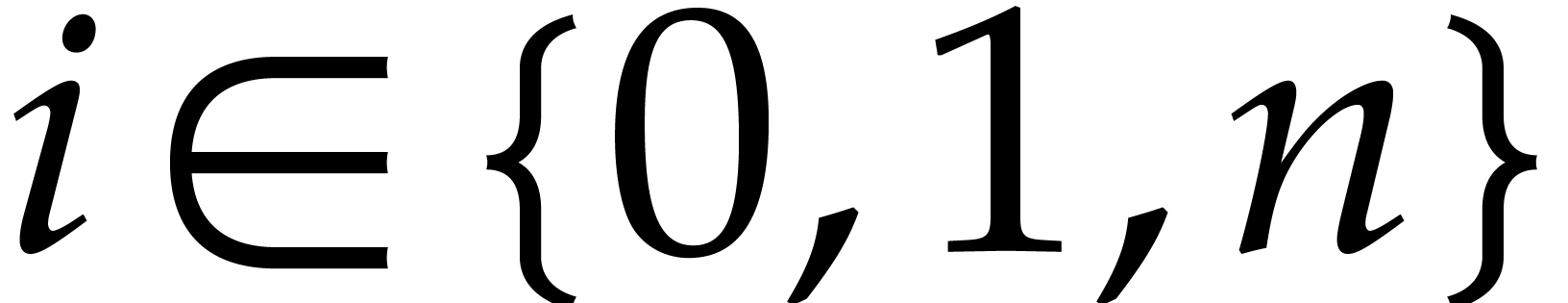 ;
;
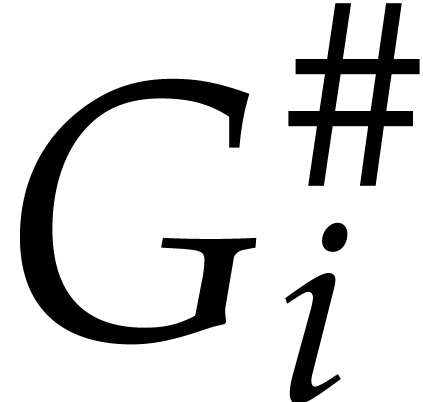 is the upper truncation of
is the upper truncation of 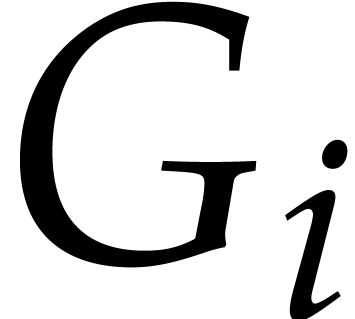 at precision
at precision 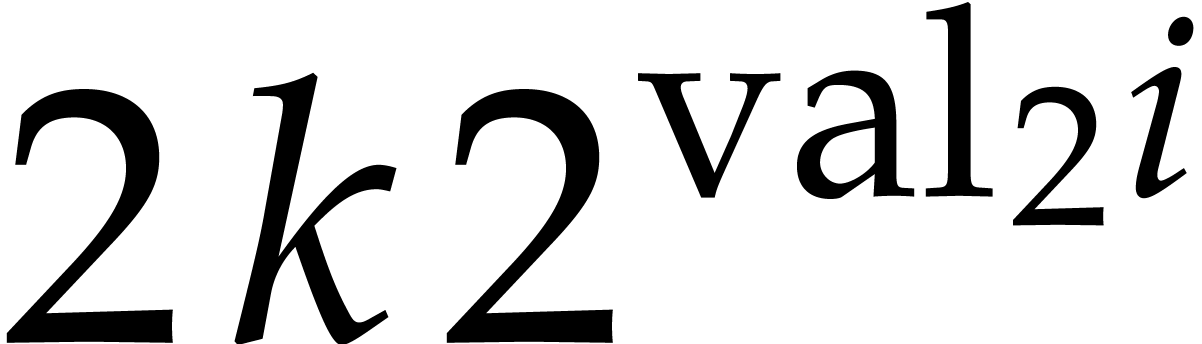 for all
other
for all
other  ;
;
the collection of all retraction coefficients 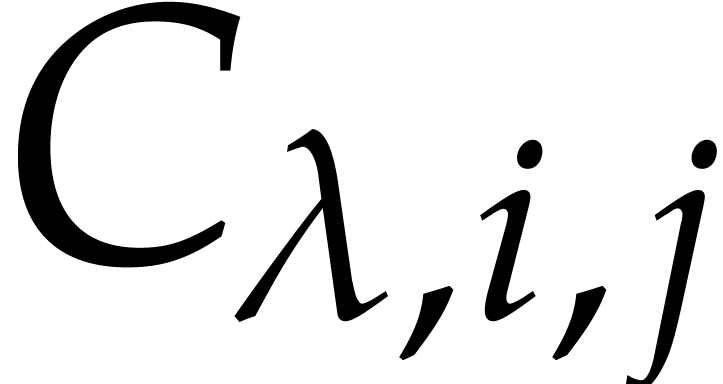 as in section 4.1.
as in section 4.1.
 fits in
space
fits in
space 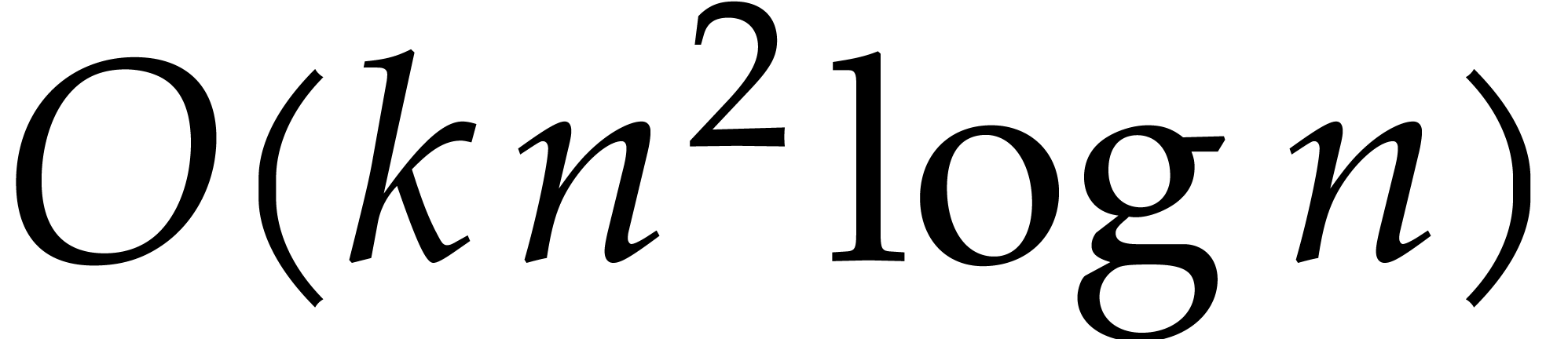 .
.
Proof. The upper truncation 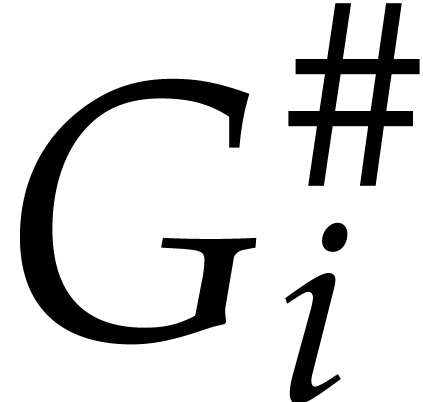 requires space
requires space 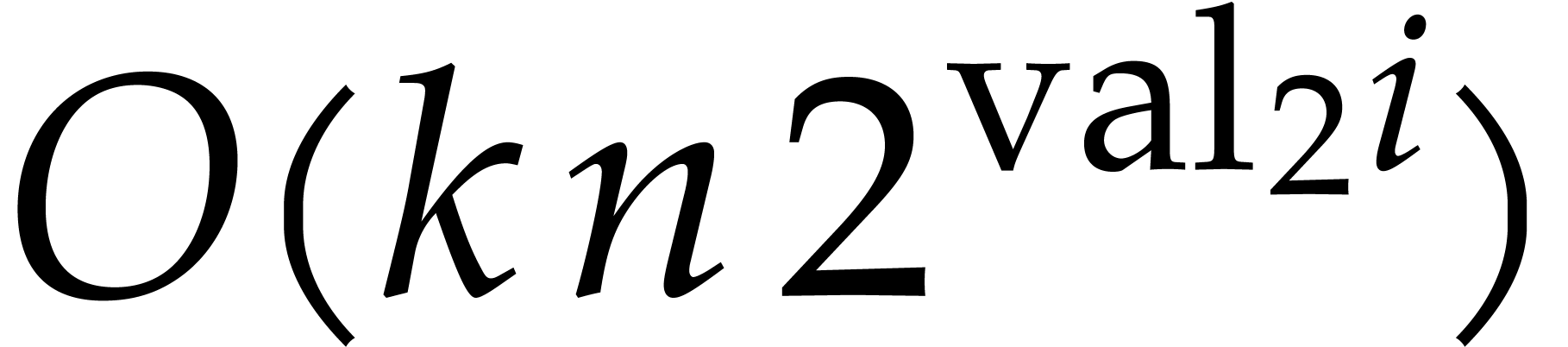 for all
for all 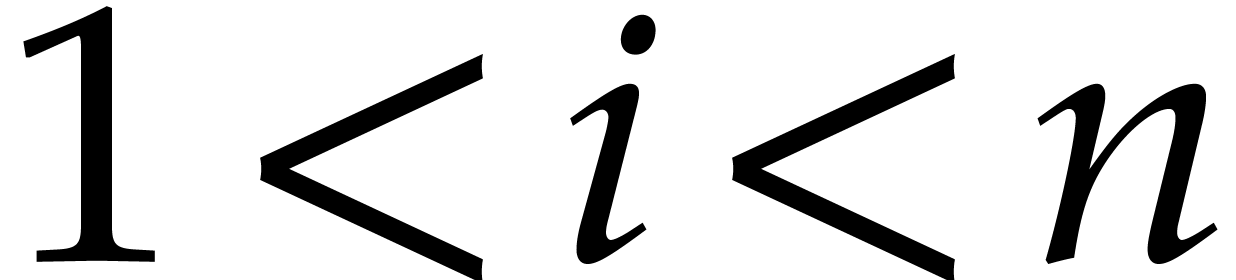 . For each
. For each 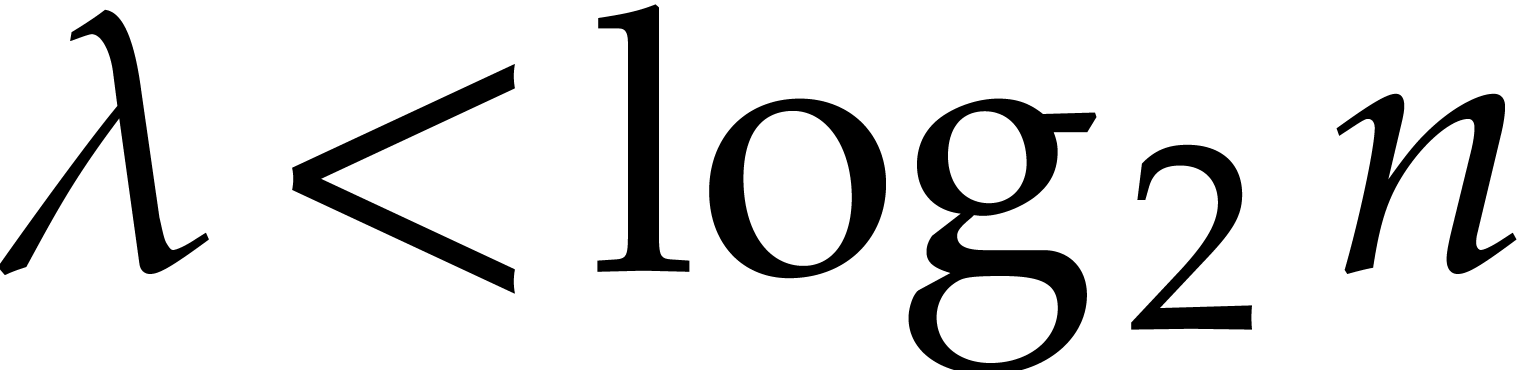 ,
there are at most
,
there are at most 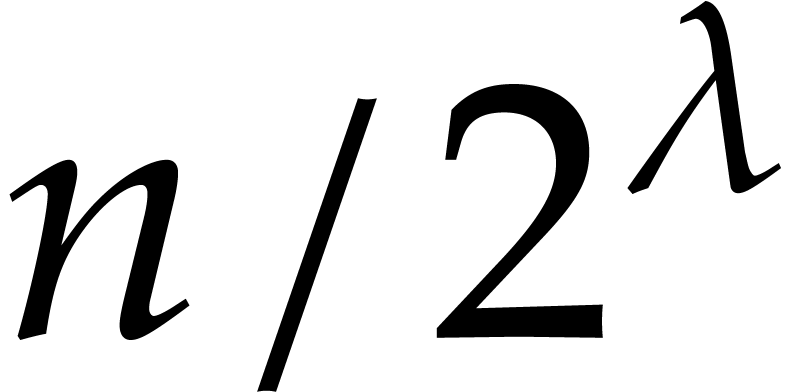 indices
indices  such that
such that 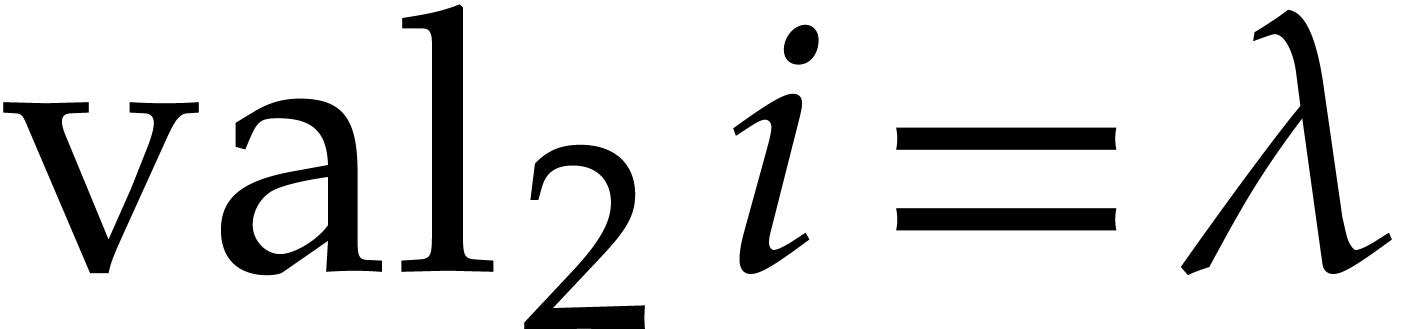 ; therefore,
; therefore, 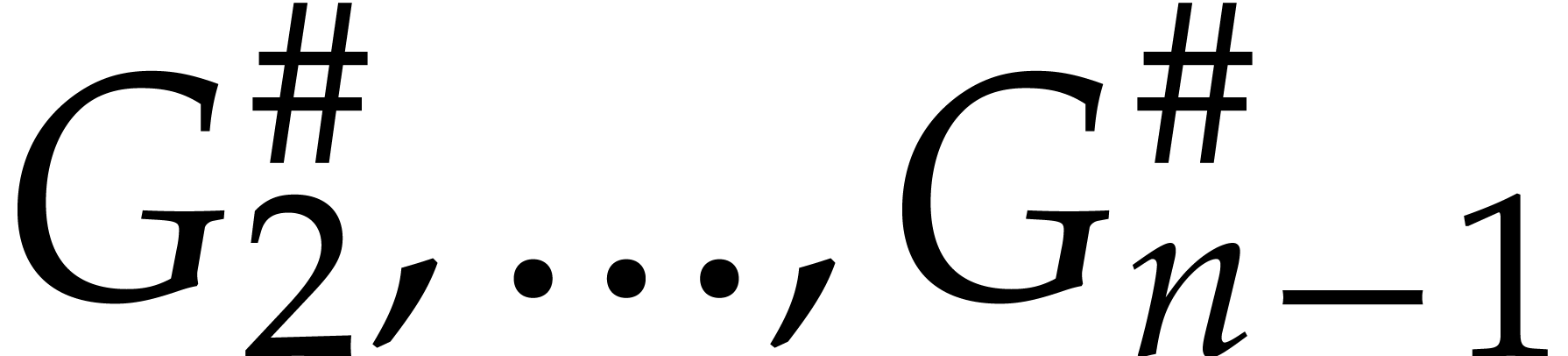 take
take 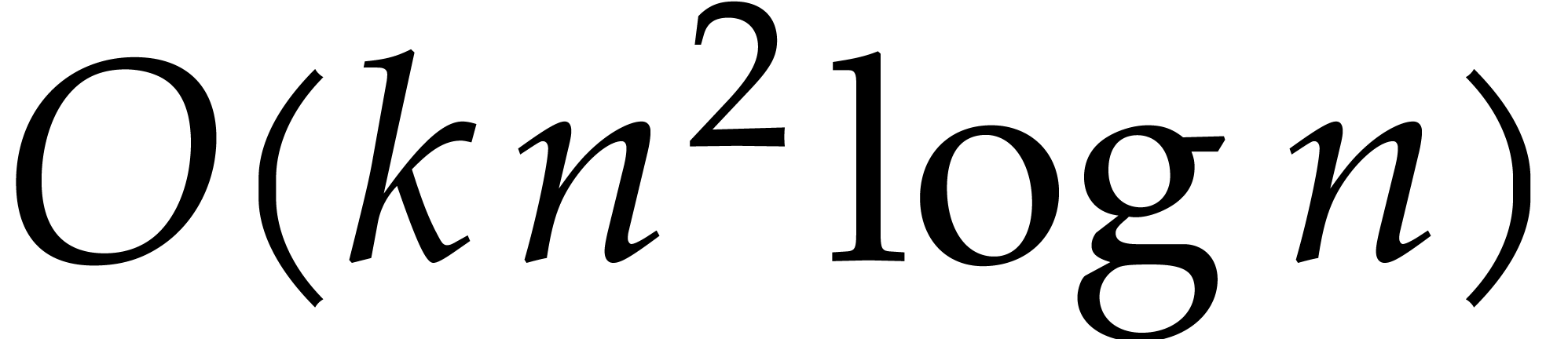 space. The elements
space. The elements
 ,
, 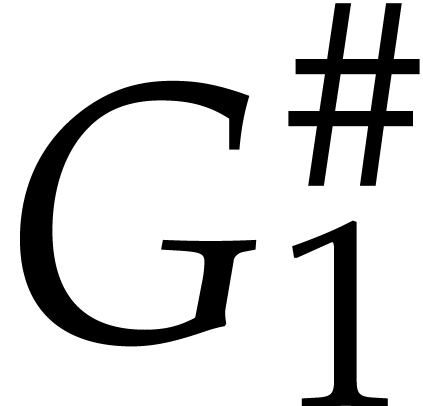 and
and
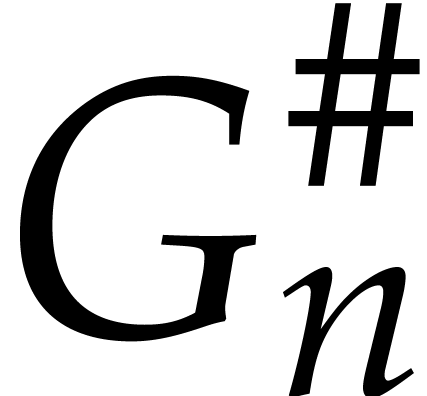 require
require 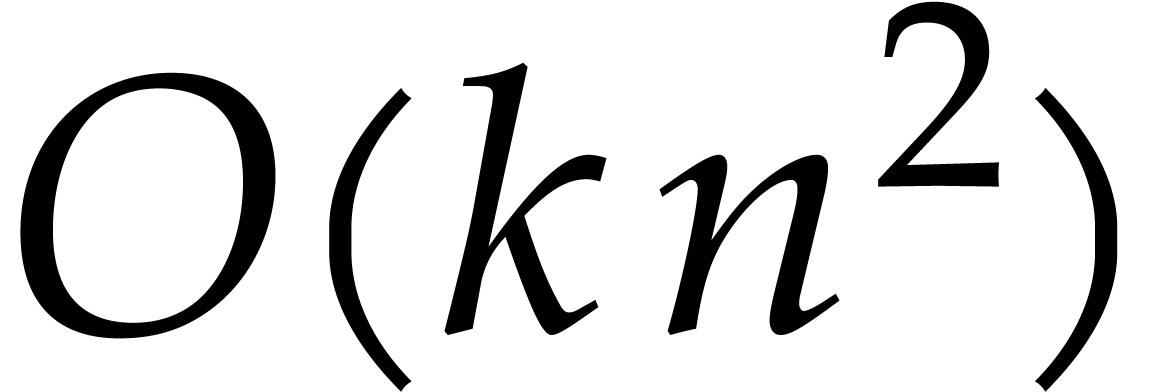 additional
space, whereas the coefficients
additional
space, whereas the coefficients 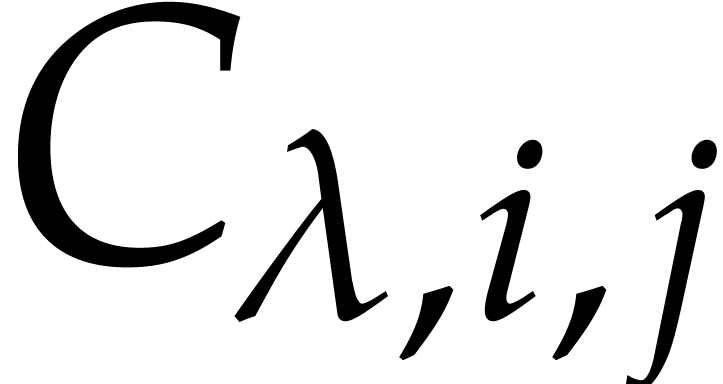 account for
account for 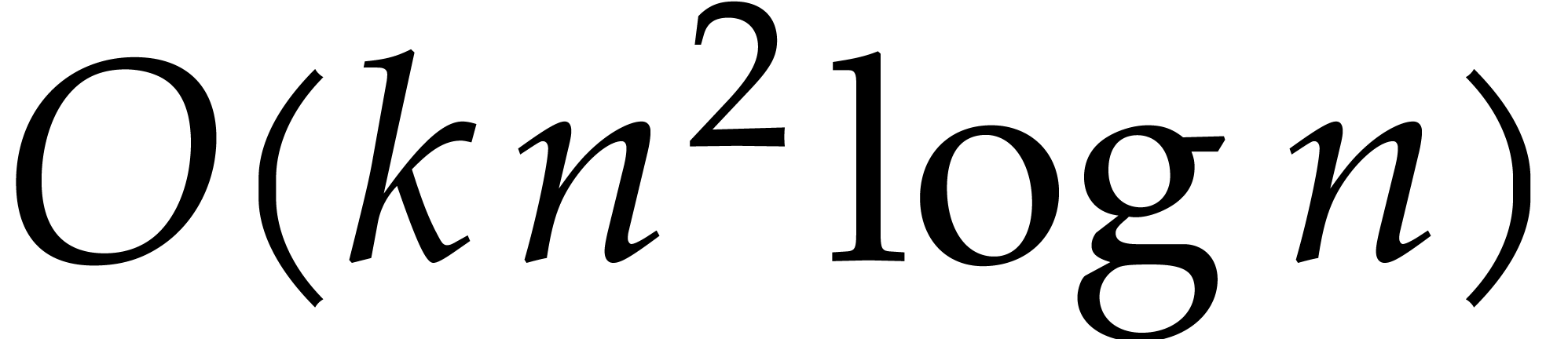 more space, by Lemma 9.
more space, by Lemma 9.
Let 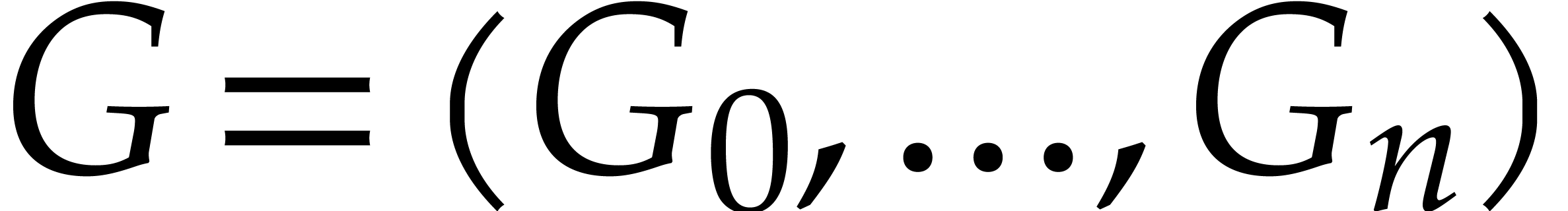 be a vanilla Gröbner basis for an ideal
be a vanilla Gröbner basis for an ideal
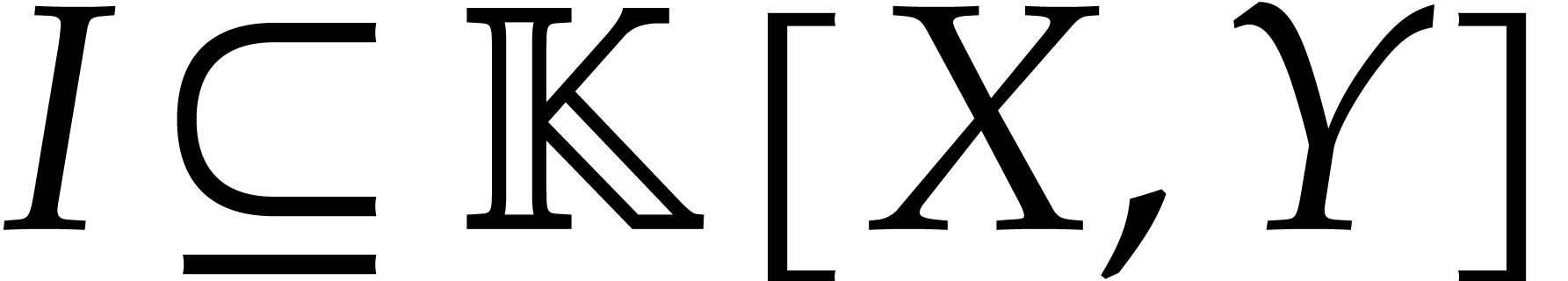 as in the previous section and assume that its
terse representation has been precomputed. The goal of this section is
to present our main algorithm that computes the extended reduction
as in the previous section and assume that its
terse representation has been precomputed. The goal of this section is
to present our main algorithm that computes the extended reduction  of a polynomial
of a polynomial 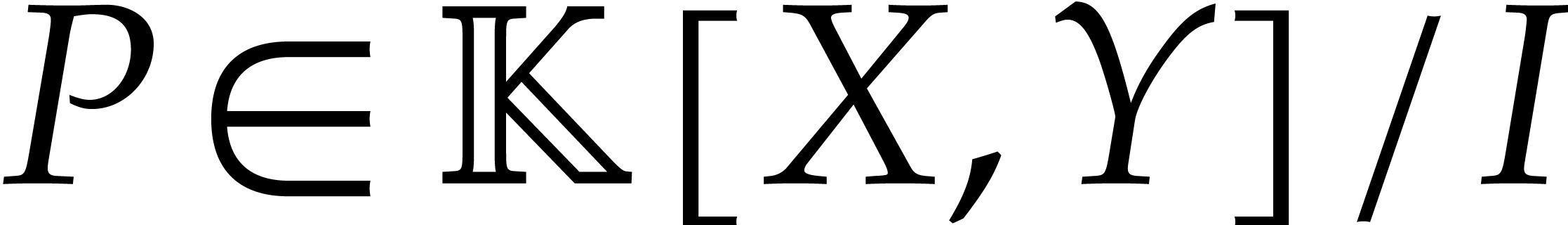 of
of 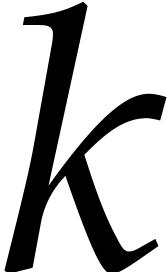 -degree
-degree  in
quasi-linear time
in
quasi-linear time 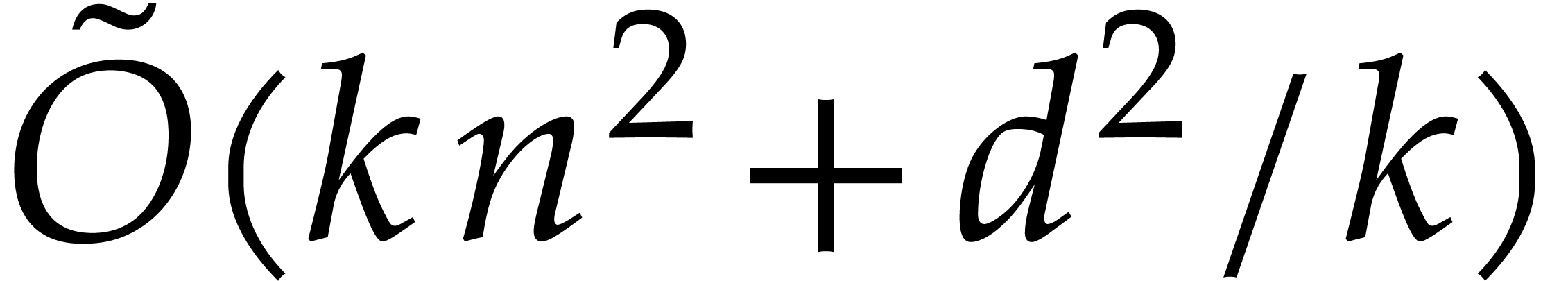 . This is
quasi-optimal with respect to the dimension of the quotient algebra
. This is
quasi-optimal with respect to the dimension of the quotient algebra 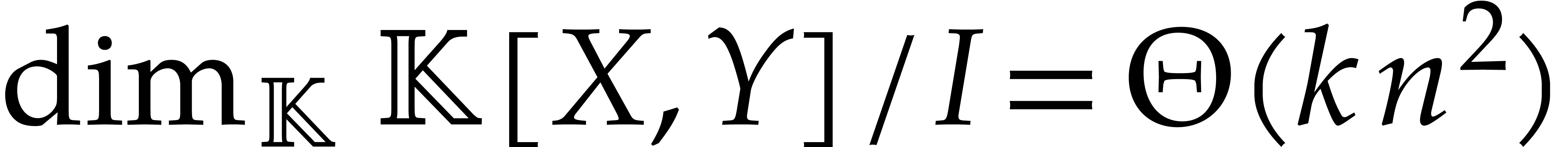 and the size of the support
and the size of the support 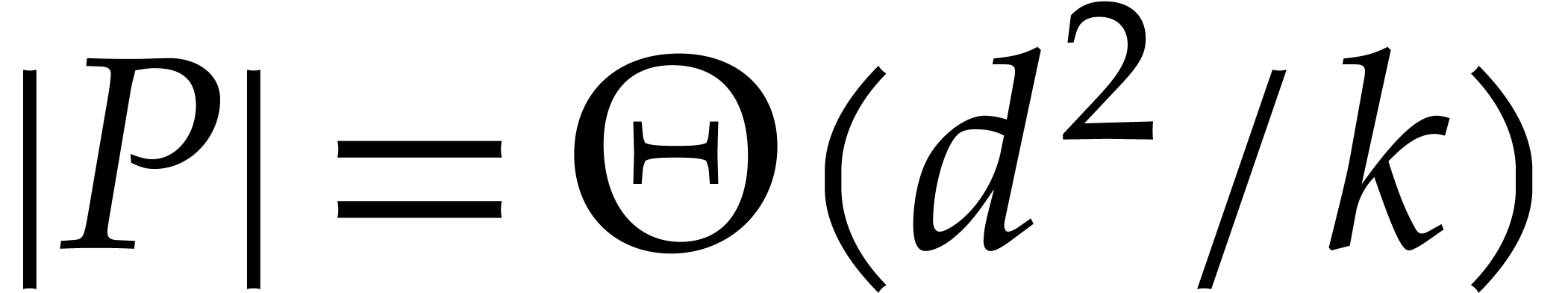 .
.
The reduction algorithm proceeds in two steps: in a first stage, we
compute the quotients  ; we
next evaluate the remainder
; we
next evaluate the remainder 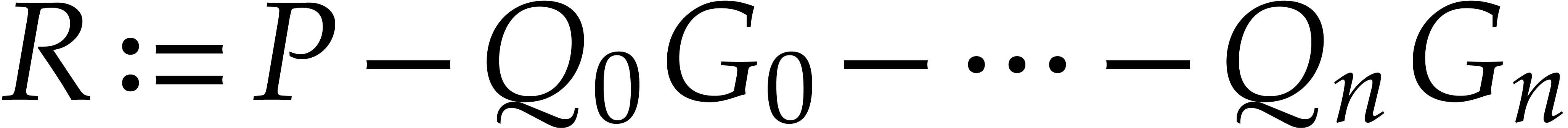 by rewriting the
linear combination
by rewriting the
linear combination  using fewer and fewer terms.
using fewer and fewer terms.
To compute the quotients, we reduce 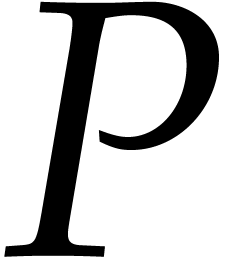 as in
section 3.3 against the tuple
as in
section 3.3 against the tuple 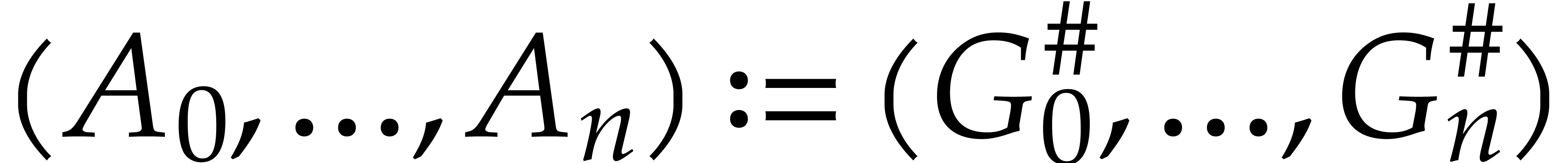 ,
in such a way that the degrees of the quotients are bounded as in
equation (4). This is done using the algorithm from [20], but with the following dichotomic selection
strategy. Given a monomial
,
in such a way that the degrees of the quotients are bounded as in
equation (4). This is done using the algorithm from [20], but with the following dichotomic selection
strategy. Given a monomial  ,
we reduce
,
we reduce 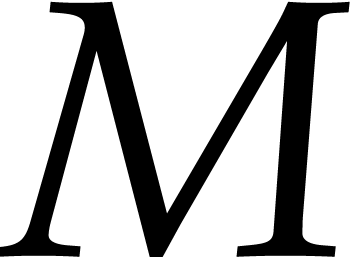 against
against 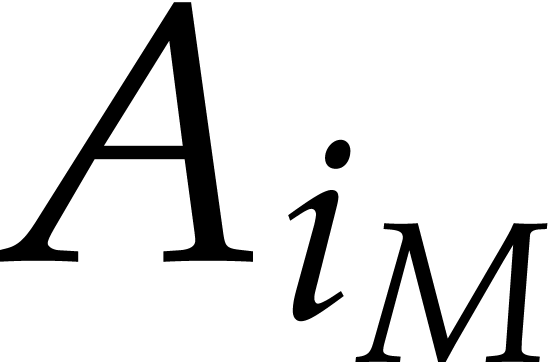 ,
where
,
where 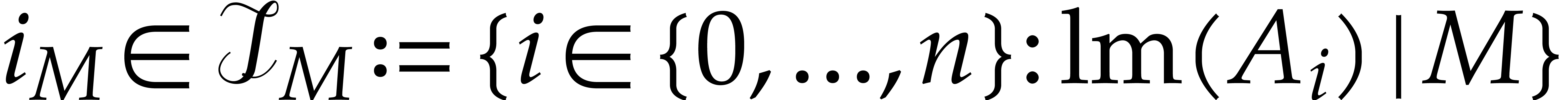 is determined as follows:
is determined as follows:
if 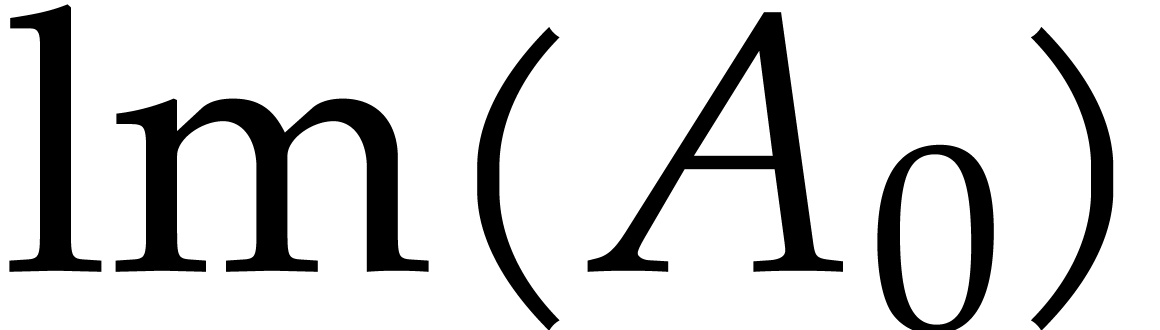 divides
divides 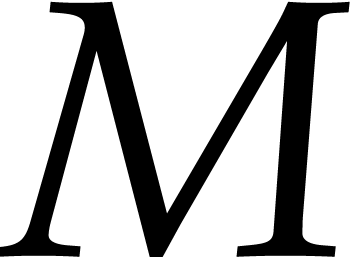 ,
then take
,
then take 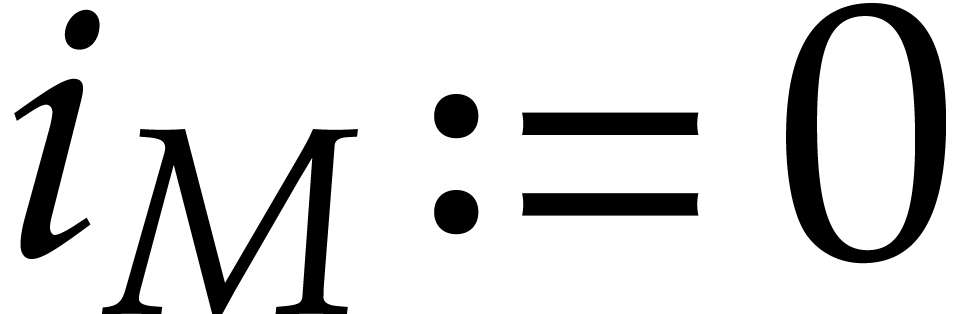 ;
;
else if  divides
divides  , then take
, then take 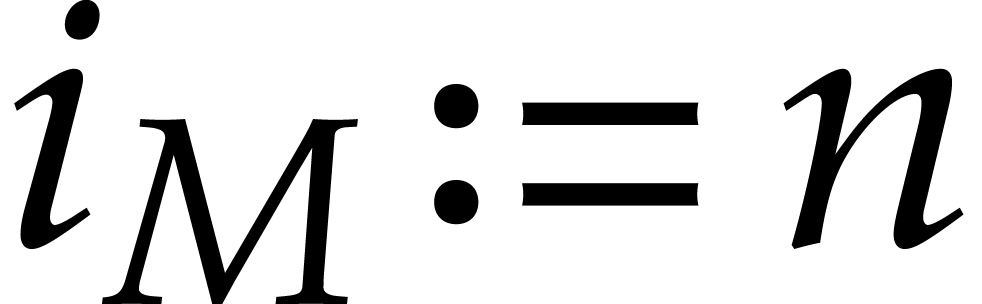 ;
;
else we take  to be the unique element in
to be the unique element in
 with
with  .
.
This selection strategy is illustrated in Figure 2 .
 be the quotients obtained for the reduction of
be the quotients obtained for the reduction of
 with respect to
with respect to 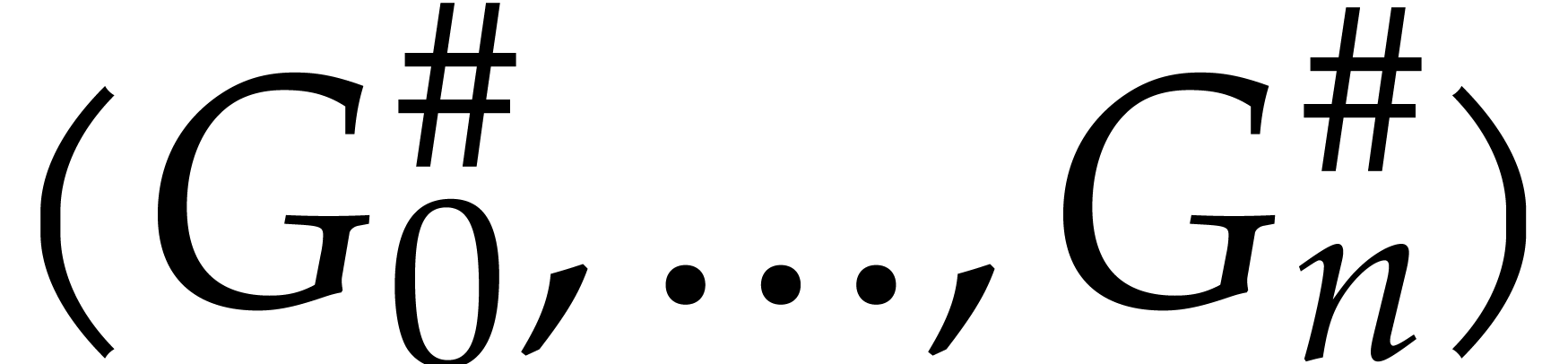 using
the dichotomic selection strategy. Then the bound
using
the dichotomic selection strategy. Then the bound
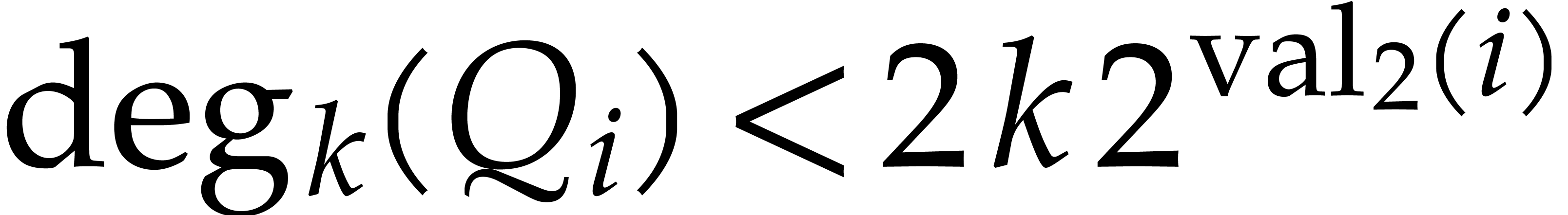
holds for all 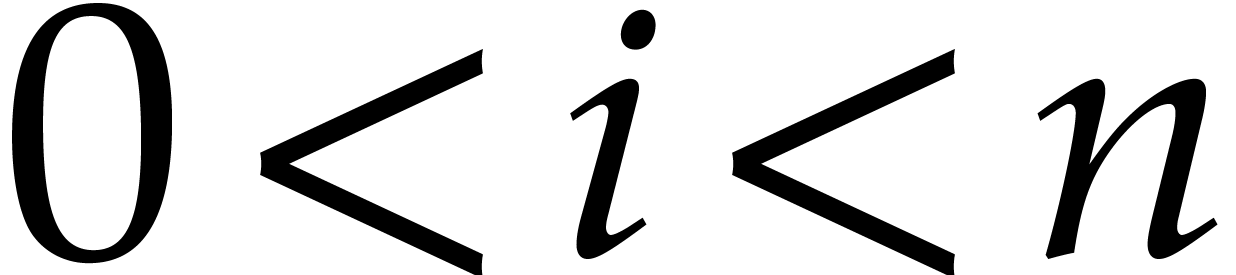 , so that
, so that
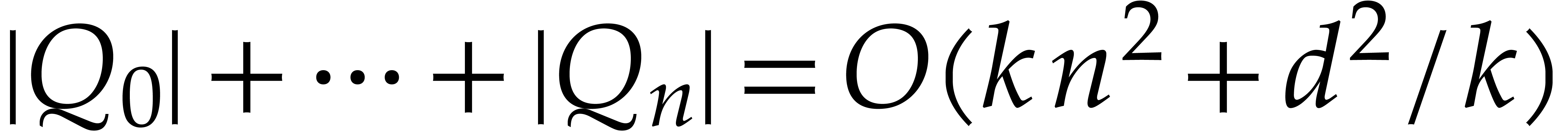 , and the extended
reduction
, and the extended
reduction  can be computed in time
can be computed in time
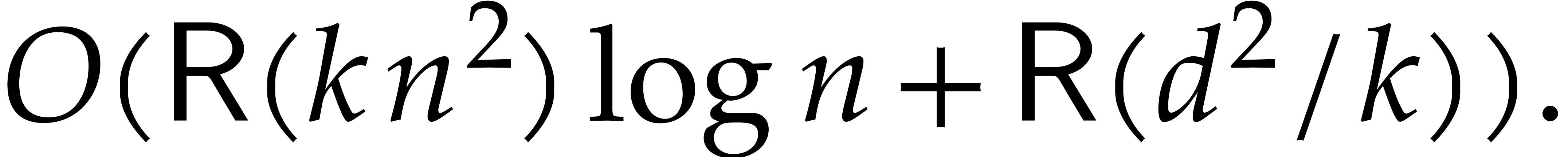
Proof. Let  with
with 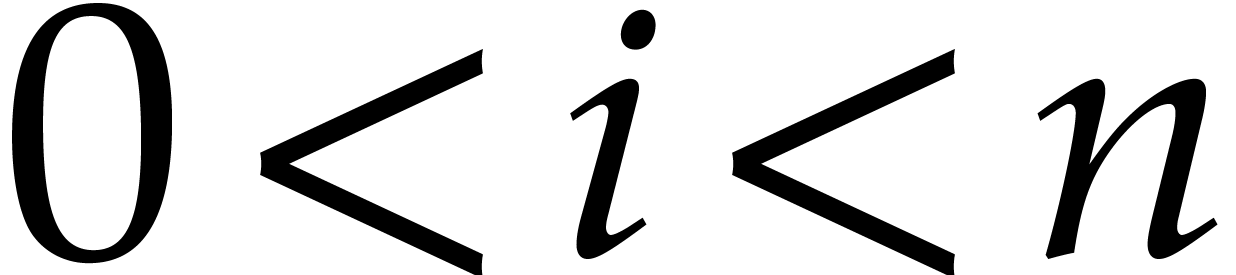 , so that
, so that 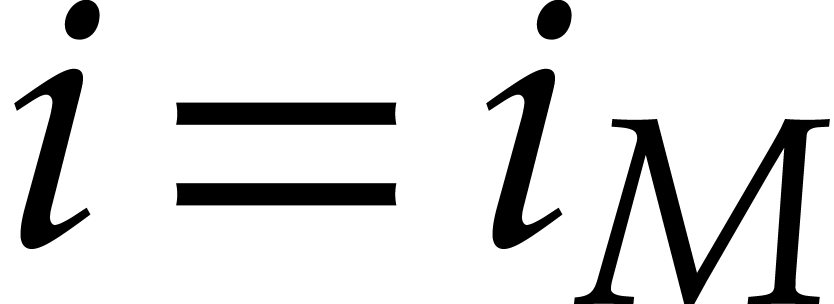 for
for 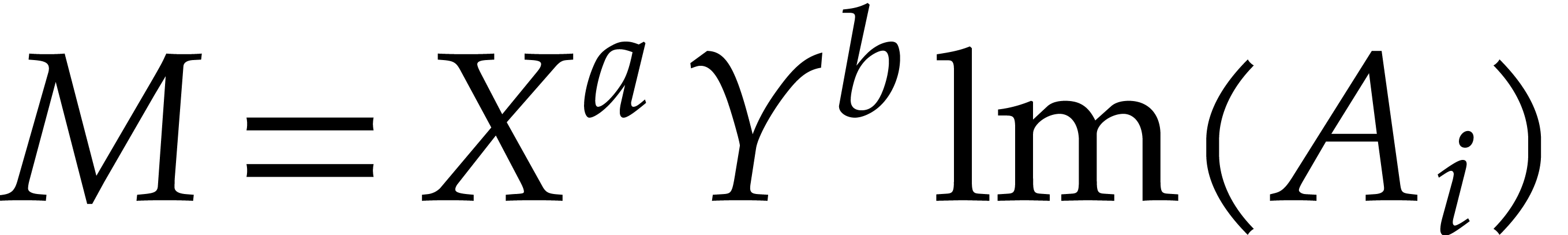 , and denote
, and denote 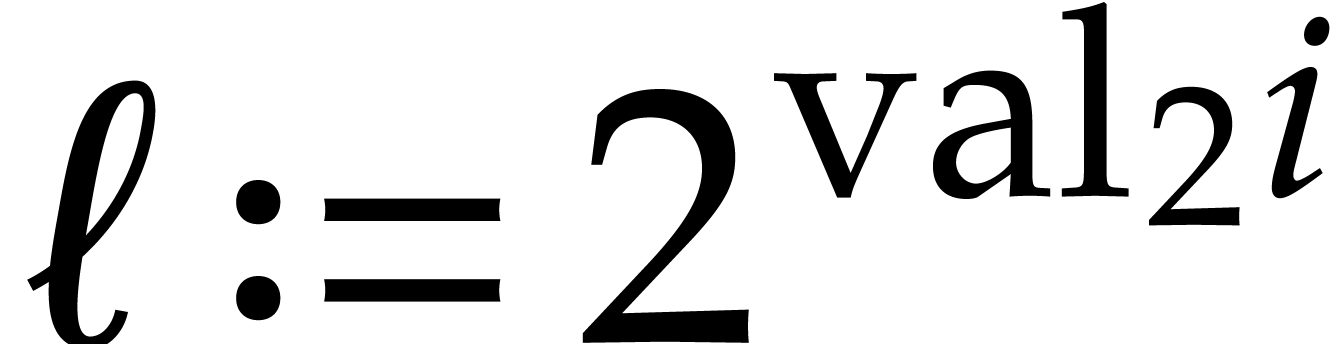 . Then we observe that
. Then we observe that  : if not, then
: if not, then 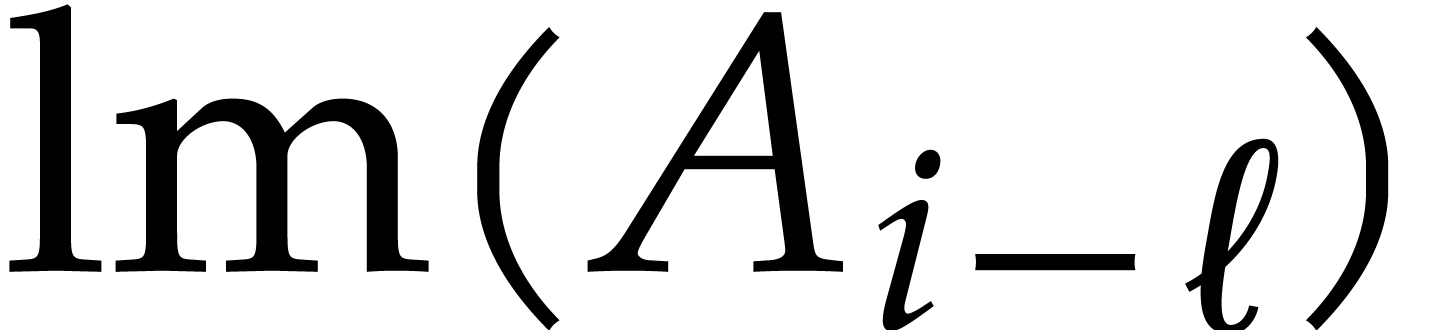 would divide
would divide
 , whereas
, whereas 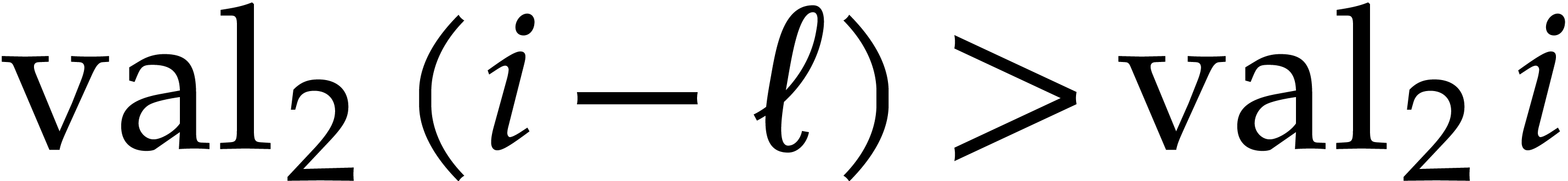 . A similar reasoning with
. A similar reasoning with 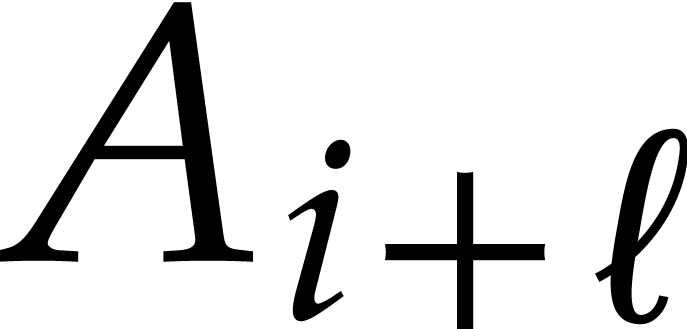 (or
(or 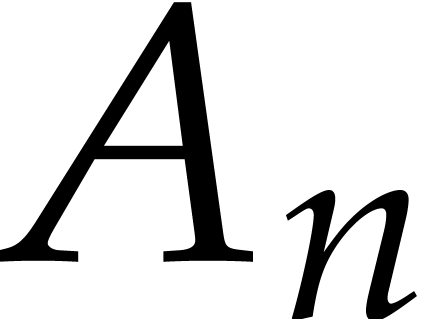 , whenever
, whenever 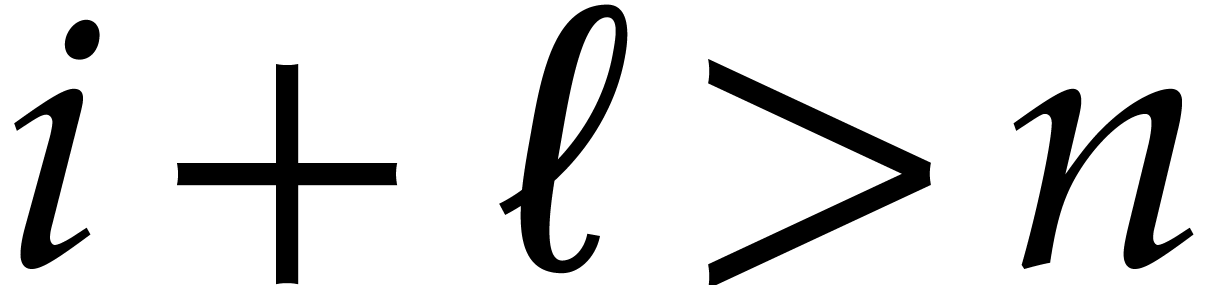 ) shows that
) shows that 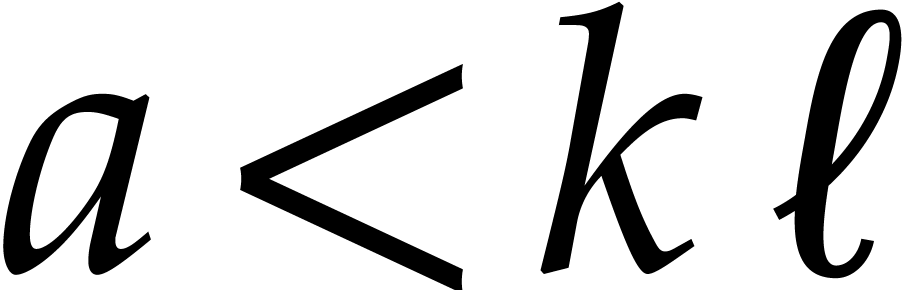 .
It follows that
.
It follows that 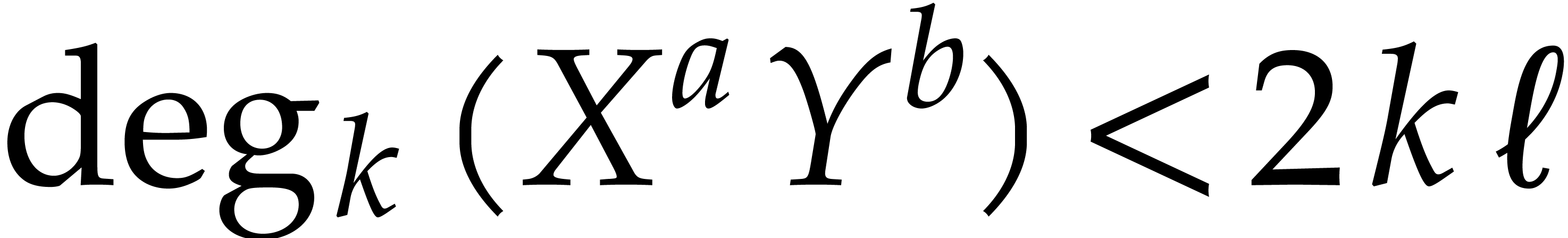 .
.
This also proves that 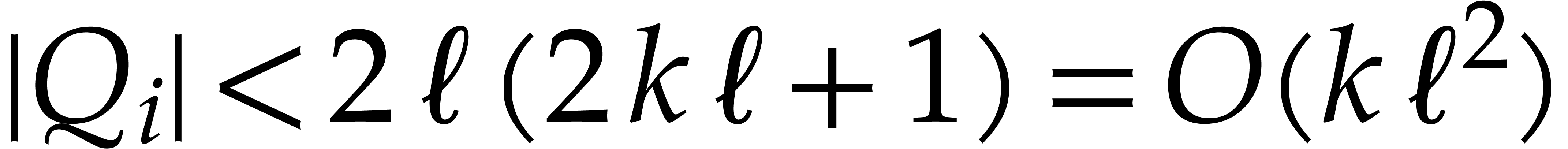 and
and 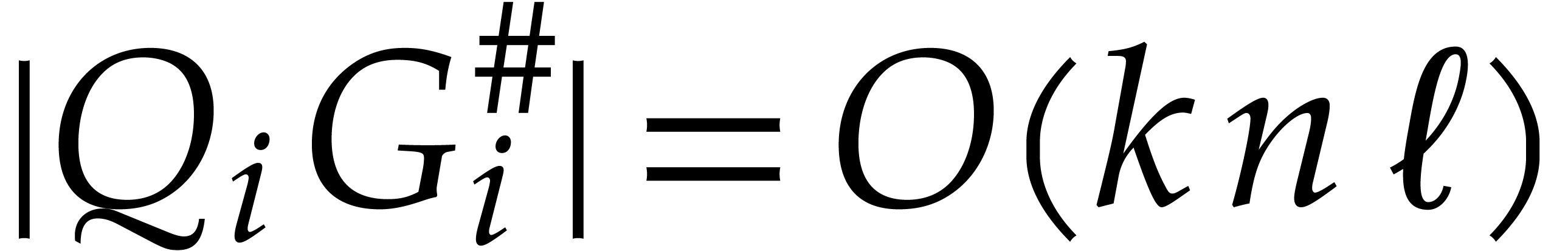 , for any
, for any 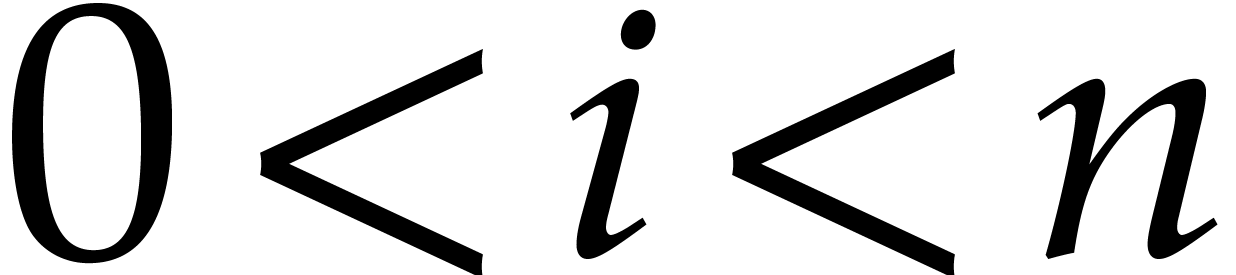 .
Since the number of indices
.
Since the number of indices 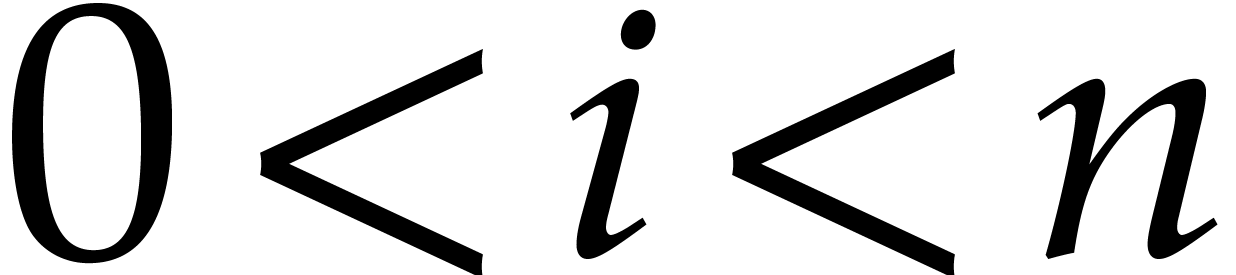 with
with  is bounded by
is bounded by  ,
we get
,
we get
On the other hand, 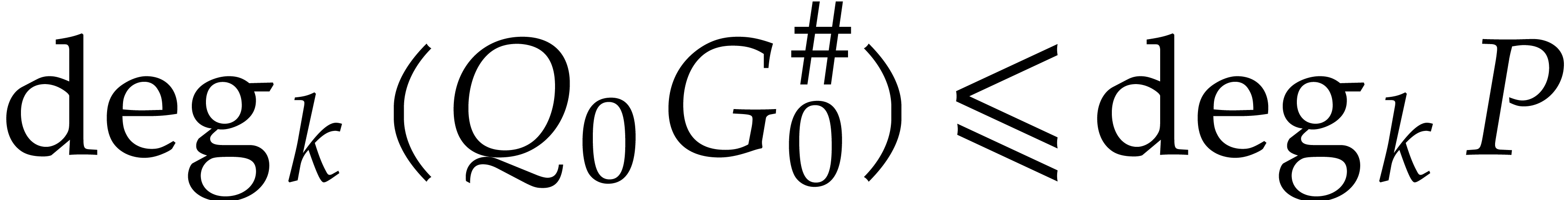 and
and 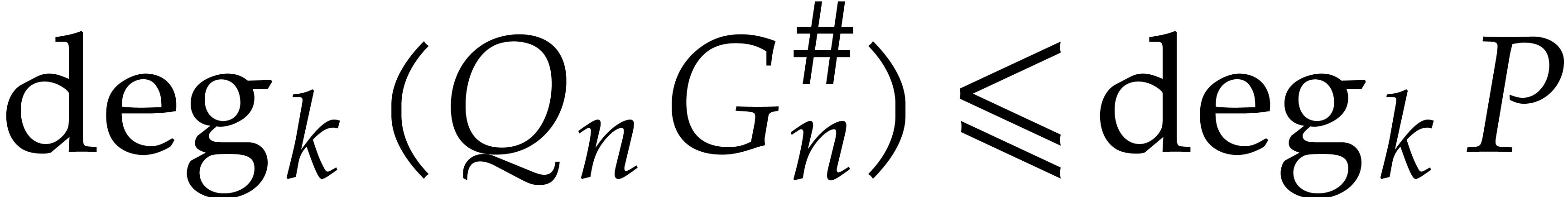 , whence
, whence 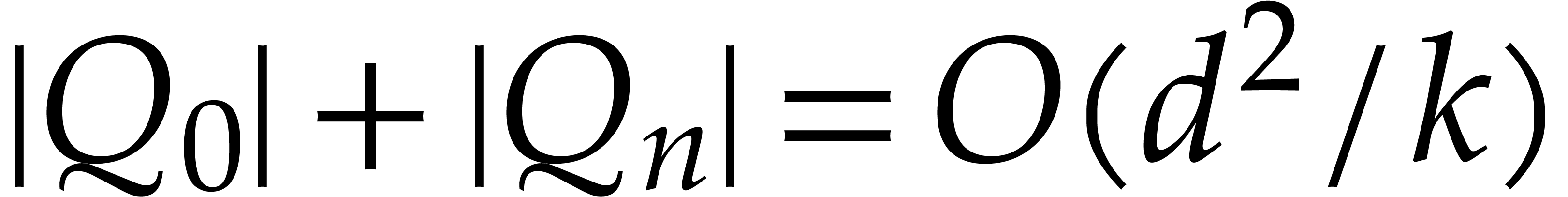 and
and 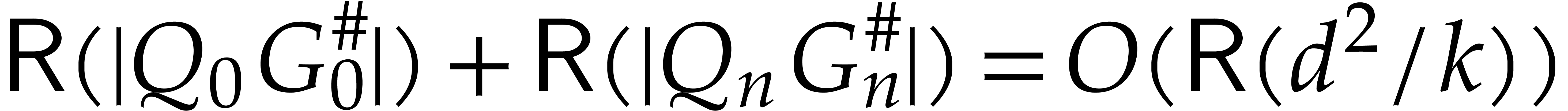 . We conclude by applying the bound (3)
for the complexity of polynomial reduction.
. We conclude by applying the bound (3)
for the complexity of polynomial reduction.
The next important observation is that the quotients  obtained in the above way can actually be used as quotients for the
extended reduction of
obtained in the above way can actually be used as quotients for the
extended reduction of 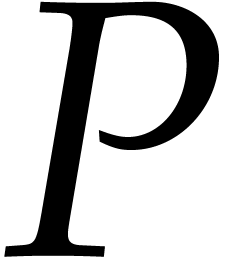 with respect to
with respect to  :
:
Proof. Let 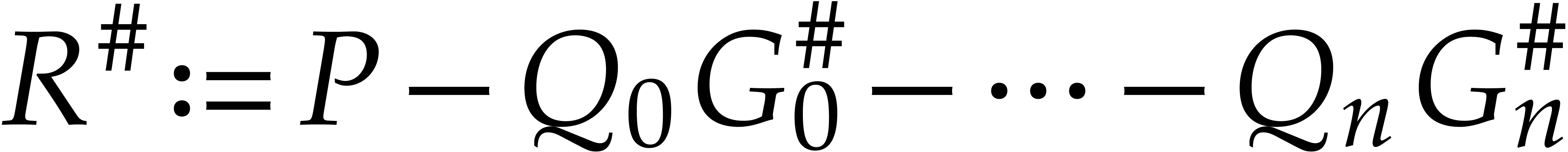 .
By construction,
.
By construction, 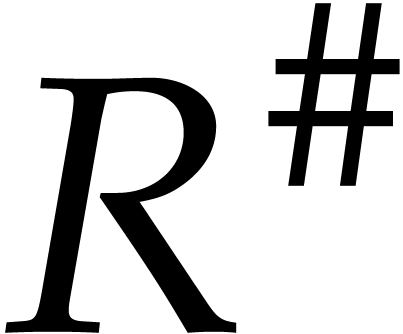 is reduced with respect to
is reduced with respect to 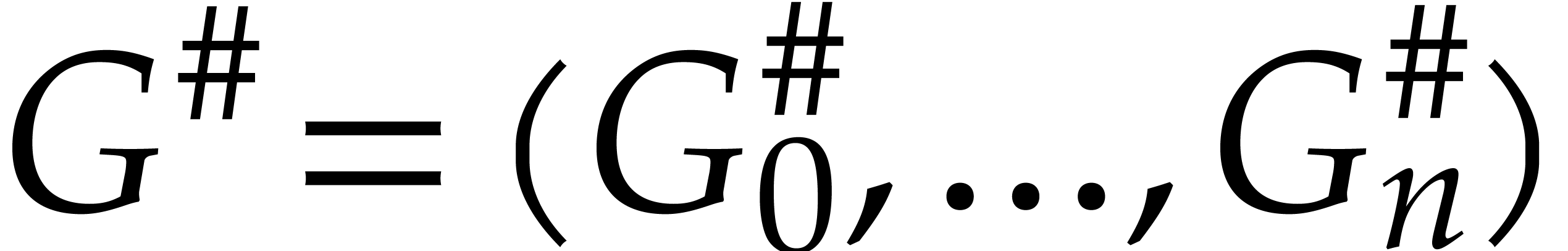 and whence with respect to
and whence with respect to  since
since 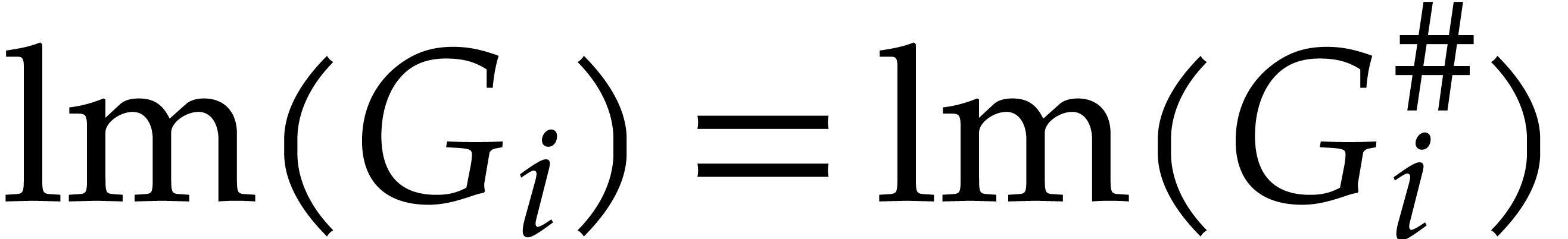 for all
for all  .
For any
.
For any 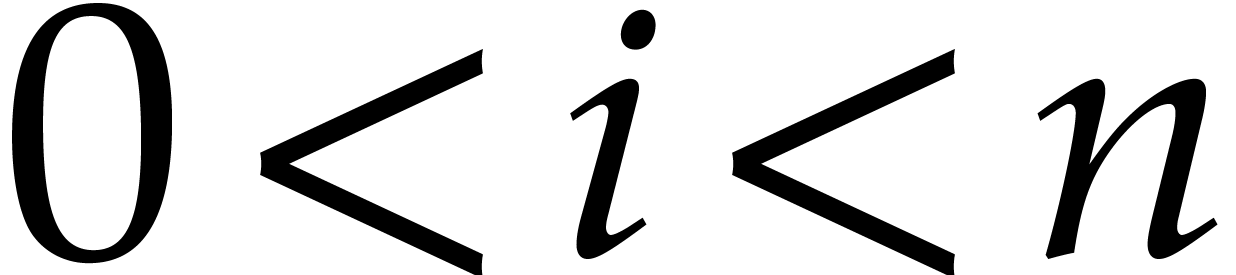 , we also have
, we also have 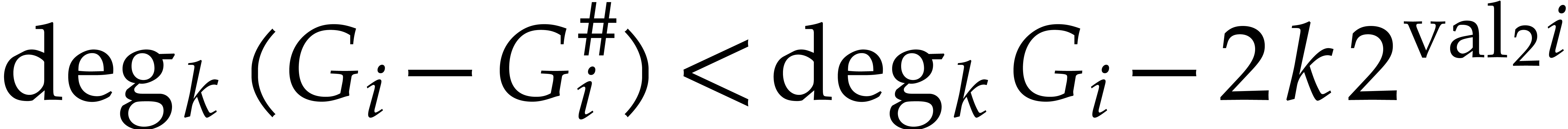 , whence
, whence
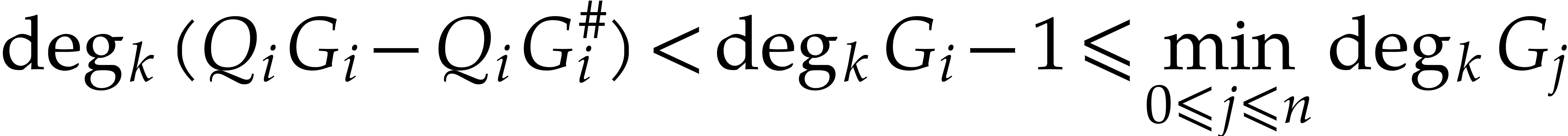
by Lemma 13 and Corollary 4. Since 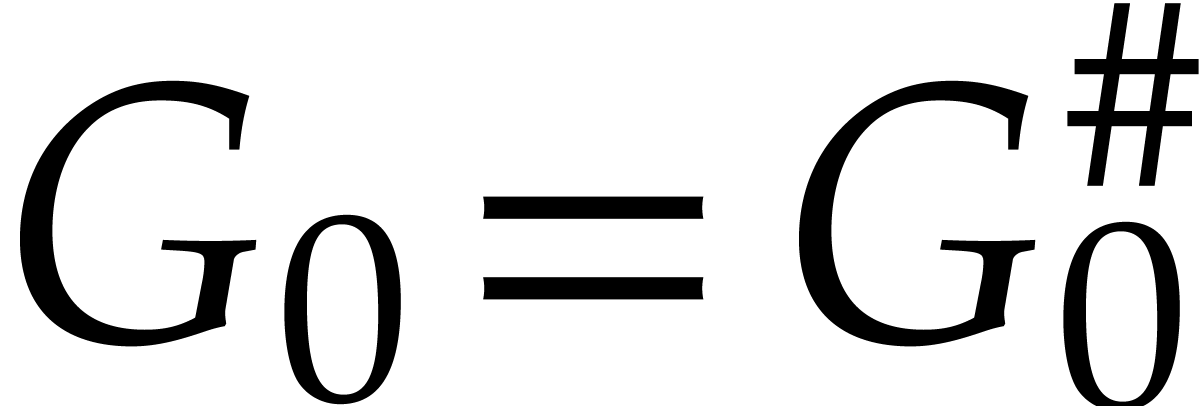 and
and 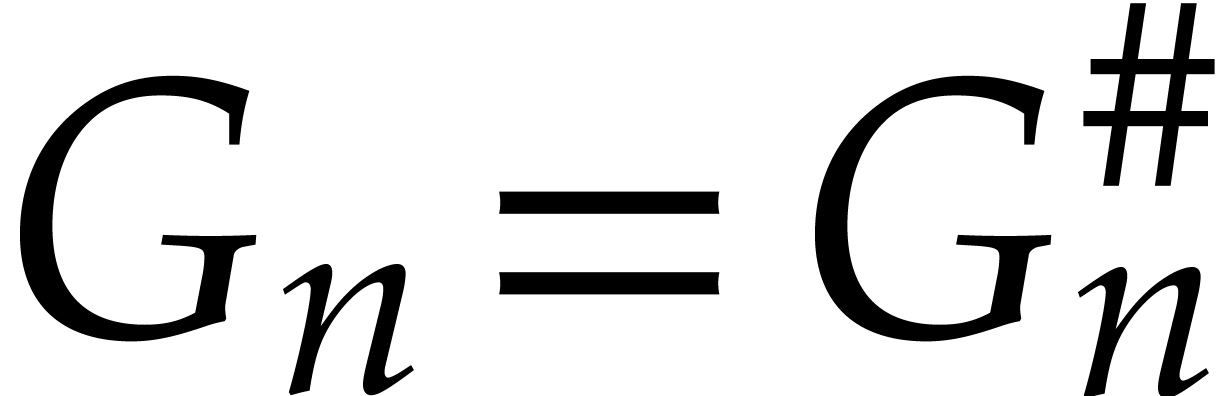 , this
means that
, this
means that
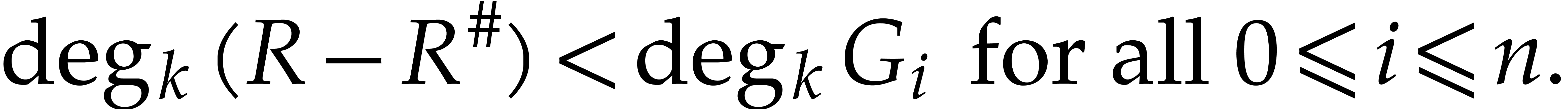
In other words, the polynomials 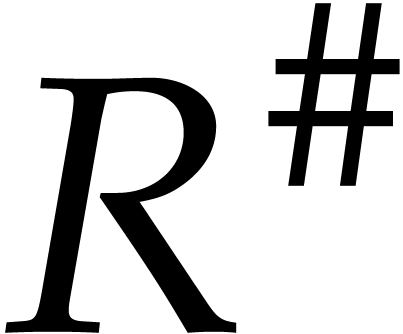 ,
,
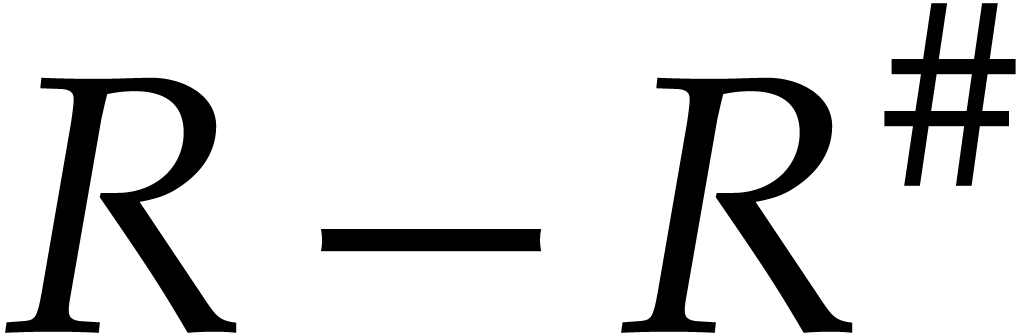 , and therefore
, and therefore  are all reduced with respect to
are all reduced with respect to  .
.
Once the quotients  are known, we need to compute
the remainder
are known, we need to compute
the remainder 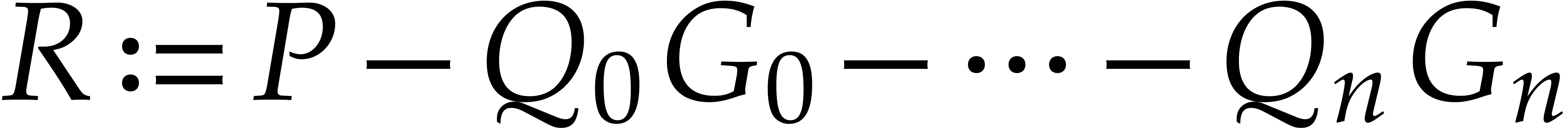 . We do this by
rewriting (or retracting) the linear combination
. We do this by
rewriting (or retracting) the linear combination  into a linear combination
into a linear combination 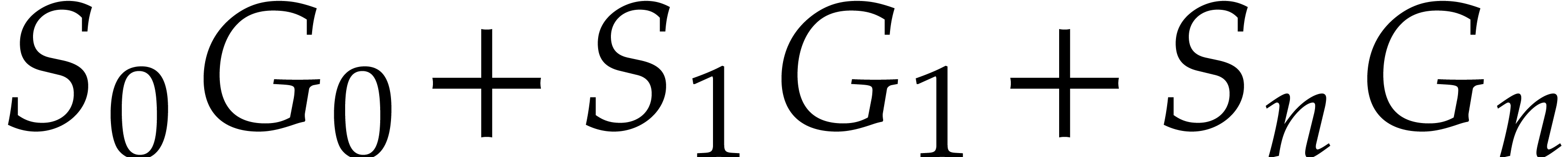 using
the following algorithm:
using
the following algorithm:
Algorithm
Output:  with
with 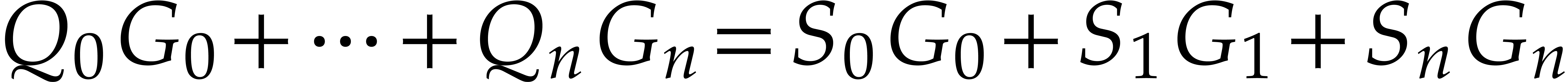
For 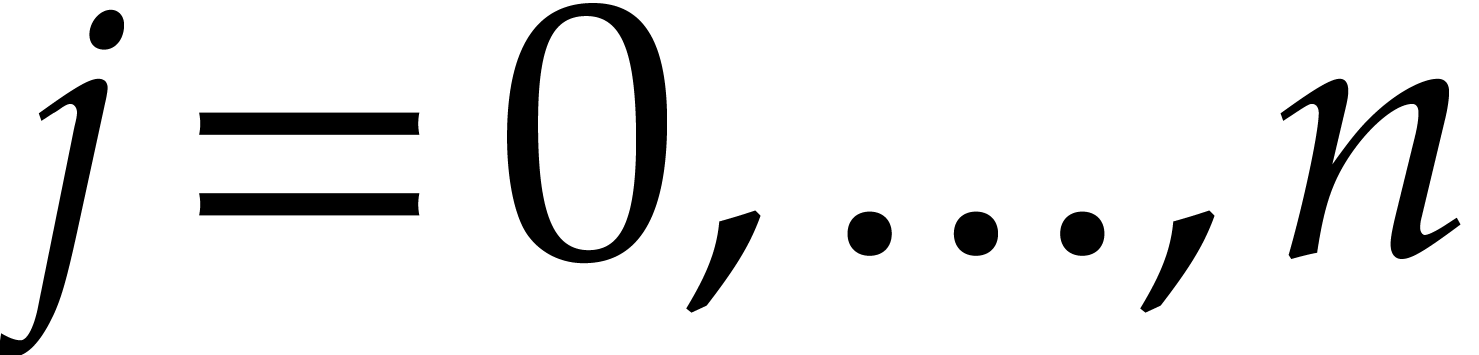 , set
, set 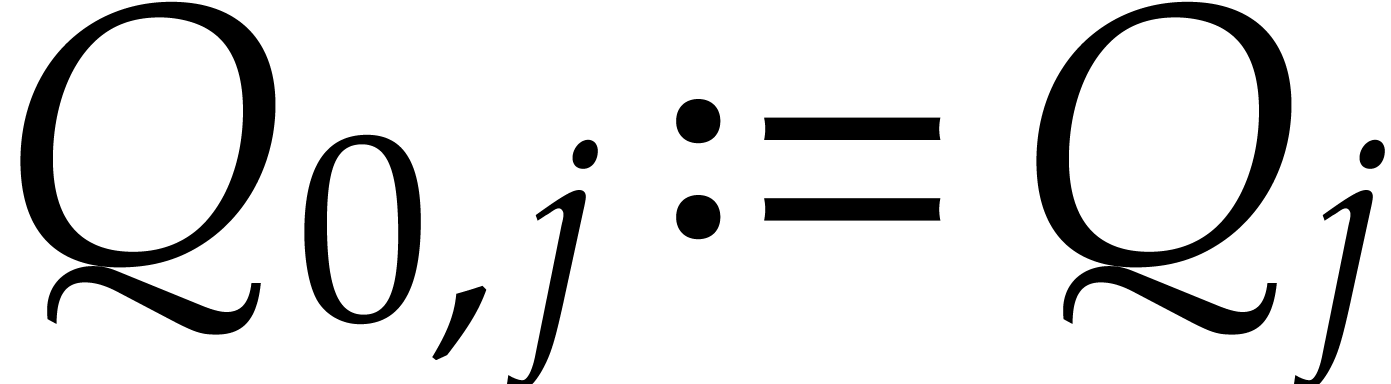
For 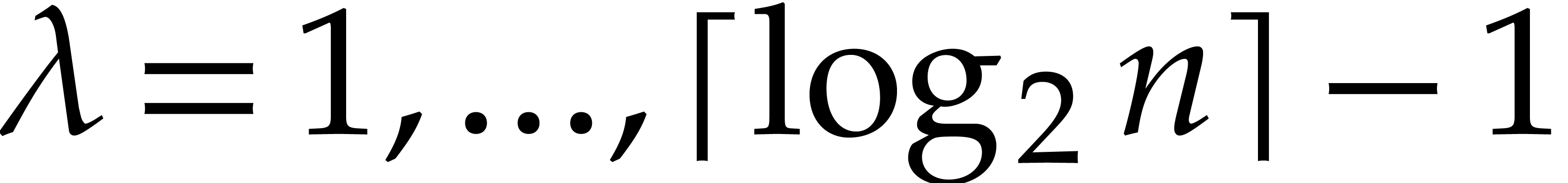 do
do
For 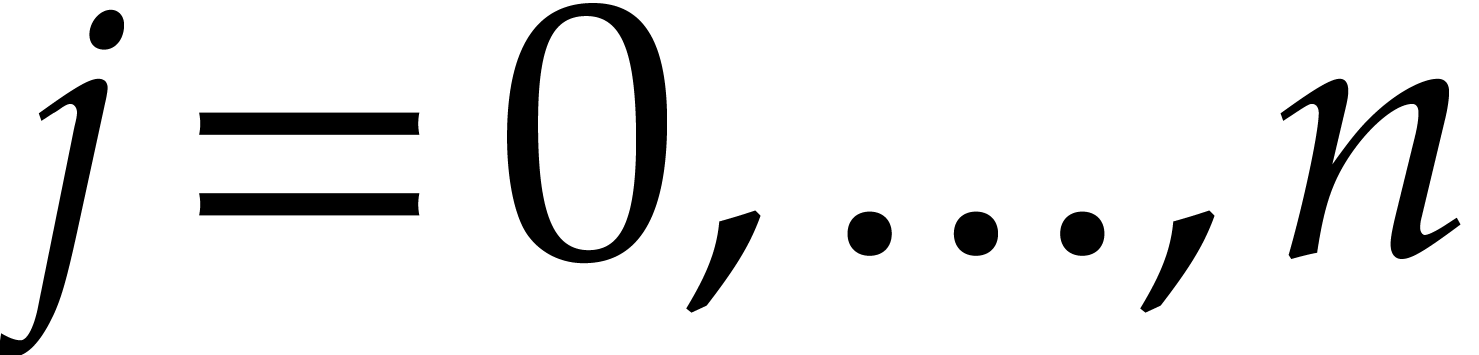 do
do
If 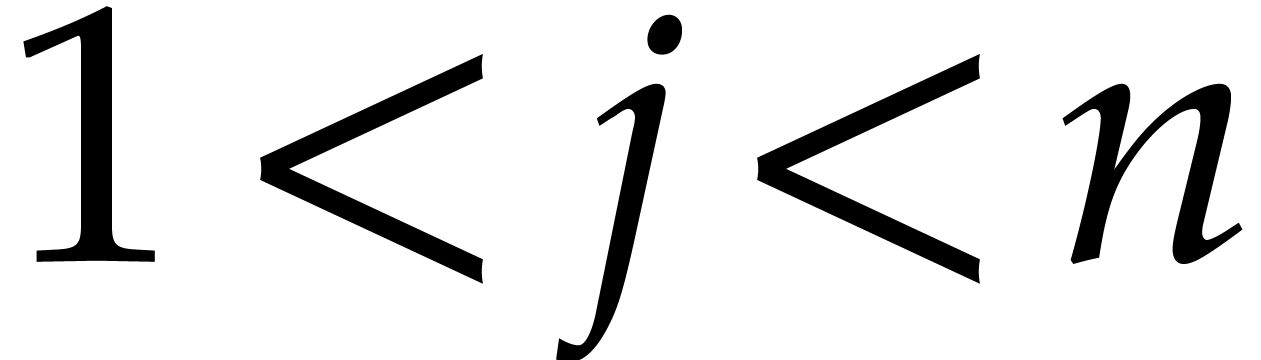 and
and 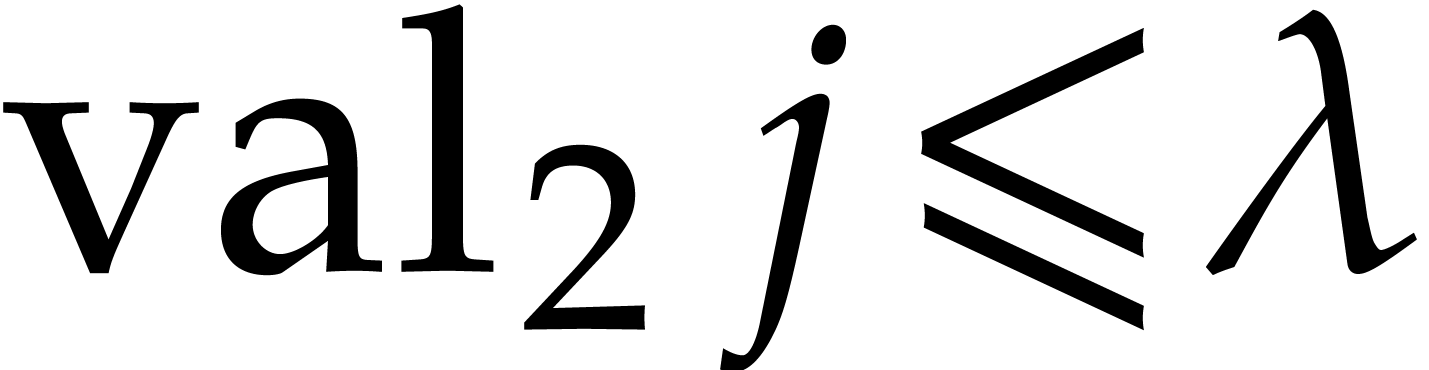 ,
then set
,
then set 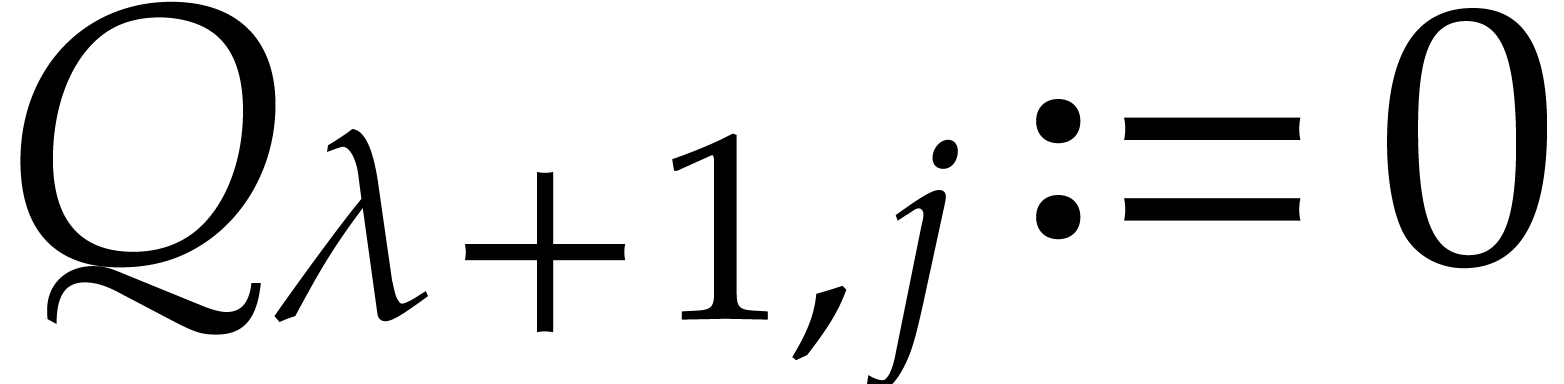
Otherwise, set 
For 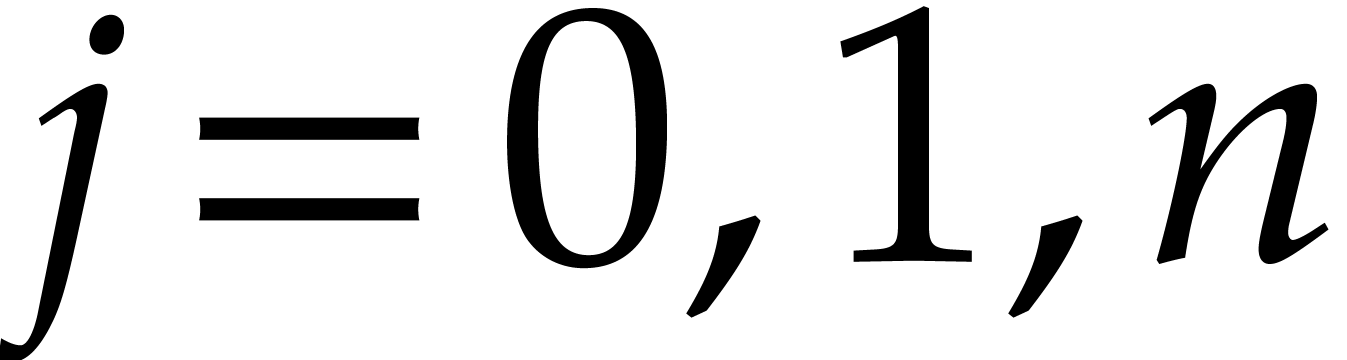 , define
, define 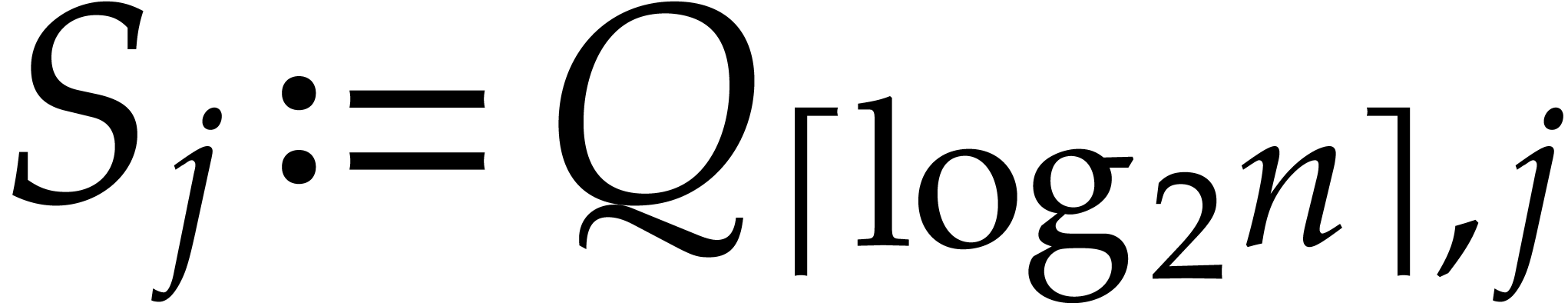 , and return
, and return 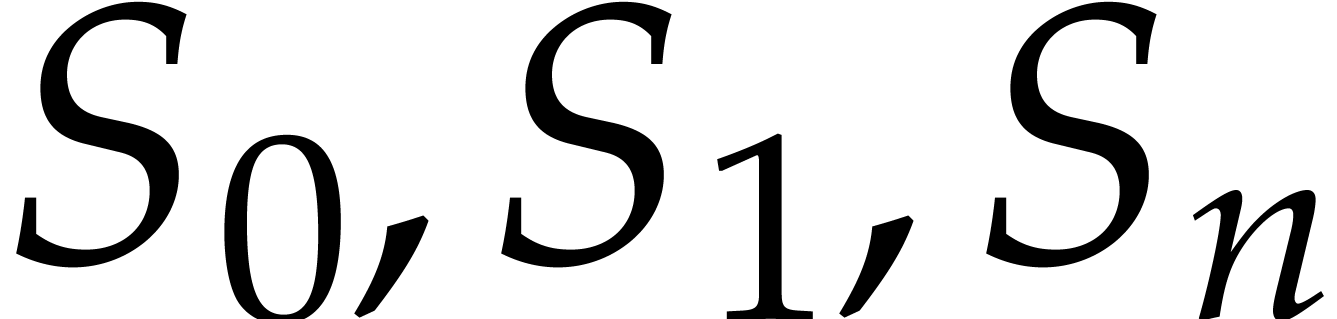
 .
.
Proof. By construction, we notice that 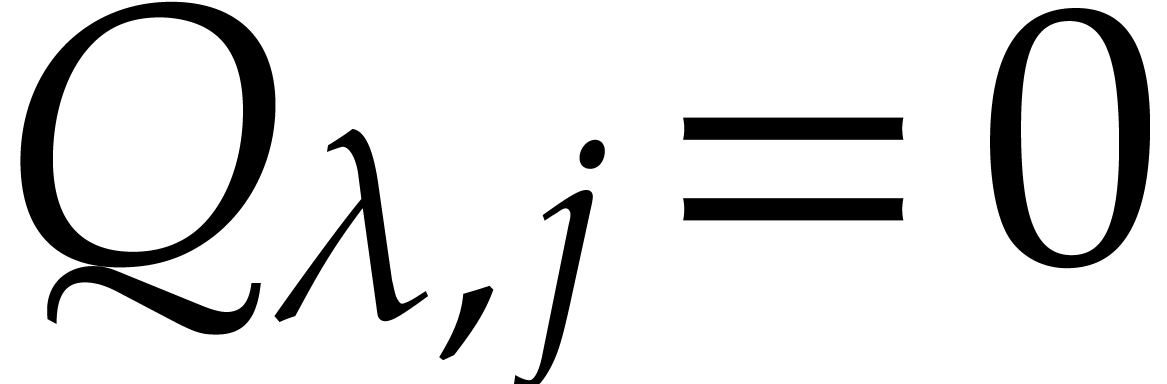 if
if 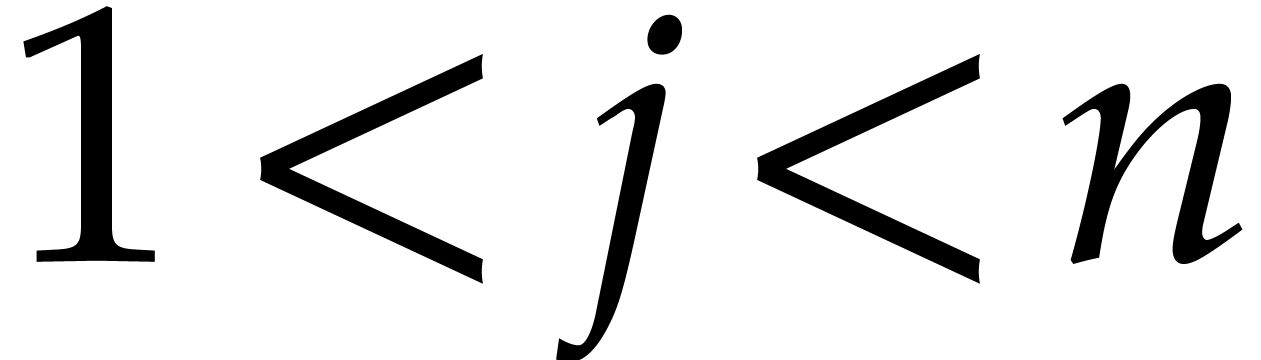 and
and 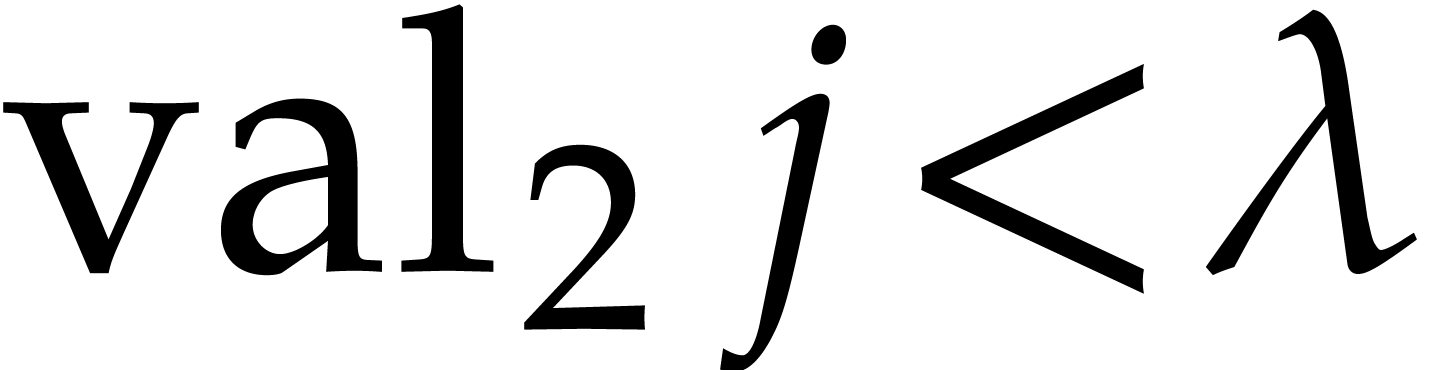 (that is
(that is 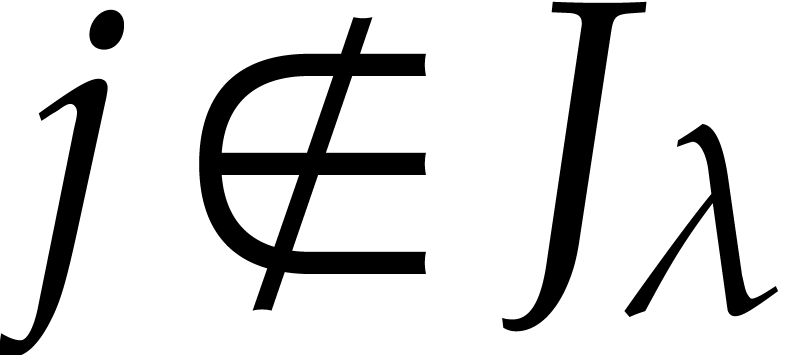 ). Let us now show
by induction over
). Let us now show
by induction over  that
that
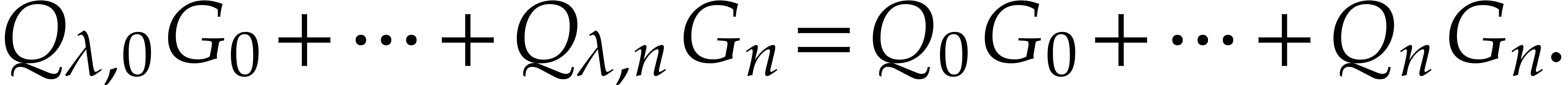
This is clearly true for 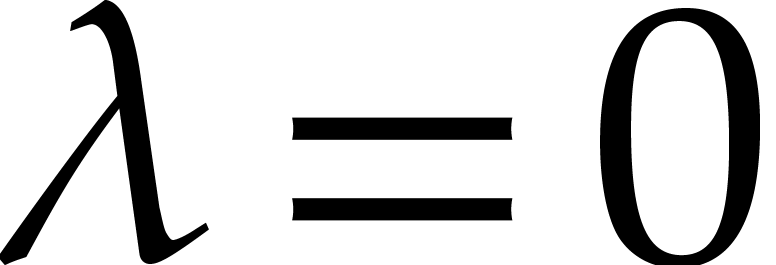 . We
have
. We
have
which proves the correctness of Algorithm 1. Again by
induction over 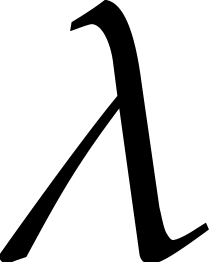 , it is not
hard to see that the bound
, it is not
hard to see that the bound 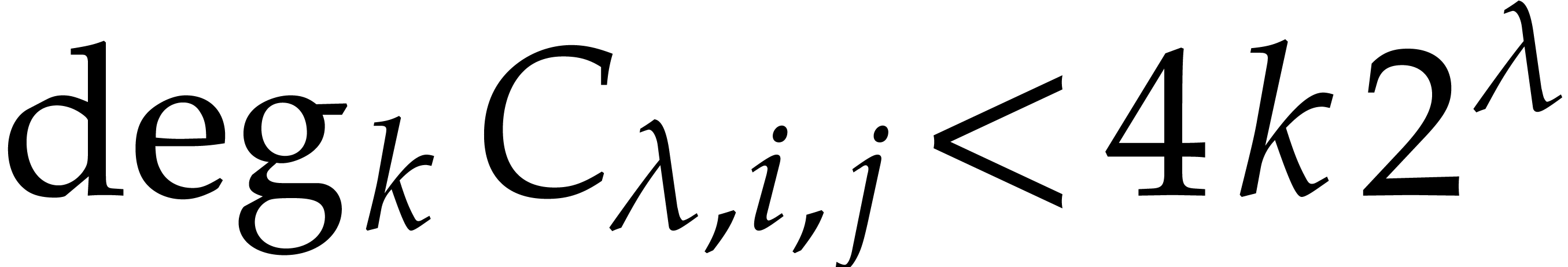 implies
implies
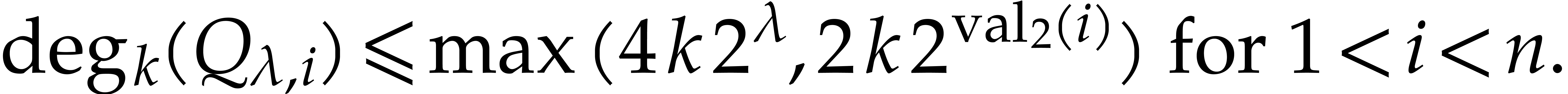 |
(5) |
Now, for 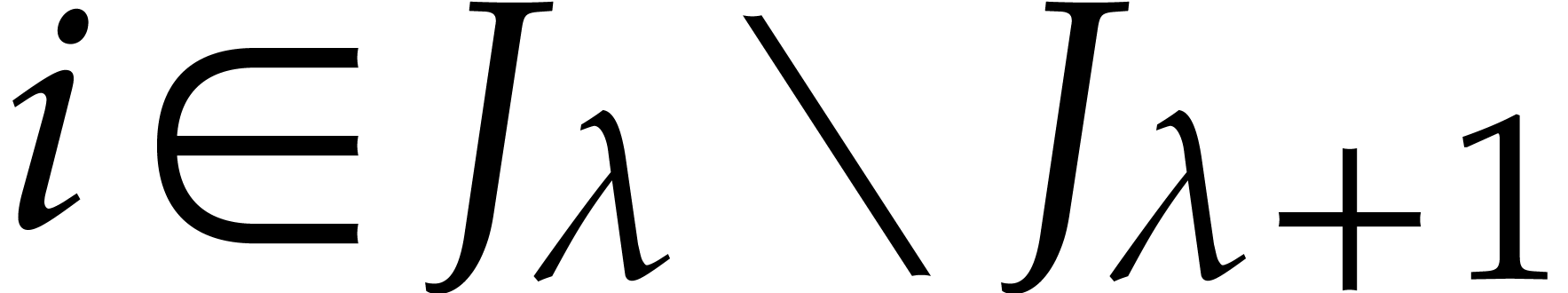 and
and  ,
the product
,
the product 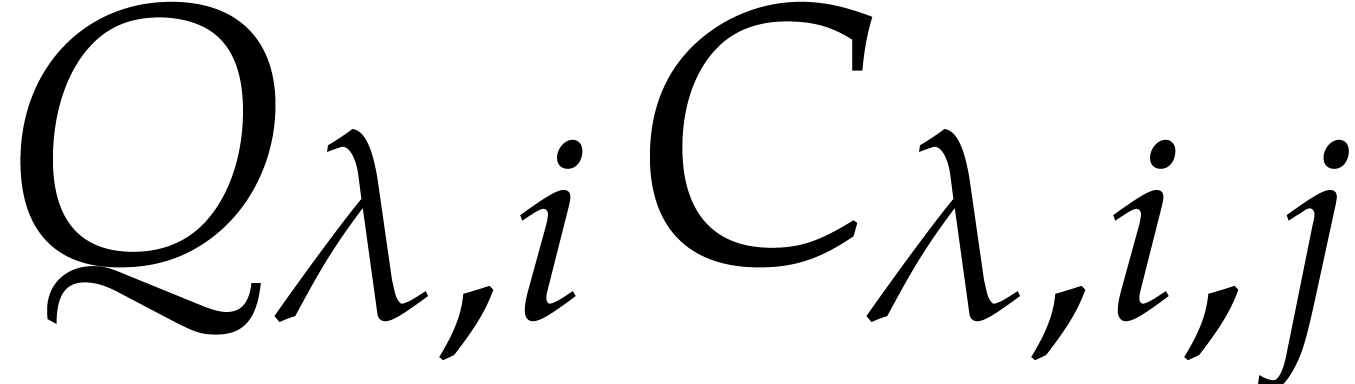 is computed in time
is computed in time 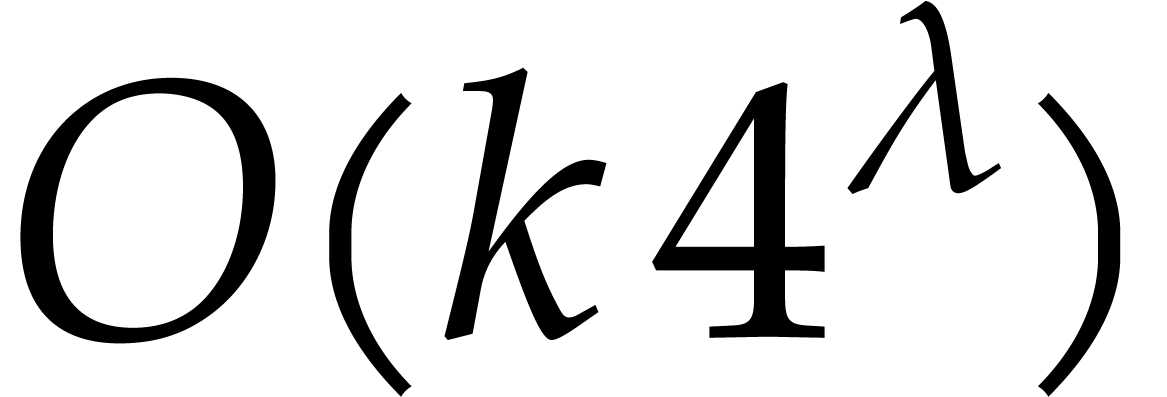 , and there are
, and there are 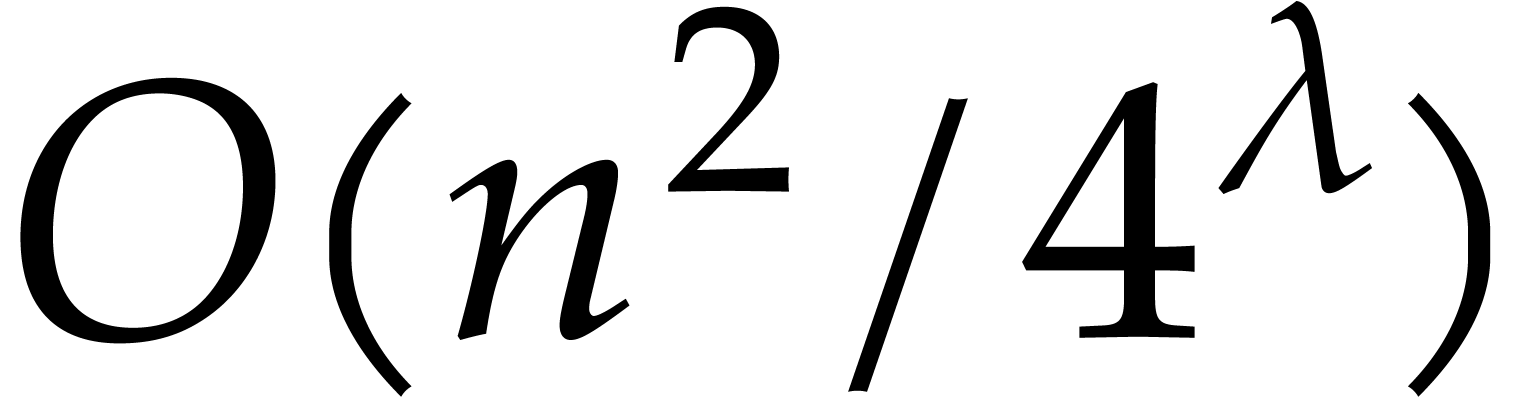 such
products (see the proof of Lemma 9). Using that
such
products (see the proof of Lemma 9). Using that 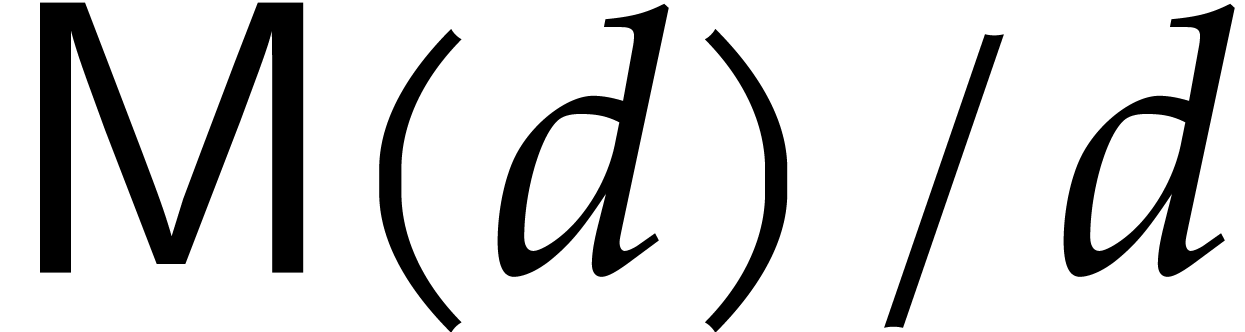 is non-decreasing, we conclude that each step can be
computed in time
is non-decreasing, we conclude that each step can be
computed in time 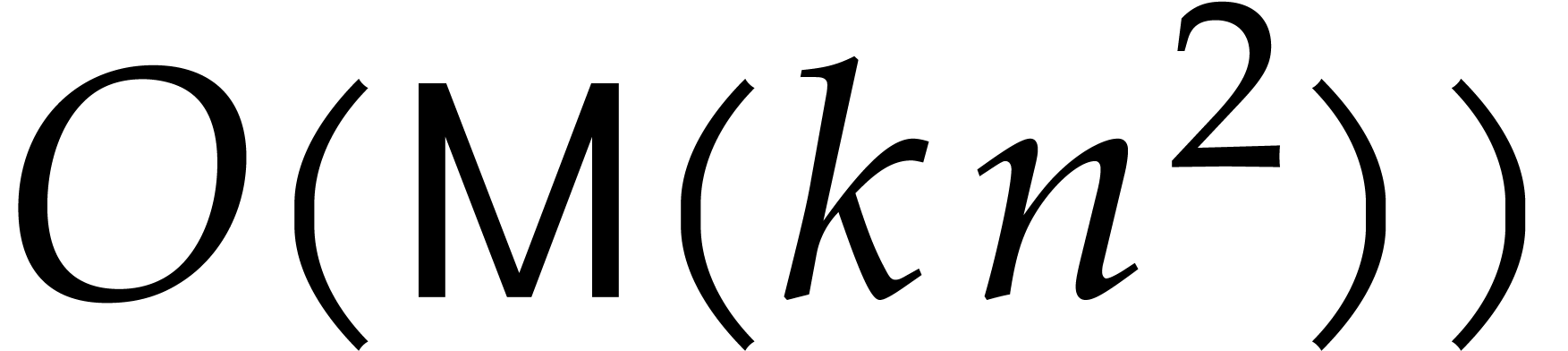 .
.
Combining our subalgorithms, we obtain our algorithm for extended reduction.
Algorithm
Output: An extended reduction 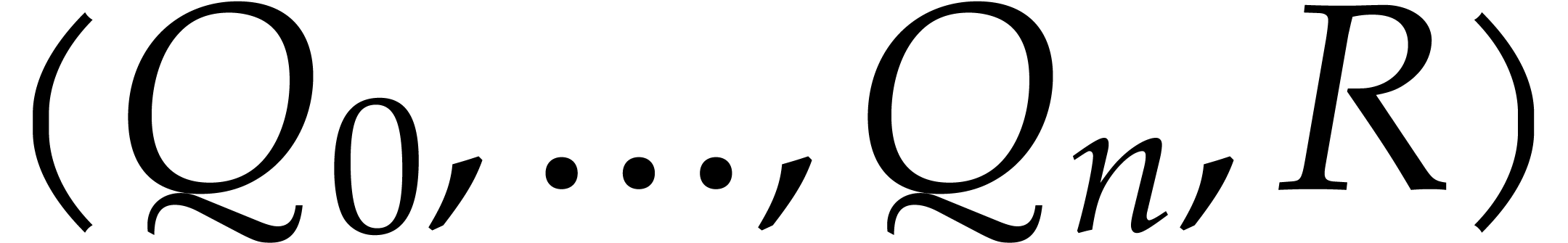 of
of  modulo
modulo 
Compute the extended reduction 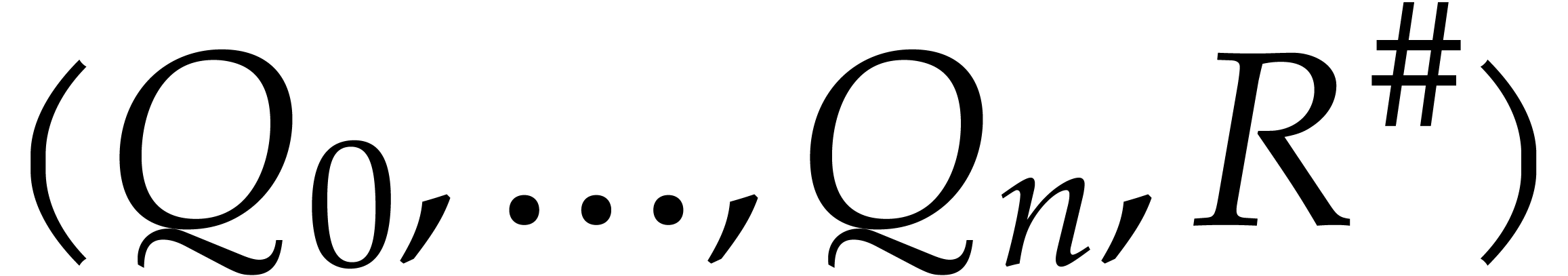 with respect to
with respect to
Compute 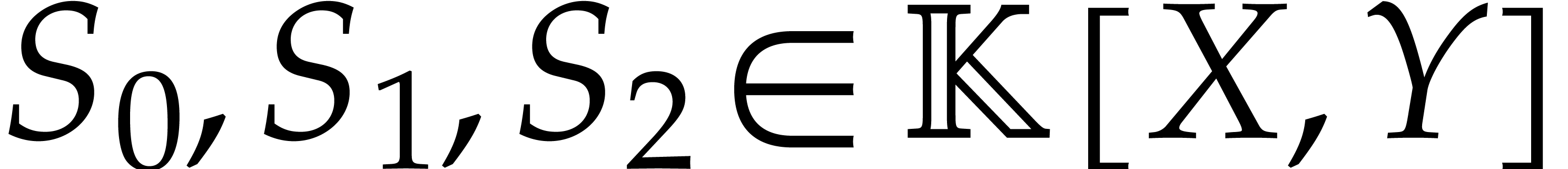 as a function of
as a function of  using Algorithm 1
using Algorithm 1
Compute 
Return 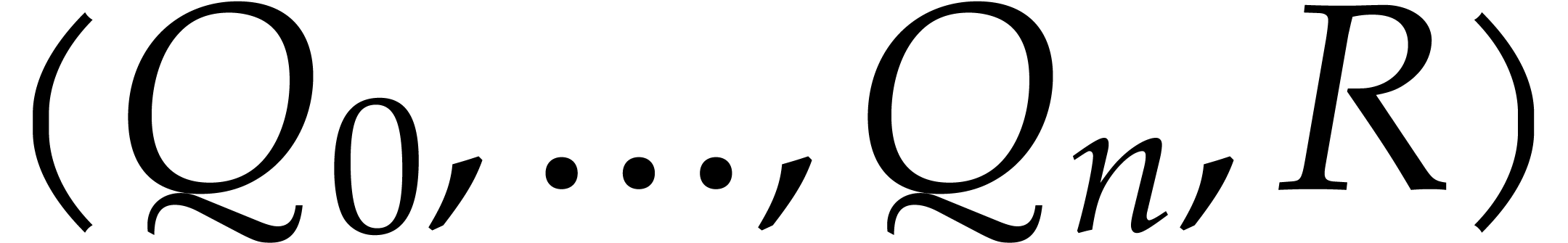 .
.
Proof. Because of Lemma 13, the
extended reduction with respect to 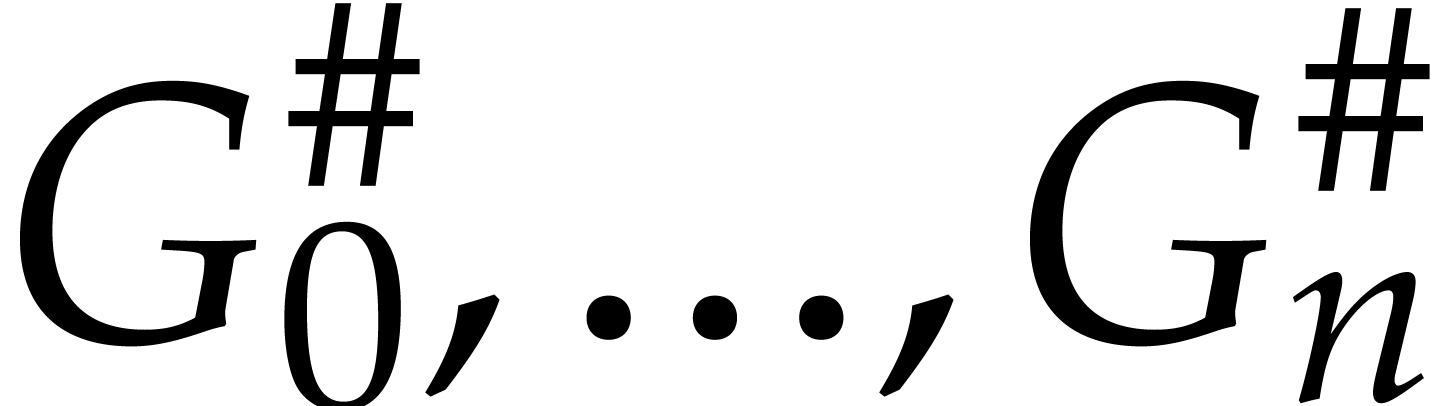 is computed
in time
is computed
in time
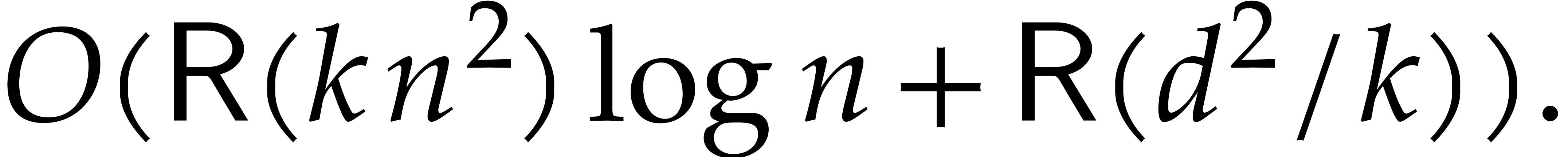
Proposition 14 ensures that the quotients are also valid
with respect to  . The next
step is to evaluate the remainder
. The next
step is to evaluate the remainder 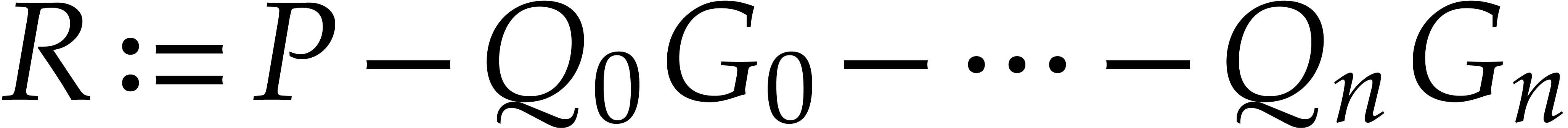 .
The
.
The 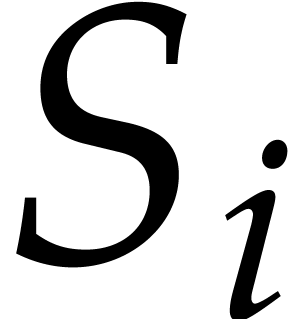 's are computed in time
's are computed in time
 using Lemma 15 and we have
using Lemma 15 and we have
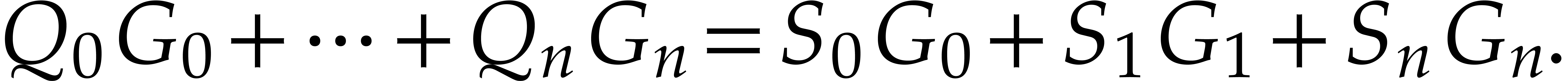
For 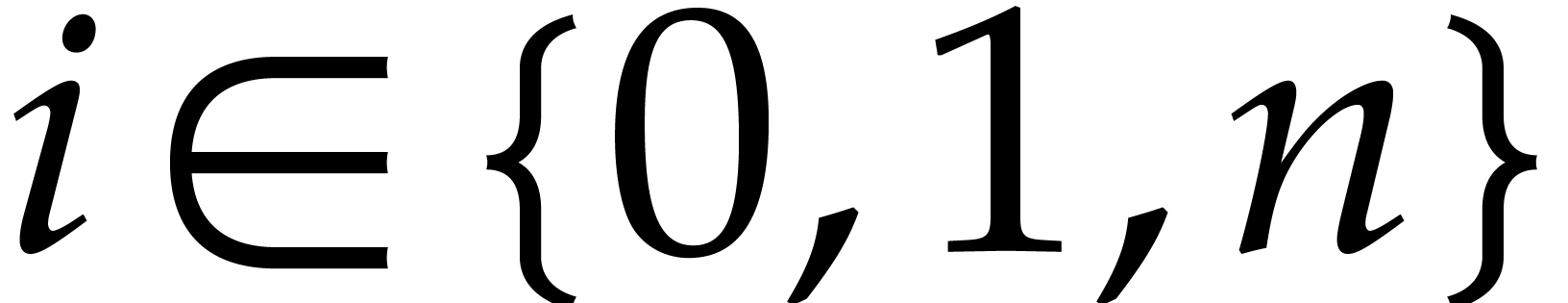 , it follows from (5) that
, it follows from (5) that 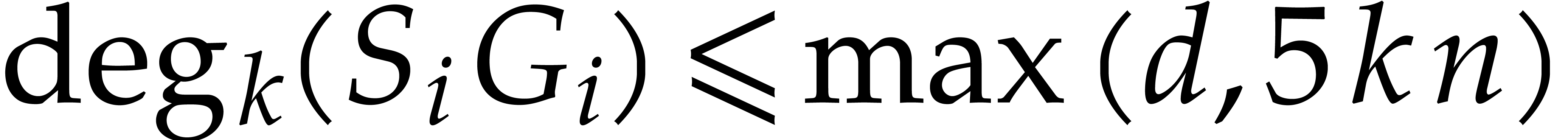 .
Consequently, the evaluation of
.
Consequently, the evaluation of 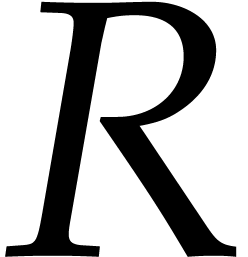 takes time
takes time
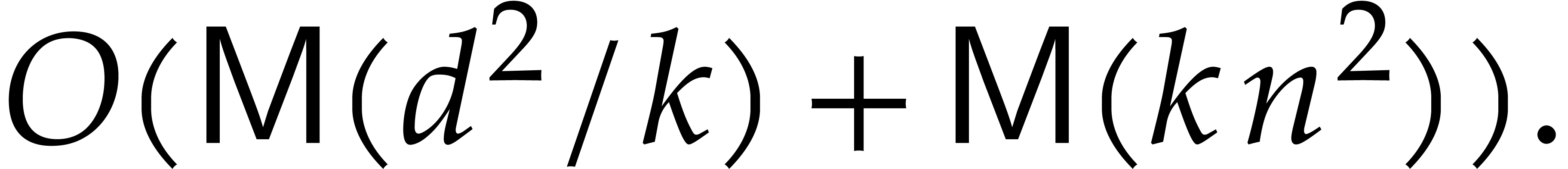

Let 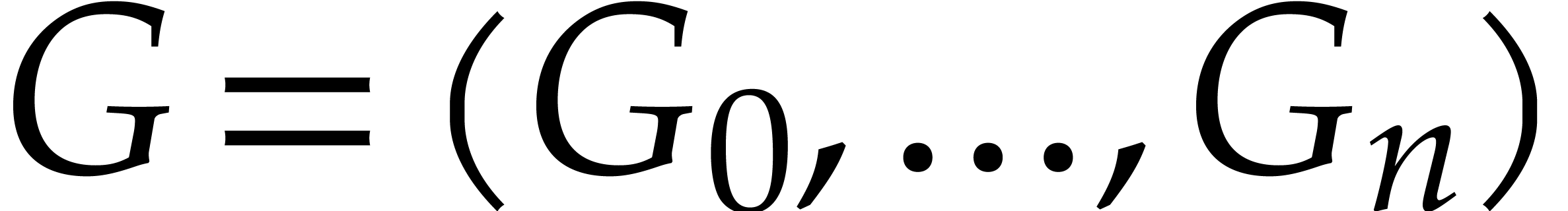 be a vanilla Gröbner basis for an ideal
be a vanilla Gröbner basis for an ideal
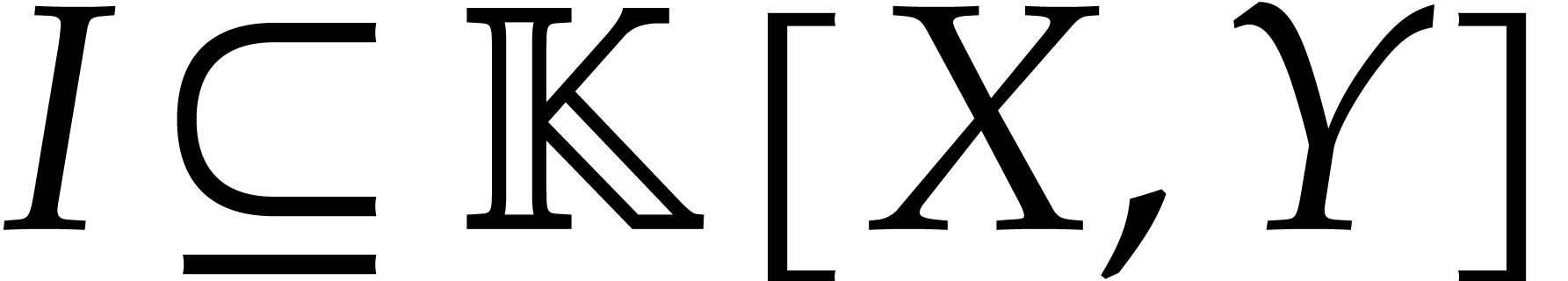 with respect to
with respect to  and
assume that we we have precomputed a terse representation for
and
assume that we we have precomputed a terse representation for  . Elements in the quotient algebra
. Elements in the quotient algebra
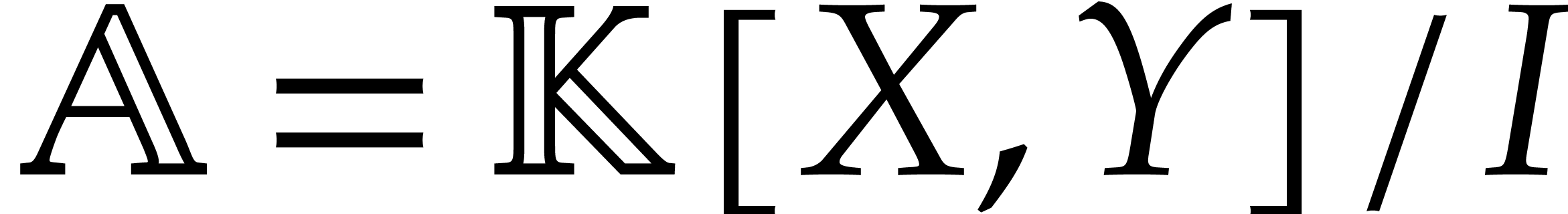 can naturally be represented as polynomials in
can naturally be represented as polynomials in
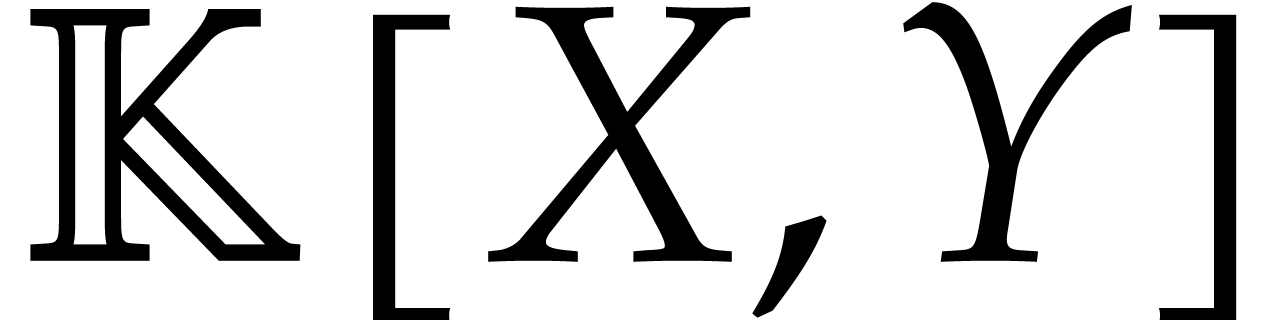 that are reduced with respect to
that are reduced with respect to  . An immediate application of Theorem 16
is a multiplication algorithm for
. An immediate application of Theorem 16
is a multiplication algorithm for  that runs in
quasi-linear time.
that runs in
quasi-linear time.
More precisely, with the notations from Proposition 3,
given two polynomials  that are reduced with
respect to
that are reduced with
respect to  , we have
, we have 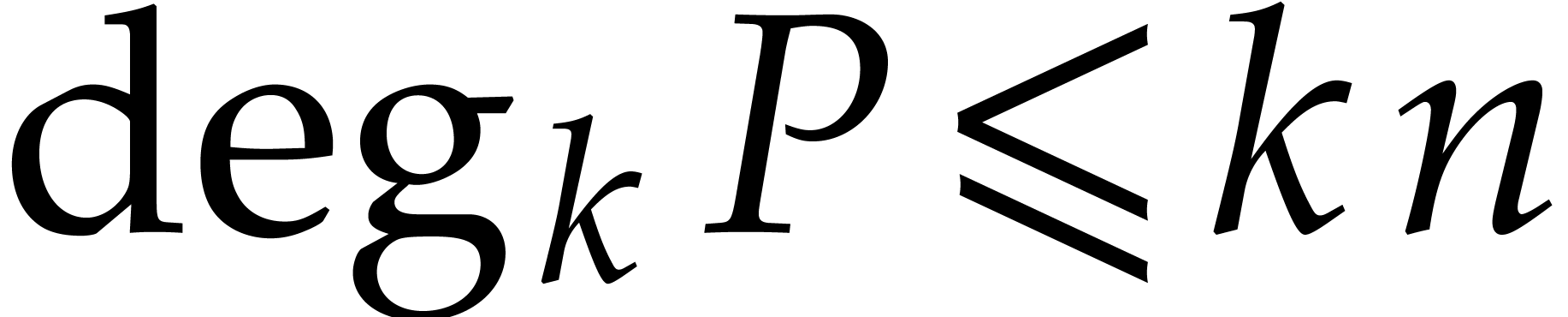 and
and  ,
whence
,
whence  and
and 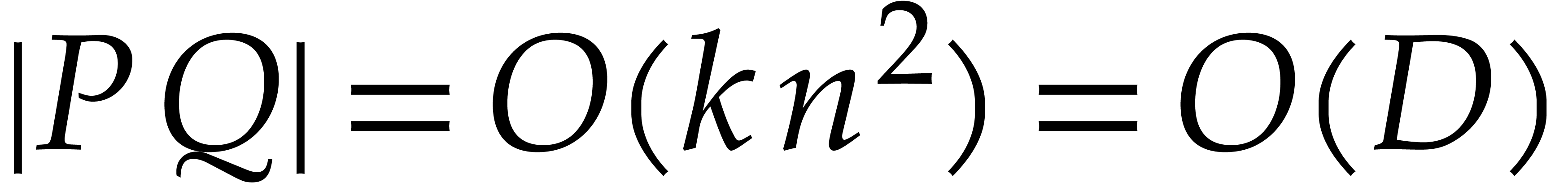 .
It follows that
.
It follows that  can be computed in time
can be computed in time 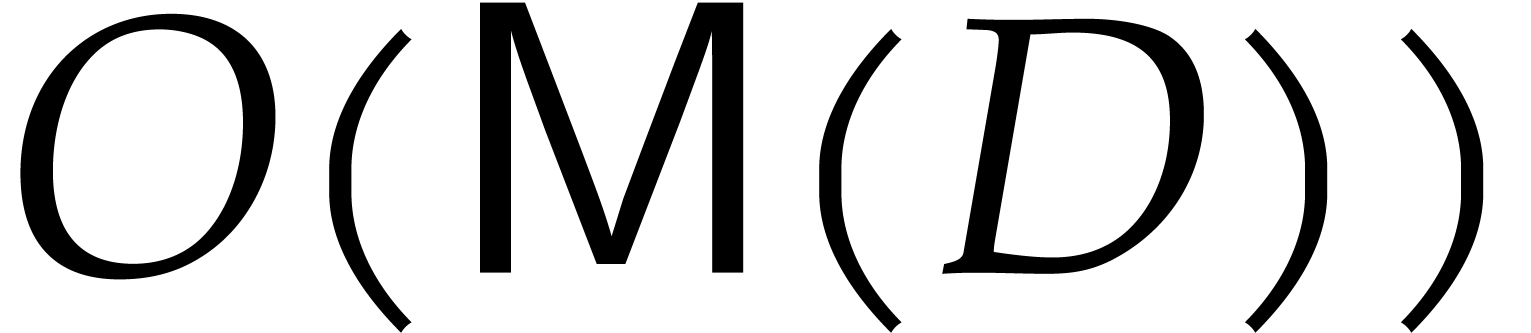 , whereas the reduction of
, whereas the reduction of  with respect to
with respect to  takes time
takes time
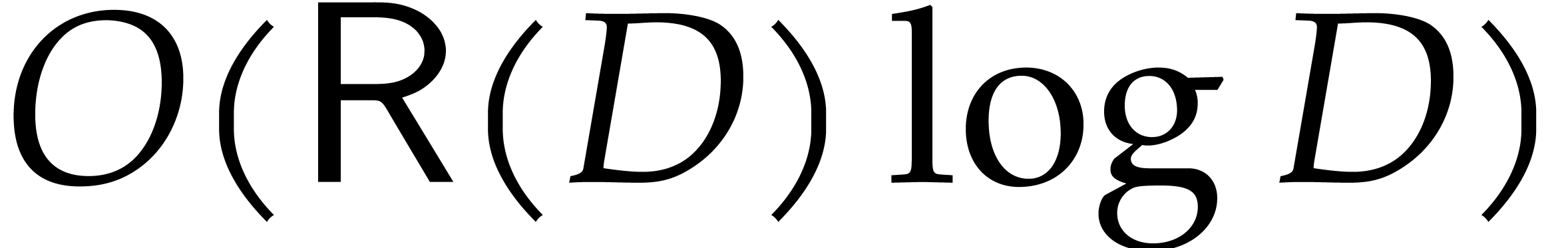 . This yields:
. This yields:
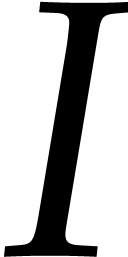 as above, multiplication in the quotient
algebra
as above, multiplication in the quotient
algebra 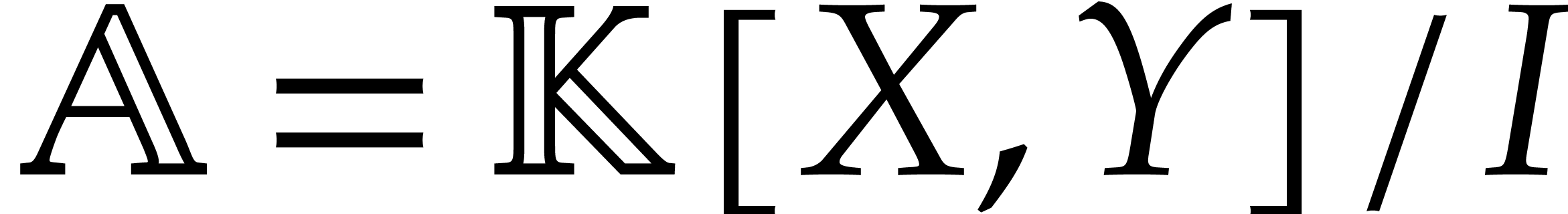 can be performed in time
can be performed in time
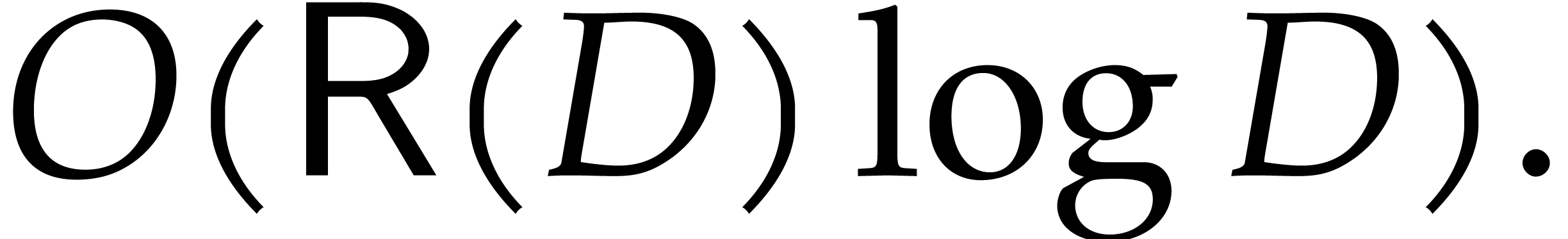
Let us now assume that our ideal 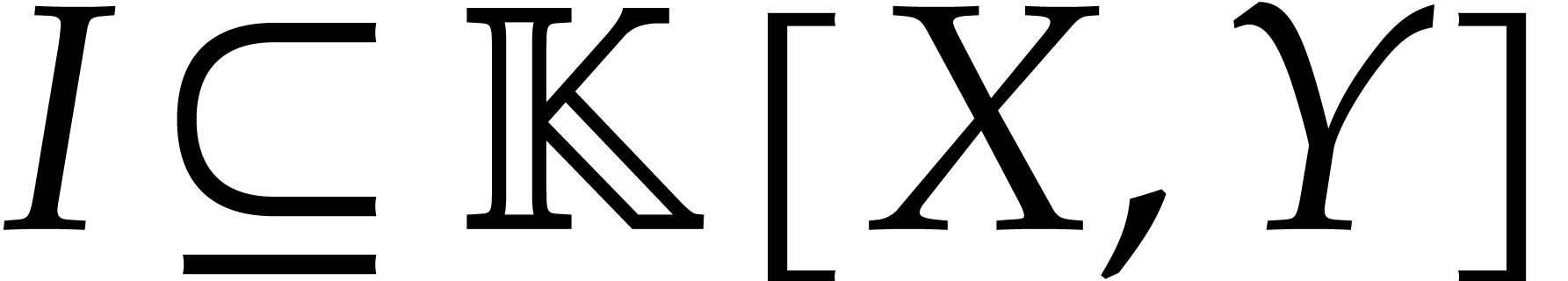 admits a
vanilla Gröbner basis
admits a
vanilla Gröbner basis 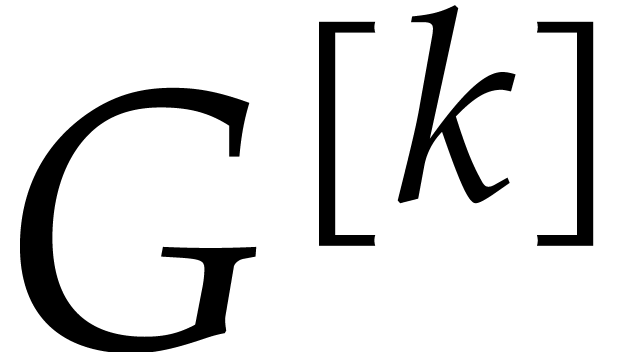 with respect to the
ordering
with respect to the
ordering  for all
for all 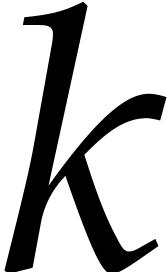 .
We will write
.
We will write 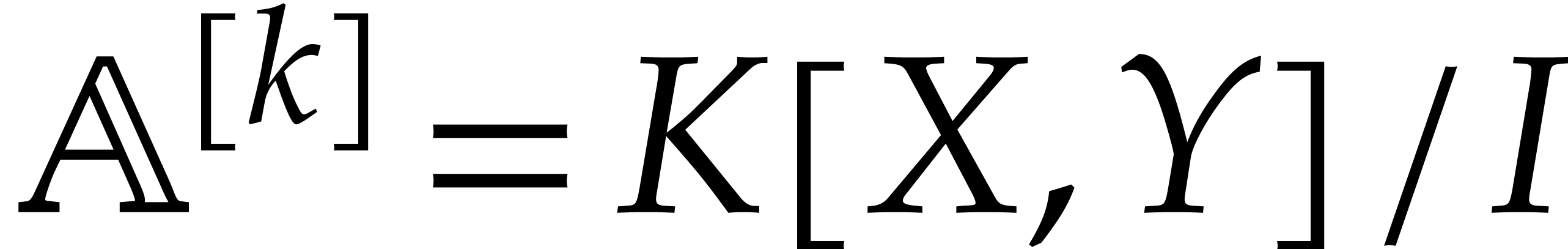 for the quotient algebra when
representing elements using normal forms with respect to
for the quotient algebra when
representing elements using normal forms with respect to 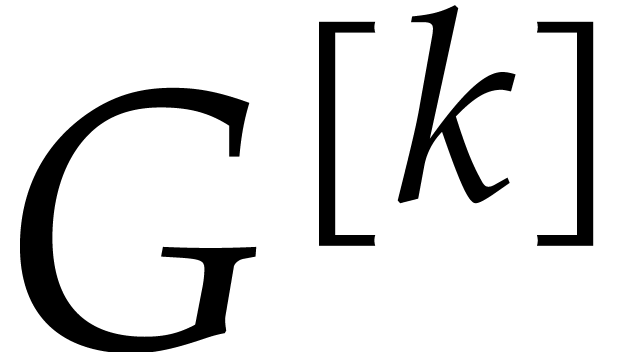 . If
. If 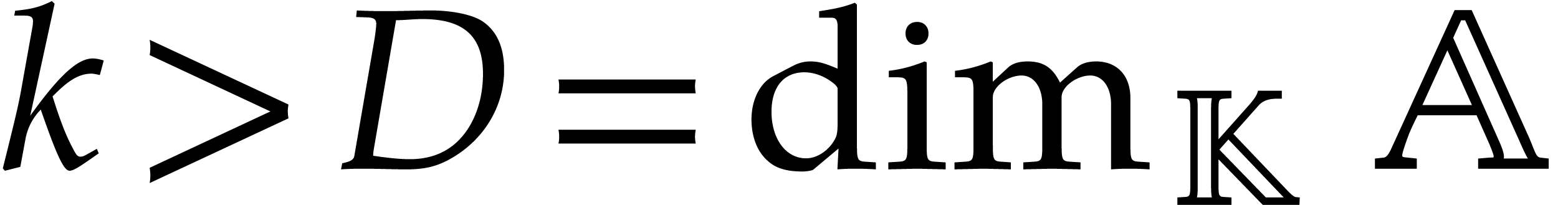 ,
then we notice that
,
then we notice that 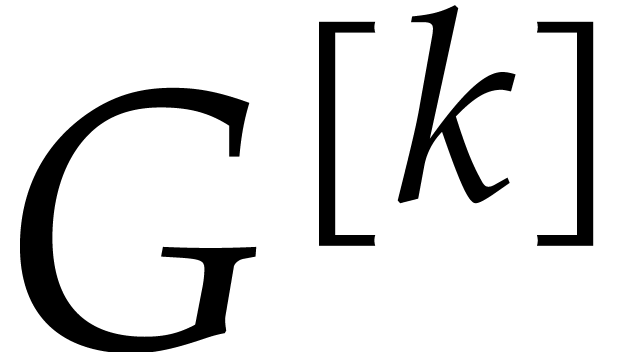 is also a Gröbner basis
with respect to the lexicographical monomial ordering
is also a Gröbner basis
with respect to the lexicographical monomial ordering 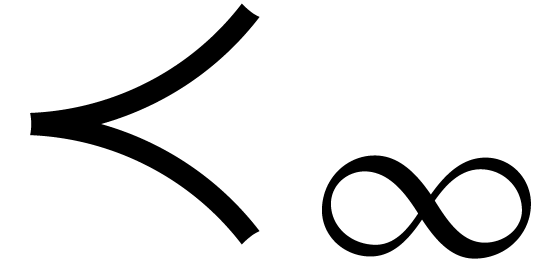 . In order to efficiently convert between
. In order to efficiently convert between 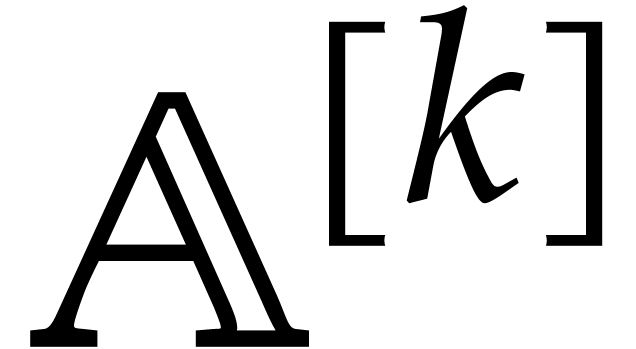 and
and 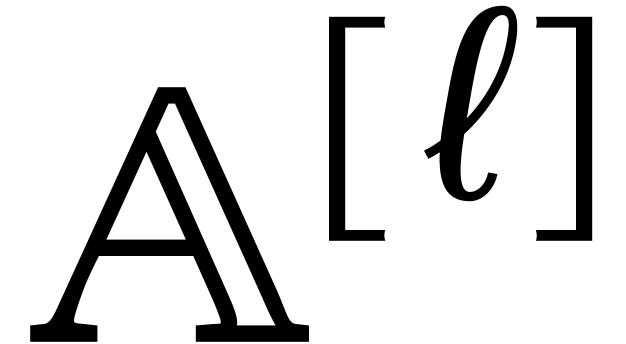 with
with  , we first consider the case when
, we first consider the case when 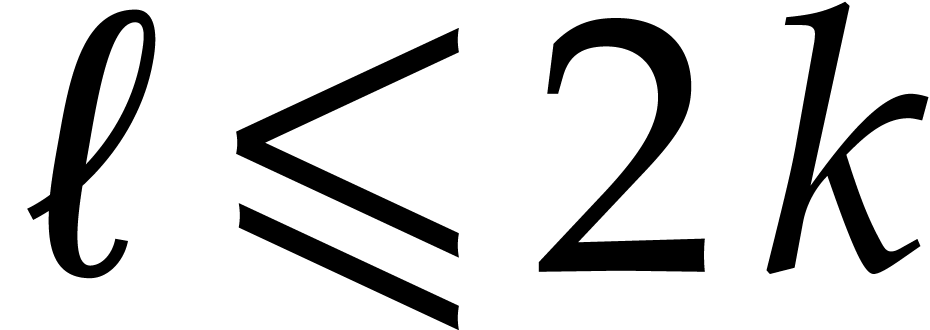 :
:
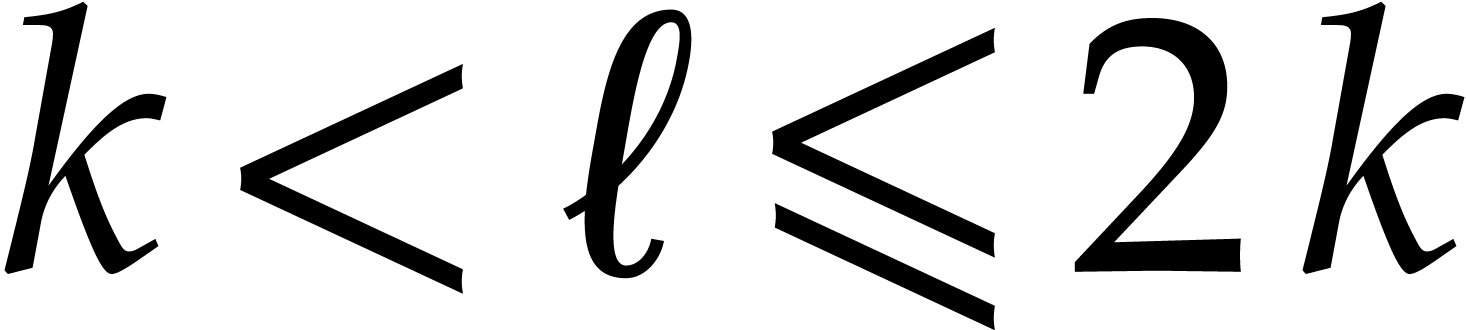 ,
assume that we have precomputed terse representations for
,
assume that we have precomputed terse representations for 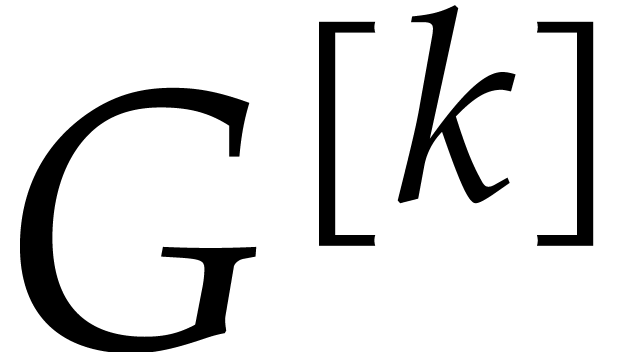 and
and 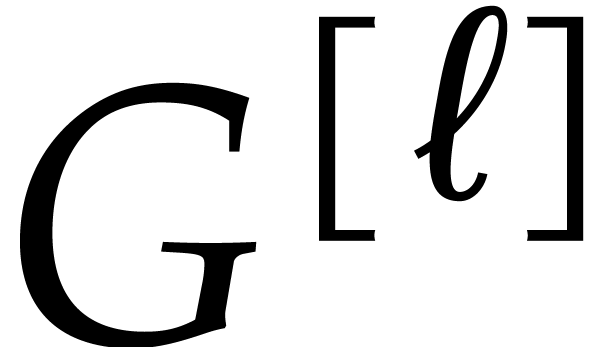 . Then
back and forth conversions between
. Then
back and forth conversions between 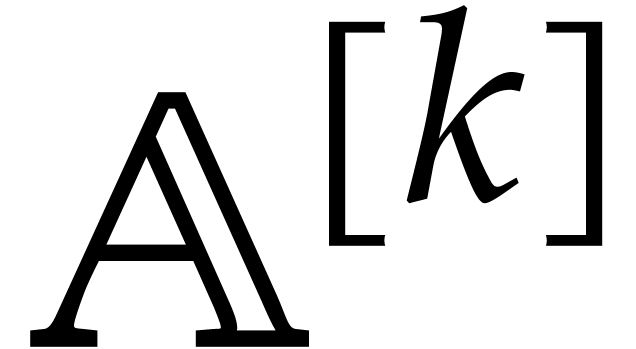 and
and 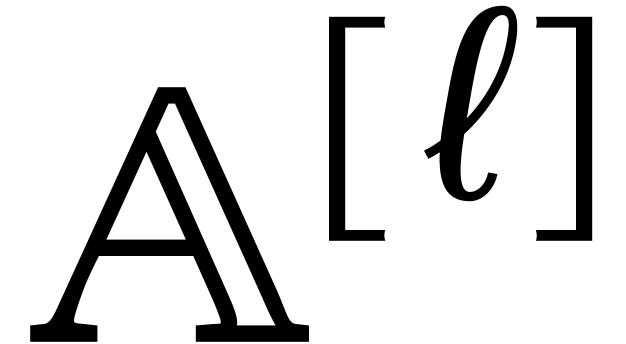 can be computed in time
can be computed in time
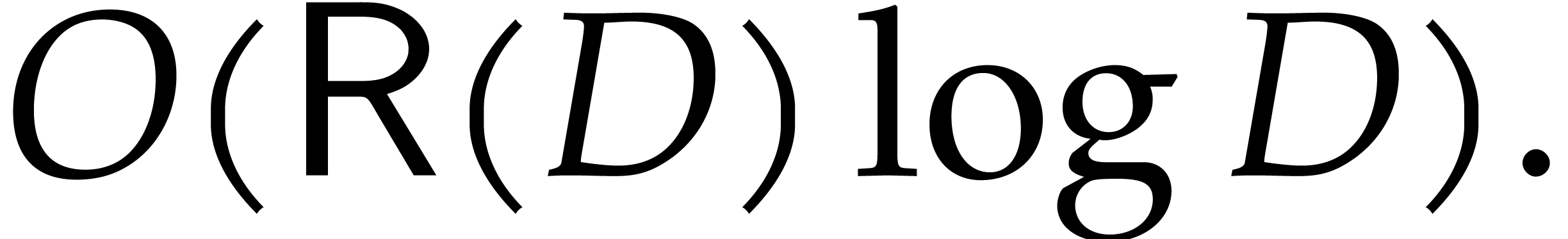
Proof. Assume that 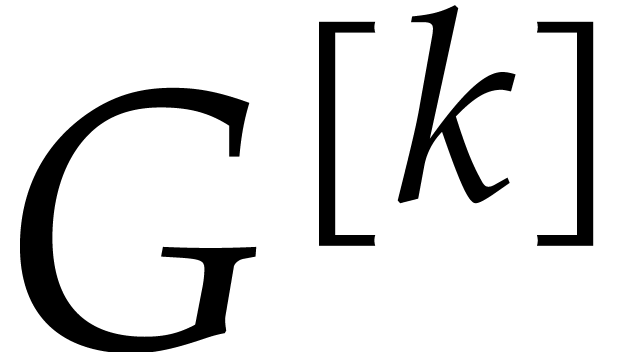 has
has
 elements
elements 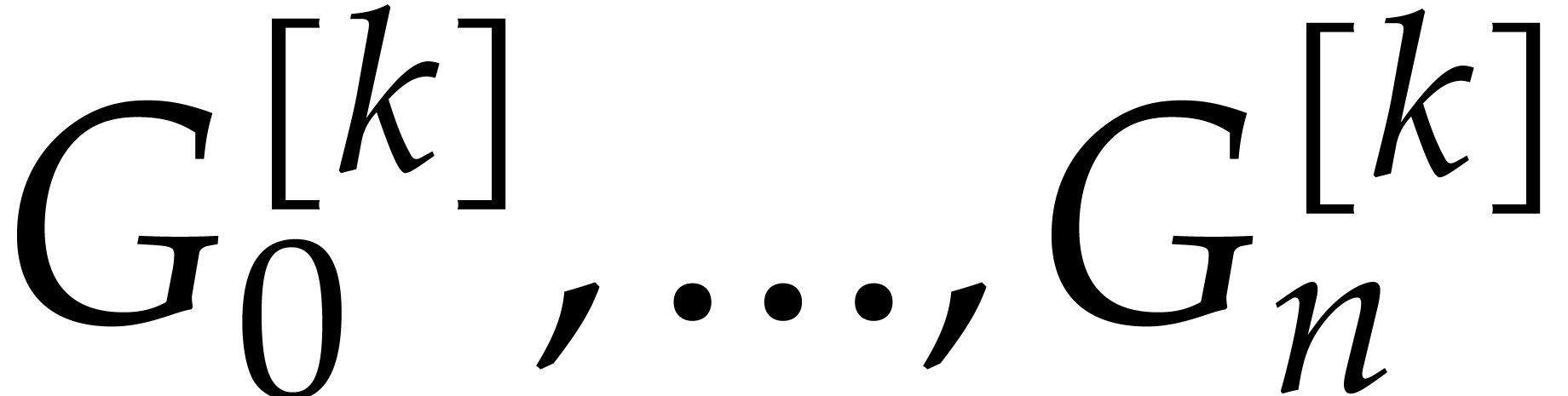 and
and 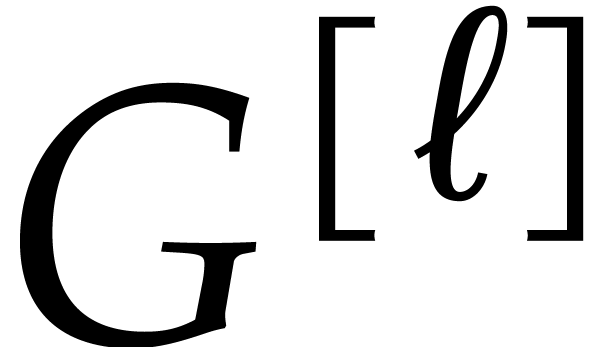 has
has  elements
elements 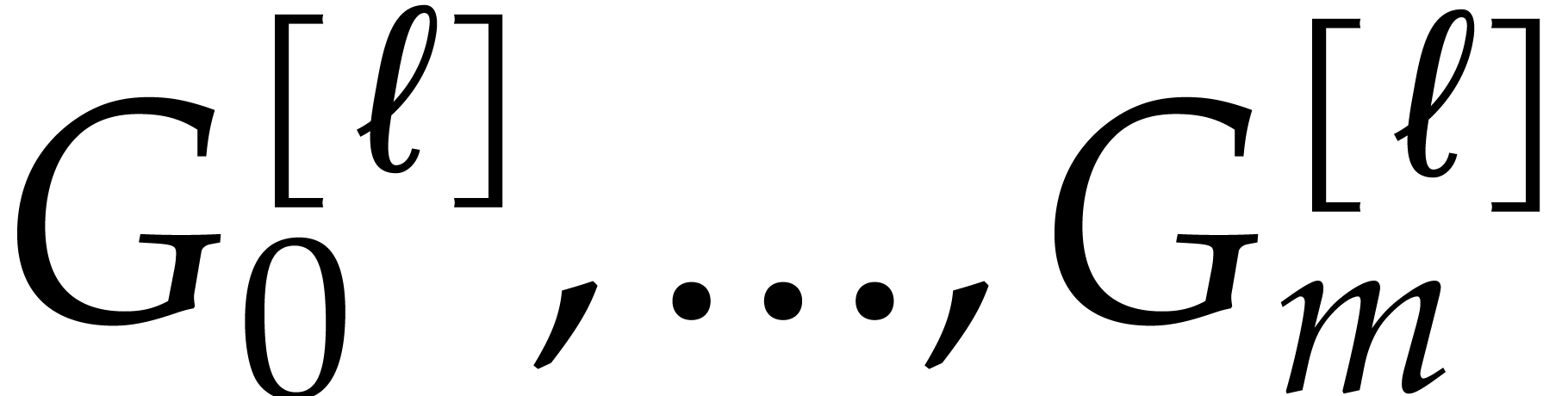 . We know from Proposition 3 that
. We know from Proposition 3 that
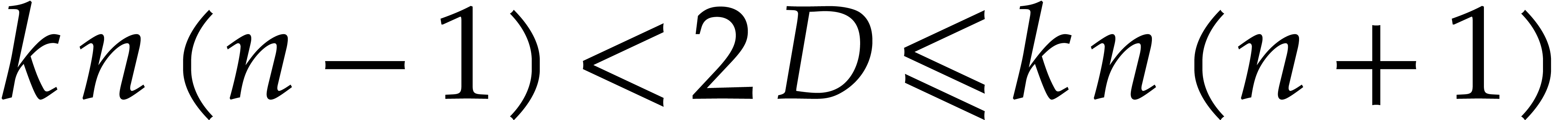 and similarly
and similarly 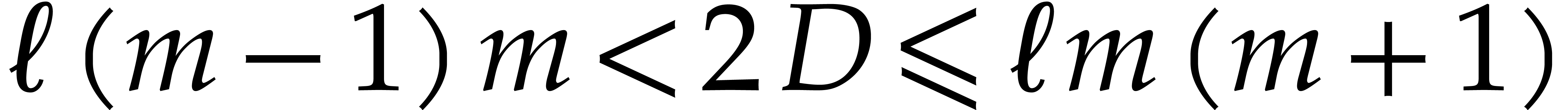 .
Now given
.
Now given 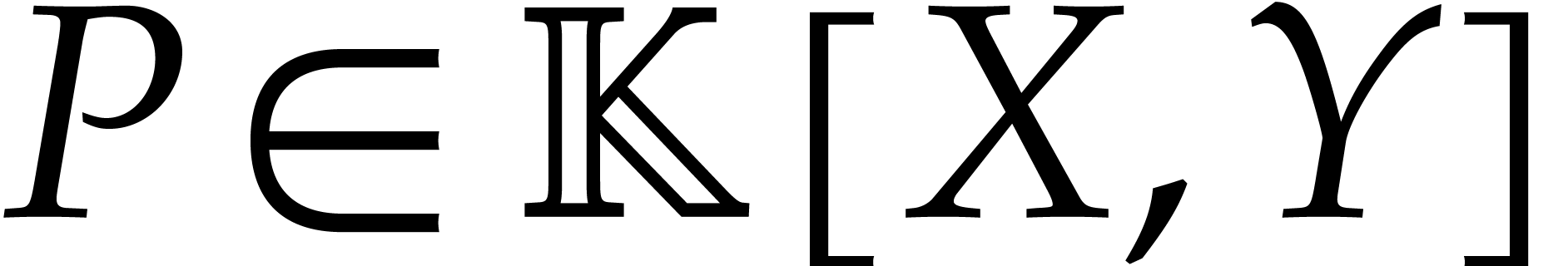 that is reduced with respect to
that is reduced with respect to 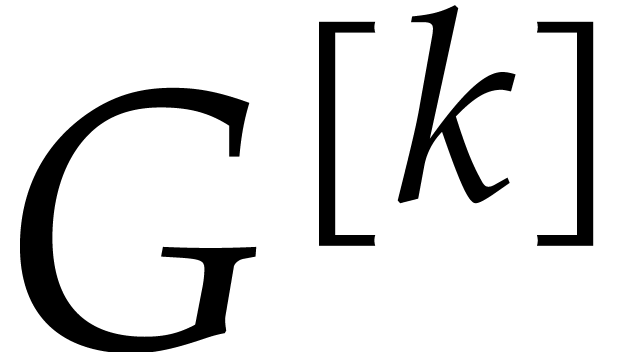 , we have
, we have 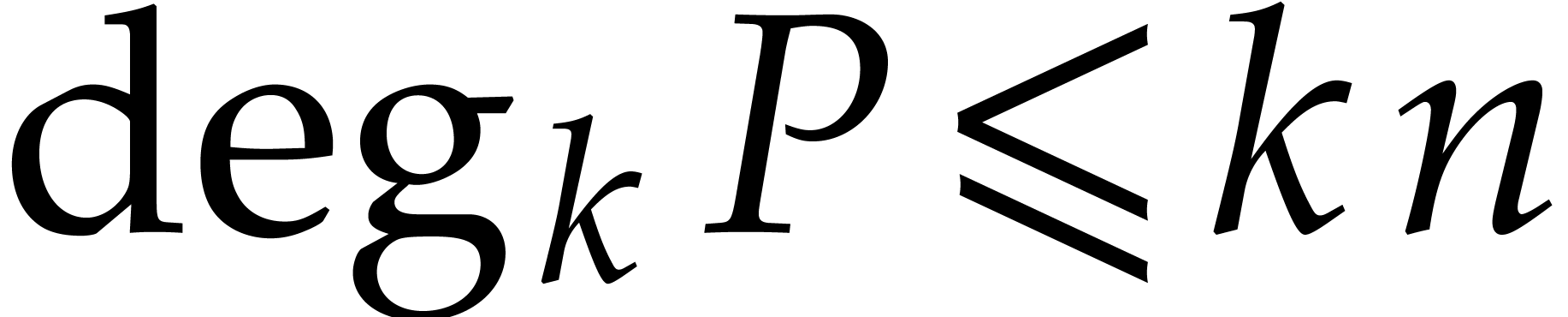 , whence
, whence 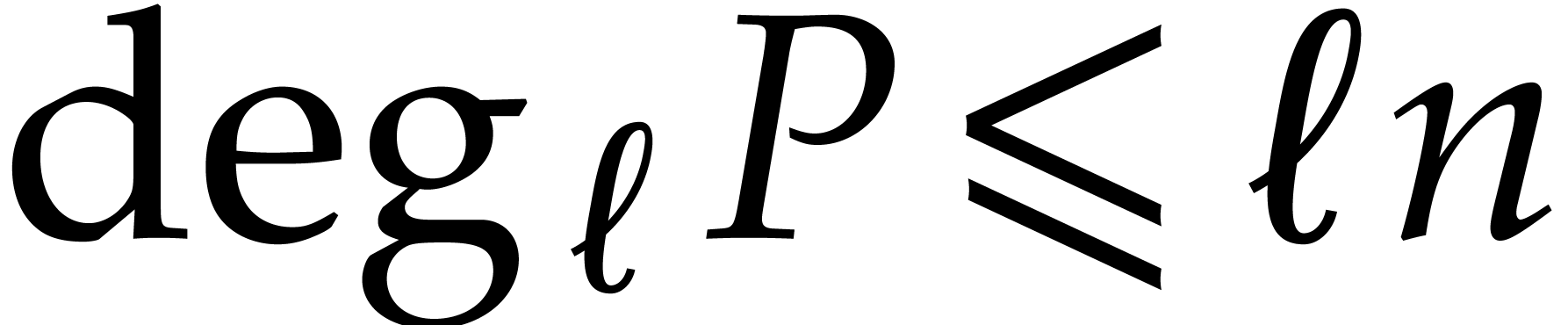 and
and 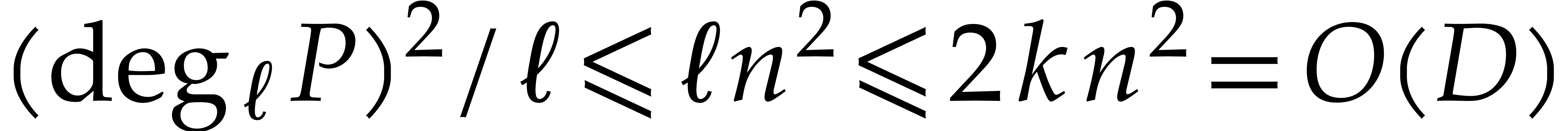 . Theorem 16 therefore implies
that normal form of
. Theorem 16 therefore implies
that normal form of 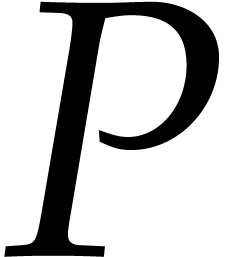 w.r.t.
w.r.t. 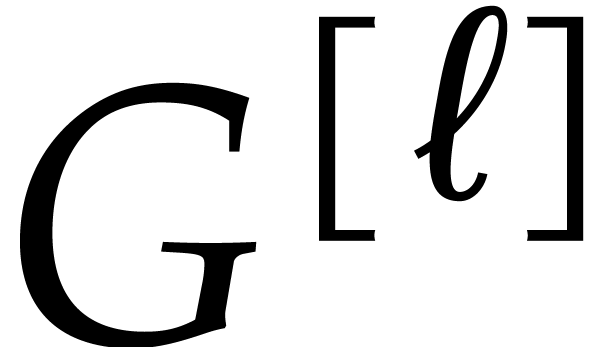 can be computed in time
can be computed in time
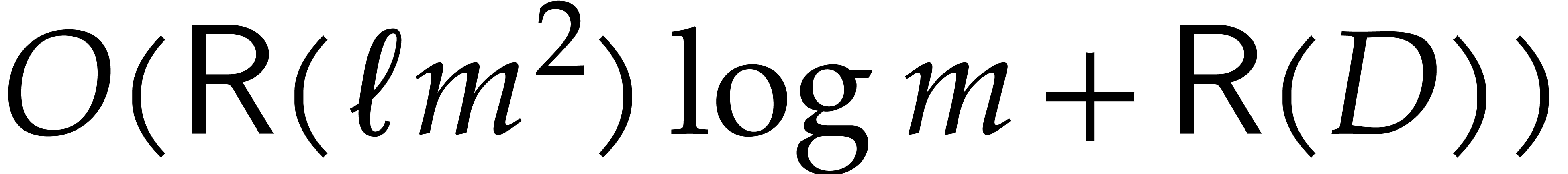
and we conclude using 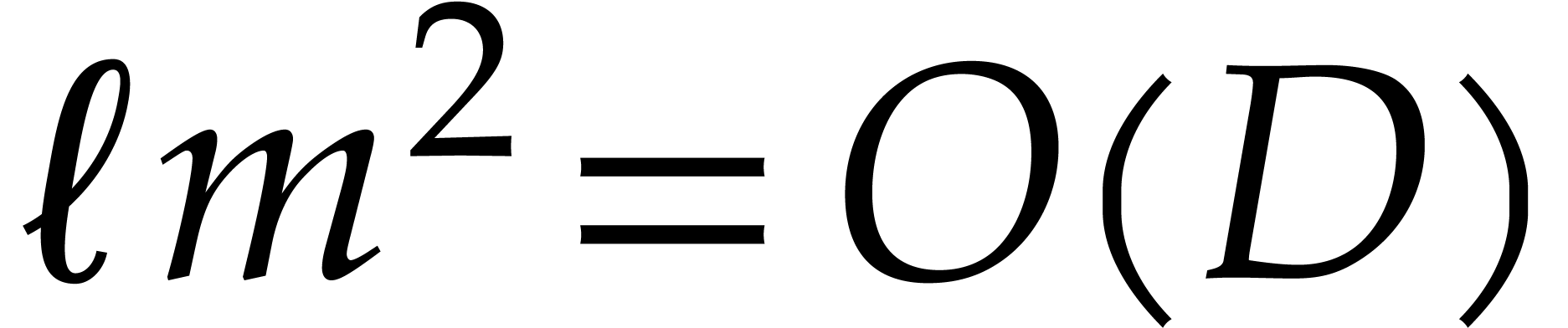 . The
proof for the backward conversion is similar.
. The
proof for the backward conversion is similar.
For general  , let
, let  be such that
be such that 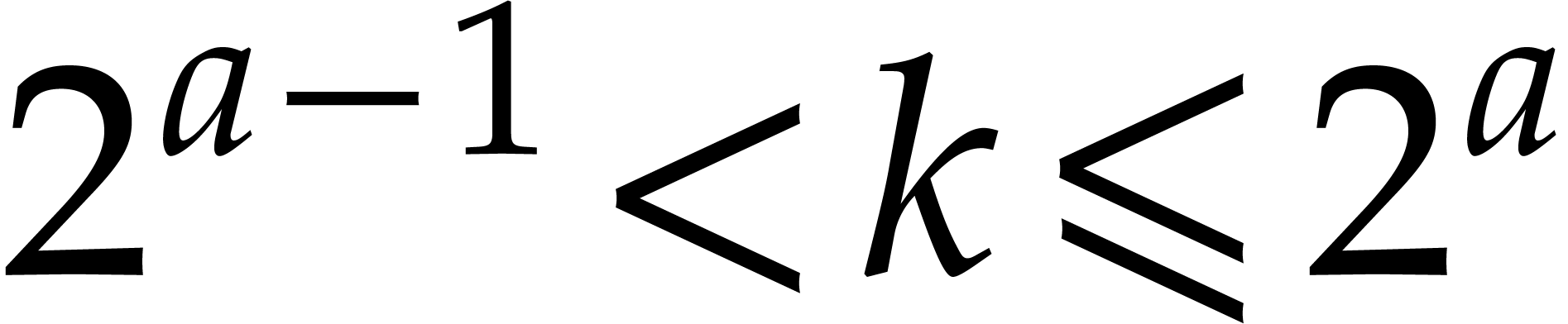 and
and 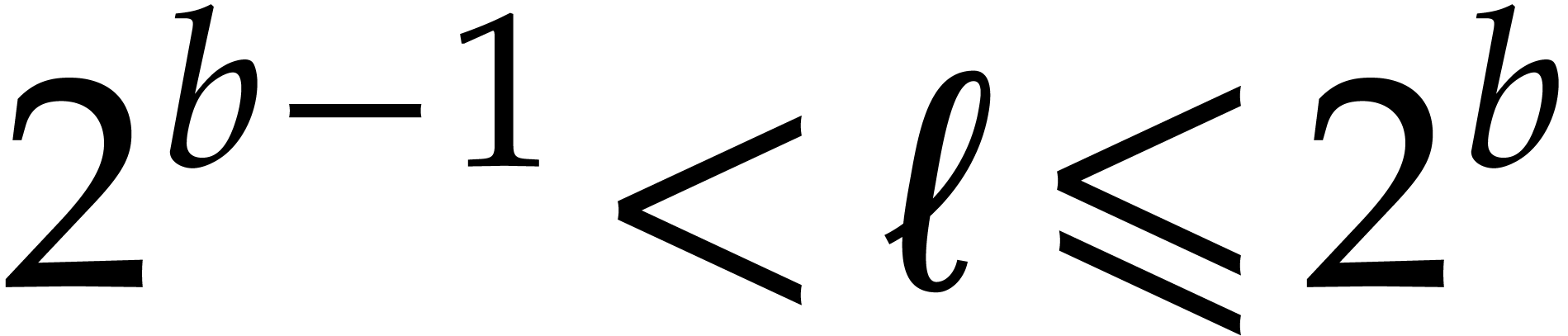 . Then we may perform conversions between
. Then we may perform conversions between 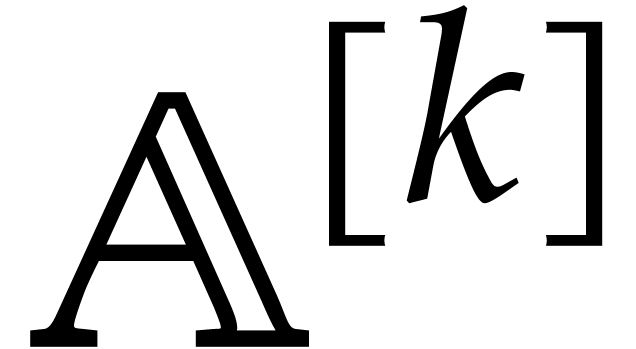 and
and 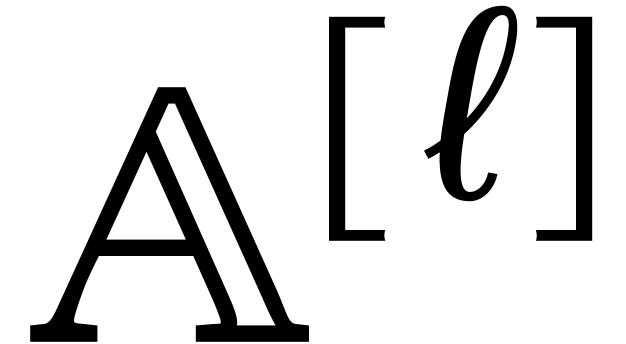 using a Gröbner walk
using a Gröbner walk
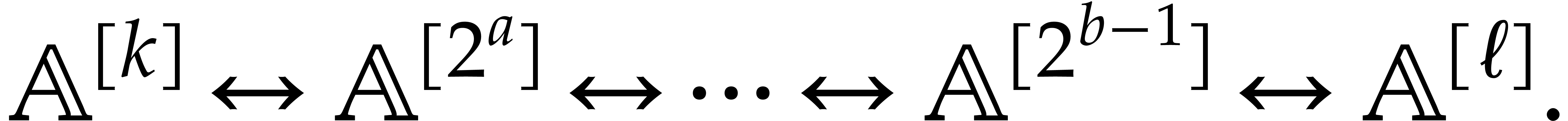
All 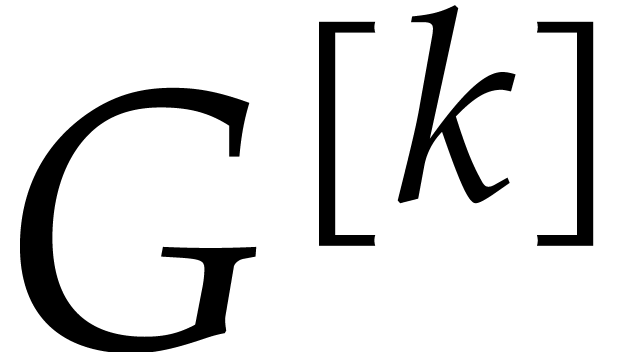 coincide for
coincide for 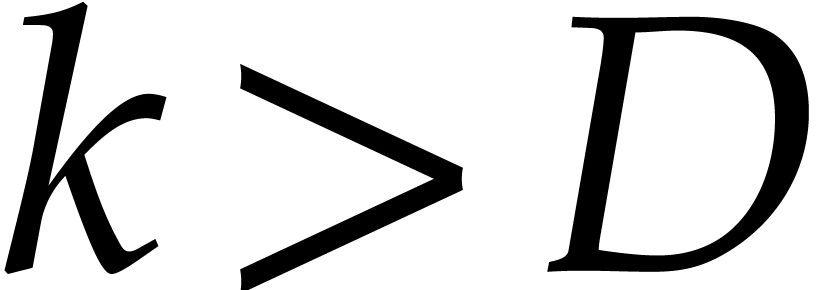 ,
so we can assume that
,
so we can assume that 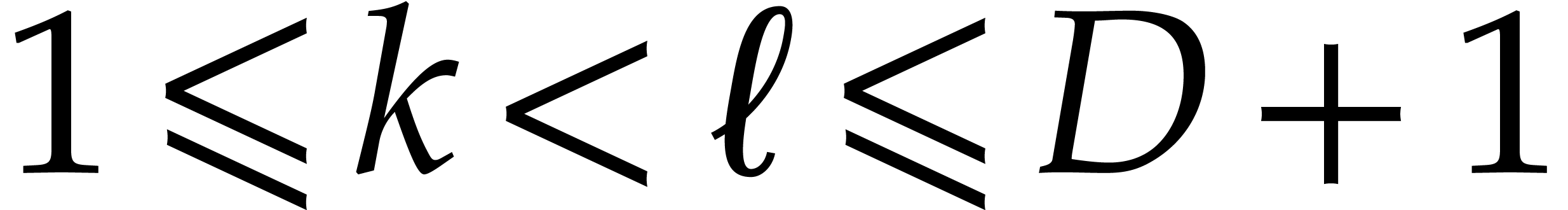 . Then
there are at most
. Then
there are at most 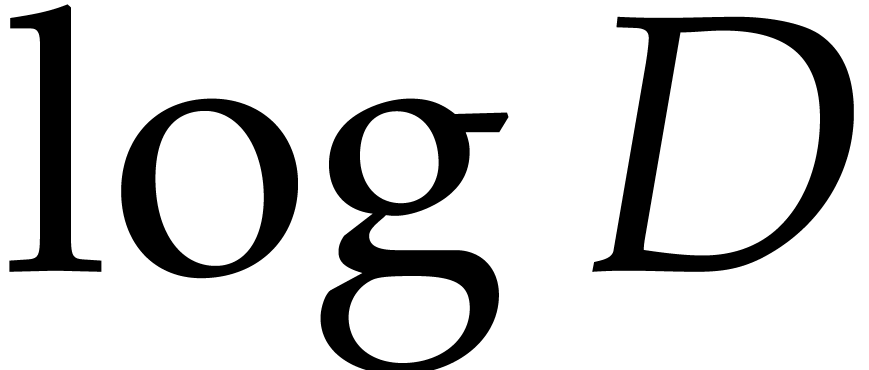 conversions as above, so that:
conversions as above, so that:
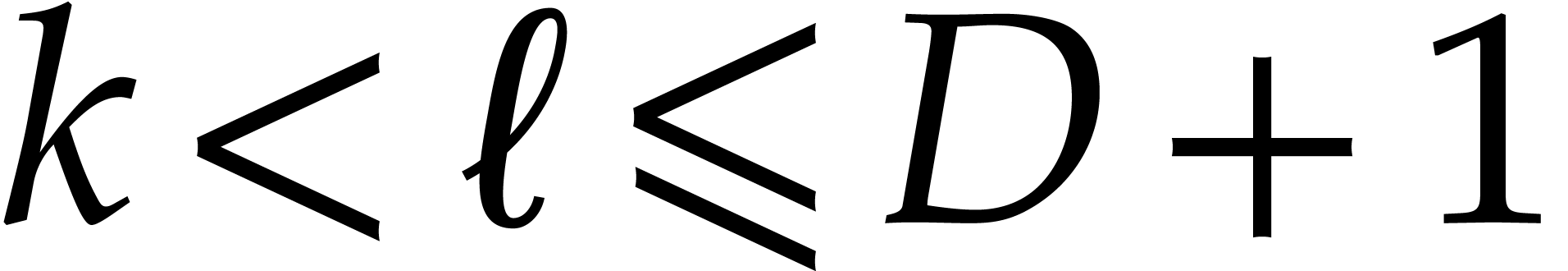 ,
assume that we have precomputed terse representations for
,
assume that we have precomputed terse representations for  . Then back and forth conversions between
. Then back and forth conversions between
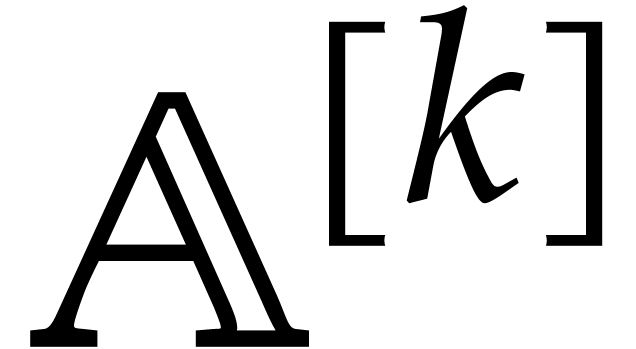 and
and 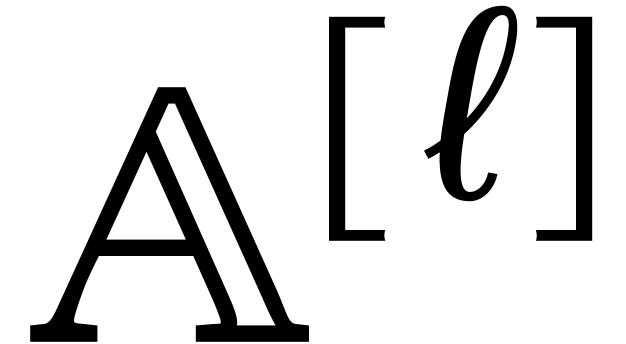 can be computed in
time
can be computed in
time
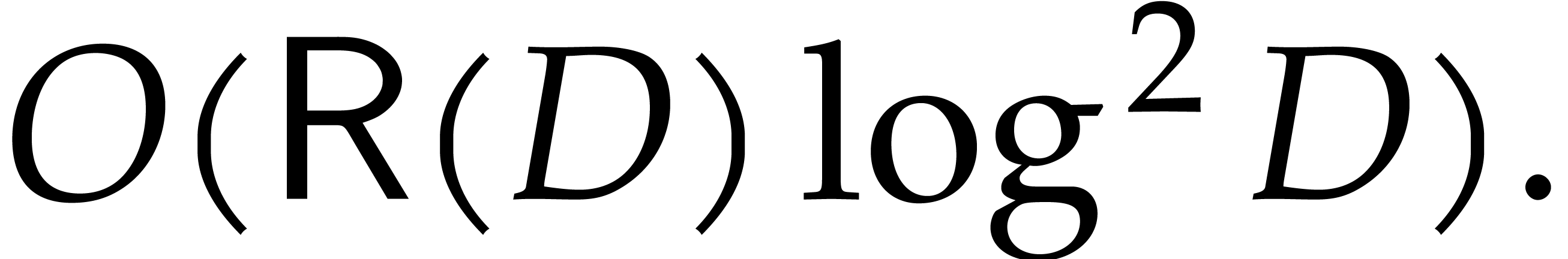
As explained in the introduction, we deliberately chose to present our results in the simplest possible setting. As a future work, it would be interesting to generalize our algorithms. The following two extensions should be rather straightforward:
The consideration of general monomial orderings, starting with  for
for  .
.
Generalizations to multivariate polynomials in 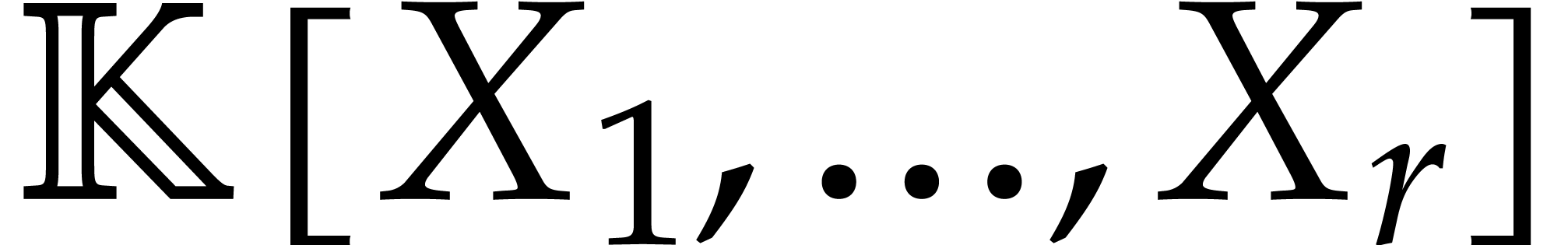 . We expect no essential problems for fixed
. We expect no essential problems for fixed
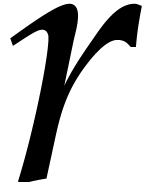 . However, the dependence
of the complexity on
. However, the dependence
of the complexity on 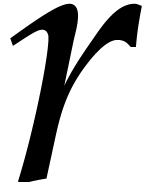 is likely to be
polynomial in
is likely to be
polynomial in 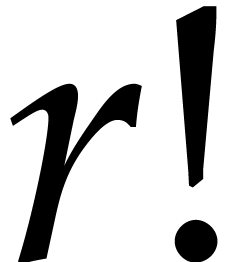 .
.
Some of the more challenging problems are as follows:
Is it true that a “sufficiently generic”
zero-dimensional ideal 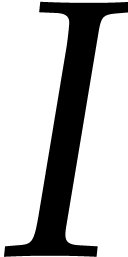 of fixed degree
of fixed degree 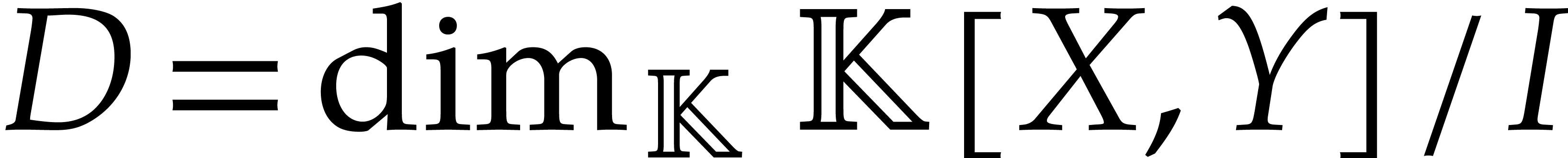 necessarily admits a vanilla Gröbner basis?
necessarily admits a vanilla Gröbner basis?
Given a vanilla Gröbner basis, what is the actual complexity of
computing its terse representation? Our first analysis suggests a
bound 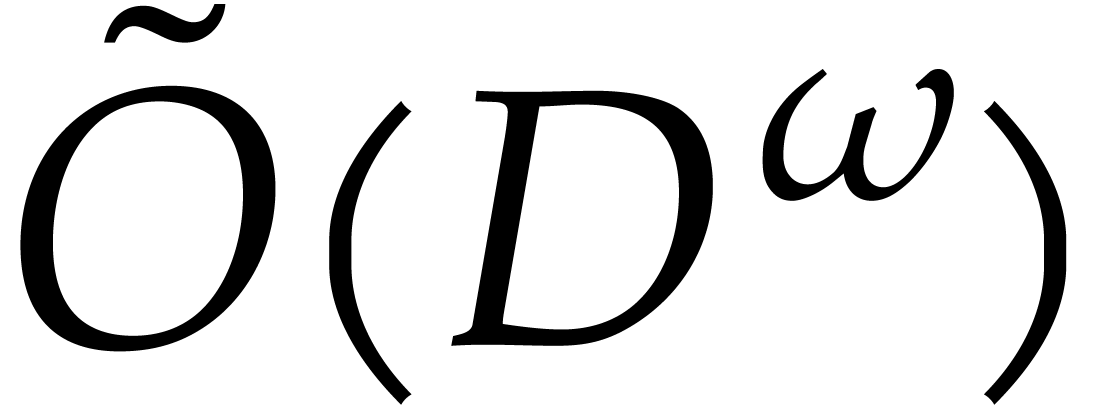 , but we suspect
that the computation of the retraction coefficients
, but we suspect
that the computation of the retraction coefficients 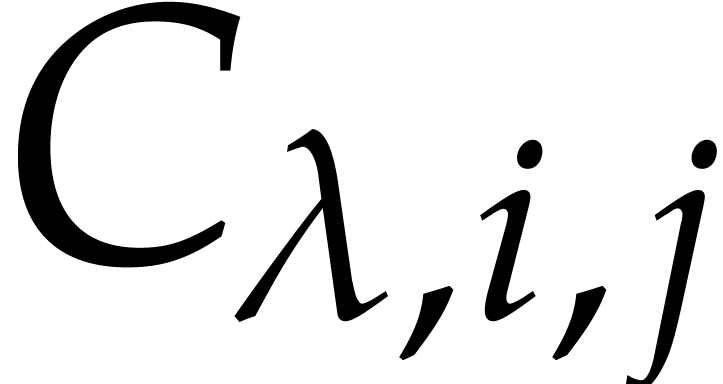 can be accelerated by using the sygyzies that result from reducing
the
can be accelerated by using the sygyzies that result from reducing
the 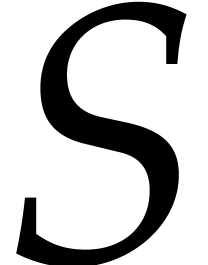 -polynomials of basis
elements to zero.
-polynomials of basis
elements to zero.
Can our results be generalized to the degenerate case of non-vanilla
Gröbner bases  ?
?
On the long run, one might also wonder whether some of the new
techniques can be used for the efficient computation of Gröbner
bases themselves. For the moment, this seems far beyond reach.
Nevertheless, a quasi-optimal algorithm does exist for the particular
case of an ideal 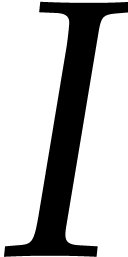 generated by two generic
polynomials
generated by two generic
polynomials  of total degree
of total degree  , when working with respect to the monomial
ordering
, when working with respect to the monomial
ordering  . We intend to
report on the details in a forthcoming paper.
. We intend to
report on the details in a forthcoming paper.
W. Auzinger and H. J. Stetter. An elimination algorithm for the computation of all zeros of a system of multivariate polynomial equations. In Ravi P. Agarwal, Y. M. Chow, and S. J. Wilson, editors, Proceedings of the International Conference on Numerical Mathematics, pages 11–30. Basel, 1988. Birkhäuser Basel.
Magali Bardet, Jean-Charles Faugère, and Bruno Salvy. On the complexity of the F5 Gröbner basis algorithm. Journal of Symbolic Computation, pages 1–24, sep 2014.
Thomas Becker and Volker Weispfenning. Gröbner bases: a computational approach to commutative algebra, volume 141 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1993.
Bruno Buchberger. Ein Algorithmus zum Auffinden der Basiselemente des Restklassenrings nach einem nulldimensionalen Polynomideal. PhD thesis, Universitat Innsbruck, Austria, 1965.
David G Cantor and Erich Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28(7):693–701, 1991.
Stéphane Collart, Michael Kalkbrener, and Daniel Mall. Converting bases with the gröbner walk. Journal of Symbolic Computation, 24(3-4):465–469, 1997.
Jean-Charles Faugère. A new efficient algorithm for computing Gröbner bases (F4). Journal of Pure and Applied Algebra, 139(1–3):61–88, 1999.
Jean-Charles Faugère. A new efficient algorithm for computing Gröbner bases without reduction to zero (F5). In Proceedings of the 2002 international symposium on Symbolic and algebraic computation, ISSAC '02, pages 75–83. New York, NY, USA, 2002. ACM.
Jean-Charles Faugère, Patrizia Gianni, Daniel Lazard, and Teo Mora. Efficient computation of zero-dimensional Gröbner bases by change of ordering. Journal of Symbolic Computation, 16(4):329–344, 1993.
M. J. Fischer and L. J. Stockmeyer. Fast on-line integer multiplication. Proc. 5th ACM Symposium on Theory of Computing, 9:67–72, 1974.
F. Le Gall. Powers of tensors and fast matrix multiplication. In Proc. ISSAC 2014, pages 296–303. Kobe, Japan, July 23–25 2014.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 3rd edition, 2013.
Vladimir P. Gerdt and Yuri A. Blinkov. Involutive bases of polynomial ideals. Mathematics and Computers in Simulation, 45(5):519–541, 1998.
M. Giusti. Some effectivity problems in polynomial ideal theory. In Proc. Eurosam '84, volume 174 of Lecture Notes in Computer Science, pages 159–171. Cambridge, 1984. Springer, Berlin.
M. Giusti. A note on the complexity of constructing standard bases. In Proc. Eurocal '85, volume 204 of Lecture Notes in Computer Science, pages 411–412. Springer-Verlag, 1985.
M. Giusti, G. Lecerf, and B. Salvy. A Gröbner free alternative for polynomial system solving. Journal of Complexity, 17(1):154–211, 2001.
D. Harvey and J. van der Hoeven. Faster integer and polynomial multiplication using cyclotomic coefficient rings. Technical Report, ArXiv, 2017. http://arxiv.org/abs/1712.03693.
David Harvey, Joris van der Hoeven, and Grégoire Lecerf. Faster polynomial multiplication over finite fields. Technical Report, ArXiv, 2014. http://arxiv.org/abs/1407.3361.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. On the complexity of polynomial reduction. In I. Kotsireas and E. Martínez-Moro, editors, Proc. Applications of Computer Algebra 2015, volume 198 of Springer Proceedings in Mathematics and Statistics, pages 447–458. Cham, 2015. Springer.
Joris van der Hoeven. Faster relaxed multiplication. In Proc. ISSAC '14, pages 405–412. Kobe, Japan, Jul 2014.
D. Lazard. Gröbner bases, Gaussian elimination and resolution of systems of algebraic equations. In J. A. van Hulzen, editor, Proc. EUROCAL'83, number 162 in Lect. Notes in Computer Sc., pages 146–156. Springer Berlin Heidelberg, 1983.
Ernst Mayr. Membership in polynomial ideals over 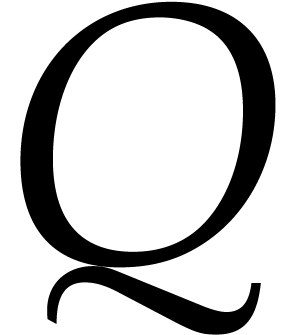 is exponential space complete. STACS
89, pages 400–406, 1989.
is exponential space complete. STACS
89, pages 400–406, 1989.
L. Robbiano. Term orderings on the polynominal ring. In European Conference on Computer Algebra (2), pages 513–517. 1985.
Fabrice Rouillier. Solving zero-dimensional systems through the rational univariate representation. Applicable Algebra in Engineering, Communication and Computing, 9(5):433–461, May 1999.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Infor., 7:395–398, 1977.
A. Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.