| Efficient root counting for analytic functions on a disk  |
|
| August 2, 2011 |
|
 . This work has
been supported by the ANR-09-JCJC-0098-01
. This work has
been supported by the ANR-09-JCJC-0098-01
In this note, we present a variant of an algorithm by Schönhage for counting the number of zeros of a complex polynomial in a disk. Our algorithm implements a few optimizations and also applies to more general analytic functions.
|
Many algorithms have been proposed for the reliable computation of zeros of complex polynomials [Sch82, Gou96, KvB00, Pan02], assuming multiple precision arithmetic. A slightly less ambitious problem is to count the number of zeros in a given disk; see also [Rum10, Sections 13.2 and 13.3]. In this paper, we present a variant of Schönhage's method [Sch82], based on iterated Graeffe transforms, but with a few advantages.
We present our algorithm in the setting of ball arithmetic [vdH09], which is our preferred variant of interval arithmetic [Moo66, AH83, MKC09, Rum10]. In this framework, a large part of the burden of bound computations is taken away from our shoulders and moved to the underlying arithmetic. Moreover, the algorithm naturally applies for analytic functions, which are represented by an approximating polynomial and a bound for the error. Finally, during the iterated application of Graeffe transforms, some coefficients of the polynomial become very small. Ball arithmetic allows us to move such coefficients to a global error term and reduce the degree of the polynomial, thereby speeding up the overall algorithm.
Our algorithm is presented for analytic functions whose power series
expansion is given explicitly up to a given order, together with an
error bound for the tail. In practice, we are often given a program
which may compute the expansion (and tail bound) up to any required
order. If we are expecting a 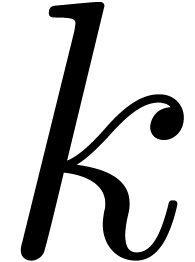 -fold
multiple root, then it is a good practice to compute the expansion up to
order
-fold
multiple root, then it is a good practice to compute the expansion up to
order 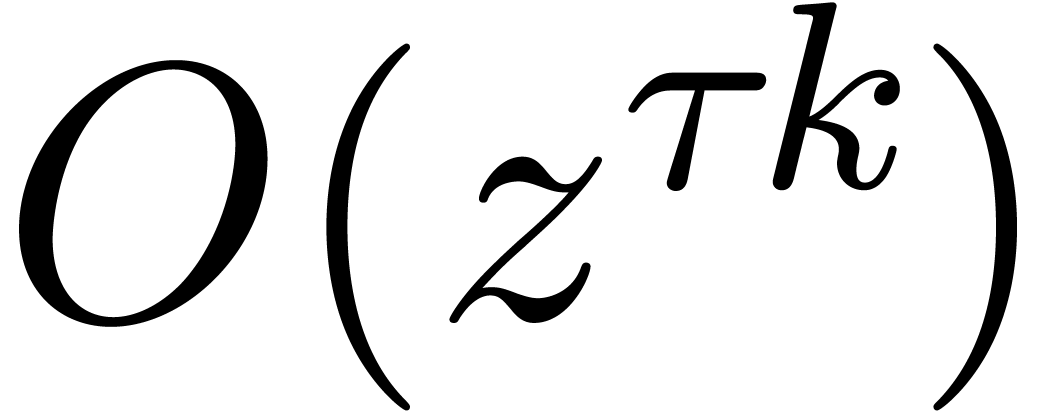 for some
for some  :
this is usually only a constant times more expensive than the
computation of an expansion up to order
:
this is usually only a constant times more expensive than the
computation of an expansion up to order 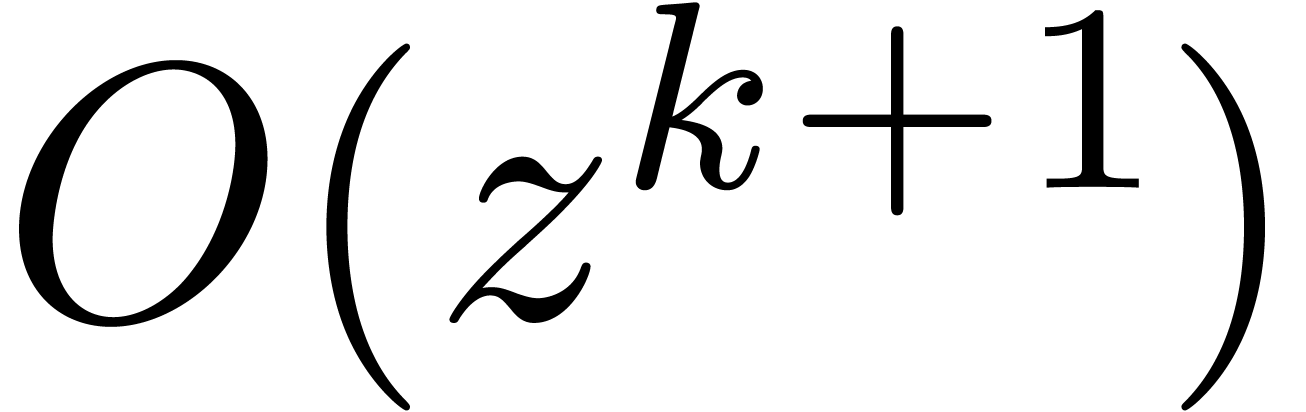 ,
but greatly improves the quality of the error bounds and the probability
that our root counting algorithm will be successful.
,
but greatly improves the quality of the error bounds and the probability
that our root counting algorithm will be successful.
Let us briefly recall the principles behind ball arithmetic, while
referring to [vdH09] for details. Given a normed vector
space  , we will denote by
, we will denote by
 or
or 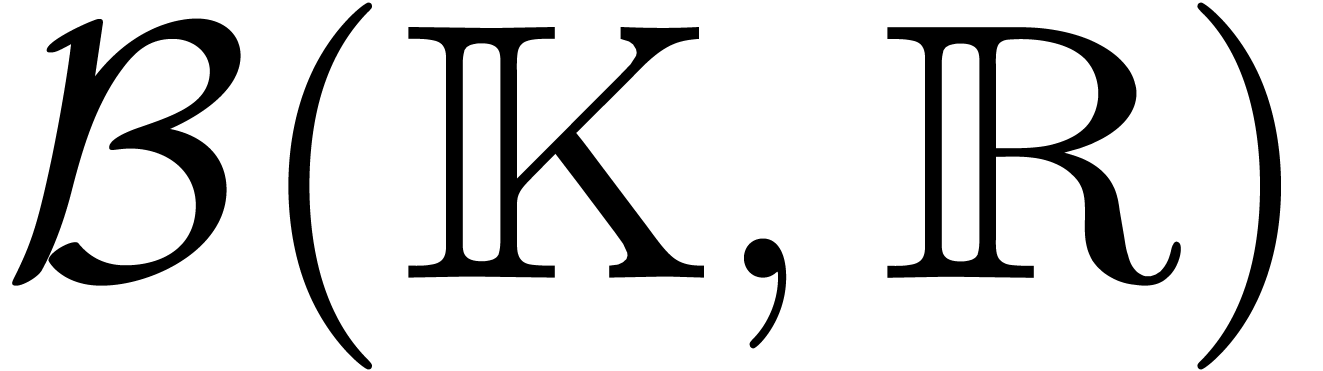 the set of closed
balls with centers in
the set of closed
balls with centers in  and radii in
and radii in 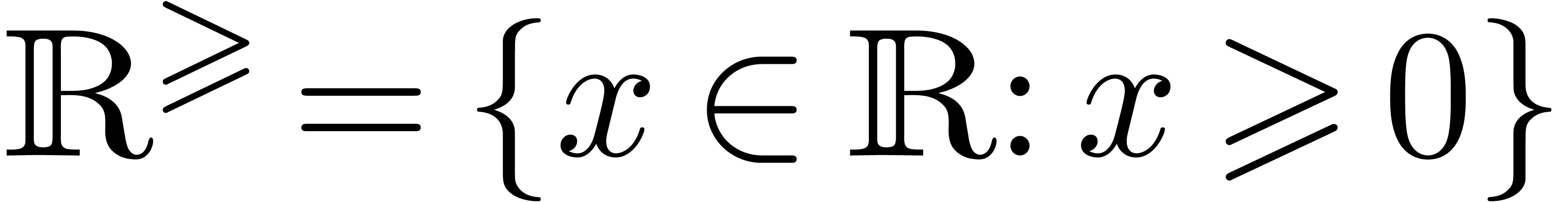 . Given such a ball
. Given such a ball 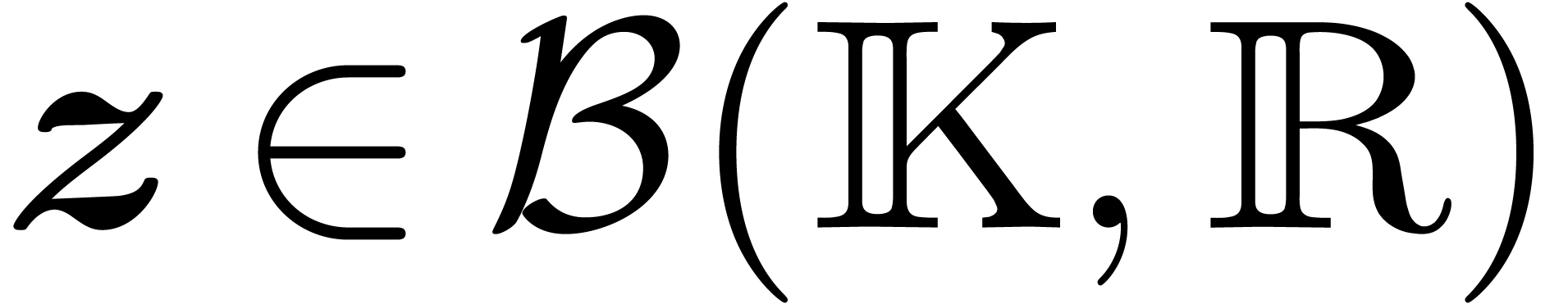 , we will denote its center by
, we will denote its center by 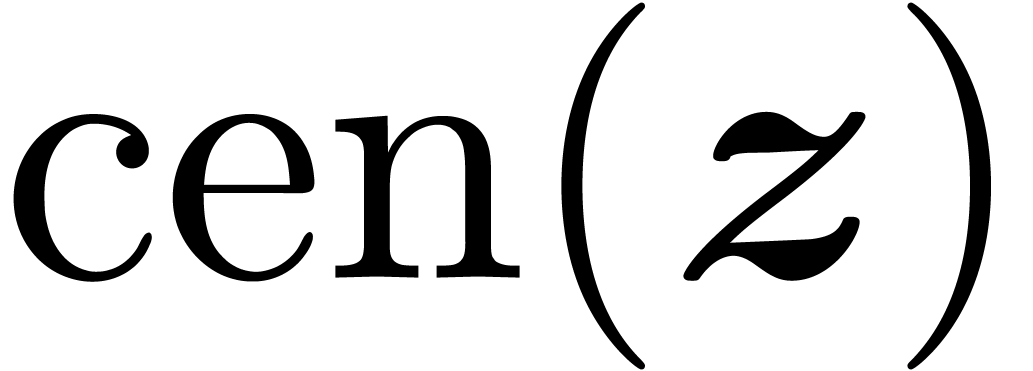 and its radius by
and its radius by 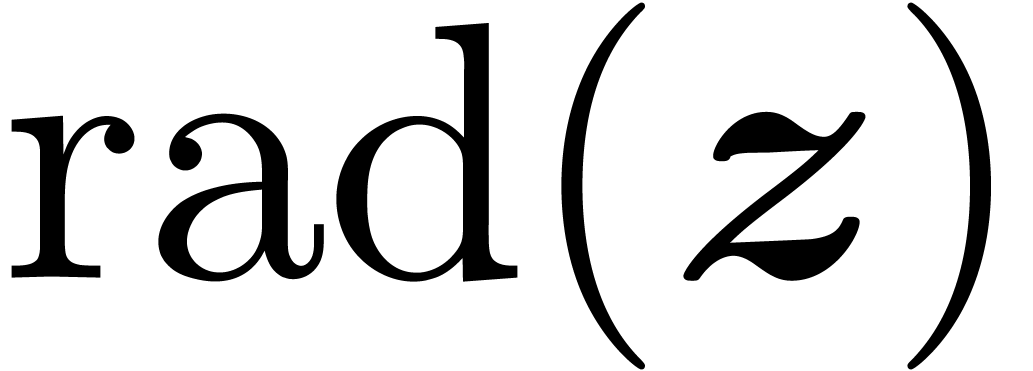 .
Conversely, given
.
Conversely, given 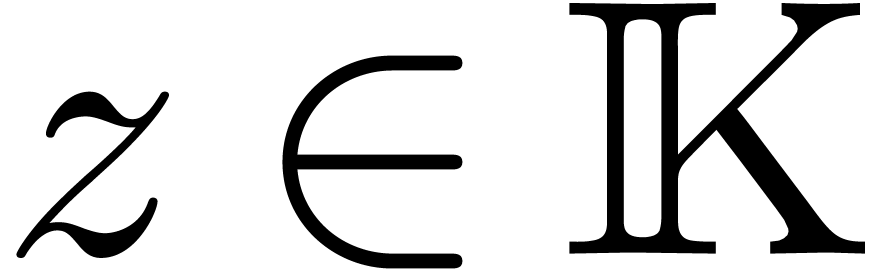 and
and 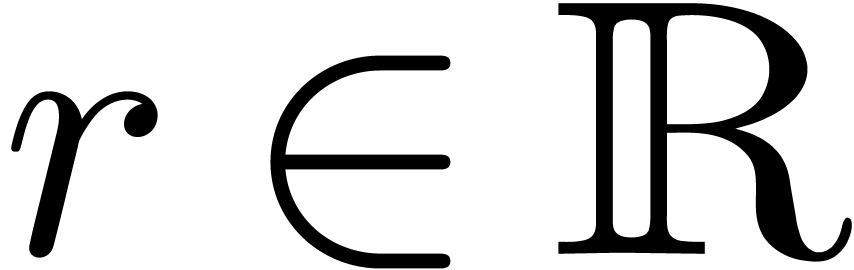 , we will denote by
, we will denote by 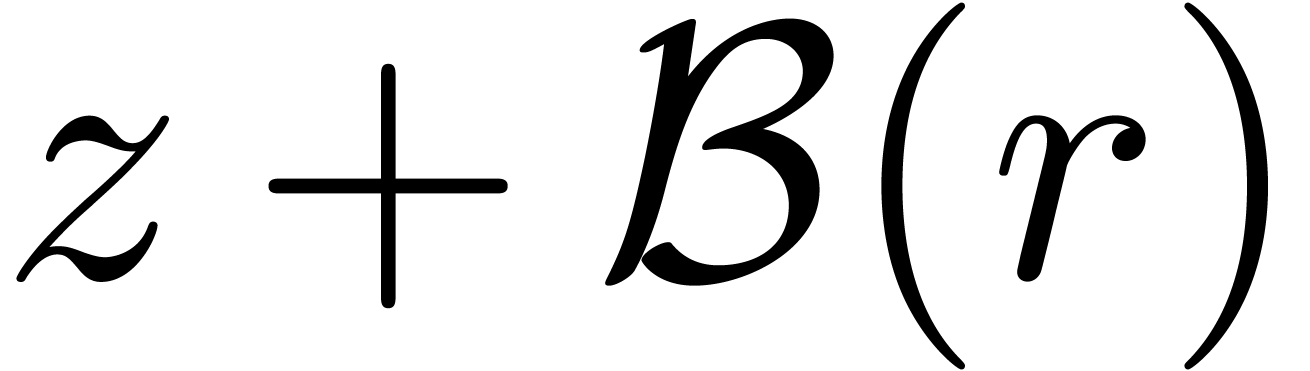 the
closed ball with center
the
closed ball with center  and radius
and radius 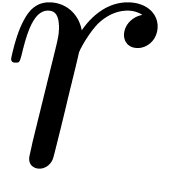 .
.
A continuous operation 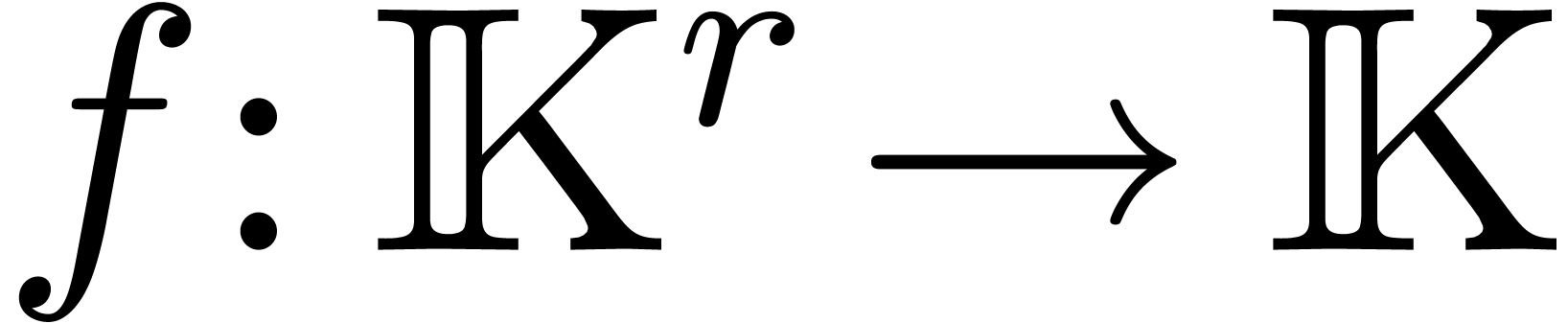 is said to lift
into an operation
is said to lift
into an operation 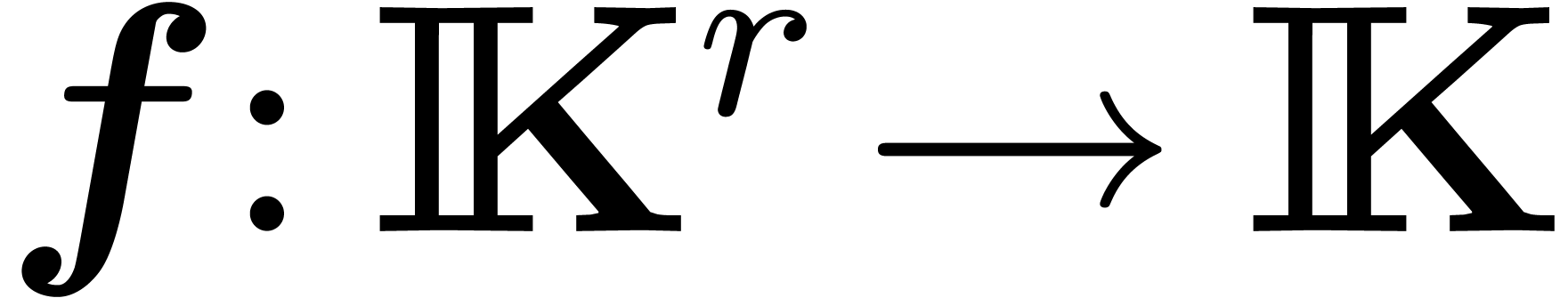 on balls, which is usually
also denoted by
on balls, which is usually
also denoted by  , if the
inclusion property
, if the
inclusion property
is satisfied for any 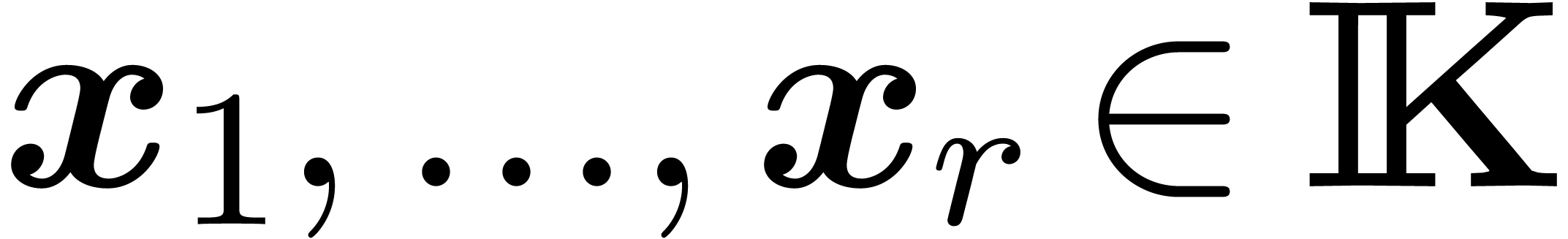 and
and  . For instance, if
. For instance, if  is a
Banach algebra, then we may take
is a
Banach algebra, then we may take
Similar formulas can be given for division and elementary functions.
In concrete machine computations, numbers are usually approximated by
floating point numbers with a finite precision. Let 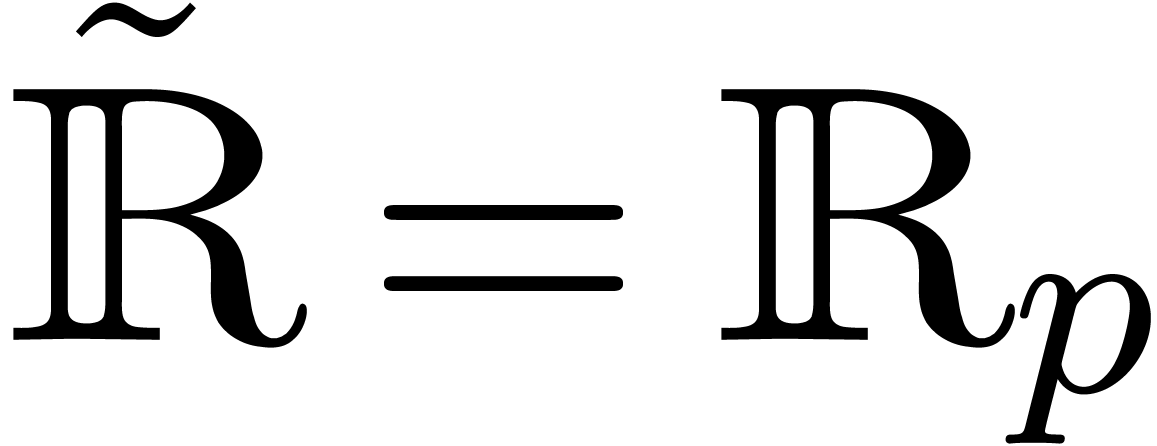 be the set of floating point numbers at a working precision of
be the set of floating point numbers at a working precision of 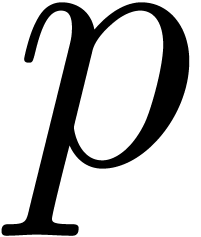 bits. It is customary to include the infinities
bits. It is customary to include the infinities 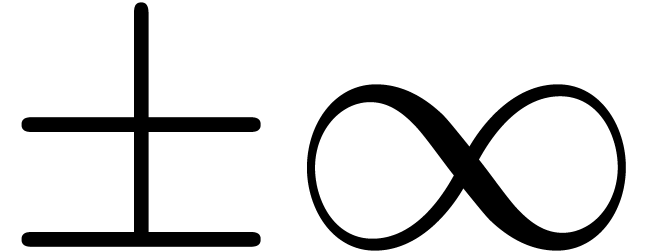 in
in  as well. The IEEE754 standard
[ANS08] specifies how to perform basic arithmetic with
floating point numbers in a predictable way, by specifying a rounding
mode
as well. The IEEE754 standard
[ANS08] specifies how to perform basic arithmetic with
floating point numbers in a predictable way, by specifying a rounding
mode 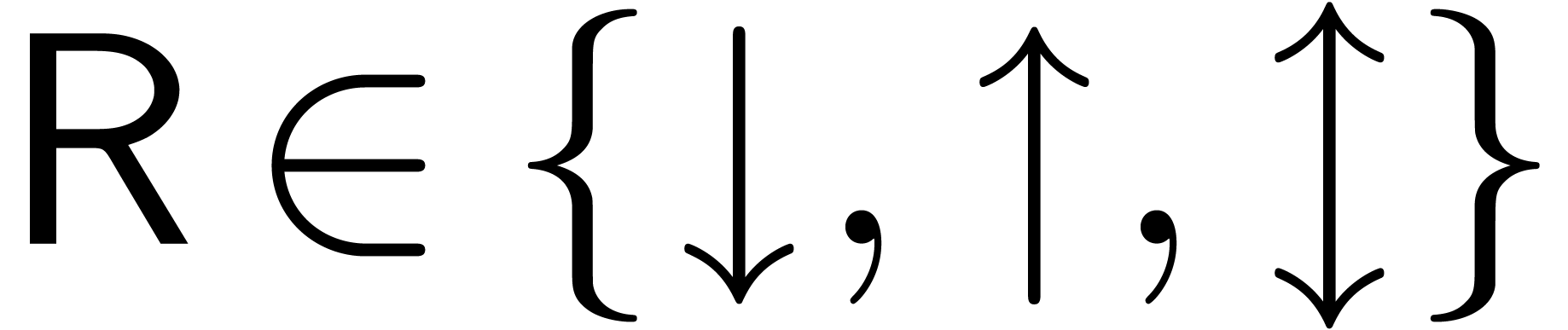 among “down”, “up”
and “nearest”. A multiple precision implementation of this
standard is available in the
among “down”, “up”
and “nearest”. A multiple precision implementation of this
standard is available in the 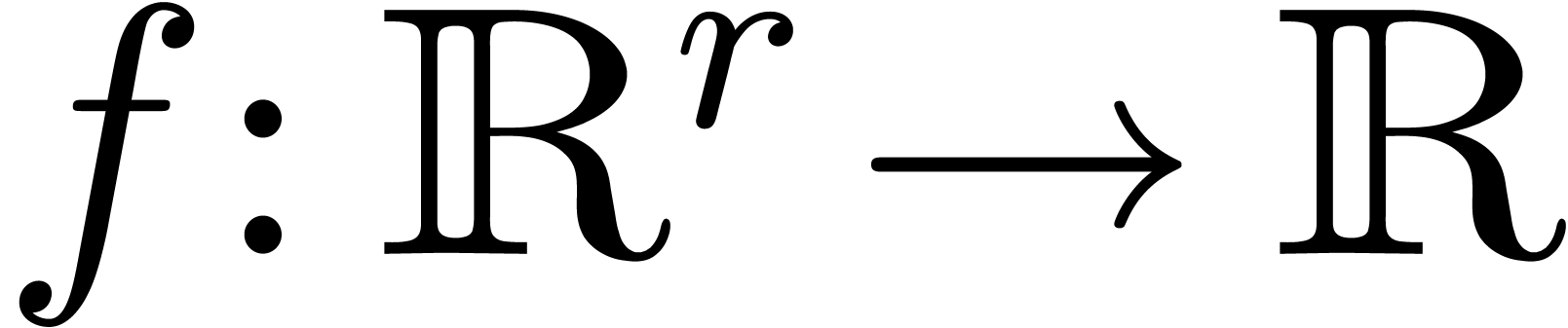 ,
we will denote by
,
we will denote by  its approximation using
floating pointing arithmetic with rounding mode
its approximation using
floating pointing arithmetic with rounding mode  . This notation extends to the case when
. This notation extends to the case when  and
and  are replaced by their
complexifications
are replaced by their
complexifications  and
and 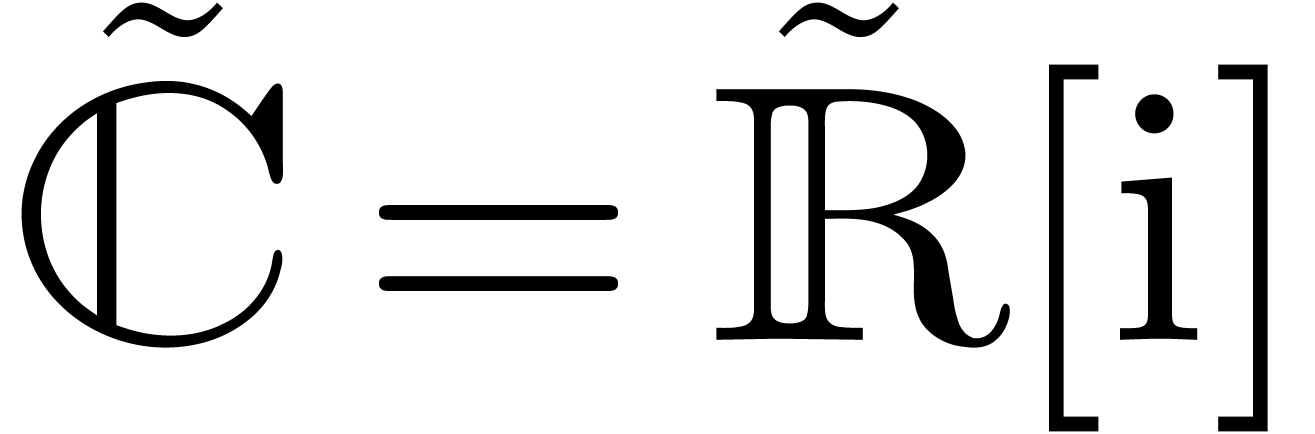 .
.
Setting 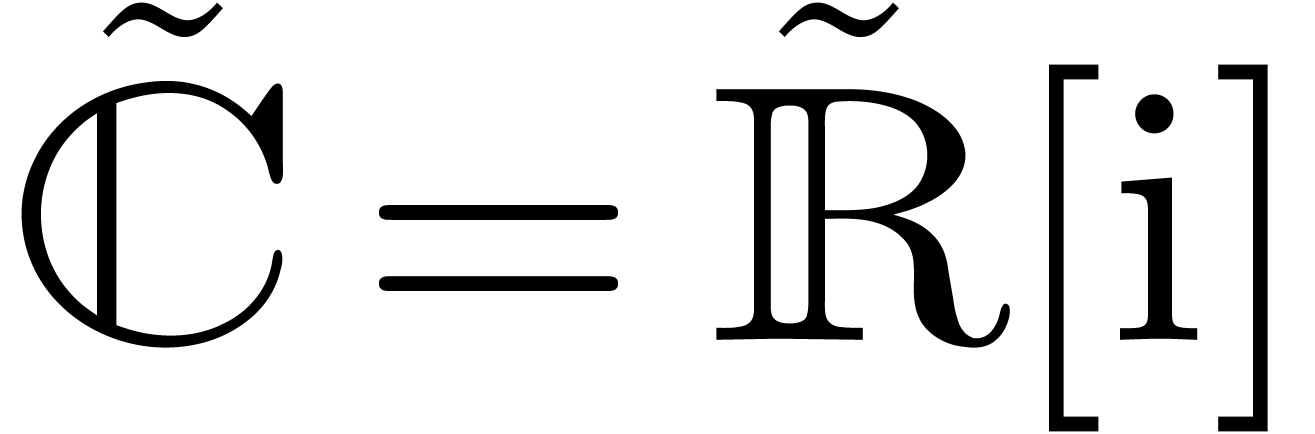 , we will denote by
, we will denote by
 or
or  the set of closed
balls in
the set of closed
balls in  with centers in
with centers in  and radii in
and radii in  . In this case,
we will also allow for balls with an infinite radius. A continuous
operation
. In this case,
we will also allow for balls with an infinite radius. A continuous
operation 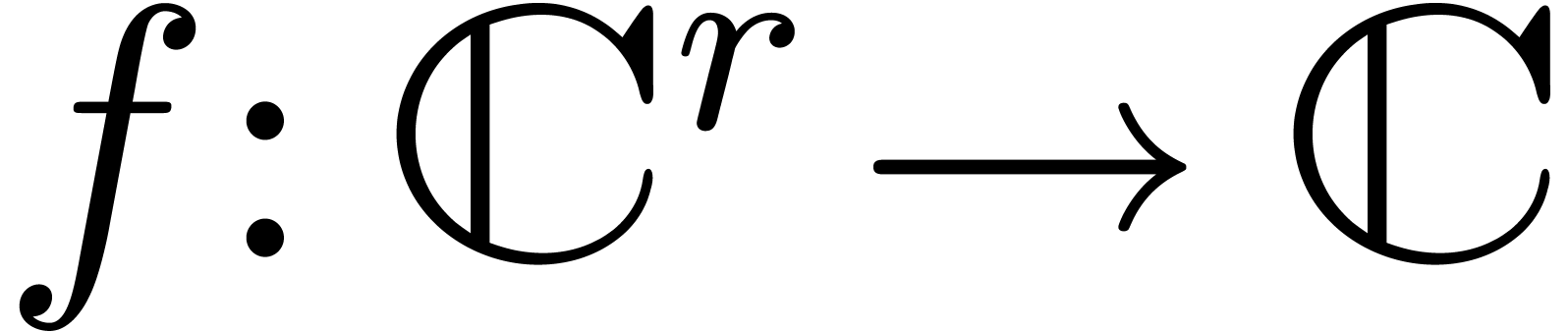 is again said to lift to an operation
is again said to lift to an operation
 on balls if (1) holds for any
on balls if (1) holds for any  and
and  . The
formulas for the ring operations may now be adapted to
. The
formulas for the ring operations may now be adapted to
where 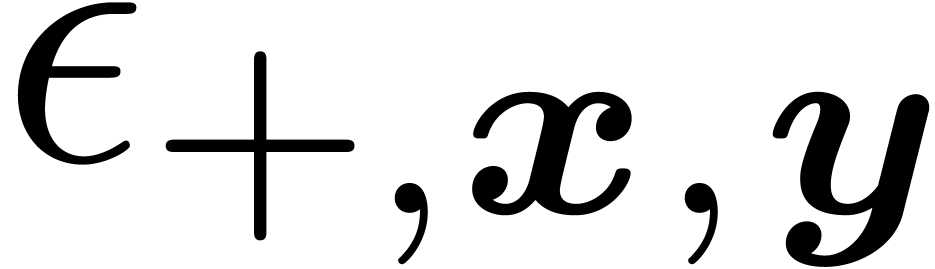 ,
, 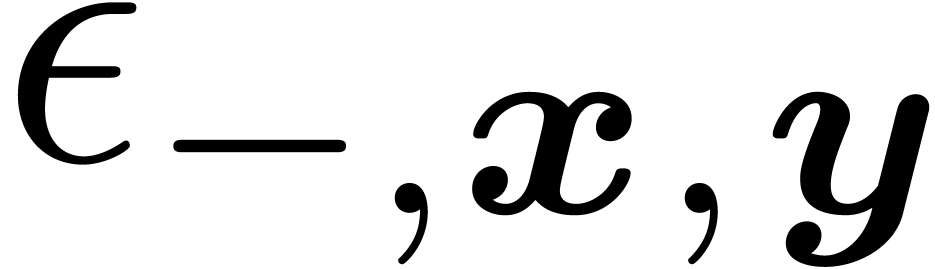 and
and 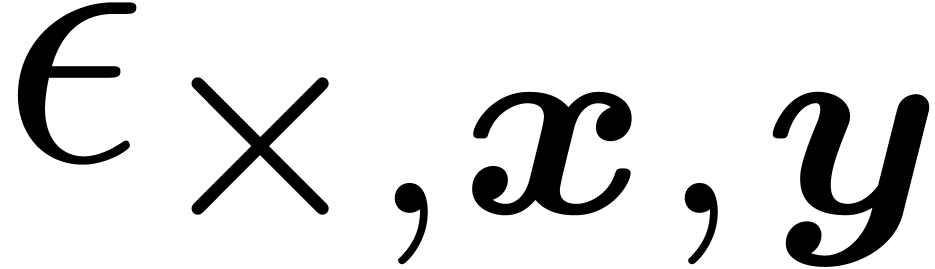 are reliable bounds for the rounding errors
induced by the corresponding floating point operations on the centers;
see [vdH09] for more details. Given
are reliable bounds for the rounding errors
induced by the corresponding floating point operations on the centers;
see [vdH09] for more details. Given  , it will be convenient to denote by
, it will be convenient to denote by 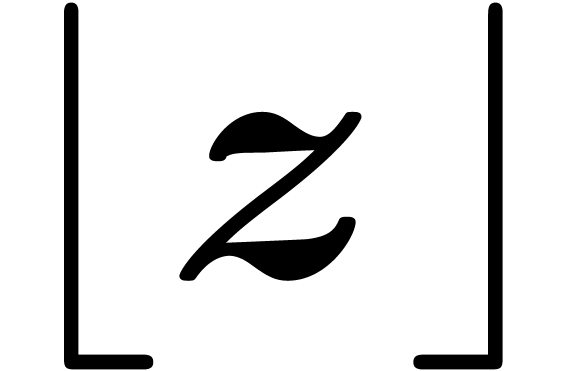 and
and 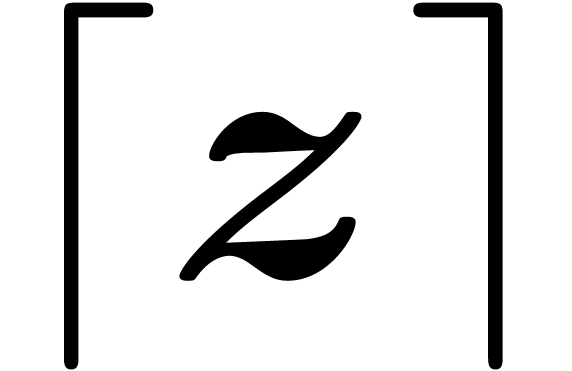 certified lower and upper
bounds for
certified lower and upper
bounds for  .
.
Let 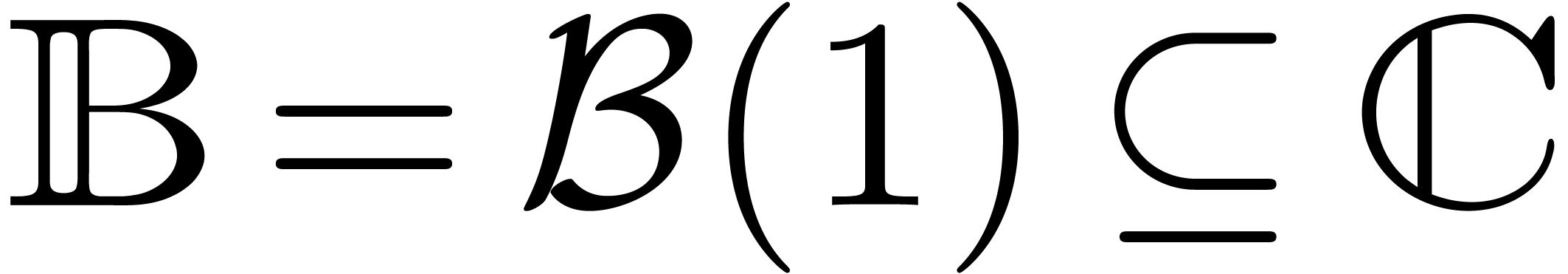 denote the closed unit disk and
denote the closed unit disk and 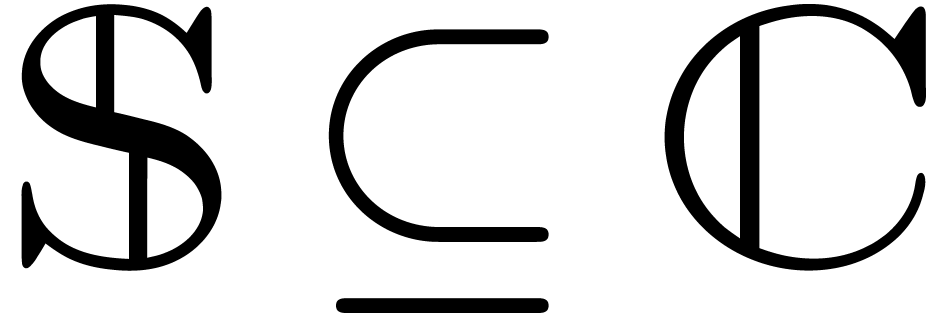 the closed unit circle. Let
the closed unit circle. Let  and
and
 denote the rings of analytic functions on
denote the rings of analytic functions on  resp.
resp.  .
We define norms on
.
We define norms on  and
and  by
by
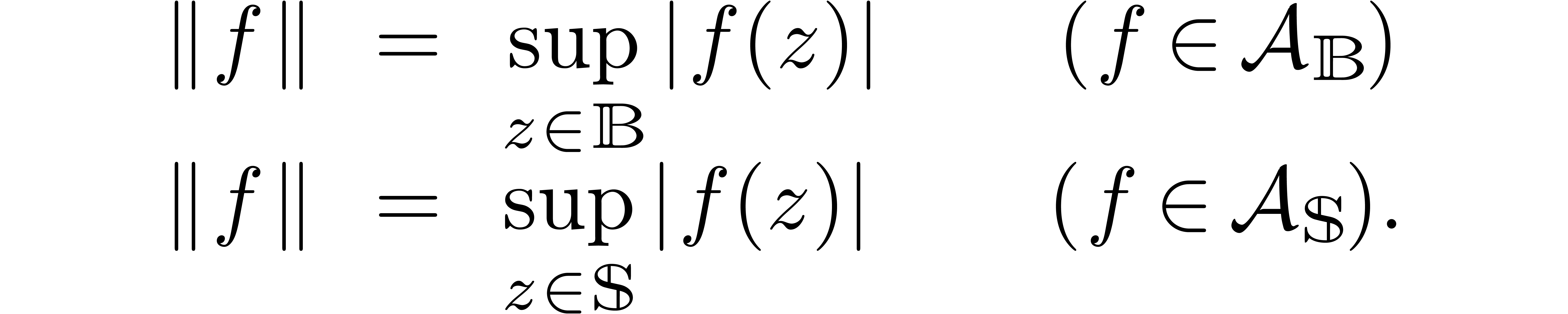
By the maximum modulus principle, the inclusion 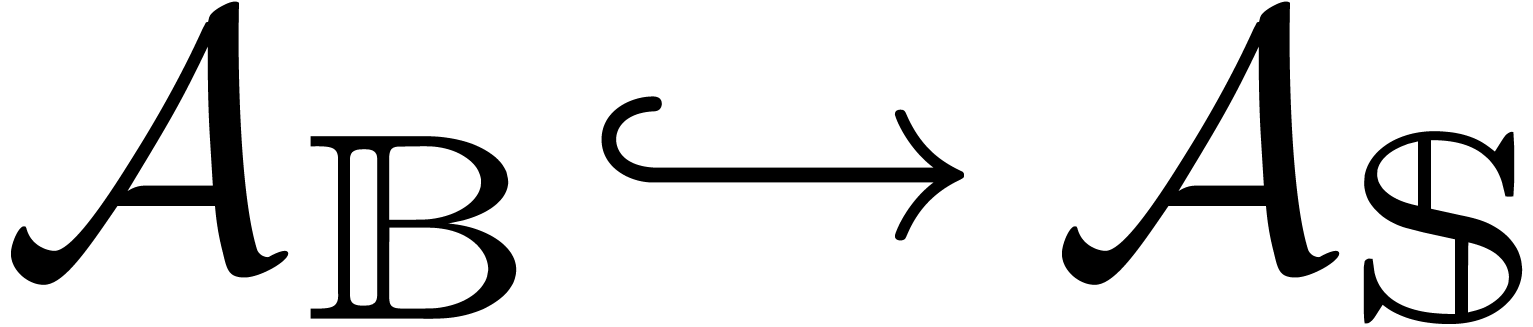 preserves norms. Since our criterion for root counting will be based on
a variant of Rouché's theorem, we will mainly consider analytic
functions on
preserves norms. Since our criterion for root counting will be based on
a variant of Rouché's theorem, we will mainly consider analytic
functions on  in what follows. In order to avoid
confusion with
in what follows. In order to avoid
confusion with 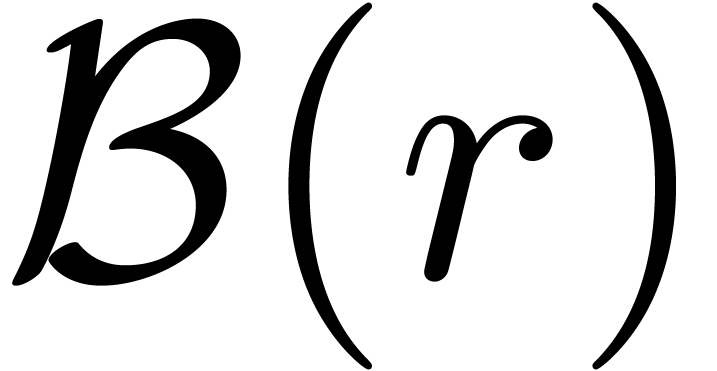 , we will
denote by
, we will
denote by 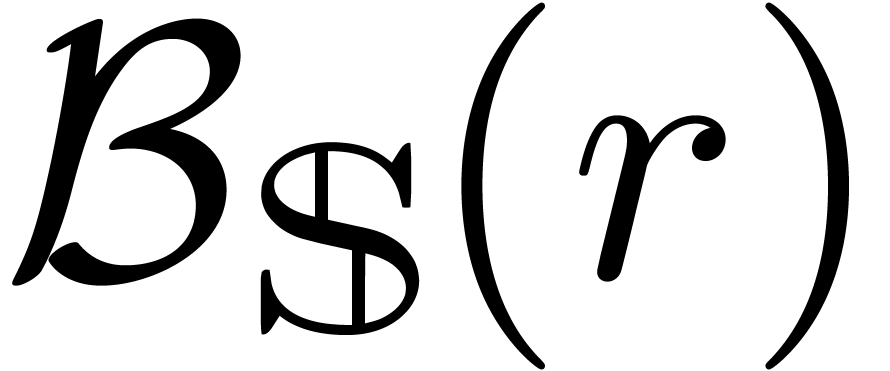 the closed ball of radius
the closed ball of radius 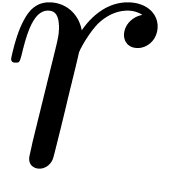 in
in  :
:
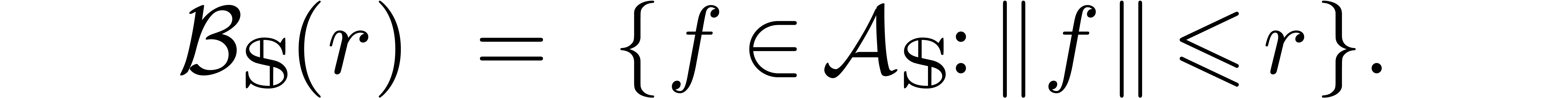
In view of section 2.1, we may then consider the space 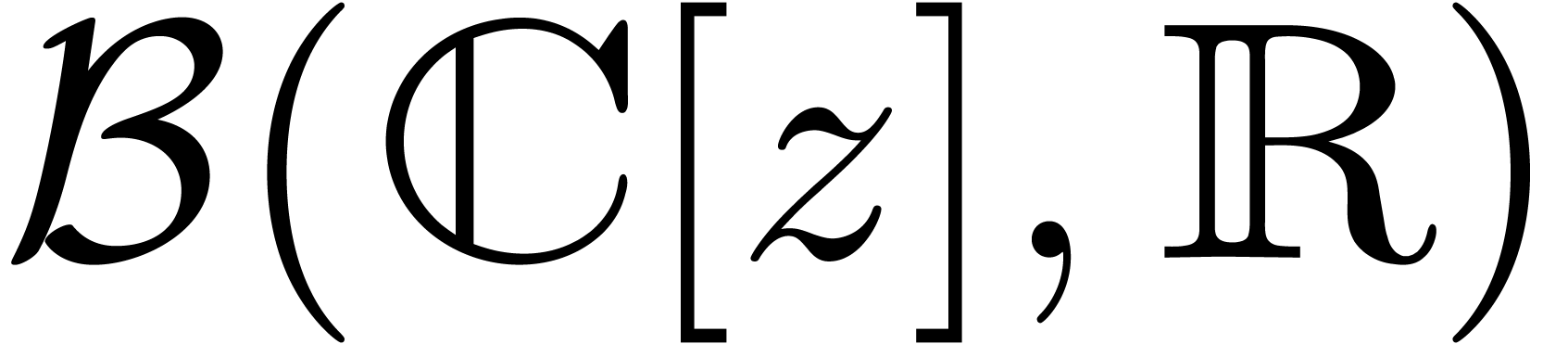 of balls with centers in
of balls with centers in 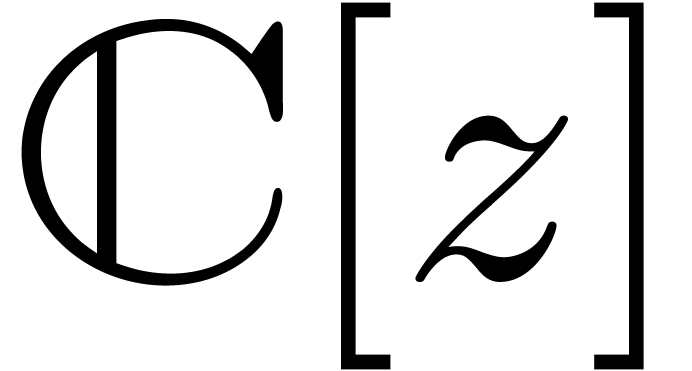 and
radii in
and
radii in  . Any such ball can
be written
. Any such ball can
be written  for
for 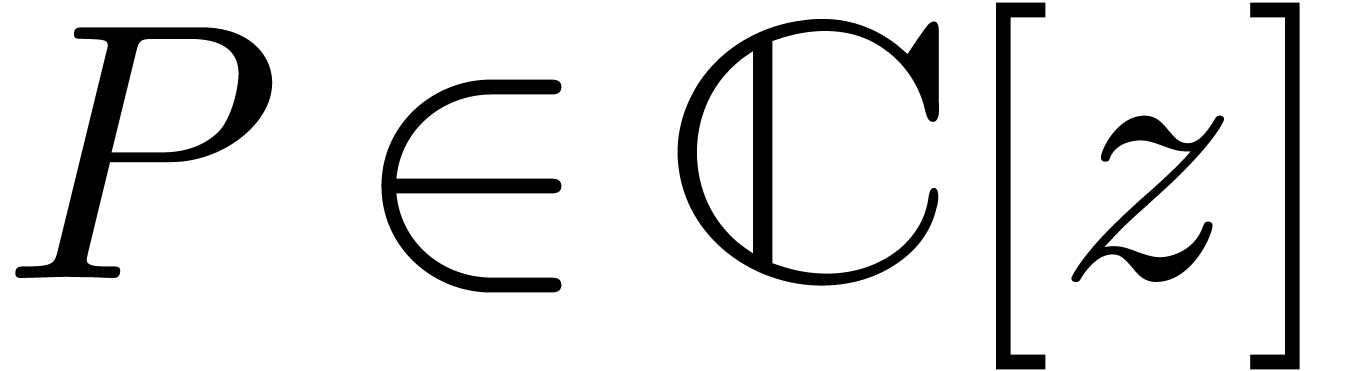 and
and  . For concrete machine
computations, and in a similar way as in section 2.2, we
may also consider the space
. For concrete machine
computations, and in a similar way as in section 2.2, we
may also consider the space 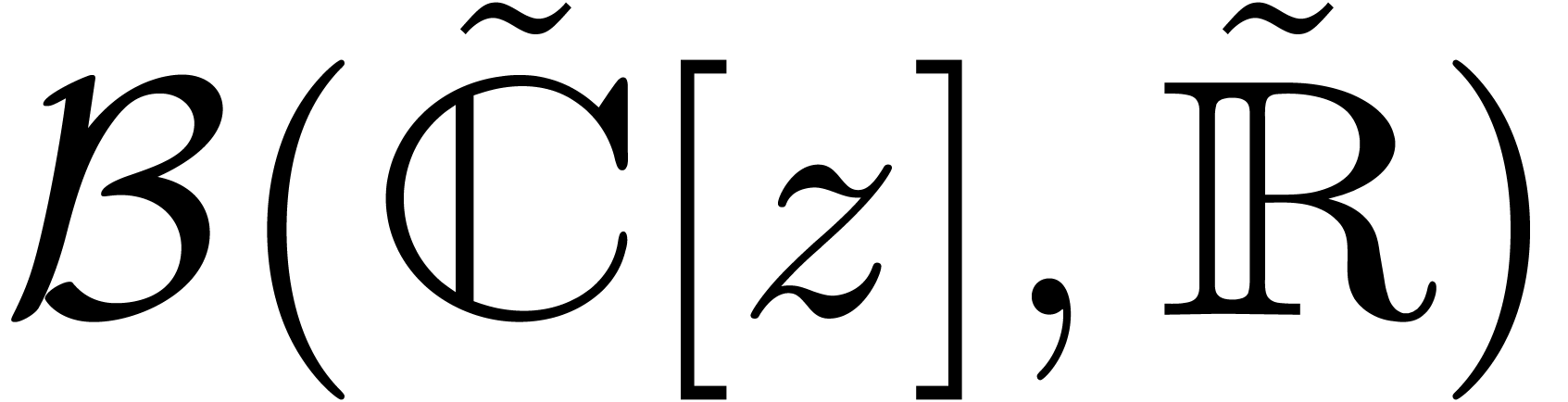 of balls with
centers in
of balls with
centers in 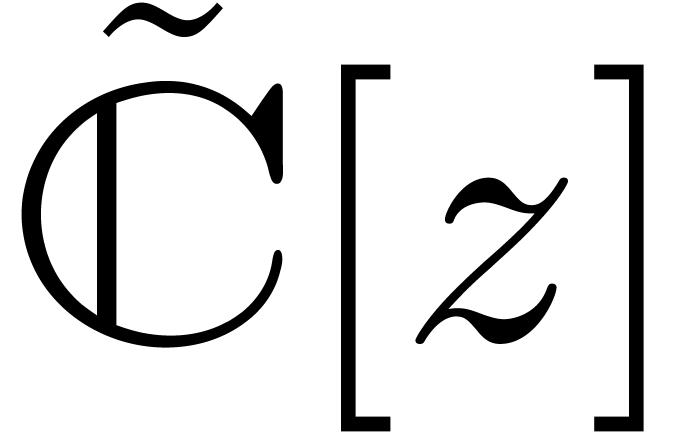 and radii in
and radii in 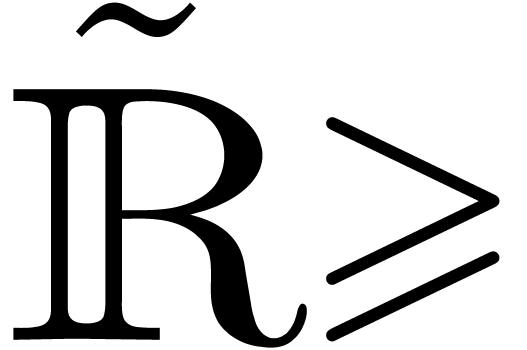 . Given
. Given 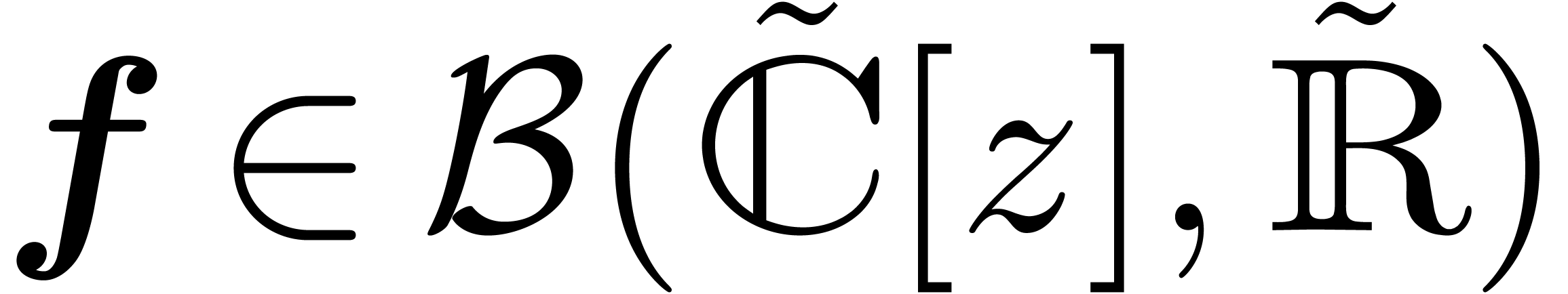 ,
we will denote by
,
we will denote by 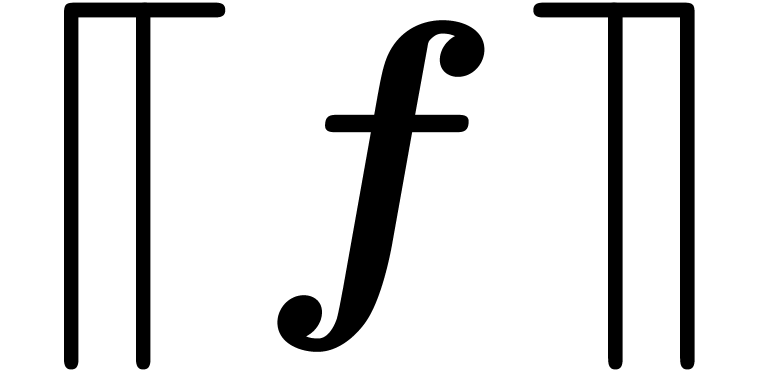 a certified upper bound for
a certified upper bound for
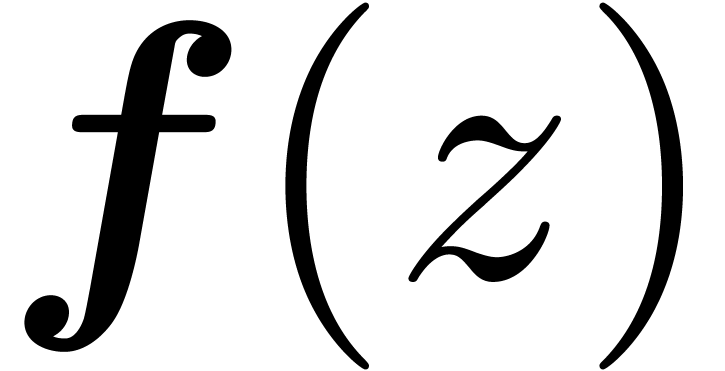 on
on  .
If
.
If 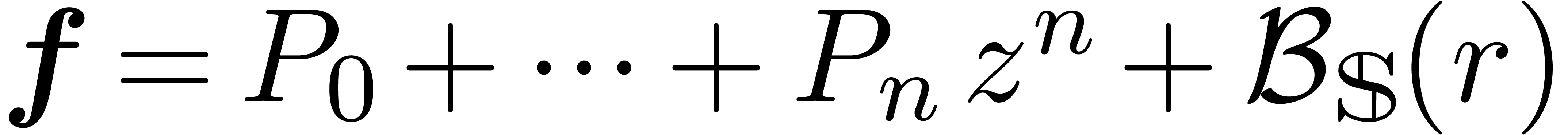 , then we may for instance
take
, then we may for instance
take  .
.
Consider a ball 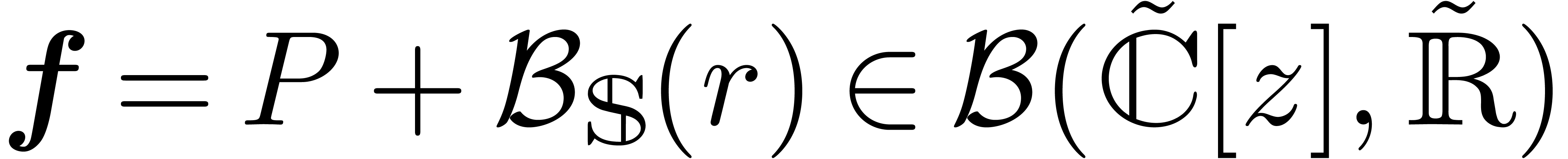 with
with 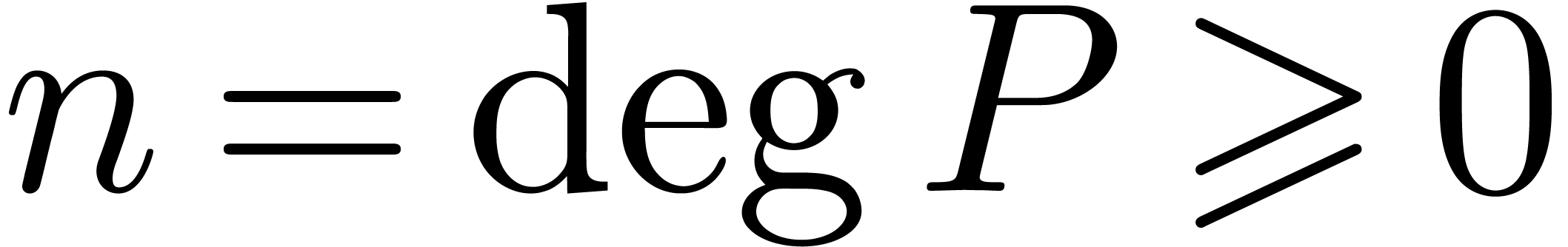 and
let
and
let  be the maximum of the exponents of the
coefficients of
be the maximum of the exponents of the
coefficients of 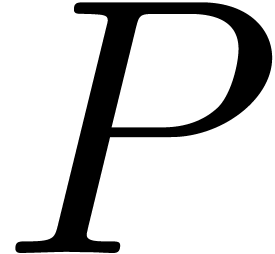 . Let
. Let 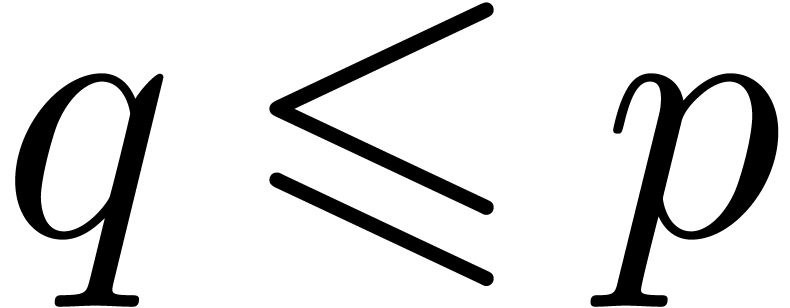 be maximal such that
be maximal such that
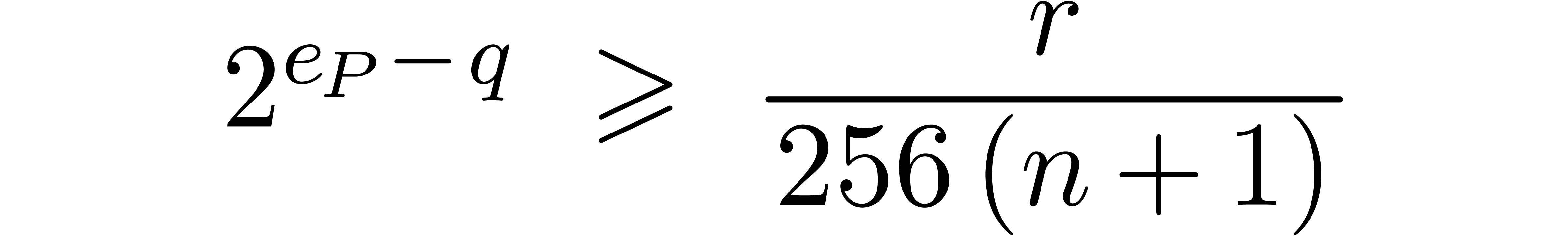
and take 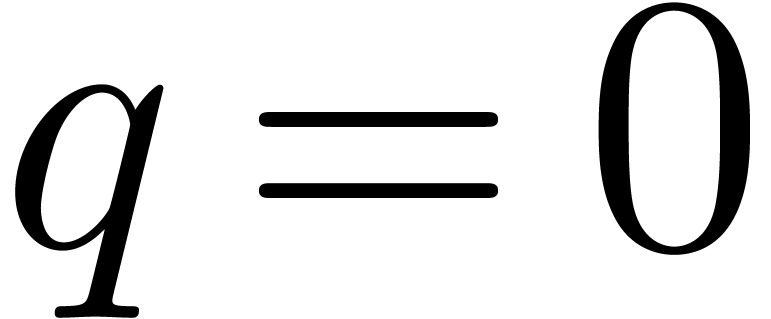 if
if 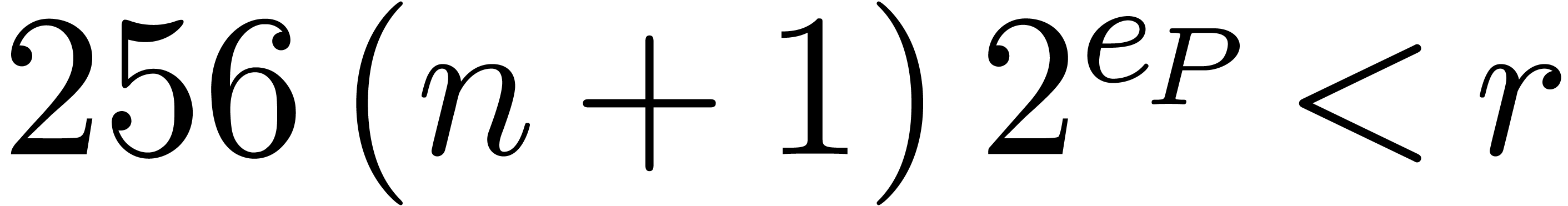 .
Denote
.
Denote  . Truncation of the
mantissas of the coefficients of
. Truncation of the
mantissas of the coefficients of 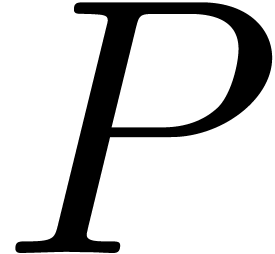 leads to a
decomposition
leads to a
decomposition

where
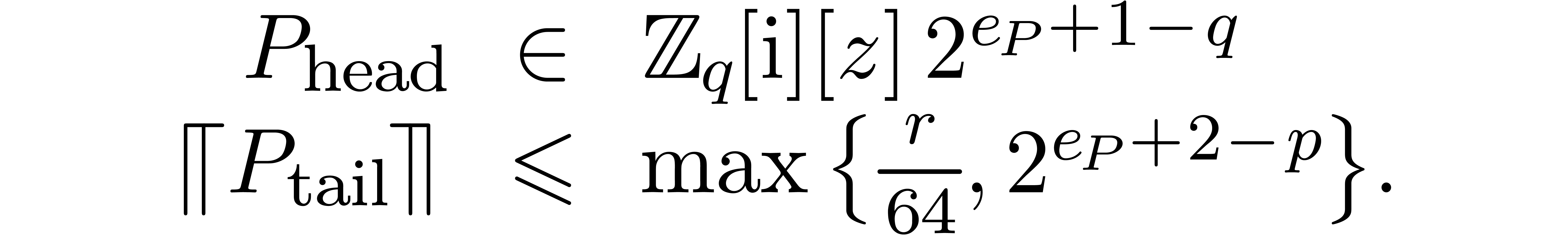
We define the simplification 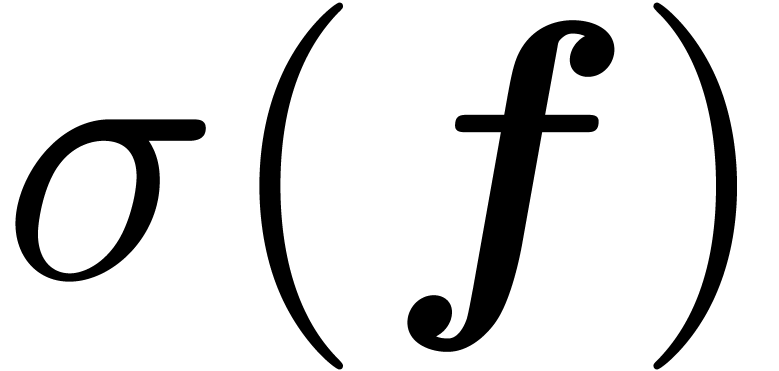 of
of  by
by

and notice that 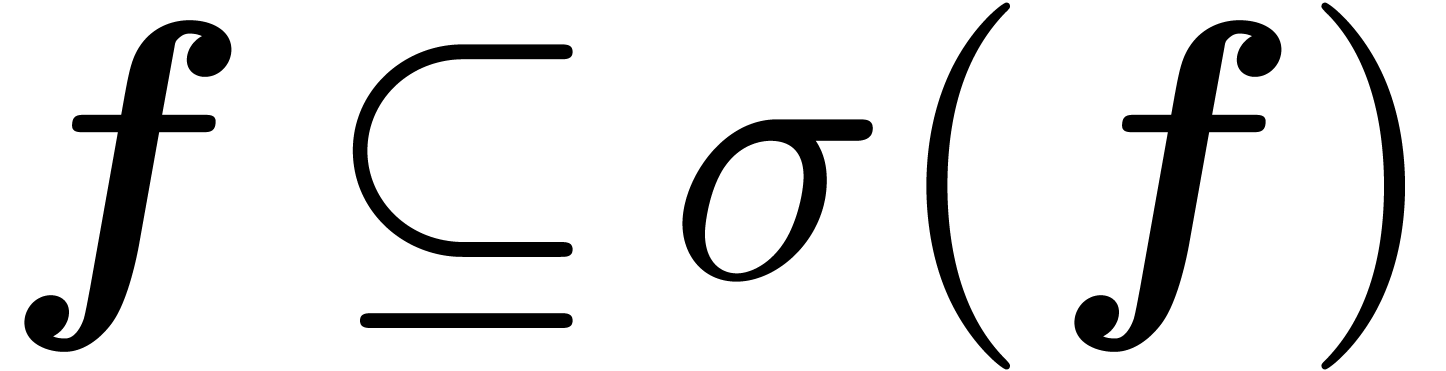 .
.
Assume now that we want to multiply two balls  and
and  in an efficient way. Modulo simplification,
we may assume without loss of generality that
in an efficient way. Modulo simplification,
we may assume without loss of generality that 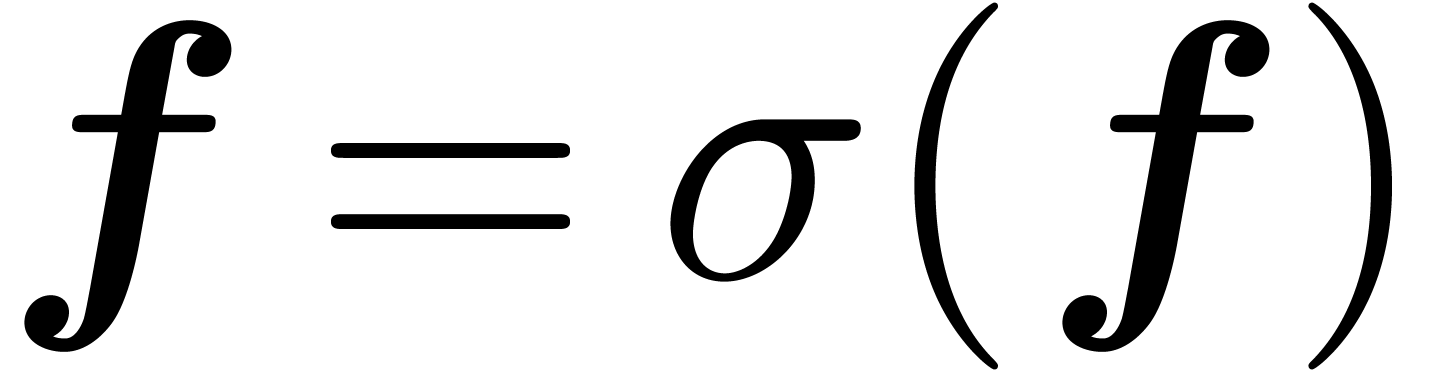 and
and 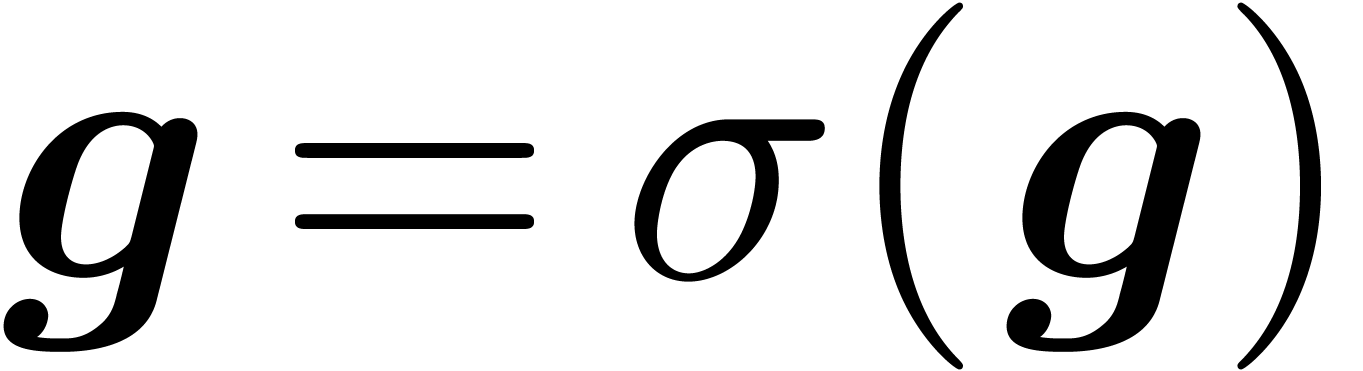 . For some common
. For some common  , we thus have
, we thus have
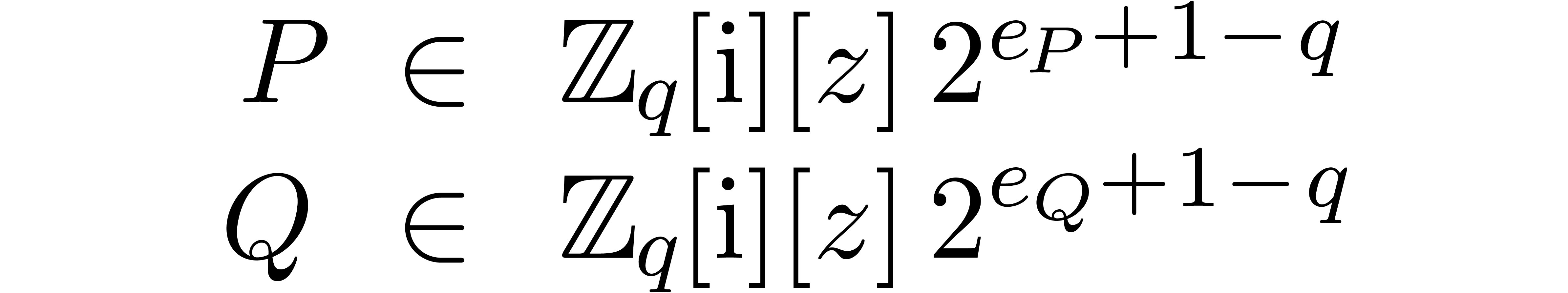
We may multiply the integer polynomials 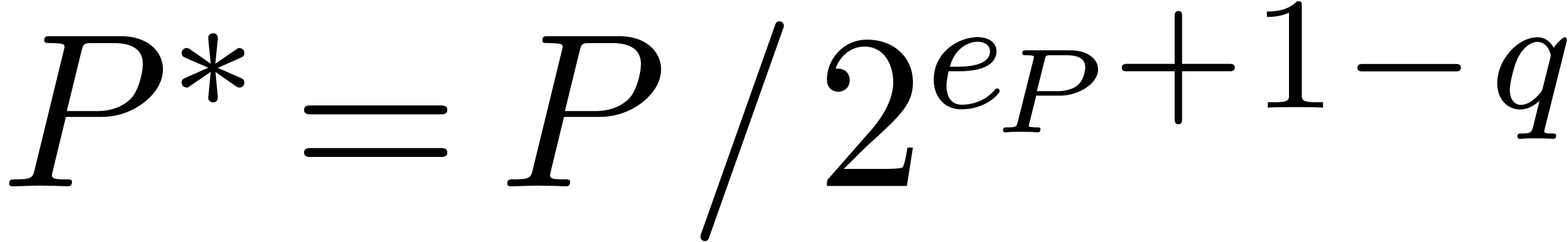 and
and 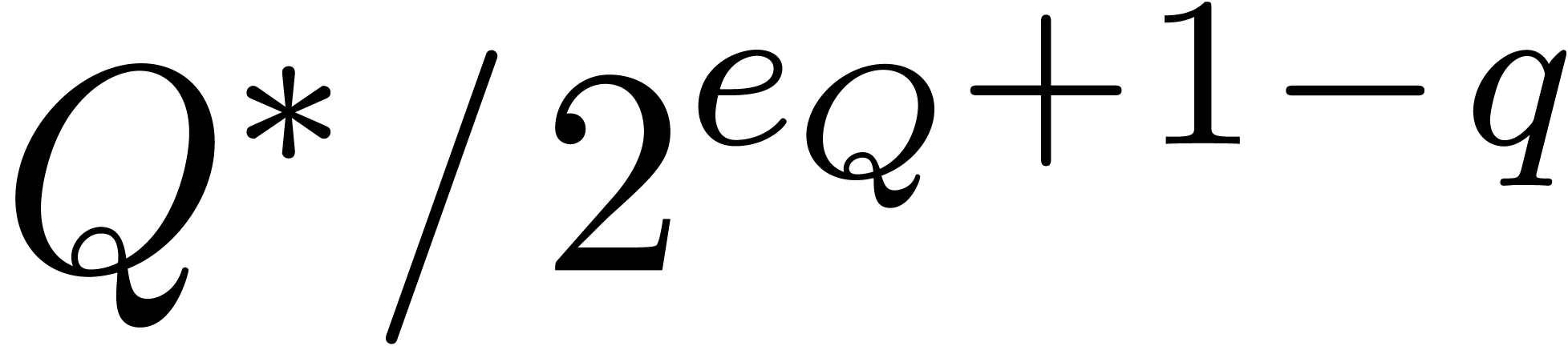 using any fast classical algorithm, such as Kronecker
substitution [PB94, GG02]. When truncating
using any fast classical algorithm, such as Kronecker
substitution [PB94, GG02]. When truncating
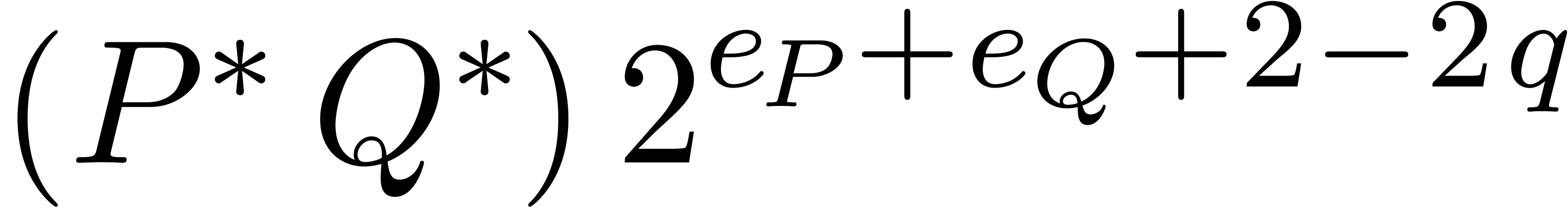 back to a complex floating polynomial
back to a complex floating polynomial 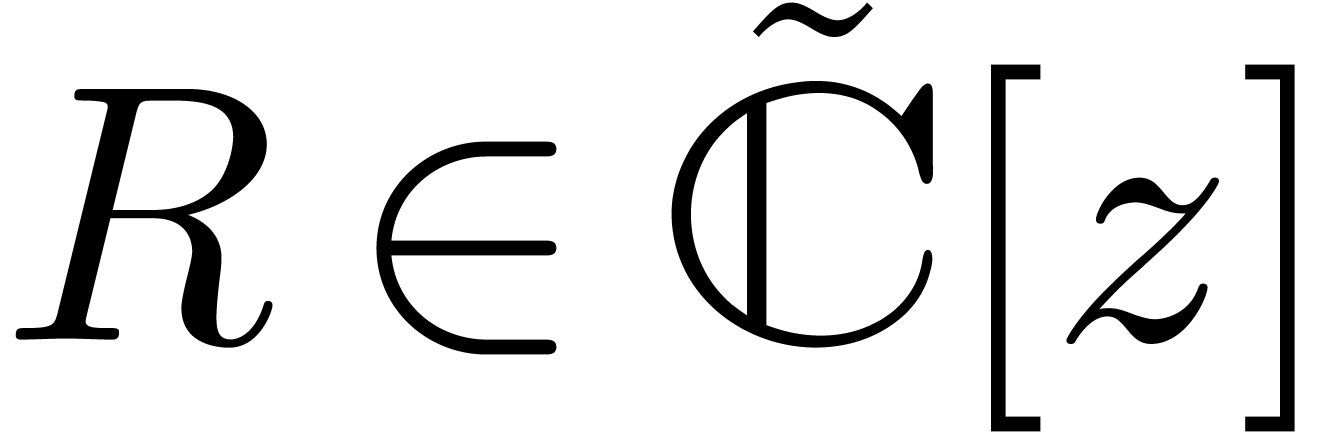 , we have
, we have
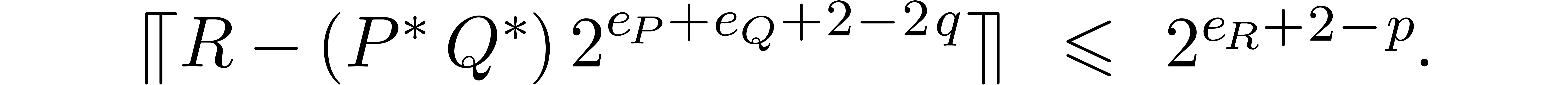
Consequently, we may take

Given an analytic function 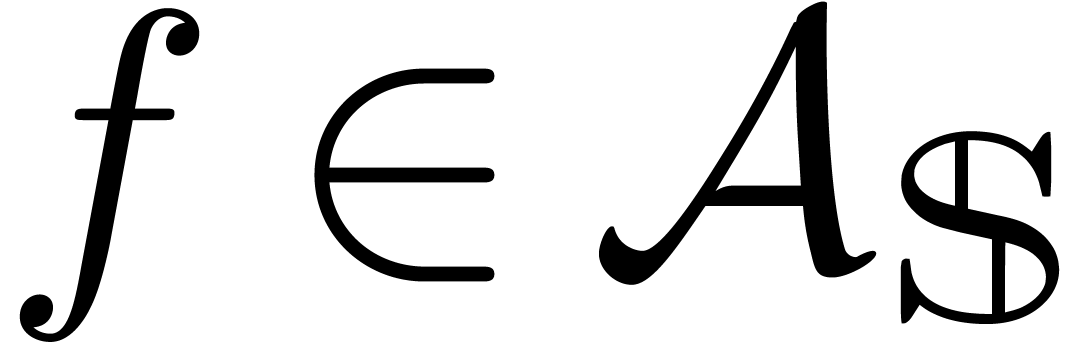 with no zeros on
with no zeros on
 , we will denote
, we will denote
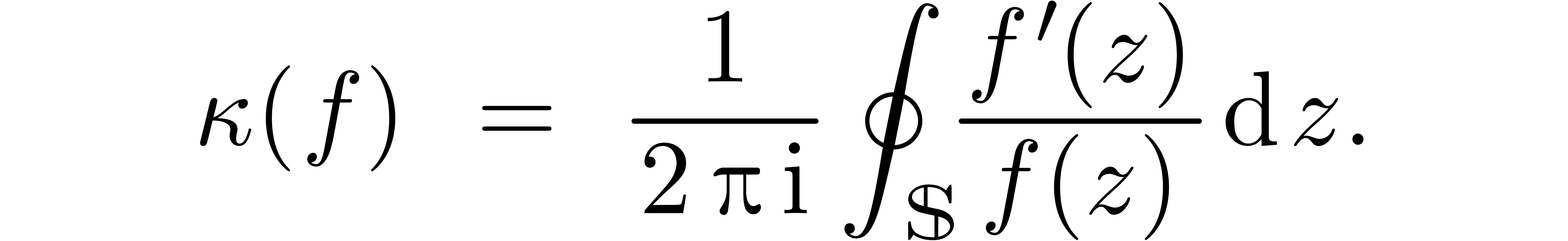
If  , then
, then 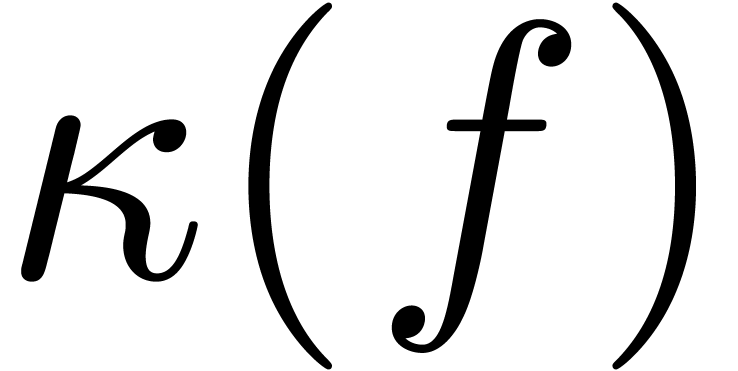 counts the number of zeros of
counts the number of zeros of 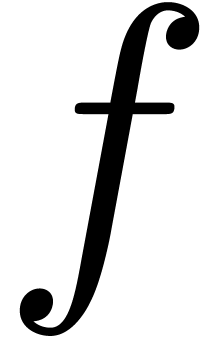 in the open unit
disk. Now consider a ball
in the open unit
disk. Now consider a ball 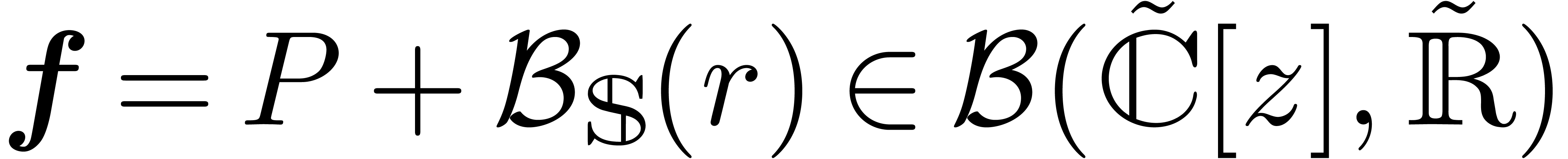 of analytic functions.
Whenever no
of analytic functions.
Whenever no  admits a zero on
admits a zero on  , then
, then 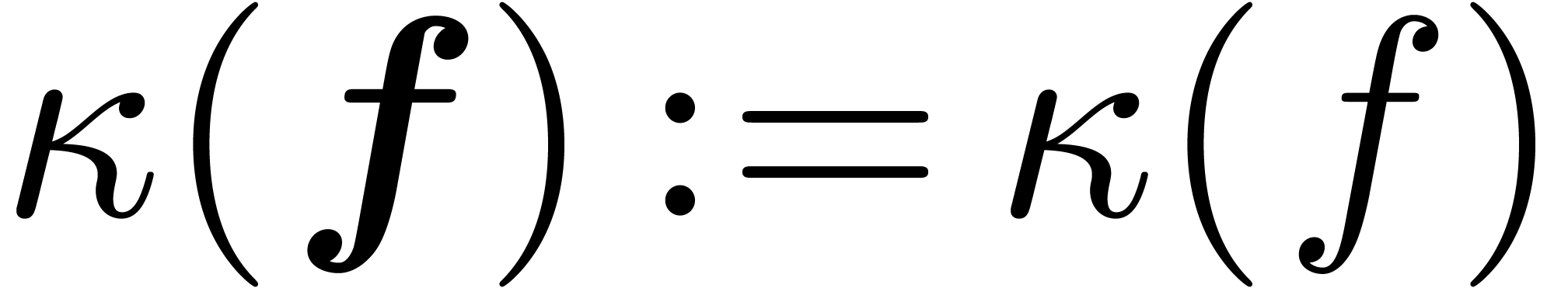 does not depend
on the choice of
does not depend
on the choice of  . The aim of
this paper is to compute
. The aim of
this paper is to compute 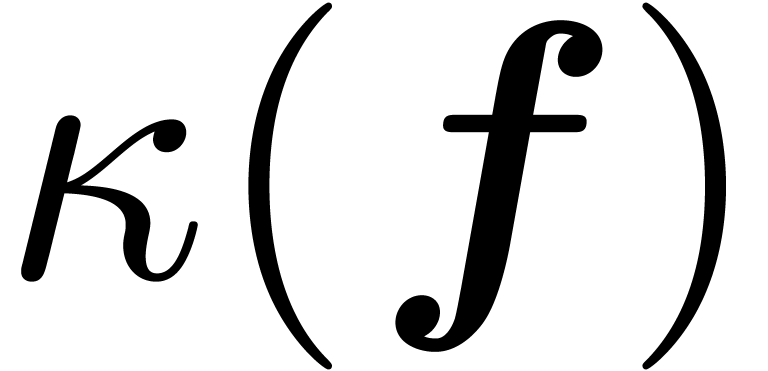 in this case. If some
in this case. If some
 admit zeros which are too close to
admit zeros which are too close to  , then the algorithm is allowed to fail.
, then the algorithm is allowed to fail.
The method that we will use for certifying the number of roots relies on the following variant of Rouché's theorem.
Proof. We will use a similar argument as in [Lan76, page 158]. Let 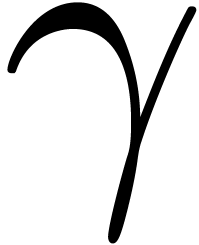 be the path on
be the path on
 which turns one time around the origin and let
which turns one time around the origin and let
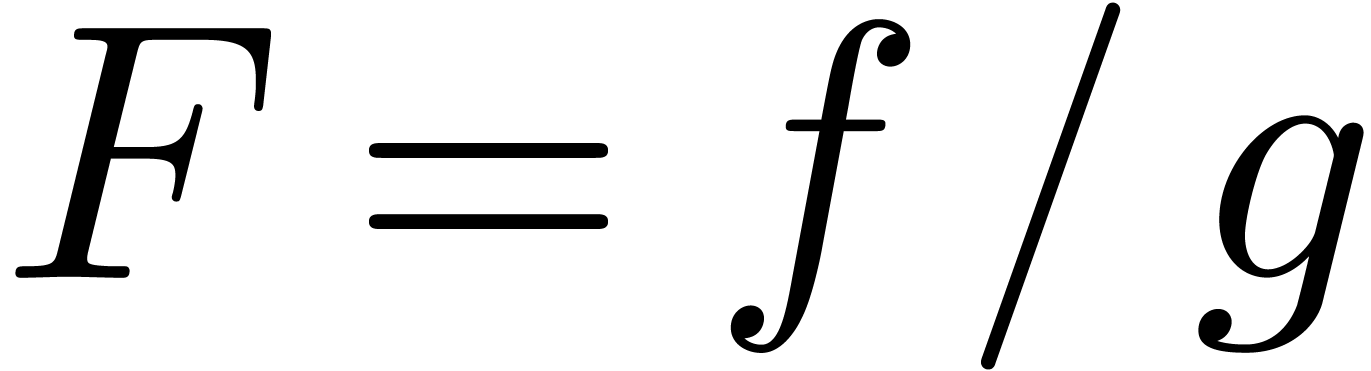 . By our assumption, the path
. By our assumption, the path
 is contained in the open disk with center one
and radius one. Since this disk does not contain the origin, we have [Lan76, Lemma 3, page 116]
is contained in the open disk with center one
and radius one. Since this disk does not contain the origin, we have [Lan76, Lemma 3, page 116]
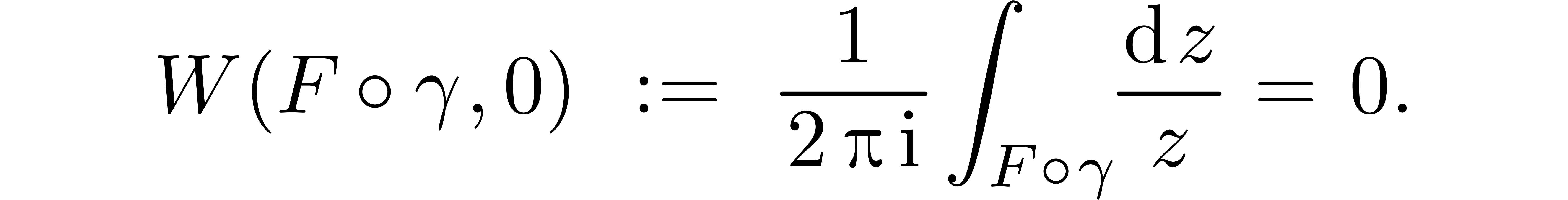
But
whence 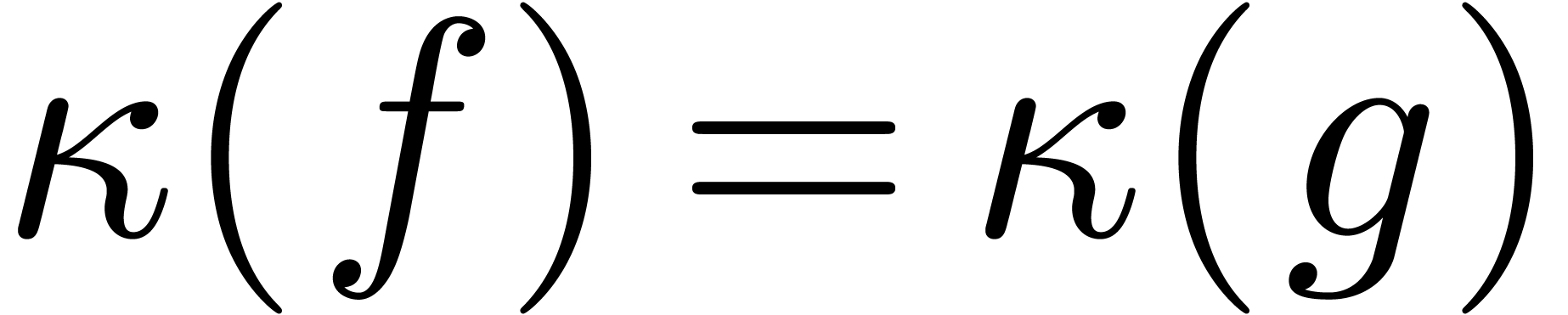 .
.
Given a polynomial 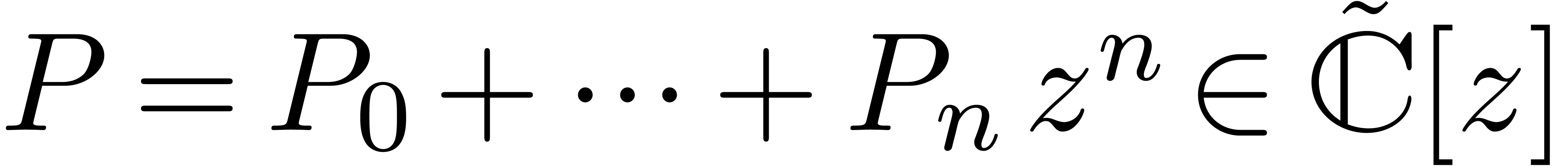 and
and  , let us denote by
, let us denote by 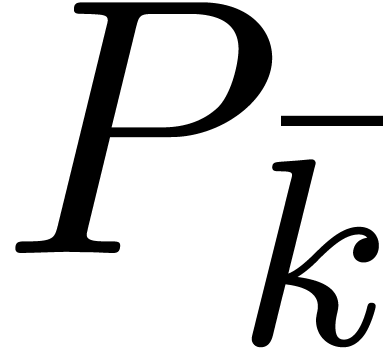 the
polynomial
the
polynomial 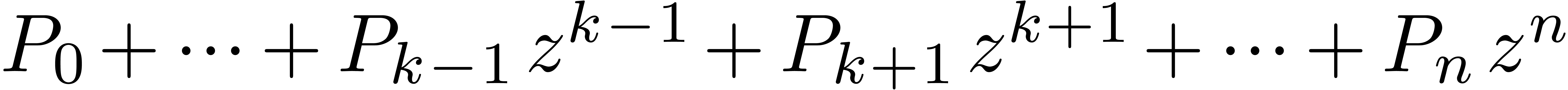 .
.
 and let
and let  be the index for which
be the index for which 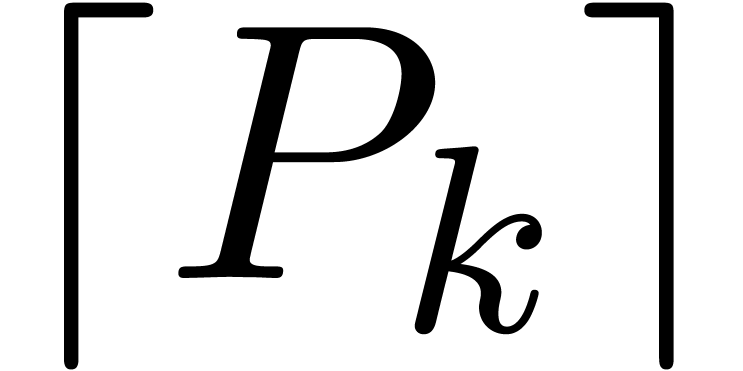 is
maximal. If
is
maximal. If
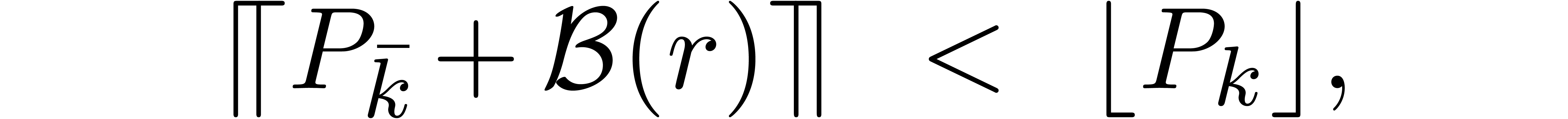
then 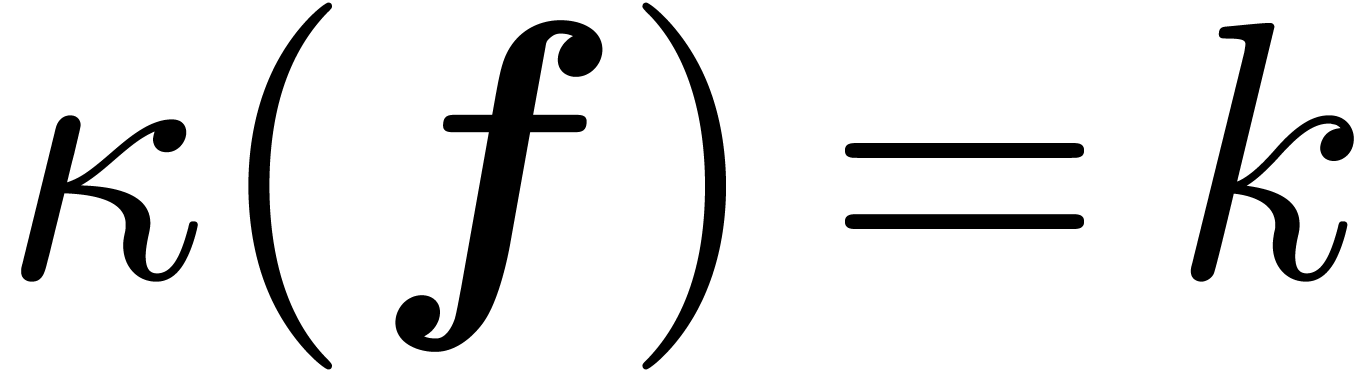 .
.
Proof. Let 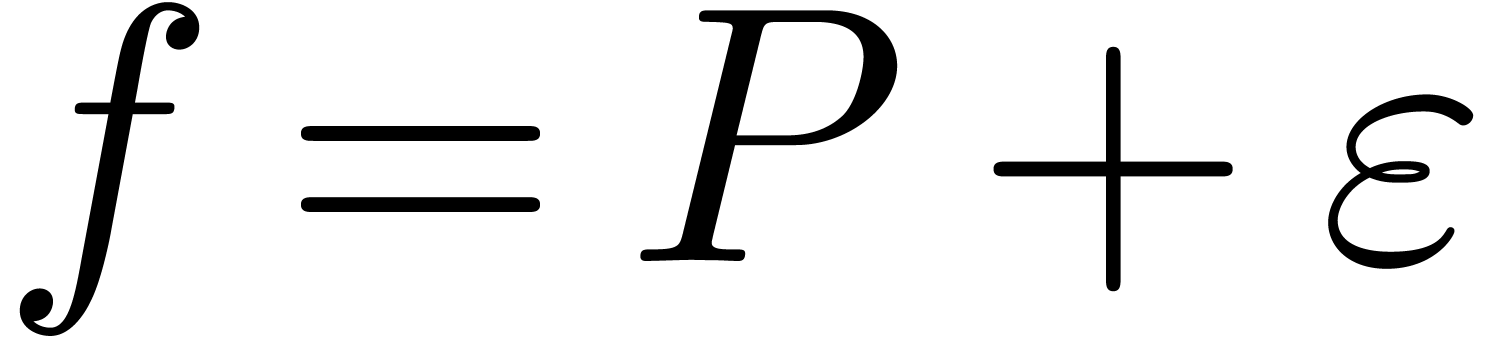 with
with 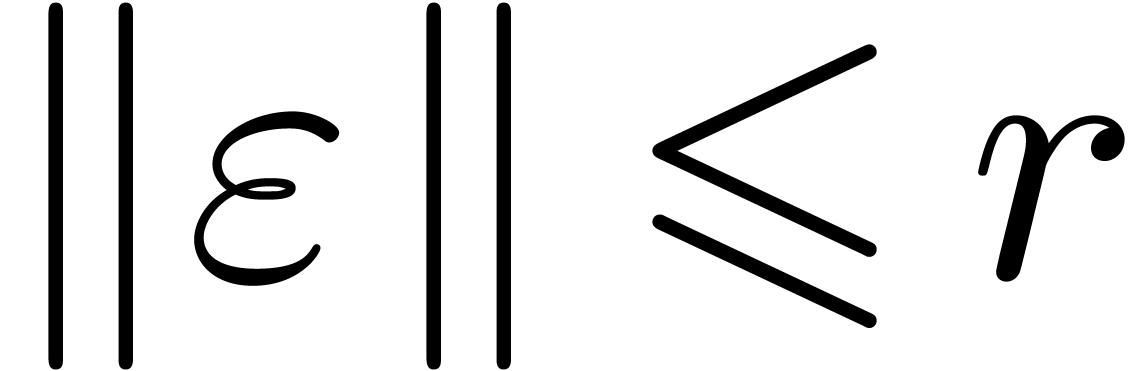 . Setting
. Setting 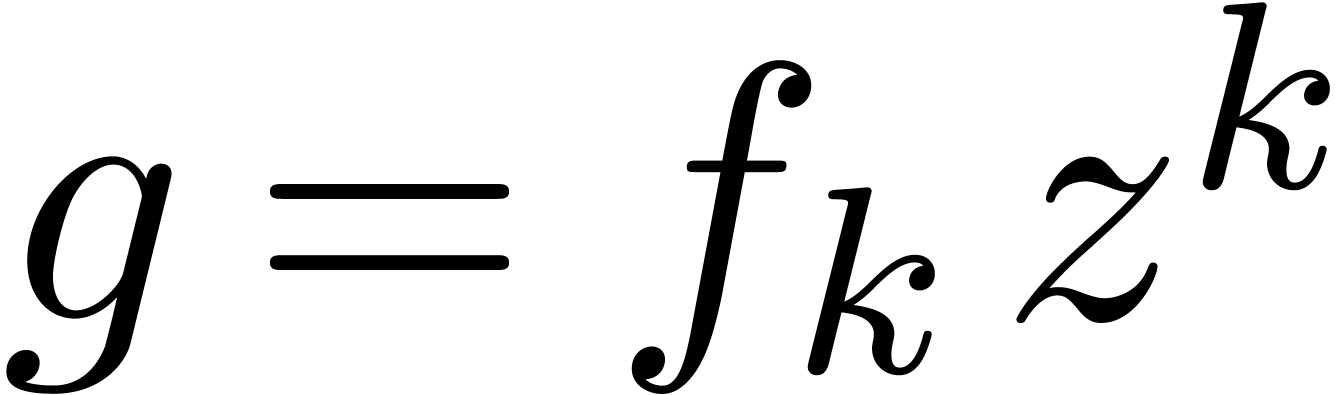 , our assumption implies
, our assumption implies
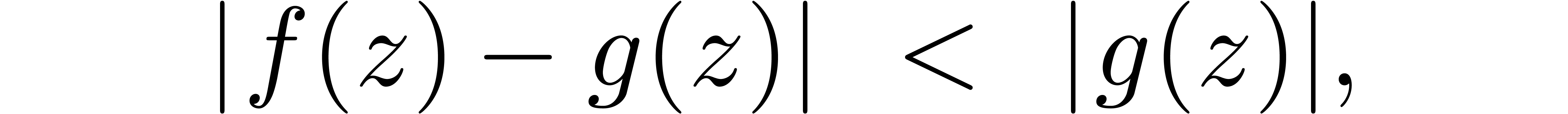
for all  . By theorem 1,
we conclude that
. By theorem 1,
we conclude that 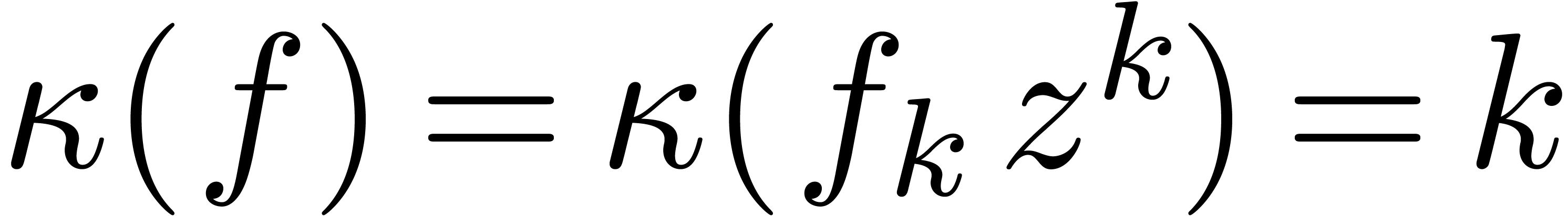 .
.
The second ingredient for our algorithm is the Graeffe transform, which
we will use for analytic functions. Given 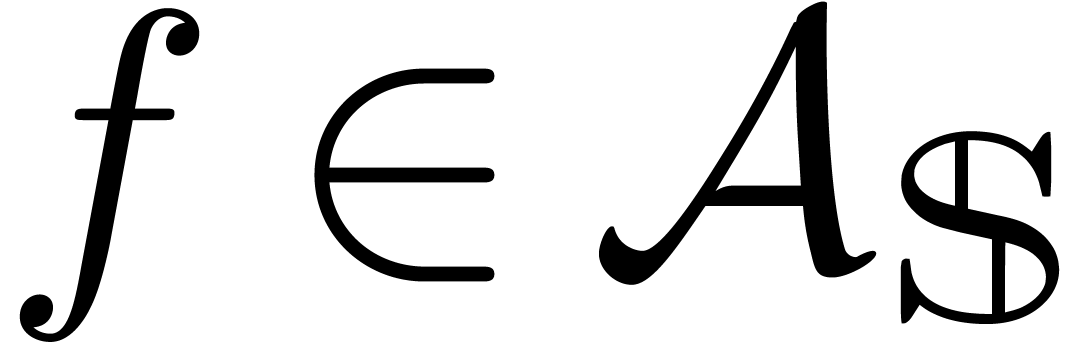 ,
we define its Graeffe transform
,
we define its Graeffe transform 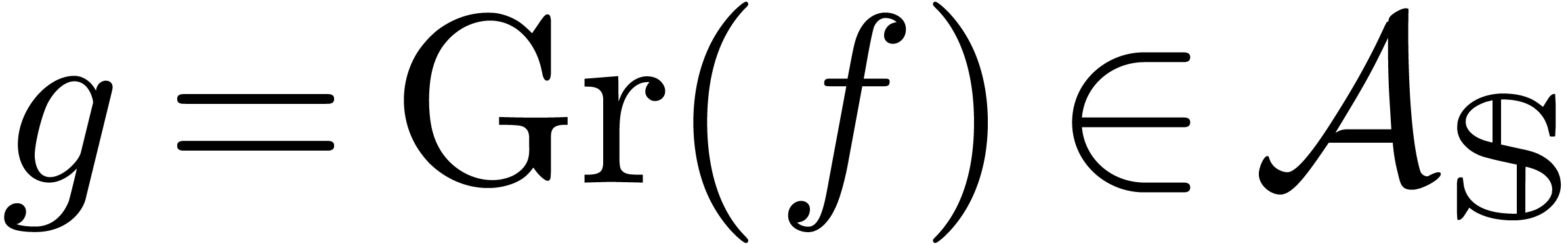 by
by
If 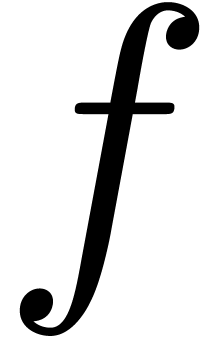 is actually a polynomial, then we notice that
is actually a polynomial, then we notice that
 has the same degree as
has the same degree as 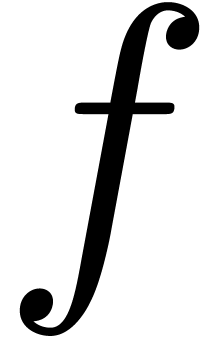 . The fundamental property of Graeffe transforms is:
. The fundamental property of Graeffe transforms is:
 ,
the roots of
,
the roots of  are precisely the squares of the
roots of
are precisely the squares of the
roots of 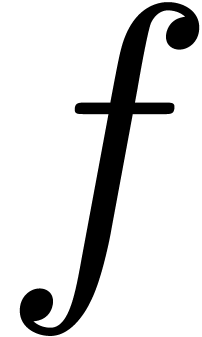 , when counting
with multiplicities.
, when counting
with multiplicities.
Proof. By continuity under small deformations,
it suffices to consider the case when  has only
simple zeros
has only
simple zeros  near
near  .
Now
.
Now
for all  near
near  .
.
Let us show that the Graeffe transform can be lifted to an operation
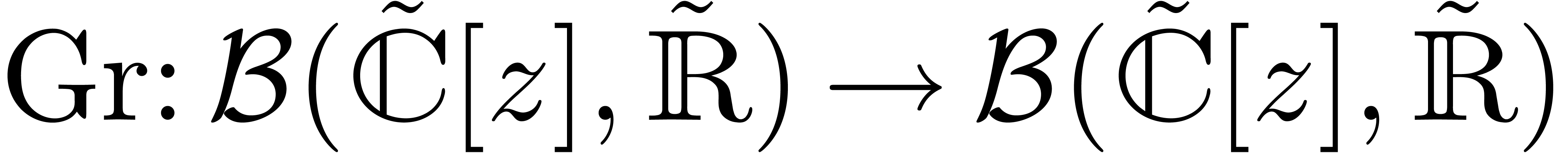 which satisfies the inclusion property
which satisfies the inclusion property
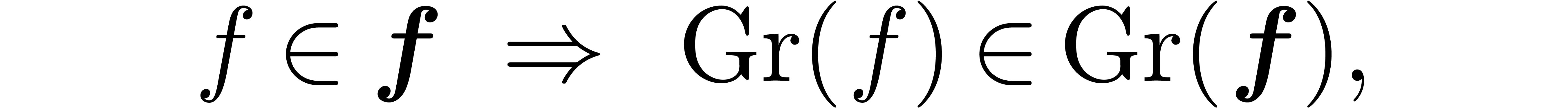
for all 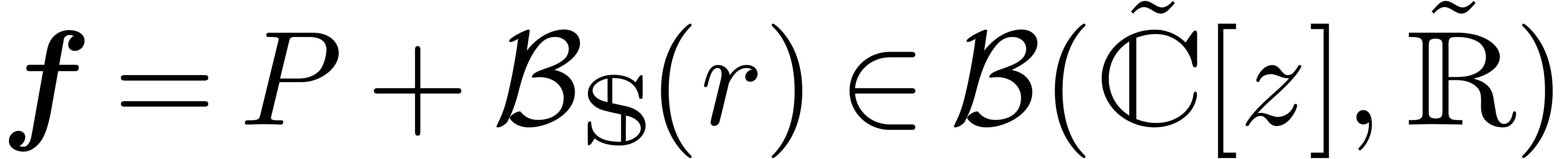 and
and  .
If
.
If 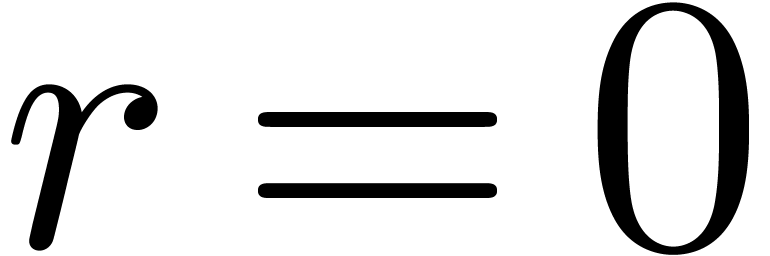 , then we may directly use
the formula
, then we may directly use
the formula 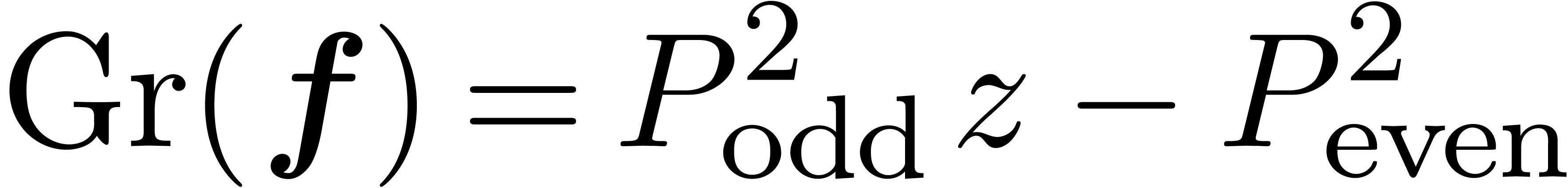 , assuming that
the squares are computed using the algorithm for ball multiplication in
section 2.5. In general, we take
, assuming that
the squares are computed using the algorithm for ball multiplication in
section 2.5. In general, we take
and claim that this definition satisfies the inclusion property. Indeed,
given  , there exists an
, there exists an  with
with 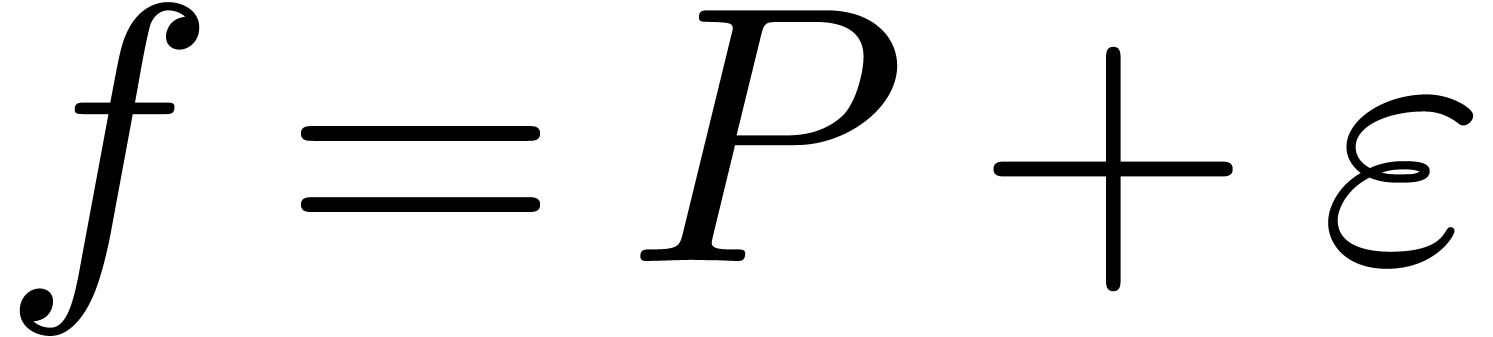 .
Hence,
.
Hence,
Since 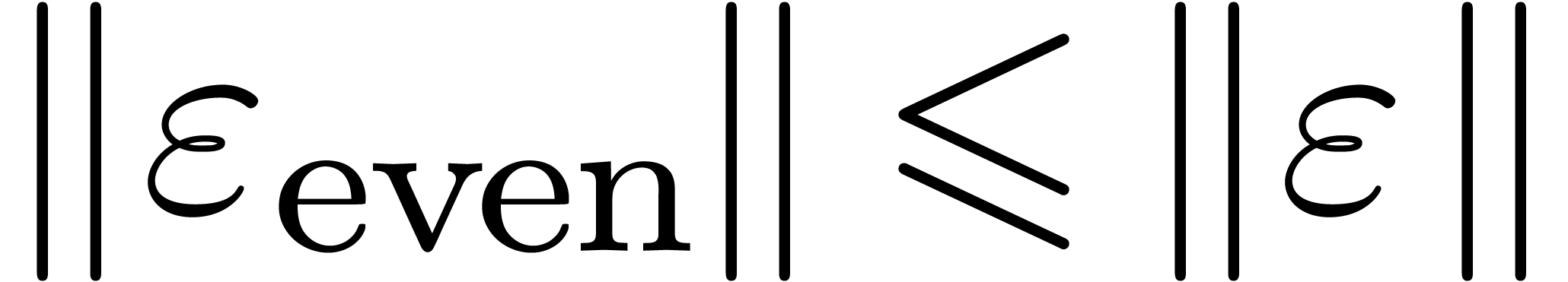 and
and 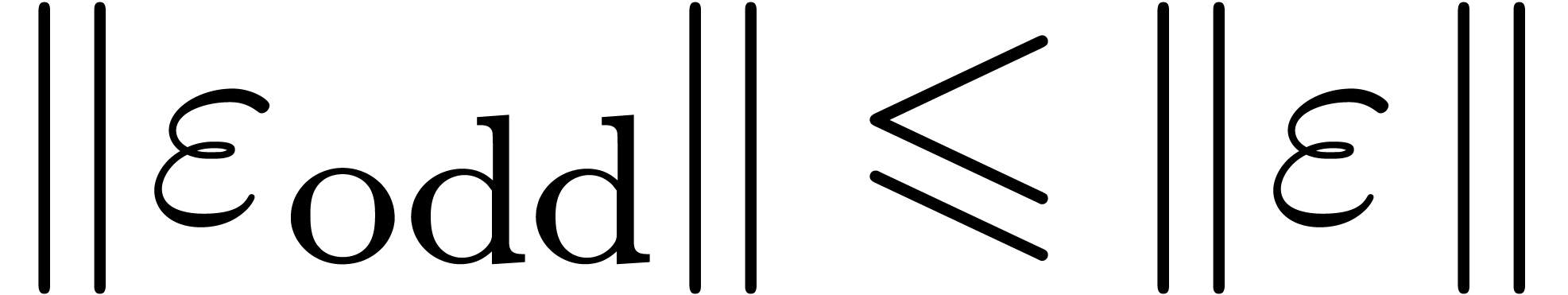 ,
we thus have
,
we thus have
This proves our claim.
Putting together the various pieces, we now have the following algorithm
for root counting. Optionally, one may add an extra integer parameter in
order to limit the number of recursive calls to, say, 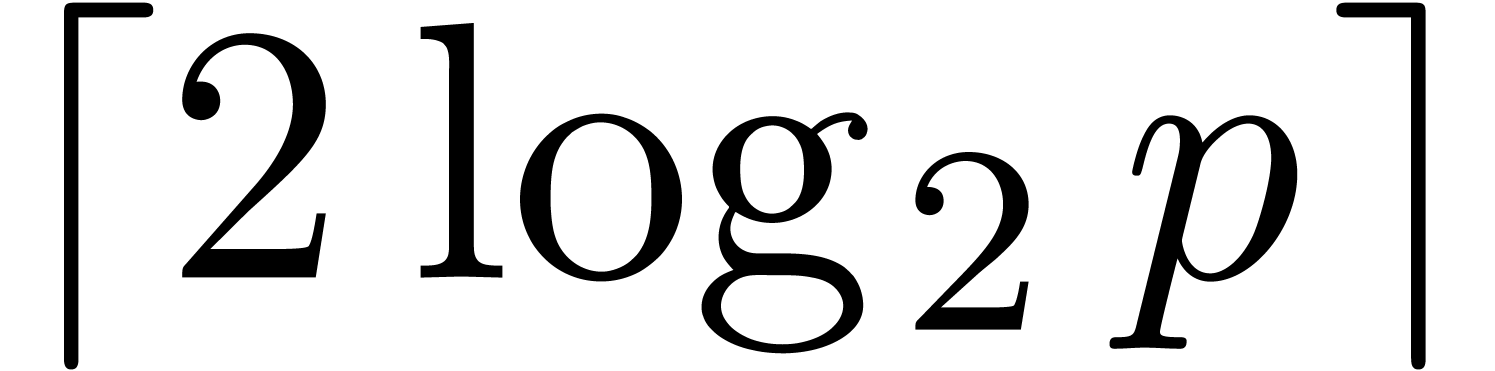 .
.
Algorithm 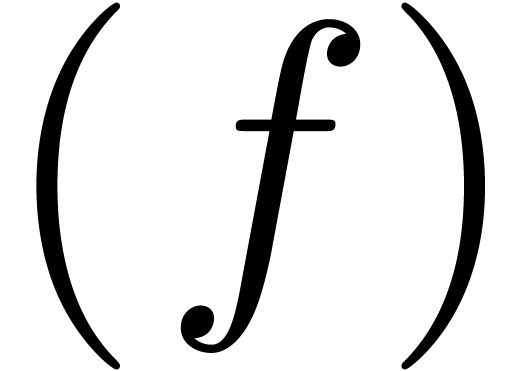
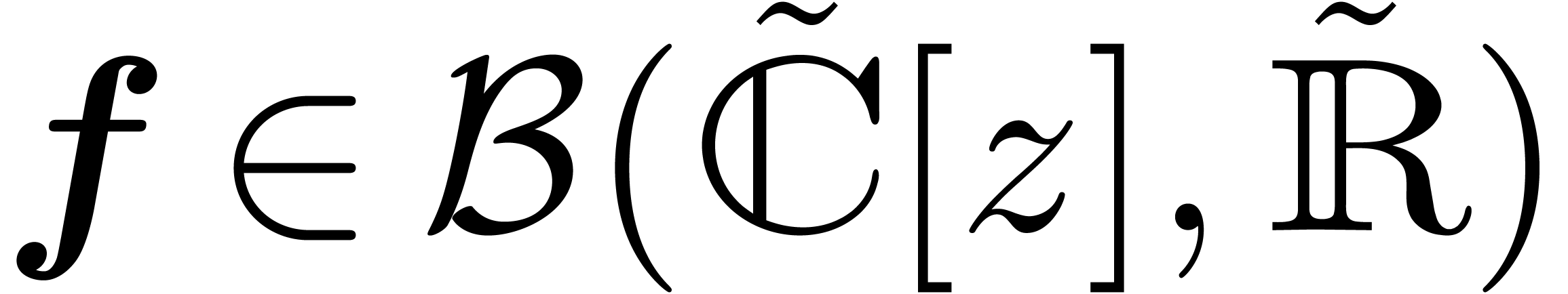
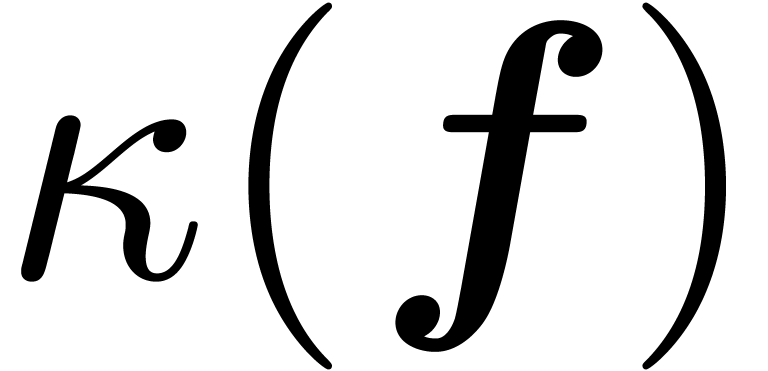 or failure
or failure
Let 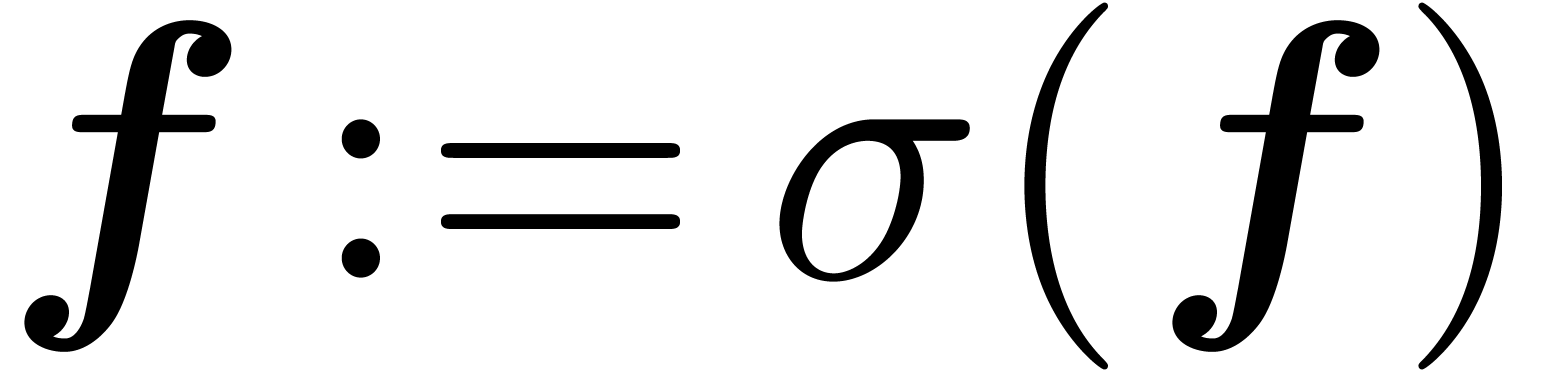 and write
and write 
If 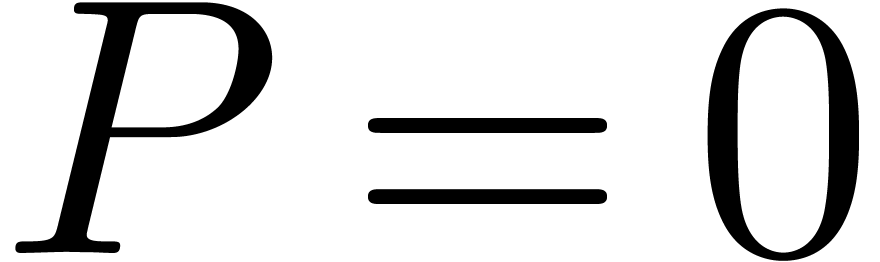 , then
abort
, then
abort
Let 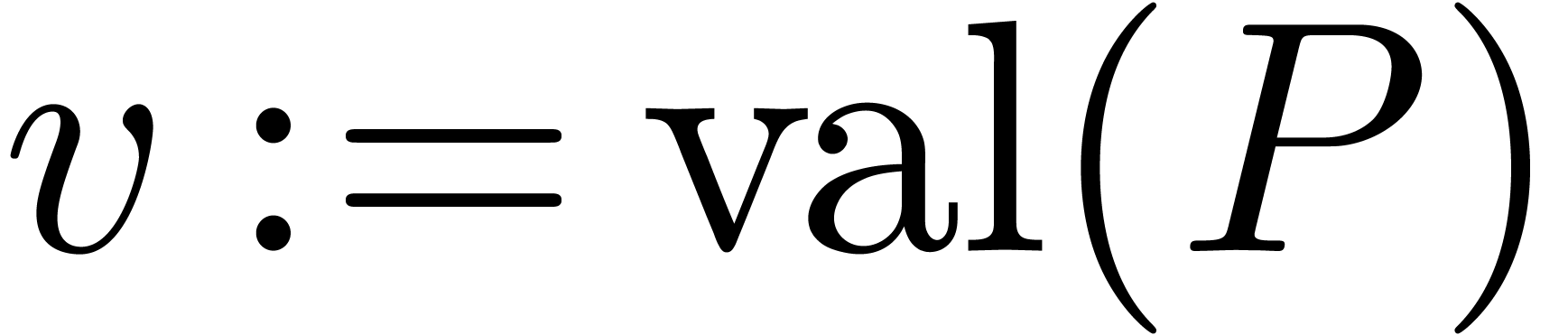 and
and 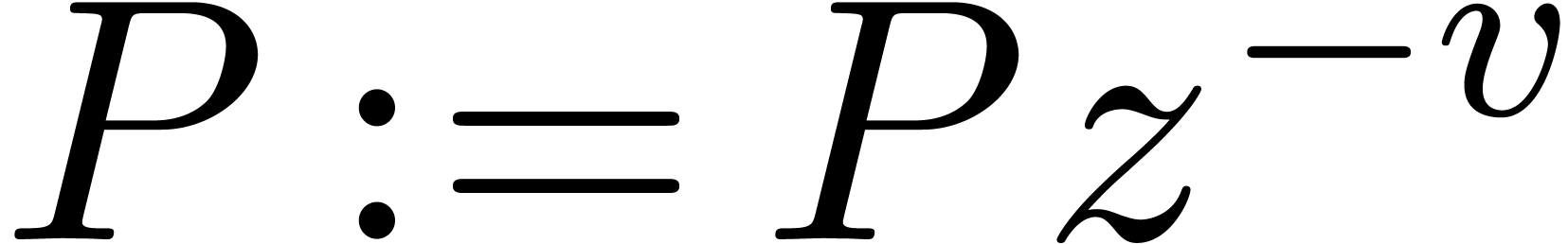
Let 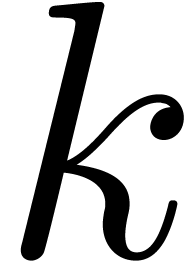 be such that
be such that 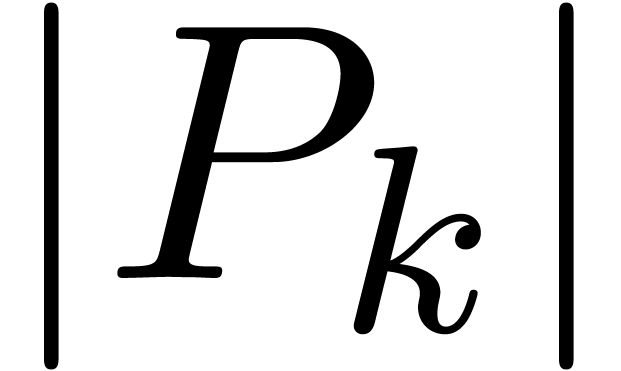 is
maximal
is
maximal
If 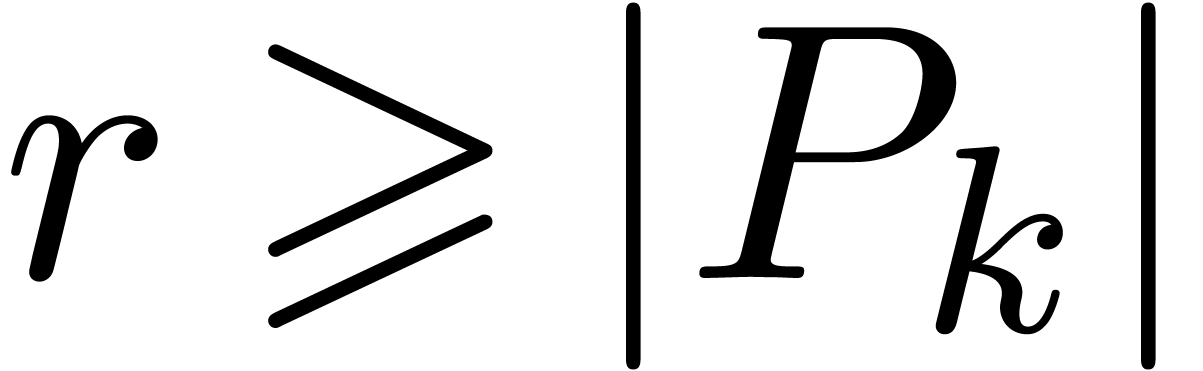 , then
abort
, then
abort
If 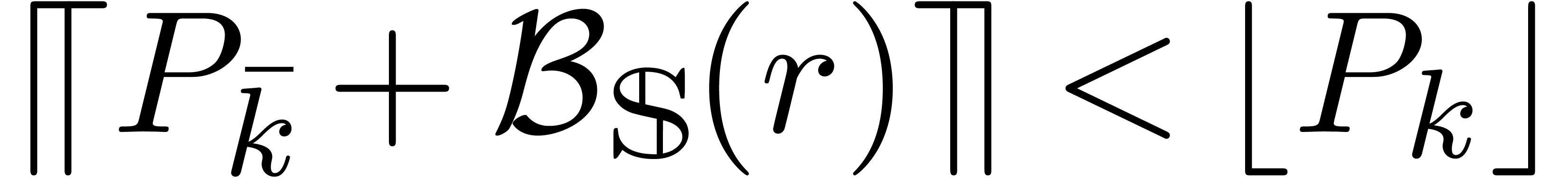 , then return
, then return 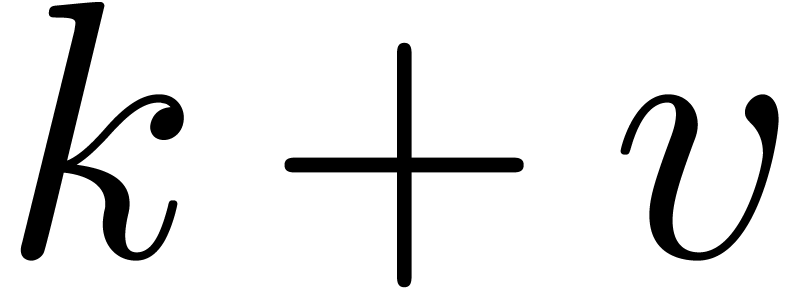
Return root-count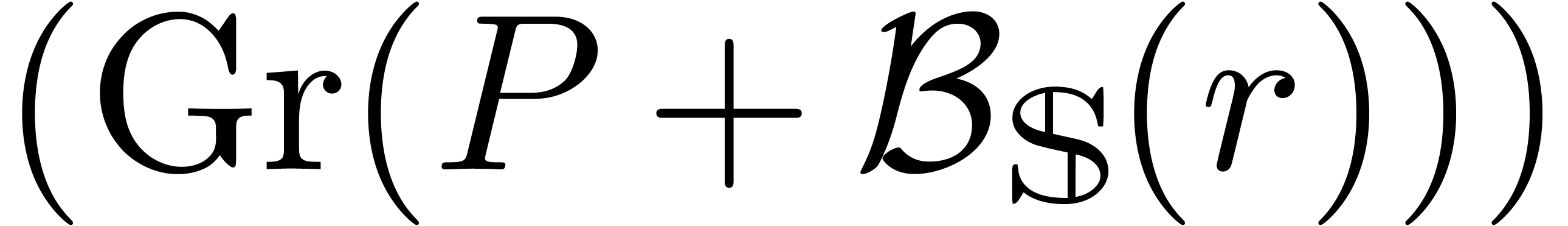
One nice property of this algorithm is that the degree of 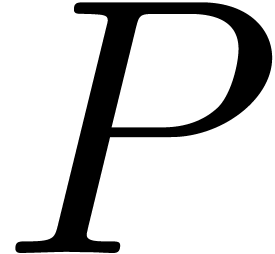 often quickly decreases during successive recursive calls.
More precisely, let
often quickly decreases during successive recursive calls.
More precisely, let  be the zeros of
be the zeros of 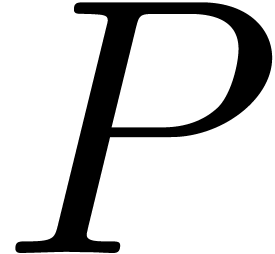 , ordered such that
, ordered such that  . Then
. Then
In the right hand size, all coefficients which smaller than 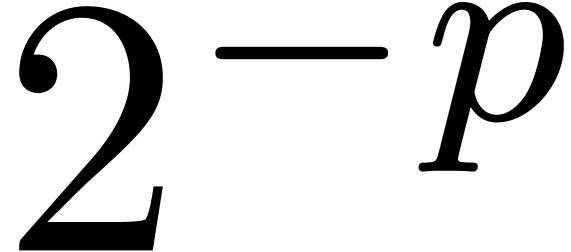 are discarded via simplification. Roughly speaking, for
are discarded via simplification. Roughly speaking, for
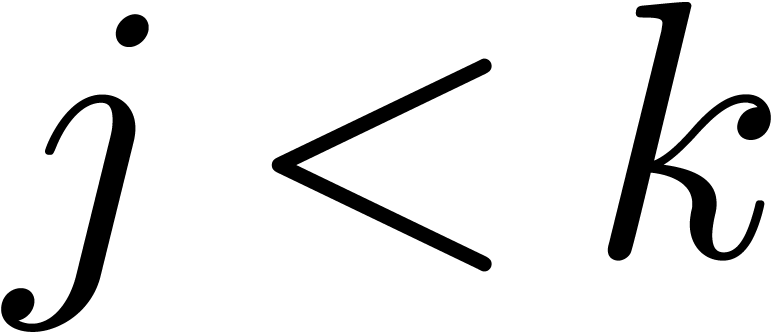 , the
, the  -th coefficient therefore only survives as long as
-th coefficient therefore only survives as long as
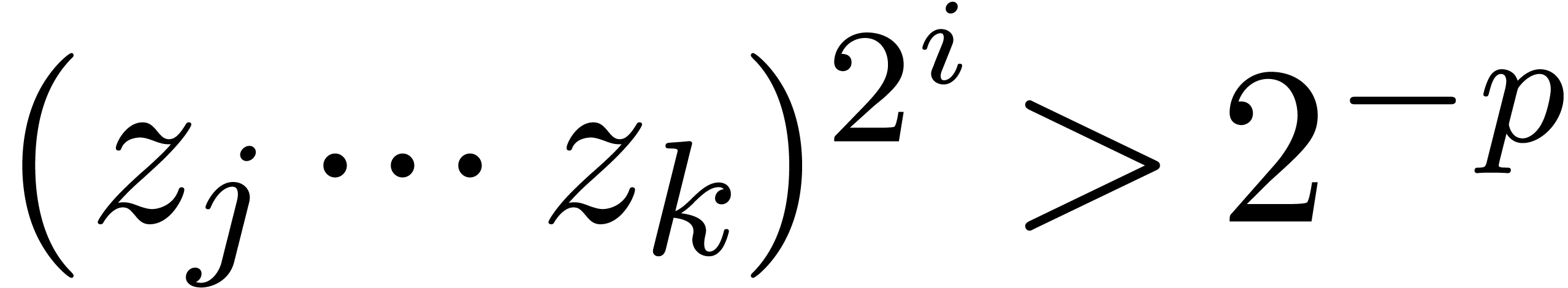 .
.
In our algorithm, satisfaction of the condition 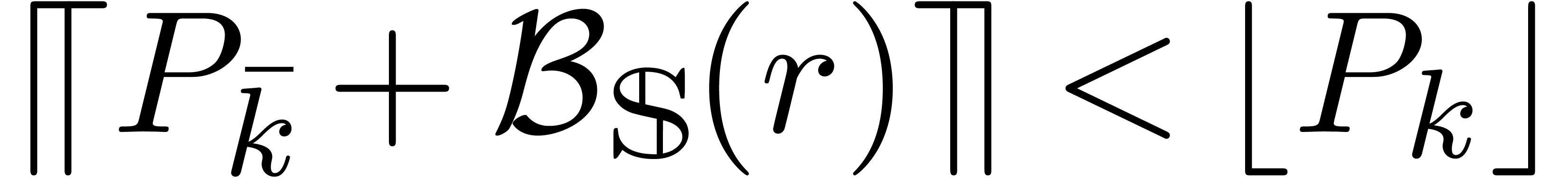 enabled us to produce a final certified root count. It may be possible
to design quick certified root counts for other favourable cases. Any
alternative root counting strategy may actually be tried before applying
our algorithm, or even at every stage as a replacement of the default
strategy based on the condition
enabled us to produce a final certified root count. It may be possible
to design quick certified root counts for other favourable cases. Any
alternative root counting strategy may actually be tried before applying
our algorithm, or even at every stage as a replacement of the default
strategy based on the condition 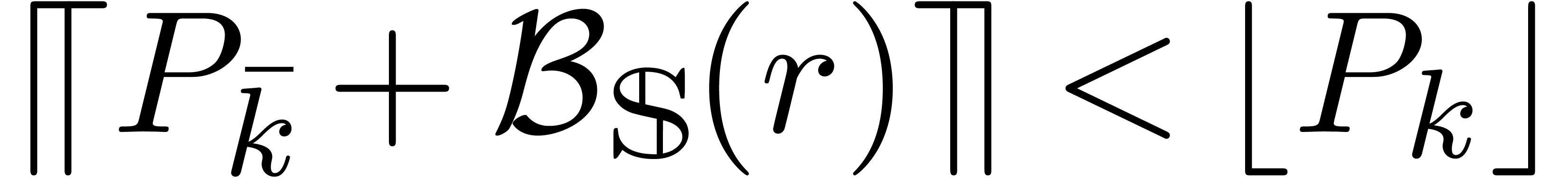 .
.
One natural alternative root counting strategy is based on the
evaluation of 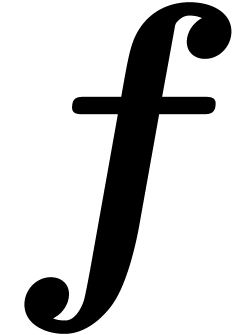 at many points on
at many points on  . Let
. Let 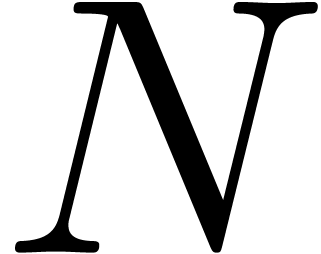 to be the
smallest power of two which is larger than
to be the
smallest power of two which is larger than 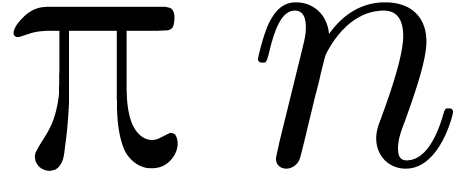 and
take
and
take 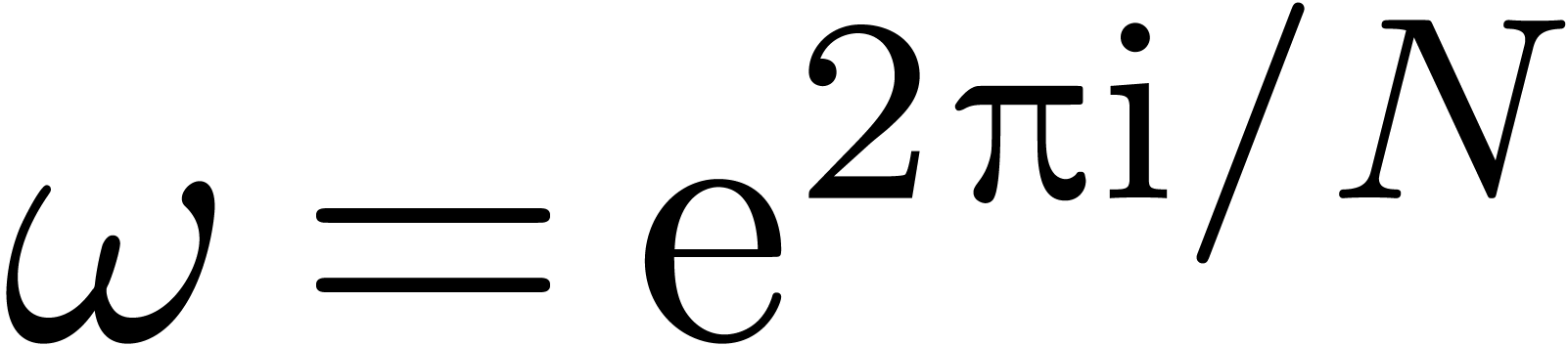 . Then we may
efficiently evaluate
. Then we may
efficiently evaluate 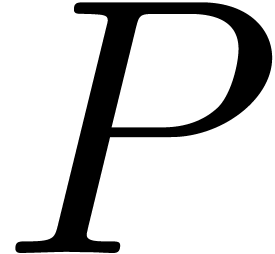 at
at 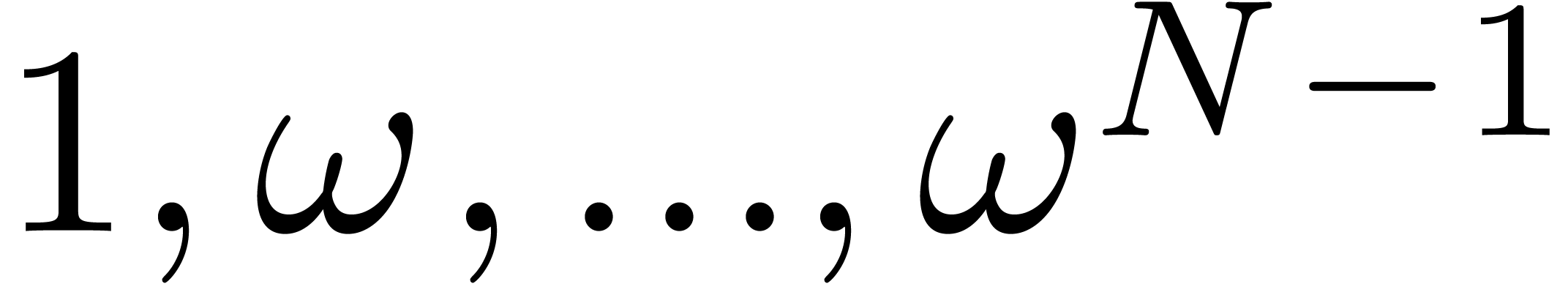 using the FFT. Furthermore, the distance between two successive powers
of
using the FFT. Furthermore, the distance between two successive powers
of  is bounded by
is bounded by 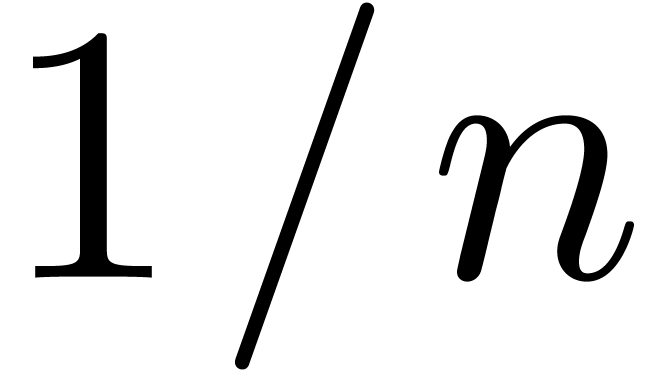 .
Now assume that
.
Now assume that
for all 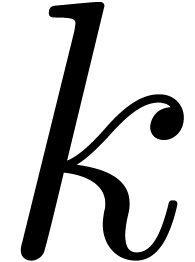 . Then it is
guaranteed that
. Then it is
guaranteed that 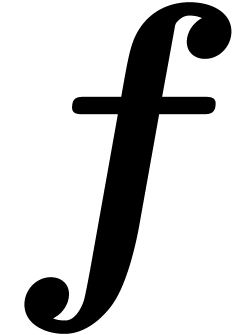 admits no zeros on
admits no zeros on  . Hence,
. Hence,
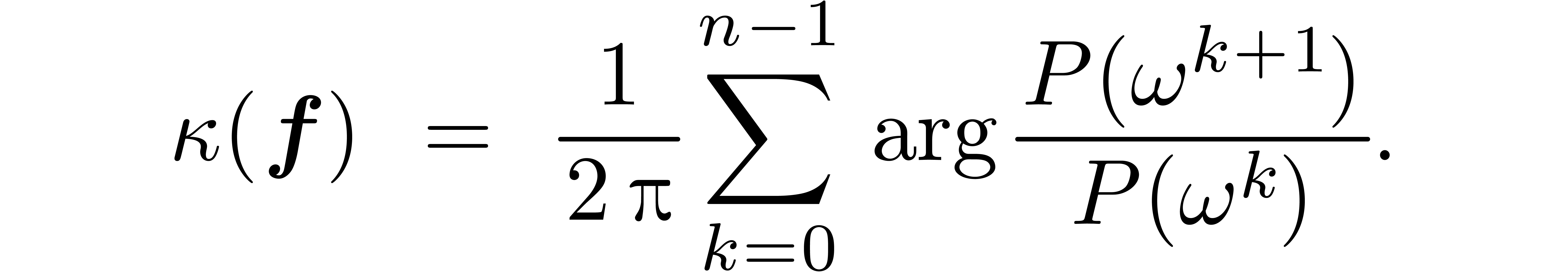
When multiplying the number of points 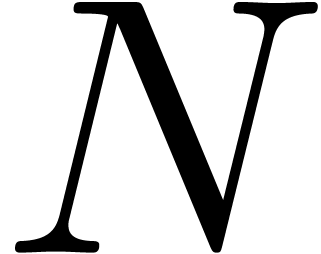 by a
constant
by a
constant 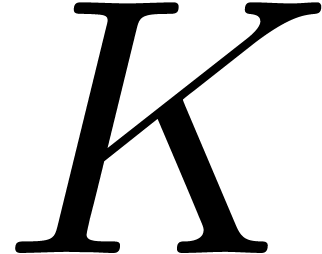 , we may replace
, we may replace
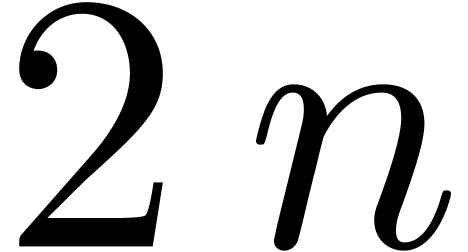 by
by 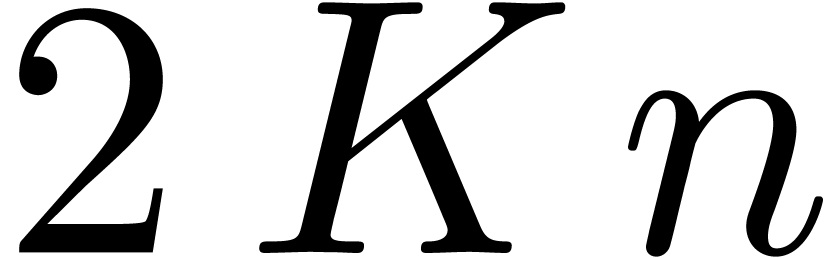 in the denominator of
(2). We may also consider the second order condition
in the denominator of
(2). We may also consider the second order condition
instead of (2), which requires the additional evaluation of
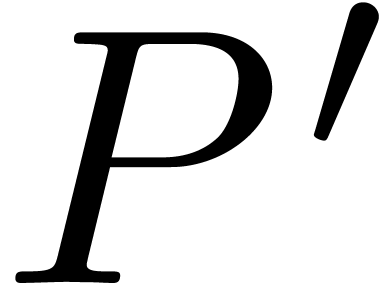 at the powers
at the powers 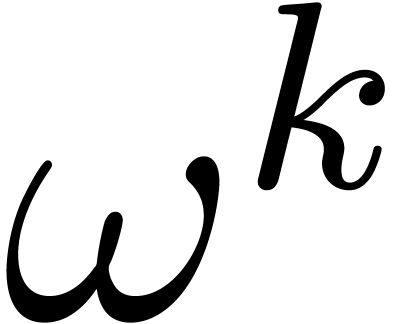 .
The conditions (2) and (3) have a reasonable
chance of being satisfied if the closest root of
.
The conditions (2) and (3) have a reasonable
chance of being satisfied if the closest root of 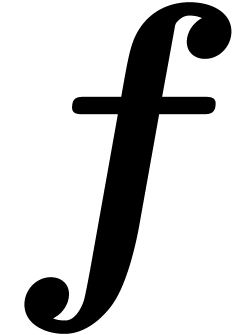 with respect to
with respect to  is at distance at least
is at distance at least 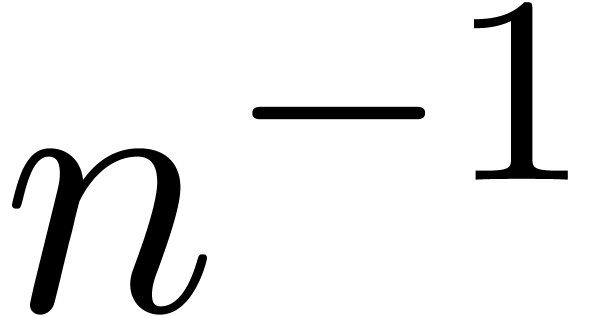 .
.
G. Alefeld and J. Herzberger. Introduction to interval analysis. Academic Press, New York, 1983.
ANSI/IEEE. IEEE standard for binary floating-point arithmetic. Technical report, ANSI/IEEE, New York, 2008. ANSI-IEEE Standard 754-2008. Revision of IEEE 754-1985, approved on June 12, 2008 by IEEE Standards Board.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
X. Gourdon. Combinatoire, algorithmique et géométrie des polynômes. PhD thesis, École polytechnique, 1996.
G. Hanrot, V. Lefèvre, K. Ryde, and P. Zimmermann. MPFR, a C library for multiple-precision floating-point computations with exact rounding. http://www.mpfr.org, 2000.
P. Kravanja and M. van Barel. Computing the zeros of analytic functions, volume 1727 of Lecture Notes in Mathematics. Springer-Verlag, 2000.
R.E. Moore, R.B. Kearfott, and M.J. Cloud. Introduction to Interval Analysis. SIAM Press, 2009.
R.E. Moore. Interval Analysis. Prentice Hall, Englewood Cliffs, N.J., 1966.
V. Y. Pan. Univariate polynomials: nearly optimal algorithms for numerical factorization and root-finding. J. Symbolic Comput., 33(5):701–733, 2002.
V. Pan and D. Bini. Polynomial and matrix computations. Birkhauser, 1994.
S.M. Rump. Verification methods: Rigorous results using floating-point arithmetic. Acta Numerica, 19:287–449, 2010.
A. Schönhage. The fundamental theorem of algebra in terms of computational complexity. Technical report, Math. Inst. Univ. of Tübingen, 1982.
J. van der Hoeven. Ball arithmetic. Technical report, HAL, 2009. http://hal.archives-ouvertes.fr/hal-00432152/fr/.