Towards semantic mathematical
editing |
|
| January 12, 2011 |
|
 . This work has
been supported by the ANR-09-JCJC-0098-01
. This work has
been supported by the ANR-09-JCJC-0098-01
Currently, there exists a big gap between formal computer-understandable mathematics and informal mathematics, as written by humans. When looking more closely, there are two important subproblems: making documents written by humans at least syntactically understandable for computers, and the formal verification of the actual mathematics in the documents. In this paper, we will focus on the first problem.
For the time being, most authors use TeX, LaTeX, or one of its
graphical front-ends in order to write documents with many
mathematical formulas. In the past decade, we have developed an
alternative wysiwyg system GNU TeXmacs, which is not based on TeX.
All these systems are only adequate for visual typesetting and do
not carry much semantics. Stated in the In recent versions of TeXmacs, we have started to integrate facilities for the semantic editing of formulas. In this paper, we will describe these facilities and expand on the underlying motivation and design choices. To go short, we continue to allow the user to enter formulas in a visually oriented way. In the background, we continuously run a packrat parser, which attempts to convert (potentially incomplete) formulas into content markup. As long as all formulas remain sufficiently correct, the editor can then both operate on a visual or semantic level, independently of the low-level representation being used. An important related topic, which will also be discussed at length, is the automatic correction of syntax errors in existing mathematical documents. In particular, the syntax corrector that we have implemented enables us to upgrade existing documents and test our parsing grammar on various books and papers from different sources. We will provide a detailed analysis of these experiments.
|
One major challenge for the design of mathematical text editors is the
possibility to give mathematical formulas more semantics. There are many
potential applications of mathematical texts with a richer semantics: it
would be easier and more robust to copy and paste formulas between a
text and a computer algebra system, one might search for formulas on
websites such as
Currently, most mathematicians write their documents in TeX, LaTeX, or one of its graphical front-ends [15, 17, 5, 29, 21]. Such documents usually focus on presentation and not on mathematical correctness, not even syntactic correctness. In the past decade, we have developed GNU TeXmacs [32, 33] as an alternative structured wysiwyg text editor. TeXmacs does not rely on LaTeX, and can be freely downloaded from http://www.texmacs.org. The main aims of TeXmacs are user-friendliness, high quality typesetting, and its use as an interface for external systems [12, 2, 13, 18]. However, until recently, mathematical formulas inside TeXmacs only carried presentation semantics.
Giving mathematical formulas more semantics can be regarded as a gradual process. Starting with formulas which only carry presentation semantics, we ultimately would like to reach the stage where all formulas can be checked by a formal proof checker [28, 30, 20, 19]. In between, the formulas might at least be correct from the syntactic point of view, or only involve non ambiguous symbols.
In this paper, we focus on techniques for making it easy for authors to
create papers in which all formulas are correct from the syntactic point
of view. In the  we
merely want to detect or enforce that the operator
we
merely want to detect or enforce that the operator  applies to
applies to  and
and  ;
we are not interested in the actual mathematical meaning of addition.
;
we are not interested in the actual mathematical meaning of addition.
If we are allowed to constraint the user to enter all texts in a way which is comfortable for the designer of the editor, then syntactic correctness can easily be achieved: we might constrain the user to directly enter content markup. Similarly, if the author is only allowed to write text in a specific mathematical sub-language (e.g. all formulas which can be parsed by some computer algebra system), then it might be possible to develop ad hoc tools which fulfill our requirements.
Therefore, the real challenge is to develop a general purpose
mathematical editor, which imposes minimal extra constraints on the user
with respect to a presentation-oriented editor, yet allows for the
production of syntactically correct documents. As often in the area of
user interfaces, there is a psychological factor in whether a particular
solution is perceived as satisfactory: certain hackers might happily
enter
One of the central ideas behind our approach is to stick as much as possible to an existing user friendly and presentation-oriented editor, while using a “syntax checker/corrector” in the background. This syntax checker will ensure that it always possible to formally parse the formulas in the document, while these formulas are represented using presentation markup. We will see that this is possible after a few minor modifications of the editor and the development of a suitable series of tools for the manipulation of formal languages. All our implementations were done in TeXmacs, but our techniques might be implemented in other editors.
An interesting related question is whether the production of syntactically correct documents is indeed best achieved during the editing phase: there might exist some magical algorithm for giving more semantics to most existing LaTeX documents. In this paper, we will also investigate this idea and single out some of the most important patterns which cause problems. Of course, from the perspective of a software with a non trivial user base, it is desirable that the provided syntax corrector can also be used in order to upgrade existing documents.
The paper is organized into two main parts: the first part (sections 2, 4 and 3) does not depend on the packrat-based formal language tools, whereas the second part (sections 5, 6 and 7) crucially depends on these tools. The last section 8 contains some applications and ideas for future developments.
In section 2, we first review the specificities of various formats for mathematical formulas. In section 3, we discuss elementary techniques for giving existing documents more semantics and the main obstacles encountered in this process. In section 4, we present a few minimal changes which were made inside TeXmacs in order to remedy some of these obstacles.
In section 5, we recall the concept of a packrat parser [9, 10]. This kind of grammars are both natural to specify, quick to parse and convenient for the specification of on-the-fly grammars, which can be locally modified inside a text. We have implemented a formal language facility inside TeXmacs, which is based on packrat parsing, but also contains a few additional features. In section 6, we will discuss the development of a standard grammar for mathematics, and different approaches for customizating this grammar. In section 7, we present several grammar-assisted editing tools which have been implemented inside TeXmacs.
In order to analyze the adequacy of the proposals in this paper, we have made a selection of a few books and other documents from various sources, and tested our algorithms on this material (1303 pages with 59504 formulas in total). These experiments, which are discussed in detail in sections 3.4 and 6.4, have given us a better understanding of the most common syntactical errors, how to correct them, the quality of our parsing grammar and remaining challenges.
We have one our best to make our experiments as reproducible as
possible. Our results were obtained using the SVN development revision
4088 of TeXmacs, which should be more or less equivalent to the unstable
release 1.0.7.10. For detailed information on how to use the semantic
editing features, please consult the integrated documentation by
clicking on the menu entry 
http://www.texmacs.org/Data/semedit-data.tar.gz
http://perso.univ-rennes1.fr/marie-francoise.roy/bpr-ed2-posted2.tar.gz
As a disclaimer, we would like to add that we take responsibility for any bad usage that the authors may have made of TeXmacs. Except for a few genuine typos, the semantic errors which were detected in their work are mostly due to current imperfections in TeXmacs.
Taking into account the numerous existing formula editors, it is a subtle task to compare every single idea in this paper to previous work. Indeed, many of the individual ideas and remarks can probably be traced back to earlier implementations. However, such earlier implementations are often experiments in a more restricted context. We recall that the aim of the current paper is to provide a general purpose tool with the average “working mathematician” (or scientist) as its prototype user. The main challenge is thus to fit the various building bricks together such that this goal is achieved.
Nevertheless, we would like to mention a few people who directly
influenced this paper. First of all, the decision to make the user
interface of TeXmacs purely graphically oriented was inspired by a talk
of O.
We finally notice that some semantic editing features are integrated
into the proprietary computer algebra systems
The current standard for mathematical documents is TeX/LaTeX [15, 17]. There are three main features which make TeX convenient for typing mathematical documents:
The use of a cryptic, yet suggestive pseudo-language for ASCII source code.
The possibility for the user to extend the language with new macros.
A high typographic quality.
In addition, LaTeX provides the user with some rudimentary support for structuring documents.
One major drawback of TeX/LaTeX is that it is not really a data format, but rather a programming language. This language is very unconventional in the sense that it does not admit a formal syntax. Indeed, the syntax of TeX can be “hacked” on the fly, and may for instance depend on the parity of the current page. This is actually one important reason for the “success” of the system: the ill-defined syntax makes it very hard to reliably convert existing documents into other formats. In particular, the only reliable parser for TeX is TeX itself.
If, for convenience, we want to consider TeX/LaTeX as a format, then we have to restrict ourselves to a sublanguage, on which we impose severe limits to the definability of new macros and syntax extensions. Unfortunately, in practice, few existing documents conform to such more rigourous versions of LaTeX, so the conversion of TeX/LaTeX to other formats necessarily involves a certain amount of heuristics. This is even true for papers which conform to a journal style with dedicated macros, since the user is not forced to use only a restricted subset of the available primitives.
Even if we ignore the inconsistent syntax of TeX, another drawback of TeX/LaTeX is its lack of formal semantics. Consider for instance the TeX formulas $a(b+c)$ and $f(x+y)$. Are a and f variables or functions? In the formulas $\sum_i a_i+C$ and $\sum_i a_i+b_i$, what is the scope of the big summation? Should we consider $[a,b[$ to be incorrect, or did we intend to write a french-style interval? Some heuristics for answering these questions will be discussed below.
There are more problems with TeX/LaTeX, such as inconsistencies in semantics of the many existing style packages, but these problems will be of lesser importance for what follows.
The
Having a standard format for mathematics on the web, which assumes
compatibility with existing
Defining a DTD with a precise semantics, which is sufficient for the representation of mathematical formulas.
In particular, the
In fact,
For instance, returning to the TeX formula $a(b+c)$, the typical presentation markup would be as follows
<mrow>
<mi>a</mi>
<mo>⁢<!-- ⁢ --></mo>
<mrow>
<mo>(</mo>
<mi>b</mi>
<mo>+</mo>
<mi>c</mi>
<mo>)</mo>
</mrow>
</mrow> |
We observe two interesting things here: first of all, the invisible
multiplication makes it clear that we intended to multiply  with
with  in the formula
in the formula 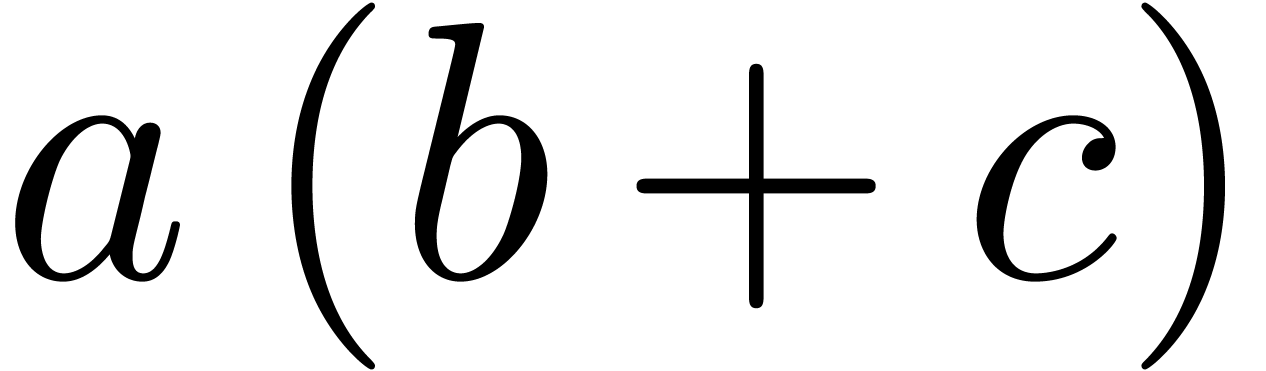 . Secondly, the (optional) inner <mrow>
and </mrow> suggest the scope and intended meaning
of the brackets.
. Secondly, the (optional) inner <mrow>
and </mrow> suggest the scope and intended meaning
of the brackets.
In principle, the above piece of presentation markup therefore already carries enough semantics so as to produce the corresponding content markup:
<apply>
<times/>
<ci>a<ci>
<apply>
<plus/>
<ci>b</ci>
<ci>c</ci>
</apply>
</apply> |
This fragment of code can be regarded as a verbose variant of the
(* a (+ b c)) |
More generally, as illustrated by the above examples,
The three main objects of the original TeXmacs project were the following:
Provide a free and user friendly wysiwyg editor for mathematical formulas.
Provide a typesetting quality which is as least as good as the quality of TeX.
Make it possible to use TeXmacs as an interface for other software, such as computer algebra systems, while keeping a good typesetting quality for large formulas.
One consequence of the first point is that we require an internal format
for formulas which is not read-only, but also suitable for
modifications. For a wysiwyg editor, it is also more convenient to work
with tree representations of documents, rather than ASCII strings.
TeXmacs provides three ways to “serialize” internal trees as
strings (native human readable, XML and
In order to be as compatible with TeX/LaTeX as possible, the original
internal TeXmacs format very much corresponded to a “clean”
tree representation for TeX/LaTeX documents. Some drawbacks of TeX, such
as lacking scopes of brackets and big operators, were therefore also
present in TeXmacs. On the other hand, TeXmacs incites users to make a
distinction between multiplication and function application, which is
important for the use of TeXmacs as an interface to computer algebra
systems. For instance, 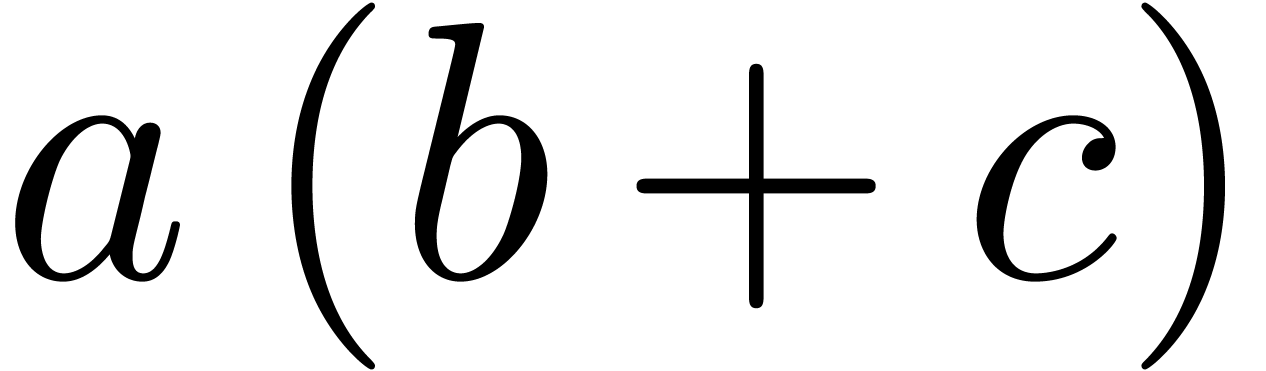 is entered by typing
a*(b+c), and internally
represented as a string leaf
is entered by typing
a*(b+c), and internally
represented as a string leaf
a*(b+c) |
in all TeXmacs versions prior to 1.0.7.6. More generally, TeXmacs
provides non ambiguous symbols for various mathematical constants ( ,
,  ,
,
 , etc.) and
operators. However, as a general rule, traditional TeXmacs documents
remain presentation oriented.
, etc.) and
operators. However, as a general rule, traditional TeXmacs documents
remain presentation oriented.
There are many other formats for the machine representation of
mathematical texts.
For some applications, such as automatic theorem proving [28,
30, 20, 19] and communication
between computer algebra systems, it is important to develop
mathematical data formats with even more semantics. Some initiatives in
this direction are
The multiplication versus function application ambiguity mentioned in section 2.1 is probably the most important obstacle to the automatic association of a semantics to mathematical formulas. There are several other annoying notational ambiguities, which are mostly due to the use of the same glyph for different purposes. In this section, we will list the most frequent ambiguities, which were encountered in our own documents and in a collection of third party documents to be described in section 3.4 below.
Besides multiplication and function application, there are several other invisible operators and symbols:
Invisible separators, as in matrix or tensor notation  .
.
Invisible addition, as in  .
.
Invisible “wildcards”, as in the increment
operator 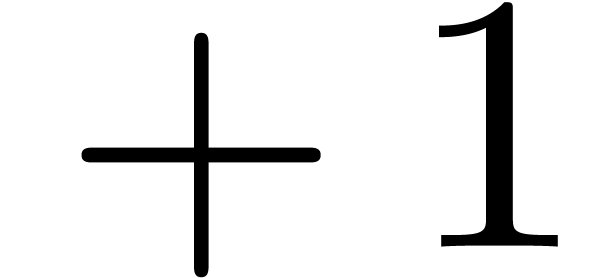 (also denoted by
(also denoted by  )
)
Invisible brackets, for forced matching if we want to omit a bracket.
Invisible ellipses as in the center of the matrix 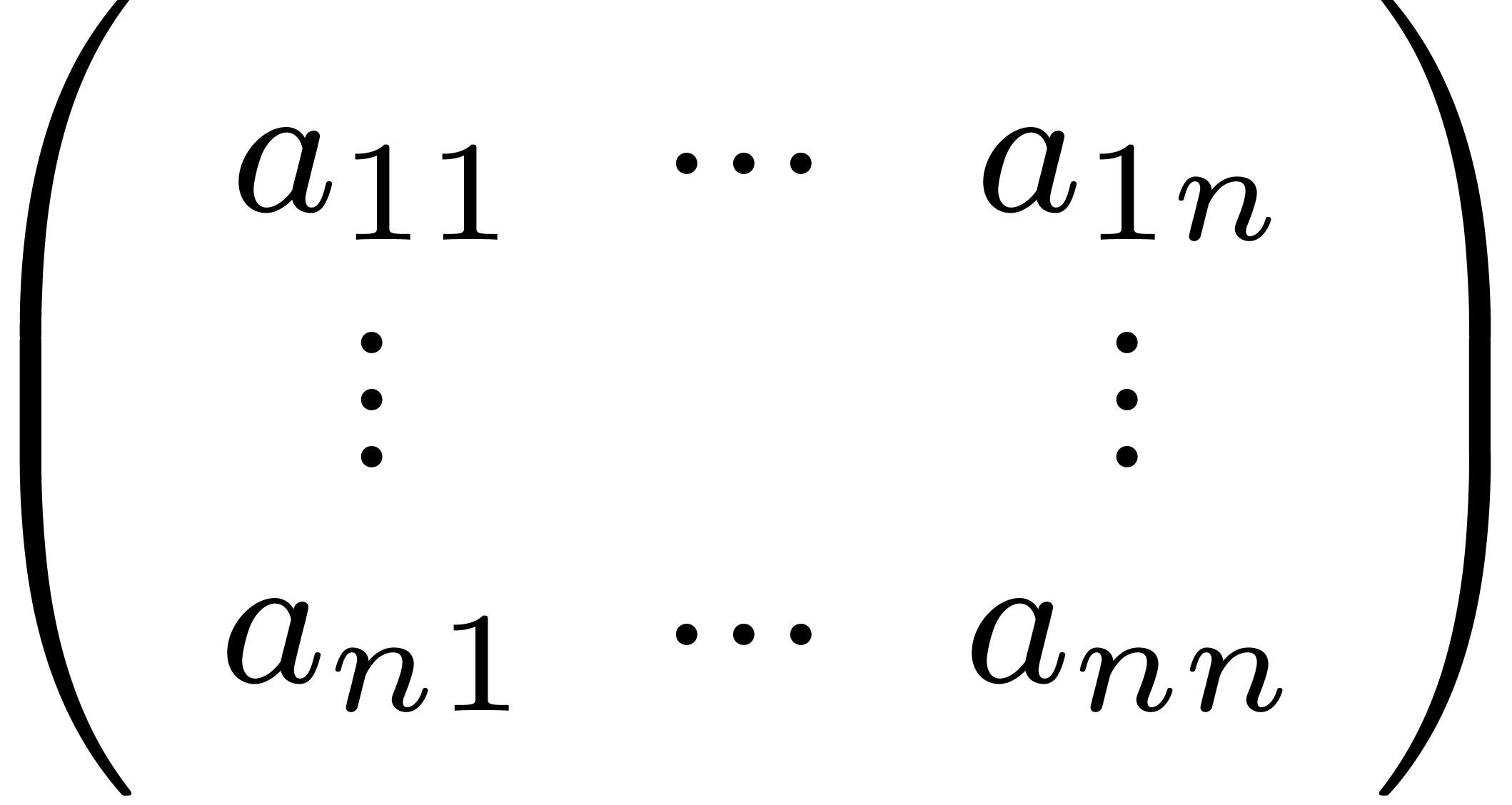 .
.
Invisible zeros as in 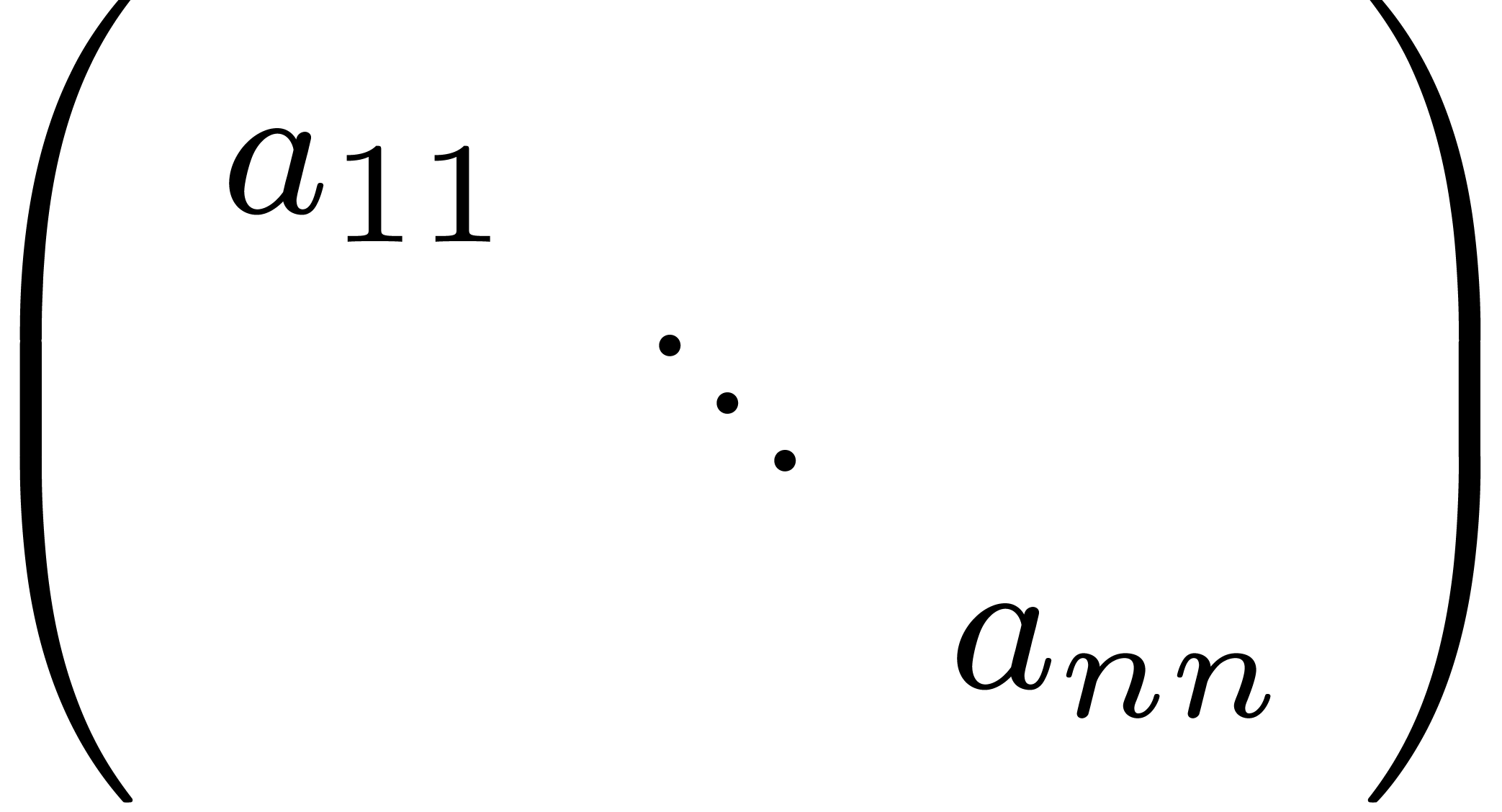 .
.
Invisible operators have been incorporated in the  and explicit in formulas such as
and explicit in formulas such as  or
or 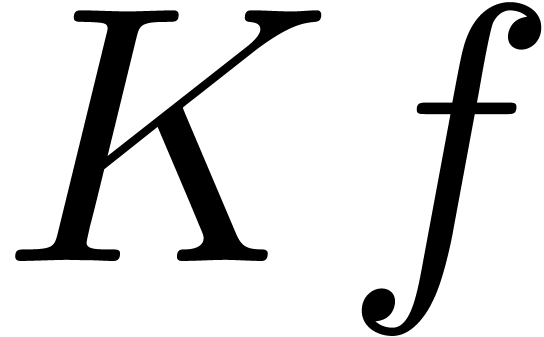 .
.
Vertical bars are used in many circumstances:
As brackets in absolute values  or
“ket” notation
or
“ket” notation 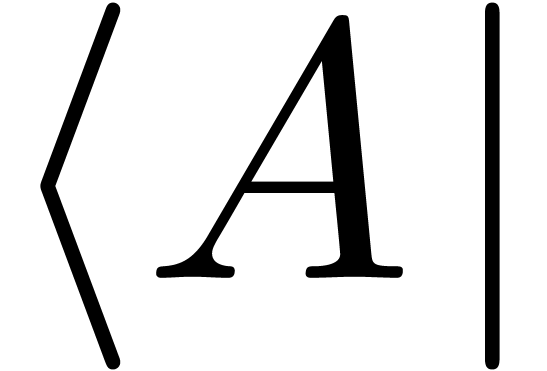 .
.
As “such that” separators in sets 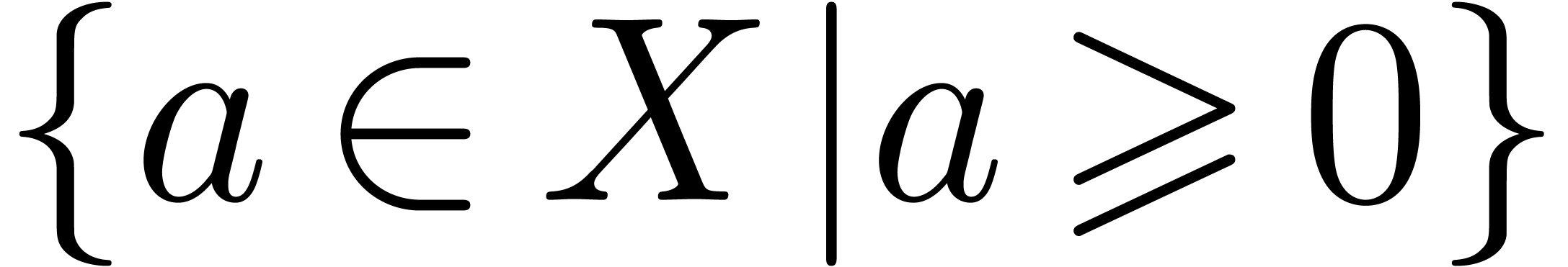 or lists.
or lists.
As the “divides” predicate 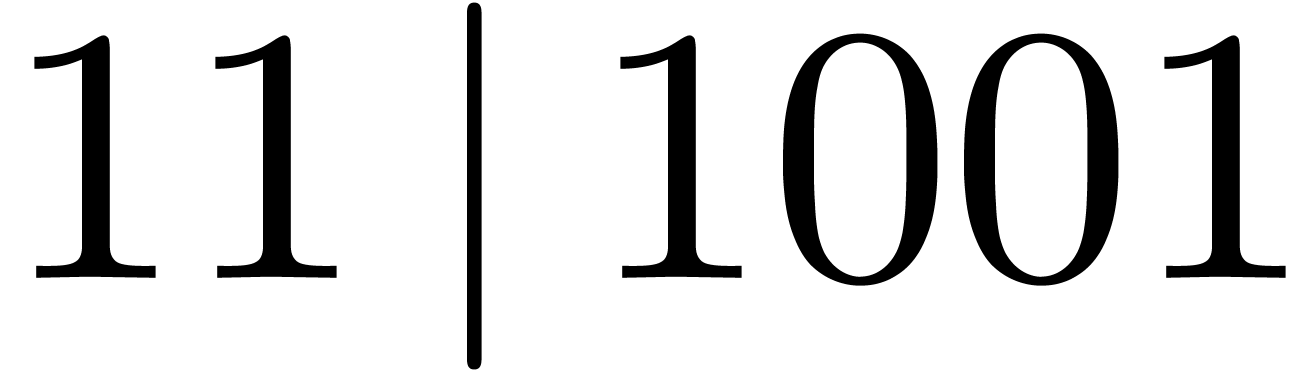 (both in binary and decimal notation).
(both in binary and decimal notation).
As separators  .
.
For restricting domains or images of applications: 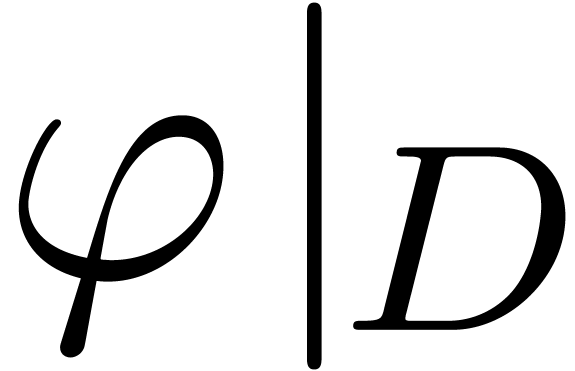 ,
, 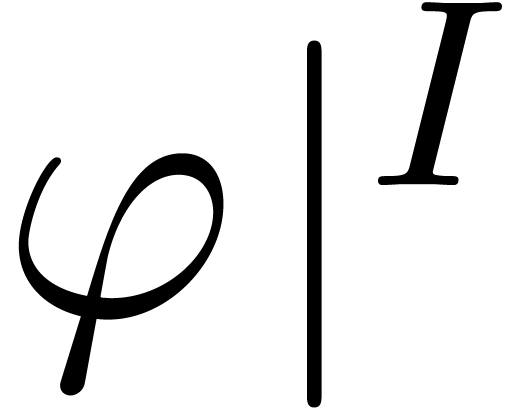 .
.
The possibility to use bars as brackets is particularly problematic for parsers, since it is not known whether we are dealing with an opening bracket, a closing bracket, or no bracket at all.
The comma may either be a separator, as in 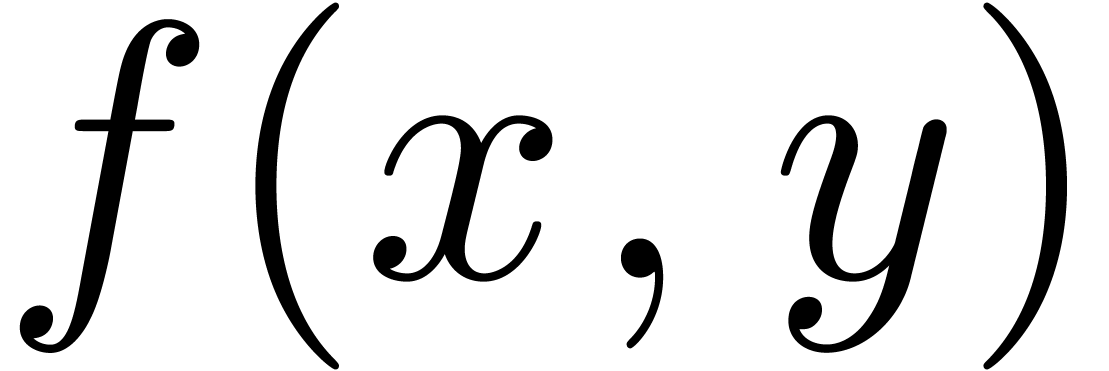 , or a decimal comma, as in
, or a decimal comma, as in 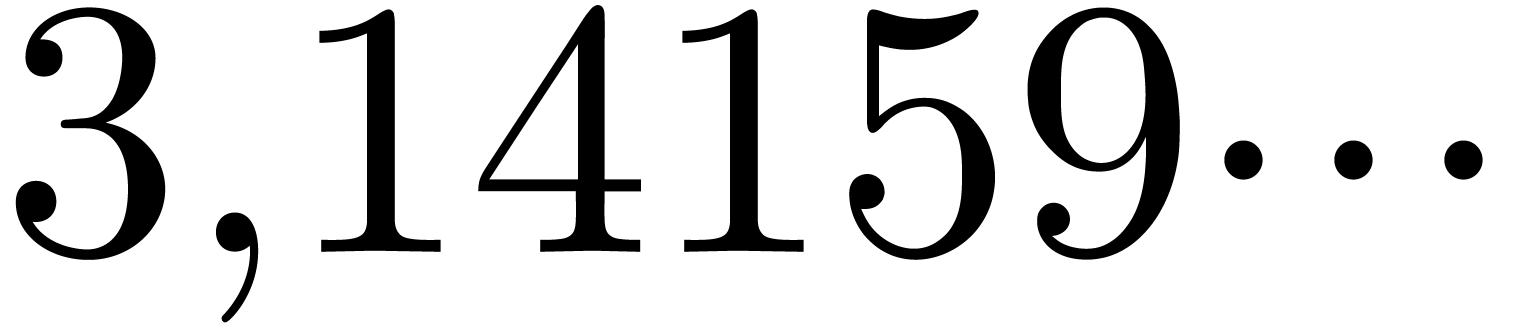 , or a grouping symbol, as in
, or a grouping symbol, as in 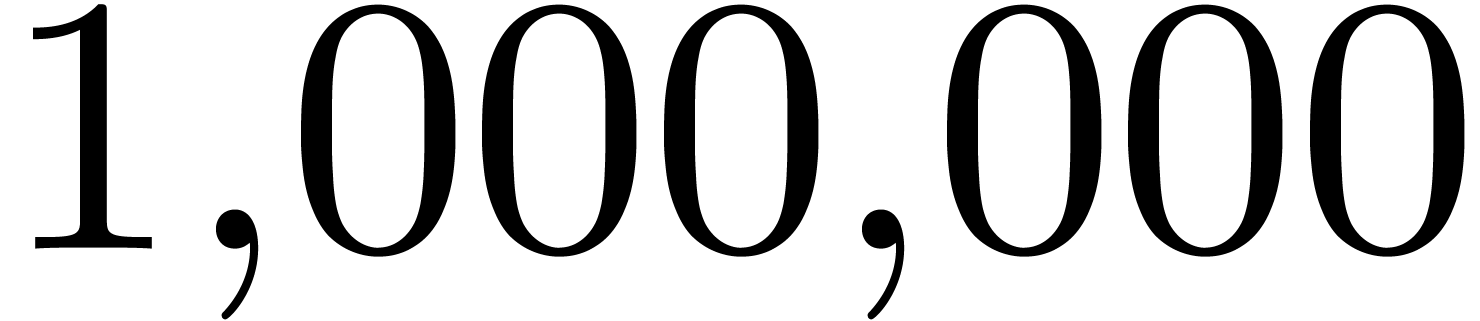 . The period symbol
“.” can be used instead of a comma in numbers, but
also as a data access operator
. The period symbol
“.” can be used instead of a comma in numbers, but
also as a data access operator 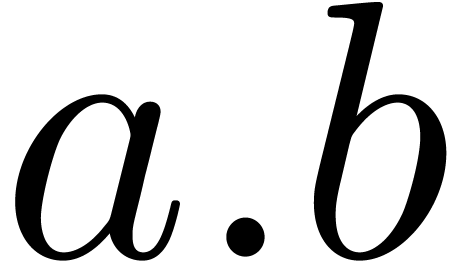 ,
or as a connector in lambda expressions
,
or as a connector in lambda expressions 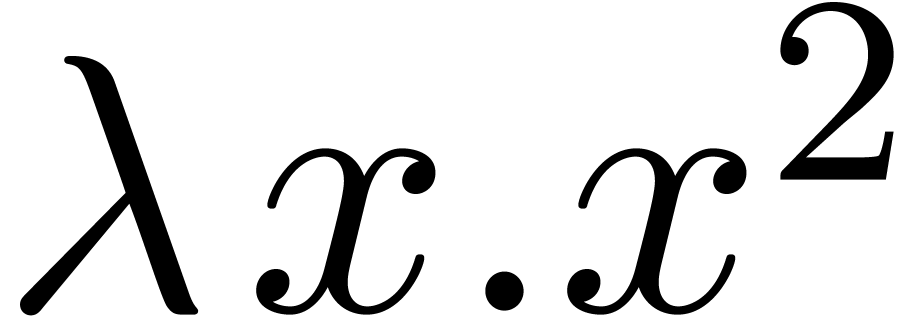 . Moreover, in the formula
. Moreover, in the formula
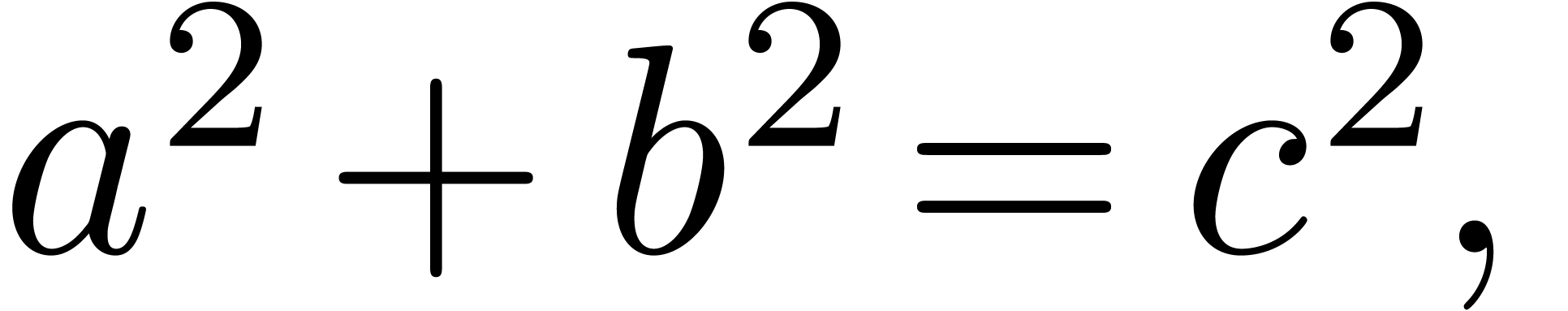
ponctuation is used in the traditional, non-mathematical way. The
semicolon “ ”
is sometimes used as an alternative for such that (example:
”
is sometimes used as an alternative for such that (example: 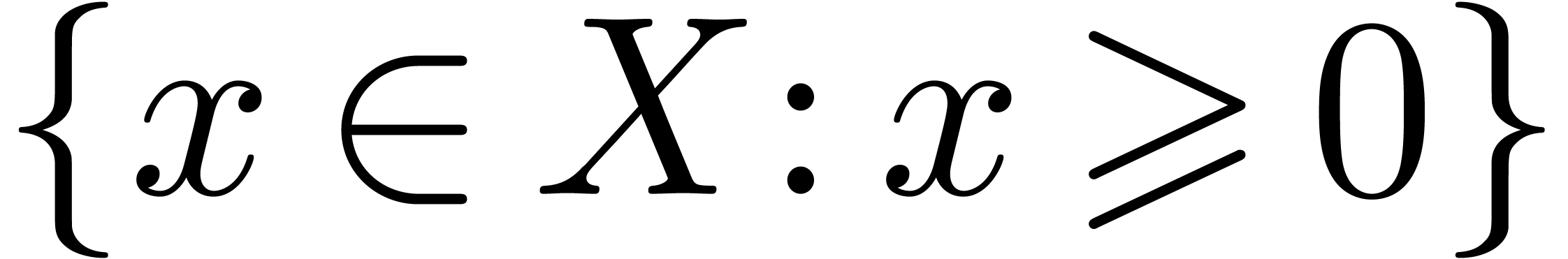 ), but might also indicate
division or the binary infix “of type”, as in
), but might also indicate
division or the binary infix “of type”, as in  .
.
In what follows, homoglyphs will refer to two semantically different symbols which are graphically depicted by the same glyph (and a potentially different spacing). In particular, the various invisible operators mentioned above are homoglyphs. Some other common homoglyphs are as follows:
The backslash  is often used for
“subtraction” of sets
is often used for
“subtraction” of sets 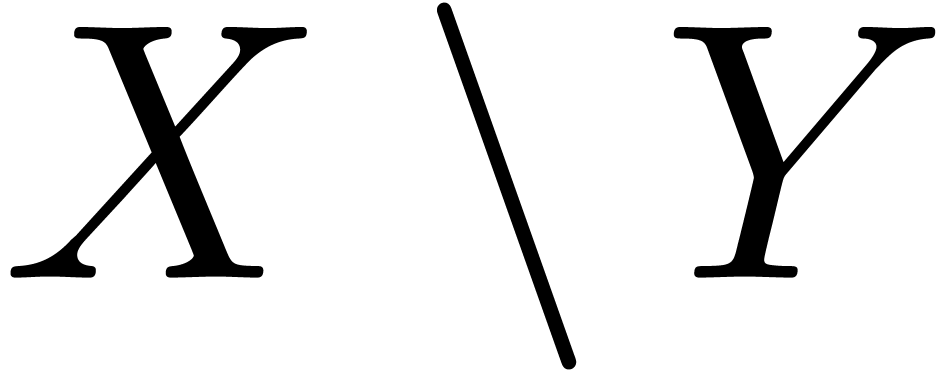 .
.
The dot  can be used as a symbol for
multiplication (example:
can be used as a symbol for
multiplication (example:  )
or as a wildcard (example: the norm
)
or as a wildcard (example: the norm 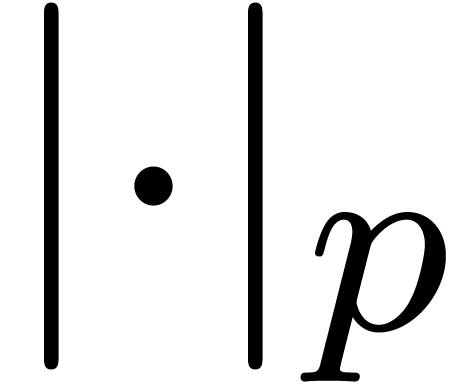 ).
).
The wedge  can be used as the logical
and operator or as the wedge product.
can be used as the logical
and operator or as the wedge product.
It should be noticed that
Authors who are not aware of the ambiguities described in the previous section are inclined to produce documents with syntax errors. Following TeX/LaTeX habits, some authors consistently omit multiplications and function applications. Others systematically replace multiplications by function applications. Besides errors due to ambiguities, the following kinds of errors are also quite common:
Inside TeXmacs, where we recall that spaces correspond to function application, users often leave superfluous spaces at the end of formulas (after changing their mind on completing a formula) or around operators (following habits for typing ASCII text).
In wysiwyg editors, context changes (such as font changes, or switches between text mode and math mode) are invisible. Even though TeXmacs provides visual hints to indicate the current context, misplaced context changes are a common mistake. Using LaTeX notation, the most common erroneous or inappropriate patterns are as follows:
Misplaced parts: \begin{math}f(x\end{math}).
Breaks: \begin{math}a+\end{math}\begin{math}b\end{math}.
Redundancies I: \begin{math}a+\begin{math}b\end{math}\end{math}.
Redundancies II: \begin{math}\text{hi}\end{math}.
Notice that some of these patterns are introduced in a natural way through certain operations, such as copy and paste, if no special routines are implemented in order to avoid this kind of nuisance.
Both in ASCII-based and wysiwyg presentation-oriented editors,
there is no reliable way to detect matching brackets, if no
special markup is introduced to distinguish between opening and
closing brackets. A reasonable heuristic is that opening and
closing brackets should be of the same “type”, such as
 and
and  or
or  and
and  .
However, this heuristic is violated for several common notations:
.
However, this heuristic is violated for several common notations:
Interval notation 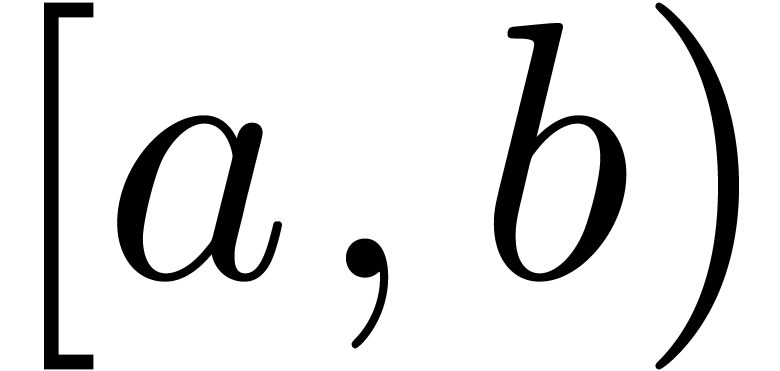 or
or 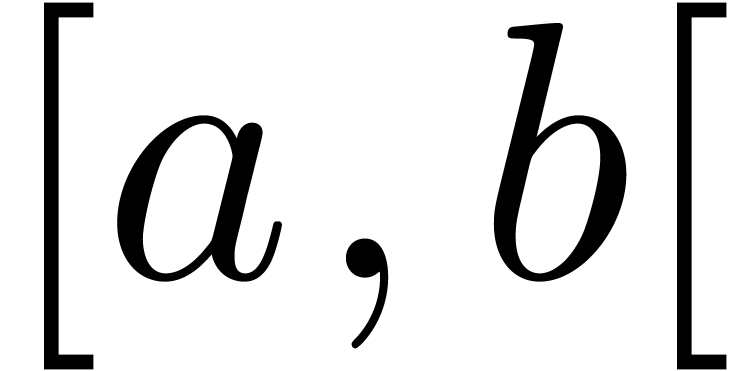 .
.
Ket notation 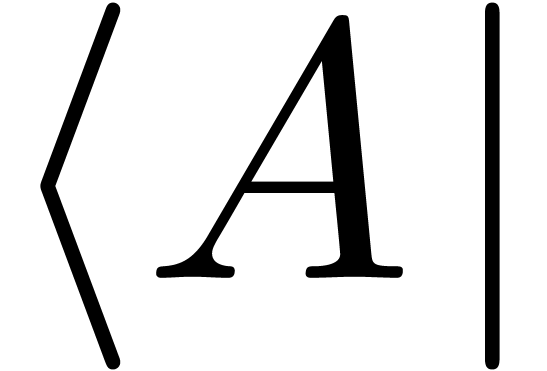 .
.
Absolute values are also particularly difficult to handle, since the opening and closing brackets coincide.
If no special markup is present to indicate the scope of a big operator, then it is difficult to determine appropriate scopes in formulas such as \sum_i a_i + K and \sum_i a_i + b_i. Although TeXmacs provided an invisible closing bracket, users (including ourselves) tended to ignore or misuse it (of course, this really means that the introduction of invisible closing brackets was not the right solution to the scoping problem).
One common aspect of all these errors is that authors who only care about presentation will usually not notice them at all: the printed versions of erroneous and correct texts are generally the same, or only differ in their spacings.
TeXmacs implements several heuristics to detect and correct syntax errors. Some of these heuristics are “conservative” in the sense that they will only perform corrections on incorrect texts and when we are sure or pretty sure that the corrections are right. Other heuristics are more “agressive” and may for instance replace spaces by multiplications or vice versa whenever this seems reasonable. However, in unlucky cases, the agressive heuristics might replace a correct symbol by an unwanted one. Notice that none of the syntactic corrections alters the presentation of the document, except for some differences in the spacing.
One major technique which is used in many of the heuristics is to
associate a symbol type to each symbol in a mathematical expression. For
instance, we associate the type “infix” to  , “opening bracket” to
, “opening bracket” to  , and special types to subscripts, superscripts
and primes. Using these types, we can detect immediately the
incorrectness of an expression such as
, and special types to subscripts, superscripts
and primes. Using these types, we can detect immediately the
incorrectness of an expression such as 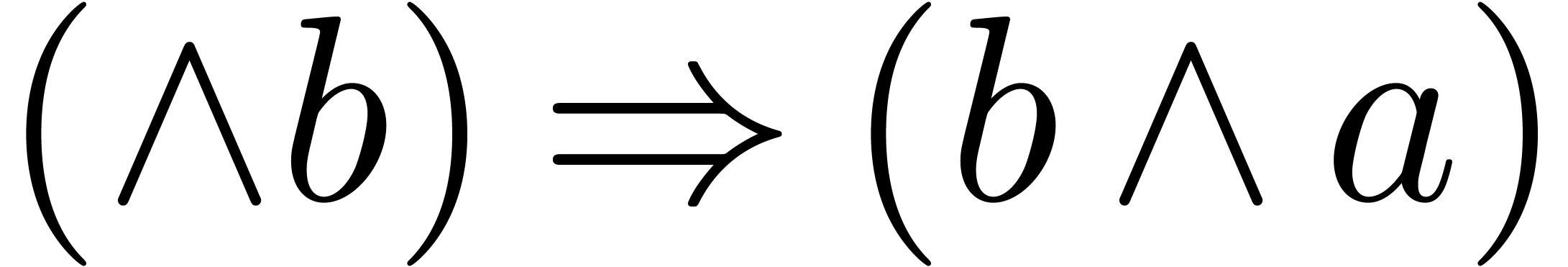 .
Some of our algorithms also rely on the binding forces of mathematical
symbols. For instance, the binding force of multiplication is larger
than the binding force of addition.
.
Some of our algorithms also rely on the binding forces of mathematical
symbols. For instance, the binding force of multiplication is larger
than the binding force of addition.
It is important to apply the different algorithms for syntax correction in an appropriate order, since certain heuristics may become more efficient on partially corrected text. For instance, it is recommended to replace $f($) by $f(x)$ before launching the heuristic for determining matching brackets. We will now list, in the appropriate order, the most important heuristics for syntax correction which are implemented in TeXmacs.
It is fairly easy to correct misplaced invisible markup, via detection and correction of the various patterns that we have described in the previous section.
There are several heuristics for the determination of matching
brackets, starting with the most conservative ones and ending with
the most agressive ones if no appropriate matches were found. The
action of the routine for bracket matching can be thought of as
the insertion of appropriate mrow tags in
Each of the heuristics proposes an “opening”,
“closing”, “middle” or
“unknown” status for each of the brackets in the
formula and then launches a straightforward matching algorithm.
The first most conservative heuristic first checks whether there
are any possibly incorrect brackets in the formula, such as the
closing 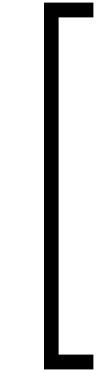 bracket in
bracket in 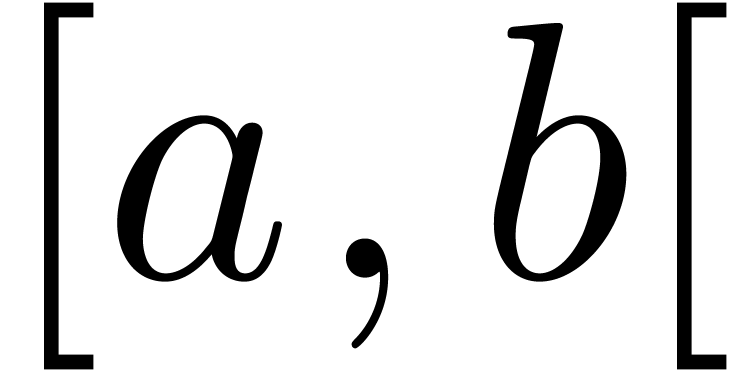 , and turns their status into
“unknown”. The status of the remaining brackets is the
default one: opening for
, and turns their status into
“unknown”. The status of the remaining brackets is the
default one: opening for  ,
,
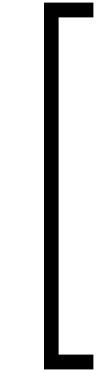 ,
,  , etc. and closing for
, etc. and closing for  ,
, 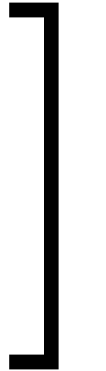 ,
, 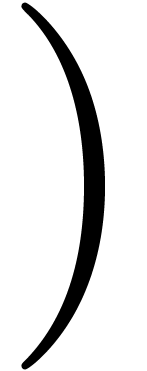 .
.
We next launch a series of more and more agressive heuristics for
the detection of particular patters, such as french intervals
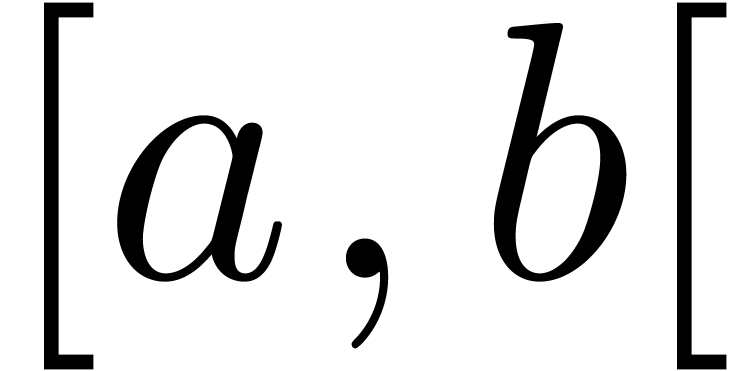 , absolute values
, absolute values  , ket notation
, ket notation 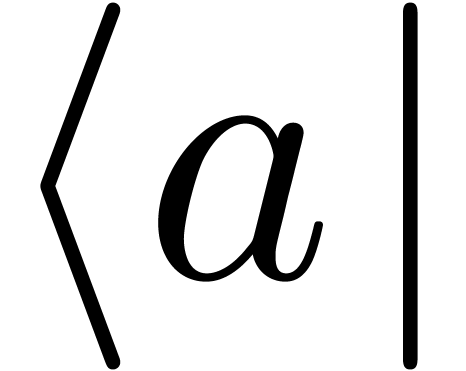 , etc. If, at the end of all these
heuristics, some brackets still do not match, then we (optionally)
match them with empty brackets. For instance, $\left(a$
will be turned into $\left(a\right.$.
, etc. If, at the end of all these
heuristics, some brackets still do not match, then we (optionally)
match them with empty brackets. For instance, $\left(a$
will be turned into $\left(a\right.$.
We notice that the heuristics may benefit from matching brackets
which are detected by earlier heuristics. For instance, in the
formula 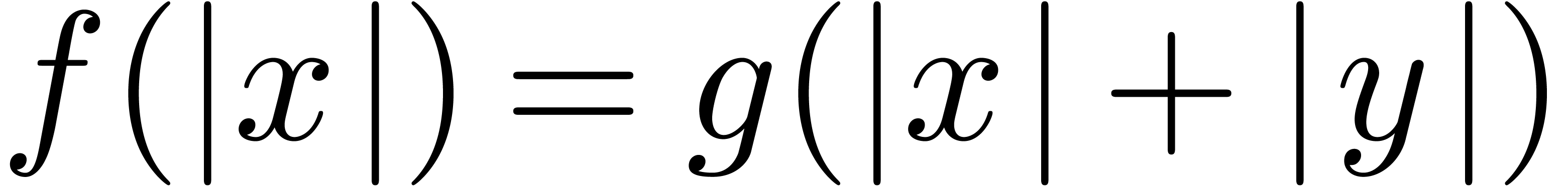 , the brackets
, the brackets
 are matched at an early stage, after which
we only need to correct the subformulas
are matched at an early stage, after which
we only need to correct the subformulas  and
and  instead of the formula as a whole.
instead of the formula as a whole.
The determination of scopes of big operators is intertwined with bracket matching. The main heuristic we use is based on the binding forces of infix operations inside the formula and the binding forces of the big operators themselves. For instance, in the formula
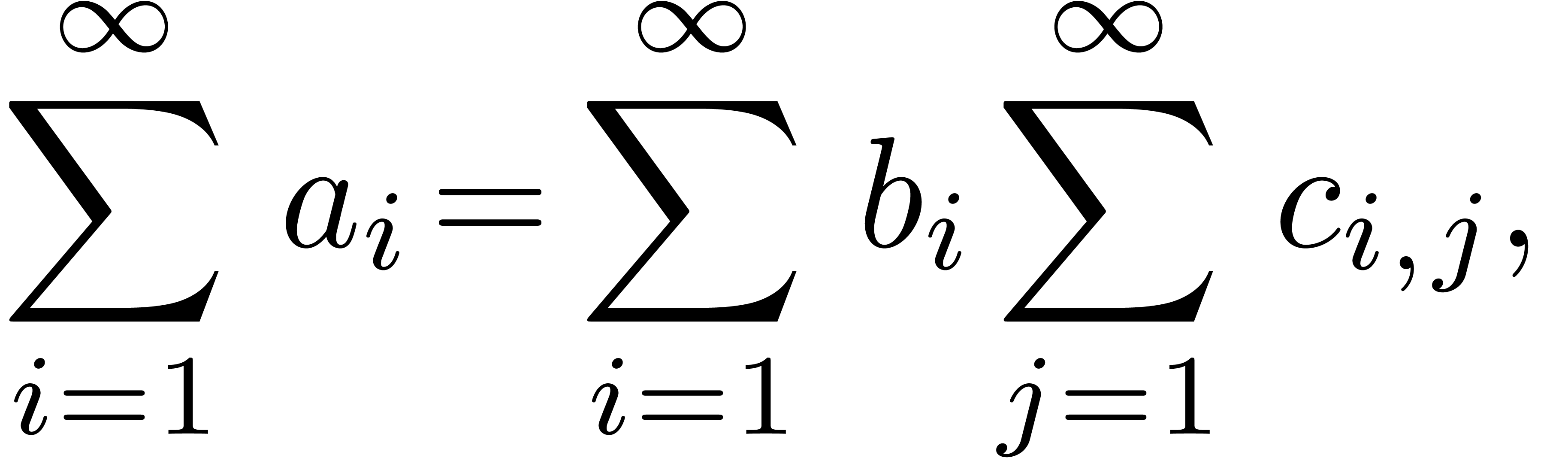 |
(1) |
the binding force of the equality is weaker than the binding force of a summation, whereas the binding force of the invisible multiplication is larger. This heuristic turns out to be extremely reliable, even though it would be incorrect on the formula
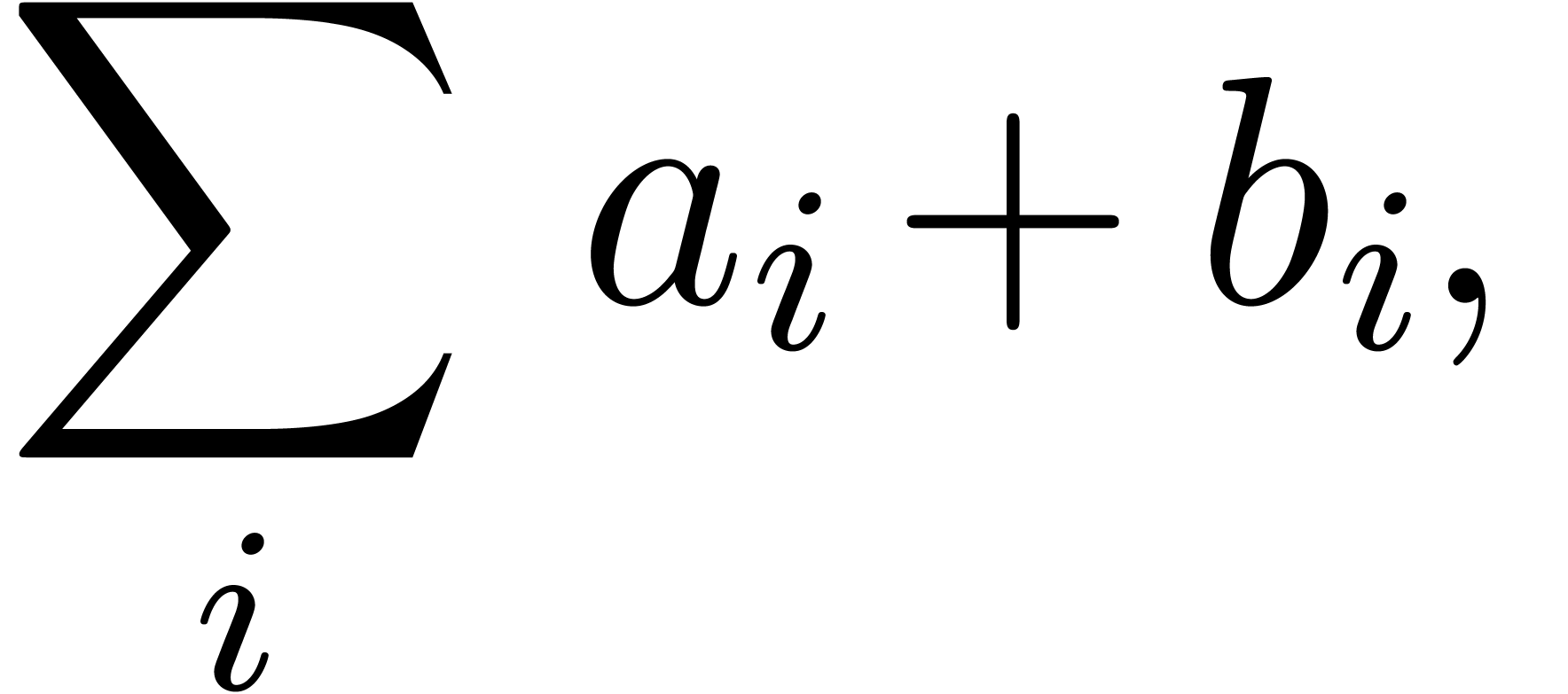
where the big summation is taken to have a slightly larger binding
force than the addition. The heuristic might be further improved
by determining which summation variables occur in which summands.
For instance, in the formula (1), the occurrence of
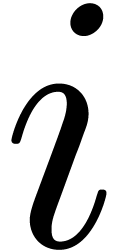 inside
inside 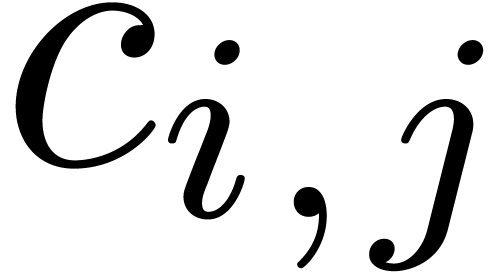 gives a
second indication that we are dealing with a nested summation.
gives a
second indication that we are dealing with a nested summation.
Trailing or other superfluous invisible symbols are easily detected and removed from formulas.
Another easy task is the detection of errors which can be repaired
through the replacement of a symbol by a homoglyph. For instance,
if the backslash symbol (with type “basic symbol”)
occurs between two letters (also with types “basic
symbol”), as in  ,
then we may replace it by the “setminus” infix.
,
then we may replace it by the “setminus” infix.
The insertion of missing invisible symbols (or replacement of incorrect ones) is one of the hardest tasks for syntax correction. Two main situations need to be distinguished:
The text to be corrected was written with TeXmacs and we may assume that most of the multiply/apply ambiguities were already resolved by the author.
The text to be corrected was imported from TeX/LaTeX, so that no multiplications or function applications were present in the source document.
In the first case, most multiplications and function applications are already correct, so the correction algorithm should be very conservative. In the second case, the insertions should be very agressive, at the risk of being incorrect in many cases.
At a first stage, it is important to determine situations in which
it is more or less clear whether to insert a multiplication or a
function application. For instance, between a number and a letter,
it is pretty sure that we have to insert a multiplication.
Similarly, after operators such as  ,
it is pretty sure that we have to insert a space.
,
it is pretty sure that we have to insert a space.
At a second stage, we determine how all letter symbols occurring in the document are “used”, i.e. whether they occur as lefthand or righthand arguments of multiplications or function applications. It is likely that they need to be used in a similar way throughout the document, thereby providing useful hints on what to do.
At the end, we insert the remaining missing symbols, while pondering our decisions as a function of the hints and whether we need to be conservative or not.
In this section, we report on the performance of the TeXmacs syntax
corrector. The results were obtained by activating the debugging tool
inside TeXmacs as well as the 
This book on algorithms in real algebraic geometry was originally written in LaTeX [4] and then converted to TeXmacs and transformed into a book with extra interactive features [3].
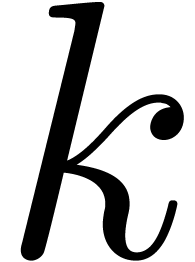
The 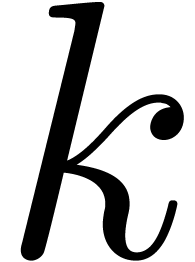 -th chapter of BPR.
-th chapter of BPR.
This corresponds to a collection [6] of six courses for students on various topics in mathematics.
The third paper in COL on information theory.
This Master's Thesis [23] was written by an early TeXmacs user and physicist.
Our own book on transseries, which was started quite long ago with an early version of TeXmacs and completed during the last decade [34].
This habilitation thesis [35] was written more recently.
The 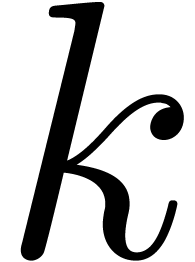 -th chapter of HAB.
-th chapter of HAB.
In the introduction, we have mentioned URLs where these documents can be downloaded. We also repeat that TeXmacs (and not the authors) should be held responsible for most of the semantic errors which were found in these documents.
In table 1, we have compiled the main results of the syntax corrector. Concerning the total number of formulas, we notice that each non empty entry of an equation array is counted as a separate formula. For the books, we only ran the corrector on the main chapters, not on the glossaries, indexes, etc. The concept of “error” will be described in more detail in section 7.1 below. Roughly speaking, a correct formula is a formula that can be parsed in suitable (tolerant) grammar, which will be described in section 6. In section 6.4, we will discuss in more detail to which extent our notion of “error” corresponds to the intuitive notion of a syntax error or “typo”.
The corrector tends to reduce the number of errors by a factor between
 and
and 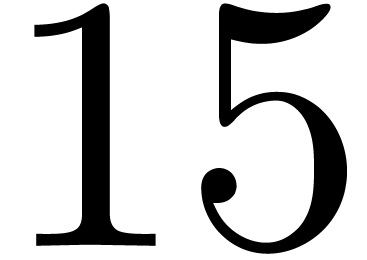 .
The typical percentage of remaining errors varies between
.
The typical percentage of remaining errors varies between 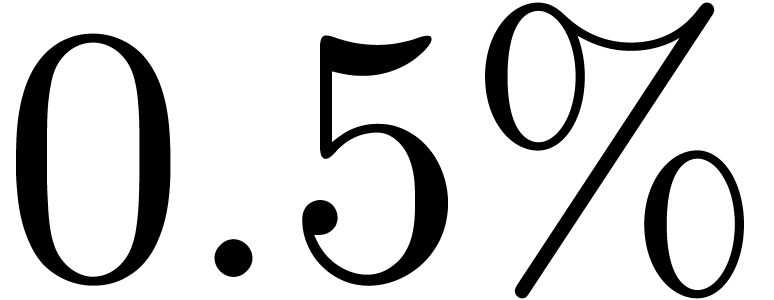 and
and  . This
error rate tends to be slightly higher for documents with many complex
formulas, such as MT; in ordinary mathematical documents, most formulas
are very short, whence trivially correct. Furthermore, many errors tend
to be concentrated at certain portions of a document. For instance, the
error rate of the individual document COL3 is as about twice
as low as the error rate of the collection COL. Similarly, the bulk of
the errors in LN are concentrated in the first chapters. Finally, errors
tend to be repeated according to patterns, induced by systematic
erroneous notation.
. This
error rate tends to be slightly higher for documents with many complex
formulas, such as MT; in ordinary mathematical documents, most formulas
are very short, whence trivially correct. Furthermore, many errors tend
to be concentrated at certain portions of a document. For instance, the
error rate of the individual document COL3 is as about twice
as low as the error rate of the collection COL. Similarly, the bulk of
the errors in LN are concentrated in the first chapters. Finally, errors
tend to be repeated according to patterns, induced by systematic
erroneous notation.
|
|||||||||||||||||||||||||||||||||||||||||||||
It is interesting to study the relative correction rates of the techniques described in the previous section. More precisely, we have implemented the following algorithms:
Correction of invisible structured markup.
Since all documents were written with older versions of TeXmacs in which bracket matching was not enforced (see also section 4.2 below), this algorithm implements a collection of heuristics to make all brackets match. In the case of absolute values, which cannot be parsed before this step, this typically decreases the number of errors. The algorithm also determines the scopes of big operators.
This algorithm detects and moves incorrectly placed brackets with respect to invisible structured markup. For instance, the LaTeX formula Let $y=f(x$). would be corrected into Let $y=f(x)$.
Removal of superfluous invisible symbols.
Heuristic insertion of missing invisible symbols, either function applications or multiplications.
Replacing symbols by appropriate homoglyphs.
Various other useful corrections.
The results are shown in table 2.
In a sense, among the original errors, one should not really count the
errors which are corrected by the bracket matching algorithm. Indeed,
the versions of TeXmacs which were used for authoring the documents
contained no standard support for, say, absolute values or big operator
scopes. Hence, the author had no real possibility to avoid parsing
errors caused by such constructs. Fortunately, our bracket matching
algorithm is highly effective at finding the correct matches. One rare
example where the algorithm “fails” is the formula 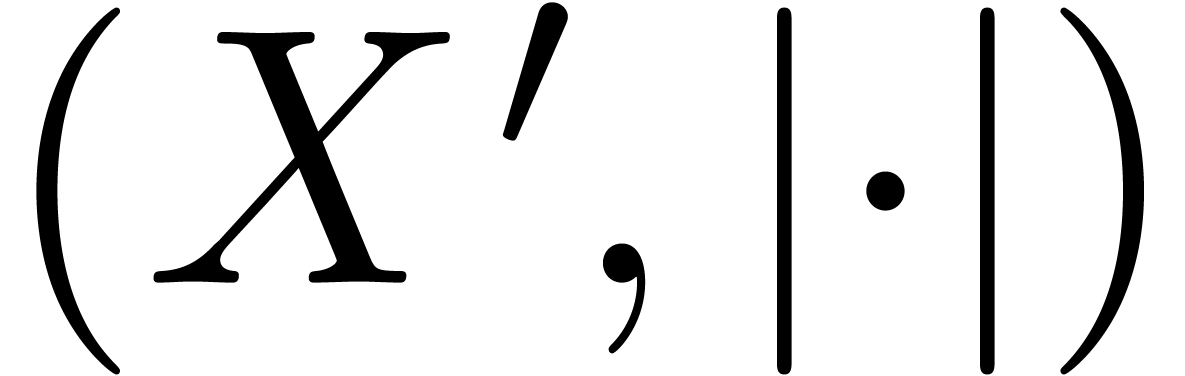 from COL, where
from COL, where  was tagged to be a
multiplication.
was tagged to be a
multiplication.
The overwhelming source of remaining error corrections is due to missing, wrong or superfluous invisible multiplications and function applications. This fact is not surprising for documents such as BPR, which were partially imported from LaTeX. Curiously, the situation seems not much better for MT, COL and IT, which were all written using TeXmacs. Even in our own documents LN and HAB, there are still a considerable number of “invisible errors”. This fact illustrates that TeXmacs provides poor incitation to correctly enter meaningful invisible content. In COL, the author actually took the habit to systematically replace multiplications by function applications. Consequently, many of the “correct” formulas do not have the intended meaning.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In section 3, we have described many common ambiguities and syntactical errors, and provided heuristics for correcting them. Of course, a more satisfactory solution would be to develop mathematical editors in such a way that these errors are ruled out right from the start, or at least, that it is harder for the user to enter obviously incorrect formulas.
In the process of making mathematical editors more sophisticated, one should nevertheless keep in mind that most authors are only interested in the presentation of the final document, and not in its correctness. For most users, presentation oriented interfaces are therefore the most intuitive ones. In particular, every time that we deviate from being presentation oriented, it should be clear for the user that it buys him more than he looses.
There are three basic techniques for inciting the user to write syntactically correct documents:
Enforcing correctness via the introduction of suitable markup.
Providing visual hints about the semantics of a formula.
Writing documentation.
Of course, the main problem with the first method is that it may violate the above principle of insisting on presentation oriented editing. The problem with the second method is that hints are either irritating or easily ignored. The third option is well-intentioned, but who reads and follows the documentation? One may also wish to introduce one or more user preferences for the desired degree of syntactic correctness.
In some cases, correctness can also be ensured by running appropriate syntax correction methods from section 3.3. For instance, the algorithms for the correction of invisible markup can be applied by default. Alternatively, one may redesign the most basic editing routines so as to ensure correctness all the way along.
Matching brackets and well-scoped big operators are particularly important for structuring mathematical formulas. It is therefore reasonable to adapt markup so as to enforce these properties. In a formula with many brackets, this is usually helpful for the user as well, since it can be tedious to count opening and closing brackets. Highlighting matching brackets consists an alternative solution, which is used in many editors for programming languages.
In TeXmacs 1.0.7.7, we have introduced a special ternary markup element
around (similar to fenced in
When typing an opening bracket, such as  , the corresponding closing bracket
, the corresponding closing bracket  is inserted automatically and the cursor is placed in
between
is inserted automatically and the cursor is placed in
between  .
.
The brackets are removed on pressing backspace or delete inside a pair of matching brackets with nothing in between.
The around tag has “no border”, in the
sense that, in the formula 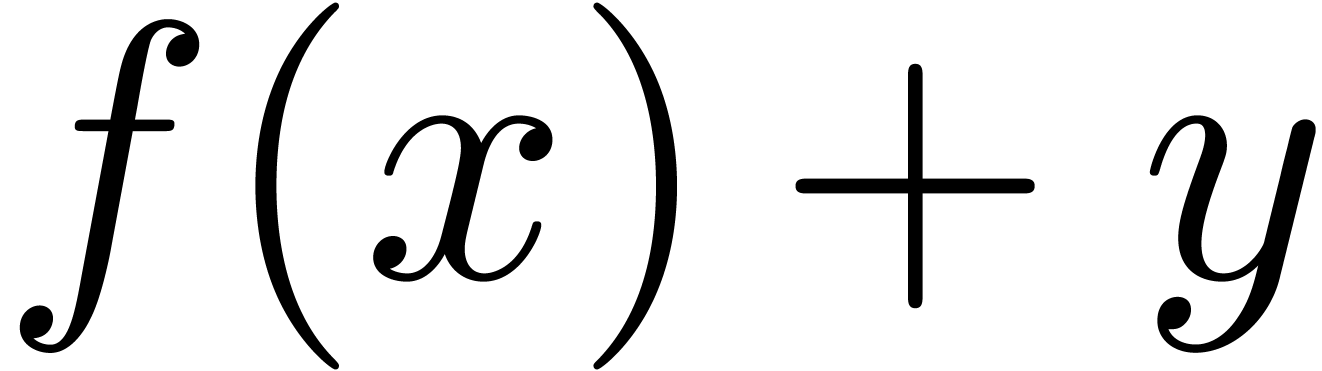 ,
there is only one accessible cursor position between
,
there is only one accessible cursor position between  and
and  resp.
resp.  and
and  .
.
In addition, one has to decide on ways to replace the opening and
closing brackets, if necessary, thereby enabling the user to type
intervals such as 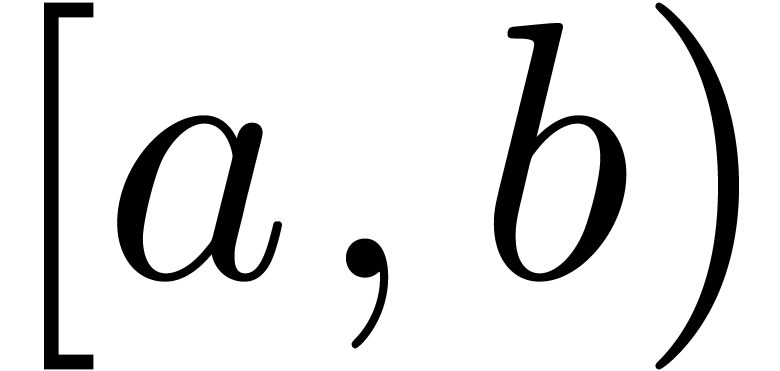 or
or 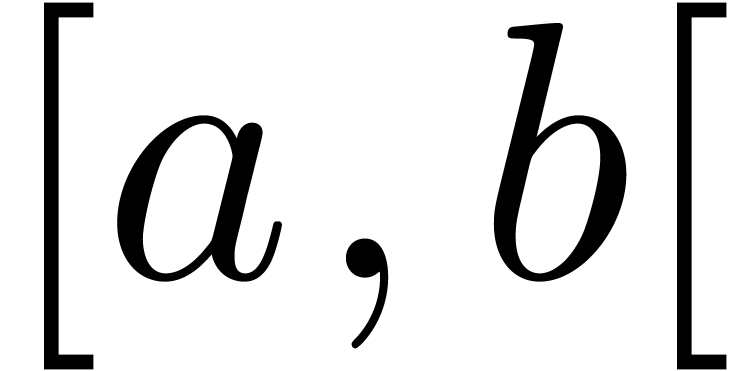 , or other kinds of “matching brackets”.
In TeXmacs, this is currently done as follows:
, or other kinds of “matching brackets”.
In TeXmacs, this is currently done as follows:
When removing an opening or closing bracket, it is actually replaced by an invisible bracket. In the special case that there was nothing between the brackets, or when both brackets become invisible, we remove the brackets. Notice that the cursor can be positioned before or after an invisible bracket.
If we type an opening or closing bracket just before or after an invisible bracket, then we replace the invisible bracket by the new bracket.
For instance, we may enter 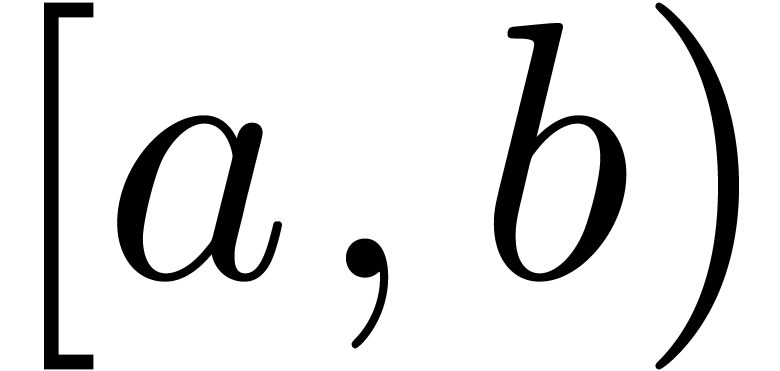 by typing [a,bdelete). In addition, we use the following
convenient rule:
by typing [a,bdelete). In addition, we use the following
convenient rule:
When typing a closing bracket just before the closing bracket of an around tag, we replace the existing closing bracket by the new one.
An alternative way for entering 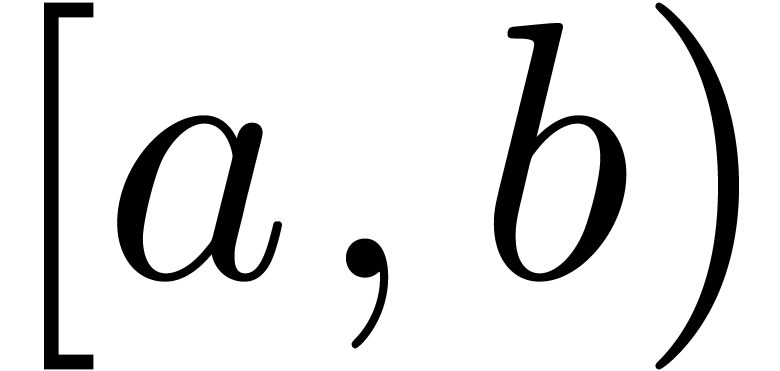 is therefore to
type [a,b). Notice that the
last rule also makes the “matching bracket mode” more
compatible with the naive presentation oriented editing mode. Indeed,
the following table shows in detail what happens when typing
is therefore to
type [a,b). Notice that the
last rule also makes the “matching bracket mode” more
compatible with the naive presentation oriented editing mode. Indeed,
the following table shows in detail what happens when typing 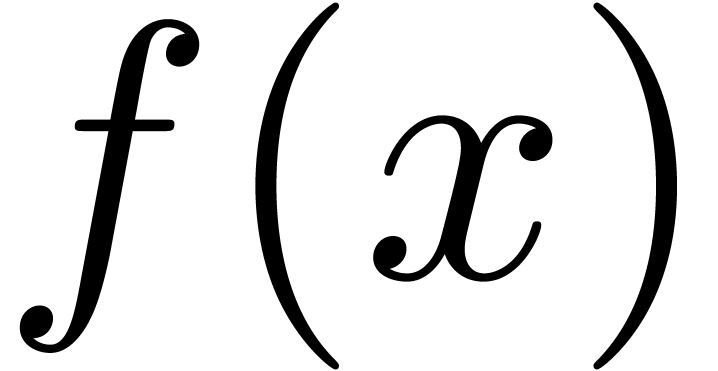 in both modes:
in both modes:
| presentation oriented mode | matching bracket mode | |
| f |  |
 |
| f( |  |
 |
| f(x | 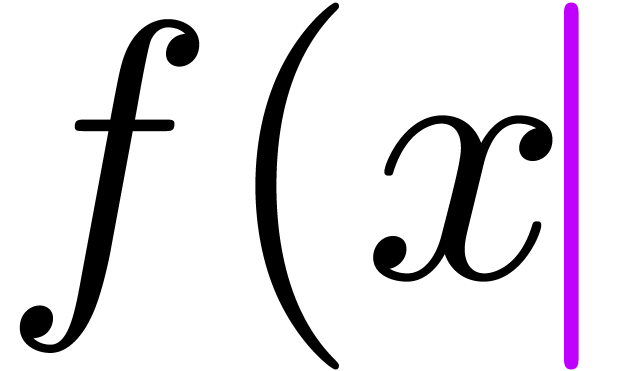 |
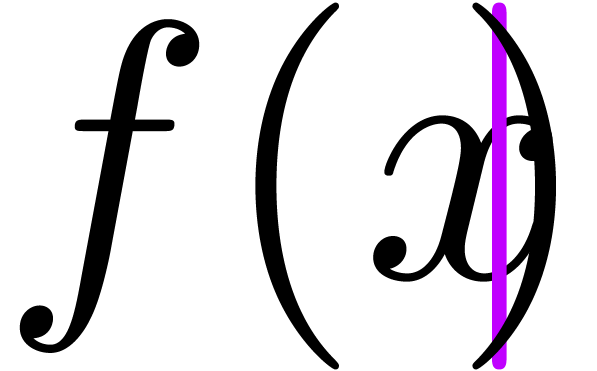 |
| f ( x ) | 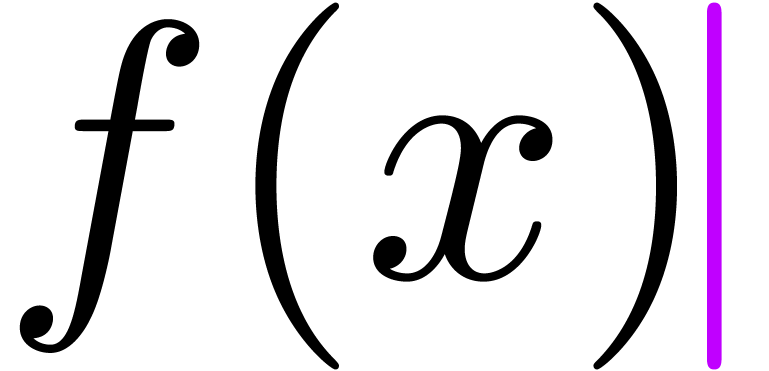 |
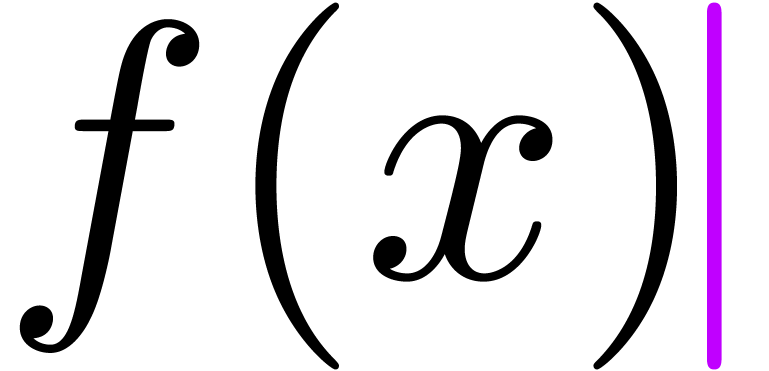 |
Notice that the shortcut f(x is equivalent to f(x) in this example.
is equivalent to f(x) in this example.
The above rules also apply for bar-like brackets, except that the bar is
either regarded as an opening or closing bracket, depending on the
context. For instance, when typing |
in an empty formula, we start an absolute value  . On the other hand, when the cursor is just before
a closing bracket, as in
. On the other hand, when the cursor is just before
a closing bracket, as in  ,
then typing |
results in the replacement of the closing bracket by a bar:
,
then typing |
results in the replacement of the closing bracket by a bar:  . As will be explained below, other bar-like
symbols can be obtained using the tab
key.
. As will be explained below, other bar-like
symbols can be obtained using the tab
key.
The matching bracket mode in TeXmacs also enforces all big operators to be scoped. As in the case of an invisible bracket, there are two cursor positions next to the invisible righthand border of a scoped big operator: inside and outside the scope of the operator. We use light cyan boxes in order to indicate the precise position of the cursor:
 |
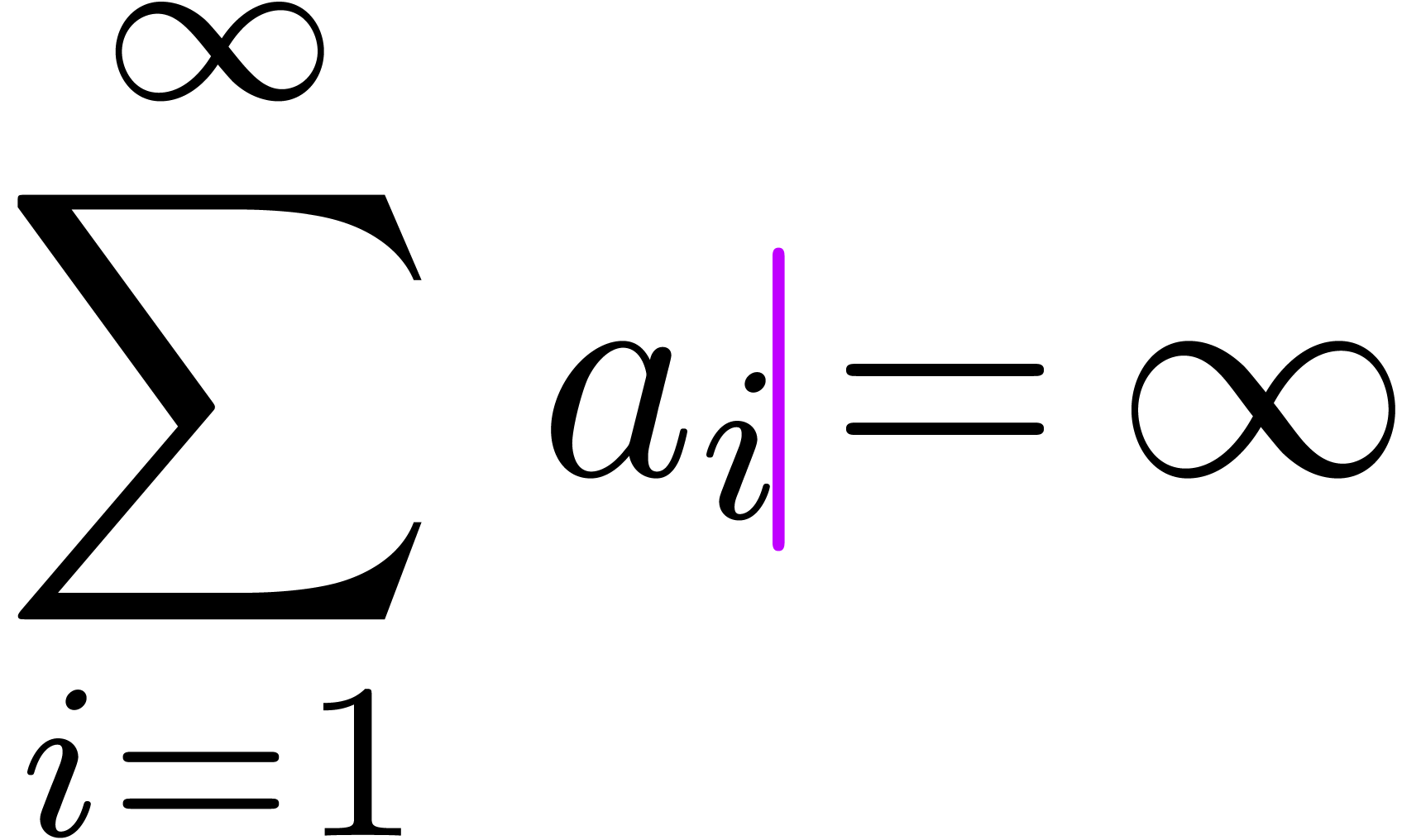 |
|
| Inside the scope | Outside the scope |
Currently, the TeXmacs implementation of subscripts and superscripts is
still presentation oriented. The problem here is the following: when
entering an expression such as 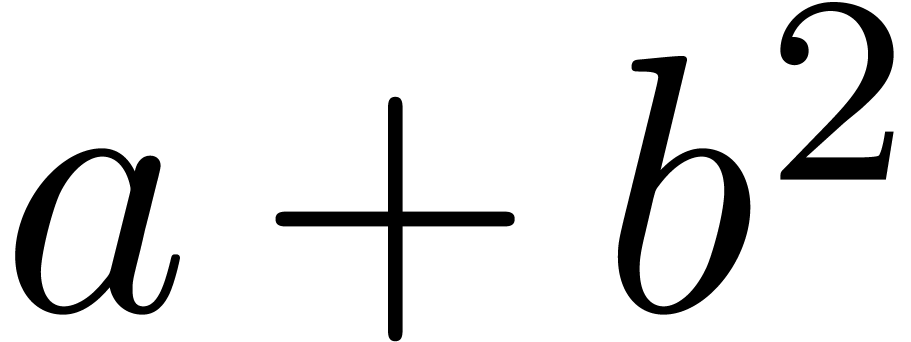 ,
there are two options for detecting that
,
there are two options for detecting that  is the
base for superscript:
is the
base for superscript:
By parsing the complete expression.
By forcing the user to specify the base by means of special markup.
The first option is out of scope for “cheap semantic editing” and only realistic in combination with the tools described in the second part of this paper. As in the case of big operators for the right border, the second option requires the introduction of an invisible left border with two adjacent cursor positions. However, such invisible borders turn out to be less natural for left borders than for right borders, partly because we have to start entering the script before entering the base.
Remark 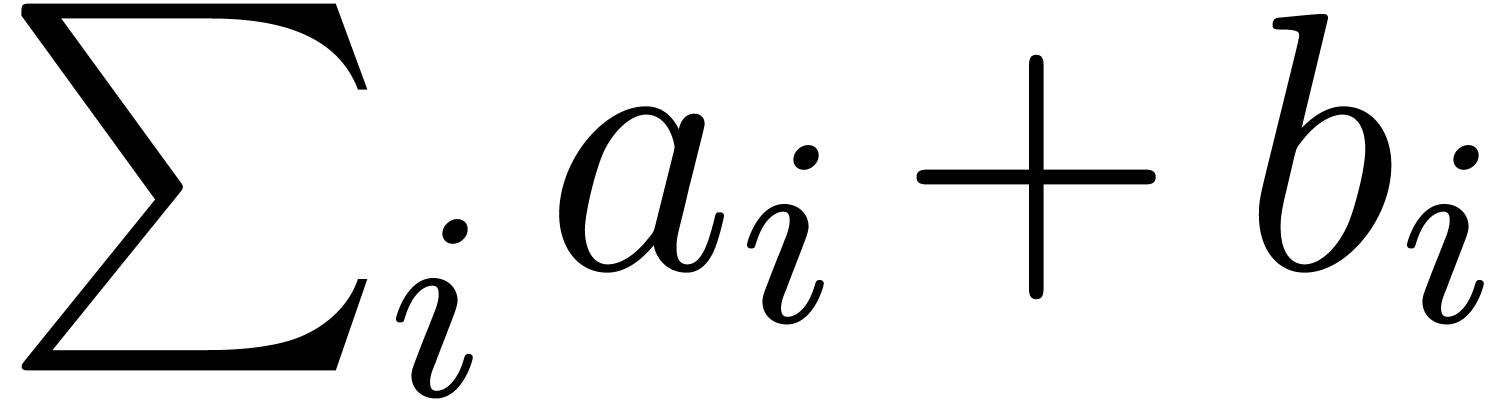 , for which our heuristic fails,
the formula would actually be more readable if we put brackets around
, for which our heuristic fails,
the formula would actually be more readable if we put brackets around
 . If we want to consider big
operators just as prefixes, then this does require some modifications in
our universal grammar, which will be specified in section 6
below. For instance, the non-terminal symbol Sum would
admit additional rules for
. If we want to consider big
operators just as prefixes, then this does require some modifications in
our universal grammar, which will be specified in section 6
below. For instance, the non-terminal symbol Sum would
admit additional rules for  ,
,
 , etc.
, etc.
TeXmacs provides a simple “variant” mechanism, based on
using the tab
key. For instance, Greek letters  ,
,
 ,
,  , etc. can be entered by typing atab, btab,
Ltab, etc. Similarly, the variants
, etc. can be entered by typing atab, btab,
Ltab, etc. Similarly, the variants 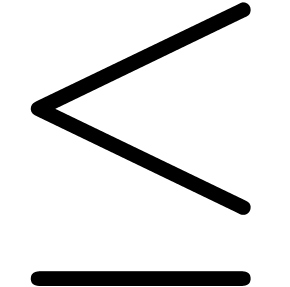 ,
, 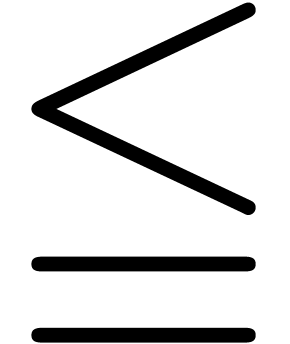 and
and 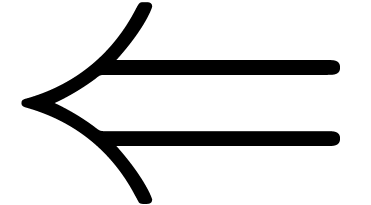 of
of 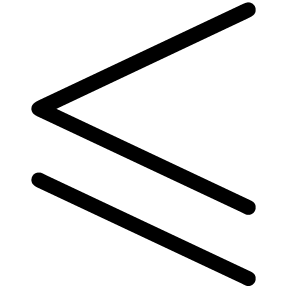 can be obtained by typing
<= and pressing the tab key several
times. Using the variant mechanism, there are also simple shortcuts
etabtab,
ptabtab,
itabtab
and gtabtab for the most frequent mathematical
constants
can be obtained by typing
<= and pressing the tab key several
times. Using the variant mechanism, there are also simple shortcuts
etabtab,
ptabtab,
itabtab
and gtabtab for the most frequent mathematical
constants  ,
,  ,
,  and
and  . Similarly, dtabtab can be used for
typing the operator
. Similarly, dtabtab can be used for
typing the operator  in
in 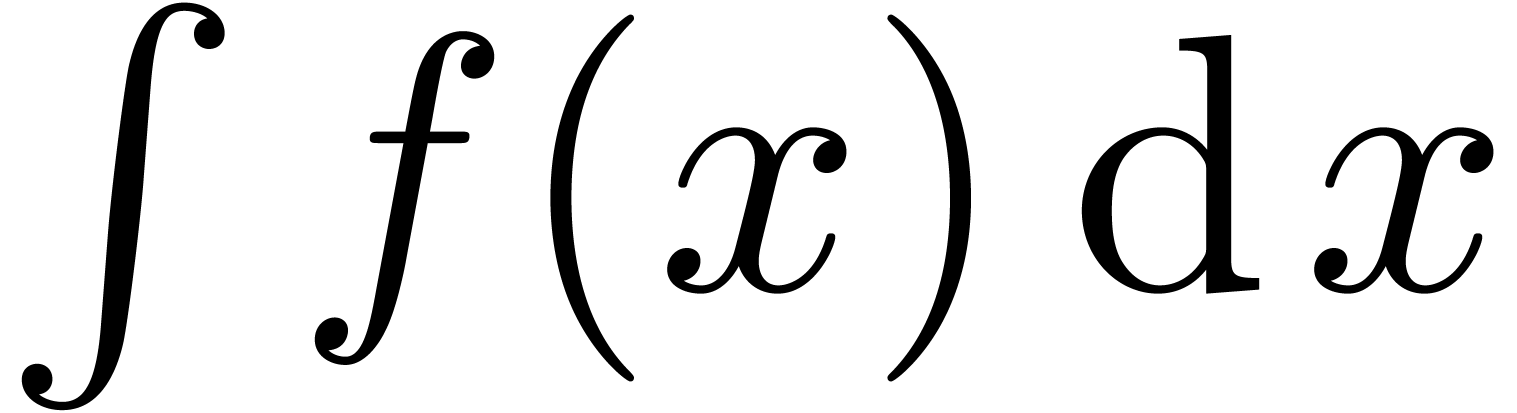 .
.
It is natural to use the variant mechanism for disambiguating homoglyphs as well. In table 3, we have displayed the current keyboard shortcuts for some of the most common homoglyphs.
|
|||||||||||||||||||||||||||||||||||||||
Regarding invisible operators, there are a few additional rules. First
of all, letters which are not separated by invisible operators are
considered as operators. For instance, typing ab
yields  and not
and not 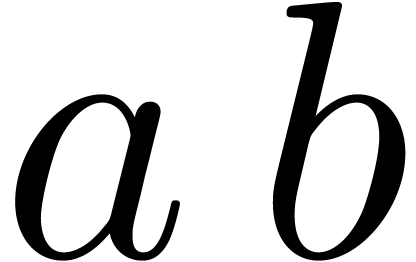 ,
as in LaTeX. This provides some incitation for the user to explicitly
enter invisible multiplications or function applications. Also, the
editor forbids entering sequences of more than one invisible
multiplication or function application. In other words, typing a**b has the same effect
as typing a*b.
,
as in LaTeX. This provides some incitation for the user to explicitly
enter invisible multiplications or function applications. Also, the
editor forbids entering sequences of more than one invisible
multiplication or function application. In other words, typing a**b has the same effect
as typing a*b.
Besides making it easy for the user to disambiguate homoglyphs, the editor also provides visual hints. For instance, the difference between the vertical bar as a separator or a division is made clear through the added spacing in the case of divisions. The status bar also provides information about the last symbol which has been entered.
Despite the above efforts, many users don't care about syntactic correctness and disambiguating homoglyphs, or are not even aware of the possibilities offered by the editor. Unfortunately, it is hard to improve this situation: a very prominent balloon with relevant hints would quickly irritate authors. Yet, for users who do not notice spacing subtleties or discrete messages on the status bar, more agressive messages are necessary in order to draw their attention.
One possible remedy would be to display more agressive help balloons only if the user's negligence leads to genuine errors. For instance, whenever the user types aspace+, the space is clearly superfluous, thereby providing us a good occasion for pointing the user to the documentation.
In the case of invisible operators, we might also display the corresponding visible operator in a somewhat dimmed color, while reducing its size, so as to leave the spacing invariant. Optionally, these hints might only be displayed if the cursor is inside the formula.
The grammars of most traditional computer languages are LALR-1 [7],
which makes it possible to generate parsers using standard tools such as
A finite alphabet  of non-terminal
symbols.
of non-terminal
symbols.
A finite alphabet  of terminal
symbols (disjoint from
of terminal
symbols (disjoint from  ).
).
One parsing rule  for each
non-terminal symbol
for each
non-terminal symbol  in
in  .
.
The set 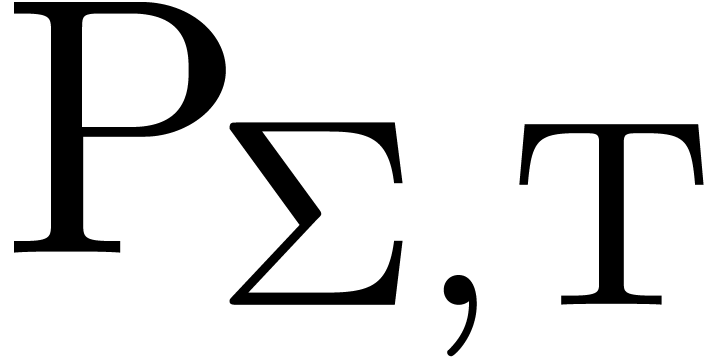 stands for the set of packrat
parsing expressions. There are various possibilities for the
precise definition of
stands for the set of packrat
parsing expressions. There are various possibilities for the
precise definition of 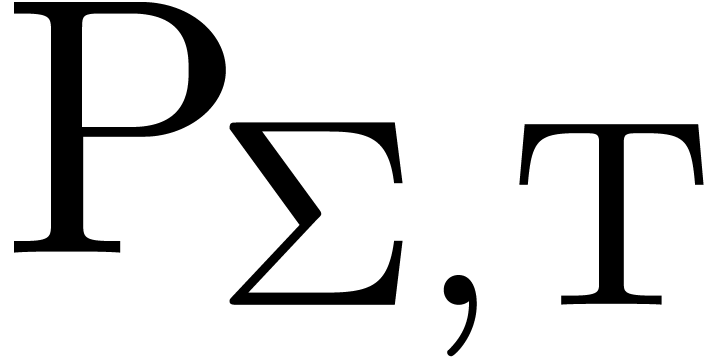 . In
what follows, each parsing expression is either of one of the following
forms:
. In
what follows, each parsing expression is either of one of the following
forms:
A non-terminal or terminal symbol in  .
.
A (possibly empty) concatenation  of parsing
expressions
of parsing
expressions  in
in 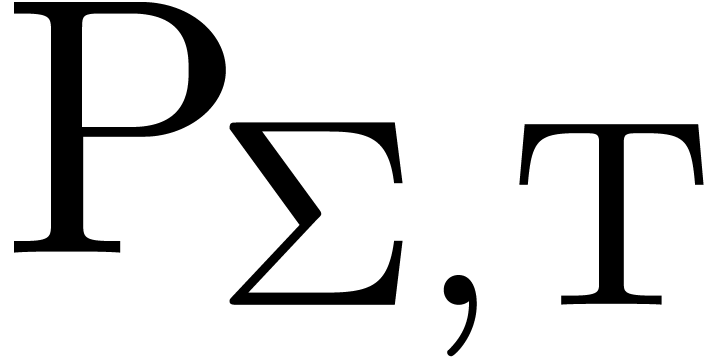 .
.
A (possibly empty) sequential disjunction  of
of 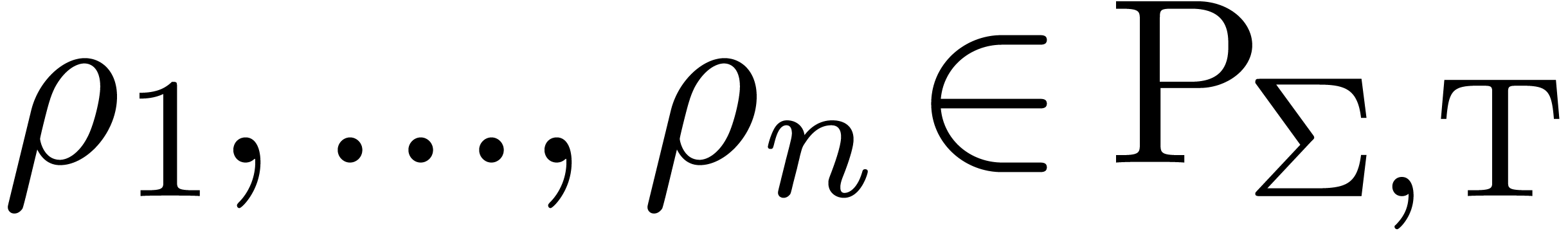 .
.
A repetition 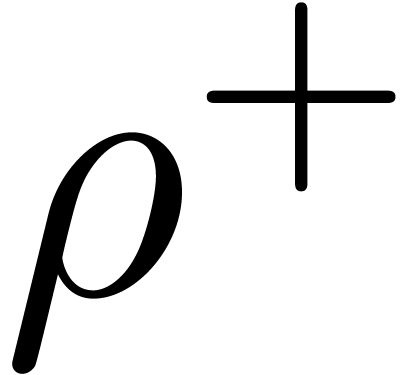 or possibly empty repetition
or possibly empty repetition
 of
of  .
.
And-predicate  , with
, with
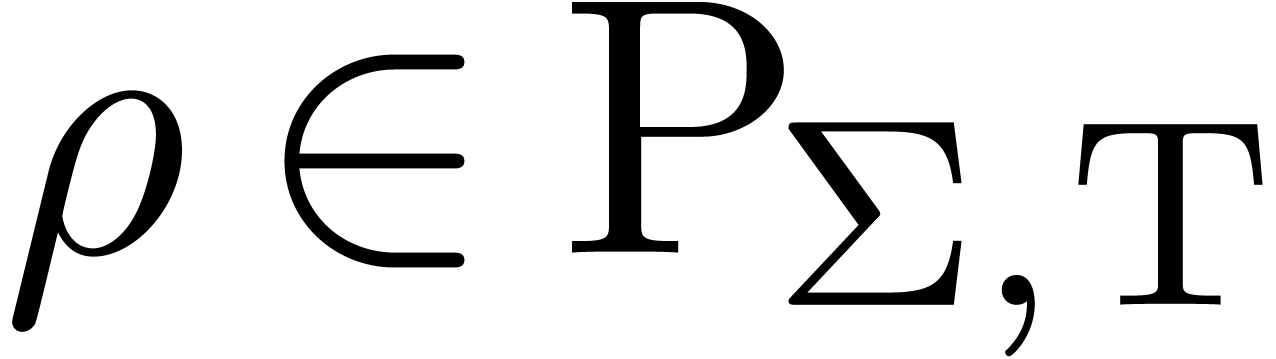 .
.
Not-predicate  , with
, with
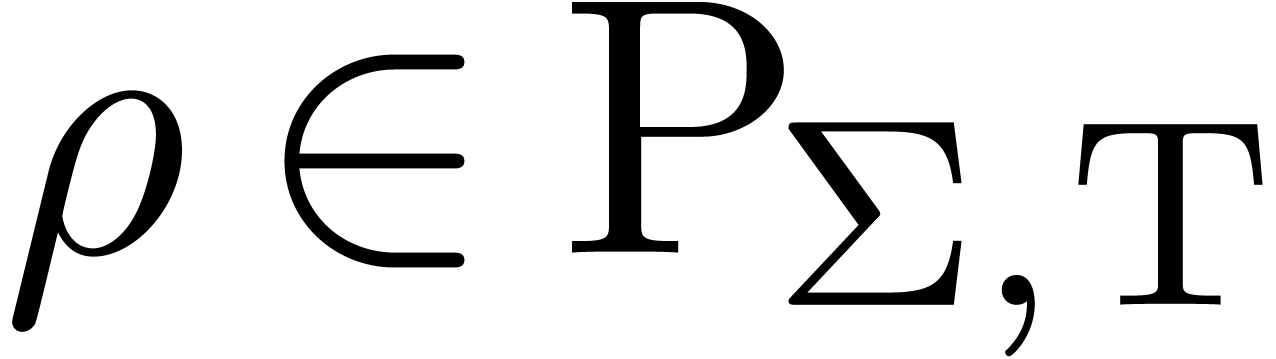 .
.
The meanings of the and-predicate and not-predicate will be made clear below.
The semantics of a packrat grammar and the implementation of a parser
are very simple. Given an input string  ,
an input position
,
an input position  and a parsing expression
and a parsing expression 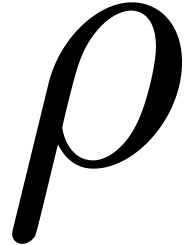 , a packrat parser will attempt to
parse
, a packrat parser will attempt to
parse  at
at  according to
according to
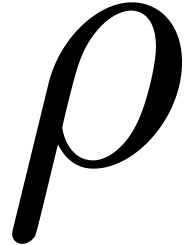 as far as possible. The result is either
“false” or a new position
as far as possible. The result is either
“false” or a new position  .
More precisely, the parser works as follows:
.
More precisely, the parser works as follows:
If 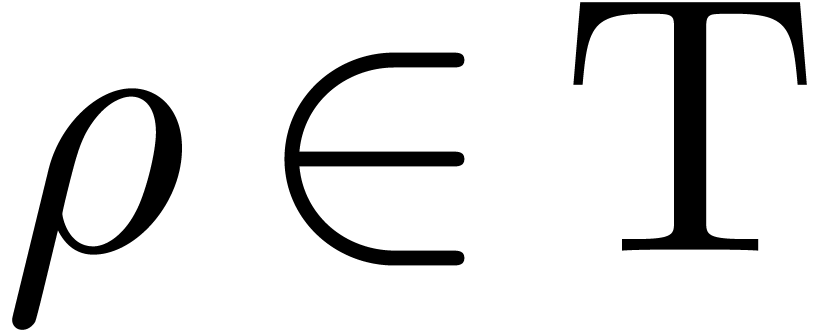 , then we try to read
, then we try to read
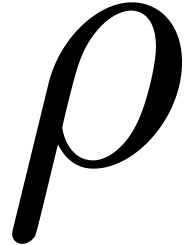 from the string
from the string  at
position
at
position  .
.
If 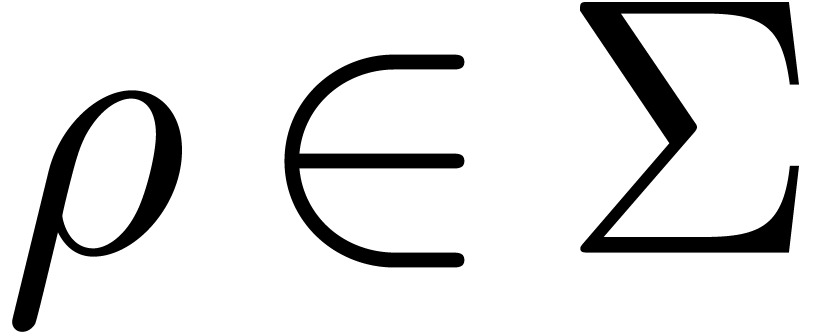 , then we parse
, then we parse  at
at  .
.
If  , then we parse
, then we parse  in sequence while updating
in sequence while updating  with the new returned positions. If one of the
with the new returned positions. If one of the  fails, then so does
fails, then so does  .
.
If 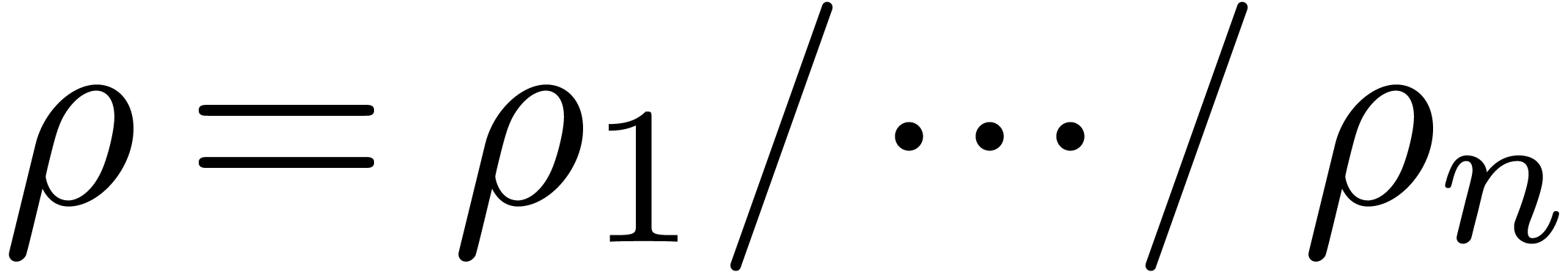 , then we try to parse
, then we try to parse
 at
at  in sequence. As
soon as one of the
in sequence. As
soon as one of the  succeeds at
succeeds at  (and yields a position
(and yields a position  ),
then so does
),
then so does  (and we return
(and we return  ).
).
In case of repetitions, say 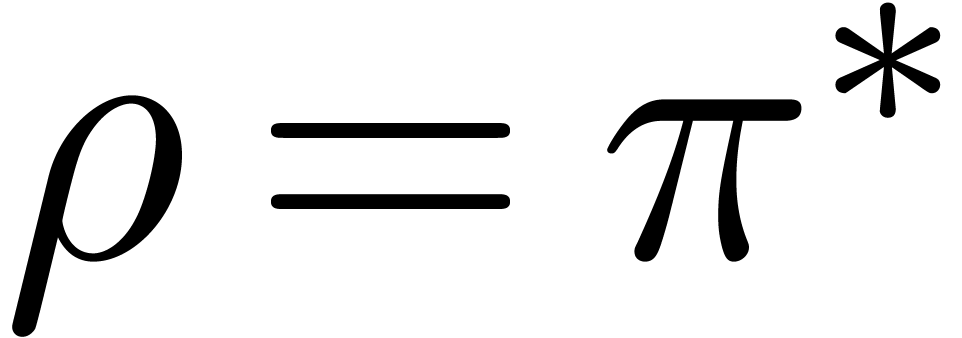 ,
we keep parsing
,
we keep parsing  at
at  until failure, while updating
until failure, while updating  with the new
positions.
with the new
positions.
If 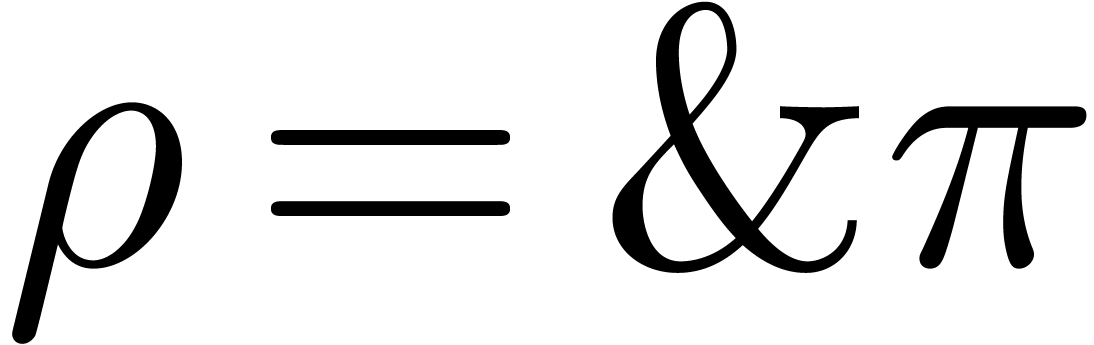 , then we try to parse
, then we try to parse
 at
at  .
In case of success, then we return the original
.
In case of success, then we return the original  (i.e. we do not consume any input). In case of failure,
we return “false”.
(i.e. we do not consume any input). In case of failure,
we return “false”.
If 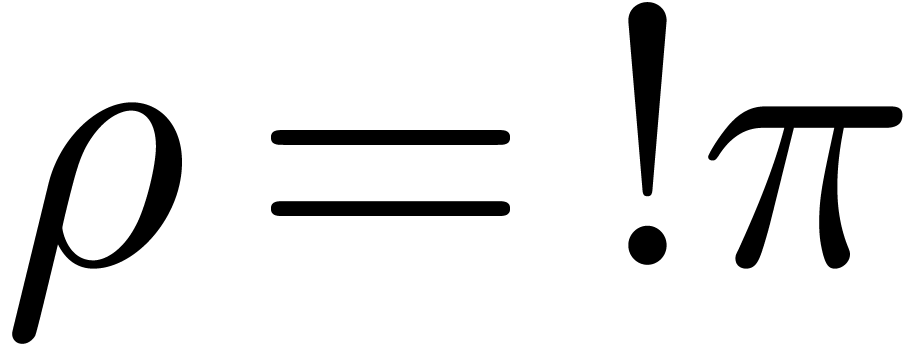 , then we try to parse
, then we try to parse
 at
at  .
In case of success, we return “false”. In case of
failure, we return the original position
.
In case of success, we return “false”. In case of
failure, we return the original position  .
.
For efficiency reasons, parse results are systematically cached.
Consequently, the the running time is always bounded by the length of
string  times the number of parsing expressions
occurring in the grammar.
times the number of parsing expressions
occurring in the grammar.
The main difference between packrat grammars and LALR-1 grammars is due
to the introduction of sequential disjunction. In the case of LALR-1
grammars, disjunctions may lead to ambiguous grammars, in which case the
generation of a parser aborts with an error message. Packrat grammars
are never ambiguous, since all disjunctions are always parsed in a
“first fit” manner. Of course, this also implies that
disjunction is non commutative. For instance, for terminal symbols  and
and 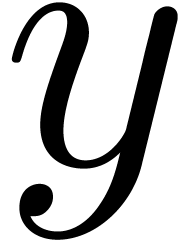 , the
parsing expression
, the
parsing expression 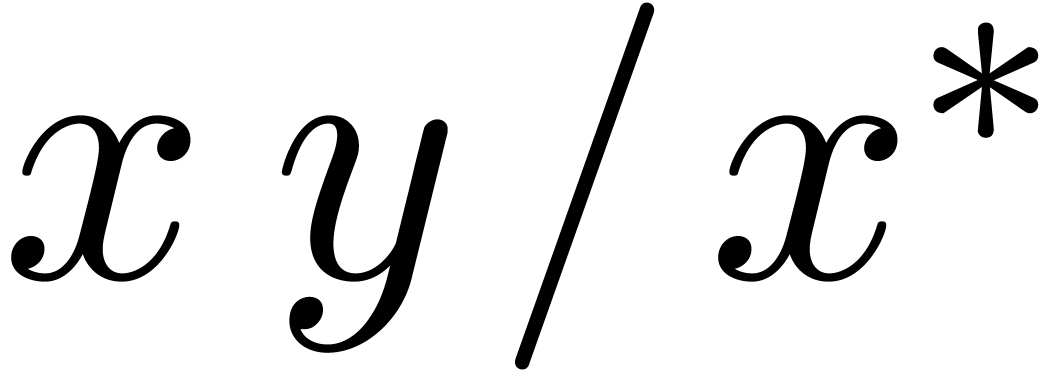 parses the string
parses the string 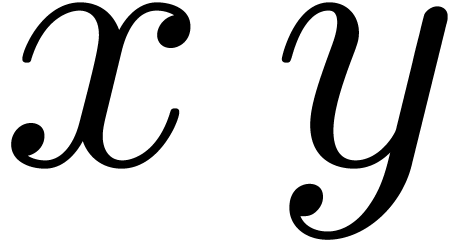 , unlike the expression
, unlike the expression 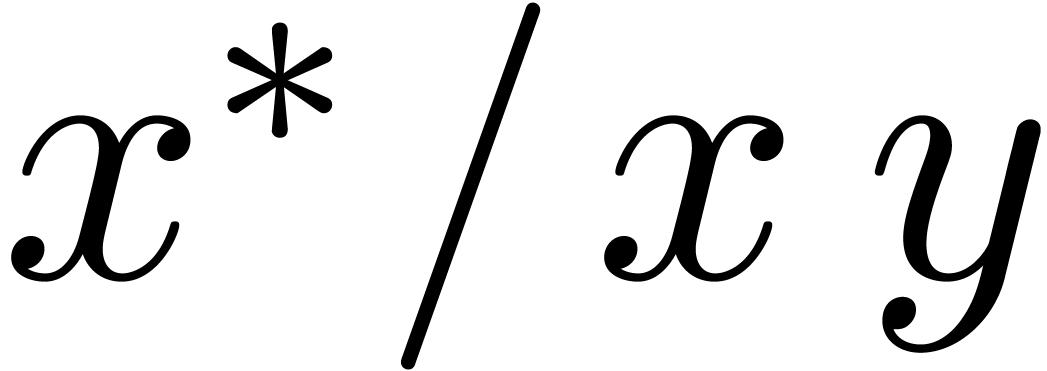 . More precisely, parsing the
string
. More precisely, parsing the
string  at position
at position  according to the expression
according to the expression 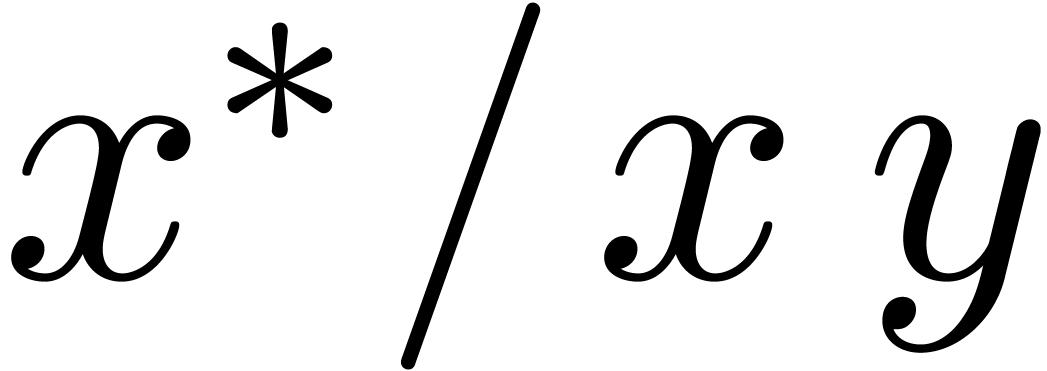 succeeds, but
returns
succeeds, but
returns  as the end position.
as the end position.
In practice, writing a packrat grammar is usually easier than writing an LALR-1 grammar. First of all, thanks to sequential disjunctions, we do not need to spend any effort in making the grammars non ambiguous (of course, the disjunctions have to be ordered with more care). Secondly, there is no limitation in the size of the “look-ahead” for packrat grammars. In particular, there is no need for a separate “lexer”.
Another important advantage is the ability to parse a string on the fly according to a given grammar. In contrast, LALR-1 grammars first apply formal language techniques in order to transform the grammar into an automaton. Although parsers based on such automata are usually an order of magnitude faster than packrat parsers, the generation of the automaton is a rather expensive precomputation. Consequently, packrat grammars are more suitable if we want to locally modify grammars inside documents.
On the negative side, packrat grammars do not support left recursion in a direct way. For instance, the grammar
leads to an infinite recursion when parsing the string  . Fortunately, this is not a very serious
drawback, because most left-recursive rules are “directly”
left-recursive in the sense that the left-recursion is internal to a
single rule. Directly left-recursive grammars can easily be rewritten
into right-recursive grammars. For instance, the above grammar can be
rewritten as
. Fortunately, this is not a very serious
drawback, because most left-recursive rules are “directly”
left-recursive in the sense that the left-recursion is internal to a
single rule. Directly left-recursive grammars can easily be rewritten
into right-recursive grammars. For instance, the above grammar can be
rewritten as
Furthermore, it is easy to avoid infinite loops as follows. Before
parsing an expression 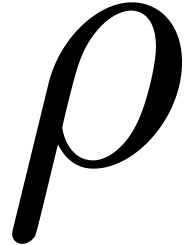 at the position
at the position 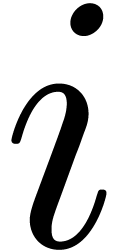 , we first put “false”
in the cache table for the pair
, we first put “false”
in the cache table for the pair 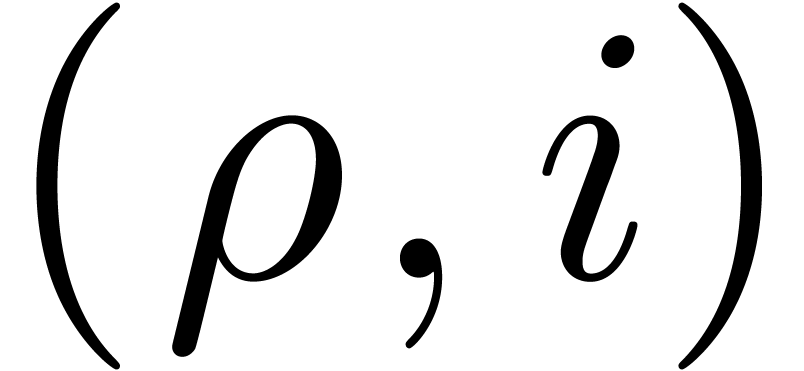 .
Any recursive attempt to parse
.
Any recursive attempt to parse 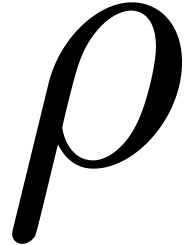 at the same
position will therefore fail.
at the same
position will therefore fail.
A negative side effect of the elimination of lexers is that whitespace
is no longer ignored. The treatment of whitespace can therefore be more
problematic for packrat parsers. For various reasons, it is probably
best to manually parse whitespace. For instance, every infix operator
such as  is replaced by a non-terminal symbol
is replaced by a non-terminal symbol
 , which automatically
“eats” the whitespace around the operator. An alternative
solution, which provides less control, is to implement a special
construct for removing all whitespace. A more elegant solution is to
introduce a second packrat grammar with associated productions, whose
only task is to eliminate whitespace, comments, etc.
, which automatically
“eats” the whitespace around the operator. An alternative
solution, which provides less control, is to implement a special
construct for removing all whitespace. A more elegant solution is to
introduce a second packrat grammar with associated productions, whose
only task is to eliminate whitespace, comments, etc.
In fact, TeXmacs documents are really trees. As we will see in section 5.4 below, we will serialize these trees into strings before applying a packrat parser. This serialization step can be used as an analogue for the lexer and an occasion to remove whitespace.
An efficient generic parser for packrat grammars, which operators on
strings of 32-bit integers, has been implemented in the C++ part of
TeXmacs. Moreover, we provide a
(define-language pocket-calculator
(define Sum
(Sum "+" Product)
(Sum "-" Product)
Product)
(define Product
(Product "*" Number)
(Product "/" Number)
Number)
(define Number
((+ (- "0" "9")) (or ("." (+ (- "0" "9"))) "")))) |
For top-level definitions of non-terminal symbols, we notice the
presence of an implicit or for sequential disjunctions.
The notation (- "0" "9") is a
convenient abbreviation for the grammar 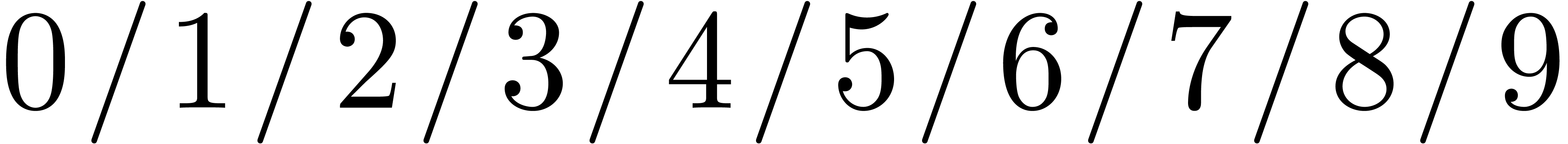 .
.
TeXmacs also allows grammars to inherit from other grammars. This makes it for instance possible to put the counterpart of a lexer in a separate grammar:
(define-language pocket-calculator-lexer
(define Space (* " "))
(define Plus (Space "+" Space))
(define Minus (Space "-" Space))
(define Times (Space "*" Space))
(define Over (Space "/" Space)))
(define-language pocket-calculator
(inherit pocket-calculator-lexer)
(define Sum
(Sum Plus Product)
(Sum Minus Product)
Product)
…) |
In a similar manner, common definitions can be shared between several grammars.
In traditional parser generators, such as
(define Sum
(-> (Sum Plus Product) ("(" 2 " " 1 " " 3 ")"))
(-> (Sum Minus Product) ("(" 2 " " 1 " " 3 ")"))
Product) |
For the last case Product, we understand that the default production is identity. In the case of left-recursive grammars, we also have to adapt the productions, which can be achieved via the use of suitable lambda expressions [10].
Notice that the productions actually define a second packrat grammar. In
principle, we might therefore translate into other languages than  and the reverse
translation might insert an invisible wildcard. Finally, we might
compose “packrat converters” so as to define new converters
or separate certain tasks which are traditionally carried out by a lexer
from the main parsing task. We intend to return to these possible
extensions in a forthcoming paper.
and the reverse
translation might insert an invisible wildcard. Finally, we might
compose “packrat converters” so as to define new converters
or separate certain tasks which are traditionally carried out by a lexer
from the main parsing task. We intend to return to these possible
extensions in a forthcoming paper.
Apart from the not yet implemented productions, there are various other kinds of annotations which have been implemented in TeXmacs. First of all, we may provide short descriptions of grammars using the :synopsis keyword:
(define-language pocket-calculator (:synopsis "grammar demo for a simple pocket calculator") …) |
Secondly, one may specify a physical or logical “color” for syntax highlighting:
(define Number
(:highlight constant_number)
((+ (- "0" "9")) (or "" ("." (+ (- "0" "9")))))) |
We may also associate types and typesetting properties to symbols:
(define And-symbol (:type infix) (:penalty 10) (:spacing default default) "<wedge>" "<curlywedge>") |
These types were for instance used in our heuristics for syntax correction (see section 3.3). Finally, we implemented the additional properties :operator and :selectable, which will be detailed in section 7 on grammar assisted editing. More kinds of annotations will probably be introduced in the future.
We recall that TeXmacs documents are internally represented by trees. Therefore, we have two options for applying packrat parsing techniques to TeXmacs documents:
Generalizing packrat grammars to “tree grammars”.
Flattening trees as strings before parsing them.
For the moment, we have opted for the second solution.
More precisely, a TeXmacs document snippet is either a string leaf or a
compound tree which consists of a string label and an arbitrary number
of children, which are again trees. String leafs are represented in
“enriched ASCII”, using the convention that special
characters can be represented by alphanumeric strings between the
special symbols < and >. For
instance, <alpha> represents  , whereas < and >
are represented by <less> and <gtr>.
Although this is currently not exactly the case, one may think of
enriched ASCII strings as unicode strings.
, whereas < and >
are represented by <less> and <gtr>.
Although this is currently not exactly the case, one may think of
enriched ASCII strings as unicode strings.
A straightforward way to serialize a compound tree  with a given label and children
with a given label and children  is as follows. Assuming that
is as follows. Assuming that  are recursively
serialized as u1,
are recursively
serialized as u1,  ,
un, we serialize
,
un, we serialize  as <\label>u1<|>…<|>un</>.
For instance, the expression
as <\label>u1<|>…<|>un</>.
For instance, the expression
would be serialized as
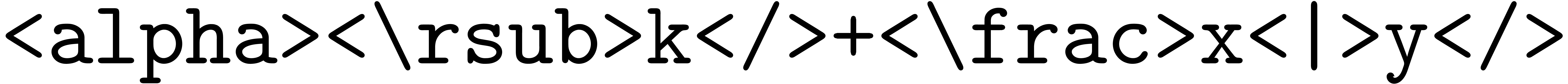
An interesting possibility is to serialize special kinds of trees in alternative ways. For instance, whitespace may be ignored and a document with several paragraphs may be serialized by inserting newline characters instead of the special “characters” <\document>, <|> and </>. In this respect, the serialization step is somewhat analogous to the lexing step for traditional parsers. For user defined macros, it is also convenient to make the serialization customizable, as will be discussed in section 6.3 below.
Recall that our generic packrat parser operates on 32 bit integer strings. Internally, part of the 32 bit integer range is reserved for characters in our enriched alphabet, including the additional “characters” <\label>, <|> and </>. Another part is reserved for non terminal symbols. The remaining part is reserved for constructs of parsing expressions.
In order to simplify the task of writing
The
:any, for any well formed TeXmacs tree.
:args as a shorthand for (:arg (* (:/ :arg))).
:leaf, for any well formed leaf.
:char, for any enriched ASCII character, such as a or <alpha>.
For instance, the Product rule in our pocket calculator might be replaced by
(define Product (Product Times Number) (Product Over Number) Fraction) (define Fraction (:<frac Sum :/ Sum :>) Number) |
Having implemented a good mechanism for the construction of parsers, we are confronted to the next question: which grammar should we use for general purpose mathematical formulas? In fact, we first have to decide whether we should provide a universal well-designed grammar or make it easy for users to define their own customized grammars.
One important argument in favour of the first option is that a standard
well-designed grammar makes communication either, since the reader or
coauthors do not have to learn different notational conventions for each
document. In the same way as presentation
Another argument in favour of a universal grammar is the fact that the design of new grammars might not be so easy for non experts. Consequently, there is a high risk that customized grammars will be ill-designed and lead to errors which are completely unintelligible for other users. Stated differently: if we choose the second option, then customizations should be made really easy. For instance, we might only allow users to introduce new operators of standard types (prefix, postfix, infix) with a given priority.
The main argument in favour of customizable grammars is that we might not be able to anticipate the kind of notation an author wishes to use, so we prefer to keep a door open for customizing the default settings. External systems, such as proof assistants or computer algebra systems, may also have built-in ways to define new notations, which we may wish to reflect inside TeXmacs.
At any rate, before adding facilities for customization, it is an interesting challenge to design a grammar which recognizes as much of the traditional mathematical notation as possible. For the moment, we have concentrated ourselves on this task, while validating the proposed grammars on a wide variety of existing documents. Besides, as we will see in section 6.3, although we do not provide easy ways for the user to customize the grammar, we do allow users to customize the tree serialization procedure. This is both a very natural extension of the existing TeXmacs macro system and probably sufficient for most situations when users need customized notations.
Having opted for a universal grammar, a second major design issue
concerns potential ambiguities. Consider the expression 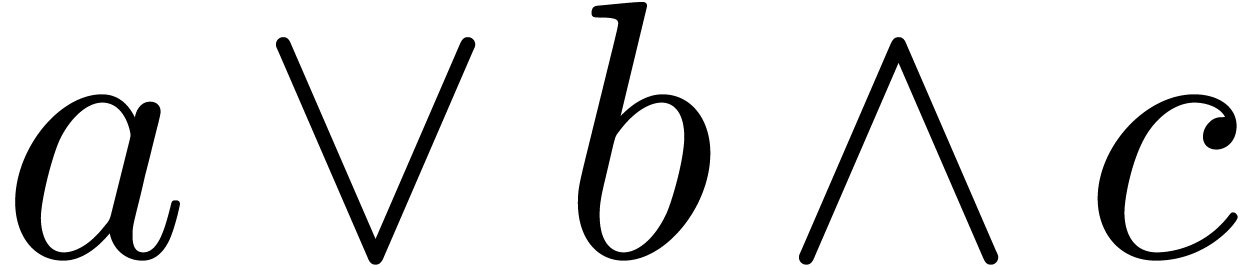 . In analogy with
. In analogy with 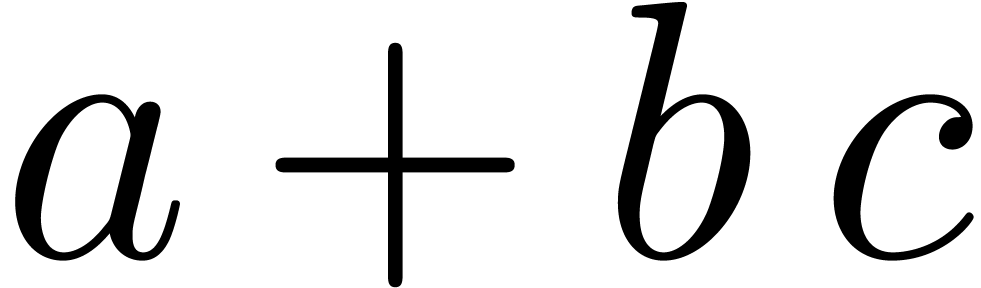 ,
this expression is traditionally parsed as
,
this expression is traditionally parsed as 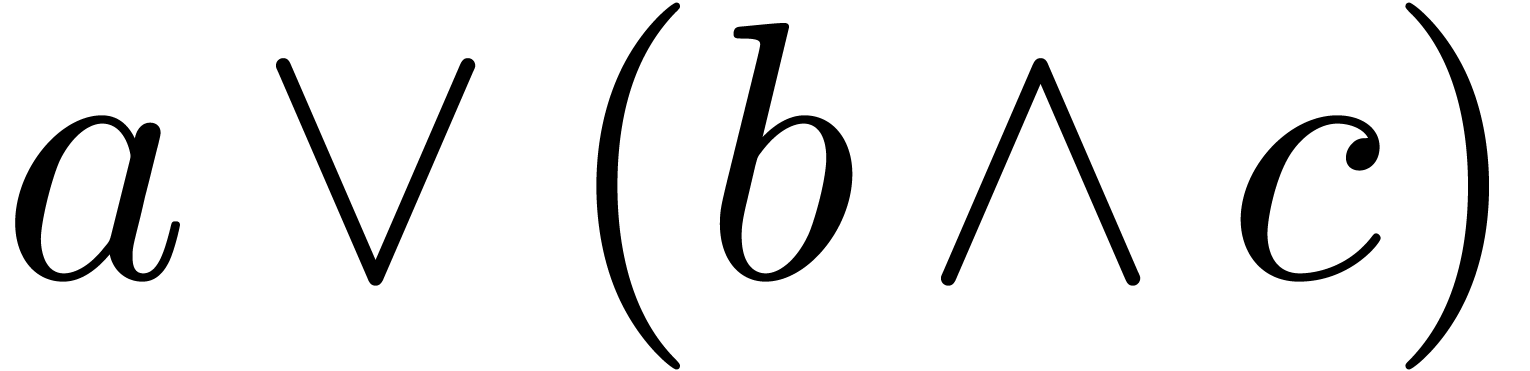 .
However, this may be non obvious for some readers. Should we punish
authors who enter such expressions, or re-lax and leave it as a task to
the reader to look up the notational conventions?
.
However, this may be non obvious for some readers. Should we punish
authors who enter such expressions, or re-lax and leave it as a task to
the reader to look up the notational conventions?
In other words, since language of a matter of communication, we have to decide whether the burden of disambiguating formulas should rather incomb to the author or to the reader. For an authoring tool such as TeXmacs, it is natural to privilege the author in this respect. We also notice that the reader might have access to the document in electronic or TeXmacs form. In that case, we will discuss in section 7 how the reading tool may incorporate facilities for providing details on the notational conventions to the reader.
The current TeXmacs grammar for mathematics is subdivided into three subgrammars:
A lowest level grammar std-symbols which mainly contains all supported mathematical symbols, grouped by category.
An intermediate grammar std-math-operators which mainly describes the mathematical operators occurring in the grammar.
The actual grammar std-math-grammar.
The purpose of the lowest level grammar is to group all supported mathematical symbols by category and describe the purpose and typesetting properties of each category. A typical non terminal symbol defined in this grammar is the following:
(define And-symbol (:type infix) (:penalty 10) (:spacing default default) "<wedge>" "<curlywedge>") |
The category contains two actual symbols <wedge>
( ) and <curlywedge>
(
) and <curlywedge>
( ). The :type
annotation specifies the purpose of the symbol, i.e. that
it will be used as an infix operator. The :penalty and
:spacing annotations specify a penalty for the symbols
during line-breaking and the usual spacing around the symbols. For some
symbols and operators, subscripts and superscripts are placed below
resp. above:
). The :type
annotation specifies the purpose of the symbol, i.e. that
it will be used as an infix operator. The :penalty and
:spacing annotations specify a penalty for the symbols
during line-breaking and the usual spacing around the symbols. For some
symbols and operators, subscripts and superscripts are placed below
resp. above:
(define N-ary-operator-symbol (:type n-ary) (:penalty panic) (:spacing none default) (:limits display) "inf" "lim" "liminf" "limsup" "max" "min" "sup") |
The symbol grammar also describes those TeXmacs tags which play a special role in the higher level grammars:
(define Reserved-symbol :<frac :<sqrt :<wide …) |
The purpose of std-math-operators is to describe all mathematical operators which will be used in the top-level grammar std-math-grammar. Roughly speaking, the operators correspond to the symbols defined in std-symbols, with this difference that they may be “decorated”, typically by primes or scripts. For instance, the counterpart of And-symbol is given by
(define And-infix (:operator) (And-infix Post) (Pre And-infix) And-symbol) |
where Pre and Post are given by
(define Pre (:operator) (:<lsub Script :>) (:<lsup Script :>) (:<lprime (* Prime-symbol) :>)) (define Post (:operator) (:<rsub Script :>) (:<rsup Script :>) (:<rprime (* Prime-symbol) :>)) |
The :operator annotation states that And-infix should be considered as an operator during selections and other structured editing operations (see section 7).
Roughly speaking, the main grammar for mathematics std-math-grammar defines the following kinds of non terminal symbols:
The main symbol Expression for mathematical expressions.
A relaxed variant Relaxed-expression of Expression,
for which operators  and formulas such as
and formulas such as
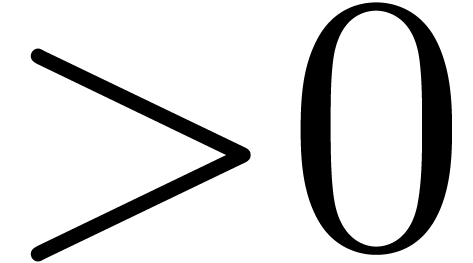 are valid expressions. Relaxed expressions
typically occur inside scripts:
are valid expressions. Relaxed expressions
typically occur inside scripts: 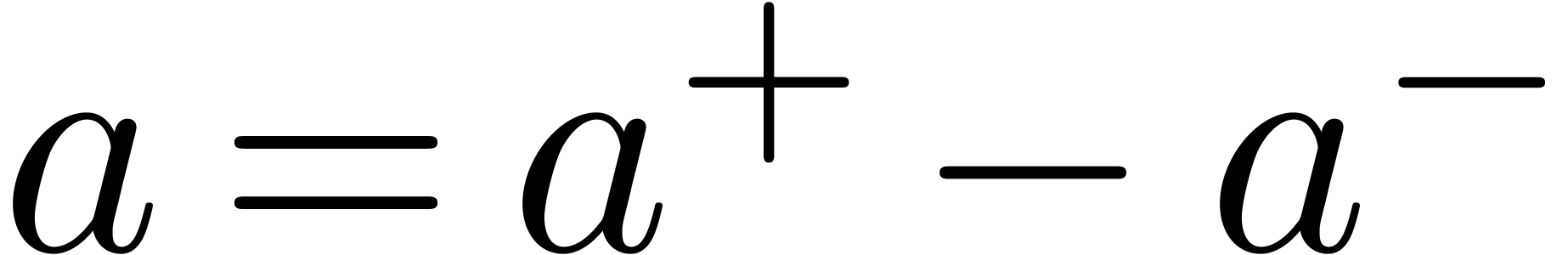 ,
,
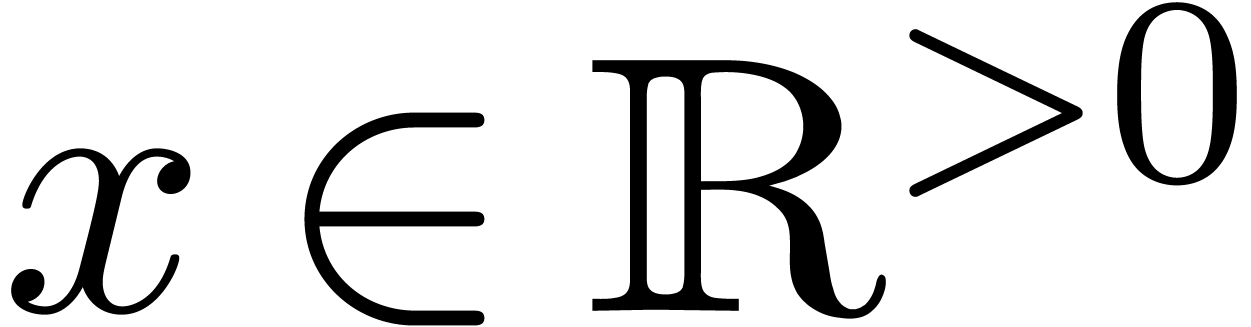 , etc.
, etc.
The symbol Main for the “public interface”, which is a relaxed expression with possible trailing ponctuation symbols and whitespace.
Symbols corresponding to each of the operator types, ordered by priority.
Some special mathematical notations, such as quantifier notation.
Prefix-expressions postfix-expressions and radicals.
For instance, the “arithmetic part” of the grammar is given by
(define Sum (Sum Plus-infix Product) (Sum Minus-infix Product) Sum-prefix) (define Sum-prefix (Plus-prefix Sum-prefix) (Minus-prefix Sum-prefix) Product) (define Product (Product Times-infix Power) (Product Over-infix Power) Power) |
The grammatical specification of relations 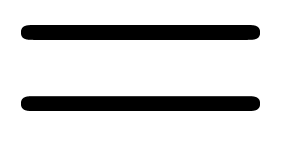 ,
,
 ,
,  ,
,  ,
etc. is similar to the specification of infix operators,
but relations carry the following special semantics:
,
etc. is similar to the specification of infix operators,
but relations carry the following special semantics:
Quantified expressions are defined by
(define Quantified (Quantifier-prefixes Ponctuation-infix Quantified) (Quantifier-fenced Quantified) (Quantifier-fenced Space-infix Quantified) Implication) |
where
(define Quantifier-prefix (Quantifier-prefix-symbol Relation)) (define Quantifier-prefixes (+ Quantifier-prefix)) (define Quantifier-fenced (Open Quantifier-prefixes Close) (:<around :any :/ Quantifier-prefixes :/ :any :>)) |
Hence, the most common forms of quantifier notation are all supported:
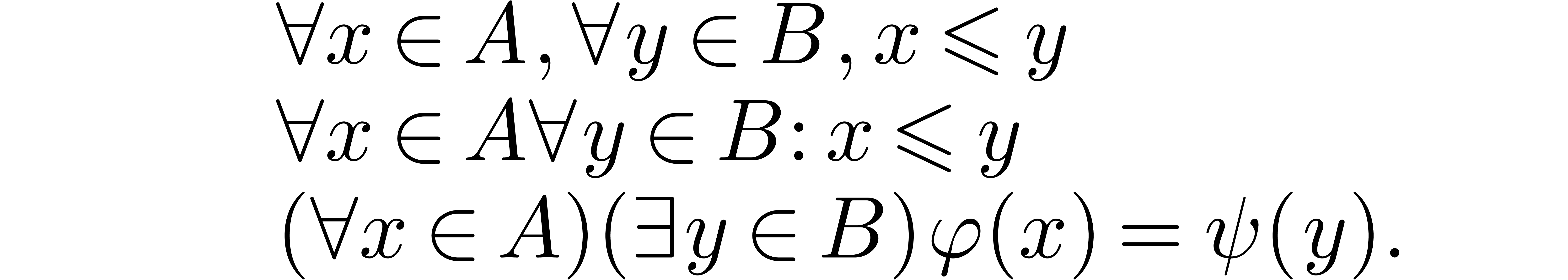
It would also be natural to replace the quantifiers  and
and  by big operators, as in the formula
by big operators, as in the formula
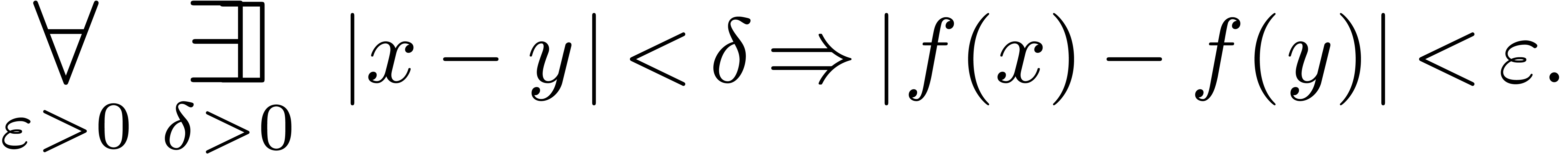
Unfortunately these big symbols are not supported by
In the treatment of postfixed expressions:
(define Postfixed (Postfixed Postfix-postfix) (Postfixed Post) (Postfixed Fenced) (Postfixed Restrict) Radical) |
we consider function application as a postfix:
(define Fenced (Open Close) (Open Expressions Close) (:<around :any :/ (* Post) (* Pre) :/ :any :>) (:<around :any :/ (* Post) Expressions (* Pre) :/ :any :>)) |
Similarly, explicit function application using the invisible apply symbol is handled inside the rule for prefixed expressions. Radical expressions are either identifiers, numbers, special symbols, fenced expressions, or special TeXmacs markup:
(define Radical Fenced Identifier Number (:<sqrt Expression :>) (:<frac Expression :/ Expression :>) (:<wide Expression :/ :args :>) ((except :< Reserved-symbol) :args :>) …) |
Although we have argued that the design or modification of packrat grammars may be difficult for the average user, it still remains desirable to provide a way to introduce new kinds of notation.
One traditional approach is to allow for the introduction of new mathematical operators of a limited number of types (prefix, postfix, infix, bracket, etc.), but with arbitrary binding forces. Such operator grammars are still easy to unterstand and modify for most users. Instead of using numerical binding forces, a nice variant of this idea is to allow for arbitrary partial orders specified by rules such as Product > Sum.
Remark 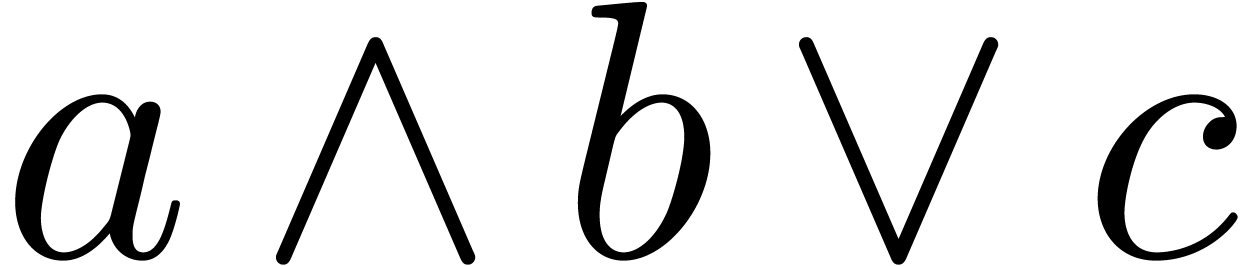 )
and provide hints on how to release the grammar. In practice, these
complications might not be worth it, since the current focus (see
section 7.3) already gives a lot of visual feedback to the
author on how formulas are interpreted.
)
and provide hints on how to release the grammar. In practice, these
complications might not be worth it, since the current focus (see
section 7.3) already gives a lot of visual feedback to the
author on how formulas are interpreted.
Inside TeXmacs, a more straightforward alternative approach is to capitalize on the existing macro system. On the one hand (and before the recent introduction of semantic editing facilities), this system was already used for the introduction of new notations and abbreviations. On the other hand, the system can be extended with a user friendly “behaves as” construct, after which it should be powerful enough for the definition of most practically useful notations.
We recall that TeXmacs macros behave in a quite similar way as LaTeX macros, except that clean names can be used for the arguments. For instance, the macro
<assign|cbrt|<macro|x|<sqrt|x|3>>> |
may be used for defining a macro for producing cubic roots 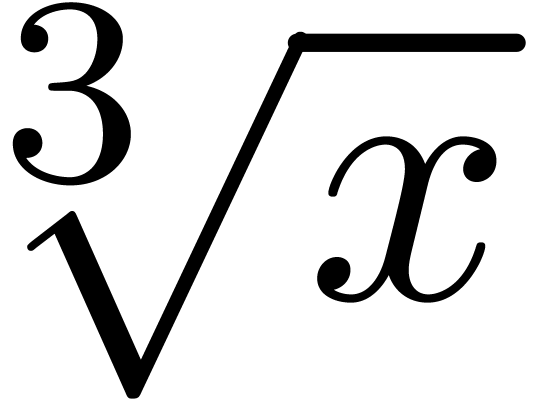 . Our serialization procedure from section 5.3 has been designed in such a way that all user defined
macros are simply expanded by default. In particular, from the semantic
point of view, there is no noticeable difference between the newly
introduced cubic roots and the built-in
. Our serialization procedure from section 5.3 has been designed in such a way that all user defined
macros are simply expanded by default. In particular, from the semantic
point of view, there is no noticeable difference between the newly
introduced cubic roots and the built-in 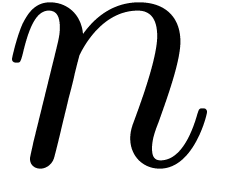 -th
roots with
-th
roots with 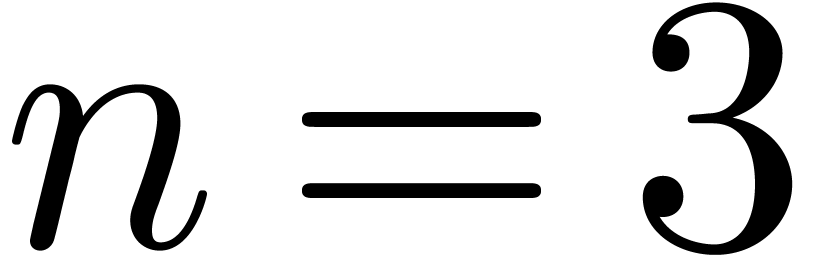 , except that the
, except that the
 in the cubic root is not editable.
in the cubic root is not editable.
The next idea is to allow users to override the default serialization of a macro. For instance, assume that we defined a macro
<assign|twopii|<macro|2*π*i>> |
By default, the line 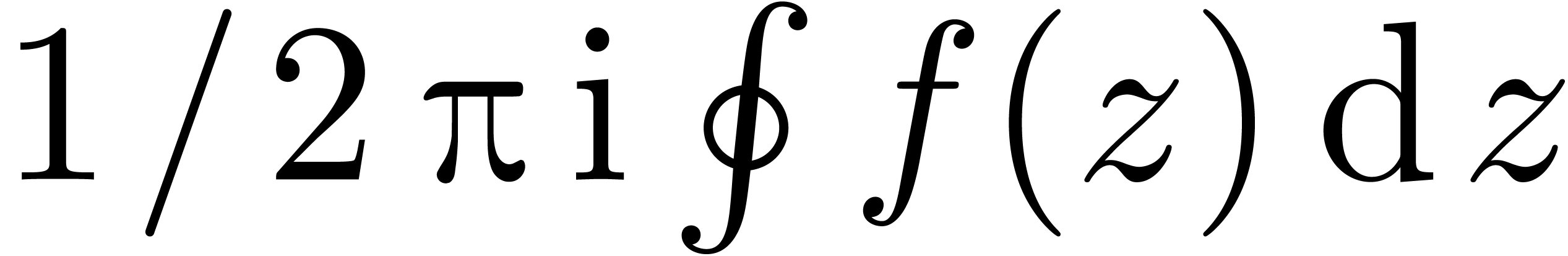 is interpreted as
is interpreted as 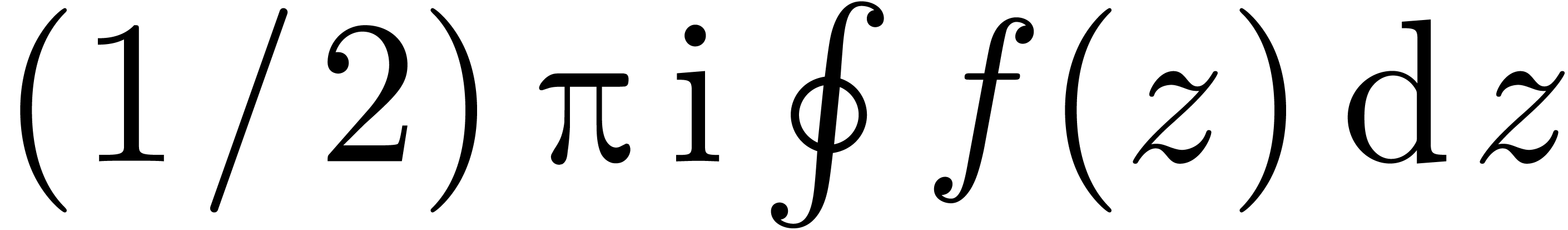 . By specifying a serialization
macro for
. By specifying a serialization
macro for
<drd-props|twopii|syntax|<macro|(2*π*i)>> |
and after entering  using our macro, the formula
using our macro, the formula
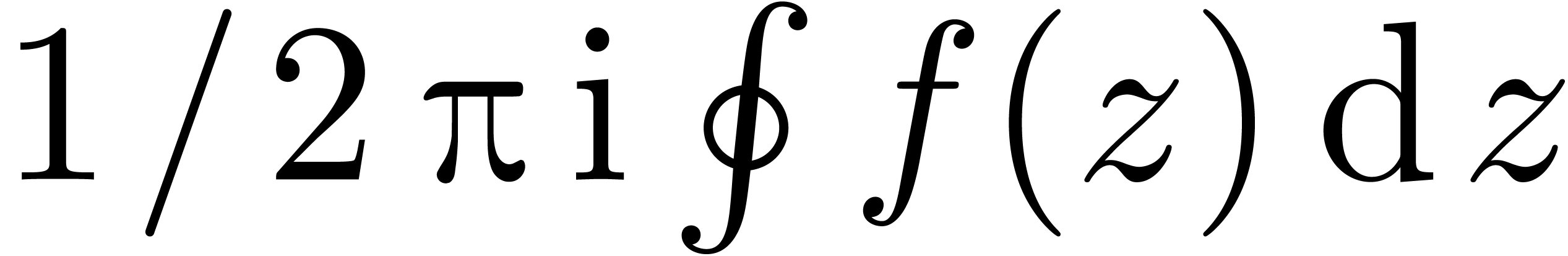 will be interpreted in the intended way
will be interpreted in the intended way 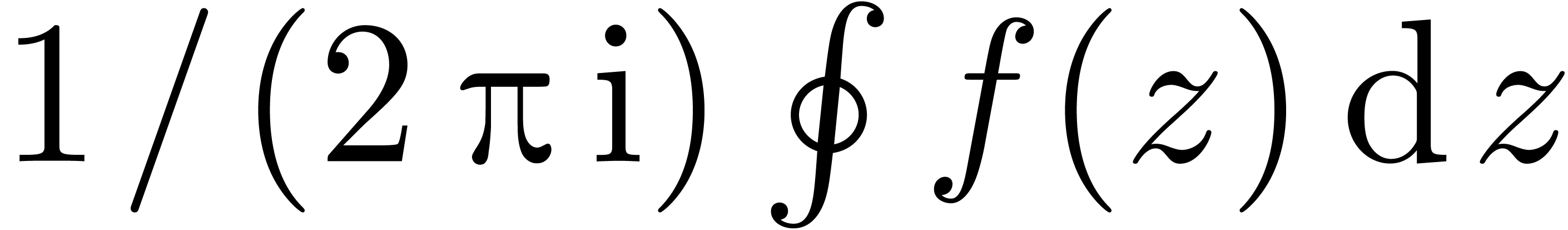 .
.
This very simple idea is both very user friendly (we basically specify
how the macro behaves from a semantic point of view) and quite powerful.
For instance, if we define a  operator with the
binding force of the logical or
operator with the
binding force of the logical or  ,
we simply invent a suitable name, such as “logical-plus”,
use a
,
we simply invent a suitable name, such as “logical-plus”,
use a  for the rendering and a
for the rendering and a  for the serialization. Of course, this scheme is limited to reduce to
those operators which are already present in our predefined universal
grammar. Nevertheless, after some years of maturing, we expect that the
universal grammar will be sufficiently rich for covering most notational
patterns used in practice.
for the serialization. Of course, this scheme is limited to reduce to
those operators which are already present in our predefined universal
grammar. Nevertheless, after some years of maturing, we expect that the
universal grammar will be sufficiently rich for covering most notational
patterns used in practice.
As a side note, it is interesting to observe once more that the serialization procedure plays the role of a “structured” lexer, except that we are rather destroying or transforming tree structure in a customizable way than detecting lexical structure inside strings.
In section 3.4, we have described the performance of the TeXmacs syntax corrector on several large sample documents. In this section, we will analyze in more detail the causes of the remaining “errors”. We will also investigate up to which extent “correct” formulas are interpreted in the way the author probably had in mind.
Throughout the section, one should bear in mind that our test documents were not written using the newly incorporated semantic editing features. On the one hand, our analysis will therefore put the finger on some of the more involved difficulties if we want to make a visually authored document semantically correct. On the other hand, we will get indications on what can be further improved in the syntax corrector and our universal grammar. Of course, our study is limited in the sense that our document base is relatively small. Nevertheless, we think that the most general trends can already be detected.
We have analyzed in detail the remaining errors in BPR1, BPR2, CH3 and HAB, which can be classified according to several criteria, such as severeness, eligibility for automatic correction, and the extent to which the author was to blame for the error. The results of our analysis have been summarized in table 4, where we have distinguished the following few main categories for sorting out the errors:
Sometimes, large whitespaces are used in a semantically meaningful way. For instance, in BPR1 and BPR2, the notation
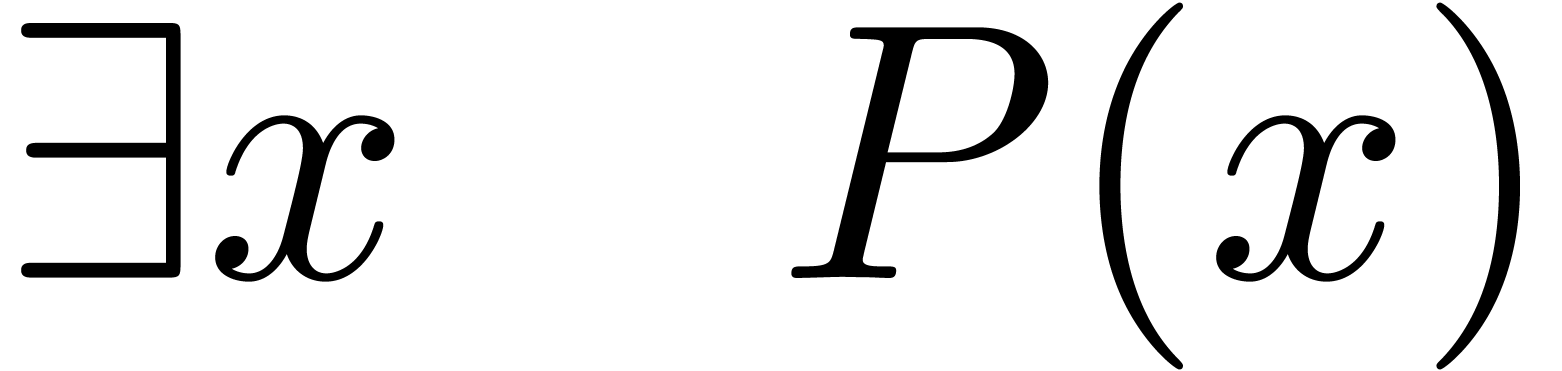 |
(2) |
is frequently used as a substitute for 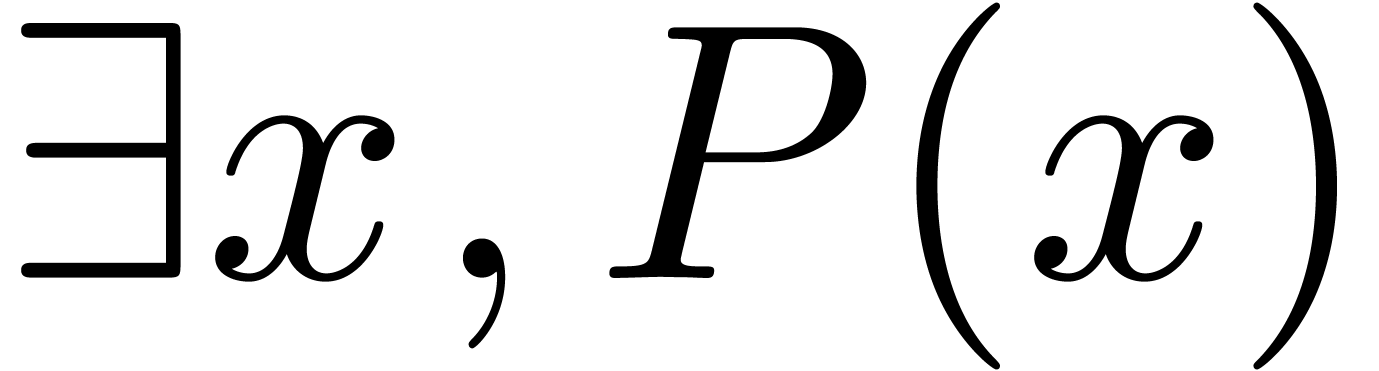 . Although potentially correctable, it should
be noticed that the (currently supported) notation
. Although potentially correctable, it should
be noticed that the (currently supported) notation 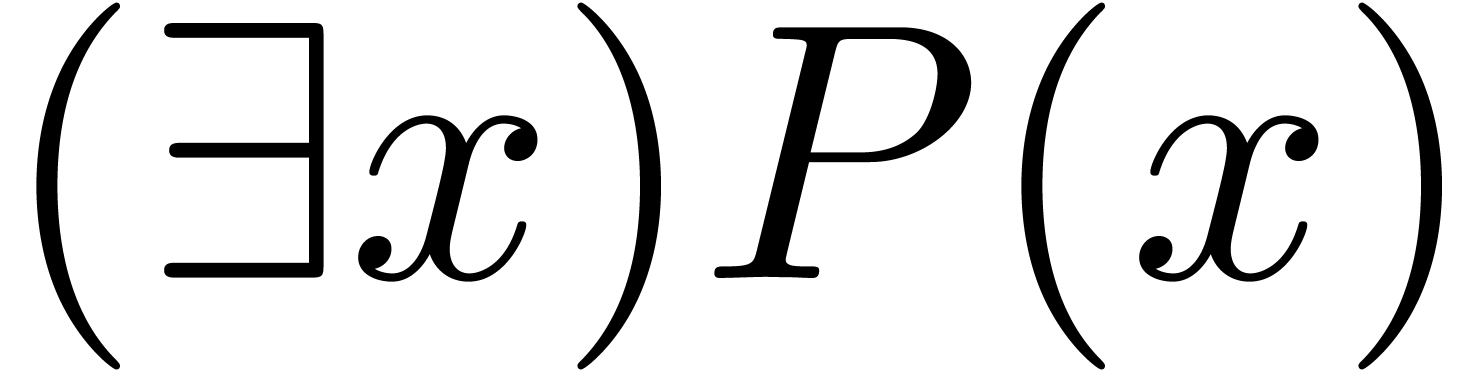 is also used in BPR. Hence, we detected “at
least” an inconsistency in the notational system of BPR.
is also used in BPR. Hence, we detected “at
least” an inconsistency in the notational system of BPR.
We have already mentioned the fact that the universal grammar
should be sufficiently friendly so as to recognize the formula
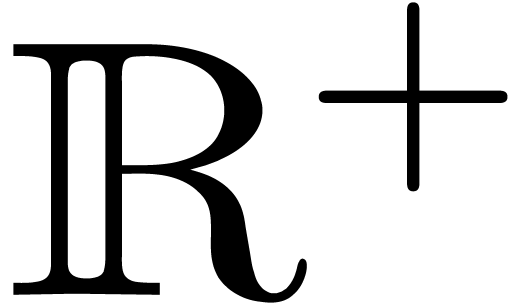 , where the operator
, where the operator
 occurs in a script. More generally, in the
formula
occurs in a script. More generally, in the
formula  from BPR1, the
operators
from BPR1, the
operators  and
and  are
sometimes used “as such”. Although it does not seem a
good idea to extend the grammar indefinitely so as to incorporate
such notations, we might extend the corrector so as to detect
these cases and automatically insert “invisible
operator” annotations.
are
sometimes used “as such”. Although it does not seem a
good idea to extend the grammar indefinitely so as to incorporate
such notations, we might extend the corrector so as to detect
these cases and automatically insert “invisible
operator” annotations.
In tables or equation arrays, large formulas are sometimes manually split across cells. One example from BPR1 is given by
In this example, the curly opening bracket in the right-hand cell of the second line is only closed on the third line. Another (truncated) example from BPR2 is
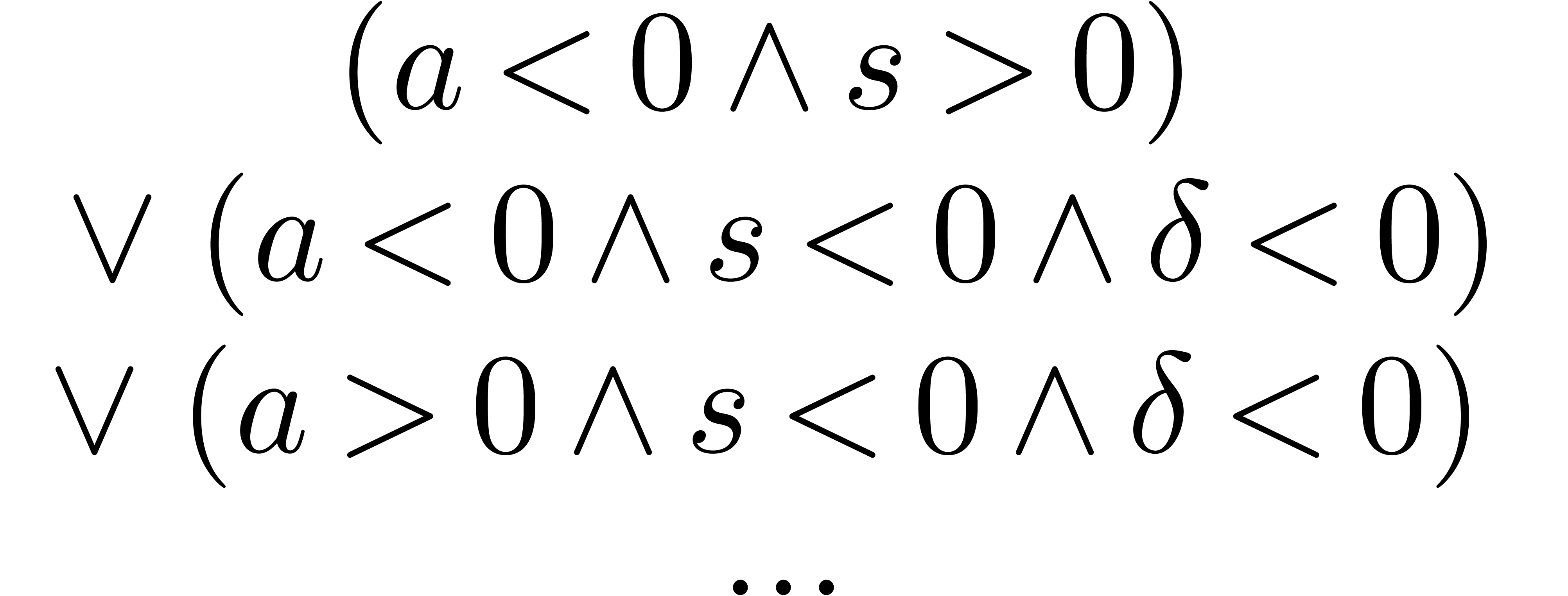
The problem here is that formulas of the form  are incorrect.
are incorrect.
The first example is more severe, and obliges the checker to try
concatenations of various cells. The second example could also be
solved by relaxing the grammar for formulas inside cells. This was
already done for formulas of the form  .
.
This problem is by far the most frequent one. Especially in CH3 the job is made hard for the corrector by the author's habit to replace multiplications by function applications. As a consequence, many symbols which would usually be detected as being variables might also be functions; this confusion pushes the corrector not to touch any of such formulas. Indeed, we consider it better to leave an incorrect formula than to make a wrong “correction”.
Although the juxtaposition of two formulas {$a+$}{$b$} is simplified into $a+b$, such simplifications can be confused by the presence of whitespace, as in $a+$ $b$.
One example from BPR2 is the formula
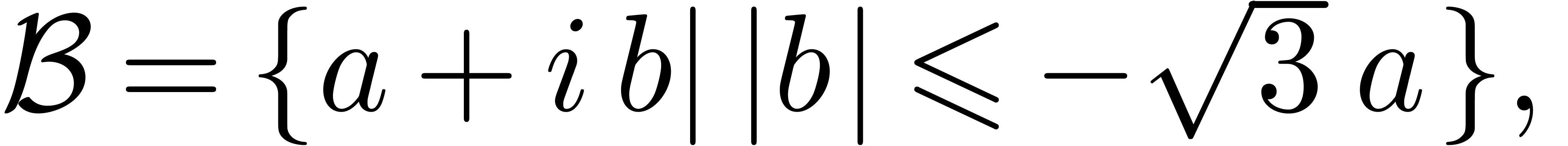
in which the absolute value 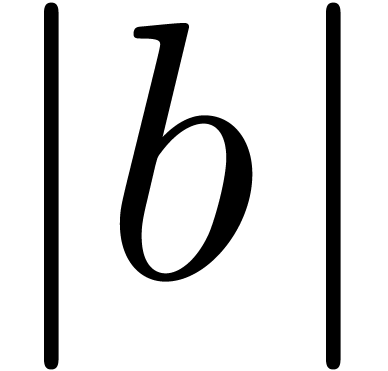 was not
recognized as such. We already mentioned another similar example
from COL before:
was not
recognized as such. We already mentioned another similar example
from COL before:  .
.
Sometimes, authors may use apparently standard notation in a non standard way, by making non conventional assumptions on operator precedence. Consider for instance the following fragment from BPR1:
Given a formula  ,where
,where
 is
is
In this case, the binding force of  is
higher than the binding force of
is
higher than the binding force of  ,
which makes the formula incorrect. Such formulas are on the limit
of being typos: it would be better to insert (possibly invisible)
brackets. This kind of error is rare though, since non standard
operator precedences usually do not prevent formulas from being
parsed, but rather result in non intended interpretations of the
formulas.
,
which makes the formula incorrect. Such formulas are on the limit
of being typos: it would be better to insert (possibly invisible)
brackets. This kind of error is rare though, since non standard
operator precedences usually do not prevent formulas from being
parsed, but rather result in non intended interpretations of the
formulas.
Consider the formula
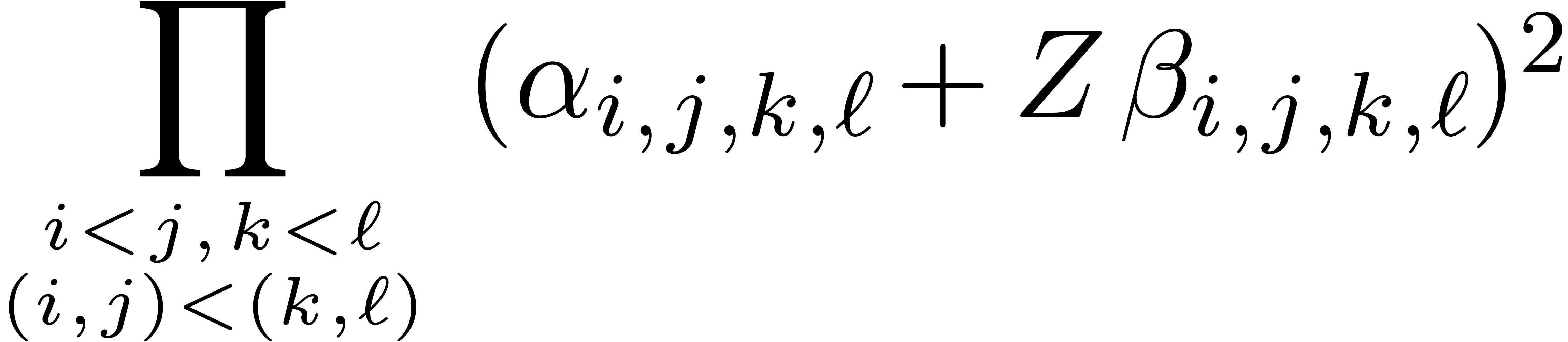
from BPR1. The authors intended to typeset the
subscript of the big product using an extra small font size, and
inserted a double subscript to achieve this visual effect. In
TeXmacs, they should have used the 
It often occurs that one needs to insert some accompanying text inside formulas, as in the formula
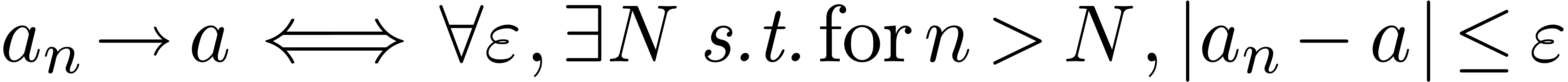
occurring in COL3. The problem here is that the text “s.t. for” was entered in math mode, so it will not be ignored by the parser. Other similar examples from BPR are
There are indeed 4 real roots:  .
.
It is obvious since the  th
entry of
th
entry of  is
is 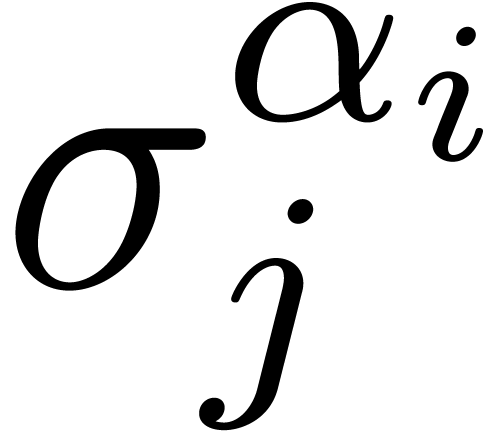 .
.
In each of these examples, we notice that the obtained visual result is actually incorrect: the errors are easily committed by users who do not pay attention to the font slant, the shapes of characters and the spacing between words. For instance, the corrected versions of the last examples read
There are indeed 4 real roots:  ,
and
,
and  .
.
It is obvious since the  -th
entry of
-th
entry of  is
is 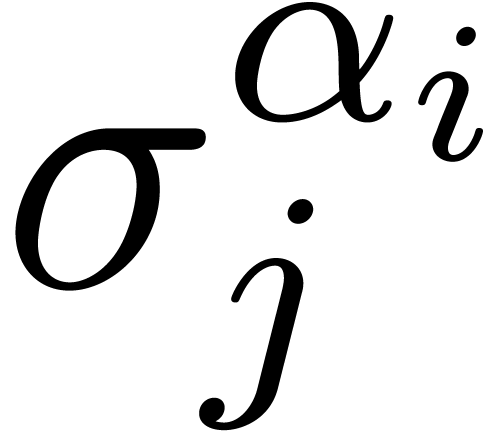 .
.
Notice also that correctly entered text inside mathematical formulas is ignored by the parser. Consequently, the use of meaningful text inside formulas may raise the same problems as the before-mentioned use of meaningful whitespace.
In BPR, there is a general tendency of typesetting implications
between substatements in math-mode, as in the example
“a) b)”.
Clearly, this is an abuse of notation, although it is true that
convenient ways to achieve the same result in text mode do not
necessarily exist.
b)”.
Clearly, this is an abuse of notation, although it is true that
convenient ways to achieve the same result in text mode do not
necessarily exist.
In some less frequent cases, it is convenient to use certain kinds of suggestive notations with ad hoc semantics. Three examples from BPR1, COL3 and HAB respectively are
The signs of the polynomials in the Sturm sequence are 
No other code word is of the form 
Clearly, there is no hope to conceive a “universal grammar” which automatically recognizes this kind of ad hoc notations. The only reasonable way to incorporate such constructs is to provide a few basic annotation tags which allow the user to manually specify the semantics.
Indeed, there is a  missing at the end of the
formula.
missing at the end of the
formula.
|
|||||||||||||||||||||||||||||||||||
The above analysis of the remaining errors takes advantage of the possibility to highlight all syntax errors in a TeXmacs document. Unfortunately, there is no automatic way to decide whether a correct formula is interpreted in the way intended by the author. Therefore, it requires far more work to give a complete qualitative and quantitative analysis of the “parse results”. Nevertheless, it is possible to manually check the interpretations of the formulas, by careful examination of the semantic focus (see 7.3 below for a definition and more explanations on this concept) at the accessible cursor positions in a formula.
We have carefully examined the documents BPR1, COL3, HAB1 and HAB5 in this way. The number of misinterpretations in BPR1 and HAB are of the same order of magnitude as the number of remaining errors. The number of misinterpretations in COL3 is very high, due to the fact that most multiplications were replaced by function applications. This paper also makes quite extensive use of semantically confusing text inside formulas. When ignoring these two major sources of misinterpretation, the universal grammar correctly parses most of the formulas.
The results of our analysis have been summarized in table 5. Let us now describe in more details the various sources of misinterpretation:
Again, the multiply/apply ambiguity constitutes a major source of confusion. Several kinds of misinterpretation are frequent:
Replacing a multiplication by a function application or
vice versa rarely modifies the parsability of a
formula, but it completely alters its sense. For instance 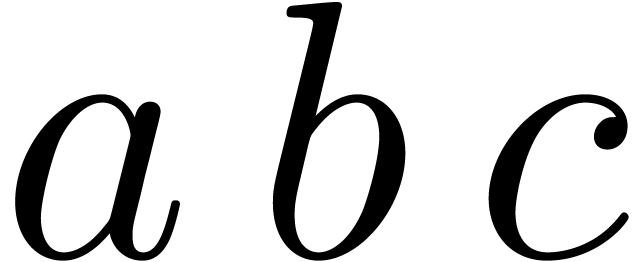 might either be interpreted as
might either be interpreted as 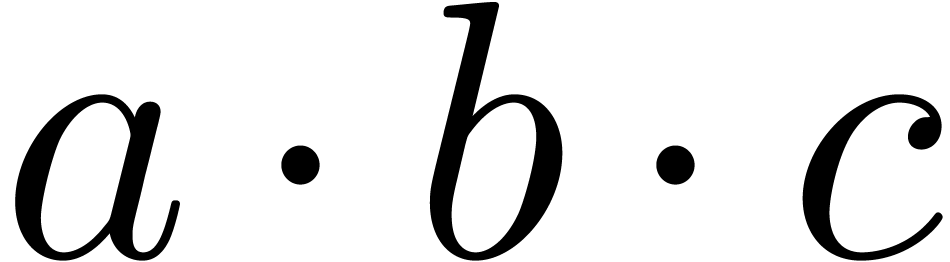 or
or 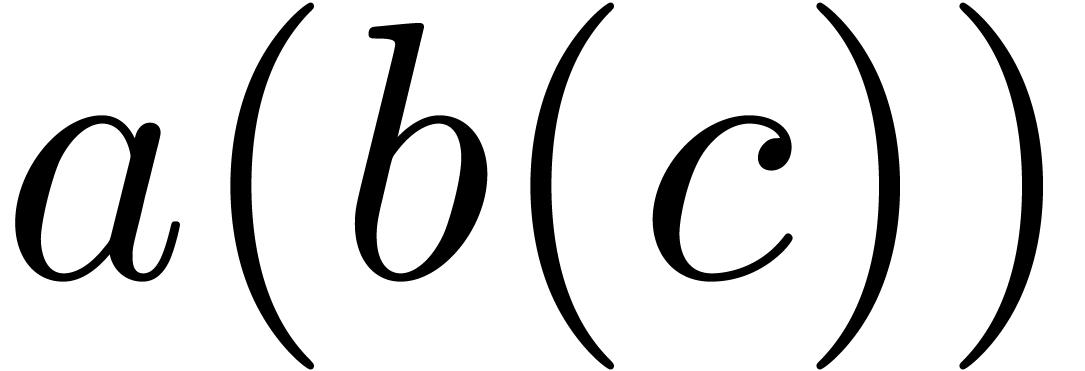 .
Fortunately, this kind of misinterpretations only occurs if
the author explicitly entered the wrong operators.
.
Fortunately, this kind of misinterpretations only occurs if
the author explicitly entered the wrong operators.
A more subtle problem occurs when the author forgets to enter
certain multiplications (or if the syntax corrector failed to
insert them). One example is the subformula 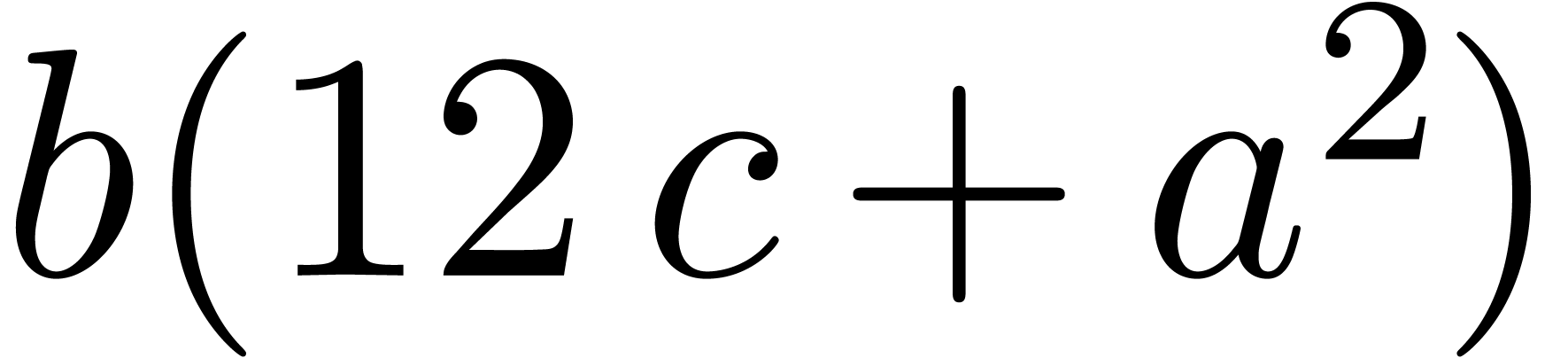 , occurring in BPR1. In
this formula,
, occurring in BPR1. In
this formula,  is interpreted as a
function applied to
is interpreted as a
function applied to  .
.
An even more subtle variant of the above misinterpretation
occurs at the end of HAB5 in the formula  . In order to avoid
trailing spaces, the
. In order to avoid
trailing spaces, the  was explicitly
marked to be an operator and an explicit space was inserted
manually after it. Consequently, the formula is interpreted as
was explicitly
marked to be an operator and an explicit space was inserted
manually after it. Consequently, the formula is interpreted as
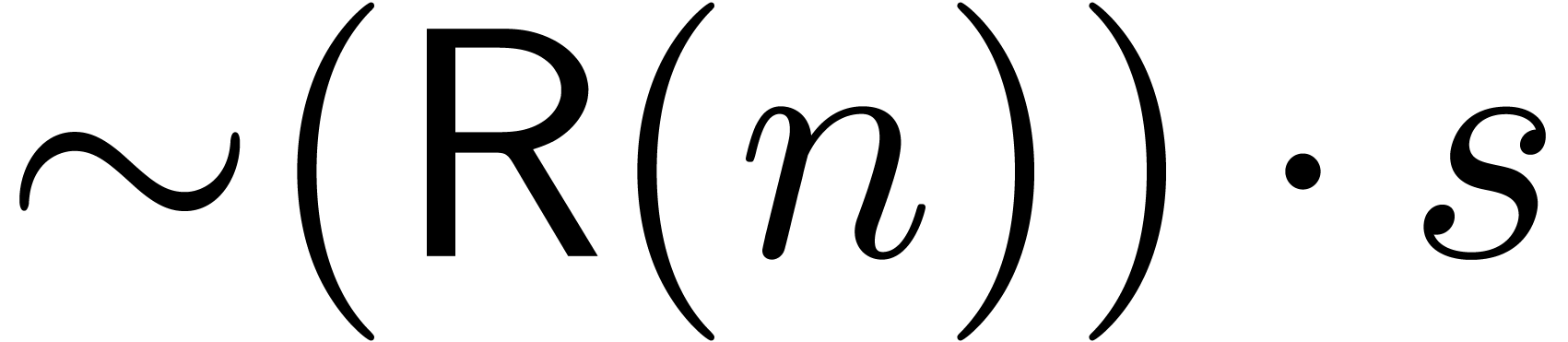 instead of the intended
instead of the intended 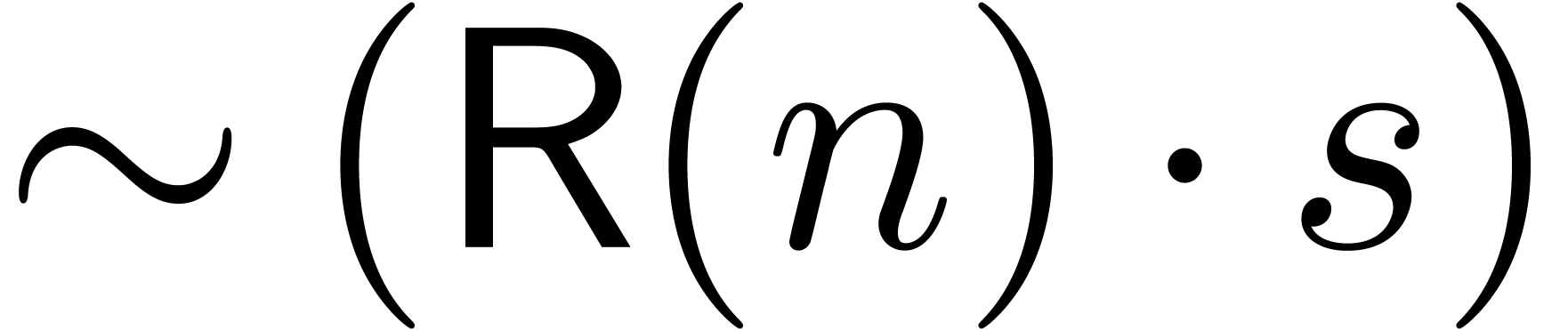 . In recent versions of TeXmacs the
precaution to mark
. In recent versions of TeXmacs the
precaution to mark  as an operator has
become superfluous.
as an operator has
become superfluous.
The informal, but widely accepted notation  is used quite often in order to signify
is used quite often in order to signify  . However, the “natural”
interpretation of this formula is
. However, the “natural”
interpretation of this formula is  .
This is an interesting case where it might be useful to insert an
additional rule into the grammar (the general form being
.
This is an interesting case where it might be useful to insert an
additional rule into the grammar (the general form being 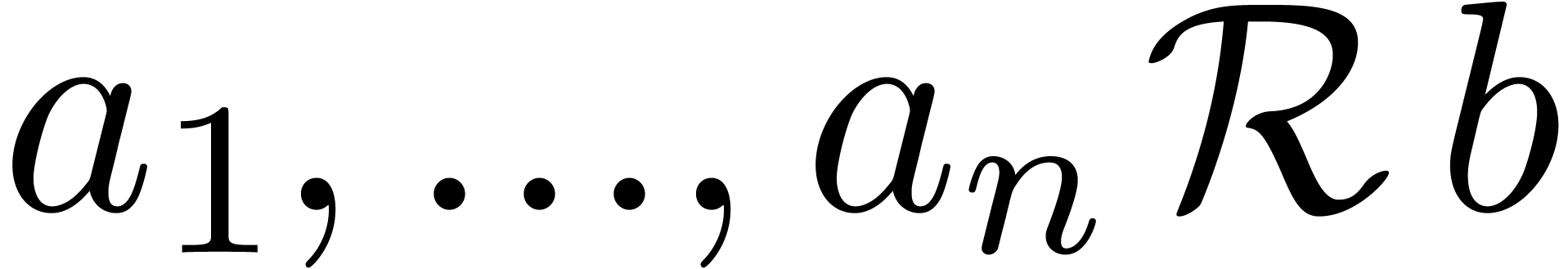 , for a relation infix
, for a relation infix  ). This rule should only
apply for top-level formulas and not for subformulas
(e.g.
). This rule should only
apply for top-level formulas and not for subformulas
(e.g. 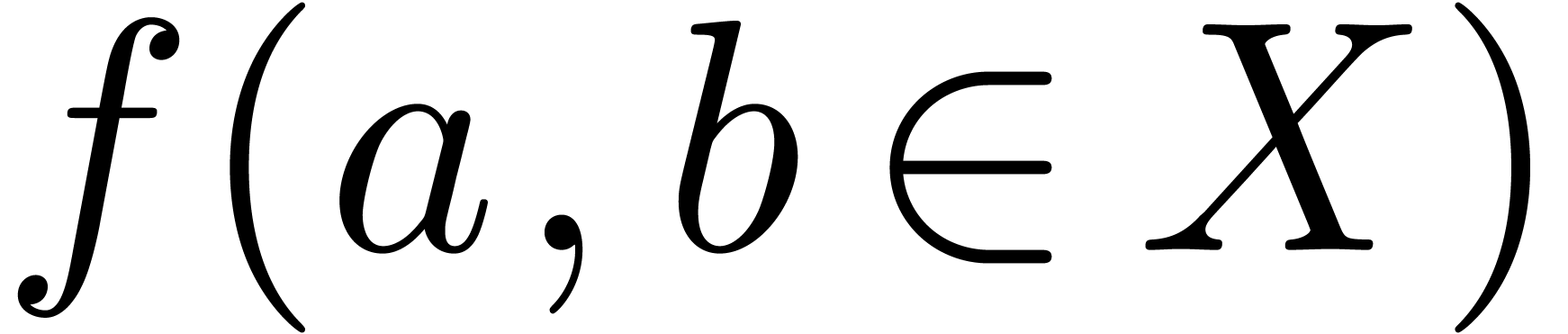 ).
Furthermore, it should be tested before the default interpretation
).
Furthermore, it should be tested before the default interpretation
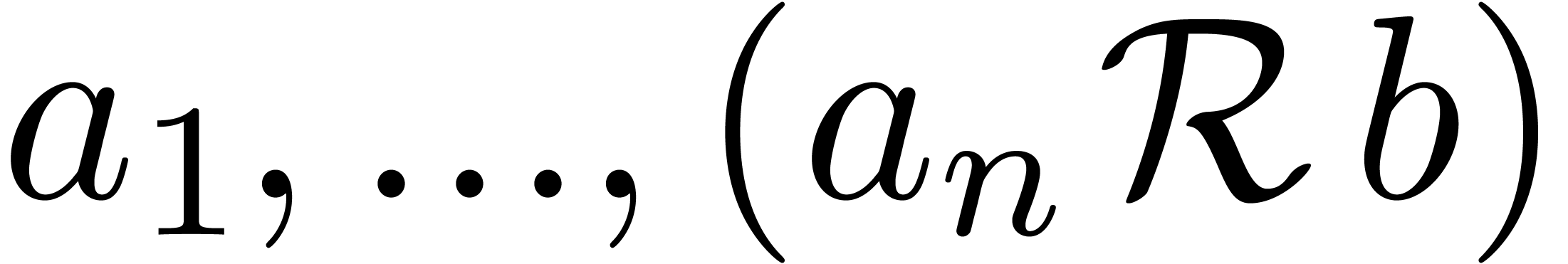 . Here we point out
that this is easy to do for packrat grammars, but not for more
conventional LALR-1 grammars, where such a test would introduce
various kinds of ambiguities.
. Here we point out
that this is easy to do for packrat grammars, but not for more
conventional LALR-1 grammars, where such a test would introduce
various kinds of ambiguities.
In BPR1, one may also find variant of the above
notation: “we define the signed remainder sequence of  and
and  ,
,
In this case, it would have been appropriate to insert invisible brackets around the sequence. Yet another blend of list notation occurs frequently in [31]:
The subsets of affine spaces  for
for  that are
that are 
Here one might have used the more verbose notation 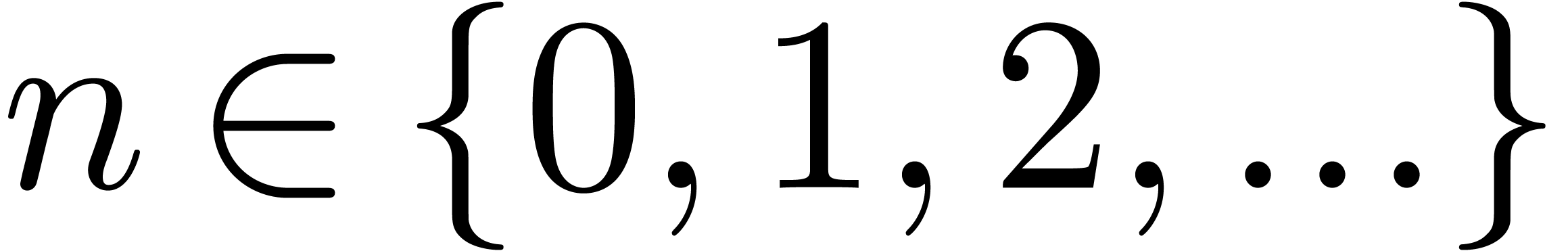 instead. However, it seems preferable to investigate
whether this example justifies another exceptional rule in the
universal grammar. Let us finally consider
instead. However, it seems preferable to investigate
whether this example justifies another exceptional rule in the
universal grammar. Let us finally consider
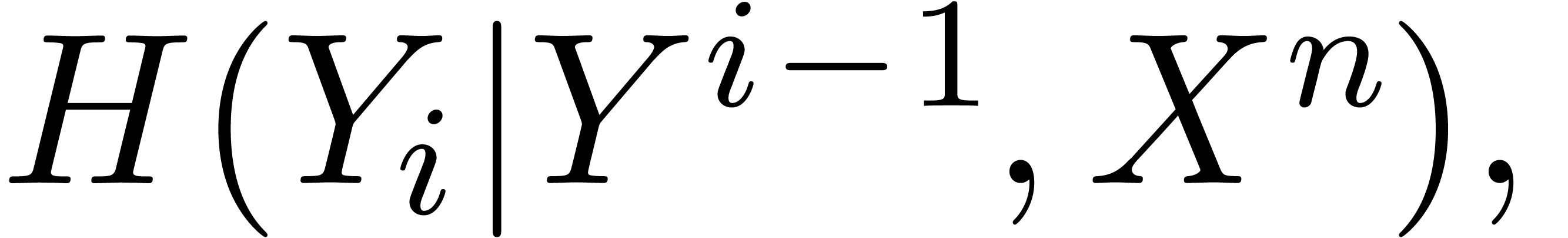
which occurs as a subformula in COL3. Currently, the
separators  and , have the same precedence
in our universal grammar. In view of the above example, we might
want to give , a higher binding force.
and , have the same precedence
in our universal grammar. In view of the above example, we might
want to give , a higher binding force.
Notice that “informal list notation” is a special instance of a potentially more general situation in which certain precedence rules need to be overridden under “certain circumstances”.
If informal text is not being marked as such inside formulas, then it gives rise to a wide variety of errors and potential misinterpretations. Consider for instance the formula
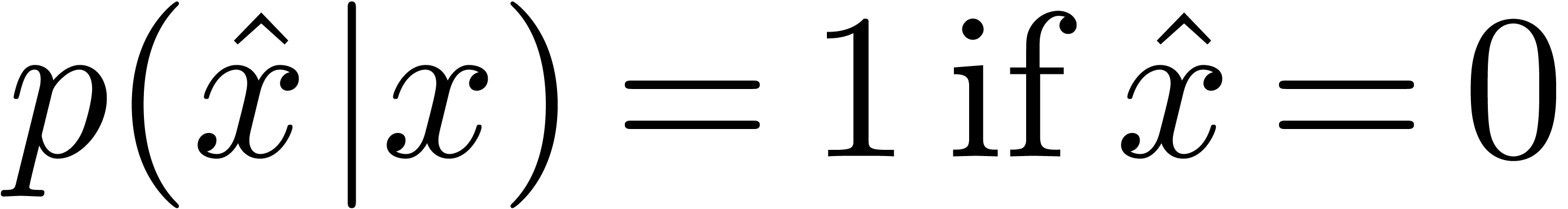
from COL3. Since the word “if” was entered in math mode, the formula is parsed as
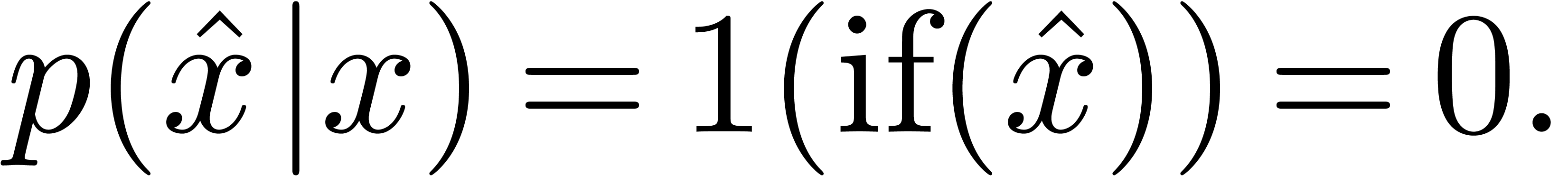
Vice versa, it sometimes happens that a mathematical formula (or part of it) was entered in text mode. Indeed, consider the following fragment from BPR1:
In the above, each  (P,Q)
is the negative of the remainder in the euclidean division of
(P,Q)
is the negative of the remainder in the euclidean division of
 (P,Q) by
(P,Q) by  for
for 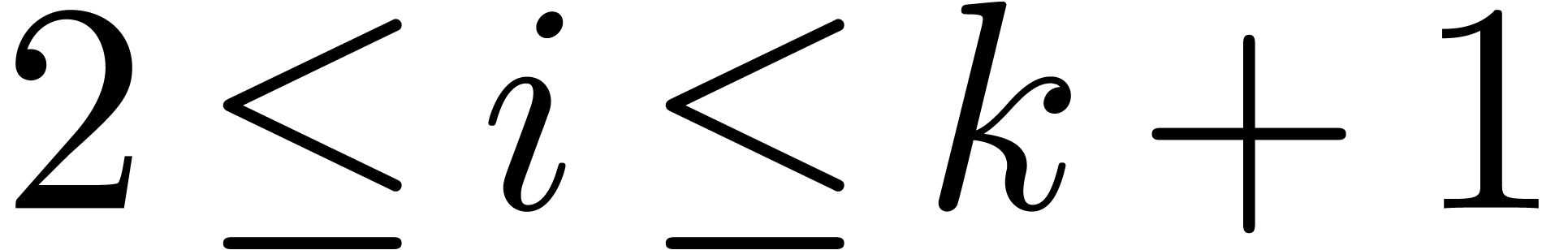 ,
,

At two occasions, the subformula  was
entered in text mode. This might have been noticed by the authors
through the use of an upright font shape.
was
entered in text mode. This might have been noticed by the authors
through the use of an upright font shape.
At several places in HAB1 we have used the following notation:

Contrary to (2), this formula can be parsed, but its meaning
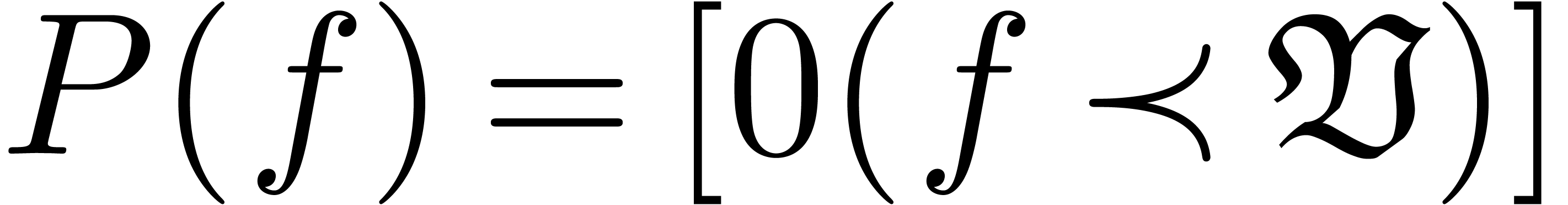
is not what the author intended. This example provides yet more rationale for the design of a good criterion for when a large whitespace really stands for a comma.
One final misinterpreted formula from the document COL3 is
Indeed, the subformula 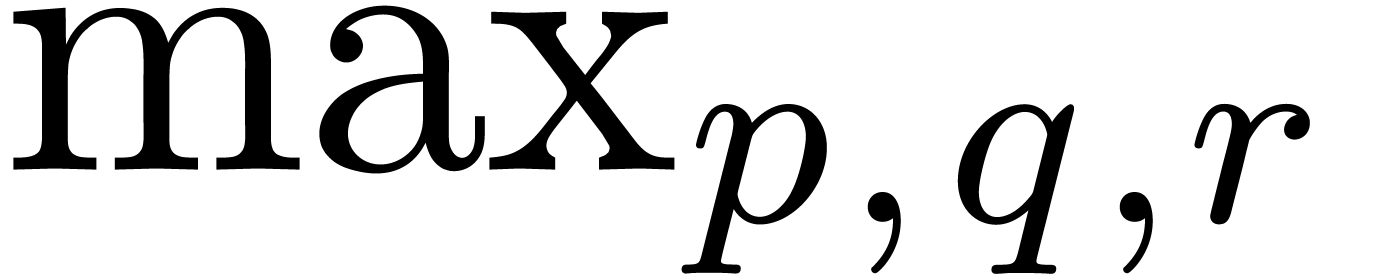 is interpreted as a
summand instead of an
is interpreted as a
summand instead of an  -ary
operator.
-ary
operator.
Despite the existence of the above misinterpretations, we have to conclude that our universal grammar is surprisingly good at interpreting formulas in the intended way. On the one hand (and contrary to the remaining errors from the previous subsection), most misinterpretations tend to fall in a small number of categories, which are relatively well understood. A large number of misinterpretations can probably be eliminated by further tweaking of the universal grammar and the syntax corrector. Most of the remaining misinterpretation can easily be eliminated by the author, if two basic rules are being followed:
Correct manual resolution of the multiply/apply ambiguity.
Correct annotations of all exceptional non mathematical markup inside formulas, such as text and meaningful whitespace.
However, TeXmacs can probably do a better job at inciting authors to follow these rules. We will come back to this point in section 8.
Of course, our conclusions are drawn on the basis of an ever shrinking
number of documents. Rapid investigation of a larger number of documents
shows that certain areas, such as  -calculus
or quantum physics, use various specialized notations. Nevertheless,
instead of designing a completely new grammar, it seems sufficient to
add a few rules to the universal grammar, which can be further
customized using macros in style files dedicated to such areas. For
instance, certain notational extensions involving
-calculus
or quantum physics, use various specialized notations. Nevertheless,
instead of designing a completely new grammar, it seems sufficient to
add a few rules to the universal grammar, which can be further
customized using macros in style files dedicated to such areas. For
instance, certain notational extensions involving  and
and  signs may both be useful in real algebraic
geometry and quantum physics. Such notations might be activated via
certain macros and keybindings defined in dedicated style packages.
signs may both be useful in real algebraic
geometry and quantum physics. Such notations might be activated via
certain macros and keybindings defined in dedicated style packages.
|
|||||||||||||||||||||||||||||||||||
Traditionally, a formal introduction of mathematical formulas starts
with the selection of a finite or countable alphabet 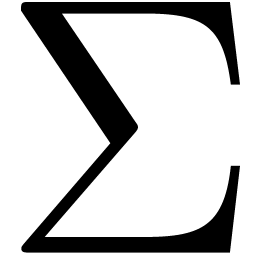 . The alphabet is partitioned into a subset of
logical symbols
. The alphabet is partitioned into a subset of
logical symbols  , a subset of
relation symbols
, a subset of
relation symbols  , a subset
of function symbols
, a subset
of function symbols  and a subset of constant
symbols. Each non-constant symbol
and a subset of constant
symbols. Each non-constant symbol  also carries a
set
also carries a
set 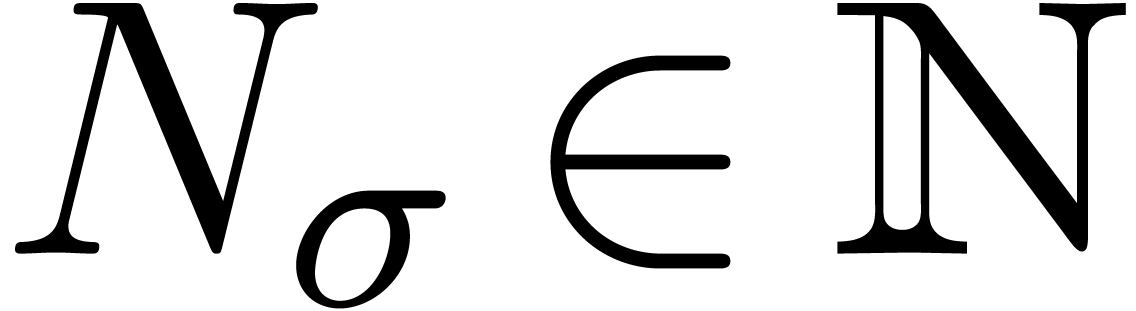 of possible arities. An abstract syntax
tree a finite
of possible arities. An abstract syntax
tree a finite  -labeled
tree, such that the leafs are labeled by constant symbols and such that
the number of children of each inner
-labeled
tree, such that the leafs are labeled by constant symbols and such that
the number of children of each inner  -labeled
node is in
-labeled
node is in 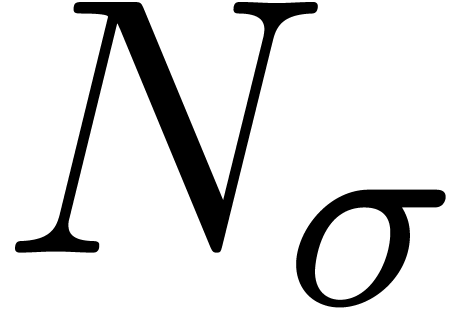 .
.
From now on, a syntactically correct formula is understood to be a formula which corresponds to an abstract syntax tree. For instance, the abstract syntax tree
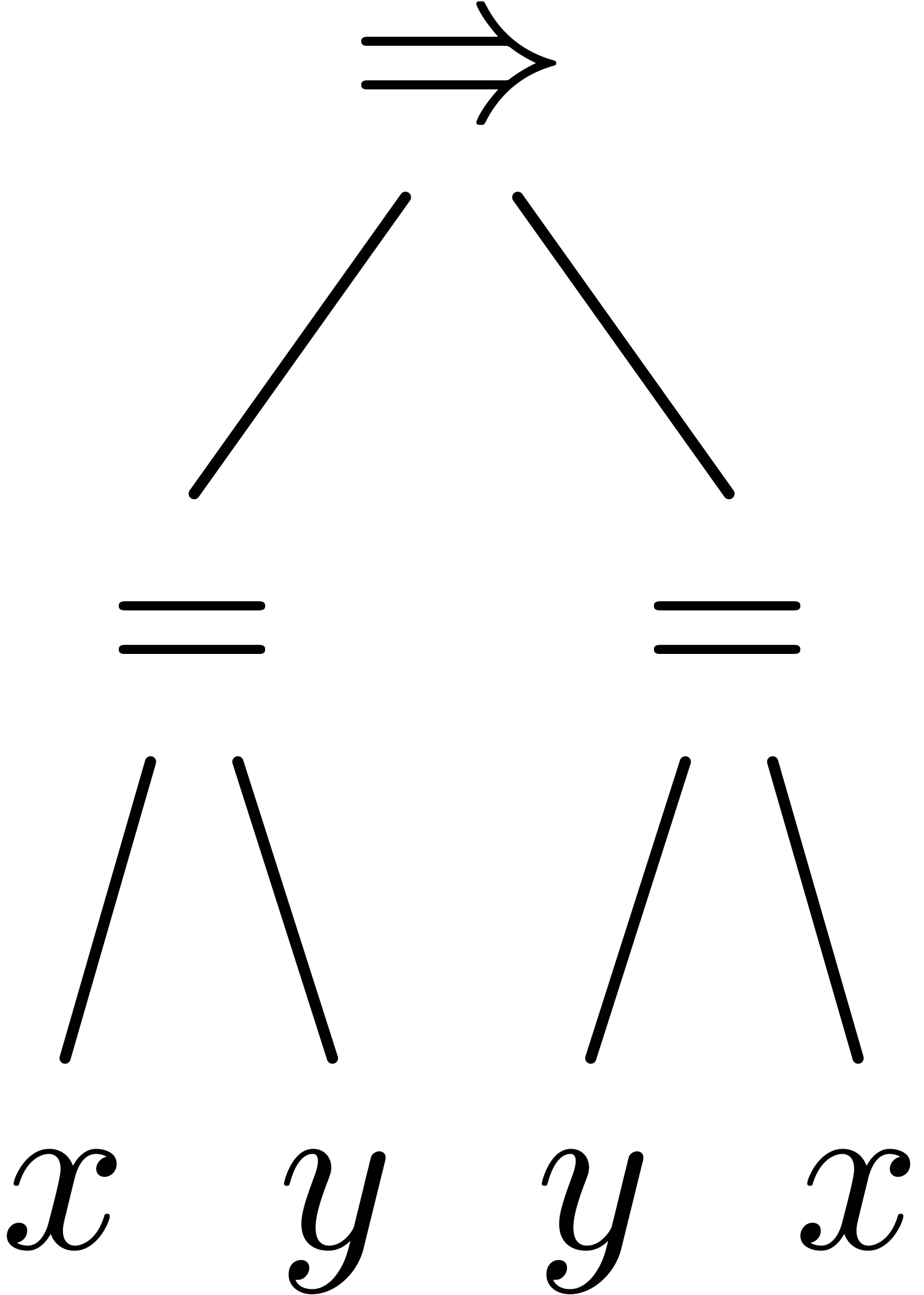
corresponds to the formula  .
For concrete document formats, our definition of syntactic correctness
assumes a way to make this correspondance more precise.
.
For concrete document formats, our definition of syntactic correctness
assumes a way to make this correspondance more precise.
The simplest content oriented formats are those for which the
correspondence is straightforward. For instance, in
by ( T1 … Tn), where T1,
T1 … Tn), where T1,  , Tn
are the representations of
, Tn
are the representations of  .
Content
.
Content
Of course, content oriented formats usually do not specify how to render formulas in a human readable form. This makes them less convenient for the purpose of wysiwyg editing. Instead of selecting a format for which the correspondence between abstract syntax trees and syntactically correct formulas is straightforward, we therefore propose to focus on convenient ways to specify non trivial correspondances, using the theory developed in sections 5 and 6. In principle, as soon as a reliable correspondance between content and presentation markup is established, the precise internal document format is not that important: at any stage, a reliable correspondance would mean that we can switch at will between the abstract syntax tree and a more visual representation.
Unfortunately, a perfectly bijective correspondence is hard to achieve.
Technically speaking, this would require an invertible grammar with
productions, which cannot only parse and transform presentation markup
into content markup, but also pretty print content markup as
presentation markup. Obviously, this is impossible as soon as certain
formulas, such as  and
and  , are parsed in the same way. Apart from this
trivial obstacle, presentation markup usually also allows for various
annotations with undefined mathematical semantics. For instance: what
would be the abstract syntax tree for a blinking formula, or a formula
in which the positions of some subformulas were adjusted so as to
“look nice”?
, are parsed in the same way. Apart from this
trivial obstacle, presentation markup usually also allows for various
annotations with undefined mathematical semantics. For instance: what
would be the abstract syntax tree for a blinking formula, or a formula
in which the positions of some subformulas were adjusted so as to
“look nice”?
These examples show that presentation markup is usually richer than
content markup. Consequently, we have opted for presentation markup as
our native format and concentrated ourselves on the one-way
correspondence from presentation markup to content markup, using a
suitable packrat grammar. In fact, for the semantic editing purposes in
the remainder of this section, the grammar does not even need to admit
production for the generation of the actual abstract syntax tree. Of
course, productions should be implemented if we want actual conversions
into
As we will detail below, it should also be noticed that we do not only need a correspondance between presentation and content markup, but also between several editor-related derivatives, such as cursor positions and selections. We finally have to decide what kind of action to undertake in cases of error. For instance, do we accept documents to be temporarily incorrect, or do we require parsability at all stages?
Remark  admit a
“Galois”-inverse
admit a
“Galois”-inverse  with the property
that
with the property
that  and
and  ?
Also, how to define a mathematical semantics for annotated formulas? In
particular, how would they behave during computations? For instance, we
might have a data type “annotated number” which joins the
annotation for any operation. When annotating a subset of the input
data, this semantics might be used to visualize the part of the output
whose computation depends on this annotated subset.
?
Also, how to define a mathematical semantics for annotated formulas? In
particular, how would they behave during computations? For instance, we
might have a data type “annotated number” which joins the
annotation for any operation. When annotating a subset of the input
data, this semantics might be used to visualize the part of the output
whose computation depends on this annotated subset.
In order to benefit from semantic editing facilities, we first have to ensure that the formulas in our document are correct. For similar reasons as in section 4.1, we have two main options:
Enforce correctness at every stage.
Incite the user to type correct formulas by providing suitable visual hints.
It depends very much on personal taste of the user which option should be preferred. For the moment, we have opted for mere incitation in our TeXmacs implementation, but we will now address the issues which arise for both points of view.
If we decide to enforce correctness at every stage, then we are immediately confronted to following problem: what happens if we type + in the example
 |
(3) |
while taking into account that the formula 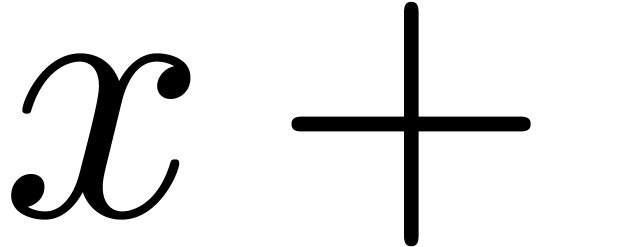 is
incorrect? Obviously, we will have to introduce some kind of markup
which will replace
is
incorrect? Obviously, we will have to introduce some kind of markup
which will replace 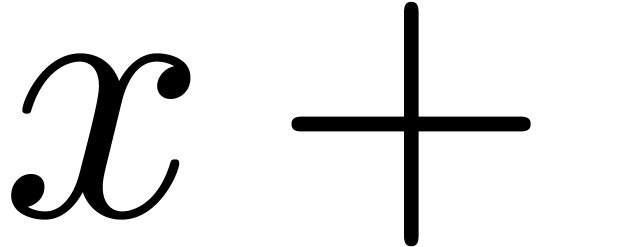 by a correct formula, such as
by a correct formula, such as
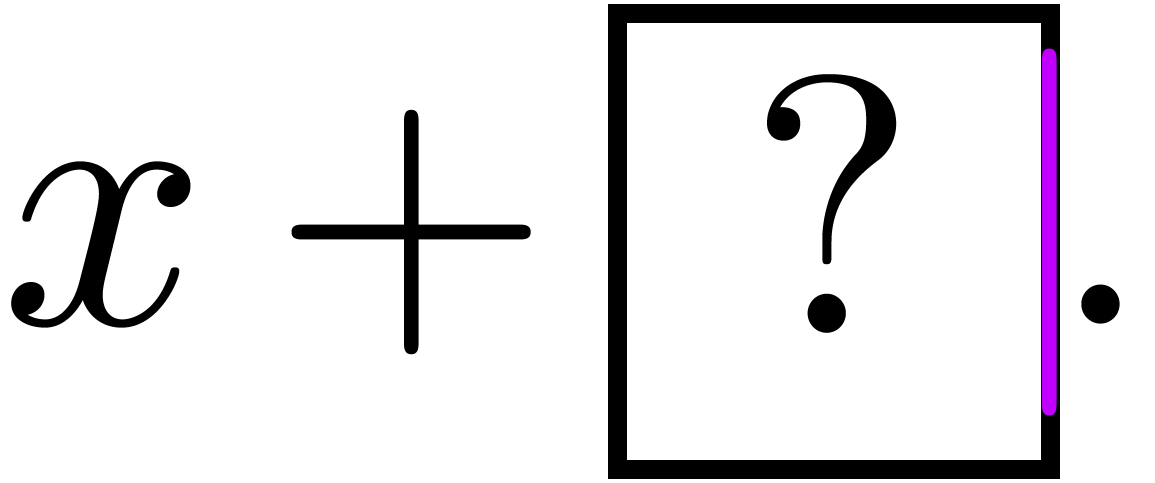
The automatically inserted dummy box  is parsed
as an ordinary variable, but transient in the sense that it
will be removed as soon as we type something new at its position. We
will call such boxes slots in what follows. Several existing
mathematical editors [29, 21] use slots in
order to keep formulas correct and indicate missing subformulas.
is parsed
as an ordinary variable, but transient in the sense that it
will be removed as soon as we type something new at its position. We
will call such boxes slots in what follows. Several existing
mathematical editors [29, 21] use slots in
order to keep formulas correct and indicate missing subformulas.
Of course, we need an automated way to decide when to insert and remove slots. This can be done by writing wrappers around the event handlers. On any document modification event, the following actions should be undertaken:
Pass the event to the usual, non-wrapped handler.
For each modified formula, apply a post-correction routine, which inserts or removes slots when appropriate.
If the post-correction routine does not succeed to make the formula correct, then undo the operation.
These wrappers have to be designed with care: for instance, the usual undo handling has to be done outside the wrapper, in order to keep the tab-variant system working (see section 4.3).
The post-correction routine should start by trying to make local changes at the old and the new cursor positions. For instance, if a slot is still present around the old cursor position, then attempt to remove it; after that, if the formula is not correct, attempt to make the formula correct by inserting a slot at the new cursor position. Only when the local corrections failed to make the entire formula correct, we launch a more global and expensive correction routine (which corrects outwards, starting at the cursor position). Such more expensive correction routines might for instance insert slots in the numerator and denominator of a newly created fraction.
Remark
Assume now that we no longer insist on correctness at all stages. In that case, an interesting question is how to provide maximal correctness without making a posteriori modifications such as the insertion and removal of slots. Following this requirement, the idea in example (3) would be to consider the formula
as being correct, provided that the cursor is positioned after
the  . In other words, if the
current formula is incorrect, then we check whether the current formula
with a dummy variable substituted for the cursor is correct. If this
check again fails, then we notify the user that he made a mistake, for
instance by highlighting the formula in red.
. In other words, if the
current formula is incorrect, then we check whether the current formula
with a dummy variable substituted for the cursor is correct. If this
check again fails, then we notify the user that he made a mistake, for
instance by highlighting the formula in red.
The second approach usually requires a grammar which is more tolerant
towards empty subformulas in special constructs such as fractions,
matrices, etc. For instance, it is reasonable to consider the empty
fraction  as being correct. Again, it really
comes down to personal taste whether one is willing to accept this: the
fraction
as being correct. Again, it really
comes down to personal taste whether one is willing to accept this: the
fraction  definitely makes it clear that some
information is missing, but the document also gets clobbered, at least
momentaneously by dummy boxes, which also give rise to
“flickering” when editing formulas. Moreover, in the case of
a matrix
definitely makes it clear that some
information is missing, but the document also gets clobbered, at least
momentaneously by dummy boxes, which also give rise to
“flickering” when editing formulas. Moreover, in the case of
a matrix
it is customary to leave certain entries blank. Semantically speaking, such blank entries correspond to invisible zeros or ellipses.
Another thing should be noticed at this point. Recall that we defined
correctness in terms of our ability to maintain a correspondance between
our presentation markup and the intended abstract syntax tree. Another
view on the above approach is to consider it as a way to build some
degree of auto-correction right into the correspondance. For instance,
the formula 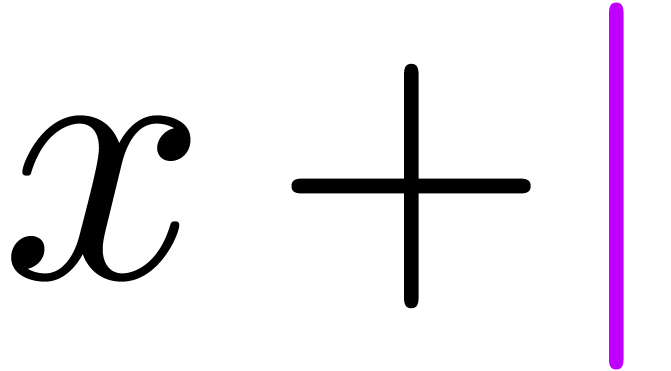 can be considered to be
“correct”, because we still have a way to make it
correct (e.g. by inserting a slot at the cursor position).
The correction might even involve the history of the formula (so that
the formula remains correct when moving the cursor). Of course, the same
visual behaviour could be achieved by inserting invisible slots, or, if
we insist on not modifying the document, by annotating the formula by
its current correction.
can be considered to be
“correct”, because we still have a way to make it
correct (e.g. by inserting a slot at the cursor position).
The correction might even involve the history of the formula (so that
the formula remains correct when moving the cursor). Of course, the same
visual behaviour could be achieved by inserting invisible slots, or, if
we insist on not modifying the document, by annotating the formula by
its current correction.
In order to describe the first grammar assisted editing feature inside TeXmacs, we first have to explain the concept of current focus.
Recall that a TeXmacs document is represented by a tree. Cursor
positions are represented by a list  of integers:
the integers
of integers:
the integers  encode a path to a subtree in the
document. If this subtree is a string leaf, then
encode a path to a subtree in the
document. If this subtree is a string leaf, then  encodes a position inside the string. Otherwise
encodes a position inside the string. Otherwise  is either
is either  or
or  ,
depending whether the cursor is before or behind the subtree. For
instance, in the formula
,
depending whether the cursor is before or behind the subtree. For
instance, in the formula
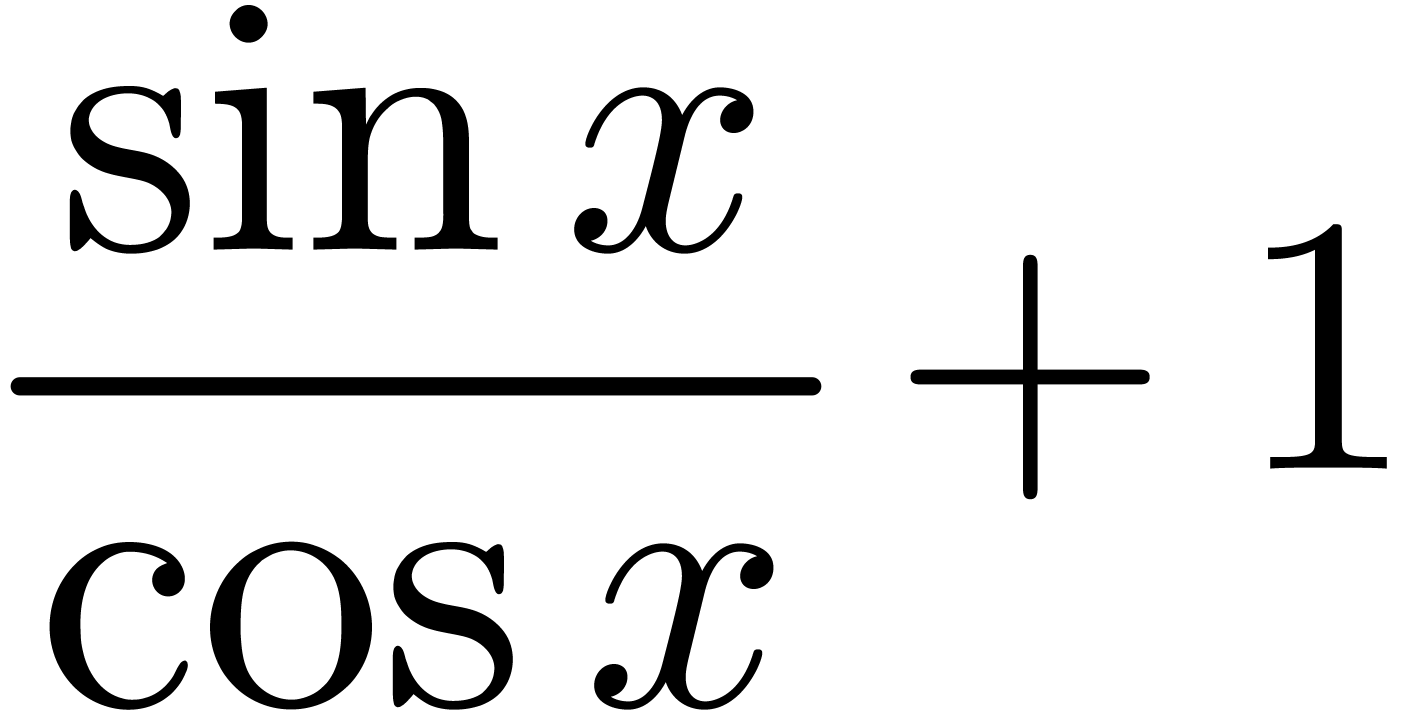
which is represented by the tree

the list  encodes the cursor position right after
encodes the cursor position right after
 and
and 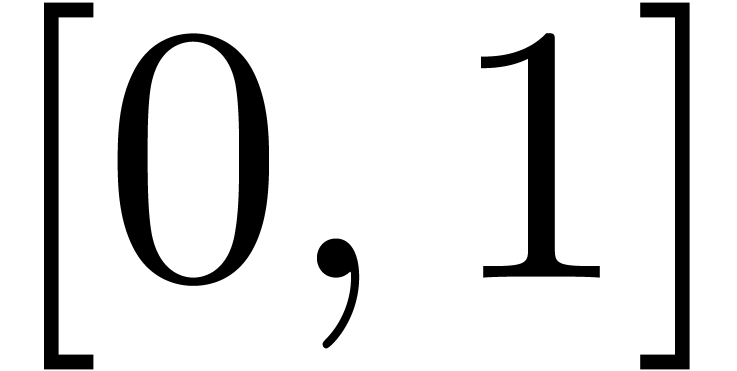 the cursor position
right after the fraction and before the
the cursor position
right after the fraction and before the  .
Notice that we prefer the leftmost position
.
Notice that we prefer the leftmost position 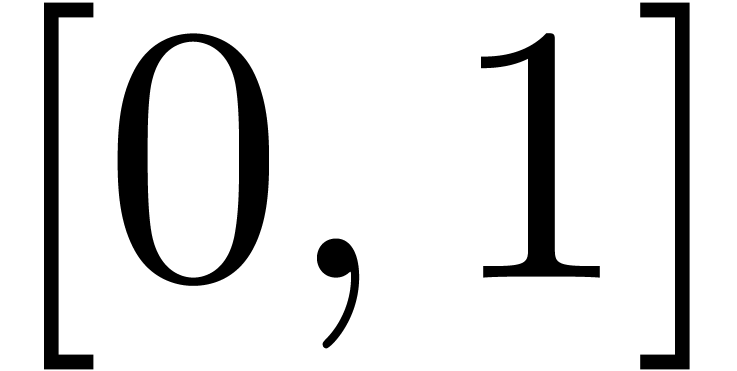 over
the equivalent position
over
the equivalent position  in the second example.
in the second example.
At a certain cursor position, we may consider all subtrees of the
document which contain the cursor. Each of these subtrees are visualized
by a light cyan bounding box inside TeXmacs. For instance, at the cursor
position  , the above formula
would typically be displayed as
, the above formula
would typically be displayed as

The innermost subtree (in this case the fraction) is called the current focus. In absence of selections, several so called structured editing operations operate on the current focus.
It is natural to generalize the above behaviour to semantic subformulas according to the current grammar. For instance, from a semantic point of view, the above formula corresponds to another tree:
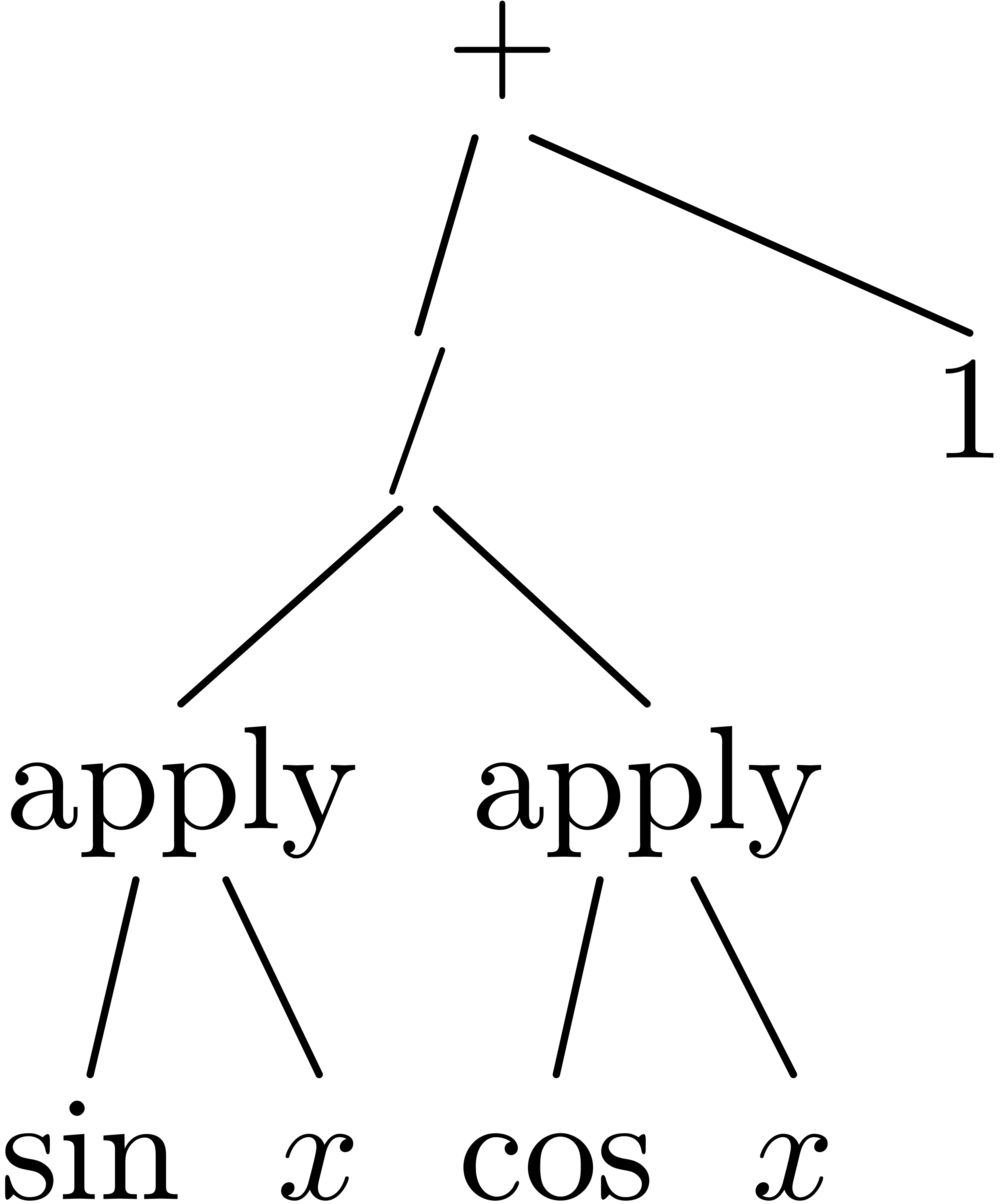 |
(4) |
For the cursor position just after  ,
it would thus be natural to consider
,
it would thus be natural to consider  as the
semantic current focus and also surround this subexpression by
a cyan box.
as the
semantic current focus and also surround this subexpression by
a cyan box.
Let us describe how this can be done. The tree serializer for our
packrat parser, which has been described in section 5.3,
also maintains a correspondance between the cursor positions. For
instance, the cursor position 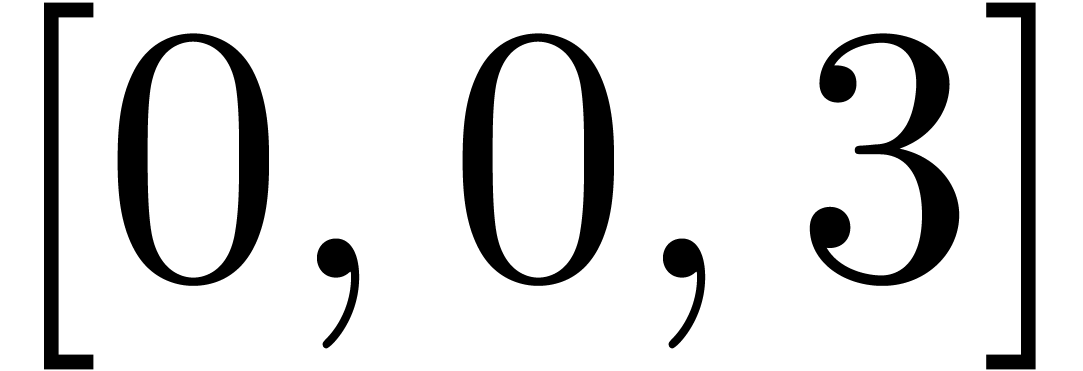 is automatically
transformed into the cursor position
is automatically
transformed into the cursor position  inside
inside
<\frac>sin x<|>cos x</f>+1
Now a successful parse of a formula naturally induces a parse tree,
which is not necessarily the same as the intended abstract syntax tree,
but usually very close. More precisely, consider the set  of all successful parses of substrings (represented by
pairs of start and end positions) involved in the complete parse.
Ordering this set by inclusion defines a tree, which is called the parse
tree.
of all successful parses of substrings (represented by
pairs of start and end positions) involved in the complete parse.
Ordering this set by inclusion defines a tree, which is called the parse
tree.
In our example, the parse tree coincides with the abstract syntax tree.
Each of the substrings in  which contains the
cursor position can be converted back into a selection (determined by a
start and an end cursor position) inside the original TeXmacs tree. In
order to find the current focus, we first determine the innermost
substring sin x in
which contains the
cursor position can be converted back into a selection (determined by a
start and an end cursor position) inside the original TeXmacs tree. In
order to find the current focus, we first determine the innermost
substring sin x in  (represented
by the pair
(represented
by the pair  ) which contains
the cursor. This substring is next converted back into the selection
) which contains
the cursor. This substring is next converted back into the selection
 .
.
In general, the parse tree does not necessarily coincide with the abstract syntax tree. In this case, some additional tweaking may be necessary. One source of potential discrepancies is the high granularity of packrat parsers, which are also used for the lexical analysis. For instance, floating point numbers might be defined using the following grammar:
(define Integer (+ (- "0" "9"))) (define Number Integer (Integer "." Integer) (Integer "." Integer "e" Integer) (Integer "." Integer "e-" Integer)) |
However, in the example
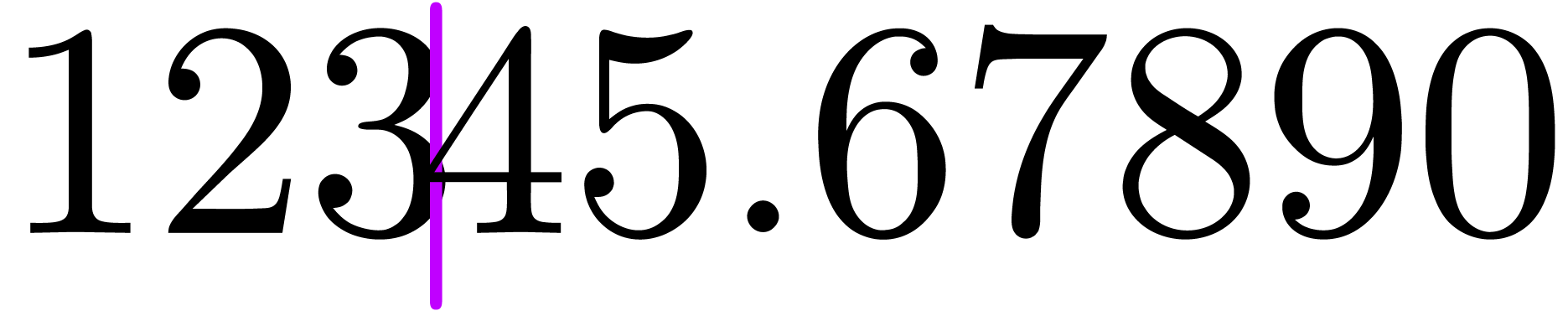
the substring  would be regarded as the current
focus. We thus have to add an annotation to the packrat grammar and (at
least for the purpose of determining the current focus) either specify
that Integer expressions should not be considered as
valid subexpressions, or specify that Number expressions
should be considered as atomic (i.e. without any
subexpressions).
would be regarded as the current
focus. We thus have to add an annotation to the packrat grammar and (at
least for the purpose of determining the current focus) either specify
that Integer expressions should not be considered as
valid subexpressions, or specify that Number expressions
should be considered as atomic (i.e. without any
subexpressions).
Other expressions for which parse trees and abstract syntax trees may differ are formulas which involve an associative operator. For instance, we might want to associate the abstract syntax tree
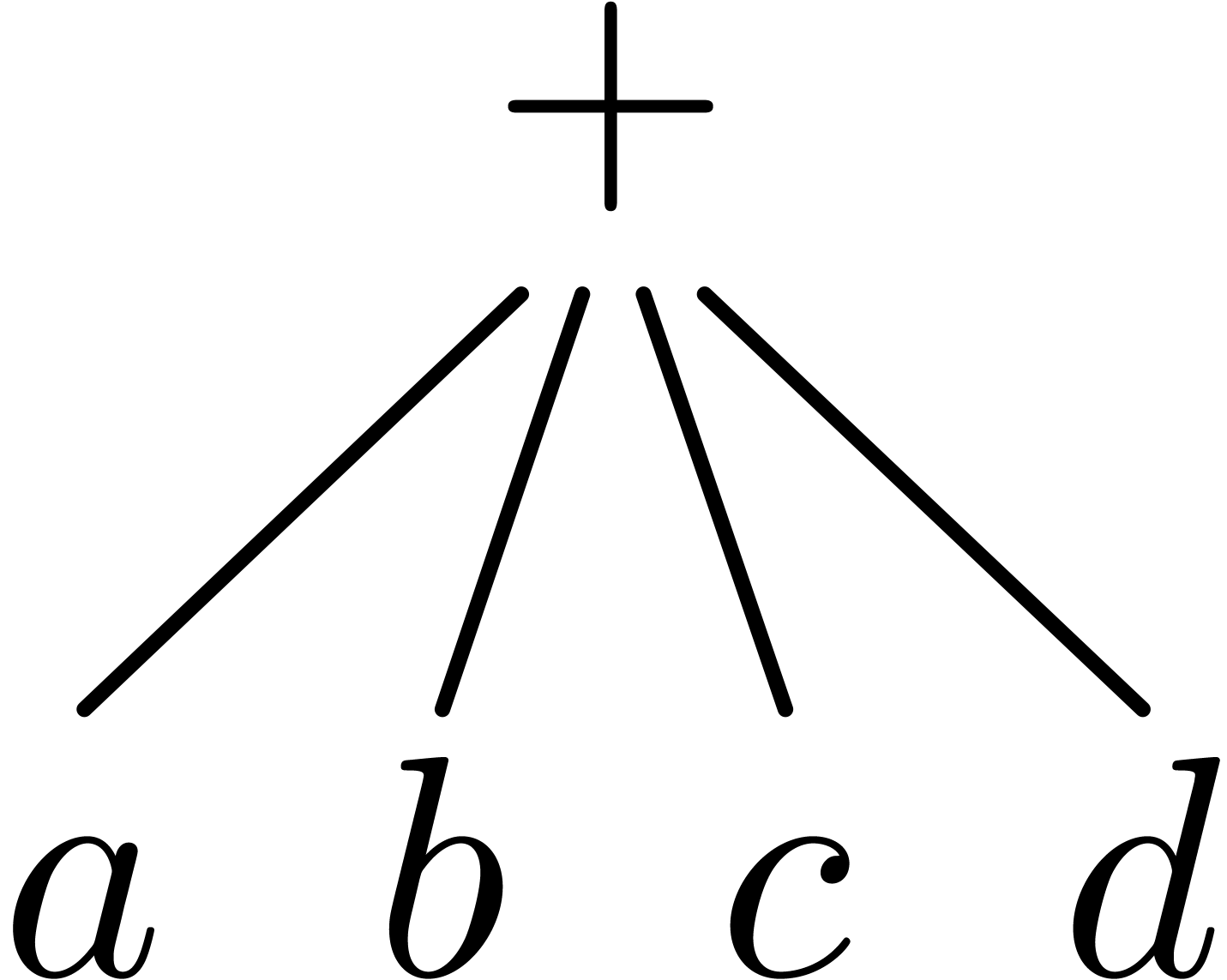
to the expression
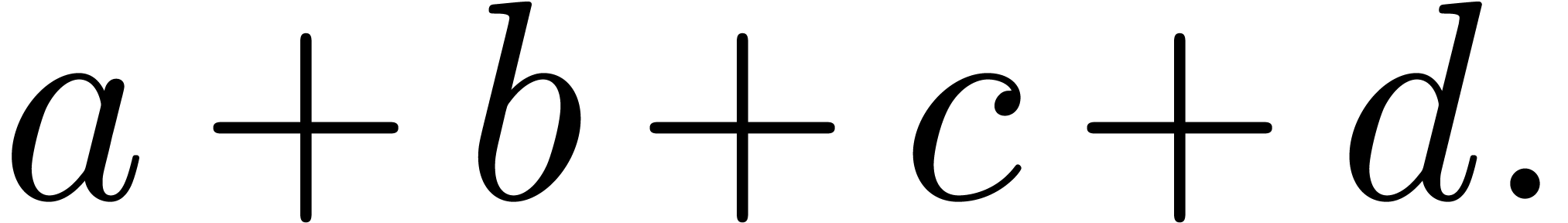
This would make the parse-subexpression  “ineligible” for use as the current focus. In our current
implementation, this behaviour is the default.
“ineligible” for use as the current focus. In our current
implementation, this behaviour is the default.
From the graphical point of view, it should noticed that many mathematical formulas do not require any two-dimensional layout:
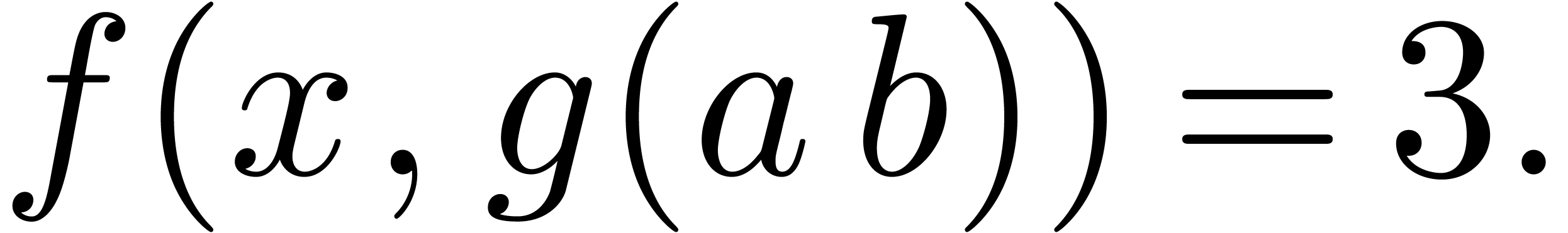
In such examples, the usual convention of surrounding all subexpressions containing the current cursor may lead to an excessive number of boxes:

For this reason, we rather decided to surround only the current semantic focus, in addition to the subexpression which correspond to native TeXmacs markup. In fact, maybe the usual convention was not a good idea after all: we should at least implement a user preference to only surround the current focus.
The semantic focus is a key ingredient for semantic mathematical editors, since it provides instant visual feedback on the meaning of formulas while they are being entered. For instance, when putting the cursor at the right hand side of an operator, the semantic focus contains all arguments of the operator. In particular, at the current cursor position, operator precedence is made transparent to the user via the cyan bounding boxes. On the one hand this makes it possible to check the semantics of a formula by traversing all accessible cursor positions (as we did in section 6.4.2).
On the other hand, in cases of doubt on the precedence of operators, the
semantic focus informs us about the default interpretation. Although the
default interpretation of a formula such as 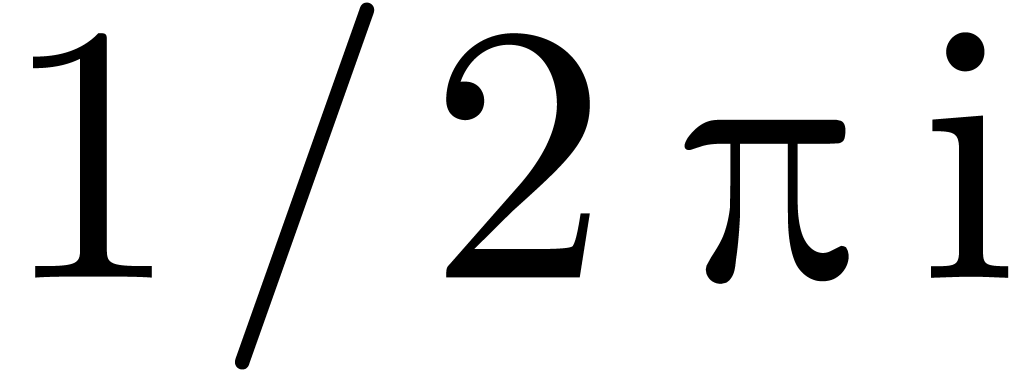 might be wrong, the editor's interpretation is at least made
transparent, and it could be overridden through the insertion of
invisible brackets. In other words, we advocate an a posteriori
approach to the resolution of common mathematical precedence
ambiguities, rather than the a priori approach mentioned in
remark 2.
might be wrong, the editor's interpretation is at least made
transparent, and it could be overridden through the insertion of
invisible brackets. In other words, we advocate an a posteriori
approach to the resolution of common mathematical precedence
ambiguities, rather than the a priori approach mentioned in
remark 2.
Semantic selections can be implemented along similar lines as the semantic focus, but it is worth it to look a bit closer at the details. We recall that a TeXmacs selection is represented by a pair with a cursor starting position and a cursor end position.
The natural way to implement semantic selections is as follows. We first
convert the selection into a substring (encoded by a starting and end
position) of the string serialization of the TeXmacs tree. We next
extend the substring to the smallest “eligible” substring in
 , for a suitable customizable
definition of “eligibility”. We finally convert the larger
substring back into a selection inside the original TeXmacs document,
which is returned as the semantic selection.
, for a suitable customizable
definition of “eligibility”. We finally convert the larger
substring back into a selection inside the original TeXmacs document,
which is returned as the semantic selection.
In the above algorithm, the definition of eligible substring for
selection may differ from the one which was used for the current focus.
For instance, for an associative operator  ,
it is natural to consider both
,
it is natural to consider both 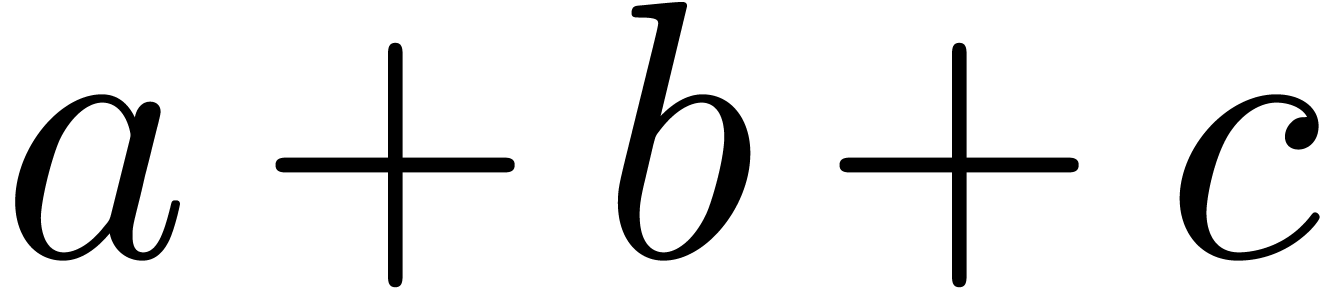 and
and  as eligible substrings of
as eligible substrings of  .
Actually, we might even want to select
.
Actually, we might even want to select  as a
substring of
as a
substring of  .
.
In the presence of subtractions, things get even more involved, since we need an adequate somewhat ad hoc notion of abstract syntax tree. For instance,

would typically be encoded as
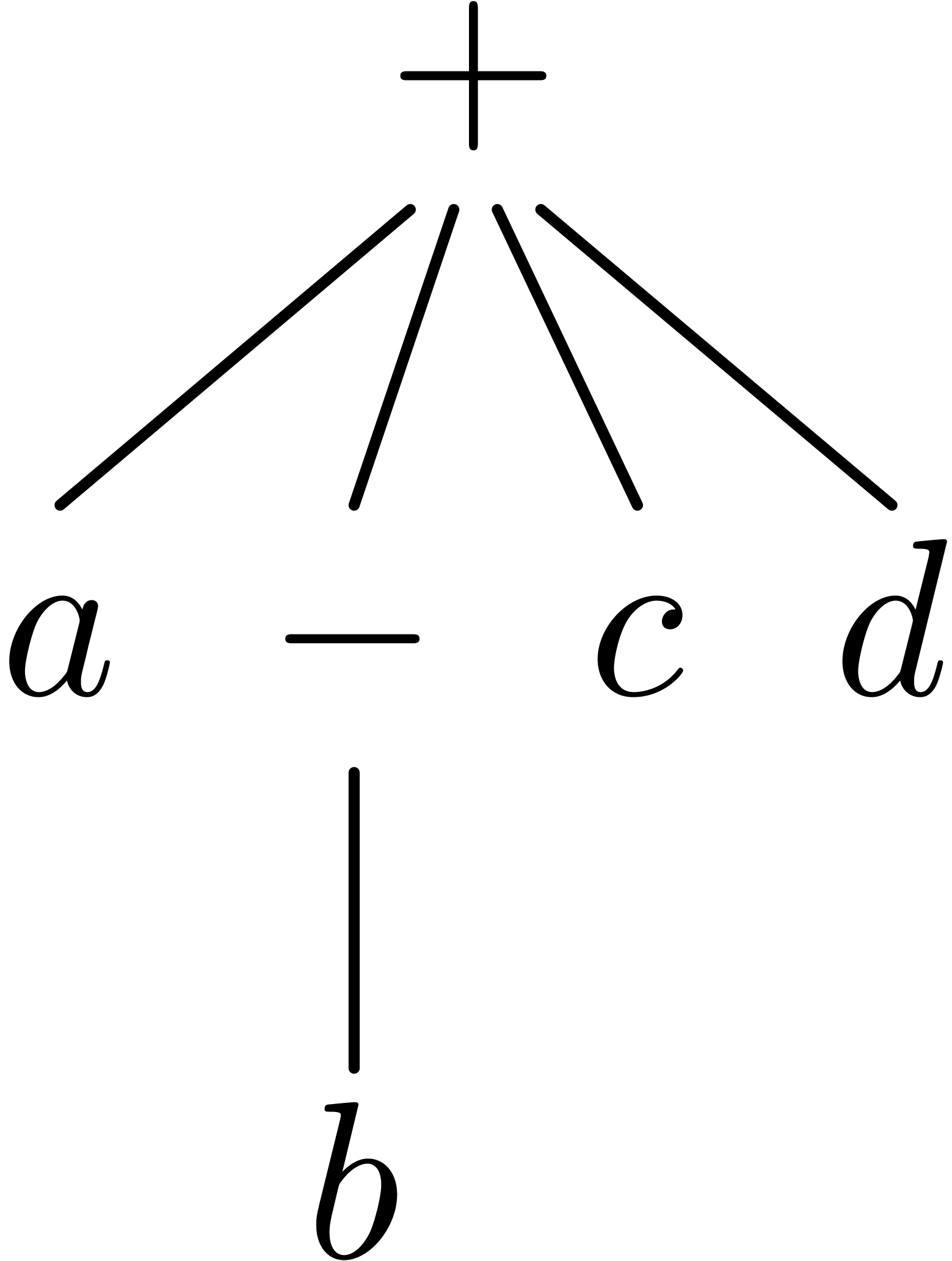
after which 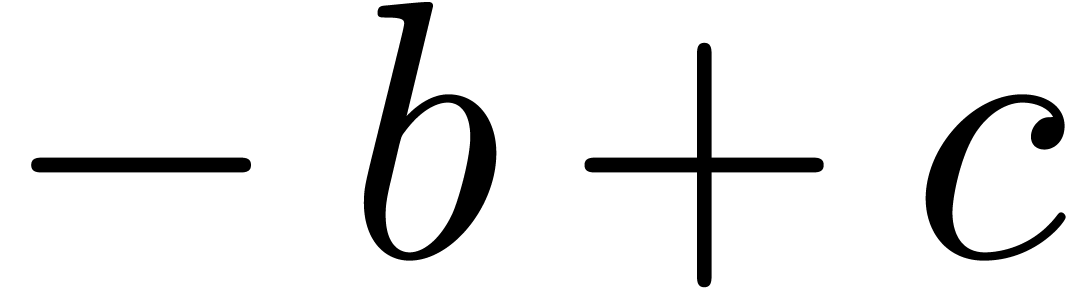 becomes an eligible substring for
selection, but not
becomes an eligible substring for
selection, but not  .
.
Furthermore, it is sometimes useful to select the subexpression 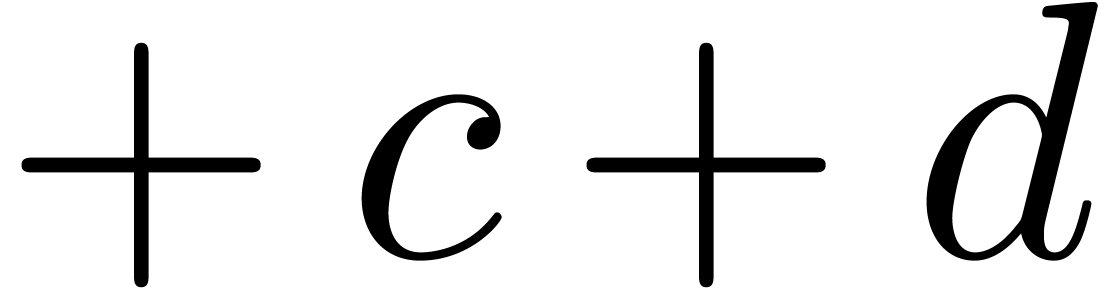 of
of  . This
occurs for instance if we want to replace
. This
occurs for instance if we want to replace  by
by
 . However, when adopting a
naive point of view on semantic selections, which might even integrate
the above remarks,
. However, when adopting a
naive point of view on semantic selections, which might even integrate
the above remarks, 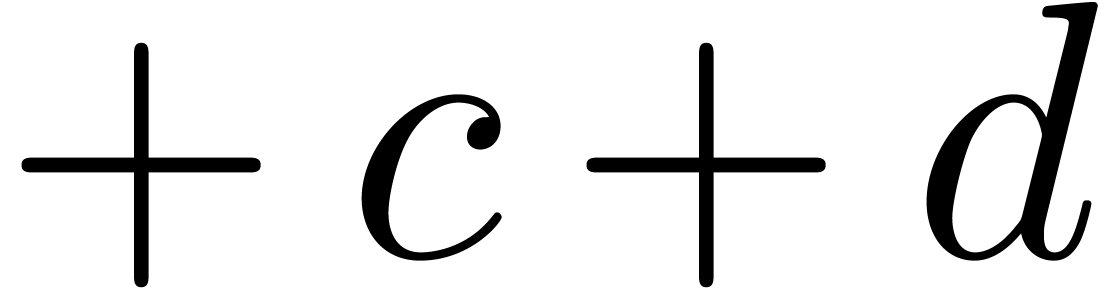 remains non eligible as a
substring of
remains non eligible as a
substring of  . Nevertheless,
such substrings do admit operator semantics. More precisely, we
may consider the selection
. Nevertheless,
such substrings do admit operator semantics. More precisely, we
may consider the selection 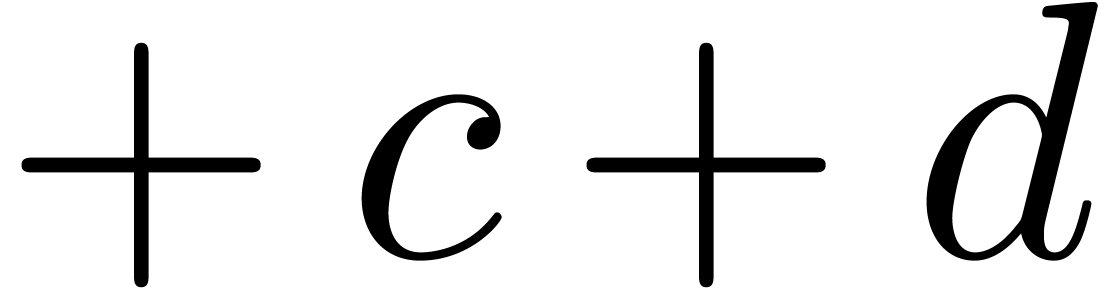 as an operator
as an operator

which will be applied to a suitable subexpression at the position where we perform a “paste”. A less trivial example would be the “selection operator”
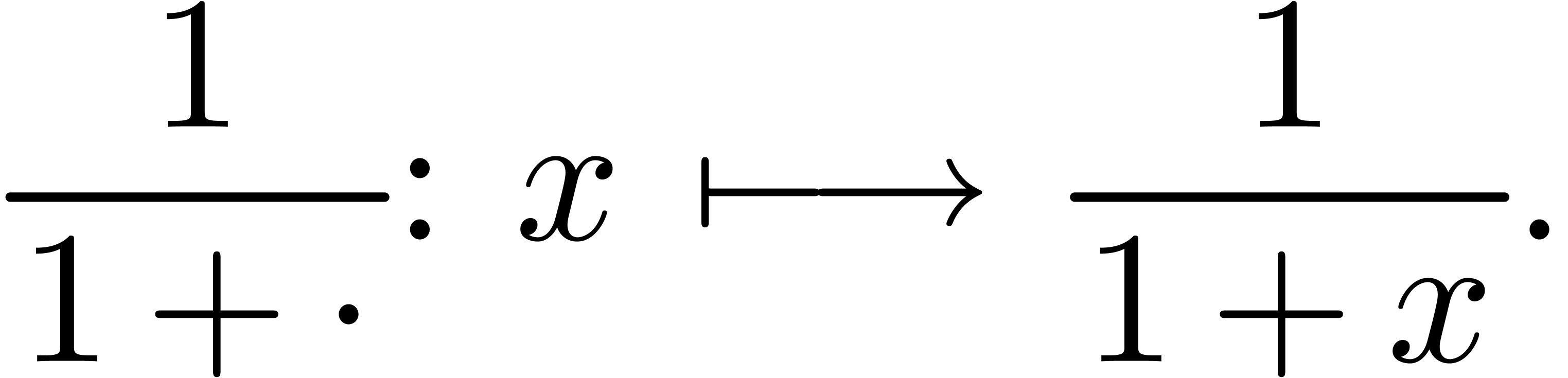
Although it is harder to see how we would select such an operator, this generalization might be useful for rapidly typing the continued fraction
Notice that this kind of semantics naturally complements the idea to use
the paste operation for substitutions of expressions (usually variables)
by other expressions. This idea was heard in a conference talk by
O.
It should be noticed that there are situations in which non semantic
selections are useful. This typically occurs when the default semantics
of the formula is non intended. For instance, the default interpretation
of the formula 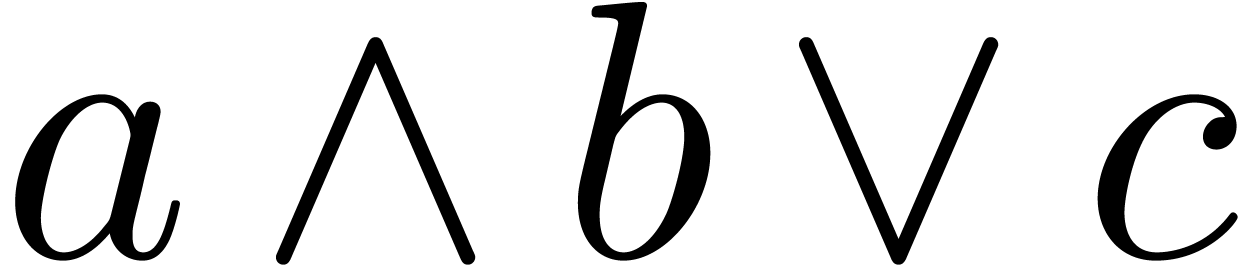 is
is 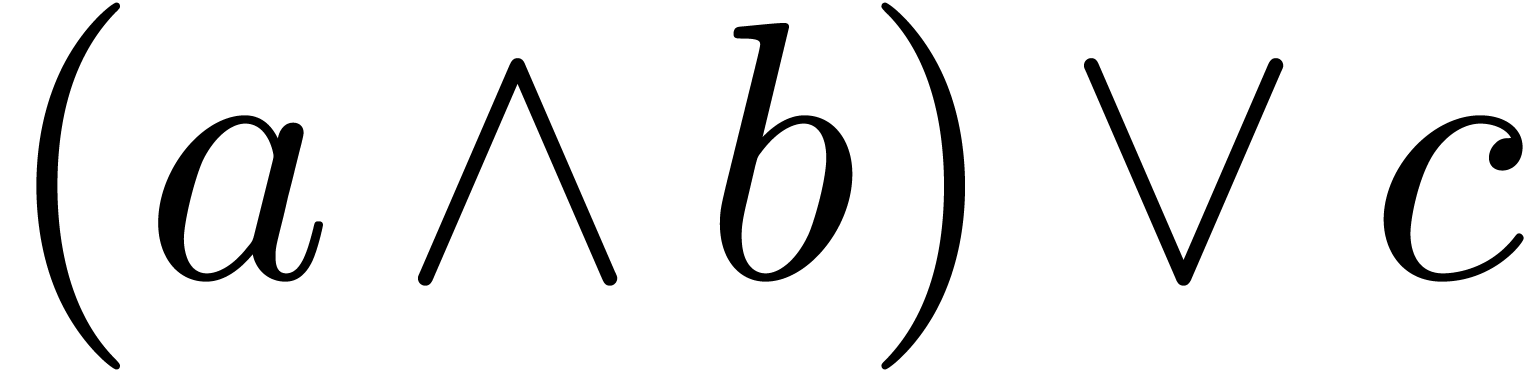 .
Imagine a context in which the desired meaning is rather
.
Imagine a context in which the desired meaning is rather 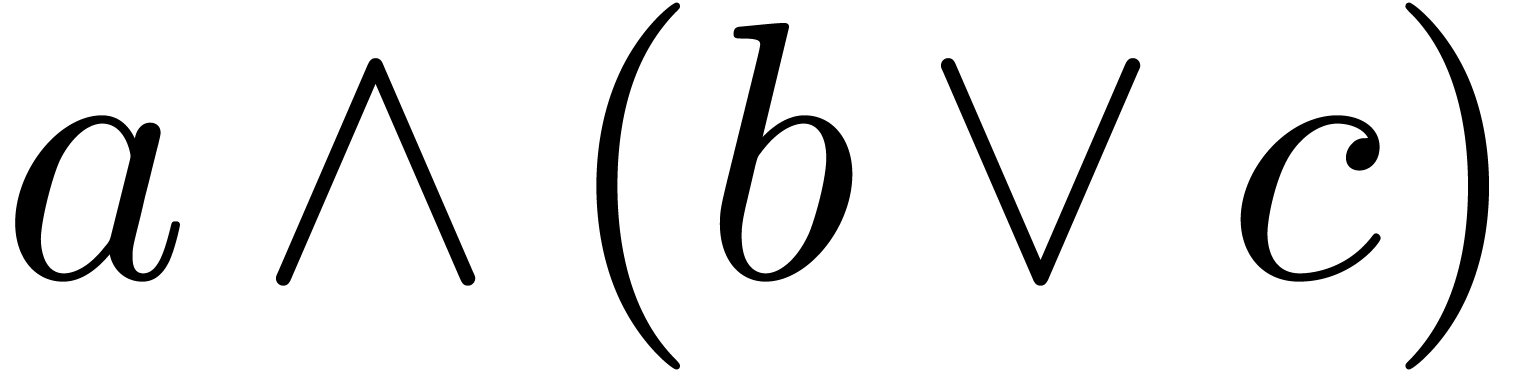 . In that case, the user might want to select
the formula
. In that case, the user might want to select
the formula  and put (possibly invisible)
brackets around it. An easy way to achieve this might be to hold a
modifier key while making the selection. Alternatively, we might
introduce shortcuts for modifying the binding forces of operators.
and put (possibly invisible)
brackets around it. An easy way to achieve this might be to hold a
modifier key while making the selection. Alternatively, we might
introduce shortcuts for modifying the binding forces of operators.
Remark
Mathematical grammars can also be useful at the typesetting phase in several ways.
First of all, the spacing around operators may depend on the way the
operator is used. Consider for instance the case of the subtraction
operator  . There should be
some space around it in a usual subtraction
. There should be
some space around it in a usual subtraction  , but not in a unary negation
, but not in a unary negation  . We also should omit the space when using the
subtraction as a pure operation:
. We also should omit the space when using the
subtraction as a pure operation: 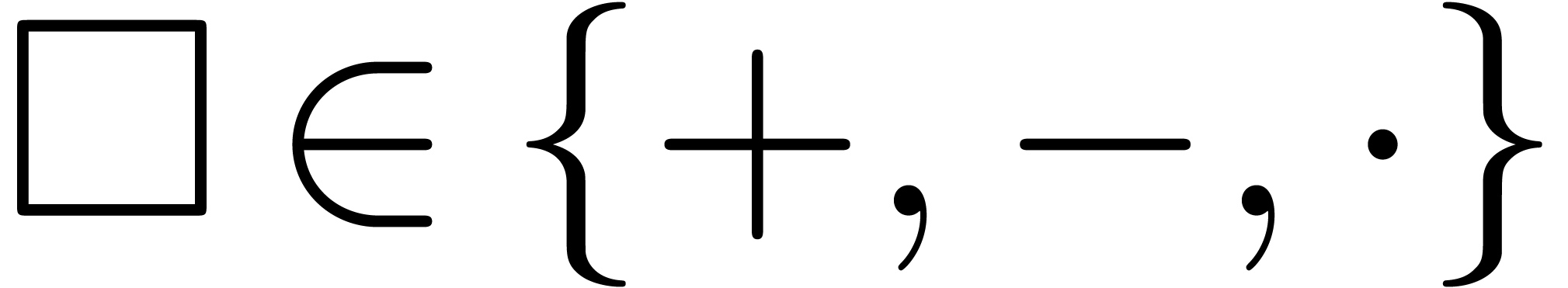 .
Usually, no parsing is necessary in order to determine the right amount
of spacing: only the general symbol types of the operator itself and its
neighbours should be known for this task. We have seen in section 5.3 how to annotate packrat grammars (using :type
and :spacing) in order to provide this information.
Notice that this kind of refined spacing algorithms are also present in
TeX [15].
.
Usually, no parsing is necessary in order to determine the right amount
of spacing: only the general symbol types of the operator itself and its
neighbours should be known for this task. We have seen in section 5.3 how to annotate packrat grammars (using :type
and :spacing) in order to provide this information.
Notice that this kind of refined spacing algorithms are also present in
TeX [15].
In a similar vein, we may provide penalties for line breaking
algorithms. In fact, grammar based line breaking algorithms might go
much further than that. For instance, we may decide to replace fractions
 with very wide numerators or denominators by
with very wide numerators or denominators by
 , thereby making them easier
to hyphenate. Such replacements can only be done in a reliable way when
semantic information is available about when to use brackets. For
instance,
, thereby making them easier
to hyphenate. Such replacements can only be done in a reliable way when
semantic information is available about when to use brackets. For
instance,  should be transformed into
should be transformed into 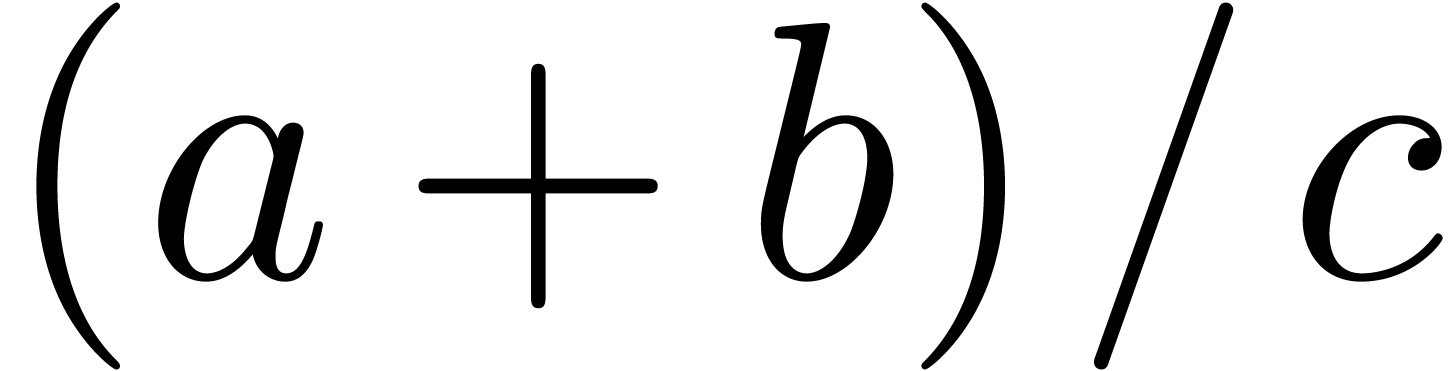 , but
, but 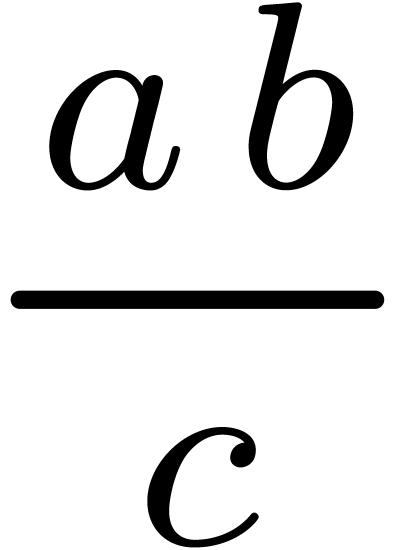 into
into
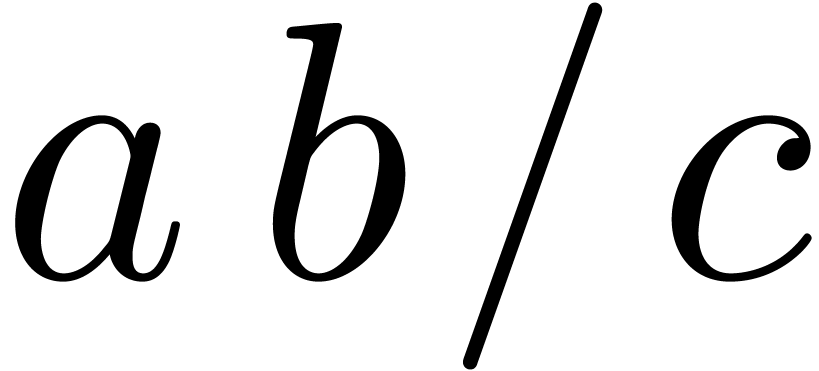 . In order to avoid expensive
parsing during the typesetting phase, we may store this bracketing
information in the document or suitable annotations during the editing
phase.
. In order to avoid expensive
parsing during the typesetting phase, we may store this bracketing
information in the document or suitable annotations during the editing
phase.
Notice that semantic hyphenation strategies should be applied with some caution: if one decides to transform a fraction occurring in a long power series with rational coefficients, then it is usually better to transform all fractions: a mixture of transformed and untransformed fractions will look a bit messy to the human eye. For similar reasons, one should systematically transform fractions when a certain width is exceeded, rather than trying to mix the usual hyphenation algorithm with semantic transformations.
Finally, in formulas with more nesting levels, one should carefully choose the level where transformations are done. For instance, if a large polynomial matrix
does not fit on a line, then we may transform the matrix into a double list:
Nevertheless, a more elegant solution might be to break the polynomials inside the matrix:
For the moment, our implementation is not yet at this level of sophistication; it would already be nice if the user could easily perform this kind of transformations by hand.
In section 3.1, we have seen that homoglyphs are a major source of ambiguity and one of the bottlenecks for the design of semantic editors. This means that we should carefully design input methods which incite the user to enter the appropriate symbols, without being overly pedantic. Furthermore, there should be more visual feedback on the current interpretation of symbols, while avoiding unnecessary clobbering of the screen. We are investigating the following ideas for implementation in TeXmacs:
An a priori way to disambiguate homoglyphs, while they are being entered, is to introduce the following new keyboard shortcut convention: if we want to override the default rendering of a symbol or operator, then type the appropriate key for the intended rendering just afterwards. For instance, we might use +space to enter an invisible space or *& to enter the wedge product. This convention benefits from the fact that many homoglyphs are infix operators, so that the above kind of shortcuts have no other natural meaning.
An alternative a posteriori approach would be to introduce a new shortcut for cycling through “homoglyph variants”. The usual variant key might also be used for this purpose, although the list of possible variants would become a bit too long for certain symbols.
Slightly visible graphical hints might be provided to users in order
to inform on the current interpretation of a symbol. For instance,
multiplication might be rendered as  ,
function application as
,
function application as  ,
and the wedge product as
,
and the wedge product as  ,
without changing any of the spacing properties. The rendering might
also be altered more locally, when the cursor is inside the formula,
or next to the operator itself.
,
without changing any of the spacing properties. The rendering might
also be altered more locally, when the cursor is inside the formula,
or next to the operator itself.
Besides, we are in the process of dressing up a list with the most common homoglyphs.
Unfortunately, at the time of writing, the
« Semantics. Mathematical
operators often have more than one meaning in different
subdisciplines or different contexts. For example, the “ ” symbol normally denotes
addition in a mathematical context, but might refer to concatenation
in a computer science context dealing with strings, or
incrementation, or have any number of other functions in given
contexts. Therefore the Unicode Standard only encodes a single
character for a single symbolic form. There are numerous other
instances in which several semantic values can be attributed to the
same Unicode value. For example, U+2218
” symbol normally denotes
addition in a mathematical context, but might refer to concatenation
in a computer science context dealing with strings, or
incrementation, or have any number of other functions in given
contexts. Therefore the Unicode Standard only encodes a single
character for a single symbolic form. There are numerous other
instances in which several semantic values can be attributed to the
same Unicode value. For example, U+2218  RING
OPERATOR may be the equivalent of white small circle or composite
function or apl jot. The Unicode Standard does not attempt to
distinguish all possible semantic values that may be applied to
mathematical operators or relational symbols. It is up to the
application or user to distinguish such meanings according to the
appropriate context. Where information is available about the usage
(or usages) of particular symbols, it has been indicated in the
character annotations in the code charts printed in [Unicode] and in
the online code charts [Charts]. »
RING
OPERATOR may be the equivalent of white small circle or composite
function or apl jot. The Unicode Standard does not attempt to
distinguish all possible semantic values that may be applied to
mathematical operators or relational symbols. It is up to the
application or user to distinguish such meanings according to the
appropriate context. Where information is available about the usage
(or usages) of particular symbols, it has been indicated in the
character annotations in the code charts printed in [Unicode] and in
the online code charts [Charts]. »
It is interesting to examine the reason which is advanced here: as a
binary operator, the  might both be used for
addition and string concatenation. In a similar way, the latin O might
be pronounced differently in english, hungarian or dutch. From the
syntactical point of view, these distinctions are completely
irrelevant: both when used as an addition or string concatenation, the
might both be used for
addition and string concatenation. In a similar way, the latin O might
be pronounced differently in english, hungarian or dutch. From the
syntactical point of view, these distinctions are completely
irrelevant: both when used as an addition or string concatenation, the
 remains an associative infix operator with a
fixed precedence.
remains an associative infix operator with a
fixed precedence.
For genuine homoglyphs, such as the logical or and the wedge product, the syntactical status usually changes as a function of the desired interpretation. For instance, the binding force of a wedge product is the same as the binding force of a product. Furthermore, such operators would usually be placed in different categories. For instance, the logical or can be found in the category “isotech” of general technical symbols. It would have been natural to add the wedge product in the category “isoamsb” of binary operators.
In fact,  is the ugly-looking
is the ugly-looking  (U+2147).
(U+2147).
Yet another example concerns the added code charts for sans serif and monospaced characters. For newly developed mathematical fonts, such as the proprietary STIX fonts, these characters tend to be misused as a replacement for typesetting formulas or text in special fonts. For instance, monospaced characters are suggested for typesetting identifiers in computer programs, which would thereby become invisible for standard search tools. We don't know of any classical mathematical notation which uses monospaced symbols and would have justified the introduction of such curiousities.
When taking a look at the existing mathematical  symbol for operations which behave
like additions in many respects; why would they use it to denote, say,
existential quantification?
symbol for operations which behave
like additions in many respects; why would they use it to denote, say,
existential quantification?
Currently, the mainstream mathematical editing tools are presentation oriented and unsuitable for the production of documents in which all formulas are at least syntactically correct. In the present paper, we have described a series of techniques which might ultimately make the production of such documents as user friendly as the existing presentation oriented programs.
The general philosophy behind our approach is that the behaviour of the editor should remain as close as possible to the behaviour of a presentation oriented editor, except, of course, for those editing actions which may benefit from the added semantics. One major consequence is that the editor naturally adapts itself to the editing habits of the user, rather than the converse. Indeed, it is tempting to “teach” the user how to write content markup, but the extra learning efforts should be rewarded by a proportional number of immediate benefits for the user. This holds especially for those users whose primary interest is a paper which looks nice, and who do not necessarily care about the “added value” of content markup.
Technically speaking, our approach relies on decoupling the visual editing facilities from the semantic checking and correction part. This is achieved through the development of a suitable collection of packrat grammar tools which allow us to maintain a robust correspondance between presentation and content markup. This correspondance comprises cursor positions, selections, and anything else needed for editing purposes. So far, our collection of grammar tools allowed us to naturally extend the most basic editing features of TeXmacs to the semantic context. Although we found it convenient to use packrat grammars, it should be noticed that other types of grammars might be used instead, modulo an additional implementation effort.
One main difficulty for the development of a general purpose semantic editor is the wide variety of users. Although we should avoid the pitfall of introducing a large number of user preferences (which would quickly become unintelligible to most people), we will probably need to introduce at least a few of them, so as to address the wide range of potential usage patterns. It will take a few years of user feedback before we will be able to propose a sufficiently stable selection of user preferences. In this paper, we have contented ourselves to investigate various possible solutions to problems in which personal taste plays an important role.
Another aspect of customization concerns the underlying mathematical grammar. We have argued that the design of grammars should be left to experts. Indeed, designing grammars is non trivial, and non standard grammars will mostly confuse potential readers. We are thus left with two main questions: the design of a “universal” grammar which is suitable for most mathematical texts, and an alternative way for the user to introduce customized notation. In section 6, we both introduced such a grammar and described our approach of using TeXmacs macros for introducing new notations. Such macros can be grouped in style packages dedicated to specific areas. Of course, our proposal for a “universal” grammar will need to be tested and worked out further.
In some cases though, it is important to allow for customizable grammars. One good example is the use of TeXmacs as an interface to an automatic theorem prover. Such systems often come with their own grammar tools for customizing notations. In such cases, it should not be hard to convert the underlying grammars into our packrat format. Moreover, packrat grammars are very well adapted to this situation, since they are incremental by nature, so it easy and efficient to use different grammars at different places inside the document. An alternative approach, which might actually be even more user friendly, would be to automatically convert standard notation into the notation used by the prover.
In sections 3.4 and 6.4, we have tested the newly implemented semantic tools on some large existing TeXmacs documents from various sources. These experiments made as reasonably optimistic about our ultimate goal of building a user friendly semantic editor for the working mathematician. We have identified a few main bottlenecks, which suggest several improvements and enhancements for the current editor:
We should provide better visual feedback to the user on homoglyphs. In particular, the difference between invisible multiplication and function application should be made more apparent.
The concept of current semantic focus should be thought out very carefully. We might want to suppress the traditional behaviour of TeXmacs to surround all ancestors of the current focus.
TeXmacs traditionally does not use slots for displaying missing subformulas. Along the lines described in section 7.2, we plan to experiment with an editing mode which will use them in a systematic way so as to keep formulas correct at all stages.
The “universal grammar” should be tested on a wider range of documents and carefully enhanced to cover most standard notations.
We should work out a comprehensible set of annotation primitives, which users will find natural when they need to put text inside their formulas or resort to ad hoc notations.
Since the current implementation is very recent, many additional tweaking will be necessary in response to user feedback.
We also have various other plans for future extensions:
We plan to add productions to our packrat grammars, which will
enable us to automatically generate, say,
We intend to implement at least some rudimentary support for grammar based typesetting, starting with line breaking, as outlined in section 7.5.
Systematic generalization of all currently supported editing operations (such as search and replace, tab-completion, structured navigation, etc.) to the semantic context.
Using the packrat grammar tools for programming languages as well, so as to support syntax highlighting, automatic indentation, etc. After dealing with purely textual programs, we will next investigate the possibility to insert mathematical formulas directly into the source code.
Exploit the extra semantics in our interfaces with external systems.
Olivier Arsac, Stéphane Dalmas et Marc Gaëtano. The design of a customizable component to display and edit formulas. In ACM Proceedings of the 1999 International Symposium on Symbolic and Algebraic Computation, July 28 - 31, pages 283–290. 1999.
Philippe Audebaud et Laurence Rideau. Texmacs as authoring tool for formal developments. Electr. Notes Theor. Comput. Sci.Volume, 103:27–48, 2004.
S. Basu, R. Pollack et M.-F. Roy. Algorithms in real algebraic geometry, volume 10 of Algorithms and Computation in Mathematics. Springer-Verlag, 2006. 2-nd edition to appear.
S. Basu, R. Pollack et M.F. Roy. Algorithms in real algebraic geometry, volume 10 of Algorithms and computation in mathematics. Springer-Verlag, Berlin, Heidelberg, New York, 2003.
T. Braun, H. Danielsson, M. Ludwig, J. Pechta et F. Zenith. Kile: an integrated latex environment. Http://kile.sourceforge.net/, 2003.
E. Chou. Collected course material. http://math.nyu.edu/~chou/, 2010.
F. DeRemer. Practical LR(k) Translators. PhD thesis, Massachusetts Institute of Technology, 1969.
B. Ford. Packrat parsing: a practical linear-time algorithm with backtracking. Master's thesis, Massachusetts Institute of Technology, September 2002.
Bryan Ford. Packrat parsing: simple, powerful, lazy, linear time. In Proceedings of the seventh ACM SIGPLAN international conference on Functional programming, ICFP '02, pages 36–47. New York, NY, USA, 2002. ACM.
K. Geddes, G. Gonnet et Maplesoft. Maple. http://www.maplesoft.com/products/maple/, 1980.
A.G. Grozin. TeXmacs interfaces to Maxima, MuPAD and Reduce. In V.P. Gerdt, editor, Proc. Int. Workshop Computer algebra and its application to physics, volume JINR E5, page 149. Dubna, June 2001. Arxiv cs.SC/0107036.
A.G. Grozin. TeXmacs-Maxima interface. Arxiv cs.SC/0506226, June 2005.
L. Lamport. LaTeX, a document preparation system. Addison Wesley, 1994.
L. Mamane et H. Geuvers. A document-oriented Coq plugin for TeXmacs. In Mathematical User-Interfaces Workshop 2006. St Anne's Manor, Workingham, UK, 2006.
T. Nipkow, L. Paulson et M. Wenzel. Isabelle/Hol.
http://www.cl.cam.ac.uk/research/hvg/Isabelle/,
1993.
S. Owre, N. Shankar et J. Rushby. Pvs specification and verification system. http://pvs.csl.sri.com/, 1992.
MacKichan Software. Scientific workplace.
http://www.mackichan.com/index.html?products/swp.html~mainFrame,
1998.
G.J. Sussman et G.L. Steele Jr. Scheme. http://www.schemers.org/, 1975.
A. Tejero-Cantero. Interference and entanglement of two massive particles. Master's thesis, Ludwig-Maximilians Universität München, September 2005. http://alv.tiddlyspace.com/I2P.
The OpenMath Society. OpenMath. http://www.openmath.org/, 2003.
Wolfram Research. Mathematica. http://www.wolfram.com/mathematica/, 1988.
N.G. de Bruijn. The mathematical language automath, its usage, and some of its extensions. In Symposium on Automatic Demonstration, volume 125 of Lect. Notes in Math., pages 29–61. Versailles, December 1968, 1970. Springer Verlag.
M. Ettrich et al. The LyX document processor. http://www.lyx.org, 1995.
T. Coquand et al. The Coq proof assistant. http://coq.inria.fr/, 1984.
L. van den Dries. Tame topology and o-minimal structures, volume 248 of London Math. Soc. Lect. Note. Cambridge university press, 1998.
J. van der Hoeven. GNU TeXmacs: a free, structured, wysiwyg and technical text editor. In Daniel Flipo, editor, Le document au XXI-ième siècle, volume 39–40, pages 39–50. Metz, 14–17 mai 2001. Actes du congrès GUTenberg.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
J. van der Hoeven. Transséries et analyse complexe effective. PhD thesis, Univ. d'Orsay, 2007. Mémoire d'habilitation.