| Modular SIMD arithmetic in |
|
| Version of June 29, 2014 |
|
Modular integer arithmetic occurs in many algorithms for computer
algebra, cryptography, and error correcting codes. Although recent
microprocessors typically offer a wide range of highly optimized
arithmetic functions, modular integer operations still require
dedicated implementations. In this article, we survey existing
algorithms for modular integer arithmetic, and present detailed
vectorized counterparts. We also present several applications,
such as fast modular Fourier transforms and multiplication of
integer polynomials and matrices. The vectorized algorithms have
been implemented in C++ inside the free computer algebra and
analysis system |
Categories and Subject Descriptors: G.4 [Mathematical Software]: Parallel and vector implementations
General Terms: Algorithms, Performance
Additional Key Words and Phrases: modular integer arithmetic, fast Fourier transform, integer product, polynomial product, matrix product, Mathemagix
During the past decade, major manufacturers of microprocessors have
changed their focus from ever increasing clock speeds to putting as many
cores as possible on one chip and to lower power consumption. One
approach followed by leading constructors such as  and
and  is to put as many x86 compatible
processors on one chip. Another approach is to rely on new simplified
processing units, which allows to increase the number of cores on each
chip. Modern Graphics Processing Units (
is to put as many x86 compatible
processors on one chip. Another approach is to rely on new simplified
processing units, which allows to increase the number of cores on each
chip. Modern Graphics Processing Units (
As powerful as multicore architectures may be, this technology also comes with its drawbacks. Besides the increased development cost of parallel algorithms, the main disadvantage is that the high degree of concurrency allowed by multicore architecture often constitutes an overkill. Indeed, many computationally intensive tasks ultimately boil down to classical mathematical building blocks such as matrix multiplication or fast Fourier transforms (FFTs).
In many cases, the implementation of such building blocks is better
served by simpler parallel architectures, and more particularly by the
Single Instruction, Multiple Data (
 and
and
More specifically, this paper concerns the efficiency of the
One important mathematical building block for  with
with 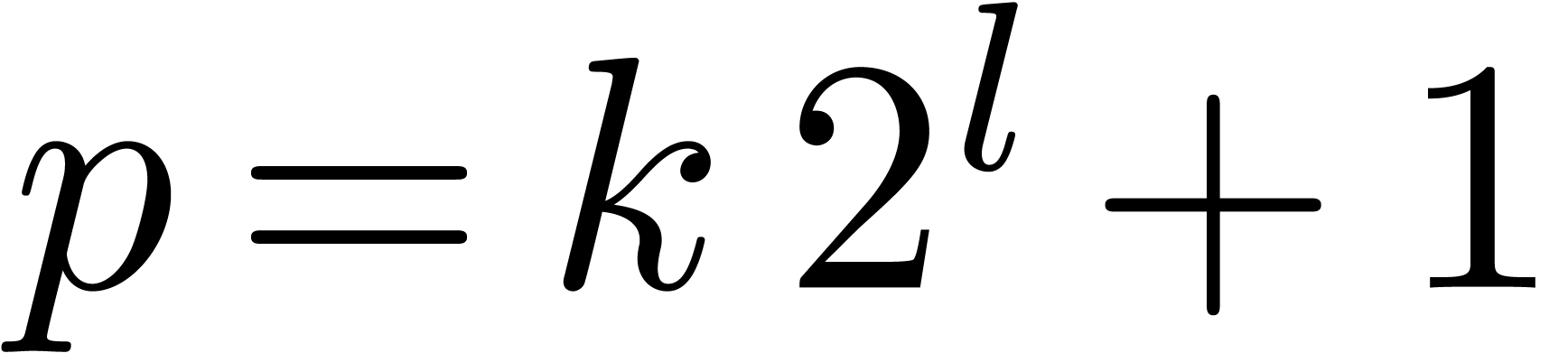 , where
, where  typically fits
within 32 or 64 bits, and
typically fits
within 32 or 64 bits, and 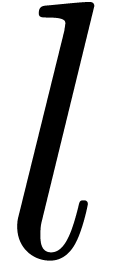 is as large as
possible under this constraint [55]. Similarly, integer
matrices can be multiplied efficiently using such
is as large as
possible under this constraint [55]. Similarly, integer
matrices can be multiplied efficiently using such
The aim of this paper is twofold. First of all, we adapt known
algorithms for modular integer arithmetic to the
The descriptions of the algorithms are self-contained and we provide
implementation details for the 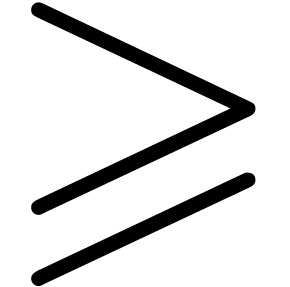
 ).
).
There is large literature on modular integer arithmetic. The main
operation to be optimized is multiplication modulo a fixed integer  . This requires an efficient
reduction of the product modulo
. This requires an efficient
reduction of the product modulo  .
The naive way of doing this reduction would be to compute the remainder
of the division of the product by
.
The naive way of doing this reduction would be to compute the remainder
of the division of the product by  .
However, divisions tend to be more expensive than multiplications in
current hardware. The classical solution to this problem is to
pre-compute the inverse
.
However, divisions tend to be more expensive than multiplications in
current hardware. The classical solution to this problem is to
pre-compute the inverse 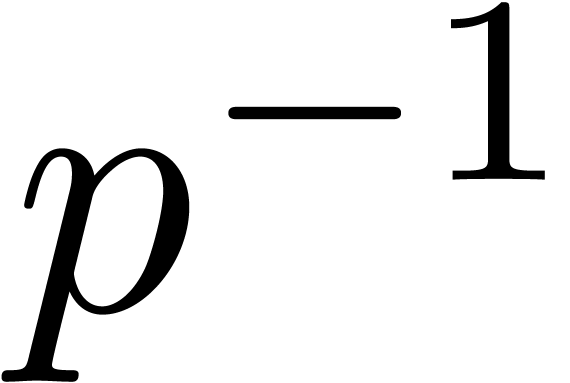 so that all divisions by
so that all divisions by
 can be transformed into multiplications.
can be transformed into multiplications.
In order to compute the product  of
of  and
and 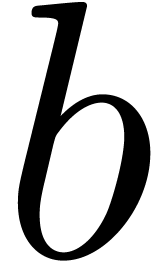 modulo
modulo  , it suffices to compute the integer floor part
, it suffices to compute the integer floor part  of the rational number
of the rational number 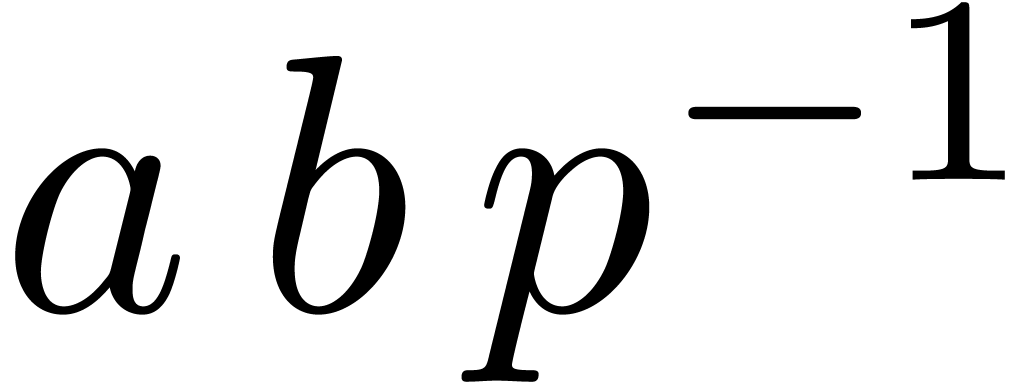 and to
deduce
and to
deduce 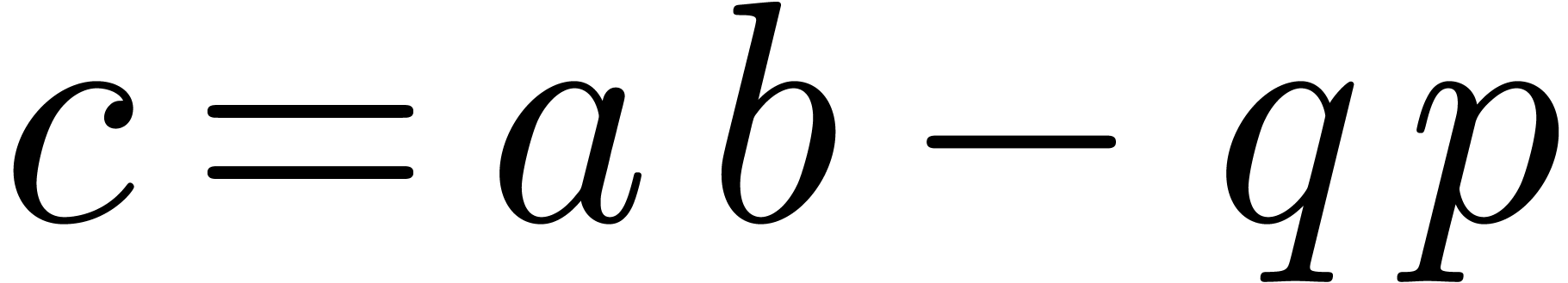 . The most obvious
algorithm is to compute
. The most obvious
algorithm is to compute  using floating point
arithmetic. However, this approach suffers from a few drawbacks. First,
in order to ensure portability, the processor should comply to the
using floating point
arithmetic. However, this approach suffers from a few drawbacks. First,
in order to ensure portability, the processor should comply to the
Barrett's algorithm [7] provides an alternative to
the floating point approach. The idea is to rescale the floating point
inverse of 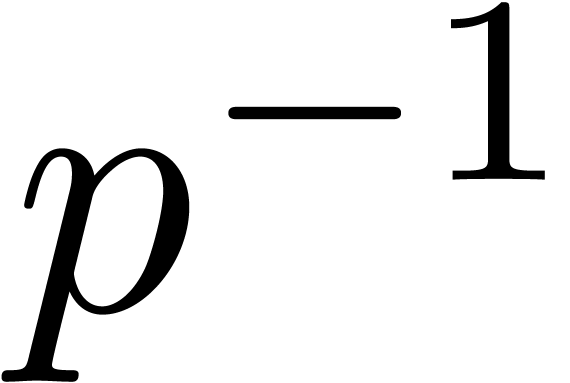 and to truncate it into an integer
type. For some early comparisons between integer and floating point
operations and a branch-free variant, we refer to [32].
This approach is also discussed in [23, Section 16.9] for
particular processors. For multiple precision integers, algorithms were
given in [6, 39].
and to truncate it into an integer
type. For some early comparisons between integer and floating point
operations and a branch-free variant, we refer to [32].
This approach is also discussed in [23, Section 16.9] for
particular processors. For multiple precision integers, algorithms were
given in [6, 39].
Another alternative approach is to precompute the inverse 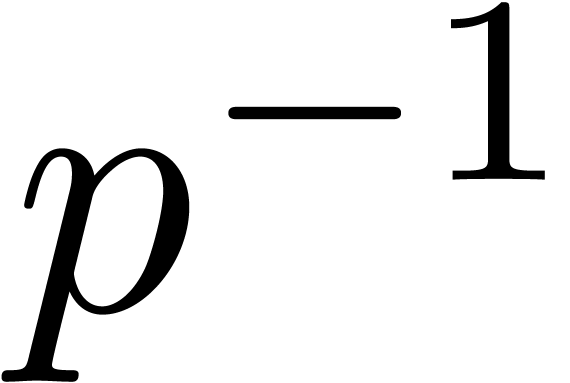 of the modulus
of the modulus  as a
as a  -adic integer. This technique, which is
essentially equivalent to Montgomery's algorithm [52],
only uses integer operations, but requires
-adic integer. This technique, which is
essentially equivalent to Montgomery's algorithm [52],
only uses integer operations, but requires  to be
odd. Furthermore, modular integers need to be encoded and decoded (with
a cost similar to one modular product), which is not always convenient.
Implementations have been discussed in [49]. A
generalization to even moduli was proposed in [48]. It
relies on computing separately modulo
to be
odd. Furthermore, modular integers need to be encoded and decoded (with
a cost similar to one modular product), which is not always convenient.
Implementations have been discussed in [49]. A
generalization to even moduli was proposed in [48]. It
relies on computing separately modulo 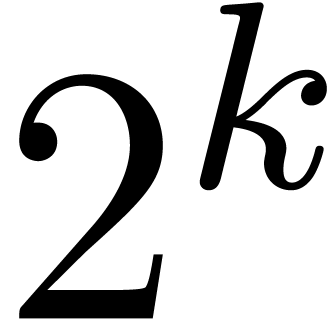 and
and  (such that
(such that  is odd, and
is odd, and  ) via Chinese
remaindering. Unfortunately, this leads to a significant overhead for
small moduli. Comparisons between Barrett's and Montgomery's product
were given in [15] for values of
) via Chinese
remaindering. Unfortunately, this leads to a significant overhead for
small moduli. Comparisons between Barrett's and Montgomery's product
were given in [15] for values of 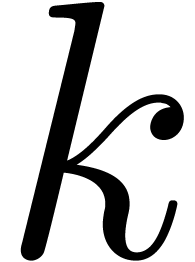 corresponding to a few machine words. A recent survey can be found in
[54] with a view towards hardware implementation.
corresponding to a few machine words. A recent survey can be found in
[54] with a view towards hardware implementation.
Modular arithmetic and several basic mathematical operations on
polynomials and matrices have been implemented before on several types
of parallel hardware (multicore architectures and
Our applications to matrix product over large polynomials or integers are central tasks to many algorithms in computer algebra [2, 12, 26, 50]. For a sample of recent targeted implementations, the reader might consult [30, 38, 53].
One difficulty with modular arithmetic is that the most efficient
algorithms are strongly dependent on the bit-size of the modulus  , as well as the availability and
efficiency of specific instructions in the hardware. This is especially
so in the case of
, as well as the availability and
efficiency of specific instructions in the hardware. This is especially
so in the case of
The fast sequential algorithms for modular reduction from the previous
section all involve some branching in order to counterbalance the effect
of rounding. Our first contribution is to eliminate all branching so as
to make vectorization possible and efficient. Our second contribution is
a complete implementation of the various approaches as a function of the
available
High performance libraries such as
A third contribution of this article is the application of our modular
arithmetic to an 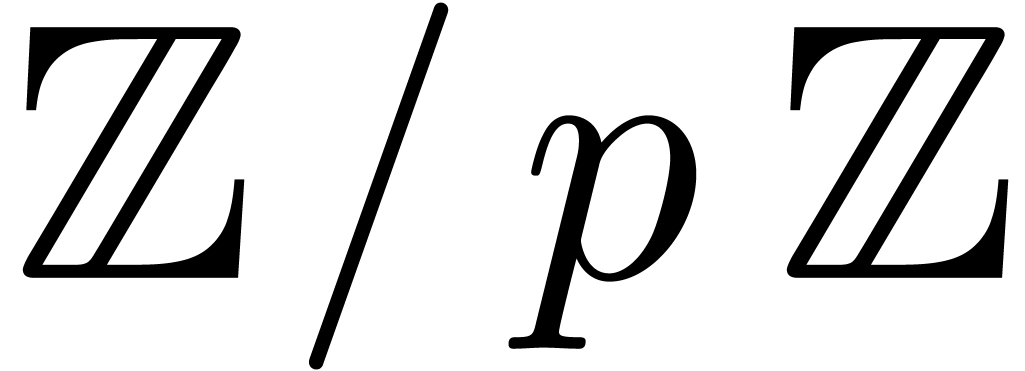 , where
, where  is a multiple of a
large power of two. Our implementations outperform existing software and
we report on timings and comparisons for integer, polynomial and matrix
products.
is a multiple of a
large power of two. Our implementations outperform existing software and
we report on timings and comparisons for integer, polynomial and matrix
products.
Besides low level software design considerations, our main research
goals concern algorithms for solving polynomial systems, for effective
complex analysis, and error correcting codes.
Throughout this article, timings are measured on a platform equipped
with an 

 kernel version 3.12 in 64
bit mode. Care has been taken for avoiding
kernel version 3.12 in 64
bit mode. Care has been taken for avoiding  always implements the right
arithmetic shift.
always implements the right
arithmetic shift.
For completeness, we conclude this introduction with recalling basic
facts on
The scalar data types which are supported;
The total bit-size 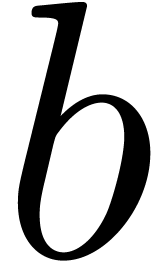 of vector registers;
of vector registers;
The number 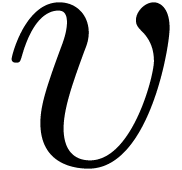 of vector registers;
of vector registers;
For each scalar data type  ,
the instruction set for vector operations over
,
the instruction set for vector operations over  ;
;
The instruction set for other operations on
Modern  of bit-size
of bit-size 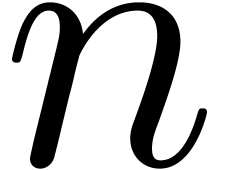 ,
we operate on vectors of
,
we operate on vectors of 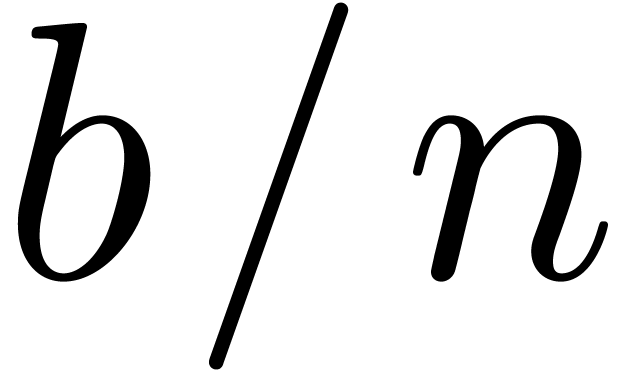 coefficients in
coefficients in  .
.
Currently, the most common  and
and  ),
), 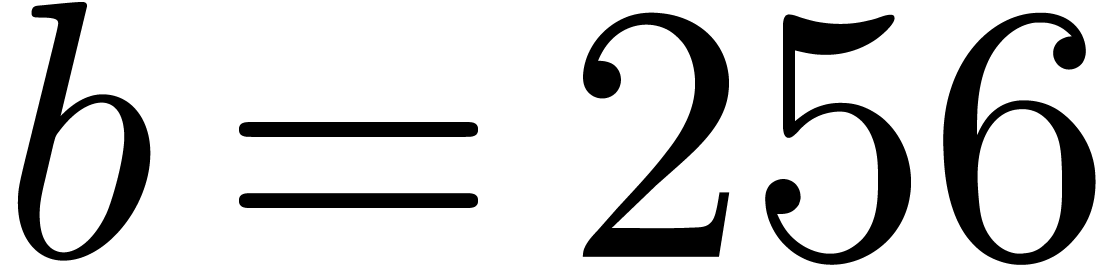 and
and 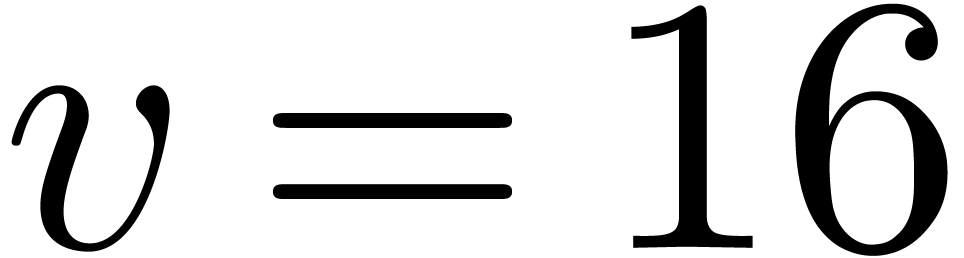 ) and
) and
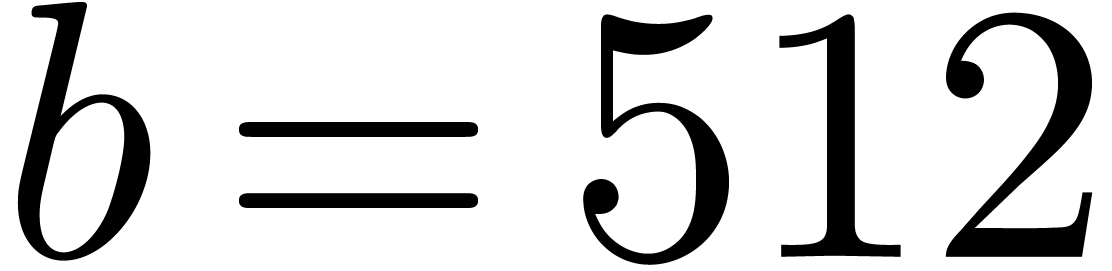 and
and 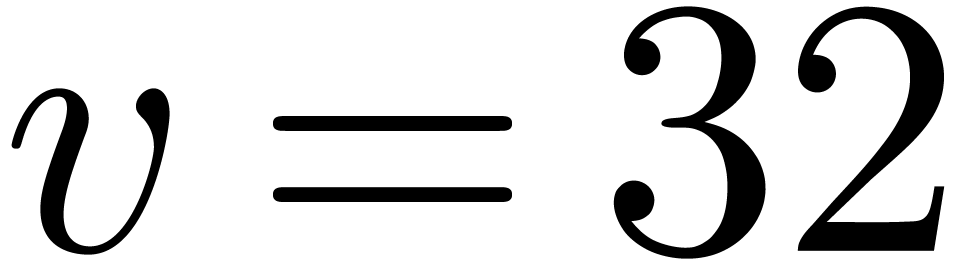 ). For instance, an
). For instance, an  integers of bit-size
integers of bit-size  in unit time.
It should be noticed that these bit-sizes
in unit time.
It should be noticed that these bit-sizes 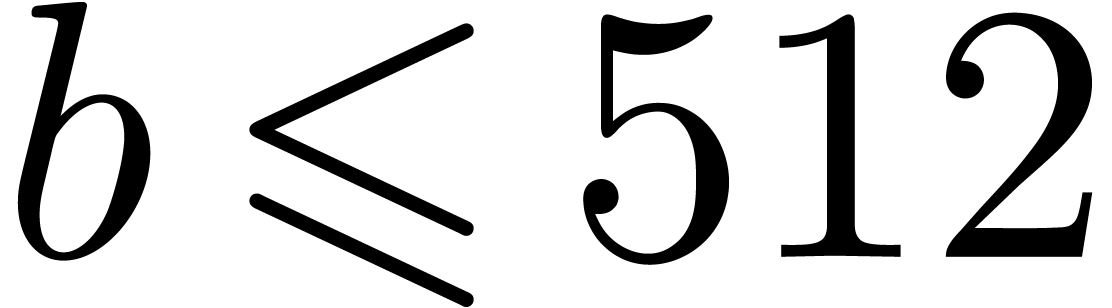 are
rather modest in comparison to their historical ancestors, such as the
are
rather modest in comparison to their historical ancestors, such as the
 vector computers (
vector computers (
In this paper, our
The types __m128i and __m128d
correspond to packed 128-bit integer and floating point vectors.
They are supported by
The instruction _mm_add_epi64 corresponds to the
addition of two vectors of 64-bit signed integers of type __m128i
(so the vectors are of length  ).
).
The predicate _mm_cmpgt_epi64 corresponds to a
component-wise 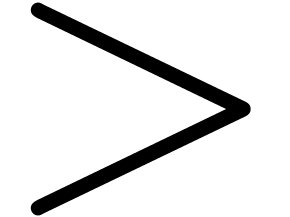 test on two vectors of 64-bit
signed integers of type __m128i. The boolean results
true and false are encoded by the
signed integers -1 and 0.
test on two vectors of 64-bit
signed integers of type __m128i. The boolean results
true and false are encoded by the
signed integers -1 and 0.
The instruction _mm_mul_pd corresponds to the
multiplication of two vectors of double precision floating point
numbers of type __m128d (so the vectors are of
length  ).
).
We notice that all floating point arithmetic conforms to the IEEE-754 standard. In particular, results of floating point operations are obtained through correct rounding of their exact mathematical counterparts, where the global rounding mode can be set by the user. Some processors also provide fused multiply add (FMA) and subtract instructions _mm_fmadd_pd and _mm_fmsub_pd which are useful in Section 3. Another less obvious but useful instruction that is provided by some processors is:
_mm_blendv_pd ( ,
,
 ,
, 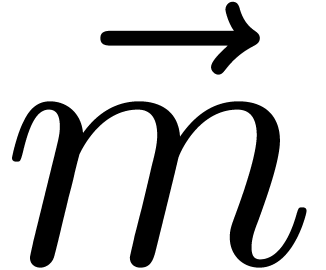 ) returns a vector
) returns a vector  with
with  whenever the most significant bit of
whenever the most significant bit of
 is set and
is set and  otherwise
(for each
otherwise
(for each 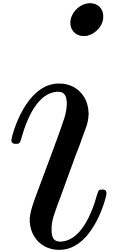 ). For floating
point numbers, it should be noticed that the most significant bit of
). For floating
point numbers, it should be noticed that the most significant bit of
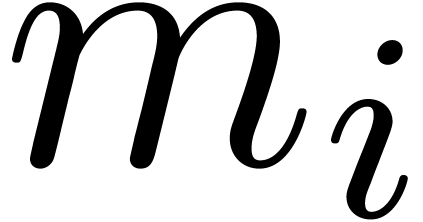 corresponds to the sign bit.
corresponds to the sign bit.
For more details about  intrinsic guides [46, 47], and also to [21] for useful comments and practical recommendations.
intrinsic guides [46, 47], and also to [21] for useful comments and practical recommendations.
Let us mention that a standard way to benefit from
If  and
and 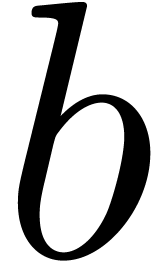 are nonnegative
integers, then
are nonnegative
integers, then 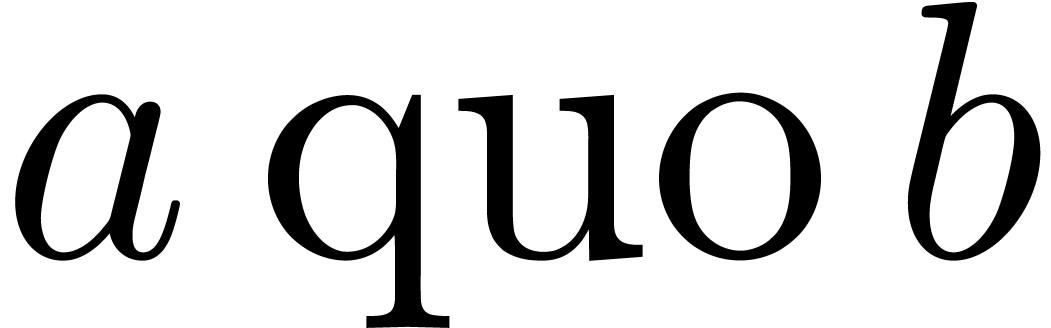 and
and  represent the quotient and the remainder in the long
division of
represent the quotient and the remainder in the long
division of  by
by 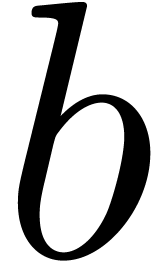 respectively. We let U denote an unsigned integer type
of bit-size
respectively. We let U denote an unsigned integer type
of bit-size 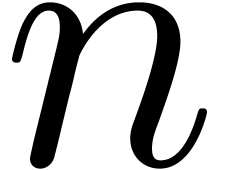 assumed to be at least
assumed to be at least  for convenience. This means that all the integers in the
range from
for convenience. This means that all the integers in the
range from  to
to  can be
represented in U by their binary expansion. The
corresponding type for signed integers of bit-size
can be
represented in U by their binary expansion. The
corresponding type for signed integers of bit-size 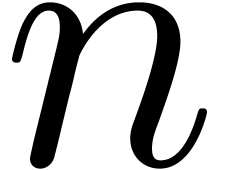 is written I: all integers from
is written I: all integers from 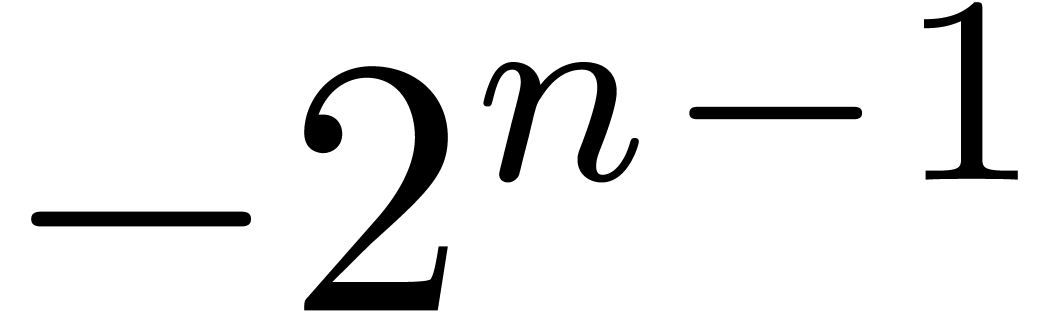 to
to 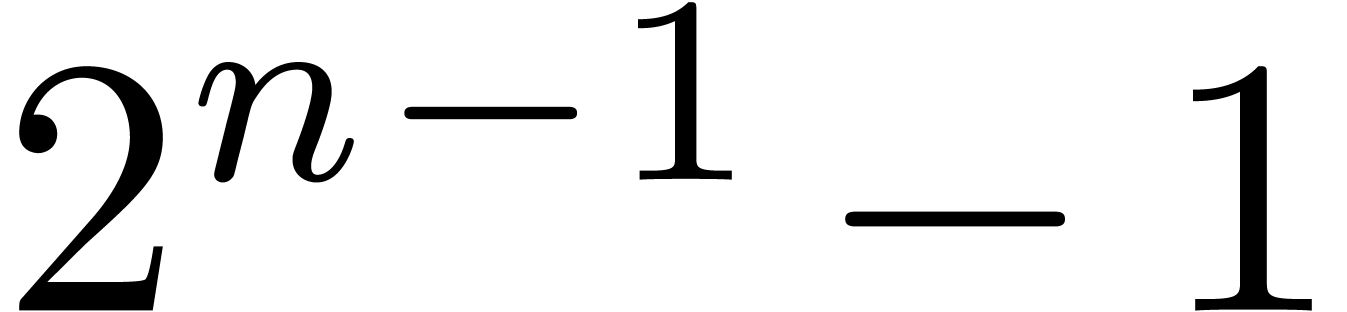 can be represented in I. The
type
can be represented in I. The
type  represents unsigned integers of size at
least
represents unsigned integers of size at
least 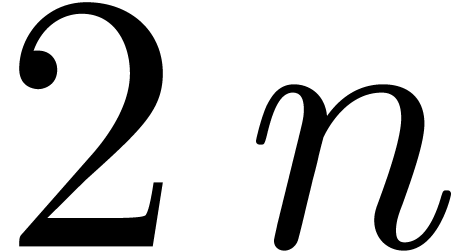 . Let
. Let  be a nonnegative integer of bit-size at most
be a nonnegative integer of bit-size at most 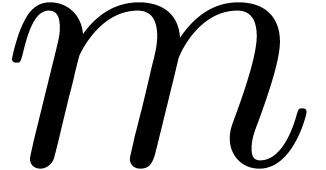 with
with 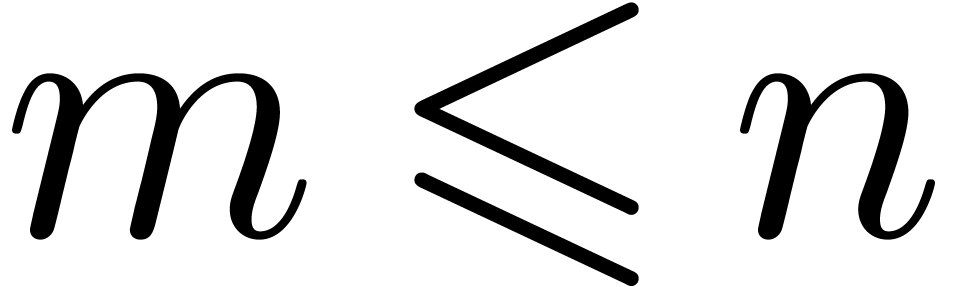 . For efficiency reasons
we consider that
. For efficiency reasons
we consider that 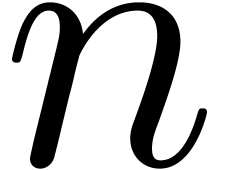 and
and 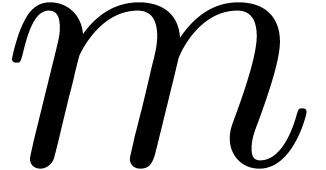 are
quantities known at compilation time, whereas the actual value of
are
quantities known at compilation time, whereas the actual value of  is only known at execution time. In fact, deciding
which elementary modular arithmetic algorithm to use at runtime
according to the bit-size of
is only known at execution time. In fact, deciding
which elementary modular arithmetic algorithm to use at runtime
according to the bit-size of  is of course too
expensive. For convenience we identify the case
is of course too
expensive. For convenience we identify the case 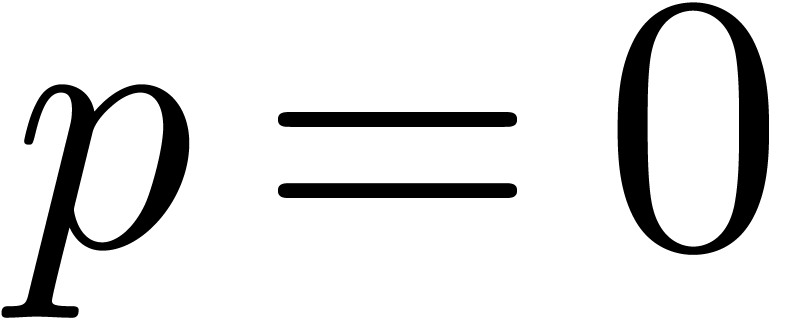 to computing modulo
to computing modulo  . Modulo
. Modulo
 integers are stored as their representative in
integers are stored as their representative in
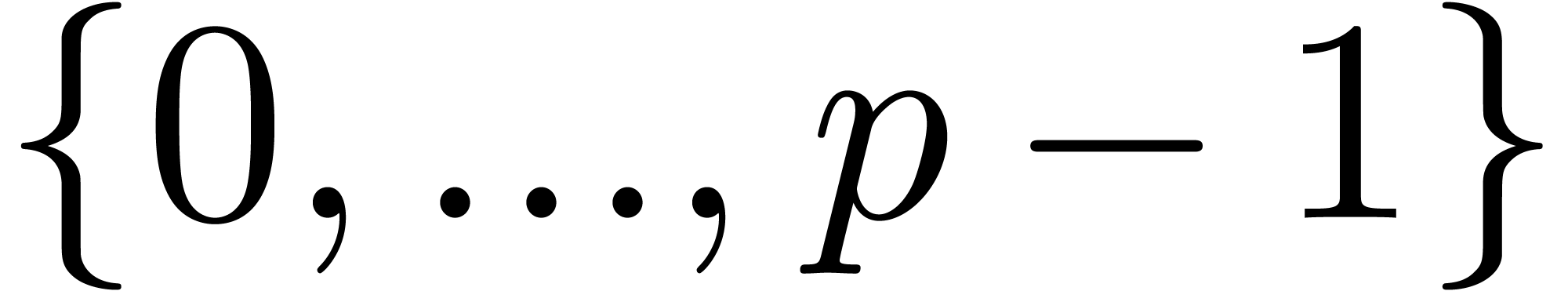 .
.
Although modular sum seems rather easy at first look, we quickly summarize the known techniques and pitfalls.
Given  and
and  modulo
modulo  , in order to compute
, in order to compute 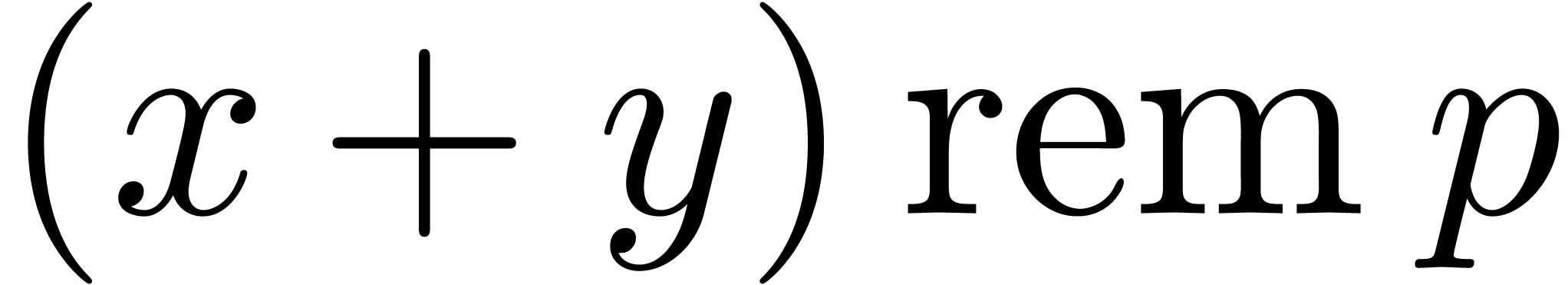 , we can first compute
, we can first compute  in U and subtract
in U and subtract  when an
overflow occurs or when
when an
overflow occurs or when 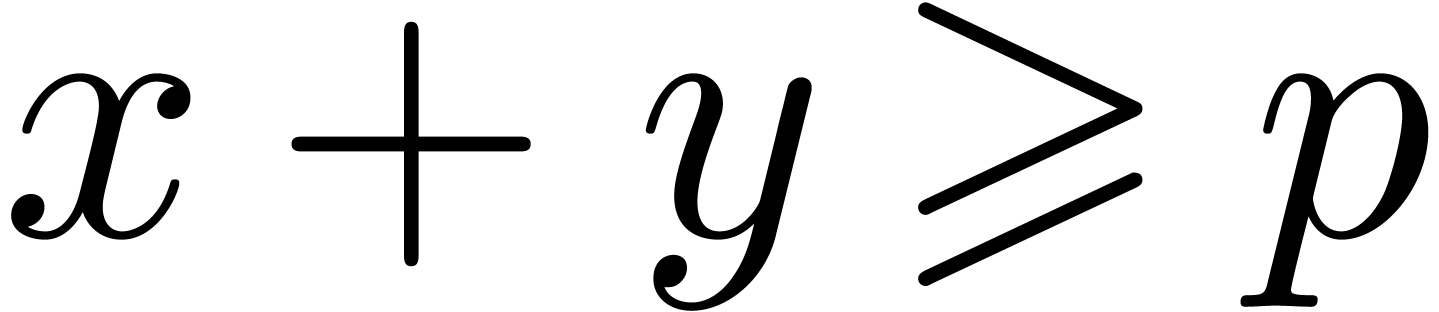 , as
detailed in the following function:
, as
detailed in the following function:
Function
Output. 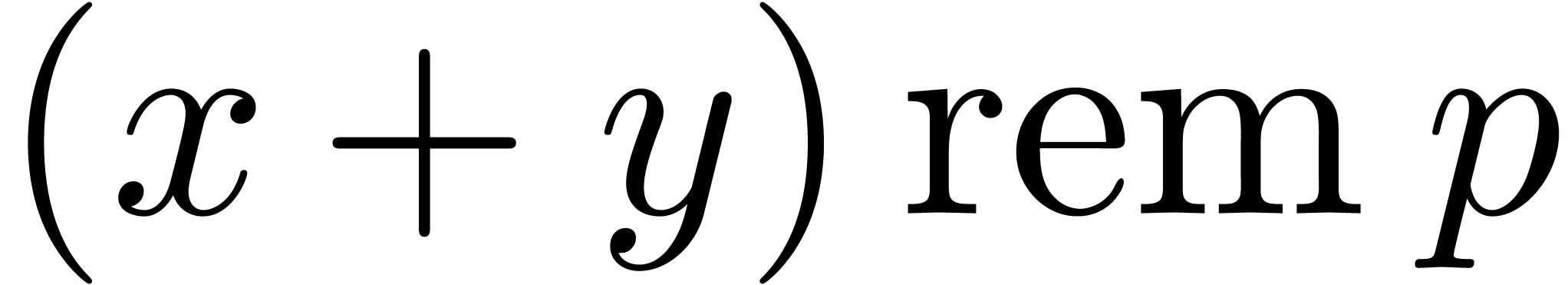 .
.
U add_mod (U  , U
, U 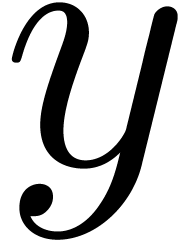 )
{
)
{
U  =
=  +
+  ;
;
if ( <
<
 ) return
) return  -
-  ;
;
return ( >=
>=  ) ?
) ?  -
-  :
:  ; }
; }
Of course, when  , no overflow
occurs in the sum of line 1, and line 2 is useless. If branching is more
expensive than shifting and if
, no overflow
occurs in the sum of line 1, and line 2 is useless. If branching is more
expensive than shifting and if  ,
then one can compute I
,
then one can compute I  =
=  +
+  -
-  and return
and return  + ((
+ (( >> (
>> ( -1)) &
-1)) &  ), where we recall that
), where we recall that  implements the right arithmetic shift. It is
important to program both versions and determine which approach is the
fastest for a given processor. Negation and subtraction can be easily
implemented in a similar manner.
implements the right arithmetic shift. It is
important to program both versions and determine which approach is the
fastest for a given processor. Negation and subtraction can be easily
implemented in a similar manner.
Arithmetic operations on packed integers are rather well supported by
 represent the packed
represent the packed  -bit integer of type __m128i, whose
entries are filled with
-bit integer of type __m128i, whose
entries are filled with  . In
order to avoid branching in Function 1, one can compute U
. In
order to avoid branching in Function 1, one can compute U  =
=  +
+  and return min (
and return min ( ,
,  -
-  ) when
) when 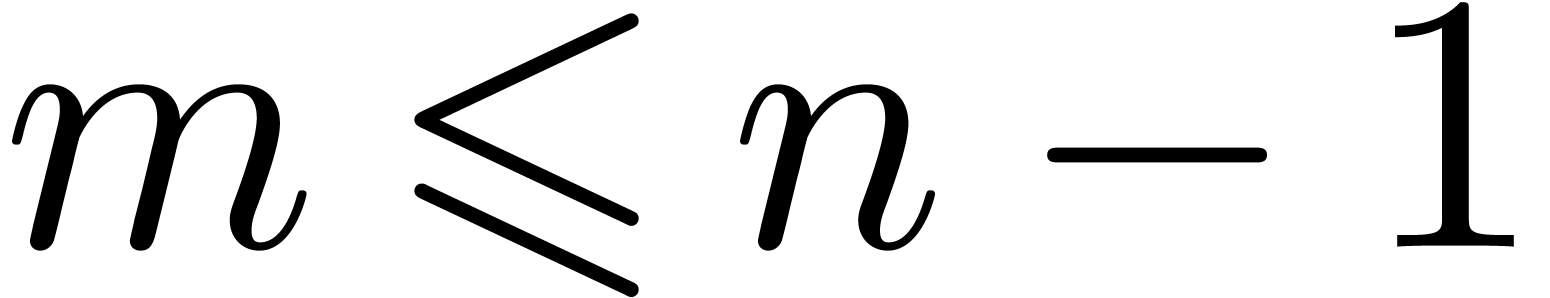 .
This approach can be straightforwardly vectorized for packed integers of
bit-sizes
.
This approach can be straightforwardly vectorized for packed integers of
bit-sizes 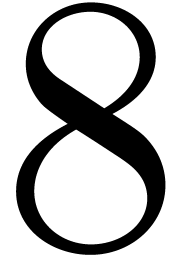 , 16 and 32, as
exemplified in the following function:
, 16 and 32, as
exemplified in the following function:
Function
Output. 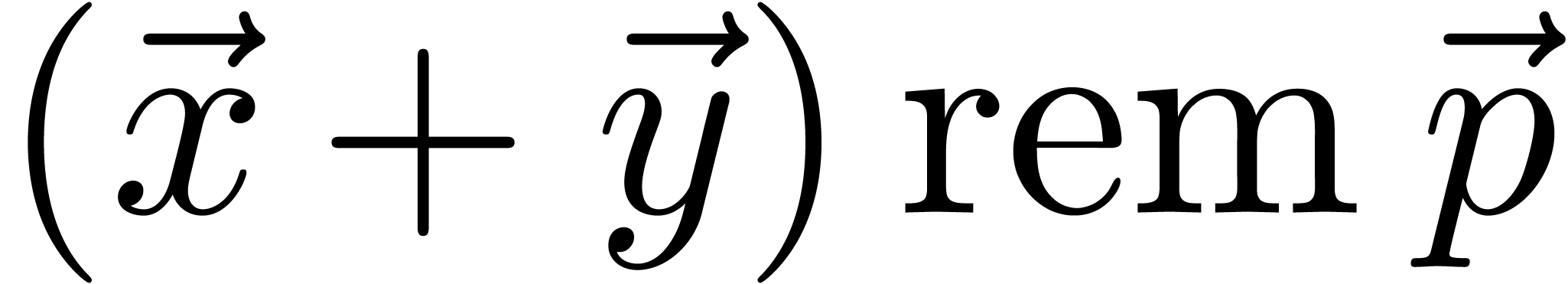 .
.
__m128i add_mod_1_epu32 (__m128i 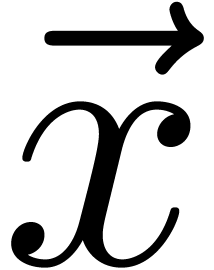 , __m128i
, __m128i 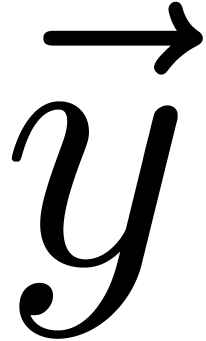 ) {
) {
__m128i 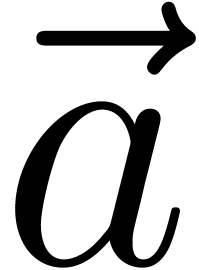 =
_mm_add_epi32 (
=
_mm_add_epi32 (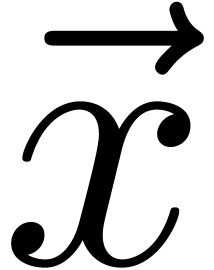 ,
, 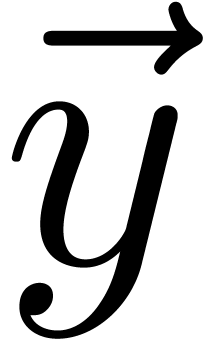 );
);
return _mm_min_epu32 ( , _mm_sub_epi32 (
, _mm_sub_epi32 ( ,
, 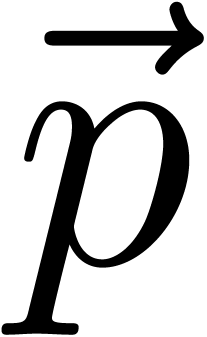 ));
}
));
}
Since the min operation does not exist on packed 64-bit
integers, we use the following function, where  represents the packed
represents the packed 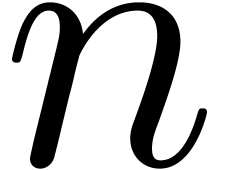 -bit
integer of type __m128i filled with
-bit
integer of type __m128i filled with  :
:
Function
Output.  .
.
__m128i add_mod_1_epu64 (__m128i  , __m128i
, __m128i  ) {
) {
__m128i  =
_mm_sub_epi64 (_mm_add_epi64 (
=
_mm_sub_epi64 (_mm_add_epi64 ( ,
,
 ),
),  );
);
__m128i  =
_mm_cmpgt_epi64 (
=
_mm_cmpgt_epi64 ( ,
,
 );
);
return _mm_add_epi64 ( , _mm_and_si128 (
, _mm_and_si128 ( ,
, 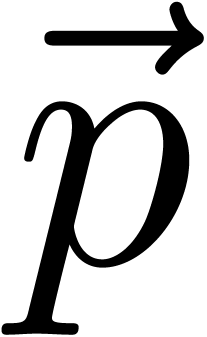 ));
}
));
}
If  , we can proceed as
follows:
, we can proceed as
follows: 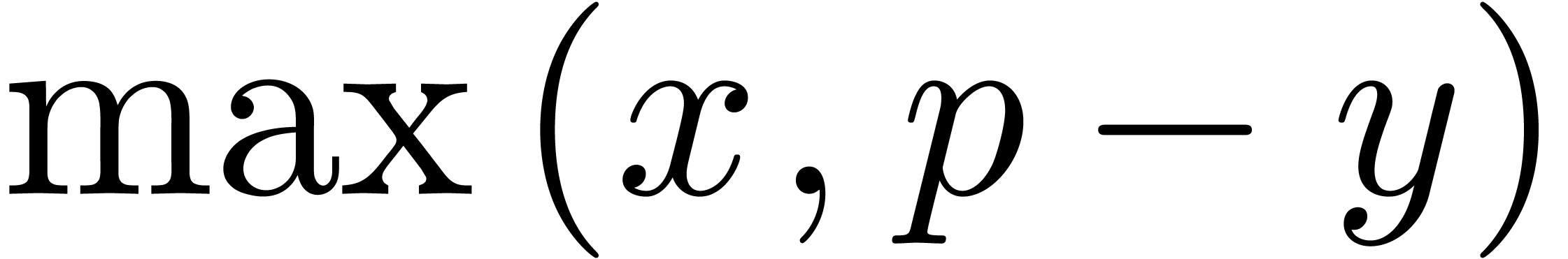 equals
equals  if, and
only if,
if, and
only if, 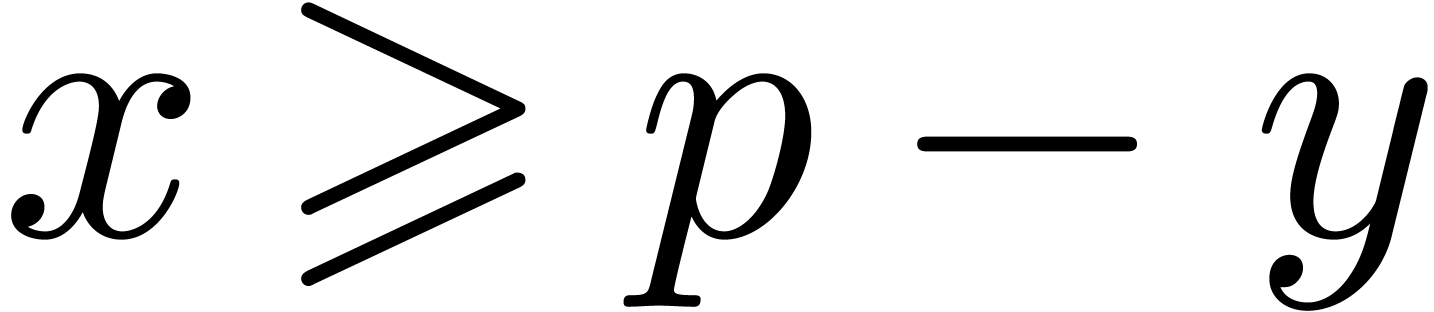 . In the latter case
. In the latter case
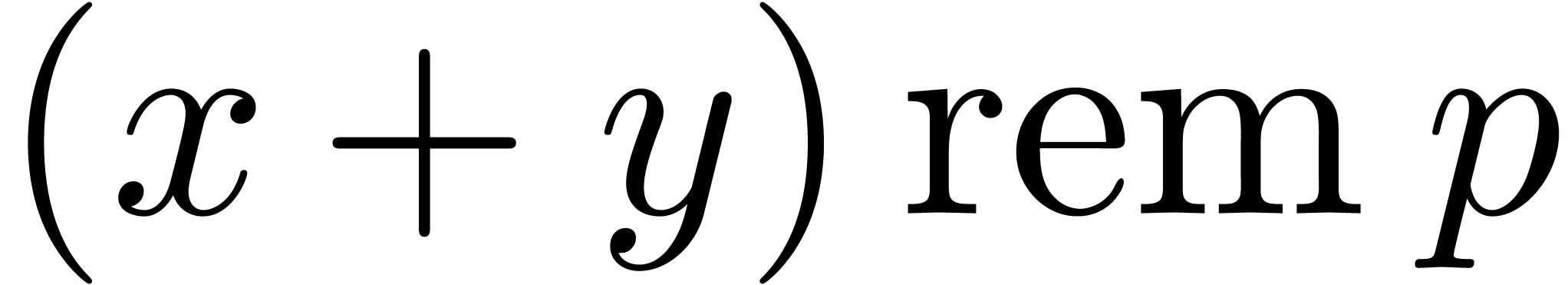 can be obtained as
can be obtained as 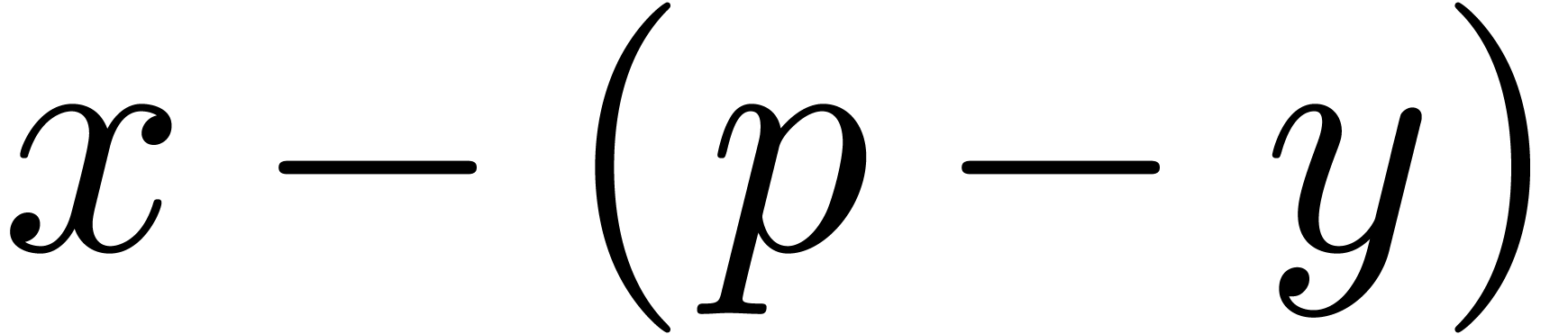 ,
and otherwise as
,
and otherwise as  . If
. If  , an overflow only occurs when
, an overflow only occurs when
 . Nevertheless, max
(
. Nevertheless, max
( ,
,  -
-
 ) equals
) equals  when computed in U and
when computed in U and  - (
- ( -
-  ) is the correct value. These calculations can
be vectorized for packed integers of bit-size
) is the correct value. These calculations can
be vectorized for packed integers of bit-size  , 16, and
, 16, and  as follows:
as follows:
Function
Output.  .
.
__m128i add_mod_epu32 (__m128i  , __m128i
, __m128i  ) {
) {
__m128i  =
_mm_sub_epi32 (
=
_mm_sub_epi32 ( ,
,  );
);
__m128i  =
_mm_cmpeq_epi32 (_mm_max_epu32 (
=
_mm_cmpeq_epi32 (_mm_max_epu32 ( ,
,
 ),
),  );
);
__m128i  =
_mm_andnot_si128 (
=
_mm_andnot_si128 ( ,
,
 );
);
return _mm_add_epi32 (_mm_sub_epi32
( ,
,  ),
),  );
}
);
}
The minimum operator and comparisons do not exist for packed 64-bit
integers so we declare the function _mm_cmpgt_epu64 (__m128i
 , __m128i
, __m128i  ) as:
) as:
_mm_cmpgt_epi64 (_mm_sub_epi64 (,
), _mm_sub_epi64 (
,
))
where  represents the packed 64-bit integer
filled with
represents the packed 64-bit integer
filled with  . The modular
addition can be realized as follows:
. The modular
addition can be realized as follows:
Function
Output.  .
.
__m128i add_mod_epu64 (__m128i 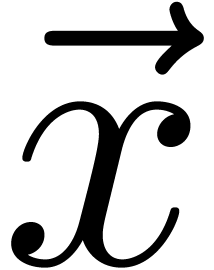 , __m128i
, __m128i 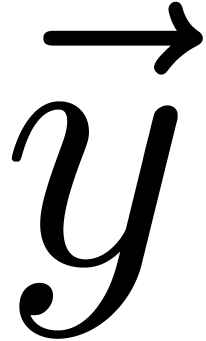 ) {
) {
__m128i  =
_mm_add_epi64 (
=
_mm_add_epi64 (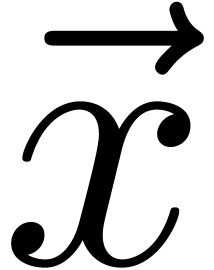 ,
, 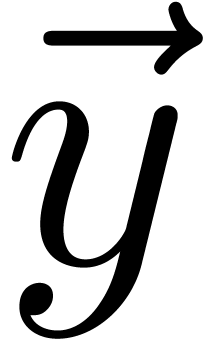 );
);
__m128i 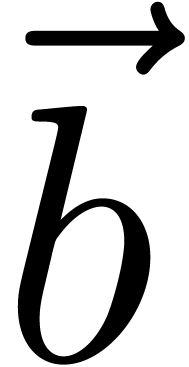 =
_mm_or_si128 (_mm_cmpgt_epu64 (
=
_mm_or_si128 (_mm_cmpgt_epu64 (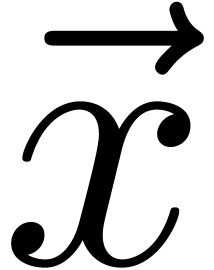 ,
,
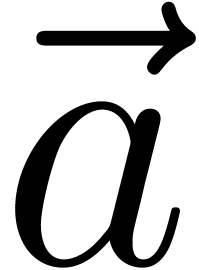 ),
),
_mm_cmpgt_epu64 ( ,
,  -
-  ));
));
return _mm_sub_epi64 ( , _mm_and_si128 (
, _mm_and_si128 ( ,
, 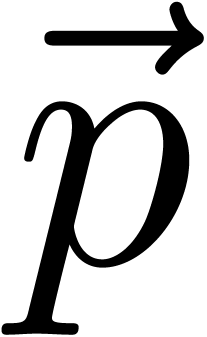 ));
}
));
}
It is straightforward to adapt these functions to the
Table 1 displays timings for arithmetic operations over
integer types of all possible bit-sizes 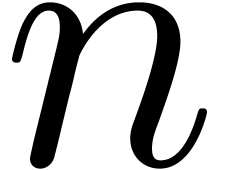 supported by the compiler. Timings are the average number of clock
cycles when applying the addition on two vectors of byte-size 4096
aligned in memory, and writing the result into the first vector. In
particular, timings include load and store instructions. The row
Scalar corresponds to disabling vectorization extensions with
the command line option -fno-tree-vectorize of the
compiler. For better performance, loops are unrolled and the
optimization option -O3 of the compiler is used. For
conciseness, we restrict tables to addition; subtraction and negation
behave in a similar way. Operations which are not supported are
indicated by
supported by the compiler. Timings are the average number of clock
cycles when applying the addition on two vectors of byte-size 4096
aligned in memory, and writing the result into the first vector. In
particular, timings include load and store instructions. The row
Scalar corresponds to disabling vectorization extensions with
the command line option -fno-tree-vectorize of the
compiler. For better performance, loops are unrolled and the
optimization option -O3 of the compiler is used. For
conciseness, we restrict tables to addition; subtraction and negation
behave in a similar way. Operations which are not supported are
indicated by
|
||||||||||||||||||||||||
Table 2 shows timings for modular sums. In absence of
vectorization, 8-bit and 16-bit arithmetic operations are in fact
performed by 32-bit operations. Indeed, 8-bit and 16-bit arithmetic is
handled in a suboptimal way by current processors and compilers. For the
vectorized implementations, we observe significant speedups when 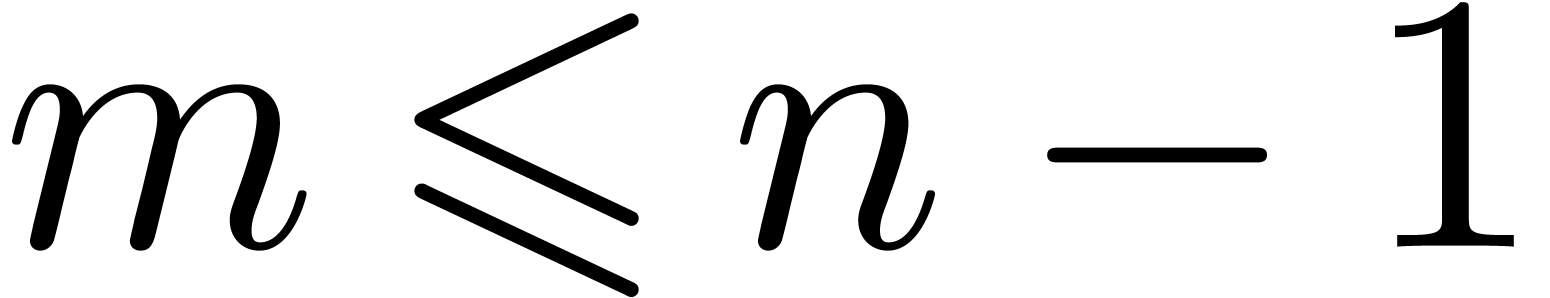 . Nevertheless, when
. Nevertheless, when  , the lack of performance is not dramatic
enough to justify the use of larger integers and double memory space.
, the lack of performance is not dramatic
enough to justify the use of larger integers and double memory space.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
The first modular product we describe is the one classically attributed
to Barrett. It has the advantage to operate on integer types with no
assumption on the modulus. For any nonnegative real number  , we write
, we write 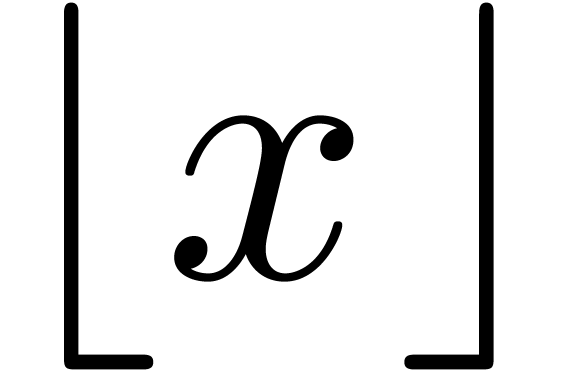 for the
largest integer less or equal to
for the
largest integer less or equal to  ,
and
,
and 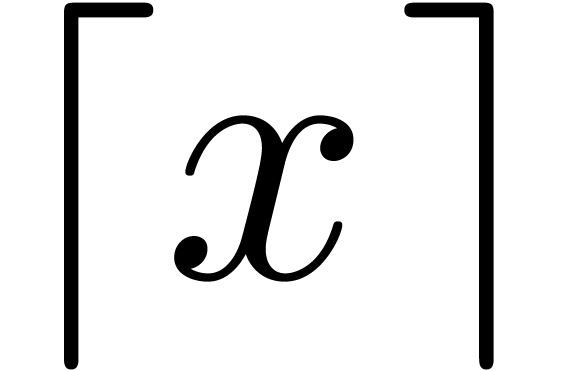 for the smallest integer greater or equal to
for the smallest integer greater or equal to
 . We use the following
auxiliary quantities:
. We use the following
auxiliary quantities:
the nonnegative integer  of
of  with
with  ;
;
nonnegative integers  and
and  such that
such that 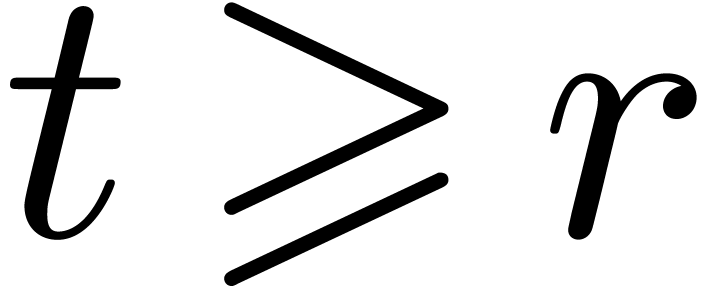 and
and 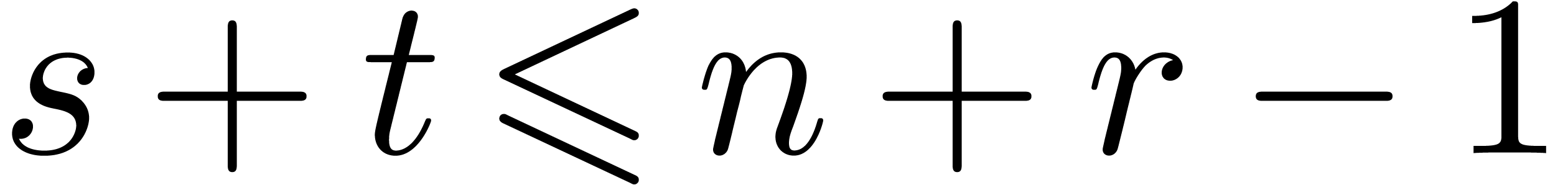 ;
;
the integer 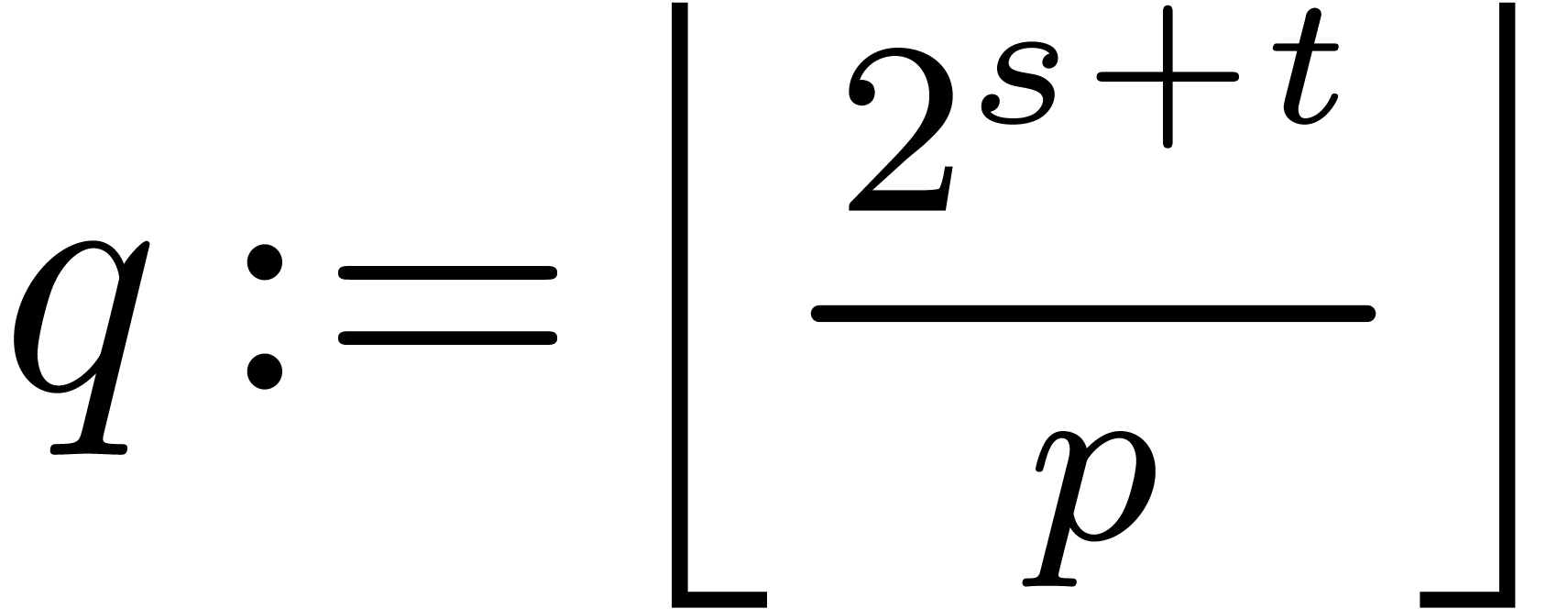 represents an approximation of a
rescaled numerical inverse of
represents an approximation of a
rescaled numerical inverse of  .
.
Since 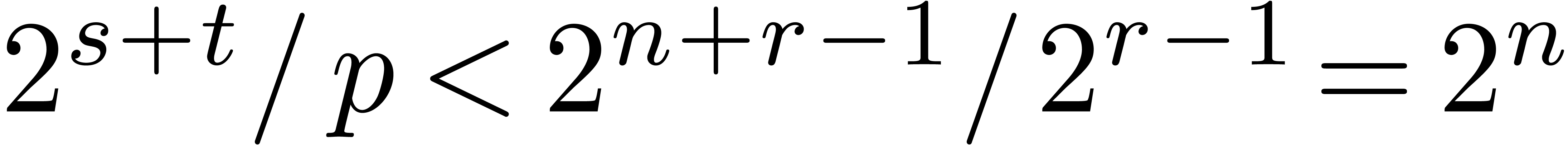 , the integer
, the integer  fits in U. We call
fits in U. We call  the pre-inverse of
the pre-inverse of  .
Since
.
Since 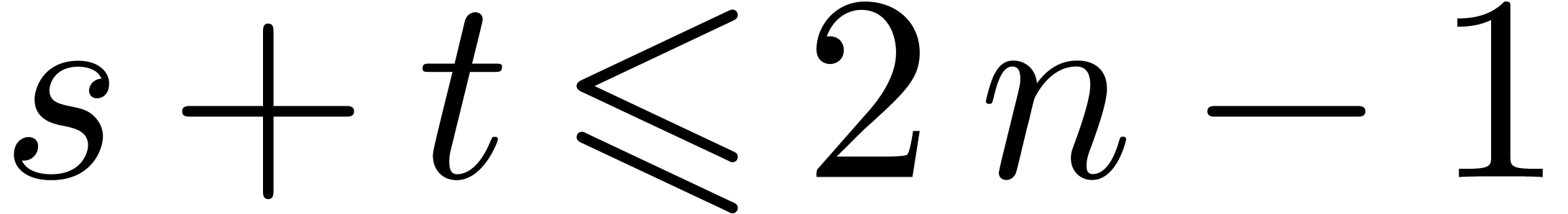 , the computation of
, the computation of
 just requires one division in
just requires one division in  . In this subsection both integers
. In this subsection both integers  and
and  are assumed to be of type U. We describe below how to set suitable values for
are assumed to be of type U. We describe below how to set suitable values for  and
and  in terms of
in terms of  (see Table 3).
(see Table 3).
Let  be one more auxiliary quantity with
be one more auxiliary quantity with 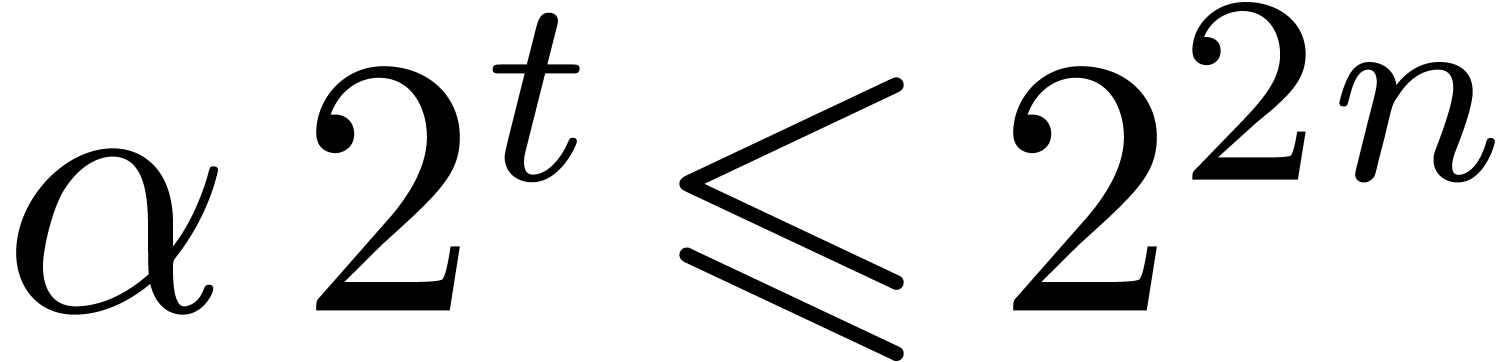 . If
. If  is an
integer such that
is an
integer such that 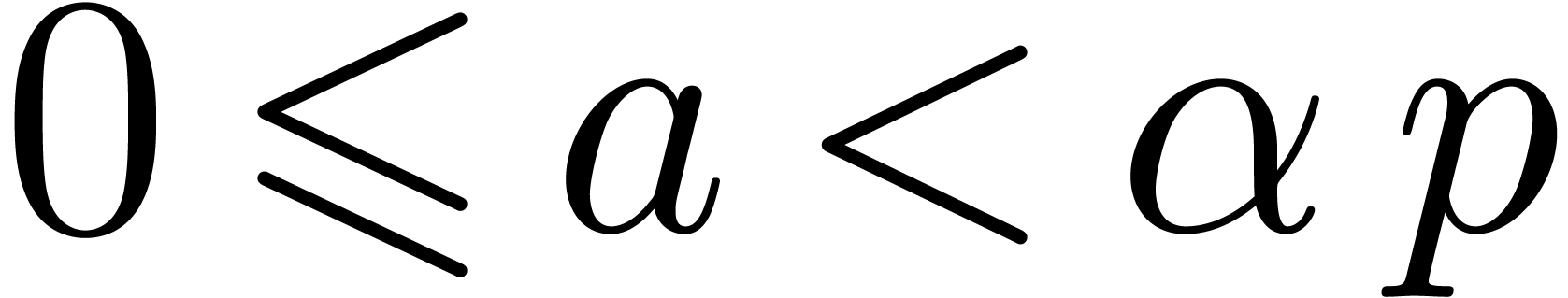 , Barrett's
algorithm computes
, Barrett's
algorithm computes  as follows:
as follows:
Function
Output.  .
.
U reduce_barrett (L  ) {
) {
L  =
=  >>
>>  ;
;
L  = (
= ( *
*  )
>>
)
>>  ;
;
L  =
=  -
-  *
*  ;
;
while ( >=
>=  )
)  =
=  -
-  ;
;
return  ; }
; }
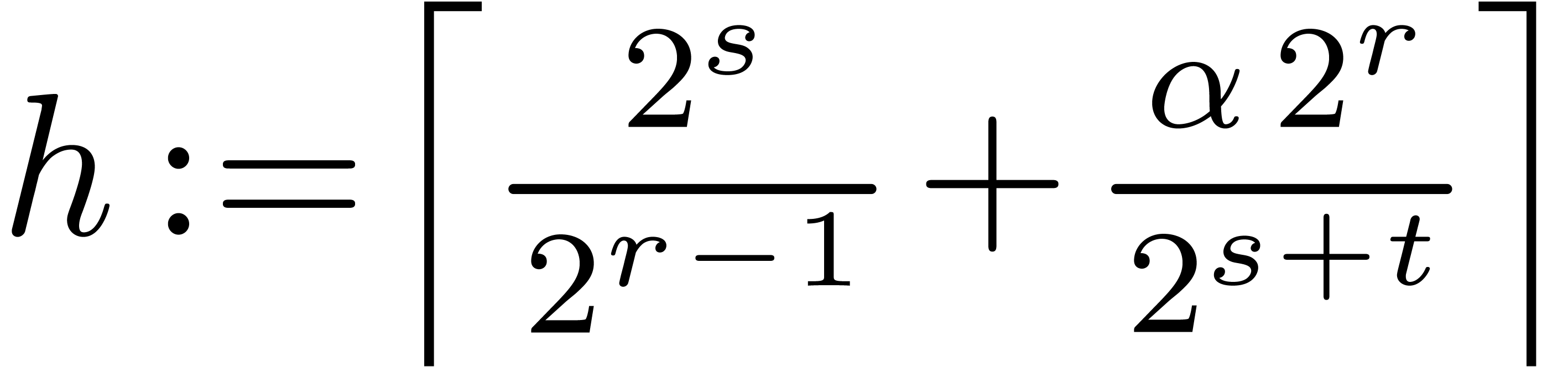 if
if 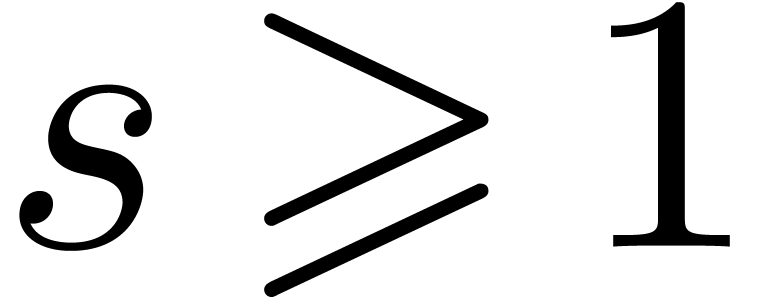 and
and 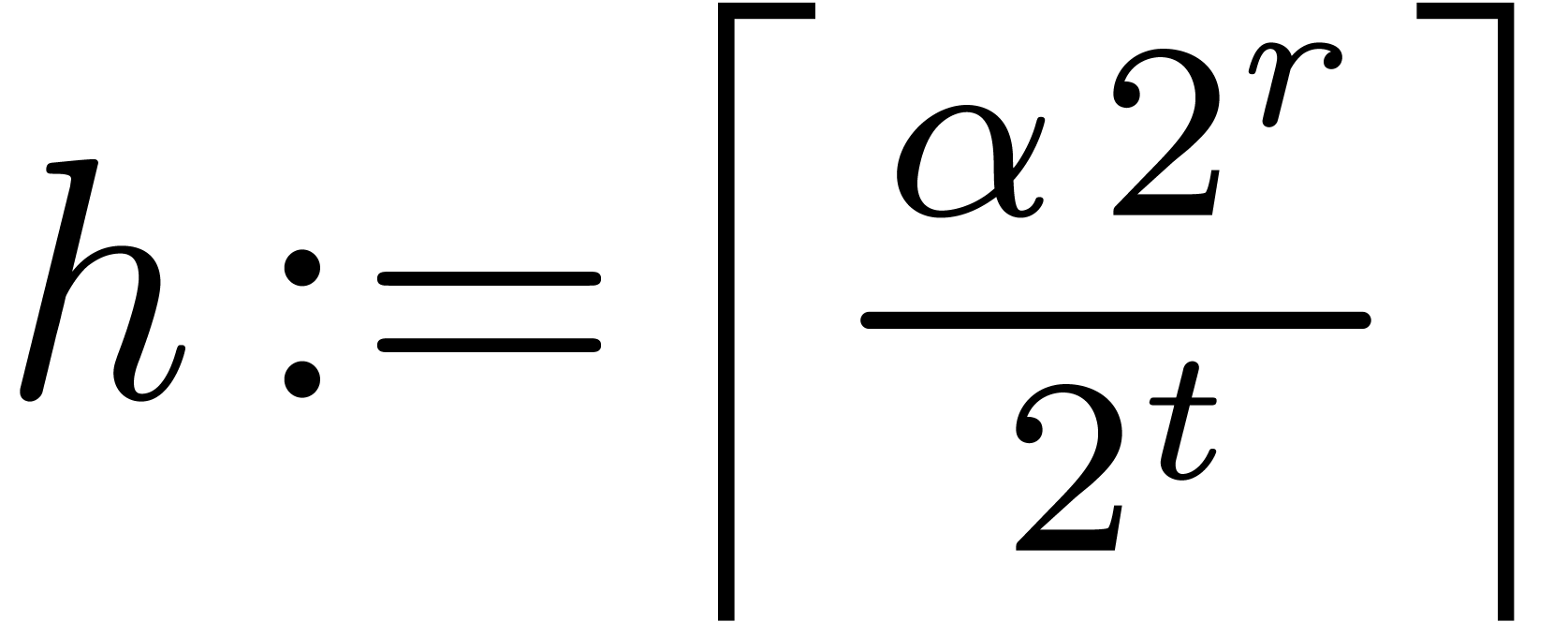 if
if 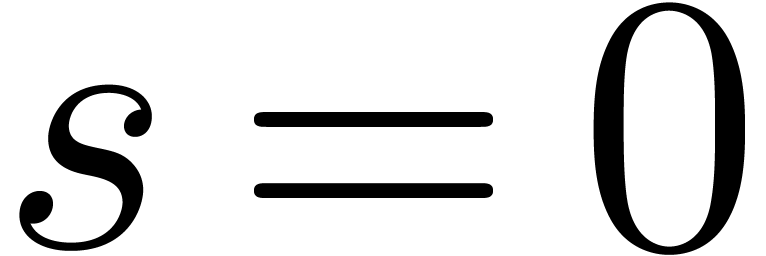 . In
addition,
. In
addition,  and
and  fit in
L.
fit in
L.
Proof. From 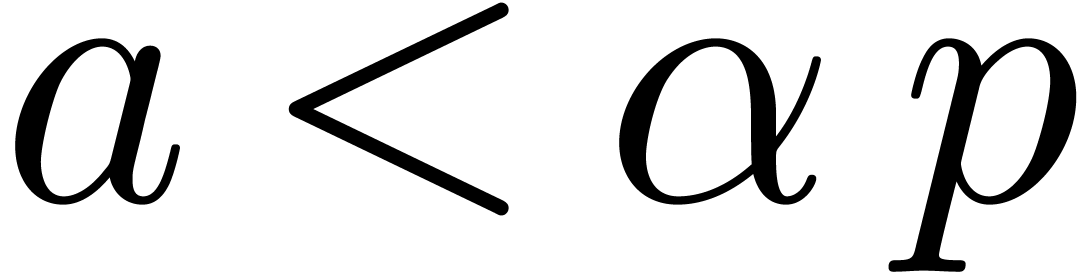 ,
it follows that
,
it follows that 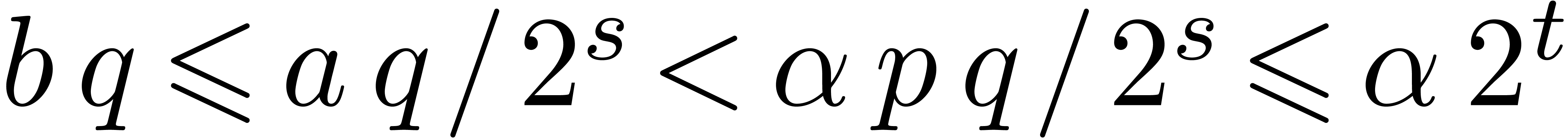 . Therefore,
. Therefore,
 has bit-size at most
has bit-size at most  , and
, and 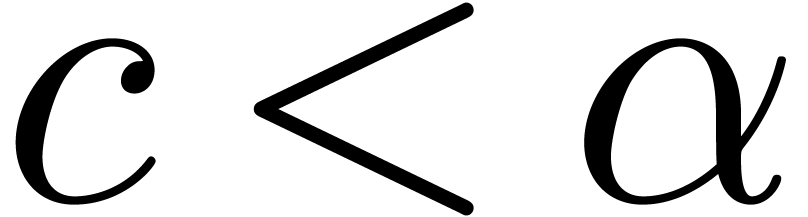 .
Since
.
Since 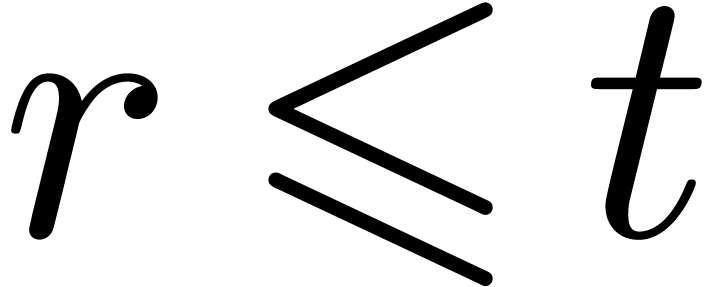 the product
the product 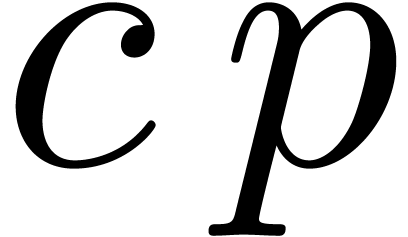 fits
in L. From
fits
in L. From
we obtain 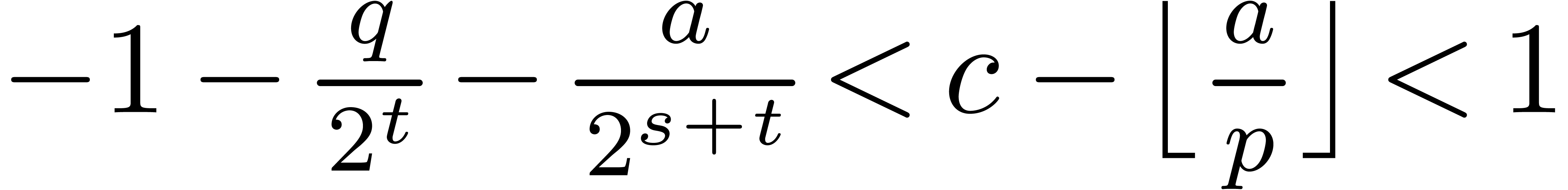 . If
. If  , then
, then 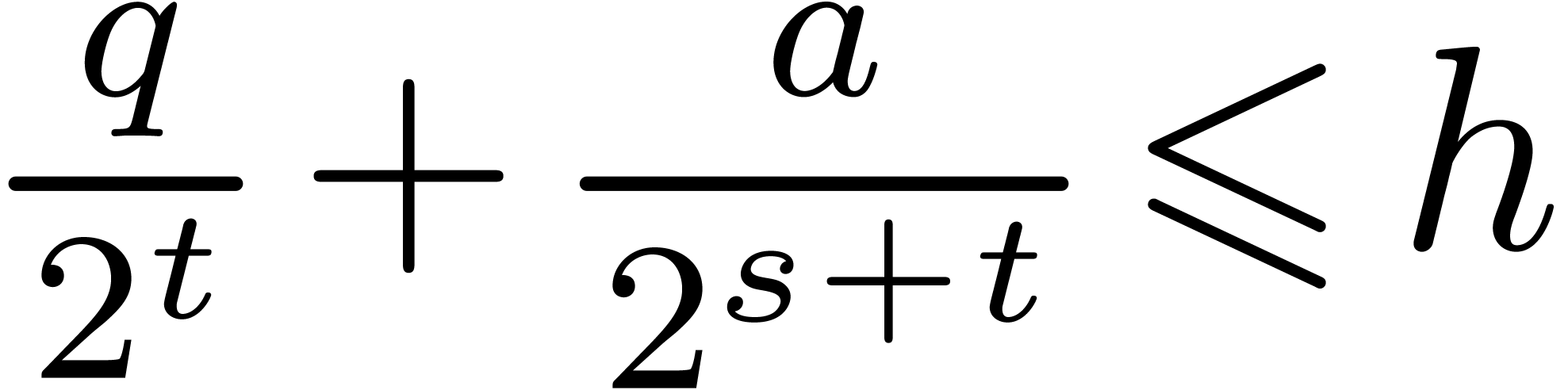 ,
so that
,
so that 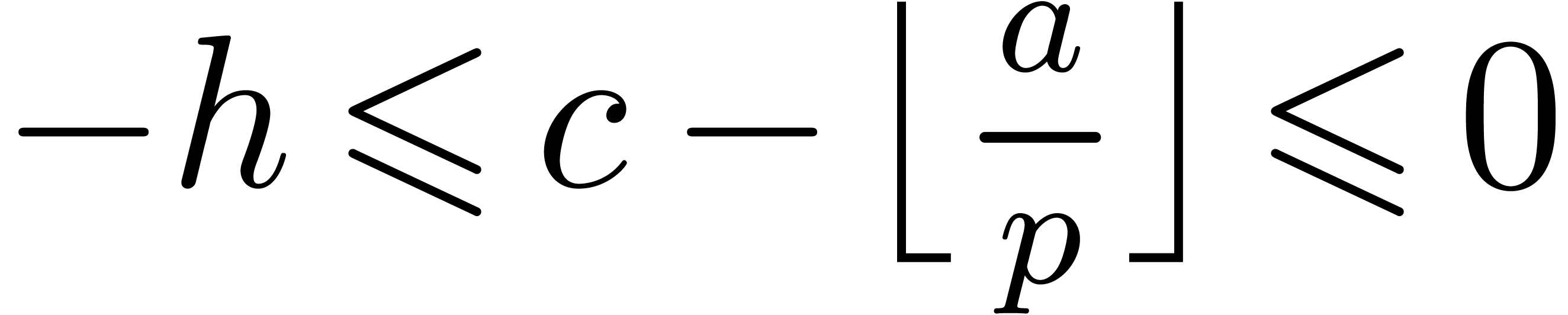 , whence the
conclusion follows. If
, whence the
conclusion follows. If 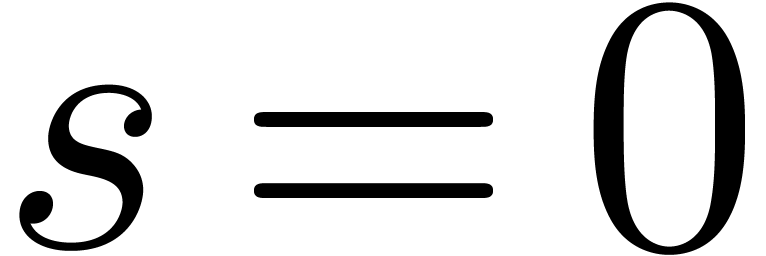 , then
, then
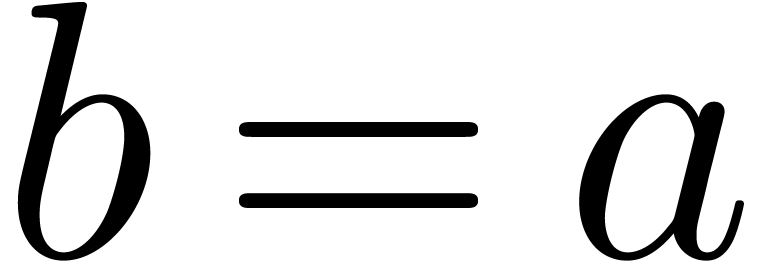 , and we still have
, and we still have 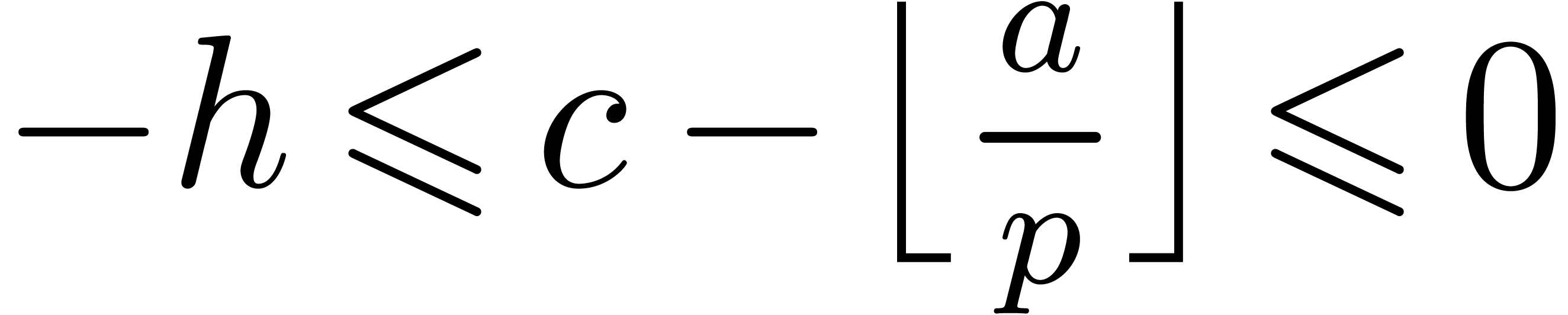 .
.
If  is an integer modulo
is an integer modulo  , and
, and 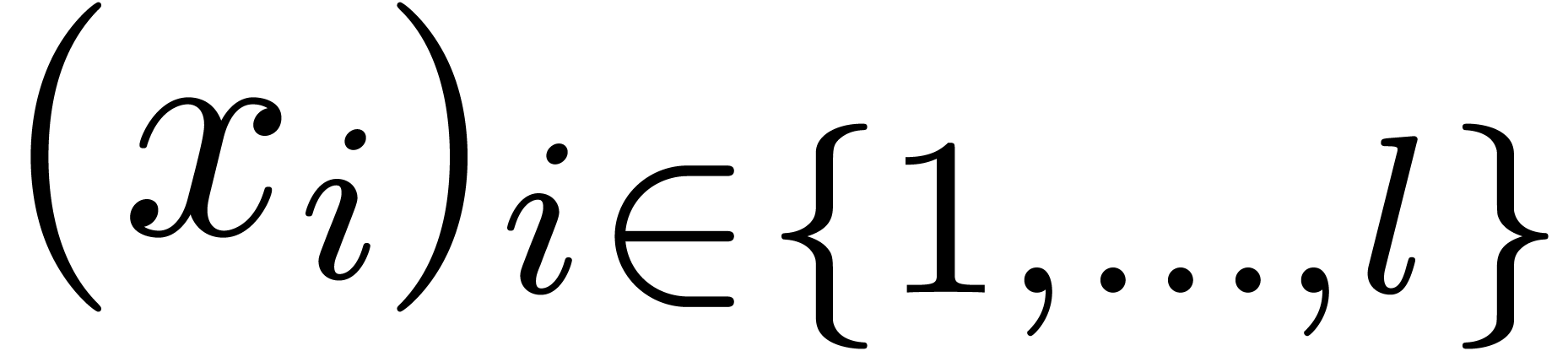 and
and 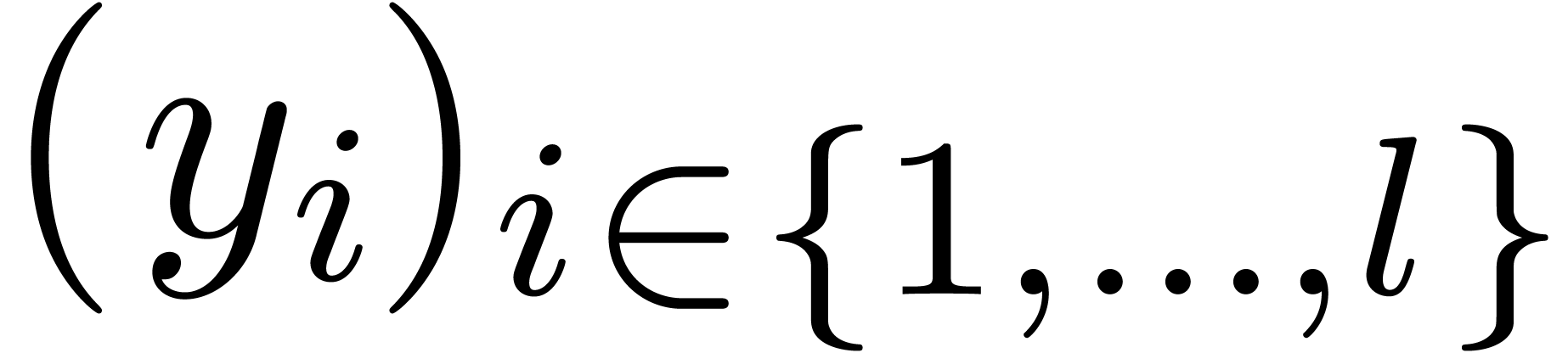 are sequences of integers modulo
are sequences of integers modulo  ,
computing
,
computing  is a central task to matrix and
polynomial products. In order to minimize the number of reductions to be
done, we wish to take
is a central task to matrix and
polynomial products. In order to minimize the number of reductions to be
done, we wish to take  as large as possible. In
general, in Barrett's algorithm, we can always take
as large as possible. In
general, in Barrett's algorithm, we can always take 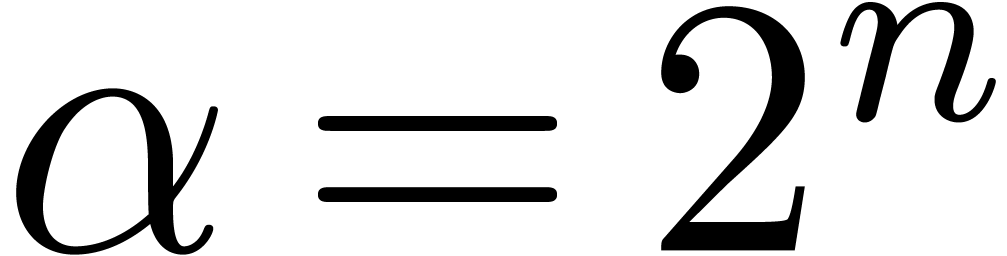 ,
,  and
and  , which leads to
, which leads to  .
When
.
When 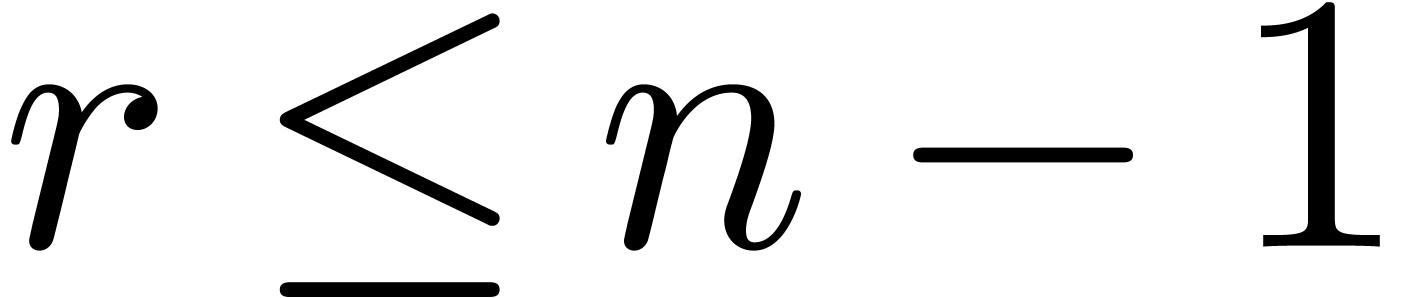 , we can achieve
, we can achieve 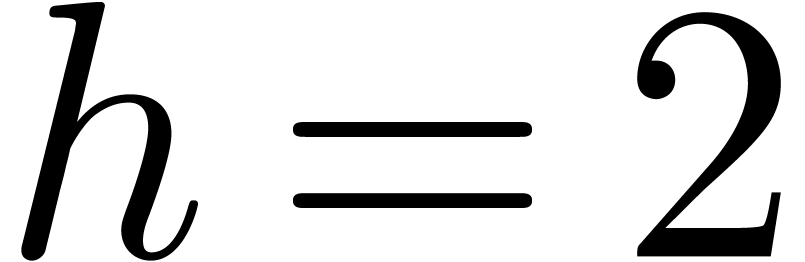 if we restrict to
if we restrict to 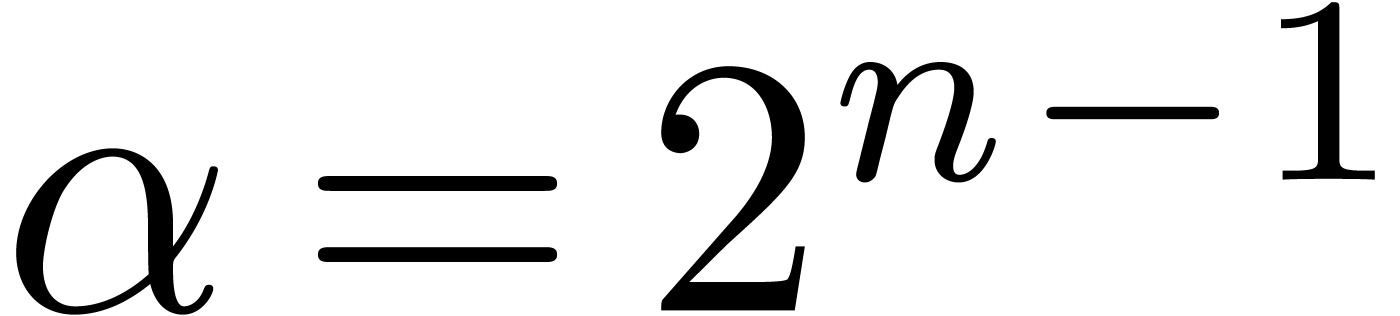 with
with 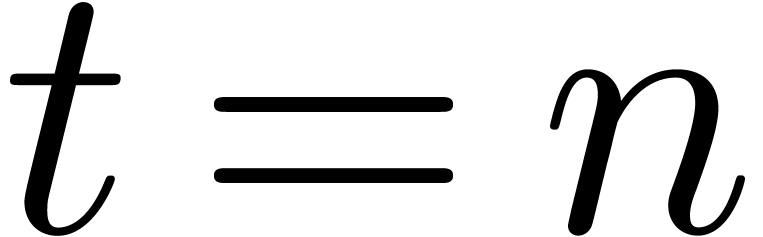 and
and 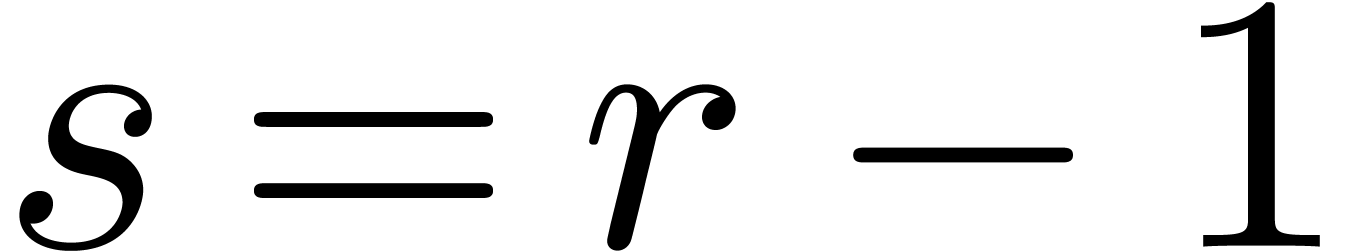 . When
. When
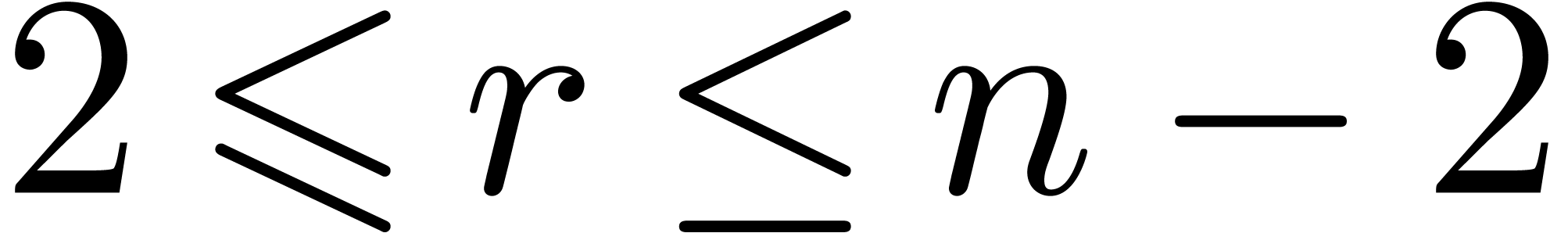 , it is even better to take
, it is even better to take
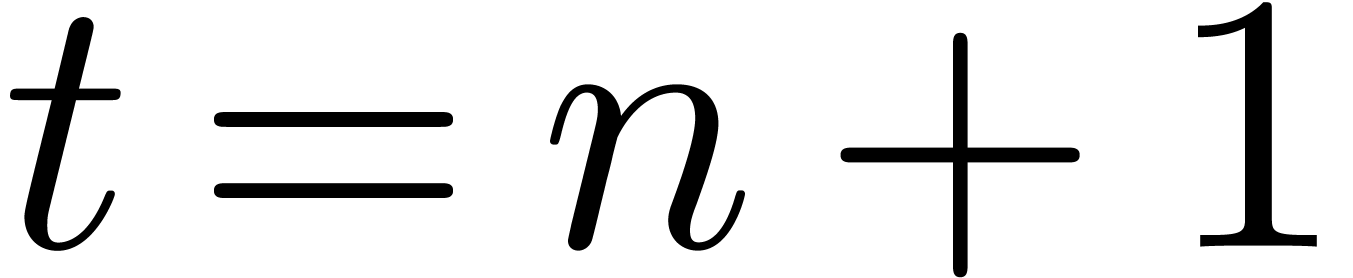 and
and 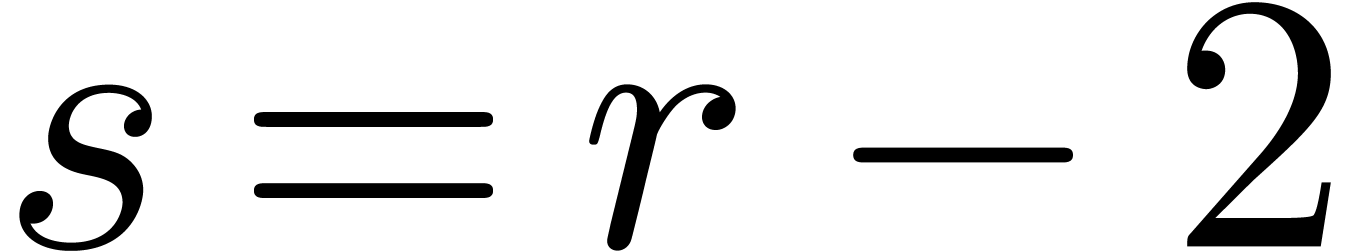 so that
so that 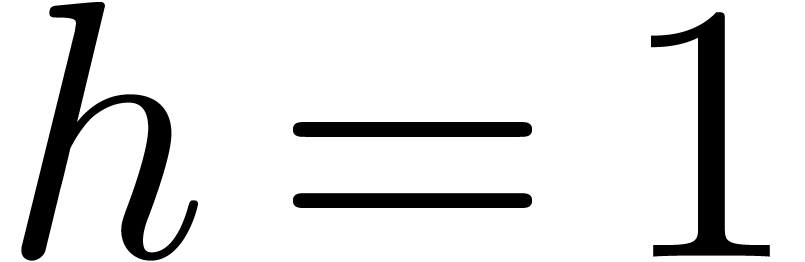 when
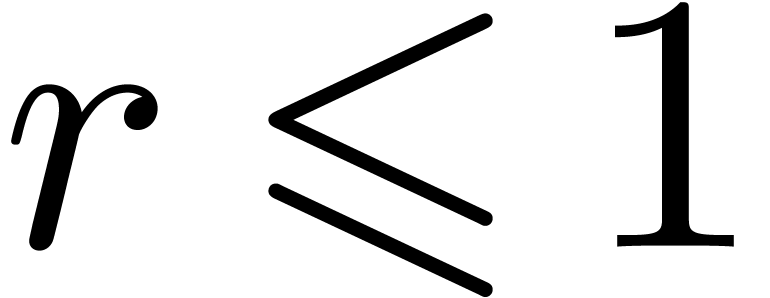
when 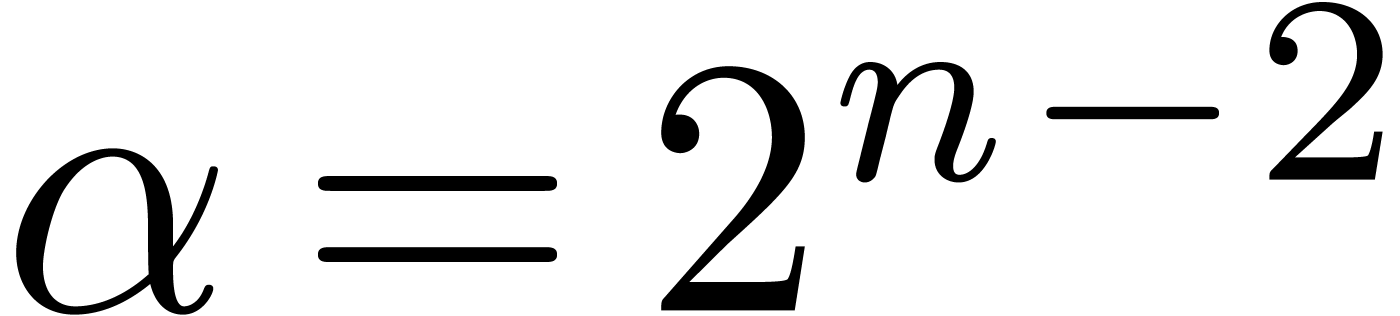 . When
. When
 , then we let
, then we let 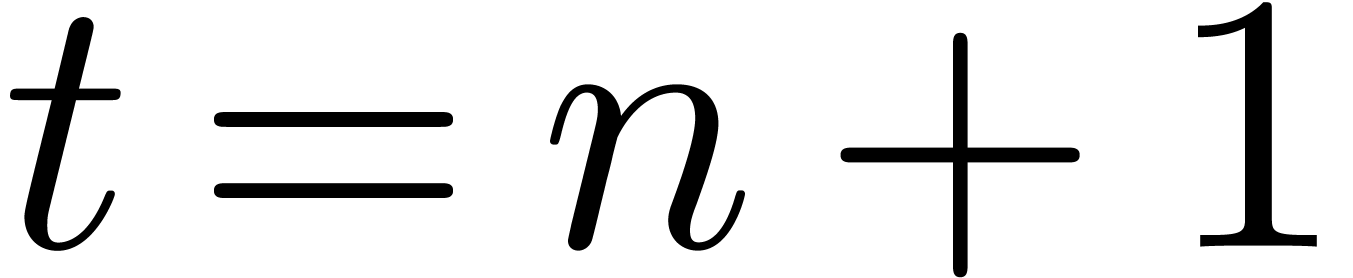 and
and 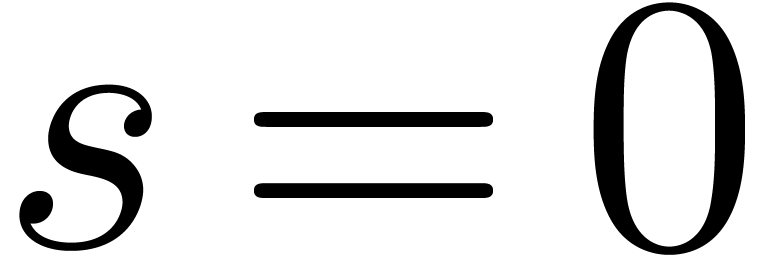 when
when 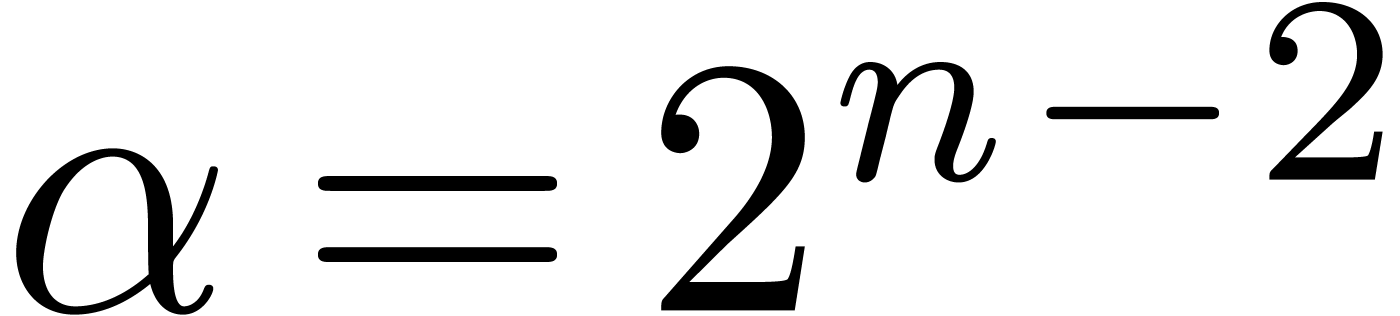 to get
to get 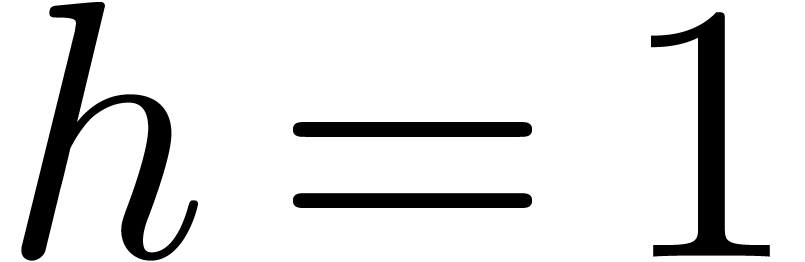 . These possible
settings are summarized in Table 3.
. These possible
settings are summarized in Table 3.
We could consider taking 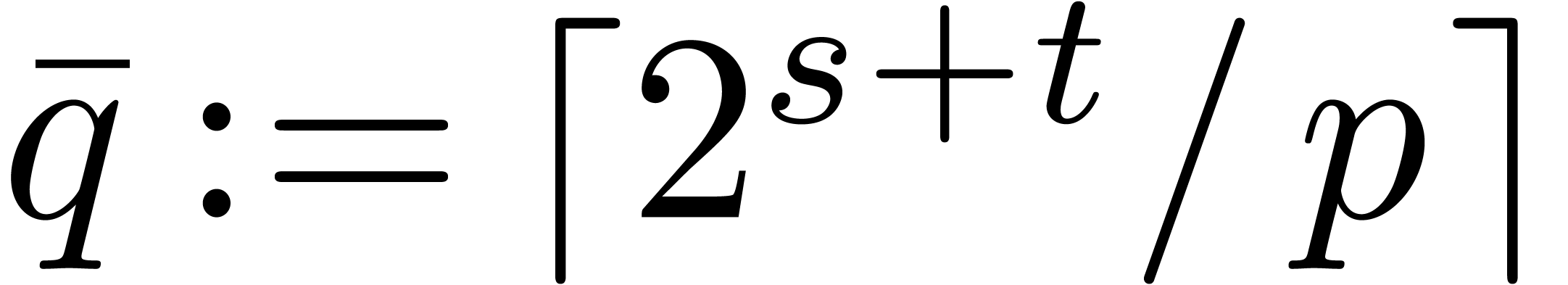 instead of
instead of  . From
. From 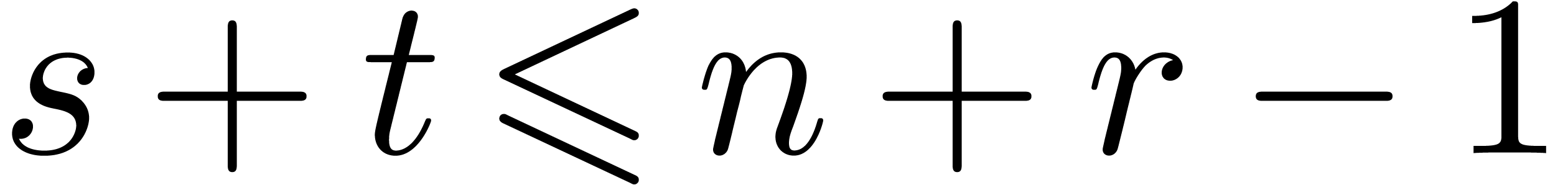 and
and 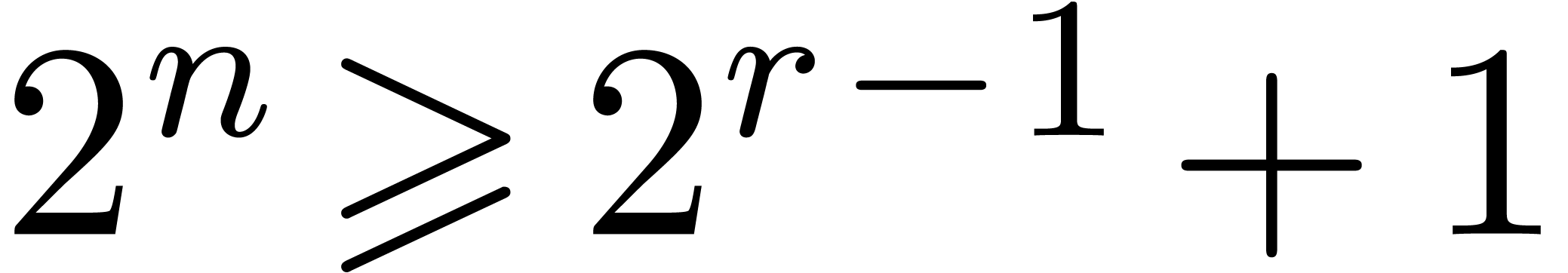 we obtain
we obtain  .
Therefore the inequalities
.
Therefore the inequalities 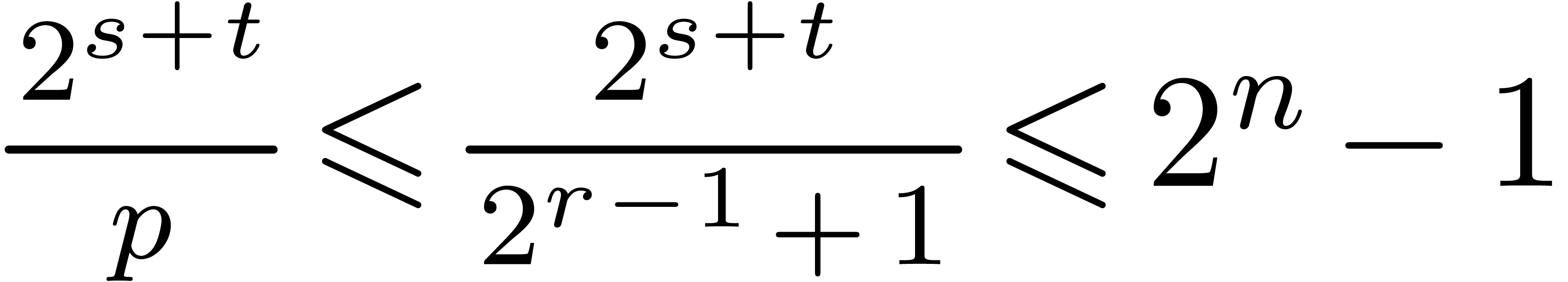 imply that
imply that  fits in U. Using
fits in U. Using  instead of
instead of  in Function 6 leads to
the following inequalities:
in Function 6 leads to
the following inequalities:
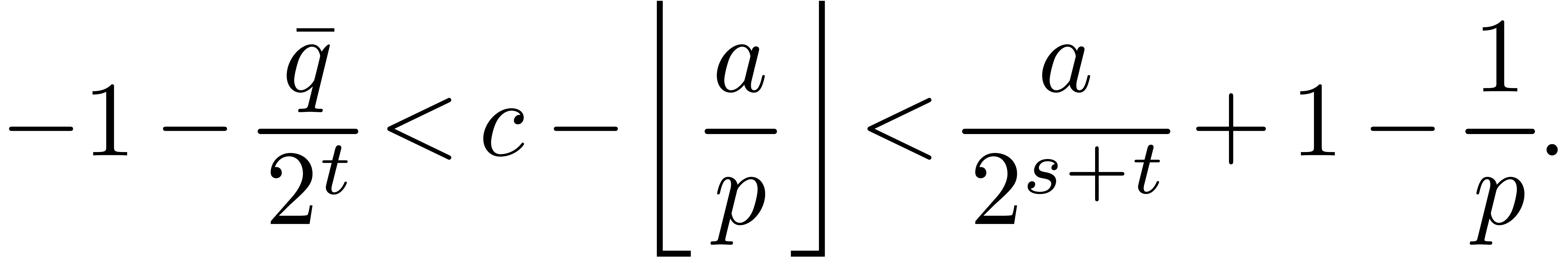
If 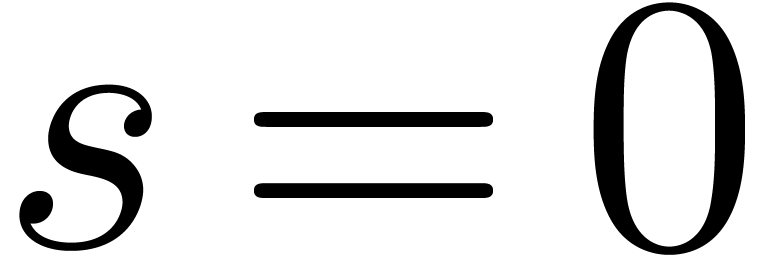 , then the term
, then the term  disappears. If
disappears. If  is sufficiently
small, then
is sufficiently
small, then 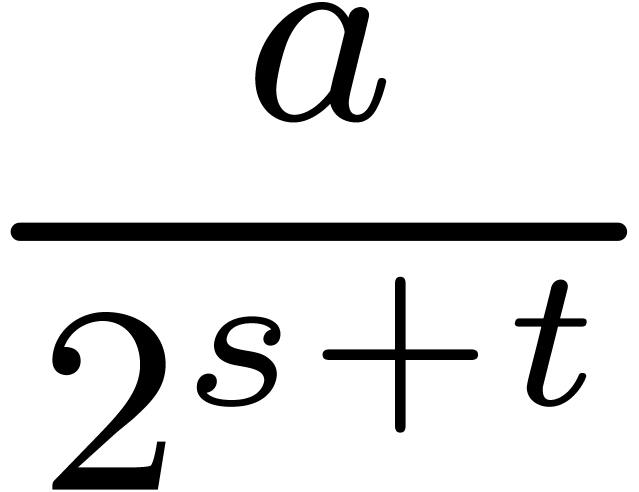 can be bounded by
can be bounded by  . Therefore line 4 of Function 6
can be discarded. More precisely, if we assume that
. Therefore line 4 of Function 6
can be discarded. More precisely, if we assume that 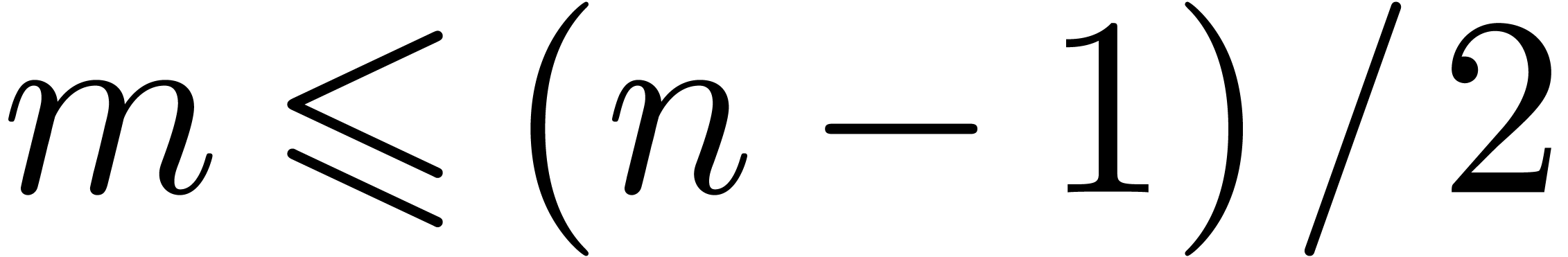 and letting
and letting 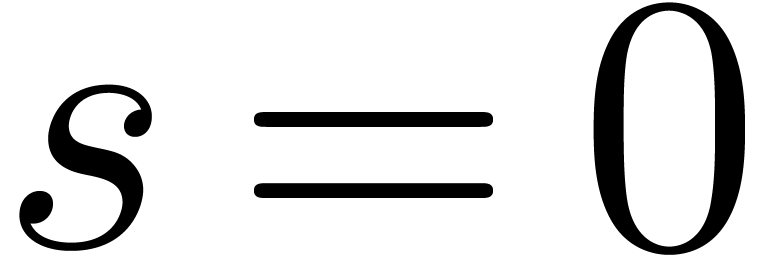 ,
,  , and
, and 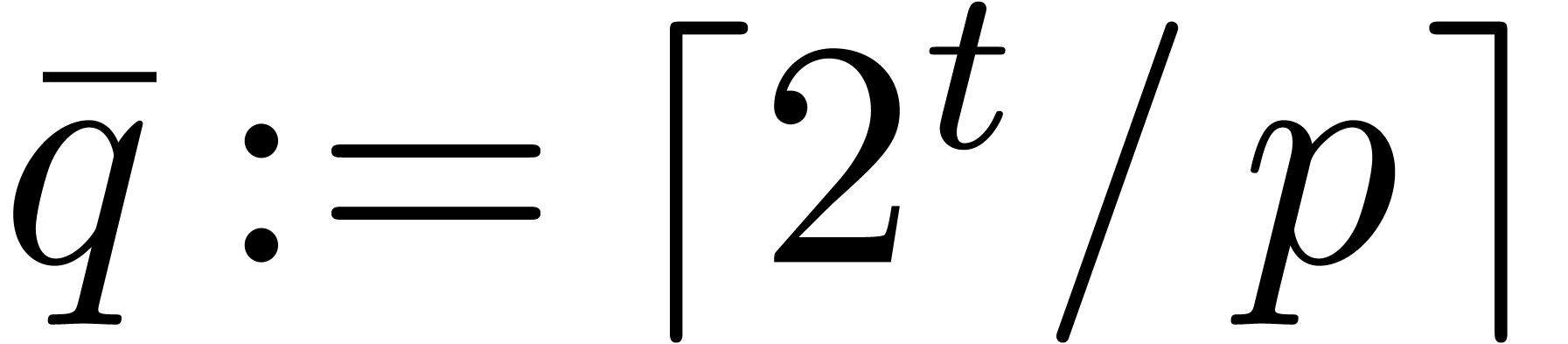 ,
then we have the following faster function:
,
then we have the following faster function:
Function
Output.  .
.
U reduce_barrett_half (U  ) {
) {
U  = (
= ( * ((L)
* ((L)  ))
>>
))
>>  ;
;
return  -
-
 *
*  ;
}
;
}
Proof. Letting  ,
the proof follows from
,
the proof follows from 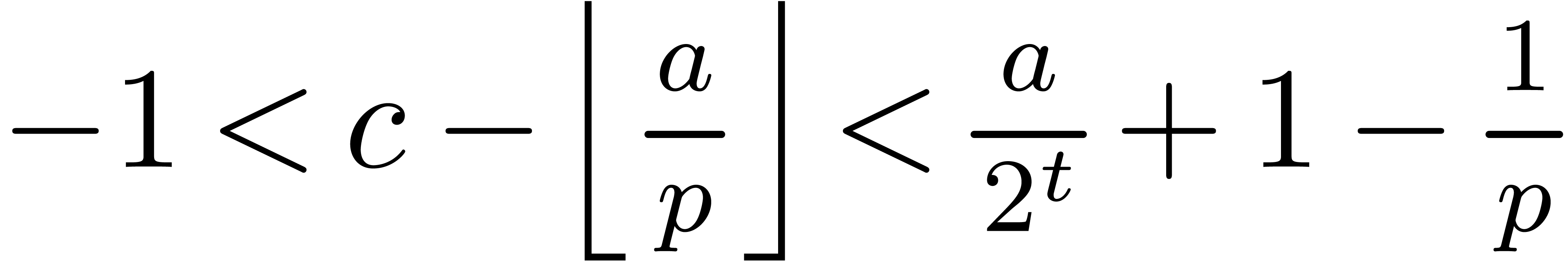 and
and 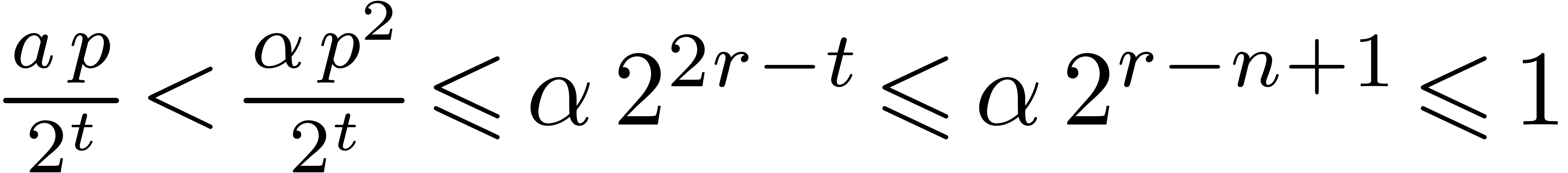 .
.
Remark  has to be computed by alternative methods such as the classical
Newton-Raphson division [57] (see also our implementation
in numerix/modular_int.hpp inside
has to be computed by alternative methods such as the classical
Newton-Raphson division [57] (see also our implementation
in numerix/modular_int.hpp inside
Assume that we wish to compte several modular products, where one of the
multiplicands is a fixed modular integer 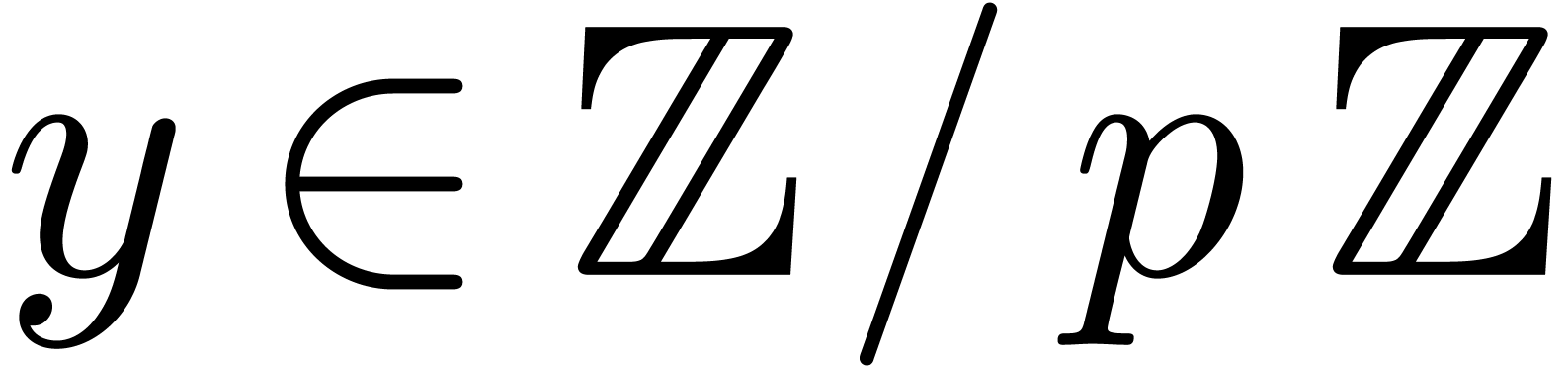 .
A typical application is the computation of
.
A typical application is the computation of  and obtain a speed-up
within each product by
and obtain a speed-up
within each product by  thanks to the following
function:
thanks to the following
function:
Function
Output. 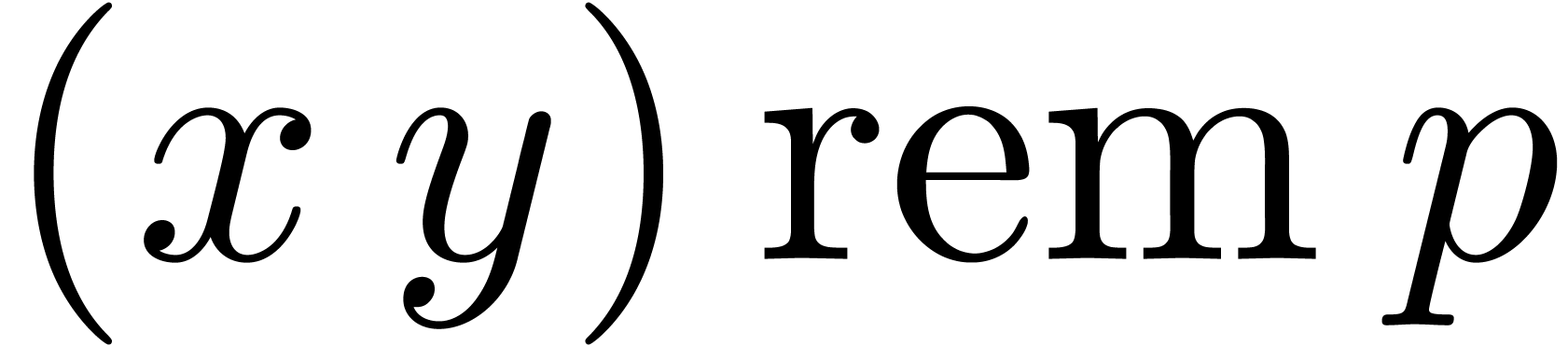 .
.
U mul_mod_barrett (U  , U y, U
, U y, U  )
{
)
{
U  = (
= ( * ((L)
* ((L)  ))
>>
))
>> 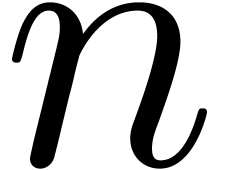 ;
;
L  = ((L)
= ((L)
 ) *
) *  - ((L)
- ((L)  ) *
) *  ;
;
return ( >=
>=  ) ?
) ?  -
-  :
:  ; }
; }
Proof. From  we obtain
we obtain
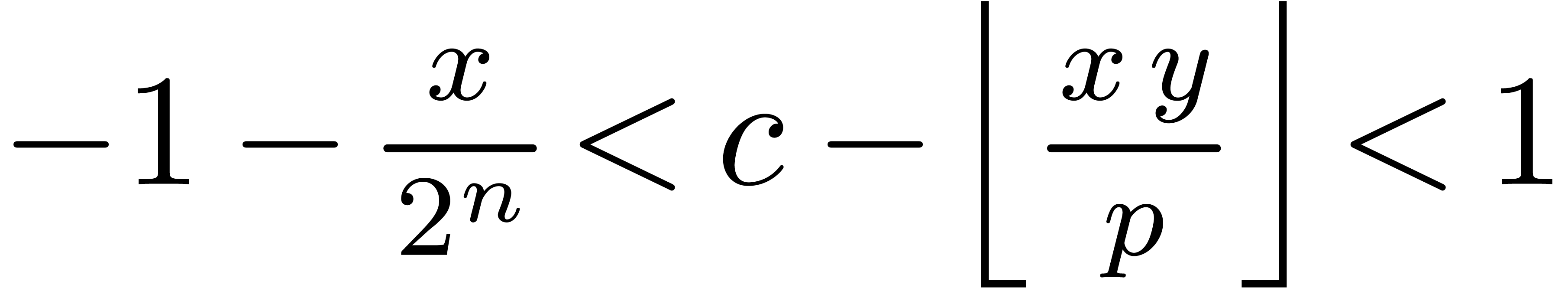 , whence the
correctness.
, whence the
correctness.
Notice that Function 8 does not depend on  ,
,  ,
,
 or
or 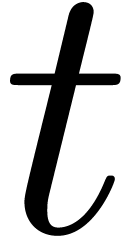 .
If
.
If 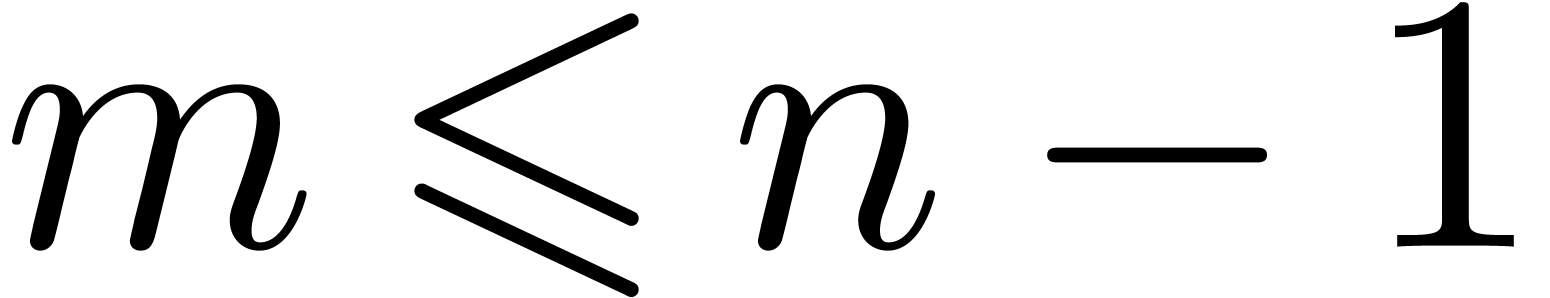 , then line 2 can be
replaced by U
, then line 2 can be
replaced by U  =
=  *
* 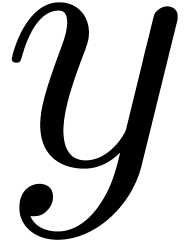 -
-  *
*  .
If
.
If 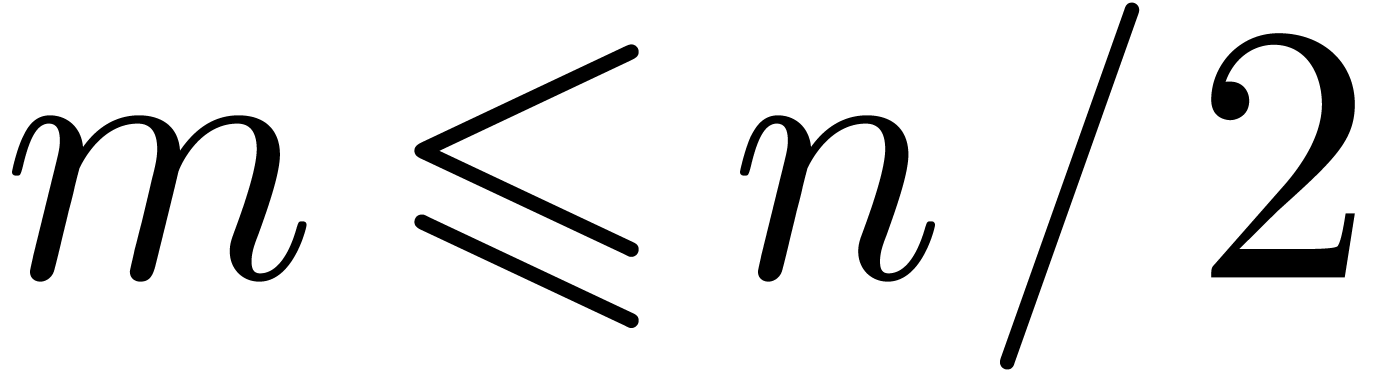 , then
, then 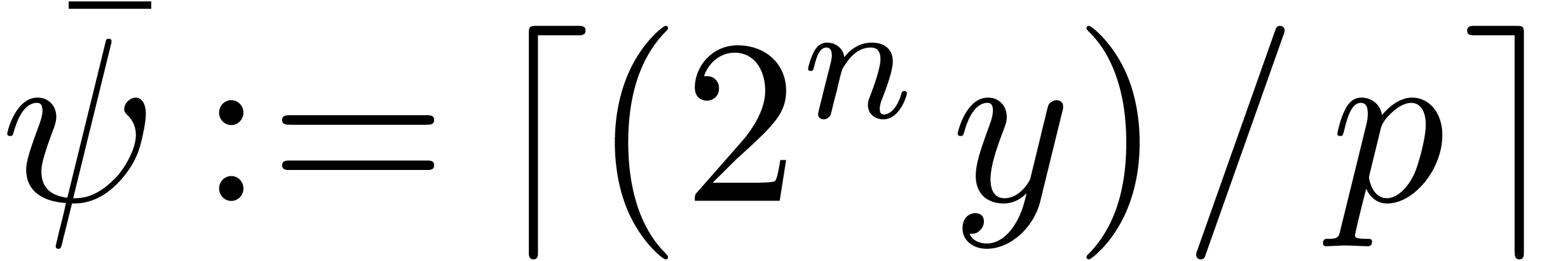 fits in U since
fits in U since 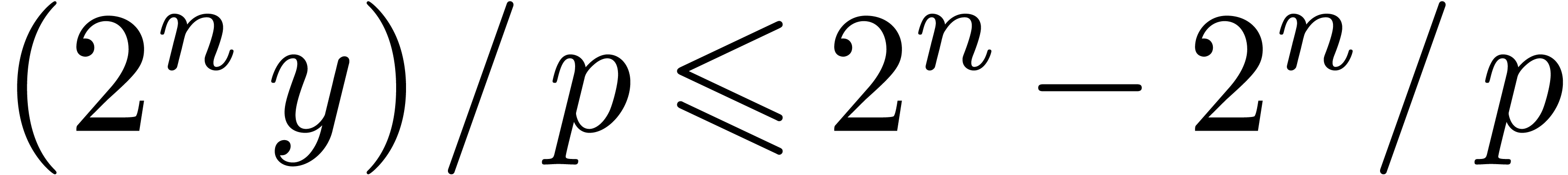 ,
and Function 8 can be improved along the same lines as
Function 7:
,
and Function 8 can be improved along the same lines as
Function 7:
Function
Output. 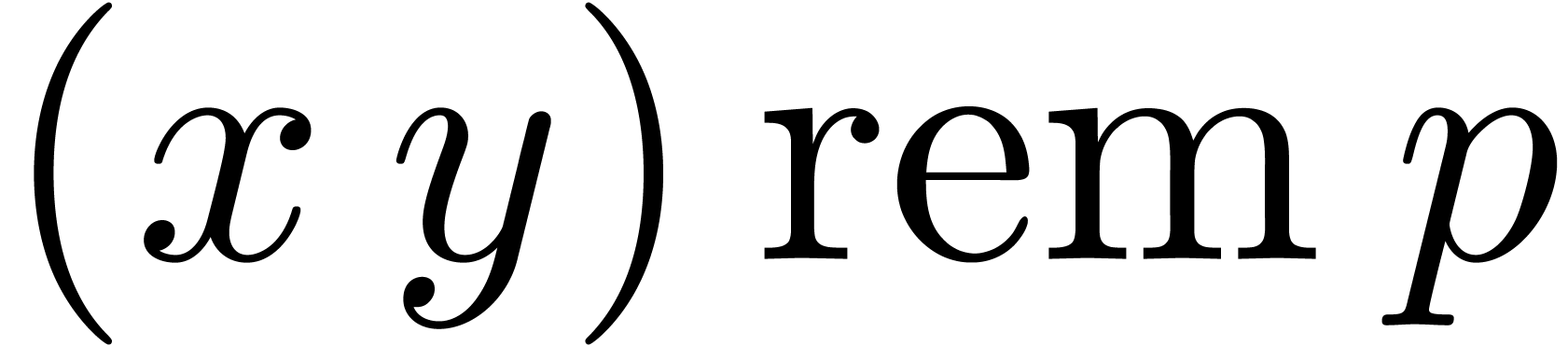 .
.
U mul_mod_barrett_half (U  , U y, U
, U y, U 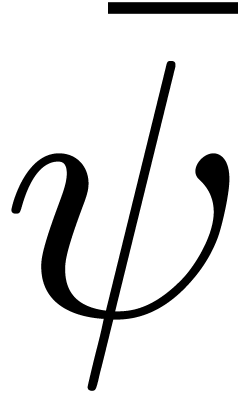 )
{
)
{
U  = (
= ( * ((L)
* ((L)  ))
>>
))
>>  ;
;
return  *
*
 -
-  *
*  ; }
; }
Proof. Similarly to previous proofs, we have
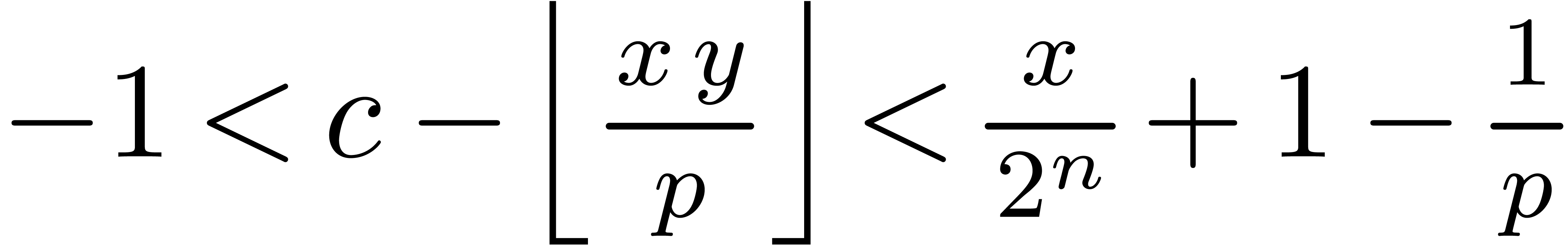 , whence the
correctness.
, whence the
correctness.
Function 6 could be easily vectorized if all the necessary
elementary operations were available within the  = min (
= min ( ,
,  -
-  ) as many times as specified by Proposition 1. In the functions below we consider the case when
) as many times as specified by Proposition 1. In the functions below we consider the case when 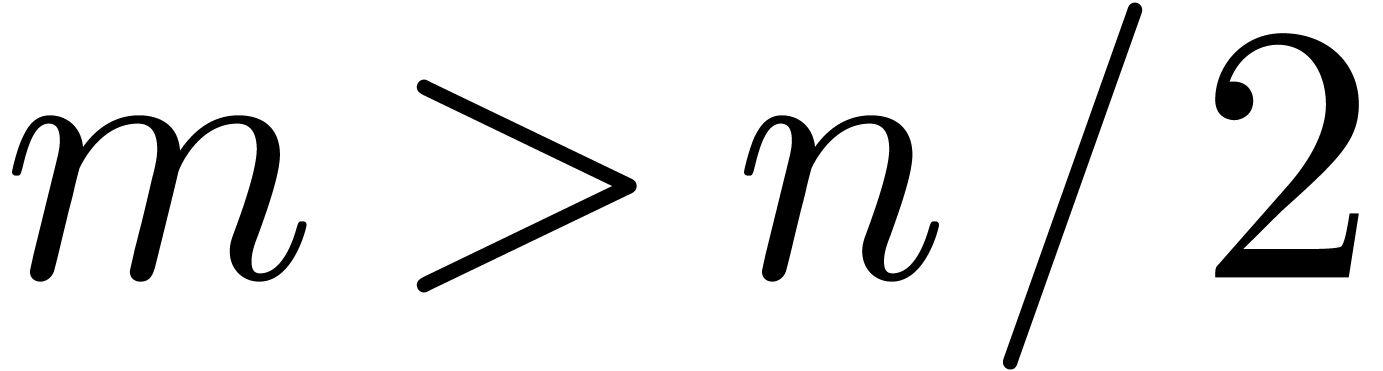 . The other case is more
straightforward. The packed
. The other case is more
straightforward. The packed 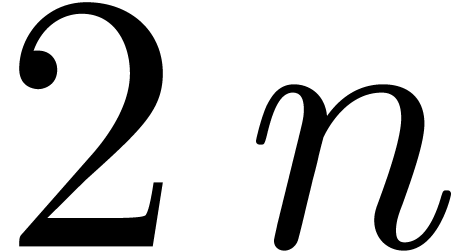 -bit
integer filled with
-bit
integer filled with  (resp.
(resp.  ) seen of type L is written
) seen of type L is written
 (resp.
(resp.  ).
The constant
).
The constant 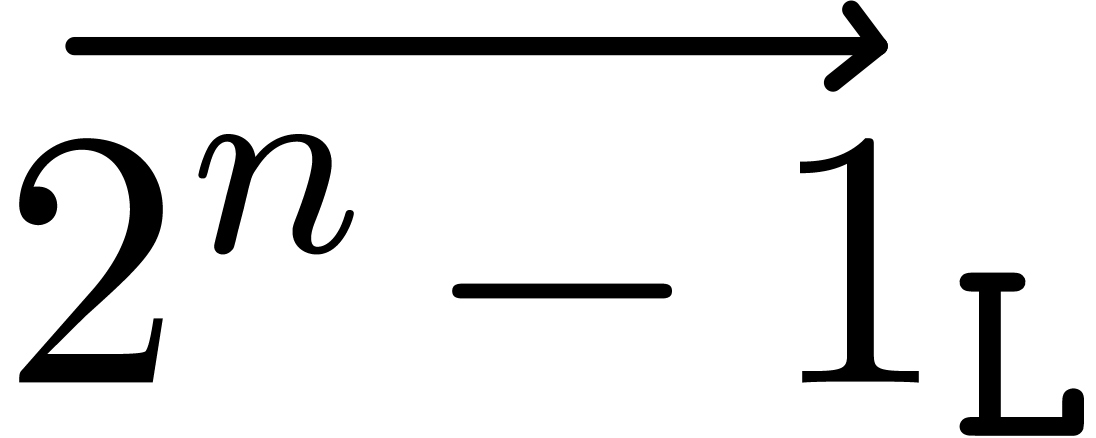 corresponds to the packed
corresponds to the packed 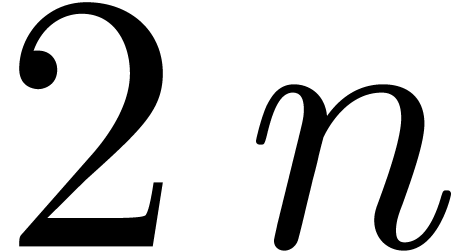 -bit integer filled with
-bit integer filled with  . We start with the simplest case
of packed 16-bit integers. If
. We start with the simplest case
of packed 16-bit integers. If 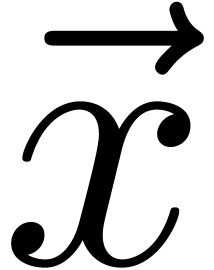 and
and 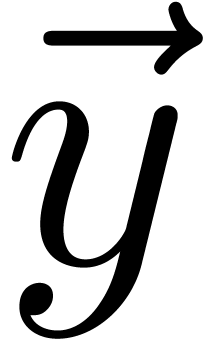 are the two vectors of scalar type U to be
multiplied modulo
are the two vectors of scalar type U to be
multiplied modulo  , then we
unpack each of them into two vectors of scalar type L,
we perform all the needed SIMD arithmetic over L, and
then we pack the result back to vectors over U.
, then we
unpack each of them into two vectors of scalar type L,
we perform all the needed SIMD arithmetic over L, and
then we pack the result back to vectors over U.
Function
Output. 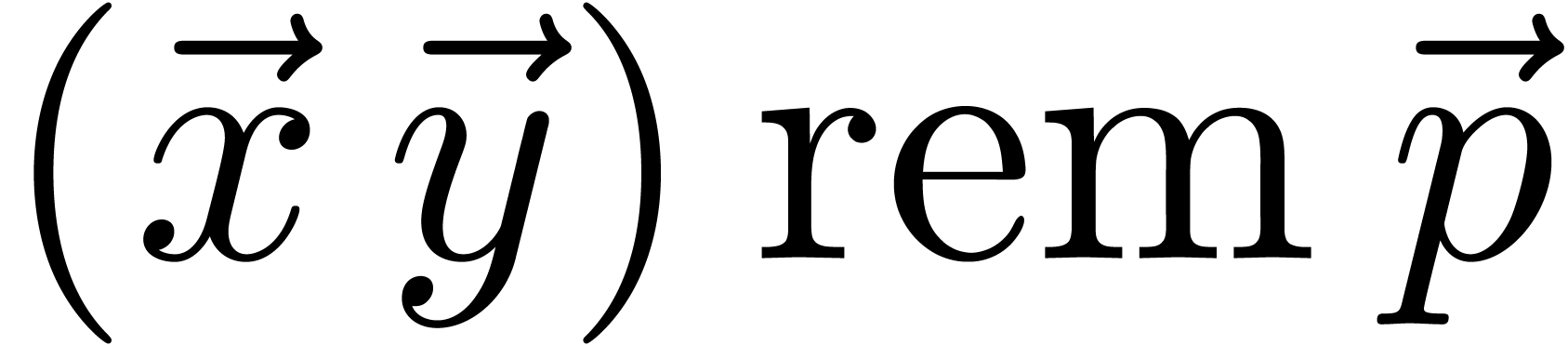 .
.
__m128i mul_mod_2_epu16 (__m128i 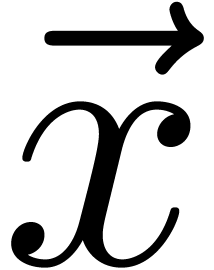 , __m128i
, __m128i 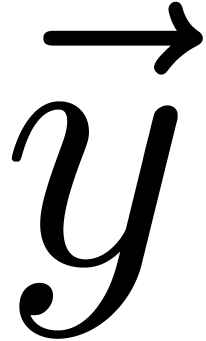 ) {
) {
__m128i  =
_mm_unpacklo_epi16 (
=
_mm_unpacklo_epi16 ( ,
,
 );
);
__m128i 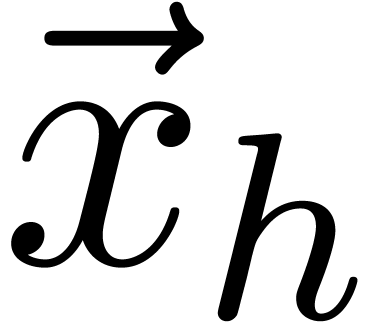 =
_mm_unpackhi_epi16 (
=
_mm_unpackhi_epi16 ( ,
,
 );
);
__m128i 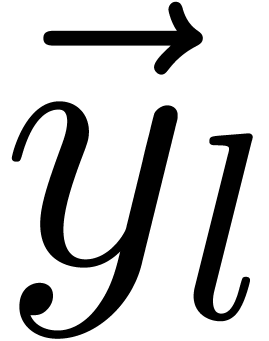 =
_mm_unpacklo_epi16 (
=
_mm_unpacklo_epi16 ( ,
,
 );
);
__m128i  =
_mm_unpackhi_epi16 (
=
_mm_unpackhi_epi16 ( ,
,
 );
);
__m128i  =
_mm_mullo_epi32 (
=
_mm_mullo_epi32 ( ,
,
 );
);
__m128i  =
_mm_mullo_epi32 (
=
_mm_mullo_epi32 ( ,
,
 );
);
__m128i  =
_mm_srli_epi32 (
=
_mm_srli_epi32 ( ,
,  );
);
__m128i  =
_mm_srli_epi32 (
=
_mm_srli_epi32 ( ,
,  );
);
__m128i  =
_mm_srli_epi32 (_mm_mullo_epi32 (
=
_mm_srli_epi32 (_mm_mullo_epi32 ( ,
,
 ),
), 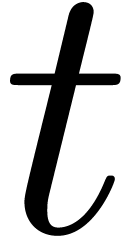 );
);
__m128i  =
_mm_srli_epi32 (_mm_mullo_epi32 (
=
_mm_srli_epi32 (_mm_mullo_epi32 ( ,
,
 ),
), 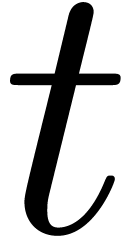 );
);
__m128i  =
_mm_packus_epi32 (
=
_mm_packus_epi32 ( ,
,
 );
);
__m128i 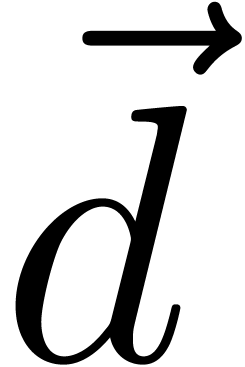 =
_mm_sub_epi16 (_mm_mullo_epi16 (
=
_mm_sub_epi16 (_mm_mullo_epi16 (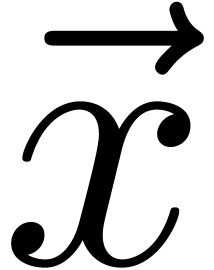 ,
,
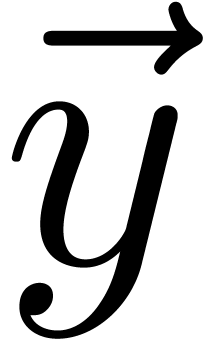 ),
),
_mm_mullo_epi16 (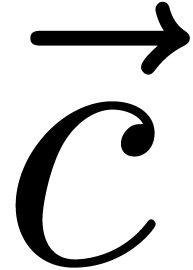 ,
,  );
);
return _mm_min_epu16 ( , _mm_sub_epi16 (
, _mm_sub_epi16 ( ,
,  ));
));
If 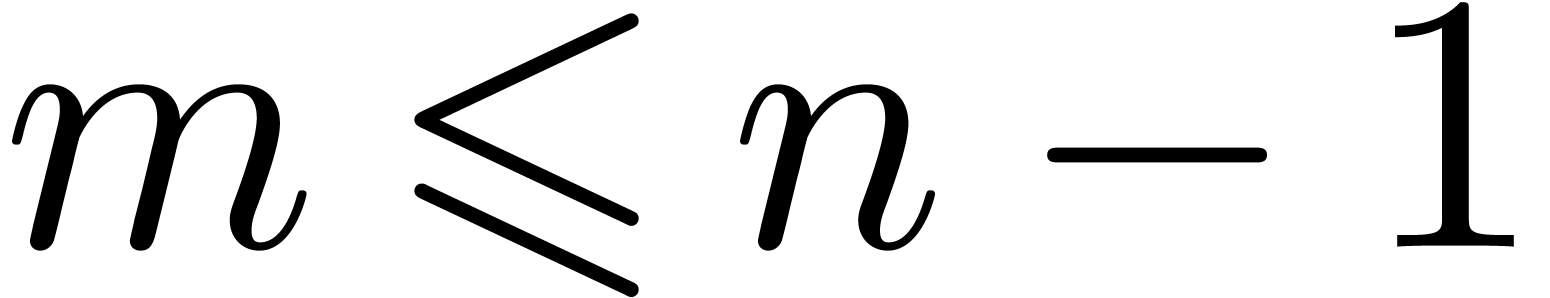 , then the computations up
to line 10 are the same but the lines after are replaced
by:
, then the computations up
to line 10 are the same but the lines after are replaced
by:
Under the only assumption that  ,
ones needs to duplicate latter lines 13 and 14.
,
ones needs to duplicate latter lines 13 and 14.
For packed 8-bit integers since no packed product is natively available, we simply perform most of the computations over packed 16-bit integers as follows:
Function
Output.  .
.
__m128i muladd_mod_2_epu8 (__m128i
 , __m128i
, __m128i  ) {
) {
__m128i 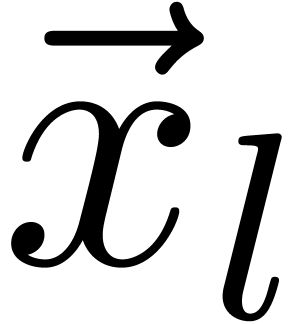 =
_mm_unpacklo_epi8 (
=
_mm_unpacklo_epi8 (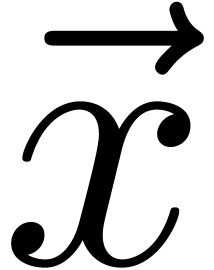 ,
,
 );
);
__m128i 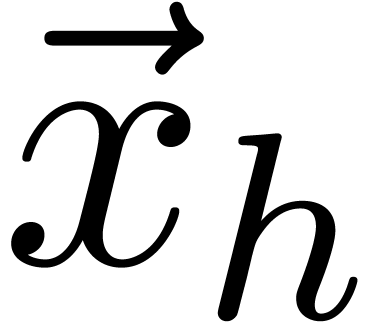 =
_mm_unpackhi_epi8 (
=
_mm_unpackhi_epi8 (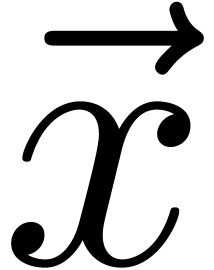 ,
,
 );
);
__m128i  =
_mm_unpacklo_epi8 (
=
_mm_unpacklo_epi8 ( ,
,
 );
);
__m128i  =
_mm_unpackhi_epi8 (
=
_mm_unpackhi_epi8 ( ,
,
 );
);
__m128i  =
_mm_mullo_epi16 (
=
_mm_mullo_epi16 ( ,
,
 );
);
__m128i  =
_mm_mullo_epi16 (
=
_mm_mullo_epi16 ( ,
,
 );
);
__m128i  =
_mm_srli_epi16 (
=
_mm_srli_epi16 ( ,
,  );
);
__m128i  =
_mm_srli_epi16 (
=
_mm_srli_epi16 ( ,
,  );
);
__m128i  =
_mm_srli_epi16 (_mm_mullo_epi16 (
=
_mm_srli_epi16 (_mm_mullo_epi16 ( ,
,
 ),
),  );
);
__m128i  =
_mm_srli_epi16 (_mm_mullo_epi16 (
=
_mm_srli_epi16 (_mm_mullo_epi16 ( ,
,
 ),
),  );
);
__m128i  =
_mm_sub_epi16 (
=
_mm_sub_epi16 ( ,
_mm_mullo_epi16 (
,
_mm_mullo_epi16 ( ,
,
 ));
));
__m128i  =
_mm_sub_epi16 (
=
_mm_sub_epi16 ( ,
_mm_mullo_epi16 (
,
_mm_mullo_epi16 ( ,
,
 ));
));
__m128i  =
_mm_packus_epi16 (
=
_mm_packus_epi16 ( ,
,
 );
);
return _mm_min_epu16 ( , _mm_sub_epi8 (
, _mm_sub_epi8 ( ,
,  ));
));
If  does not hold, then the same modifications as
with packed 16-bit integers are applied.
does not hold, then the same modifications as
with packed 16-bit integers are applied.
For packed  -bit integers, a
similar extension using packing and unpacking instructions is not
possible. We take advantage of the _mm_mul_epu32
instruction. If
-bit integers, a
similar extension using packing and unpacking instructions is not
possible. We take advantage of the _mm_mul_epu32
instruction. If  , then we use
the following code:
, then we use
the following code:
Function
Output.  .
.
__m128i mul_mod_2_epu32 (__m128i 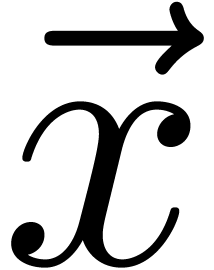 , __m128i
, __m128i 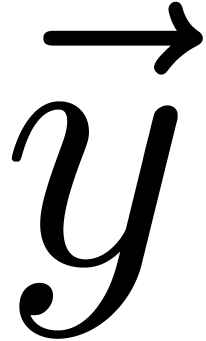 ) {
) {
__m128i  =
_mm_mul_epu32 (
=
_mm_mul_epu32 ( ,
,  );
);
__m128i  =
_mm_srli_epi64 (
=
_mm_srli_epi64 ( ,
,  );
);
__m128i  =
_mm_srli_epi64 (_mm_mullo_epi32 (
=
_mm_srli_epi64 (_mm_mullo_epi32 ( ,
,
 ),
),  );
);
__m128i  =
_mm_srli_si128 (
=
_mm_srli_si128 ( ,
4);
,
4);
__m128i  =
_mm_srli_si128 (
=
_mm_srli_si128 (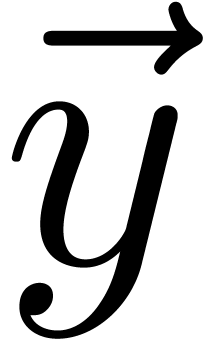 ,
4);
,
4);
__m128i 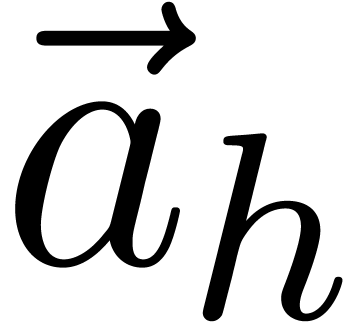 =
_mm_mul_epu32 (
=
_mm_mul_epu32 (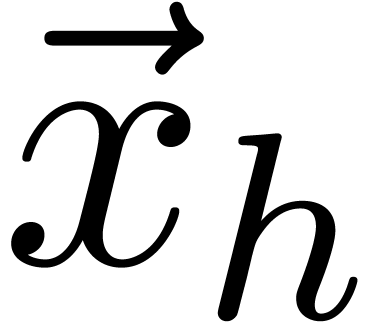 ,
, 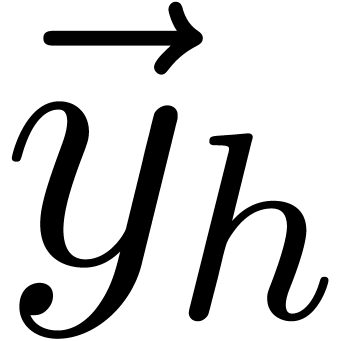 );
);
__m128i  =
_mm_srli_epi64 (
=
_mm_srli_epi64 ( ,
,  );
);
__m128i  =
_mm_srli_epi64 (_mm_mullo_epi32 (
=
_mm_srli_epi64 (_mm_mullo_epi32 ( ,
,
 ),
),  );
);
__m128i  =
_mm_blend_epi16 (
=
_mm_blend_epi16 ( ,
_mm_slli_si128 (
,
_mm_slli_si128 ( ,
4),4+8+64+128);
,
4),4+8+64+128);
__m128i  =
_mm_or_si128 (
=
_mm_or_si128 ( ,
_mm_slli_si128 (
,
_mm_slli_si128 ( ,
4));
,
4));
__m128i  =
_mm_sub_epi32 (
=
_mm_sub_epi32 ( ,
_mm_mullo_epi32 (
,
_mm_mullo_epi32 ( ,
,
 ));
));
return _mm_min_epu32 ( , _mm_sub_epi32 (
, _mm_sub_epi32 ( ,
,  ));
));
When 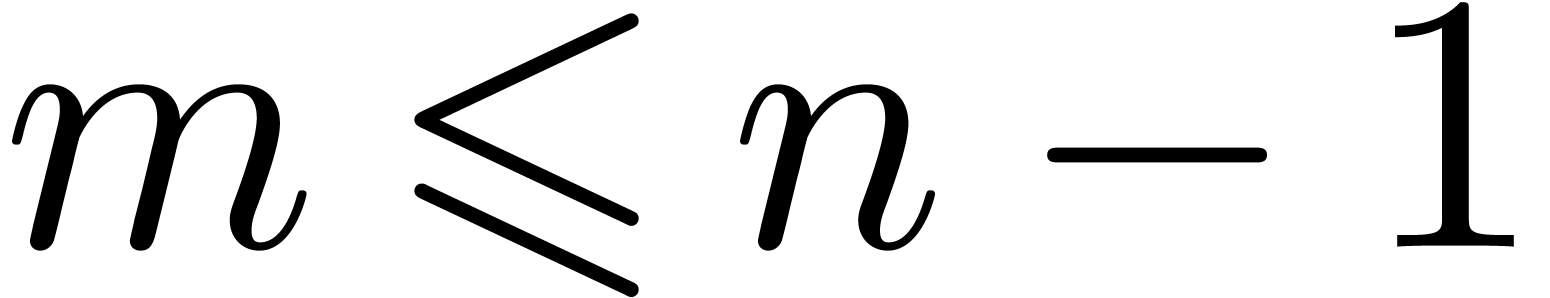 , the same kind of
modifications as before have to be done:
, the same kind of
modifications as before have to be done:  must be
computed with vectors of unsigned 64-bit integers. Since these vectors
do not support the computation of the minimum, one has to use _mm_cmpgt_epi64.
must be
computed with vectors of unsigned 64-bit integers. Since these vectors
do not support the computation of the minimum, one has to use _mm_cmpgt_epi64.
In Table 4 we display timings for multiplying machine
integers, using the same conventions as in Table 1. Recall
that packed  -bit integers
have no dedicated instruction for multiplication: it is thus done
through the 16-bit multiplication via unpacking/packing.
-bit integers
have no dedicated instruction for multiplication: it is thus done
through the 16-bit multiplication via unpacking/packing.
|
||||||||||||||||||||||||
Table 5 shows the performance of the above algorithms. The
row “Naive” corresponds to the scalar approach using the
 is significantly faster than the case
is significantly faster than the case  .
.
In the scalar approach, compiler optimizations and hardware operations
are not always well supported for small sizes, so it makes sense to
perform computations on a larger size. On our test platform, 32-bit
integers typically provide the best performance. The resulting timings
are given in the row “padded Barrett”. For 8-bit integers,
the best strategy is in fact to use lookup tables yielding  cycles in average, but this strategy cannot be vectorized.
Finally the last two rows correspond to the vectorized versions of
Barrett's approach.
cycles in average, but this strategy cannot be vectorized.
Finally the last two rows correspond to the vectorized versions of
Barrett's approach.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For larger integers, the performance is shown in Table 6.
Let us mention that in the row “Barrett” with 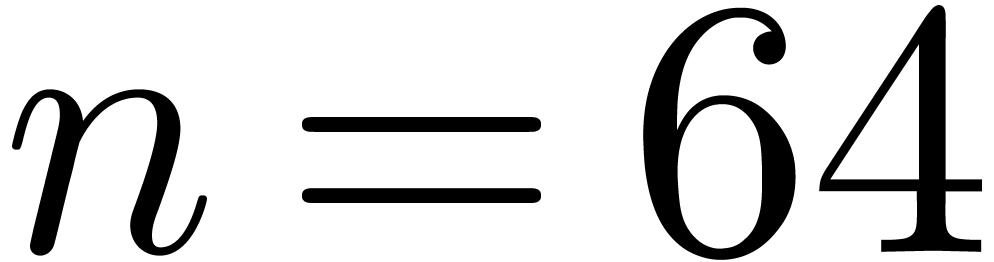 we actually make use of __int128 integer
arithmetic.
we actually make use of __int128 integer
arithmetic.
|
||||||||||||||||||||||||||||||||||||
Table 7 shows the average cost of one product with a fixed multiplicand. In comparison with Table 5, we notice a significant speedup, especially for the vectorial algorithms.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Remark 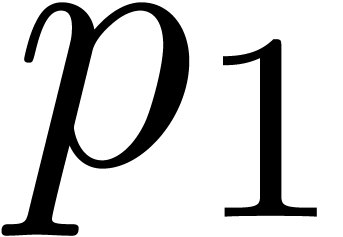 ,
,
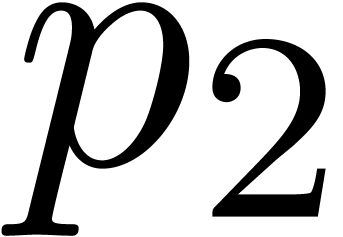 ,
, 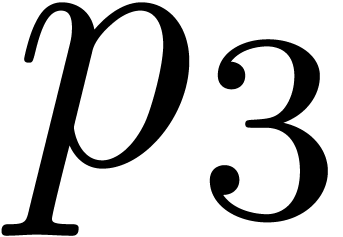 ,
,  ,
assuming they share the same parameters
,
assuming they share the same parameters 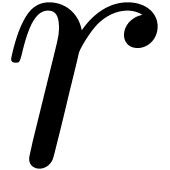 ,
,
 and
and 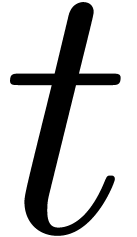 .
Nevertheless, instead of using vectors
.
Nevertheless, instead of using vectors 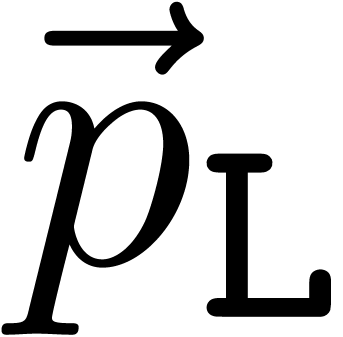 filled
with the same modulus, this requires one vector of type L
to be filled with
filled
with the same modulus, this requires one vector of type L
to be filled with 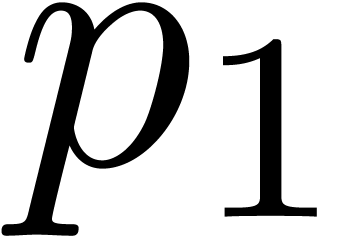 and
and 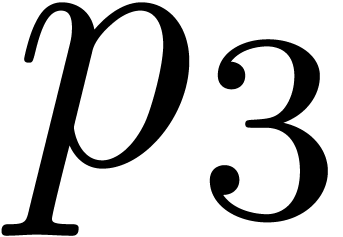 and a second one with
and a second one with 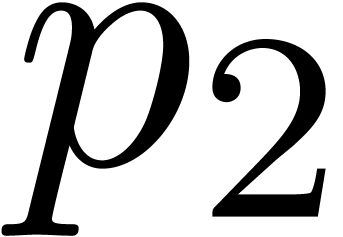 and
and  ; the same consideration holds for
; the same consideration holds for 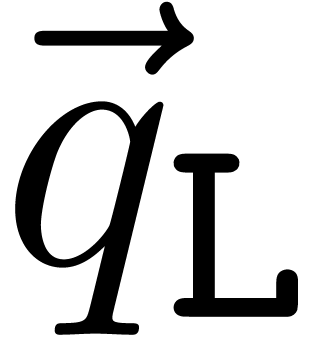 . These modifications involve to cache more
pre-computations and a small overhead in each operation.
. These modifications involve to cache more
pre-computations and a small overhead in each operation.
For Montgomery's algorithm [52], one needs to assume that
 is odd. Let
is odd. Let 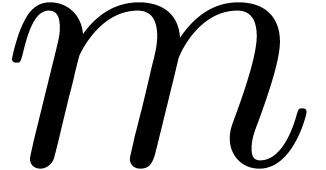 be such that
be such that
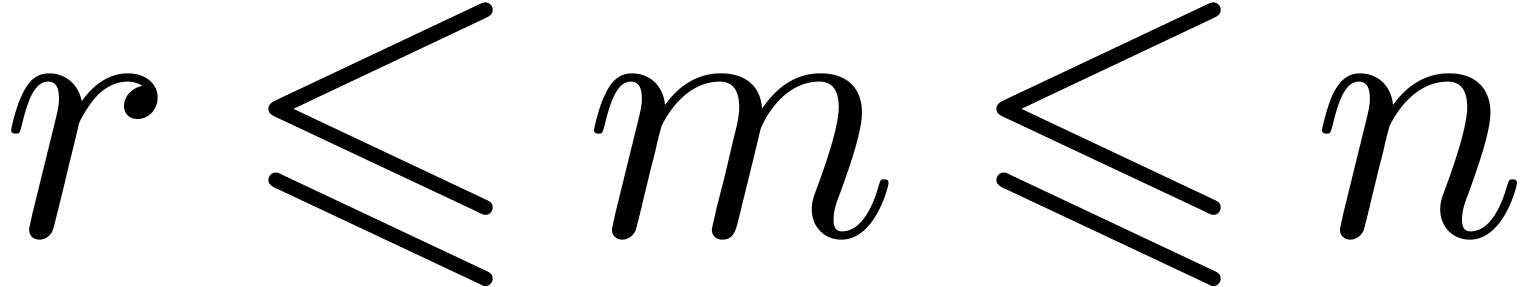 and let
and let 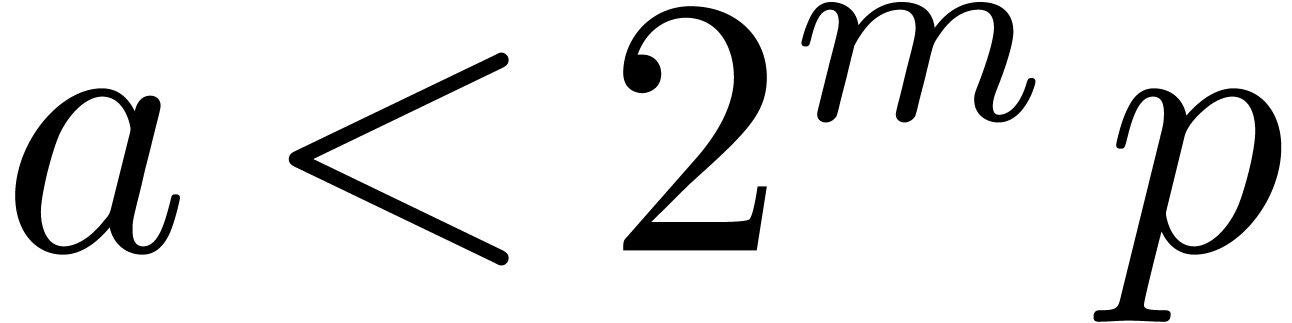 .
We need the auxiliary quantities
.
We need the auxiliary quantities 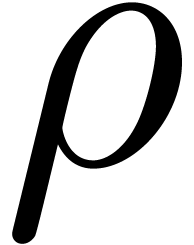 and
and  defined by
defined by 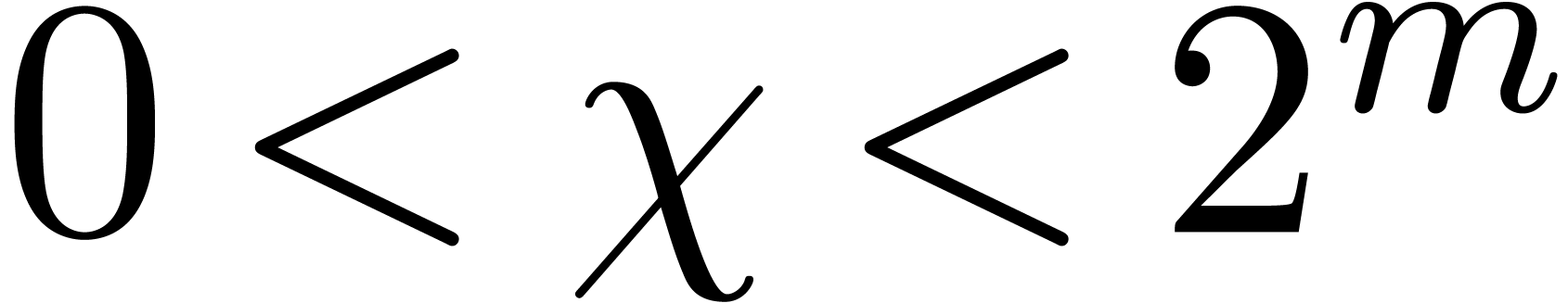 ,
,
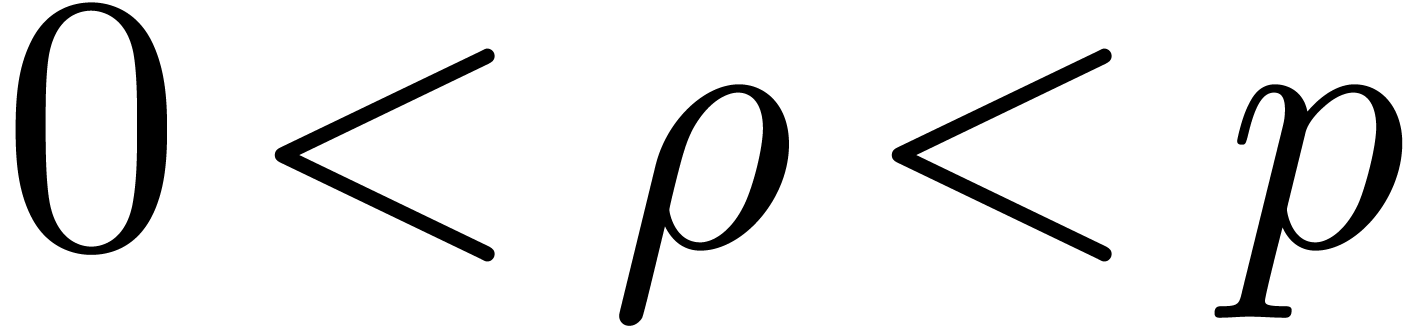 , and
, and 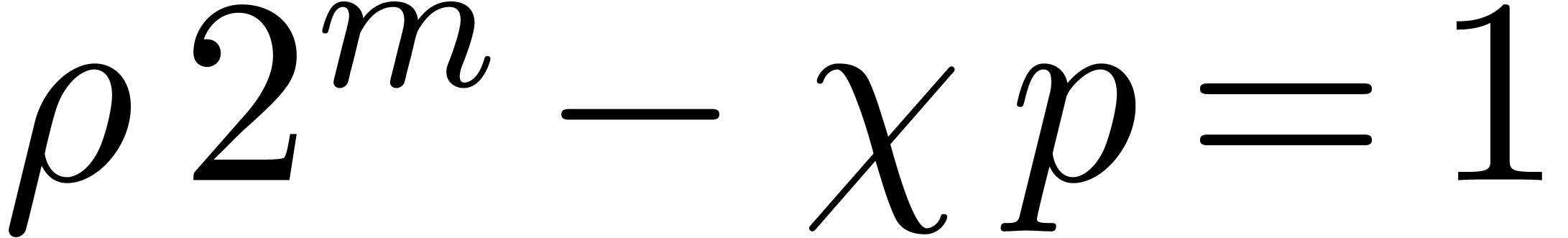 . They can be classically computed with the extended
Euclidean algorithm [26, Chapter 3].
. They can be classically computed with the extended
Euclidean algorithm [26, Chapter 3].
For convenience we introduce 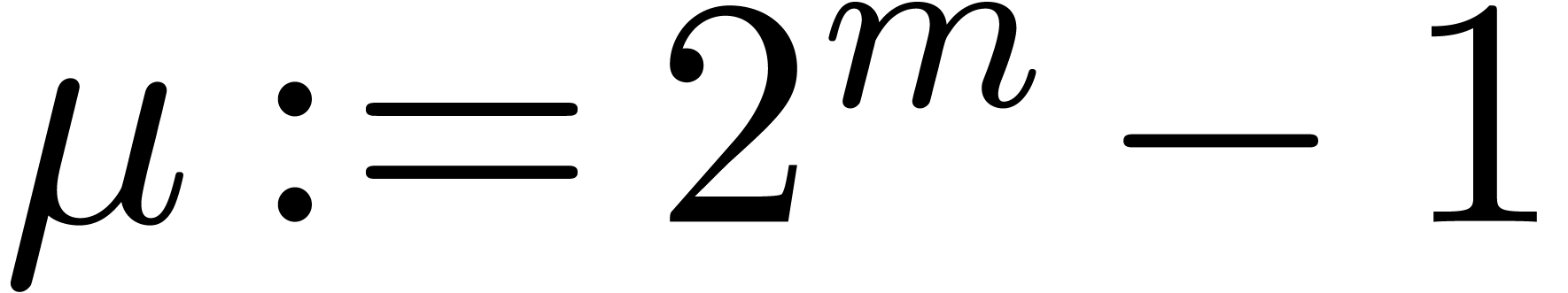 .
The core of Montgomery's algorithm is the following reduction function:
.
The core of Montgomery's algorithm is the following reduction function:
Function
Output. 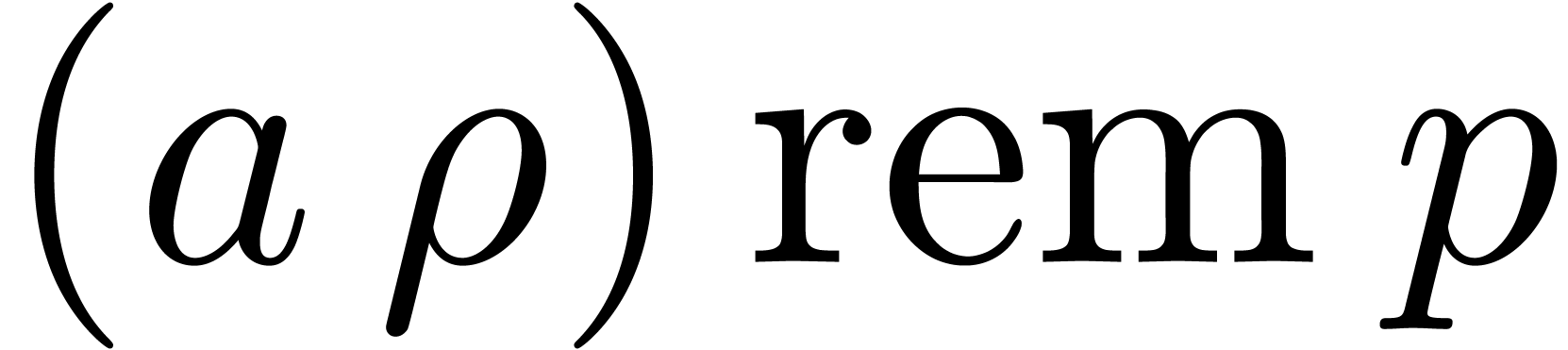 .
.
U reduce_montgomery (U  ) {
) {
U 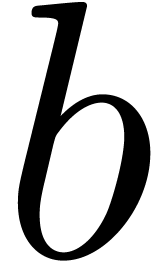 = (
= ( *
*  )
&
)
&  ;
;
L  =
=  +
+  *
*  ;
;
U  =
=  >> m;
>> m;
if ( <
<
 ) return
) return  -
-  ;
;
return ( >=
>=  ) ?
) ?  -
-  :
:  ; }
; }
 , then line 4 can be discarded.
, then line 4 can be discarded.
Proof. First one verifies that  . Therefore
. Therefore  is a
multiple of
is a
multiple of 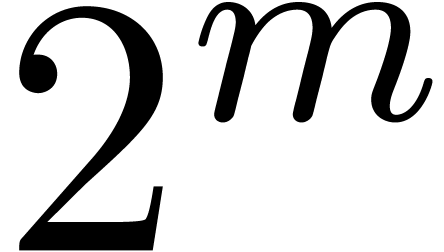 . If
. If 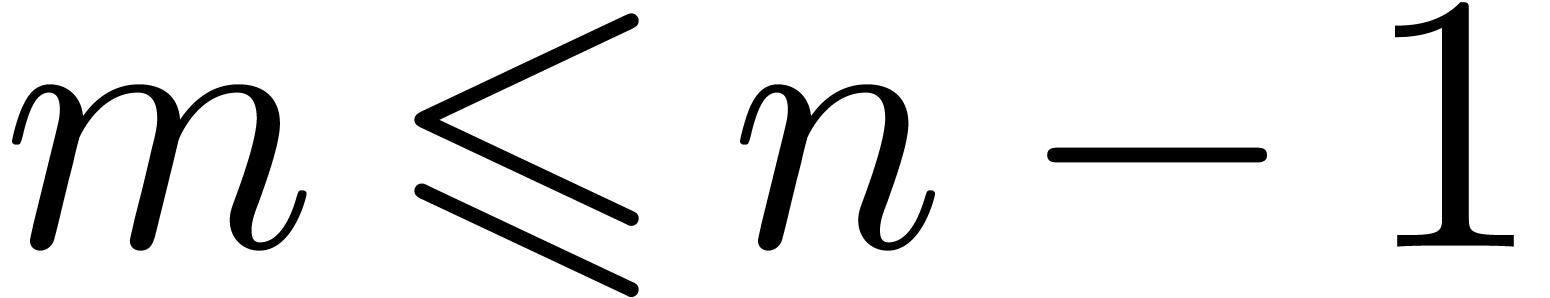 , then no overflow occurs in the sum of line 2,
and the division in line
, then no overflow occurs in the sum of line 2,
and the division in line  is exact. We then have
is exact. We then have
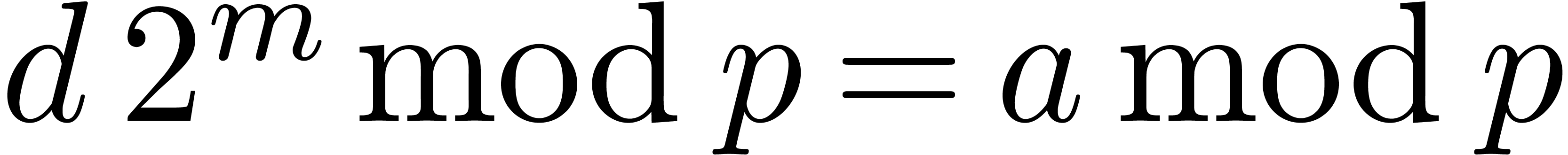 , and the correctness follows
from
, and the correctness follows
from 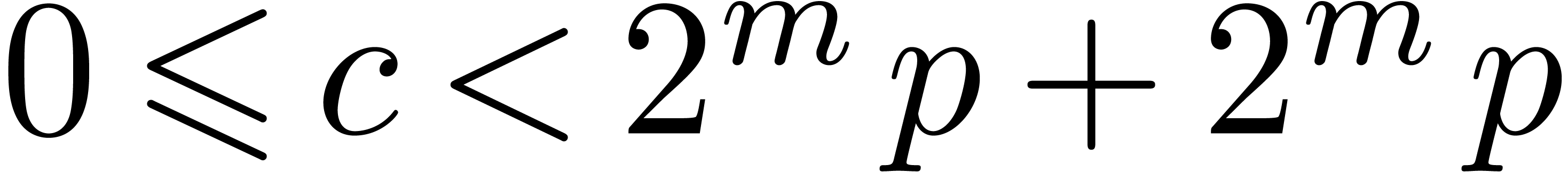 and thus
and thus 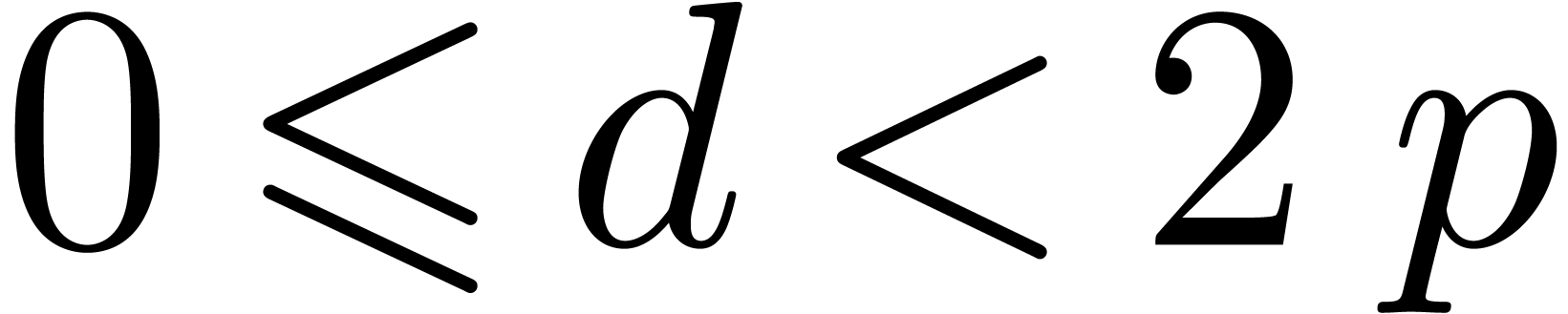 .
If
.
If  , then the casual overflow
in line 2 is tested in line 4, and
, then the casual overflow
in line 2 is tested in line 4, and 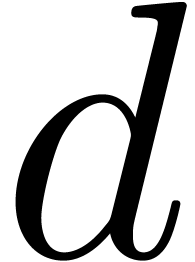 is the value
in U of
is the value
in U of 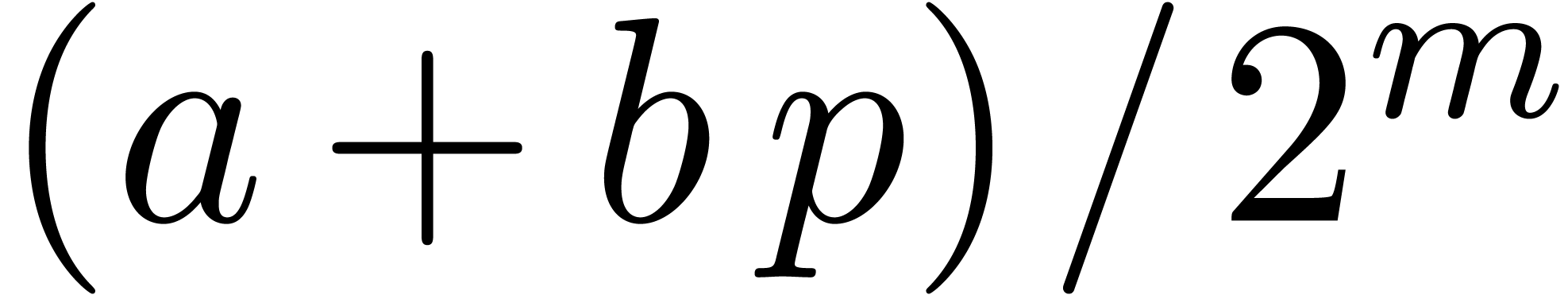 .
.
Let  be a modulo
be a modulo  integer.
We say that
integer.
We say that  is in Montgomery's
representation if stored as
is in Montgomery's
representation if stored as  .
The product of two modular integers
.
The product of two modular integers  and
and 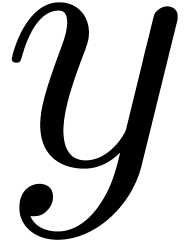 , of respective Montgomery's
representations
, of respective Montgomery's
representations  and
and 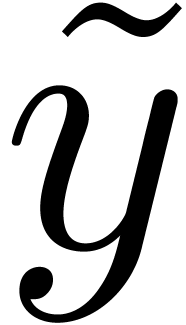 , can be obtained in Montgomery's representation
, can be obtained in Montgomery's representation
 by applying Function 13 to
by applying Function 13 to 
 since
since 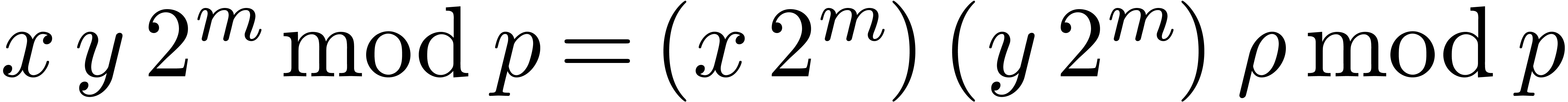 .
.
If  , then the mask in line 1
can be avoided, and the shift in line 3 might be more favorable than a
general shift, according to the compiler. In total, if
, then the mask in line 1
can be avoided, and the shift in line 3 might be more favorable than a
general shift, according to the compiler. In total, if  or
or 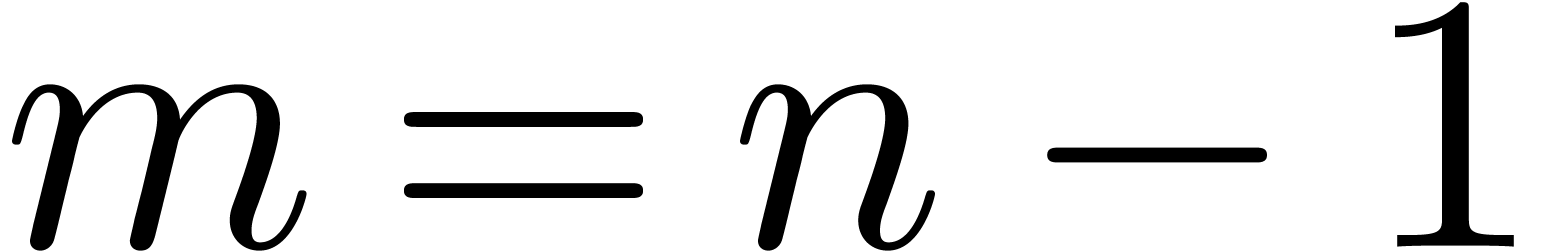 , Montgomery's approach is
expected to be faster than Barrett's one. Otherwise costs should be
rather similar. Of course these cost considerations are rather informal
and the real cost very much depends on the processor and the compiler.
, Montgomery's approach is
expected to be faster than Barrett's one. Otherwise costs should be
rather similar. Of course these cost considerations are rather informal
and the real cost very much depends on the processor and the compiler.
Remark 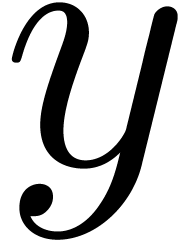 . Writing
. Writing 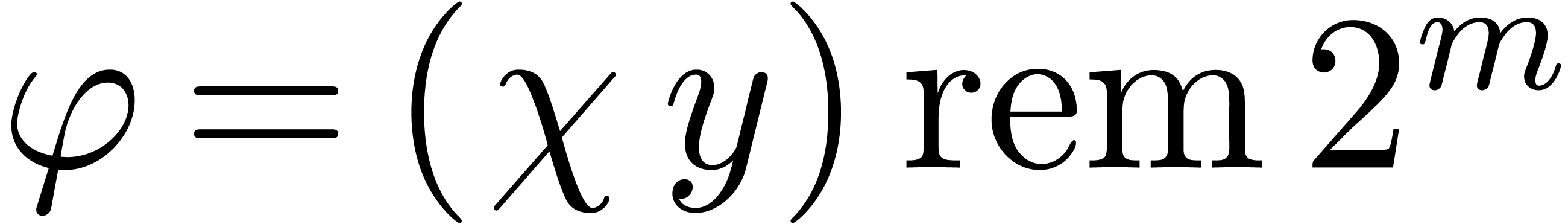 ,
the only simplification appears in line 1, where
,
the only simplification appears in line 1, where 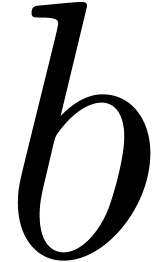 can be obtained as
can be obtained as 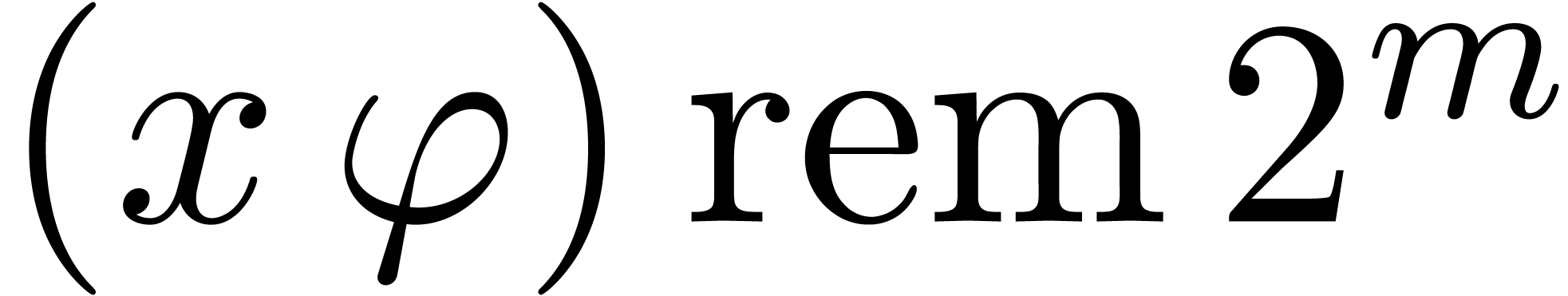 , which
saves one product in U. Therefore Barrett's approach is
expected to be always faster for this task. Precisely, if
, which
saves one product in U. Therefore Barrett's approach is
expected to be always faster for this task. Precisely, if 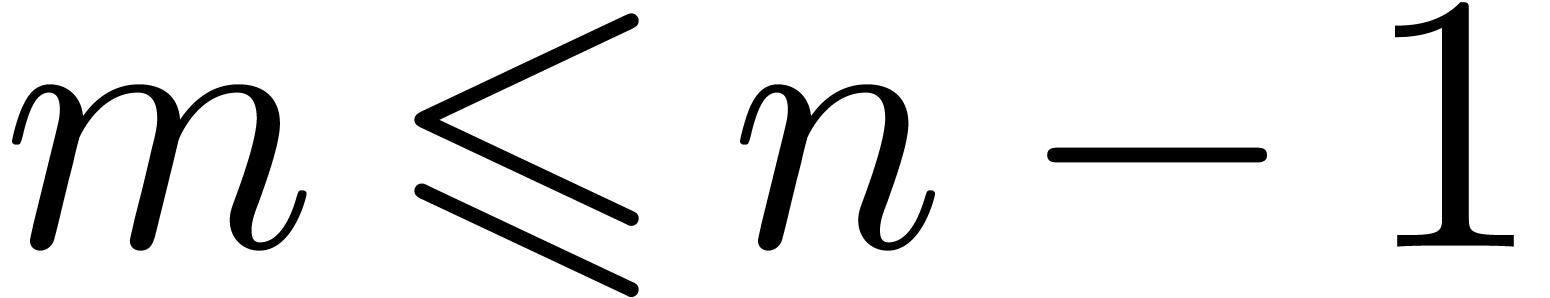 , this is to be compared to Function 8
which performs only one high product in line 1.
, this is to be compared to Function 8
which performs only one high product in line 1.
Remark 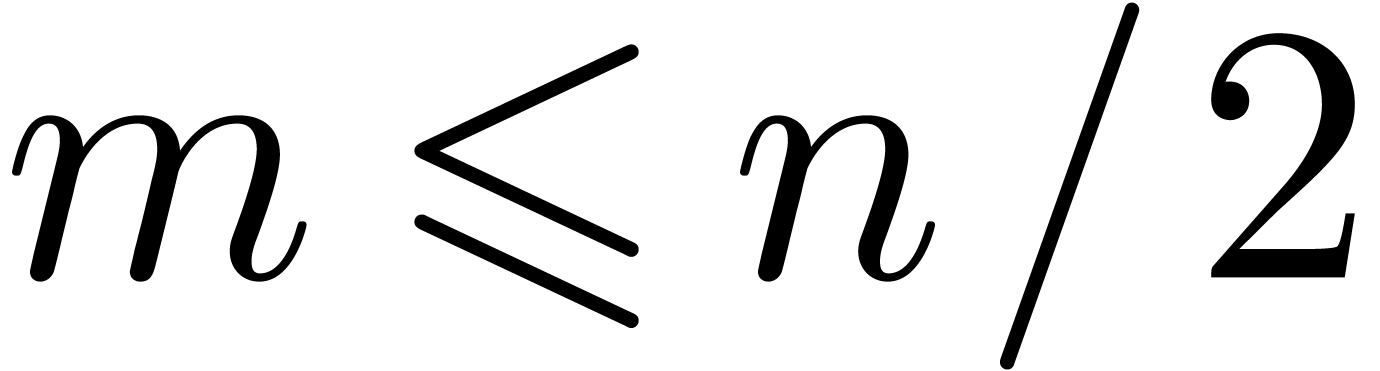 .
.
Table 8 contains timings measured in the same manner as in
the previous subsection. Compared to Tables 5 and 6
we observe that Montgomery's product is not interesting in the scalar
case for 8 and 16-bit integers but it outperforms Barrett's approach in
larger sizes, especially when  .
Compared to Table 7, Montgomery's product is only faster
for when
.
Compared to Table 7, Montgomery's product is only faster
for when 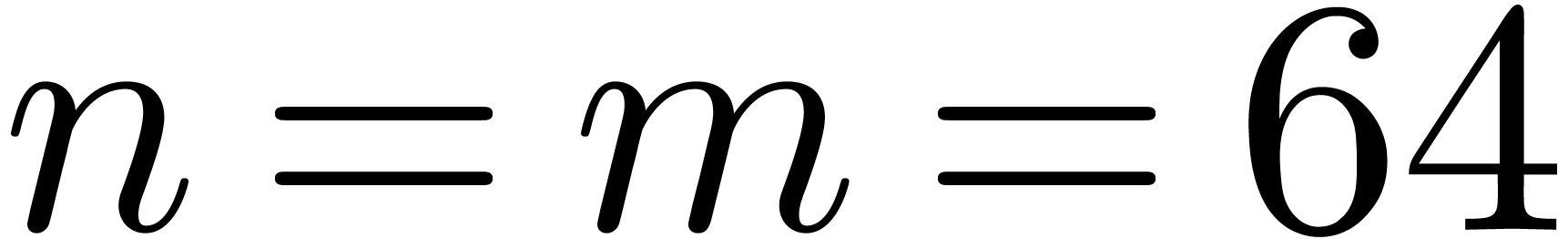 and
and 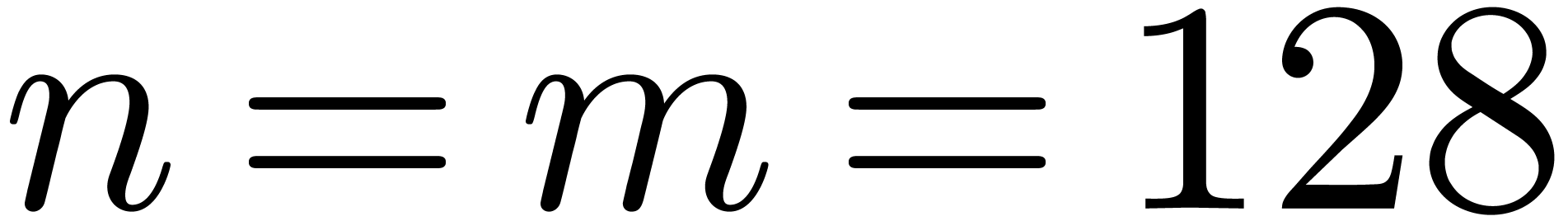 .
.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Instead of integer types, we can use numeric types such as float
or double to perform modular operations. Let us write
F such a type, and let 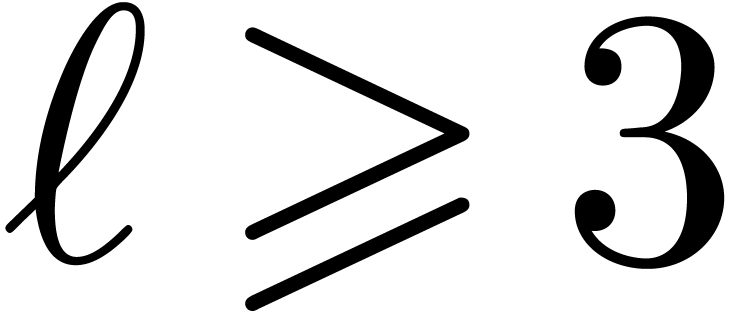 represent
the size of the mantissa of F minus one,
i.e. 23 bits for float and 52 bits for double. This number of bits corresponds to the size of the
so called trailing significant field of F,
which is explicitly stored. The modular product of
represent
the size of the mantissa of F minus one,
i.e. 23 bits for float and 52 bits for double. This number of bits corresponds to the size of the
so called trailing significant field of F,
which is explicitly stored. The modular product of 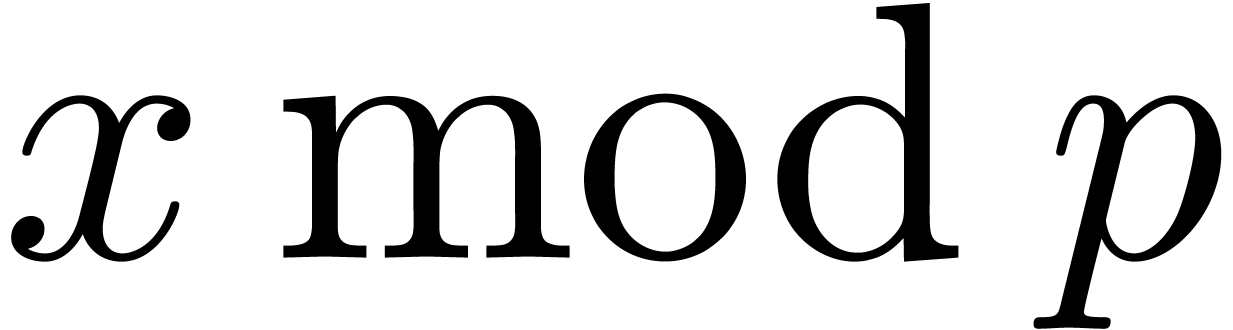 and
and 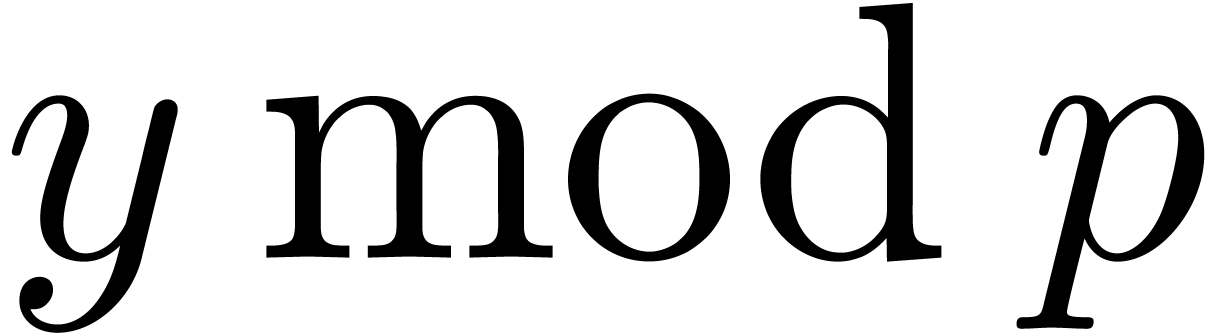 begins with the computation of an integer
approximation
begins with the computation of an integer
approximation  of
of  .
Then
.
Then 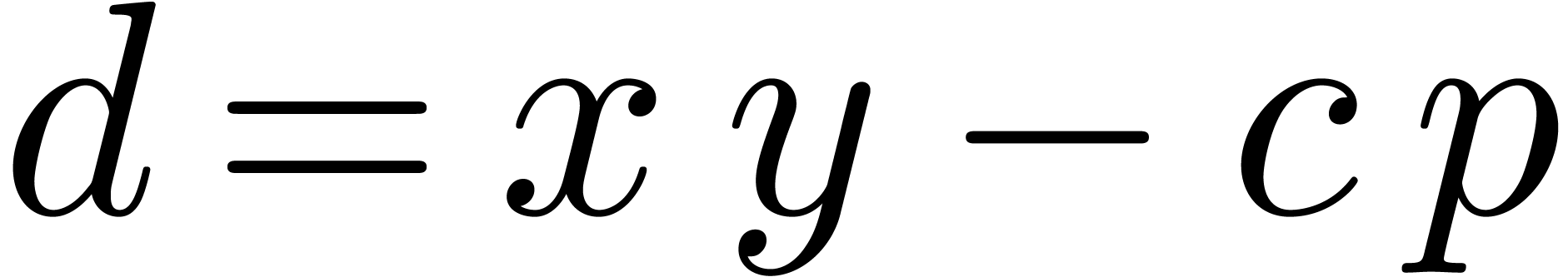 is an approximation of
is an approximation of 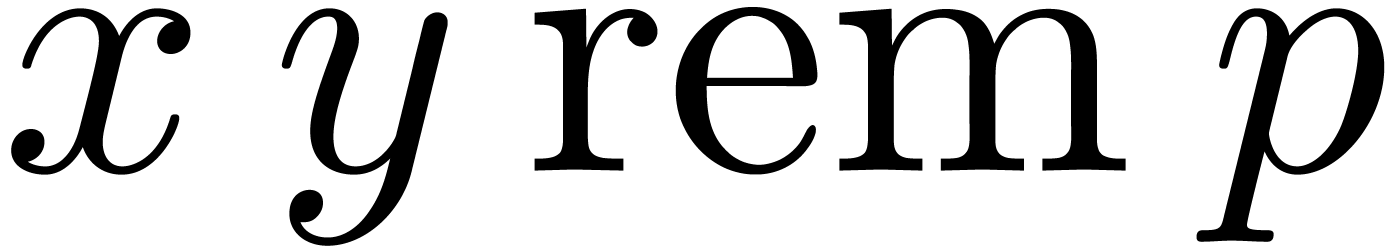 at distance
at distance  . The constant
hidden behind the latter
. The constant
hidden behind the latter  depends on rounding
modes. In this section we conform to IEEE-754 standard. We
first analyze the case when
depends on rounding
modes. In this section we conform to IEEE-754 standard. We
first analyze the case when  fills less than half
of the mantissa. We next propose a general algorithm using the fused
multiply-add operation.
fills less than half
of the mantissa. We next propose a general algorithm using the fused
multiply-add operation.
The following notations are used until the end of the present section.
We write  for the value of
for the value of  computed in F by applying the division operator on 1.0 and (F)
computed in F by applying the division operator on 1.0 and (F)  . Still
following IEEE-754, the trailing significant field of
. Still
following IEEE-754, the trailing significant field of  is written
is written  and its exponent
and its exponent
 . These quantities precisely
depend on the active rounding mode used to compute
. These quantities precisely
depend on the active rounding mode used to compute  . But for all rounding modes, they satisfy the
following properties:
. But for all rounding modes, they satisfy the
following properties:
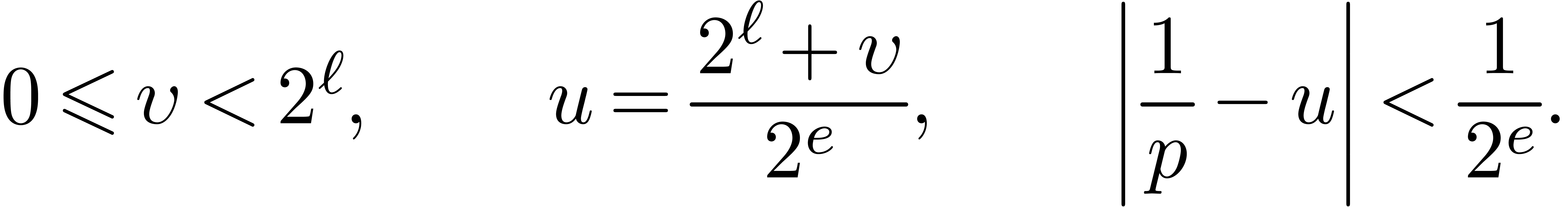 |
(1) |
From the latter inequality we obtain
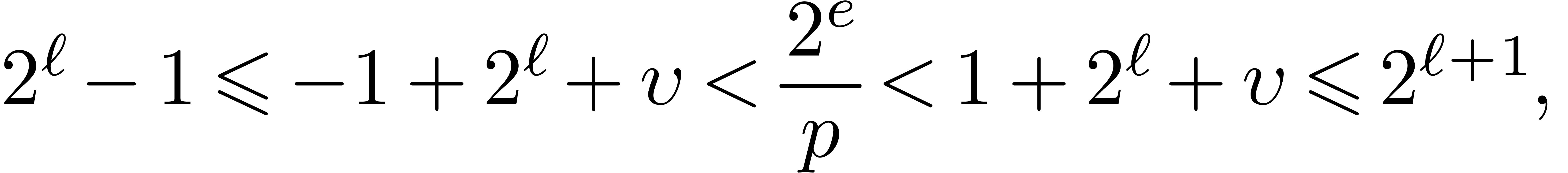
and thus
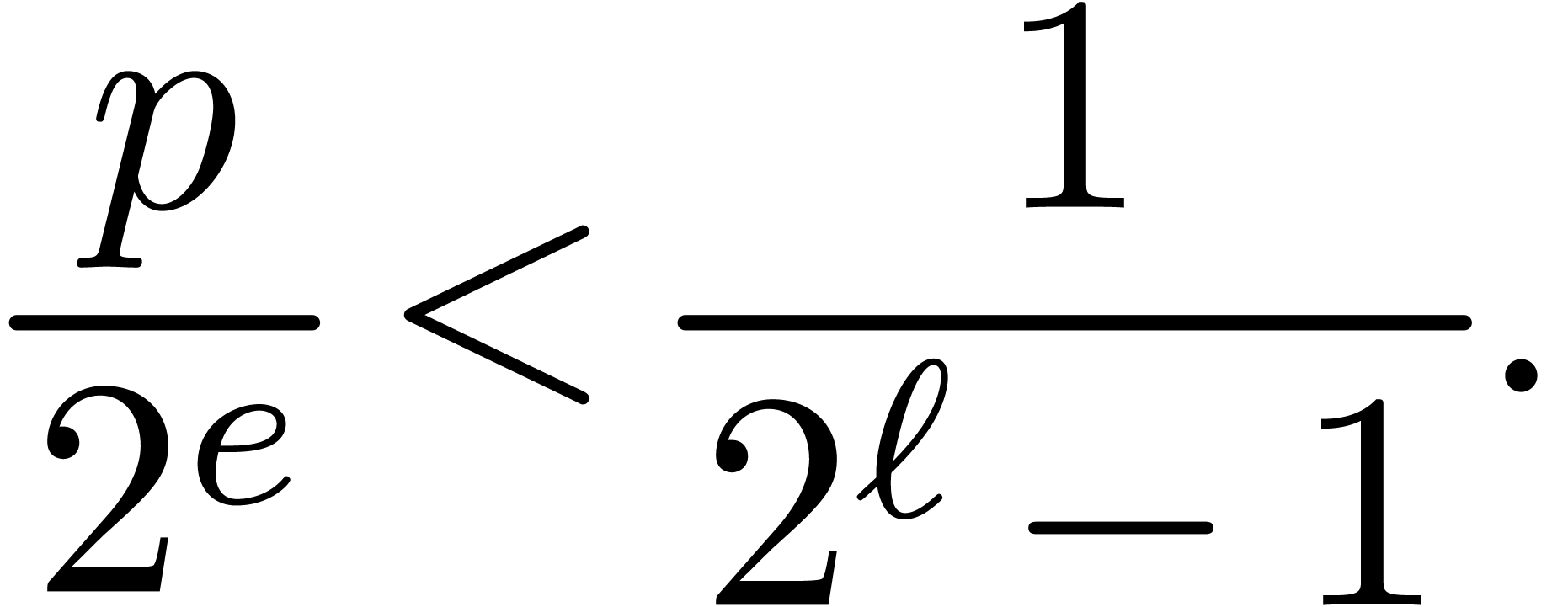 |
(2) |
Let  be a real number of type F,
and let F
be a real number of type F,
and let F  =
=  *
*
 be the approximation of
be the approximation of  computed in F. Again, independently of the rounding
mode, there exist integers
computed in F. Again, independently of the rounding
mode, there exist integers  and
and  , for the trailing significant field and the
exponent of
, for the trailing significant field and the
exponent of  , such that
, such that
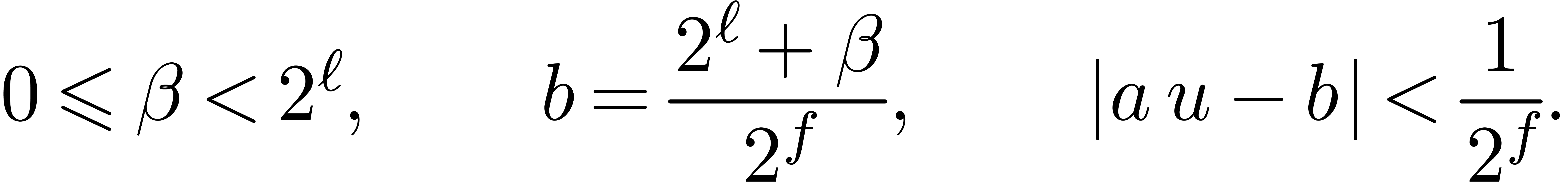 |
(3) |
From 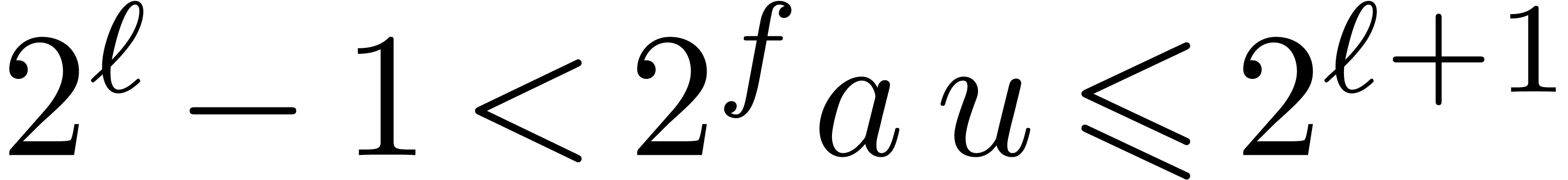 we deduce
we deduce
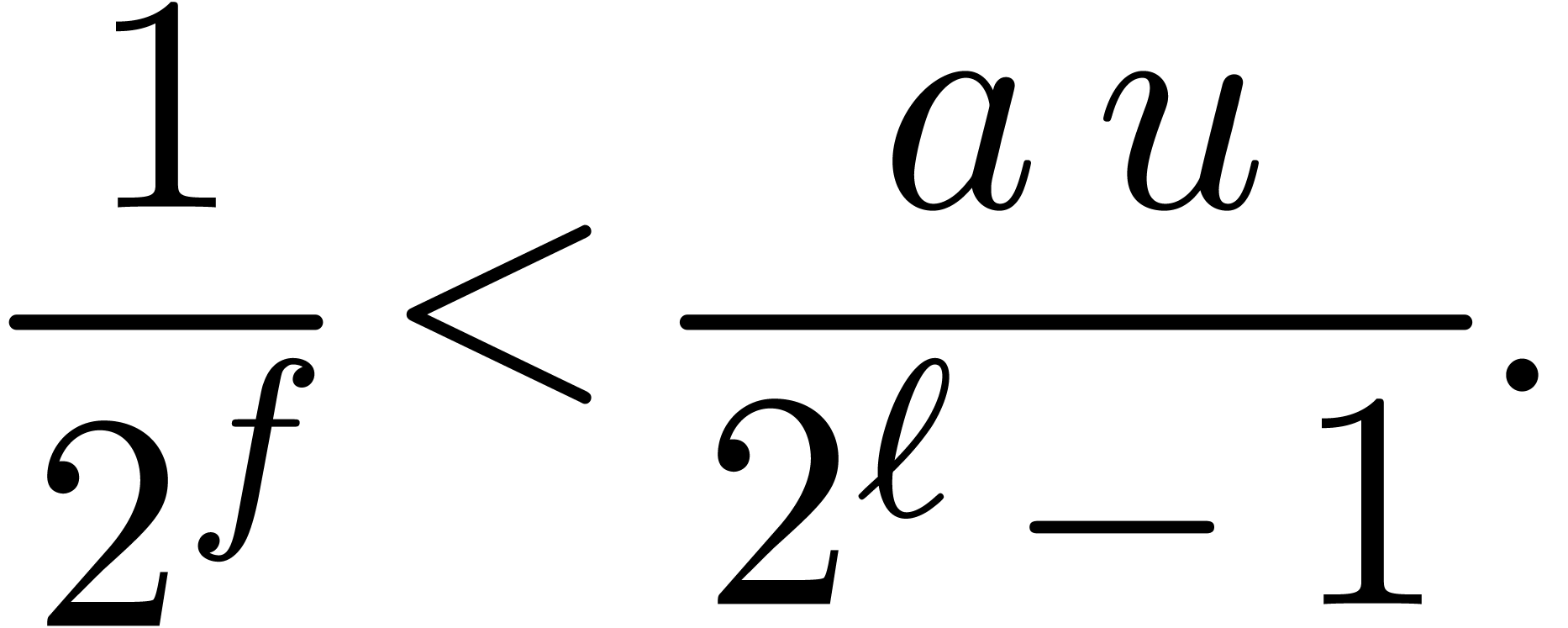 |
(4) |
We also use the approximation  of 1.0
/ ((F)
of 1.0
/ ((F)  ) computed in F with rounding mode set towards infinity, so that
) computed in F with rounding mode set towards infinity, so that 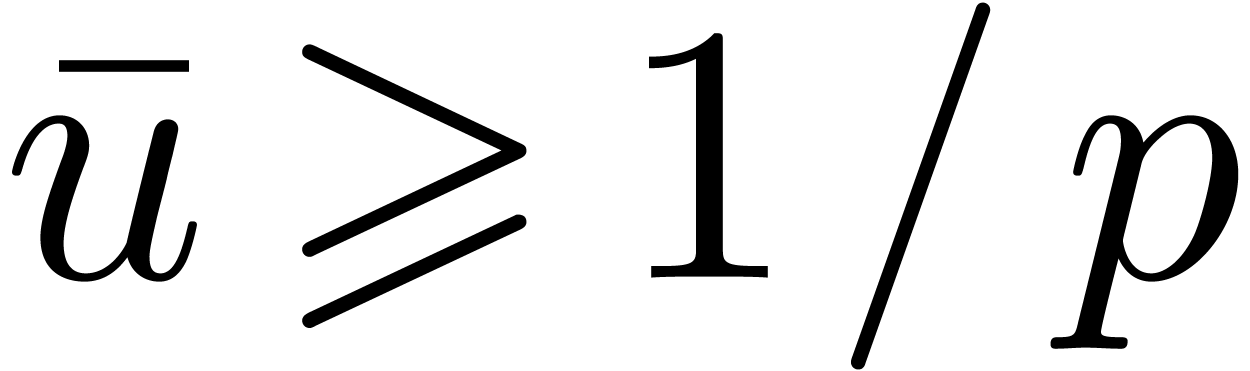 holds.
holds.
When  fills no more than half of the mantissa,
that is when
fills no more than half of the mantissa,
that is when 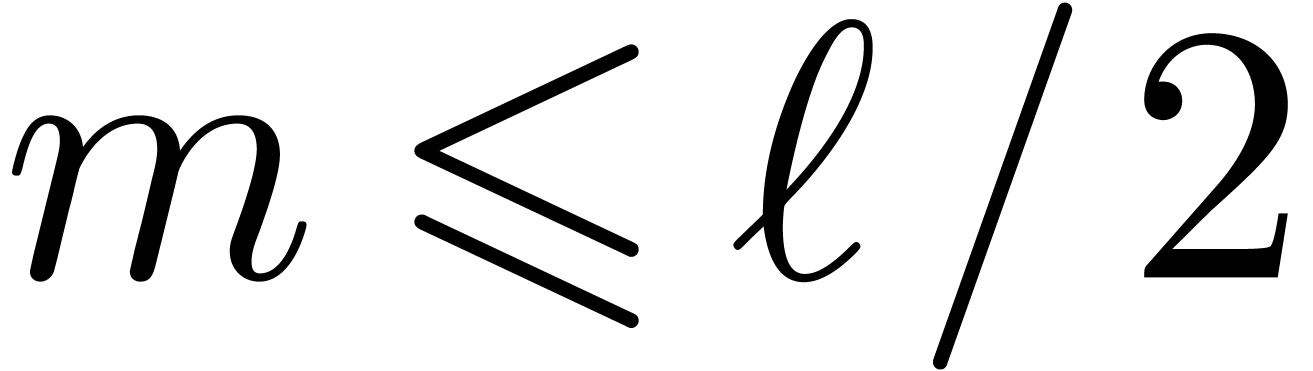 , it is possible
to perform modular products in F easily. Let the floor function return the largest integral value less than
or equal to its argument, as defined in
, it is possible
to perform modular products in F easily. Let the floor function return the largest integral value less than
or equal to its argument, as defined in
Function
Output. 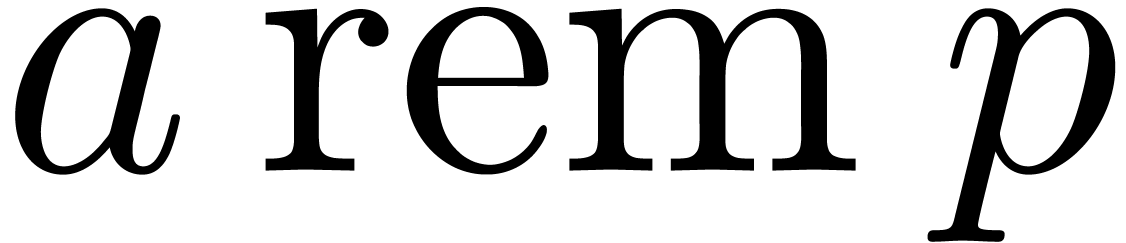 .
.
F reduce_numeric_half (F  ) {
) {
F 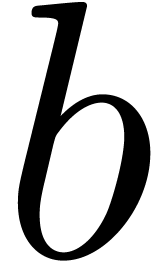 =
=  *
*  ;
;
F  = floor
(
= floor
(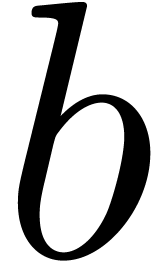 );
);
F  =
=  -
-  *
*  ;
;
if ( >=
>=
 ) return
) return  -
-  ;
;
if ( < 0)
return
< 0)
return  +
+  ;
;
return  ; }
; }
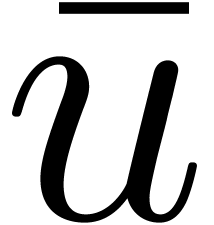 is used
instead of
is used
instead of  in line 1, and if the rounding mode
is set towards infinity, then line 4 can be discarded.
in line 1, and if the rounding mode
is set towards infinity, then line 4 can be discarded.
Proof. Using 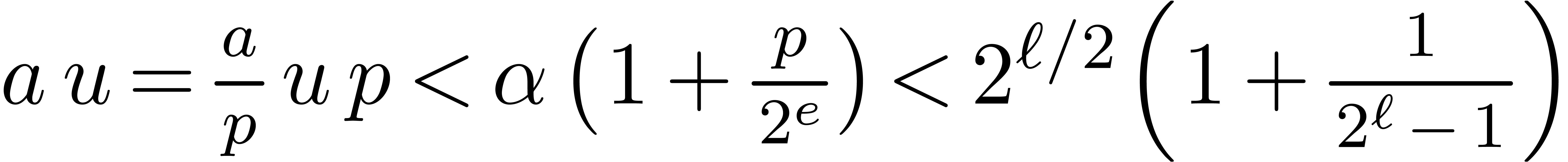 , hence the floor function
actually returns
, hence the floor function
actually returns 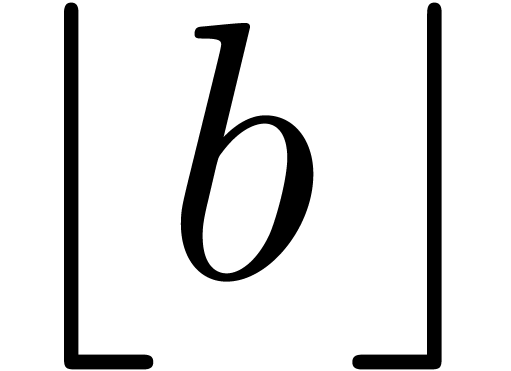 in
in  . From the decomposition
. From the decomposition
 |
(5) |
we deduce
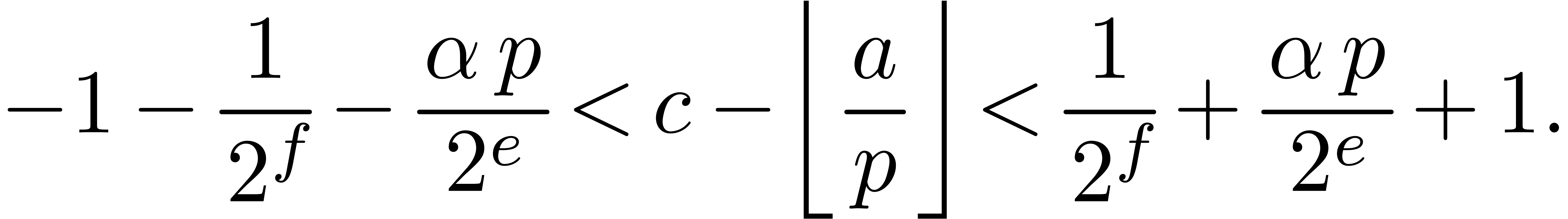
From 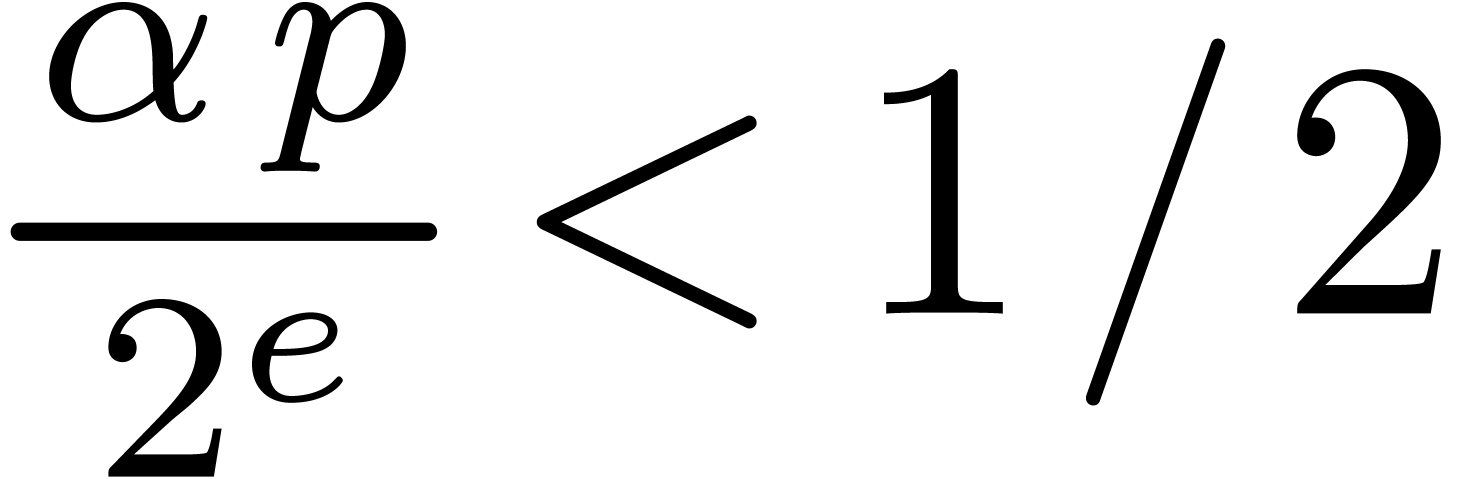 , and from
, and from  . It follows that
. It follows that
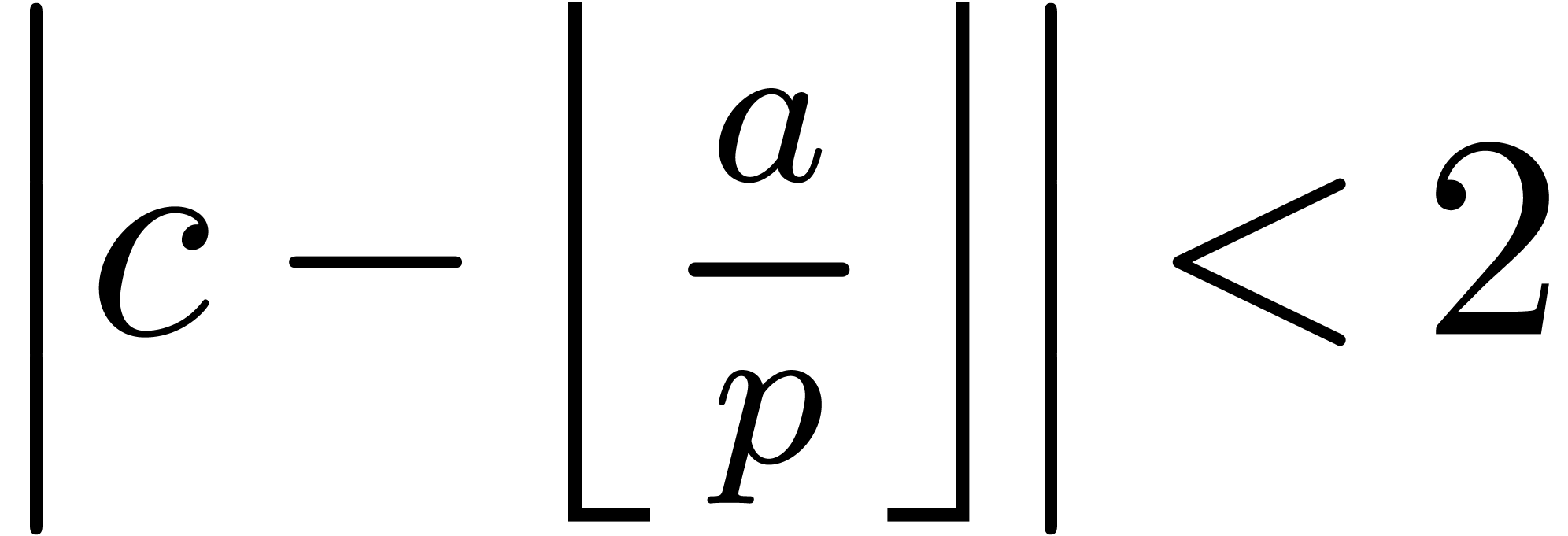 hence that
hence that 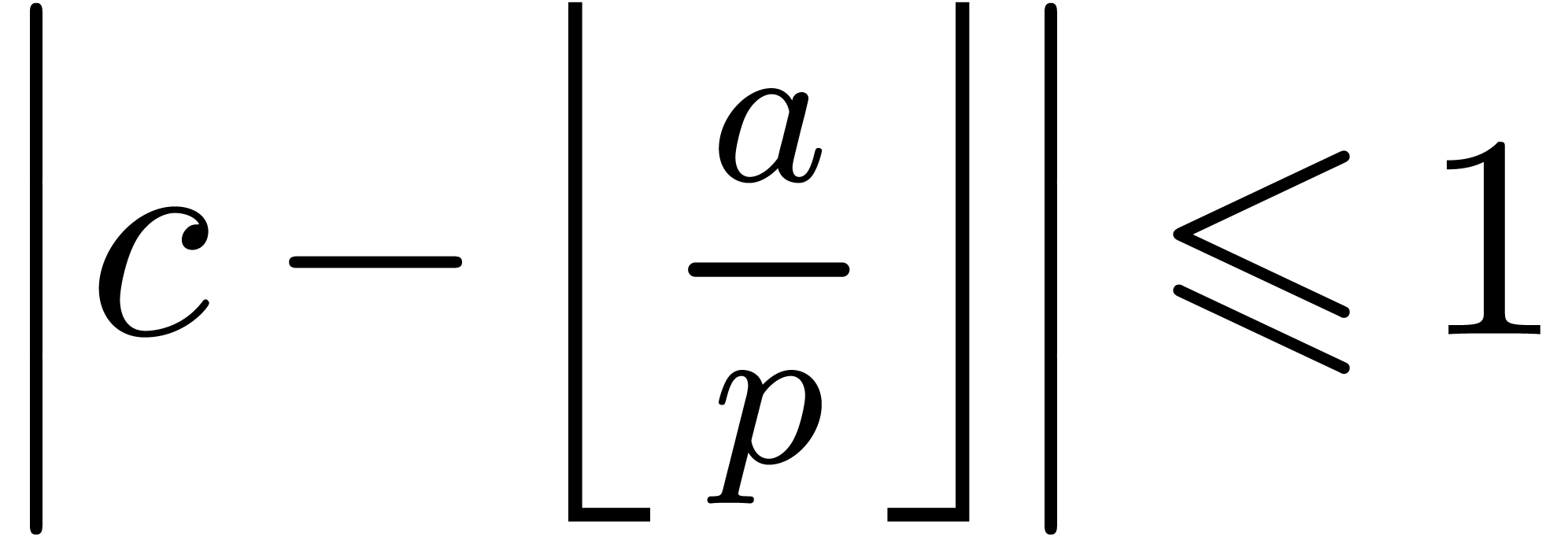 .
.
If using 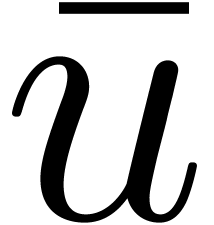 instead of
instead of  , and if the rounding mode is set towards infinity,
then
, and if the rounding mode is set towards infinity,
then 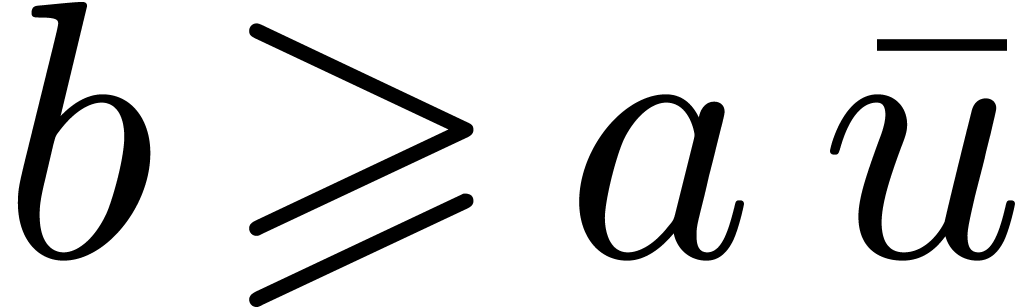 , and then
, and then 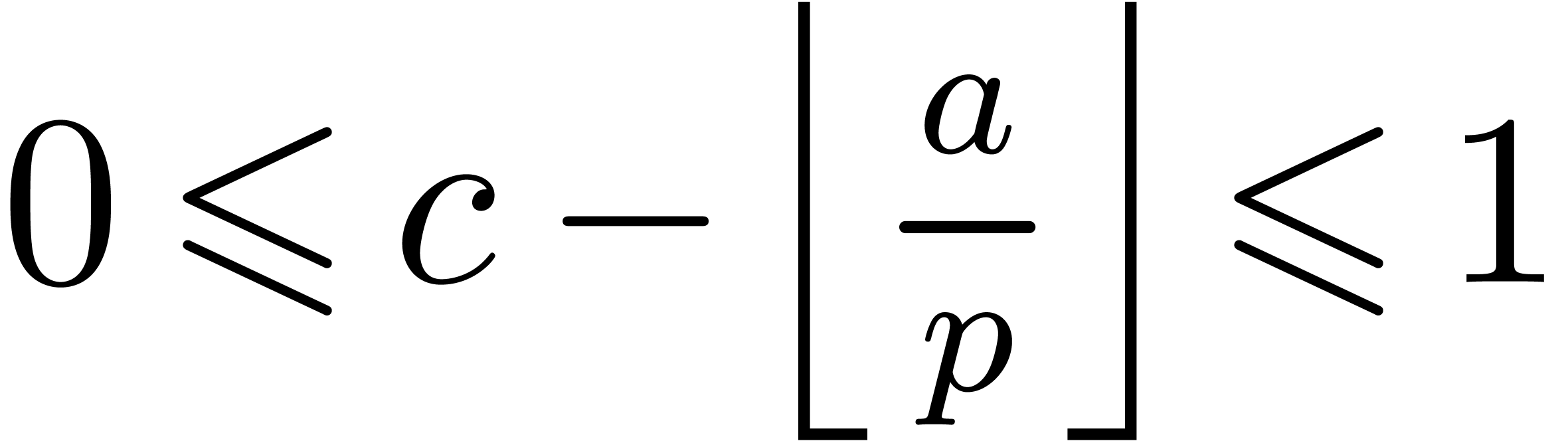 , which allows us to discard line 4.
, which allows us to discard line 4.
In the same way we did for Barrett's product, and under mild
assumptions, we can improve the latter function whenever 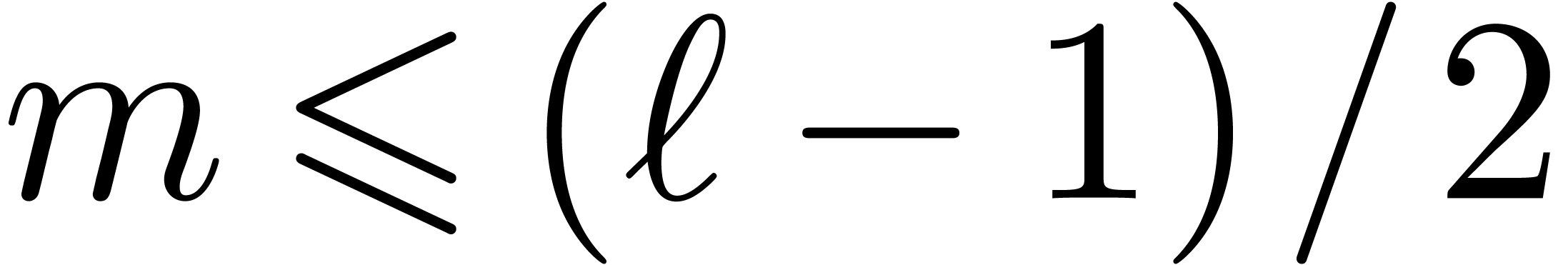 .
.
Function
Hypothesis. The current rounding mode rounds towards infinity.
Output. 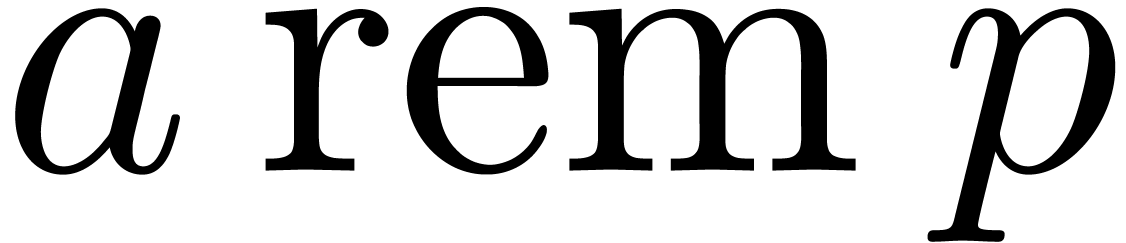 .
.
F reduce_numeric_half_1 (F  ) {
) {
F  =
=  *
*  ;
;
F  = floor
(
= floor
( );
);
return  -
-
 *
*  ;
}
;
}
Proof. We claim that
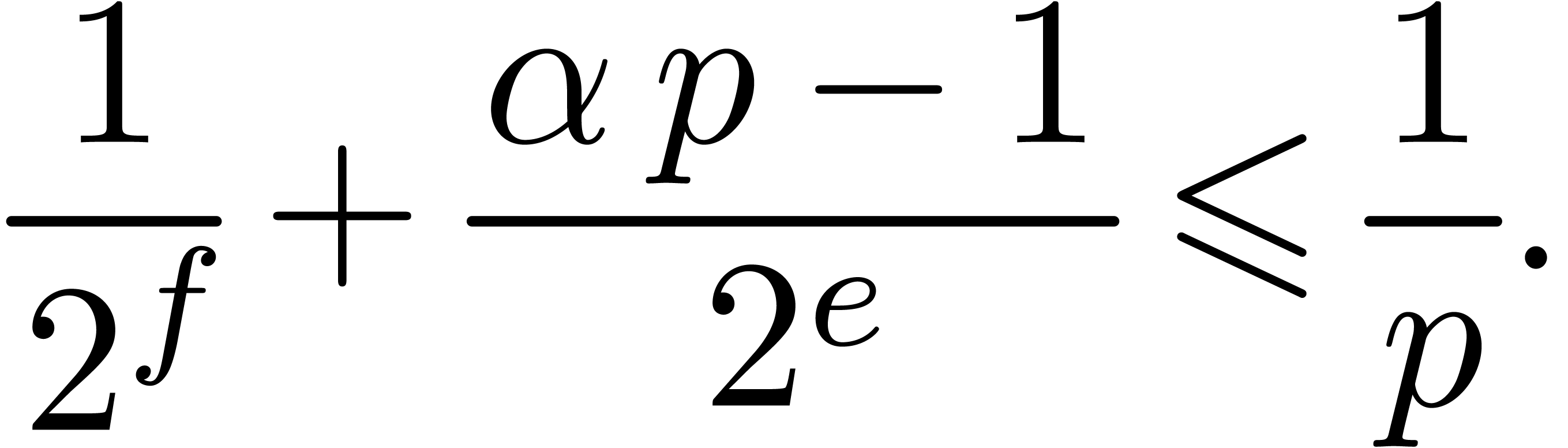 |
(6) |
By 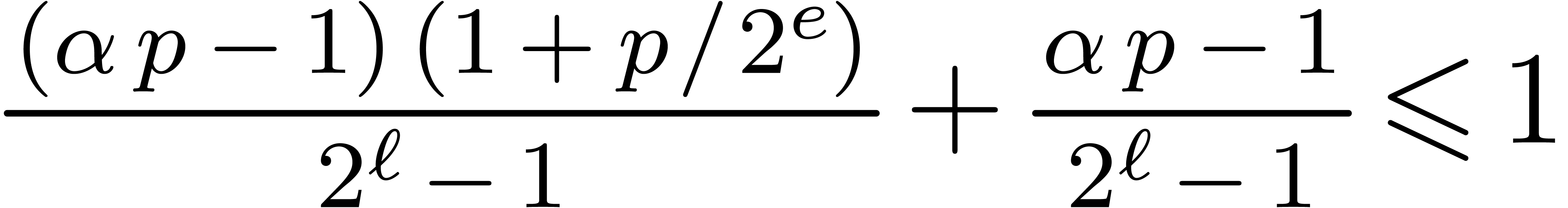 ,
which is itself implied by
,
which is itself implied by 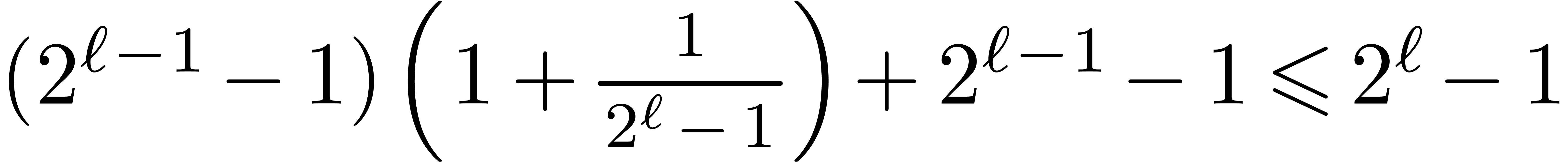 ,
that is correct since it rewrites into
,
that is correct since it rewrites into 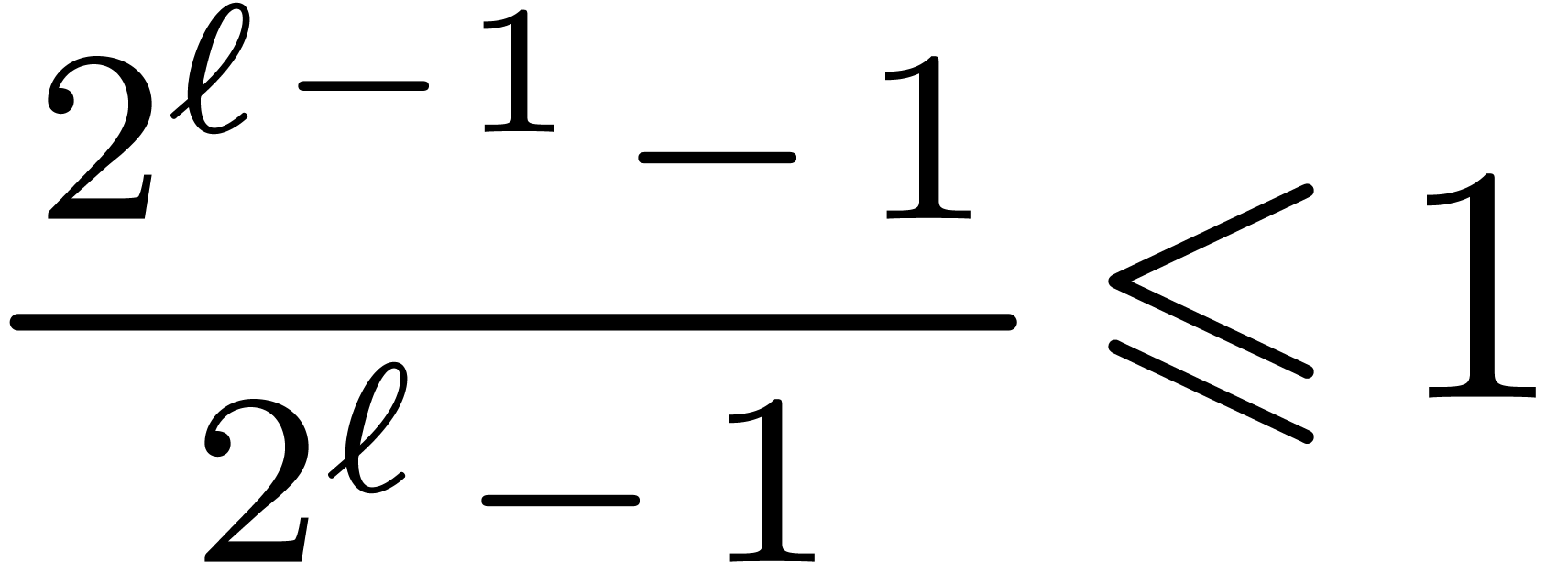 by
expanding the product.
by
expanding the product.
From 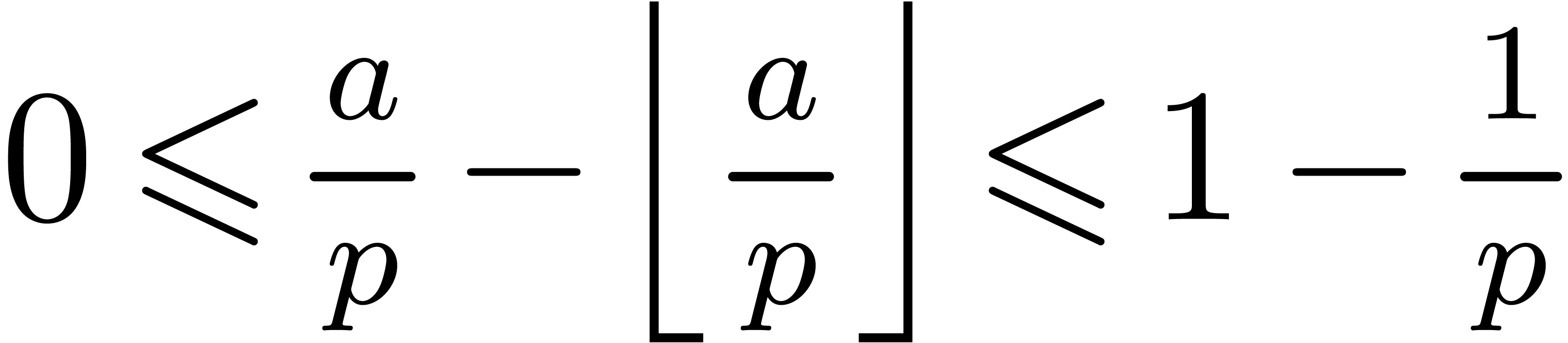 and
and
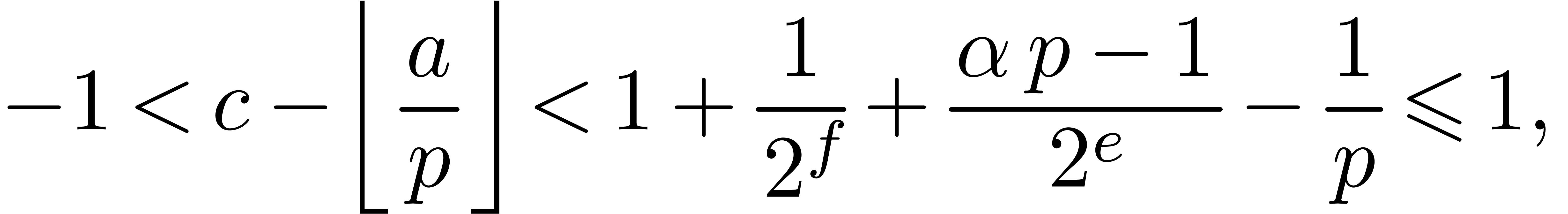
which proves the correctness.
Remark 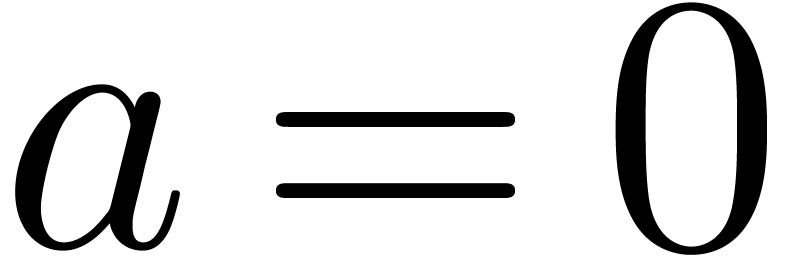 or
or 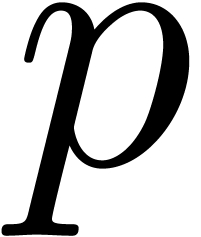 does not divide
does not divide  .
This is in particular case, if
.
This is in particular case, if 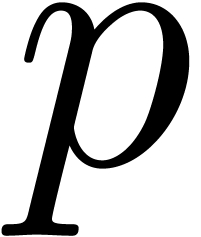 is prime and
is prime and  is the product of two numbers in
is the product of two numbers in 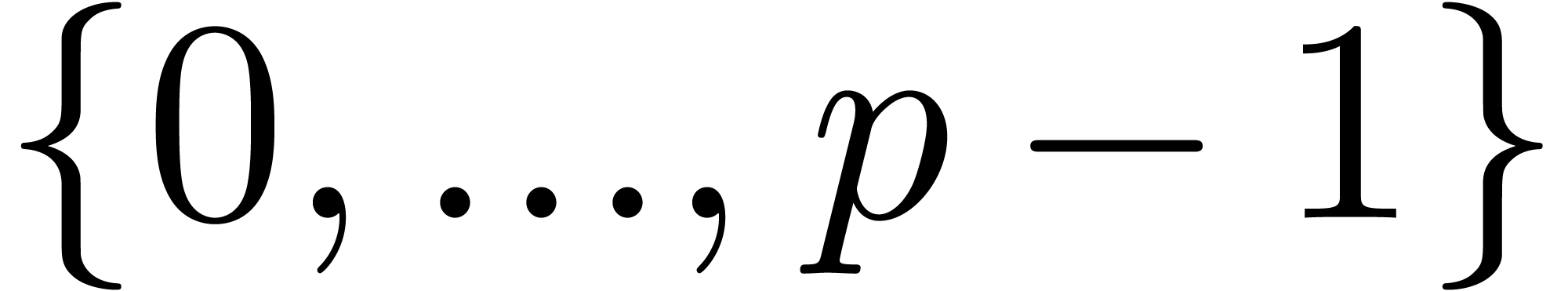 . Indeed, if
. Indeed, if 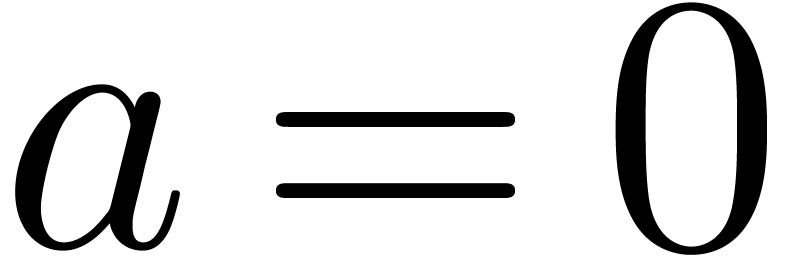 ,
then the algorithm is clearly correct. If
,
then the algorithm is clearly correct. If 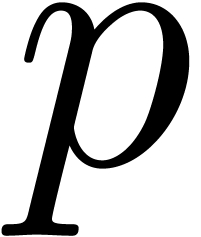 does
not divide
does
not divide  , then we have
, then we have
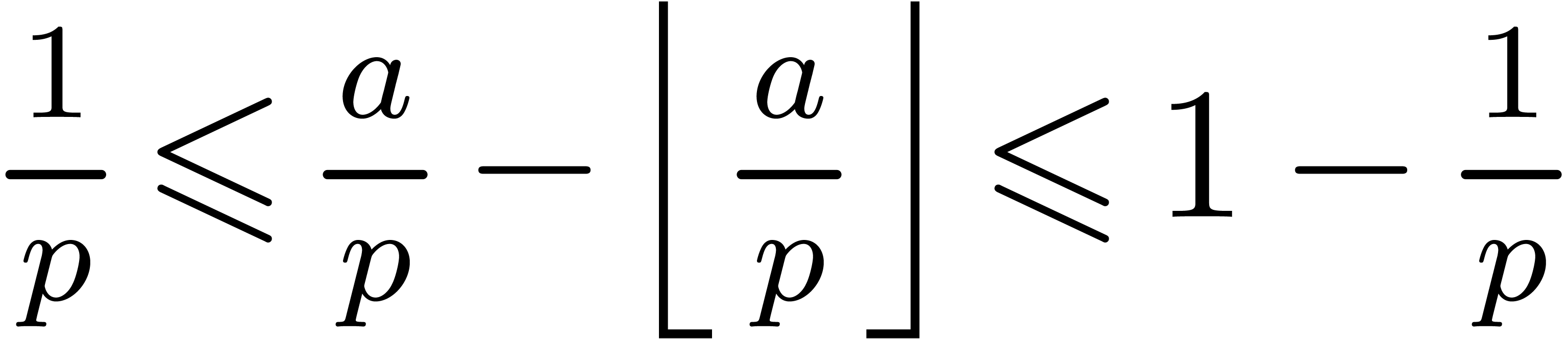 . Combining the latter
inequality with
. Combining the latter
inequality with 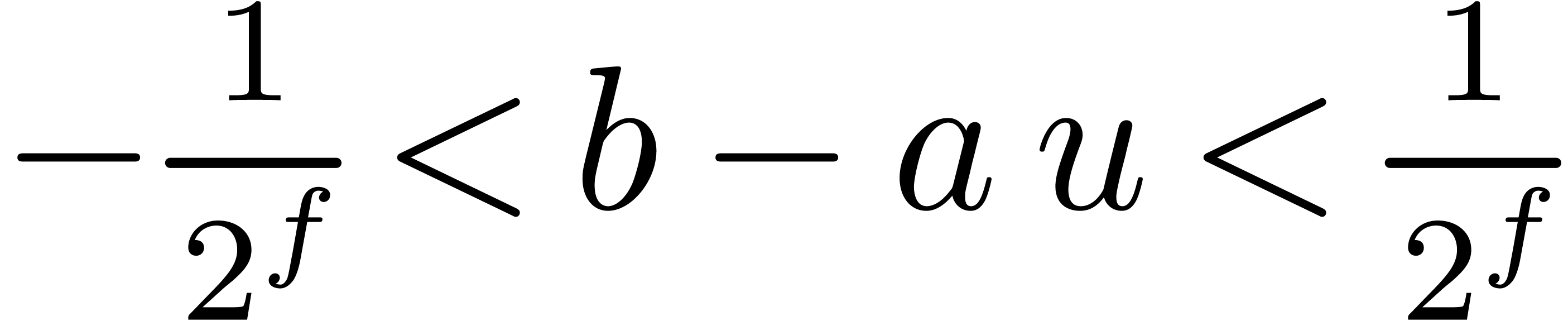 and
and 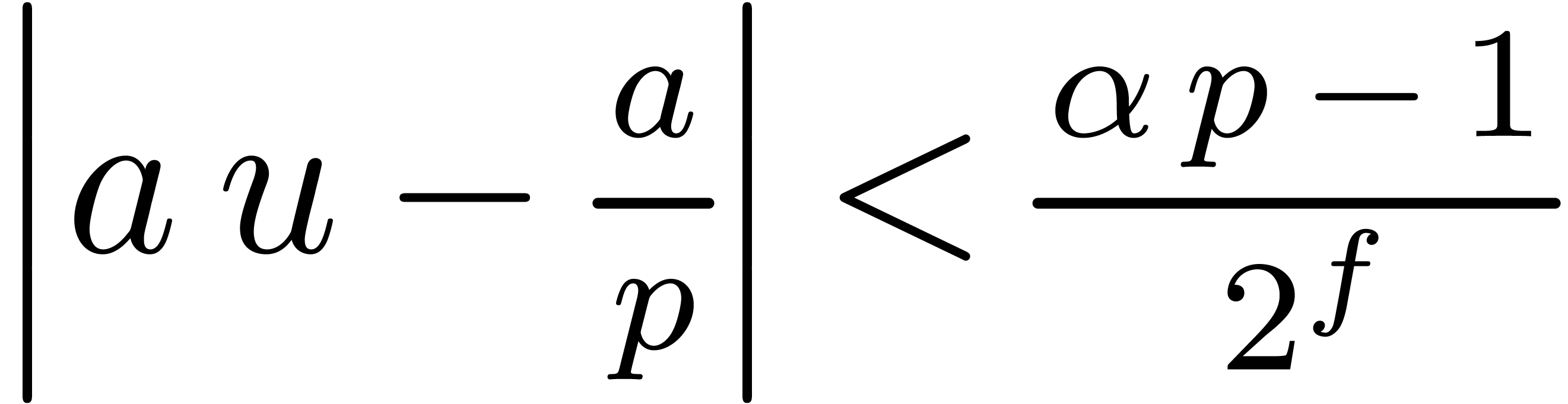 yields
yields
Inequality 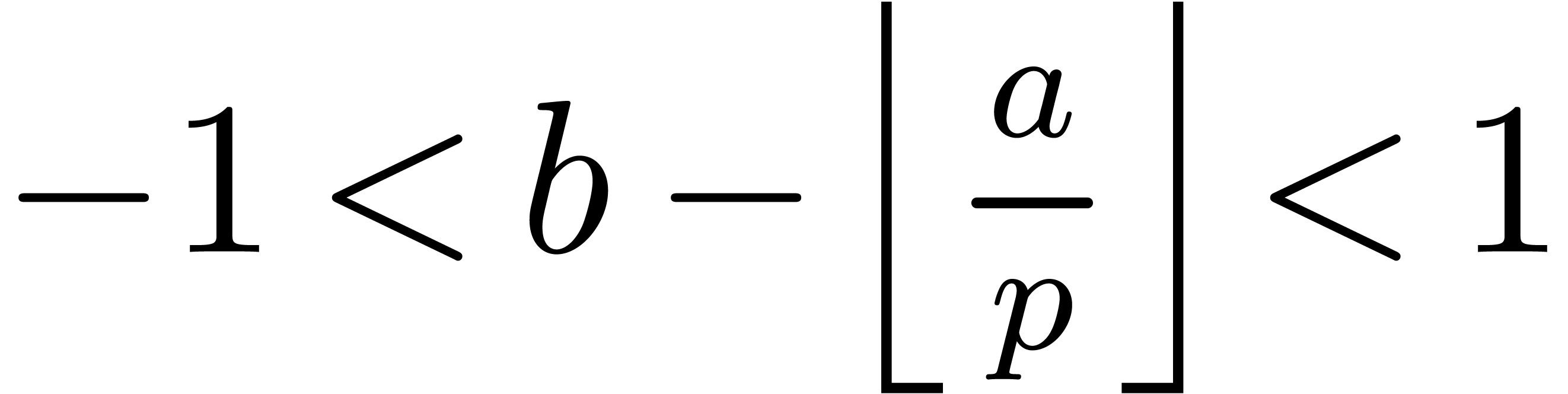 .
.
Until now we have not exploited the whole mantissa of F. To
release the assumption  in Function 14,
the value for
in Function 14,
the value for  could be computed over a
sufficiently large integer type. Over double one can use
could be computed over a
sufficiently large integer type. Over double one can use
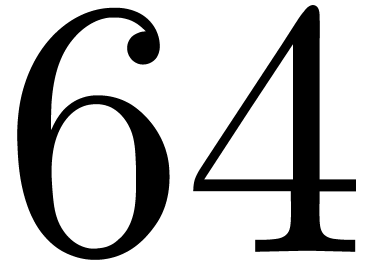 -bit integers, as implemented
for instance in [58]. The drawbacks of this approach are
the extra conversions between numeric and integer types, and the fact
that the vectorization is compromised since
-bit integers, as implemented
for instance in [58]. The drawbacks of this approach are
the extra conversions between numeric and integer types, and the fact
that the vectorization is compromised since 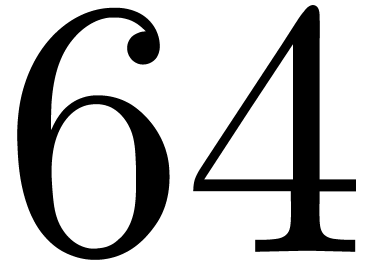 -bit integer products are not natively available in
the
-bit integer products are not natively available in
the 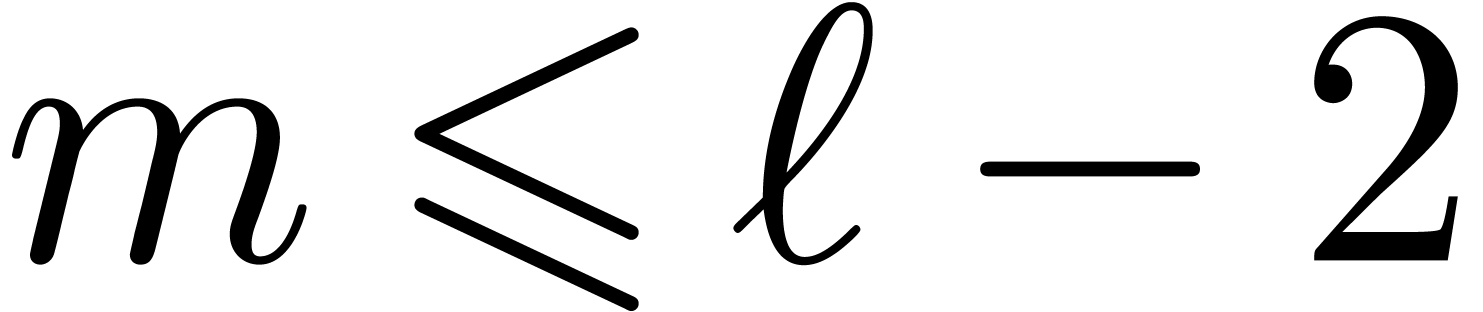 , using the fused
multiply-add operation from the IEEE 754-2008 standard. We
write fma (
, using the fused
multiply-add operation from the IEEE 754-2008 standard. We
write fma ( ,
, 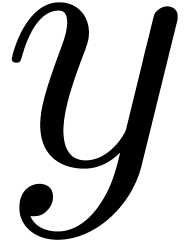 ,
,  )
for the evaluation of
)
for the evaluation of  using the current rounding
mode.
using the current rounding
mode.
Function
Output.  .
.
F mul_mod_fma (F  , F
, F  )
{
)
{
F  =
=  *
* 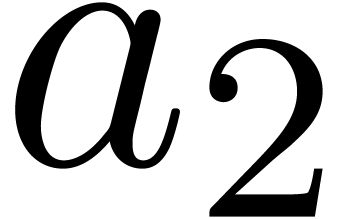 ;
;
F 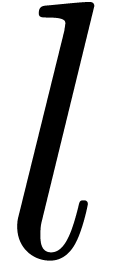 = fma
(
= fma
( ,
, 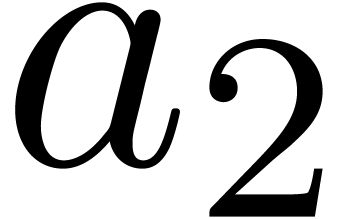 ,
, 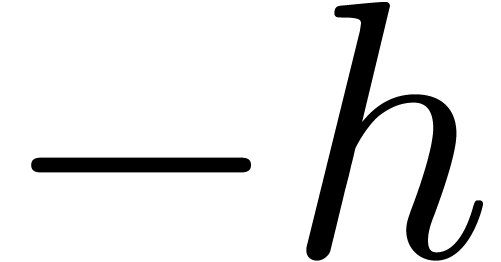 );
);
F  =
=  *
*
 ;
;
F  = floor (
= floor ( );
);
F  = fma
(
= fma
( ,
,  ,
, 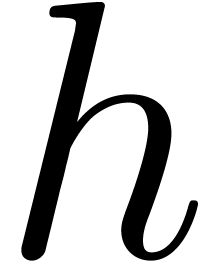 );
);
F  =
=  +
+
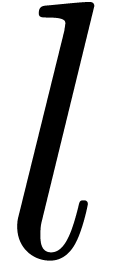 ;
;
if ( >=
>=
 ) return
) return  -
-  ;
;
if ( < 0)
return
< 0)
return  +
+  ;
;
return  ; }
; }
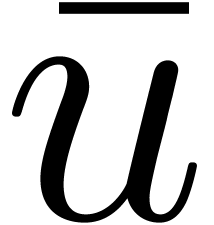 is used instead of
is used instead of  in line 3, and if the rounding mode is set towards
infinity, then line 7 can be discarded.
in line 3, and if the rounding mode is set towards
infinity, then line 7 can be discarded.
Proof. Let 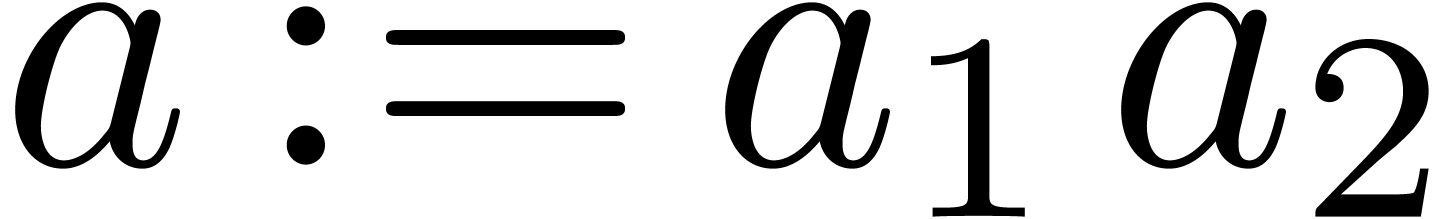 .
We have
.
We have 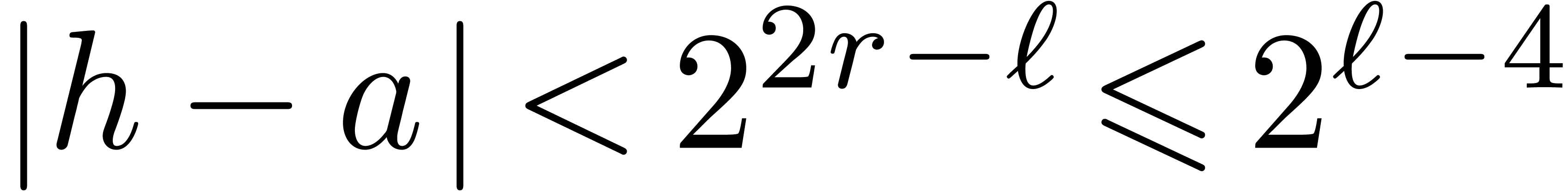 , so that
, so that 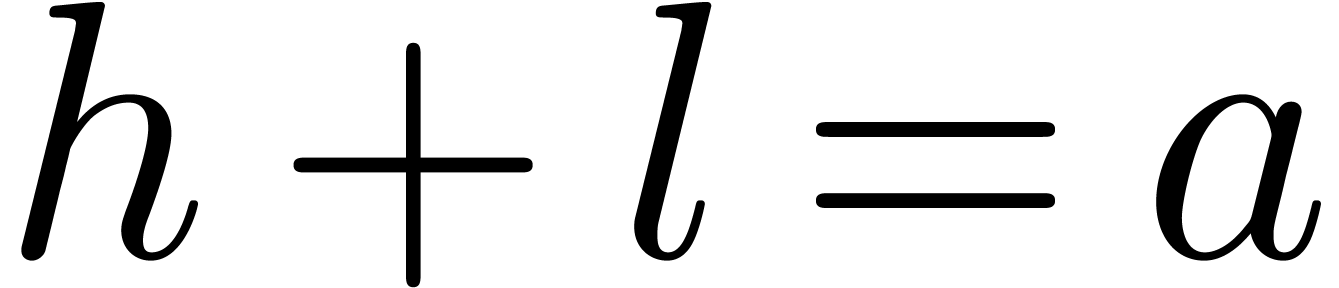 . We also verify that
. We also verify that 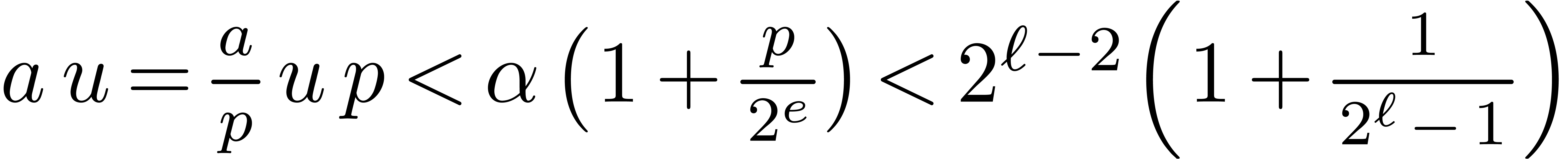 , which implies that
, which implies that 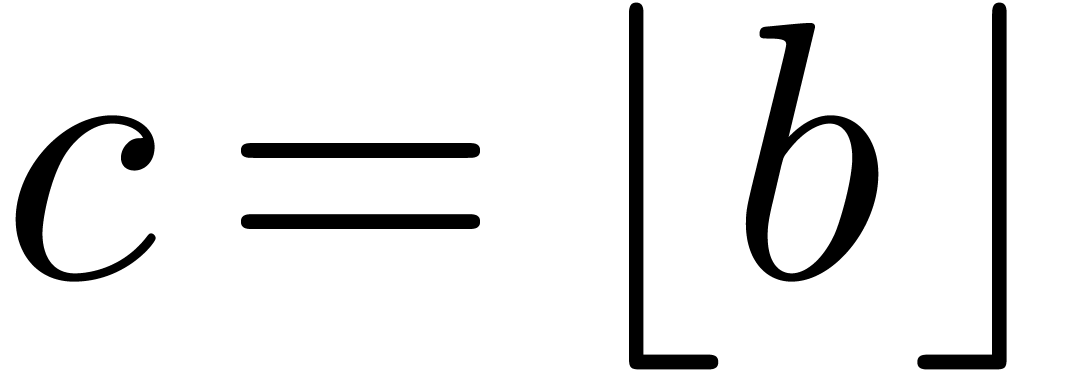 . Using
. Using
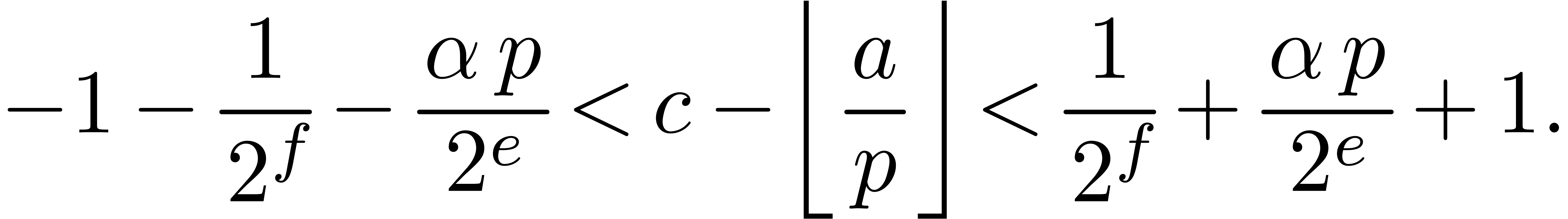
From 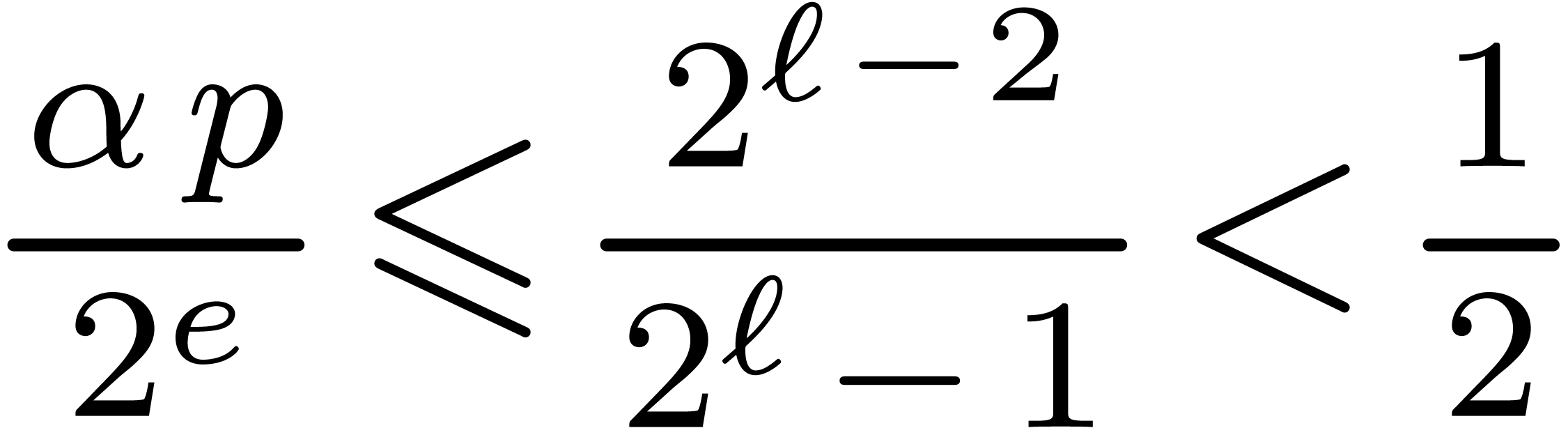 , and from
, and from 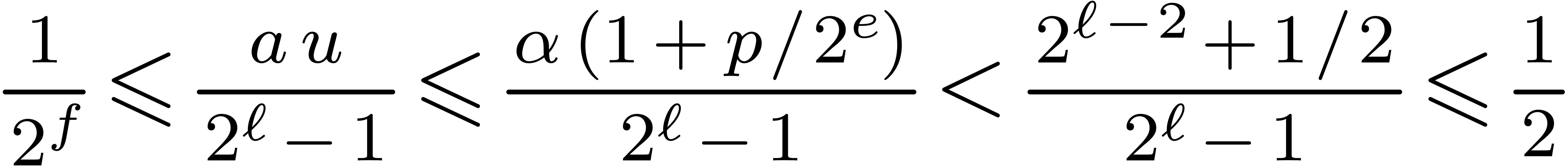 . It follows that
. It follows that
 . In particular this implies
. In particular this implies
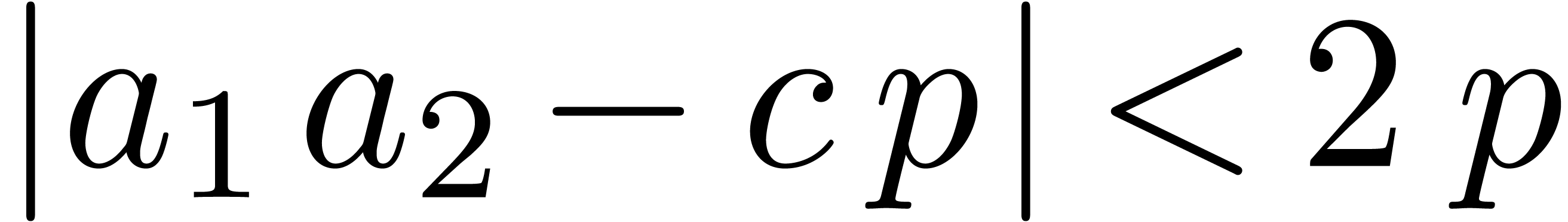 , whence
, whence 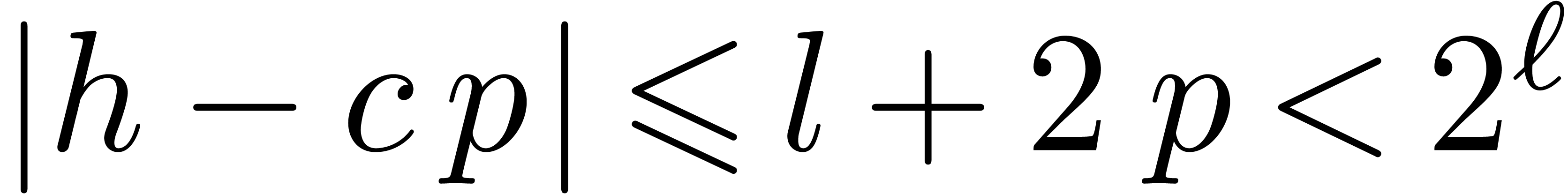 . This proves that
. This proves that 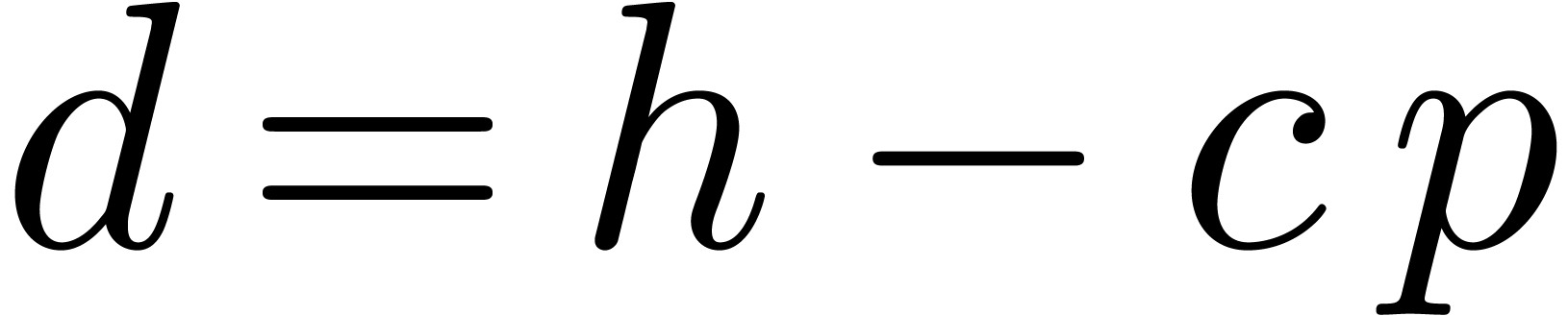 and
therefore
and
therefore 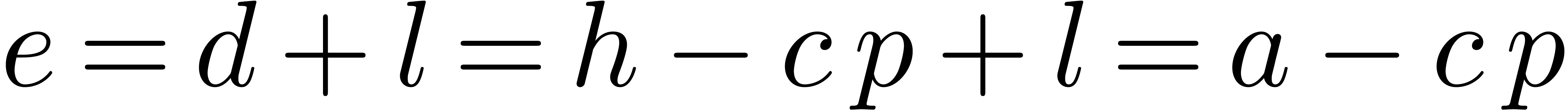 , which finally
implies the correctness of Function 16.
, which finally
implies the correctness of Function 16.
Now suppose that 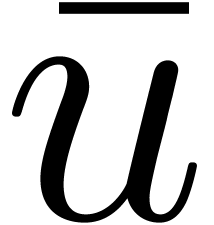 is used and that the rounding
mode is set towards infinity. Then
is used and that the rounding
mode is set towards infinity. Then 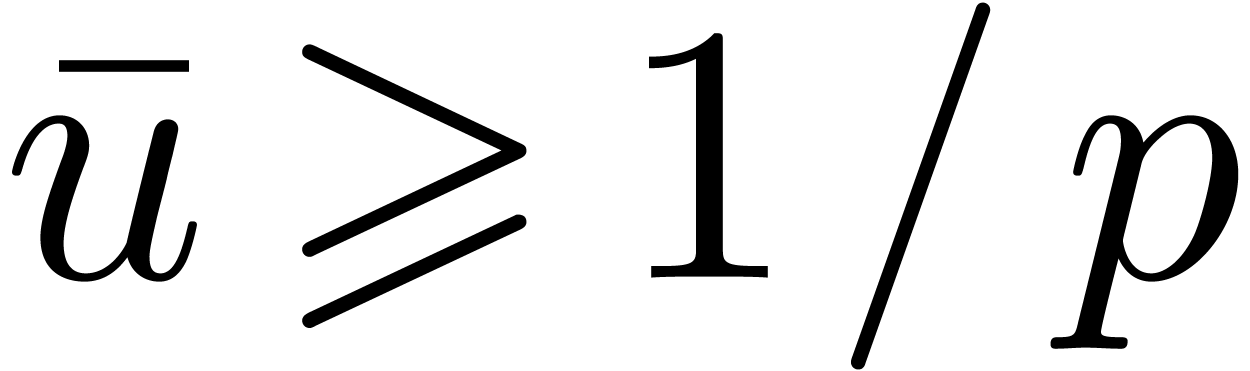 ,
,
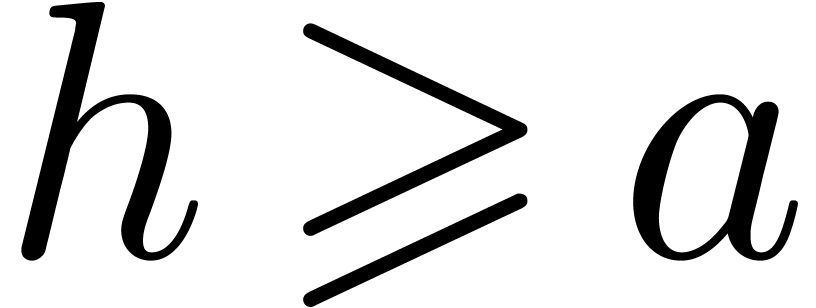 and
and 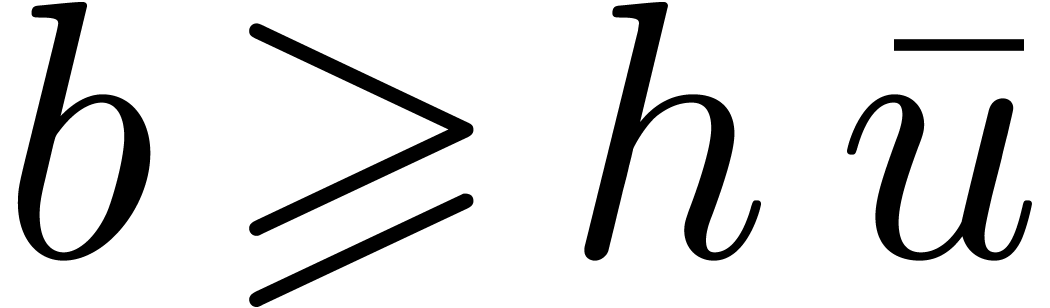 so that
so that 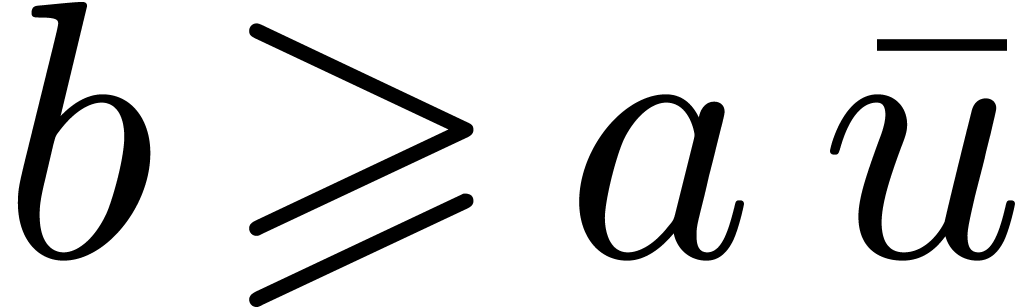 , and therefore
, and therefore  .
.
Remark 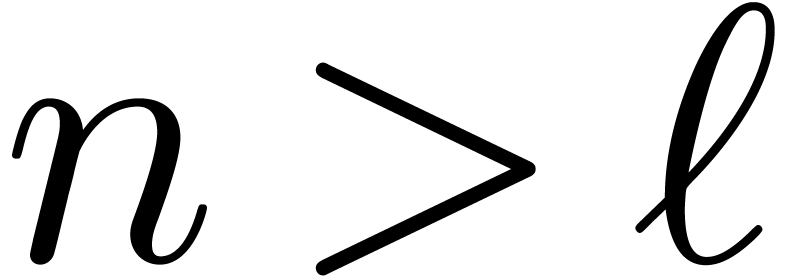 bits.
In the above functions the executable code generated for the
floor instruction heavily depends on the compiler, its version,
and its command line arguments. This makes timings for this numeric
approach rather unpredictable. We have run tests with
bits.
In the above functions the executable code generated for the
floor instruction heavily depends on the compiler, its version,
and its command line arguments. This makes timings for this numeric
approach rather unpredictable. We have run tests with 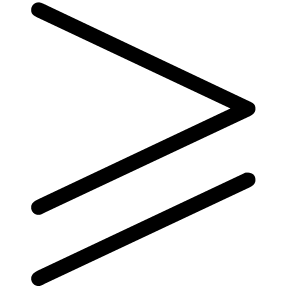 4.7 and
4.7 and  3.4 and observed that
3.4 and observed that
 = (F) ((I)
= (F) ((I) 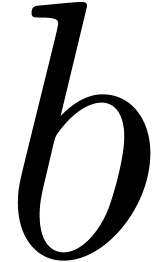 )
always generates cvttsd2si, cvtsi2sd instructions
which are the x86 cast instructions, whereas
)
always generates cvttsd2si, cvtsi2sd instructions
which are the x86 cast instructions, whereas  = floor (
= floor ( ) is compiled
into a call to the floor function from the math library. In
order to force the compiler to use a special purpose instruction such as
roundsd from
) is compiled
into a call to the floor function from the math library. In
order to force the compiler to use a special purpose instruction such as
roundsd from
For efficiency, we assume that
Function
Output. 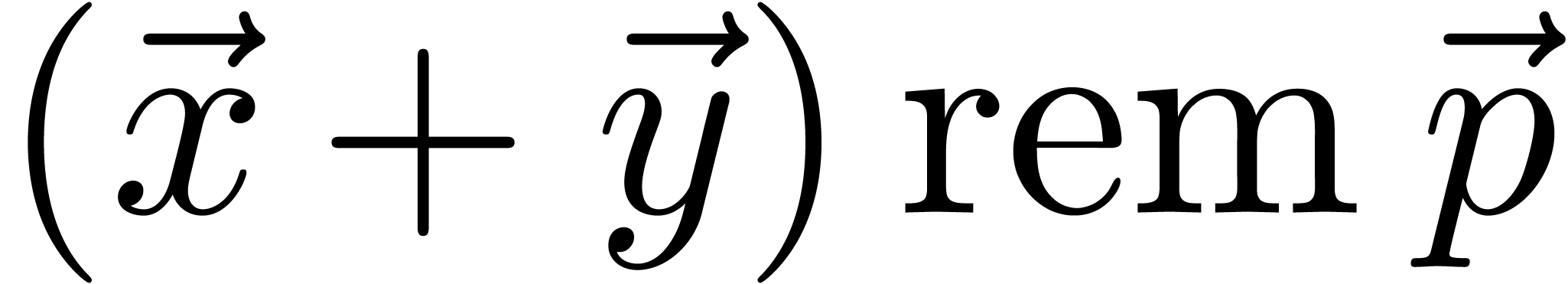 .
.
__m128d add_mod_1 (__m128d 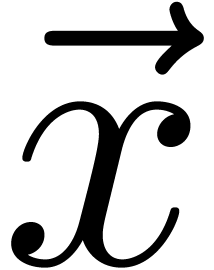 , __m128d
, __m128d 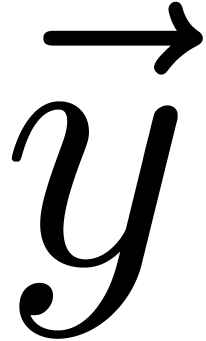 )
{
)
{
__m128d  =
_mm_add_pd (
=
_mm_add_pd ( ,
,  );
);
__m128d  =
_mm_sub_pd (
=
_mm_sub_pd ( ,
,  );
);
return _mm_blendv_pd ( ,
,  ,
,
 ); }
); }
Assuming that
Function
Output.  .
.
__m128d mul_mod_1 (__m128d  , __m128d
, __m128d  )
{
)
{
__m128d  =
_mm_mul_pd (
=
_mm_mul_pd ( ,
,  );
);
__m128d  =
_mm_fmsub_pd (
=
_mm_fmsub_pd (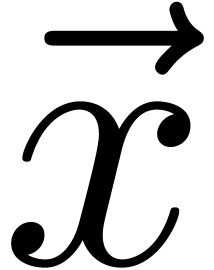 ,
, 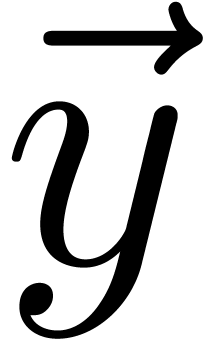 ,
, 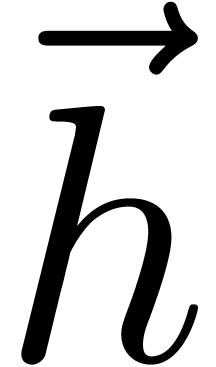 );
);
__m128d 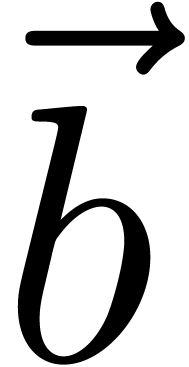 =
_mm_mul_pd (
=
_mm_mul_pd ( ,
,  );
);
__m128d  =
_mm_floor (
=
_mm_floor ( );
);
__m128d 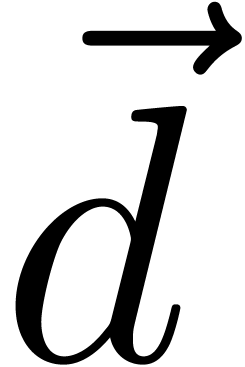 =
_mm_fnmadd_pd (
=
_mm_fnmadd_pd ( ,
,  ,
,  );
);
__m128d  =
_mm_add_pd (
=
_mm_add_pd ( ,
,  );
);
__m128d  =
_mm_sub_pd (
=
_mm_sub_pd ( ,
,  );
);
 =
_mm_blendv_pd (
=
_mm_blendv_pd ( ,
,  ,
,  );
);
 =
_mm_add_pd (
=
_mm_add_pd ( ,
,  );
);
return _mm_blendv_pd ( ,
, 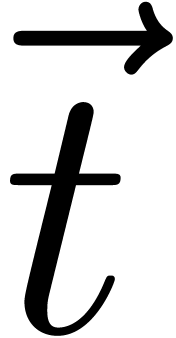 ,
,
 ); }
); }
Our
Table 9 is obtained under similar conditions as Tables 1 and 4, but for the types float
and double. The row “Scalar” corresponds to
the unvectorized implementation with unrolled loops, and preventing the
compiler from using auto-vectorization. The next rows concern timings
using
|
|||||||||||||||||||||||||
In Table 10 we have shown timings for the modular sum and
product functions from this section. The row “Scalar”
excludes auto-vectorization and does not use the processor built-in
|
||||||||||||||||||||||||||||||||||||||||||||||||
We notice that the timings in Table 10 are interesting when compared to those in Table 5. However, for multiplications with a fixed multiplicand, the approach from Table 7 becomes more attractive, and this will indeed be used in Section 5 below.
We also notice that efficient hardware quadruple precision arithmetic
would allow us to consider moduli with larger bit sizes. An alternative
to hardware quadruple precision arithmetic would be to provide an
efficient “three-sum” 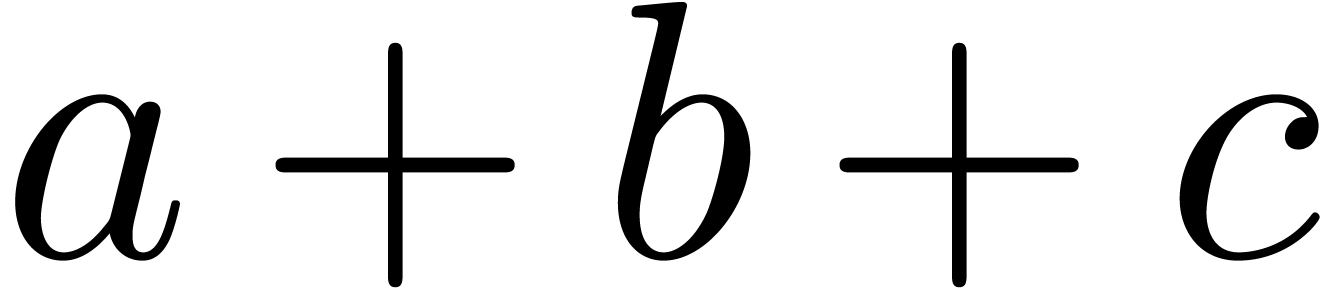 instruction
with correct
instruction
with correct
The
Consider a typical template class in
For example, the class vector<C,V> (defined in basix/vector.hpp) corresponds to dense vectors with entries
in C, stored in a contiguous segment of memory. A vector
of this type consists of a pointer of type C* to the
first element of the vector, the size 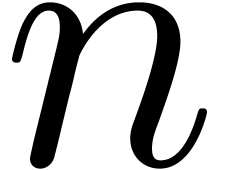 of the
vector, and the size
of the
vector, and the size  of the allocated memory.
For the sake of simplicity we omit that our vectors are endowed with
reference counters. At the top level user interface, for instance, the
sum of two vectors is defined as follows:
of the allocated memory.
For the sake of simplicity we omit that our vectors are endowed with
reference counters. At the top level user interface, for instance, the
sum of two vectors is defined as follows:
template<typename C, typename V>
vector<C,V> operator + (const vector<C,V>& v, const vector<C,V>& w) {
typedef implementation<vector_linear, V> Vec;
nat n= N(v); nat l= aligned_size<C,V> (n);
C* t= mmx_new<C> (l);
Vec::add (t, seg (v), seg (w), n);
return vector<C,V> (t, n, l); }
In this piece of code N(v) represents the size of  , aligned_size<C,V>
(n) computes the length to be allocated in order to store vectors
of size n over C in memory. According to
the values of C and V, we can force the
allocated memory segment to start at an address multiple of a given
value, such as 16 bytes when using
, aligned_size<C,V>
(n) computes the length to be allocated in order to store vectors
of size n over C in memory. According to
the values of C and V, we can force the
allocated memory segment to start at an address multiple of a given
value, such as 16 bytes when using
The classes containing the implementations are specializations of the following class:
template<typename F, typename V, typename W=V> struct implementation;
The first template argument F is usually an empty class which names a set of functionalities. In the latter example we introduced vector_linear, which stands for the usual entry-wise vector operations, including addition, subtraction, component-wise product, etc. The value of the argument V for naive implementations of vector operations is vector_naive. The role of the third argument W will be explained later. The naive implementation of the addition of two vectors is then declared as a static member of implementation<vector_linear, vector_naive> as follows:
template<typename V>
struct implementation<vector_linear, V, vector_naive> {
static inline void
add (C* dest, const C* s1, const C* s2, nat n) {
for (nat i= 0; i < n; i++)
dest[i]= s1[i] + s2[i]; } ../..
Four by four loop unrolling can for instance be implemented within another variant, say vector_unrolled_4, as follows:
template<typename V>
struct implementation<vector_linear, V, vector_unrolled_4> {
static inline void
add (C* dest, const C* s1, const C* s2, nat n) {
nat i= 0;
for (; i + 4 < n; i += 4) {
dest[i ]= s1[i ] + s2[i ]; dest[i+1]= s1[i+1] + s2[i+1];
dest[i+2]= s1[i+2] + s2[i+2]; dest[i+3]= s1[i+3] + s2[i+3]; }
for (; i < n; i++)
dest[i]= s1[i] + s2[i]; } ../..
When defining a new variant we hardly ever want to redefine the whole set of functionalities of other variants. Instead we wish to introduce new algorithms for a subset of functionalities, and to have the remaining implementations inherit from other variants. We say that a variant V inherits from W when the following partial specialization is active:
template<typename F, typename U>
struct implementation<F,U,V>: implementation<F,U,W> {};
For instance, if the variant V inherits from vector_naive, then the add function from implementation<vector_linear,V> is inherited from implementation<vector_linear, vector_naive>, unless the following partial template specialization is implemented: template<typename U> implementation<vector_linear,U,V>.
It remains to explain the role of the three parameters of implementation. In fact the second parameter keeps track of the top level variant from which V inherits. Therefore, in a static member of implementation<F,U,V>, when one needs to call a function related to another set of functionalities G, then it is fetched in implementation<G,U>. In order to illustrate the interest of this method, let us consider polynomials in the next paragraphs.
Our class polynomial<C,V> (defined in algebramix/polynomial.hpp) represents polynomials with coefficients in C using implementation variant V. Each instance of a polynomial is represented by a vector, that is a pointer with a reference counter to a structure containing a pointer to the array of coefficients of type C* with its allocated size, and an integer for the length of the considered polynomial (defined as the degree plus one). The set of functionalities includes linear operations, mainly inherited from those of the vectors (since the internal representations are the same), multiplication, division, composition, Euclidean sequences, subresultants, evaluations, Chinese remaindering, etc. All these operations are implemented for the variant polynomial_naive (in the file algebramix/polynomial_naive.hpp) with the most general but naive algorithms (with quadratic cost for multiplication and division).
The variant polynomial_dicho<W> inherits from the parameter variant W and contains implementations of classical divide and conquer algorithms: Karatsuba for the product, Sieveking's polynomial division, half-gcd, divide and conquer evaluation and interpolations [26, Chapters 8–11]. Polynomial product functions belong to the set of functionalities polynomial_multiply, and division functions to the set polynomial_divide. The division functions of polynomial_dicho<W> are implemented as static members of
template<typename U, typename W> struct implementation<polynomial_divide,U,polynomial_dicho<W> >
They make use of the product functions of implementation<polynomial_multiply,U>.
Let us now consider polynomials with modular integer coefficients and let us describe how the Kronecker substitution product is plugged in. In a nutshell, the coefficients of the polynomials are first lifted into integers. The lifted integer polynomials are next evaluated at a sufficiently large power of two, and we compute the product of the resulting integers. The polynomial product is retrieved by splitting the integer product into chunks and reducing them by the modulus. For details we refer the reader for instance to [26, Chapter 8]. As to our implementation, we first create the new variant polynomial_kronecker<W> on top of another variant W (see file algebramix/polynomial_kronecker.hpp), which inherits from W, but which only redefines the implementation of the product in
template<typename U, typename W> struct implementation<polynomial_multiply,U,polynomial_kronecker<W> >
When using the variant K defined by
typedef polynomial_dicho<polynomial_kronecker<polynomiam_naive> > > K;
the product functions in implementation<polynomial_multiply, K> correspond to the Kronecker substitution. The functions in implementation<polynomial_division, K> are inherited from
implementation<polynomial_division, K,
polynomial_dicho<polynomial_naive> >
and thus use Sieveking's division algorithm. The divisions rely in their turn on the multiplication from implementation<polynomial_multiply, K>, which benefits from Kronecker substitution. In this way, it is very easy for a user to redefine a new variant and override given functions a posteriori, without modifying existing code.
Finally, for a given mathematical template type, we define a default variant as a function of the remaining template parameters. For instance, the default variant of the parameter V in vector<C,V> is typename vector_variant<C>::type which is intended to provide users with reasonable performance. This default value is set to vector_naive, but can be overwritten for special coefficients. The default variant is also the default value of the variant parameter in the declaration of vector. Users can thus simply write vector<C>. The same mechanism applies to polynomials, series, matrices, etc.
In
Operations on vectors of integer and numeric types are implemented in a hierarchy of variants. One major variant controls the way loops are unrolled. Another important variant is dedicated to memory alignement.
In order to benefit from vectorized modular arithmetic within the fast Fourier transform, we implemented a vectorized variant of the classical in-place algorithm. In this section, we describe this variant and its applications to polynomial and matrix multiplication.
Let 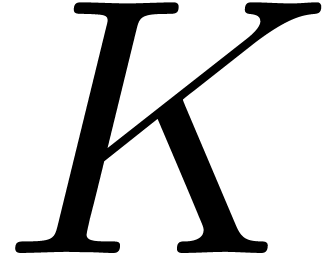 be a commutative field, let
be a commutative field, let  with
with 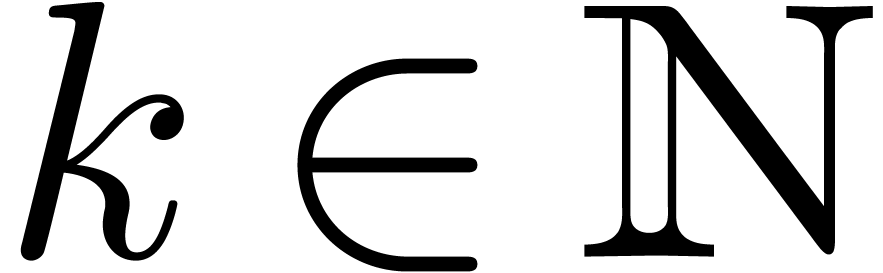 , and let
, and let 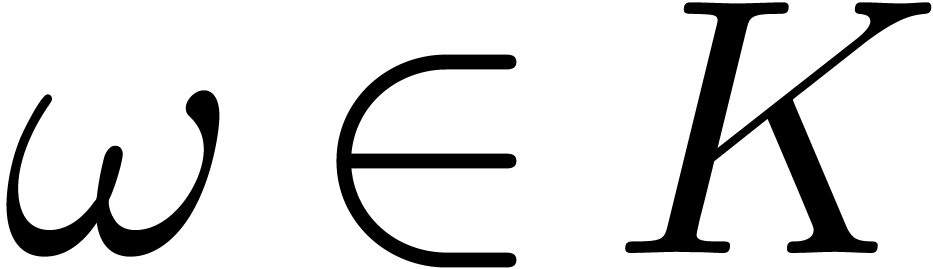 be a primitive
be a primitive 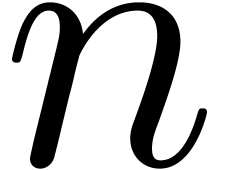 -th
root of unity, which means that
-th
root of unity, which means that 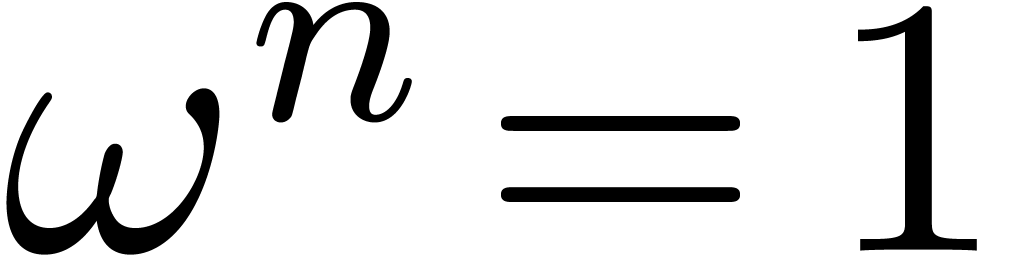 ,
and
,
and 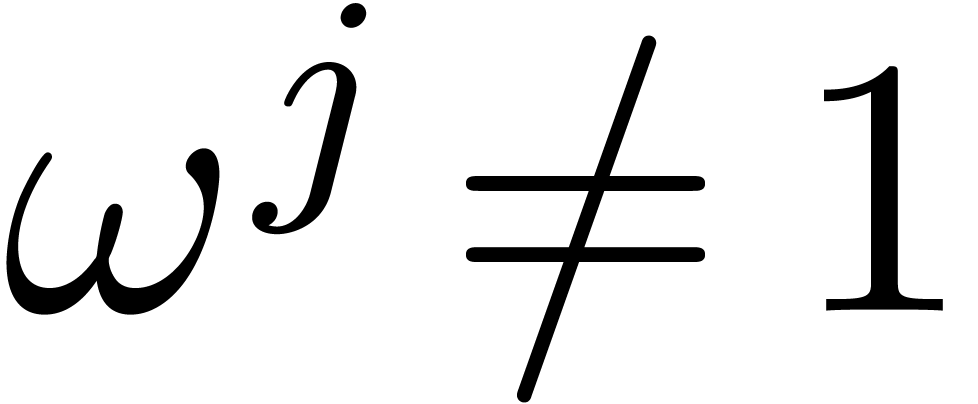 for all
for all  .
Let
.
Let  be a
be a 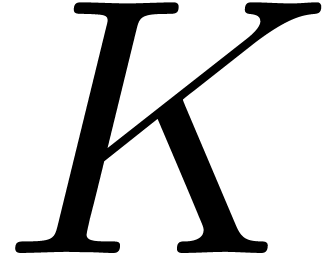 -vector
space. The fast Fourier transform (with respect to
-vector
space. The fast Fourier transform (with respect to  ) of an
) of an 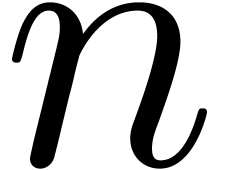 -tuple
-tuple
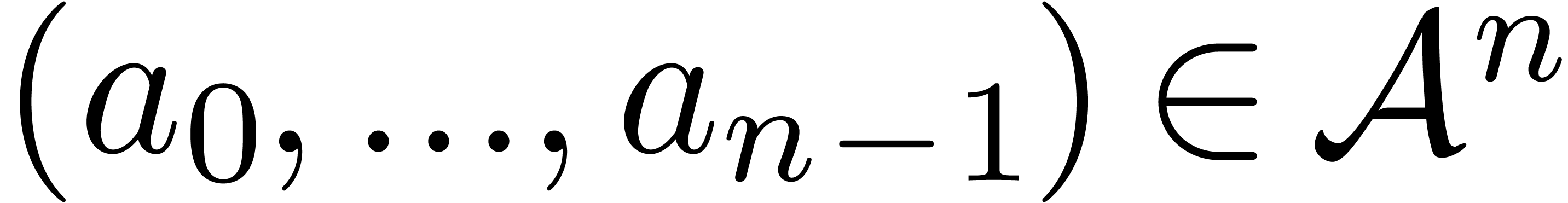 is the
is the  -tuple
-tuple
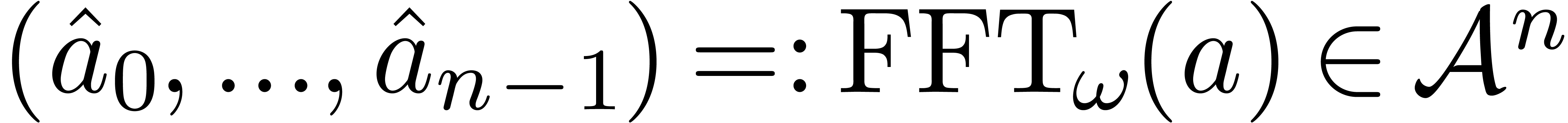 with
with
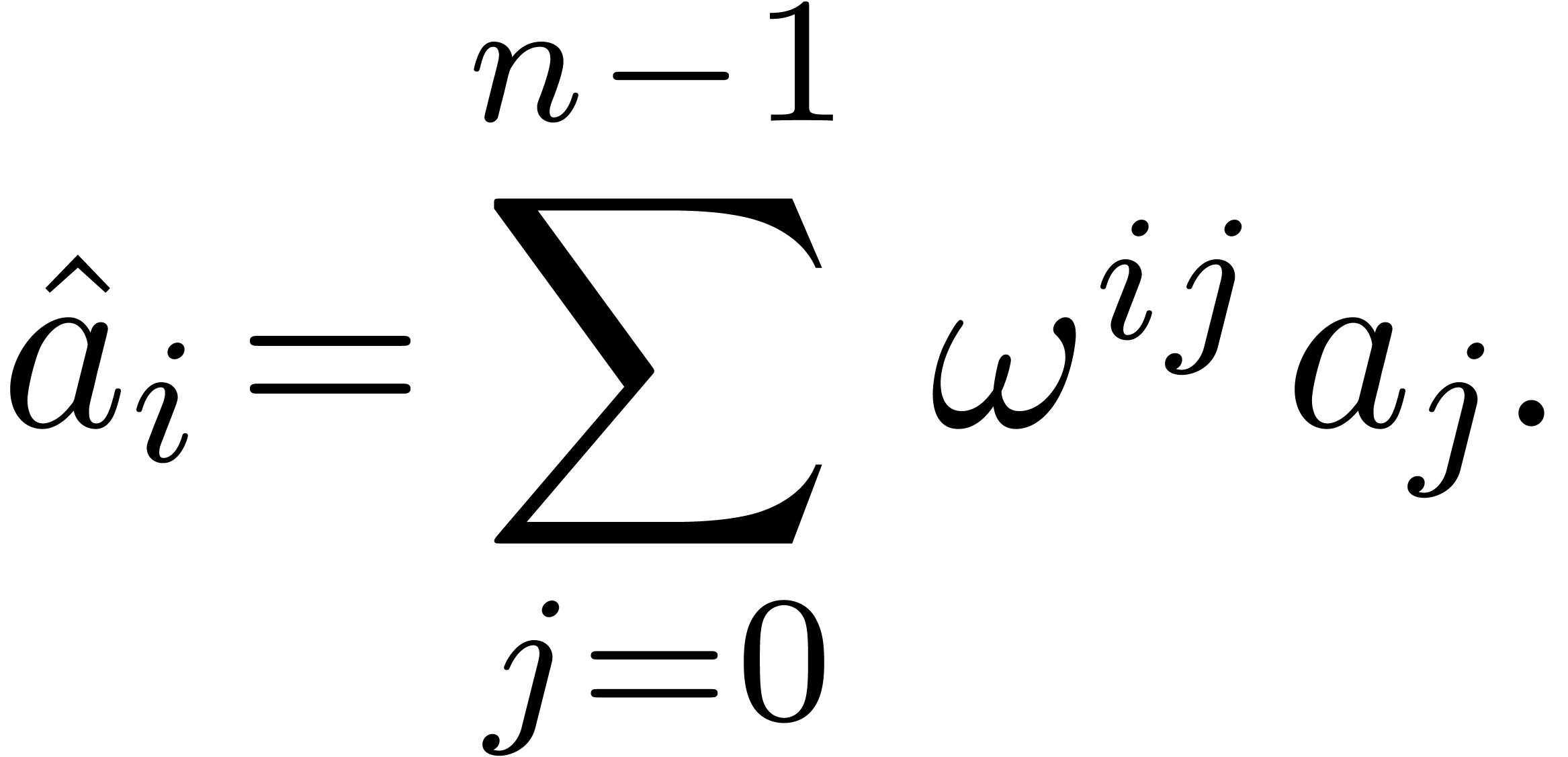
In other words, 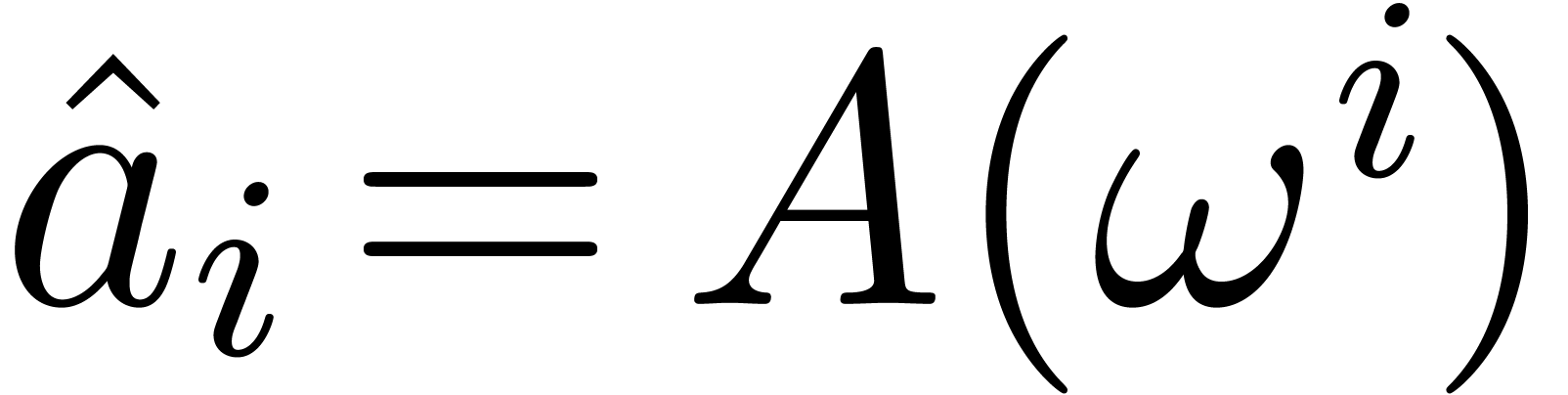 , where
, where 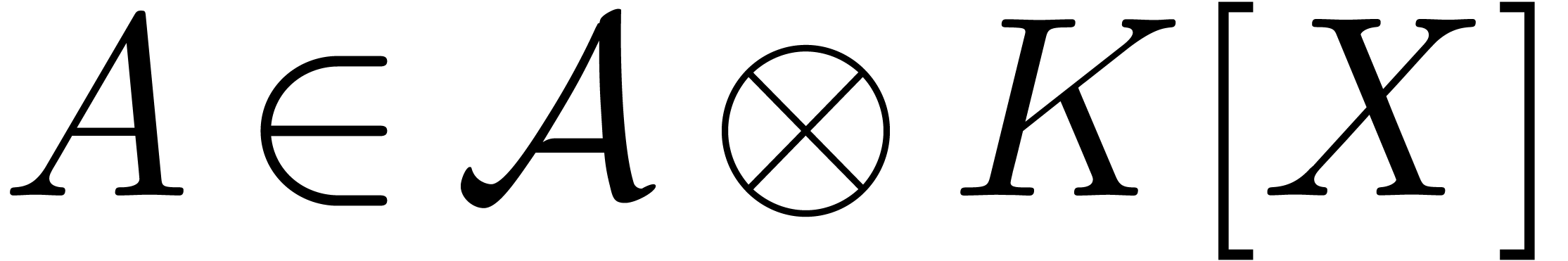 denotes the element
denotes the element 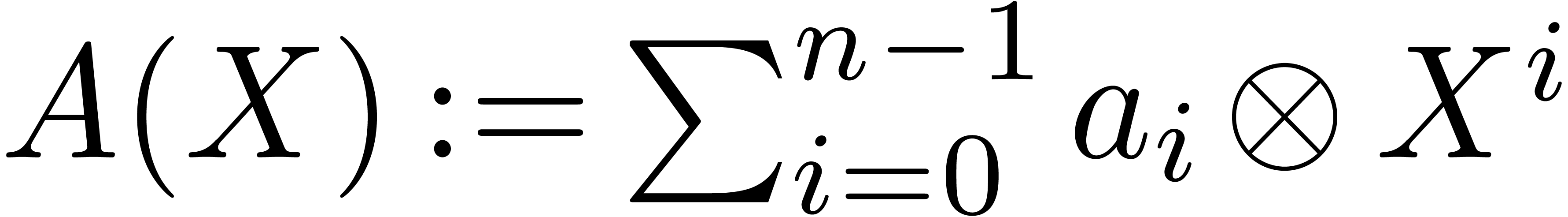 .
If
.
If  has binary expansion
has binary expansion 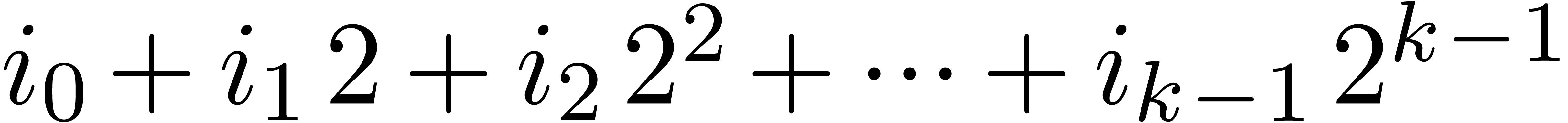 , then we write
, then we write 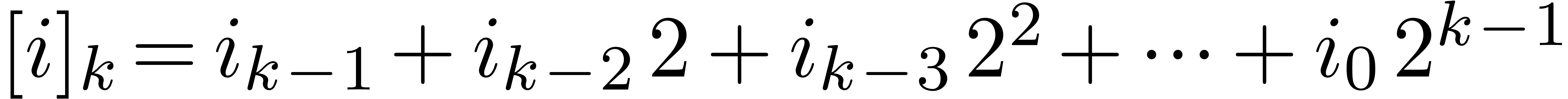 for the
bitwise mirror of
for the
bitwise mirror of 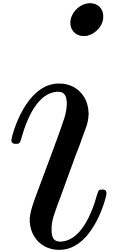 in length
in length 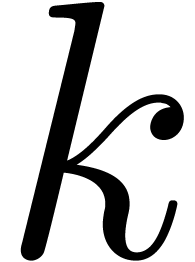 . Following the terminology of [40], the truncated Fourrier transform (
. Following the terminology of [40], the truncated Fourrier transform (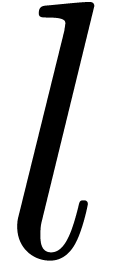 -tuple
-tuple 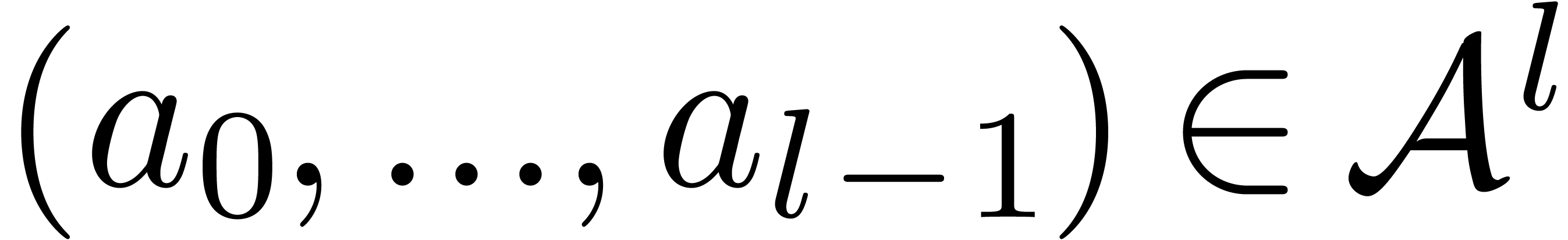 (with respect to
(with respect to  ) is
) is
The classical FFT and 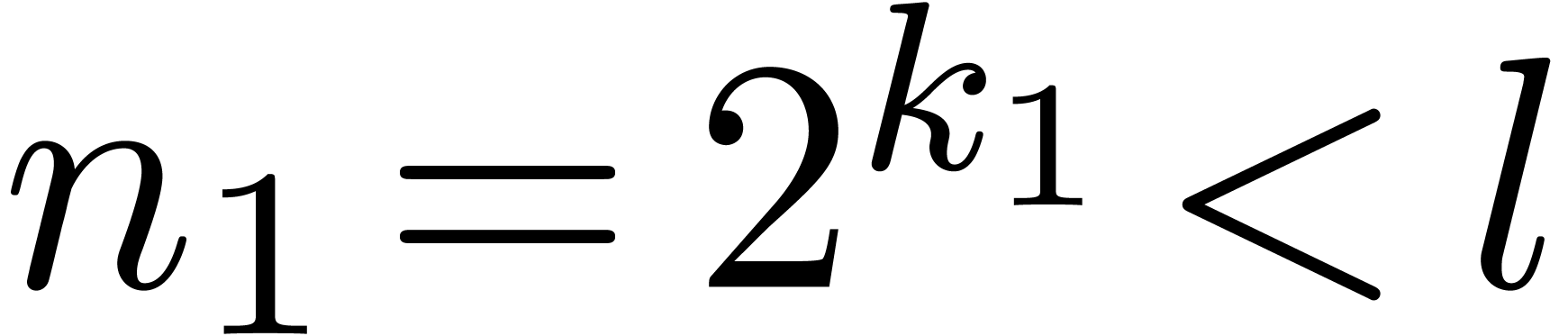 be a
divisor of
be a
divisor of  . The following
algorithm reduces one
. The following
algorithm reduces one 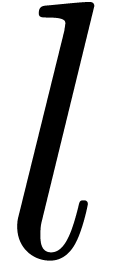 over
over 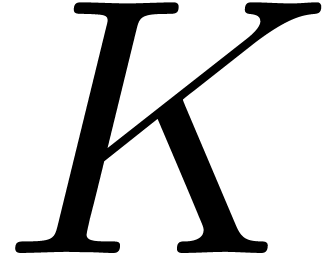 into one
into one 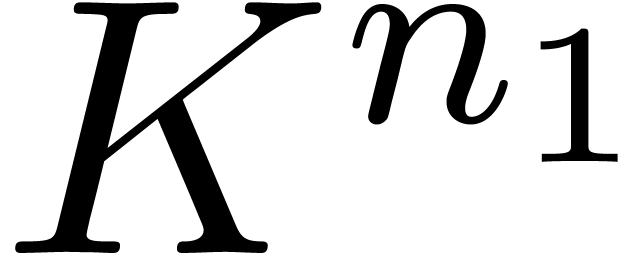 of size
of size  and into one
and into one
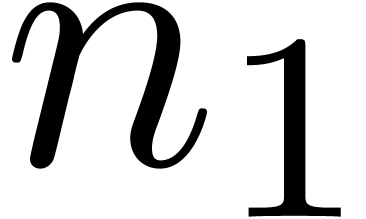 over
over 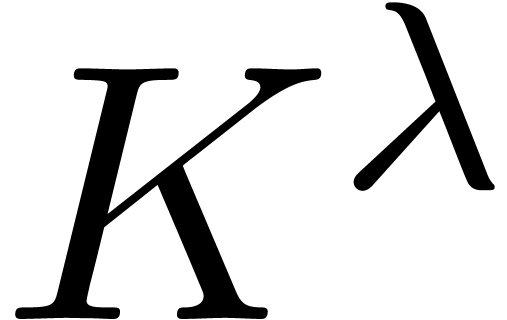 .
.
Algorithm
For convenience we consider that  for all
for all
 .
.
Let  for all
for all  .
.
Compute 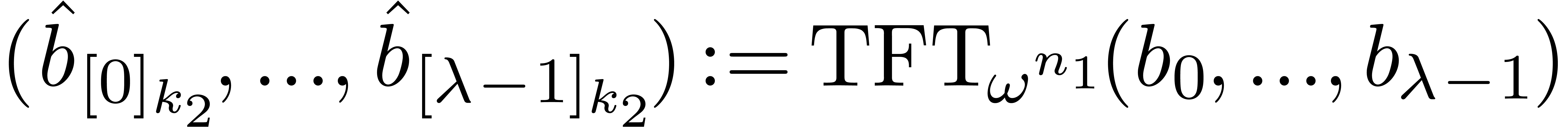 .
.
Let  for all
for all  .
.
Compute 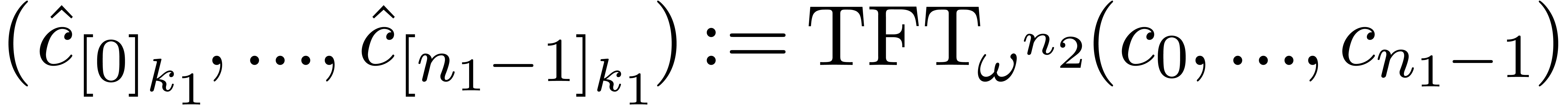 .
.
Return  .
.
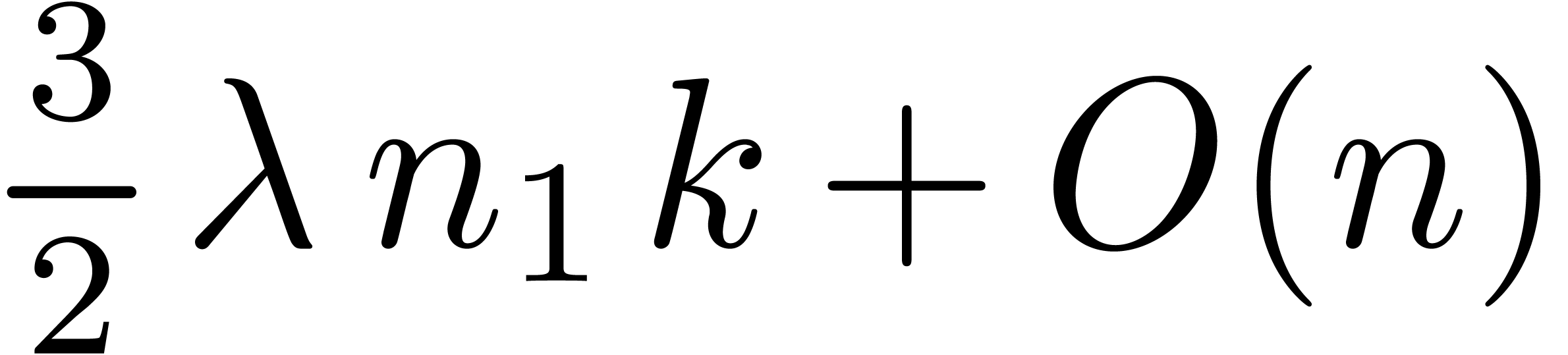 operations in
operations in 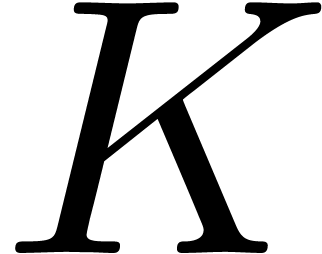 ,
assuming given all the powers of
,
assuming given all the powers of  .
.
Proof. Let  for
for  , so that we have
, so that we have  and
and 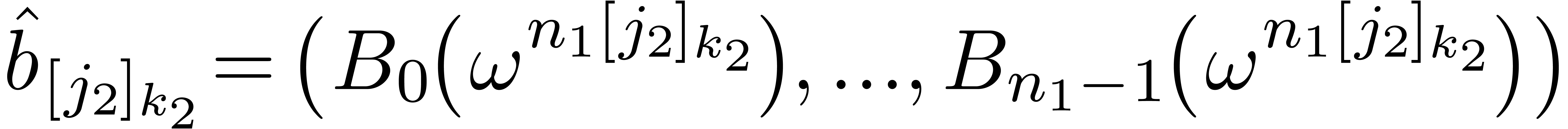 for all
for all  .
Let
.
Let  and
and  .
A straightforward calculation leads to
.
A straightforward calculation leads to 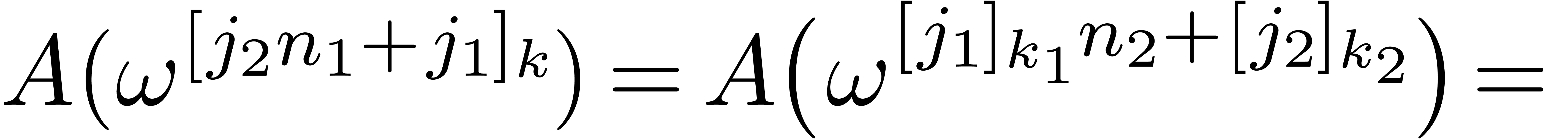
By [40, Theorem 1] step 1 can be done with 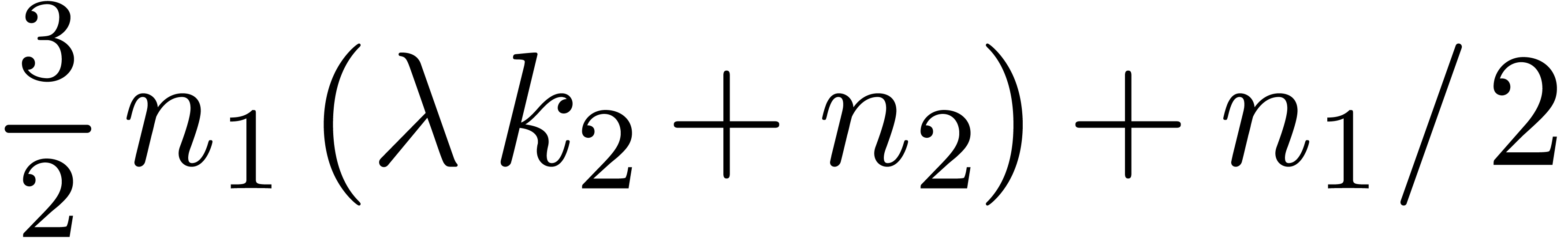 operations in
operations in  . Step 2
involves
. Step 2
involves 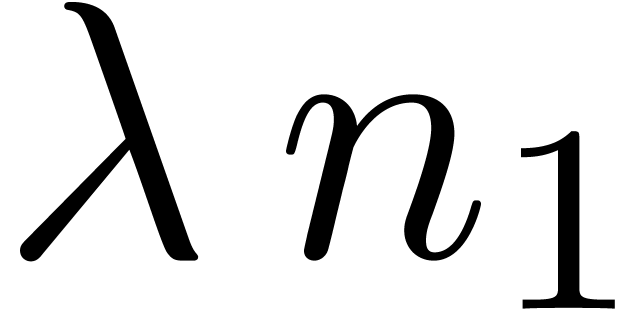 operations and step 3 takes
operations and step 3 takes 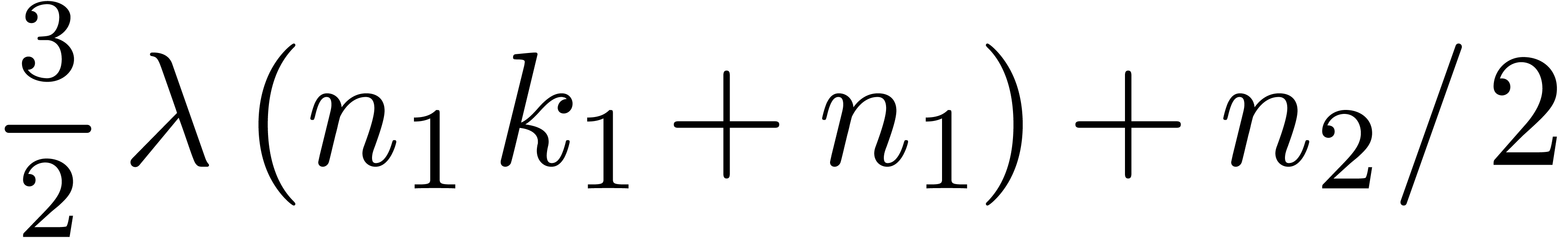 more operations.
more operations.
Inverting Algorithm 1 is straightforward: it suffices to
invert steps from 4 to 1 and use the inverse of the 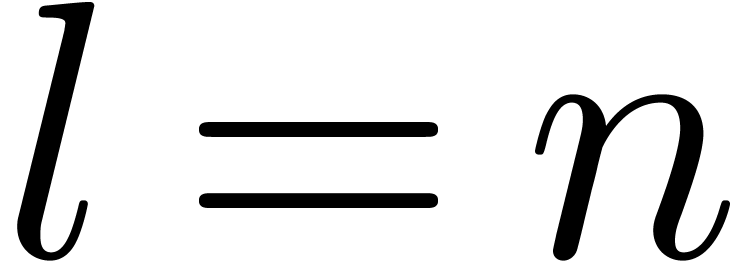 , then Algorithm 1
can be used to compute the
, then Algorithm 1
can be used to compute the 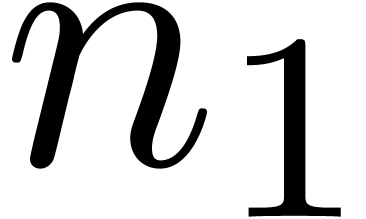 is taken to be the size corresponding to a machine vector,
then most of the
is taken to be the size corresponding to a machine vector,
then most of the 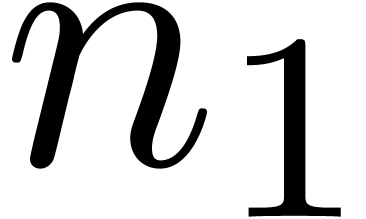 much larger, for instance of
order
much larger, for instance of
order 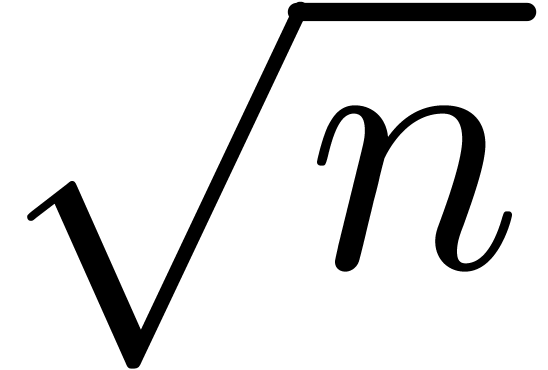 , so that the
, so that the 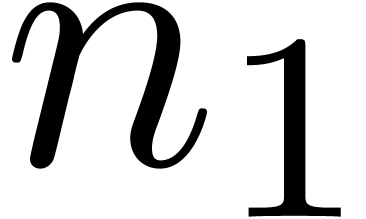 of order
of order 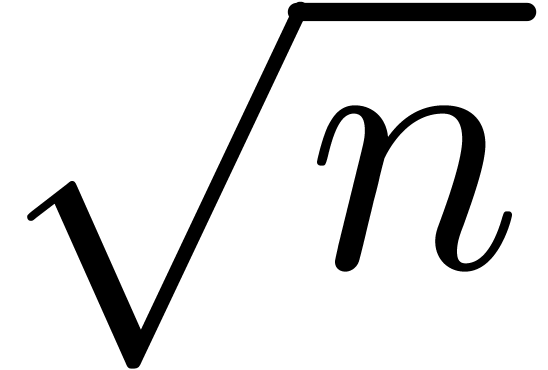 , this algorithm is
very close to the cache-friendly version of the
, this algorithm is
very close to the cache-friendly version of the
A critical point in large sizes becomes the matrix transposition,
necessary to reorganize data in steps 1 and 4 of Algorithm 1.
We designed ad hoc cache-friendly 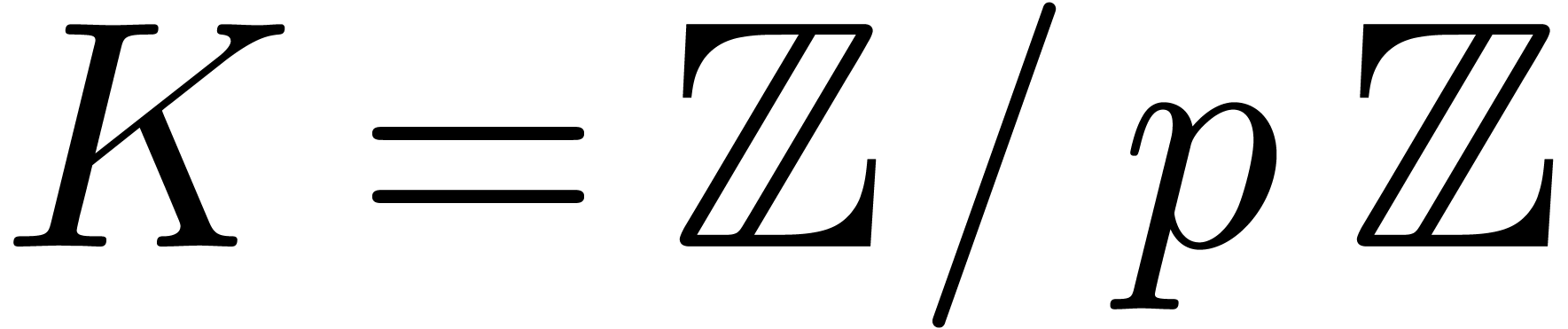 with
with 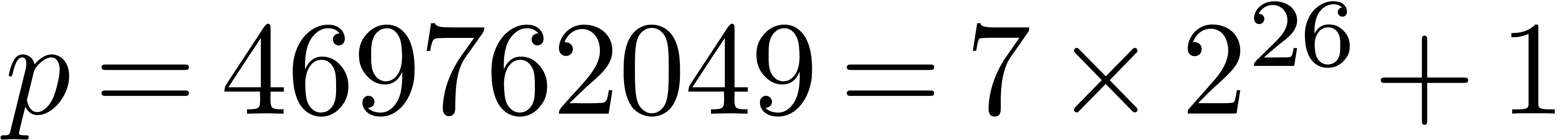 in
in
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 12 concerns 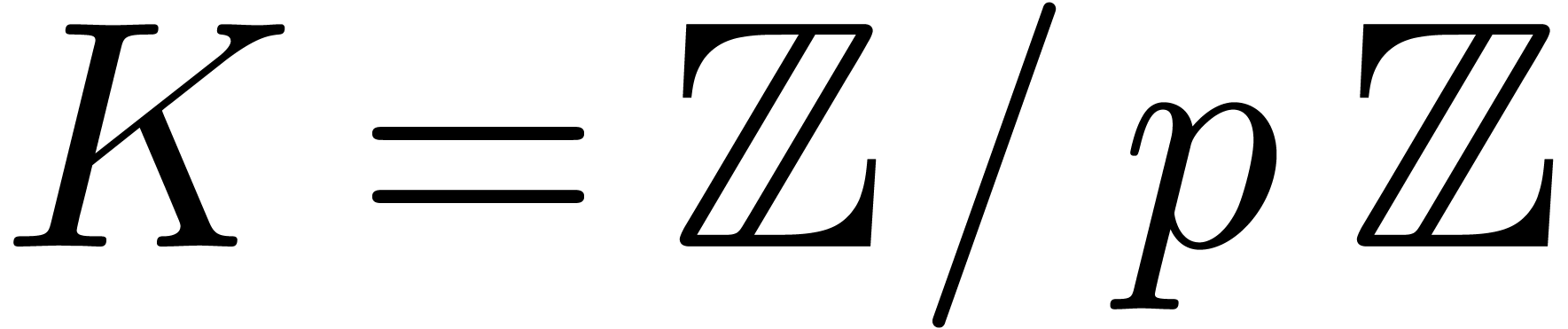 and
and 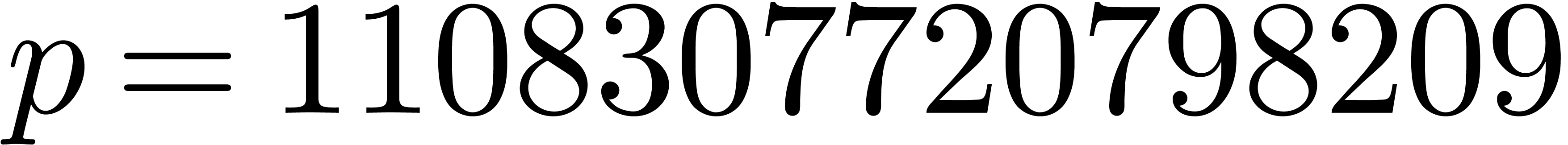 . We
compare
. We
compare
|
||||||||||||||||||||||||||||||||||||||||||
For the sake of comparison, we also report on the performance of the
|
||||||||||||||||||||||||||||||||||||||||||
One major application of the 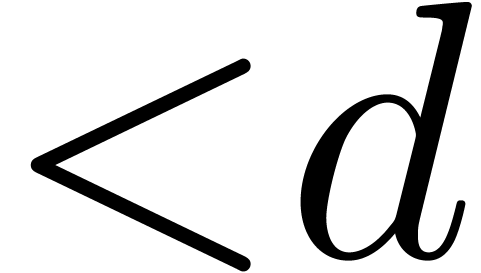 over
over  . For this task, we
compare
. For this task, we
compare
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If 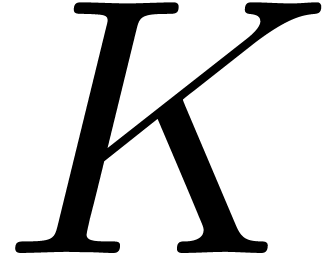 is a field with sufficiently many primitive
roots of unity of order a power of two, then two
is a field with sufficiently many primitive
roots of unity of order a power of two, then two  matrices
matrices  and
and  with
coefficients in
with
coefficients in 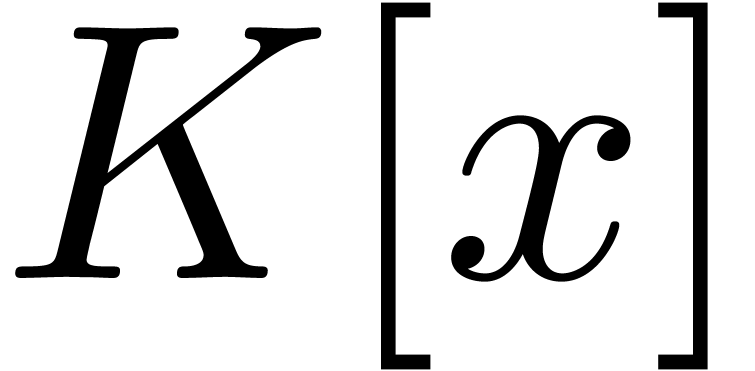 of degrees
of degrees 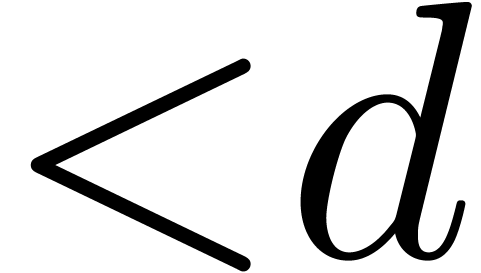 can be multiplied by performing
can be multiplied by performing 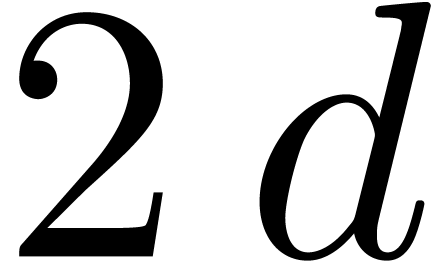 on each of the coefficients of
on each of the coefficients of  and
and  , by
multiplying
, by
multiplying 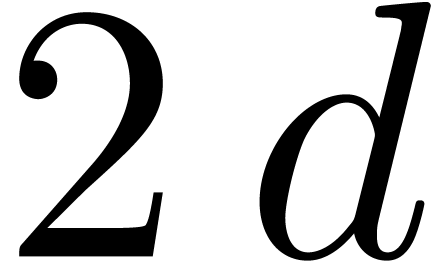 matrices over
matrices over 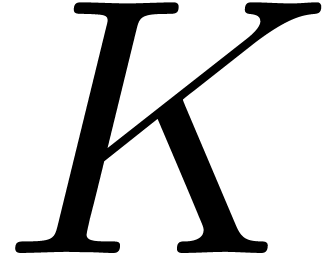 , and finally by recovering the matrix product
through coefficient-wise inverse transforms. This requires
, and finally by recovering the matrix product
through coefficient-wise inverse transforms. This requires 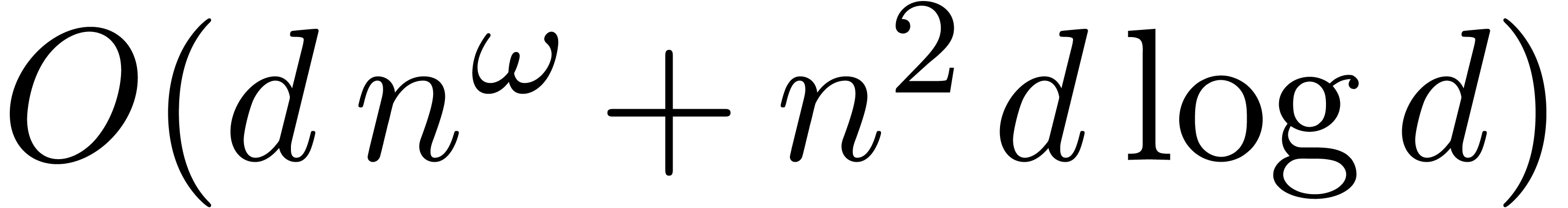 operations in
operations in 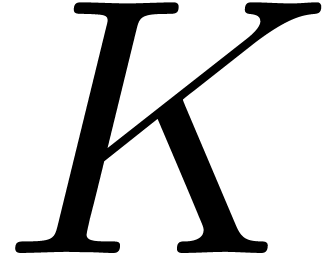 ,
where
,
where 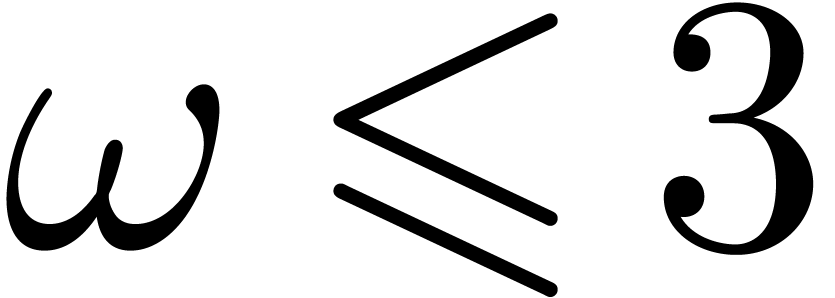 is the exponent of
is the exponent of  matrix multiplication over
matrix multiplication over 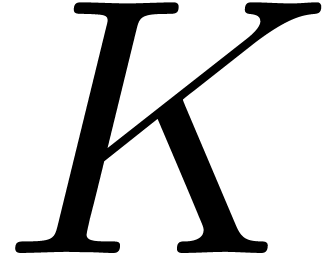 .
In general, most of the time is spent in the matrix products over
.
In general, most of the time is spent in the matrix products over 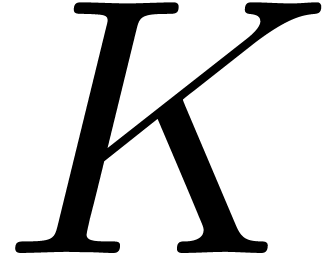 . Nevertheless, if
. Nevertheless, if 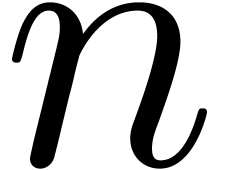 remains sufficiently small with respect to
remains sufficiently small with respect to  ,
then most of the time is spent in the fast Fourier transforms, and our
method becomes most efficient. Table 15 compares this
approach to naive multiplication, and to
,
then most of the time is spent in the fast Fourier transforms, and our
method becomes most efficient. Table 15 compares this
approach to naive multiplication, and to
|
||||||||||||||||||||||||||||
Another important application of fast Fourier transforms is integer
multiplication. The method that we have implemented is based on
Kronecker segmentation and the three-prime FFT (see
[55] and [26, Section 8.3]). Let 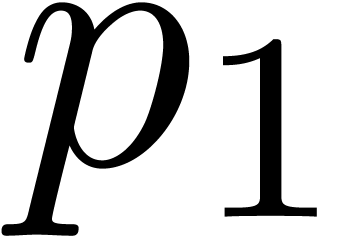 ,
, 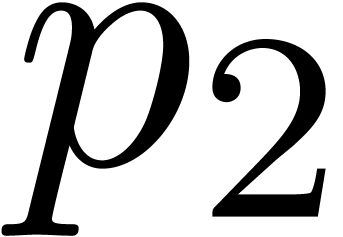 and
and 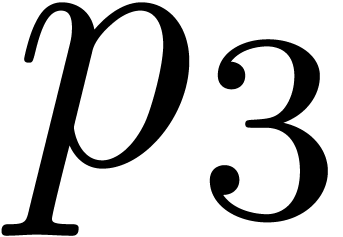 be three prime numbers. The two integers
be three prime numbers. The two integers  and
and
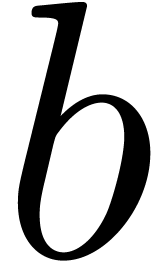 of at most
of at most 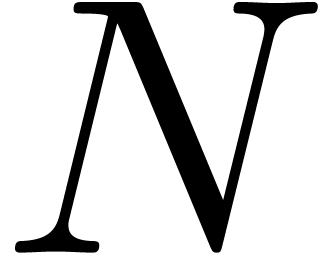 bits to be
multiplied are split into chunks of a suitable bit-size
bits to be
multiplied are split into chunks of a suitable bit-size 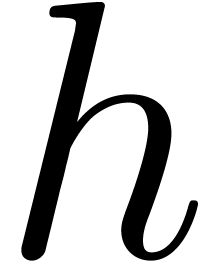 and converted into polynomials
and converted into polynomials  and
and  of
of  of degrees
of degrees 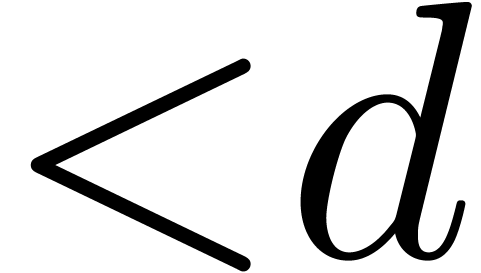 , with
, with  ,
,
 and
and  .
The maximum bit-size of the coefficients of the product
.
The maximum bit-size of the coefficients of the product 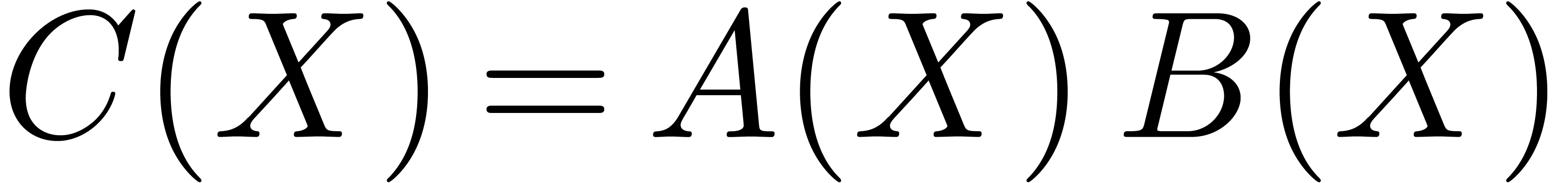 is at most
is at most 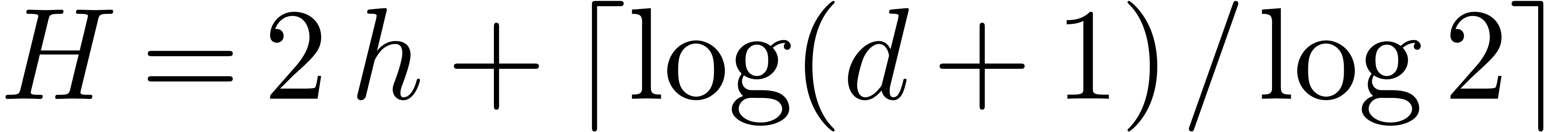 . The parameter
. The parameter
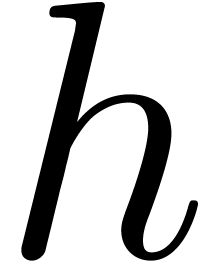 is taken such that
is taken such that  is
minimal under the constraint that
is
minimal under the constraint that 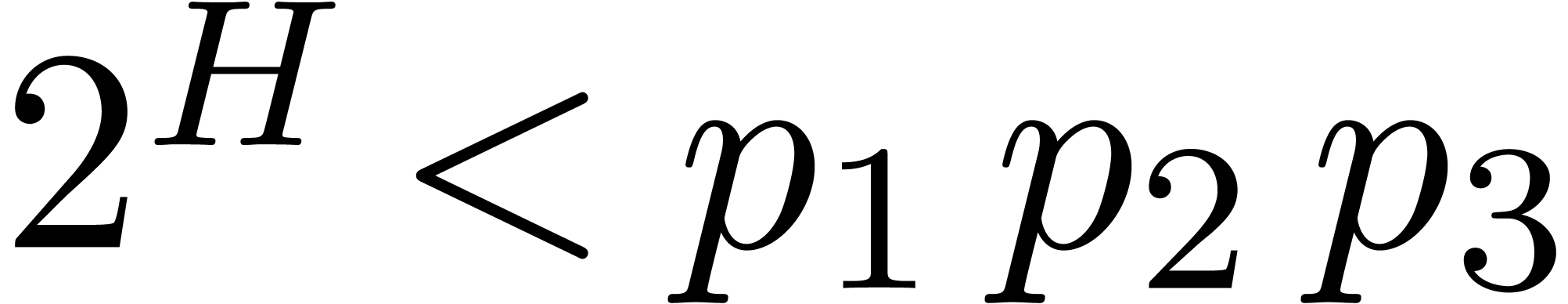 .
The polynomial
.
The polynomial  can then be recovered from its
values computed modulo
can then be recovered from its
values computed modulo 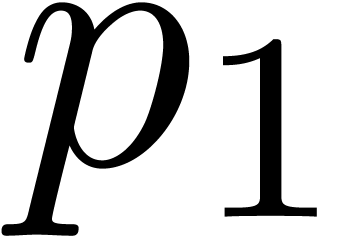 ,
, 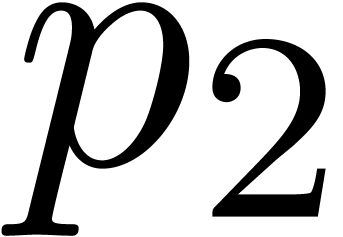 and
and 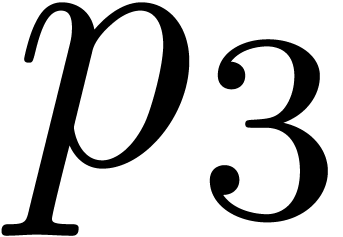 using
using 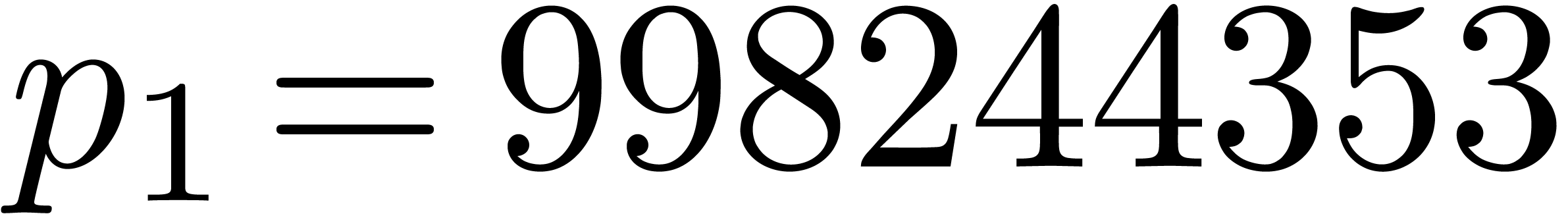 ,
, 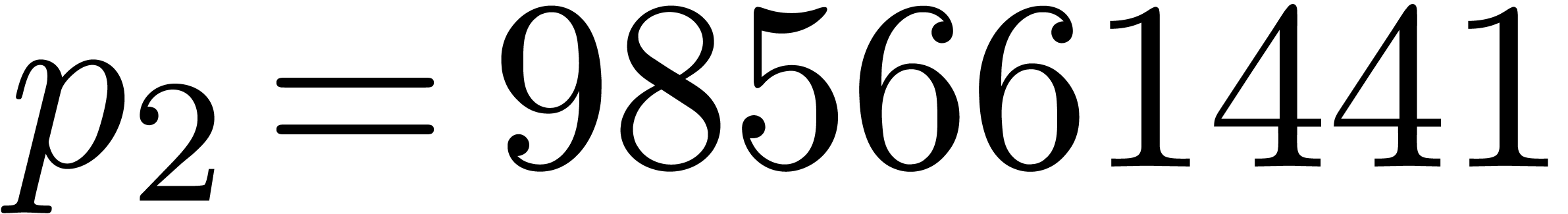 and
and 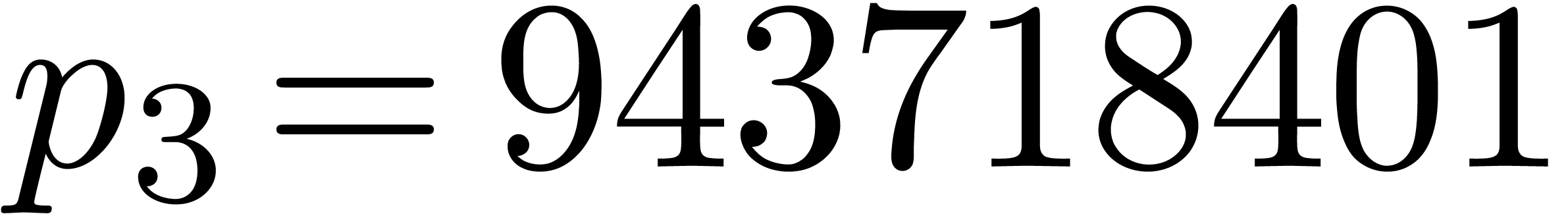 . We
compare with the timings of
. We
compare with the timings of
|
||||||||||||||||||||||||||||||||||||||||||
Similarly to polynomial matrices, small matrices over large integers can
be multiplied efficiently using modular
|
|||||||||||||||||||||||||||||||||||
Nowadays
The use of  matrices of 32-bit
integers using
matrices of 32-bit
integers using
As a final comment we would like to emphasize that
D. Abrahams and A. Gurtovoy. C++ Template Metaprogramming: Concepts, Tools, and Techniques from Boost and Beyond. Addison Wesley, 2004.
A. V. Aho, J. E. Hopcroft, and J. D. Ullman. The design and analysis of computer algorithms. Addison-Wesley series in computer science and information processing. Addison-Wesley Pub. Co., 1974.
R. Alverson. Integer division using reciprocals. In Proceedings of the Tenth Symposium on Computer Arithmetic, pages 186–190. IEEE Computer Society Press, 1991.
H. G. Baker. Computing A*B (mod N) efficiently in ANSI C. SIGPLAN Not., 27(1):95–98, 1992.
B. Bank, M. Giusti, J. Heintz, G. Lecerf, G. Matera, and P. Solernó. Degeneracy loci and polynomial equation solving. Accepted for publication to Foundations of Computational Mathematics. Preprint available from http://arxiv.org/abs/1306.3390, 2013.
N. Bardis, A. Drigas, A. Markovskyy, and J. Vrettaros. Accelerated modular multiplication algorithm of large word length numbers with a fixed module. In M. D. Lytras, P. Ordonez de Pablos, A. Ziderman, A. Roulstone, H. Maurer, and J. B. Imber, editors, Organizational, Business, and Technological Aspects of the Knowledge Society, volume 112 of Communications in Computer and Information Science, pages 497–505. Springer Berlin Heidelberg, 2010.
P. Barrett. Implementing the Rivest Shamir and Adleman public key encryption algorithm on a standard digital signal processor. In A. Odlyzko, editor, Advances in Cryptology – CRYPTO' 86, volume 263 of Lect. Notes Comput. Sci., pages 311–323. Springer Berlin Heidelberg, 1987.
D. J. Bernstein, Hsueh-Chung Chen, Ming-Shing Chen, Chen-Mou Cheng, Chun-Hung Hsiao, Tanja Lange, Zong-Cing Lin, and Bo-Yin Yang. The billion-mulmod-per-second PC. In SHARCS'09 Special-purpose Hardware for Attacking Cryptographic Systems: 131, 2009. http://cr.yp.to/djb.html.
D. J. Bernstein, Tien-Ren Chen, Chen-Mou Cheng, Tanja Lange, and Bo-Yin Yang. ECM on graphics cards. In A. Joux, editor, Advances in Cryptology - EUROCRYPT 2009, volume 5479 of Lect. Notes Comput. Sci., pages 483–501. Springer Berlin Heidelberg, 2009.
J. Berthomieu, G. Lecerf, and G. Quintin. Polynomial root finding over local rings and application to error correcting codes. Appl. Alg. Eng. Comm. Comp., 24(6):413–443, 2013.
J. Berthomieu, J. van der Hoeven, and G. Lecerf.
Relaxed algorithms for  -adic
numbers. J. Théor. Nombres Bordeaux,
23(3):541–577, 2011.
-adic
numbers. J. Théor. Nombres Bordeaux,
23(3):541–577, 2011.
D. Bini and V. Y. Pan. Polynomial and Matrix Computations: Fundamental Algorithms. Progress in Theoretical Computer Science. Birkhauser Verlag GmbH, 2012.
Boost team. Boost (C++ libraries). Software available at http://www.boost.org, from 1999.
W. Bosma, J. Cannon, and C. Playoust. The Magma algebra system. I. The user language. J. Symbolic Comput., 24(3-4):235–265, 1997.
A. Bosselaers, R. Govaerts, and J. Vandewalle. Comparison of three modular reduction functions. In D. R. Stinson, editor, Advances in Cryptology — CRYPTO' 93, volume 773 of Lect. Notes Comput. Sci., pages 175–186. Springer Berlin Heidelberg, 1994.
British Standards Institution. The C standard: incorporating Technical Corrigendum 1: BS ISO/IEC 9899/1999. John Wiley, 2003.
CLANG, a C language family frontend for LLVM. Software available at http://clang.llvm.org, from 2007.
J.-G. Dumas, T. Gautier, C. Pernet, and B. D. Saunders. LinBox founding scope allocation, parallel building blocks, and separate compilation. In K. Fukuda, J. van der Hoeven, M. Joswig, and N. Takayama, editors, Mathematical Software – ICMS 2010, volume 6327 of Lect. Notes Comput. Sci., pages 77–83. Springer Berlin Heidelberg, 2010.
J.-G. Dumas, P. Giorgi, and C. Pernet. FFPACK: Finite field linear algebra package. In J. Schicho, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 119–126. ACM Press, 2004.
J.-G. Dumas, P. Giorgi, and C. Pernet. Dense linear algebra over word-size prime fields: The FFLAS and FFPACK packages. ACM Trans. Math. Softw., 35(3):19:1–19:42, 2008.
A. Fog. Instruction tables. Lists of instruction latencies, throughputs and micro-operation breakdowns for Intel, AMD and VIA CPUs. http://www.agner.org/optimize, Copenhagen University College of Engineering, 2012.
A. Fog. Optimizing software in C++. An optimization guide for Windows, Linux and Mac platforms. http://www.agner.org/optimize, Copenhagen University College of Engineering, 2012.
A. Fog. Optimizing subroutines in assembly language. An optimization guide for x86 platforms. http://www.agner.org/optimize, Copenhagen University College of Engineering, 2012.
L. Fousse, G. Hanrot, V. Lefèvre, P. Pélissier, and P. Zimmermann. MPFR: A multiple-precision binary floating-point library with correct rounding. ACM Trans. Math. Software, 33(2), 2007. Software available at http://www.mpfr.org.
M. Frigo and S. G. Johnson. The design and implementation of FFTW3. Proc. IEEE, 93(2):216–231, 2005.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge Univ. Press, 2nd edition, 2003.
GCC, the GNU Compiler Collection. Software available at http://gcc.gnu.org, from 1987.
K. Geddes, G. Gonnet, and Maplesoft. Maple (TM). http://www.maplesoft.com/products/maple, from 1980.
P. Giorgi, Th. Izard, and A. Tisserand. Comparison of modular arithmetic algorithms on GPUs. In B. Chapman, F. Desprez, G. R. Joubert, A. Lichnewsky, F. Peters, and Th. Priol, editors, Parallel Computing: From Multicores and GPU's to Petascale, volume 19 of Advances in Parallel Computing, pages 315–322. IOS Press, 2010.
P. Giorgi and R. Lebreton. Online order basis algorithm and its impact on block Wiedemann algorithm. In Proceedings of the 2014 International Symposium on Symbolic and Algebraic Computation, ISSAC '14. ACM Press, 2014. To appear.
T. Granlund et al. GMP, the GNU multiple precision arithmetic library, from 1991. Software available at http://gmplib.org.
T. Granlund and P. L. Montgomery. Division by invariant integers using multiplication. In Proceedings of the ACM SIGPLAN 1994 conference on Programming language design and implementation, PLDI '94, pages 61–72, New York, NY, USA, 1994. ACM Press.
Sardar Anisul Haque and Marc Moreno Maza. Plain polynomial arithmetic on GPU. Journal of Physics: Conference Series, 385(1):012014, 2012.
W. Hart and the FLINT Team. FLINT: Fast Library for Number Theory, from 2008. Software available at http://www.flintlib.org.
W. Hart and the MPIR Team. MPIR, Multiple Precision Integers and Rationals, from 2010. Software available at http://www.mpir.org.
D. Harvey. A cache-friendly truncated FFT. Theoret. Comput. Sci., 410(27–29):2649–2658, 2009.
D. Harvey and D. S. Roche. An in-place truncated Fourier transform and applications to polynomial multiplication. In S. M. Watt, editor, Proceedings of the 2010 International Symposium on Symbolic and Algebraic Computation, ISSAC '10, pages 325–329, New York, NY, USA, 2010. ACM Press.
D. Harvey and A. V. Sutherland. Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time. Algorithmic Number Theory 11th International Symposium (ANTS XI), 2014. To appear.
W. Hasenplaugh, G. Gaubatz, and V. Gopal. Fast modular reduction. In P. Kornerup and J.-M. Muller, editors, 18th IEEE Symposium on Computer Arithmetic, ARITH '07, pages 225–229. IEEE Computer Society, 2007.
J. van der Hoeven. The truncated Fourier transform and applications. In J. Schicho, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 290–296. ACM Press, 2004.
J. van der Hoeven and G. Lecerf. Interfacing Mathemagix with C++. In M. Monagan, G. Cooperman, and M. Giesbrecht, editors, Proceedings of the 2013 International Symposium on Symbolic and Algebraic Computation, ISSAC '13, pages 363–370. ACM Press, 2013.
J. van der Hoeven and G. Lecerf. Mathemagix User
Guide. HAL, 2013.
http://hal.archives-ouvertes.fr/hal-00785549.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial and series multiplication. J. Symbolic Comput., 50:227–254, 2013.
J. van der Hoeven, G. Lecerf, B. Mourain, Ph. Trébuchet, J. Berthomieu, D. Diatta, and A. Mantzaflaris. Mathemagix, the quest of modularity and efficiency for symbolic and certified numeric computation. ACM SIGSAM Communications in Computer Algebra, 177(3), 2011. In Section "ISSAC 2011 Software Demonstrations", edited by M. Stillman, p. 166–188.
J. van der Hoeven, G. Lecerf, B. Mourrain, et al. Mathemagix, 2002–2014. Software available at http://www.mathemagix.org.
Intel Corporation. Intel (R) intrinsics guide.
Version 3.0.1, released 7/23/2013.
http://software.intel.com/en-us/articles/intel-intrinsics-guide.
Intel Corporation, 2200 Mission College Blvd., Santa
Clara, CA 95052-8119, USA. Intel (R) Architecture Instruction
Set Extensions Programming Reference, 2013. Ref.
319433-015.
http://software.intel.com/en-us/intel-isa-extensions.
Ç. Kaya Koç. Montgomery reduction with even modulus. IEE Proceedings - Computers and Digital Techniques, 141(5):314–316, 1994.
Ç. Kaya Koç, T. Acar, and Jr. Kaliski, B. S. Analyzing and comparing Montgomery multiplication algorithms. Micro, IEEE, 16(3):26–33, 1996.
D. E. Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms. Pearson Education, 3rd edition, 1997.
G. Lecerf. Mathemagix: towards large scale programming for symbolic and certified numeric computations. In K. Fukuda, J. van der Hoeven, M. Joswig, and N. Takayama, editors, Mathematical Software - ICMS 2010, Third International Congress on Mathematical Software, Kobe, Japan, September 13-17, 2010, volume 6327 of Lect. Notes Comput. Sci., pages 329–332. Springer, 2010.
P. L. Montgomery. Modular multiplication without trial division. Math. Comp., 44(170):519–521, 1985.
M. Moreno Maza and Y. Xie. FFT-Based Dense Polynomial Arithmetic on Multi-cores. In D. J. K. Mewhort, N. M. Cann, G. W. Slater, and T. J. Naughton, editors, High Performance Computing Systems and Applications, volume 5976 of Lect. Notes Comput. Sci., pages 378–399. Springer Berlin Heidelberg, 2010.
N. Nedjah and L. de Macedo Mourelle. A review of modular multiplication methods and respective hardware implementations. Informatica, 30(1):111–129, 2006.
J. M. Pollard. The fast Fourier transform in a finite field. Math. Comp., 25(114):365–374, 1971.
G. van Rossum and J. de Boer. Interactively testing remote servers using the Python programming language. CWI Quarterly, 4(4):283–303, 1991. Software available at http://www.python.org.
M. J. Schulte, J. Omar, and E. E. Jr. Swartzlander. Optimal initial approximations for the Newton-Raphson division algorithm. Computing, 53(3-4):233–242, 1994.
V. Shoup. NTL: A Library for doing Number
Theory, 2014. Software, version 6.1.0.
http://www.shoup.net/ntl.
W. A. Stein et al. Sage Mathematics Software. The Sage Development Team, from 2004. Software available at http://www.sagemath.org.
E. Thomé. Théorie algorithmique des nombres et applications à la cryptanalyse de primitives cryptographiques. http://www.loria.fr/~thome/files/hdr.pdf, 2012. Mémoire d'habilitation à diriger des recherches de l'Université de Lorraine, France.
Registered trademarks.