Guessing singular dependencies |
|
| November 4, 2023 |
|
 . This work was
partially supported by the ANR Gecko project.
. This work was
partially supported by the ANR Gecko project.
Given
|
Consider an infinite sequence 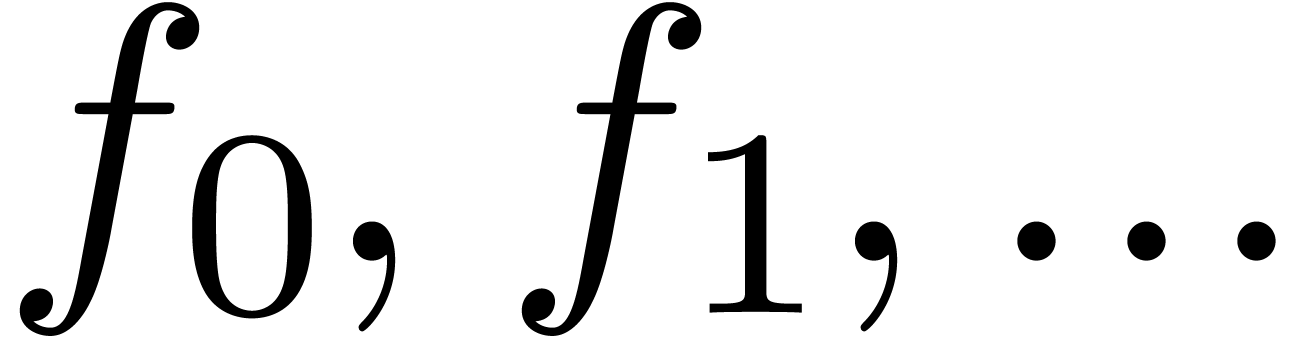 of complex
numbers. If
of complex
numbers. If 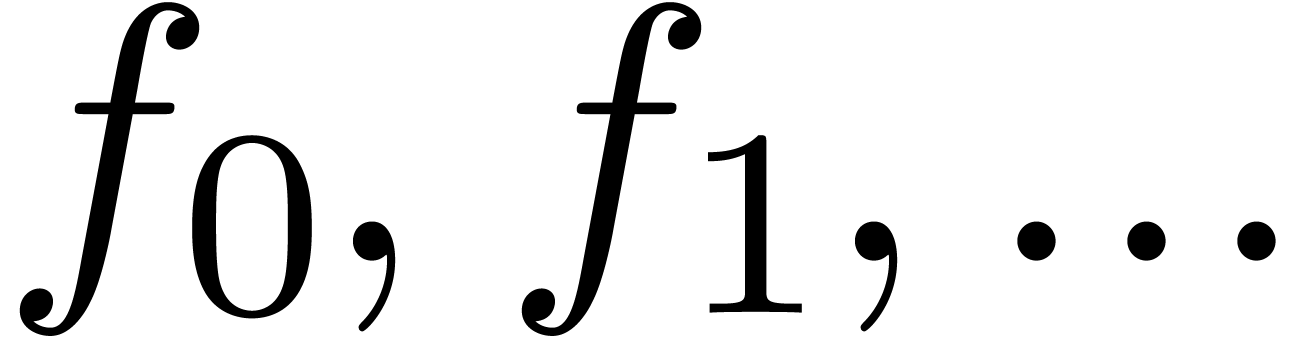 are the coefficients of a formal
power series
are the coefficients of a formal
power series  , then it is
well-known [Pól37, Wil04, FS96]
that a lot of information about the behaviour of
, then it is
well-known [Pól37, Wil04, FS96]
that a lot of information about the behaviour of  near its dominant singularity can be obtained from the asymptotic
behaviour of the sequence
near its dominant singularity can be obtained from the asymptotic
behaviour of the sequence 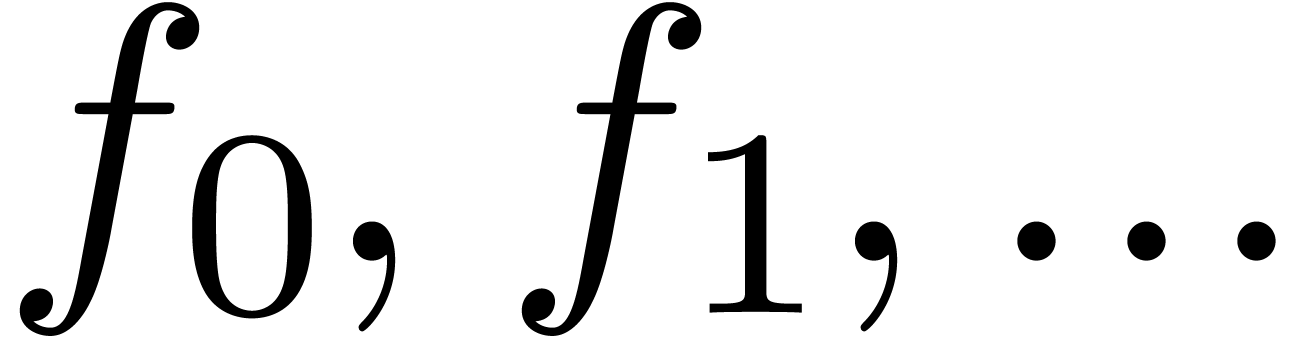 .
However, if
.
However, if  is the solution to some complicated
equation, then it can be hard to compute the asymptotic behaviour using
formal methods. On the other hand, the coefficients
is the solution to some complicated
equation, then it can be hard to compute the asymptotic behaviour using
formal methods. On the other hand, the coefficients 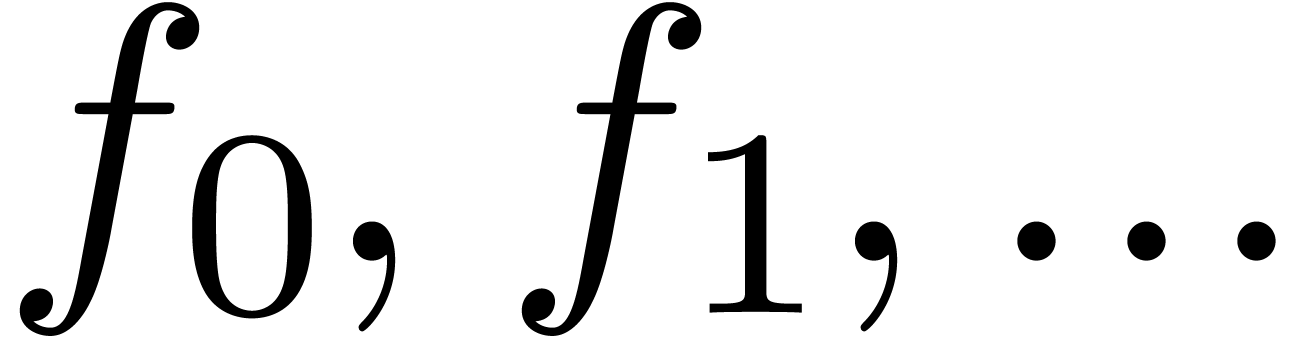 of such a solution
of such a solution  can often be computed
numerically up to a high order. This raises the question of how to
guess the asymptotic behaviour of
can often be computed
numerically up to a high order. This raises the question of how to
guess the asymptotic behaviour of 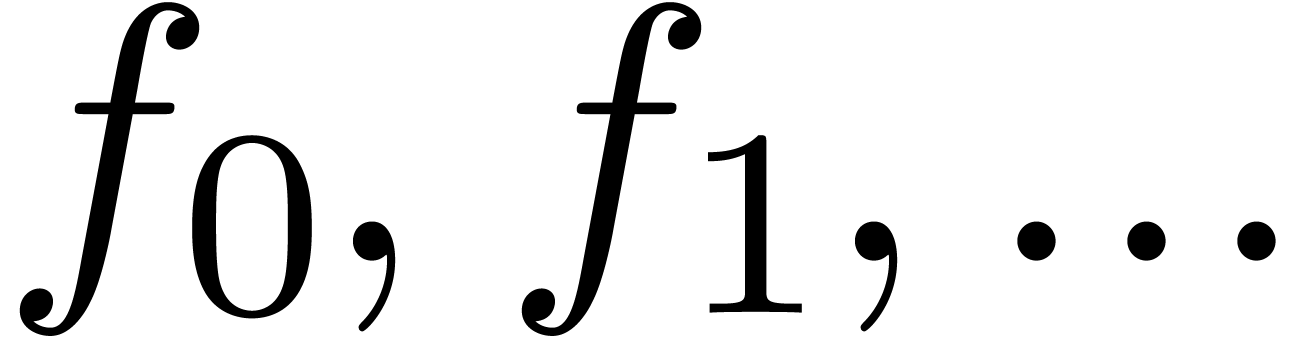 ,
based on this numerical evidence.
,
based on this numerical evidence.
In fact, the systematic integration of “guessing tools” into
symbolic computation packages would be a useful thing. Indeed, current
systems can be quite good at all kinds of formal manipulations. However,
in the daily practice of scientific discovery, it would be helpful if
these systems could also detect hidden properties, which may not be
directly apparent or expected, and whose validity generally depends on
heuristics. One well-known tool in this direction is the LLL-algorithm.
Given 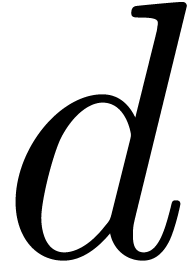 numbers
numbers 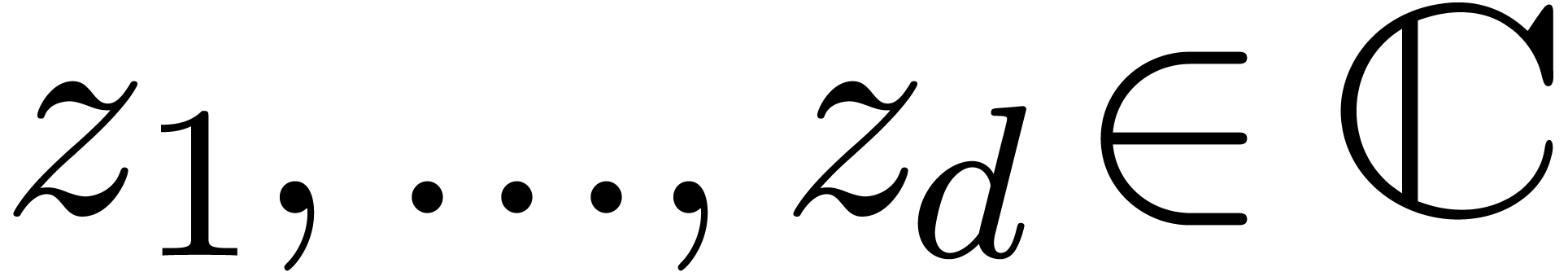 ,
it can be used in order to guess relations of the form
,
it can be used in order to guess relations of the form
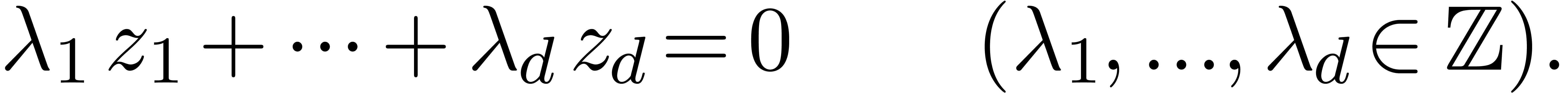 |
(1) |
Given 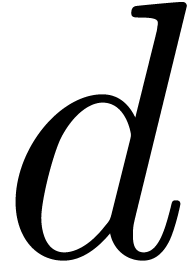 formal power series
formal power series 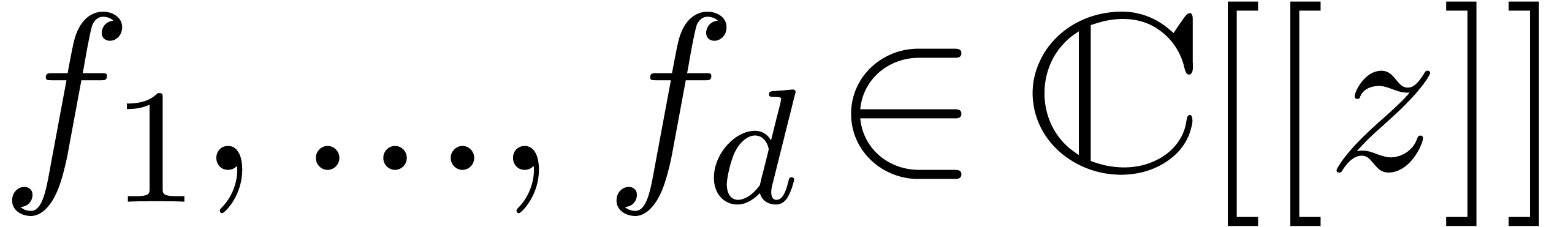 , algorithms for the computation of
Padé-Hermite forms [BL94, Der94] can be
used in order to guess linear relations
, algorithms for the computation of
Padé-Hermite forms [BL94, Der94] can be
used in order to guess linear relations
 |
(2) |
A well-known implementation is provided by the  , the
, the
 or a linear differential equation
with coefficients in
or a linear differential equation
with coefficients in 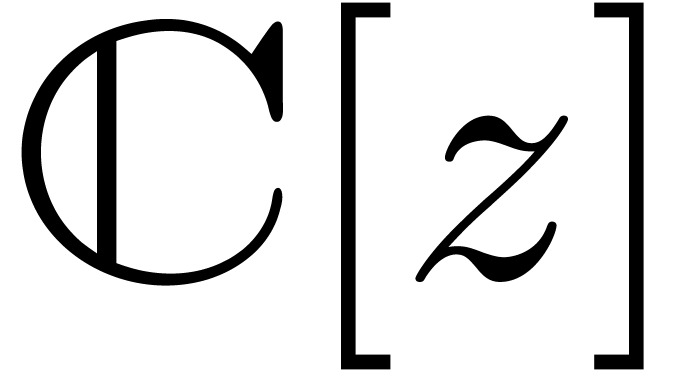 satisfied by
satisfied by  .
.
Unfortunately, many interesting formal power series  do not admit closed form formulas and are not holonomic. In that case,
we can still use asymptotic extrapolation [vdH06] in order
to guess the asymptotic behaviour of the coefficients. However, this
only provides us some rough idea about the behaviour of
do not admit closed form formulas and are not holonomic. In that case,
we can still use asymptotic extrapolation [vdH06] in order
to guess the asymptotic behaviour of the coefficients. However, this
only provides us some rough idea about the behaviour of  at its dominant singularity. In practice, it often happens that
at its dominant singularity. In practice, it often happens that  locally satisfies an algebraic or differential
equation with analytic coefficients, even though these coefficients fail
to be polynomials. In this paper, we will shall describe two approaches
to deal with this situation.
locally satisfies an algebraic or differential
equation with analytic coefficients, even though these coefficients fail
to be polynomials. In this paper, we will shall describe two approaches
to deal with this situation.
In section 2, we first present a numerical algorithm for
approximating the radius of convergence of  ,
assuming that only a finite number of its coefficients are known. In the
case when
,
assuming that only a finite number of its coefficients are known. In the
case when  admits a unique dominant isolated
singularity
admits a unique dominant isolated
singularity  , we will also
describe several approaches to find
, we will also
describe several approaches to find  .
.
In section 3, we consider the favourable situation when
there exists an algorithm for the analytic continuation of  . This algorithm should allow us to compute the
Taylor series expansion of
. This algorithm should allow us to compute the
Taylor series expansion of  not only at the
origin, but at any point on its Riemann surface. This is typically the
case when
not only at the
origin, but at any point on its Riemann surface. This is typically the
case when  is the solution of an initial value
problem [vdH07]. We will show how to exploit the mechanism
of analytic continuation in order to find so called algebraic or
Fuchsian dependencies at singularities.
is the solution of an initial value
problem [vdH07]. We will show how to exploit the mechanism
of analytic continuation in order to find so called algebraic or
Fuchsian dependencies at singularities.
In the remainder of the paper, we let 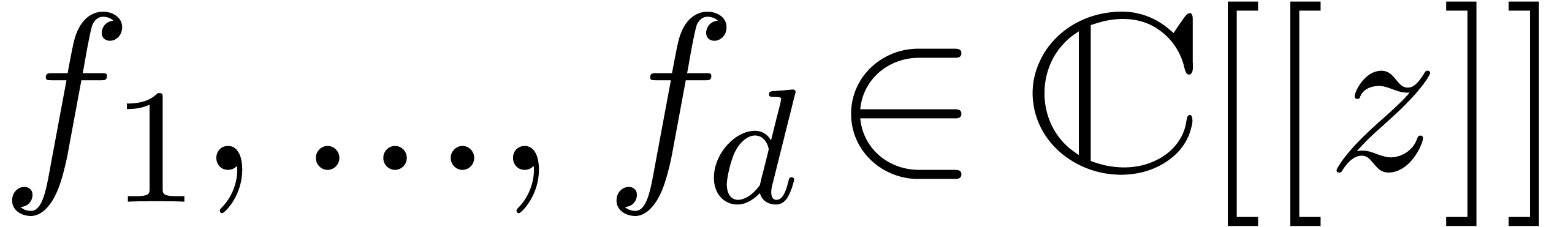 be power
series with radii of convergence at least
be power
series with radii of convergence at least  .
We assume that the coefficients of the
.
We assume that the coefficients of the 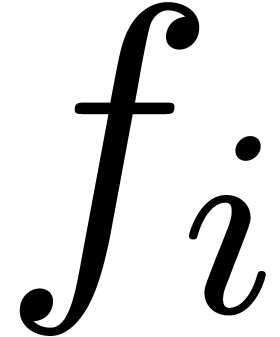 can be
computed up to a high order and with great accuracy. This is typically
the case if the
can be
computed up to a high order and with great accuracy. This is typically
the case if the 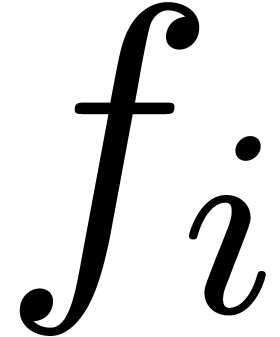 are given as explicit generating
functions or solutions to functional equations. Given a radius
are given as explicit generating
functions or solutions to functional equations. Given a radius 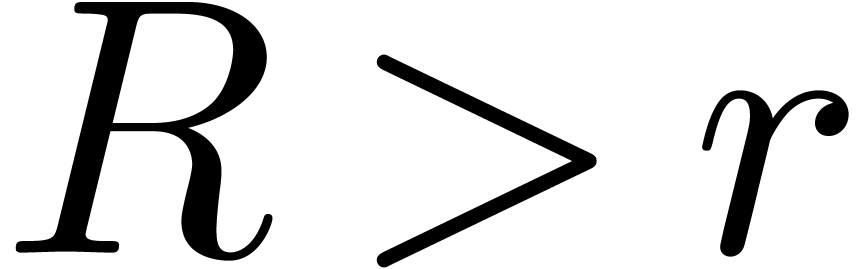 , we are interested in the
determination of linear dependencies
, we are interested in the
determination of linear dependencies
 |
(3) |
where 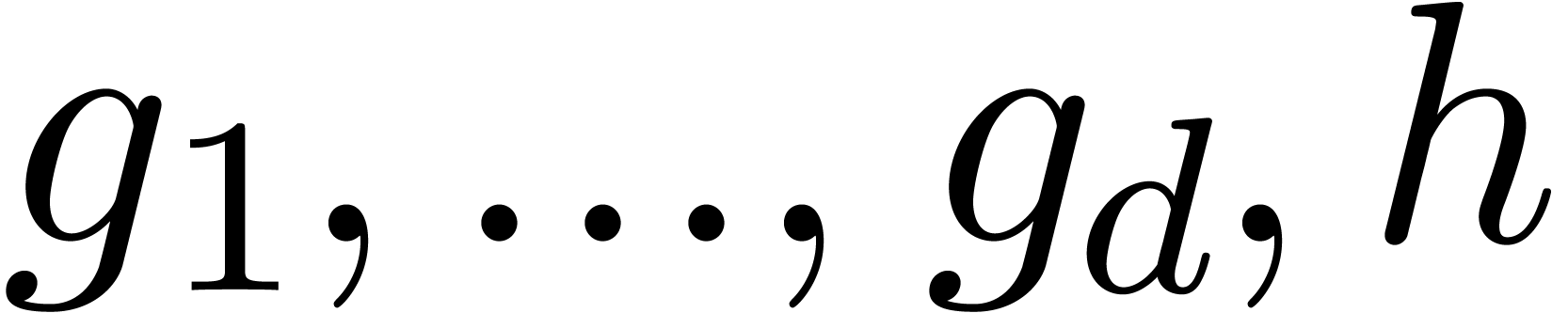 have radii of convergence strictly larger
than
have radii of convergence strictly larger
than  . In section 4,
we will describe an algorithm for doing this, based on Gram-Schmidt
orthogonalization. Modulo the change of variables
. In section 4,
we will describe an algorithm for doing this, based on Gram-Schmidt
orthogonalization. Modulo the change of variables 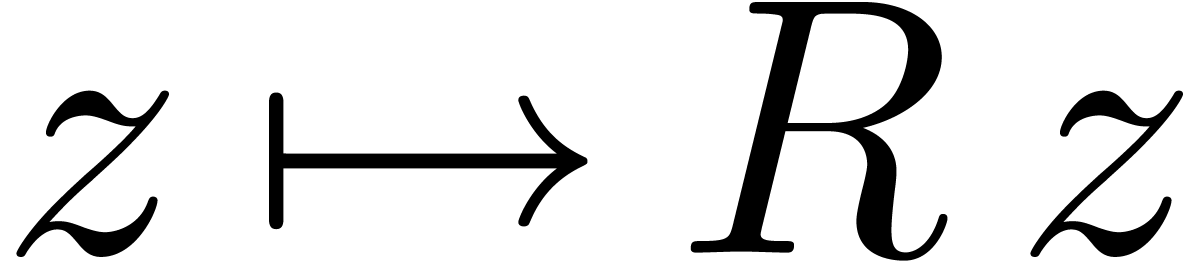 , it actually suffices to consider the case when
, it actually suffices to consider the case when
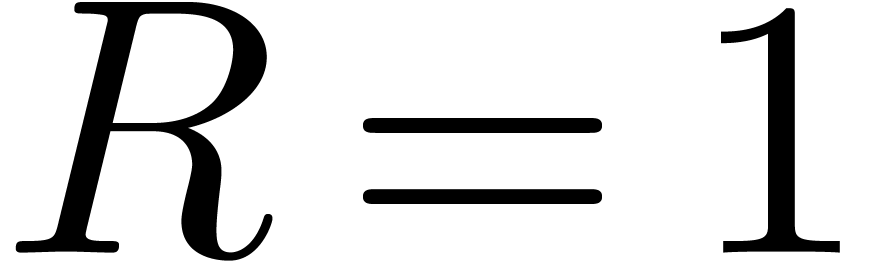 . In section 5,
we will present some relations which were recognized by the algorithm.
In section 6, we will also examine the behaviour of the
algorithm in the case when
. In section 5,
we will present some relations which were recognized by the algorithm.
In section 6, we will also examine the behaviour of the
algorithm in the case when  are analytically
independent. Section 7 contains a discussion of the
algorithm and perspectives.
are analytically
independent. Section 7 contains a discussion of the
algorithm and perspectives.
Let  be an analytic function which is given by
its power series
be an analytic function which is given by
its power series 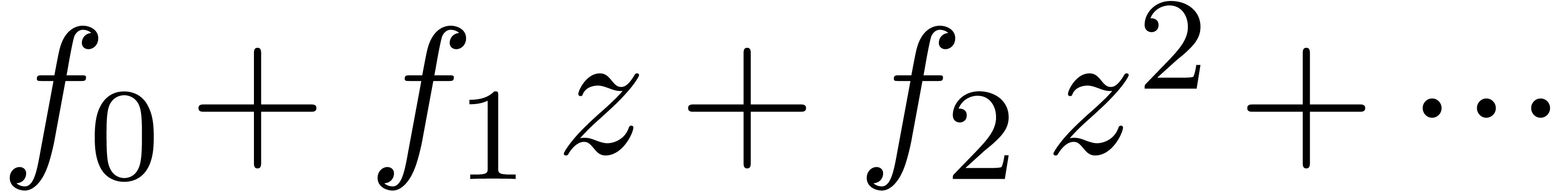 at the origin. A first natural
question is how to compute the radius of convergence
at the origin. A first natural
question is how to compute the radius of convergence 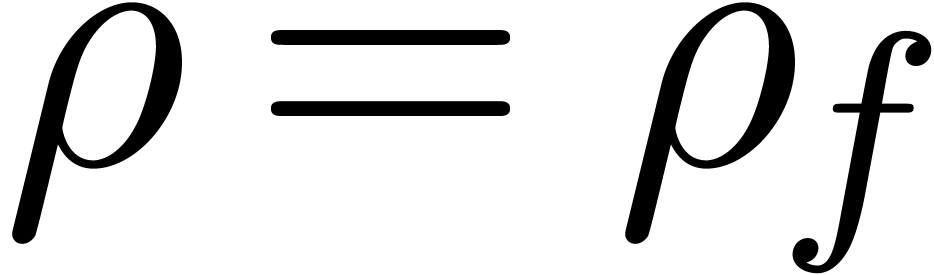 of
of  at the origin, assuming that we have an
algorithm for computing the coefficients
at the origin, assuming that we have an
algorithm for computing the coefficients 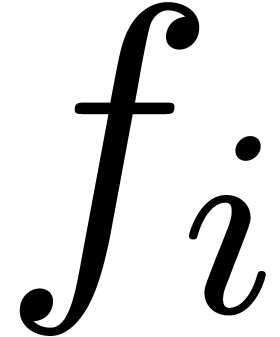 .
In what follows, we will only be interested in heuristic algorithms. In
general, good lower bounds for
.
In what follows, we will only be interested in heuristic algorithms. In
general, good lower bounds for 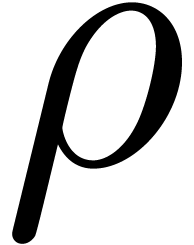 can often be
obtained efficiently, but the computation of sharp upper bounds can be
undecidable. For some results on the exact computation of
can often be
obtained efficiently, but the computation of sharp upper bounds can be
undecidable. For some results on the exact computation of 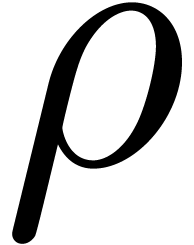 , we refer to [DL89, vdH07].
, we refer to [DL89, vdH07].
Theoretically speaking, the radius of convergence is given by
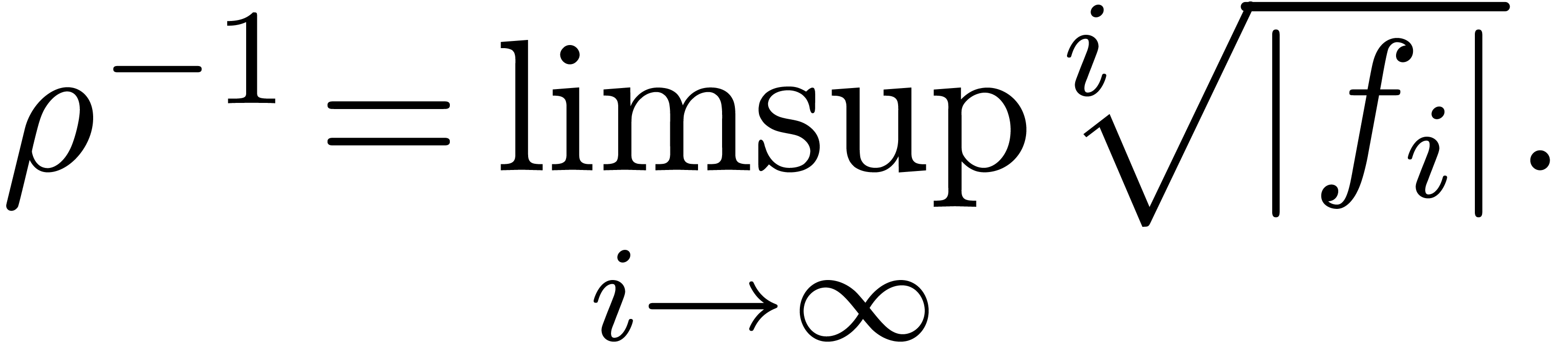
After the computation of 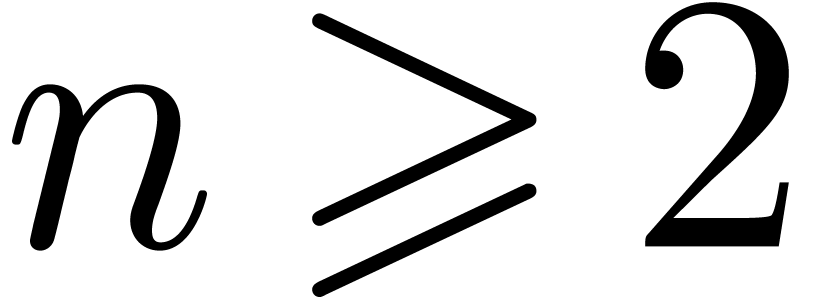 coefficients
coefficients 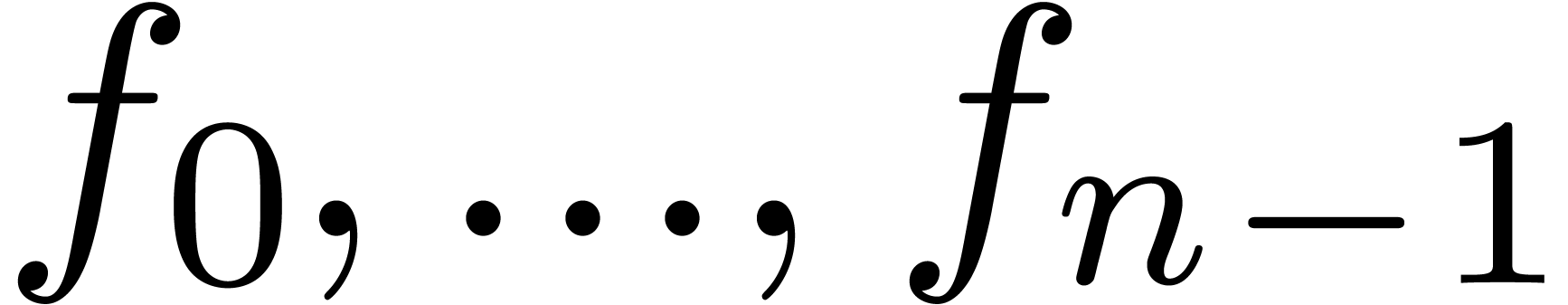 of
of  , this
yields the approximation
, this
yields the approximation
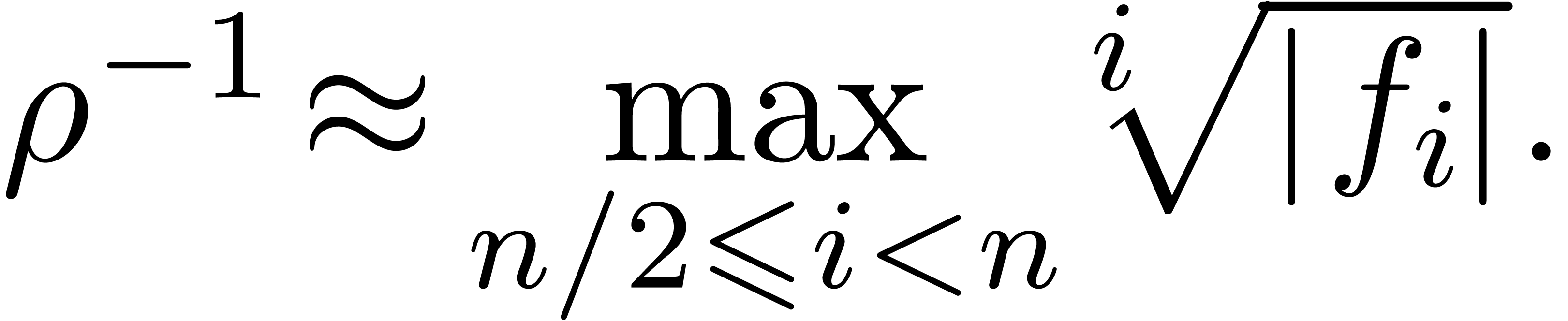 |
(4) |
For most convergent power series  ,
this formula is ultimately exact in the sense that
,
this formula is ultimately exact in the sense that
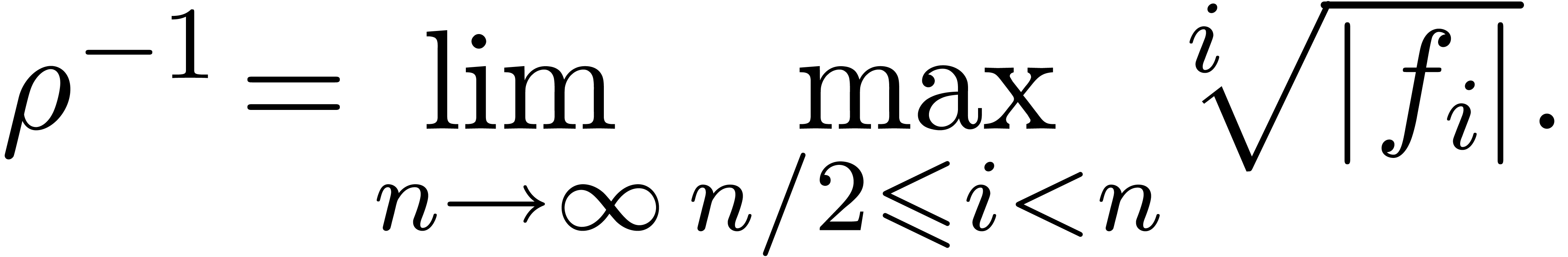 |
(5) |
This is for instance the case when 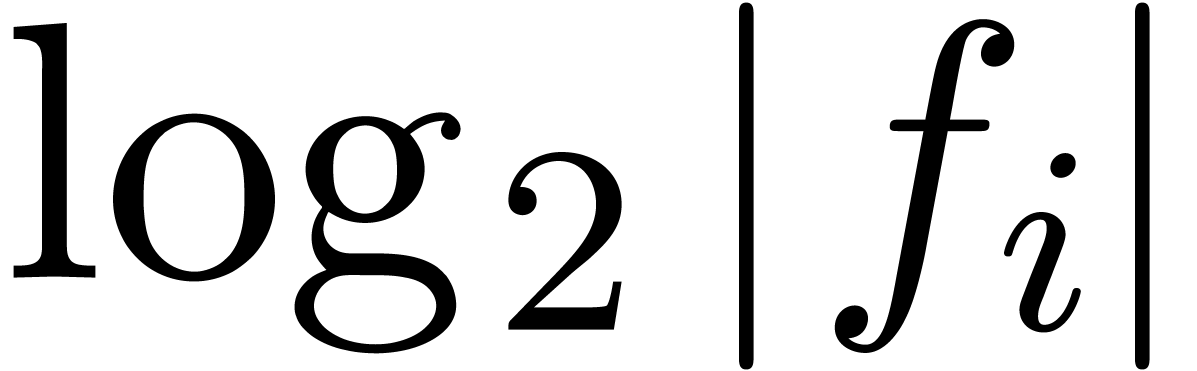 is ultimately
convex or ultimately concave. The set of
is ultimately
convex or ultimately concave. The set of  for
which (5) holds is also stable under the transformation
for
which (5) holds is also stable under the transformation
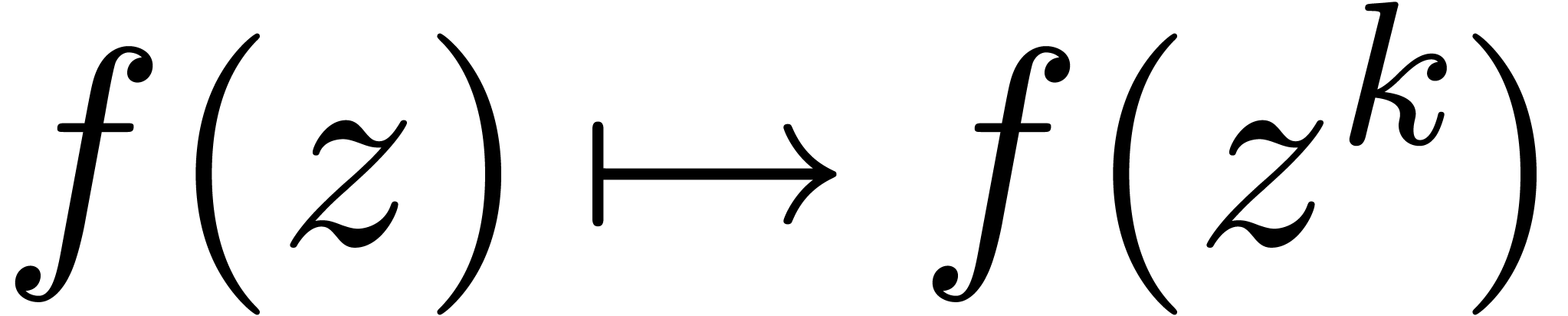 for any
for any 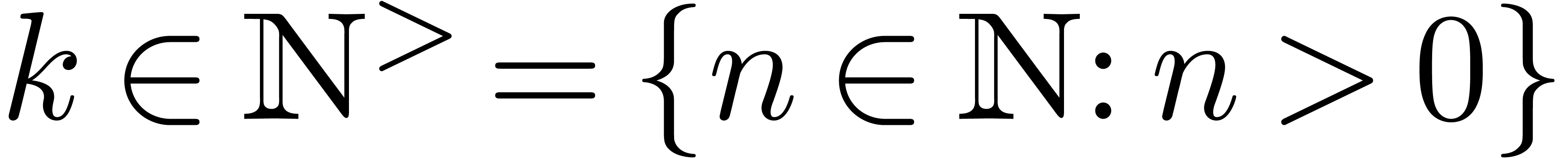 .
Of course, we may replace
.
Of course, we may replace 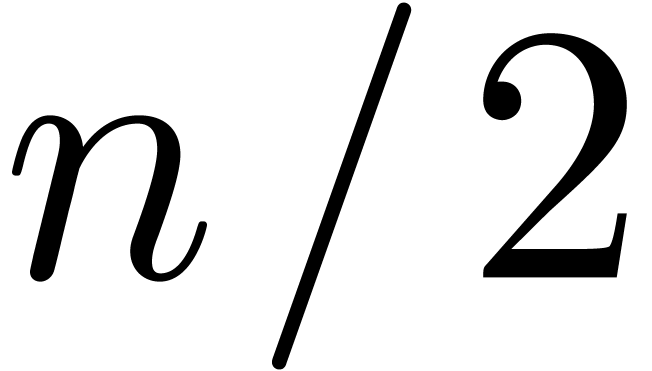 by
by 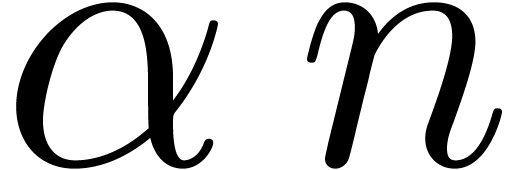 in (5) for any
in (5) for any 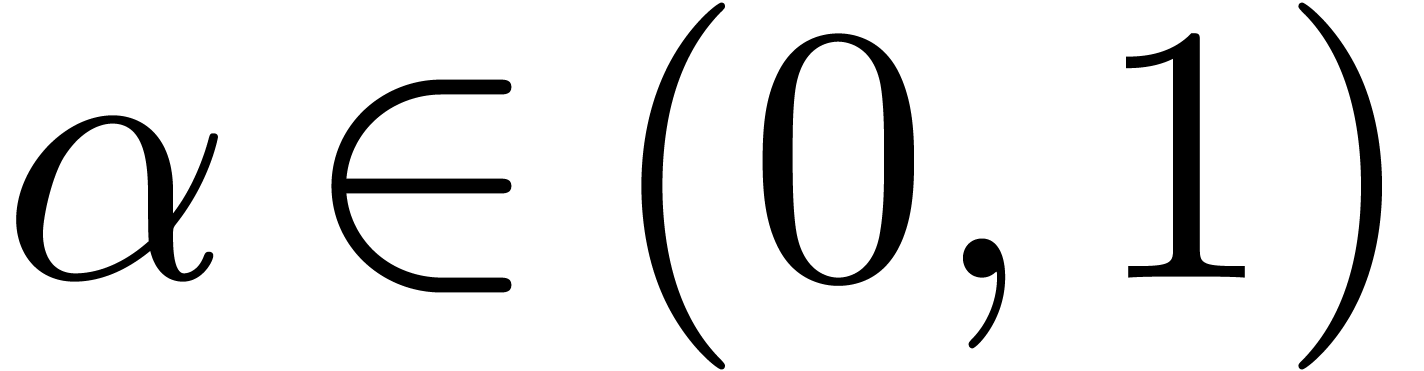 .
.
The formula (4) has the disadvantage that it has not been
scaled appropriately: when replacing  by
by  , where
, where 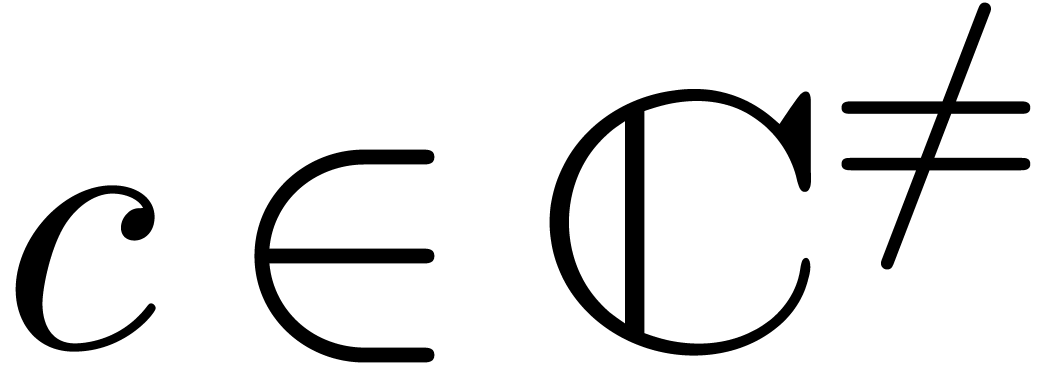 is
such that
is
such that  , we obtain
different approximations for
, we obtain
different approximations for  and
and  . Therefore, it is better to replace
. Therefore, it is better to replace  by
by 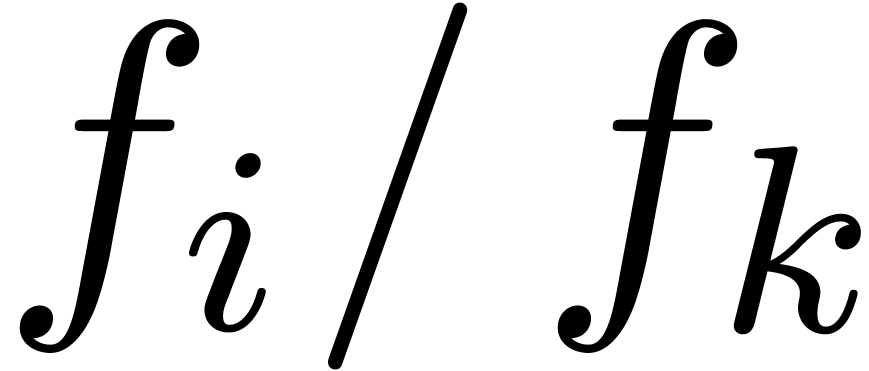 for some appropriate
coefficient
for some appropriate
coefficient 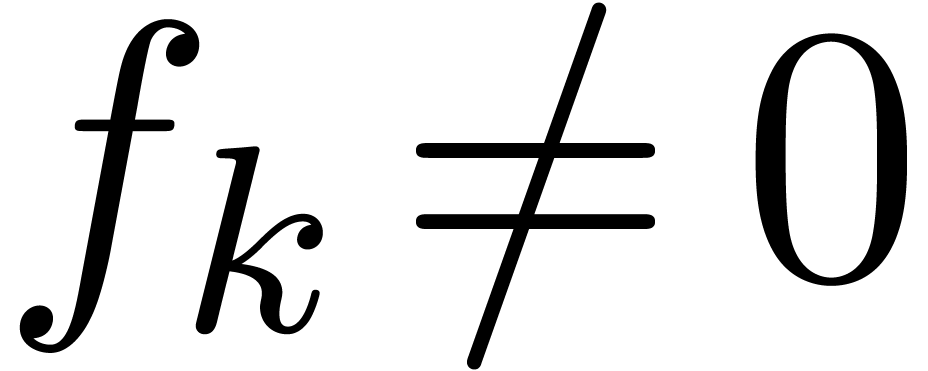 with
with 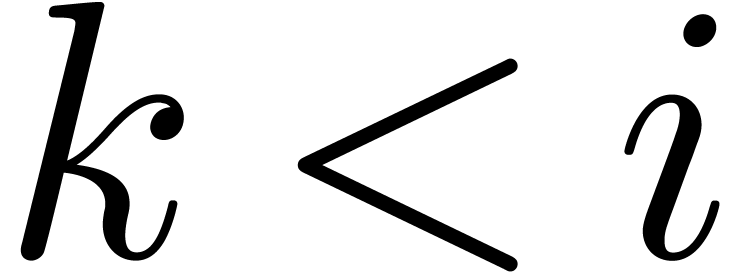 .
One way to choose appropriate indices
.
One way to choose appropriate indices 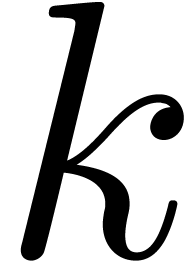 is to
consider the numerical Newton polygon of
is to
consider the numerical Newton polygon of  ,
where
,
where 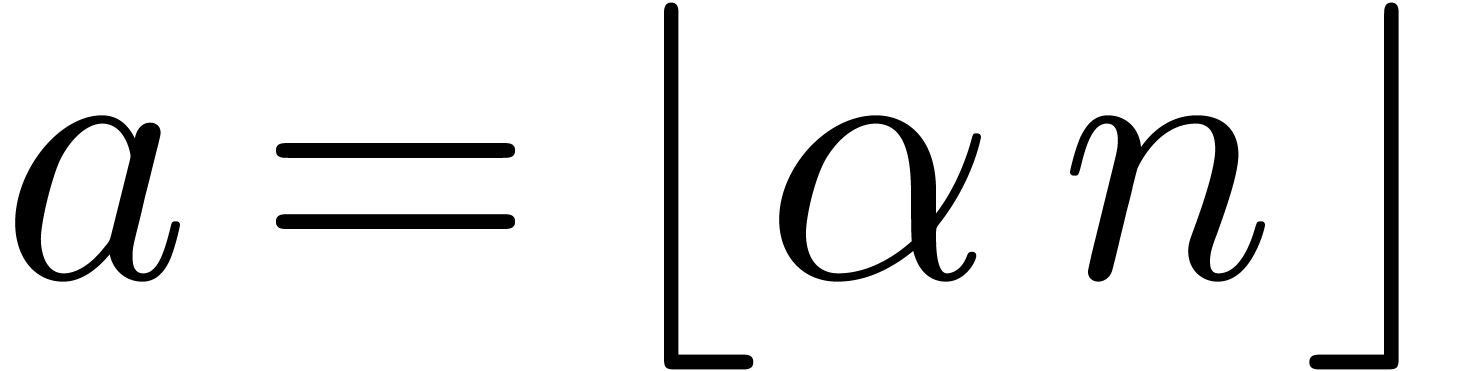 ,
, 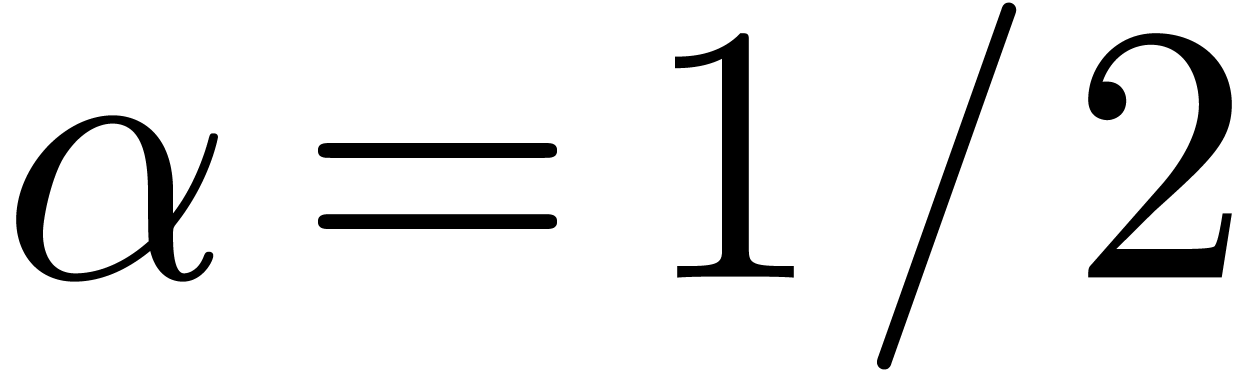 .
.
Let 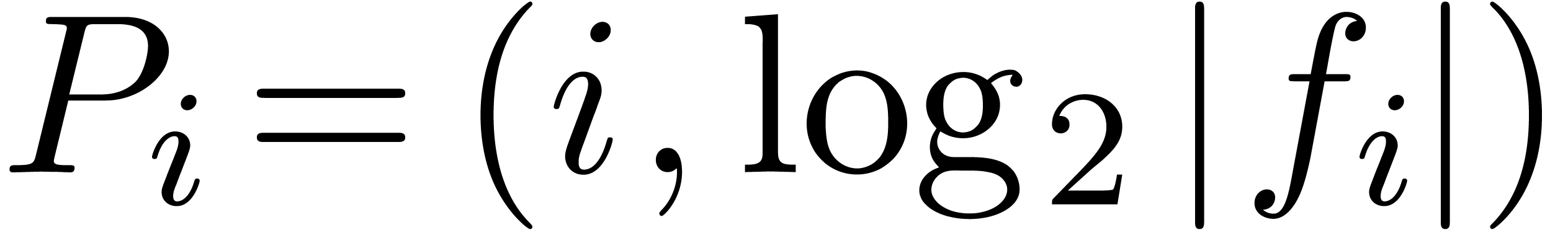 for
for 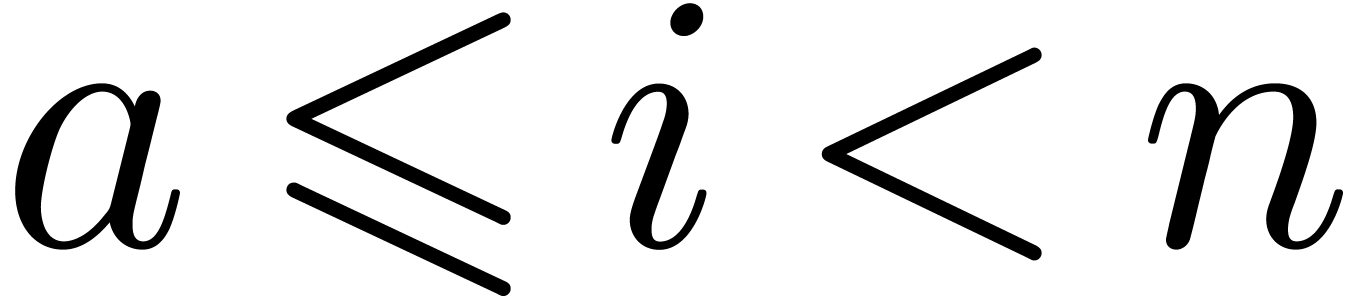 ,
where we understand that
,
where we understand that 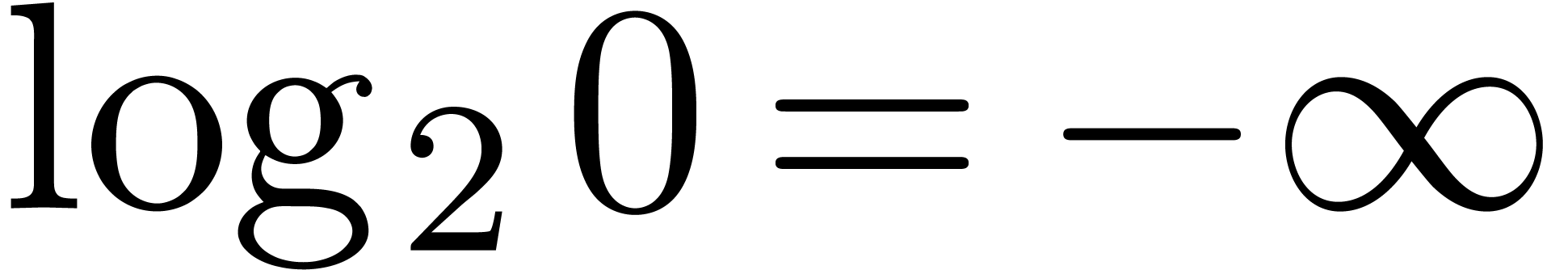 .
Then the Newton diagram of
.
Then the Newton diagram of  is the convex hull of
the half lines
is the convex hull of
the half lines 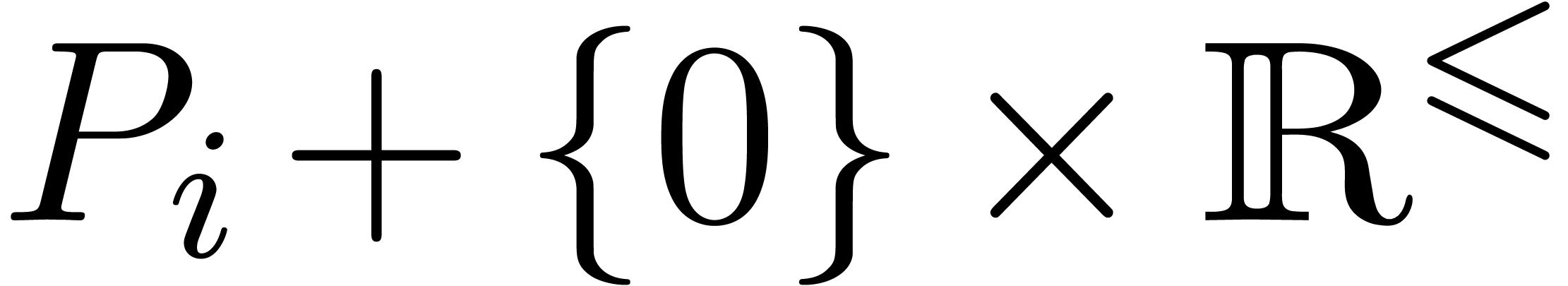 for
for 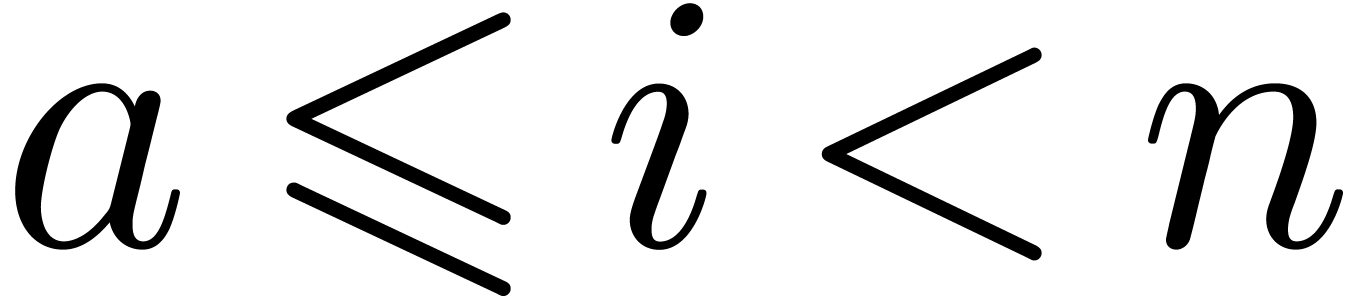 .
There exists a minimal subset
.
There exists a minimal subset 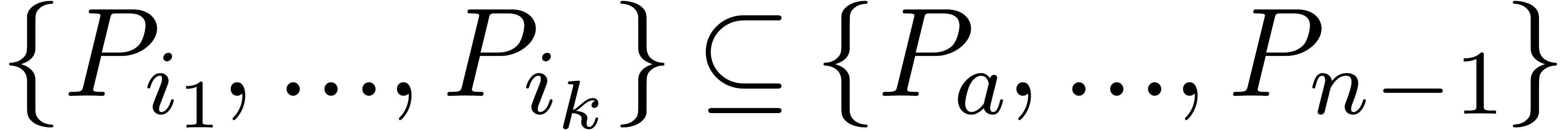 with
with  , such that the Newton diagram is also the
convex hull of the half lines
, such that the Newton diagram is also the
convex hull of the half lines 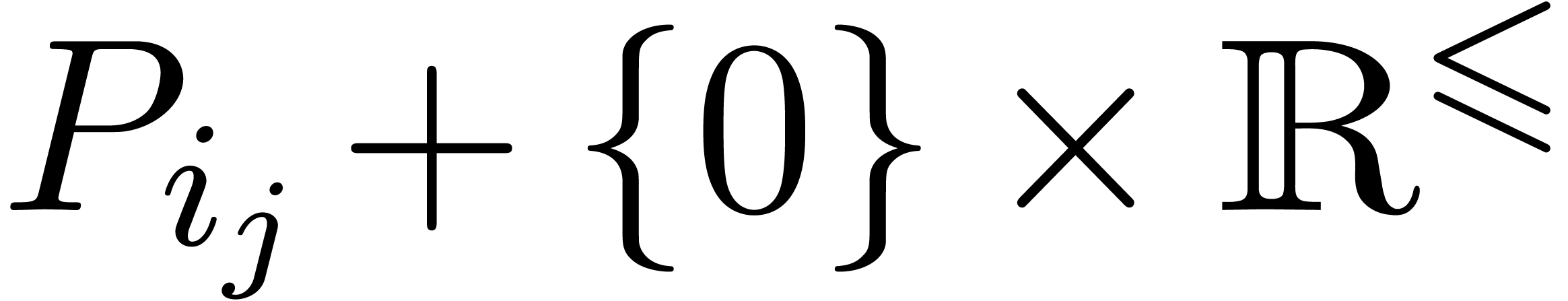 for
for 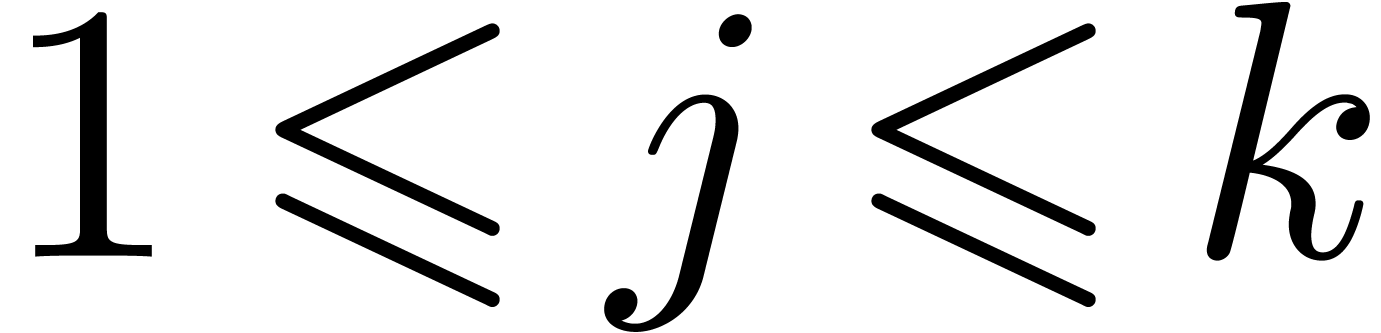 . Graphically speaking, the
. Graphically speaking, the 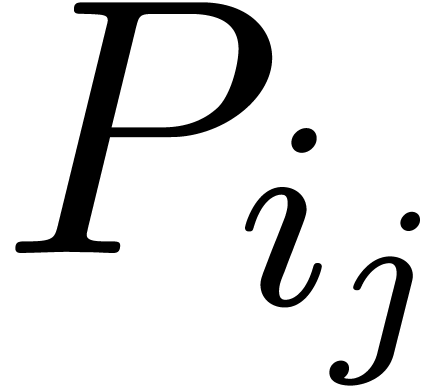 are the vertices of the Newton diagram.
are the vertices of the Newton diagram.
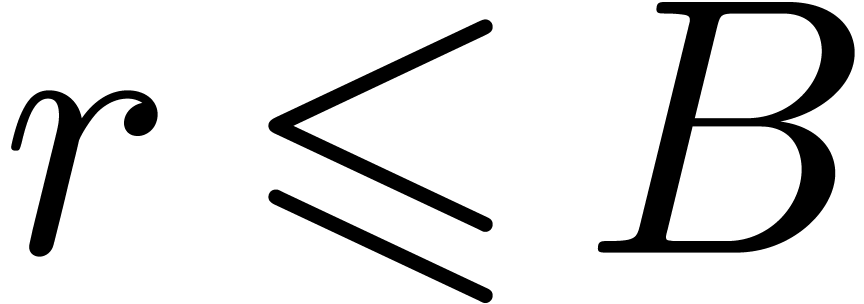
For a fixed 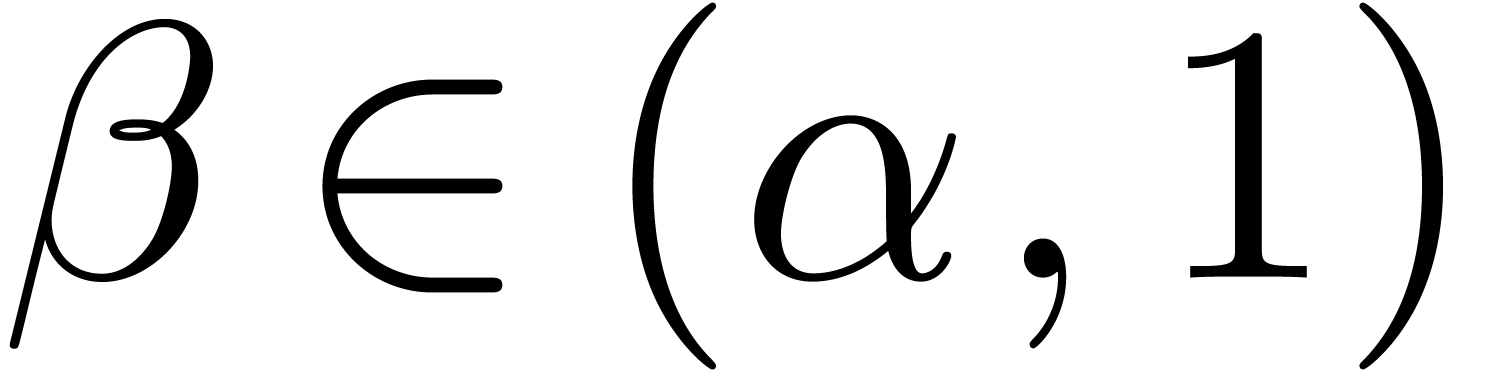 , say
, say 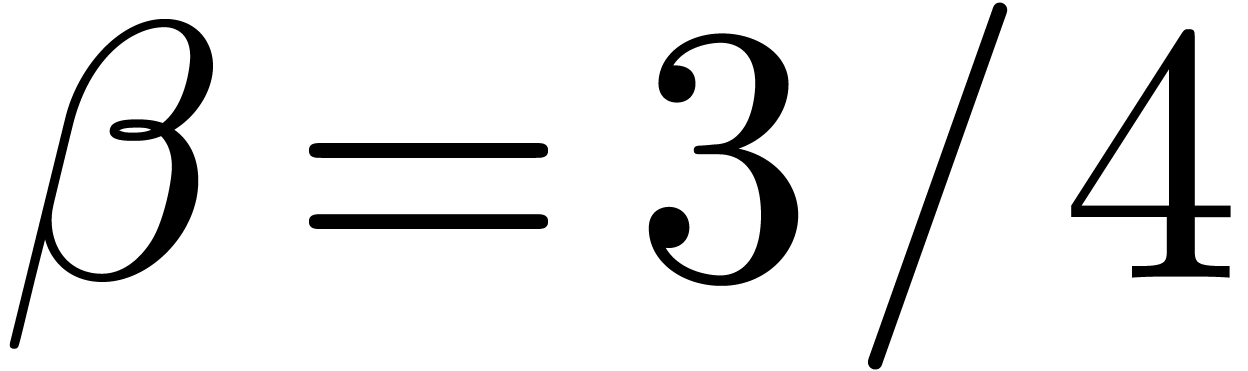 , we may now determine the unique
edge
, we may now determine the unique
edge 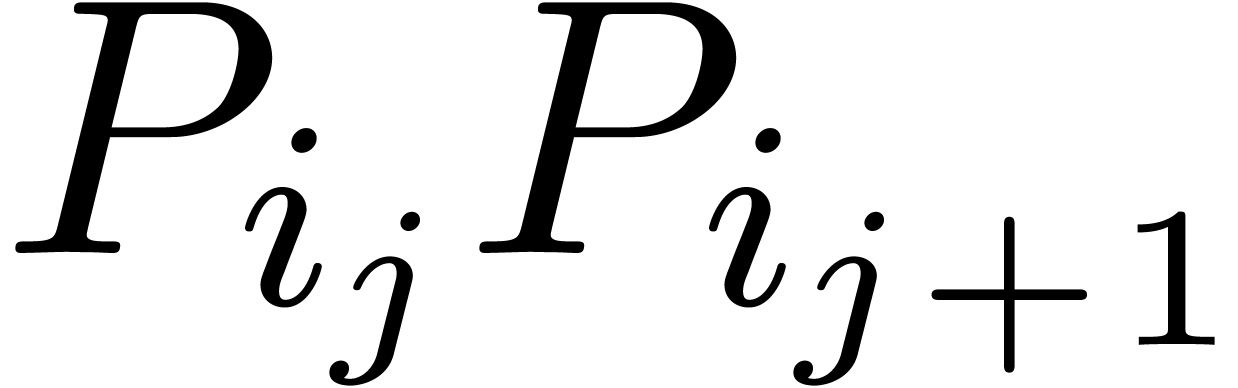 of the Newton diagram such that
of the Newton diagram such that 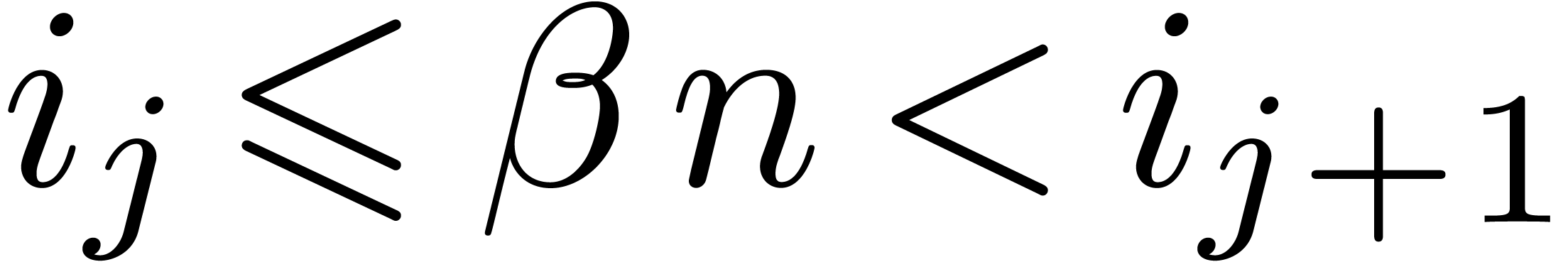 , and replace the formula (4)
by
, and replace the formula (4)
by
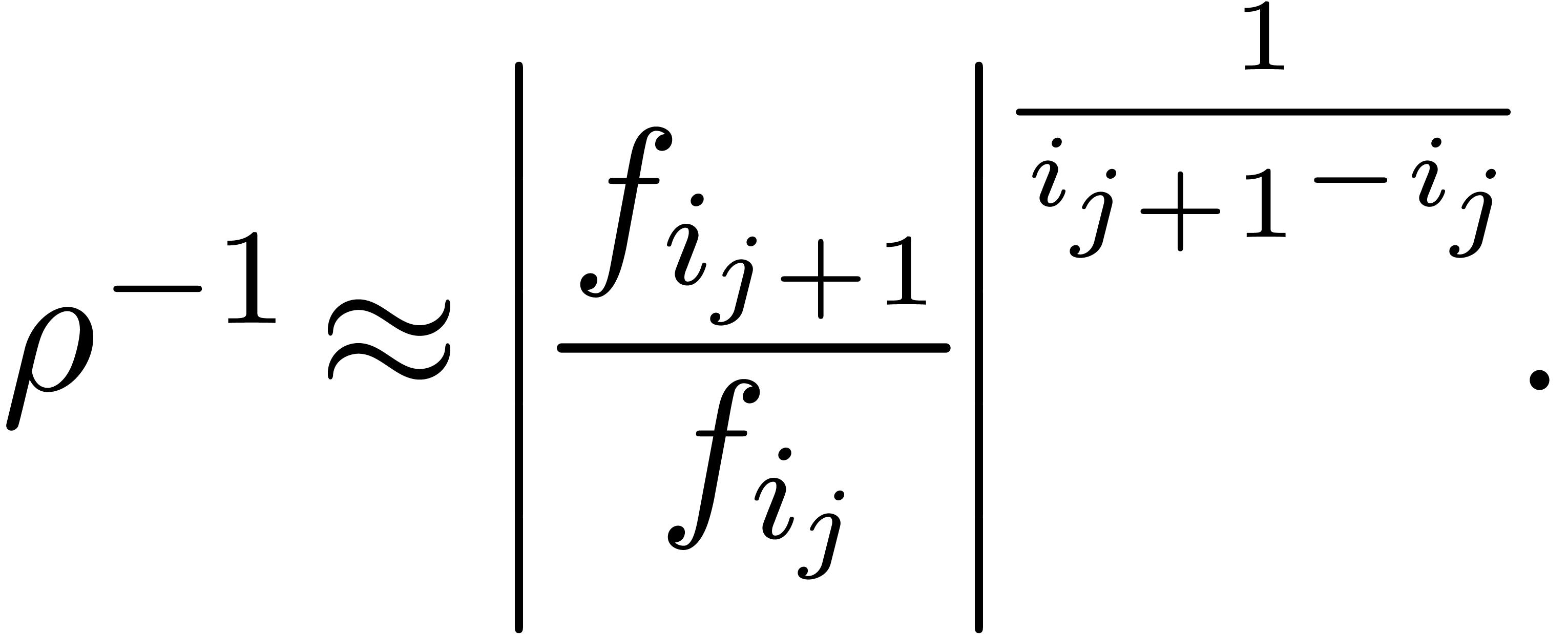 |
(6) |
For most convergent power series  ,
the formula (6) is again ultimately exact. The indices
,
the formula (6) is again ultimately exact. The indices  can be computed from the coefficients
can be computed from the coefficients 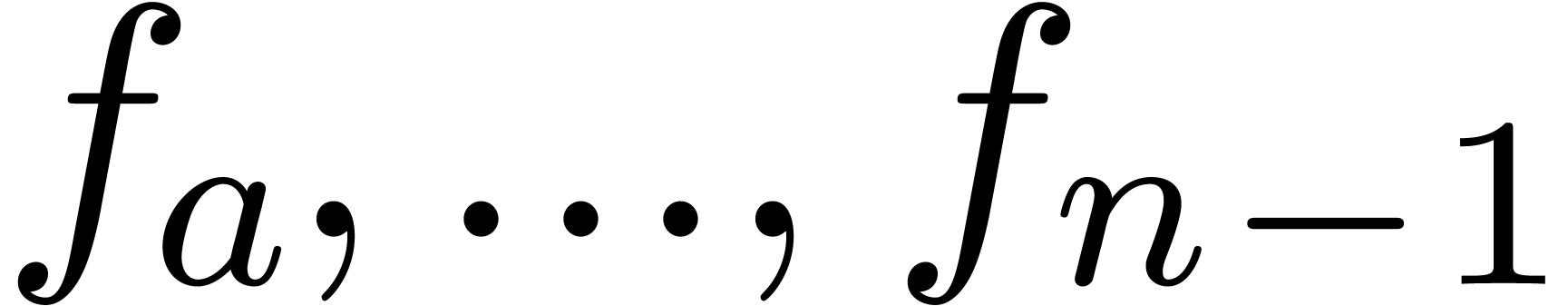 using a linear traversal in time
using a linear traversal in time 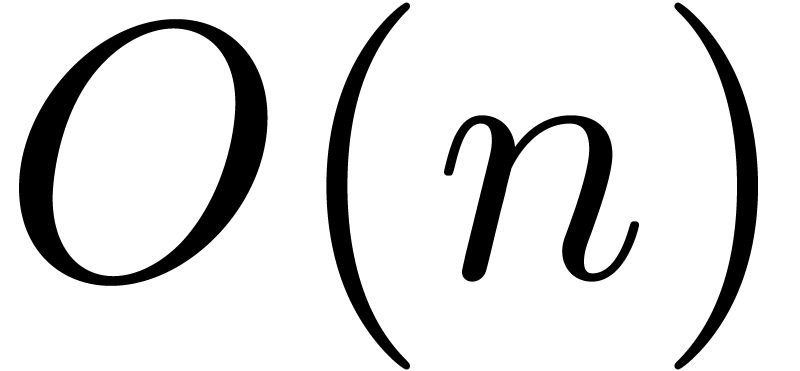 . Modulo a tiny extra cost, this enables us to
compute a more accurate approximation of
. Modulo a tiny extra cost, this enables us to
compute a more accurate approximation of 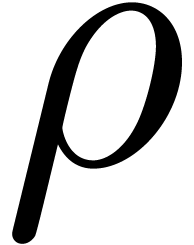 than
(4). The formula (6) has been implemented in
the
than
(4). The formula (6) has been implemented in
the  , the computed radius is
usually correct up to one decimal digit.
, the computed radius is
usually correct up to one decimal digit.
The formula (6) usually yields a reasonable estimate for
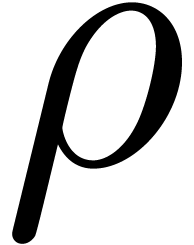 , even in very degenerate
cases when there are several singularities at distance
, even in very degenerate
cases when there are several singularities at distance 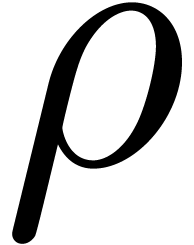 or close to
or close to 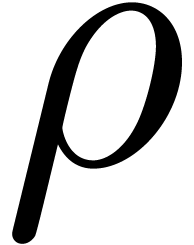 . If
. If  admits an isolated singularity
admits an isolated singularity  at
distance
at
distance 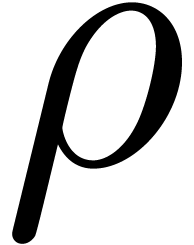 , with no other
singularities at distance close to
, with no other
singularities at distance close to 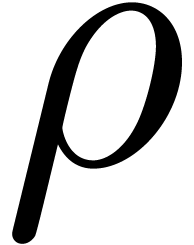 ,
then the quotient
,
then the quotient 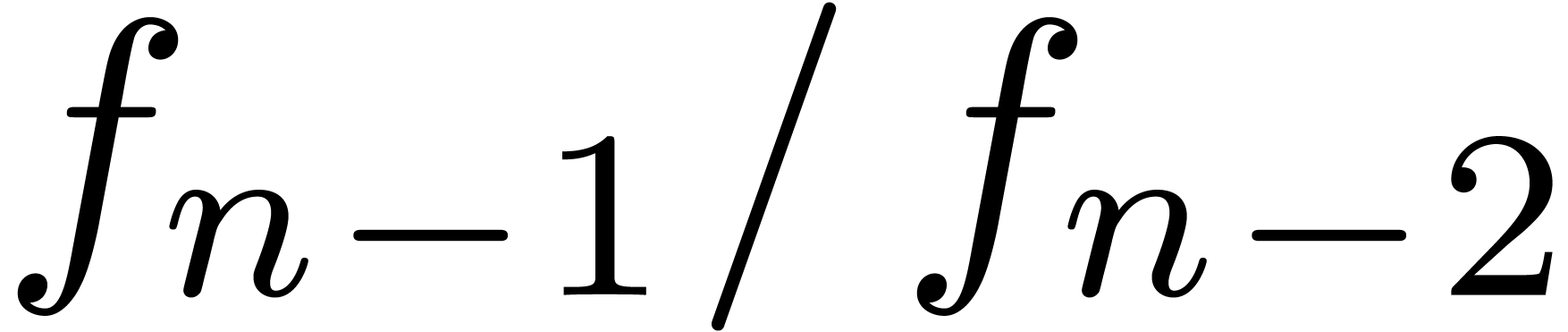 usually tends to
usually tends to  for large
for large 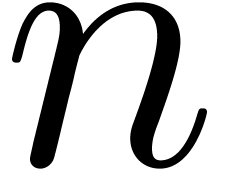 .
When the singularity at
.
When the singularity at  has a known type, then
the approximation
has a known type, then
the approximation 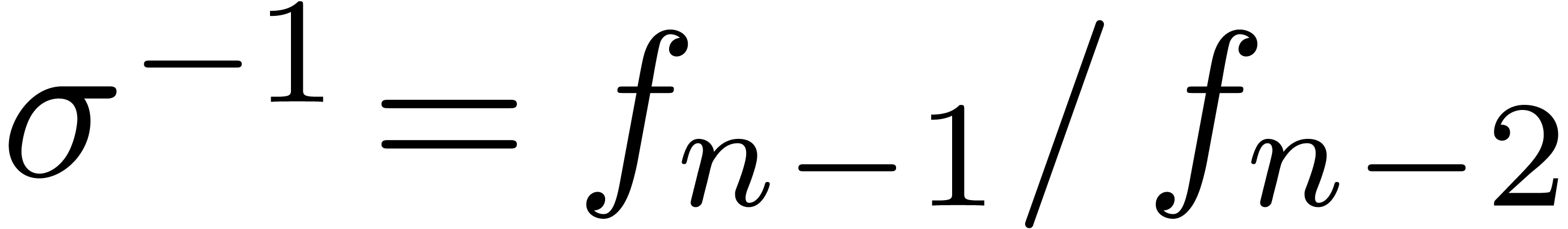 can be further improved.
can be further improved.
For instance, in the case of algebraic singularities, we have
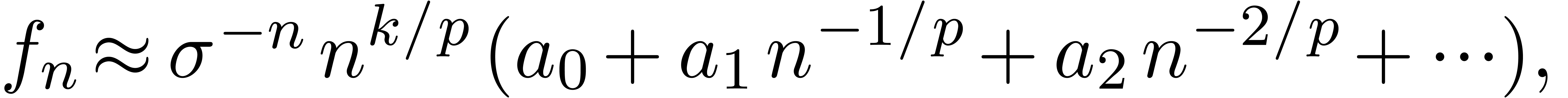
with 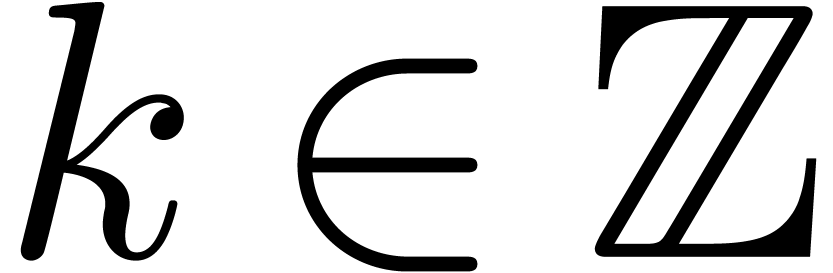 and ramification index
and ramification index 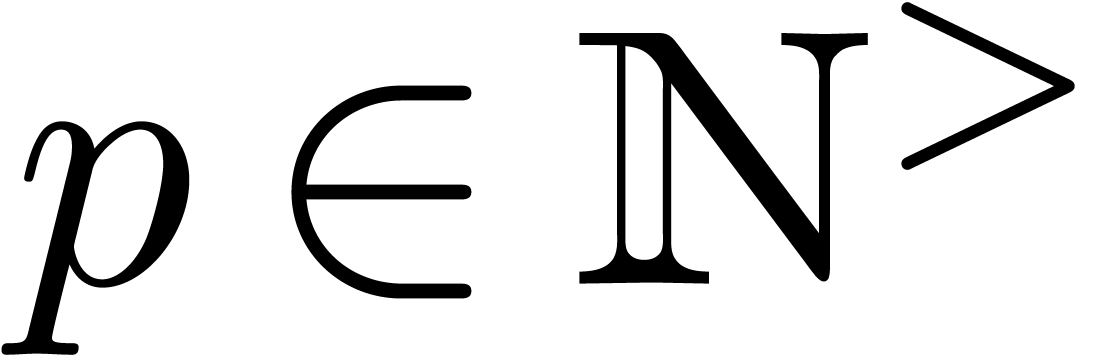 , whence
, whence
 |
(7) |
Using the E-algorithm [Wen01, BZ91], we may
now compute simultaneous approximations for the first coefficients 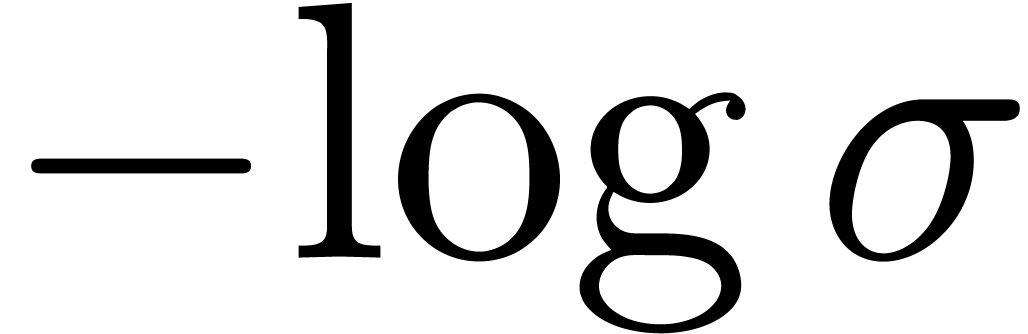 ,
, 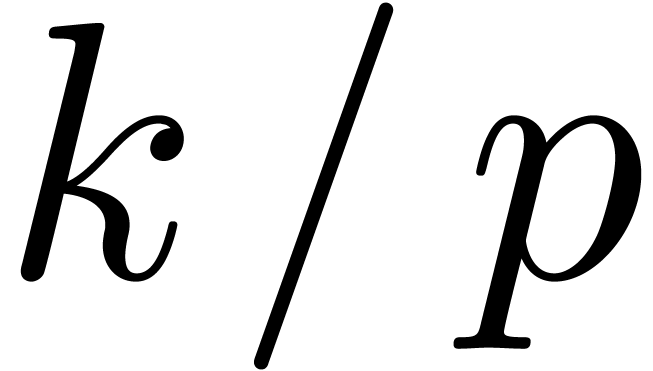 ,
,
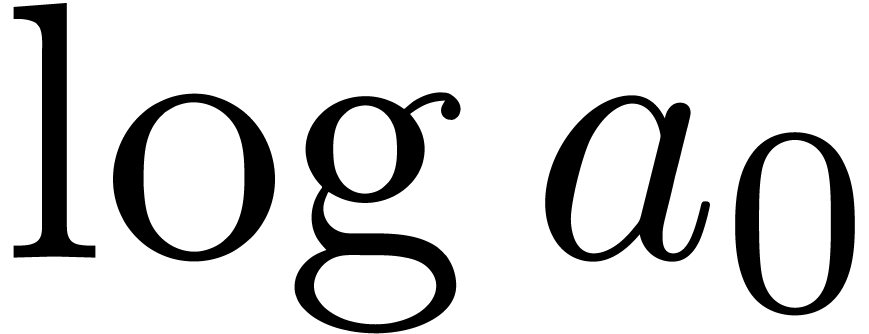 ,
, 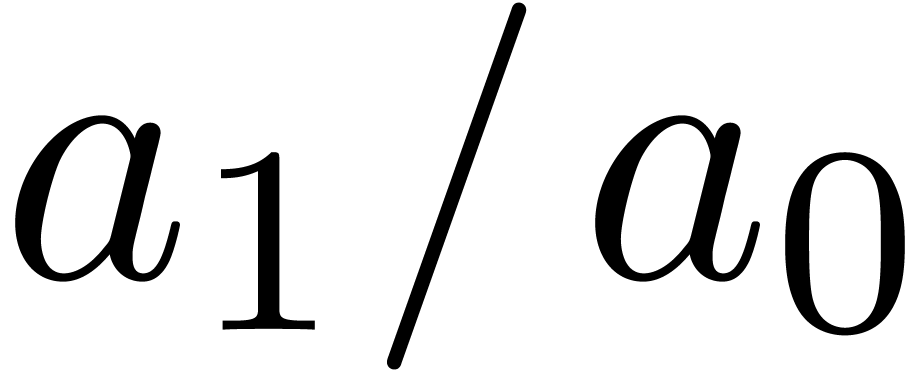 , etc. of the expansion (7).
It turns out that this strategy greatly improves the accuracy of the
approximation of
, etc. of the expansion (7).
It turns out that this strategy greatly improves the accuracy of the
approximation of  (see also [vdH06]).
(see also [vdH06]).
Similarly, we say that  is Fuchsian at
is Fuchsian at  , if
, if  satisfies a linear differential equation
satisfies a linear differential equation
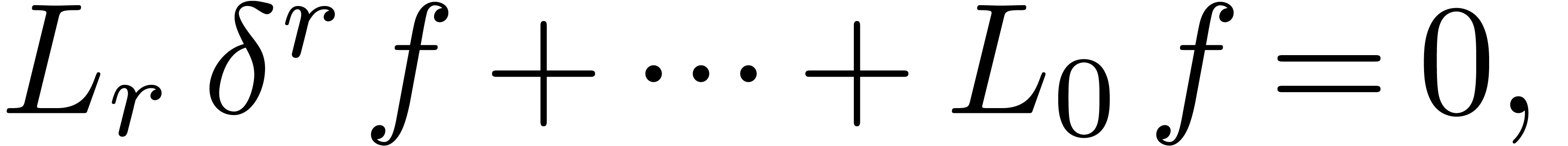
where 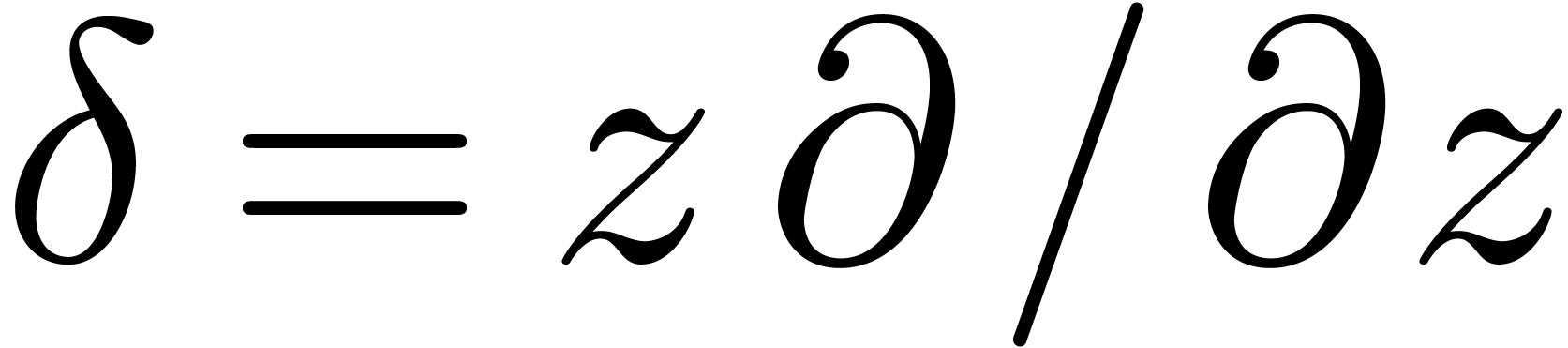 and
and  are analytic
functions at
are analytic
functions at  with
with 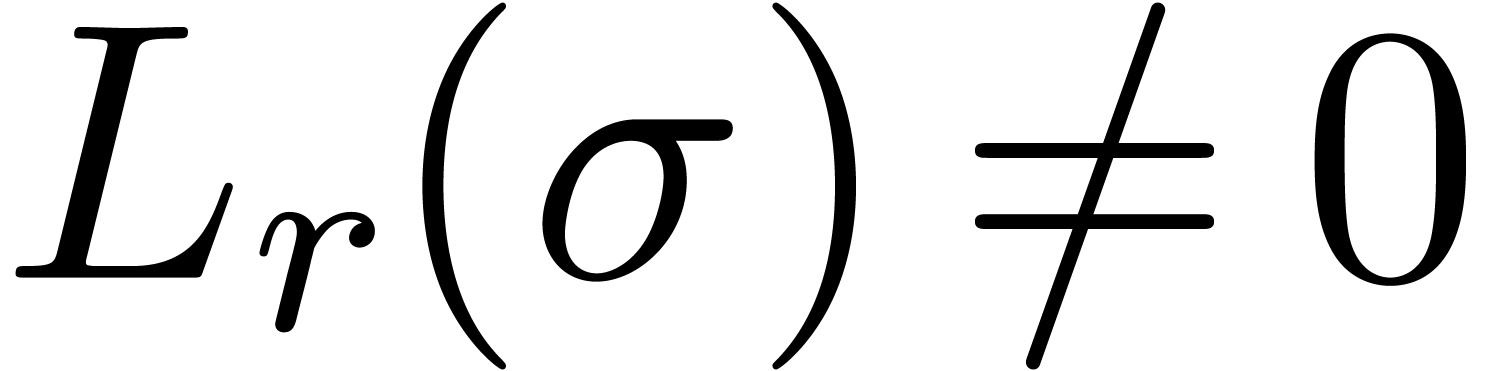 .
In that case, the Taylor coefficients
.
In that case, the Taylor coefficients  satisfy
the asymptotic expansion
satisfy
the asymptotic expansion
where 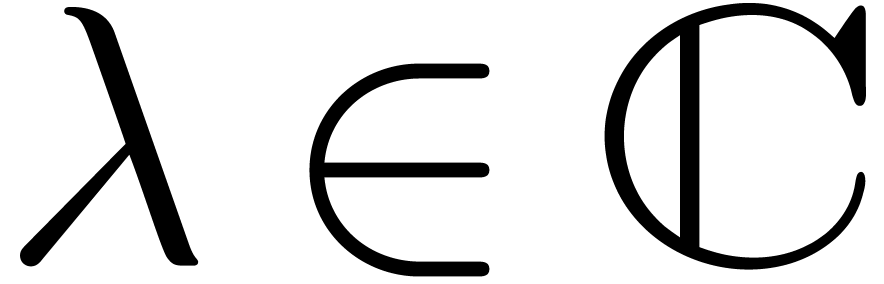 ,
, 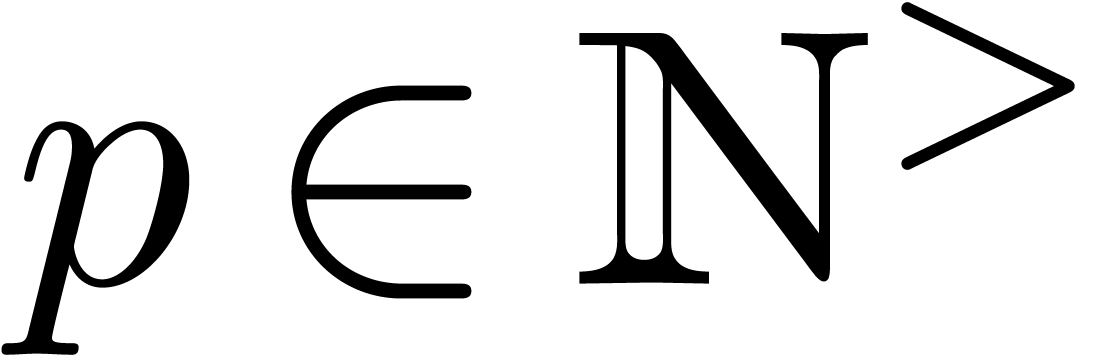 and the
and the 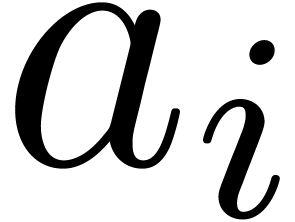 are polynomials in
are polynomials in 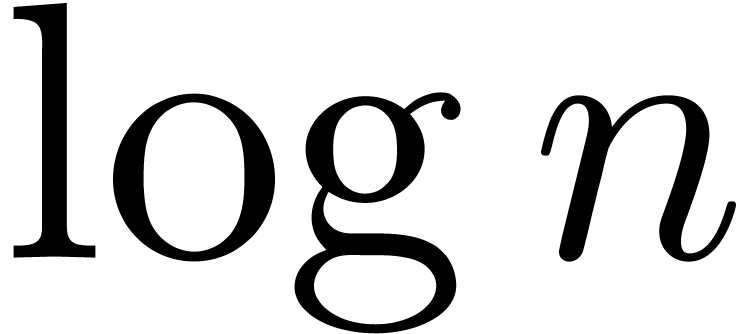 of degrees
of degrees 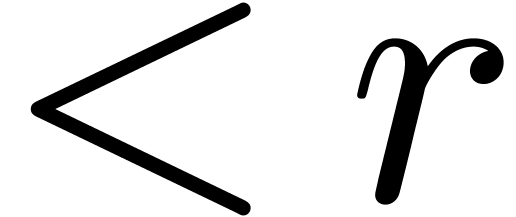 . Again, the
E-algorithm or more general algorithms for asymptotic extrapolation [vdH06] can be used to compute
. Again, the
E-algorithm or more general algorithms for asymptotic extrapolation [vdH06] can be used to compute  with a
high accuracy. Notice that these algorithms also provide estimates for
the accuracies of the computed approximations.
with a
high accuracy. Notice that these algorithms also provide estimates for
the accuracies of the computed approximations.
In the case when the closest singularity  is a
simple pole, we may directly try to find the polynomial
is a
simple pole, we may directly try to find the polynomial  . This polynomial has the property that the
radius of convergence of
. This polynomial has the property that the
radius of convergence of 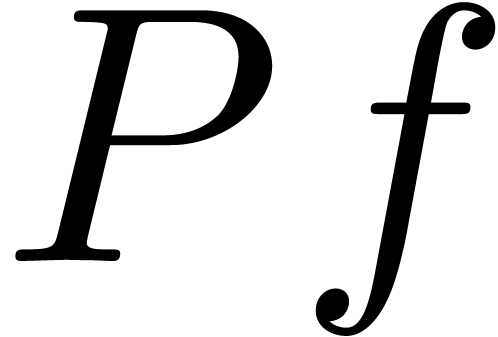 is strictly larger than
is strictly larger than
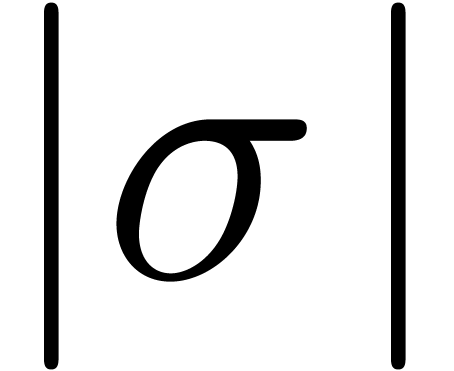 . More generally, if
. More generally, if  is meromorphic on the compact disc
is meromorphic on the compact disc  of radius
of radius 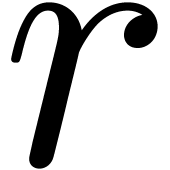 , then we may
search for a polynomial
, then we may
search for a polynomial 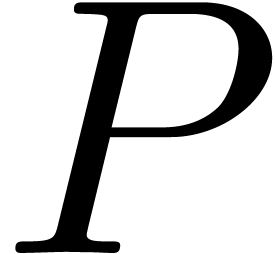 such that the radius of
convergence of
such that the radius of
convergence of 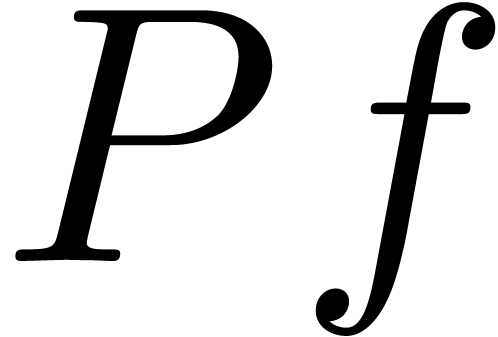 is strictly larger than
is strictly larger than 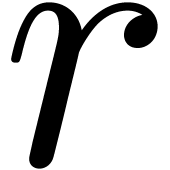 . This can be done using simple
linear algebra, as follows:
. This can be done using simple
linear algebra, as follows:
Algorithm denom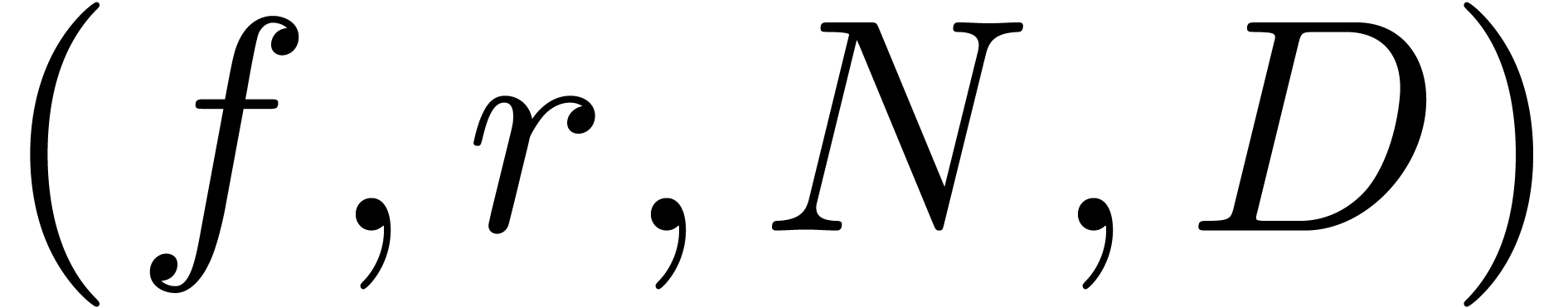
 coefficients of
coefficients of 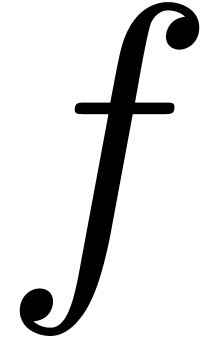 , a radius
, a radius
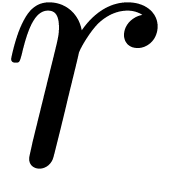 and a degree bound
and a degree bound 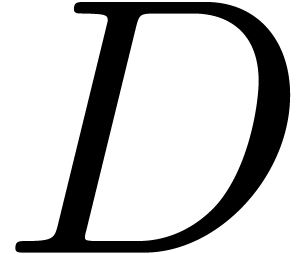
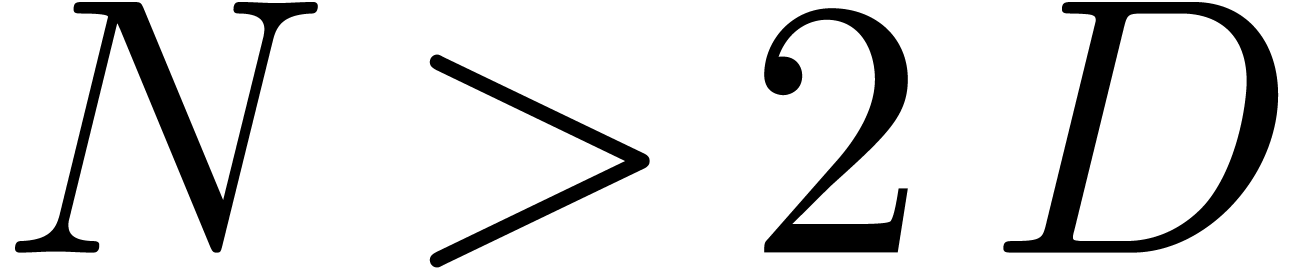
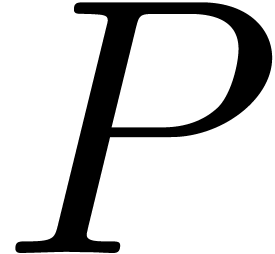 with
with  ,
,
chosen of minimal degree 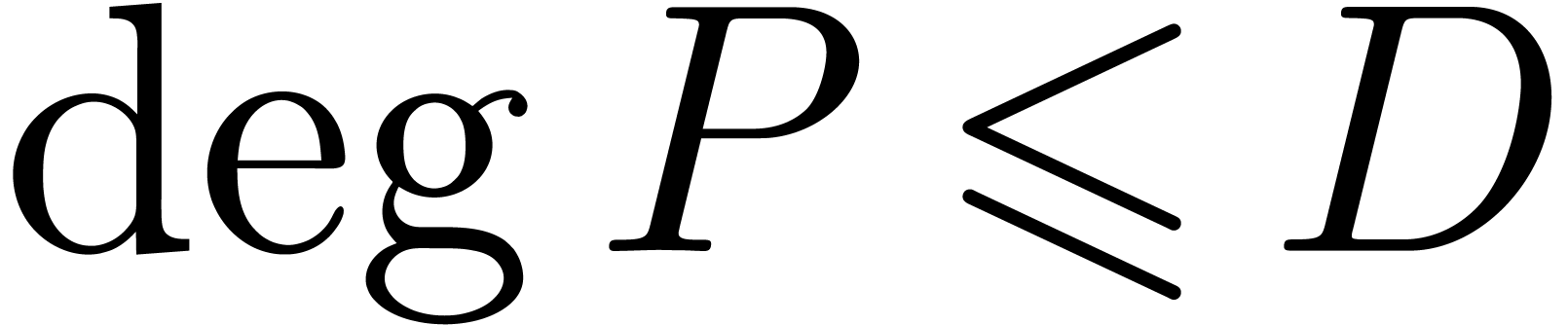 ,
or failed
,
or failed
Step 1. [Initialize]
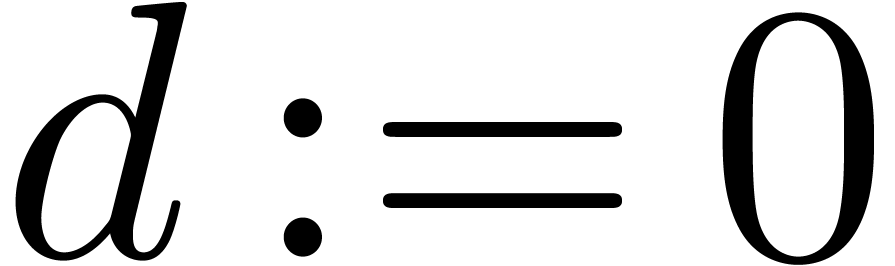
Step 2. [Determine 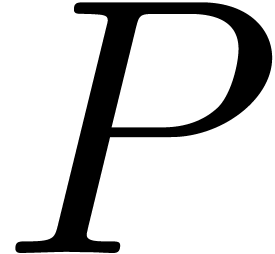 ]
]
Solve the linear system
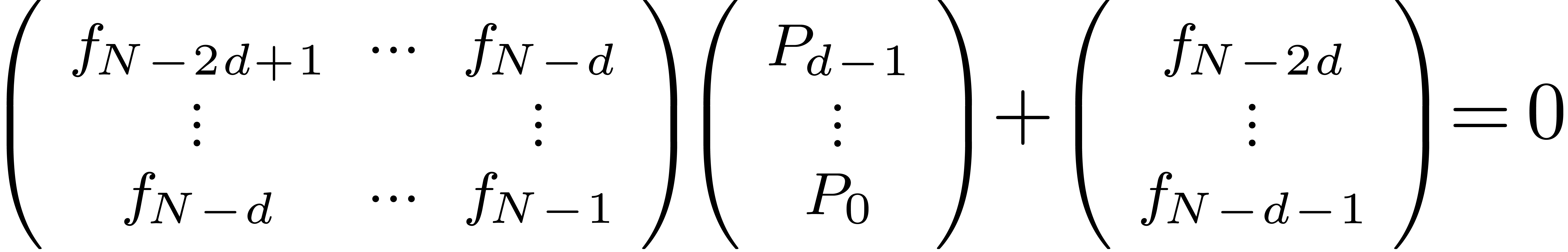 |
(8) |
Set 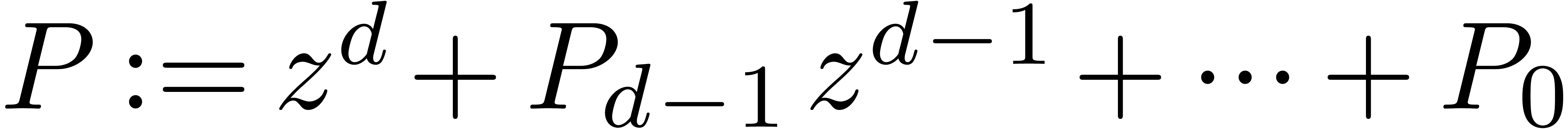
Step 3. [Terminate or loop]
Heuristically determine 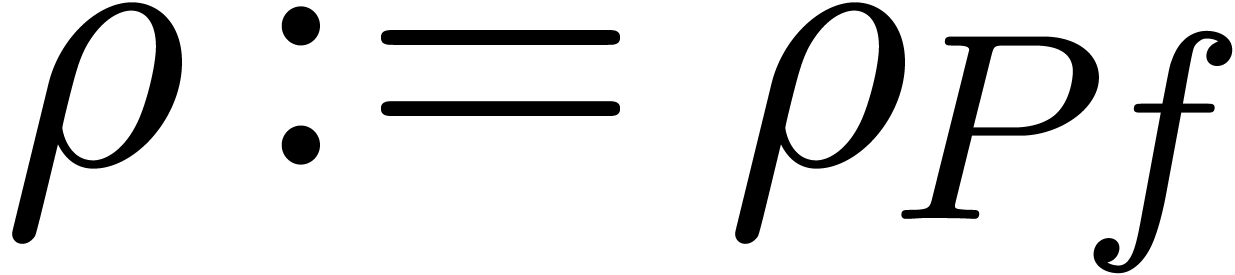 ,
based on the first
,
based on the first 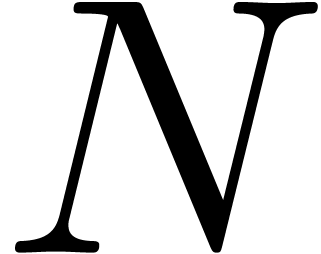 coefficients of
coefficients of 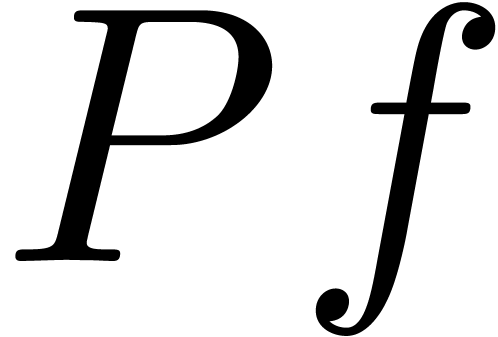
If 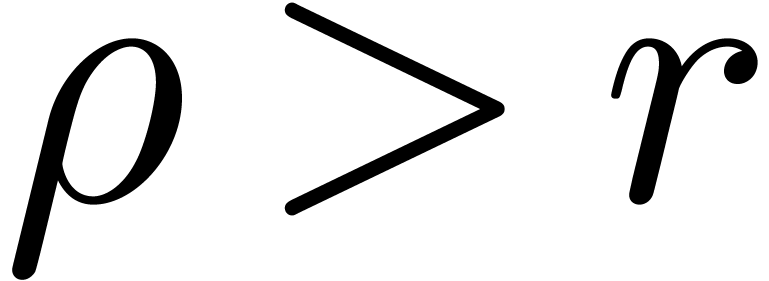 then return
then return 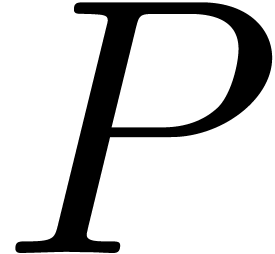
If 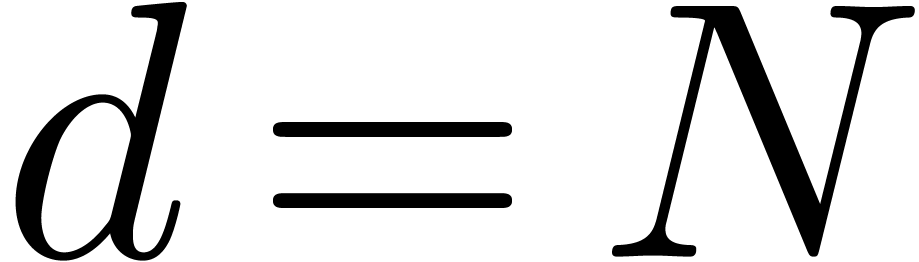 then return failed
then return failed
Set 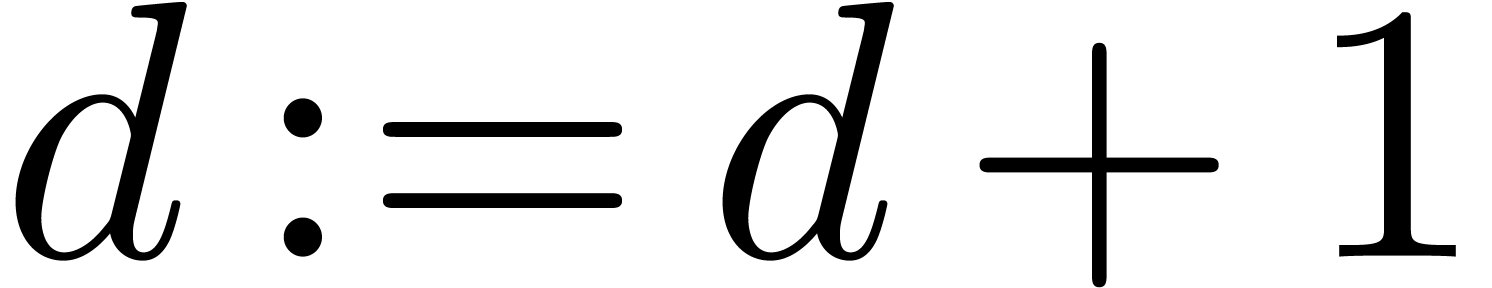 and go to step 2
and go to step 2
Proof. Modulo a scaling 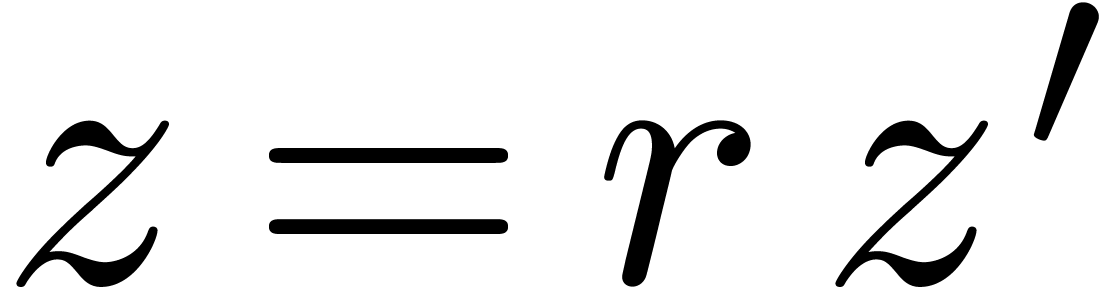 , we may assume without loss of generality that
, we may assume without loss of generality that
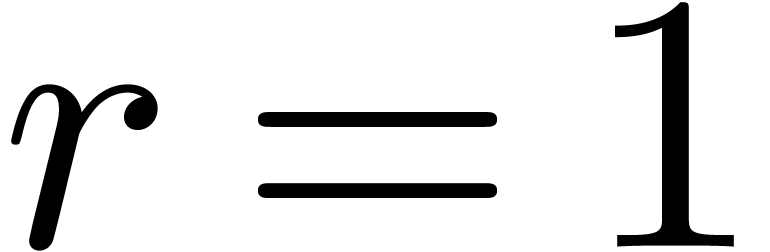 . Furthermore, the proof is
clear if
. Furthermore, the proof is
clear if 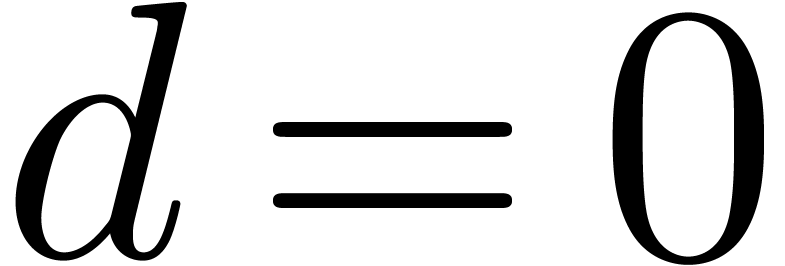 , so we will assume
that
, so we will assume
that 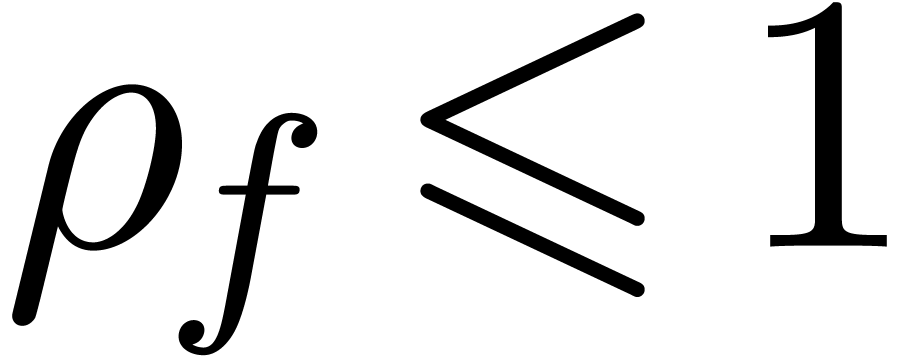 . Assume that there
exists a polynomial
. Assume that there
exists a polynomial  with
with 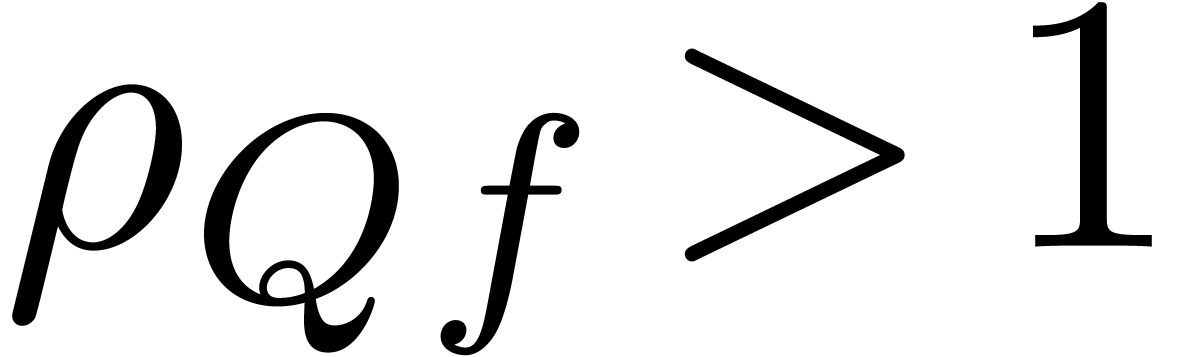 and choose
and choose
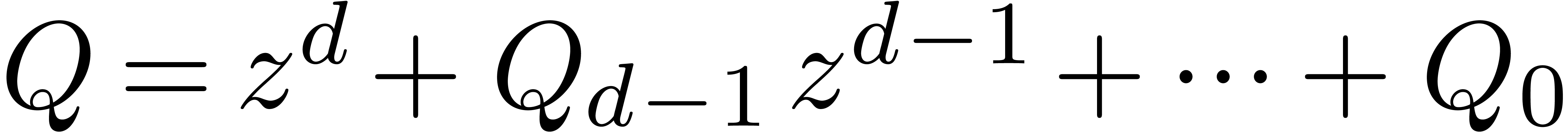
monic and of minimal degree 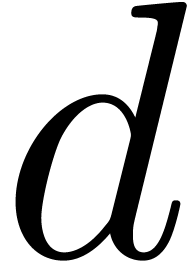 .
Notice that such a polynomial
.
Notice that such a polynomial  exists in
particular, if (8) admits no solution for some
exists in
particular, if (8) admits no solution for some 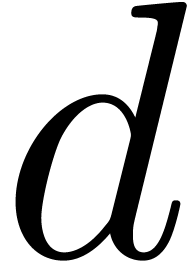 . We have
. We have
 |
(9) |
Since we assumed that 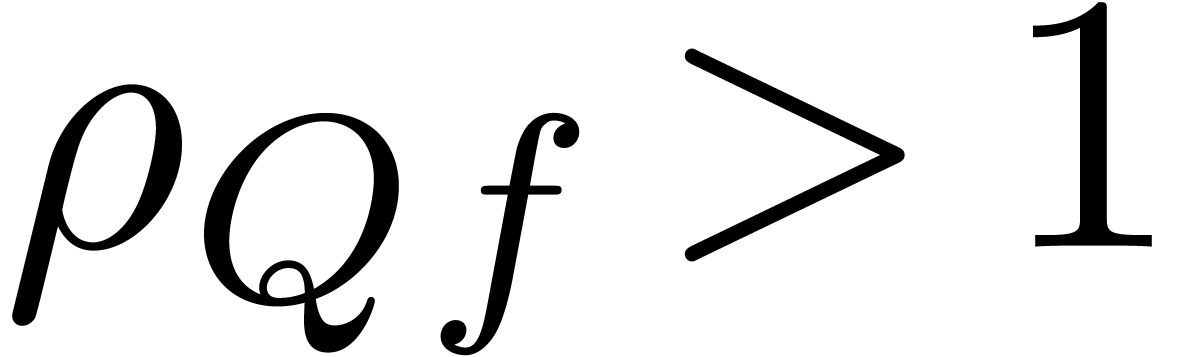 , the
coefficients
, the
coefficients 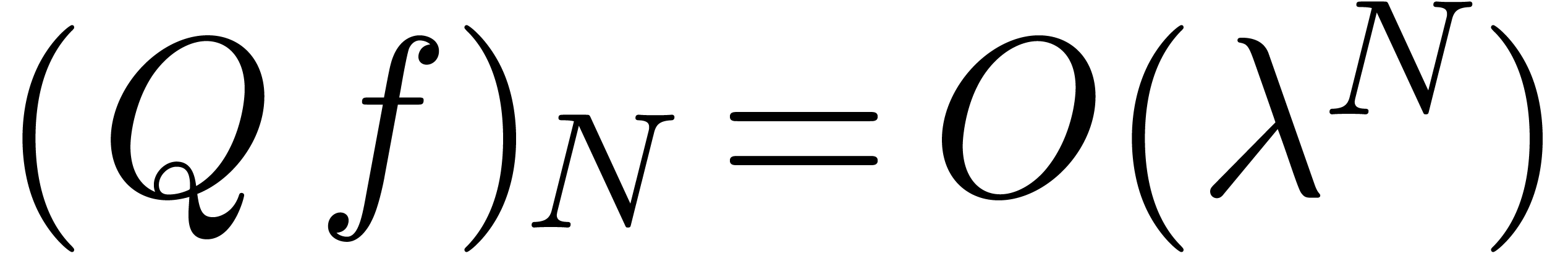 have exponential decay for some
have exponential decay for some
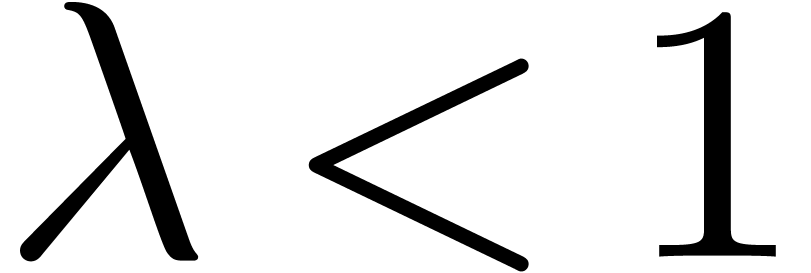 . Now consider a polynomial
. Now consider a polynomial
 of degree
of degree 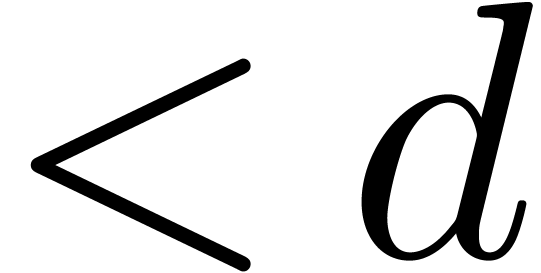 and let
and let 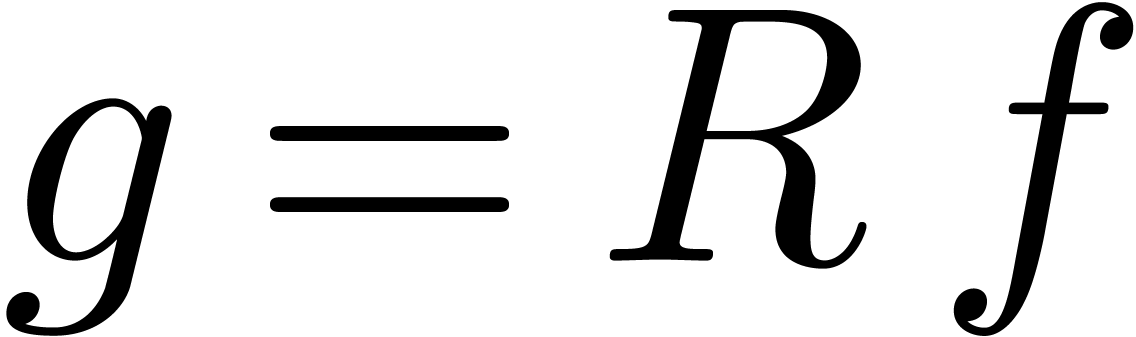 , so that
, so that
By the minimality hypothesis of 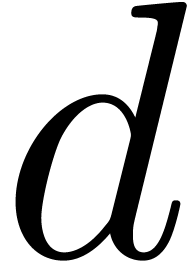 ,
we have
,
we have 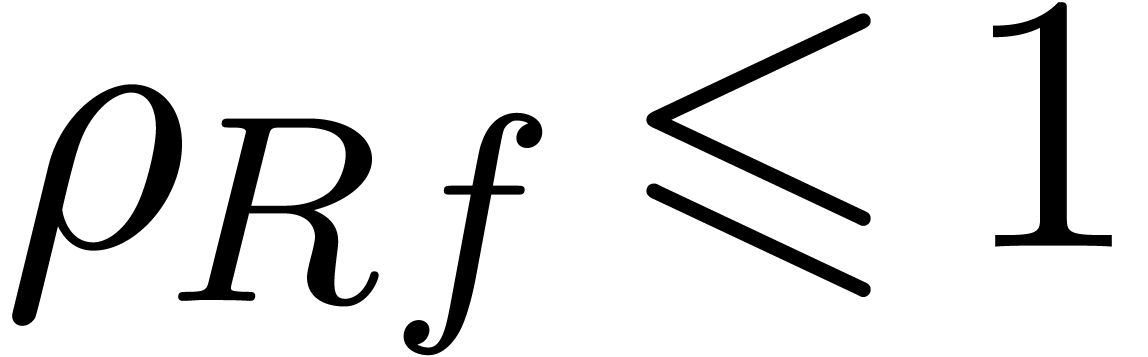 , whence the
coefficients
, whence the
coefficients 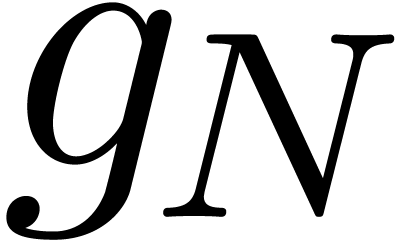 have polynomial or exponential
growth in
have polynomial or exponential
growth in 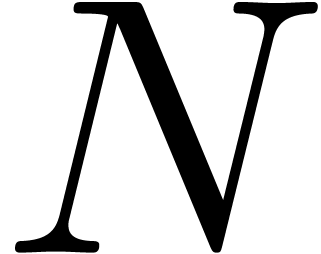 . Since this
property holds for all
. Since this
property holds for all 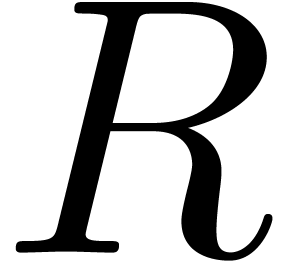 , it
follows that the matrix norm
, it
follows that the matrix norm 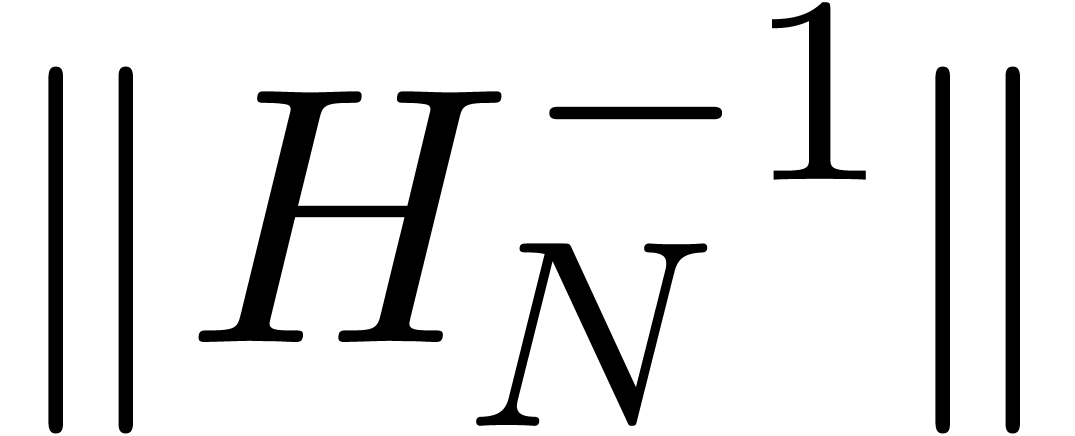 remains bounded for
large
remains bounded for
large 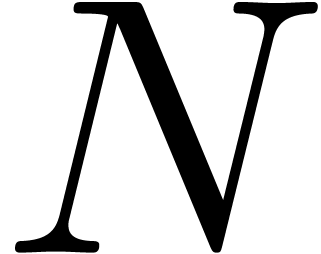 . In particular, the
solution to (8) is only an exponentially small perturbation
of the solution to (9) for large values of
. In particular, the
solution to (8) is only an exponentially small perturbation
of the solution to (9) for large values of 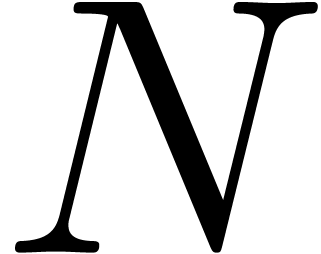 .
.
Remark  -step
search for the optimal degree
-step
search for the optimal degree 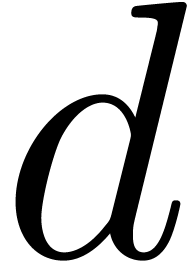 .
Using a binary search (doubling
.
Using a binary search (doubling 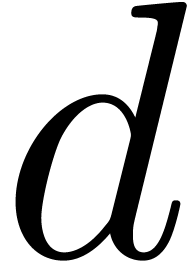 at each step at
a first stage, and using a dichotomic search at a second stage), the
number of steps can be reduced to
at each step at
a first stage, and using a dichotomic search at a second stage), the
number of steps can be reduced to 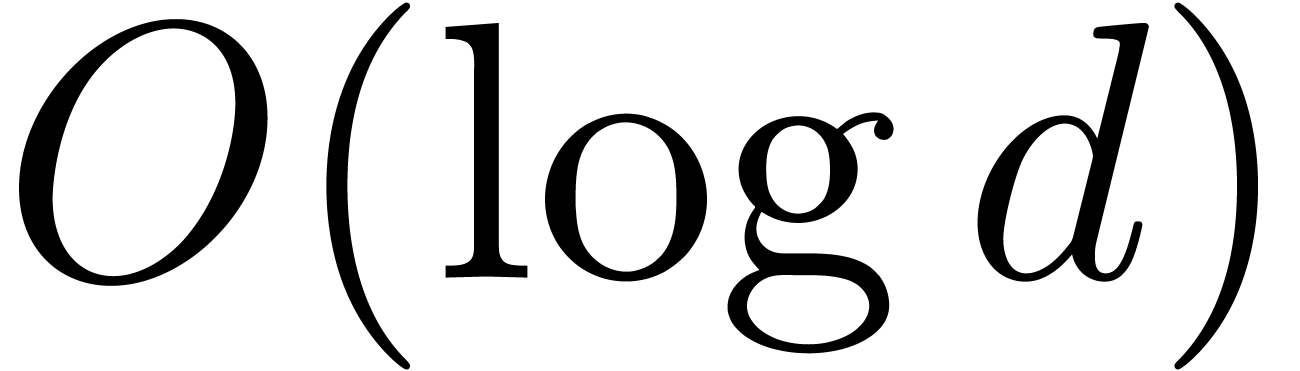 .
.
Let  be an analytic function which is given by
its power series
be an analytic function which is given by
its power series 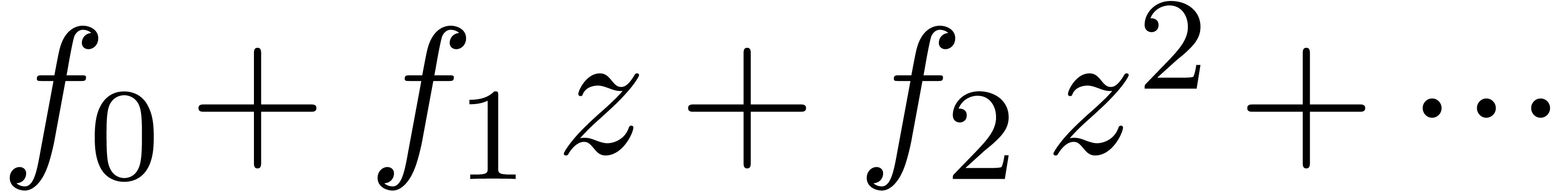 at the origin. Assume that
at the origin. Assume that  can be continued analytically on a Riemann surface
can be continued analytically on a Riemann surface
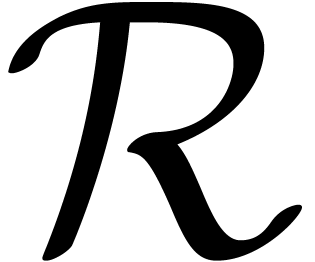 above the closed disk
above the closed disk  of
radius
of
radius  minus a finite set of points
minus a finite set of points  . Let
. Let  be the set of
analytic functions on
be the set of
analytic functions on  . We
say that
. We
say that  is algebraic on
is algebraic on 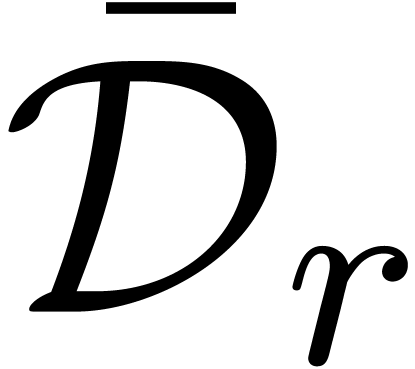 if
if  only admits algebraic singularities inside
only admits algebraic singularities inside
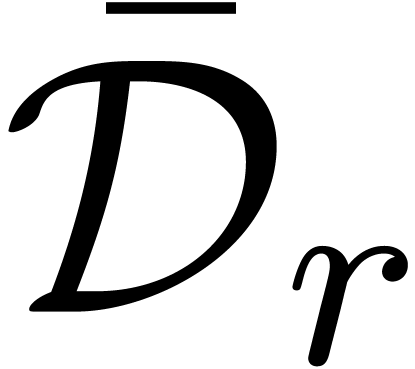 . This is the case if and
only if there exists a polynomial dependency
. This is the case if and
only if there exists a polynomial dependency
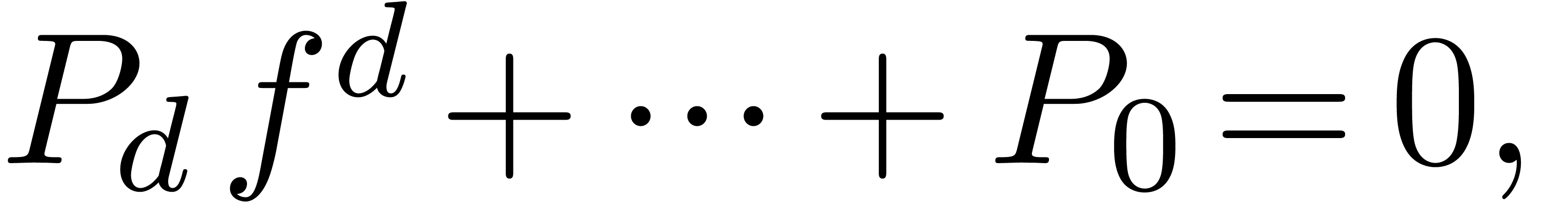 |
(10) |
where  . In that case, we may
normalize the relation such that
. In that case, we may
normalize the relation such that 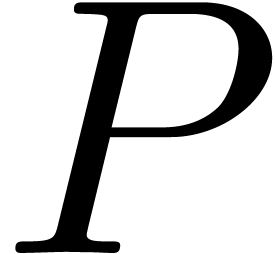 has minimal
degree and such that
has minimal
degree and such that 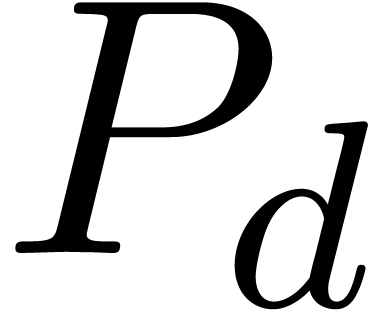 is a monic polynomial of
minimal degree. In particular, all roots of
is a monic polynomial of
minimal degree. In particular, all roots of 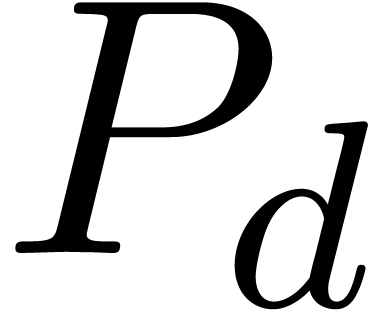 are
inside the disc
are
inside the disc 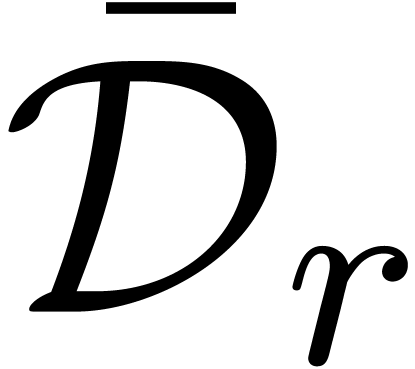 . We say that
. We say that
 is Fuchsian on
is Fuchsian on 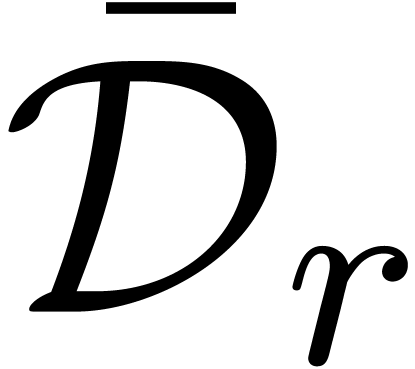 ,
if
,
if  only admits Fuchsian singularities inside
only admits Fuchsian singularities inside
 . This implies the existence
of a dependency
. This implies the existence
of a dependency
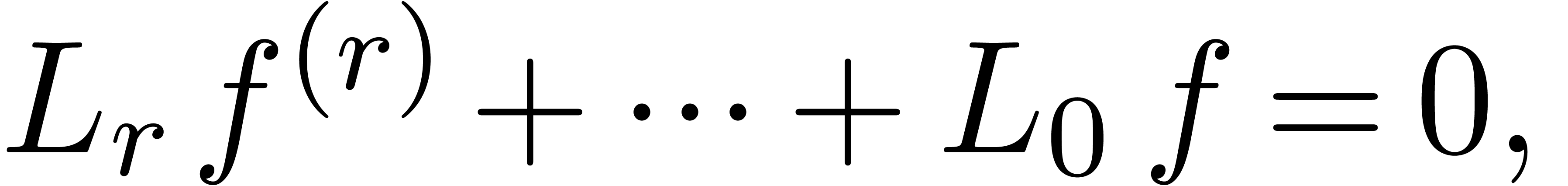 |
(11) |
where  . Again, we may
normalize (11) such that
. Again, we may
normalize (11) such that  has
minimal order
has
minimal order  and such that
and such that 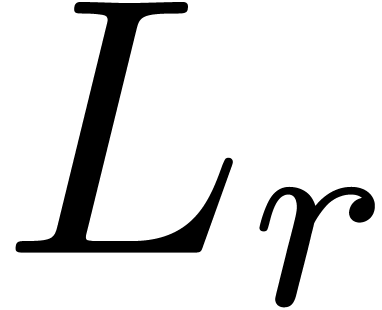 is a monic polynomial of minimal degree. Assuming that we have a high
accuracy algorithm for the analytic continuation of
is a monic polynomial of minimal degree. Assuming that we have a high
accuracy algorithm for the analytic continuation of  , we will give heuristic algorithms for the
computation of dependencies of the form (10) or (11),
if they exist.
, we will give heuristic algorithms for the
computation of dependencies of the form (10) or (11),
if they exist.
Remark 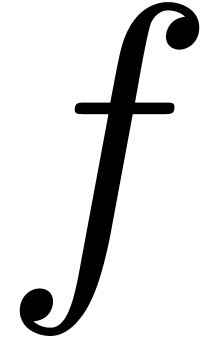 is
the solution of an initial value problem. For a precise definition of a
computable analytic function, we refer to [vdH07]. For the
heuristic purposes of this section, the existence of a numerical
algorithm for the continuation of
is
the solution of an initial value problem. For a precise definition of a
computable analytic function, we refer to [vdH07]. For the
heuristic purposes of this section, the existence of a numerical
algorithm for the continuation of 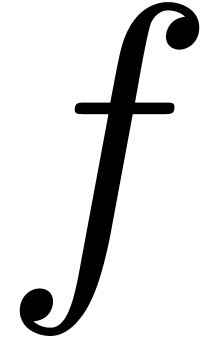 will be
sufficient.
will be
sufficient.
Assume that  is algebraic on
is algebraic on 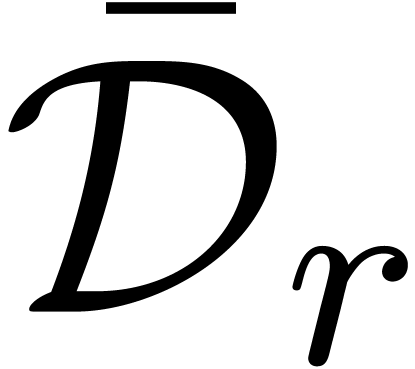 . For each singularity
. For each singularity 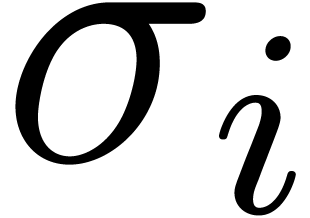 , choose a path
, choose a path 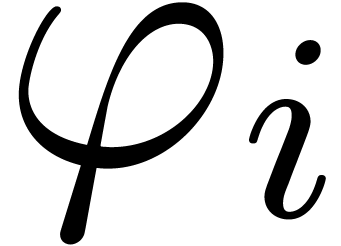 from the
origin to a point near
from the
origin to a point near 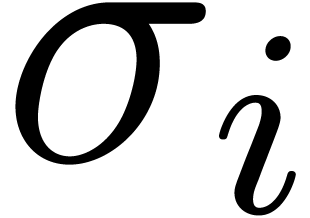 which avoids the other
singularities, and let
which avoids the other
singularities, and let 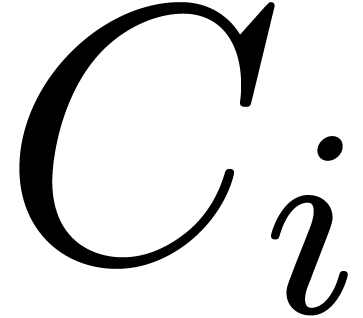 be the operator which
performs an analytic continuation along
be the operator which
performs an analytic continuation along 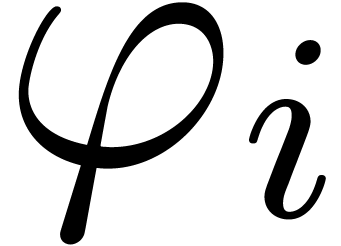 ,
one turn around
,
one turn around 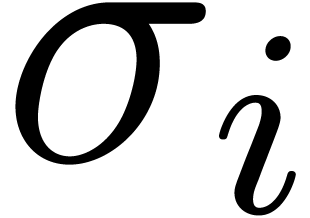 , followed by
an analytic continuation along
, followed by
an analytic continuation along 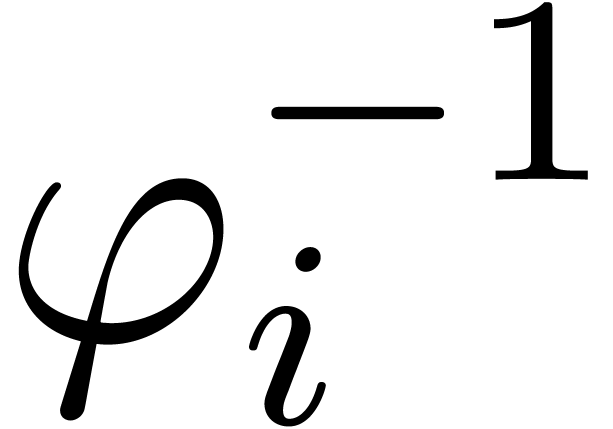 .
In the following algorithm for the detection of algebraic dependencies,
we assume a heuristic equality test for analytic functions at a point,
for instance by checking
.
In the following algorithm for the detection of algebraic dependencies,
we assume a heuristic equality test for analytic functions at a point,
for instance by checking 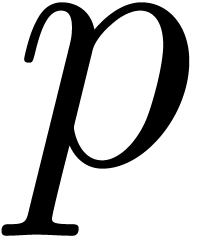 -bit
equality of the first
-bit
equality of the first 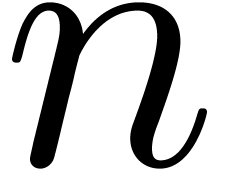 terms of the Taylor series
expansions.
terms of the Taylor series
expansions.
Algorithm alg_dep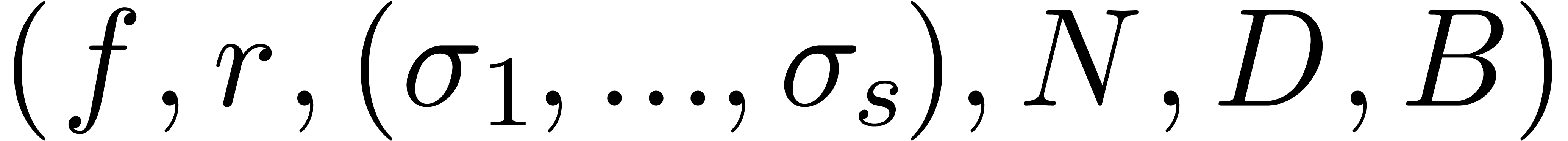
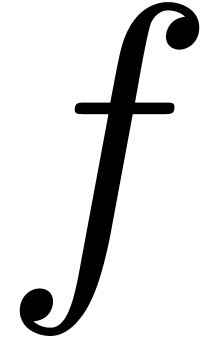 above
above 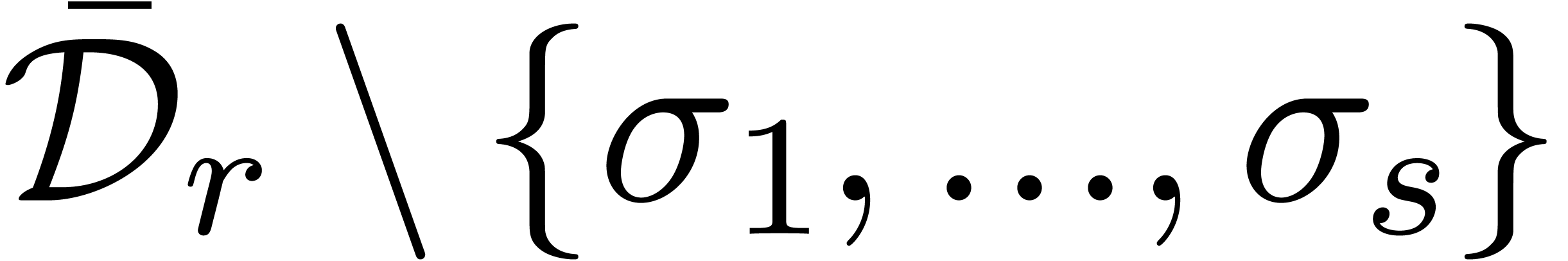 and bounds
and bounds 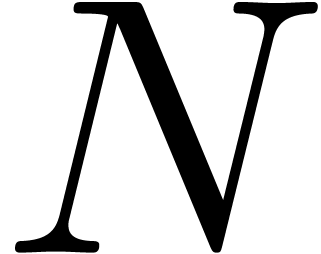 ,
,
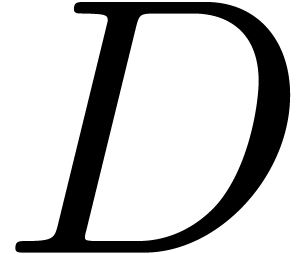 and
and 
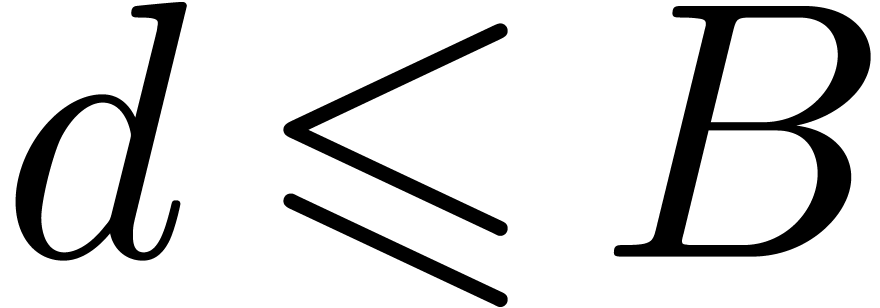 and
and 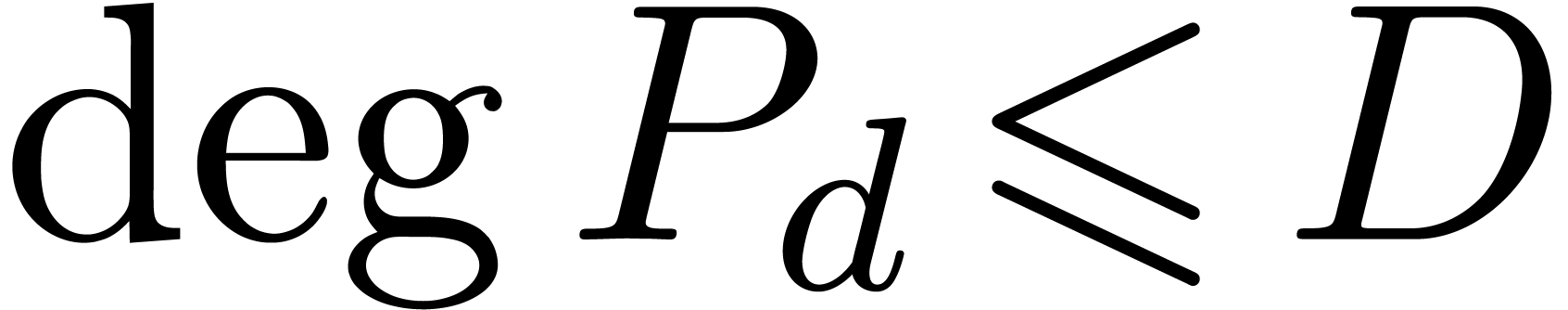 , or failed
, or failed
Step 1. [Initialize]
Set 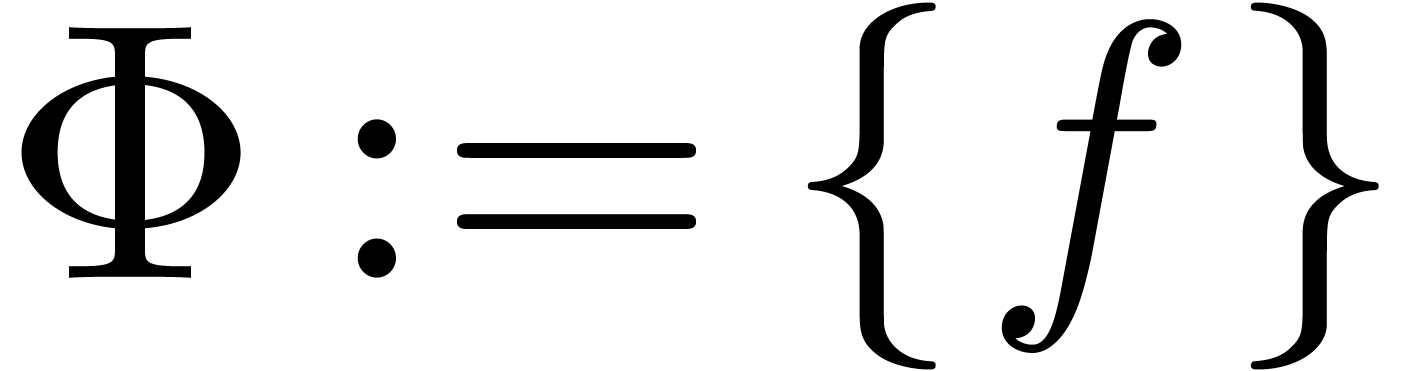
Step 2. [Saturate]
If 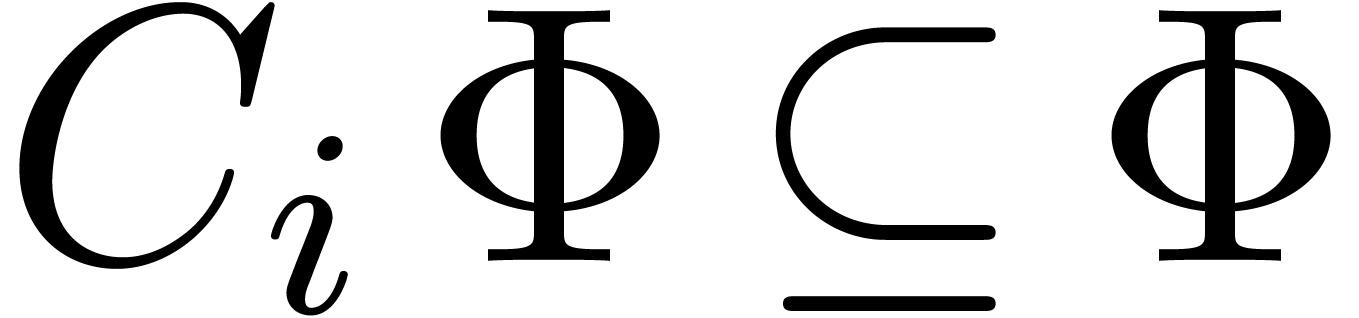 for all
for all 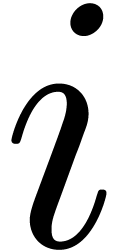 ,
then go to step 3
,
then go to step 3
If  then return failed
then return failed

Repeat step 2
Step 3. [Terminate]
Denote 
Compute 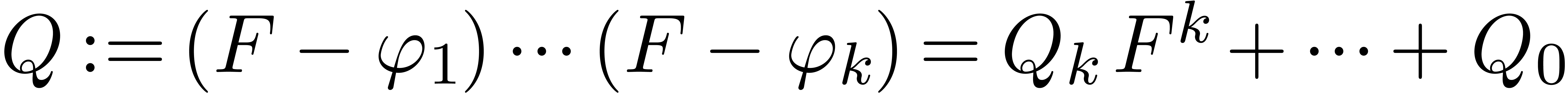
For each 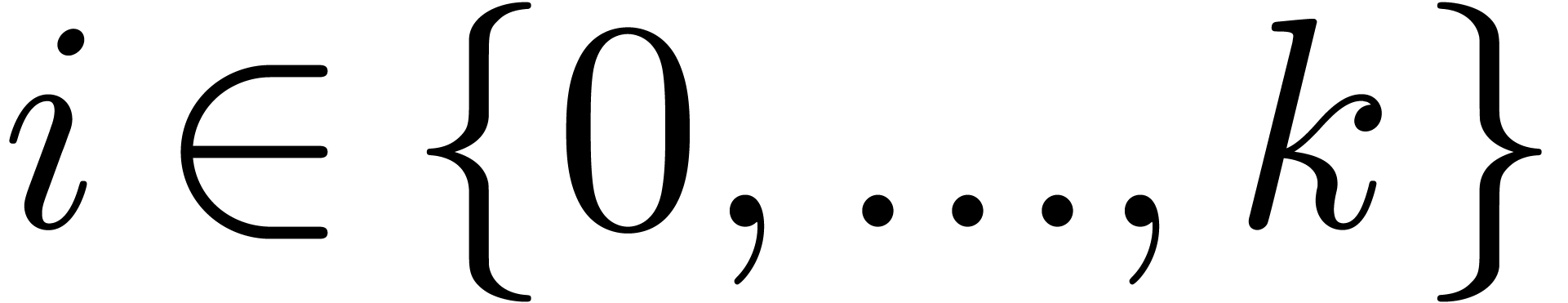 , compute
, compute 
If 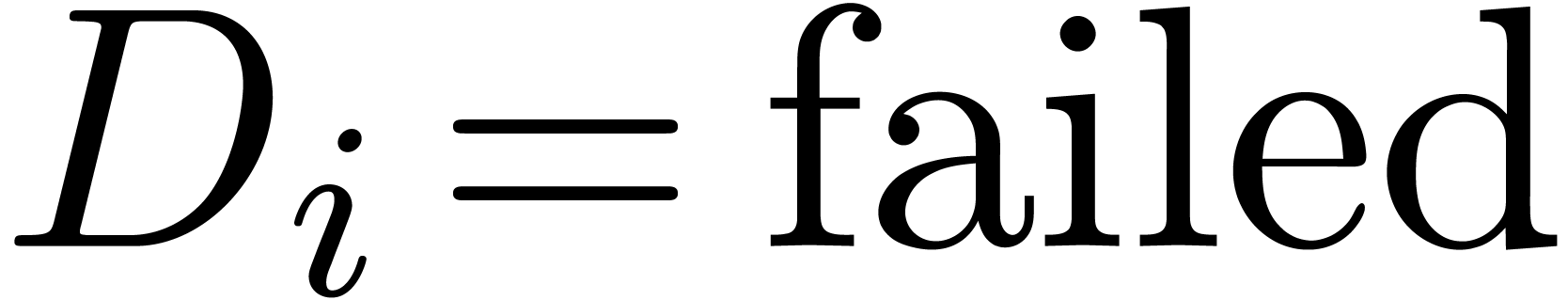 for some
for some  ,
then return failed
,
then return failed
Return 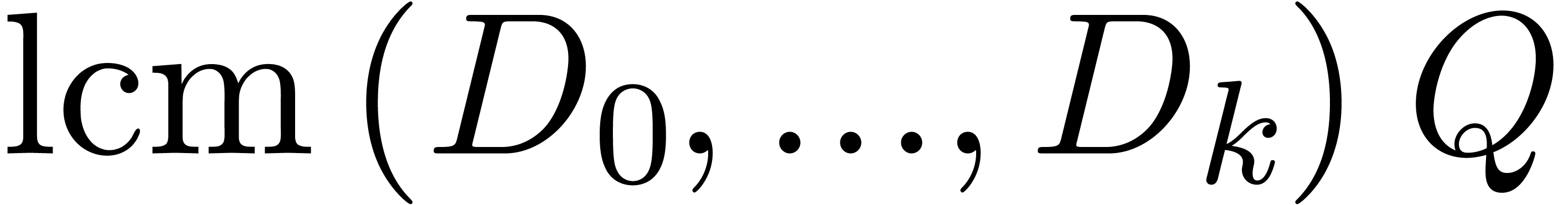
Proof. Assume that 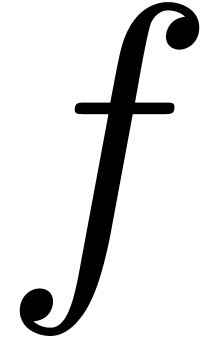 satisfies a normalized relation (10), with
satisfies a normalized relation (10), with  and
and  . Since
. Since  only contains distinct roots of
only contains distinct roots of 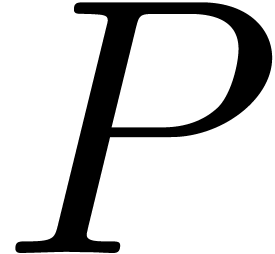 ,
we have
,
we have 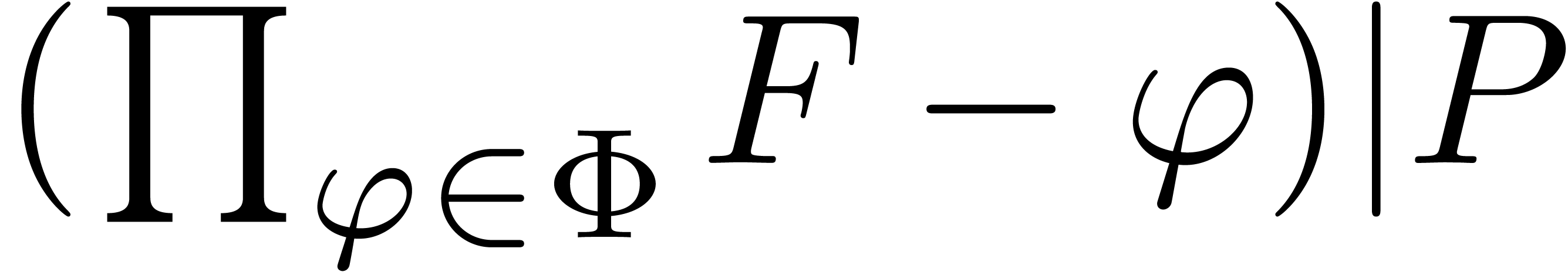 in
in 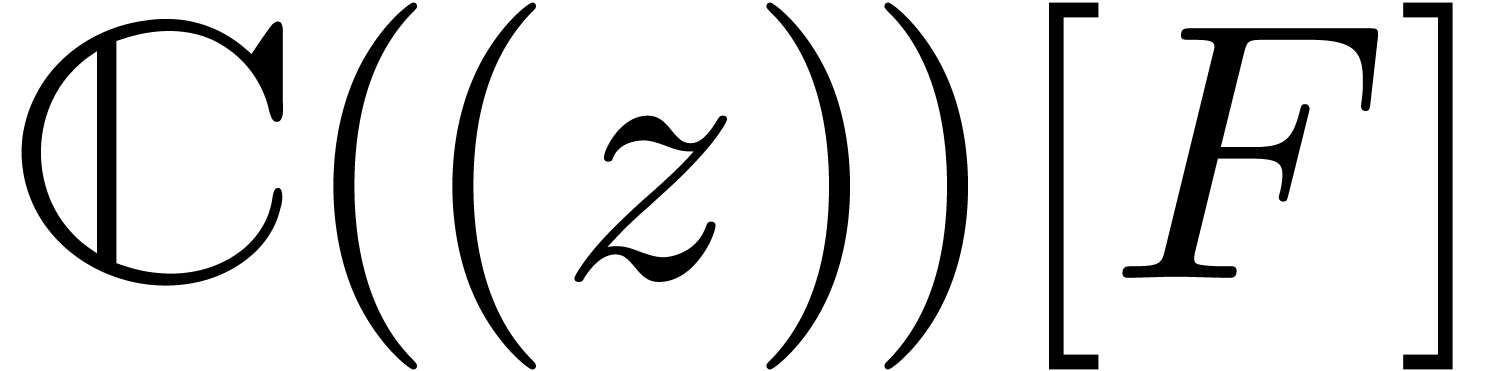 throughout
the algorithm. In particular
throughout
the algorithm. In particular  ,
and we ultimately obtain stabilization
,
and we ultimately obtain stabilization  .
.
At this point, analytic continuation around any of the points  leaves the polynomial
leaves the polynomial  invariant,
so the coefficients of
invariant,
so the coefficients of  are analytic and
single-valued on
are analytic and
single-valued on 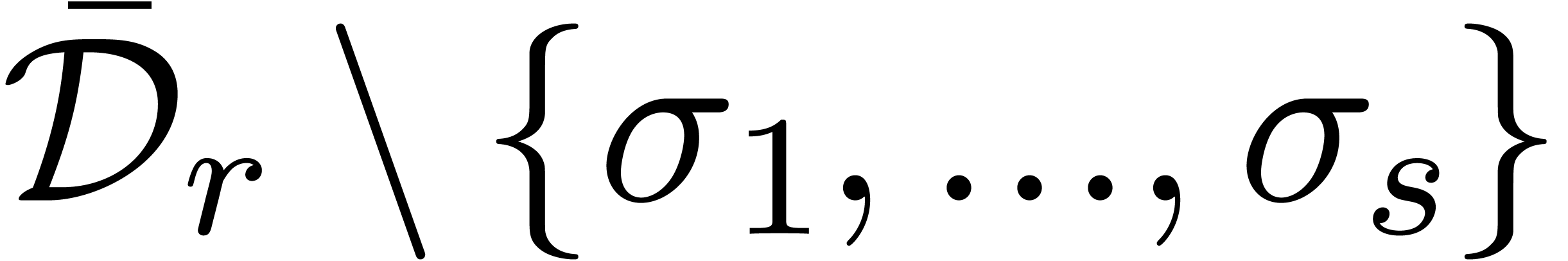 . On the
other hand, given a singularity
. On the
other hand, given a singularity 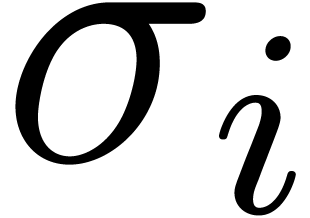 ,
each solution
,
each solution 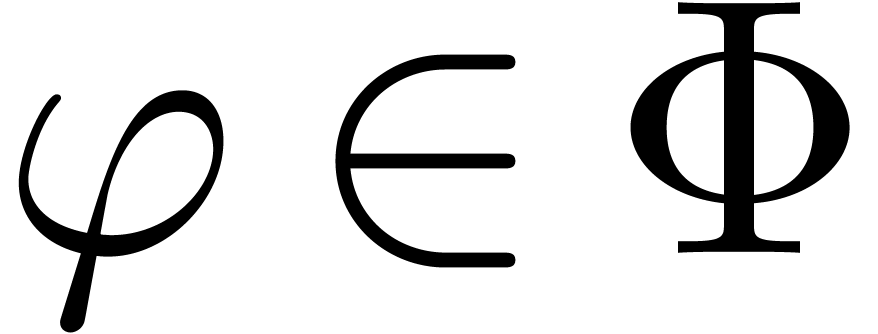 is also given by a convergent
Puiseux series near
is also given by a convergent
Puiseux series near 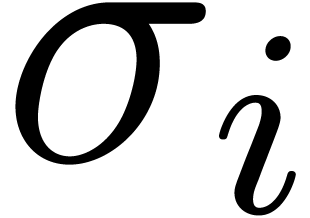 , whence
so are the coefficients of
, whence
so are the coefficients of  .
Since the only Puiseux series without monodromy around
.
Since the only Puiseux series without monodromy around 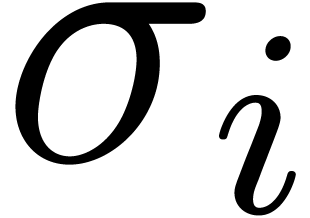 are Laurent series, it follows that the coefficients of
are Laurent series, it follows that the coefficients of  are meromorphic on
are meromorphic on 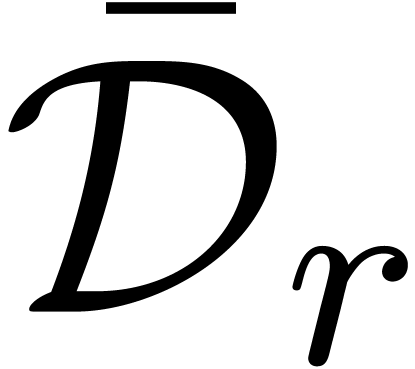 .
.
By the minimality assumption on  ,
it follows that
,
it follows that  and
and 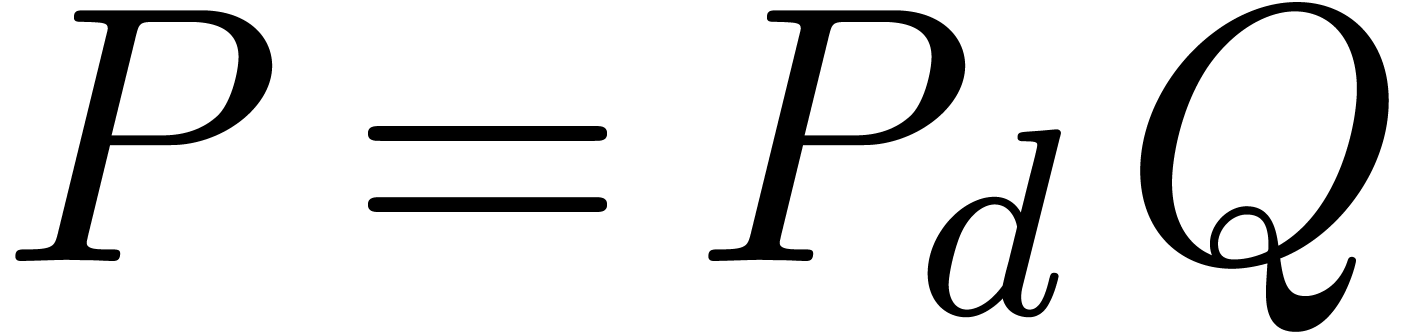 . Since each coefficient
. Since each coefficient 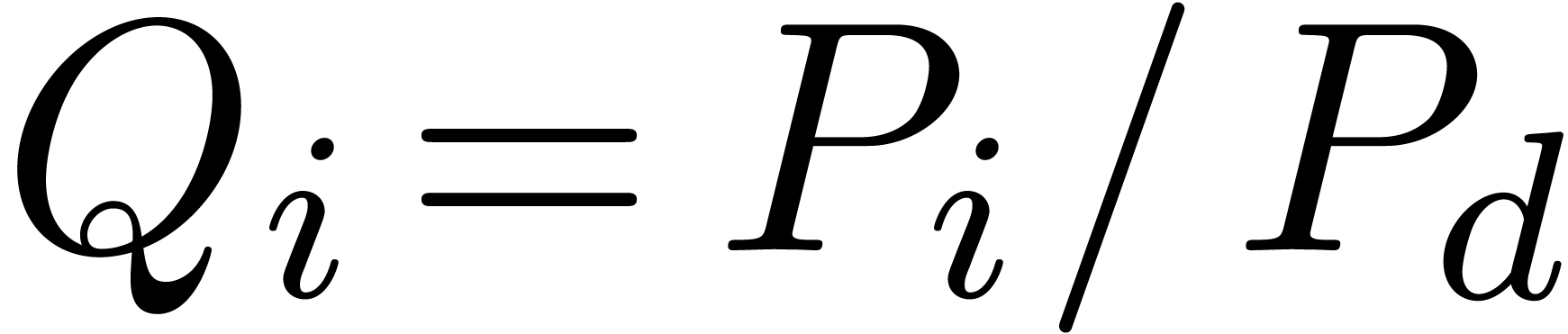 is
meromorphic on
is
meromorphic on 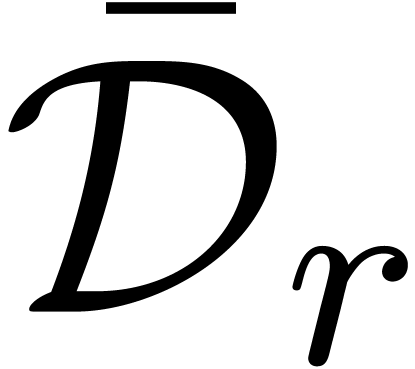 , we may use
the algorithm denom from the previous section in order
to compute a polynomial
, we may use
the algorithm denom from the previous section in order
to compute a polynomial 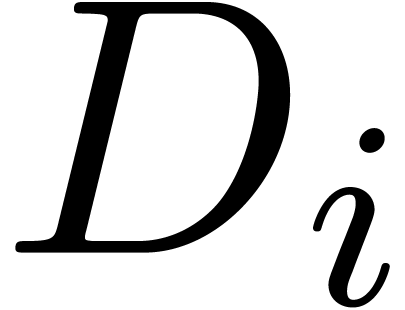 of minimal degree
of minimal degree  such that
such that 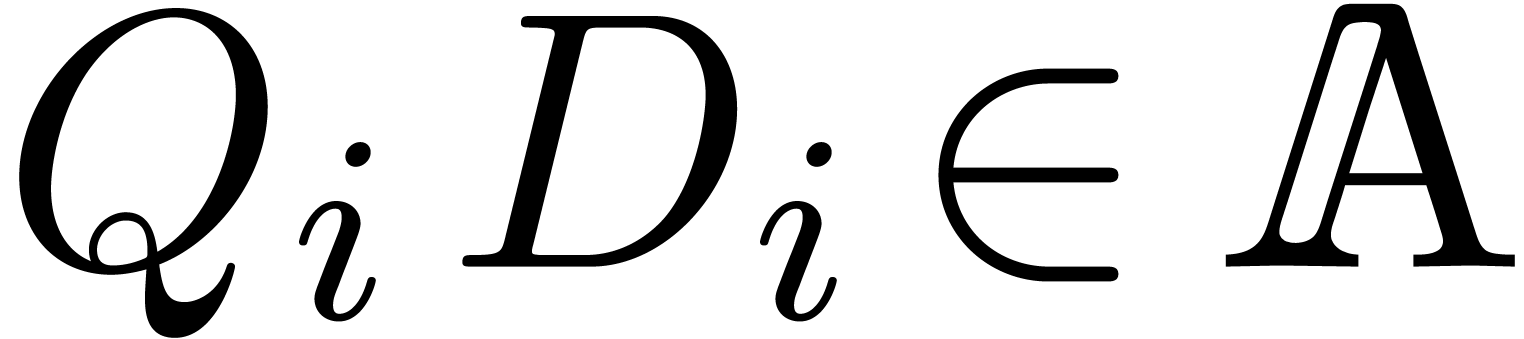 .
The monic least common multiple
.
The monic least common multiple 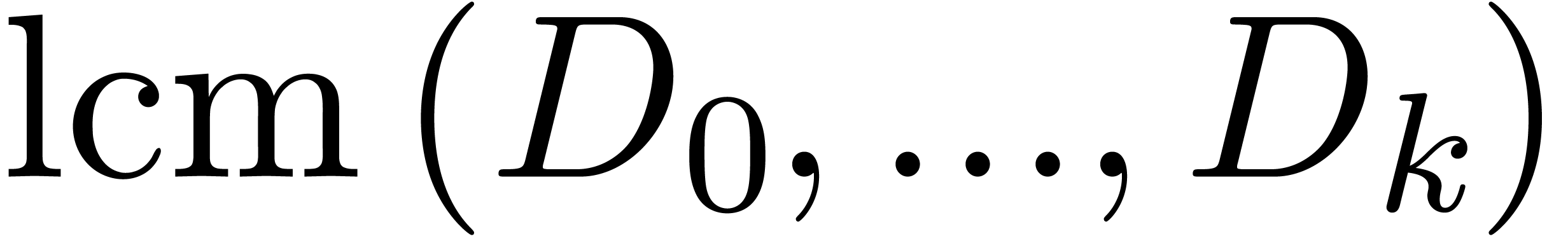 is nothing but
the monic polynomial
is nothing but
the monic polynomial 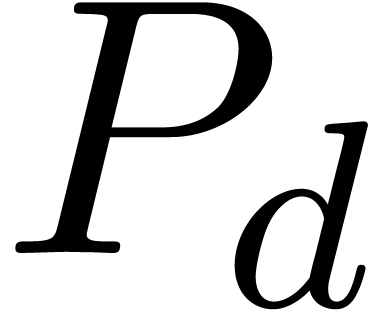 of minimal degree such that
of minimal degree such that
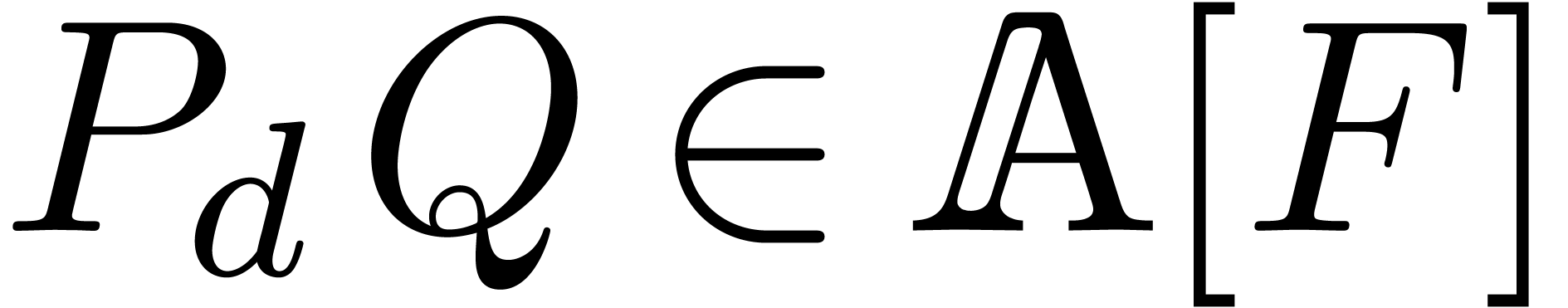 .
.
Remark  and check whether they are indeed superior to
and check whether they are indeed superior to 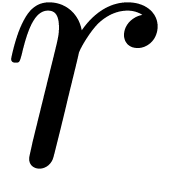 .
.
Algorithm fuch_dep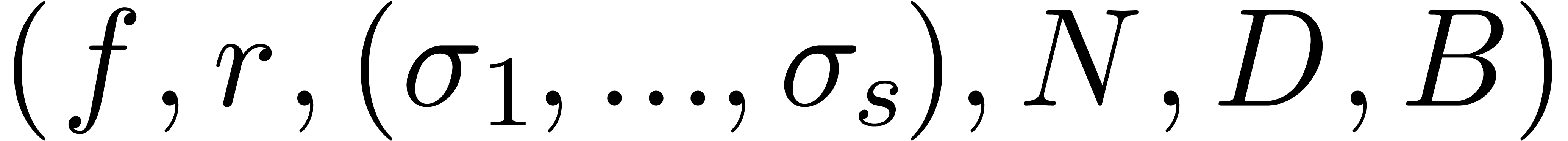
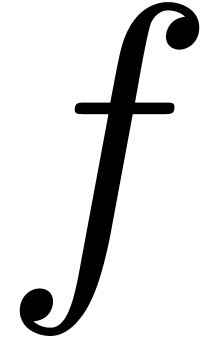 above
above 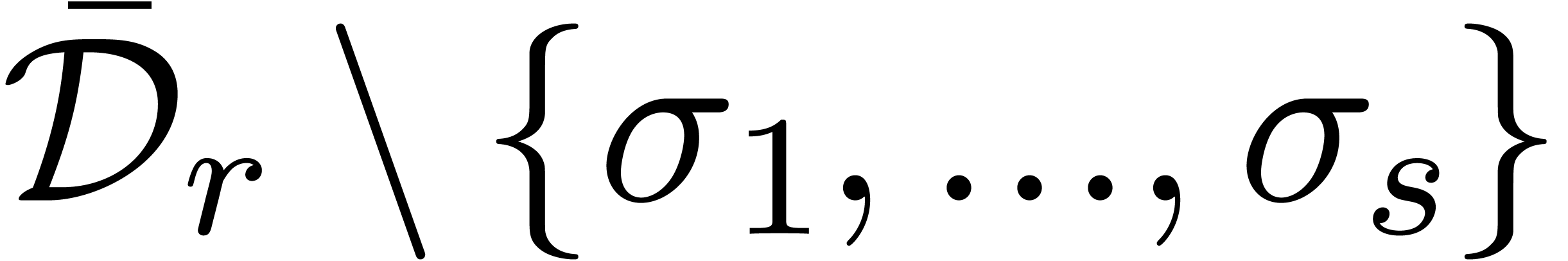 and bounds
and bounds 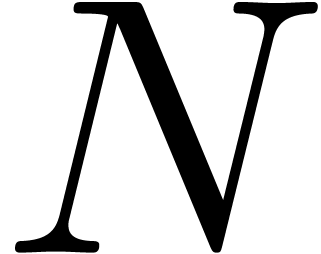 ,
,
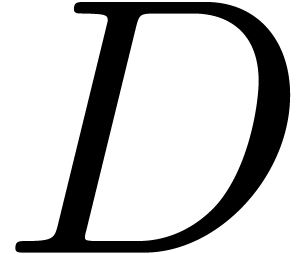 and
and 
 and
and 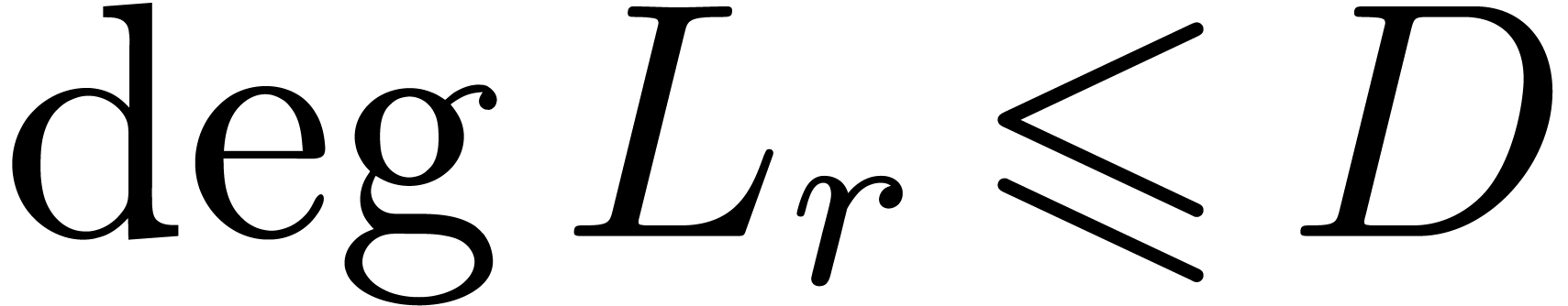 , or failed
, or failed
Step 1. [Initialize]
Set 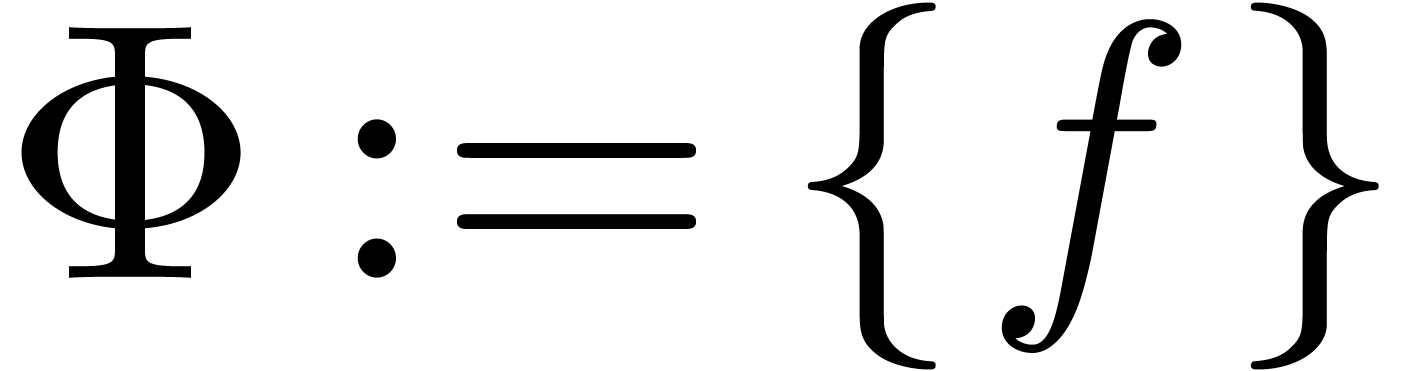
Step 2. [Saturate]
If 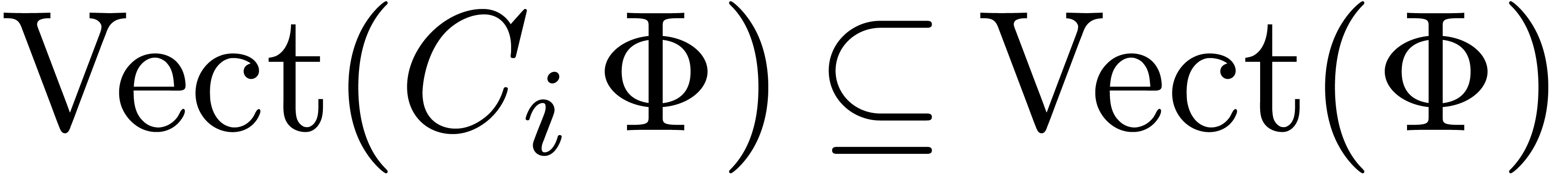 for all
for all  ,
then go to step 3
,
then go to step 3
If  then return failed
then return failed
 for
for  and
and 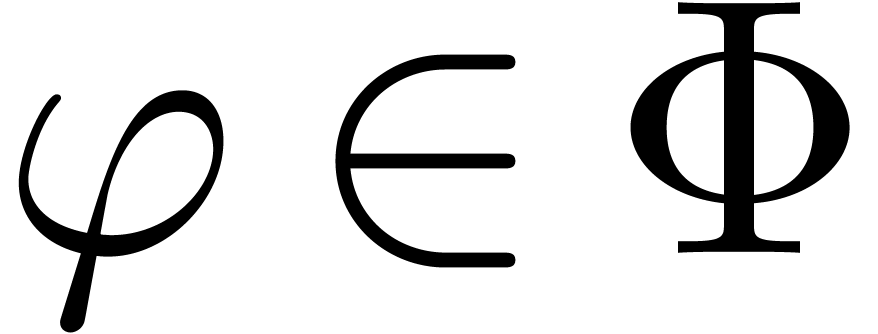 with
with 
Repeat step 2
Step 3. [Terminate]
Denote 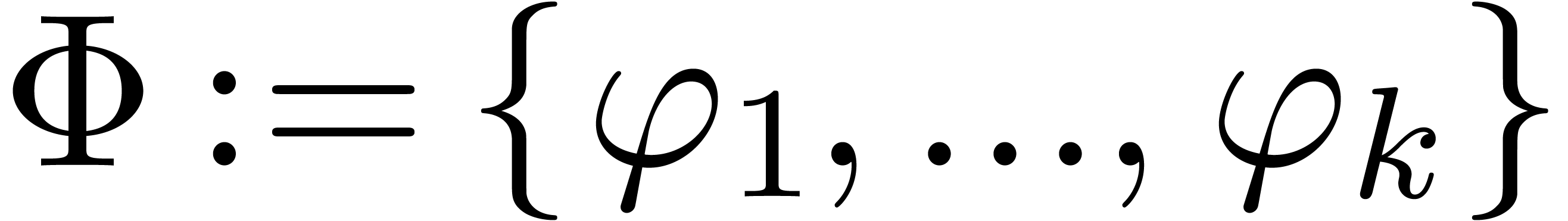
Compute 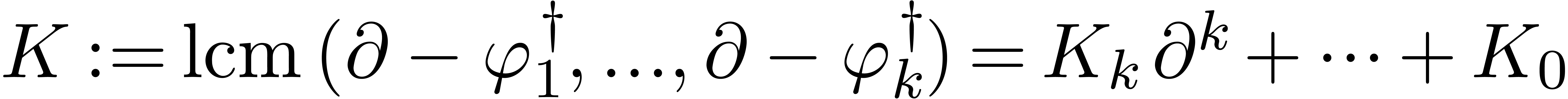
in the skew polynomial ring 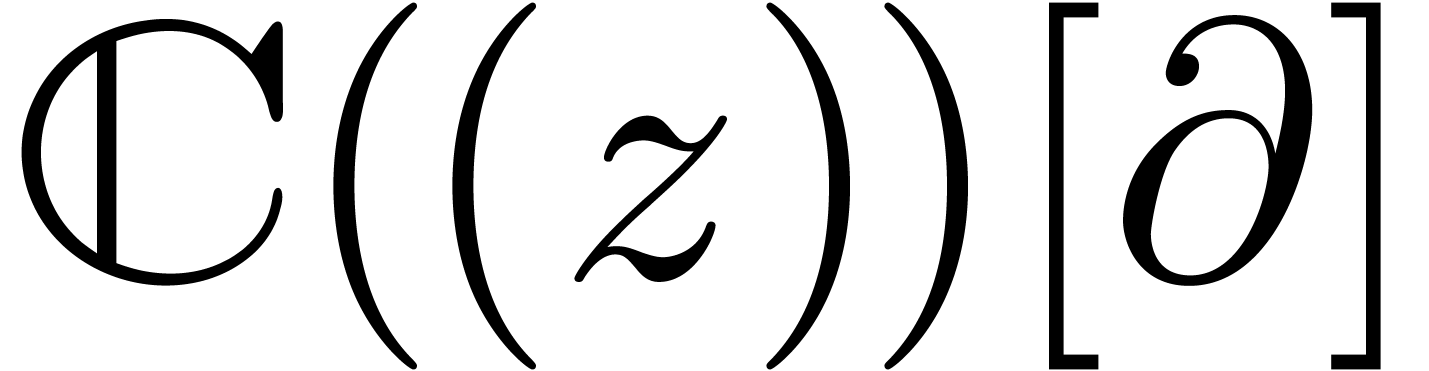 ,
where
,
where  denotes
denotes 
For each 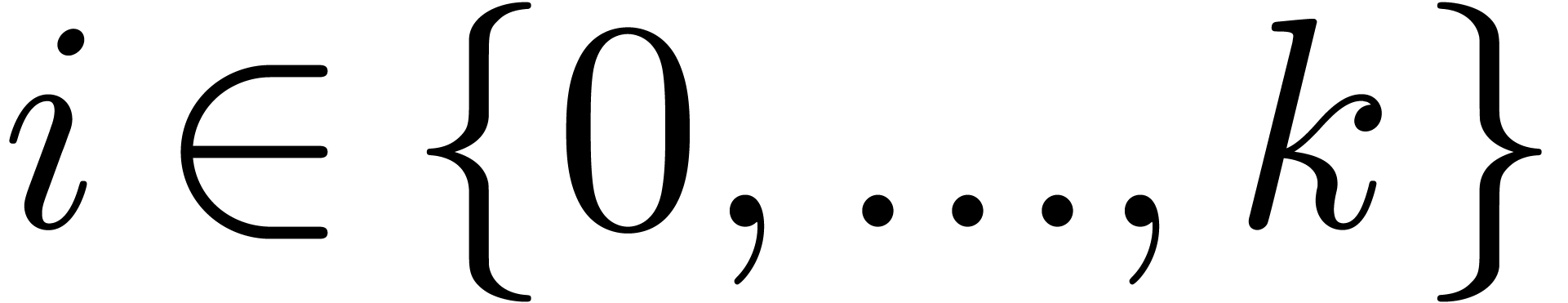 , compute
, compute 
If 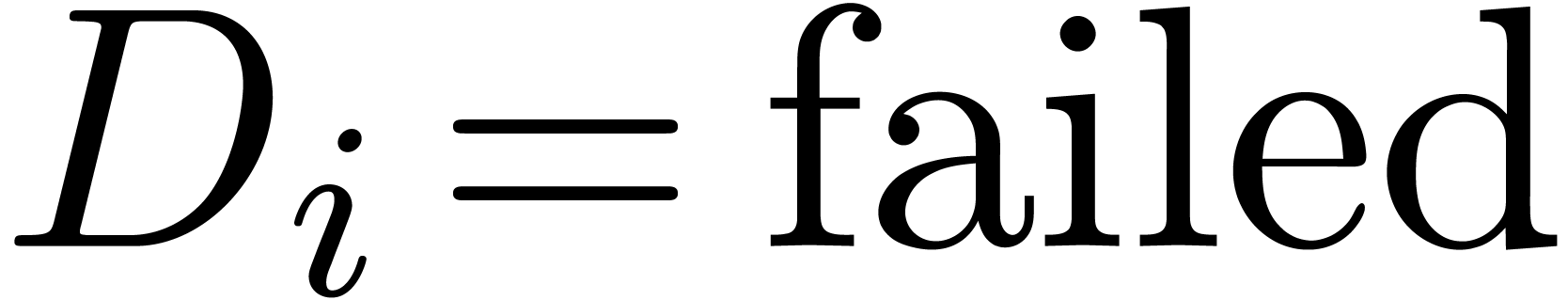 for some
for some 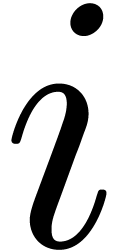 ,
then return failed
,
then return failed
Return 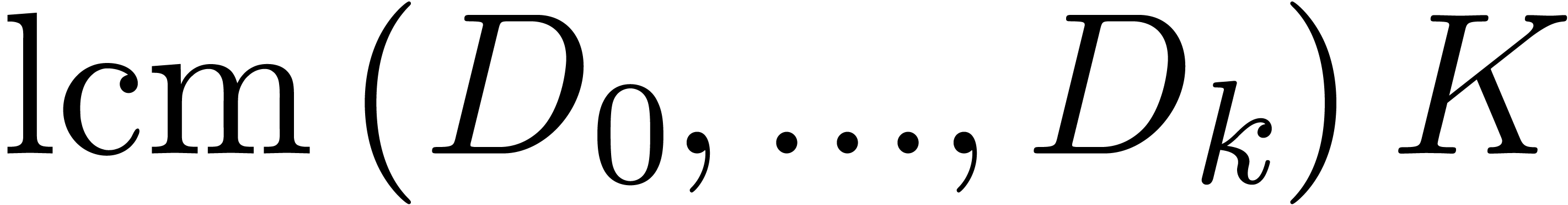
Proof. Assume that 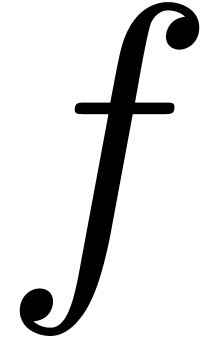 satisfies a normalized Fuchsian relation (11), with
satisfies a normalized Fuchsian relation (11), with  and
and 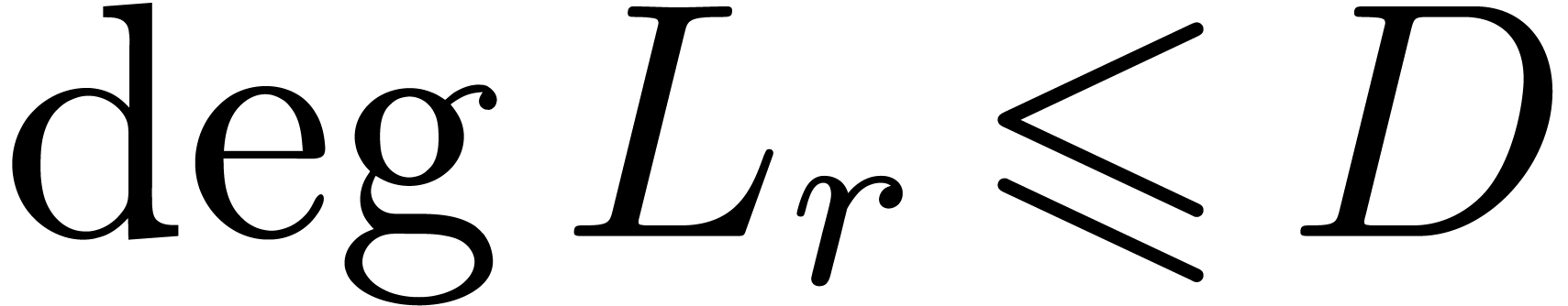 .
Throughout the algorithm, the set
.
Throughout the algorithm, the set  only contains
linearly independent solutions to
only contains
linearly independent solutions to 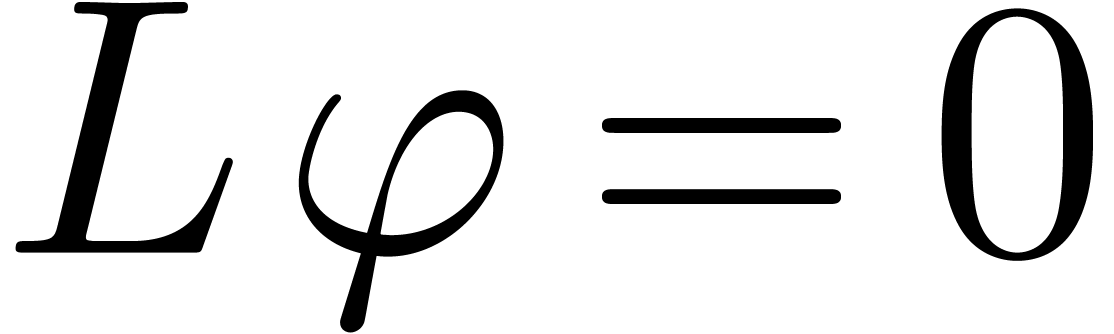 .
Therefore, the smallest operator
.
Therefore, the smallest operator 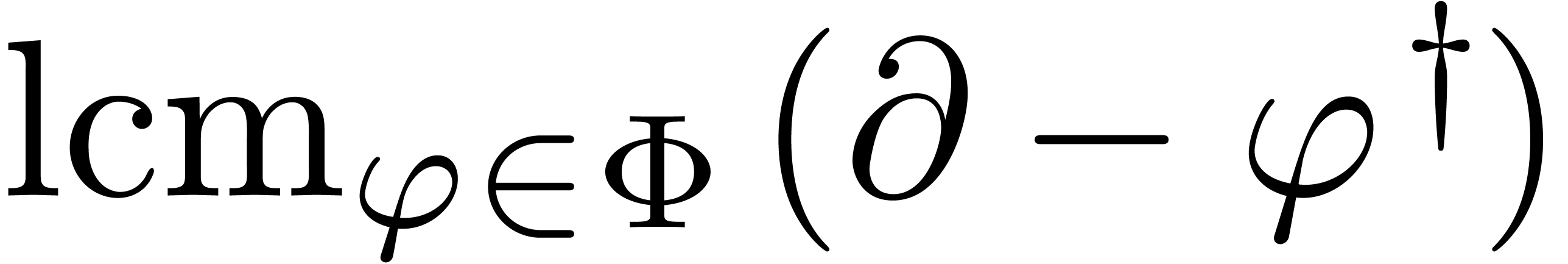 which vanishes
on
which vanishes
on  divides
divides  in
in 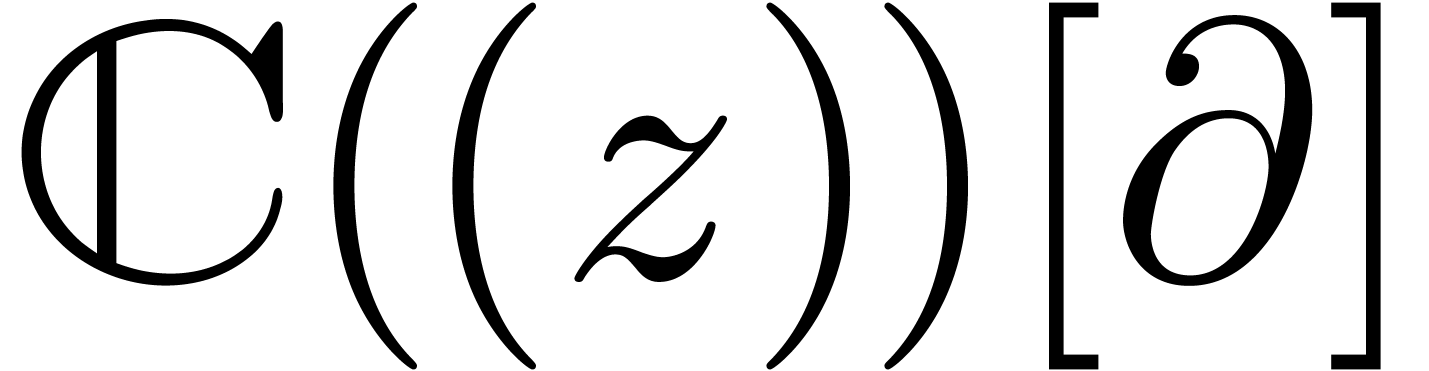 . In particular
. In particular  , and we ultimately obtain stabilization
, and we ultimately obtain stabilization  .
.
Consider one of the singularities 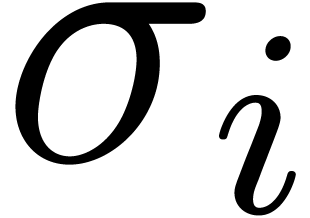 .
Since
.
Since 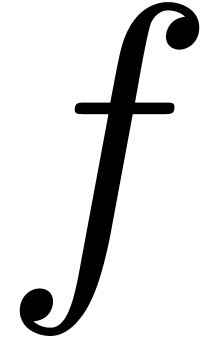 is Fuchsian at
is Fuchsian at 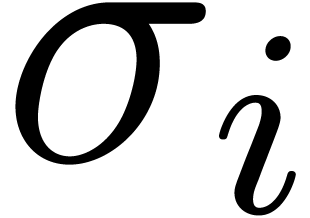 , the equation
, the equation 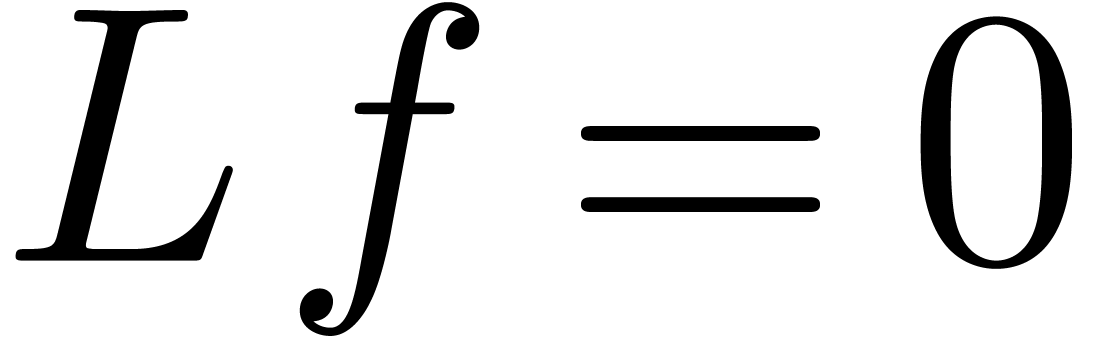 admits a
fundamental system of solutions of the form
admits a
fundamental system of solutions of the form
where 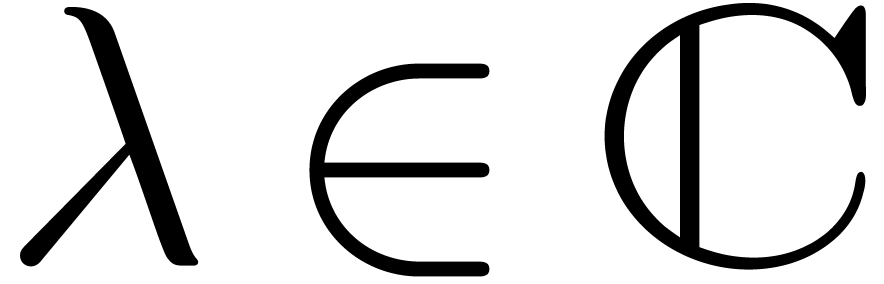 and
and  are convergent
power series. The coefficients of
are convergent
power series. The coefficients of 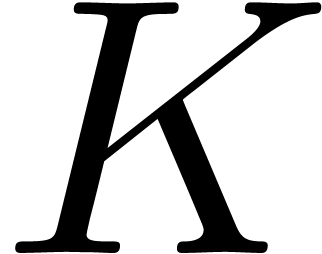 lay in the
field
lay in the
field  generated by all generalized power series
of this form. Again, the only elements of
generated by all generalized power series
of this form. Again, the only elements of  with a
trivial monodromy around
with a
trivial monodromy around  are convergent Laurent
series at
are convergent Laurent
series at  . Since analytic
continuation around
. Since analytic
continuation around 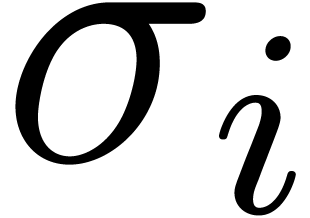 leaves the operator
leaves the operator 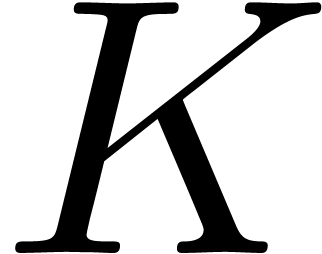 unchanged, it follows that the coefficients of
unchanged, it follows that the coefficients of 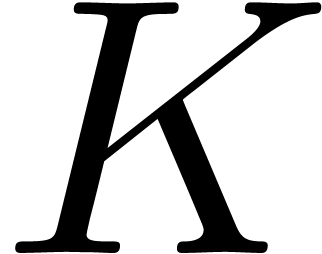 are meromorphic on
are meromorphic on 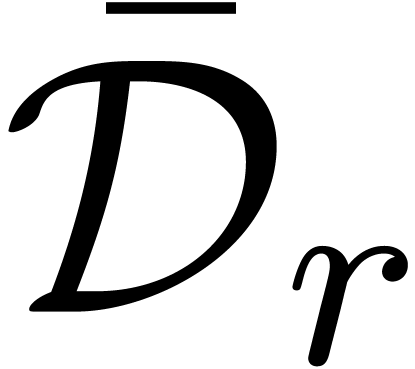 .
We conclude in a similar way as in the proof of theorem 4.
.
We conclude in a similar way as in the proof of theorem 4.
Remark 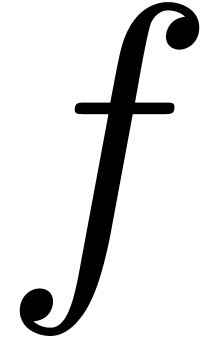 admits at worse a Fuchsian singularity at
admits at worse a Fuchsian singularity at
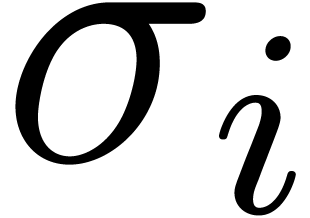 is essential for the algorithm to work. For
instance, in the case of the function
is essential for the algorithm to work. For
instance, in the case of the function
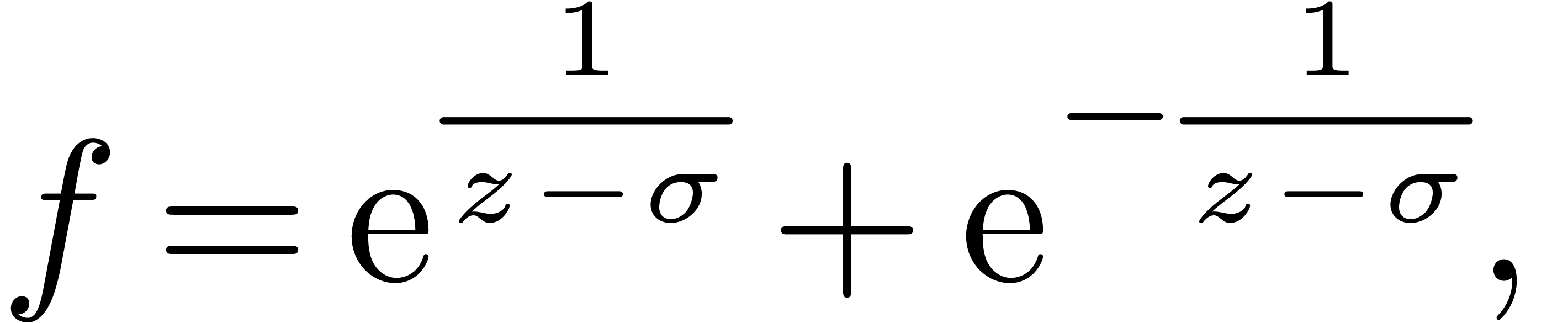
the monodromy around  is trivial, whence applying
the algorithm for
is trivial, whence applying
the algorithm for 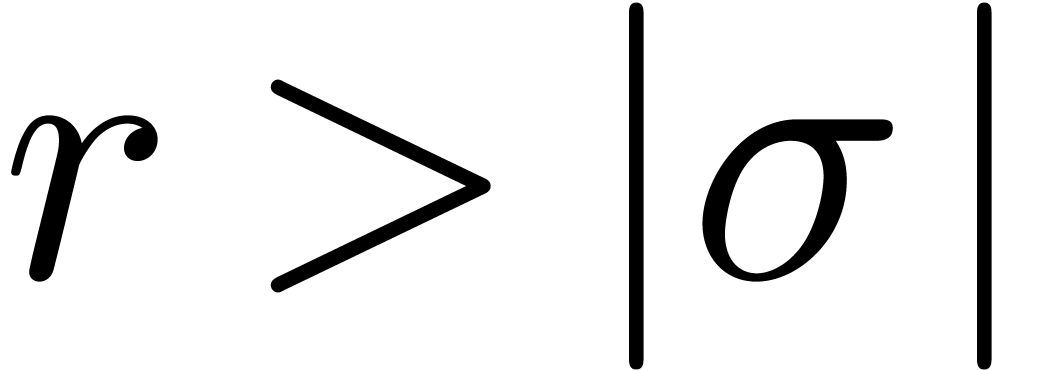 would simply result in having
would simply result in having
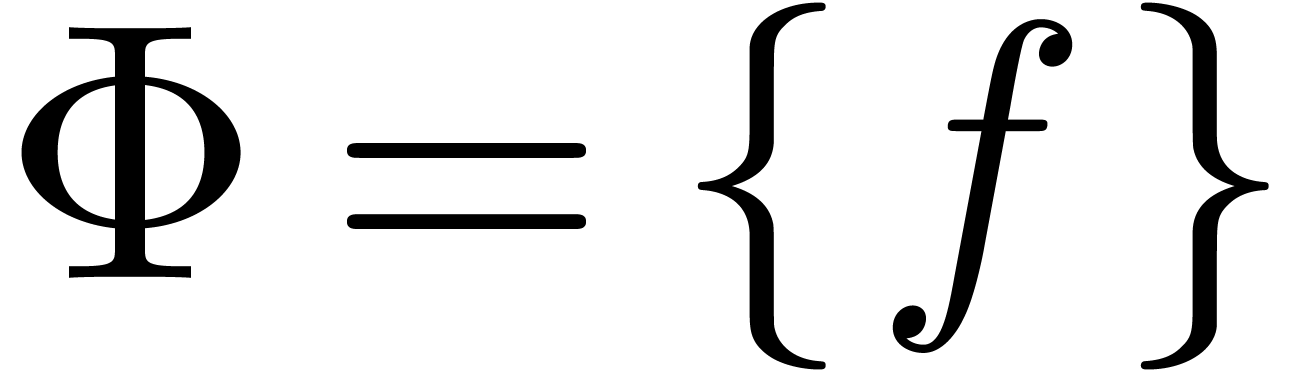 at step 3. Although
at step 3. Although 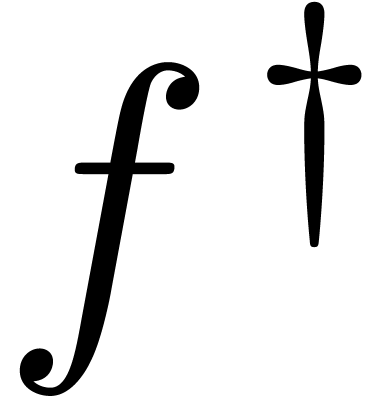 has
no monodromy around
has
no monodromy around  , this
function is no longer a Laurent series. In fact, the desired vanishing
operator has second order in this case, but it cannot be read off
directly from
, this
function is no longer a Laurent series. In fact, the desired vanishing
operator has second order in this case, but it cannot be read off
directly from  .
.
So far, our algorithms assume that we know the locations of the
singularities  inside the disc
inside the disc 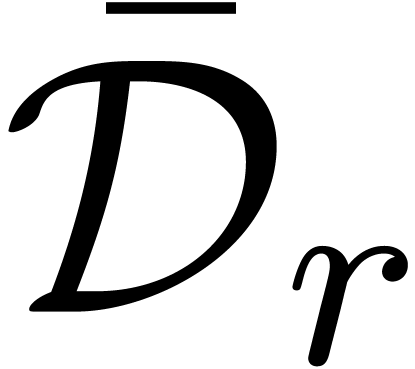 . Using the techniques from the previous
section, we still need an algorithm to determine these locations.
. Using the techniques from the previous
section, we still need an algorithm to determine these locations.
Assume that we have localized some of the singularities  and that
and that  has been stabilized under the
corresponding operators
has been stabilized under the
corresponding operators 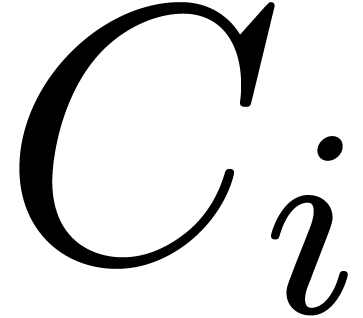 .
Given one of the singularities
.
Given one of the singularities 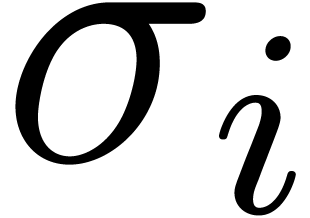 ,
one subtask is to determine a small radius
,
one subtask is to determine a small radius  such
that
such
that  does not admit other singularities above
the disc with center
does not admit other singularities above
the disc with center 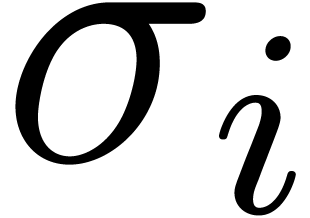 and radius
and radius  . For a given candidate
. For a given candidate  , this condition can be checked as follows. We
choose a sufficient number
, this condition can be checked as follows. We
choose a sufficient number 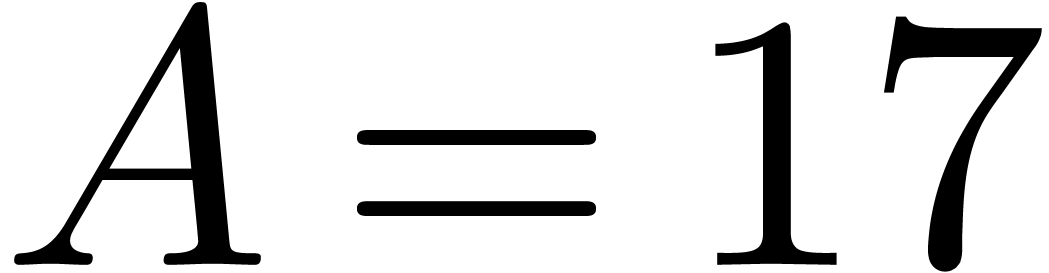 of equally spaced
points
of equally spaced
points
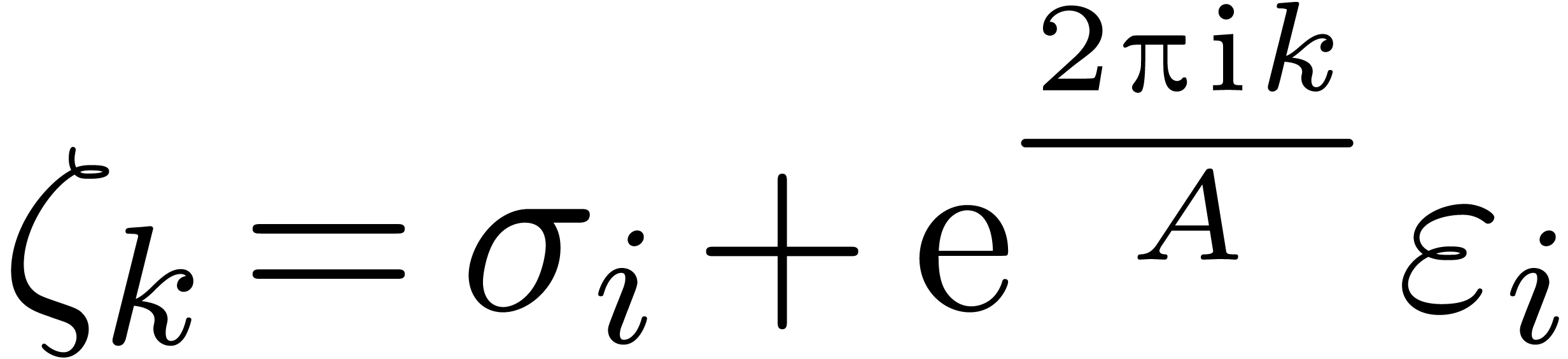
on the Riemann surface of  above the circle with
center
above the circle with
center 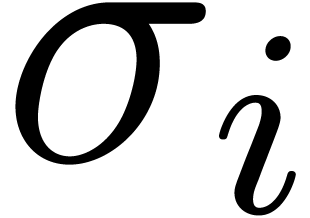 and radius
and radius  .
For each
.
For each 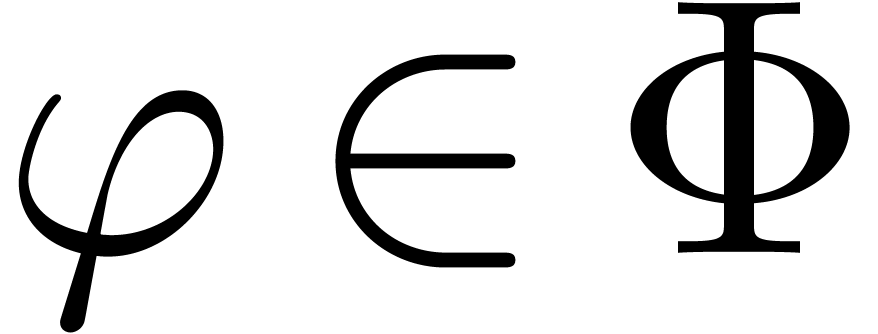 and each point
and each point  , we may use the techniques from the previous
section in order to determine the closest singularity
, we may use the techniques from the previous
section in order to determine the closest singularity  of
of  to
to  .
Now our check succeeds if
.
Now our check succeeds if 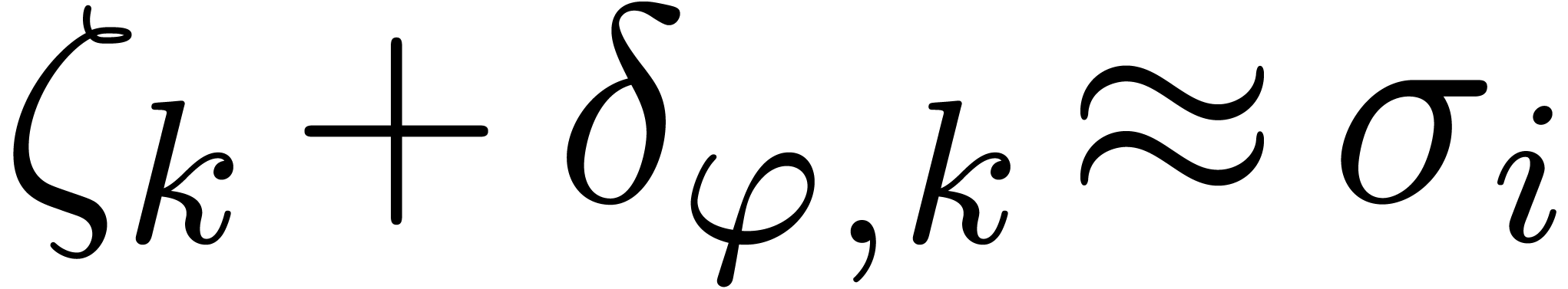 or
or 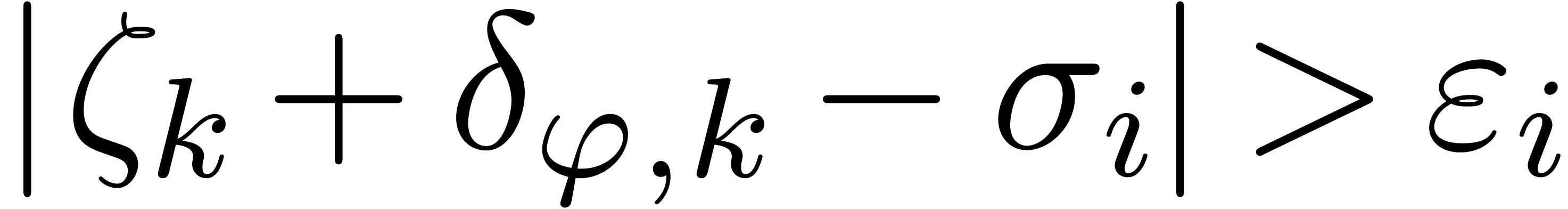 for all
for all  and
and  .
If it fails, then we retry with a smaller
.
If it fails, then we retry with a smaller  .
As soon as
.
As soon as  becomes smaller than a fixed
threshold, then we abort.
becomes smaller than a fixed
threshold, then we abort.
A second subtask is to guarantee the absence of singularities on the
remaining part of the Riemann surface of  above
above
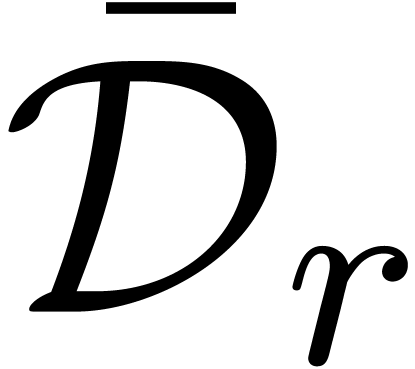 . We construct a sequence of
open balls
. We construct a sequence of
open balls 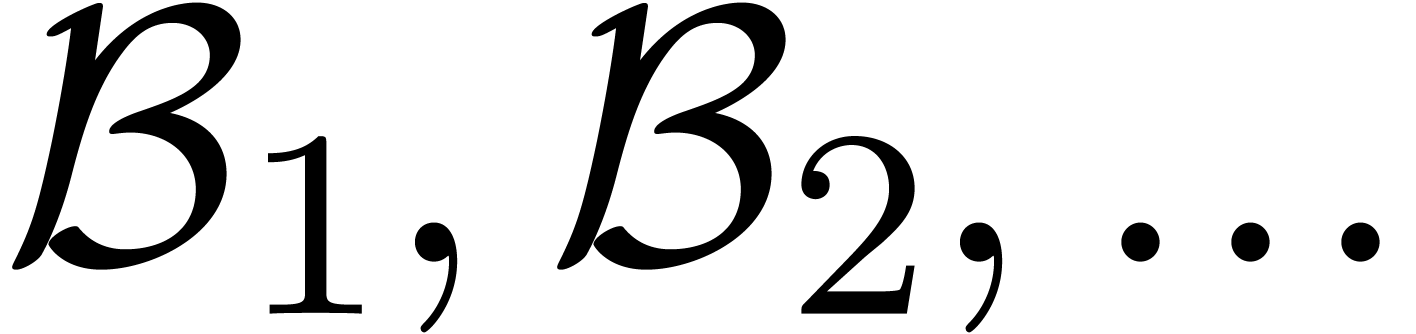 as follows. For
as follows. For  , we let
, we let 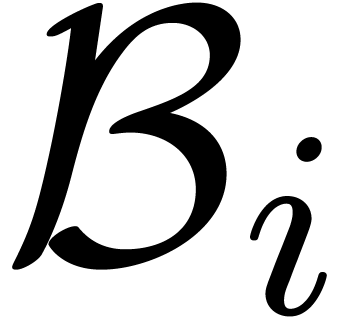 be the ball
with center
be the ball
with center 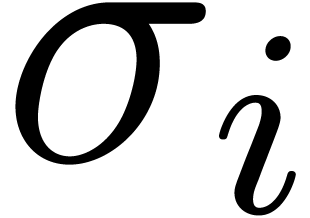 and radius
and radius  . The remaining
. The remaining 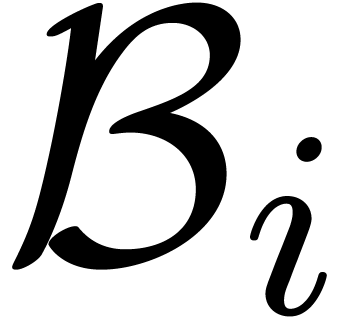 are
constructed by induction over
are
constructed by induction over 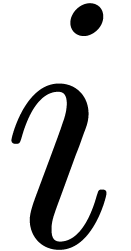 .
We arbitrarily chose the center
.
We arbitrarily chose the center  of
of 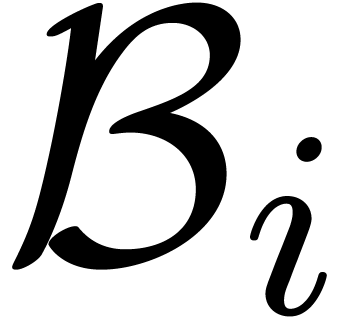 in
in  and heuristically determine the
minimum
and heuristically determine the
minimum 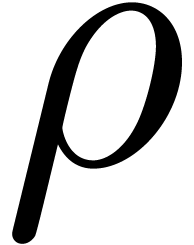 of the convergence radii of the elements
in
of the convergence radii of the elements
in  above
above  .
If
.
If 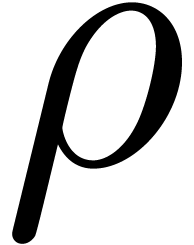 is significantly smaller than
is significantly smaller than  , then this indicates a missing singularity: we
heuristically determine the closest singularity
, then this indicates a missing singularity: we
heuristically determine the closest singularity  to
to  and add it to the set
and add it to the set  . Since
. Since  was chosen
arbitrarily, there usually is at most one closest singularity. As an
additional security check, we may also determine the closest singularity
to
was chosen
arbitrarily, there usually is at most one closest singularity. As an
additional security check, we may also determine the closest singularity
to 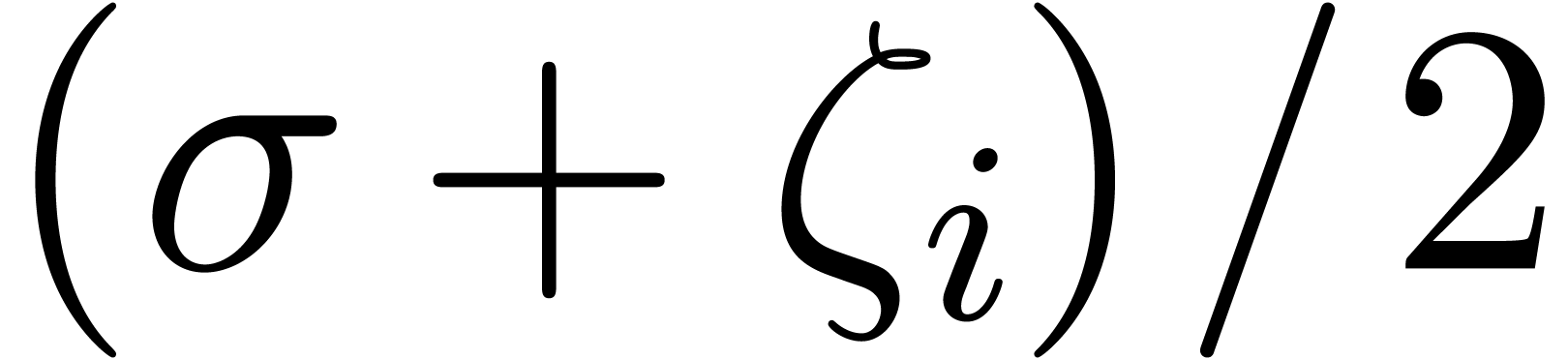 and check that it coincides with
and check that it coincides with  . If
. If 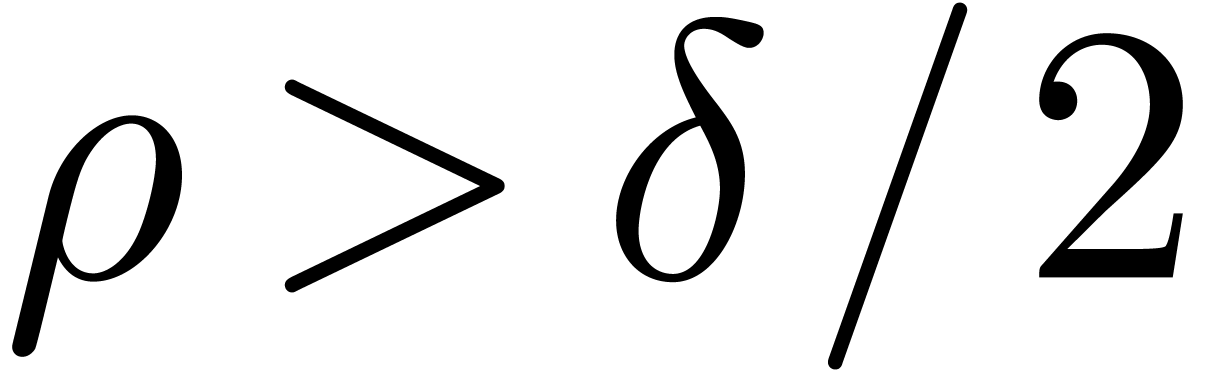 ,
then we take
,
then we take 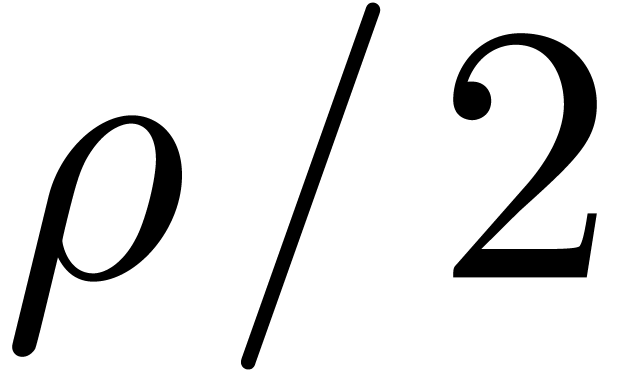 to be the radius of
to be the radius of  and continue our construction. Since
and continue our construction. Since  is compact, the construction will eventually terminate, unless we find a
new singularity.
is compact, the construction will eventually terminate, unless we find a
new singularity.
The above algorithms either enable us to find new singularities above
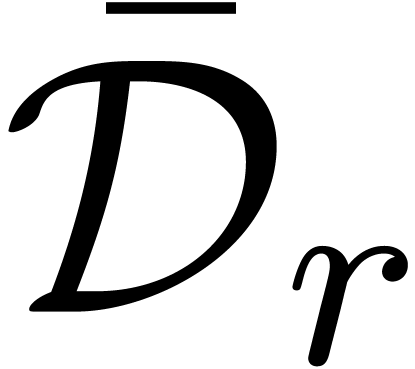 or obtain a certificate that there are no other
singularities. We may insert them in the saturation steps of alg_dep
and fuch_dep, just before jumping to step 3: we only
jump if
or obtain a certificate that there are no other
singularities. We may insert them in the saturation steps of alg_dep
and fuch_dep, just before jumping to step 3: we only
jump if  is saturated under the
is saturated under the 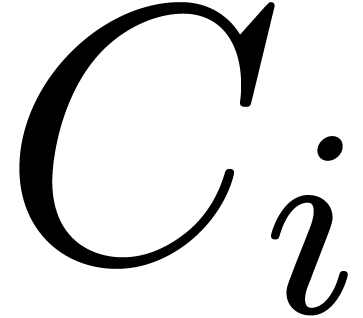 and no new singularities are found. We keep repeating step 2 in the
contrary case. Of course, we may introduce an additional threshold
parameter
and no new singularities are found. We keep repeating step 2 in the
contrary case. Of course, we may introduce an additional threshold
parameter 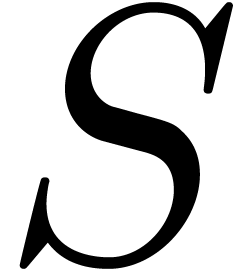 in order to abort the algorithm
whenever
in order to abort the algorithm
whenever 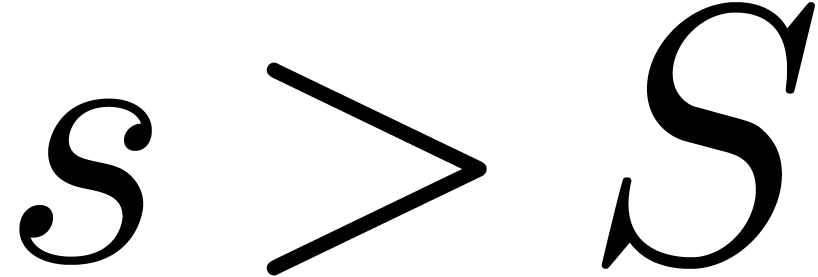 .
.
Given an order 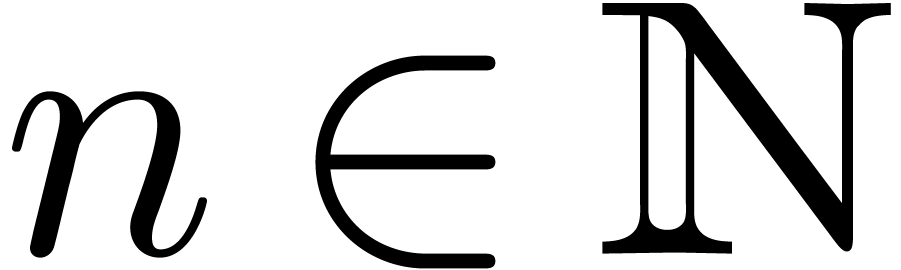 , we will
denote by
, we will
denote by 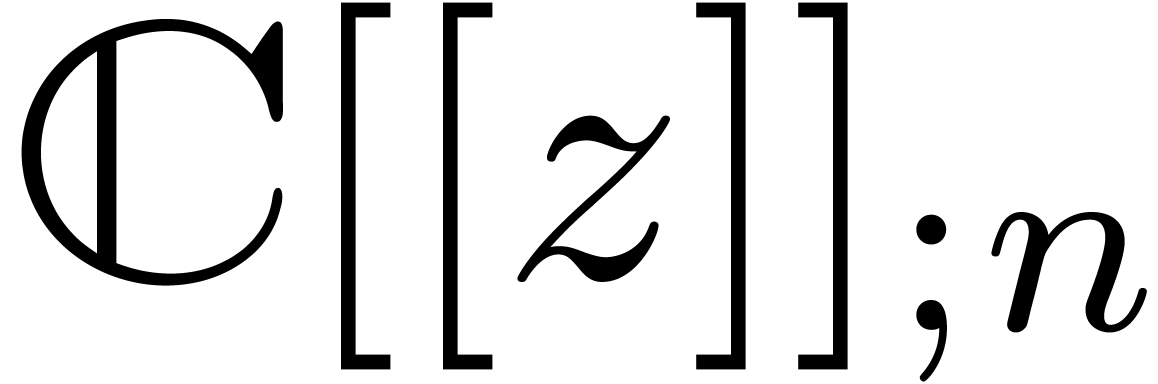 the set of power series
the set of power series  with
with  for all
for all  . When truncating the usual multiplication on
. When truncating the usual multiplication on
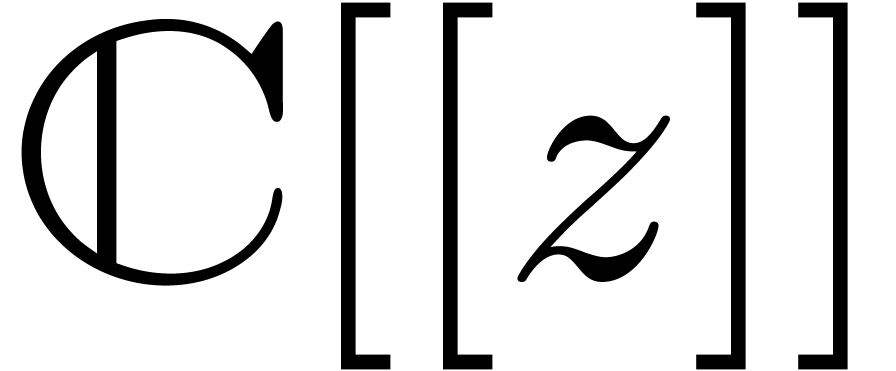 at order
at order 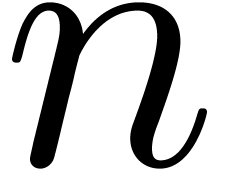 ,
we give
,
we give  a ring structure, which is isomorphic to
a ring structure, which is isomorphic to
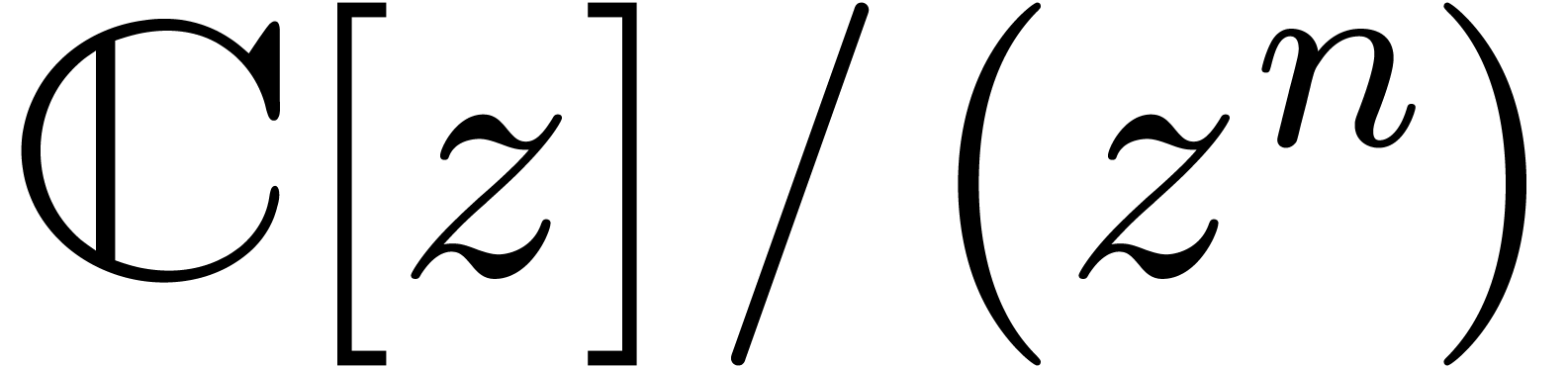 . We will denote by
. We will denote by 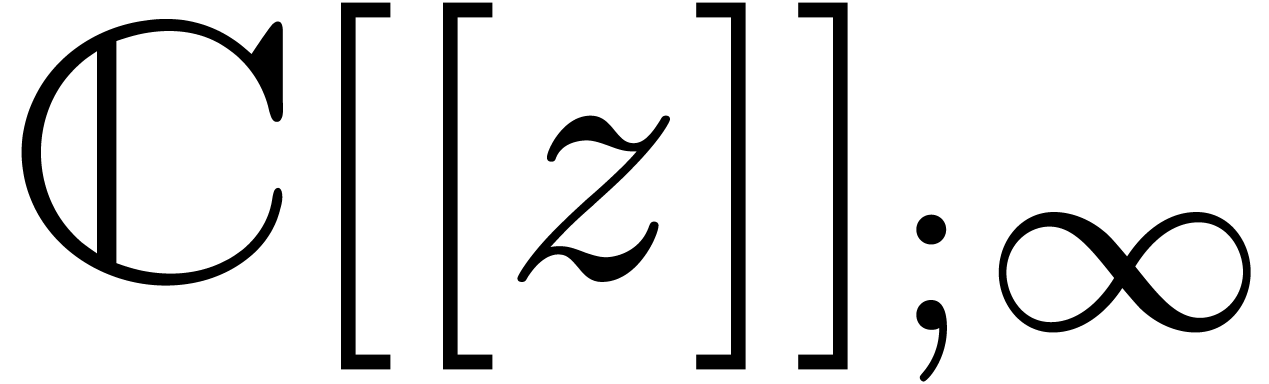 the Hilbert space of all power series
the Hilbert space of all power series  with finite
with finite  norm
norm
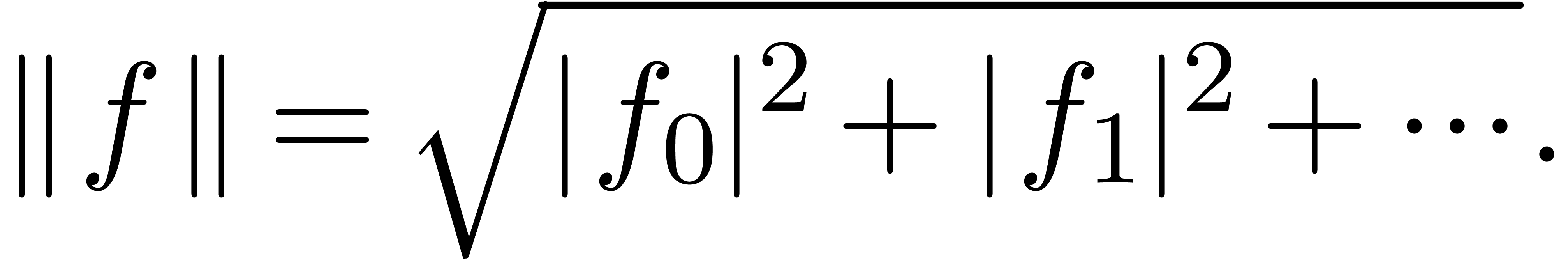
More generally, the norm of a vector 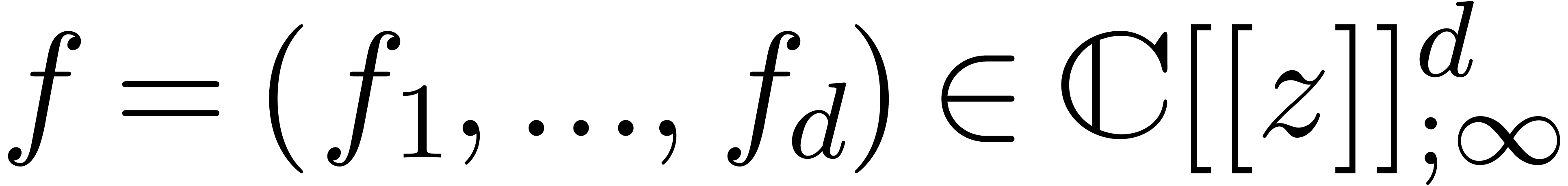 is given by
is given by
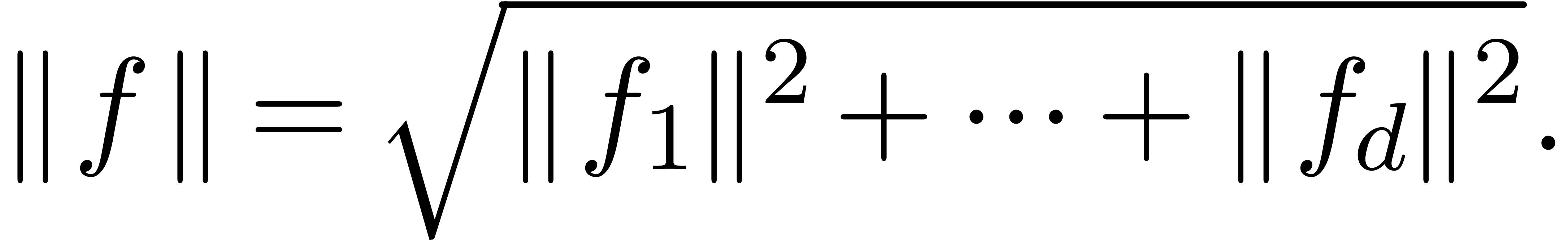
The spaces  can be considered as an increasing
sequence of Hilbert spaces, for the restrictions of the norm on
can be considered as an increasing
sequence of Hilbert spaces, for the restrictions of the norm on 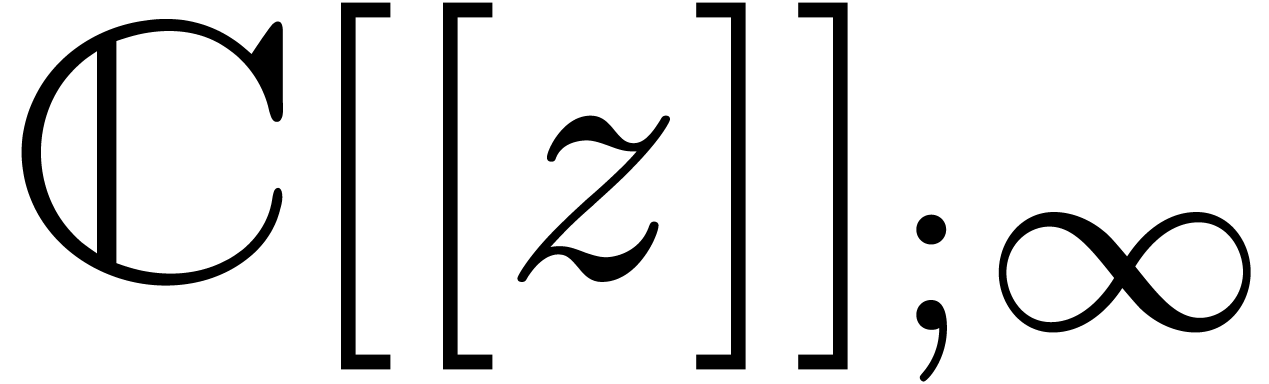 to the
to the  .
.
Let 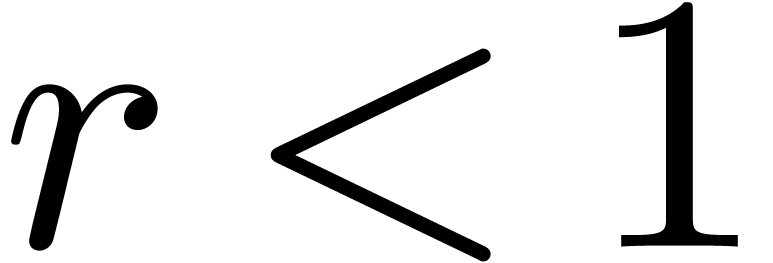 and assume that
and assume that 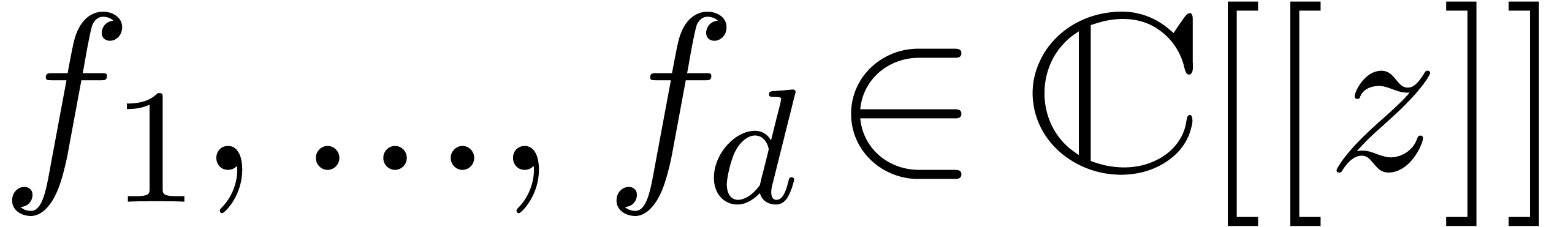 are
power series with radii of convergence at least
are
power series with radii of convergence at least 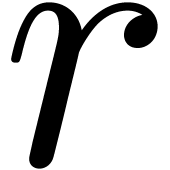 . We want to solve the equation
. We want to solve the equation
 |
(12) |
We will denote the affine space of all such relations 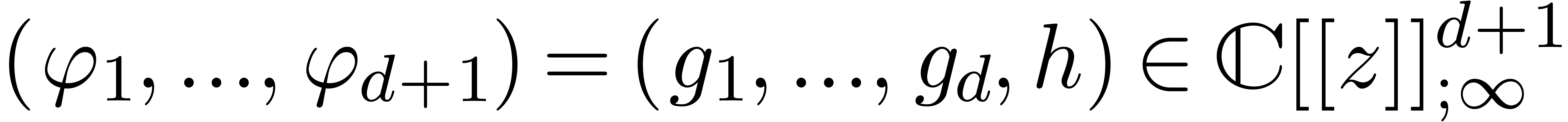 by
by 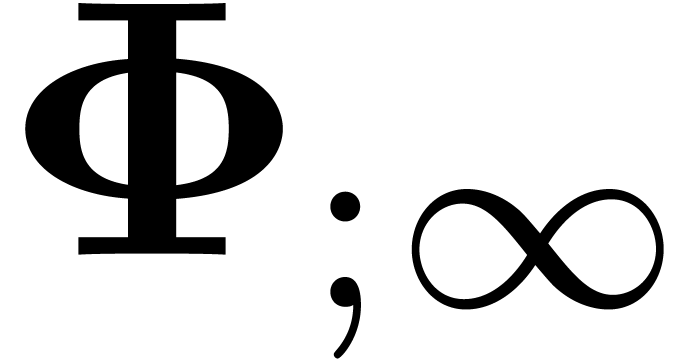 . Since the equation (12) involves an infinite number of coefficients, we need to
consider its truncated version at a finite order
. Since the equation (12) involves an infinite number of coefficients, we need to
consider its truncated version at a finite order  . Replacing
. Replacing  by their
truncations in
by their
truncations in  , we search
for non-trivial solutions of the equation
, we search
for non-trivial solutions of the equation
 |
(13) |
such that the norms of 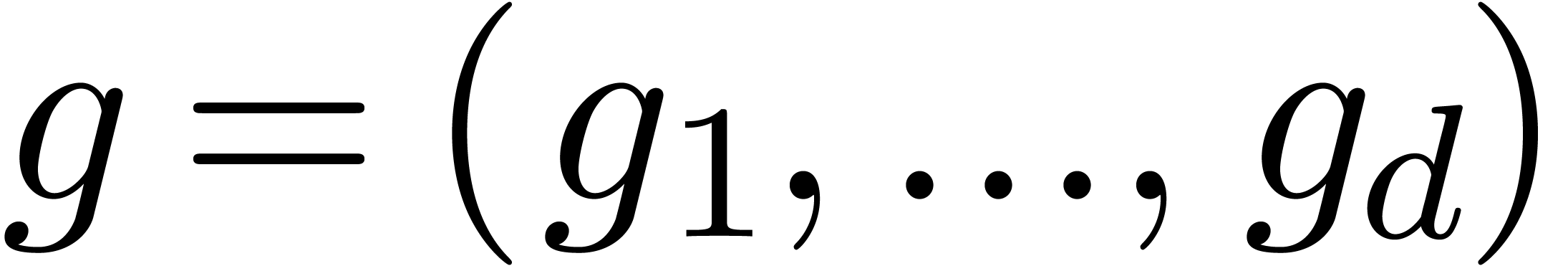 and
and 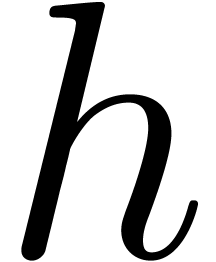 are small. We will denote by
are small. We will denote by 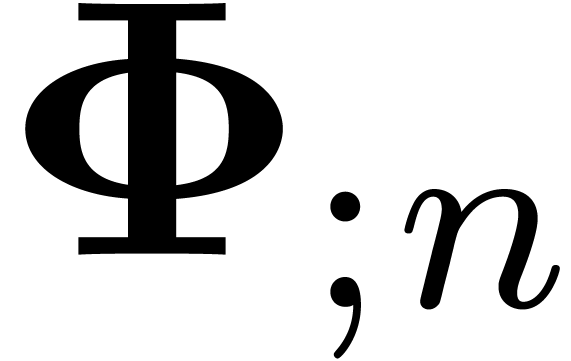 the affine space of
all
the affine space of
all 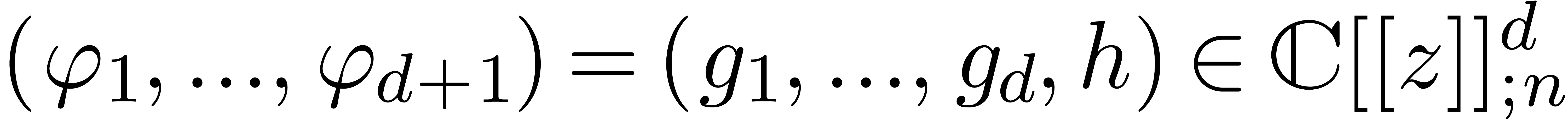 which satisfy (13).
which satisfy (13).
Let us reformulate our problem in terms of linear algebra. The series
 give rise to an
give rise to an 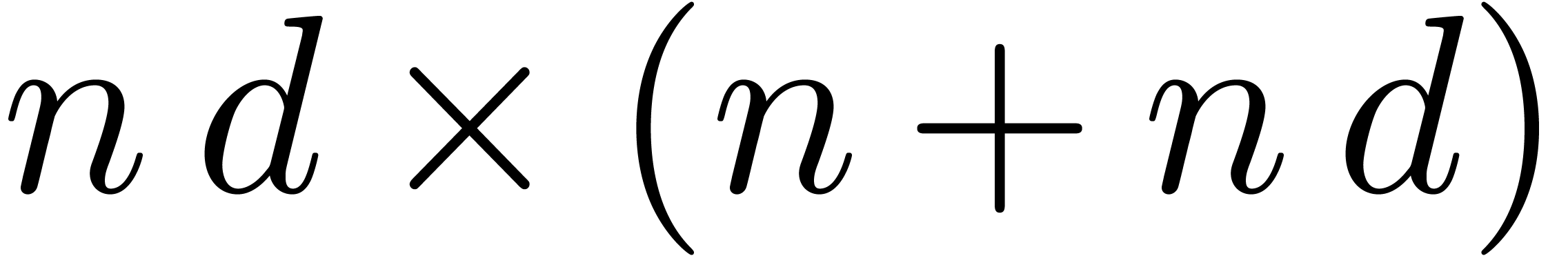 matrix
matrix
The unknown series  give rise to a row vector
give rise to a row vector
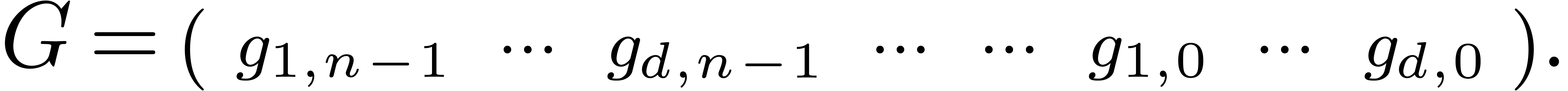
Setting  , we then have
, we then have
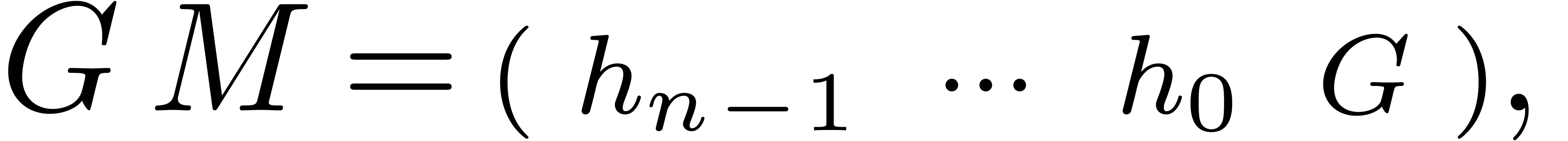
whence 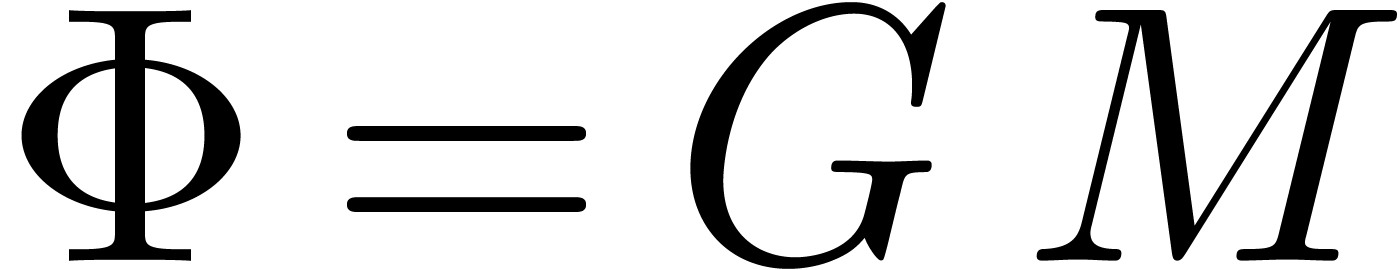 encodes the relation
encodes the relation 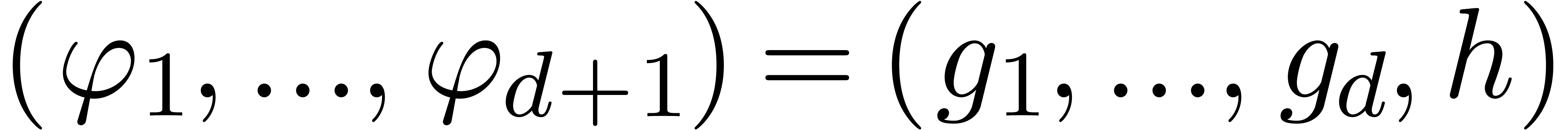 . This reduces the problem to finding those
vectors
. This reduces the problem to finding those
vectors  for which
for which 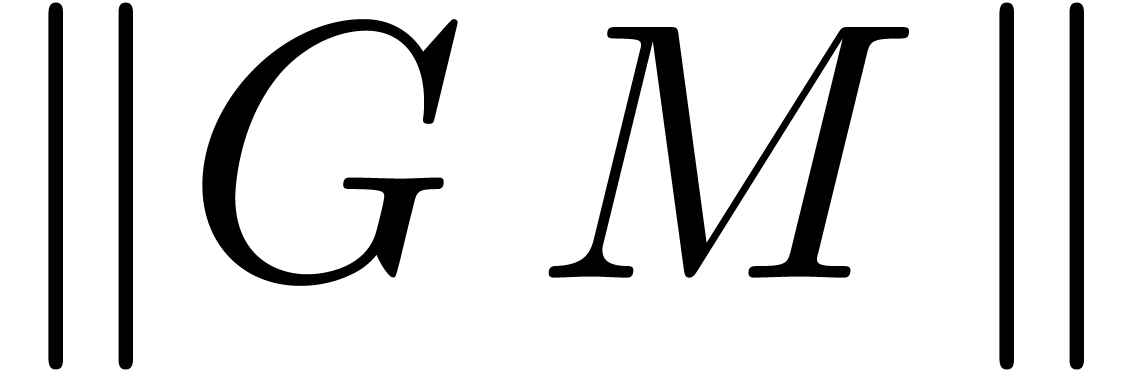 is
small, provided that at least one of the coefficients
is
small, provided that at least one of the coefficients  is reasonably large.
is reasonably large.
We start with the computation of a thin LQ decomposition of 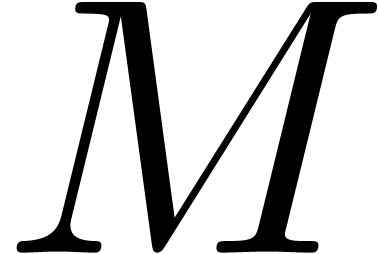 . This can for instance be done using the
Gram-Schmidt process: starting with the first row, we orthogonally
project each row on the vector space spanned by the previous rows. This
results in a decomposition
. This can for instance be done using the
Gram-Schmidt process: starting with the first row, we orthogonally
project each row on the vector space spanned by the previous rows. This
results in a decomposition
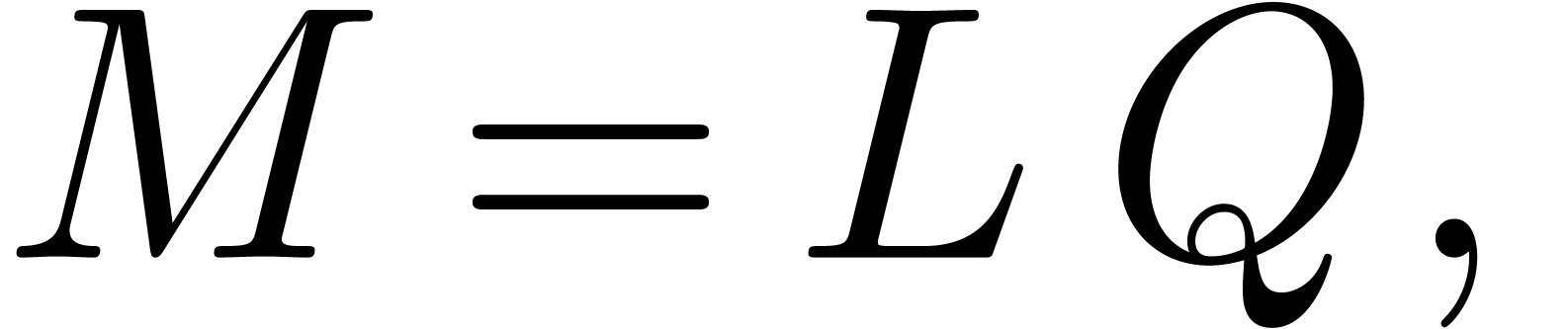
where  is a lower triangular
is a lower triangular  matrix with ones on the diagonal and
matrix with ones on the diagonal and  is an
is an 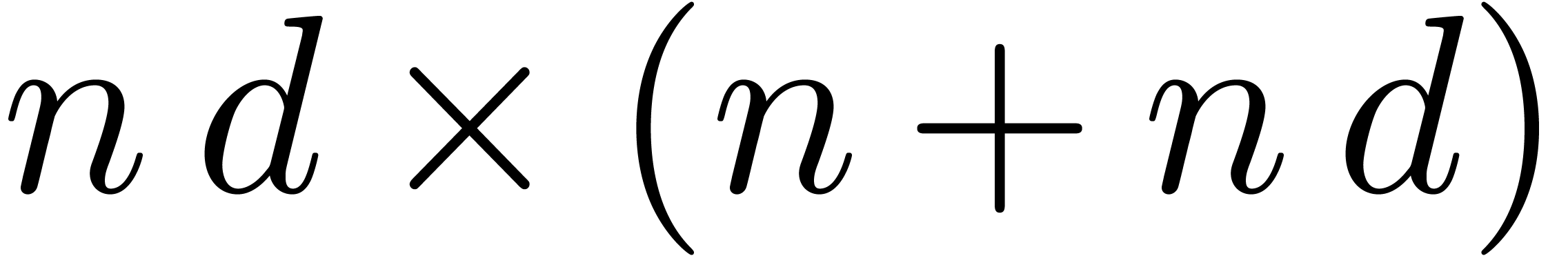 matrix, whose rows are mutually orthogonal
(i.e.
matrix, whose rows are mutually orthogonal
(i.e. 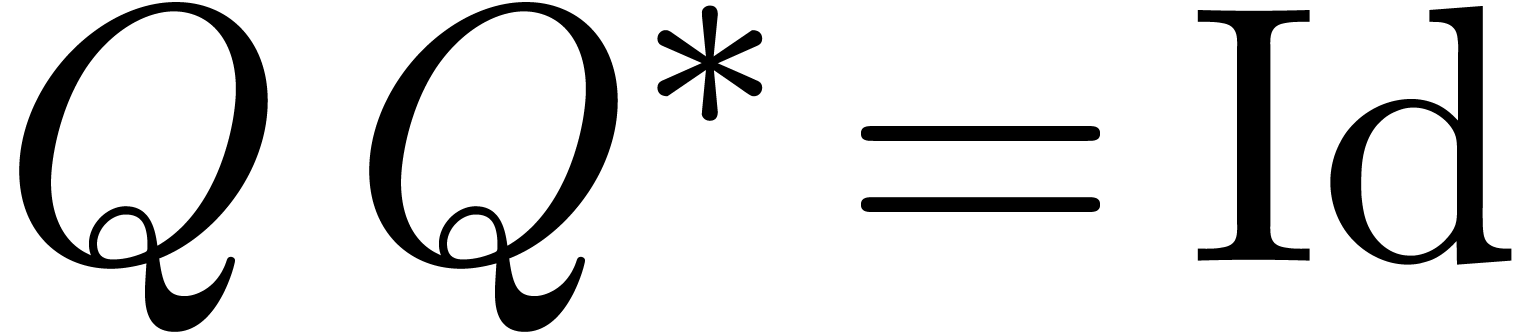 ). Since
). Since
 coincides with the righthand side of
coincides with the righthand side of  , the decomposition can be done
in-place. Now consider the matrix
, the decomposition can be done
in-place. Now consider the matrix  formed by the
formed by the
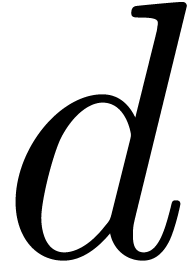 last rows of
last rows of 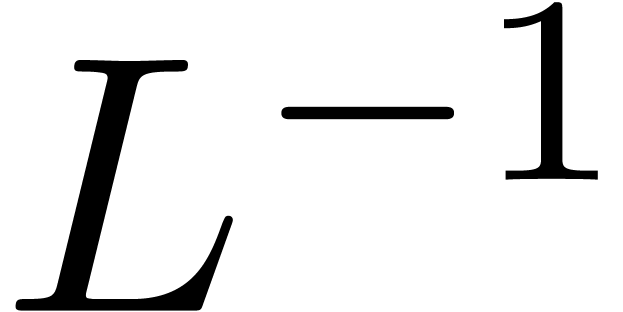 .
Then each row
.
Then each row 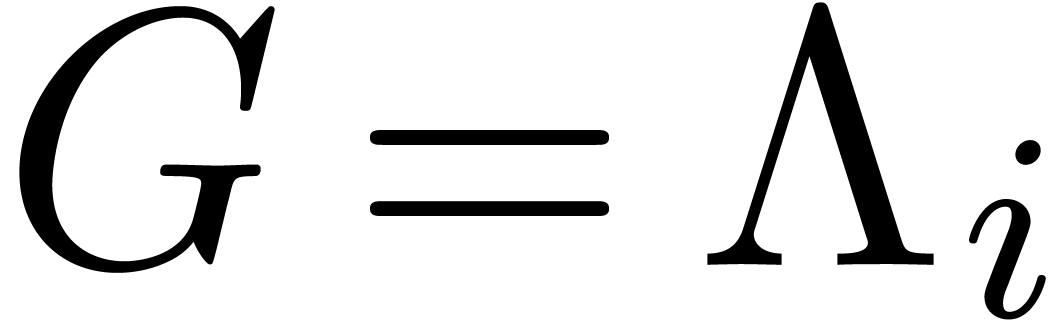 gives rise to a relation (13),
encoded by
gives rise to a relation (13),
encoded by 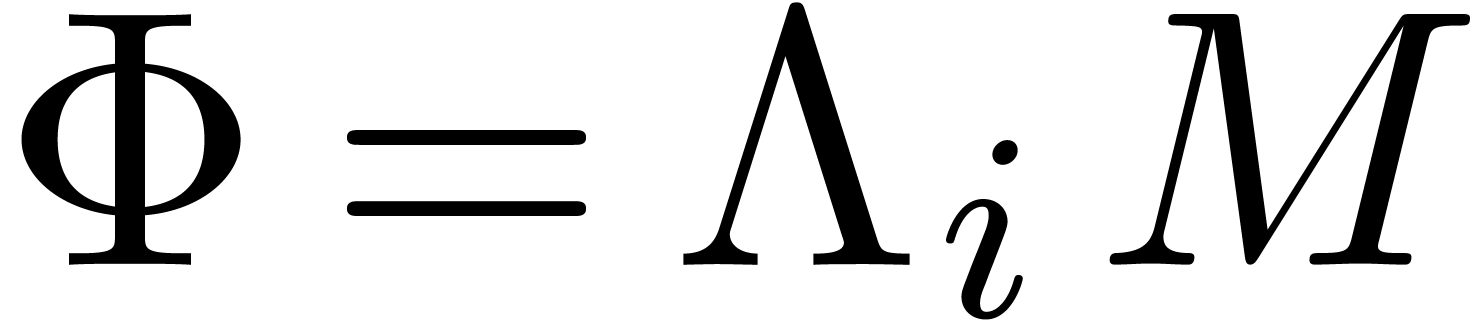 . Moreover, this
relation is normal or
. Moreover, this
relation is normal or 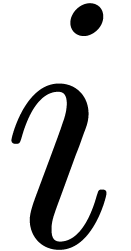 -normal,
in the sense that
-normal,
in the sense that 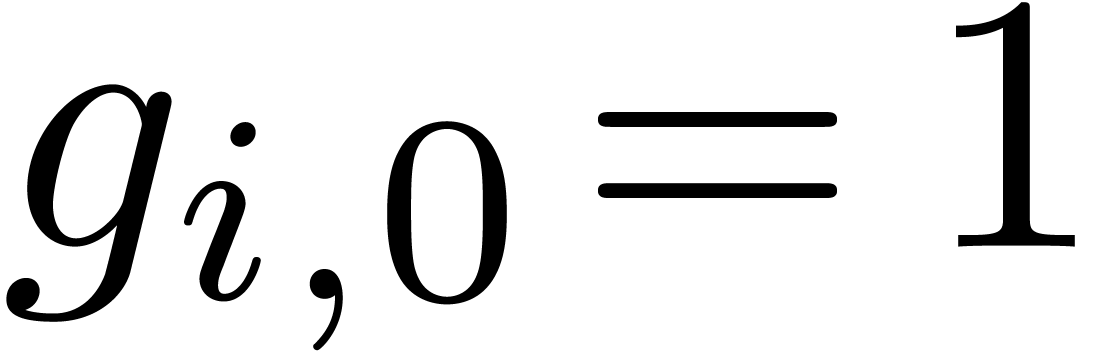 and
and 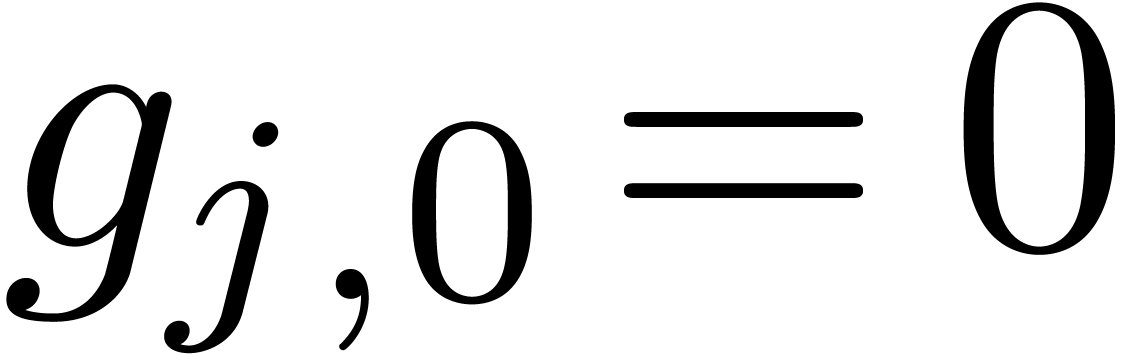 for all
for all 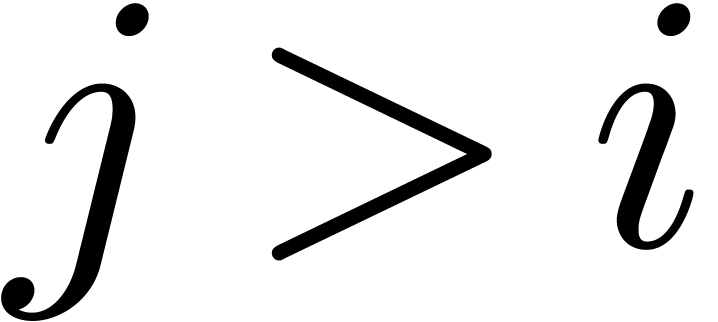 . Since
. Since 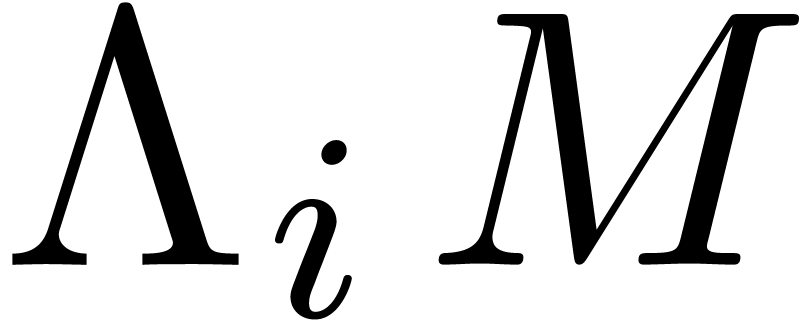 is the shortest vector in
is the shortest vector in 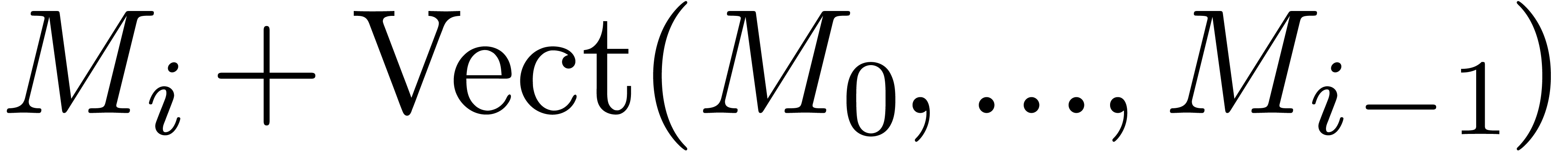 ,
the relation is also minimal in norm, among all
,
the relation is also minimal in norm, among all  -normal relations. Choosing the row
-normal relations. Choosing the row 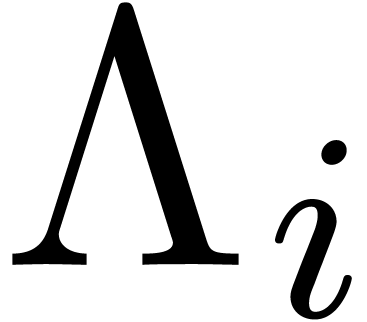 for which
for which 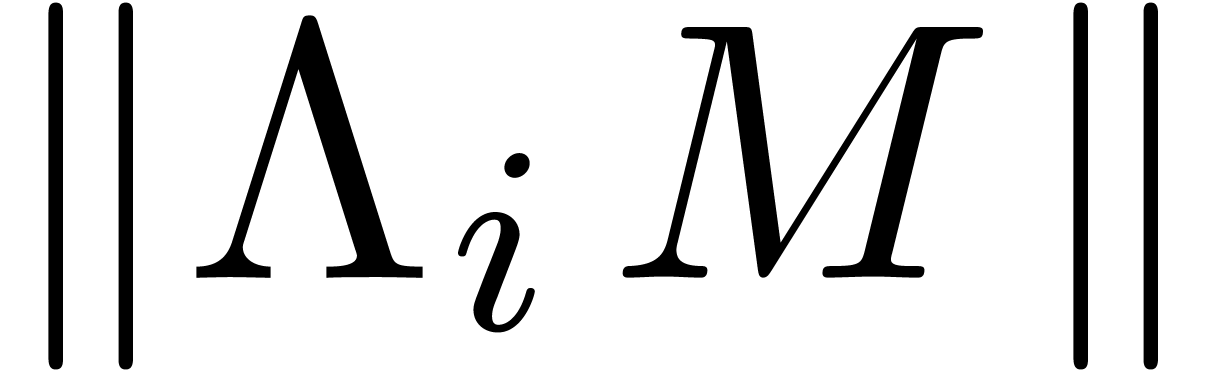 is minimal, our algorithm simply
returns the corresponding relation. Then our algorithm has the following
fundamental property:
is minimal, our algorithm simply
returns the corresponding relation. Then our algorithm has the following
fundamental property:
 for which
for which 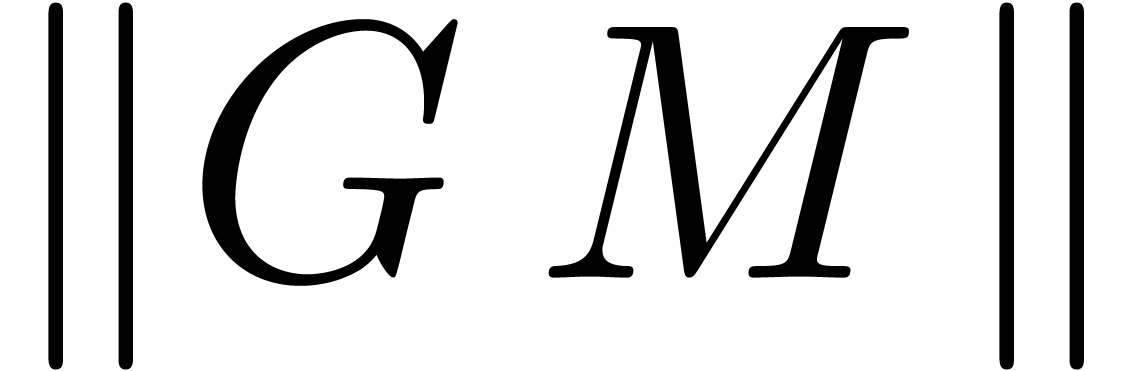 is minimal.
is minimal.
Let us now return to the case when 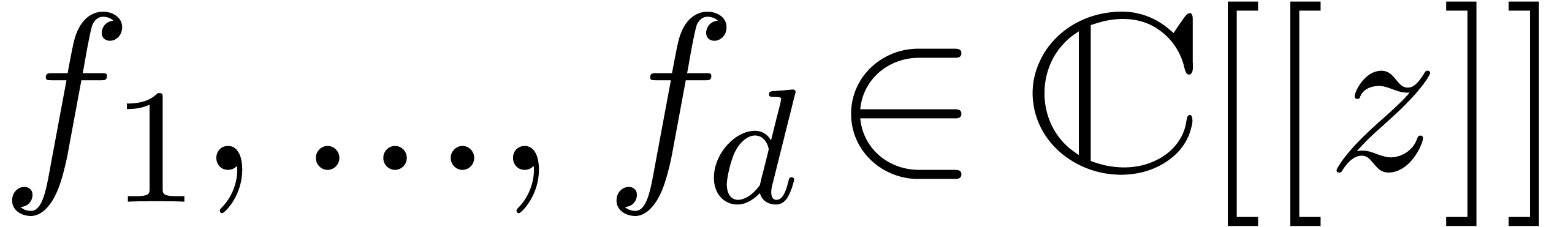 are no longer
truncated, but all have a radius of convergence
are no longer
truncated, but all have a radius of convergence 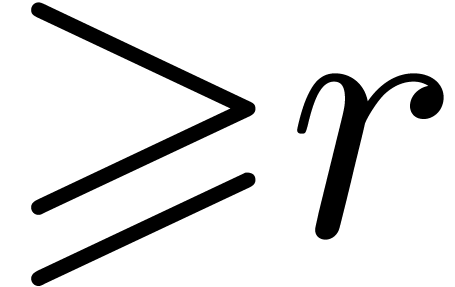 . A relation (12) is again said to be
normal or
. A relation (12) is again said to be
normal or 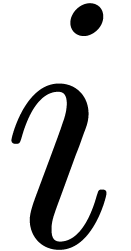 -normal
if
-normal
if 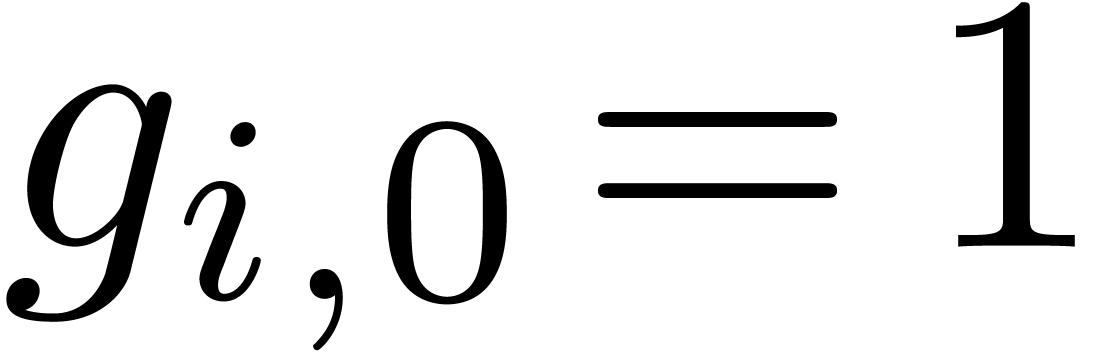 and
and 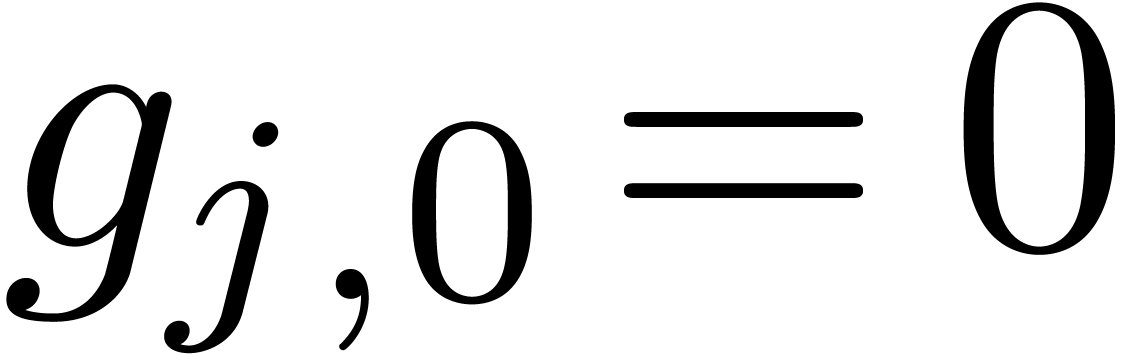 for all
for all  . Under the limit
. Under the limit  , we claim that our algorithm finds a minimal
normal relation, if there exists a relation of the form (12):
, we claim that our algorithm finds a minimal
normal relation, if there exists a relation of the form (12):
Assume that 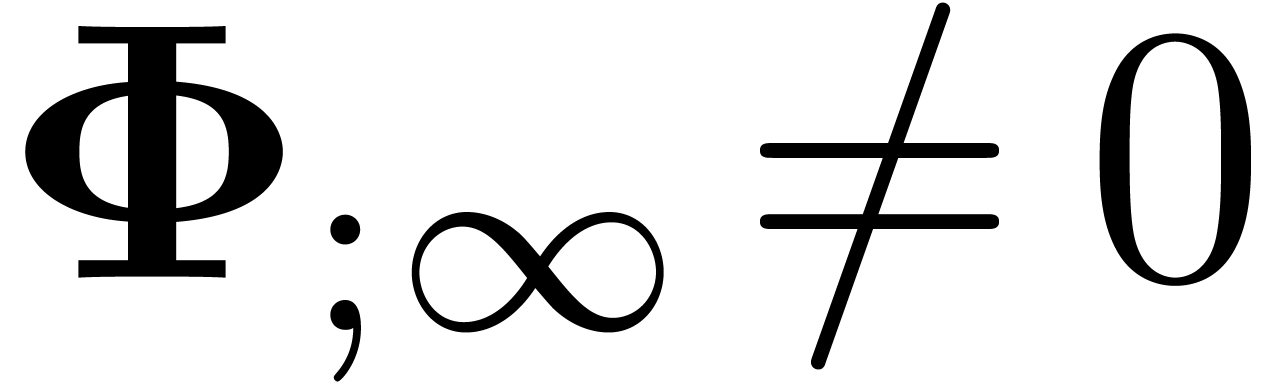 . Then
. Then
 contains a minimal normal relation.
contains a minimal normal relation.
Assume that  is a minimal
is a minimal  -normal relation. For each
-normal relation. For each  , let
, let 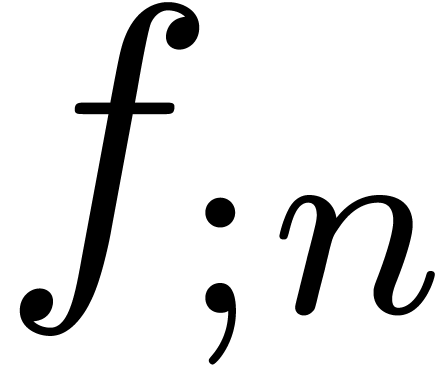 be the
truncation of
be the
truncation of  at order
at order 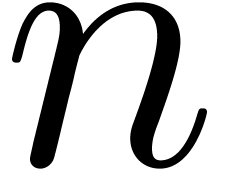 and consider the corresponding minimal
and consider the corresponding minimal 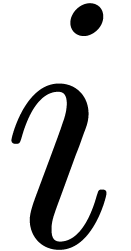 -normal relation
-normal relation 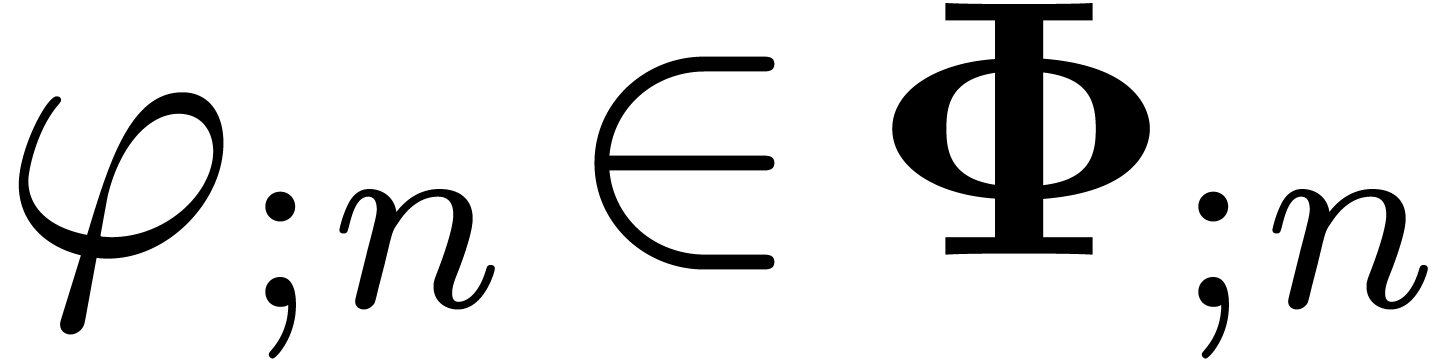 . Then the relations
. Then the relations 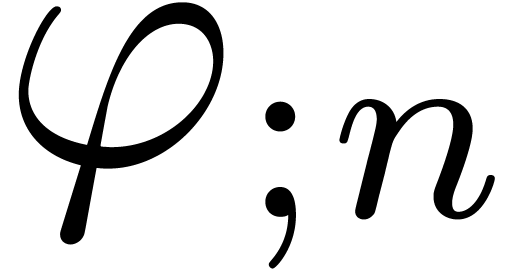 converge to
converge to  in
in 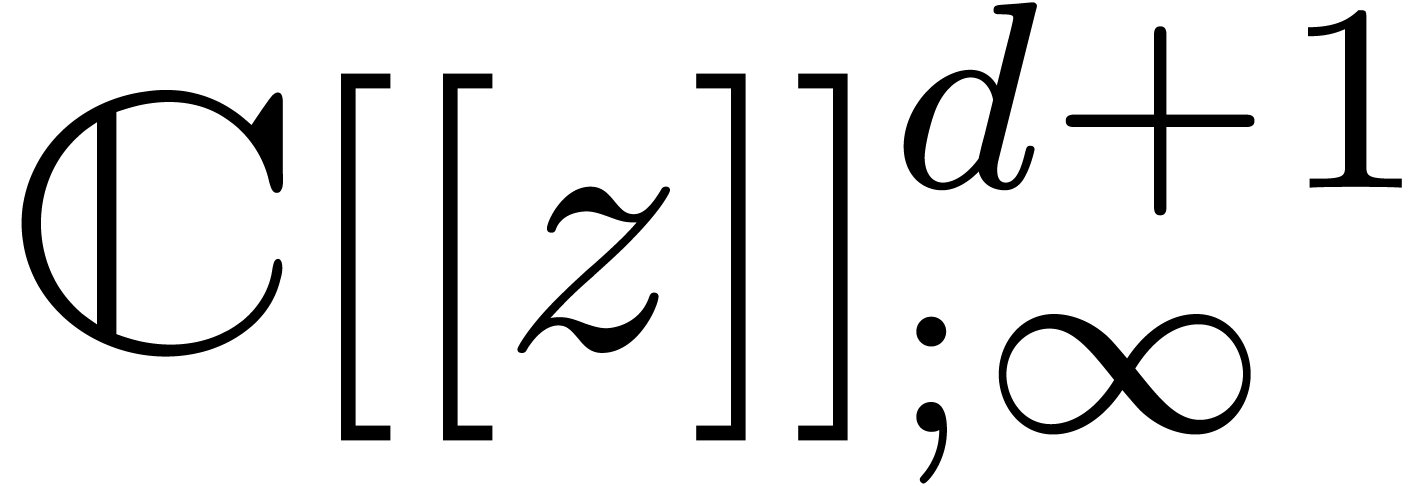 .
.
If 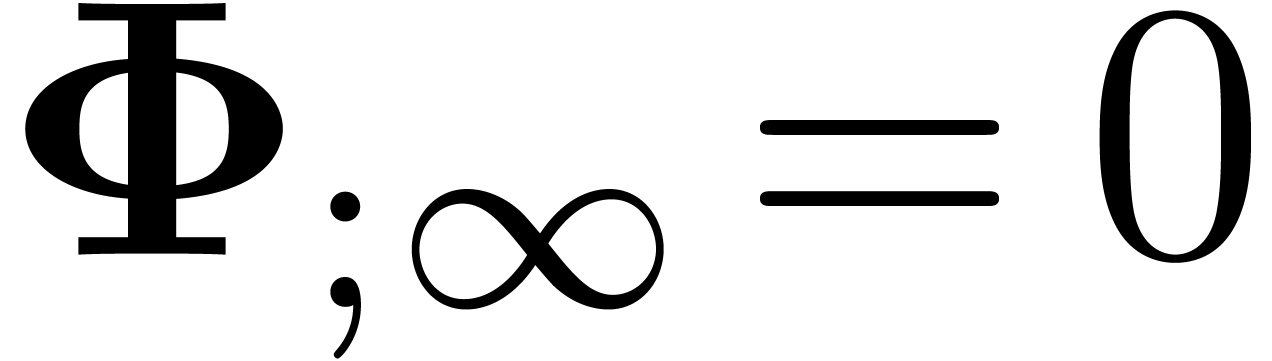 , then the norms
, then the norms
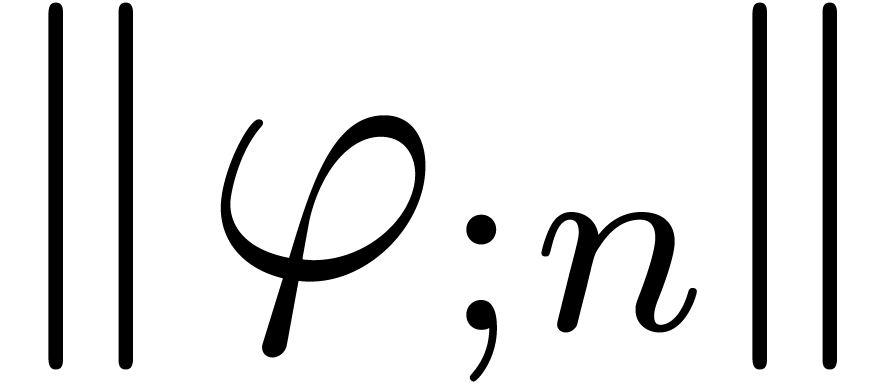 , with
, with 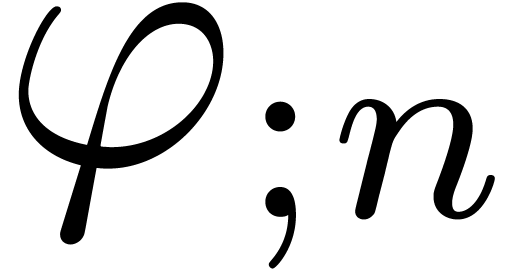 as in
as in  .
.
Proof. A non trivial relation 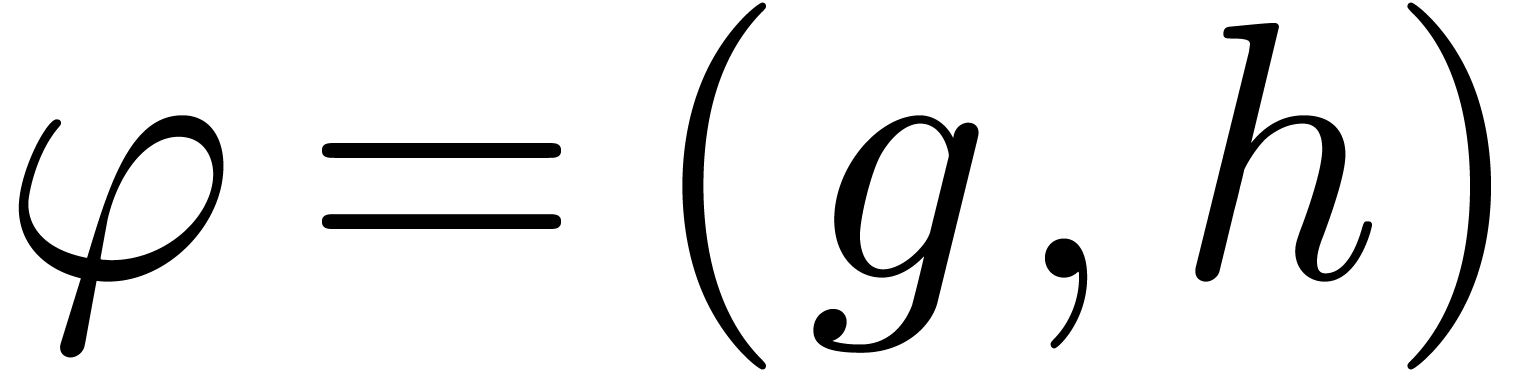 is easily normalized: we first divide
is easily normalized: we first divide  by
by 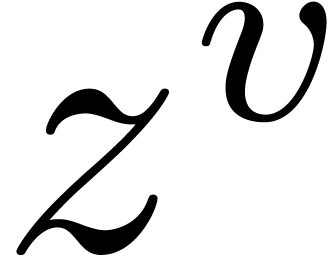 , where
, where 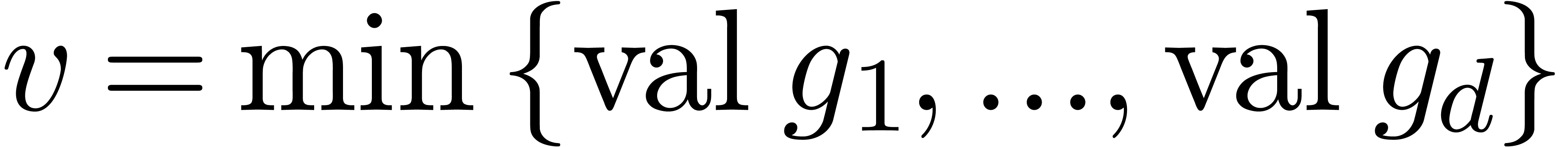 . We next divide by
. We next divide by 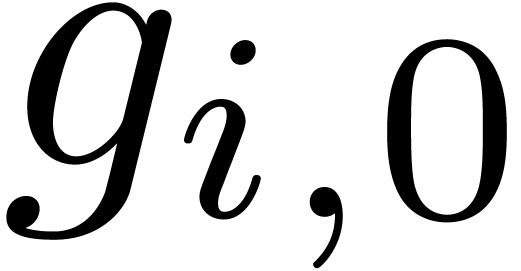 ,
where
,
where 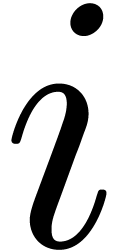 is largest with
is largest with  . Now the set of all
. Now the set of all 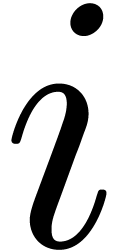 -normal
relations is a closed affine subspace of
-normal
relations is a closed affine subspace of 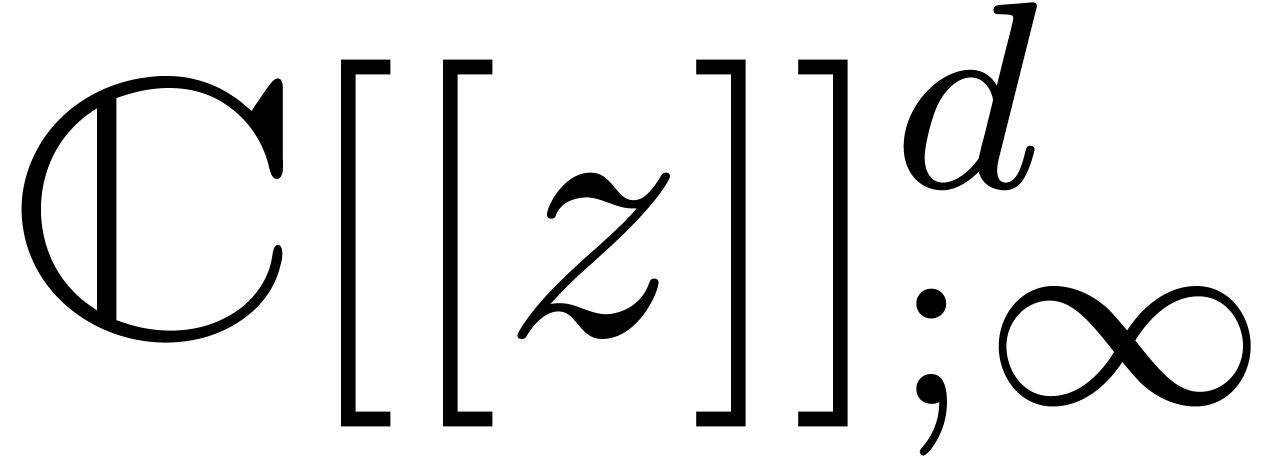 .
The orthogonal projection of
.
The orthogonal projection of  on this subspace
yields an
on this subspace
yields an 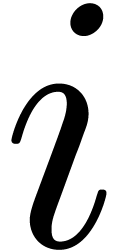 -normal relation of
minimal norm. This proves (a).
-normal relation of
minimal norm. This proves (a).
Assume that there exists an 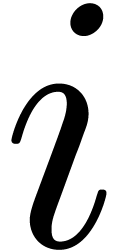 -normal
relation
-normal
relation 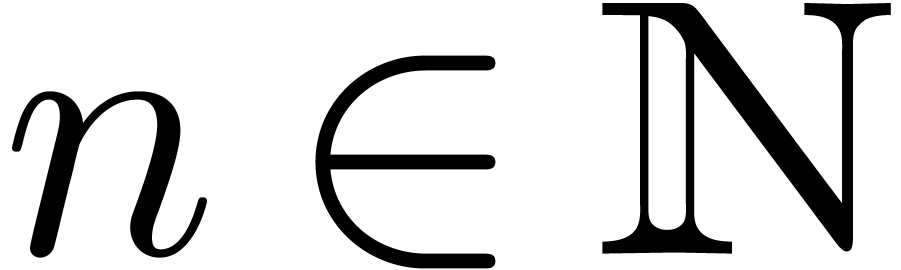 , consider the minimal
, consider the minimal 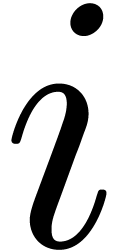 -normal relation
-normal relation 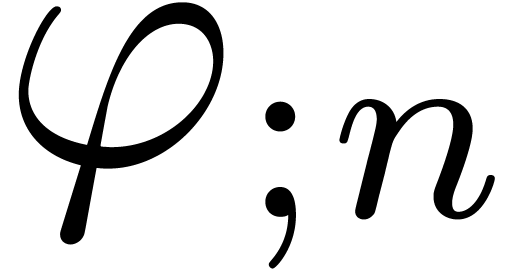 at
this order. Truncation of this relation at a smaller order
at
this order. Truncation of this relation at a smaller order 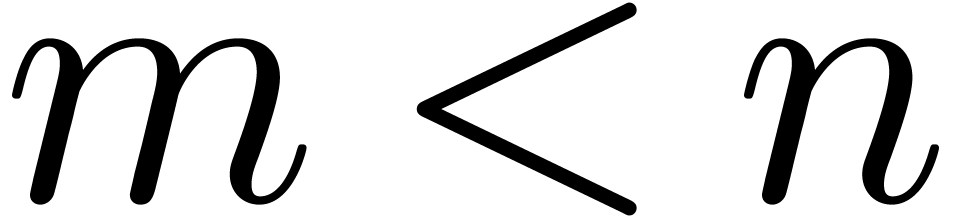 yields an
yields an  -normal
relation
-normal
relation  at order
at order  with
with
 , whence
, whence
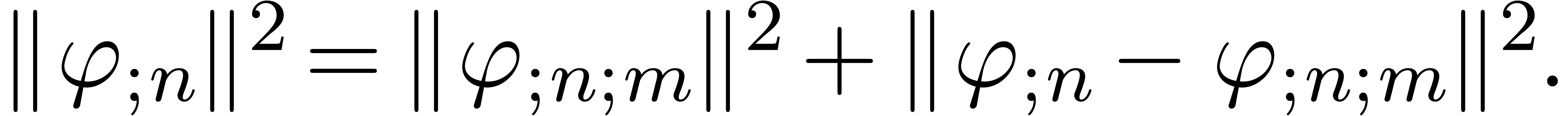 |
(14) |
Moreover, since 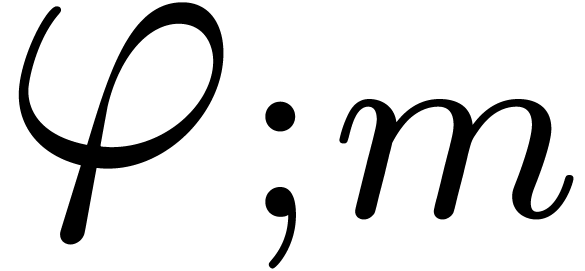 is the projection of
is the projection of  on the affine space of
on the affine space of  -normal
relations at order
-normal
relations at order  , we have
, we have
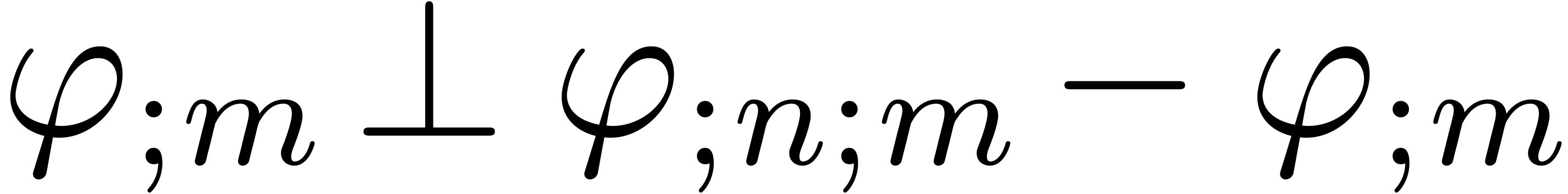 and
and
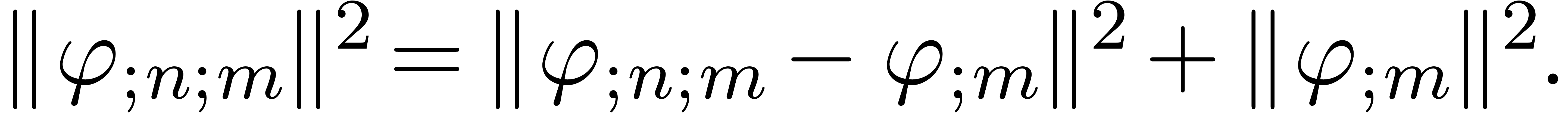 |
(15) |
In particular, 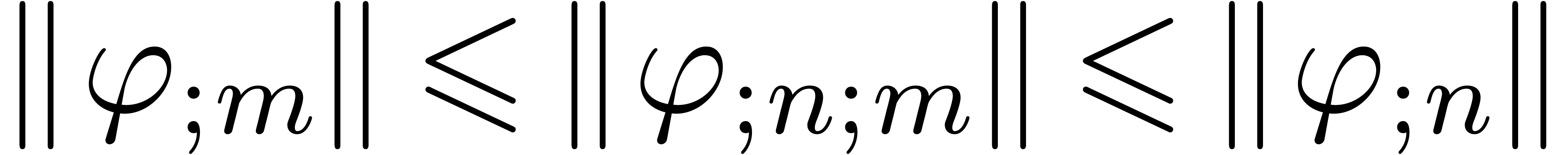 and
and
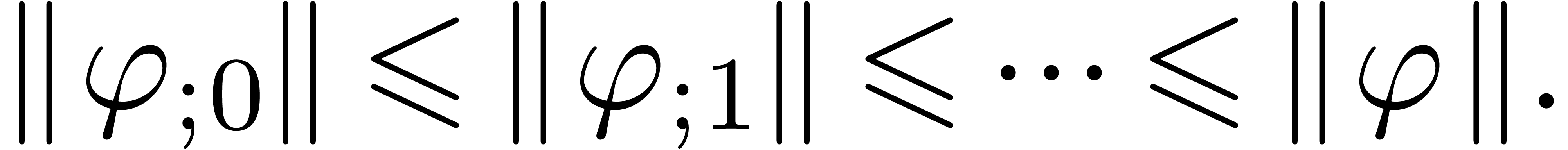
For large  , it follows that
, it follows that
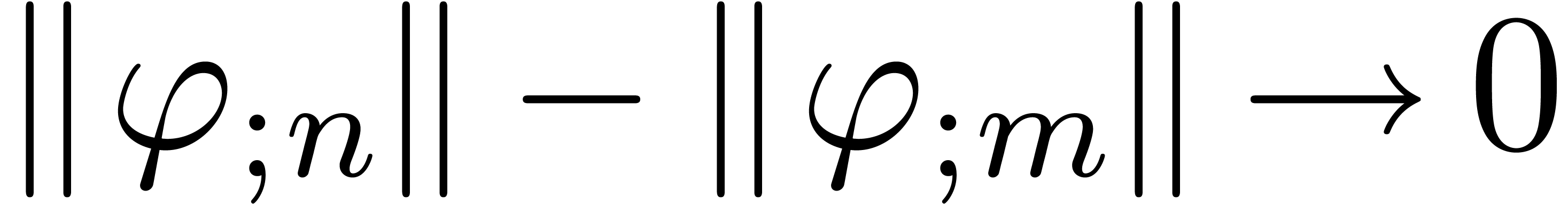 , whence
, whence
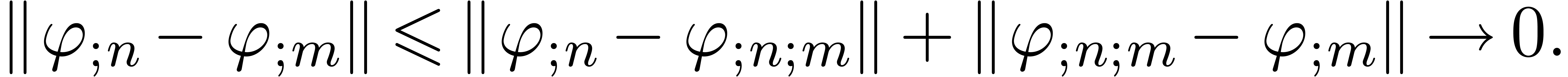
In other words, 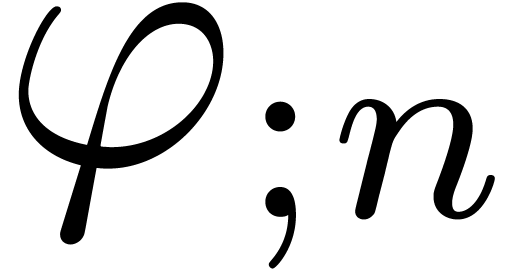 is a Cauchy sequence, which
converges to a limit
is a Cauchy sequence, which
converges to a limit 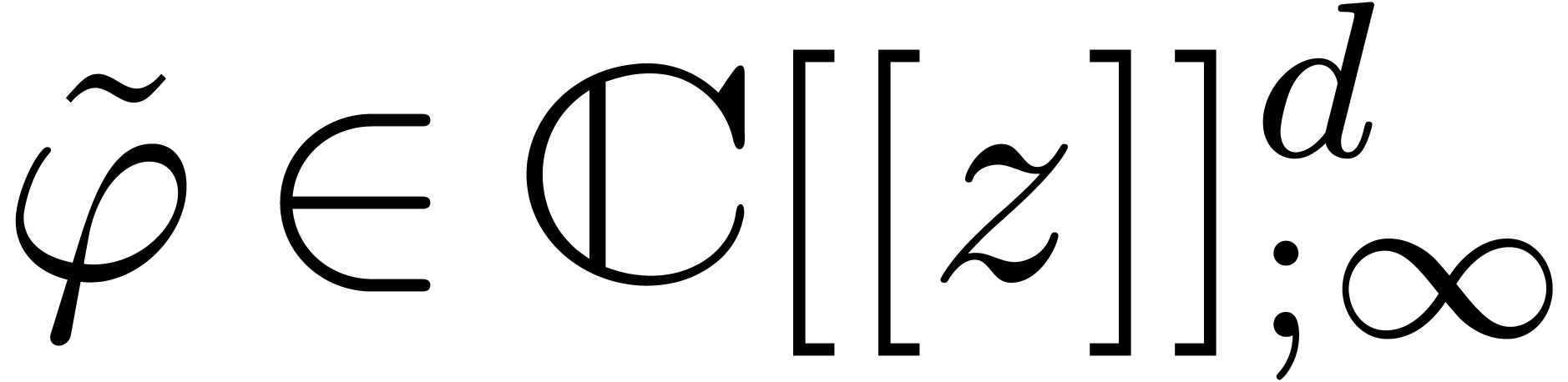 . By the
minimality hypothesis of
. By the
minimality hypothesis of  , we
have
, we
have 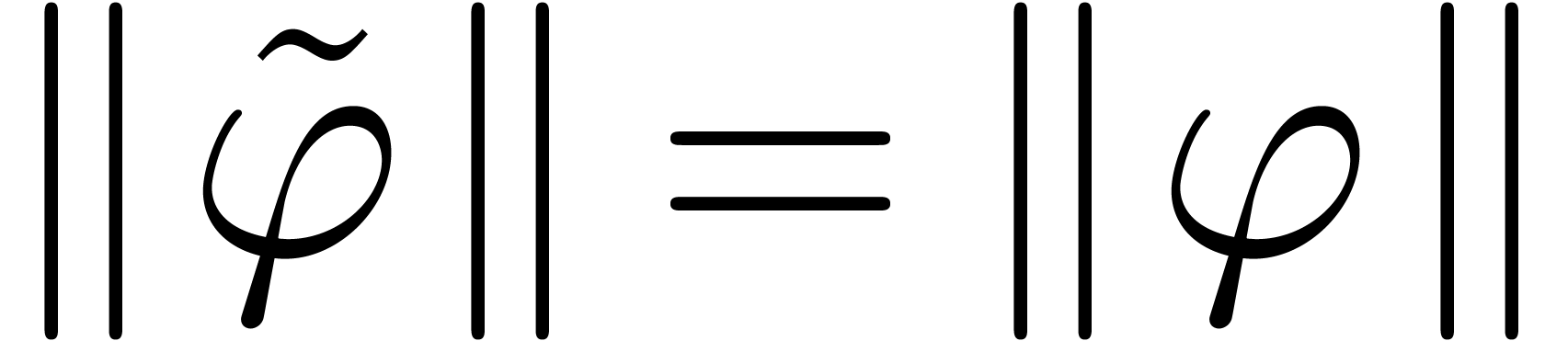 . Passing (14)
and (15) to the limit, we get
. Passing (14)
and (15) to the limit, we get  ,
whence
,
whence 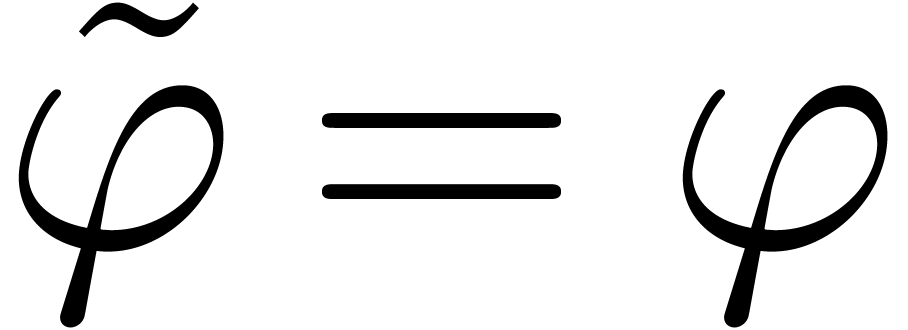 and (b).
and (b).
In general, the existence of a bound  with
with
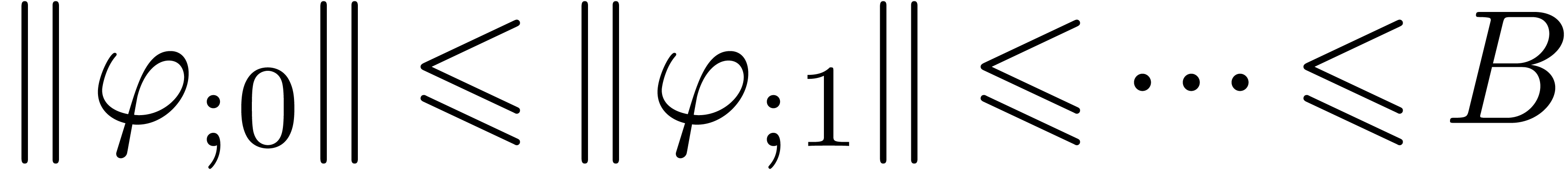
still ensures 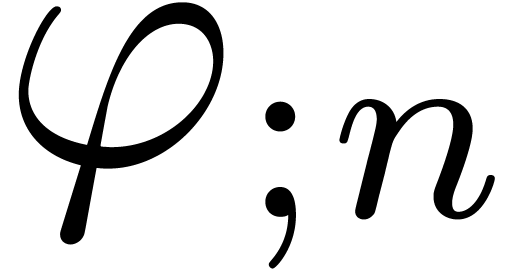 to be a Cauchy sequence, and its
limit yields an
to be a Cauchy sequence, and its
limit yields an  -normal
relation (12). This proves the last assertion
(c).
-normal
relation (12). This proves the last assertion
(c).
A first implementation of our guessing algorithm has been made in the
Here follow the values for 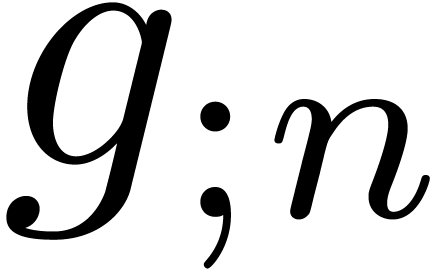 at different orders
and
at different orders
and 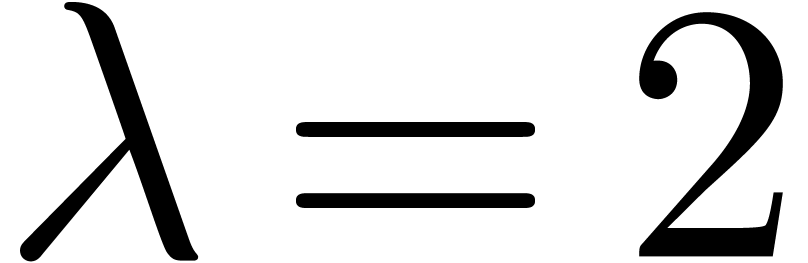 :
:
The 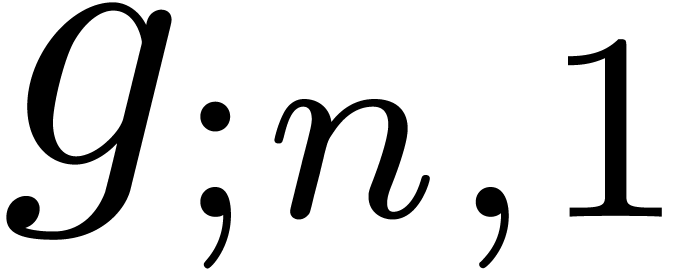 clearly convergence to a limit
clearly convergence to a limit 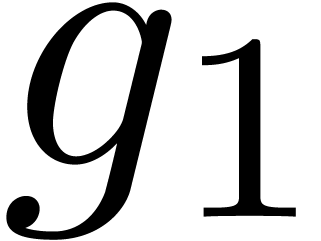 with radius of convergence
with radius of convergence 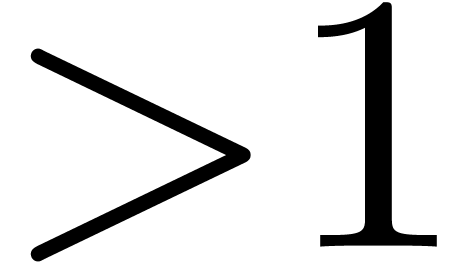 .
It should be noticed that we do not have
.
It should be noticed that we do not have 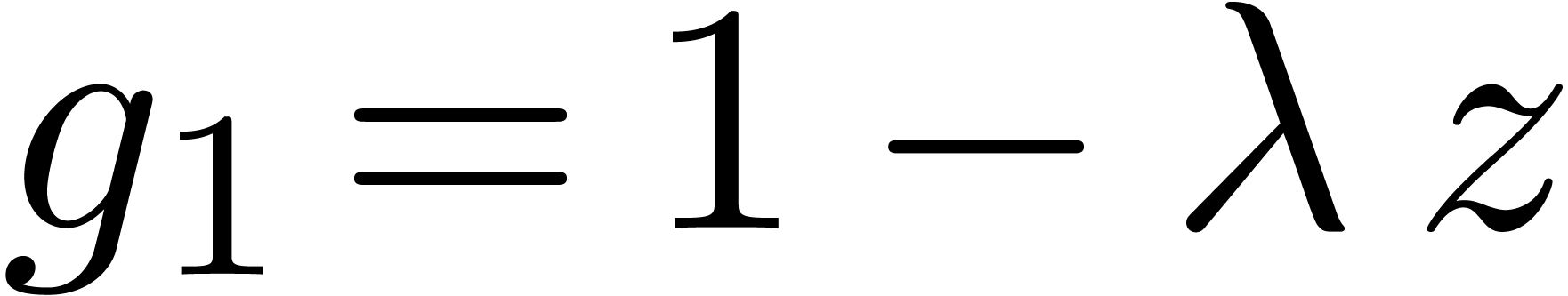 .
In other words, we did not find the “best” relation, as in
the case of Padé-Hermite approximation. A closer examination of
the result shows that
.
In other words, we did not find the “best” relation, as in
the case of Padé-Hermite approximation. A closer examination of
the result shows that
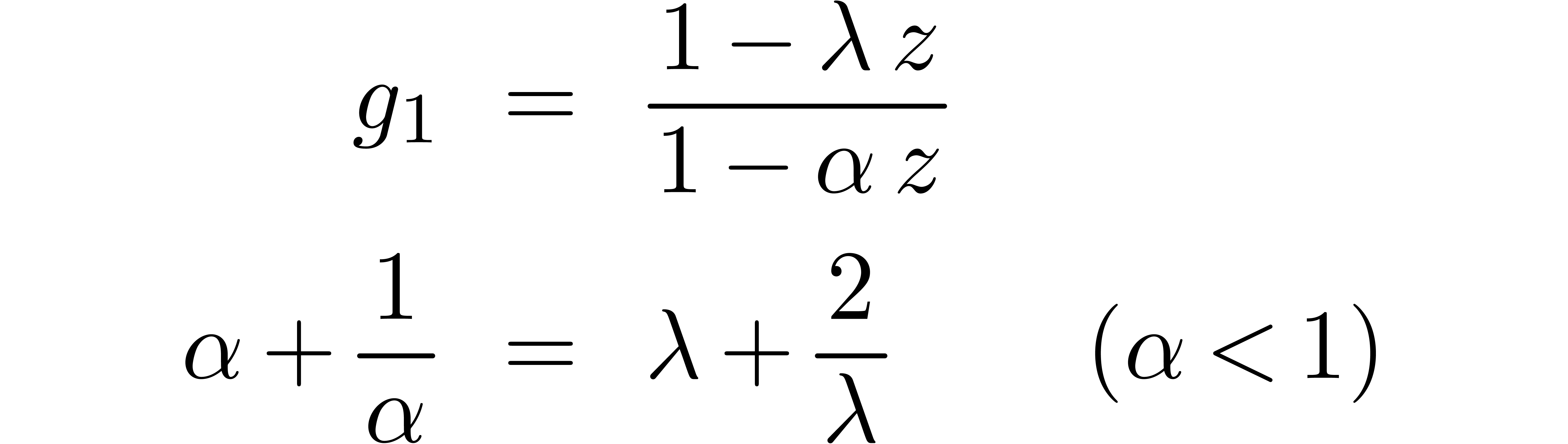
In particular,  decreases if
decreases if 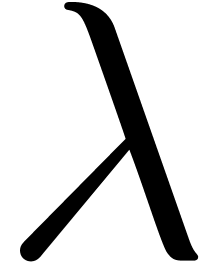 increases.
increases.
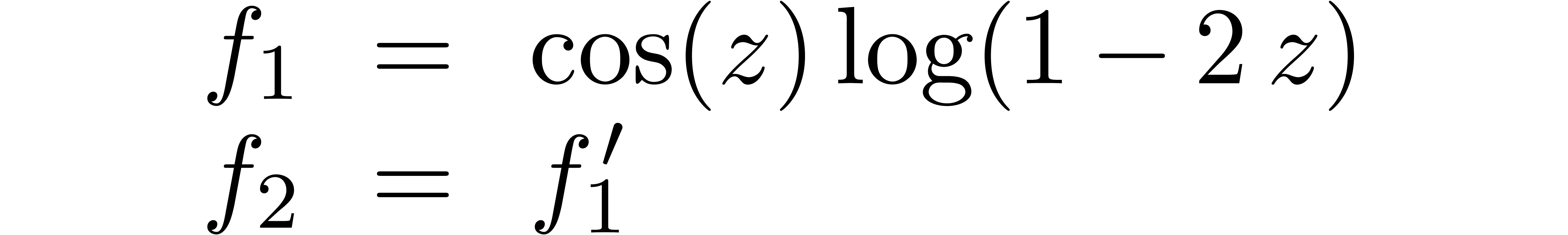
We obtain:

The convergence only becomes apparent at higher orders. Contrary to the
previous example, it seems that the series in the computed relation all
have a radius of convergence 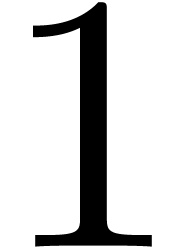 .
The norms of the computed results are given by
.
The norms of the computed results are given by 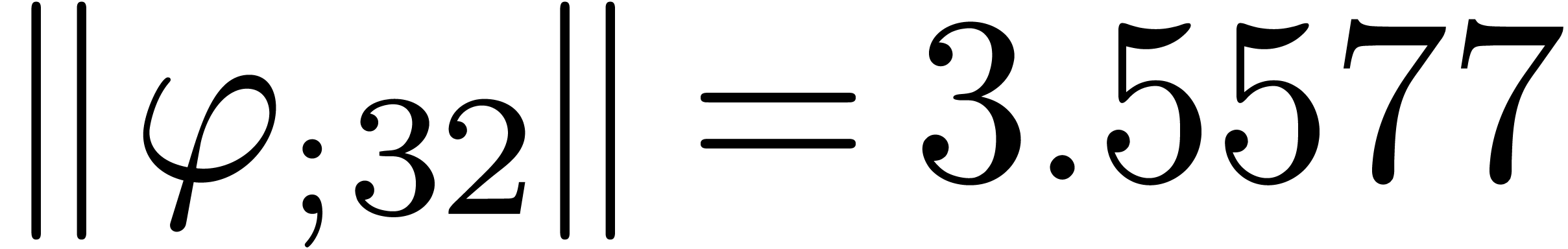 ,
, 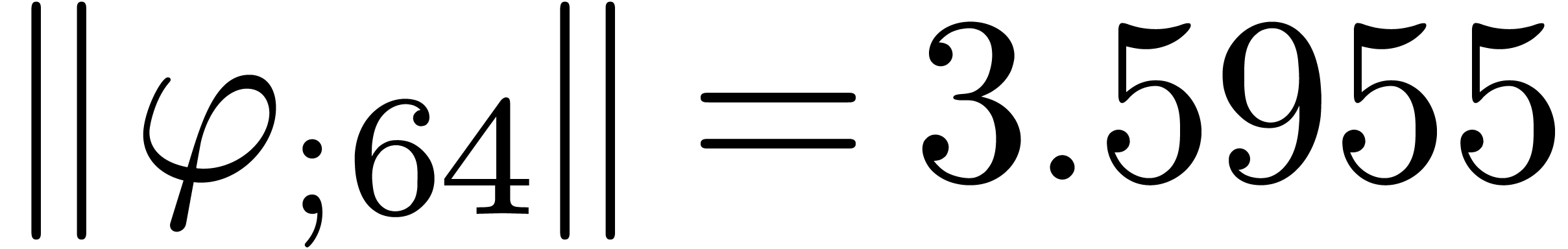 ,
, 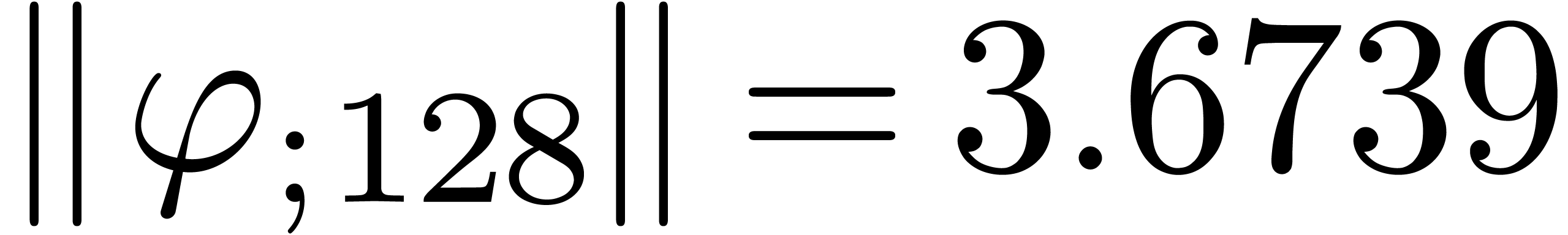 and
and 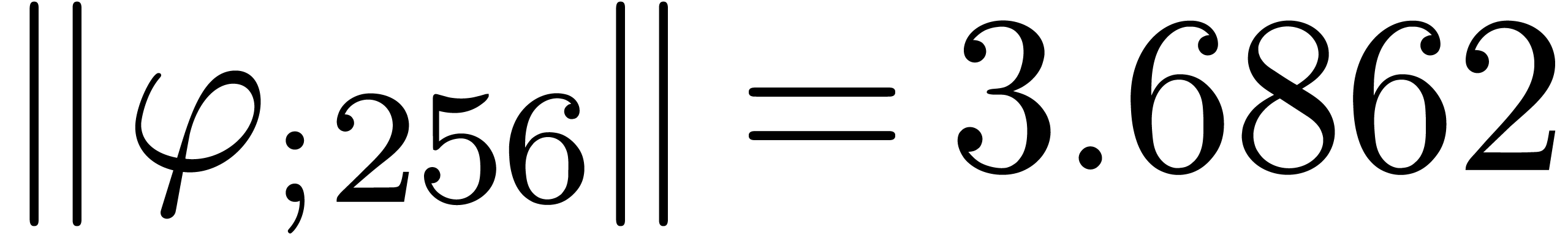 .
.
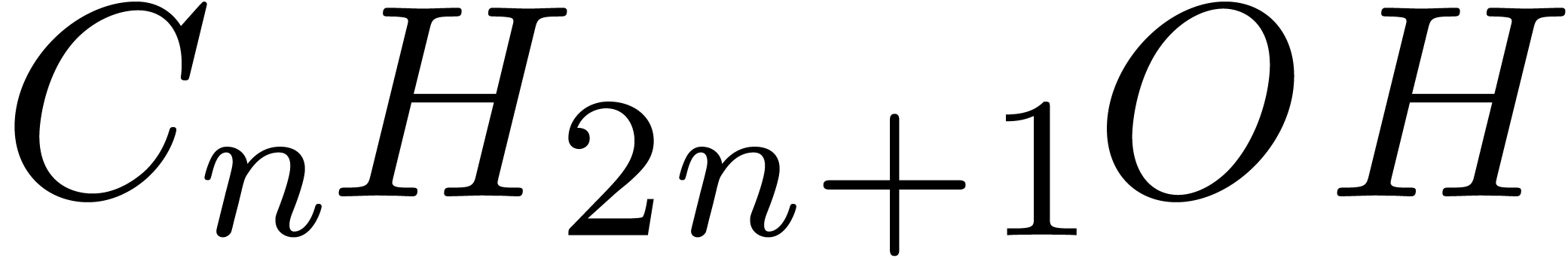 [Pól37].
Its generating series satisfies the functional equation
[Pól37].
Its generating series satisfies the functional equation
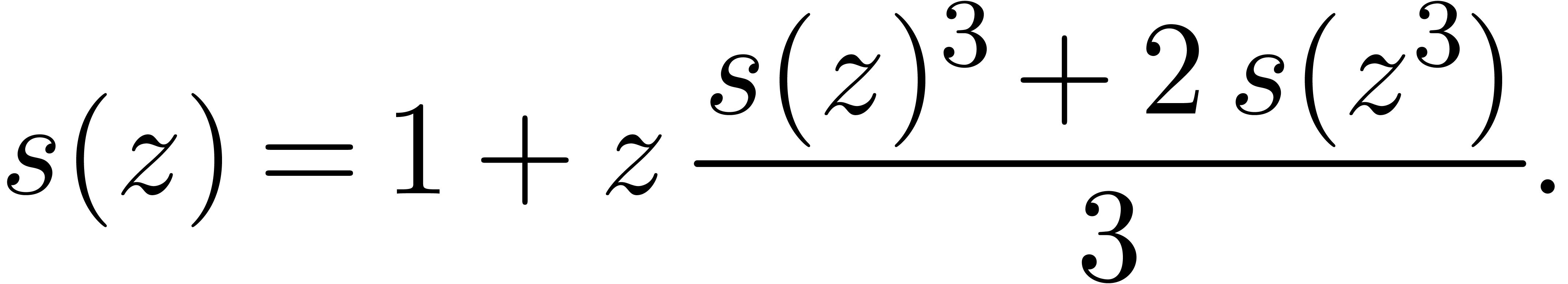
Using asymptotic extrapolation [vdH06], this series is
found to have a radius of convergence 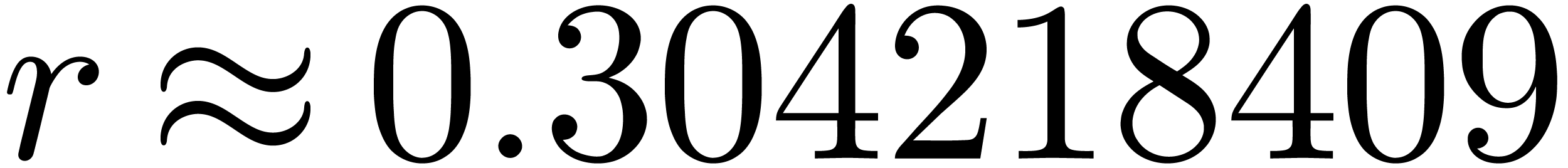 .
In order to investigate
.
In order to investigate  close to its dominant
singularity, we apply our algorithm to
close to its dominant
singularity, we apply our algorithm to
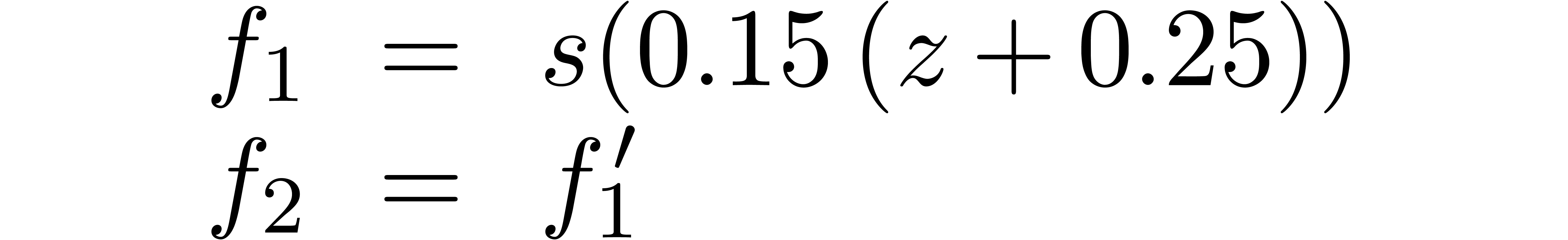
The translation 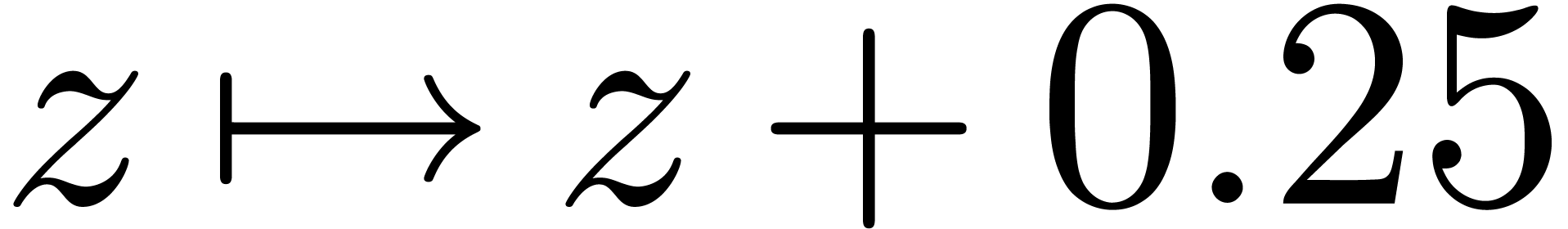 is done using power series
evaluation until stabilization at the working precision. At different
orders, we obtain:
is done using power series
evaluation until stabilization at the working precision. At different
orders, we obtain:

The corresponding norms are given by 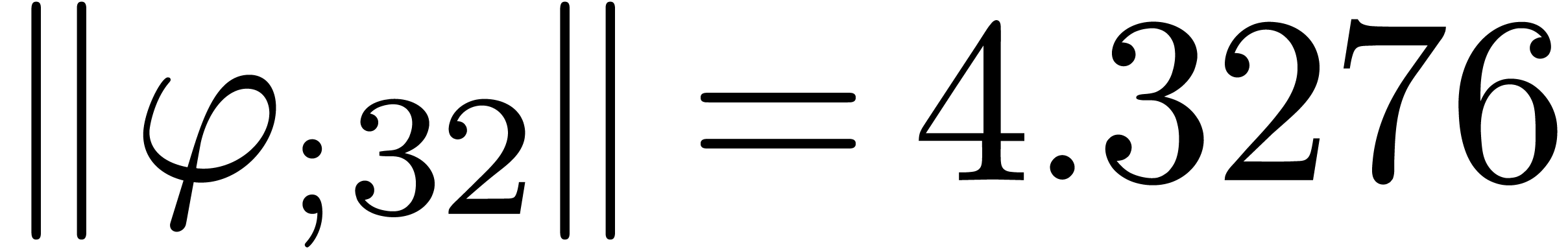 ,
,
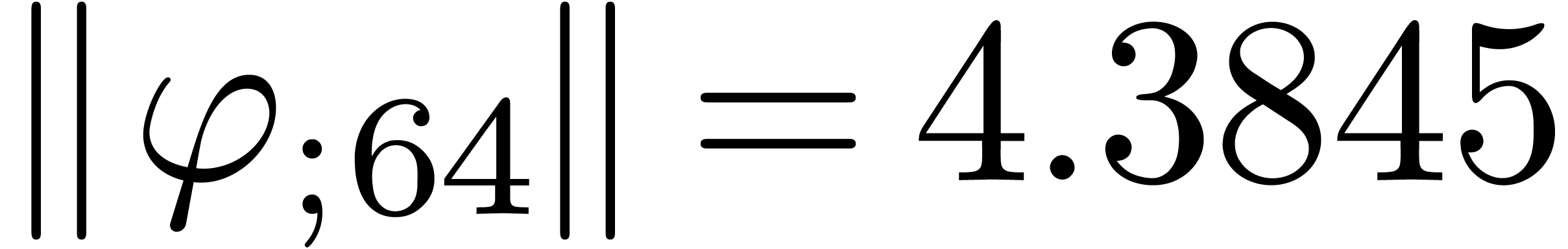 ,
, 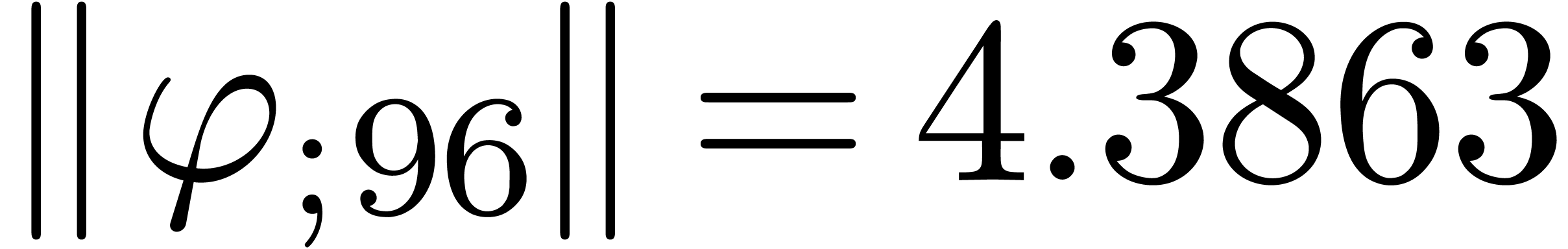 and
and
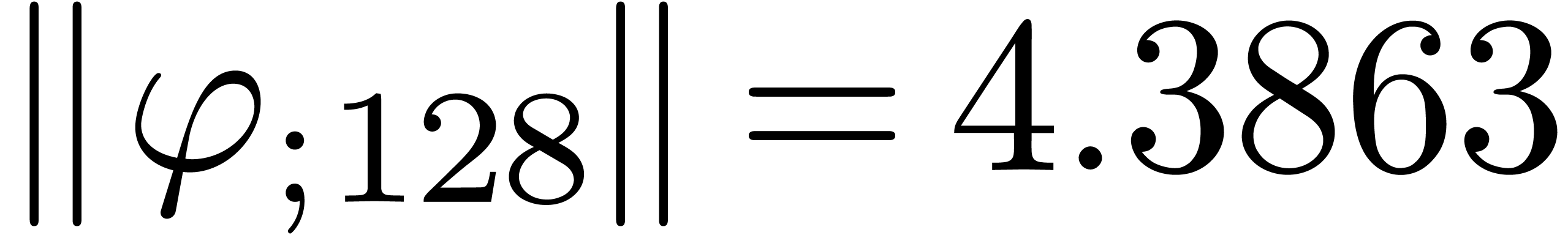 . Again, the convergence is
rather slow, and the computed series all seem to have radius of
convergence
. Again, the convergence is
rather slow, and the computed series all seem to have radius of
convergence 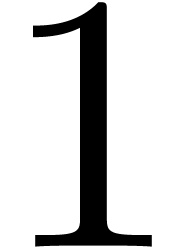 .
.
It is also instructive to run the algorithm on examples where the 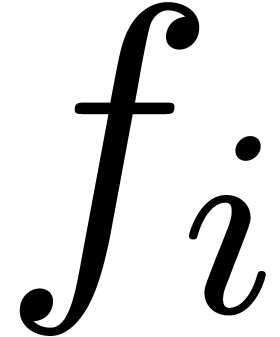 are known to be analytically independent. In that
case, it is important to examine the behaviour of the norms
are known to be analytically independent. In that
case, it is important to examine the behaviour of the norms 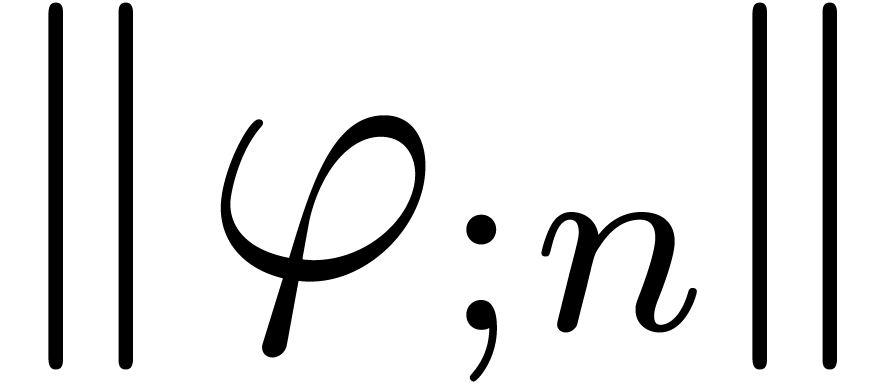 for
for  and find more precise criteria
which will enable us to discard the existence of a nice dependency with
a reasonable degree of certainty.
and find more precise criteria
which will enable us to discard the existence of a nice dependency with
a reasonable degree of certainty.
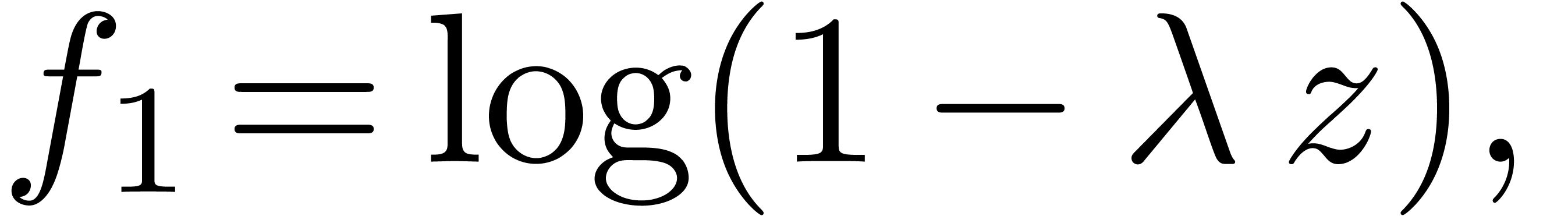
where  . Running our algorithm
directly on this function yields the following results for
. Running our algorithm
directly on this function yields the following results for 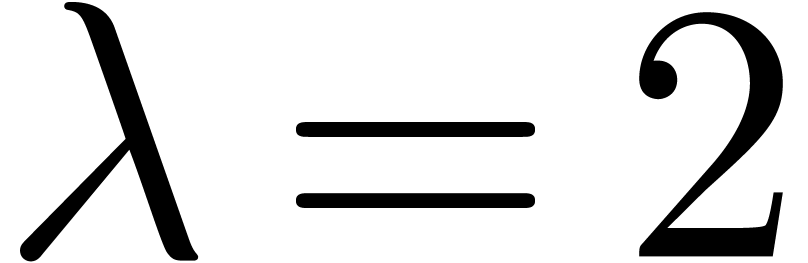 :
:
The results indeed do not converge and the corresponding sequence of
norms 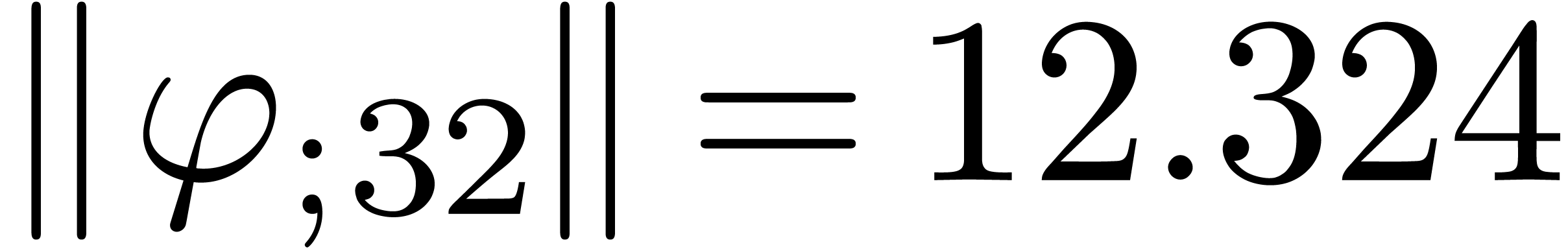 ,
, 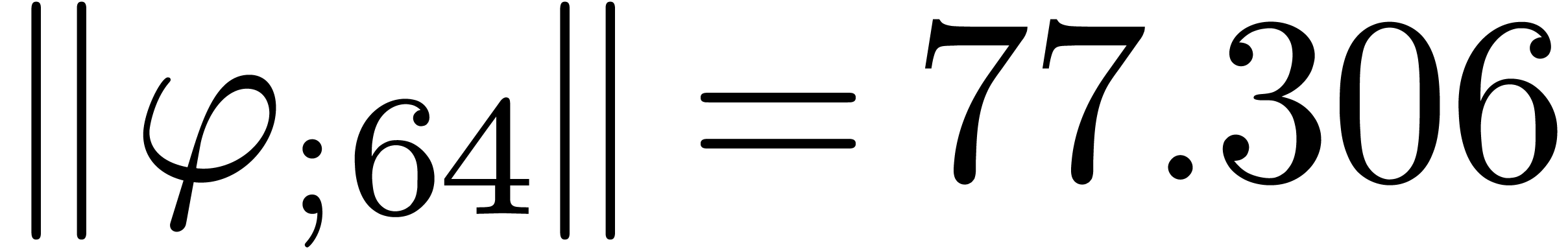 ,
, 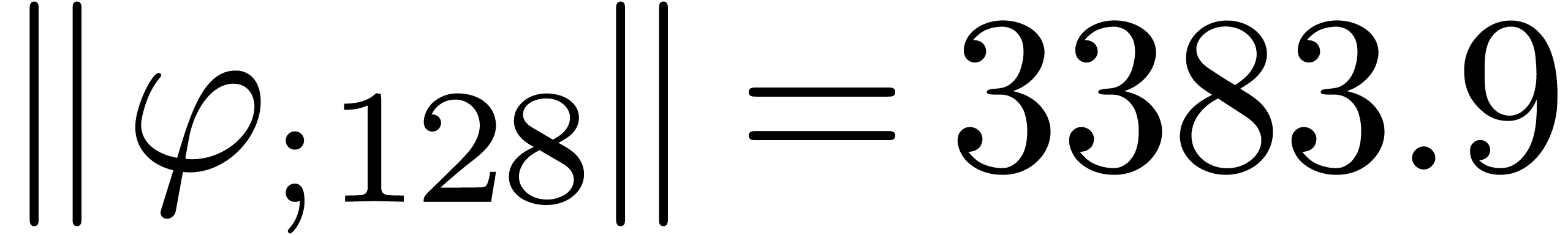 and
and 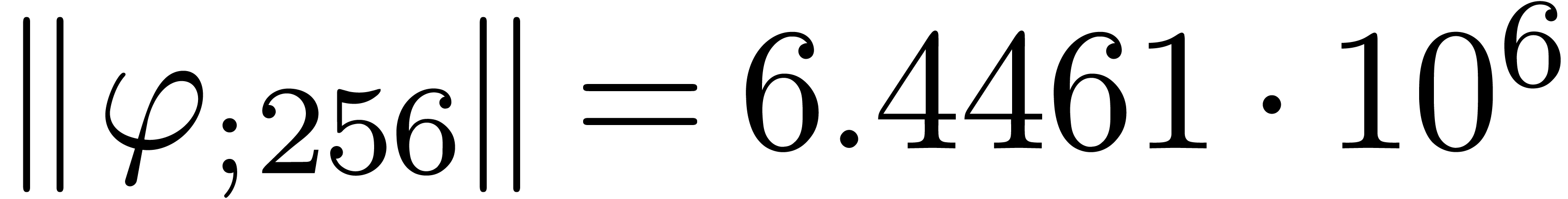 diverges at moderate speed.
diverges at moderate speed.
 . More generally, we can consider various
types of singularities, such as
. More generally, we can consider various
types of singularities, such as
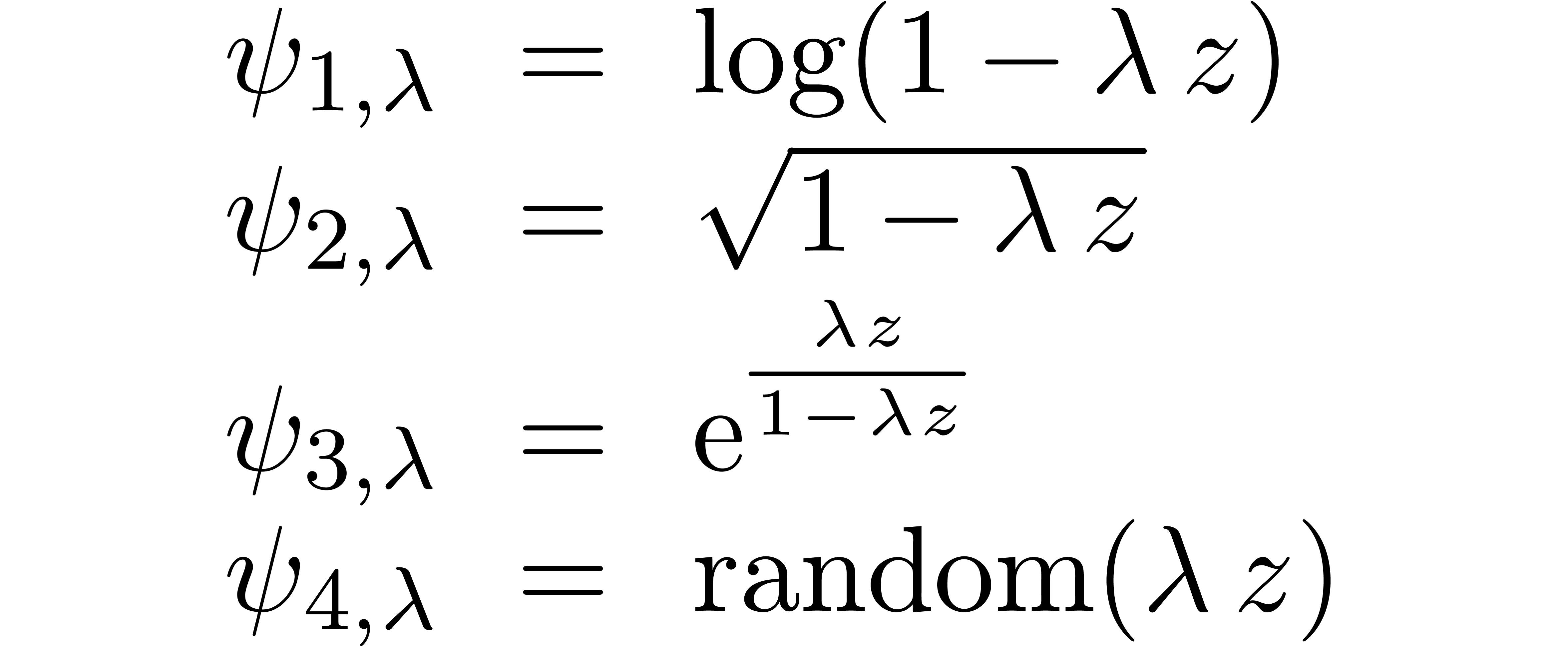
The series  is a series whose coefficients are
chosen according to a random uniform distribution on
is a series whose coefficients are
chosen according to a random uniform distribution on 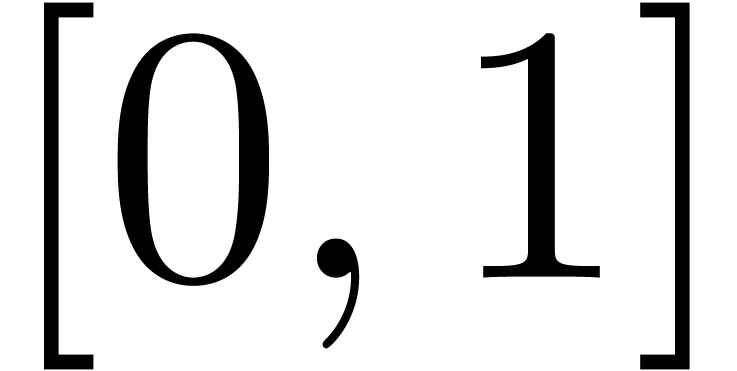 . The results are shown in table 1
below. For
. The results are shown in table 1
below. For 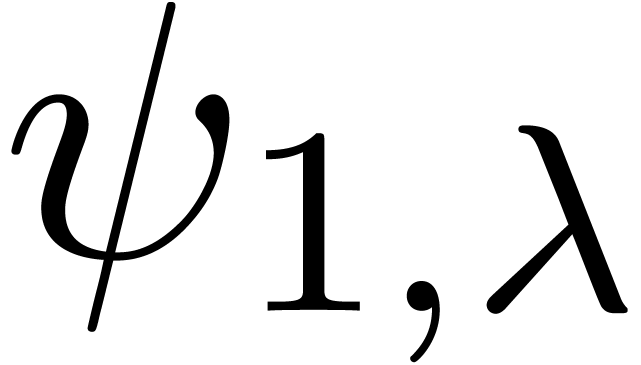 ,
, 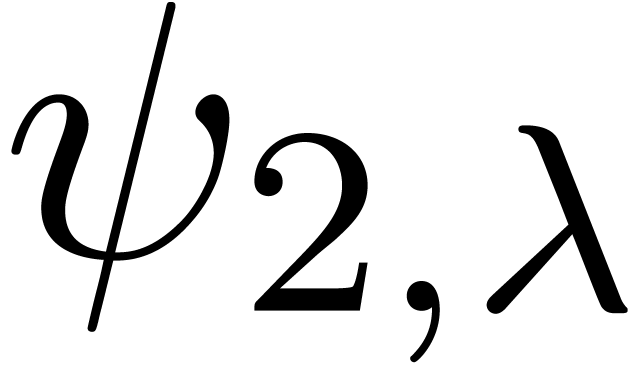 and
and 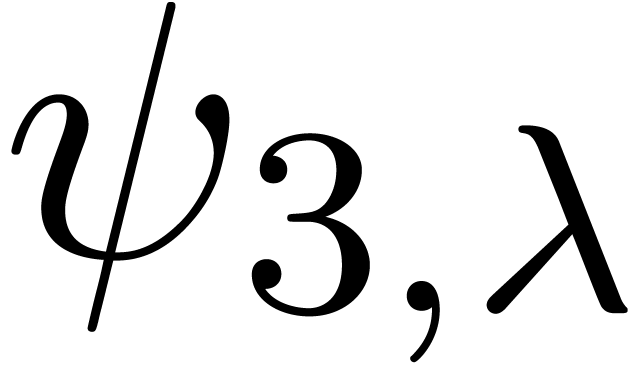 , it seems that the norm
does not much depend on the precise type of singularity, but only on
, it seems that the norm
does not much depend on the precise type of singularity, but only on
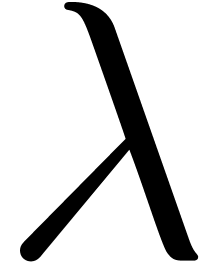 and the truncation order
and the truncation order 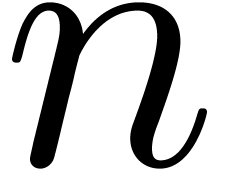 . For the last series
. For the last series 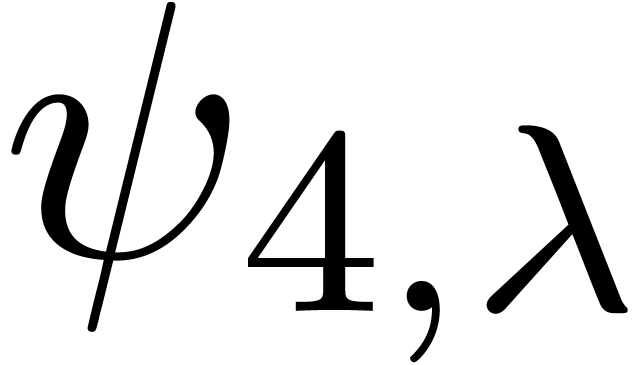 ,
the dependencies on
,
the dependencies on 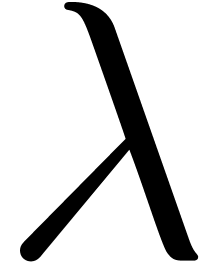 and
and 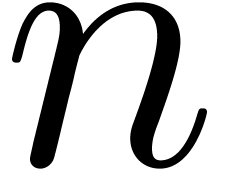 approximately seem to follow the law
approximately seem to follow the law
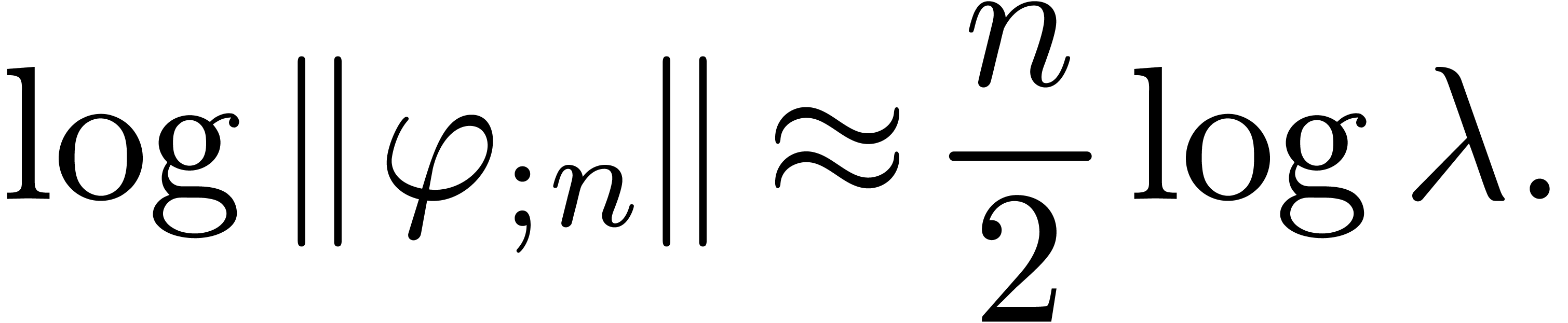 |
(16) |
This idealized law needs to be adjusted for functions 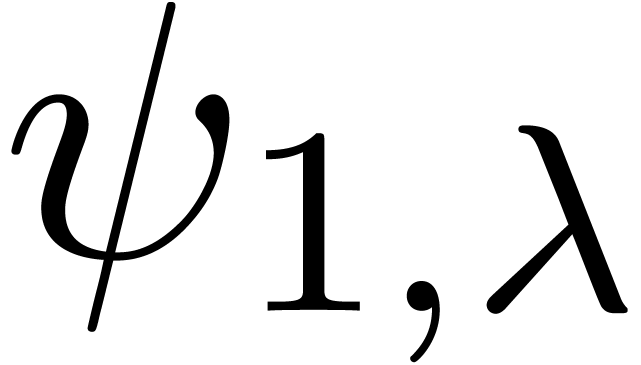 ,
, 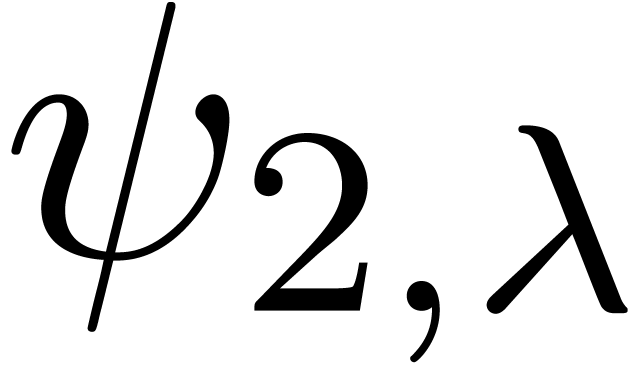 ,
,
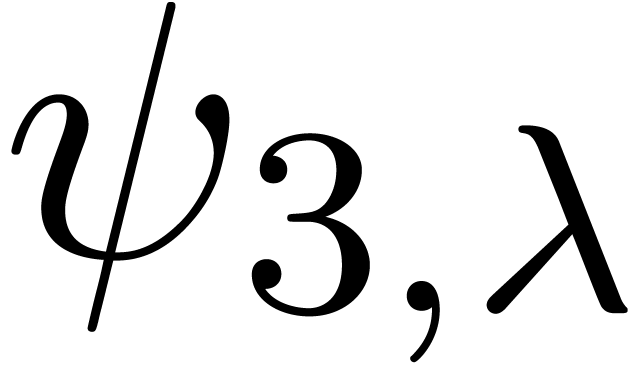 with more common types of singularities.
Although (16) remains asymptotically valid for large values
of
with more common types of singularities.
Although (16) remains asymptotically valid for large values
of 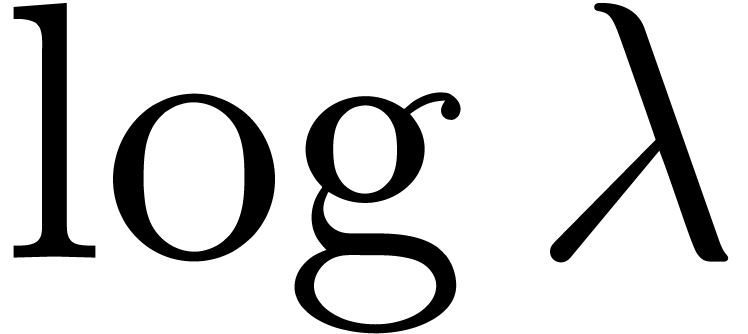 , the factor
, the factor 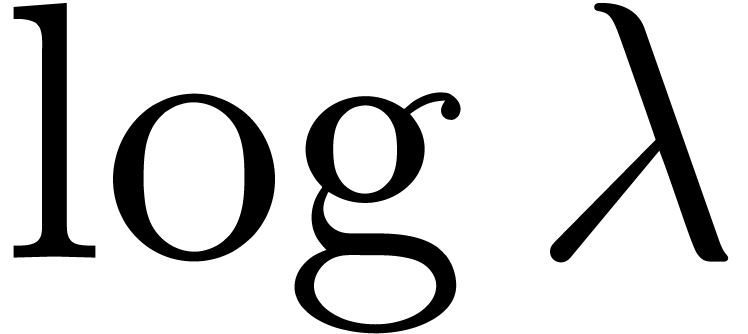 needs to be replaced by a smaller number for moderate
values. For
needs to be replaced by a smaller number for moderate
values. For 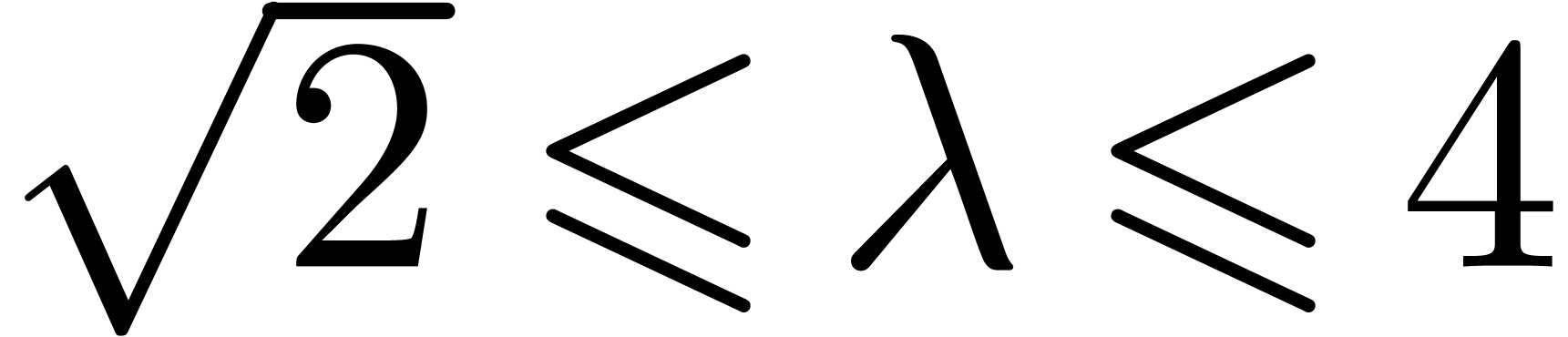 , this factor
rather seems to be of the form
, this factor
rather seems to be of the form 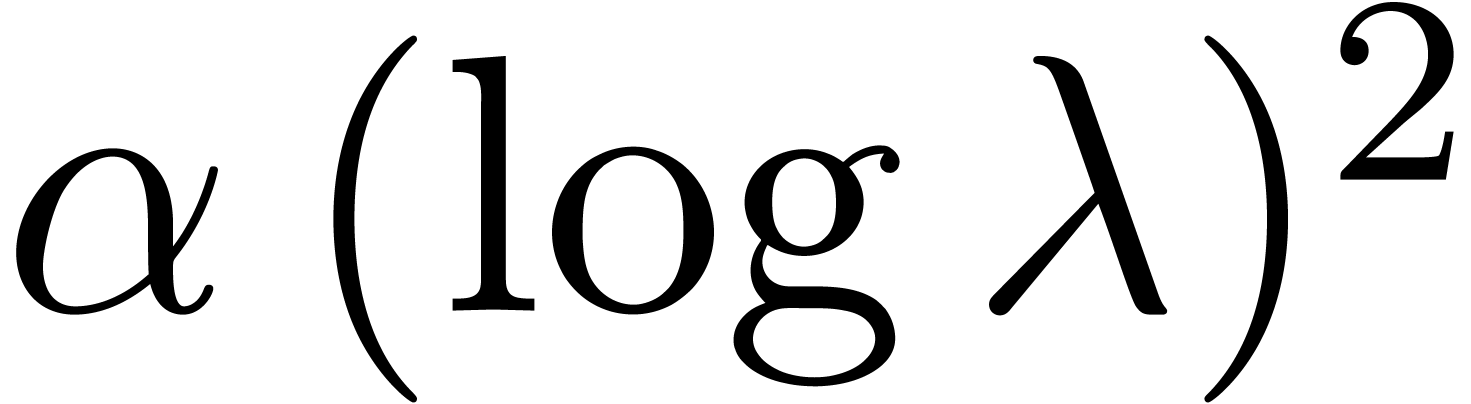 ,
where the constant
,
where the constant  depends on the nature of the
singularity. Also, the linear dependency of
depends on the nature of the
singularity. Also, the linear dependency of 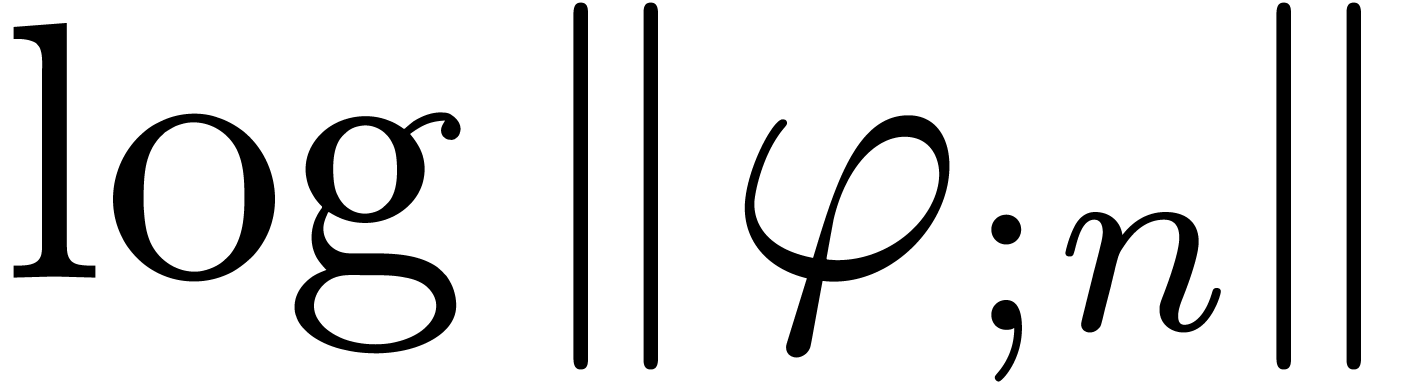 on
on
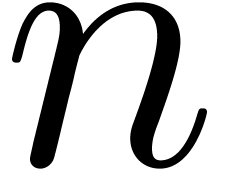 is only reached for large values of
is only reached for large values of 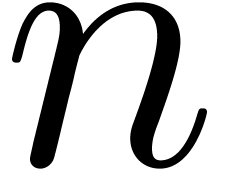 .
.
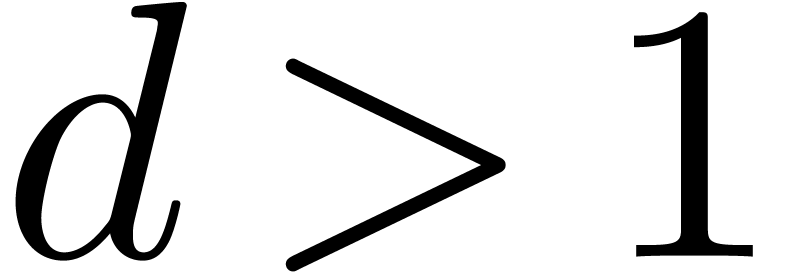
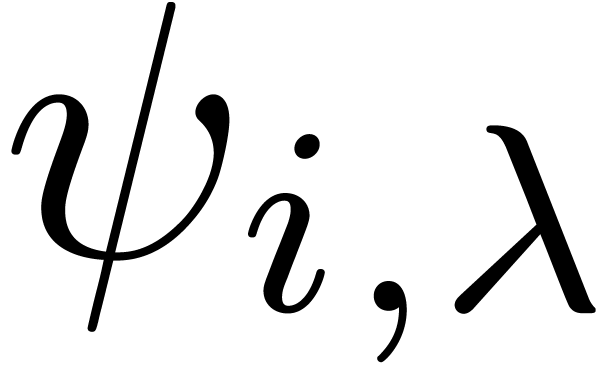 as above and studied the dependency of
as above and studied the dependency of 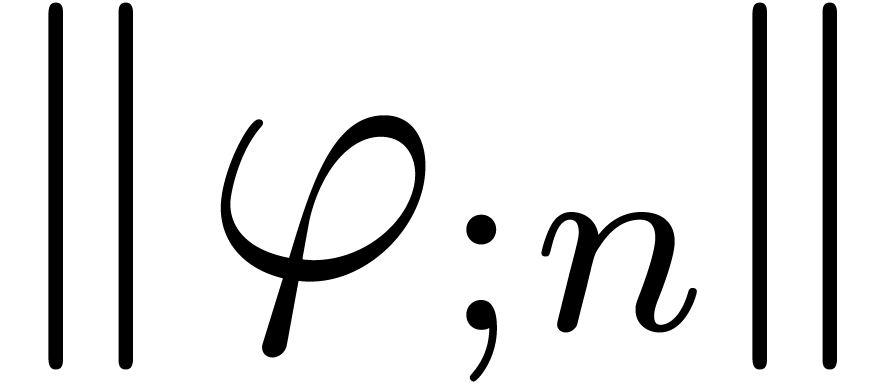 on
on
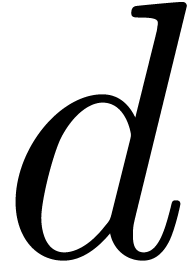 . The results are shown in
table 2 below. In the bottom rows,
. The results are shown in
table 2 below. In the bottom rows, 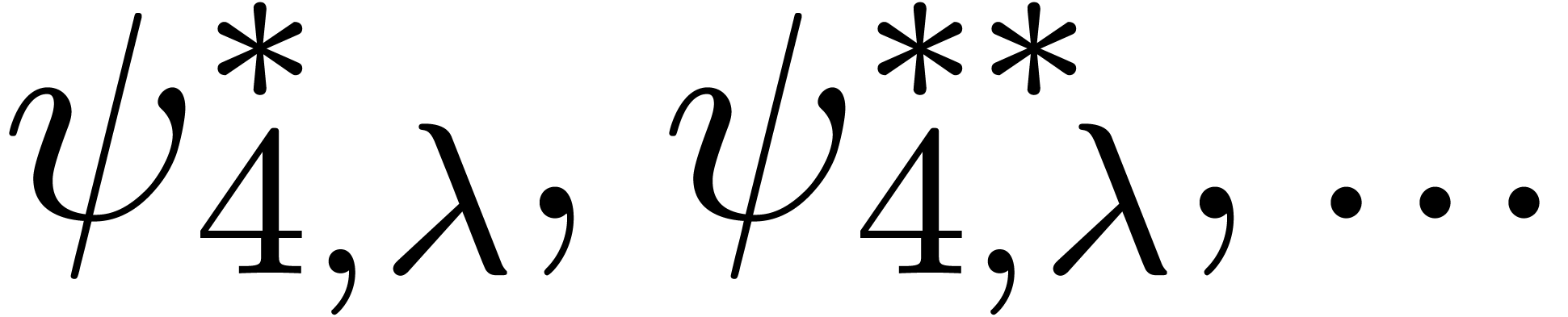 stand for distinct uncorrelated random series
stand for distinct uncorrelated random series 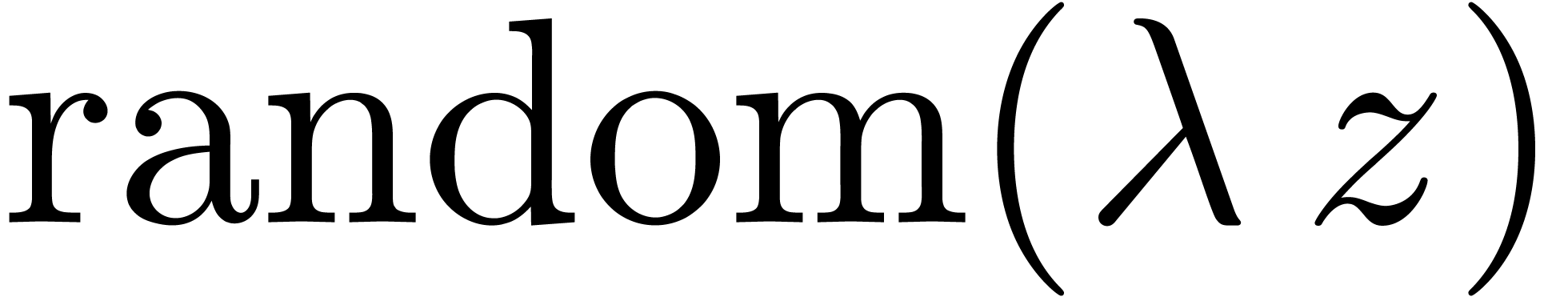 . In that case, the relation (16)
generalizes to
. In that case, the relation (16)
generalizes to
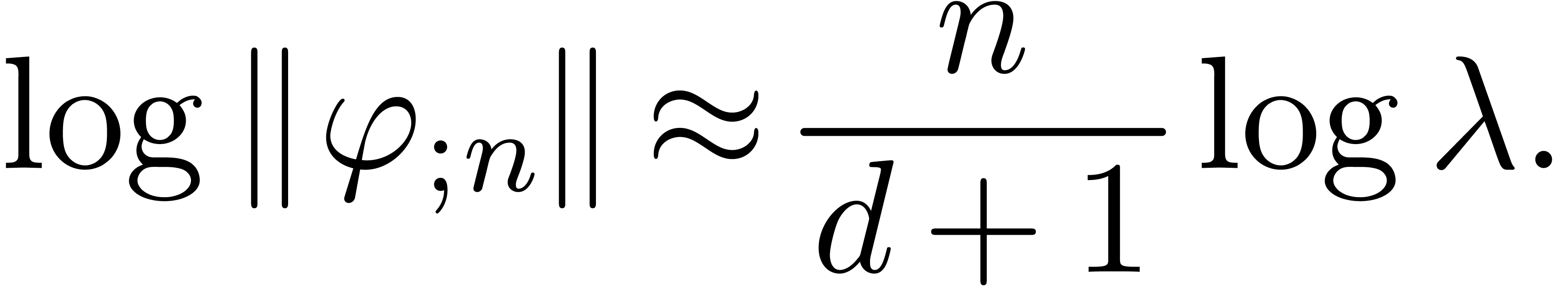 |
(17) |
It also seems that the law can be adapted to functions with more common types of singularities, along similar lines as before.
In the case when a linear relation (12) exists, we have
observed in section 5 that our algorithm usually returns a
relation whose series all have radius of convergence 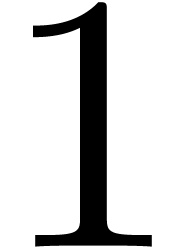 . Larger radii of convergence
. Larger radii of convergence 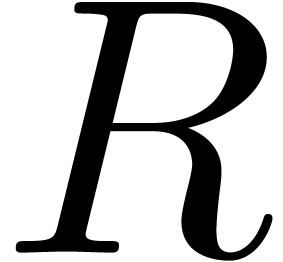 can be obtained simply by running the algorithm on
can be obtained simply by running the algorithm on 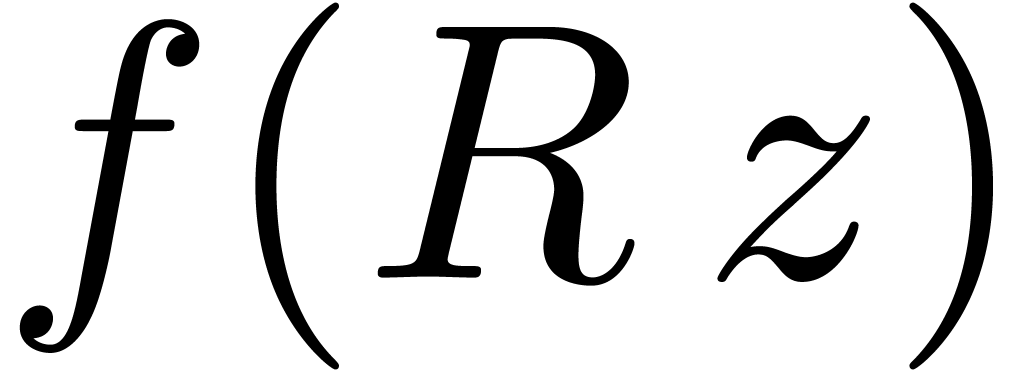 and scaling back the result.
and scaling back the result.
In the example of the enumeration of alcohols, we have also mentioned
the fact that the detection of dependencies is improved by zooming in on
the singularity. Although we used a shift  for
doing so, this is quite expensive in general: if
for
doing so, this is quite expensive in general: if 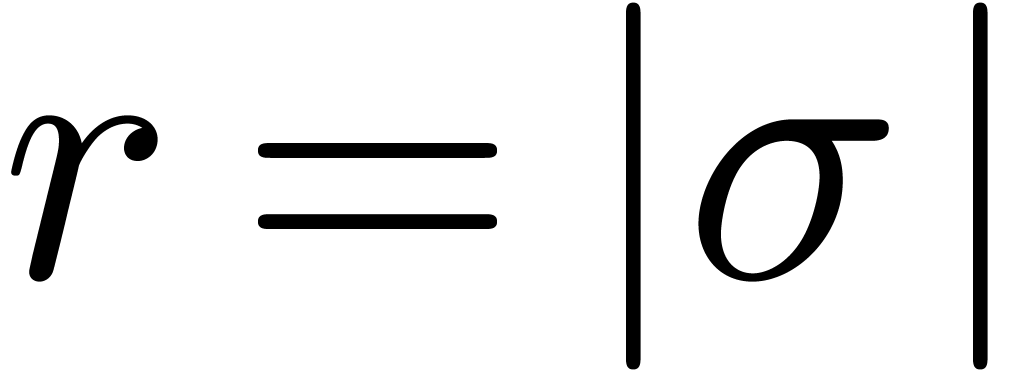 is the module of the singularity
is the module of the singularity  ,
then approximately
,
then approximately 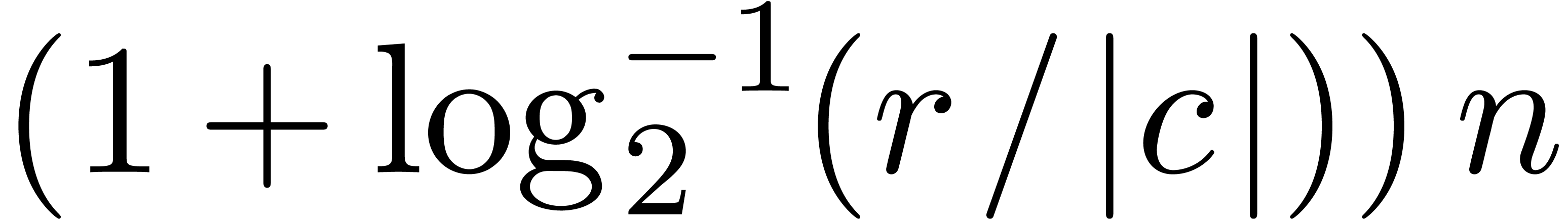 Taylor coefficients of
Taylor coefficients of 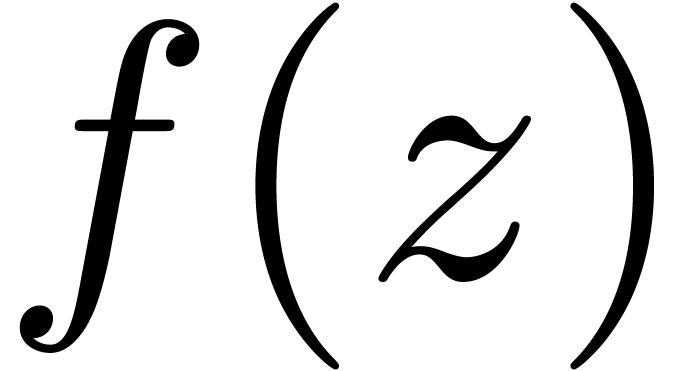 are needed in order to accurately compute
are needed in order to accurately compute 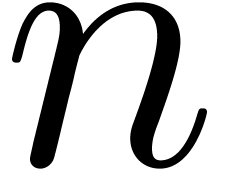 coefficients of
coefficients of 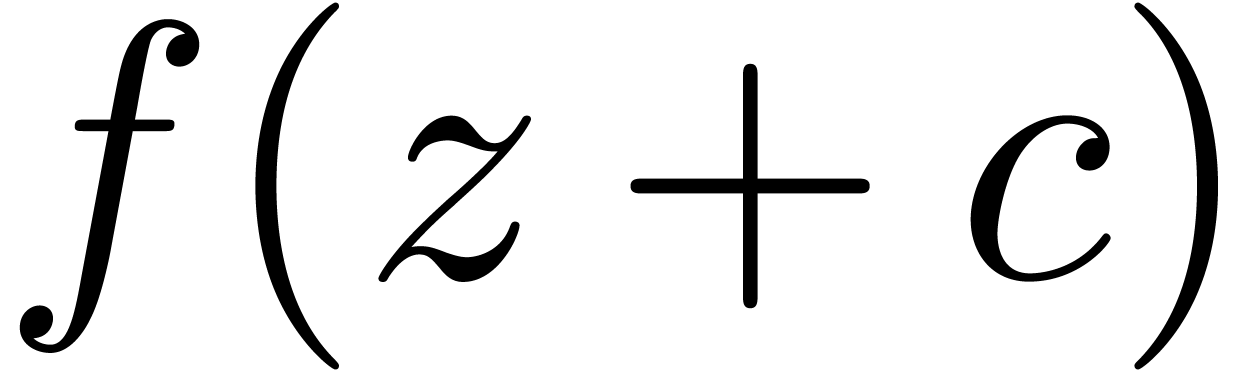 .
When possible, it is better to postcompose
.
When possible, it is better to postcompose  with
a suitable analytic function
with
a suitable analytic function 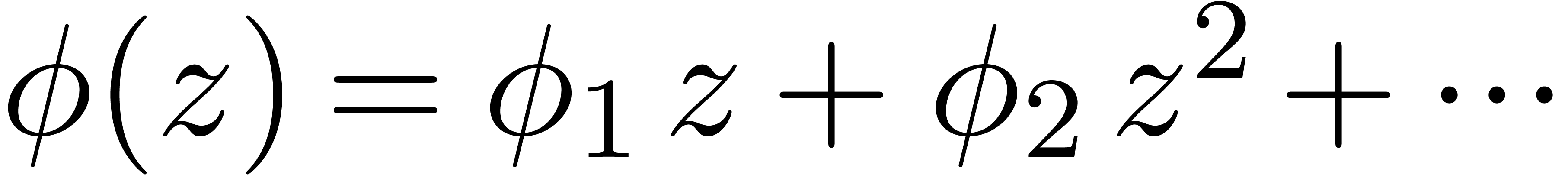 .
Here
.
Here  should be chosen in such a way that
should be chosen in such a way that  has
has 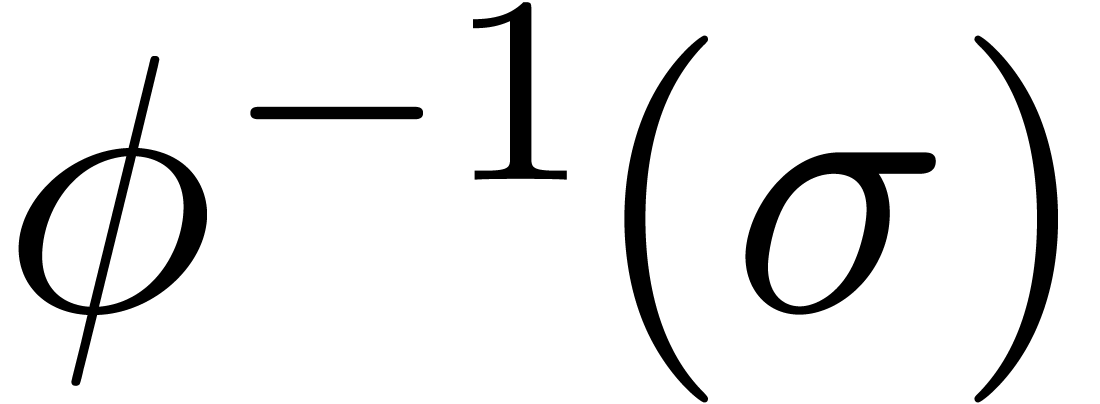 as its only singularity
in the unit disk, and such that
as its only singularity
in the unit disk, and such that 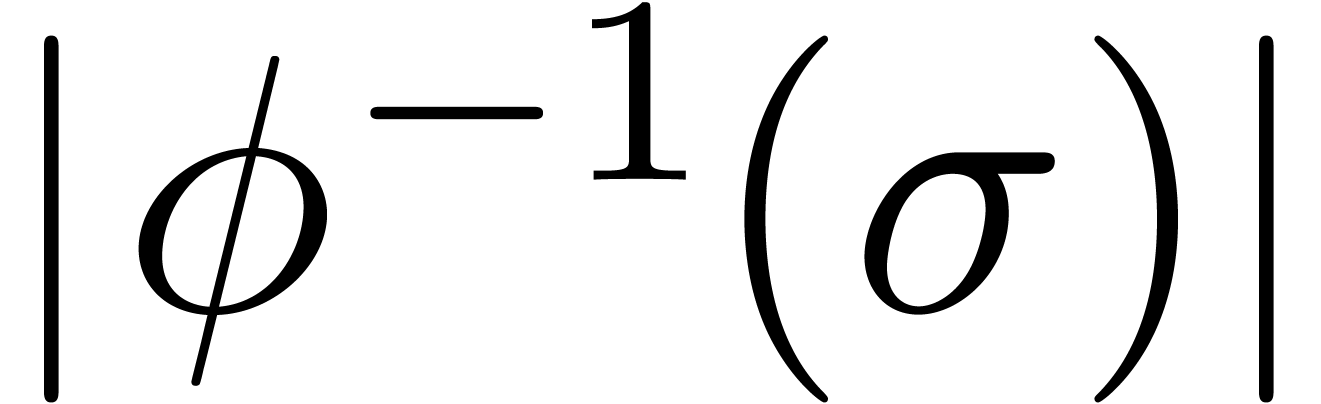 is as small as
possible. Also, if
is as small as
possible. Also, if  satisfies a differential
equation, then
satisfies a differential
equation, then  can be expanded efficiently at
can be expanded efficiently at
 by integrating the equation from its initial
conditions [BK78, vdH02a].
by integrating the equation from its initial
conditions [BK78, vdH02a].
Our empirical observations in the section 6 suggest a few
criteria for detecting the non-existence of dependencies (12).
First of all, when running the algorithm for different orders  , we should observe a more or less
geometric increase of the norm
, we should observe a more or less
geometric increase of the norm 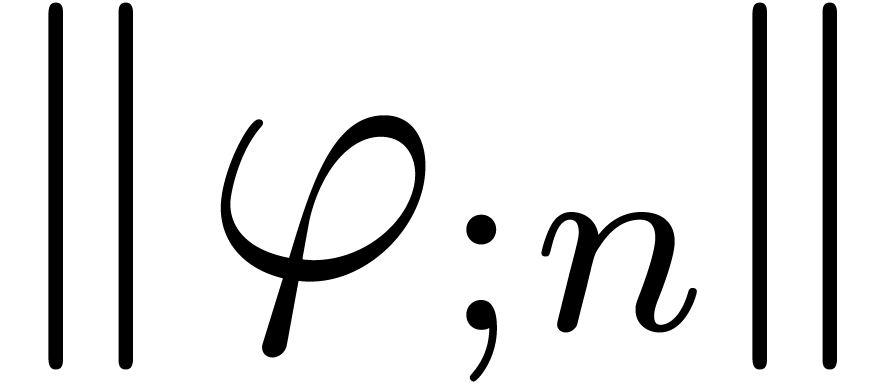 .
If we know the norm
.
If we know the norm 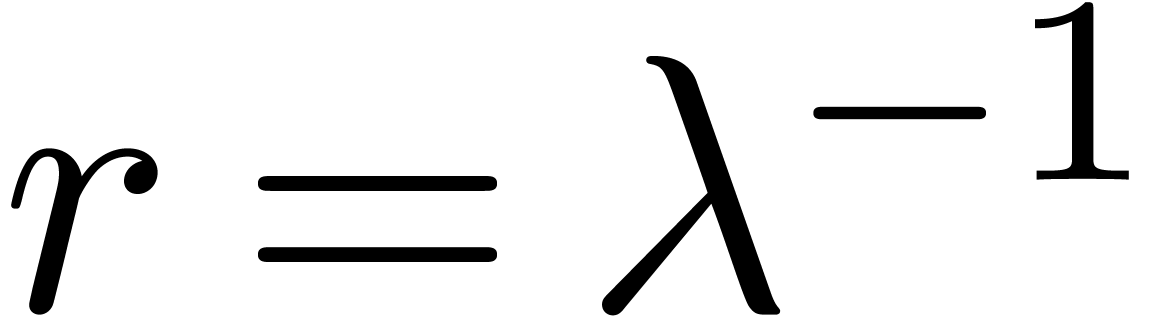 of the smallest singularity,
then this idea may be refined by comparing the computed values of
of the smallest singularity,
then this idea may be refined by comparing the computed values of 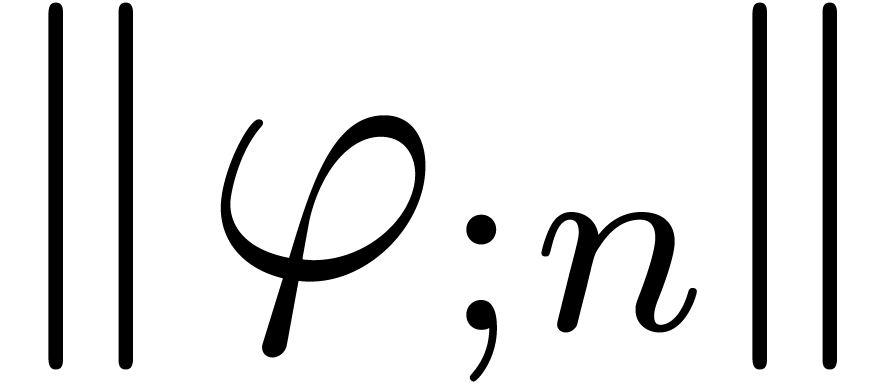 with the expected values, as given by the law (17), or a suitable adaptation of this law when
with the expected values, as given by the law (17), or a suitable adaptation of this law when 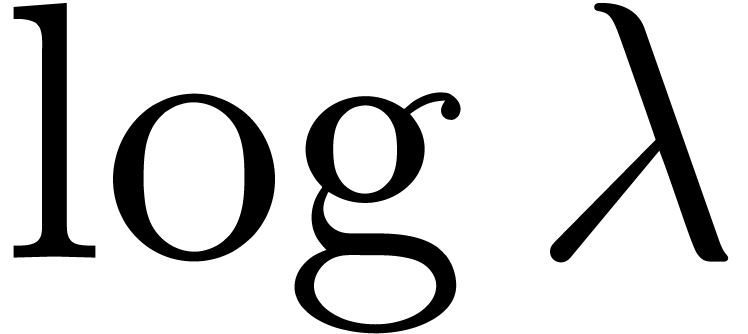 becomes small. This method is most effective when
becomes small. This method is most effective when 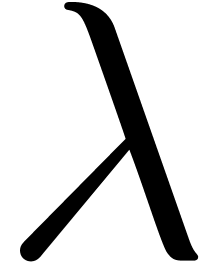 is large. When possible, it is therefore recommended
to zoom in on the singularity, as discussed above.
is large. When possible, it is therefore recommended
to zoom in on the singularity, as discussed above.
For any numerical checks based on the law (17) or a
refinement of it, we also recommend to precondition the input series
 . In particular, we recommend
to multiply each
. In particular, we recommend
to multiply each 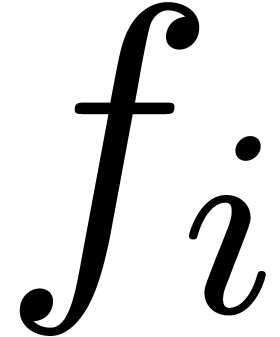 by a suitable constant,
ensuring that
by a suitable constant,
ensuring that
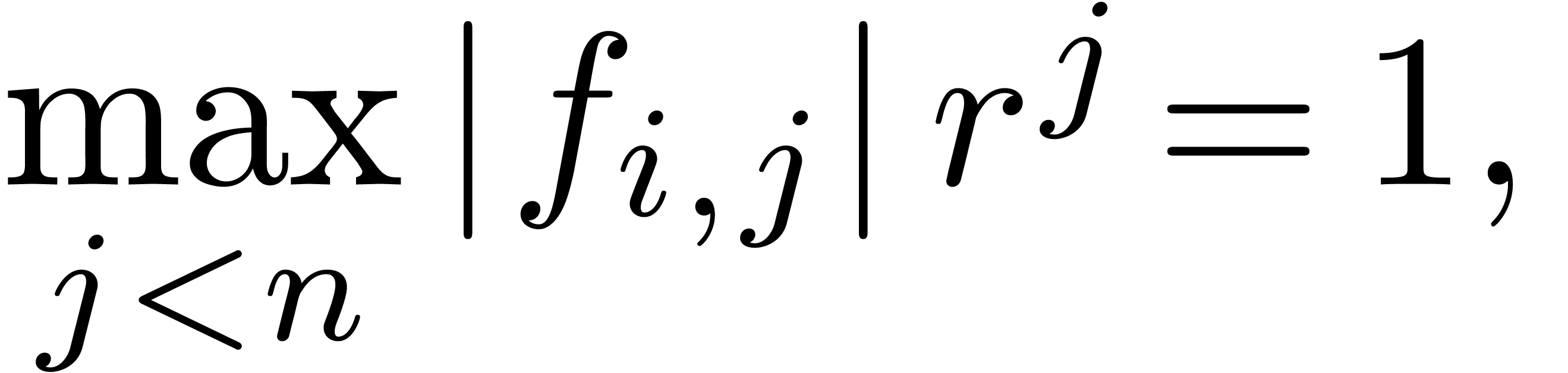
whenever we apply our algorithm at order 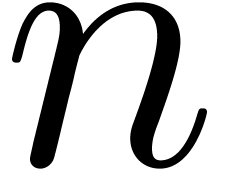 .
Here
.
Here 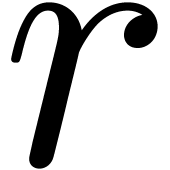 is computed using one of the algorithms
from section 2.
is computed using one of the algorithms
from section 2.
Let us now analyze the cost of the algorithm from section 4.
The current working precision 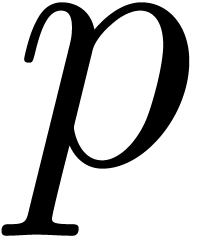 should in general
be taken larger than
should in general
be taken larger than 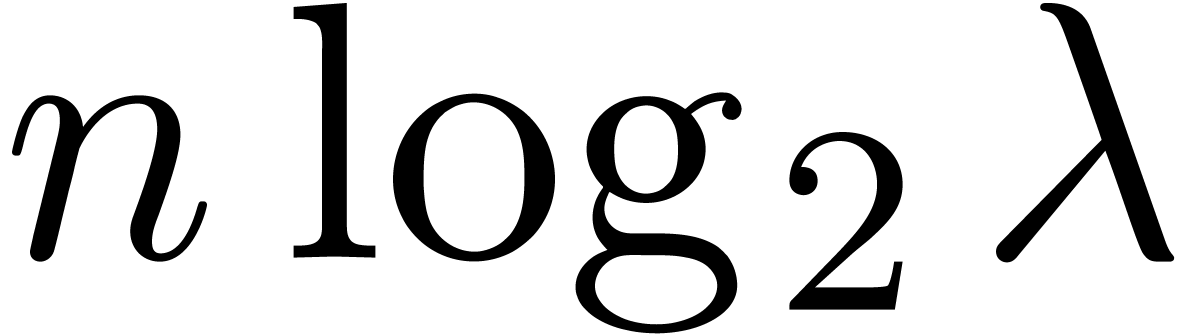 in order to keep the method
numerically stable. Denoting by
in order to keep the method
numerically stable. Denoting by 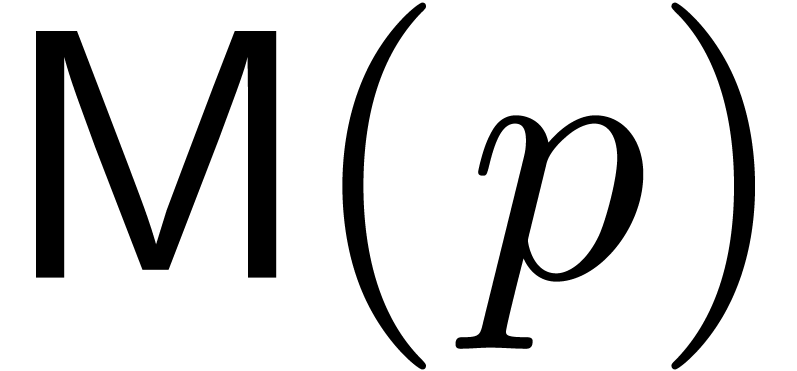 the cost for
multiplying two
the cost for
multiplying two 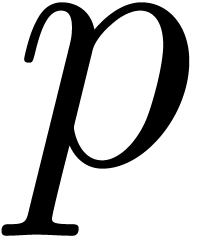 bit numbers, a naive
implementation of the Gram-Schmidt orthogonalization procedure yields a
total cost of
bit numbers, a naive
implementation of the Gram-Schmidt orthogonalization procedure yields a
total cost of 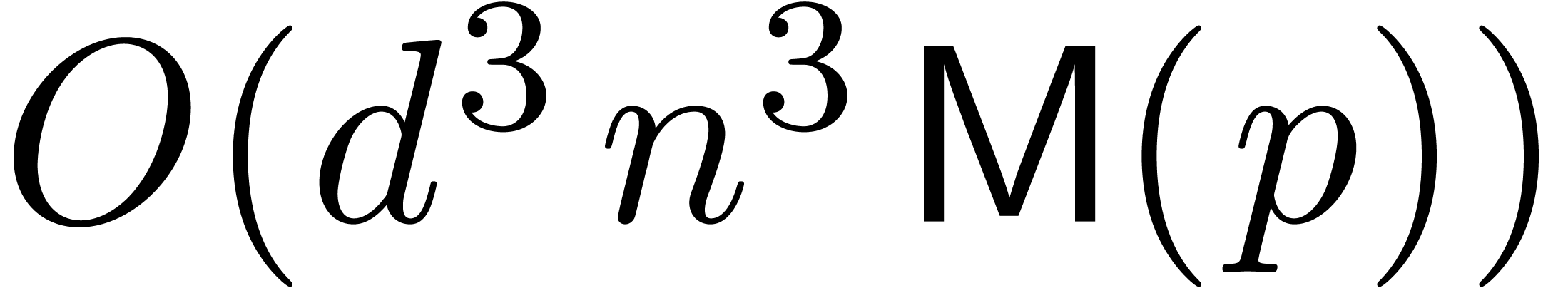 . Denoting by
. Denoting by
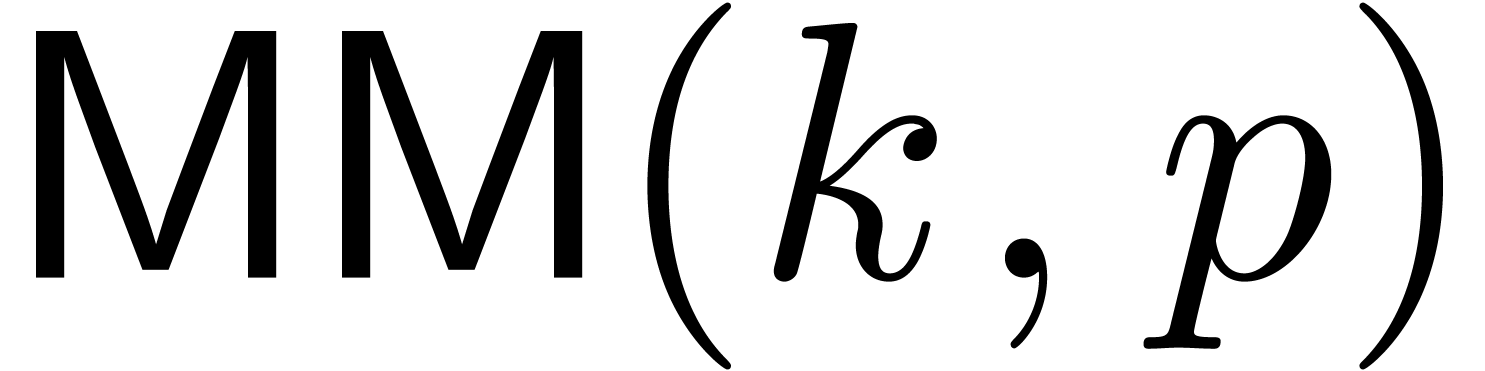 the cost of multiplying two
the cost of multiplying two  matrices with
matrices with 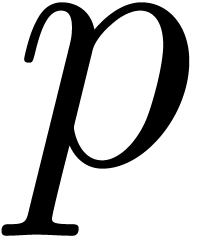 bit entries, and using a blockwise
Gram-Schmidt procedure, we obtain the better bound
bit entries, and using a blockwise
Gram-Schmidt procedure, we obtain the better bound 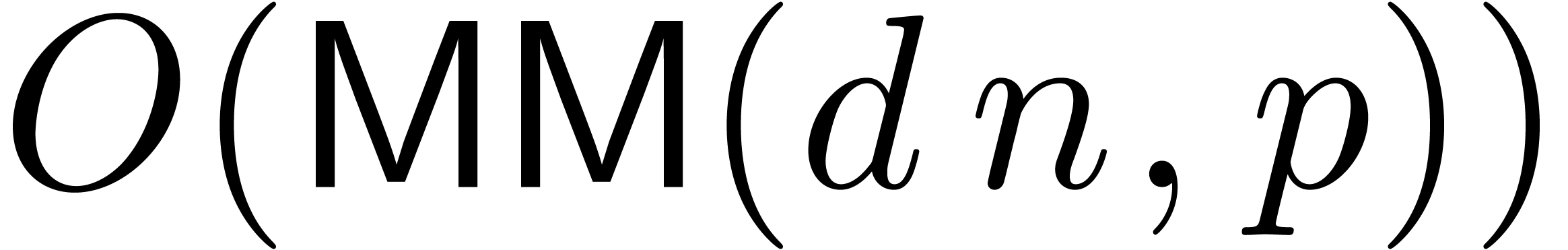 . However, the matrix
. However, the matrix 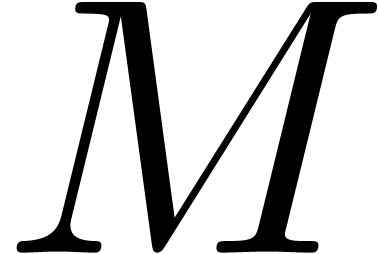 from section 4 has a very special form. With more work, it
might therefore be possible to save an additional factor
from section 4 has a very special form. With more work, it
might therefore be possible to save an additional factor 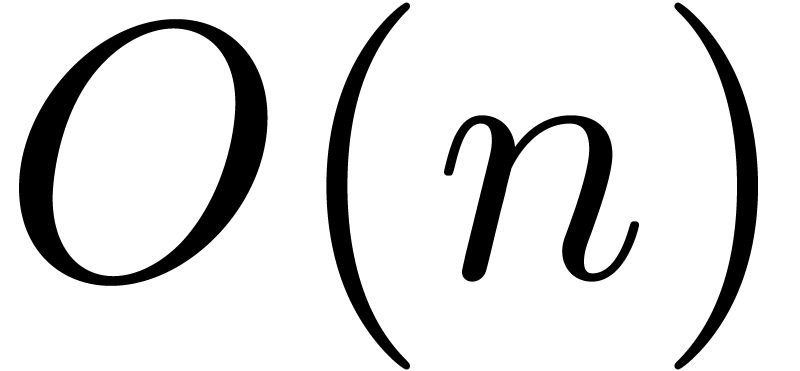 , but we have not actively tried to do so yet.
, but we have not actively tried to do so yet.
Since it is often possible to zoom in on the singularity, we may
evaluate the computational cost in terms of the desired “output
quality”. As a definition of the output quality, we may take the
expected value 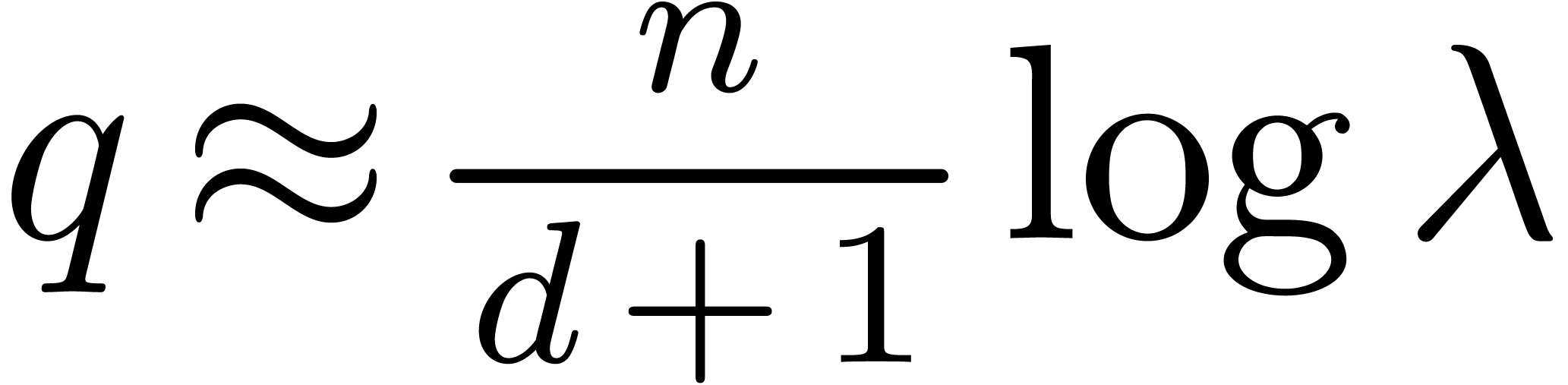 of
of 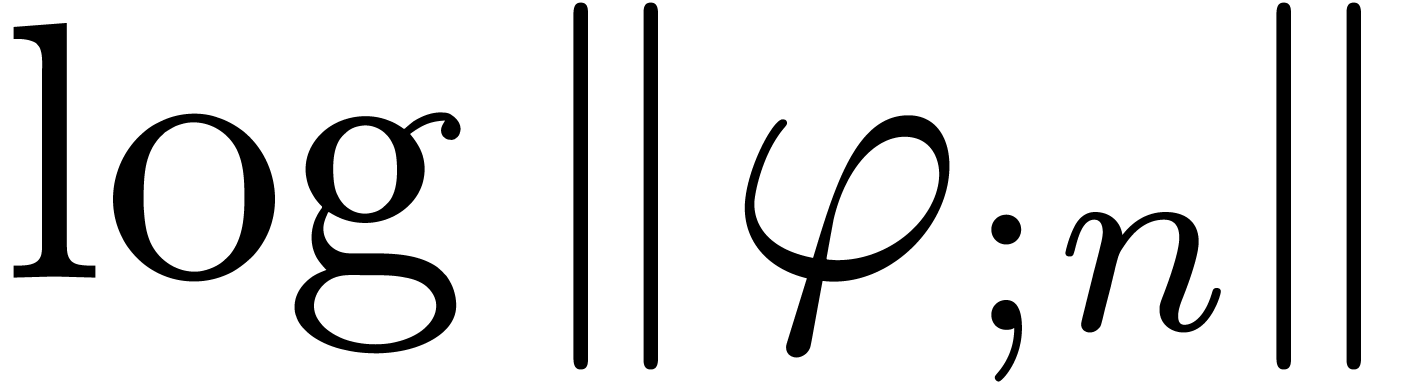 in the
case when
in the
case when  are independent. In terms of
are independent. In terms of  , the time complexity than becomes
, the time complexity than becomes
where  is the exponent of matrix multiplication.
The complexity bound makes it clear that we should put a lot of effort
into keeping
is the exponent of matrix multiplication.
The complexity bound makes it clear that we should put a lot of effort
into keeping 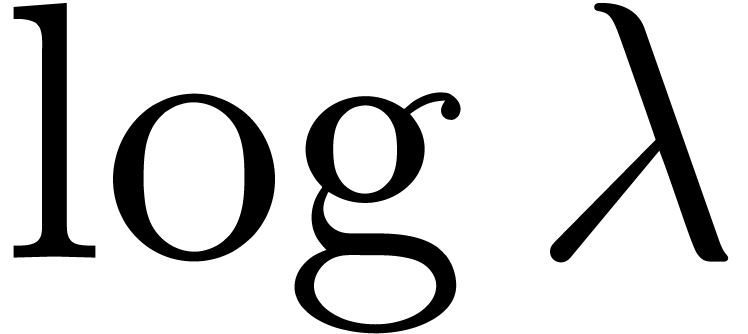 large. For instance, zooming in on
the singularity using a shift makes it possible to replace
large. For instance, zooming in on
the singularity using a shift makes it possible to replace  by
by 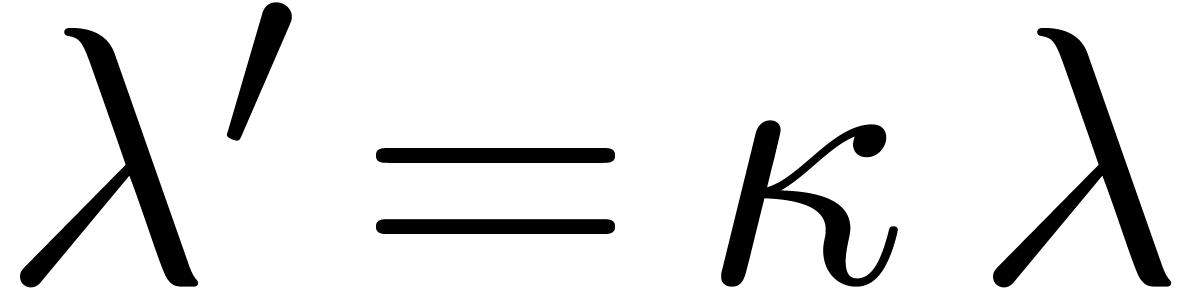 modulo the evaluation of
modulo the evaluation of  at a larger order
at a larger order 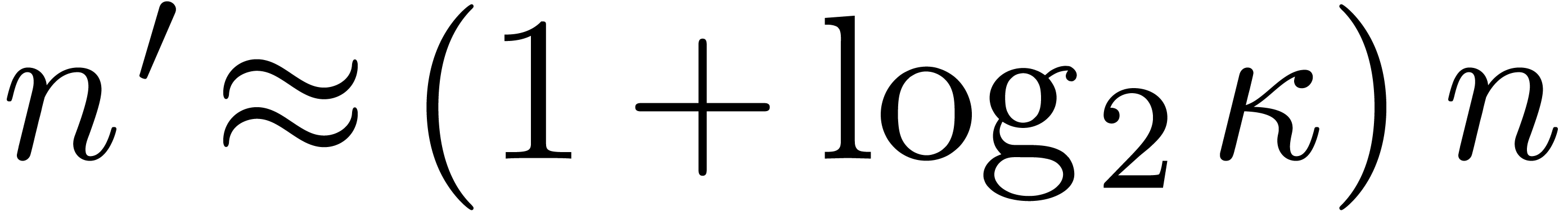 instead of
instead of
 (and a bit precision
(and a bit precision 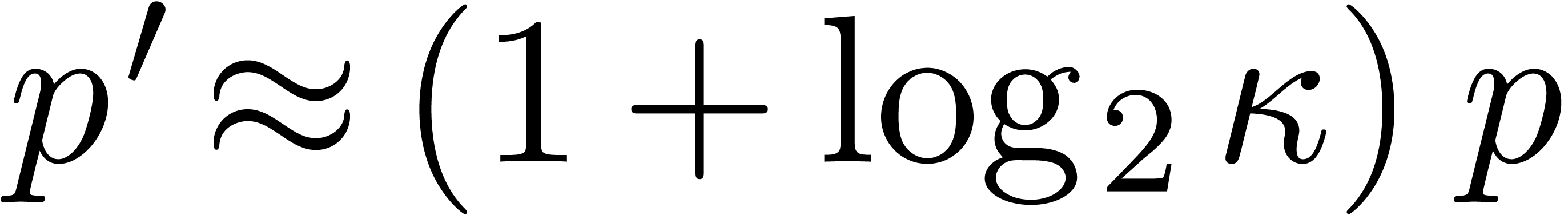 instead of
instead of 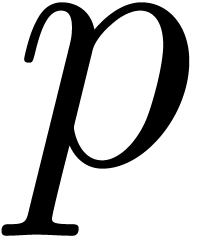 ). In many
practical cases, this can be done in time
). In many
practical cases, this can be done in time 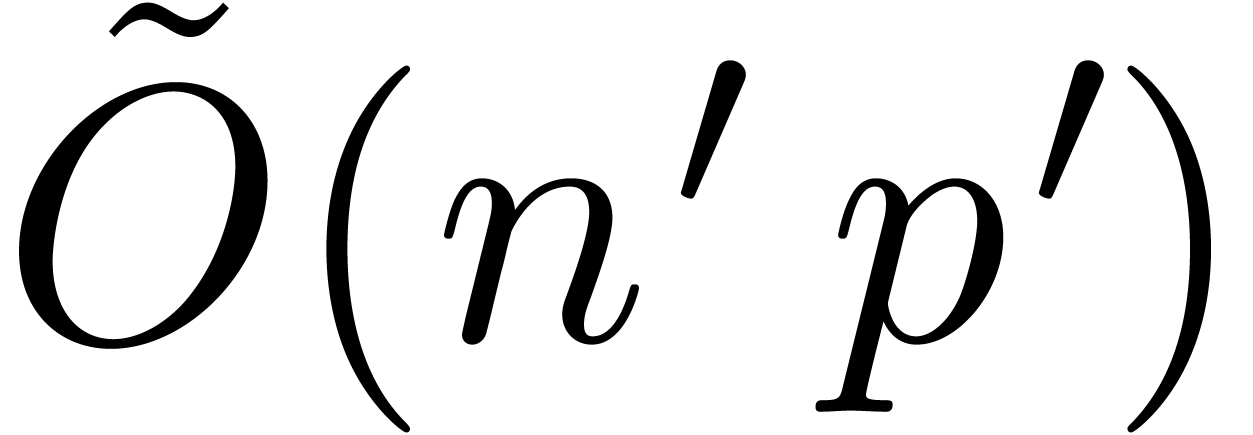 ,
which allows for a drastic reduction of the complexity. Of course, a
possible analytic relation will only be obtained on a small disk around
the singularity of interest.
,
which allows for a drastic reduction of the complexity. Of course, a
possible analytic relation will only be obtained on a small disk around
the singularity of interest.
To go short, our algorithm from section 4 mainly works well if the following conditions are satisfied:
The number 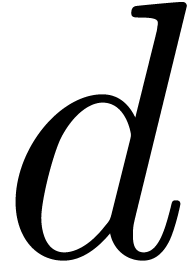 should not be too large.
should not be too large.
There exists a large constant  for which all
singularities of
for which all
singularities of  are concentrated inside the
disk of radius
are concentrated inside the
disk of radius 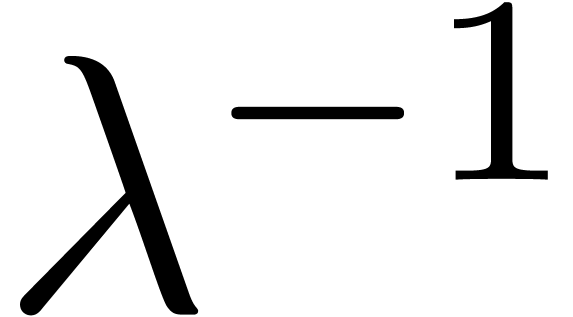 or outside the disk of radius
or outside the disk of radius
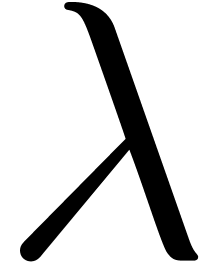 .
.
If we are interested in dependencies near an isolated singularity, then the second condition can often be achieved by zooming in on the singularity.
As a final note, we mention the fact that linear analytic dependencies
can sometimes be obtained using the process of asymptotic extrapolation
[vdH06]. For instance, given a function  with an isolated smallest singularity at
with an isolated smallest singularity at 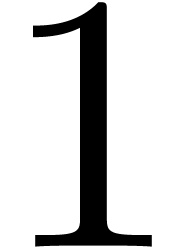 of the
form
of the
form
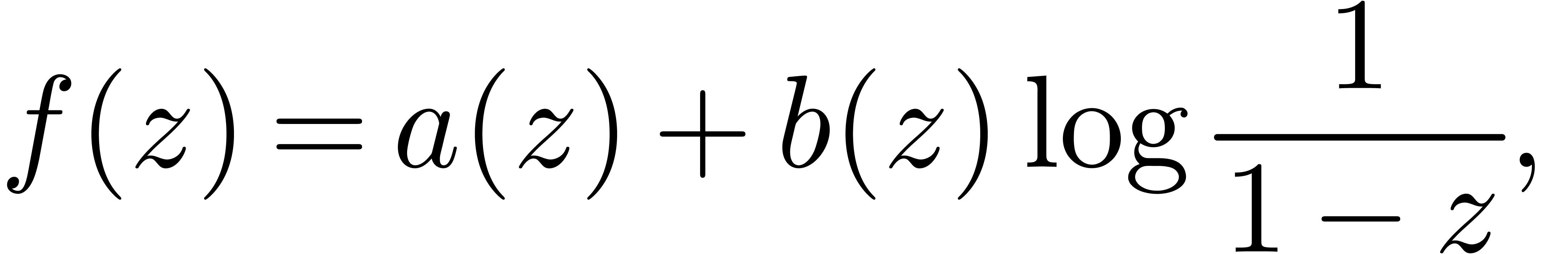
where  and
and 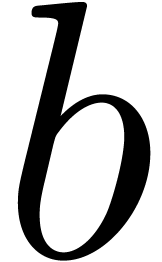 are analytic
at
are analytic
at 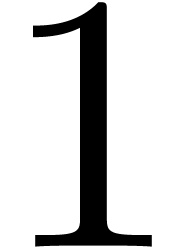 , the asymptotic
extrapolation of
, the asymptotic
extrapolation of 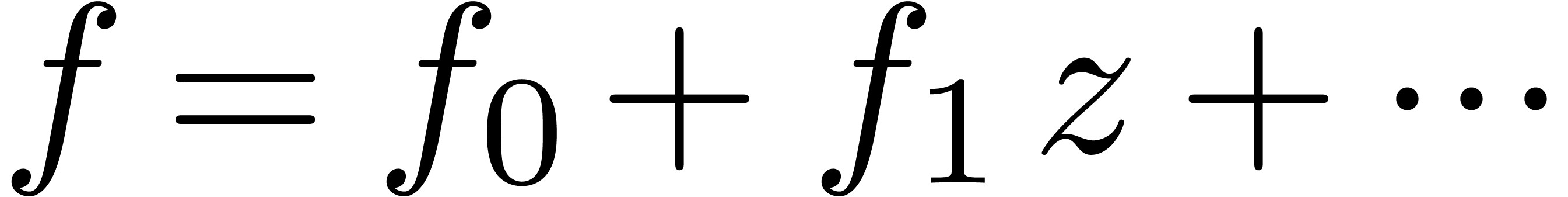 yields an asymptotic expansion
of the form
yields an asymptotic expansion
of the form
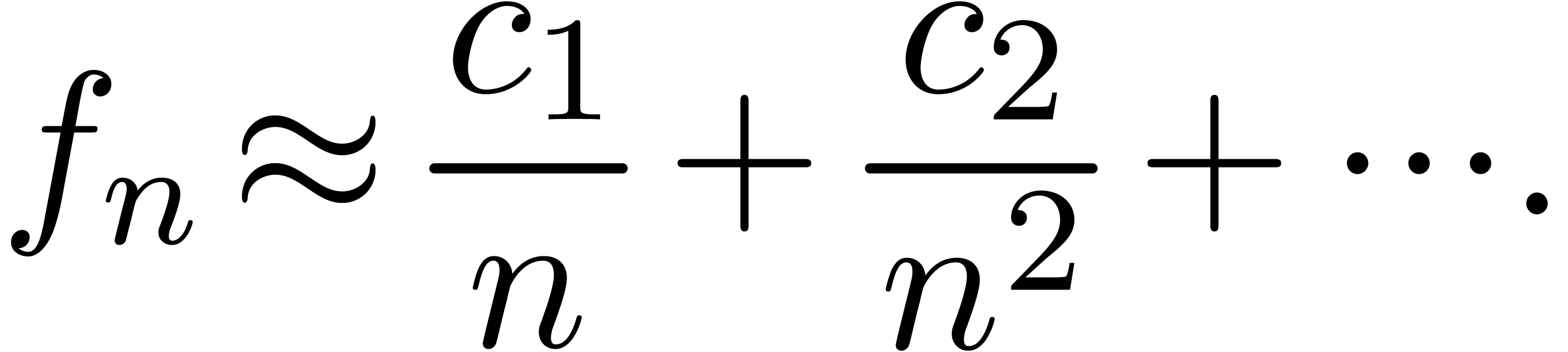
Using singularity analysis [FS96], we may then recover the
function 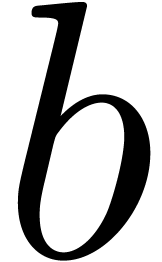 from the coefficients
from the coefficients 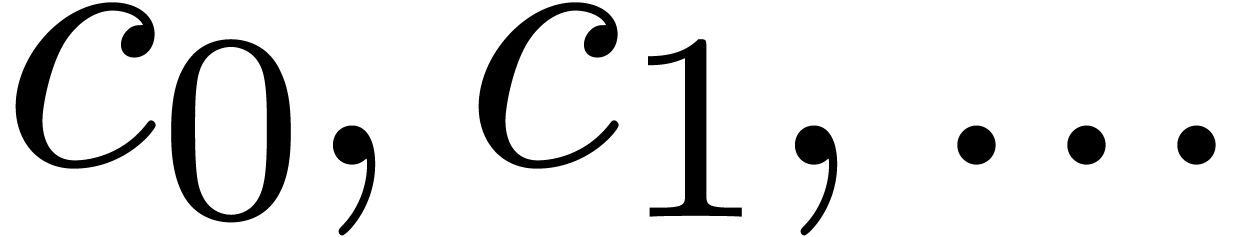 . However, this technique only works in special
cases, since the first
. However, this technique only works in special
cases, since the first  terms of the asymptotic
expansion may hide other terms, which need to be taken into account when
searching for exact dependencies.
terms of the asymptotic
expansion may hide other terms, which need to be taken into account when
searching for exact dependencies.
R.P. Brent and H.T. Kung. Fast algorithms for manipulating formal power series. Journal of the ACM, 25:581–595, 1978.
B. Beckermann and G. Labahn. A uniform approach for the fast computation of matrix-type Padé approximants. SIAM J. Matrix Analysis and Applications, pages 804–823, 1994.
C. Brezinski and R. Zaglia. Extrapolation Methods. Theory and Practice. North-Holland, Amsterdam, 1991.
H. Derksen. An algorithm to compute generalized padé-hermite forms. Technical Report Rep. 9403, Catholic University Nijmegen, January 1994.
J. Denef and L. Lipshitz. Decision problems for differential equations. The Journ. of Symb. Logic, 54(3):941–950, 1989.
P. Flajolet and R. Sedgewick. An introduction to the analysis of algorithms. Addison Wesley, Reading, Massachusetts, 1996.
G. Pólya. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen. Acta Mathematica, 68:145–254, 1937.
B. Salvy and P. Zimmermann. Gfun: a Maple package for the manipulation of generating and holonomic functions in one variable. ACM Trans. on Math. Software, 20(2):163–177, 1994.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven et al. Mathemagix, 2002. http://www.mathemagix.org.
J. van der Hoeven. Algorithms for asymptotic extrapolation. JSC, 2006. Submitted.
J. van der Hoeven. On effective analytic continuation. MCS, 1(1):111–175, 2007.
E. J. Weniger. Nonlinear sequence transformations: Computational tools for the acceleration of convergence and the summation of divergent series. Technical Report math.CA/0107080, Arxiv, 2001.
H.S. Wilf. Generatingfunctionology. Academic Press, 2nd edition, 2004. http://www.math.upenn.edu/~wilf/DownldGF.html.