| Probably faster multiplication of sparse polynomials   |
|
| February 11, 2020 |
|
 . This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
. This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
 . This article has
been written using GNU TeXmacs [22].
. This article has
been written using GNU TeXmacs [22].
In this paper, we present a probabilistic algorithm to multiply two sparse polynomials almost as efficiently as two dense univariate polynomials with a result of approximately the same size. The algorithm depends on unproven heuristics that will be made precise. |
Let 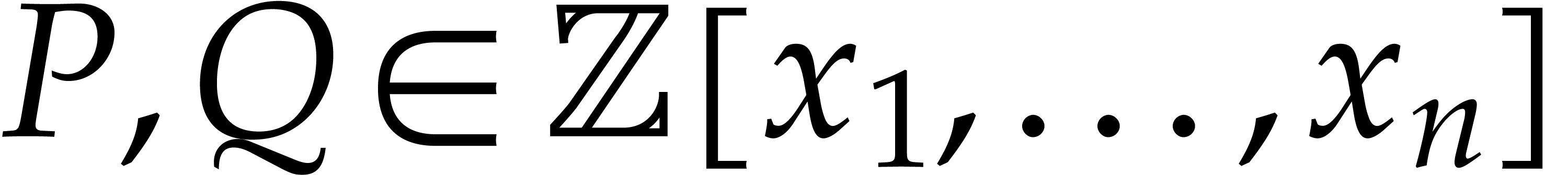 be polynomials that are represented in the
usual way as linear combinations of power products. The problem of
sparse polynomial multiplication is to compute the product
be polynomials that are represented in the
usual way as linear combinations of power products. The problem of
sparse polynomial multiplication is to compute the product 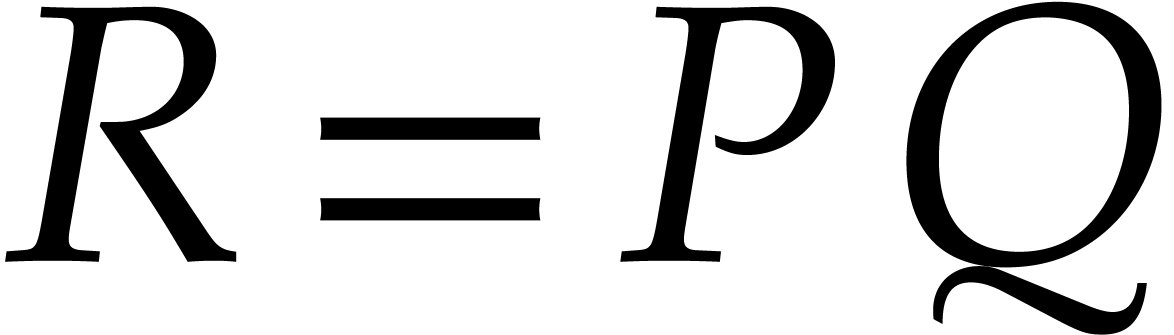 in a way that is as efficient as possible in terms of
the total bitsize of
in a way that is as efficient as possible in terms of
the total bitsize of  ,
,  , and
, and  (and
where we use a similar sparse representation for
(and
where we use a similar sparse representation for  as for
as for  and
and  ).
).
For pedagogical reasons, we mainly restrict our attention to polynomials with integer coefficients. Together with polynomials with rational coefficients, this is indeed the most important case for practical implementations inside computer algebra systems. Nevertheless, it is not hard to adapt our techniques to coefficients in more general rings (some indications to that effect are given in section 5.2). Still for pedagogical reasons, we will carry out our complexity analysis in the RAM model [11]. We expect our algorithms to adapt to the Turing model [13], but more work will be needed to prove this and some of the constant factors might deteriorate.
For polynomials of modest size, naive algorithms are often most efficient. We refer to [3, 6, 10, 19, 28, 32, 33, 37] for implementation techniques that are efficient in practice. Various types of faster algorithms have been proposed for polynomials with special supports [16, 18, 23, 35].
Asymptotically fast methods for polynomials of large sizes usually rely
on sparse interpolation. The seminal paper by Ben Or and Tiwari [4] triggered the development of many fast algorithms for the
sparse interpolation of polynomial blackbox functions [1,
5, 9, 20, 24–27, 29, 34]. In this framework, the
unknown polynomial  is given through a blackbox
functions that can be evaluated at points in suitable extensions of the
coefficient ring. We refer to [36] for a nice survey on
sparse interpolation and other algorithms to compute with sparse
polynomials. The present paper grew out of our recent preprint [21]
with Grégoire Lecerf on this topic; the idea to “exploit
colliding terms” in section 6.6 forms the starting point of our
work.
is given through a blackbox
functions that can be evaluated at points in suitable extensions of the
coefficient ring. We refer to [36] for a nice survey on
sparse interpolation and other algorithms to compute with sparse
polynomials. The present paper grew out of our recent preprint [21]
with Grégoire Lecerf on this topic; the idea to “exploit
colliding terms” in section 6.6 forms the starting point of our
work.
The most efficient algorithms for sparse interpolation are mostly probabilistic. Here we note that it is usually easy to check that the result is correct with high probability: just evaluate both the blackbox function and its supposed interpolation at a random point and verify that both evaluations coincide. In this paper, all algorithms will be probabilistic, which is suitable for the practical purposes that we are interested in. The running times of our algorithms also rely on suitable heuristics that we will make precise.
Although the multiplication problem for sparse polynomials does not
directly fit into the usual blackbox model, it does benefit from the
techniques that have been developed for sparse interpolation. Practical
algorithms along these lines have appeared in [8, 12,
19, 31]. Most algorithms operate in two
phases: we first need to determine the exponents of the product  and then its coefficients. The first phase is
typically more expensive when the coefficients of
and then its coefficients. The first phase is
typically more expensive when the coefficients of  are small, but it becomes cheap for large coefficients, due to the fact
that we may first reduce
are small, but it becomes cheap for large coefficients, due to the fact
that we may first reduce  modulo a suitable
prime. It is also customary to distinguish between the supersparse case
in which the total degree of
modulo a suitable
prime. It is also customary to distinguish between the supersparse case
in which the total degree of  is allowed to
become huge and the normally sparse case in which the total degree
remains small. In this paper, we mainly focus on the second problem,
which is most important for practical applications.
is allowed to
become huge and the normally sparse case in which the total degree
remains small. In this paper, we mainly focus on the second problem,
which is most important for practical applications.
In order to describe the complexity results, let us introduce some
notations. Given a polynomial 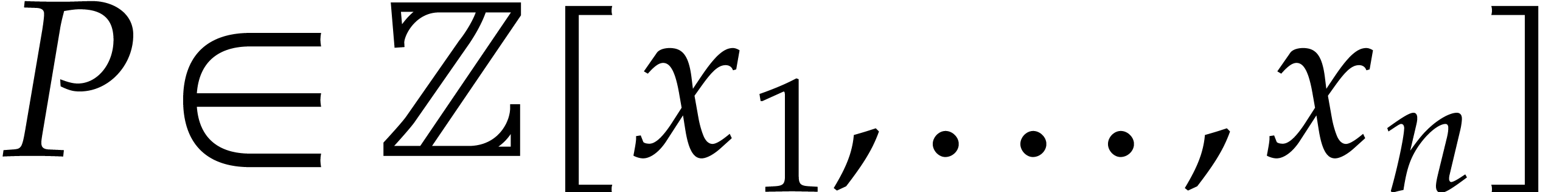 ,
we will write
,
we will write 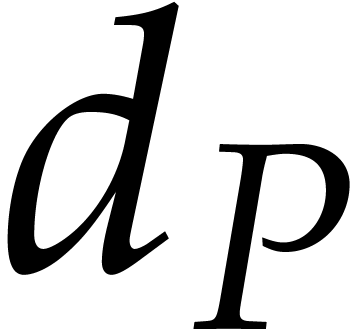 for its total degree,
for its total degree, 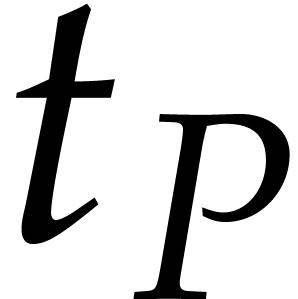 for its number of terms,
for its number of terms, 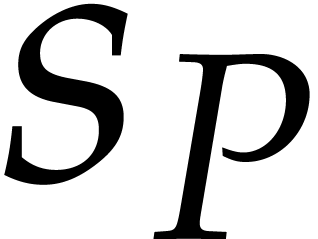 for the
number of powers
for the
number of powers 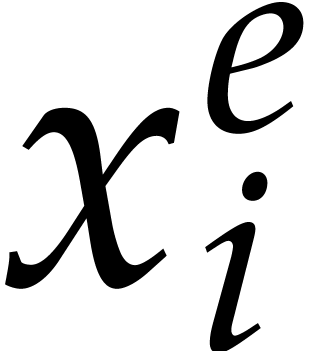 that occur in its
representation, and
that occur in its
representation, and 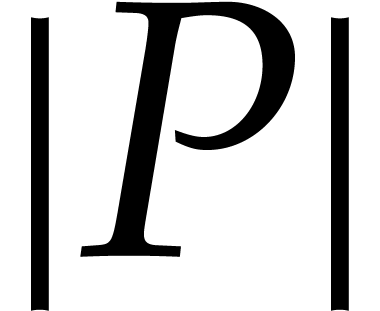 for the maximal absolute of
a coefficient. For instance, if
for the maximal absolute of
a coefficient. For instance, if 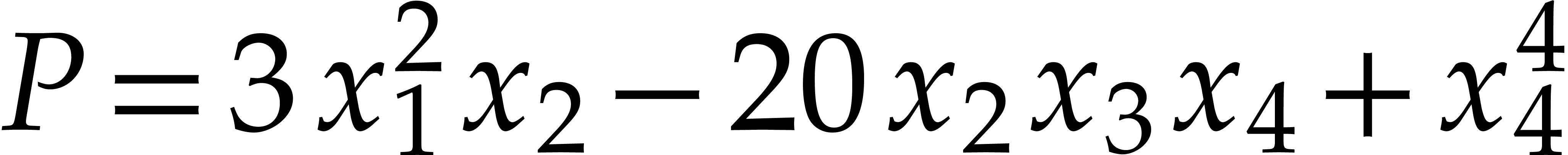 ,
then we have
,
then we have 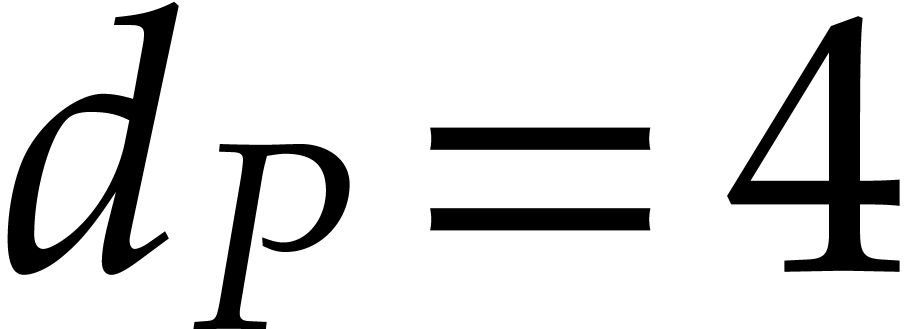 ,
, 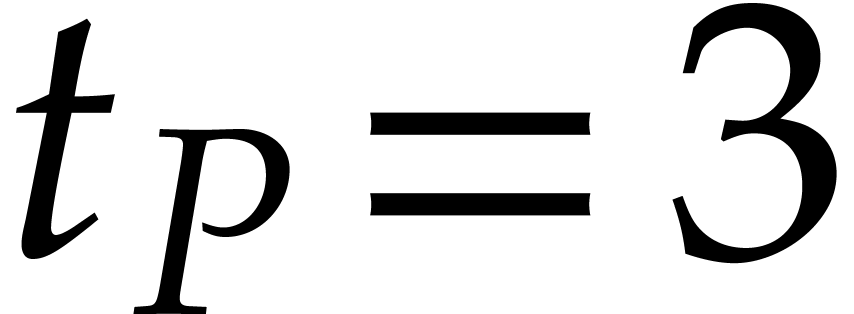 ,
, 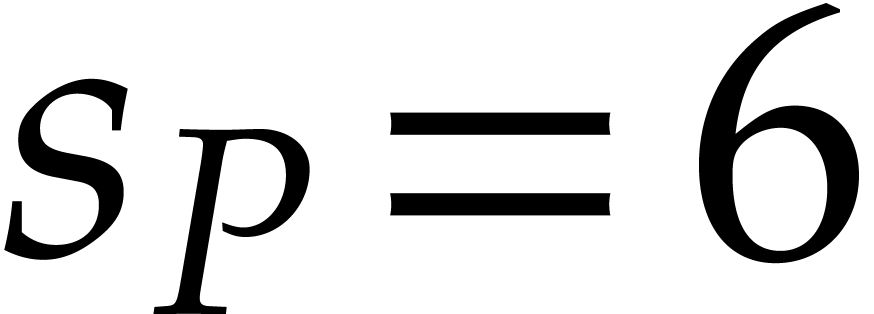 ,
and
,
and 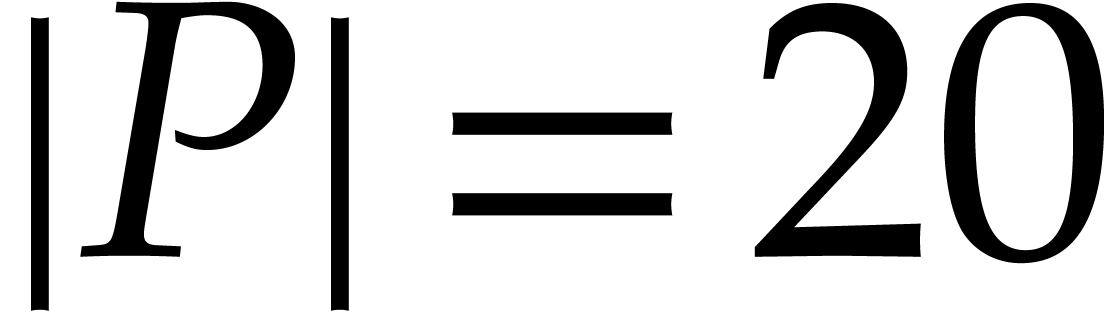 . For our multiplication
problem
. For our multiplication
problem 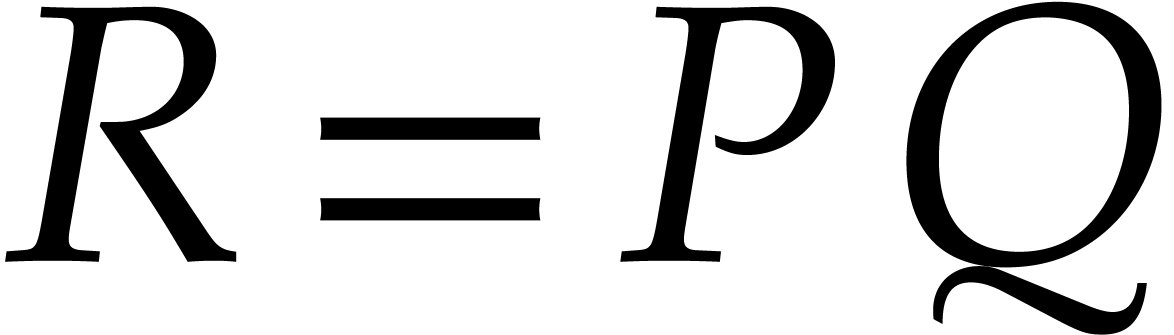 , the degree
, the degree 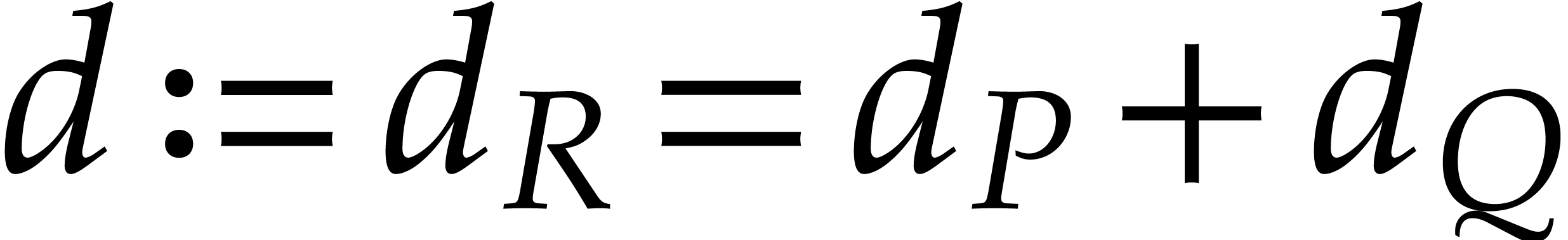 of the result is easily determined, but we usually
only assume a bound
of the result is easily determined, but we usually
only assume a bound  with
with  for its number of terms.
for its number of terms.
It is interesting to keep track of the dependency of our running times on logarithmic factors in certain parameters, but it is also convenient to ignore less important logarithmic and sublogarithmic factors. We do this by introducing the notation
We also wish to compare the cost of our algorithms with the cost of
multiplying dense univariate polynomials of approximately the same size.
Given integers 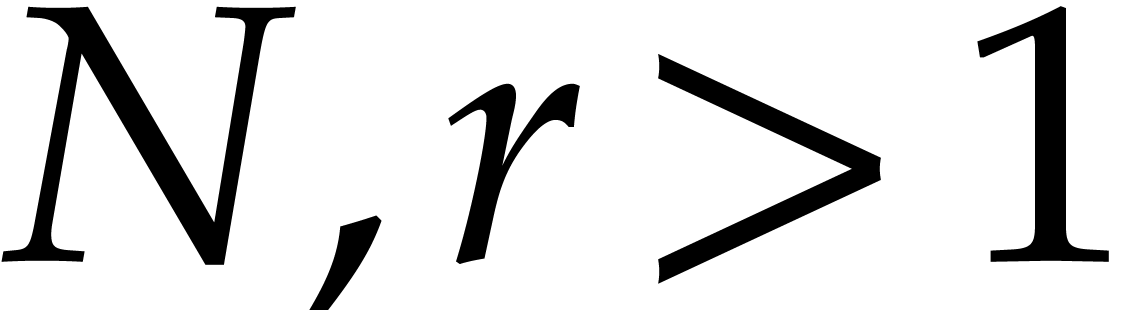 , we therefore
also introduce the following two complexities:
, we therefore
also introduce the following two complexities:
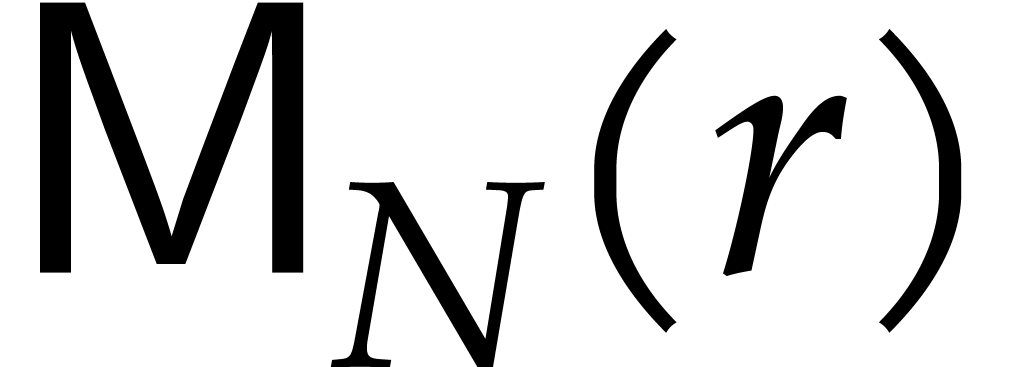 stands for the cost of multiplying two
non-zero polynomials in
stands for the cost of multiplying two
non-zero polynomials in 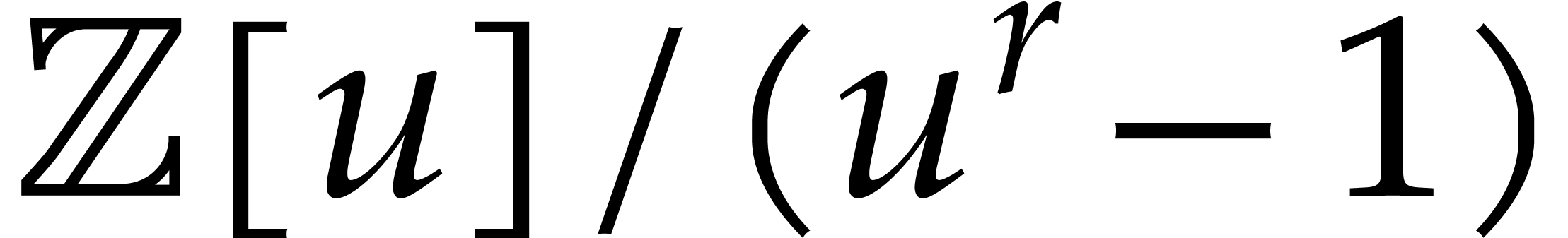 under the assumption
that the product
under the assumption
that the product  satisfies
satisfies 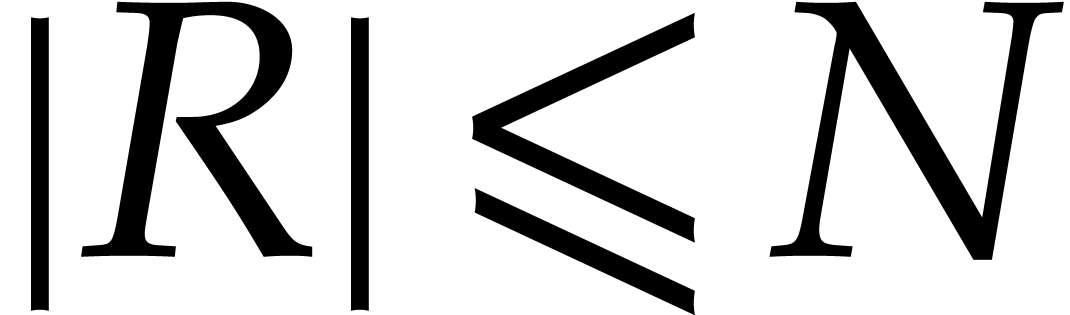 .
.
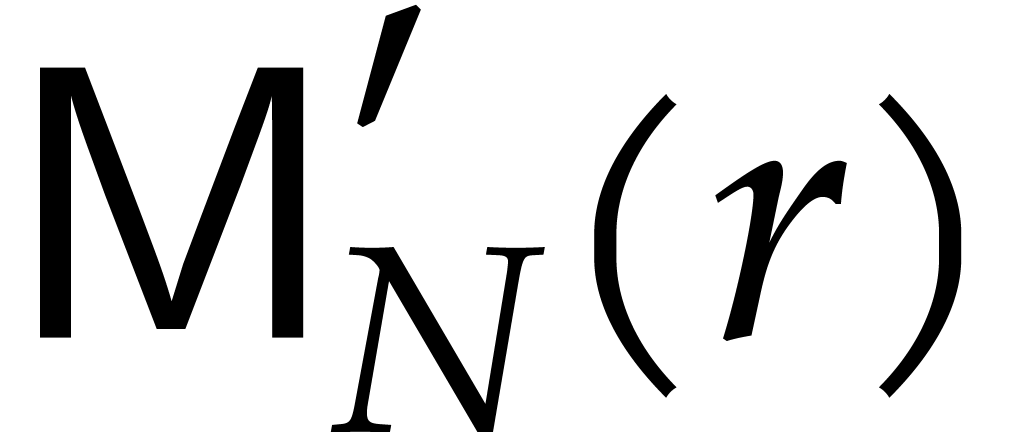 stands for the cost of multiplying two
polynomials in
stands for the cost of multiplying two
polynomials in 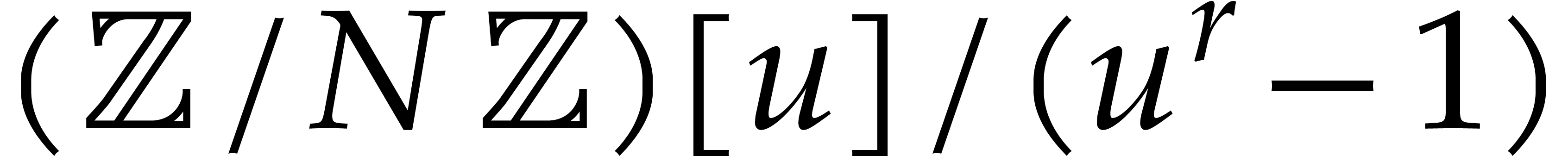 .
.
We make the customary assumption that 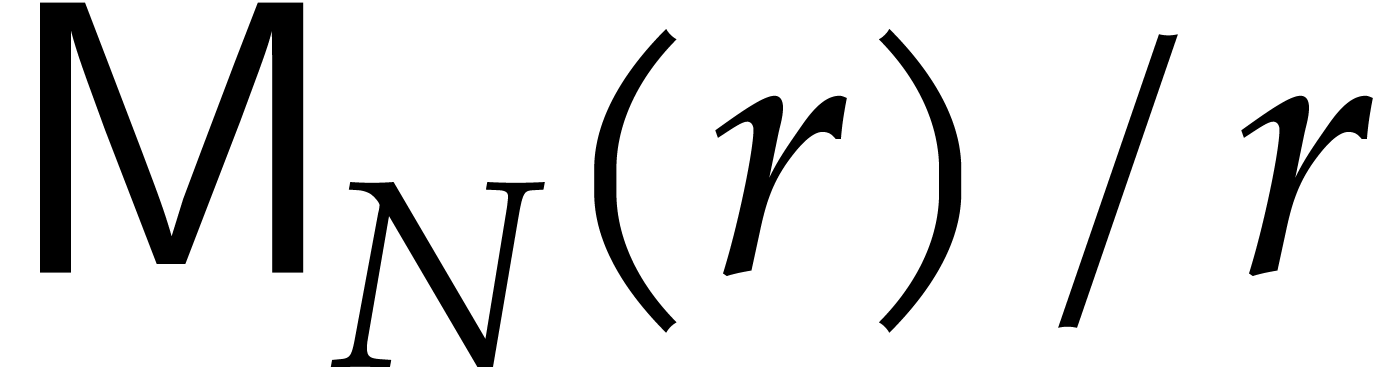 and
and 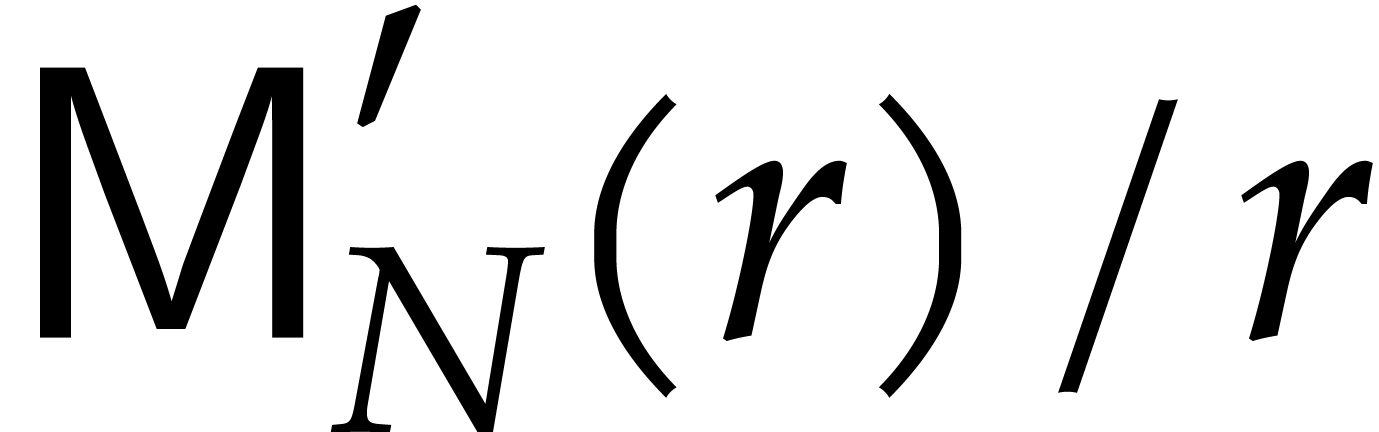 are non-decreasing as functions in
are non-decreasing as functions in 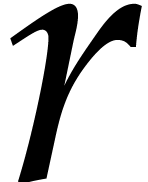 . By [14], one may take
. By [14], one may take 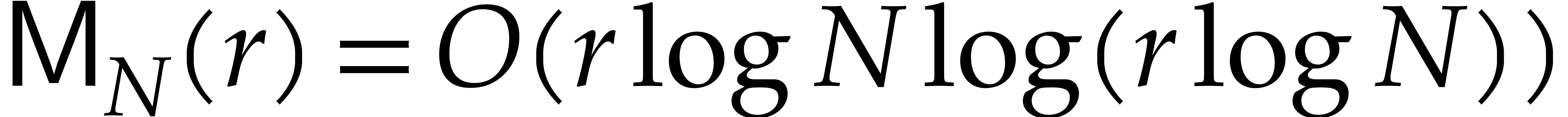 . If
. If 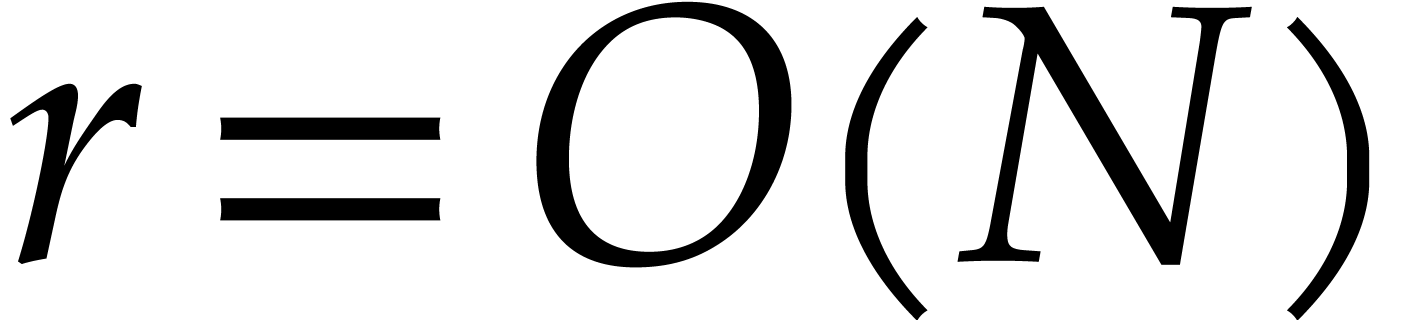 ,
then one also has
,
then one also has 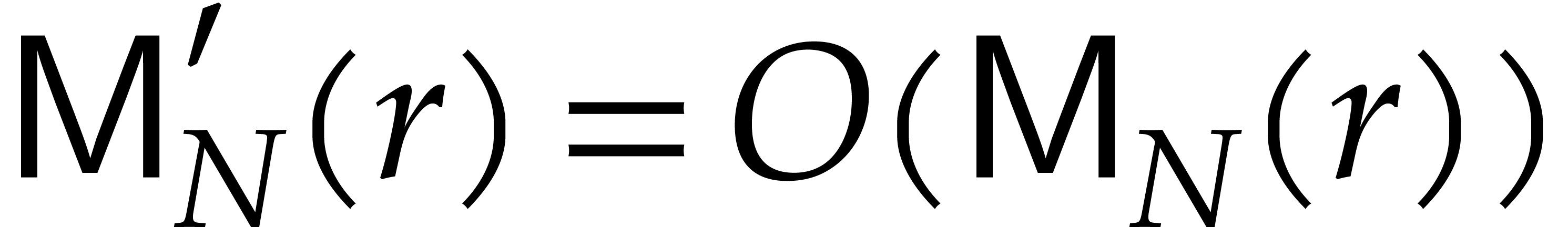 , using
Kronecker substitution [11].
, using
Kronecker substitution [11].
One traditional approach for sparse polynomial multiplication is to
evaluate  ,
,  , and
, and  at
at  points in a geometric progression
points in a geometric progression 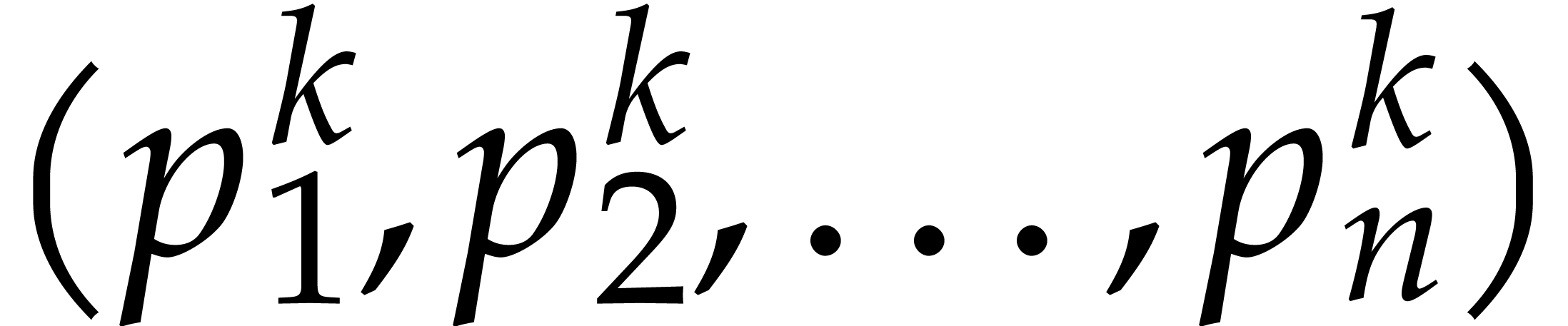 modulo a sufficiently large prime number
modulo a sufficiently large prime number 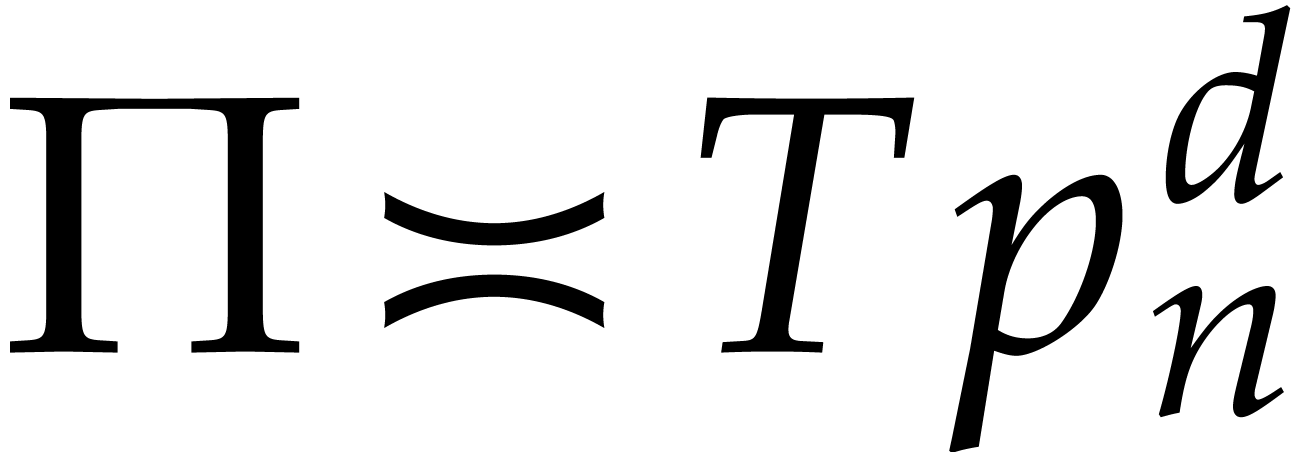 ,
where
,
where  stands for the
stands for the  -th prime number. In combination with the tangent
Graeffe method [21, sections 5 and 7.2], this approach
allows the exponents of
-th prime number. In combination with the tangent
Graeffe method [21, sections 5 and 7.2], this approach
allows the exponents of  to be computed in time
to be computed in time
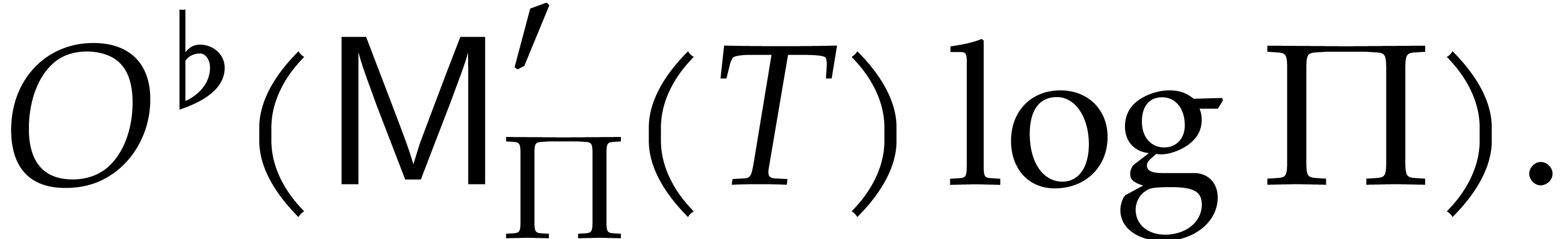 |
(1) |
The coefficients can be recovered using fast Vandermonde system solving, in time
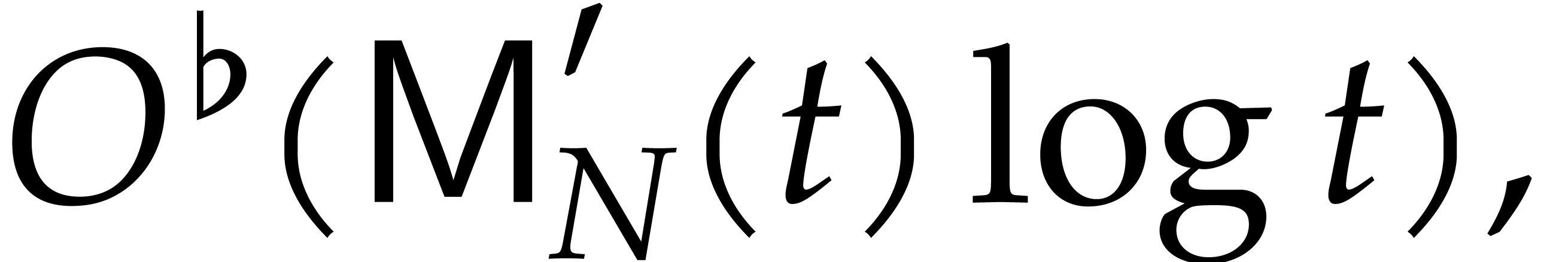 |
(2) |
where  . In our case when
. In our case when  is small, we usually have
is small, we usually have 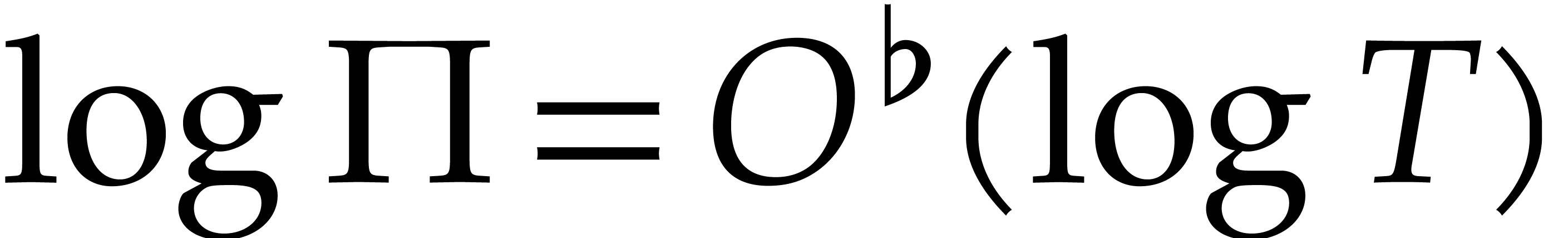 , in which case (1) simplifies into
, in which case (1) simplifies into
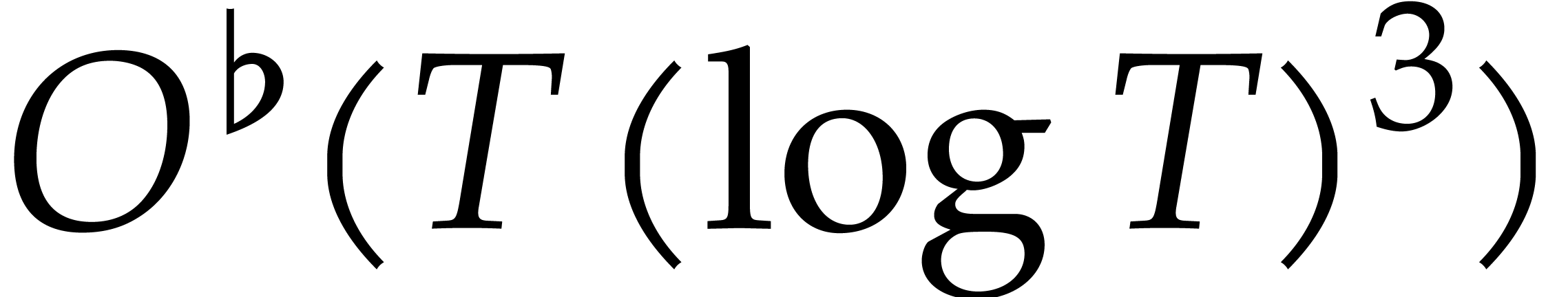 . The dependence of the
complexity on
. The dependence of the
complexity on  can be reduced using techniques
from [26], among others.
can be reduced using techniques
from [26], among others.
The main results of this paper are two faster probabilistic algorithms.
The shorter running times rely on two heuristics HE and
HC that will be detailed in section 4. For
any 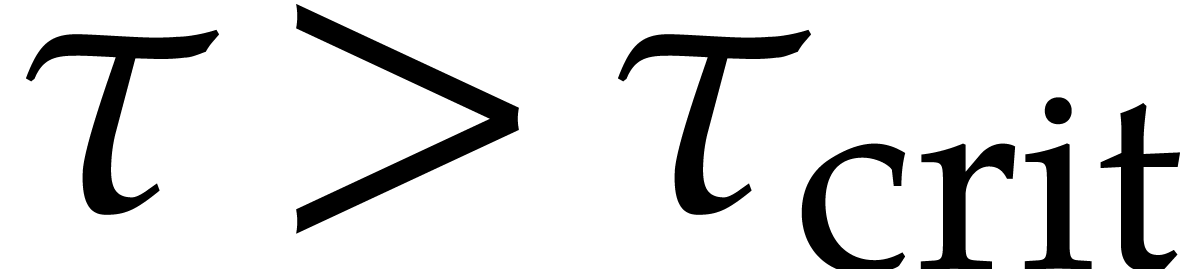 , we show (Theorem 6) that the exponents of
, we show (Theorem 6) that the exponents of  can be
computed in time
can be
computed in time
 |
(3) |
where 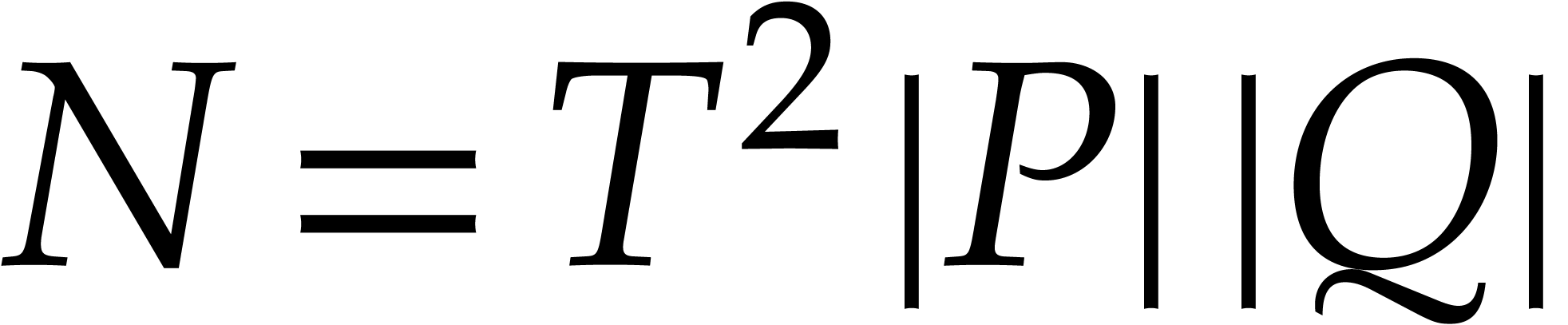 and
and 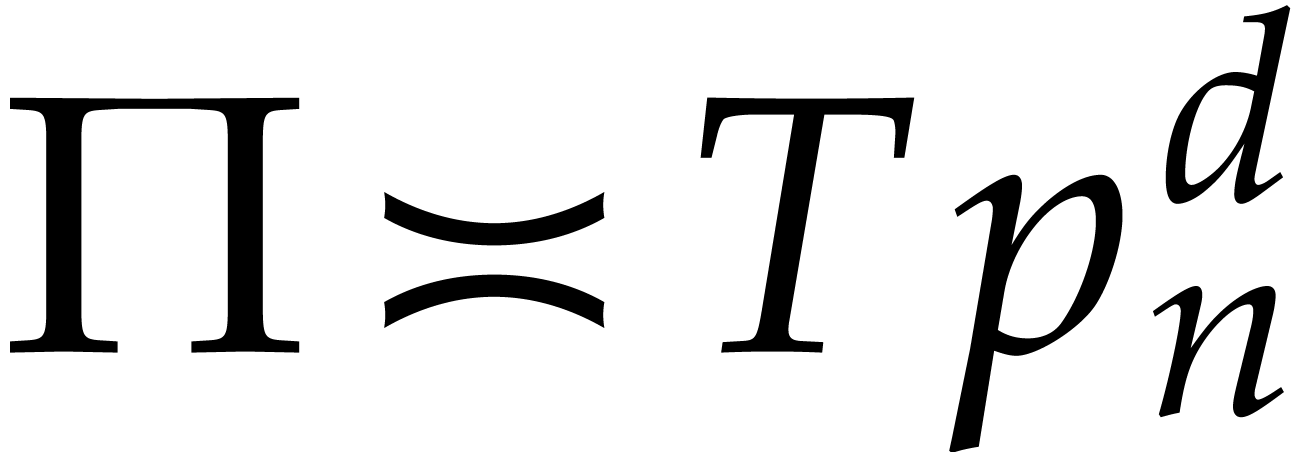 is prime. This
algorithm is probabilistic of Monte Carlo type. Based on numerical
evidence in section 3, we conjecture that
is prime. This
algorithm is probabilistic of Monte Carlo type. Based on numerical
evidence in section 3, we conjecture that 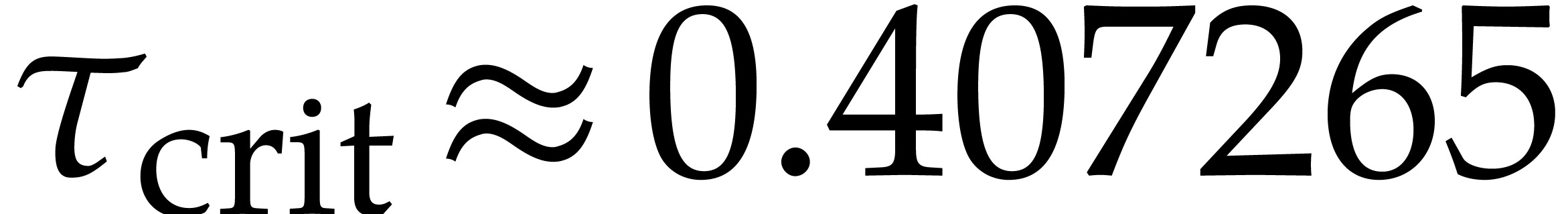 . We also show (Theorem 4) that
the coefficients may be computed in expected time
. We also show (Theorem 4) that
the coefficients may be computed in expected time
 |
(4) |
using a probabilistic algorithm of Las Vegas type. In practice, when
 is small and
is small and 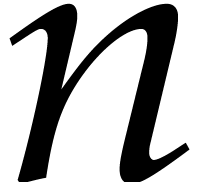 not too
large with respect to
not too
large with respect to 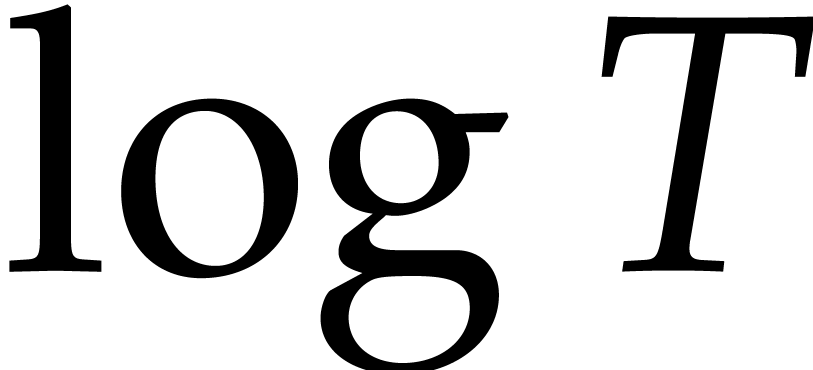 , the
corrective terms in (3) are negligible and the cost reduces
to
, the
corrective terms in (3) are negligible and the cost reduces
to 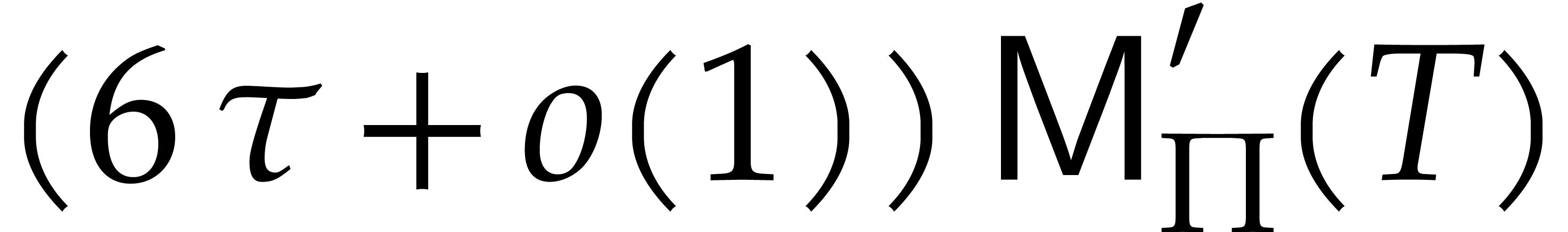 . Similarly, the cost (4) usually simplifies to
. Similarly, the cost (4) usually simplifies to 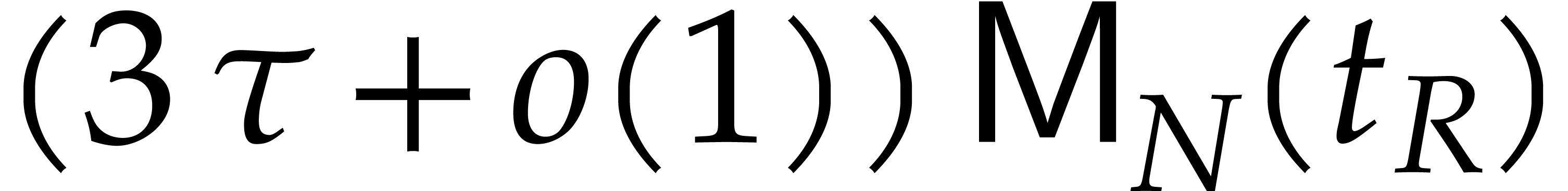 .
If we also have
.
If we also have 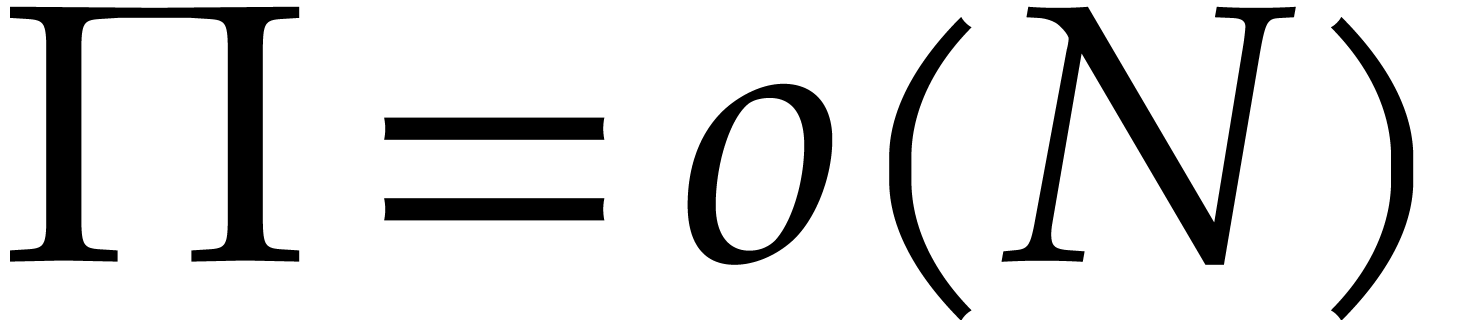 , then this
means that the cost of the entire sparse multiplication becomes
, then this
means that the cost of the entire sparse multiplication becomes 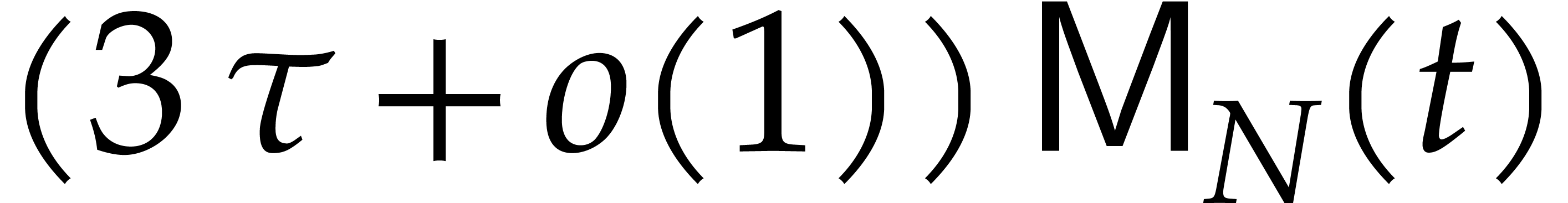 . Here we note that
. Here we note that 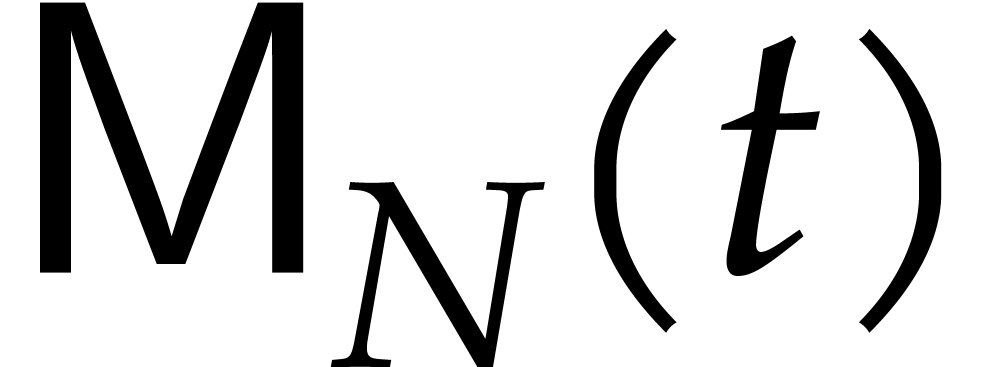 also corresponds to the time needed to multiply two dense
polynomials in
also corresponds to the time needed to multiply two dense
polynomials in 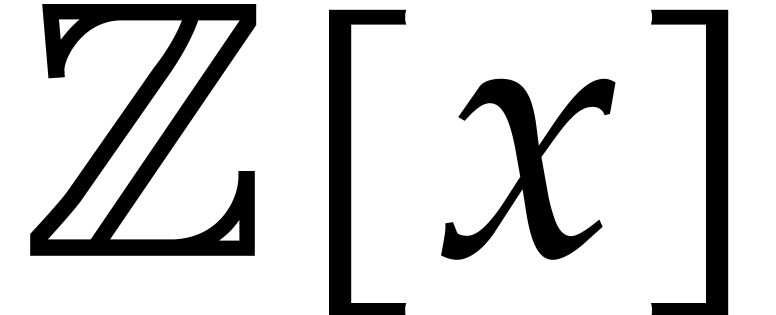 , provided
that the product
, provided
that the product  satisfies
satisfies 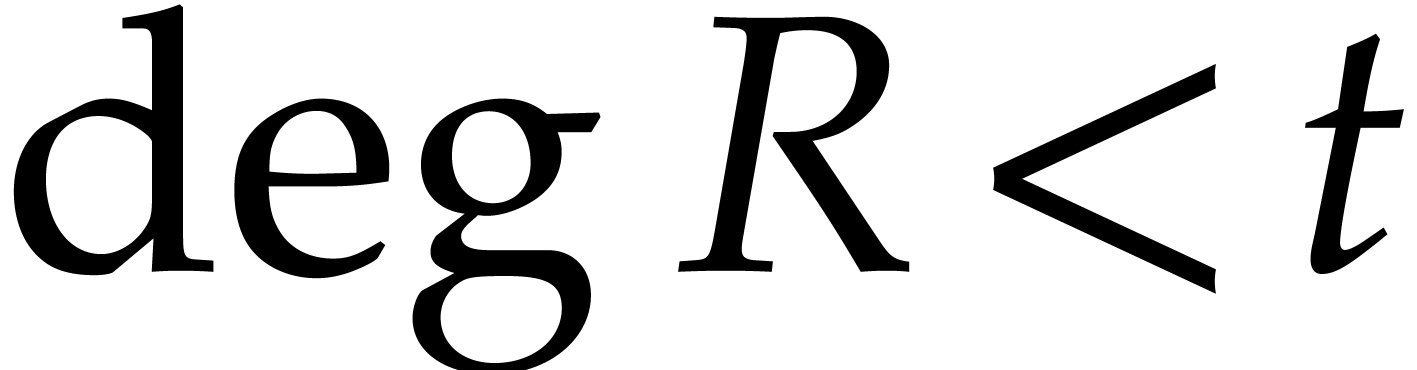 and
and 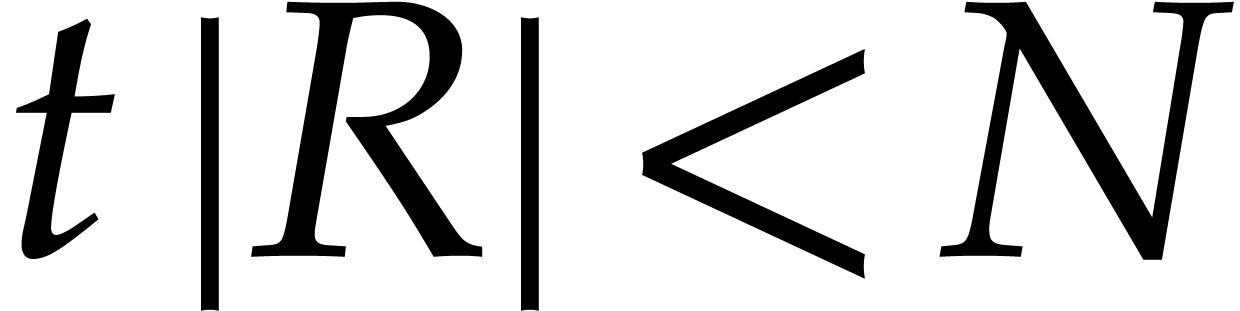 .
.
The proof of these bounds relies on the evaluation of  at three points of the form
at three points of the form  in algebras of the
form
in algebras of the
form 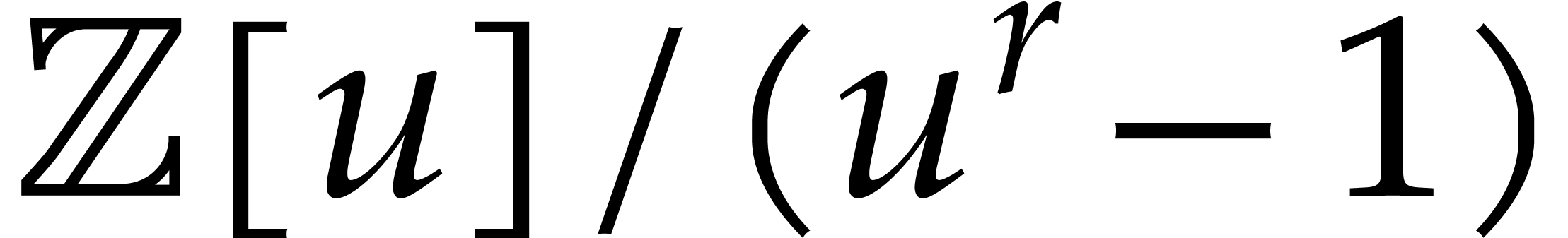 , where
, where 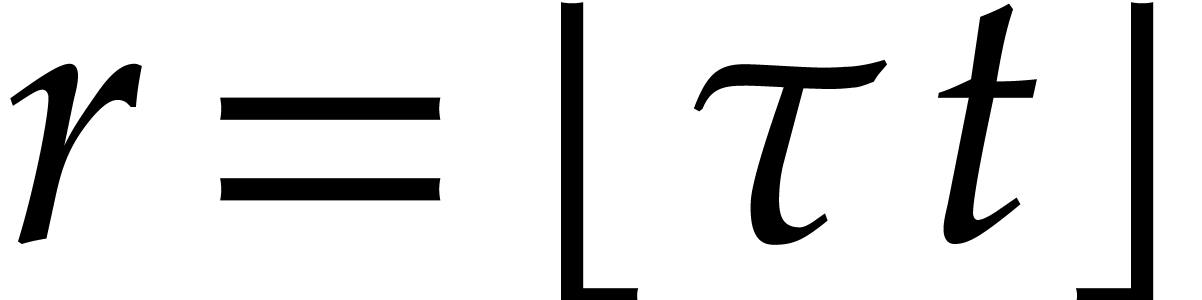 . If
. If  is sufficiently
large (namely
is sufficiently
large (namely 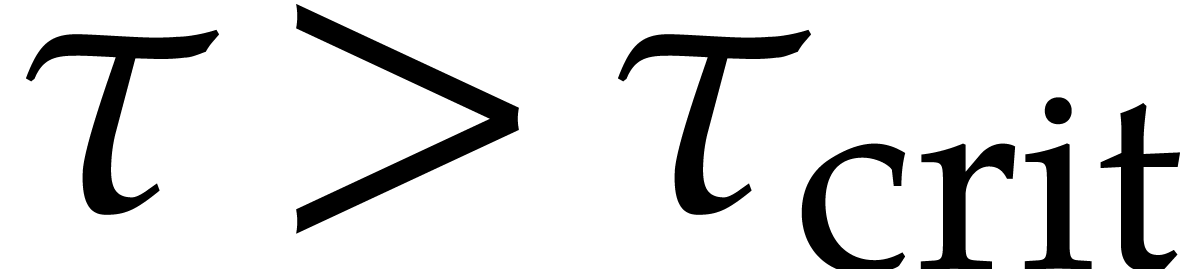 for some critical value) and we
already know the exponents of
for some critical value) and we
already know the exponents of  ,
then we show how to recover the coefficients with high probability. One
interesting feature of our algorithm is that three evaluations are
sufficient with high probability. A logarithmic number of evaluations is
necessary when using the more obvious iterative approach for which every
additional evaluation allows us to compute a constant fraction of the
unknown coefficients (with high probability). Our algorithm is first
explained with an example in section 2 and then in general
in section 4.1. The probabilistic analysis is done in
section 3. In section 4.2, we extend our
approach to the computation of the exponents, using three additional
evaluations. The last section 5 is devoted to variants and
extensions of our approach, and further remarks.
,
then we show how to recover the coefficients with high probability. One
interesting feature of our algorithm is that three evaluations are
sufficient with high probability. A logarithmic number of evaluations is
necessary when using the more obvious iterative approach for which every
additional evaluation allows us to compute a constant fraction of the
unknown coefficients (with high probability). Our algorithm is first
explained with an example in section 2 and then in general
in section 4.1. The probabilistic analysis is done in
section 3. In section 4.2, we extend our
approach to the computation of the exponents, using three additional
evaluations. The last section 5 is devoted to variants and
extensions of our approach, and further remarks.
The present paper works out an idea that was first mentioned in [21, section 6.6], in the context of general sparse interpolation. The application to polynomial multiplication is particularly suitable because of the low amortized cost of blackbox evaluations. The idea of using evaluations in (small) cyclic algebras has been used before in [2, 9, 31], but with a less optimal complexity. This approach also seems close to binning techniques that have recently been applied to compute sparse Fourier transforms [15, 30]; we plan to investigate this parallel in future work.
Consider two sparse polynomials
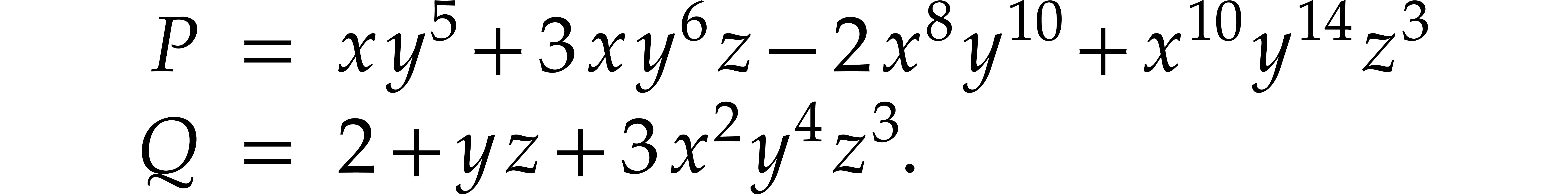
Their product  is given by
is given by
Assume that the monomials 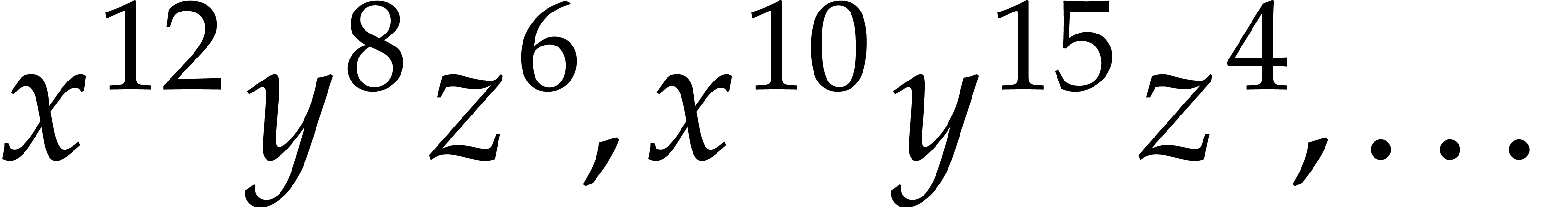 of
of  are known, but not the corresponding coefficients. Our aim is to
determine
are known, but not the corresponding coefficients. Our aim is to
determine  through its evaluations at
“points” of the form
through its evaluations at
“points” of the form 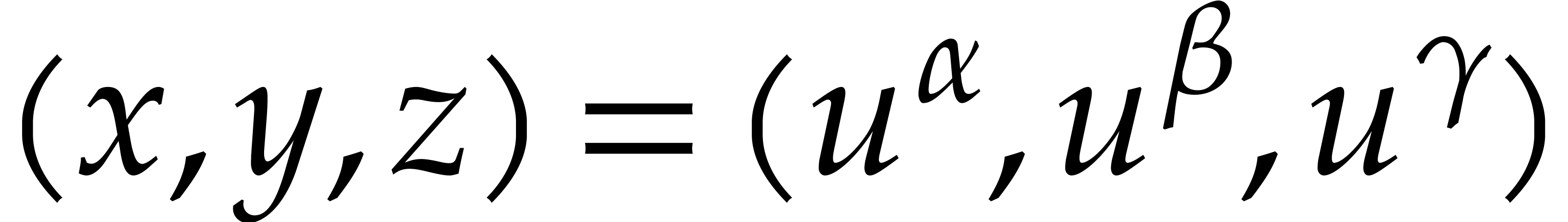 in
in 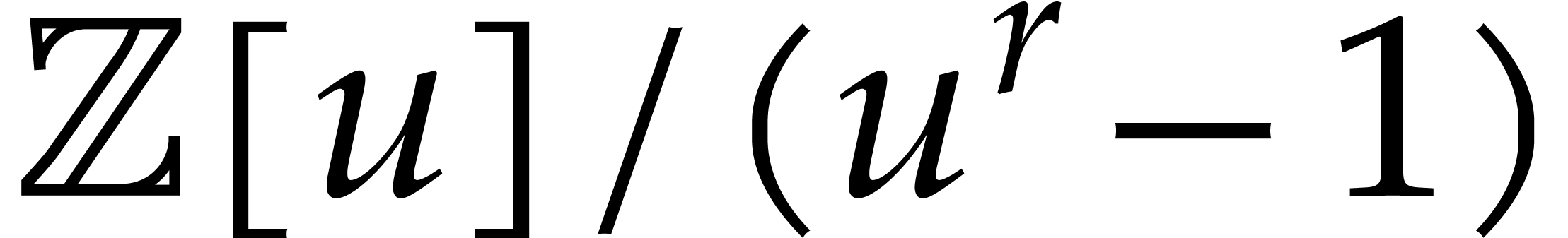 for suitable
for suitable 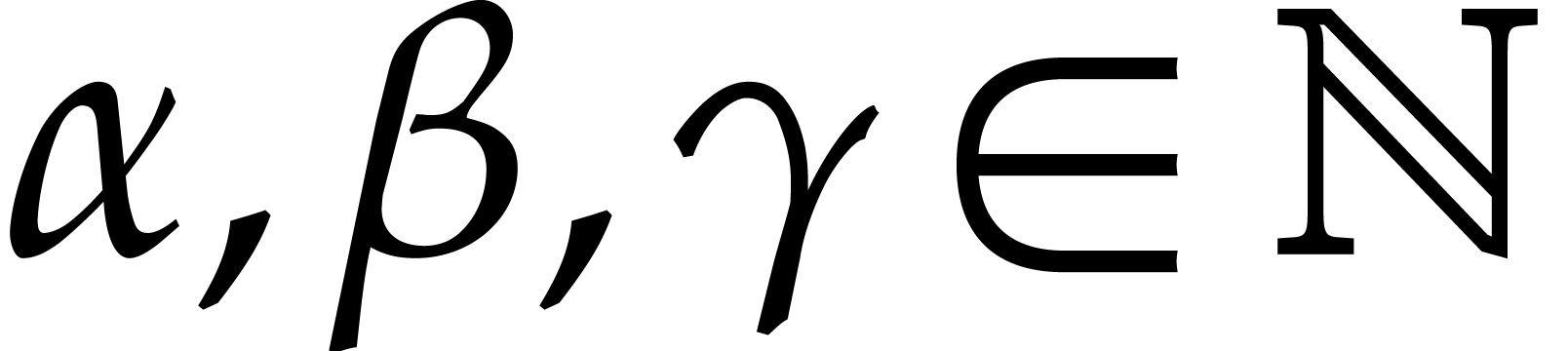 and lengths
and lengths 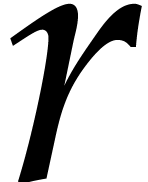 . These evaluations are obtained by
evaluating
. These evaluations are obtained by
evaluating  and
and  at the
same points and multiplying the results in
at the
same points and multiplying the results in 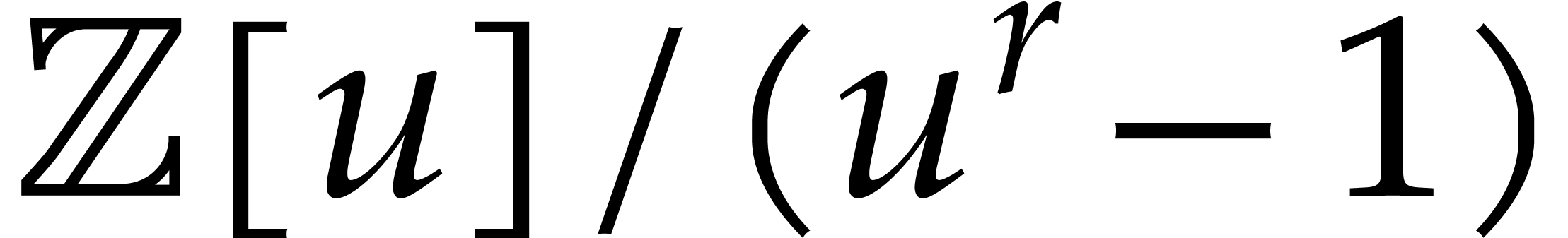 .
In what follows, we will use three evaluation points.
.
In what follows, we will use three evaluation points.
 into a “game of mystery balls”. At the start of the game,
we have one numbered ball for each term of
into a “game of mystery balls”. At the start of the game,
we have one numbered ball for each term of
 :
:
For each ball, say  , the
corresponding “mystery coefficient”
, the
corresponding “mystery coefficient”  needs to be determined (it might be hidden inside the ball), whereas the
corresponding exponents
needs to be determined (it might be hidden inside the ball), whereas the
corresponding exponents  are known (and stored in
a table or painted on the ball). In fact, our game has three identical
sets of balls, one for each of the three evaluation points. For each of
these evaluation points, we also have a set of
are known (and stored in
a table or painted on the ball). In fact, our game has three identical
sets of balls, one for each of the three evaluation points. For each of
these evaluation points, we also have a set of 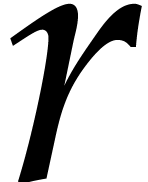 boxes, labeled by
boxes, labeled by  .
.
Now consider the evaluation of  at a point as
above, say at
at a point as
above, say at 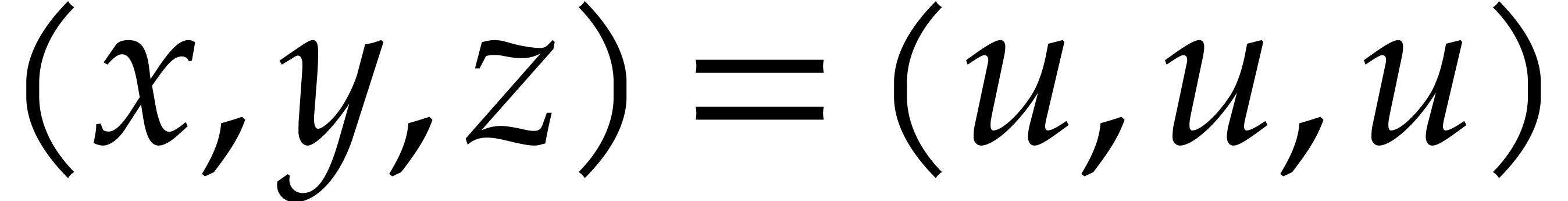 in the ring
in the ring 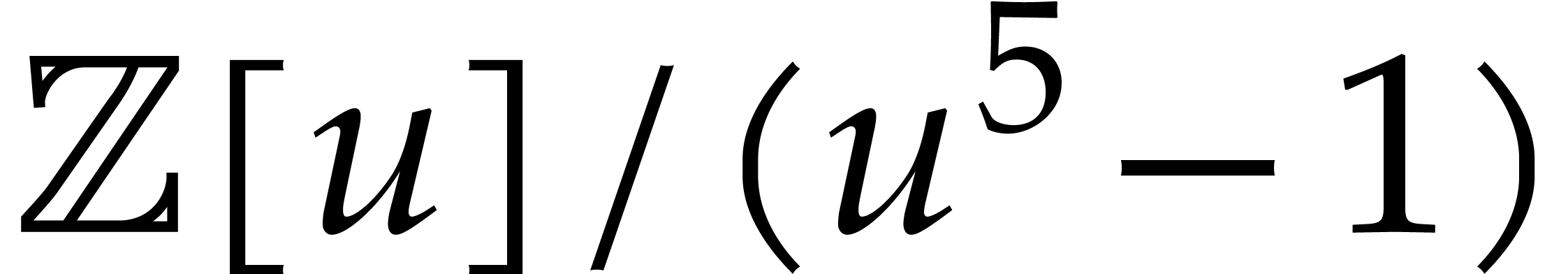 . Then each term
. Then each term 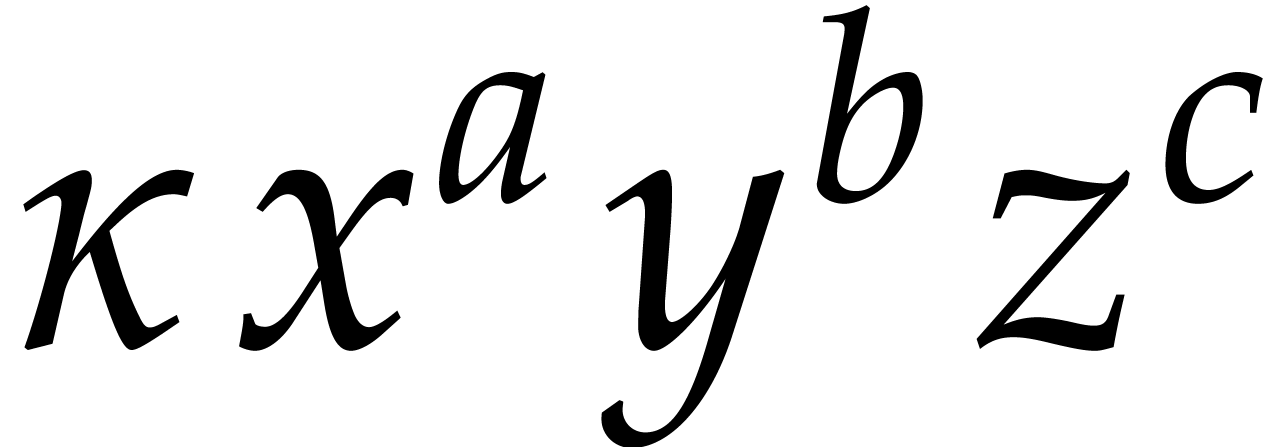 evaluates
to a term
evaluates
to a term 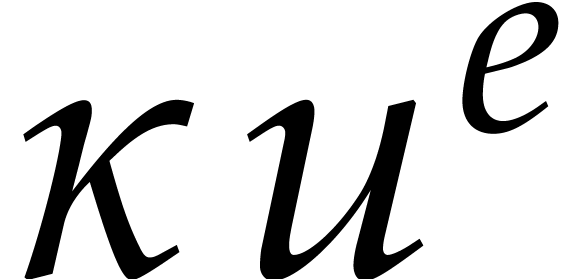 with
with 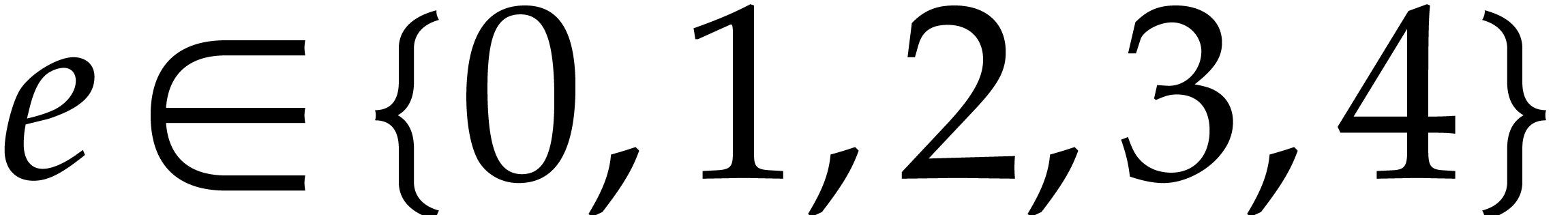 and
and  modulo
modulo 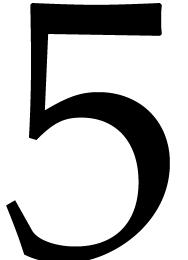 .
In our game, we throw the corresponding ball into the box that is
labeled by
.
In our game, we throw the corresponding ball into the box that is
labeled by 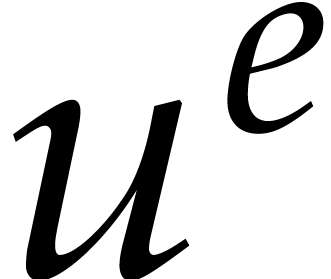 . For instance,
our first ball
. For instance,
our first ball  evaluates to
evaluates to 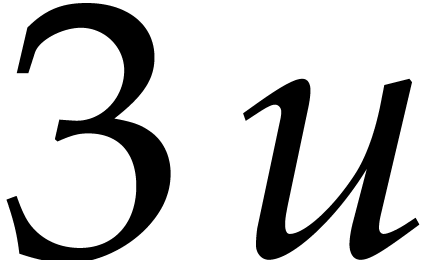 and goes into the box labeled by
and goes into the box labeled by 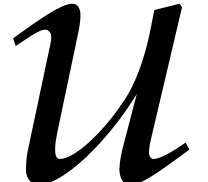 .
Our second ball
.
Our second ball  evaluates to
evaluates to 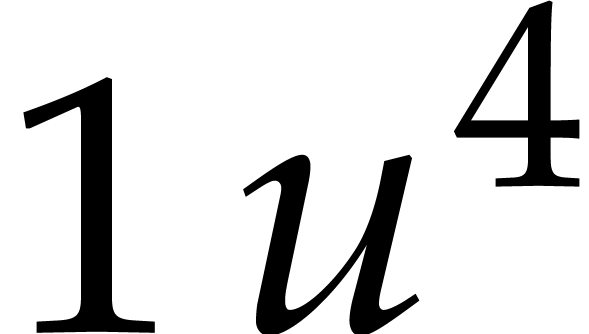 and goes into the box labeled by
and goes into the box labeled by 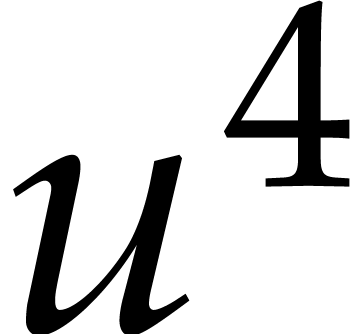 .
Continuing this way, we obtain the upper left distribution in Figure 1. Now the complete evaluation of
.
Continuing this way, we obtain the upper left distribution in Figure 1. Now the complete evaluation of  at
at
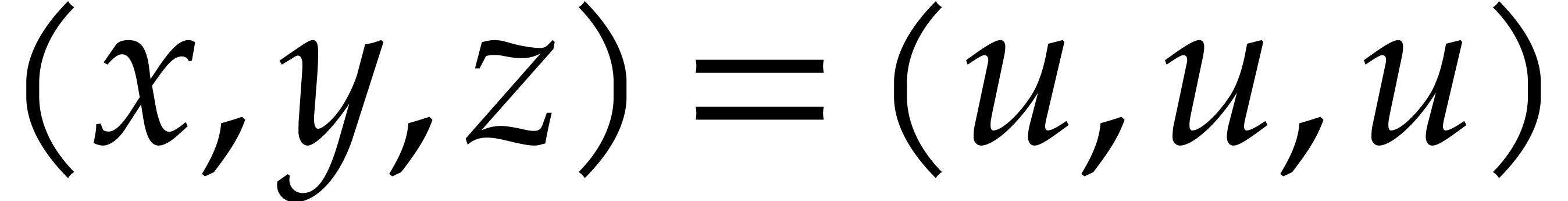 in
in 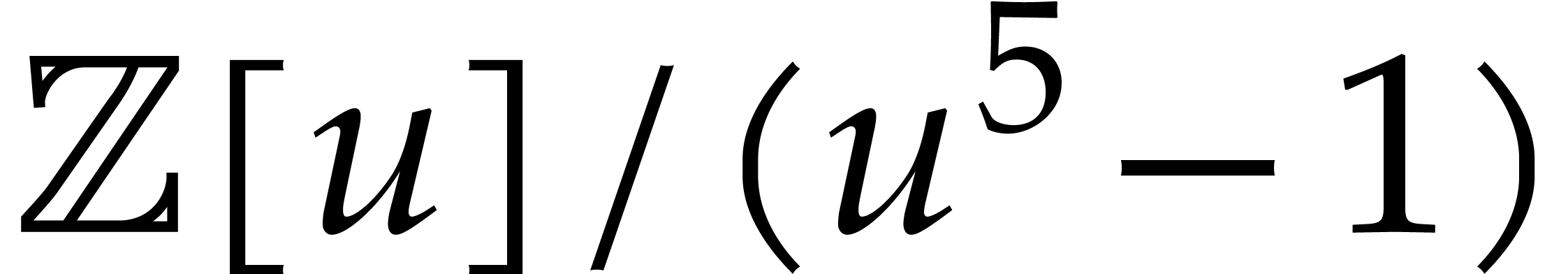 gives
gives
For each box, this means that we also know the sum of all coefficients
hidden in the balls in that box. Indeed, in our example, the first box
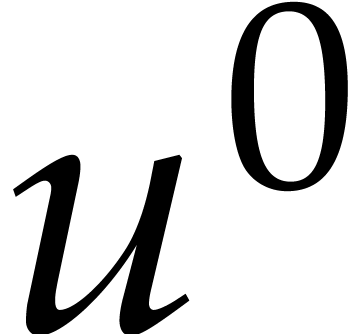 contains three balls
contains three balls  , , and
, , and  ,
with coefficients
,
with coefficients 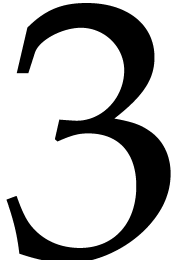 ,
, 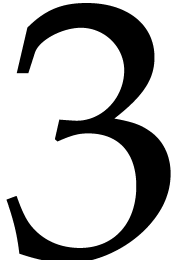 , and
, and 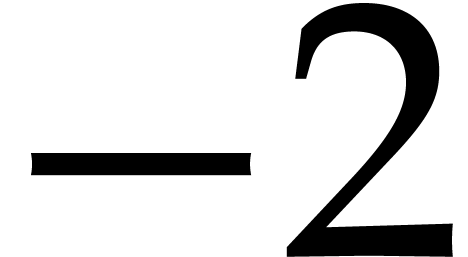 that
sum up to
that
sum up to  . In Figure 1, we indicated these sums below the boxes. In round one of
our game, we actually took our chances three times, by using the three
evaluation points
. In Figure 1, we indicated these sums below the boxes. In round one of
our game, we actually took our chances three times, by using the three
evaluation points 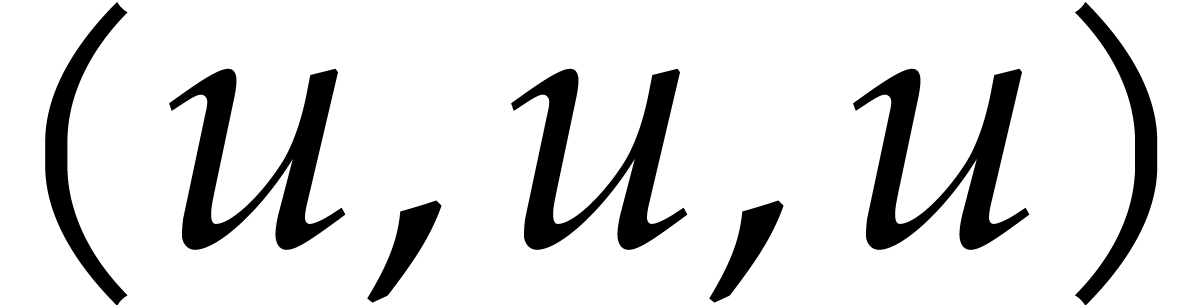 ,
, 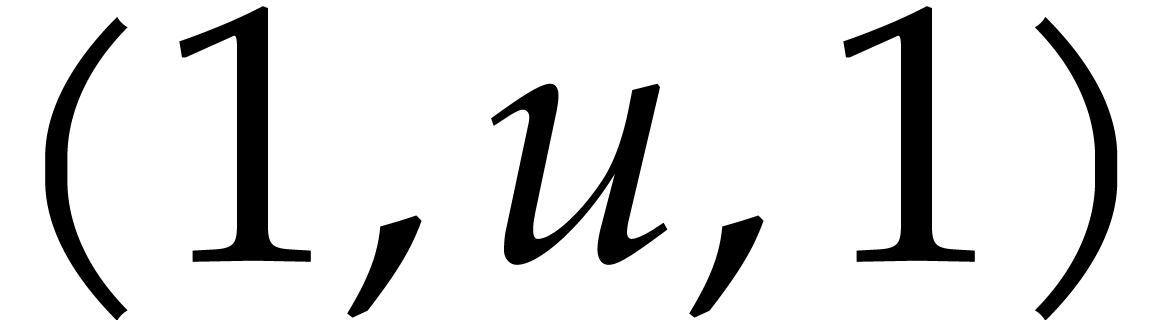 , and
, and 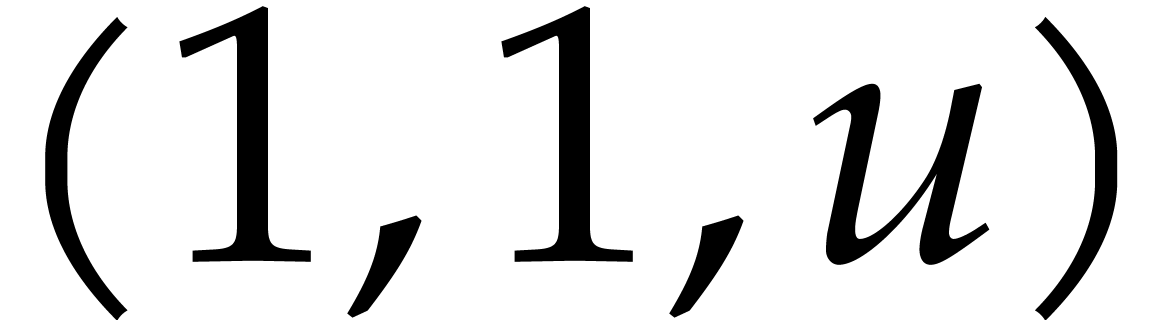 in
in
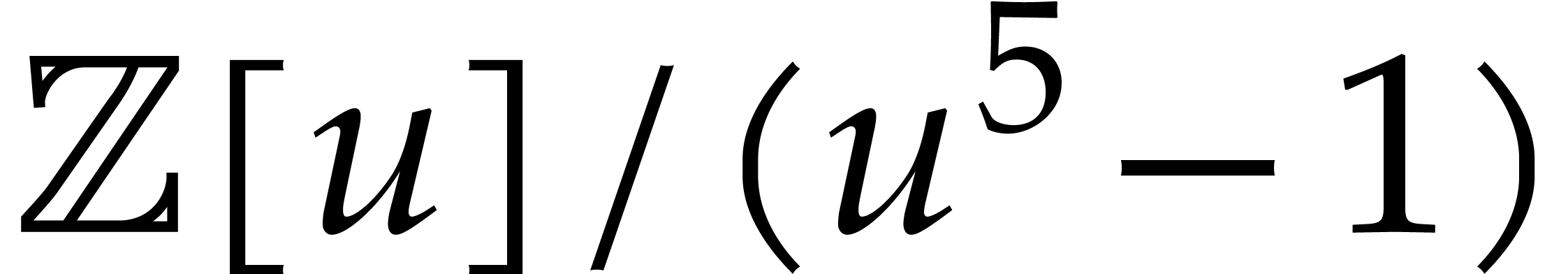 , and throwing our balls
accordingly. This corresponds to the top row in Figure 1.
, and throwing our balls
accordingly. This corresponds to the top row in Figure 1.
Now we play our game as follows. If, in a certain round, a ball ends up
alone in its box (we will also say that the ball has a private box),
then the number below it coincides with the secret coefficient inside.
At that point, we may remove the ball, as well as its copies from the
two other throws, and update the numbers below accordingly. In round one
of our running example, ball  ends up in a box of
its own for our first throw. Similarly, the balls
ends up in a box of
its own for our first throw. Similarly, the balls  and
and  both have private boxes for the second
throw. Ball
both have private boxes for the second
throw. Ball  also has a private box for the third
throw. Removing the balls
also has a private box for the third
throw. Removing the balls  ,
,
 , and
, and  from the game, we obtain the second row in Figure 1. We
also updated the numbers below the boxes: for every box, the number
below it still coincides with the sum of the mystery coefficients inside
the balls inside that box. Now that the balls
from the game, we obtain the second row in Figure 1. We
also updated the numbers below the boxes: for every box, the number
below it still coincides with the sum of the mystery coefficients inside
the balls inside that box. Now that the balls  ,
,  , and
, and
 have been removed, we observe that balls
have been removed, we observe that balls  and
and  have private boxes in
their turn. We may thus determine their mystery coefficients and remove
them from the game as well. This brings us to round three of our game
and the third row in Figure 1. Going on like this, we win
our game when all balls eventually get removed. We lose whenever there
exists a round in which there are still some balls left, but all
non-empty boxes contain at least two balls. In our example, we win after
five rounds.
have private boxes in
their turn. We may thus determine their mystery coefficients and remove
them from the game as well. This brings us to round three of our game
and the third row in Figure 1. Going on like this, we win
our game when all balls eventually get removed. We lose whenever there
exists a round in which there are still some balls left, but all
non-empty boxes contain at least two balls. In our example, we win after
five rounds.
Remark
Remark  does
not get removed in our modified game and choose
does
not get removed in our modified game and choose  in such a way that the round
in such a way that the round  in which it gets
removed in the original game is minimal. Then we observe that all balls
that were removed before round
in which it gets
removed in the original game is minimal. Then we observe that all balls
that were removed before round  in the original
game also get removed in the modified version, eventually. When this
happens,
in the original
game also get removed in the modified version, eventually. When this
happens,  is in a private box for one of the
throws: a contradiction.
is in a private box for one of the
throws: a contradiction.
Have we been lucky in our example with 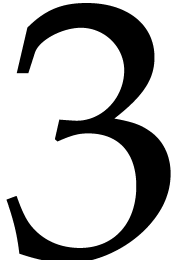 throws of
throws of
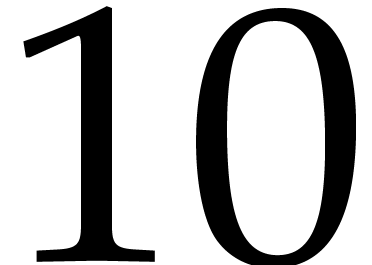 balls in
balls in 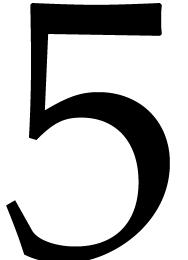 boxes? For the
probabilistic analysis in this section, we will assume that our throws
are random and independent. We will do our analysis for three throws,
because this is best, although a similar analysis could be carried out
for other numbers of throws. From now on, we will assume that we have
boxes? For the
probabilistic analysis in this section, we will assume that our throws
are random and independent. We will do our analysis for three throws,
because this is best, although a similar analysis could be carried out
for other numbers of throws. From now on, we will assume that we have
 balls and
balls and 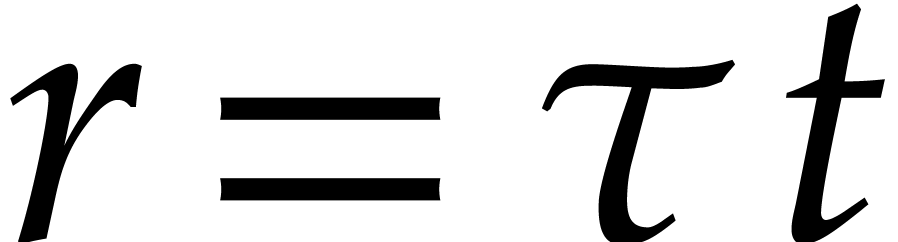 boxes.
boxes.
The experiment of throwing  balls in
balls in 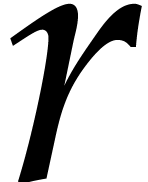 boxes has widely been studied in the literature about hash
tables [7, Chapter 9]. For a fixed ball, the probability
that all other
boxes has widely been studied in the literature about hash
tables [7, Chapter 9]. For a fixed ball, the probability
that all other  balls end up in another box is
given by
balls end up in another box is
given by
More generally, for any fixed  ,
the probability that
,
the probability that  other balls end up in the
same box and all the others in other boxes is given by
other balls end up in the
same box and all the others in other boxes is given by
Stated otherwise, we may expect with high probability that approximately
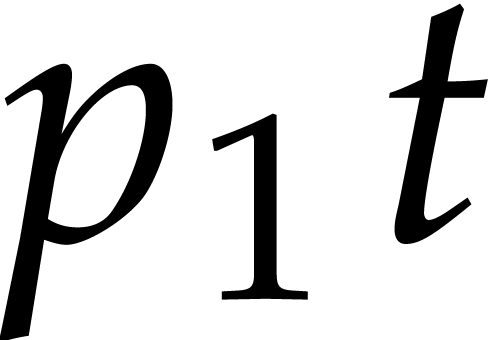 balls end up in a private box, approximately
balls end up in a private box, approximately
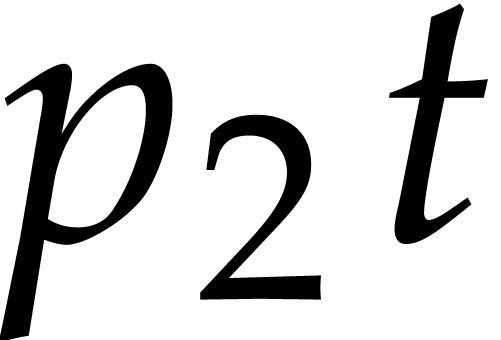 balls inside a box with one other ball, and so
on.
balls inside a box with one other ball, and so
on.
This shows how we can expect our balls to be distributed in the first
round of our game and at the limit when  gets
large. Assume more generally that we know the distribution
gets
large. Assume more generally that we know the distribution 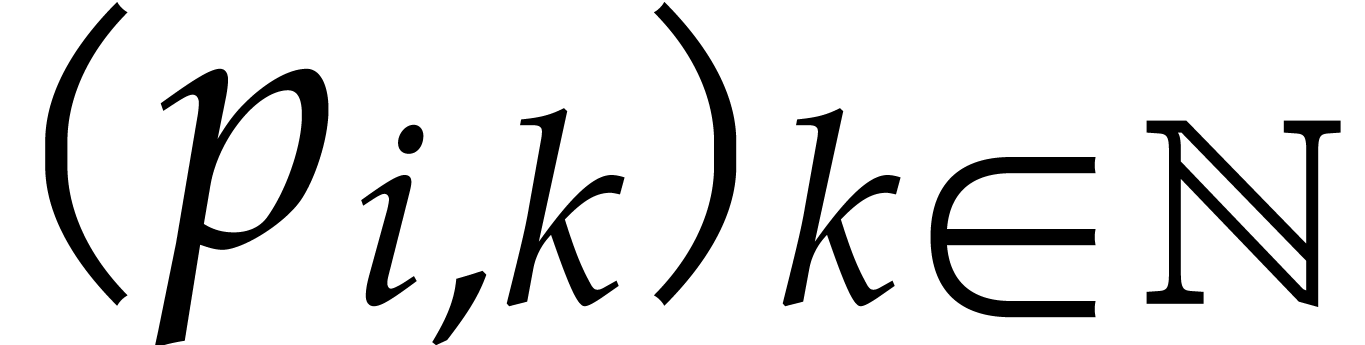 in round
in round  and let us show how to
determine the distribution
and let us show how to
determine the distribution 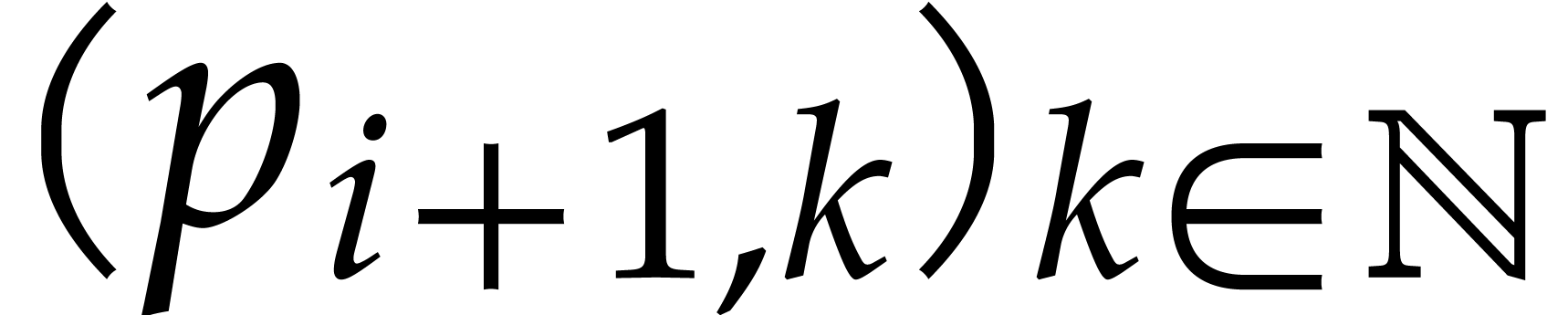 for the next round.
More precisely, assume that
for the next round.
More precisely, assume that 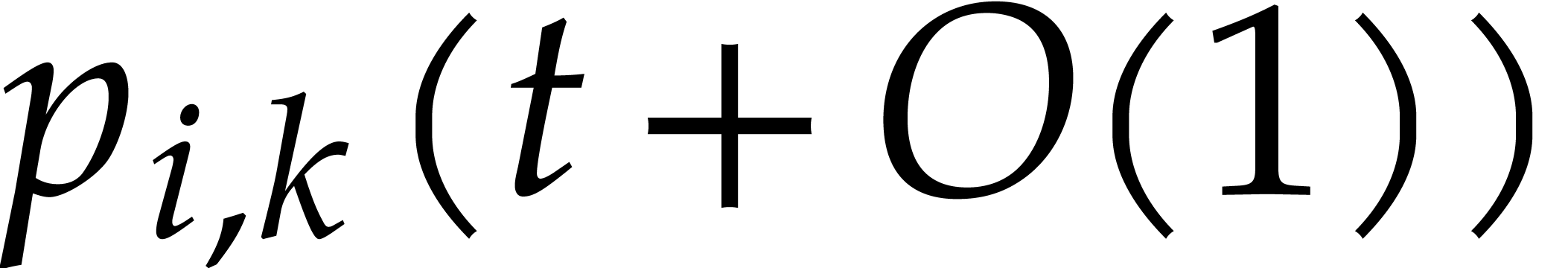 is the expected
number of balls in a box with
is the expected
number of balls in a box with  balls in round
balls in round
 , where we start with
, where we start with
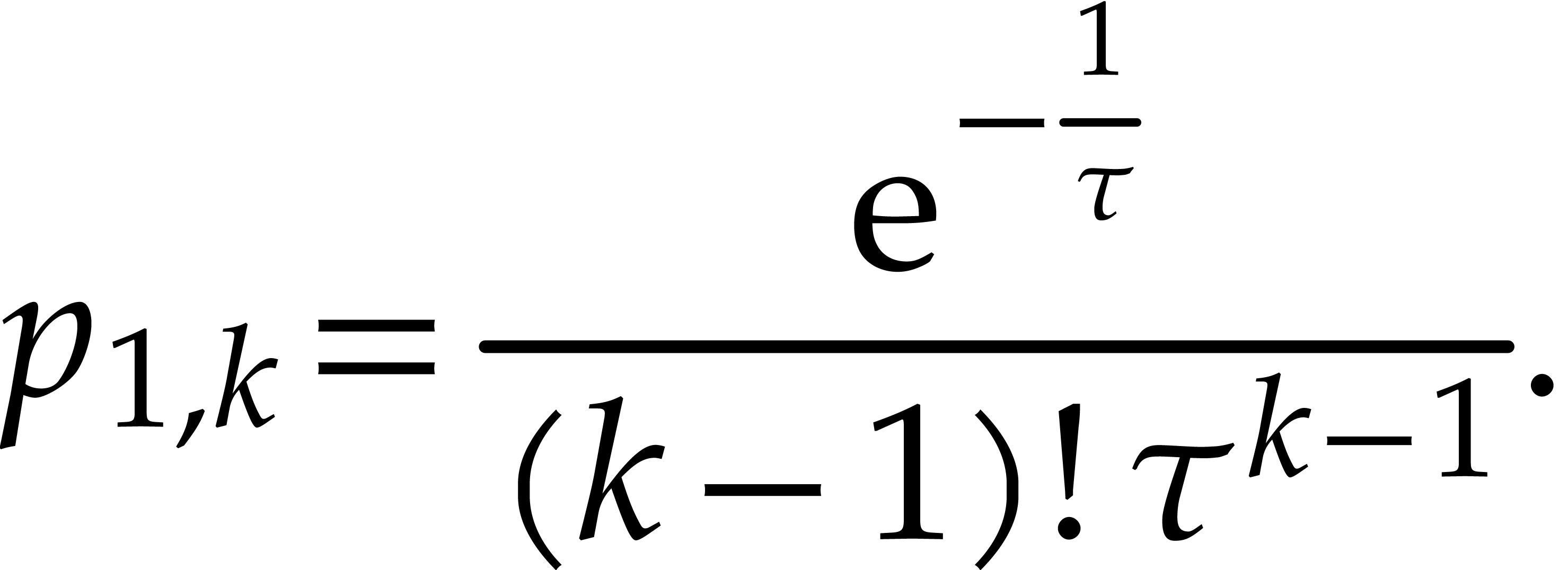
Setting
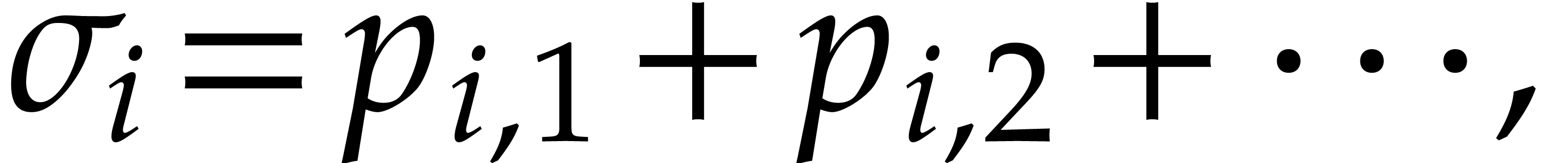
we notice that  , where
, where 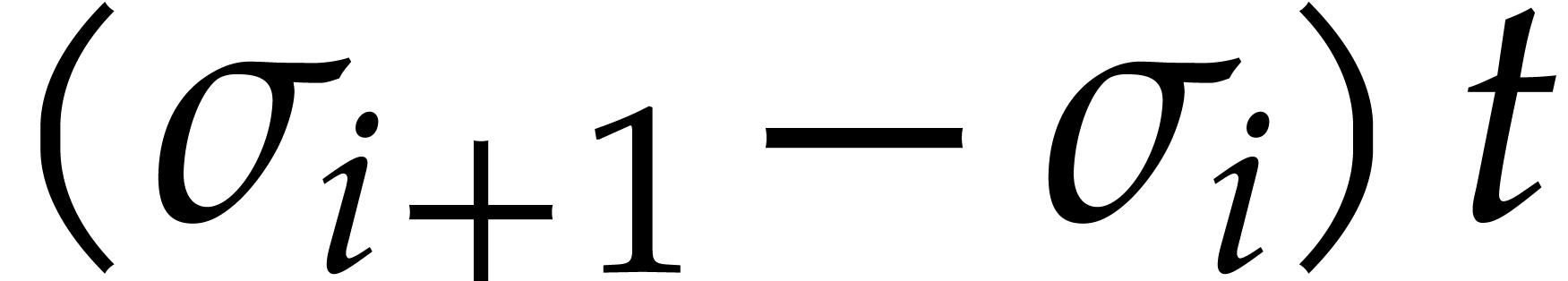 stands for the expected number of balls that are
removed during round
stands for the expected number of balls that are
removed during round  .
.
Now let us focus on the first throw in round  (the two other throws behave similarly, since they follow the same
probability distribution). There are
(the two other throws behave similarly, since they follow the same
probability distribution). There are 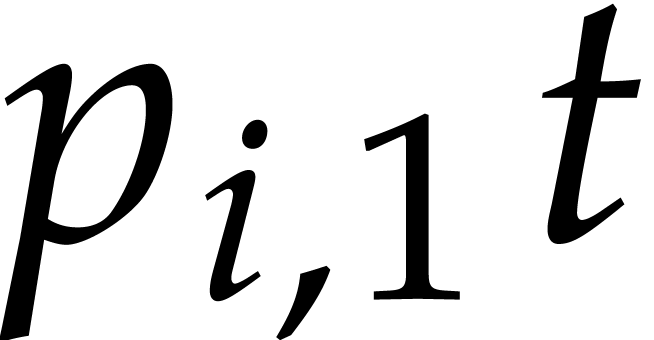 balls that
are in a private box for this throw. For each of the remaining balls,
the probability
balls that
are in a private box for this throw. For each of the remaining balls,
the probability 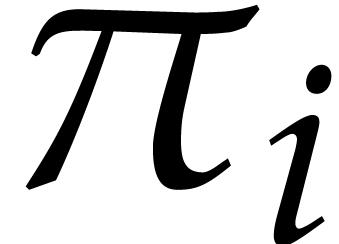 that it ended up in a private
box for at least one of the two other throws is
that it ended up in a private
box for at least one of the two other throws is
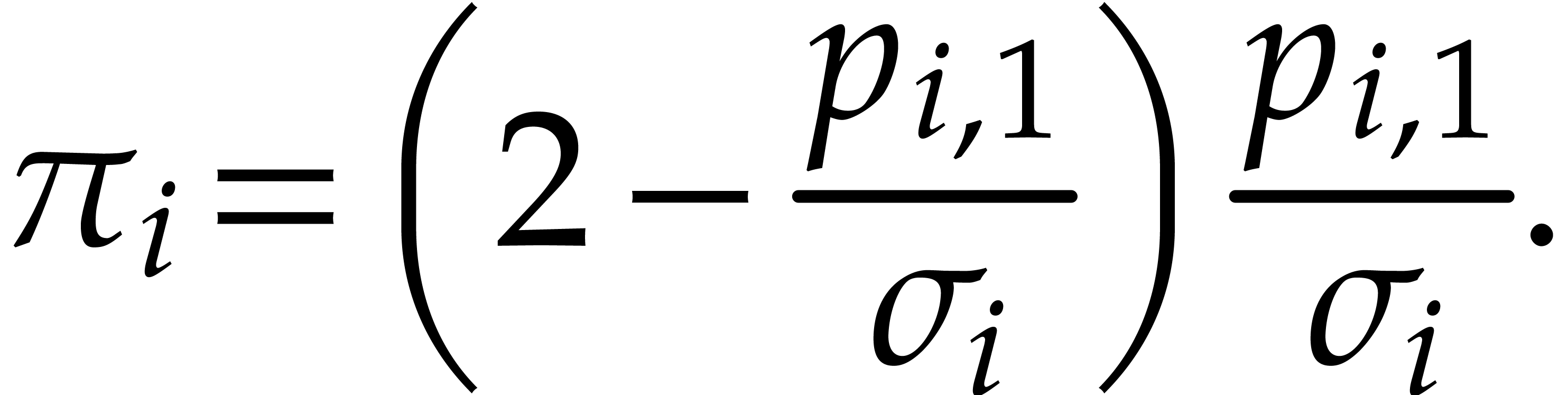
The probability that a box with 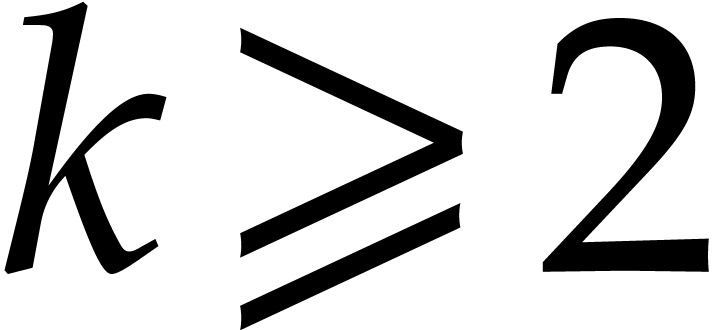 balls becomes
one with
balls becomes
one with  balls in the next round is therefore
given by
balls in the next round is therefore
given by
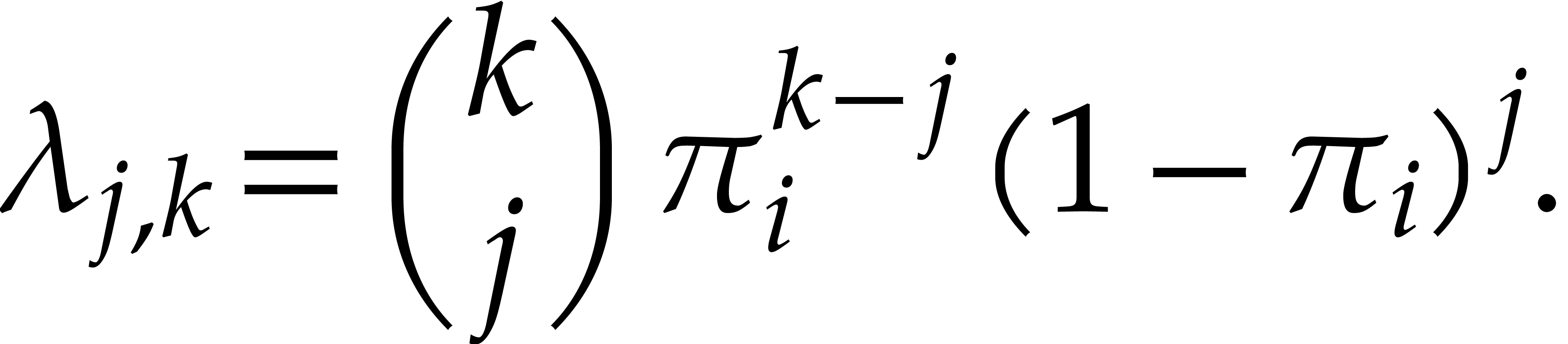
For all 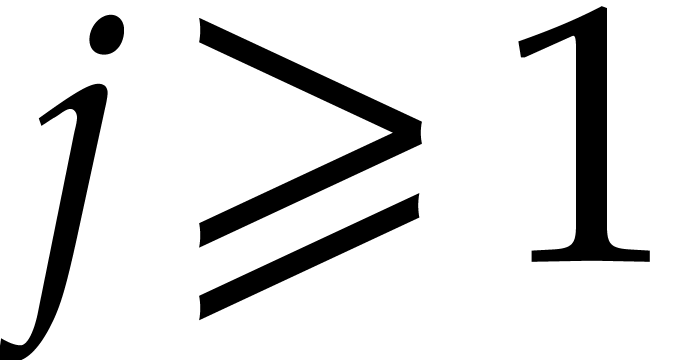 , this yields
, this yields
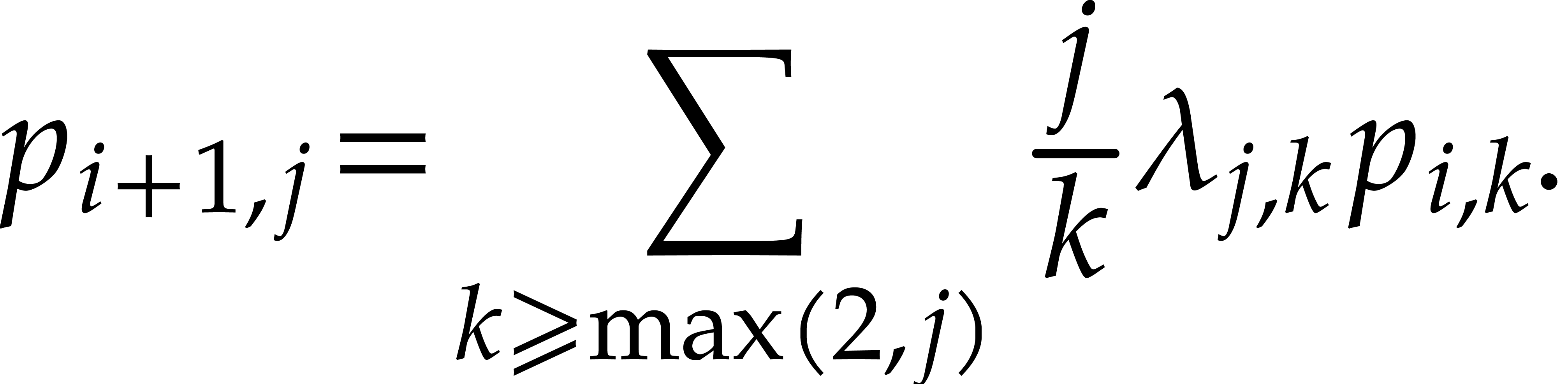
If  tends to zero for large
tends to zero for large  and
and  gets large, then we win our game with high
probability. If
gets large, then we win our game with high
probability. If  tends to a limit
tends to a limit 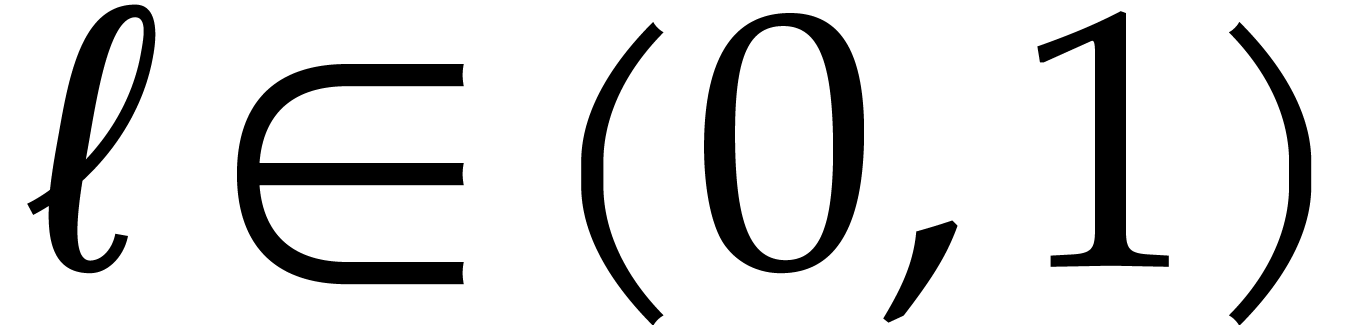 , then we will probably lose and end up with
approximately
, then we will probably lose and end up with
approximately 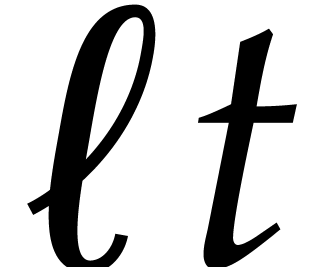 balls that can't be removed (for
each of the three throws).
balls that can't be removed (for
each of the three throws).
We have not yet been able to fully describe the asymptotic behavior of
the distribution
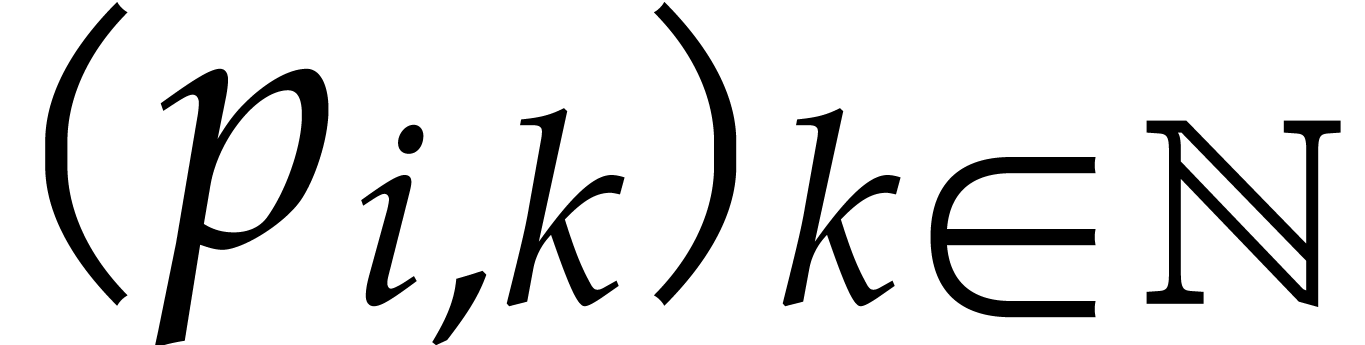 for
for
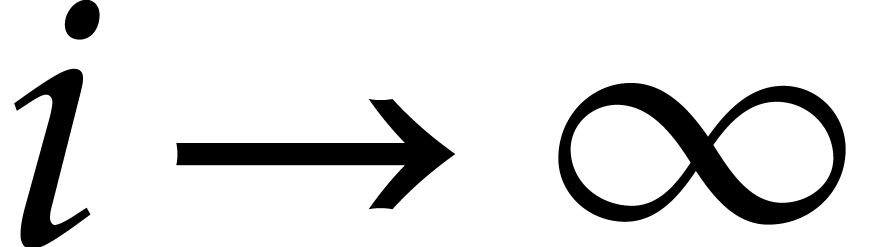 ,
which follows a non-linear dynamics. Nevertheless, it is easy to
compute reliable approximations for the coefficients
,
which follows a non-linear dynamics. Nevertheless, it is easy to
compute reliable approximations for the coefficients
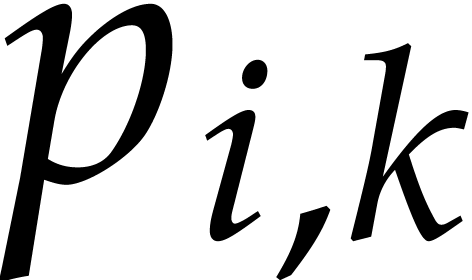 using interval or ball arithmetic [
17
]; for this purpose, it suffices to replace each coefficient
using interval or ball arithmetic [
17
]; for this purpose, it suffices to replace each coefficient
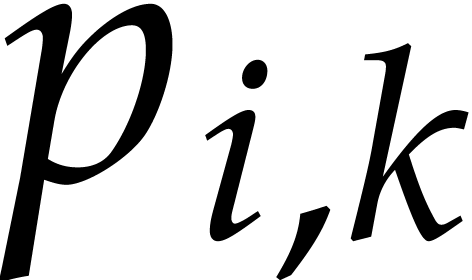 in the tail of the distribution (
i.e.
for large
in the tail of the distribution (
i.e.
for large
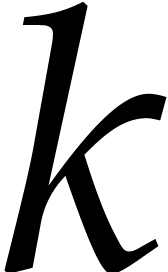 )
by the interval
)
by the interval
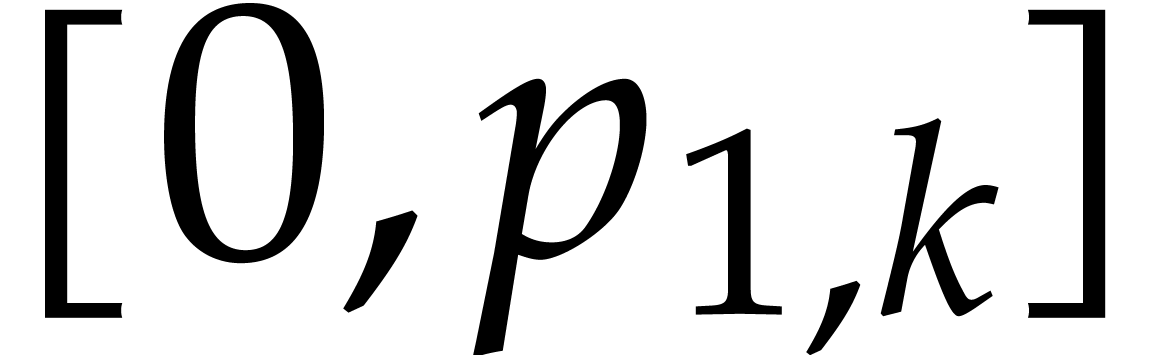 .
Tables
1
,
2
, and
3
show some numerical data that we computed in this way (the error in the
numbers being at most
.
Tables
1
,
2
, and
3
show some numerical data that we computed in this way (the error in the
numbers being at most
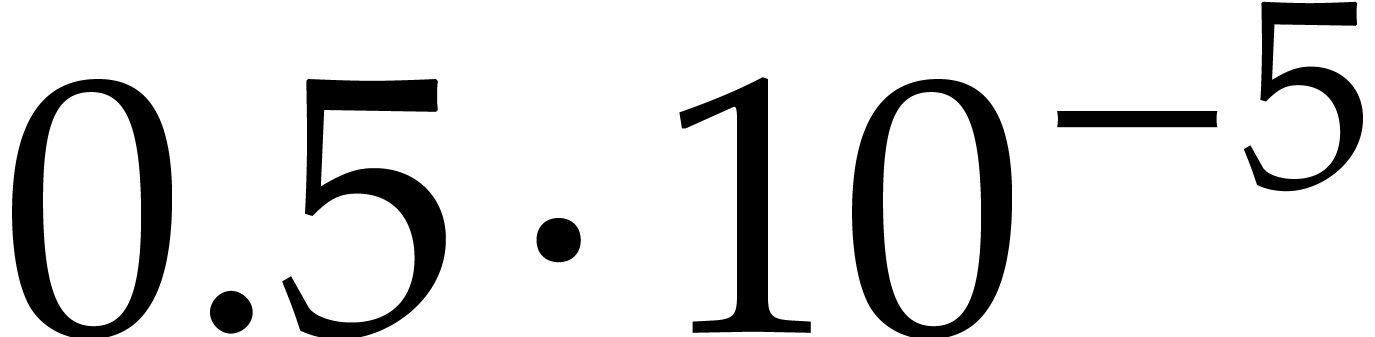 ).
Our numerical experiments indicate that the “phase change”
between winning and losing occurs at a critical value
).
Our numerical experiments indicate that the “phase change”
between winning and losing occurs at a critical value
 with
with
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Table
1
shows what happens for
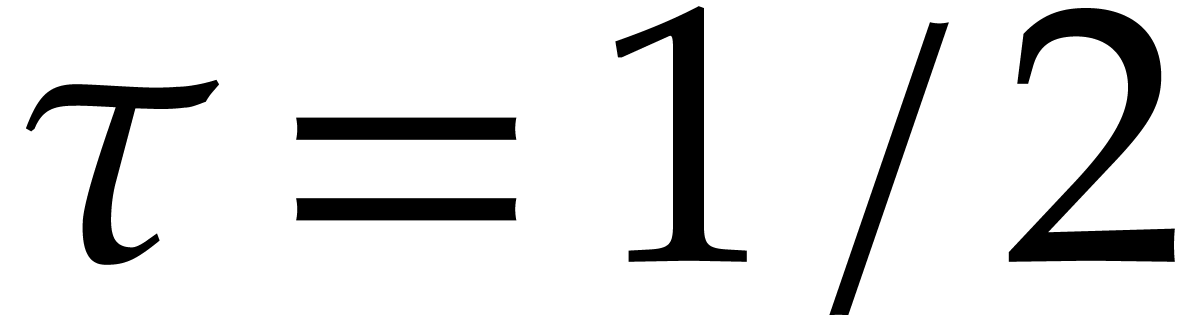 :
until the seventh round, a bit less than half of the balls get removed
at every round. After round eight, the remaining balls are removed at an
accelerated rate. For
:
until the seventh round, a bit less than half of the balls get removed
at every round. After round eight, the remaining balls are removed at an
accelerated rate. For
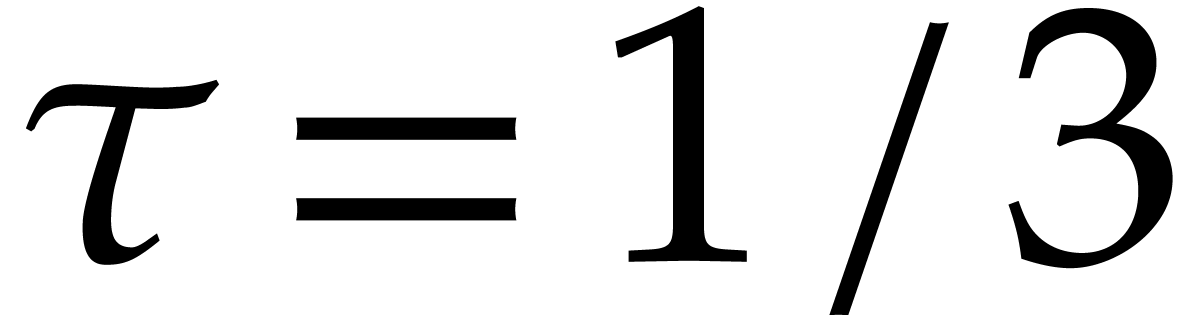 ,
the distributions
,
the distributions
 numerically tend to a non-zero limit distribution
numerically tend to a non-zero limit distribution
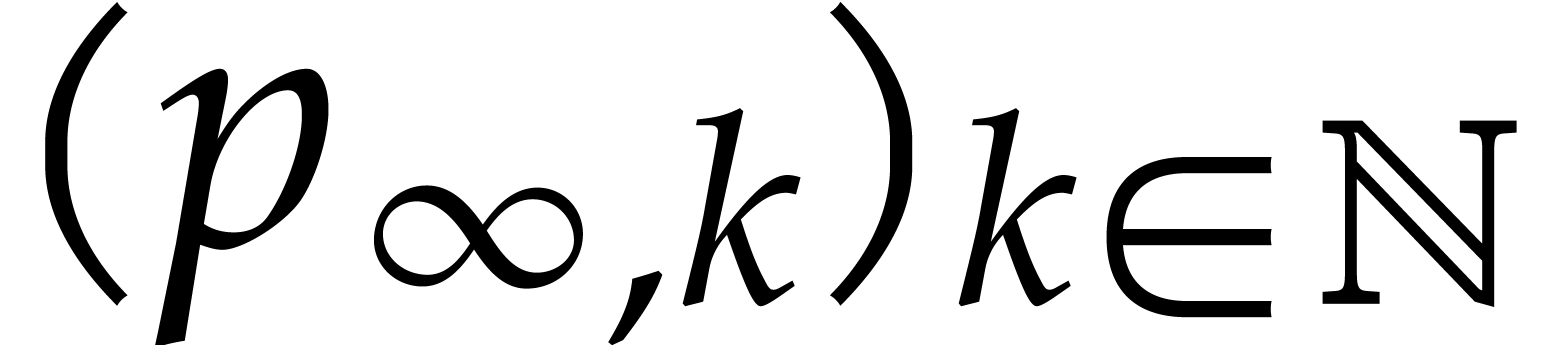 with
with
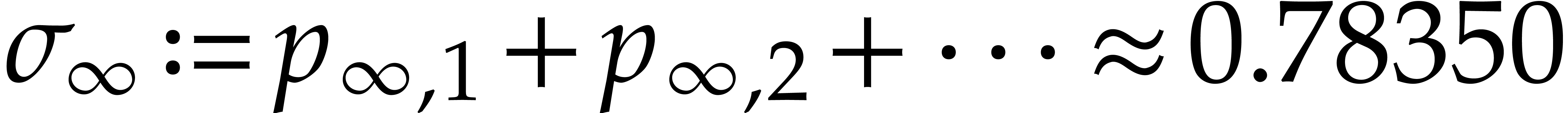 .
In Table
3
, we show some of the distributions in round ten, for
.
In Table
3
, we show some of the distributions in round ten, for
 near the critical point
near the critical point
 .
We also computed an approximation of the limit distribution at the
critical point itself.
.
We also computed an approximation of the limit distribution at the
critical point itself.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For 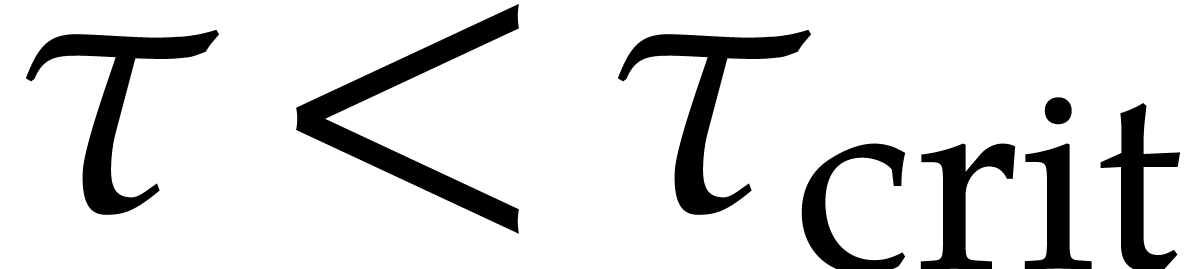 , we note that reliable
numerical computations can be turned into an actual proof that we lose
with high probability. Indeed, assume that
, we note that reliable
numerical computations can be turned into an actual proof that we lose
with high probability. Indeed, assume that 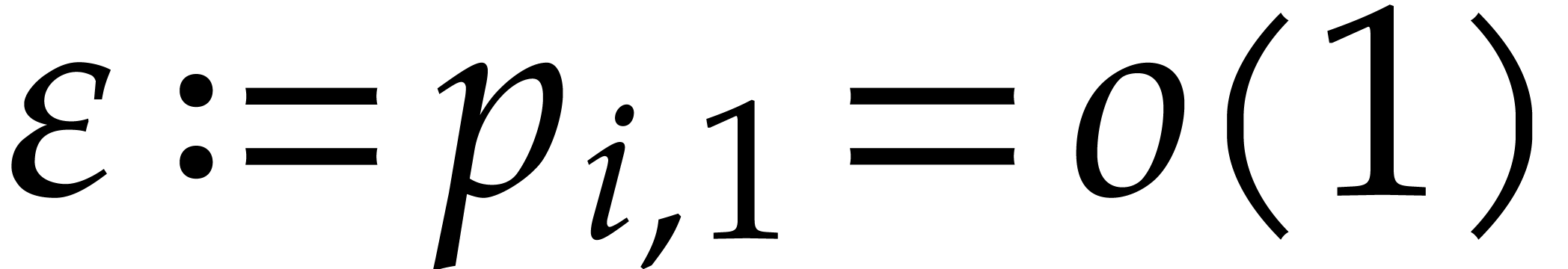 gets
very small for some
gets
very small for some  , whereas
, whereas
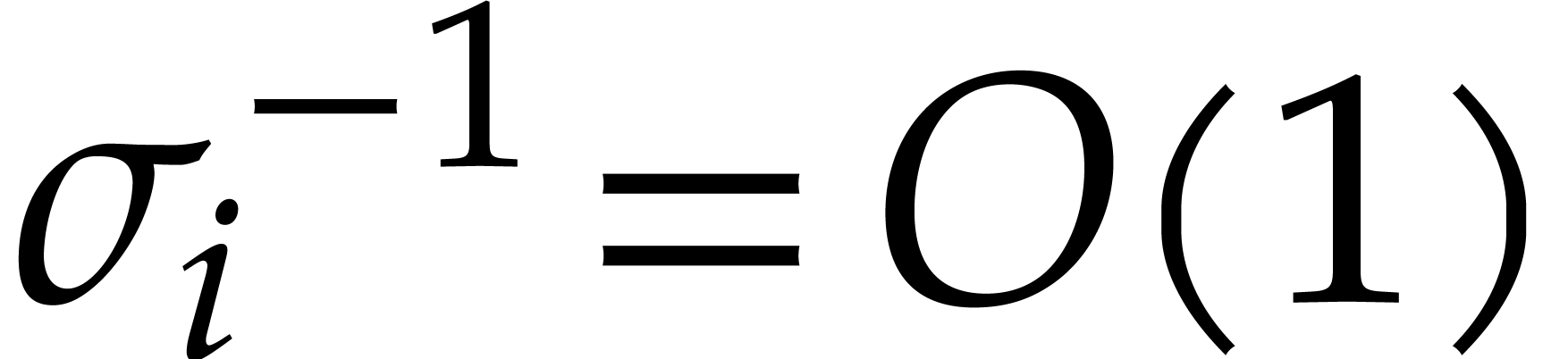 remains bounded (for instance, in Table 2,
we have
remains bounded (for instance, in Table 2,
we have 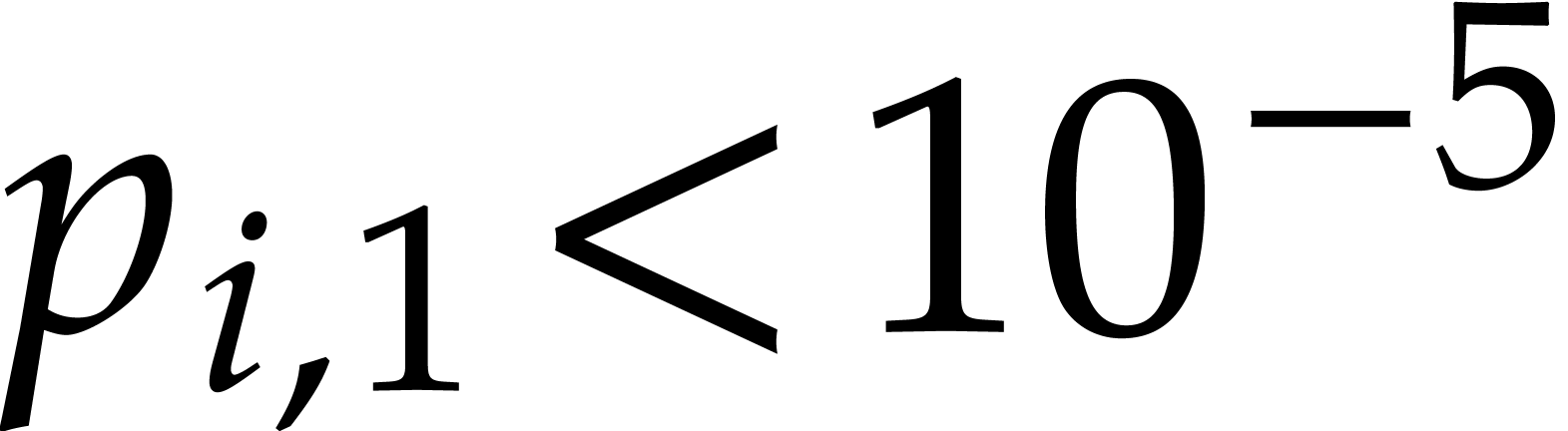 and
and 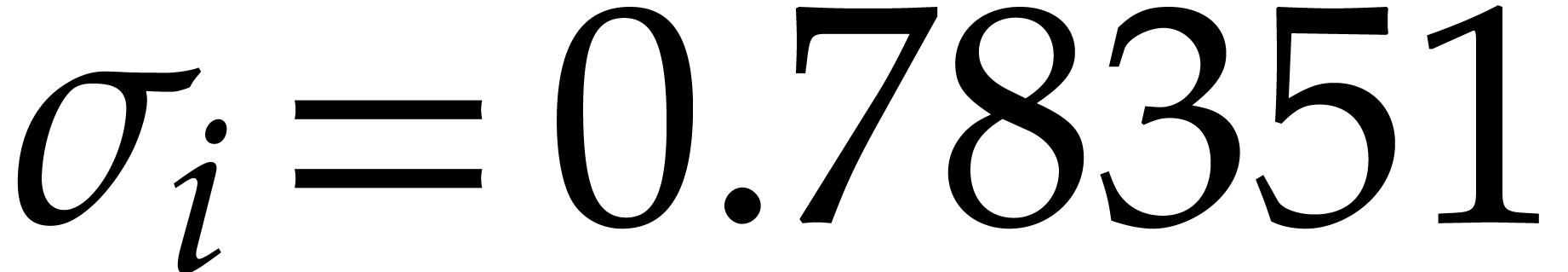 for
for 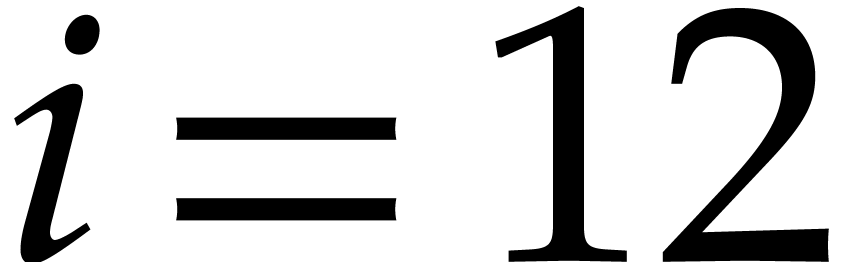 ). Then
). Then 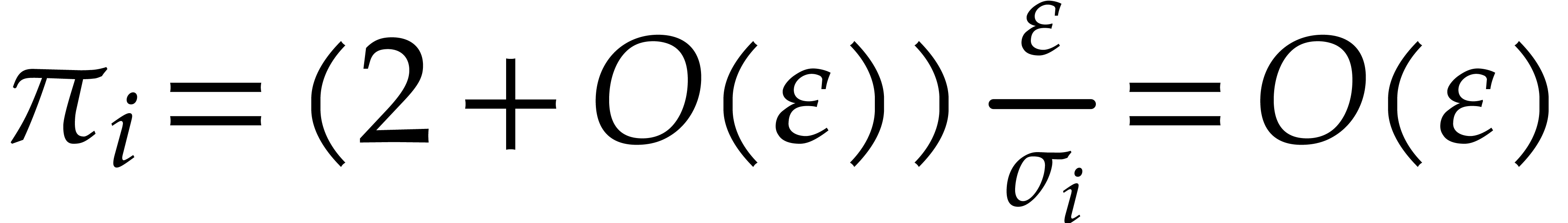 also gets very small and
also gets very small and
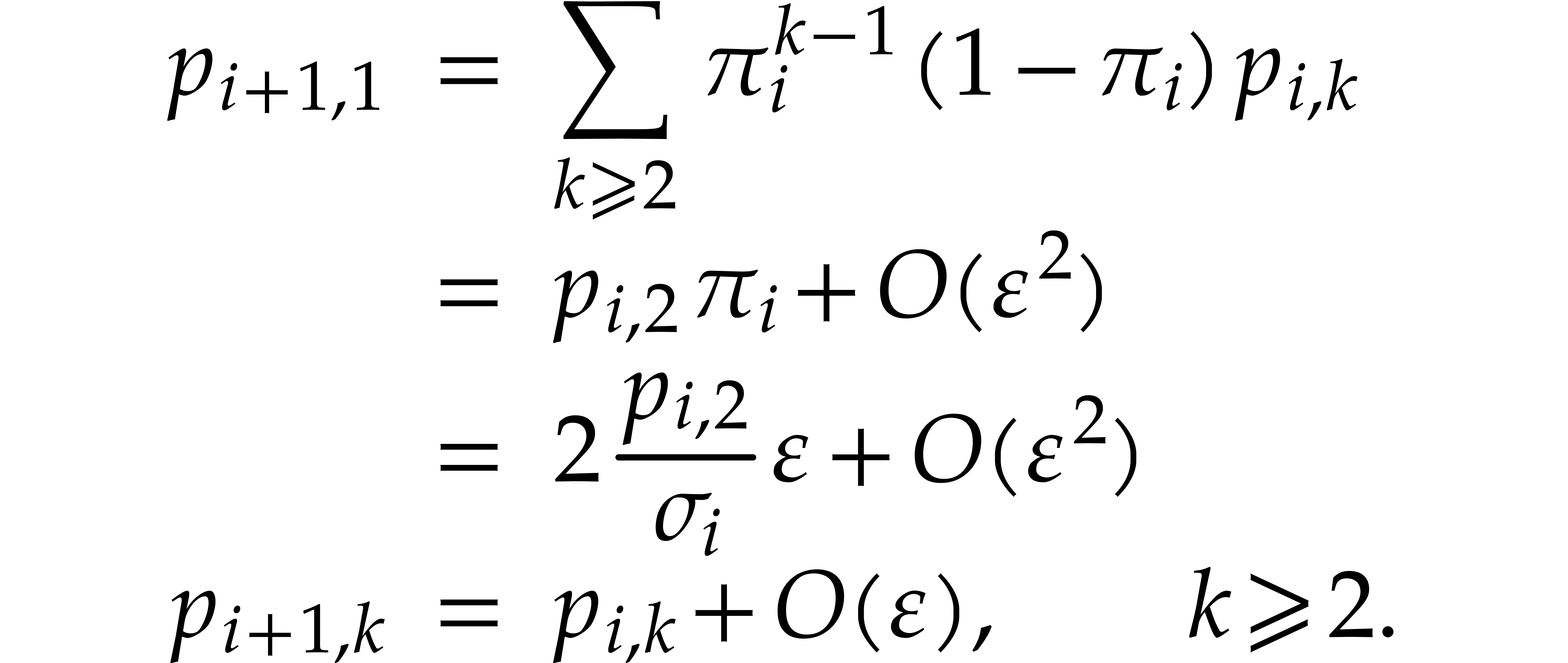
If 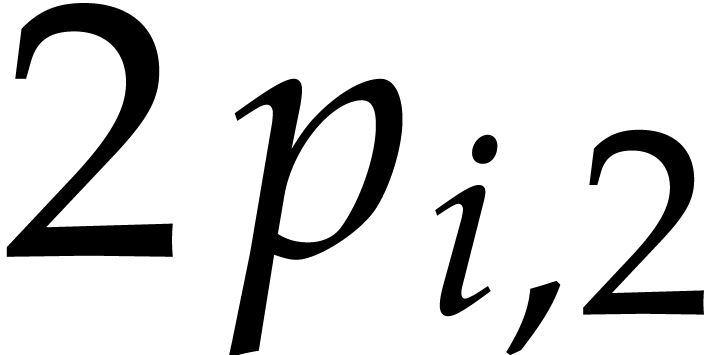 happens to be
happens to be  times
smaller than
times
smaller than  for some fixed
for some fixed 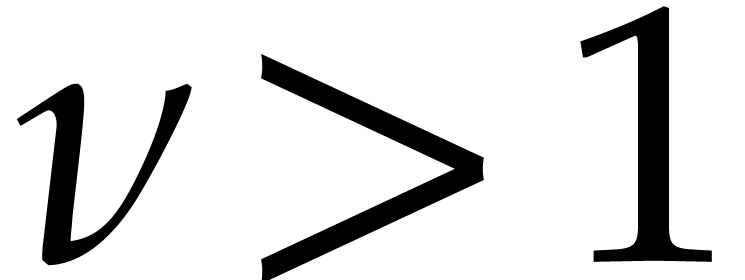 (for instance, in Table 2, we actually have
(for instance, in Table 2, we actually have 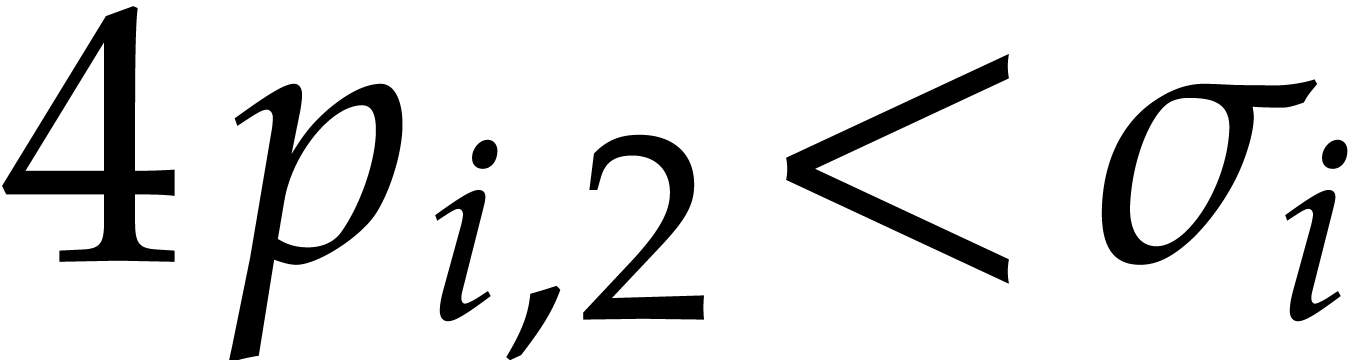 for
for 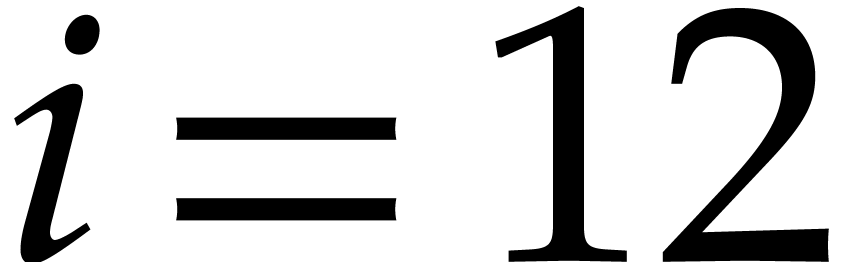 ), then a
standard contracting ball type argument can be used to prove that
), then a
standard contracting ball type argument can be used to prove that 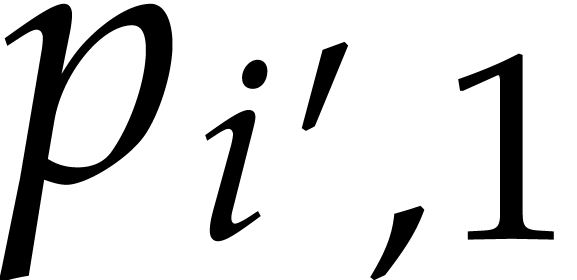 decreases to zero with geometric speed for
decreases to zero with geometric speed for 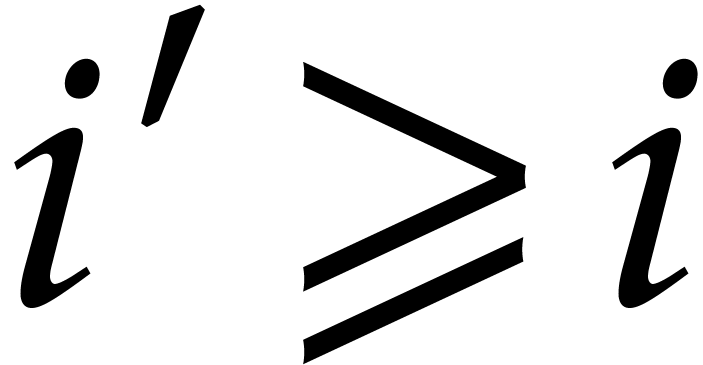 , while
, while  remains bounded away from zero.
remains bounded away from zero.
Conversely, given 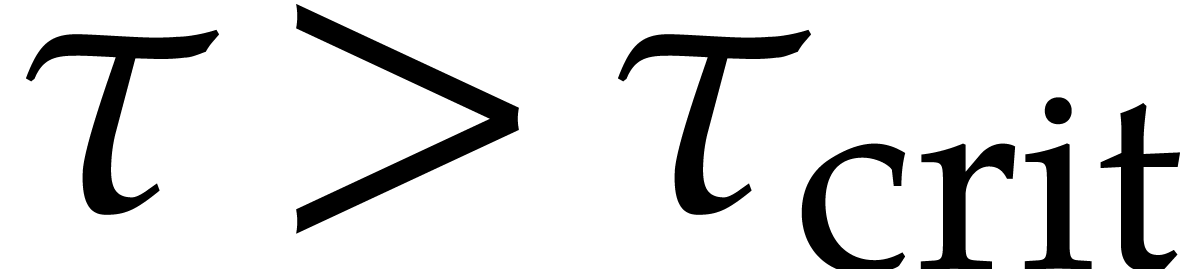 , it seems
harder to prove in a similar way that we win. Nevertheless, for any
, it seems
harder to prove in a similar way that we win. Nevertheless, for any
 , reliable computations
easily allow us to determine some round
, reliable computations
easily allow us to determine some round  with
with
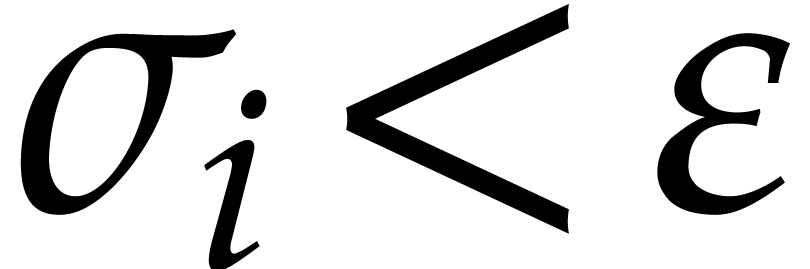 . For instance, for
. For instance, for 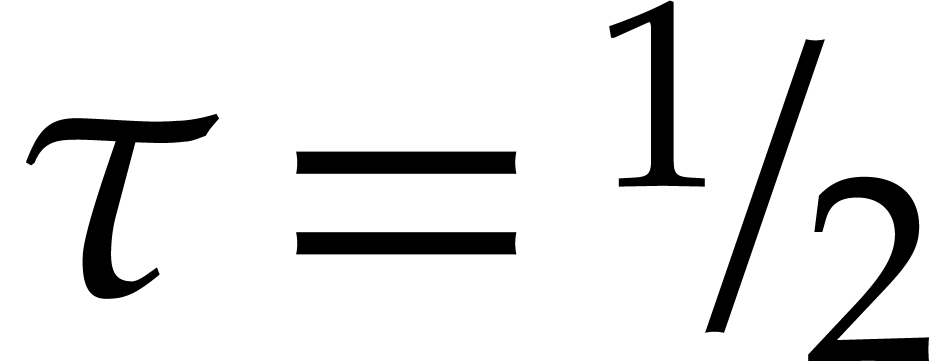 and
and 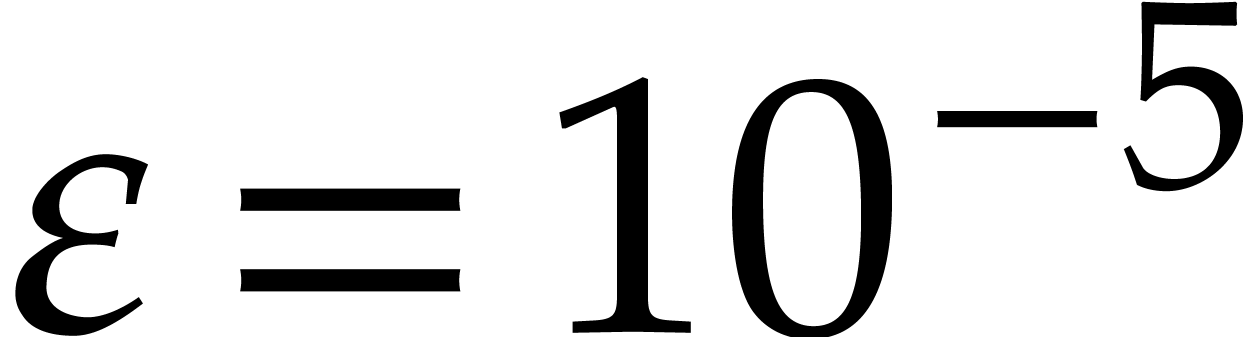 , we may
take
, we may
take 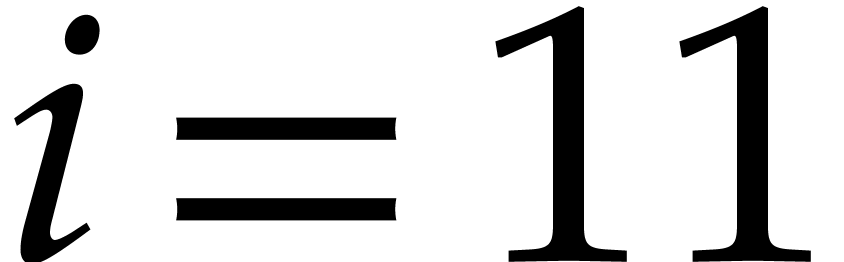 . This is good enough
for practical purposes: for
. This is good enough
for practical purposes: for 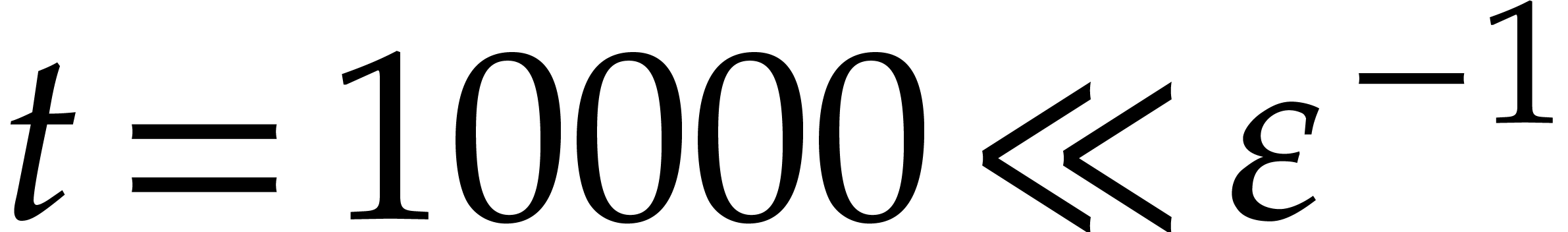 ,
it means that we indeed win with high probability. Here we also note
that a large number of rounds are generally necessary to win when
,
it means that we indeed win with high probability. Here we also note
that a large number of rounds are generally necessary to win when  approaches the critical value
approaches the critical value  . For instance, for
. For instance, for 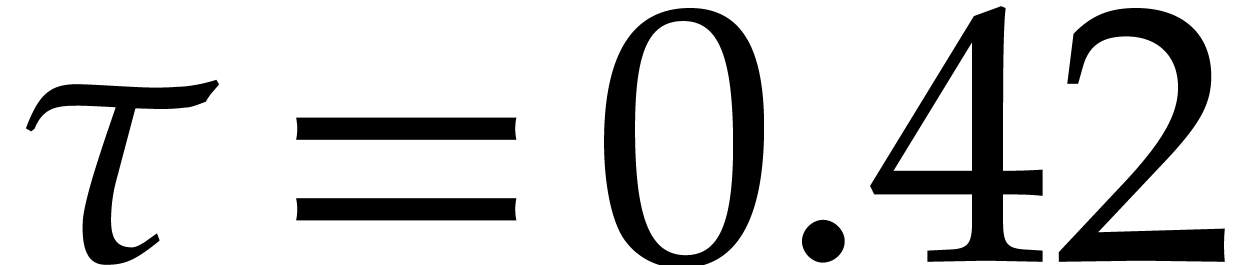 ,
we need to wait until round
,
we need to wait until round 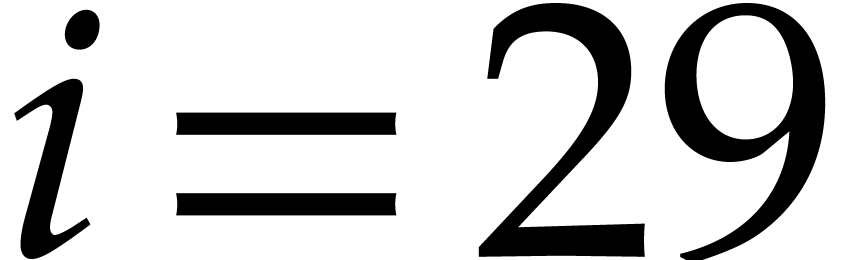 to get
to get 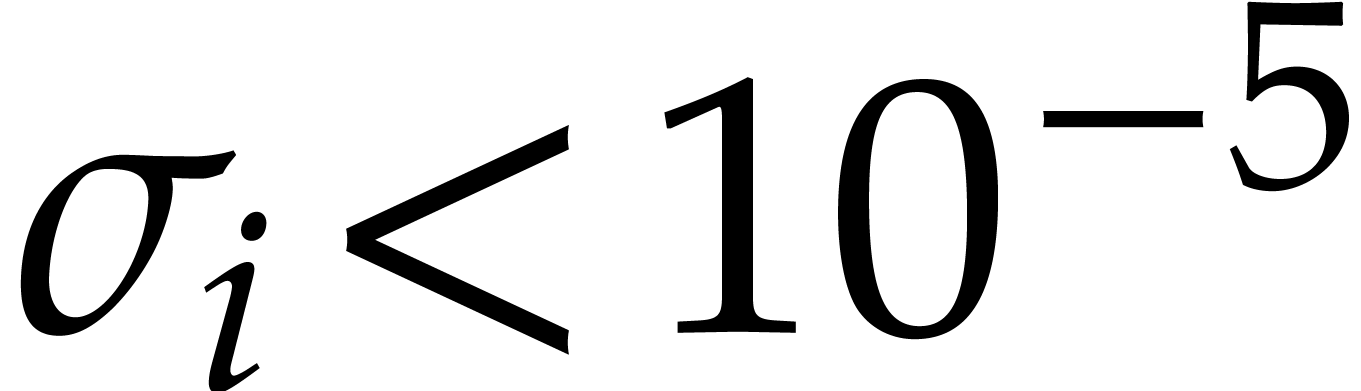 . Nevertheless, after a certain number of
rounds, it seems that
. Nevertheless, after a certain number of
rounds, it seems that  always converges to zero
with superlinear speed.
always converges to zero
with superlinear speed.
In Table
4
, we conclude with the result of a computer simulation in which we
played our game with
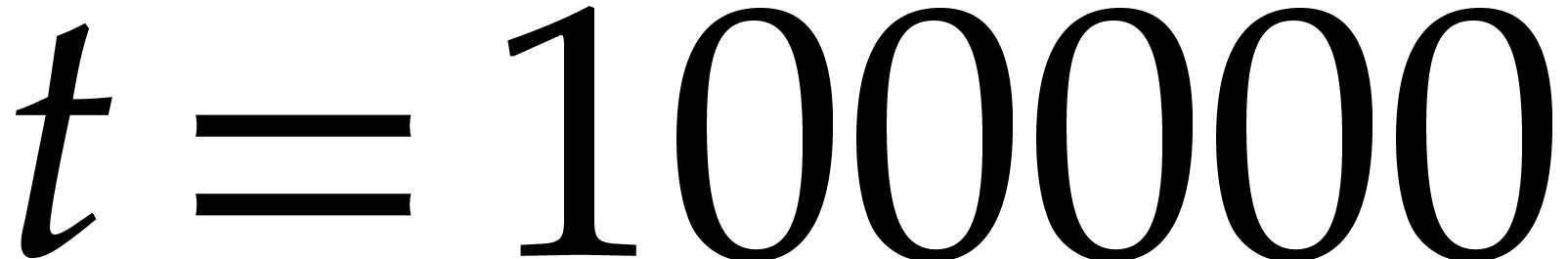 and
and
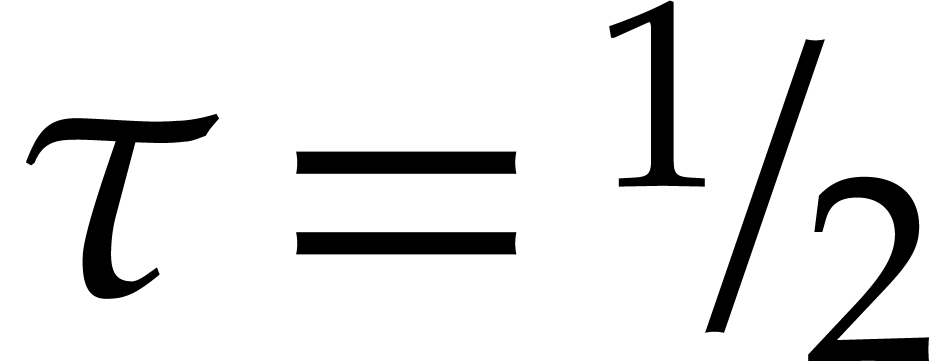 .
As one can see, the results are close to the theoretically expected
ones from Table
1
.
.
As one can see, the results are close to the theoretically expected
ones from Table
1
.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Remark
Let us now turn to the general problem of multiplying sparse
polynomials. We will focus on the multiplication 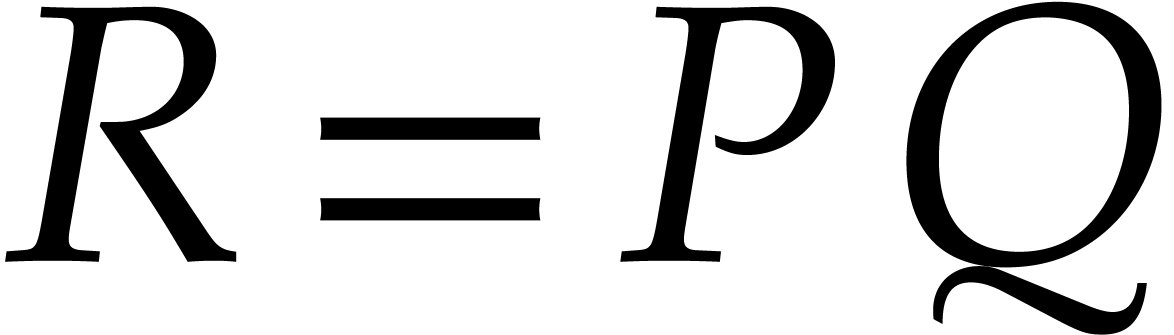 of integer polynomials
of integer polynomials 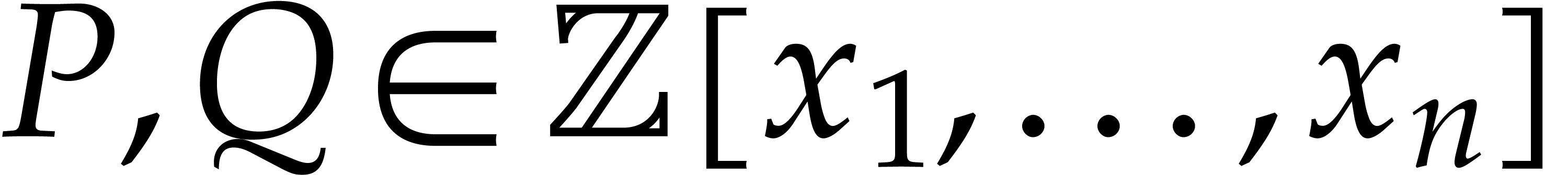 in at least two
variables. We define
in at least two
variables. We define  to be the total degree of
to be the total degree of
 and assume that we have a bound
and assume that we have a bound  for the number of terms of
for the number of terms of  .
.
As explained in the introduction, we proceed in two phases: we first
determine the exponents of the unknown product  . This part is probabilistic of Monte Carlo type,
where we tolerate a rate of failure
. This part is probabilistic of Monte Carlo type,
where we tolerate a rate of failure  that is
fixed in advance. In the second phase, we determine the unknown
coefficients, using a probabilistic algorithm of Las Vegas type. In this
section, we start with the second phase, which has already been
explained on an example in section 2.
that is
fixed in advance. In the second phase, we determine the unknown
coefficients, using a probabilistic algorithm of Las Vegas type. In this
section, we start with the second phase, which has already been
explained on an example in section 2.
Assume that our product 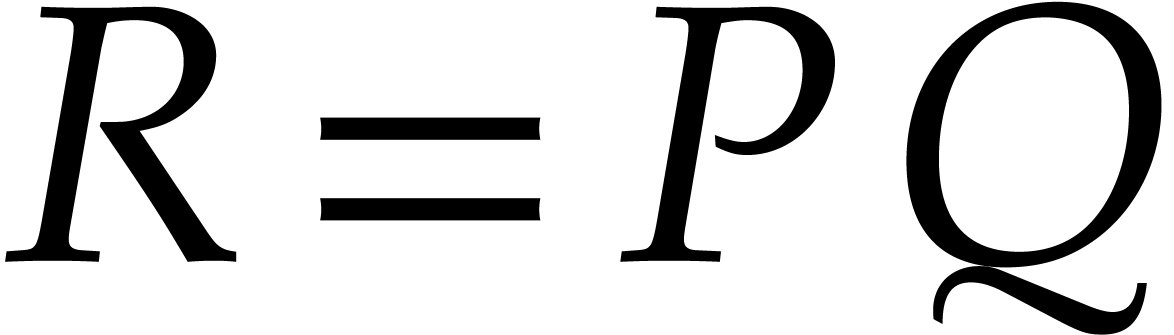 has
has  terms, so that
terms, so that 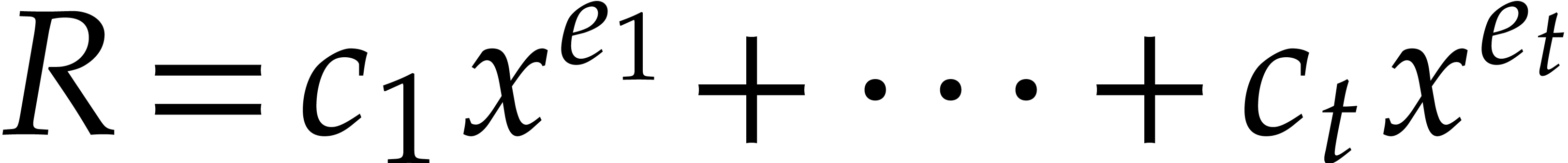 for certain
for certain 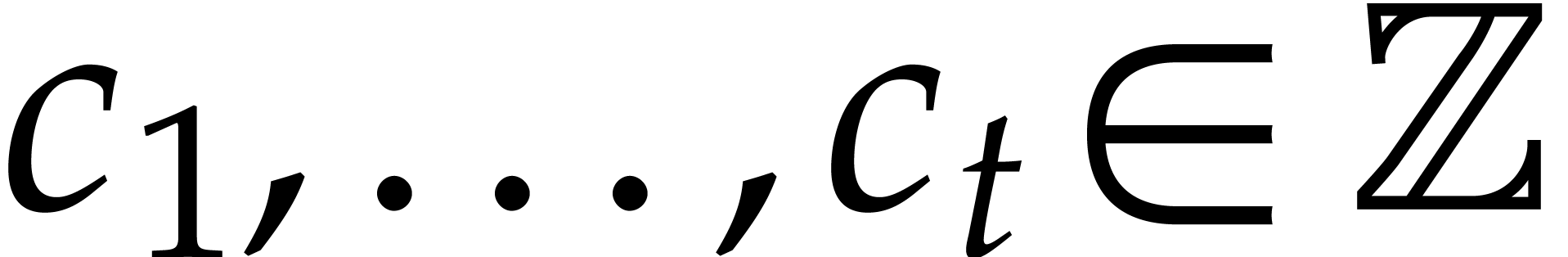 and
and 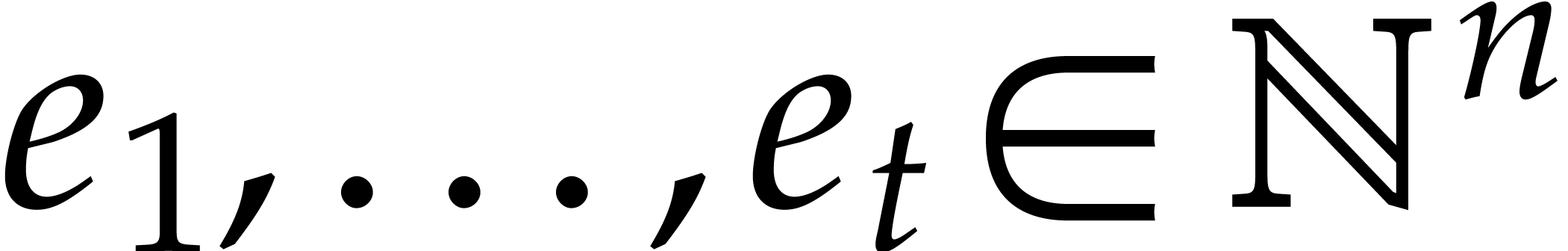 , where
, where 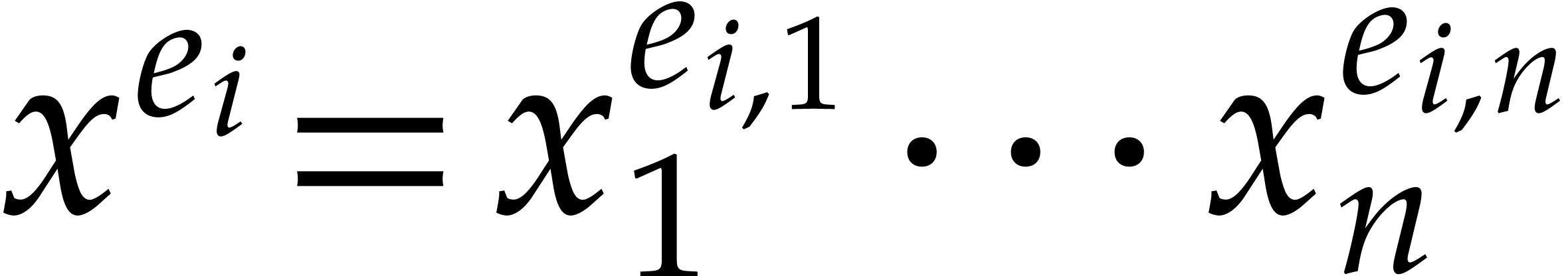 for
for 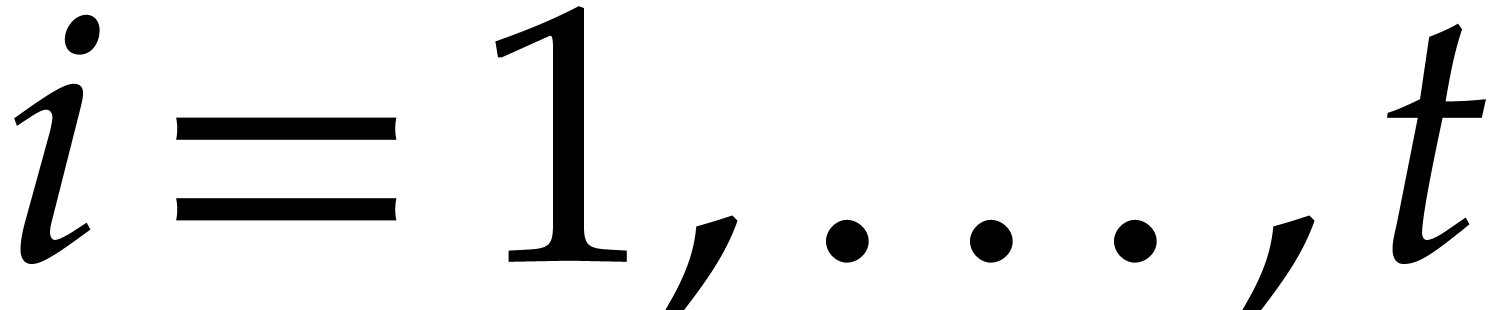 . It is obvious how to
generalize the algorithm from section 2 to this case: for
some fixed
. It is obvious how to
generalize the algorithm from section 2 to this case: for
some fixed 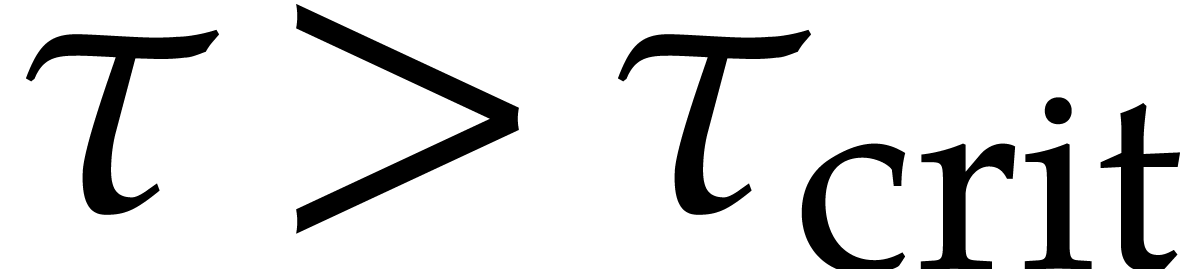 , we distribute
“our
, we distribute
“our  balls” over
balls” over 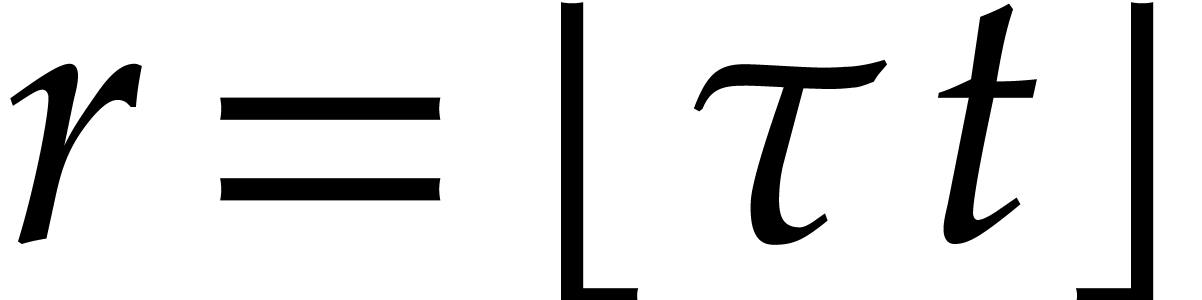 boxes, through the evaluation of
boxes, through the evaluation of  at three points
at three points
 in
in 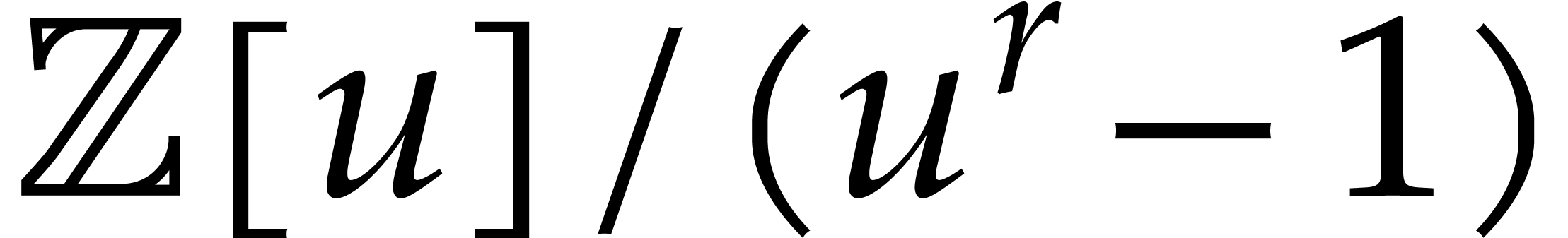 for
for  and
and 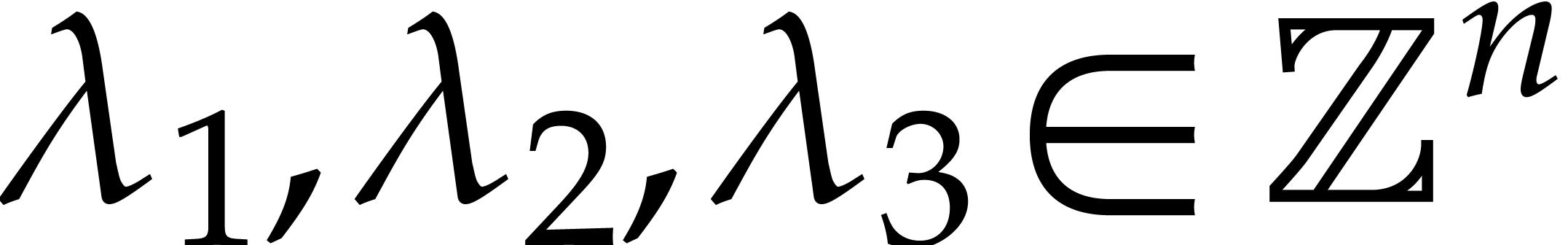 . The vectors
. The vectors 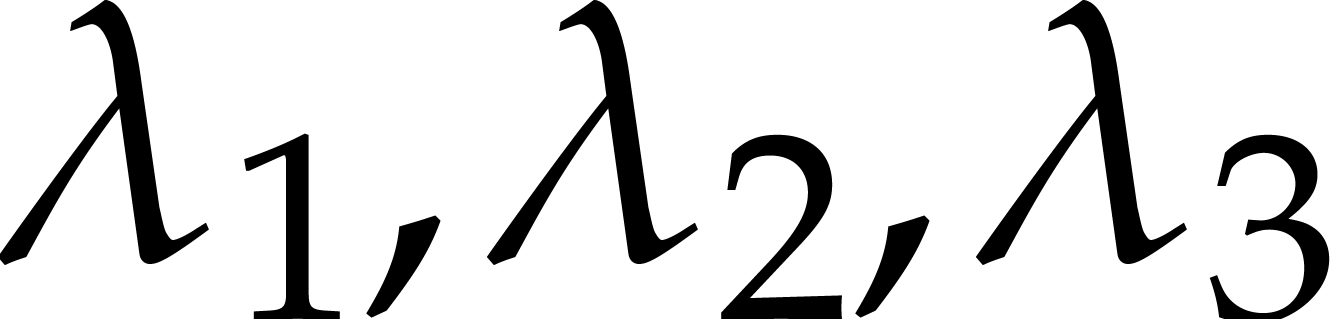 are essentially chosen at random, but it is convenient to
take them pairwise non-collinear modulo
are essentially chosen at random, but it is convenient to
take them pairwise non-collinear modulo 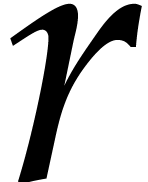 ,
so as to avoid any “useless throws”. We assume the following
heuristic:
,
so as to avoid any “useless throws”. We assume the following
heuristic:
For random vectors 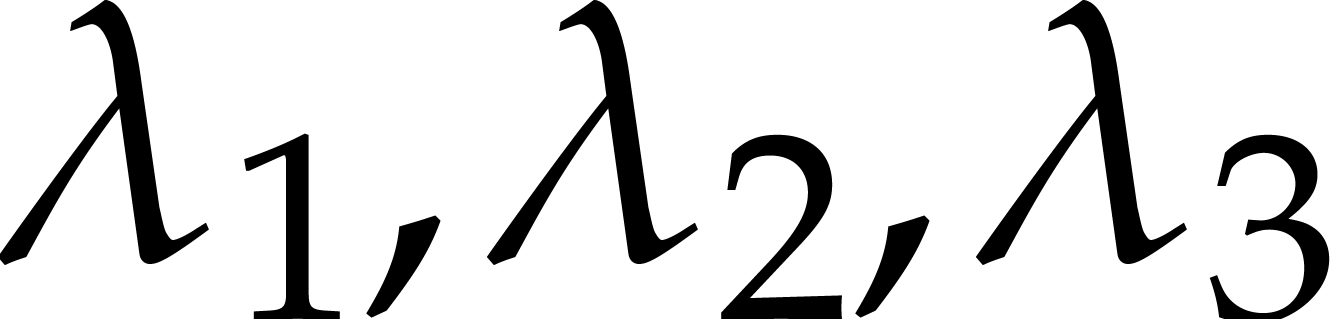 as above each of the
three throws randomly distributes the balls over the boxes, and
the three distributions are independent.
as above each of the
three throws randomly distributes the balls over the boxes, and
the three distributions are independent.
We then play our game of mystery balls as usual, which yields the
coefficients
 if we win and only a subset of these coefficients if we lose. In view
of Remark
2
, this leads to Algorithm
1
.
if we win and only a subset of these coefficients if we lose. In view
of Remark
2
, this leads to Algorithm
1
.
Algorithm
Output: the product
Assume: |
Proof. The correctness of the algorithm has been
explained in section 2. As to the running time, we first
note that none of the integer coefficients encountered during our
computation exceeds  in absolute value. Now steps
1 and 2 have negligible cost and the running
time for the remaining steps is as follows:
in absolute value. Now steps
1 and 2 have negligible cost and the running
time for the remaining steps is as follows:
In step 3, for every term 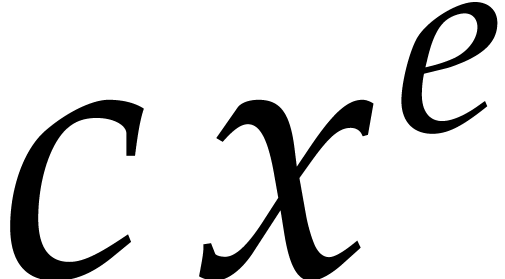 in
in
 or
or  and every
and every 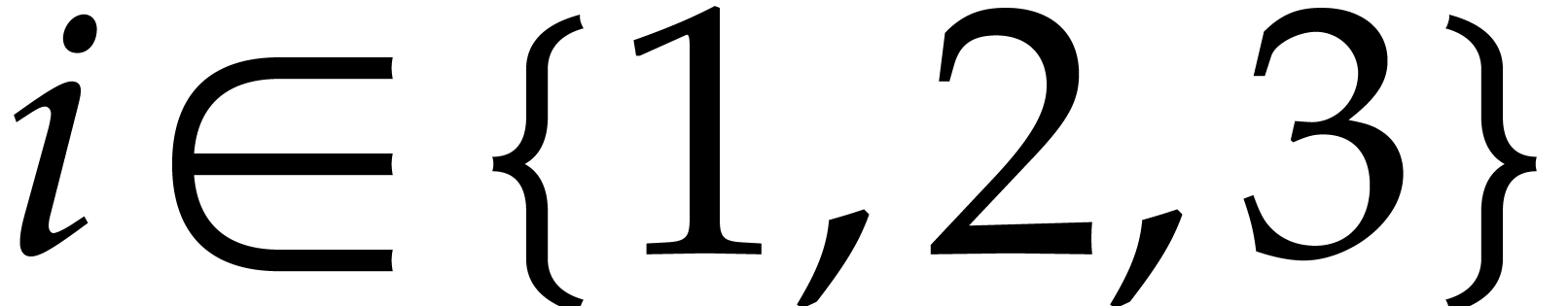 , we first have to compute
, we first have to compute 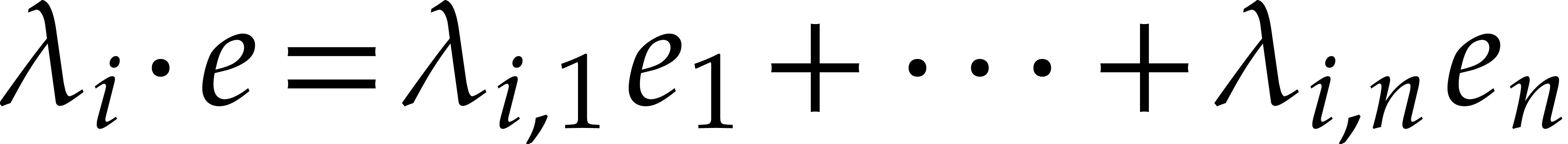 modulo
modulo  .
Since we only have to accumulate
.
Since we only have to accumulate 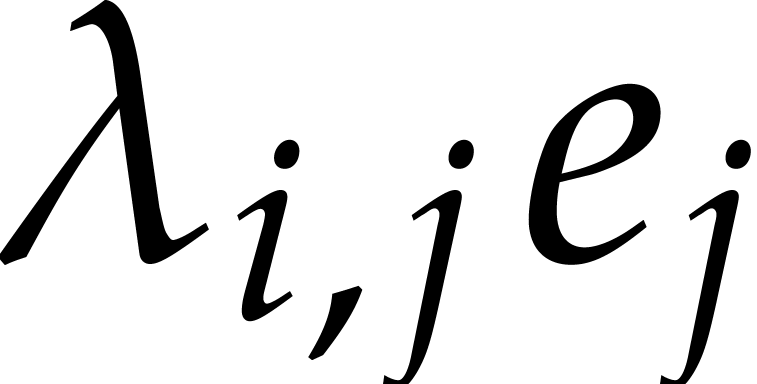 when
when 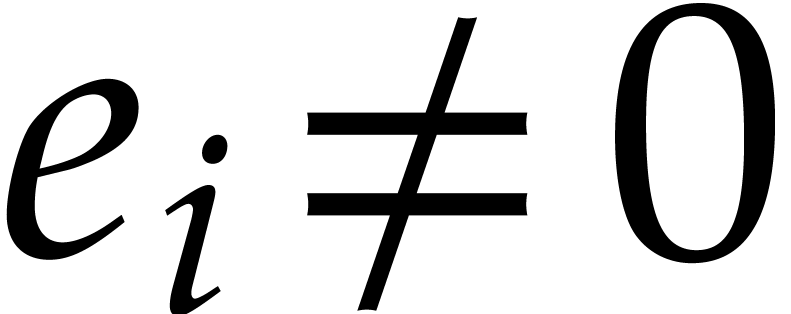 , this can be done in time
, this can be done in time
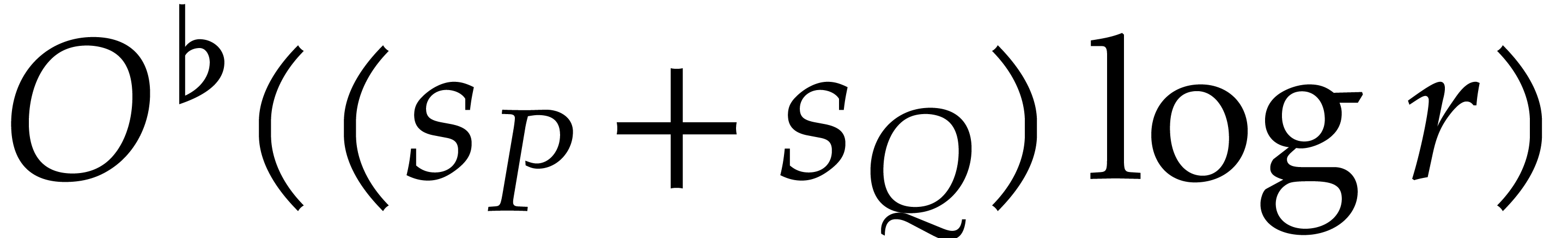 . We next have to add the
coefficients of all terms that end up in the same box, which amounts
to
. We next have to add the
coefficients of all terms that end up in the same box, which amounts
to 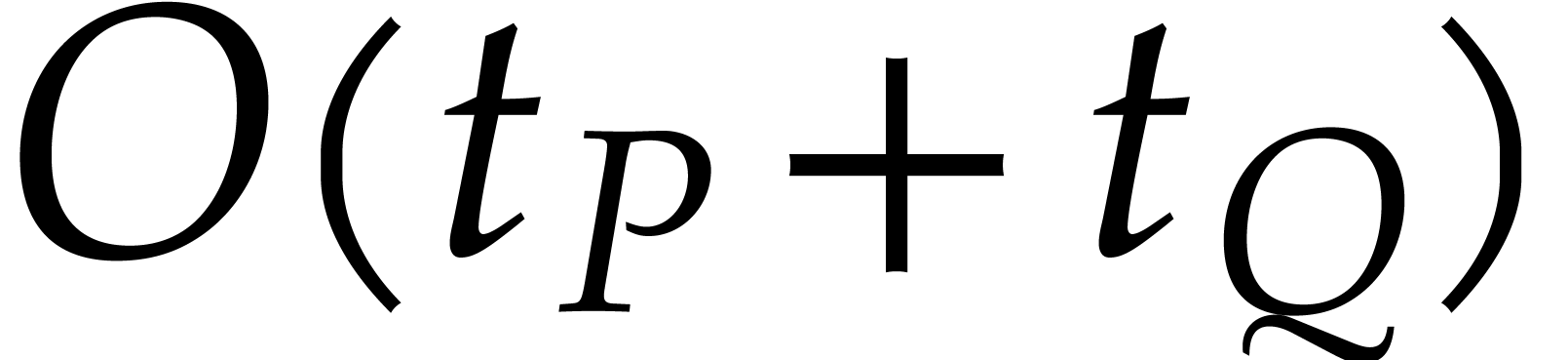 additions of cost
additions of cost 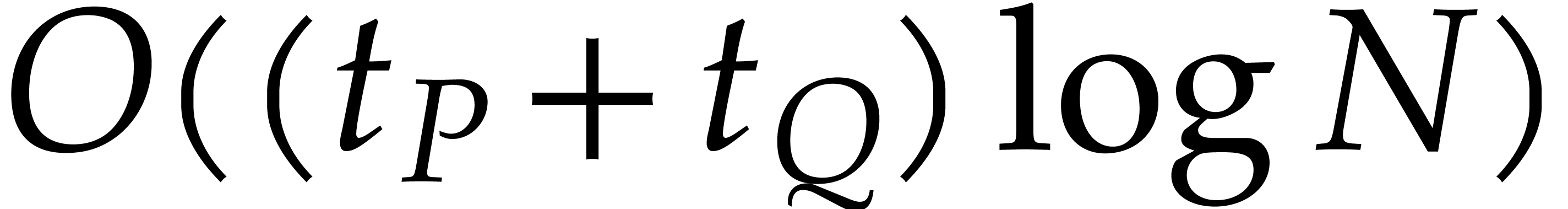 .
.
In step 4, we do three multiplications of cost 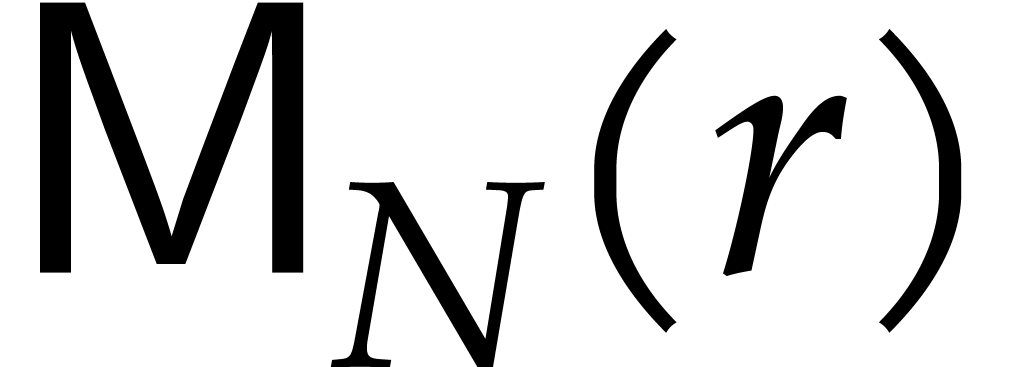 each. Since
each. Since 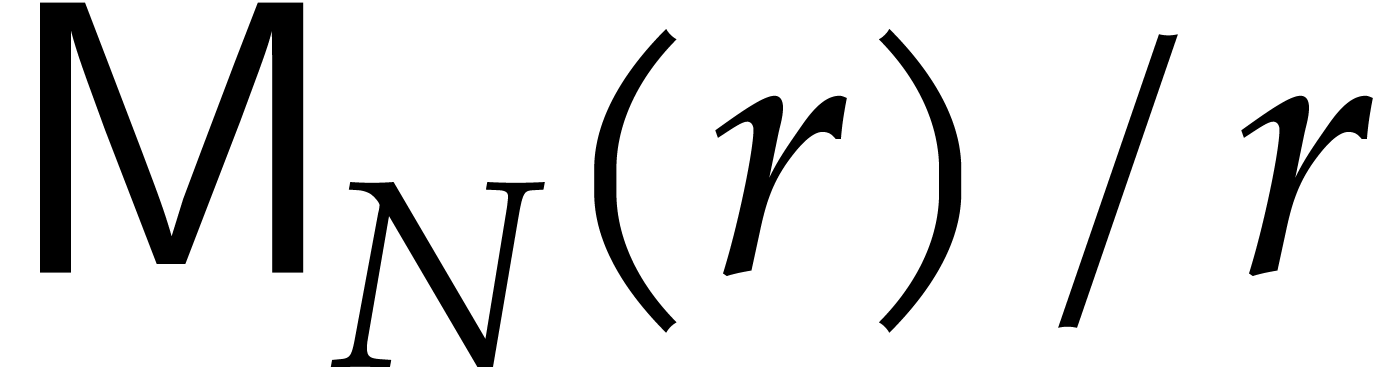 is
non-decreasing, the cost of these multiplications is bounded by
is
non-decreasing, the cost of these multiplications is bounded by
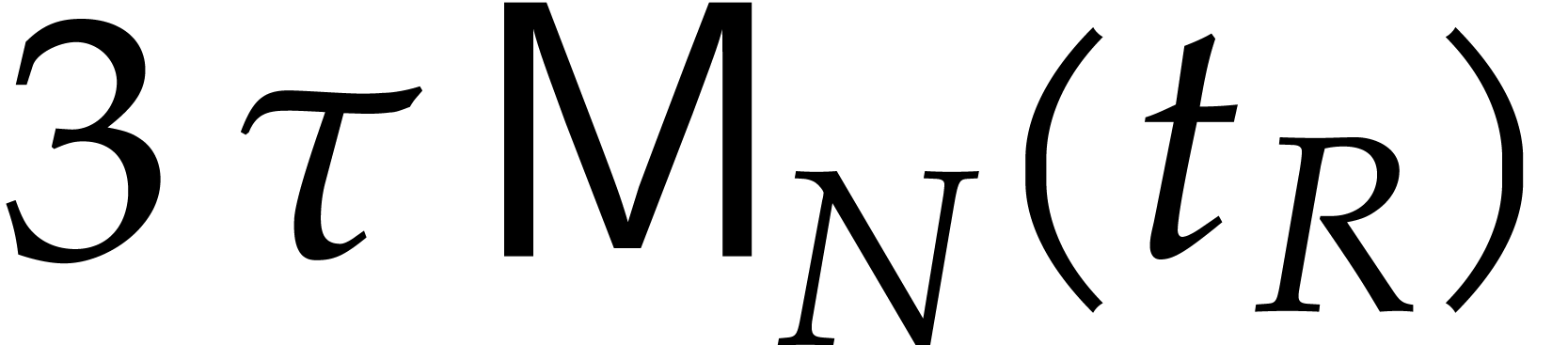 .
.
In steps 5 and 6, we play our game of
mystery balls, where 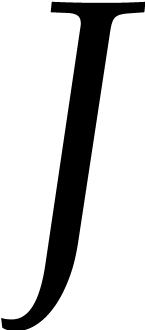 stands for the set of
ball that are still in play. Whenever ball
stands for the set of
ball that are still in play. Whenever ball  ends up in a private box for throw number
ends up in a private box for throw number  , we have to determine where this ball landed
for the other throws, by computing
, we have to determine where this ball landed
for the other throws, by computing 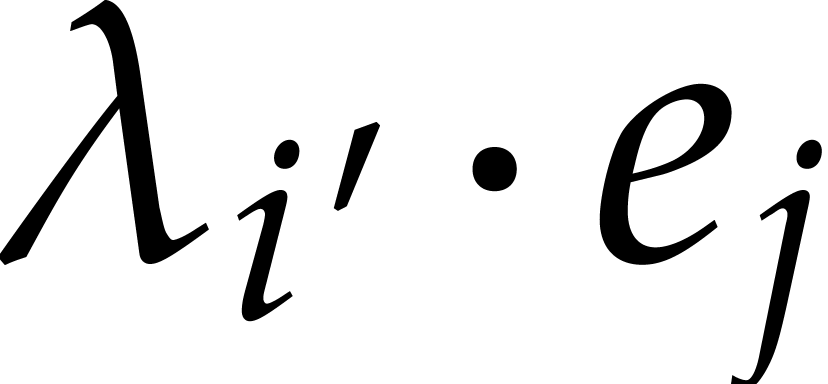 modulo
modulo
 for
for  .
We then have to update the numbers below the corresponding boxes,
which corresponds to setting
.
We then have to update the numbers below the corresponding boxes,
which corresponds to setting 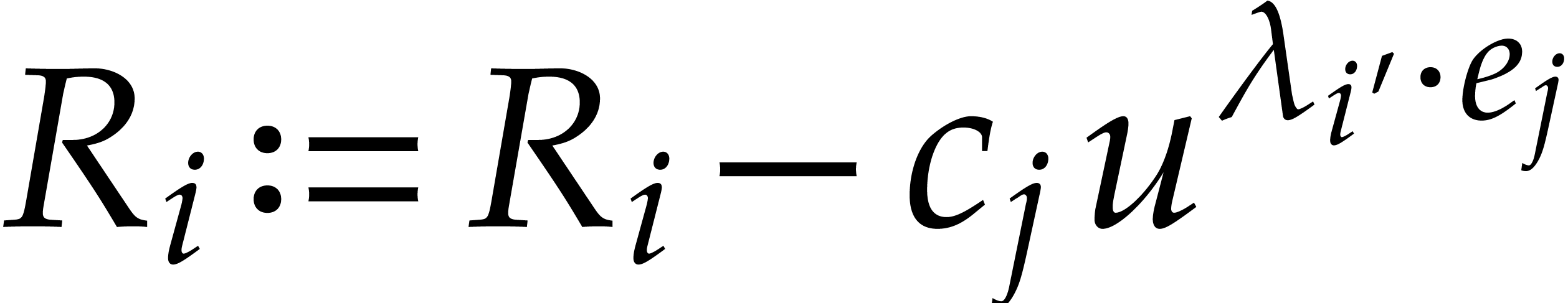 in step 6b. Since this eventually has to be done for
each of the
in step 6b. Since this eventually has to be done for
each of the  balls, step 6 takes
balls, step 6 takes
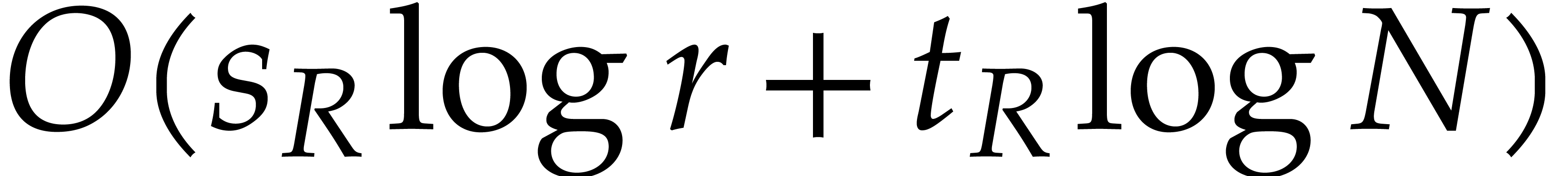 bit-operations, using a similar analysis as
for step 3.
bit-operations, using a similar analysis as
for step 3.
Let us finally investigate bookkeeping costs that are implicit in our description of the algorithm. Above all, we have to maintain the linked lists with balls inside each box (see Remark 1). This can be done in time
The other implicit costs to maintain various tables are also bounded by
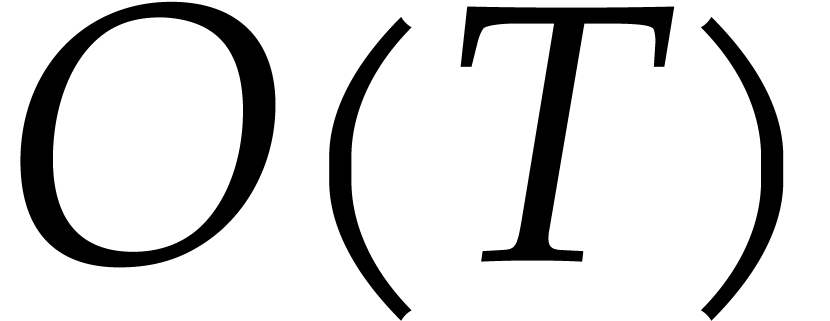 .
.
In [21], we surveyed several strategies for computing the
exponents of the product  .
Most of the approaches from sections 4, 6, and 7 of that paper can be
adapted to the present setting. We will focus on a probabilistic
strategy that we expect to be one of the most efficient ones for
practical purposes (a few variants will be discussed in section 5).
.
Most of the approaches from sections 4, 6, and 7 of that paper can be
adapted to the present setting. We will focus on a probabilistic
strategy that we expect to be one of the most efficient ones for
practical purposes (a few variants will be discussed in section 5).
For 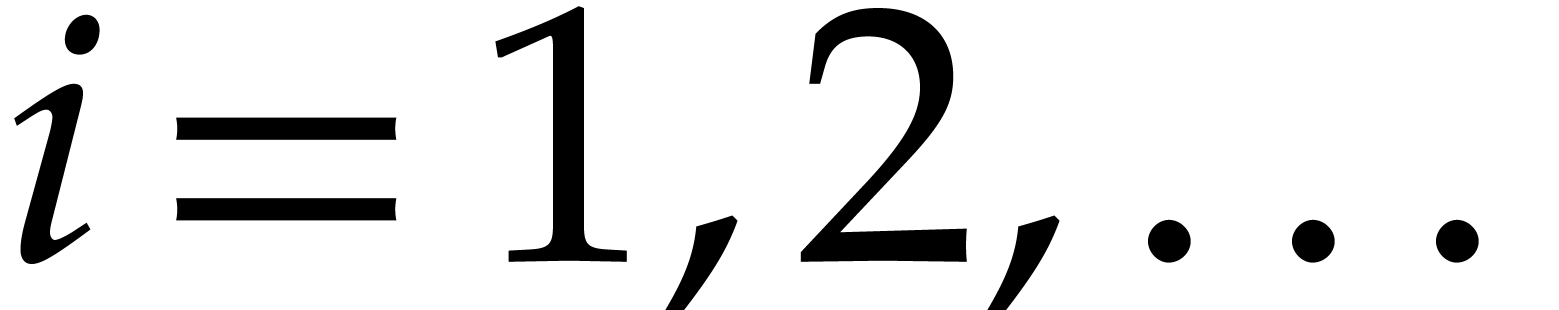 , let
, let 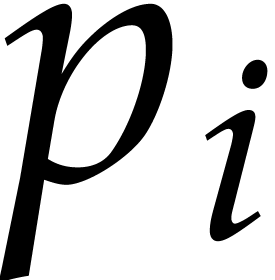 be the
be the  -th prime number and
let
-th prime number and
let 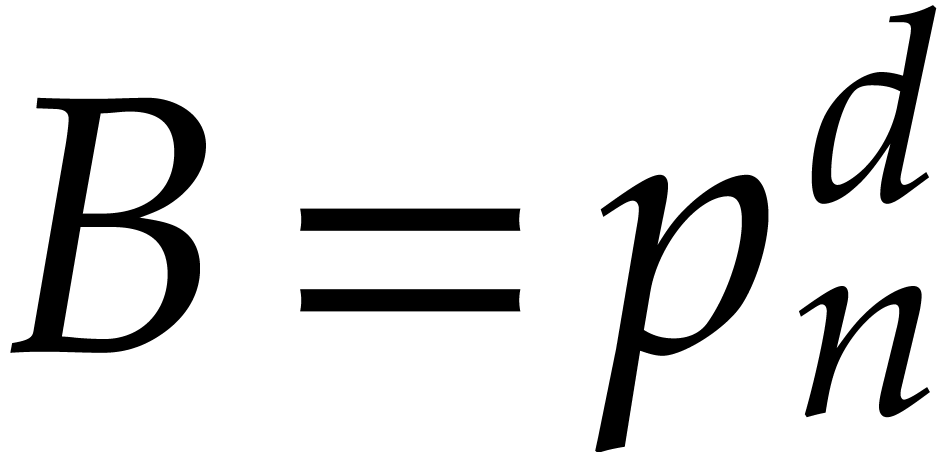 . We let
. We let  be a fixed prime number with
be a fixed prime number with 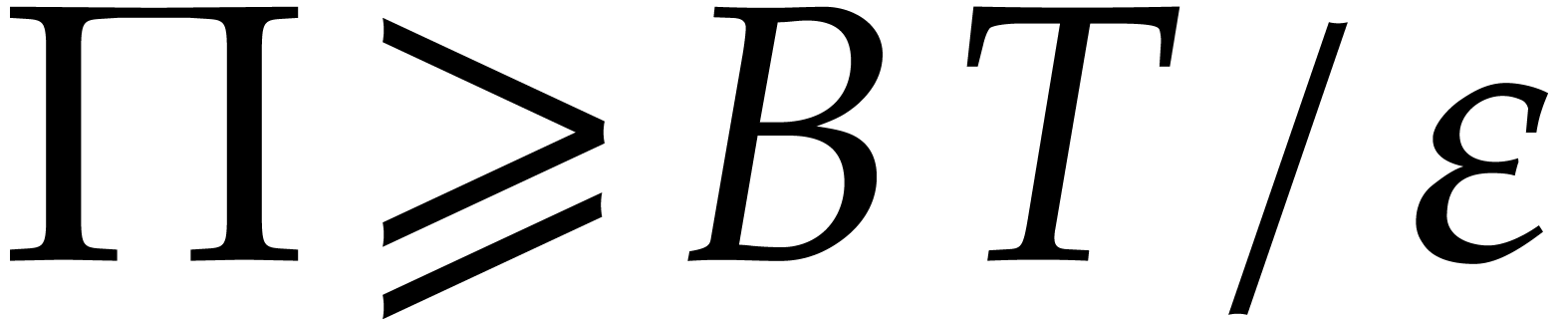 (for practical
implementations, we may also take
(for practical
implementations, we may also take  to be a
product of prime numbers that fit into machine words, and use
multi-modular arithmetic to compute modulo
to be a
product of prime numbers that fit into machine words, and use
multi-modular arithmetic to compute modulo  ).
For some fixed
).
For some fixed 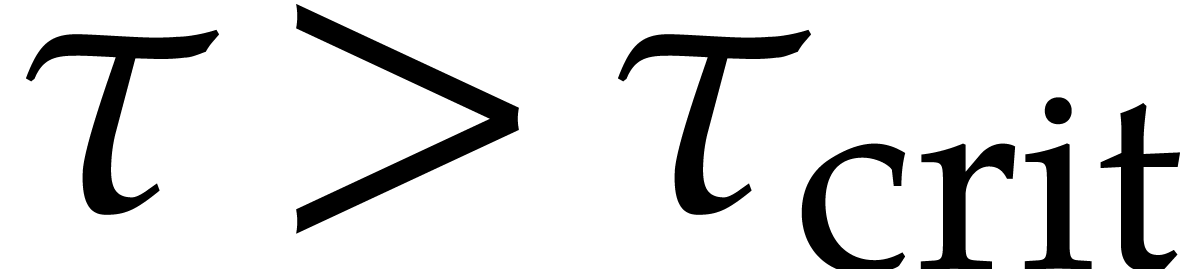 , we again use
, we again use
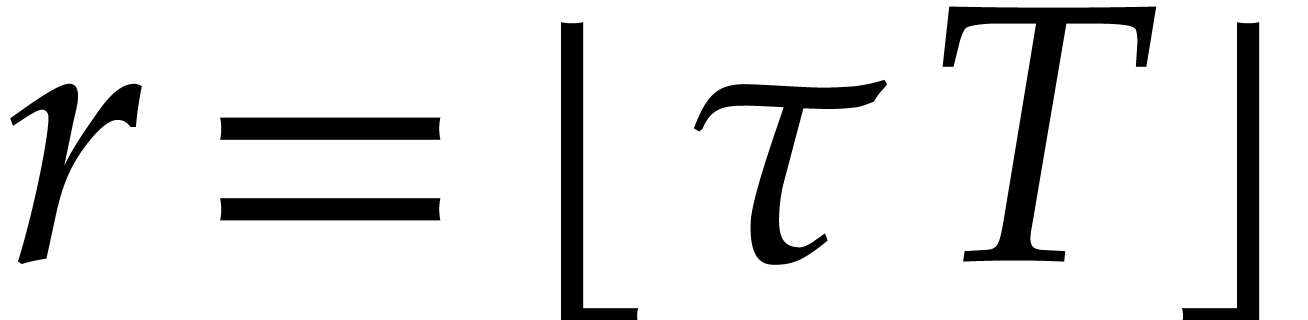 boxes, and evaluate
boxes, and evaluate  over
the ring
over
the ring 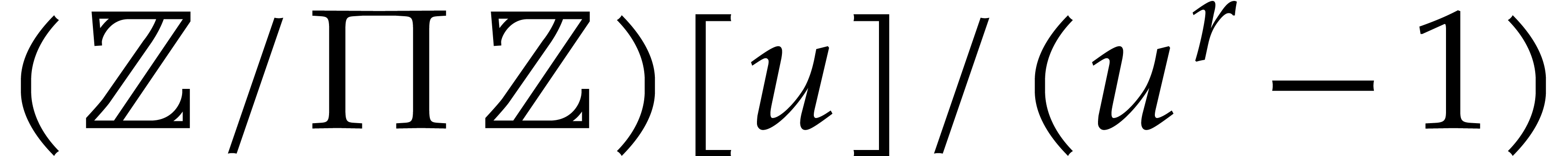 . This time, we use
six evaluation points of the form
. This time, we use
six evaluation points of the form  and
and  for
for 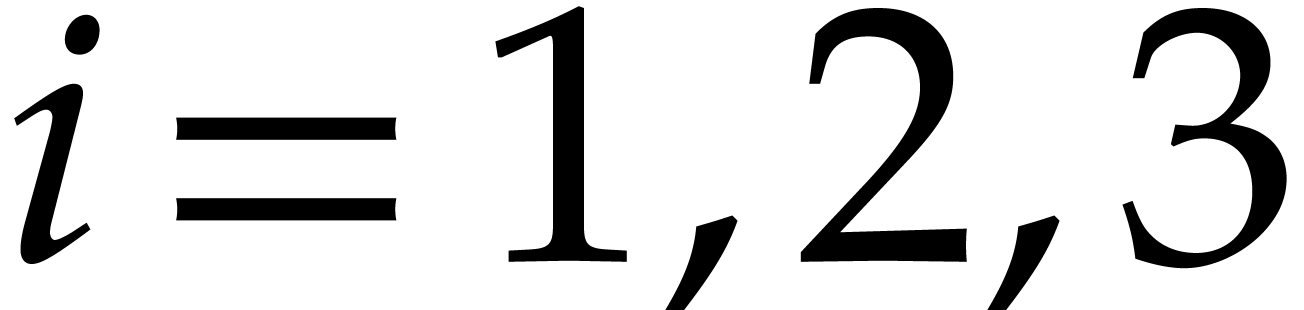 , where the
, where the
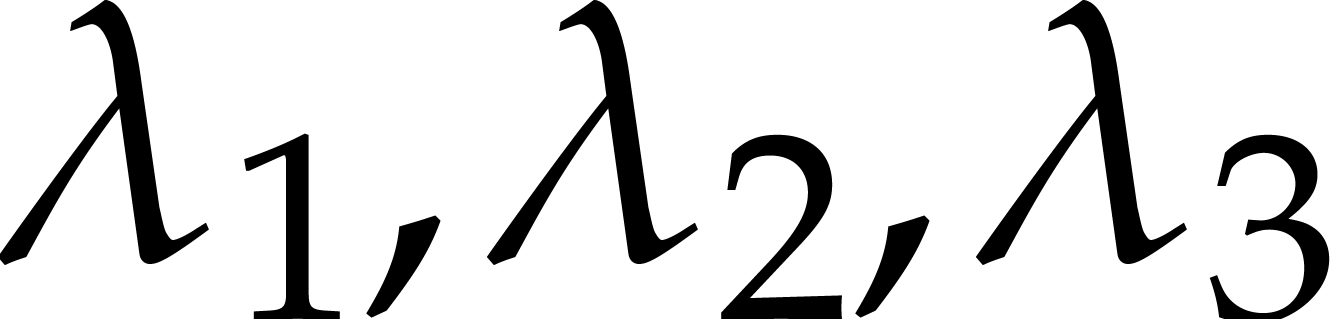 are chosen at random and pairwise non-collinear
modulo
are chosen at random and pairwise non-collinear
modulo 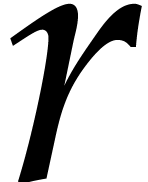 .
.
Now consider a term 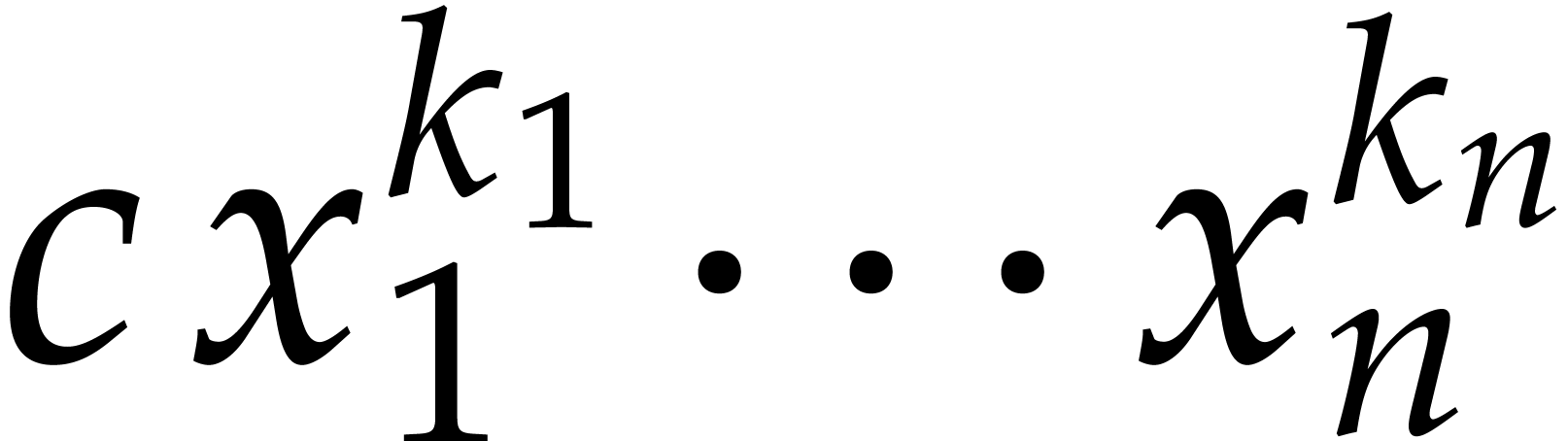 of
of  . Its evaluation at
. Its evaluation at  is
is 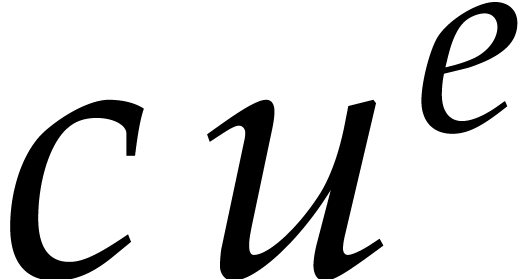 , where
, where 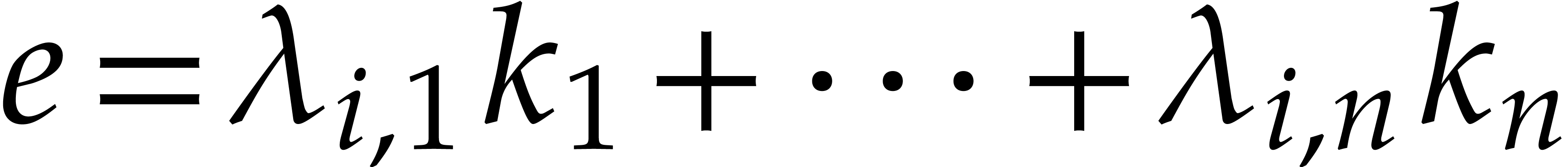 modulo
modulo 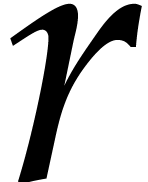 . Meanwhile, its
evaluation at
. Meanwhile, its
evaluation at  is
is 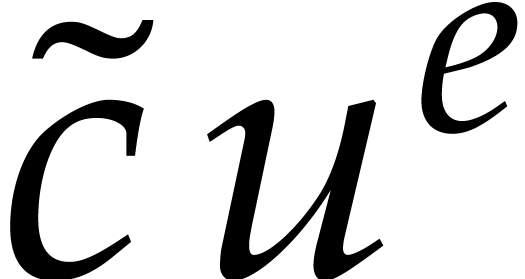 with
with
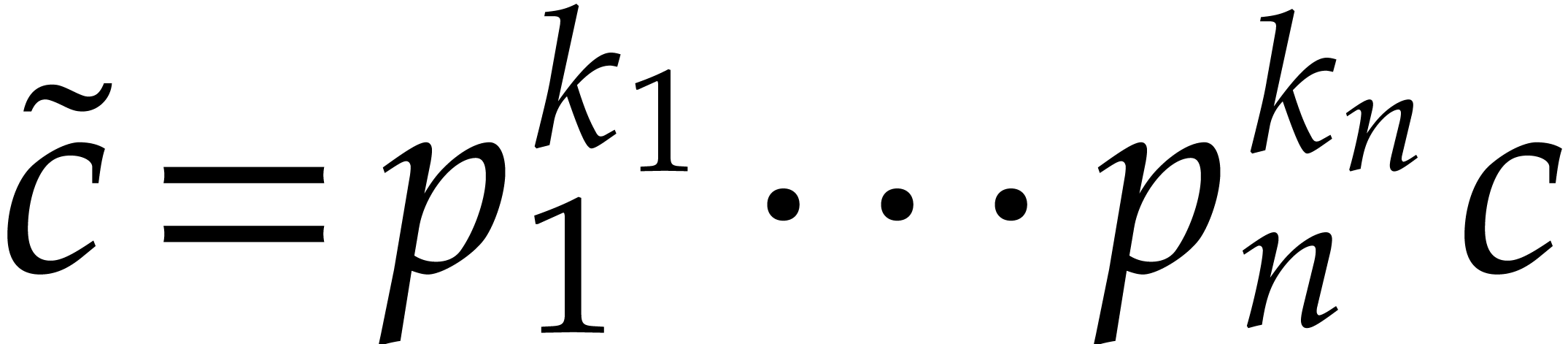 . If there is no other term
that evaluates to an expression of the form
. If there is no other term
that evaluates to an expression of the form 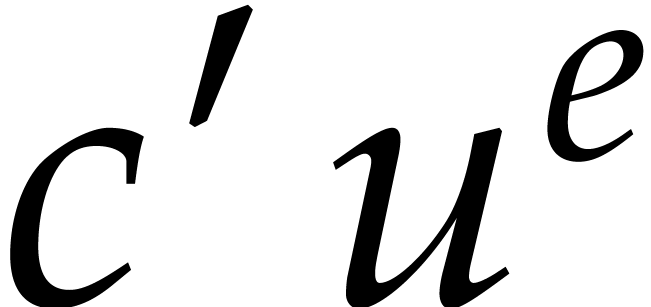 at
at
 , then the same holds for the
evaluation at
, then the same holds for the
evaluation at  . Consequently,
the unique representative
. Consequently,
the unique representative  of the quotient
of the quotient  in
in  coincides with
coincides with  (the quotient is well defined with high probability). From
this, we can determine the exponents
(the quotient is well defined with high probability). From
this, we can determine the exponents  by
factoring
by
factoring  . As additional
safeguards, we also check that
. As additional
safeguards, we also check that 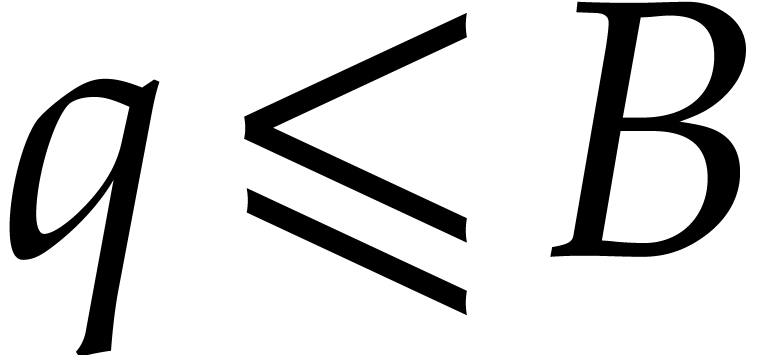 ,
that all prime factors of
,
that all prime factors of  are in
are in  , and that
, and that 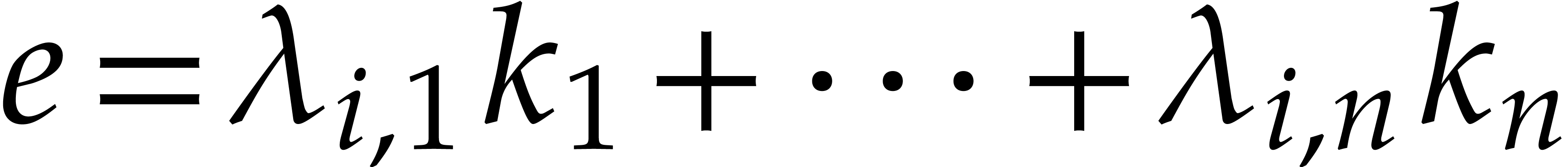 modulo
modulo  .
.
Conversely, assume that there are at least two terms of  that evaluate to an expression of the form
that evaluate to an expression of the form 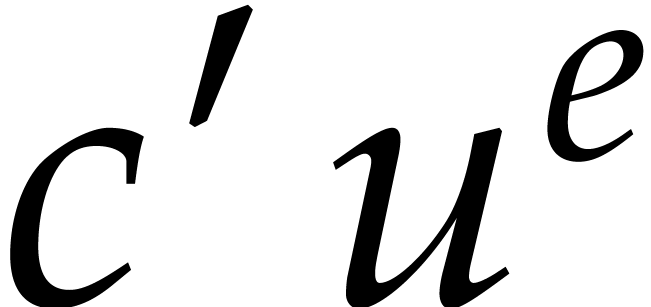 at
at
 . Let
. Let  and
and  now be the coefficients of
now be the coefficients of  in
in  and
and 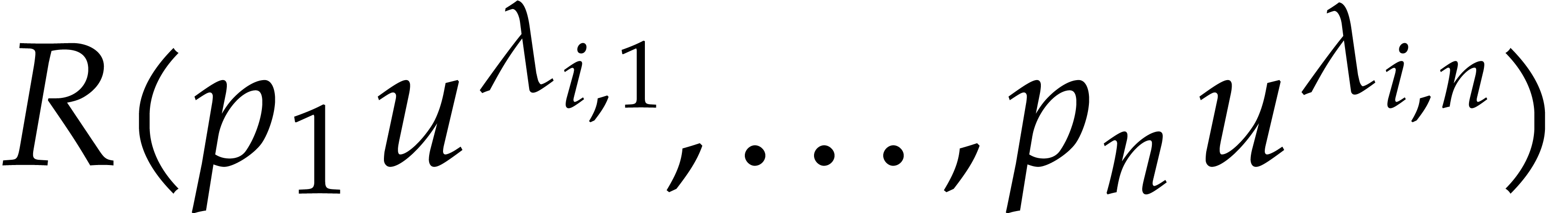 .
Then the quotient
.
Then the quotient 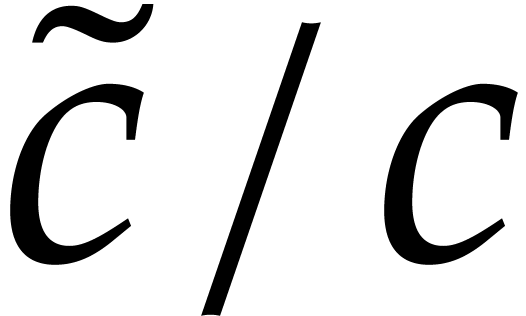 is essentially a random
element in
is essentially a random
element in  (see the heuristic
HC below for more details), so its unique
representative in
(see the heuristic
HC below for more details), so its unique
representative in  is higher than
is higher than  with probability
with probability 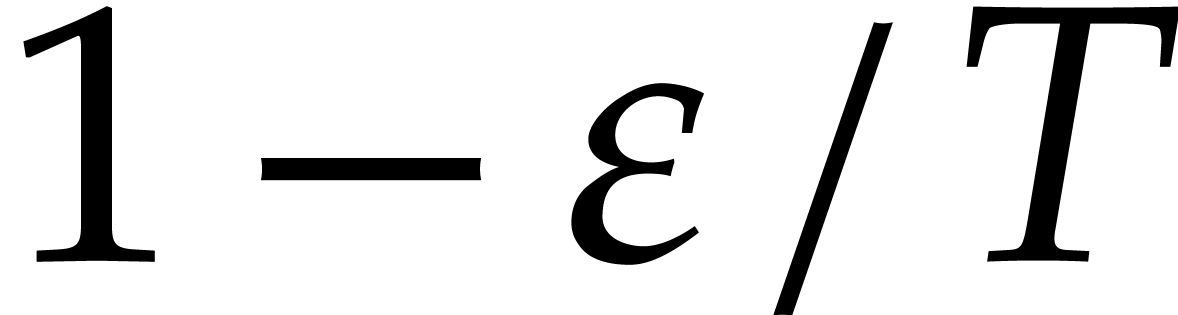 .
This allows our algorithm to detect that we are dealing with colliding
terms; for the
.
This allows our algorithm to detect that we are dealing with colliding
terms; for the 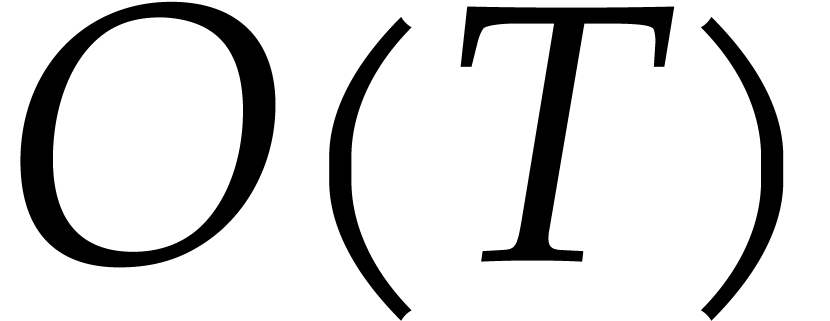 quotients that we need to
consider the probability of failure becomes
quotients that we need to
consider the probability of failure becomes 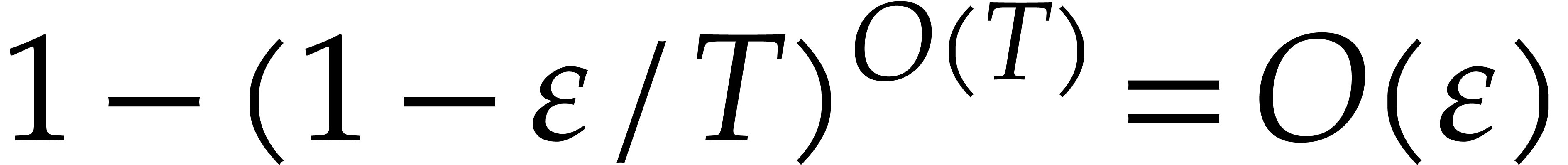 .
.
Using the above technique, the three additional evaluations at  , allow us to determine which balls
end up in a private box in our game of mystery balls. Moreover, since we
can determine the corresponding exponents, we can also find where these
balls landed for the two other throws. This allows us to play our game
modulo minor modifications. Besides maintaining the numbers below the
boxes for the first three throws, we also maintain the corresponding
numbers for the evaluations at
, allow us to determine which balls
end up in a private box in our game of mystery balls. Moreover, since we
can determine the corresponding exponents, we can also find where these
balls landed for the two other throws. This allows us to play our game
modulo minor modifications. Besides maintaining the numbers below the
boxes for the first three throws, we also maintain the corresponding
numbers for the evaluations at 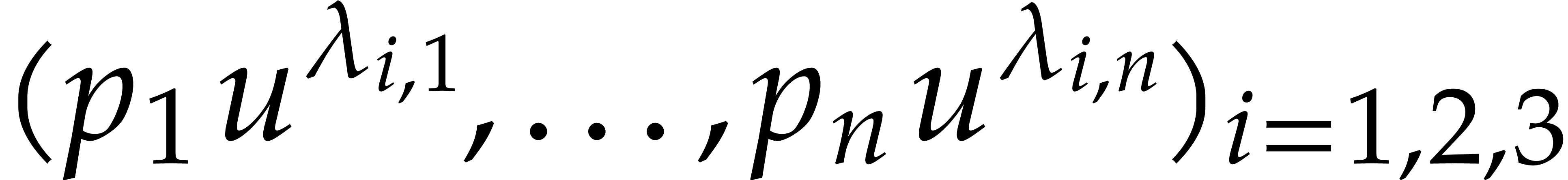 .
For every round of the game, the same technique then allows us to
determine which balls have private boxes, and iterate.
.
For every round of the game, the same technique then allows us to
determine which balls have private boxes, and iterate.
In our probabilistic analysis, it is important that the quotients 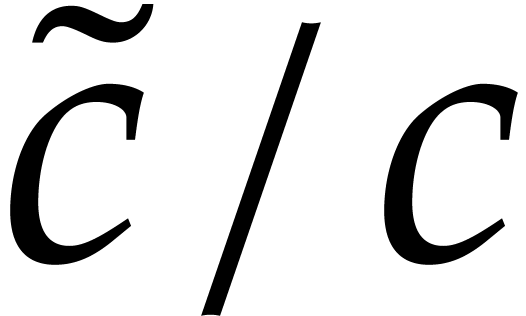 are essentially random elements in
are essentially random elements in 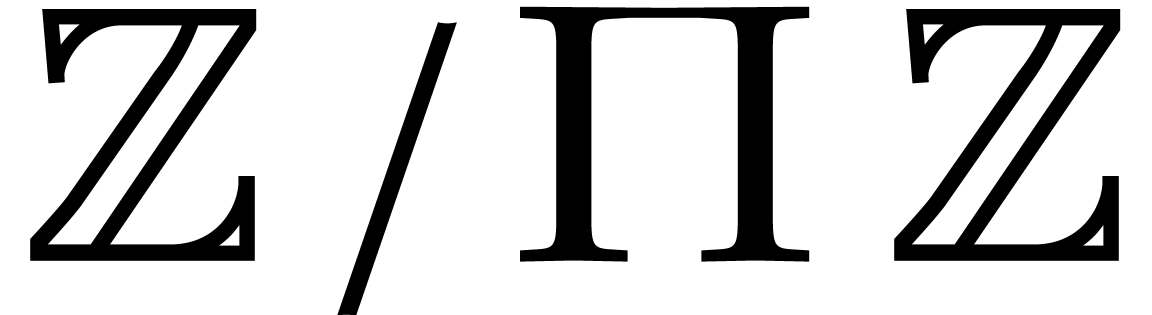 in case of collisions. This assumption might fail when the coefficients
of
in case of collisions. This assumption might fail when the coefficients
of 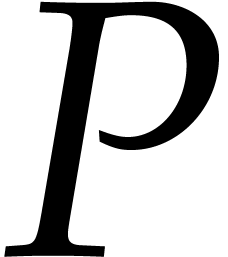 and
and  are special
(e.g. either zero or one). Nevertheless, it becomes
plausible after a change of variables
are special
(e.g. either zero or one). Nevertheless, it becomes
plausible after a change of variables 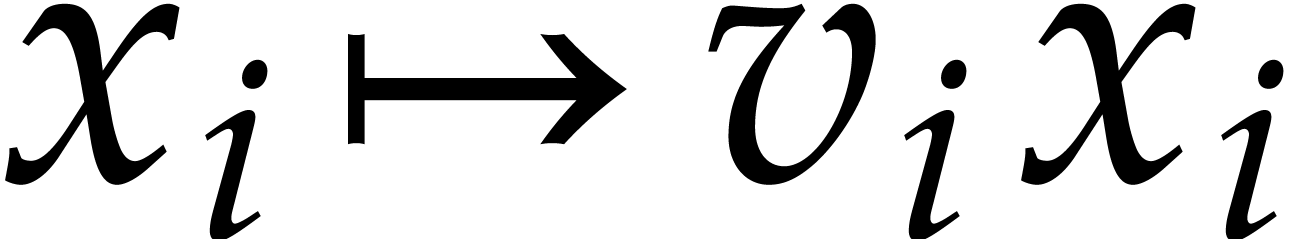 ,
,
 , where
, where  are random invertible elements in
are random invertible elements in 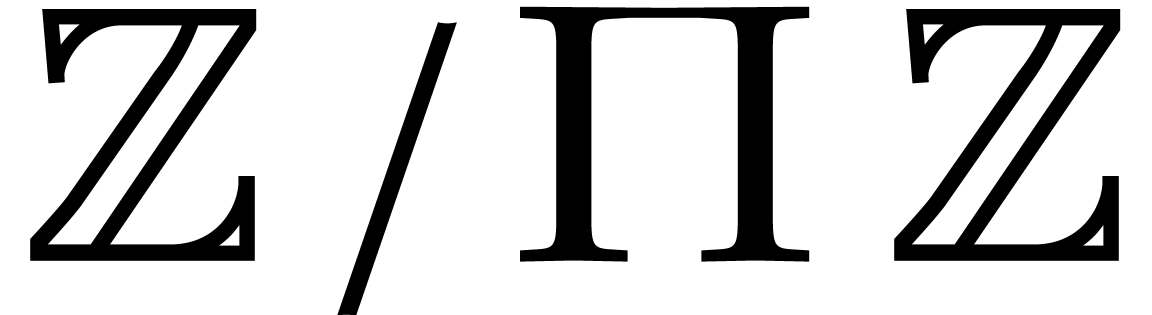 .
Let us formulate this as our second heuristic:
.
Let us formulate this as our second heuristic:
For random vectors 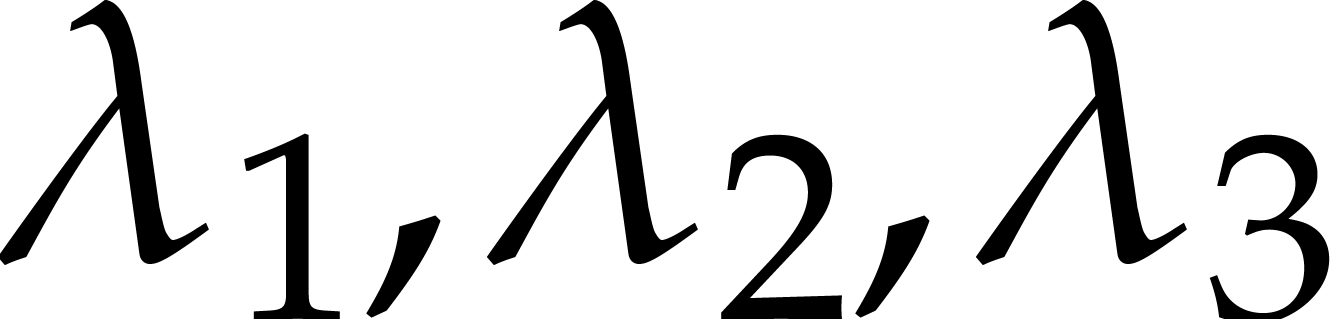 and after a random
change of variables
and after a random
change of variables 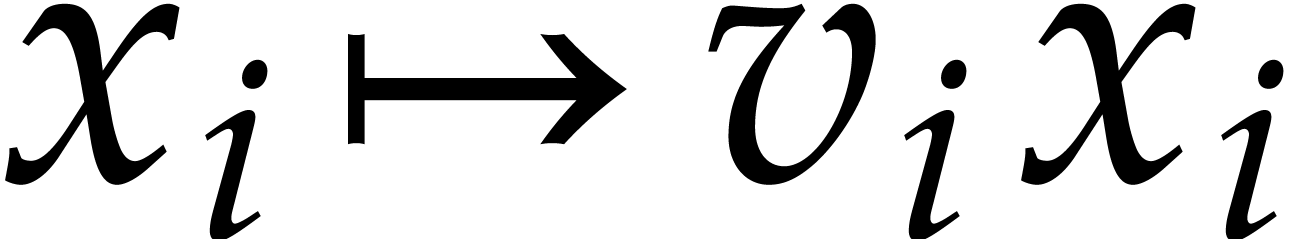 (
( ), the quotients
), the quotients 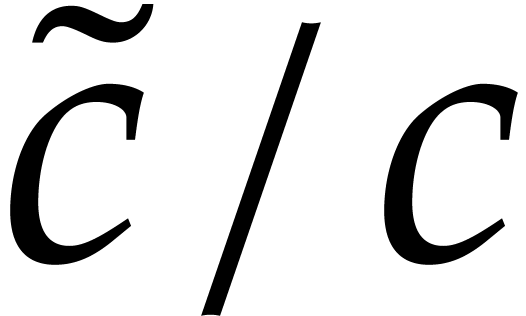 as above are uniformly distributed over
as above are uniformly distributed over 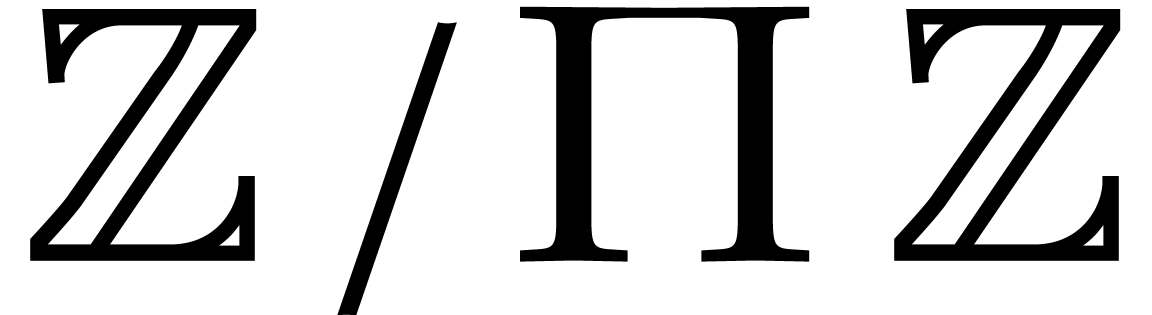 , and the distributions for different
quotients are independent.
, and the distributions for different
quotients are independent.
Algorithm 2 summarizes our method, while incorporating the random change of variables.
Algorithm
Output: the exponents of the product
Assume: |
 with distinct prime factors, it
takes
with distinct prime factors, it
takes
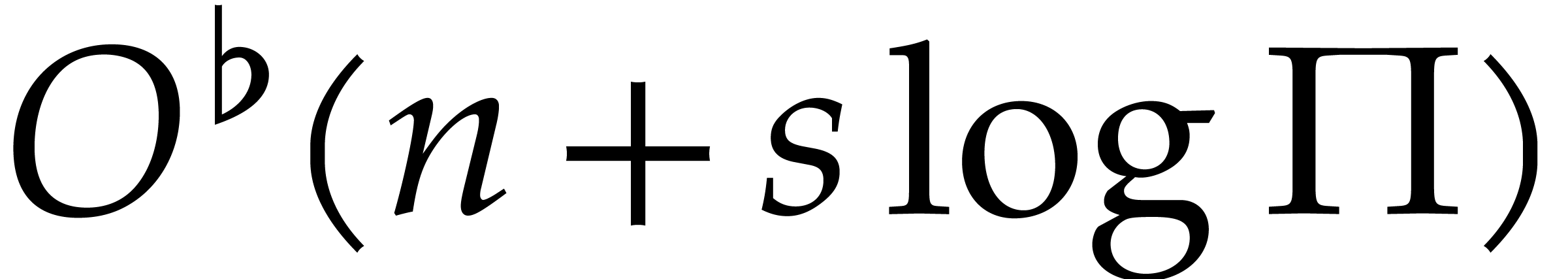
bit operations to determine the existence of a prime factorization
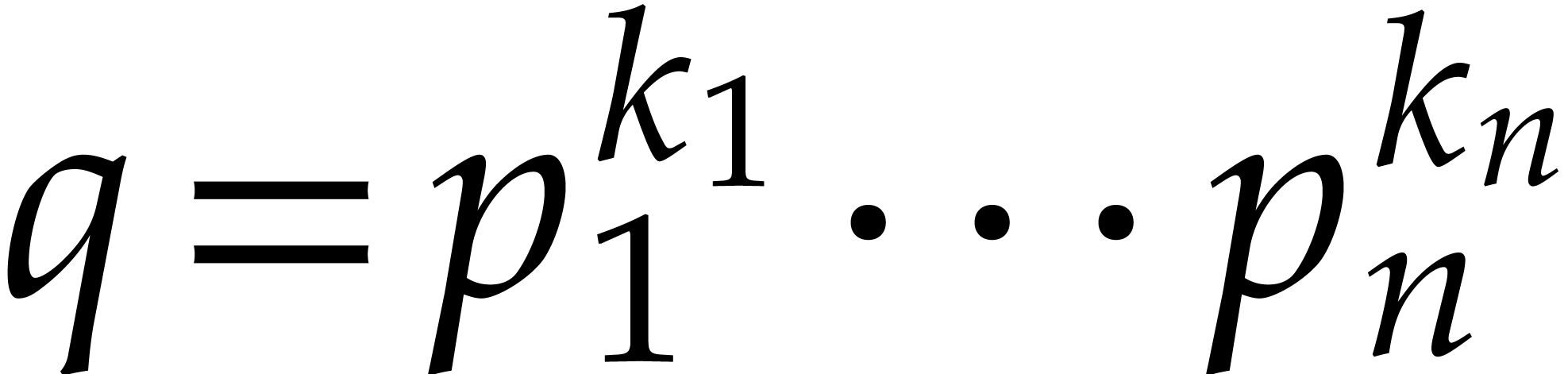 with
with  ,
and to compute it in case there is.
,
and to compute it in case there is.
Proof. We first determine the indices 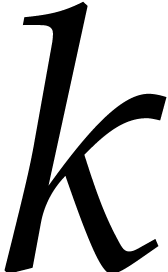 with
with 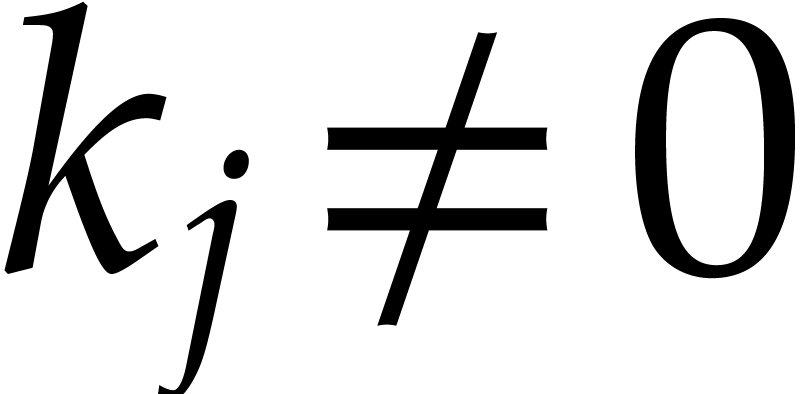 using a divide and conquer
technique. At the top level, we start with the remainder
using a divide and conquer
technique. At the top level, we start with the remainder  of the division of
of the division of  by
by  . We next compute
. We next compute 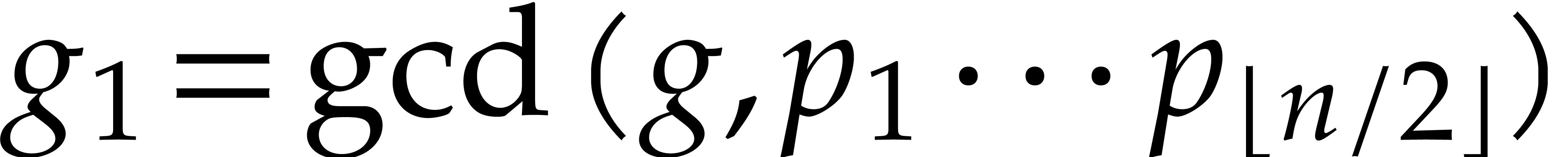 and
and
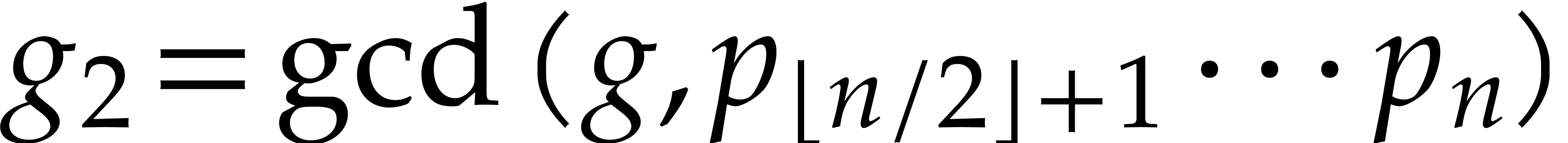 . If
. If 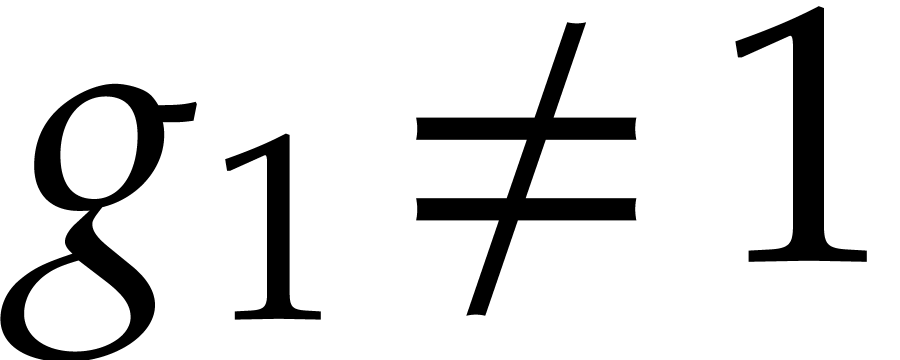 , then we go on with the computation of
, then we go on with the computation of 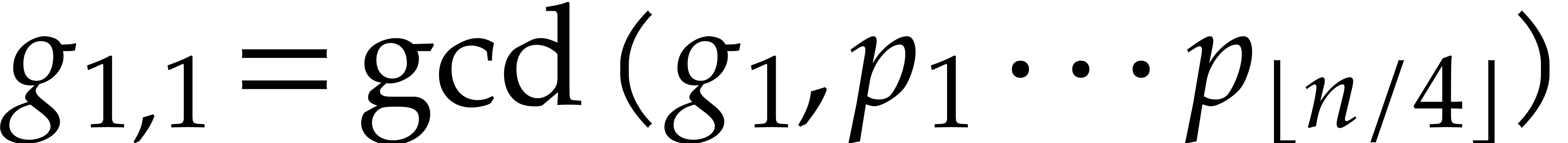 and
and 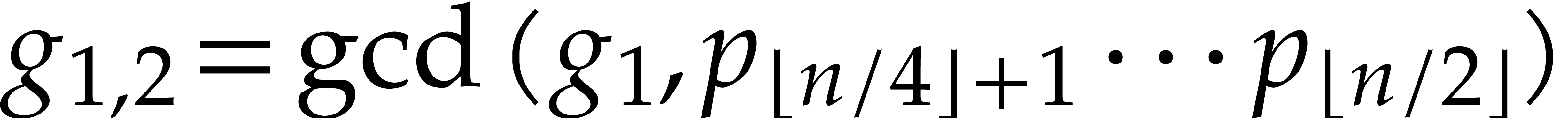 , and
similarly for
, and
similarly for 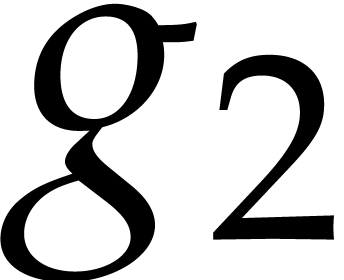 . We repeat
this dichotomic process until we have found all prime factors of
. We repeat
this dichotomic process until we have found all prime factors of 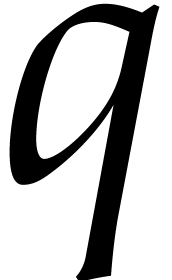 . For each of the
. For each of the  prime factors
prime factors 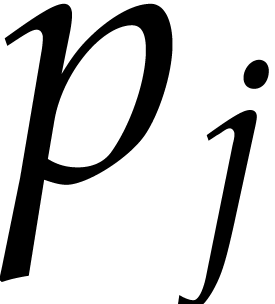 of
of 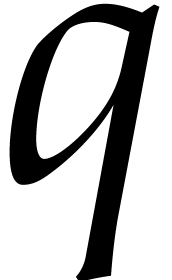 ,
we next compute
,
we next compute 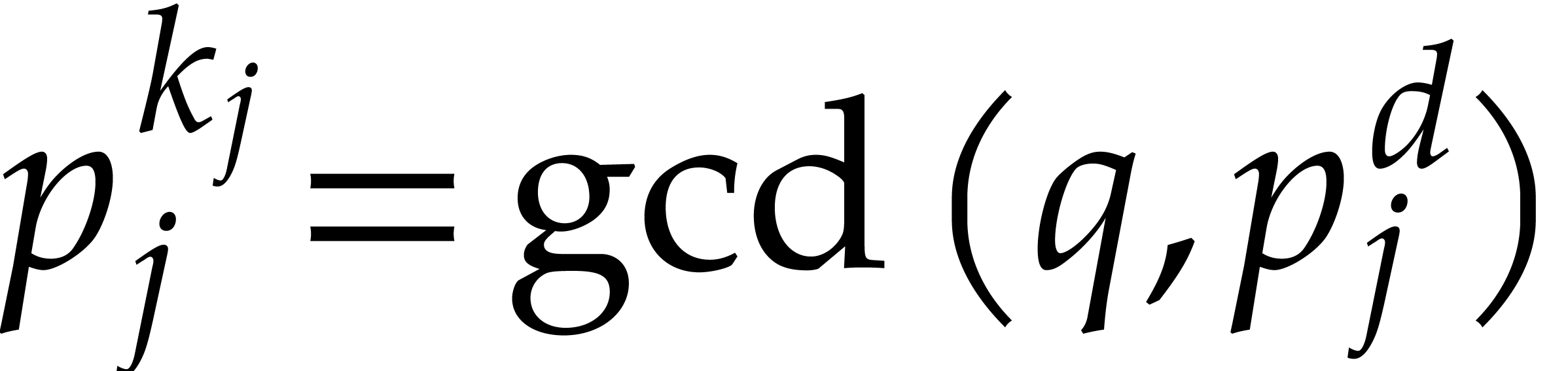 and
and 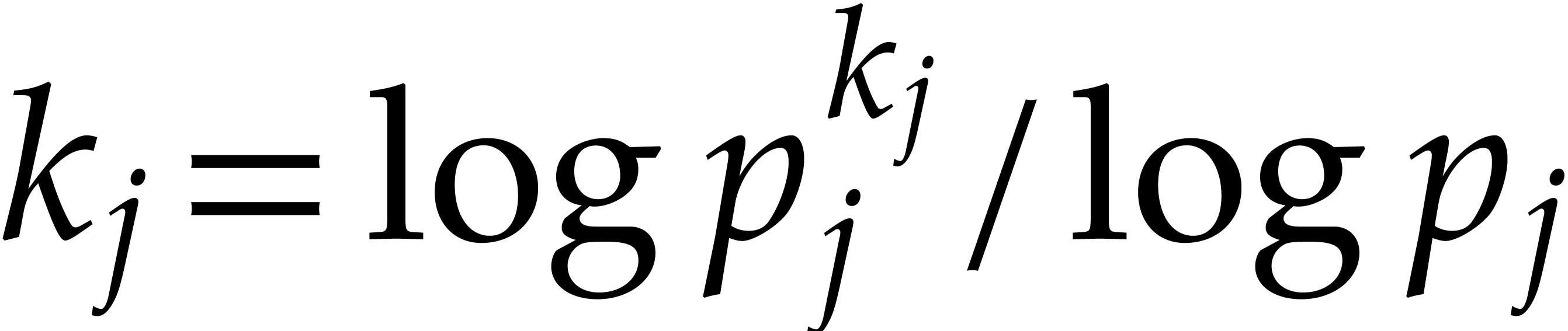 . The total running time of this algorithm is
bounded by
. The total running time of this algorithm is
bounded by 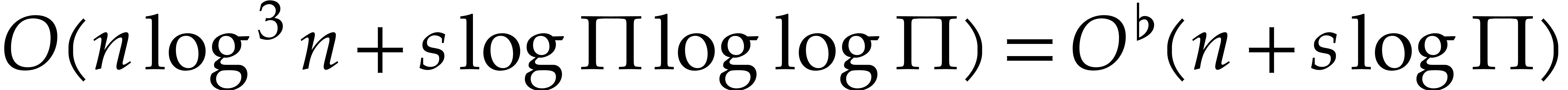 .
.
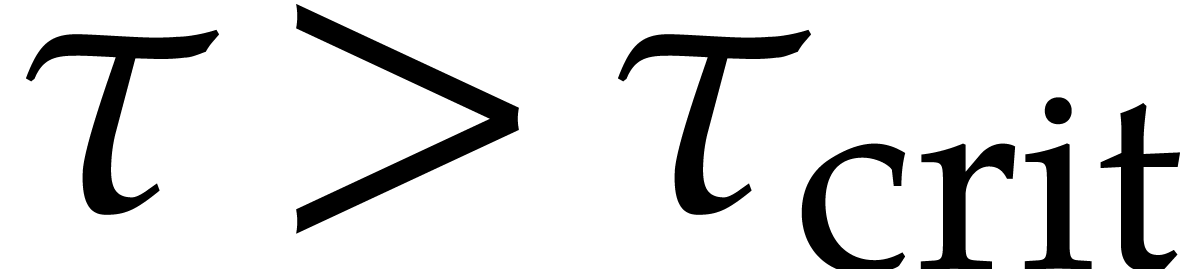 with
with 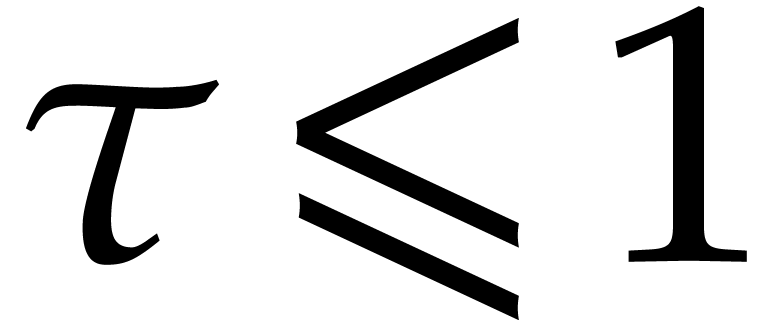 ,
, 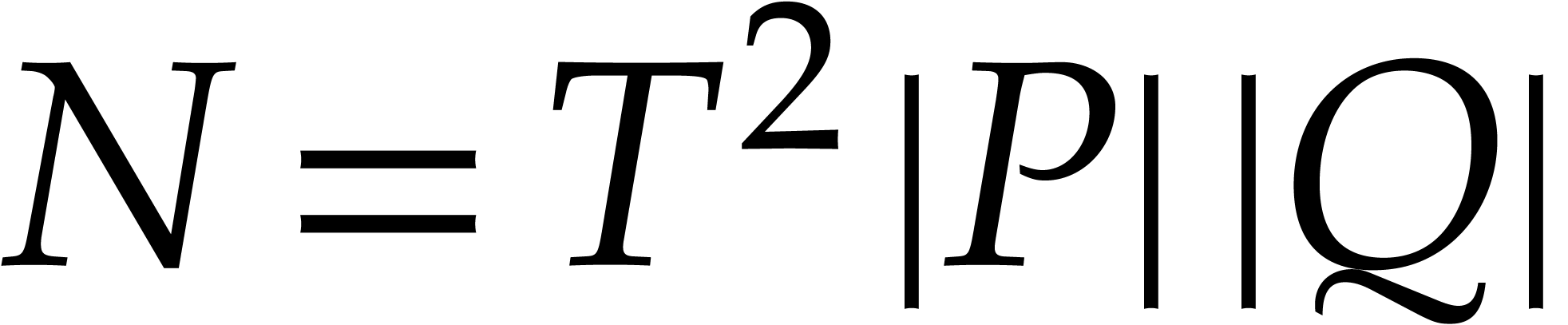 , and
, and 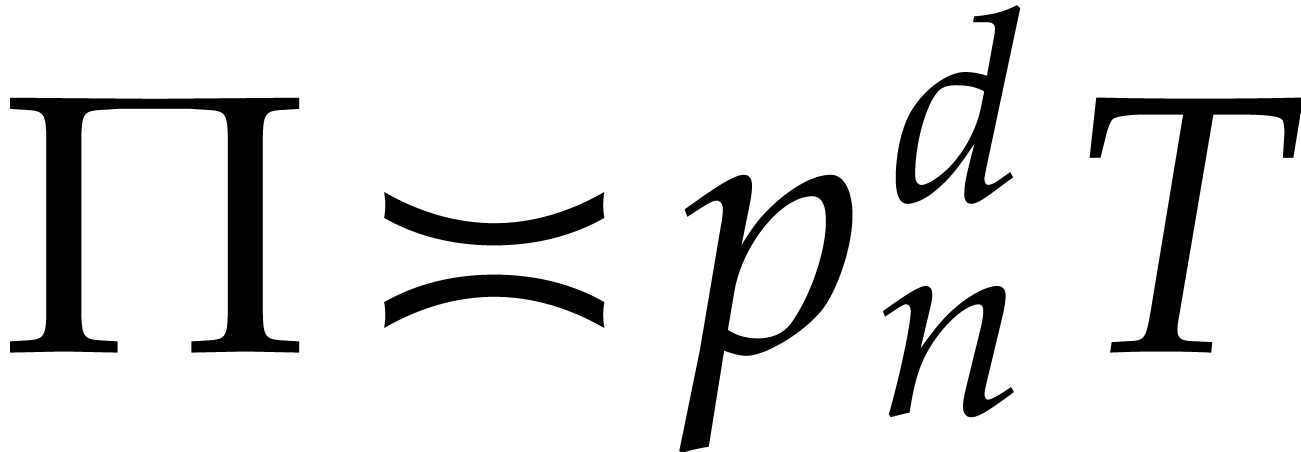 .
Then Algorithm 2 is correct and runs in time
.
Then Algorithm 2 is correct and runs in time
Proof. We have already explained why our
algorithm returns the correct answer with probability  . The complexity analysis for steps 5,
6 and 8b is similar as the one
for Algorithm 1. The running time for the other steps is as
follows:
. The complexity analysis for steps 5,
6 and 8b is similar as the one
for Algorithm 1. The running time for the other steps is as
follows:
The reductions of 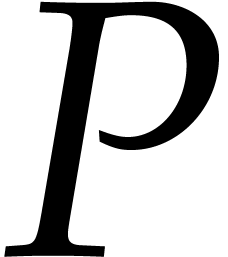 and
and  modulo
modulo  can be computed in time
can be computed in time 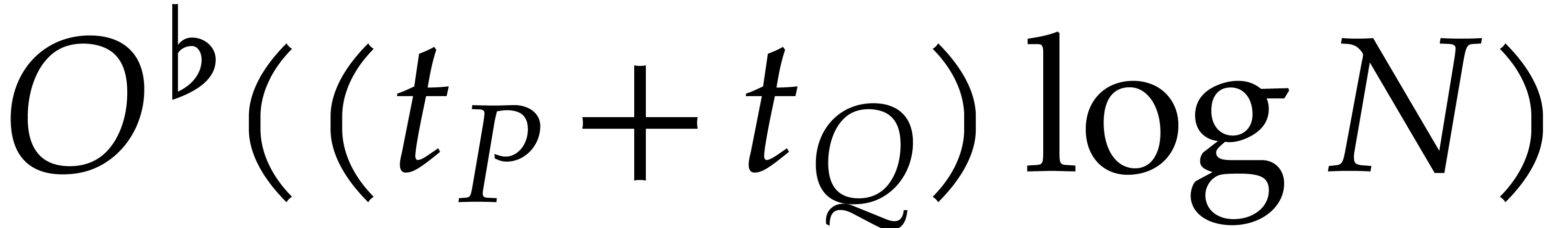 , in step 3.
, in step 3.
In step 4, we have to compute 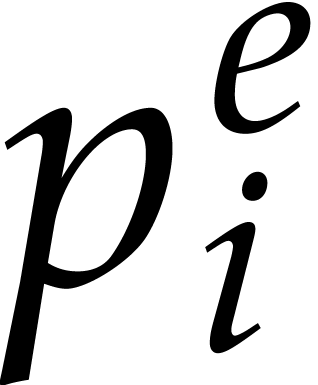 modulo
modulo  for every power
for every power 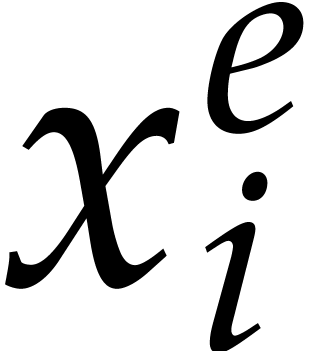 occurring in the representation of
occurring in the representation of  or
or  . Using binary powering, such a
power can be computed in time
. Using binary powering, such a
power can be computed in time 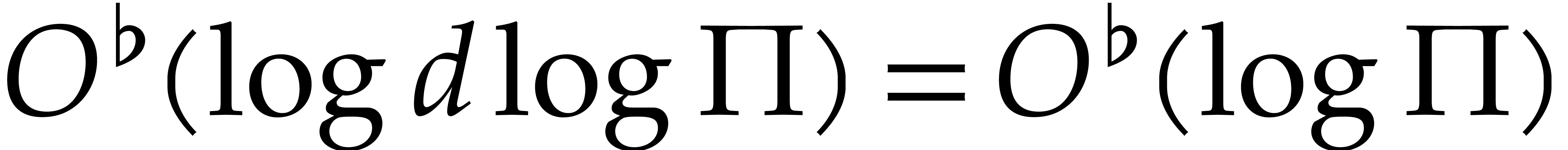 .
The total cost of this step is therefore bounded by
.
The total cost of this step is therefore bounded by 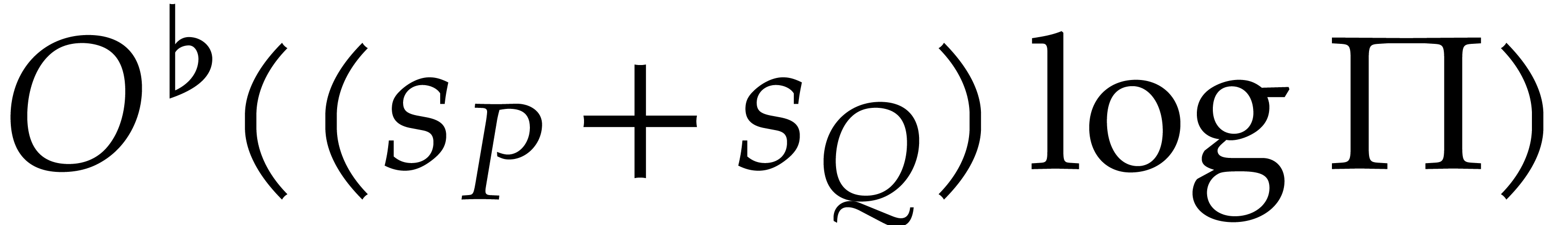 .
.
In steps 7 and 8c, we have
already shown that one factorization can be done in time 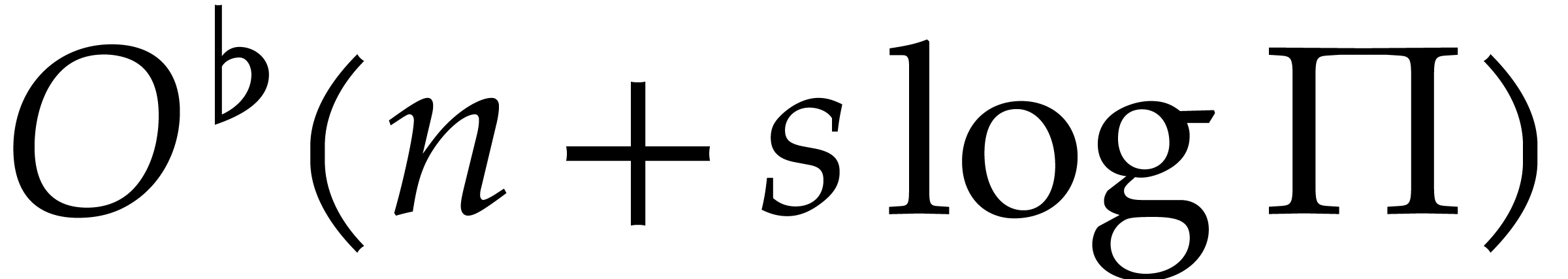 . Altogether, the cost of these
steps is therefore bounded by
. Altogether, the cost of these
steps is therefore bounded by 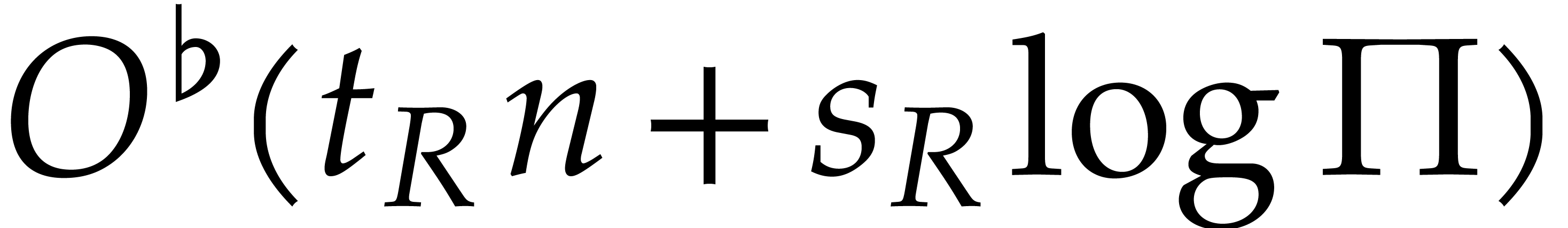 .
.

In section 4.2, we have described an efficient algorithm
for the case when the total degree  is small.
This indeed holds for most practical applications, but it attractive to
also study the case when our polynomials are “truly sparse”
with potentially large exponents. This is already interesting for
univariate polynomials, a case that we also did not consider so far.
Modulo the technique of Kronecker substitution [21, Section
7.1], it actually suffices to consider the univariate case. For
simplicity, let us restrict ourselves to this case. When
is small.
This indeed holds for most practical applications, but it attractive to
also study the case when our polynomials are “truly sparse”
with potentially large exponents. This is already interesting for
univariate polynomials, a case that we also did not consider so far.
Modulo the technique of Kronecker substitution [21, Section
7.1], it actually suffices to consider the univariate case. For
simplicity, let us restrict ourselves to this case. When 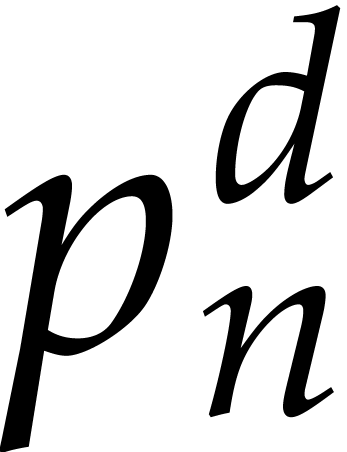 gets moderately large, it can also be interesting to
consider the incremental approach from [20] and [21,
Section 7.3].
gets moderately large, it can also be interesting to
consider the incremental approach from [20] and [21,
Section 7.3].
One first observation in the univariate case is that we can no longer
take the same number of boxes 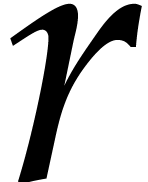 for our three
throws. Next best is to take
for our three
throws. Next best is to take 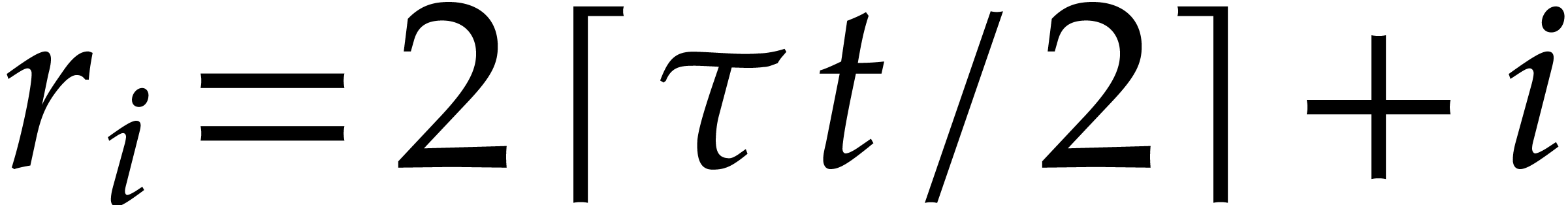 boxes for our
boxes for our  -th throw, where
-th throw, where 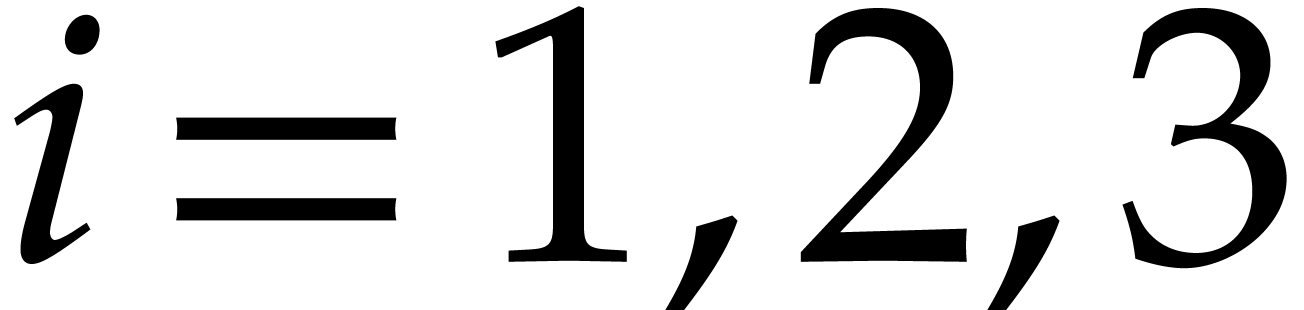 . By construction this ensures that
. By construction this ensures that 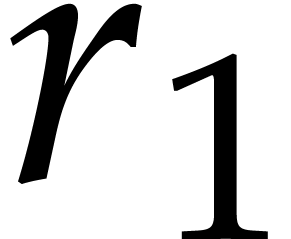 ,
, 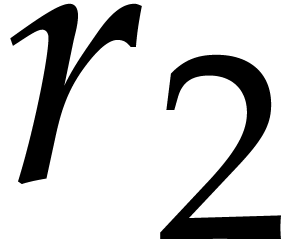 ,
and
,
and 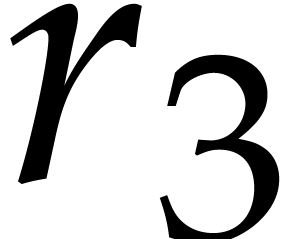 are pairwise coprime. If the exponents of
are pairwise coprime. If the exponents of
 are large, then it is also reasonable to assume
that our heuristic HE still holds.
are large, then it is also reasonable to assume
that our heuristic HE still holds.
For the efficient determination of the exponents, let 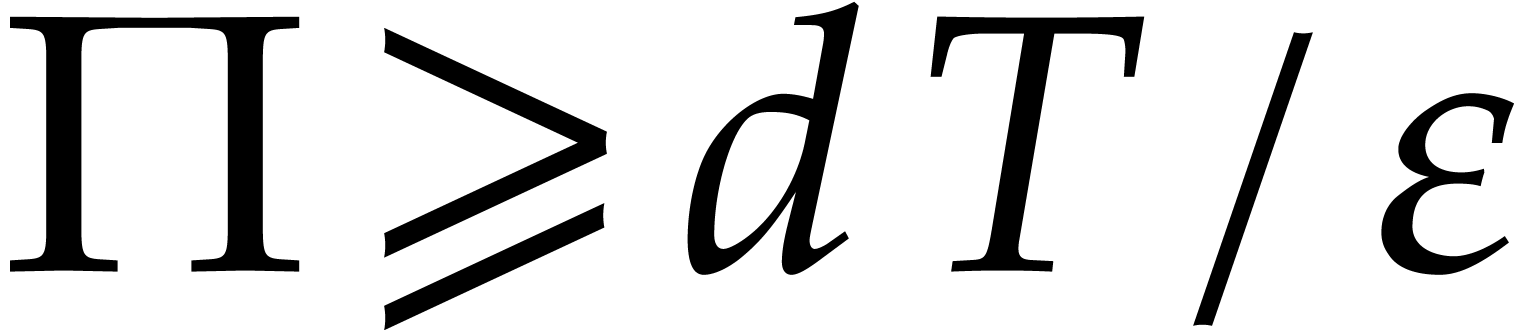 . As before, we may take
. As before, we may take  to be prime or a product of prime numbers that fit into machine words.
Following Huang [26], we now evaluate both
to be prime or a product of prime numbers that fit into machine words.
Following Huang [26], we now evaluate both 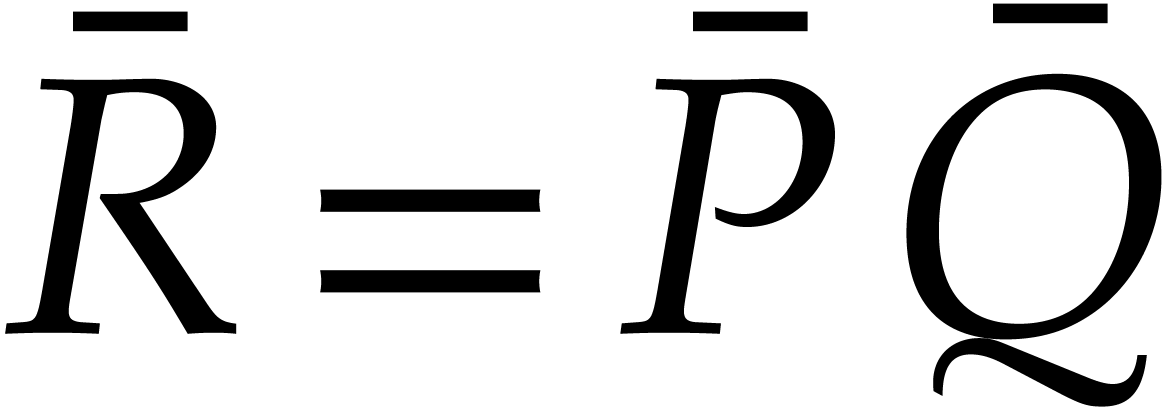 and
and 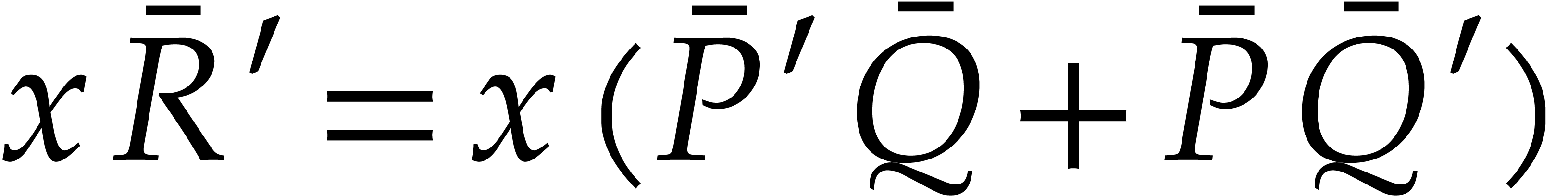 at
at  in
in 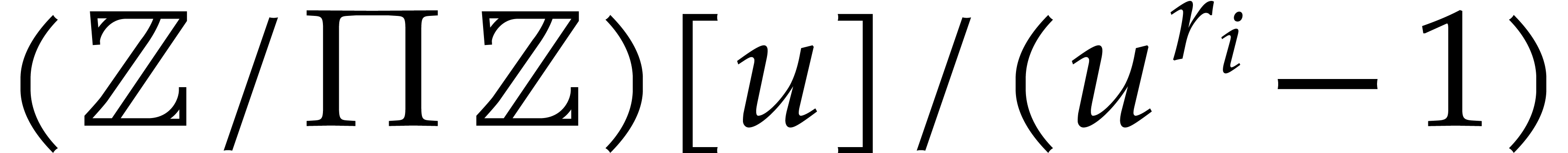 for
for 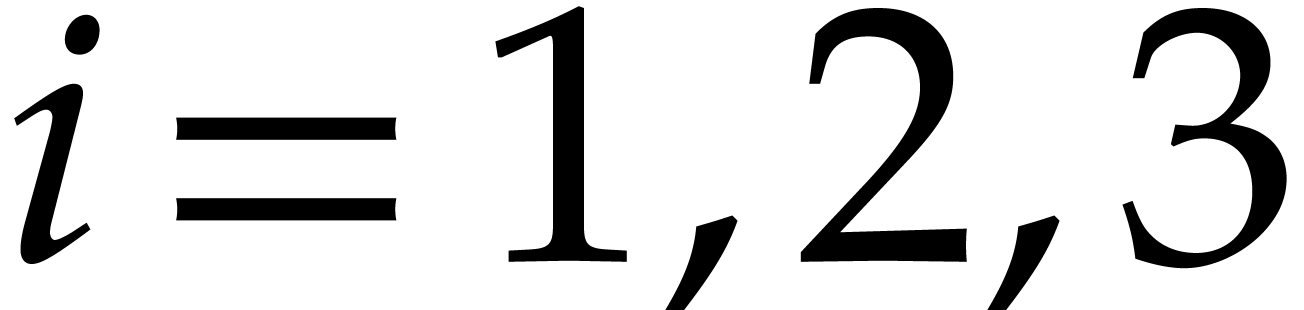 . Any term
. Any term
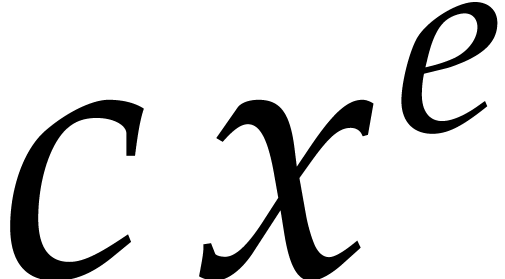 of
of 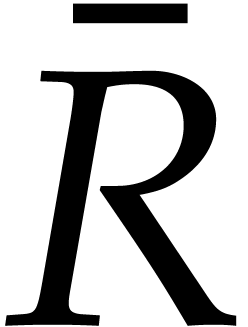 then gives rise to a
term
then gives rise to a
term 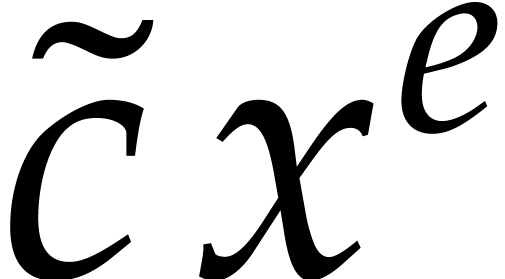 of
of 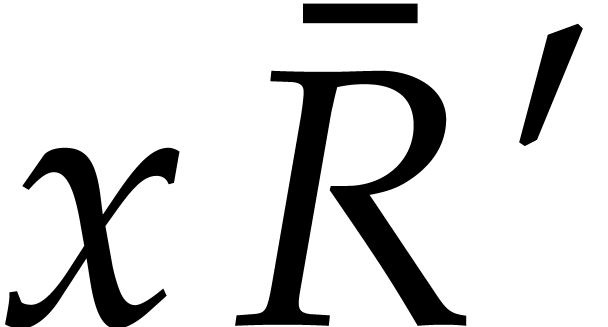 with
with  , so we can directly read off
, so we can directly read off 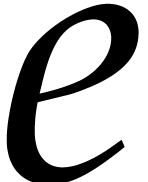 from the quotient
from the quotient 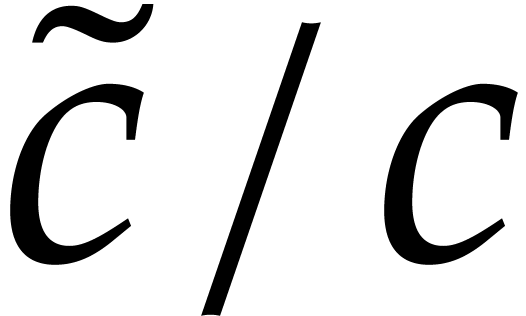 .
Modulo the above changes, this allows us to proceed as in Algorithm 2. One may prove in a similar way as before that the bit
complexity of determining the exponents in this way is bounded by
.
Modulo the above changes, this allows us to proceed as in Algorithm 2. One may prove in a similar way as before that the bit
complexity of determining the exponents in this way is bounded by
The computation of the coefficients can be done in time
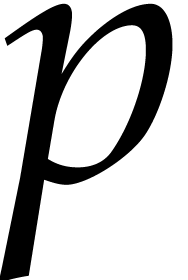 ,
it is also possible to use coefficients in
,
it is also possible to use coefficients in  , while using a fixed point number representation.
Provided that all coefficients have the same order of magnitude, the
floating point case can be reduced to this case. Indeed, the
reductions modulo
, while using a fixed point number representation.
Provided that all coefficients have the same order of magnitude, the
floating point case can be reduced to this case. Indeed, the
reductions modulo  are remarkably stable from a
numerical point of view, and we may use FFT-multiplication in
are remarkably stable from a
numerical point of view, and we may use FFT-multiplication in 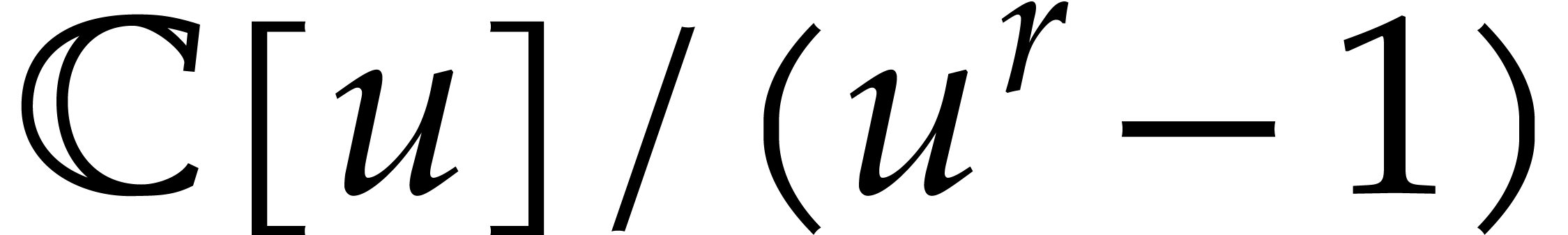 . Algorithm 2 can
also be adapted, provided that
. Algorithm 2 can
also be adapted, provided that  .
.
 small in
Algorithm 2 by using the incremental technique from [20] and [21, Section 7.3]. Over finite fields
small in
Algorithm 2 by using the incremental technique from [20] and [21, Section 7.3]. Over finite fields
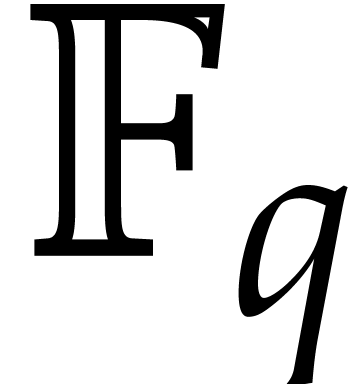 of small characteristic, one needs to use
other techniques from [21].
of small characteristic, one needs to use
other techniques from [21].
Instead of taking our three additional evaluation points of the form
 , we may for instance take
them of the form
, we may for instance take
them of the form 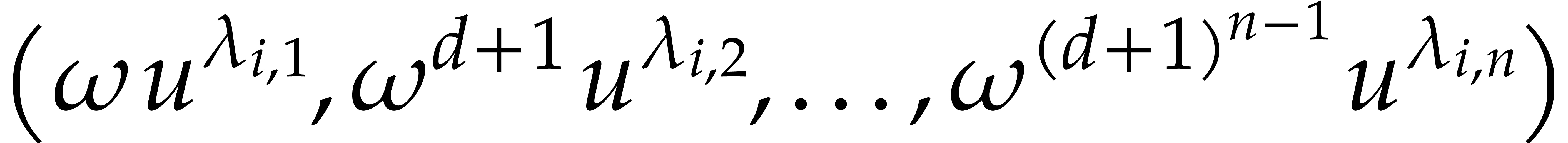 , where
, where 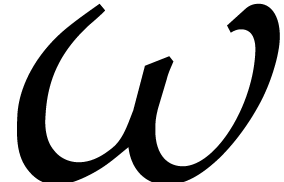 is a primitive root of unity of large smooth order
(this may force us to work over an extension field; alternatively, one
may use the aforementioned incremental technique and roots
is a primitive root of unity of large smooth order
(this may force us to work over an extension field; alternatively, one
may use the aforementioned incremental technique and roots  of lower orders). Thanks to the smoothness assumption,
discrete logarithms of powers of
of lower orders). Thanks to the smoothness assumption,
discrete logarithms of powers of  can be computed
efficiently using Pohlig–Hellman's algorithm. This allows us to
recover exponents
can be computed
efficiently using Pohlig–Hellman's algorithm. This allows us to
recover exponents  from quotients of the form
from quotients of the form
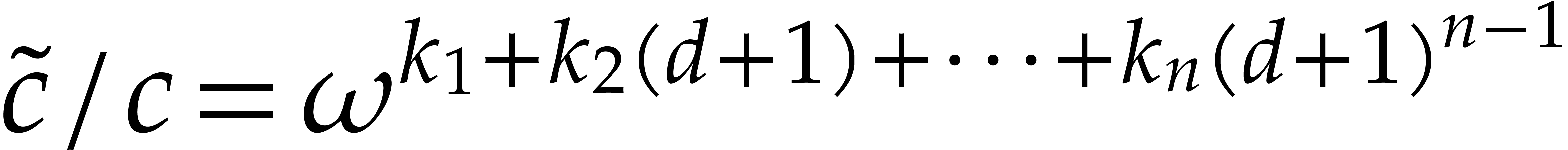 .
.
 , in which case complexities are
measured in terms of the number of operations in
, in which case complexities are
measured in terms of the number of operations in  . For rings of sufficiently large
characteristic, one may directly adapt the algorithms from section 4. For rings of small characteristic, it is possible to
generalize the techniques from the finite field case.
. For rings of sufficiently large
characteristic, one may directly adapt the algorithms from section 4. For rings of small characteristic, it is possible to
generalize the techniques from the finite field case.
The techniques from this paper can also be used for general purpose
sparse interpolation. In that case the polynomial 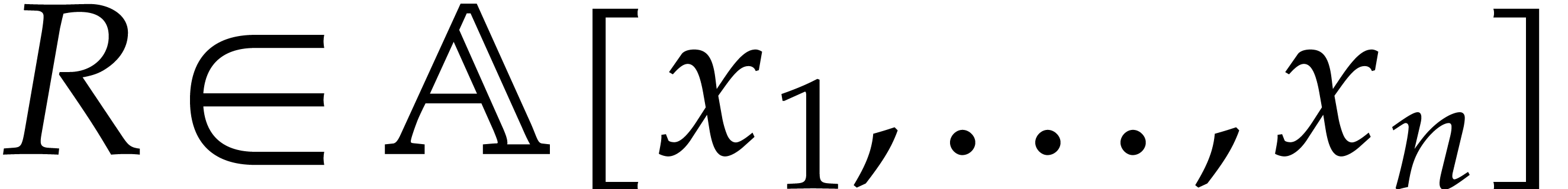 is given through an arbitrary blackbox function that can be evaluated at
points in
is given through an arbitrary blackbox function that can be evaluated at
points in  -algebras over some
ring
-algebras over some
ring  . This problem was
studied in detail in [21]. In section 6, we investigated in
particular how to replace expensive evaluations in cyclic
. This problem was
studied in detail in [21]. In section 6, we investigated in
particular how to replace expensive evaluations in cyclic  -algebras of the form
-algebras of the form 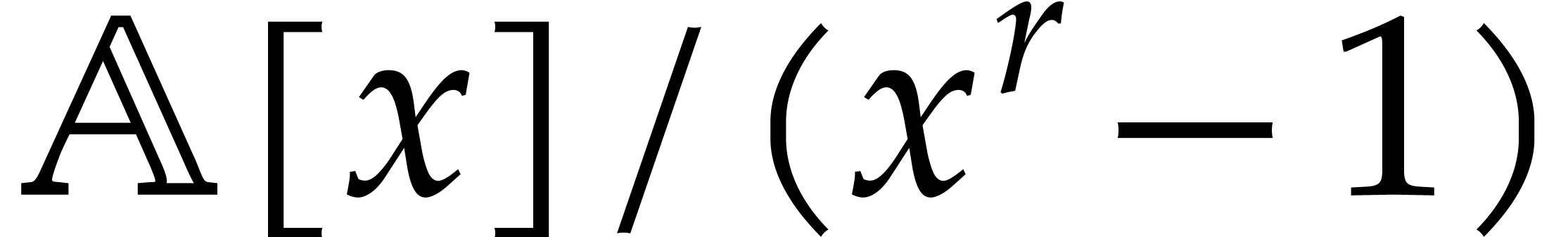 by cheaper evaluations at suitable
by cheaper evaluations at suitable 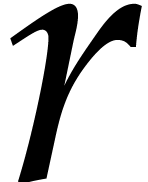 -th
roots of unity in
-th
roots of unity in  or a small extension of
or a small extension of  . The main new techniques from this
paper were also anticipated in section 6.6.
. The main new techniques from this
paper were also anticipated in section 6.6.
The algorithms from this paper become competitive with the geometric
sequence approach if the blackbox function is particularly cheap to
evaluate. Typically, the cost  of one evaluation
should be
of one evaluation
should be 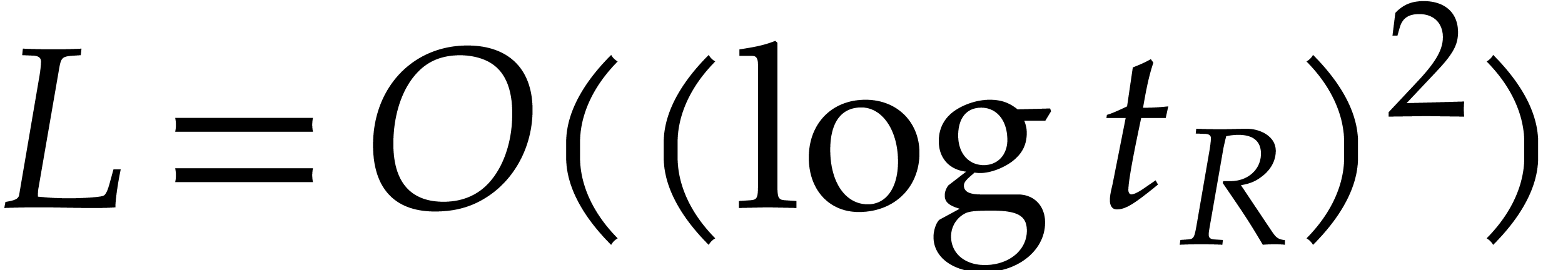 or
or 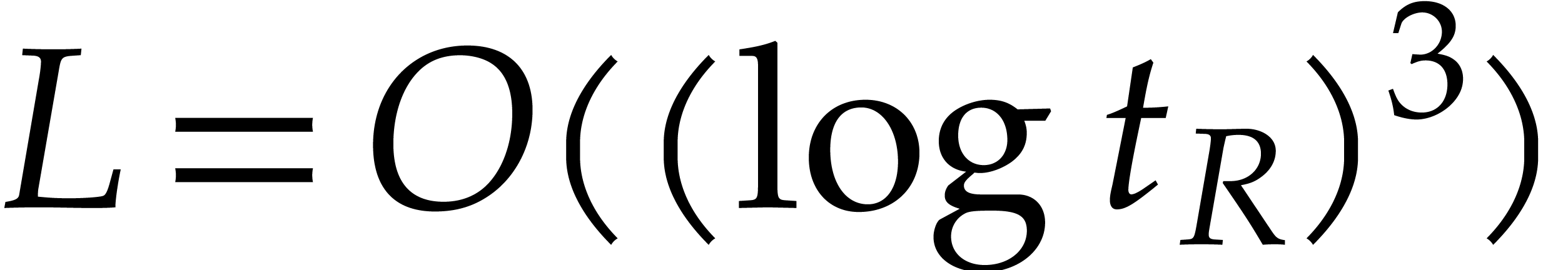 ,
depending on the specific variant of the geometric sequence approach
that we use.
,
depending on the specific variant of the geometric sequence approach
that we use.
Technically speaking, it is interesting to note that the problem from
this paper actually does not fit into this framework. Indeed,
if 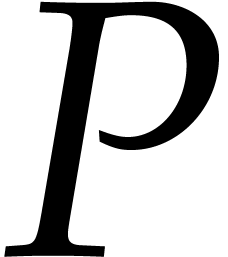 and
and 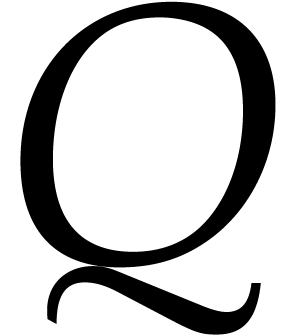 are sparse
polynomial that are represented in their standard expanded form, then
the evaluation of
are sparse
polynomial that are represented in their standard expanded form, then
the evaluation of 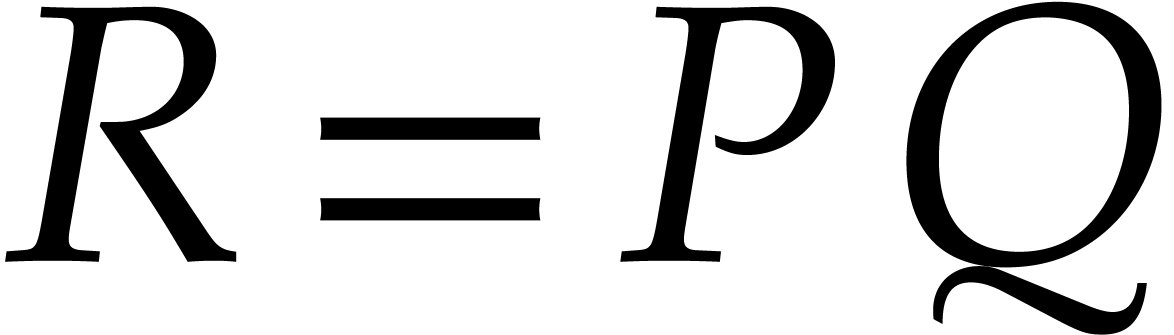 at a single point requires
at a single point requires
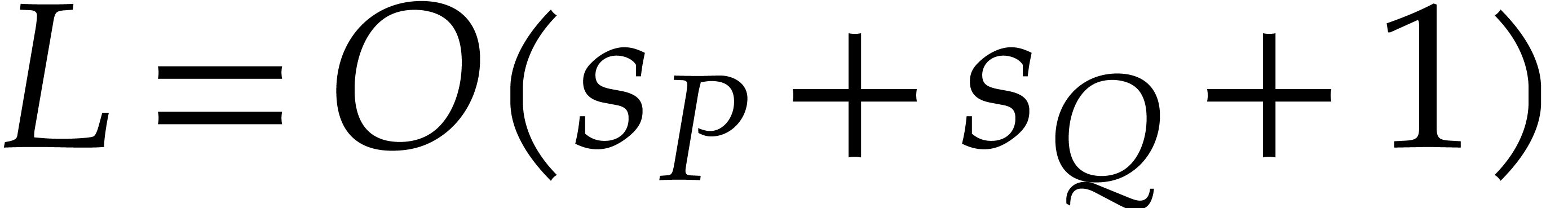 operations in
operations in  ,
and we typically have
,
and we typically have 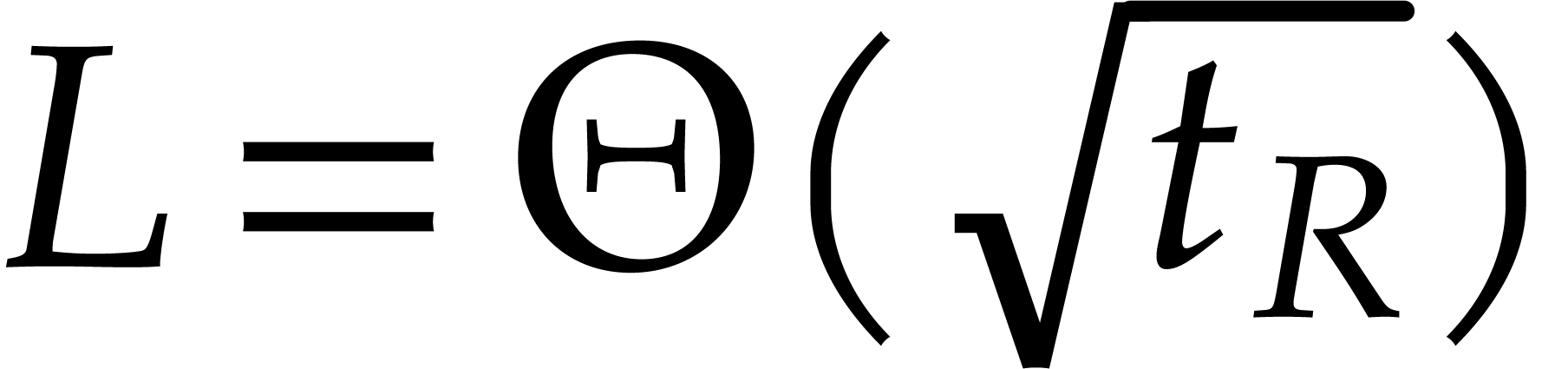 . This
is due to the fact that the standard blackbox model does not take into
account possible speed-ups if we evaluate our function at many points in
geometric progression or at
. This
is due to the fact that the standard blackbox model does not take into
account possible speed-ups if we evaluate our function at many points in
geometric progression or at 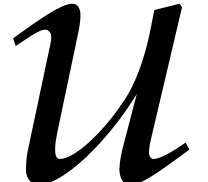 in a cyclic algebra
in a cyclic algebra
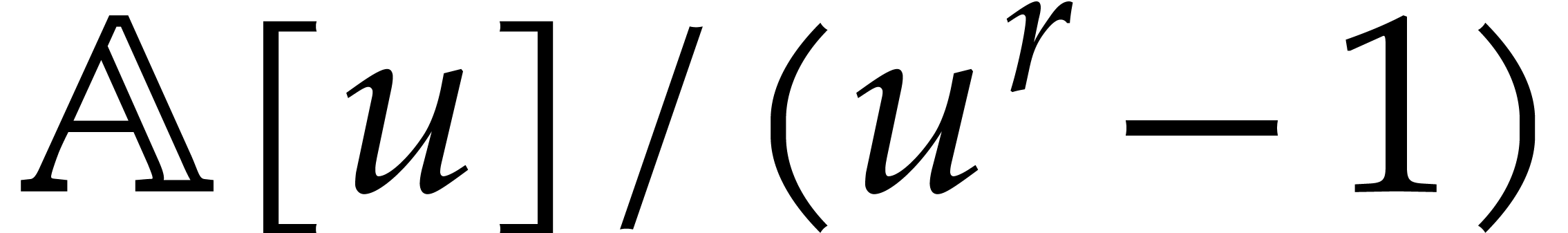 .
.
Both in theory and for practical applications, it would be better to
extend the blackbox model by allowing for polynomials  of the form
of the form
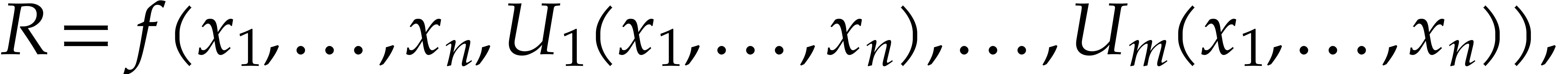
where 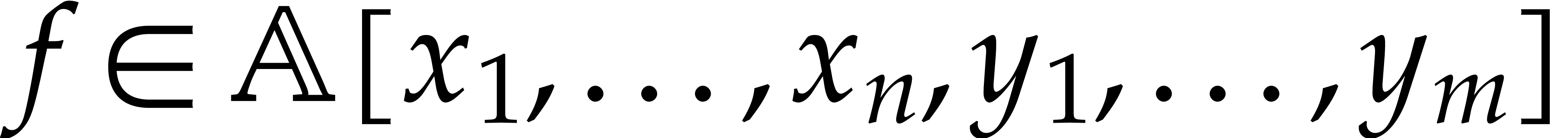 is a blackbox function and
is a blackbox function and  are sparse polynomials in their usual expanded
representation. Within this model, the techniques from this paper should
become efficient for many other useful operations on sparse polynomials,
such as the computation of gcds or determinants of matrices whose
entries are large sparse polynomials.
are sparse polynomials in their usual expanded
representation. Within this model, the techniques from this paper should
become efficient for many other useful operations on sparse polynomials,
such as the computation of gcds or determinants of matrices whose
entries are large sparse polynomials.
The heuristic HE plays an important role in our
complexity analysis. It is an interesting question whether it is
satisfied for polynomials  whose support is
highly regular and not random at all. A particularly important case is
when
whose support is
highly regular and not random at all. A particularly important case is
when 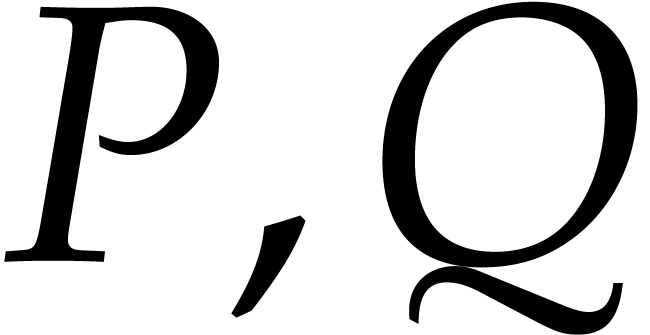 and
and  are dense
polynomials in
are dense
polynomials in 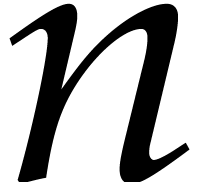 variables of total degrees
variables of total degrees 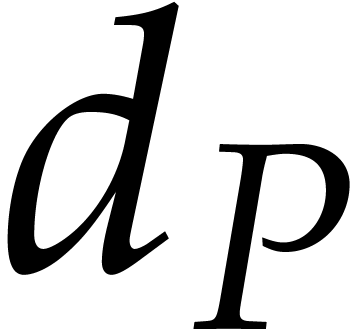 ,
, 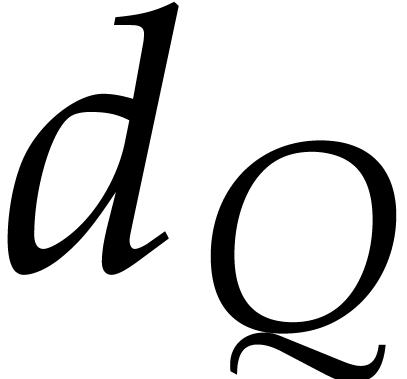 and
and 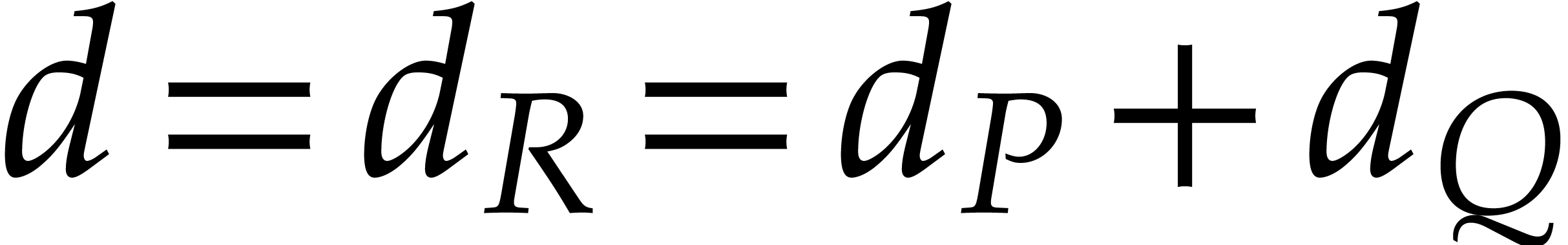 . Such polynomials are often
considered to be sparse, due to the fact that
. Such polynomials are often
considered to be sparse, due to the fact that  contains about
contains about 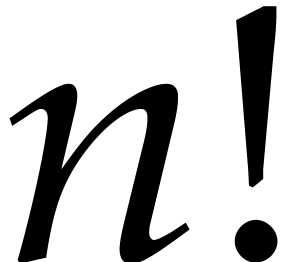 times less terms than a fully
dense polynomial of degree
times less terms than a fully
dense polynomial of degree  in each variable.
in each variable.
If  is bivariate or trivariate and of very high
degree, then it has been shown in [16] that
is bivariate or trivariate and of very high
degree, then it has been shown in [16] that  can be computed in approximately the same time as the
product of two dense univariate polynomials which has the same number of
terms as
can be computed in approximately the same time as the
product of two dense univariate polynomials which has the same number of
terms as  . An algorithm for
arbitrary dimensions
. An algorithm for
arbitrary dimensions 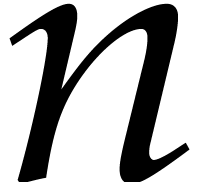 has been presented in [23], whose cost is approximately
has been presented in [23], whose cost is approximately 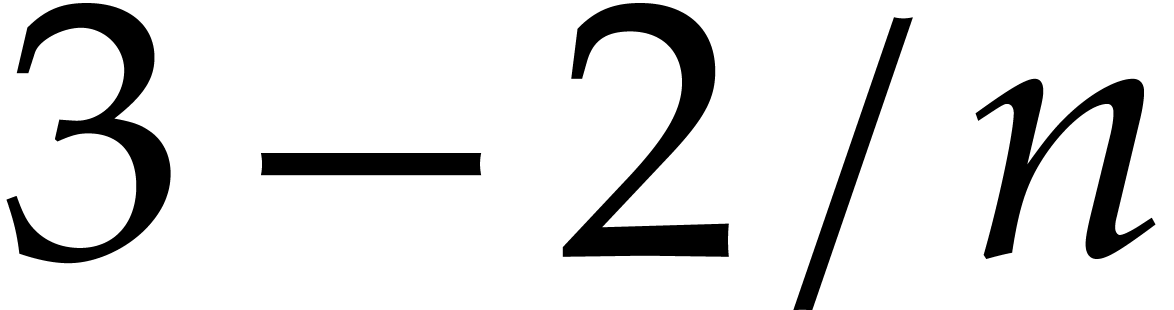 times
larger than the cost of a univariate product of the same size. The
problem has also been studied in [18, 19] and
it is often used as a benchmark [12, 32].
times
larger than the cost of a univariate product of the same size. The
problem has also been studied in [18, 19] and
it is often used as a benchmark [12, 32].
What about the techniques from this paper? We first note that the
exponents of  are known, so we can directly focus
on the computation of the coefficients. In case that we need to do
several product computations for the same
are known, so we can directly focus
on the computation of the coefficients. In case that we need to do
several product computations for the same 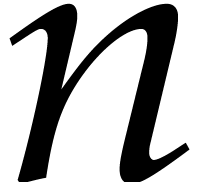 and
and
 , we can also spend some time
on computing a small
, we can also spend some time
on computing a small  and vectors
and vectors 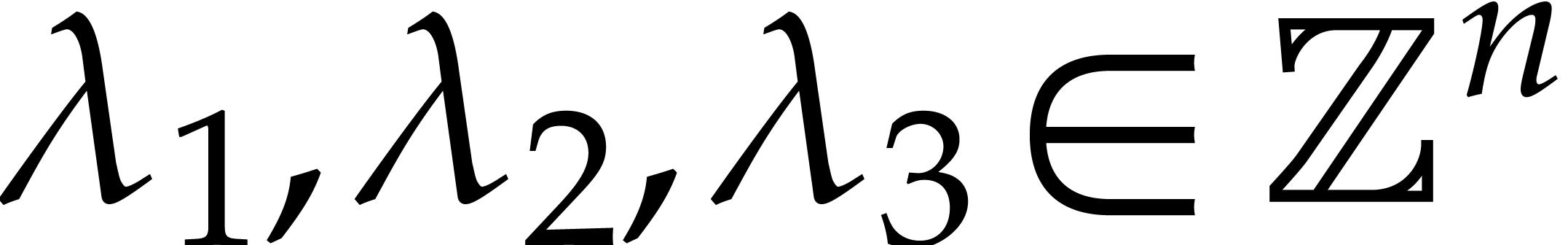 for which we know beforehand that we will win our game of
mystery balls. For our simulations, we found it useful to chose each
for which we know beforehand that we will win our game of
mystery balls. For our simulations, we found it useful to chose each
 among a dozen random vectors in a way that
minimizes the sum of the squares of the number of balls in the boxes
(this sum equals
among a dozen random vectors in a way that
minimizes the sum of the squares of the number of balls in the boxes
(this sum equals  for the first throw in Figure
1).
for the first throw in Figure
1).
For various  ,
,  , and
, and  ,
we played our game several times for different triples of vectors
,
we played our game several times for different triples of vectors 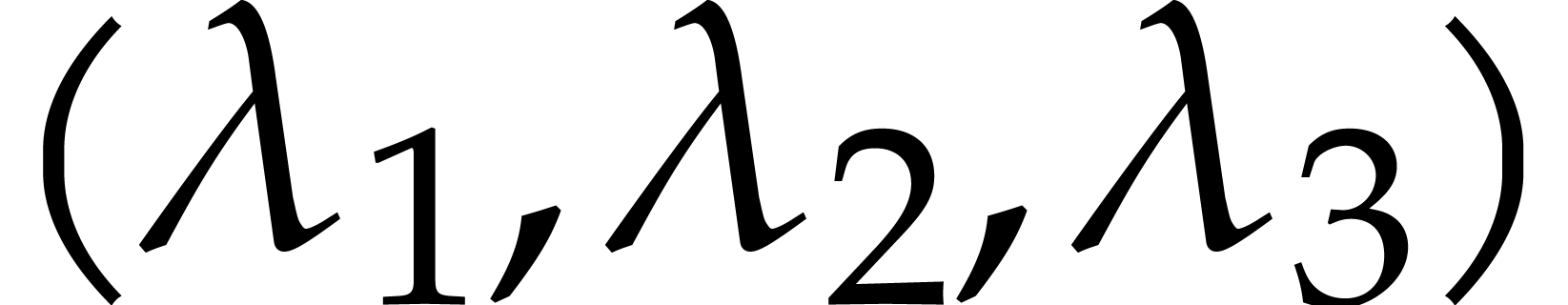 . The critical value for
. The critical value for  for this specific type of support seems to be close to
for this specific type of support seems to be close to
 . In Table 5
below, we report several cases for which we managed to win for this
value of
. In Table 5
below, we report several cases for which we managed to win for this
value of  . This
proves that optimal polynomial multiplication algorithms for
supports of this type are almost as efficient as dense univariate
polynomial products of the same size.
. This
proves that optimal polynomial multiplication algorithms for
supports of this type are almost as efficient as dense univariate
polynomial products of the same size.
|
||||||||||||||||||||||||||||||||||||||||||||||||
A. Arnold, M. Giesbrecht, and D. S. Roche. Sparse interpolation over finite fields via low-order roots of unity. In ISSAC '14: Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, pages 27–34. ACM Press, 2014.
A. Arnold, M. Giesbrecht, and D. S. Roche. Faster sparse multivariate polynomial interpolation of straight-line programs. JSC, 75:4–24, 2016.
M. Asadi, A. Brandt, R. Moir, and M. M. Maza. Sparse polynomial arithmetic with the BPAS library. In International Workshop on Computer Algebra in Scientific Computing, pages 32–50. Springer, 2018.
M. Ben-Or and P. Tiwari. A deterministic algorithm for sparse multivariate polynomial interpolation. In STOC '88: Proceedings of the twentieth annual ACM symposium on Theory of computing, pages 301–309. ACM Press, 1988.
J. Canny, E. Kaltofen, and Y. Lakshman. Solving systems of non-linear polynomial equations faster. In Proceedings of the ACM-SIGSAM 1989 International Symposium on Symbolic and Algebraic Computation, pages 121–128. ACM Press, 1989.
C. Fieker, W. Hart, T. Hofmann, and F. Johansson. Nemo/Hecke: computer algebra and number theory packages for the Julia programming language. In Proc. ISSAC 2017, pages 157–164. 2017.
Ph. Flajolet and R. Sedgewick. An introduction to the analysis of algorithms. Addison Wesley, Reading, Massachusetts, 2nd edition, 1996.
T. S. Freeman, G. M. Imirzian, E. Kaltofen, and Y. Lakshman. DAGWOOD: a system for manipulating polynomials given by straight-line programs. ACM Trans. Math. Software, 14:218–240, 1988.
S. Garg and É. Schost. Interpolation of polynomials given by straight-line programs. Theor. Comput. Sci., 410(27-29):2659–2662, 2009.
Mickaël Gastineau and Jacques Laskar. Development of trip: fast sparse multivariate polynomial multiplication using burst tries. In International Conference on Computational Science, pages 446–453. Springer, 2006.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
A. W. Groves and D. S. Roche. Sparse polynomials in FLINT. ACM Communications in Computer Algebra, 50(3):105–108, 2016.
C. H.Papadimitriou. Computational Complexity. Addison-Wesley, 1994.
D. Harvey and J. van der Hoeven. Integer
multiplication in time 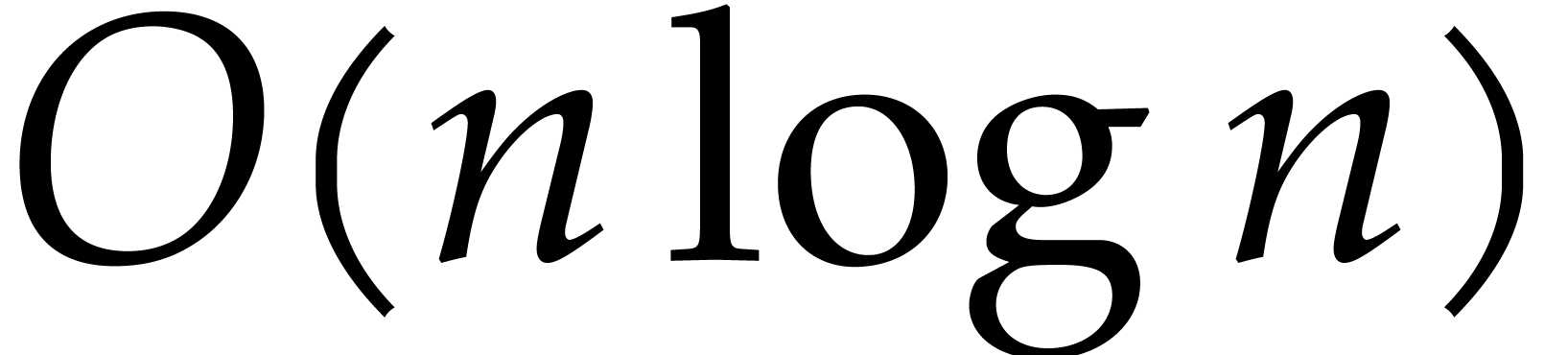 .
Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070778.
.
Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070778.
H. Hassanieh, P. Indyk, D. Katabi, and E. Price. Nearly optimal sparse Fourier transform. In Proceedings of the forty-fourth annual ACM symposium on Theory of computing, pages 563–578. 2012.
J. van der Hoeven. The truncated Fourier transform and applications. In J. Gutierrez, editor, Proc. ISSAC 2004, pages 290–296. Univ. of Cantabria, Santander, Spain, July 4–7 2004.
J. van der Hoeven. Ball arithmetic. Technical Report, HAL, 2009. http://hal.archives-ouvertes.fr/hal-00432152.
J. van der Hoeven and G. Lecerf. On the complexity of blockwise polynomial multiplication. In Proc. ISSAC '12, pages 211–218. Grenoble, France, July 2012.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial multiplication. JSC, 50:227–254, 2013.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation in practice. ACM Commun. Comput. Algebra, 48(3/4):187–191, 2015.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation. Exploring fast heuristic algorithms over finite fields. Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02382117.
J. van der Hoeven et al. GNU TeXmacs. http://www.texmacs.org, 1998.
J. van der Hoeven and É. Schost. Multi-point evaluation in higher dimensions. AAECC, 24(1):37–52, 2013.
M. A. Huang and A. J. Rao. Interpolation of sparse multivariate polynomials over large finite fields with applications. In SODA '96: Proceedings of the seventh annual ACM-SIAM symposium on Discrete algorithms, pages 508–517. Philadelphia, PA, USA, 1996. Society for Industrial and Applied Mathematics.
Q. L. Huang and X. S. Gao. Sparse Polynomial Interpolation with Finitely Many Values for the Coefficients. In V. Gerdt, V. Koepf, W. Seiler, and E. Vorozhtsov, editors, Computer Algebra in Scientific Computing. 19th International Workshop, CASC 2017, Beijing, China, September 18-22, 2017, Proceedings., volume 10490 of Lecture Notes in Computer Science. Springer, Cham, 2017.
Q.-L. Huang. Sparse polynomial interpolation over fields with large or zero characteristic. In Proc. ISSAC '19, pages 219–226. ACM, 2019.
M. Javadi and M. Monagan. Parallel sparse polynomial interpolation over finite fields. In M. Moreno Maza and J.-L. Roch, editors, PASCO '10: Proceedings of the 4th International Workshop on Parallel and Symbolic Computation, pages 160–168. ACM Press, 2010.
S. C. Johnson. Sparse polynomial arithmetic. SIGSAM Bull., 8(3):63–71, 1974.
E. Kaltofen and L. Yagati. Improved sparse multivariate polynomial interpolation algorithms. In ISSAC '88: Proceedings of the International Symposium on Symbolic and Algebraic Computation, pages 467–474. Springer Verlag, 1988.
M. Kapralov. Sparse Fourier transform in any constant dimension with nearly-optimal sample complexity in sublinear time. In Proceedings of the forty-eighth annual ACM symposium on Theory of Computing, pages 264–277. 2016.
Mohamed Khochtali, Daniel S Roche, and Xisen Tian. Parallel sparse interpolation using small primes. In Proceedings of the 2015 International Workshop on Parallel Symbolic Computation, pages 70–77. 2015.
M. Monagan and R. Pearce. Parallel sparse polynomial multiplication using heaps. In ISSAC '09: Proceedings of the 2009 International Symposium on Symbolic and Algebraic Computation, pages 263–270. ACM Press, 2009.
M. Monagan and R. Pearce. Sparse polynomial multiplication and division in Maple 14. Available from http://cgi.cecm.sfu.ca/~pborwein/MITACS/highlights/SDMPmaple14.pdf, 2009.
H. Murao and T. Fujise. Modular algorithm for sparse multivariate polynomial interpolation and its parallel implementation. JSC, 21:377–396, 1996.
D. S. Roche. Chunky and equal-spaced polynomial multiplication. JSC, 46(7):791–806, 2011.
D. S. Roche. What can (and can't) we do with sparse polynomials? In C. Arreche, editor, ISSAC '18: Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, pages 25–30. ACM Press, 2018.
T. Yan. The geobucket data structure for polynomials. JSC, 25(3):285–293, 1998.