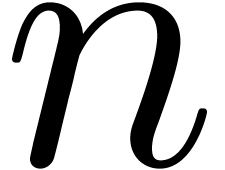 can be
multiplied in time
can be
multiplied in time 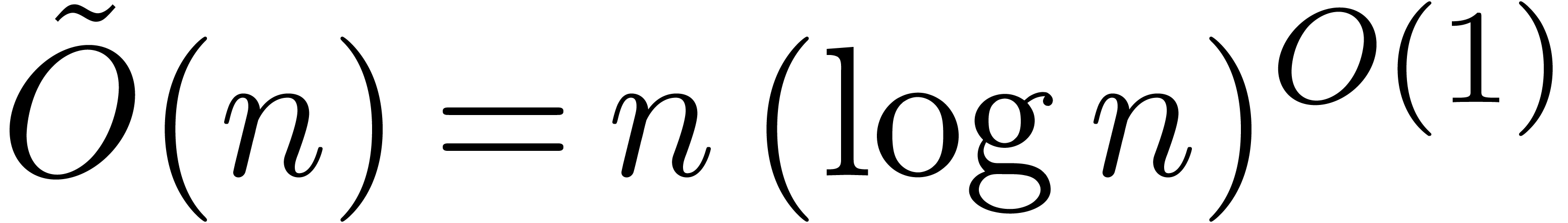 on a Turing machine, and the
product of two univariate polynomials can be done with
on a Turing machine, and the
product of two univariate polynomials can be done with 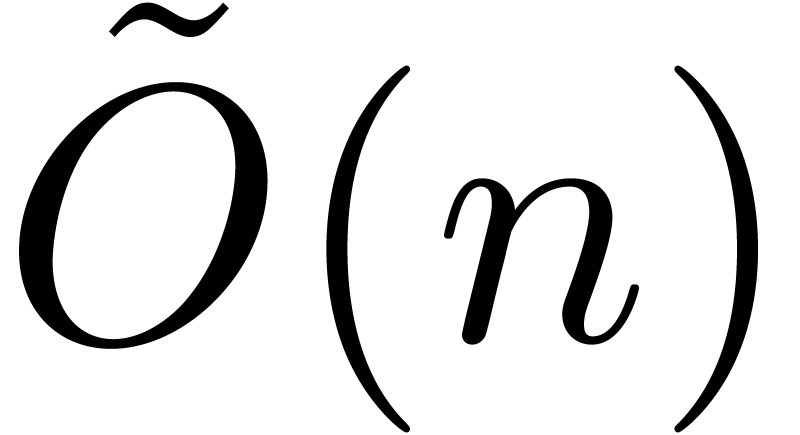 arithmetic operations in the coefficient ring.
arithmetic operations in the coefficient ring.
|
In this paper, we present fast algorithms for the product of two
multivariate polynomials in sparse representation. The bit
complexity of our algorithms are studied in detail for various
types of coefficients, and we derive new complexity results for
the power series multiplication in many variables. Our algorithms
are implemented and freely available within the
|
It is classical [SS71, Sch77, CK91,
Für07] that the product of two integers, or two
univariate polynomials over any ring, can be performed in softly
linear time for the usual dense representations. More precisely,
two integers of bit-size at most 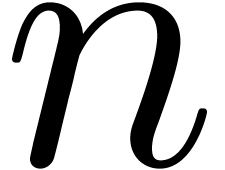 can be
multiplied in time
can be
multiplied in time 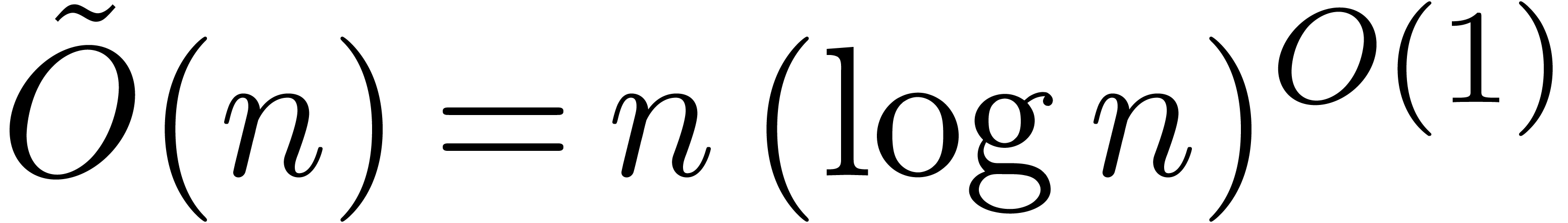 on a Turing machine, and the
product of two univariate polynomials can be done with
on a Turing machine, and the
product of two univariate polynomials can be done with 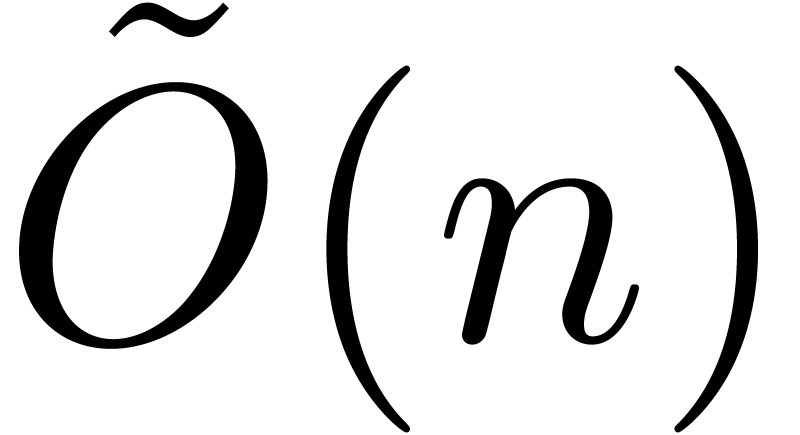 arithmetic operations in the coefficient ring.
arithmetic operations in the coefficient ring.
Multivariate polynomials often admit many zero coefficients, so a
sparse representation is usually preferred over a dense one:
each monomial is a pair made of a coefficient and an exponent written in
the dense binary representation. A natural problem is whether the
product 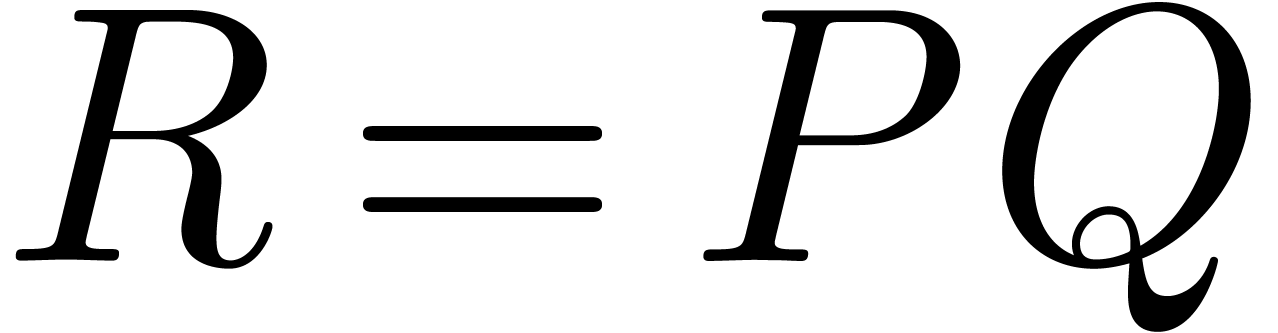 of two sparse multivariate polynomials
in
of two sparse multivariate polynomials
in  can be computed in softly linear time. We
will assume to be given a subset
can be computed in softly linear time. We
will assume to be given a subset 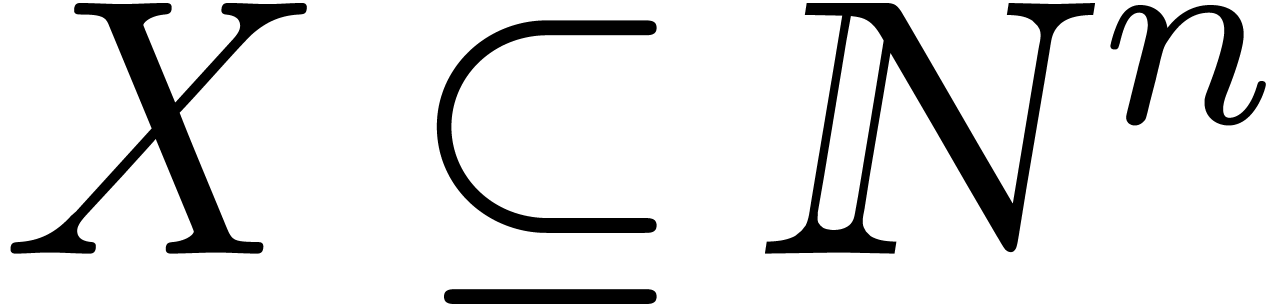 of size
of size  that contains the support of
that contains the support of 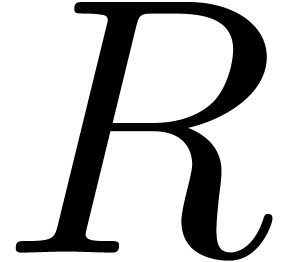 . We also let
. We also let 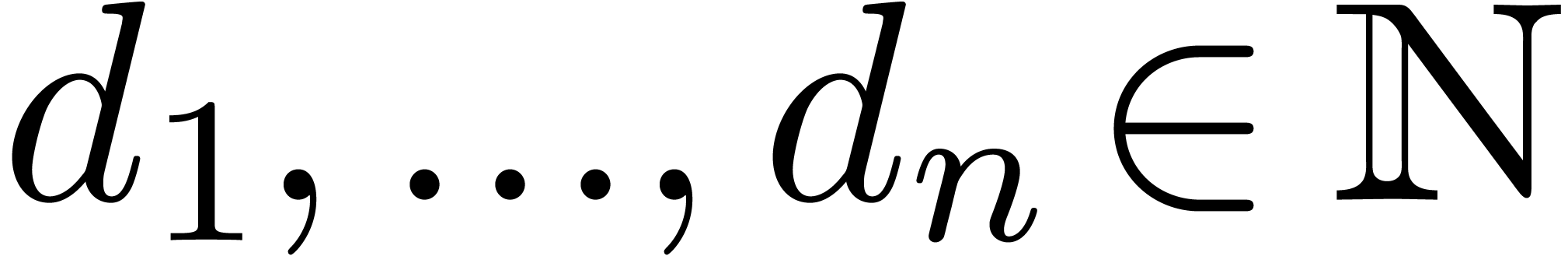 be the minimal
numbers with
be the minimal
numbers with 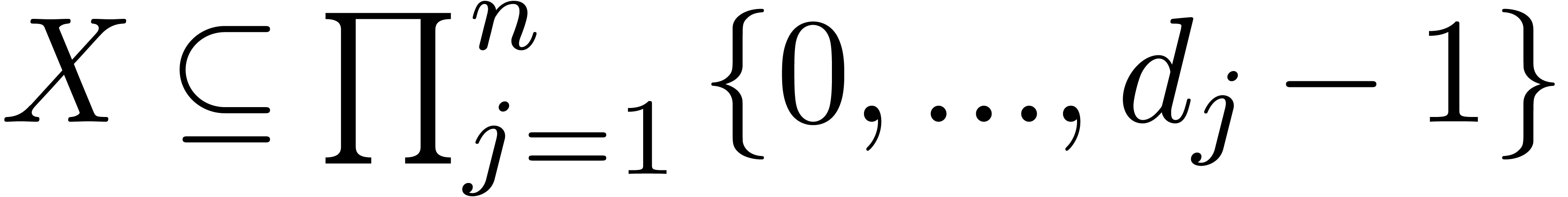 .
.
For coefficient fields of characteristic zero, it is proved in [CKL89]
that 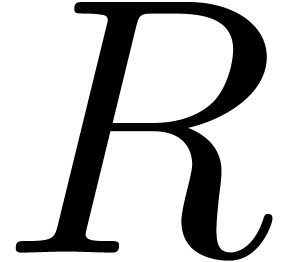 can be computed using
can be computed using 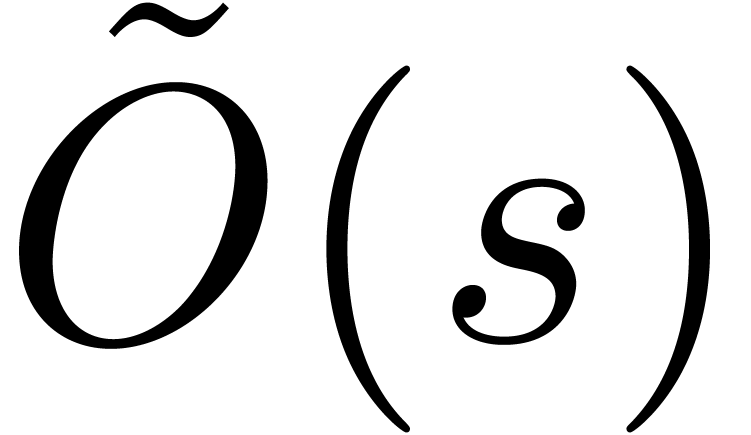 operations over the ground field. This algorithm uses fast evaluation
and interpolation at suitable points built from prime numbers.
Unfortunately, the method hides an expensive growth of intermediate
integers involved in the linear transformations, which prevents the
algorithm from being softly linear in terms of bit-complexity.
operations over the ground field. This algorithm uses fast evaluation
and interpolation at suitable points built from prime numbers.
Unfortunately, the method hides an expensive growth of intermediate
integers involved in the linear transformations, which prevents the
algorithm from being softly linear in terms of bit-complexity.
In this paper, we turn our attention to various concrete coefficient
rings for which it makes sense to study the problem in terms of
bit-complexity. For these rings, we will present multiplication
algorithms which admit softly linear bit-complexities, under the mild
assumption that 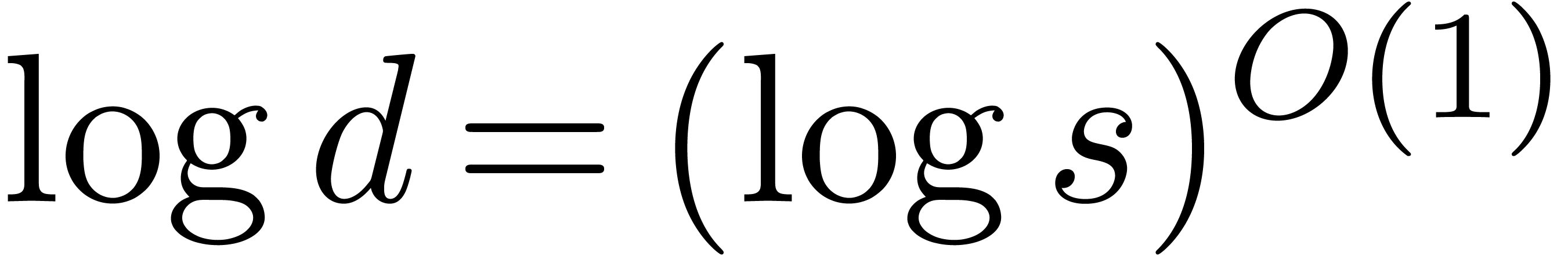 . Our
approach is similar to [CKL89], but relies on a different
kind of evaluation points. Furthermore, finite fields form an important
special case for our method.
. Our
approach is similar to [CKL89], but relies on a different
kind of evaluation points. Furthermore, finite fields form an important
special case for our method.
Let us briefly outline the structure of this paper. In section 2,
we start with a presentation of the main algorithm over an arbitrary
effective algebra  with elements of sufficiently
high order. In section 3, we treat various specific
coefficient rings. In section 4 we give an application to
multivariate power series multiplication. In the last section 5,
we report on timings with our
with elements of sufficiently
high order. In section 3, we treat various specific
coefficient rings. In section 4 we give an application to
multivariate power series multiplication. In the last section 5,
we report on timings with our
Let  be an effective algebra over an effective
field
be an effective algebra over an effective
field 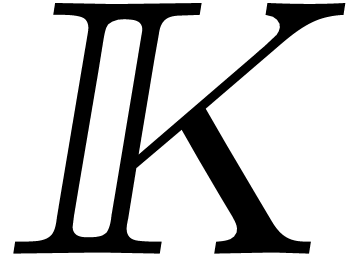 , i.e. all
algebra and field operations can be performed by algorithm.
, i.e. all
algebra and field operations can be performed by algorithm.
We will denote by 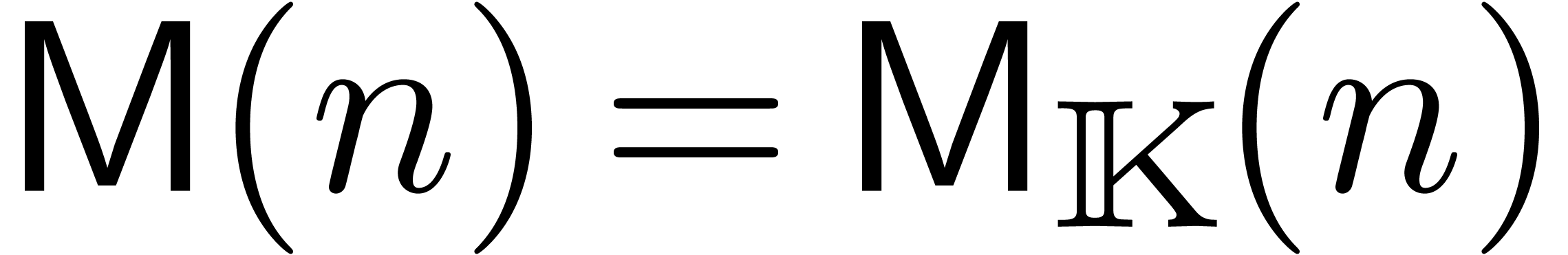 the cost for multiplying two
univariate polynomials of degree
the cost for multiplying two
univariate polynomials of degree 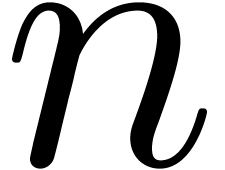 over
over  in terms of the number of arithmetic operations in
in terms of the number of arithmetic operations in  . Similarly, we denote by
. Similarly, we denote by 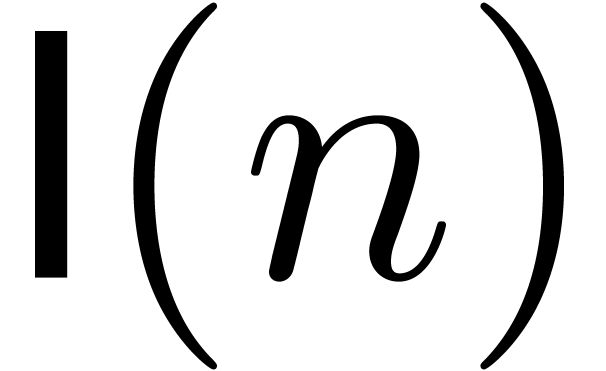 the time needed to multiply two integers of bit-size at
most
the time needed to multiply two integers of bit-size at
most 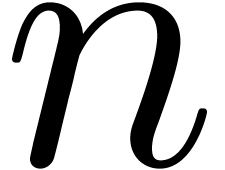 . One can take
. One can take 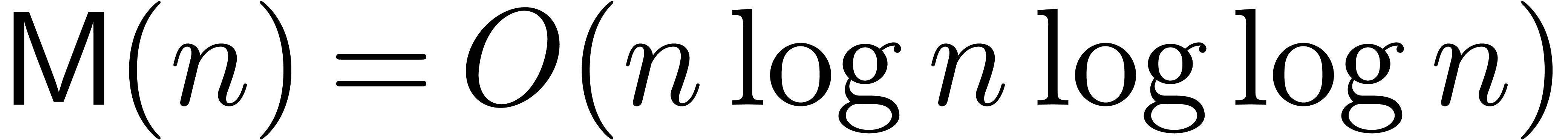 [CK91] and
[CK91] and 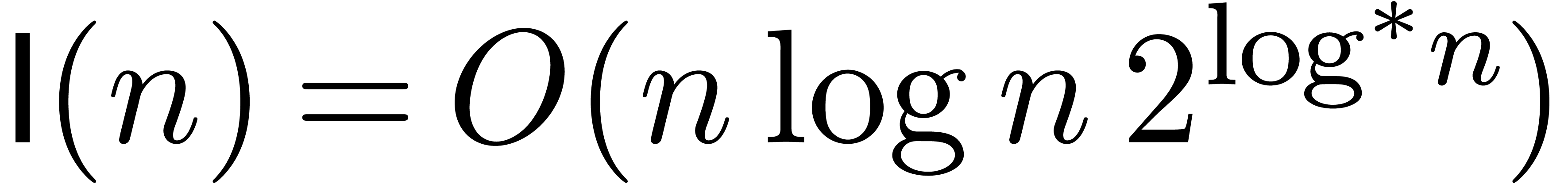 [Für07],
where
[Für07],
where 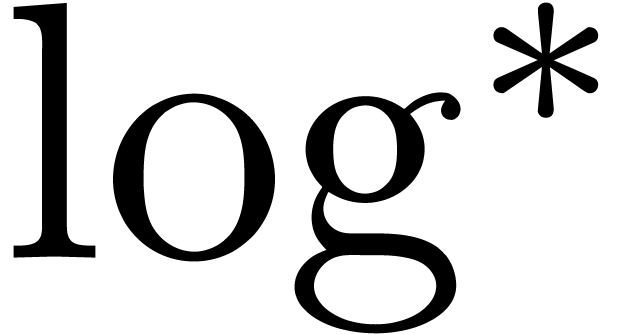 represents the iterated logarithm of
represents the iterated logarithm of  . Throughout the paper, we will
assume that
. Throughout the paper, we will
assume that 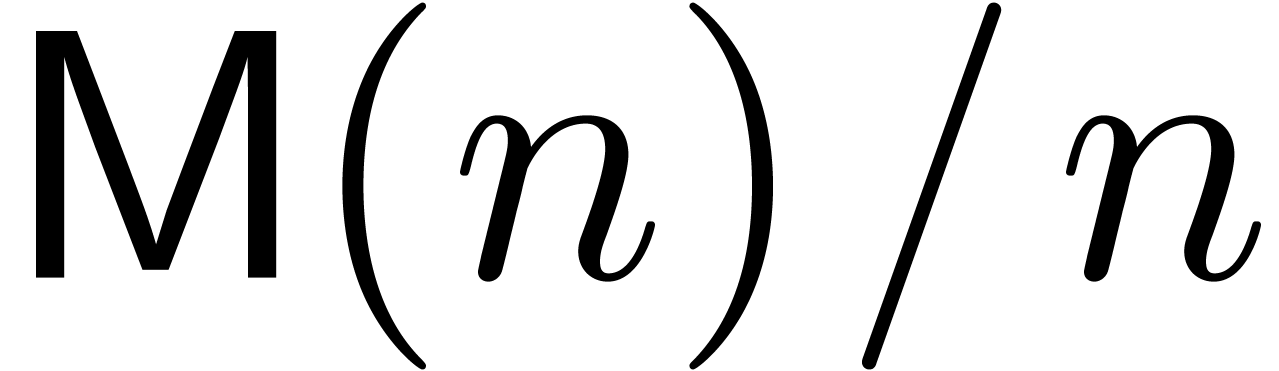 and
and 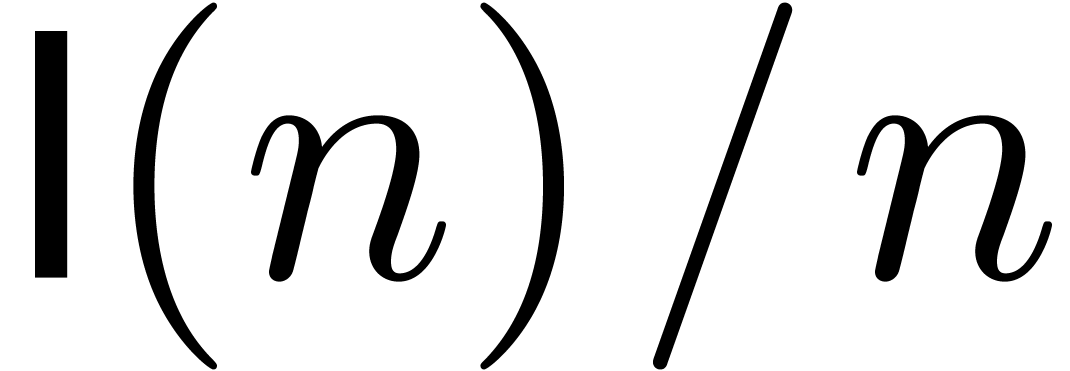 are
increasing. We also assume that
are
increasing. We also assume that  and
and  .
.
Given a multivariate polynomial 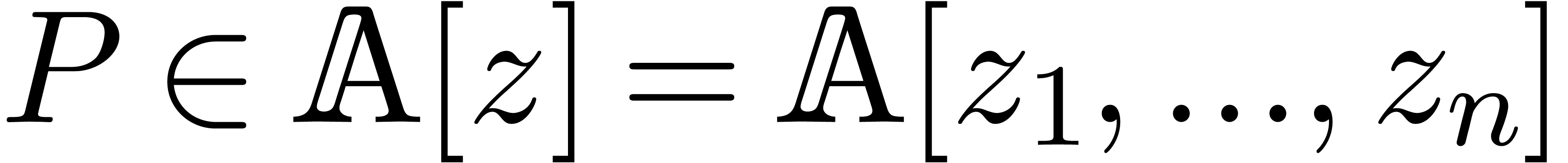 and an index
and an index
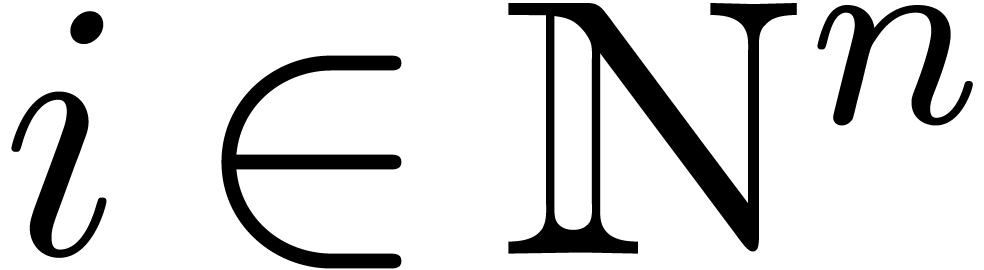 , we denote
, we denote 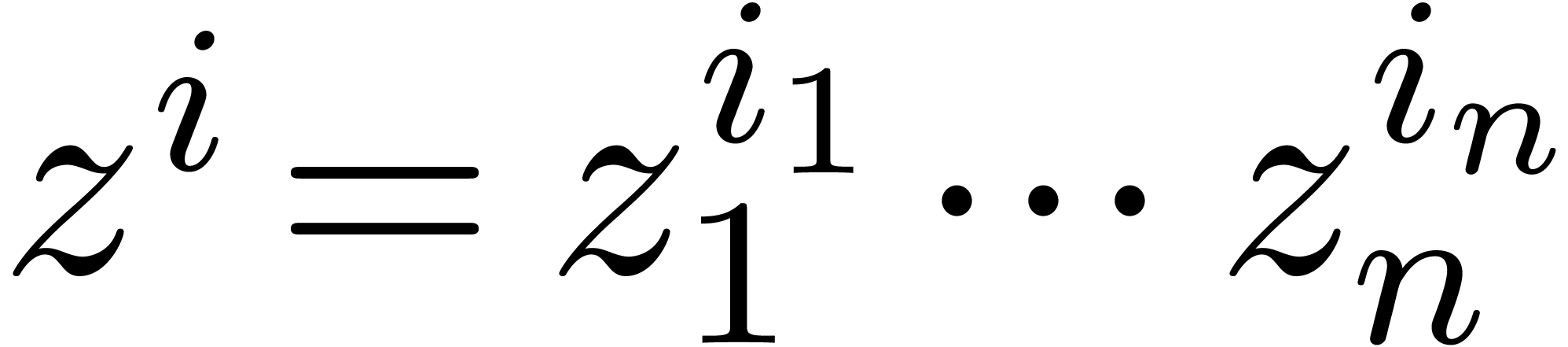 and let
and let  be the coefficient of
be the coefficient of  in
in 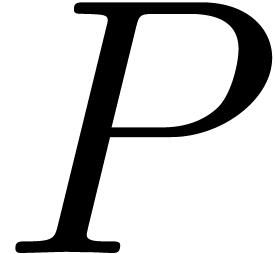 . The support of
. The support of
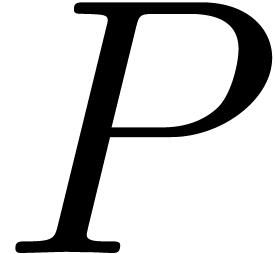 is defined by
is defined by 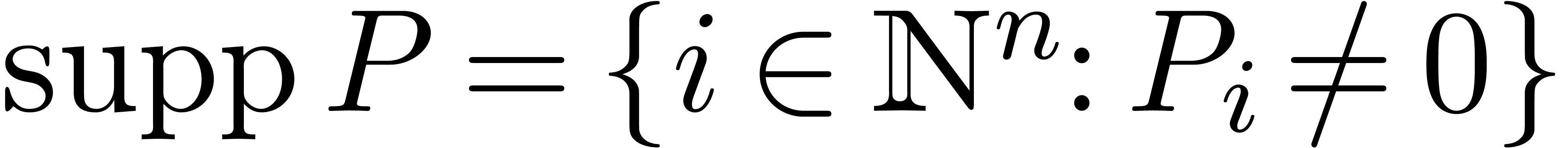 and we
denote by
and we
denote by  its cardinality.
its cardinality.
In the sparse representation, the polynomial 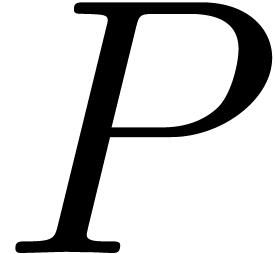 is
stored as a sequence of exponent-coefficient pairs
is
stored as a sequence of exponent-coefficient pairs 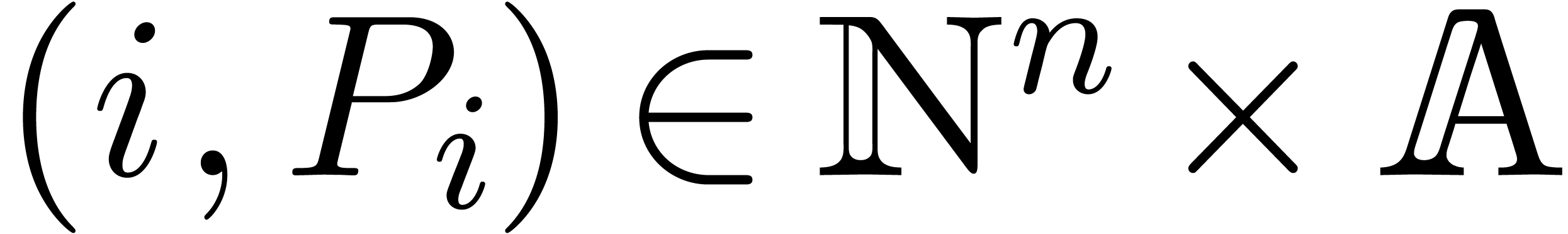 . Natural numbers are represented by their
sequences of binary digits. The bit-size of an exponent
. Natural numbers are represented by their
sequences of binary digits. The bit-size of an exponent 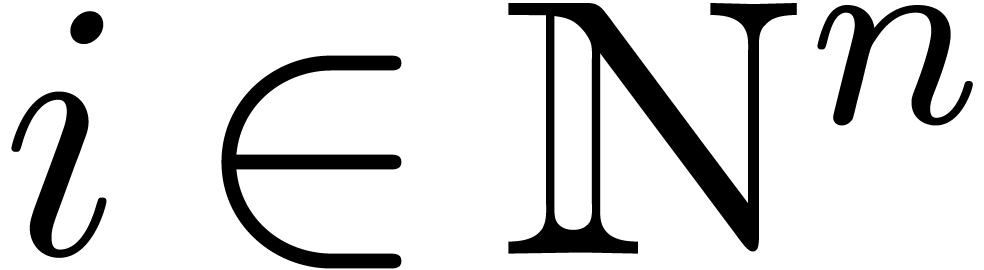 is
is 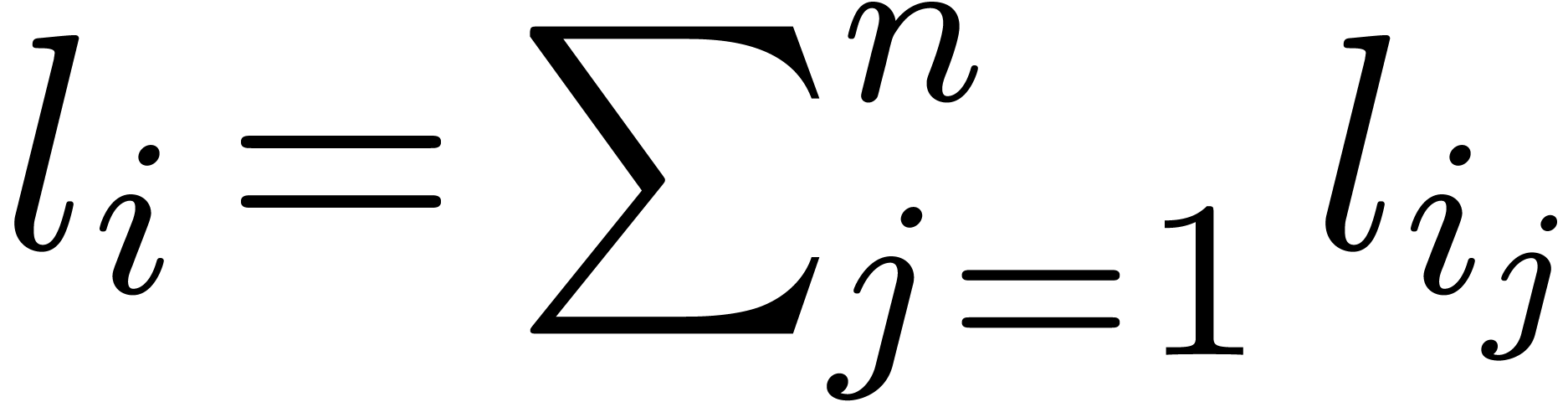 , where
, where
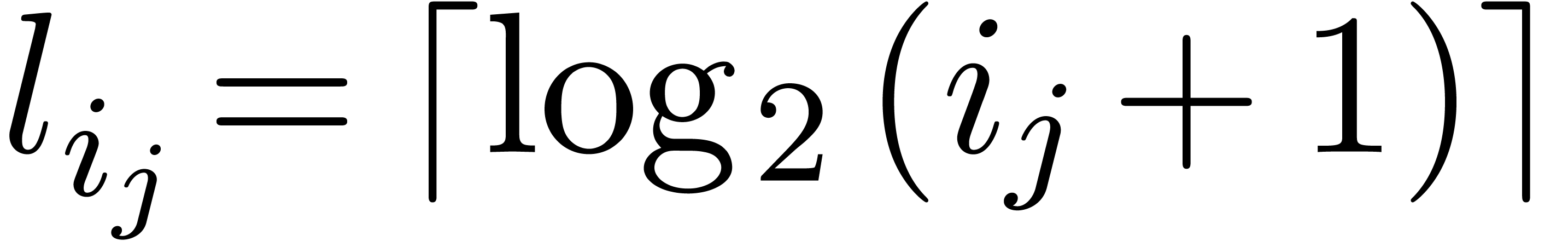 . We let
. We let  be the bit-size of
be the bit-size of 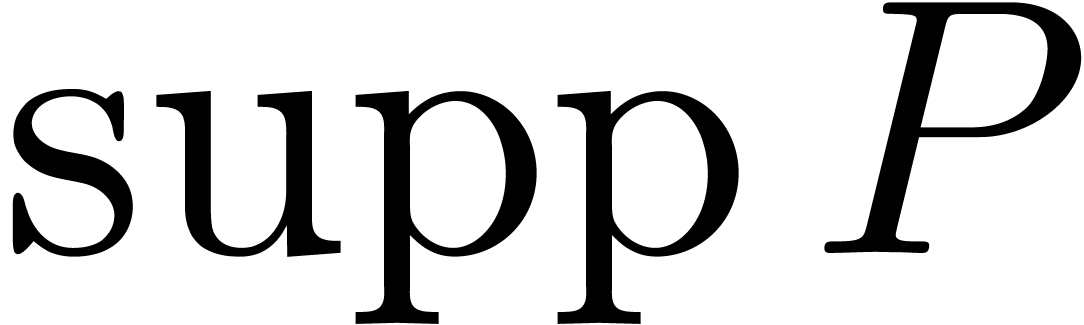 .
.
In this and the next section, we are interested in the multiplication
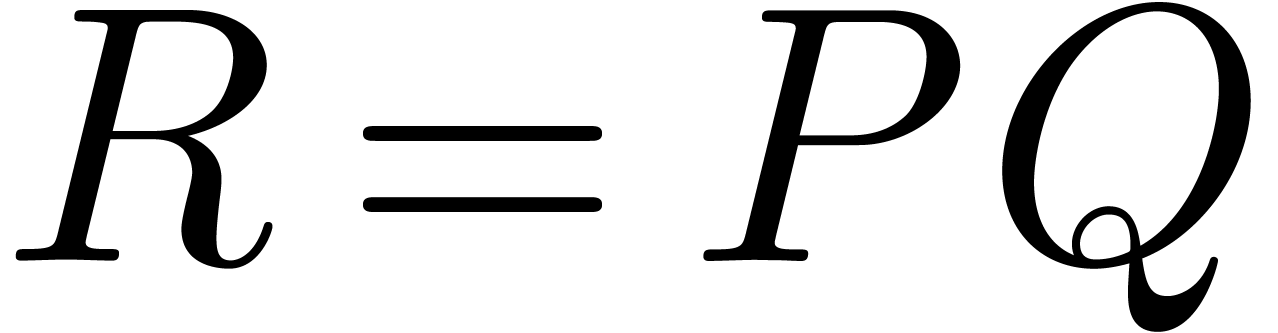 of two sparse polynomials
of two sparse polynomials 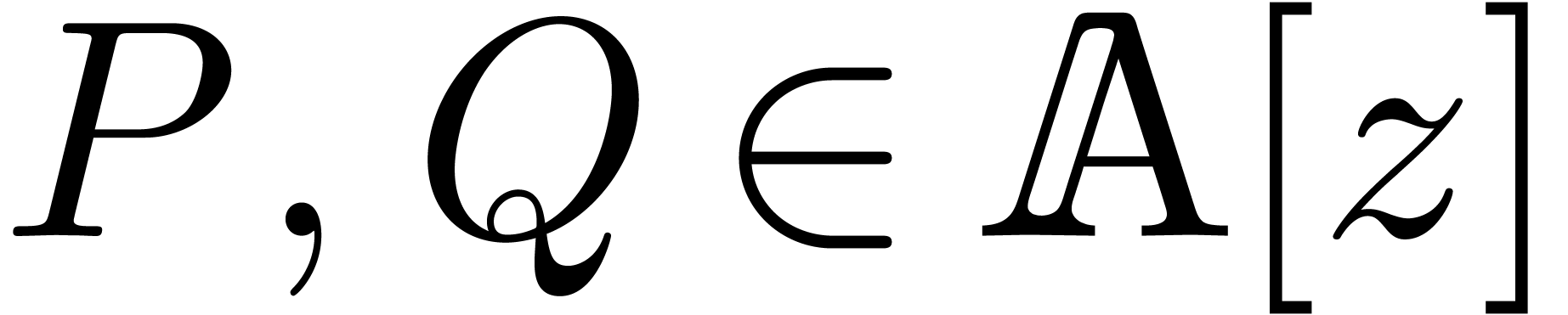 . We assume given a finite set
. We assume given a finite set 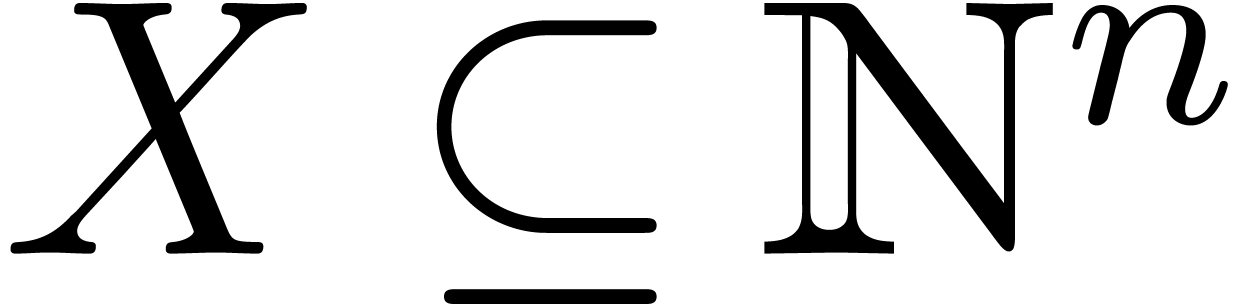 , such that
, such that  .
We will write
.
We will write 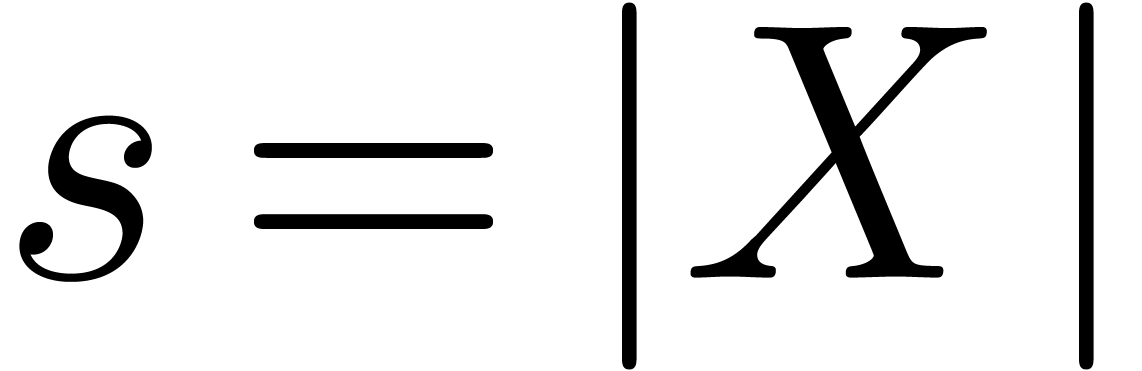 for its size and
for its size and 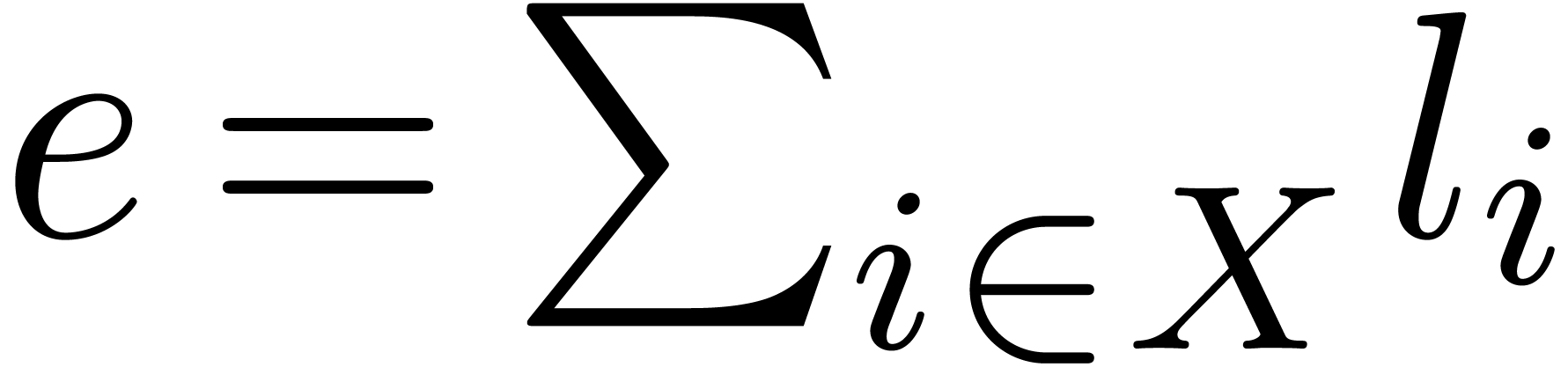 for its bit-size. We also denote
for its bit-size. We also denote  and
and  . For each
. For each  , we introduce
, we introduce 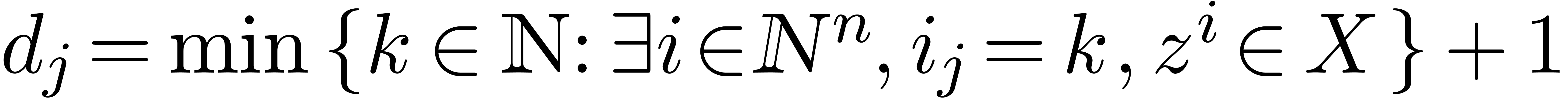 ,
which sharply bounds the partial degree in
,
which sharply bounds the partial degree in 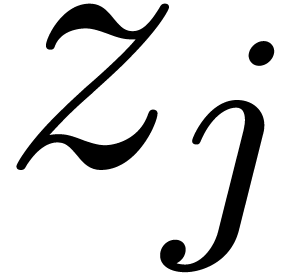 for
each monomial in
for
each monomial in  . We denote
. We denote
 .
.
Given  pairwise distinct points
pairwise distinct points 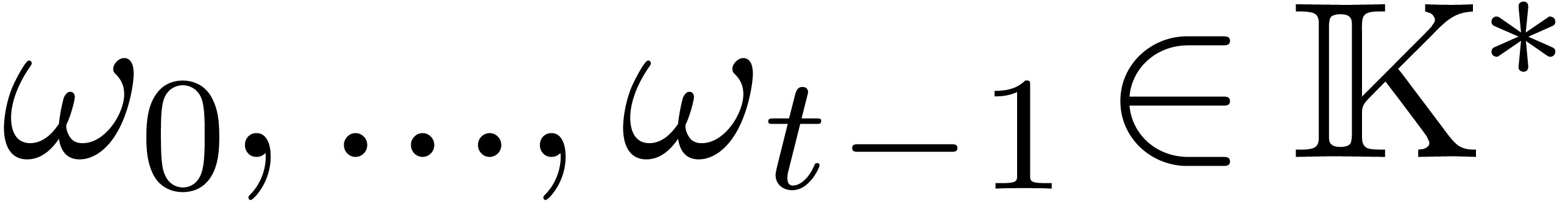 and
and 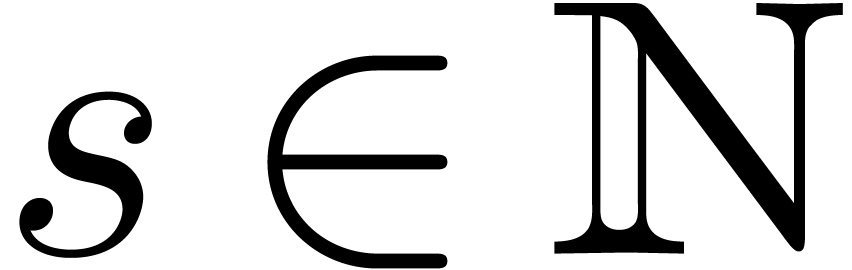 , let
, let 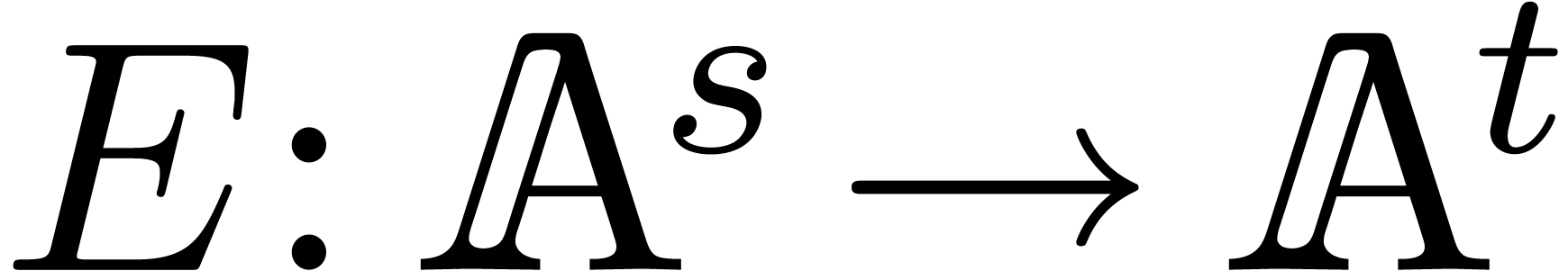 be the linear map which sends
be the linear map which sends 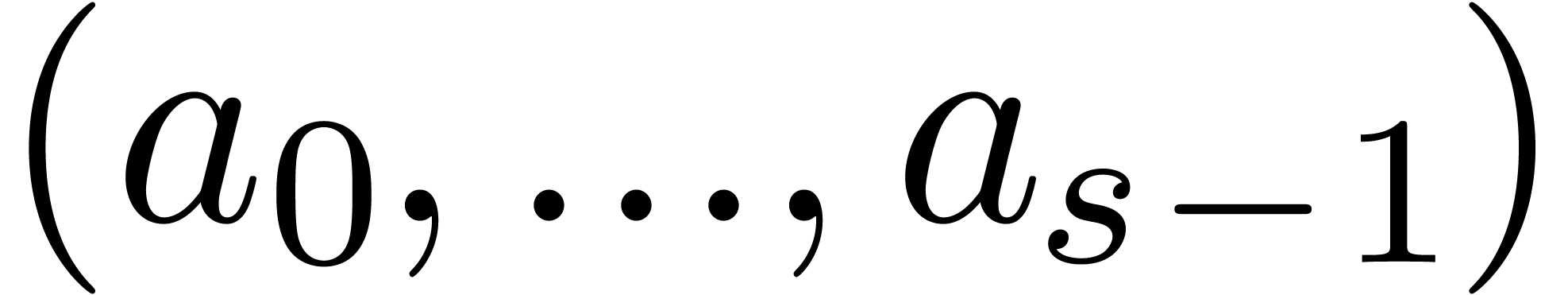 to
to 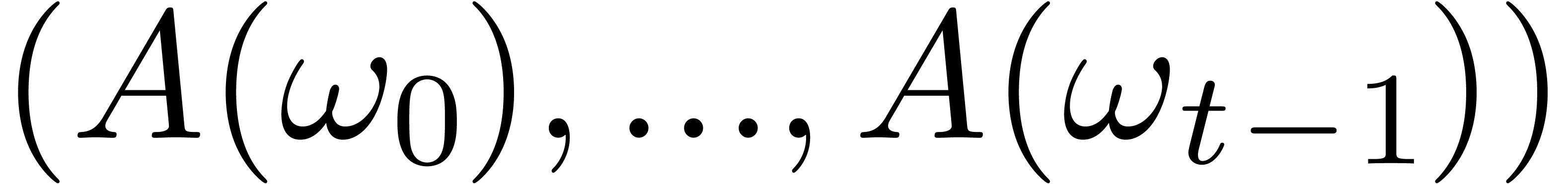 , with
, with 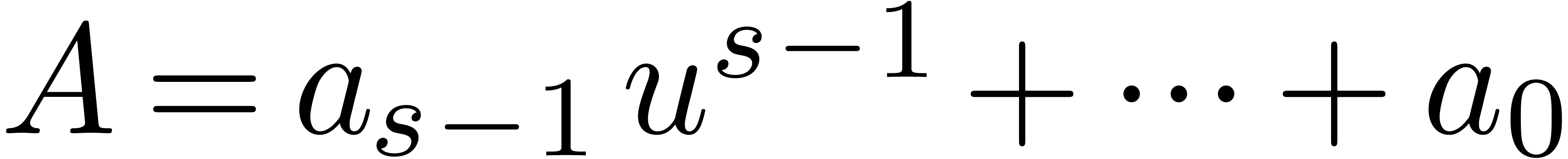 .
In the canonical basis, this map corresponds to left multiplication by
the generalized Vandermonde matrix
.
In the canonical basis, this map corresponds to left multiplication by
the generalized Vandermonde matrix
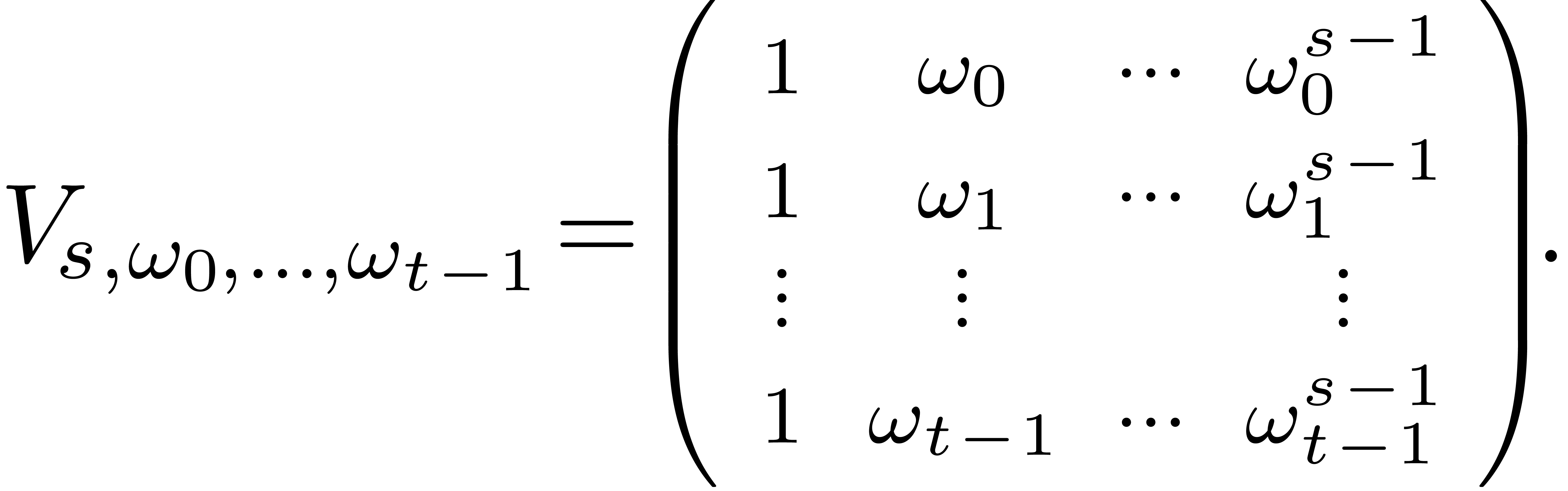
The computation of  and its inverse
and its inverse 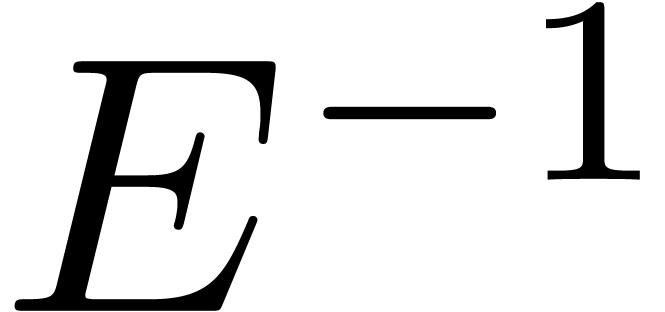 (if
(if  )
correspond to the problems of multi-point evaluation and interpolation
of a polynomial. Using binary splitting, it is classical [MB72,
Str73, BM74] that both problems can be solved
in time
)
correspond to the problems of multi-point evaluation and interpolation
of a polynomial. Using binary splitting, it is classical [MB72,
Str73, BM74] that both problems can be solved
in time  . Notice that the
algorithms only require vectorial operations in
. Notice that the
algorithms only require vectorial operations in  (additions, subtractions and multiplications with elements in
(additions, subtractions and multiplications with elements in  ).
).
Our main algorithm relies on the efficient computations of the
transpositions 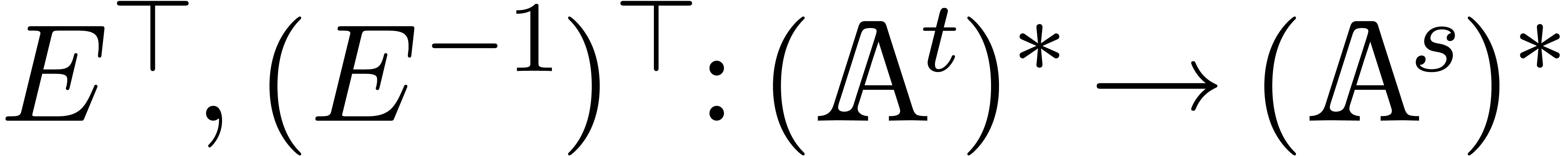 of
of  and
and
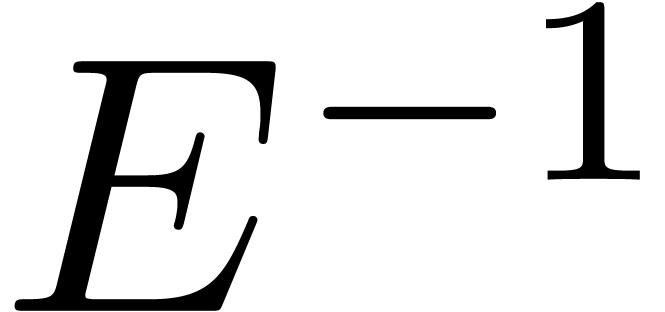 . The map
. The map  corresponds to left multiplication by
corresponds to left multiplication by
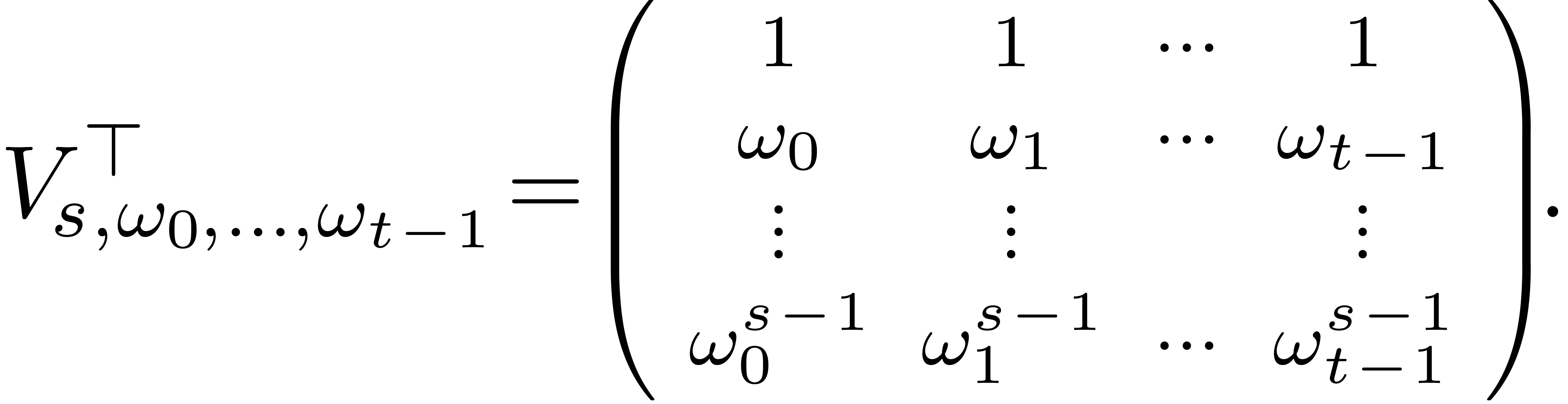
By the transposition principle [Bor56, Ber],
the operations  and
and 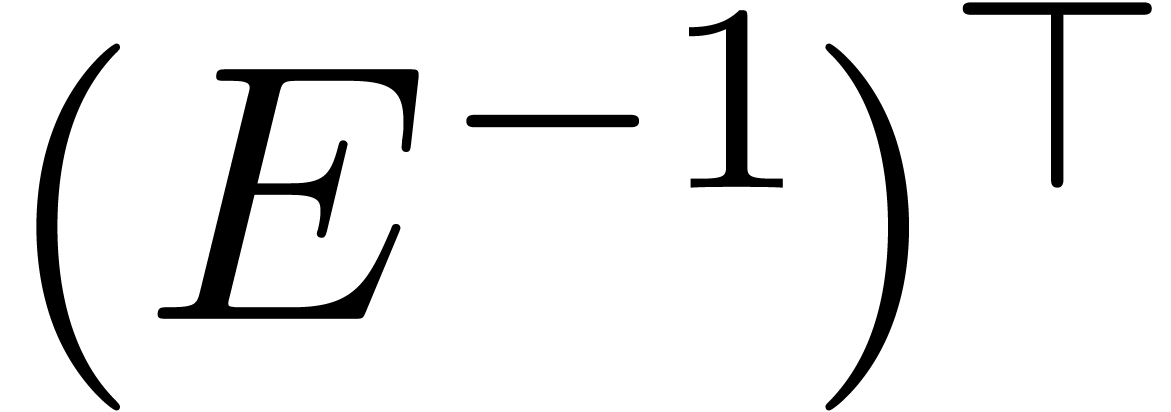 can
again be computed in time
can
again be computed in time  .
.
There is an efficient direct approach for the computation of  [BLS03]. Given a vector
[BLS03]. Given a vector 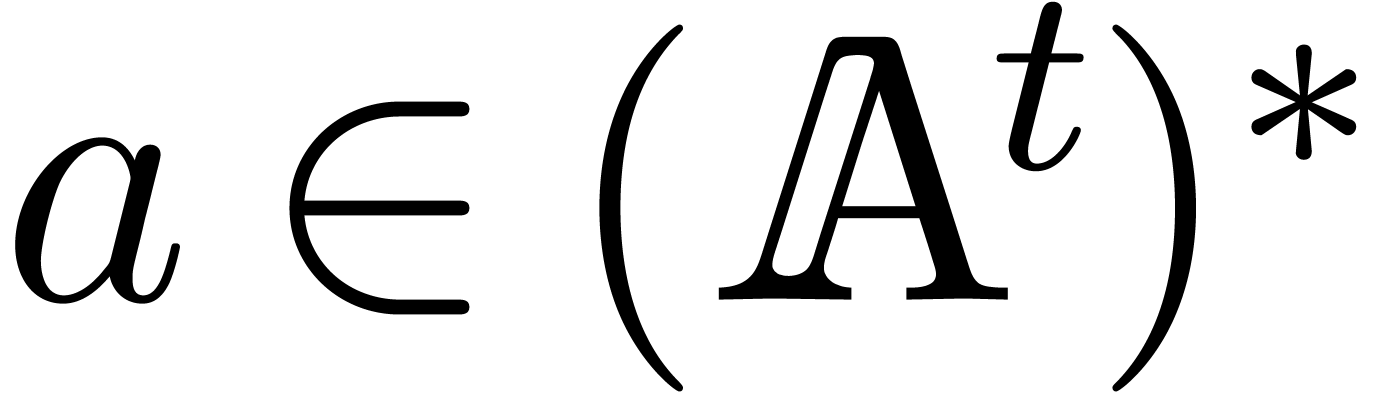 with entries
with entries  , the entries
, the entries
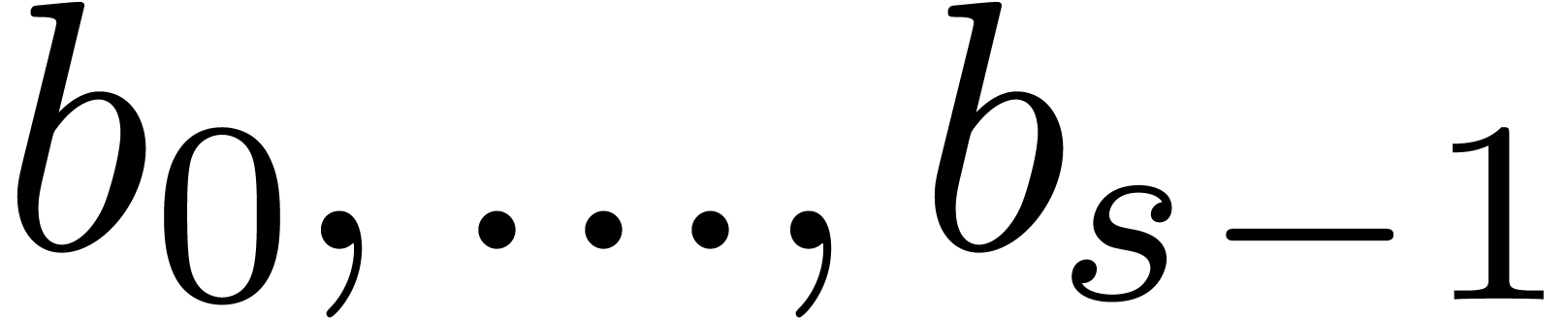 of
of 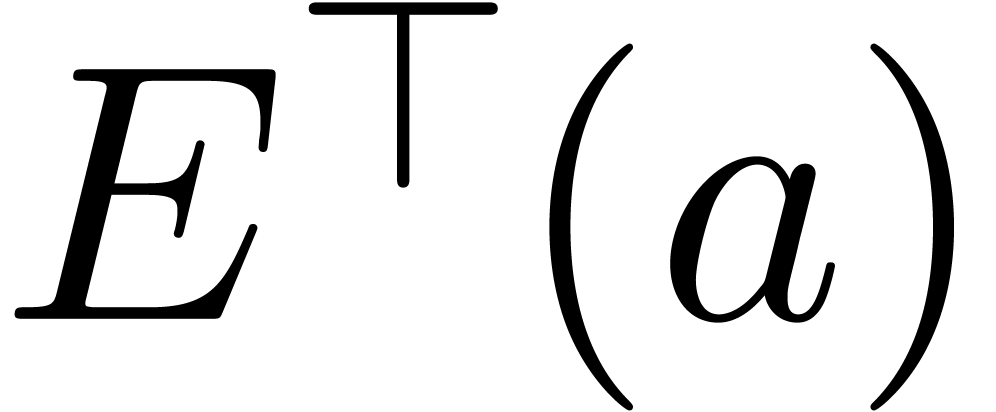 are identical to the
first
are identical to the
first  coefficients of the power series
coefficients of the power series
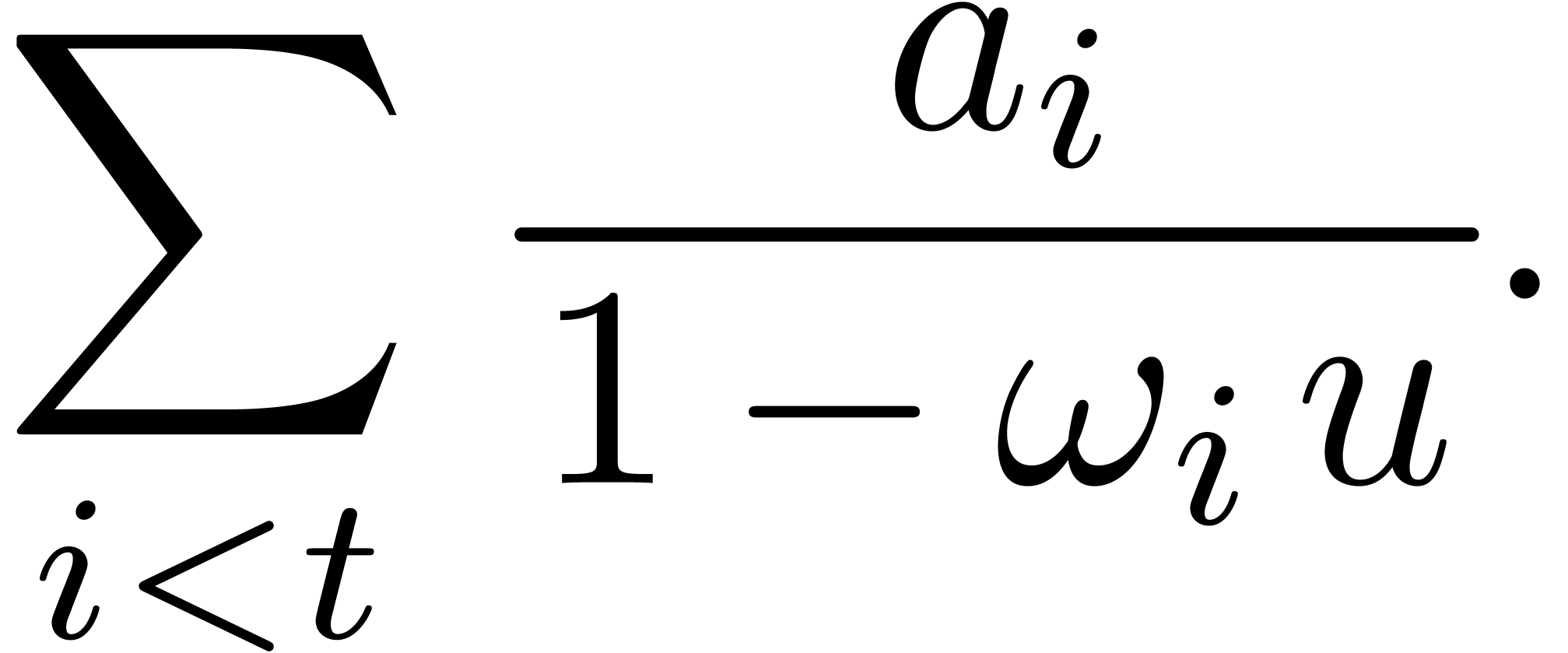
The numerator and denominator of this rational function can be computed
using binary splitting. If 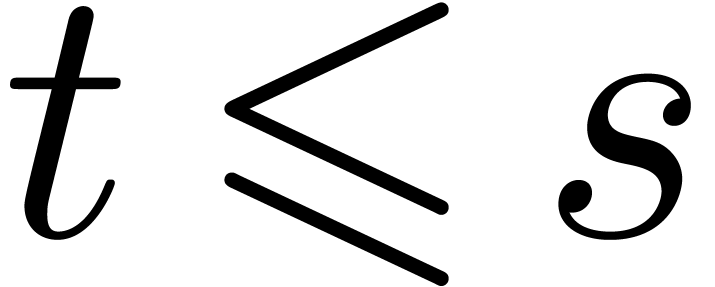 ,
then this requires
,
then this requires  vectorial operations in
vectorial operations in  [GG02, Theorem 10.10]. The truncated
division of the numerator and denominator at order
[GG02, Theorem 10.10]. The truncated
division of the numerator and denominator at order  requires
requires 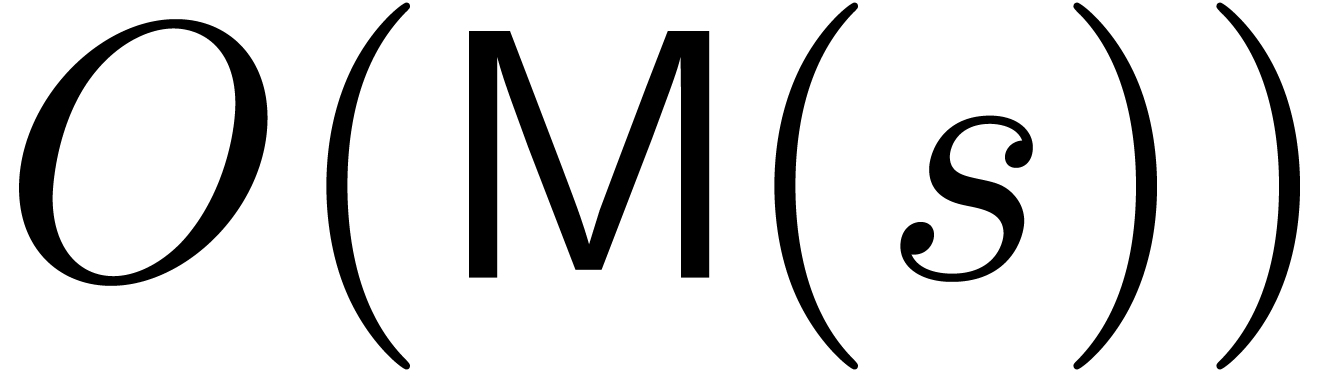 vectorial operations in
vectorial operations in  . If
. If 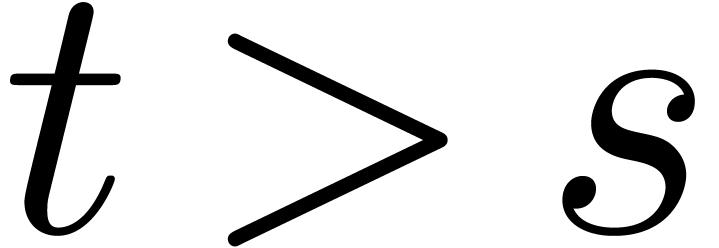 ,
then we cut the sum into
,
then we cut the sum into 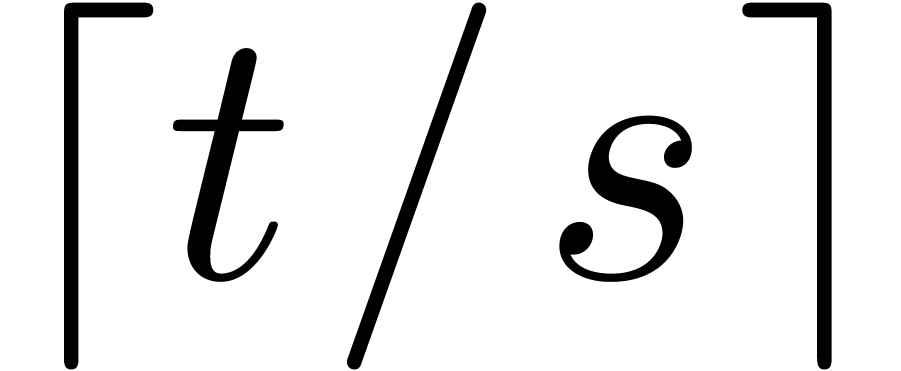 parts of size
parts of size 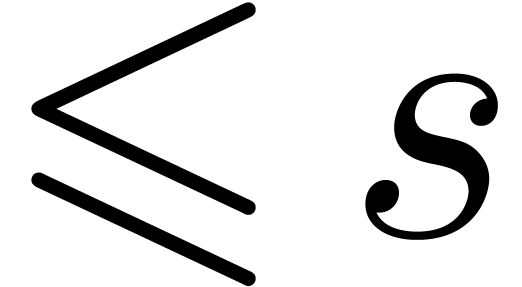 , and obtain the complexity bound
, and obtain the complexity bound
 .
.
Inversely, assume that we wish to recover  from
from
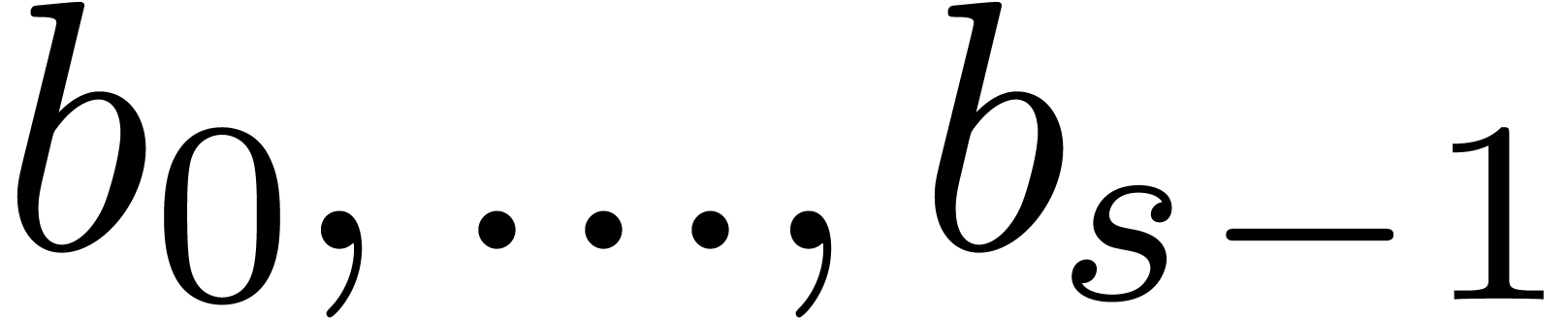 , when
, when  . For simplicity, we assume that the
. For simplicity, we assume that the  are non-zero (this will be the case in the sequel).
Setting
are non-zero (this will be the case in the sequel).
Setting 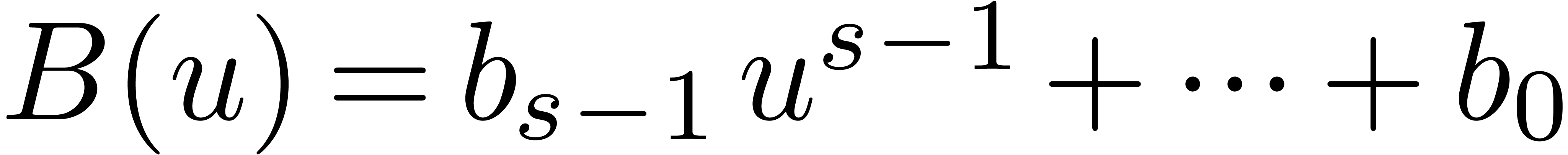 ,
, 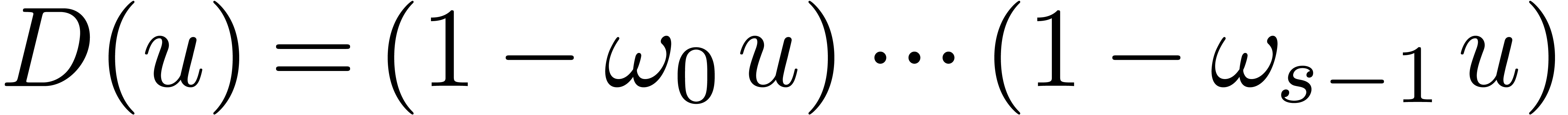 and
and 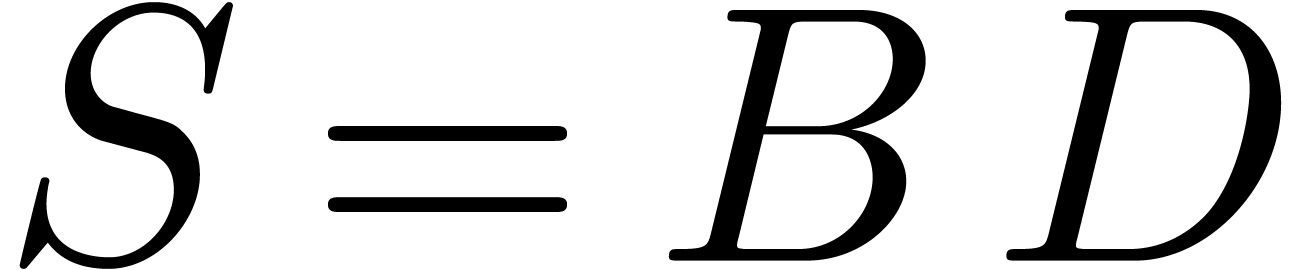 , we notice that
, we notice that 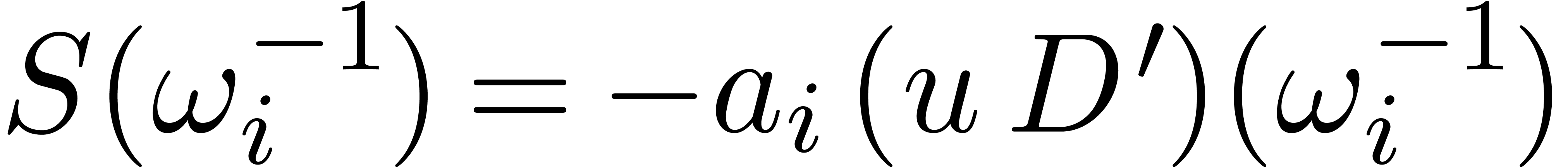 for all
for all 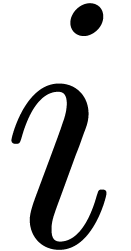 .
Hence, the computation of the
.
Hence, the computation of the 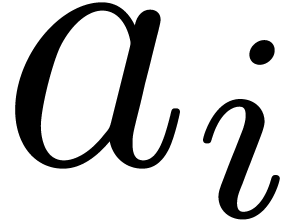 reduces to two
multi-point evaluations of
reduces to two
multi-point evaluations of  and
and 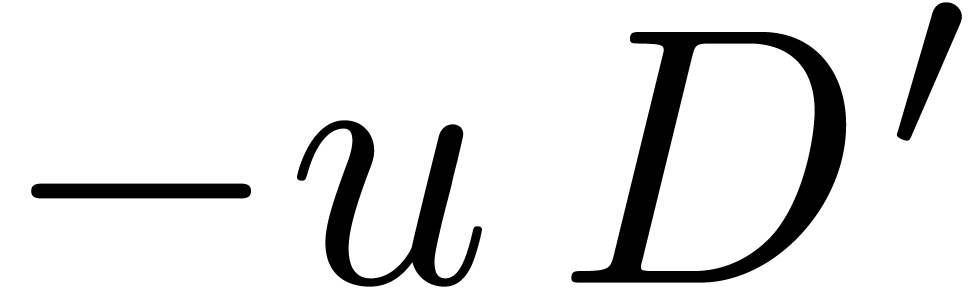 at
at  and
and  divisions. This
amounts to a total of
divisions. This
amounts to a total of  vectorial operations in
vectorial operations in
 and
and 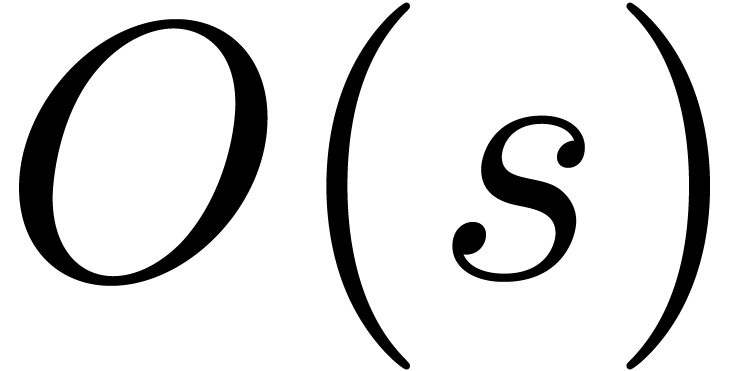 divisions in
divisions in  .
.
Let  be a new variable. We introduce the vector
spaces
be a new variable. We introduce the vector
spaces
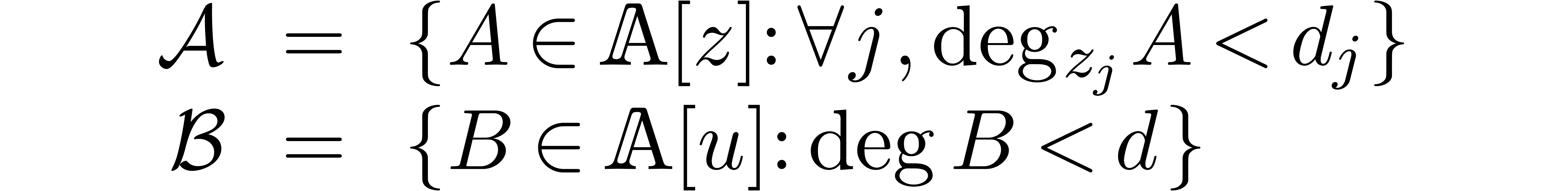
Given 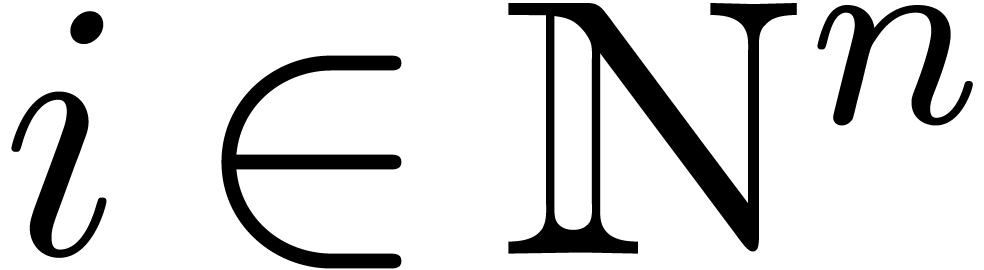 , let
, let 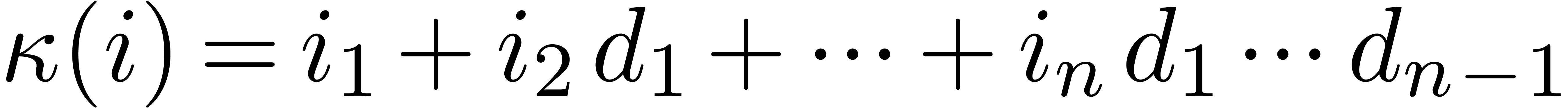 . The Kronecker isomorphism
. The Kronecker isomorphism 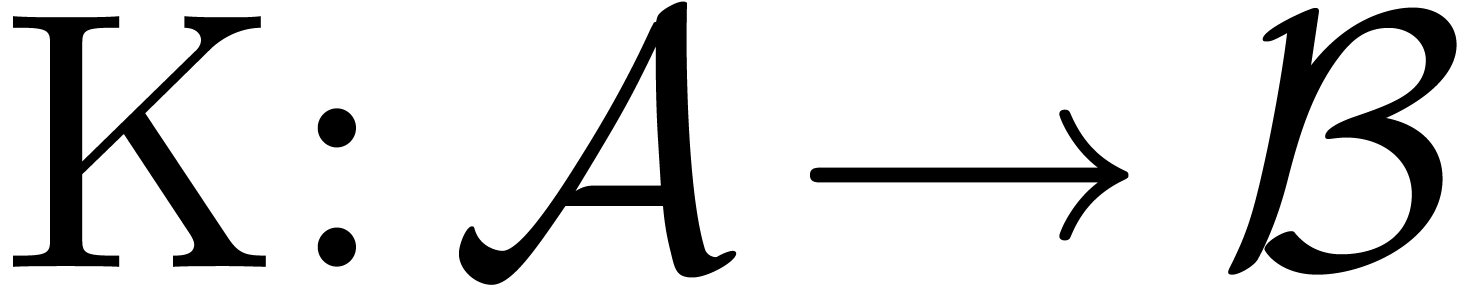 , is the unique
, is the unique  -linear map with
-linear map with

It corresponds to the evaluation at  ,
so that
,
so that 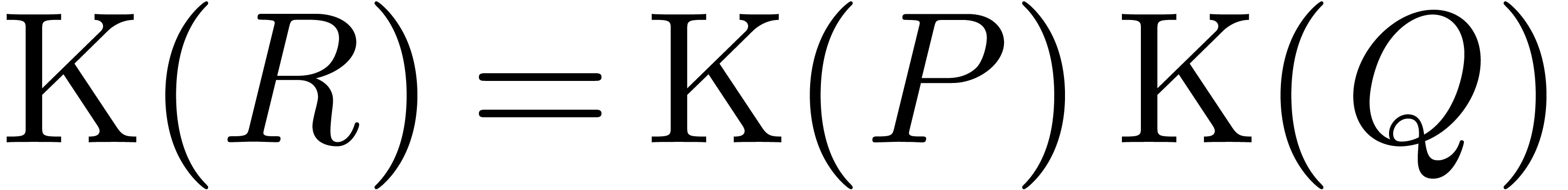 .
.
Assume now that we are given an element  of
multiplicative order at least
of
multiplicative order at least  and consider the
following evaluation map
and consider the
following evaluation map
We propose to compute  though the equality
though the equality 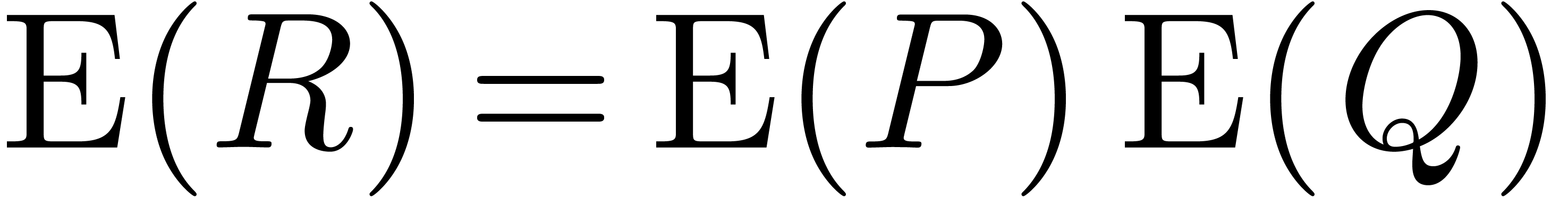 .
.
Given  , let
, let 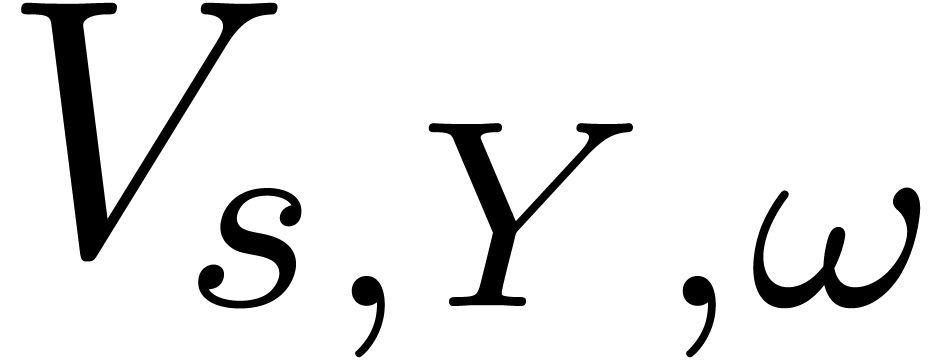 be the matrix of
be the matrix of  restricted to the space of
polynomials with support included in
restricted to the space of
polynomials with support included in 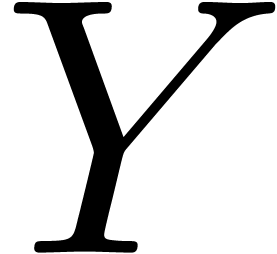 .
Setting
.
Setting  , we have
, we have
Taking  resp.
resp.  , this allows us to compute
, this allows us to compute 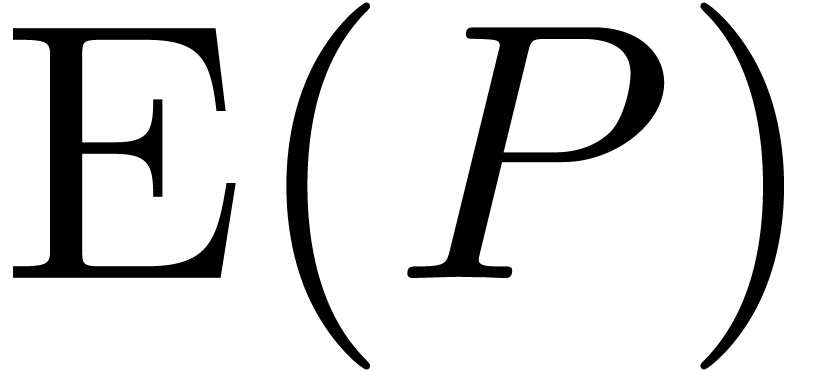 and
and  using our algorithm for transposed
multi-point evaluation from section 2.2. We obtain
using our algorithm for transposed
multi-point evaluation from section 2.2. We obtain 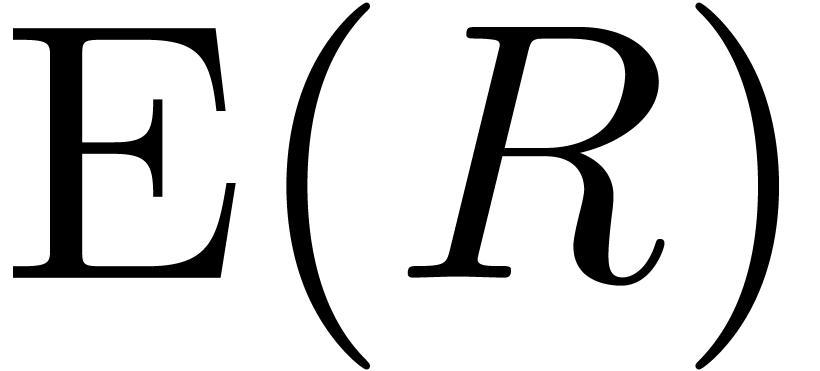 using one Hadamard product
using one Hadamard product 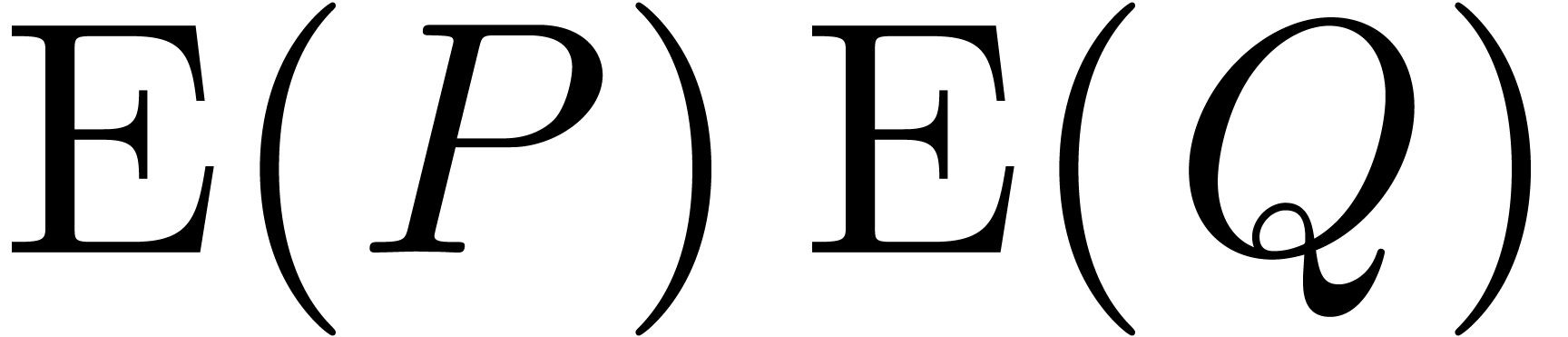 . Taking
. Taking  ,
the points
,
the points  are pairwise distinct, since the
are pairwise distinct, since the 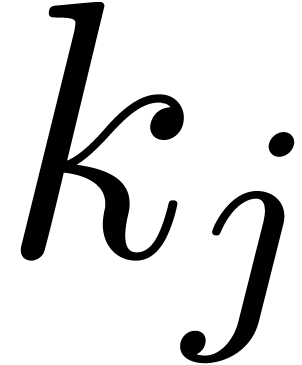 are smaller than the order of
are smaller than the order of  . Hence
. Hence 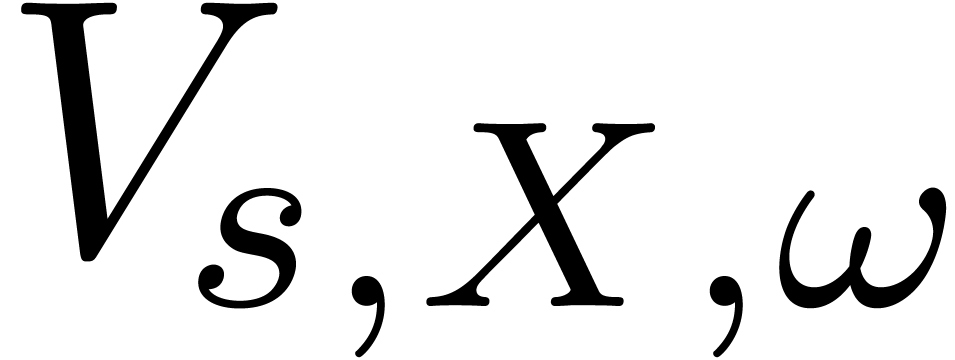 is invertible and we
recover
is invertible and we
recover 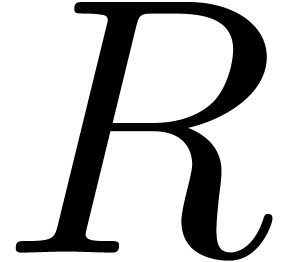 from
from  using
transposed multi-point interpolation.
using
transposed multi-point interpolation.
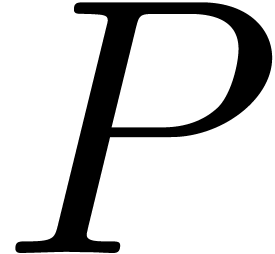 and
and  in
in 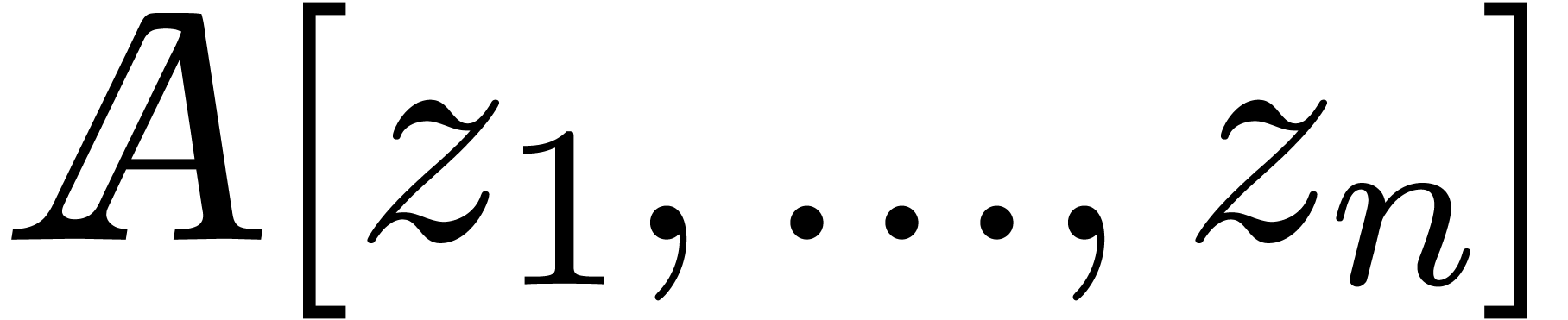 and an element
and an element 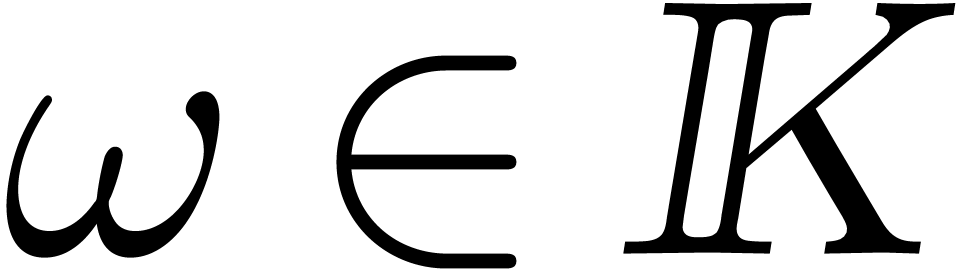 of order at least d, then the product
of order at least d, then the product 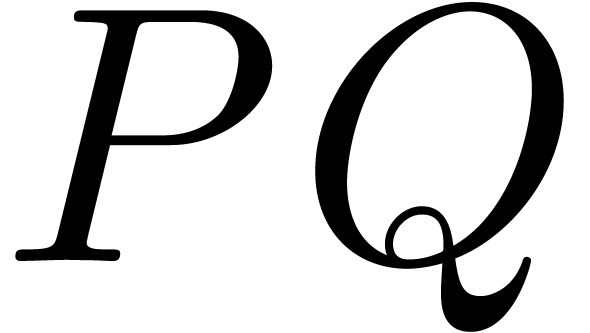 can be computed using
can be computed using  products in
products in 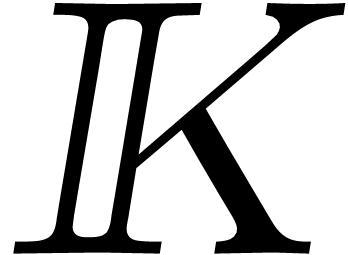 ,
,  inversions in
inversions in 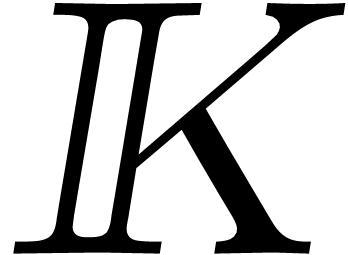 ,
, 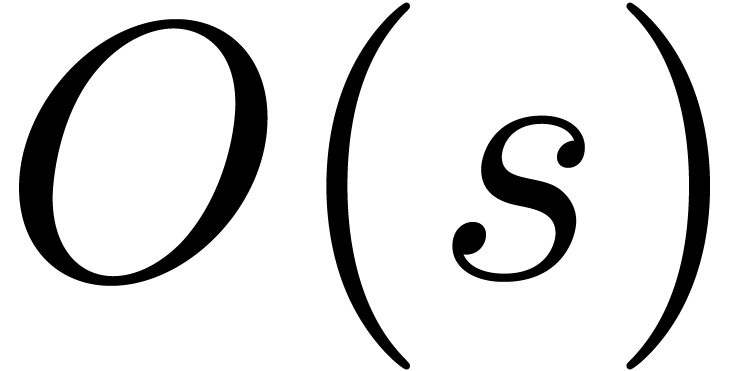 products in
products in  , and
, and 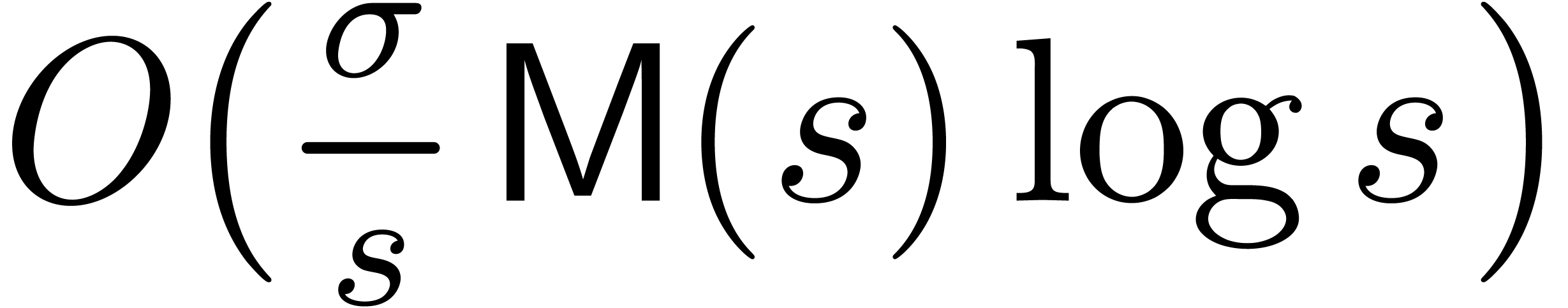 vectorial operations in
vectorial operations in  .
.
Proof. By classical binary powering, the
computation of the sequence 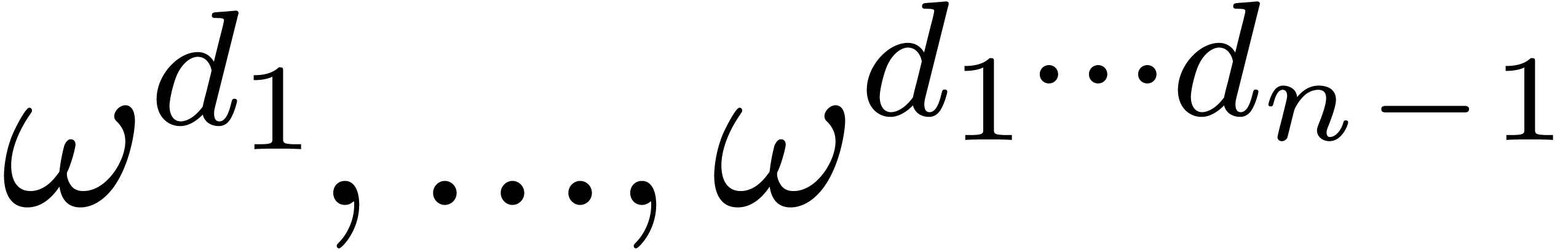 takes
takes 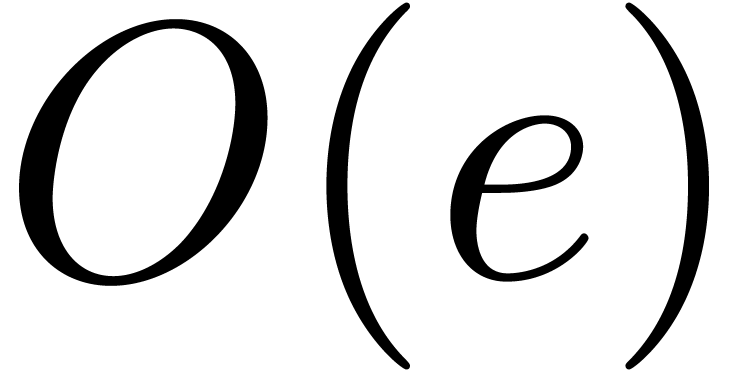 operations in
operations in  because each
because each 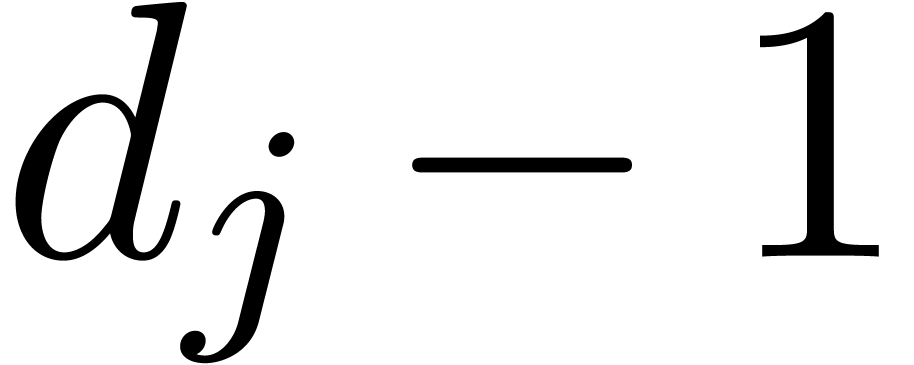 does appear in the entries of
does appear in the entries of 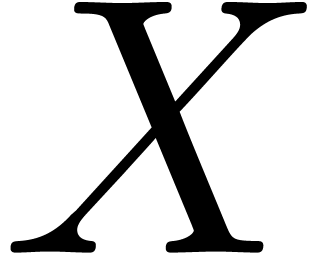 . Then the computation of all the
. Then the computation of all the 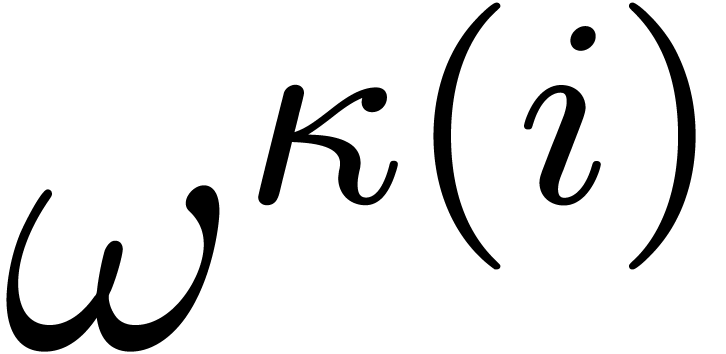 for
for 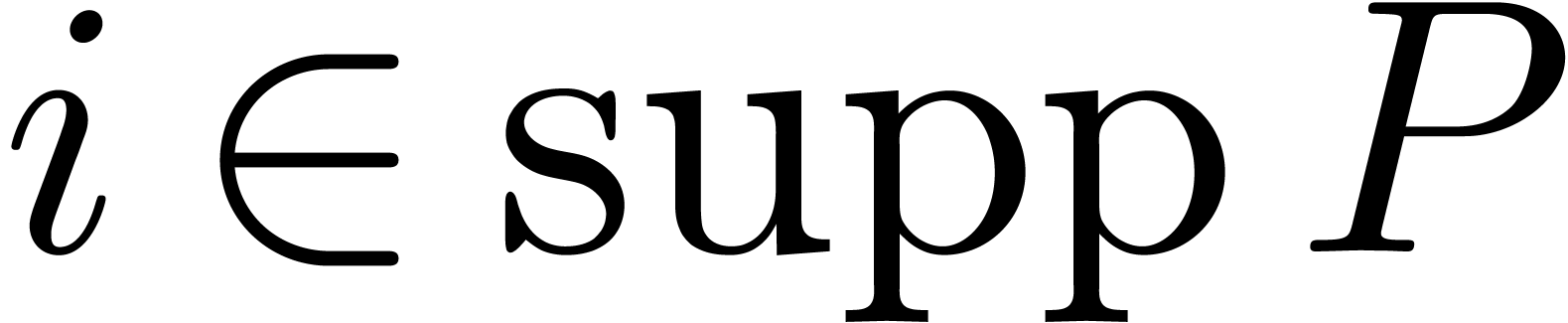 (resp.
(resp. 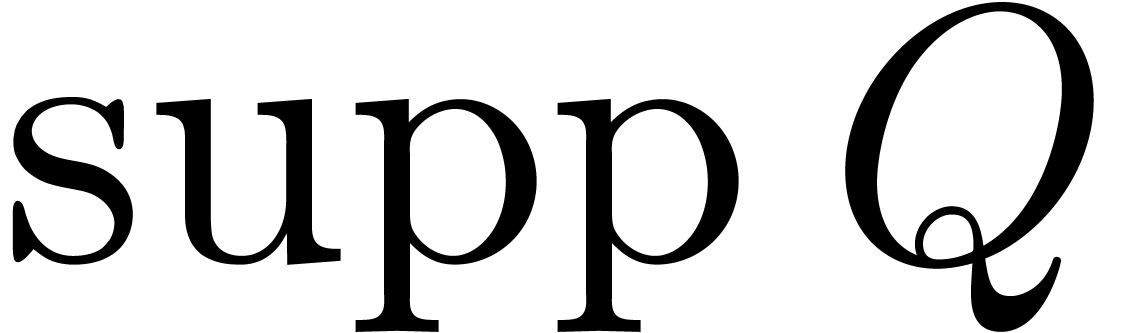 and
and 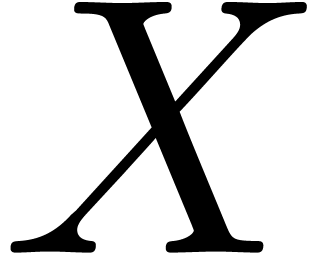 ) requires
) requires 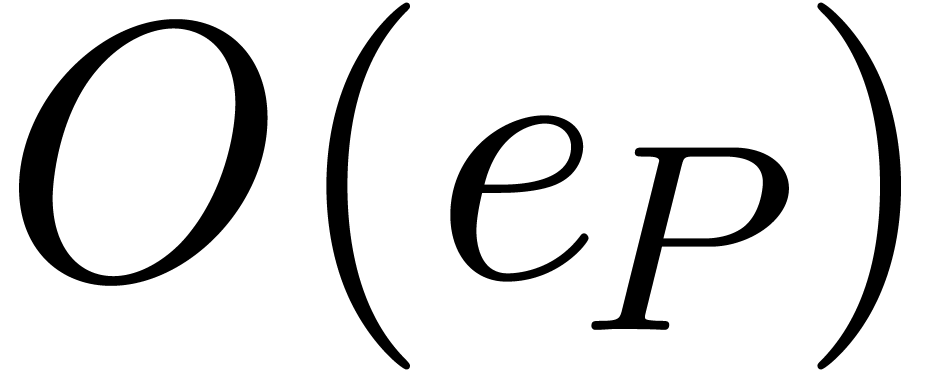 (resp.
(resp. 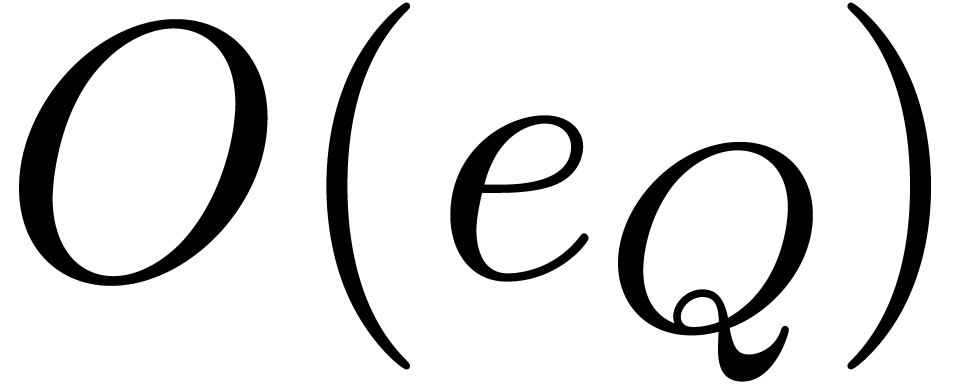 and
and 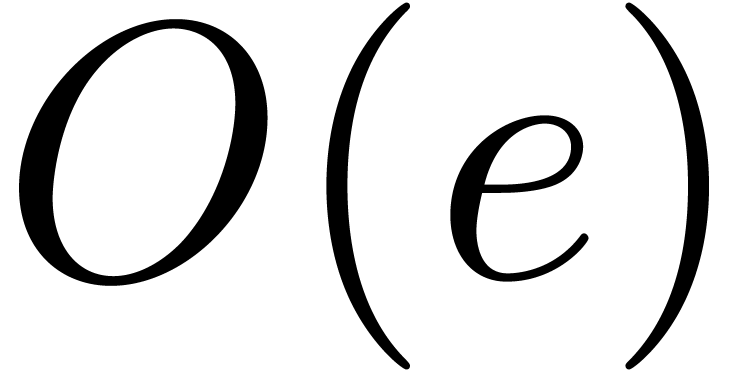 )
products in
)
products in 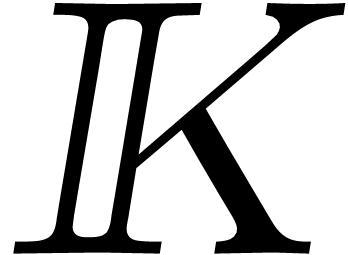 . Using the
complexity results from section 2.2, we may compute
. Using the
complexity results from section 2.2, we may compute 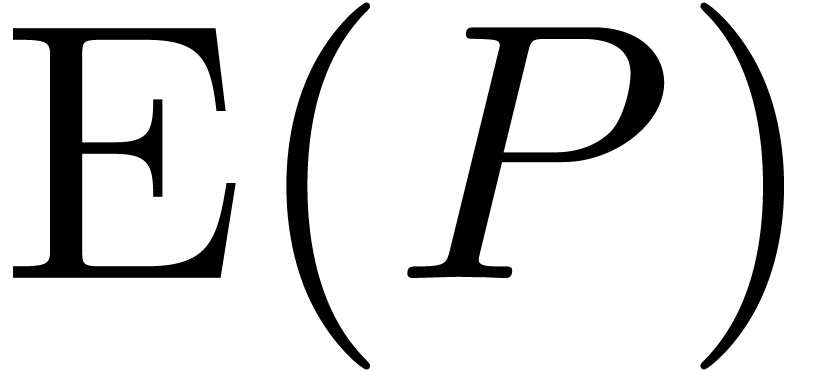 and
and  using
using 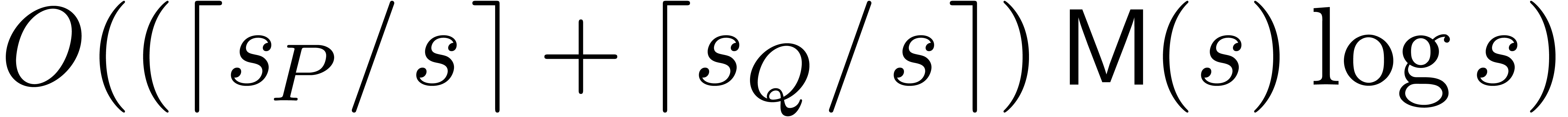 vectorial operations in
vectorial operations in  . We
deduce
. We
deduce 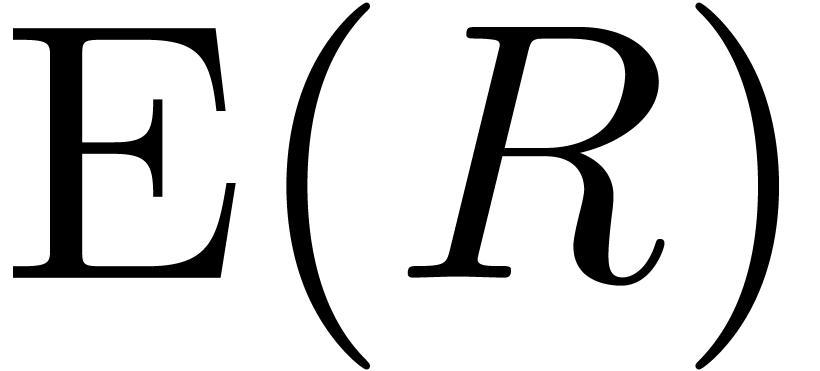 using
using 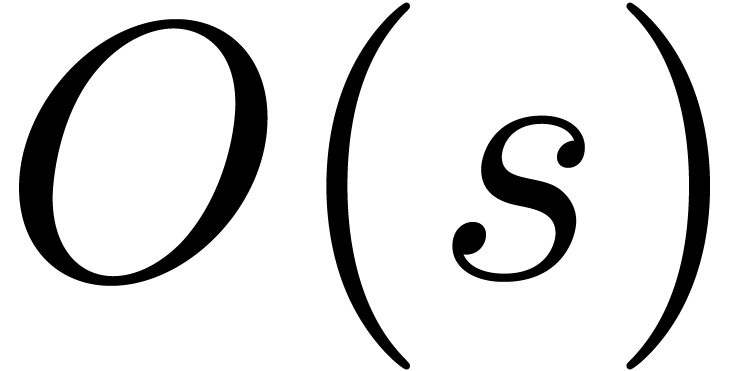 more
multiplications in
more
multiplications in  . Again
using the results from section 2.2, we retrieve the
coefficients
. Again
using the results from section 2.2, we retrieve the
coefficients 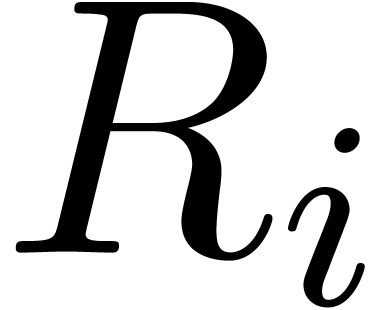 after
after  further vectorial operations in
further vectorial operations in  and
and 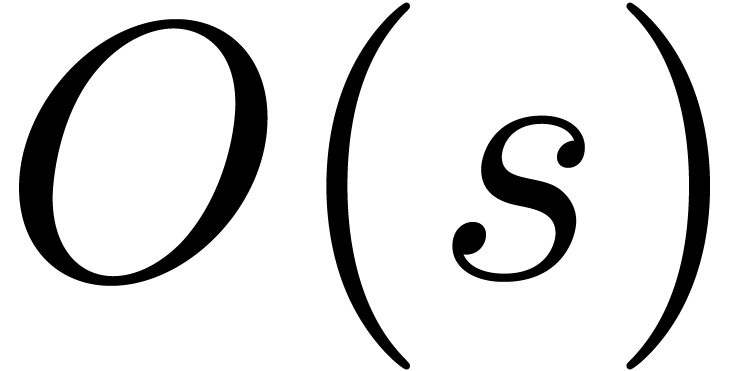 divisions in
divisions in  .
Adding up the various contributions, we obtain the theorem.
.
Adding up the various contributions, we obtain the theorem.
Remark
If 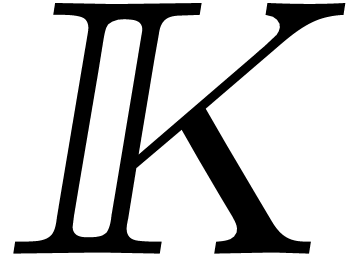 is the finite field
is the finite field 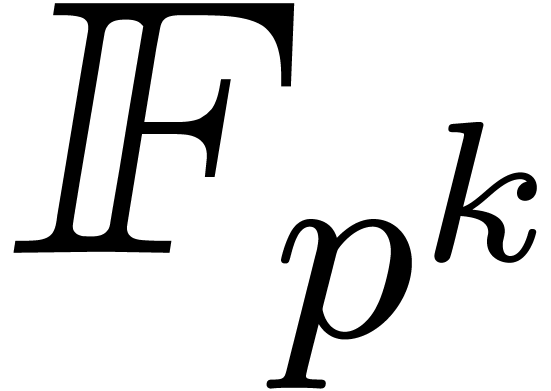 with
with 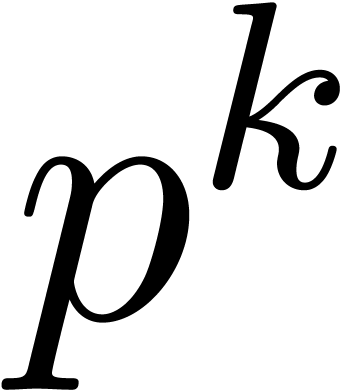 elements, then its multiplicative group is
cyclic of order
elements, then its multiplicative group is
cyclic of order 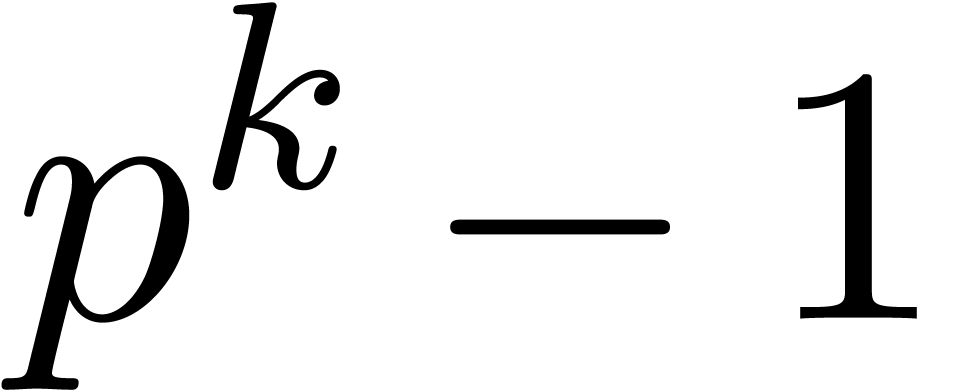 . Whenever
. Whenever
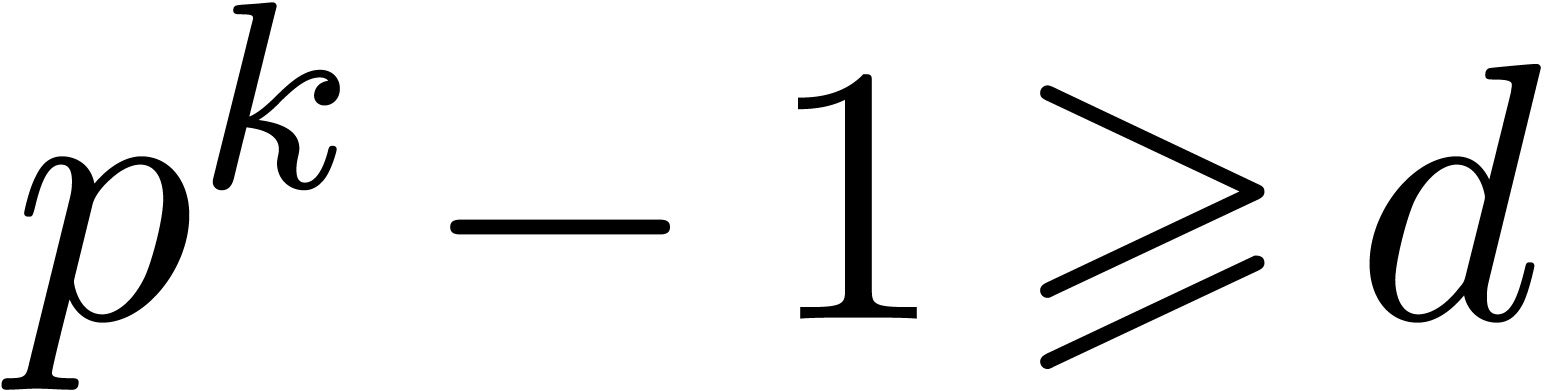 , it follows that the main
theorem 1 applies for any primitive element
, it follows that the main
theorem 1 applies for any primitive element  of this group.
of this group.
Usually, 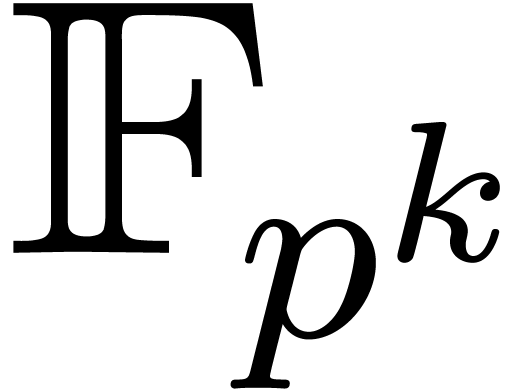 is given as the quotient
is given as the quotient 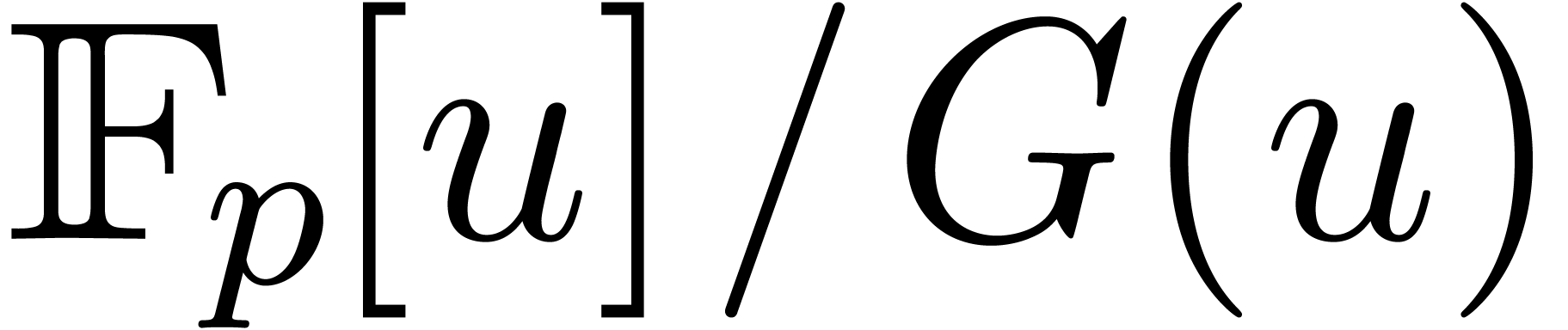 for some monic and irreducible polynomial
for some monic and irreducible polynomial  of degree
of degree 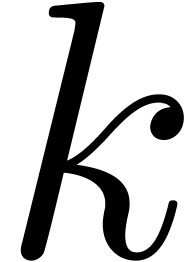 . In that case, a
multiplication in
. In that case, a
multiplication in  amounts to
amounts to 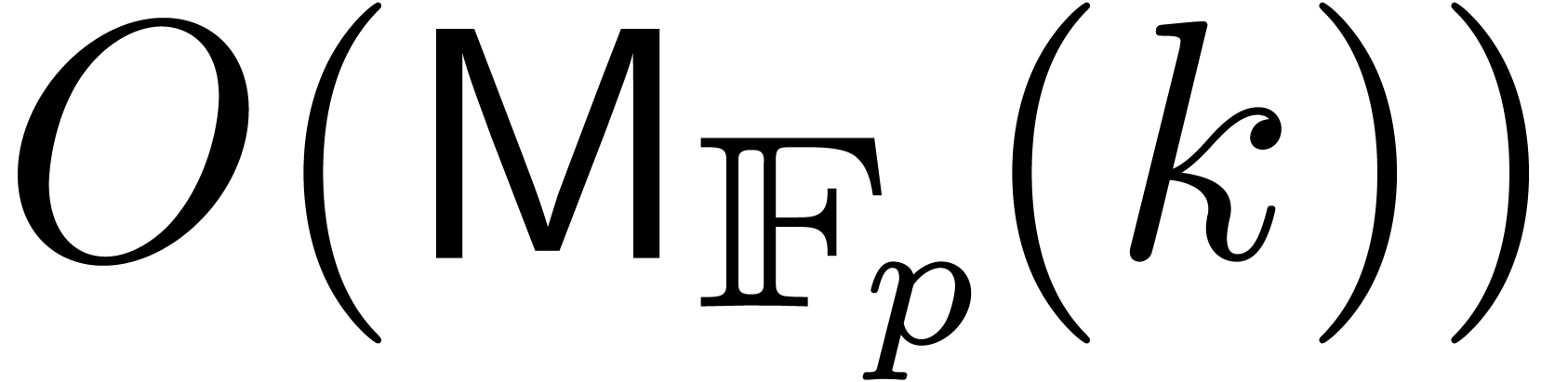 ring operations in
ring operations in 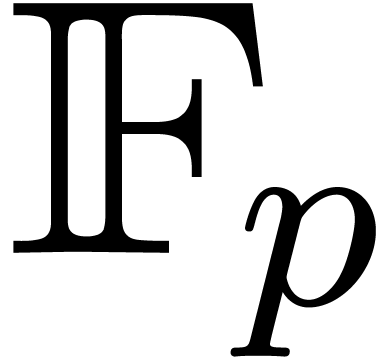 . An
inversion in
. An
inversion in  requires an extended gcd
computation in
requires an extended gcd
computation in 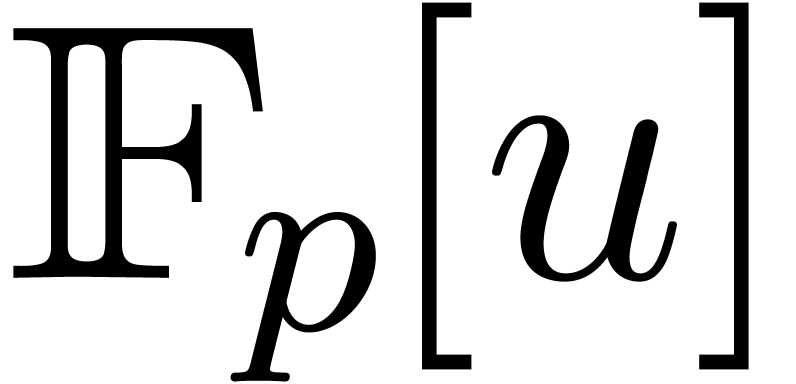 and gives rise to
and gives rise to 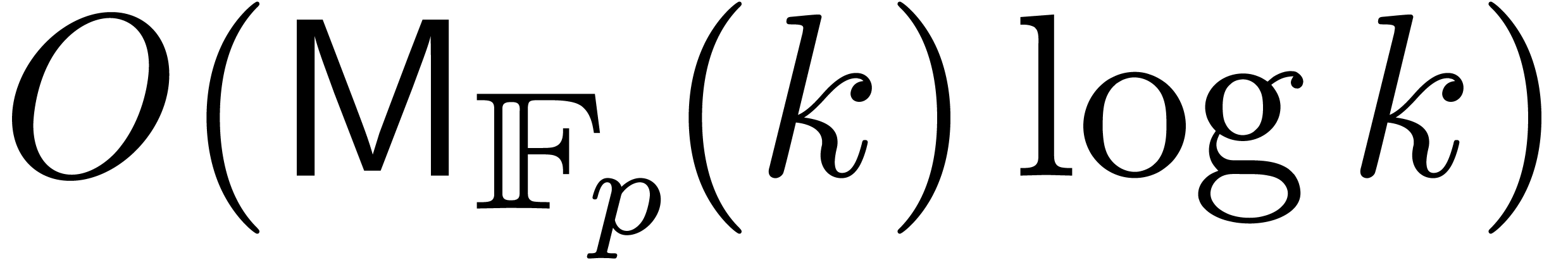 operations in
operations in 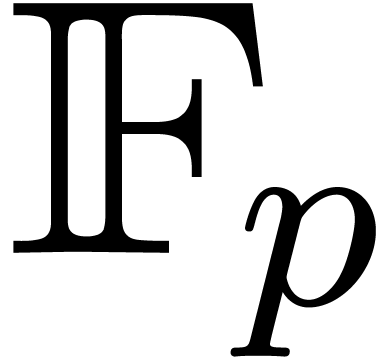 .
Using Kronecker multiplication, we can also take
.
Using Kronecker multiplication, we can also take 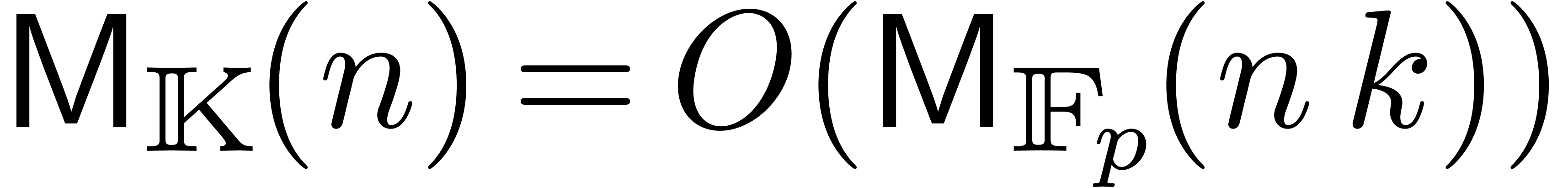 . Using these estimates, Theorem 1
implies:
. Using these estimates, Theorem 1
implies:
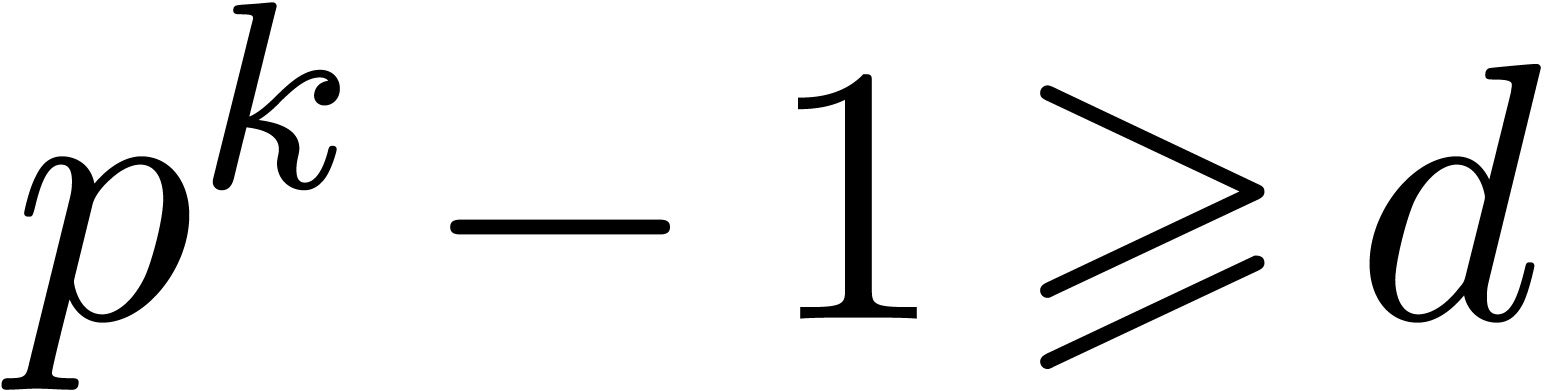 . Given two
polynomials
. Given two
polynomials 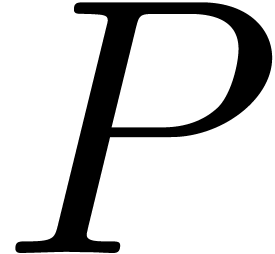 and
and  in
in
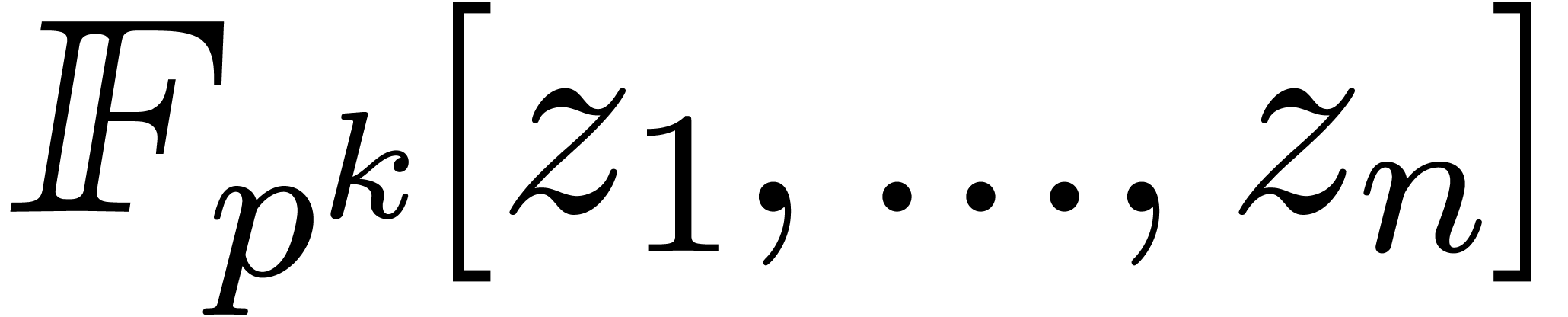 , the product
, the product 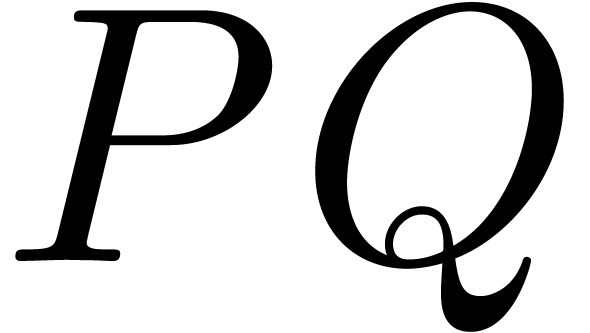 can be computed using
can be computed using
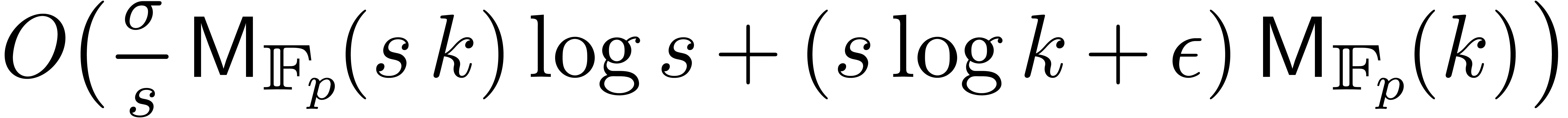
ring operations in 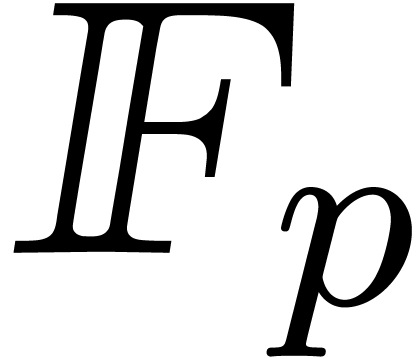 and
and 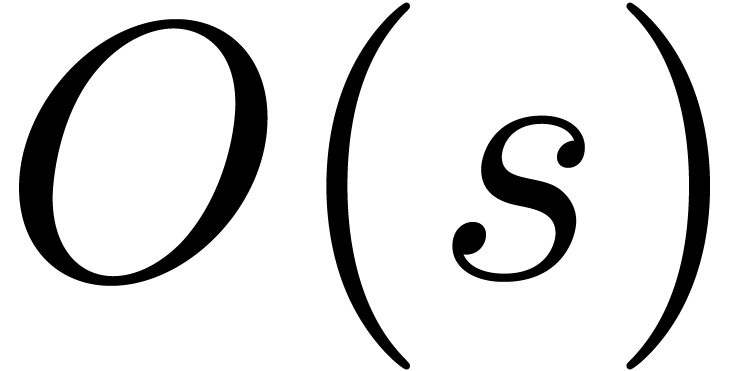 inversions in
inversions in 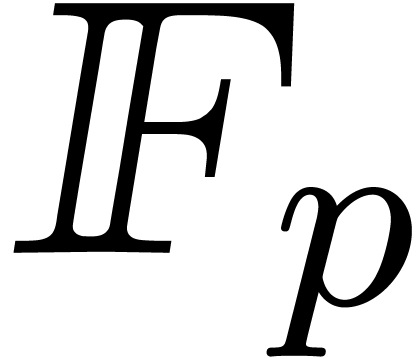 .
.
Applying the general purpose algorithm from [CK91], two
polynomials of degree 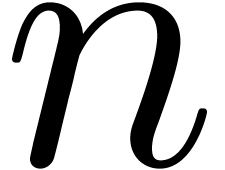 over
over 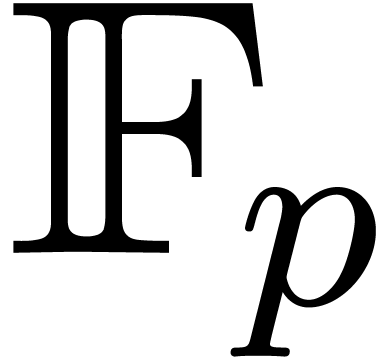 can be multiplied in time
can be multiplied in time 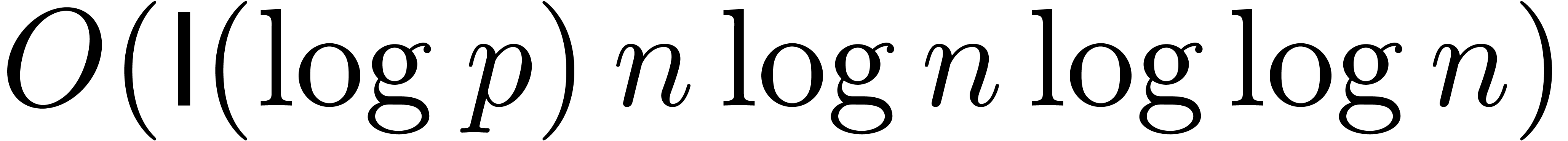 .
Alternatively, we may lift the multiplicants to polynomials in
.
Alternatively, we may lift the multiplicants to polynomials in 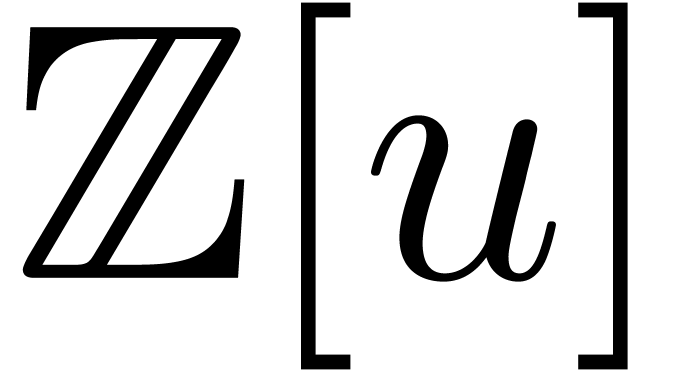 , use Kronecker multiplication and
reduce modulo
, use Kronecker multiplication and
reduce modulo 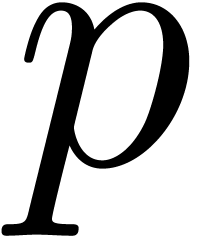 . As long as
. As long as
 , this yields the better
complexity bound
, this yields the better
complexity bound 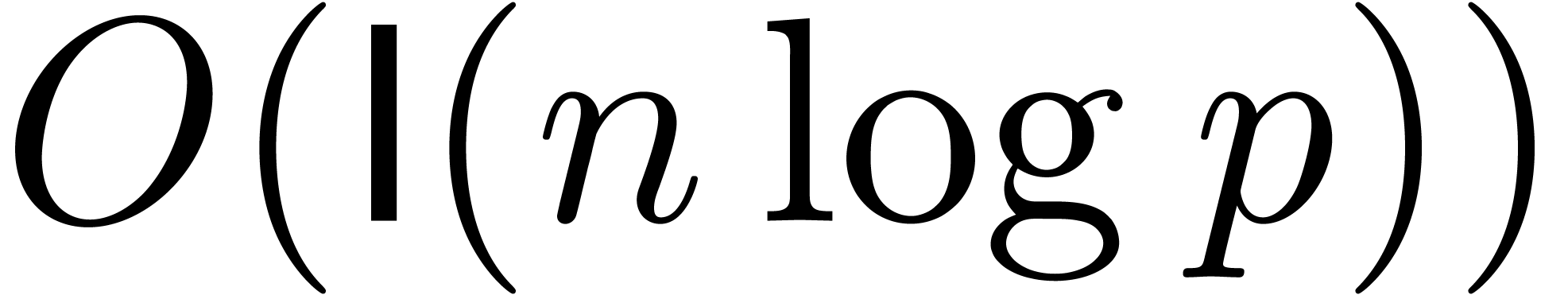 . Theorem 1 therefore implies:
. Theorem 1 therefore implies:
Remark 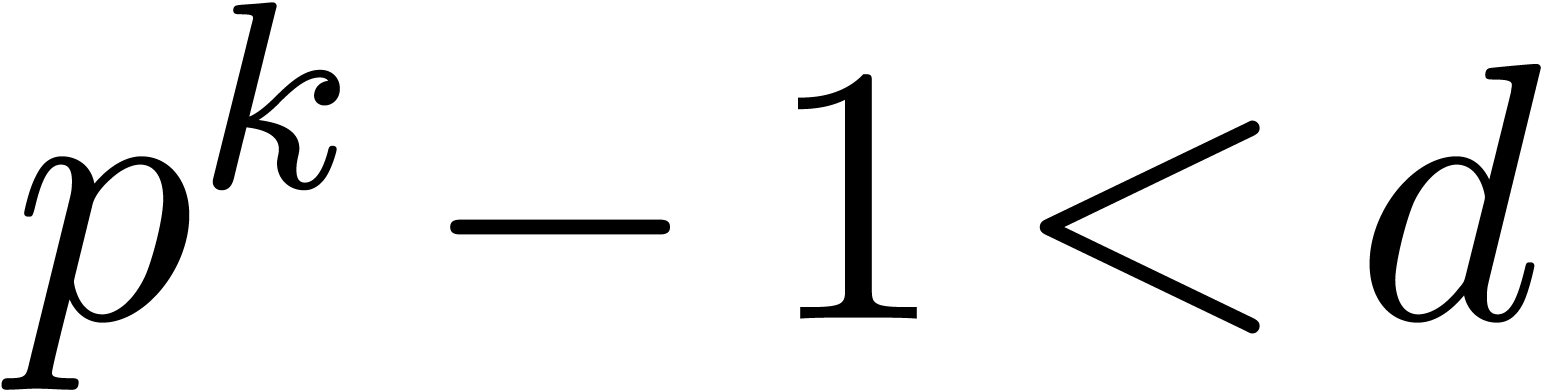 then it is always possible to build an algebraic extension
of suitable degree
then it is always possible to build an algebraic extension
of suitable degree 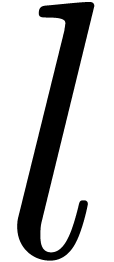 in order to apply the
corollary. Such constructions are classical, see for instance [GG02,
Chapter 14]. We need to have
in order to apply the
corollary. Such constructions are classical, see for instance [GG02,
Chapter 14]. We need to have 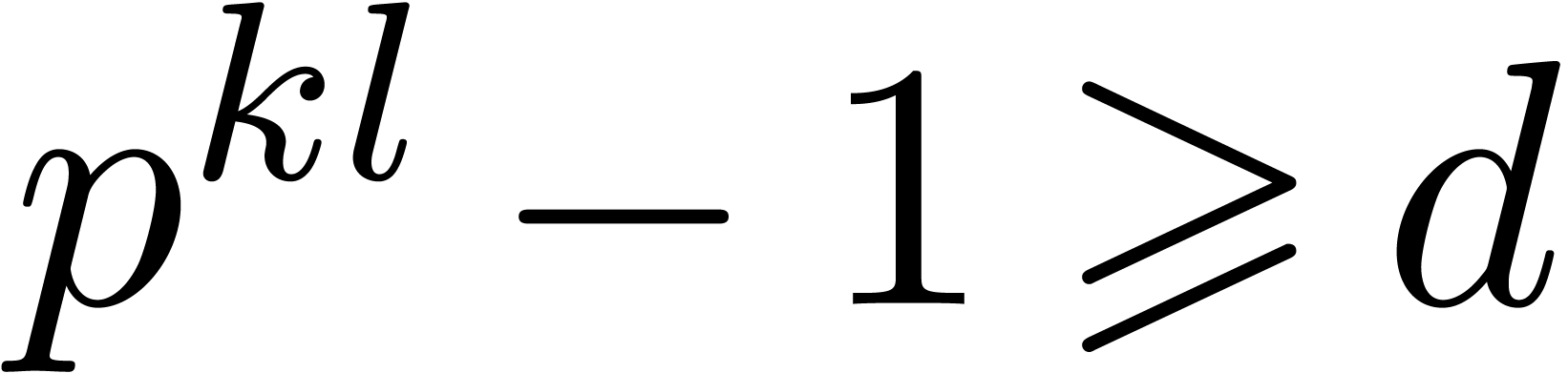 ,
so
,
so 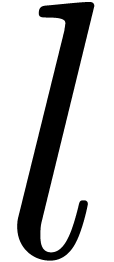 should be taken of the order
should be taken of the order 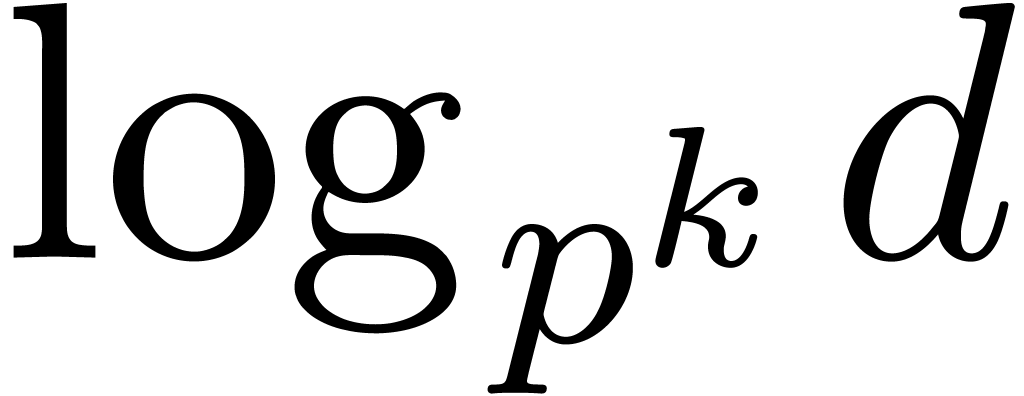 , which also corresponds to the additional
overhead induced by this method.
, which also corresponds to the additional
overhead induced by this method.
Remark 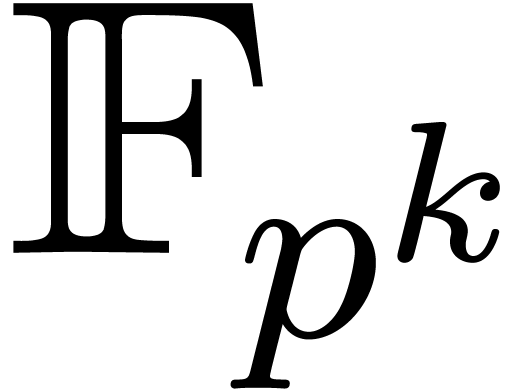 can be constructed in polynomial time [BS91]. If
can be constructed in polynomial time [BS91]. If 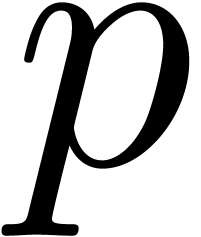 is odd, then
is odd, then  is a primive element
if and only if
is a primive element
if and only if 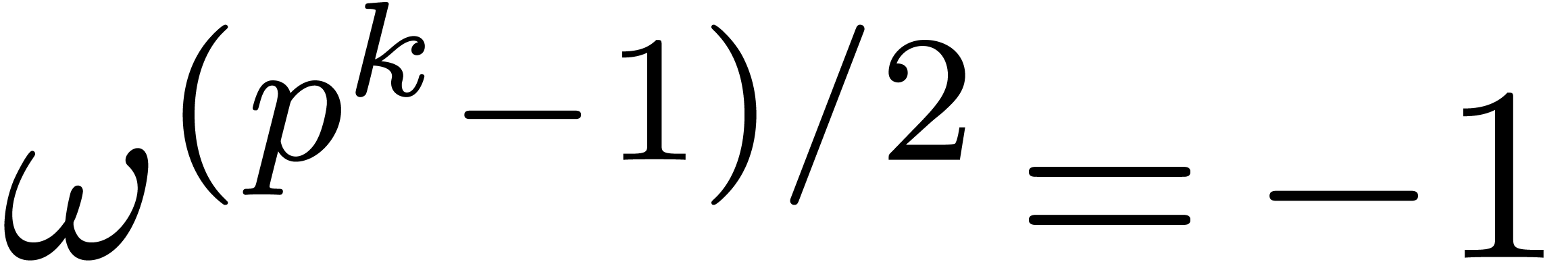 . In
. In 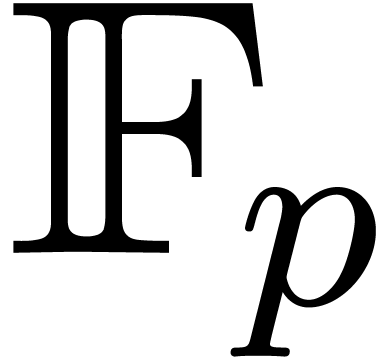 , the smallest
, the smallest  such that
such that 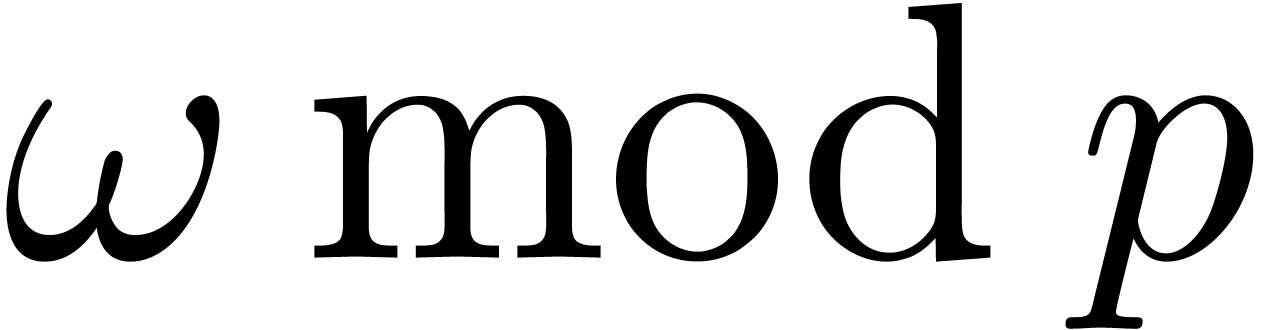 is a primitive element satisfies
is a primitive element satisfies 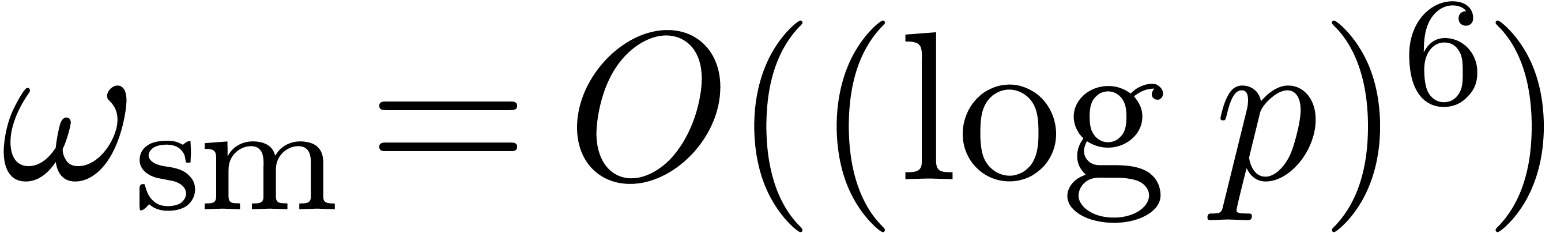 .
.
One approach for the multiplication 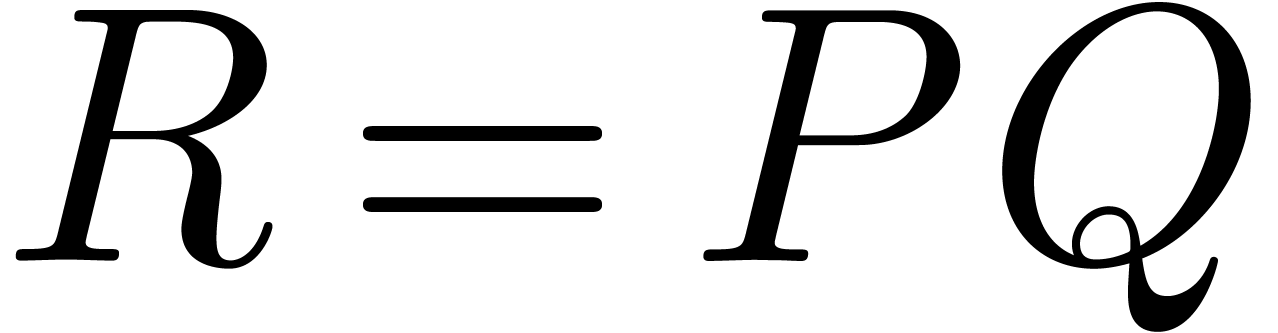 of
polynomials with integer coefficients is to reduce the problem modulo a
suitable prime number
of
polynomials with integer coefficients is to reduce the problem modulo a
suitable prime number 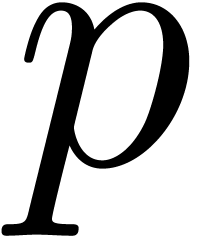 . This
prime number should be sufficiently large such that
. This
prime number should be sufficiently large such that 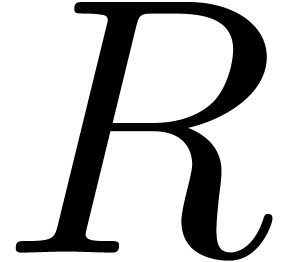 can be read off from
can be read off from 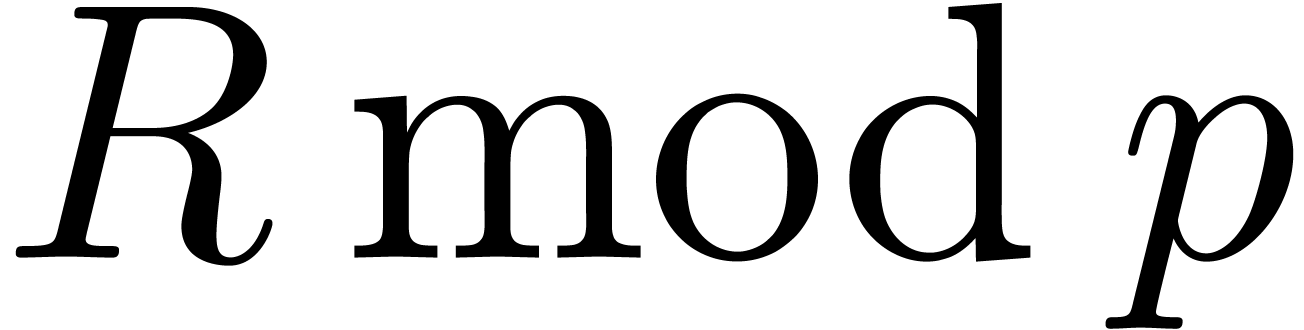 and such that
and such that 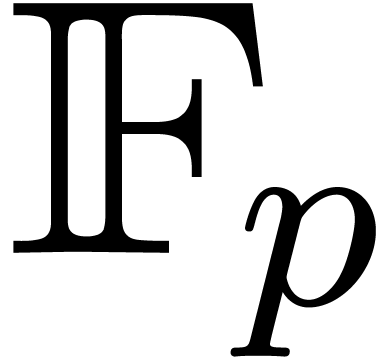 admits elements of order
admits elements of order 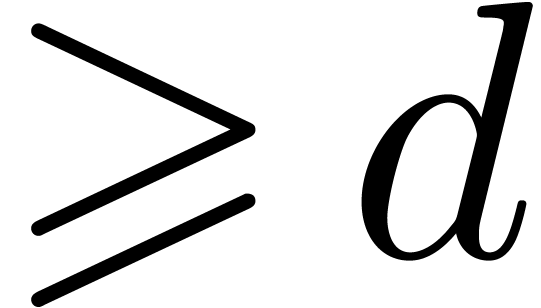 .
.
Let 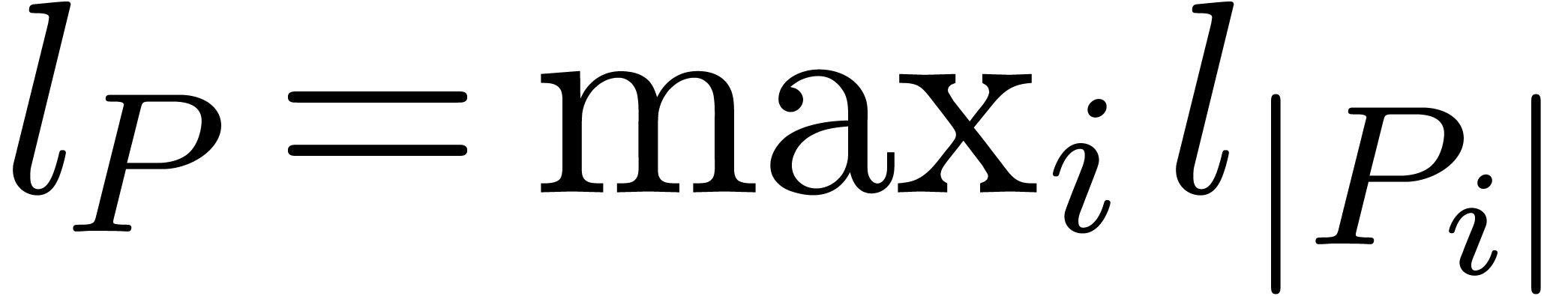 denote the maximal bit-length of the
coefficients of
denote the maximal bit-length of the
coefficients of 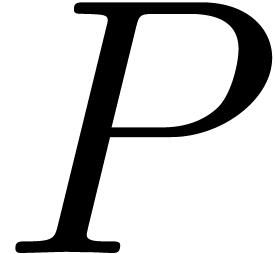 and similarly for
and similarly for  and
and 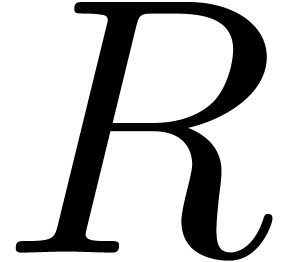 . Since
. Since
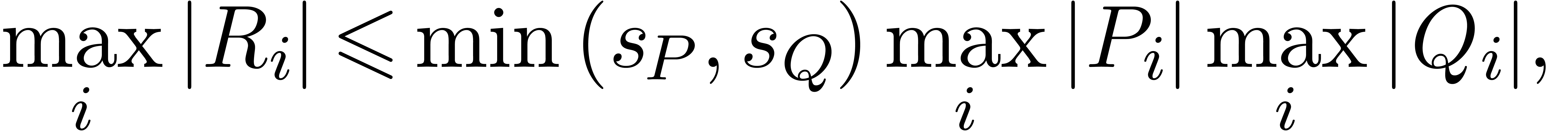
we have
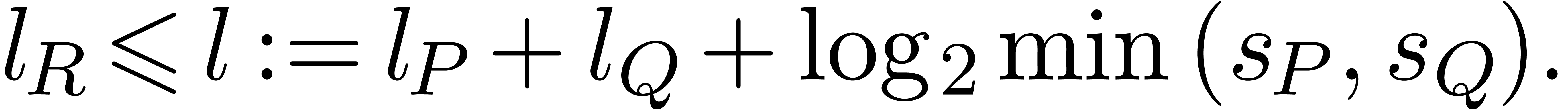
It therefore suffices to take 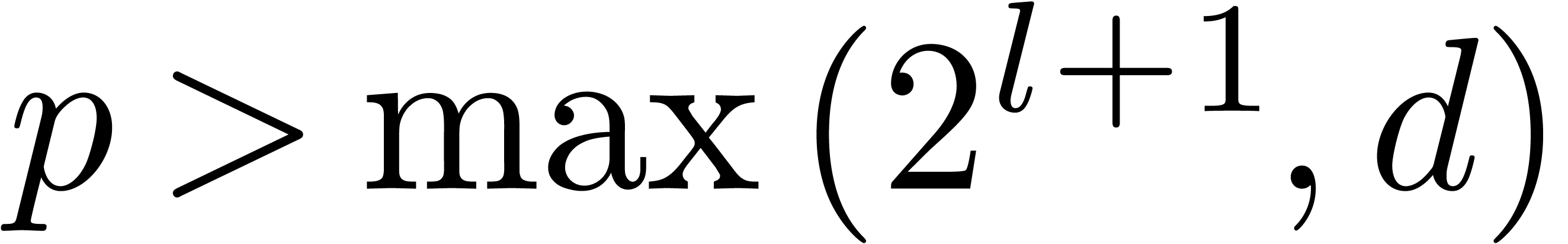 .
Corollary 4 now implies:
.
Corollary 4 now implies:
Remark 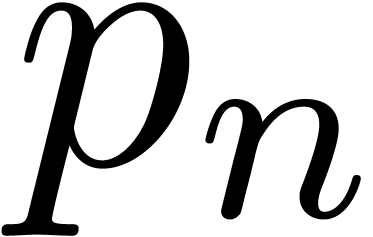 denote the
denote the 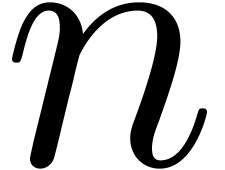 -th
prime number. The prime number theorem implies that
-th
prime number. The prime number theorem implies that 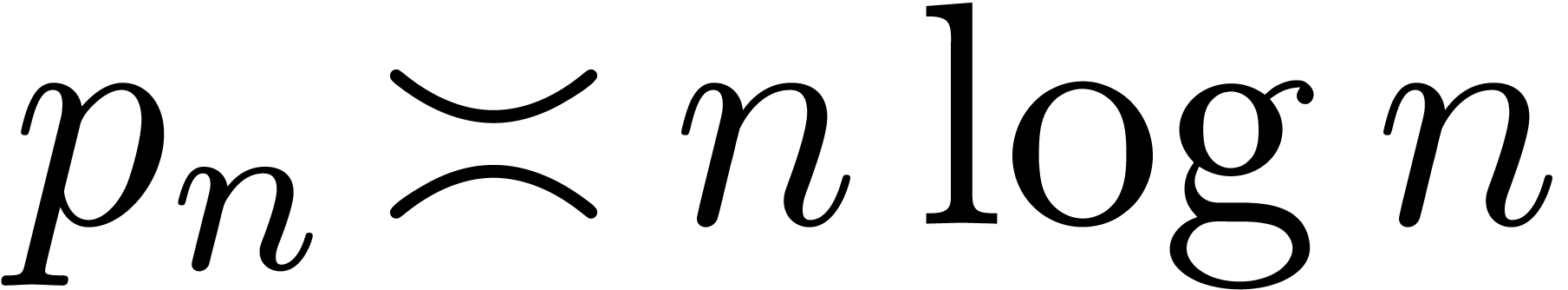 . Cramér's conjecture [Cra36]
states that
. Cramér's conjecture [Cra36]
states that
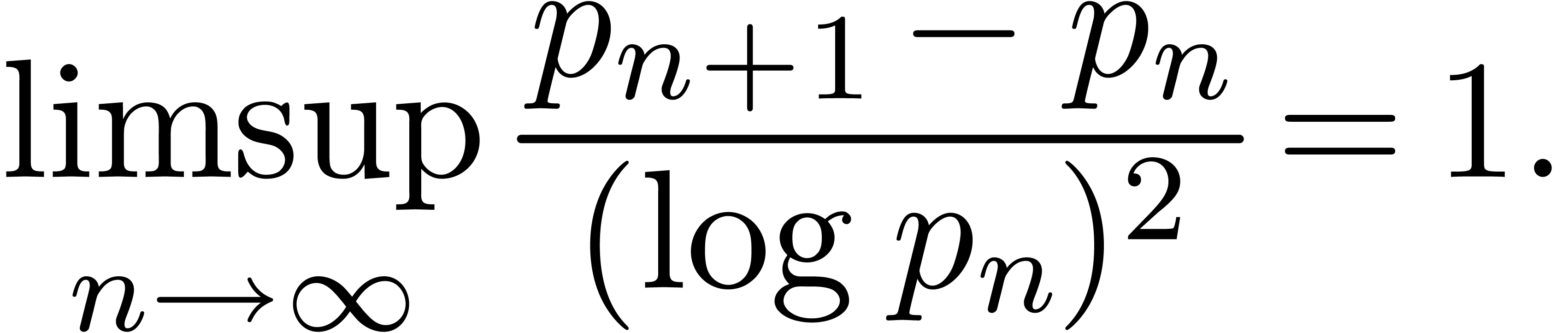
This conjecture is supported by numerical evidence. Setting
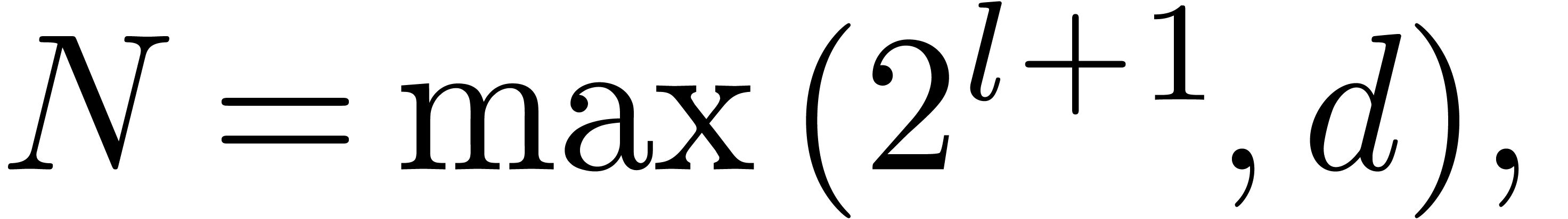
the conjecture implies that the smallest prime number  with
with 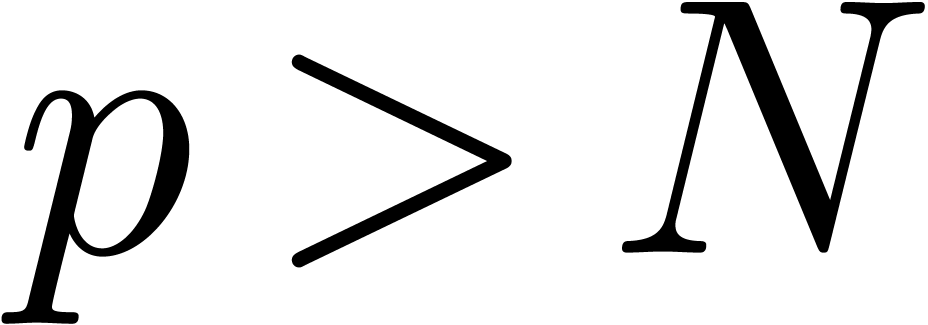 satisfies
satisfies 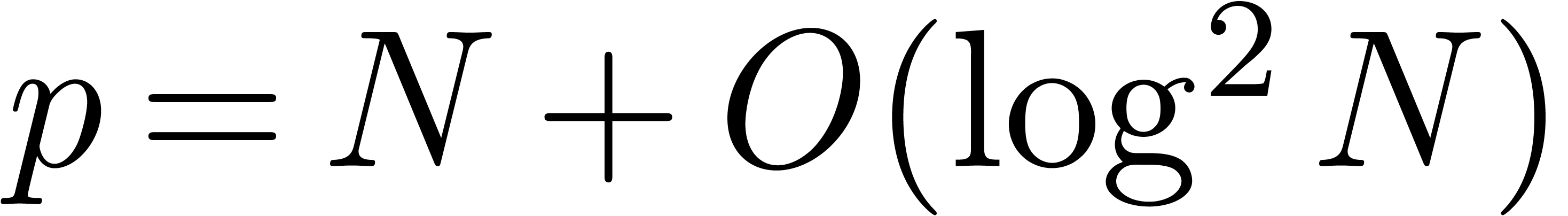 .
Using a polynomial time primality test [AKS04], it follows
that this number can be computed by brute force in time
.
Using a polynomial time primality test [AKS04], it follows
that this number can be computed by brute force in time 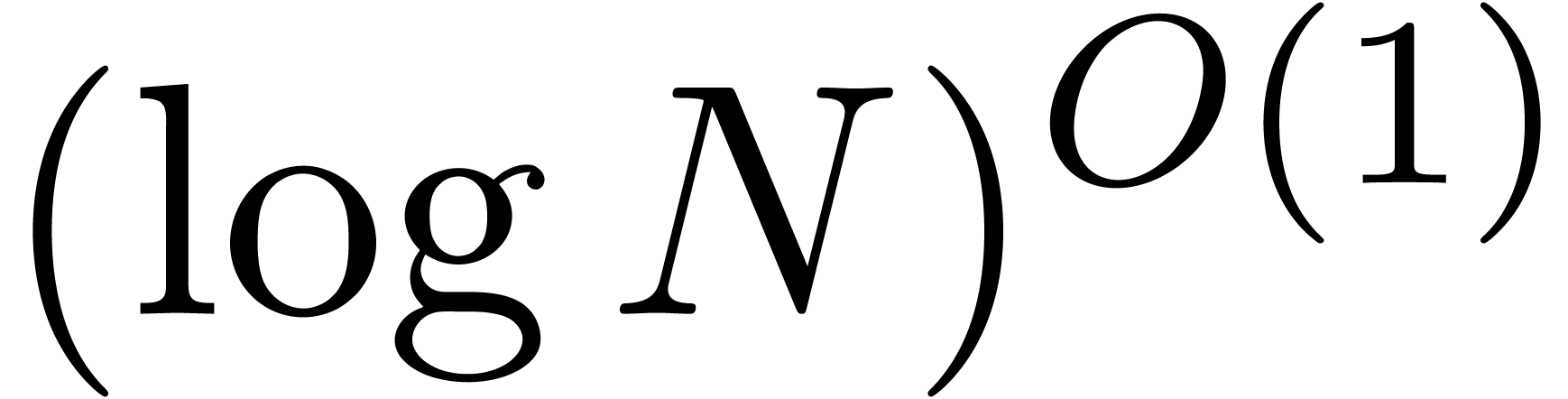 . In addition, in order to satisfy the
complexity bound it suffices to tabulates prime numbers of sizes 2, 4,
8, 16, etc.
. In addition, in order to satisfy the
complexity bound it suffices to tabulates prime numbers of sizes 2, 4,
8, 16, etc.
In our algorithm and Theorem 1, we regard the computation
of a prime number 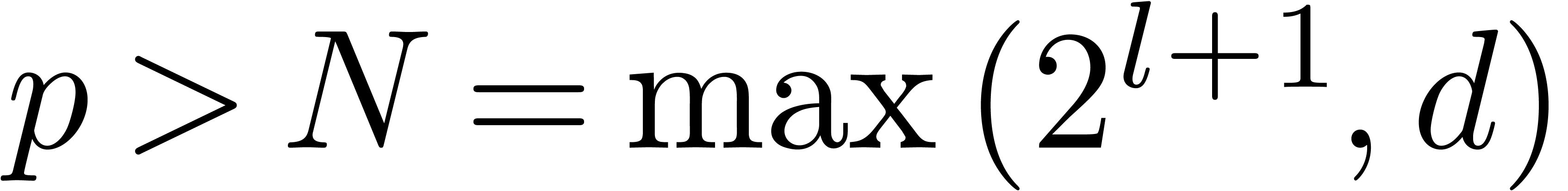 as a precomputation. This is
reasonable if
as a precomputation. This is
reasonable if  is not too large. Now the quantity
is not too large. Now the quantity
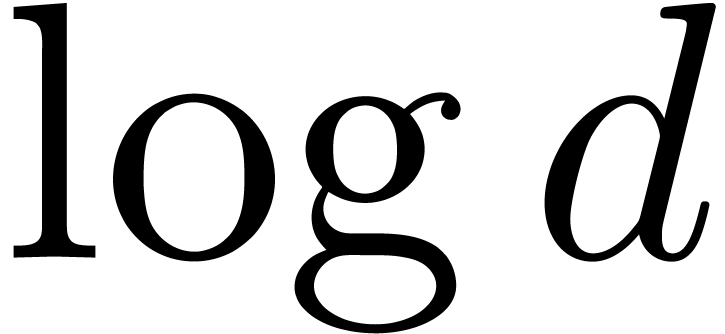 usually remains reasonably small. Hence, our
assumption that
usually remains reasonably small. Hence, our
assumption that  is not too large only gets
violated if
is not too large only gets
violated if  becomes large. In that case, we will
rather use Chinese remaindering. We first compute
becomes large. In that case, we will
rather use Chinese remaindering. We first compute 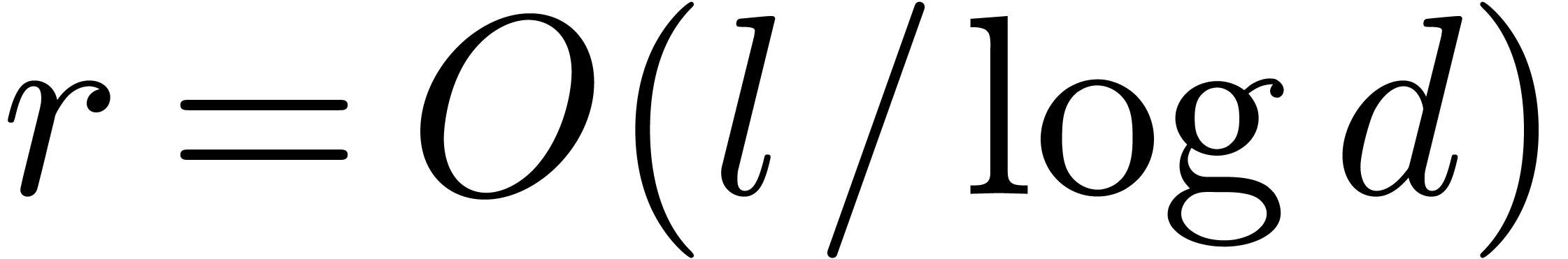 prime numbers
prime numbers  with
with
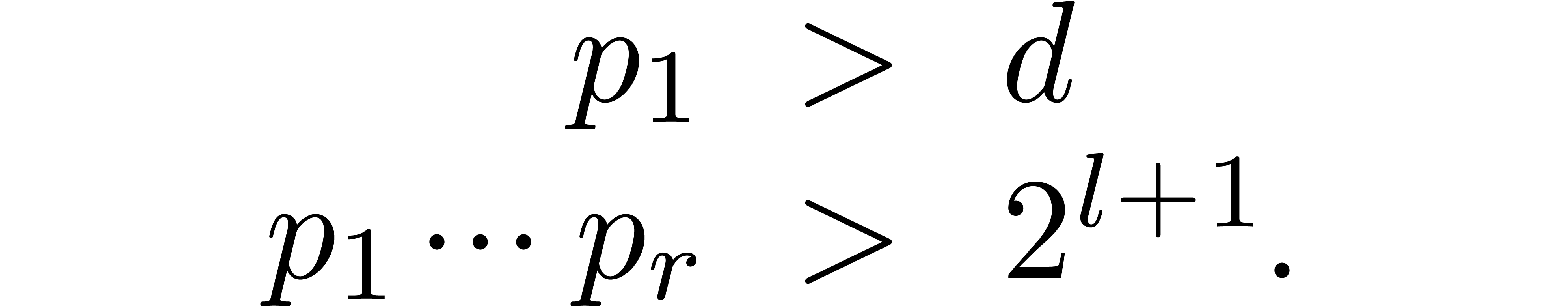
Each 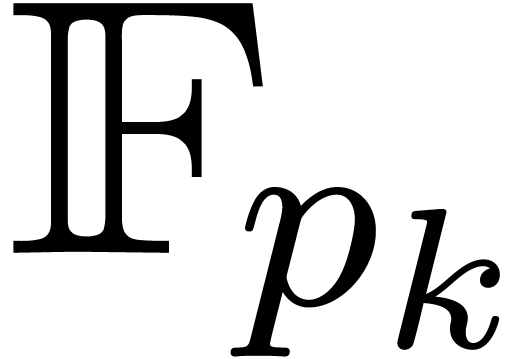 contains a primitive root of unity
contains a primitive root of unity 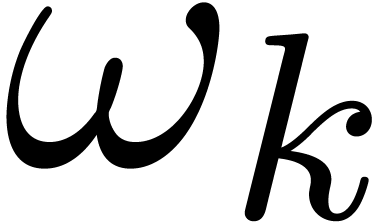 of order
of order 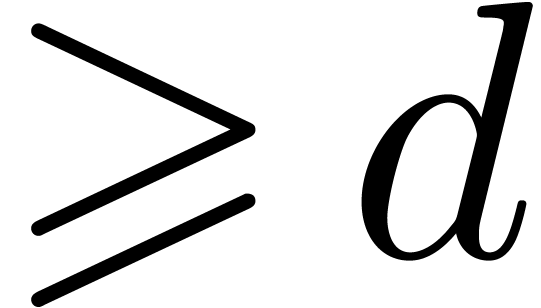 .
We next proceed as before, with
.
We next proceed as before, with 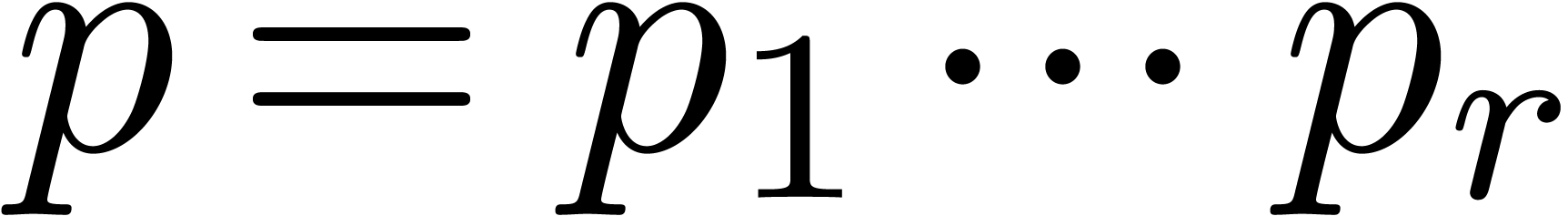 and
and 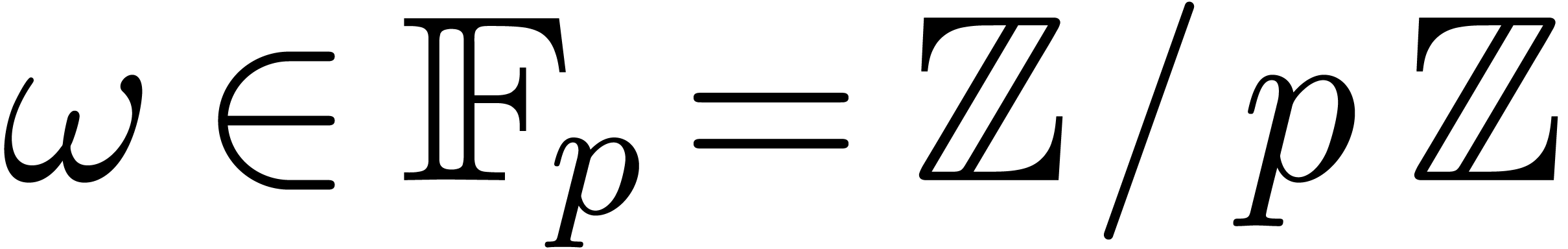 such that
such that 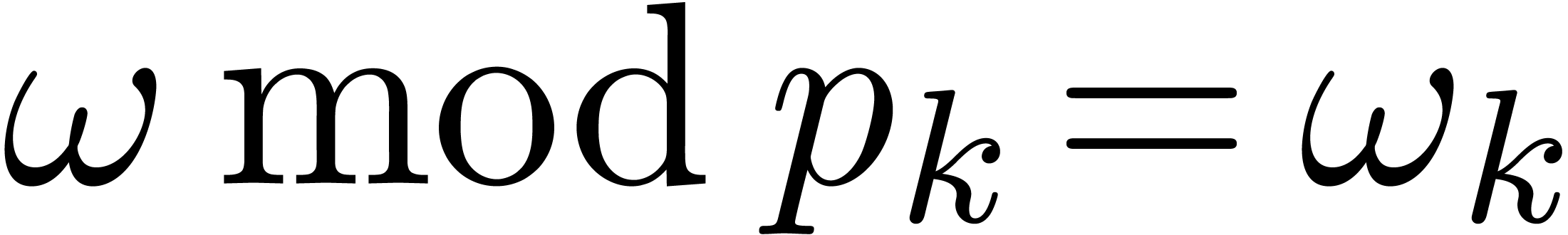 for each
for each 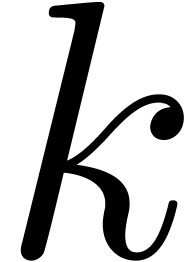 . Indeed, the fact that each
. Indeed, the fact that each 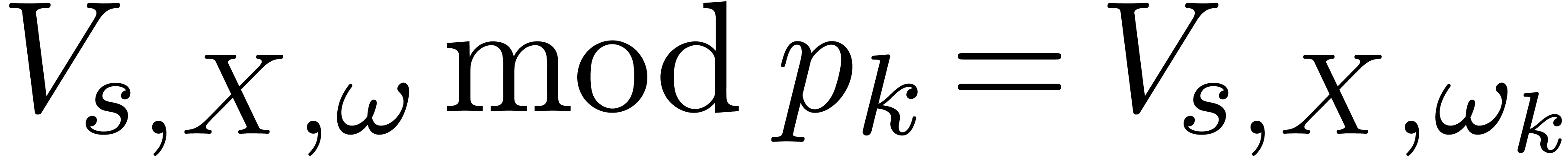 is invertible implies that
is invertible implies that 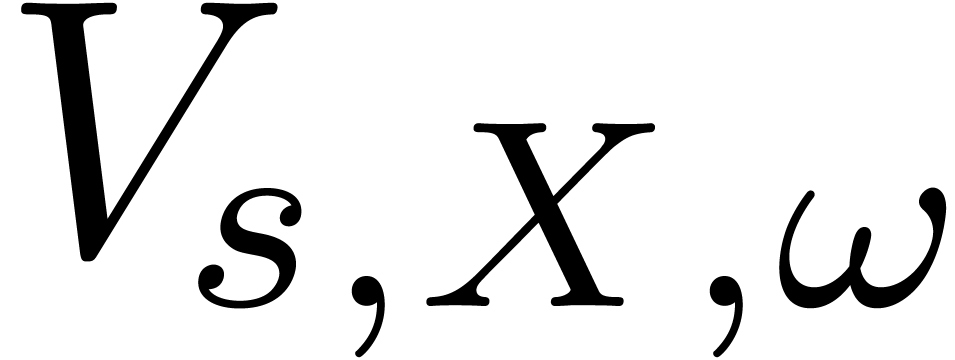 is invertible.
is invertible.
We will say that  form a reduced sequence of
prime moduli with order
form a reduced sequence of
prime moduli with order 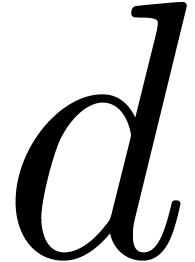 and capacity
and capacity  , whenever
, whenever 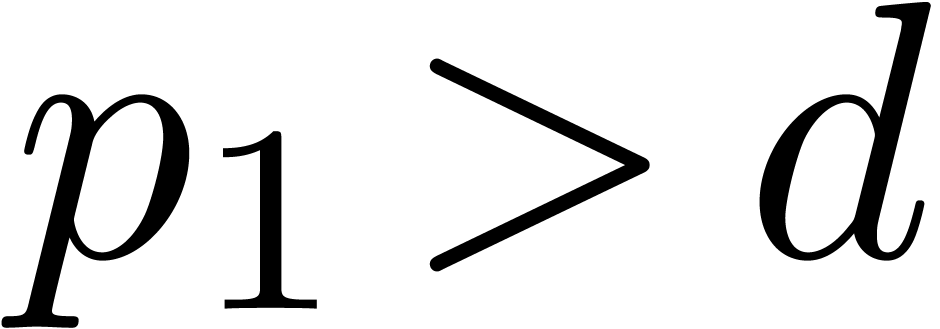 ,
, 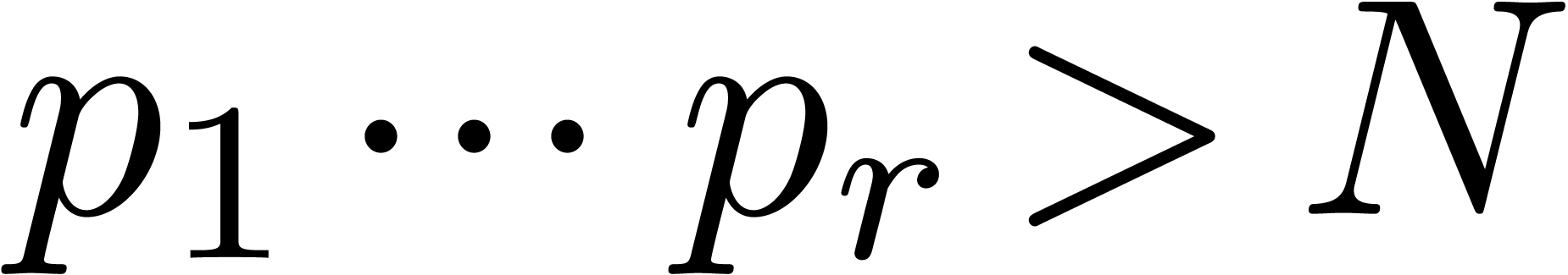 ,
, 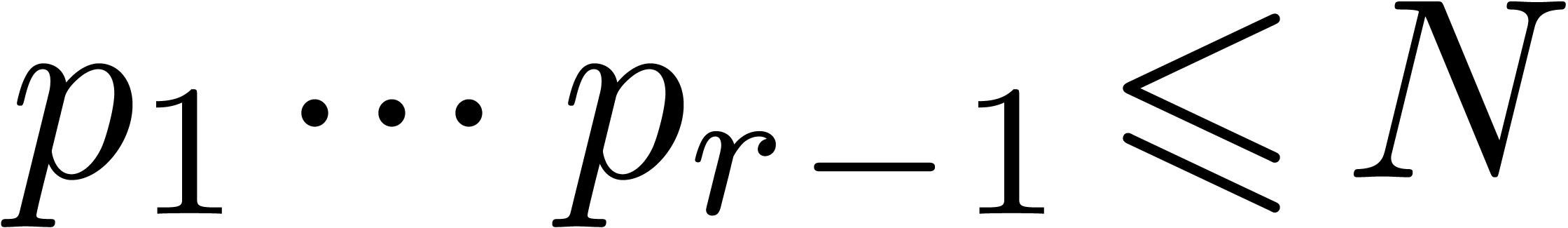 and
and 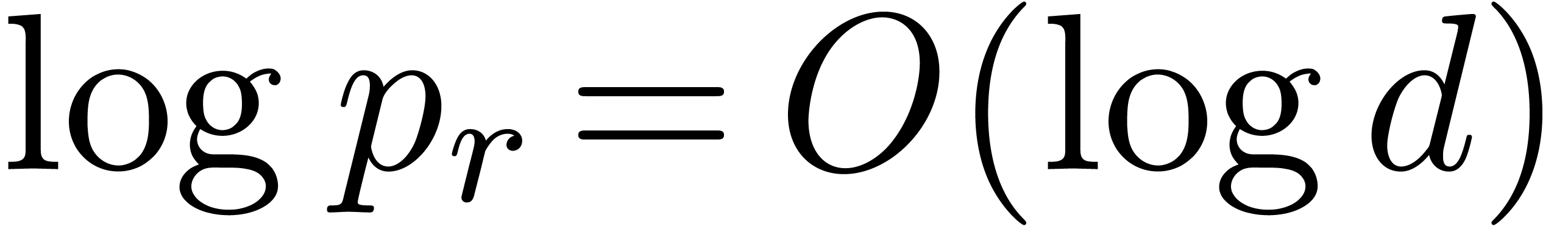 . We
then have the following refinement of Corollary 7:
. We
then have the following refinement of Corollary 7:
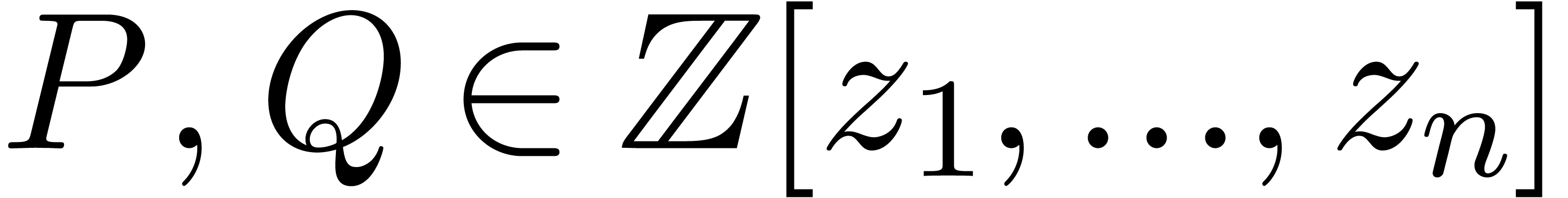 and a reduced sequence
and a reduced sequence  of prime moduli with order
of prime moduli with order 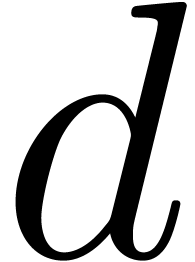 and
capacity
and
capacity 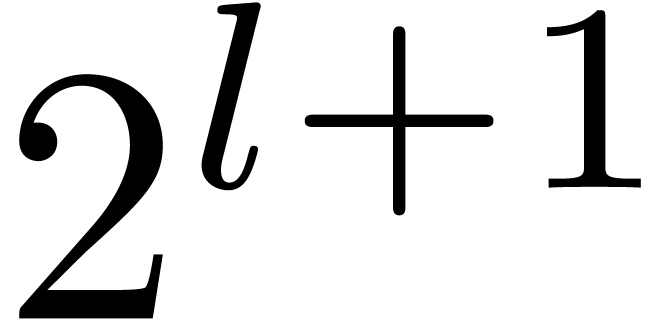 , we can compute
, we can compute
 in time
in time
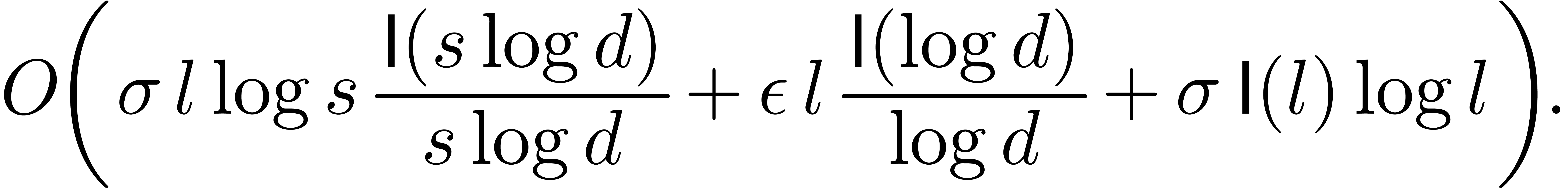
An important kind of sparse polynomials are power series in several
variables, truncated by total degree. Such series are often used in long
term integration of dynamical systems [MB96, MB04],
in which case their coefficients are floating point numbers rather than
integers. Assume therefore that 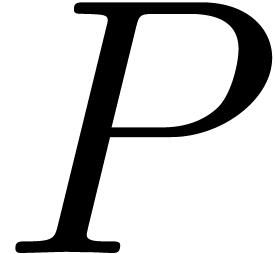 and
and  are polynomials with floating coefficients with a
precision of
are polynomials with floating coefficients with a
precision of  bits.
bits.
Let  be the maximal exponent of the coefficients
of
be the maximal exponent of the coefficients
of 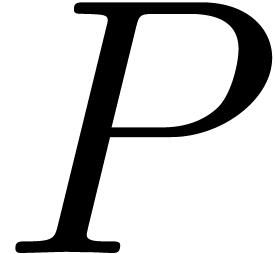 . For a so called
discrepancy
. For a so called
discrepancy 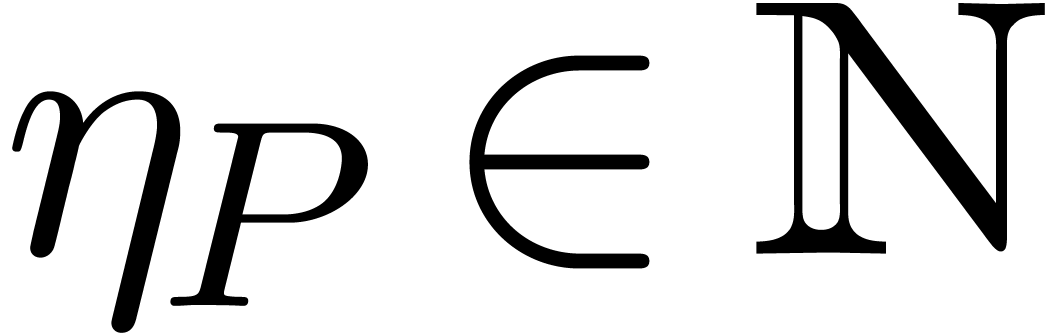 , fixed
by the user, we let
, fixed
by the user, we let 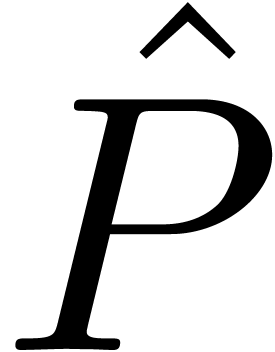 be the integer polynomial
with
be the integer polynomial
with
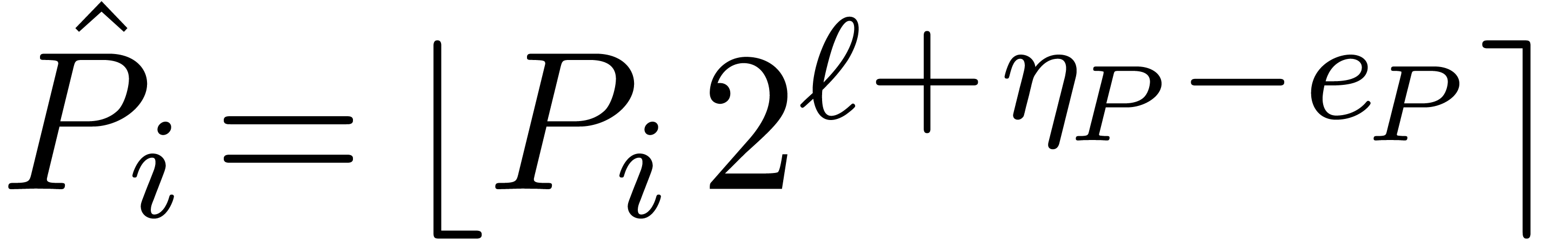
for all 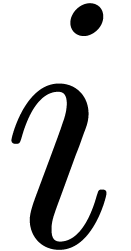 . We have
. We have 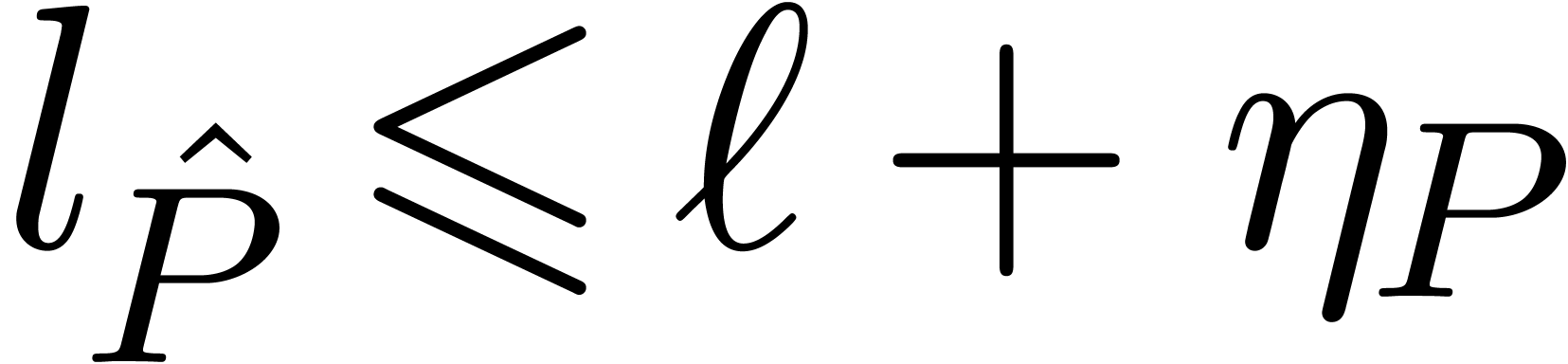 and
and
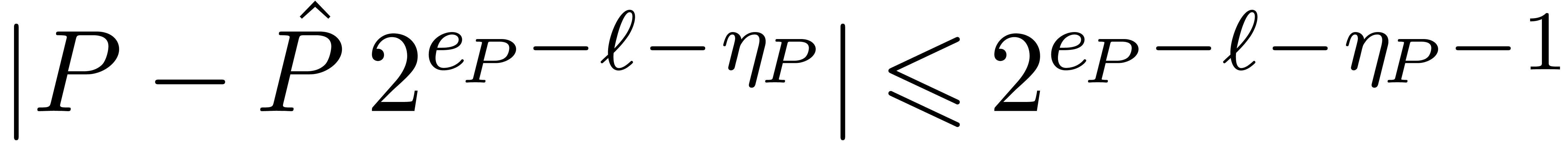
for the sup-norm on the coefficients. If all coefficients of 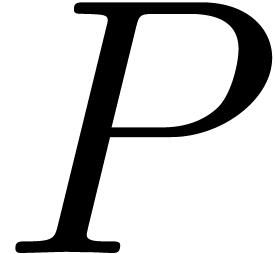 have a similar order of magnitude, in the sense that the
minimal exponent of the coefficients is at least
have a similar order of magnitude, in the sense that the
minimal exponent of the coefficients is at least  , then we actually have
, then we actually have 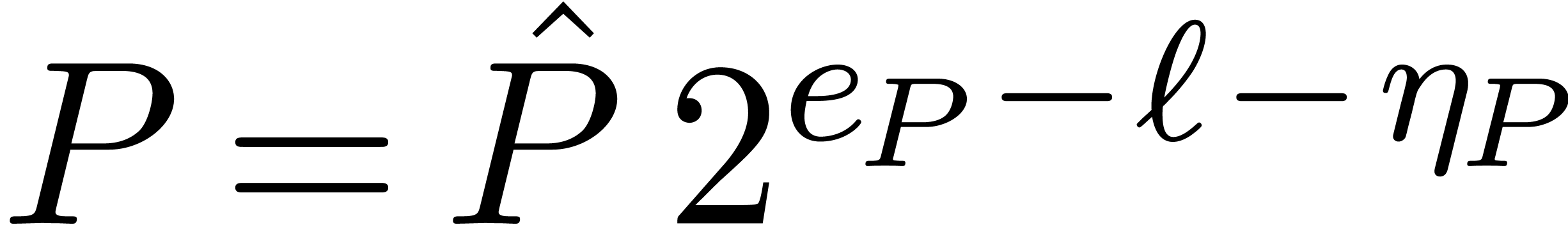 . Applying a similar decomposition to
. Applying a similar decomposition to  , we may compute the product
, we may compute the product
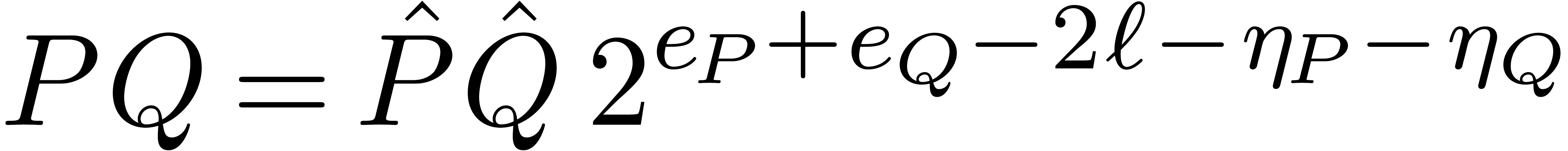
using the algorithm from section 2 and convert the resulting coefficients back into floating point format.
Usually, the coefficients 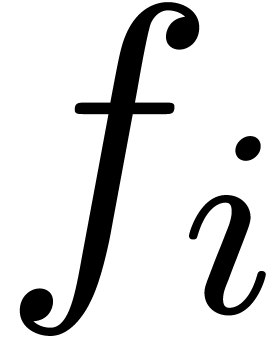 of a univariate power
series
of a univariate power
series 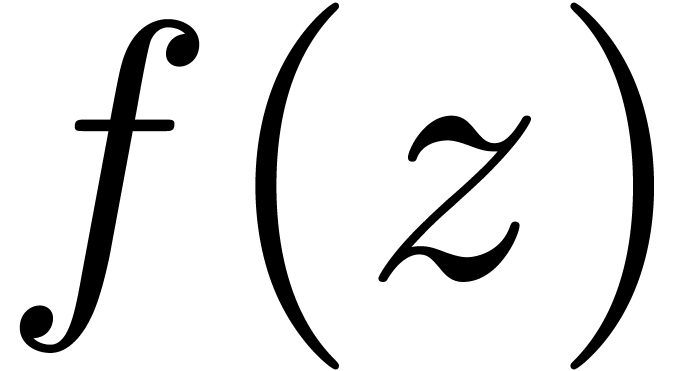 are approximately in a geometric
progression
are approximately in a geometric
progression 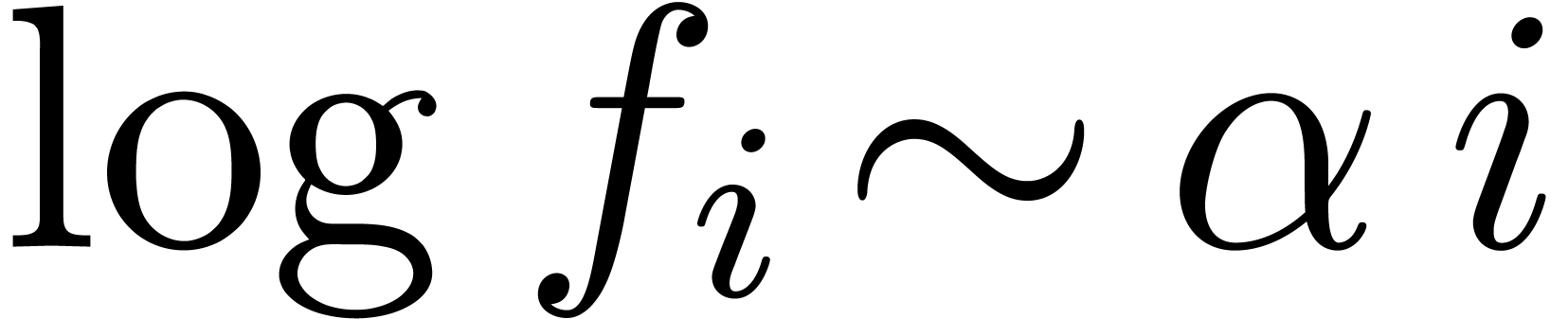 . In that case,
the coefficients of the power series
. In that case,
the coefficients of the power series 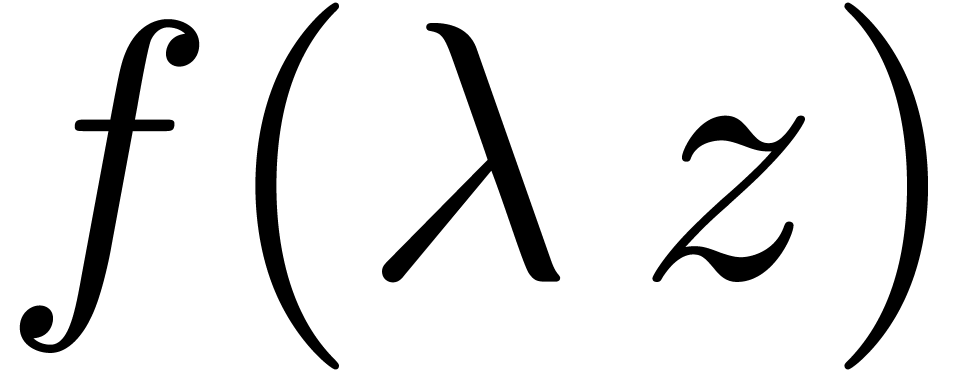 with
with 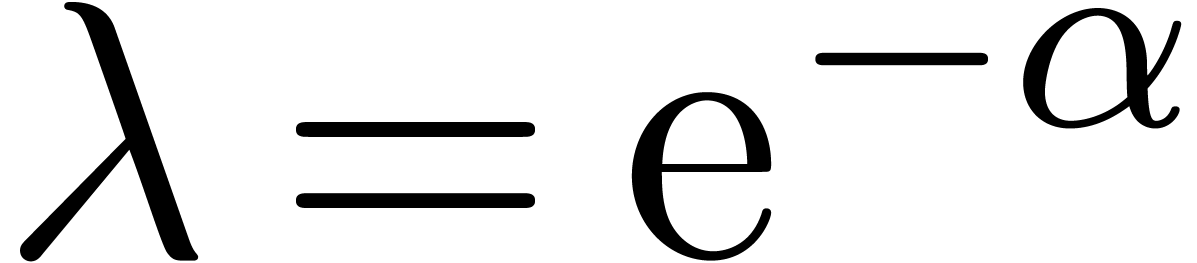 are approximately of the same order of magnitude. In
the multivariate case, the coefficients still have a geometric increase
on diagonals
are approximately of the same order of magnitude. In
the multivariate case, the coefficients still have a geometric increase
on diagonals 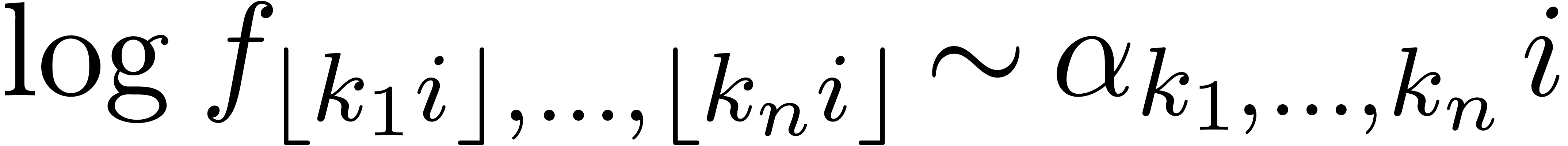 , but the
parameter
, but the
parameter 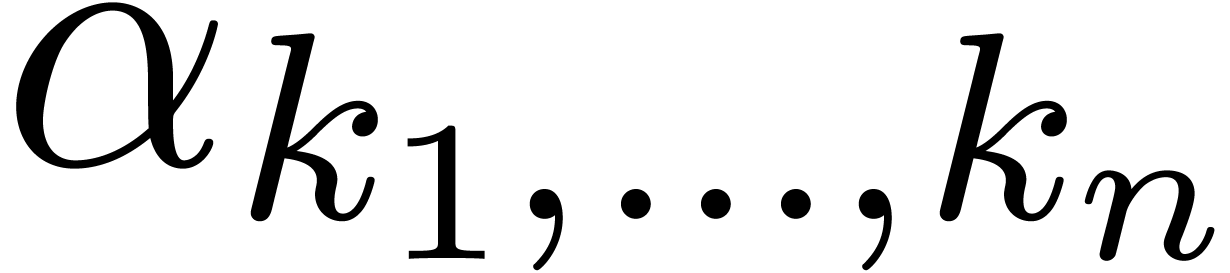 depends on the diagonal. After a
suitable change of variables
depends on the diagonal. After a
suitable change of variables 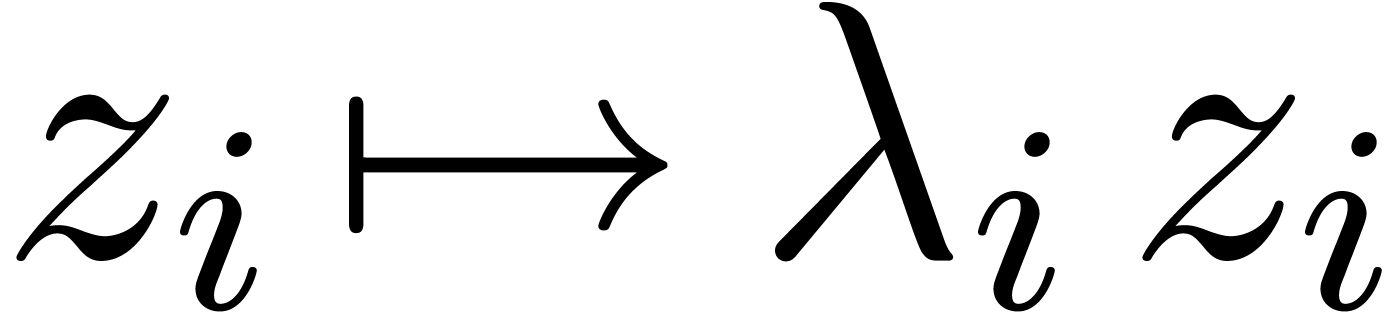 ,
the coefficients in a big zone near the main diagonal become of
approximately the same order of magnitude. However, the discrepancy
usually needs to be chosen proportional to the total truncation degree
in order to ensure sufficient accuracy elsewhere.
,
the coefficients in a big zone near the main diagonal become of
approximately the same order of magnitude. However, the discrepancy
usually needs to be chosen proportional to the total truncation degree
in order to ensure sufficient accuracy elsewhere.
Let us now consider the case when 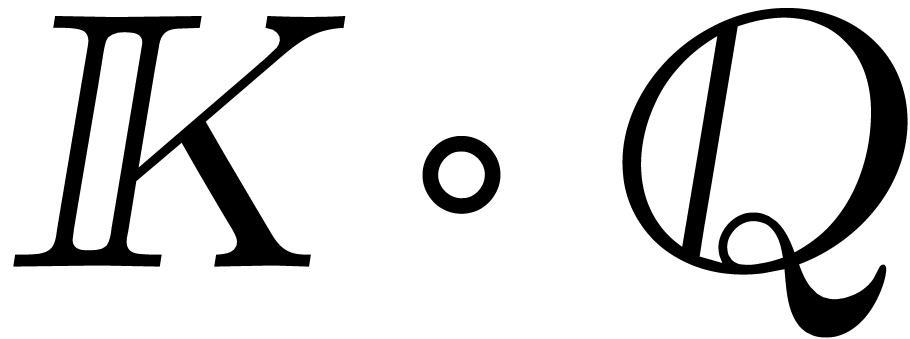 .
Let
.
Let 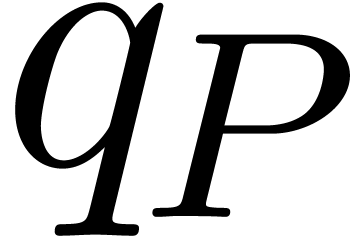 and
and  denote the least
common multiples of the denominators of the coefficients of
denote the least
common multiples of the denominators of the coefficients of  resp.
resp.  .
One obvious way to compute
.
One obvious way to compute  is to set
is to set 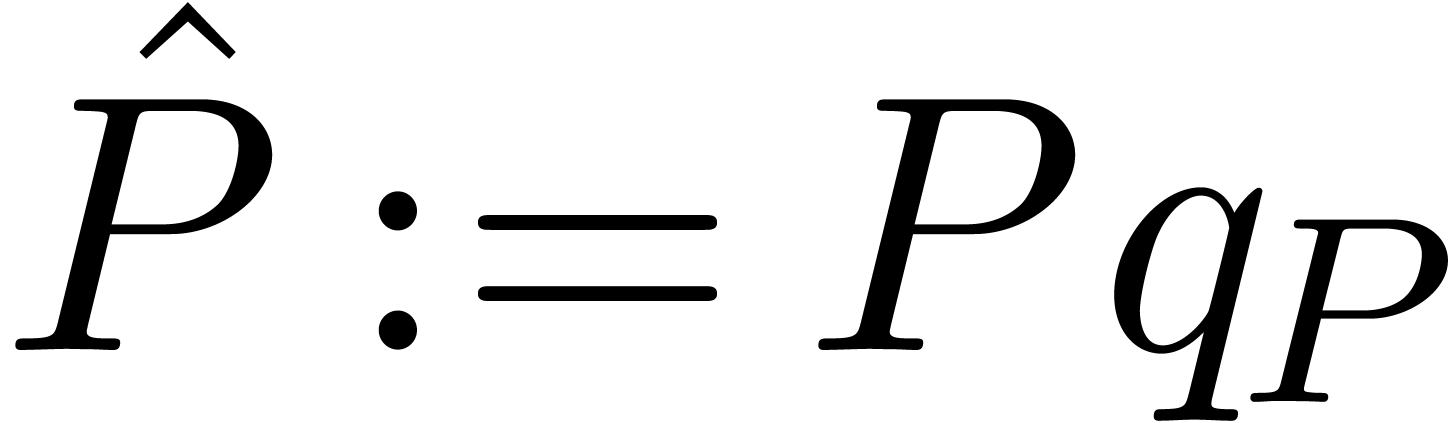 ,
, 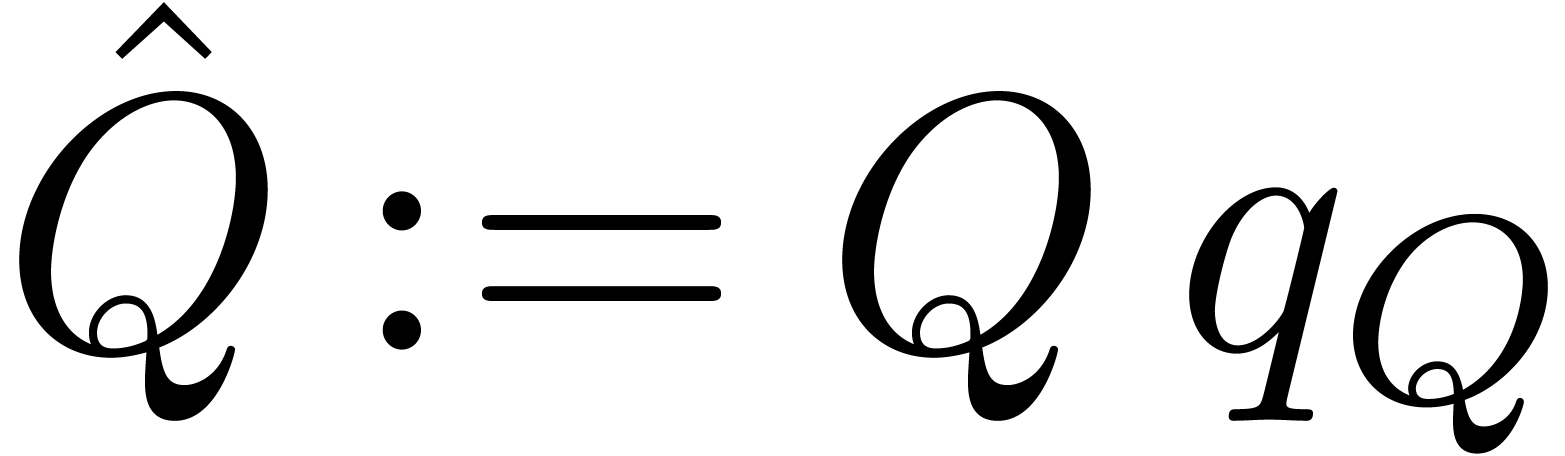 ,
and compute
,
and compute  using one of the methods from
section 3.2. This approach works well in many cases
(e.g. when
using one of the methods from
section 3.2. This approach works well in many cases
(e.g. when  and
and  are truncations of exponential generating series). Unfortunately, this
approach is deemed to be very slow if the size of
are truncations of exponential generating series). Unfortunately, this
approach is deemed to be very slow if the size of 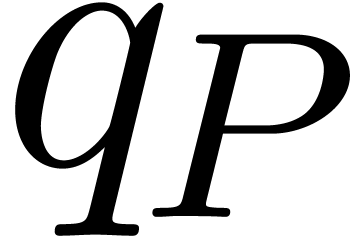 or
or  is much larger than the size of any of the
coefficients of
is much larger than the size of any of the
coefficients of  .
.
An alternative, more heuristic approach is the following. Let 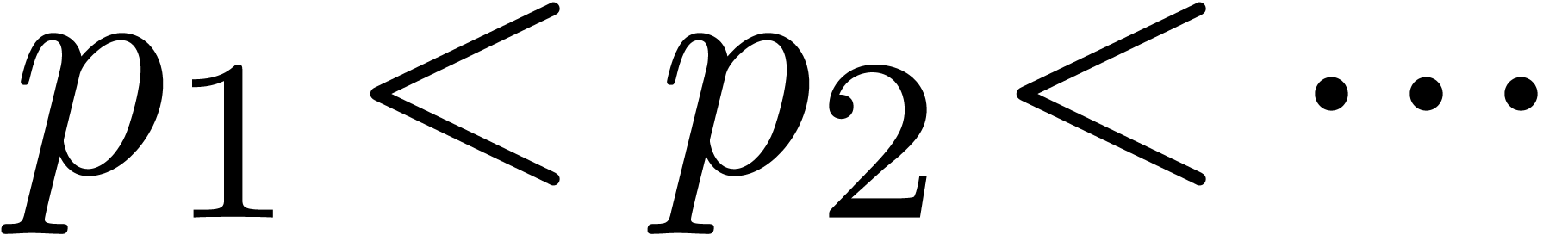 be an increasing sequence of prime numbers with
be an increasing sequence of prime numbers with 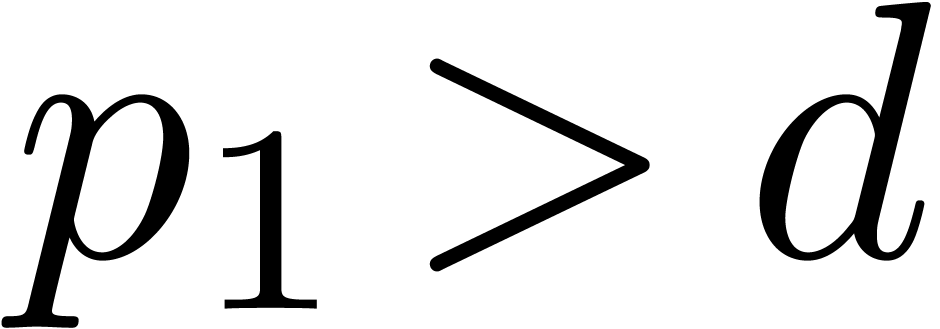 and such that each
and such that each 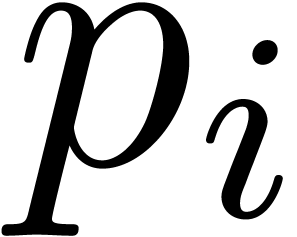 is relatively
prime to the denominators of each of the coefficients of
is relatively
prime to the denominators of each of the coefficients of 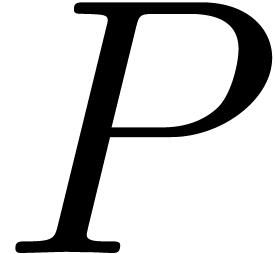 and
and  . For each
. For each
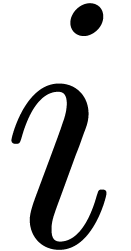 , we may then multiply
, we may then multiply 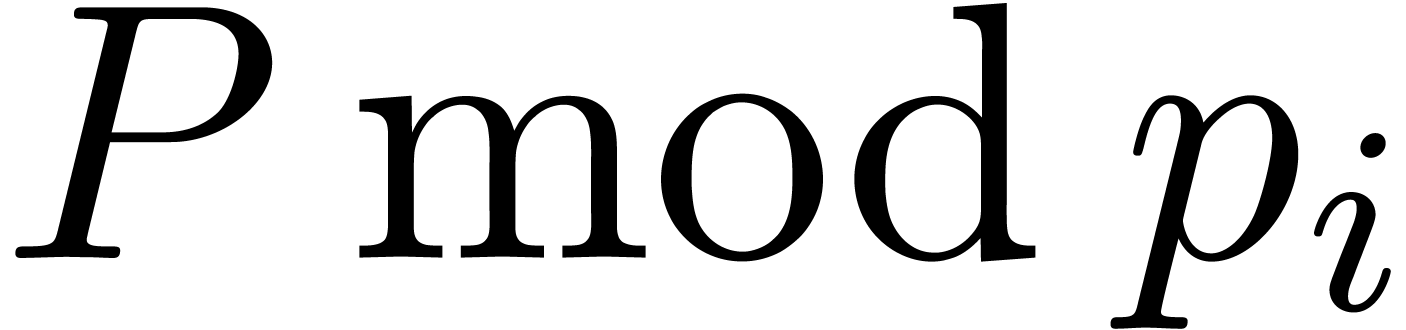 and
and 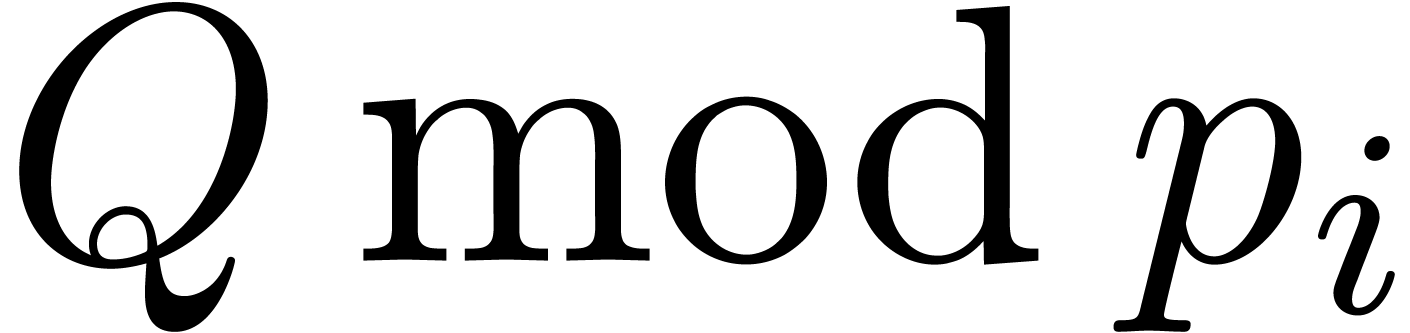 using the algorithm from
section 2. For
using the algorithm from
section 2. For 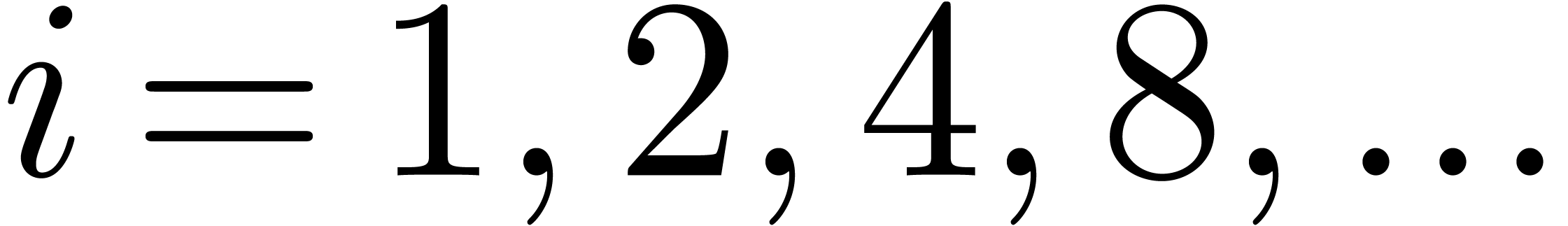 ,
we may recover
,
we may recover 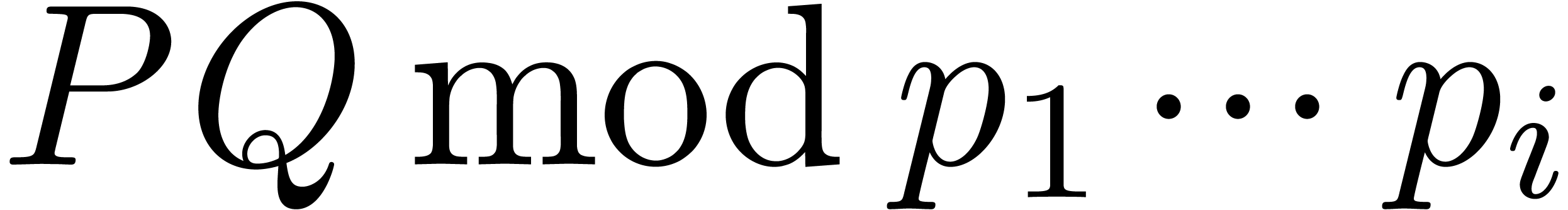 using Chinese remaindering and
attempt to reconstruct
using Chinese remaindering and
attempt to reconstruct 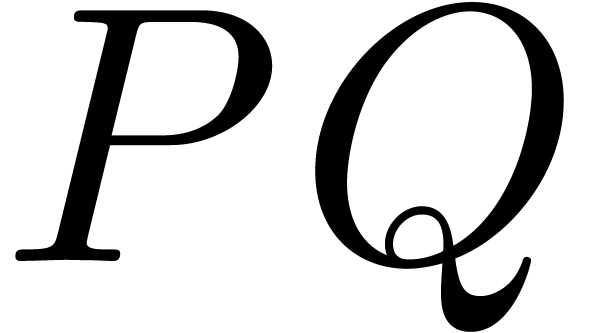 from
from 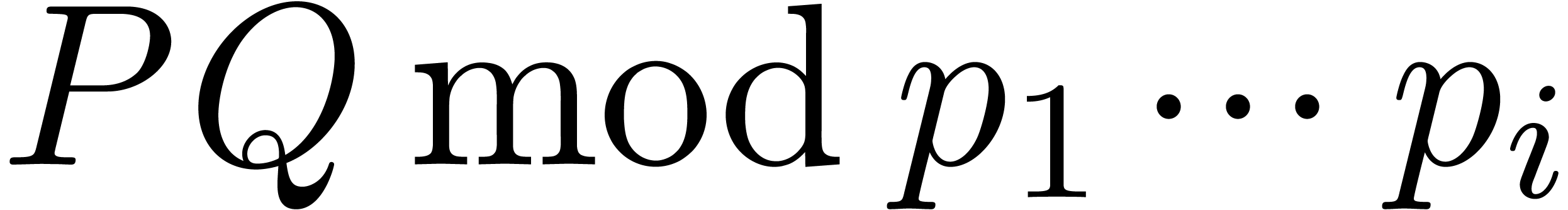 using rational number reconstruction [GG02, Chapter 5]. If
this yields the same result for a given
using rational number reconstruction [GG02, Chapter 5]. If
this yields the same result for a given 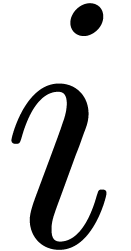 and
and
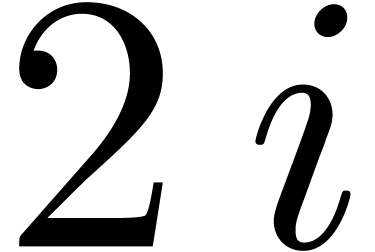 , then the reconstructed
, then the reconstructed  is likely to be correct at those stages.
is likely to be correct at those stages.
Of course, if we have an a priori bound on the bit sizes of the
coefficients of  , then we may
directly take a sufficient number of primes
, then we may
directly take a sufficient number of primes  such
that
such
that  can be reconstructed from its reduction
modulo
can be reconstructed from its reduction
modulo  .
.
Let  be an algebraic number field. For some
algebraic integer
be an algebraic number field. For some
algebraic integer  , we may
write
, we may
write 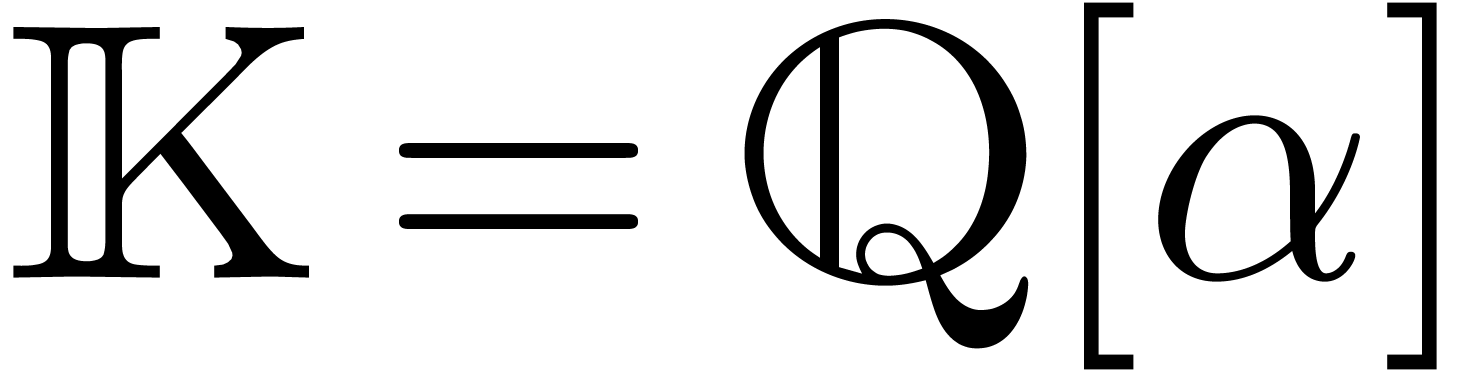 . Let
. Let 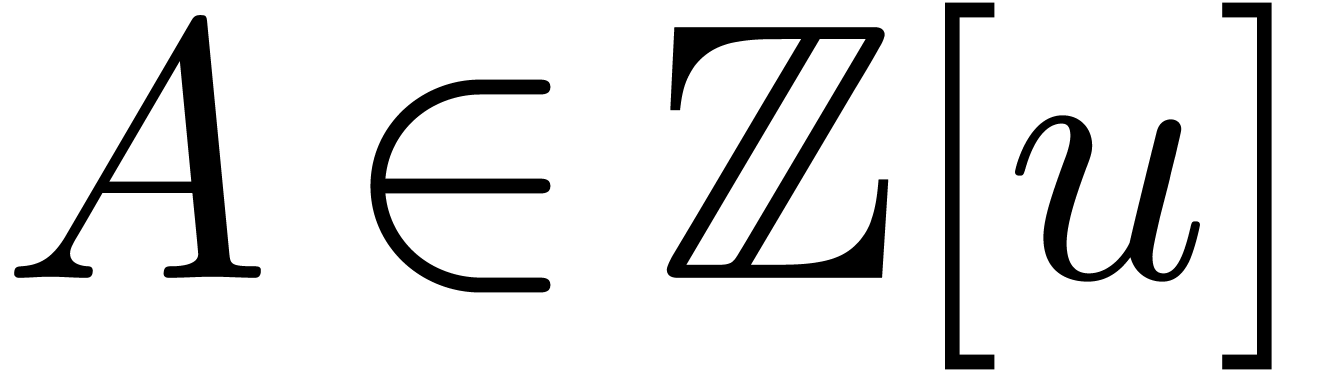 be the monic polynomial of minimal degree
be the monic polynomial of minimal degree 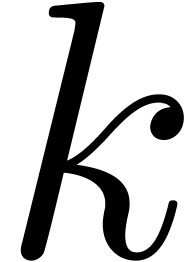 with
with
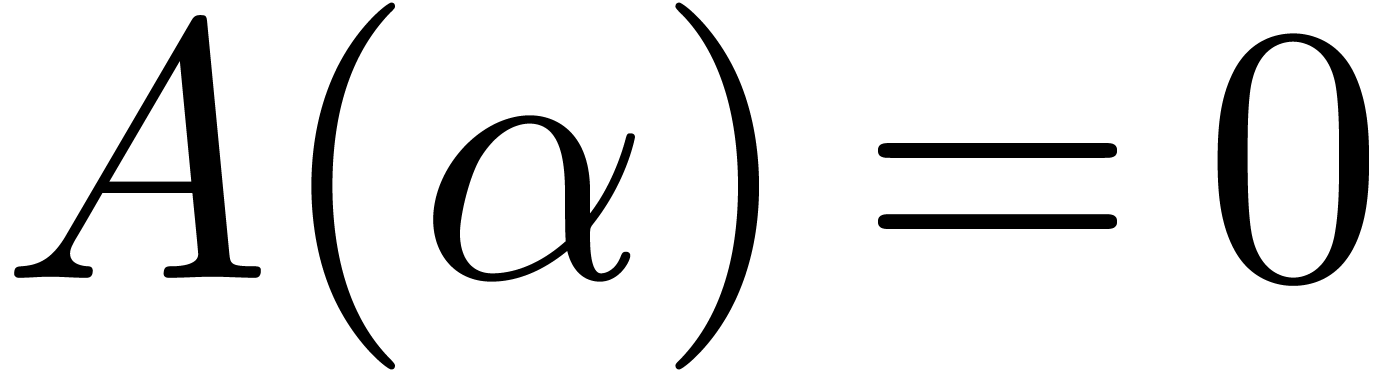 . Given a prime number
. Given a prime number 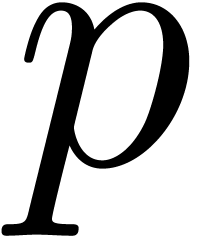 , the polynomial
, the polynomial 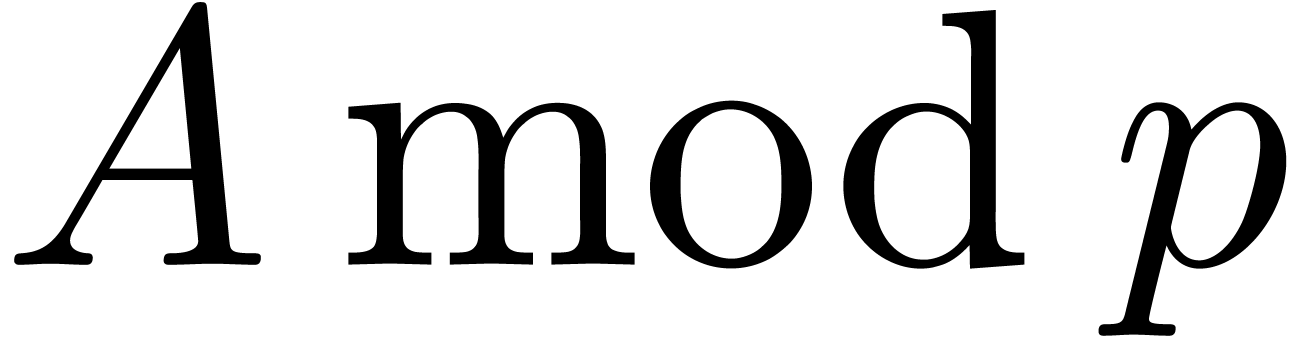 induces an algebraic extension
induces an algebraic extension 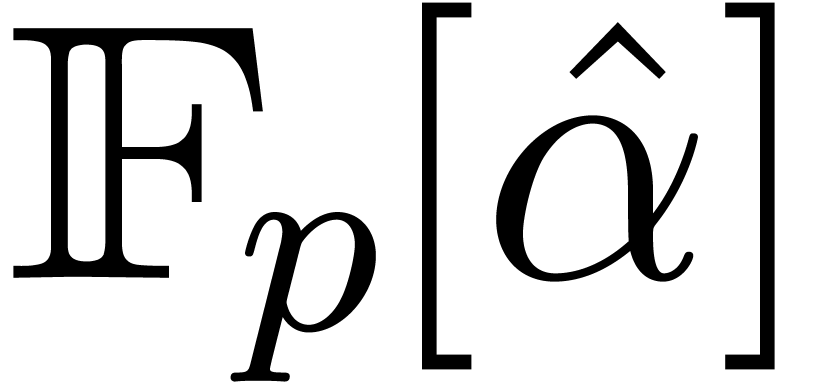 of
of 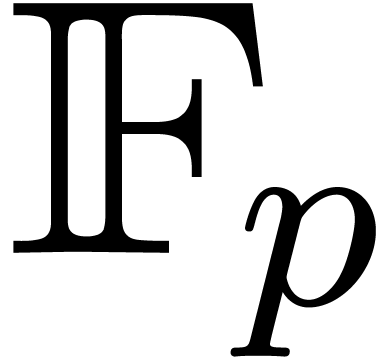 , where
, where 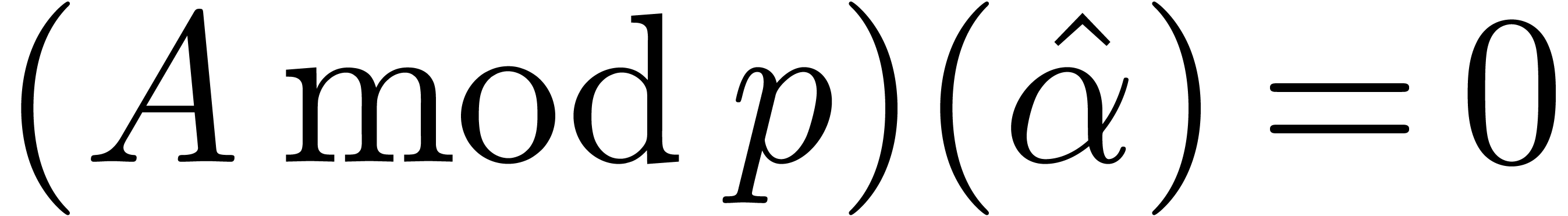 .
Reduction modulo
.
Reduction modulo 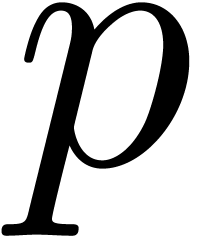 of a sparse polynomial
of a sparse polynomial 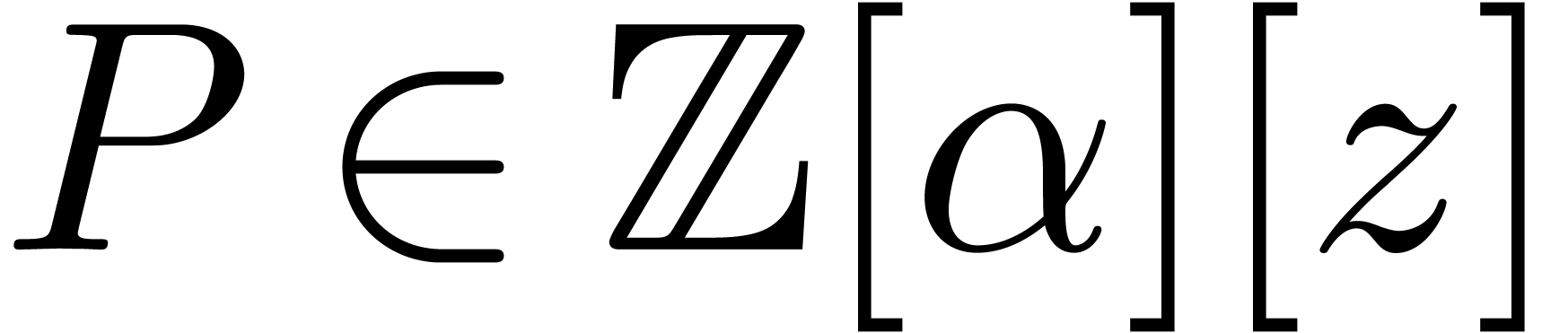 then yields a sparse polynomial
then yields a sparse polynomial 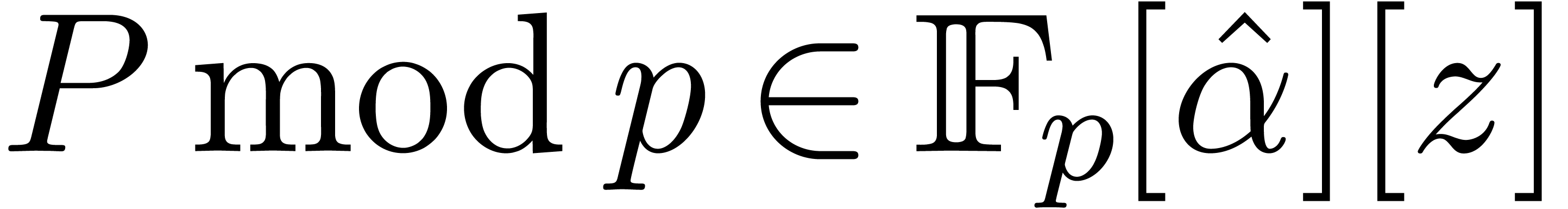 . We have seen in section 3.1 how
to multiply sparse polynomials over the finite field
. We have seen in section 3.1 how
to multiply sparse polynomials over the finite field 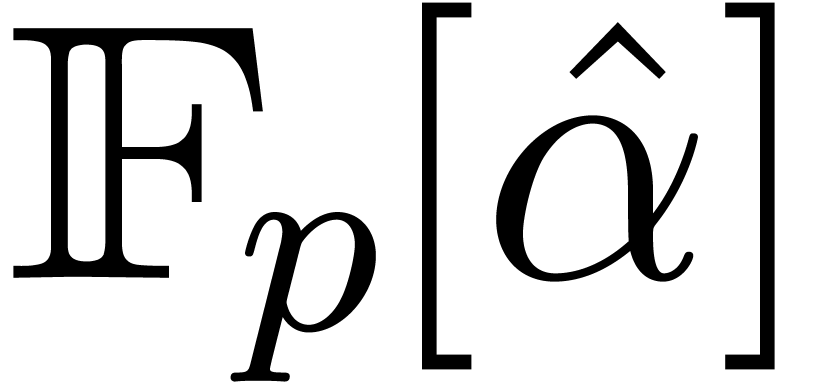 . Choosing one or more sufficiently large prime
numbers
. Choosing one or more sufficiently large prime
numbers 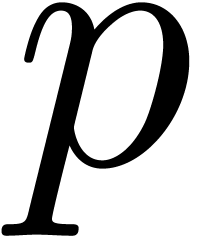 , we may thus apply
the same approaches as in section 3.2 in order to multiply
sparse polynomials over
, we may thus apply
the same approaches as in section 3.2 in order to multiply
sparse polynomials over 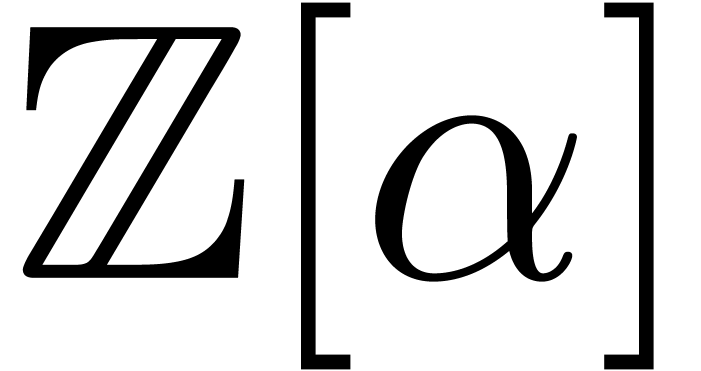 .
Using the techniques from section 3.4, we next deal with
the case of sparse polynomials over
.
Using the techniques from section 3.4, we next deal with
the case of sparse polynomials over 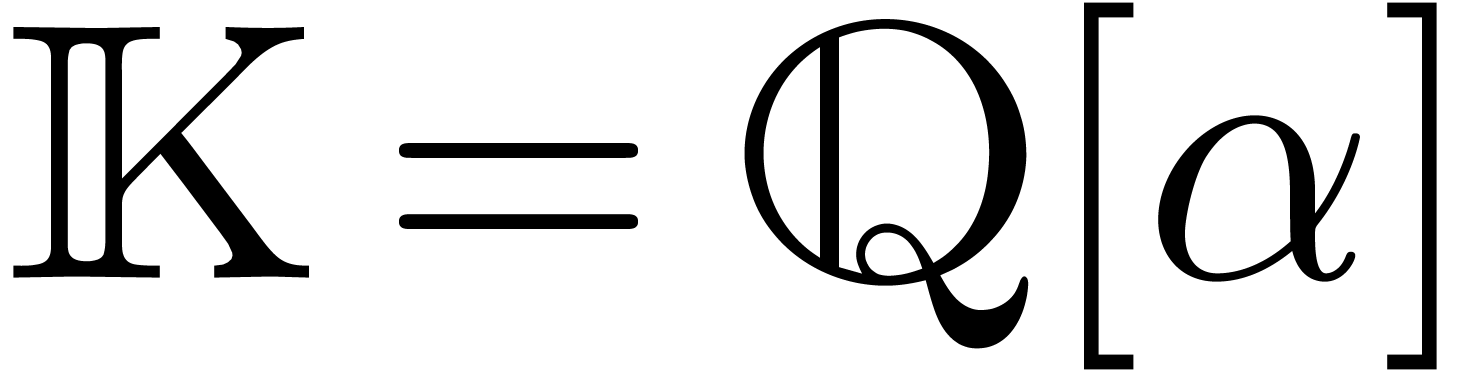 .
.
Given 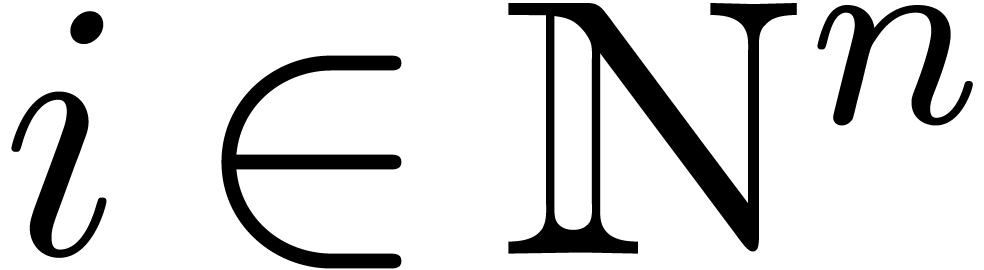 , let
, let  . The total degree of a polynomial
. The total degree of a polynomial
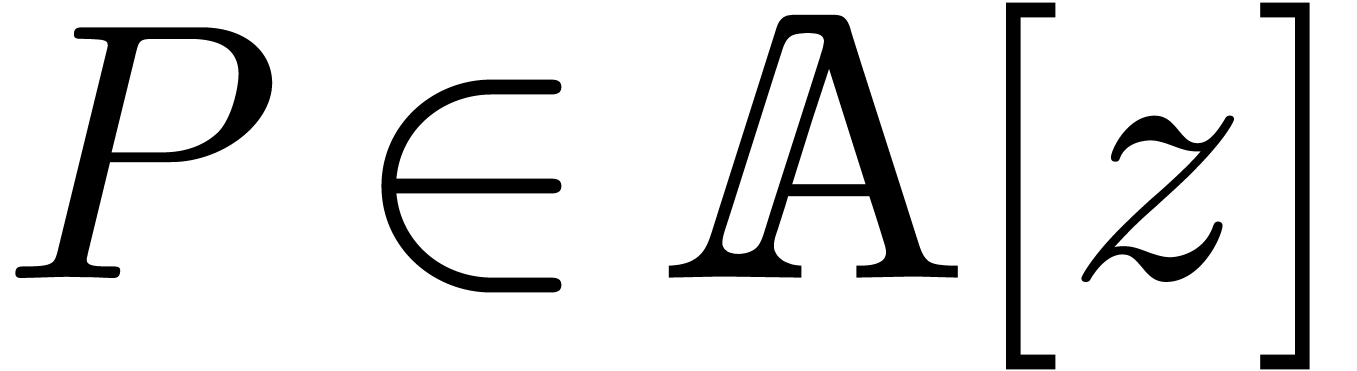 is defined by
is defined by
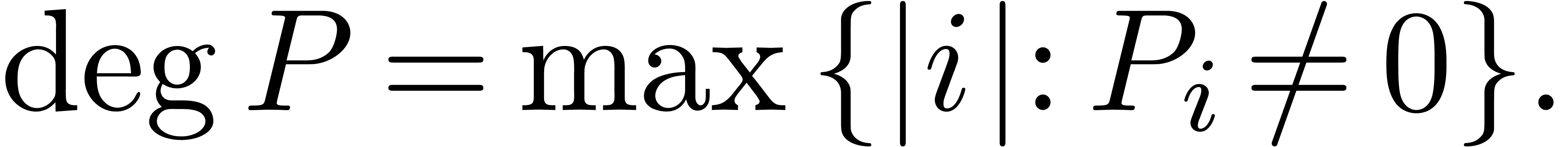
Given a subset 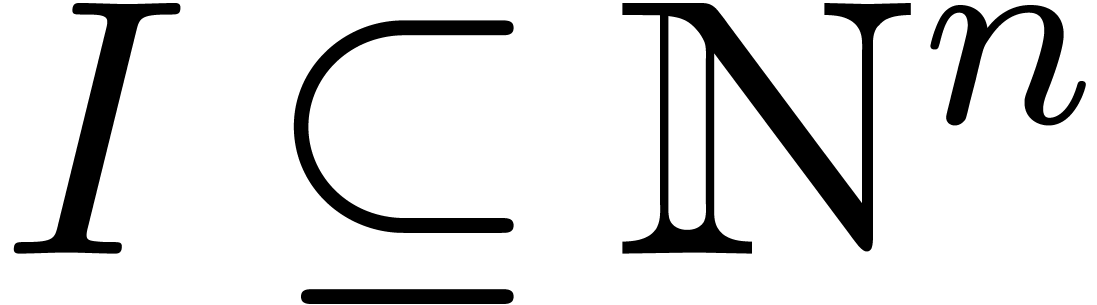 , we define
the restriction
, we define
the restriction 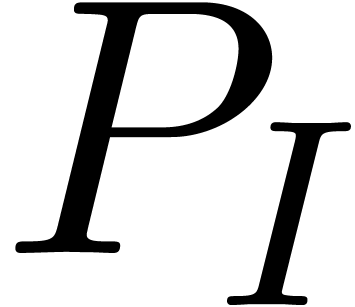 of
of  to
to 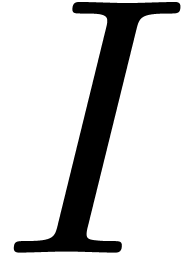 by
by
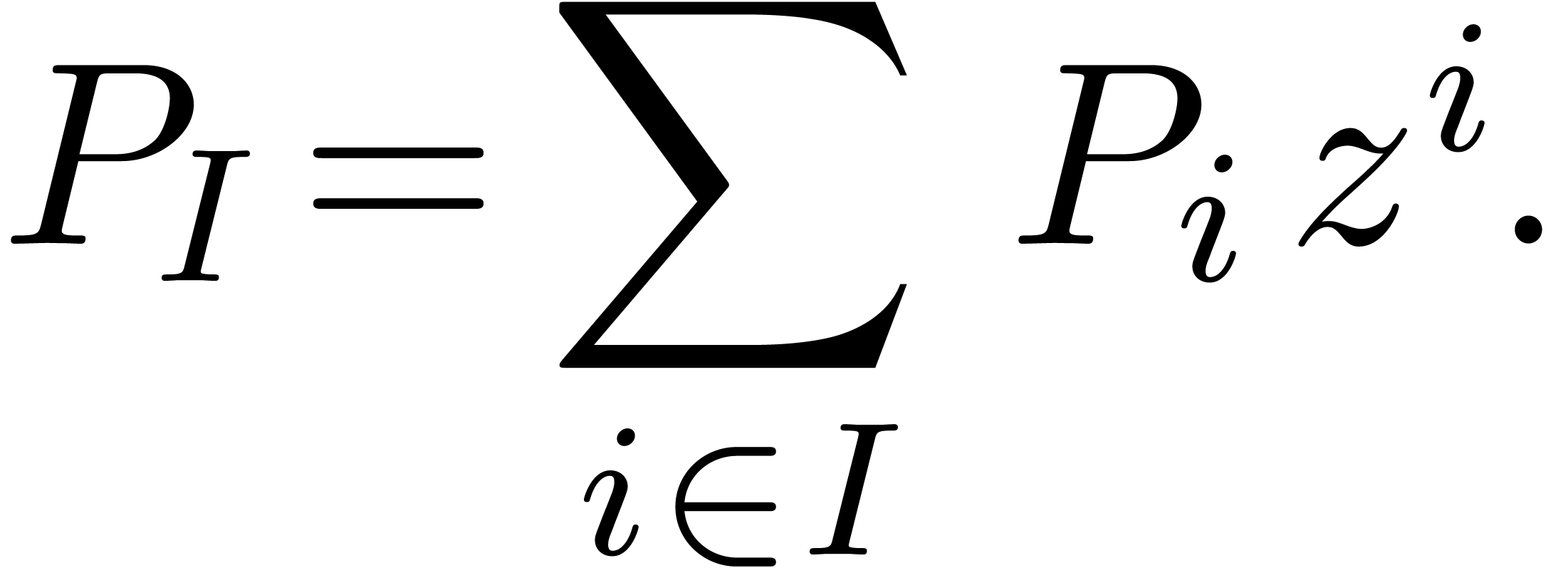
For 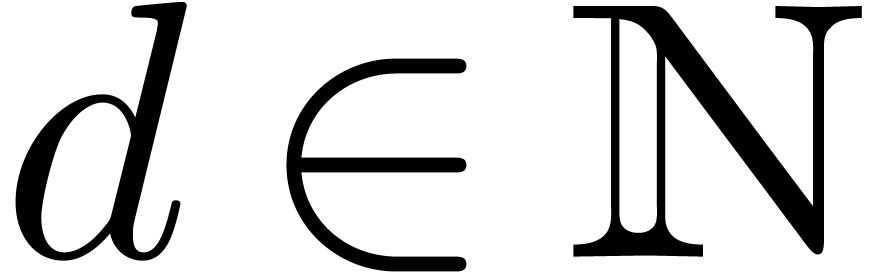 , we define initial
segments
, we define initial
segments 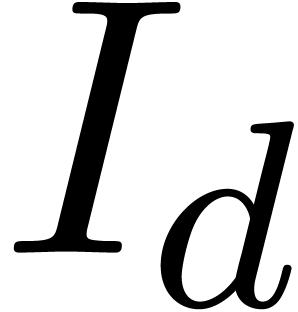 of
of 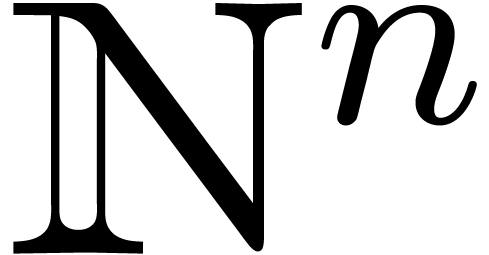 by
by
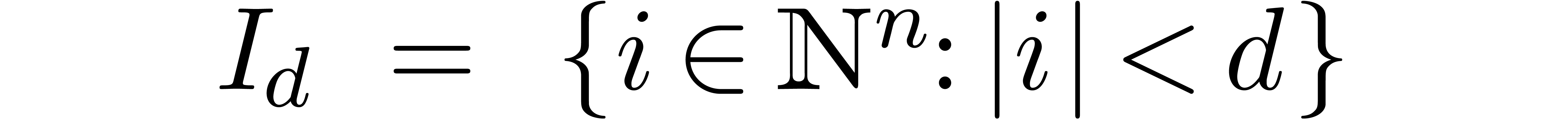
Then
is the set of polynomials of total degree 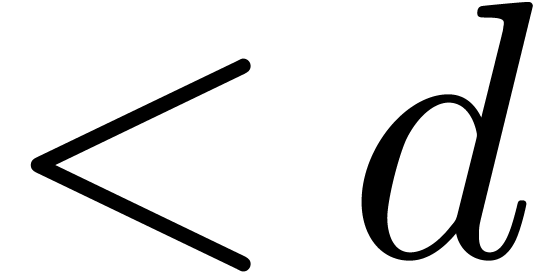 .
Given
.
Given 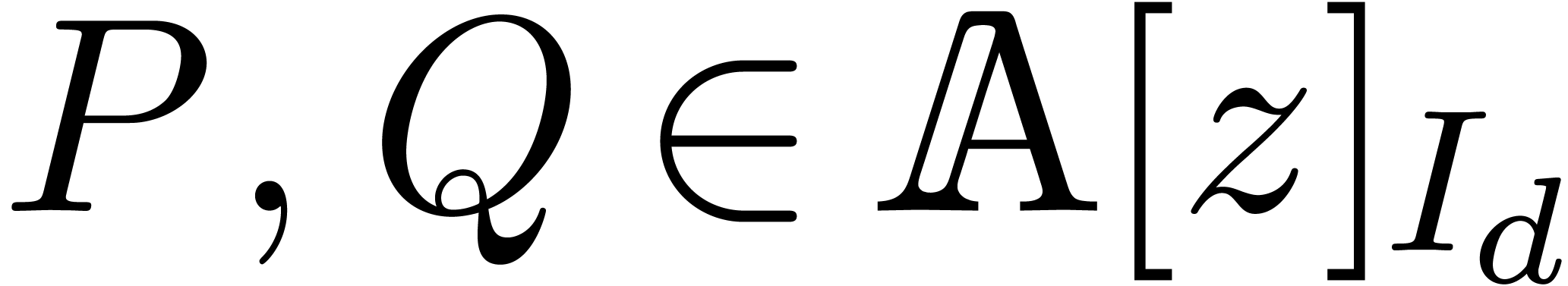 , the aim of this
section is to describe efficient algorithms for the computation of
, the aim of this
section is to describe efficient algorithms for the computation of 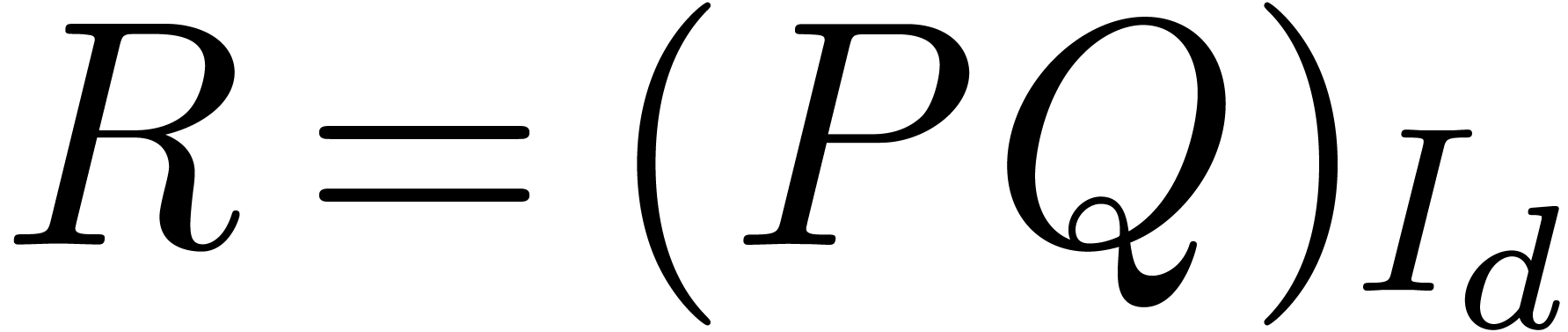 . We will follow and extend the
strategy described in [LS03].
. We will follow and extend the
strategy described in [LS03].
Remark  with
with  ,
but for the sake of simplicity, we will stick to ordinary total degrees.
,
but for the sake of simplicity, we will stick to ordinary total degrees.
Given a polynomial 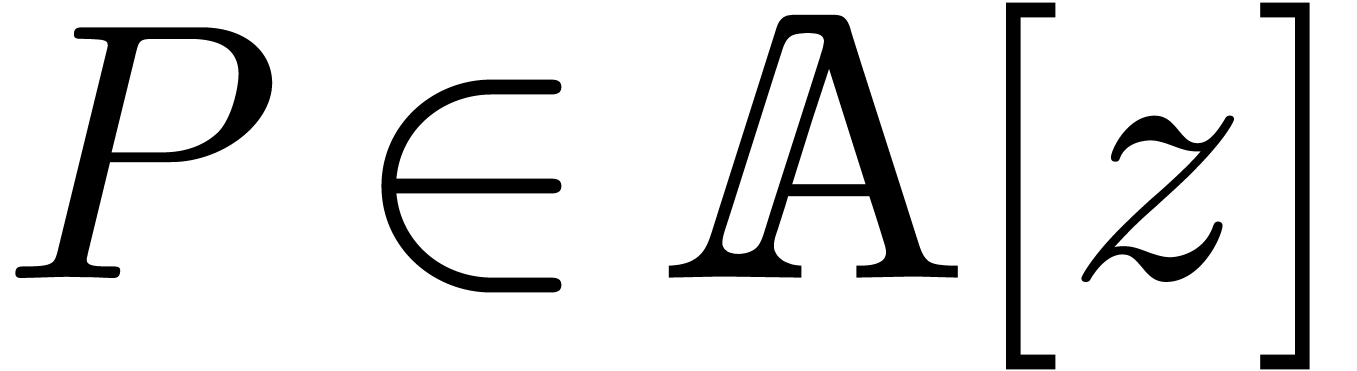 , we
define its projective transform
, we
define its projective transform 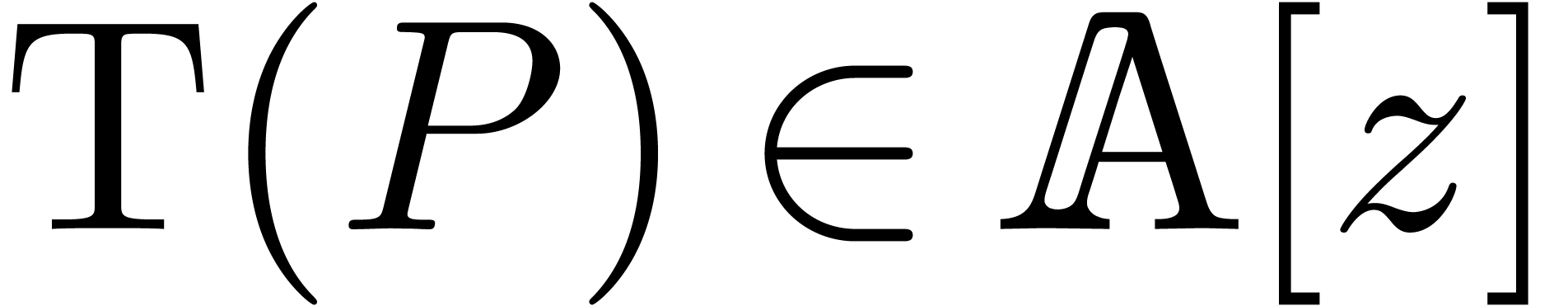 by
by
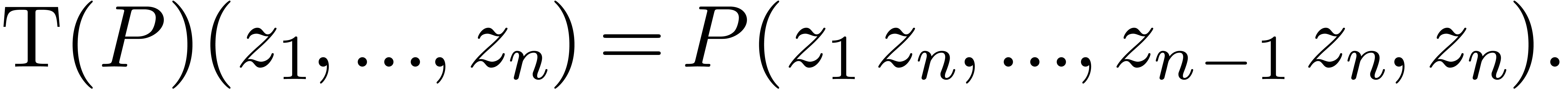
If 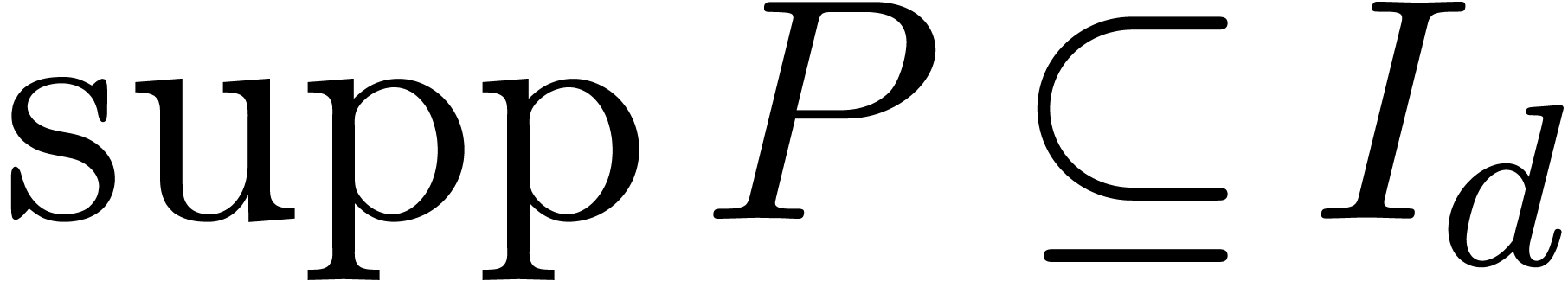 , then
, then 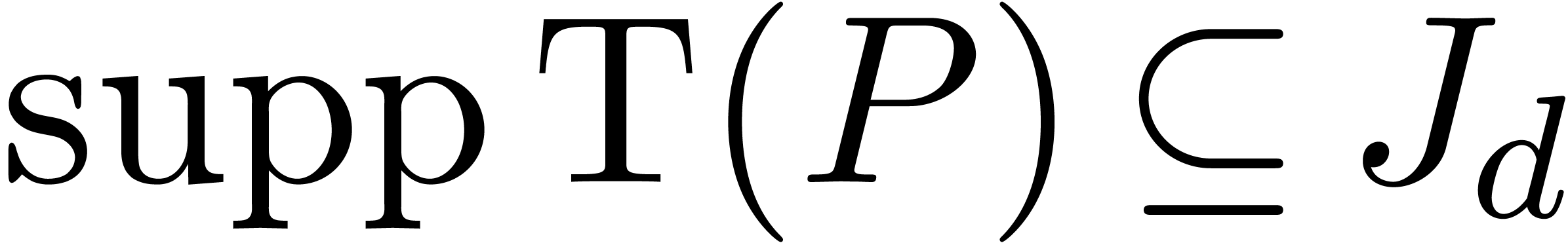 , where
, where
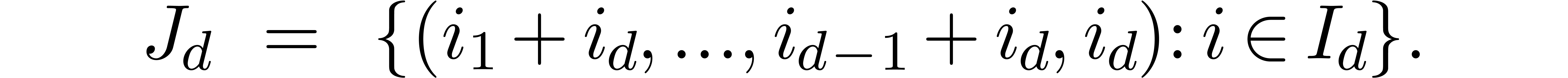
Inversely, for any  , there
exists a unique
, there
exists a unique 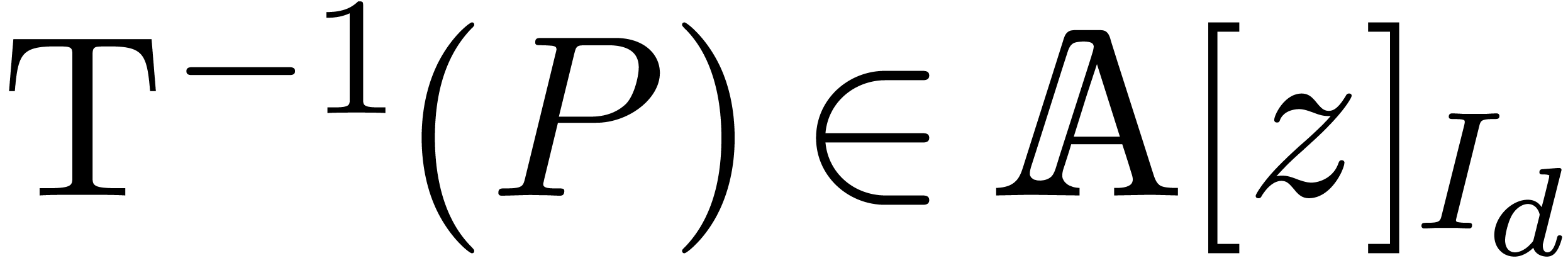 with
with 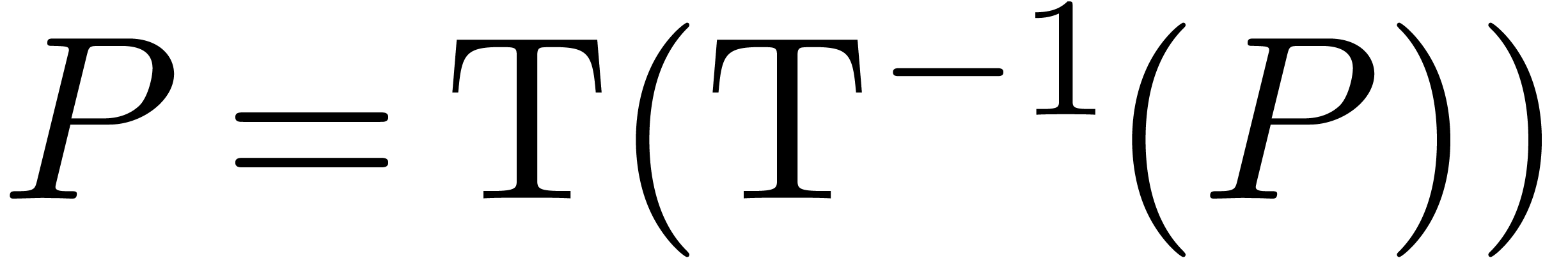 . The transformation
. The transformation  is an
injective morphism of
is an
injective morphism of  -algebras.
Consequently, given
-algebras.
Consequently, given 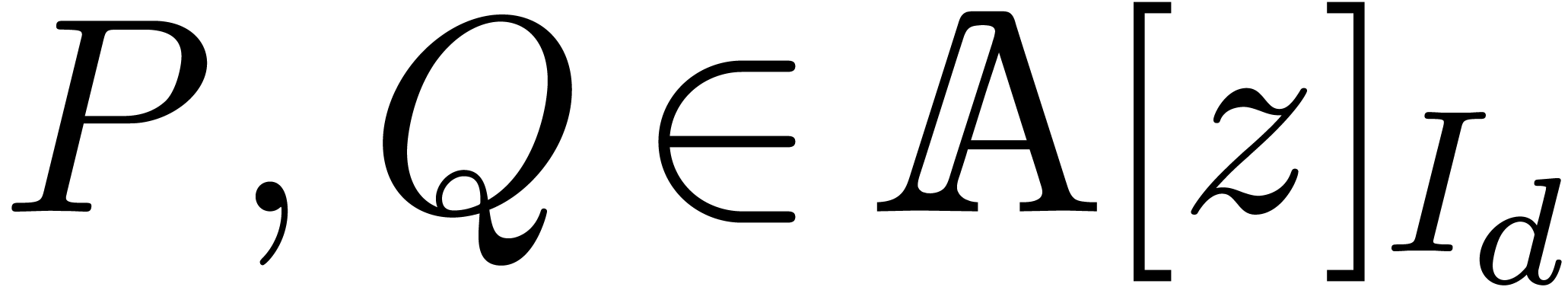 , we will
compute the truncated product
, we will
compute the truncated product  using
using
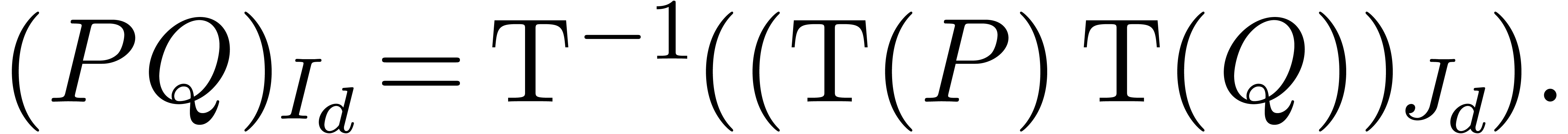
Given a polynomial 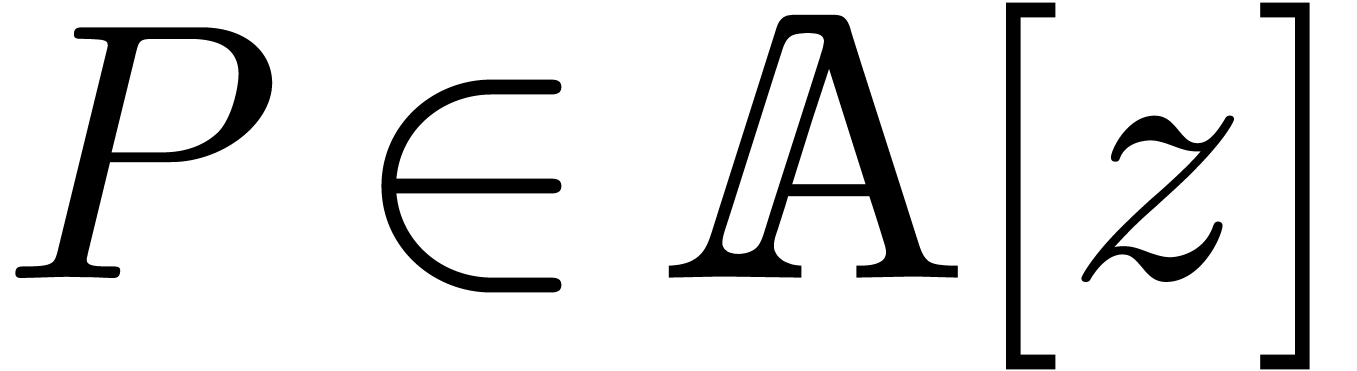 and
and  , let
, let
If 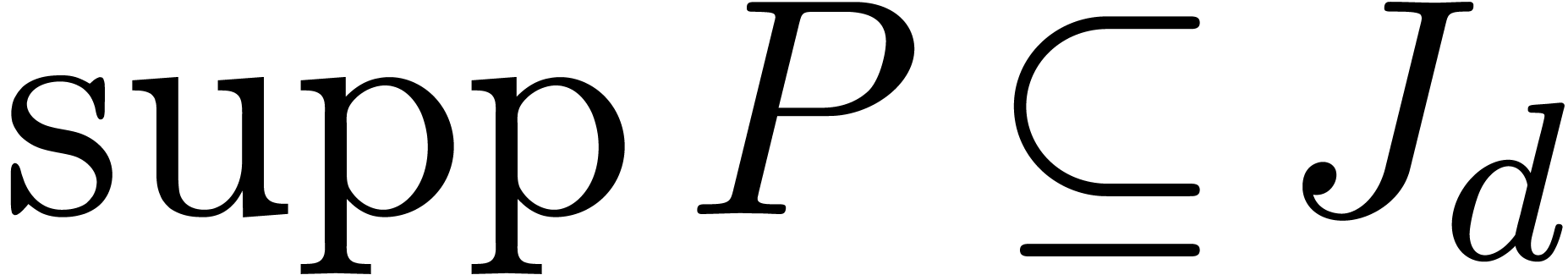 , then
, then 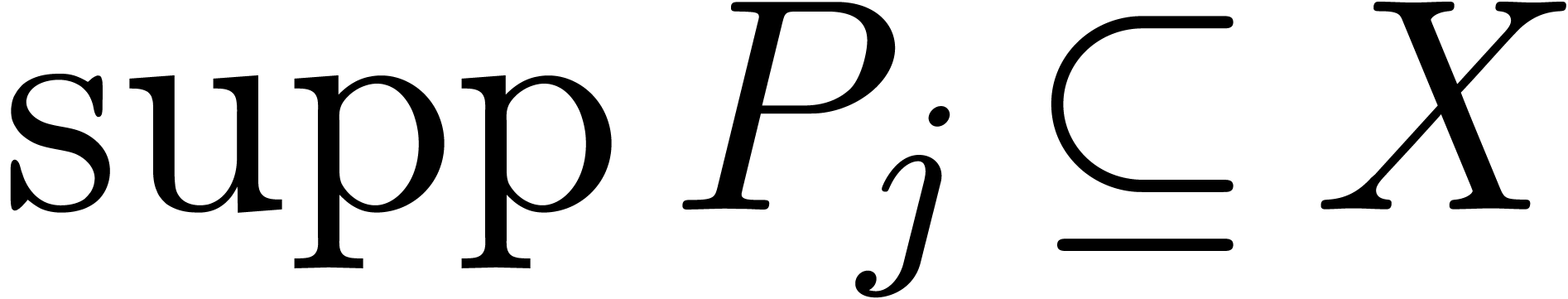 , with
, with
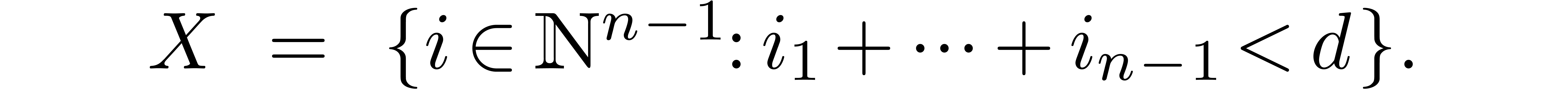
Let  be an element of
be an element of  of
sufficiently high order
of
sufficiently high order 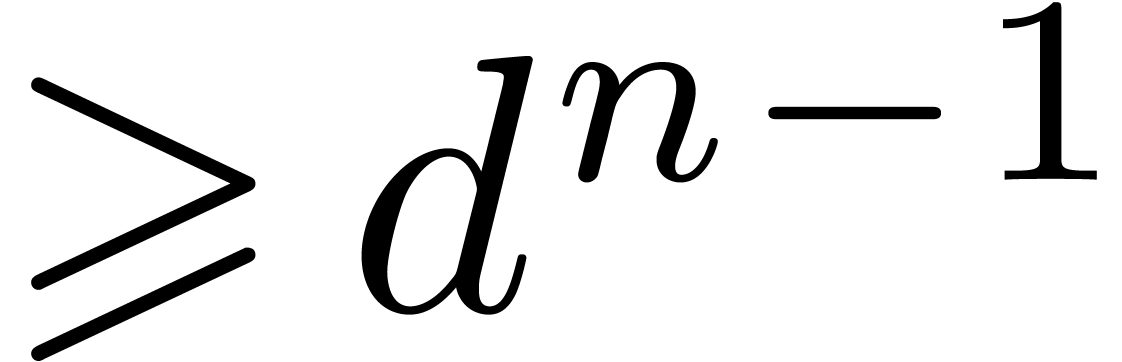 .
Taking
.
Taking  as above, the construction in section 2.3 yields a
as above, the construction in section 2.3 yields a  -linear
and invertible evaluation mapping
-linear
and invertible evaluation mapping
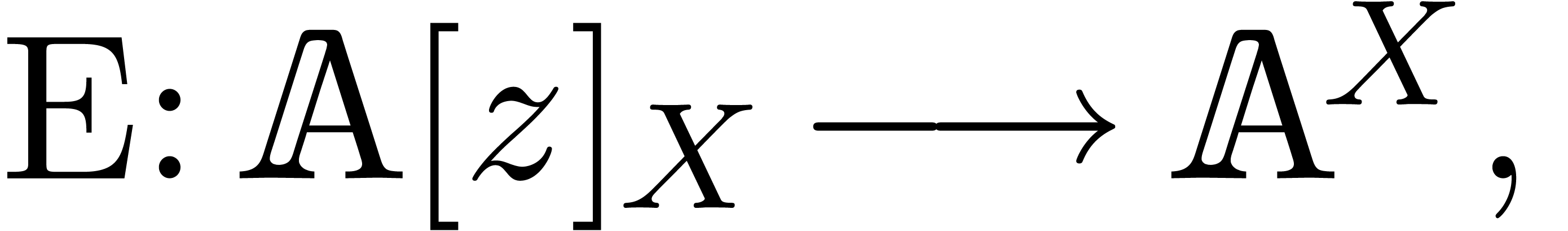
such that for all 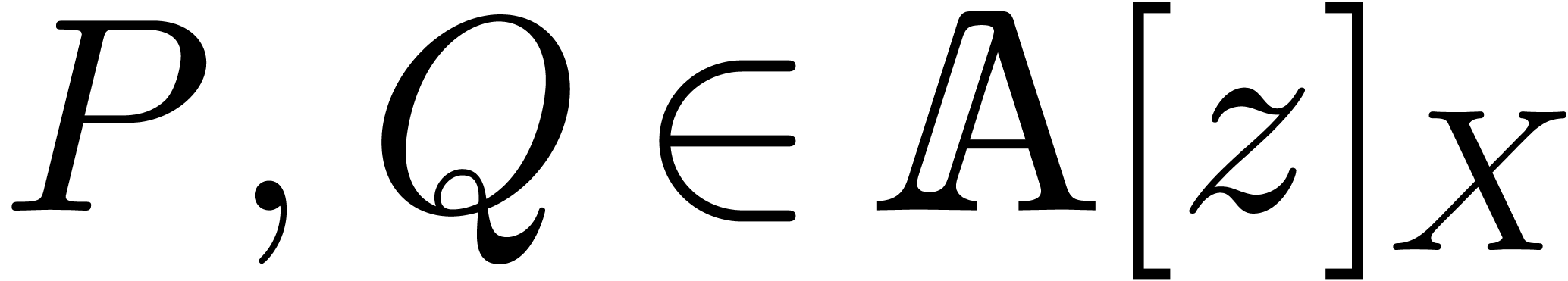 with
with 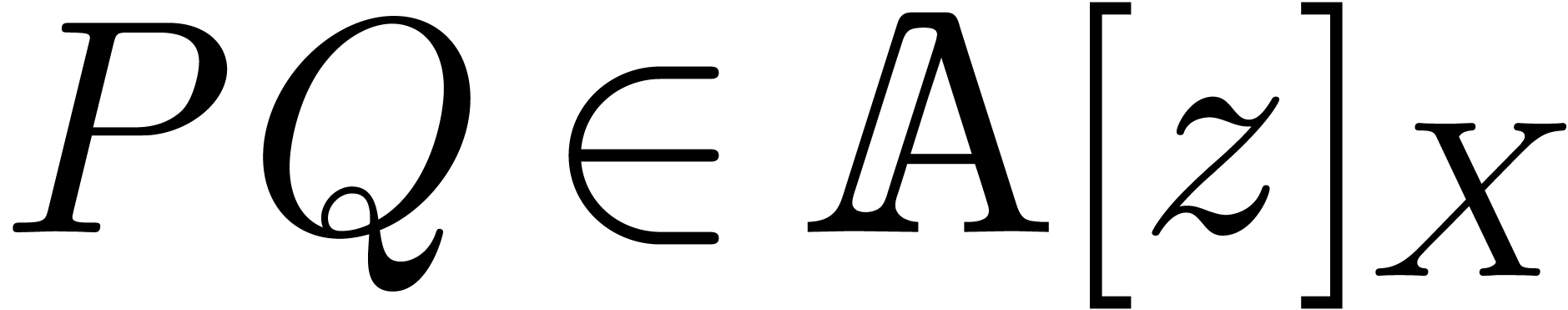 , we have
, we have
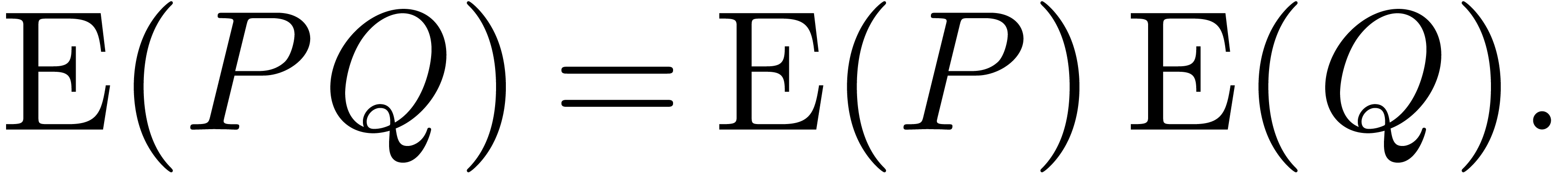 |
(1) |
This map extends to 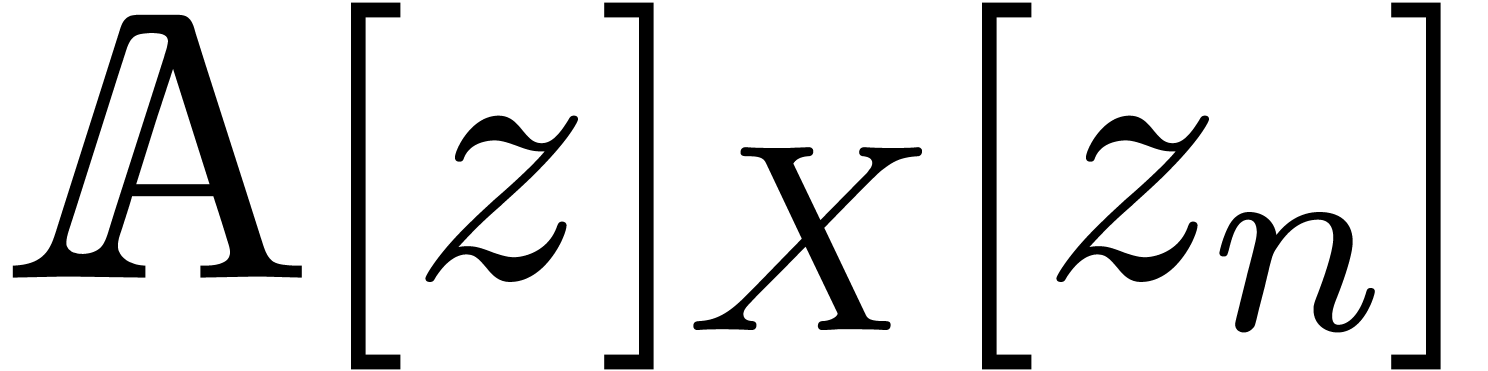 using
using
Given 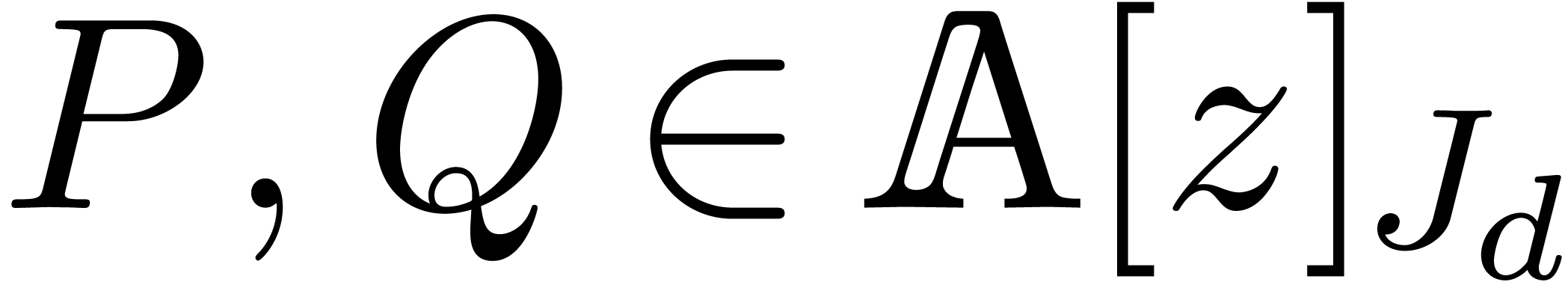 and
and 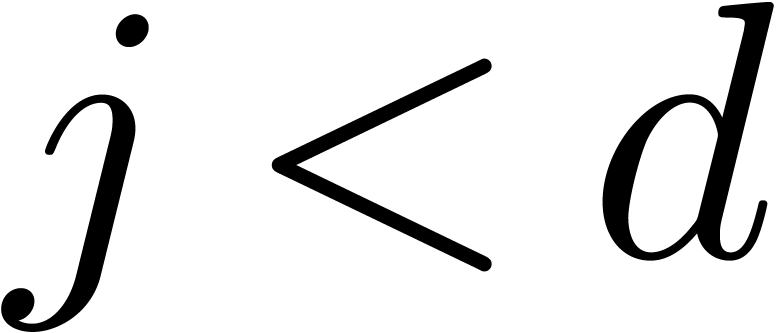 ,
the relation (1) yields
,
the relation (1) yields
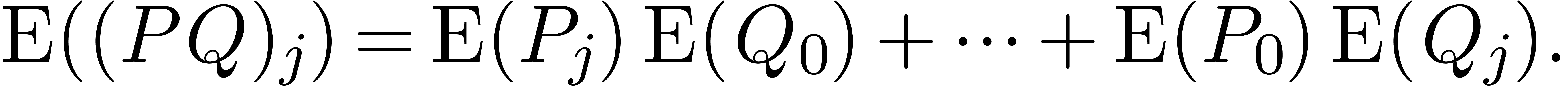
In particular, if 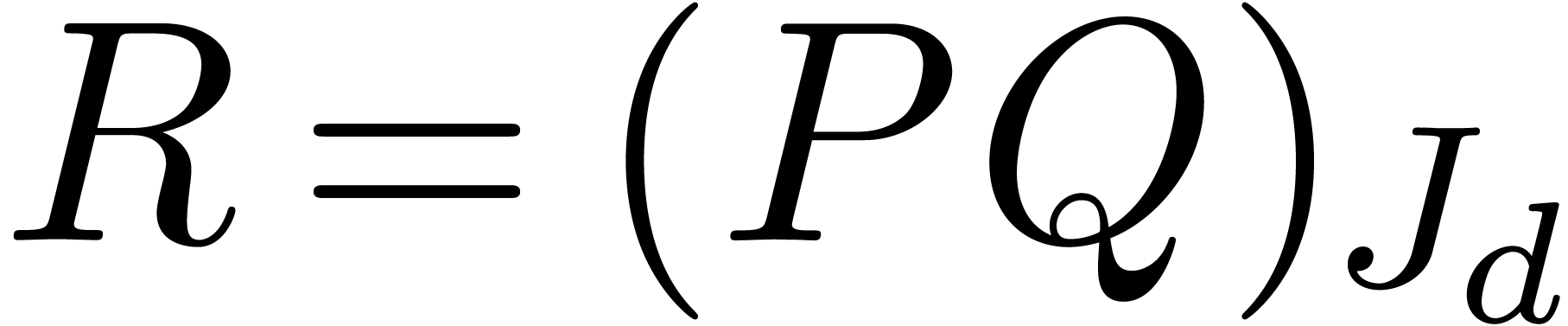 , then
, then
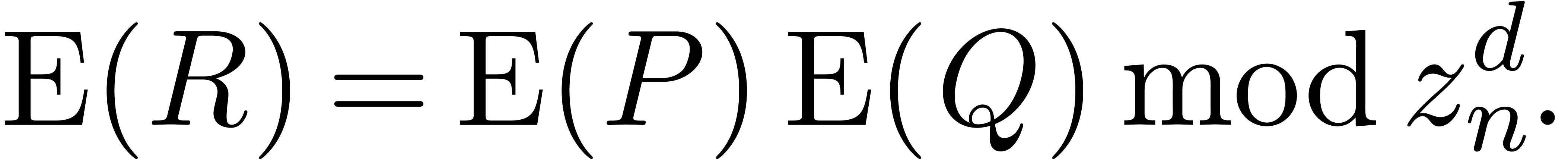
Since  is invertible, this yields an efficient
way to compute
is invertible, this yields an efficient
way to compute  .
.
The number of coefficients of a truncated series in 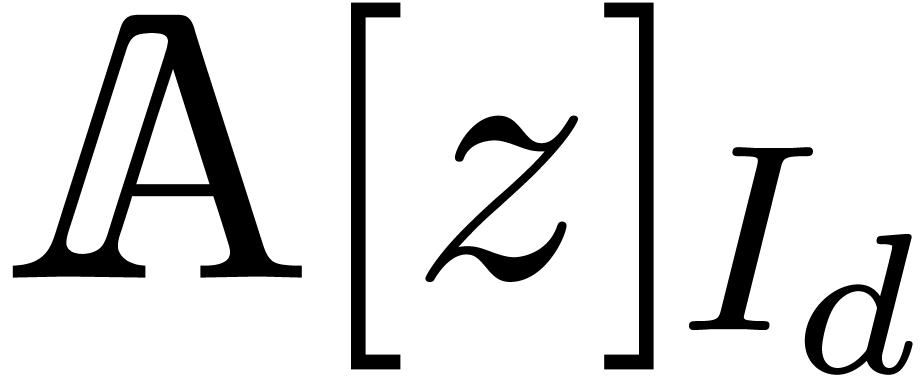 is given by
is given by
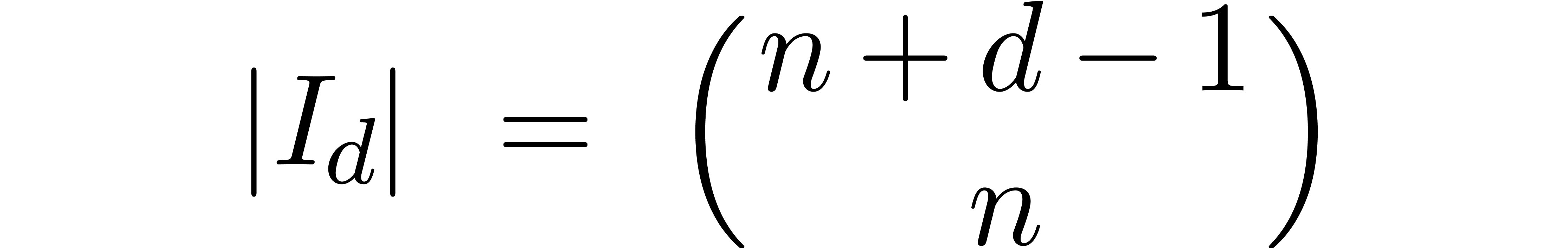
The size 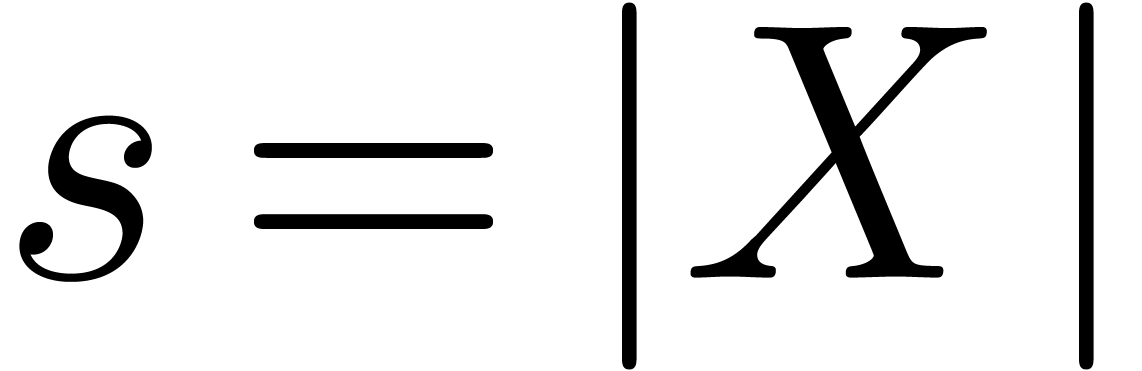 of
of 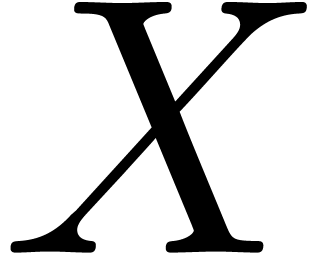 is smaller
by a factor between
is smaller
by a factor between 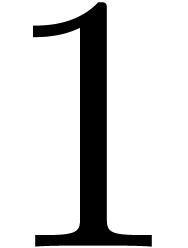 and
and 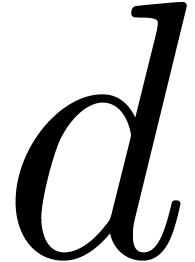 :
:
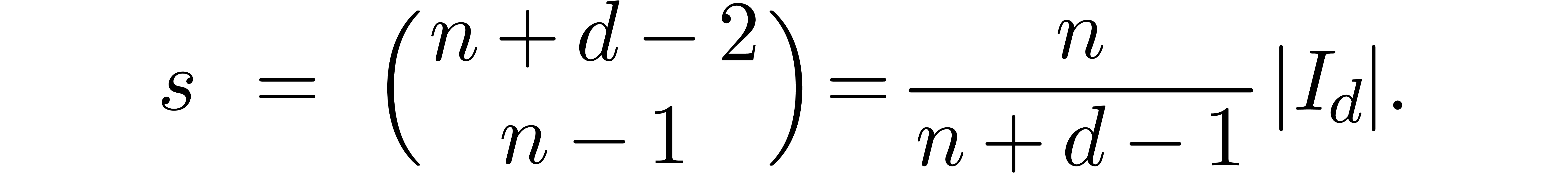
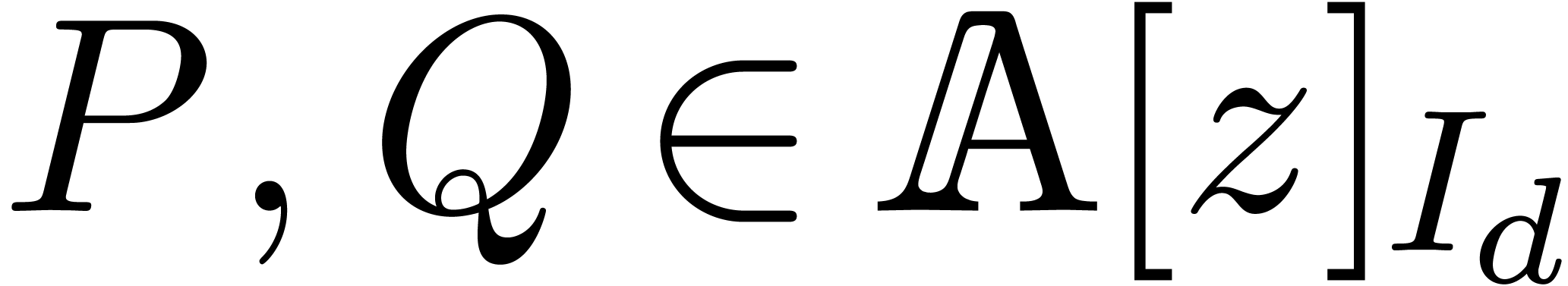 and an element
and an element 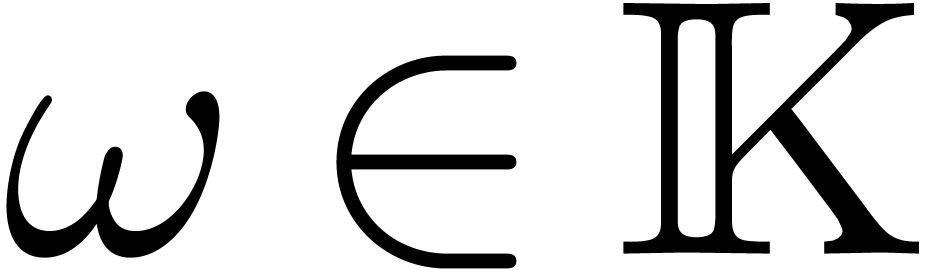 of order at least
of order at least 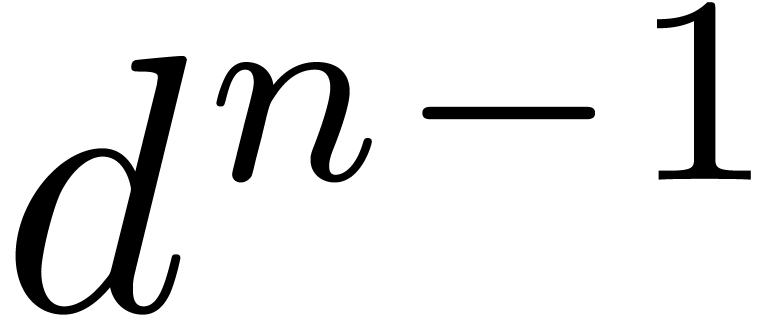 , we can
compute
, we can
compute  using
using  inversions in
inversions in  ,
, 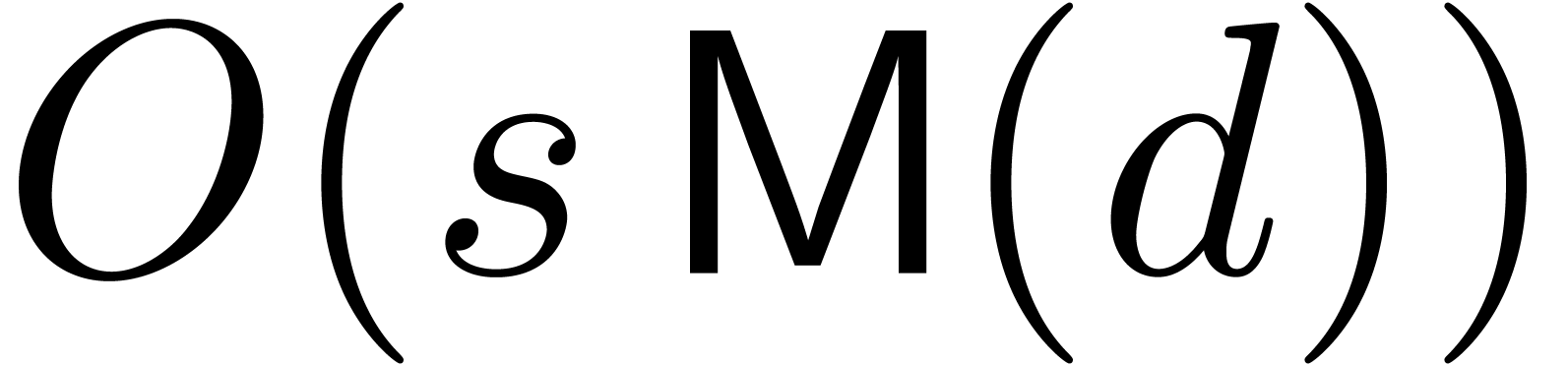 general operations in
general operations in  ,
and
,
and  vectorial operations in
vectorial operations in  .
.
Proof. The transforms  and
and 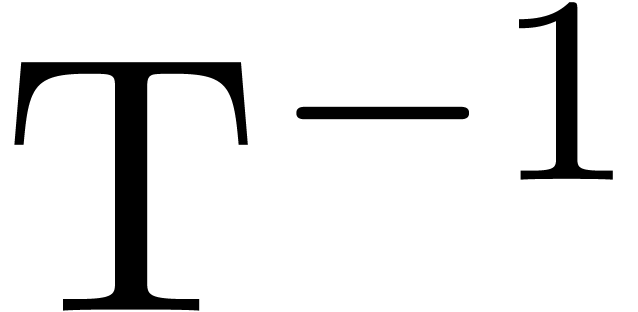 require a negligible amount of time. The
computation of the evaluation points
require a negligible amount of time. The
computation of the evaluation points 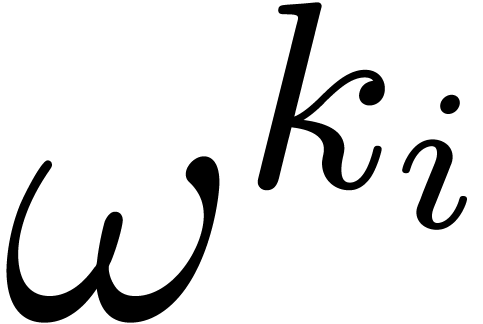 only
involves
only
involves 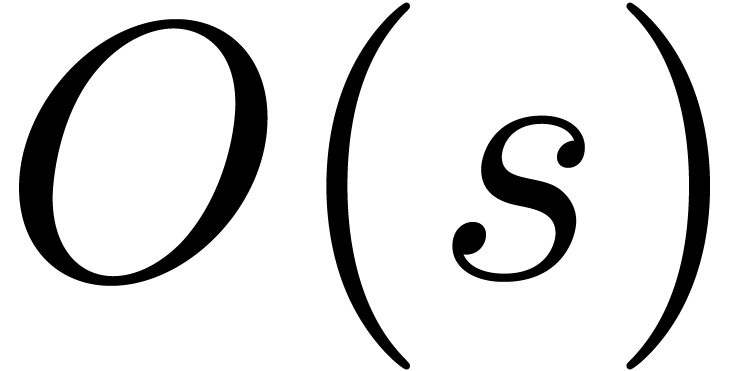 products in
products in  , when exploiting the fact that
, when exploiting the fact that  is an initial segment. The computation of
is an initial segment. The computation of 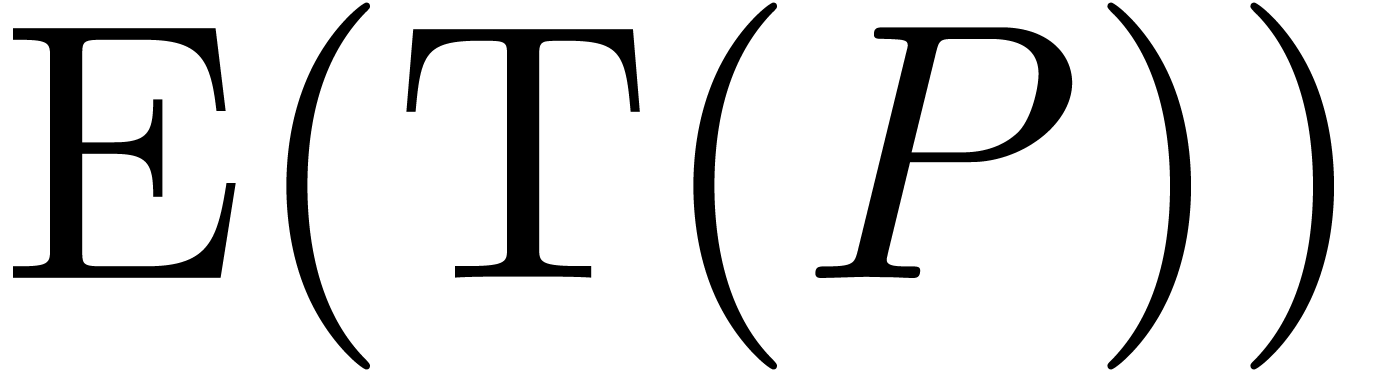 and
and
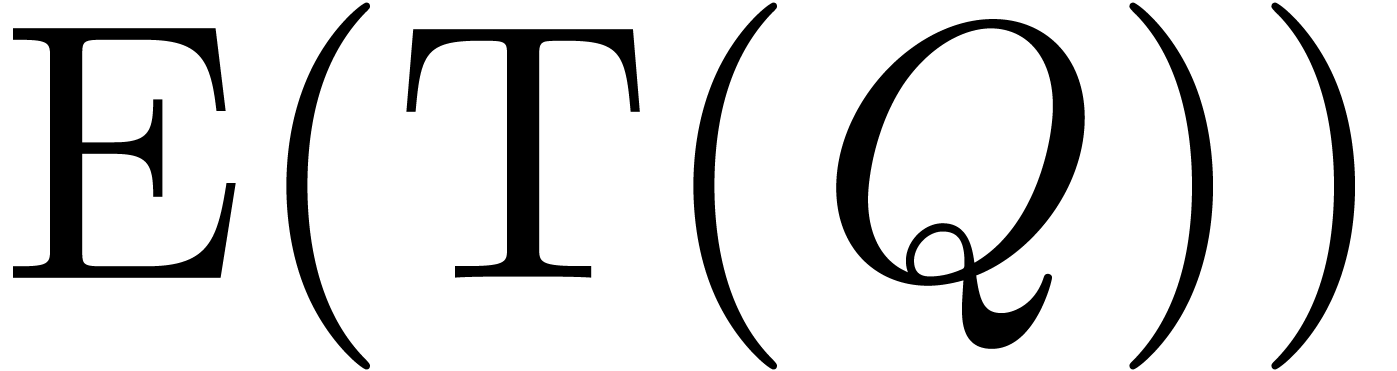 requires
requires  vectorial
operations in
vectorial
operations in  . The
computation of
. The
computation of 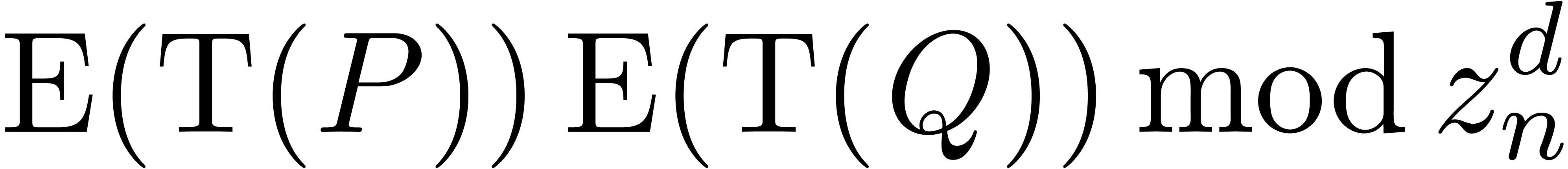 can be done using
can be done using 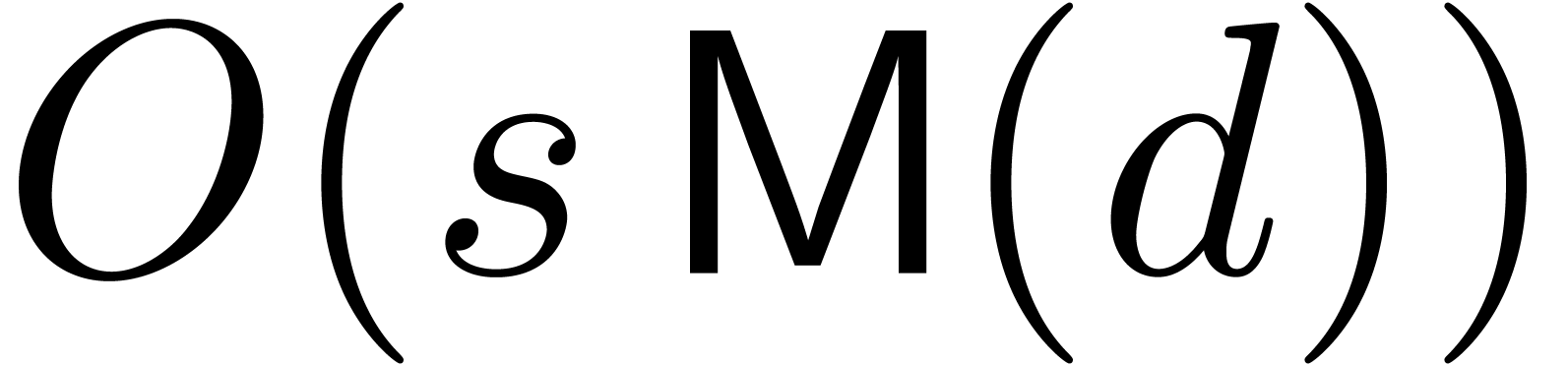 general operations in
general operations in  .
Recovering
.
Recovering 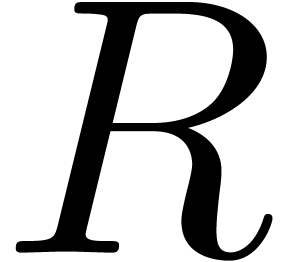 again requires
again requires  vectorial operations in
vectorial operations in  , as
well as
, as
well as 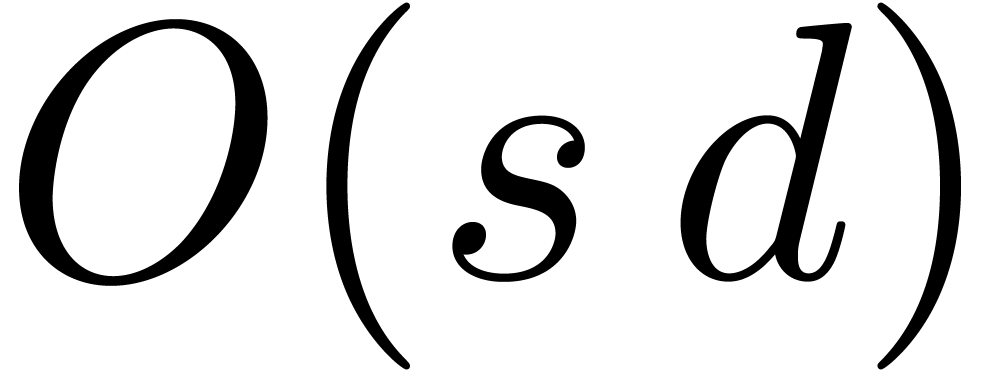 divisions in
divisions in  .
.
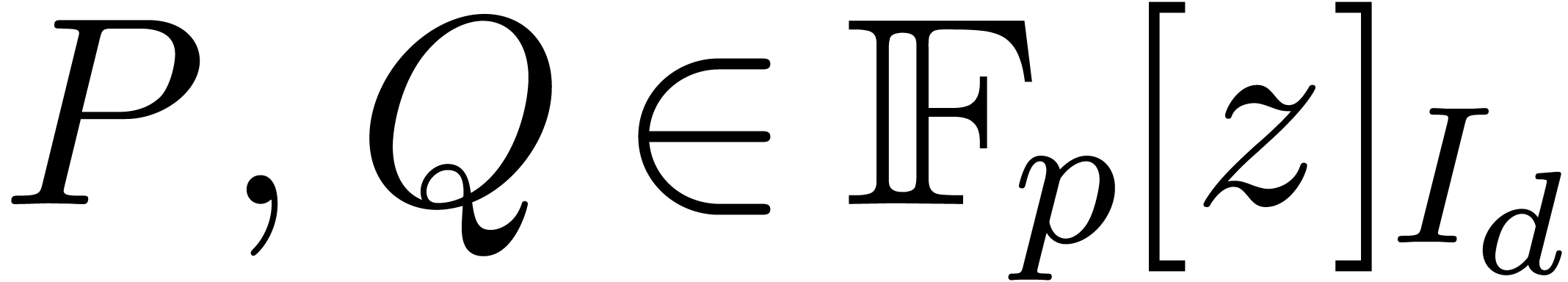 , where
, where
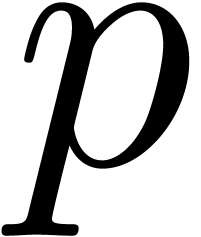 is a prime number with
is a prime number with 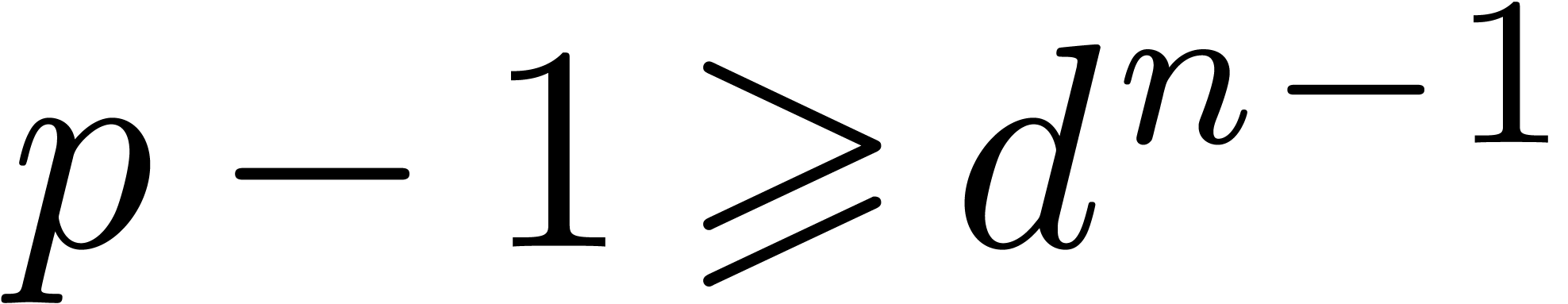 , we can compute
, we can compute  in time
in time
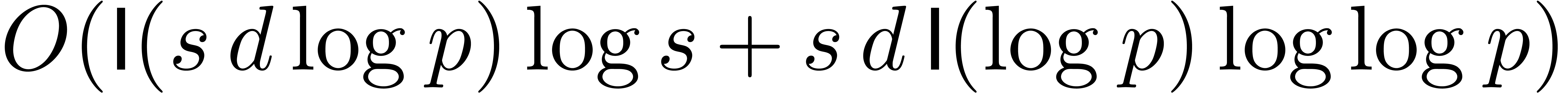 .
.
In the case when  , the
assumption
, the
assumption 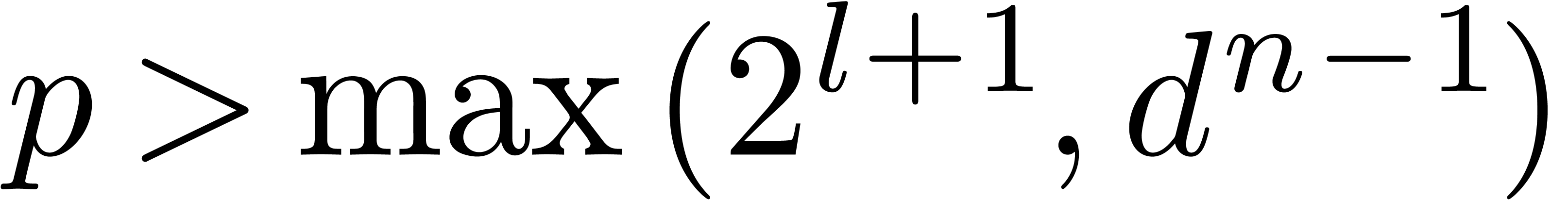 , with
, with 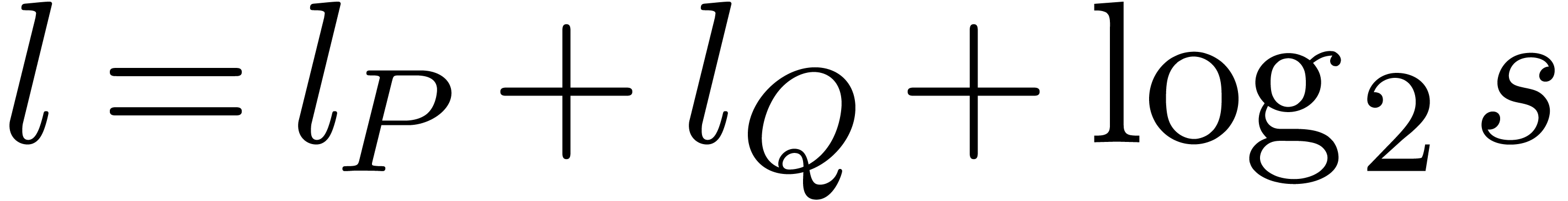 , guarantees that the coefficients
of the result
, guarantees that the coefficients
of the result  can be reconstructed from their
reductions modulo
can be reconstructed from their
reductions modulo  . Combining
this observation with Chinese remaindering, we obtain:
. Combining
this observation with Chinese remaindering, we obtain:
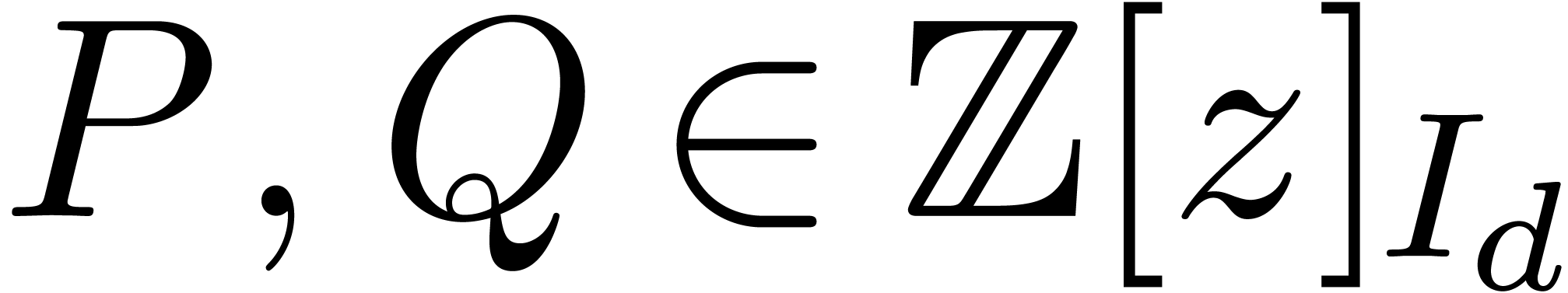 and a reduced sequence
and a reduced sequence  of prime moduli with order
of prime moduli with order 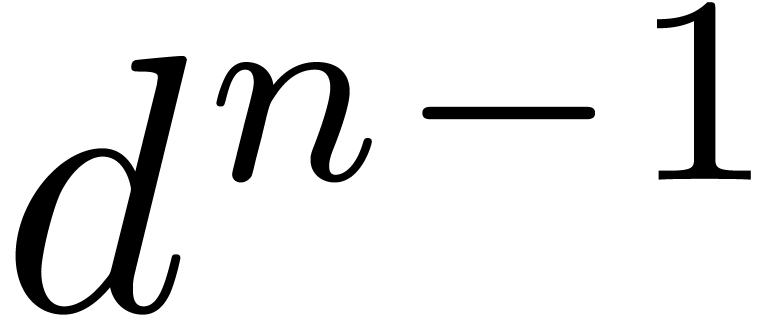 and capacity
and capacity 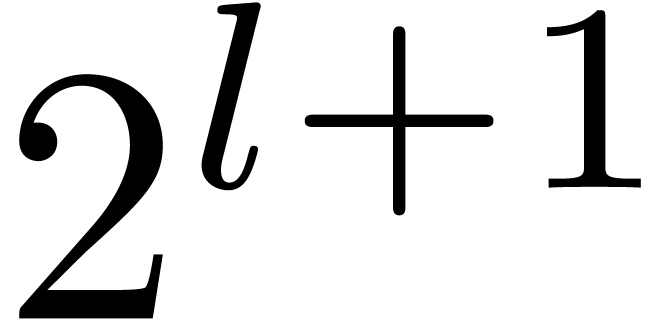 , we can
compute
, we can
compute  in time
in time
We have implemented the fast series product of the previous section
within the C++ library multimix of
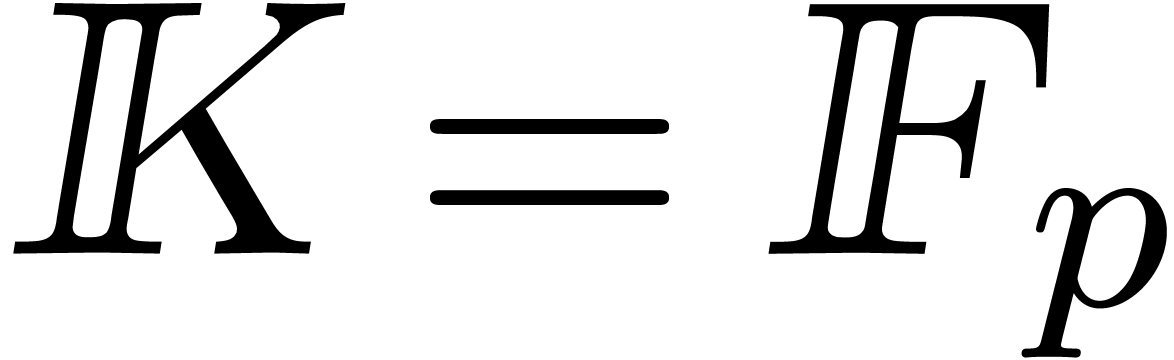 , with
, with 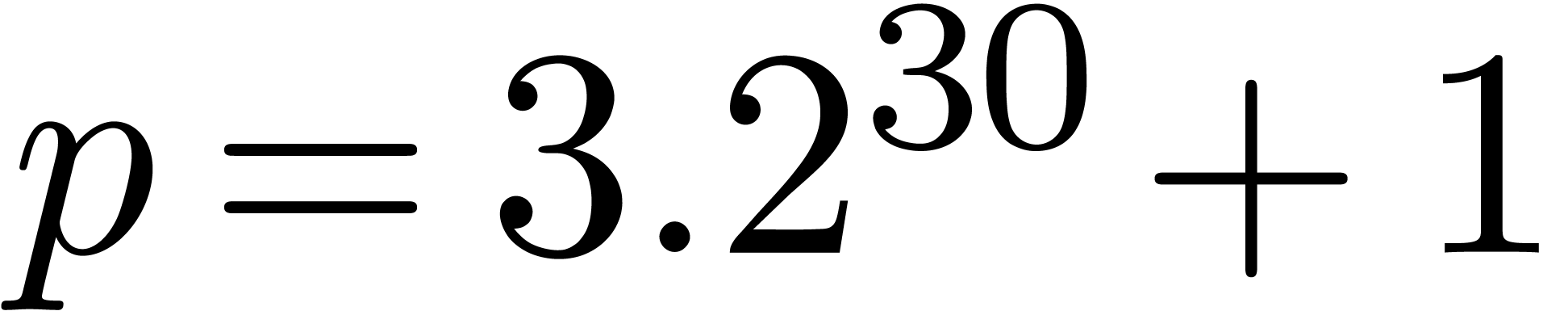 , on a 2.4 GHz Intel(R) Core(TM)2
Duo platform. Recall that
, on a 2.4 GHz Intel(R) Core(TM)2
Duo platform. Recall that 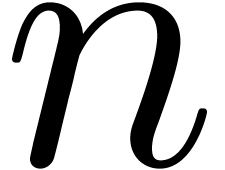 is the number of the
variables and
is the number of the
variables and 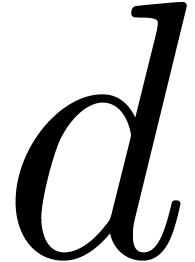 the truncation order. Timings are
given in milliseconds. The line naive corresponds to the naive
multiplication, that performs all the two by two monomial products,
while the line fast stands for the algorithm of the previous
section. We have added the size
the truncation order. Timings are
given in milliseconds. The line naive corresponds to the naive
multiplication, that performs all the two by two monomial products,
while the line fast stands for the algorithm of the previous
section. We have added the size 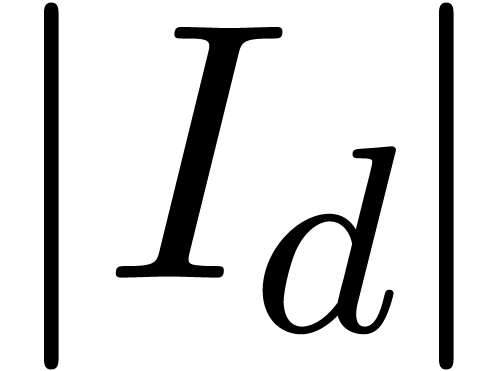 of the support
of the series, together with the cost
of the support
of the series, together with the cost 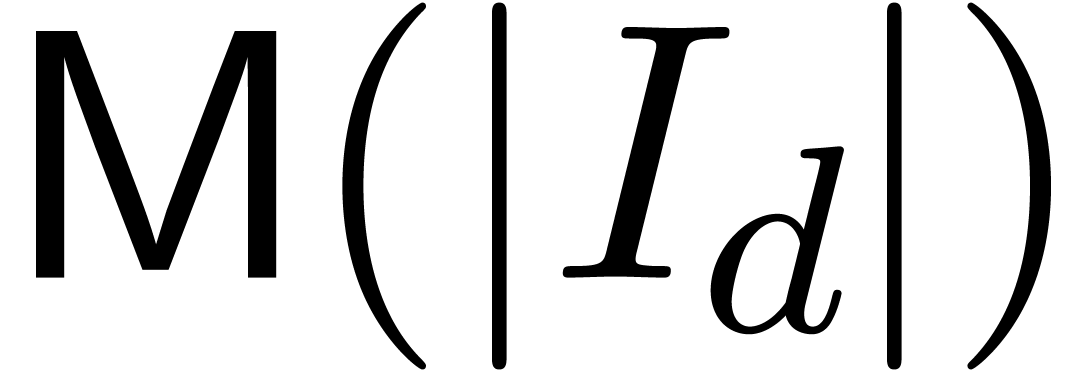 of our
univariate multiplication in size
of our
univariate multiplication in size 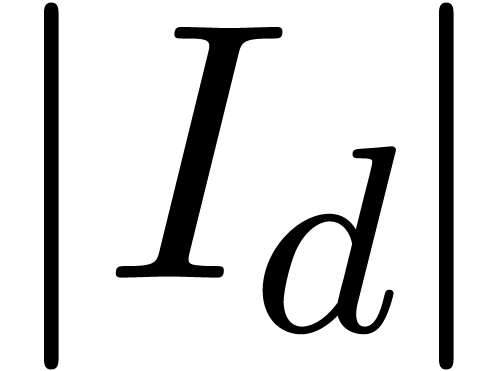 for
comparison. An empty cell corresponds to a computation that needed more
than 10 minutes. The following tables demonstrate that the new fast
algorithms are relevant to practice and that the theoretical soflty
linear asymptotic cost can really be observed.
for
comparison. An empty cell corresponds to a computation that needed more
than 10 minutes. The following tables demonstrate that the new fast
algorithms are relevant to practice and that the theoretical soflty
linear asymptotic cost can really be observed.
|
||||||||||||||||||||||||||||||
|
||||||||||||||||||||
|
||||||||||||||||||||||||||||||
M. Agrawal, N. Kayal, and N. Saxena. Primes is in p. Annals of Mathematics, 160(2):781–793, 2004.
D. Bernstein. The transposition principle. Available
from
http://cr.yp.to/transposition.html.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In Proceedings of ISSAC 2003, pages 37–44. ACM, 2003.
A. Borodin and R.T. Moenck. Fast modular transforms. Journal of Computer and System Sciences, 8:366–386, 1974.
J. L. Bordewijk. Inter-reciprocity applied to electrical networks. Applied Scientific Research B: Electrophysics, Acoustics, Optics, Mathematical Methods, 6:1–74, 1956.
Johannes Buchmann and Victor Shoup. Constructing nonresidues in finite fields and the extended riemann hypothesis. In STOC '91: Proceedings of the twenty-third annual ACM symposium on Theory of computing, pages 72–79, New York, NY, USA, 1991. ACM.
D.G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
J. Canny, E. Kaltofen, and Y. Lakshman. Solving systems of non-linear polynomial equations faster. In Proc. ISSAC '89, pages 121–128, Portland, Oregon, A.C.M., New York, 1989. ACM Press.
H. Cramér. On the order of magnitude of the difference between consecutive prime numbers. Acta Arithmetica, 2:23–46, 1936.
M. Fürer. Faster integer multiplication. In Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing (STOC 2007), pages 57–66, San Diego, California, 2007.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
G. Lecerf and É. Schost. Fast multivariate power series multiplication in characteristic zero. SADIO Electronic Journal on Informatics and Operations Research, 5(1):1–10, September 2003.
R.T. Moenck and A. Borodin. Fast modular transforms via division. In Thirteenth annual IEEE symposium on switching and automata theory, pages 90–96, Univ. Maryland, College Park, Md., 1972.
K. Makino and M. Berz. Remainder differential algebras and their applications. In M. Berz, C. Bischof, G. Corliss, and A. Griewank, editors, Computational differentiation: techniques, applications and tools, pages 63–74, SIAM, Philadelphia, 1996.
K. Makino and M. Berz. Suppression of the wrapping effect by Taylor model-based validated integrators. Technical Report MSU Report MSUHEP 40910, Michigan State University, 2004.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Informatica, 7:395–398, 1977.
A. Schönhage and V. Strassen. Schnelle Multiplikation grosser Zahlen. Computing, 7:281–292, 1971.
V. Strassen. Die Berechnungskomplexität von elementarsymmetrischen Funktionen und von Interpolationskoeffizienten. Numer. Math., 20:238–251, 1973.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven et al. Mathemagix, 2002. http://www.mathemagix.org.