| On the complexity of multivariate polynomial division  |
|
| April 30, 2017 |
|
 . This work has
been supported by the ANR-09-JCJC-0098-01
. This work has
been supported by the ANR-09-JCJC-0098-01
Abstract
In this paper, we present a new algorithm for reducing a multivariate polynomial with respect to an autoreduced tuple of other polynomials. In a suitable sparse complexity model, it is shown that the execution time is essentially the same (up to a logarithmic factor) as the time needed to verify that the result is correct.
Keywords: sparse reduction, complexity, division, algorithm
Sparse interpolation [1, 5, 2, 13] provides an interesting paradigm for efficient computations with multivariate polynomials. In particular, under suitable hypothesis, multiplication of sparse polynomials can be carried out in quasi-linear time, in terms of the expected output size. More recently, other multiplication algorithms have also been investigated, which outperform naive and sparse interpolation under special circumstances [14, 12]. An interesting question is how to exploit such asymptotically faster multiplication algorithms for the purpose of polynomial elimination. In this paper, we will focus on the reduction of a multivariate polynomial with respect to an autoreduced set of other polynomials and show that fast multiplication algorithms can indeed be exploited in this context in an asymptotically quasi-optimal way.
Consider the polynomial ring 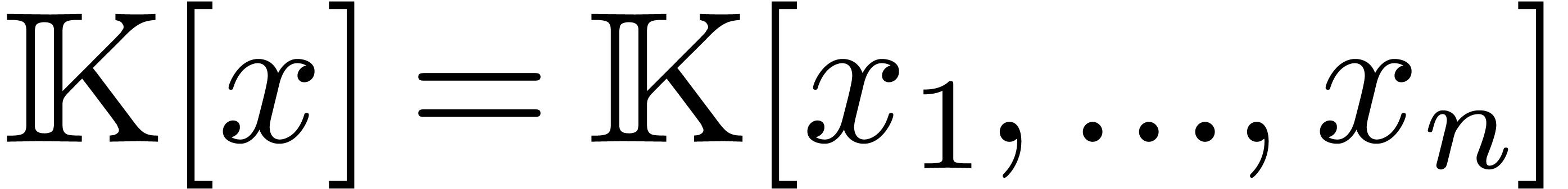 over an effective
field
over an effective
field  with an effective zero test. Given a
polynomial
with an effective zero test. Given a
polynomial 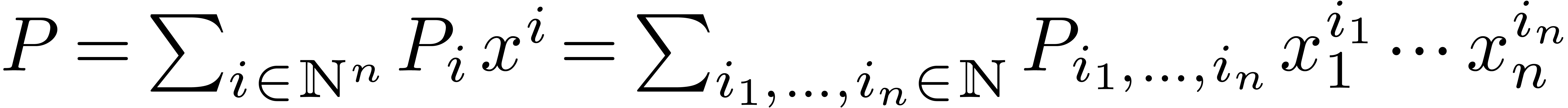 , we call
, we call 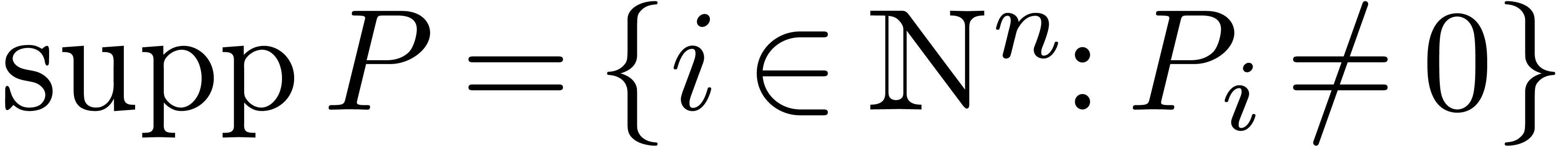 the support of
the support of  .
The naive multiplication of two sparse polynomials
.
The naive multiplication of two sparse polynomials  requires a priori
requires a priori  operations in
operations in  . This upper bound is sharp if
. This upper bound is sharp if 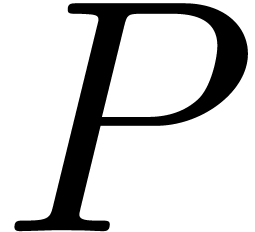 and
and  are very sparse, but
pessimistic if
are very sparse, but
pessimistic if 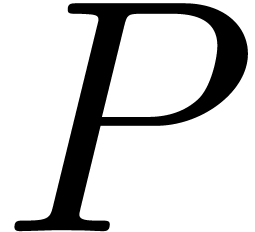 and
and  are
dense.
are
dense.
Assuming that  has characteristic zero, a better
algorithm was proposed in [2] (see also [1, 5] for some background). The complexity of this algorithm can
be expressed in the expected size
has characteristic zero, a better
algorithm was proposed in [2] (see also [1, 5] for some background). The complexity of this algorithm can
be expressed in the expected size 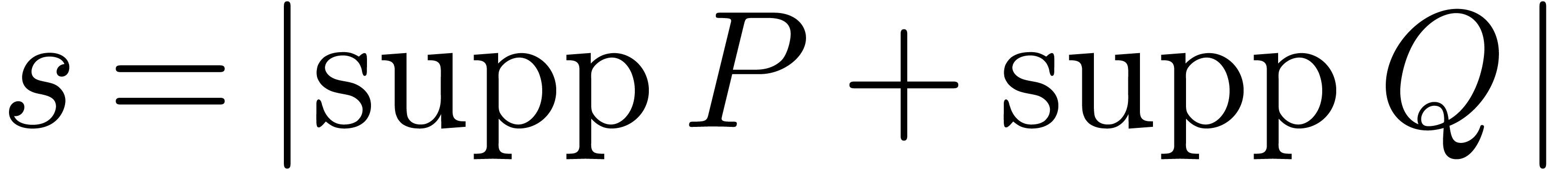 of the
output (when no cancellations occur). It is shown that
of the
output (when no cancellations occur). It is shown that  and
and  can be multiplied using
only
can be multiplied using
only  operations in
operations in  ,
where
,
where 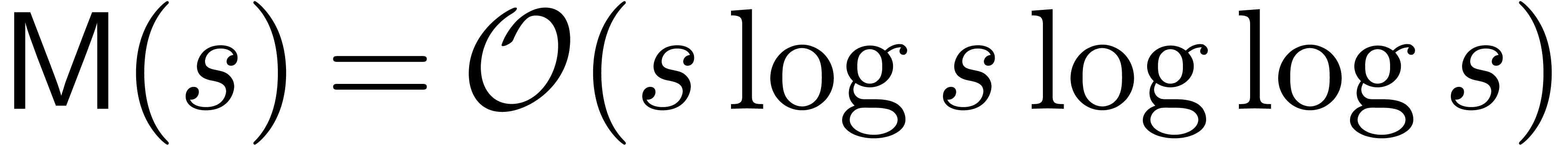 stands for the complexity of multiplying
two univariate polynomials in
stands for the complexity of multiplying
two univariate polynomials in 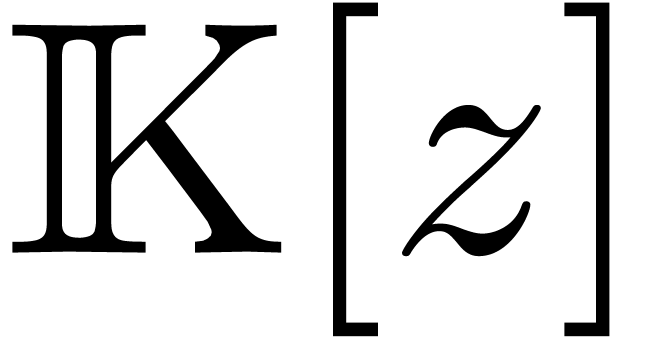 of degrees
of degrees  . Unfortunately, the algorithm in
[2] has two drawbacks:
. Unfortunately, the algorithm in
[2] has two drawbacks:
The algorithm leads to a big growth for the sizes of the coefficients, thereby compromising its bit complexity (which is often worse than the bit complexity of naive multiplication).
It requires 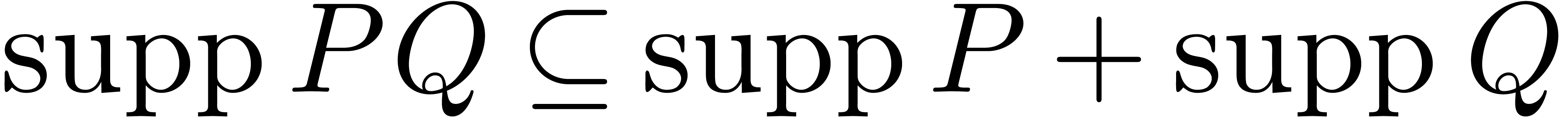 to be known beforehand. More
precisely, whenever a bound
to be known beforehand. More
precisely, whenever a bound 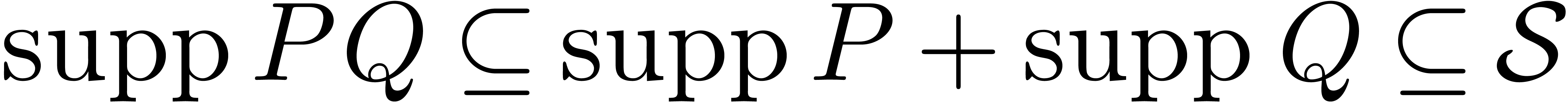 is known, then
we really obtain a multiplication algorithm of complexity
is known, then
we really obtain a multiplication algorithm of complexity 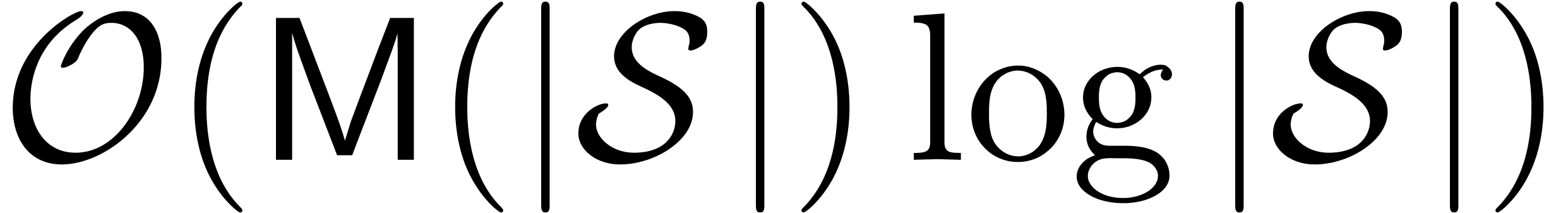 .
.
In practice, the second drawback is of less importance. Indeed,
especially when the coefficients in  can become
large, then the computation of
can become
large, then the computation of  is often cheap
with respect to the multiplication
is often cheap
with respect to the multiplication 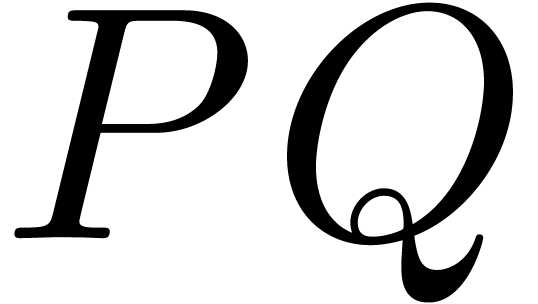 itself, even
if we compute
itself, even
if we compute  in a naive way.
in a naive way.
Recently, several algorithms were proposed for removing the drawbacks of
[2]. First of all, in [13] we proposed a
practical algorithm with essentially the same advantages as the original
algorithm from [2], but with a good bit complexity and a
variant which also works in positive characterisic. However, it still
requires a bound for 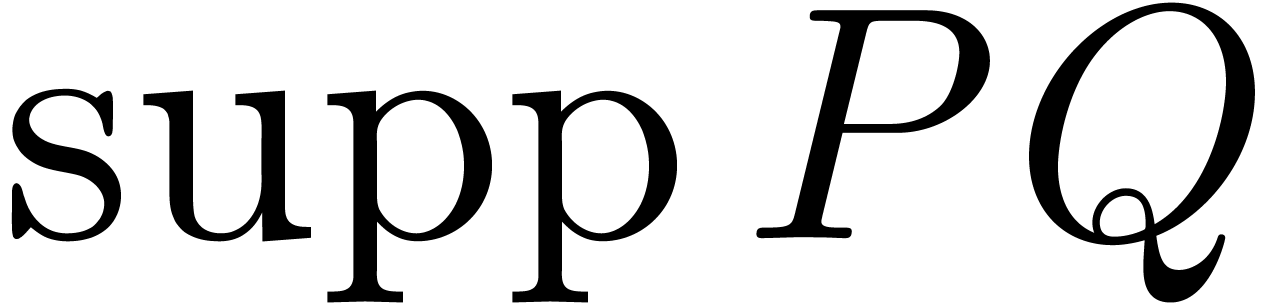 and it only works for
special kinds of fields
and it only works for
special kinds of fields  (which nevertheless
cover the most important cases such as
(which nevertheless
cover the most important cases such as 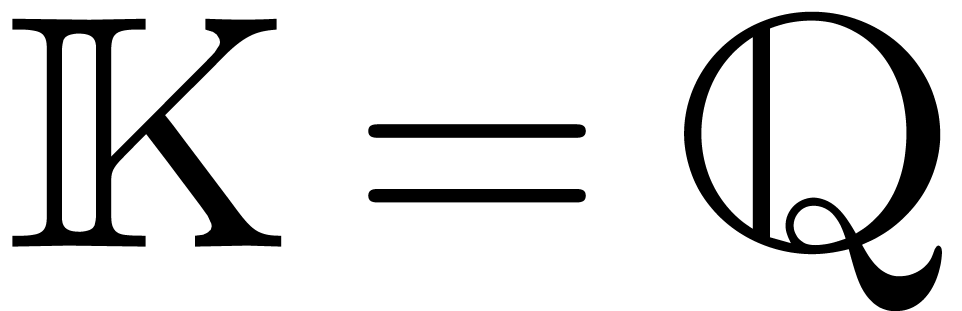 and
finite fields). Even faster algorithms were proposed in [9,
14], but these algorithms only work for special supports.
Yet another algorithm was proposed in [7, 12].
This algorithm has none of the drawbacks of [2], but its
complexity is suboptimal (although better than the complexity of naive
multiplication).
and
finite fields). Even faster algorithms were proposed in [9,
14], but these algorithms only work for special supports.
Yet another algorithm was proposed in [7, 12].
This algorithm has none of the drawbacks of [2], but its
complexity is suboptimal (although better than the complexity of naive
multiplication).
At any rate, these recent developments make it possible to rely on fast sparse polynomial multiplication as a building block, both in theory and in practice. This makes it natural to study other operations on multivariate polynomials with this building block at our disposal. One of the most important such operations is division.
The multivariate analogue of polynomial division is the reduction of a
polynomial 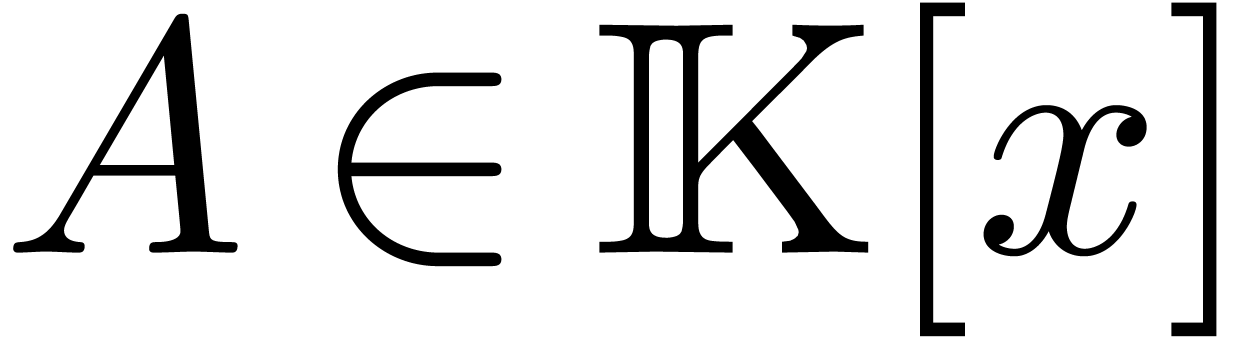 with respect to an autoreduced tuple
with respect to an autoreduced tuple
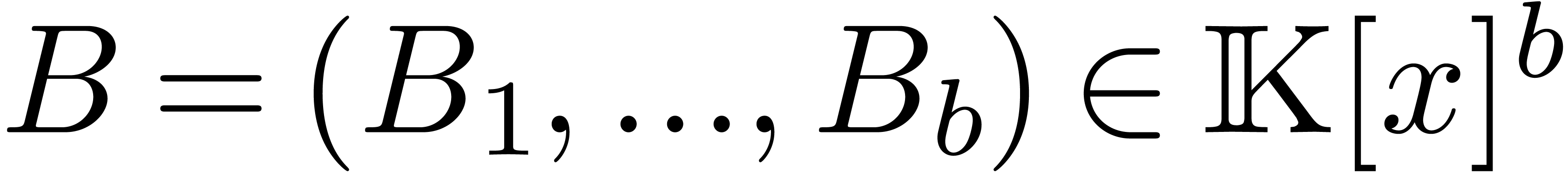 of other polynomials. This leads to a relation
of other polynomials. This leads to a relation
such that none of the terms occurring in  can be
further reduced with respect to
can be
further reduced with respect to  .
In this paper, we are interested in the computation of
.
In this paper, we are interested in the computation of  as well as
as well as  . We will call
this the problem of extended reduction, in analogy with the
notion of an “extended g.c.d.”.
. We will call
this the problem of extended reduction, in analogy with the
notion of an “extended g.c.d.”.
Now in the univariate context, “relaxed power series”
provide a convenient technique for the resolution of implicit equations
[6, 7, 8, 10]. One
major advantage of this technique is that it tends to respect most
sparsity patterns which are present in the input data and in the
equations. The main technical tool in this paper (see section 3)
is to generalize this technique to the setting of multivariate
polynomials, whose terms are ordered according to a specific admissible
ordering on the monomials. This will make it possible to rewrite (1) as a so called recursive equation (see section 4.2),
which can be solved in a relaxed manner. Roughly speaking, the cost of
the extended reduction then reduces to the cost of the relaxed
multiplications  . Up to a
logarithmic overhead, we will show (theorem 7) that this
cost is the same as the cost of checking the relation (1).
. Up to a
logarithmic overhead, we will show (theorem 7) that this
cost is the same as the cost of checking the relation (1).
In order to simplify the exposition, we will adopt a simplified sparse
complexity model throughout this paper. In particular, our complexity
analysis will not take into account the computation of support bounds
for products or results of the extended reduction. Bit complexity issues
will also be left aside in this paper. We finally stress that our
results are mainly of theoretical interest since none of the proposed
algorithms have currently been implemented. Nevertheless, practical
gains are not to be excluded, especially in the case of small 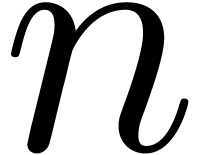 , high degrees and dense supports.
, high degrees and dense supports.
Let  be an effective field with an effective zero
test and let
be an effective field with an effective zero
test and let  be indeterminates. We will denote
be indeterminates. We will denote
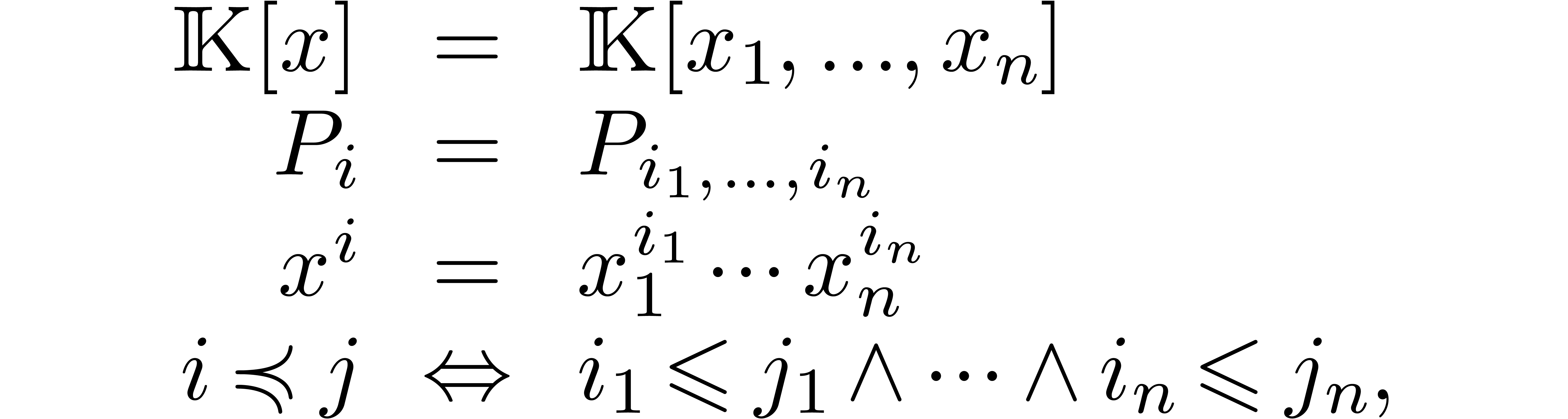
for any  and
and 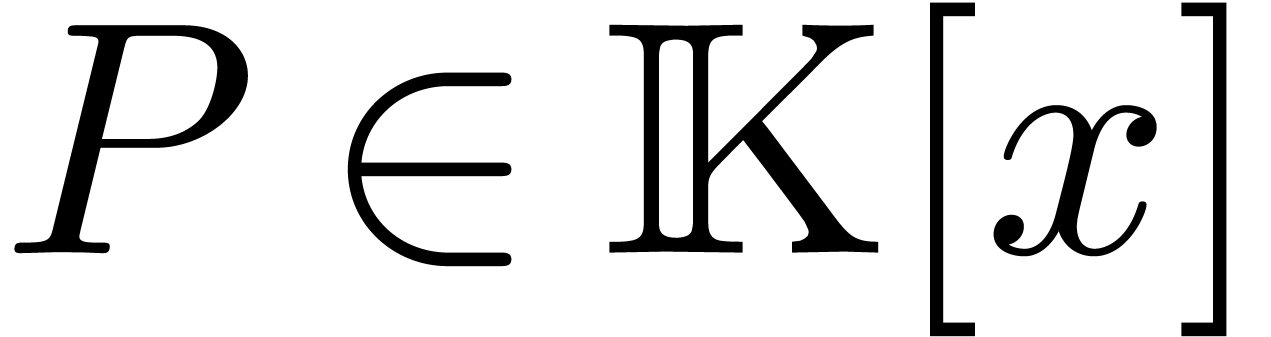 .
In particular,
.
In particular,  . For any
subset
. For any
subset 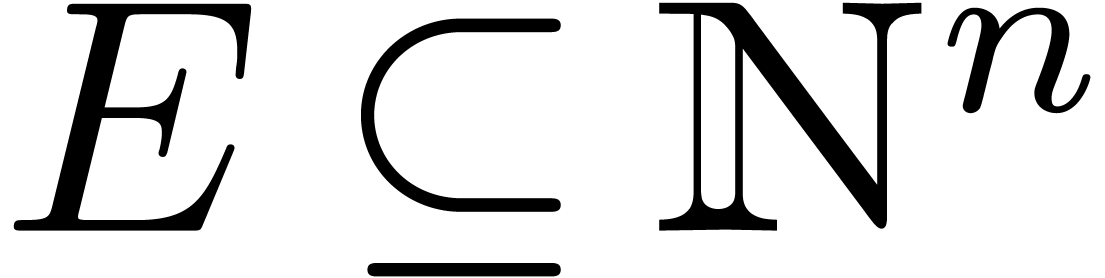 we will denote by
we will denote by 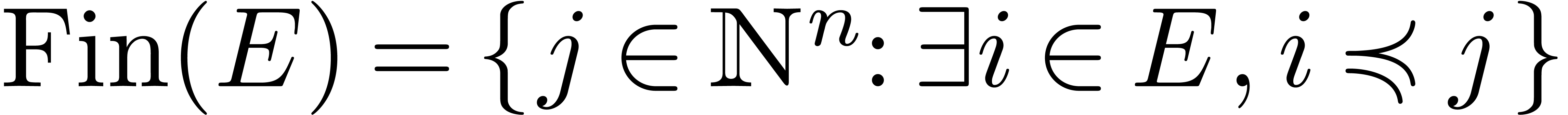 the final segment generated by
the final segment generated by  for the
partial ordering
for the
partial ordering  .
.
Let 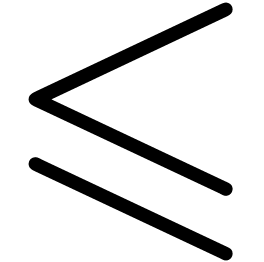 be a total ordering on
be a total ordering on 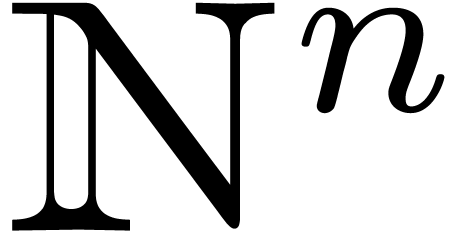 which is compatible with addition. Two particular such orderings are the
lexicographical ordering
which is compatible with addition. Two particular such orderings are the
lexicographical ordering 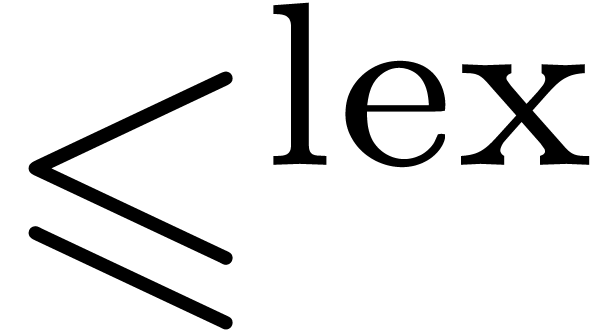 and the reverse
lexicographical ordering
and the reverse
lexicographical ordering 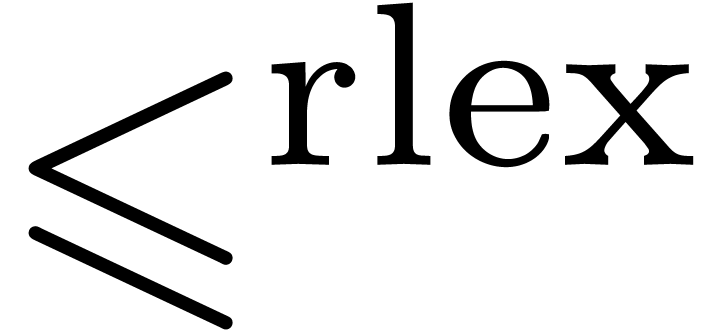 :
:
In general, it can be shown [16] that there exist real
vectors 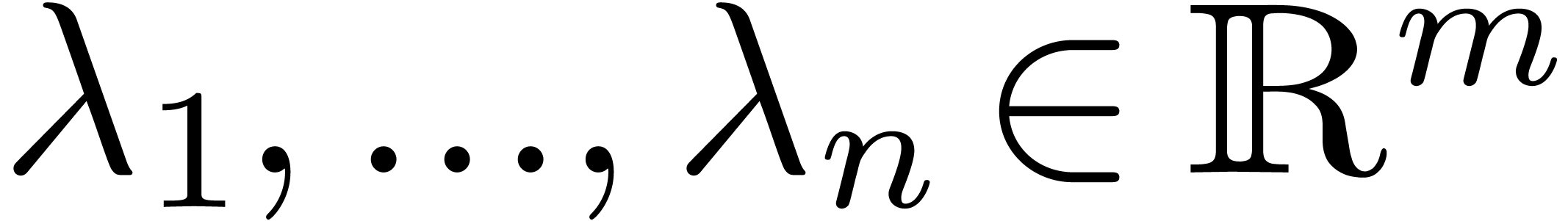 with
with  ,
such that
,
such that
In what follows, we will assume that 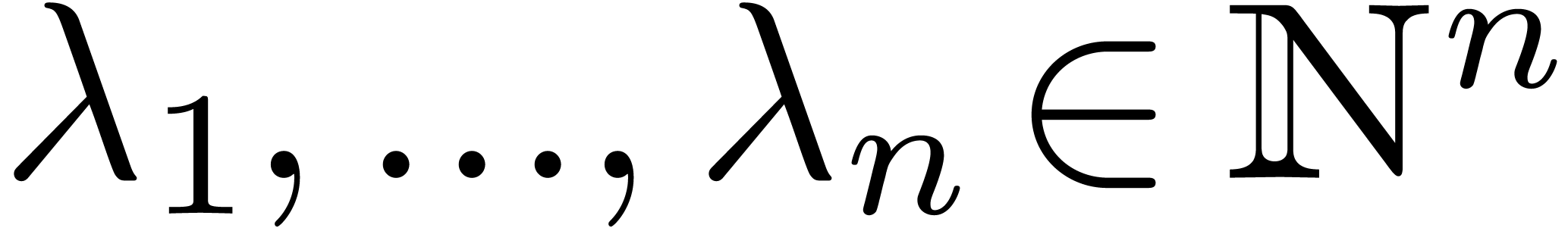 and
and  for all
for all 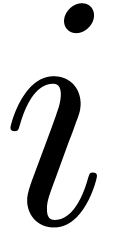 .
We will also denote
.
We will also denote
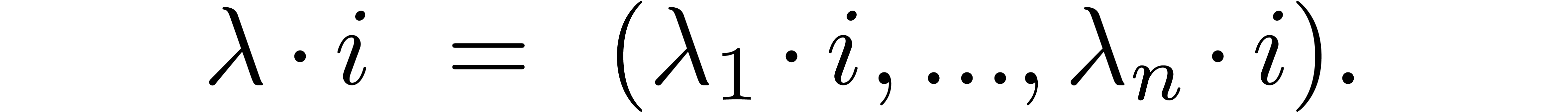
For instance, the graded reverse lexicographical ordering 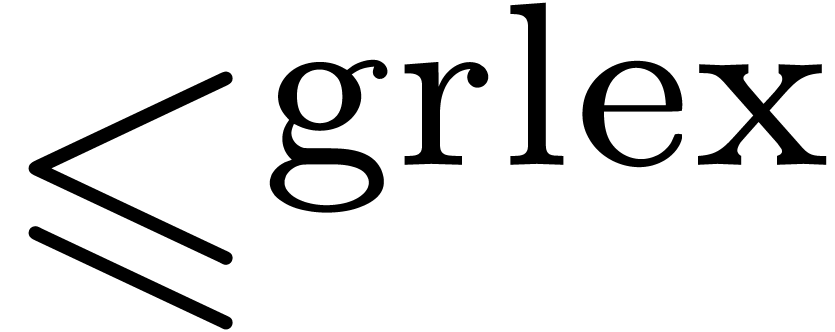 is obtained by taking
is obtained by taking 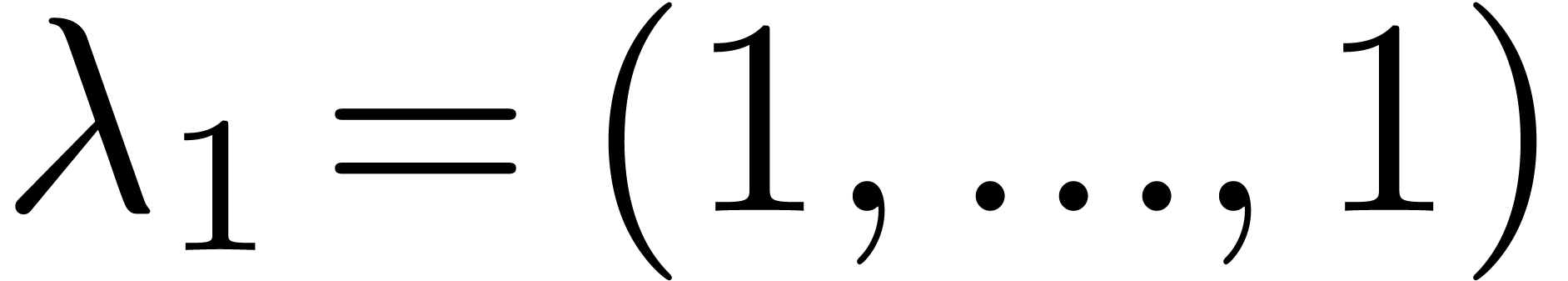 ,
,
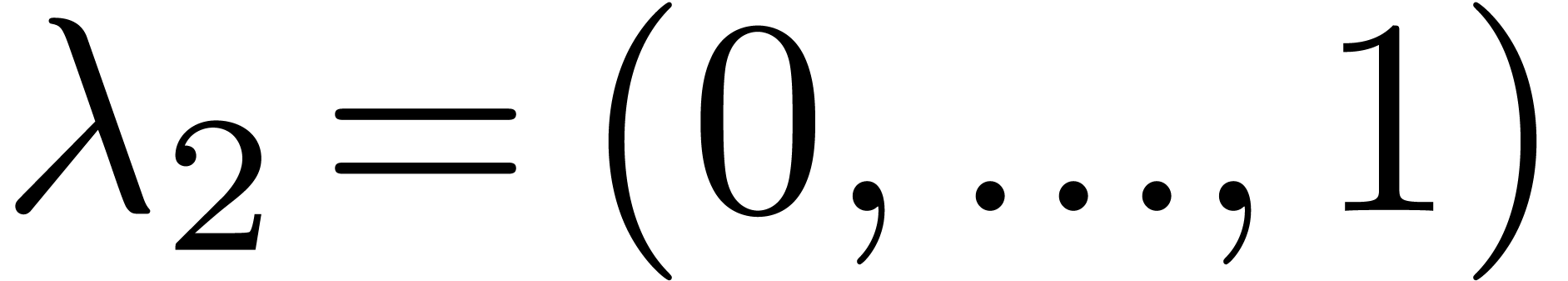 ,
,  ,
,  ,
, 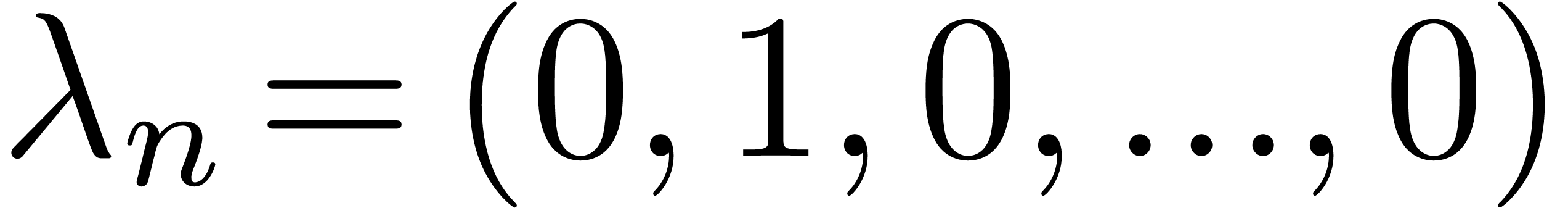 .
.
Given 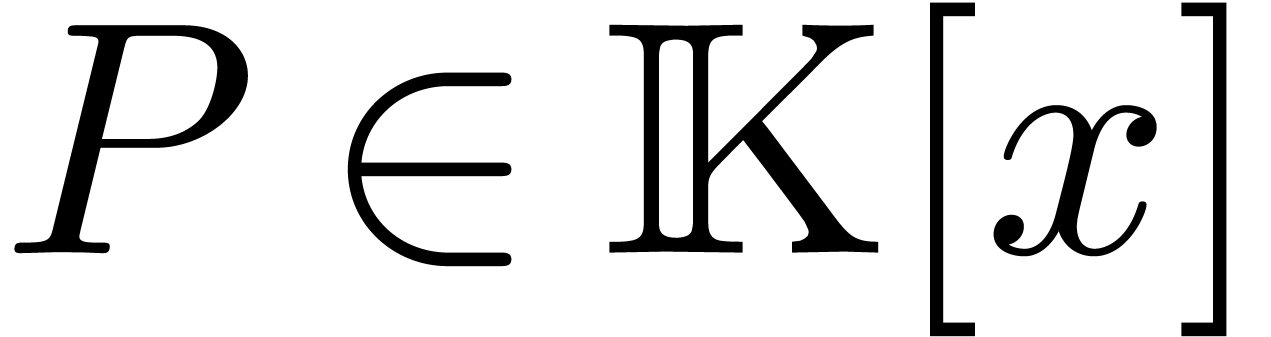 , we define its
support by
, we define its
support by
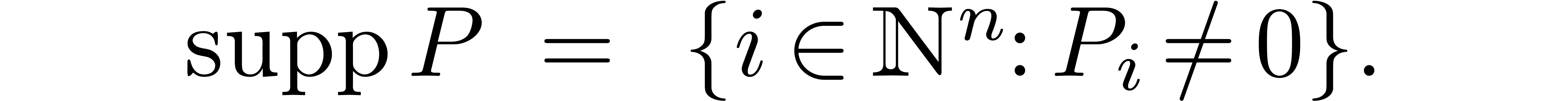
If 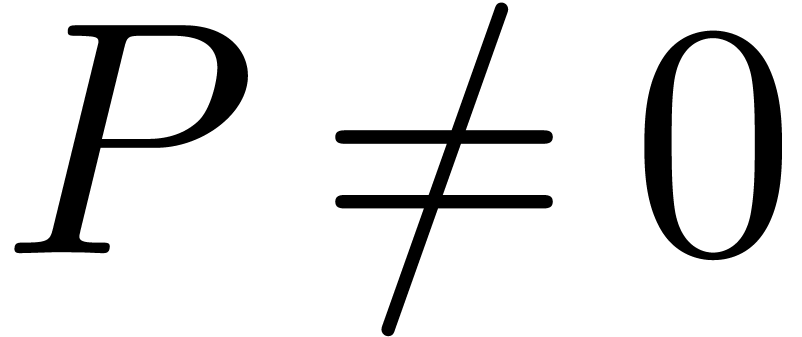 , then we also define its
leading exponent
, then we also define its
leading exponent 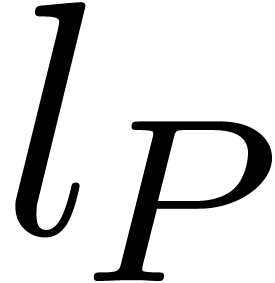 and
coefficient
and
coefficient 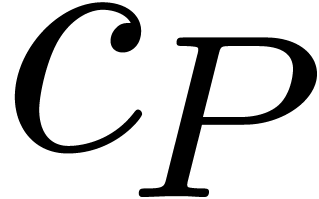 by
by
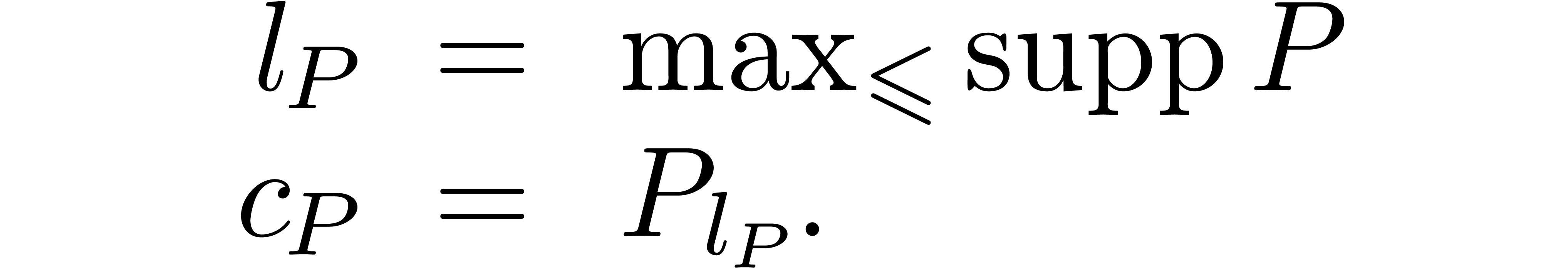
Given a finite set  , we will
denote its cardinality by
, we will
denote its cardinality by  .
.
Let us briefly recall the technique of relaxed power series
computations, which is explained in more detail in [7]. In
this computational model, a univariate power series  is regarded as a stream of coefficients
is regarded as a stream of coefficients 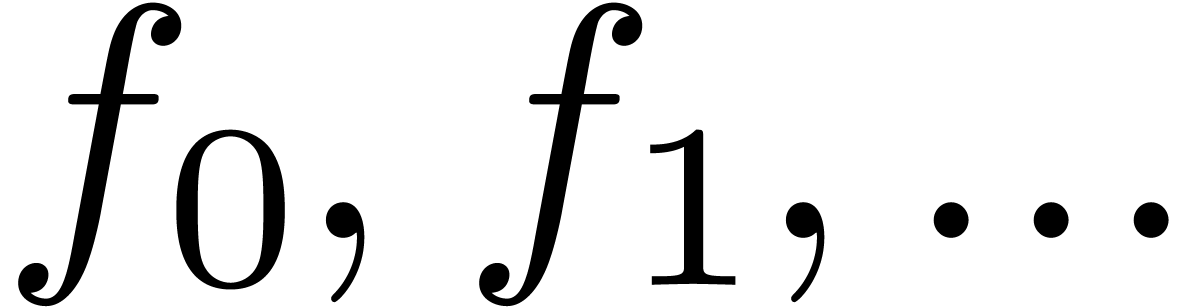 .
When performing an operation
.
When performing an operation 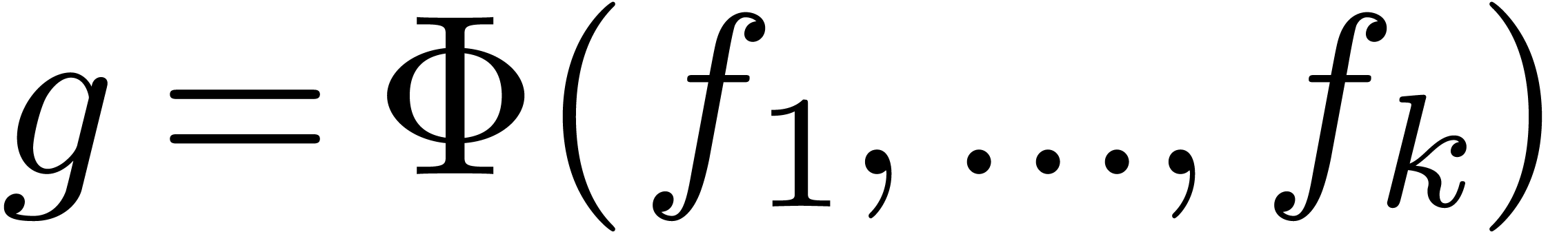 on power series it
is required that the coefficient
on power series it
is required that the coefficient  of the result
is output as soon as sufficiently many coefficients of the inputs are
known, so that the computation of
of the result
is output as soon as sufficiently many coefficients of the inputs are
known, so that the computation of 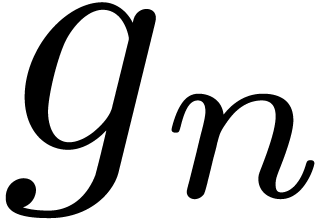 does not
depend on the further coefficients. For instance, in the case of a
multiplication
does not
depend on the further coefficients. For instance, in the case of a
multiplication 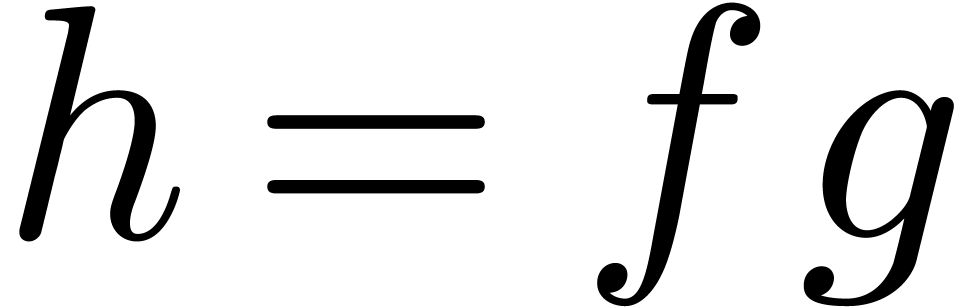 , we require
that
, we require
that 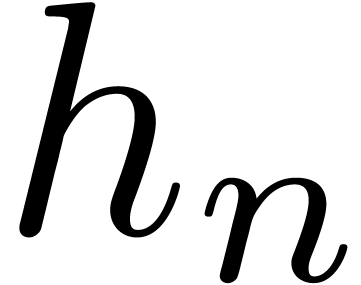 is output as soon as
is output as soon as  and
and  are known. In particular, we may use the
naive formula
are known. In particular, we may use the
naive formula 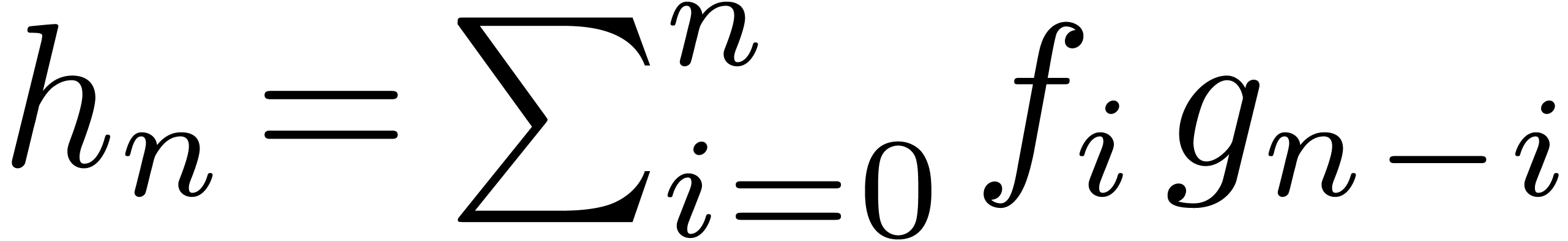 for the computation of
for the computation of 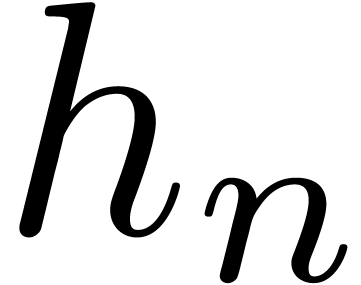 .
.
The additional constraint on the time when coefficients should be output
admits the important advantage that the inputs may depend on the output,
provided that we add a small delay. For instance, the exponential  of a power series
of a power series 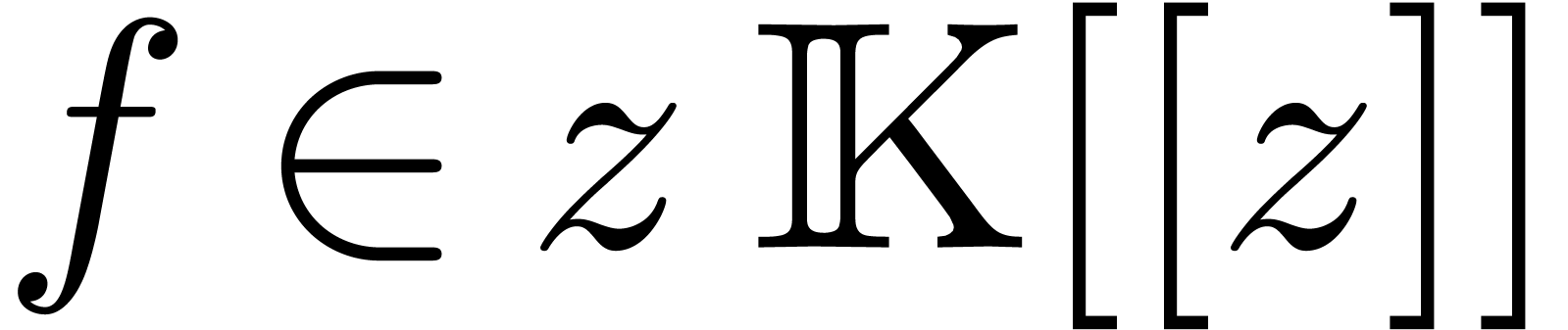 may be
computed in a relaxed way using the formula
may be
computed in a relaxed way using the formula
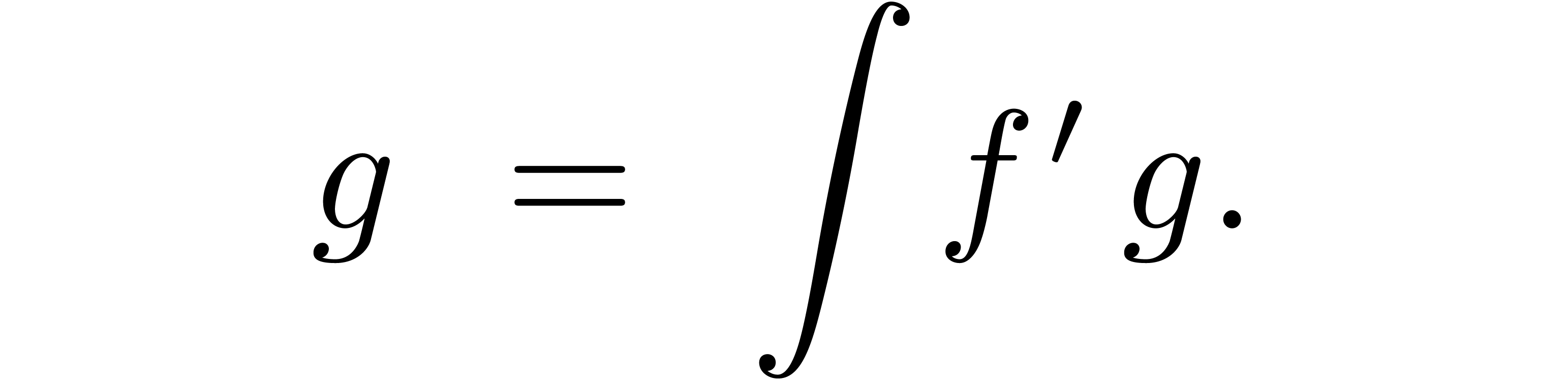
Indeed, when using the naive formula for products, the coefficient 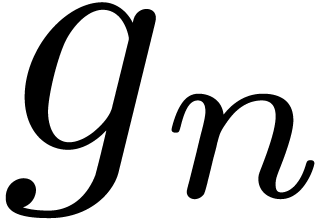 is given by
is given by
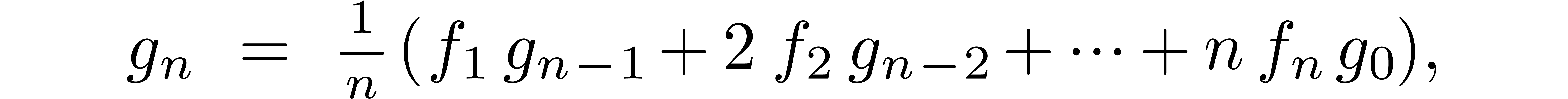
and the right-hand side only depends on the previously computed
coefficients 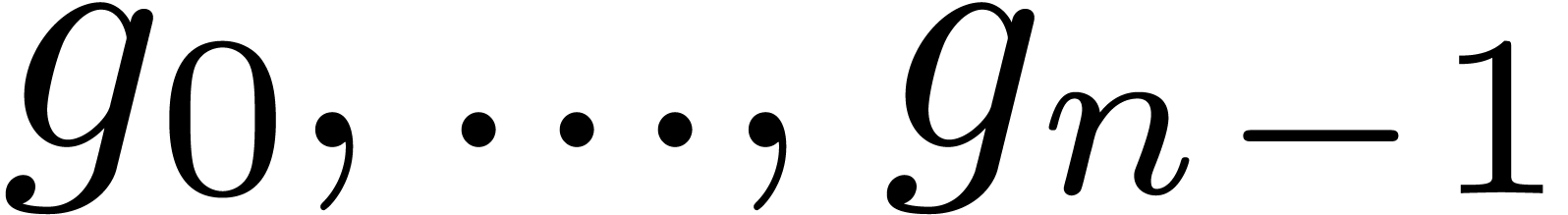 . More
generally, equations of the form
. More
generally, equations of the form 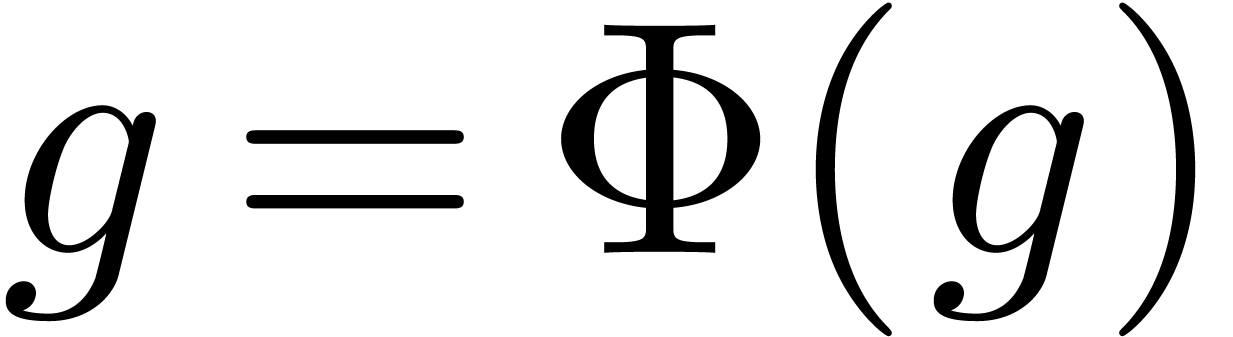 which have this
property are called recursive equations and we refer to [11] for a mechanism to transform fairly general implicit
equations into recursive equations.
which have this
property are called recursive equations and we refer to [11] for a mechanism to transform fairly general implicit
equations into recursive equations.
The main drawback of the relaxed approach is that we cannot directly use
fast algorithms on polynomials for computations with power series. For
instance, assuming that  has sufficiently many
has sufficiently many
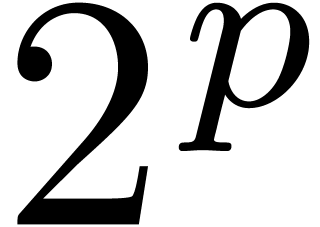 -th roots of unity and that
field operations in
-th roots of unity and that
field operations in  can be done in time
can be done in time 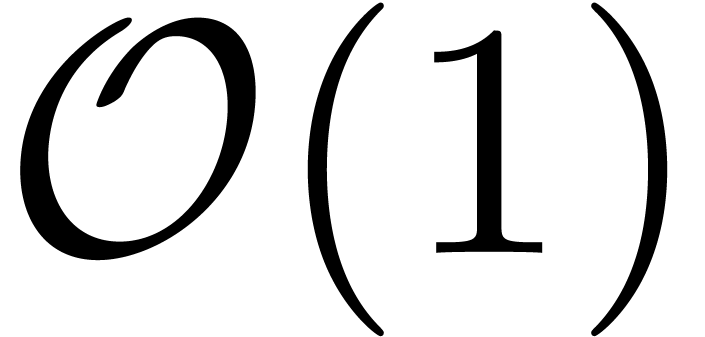 , two polynomials of degrees
, two polynomials of degrees 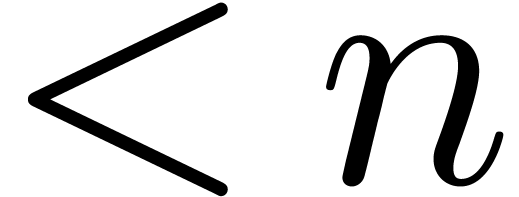 can be multiplied in time
can be multiplied in time 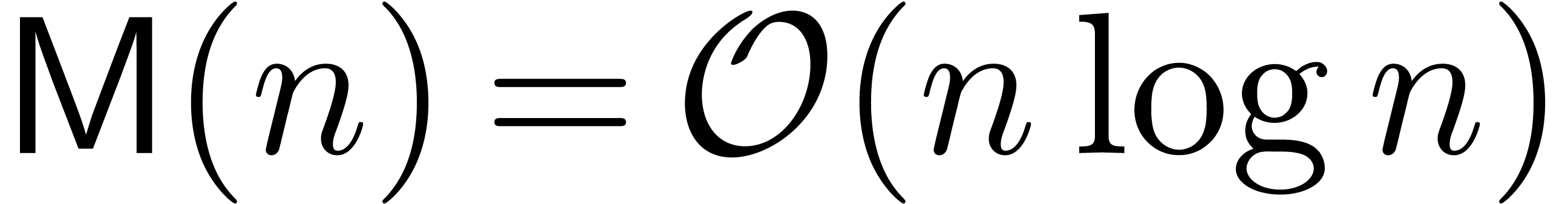 , using FFT multiplication [3]. Given
the truncations
, using FFT multiplication [3]. Given
the truncations 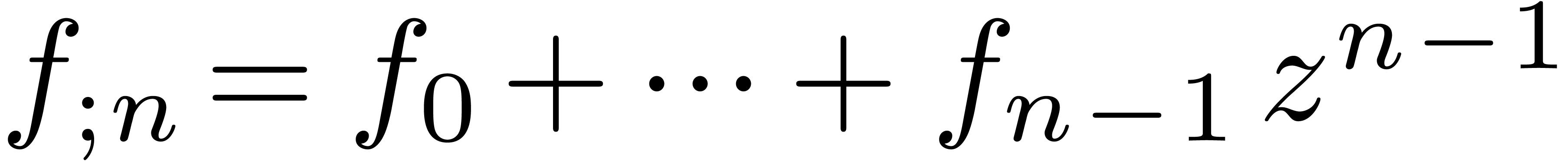 and
and 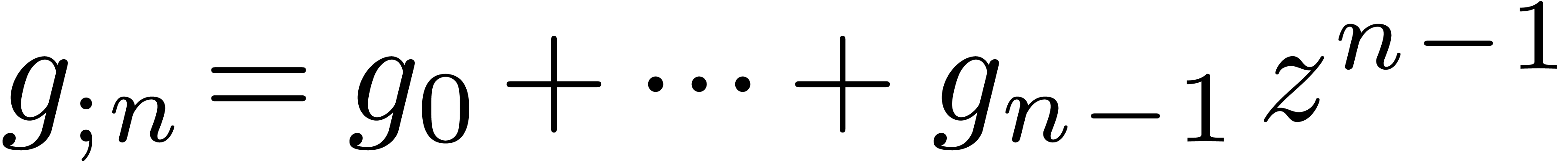 at
order
at
order  of power series
of power series 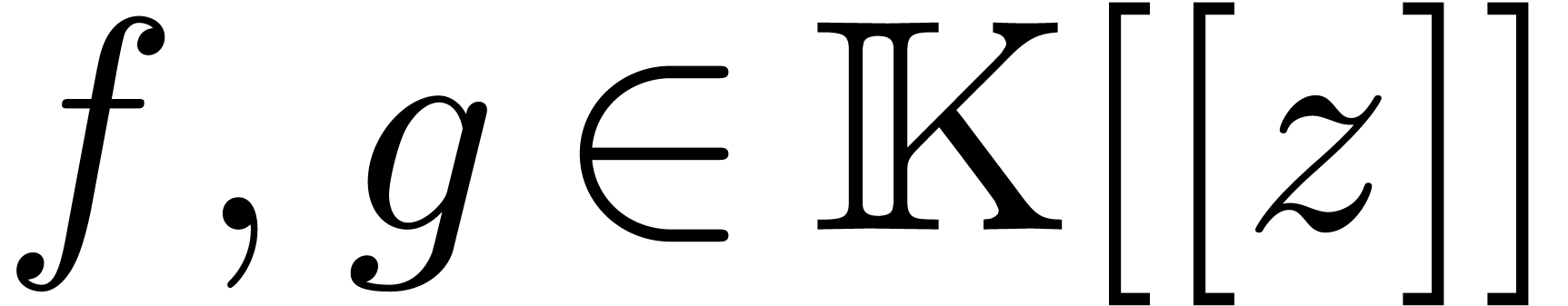 , we may thus compute the truncated product
, we may thus compute the truncated product  in time
in time 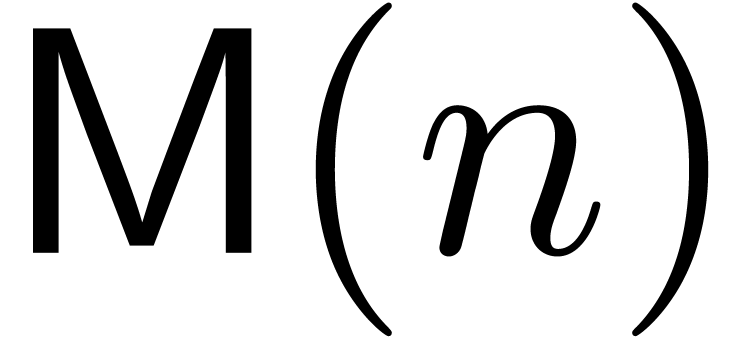 as well. This is much
faster than the naive
as well. This is much
faster than the naive 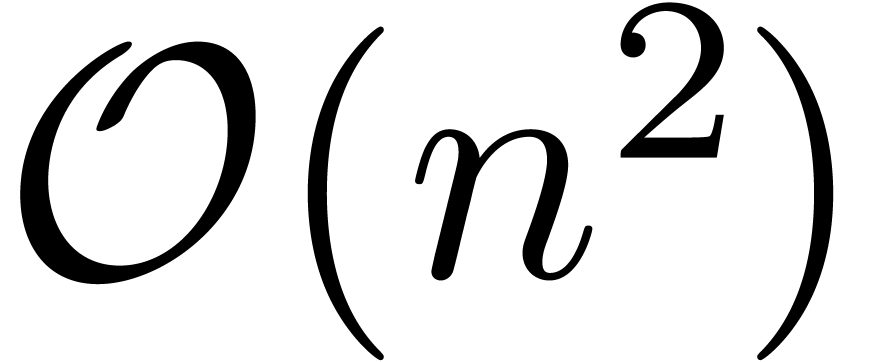 relaxed multiplication
algorithm for the computation of
relaxed multiplication
algorithm for the computation of  .
However, the formula for
.
However, the formula for 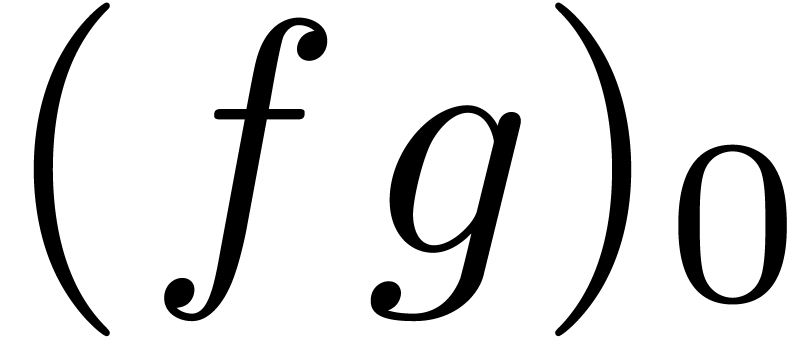 when using FFT
multiplication depends on all input coefficients
when using FFT
multiplication depends on all input coefficients 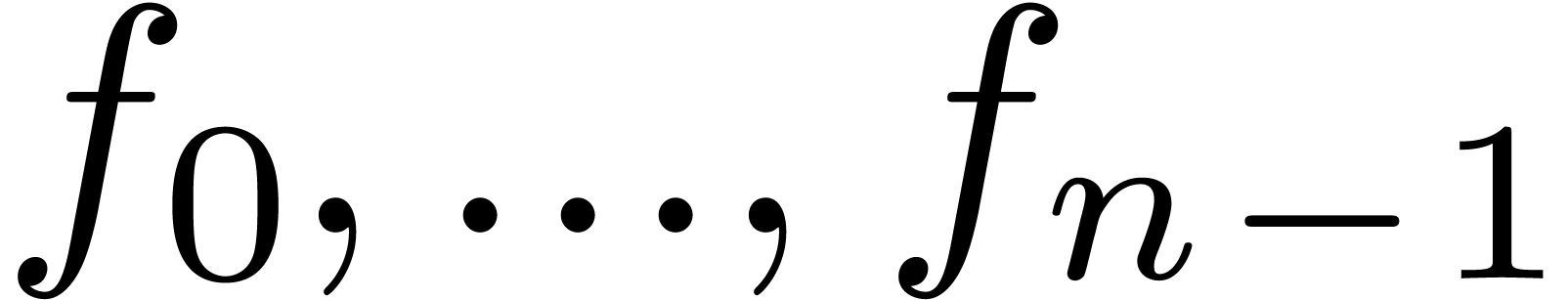 and
and 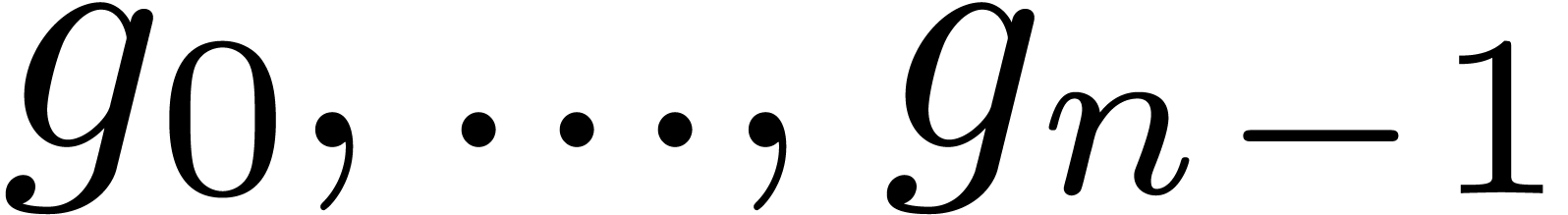 , so the fast algorithm
is not relaxed (we will say that FFT multiplication is a
zealous algorithm). Fortunately, efficient relaxed
multiplication algorithms do exist:
, so the fast algorithm
is not relaxed (we will say that FFT multiplication is a
zealous algorithm). Fortunately, efficient relaxed
multiplication algorithms do exist:
Theorem 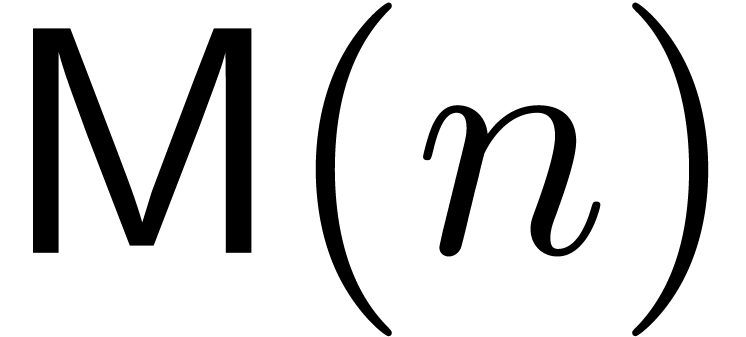 be the time complexity for the
multiplication of polynomials of degrees
be the time complexity for the
multiplication of polynomials of degrees 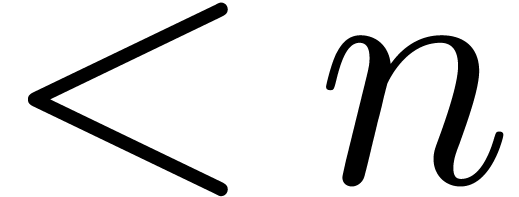 in
in
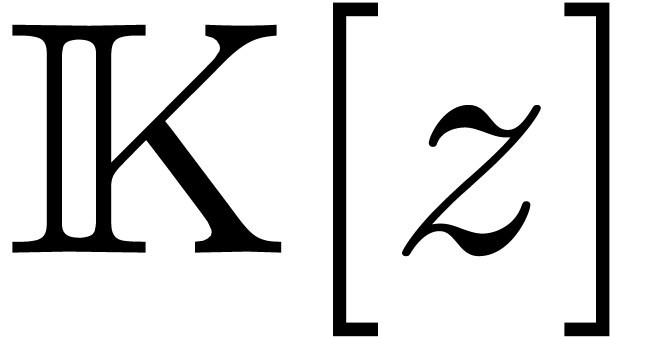 . Then there exists a relaxed
multiplication algorithm for series in
. Then there exists a relaxed
multiplication algorithm for series in 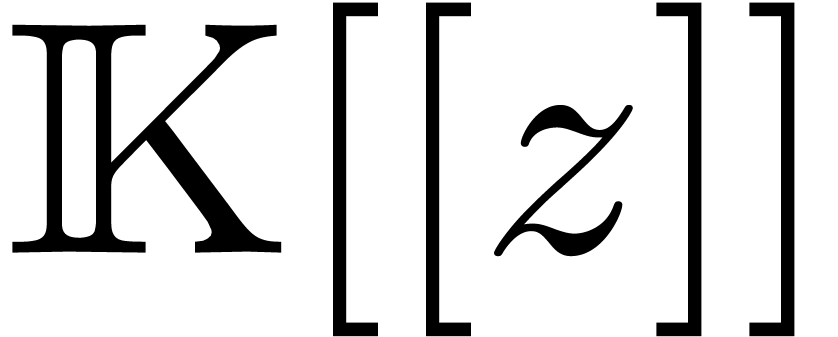 at order
at order
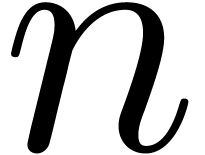 of time complexity
of time complexity 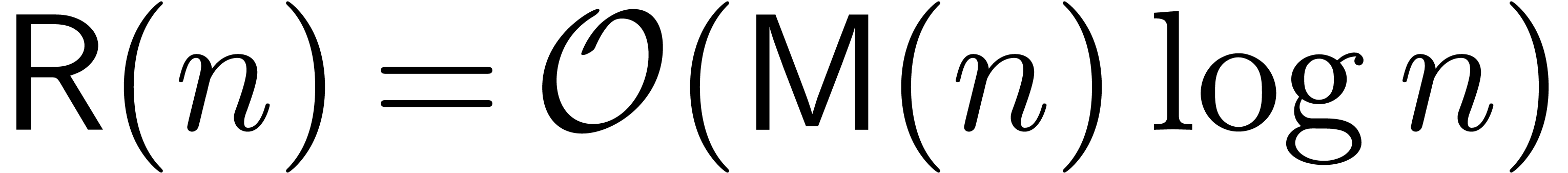 .
.
Remark  is replaced by an arbitrary
bilinear “multiplication”
is replaced by an arbitrary
bilinear “multiplication” 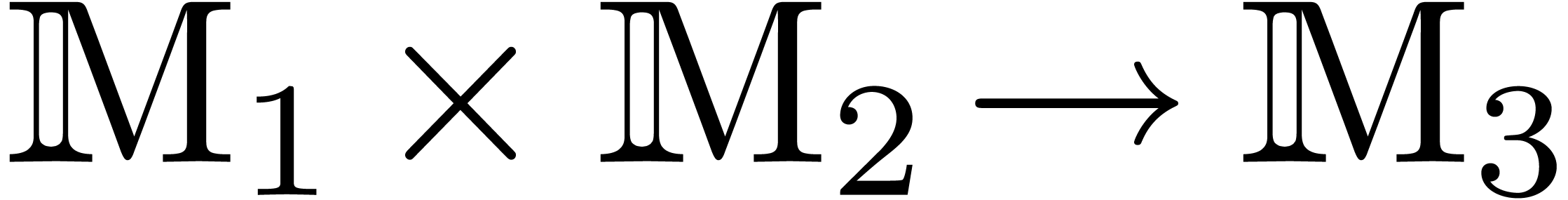 ,
where
,
where 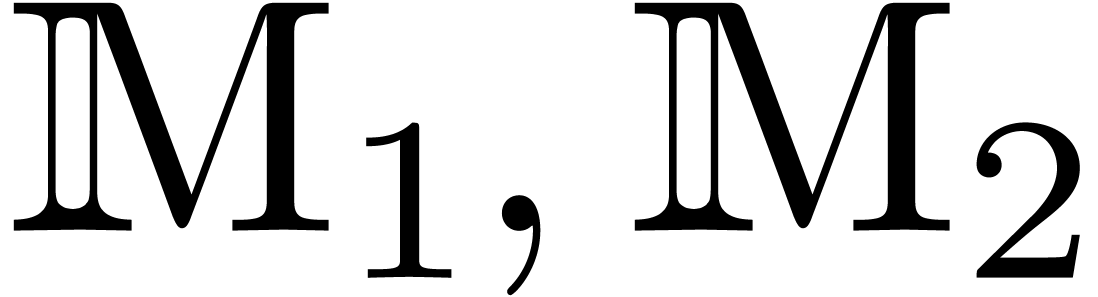 and
and  are effective
modules over an effective ring
are effective
modules over an effective ring  .
If
.
If 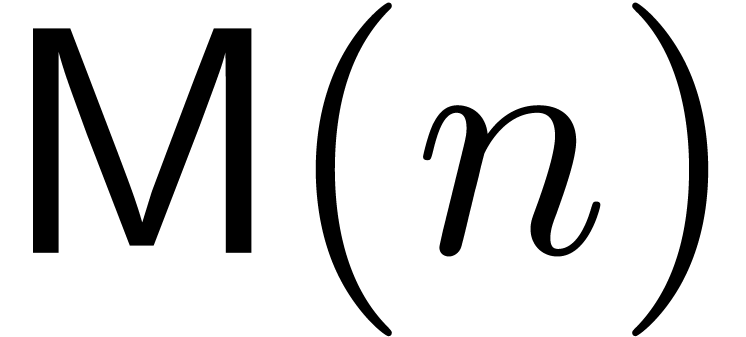 denotes the time complexity for multiplying
two polynomials
denotes the time complexity for multiplying
two polynomials  and
and  of
degrees
of
degrees  , then we again
obtain a relaxed multiplication for series
, then we again
obtain a relaxed multiplication for series 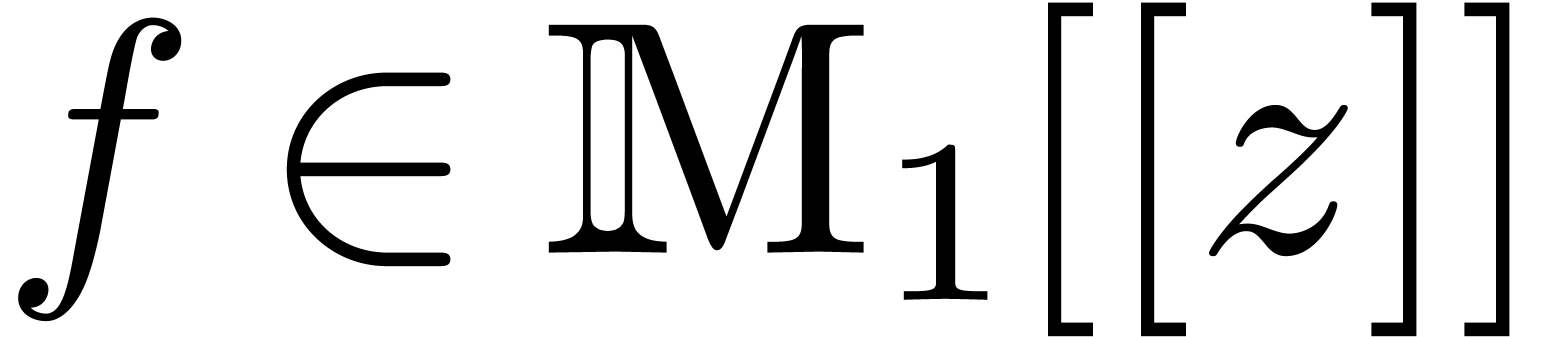 and
and
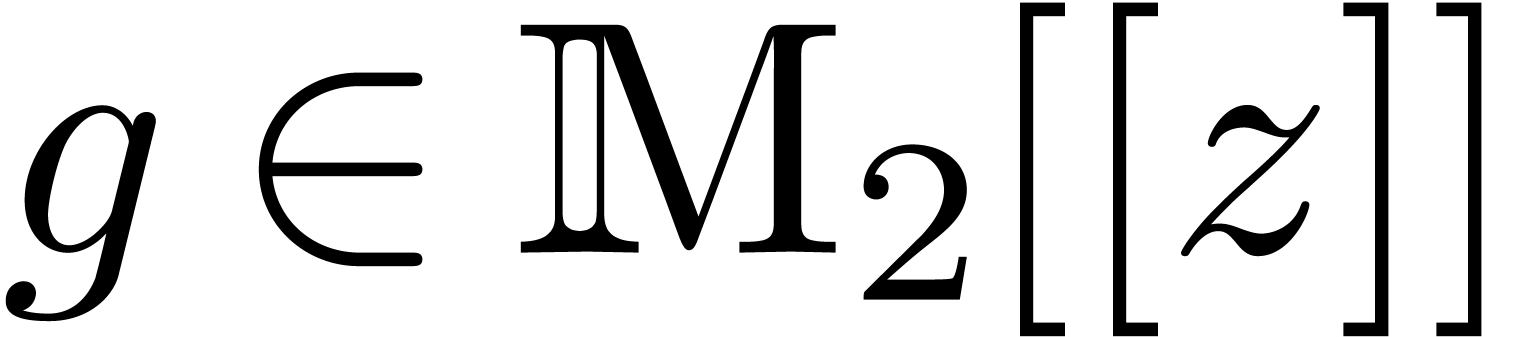 at order
at order 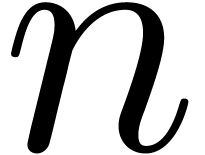 of time
complexity
of time
complexity 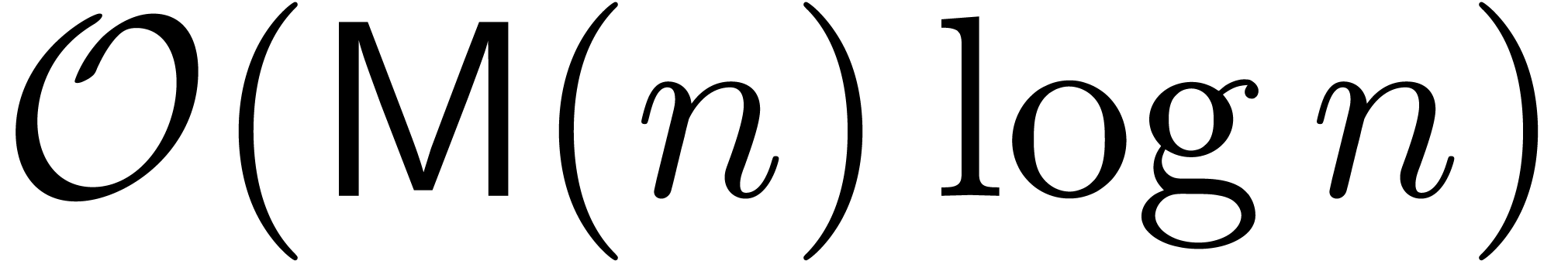 .
.
Theorem  admits a primitive
admits a primitive 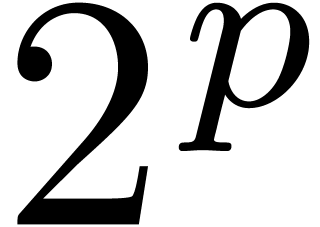 -th root
of unity for all
-th root
of unity for all 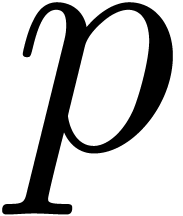 , then there
exists a relaxed multiplication algorithm of time complexity
, then there
exists a relaxed multiplication algorithm of time complexity 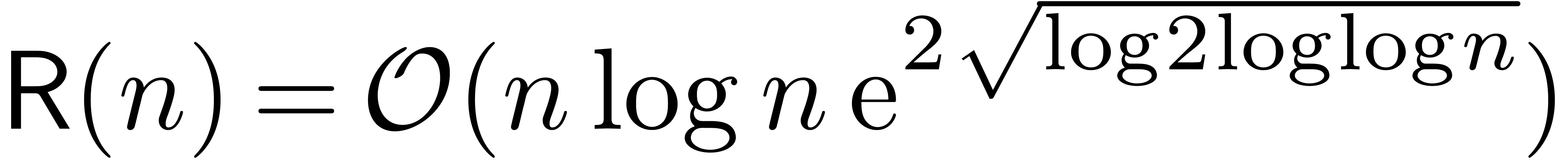 . In practice, the existence of a
. In practice, the existence of a
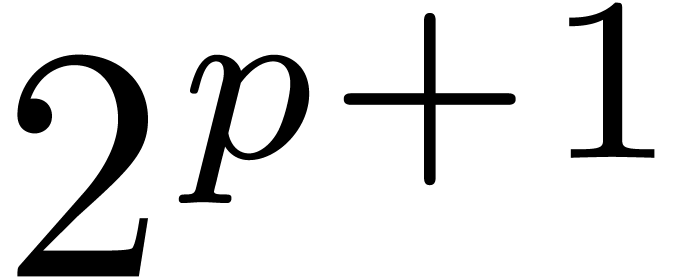 -th root of unity with
-th root of unity with 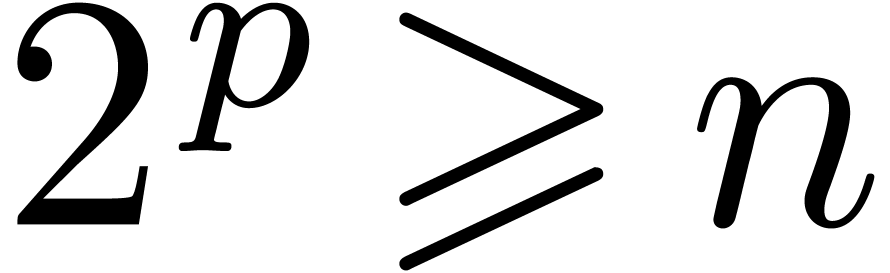 suffices for multiplication up to order
suffices for multiplication up to order 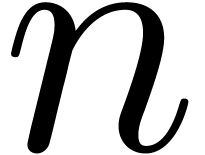 .
.
Let  be an effective ring. A power series
be an effective ring. A power series  is said to be computable if there is an
algorithm which takes
is said to be computable if there is an
algorithm which takes 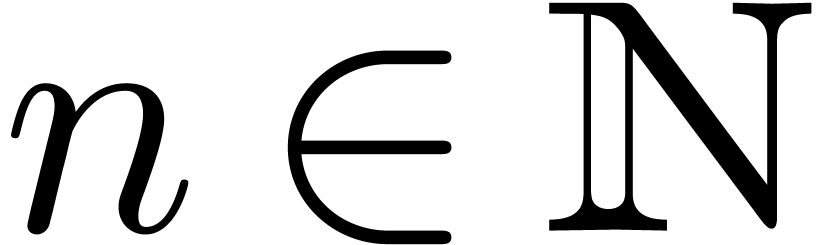 on input and produces the
coefficient
on input and produces the
coefficient 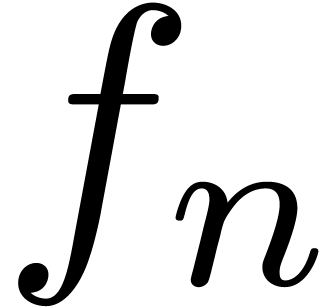 on output. We will denote by
on output. We will denote by 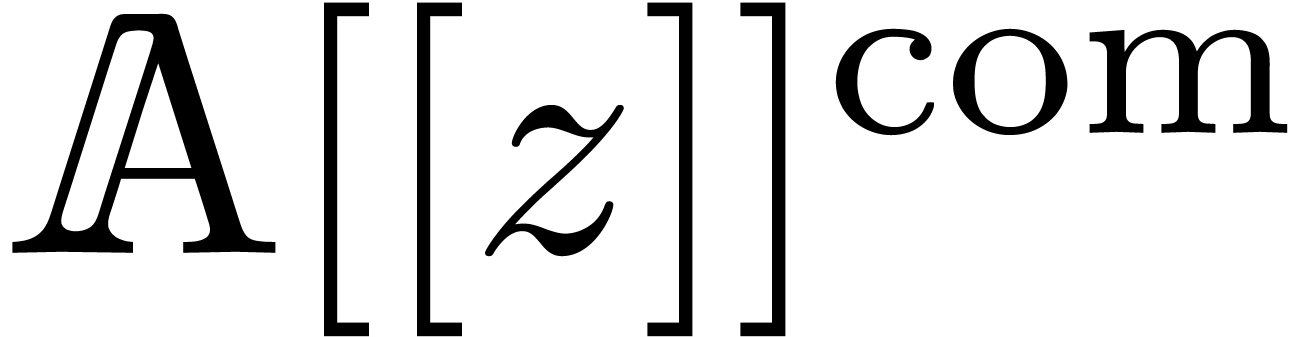 the set of such series. Then
the set of such series. Then 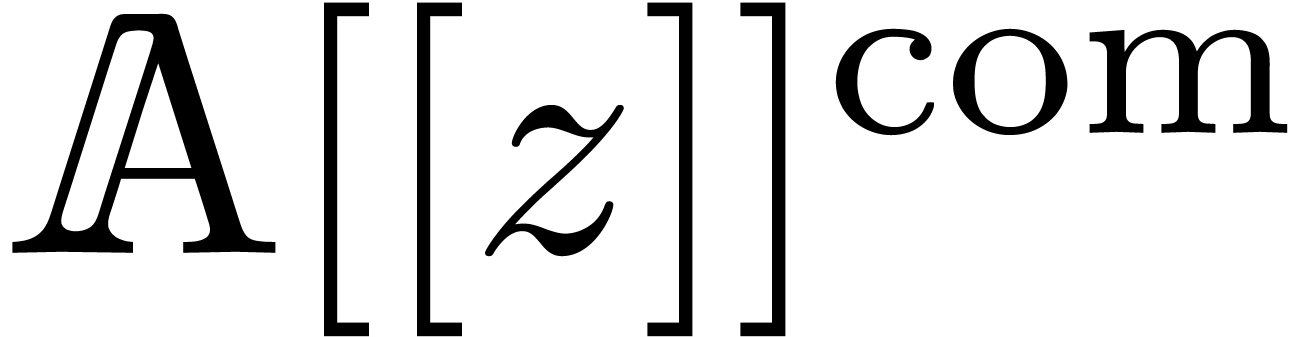 is an effective ring for relaxed addition, subtraction and
multiplication.
is an effective ring for relaxed addition, subtraction and
multiplication.
A computable Laurent series is a formal product 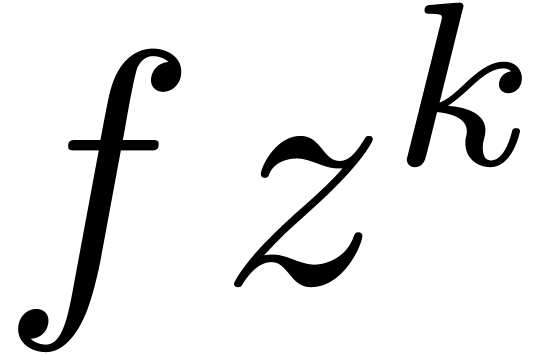 with
with  and
and  .
The set
.
The set 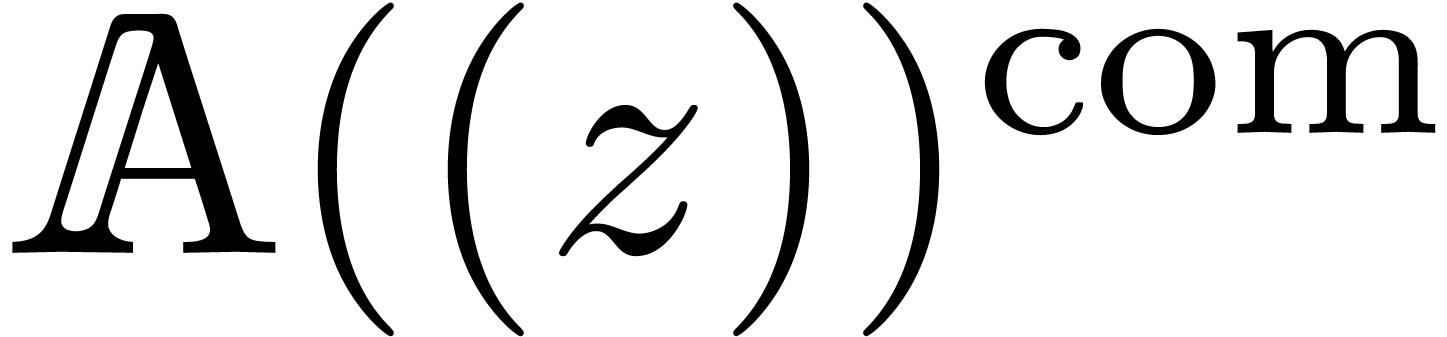 of such series forms an effective ring
for the addition, subtraction and multiplication defined by
of such series forms an effective ring
for the addition, subtraction and multiplication defined by
If  is an effective field with an effective zero
test, then we may also define an effective division on
is an effective field with an effective zero
test, then we may also define an effective division on 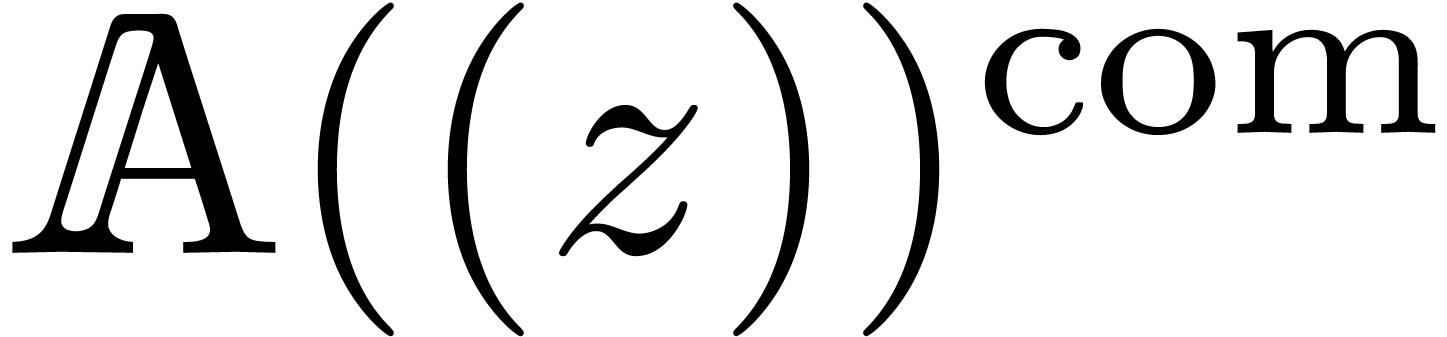 , but this operation will not be needed in what
follows.
, but this operation will not be needed in what
follows.
Assume now that  is replaced by a finite number
of variables
is replaced by a finite number
of variables 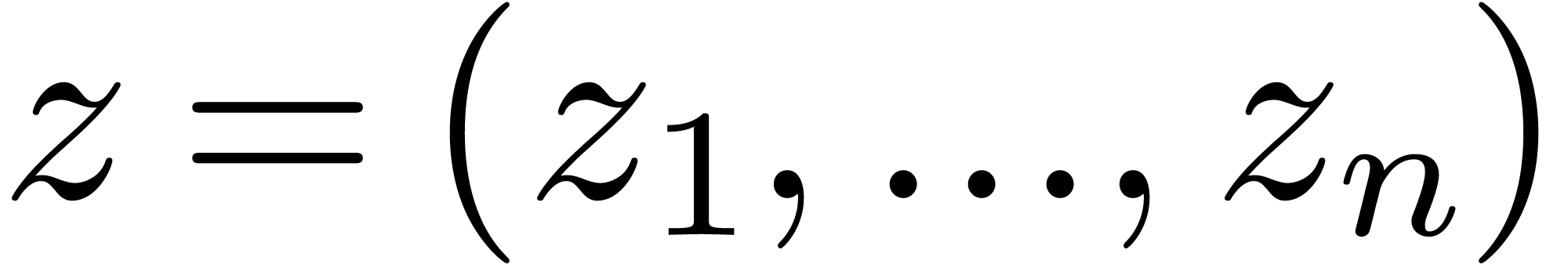 . Then an
element of
. Then an
element of
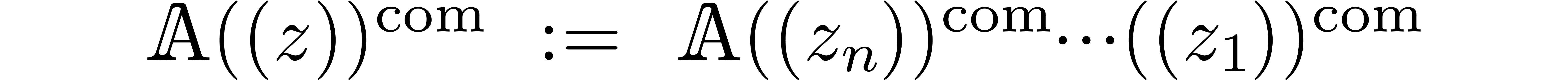
will also be called a “computable lexicographical Laurent
series”. Any non zero  has a natural
valuation
has a natural
valuation  , by setting
, by setting 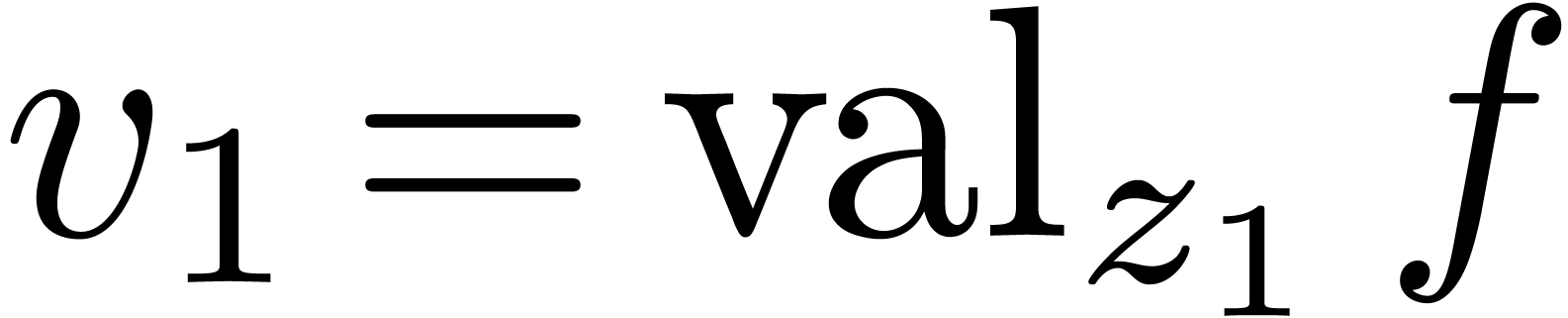 ,
, 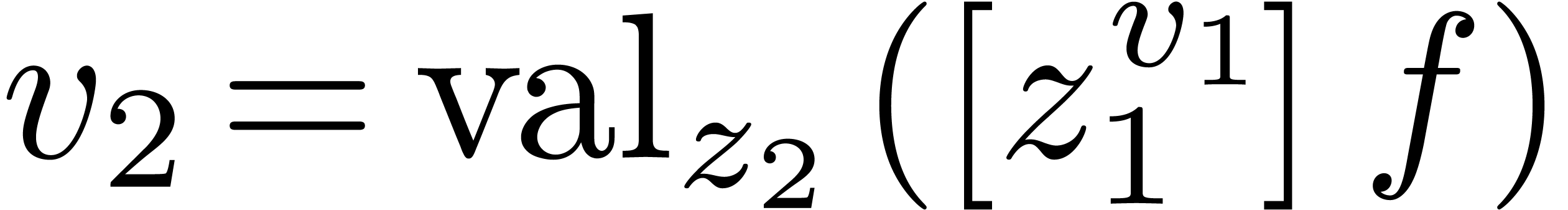 ,
etc. The concept of recursive equations naturally generalizes to the
multivariate context. For instance, for an infinitesimal Laurent series
,
etc. The concept of recursive equations naturally generalizes to the
multivariate context. For instance, for an infinitesimal Laurent series
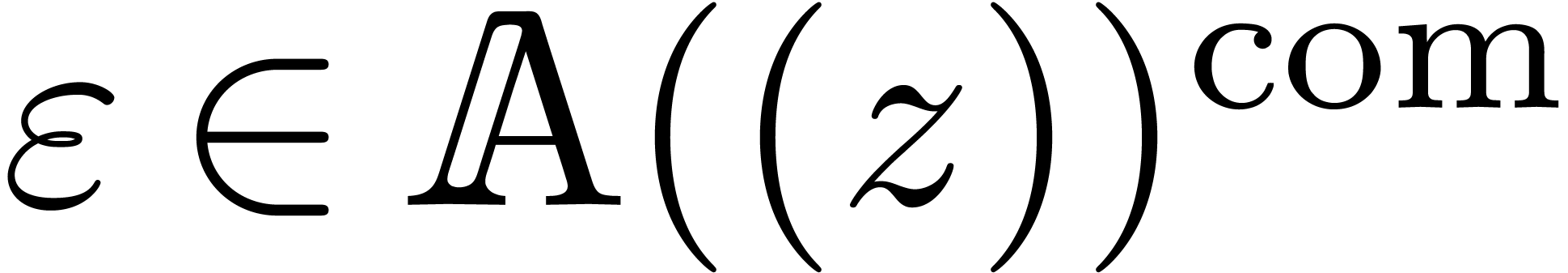 (that is,
(that is, 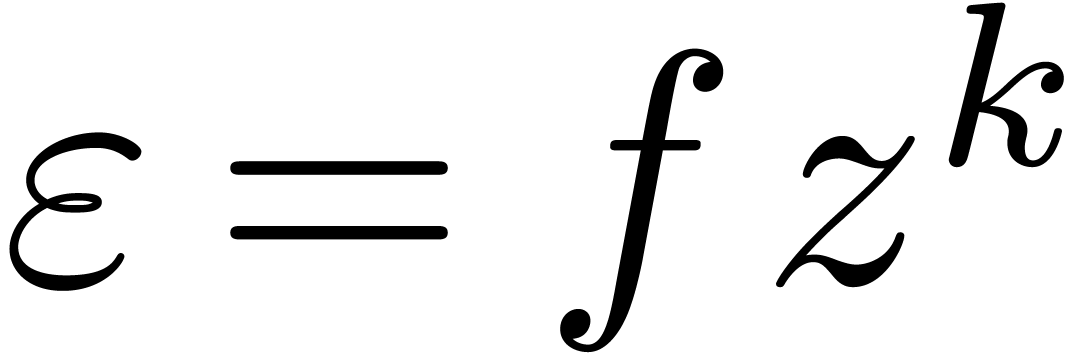 ,
where
,
where 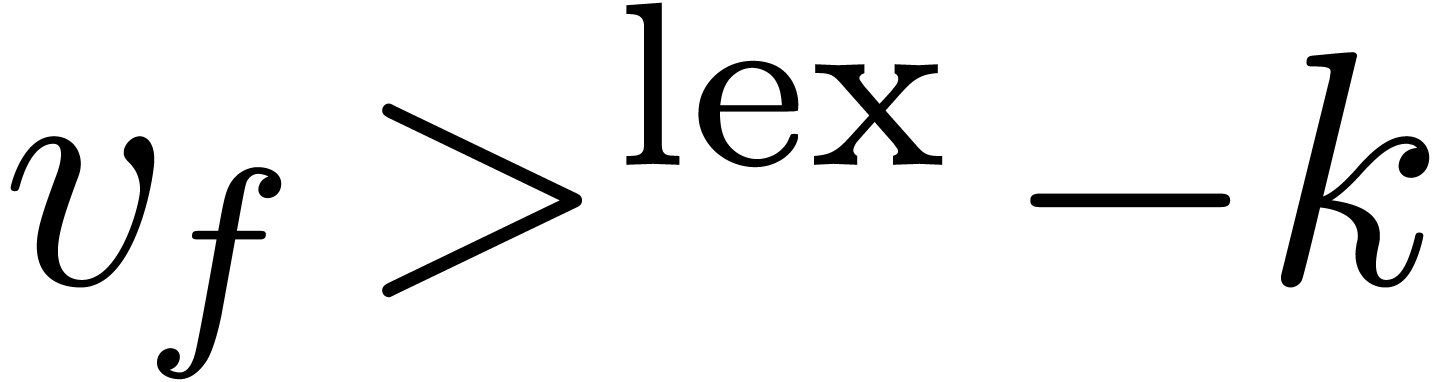 ), the formula
), the formula
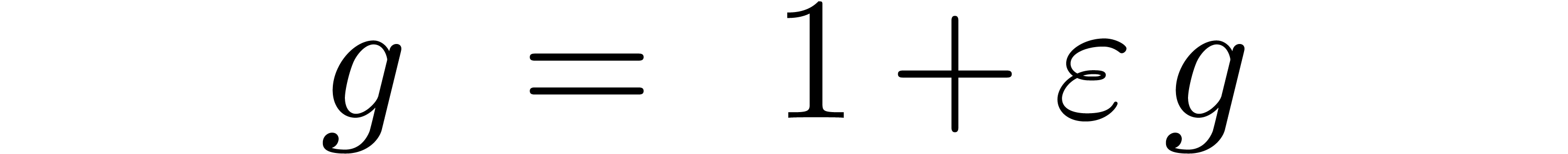
allows us to compute 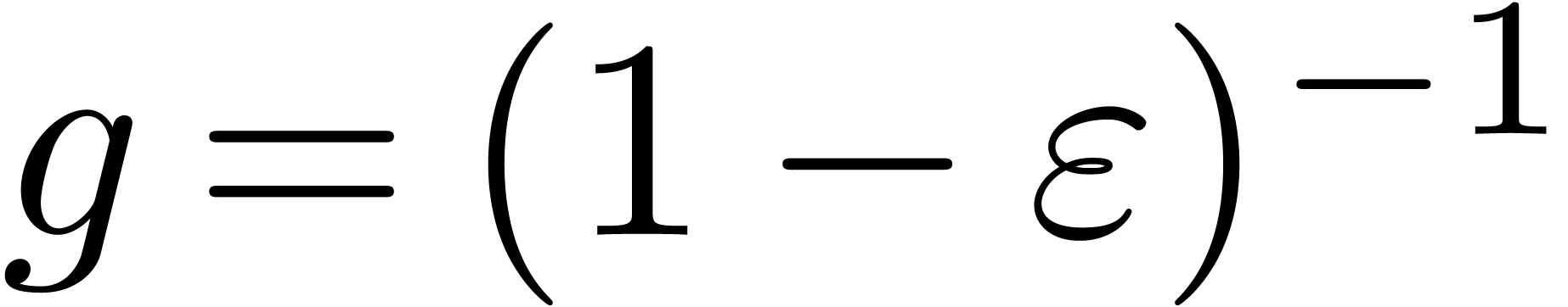 using a single relaxed
multiplication in
using a single relaxed
multiplication in 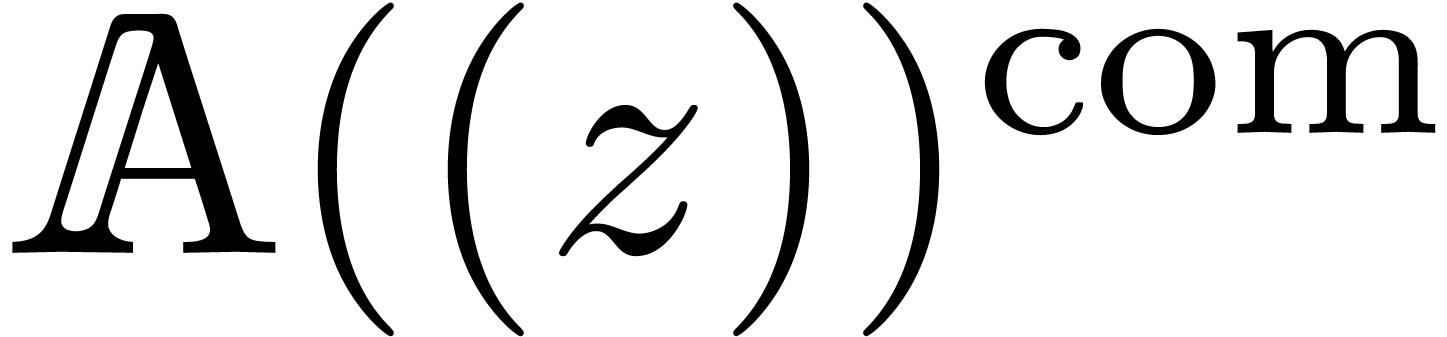 .
.
Now take 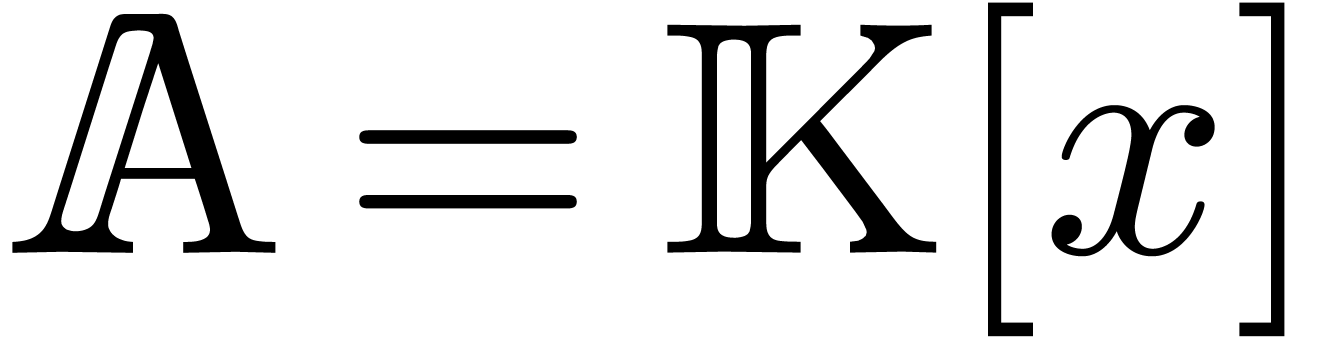 and consider a polynomial
and consider a polynomial 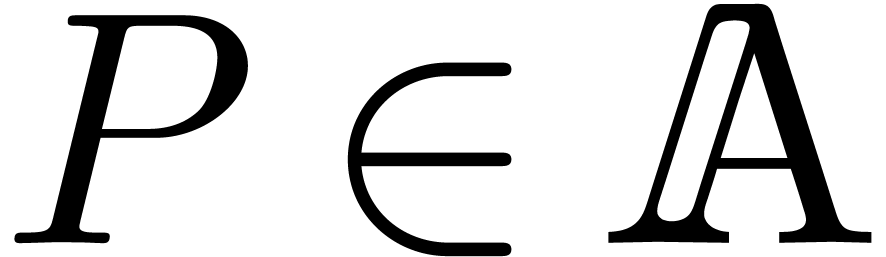 . Then we define the Laurent polynomial
. Then we define the Laurent polynomial 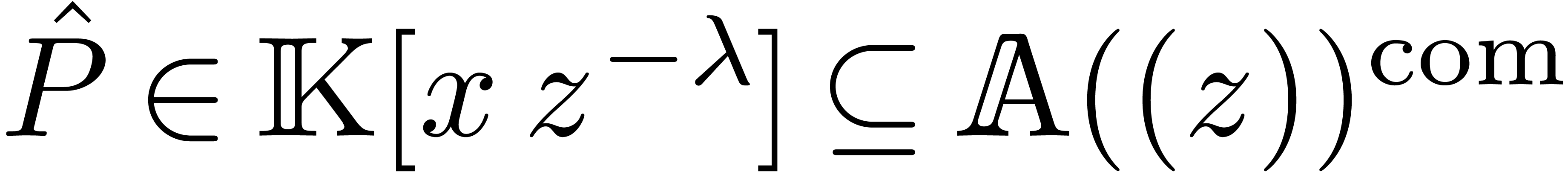 by
by
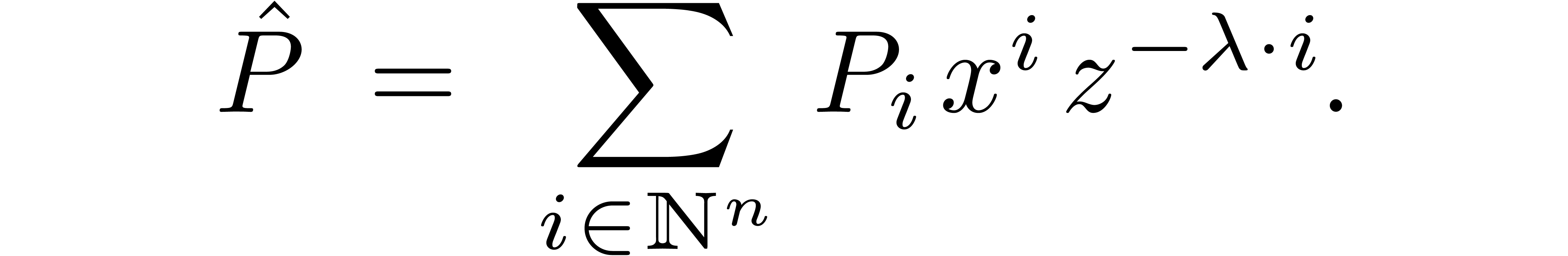
Conversely, given 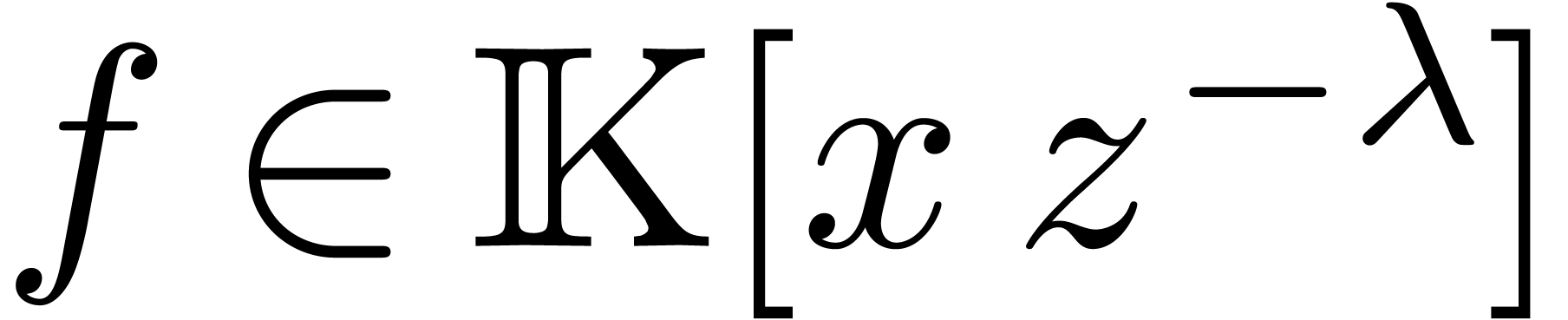 , we define
, we define
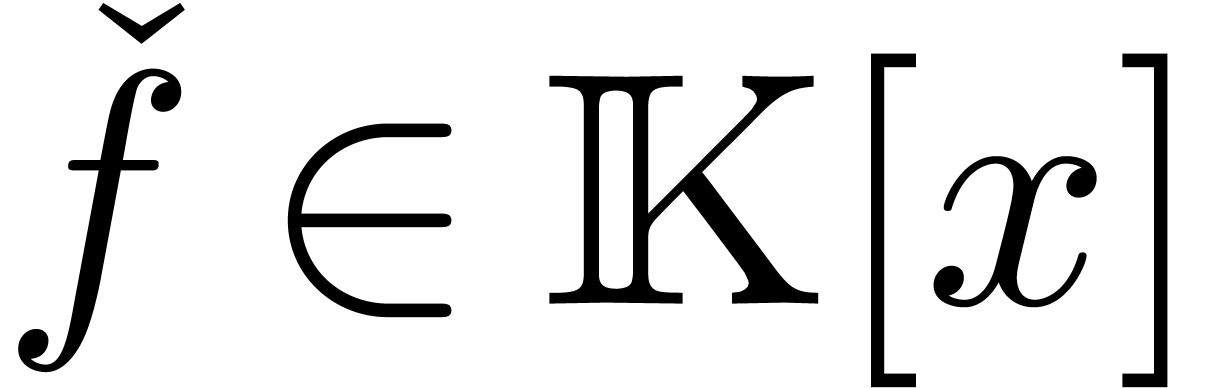 by substituting
by substituting  in
in  . We will call the transformations
. We will call the transformations
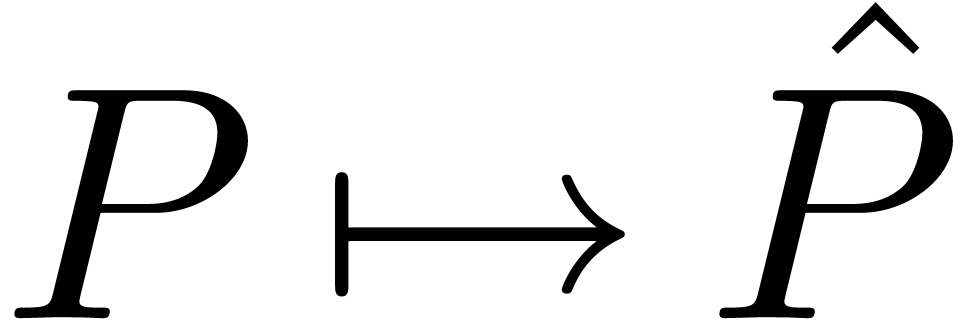 and
and 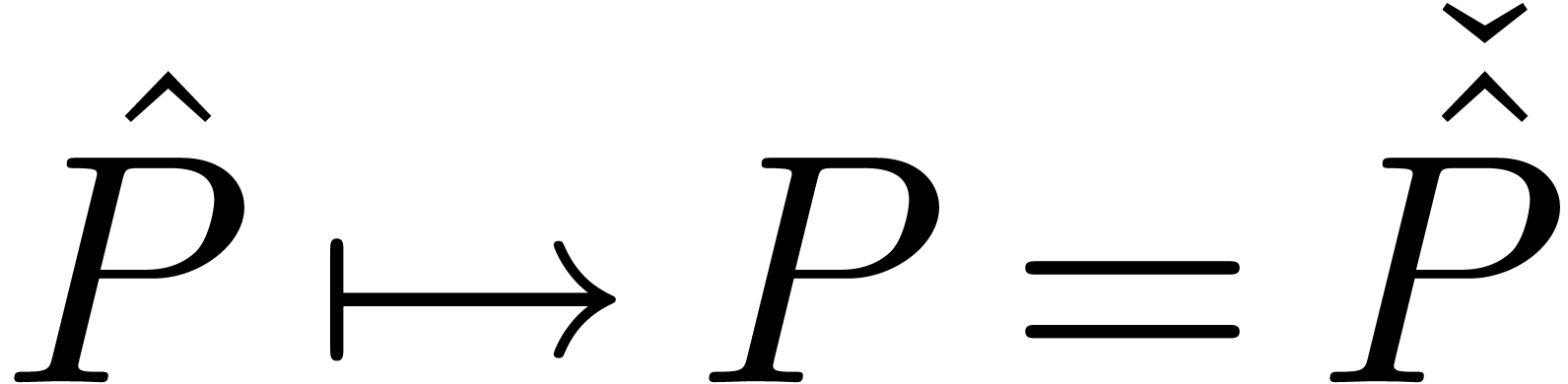 tagging
resp. untagging; they provide us with a relaxed
mechanism to compute with multivariate polynomials in
tagging
resp. untagging; they provide us with a relaxed
mechanism to compute with multivariate polynomials in 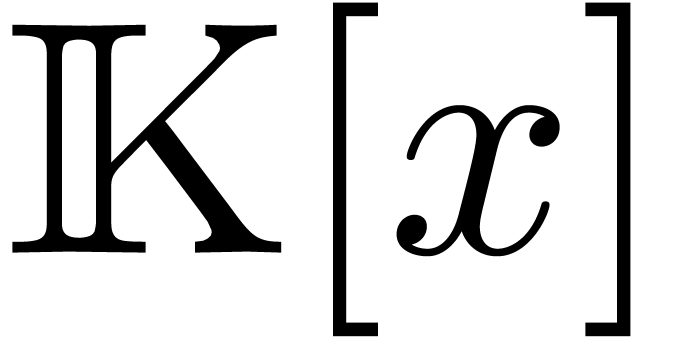 , such that the admissible ordering
, such that the admissible ordering  on
on 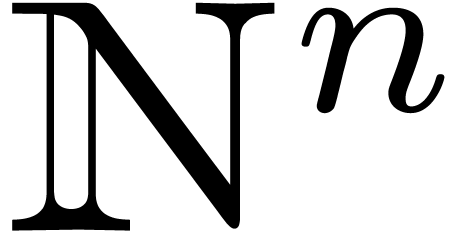 is respected. For instance, we
may compute the relaxed product of two polynomials
is respected. For instance, we
may compute the relaxed product of two polynomials  by computing the relaxed product
by computing the relaxed product 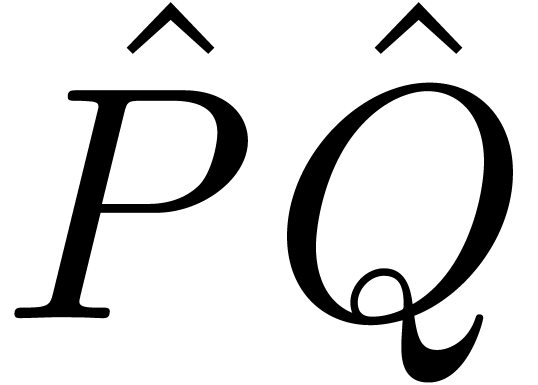 and
substituting
and
substituting 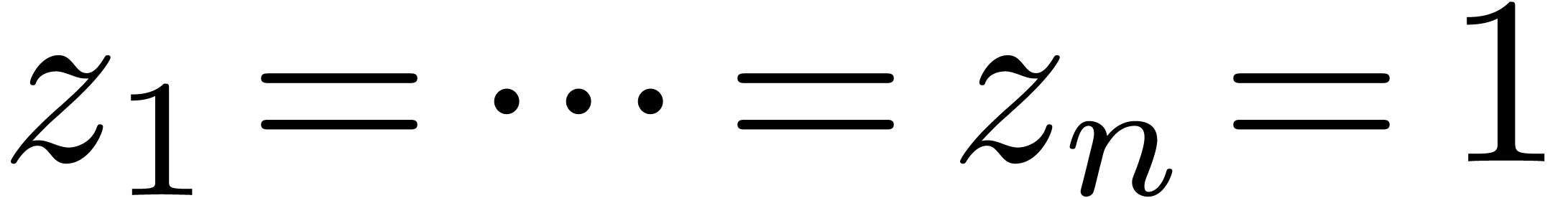 in the result. We notice that
tagging is an injective operation which preserves the size of the
support.
in the result. We notice that
tagging is an injective operation which preserves the size of the
support.
Assume now that we are given  and a set
and a set 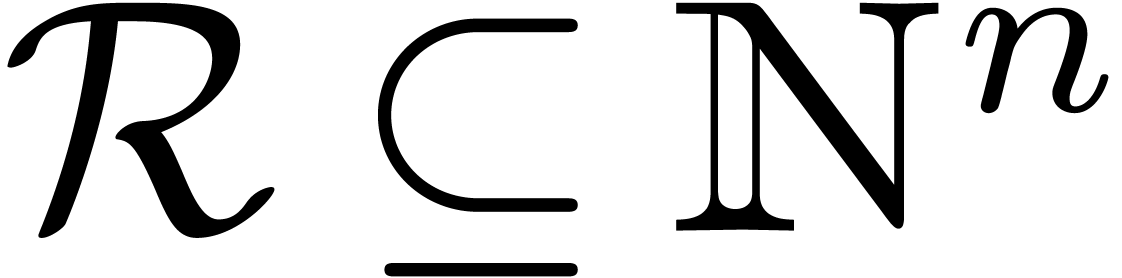 such that
such that 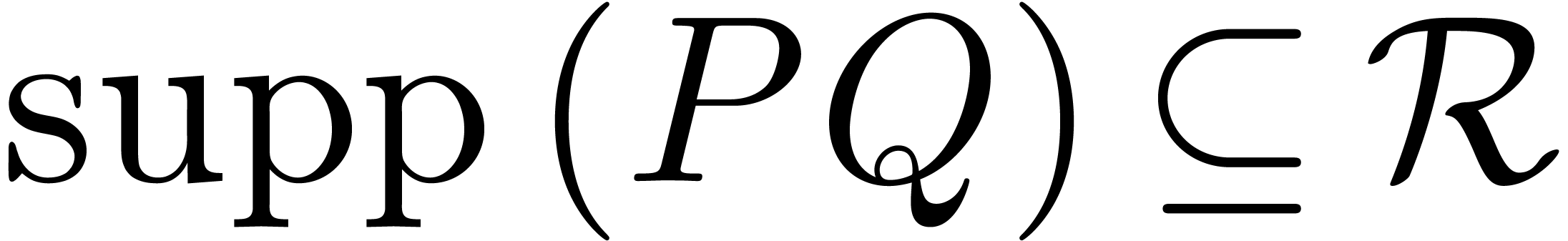 . We
assume that
. We
assume that 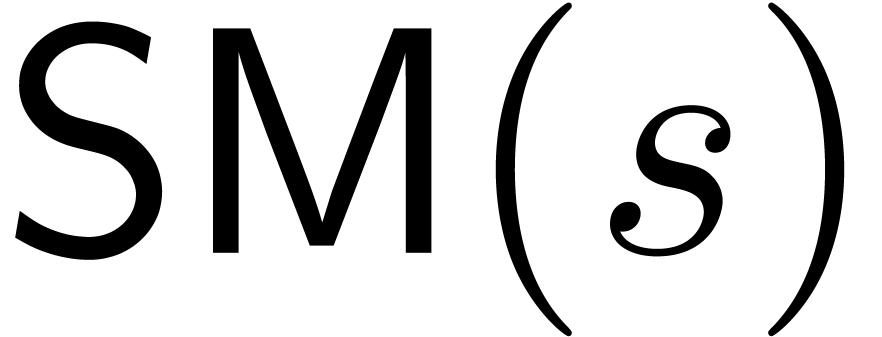 is a function such that the
(zealous) product
is a function such that the
(zealous) product 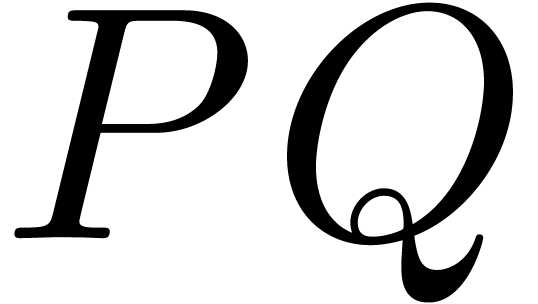 can be computed in time
can be computed in time 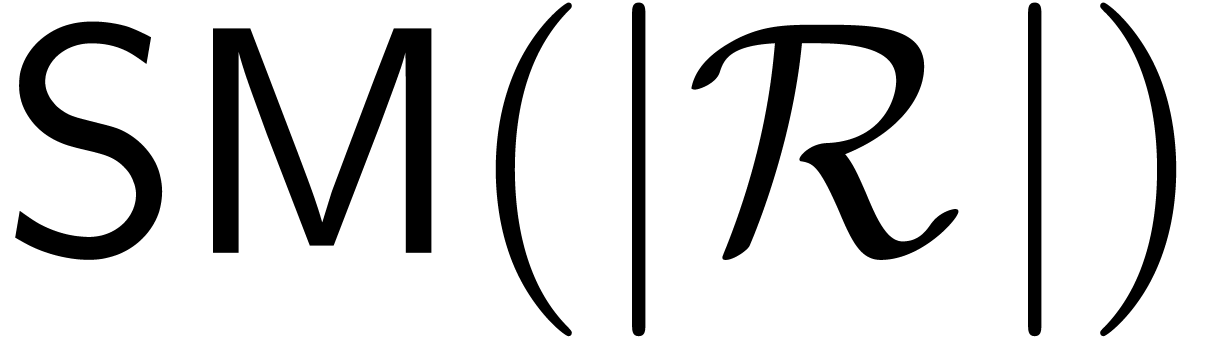 . We will also assume that
. We will also assume that 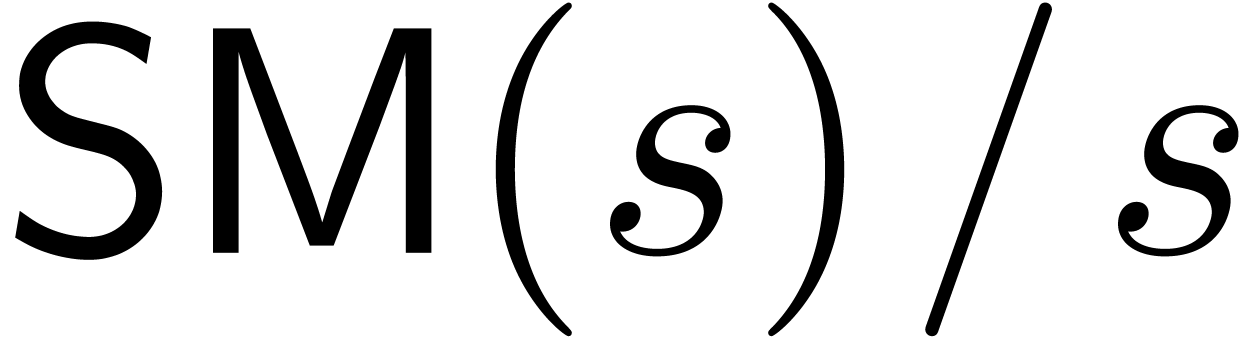 is an increasing function of
is an increasing function of  . In [2, 15], it is shown
that we may take
. In [2, 15], it is shown
that we may take 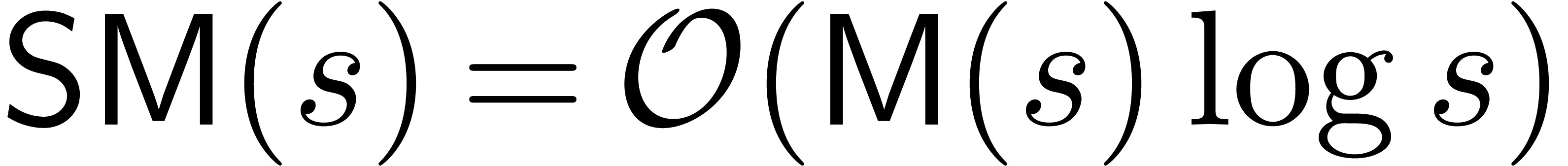 .
.
Let us now study the complexity of sparse relaxed multiplication of 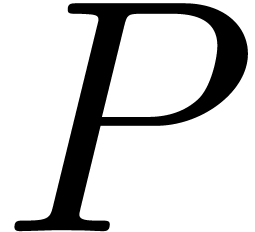 and
and  . We
will use the classical algorithm for fast univariate relaxed
multiplication from [6, 7], of time complexity
. We
will use the classical algorithm for fast univariate relaxed
multiplication from [6, 7], of time complexity
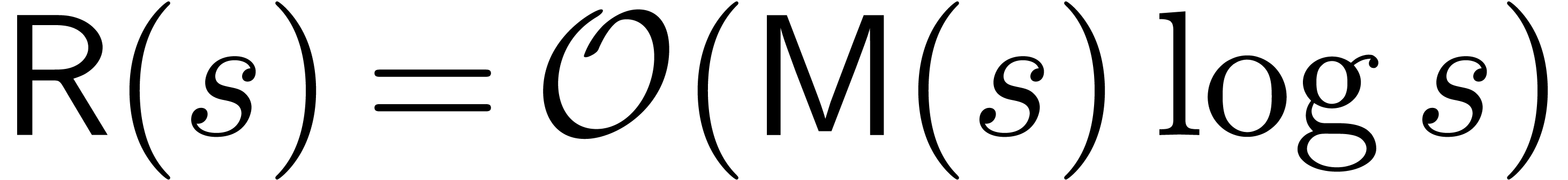 . We will also consider
semi-relaxed multiplication as in [8], where one of the
arguments
. We will also consider
semi-relaxed multiplication as in [8], where one of the
arguments 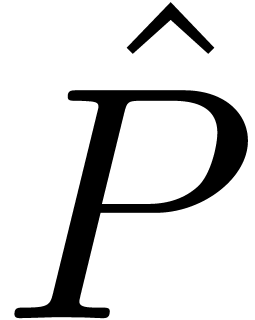 or
or  is
completely known in advance and only the other one is computed in a
relaxed manner.
is
completely known in advance and only the other one is computed in a
relaxed manner.
Given 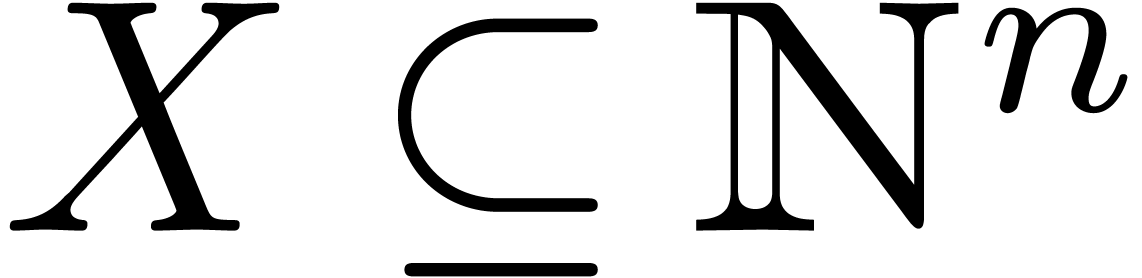 and
and 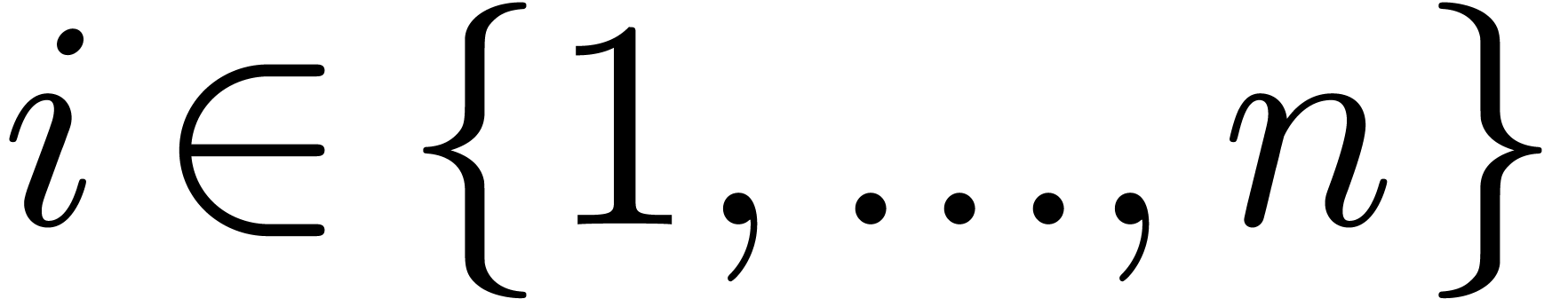 ,
we will denote
,
we will denote
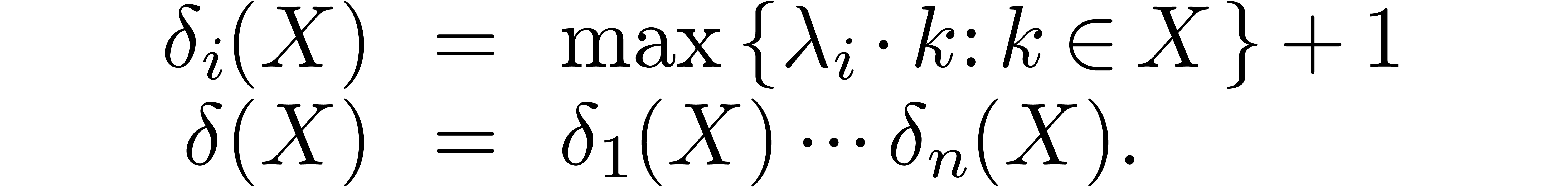
We now have the following:
Theorem  and
and  can be computed in time
can be computed in time
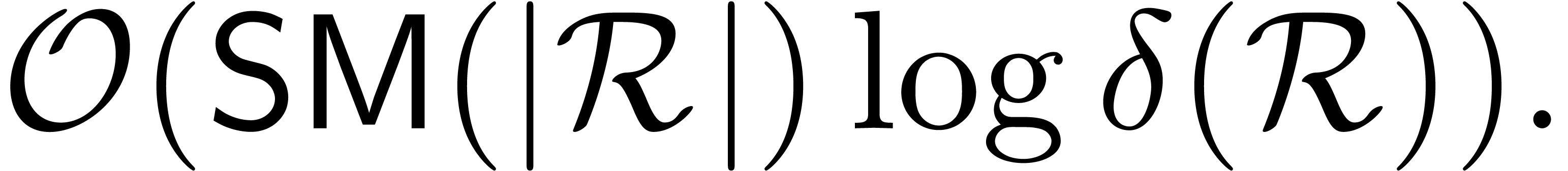
Proof. In order to simplify our exposition, we will
rather prove the theorem for a semi-relaxed product of 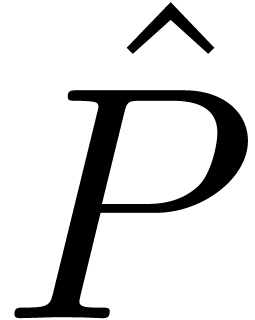 (relaxed) and
(relaxed) and  (known in advance). As shown in
[8], the general case reduces to this special case. We will
prove by induction over
(known in advance). As shown in
[8], the general case reduces to this special case. We will
prove by induction over 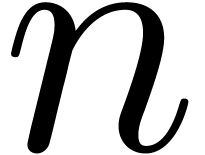 that the semi-relaxed
product can be computed using at most
that the semi-relaxed
product can be computed using at most 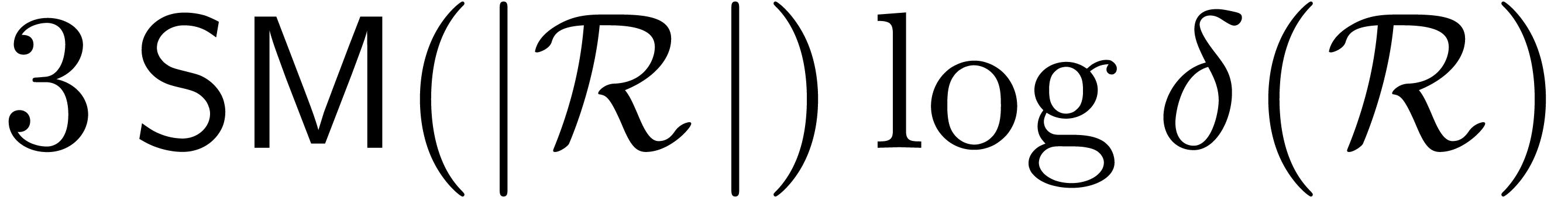 operations
in
operations
in  if
if  is sufficiently
large. For
is sufficiently
large. For 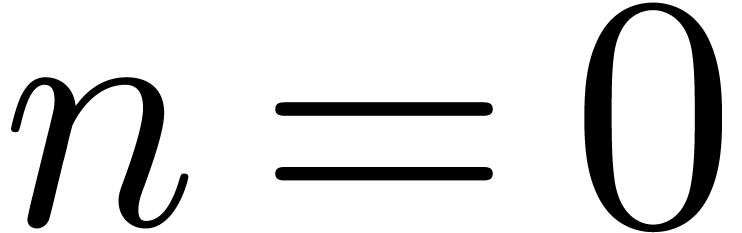 , we have nothing
to do, so assume that
, we have nothing
to do, so assume that 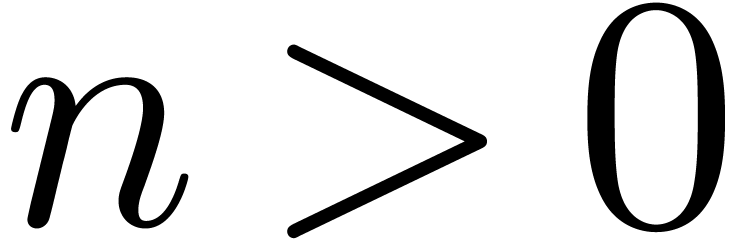 .
.
Let us first consider the semi-relaxed product of 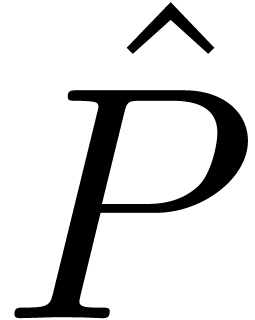 and
and  with respect to
with respect to 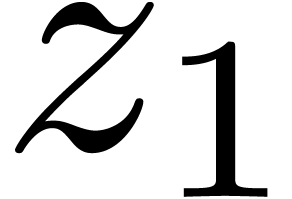 . Setting
. Setting 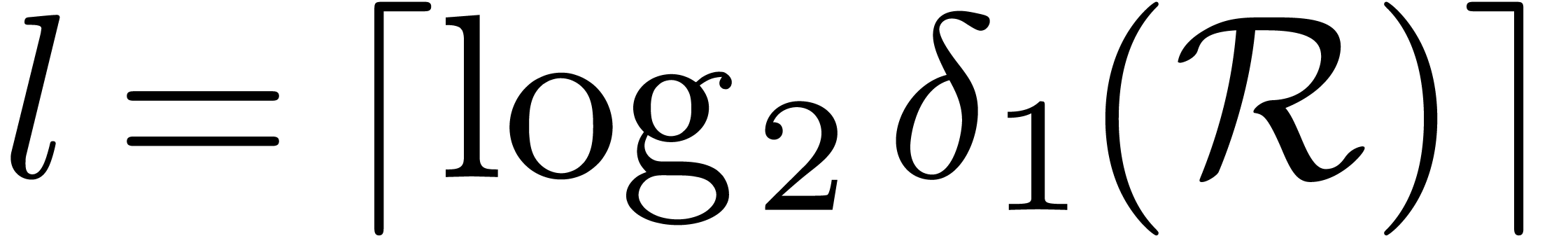 ,
the computation of this product corresponds (see the right-hand side of
figure 1) to the computation of
,
the computation of this product corresponds (see the right-hand side of
figure 1) to the computation of 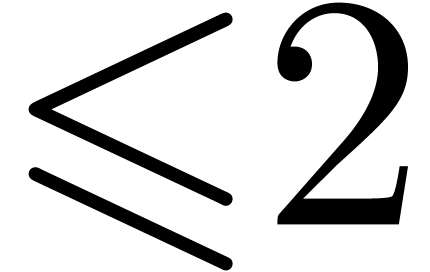 zealous
zealous  products (i.e.
products (i.e. 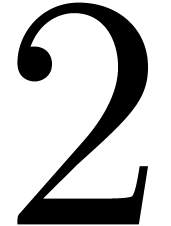 products of polynomials of degrees
products of polynomials of degrees 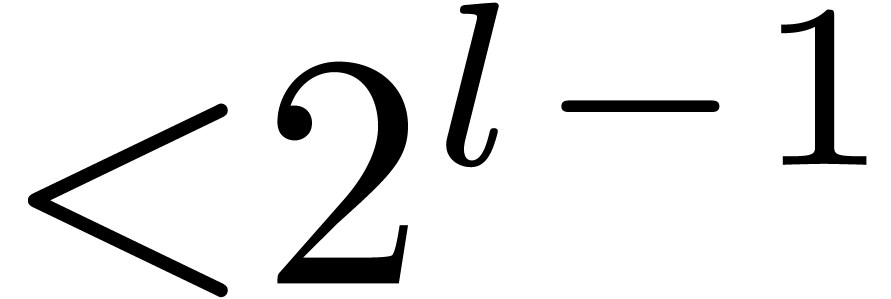 in
in  ),
), 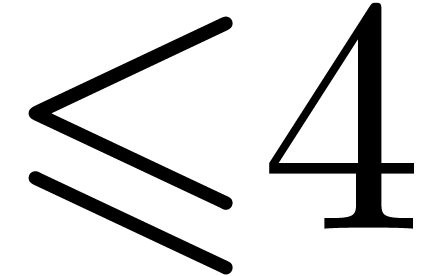 zealous
zealous  products, and so on until
products, and so on until 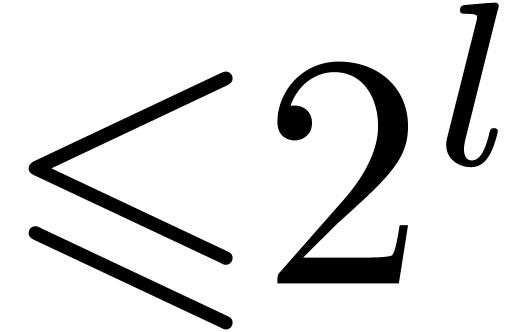 zealous
zealous  products. We finally need
to perform
products. We finally need
to perform 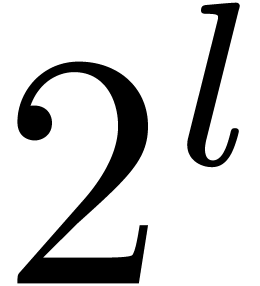 semi-relaxed
semi-relaxed  products of series in
products of series in  only.
only.
More precisely, assume that 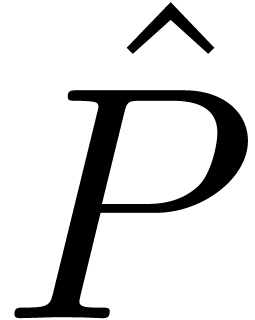 and
and  have valuations
have valuations 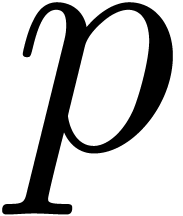 resp.
resp.  in
in  and let
and let 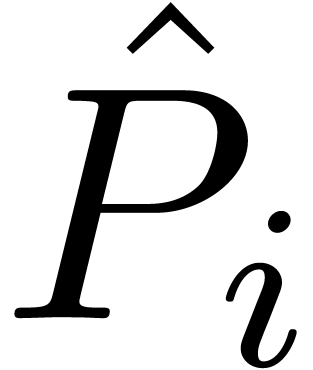 stand for the coefficient of
stand for the coefficient of 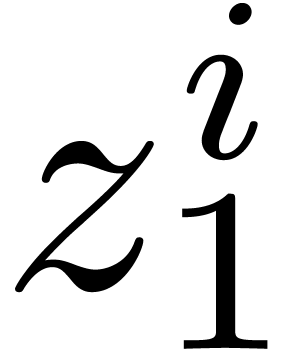 in
in  . We also define
. We also define
Now consider a block size 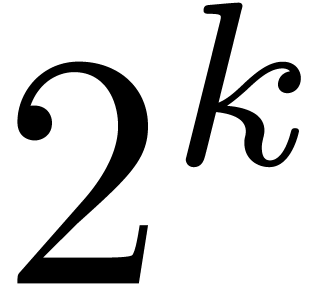 .
For each
.
For each 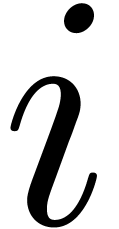 , we define
, we define
and notice that the 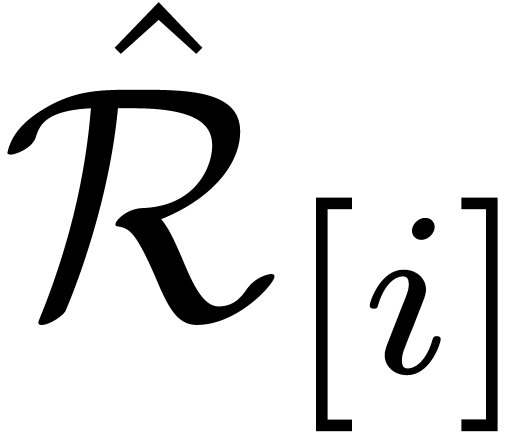 are pairwise disjoint. In
the semi-relaxed multiplication, we have to compute the zealous
are pairwise disjoint. In
the semi-relaxed multiplication, we have to compute the zealous  products
products 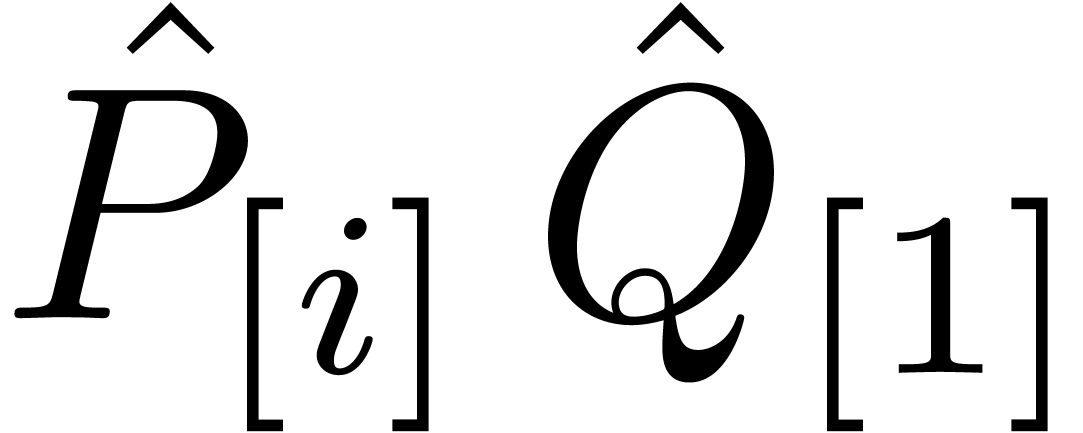 for all
for all 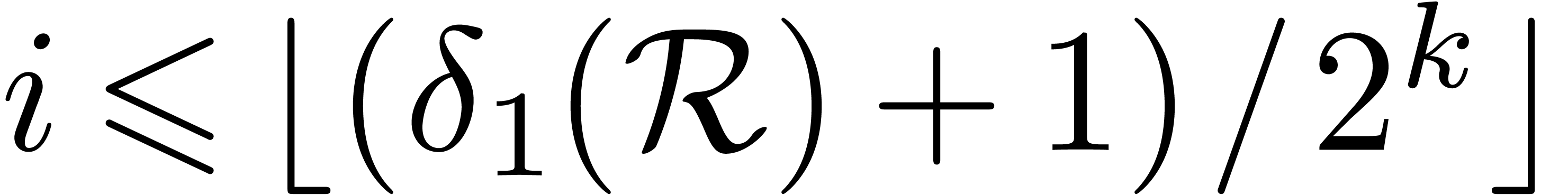 . Since
. Since
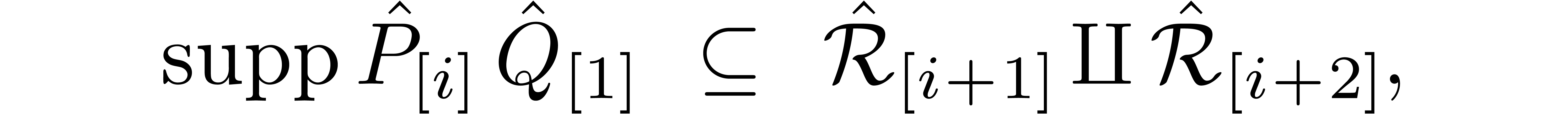
we may compute all these products in time
The total time spent in performing all zealous  block multiplications with
block multiplications with 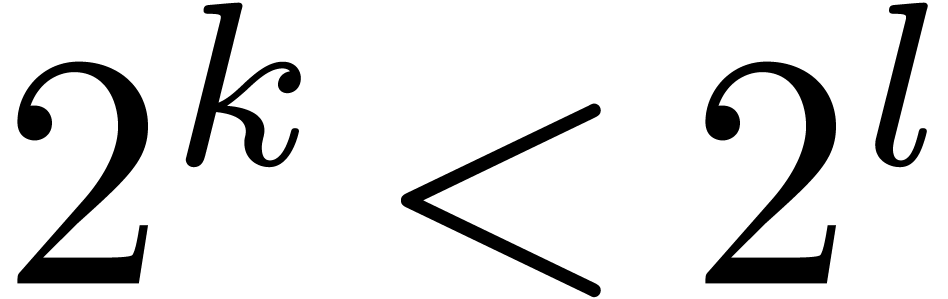 is therefore bounded
by
is therefore bounded
by 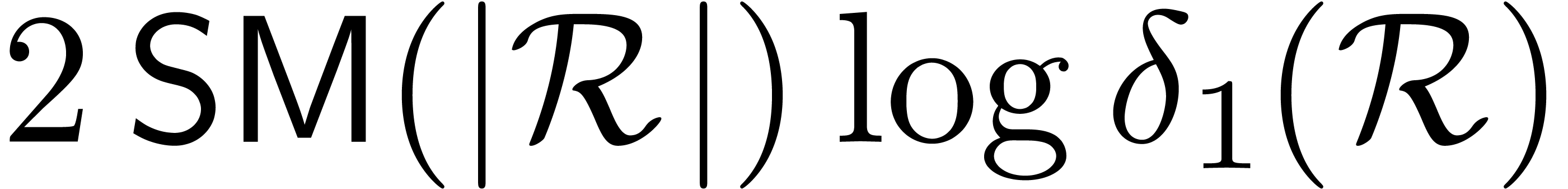 .
.
Let us next consider the remaining  semi-relaxed
products. If
semi-relaxed
products. If 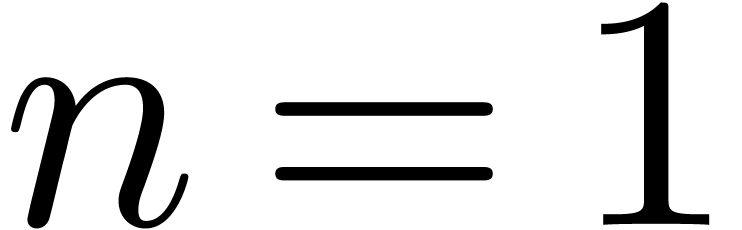 , then these are
really scalar products, whence the remaining work can clearly be
performed in time
, then these are
really scalar products, whence the remaining work can clearly be
performed in time 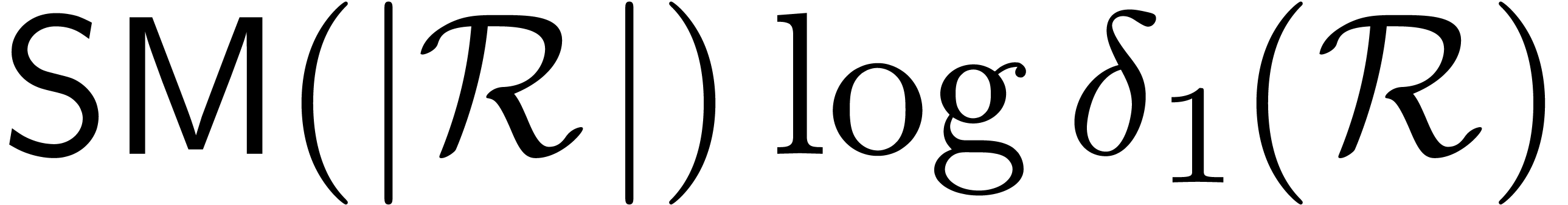 if
if  is
sufficiently large. If
is
sufficiently large. If 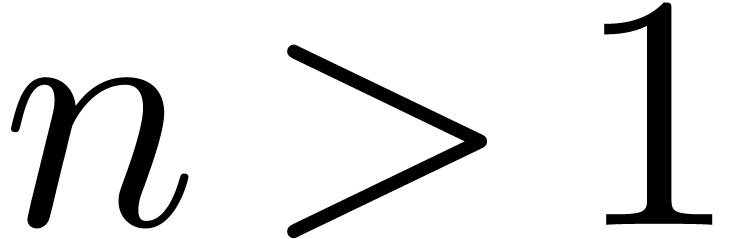 , then
for each
, then
for each 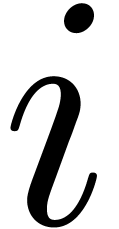 , we have
, we have
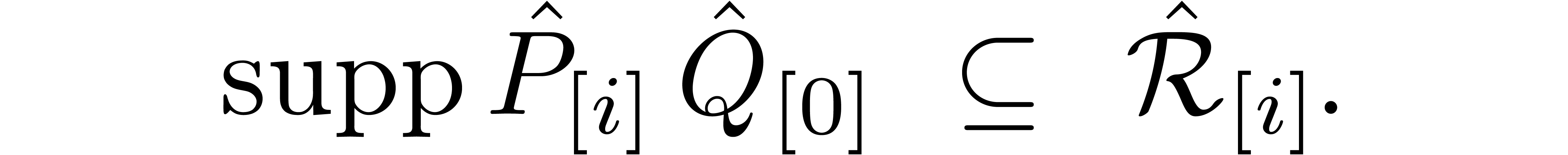
By the induction hypothesis, we may therefore perform this semi-relaxed
product in time 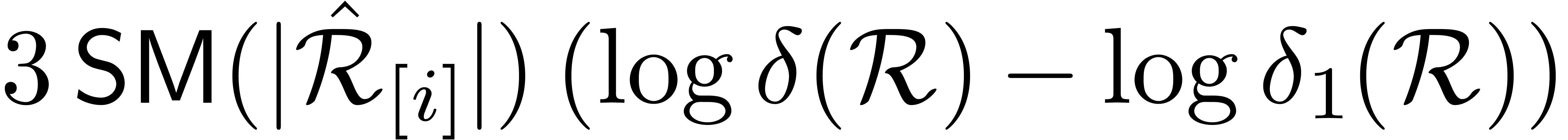 . A similar
argument as above now yields the bound
. A similar
argument as above now yields the bound 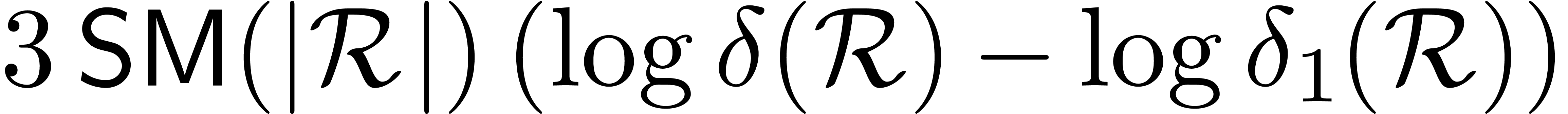 for
performing all
for
performing all  semi-relaxed block products. The
total execution time (which also takes into account the final additions)
is therefore bounded by
semi-relaxed block products. The
total execution time (which also takes into account the final additions)
is therefore bounded by 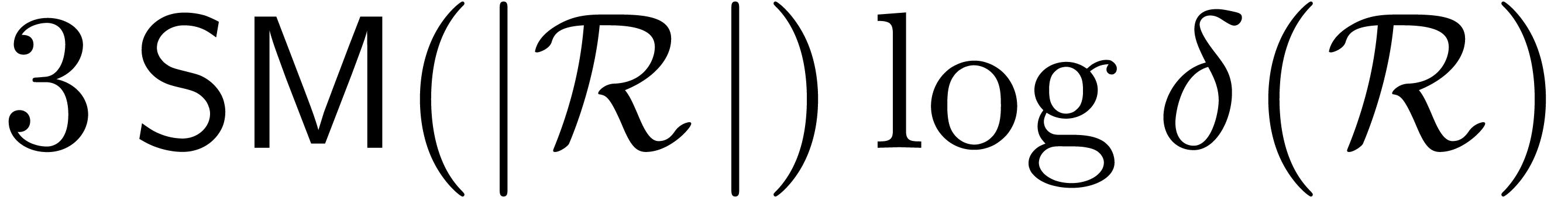 .
This completes the induction.
.
This completes the induction.
Remark 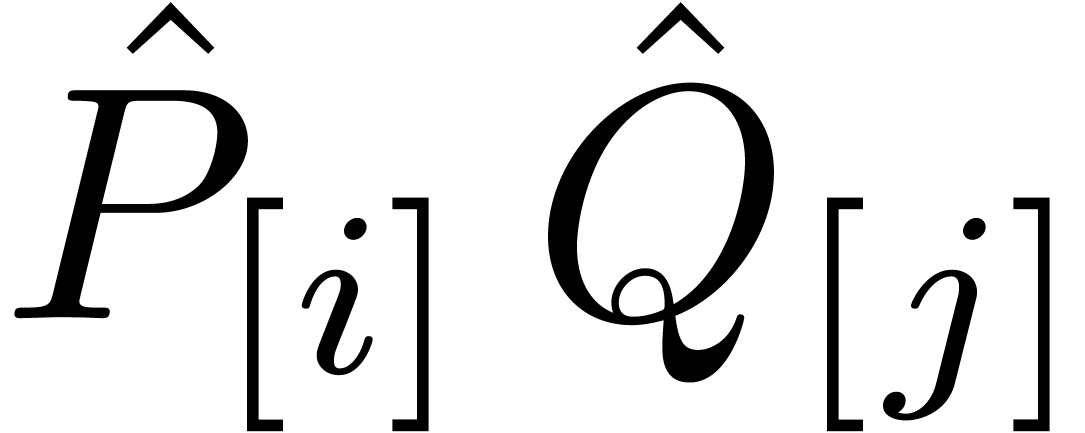 is
best done in the untagged model, i.e. using the formula
is
best done in the untagged model, i.e. using the formula
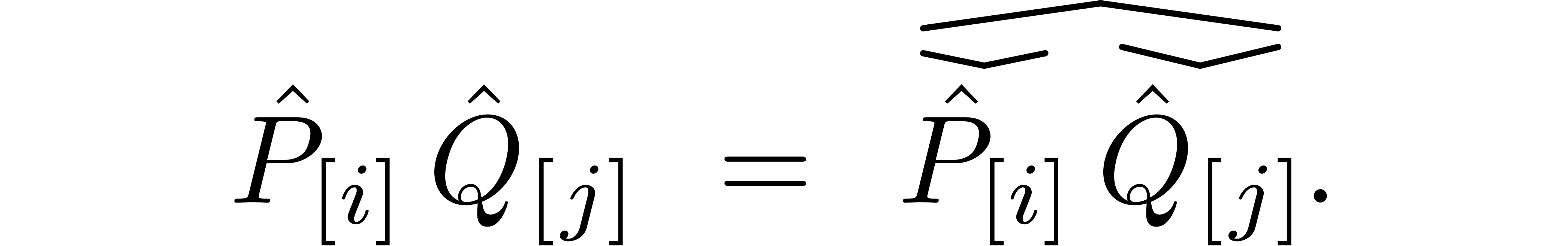
Proceeding this way allows us to use any of our preferred algorithms for sparse polynomial multiplication. In particular, we may use [14] or [12].
Consider a tuple 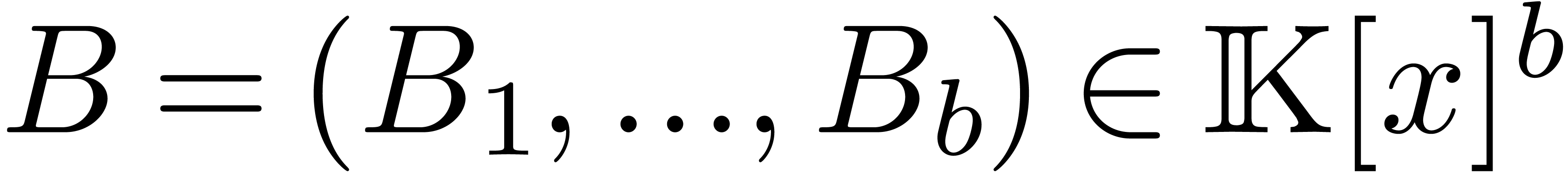 . We say
that
. We say
that  is autoreduced if
is autoreduced if 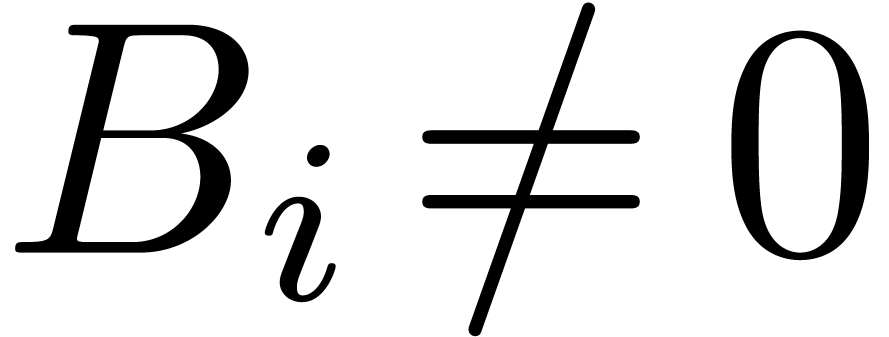 for all
for all 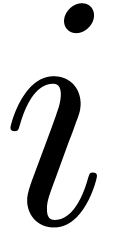 and
and  and
and  for all
for all 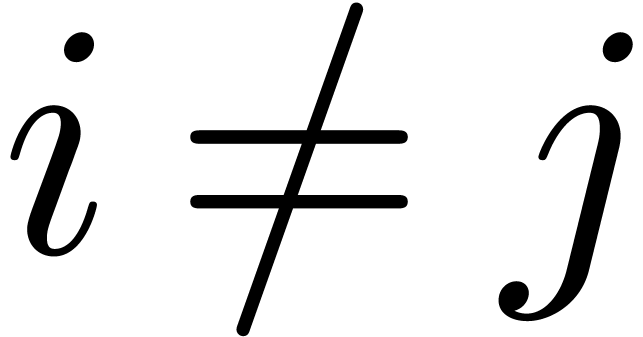 .
Given such a tuple
.
Given such a tuple  and an arbitrary polynomial
and an arbitrary polynomial
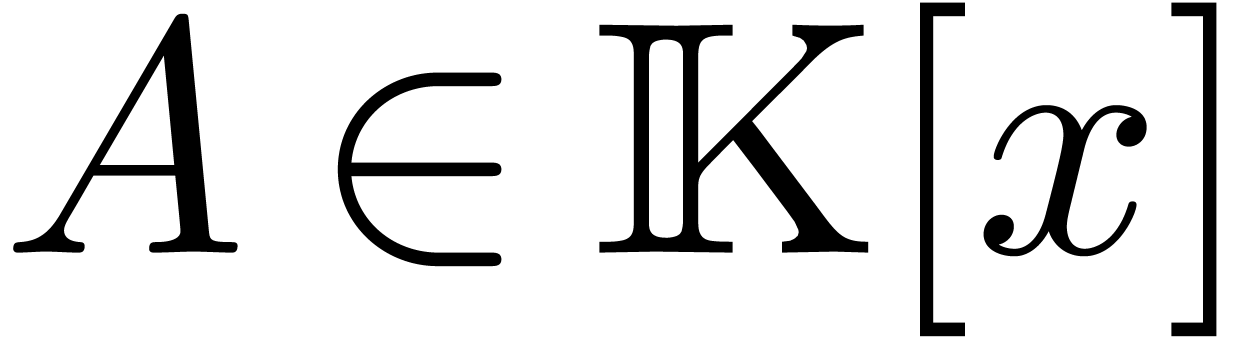 , we say that
, we say that  is reduced with respect to
is reduced with respect to  if
if  for all
for all 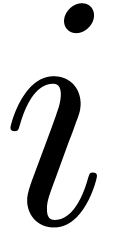 and
and 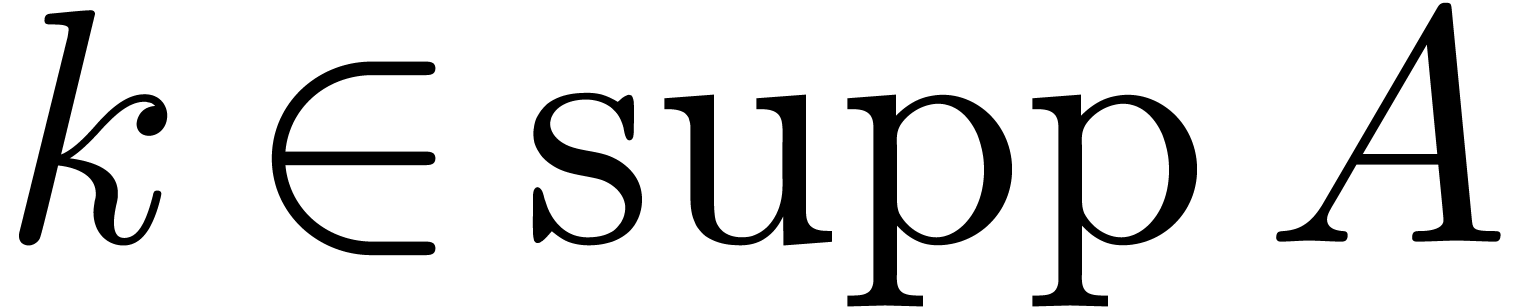 . An extended reduction of
. An extended reduction of
 with respect to
with respect to  is a
tuple
is a
tuple 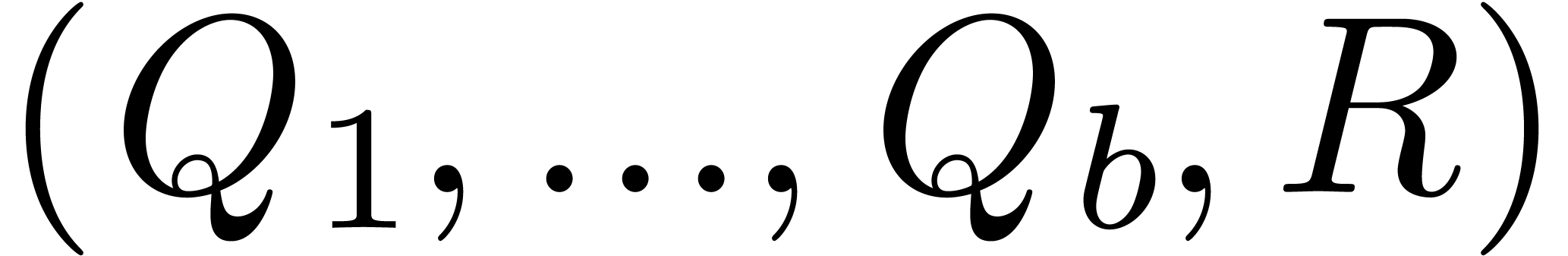 with
with
such that 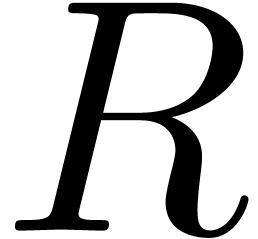 is reduced with respect to
is reduced with respect to  . The naive algorithm
extended-reduce below computes an extended reduction of
. The naive algorithm
extended-reduce below computes an extended reduction of
 .
.
Algorithm extended-reduce
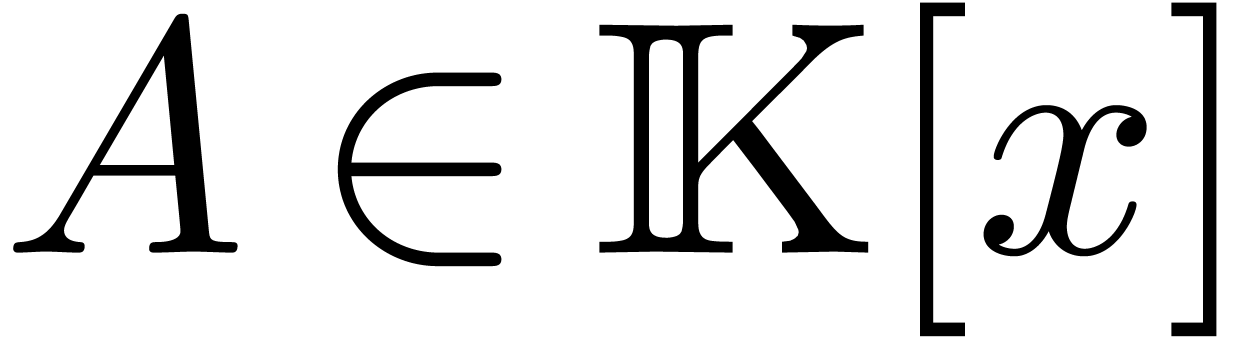 and an
autoreduced tuple
and an
autoreduced tuple 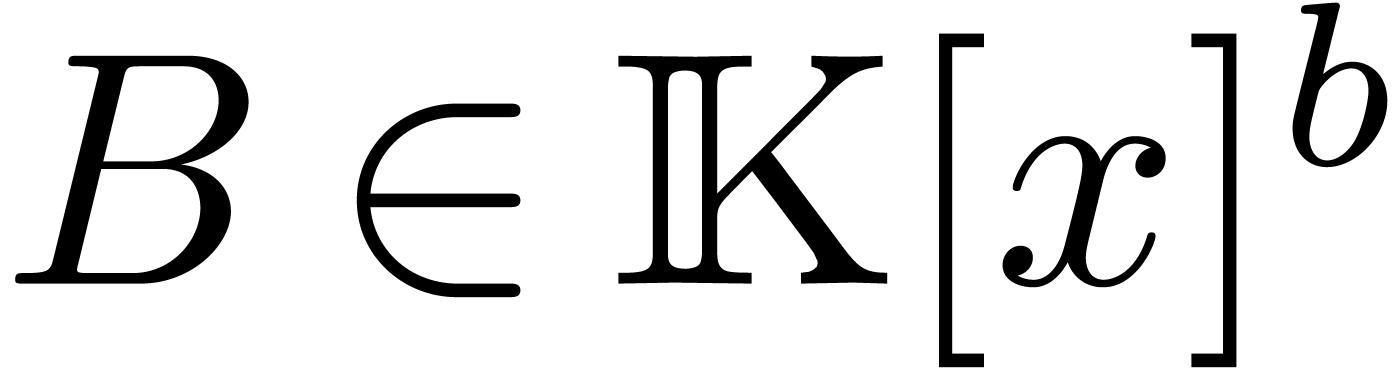
 with respect to
with respect to 
Start with 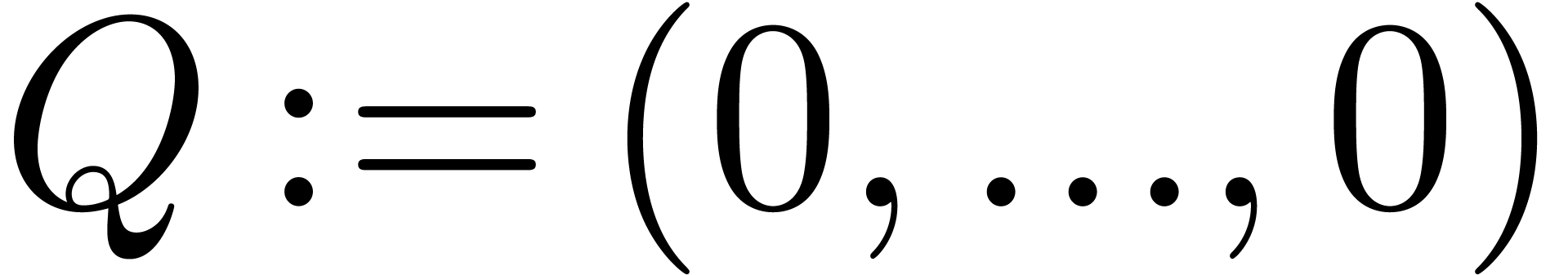 and
and 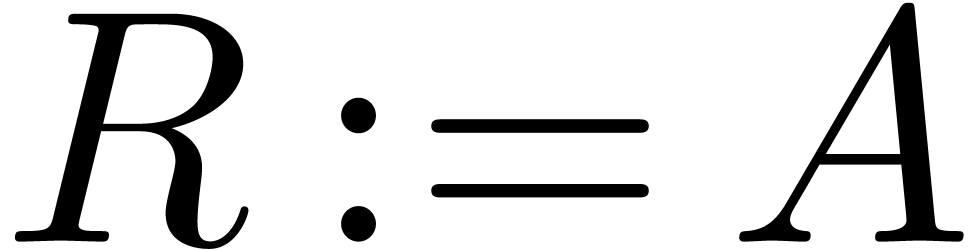
While 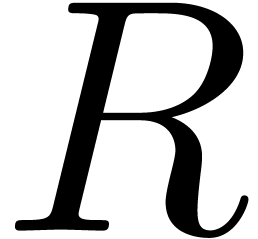 is not reduced with respect to
is not reduced with respect to  do
do
Let 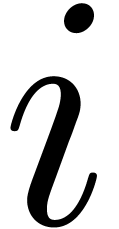 be minimal and such that
be minimal and such that  for some
for some 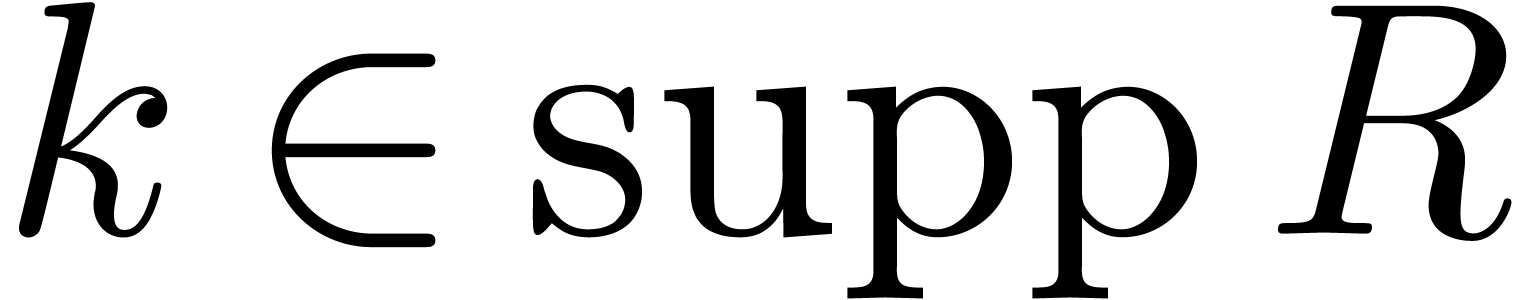
Let 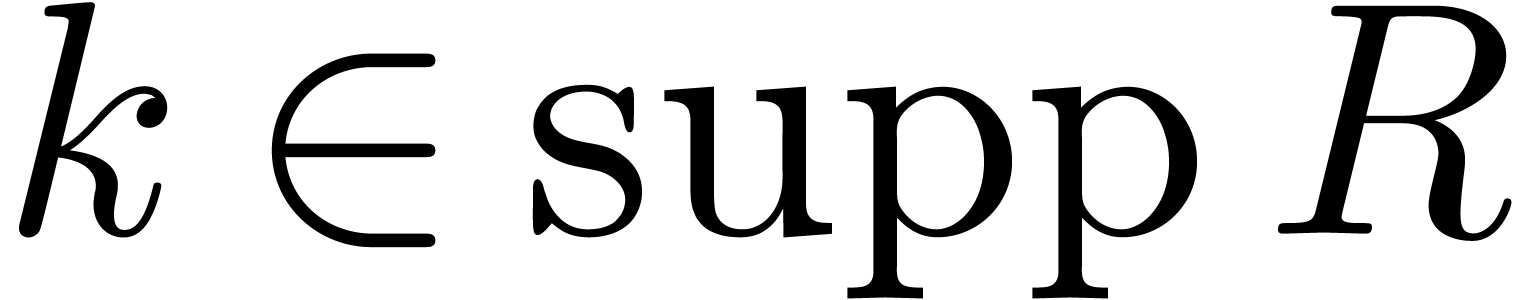 be maximal with
be maximal with 
Set 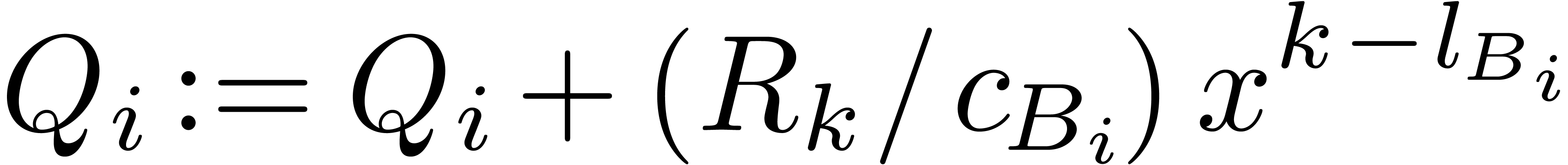 and
and 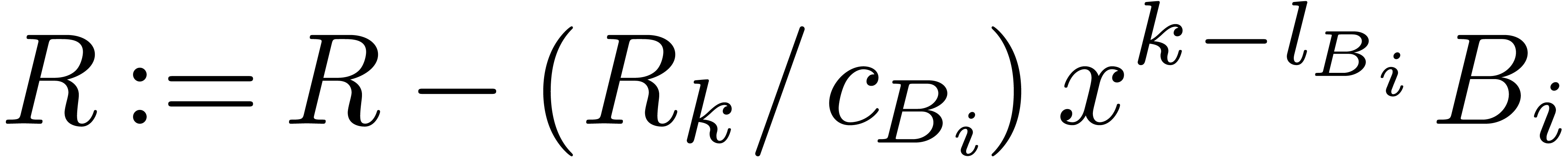
Return 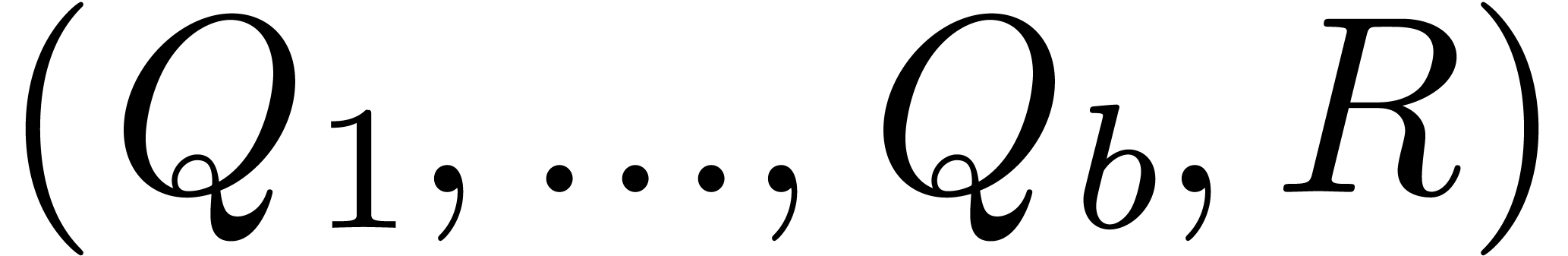
Remark  minimal with
minimal with  for some
for some 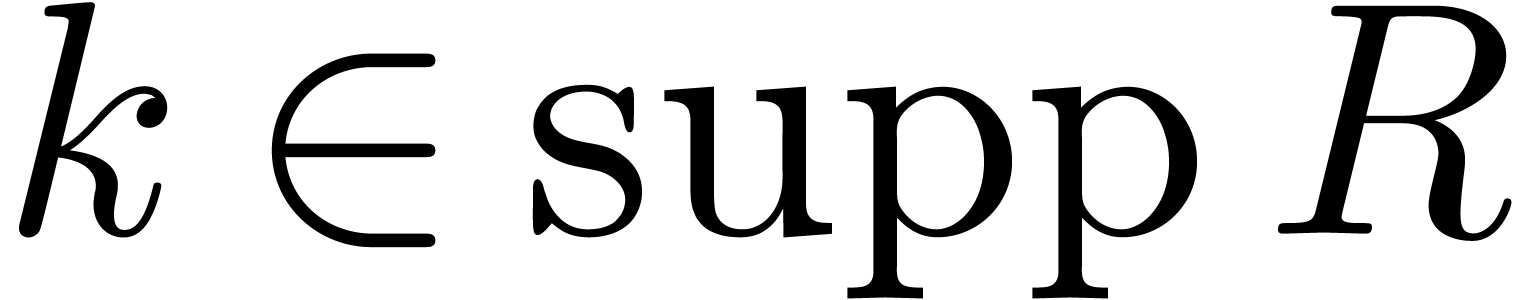 . This
particular extended reduction is also characterized by the fact that
. This
particular extended reduction is also characterized by the fact that
for each  .
.
In order to compute  and
and  in a relaxed manner, upper bounds
in a relaxed manner, upper bounds
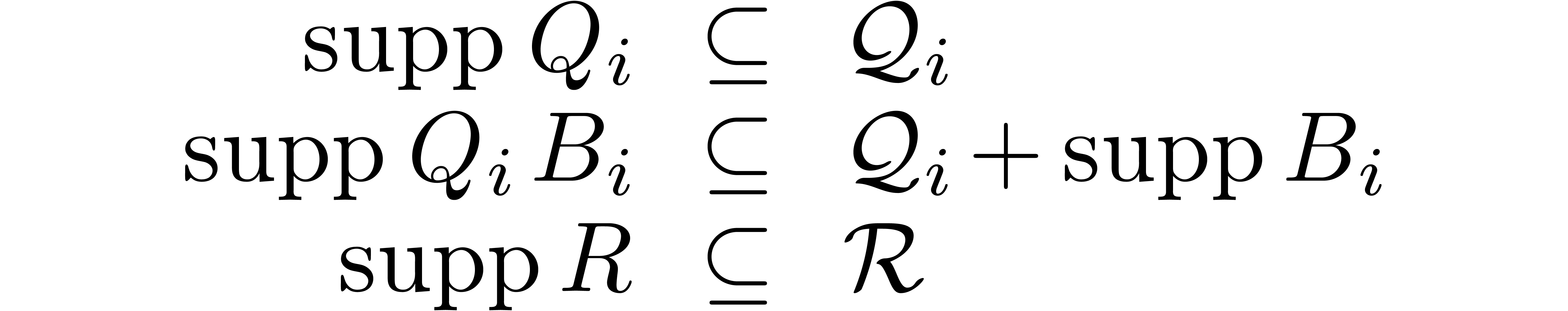
need to be known beforehand. These upper bounds are easily computed as a
function of  by the variant
supp-extended-reduce of extended-reduce below.
We recall from the end of the introduction that we do not take into
account the cost of this computation in our complexity analysis. In
reality, the execution time of supp-extended-reduce is
similar to the one of extended-reduce, except that
potentially expensive operations in
by the variant
supp-extended-reduce of extended-reduce below.
We recall from the end of the introduction that we do not take into
account the cost of this computation in our complexity analysis. In
reality, the execution time of supp-extended-reduce is
similar to the one of extended-reduce, except that
potentially expensive operations in  are replaced
by boolean operations of unit cost. We also recall that support bounds
can often be obtained by other means for specific problems.
are replaced
by boolean operations of unit cost. We also recall that support bounds
can often be obtained by other means for specific problems.
Algorithm supp-extended-reduce
 and
and  of
of 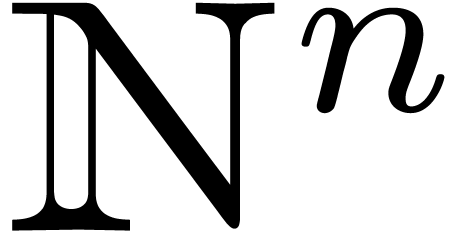 as above
as above
 and
and  of
of 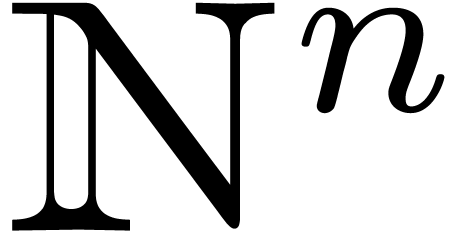 as above
as above
Start with  and
and 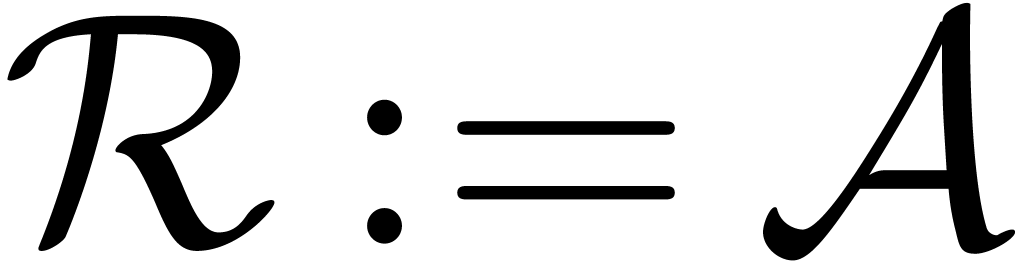
While 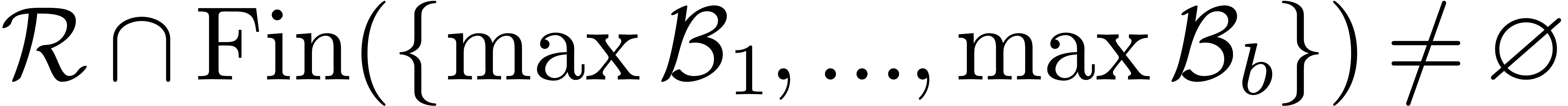 do
do
Let 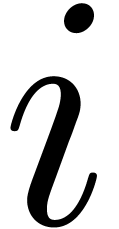 be minimal with
be minimal with 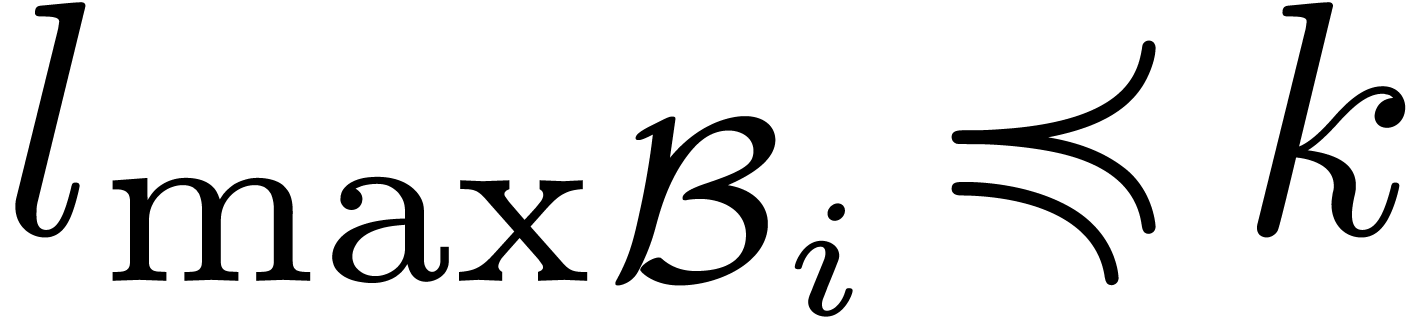 for some
for some 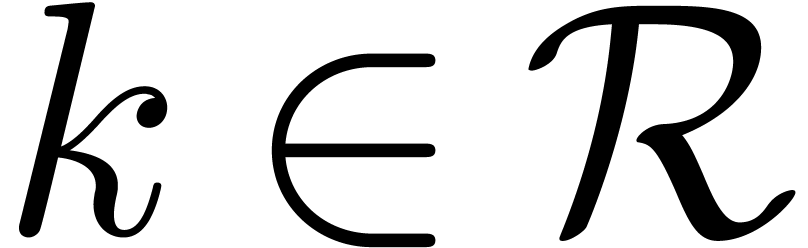
Let 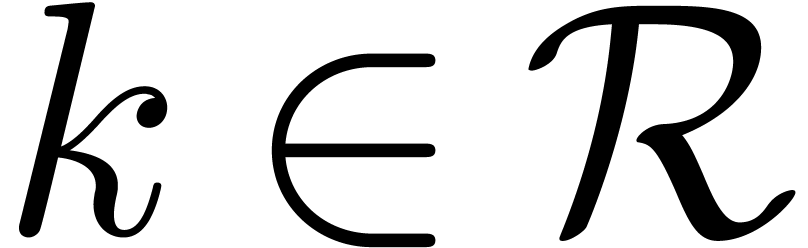 be maximal with
be maximal with 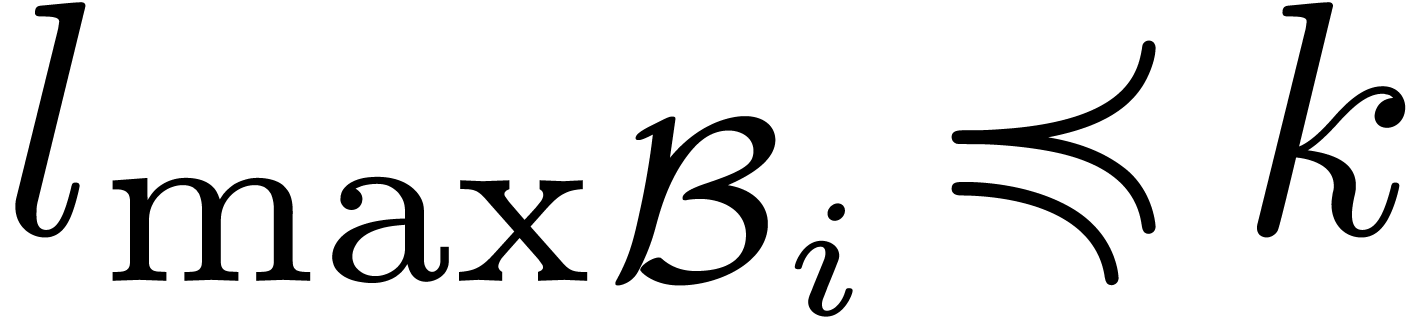
Set 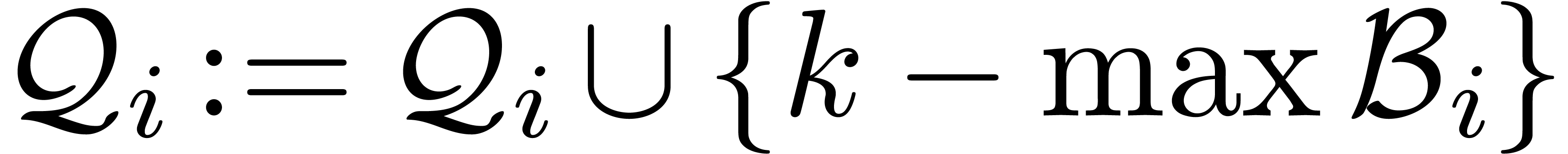 and
and
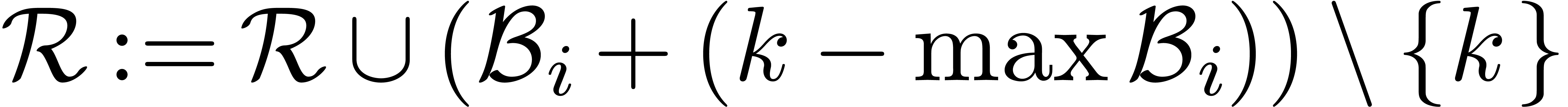
Return 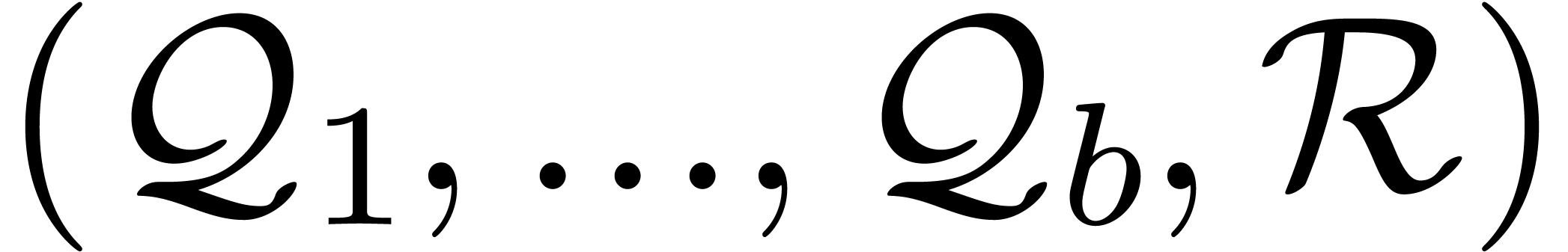
Using the relaxed multiplication from section 3, we are now
in a position to replace the algorithm extended-reduce by a
new algorithm, which directly computes  using the
equation (3). In order to do this, we still have to put it
in a recursive form which is suitable for relaxed resolution.
using the
equation (3). In order to do this, we still have to put it
in a recursive form which is suitable for relaxed resolution.
Denoting by 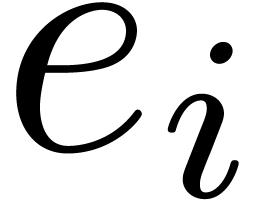 the
the 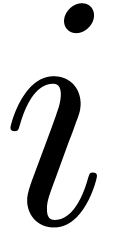 -th
canonical basis vector of
-th
canonical basis vector of 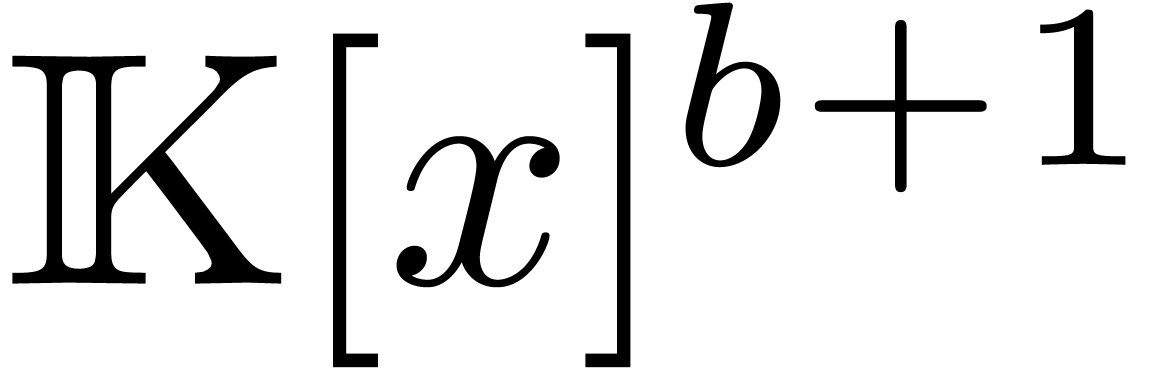 ,
we first define an operator
,
we first define an operator 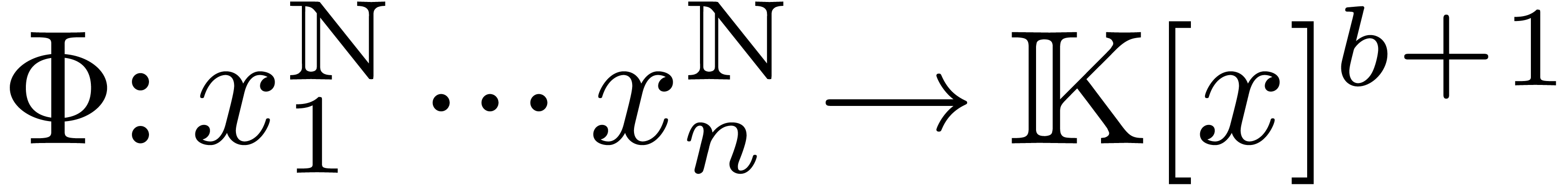 by
by
By linearity, this operator extends to 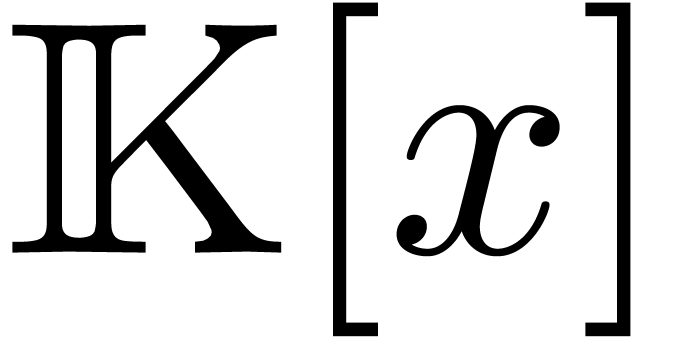
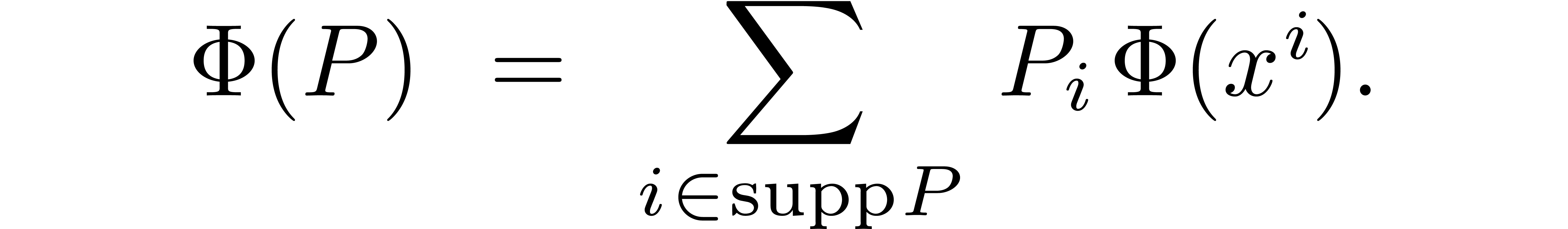
In particular, 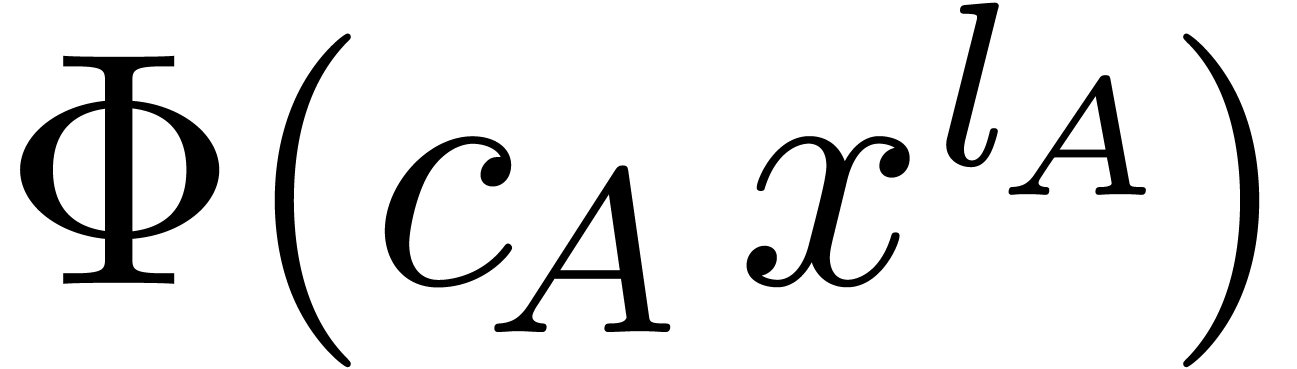 yields the “leading
term” of the extended reduction
yields the “leading
term” of the extended reduction 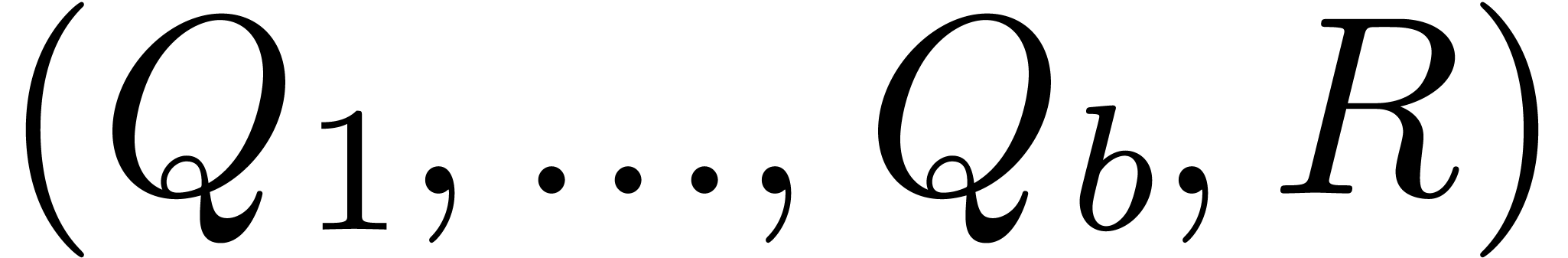 .
We also denote by
.
We also denote by  the corresponding operator
from
the corresponding operator
from 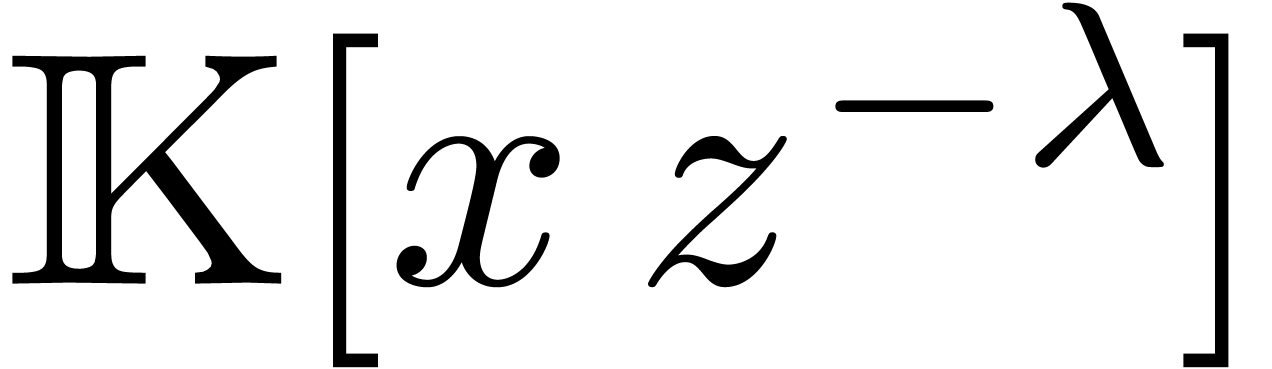 to
to 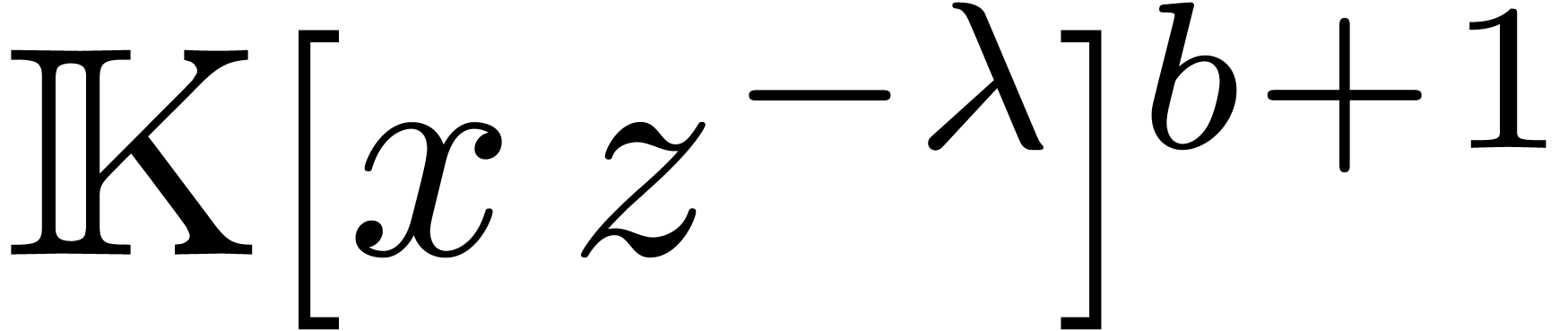 which sends
which sends 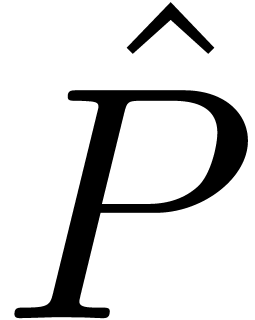 to
to 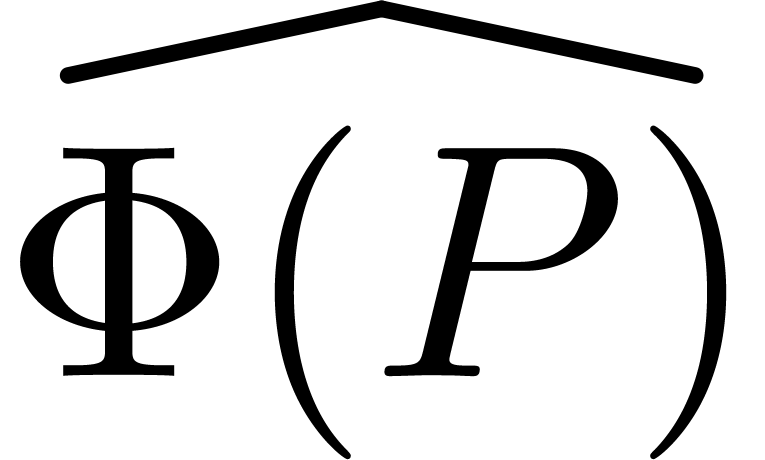 .
.
Now let  for each
for each  .
Then
.
Then
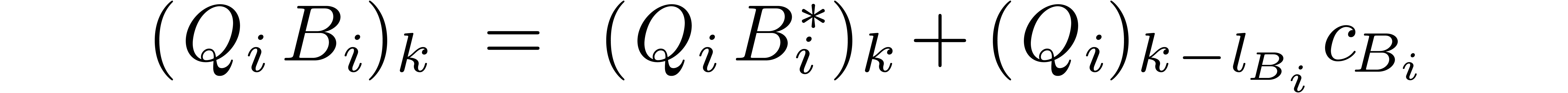
for each 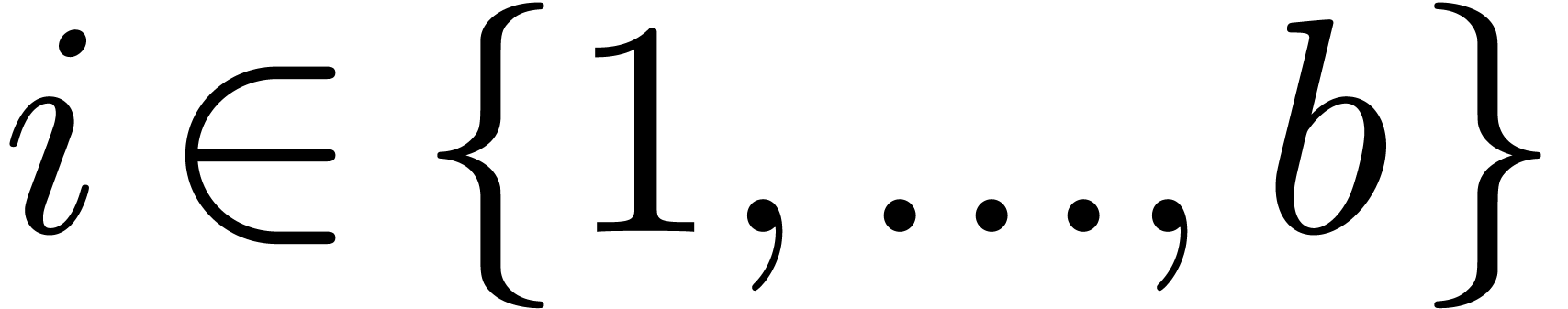 and
and  .
The equation
.
The equation
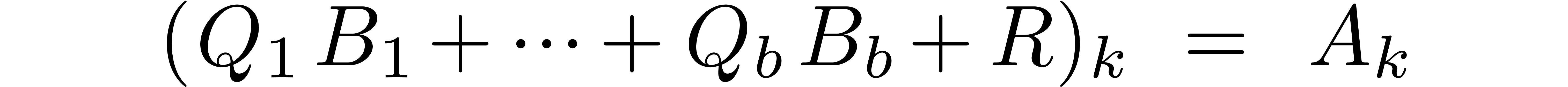
can thus be rewritten as
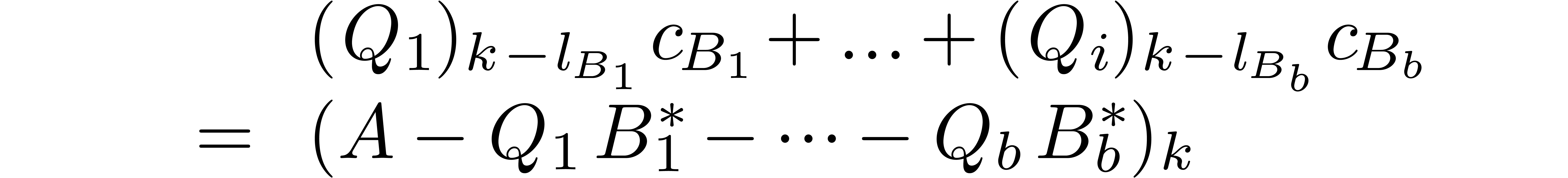
Using the operator  this equation can be
rewritten in a more compact form as
this equation can be
rewritten in a more compact form as
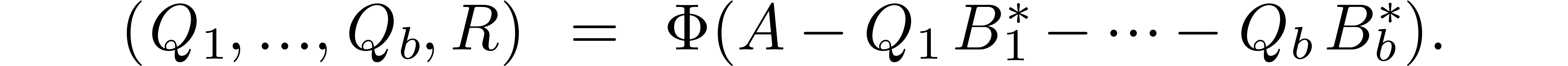
The tagged counterpart
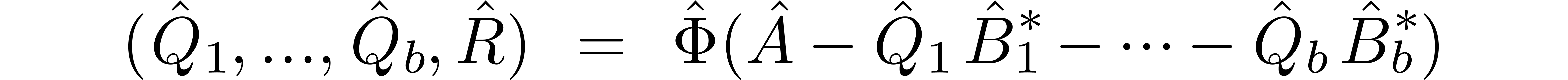
is recursive, whence the extended reduction can be computed using 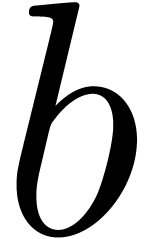 multivariate relaxed multiplications
multivariate relaxed multiplications  . With
. With 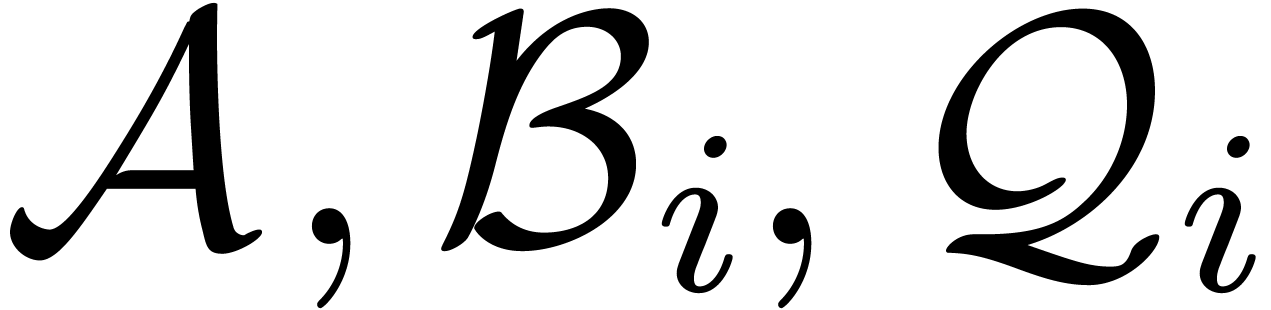 and
and  as in the previous section, theorem 4
therefore implies:
as in the previous section, theorem 4
therefore implies:
Theorem  with respect
to
with respect
to  in time
in time
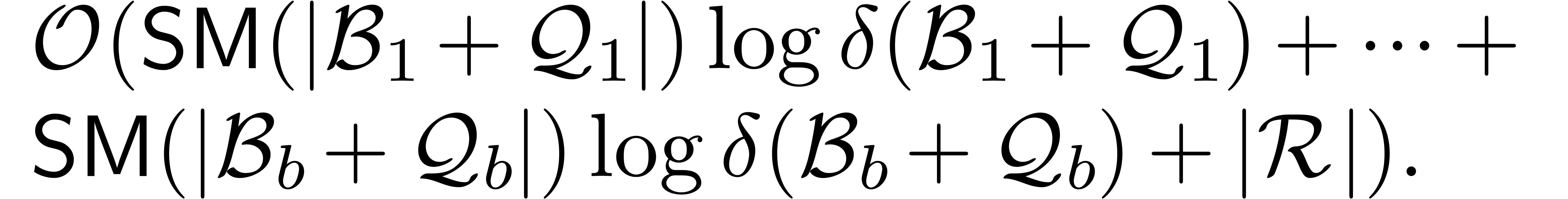
Remark  ,
the
,
the 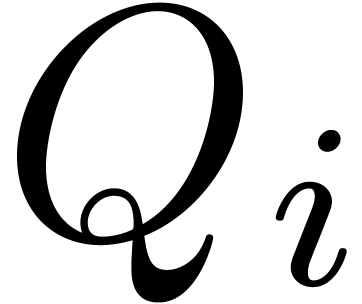 and
and  may be replaced
by vectors of polynomials in
may be replaced
by vectors of polynomials in 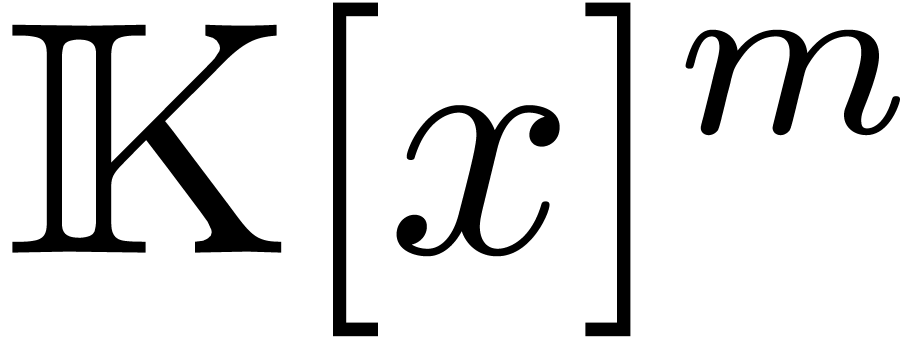 (regarded as
polynomials with coefficients in
(regarded as
polynomials with coefficients in 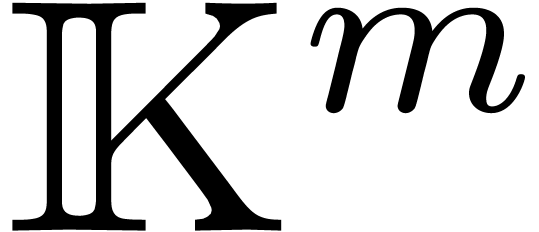 ),
in the case that several polynomials need to be reduced simultaneously.
),
in the case that several polynomials need to be reduced simultaneously.
M. Ben-Or and P. Tiwari. A deterministic algorithm for sparse multivariate polynomial interpolation. In STOC '88: Proceedings of the twentieth annual ACM symposium on Theory of computing, pages 301–309, New York, NY, USA, 1988. ACM Press.
J. Canny, E. Kaltofen, and Y. Lakshman. Solving systems of non-linear polynomial equations faster. In Proc. ISSAC '89, pages 121–128, Portland, Oregon, A.C.M., New York, 1989. ACM Press.
J.W. Cooley and J.W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
M. J. Fischer and L. J. Stockmeyer. Fast on-line integer multiplication. Proc. 5th ACM Symposium on Theory of Computing, 9:67–72, 1974.
D. Y. Grigoriev and M. Karpinski. The matching problem for bipartite graphs with polynomially bounded permanents is in NC. In Proceedings of the 28th IEEE Symposium on the Foundations of Computer Science, pages 166–172, 1987.
J. van der Hoeven. Lazy multiplication of formal power series. In W. W. Küchlin, editor, Proc. ISSAC '97, pages 17–20, Maui, Hawaii, July 1997.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Relaxed multiplication using the middle product. In Manuel Bronstein, editor, Proc. ISSAC '03, pages 143–147, Philadelphia, USA, August 2003.
J. van der Hoeven. The truncated Fourier transform and applications. In J. Gutierrez, editor, Proc. ISSAC 2004, pages 290–296, Univ. of Cantabria, Santander, Spain, July 4–7 2004.
J. van der Hoeven. New algorithms for relaxed multiplication. JSC, 42(8):792–802, 2007.
J. van der Hoeven. From implicit to recursive equations. Technical report, HAL, 2011. http://hal.archives-ouvertes.fr/hal-00583125.
J. van der Hoeven and G. Lecerf. On the complexity of blockwise polynomial multiplication. In Proc. ISSAC '12, pages 211–218, Grenoble, France, July 2012.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial multiplication. JSC, 50:227–254, 2013.
J. van der Hoeven and É. Schost. Multi-point evaluation in higher dimensions. AAECC, 24(1):37–52, 2013.
E. Kaltofen and Y. N. Lakshman. Improved sparse multivariate polynomial interpolation algorithms. In ISSAC '88: Proceedings of the international symposium on Symbolic and algebraic computation, pages 467–474. Springer Verlag, 1988.
L. Robbiano. Term orderings on the polynominal ring. In European Conference on Computer Algebra (2), pages 513–517, 1985.