Sparse polynomial interpolation in practice
|
| April 18, 2014 |
Sparse polynomial interpolation in practice
|
Sparse polynomial interpolation consists in recovering of a sparse
representation of a polynomial 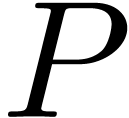 given by a
blackbox program which computes values of
given by a
blackbox program which computes values of 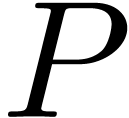 at as
many points as necessary. In practice
at as
many points as necessary. In practice 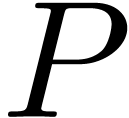 is
typically represented by DAGs (Directed Acyclic Graphs) or SPLs
(Straight Line Programs). For polynomials with at most
is
typically represented by DAGs (Directed Acyclic Graphs) or SPLs
(Straight Line Programs). For polynomials with at most  terms over a field
terms over a field 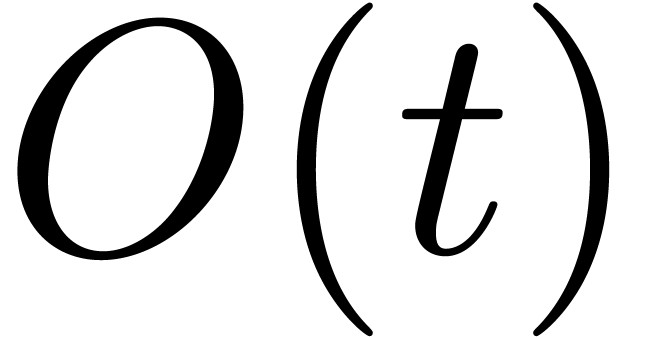 , this
task typically involves
, this
task typically involves  evaluations of
evaluations of 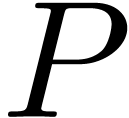 , operations on integers for
discovering the exponents of the nonzero terms of
, operations on integers for
discovering the exponents of the nonzero terms of 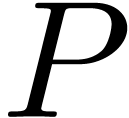 , and an additional number of operations in
, and an additional number of operations in 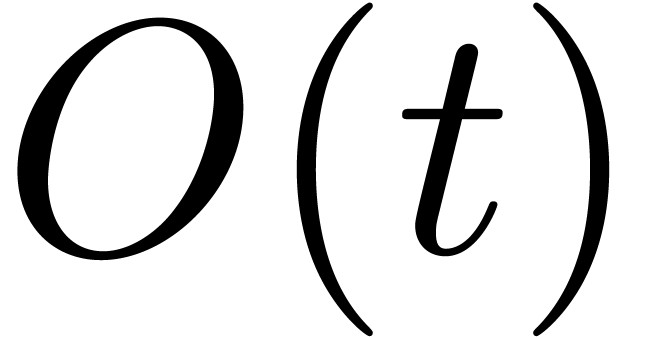 that can be bounded by
that can be bounded by 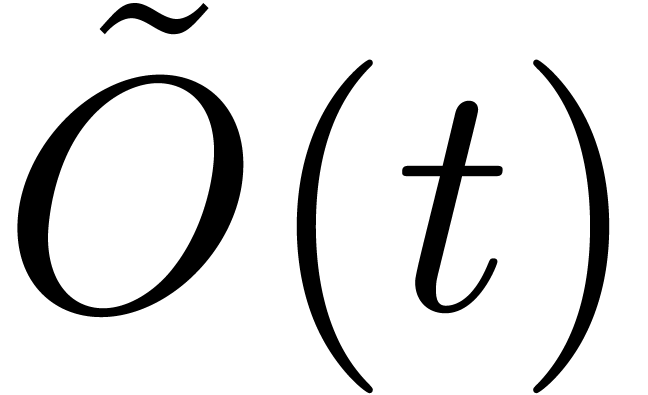
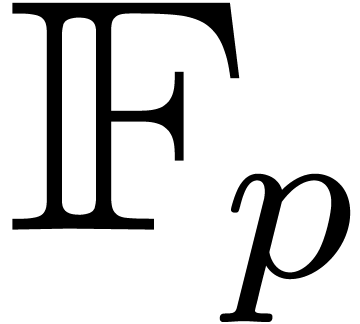 for recovering the coefficients [3].
for recovering the coefficients [3].
However, the latter complexity analysis does not take into account the
sizes of coefficients in 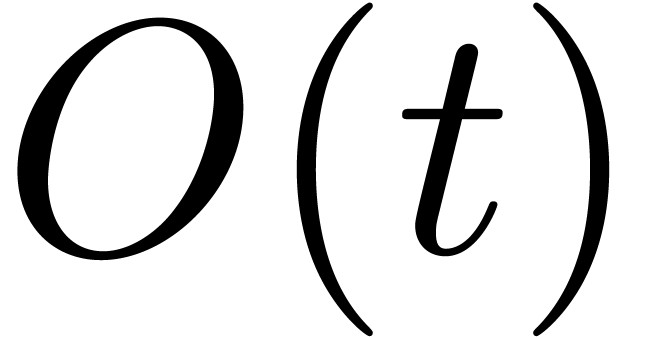 and the expression
swell that might occur when evaluating at points with high height [9]. For practical implementations, it is important to perform
most of the computations over a prime finite field
and the expression
swell that might occur when evaluating at points with high height [9]. For practical implementations, it is important to perform
most of the computations over a prime finite field 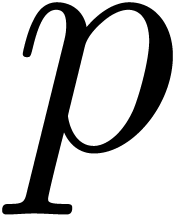 , where
, where 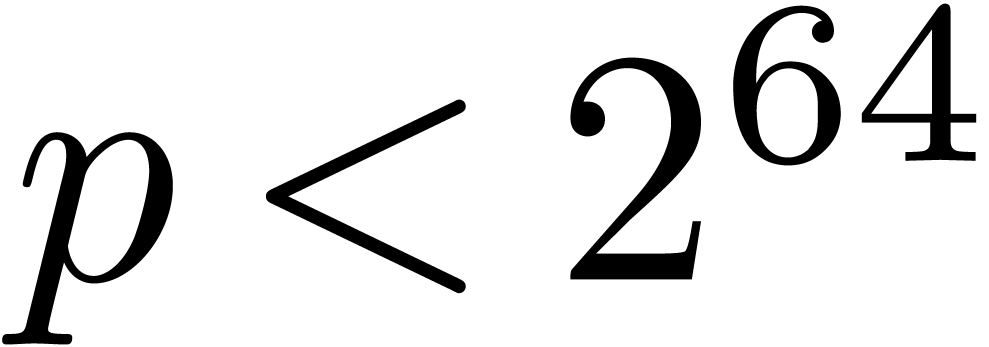 fits into a
single machine register. On modern architectures, this typically means
that
fits into a
single machine register. On modern architectures, this typically means
that 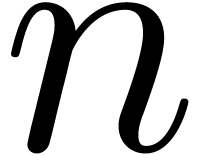 . There mainly are two
approaches which can be used over finite fields: the “prime
number” approach [9] and the “Kronecker
substitution” approach [8]. For more references and
practical point of views on known algorithms we refer the reader to [1, 2, 7] (see also [5]
in a more restricted context). We recall these approaches in Section 2. In Section 3, we present new techniques which
may be used to further enhance and combine these classical approaches.
. There mainly are two
approaches which can be used over finite fields: the “prime
number” approach [9] and the “Kronecker
substitution” approach [8]. For more references and
practical point of views on known algorithms we refer the reader to [1, 2, 7] (see also [5]
in a more restricted context). We recall these approaches in Section 2. In Section 3, we present new techniques which
may be used to further enhance and combine these classical approaches.
We report on our implementations in the
Throughout this paper, we will use vector notation for  -tuples: given variables
-tuples: given variables 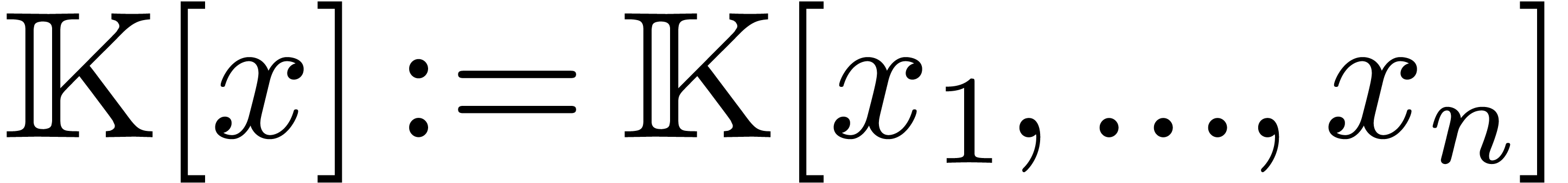 , we write
, we write  .
If
.
If 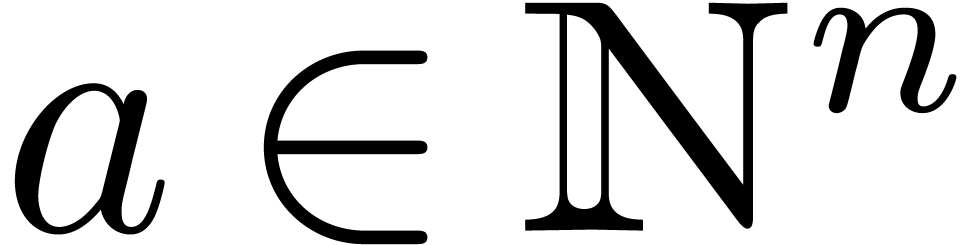 is a vector of
is a vector of  elements in
elements in  or the sequence of the variables
or the sequence of the variables
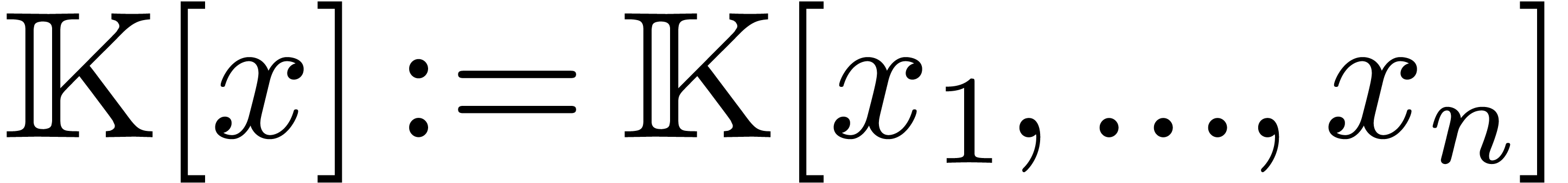 , and if
, and if 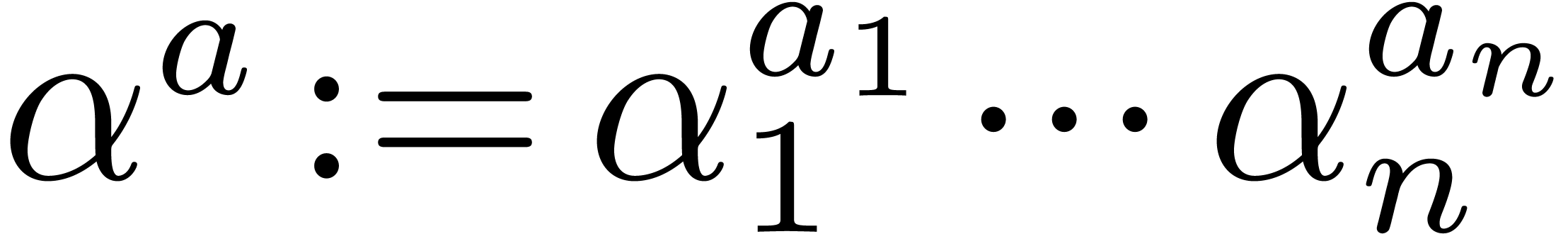 , then we write
, then we write 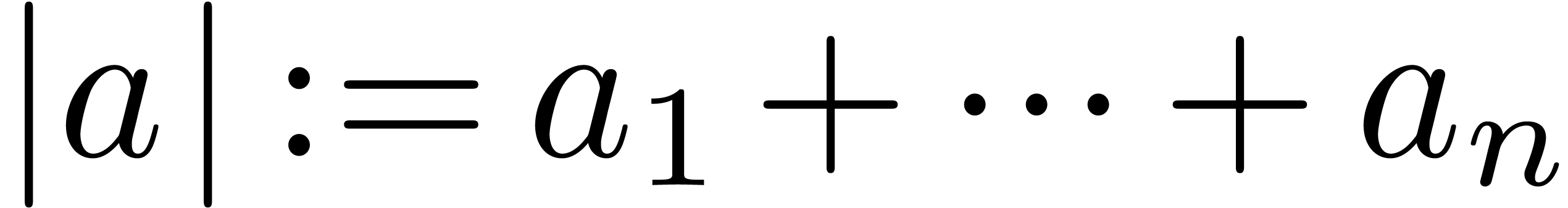 and
and
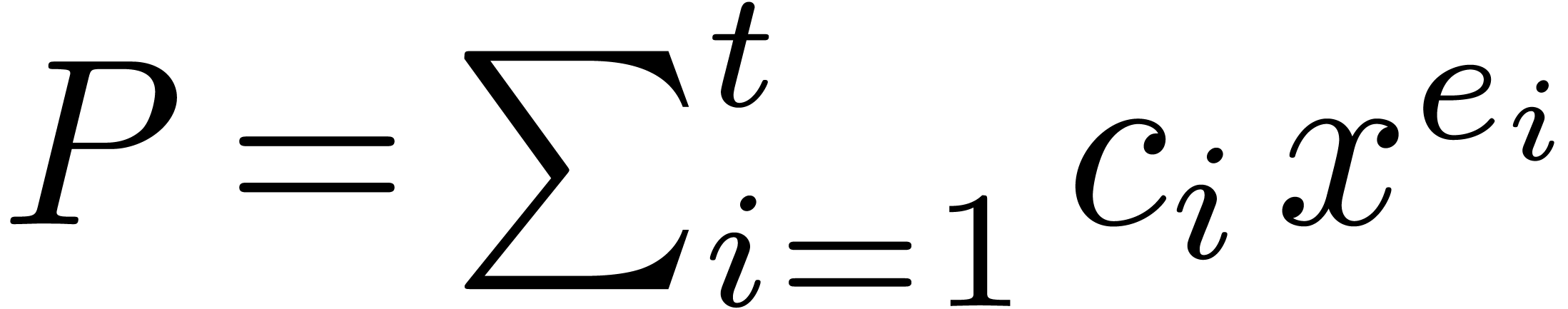 . If
. If 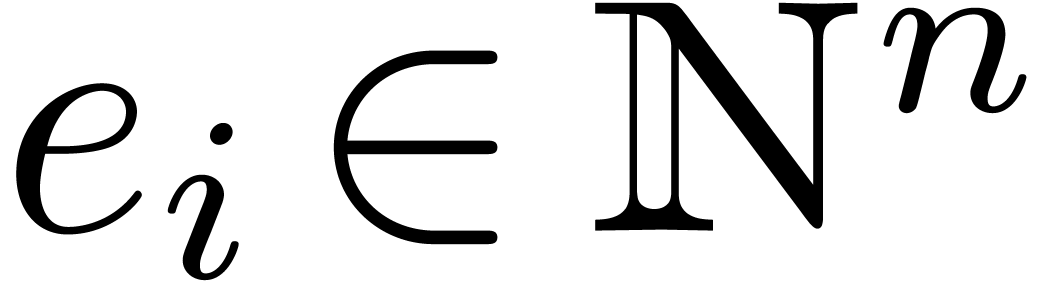 with all the exponents
with all the exponents 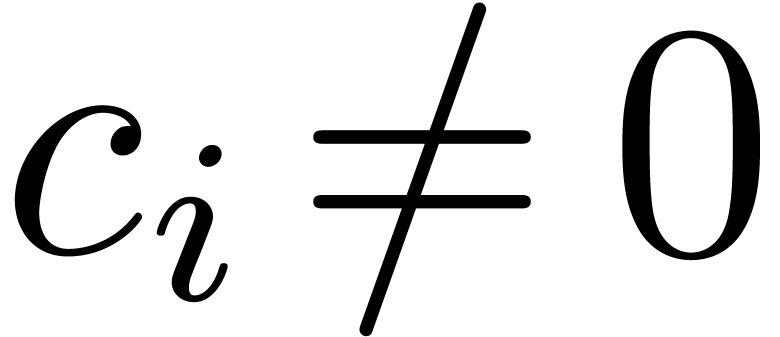 pairwise distinct and
pairwise distinct and
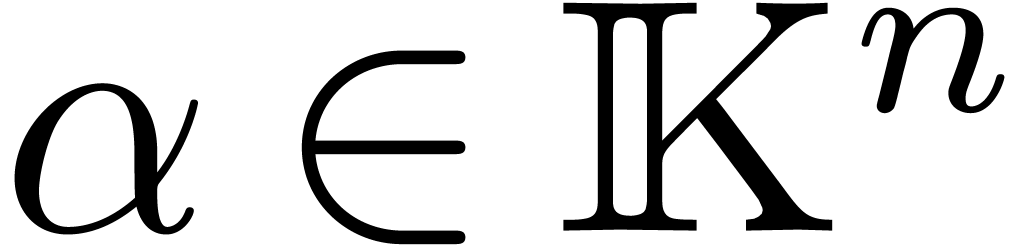 , then for all
, then for all 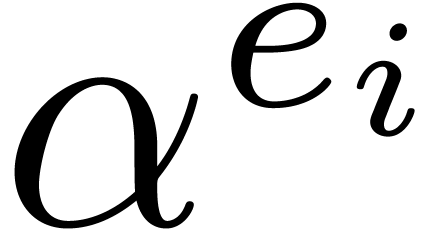 we have
we have
If the values 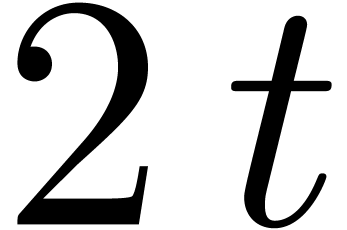 are pairwise distinct, then it is
classical that
are pairwise distinct, then it is
classical that 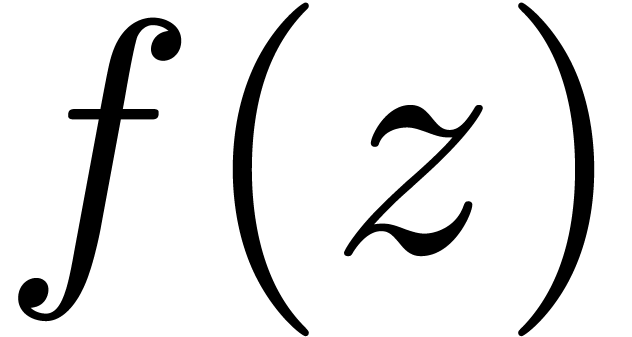 can be computed efficiently from
the first
can be computed efficiently from
the first 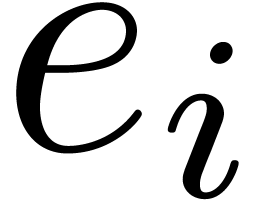 terms of the power series
terms of the power series 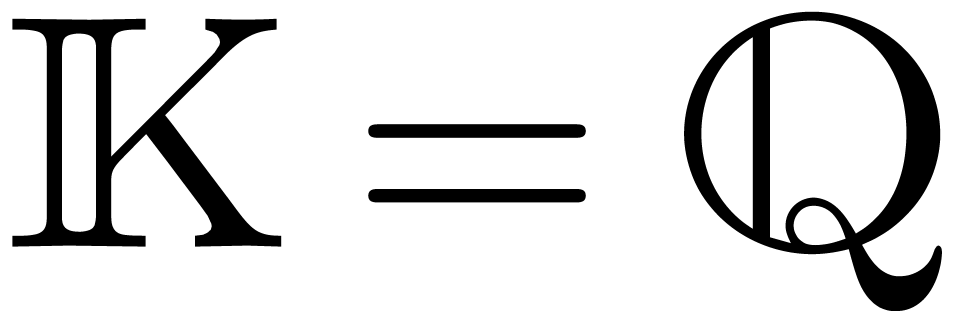 [3]. One may further recover the
[3]. One may further recover the  from the
from the 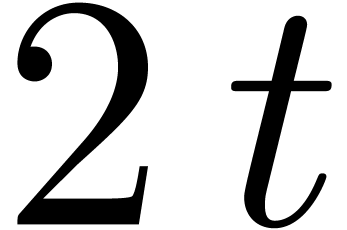 with suitable values of
with suitable values of
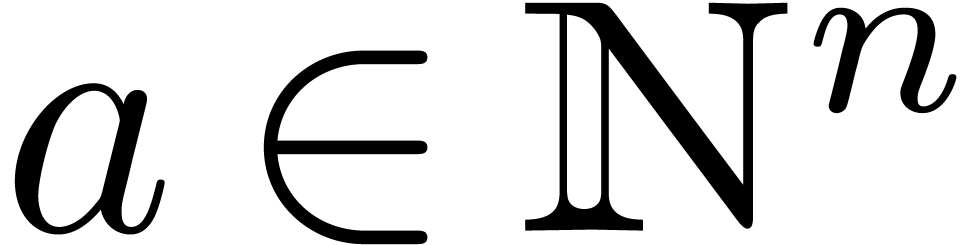 . If no bound for
. If no bound for  is known in advance, then we try to interpolate for
successive upper bounds
is known in advance, then we try to interpolate for
successive upper bounds  in geometric
progression.
in geometric
progression.
Over many common fields such as  ,
the numbers
,
the numbers 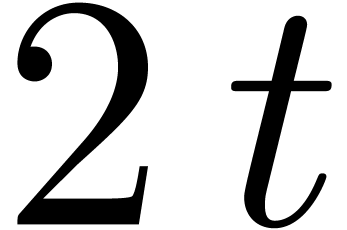 can become quite large. For
efficiency reasons, it is better to work over a finite field
can become quite large. For
efficiency reasons, it is better to work over a finite field 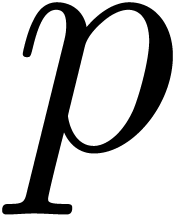 as much as possible. Moreover, we wish to take a
as much as possible. Moreover, we wish to take a 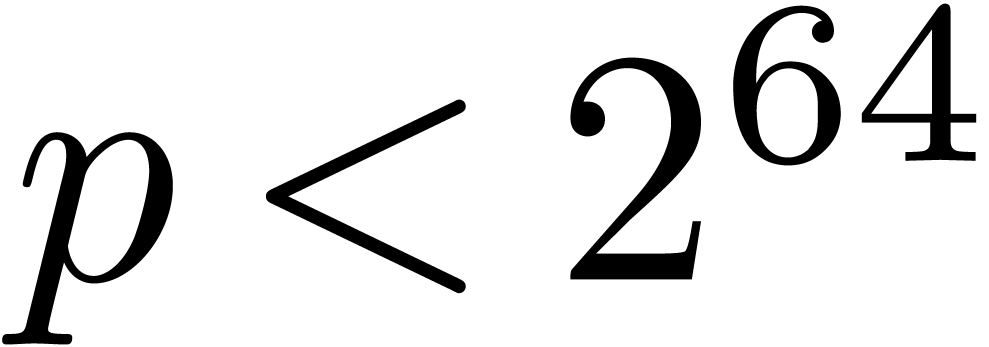 which fits into a single machine register, so that
computations in
which fits into a single machine register, so that
computations in  can be done very efficiently.
When using modular reduction, the problems of computing the
can be done very efficiently.
When using modular reduction, the problems of computing the  and computing the
and computing the  are actually
quite distinct, and are best treated separately. The
are actually
quite distinct, and are best treated separately. The  do not mostly depend on
do not mostly depend on 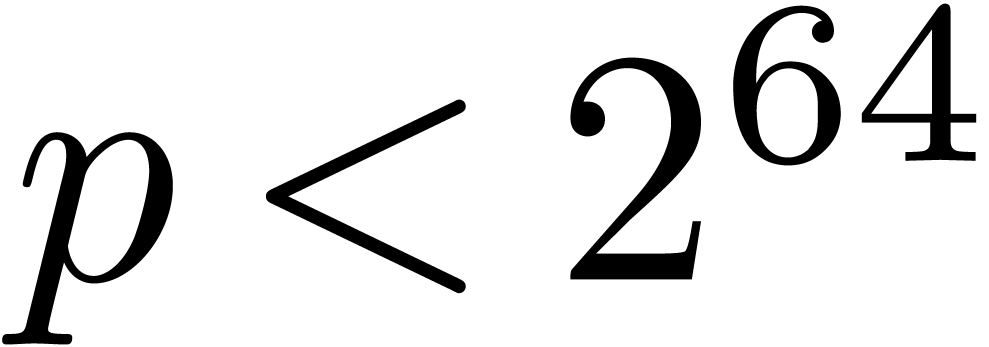 (except for a finite
number of bad values) and only need to be computed for one
(except for a finite
number of bad values) and only need to be computed for one 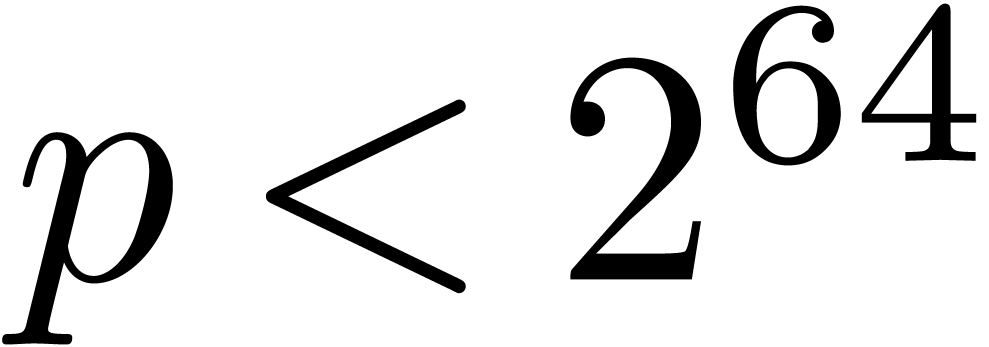 . The
. The  are potentially
large numbers in
are potentially
large numbers in 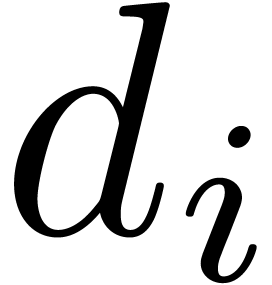 , so we may
need to compute their reductions modulo several
, so we may
need to compute their reductions modulo several 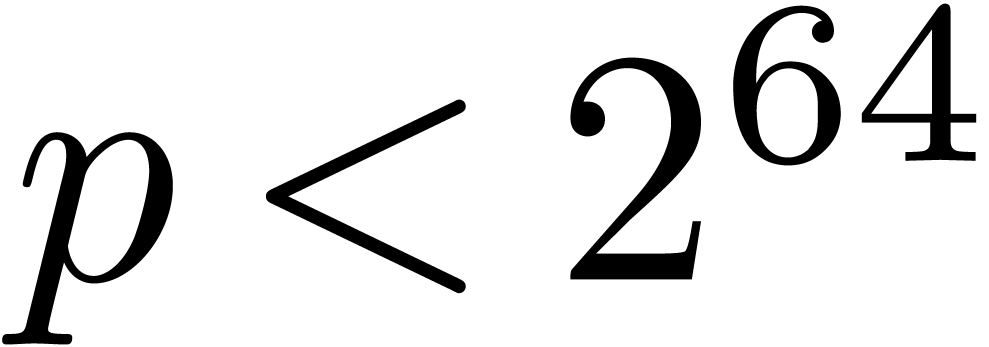 and then recover them using rational number reconstruction [4].
From now on, we focus on the computation of the support of
and then recover them using rational number reconstruction [4].
From now on, we focus on the computation of the support of  written
written 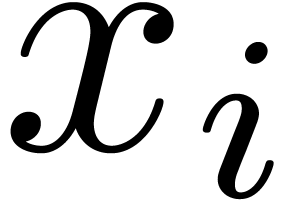 .
Let
.
Let 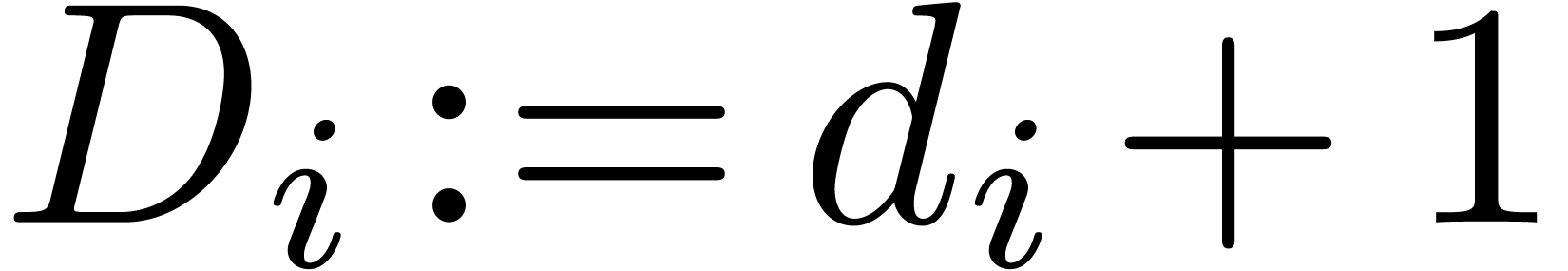 represent the partial degree of
represent the partial degree of  in
in 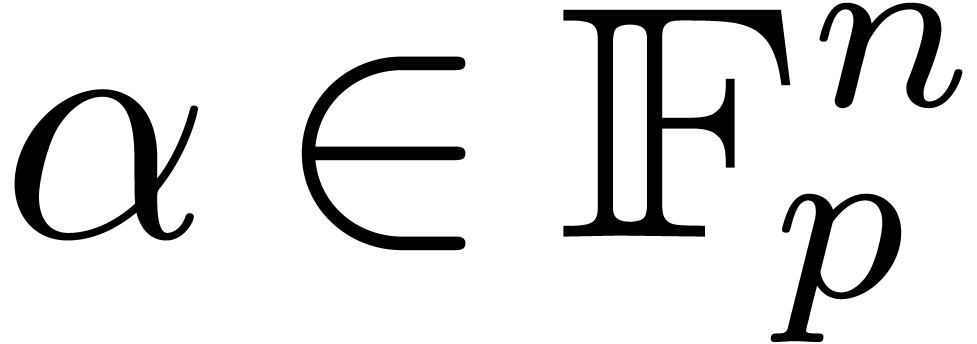 , and let
, and let
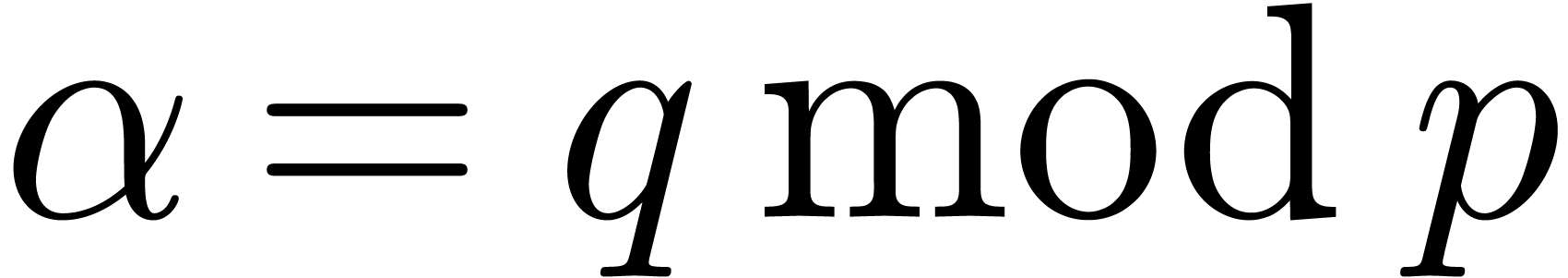 .
.
For the determination of suitable 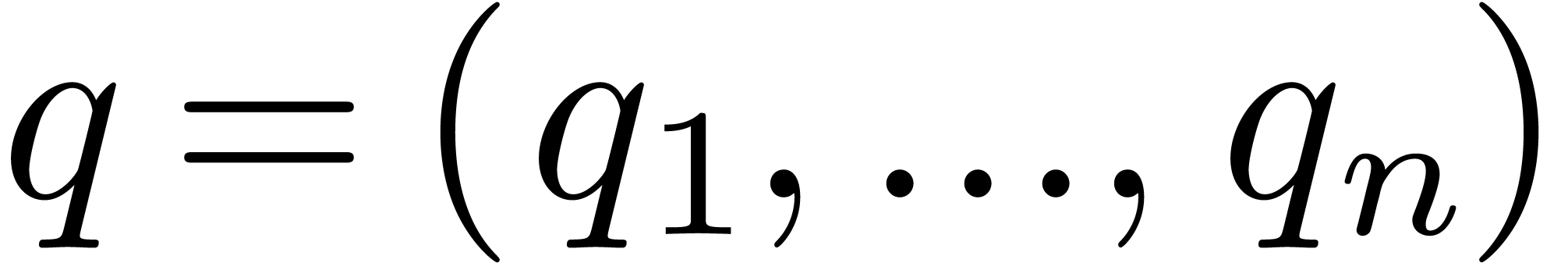 such that the
such that the
 can be reconstructed from the
can be reconstructed from the 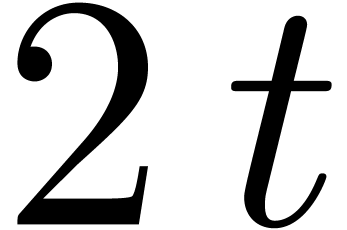 , the “prime number” approach is to
take
, the “prime number” approach is to
take 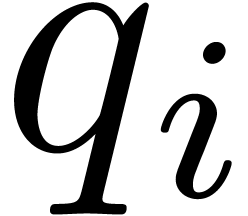 , where
, where 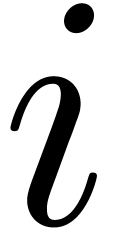 and
and 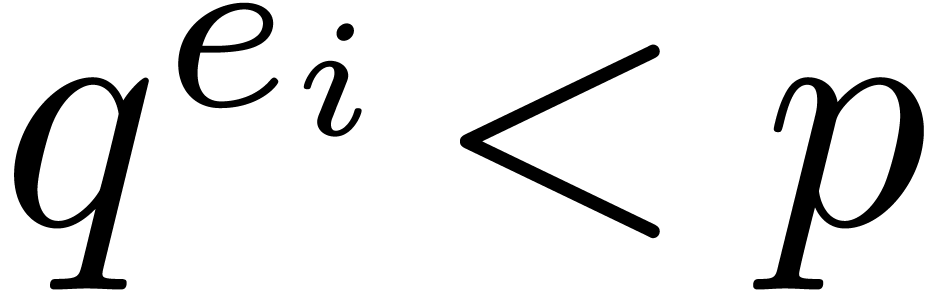 is the
is the 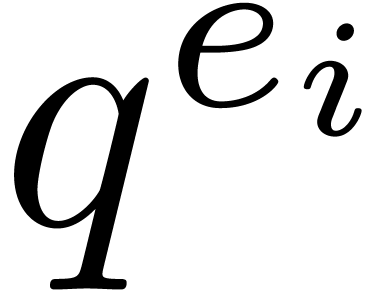 -th
prime number. As long as
-th
prime number. As long as 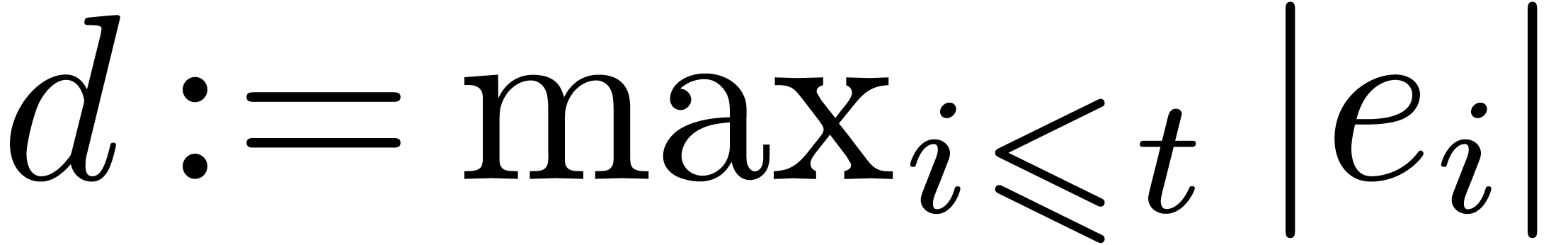 , we
may then recover
, we
may then recover  from
from 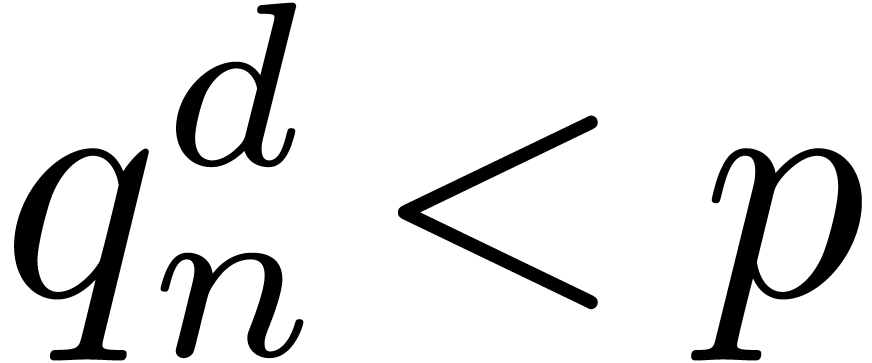 by repeated divisions. If
by repeated divisions. If 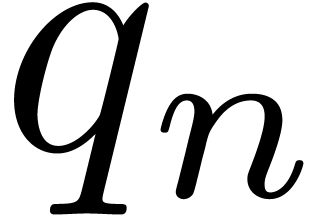 is the total degree of
is the total degree of
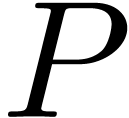 , then it suffices that
, then it suffices that 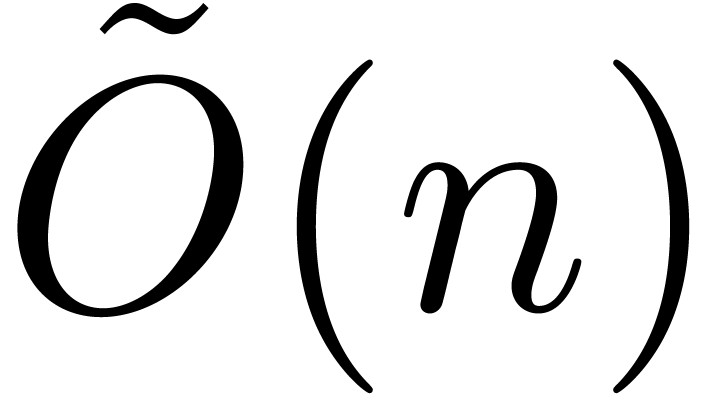 . We recall that
. We recall that  asymptotically grows as
asymptotically grows as 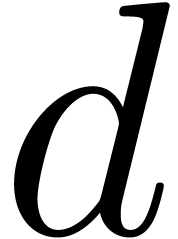 , so
that
, so
that 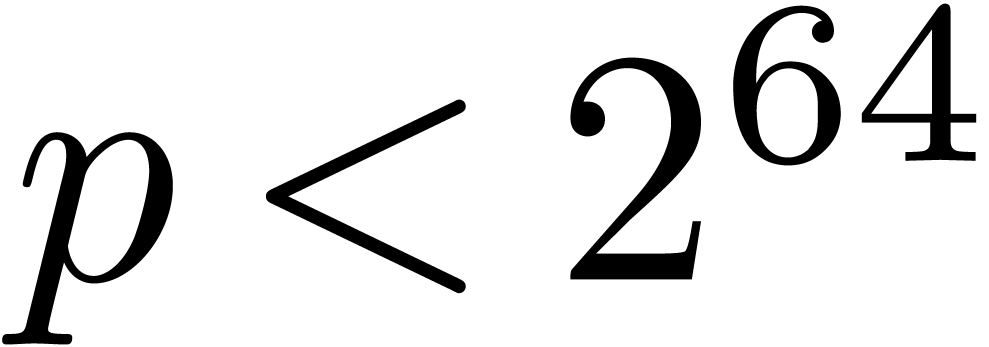 can be taken of bit-size in
can be taken of bit-size in 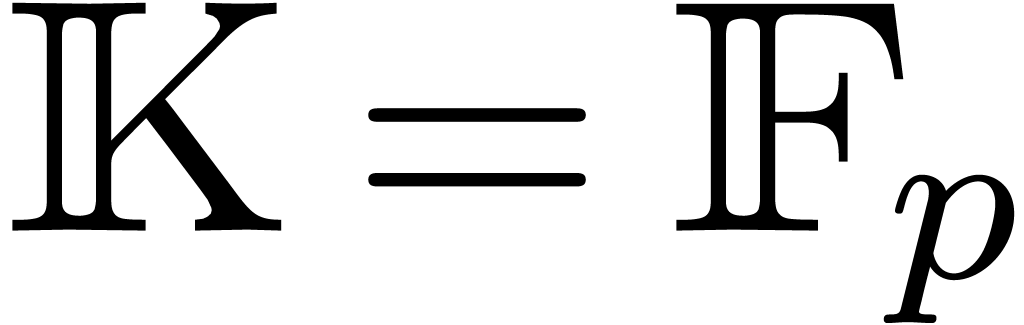 . This approach is therefore efficient when
. This approach is therefore efficient when
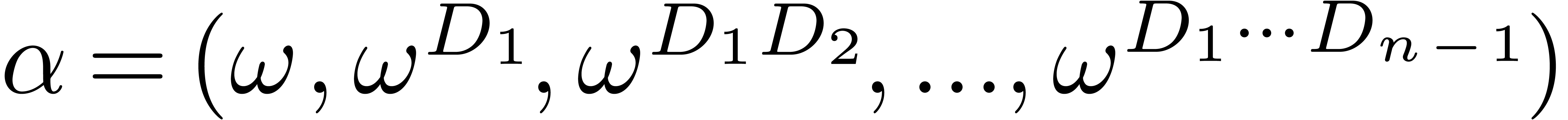 is sufficiently small.
is sufficiently small.
If 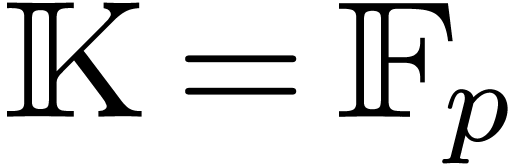 , the “Kronecker
substitution” approach is to take
, the “Kronecker
substitution” approach is to take 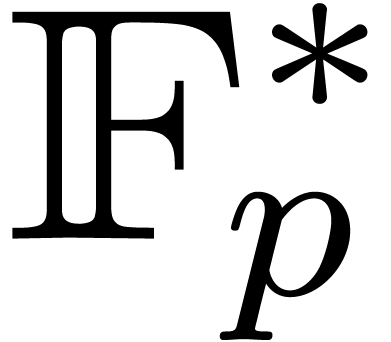 ,
where
,
where 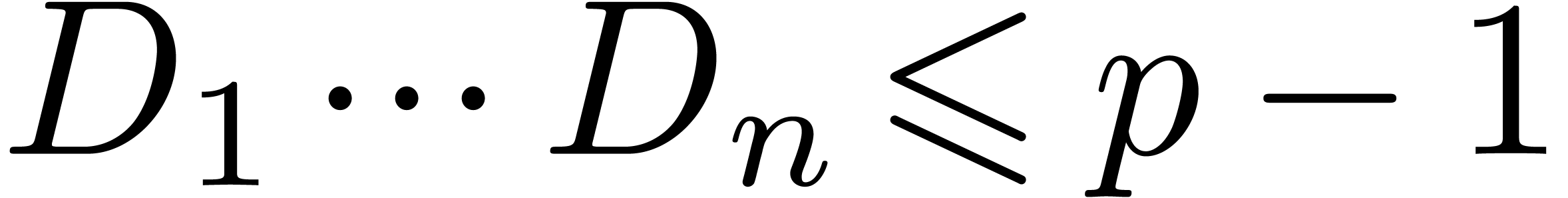 is a primitive root of the multiplicative
group
is a primitive root of the multiplicative
group 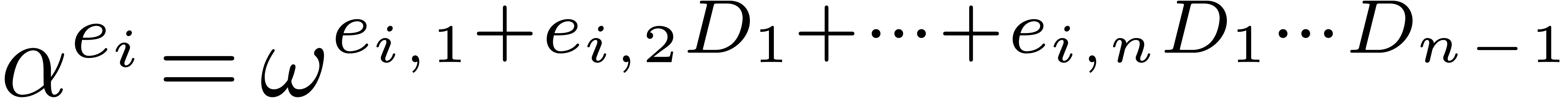 . Assuming that
. Assuming that 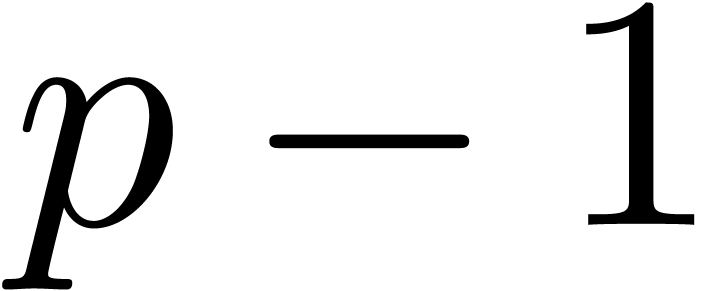 , we can compute all the value
, we can compute all the value
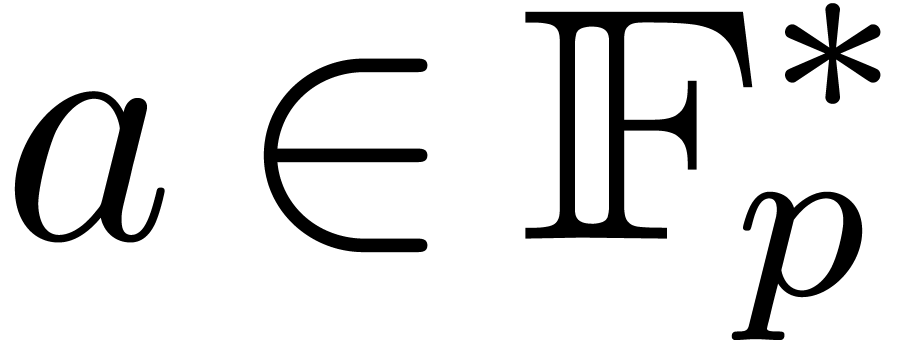 . Moreover, assuming that the
prime number
. Moreover, assuming that the
prime number 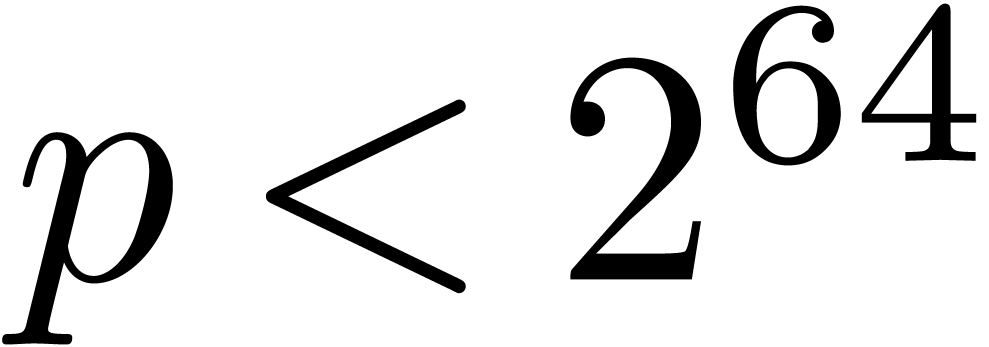 is “smooth”, meaning
that
is “smooth”, meaning
that  has only small prime factors, the discrete
logarithm problem can be solved efficiently in
has only small prime factors, the discrete
logarithm problem can be solved efficiently in 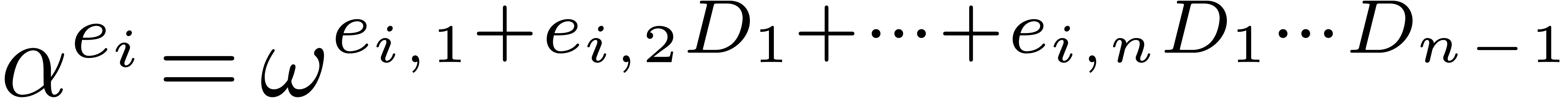 : given
: given 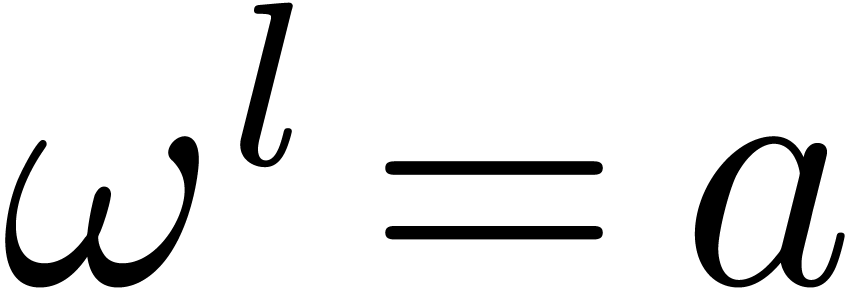 there exists a
relatively efficient algorithm to compute
there exists a
relatively efficient algorithm to compute 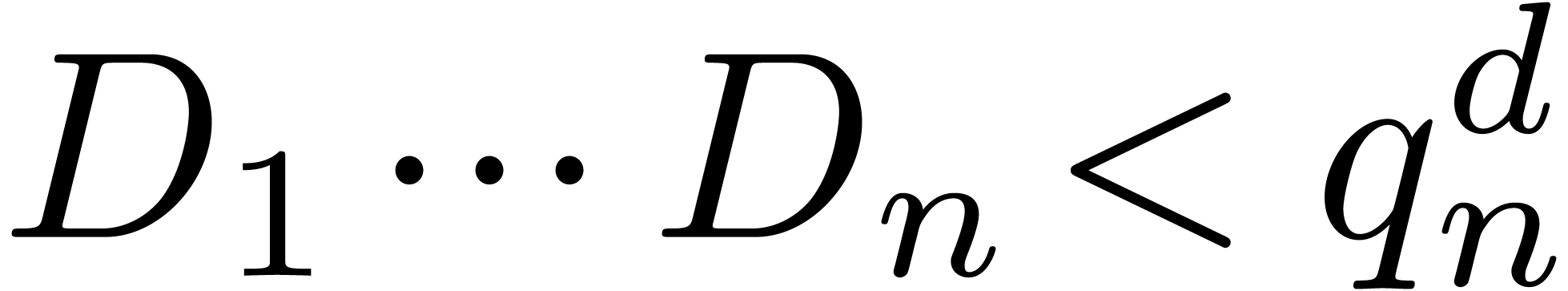 with
with
 [11]. In this way we deduce all the
[11]. In this way we deduce all the
 . This approach is efficient
when the partial degrees are small. More specifically, we prefer it over
the prime number approach if
. This approach is efficient
when the partial degrees are small. More specifically, we prefer it over
the prime number approach if 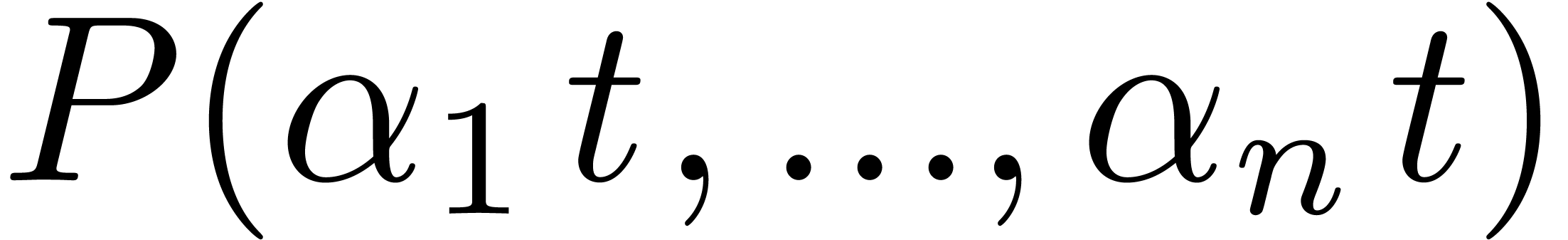 .
.
We notice that bounds for 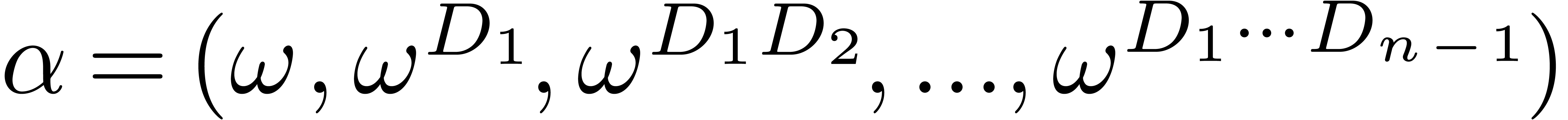 ,
,
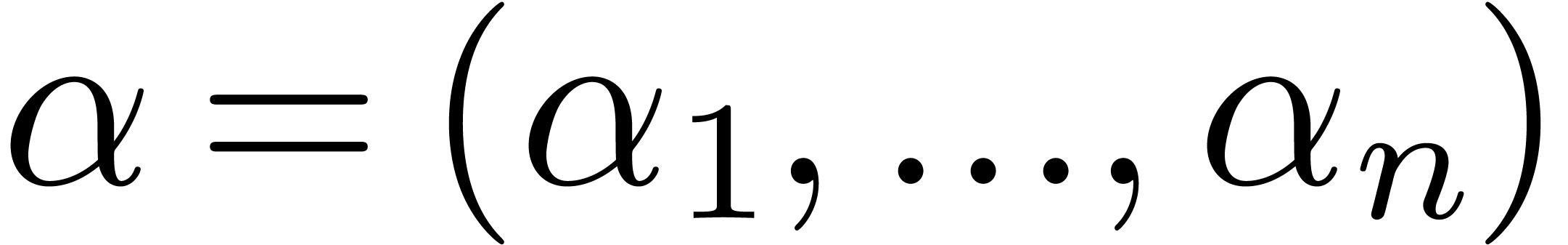 are sometimes known in advance
(e.g. from a syntactic expression for
are sometimes known in advance
(e.g. from a syntactic expression for 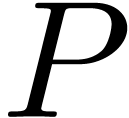 ) and sometimes have to be guessed themselves.
The total degree can be guessed efficiently by using sparse
interpolation for the univariate polynomial
) and sometimes have to be guessed themselves.
The total degree can be guessed efficiently by using sparse
interpolation for the univariate polynomial 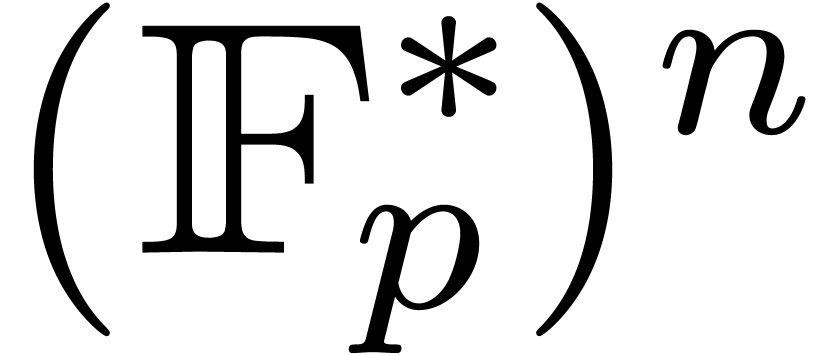 , where
, where 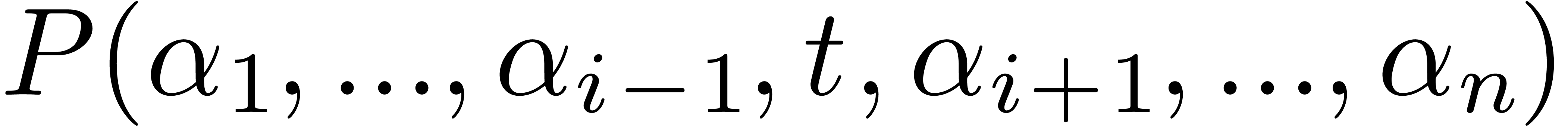 is a random point in
is a random point in
 . Similarly, the partial
degrees
. Similarly, the partial
degrees 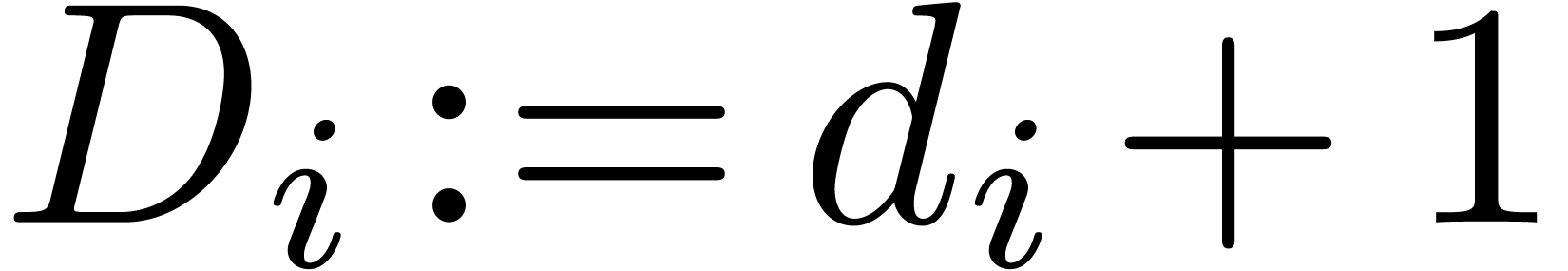 are obtained by interpolating
are obtained by interpolating 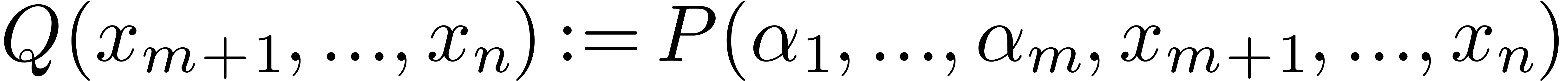 .
.
Remark. It often occurs that the expression for 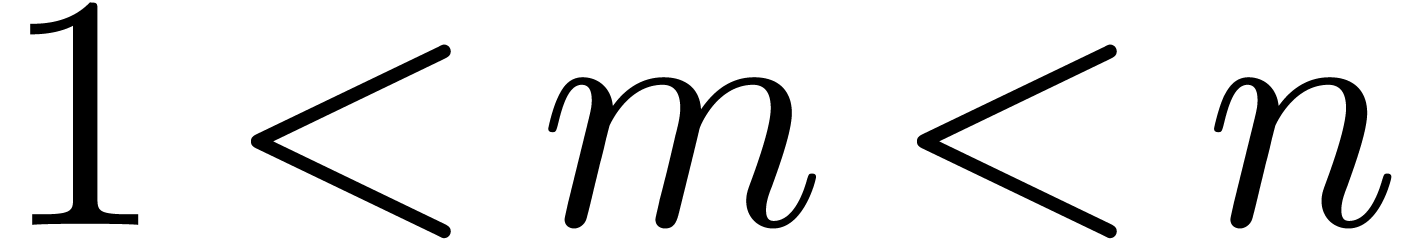 involves division even though the end result is a
polynomial; this happens for instance when computing a symbolic
determinant using Gaussian elimination. When division is allowed in the
prime number approach, then some care is required in order to avoid
systematic divisions by zero. For instance,
involves division even though the end result is a
polynomial; this happens for instance when computing a symbolic
determinant using Gaussian elimination. When division is allowed in the
prime number approach, then some care is required in order to avoid
systematic divisions by zero. For instance, 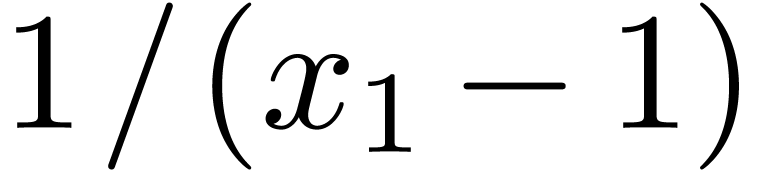 cannot be evaluated at
cannot be evaluated at 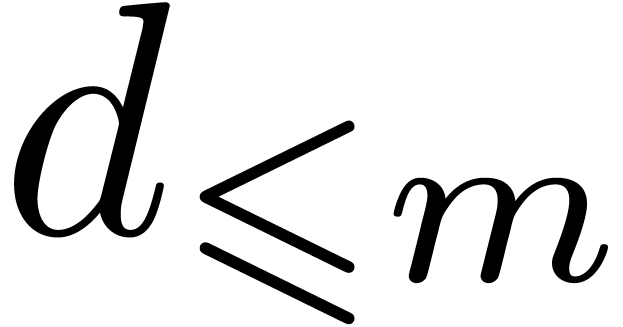 and
and 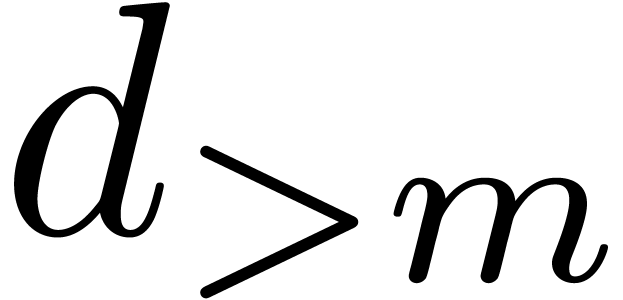 cannot be evaluated at
cannot be evaluated at  when
when 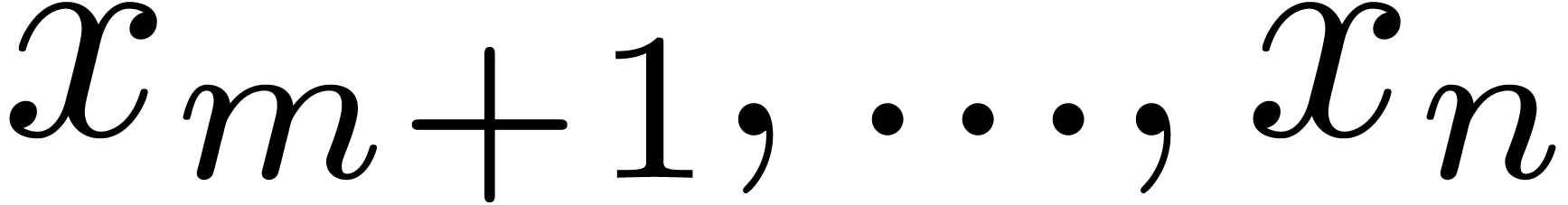 . The first problem can be avoided by taking
. The first problem can be avoided by taking
 . The nuisance of the second
problem can be reduced by replacing the
. The nuisance of the second
problem can be reduced by replacing the 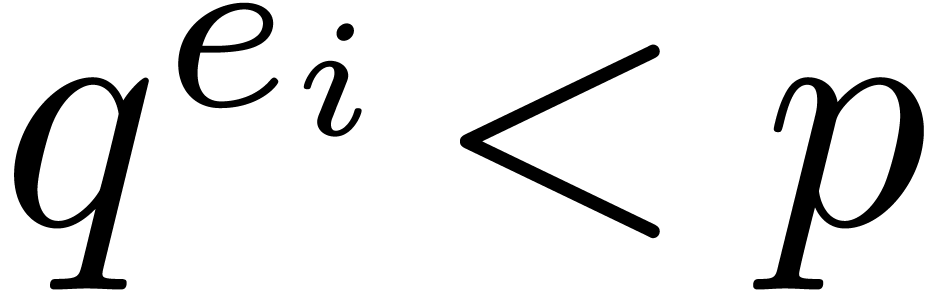 by small
random and pairwise distinct primes.
by small
random and pairwise distinct primes.
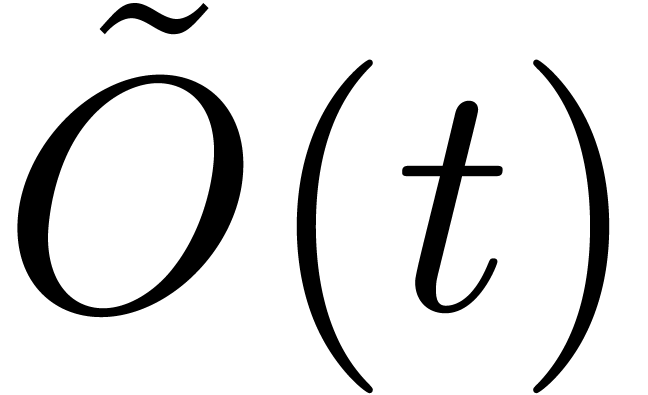 In this section we carry on
with the same notation, and
In this section we carry on
with the same notation, and 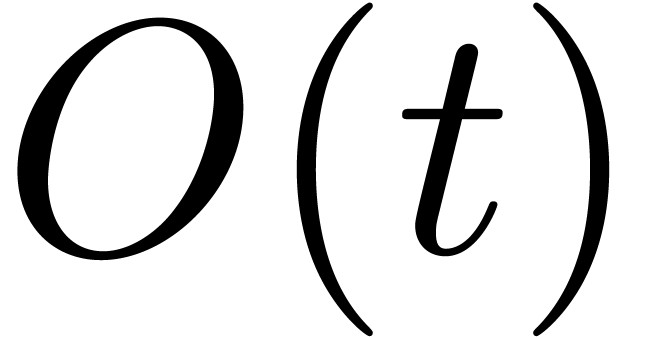 is the finite field
is the finite field
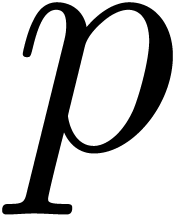 . We aim at decomposing the
interpolation problem into several ones with less variables in order to
interpolate more polynomials than with the previously known techniques.
For all our algorithms, we assume that the support
. We aim at decomposing the
interpolation problem into several ones with less variables in order to
interpolate more polynomials than with the previously known techniques.
For all our algorithms, we assume that the support 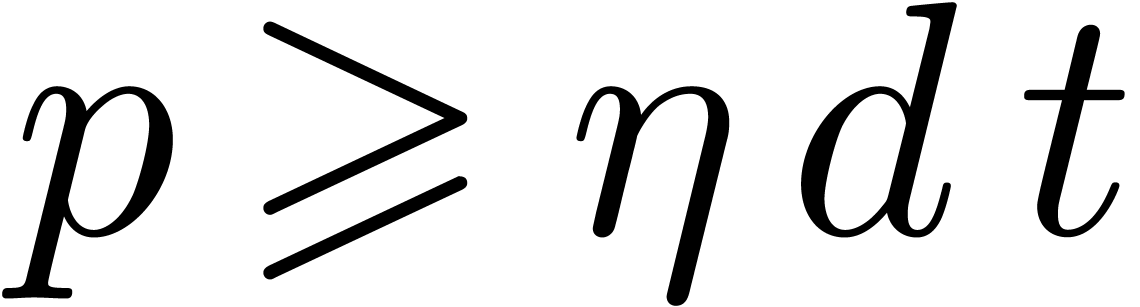 of
of 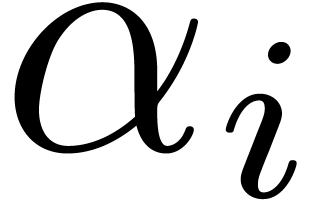 is known for some
is known for some 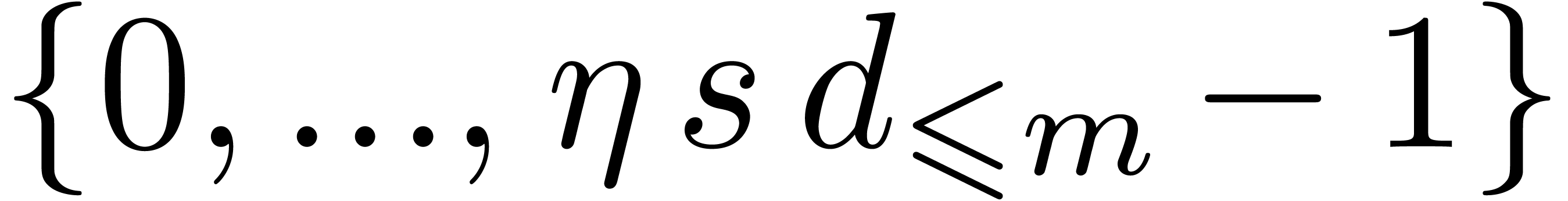 and
random
and
random 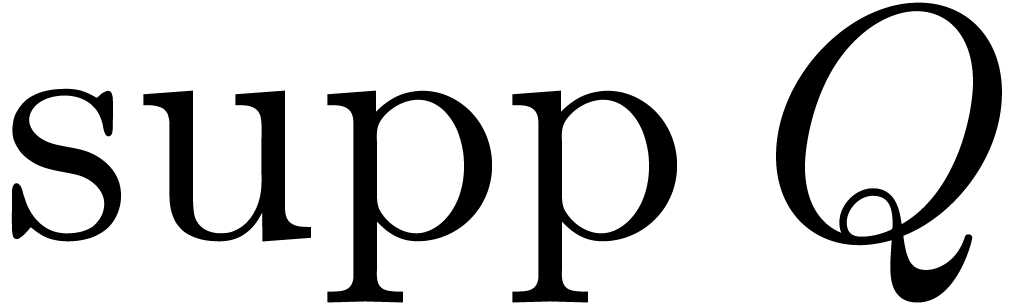 . We will write
. We will write 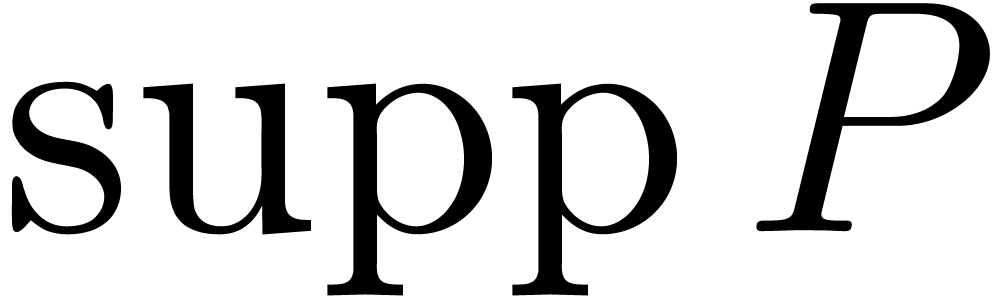 and
and 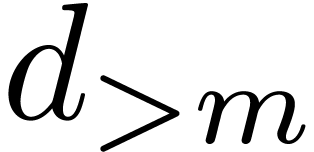 for the total degrees of
for the total degrees of
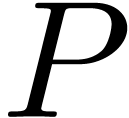 in
in 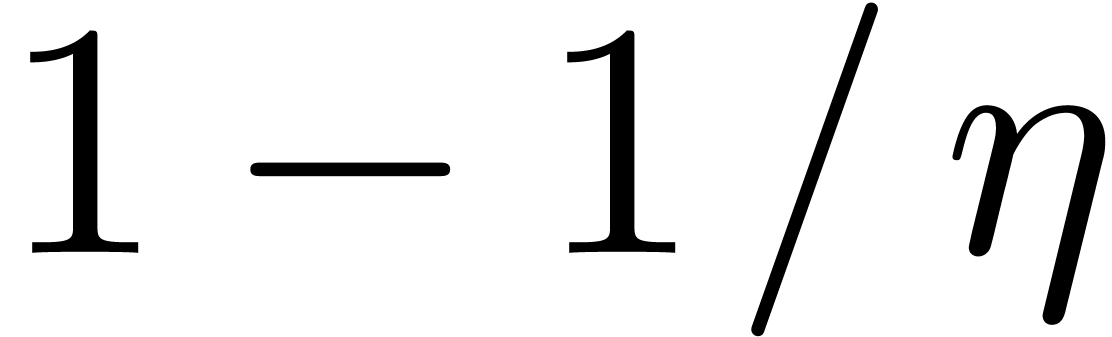 resp.
resp.
 . Let
. Let 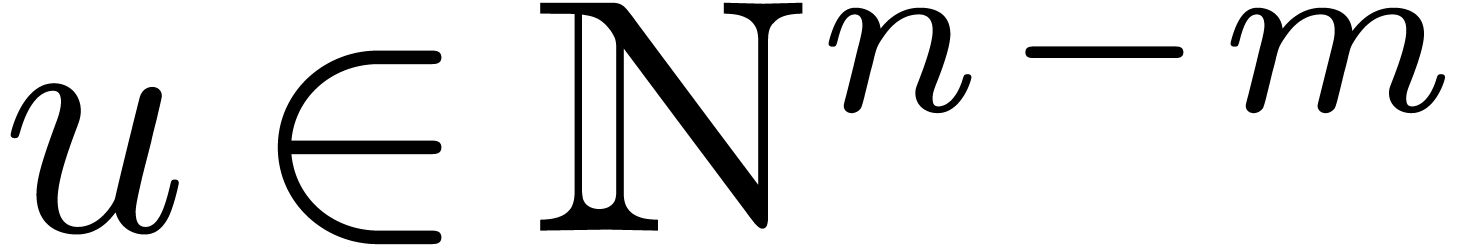 and assume that
and assume that  . By the
Schwartz-Zippel lemma, taking random
. By the
Schwartz-Zippel lemma, taking random  in
in  ensures that
ensures that 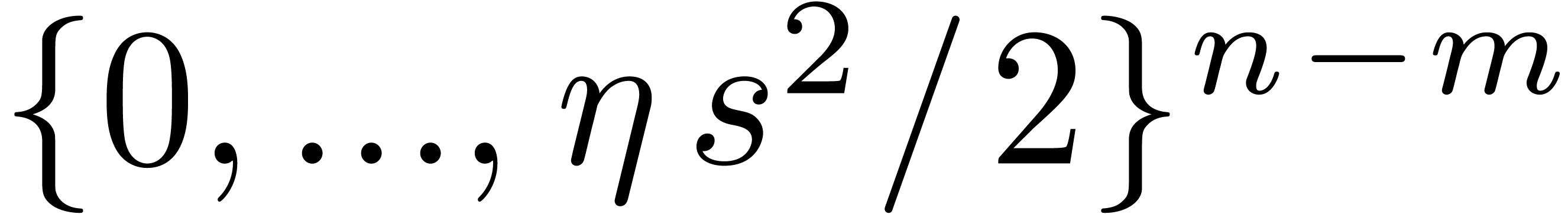 coincides with
the projection of
coincides with
the projection of 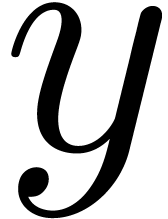 on
on 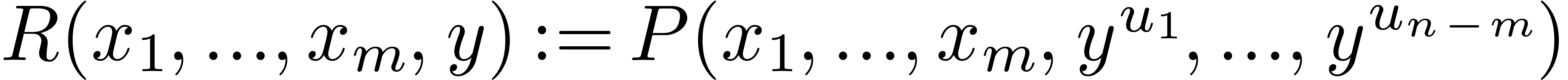 with probability at least
with probability at least  .
.
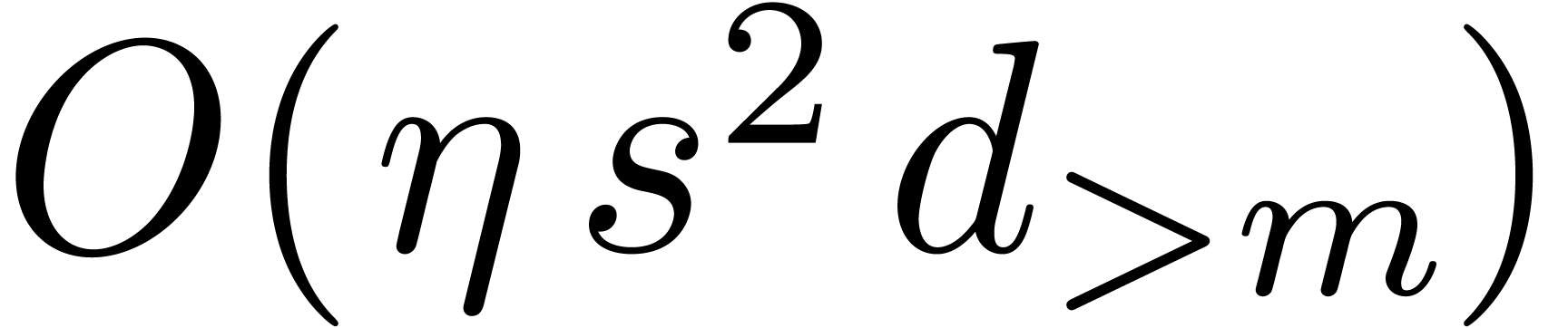 and let
and let 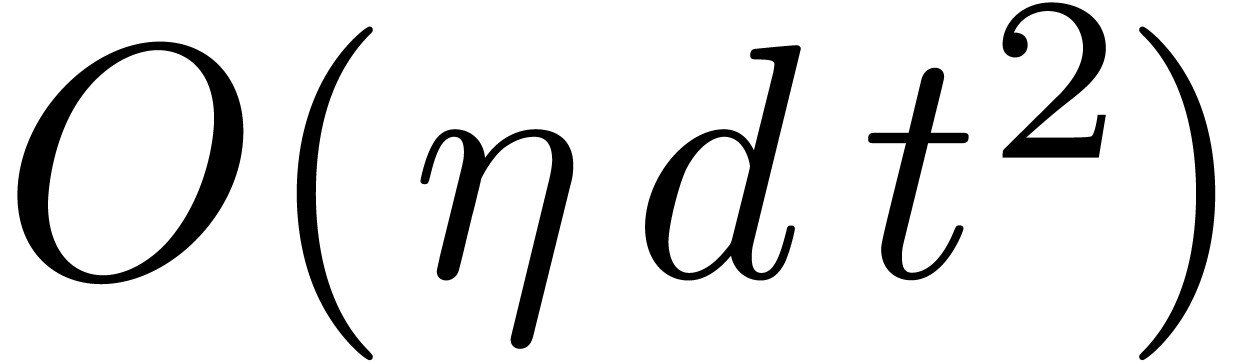 be
such that
be
such that 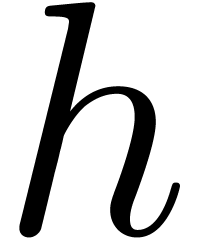 are pairwise distinct. Such a vector
are pairwise distinct. Such a vector
 , seen as a linear form
acting on the exponents, is said to separate the exponents of
, seen as a linear form
acting on the exponents, is said to separate the exponents of  . A random vector in
. A random vector in 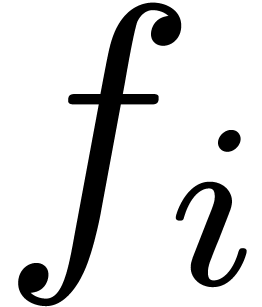 separates exponents with probability at least
separates exponents with probability at least 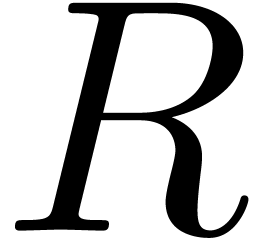 . Since one can quickly verify
that
. Since one can quickly verify
that  is a separating form, it is worth
spending time to search for
is a separating form, it is worth
spending time to search for  with small
entries.
with small
entries.
Now consider a new variable 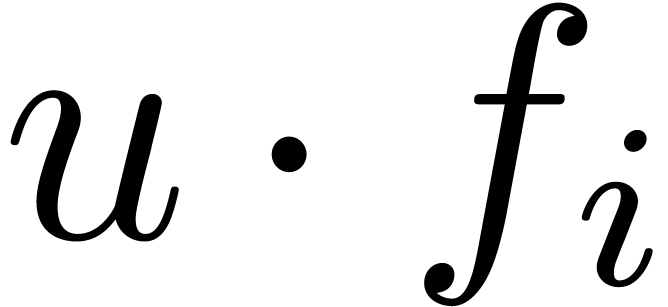 and
and  . The partial degree of
. The partial degree of 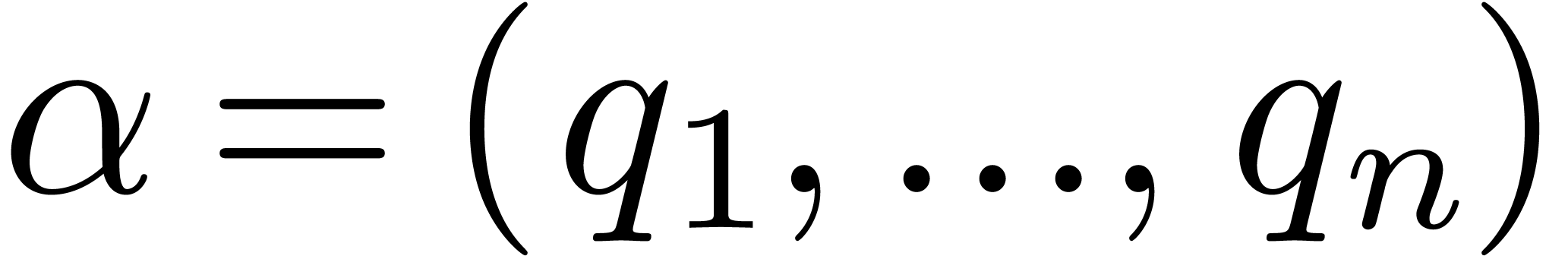 in
in 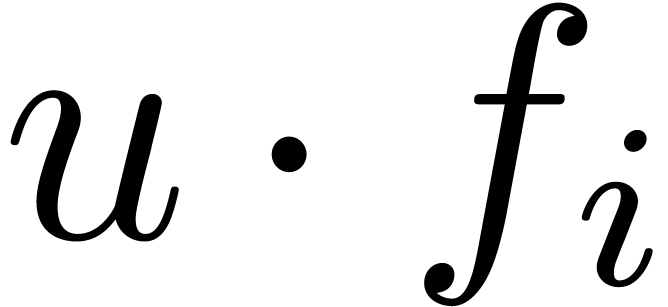 is
is 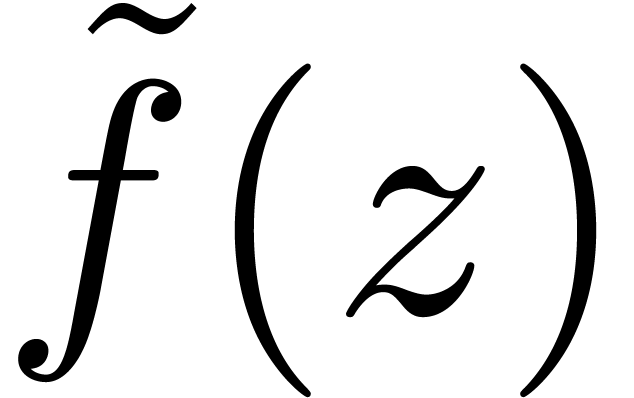 ,
hence its total degree is
,
hence its total degree is 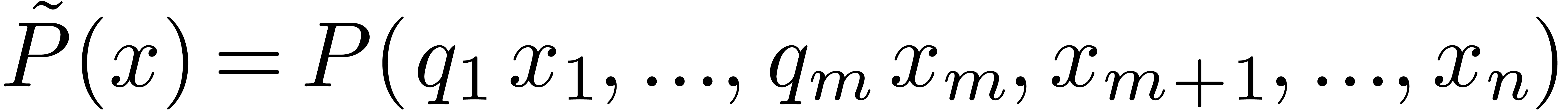 .
If
.
If 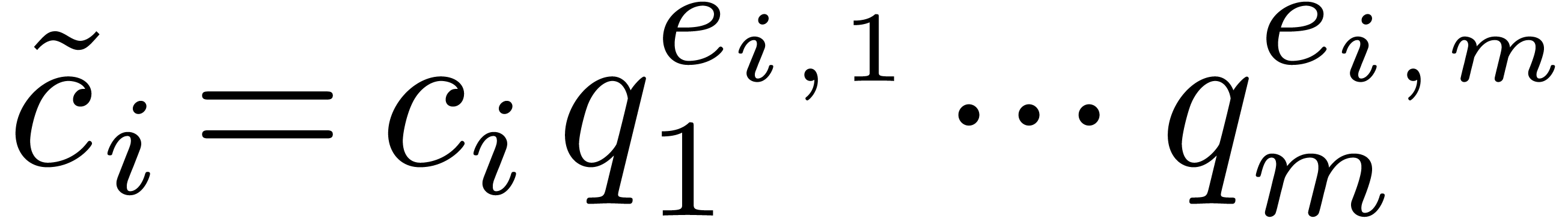 is in the support of
is in the support of 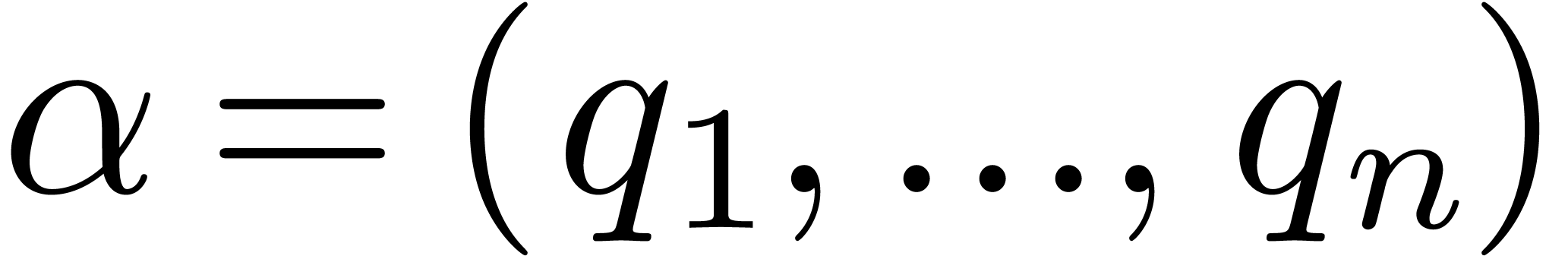 then there exists a unique exponent
then there exists a unique exponent 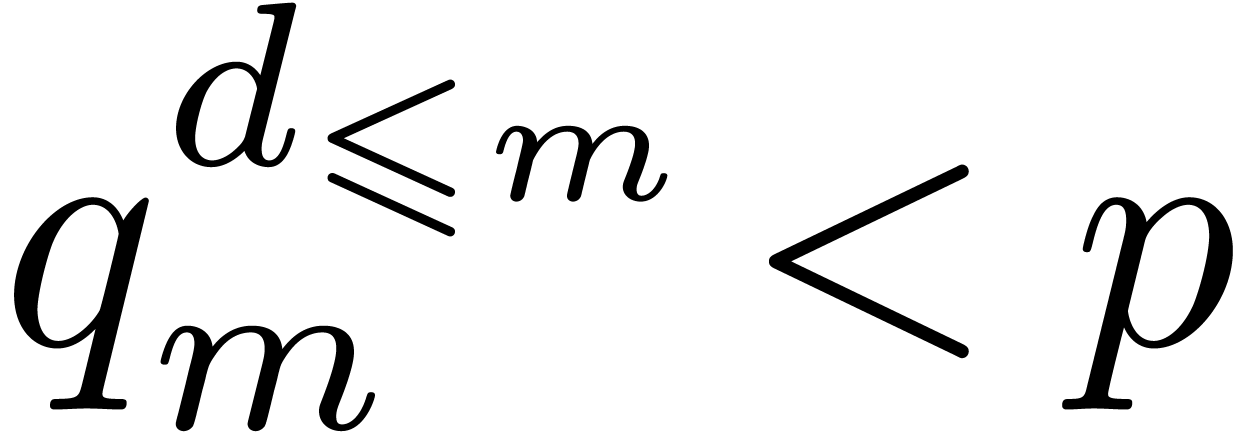 of
of  such that
such that 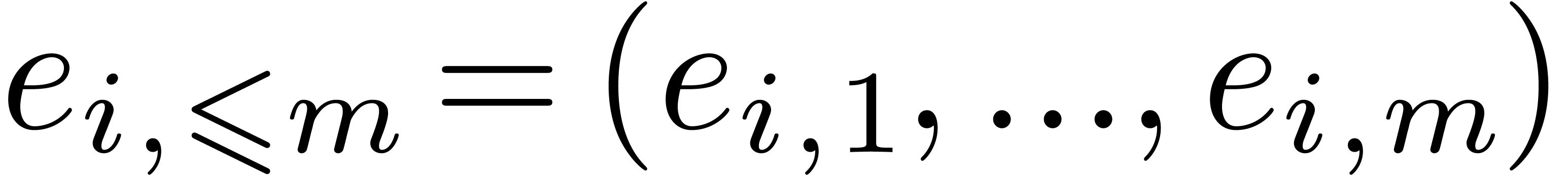 . We
can compute
. We
can compute 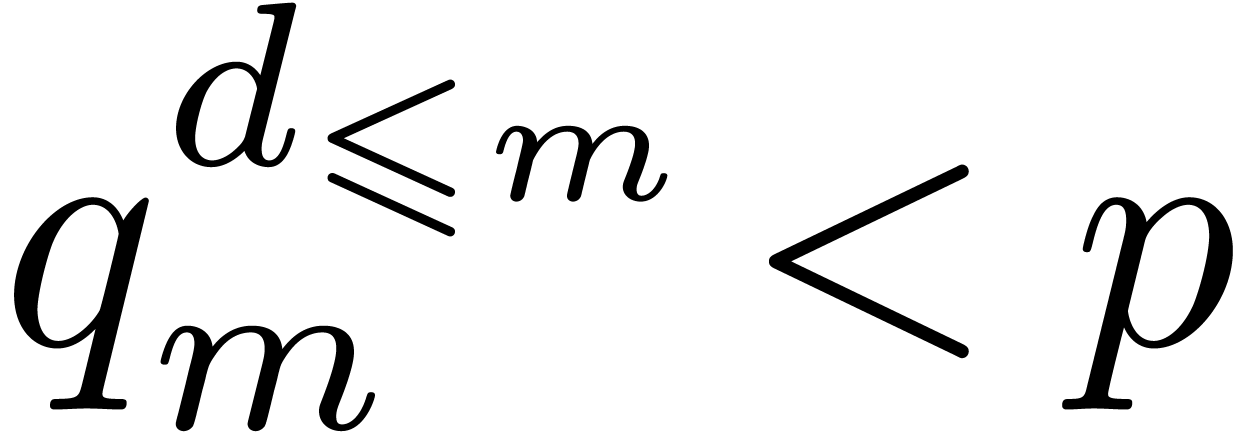 efficiently after sorting the
efficiently after sorting the 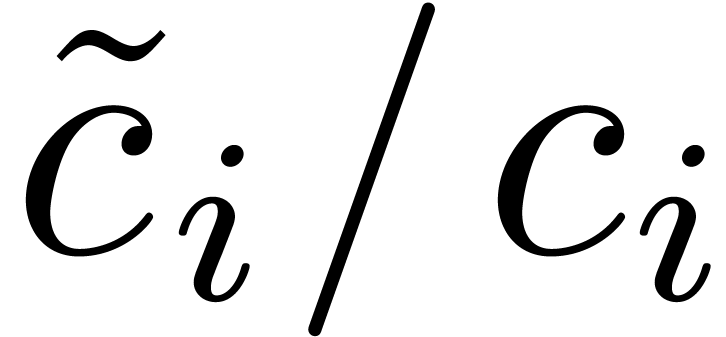 accordingly to the values
accordingly to the values 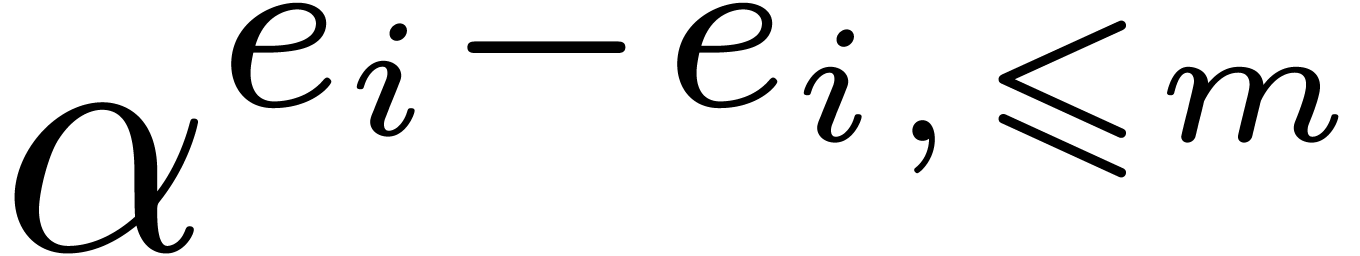 . We have thus shown how to reduce the sparse
interpolation problem for
. We have thus shown how to reduce the sparse
interpolation problem for 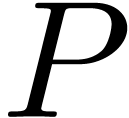 to the
“smaller” sparse interpolation problem for
to the
“smaller” sparse interpolation problem for 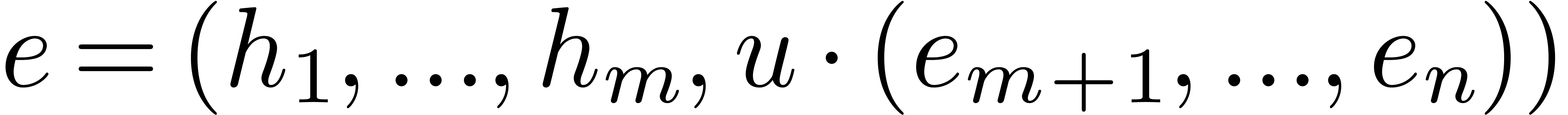 . If
. If 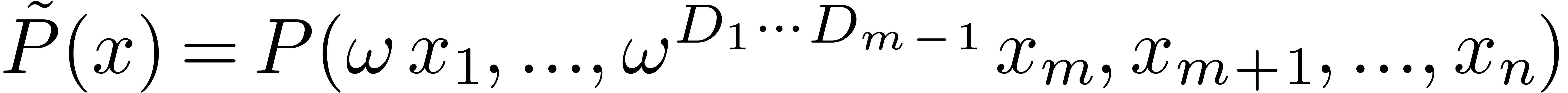 ,
then the method succeeds with high probability.
,
then the method succeeds with high probability.
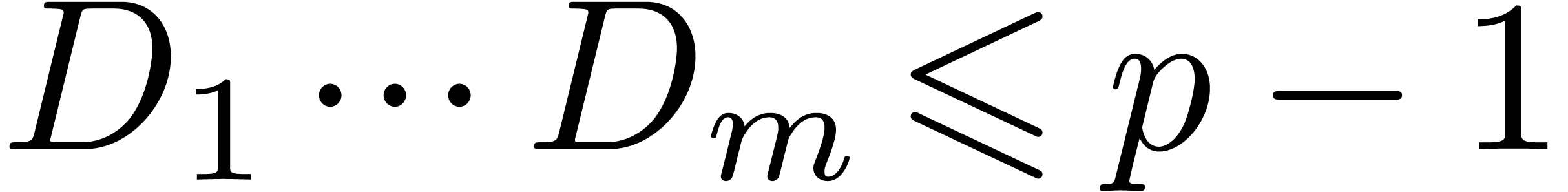 and let
and let 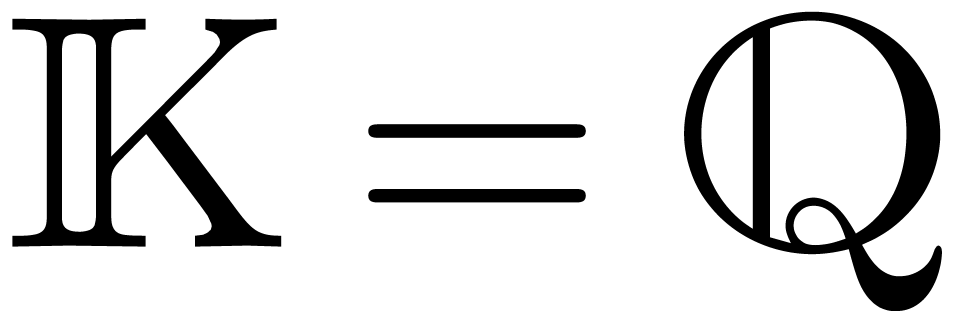 be the
generating series associated to
be the
generating series associated to 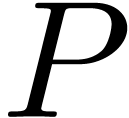 and
and 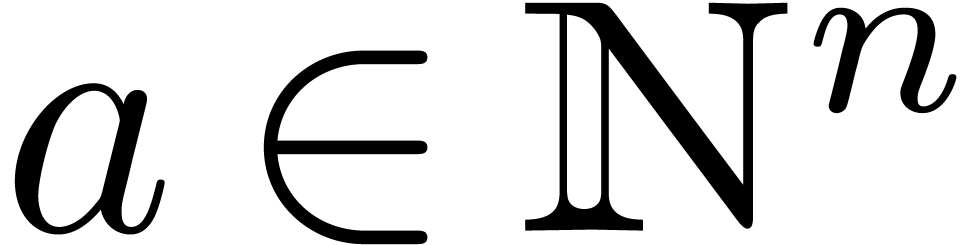 as in (1). In a similar way, we may
associate a generating series
as in (1). In a similar way, we may
associate a generating series 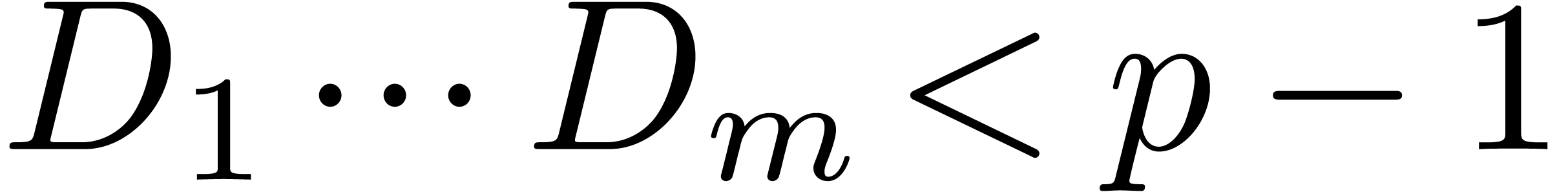 to
to 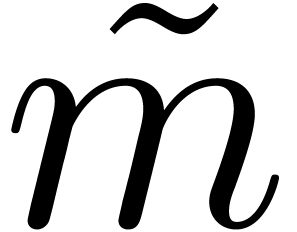 . Using sparse interpolation, we find
. Using sparse interpolation, we find  and
and 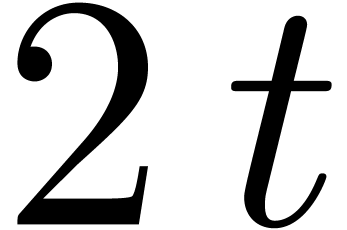 such that (1)
holds, as well as the analogous numbers
such that (1)
holds, as well as the analogous numbers 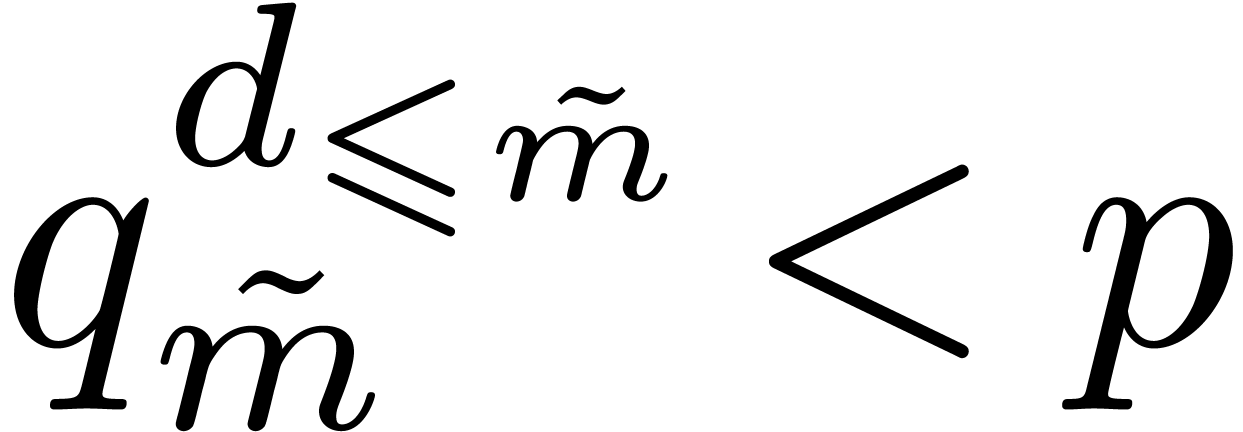 and
and
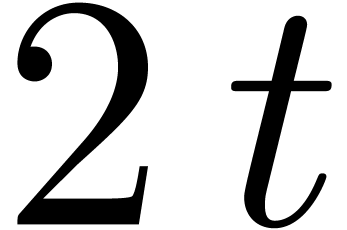 for
for 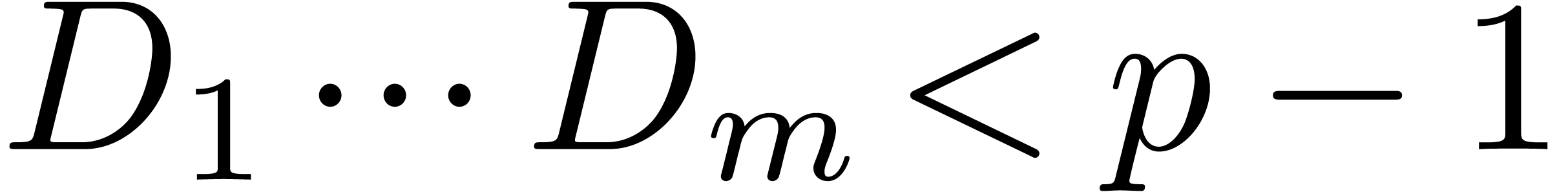 .
If
.
If 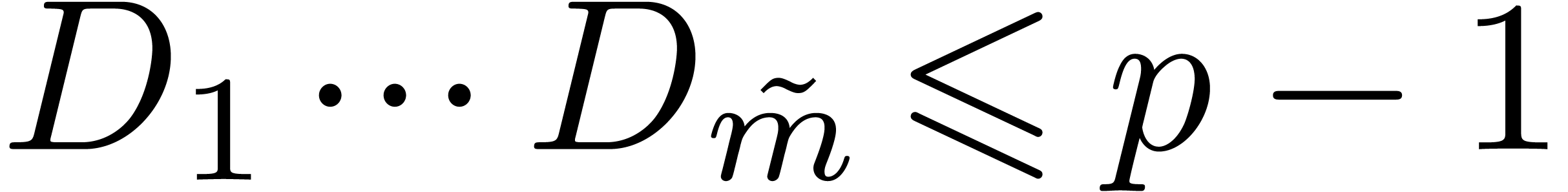 , then these data allow
us to recover the vectors
, then these data allow
us to recover the vectors 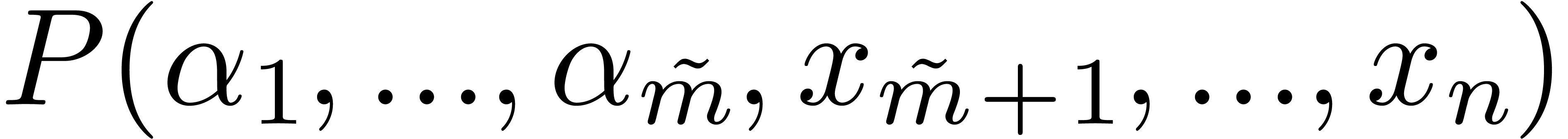 from the ratios
from the ratios
 . We may next compute the
complete
. We may next compute the
complete  from
from  ,
since we assumed
,
since we assumed 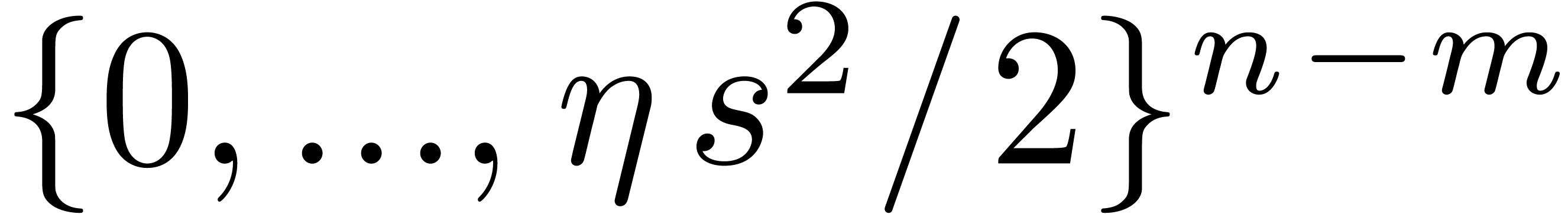 to be known. This strategy
also applies to the “Kronecker substitution” approach. In
that case, we take
to be known. This strategy
also applies to the “Kronecker substitution” approach. In
that case, we take 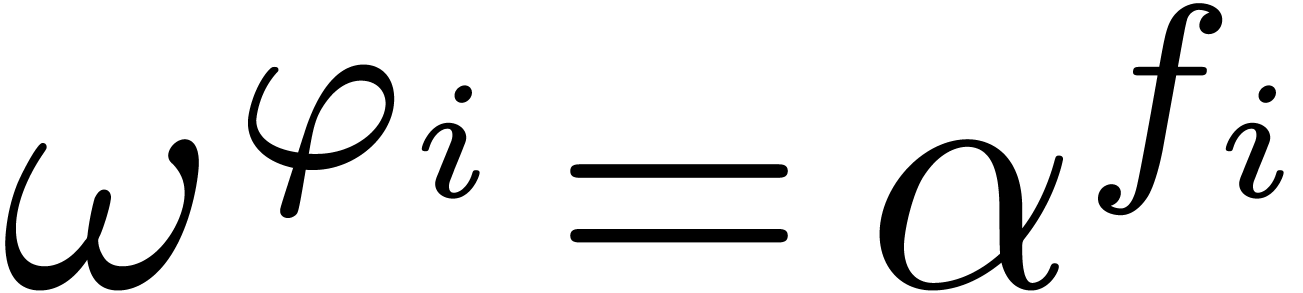 , and we
require that
, and we
require that  . If none of
the conditions
. If none of
the conditions 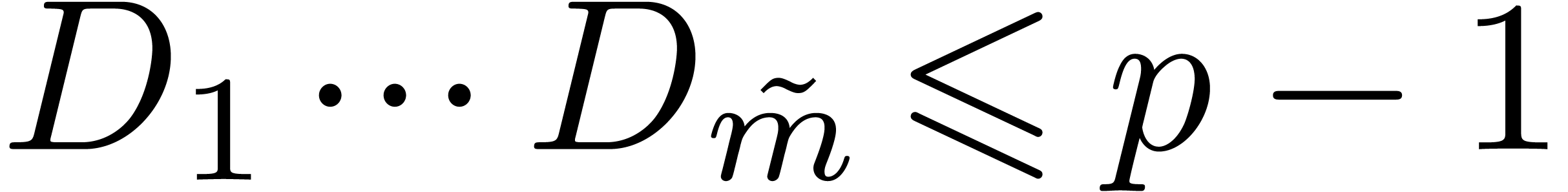 or
or 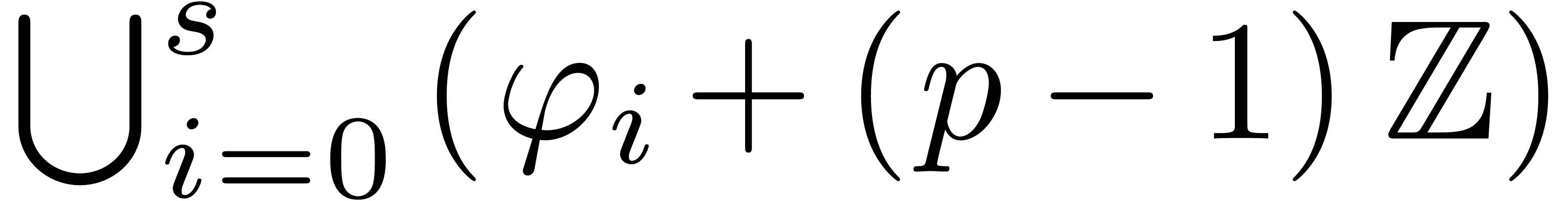 holds, then we let
holds, then we let 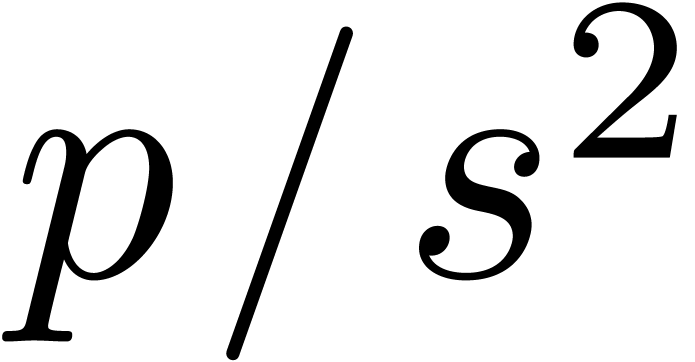 be maximal such that either
be maximal such that either
 or
or 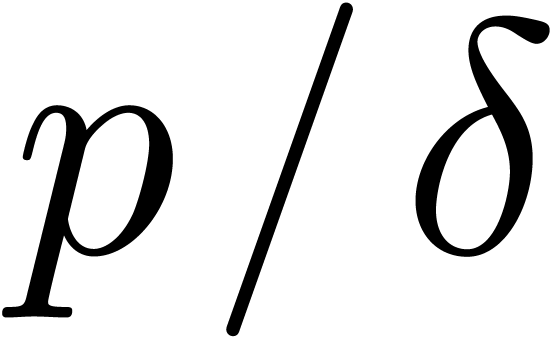 ,
and we recursively apply the strategy to
,
and we recursively apply the strategy to 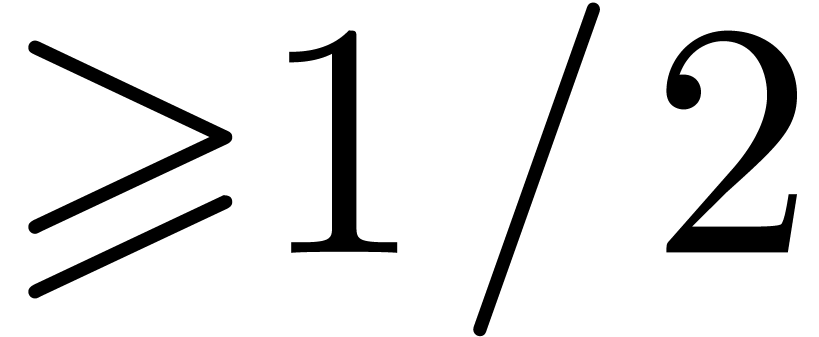 and
then to
and
then to  itself.
itself.
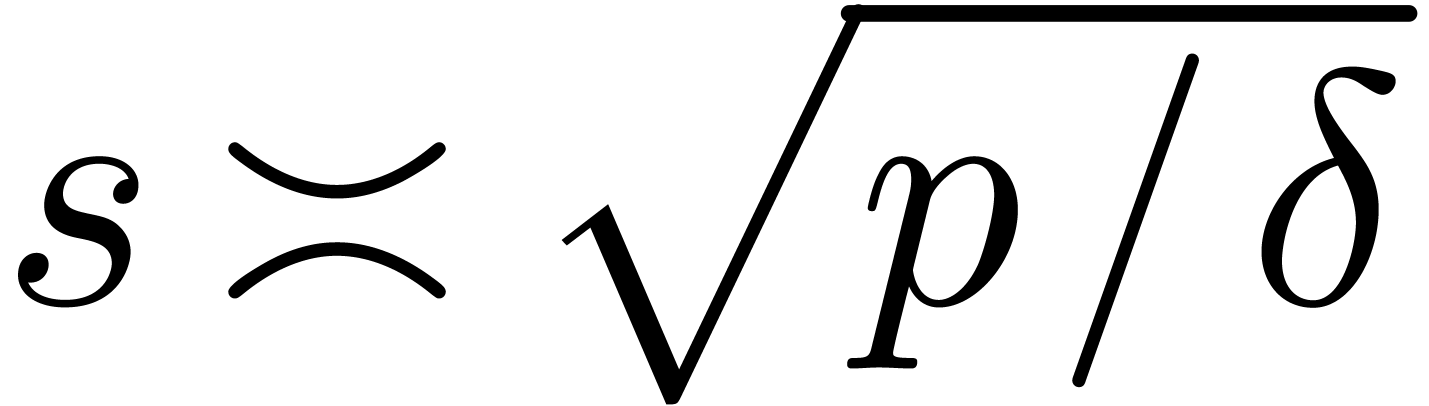 be as in the “Kronecker
substitution” approach. For each
be as in the “Kronecker
substitution” approach. For each 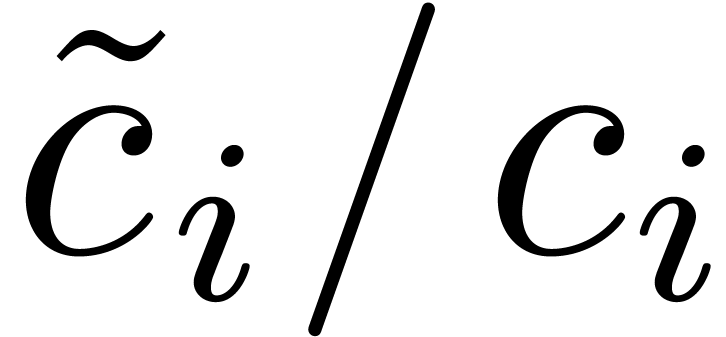 in the
support of
in the
support of 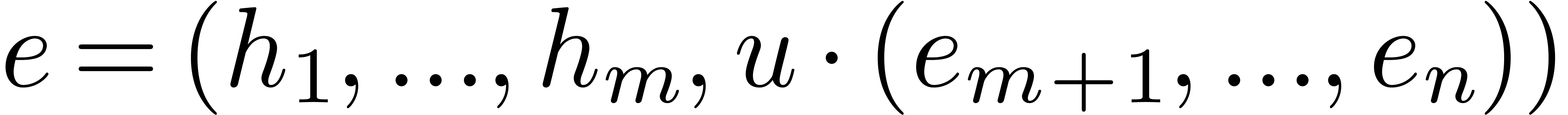 , let
, let 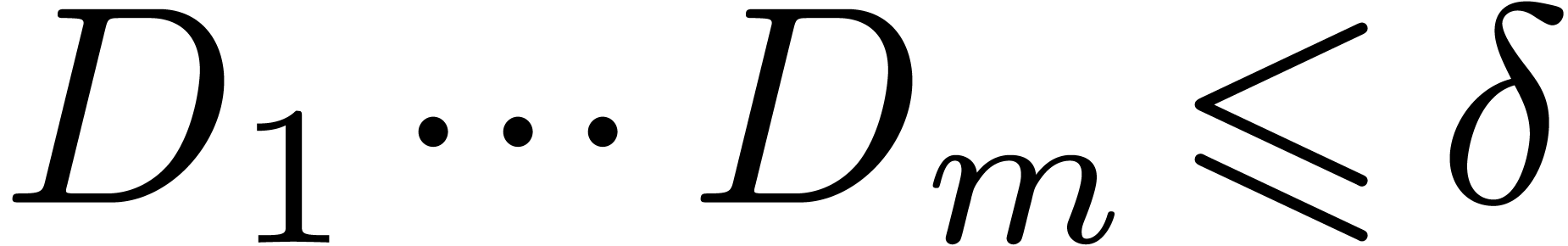 be such that
be such that  ,
and let
,
and let  be the smallest distance between any
two distinct points of
be the smallest distance between any
two distinct points of  . If
. If
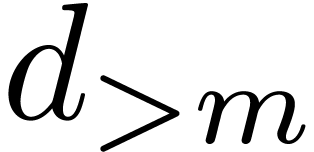 is large and the exponents of
is large and the exponents of 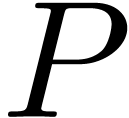 are random, then
are random, then  is expected to be of the
order
is expected to be of the
order 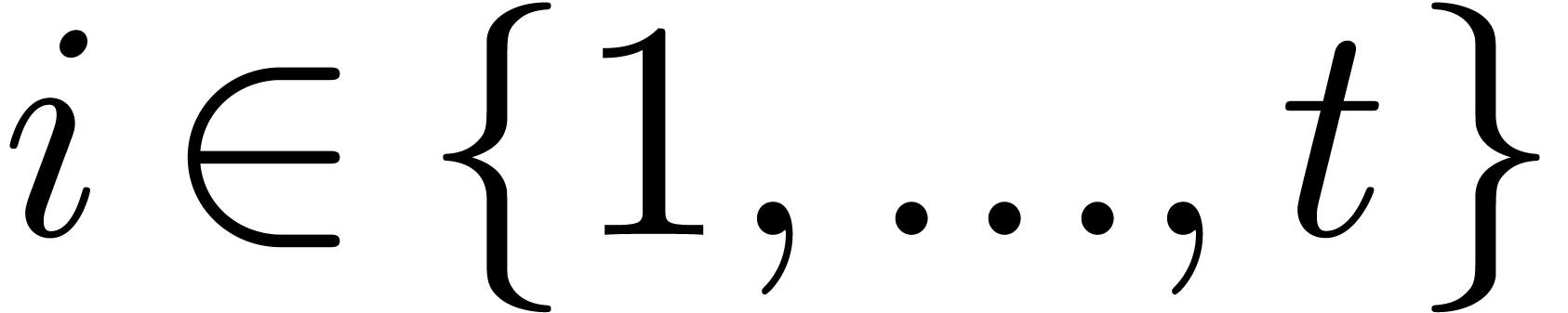 (this follows from the birthday problem:
taking
(this follows from the birthday problem:
taking 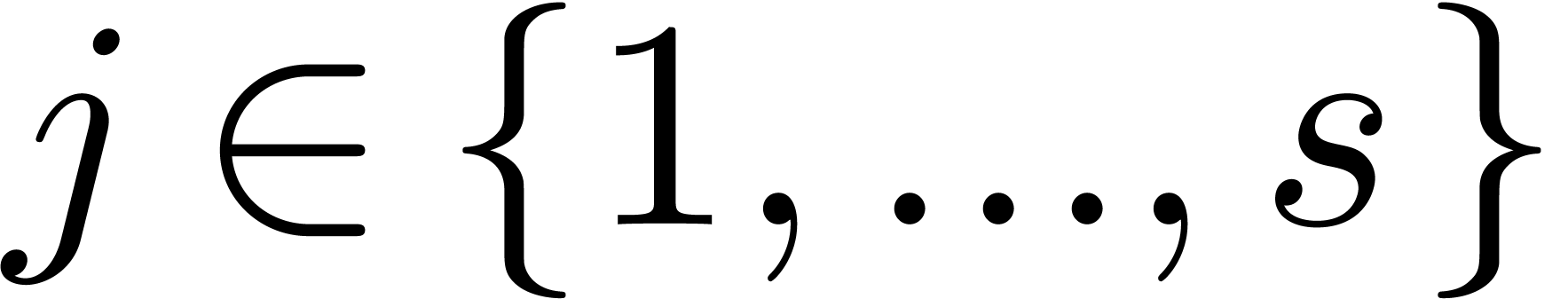 random points out of
random points out of 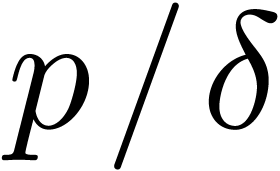 , the probability of a collision is
, the probability of a collision is  as soon as
as soon as 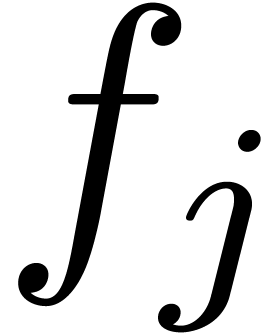 ).
Now assume that
).
Now assume that 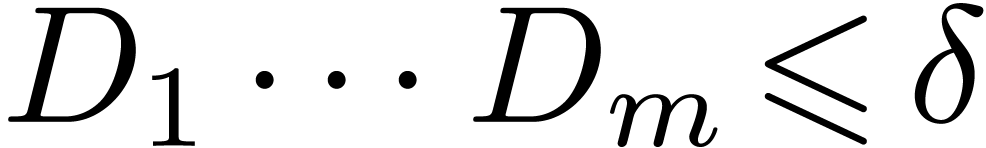 .
Performing sparse interpolation on
.
Performing sparse interpolation on  ,
we obtain numbers
,
we obtain numbers 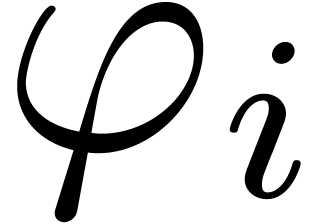 , as well
as the corresponding
, as well
as the corresponding 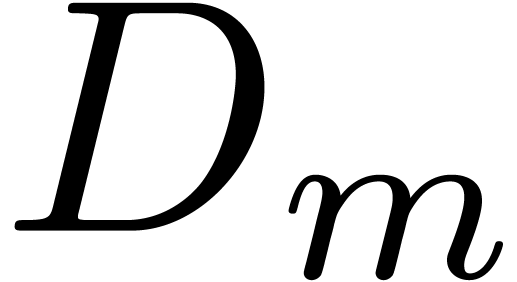 with
with 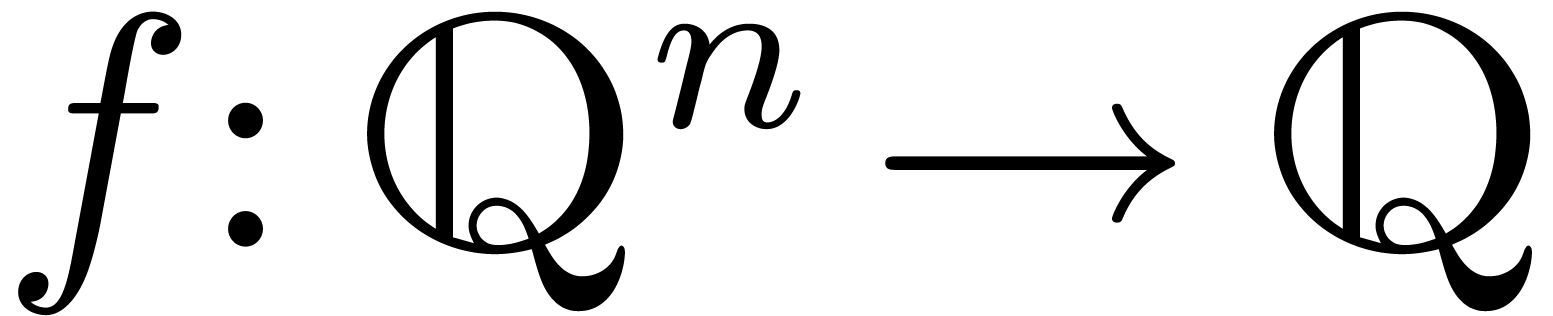 . For each
. For each 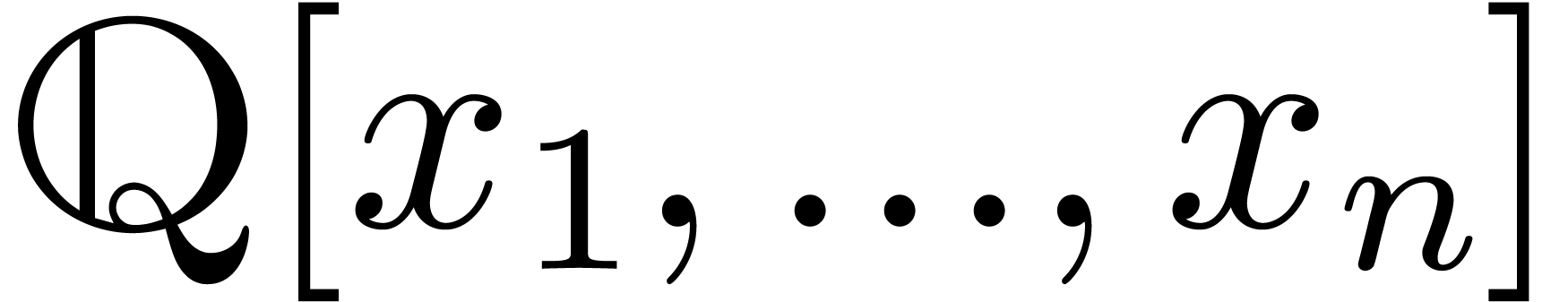 ,
there is unique
,
there is unique 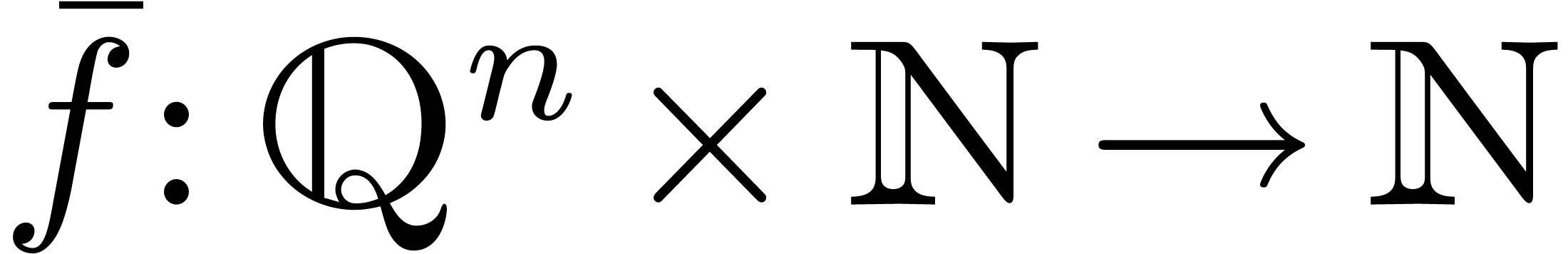 and
and  with
with  . We may thus recover
. We may thus recover
 from
from 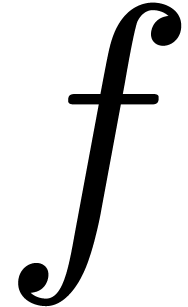 and
and 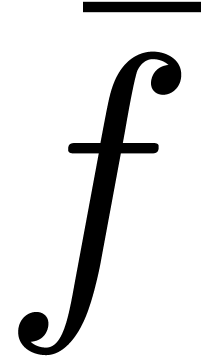 . In order to improve the randomness of the
numbers
. In order to improve the randomness of the
numbers  modulo
modulo  ,
it is recommended to replace
,
it is recommended to replace  by a random
larger number.
by a random
larger number.
The
Multivariate polynomials, power series, jets, and related algorithms are
integrated in the
Sparse interpolation is implemented in multimix/sparse_interpolation.hpp.
Complete examples of use can be found in multimix/test/sparse_interpolation_test.cpp.
If  represents the polynomial function that we
want to interpolate as a polynomial in
represents the polynomial function that we
want to interpolate as a polynomial in  ,
then our main routines take as input a function
,
then our main routines take as input a function  such that
such that  is the preimage of
is the preimage of  computed modulo a prime number
computed modulo a prime number 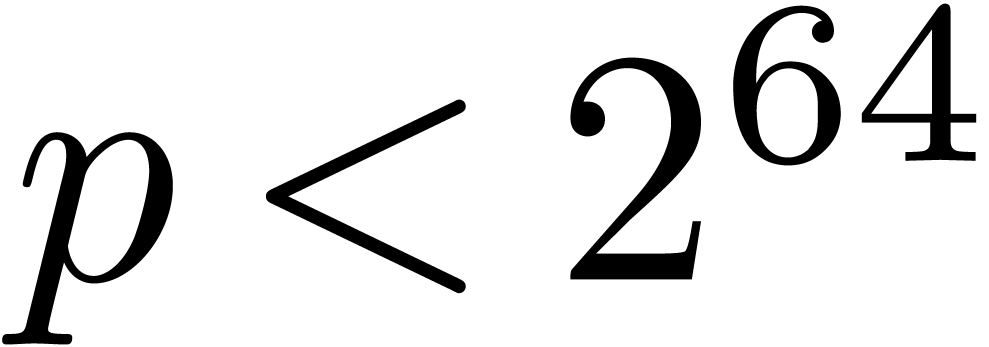 .
If computing
.
If computing  modulo
modulo 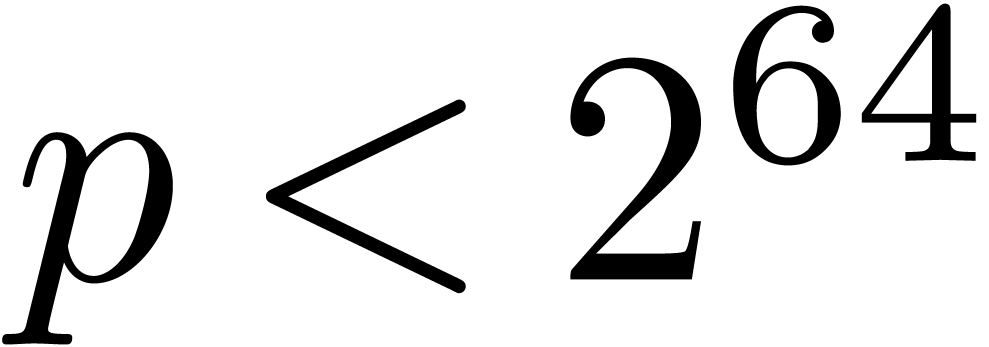 involves a division by zero, then an error is raised. For efficiency
reasons, such a function
involves a division by zero, then an error is raised. For efficiency
reasons, such a function  can be essentially a
pointer to a compiled function. Of course DAGs over
can be essentially a
pointer to a compiled function. Of course DAGs over  or
or 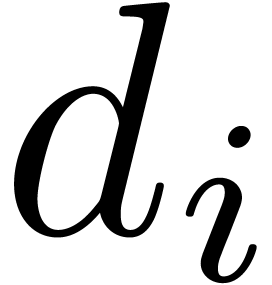 can be converted to such functions
via SLPs.
can be converted to such functions
via SLPs.
In the next examples, which can be found in multimix/bench/sparse_interpolation_bench.cpp, we illustrate the behaviours of the aforementioned algorithms on an Intel(R) Core(TM) i7-3720QM CPU @ 2.60GHz platform with 8 GB of 1600 MHz DDR3.
Example  polynomials with
polynomials with  terms, in
terms, in  variables, and with
partial degrees at most
variables, and with
partial degrees at most  , and
compute the support of their product. With
, and
compute the support of their product. With  ,
,
 ,
,  ,
,  , then
a direct use of the “Kronecker substitution” involves
computing with GMP based modular integers of bit size about 160: the
total time amounts to 171 s (91 s are spent in the Cantor-Zassenhaus
stage for root finding). With the “coefficient ratios”
approach, the set of variables is split into 3 blocks and all the
computations can be done with 64-bit integers for a total time of 31 s
(most of the time is still spent in the Cantor-Zassenhaus stages, but
relatively less in the discrete logarithm computations). With the
“closest points” technique the set of variables is split
into 5 blocks and all the computations are also done with 64-bit
integers for a total time of 47 s. The “separating form”
approach is not competitive here, since it does not manage to keep the
computations on 64 bits integers only. Nevertheless, in a
“lacunary polynomials” context, namely when
, then
a direct use of the “Kronecker substitution” involves
computing with GMP based modular integers of bit size about 160: the
total time amounts to 171 s (91 s are spent in the Cantor-Zassenhaus
stage for root finding). With the “coefficient ratios”
approach, the set of variables is split into 3 blocks and all the
computations can be done with 64-bit integers for a total time of 31 s
(most of the time is still spent in the Cantor-Zassenhaus stages, but
relatively less in the discrete logarithm computations). With the
“closest points” technique the set of variables is split
into 5 blocks and all the computations are also done with 64-bit
integers for a total time of 47 s. The “separating form”
approach is not competitive here, since it does not manage to keep the
computations on 64 bits integers only. Nevertheless, in a
“lacunary polynomials” context, namely when  becomes very large, the computation of a very large smooth prime number
becomes very expensive, and the “separating form” point of
view becomes useful.
becomes very large, the computation of a very large smooth prime number
becomes very expensive, and the “separating form” point of
view becomes useful.
Example  matrix whose entries are independent variables. This determinant is a
polynomial in
matrix whose entries are independent variables. This determinant is a
polynomial in  variables with
variables with  terms, whose total degree is
terms, whose total degree is  and whose partial
degrees are all
and whose partial
degrees are all  . The
following table displays timings for interpolating this polynomial using
the “Kronecker substitution” approach:
. The
following table displays timings for interpolating this polynomial using
the “Kronecker substitution” approach:
|
||||||||||
For  computations are performed via
computations are performed via
 -bits modular arithmetic.
Here we used a fast compiled determinant function, so that most of the
time is spent in the Cantor-Zassenhaus stage. We noticed that the
“closest points” strategy is not well suited to this
problem. The “coefficient ratios” approach allows to perform
all the computations on 64-bits for
-bits modular arithmetic.
Here we used a fast compiled determinant function, so that most of the
time is spent in the Cantor-Zassenhaus stage. We noticed that the
“closest points” strategy is not well suited to this
problem. The “coefficient ratios” approach allows to perform
all the computations on 64-bits for  within
within  s, but it is penalized by two calls to
Cantor-Zassenhaus.
s, but it is penalized by two calls to
Cantor-Zassenhaus.
For a convenient use, our sparse interpolation routine is available
inside the  for
for  in
in  s, and for
s, and for  in
in  s. As a
comparison, the function sinterp, modulo
s. As a
comparison, the function sinterp, modulo  , of
, of  , and
, and  hour for
hour for  .
.
Mmx] |
use "multimix"; n:= 5; |
Mmx] |
det_mod (v: Vector Integer, p: Integer): Integer == {
w == [ z mod modulus p | z in v ];
M == [ @(w[i * n, (i+1) * n]) || i in 0..n ];
return preimage det M; }; |
Mmx] |
coords == coordinates (coordinate ('x[i,j]) | i in 0..n | j in 0..n); |
Mmx] |
#as_mvpolynomial% (det_mod, coords, 1000) |

A. Arnold, M. Giesbrecht, and D. S. Roche. Faster sparse polynomial interpolation of straight-line programs over finite fields. Technical report, arXiv:1401.4744, 2014.
A. Arnold and D. S. Roche. Multivariate sparse interpolation using randomized Kronecker substitutions. Technical report, arXiv:1401.6694, 2014.
M. Ben-Or and P. Tiwari. A deterministic algorithm for sparse multivariate polynomial interpolation. In STOC '88: Proceedings of the twentieth annual ACM symposium on Theory of computing, pages 301–309, New York, NY, USA, 1988. ACM Press.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial multiplication. J. Symbolic Comput., 50:227–254, 2013.
J. van der Hoeven, G. Lecerf, B. Mourrain, et al. Mathemagix, 2002. http://www.mathemagix.org.
M. Javadi and M. Monagan. Parallel sparse polynomial interpolation over finite fields. In Proceedings of the 4th International Workshop on Parallel and Symbolic Computation, PASCO '10, pages 160–168. ACM Press, 2010.
E. Kaltofen. Fifteen years after DSC and WLSS2, what parallel computations I do today. Invited lecture at PASCO 2010. In Proceedings of the 4th International Workshop on Parallel and Symbolic Computation, PASCO '10, pages 10–17, New York, NY, USA, 2010. ACM Press.
E. Kaltofen, Y. N. Lakshman, and J.-M. Wiley. Modular rational sparse multivariate polynomial interpolation. In ISSAC '90: Proceedings of the international symposium on Symbolic and algebraic computation, pages 135–139, New York, NY, USA, 1990. ACM Press.
E. Kaltofen and Wen-shin Lee. Early termination in sparse interpolation algorithms. J. Symbolic Comput., 36(3–4):365–400, 2003.
S. C. Pohlig and M. E. Hellman. An improved algorithm
for computing logarithms over GF and its
cryptographic significance. IEEE Trans. Inf. Theory,
24(1):106–110, 1978.
and its
cryptographic significance. IEEE Trans. Inf. Theory,
24(1):106–110, 1978.