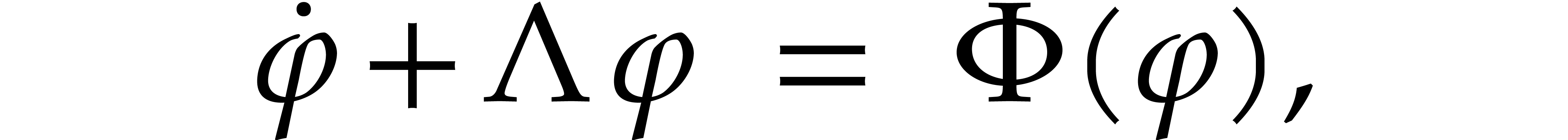 |
|
In this paper, we present various new algorithms for the integration of stiff differential equations that allow the step size to increase proportionally with time. We mainly focus on high precision integrators, which leads us to use high order Taylor schemes. We will also present various algorithms for certifying the numerical results, again with the property that the step size increases with time.
|
Consider the differential equation
where 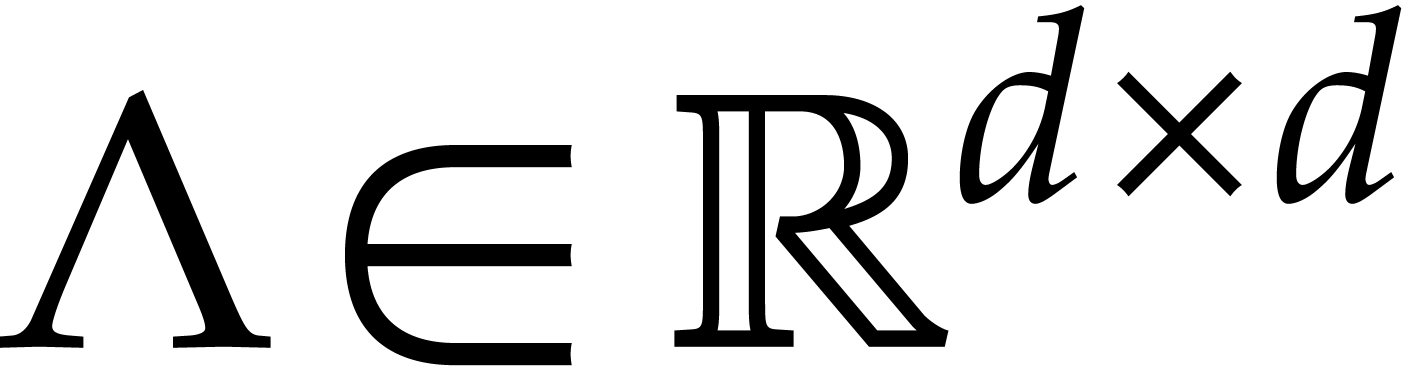 is a diagonal matrix with positive real
entries
is a diagonal matrix with positive real
entries  , and where
, and where 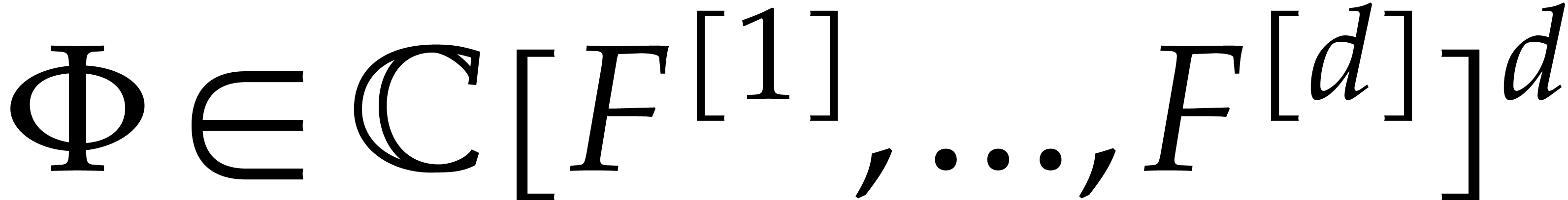 is a polynomial forcing term. We are interested in
analytic solutions
is a polynomial forcing term. We are interested in
analytic solutions 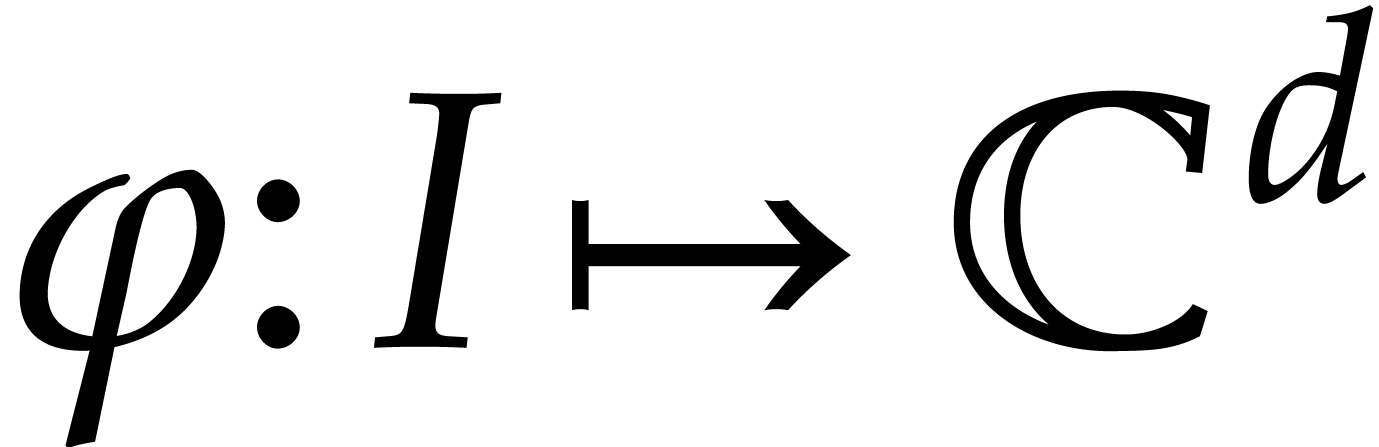 , where
, where
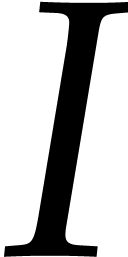 is either an interval of the form
is either an interval of the form 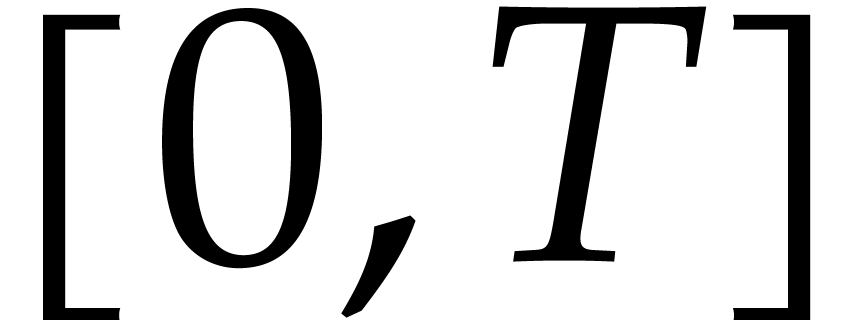 with
with  , or a
larger subset of
, or a
larger subset of  that contains an interval of
this form. The
that contains an interval of
this form. The  components of this mapping will
be written
components of this mapping will
be written 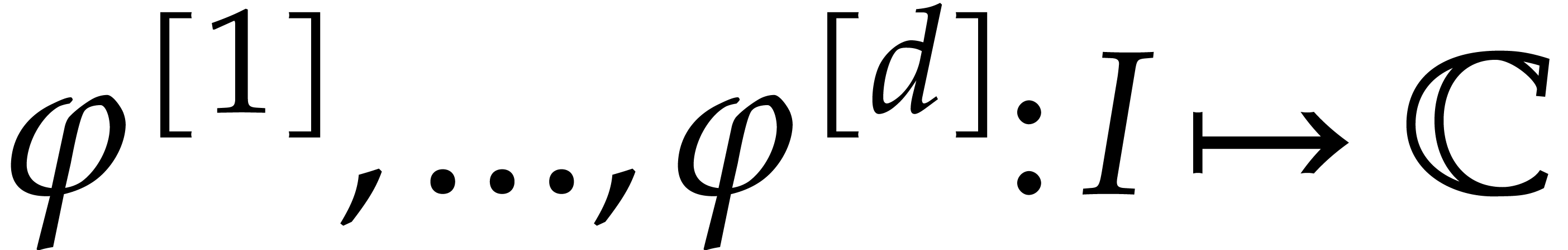 , whereas
subscripts will be reserved for the coefficients of local power series
solutions. A similar notation will be used for the components of other
vectors and matrices.
, whereas
subscripts will be reserved for the coefficients of local power series
solutions. A similar notation will be used for the components of other
vectors and matrices.
If the largest eigenvalue 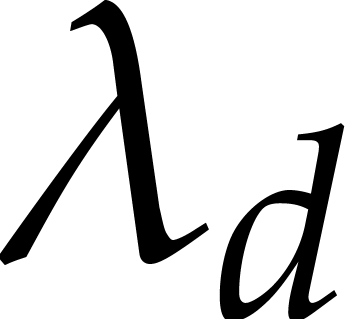 of
of  gets large with respect to the forcing term
gets large with respect to the forcing term  , then the equation (1) is said to be
stiff. Generic numerical integration schemes experience
difficulties with this kind of equations, whether we use Euler's method,
a Runge–Kutta scheme, or high order algorithms based on Taylor
expansions. Roughly speaking, the problem is that all generic methods
become inaccurate when the step size exceeds
, then the equation (1) is said to be
stiff. Generic numerical integration schemes experience
difficulties with this kind of equations, whether we use Euler's method,
a Runge–Kutta scheme, or high order algorithms based on Taylor
expansions. Roughly speaking, the problem is that all generic methods
become inaccurate when the step size exceeds 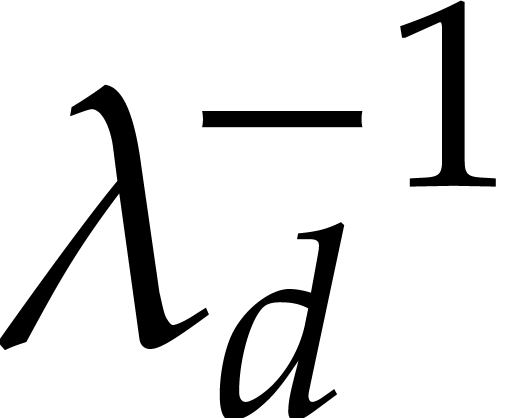 . One of the most difficult cases is when
. One of the most difficult cases is when  is large, but each of the quotients
is large, but each of the quotients 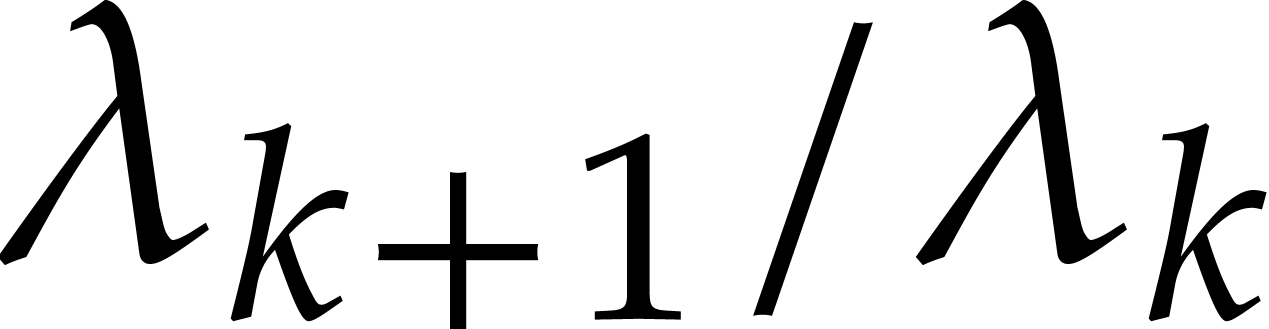 remains reasonably close to one. This happens for instance when
remains reasonably close to one. This happens for instance when 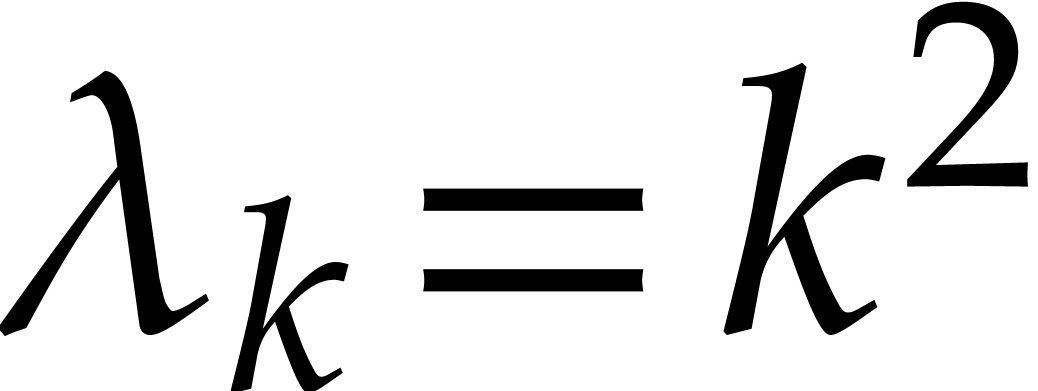 , a case that is naturally
encountered when discretizing certain partial differential equations.
, a case that is naturally
encountered when discretizing certain partial differential equations.
Implicit integration schemes allow for larger step sizes than generic
methods, but involve the computation and inversion of Jacobian matrices,
which may be expensive in high dimension  .
But even such more expensive schemes only seem to deal with the step
size issue in a somewhat heuristic manner: one typically selects a
scheme that is “stable” when applied to any equation
.
But even such more expensive schemes only seem to deal with the step
size issue in a somewhat heuristic manner: one typically selects a
scheme that is “stable” when applied to any equation 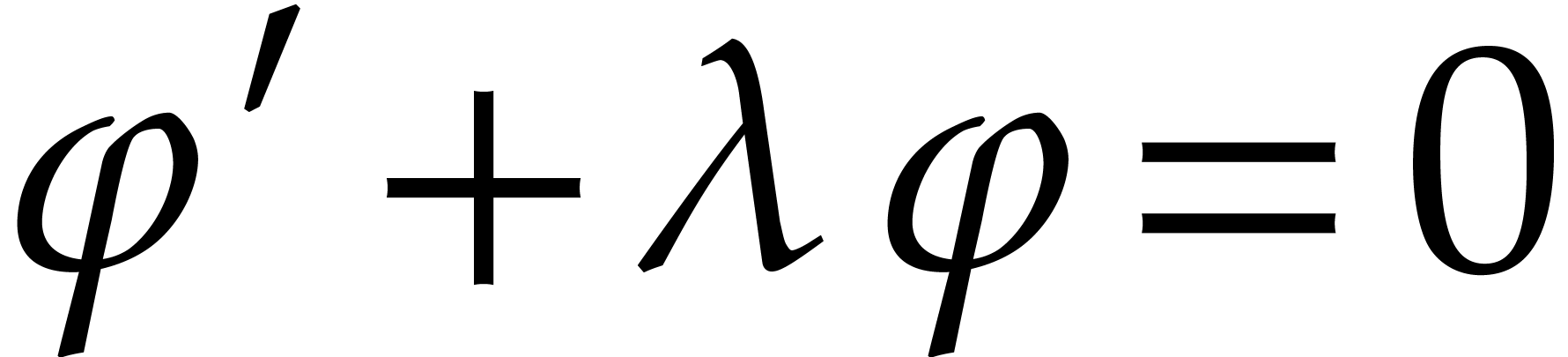 for all
for all  ,
and then hopes that the scheme continues to behave well for the actual
target equation (1). We refer to [25, Section
17.5] and [4, Section 6] for more information on classical
integration schemes for stiff differential equations.
,
and then hopes that the scheme continues to behave well for the actual
target equation (1). We refer to [25, Section
17.5] and [4, Section 6] for more information on classical
integration schemes for stiff differential equations.
We are mainly interested in high precision computations, in which case
it is natural to use high order integration schemes that are based on
Taylor expansions. In this context, we are not aware of any numerical
method that allows the step size to increase proportionally with time.
The main aim of this paper is to present such a method, together with
several variants, as well as a way to compute rigorous bounds for the
error. Our fastest method is an explicit scheme, but its convergence
deteriorates when the eigenvalues 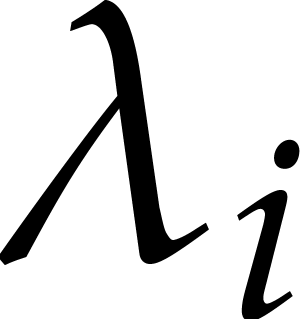 are close. The
slower and rigourous counterparts rely on the computation of Jacobian
matrices.
are close. The
slower and rigourous counterparts rely on the computation of Jacobian
matrices.
In sections 3 and 4, we recall various
approaches that can be used to compute truncated series solutions to
initial value problems and how to derive high order integration schemes
from this. More precisely, given a numerical approximation 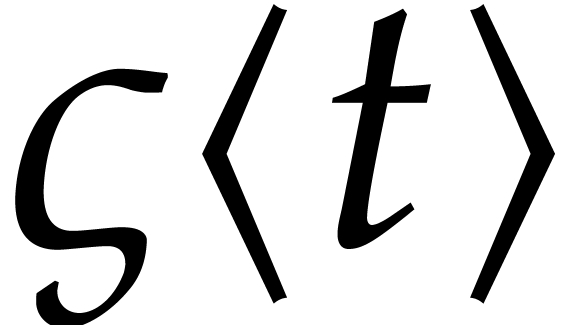 for
for 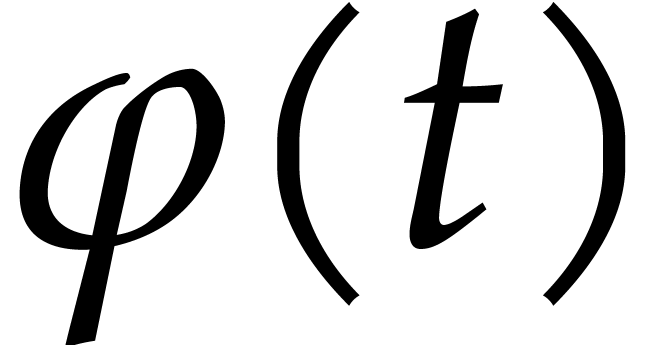 at time
at time  , we compute the first
, we compute the first  terms
of a power series solution
terms
of a power series solution 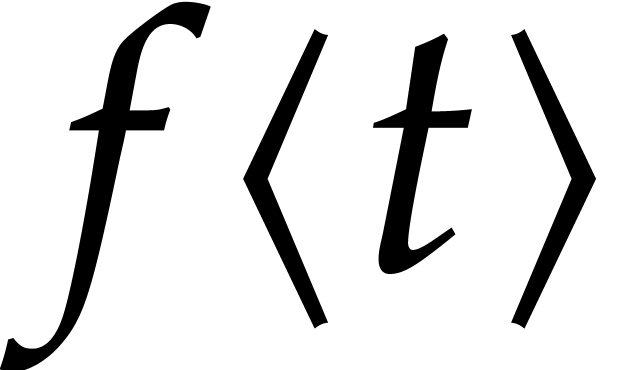 to the initial value
problem
to the initial value
problem
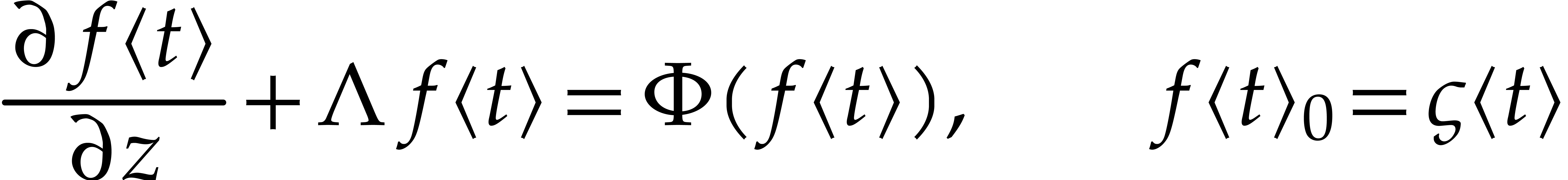 |
(2) |
and return 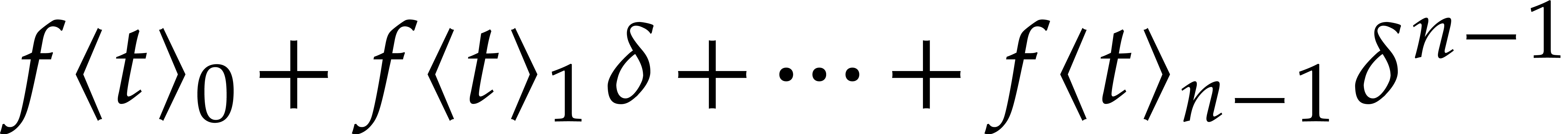 as an approximation of
as an approximation of 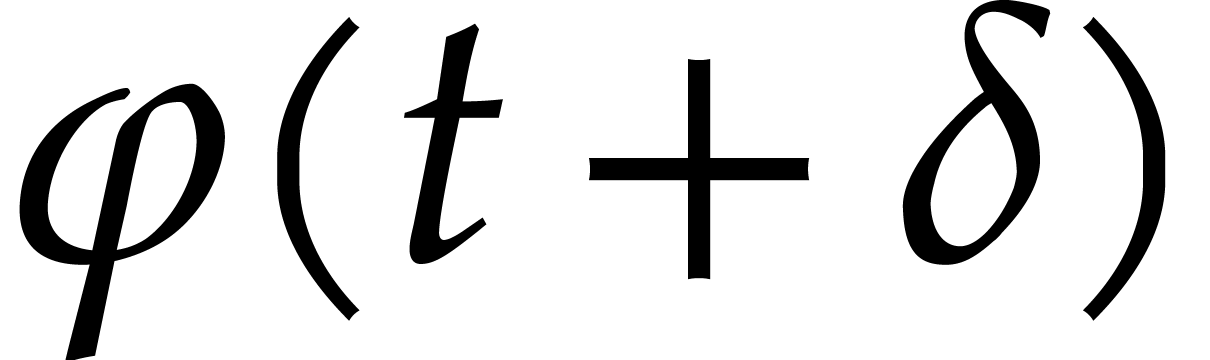 for some suitable step size
for some suitable step size  .
The inaccuracy of such schemes for larger step sizes is due to the fact
that the
.
The inaccuracy of such schemes for larger step sizes is due to the fact
that the 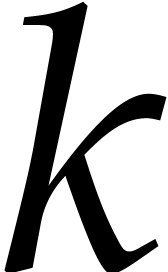 -th coefficient of
-th coefficient of
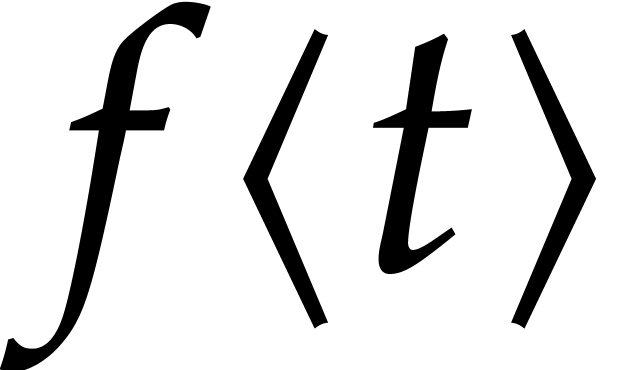 tends to change proportionally to
tends to change proportionally to 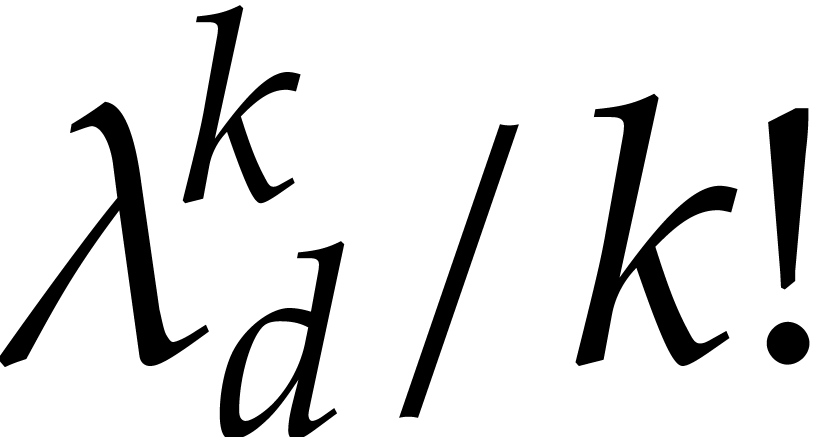 for slight perturbations of
for slight perturbations of 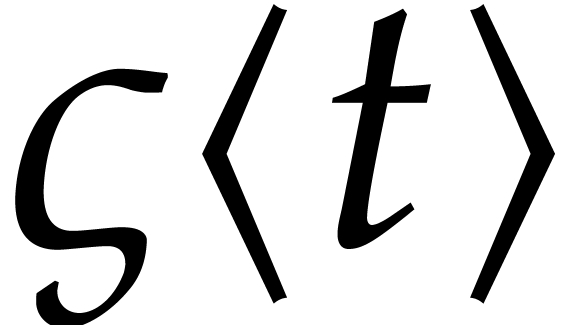 .
If
.
If 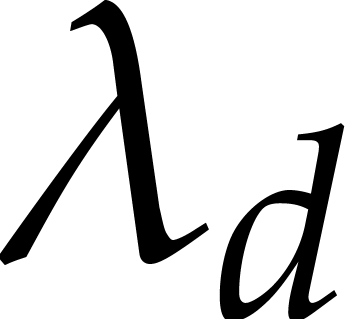 is large, then even small multiples of
is large, then even small multiples of 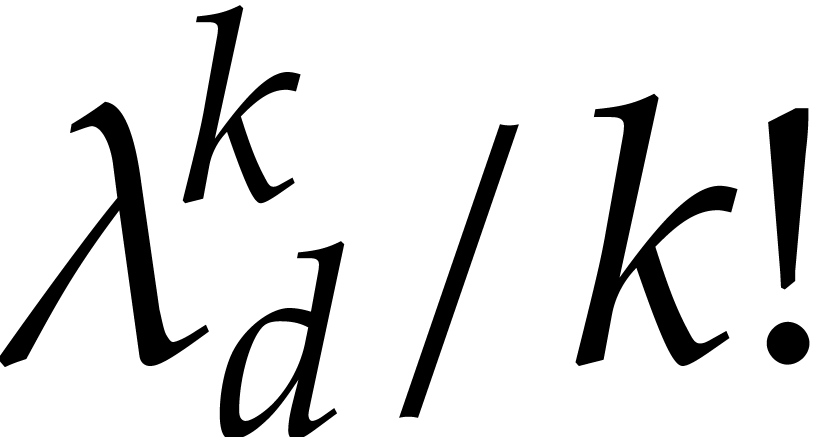 quickly dominate
quickly dominate 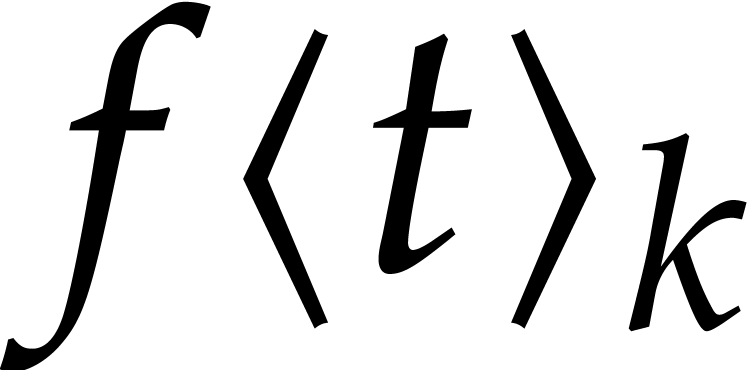 ,
which severely limits the step sizes that we can use.
,
which severely limits the step sizes that we can use.
This numerical instability is an unpleasant artifact of traditional methods for the integration of differential equations. It is well know that solutions of stiff equations tend to become very smooth after a certain period of time (in which case one says that the system has reached its steady state), but this does not lead to larger step sizes, as we would hope for.
In order to make this idea of “smoothness after a certain period
of time” more precise, it is instructive to study the analytic
continuation of  in the complex plane. In section
2, for a fixed initial condition
in the complex plane. In section
2, for a fixed initial condition 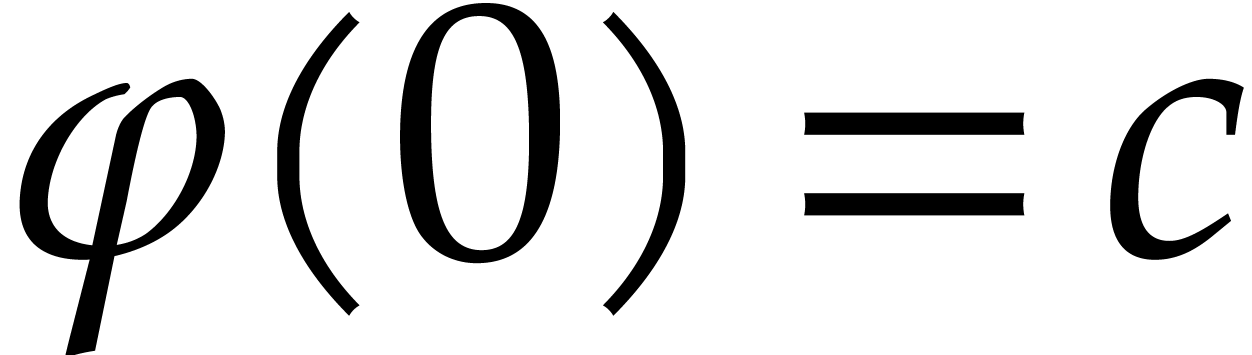 and a fixed forcing term
and a fixed forcing term  , we
show the existence of a compact half disk
, we
show the existence of a compact half disk 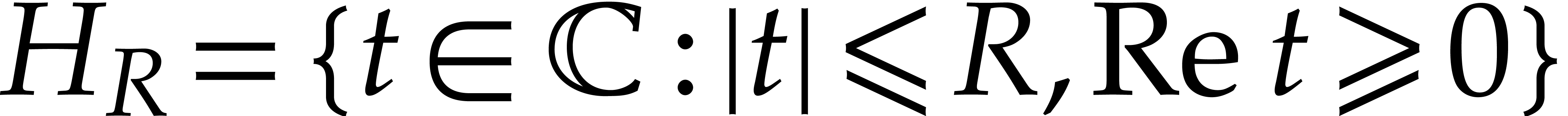 ,
,
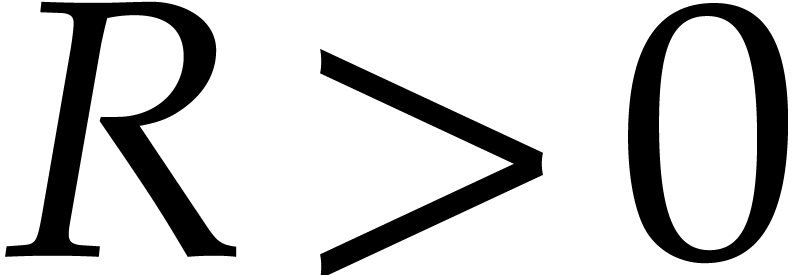 , on which the solution
, on which the solution  of (1) is analytic, for any
choice of
of (1) is analytic, for any
choice of  . In particular,
for
. In particular,
for 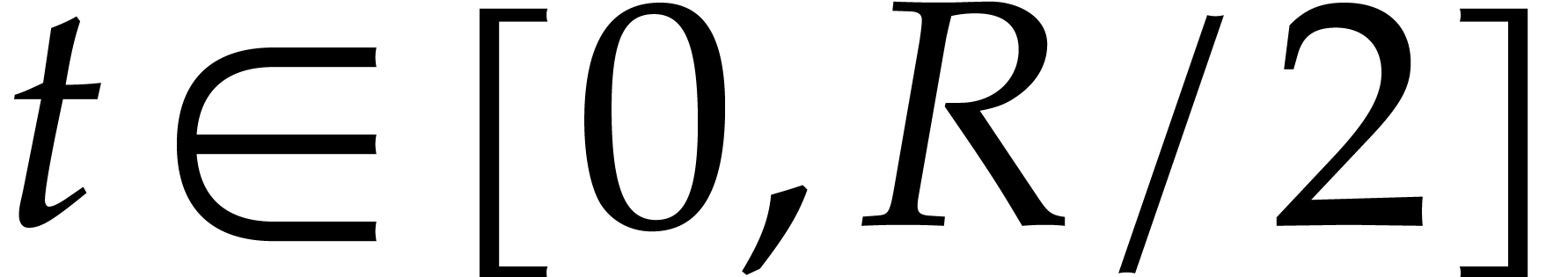 , the radius of
convergence
, the radius of
convergence 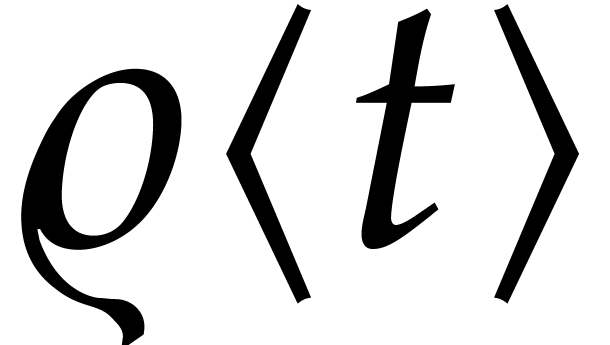 of the exact Taylor expansion
of the exact Taylor expansion 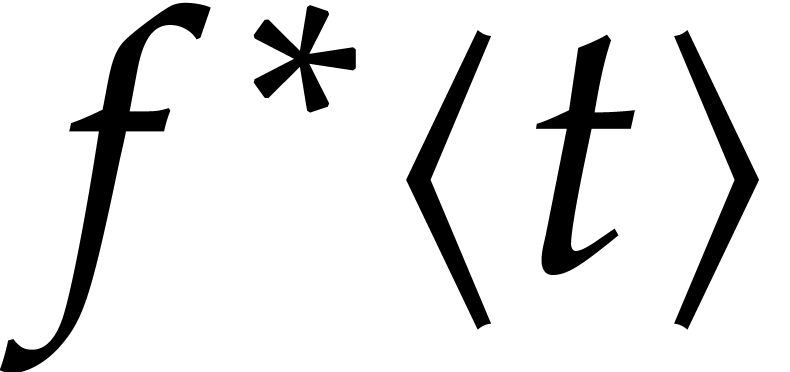 of
of  at time
at time  is at least
is at least  . Setting
. Setting 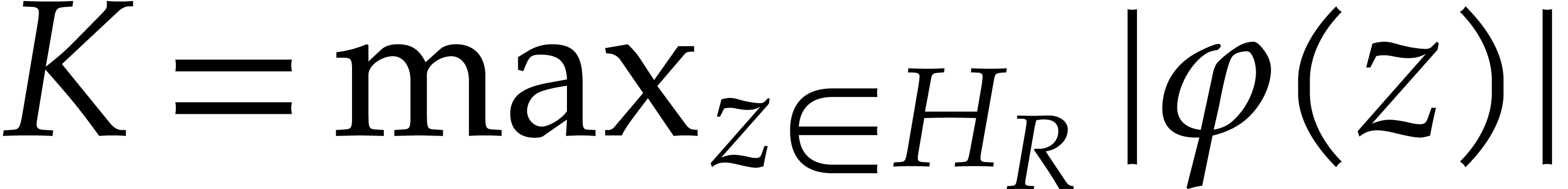 , Cauchy's formula thus yields the
bound
, Cauchy's formula thus yields the
bound 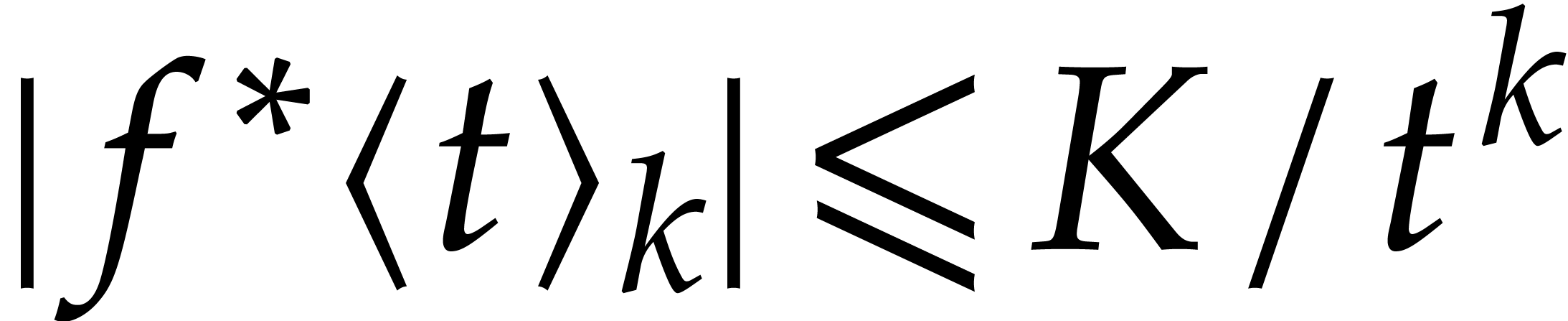 for all
for all 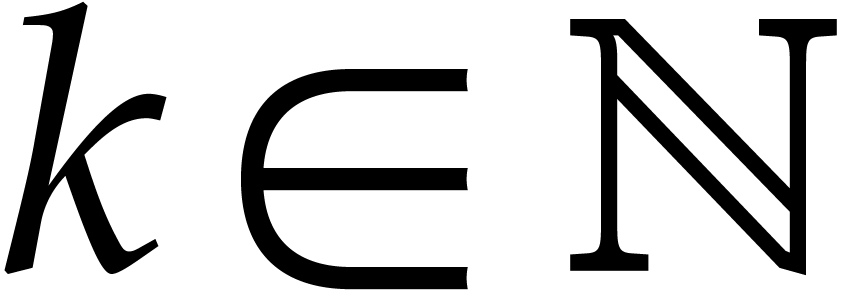 .
.
If 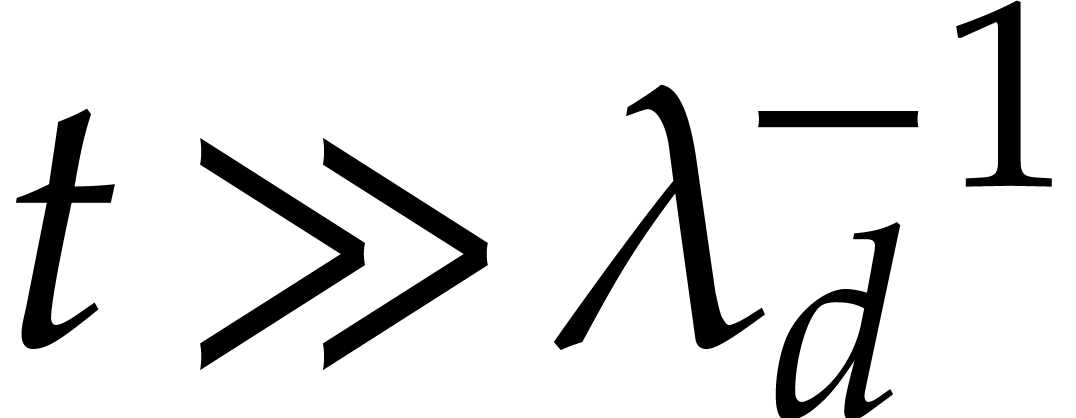 , then this means that
efficient integration schemes should allow for step sizes of the order
, then this means that
efficient integration schemes should allow for step sizes of the order
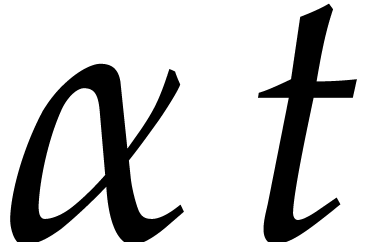 at time
at time  ,
for some fixed constant
,
for some fixed constant 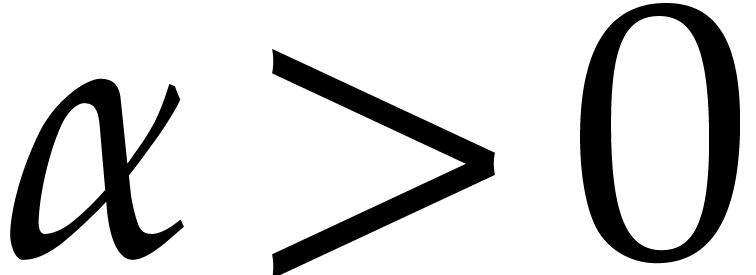 . In
section 5, we will present various such schemes. They are
all based on the computation of good approximations
. In
section 5, we will present various such schemes. They are
all based on the computation of good approximations 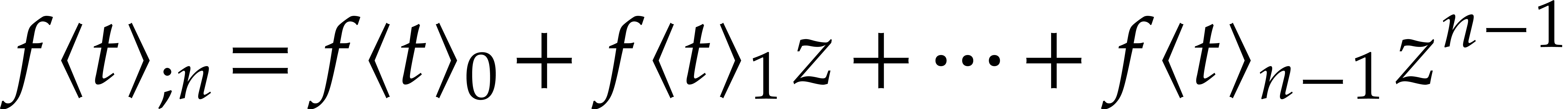 of the exact Taylor expansion
of the exact Taylor expansion 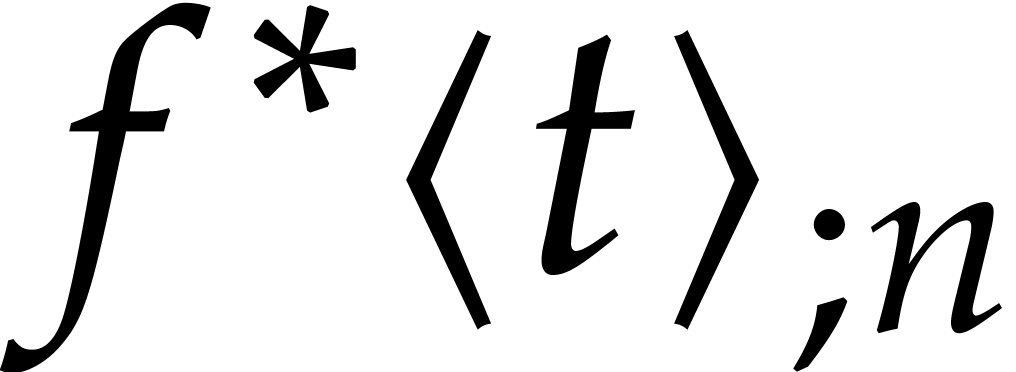 of
of  at time
at time  and order
and order  . By what precedes, such an approximation
cannot be obtained by solving (2). Instead, for a suitable
so-called critical index
. By what precedes, such an approximation
cannot be obtained by solving (2). Instead, for a suitable
so-called critical index  that depends
on
that depends
on  , we will solve the
following so-called steady-state problem:
, we will solve the
following so-called steady-state problem:
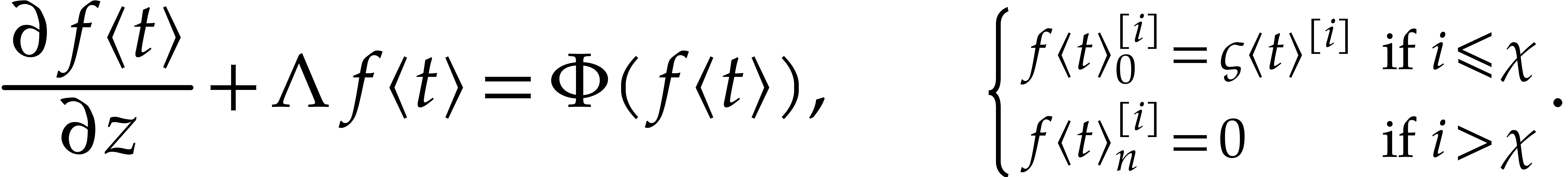 |
(3) |
Intuitively speaking, the system has reached a steady state for the
eigenvalues 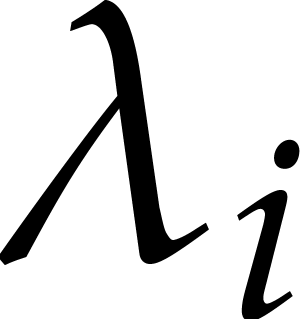 with
with 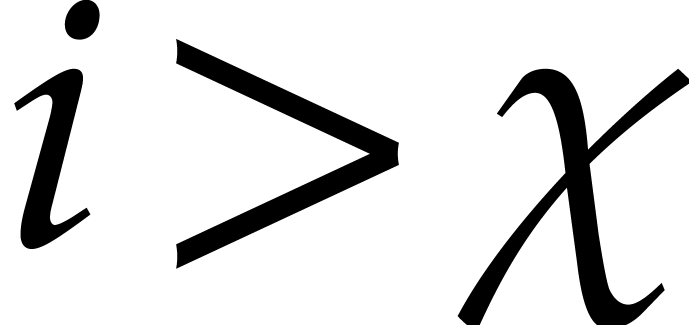 .
Such eigenvalues
.
Such eigenvalues 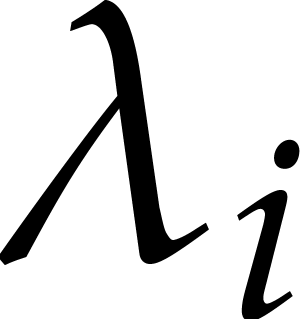 are “large”, so it
is more accurate to determine coefficients
are “large”, so it
is more accurate to determine coefficients 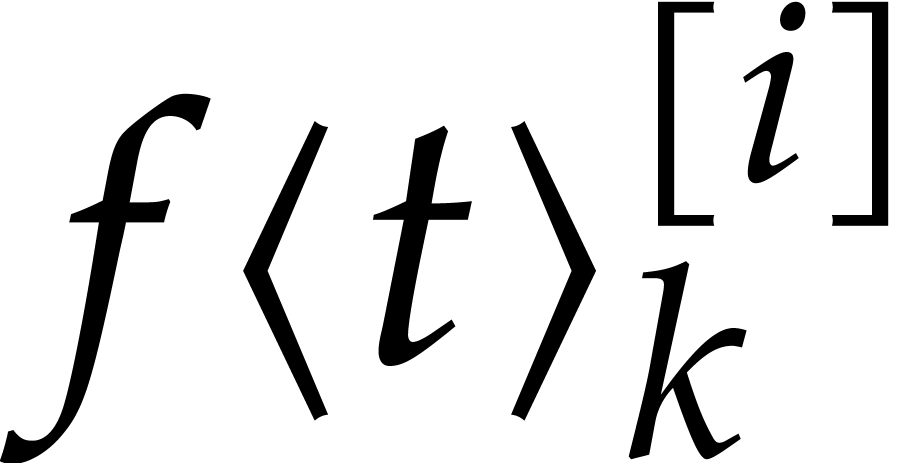 as a
function of later coefficients
as a
function of later coefficients  rather than
earlier ones. Furthermore, the coefficients
rather than
earlier ones. Furthermore, the coefficients 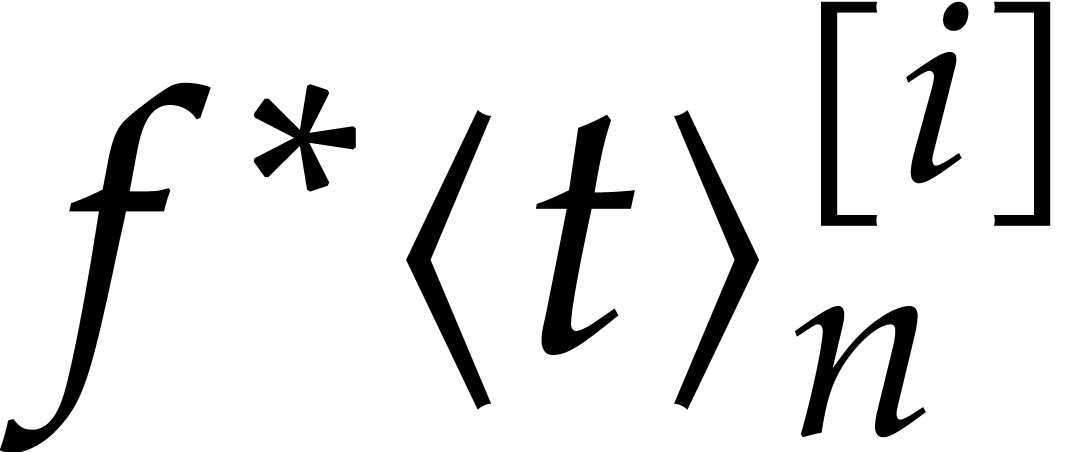 are
so “small” that they can be approximated by zeros; this
explains the steady-state conditions
are
so “small” that they can be approximated by zeros; this
explains the steady-state conditions 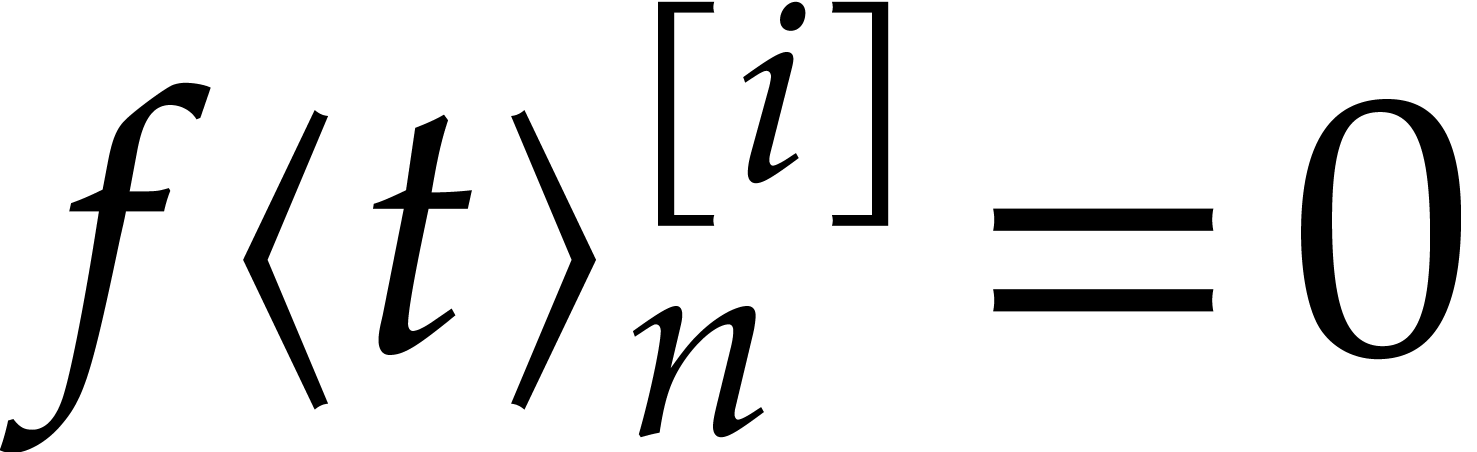 . The remaining eigenvalues
. The remaining eigenvalues  with
with 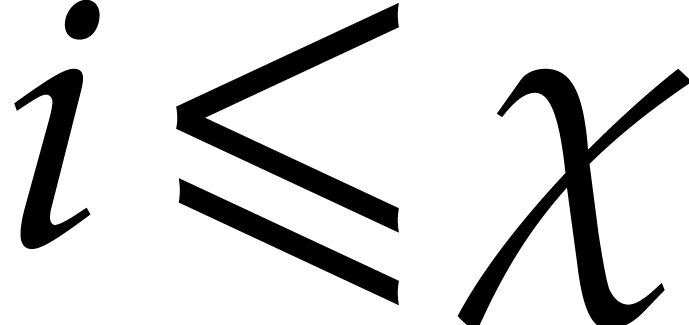 are small enough for the step size under
consideration that the dependence of
are small enough for the step size under
consideration that the dependence of  on the
initial condition
on the
initial condition  is sufficiently moderate for
(3) to admit an accurate solution. We say that the system
(1) is in a transient state for such eigenvalues
is sufficiently moderate for
(3) to admit an accurate solution. We say that the system
(1) is in a transient state for such eigenvalues
 at time
at time  .
.
A final topic is the computation of rigorous error bounds for the numerical integration process. For differential equations that are not stiff, this is a classical theme in interval analysis [21, 15, 5, 16, 18, 19, 11]. It has long been an open problem to develop efficient reliable integrators for stiff differential equations. We report on progress in this direction in section 6.
Consider the equation (1) for a fixed initial condition
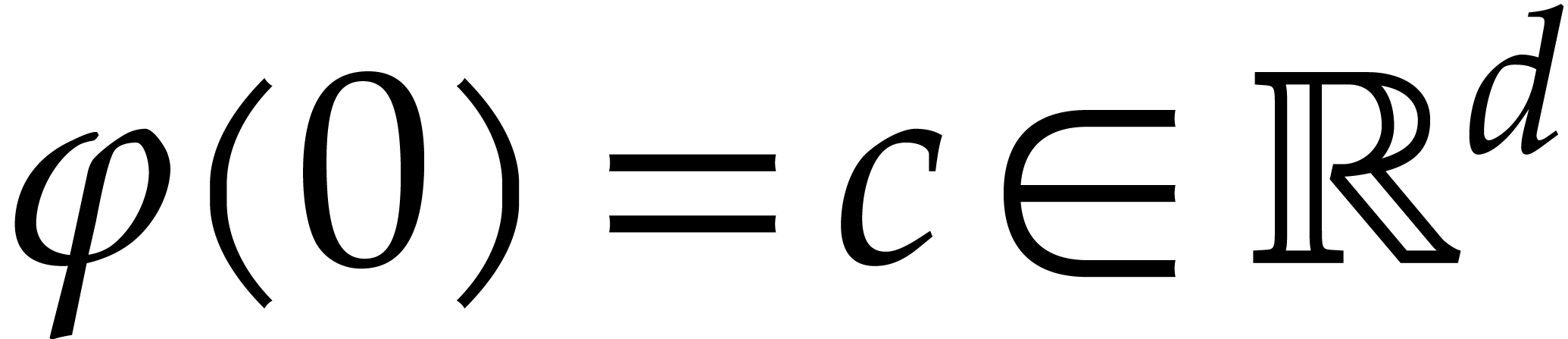 and a fixed forcing term
and a fixed forcing term  , but where we will allow ourselves to vary
, but where we will allow ourselves to vary  . Our main aim is to show that
there exists a compact “half disk”
. Our main aim is to show that
there exists a compact “half disk”
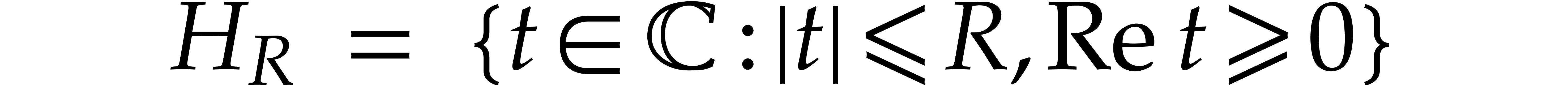
with 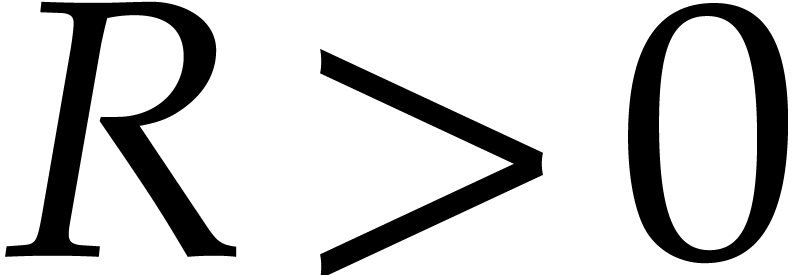 on which the solution
on which the solution  to (1) exists and is analytic, independently of the choice
of
to (1) exists and is analytic, independently of the choice
of  . We will both prove a
weak and simpler version of this result and a stronger version that
allows us to take larger radii
. We will both prove a
weak and simpler version of this result and a stronger version that
allows us to take larger radii 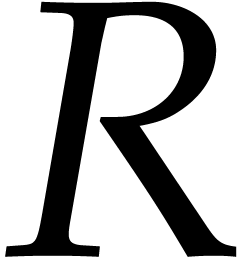 and that is also
more convenient if we want to actually compute a radius
and that is also
more convenient if we want to actually compute a radius  that works.
that works.
We will need a few more notations. We denote the interior of  by
by
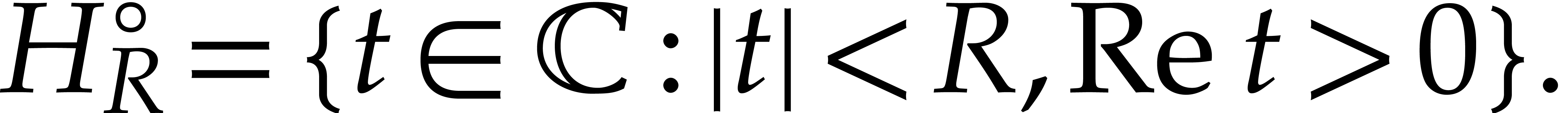
Given a non-empty open subset  ,
we write
,
we write 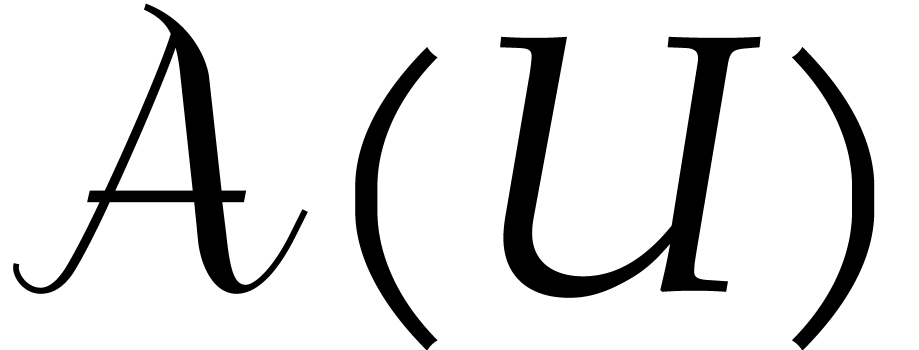 for the Banach space of analytic
functions
for the Banach space of analytic
functions 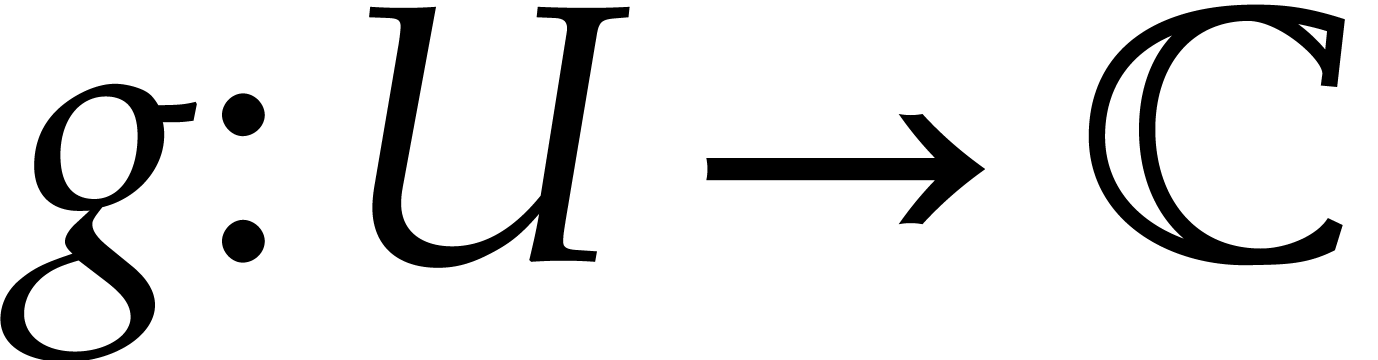 with finite sup-norm
with finite sup-norm
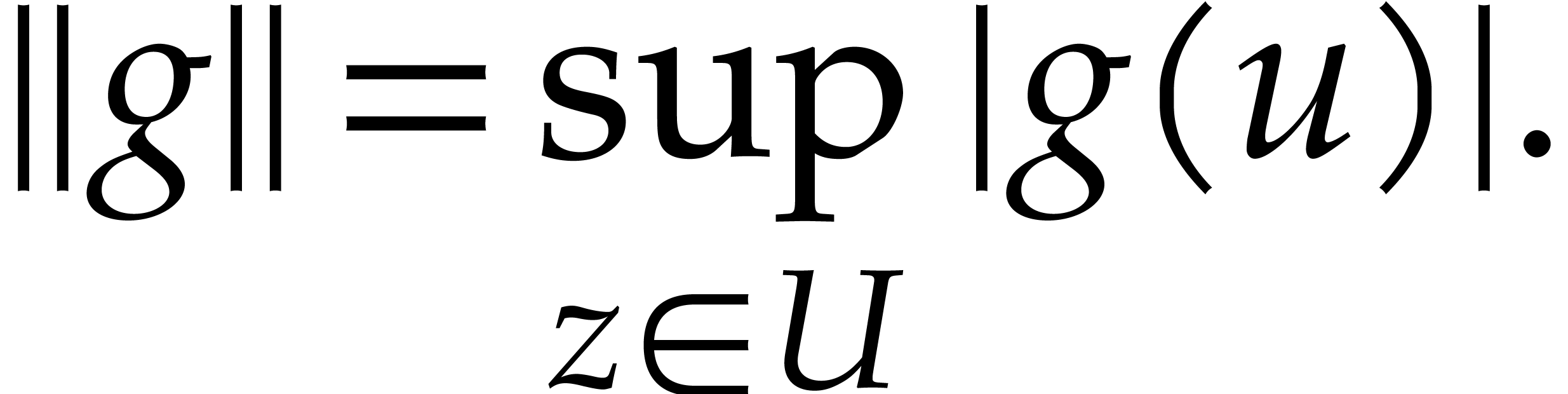
We will often use vector notation: given  ,
,
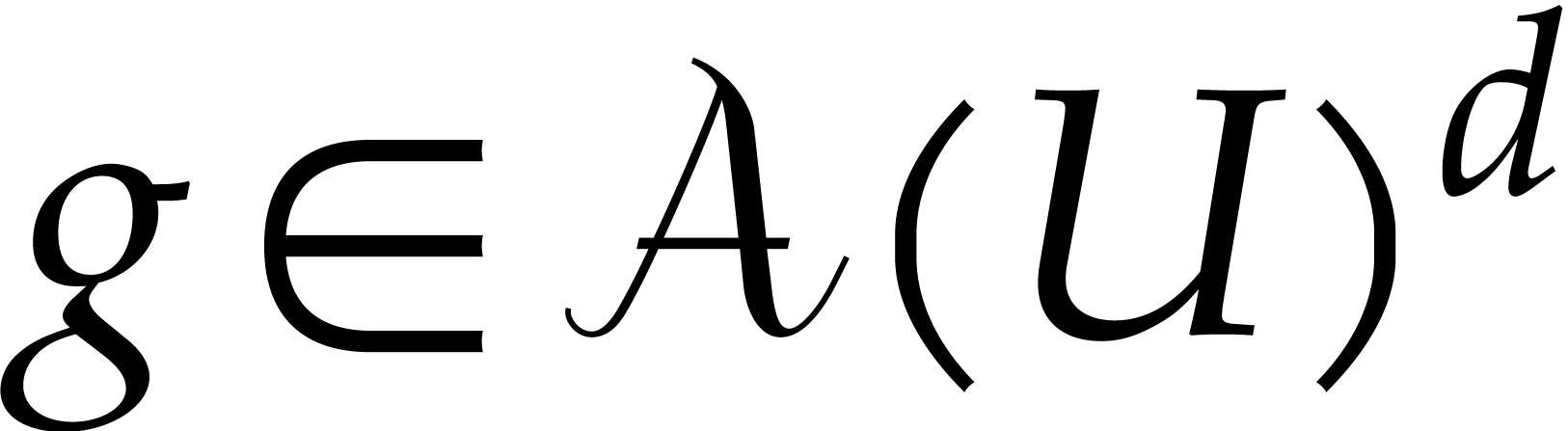 , and
, and 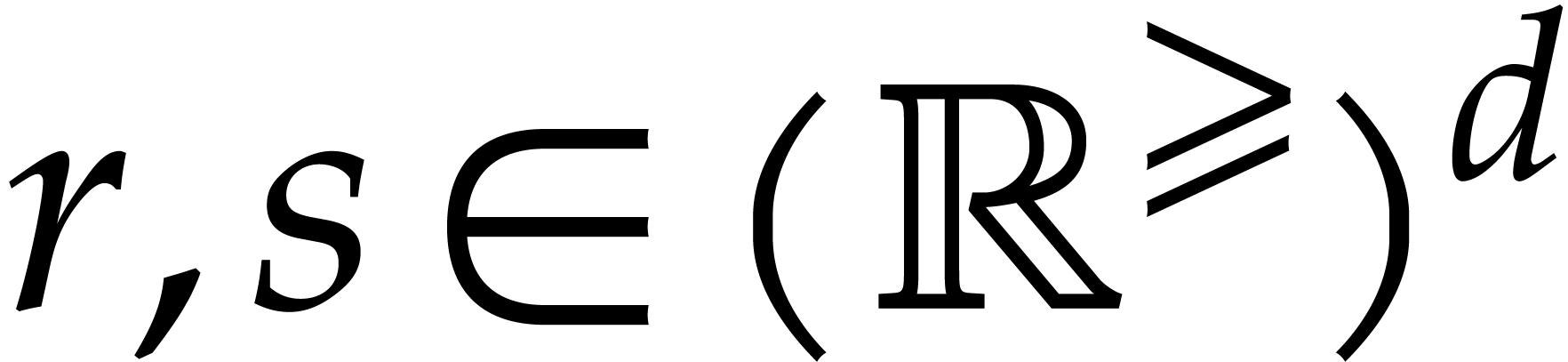 , we write
, we write
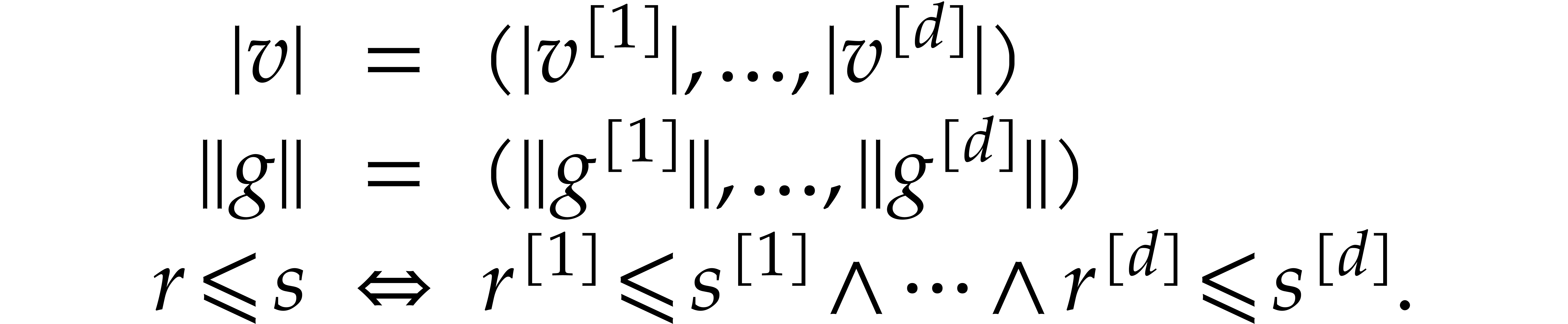
In addition to such “componentwise” norms, we will also use
more traditional sup-norms: given  ,
,
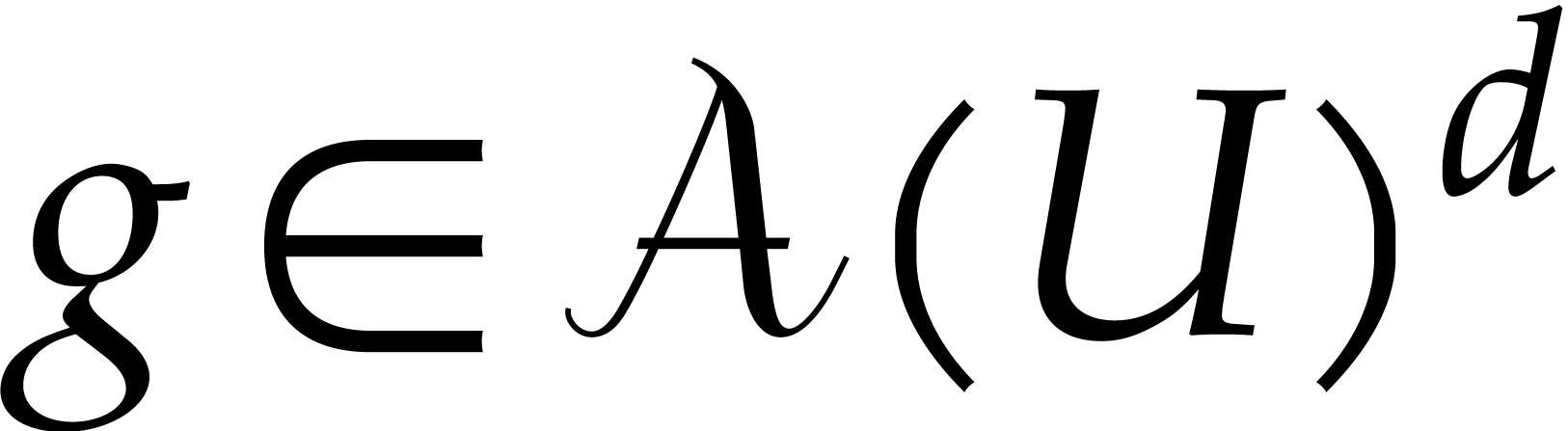 , and an
, and an  matrix
matrix  , we define
, we define
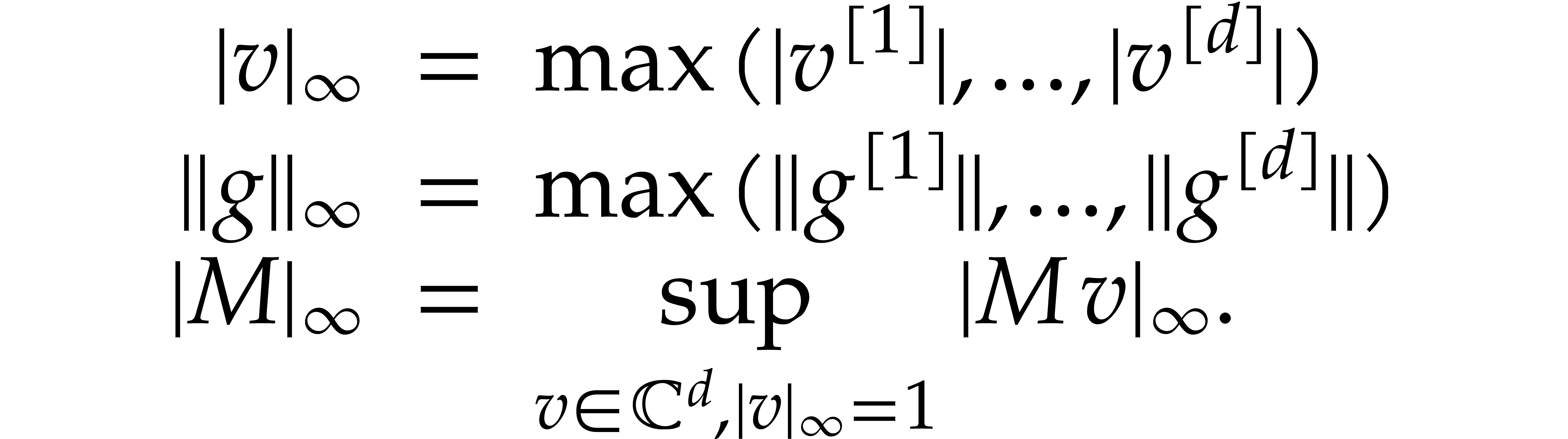
We will also need two well known results from complex analysis, namely an explicit version of Cauchy-Kovalevskaya's theorem and a variant of Montel's theorem.
 ,
,  , and consider the initial value problem
, and consider the initial value problem
Writing 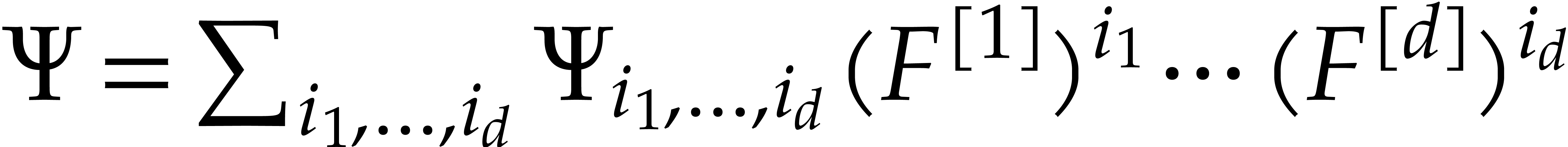 , let
, let
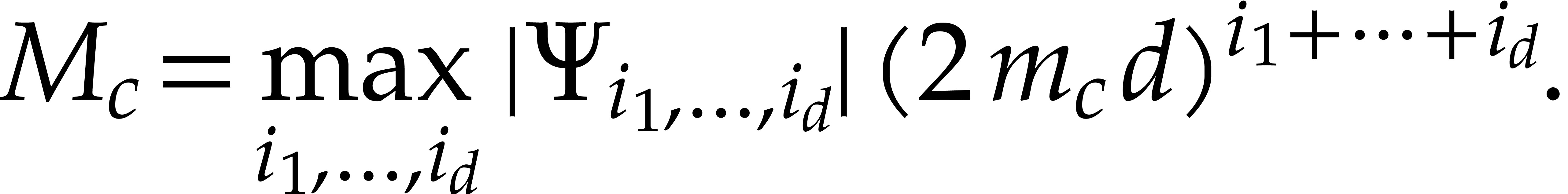
Then  and radius
and radius
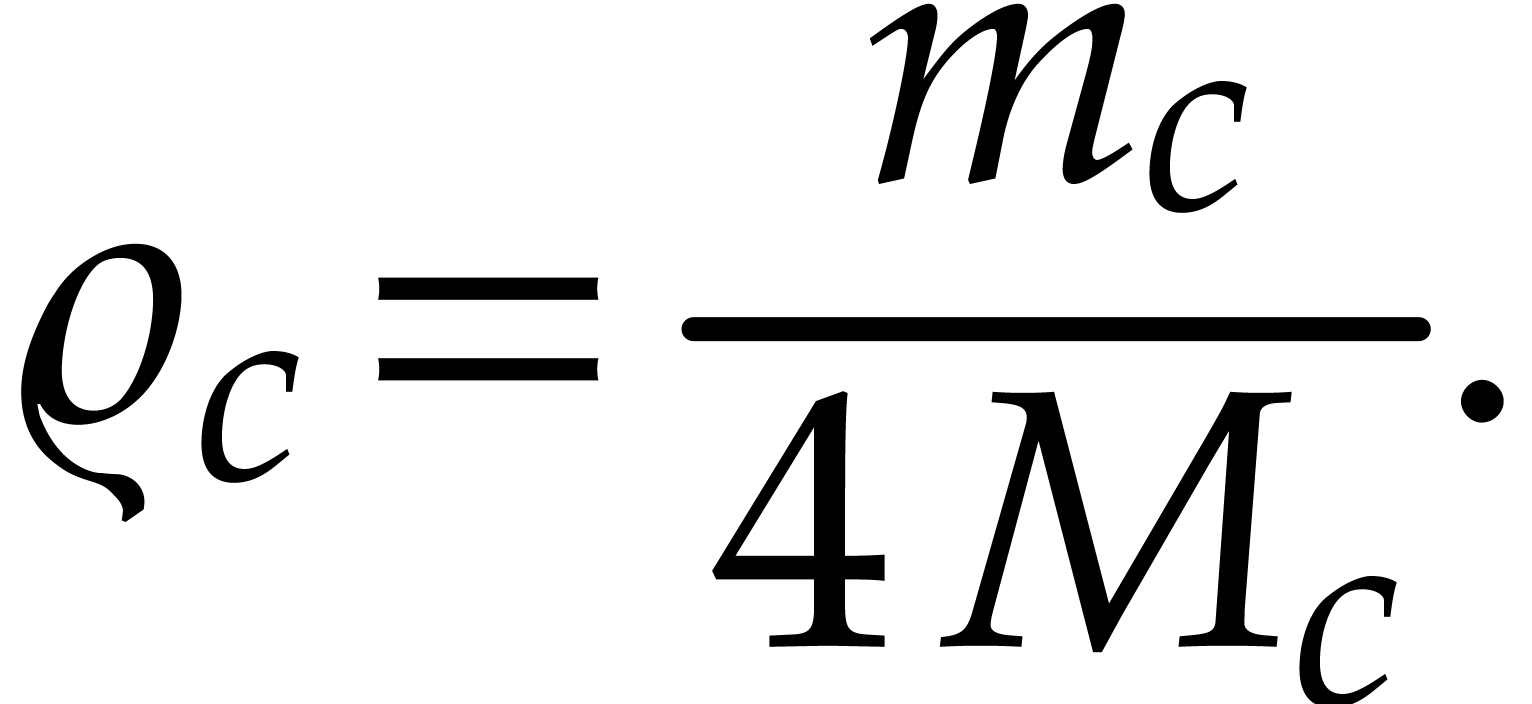
Proof. Our assumptions imply that
constitutes a “majorant equation” for (4) in
the sense of Cauchy-Kovalevskaya. By symmetry, each of the components
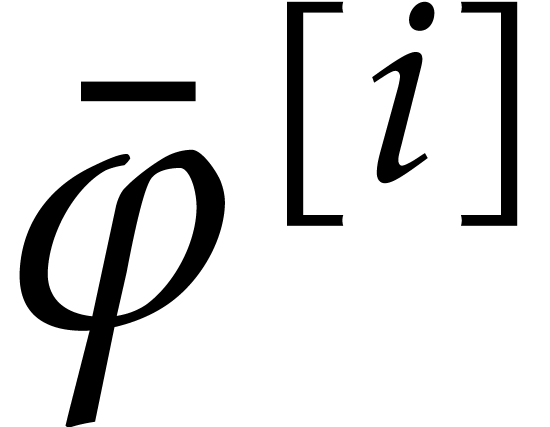 of this equation satisfies the simpler equation
of this equation satisfies the simpler equation
which admits the explicit solution
of radius  . Since the formal
power series solution of (4) satisfies
. Since the formal
power series solution of (4) satisfies 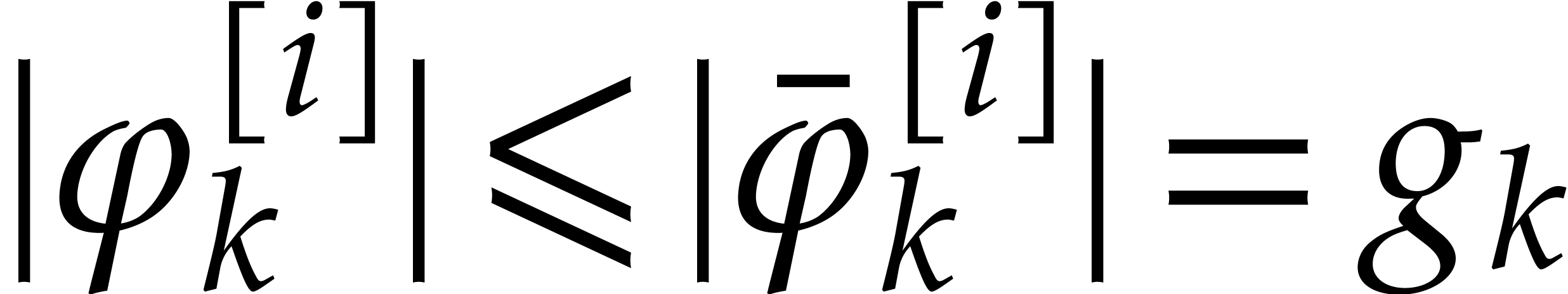 for all
for all 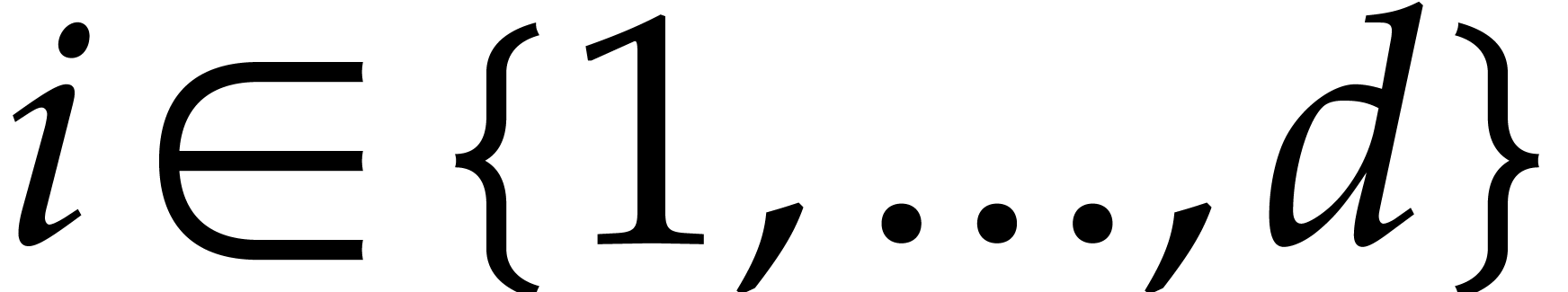 and
and 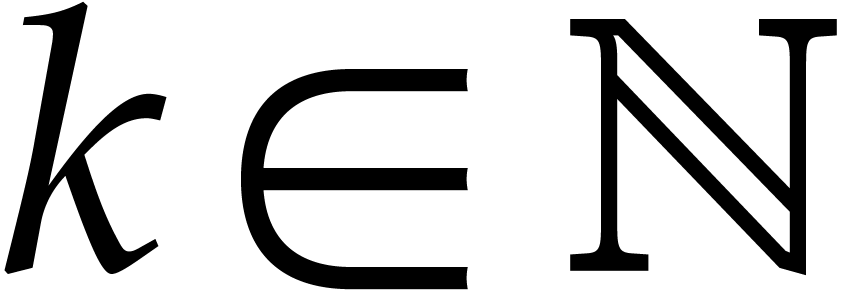 ,
it follows that
,
it follows that  has radius of convergence at
least
has radius of convergence at
least  .
.
 of
of  and a bounded sequence
and a bounded sequence  , we
can extract a subsequence
, we
can extract a subsequence  that converges
uniformly to a limit
that converges
uniformly to a limit  on every compact subset
of
on every compact subset
of  .
.
Proof. If 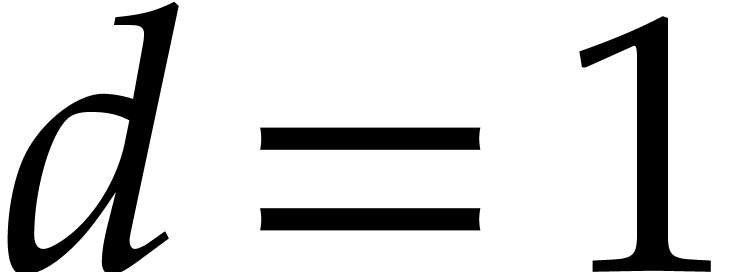 ,
then this is Montel's theorem. The general case is obtained using an
easy induction on
,
then this is Montel's theorem. The general case is obtained using an
easy induction on  : we first
extract a subsequence
: we first
extract a subsequence 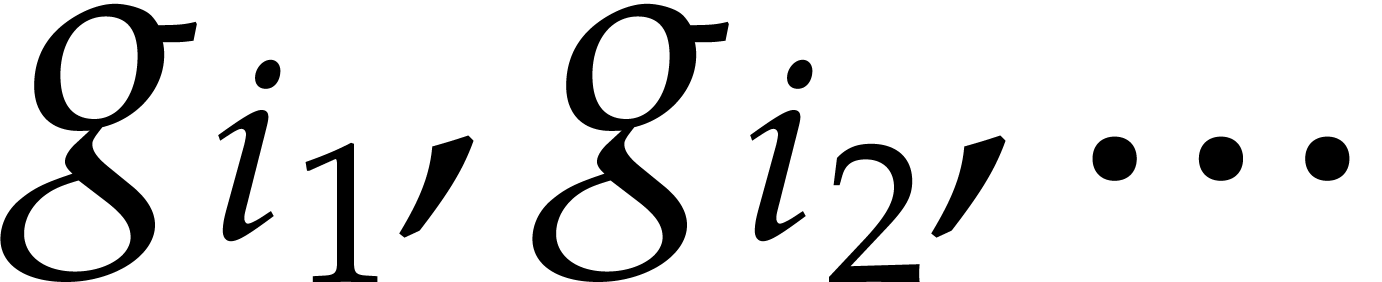 such that
such that  converges to a limit in
converges to a limit in  and then apply the
induction hypothesis to this subsequence for the remaining
and then apply the
induction hypothesis to this subsequence for the remaining  components.
components.
Let  denote the Jacobian matrix of
denote the Jacobian matrix of  .
.
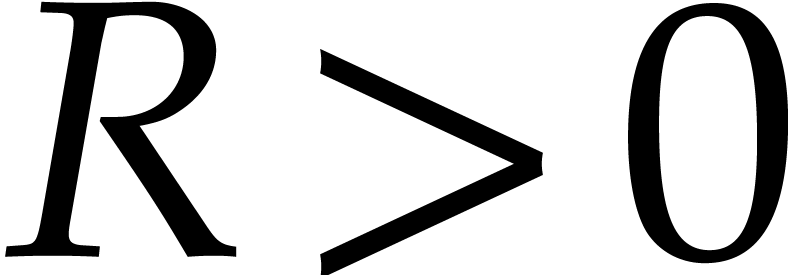 ,
, 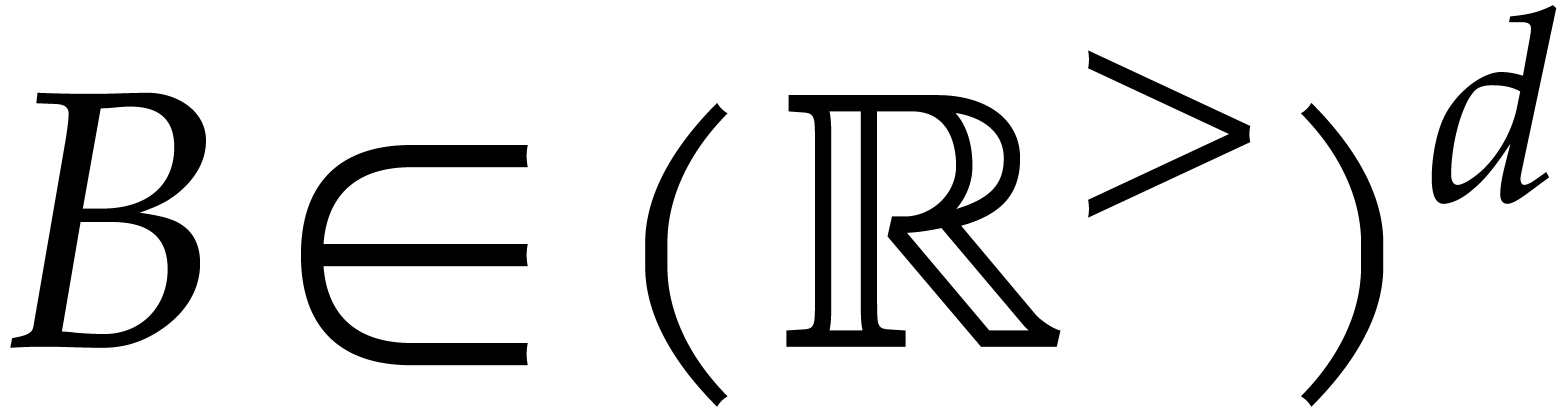 , and
, and 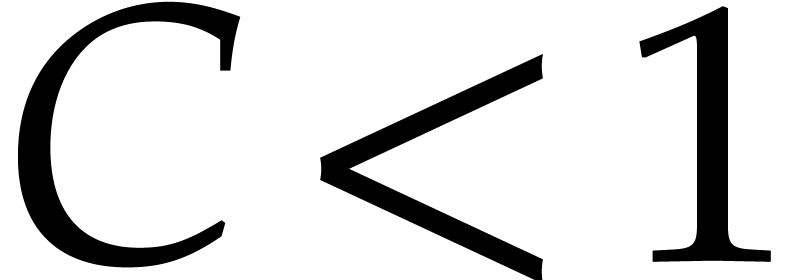 be such that
for all
be such that
for all 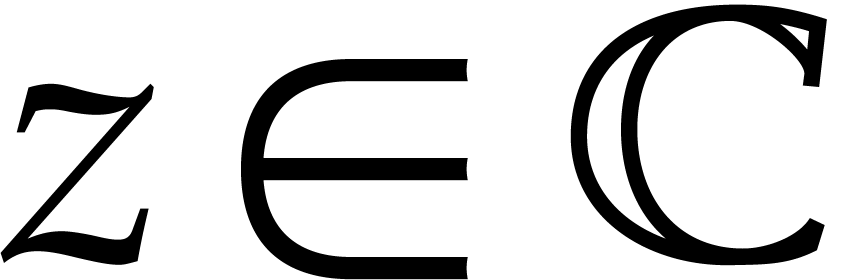 , we have
, we have
Then, for any choice of  ,
the initial value problem
,
the initial value problem
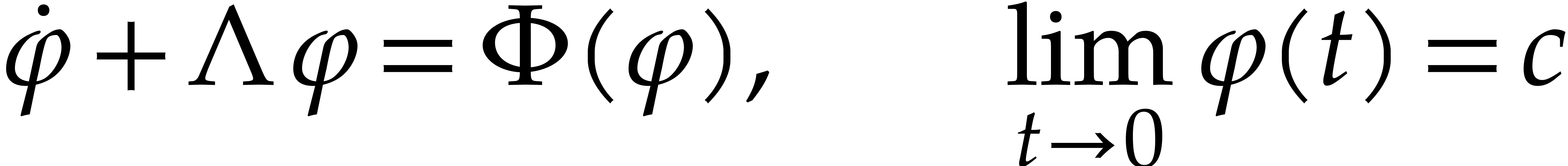 |
(7) |
admits a unique analytic solution on  .
In addition, we have
.
In addition, we have 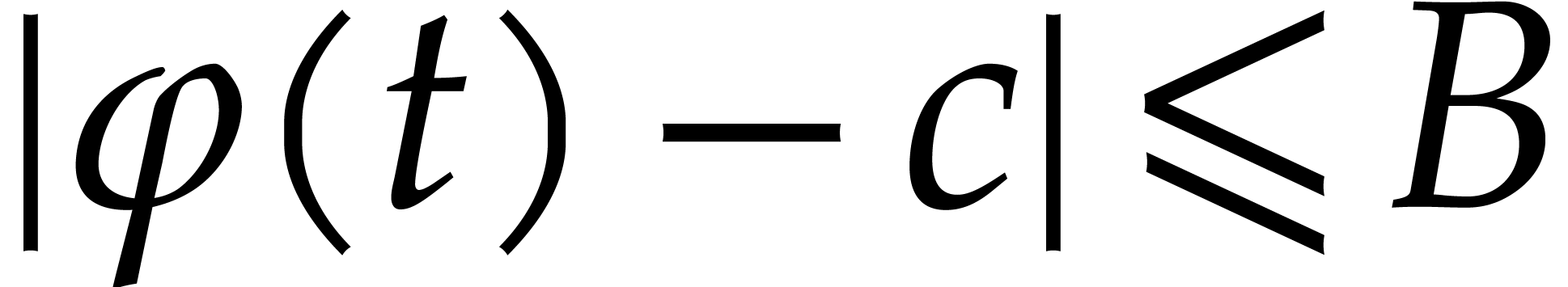 for all
for all  .
.
Proof. Consider the operator 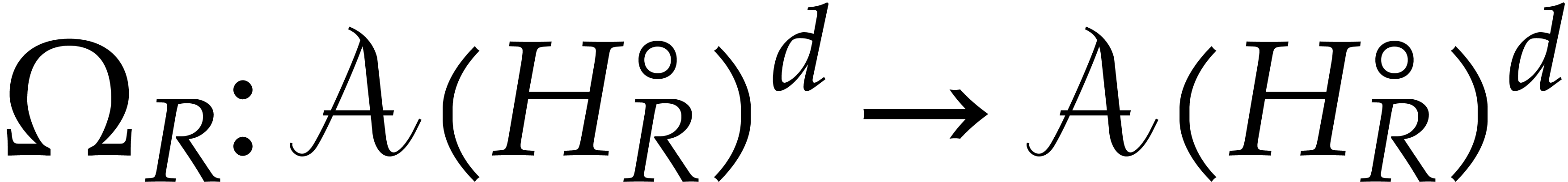 with
with
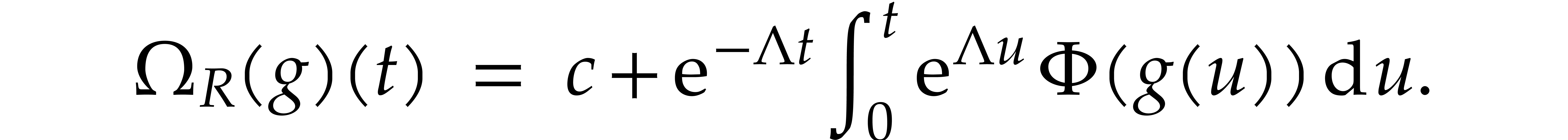
The fixed points 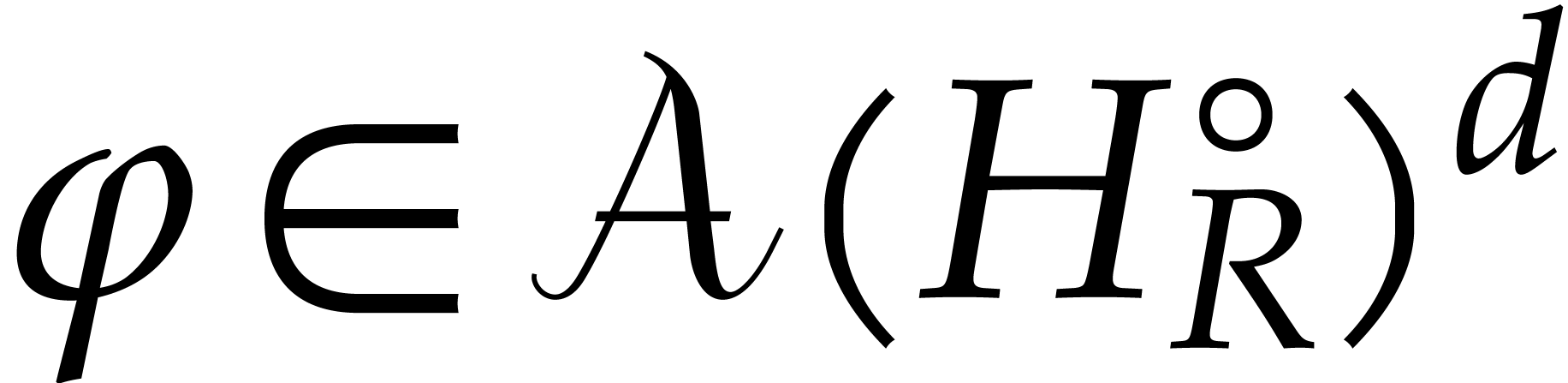 of this operator are precisely
the solutions of (7). Let us prove the existence of such a
fixed point. The uniqueness follows by analytic continuation from the
well known uniqueness of the solution of the initial value problem (7) on a neighbourhood of the origin.
of this operator are precisely
the solutions of (7). Let us prove the existence of such a
fixed point. The uniqueness follows by analytic continuation from the
well known uniqueness of the solution of the initial value problem (7) on a neighbourhood of the origin.
Let us first notice that  maps the ball
maps the ball
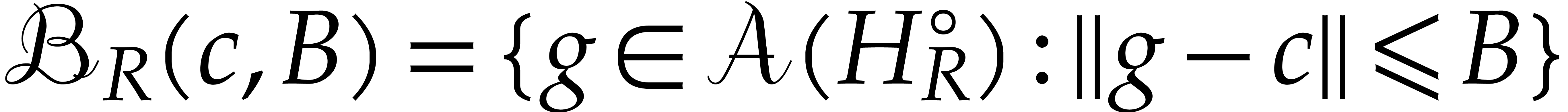
with center  and radius
and radius 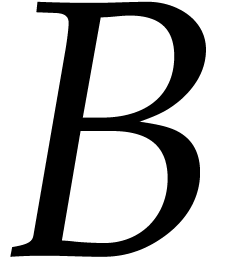 into itself. Indeed, given
into itself. Indeed, given 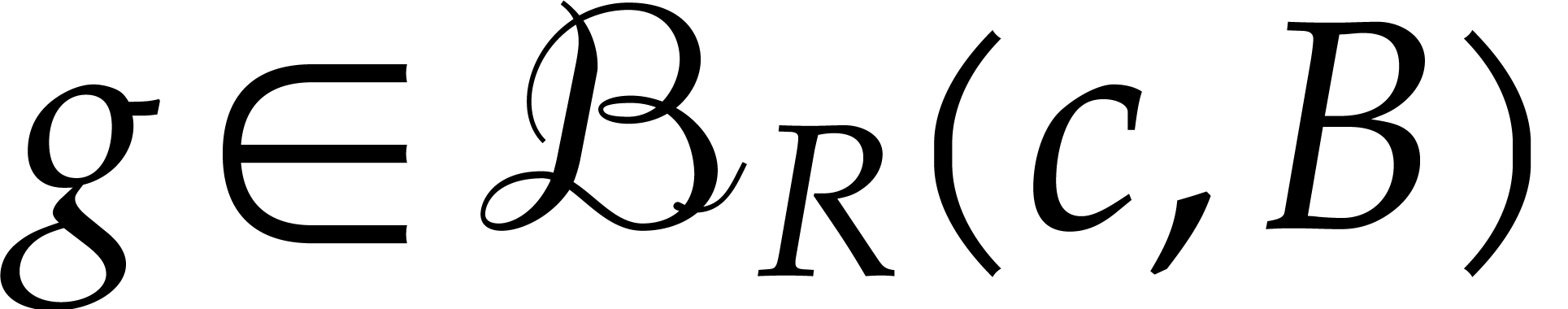 and
and 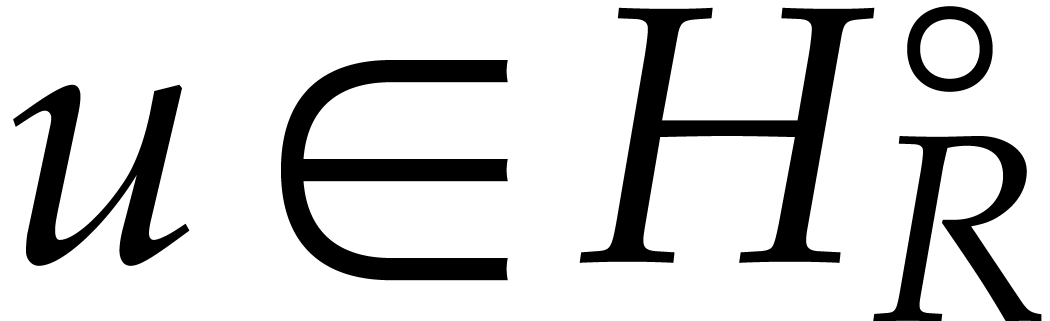 , our hypothesis (5) implies
, our hypothesis (5) implies
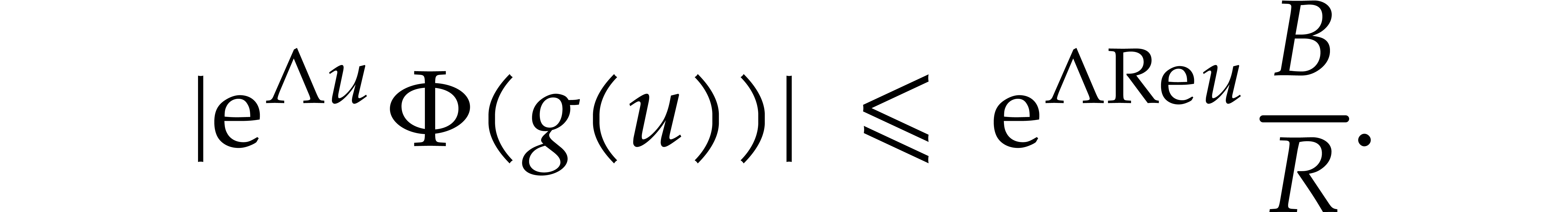
For all  , it follows that
, it follows that
whence  , as desired.
, as desired.
Let us next show that  is actually contracting on
is actually contracting on
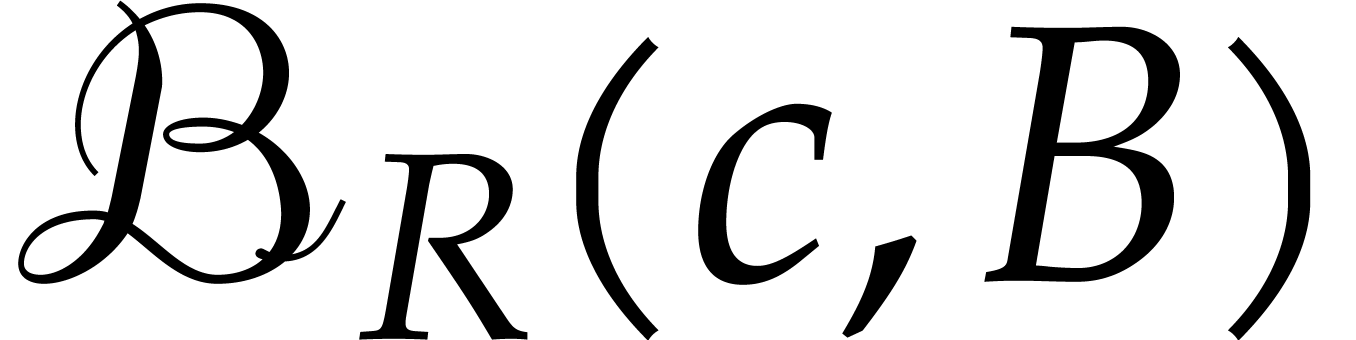 . Given
. Given 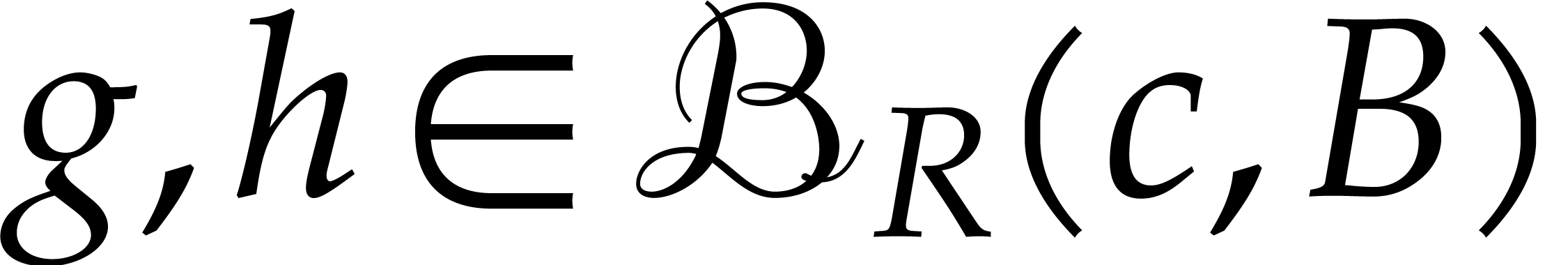 , consider the homotopy
, consider the homotopy 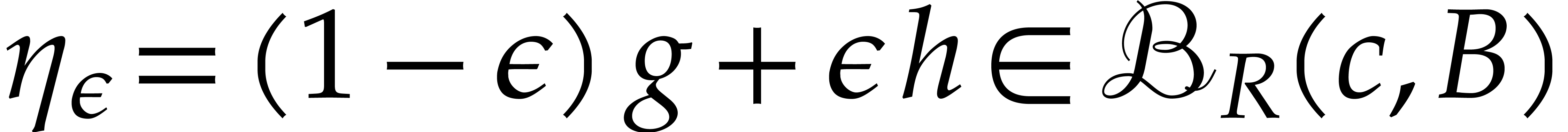 with
with 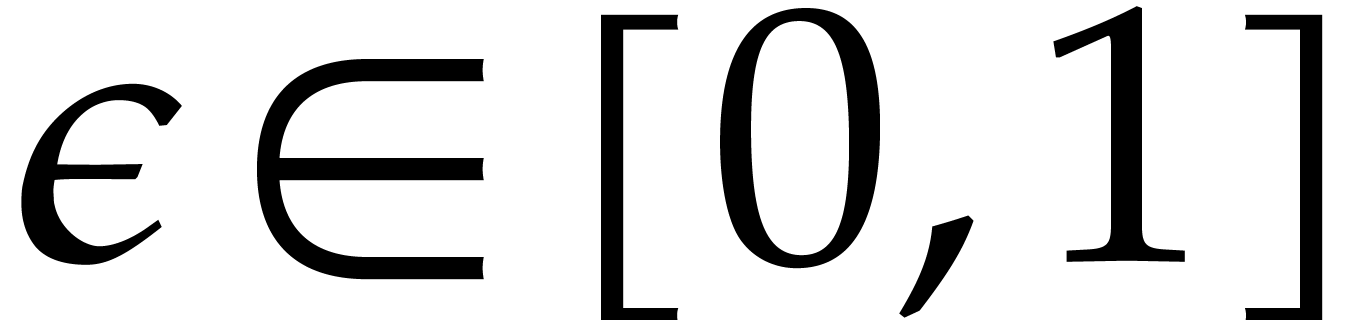 . From (6),
we get
. From (6),
we get
It follows that
and
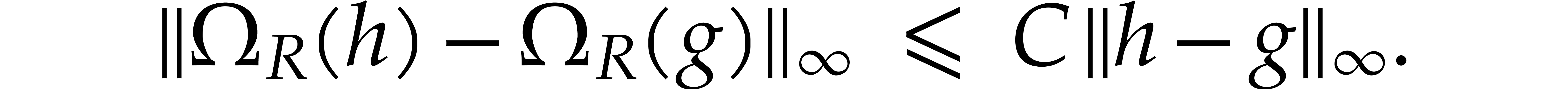
This shows that  is indeed contracting on
is indeed contracting on 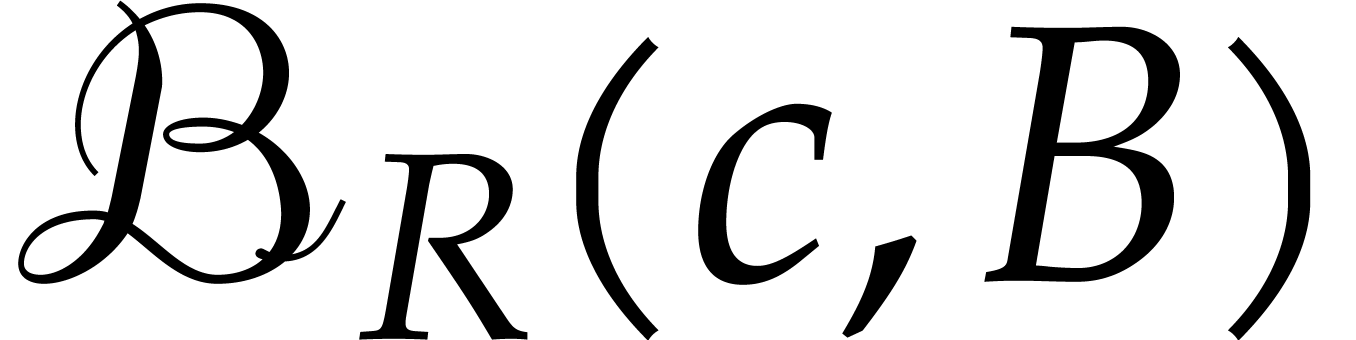 . Since
. Since 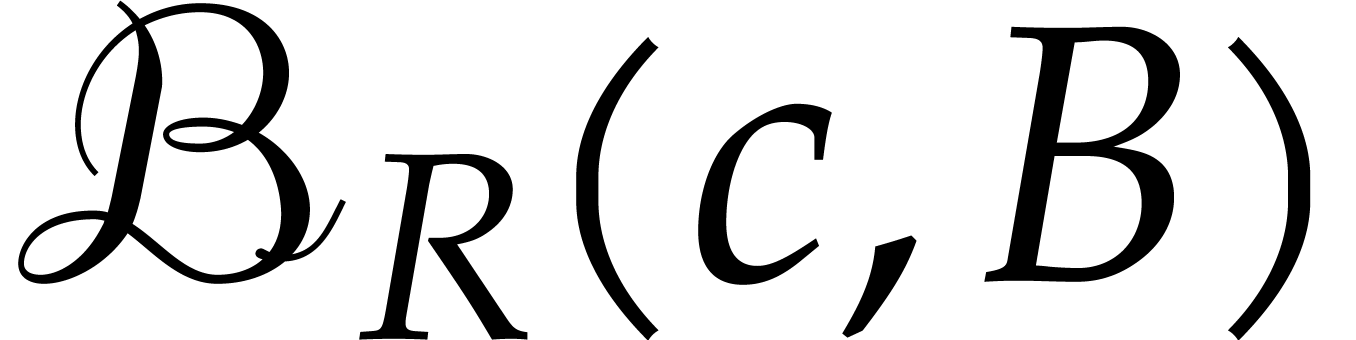 is
complete as a closed bounded subspace of
is
complete as a closed bounded subspace of 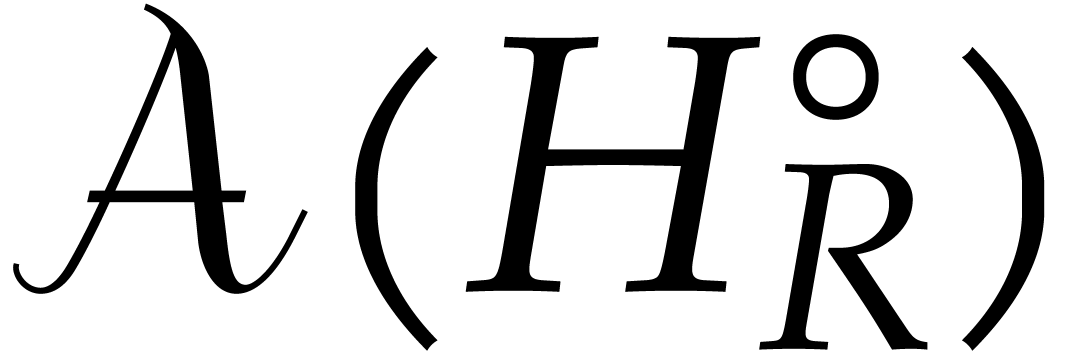 ,
we conclude that
,
we conclude that 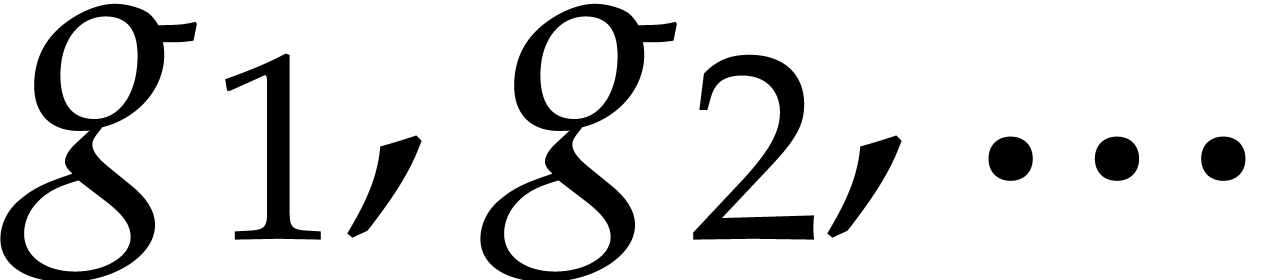 converges to a fixed point
converges to a fixed point 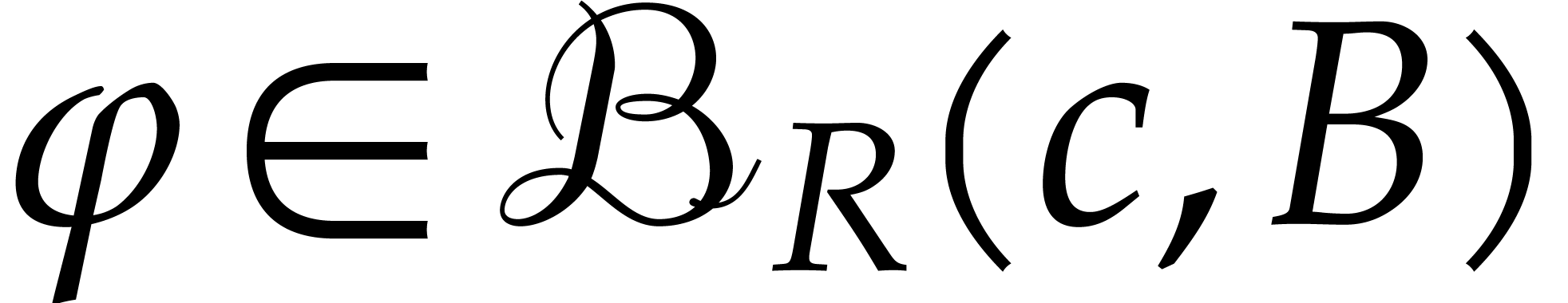 of
of 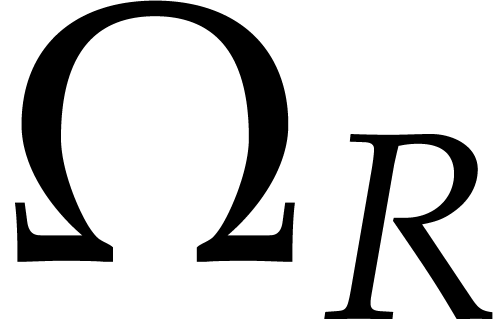 .
.
It turns out that the condition (6) on the Jacobian is not
really needed. Moreover, the solution can further be extended to the
closure  of
of  .
.
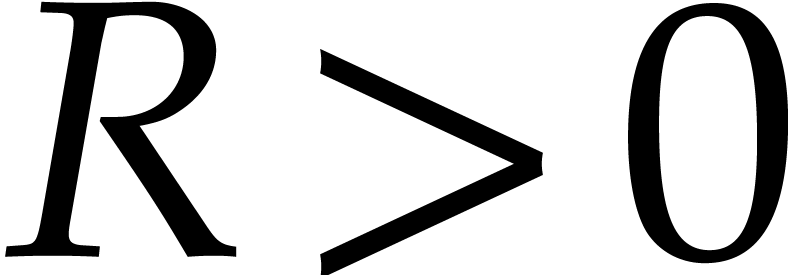 and
and 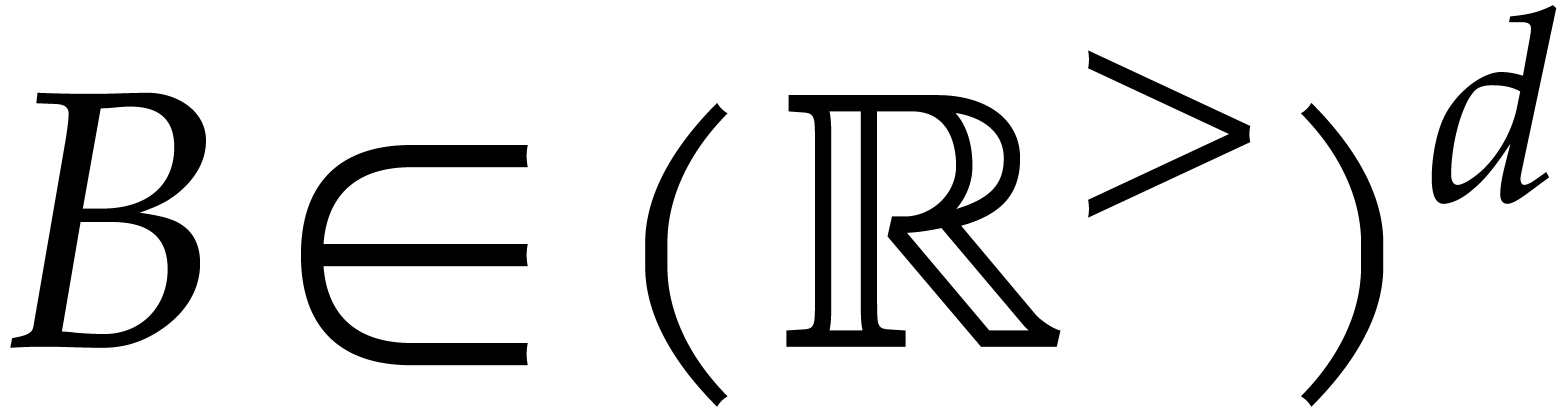 be
such that for all
be
such that for all  , we
have
, we
have
Then, for any choice of  ,
the initial value problem
,
the initial value problem
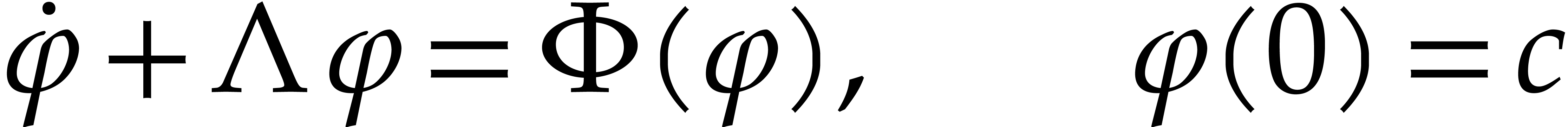 |
(9) |
admits a unique analytic solution on  .
In addition, we have
.
In addition, we have 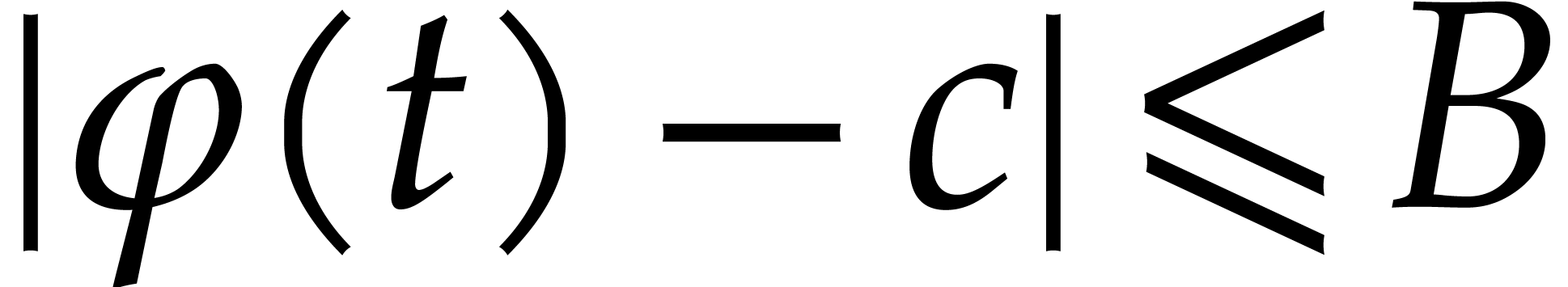 for all
for all 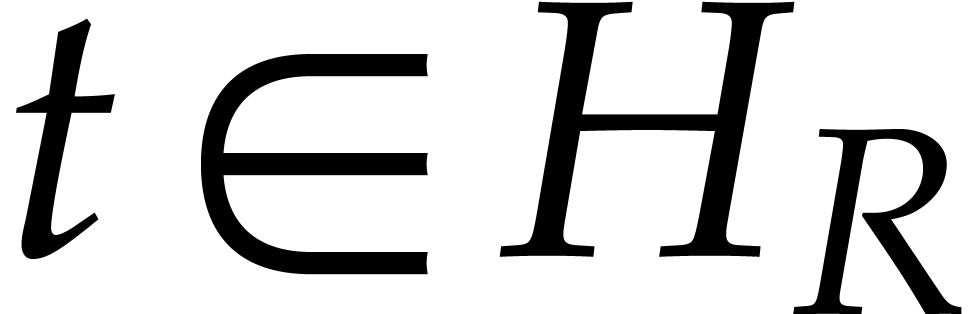 .
.
Proof. Let 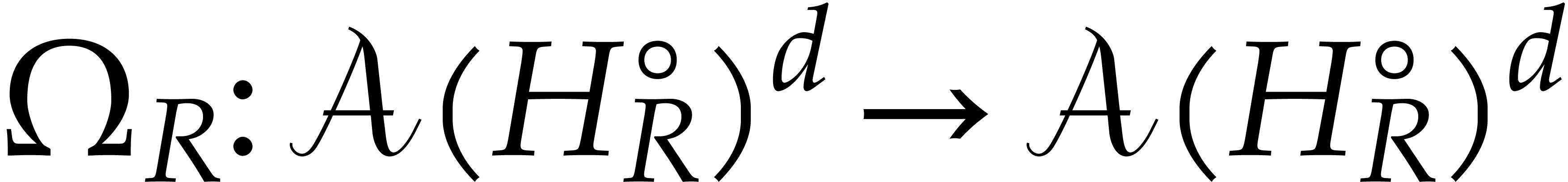 be as in the
proof of Theorem 3 and notice that
be as in the
proof of Theorem 3 and notice that 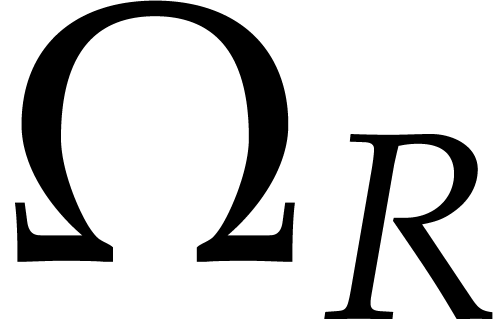 still maps
still maps  into itself. Now consider the
sequence
into itself. Now consider the
sequence  with
with 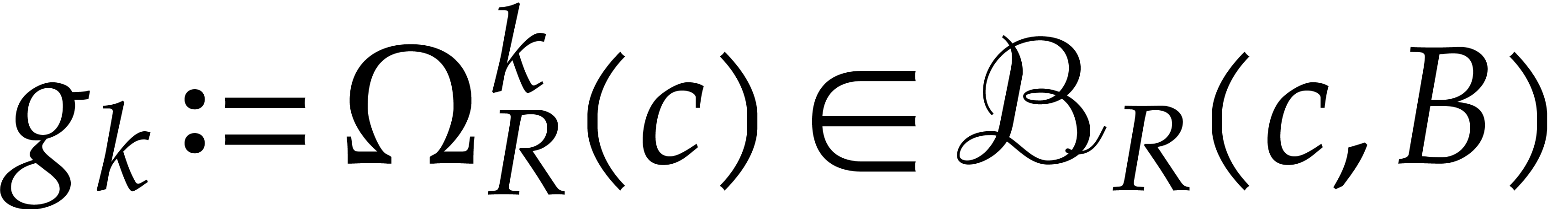 .
Applying Montel's theorem, we obtain a subsequence
.
Applying Montel's theorem, we obtain a subsequence 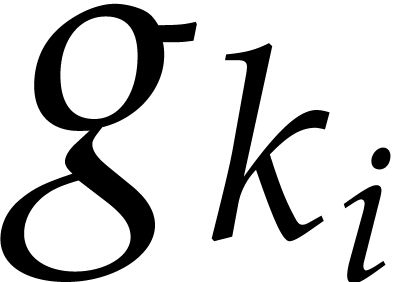 that converges uniformly to a limit
that converges uniformly to a limit 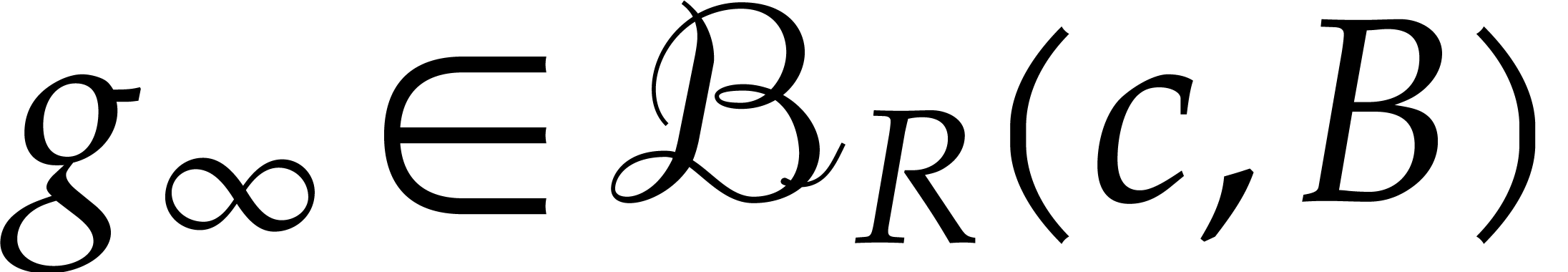 on every
compact subset of
on every
compact subset of  .
.
We claim that 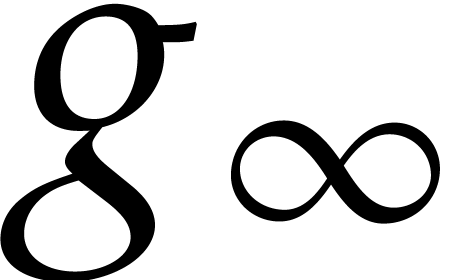 is a fixed point of
is a fixed point of 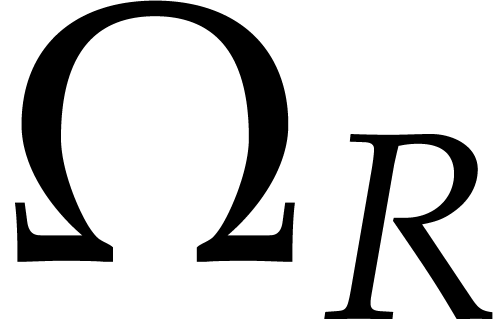 . Indeed, for a sufficiently small
. Indeed, for a sufficiently small  with
with  , we have
, we have
 for all
for all  with
with  . As in the proof of Theorem 3, this means that
. As in the proof of Theorem 3, this means that  is contracting on
is contracting on
 . Consequently, the
restrictions
. Consequently, the
restrictions 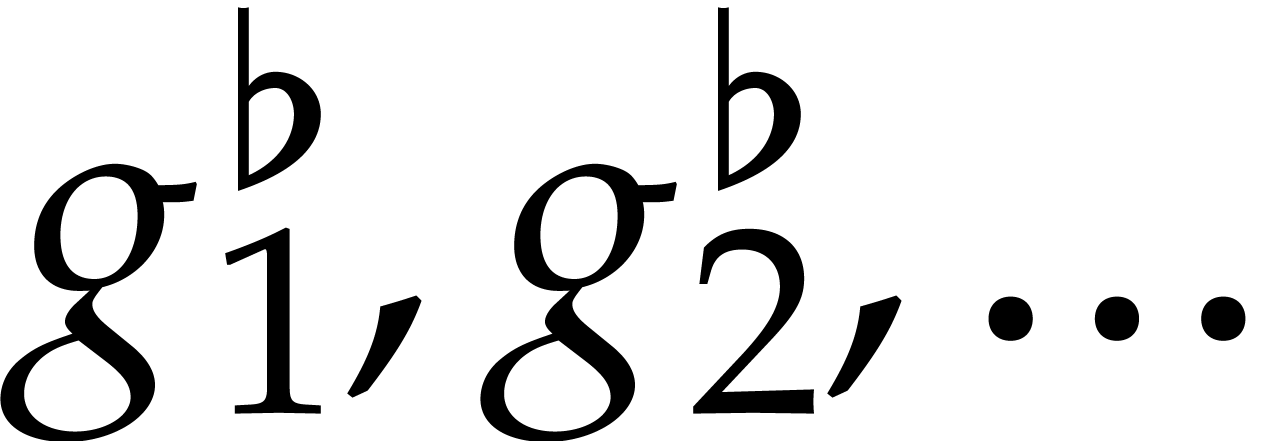 of the functions
of the functions 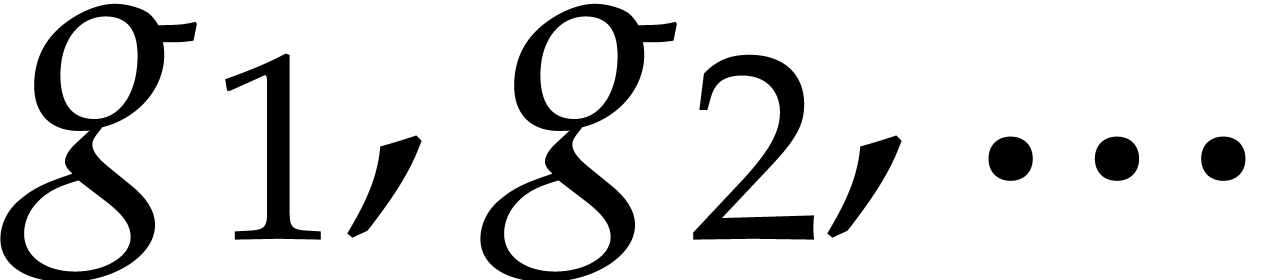 to
to 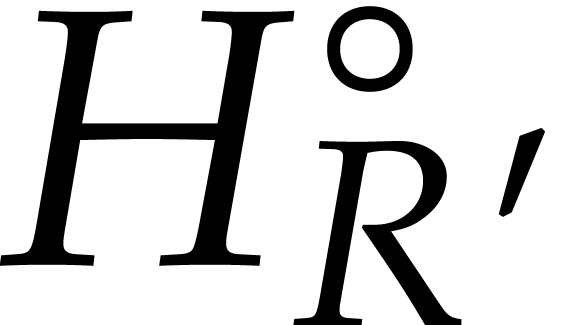 with
with 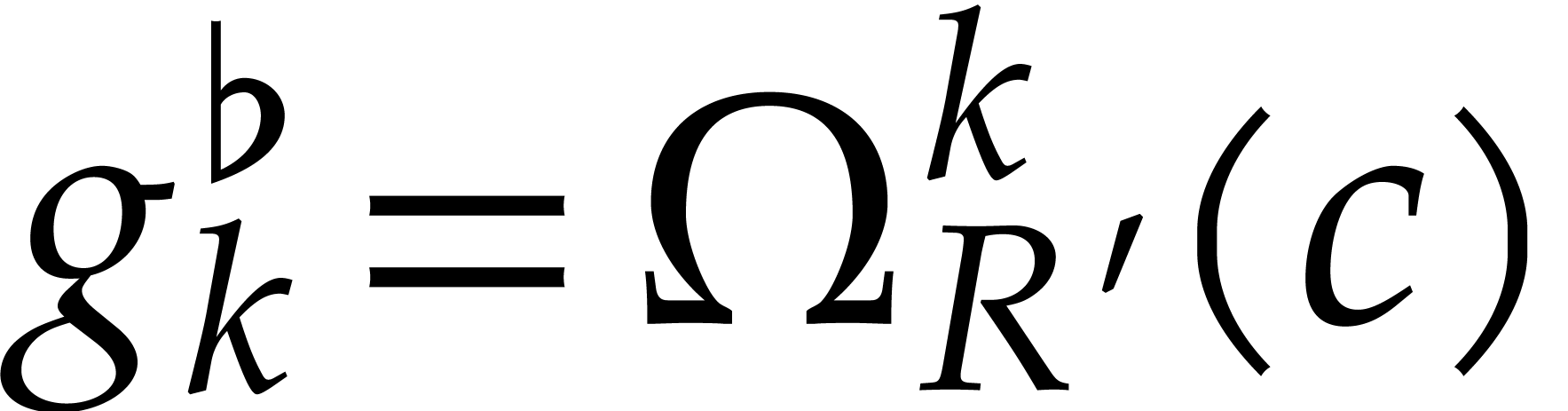 tend to a fixed
point
tend to a fixed
point  , and so does the
subsequence
, and so does the
subsequence  . Now this fixed
point
. Now this fixed
point  coincides with
coincides with 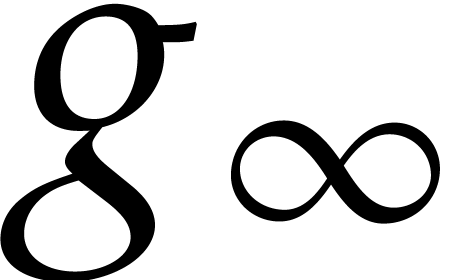 on
on
 and also solves the initial value problem (7). By analytic continuation,
and also solves the initial value problem (7). By analytic continuation, 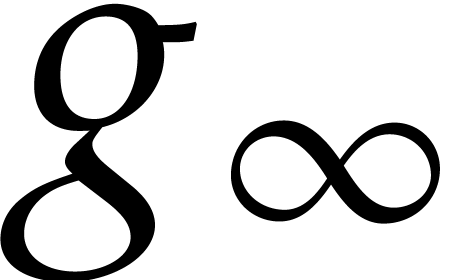 therefore solves the same initial value problem on
therefore solves the same initial value problem on  , which completes the proof of our claim.
, which completes the proof of our claim.
It remains to be shown that  can be extended to
an analytic function
can be extended to
an analytic function  on
on  that satisfies
that satisfies 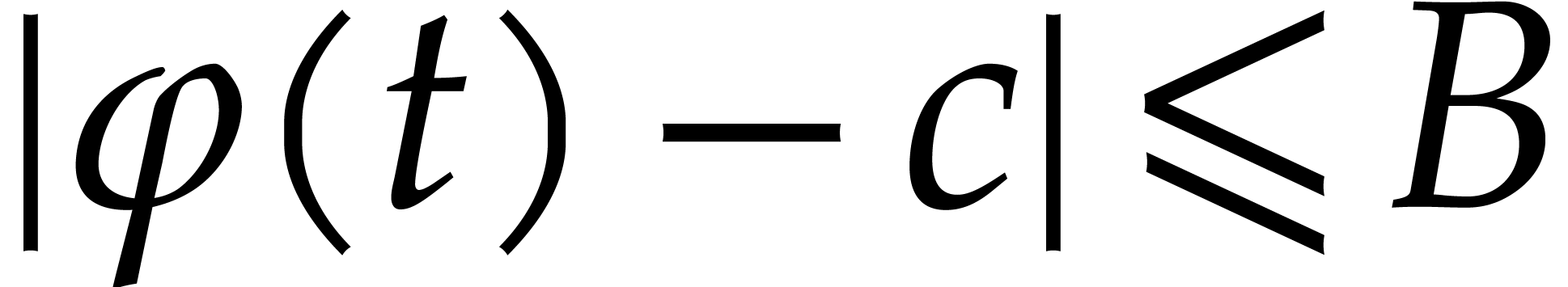 for all
for all  . Since
. Since  on
on  , we first notice that
, we first notice that  is bounded on
is bounded on  , whence
, whence  continuously extends to a function
continuously extends to a function  that is defined on the whole of
that is defined on the whole of  ,
and we clearly have
,
and we clearly have 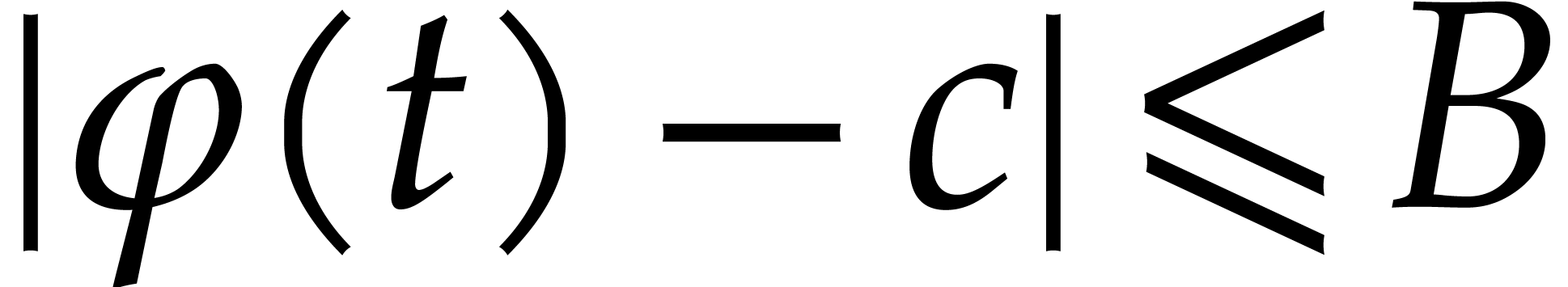 for all
for all  .
.
Now let us consider the unique solution 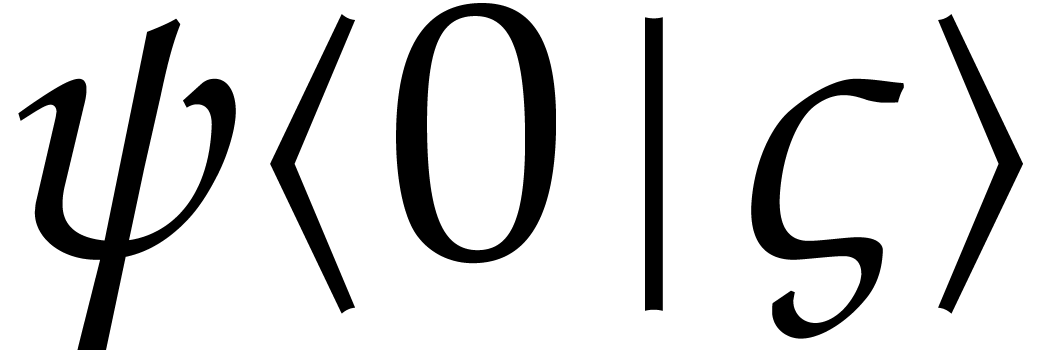 to the
initial value problem
to the
initial value problem 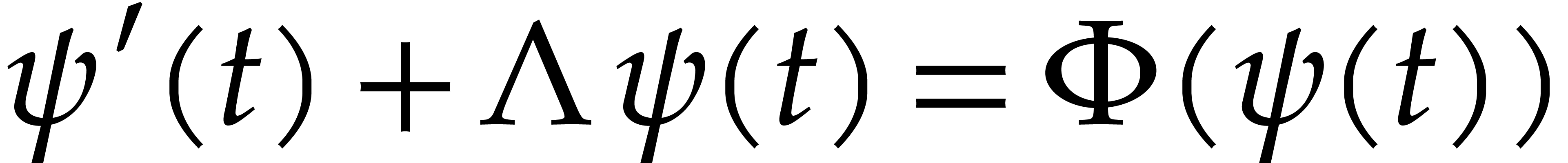 with
with 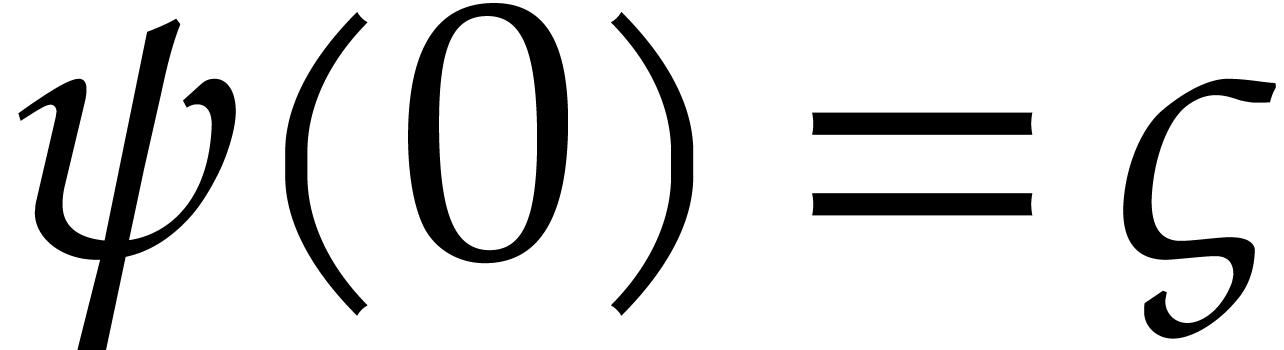 . Theorem 1 provides us with a
lower bound
. Theorem 1 provides us with a
lower bound 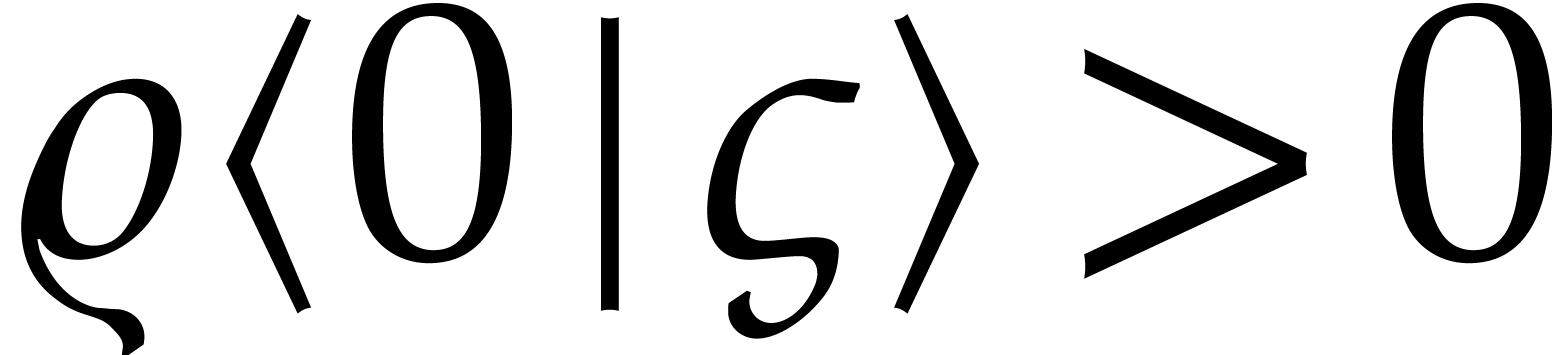 for the radius of convergence of
for the radius of convergence of
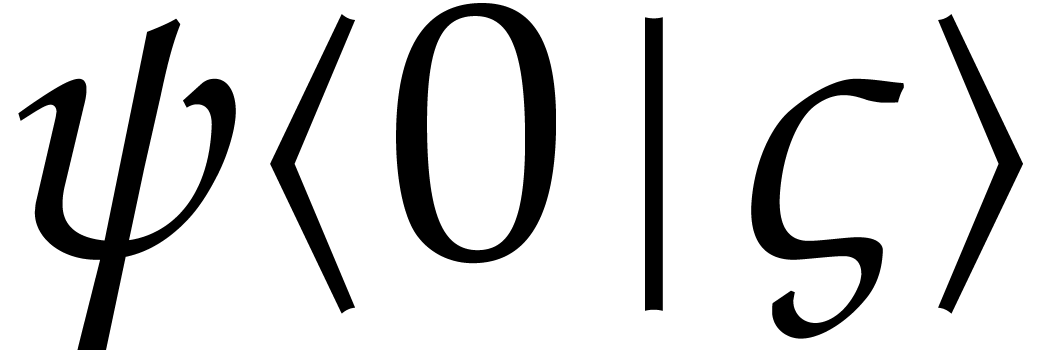 , which depends continuously
on
, which depends continuously
on  . By the compactness of
. By the compactness of
 , it follows that there
exists some
, it follows that there
exists some  with
with 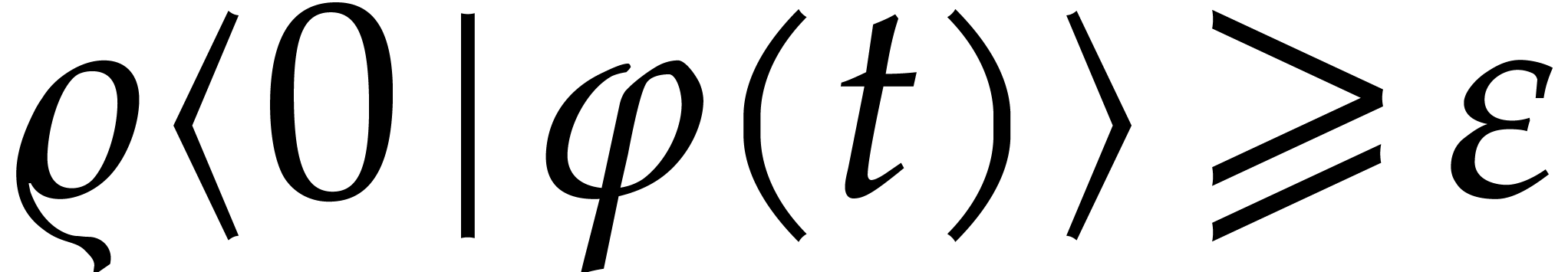 for all
for all
 . Now consider
. Now consider  on the boundary
on the boundary  of
of  and let
and let  be such that
be such that 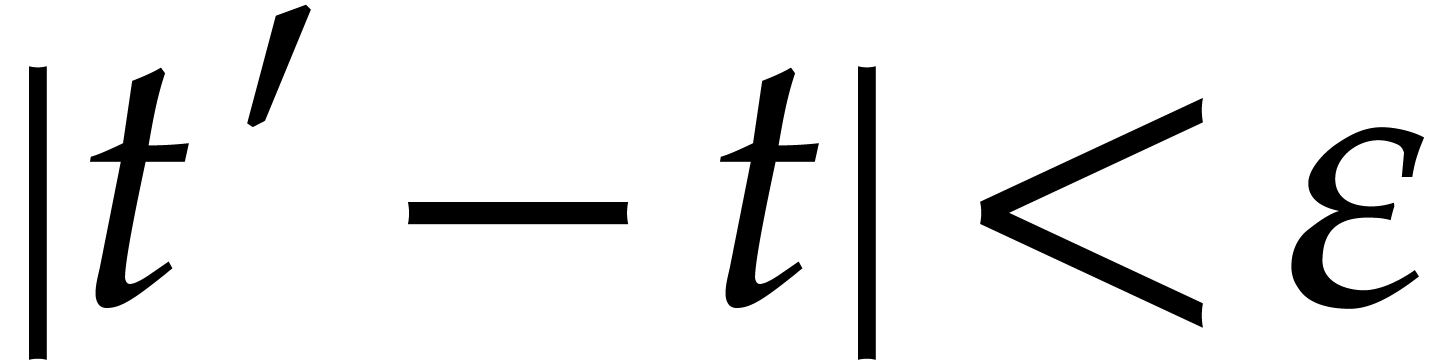 . Then
. Then 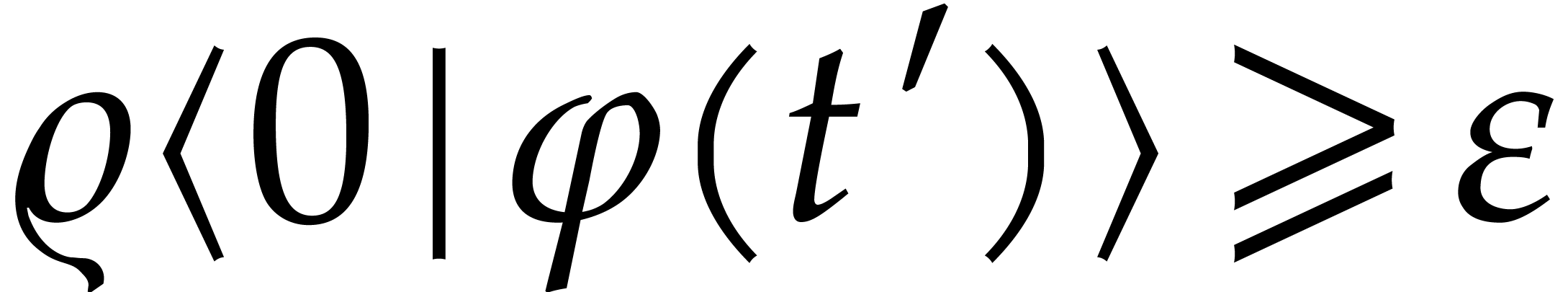 and
and 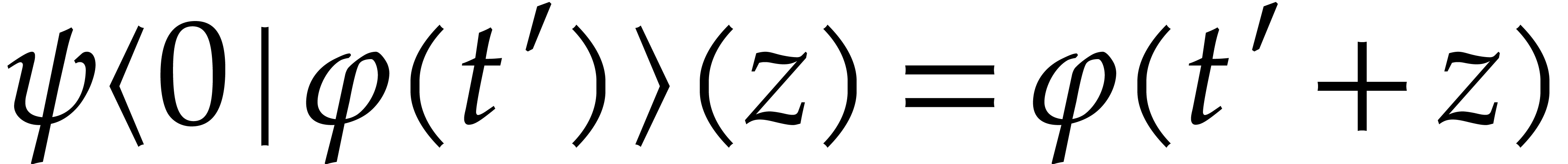 on some neighbourhood of
on some neighbourhood of 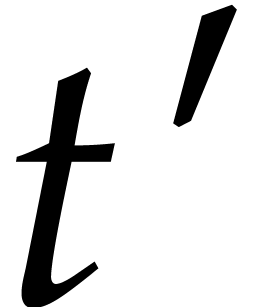 .
We conclude that
.
We conclude that 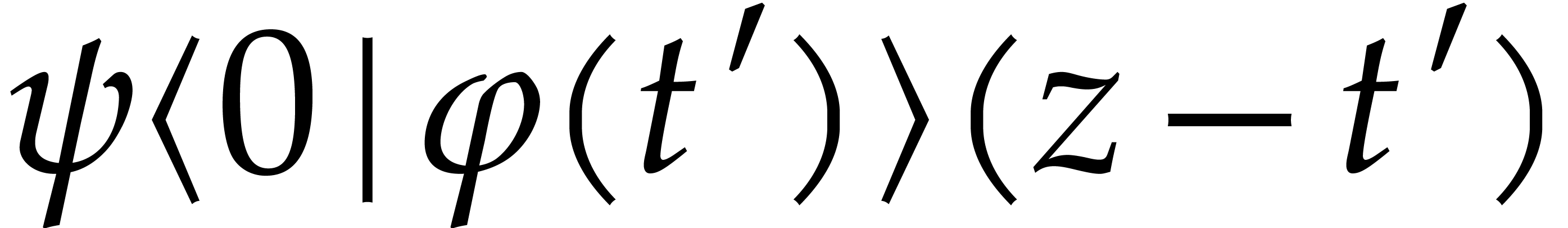 is an analytic extension of
is an analytic extension of
 to the open disk
to the open disk 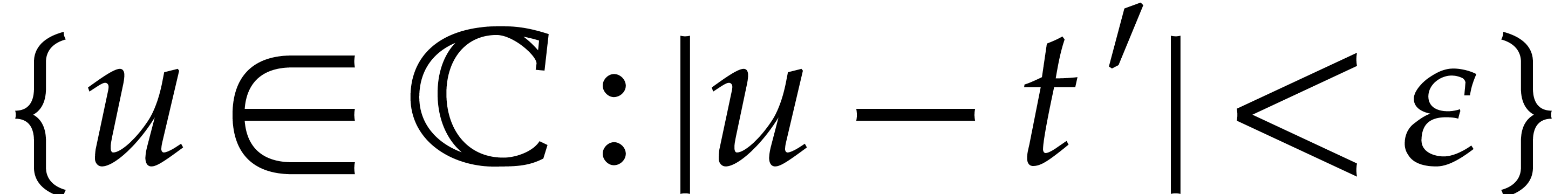 that
contains
that
contains  .
.
Before we present algorithms for the numeric integration of (1),
let us first consider the question how to compute formal power series
solutions. Since we will later be considering power series solutions at
various times  , we will use
the letter
, we will use
the letter 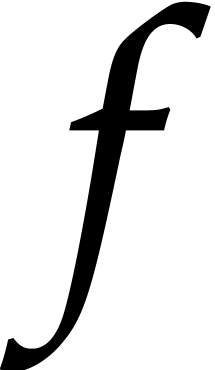 instead of
instead of  for such solutions. Notice that a vector
for such solutions. Notice that a vector 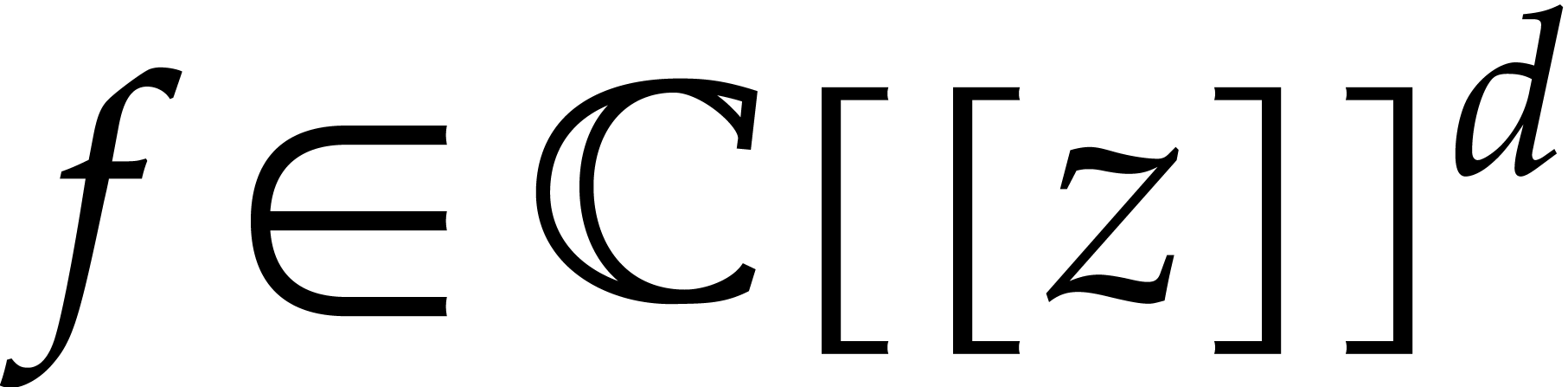 of
of  formal power series can also be regarded as a formal
power series
formal power series can also be regarded as a formal
power series 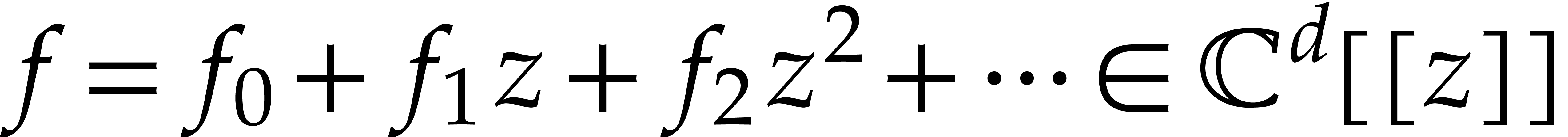 with coefficients in
with coefficients in 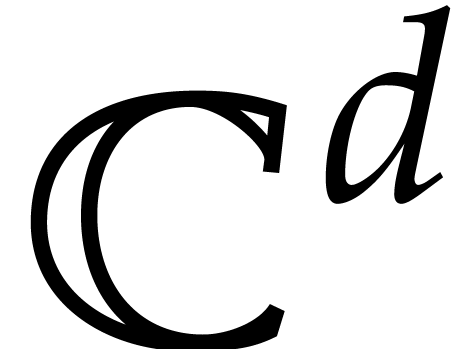 .
.
Let  be the initial condition. Setting
be the initial condition. Setting 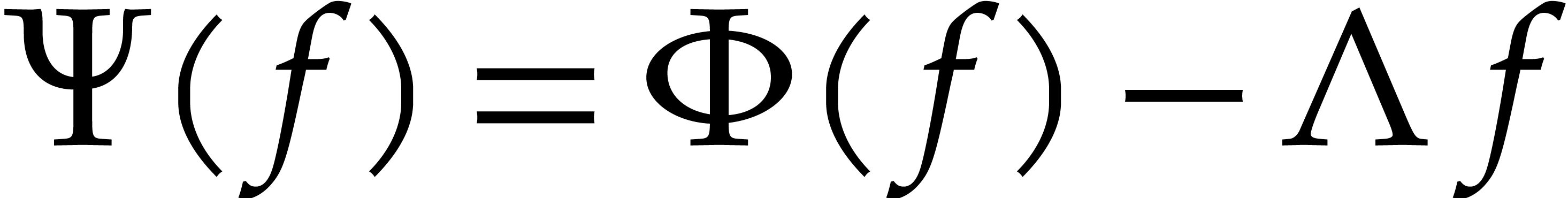 , we are thus interested in the
computation of truncated power series solutions to the equation
, we are thus interested in the
computation of truncated power series solutions to the equation
Alternatively, this equation can be rewritten in integral form
where the integration operator 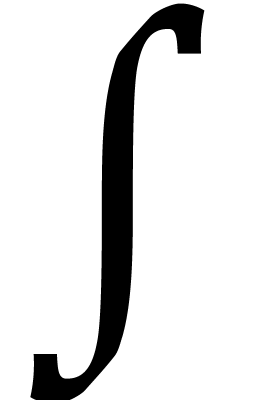 sends
sends 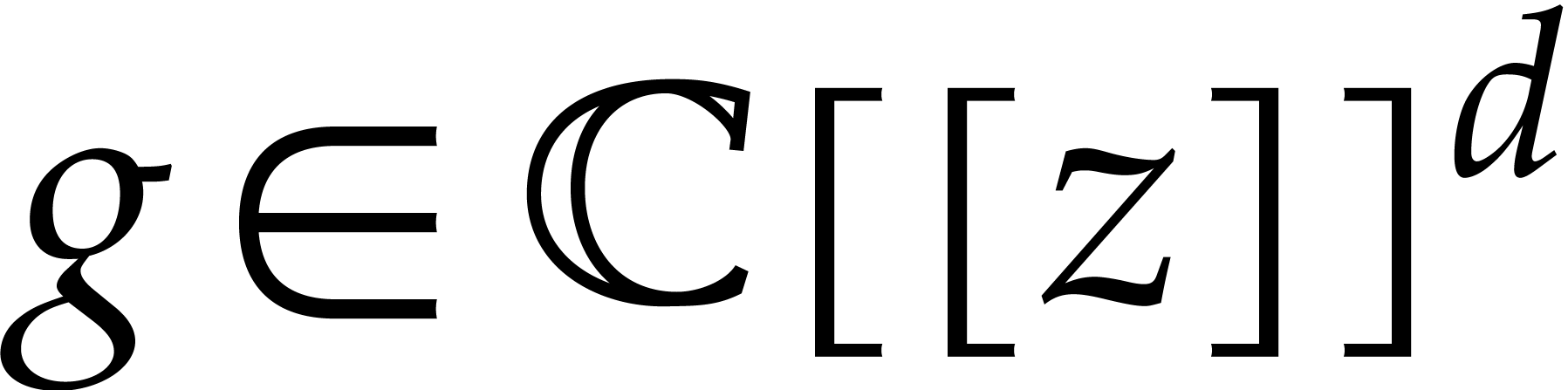 to
to 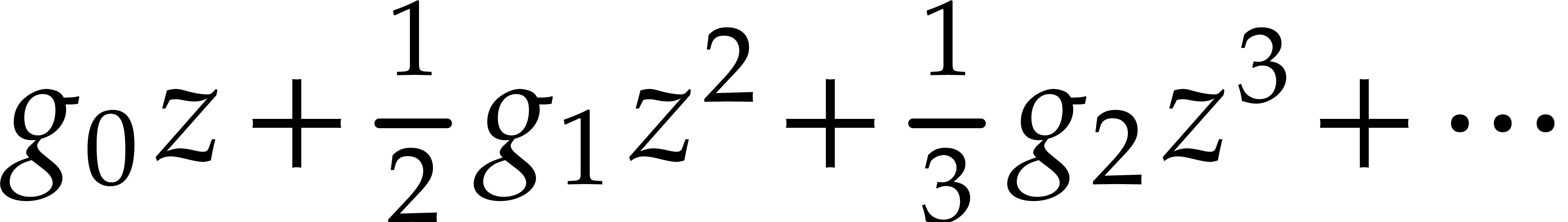 .
.
In this section, we recall several approaches to the computation of
power series solutions to such equations. The efficiency of each method
can be measured in terms of the number of field operations in  that are required to compute the first
that are required to compute the first 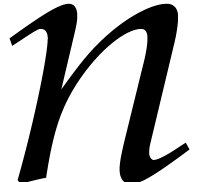 terms of the solution. For the time being, we assume that all
computations are done at a fixed bit precision
terms of the solution. For the time being, we assume that all
computations are done at a fixed bit precision 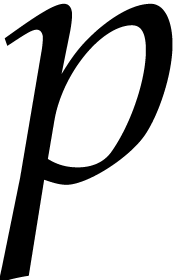 , so that operations in
, so that operations in  are
done at unit cost. One may also take into account the number
are
done at unit cost. One may also take into account the number 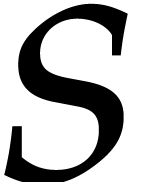 of scalar operations that are necessary for the evaluation
of
of scalar operations that are necessary for the evaluation
of  . A further refinement is
to separately count the number
. A further refinement is
to separately count the number  of
multiplications that are needed. For instance, if
of
multiplications that are needed. For instance, if 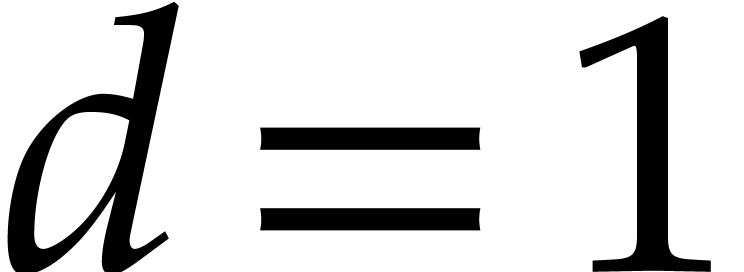 and
and 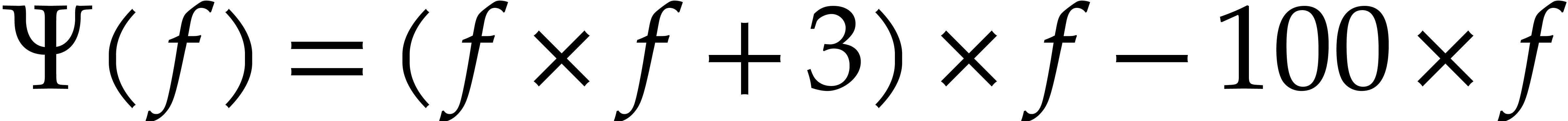 , then we have
, then we have  and
and 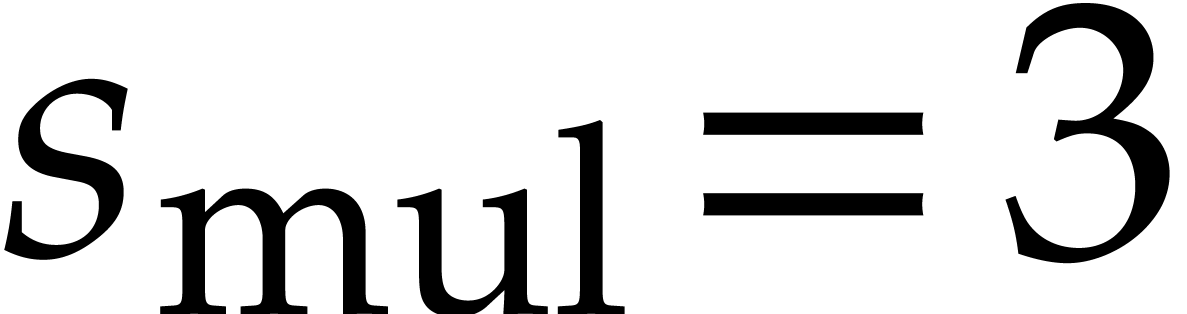 . We always
assume that
. We always
assume that  .
.
 in
in 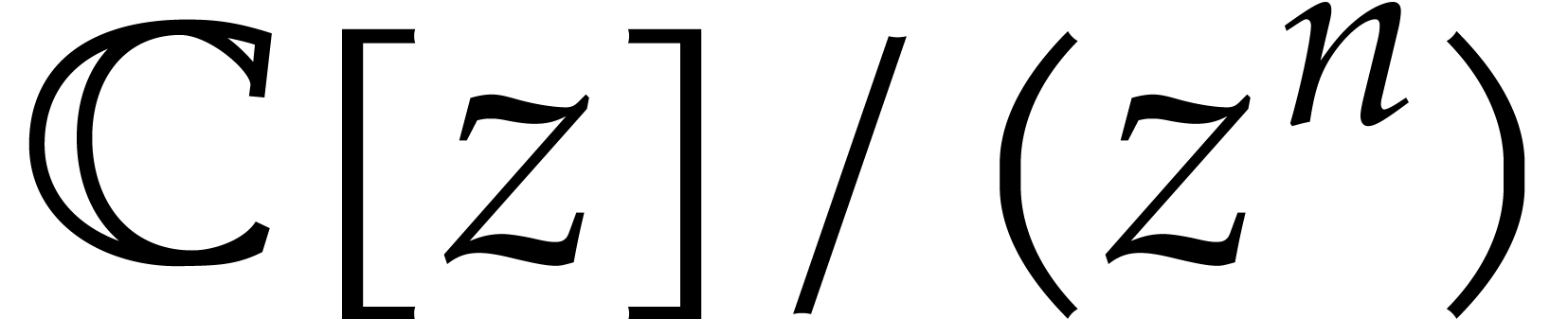 , which are also called jets of order
, which are also called jets of order
 . One addition in
. One addition in 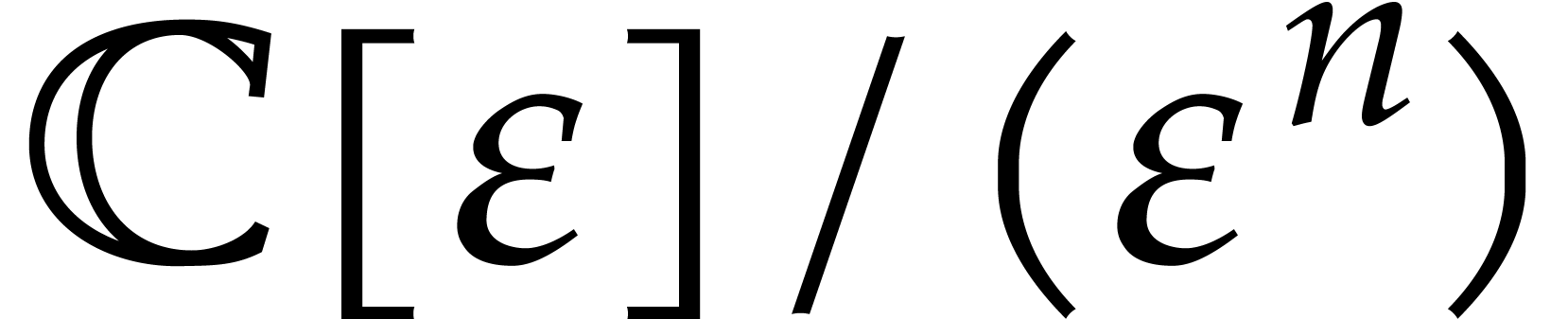 reduces to
reduces to 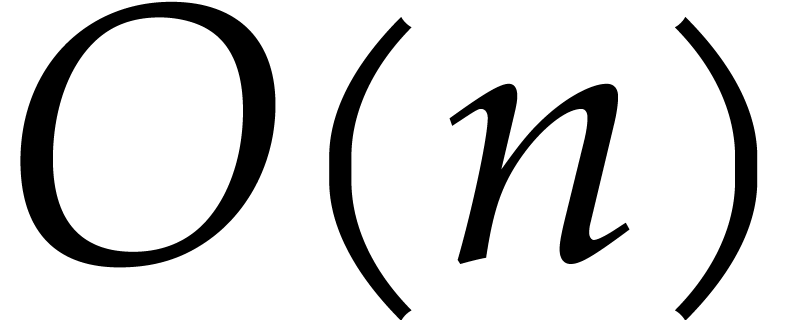 additions in
additions in  and similarly for scalar multiplications with an
element in
and similarly for scalar multiplications with an
element in  . A naive
multiplication in
. A naive
multiplication in 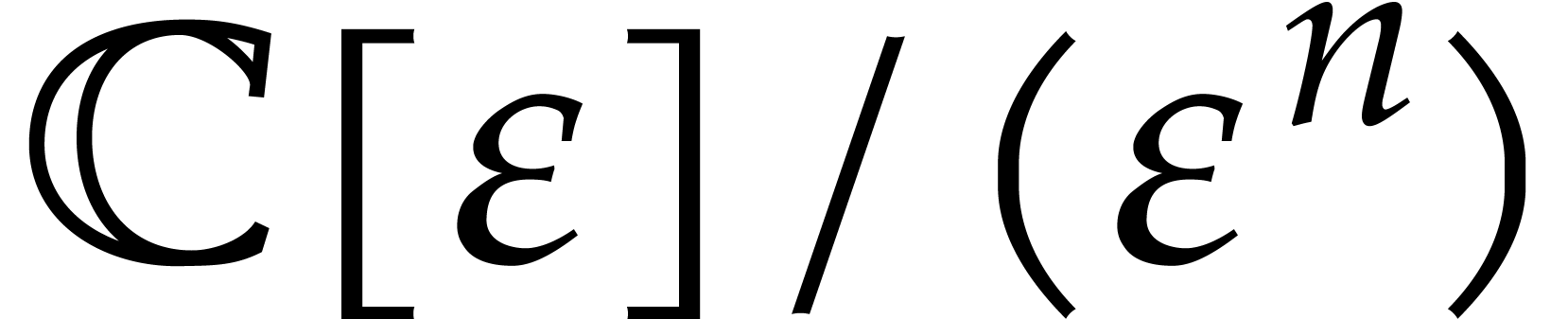 requires
requires 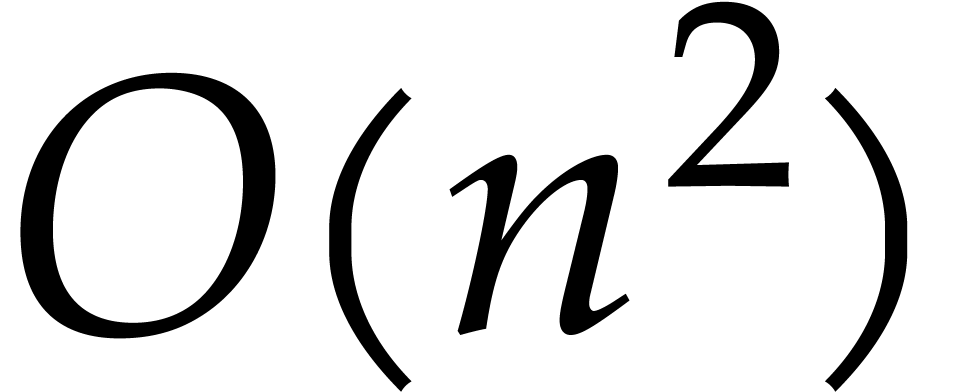 operations in
operations in  , although
this cost can be reduced to
, although
this cost can be reduced to 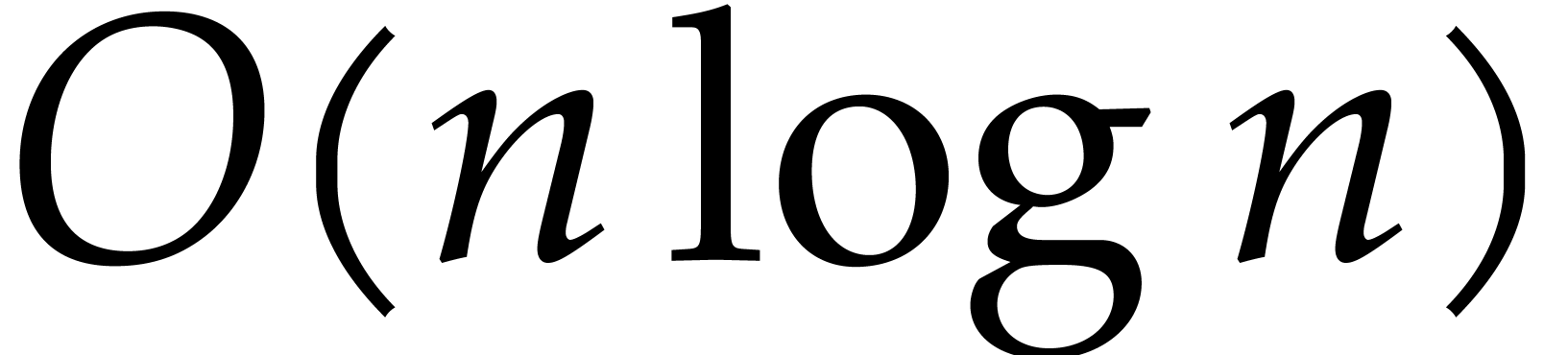 using FFT
techniques. The integration operator
using FFT
techniques. The integration operator  sends
sends
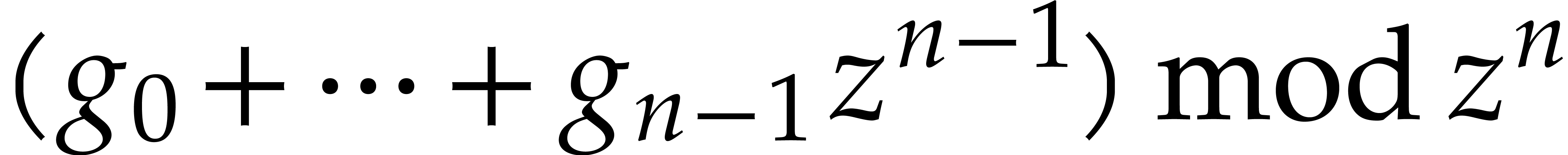 to
to 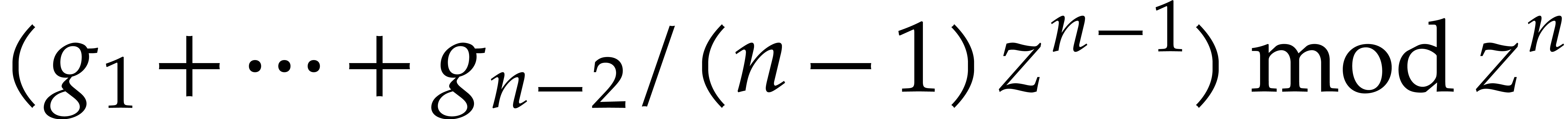 and can be computed
in linear time.
and can be computed
in linear time.
Now assume that 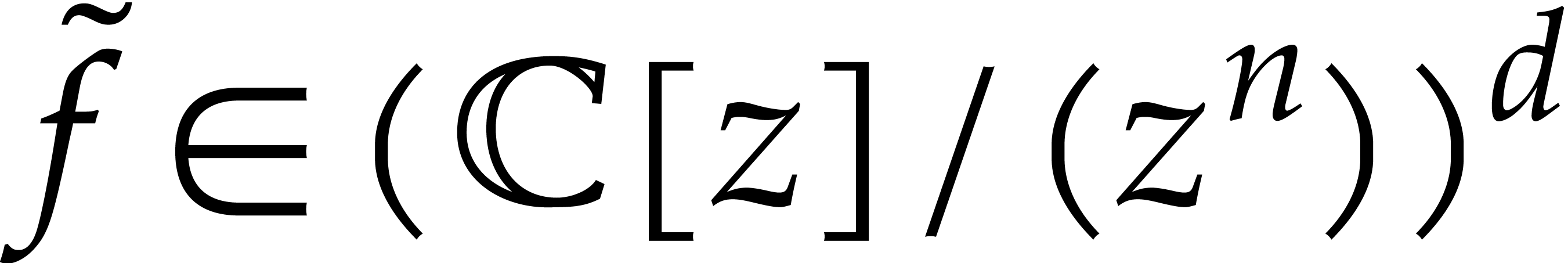 is an approximate solution to
(11) whose first
is an approximate solution to
(11) whose first 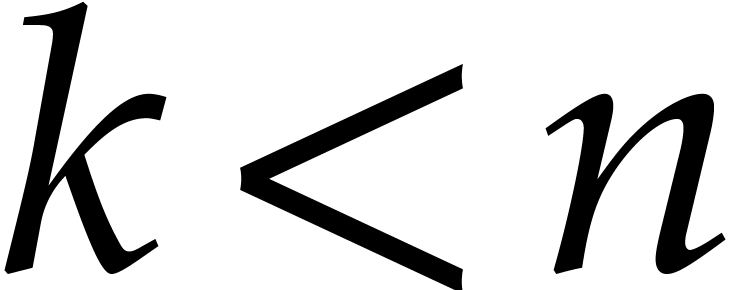 terms are correct.
In other words, if
terms are correct.
In other words, if 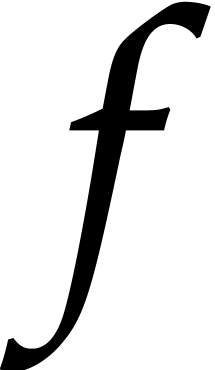 is the actual solution and
is the actual solution and
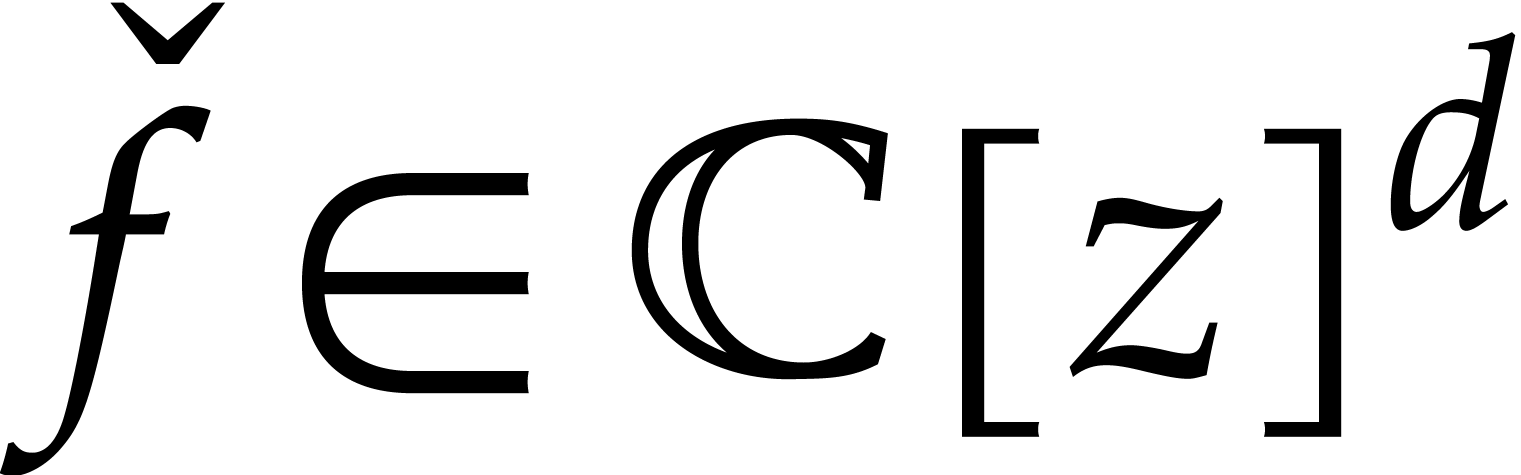 is a preimage of
is a preimage of 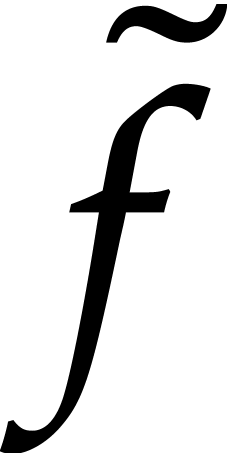 with
with
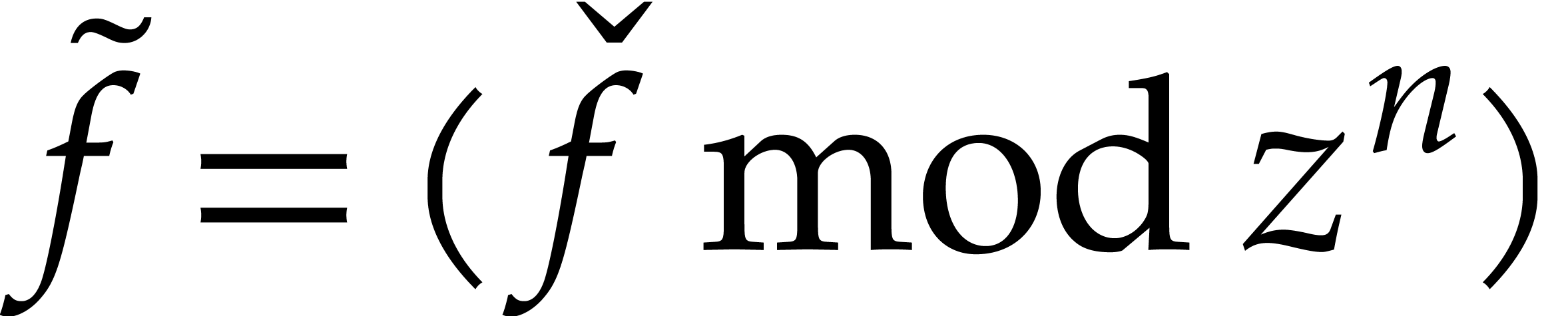 , then
, then 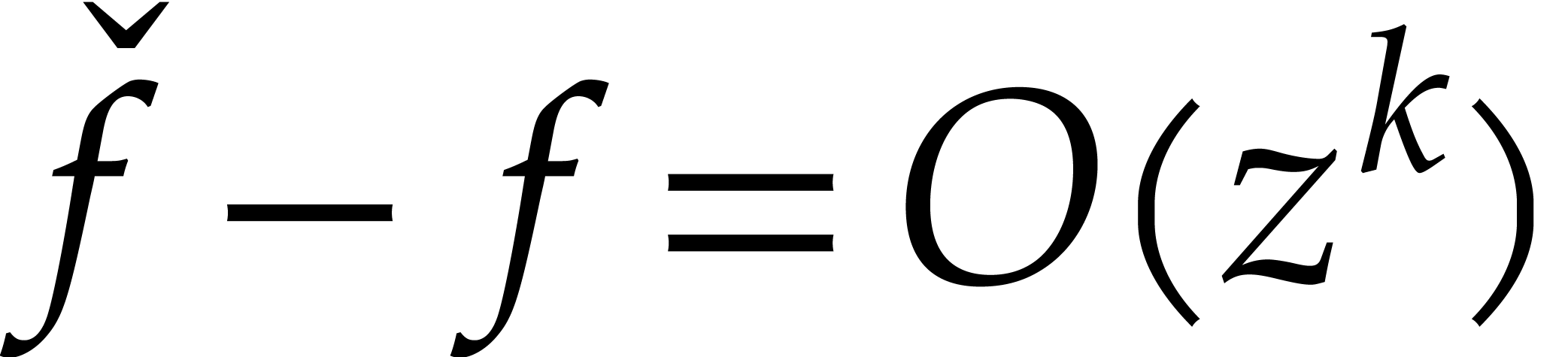 . Given such an approximation, one iteration
. Given such an approximation, one iteration
of (11) yields a new approximation whose first  terms are correct. Starting with
terms are correct. Starting with 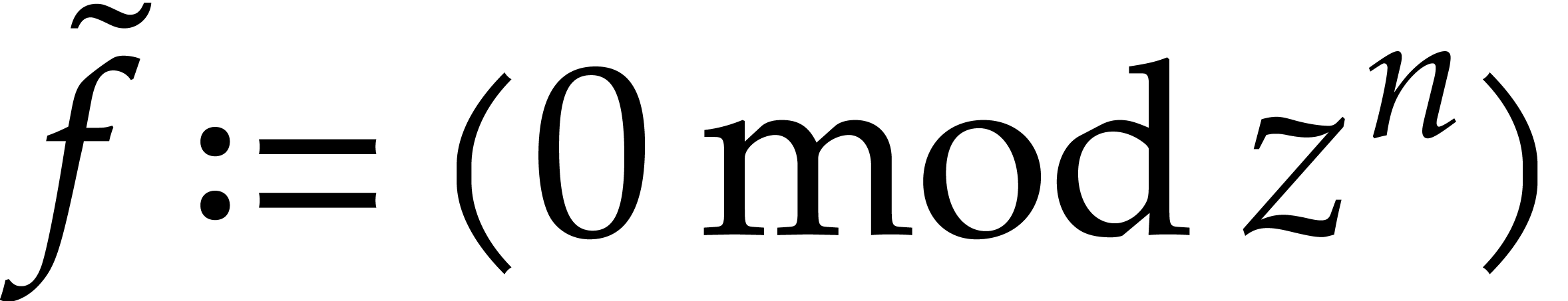 , we thus obtain a solution modulo
, we thus obtain a solution modulo 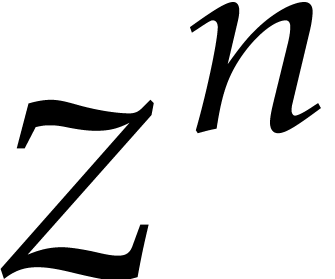 of (11) after at most
of (11) after at most 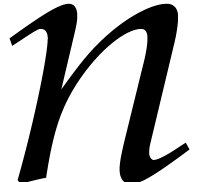 iterations.
The total cost of this computation is bounded by
iterations.
The total cost of this computation is bounded by 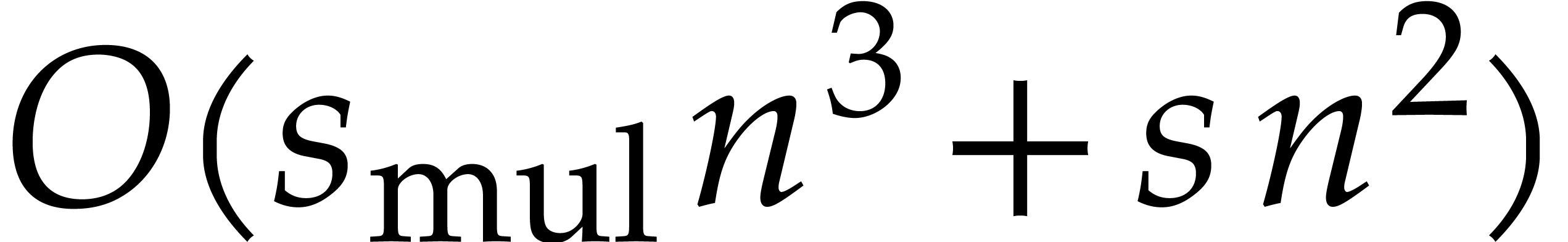 , or by
, or by 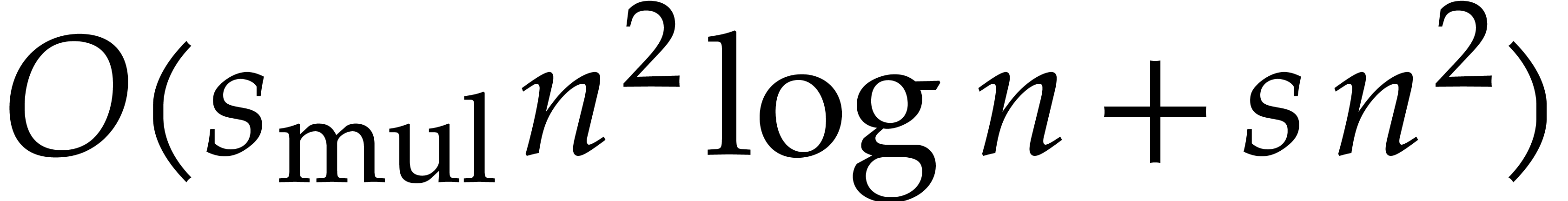 when using
FFT-techniques.
when using
FFT-techniques.
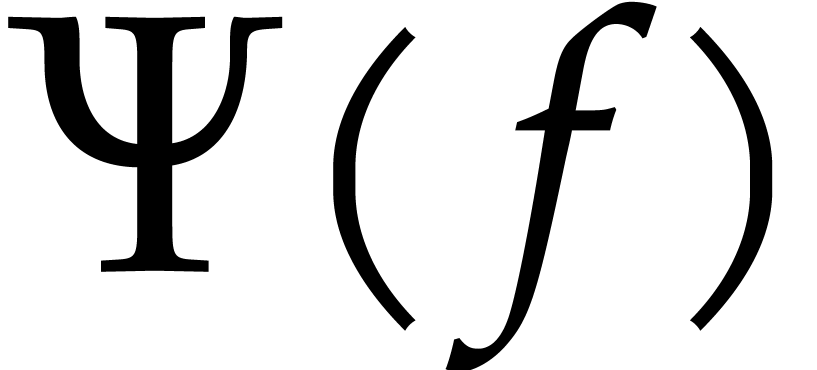 is a polynomial, it is built from the
components of
is a polynomial, it is built from the
components of  using additions,
multiplications, and scalar multiplications with constants in
using additions,
multiplications, and scalar multiplications with constants in  . For sums, scalar products,
general products, and integrals of power series, we may extract their
coefficients in
. For sums, scalar products,
general products, and integrals of power series, we may extract their
coefficients in  using the following rules
using the following rules
Applying this recursively to the polynomial expression  , the iteration (12) yields a
recursion relation
, the iteration (12) yields a
recursion relation
that allows us to compute  from
from 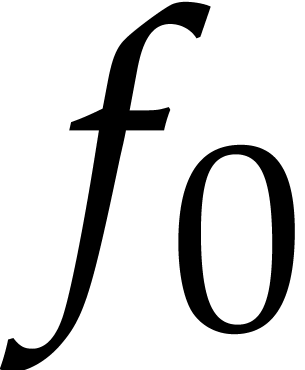 , by induction on
, by induction on 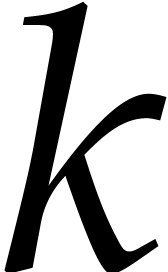 .
Proceeding in this way, the computation of the solution
.
Proceeding in this way, the computation of the solution 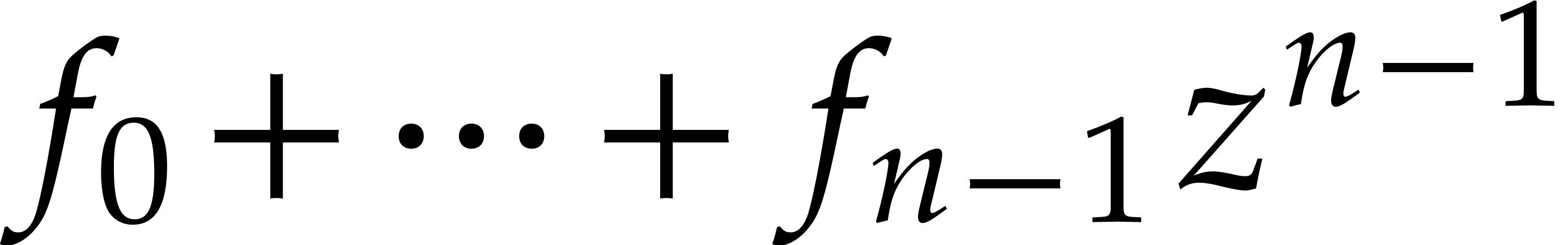 at order
at order 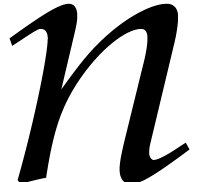 requires
requires 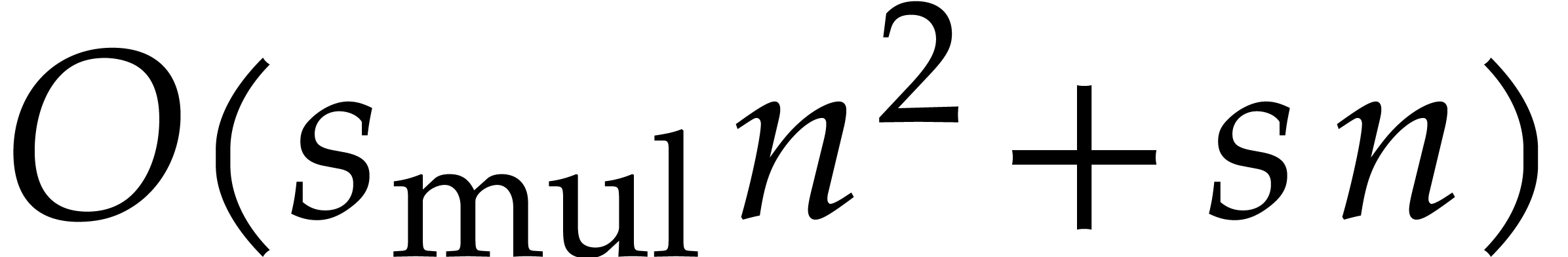 operations.
operations.
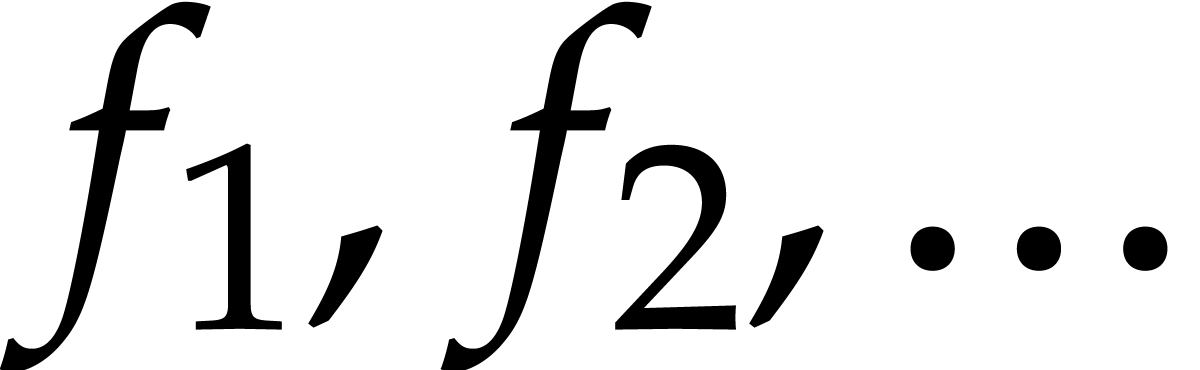 successively using the recursion relation (17) can be
reformulated elegantly in the framework of lazy power series
computations. The idea is to regard a power series
successively using the recursion relation (17) can be
reformulated elegantly in the framework of lazy power series
computations. The idea is to regard a power series  as given by its stream
as given by its stream  of coefficients. Basic
arithmetic operations on power series are implemented in a
lazy manner: when computing the
of coefficients. Basic
arithmetic operations on power series are implemented in a
lazy manner: when computing the 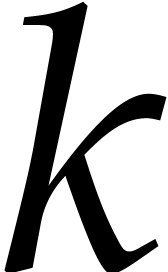 -th
coefficient of a sum
-th
coefficient of a sum 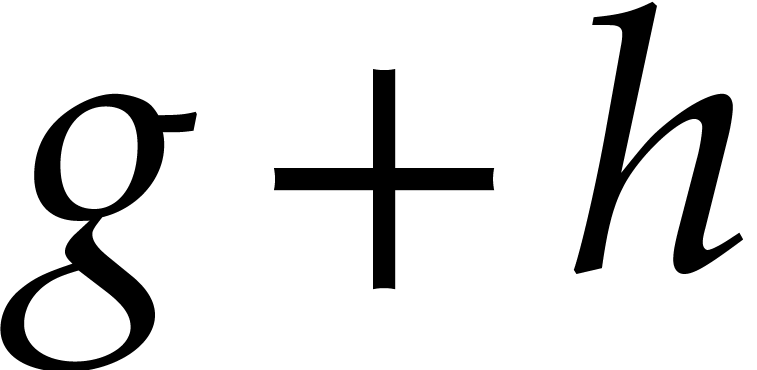 , a
product
, a
product 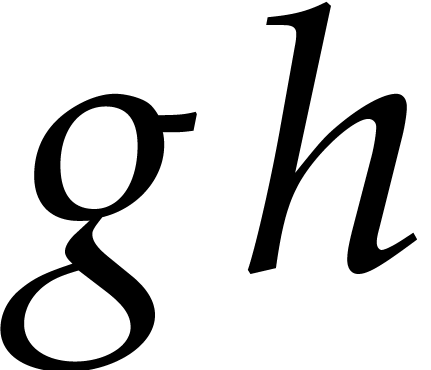 , or an integral
, or an integral
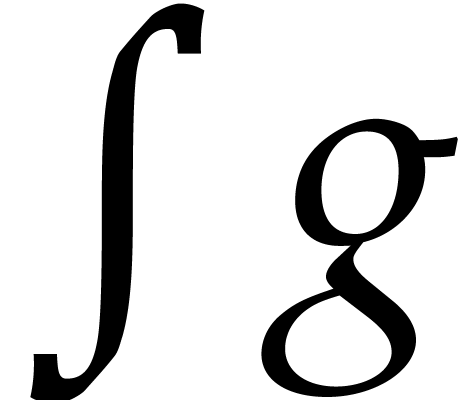 , we compute “just
the coefficients that are needed” from
, we compute “just
the coefficients that are needed” from 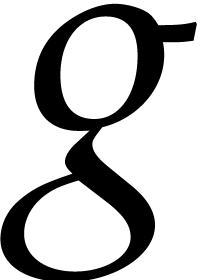 and
and 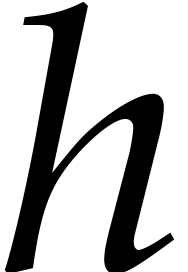 . The natural way to do
this is precisely to use the relations (13–16).
. The natural way to do
this is precisely to use the relations (13–16).
The lazy power series approach has the important property that the 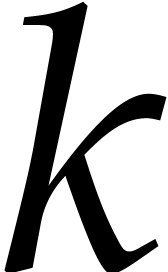 -th coefficient
-th coefficient 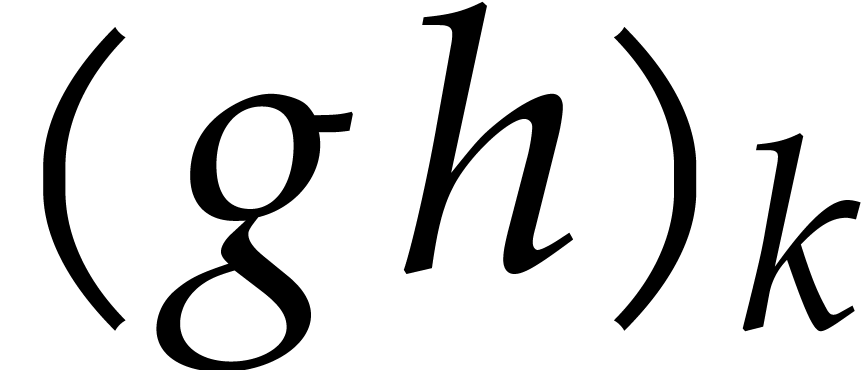 of a product (say) becomes available as soon as
of a product (say) becomes available as soon as  and
and  are given. This makes it possible to let
are given. This makes it possible to let
 and
and  depend on the result
depend on the result
 , as long as the computation
of
, as long as the computation
of  and
and 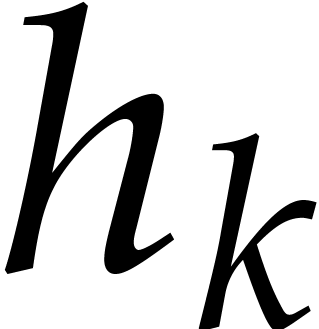 only involves
previous coefficients
only involves
previous coefficients  of
of 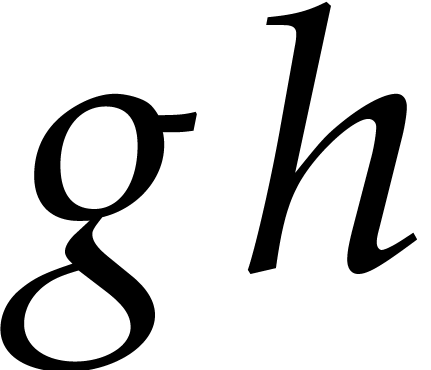 . As a consequence, the fixed point equation (11) can be solved simply by evaluating the right hand side
using lazy power series arithmetic. Indeed, the
. As a consequence, the fixed point equation (11) can be solved simply by evaluating the right hand side
using lazy power series arithmetic. Indeed, the 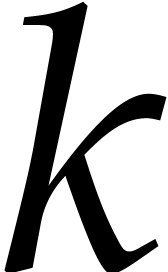 -th coefficient
-th coefficient 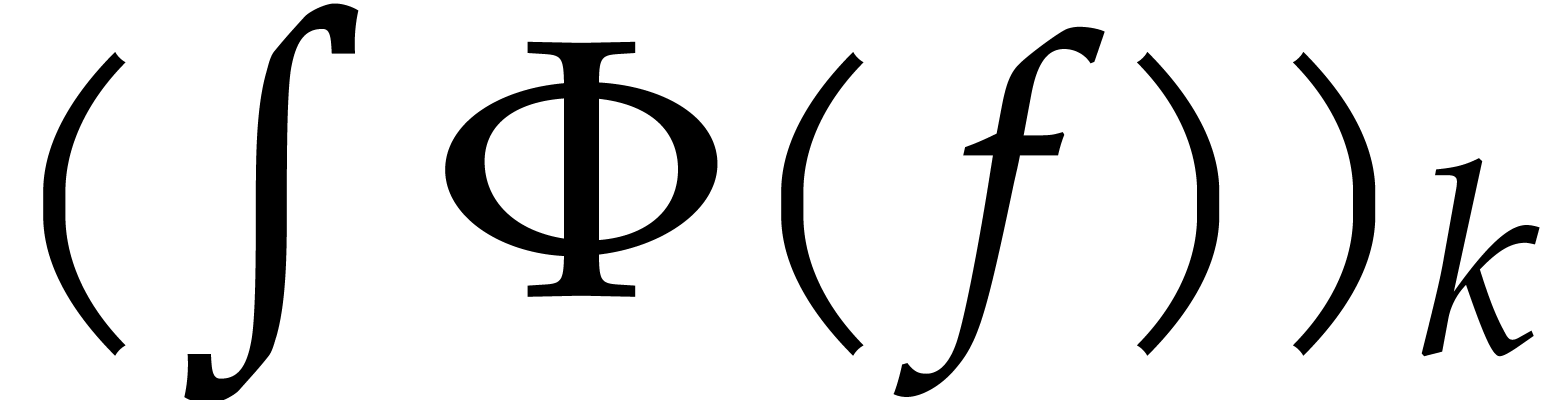 only depends
on previous coefficients
only depends
on previous coefficients  of
of  .
.
 using (15) requires
using (15) requires 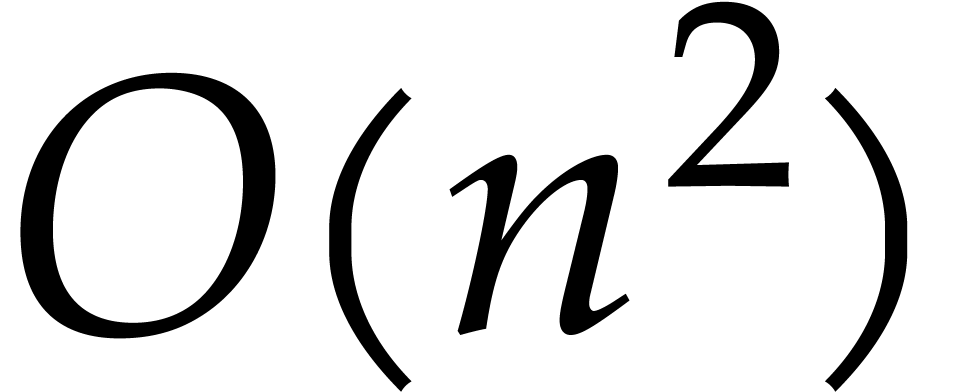 operations. Here we
recall that FFT techniques allow us to compute a product in
operations. Here we
recall that FFT techniques allow us to compute a product in 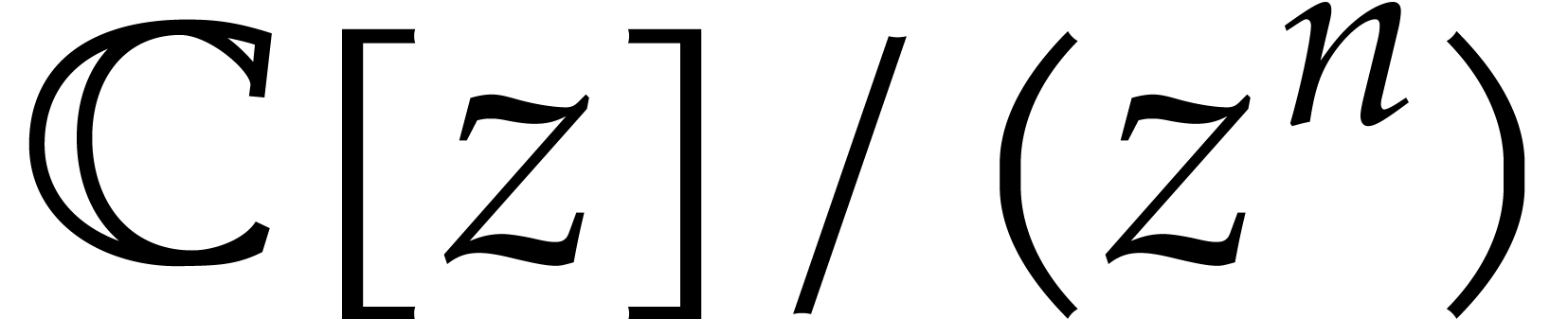 using only
using only 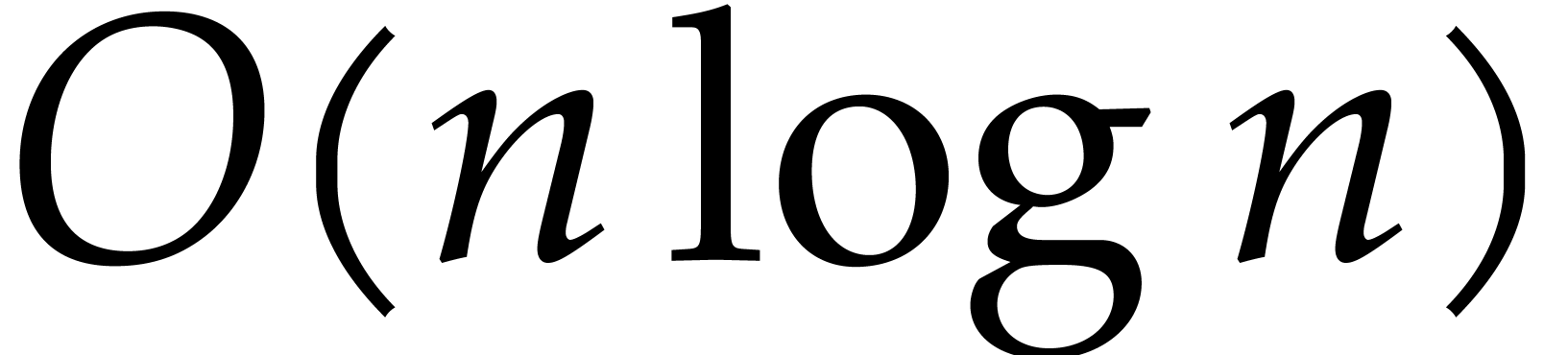 operations.
operations.
One essential observation is that, in order to solve (11)
using the lazy power series approach, we only relied on the fact that
each coefficient 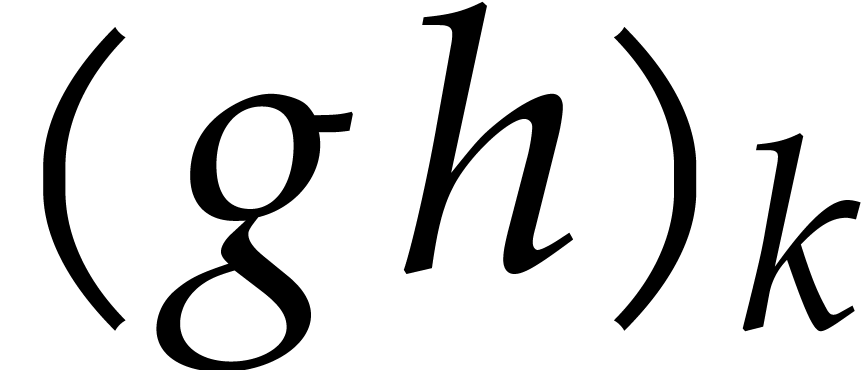 becomes available as soon as
becomes available as soon as
 and
and  are given. In fact,
it is possible to design faster multiplication methods that still have
this property; such methods are said to be relaxed or
on-line. A relaxed multiplication method that computes a
product at order
are given. In fact,
it is possible to design faster multiplication methods that still have
this property; such methods are said to be relaxed or
on-line. A relaxed multiplication method that computes a
product at order 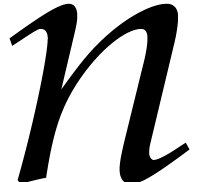 in time
in time 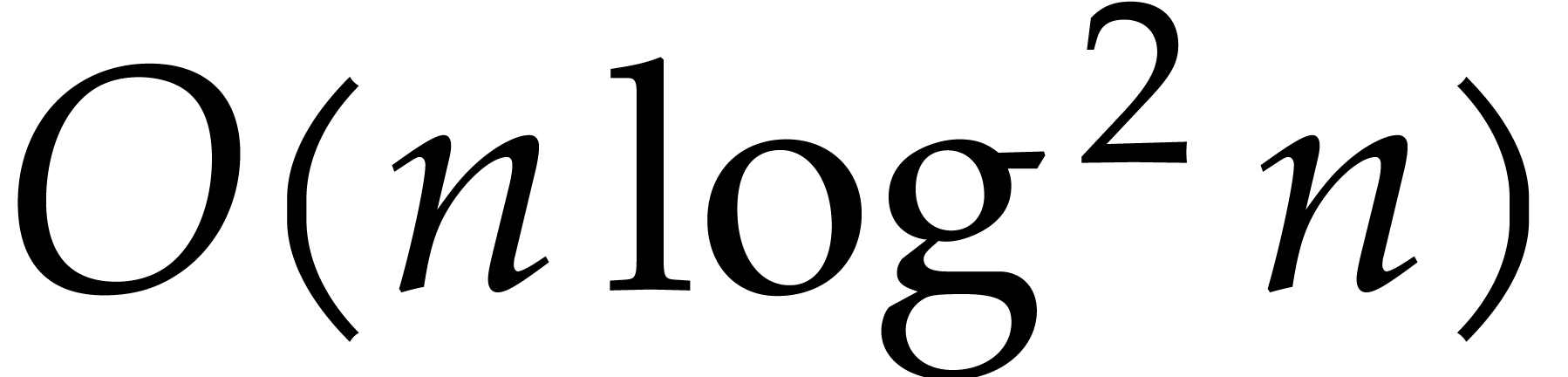 was presented in [8] and can be traced back to [6].
An even faster algorithm of time complexity
was presented in [8] and can be traced back to [6].
An even faster algorithm of time complexity 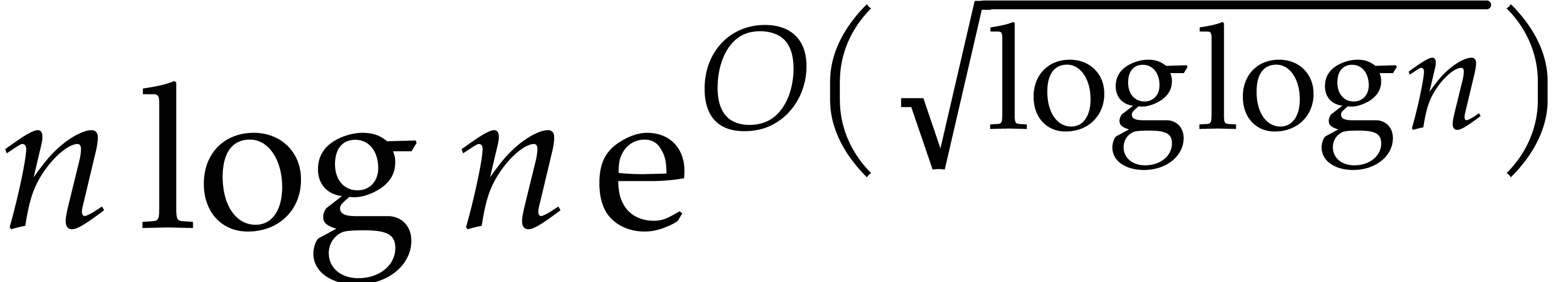 was
given in [9].
was
given in [9].
Denoting by 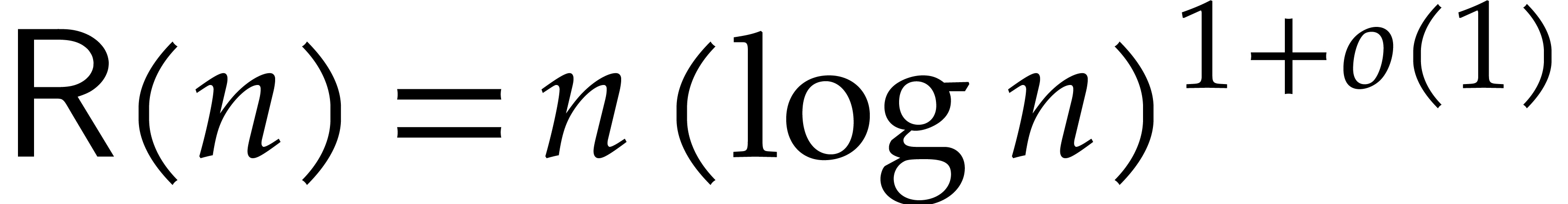 the cost of relaxed multiplication
at order
the cost of relaxed multiplication
at order 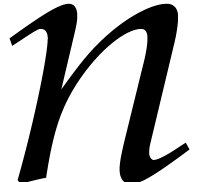 , the resolution of
(11) at order
, the resolution of
(11) at order 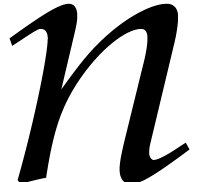 now requires only
now requires only
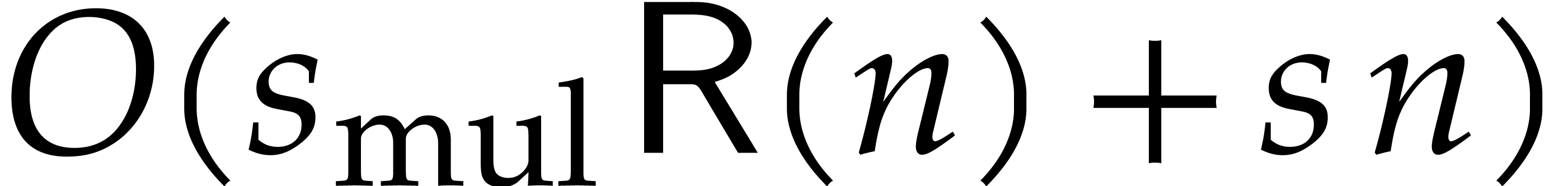 operations.
operations.
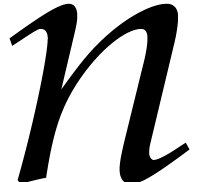 in time
in time 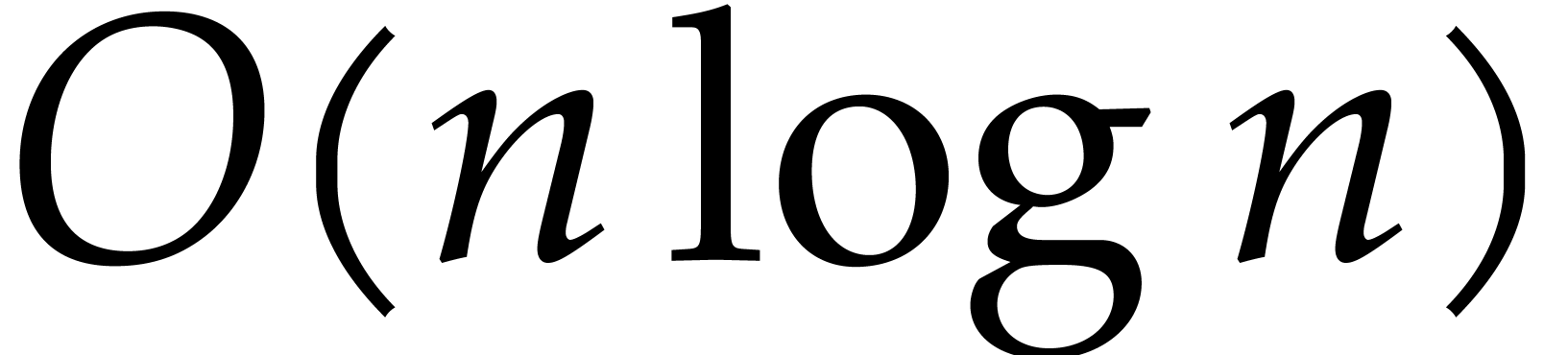 . However, this
complexity analysis does not take into account the dependence on
. However, this
complexity analysis does not take into account the dependence on  and
and 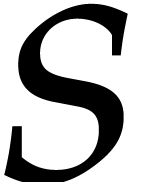 . In
particular, the dependence on
. In
particular, the dependence on  of Brent and
Kung's method is exponential [8]. Faster algorithms were
proposed in [26, 1], based on the
simultaneous computation of the solution
of Brent and
Kung's method is exponential [8]. Faster algorithms were
proposed in [26, 1], based on the
simultaneous computation of the solution 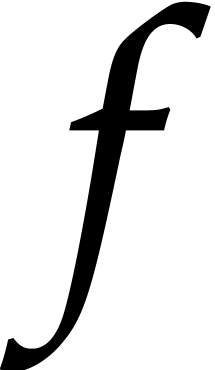 and
its first variation. This allows for the computation of a solution of
(10) at order
and
its first variation. This allows for the computation of a solution of
(10) at order 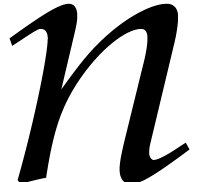 in time
in time 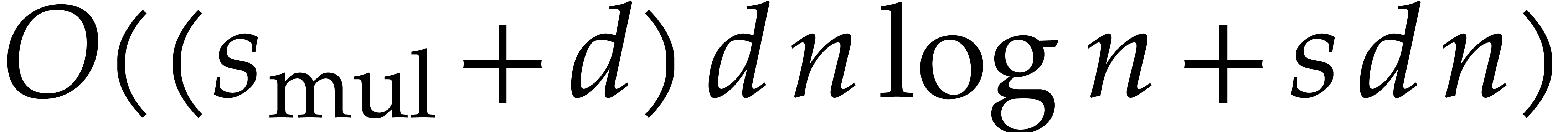 . Whenever
. Whenever 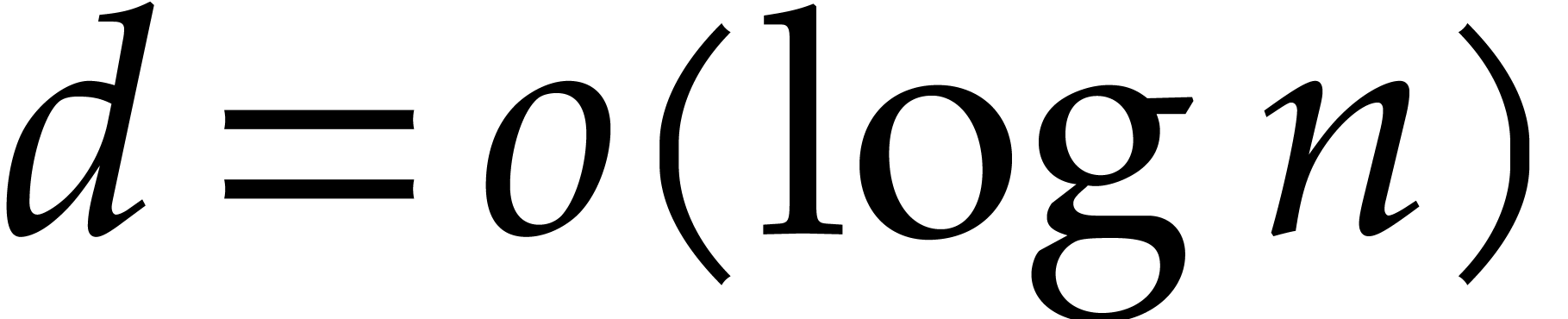 , the computation time can be further reduced to
, the computation time can be further reduced to
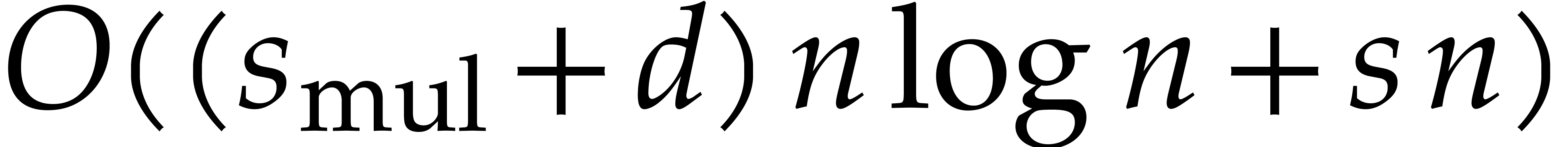 [10]. For small
[10]. For small  , this leads to the asymptotically most
efficient method for solving (10). For large
, this leads to the asymptotically most
efficient method for solving (10). For large  , the computation of the first variation
induces a
, the computation of the first variation
induces a 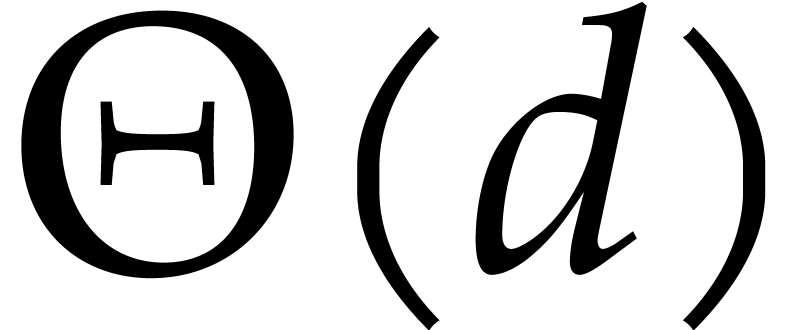 overhead, and the relaxed method
usually becomes more efficient.
overhead, and the relaxed method
usually becomes more efficient.
Let  as before. The aim of this section is to
present a naive algorithm for the numerical integration of the
differential equation
as before. The aim of this section is to
present a naive algorithm for the numerical integration of the
differential equation
based on the computation of truncated power series solutions at
successive times 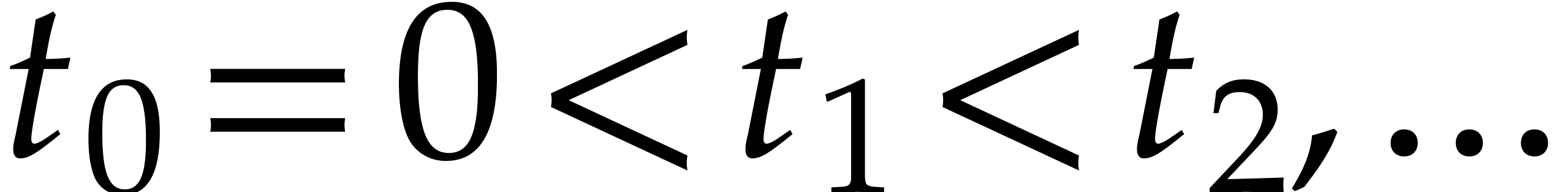 . We will
use a fixed expansion order
. We will
use a fixed expansion order 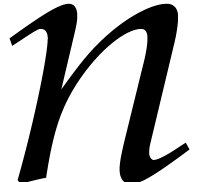 ,
a fixed bit precision
,
a fixed bit precision 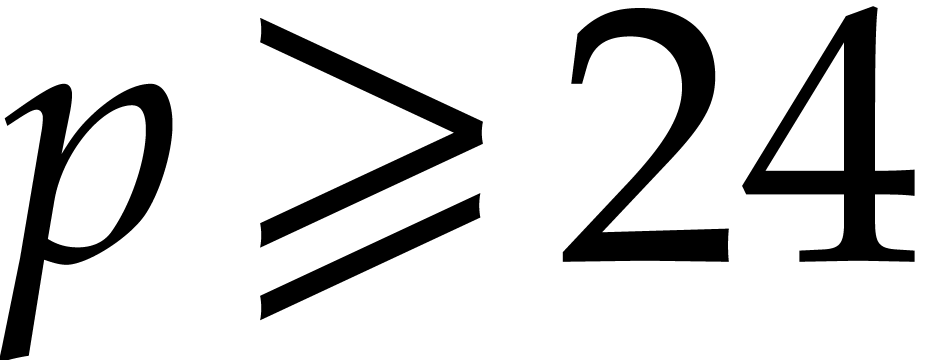 , but
an adaptive step size
, but
an adaptive step size 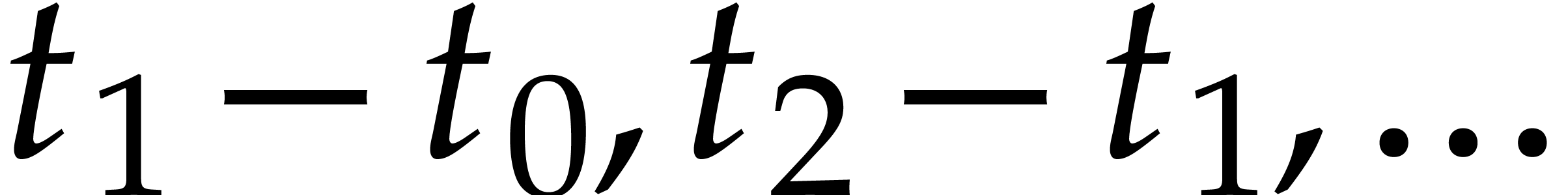 . At
. At
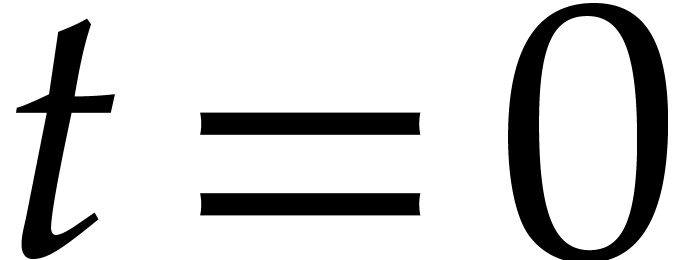 , we are given an initial
condition
, we are given an initial
condition 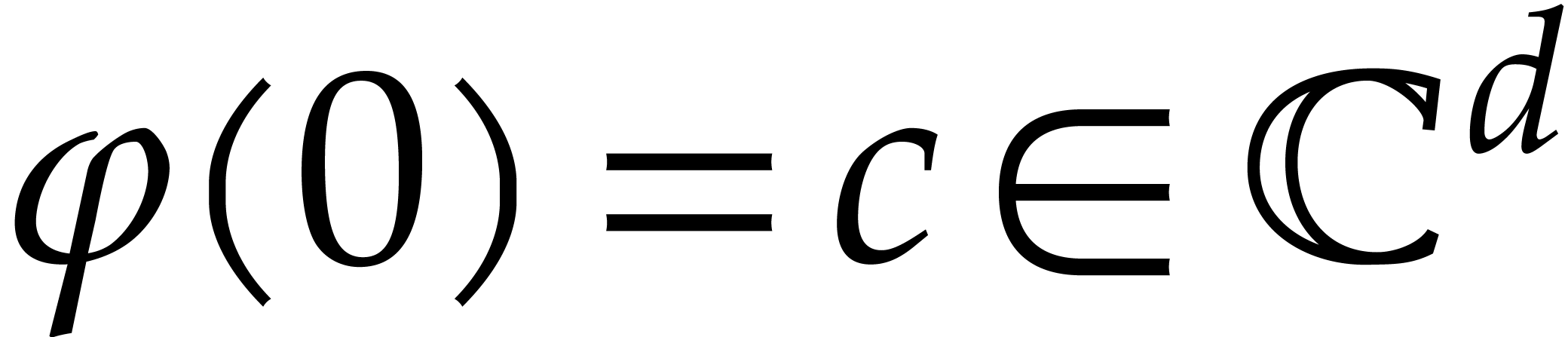 and our aim is to find a good numeric
approximation for
and our aim is to find a good numeric
approximation for 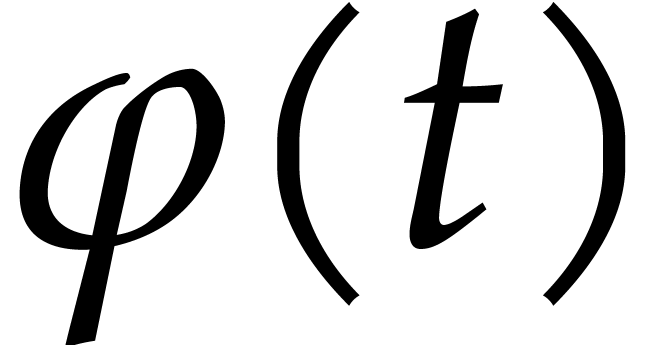 at time
at time  . The algorithm is not designed to be efficient when
the equation gets stiff and we will present a heuristic discussion on
what goes wrong when this happens.
. The algorithm is not designed to be efficient when
the equation gets stiff and we will present a heuristic discussion on
what goes wrong when this happens.
Let us write  for the Taylor series expansion of
for the Taylor series expansion of
 at time
at time  and
and 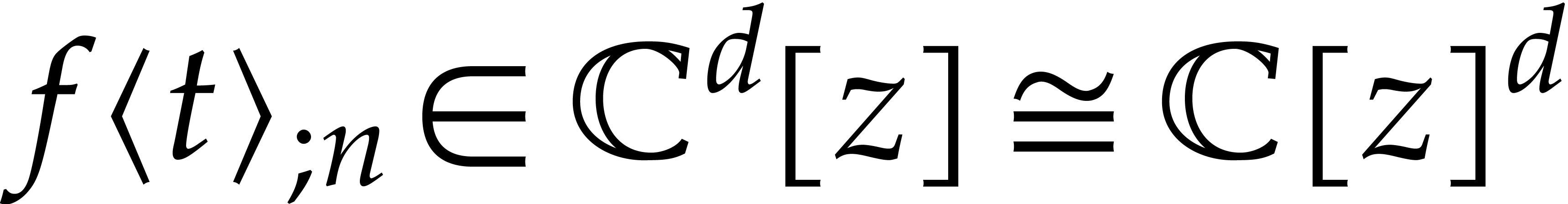 for its truncation at order
for its truncation at order 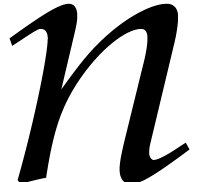 .
In other words, setting
.
In other words, setting
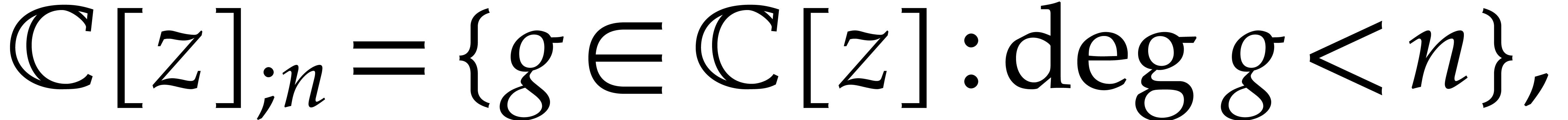
we have 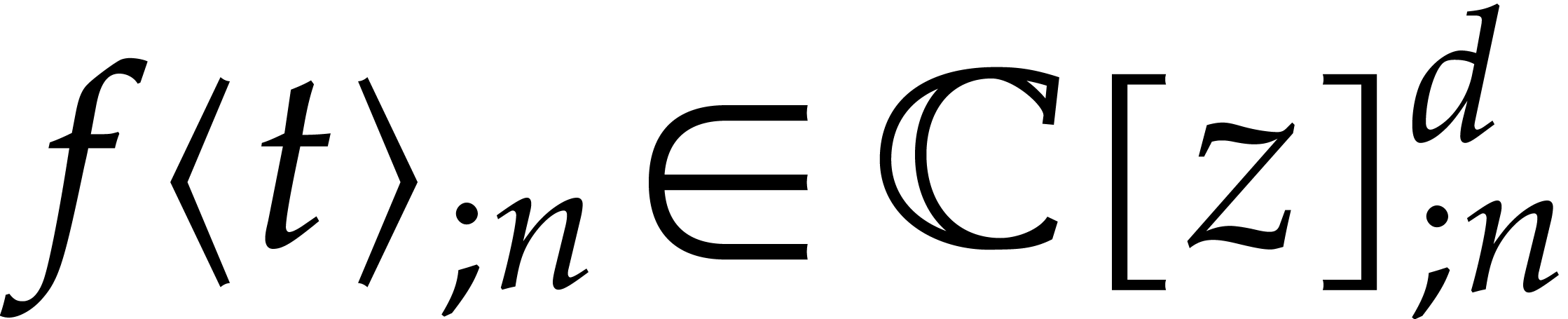 and
and
If the time  at which we expand
at which we expand  is clear from the context, then we will simply drop the postfix
is clear from the context, then we will simply drop the postfix 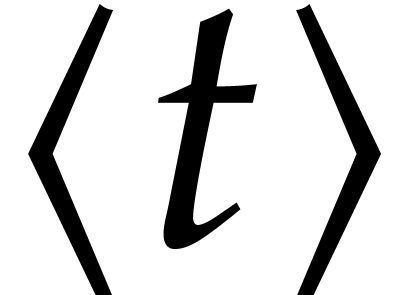 and write
and write  instead of
instead of 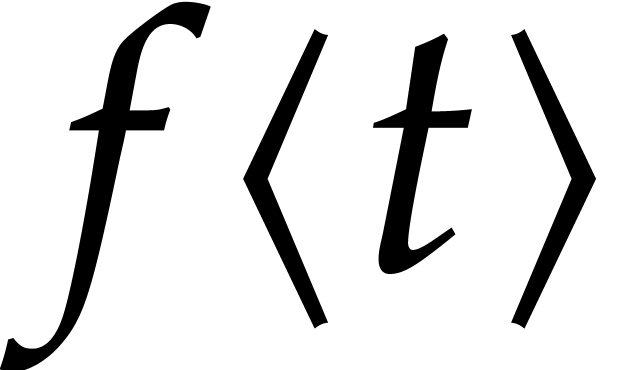 . Conversely, for any other
quantities that implicitly depend on
. Conversely, for any other
quantities that implicitly depend on  ,
we will use the postfix
,
we will use the postfix  to make this dependence
explicit.
to make this dependence
explicit.
So let  be the power series expansion of
be the power series expansion of  at a fixed time
at a fixed time  .
In view of (18), this power series satisfies the equation
.
In view of (18), this power series satisfies the equation
In the previous section, we have recalled various methods for computing
truncated power series solutions  as a function
of the initial condition
as a function
of the initial condition 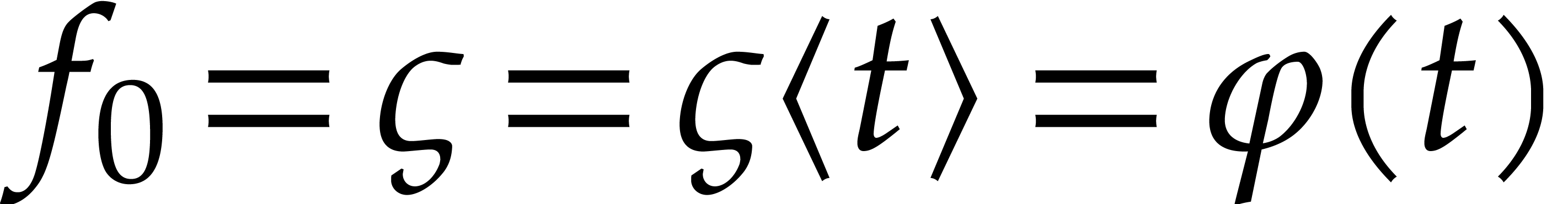 at time
at time  . In what follows, we will use any of these
algorithms as a black box, and show how to device a numerical
integration scheme from that.
. In what follows, we will use any of these
algorithms as a black box, and show how to device a numerical
integration scheme from that.
Obviously, given 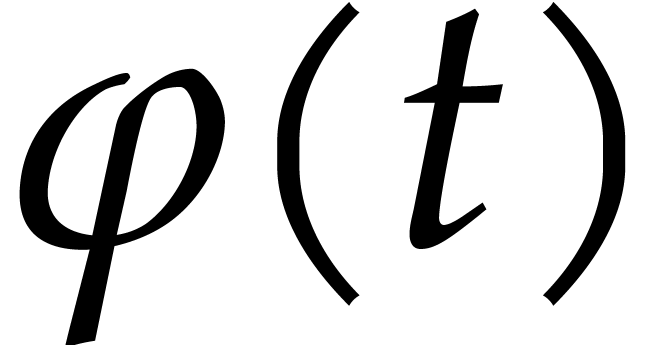 and an appropriate step size
and an appropriate step size
 at time
at time  ,
the idea is to compute
,
the idea is to compute 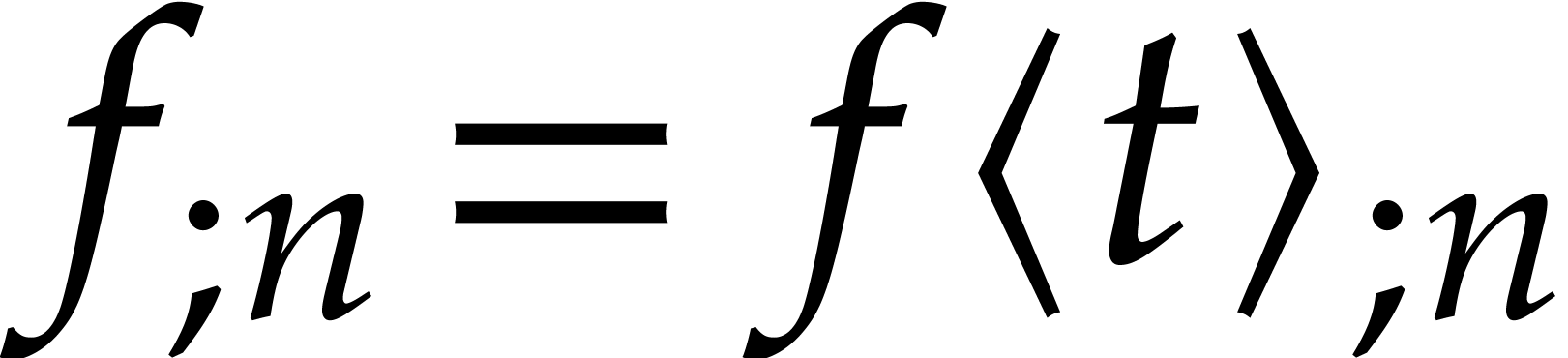 and simply evaluate
and simply evaluate
We next continue with  in the role of
in the role of  and with a suitably adapted step size
and with a suitably adapted step size  . The main question is therefore to find a
suitable step size
. The main question is therefore to find a
suitable step size  . Now the
expected order of magnitude of
. Now the
expected order of magnitude of 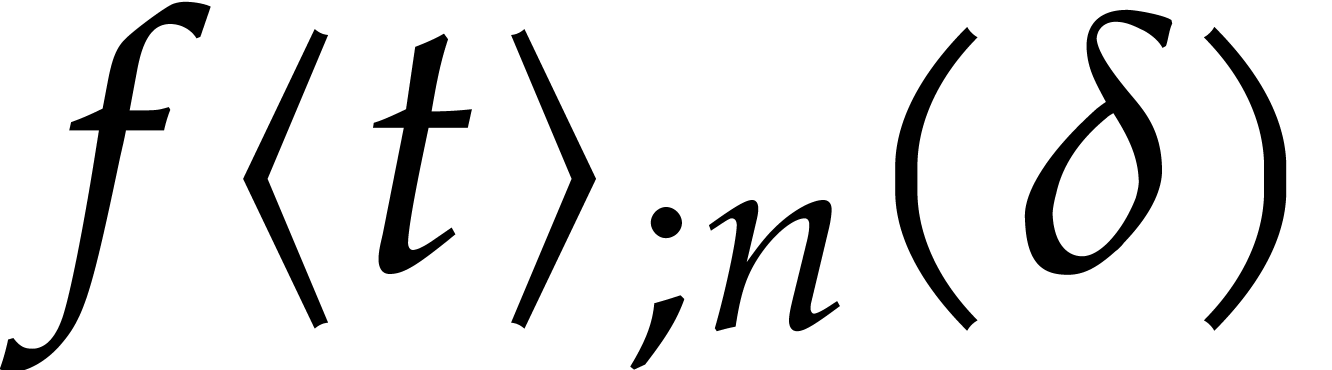 is given by
is given by
Since we are computing with  bits of precision,
we wish to keep the relative error of our numeric integration scheme
below
bits of precision,
we wish to keep the relative error of our numeric integration scheme
below 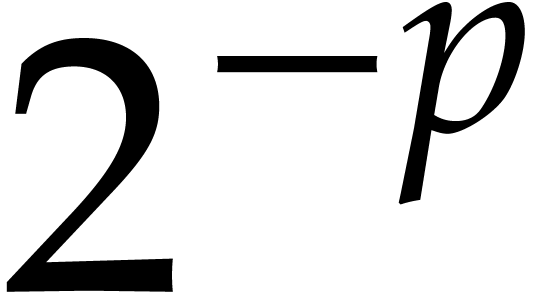 , approximately.
Therefore, we need to ensure that the truncation error
, approximately.
Therefore, we need to ensure that the truncation error
remains bounded by 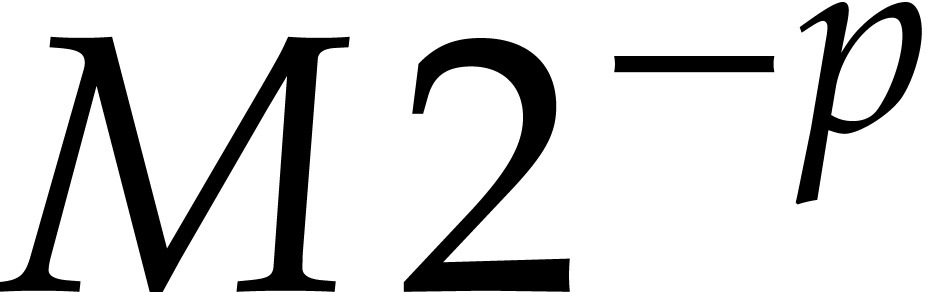 . Although
we have not computed any of the coefficients
. Although
we have not computed any of the coefficients 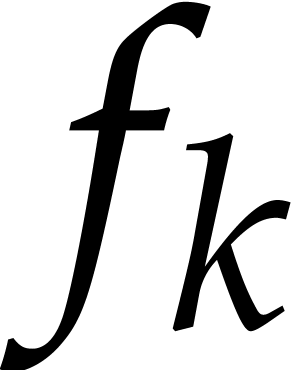 for
for
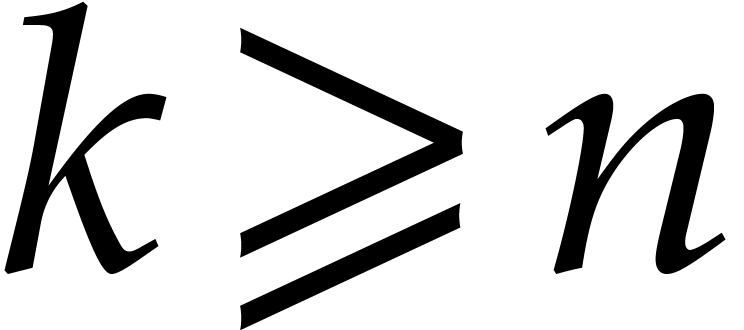 , a reasonable approximate
upper bound for
, a reasonable approximate
upper bound for  is given by
is given by
where  is a small positive integer, called the
number of guard terms. In order to protect ourselves against
the occasional vanishing of
is a small positive integer, called the
number of guard terms. In order to protect ourselves against
the occasional vanishing of 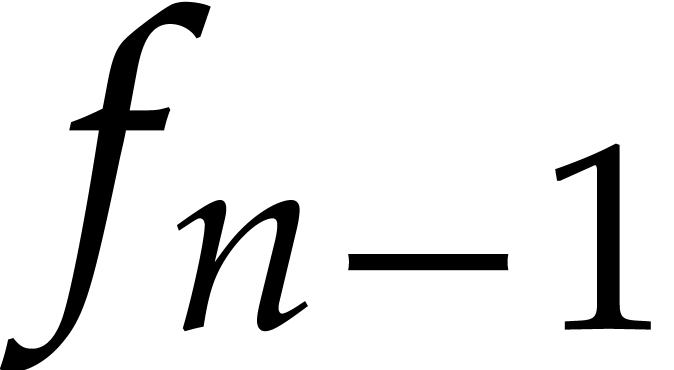 ,
it is wise to take
,
it is wise to take  .
Nevertheless, a small value such as
.
Nevertheless, a small value such as 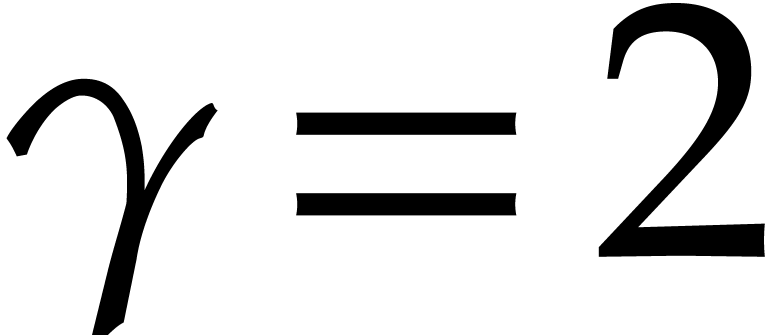 or
or 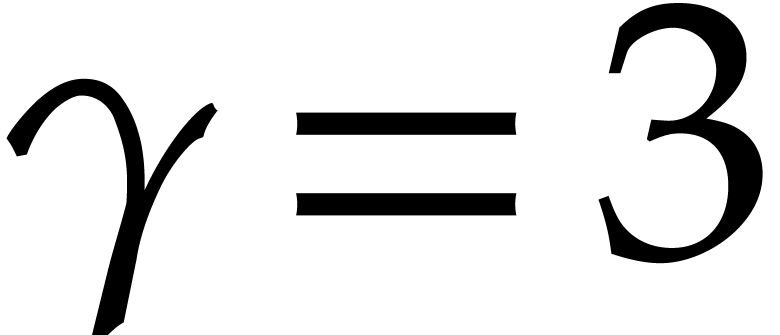 should usually provide acceptable upper estimates for
should usually provide acceptable upper estimates for
 . We now simply take the step
size
. We now simply take the step
size  to be maximal with
to be maximal with 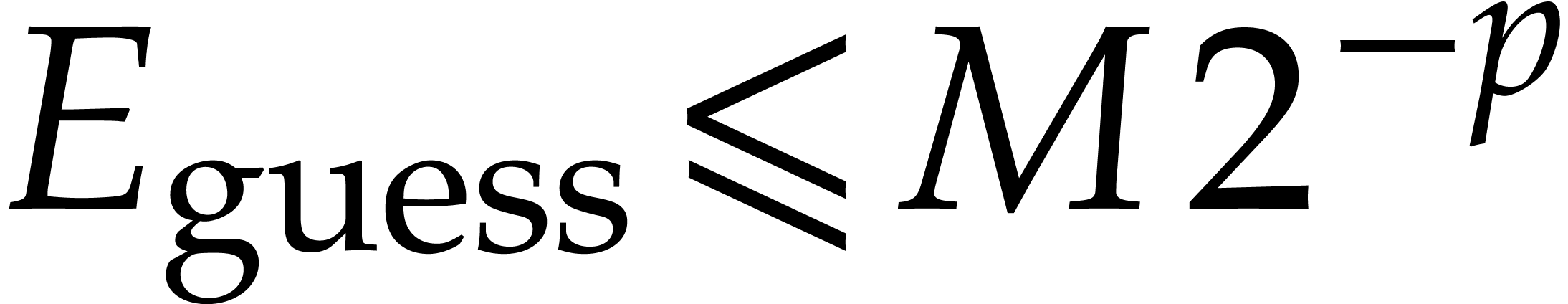 . This leads to the following algorithm for the
numerical integration of (18):
. This leads to the following algorithm for the
numerical integration of (18):
Algorithm
Output: a numerical approximation for 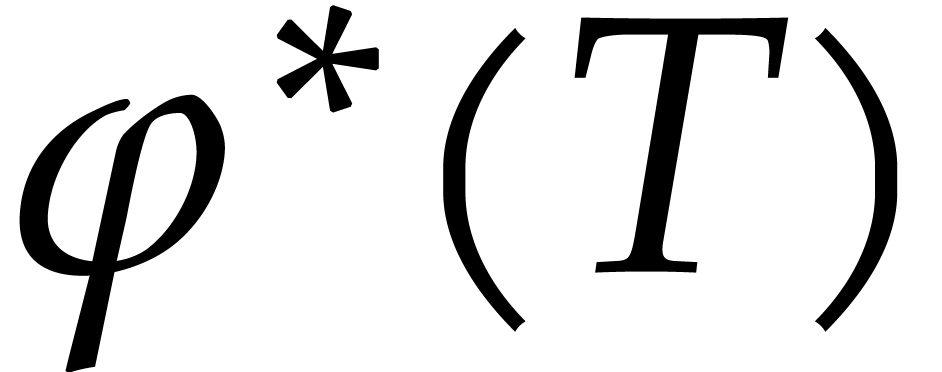 , where
, where  satisfies (18) with
satisfies (18) with 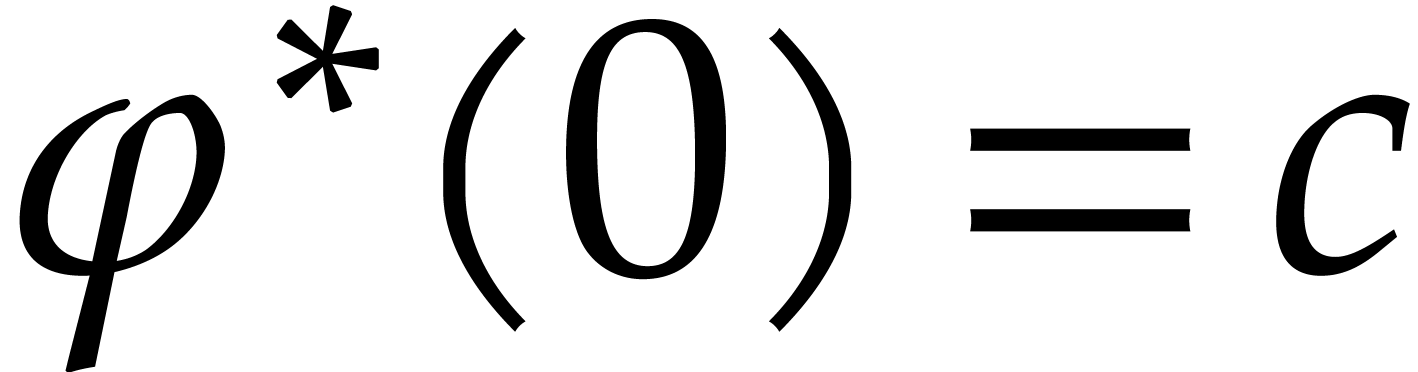
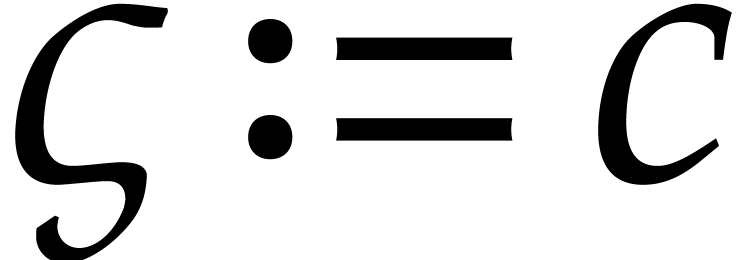 ,
, 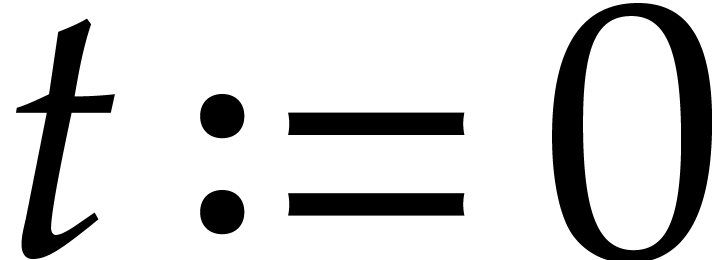
while 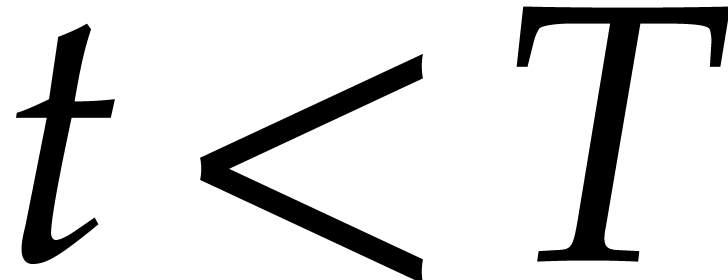 do
do
Compute the truncated solution 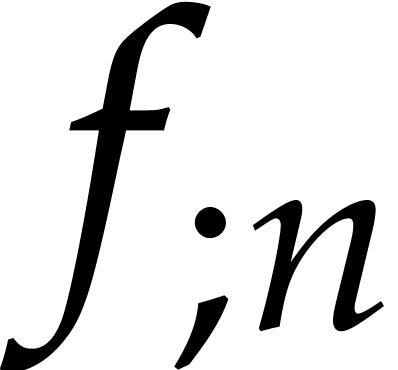 to (19)
with
to (19)
with 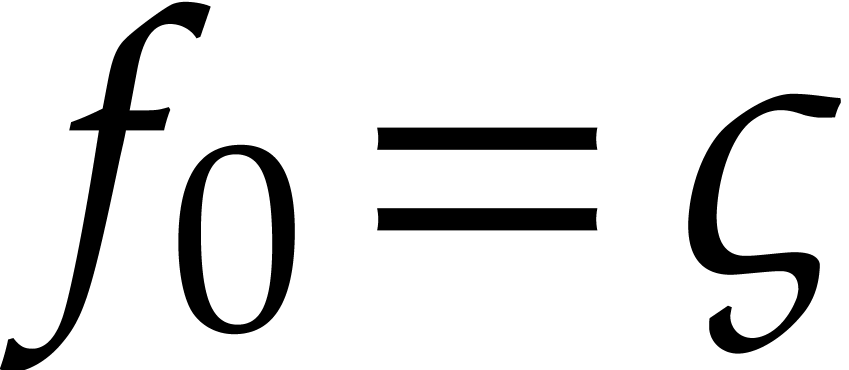
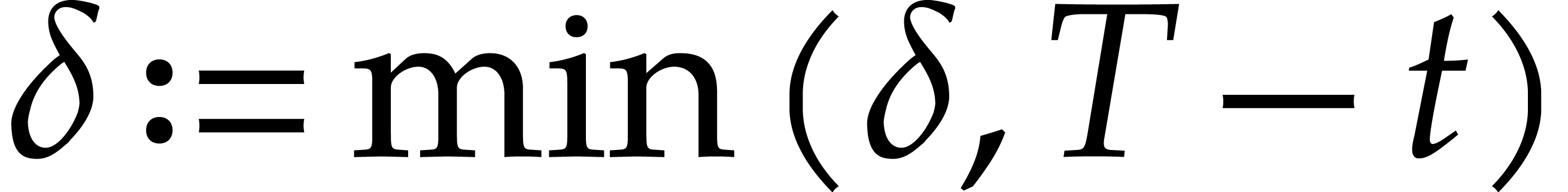
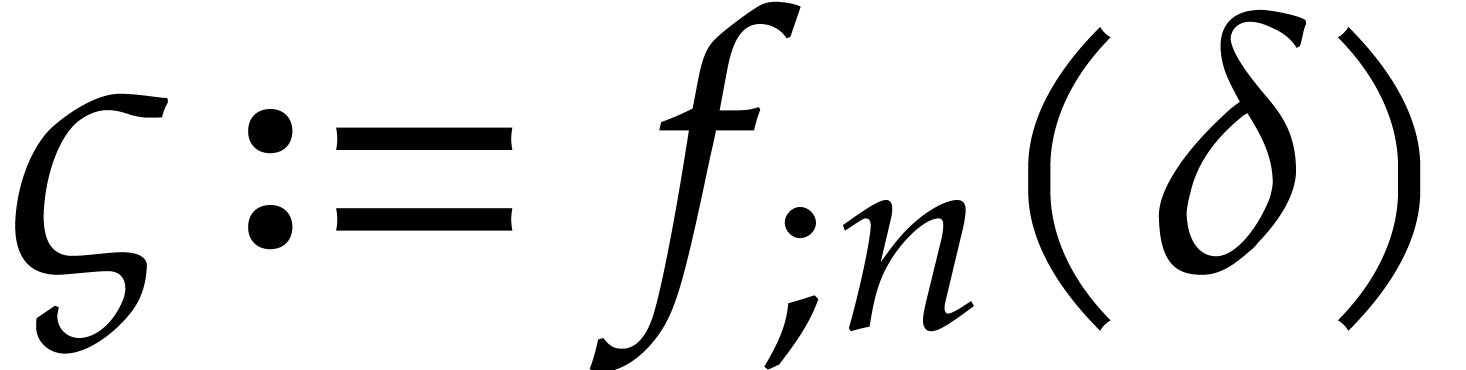 ,
, 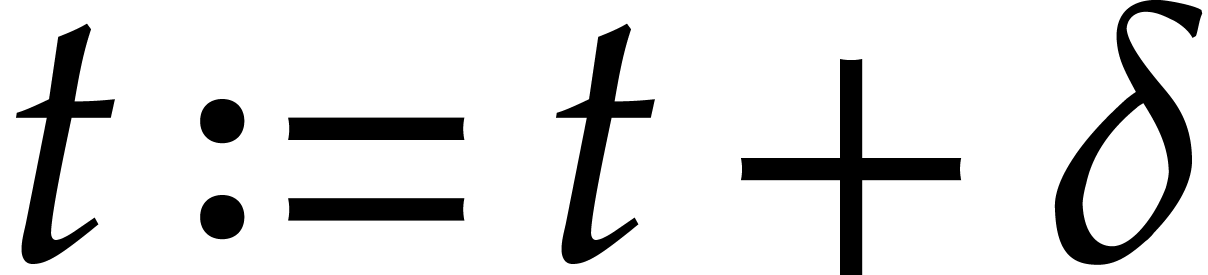
return 
Let  denote the exact solution of (18)
with
denote the exact solution of (18)
with 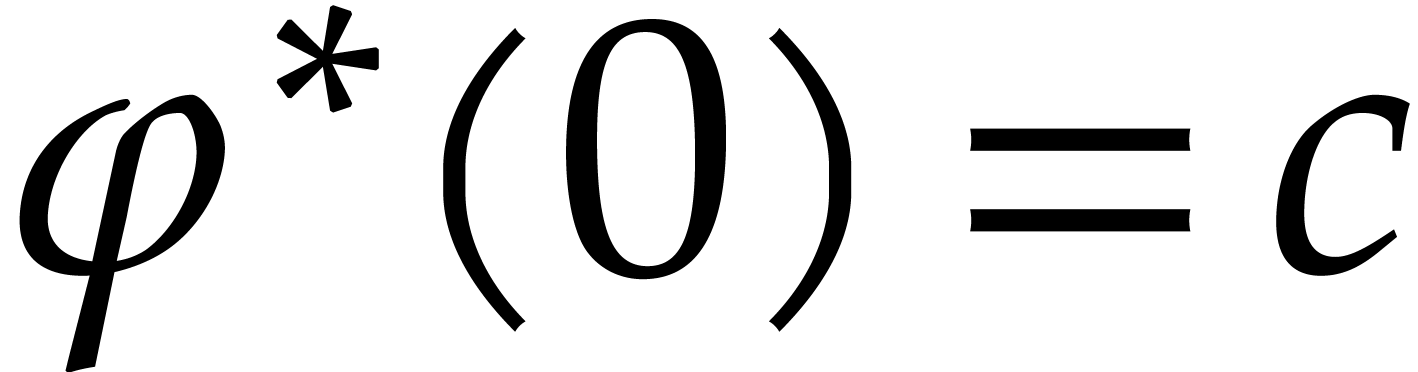 and let
and let  denote the
computed approximation by Algorithm 1. In order to analyze
various aspects of the algorithm, it is instructive to look at the
radius of convergence
denote the
computed approximation by Algorithm 1. In order to analyze
various aspects of the algorithm, it is instructive to look at the
radius of convergence  of
of  at time
at time  . Roughly speaking,
with the notations from the previous subsection, the coefficients
. Roughly speaking,
with the notations from the previous subsection, the coefficients 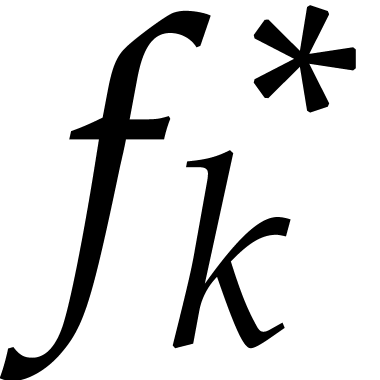 of the power series expansion
of the power series expansion 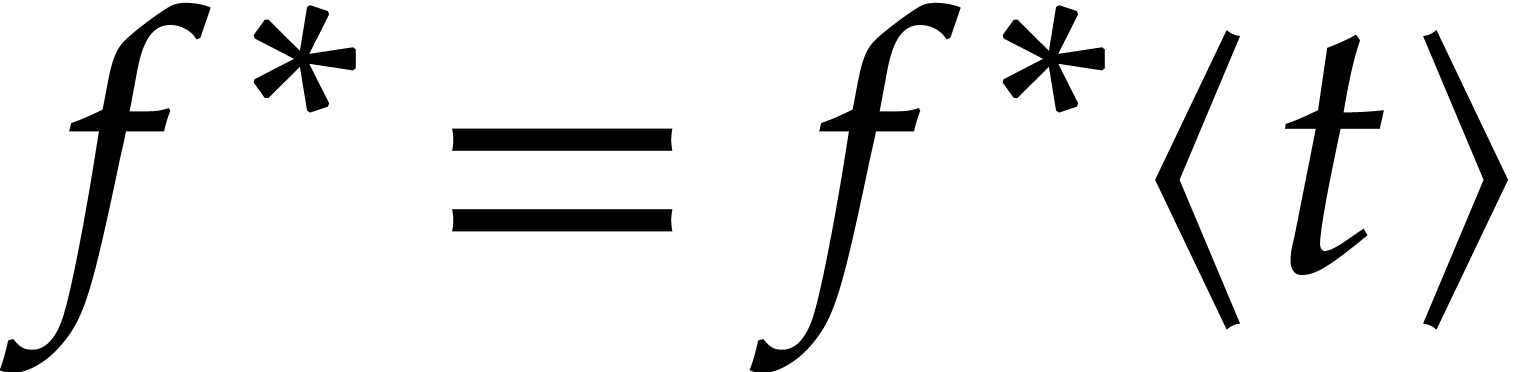 of
of  at time
at time  grow as
grow as
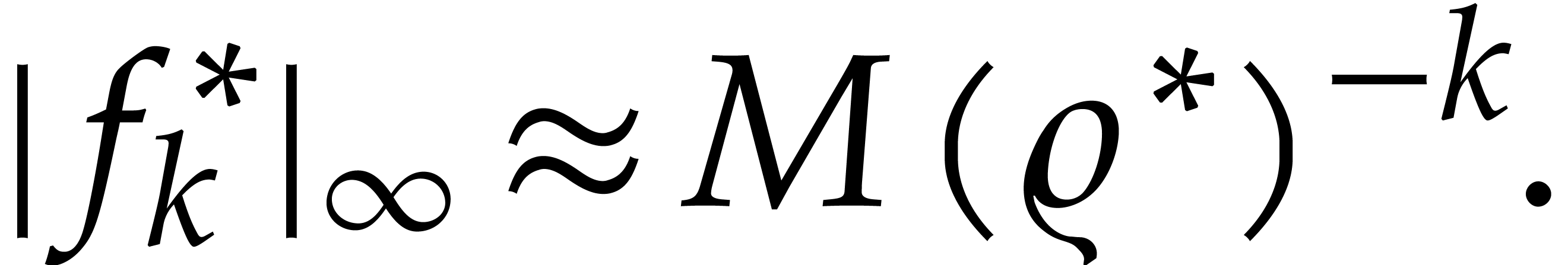
Ideally speaking, if we were able to compute  with sufficient accuracy, then the coefficients
with sufficient accuracy, then the coefficients  should grow in a similar way. Setting
should grow in a similar way. Setting 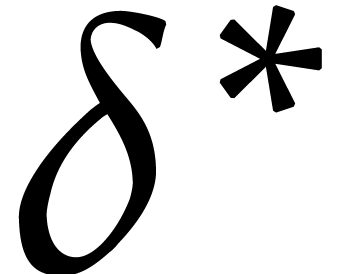 for the
step size in this ideal situation, we would then expect that
for the
step size in this ideal situation, we would then expect that 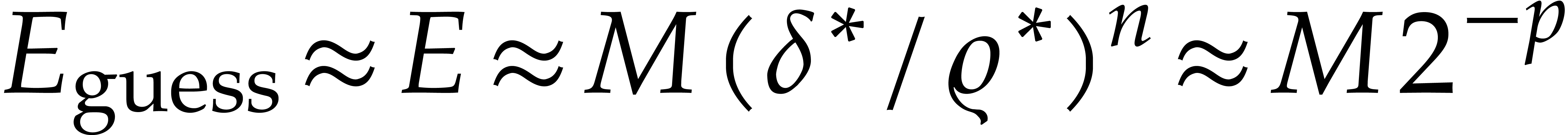 , whence
, whence
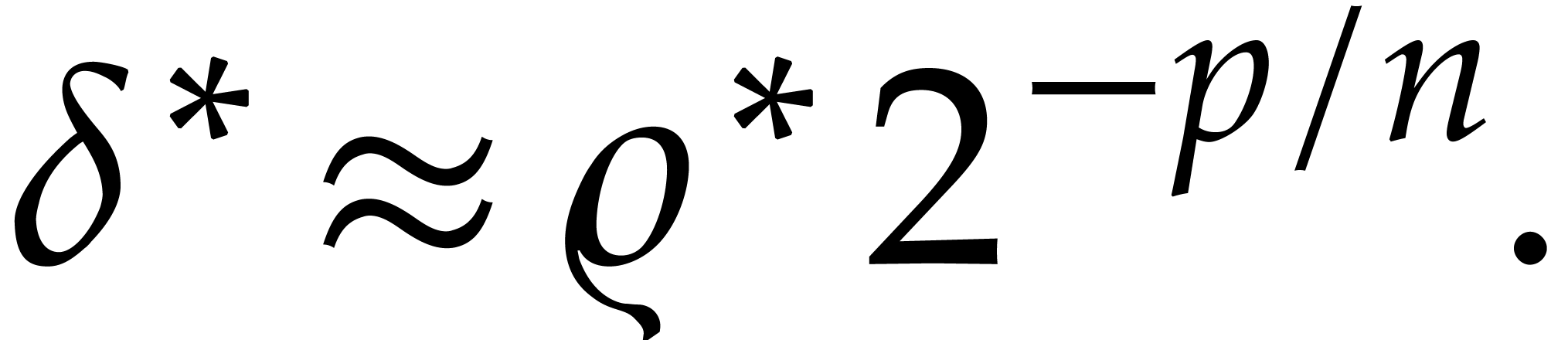 |
(23) |
This suggests to take the expansion order 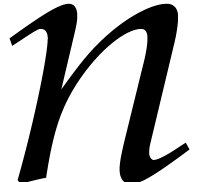 to be
proportional to
to be
proportional to 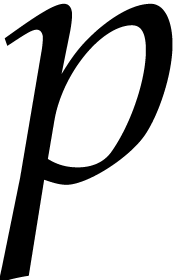 , after which
the step size
, after which
the step size  should be proportional to the
radius of convergence
should be proportional to the
radius of convergence  .
.
Let us pursue this line of wishful thinking a little further. Theorem 4 implies that  is analytic on a
compact half disk
is analytic on a
compact half disk  that is independent of
that is independent of  . In particular, we get that
. In particular, we get that 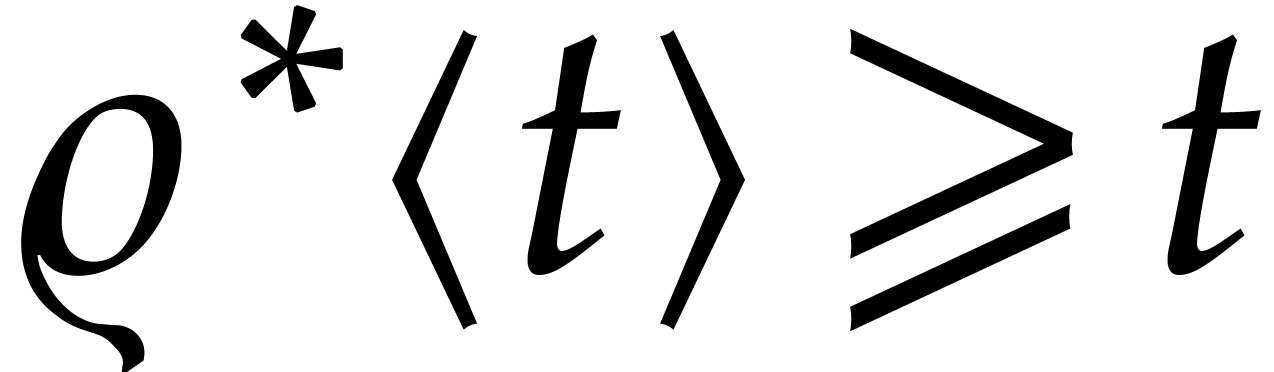 for
for  . It
can also be shown that the radius of convergence of
. It
can also be shown that the radius of convergence of  at the origin is of the order
at the origin is of the order 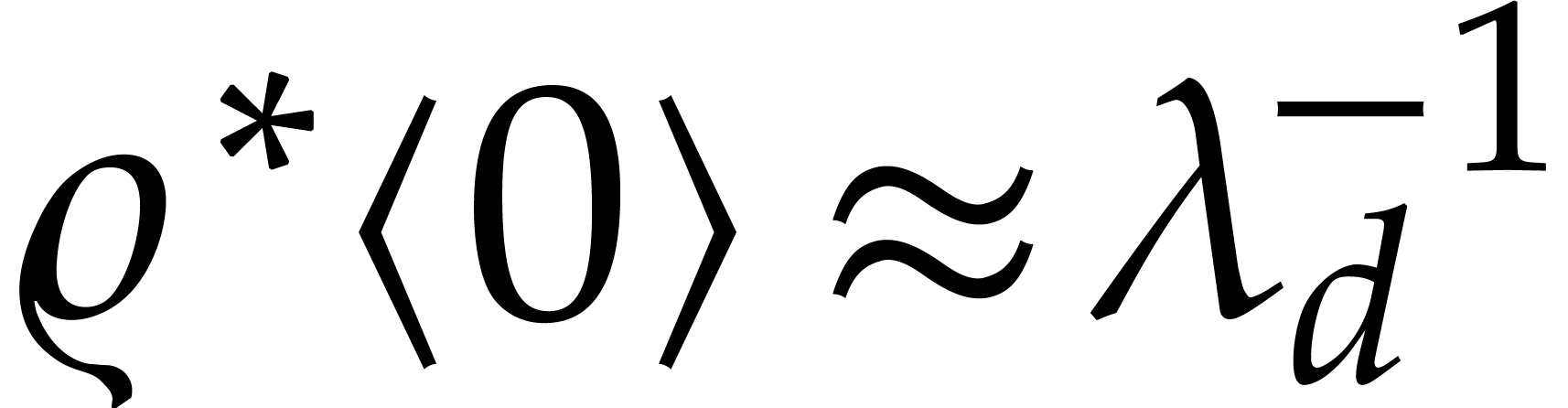 or more. For stiff
equations, we typically have
or more. For stiff
equations, we typically have 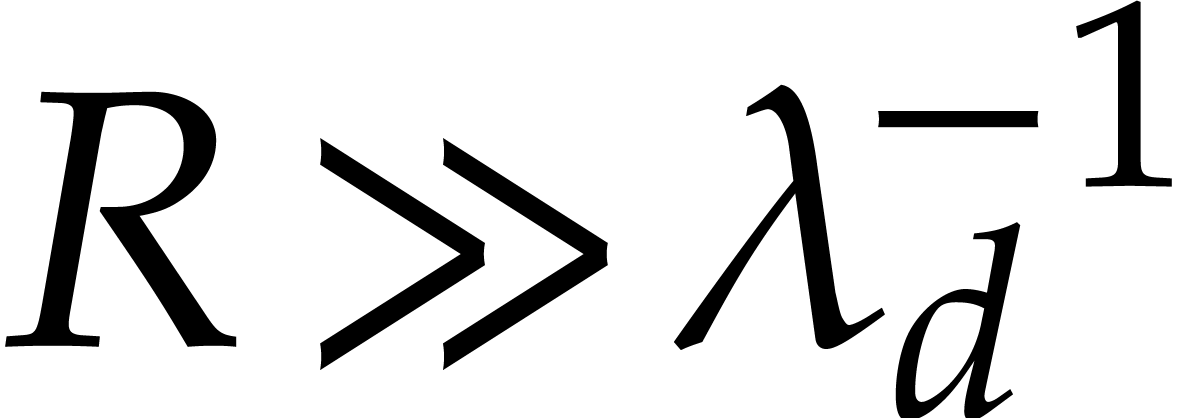 .
In order to integrate the equation until a time
.
In order to integrate the equation until a time 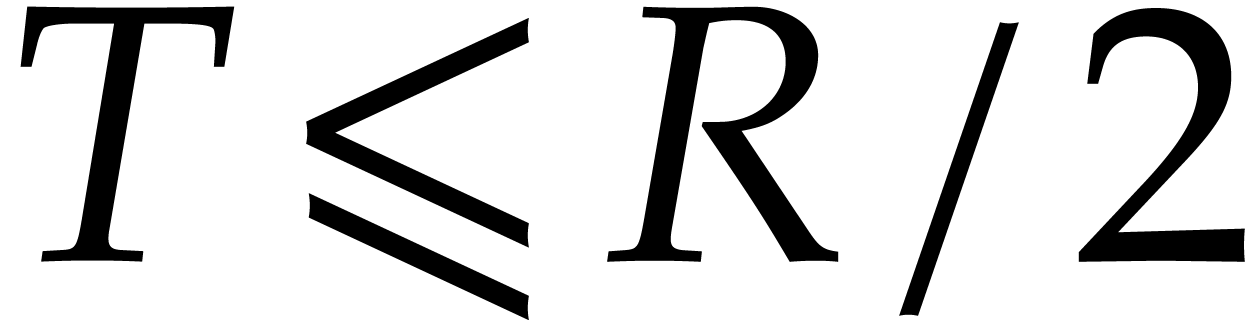 , we thus hope for a step size that increases
geometrically from
, we thus hope for a step size that increases
geometrically from 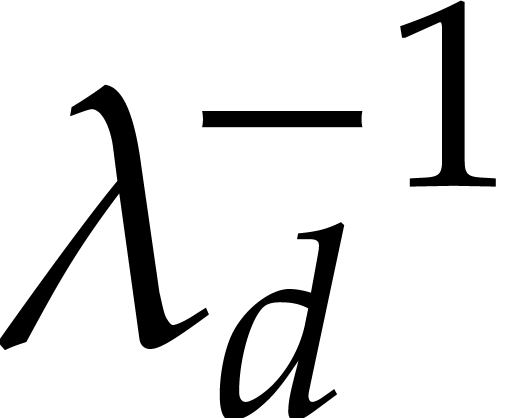 to
to 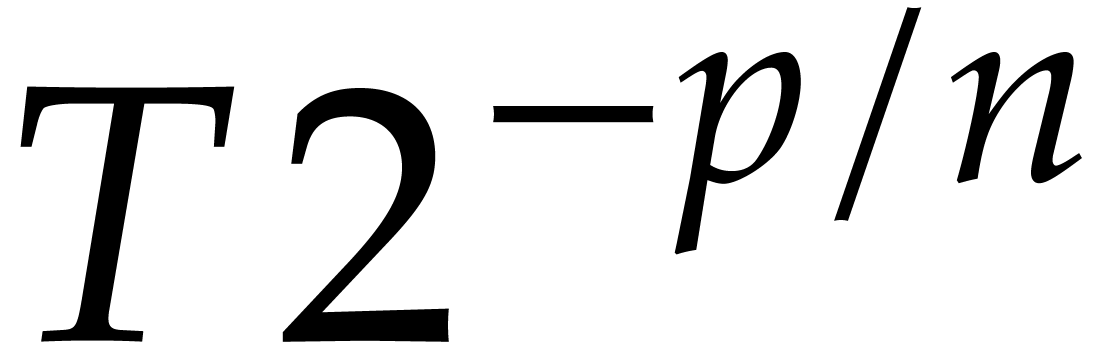 . The entire integration would then require
approximately
. The entire integration would then require
approximately 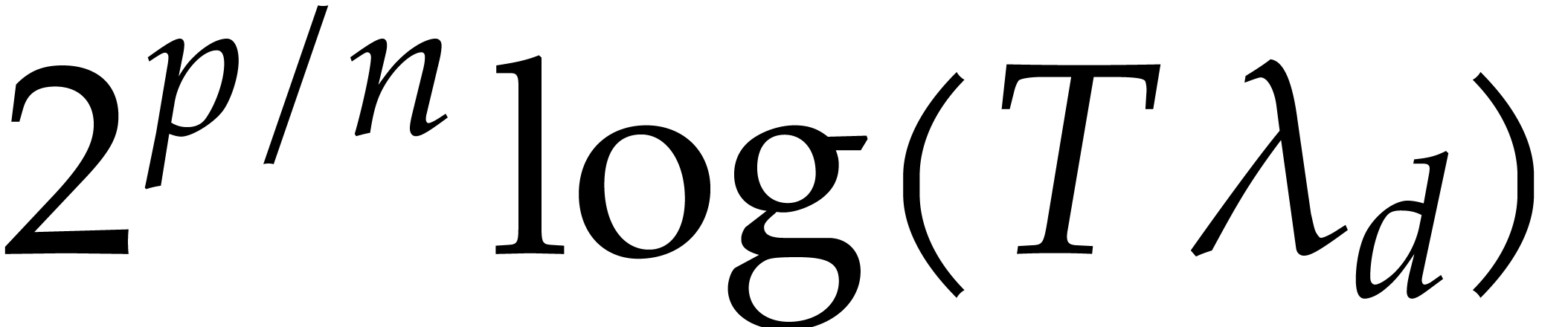 steps. Using the most efficient
algorithms from section 3, each step requires
steps. Using the most efficient
algorithms from section 3, each step requires 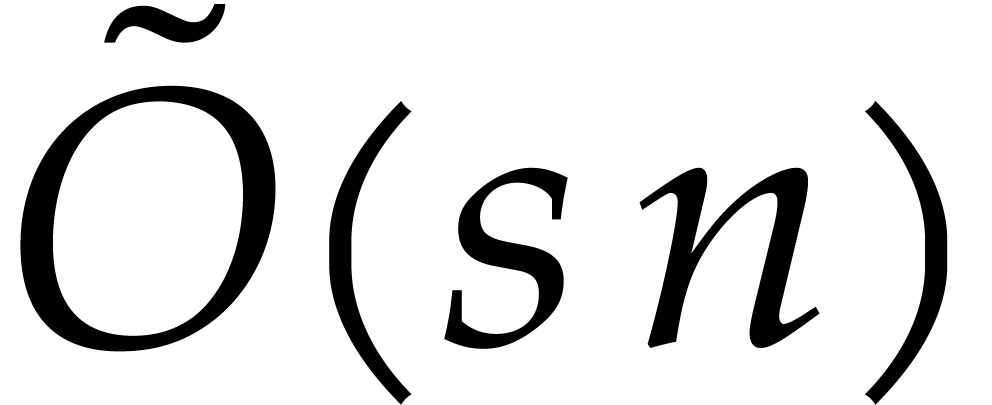 floating point operations (here the “flat Oh”
notation
floating point operations (here the “flat Oh”
notation 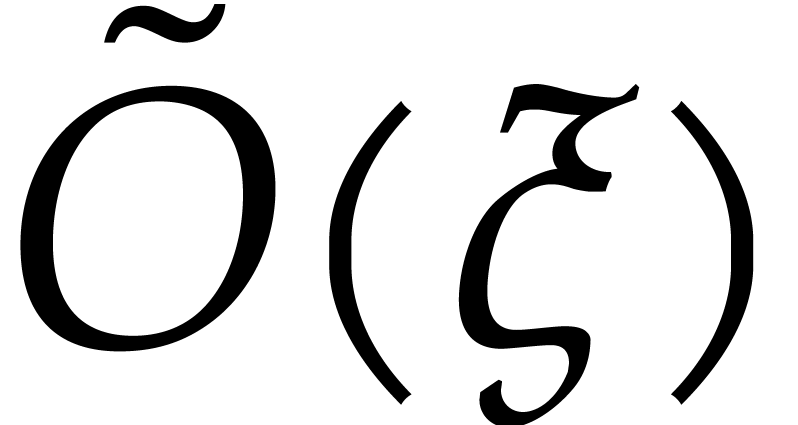 stands for
stands for 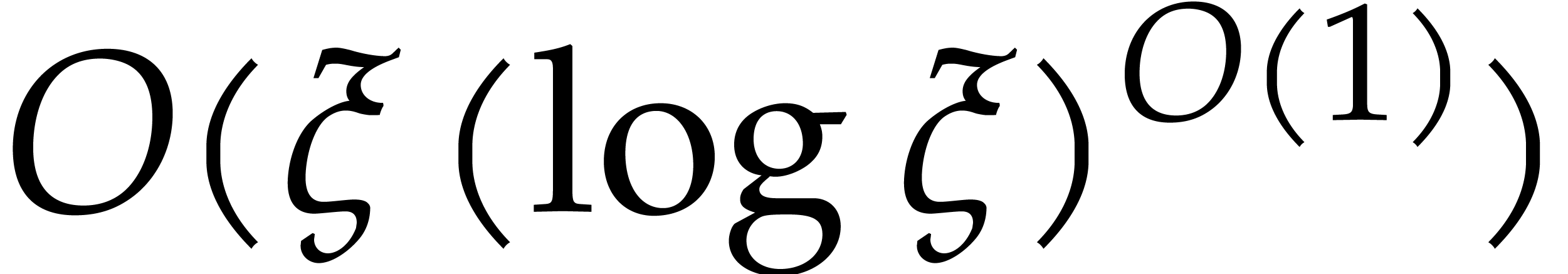 ). Since additions and multiplications of
). Since additions and multiplications of 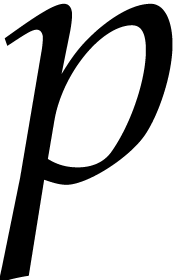 bit floating point numbers can be performed in time
bit floating point numbers can be performed in time 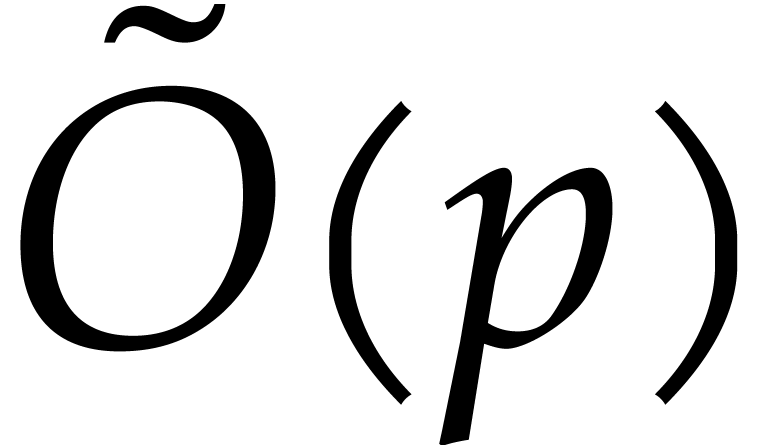 , the overall bit cost of the
entire integration would thus be bounded by
, the overall bit cost of the
entire integration would thus be bounded by 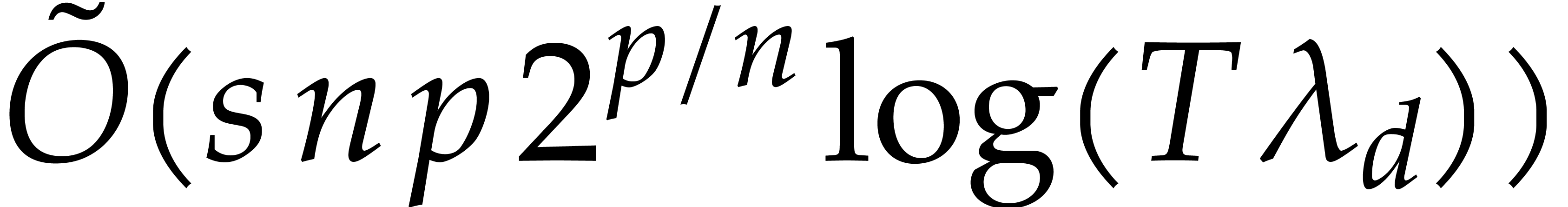 .
.
But are we indeed able to compute 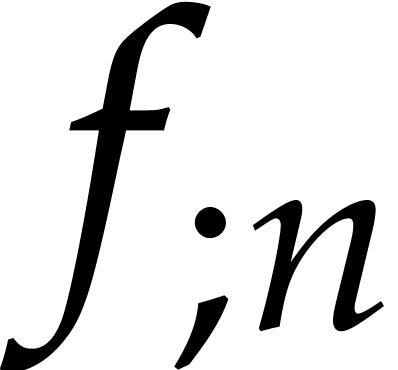 with enough
accuracy in order to ensure that the coefficients
with enough
accuracy in order to ensure that the coefficients  grow according to
grow according to  ? Let us
carefully analyze each of the sources of error for one step of our
integration scheme. By construction, we ensured the truncation error to
be of the order
? Let us
carefully analyze each of the sources of error for one step of our
integration scheme. By construction, we ensured the truncation error to
be of the order  . One of the
most intrinsic sources of error comes from the initial condition
. One of the
most intrinsic sources of error comes from the initial condition 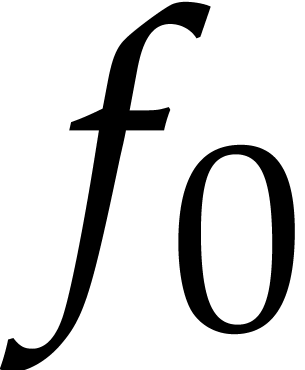 : since we are computing with a
precision of
: since we are computing with a
precision of 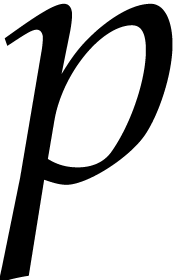 bits, the mere representation of
bits, the mere representation of
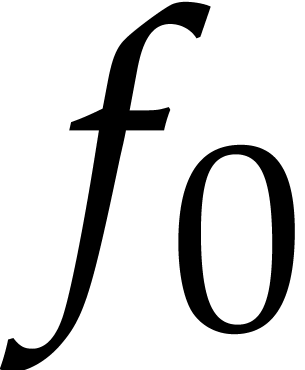 induces a relative error of the order of
induces a relative error of the order of 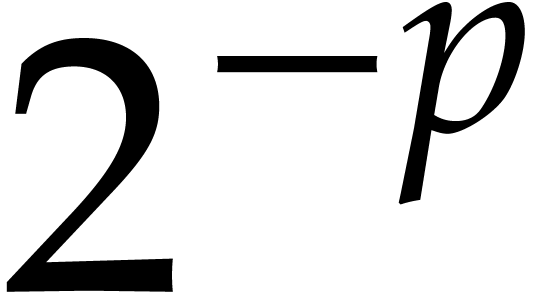 . Even when computing
. Even when computing 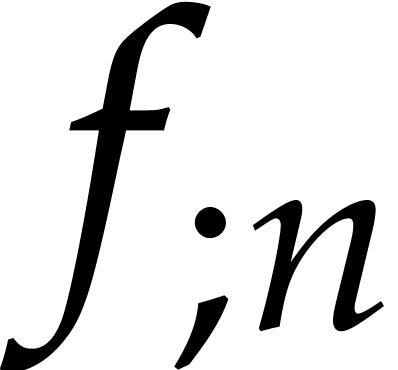 from
from 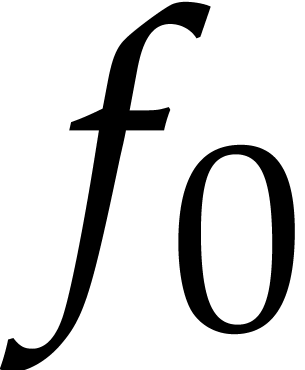 with infinite precision, this
intrinsic source of error cannot be removed.
with infinite precision, this
intrinsic source of error cannot be removed.
Let us now study how the error in the initial condition affects the
errors in the other coefficients 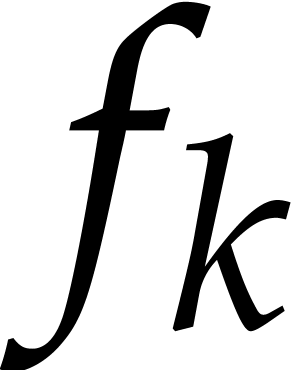 .
For this, we need to investigate the first variation of
.
For this, we need to investigate the first variation of  , which describes the sensitivity of the flow
to the initial condition. More precisely, let
, which describes the sensitivity of the flow
to the initial condition. More precisely, let 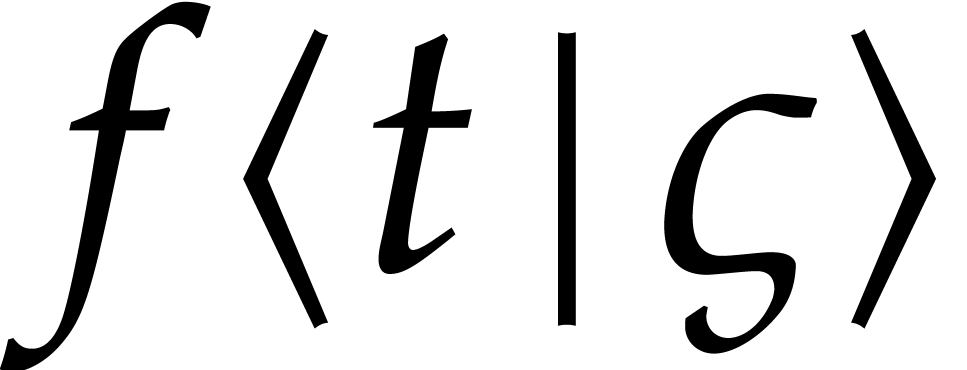 be
the power solution of (19) at time
be
the power solution of (19) at time  as a function of the initial condition
as a function of the initial condition 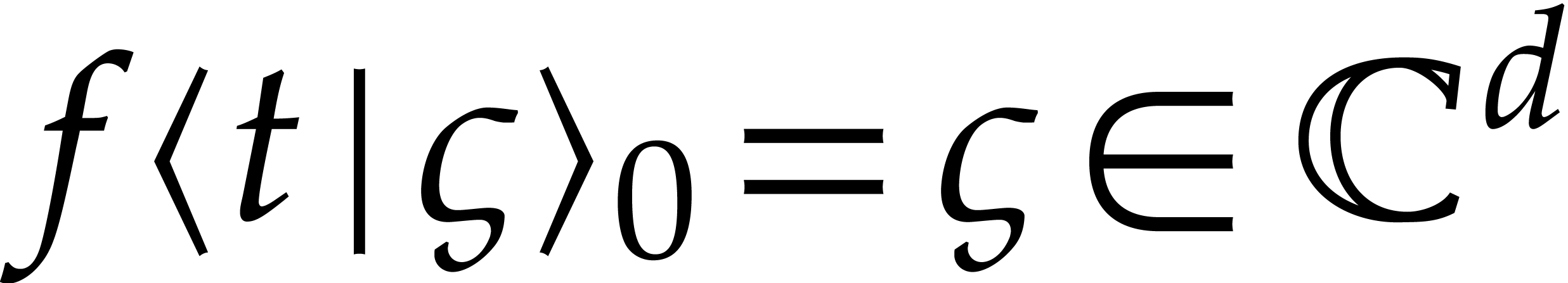 .
Then the first variation
.
Then the first variation 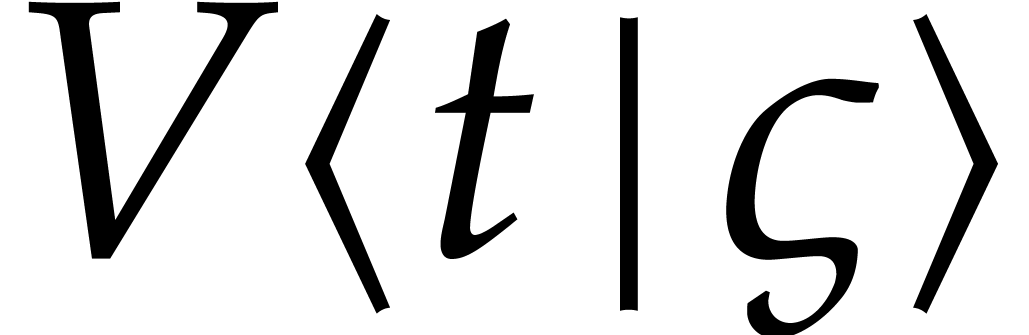 is the
is the  matrix with entries
matrix with entries 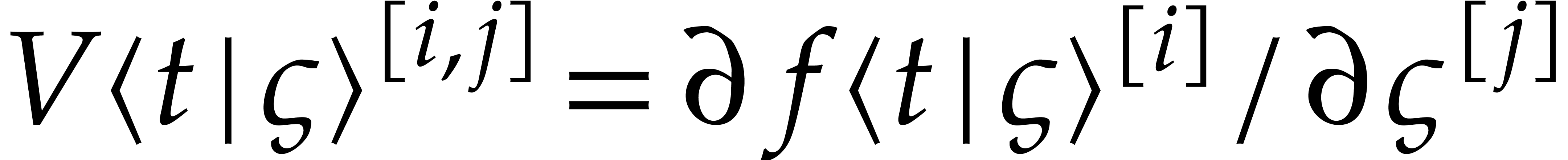 .
Dropping
.
Dropping 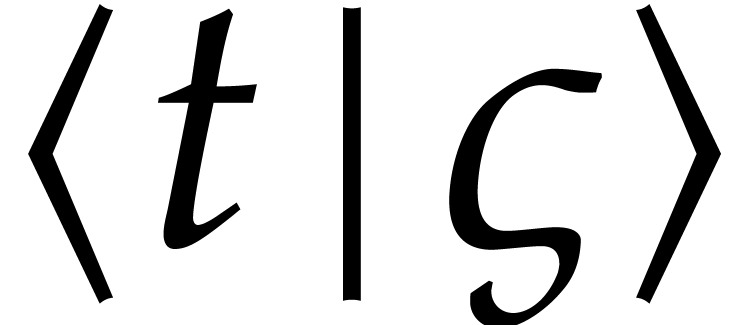 suffixes when they are clear from the
context, the first variation satisfies the linear differential equation
suffixes when they are clear from the
context, the first variation satisfies the linear differential equation
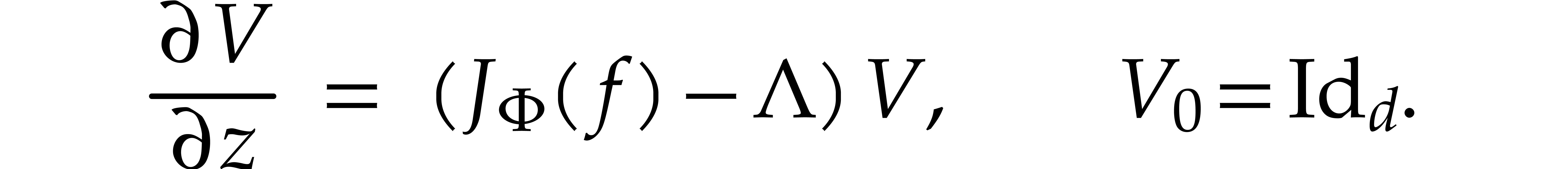
Here we recall that 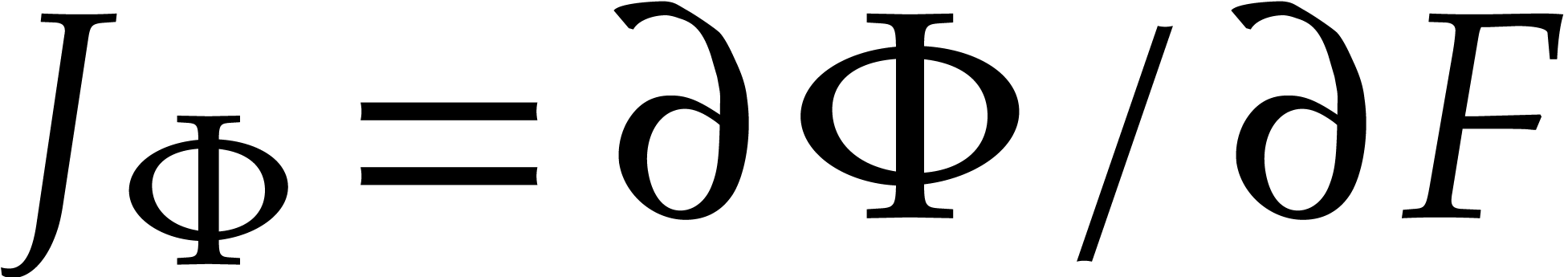 stands for the Jacobian
matrix of
stands for the Jacobian
matrix of  . If our equation
is very stiff, then
. If our equation
is very stiff, then  is small with respect to
is small with respect to
 , which leads to the
extremely crude approximation
, which leads to the
extremely crude approximation  for the first
variation.
for the first
variation.
Now the relative error in the initial condition 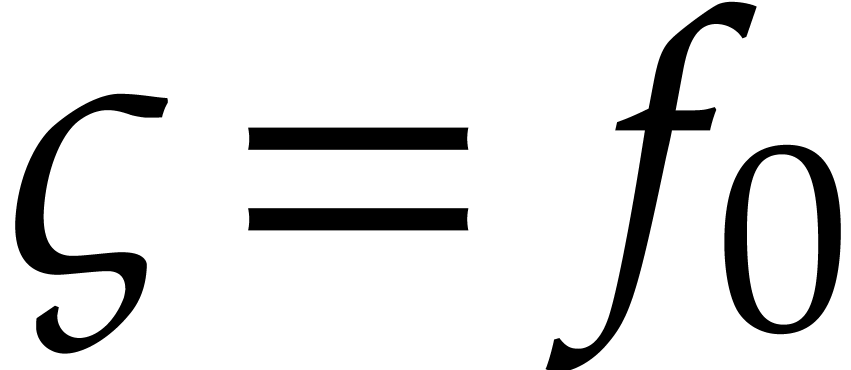 is at best
is at best 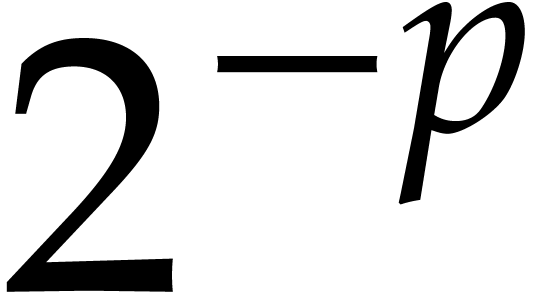 , as explained
above, which means that
, as explained
above, which means that 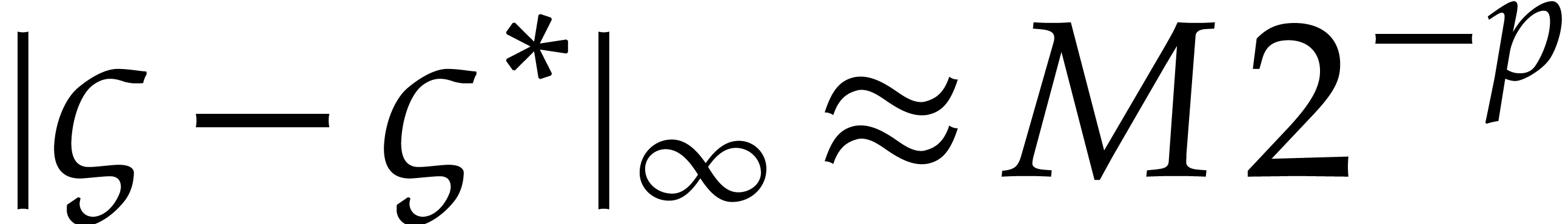 for
for 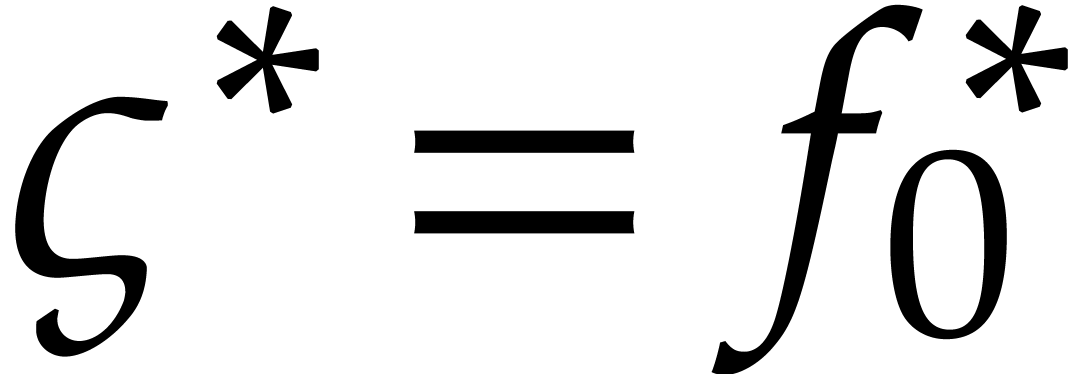 . In combination with the relation
. In combination with the relation 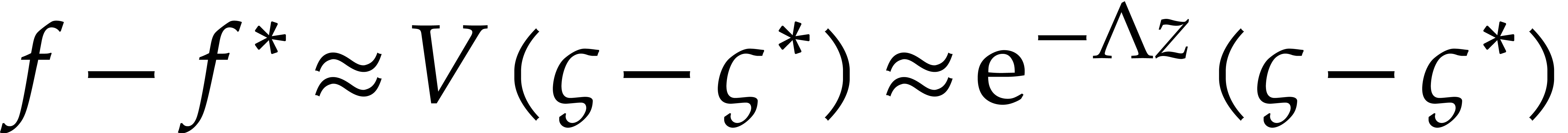 , this leads to the following errors for the
other coefficients:
, this leads to the following errors for the
other coefficients:
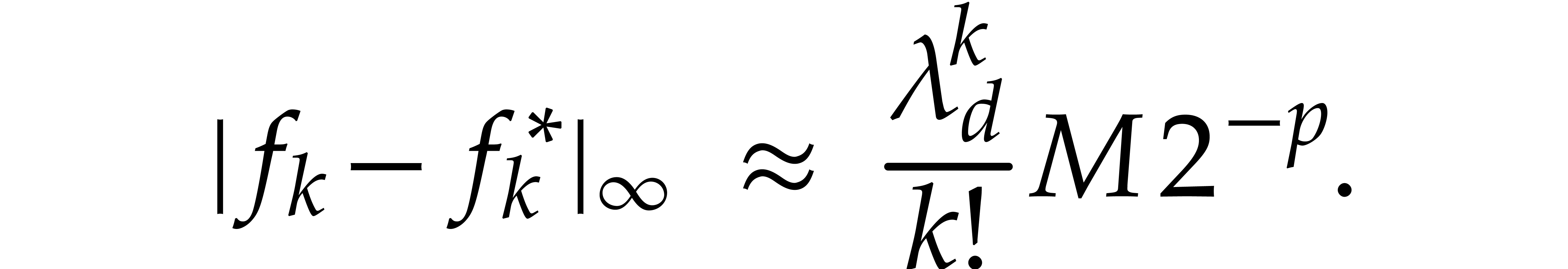
Now if 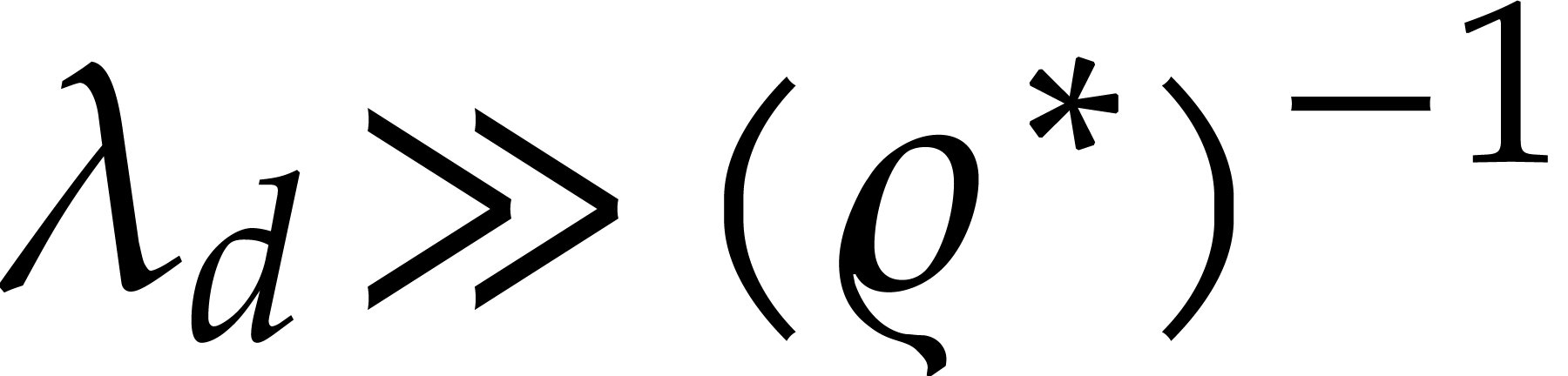 , then the error
, then the error 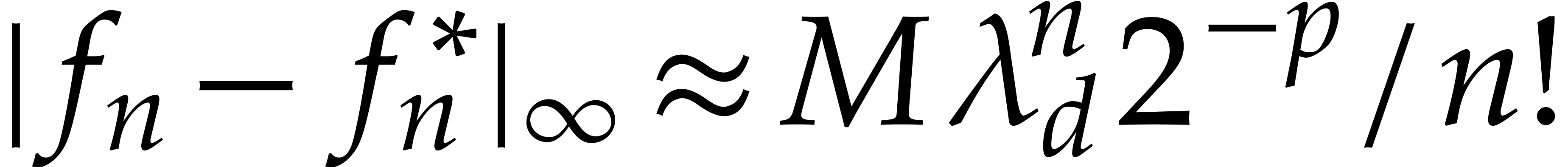 dominates the actual value
dominates the actual value 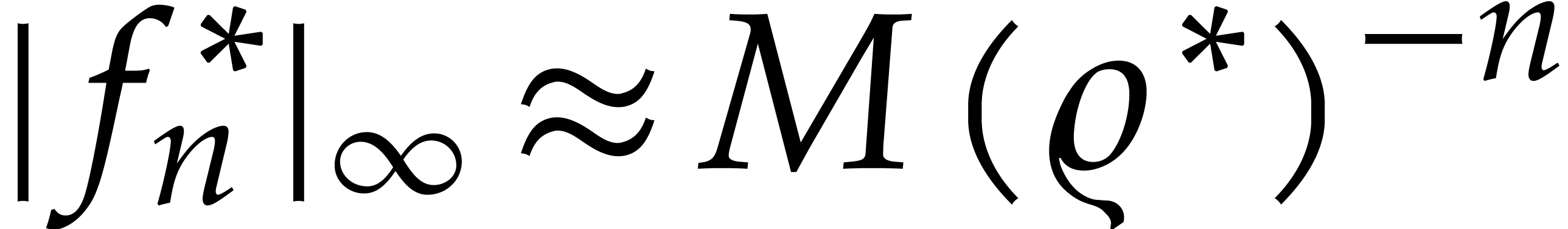 , which yields
, which yields 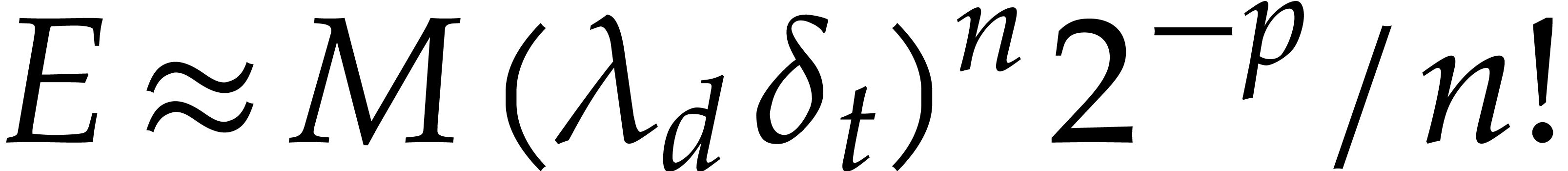 instead of
instead of
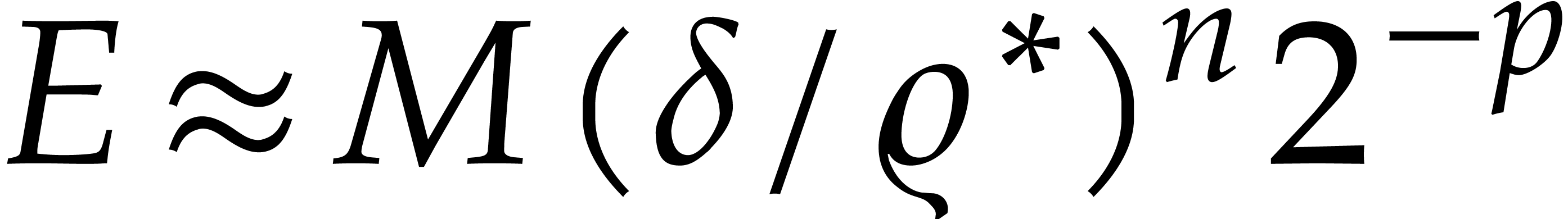 . When chosing our step size
. When chosing our step size
 such that
such that 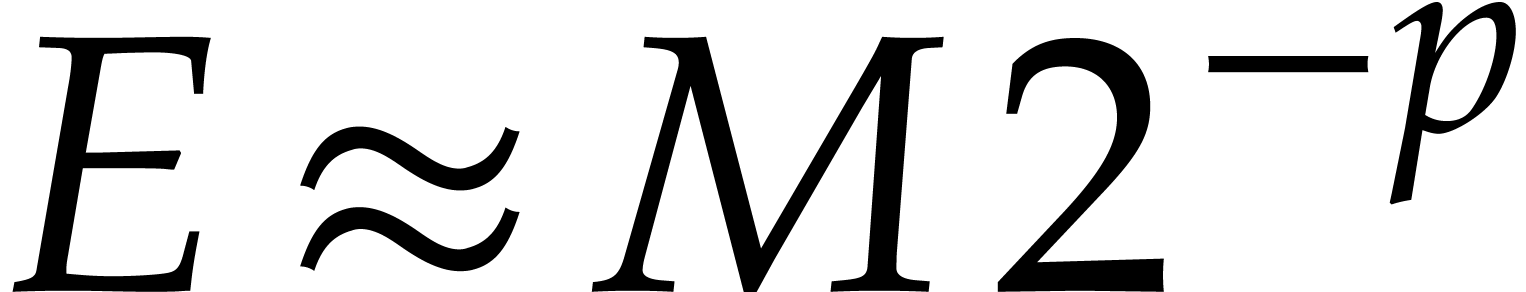 ,
as in Algorithm 1, this yields
,
as in Algorithm 1, this yields 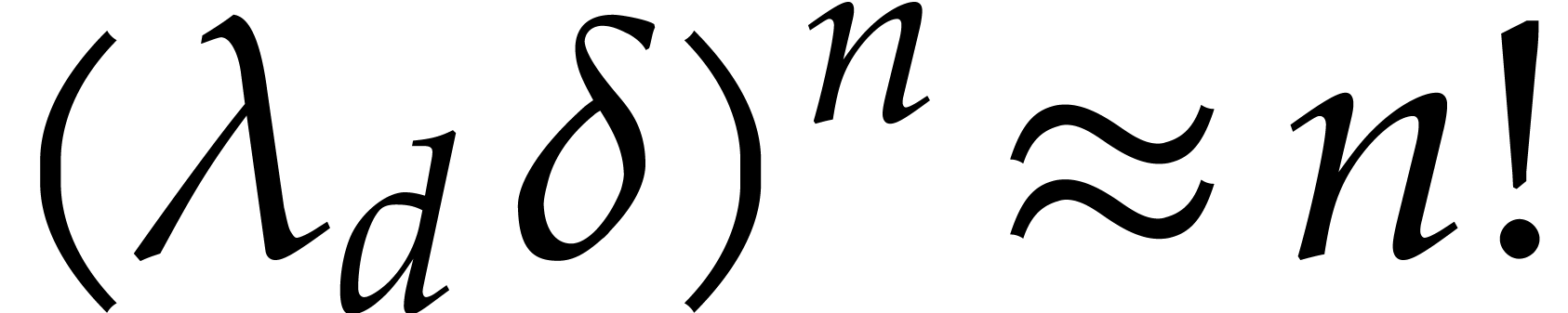 and
and
instead of the desired step size 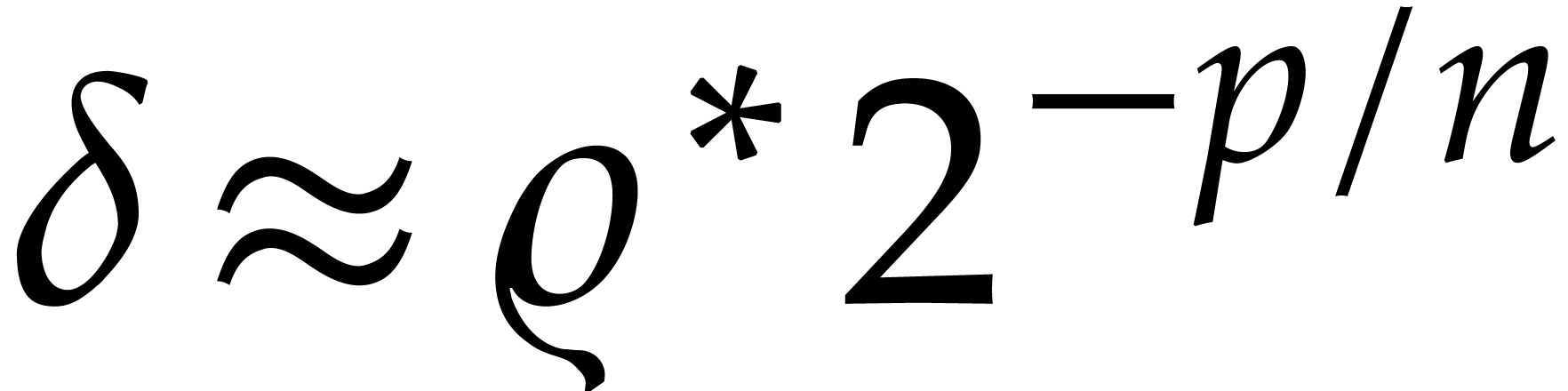 .
The actual bit cost of the complete integration is therefore bounded by
.
The actual bit cost of the complete integration is therefore bounded by
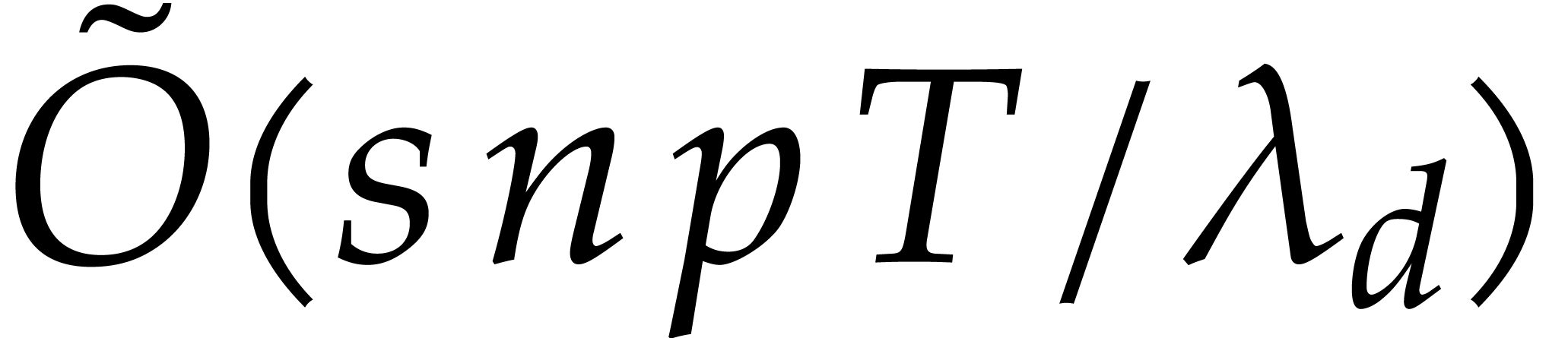 instead of
instead of 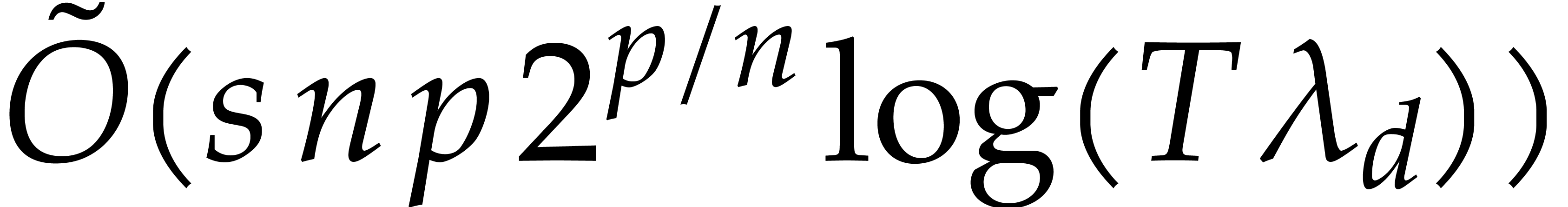 .
.
An interesting aspect of this analysis is the fact that the step size
 still turns out to be
still turns out to be 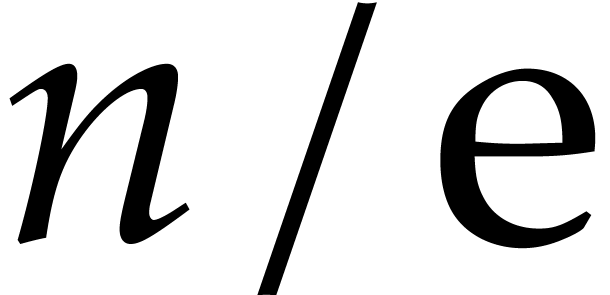 times larger than
times larger than 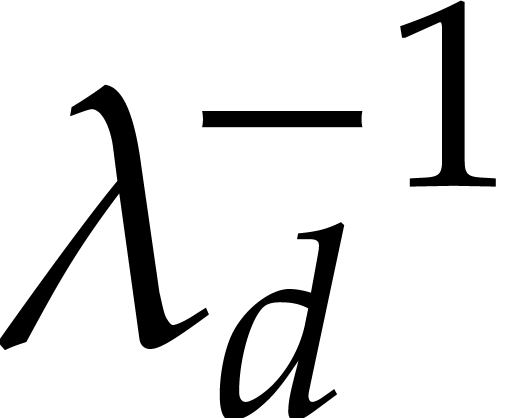 , whence
larger orders
, whence
larger orders 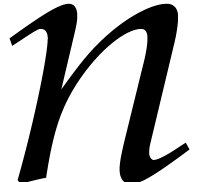 allow for larger step sizes.
However, this comes at the expense of a larger relative error than
allow for larger step sizes.
However, this comes at the expense of a larger relative error than 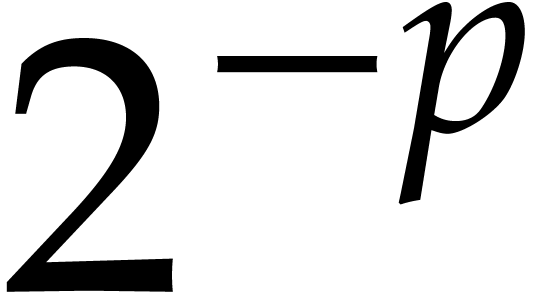 . Indeed, we have
. Indeed, we have
This error is maximal for 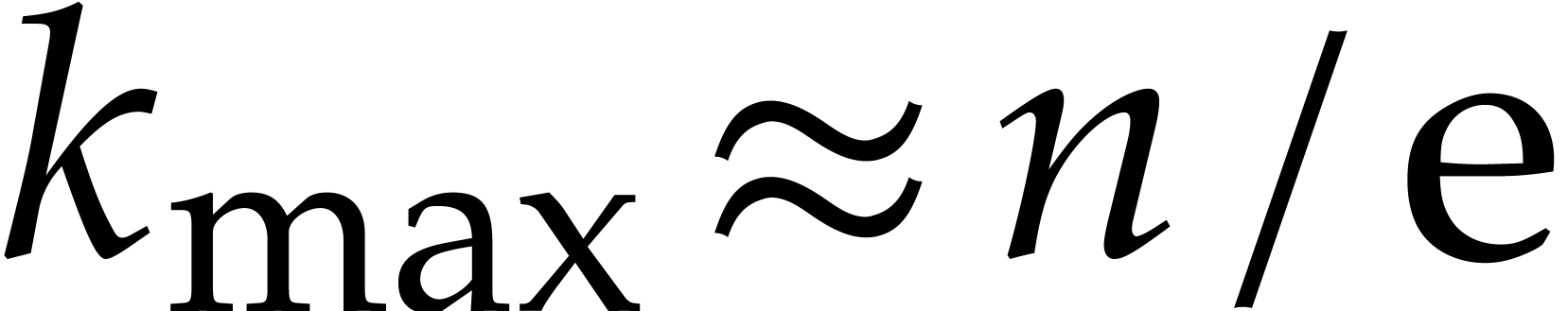 ,
in which case we have
,
in which case we have
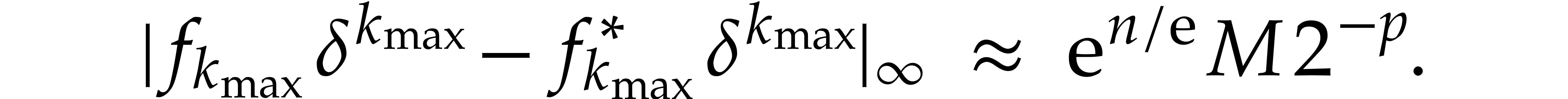
This means that the relative error for one step of our integration
method is 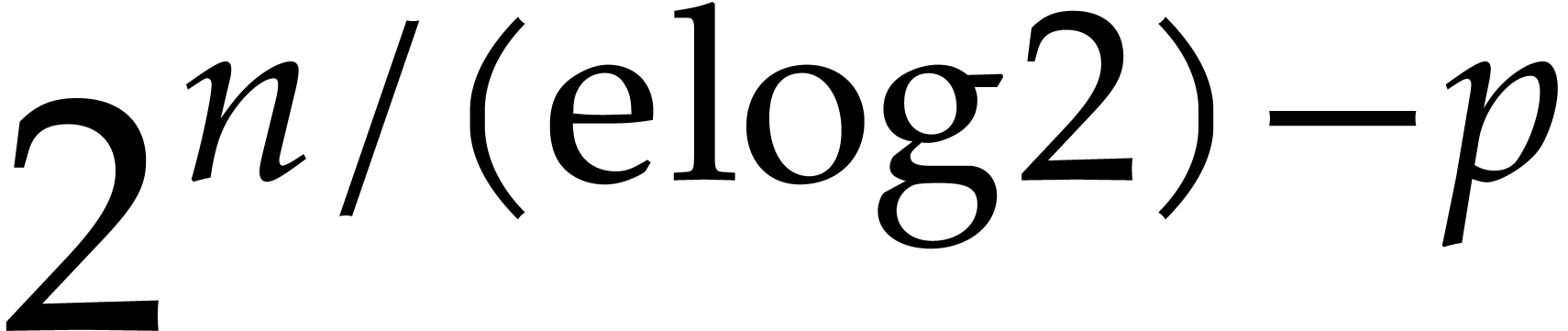 instead of
instead of 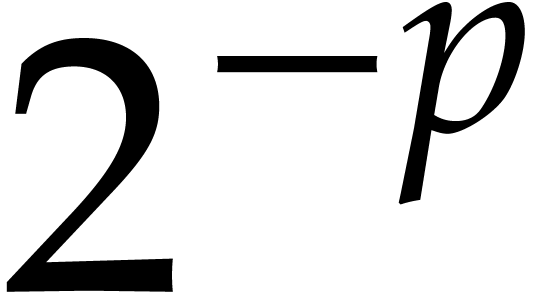 . In other words, we have “sacrificed”
. In other words, we have “sacrificed”
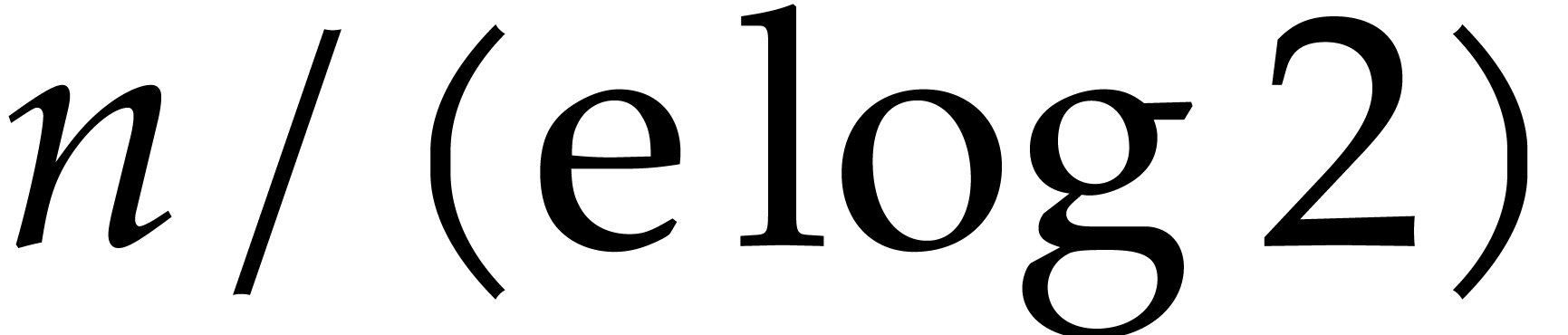 bits of precision, so that the method admits an
“effective precision” of only
bits of precision, so that the method admits an
“effective precision” of only 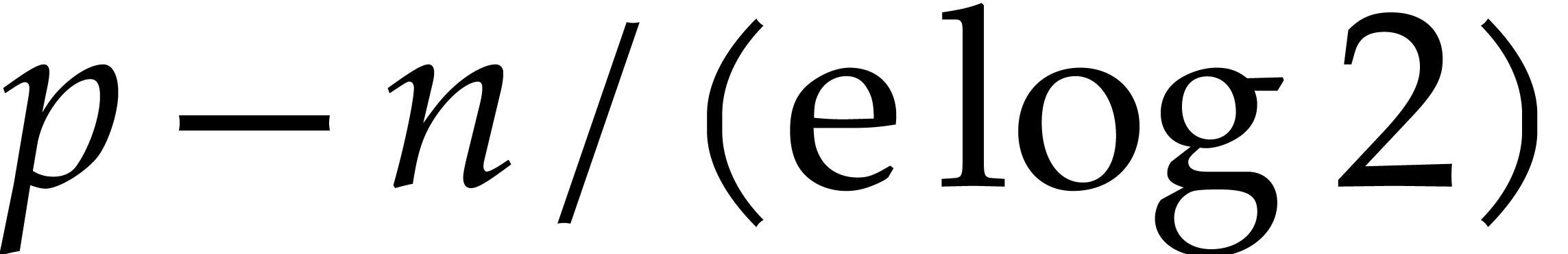 bits.
bits.
The last source of errors for Algorithm 1 comes from
rounding errors during the computation of 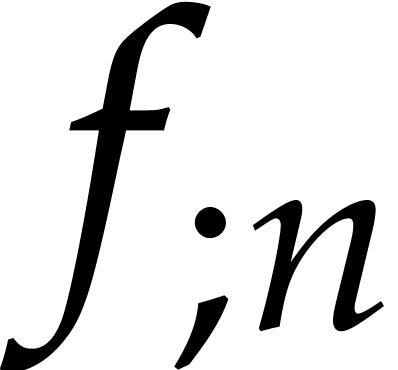 from
from
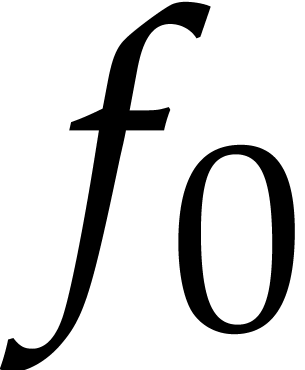 . The nature of these errors
depends on the particular method that we used for computing the power
series
. The nature of these errors
depends on the particular method that we used for computing the power
series 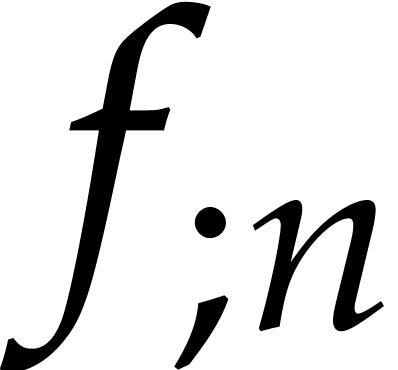 . Nevertheless, for
most methods, the rounding errors only contribute marginally to the
total error. This is due to the fact that
. Nevertheless, for
most methods, the rounding errors only contribute marginally to the
total error. This is due to the fact that 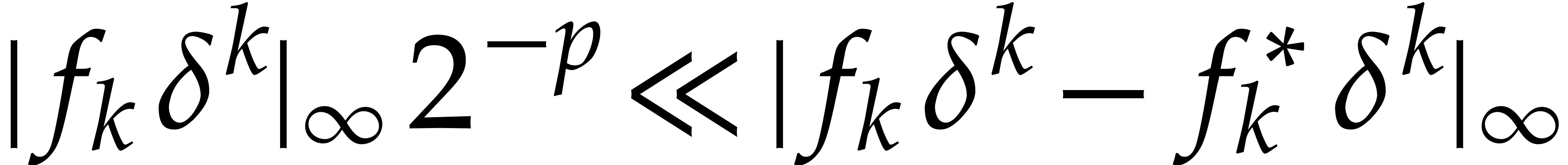 for
for
 , so the rounding errors are
absorbed by the errors induced by the error in the initial condition
, so the rounding errors are
absorbed by the errors induced by the error in the initial condition
 .
.
Let us continue with the notations from section 4 and its
subsection 4.2. In particular, we assume that the exact
solution  to (1) with initial
condition
to (1) with initial
condition  is analytic on the compact half disk
is analytic on the compact half disk
 . We also denote by
. We also denote by  an upper bound for
an upper bound for 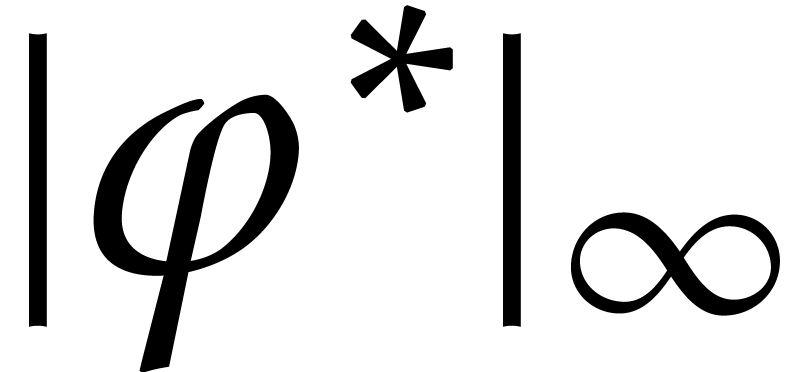 on
on  , so that
, so that 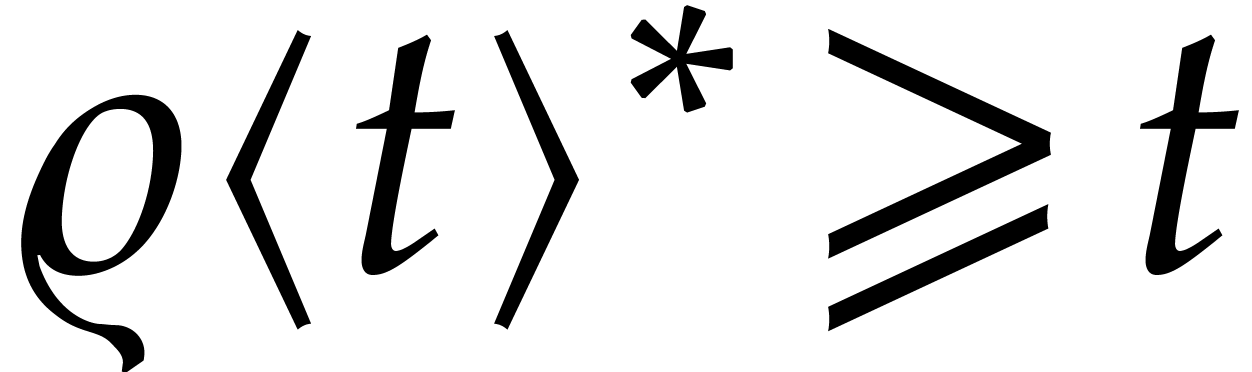 and
and

for all 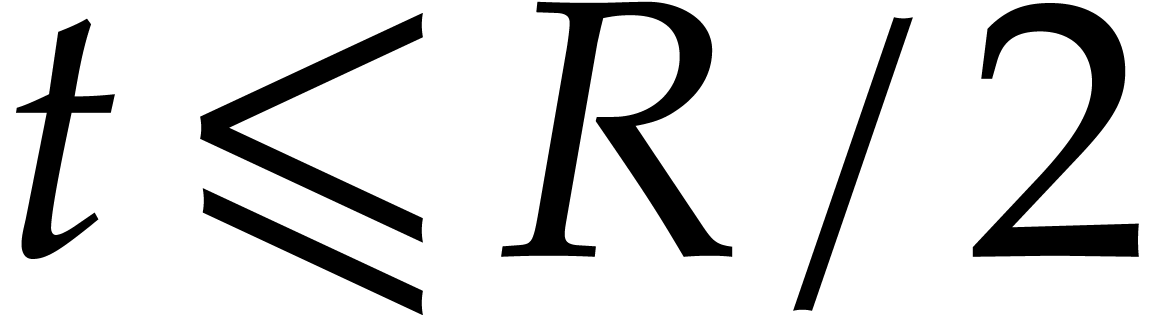 and
and 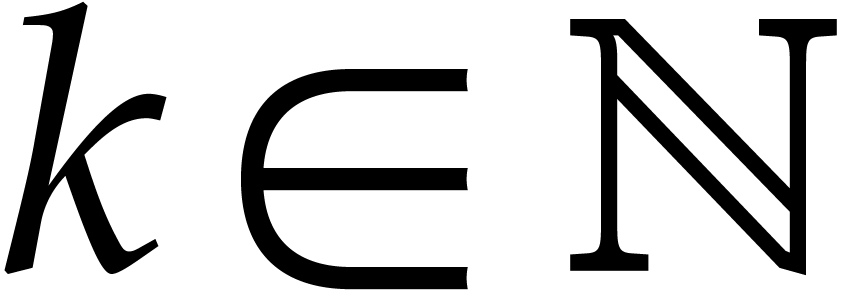 ,
by Cauchy's theorem. From now on, we assume that
,
by Cauchy's theorem. From now on, we assume that 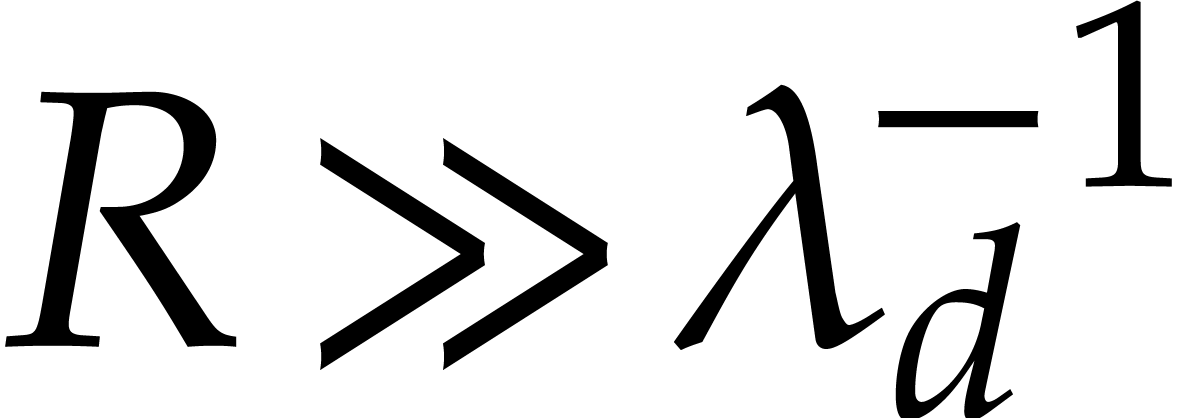 , so that Algorithm 1 only allows us to
use a step size of the order (24) instead of (23).
The aim of this section is to present a new way to compute truncated
power series solutions of the equation
, so that Algorithm 1 only allows us to
use a step size of the order (24) instead of (23).
The aim of this section is to present a new way to compute truncated
power series solutions of the equation
at time  , with the property
that
, with the property
that 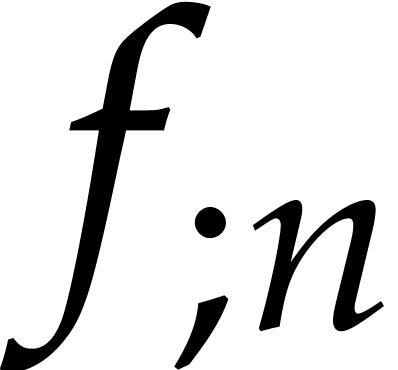 is a good approximation of the true
truncated solution
is a good approximation of the true
truncated solution 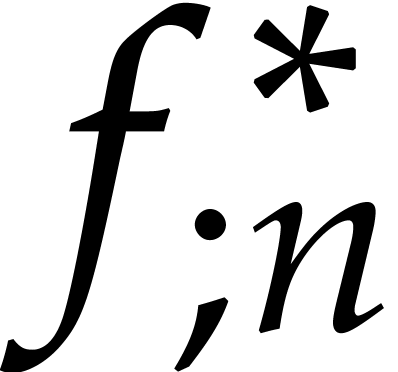 . In a
similar way as in section 4, we will then use this to
derive an algorithm for the numerical integration of (1).
Contrary to before, the property that
. In a
similar way as in section 4, we will then use this to
derive an algorithm for the numerical integration of (1).
Contrary to before, the property that 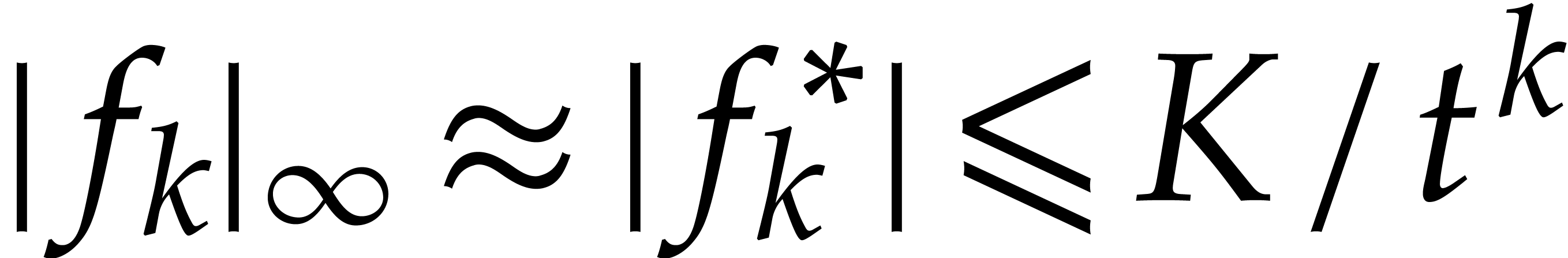 for
for  allows us to take step sizes of the desired order (23) for
allows us to take step sizes of the desired order (23) for 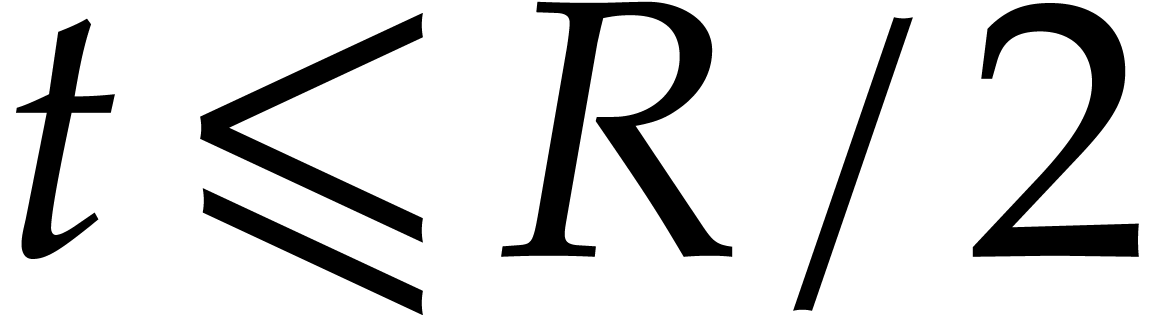 .
.
We stress once more that the reduced step size for Algorithm 1
is a consequence of our choice to compute the truncated solution 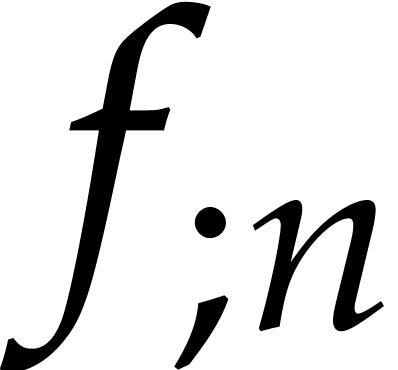 of (25) in terms of the initial
condition
of (25) in terms of the initial
condition  (that can only be known approximately)
and not of the choice of the particular algorithm that is used
for this computation.
(that can only be known approximately)
and not of the choice of the particular algorithm that is used
for this computation.
Indeed, as explained in section 4.2, only a small change in
 of the order of
of the order of 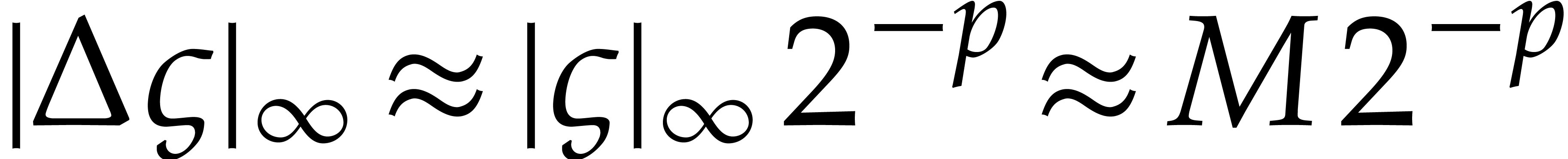 can have
a dramatic effect on the solution
can have
a dramatic effect on the solution  ,
since the coefficient
,
since the coefficient  can change by as much as
can change by as much as
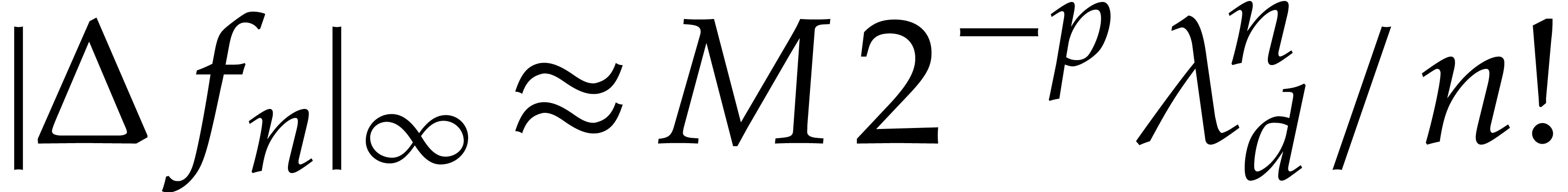 . Since
. Since  for large
for large 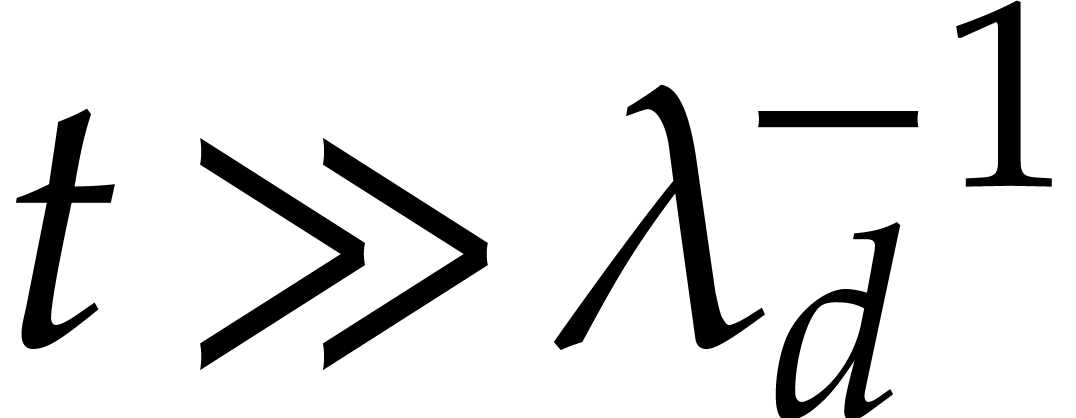 , it follows that a
minor change in
, it follows that a
minor change in  leads to a completely incorrect
computation of the coefficients
leads to a completely incorrect
computation of the coefficients 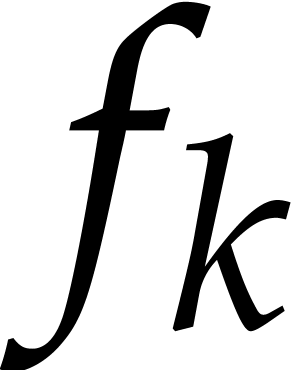 with
with 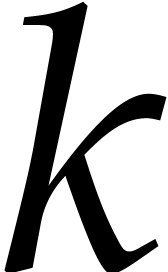 close to
close to 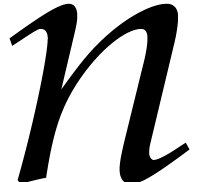 .
.
For small  , the error
, the error  generally does remain bounded by the actual value
generally does remain bounded by the actual value
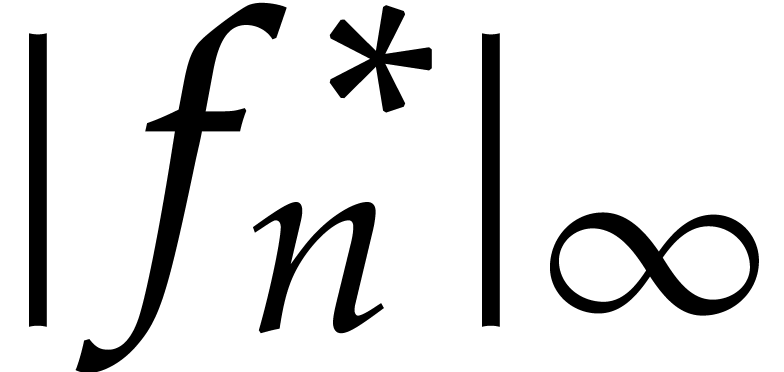 . In the theory of stiff
differential equations, it is customary to say that the system is in a
transient state for such
. In the theory of stiff
differential equations, it is customary to say that the system is in a
transient state for such  .
As soon as the error
.
As soon as the error 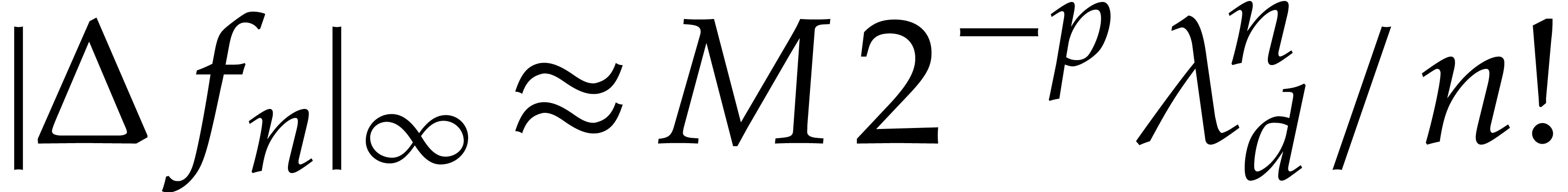 exceeds
exceeds 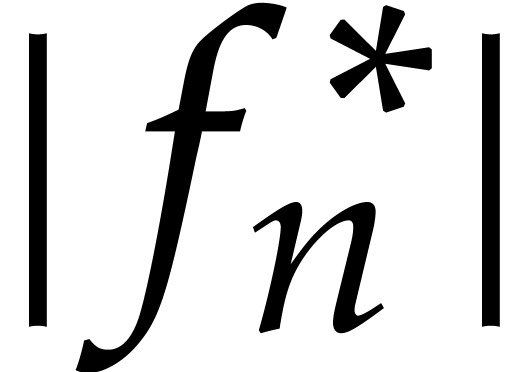 , we say that the system has reached its
steady state for the largest eigenvalue
, we say that the system has reached its
steady state for the largest eigenvalue 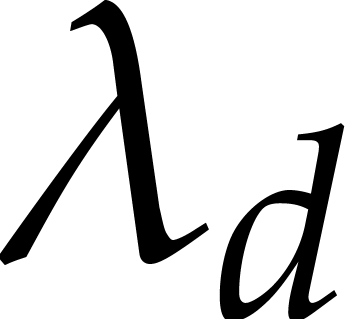 of
of  . When this happens, the
system may still be in a transient state for some of the other
eigenvalues
. When this happens, the
system may still be in a transient state for some of the other
eigenvalues 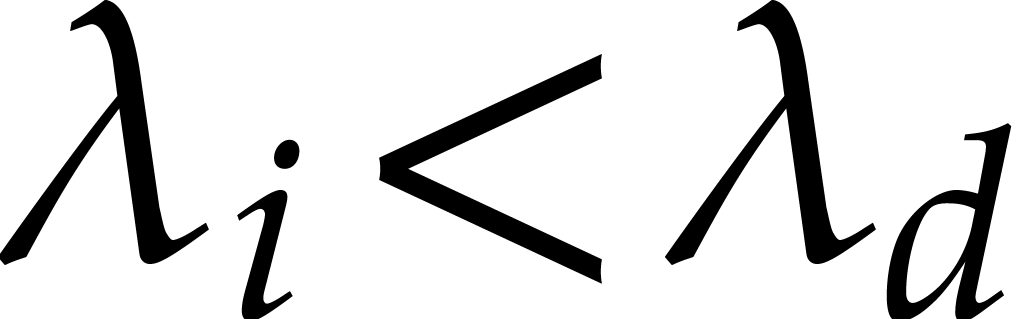 . This motivates
the definition of the critical index
. This motivates
the definition of the critical index 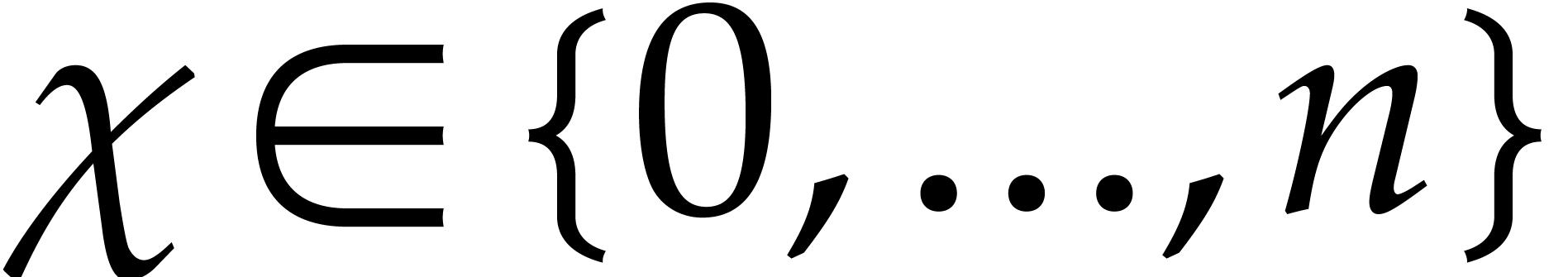 as
being the largest index
as
being the largest index  such that we are in a
transient state for
such that we are in a
transient state for 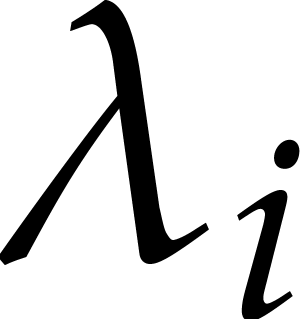 ; we take
; we take
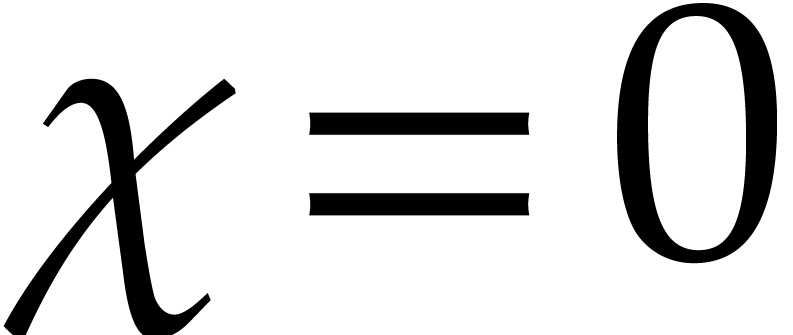 if we reached the steady state for all
eigenvalues
if we reached the steady state for all
eigenvalues 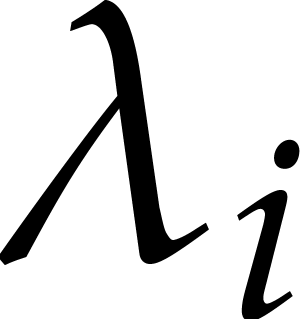 .
.
The concepts of transient state, steady state, and critical index are
deliberately somewhat vague. As a tentative definition, we might say
that we reached the steady state for 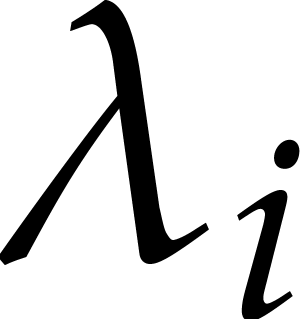 if
if 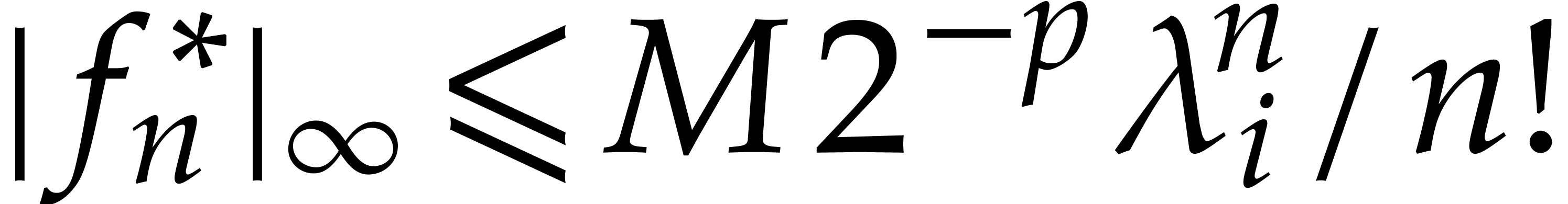 . However, for computational
purposes, it is convenient to interpret this inequality as an
approximate one. The crucial property of reaching the steady state for
. However, for computational
purposes, it is convenient to interpret this inequality as an
approximate one. The crucial property of reaching the steady state for
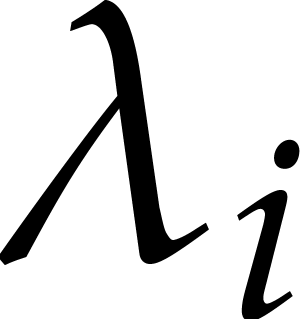 is that the smallness of
is that the smallness of 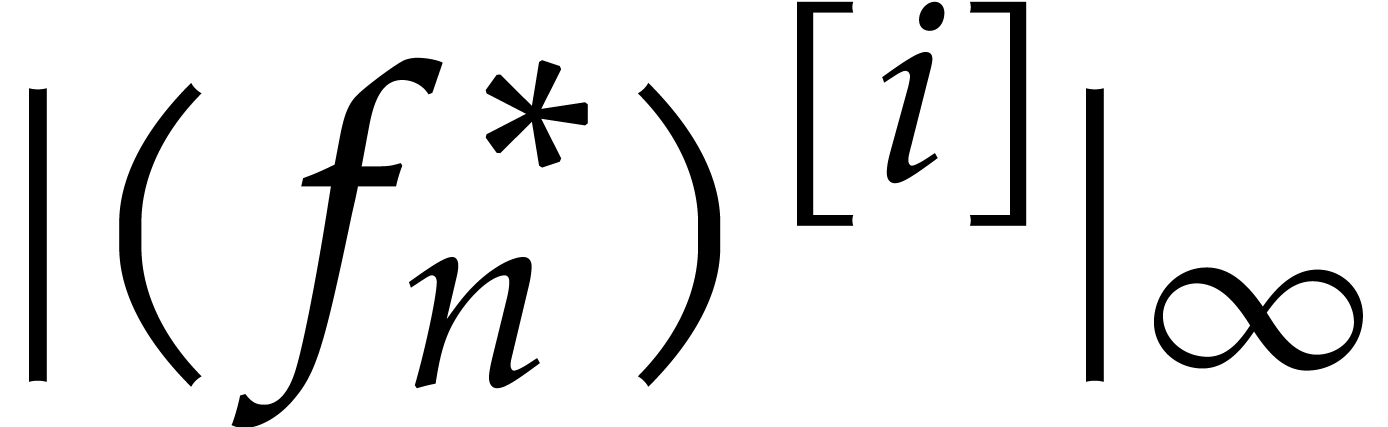 essentially determines the
essentially determines the  -th
component
-th
component 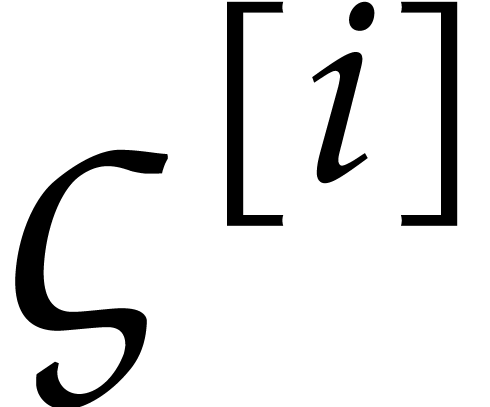 of the initial condition up to the
last
of the initial condition up to the
last  -th bit.
-th bit.
The main idea behind our algorithm is to use this property as a
“boundary condition” for the computation of  . More precisely, we boldly impose the boundary
conditions
. More precisely, we boldly impose the boundary
conditions 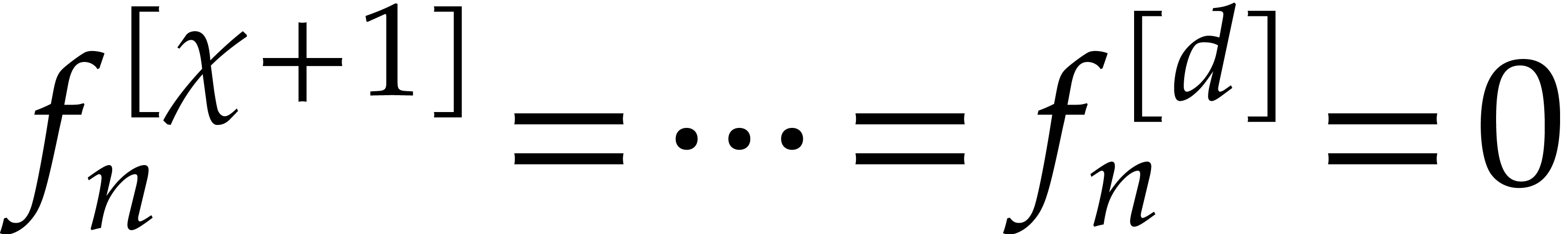 as a replacement for the initial
conditions
as a replacement for the initial
conditions 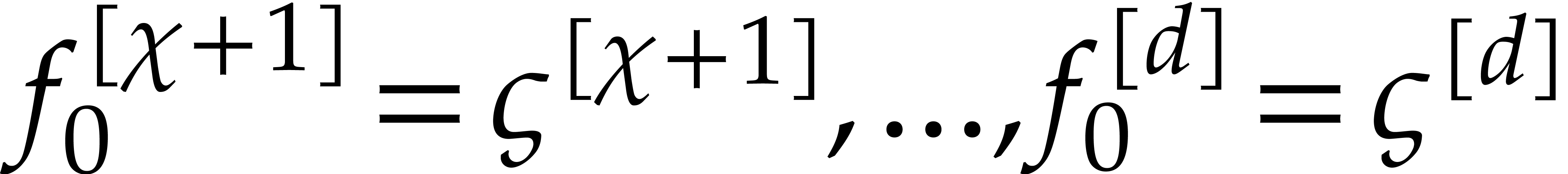 , while keeping
the remaining initial conditions
, while keeping
the remaining initial conditions  for the
transient states. In other words, we wish to find the truncated solution
for the
transient states. In other words, we wish to find the truncated solution
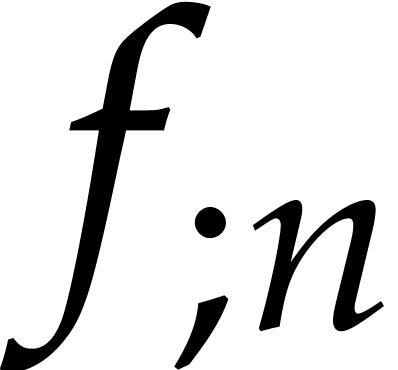 of the system
of the system
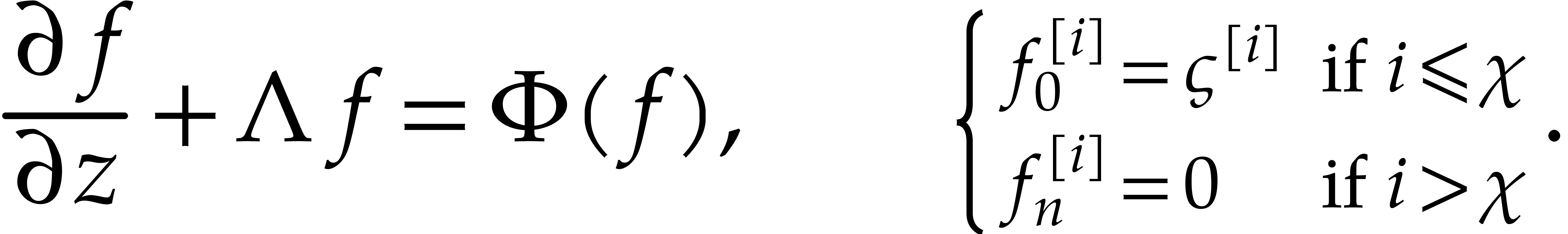 |
(26) |
We will call 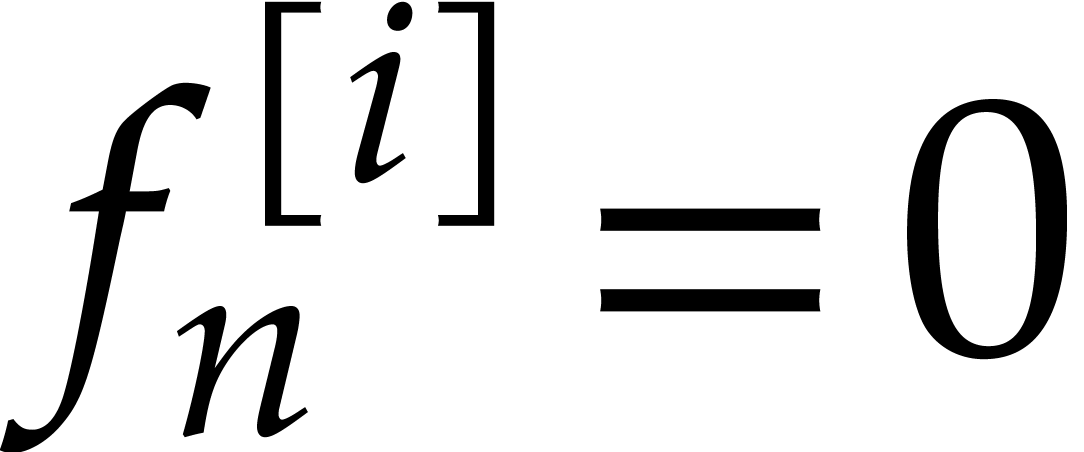 the steady-state condition
for
the steady-state condition
for 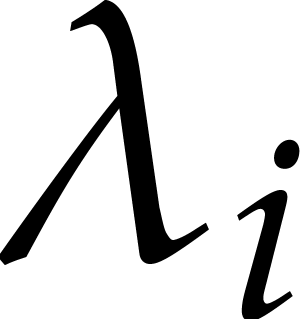 and (26) a steady-state
problem.
and (26) a steady-state
problem.
In order to solve (26), it is natural to adapt the
iterative method from section 3 and introduce the operator
 with
with
The actual arithmetic is performed over 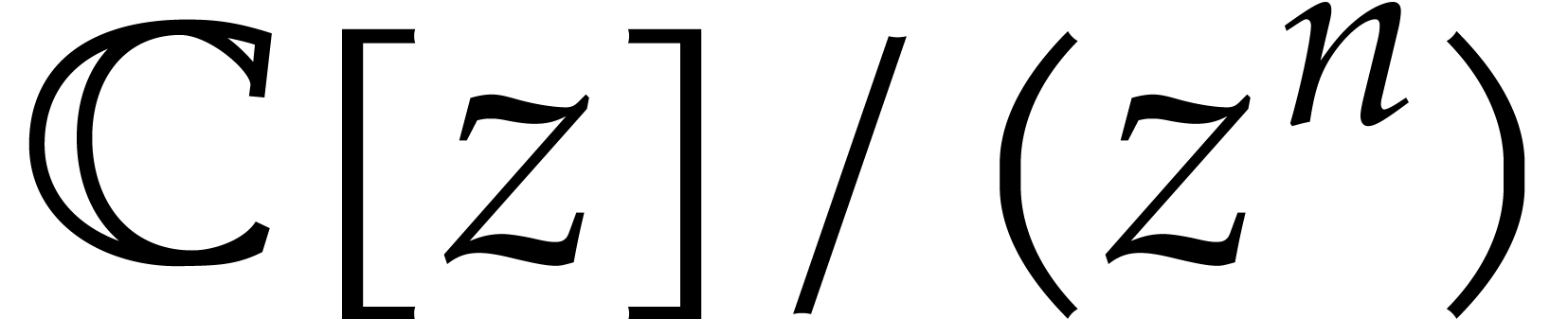 ,
but it will be more convenient to view
,
but it will be more convenient to view  as an
operator from
as an
operator from 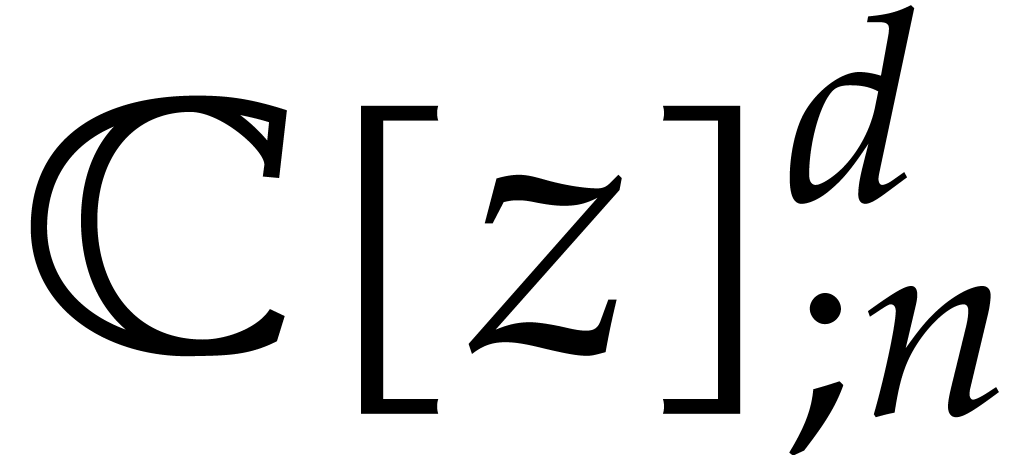 into itself. The computation of
into itself. The computation of
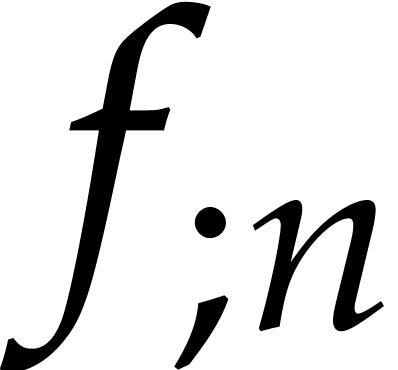 as a fixed point of
as a fixed point of  leaves us with two questions: how to chose a suitable ansatz
for the iteration
leaves us with two questions: how to chose a suitable ansatz
for the iteration 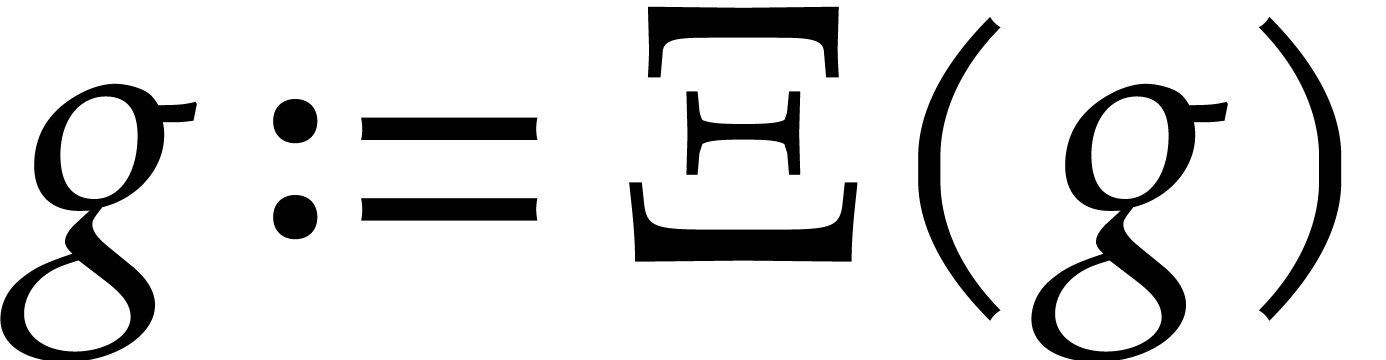 and how to determine the
critical index
and how to determine the
critical index  ?
?
For the ansatz, we go back to the solution 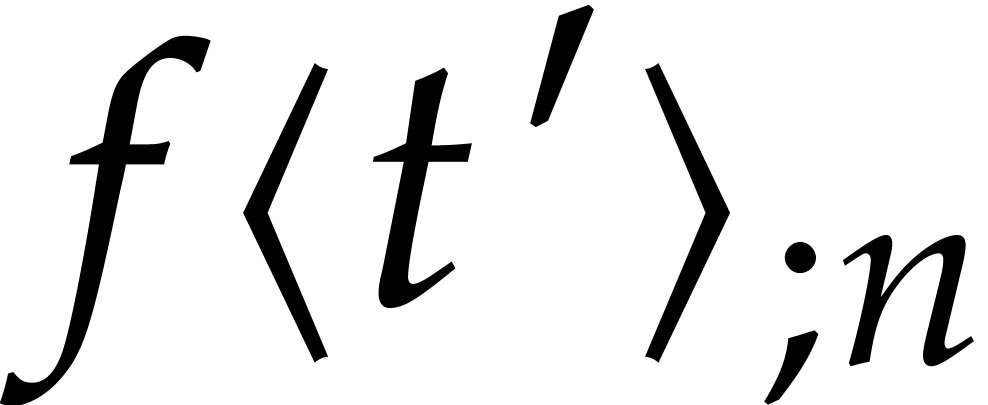 from the previous step at time
from the previous step at time 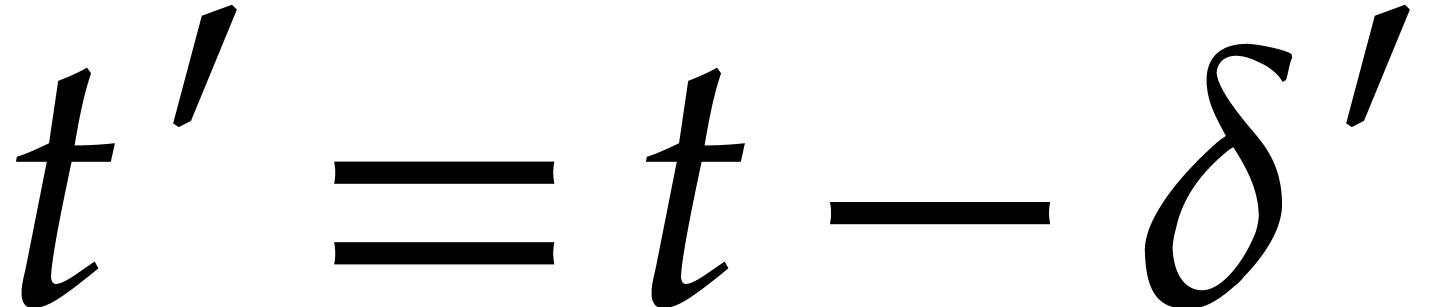 and simply use
and simply use
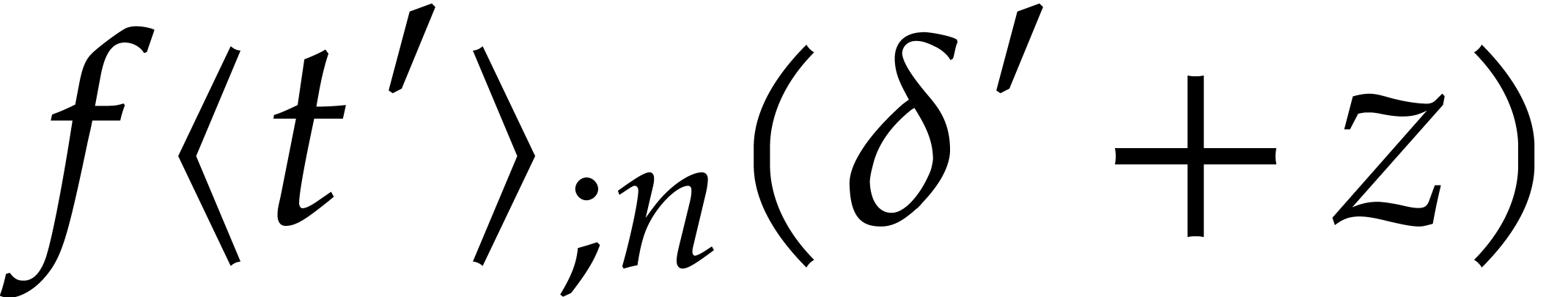 as a first approximation of the solution
as a first approximation of the solution 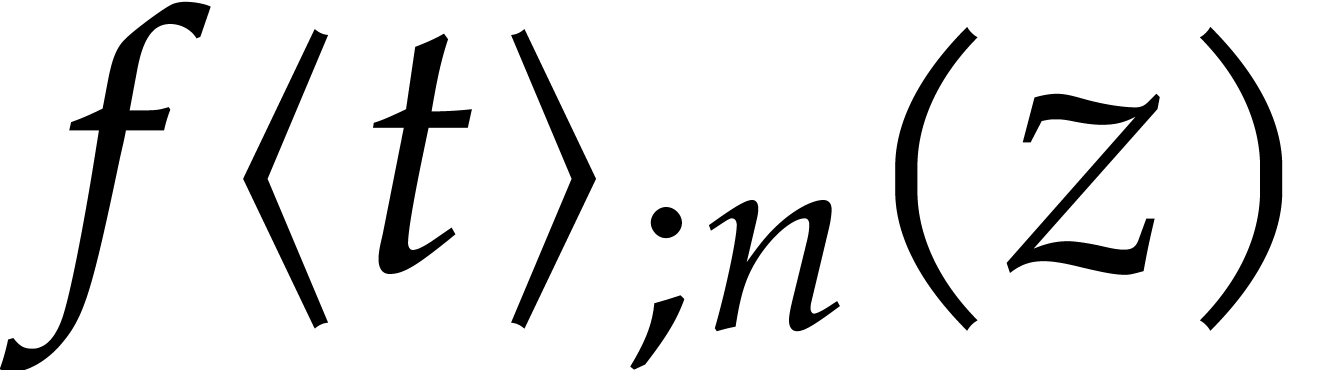 at time
at time  .
For
.
For 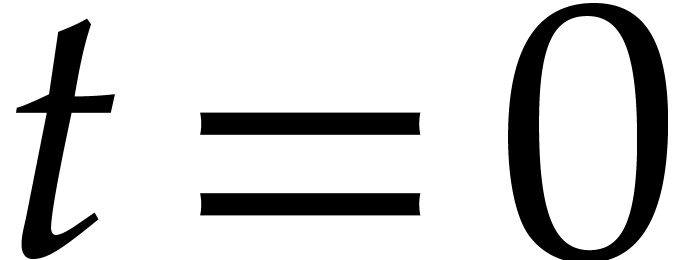 , we fall back to the
traditional method from section 4. For the initial and
steady-state conditions to “propagate to the other end”, at
least
, we fall back to the
traditional method from section 4. For the initial and
steady-state conditions to “propagate to the other end”, at
least 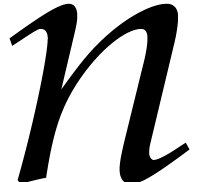 iterations are required in order to find a
fixed point of
iterations are required in order to find a
fixed point of  , whereas
, whereas 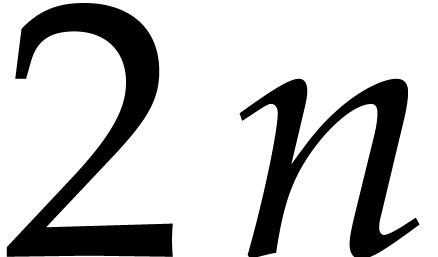 iterations usually suffice. One may thus take
iterations usually suffice. One may thus take  .
.
As to the critical index 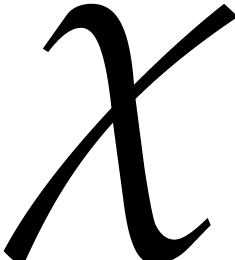 , we
determine it as a function of the step size
, we
determine it as a function of the step size  through
through
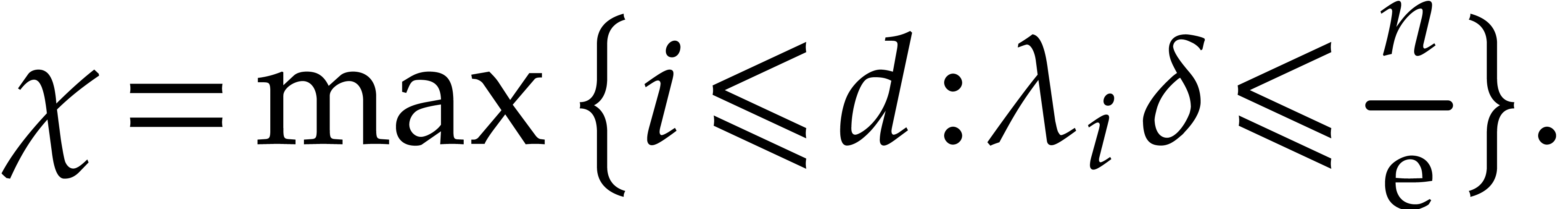 |
(28) |
This choice is meant to ensure the fastest convergence of the iteration
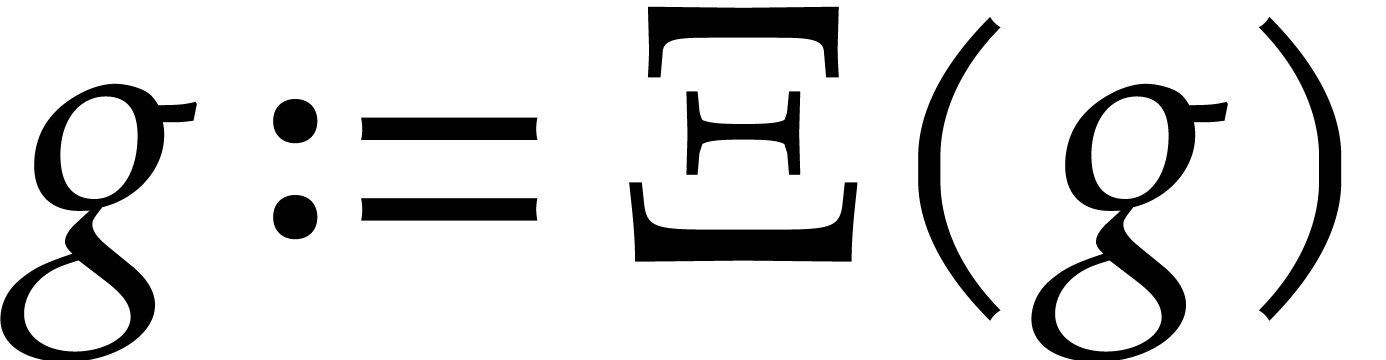 and we used
and we used 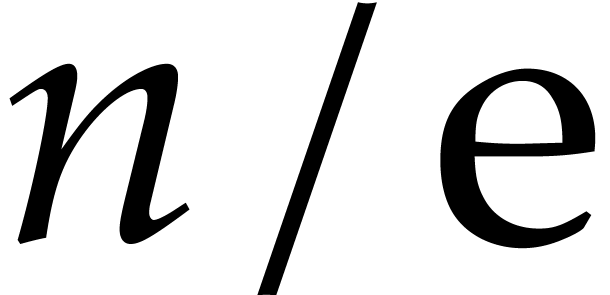 as an
approximation of
as an
approximation of 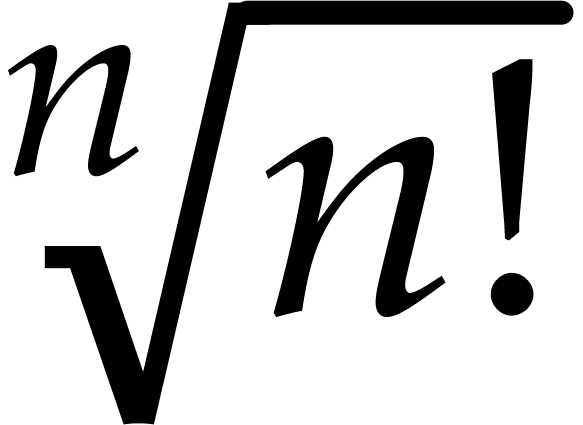 . The step
size
. The step
size  itself is chosen in the same way as in
section 4. Since
itself is chosen in the same way as in
section 4. Since 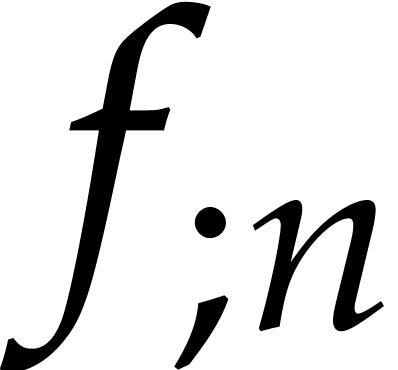 is not yet
available for the computation of
is not yet
available for the computation of  ,
we may use the previous step size
,
we may use the previous step size 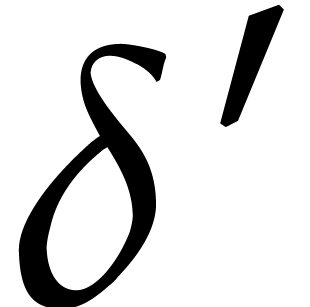 as an
approximation for
as an
approximation for  in (28).
Optionally, one may also wish to implement a few additional sanity
checks in order to ensure convergence of the
in (28).
Optionally, one may also wish to implement a few additional sanity
checks in order to ensure convergence of the  -iteration and decrease the step size in case of
failure. One useful such check is to verify that
-iteration and decrease the step size in case of
failure. One useful such check is to verify that 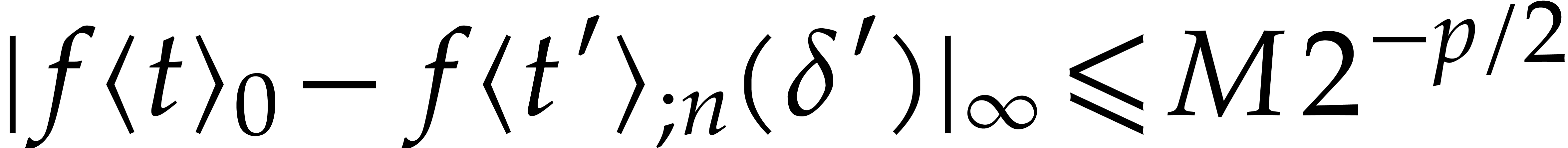 .
.
Altogether, this leads to the following algorithm:
Algorithm
Output: a numerical approximation for 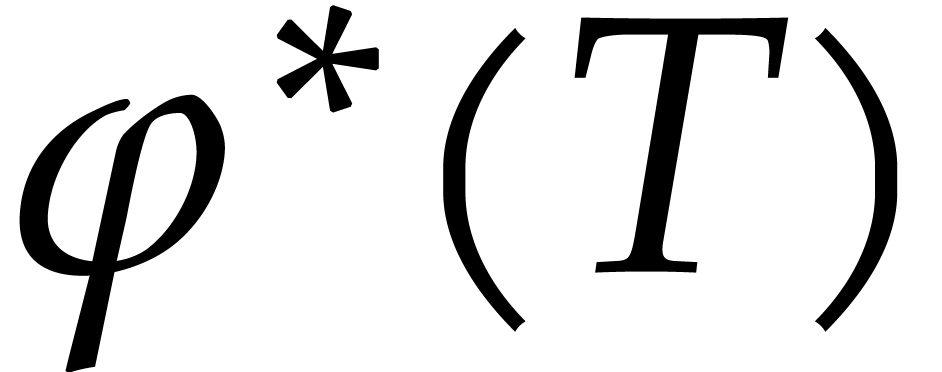 , where
, where  satisfies (1) with
satisfies (1) with 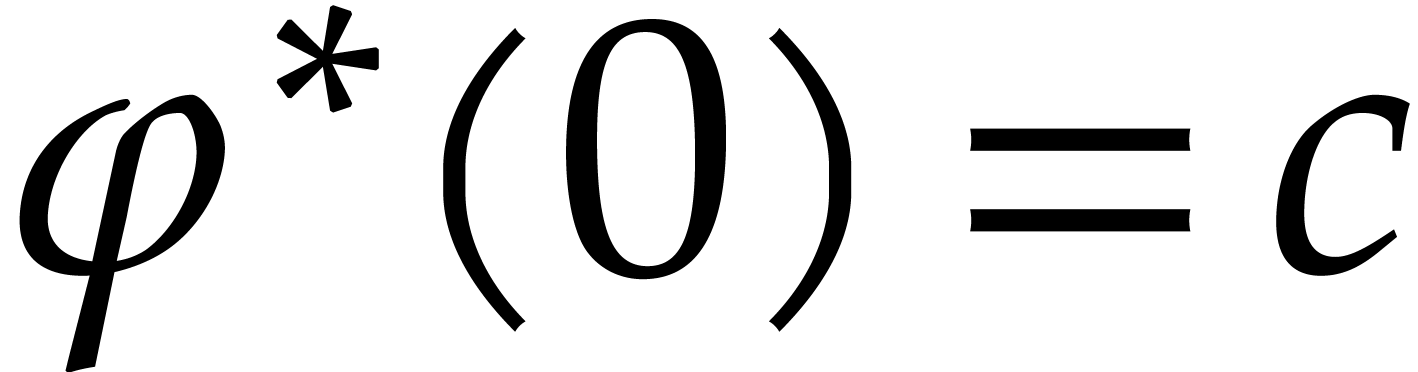
 ,
, 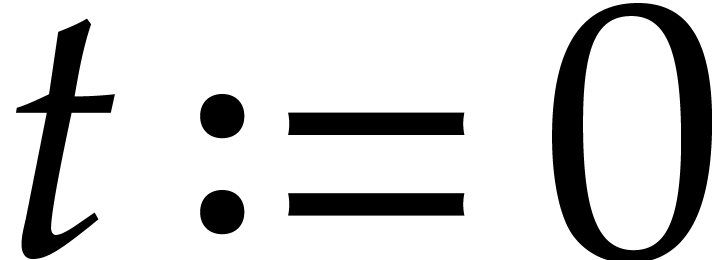
Compute the truncated solution 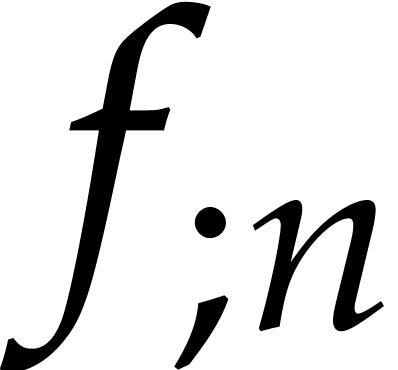 to (19)
with
to (19)
with 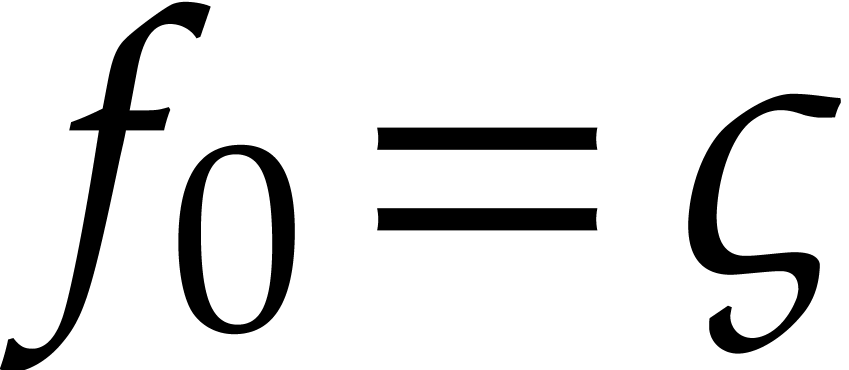
while  do
do
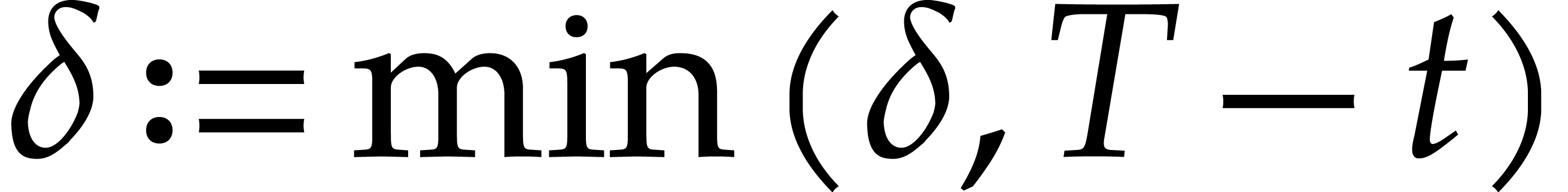
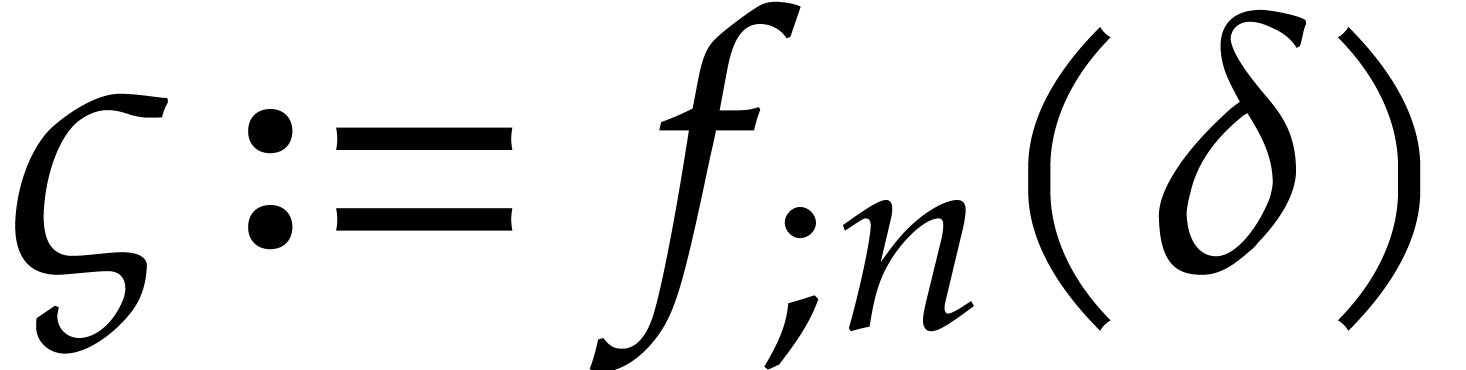 ,
, 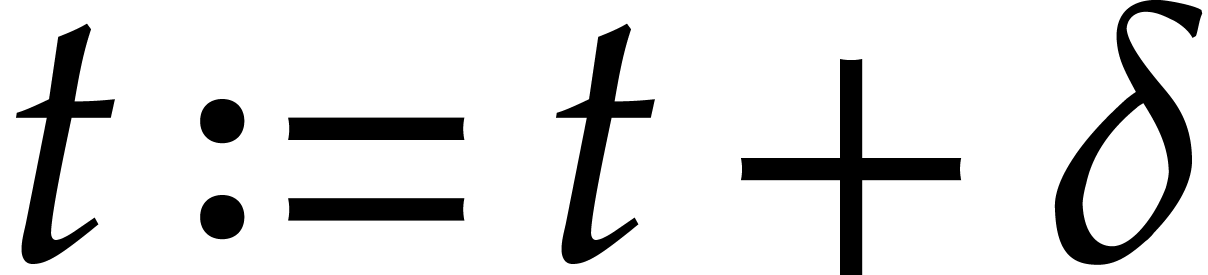
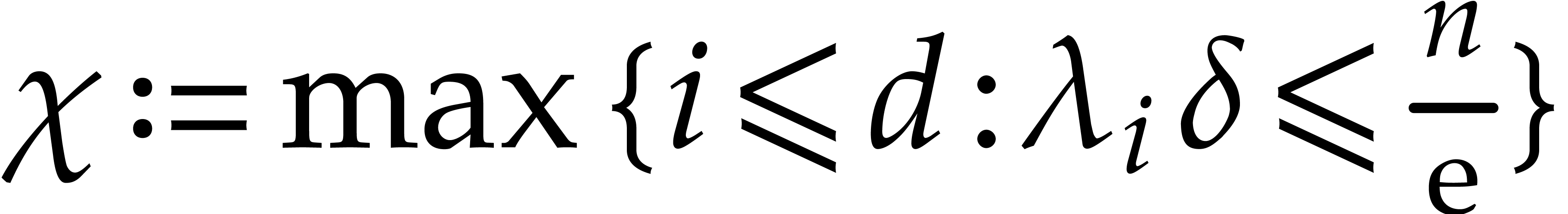
Replace 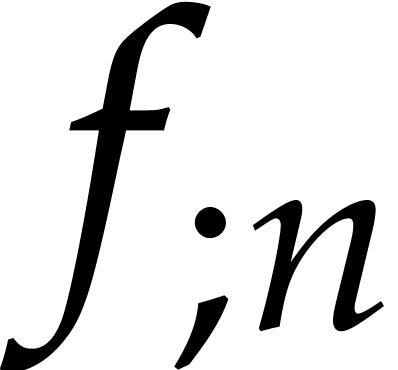 by the approximate fixed point
by the approximate fixed point 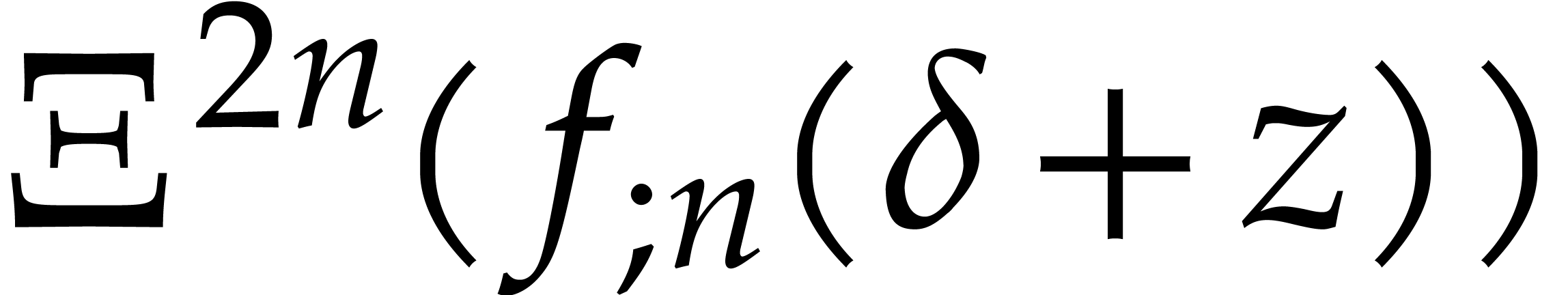 of
of  as in (27)
as in (27)
return 
 -iteration
-iteration
Let us now study the convergence of  as a mapping
on the
as a mapping
on the 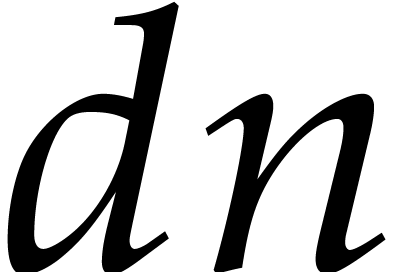 -dimensional vector
space
-dimensional vector
space 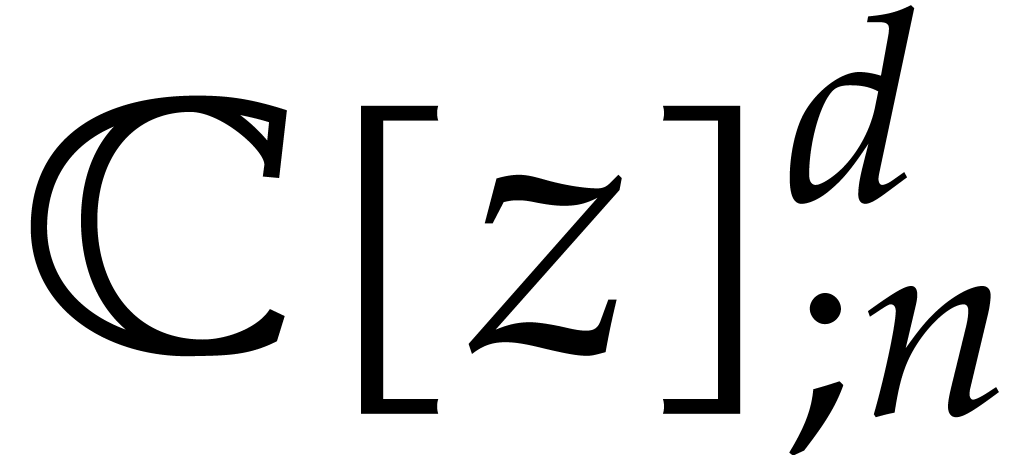 over
over  .
We define a norm
.
We define a norm  on this space by
on this space by
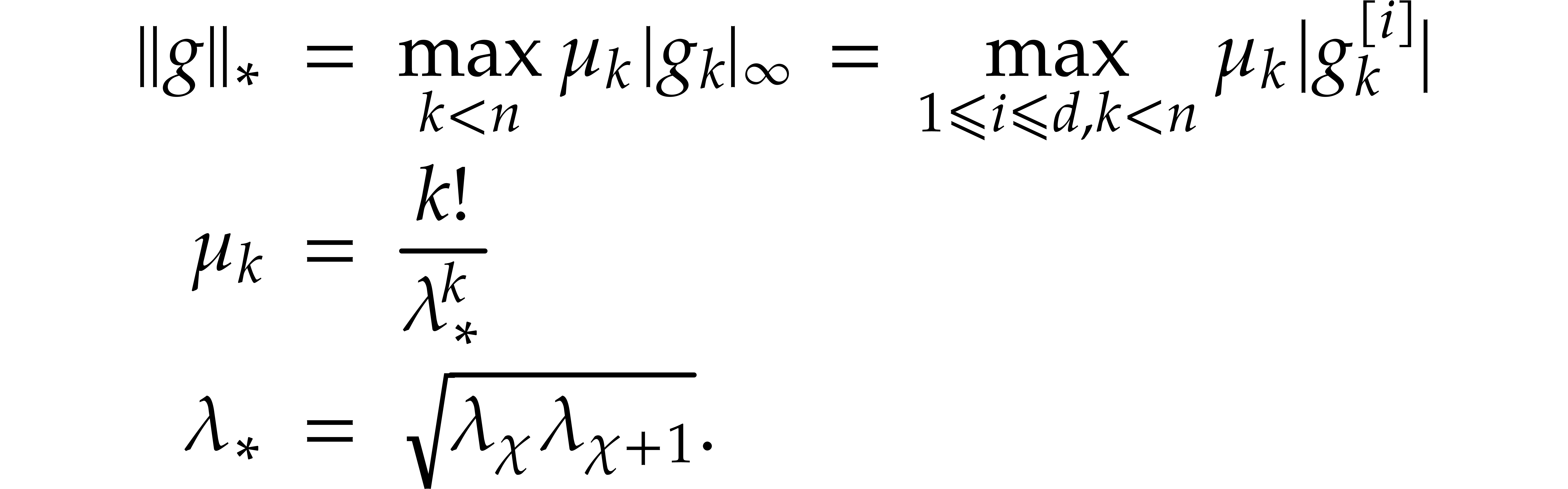
For a linear map on this space, represented as a matrix 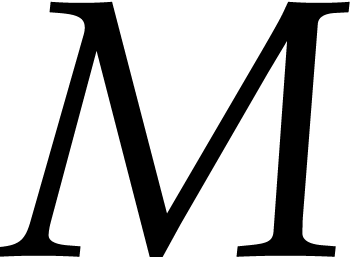 , we have the corresponding matrix norm
, we have the corresponding matrix norm
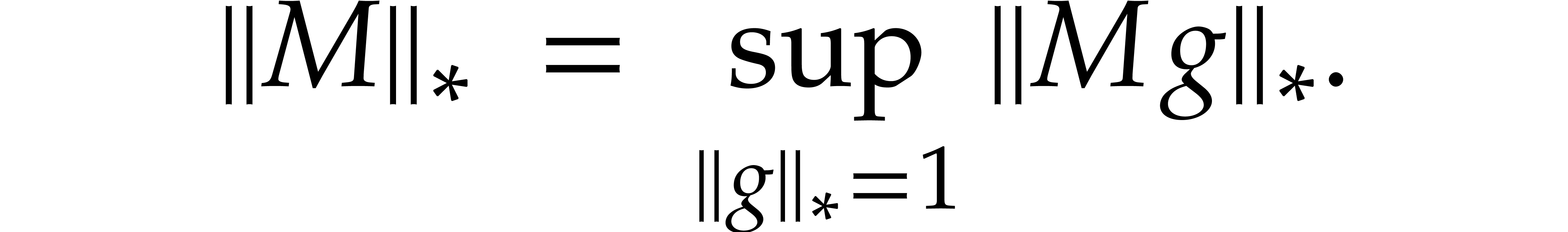
Recall that  and
and  stand
for the Jacobian matrices of
stand
for the Jacobian matrices of  and
and  .
.
Proof. Consider an infinitesimal perturbation
 of
of  with
with  . Given
. Given  and
and  , we have
, we have
Similarly, given  and
and  , we have
, we have
Putting both relations together, we obtain 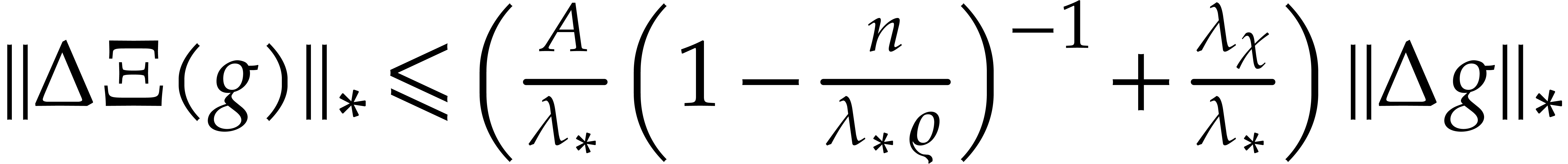 .
.
Assume that
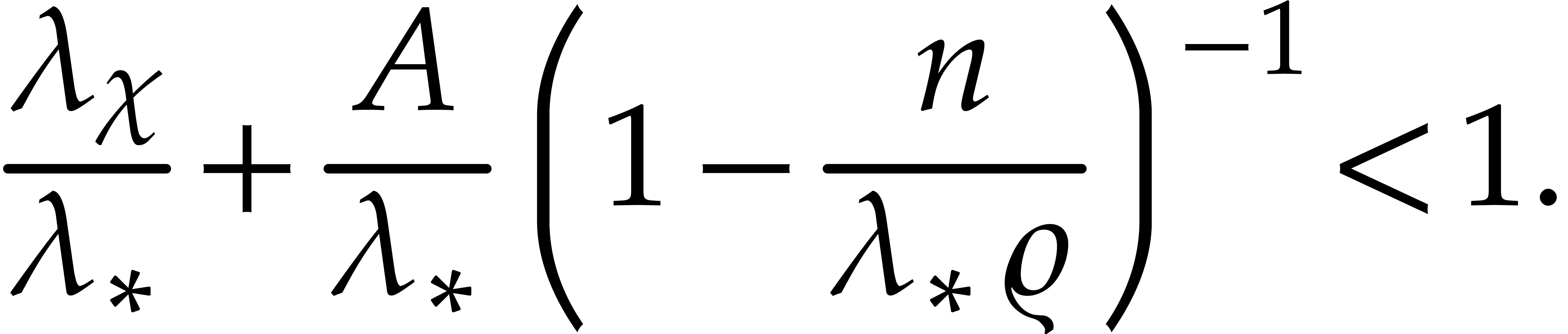 |
(29) |
Then the theorem implies the existence a small neighbourhood of the
fixed point 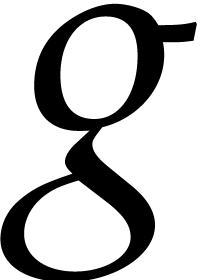 of
of  on which
the
on which
the  -iteration converges to
-iteration converges to
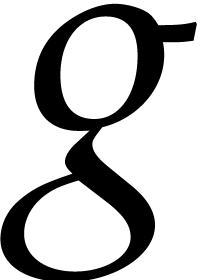 . Whenever this condition is
met, the
. Whenever this condition is
met, the  -iteration actually
tends to converge on a rather large neighbourhood that includes our
ansatz; see the next subsection for a more detailed discussion.
Intuitively speaking, the condition requires the eigenvalues
-iteration actually
tends to converge on a rather large neighbourhood that includes our
ansatz; see the next subsection for a more detailed discussion.
Intuitively speaking, the condition requires the eigenvalues 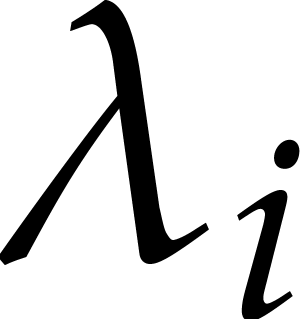 to be sufficiently separated with respect to the norm of
the forcing term
to be sufficiently separated with respect to the norm of
the forcing term  . Even when
the condition does not hold, the
. Even when
the condition does not hold, the  -iteration
usually still displays an initial convergence for our ansatz,
but the quality of the approximate solution to (26) ceases
to improve after a while.
-iteration
usually still displays an initial convergence for our ansatz,
but the quality of the approximate solution to (26) ceases
to improve after a while.
If the condition (29) is satisfied for all critical indices
 that we encounter when integrating from
that we encounter when integrating from  until time
until time  ,
then Algorithm 2 should produce an accurate result. The
idealized analysis from section 4.2 then also applies, so
the algorithm takes
,
then Algorithm 2 should produce an accurate result. The
idealized analysis from section 4.2 then also applies, so
the algorithm takes 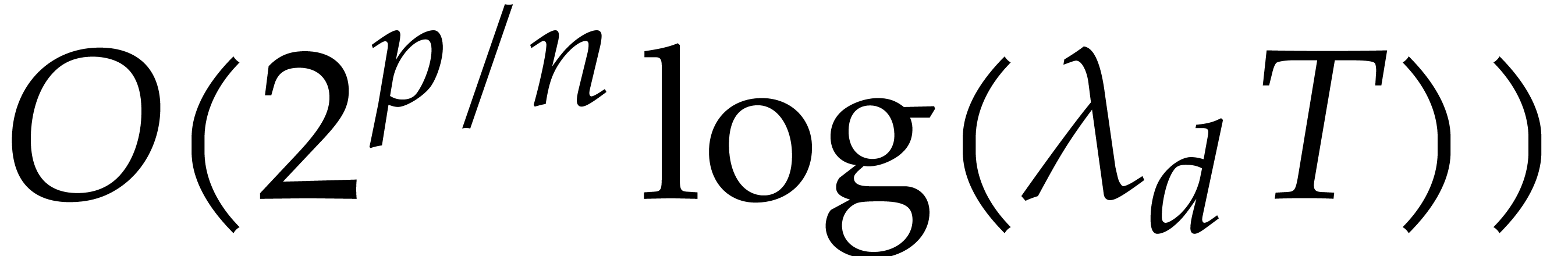 steps. Since each step now
requires
steps. Since each step now
requires  floating point operations at bit
precision
floating point operations at bit
precision 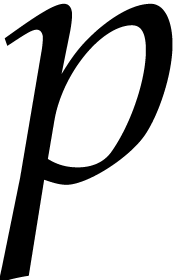 , we finally obtain
the bound
, we finally obtain
the bound 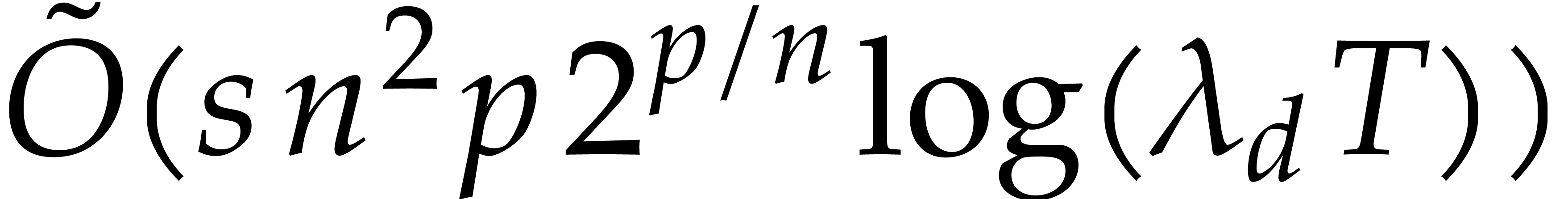 for the total running time.
for the total running time.
Let us now investigate in more detail why fixed points 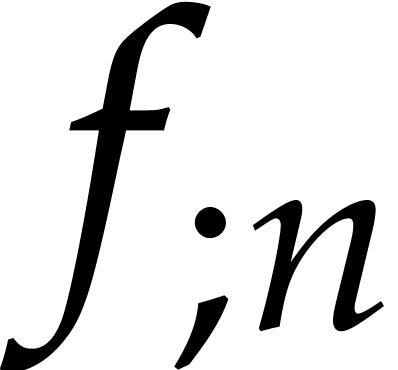 of the
of the  -iteration indeed
approximate the true solution
-iteration indeed
approximate the true solution 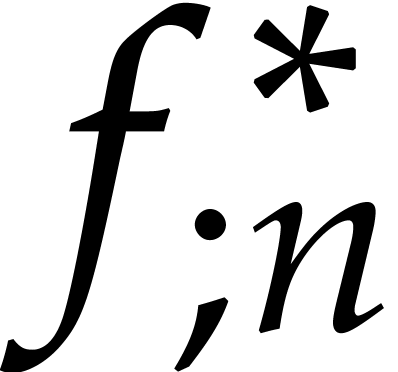 quite well. For
this, we will determine a more precise small neighbourhood of the fixed
point
quite well. For
this, we will determine a more precise small neighbourhood of the fixed
point 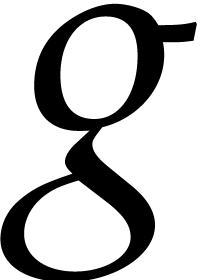 on which the
on which the  -iteration
converges and show that this neighbourhood in particular contains
-iteration
converges and show that this neighbourhood in particular contains 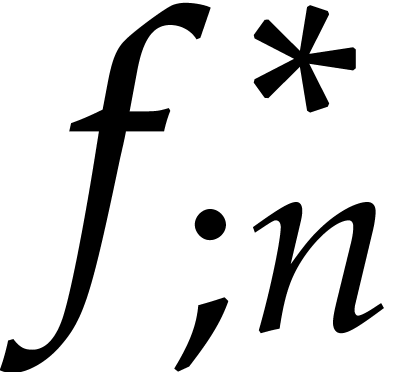 . We start with two lemmas.
. We start with two lemmas.
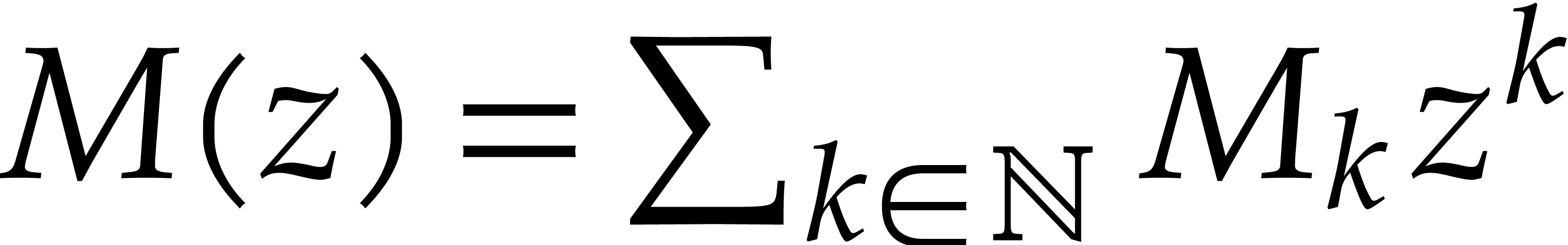 be a
be a  matrix of
analytic functions defined on the closed ball
matrix of
analytic functions defined on the closed ball 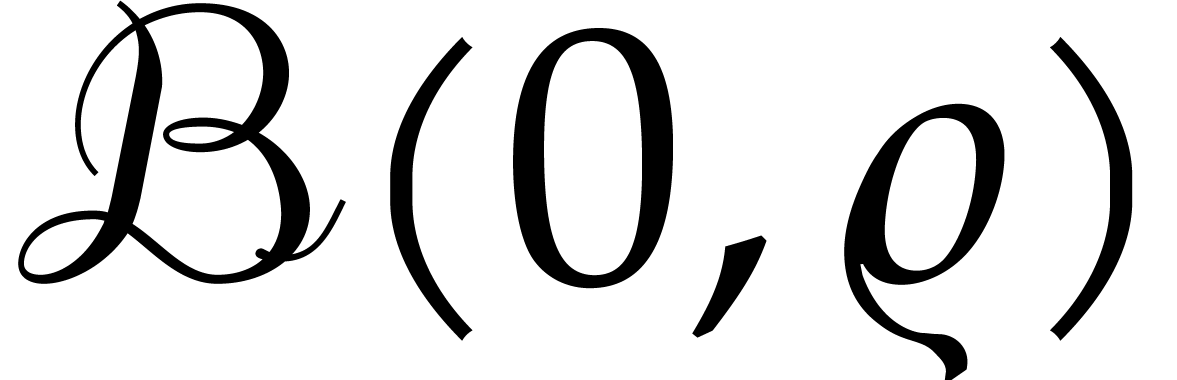 with center zero and radius
with center zero and radius  .
Let
.
Let 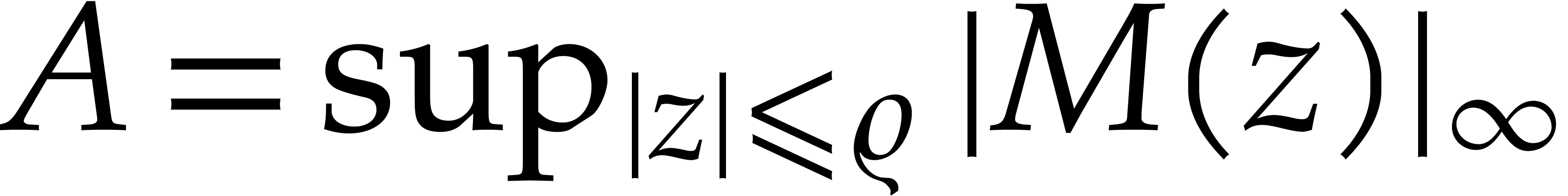 . Then
. Then 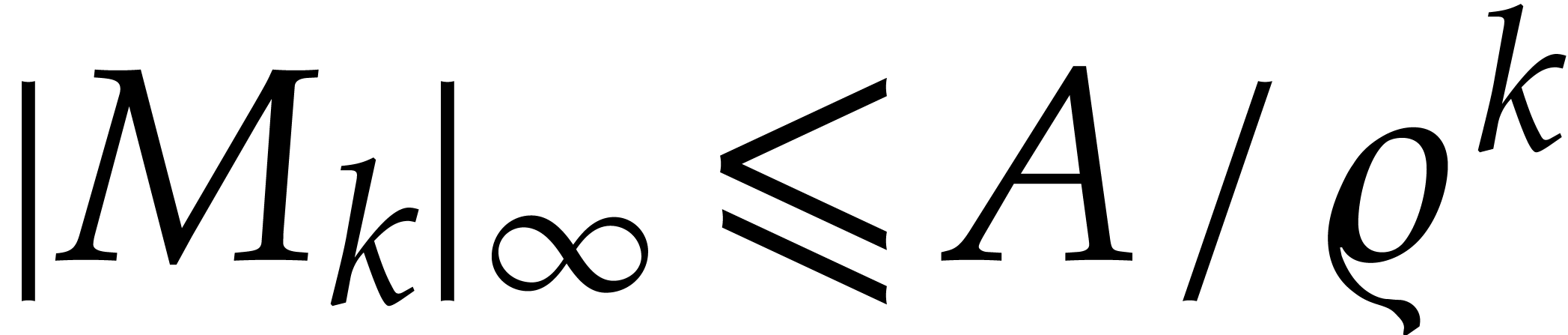 for all
for all  .
.
Proof. Given  with
with 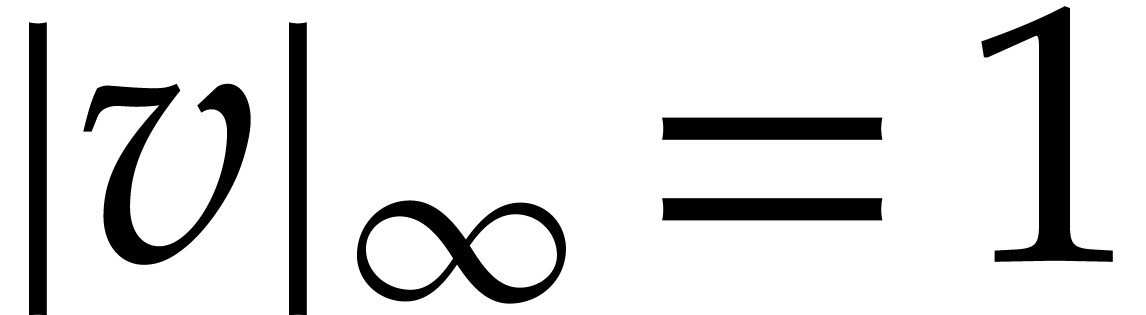 , we have
, we have
It follows that 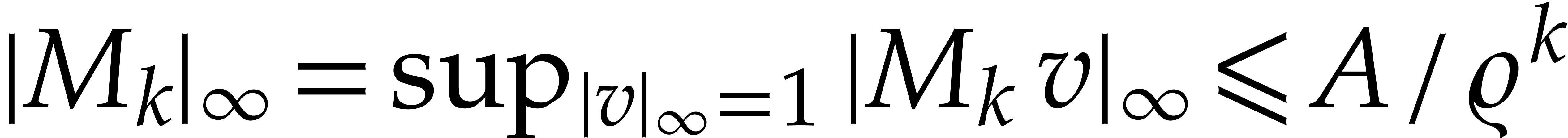 .
.
 ,
,  ,
,  ,
,
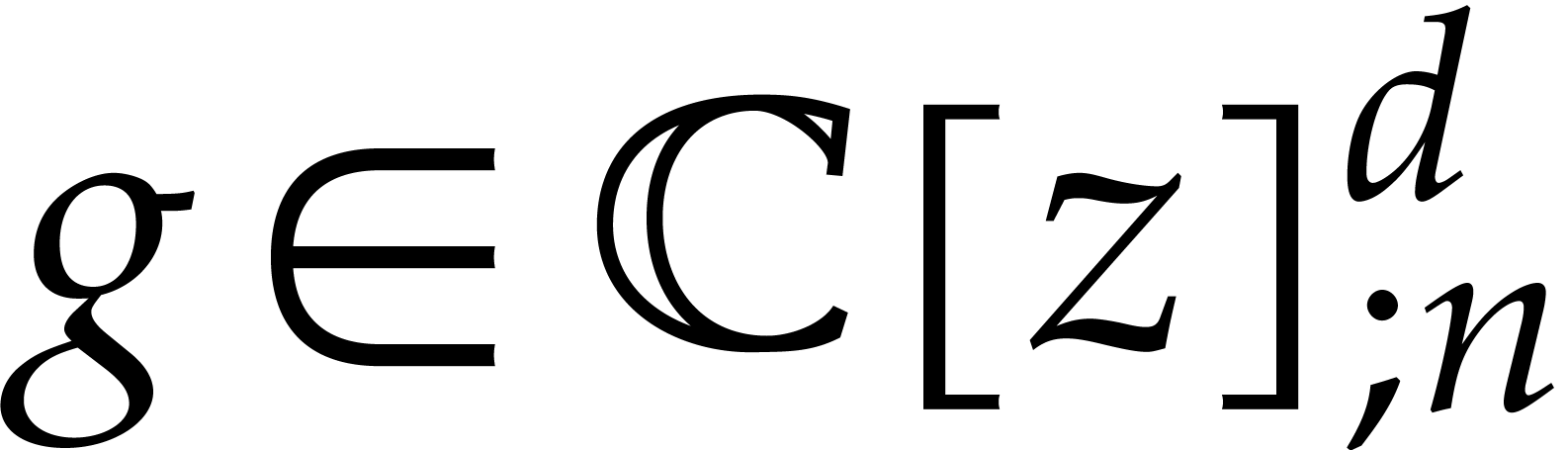 , and
, and
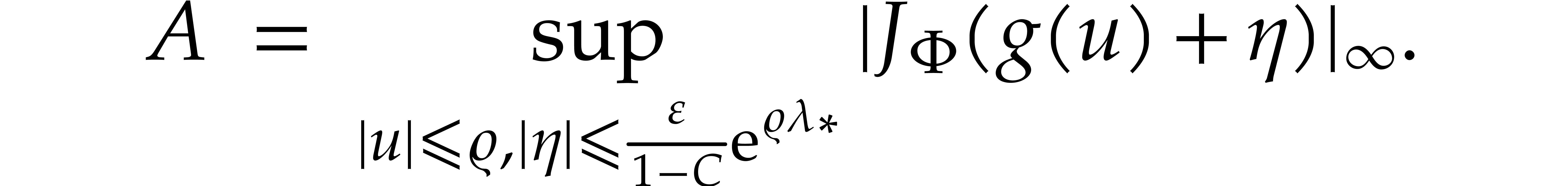
Then for all 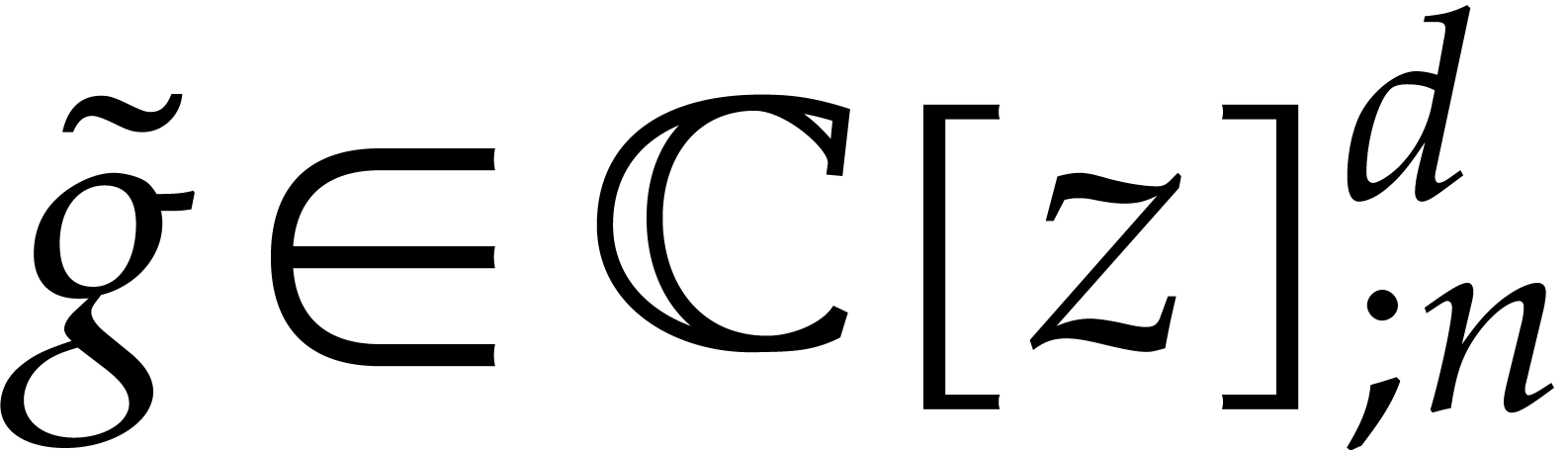 with
with 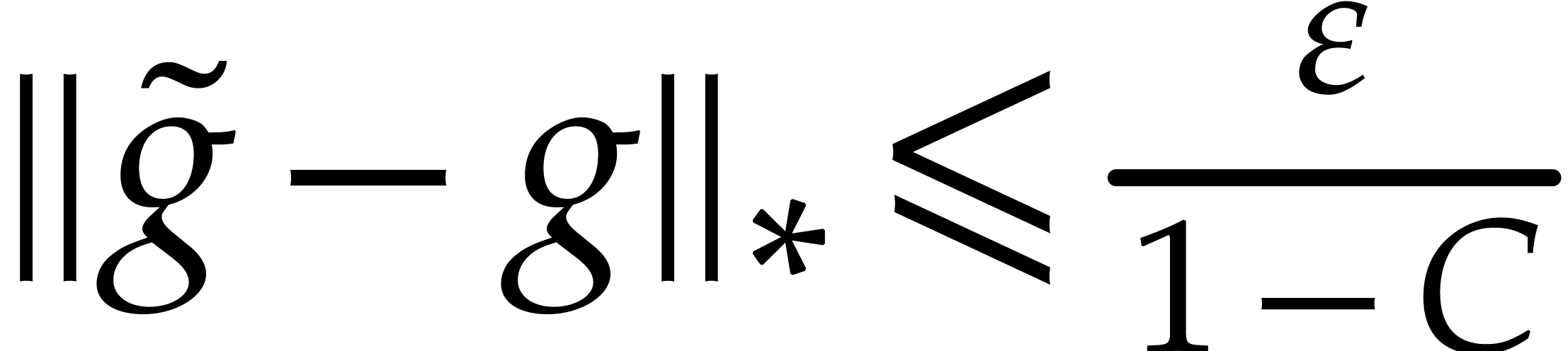 and
and  , we have
, we have
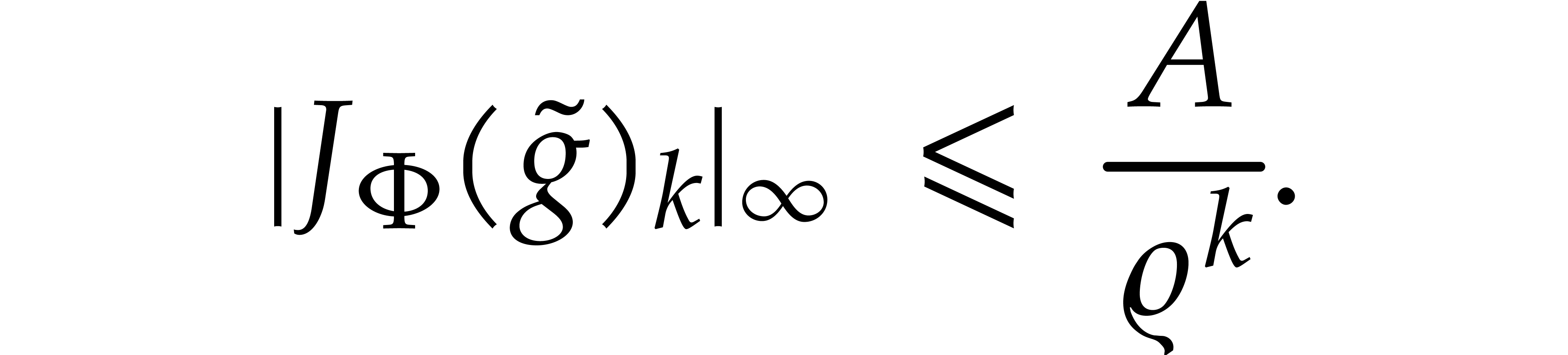
Proof. Setting 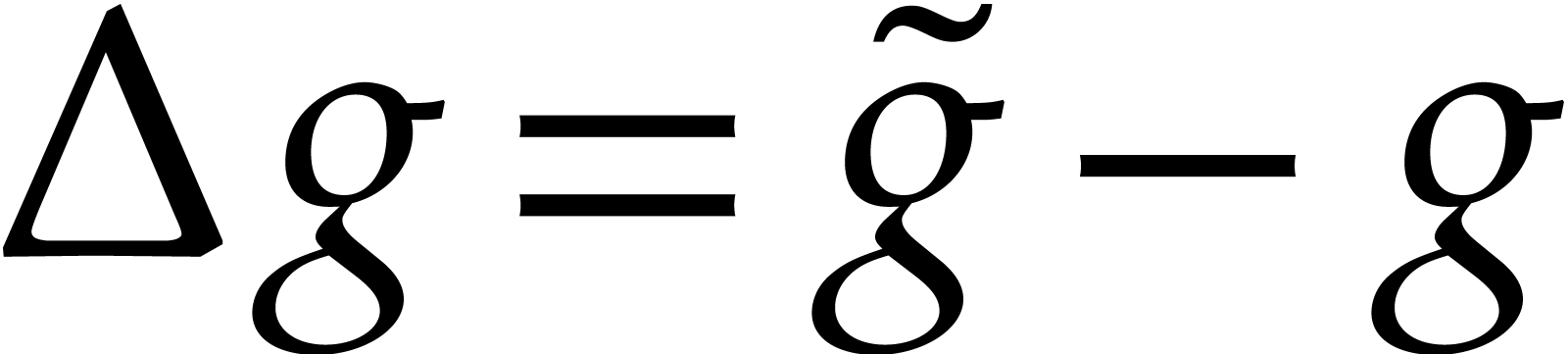 ,
we first notice that
,
we first notice that
It follows that
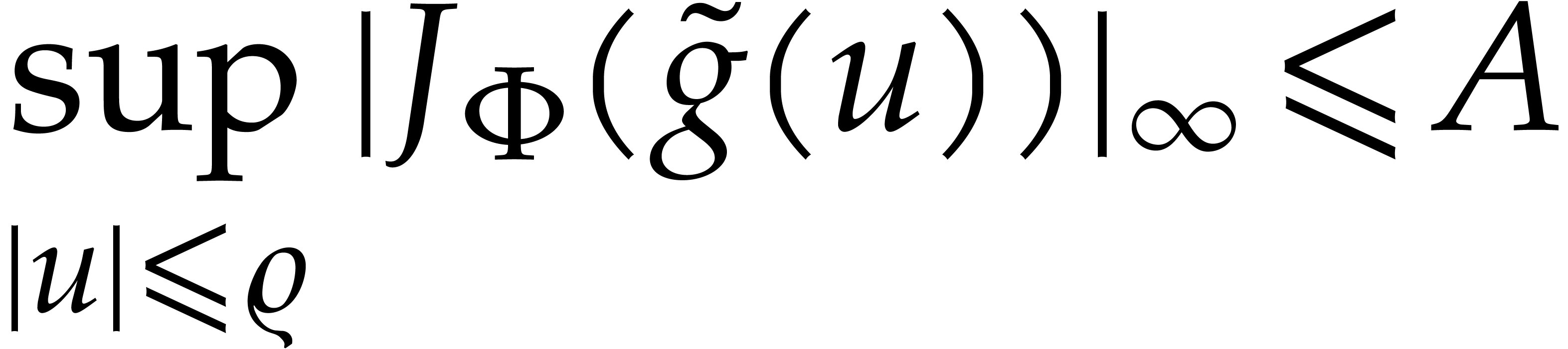
and we conclude using the previous lemma.
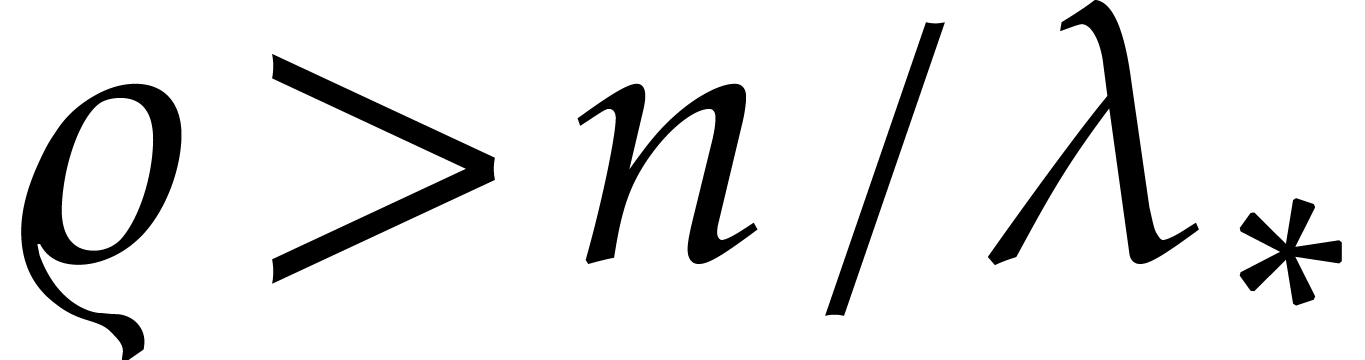 and
and 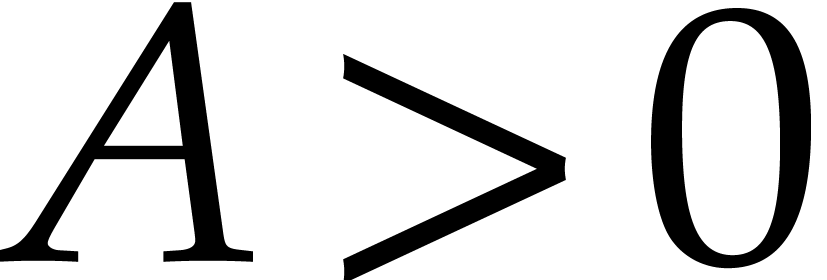 be
such that
be
such that
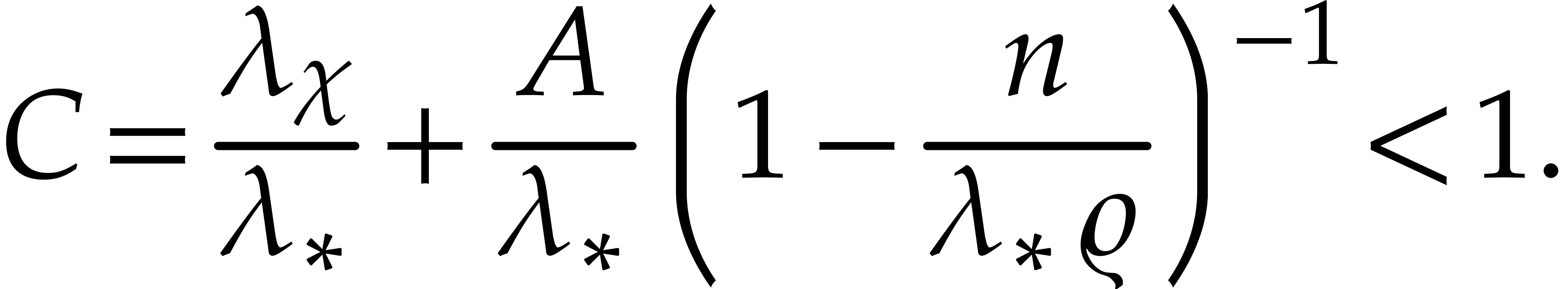
Let 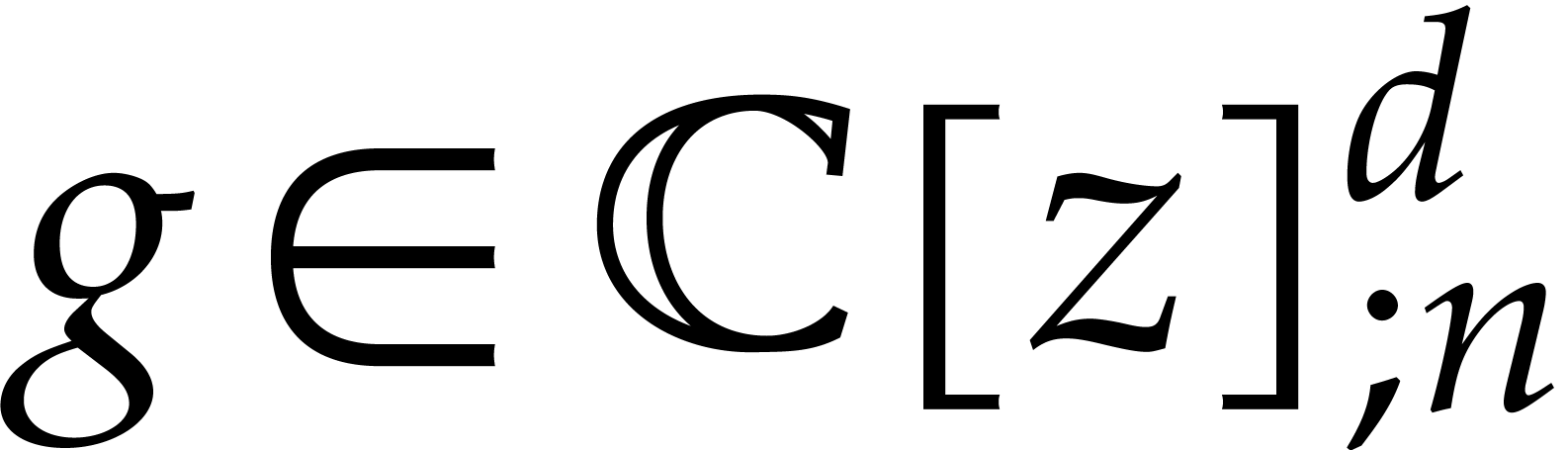 and
and 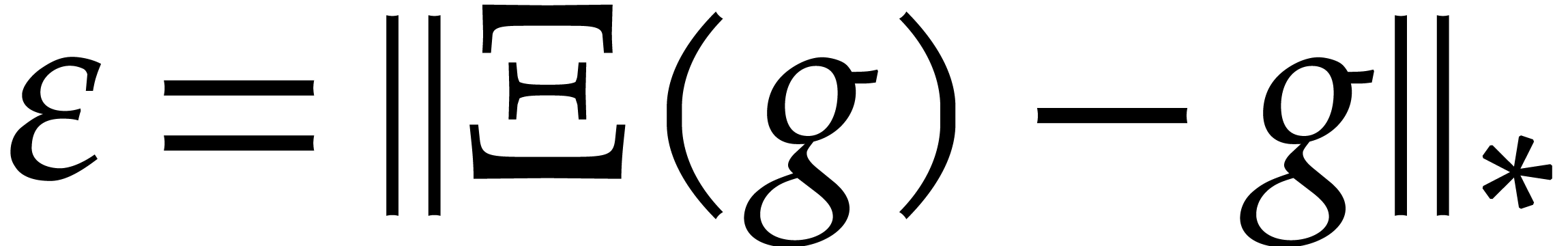 be such
that
be such
that

Then the sequence  tends to a unique fixed
point
tends to a unique fixed
point 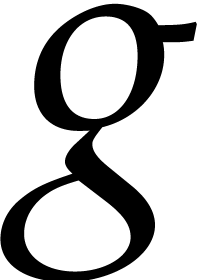 on the set
on the set
Proof. A straightforward adaptation of the proof
of Theorem 5 shows that 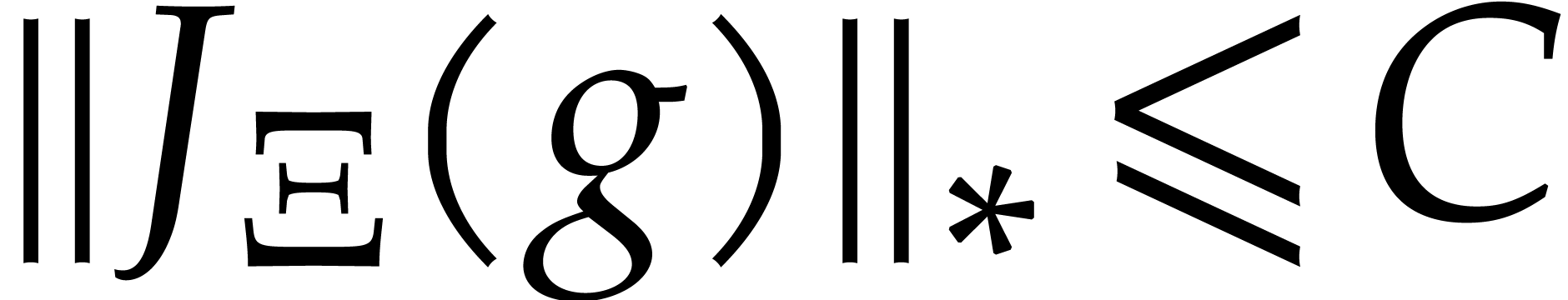 on the ball
on the ball
 , which means that
, which means that 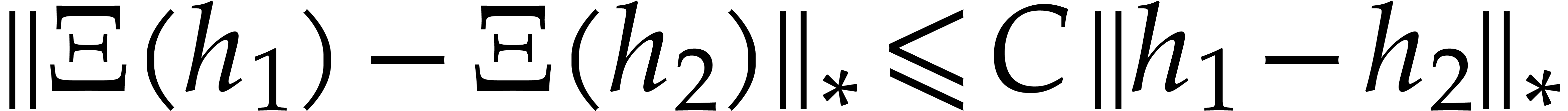 on this ball. By induction on
on this ball. By induction on  , it follows that
, it follows that 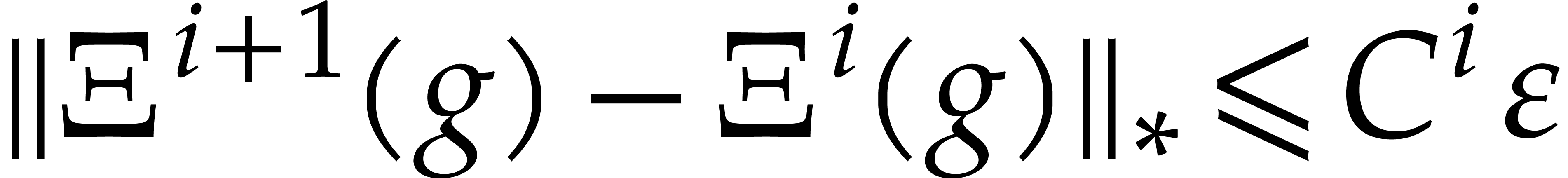 and
and 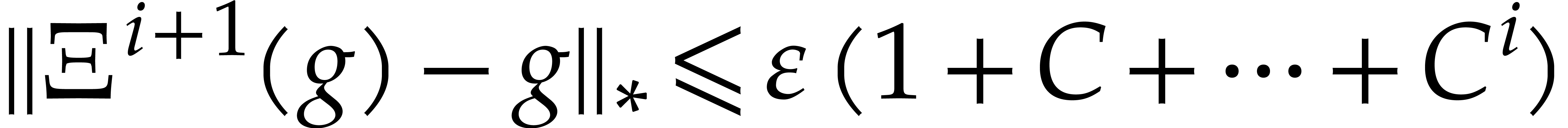 . We conclude that
. We conclude that  converges to a fixed point
converges to a fixed point  of
of  in
in 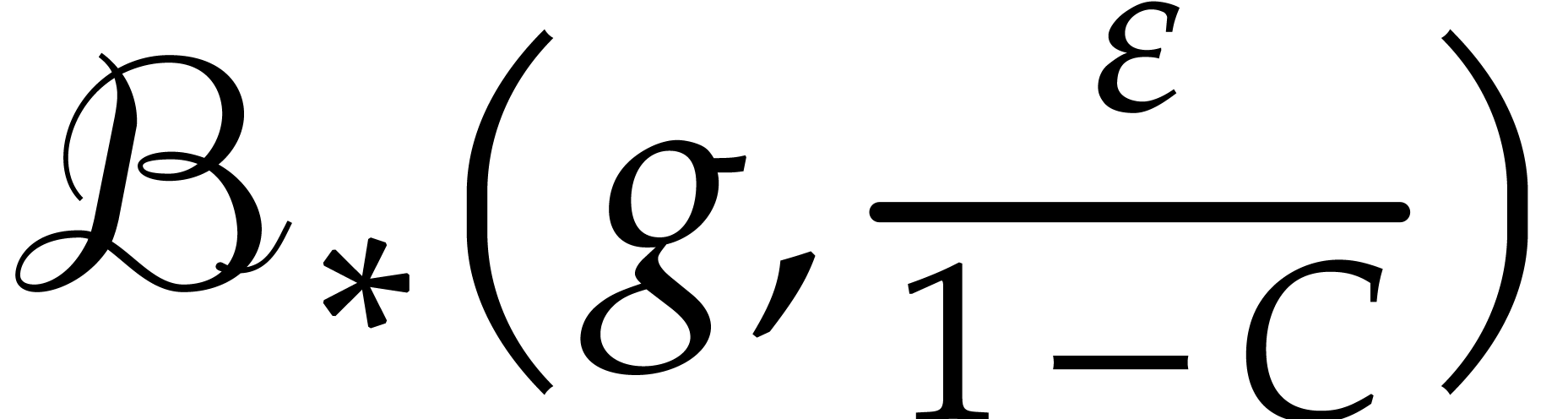 .
.
Returning to the Taylor series expansion 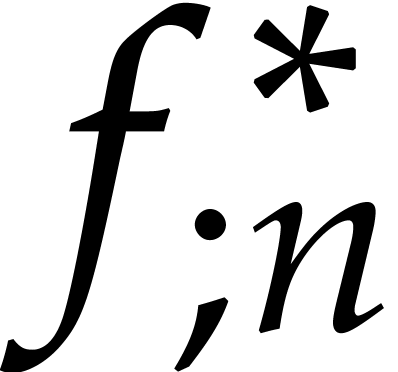 of the
exact solution of (1) at time
of the
exact solution of (1) at time  ,
we notice that
,
we notice that
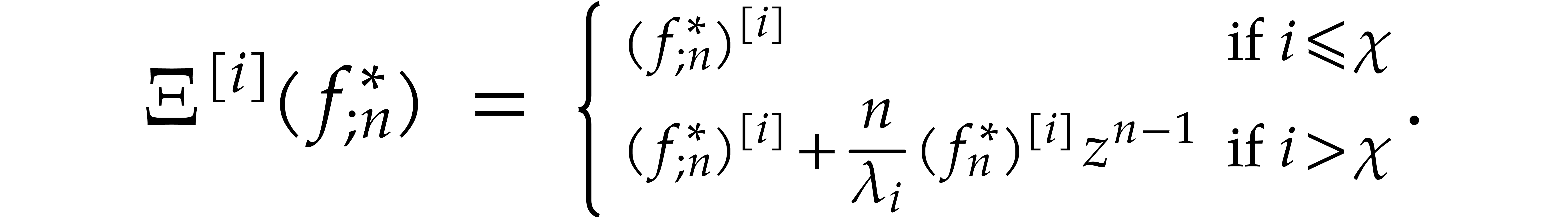
It follows that
Now assuming that the aimed step size 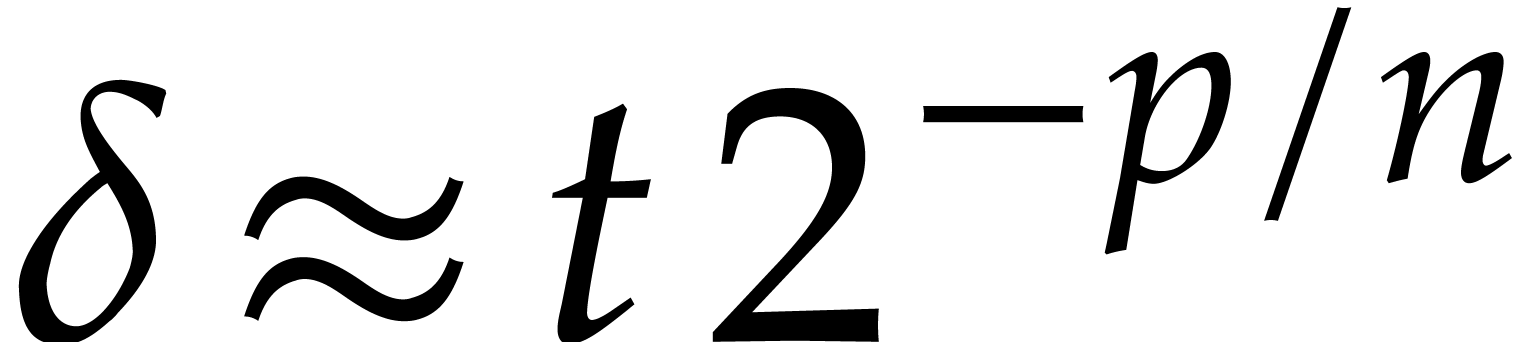 was more
or less achieved at the previous step, it follows that
was more
or less achieved at the previous step, it follows that 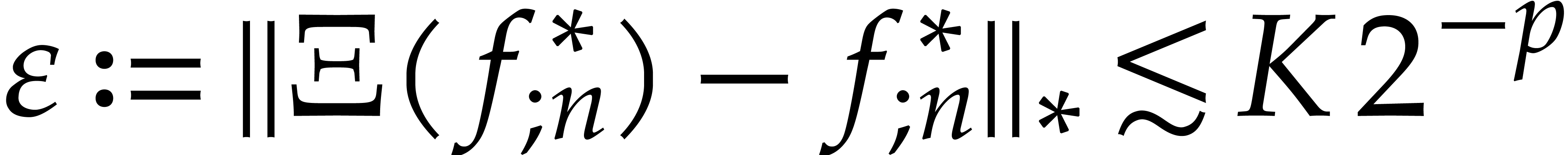 is of the desired order. If the condition (29) is indeed
satisfied for
is of the desired order. If the condition (29) is indeed
satisfied for 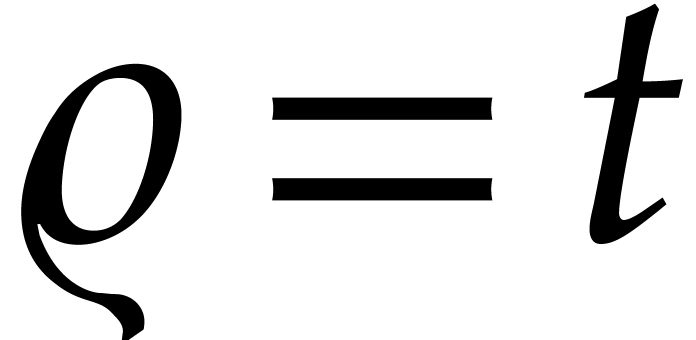 , we thus
should be able to apply Theorem 8 and conclude that the
computed fixed point
, we thus
should be able to apply Theorem 8 and conclude that the
computed fixed point  is within distance
is within distance 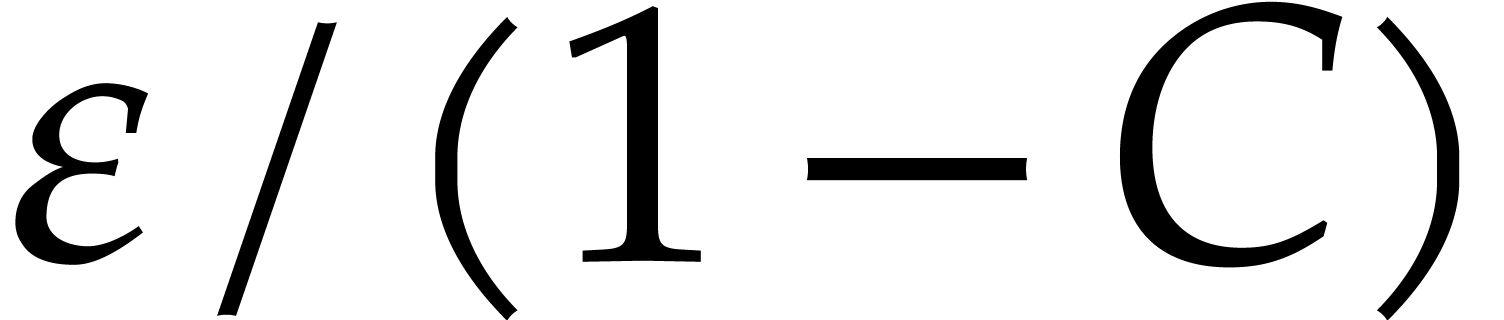 for the
for the 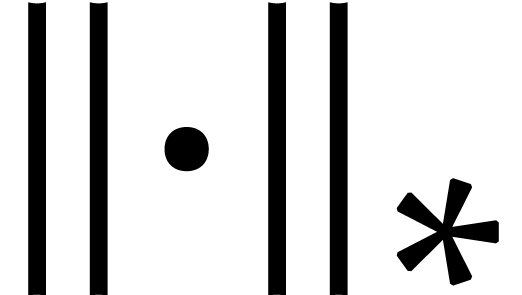 norm. Using a similar
reasoning, we also see that the ansatz at the next step will be
sufficiently close to the true solution for the
norm. Using a similar
reasoning, we also see that the ansatz at the next step will be
sufficiently close to the true solution for the  -iteration to converge.
-iteration to converge.
A more robust but costly approach to solve the steady-state problem (26) is to compute the initial values 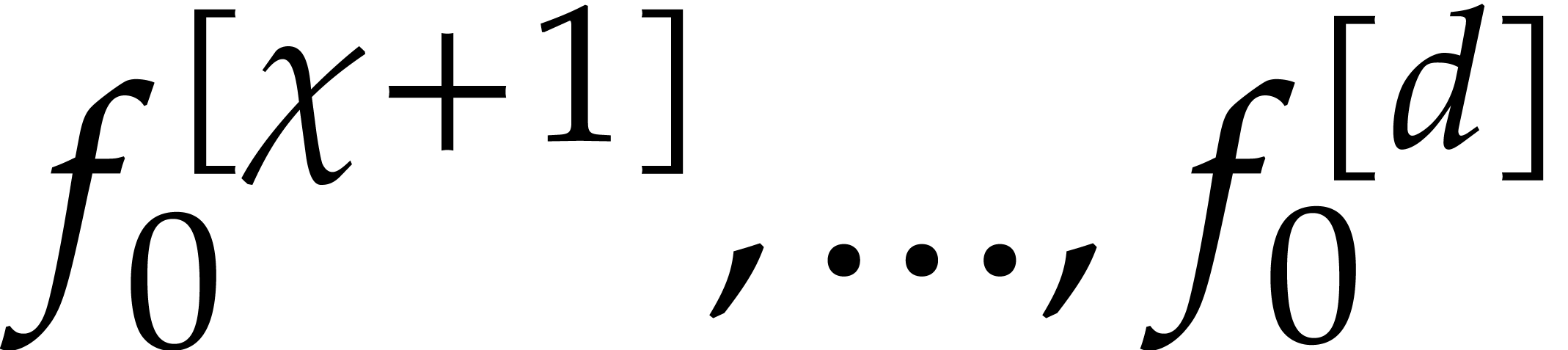 with sufficient precision using Newton's method. Given a tentative
approximation
with sufficient precision using Newton's method. Given a tentative
approximation 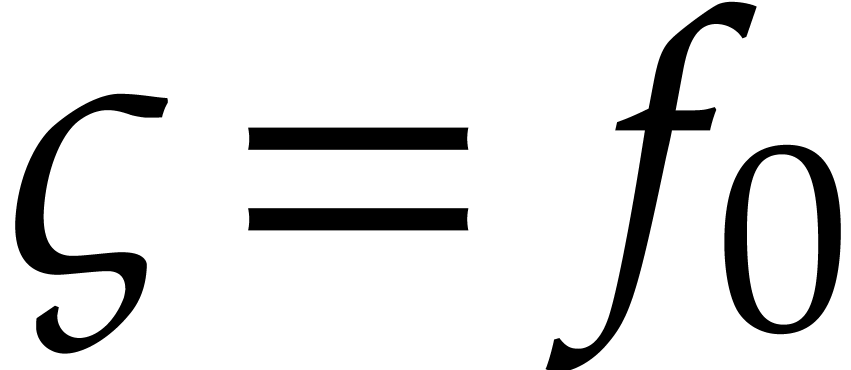 for the initial condition, we both
compute
for the initial condition, we both
compute 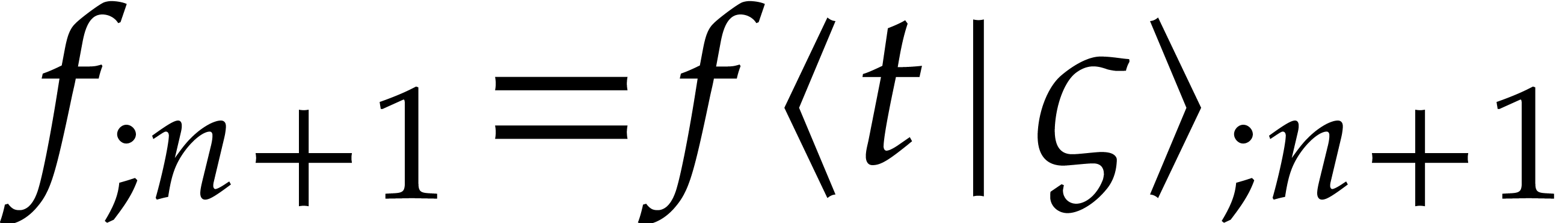 and the first variation
and the first variation 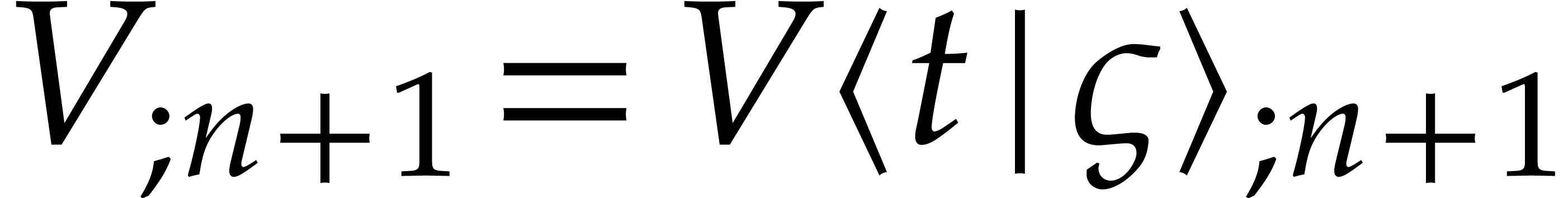 , after which we update
, after which we update 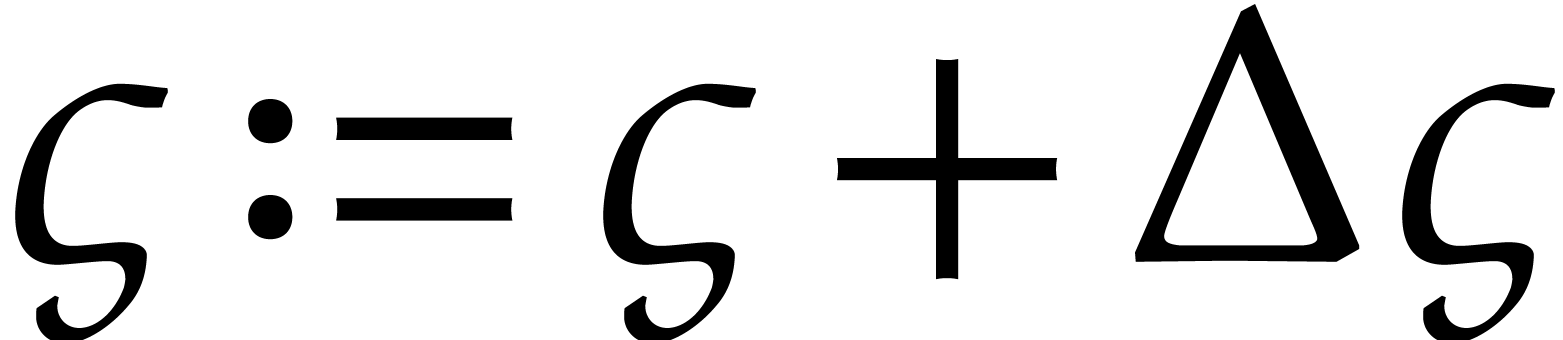 by solving the linear system
by solving the linear system

This method admits quadratic convergence, but it requires us to compute
with a precision of 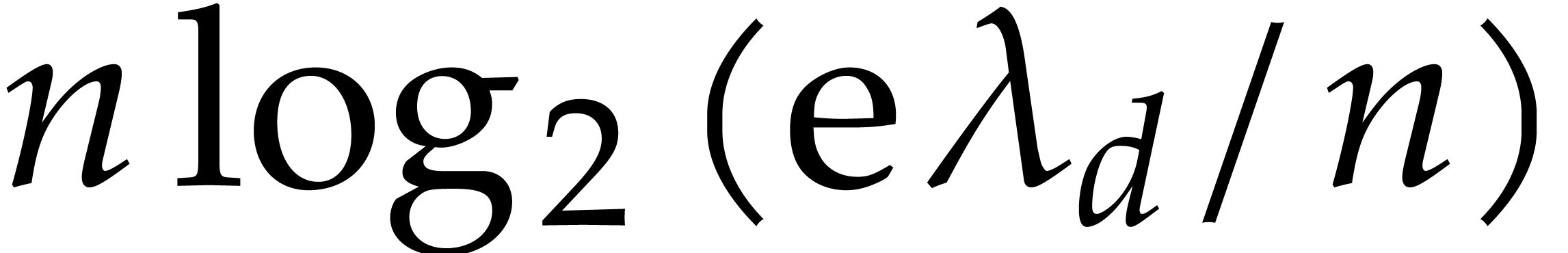 bits at least in order to be
accurate. Indeed, this comes from the fact that
bits at least in order to be
accurate. Indeed, this comes from the fact that  grows roughly as
grows roughly as 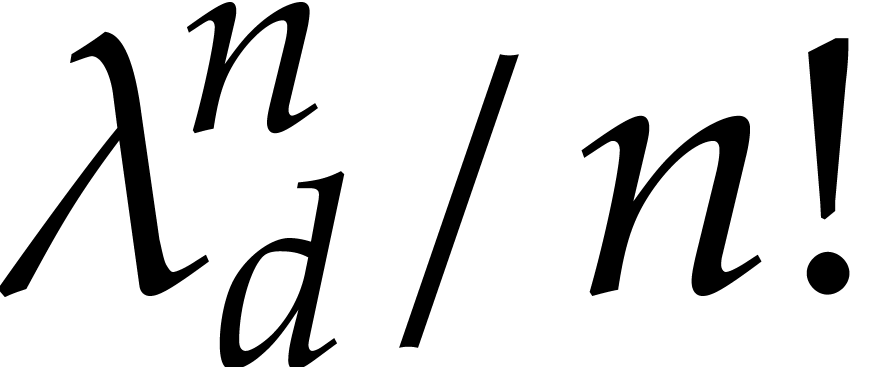 . On the
upside, we may compute
. On the
upside, we may compute 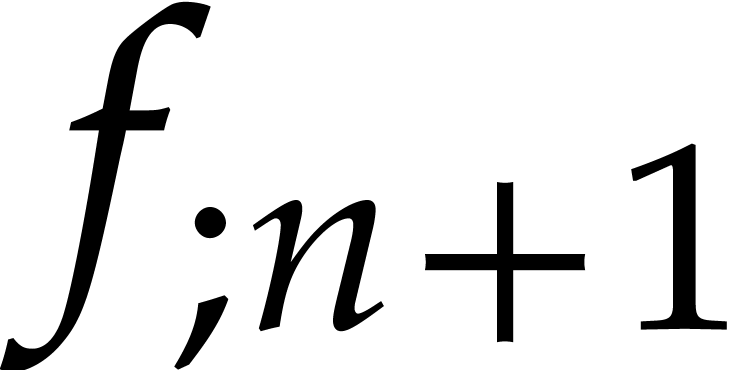 and
and 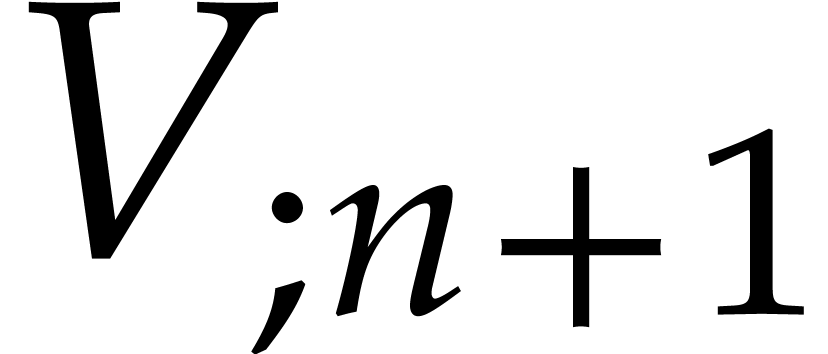 using any of the algorithms from section 3. The total
running time is therefore bounded by
using any of the algorithms from section 3. The total
running time is therefore bounded by 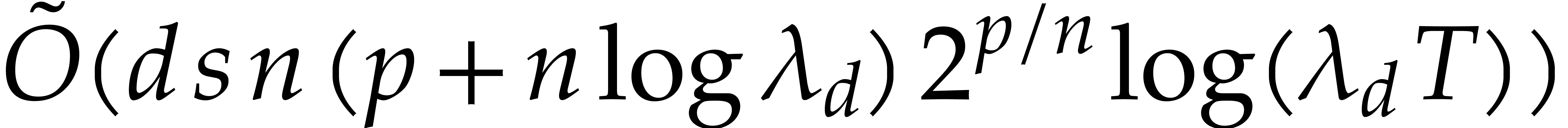 .
Notice also that it actually suffices to compute the last
.
Notice also that it actually suffices to compute the last 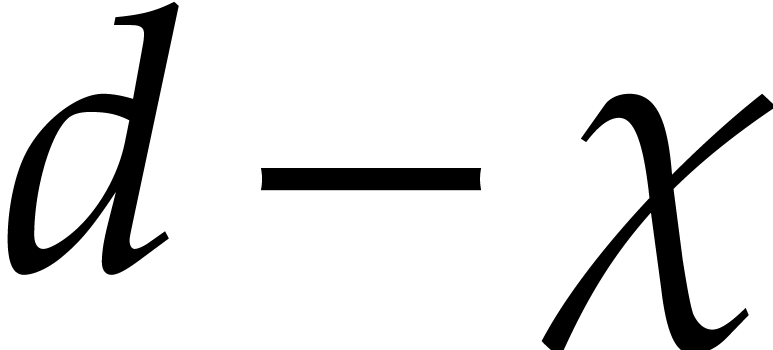 rows of
rows of 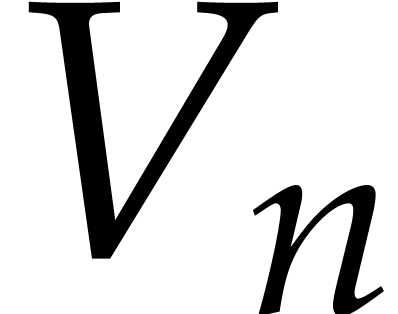 , due
to the requirement that
, due
to the requirement that 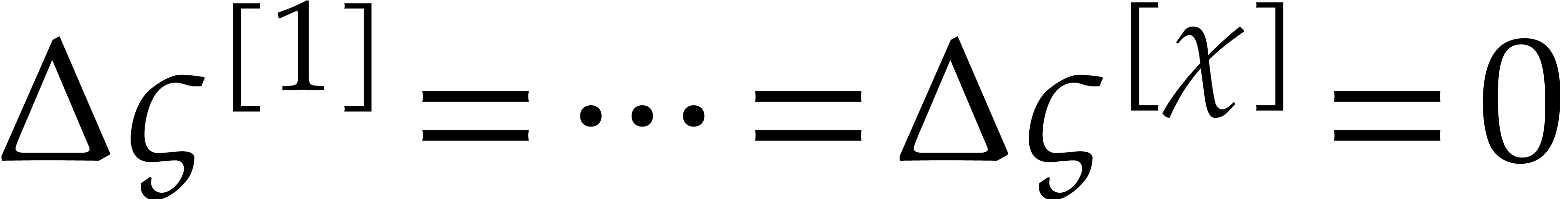 .
.
The main disadvantage of the above method is that the computation of the
first variation 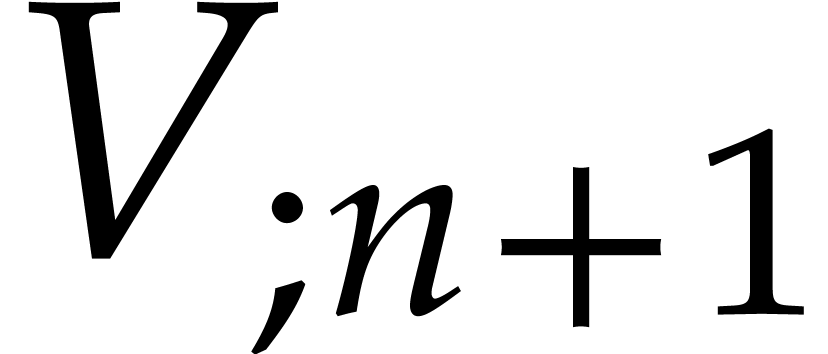 along with
along with 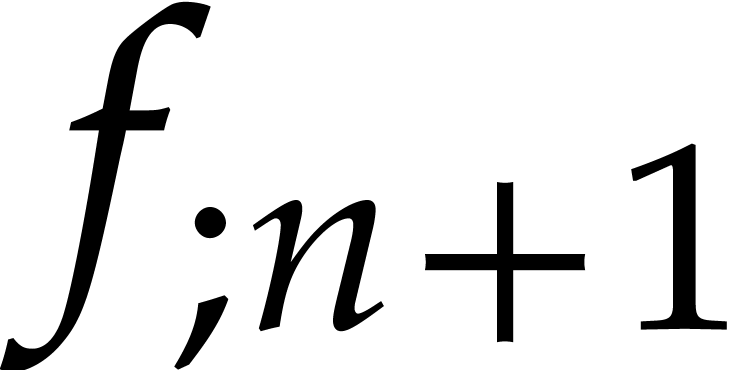 induces an overhead of
induces an overhead of  ,
which may be a problem for systems of high dimension. Let us now sketch
how one might reduce this overhead by combining the variational approach
with the
,
which may be a problem for systems of high dimension. Let us now sketch
how one might reduce this overhead by combining the variational approach
with the  -iteration. We
intend to return to a more detailed analysis in a future work.
-iteration. We
intend to return to a more detailed analysis in a future work.
Instead of using a single critical index 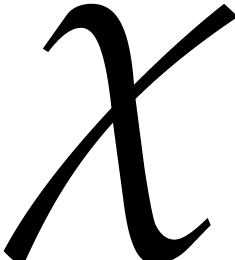 ,
the first idea is to use a range
,
the first idea is to use a range  of indices
starting at
of indices
starting at 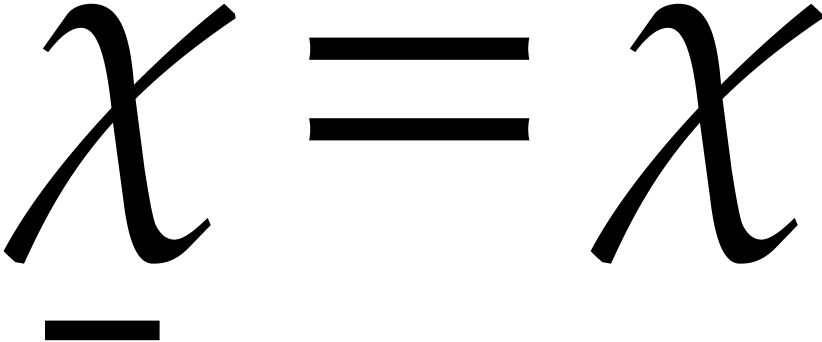 , and such that
the condition (29) holds for
, and such that
the condition (29) holds for
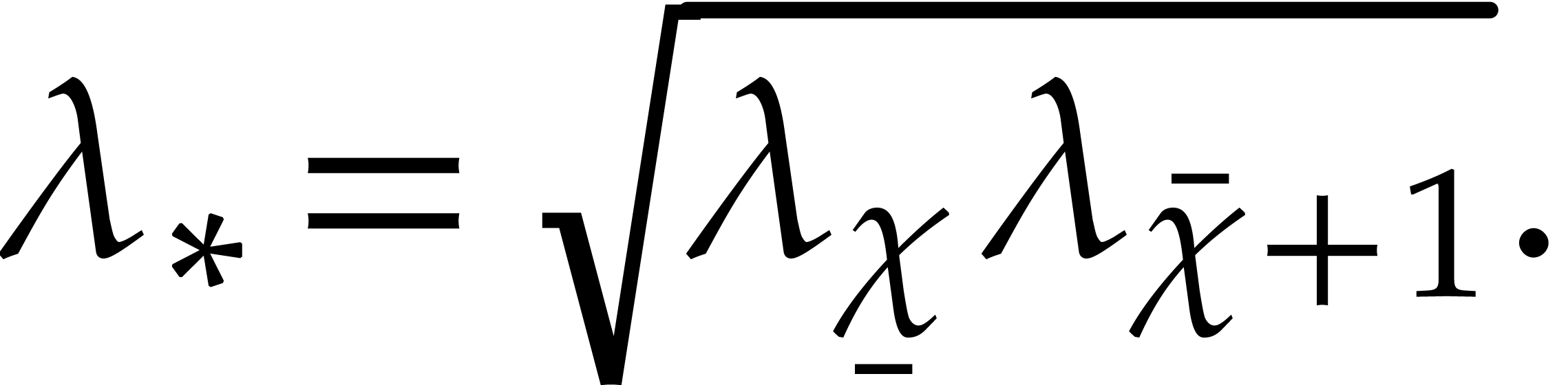
The second idea is to only vary the components 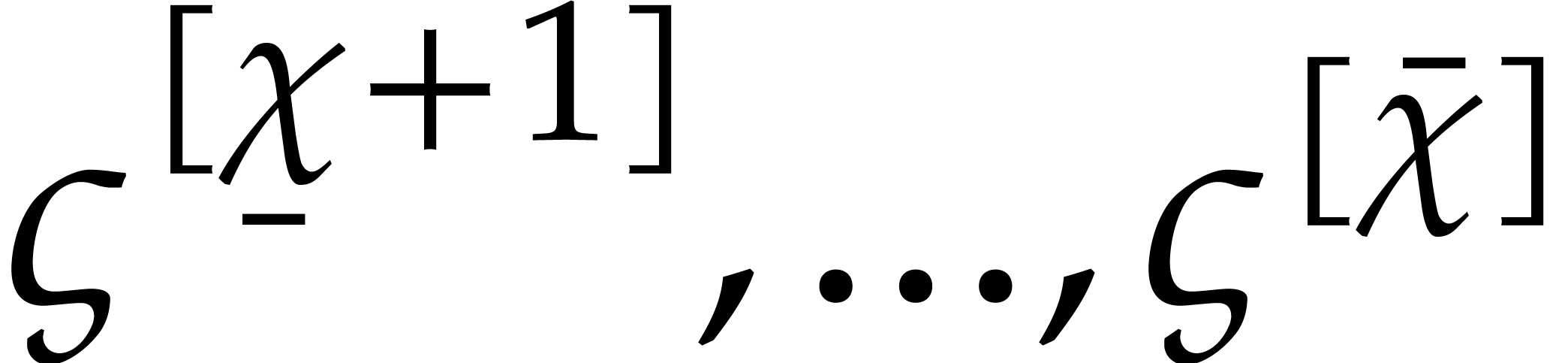 of the initial condition and use the steady-state conditions for the
indices
of the initial condition and use the steady-state conditions for the
indices 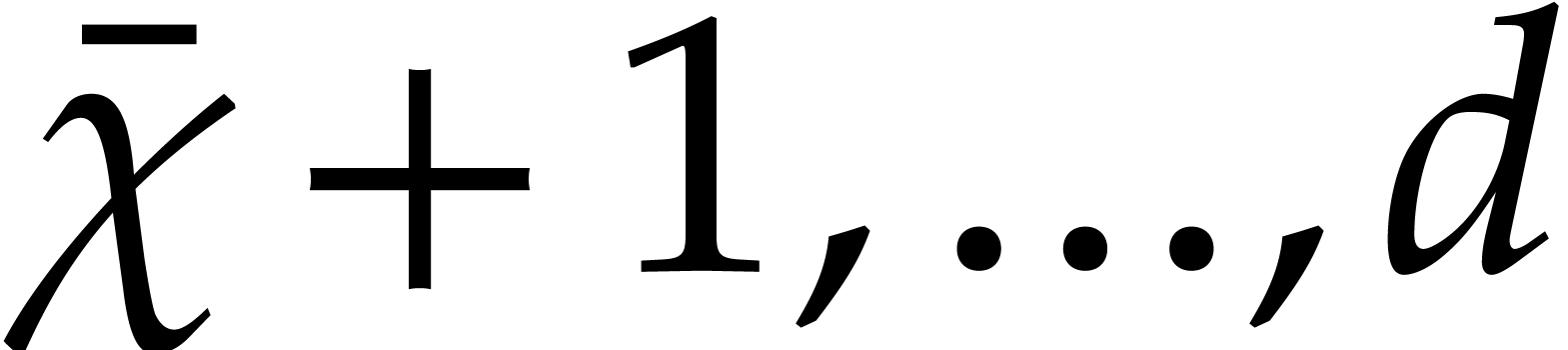 .
.
More specifically, for a tentative initial condition 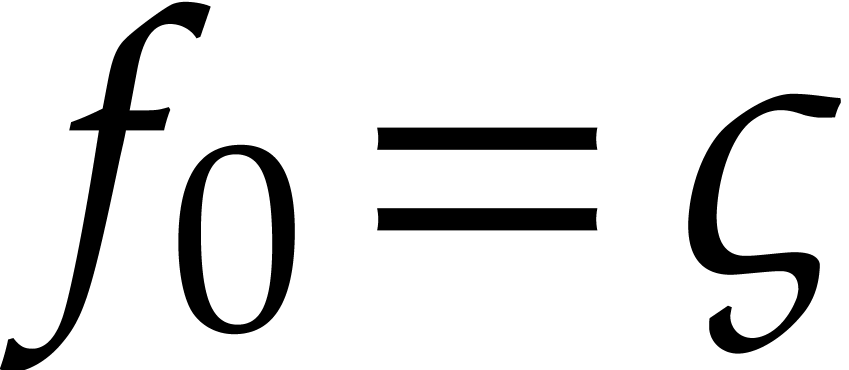 , we first solve the steady-state problem
, we first solve the steady-state problem
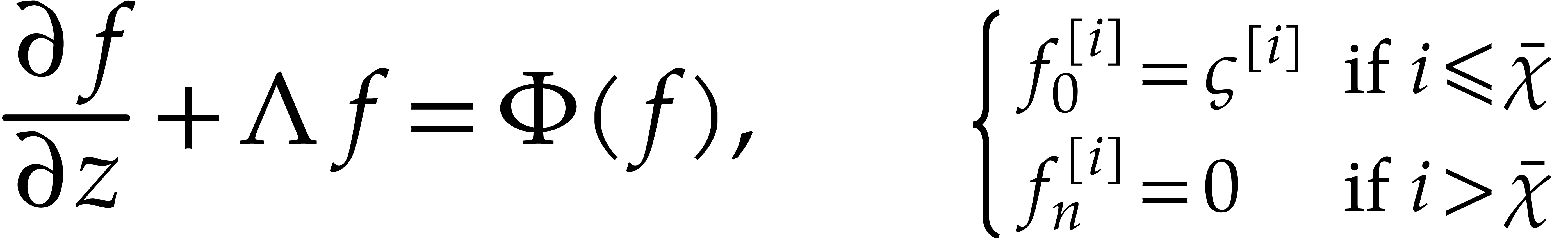
using the  -iteration
technique. In a similar way, we next solve the following variational
steady-state problem for the
-iteration
technique. In a similar way, we next solve the following variational
steady-state problem for the 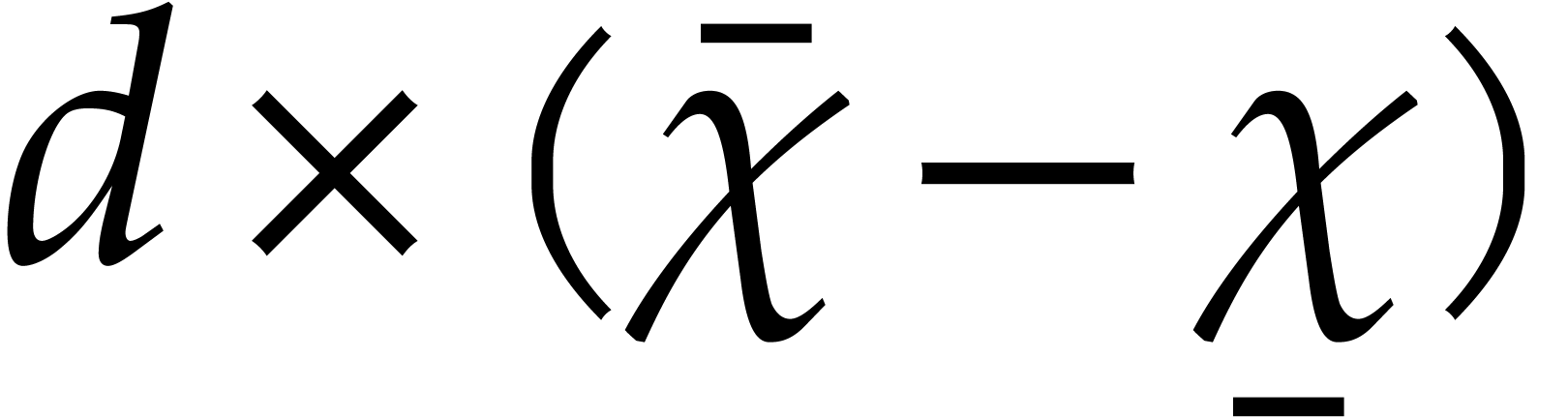 matrix
matrix  :
:
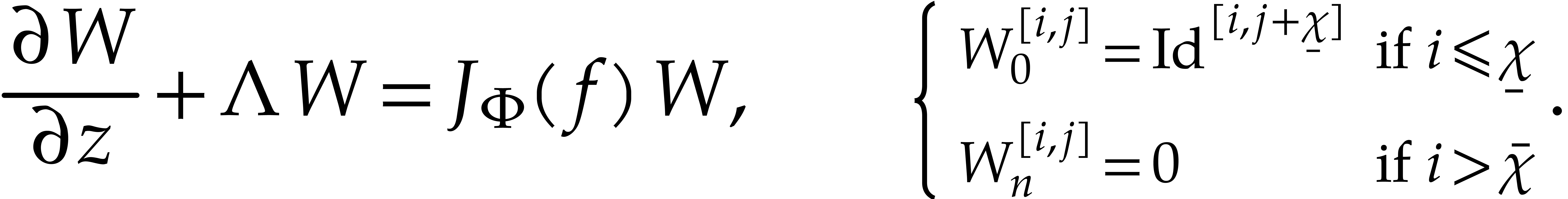
As our ansatz, we may use 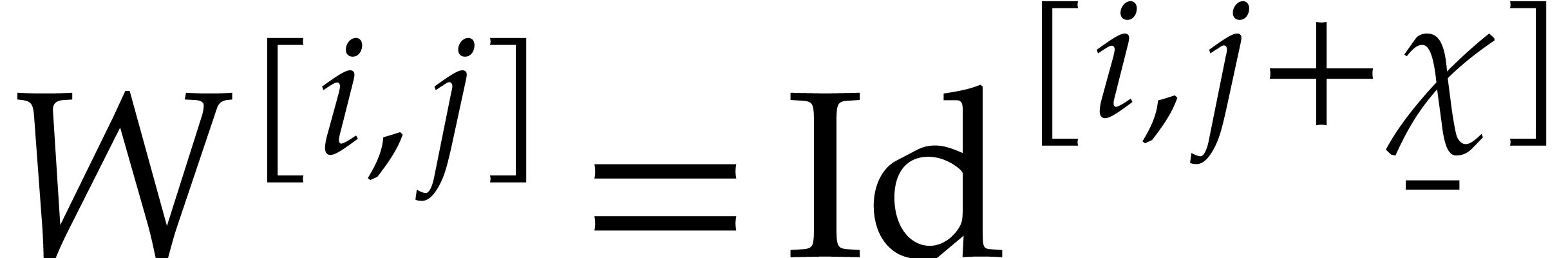 for all
for all  . Having computed
. Having computed  and
and 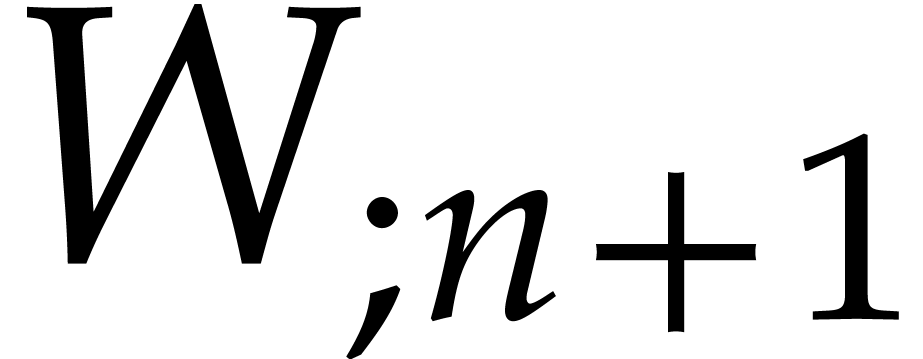 at precision
at precision  ,
we finally update
,
we finally update 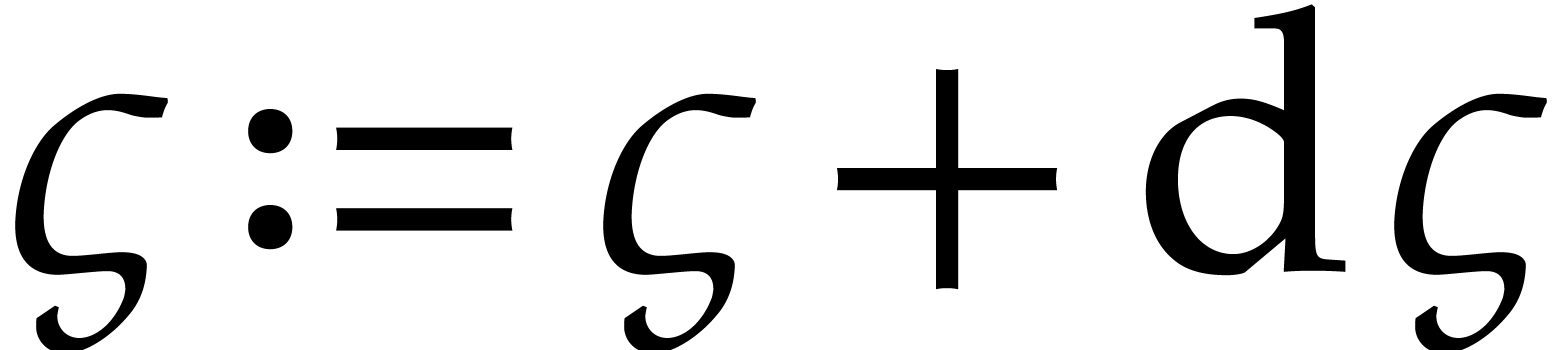 by solving the linear system
by solving the linear system
and setting 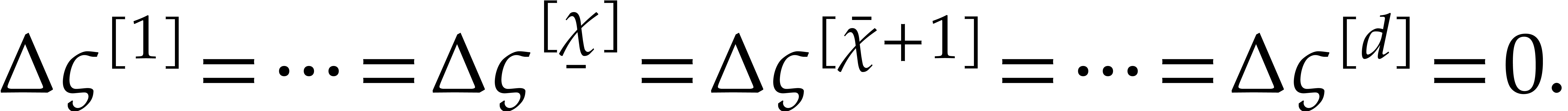 We repeat this whole process until
We repeat this whole process until
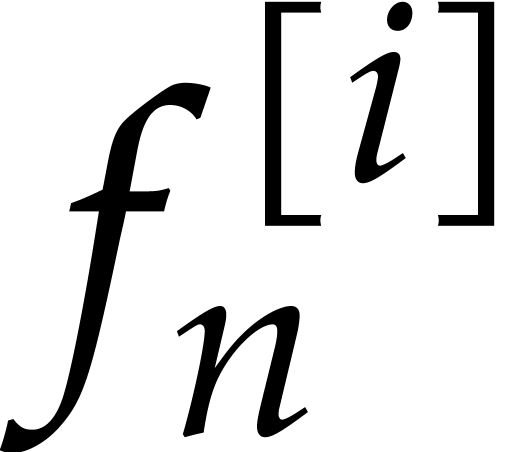 is sufficiently close to zero for
is sufficiently close to zero for 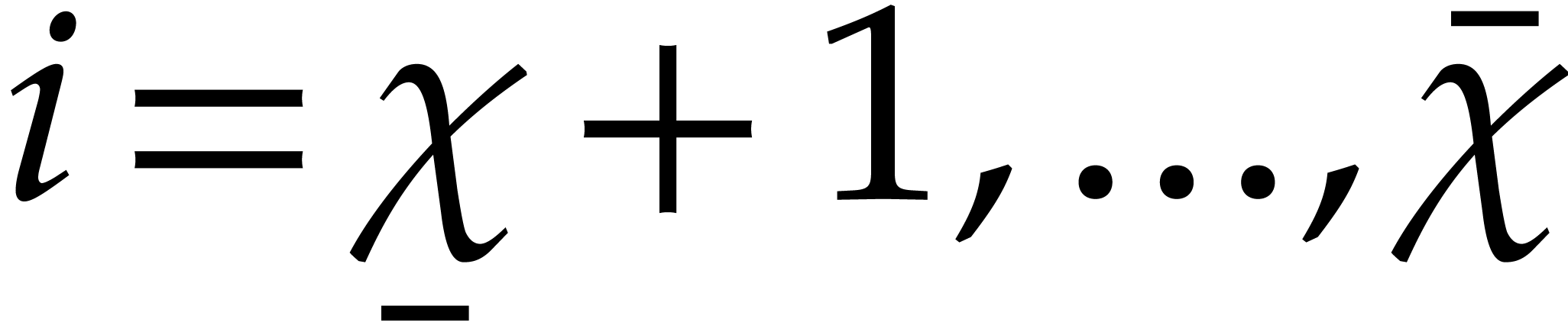 .
.
Remark
Remark 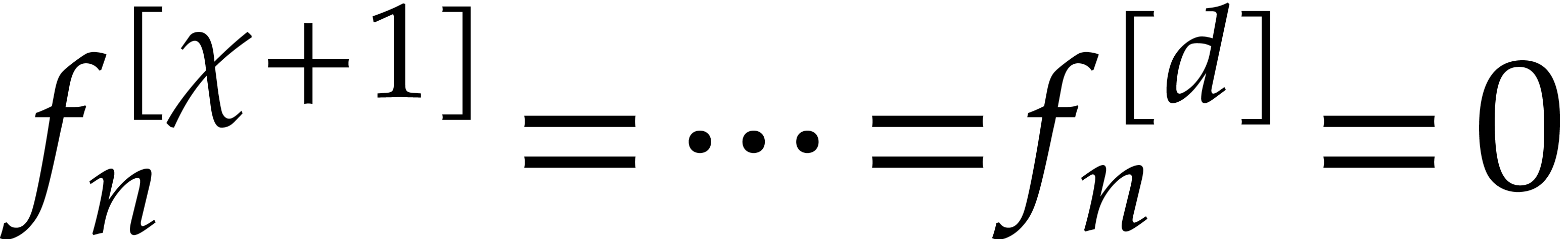 , yet another approach would be to minimize the norm
, yet another approach would be to minimize the norm
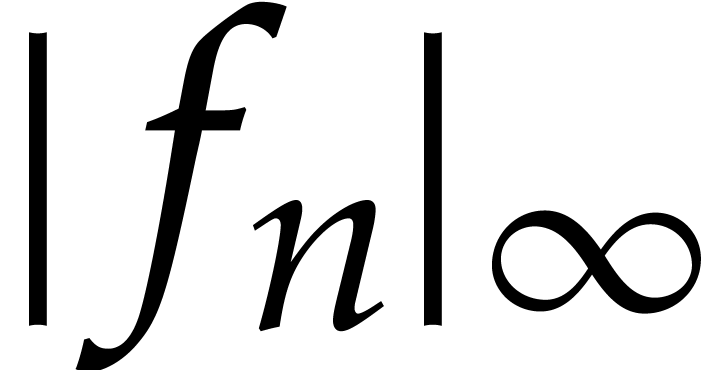 under the condition that
under the condition that 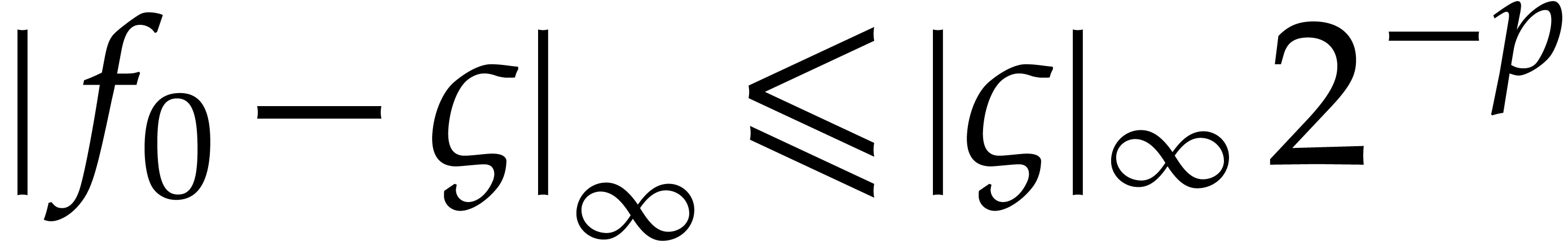 . This approach admits the advantages that one does
not need to know
. This approach admits the advantages that one does
not need to know  and that it might be applied to
more general complex matrices
and that it might be applied to
more general complex matrices  .
However, it requires the computation of the full Jacobian matrix.
.
However, it requires the computation of the full Jacobian matrix.
In the previous two sections, we have described numerical algorithms for integrating (1). An interesting question is how to compute a tight error bound such that the distance between the true and the computed solutions lies within this error bound. Ball arithmetic provides a suitable framework for such computations. This variant of interval arithmetic is well suited for high precision computations with complex numbers and we will briefly recall its basic principles in section 6.1. As a first application, we show how to make Theorem 4 more effective.
The certified integration of differential equations that are not stiff (i.e. the robust counterpart of section 4) is a classical topic in interval arithmetic [20, 21, 15, 5, 24, 16, 7, 22, 18, 14, 17, 23, 19]. For recent algorithms of good complexity, much in the spirit of the present paper, we refer to [11]. Most of the existing algorithms rely on Taylor series expansions as we do, while providing rigorous tail bounds for the truncation error.
The effective counterpart of Theorem 4 provides suitable
tail bounds in the case of stiff differential equations. In sections 6.3 and 6.4, we show how to use this for the
certified resolution of steady-state problems using the  -iteration from section 5.1.
Unfortunately, our first algorithms are rather naive and typically lead
to heavily overestimated error bounds. The classical way to reduce this
overestimation is to also compute the first variation and apply the mean
value theorem: see section 6.5 for how to do this in our
context.
-iteration from section 5.1.
Unfortunately, our first algorithms are rather naive and typically lead
to heavily overestimated error bounds. The classical way to reduce this
overestimation is to also compute the first variation and apply the mean
value theorem: see section 6.5 for how to do this in our
context.
Given  and
and  ,
we write
,
we write  for the closed ball with
center
for the closed ball with
center  and radius
and radius 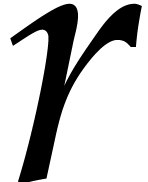 .
The set of such balls is denoted by
.
The set of such balls is denoted by 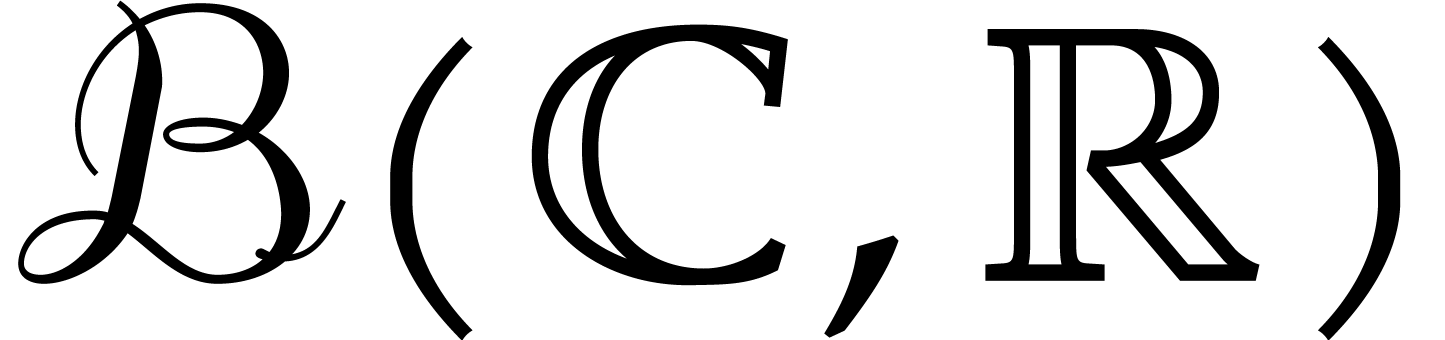 or
or  . One may lift the ring operations
. One may lift the ring operations
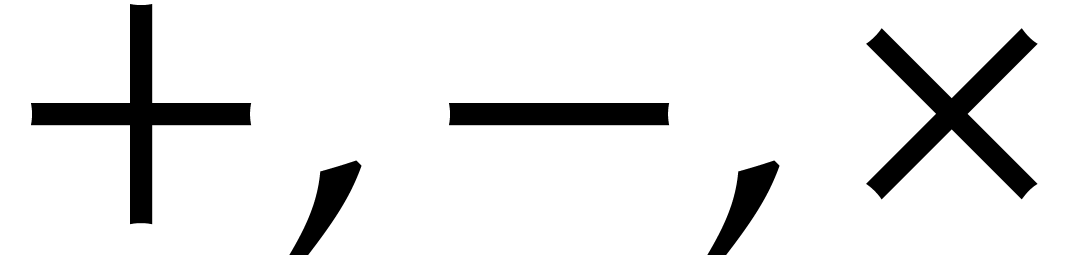 in
in  to balls in
to balls in  , by setting:
, by setting:
These formulas are simplest so as to satisfy the so called inclusion
principle: given 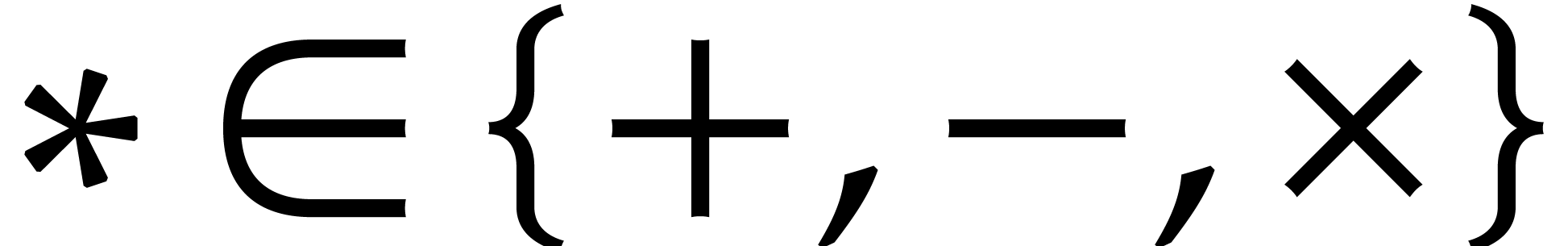 ,
, 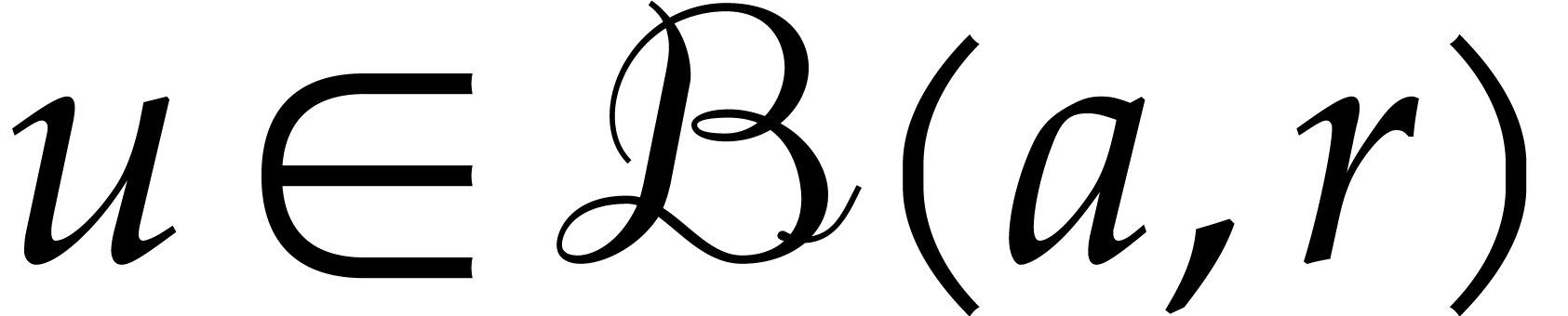 and
and 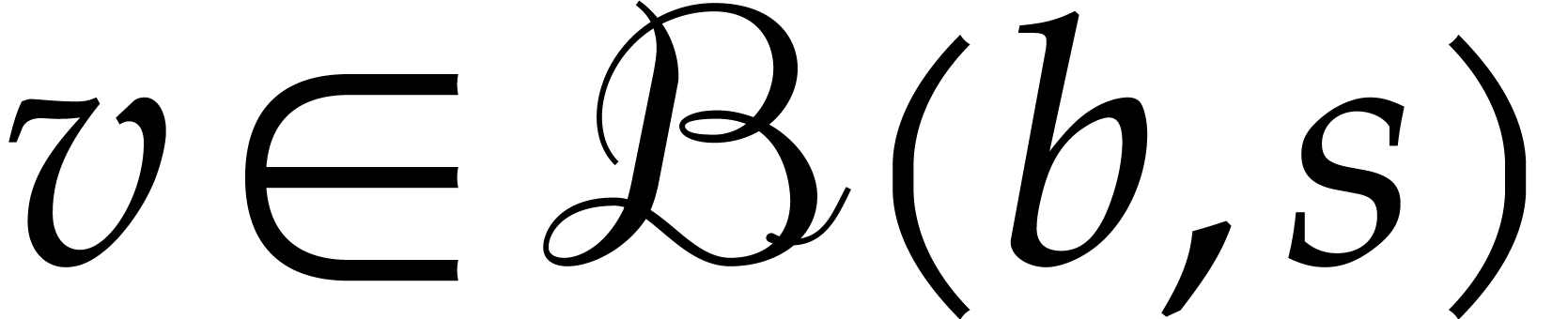 , we
have
, we
have 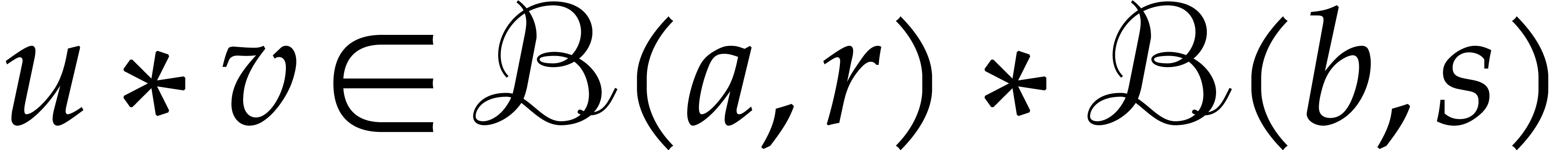 . This arithmetic for
computing with balls is called exact ball arithmetic. It
extends to other operations that might be defined on
. This arithmetic for
computing with balls is called exact ball arithmetic. It
extends to other operations that might be defined on  , as long as the ball lifts of operations
satisfy the inclusion principle. Any ordinary complex number
, as long as the ball lifts of operations
satisfy the inclusion principle. Any ordinary complex number 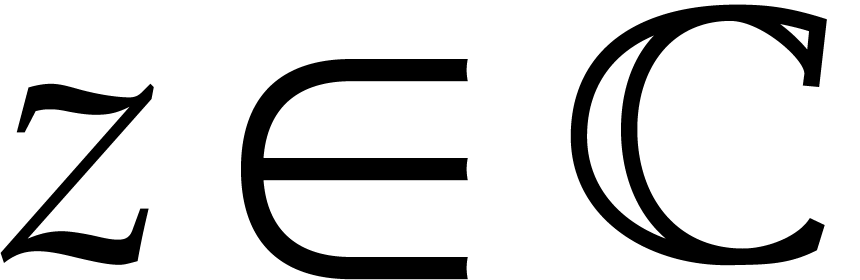 can be reinterpreted as a ball
can be reinterpreted as a ball 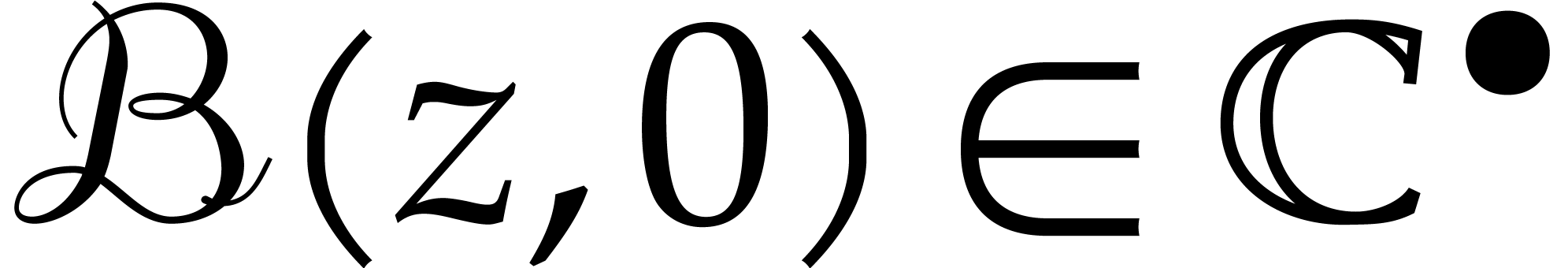 . Given a ball
. Given a ball 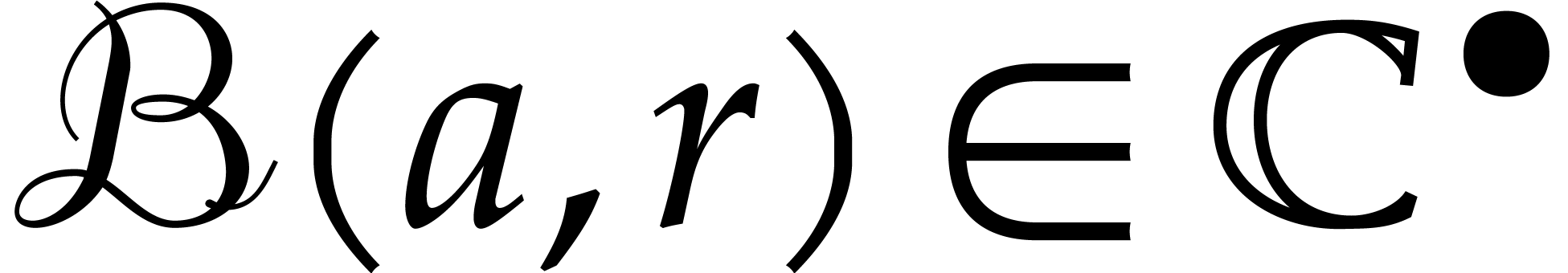 ,
we also notice that
,
we also notice that 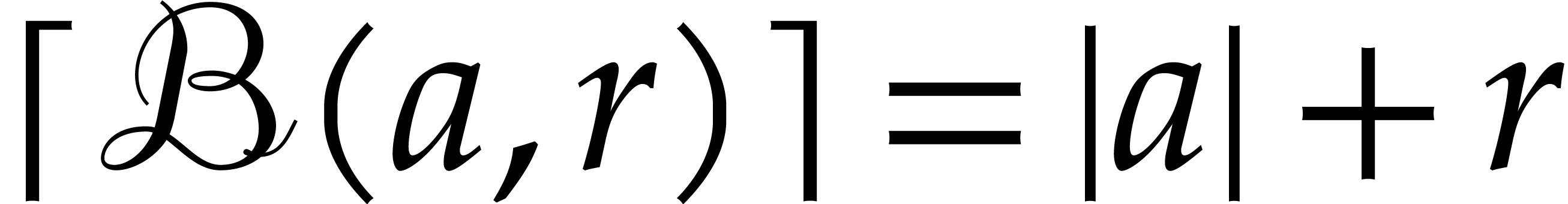 and
and 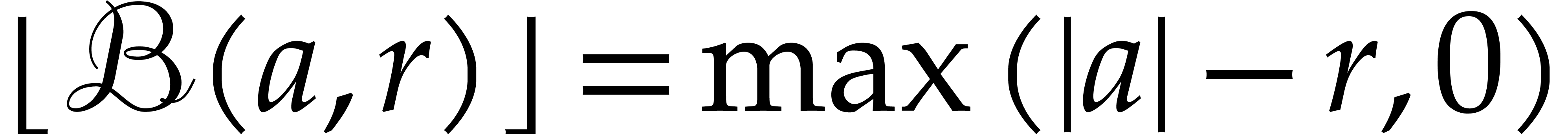 provide us with reliable upper and lower bounds for
provide us with reliable upper and lower bounds for 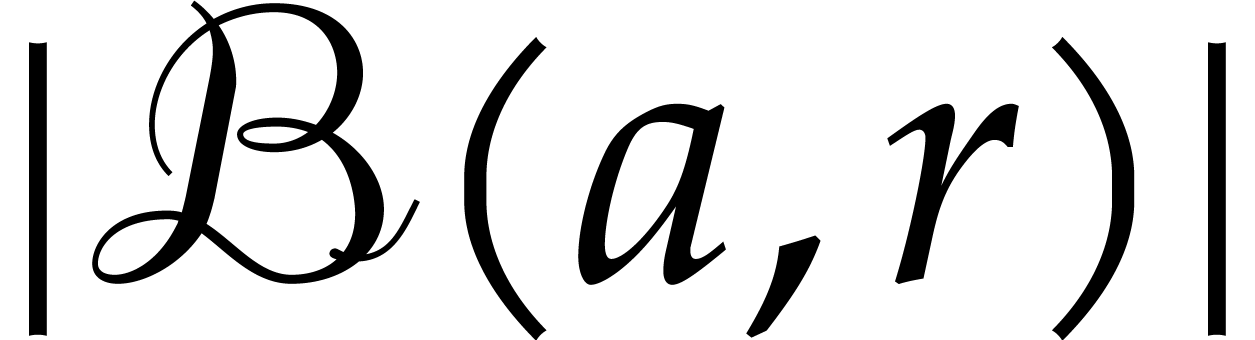 in
in 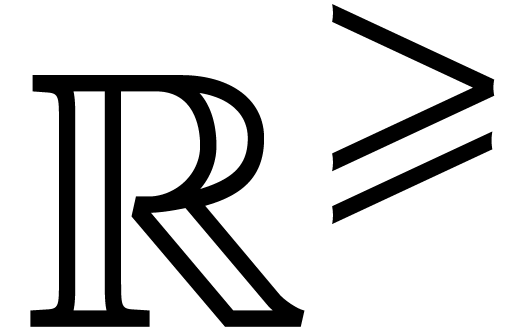 .
.
Another interesting operation on balls 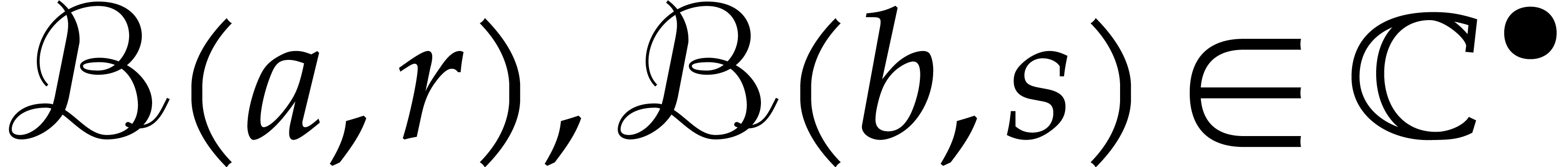 that we
will need below is intersection. Assuming that the set intersection
that we
will need below is intersection. Assuming that the set intersection 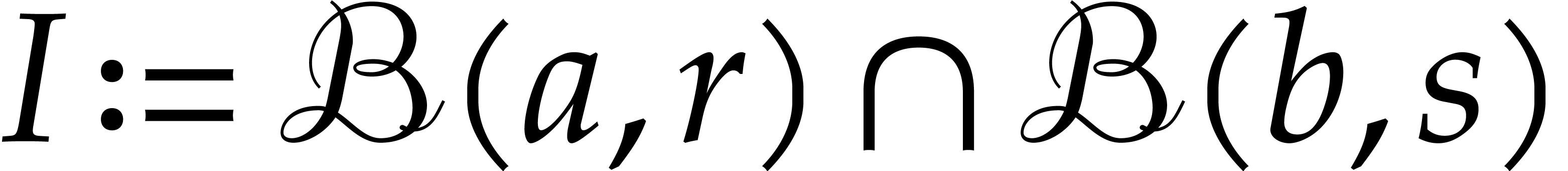 is non-empty, we define the ball intersection
is non-empty, we define the ball intersection  to be the ball of smallest radius that contains
to be the ball of smallest radius that contains 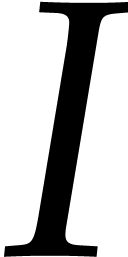 . In order to determine this ball
intersection, we may assume without loss of generality that
. In order to determine this ball
intersection, we may assume without loss of generality that 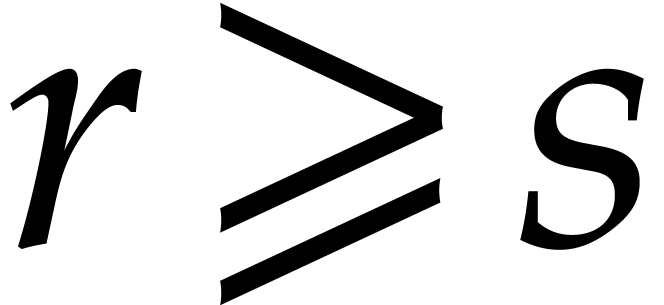 . If
. If 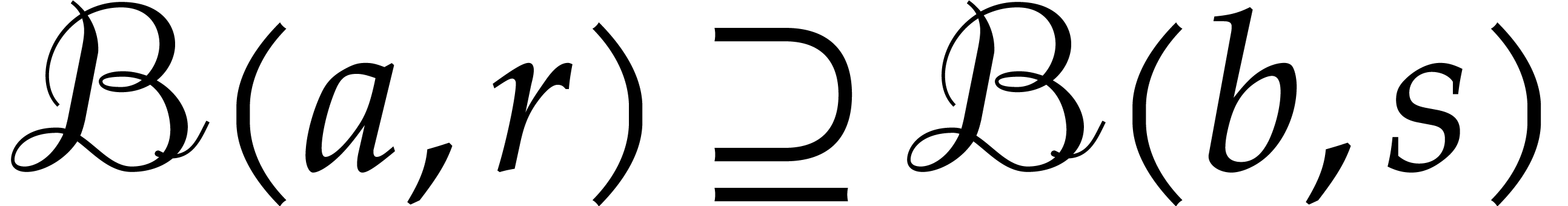 ,
then
,
then 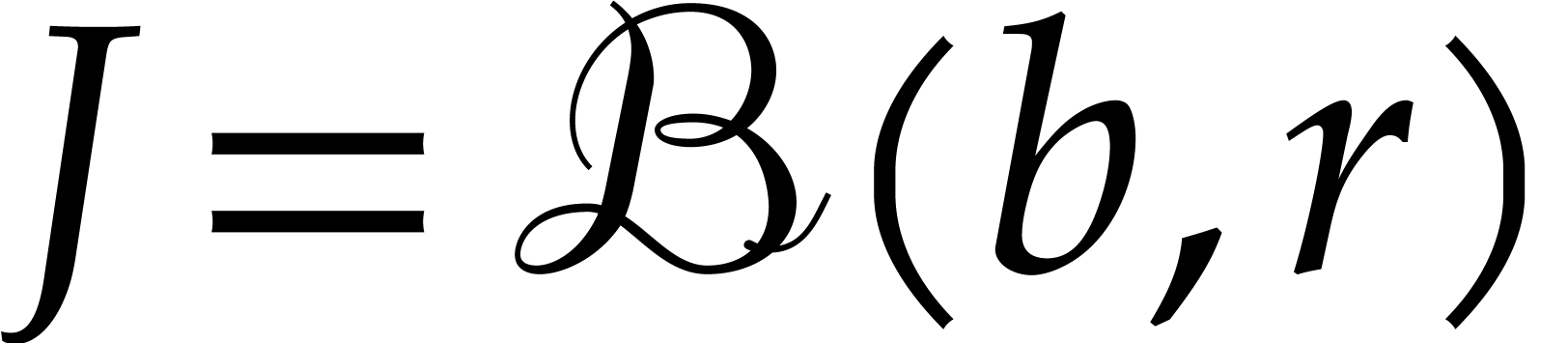 . Otherwise, let
. Otherwise, let 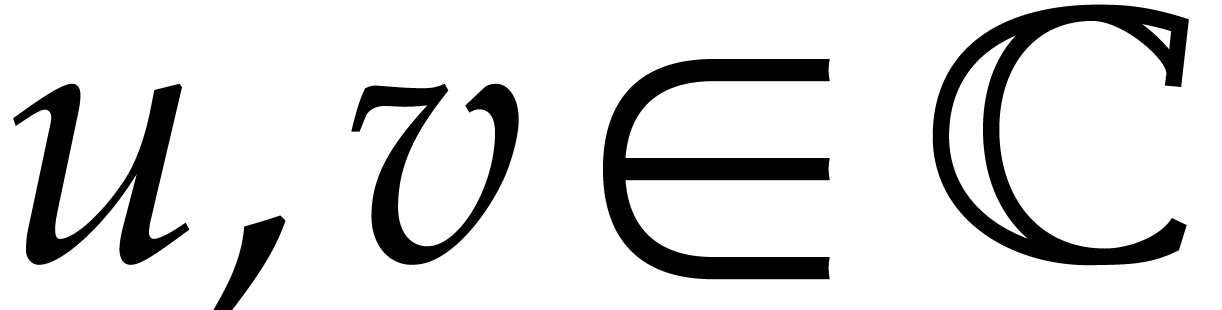 be the two (possibly identical) intersections of the
circles
be the two (possibly identical) intersections of the
circles 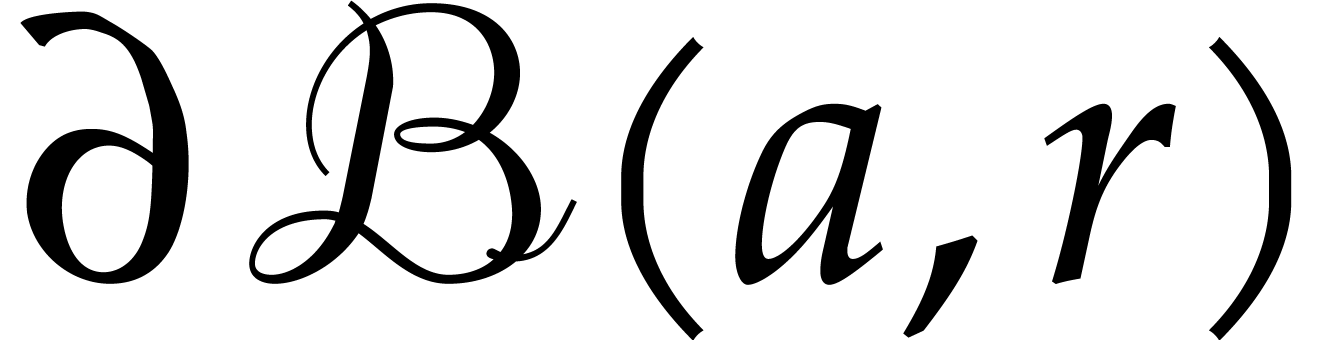 and
and 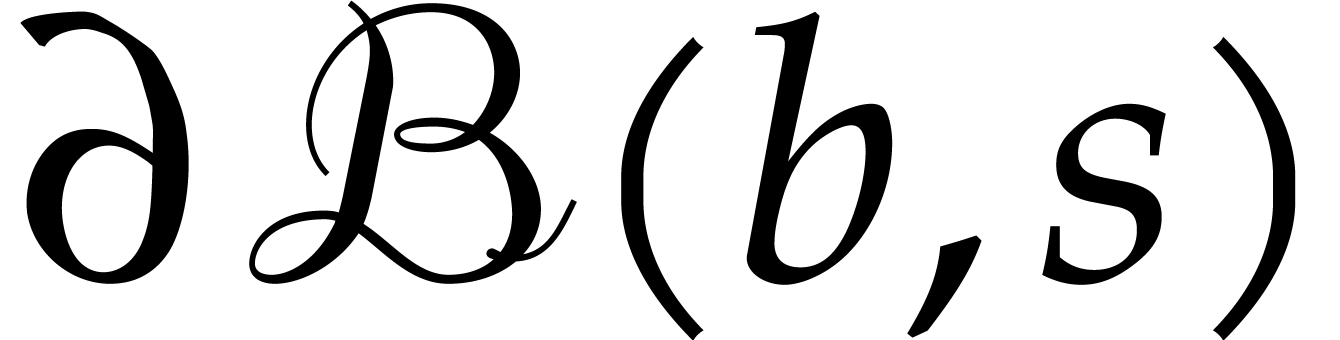 .
If
.
If 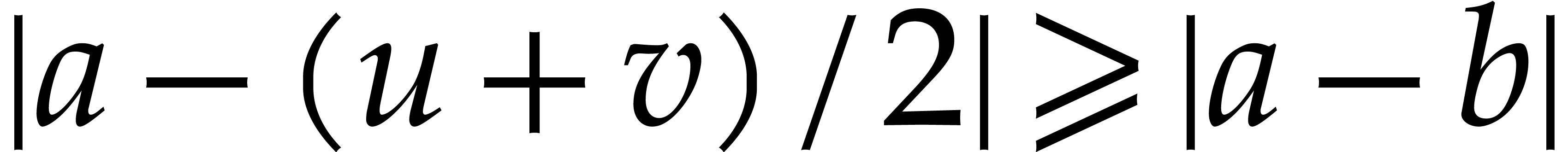 , then we still have
, then we still have 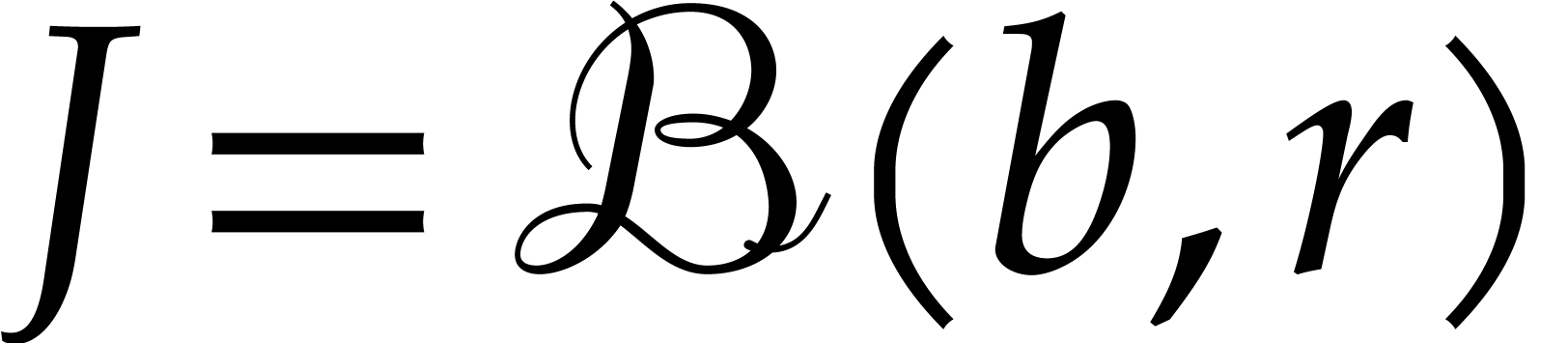 . Otherwise,
. Otherwise, 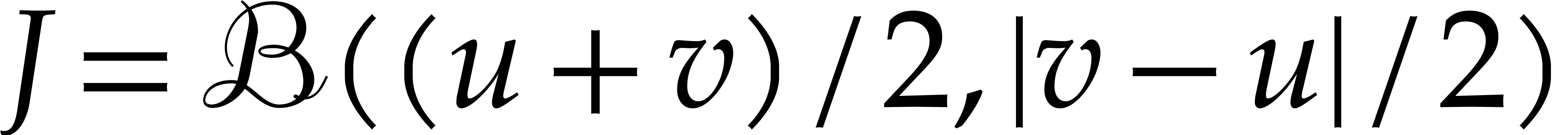 .
.
It will also be convenient to extend vector notations to balls. First of
all, we identify vectors of balls 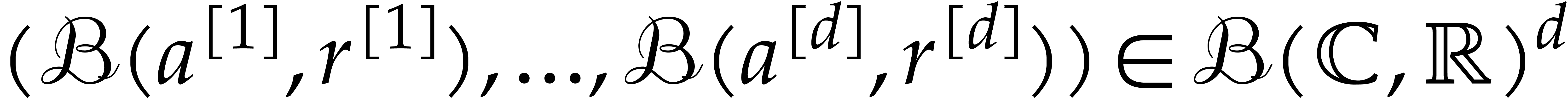 with
“ball vectors”
with
“ball vectors”  .
Given
.
Given  and
and 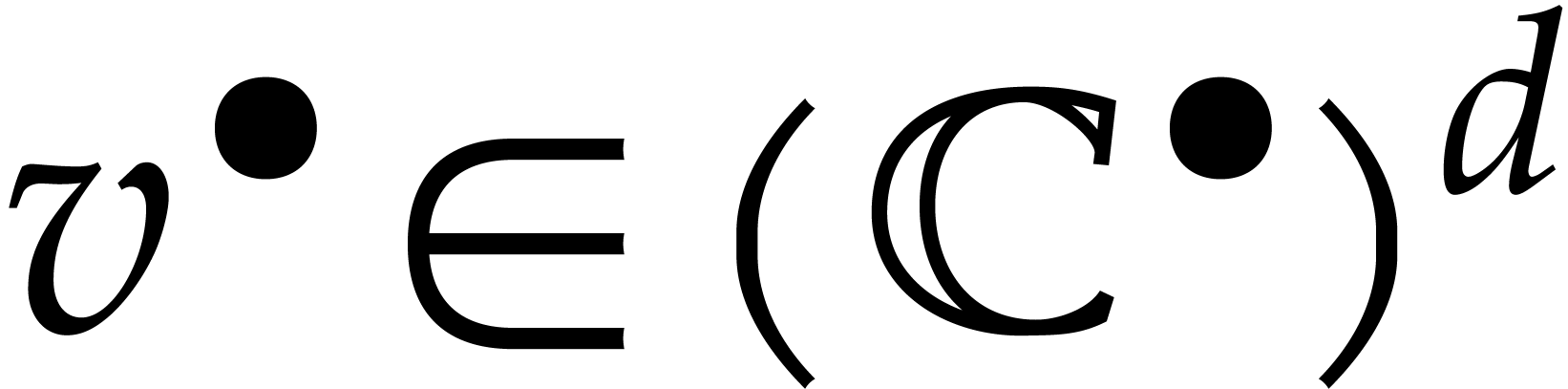 ,
we also write
,
we also write  if and only if
if and only if 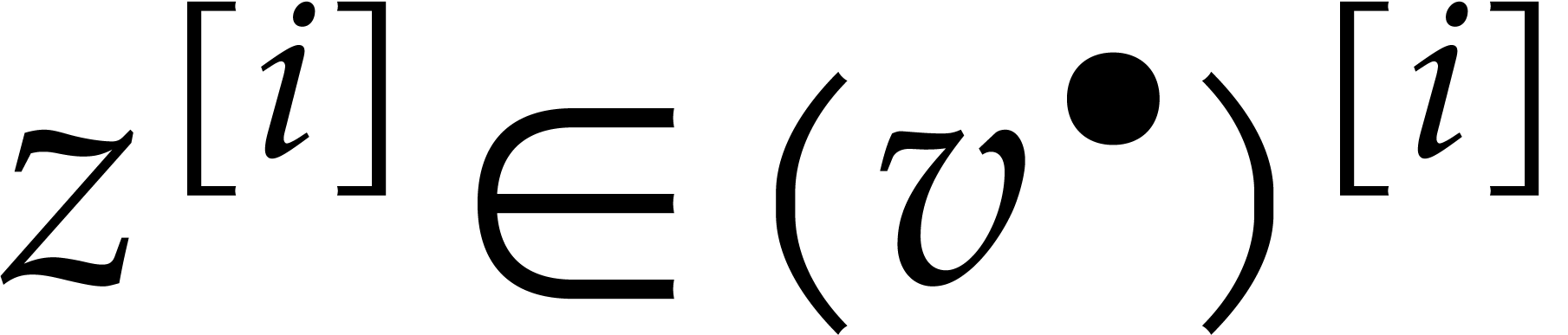 for
for  . Similar remarks apply
to ball matrices, ball series, etc.
. Similar remarks apply
to ball matrices, ball series, etc.
Remark 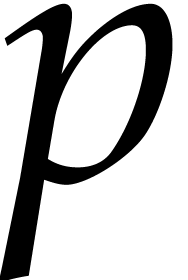 bits and an
exponent of
bits and an
exponent of  bits [3]. Let
bits [3]. Let  and
and 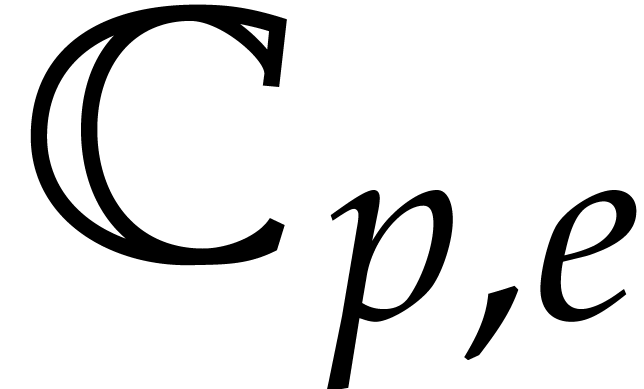 the sets of real and complex
floating point numbers of this type (strictly speaking, one also has
the sets of real and complex
floating point numbers of this type (strictly speaking, one also has
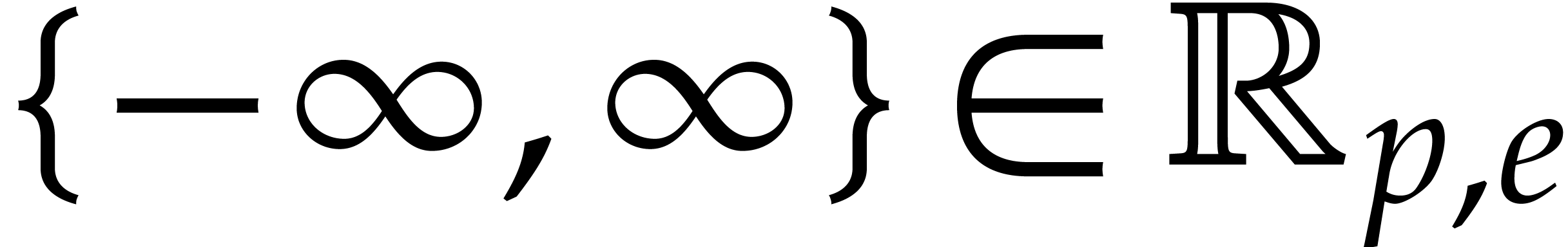 for the reliable rounding of overflowing
operations). One may adapt the above arithmetic on exact balls to
floating point balls in
for the reliable rounding of overflowing
operations). One may adapt the above arithmetic on exact balls to
floating point balls in 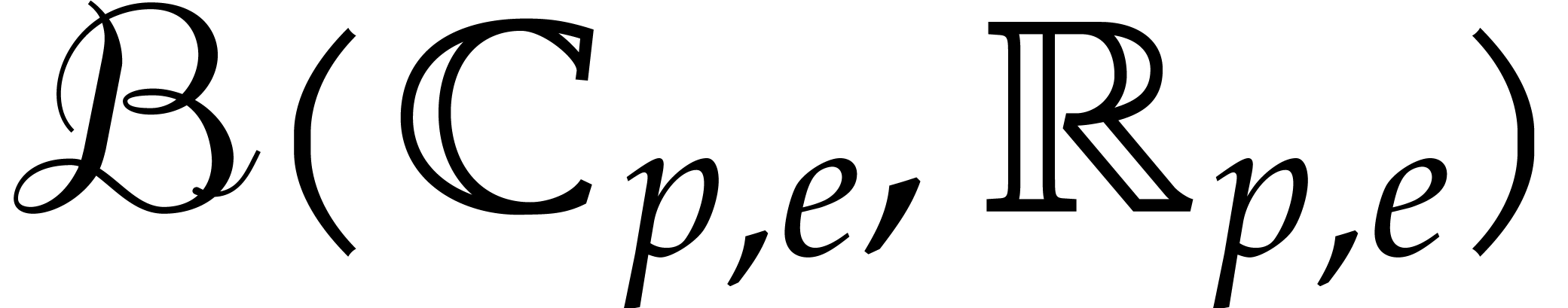 while preserving the
inclusion principle: it suffices to slightly increase the radii of
output balls so as to take care of rounding errors. For precise formulas
and interesting variations, we refer to [13]. For
simplicity, the sequel will be presented for exact ball arithmetic only,
but it is not hard to adapt the results to take into account rounding
errors.
while preserving the
inclusion principle: it suffices to slightly increase the radii of
output balls so as to take care of rounding errors. For precise formulas
and interesting variations, we refer to [13]. For
simplicity, the sequel will be presented for exact ball arithmetic only,
but it is not hard to adapt the results to take into account rounding
errors.
The polynomials 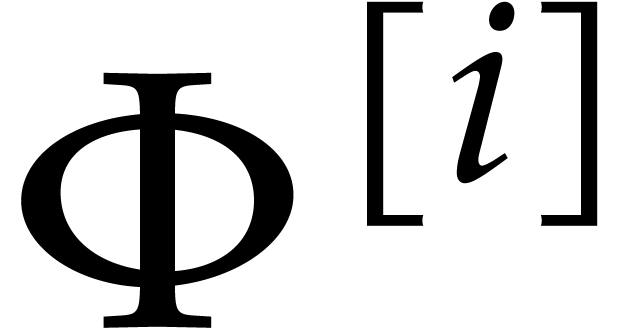 in (1) can either
be represented as linear combinations of monomials, or using a dag
(directed acyclic graph). In both cases, the ball arithmetic from the
previous subsection allows us to reliably evaluate
in (1) can either
be represented as linear combinations of monomials, or using a dag
(directed acyclic graph). In both cases, the ball arithmetic from the
previous subsection allows us to reliably evaluate  at balls in
at balls in  .
.
For the effective counterpart of Theorem 4, there is a
trade-off between the qualities of the radius 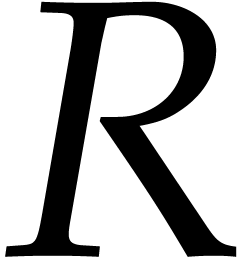 (larger radii being better) and the bound
(larger radii being better) and the bound  (smaller values of
(smaller values of 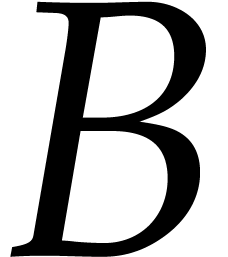 being better). For a given
being better). For a given
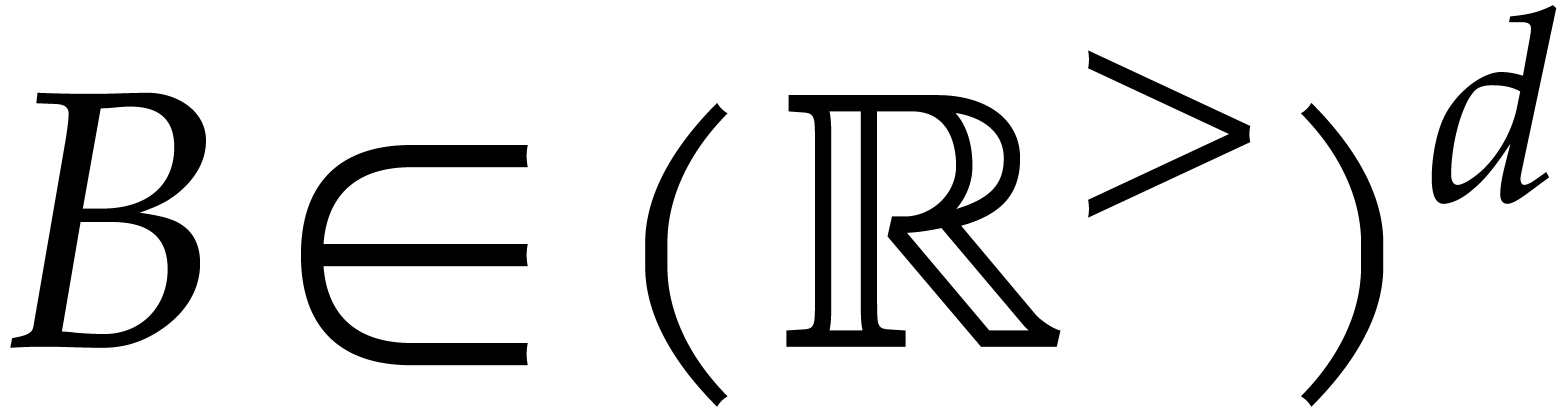 , it is simple to compute the
“best” corresponding
, it is simple to compute the
“best” corresponding  that satisfies
the condition (8), by taking
that satisfies
the condition (8), by taking 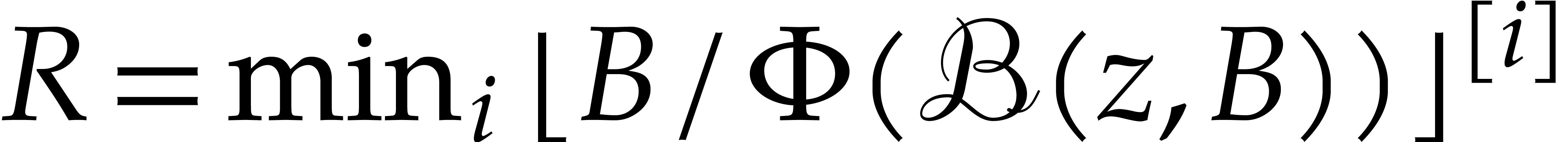 .
Conversely, for a fixed
.
Conversely, for a fixed 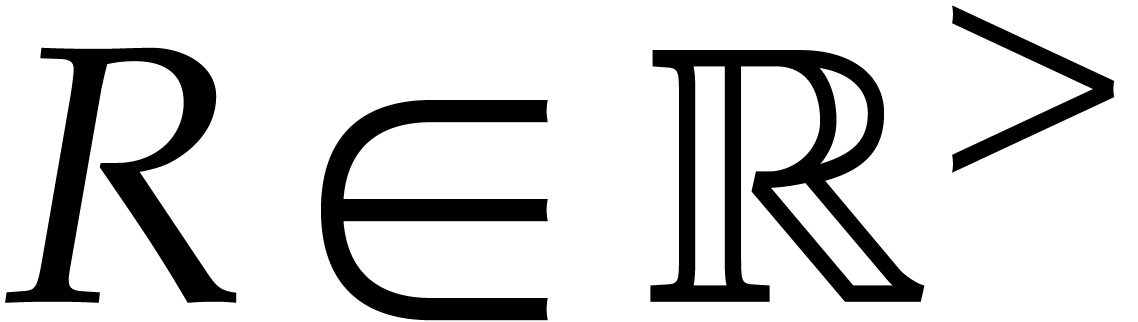 , let
us recall a classical technique from interval analysis that can be used
to compute an “almost best” corresponding bound
, let
us recall a classical technique from interval analysis that can be used
to compute an “almost best” corresponding bound 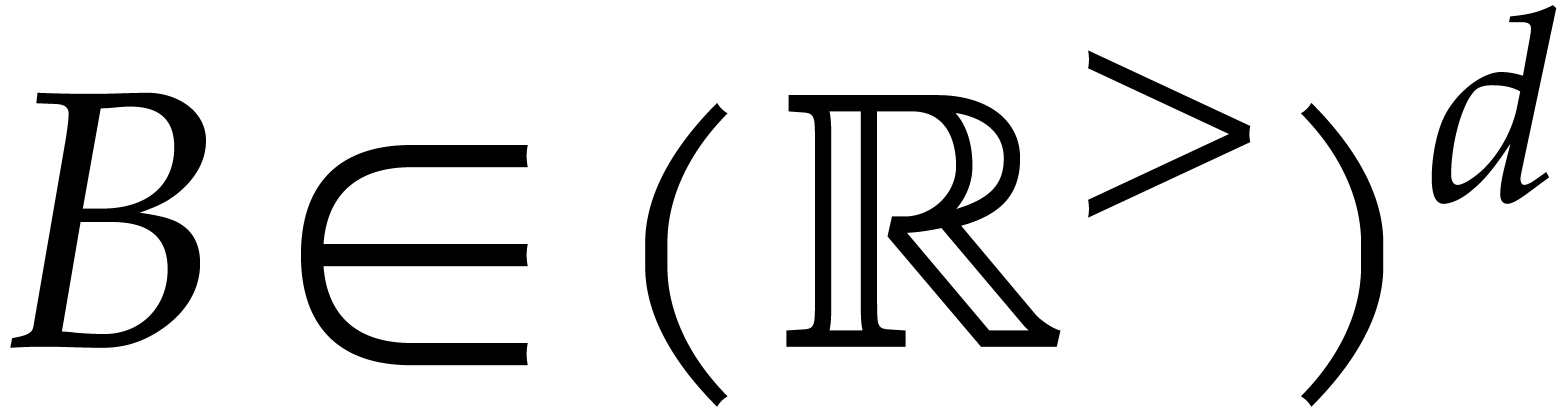 that satisfies (8).
that satisfies (8).
We simply construct a sequence  in
in 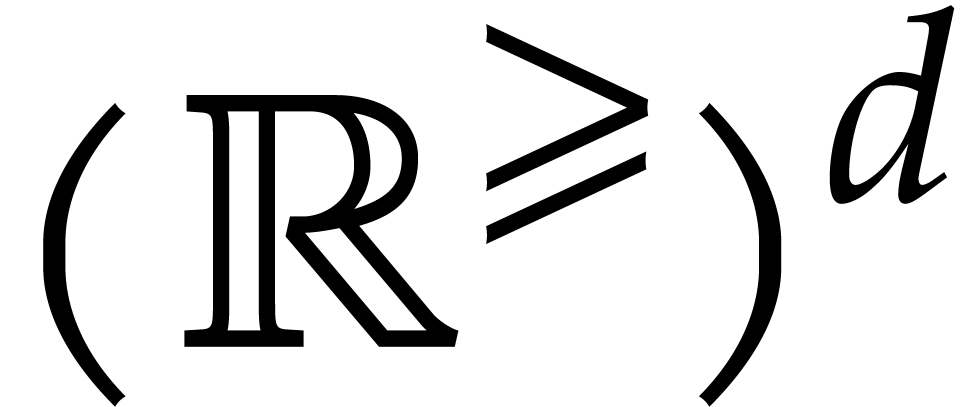 by taking
by taking 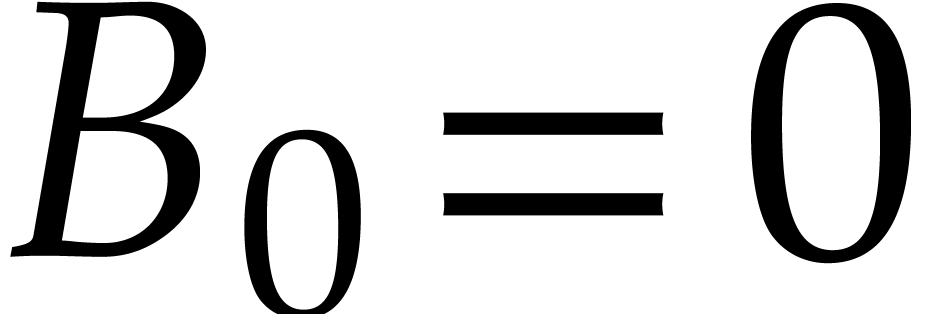 and
and 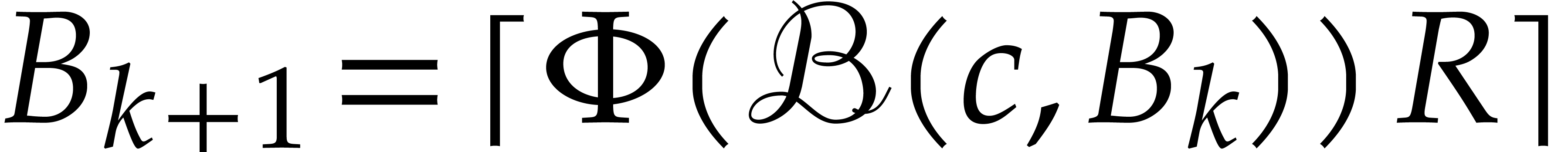 for all
for all 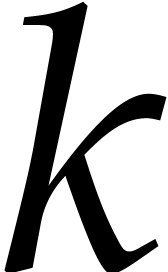 . If there exists a
finite
. If there exists a
finite 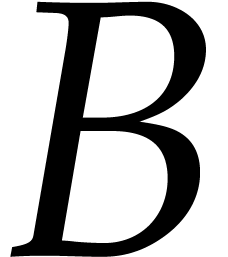 for which (8) holds, then
the sequence
for which (8) holds, then
the sequence 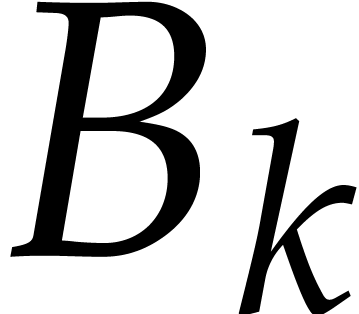 usually converges to a minimal such
usually converges to a minimal such
 quite quickly. After say ten iterations, we
should therefore have a reasonable approximation. One then slightly
inflates the last value by taking
quite quickly. After say ten iterations, we
should therefore have a reasonable approximation. One then slightly
inflates the last value by taking 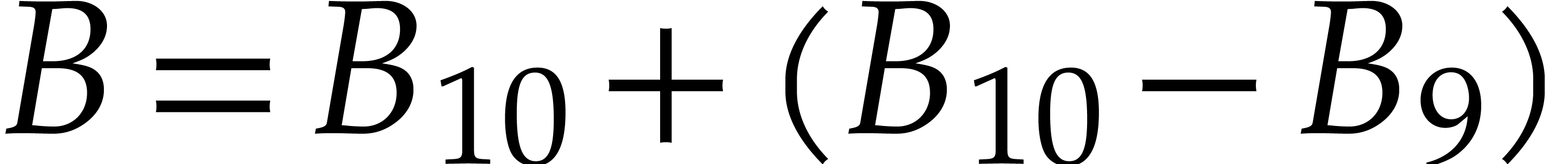 .
If
.
If 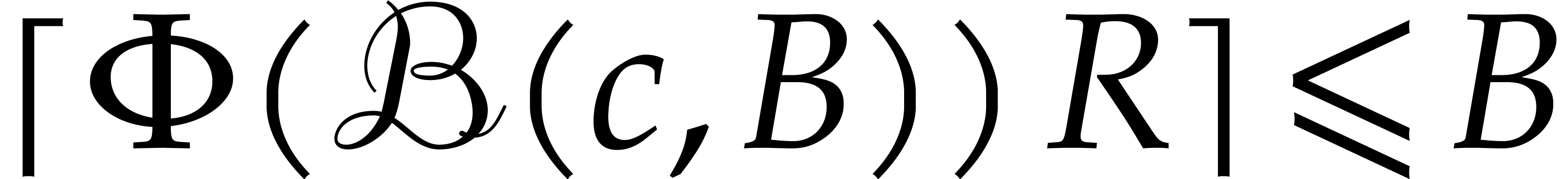 , then we have succeeded
in finding a suitable
, then we have succeeded
in finding a suitable  . If
not, then we return “failed”.
. If
not, then we return “failed”.
Using the above procedure, we may also compute a reasonably large
compact half disk  on which
on which  is analytic, together with a bound for
is analytic, together with a bound for  :
we simply perform a dichotomic search for the largest
:
we simply perform a dichotomic search for the largest 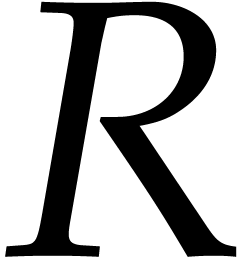 for which the computation of a corresponding
for which the computation of a corresponding 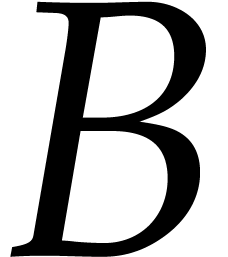 does not fail. If we also wish the bound
does not fail. If we also wish the bound 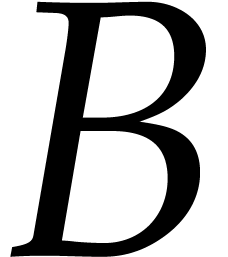 to
remain reasonably small, one may simply divide
to
remain reasonably small, one may simply divide 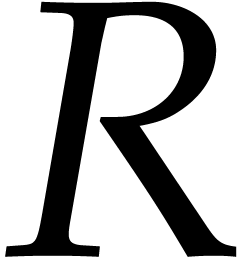 by two at the end of the search and compute the corresponding
by two at the end of the search and compute the corresponding  .
.
Let us now return to the integration of (1) and let  be the exact solution for the initial condition
be the exact solution for the initial condition 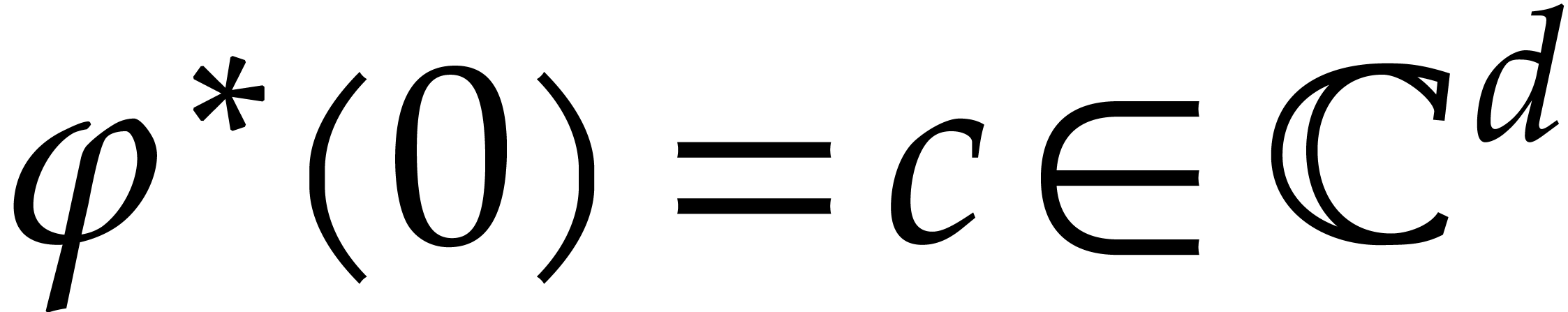 . Let
. Let  and
and
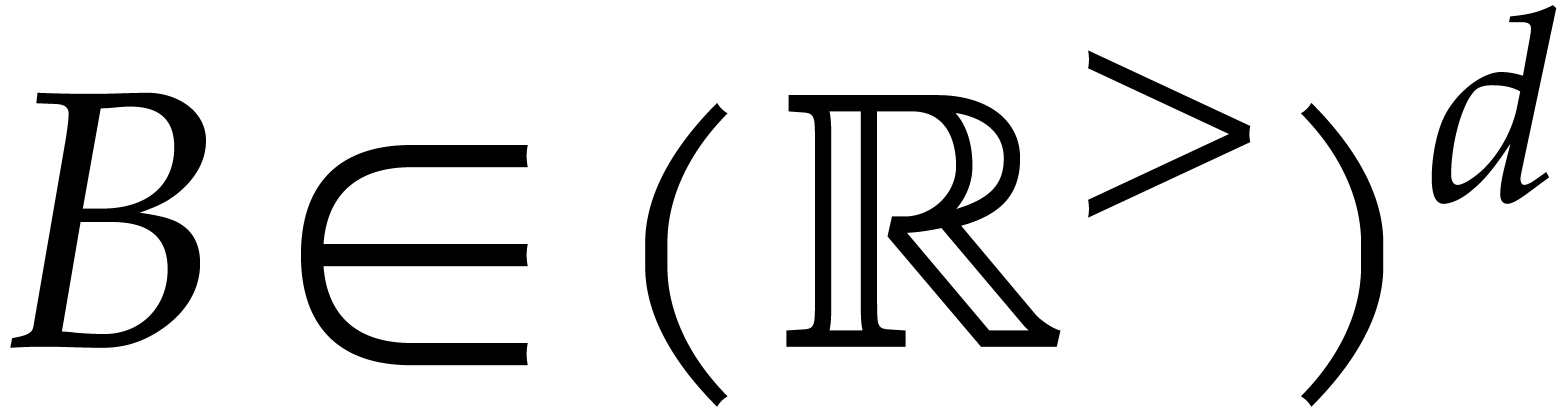 be computed as above such that (8)
holds. Assume that we were able to reliably integrate (1)
until a given time
be computed as above such that (8)
holds. Assume that we were able to reliably integrate (1)
until a given time 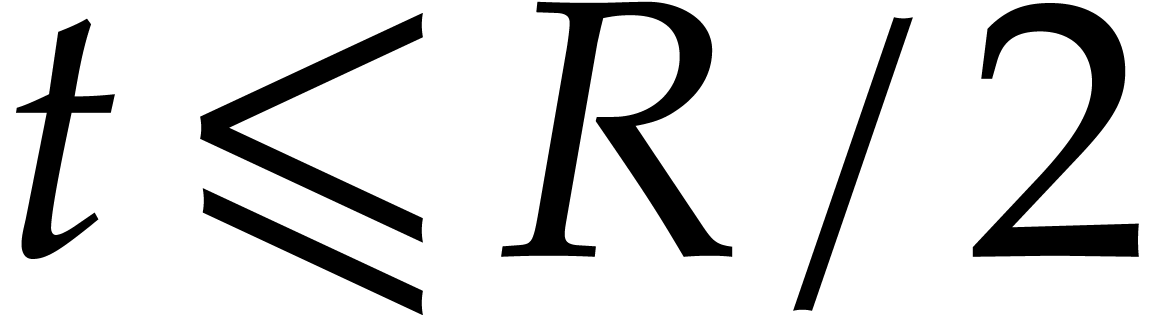 and let
and let 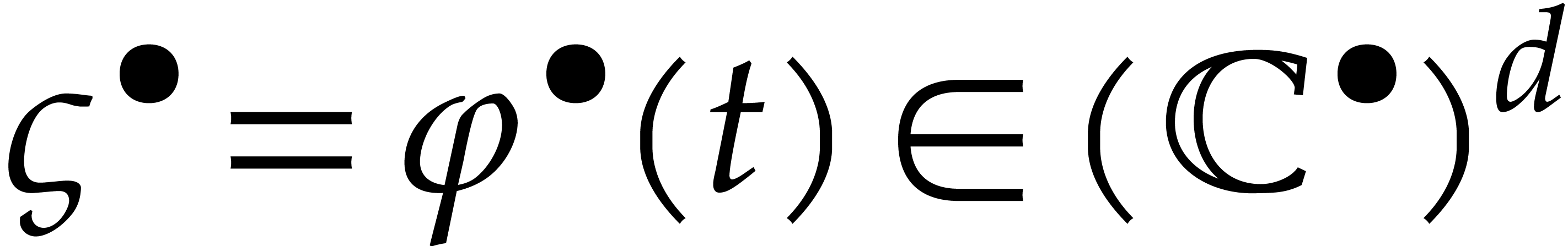 , so that
, so that 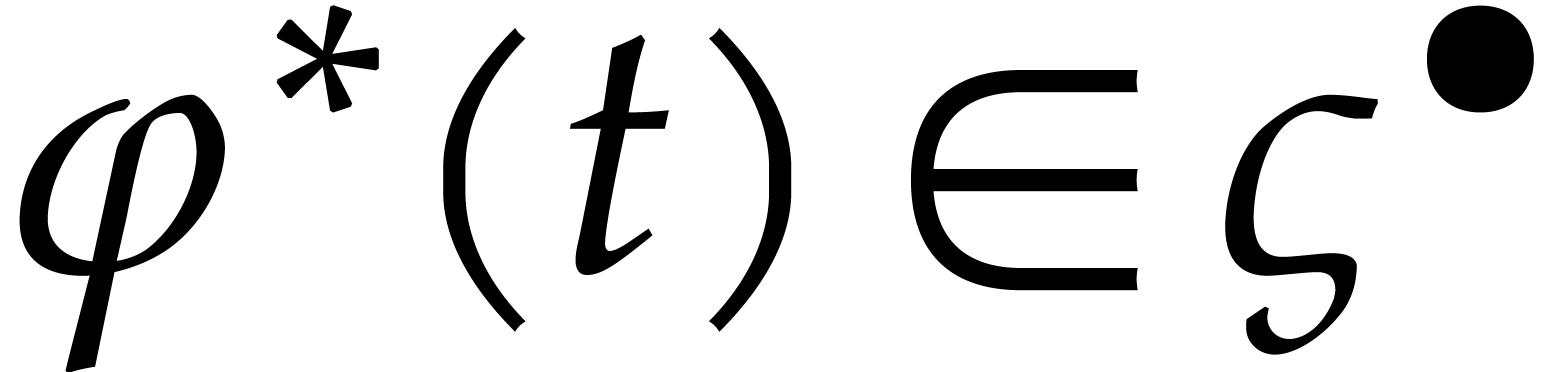 .
.
In order to adapt the  -iteration
to ball arithmetic, we first deduce from Theorem 4 that
-iteration
to ball arithmetic, we first deduce from Theorem 4 that
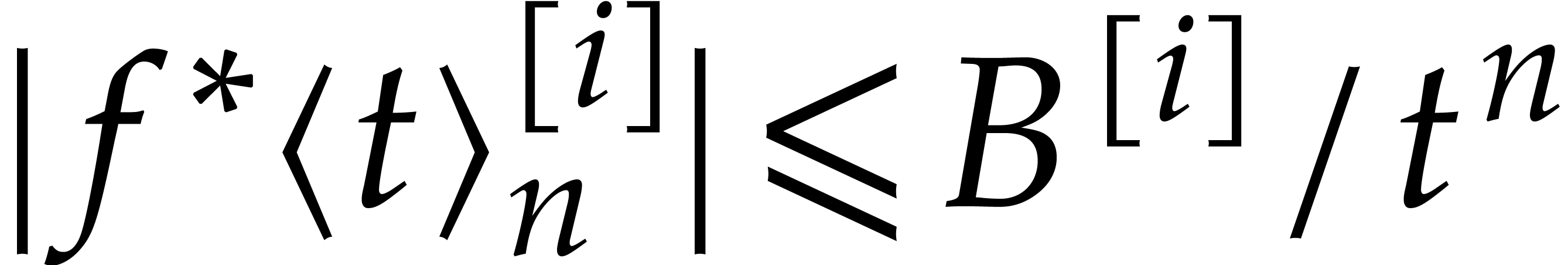 for
for 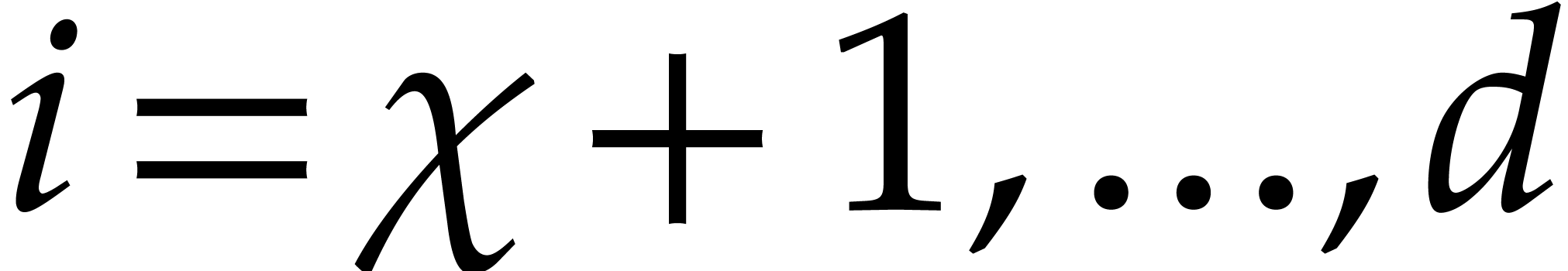 .
This provides us with the required steady-state conditions
.
This provides us with the required steady-state conditions 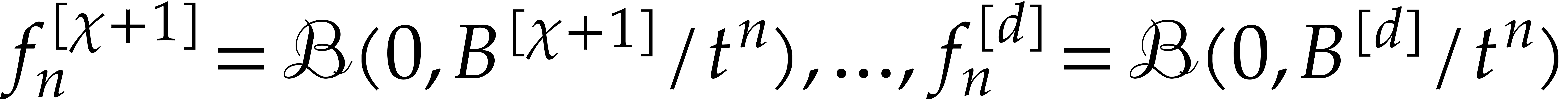 , in addition to the initial conditions
, in addition to the initial conditions  . The ball counterpart of our
steady-state problem thus becomes
. The ball counterpart of our
steady-state problem thus becomes
 |
(30) |
We correspondingly define the ball version of  for
for 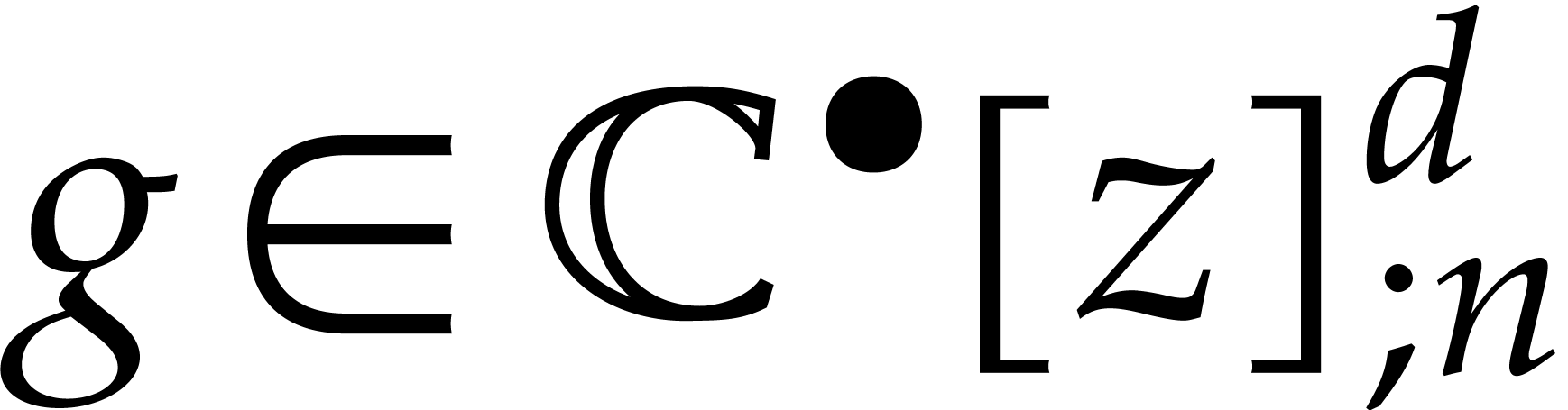 by
by
This map has the property that 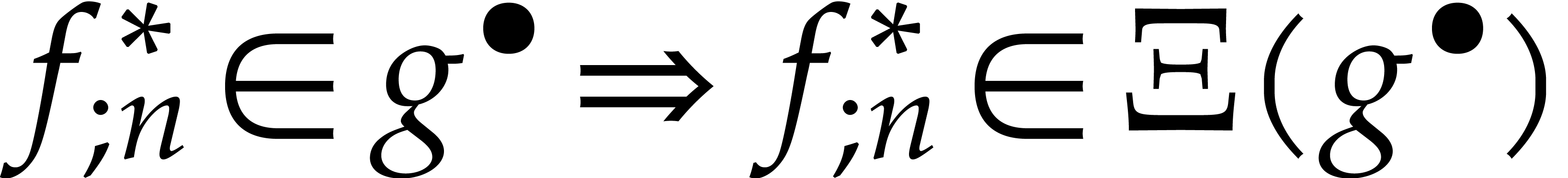 .
In our ball context, we may actually iterate using the following
improved version
.
In our ball context, we may actually iterate using the following
improved version 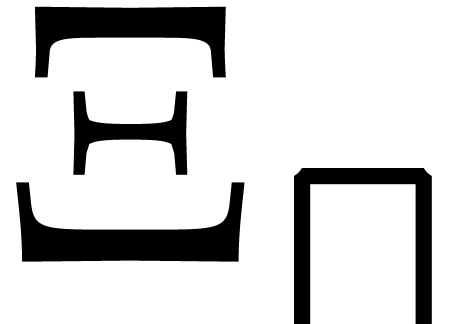 of
of  :
:

Here we understand that the intersections are taken coefficientwise.
Since iterations using  can only improve our
enclosures, we do not need to worry much about the ansatz. We
may deduce a reasonably good ansatz from the power series expansion
can only improve our
enclosures, we do not need to worry much about the ansatz. We
may deduce a reasonably good ansatz from the power series expansion 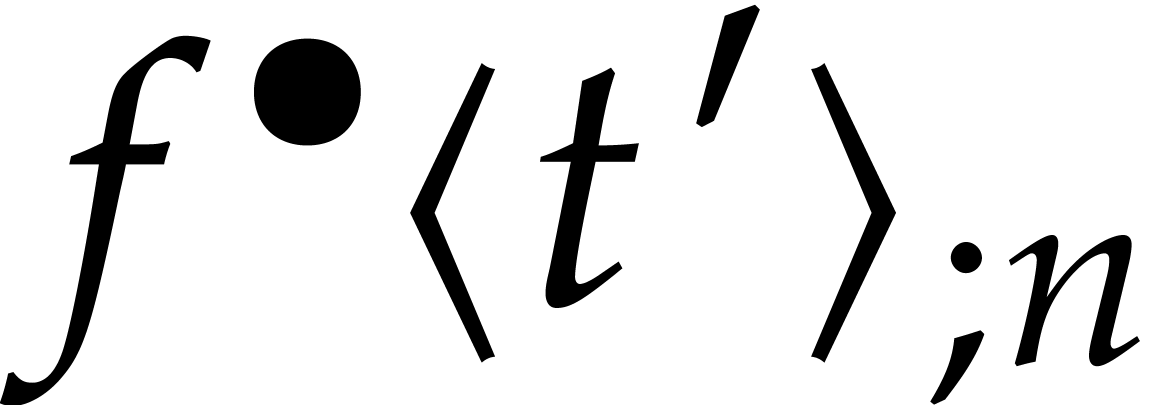 at the previous time
at the previous time 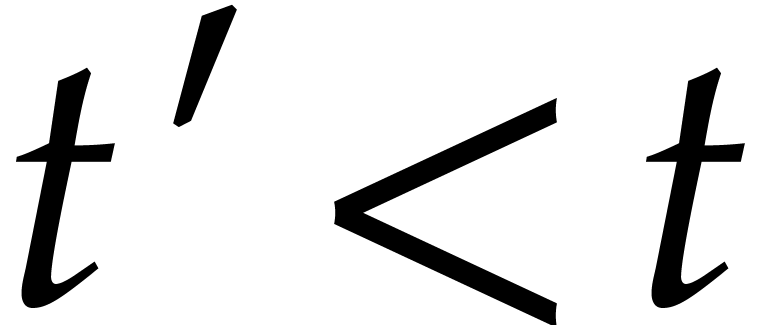 ,
and the Cauchy bounds
,
and the Cauchy bounds 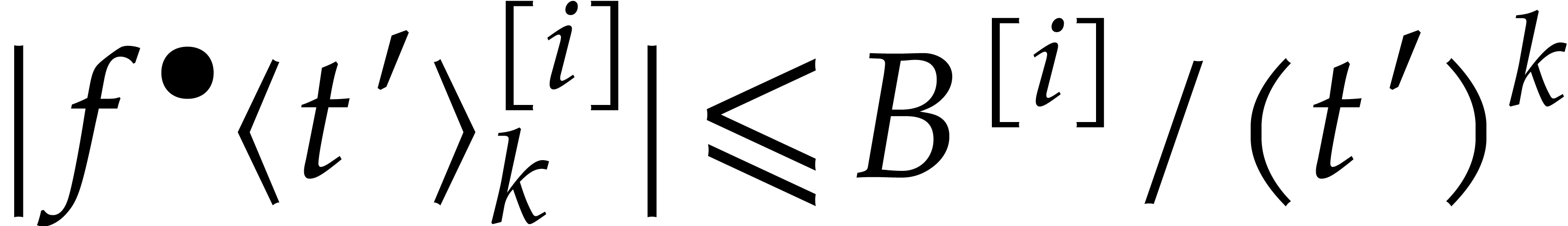 for all
for all 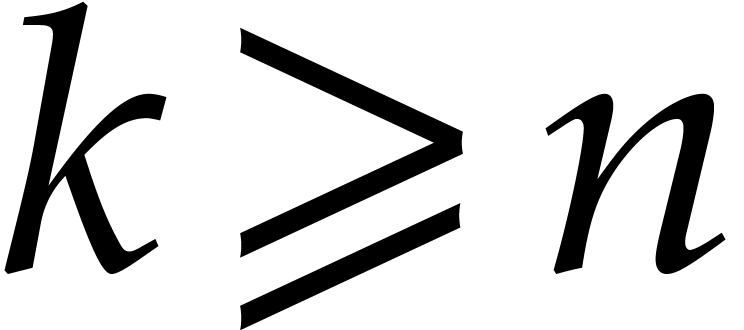 . But it is perfectly reasonable as well to use
. But it is perfectly reasonable as well to use
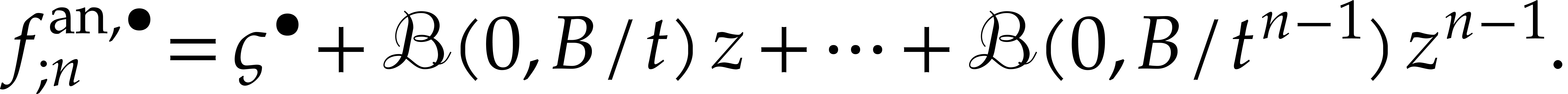
Applying  a sufficient number of times to this
ansatz, we obtain the desired ball enclosure
a sufficient number of times to this
ansatz, we obtain the desired ball enclosure 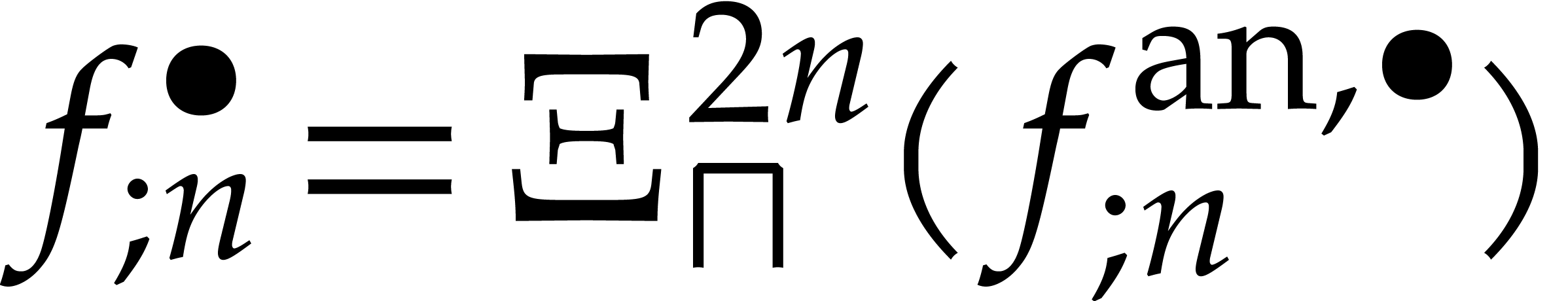 of
the truncated power series expansion of
of
the truncated power series expansion of  at time
at time
 . Assuming that
. Assuming that 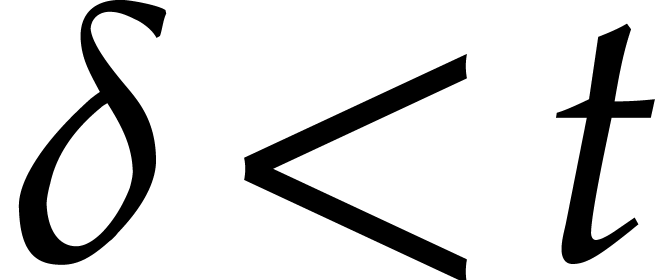 , we may then deduce the enclosure
, we may then deduce the enclosure
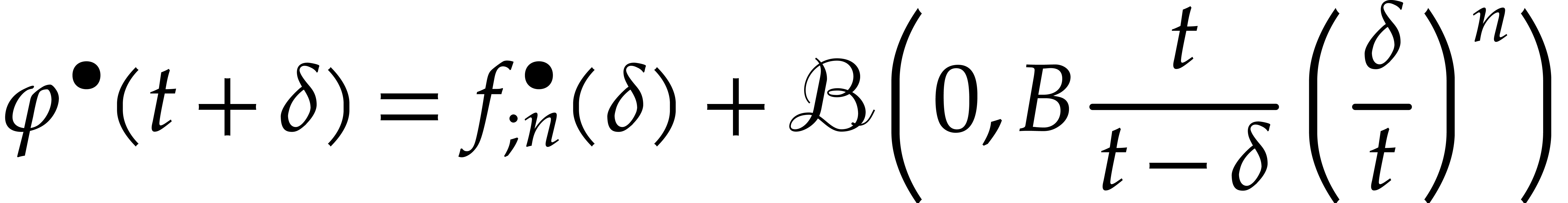 |
(31) |
of  at time
at time  .
Notice that the cost of the computation of certified solutions in this
way is similar to the cost of Algorithm 1, up to a constant
factor.
.
Notice that the cost of the computation of certified solutions in this
way is similar to the cost of Algorithm 1, up to a constant
factor.
The above method relies on the property that the steady-state problem
(30) for balls specializes into a numerical steady-state
problem that admits 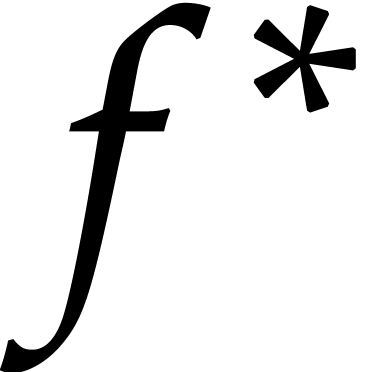 as a solution, since
as a solution, since  and
and 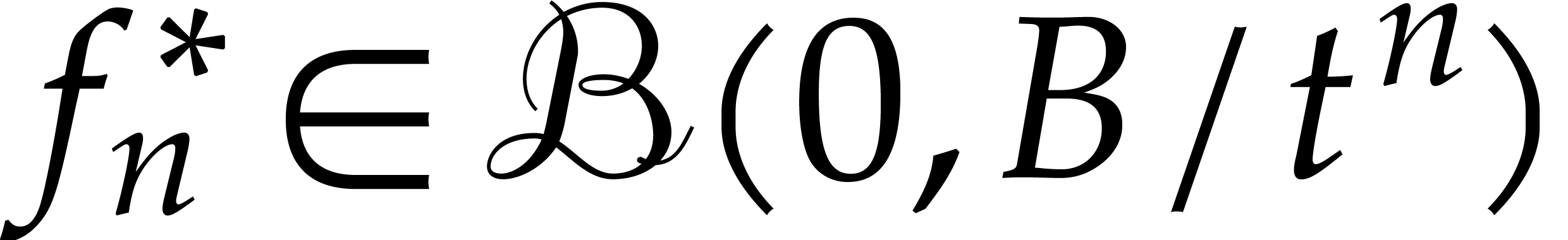 .
Given a numerical approximation of
.
Given a numerical approximation of 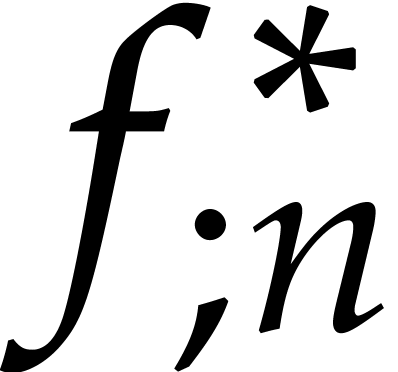 ,
as computed in section 5, a related problem is whether we
can certify the existence of an actual solution in a small neighbourhood
of the approximate solution.
,
as computed in section 5, a related problem is whether we
can certify the existence of an actual solution in a small neighbourhood
of the approximate solution.
In order to make this more precise, let us introduce a few more
notations. Given 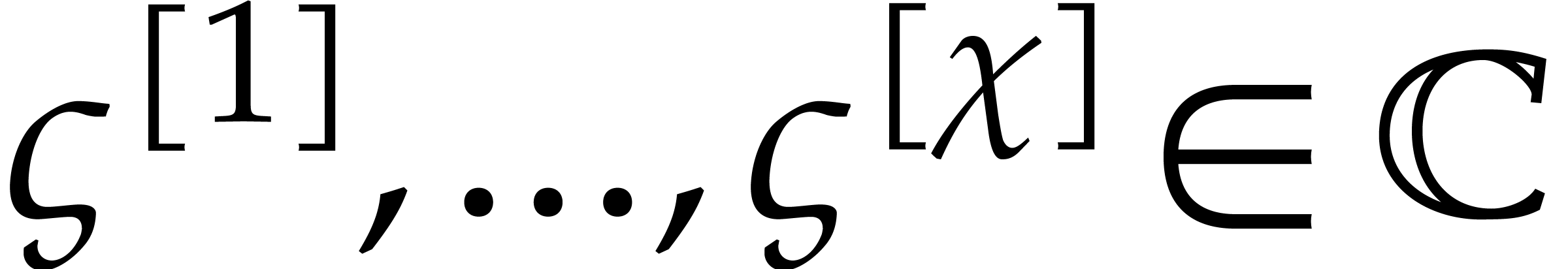 and
and  , consider the numeric steady-state problem
, consider the numeric steady-state problem
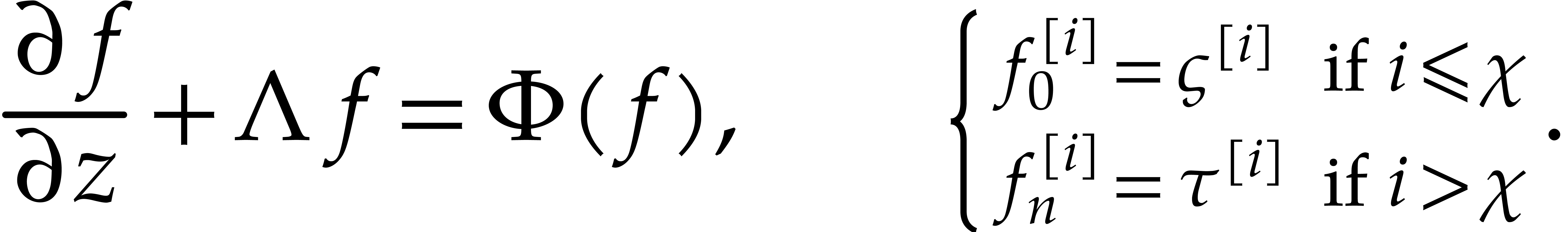 |
(32) |
We will denote by 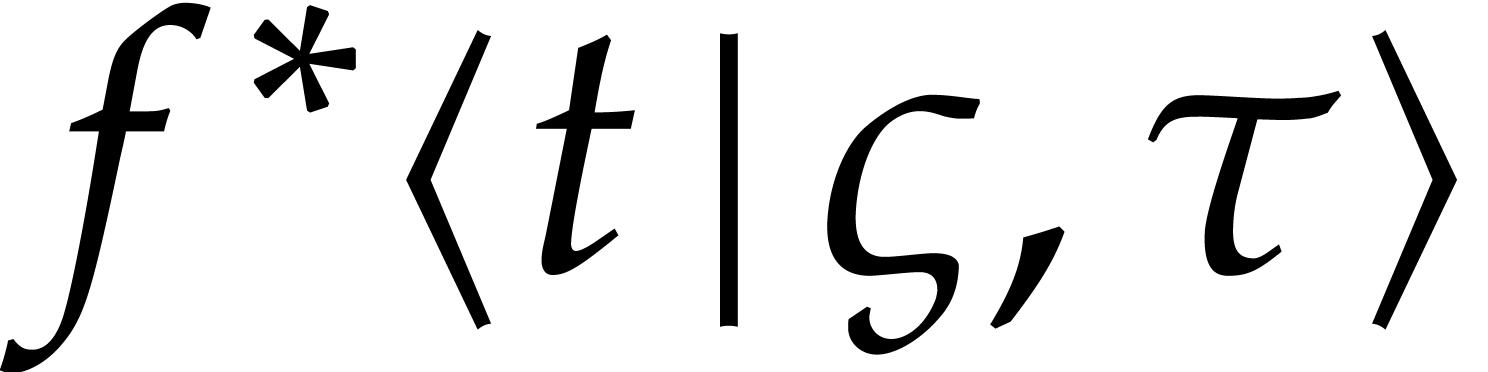 any exact solution to this
problem if such solution exists. It will be convenient to regard
any exact solution to this
problem if such solution exists. It will be convenient to regard  and
and  as elements of
as elements of 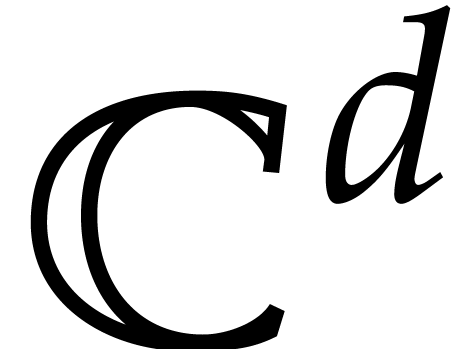 , through padding with zeros. Now
consider the operator
, through padding with zeros. Now
consider the operator 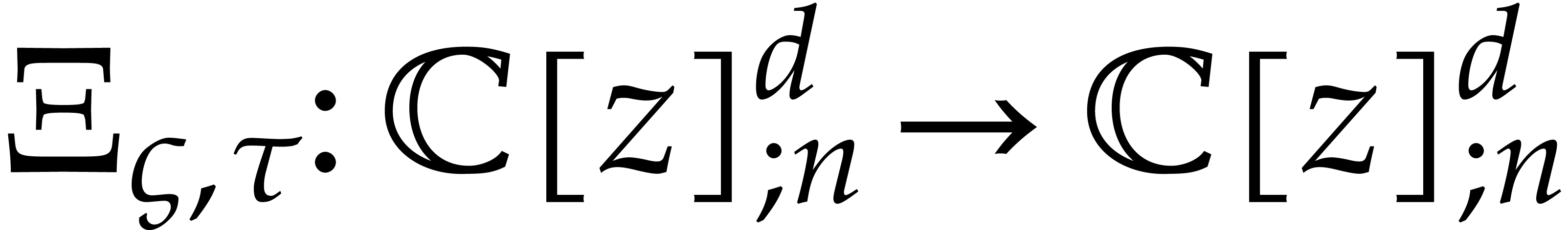 defined by
defined by
Through the iterated application of  to a
suitable ansatz, we may obtain a numerical approximation
to a
suitable ansatz, we may obtain a numerical approximation 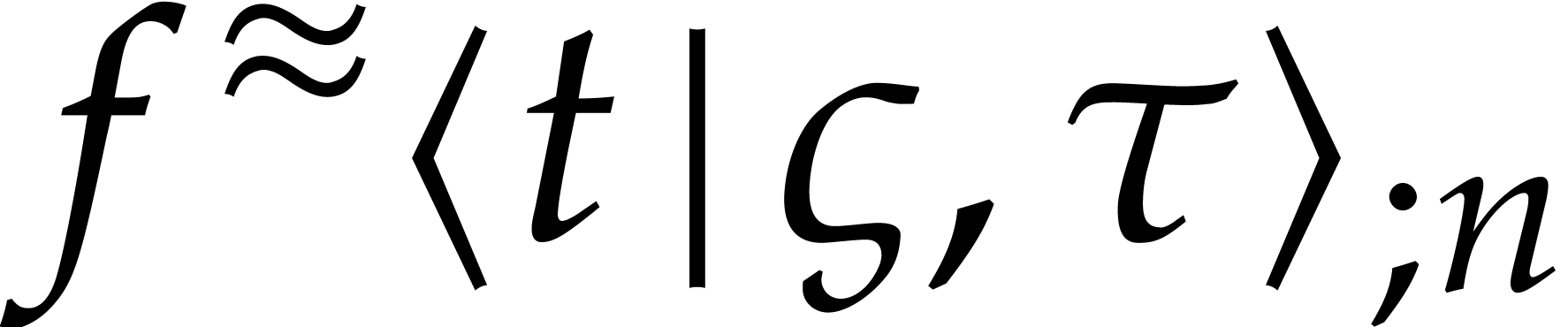 of
of 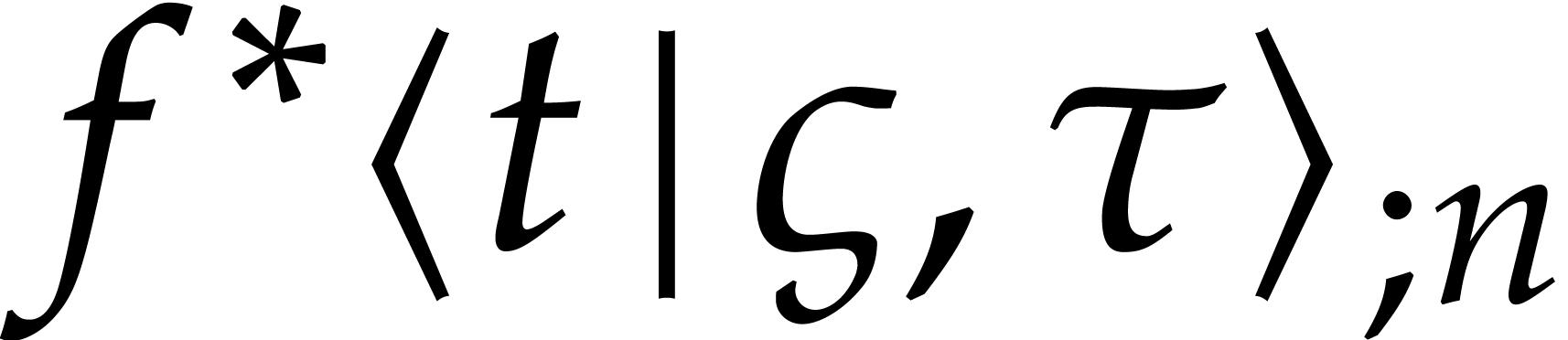 .
.
Now consider balls  and
and  , again padded with zeros. Then we have the
following ball analogue of (32):
, again padded with zeros. Then we have the
following ball analogue of (32):
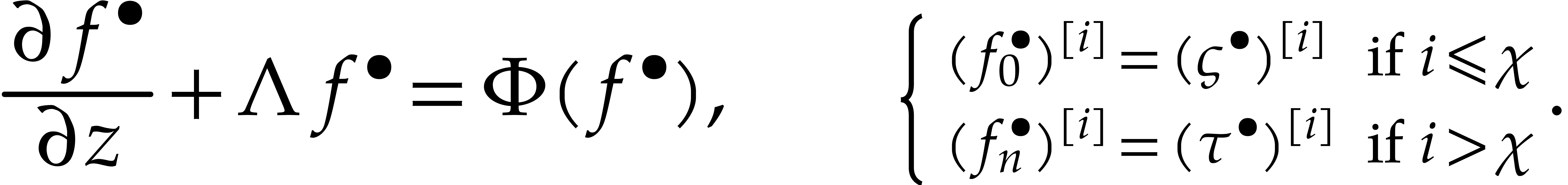 |
(33) |
Let  and
and  denote the
centers of
denote the
centers of  and
and  .
Starting from a numerical approximation
.
Starting from a numerical approximation  of
of  , we wish to compute the truncation
, we wish to compute the truncation
 of a solution to (33), with the
property that
of a solution to (33), with the
property that 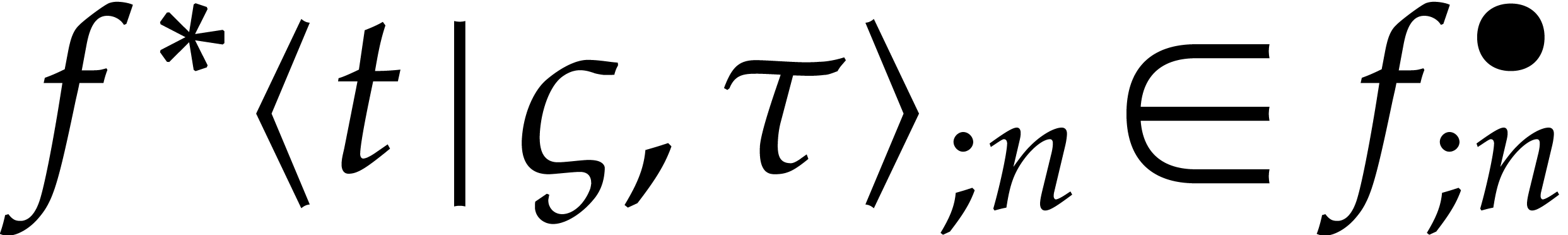 for all
for all  and
and  .
.
In order to do this, the idea is again to use a suitable ball version of
 , given by
, given by
and to keep applying 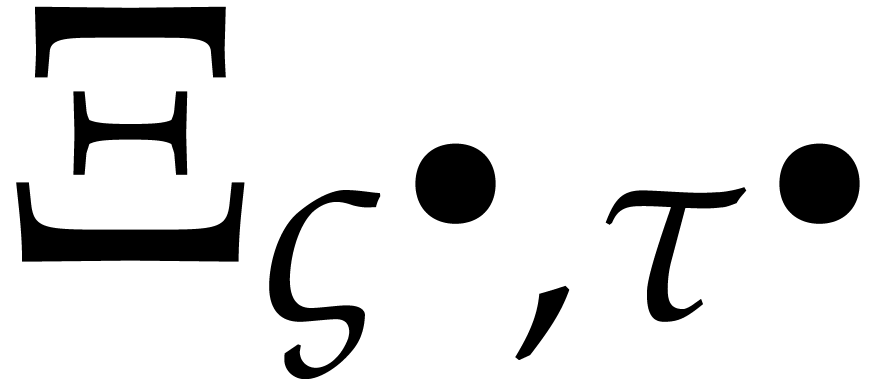 on the ansatz
on the ansatz  until we are sufficiently close to a fixed point.
Using a similar inflation technique as in section 6.2, we
finally obtain a truncated series
until we are sufficiently close to a fixed point.
Using a similar inflation technique as in section 6.2, we
finally obtain a truncated series  with
with 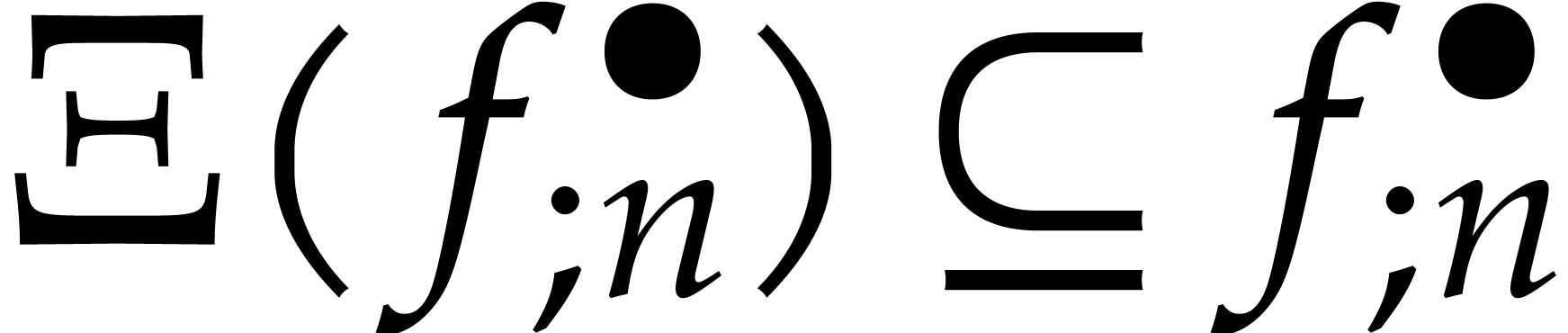 , or “failed”. Now for
any
, or “failed”. Now for
any  and
and 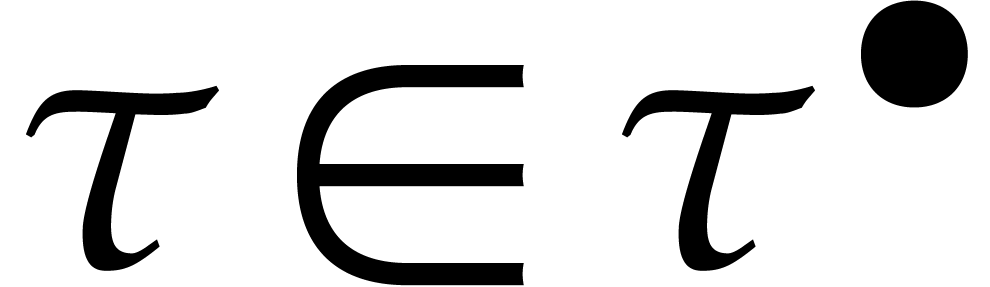 ,
we notice that this also yields
,
we notice that this also yields 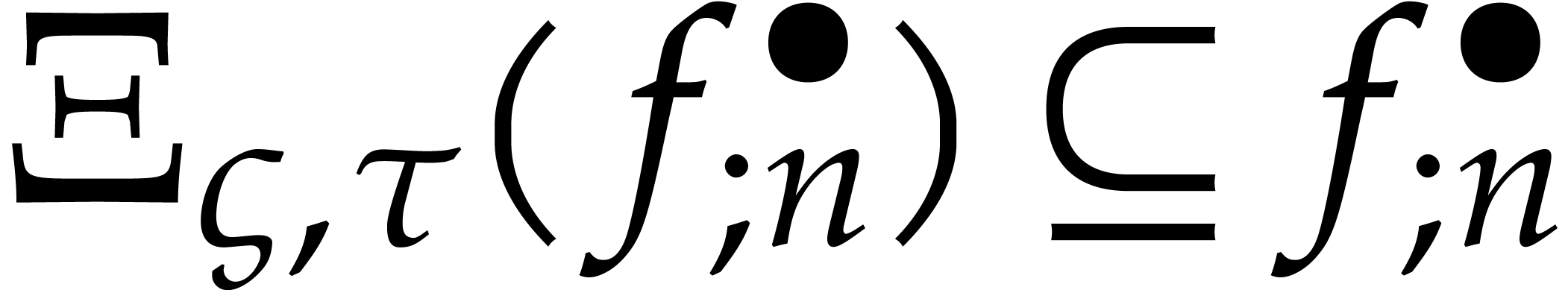 .
Thinking of
.
Thinking of  as a compact set of series in
as a compact set of series in 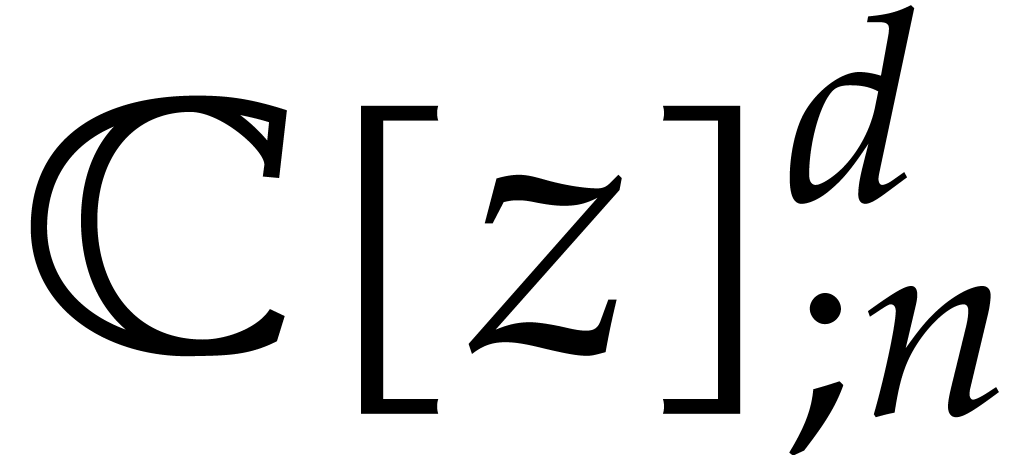 , this means in particular that
, this means in particular that
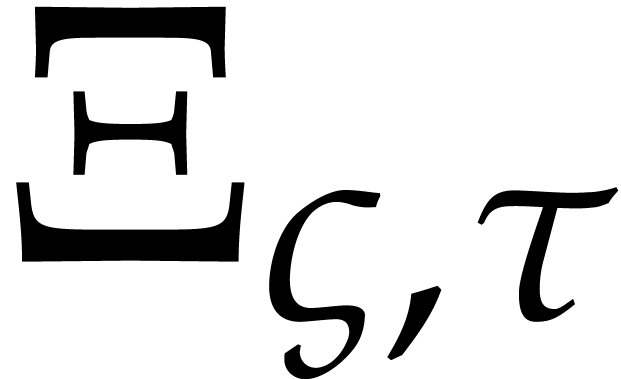 admits a fixed point
admits a fixed point 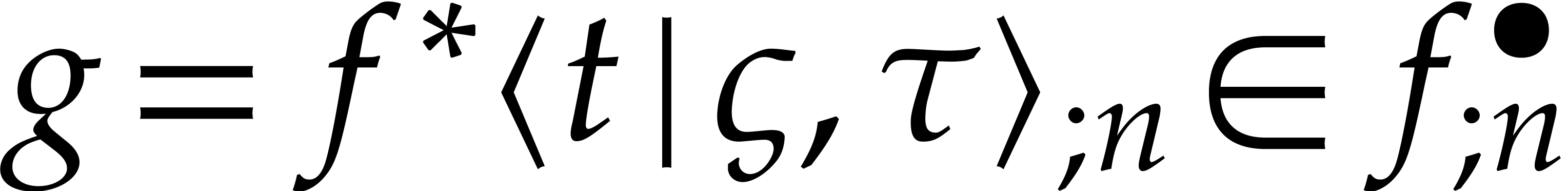 , as desired.
, as desired.
If 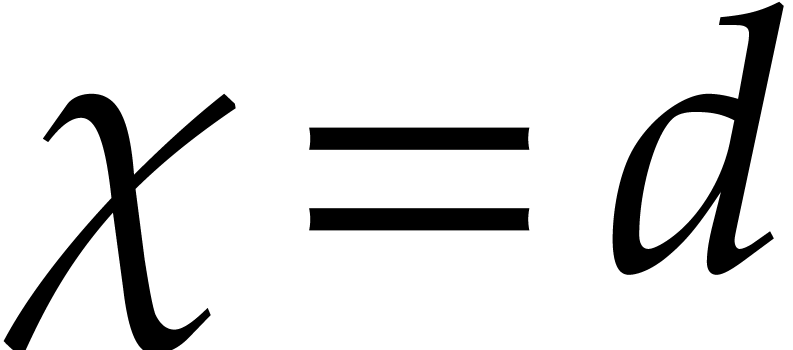 , then the algorithm from
subsection 6.3 specializes to a classical way to compute
the enclosure (31) of a solution to (1) at
time
, then the algorithm from
subsection 6.3 specializes to a classical way to compute
the enclosure (31) of a solution to (1) at
time  as a function of the enclosure
as a function of the enclosure  at time
at time  .
However, it is well known that this method suffers from a large
overestimation of the errors, due to the so-called “wrapping
effect”. A well know technique to reduce this overestimation is to
first compute a certified solution for the initial condition
.
However, it is well known that this method suffers from a large
overestimation of the errors, due to the so-called “wrapping
effect”. A well know technique to reduce this overestimation is to
first compute a certified solution for the initial condition 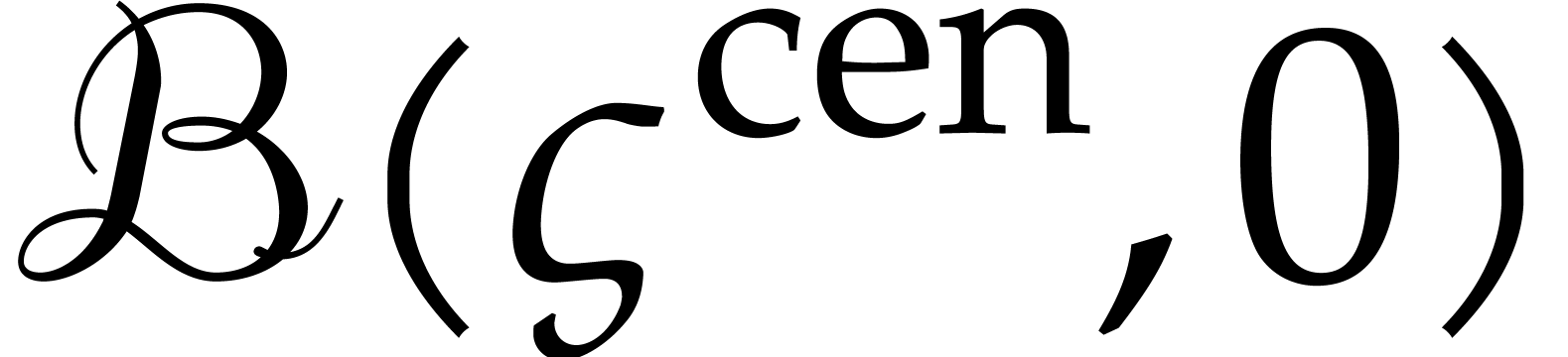 instead of
instead of  and then to bound the
error due to this replacement, by investigating the first variation. Let
us now show how to extend this technique to general critical indices
and then to bound the
error due to this replacement, by investigating the first variation. Let
us now show how to extend this technique to general critical indices
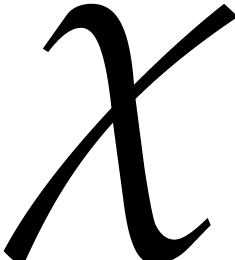 .
.
With 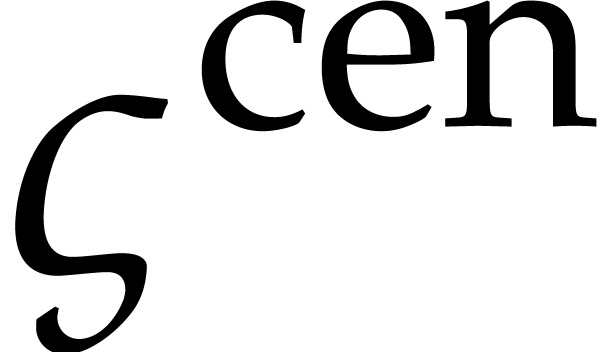 in the role of
in the role of  and
and
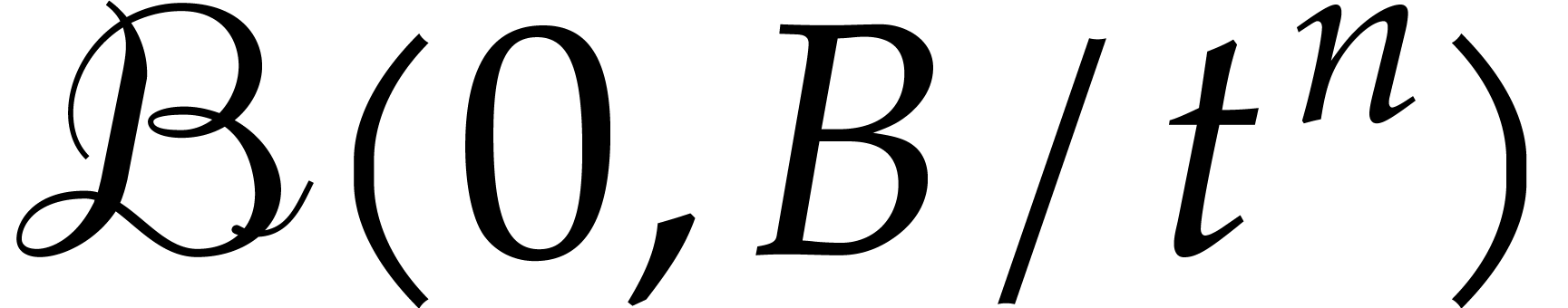 in the role of
in the role of  ,
we start with the computation of a truncated certified solution
,
we start with the computation of a truncated certified solution  to (33). Recall that this ball solution
has the property that
to (33). Recall that this ball solution
has the property that 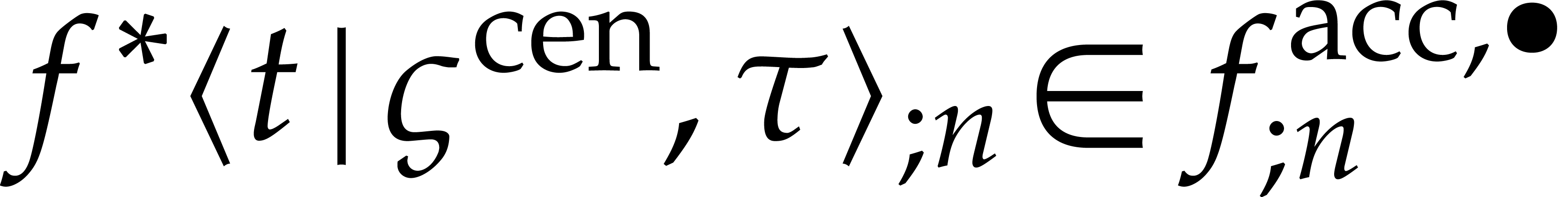 for all
for all 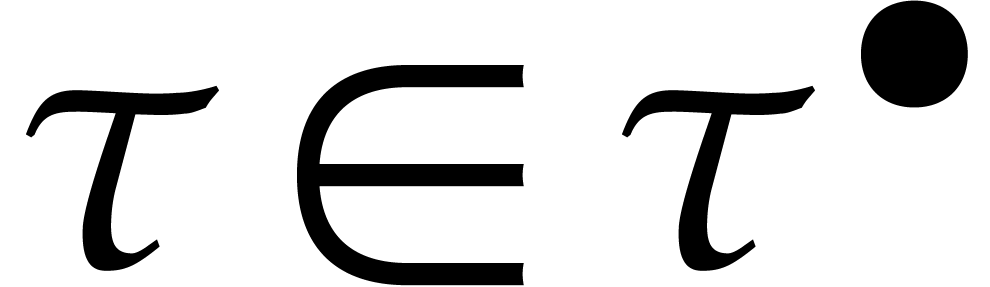 . Since the initial conditions are exact, this
solution is generally fairly accurate. Now for any
. Since the initial conditions are exact, this
solution is generally fairly accurate. Now for any 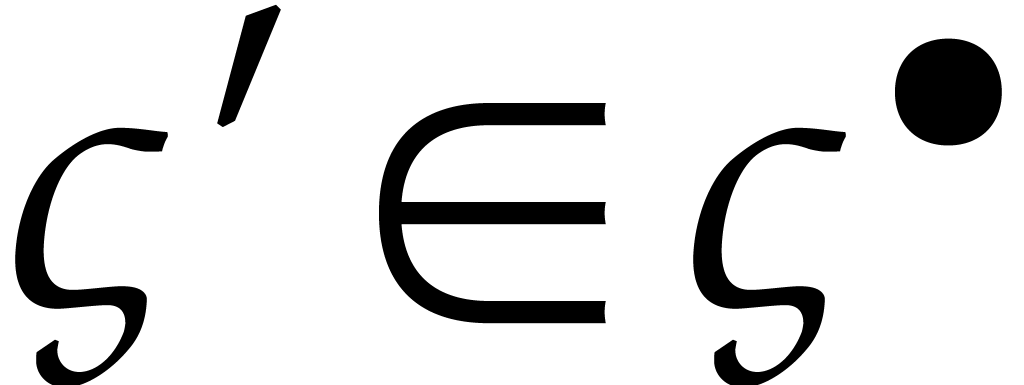 , we may write
, we may write
We next observe that
where 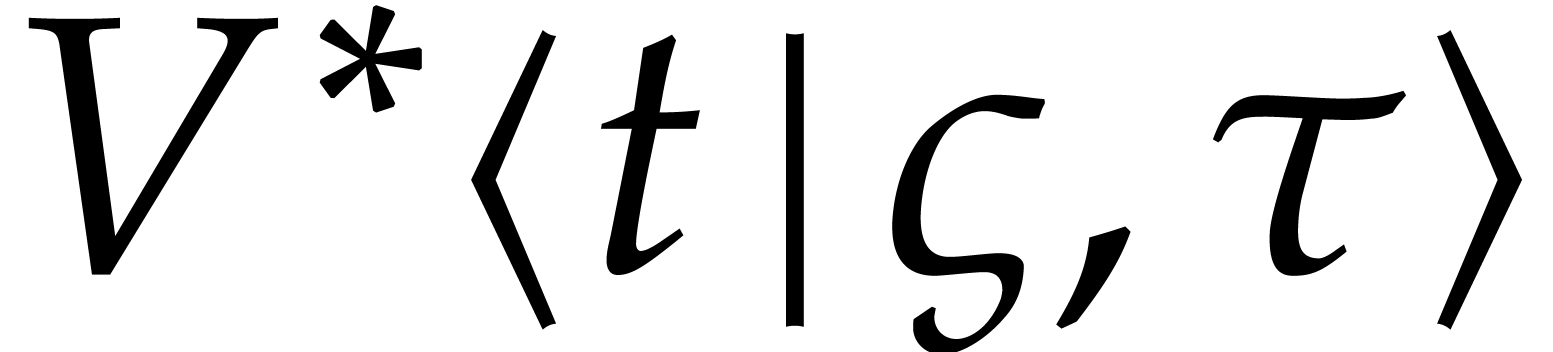 denotes the exact solution of the
following equation for the first steady-state variation:
denotes the exact solution of the
following equation for the first steady-state variation:
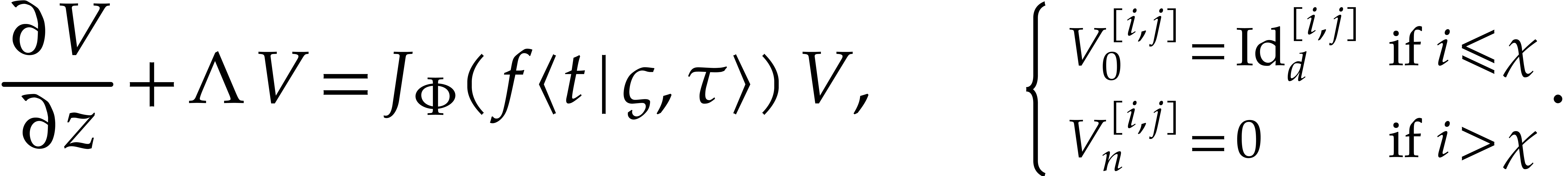
This equation again admits a ball analogue
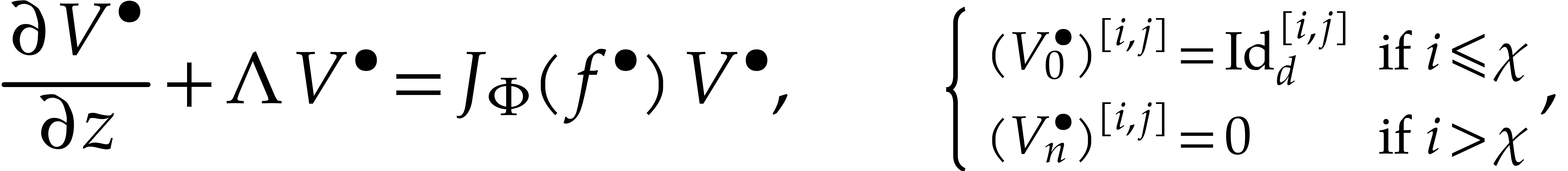
where  is a solution to (30). We
only compute a crude solution
is a solution to (30). We
only compute a crude solution  to this equation,
for a crude solution
to this equation,
for a crude solution  to (30), both
truncated to the order
to (30), both
truncated to the order  .
These solutions can be obtained using the techniques from section 6.3. From (34) we finally conclude that
.
These solutions can be obtained using the techniques from section 6.3. From (34) we finally conclude that
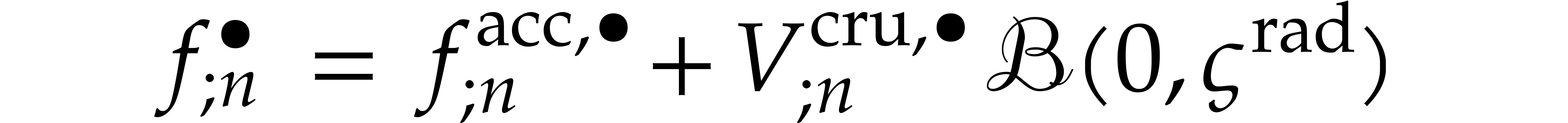
is a ball enclosure for  .
This enclosure is usually of a much better quality than
.
This enclosure is usually of a much better quality than  . However, its computational cost is roughly
. However, its computational cost is roughly
 times higher, due to the fact that we need to
determine the first variation.
times higher, due to the fact that we need to
determine the first variation.
In the case when  is too small for (29)
to hold, we may generalize the above strategy and incorporate some of
the ideas from section 5.4. With
is too small for (29)
to hold, we may generalize the above strategy and incorporate some of
the ideas from section 5.4. With  and
and  from there, let us briefly outline how to do
this. We proceed in four stages:
from there, let us briefly outline how to do
this. We proceed in four stages:
We first compute a truncated numeric solution  to (26), using the technique from section 5.4.
to (26), using the technique from section 5.4.
Let 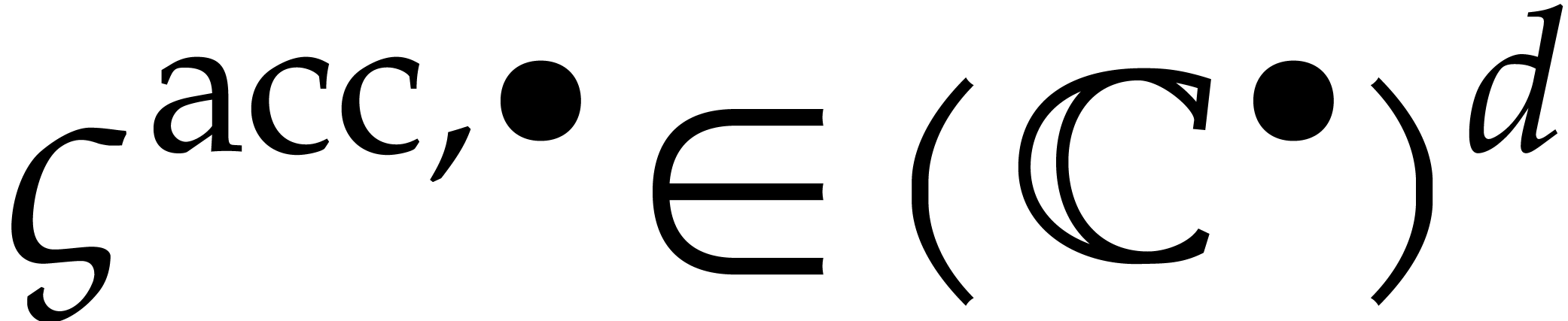 be such that
be such that 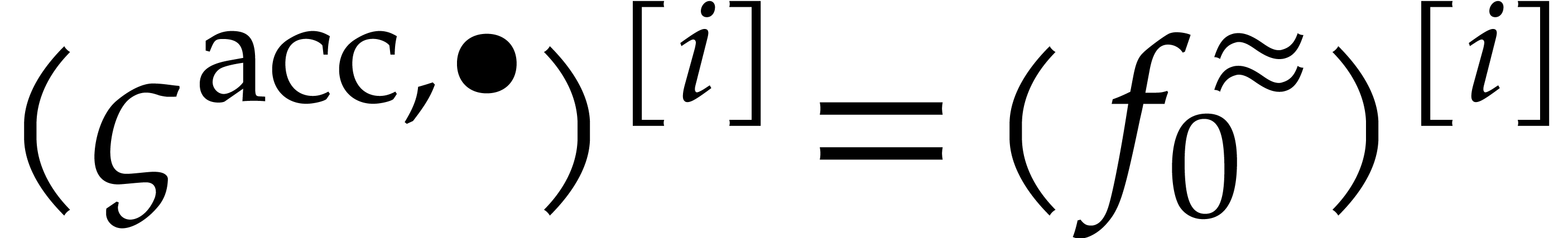 for
for
 and
and 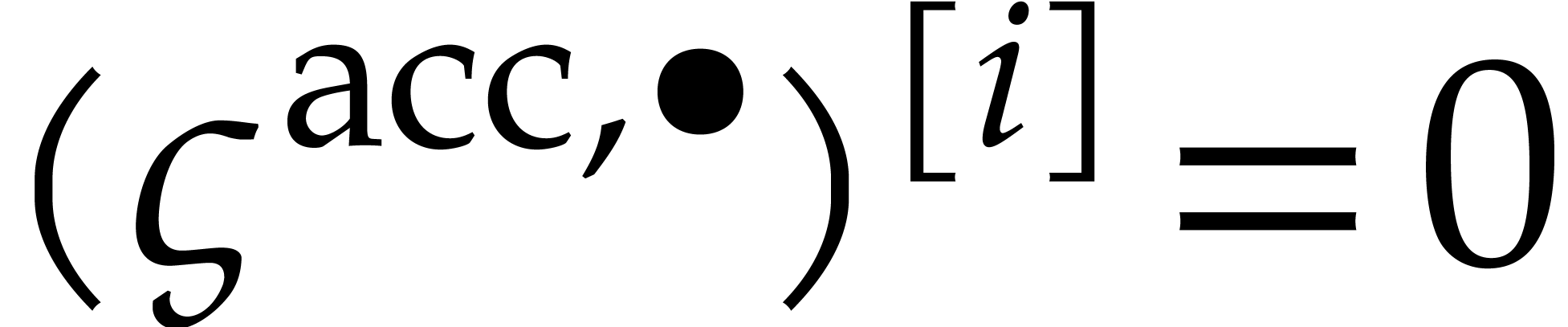 for
for 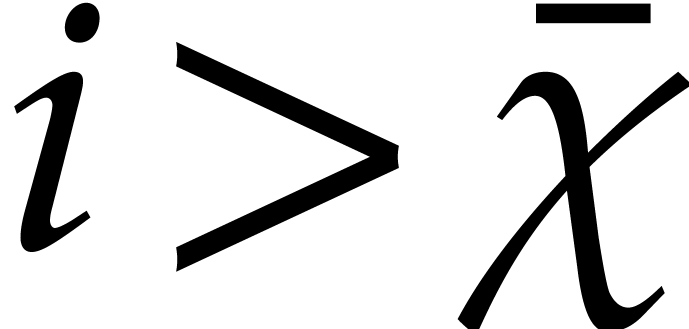 . Similarly, let
. Similarly, let 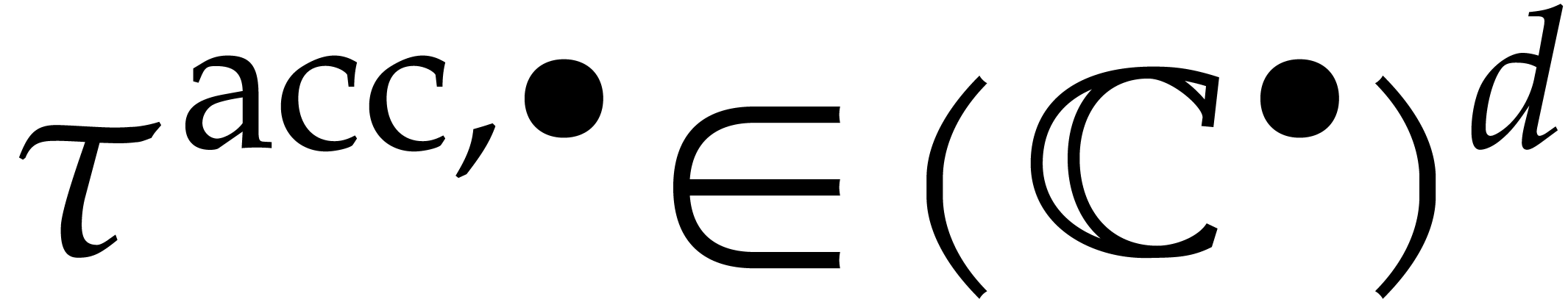 be
such that
be
such that 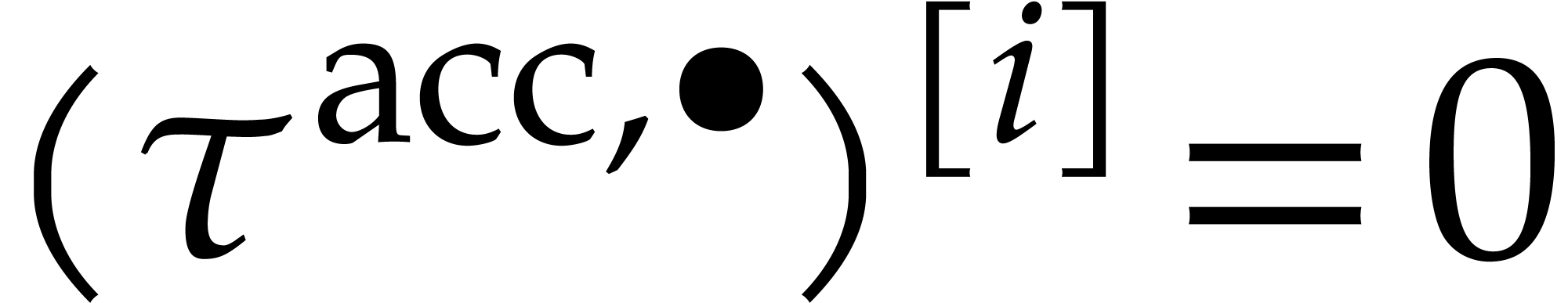 for
for 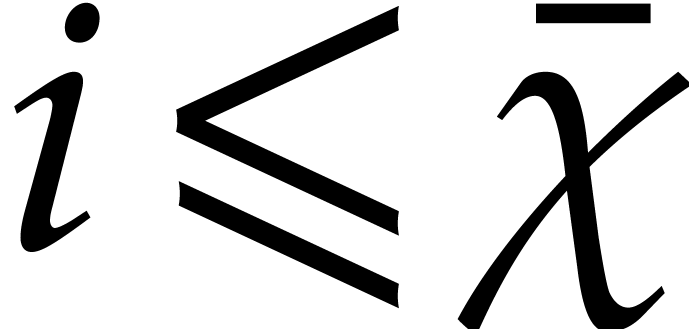 and
and
 for
for  .
We use
.
We use  as an ansatz for its
deformation into a reliable truncated solution
as an ansatz for its
deformation into a reliable truncated solution  to (33), but with
to (33), but with  in the role
of
in the role
of  , with
, with  in the role of
in the role of  ,
and
,
and 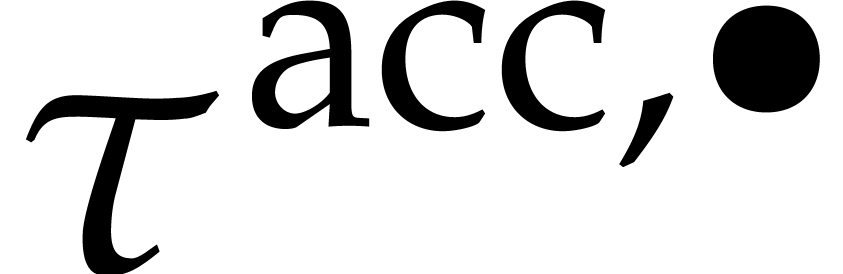 in the role of
in the role of  .
.
We further deform 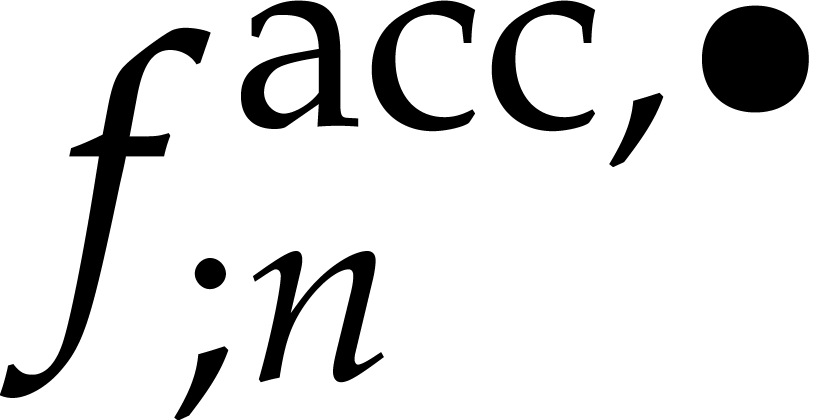 into a reliable truncated
solution
into a reliable truncated
solution 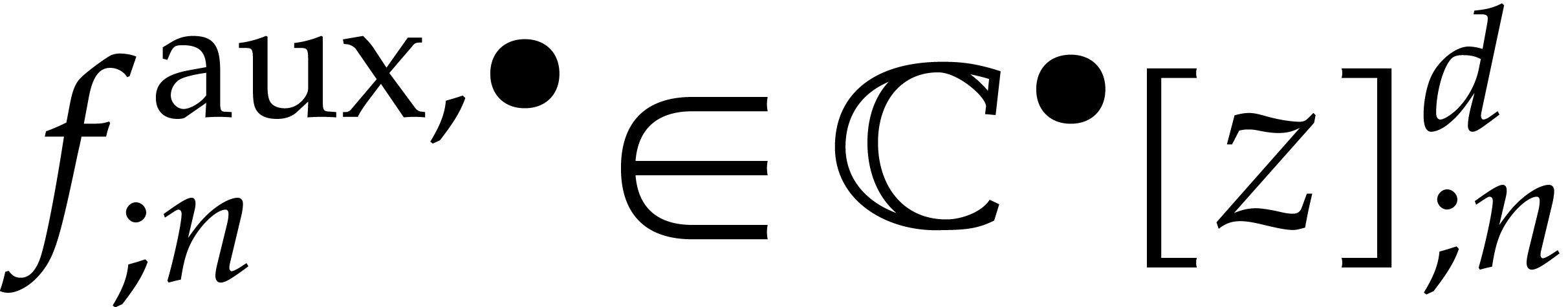 to (33), this time
with
to (33), this time
with  in the role of
in the role of  . We do this by computing
. We do this by computing  as above, together with a crude but reliable solution to the
equation
as above, together with a crude but reliable solution to the
equation
We then take
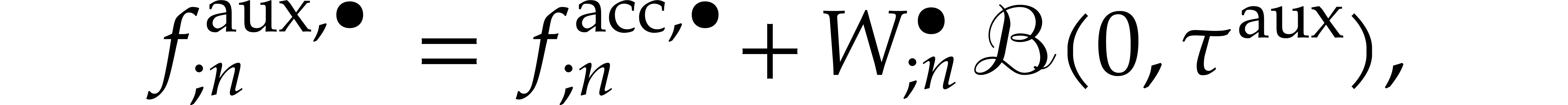
where 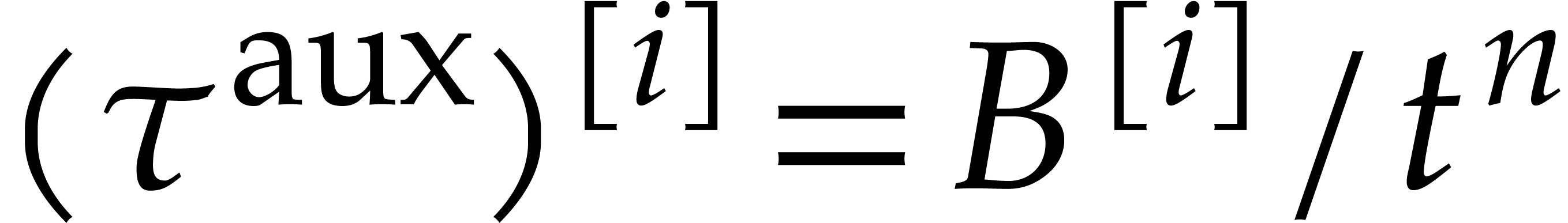 for
for 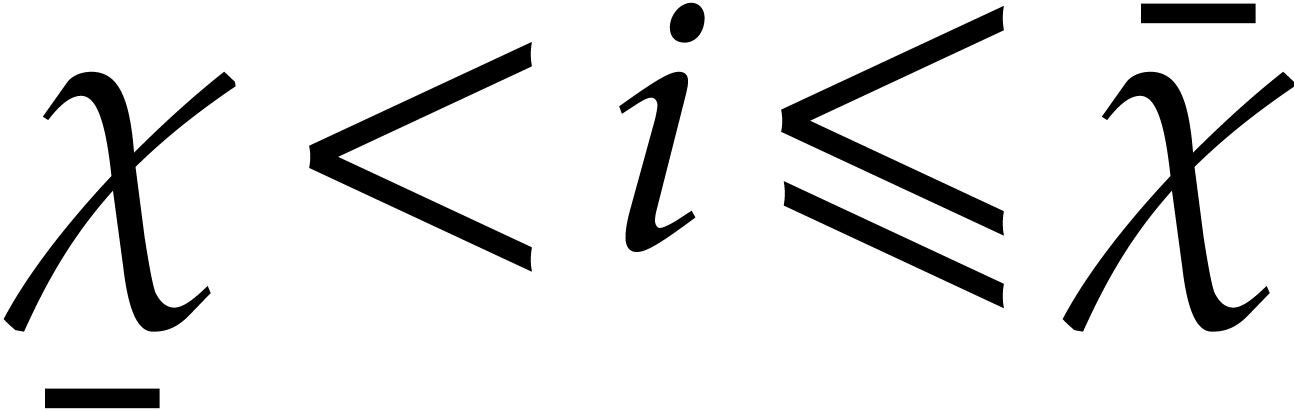 and
and 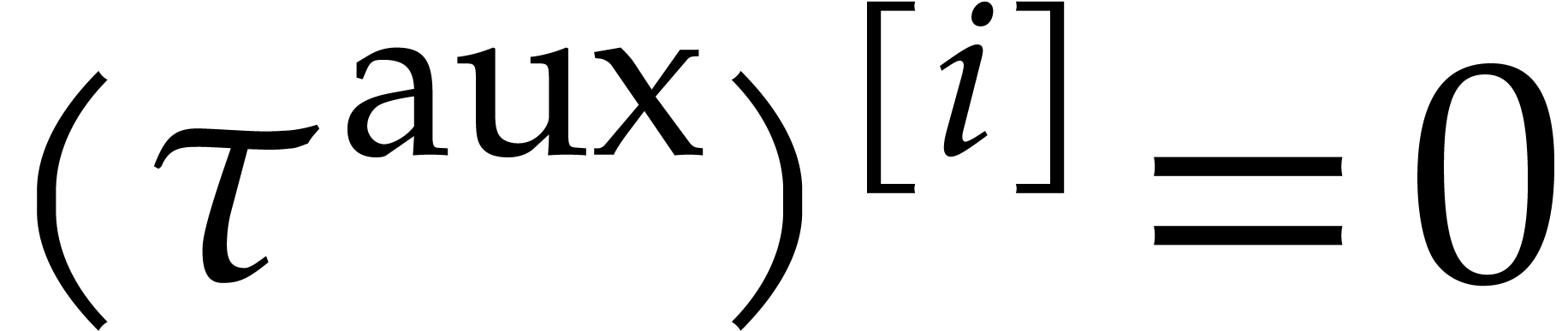 for
for 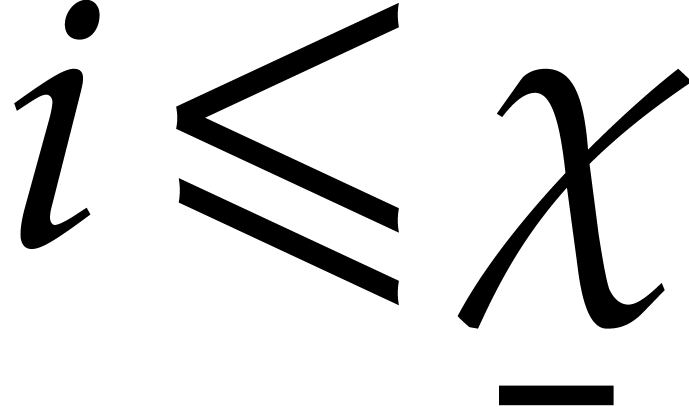 and
and  .
.
We finally compute the desired truncated solution  to (30) as
to (30) as

where  is computed as above.
is computed as above.
There are several directions for generalizations and further
improvements of the results in this paper. For simplicity, we assumed
 to be a diagonal matrix with positive
eigenvalues. It should not be hard to adapt the results to arbitrary
matrices
to be a diagonal matrix with positive
eigenvalues. It should not be hard to adapt the results to arbitrary
matrices  with positive real eigenvalues only (as
long as the forcing term
with positive real eigenvalues only (as
long as the forcing term  does not explode for
the change of coordinates that puts
does not explode for
the change of coordinates that puts  in Jordan
normal form).
in Jordan
normal form).
A more interesting generalization would be to consider complex
eigenvalues 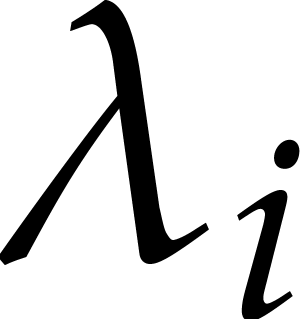 with strictly positive real parts.
In that case, the half disks
with strictly positive real parts.
In that case, the half disks  would need to be
replaced by smaller compact sectors of the form
would need to be
replaced by smaller compact sectors of the form 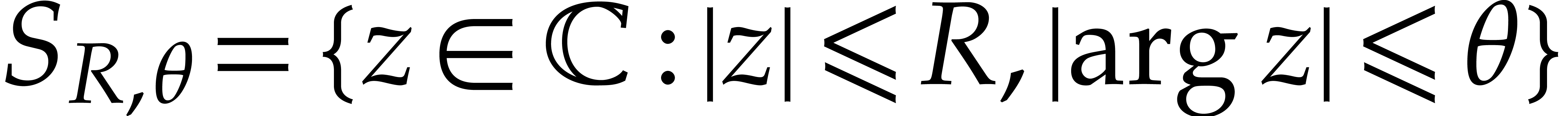 with
with 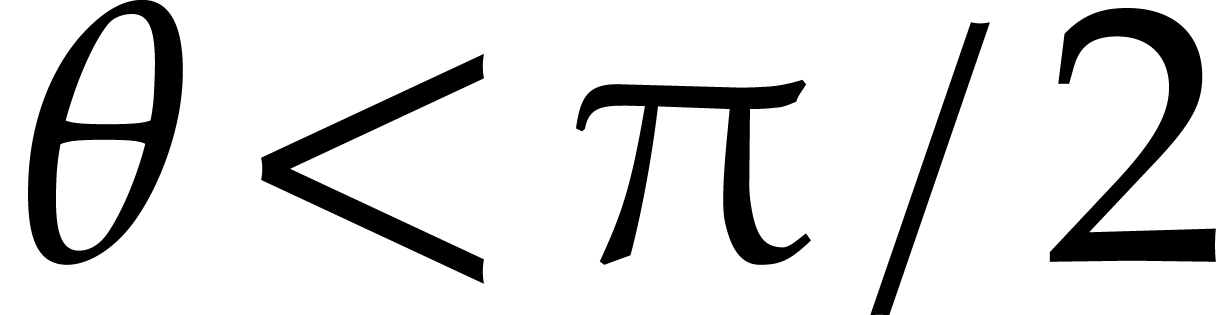 . Even more generally,
one may investigate how to develop accurate Taylor series methods for
integrating arbitrary differential equations with the property that the
step size is proportional to the radius of convergence of the exact
solution; see also Remark 10.
. Even more generally,
one may investigate how to develop accurate Taylor series methods for
integrating arbitrary differential equations with the property that the
step size is proportional to the radius of convergence of the exact
solution; see also Remark 10.
In this paper, we focussed on high precision computations using high order Taylor schemes. Another interesting question is whether it is possible to develop analogues of our methods in the same spirit as more traditional Runge–Kutta schemes. How would such analogues compare to implicit integration schemes?
Concerning certified integration, the theory of Taylor models [18,
23, 19] allows for higher order expansions of
the flow  as a function of the initial condition
as a function of the initial condition
 (that is, beyond the computation of the first
variation as in this paper). We think that it should be relatively
straightforward to adapt our techniques to such higher order expansions.
In a similar vein, we expect that the techniques from [7,
11] to further curb the wrapping effect can be adapted to
the stiff setting.
(that is, beyond the computation of the first
variation as in this paper). We think that it should be relatively
straightforward to adapt our techniques to such higher order expansions.
In a similar vein, we expect that the techniques from [7,
11] to further curb the wrapping effect can be adapted to
the stiff setting.
From a more practical point of view, it would finally be interesting to
have more and better machine implementations. For the moment, we only
did a toy implementation of the main algorithm from section 5.1
in the
A. Bostan, F. Chyzak, F. Ollivier, B. Salvy, É. Schost, and A. Sedoglavic. Fast computation of power series solutions of systems of differential equations. In Proceedings of the 18th ACM-SIAM Symposium on Discrete Algorithms, pages 1012–1021. New Orleans, Louisiana, U.S.A., January 2007.
R. P. Brent and H. T. Kung. Fast algorithms for manipulating formal power series. Journal of the ACM, 25:581–595, 1978.
R. P. Brent and P. Zimmermann. Modern Computer Arithmetic. Cambridge University Press, 2010.
J. C. Butcher. Numerical methods for ordinary differential equations in the 20th century. J. of Computational and Applied Mathematics, 125:1–29, 2000.
J.-P. Eckmann, H. Koch, and P. Wittwer. A computer-assisted proof of universality in area-preserving maps. Memoirs of the AMS, 47(289), 1984.
M. J. Fischer and L. J. Stockmeyer. Fast on-line integer multiplication. Proc. 5th ACM Symposium on Theory of Computing, 9:67–72, 1974.
T. N. Gambill and R. D. Skeel. Logarithmic reduction of the wrapping effect with application to ordinary differential equations. SIAM J. Numer. Anal., 25(1):153–162, 1988.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. New algorithms for relaxed multiplication. JSC, 42(8):792–802, 2007.
J. van der Hoeven. Newton's method and FFT trading. J. Symbolic Comput., 45(8):857–878, 2010.
J. van der Hoeven. Certifying trajectories of dynamical systems. In I. Kotsireas, S. Rump, and C. Yap, editors, Mathematical Aspects of Computer and Information Sciences: 6th International Conference, MACIS 2015, Berlin, Germany, November 11-13, 2015, Revised Selected Papers, pages 520–532. Cham, 2016. Springer International Publishing.
J. van der Hoeven, G. Lecerf, B. Mourrain et al. Mathemagix. from 2002. http://www.mathemagix.org.
Joris van der Hoeven and Grégoire Lecerf. Evaluating straight-line programs over balls. In Paolo Montuschi, Michael Schulte, Javier Hormigo, Stuart Oberman, and Nathalie Revol, editors, 2016 IEEE 23nd Symposium on Computer Arithmetic, pages 142–149. IEEE, 2016.
W. Kühn. Rigourously computed orbits of dynamical systems without the wrapping effect. Computing, 61:47–67, 1998.
O. E. Lanfort. A computer assisted proof of the Feigenbaum conjectures. Bull. of the AMS, 6:427–434, 1982.
R. Lohner. Einschließung der Lösung gewöhnlicher Anfangs- und Randwertaufgaben und Anwendugen. PhD thesis, Universität Karlsruhe, 1988.
R. Lohner. On the ubiquity of the wrapping effect in the computation of error bounds. In U. Kulisch, R. Lohner, and A. Facius, editors, Perspectives on enclosure methods, pages 201–217. Wien, New York, 2001. Springer.
K. Makino and M. Berz. Remainder differential algebras and their applications. In M. Berz, C. Bischof, G. Corliss, and A. Griewank, editors, Computational differentiation: techniques, applications and tools, pages 63–74. SIAM, Philadelphia, 1996.
K. Makino and M. Berz. Suppression of the wrapping effect by Taylor model-based validated integrators. Technical Report MSU Report MSUHEP 40910, Michigan State University, 2004.
R. E. Moore. Automatic local coordinate transformations to reduce the growth of error bounds in interval computation of solutions to ordinary differential equation. In L. B. Rall, editor, Error in Digital Computation, volume 2, pages 103–140. John Wiley, 1965.
R. E. Moore. Interval Analysis. Prentice Hall, Englewood Cliffs, N.J., 1966.
A. Neumaier. The wrapping effect, ellipsoid arithmetic, stability and confedence regions. Computing Supplementum, 9:175–190, 1993.
A. Neumaier. Taylor forms - use and limits. Reliable Computing, 9:43–79, 2002.
K. Nickel. How to fight the wrapping effect. In Springer-Verlag, editor, Proc. of the Intern. Symp. on interval mathematics, pages 121–132. 1985.
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical recipes, the art of scientific computing. Cambridge University Press, 3rd edition, 2007.
A. Sedoglavic. Méthodes seminumériques en algèbre différentielle ; applications à l'étude des propriétés structurelles de systèmes différentiels algébriques en automatique. PhD thesis, École polytechnique, 2001.