Structured FFT and TFT:
symmetric and
lattice polynomials |
|
|
Joris van der Hoeven
|
|
Laboratoire d'informatique
UMR 7161 CNRS
École polytechnique
91128 Palaiseau Cedex, France
|
|
vdhoeven@lix.polytechnique.fr
|
|
|
|
LIRMM
UMR 5506 CNRS
Université de Montpellier II
Montpellier, France
|
|
|
|
Computer Science Department
Western University
London, Ontario
Canada
|
|
|
|
Abstract
In this paper, we consider the problem of efficient computations with
structured polynomials. We provide complexity results for computing
Fourier Transform and Truncated Fourier Transform of symmetric
polynomials, and for multiplying polynomials supported on a lattice.
1.Introduction
Fast computations with multivariate polynomials and power series have
been of fundamental importance since the early ages of computer algebra.
The representation is an important issue which conditions the
performance in an intrinsic way; see [23, 31,
8] for some historical references.
It is customary to distinguish three main types of representations:
dense, sparse, and functional. A dense representation is made
of a compact description of the support of the polynomial and the
sequence of its coefficients. The main example concerns block
supports – it suffices to store the coordinates of two
opposite vertices. In a dense representation all the coefficients of the
considered support are stored, even if they are zero. If a polynomial
has only a few non-zero terms in its bounding block, we shall prefer to
use a sparse representation which stores only the sequence of
the non-zero terms as pairs of monomials and coefficients. Finally, a
functional representation stores a function that can produce
values of the polynomials at any given point. This can be a pure
blackbox (which means that its internal structure is not supposed to be
known) or a specific data structure such as straight-line
programs (see Chapter 4 of [4], for instance, and [10] for a concrete library for the manipulation of polynomials
with a functional representation).
For dense representations with block supports, it is classical that the
algorithms used for the univariate case can be naturally extended: the
naive algorithm, Karatsuba's algorithm, and even Fast Fourier Transforms
[7, 30, 6, 28, 16] can be applied recursively in each variable, with good
performance. Another classical approach is the Kronecker substitution
which reduces the multivariate product to one variable only; for all
these questions, we refer the reader to classical books such as [29, 14]. When the number of variables is fixed
and the partial degrees tend to infinity, these techniques lead to
softly linear costs.
After the discovery of sparse interpolation [2, 24,
25, 26, 11], probabilistic
algorithms with a quasi-linear complexity have been developed for sparse
polynomial multiplication [5]. It has recently be shown
that such asymptotically fast algorithms may indeed become more
efficient than naive sparse multiplication [19].
In practice however, it frequently happens that multivariate polynomials
with a dense flavor do not admit a block support. For instance, it is
common to consider polynomials of a given total degree. In a recent
series of works [15, 17, 18, 21, 20], we have studied the complexity of
polynomial multiplication in this “semi-dense” setting. In
the case when the supports of the polynomials are initial segments for
the partial ordering on 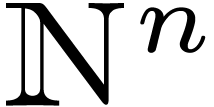 , the
truncated Fourier transform is a useful device for the design of
efficient algorithms.
, the
truncated Fourier transform is a useful device for the design of
efficient algorithms.
Besides polynomials with supports of a special kind, we may also
consider what will call “structured polynomials”. By analogy
with linear algebra, such polynomials carry a special structure which
might be exploited for the design of more efficient algorithms. In this
paper, we turn our attention to a first important example of this kind:
polynomials which are invariant under the action of certain matrix
groups. We consider only two special cases: finite subgroups of  and finite groups of diagonal matrices. These cases
are already sufficient to address questions raised e.g. in
celestial mechanics [12]; it is hoped that more general
groups can be dealt with using similar ideas.
and finite groups of diagonal matrices. These cases
are already sufficient to address questions raised e.g. in
celestial mechanics [12]; it is hoped that more general
groups can be dealt with using similar ideas.
In the limited scope of this paper, our main objective is to prove
complexity results that demonstrate the savings induced by a proper use
of the symmetries. Our complexity analyses take into account the number
of arithmetic operations in the base field, and as often, we consider
that operations with groups and lattices take a constant number of
operations. A serious implementation of our algorithms would require an
improved study of these aspects.
Of course, there already exists an abundant body of work on some of
these questions. Crystallographic FFT algorithms date back to
[32], with contributions as recent as [27],
but are dedicated to crystallographic symmetries. A more general
framework due to [1] was recently revisited under the point
of view of high-performance code generation [22]; our
treatment of permutation groups is in a similar spirit, but to our
understanding, these previous papers do not prove results such as those
we give below (and they only consider the FFT, not its truncated
version).
Similarly, our results on diagonal groups, which fit in the general
context of FFTs over lattices, use similar techniques as in a series of
papers initiated by [13] and continued as recently as [33, 3], but the actual results we prove are not
in those references.
2.The classical FFT
2.1Notation
We will work over an effective base field (or ring)  with sufficiently many roots of unity; the main objects are polynomials
with sufficiently many roots of unity; the main objects are polynomials
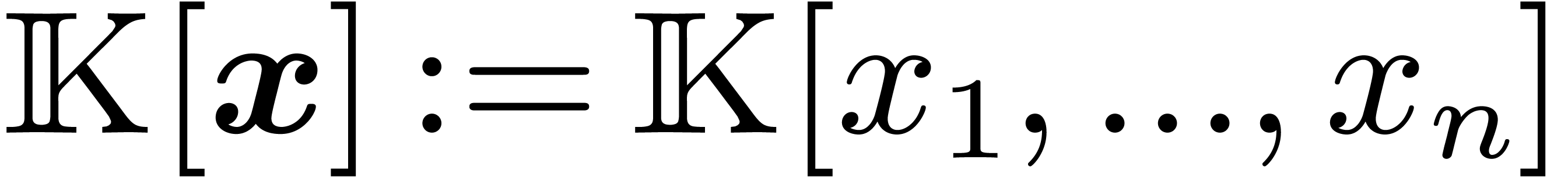 in
in 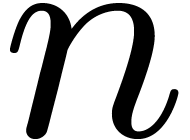 variables over
variables over  . For any
. For any  and
and 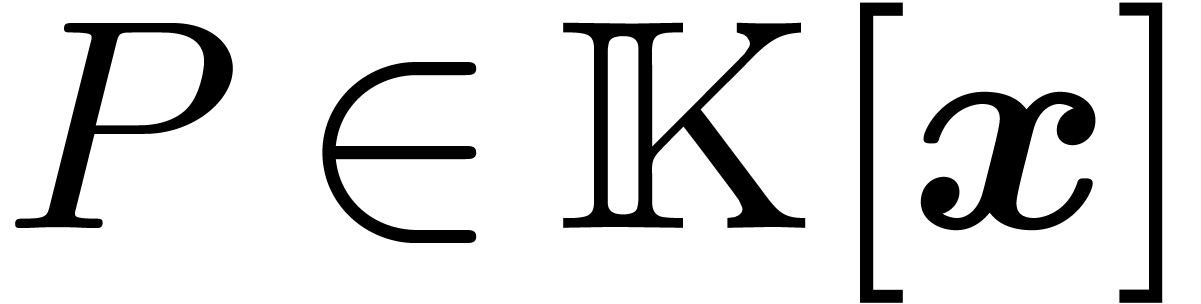 , we denote by
, we denote by 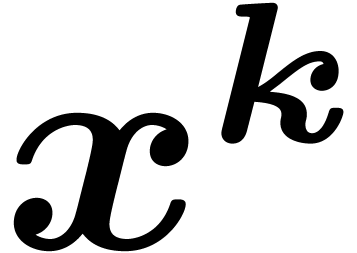 the monomial
the monomial  and by
and by  the coefficient of
the coefficient of  in
in 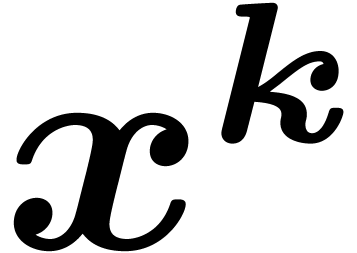 . The support
. The support 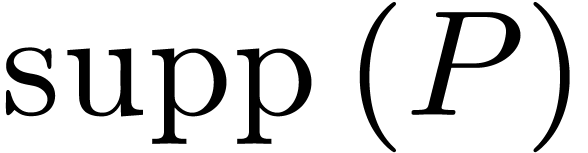 of a
polynomial
of a
polynomial 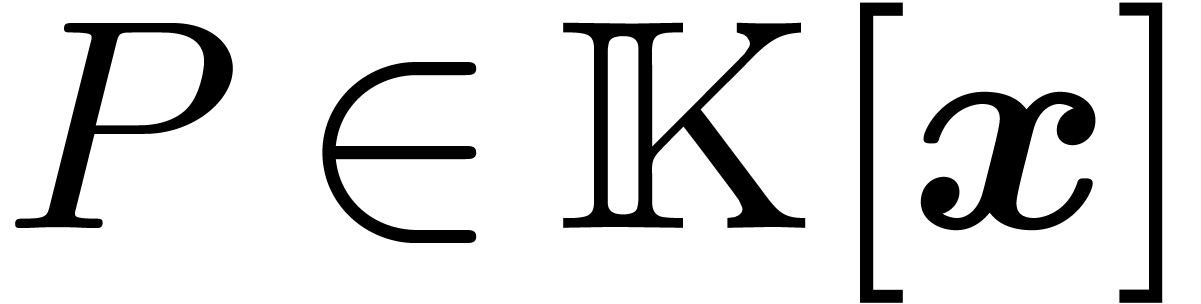 is the set of exponents
is the set of exponents  such that
such that  .
.
For any subset  of
of 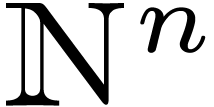 ,
we define
,
we define 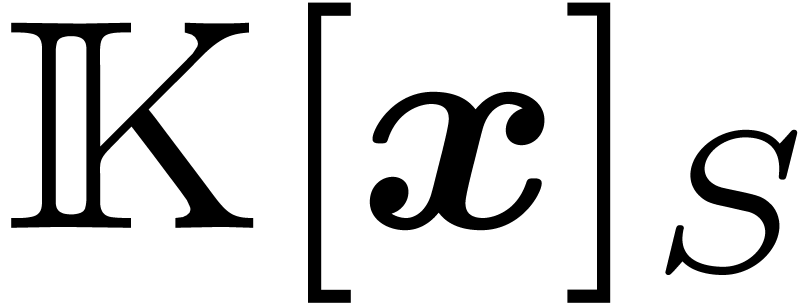 as the polynomials with support
included in
as the polynomials with support
included in  . As an important
special case, when
. As an important
special case, when 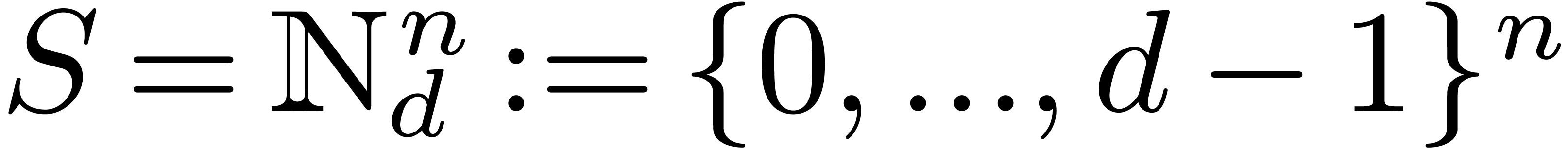 , we
denote by
, we
denote by 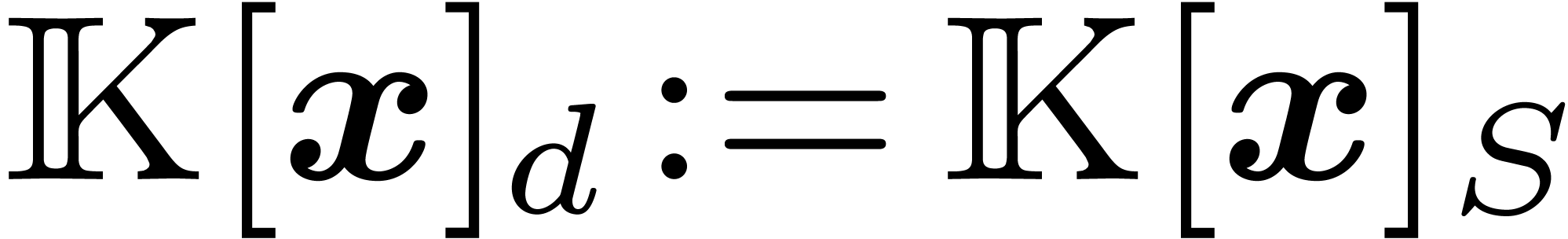 the set of polynomials with partial
degree less than
the set of polynomials with partial
degree less than 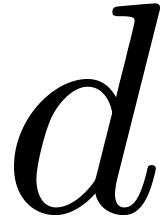 in all variables.
in all variables.
Let  be a primitive
be a primitive 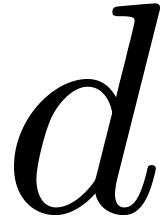 th
root of unity (in Section 4, it will be convenient to write
this root
th
root of unity (in Section 4, it will be convenient to write
this root 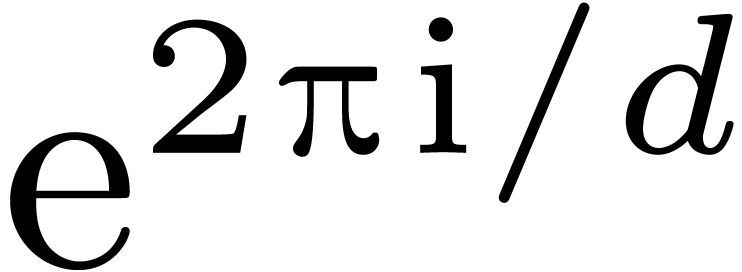 ). For any
). For any  , we define
, we define 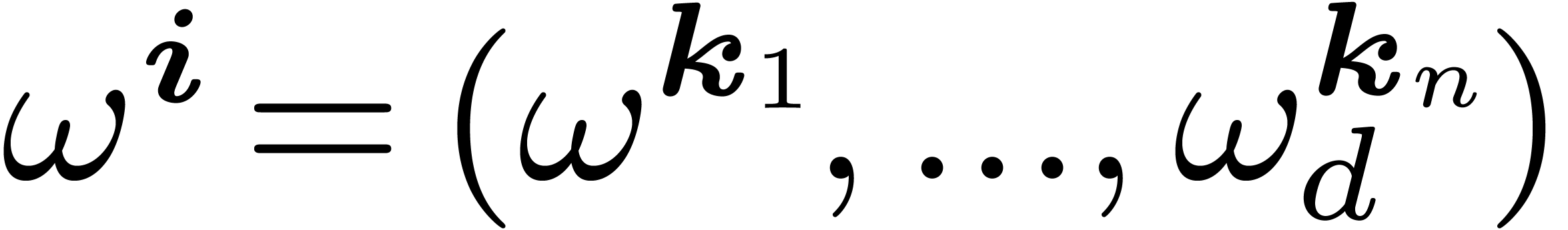 . One of our aims is to compute efficiently the map
. One of our aims is to compute efficiently the map
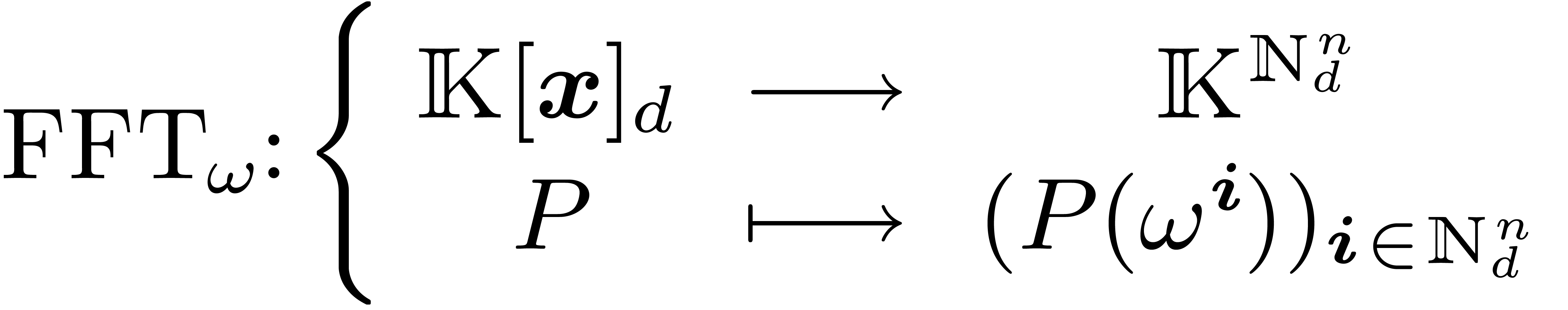
when 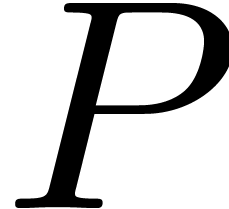 is a “structured polynomial”.
Here,
is a “structured polynomial”.
Here, 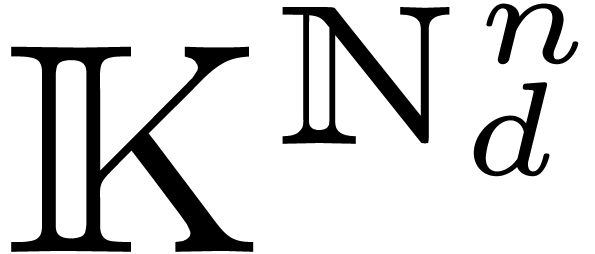 denotes the set of vectors with entries in
denotes the set of vectors with entries in
 indexed by
indexed by  ;
in other words,
;
in other words,  implies that
implies that  for all
for all  . Likewise,
. Likewise, 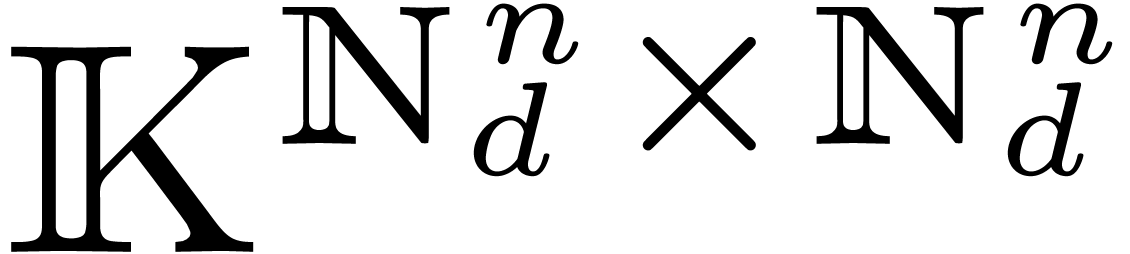 denotes the set of matrices with indices in
denotes the set of matrices with indices in 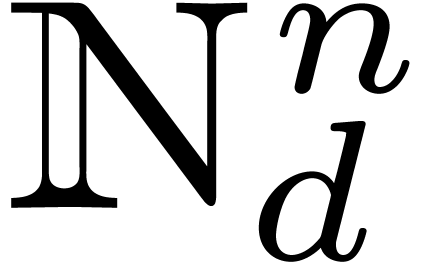 , that is,
, that is,  implies that
implies that
 for all
for all  .
.
Most of the time, we will take 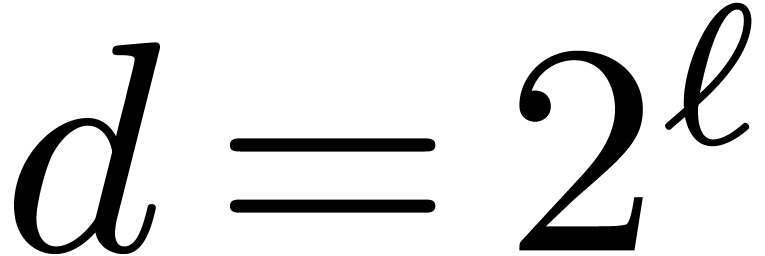 with
with 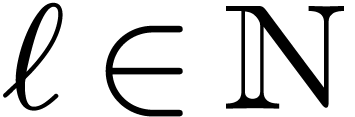 , although we will also need more general
, although we will also need more general 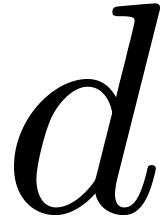 of mixed radices
of mixed radices 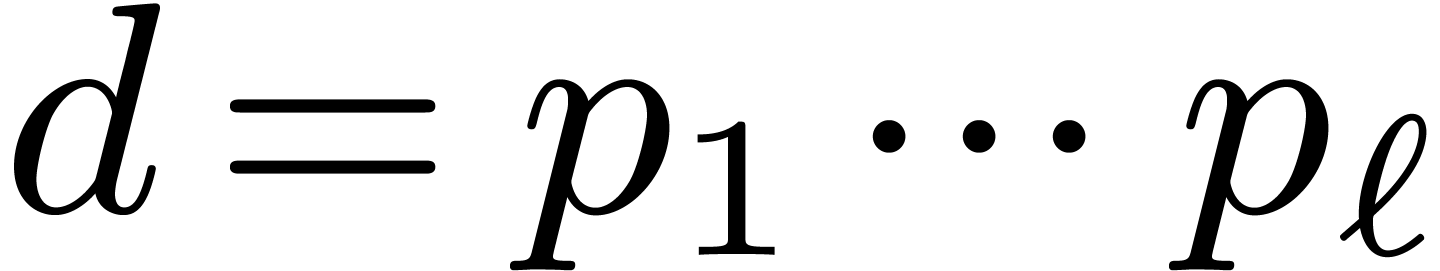 .
.
We denote by 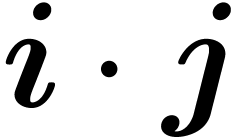 the inner product of two vectors in
the inner product of two vectors in
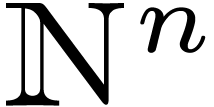 . We also let
. We also let 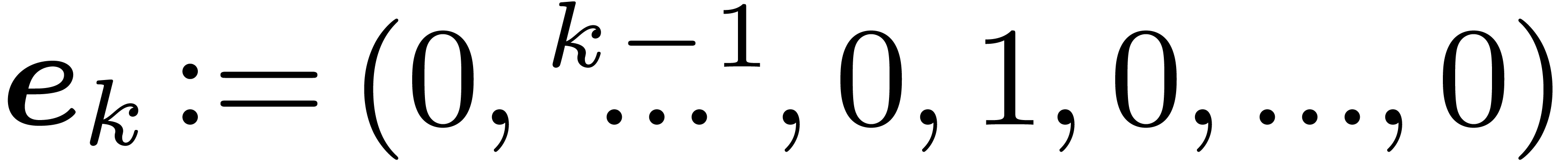 , for
, for  ,
be the
,
be the 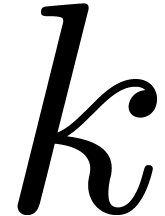 th element of the
canonical basis of
th element of the
canonical basis of 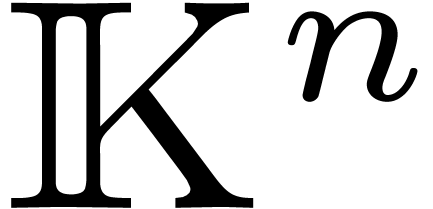 . At last,
for
. At last,
for 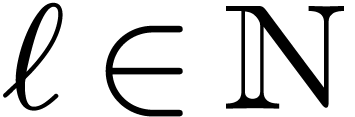 and
and 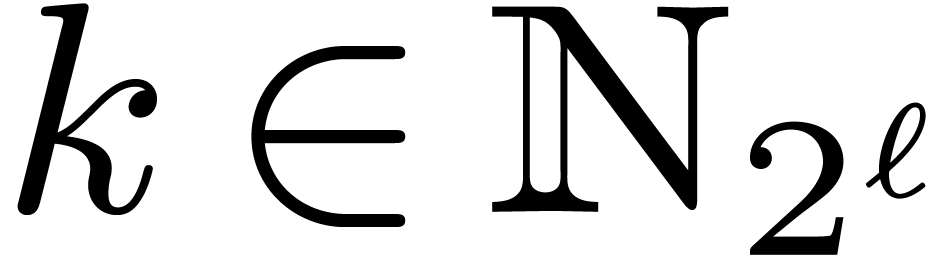 we denote by
we denote by
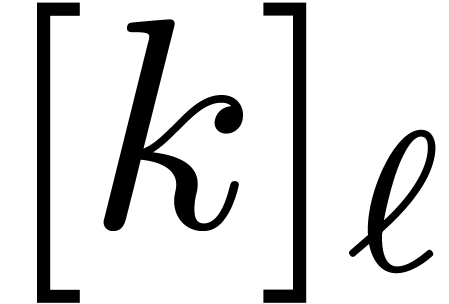 the bit reversal of
the bit reversal of 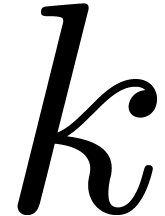 in
length
in
length 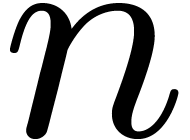 and we extend this notation to vectors by
and we extend this notation to vectors by
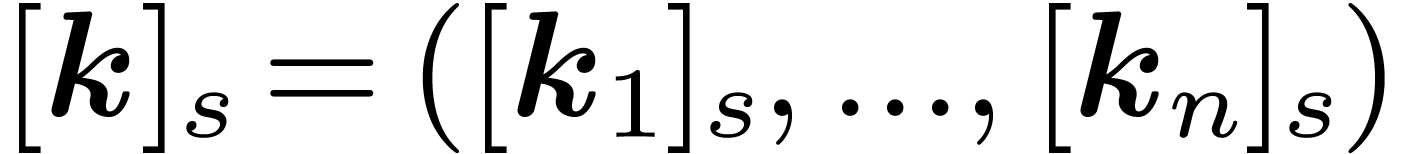 .
.
2.2The classical multivariate
FFT
Let us first consider the in-place computation of a full 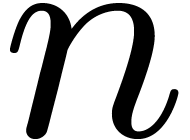 -dimensional FFT of length
-dimensional FFT of length 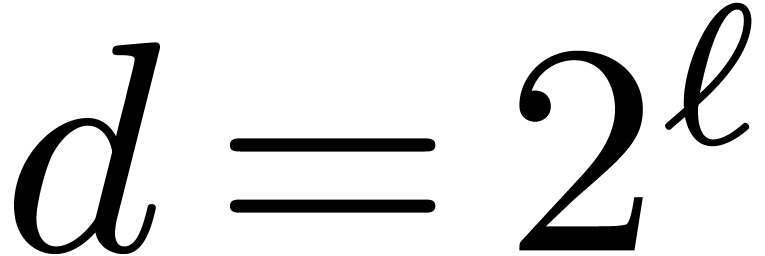 in each variable. We first recall the notations and operations of the
decimation in time variant of the FFT, and we refer the reader to [9] for more details. In what follows,
in each variable. We first recall the notations and operations of the
decimation in time variant of the FFT, and we refer the reader to [9] for more details. In what follows,  is a
is a 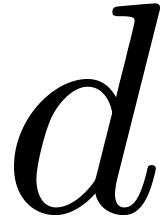 th primitive root of
unity.
th primitive root of
unity.
We start with the FFT of a univariate polynomial 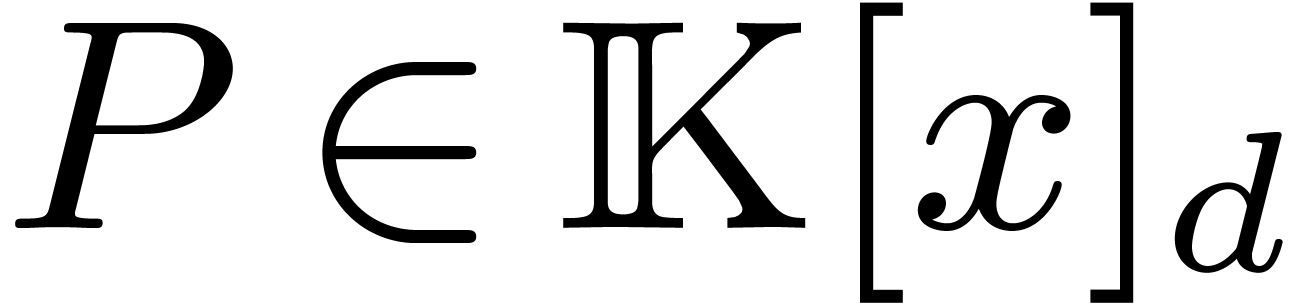 . Decimation in time amounts to decomposing
. Decimation in time amounts to decomposing  into its even and odd parts, and proceeding
recursively, by means of
into its even and odd parts, and proceeding
recursively, by means of 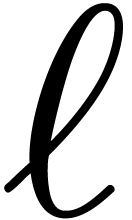 decimations applied to
the variable
decimations applied to
the variable 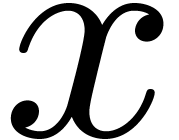 . For
. For  , we will write
, we will write 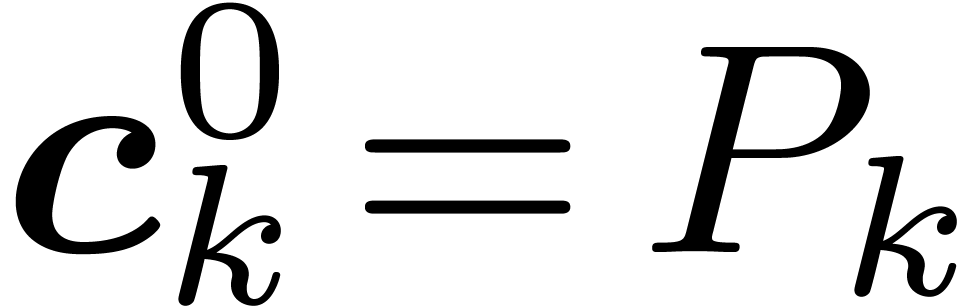 for the input and denote by
for the input and denote by 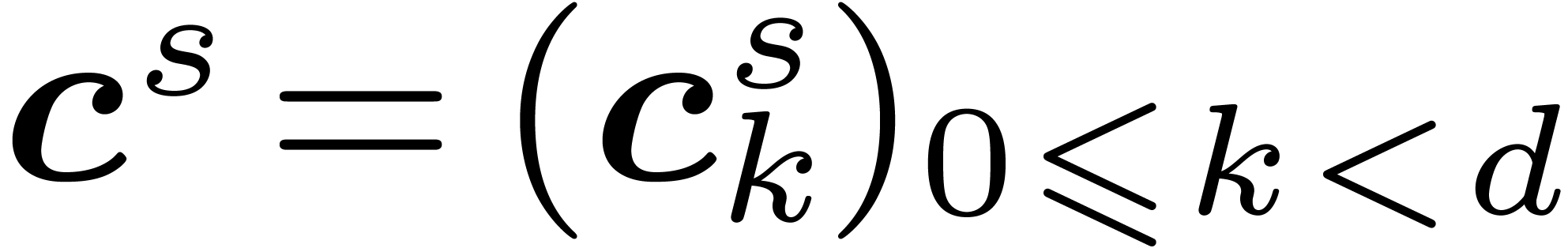 the result after
the result after
 decimation steps, for
decimation steps, for 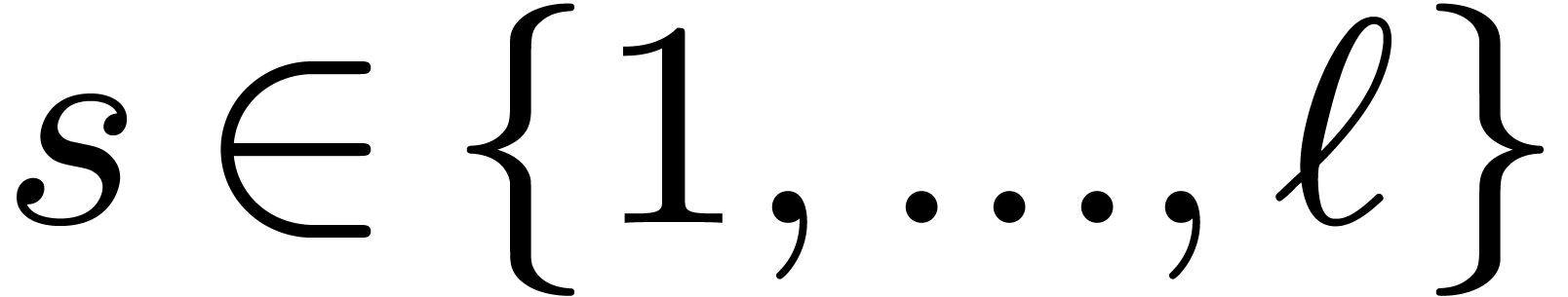 .
.
At stage  , the decimation is
computed using butterflies of span
, the decimation is
computed using butterflies of span 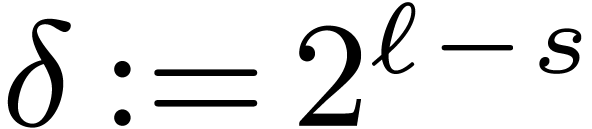 .
If
.
If 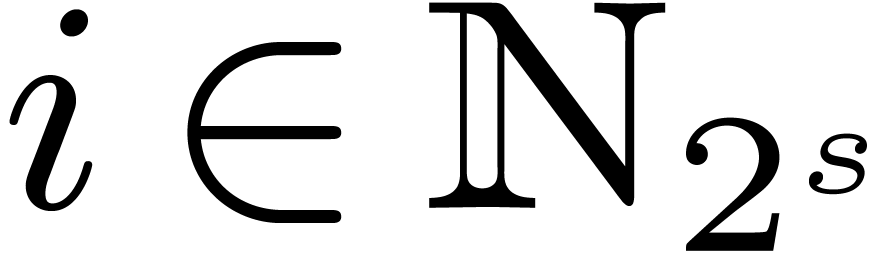 is even and
is even and  belongs
to
belongs
to  then these butterflies are given by
then these butterflies are given by
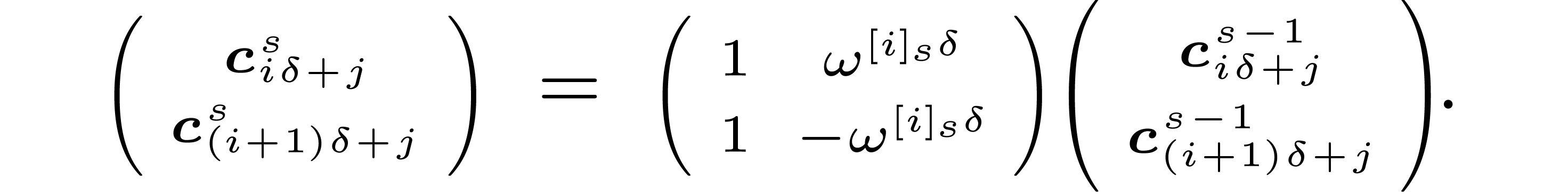
Putting the coefficients of all these linear relations in a matrix 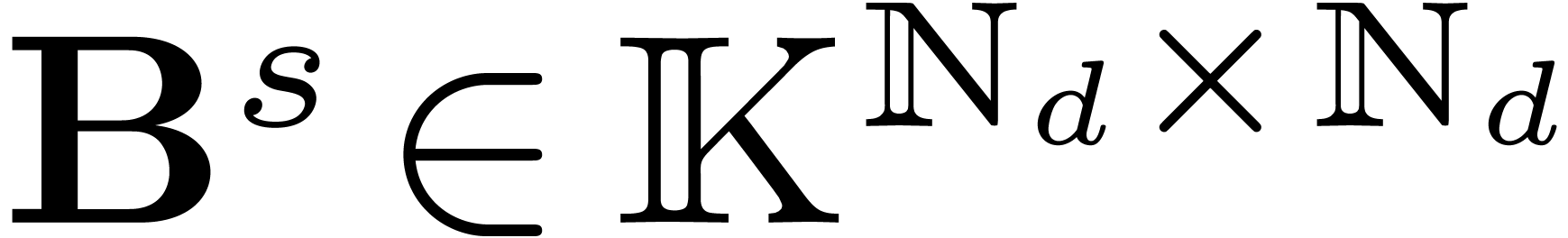 , we get
, we get 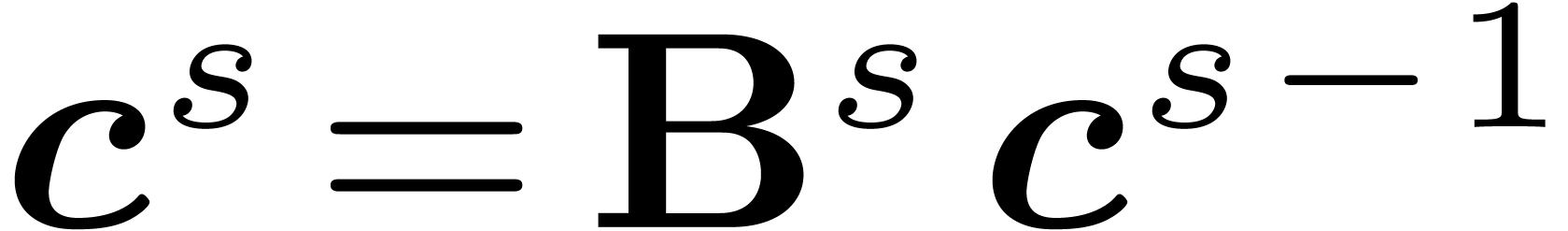 . The matrix
. The matrix 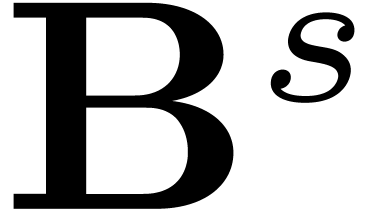 is sparse, with
at most two non-zero coefficients on each row and each column; up to
permutation, it is block-diagonal, with blocks of size 2. After
is sparse, with
at most two non-zero coefficients on each row and each column; up to
permutation, it is block-diagonal, with blocks of size 2. After  stages, we get the evaluations of
stages, we get the evaluations of 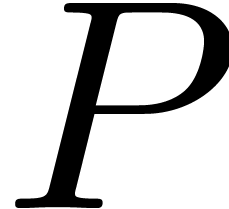 in the bit reversed order:
in the bit reversed order:
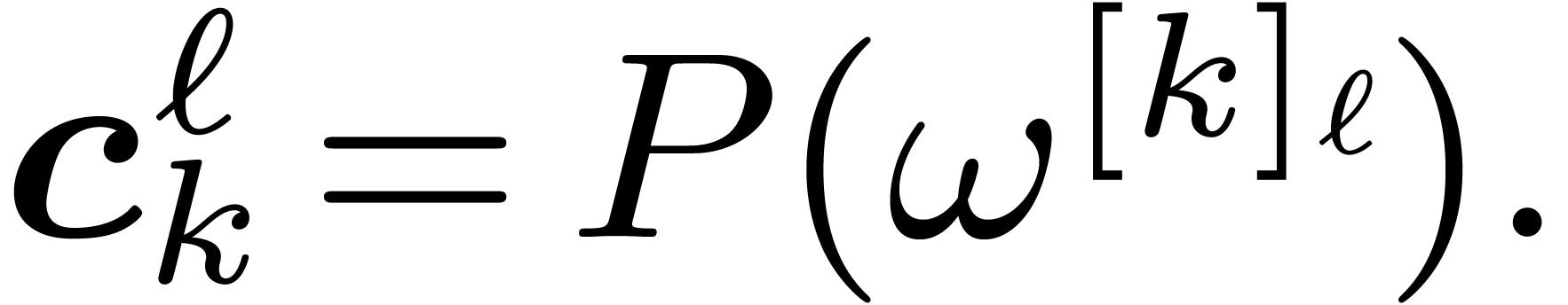
We now adapt this notation to the multivariate case. The computation is
still divided in 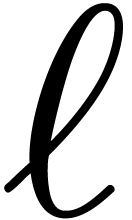 stages, each stage doing one
decimation in every variable
stages, each stage doing one
decimation in every variable  .
Therefore, we will denote by
.
Therefore, we will denote by 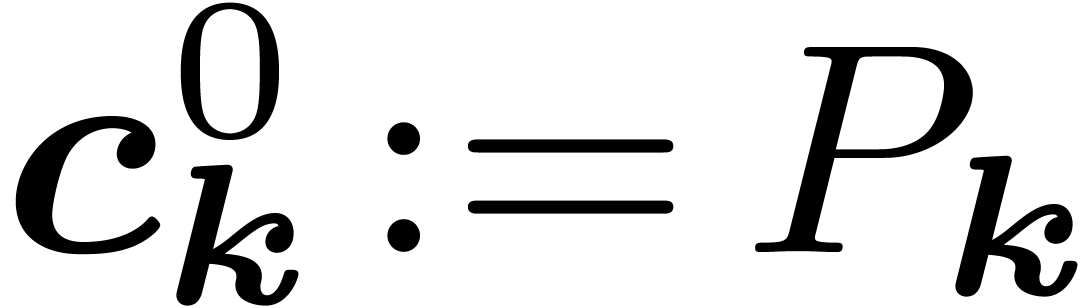 the coefficients of
the input for
the coefficients of
the input for 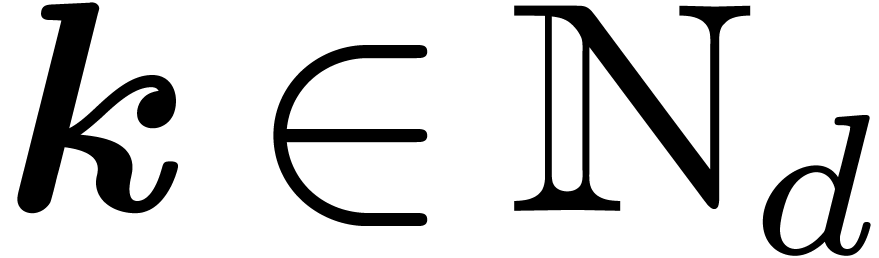 and by
and by 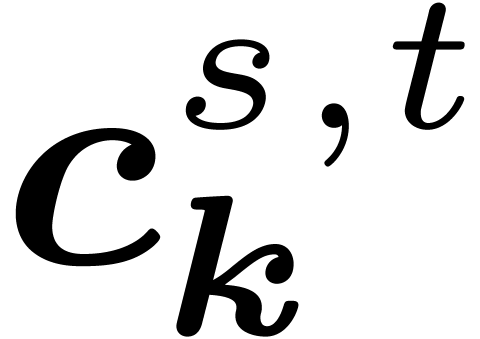 the
coefficients obtained during the
the
coefficients obtained during the  th
stage, after the decimations in
th
stage, after the decimations in  are done, with
are done, with
 and
and  ,
so that
,
so that 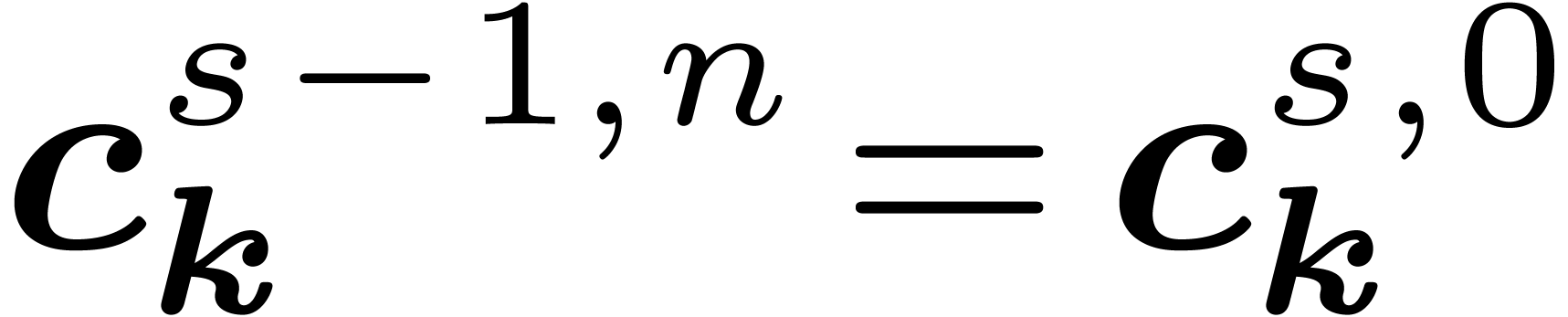 . We abbreviate
. We abbreviate 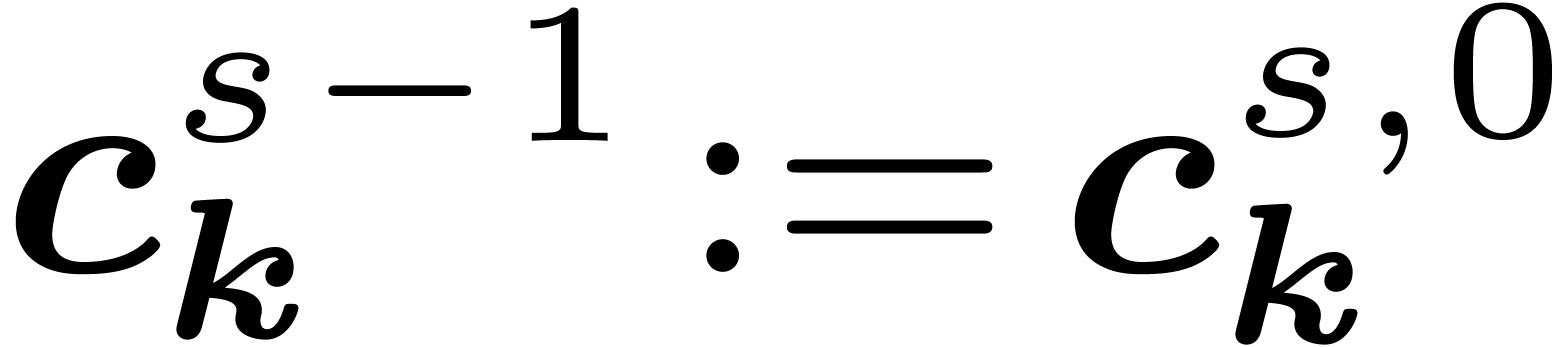 for the coefficients after
for the coefficients after  stages.
stages.
The intermediate coefficients 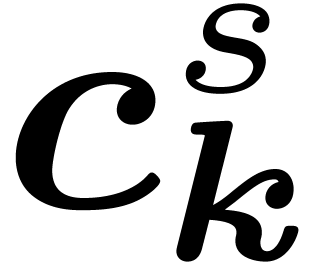 can be seen as
evaluations of intermediate polynomials: for every
can be seen as
evaluations of intermediate polynomials: for every 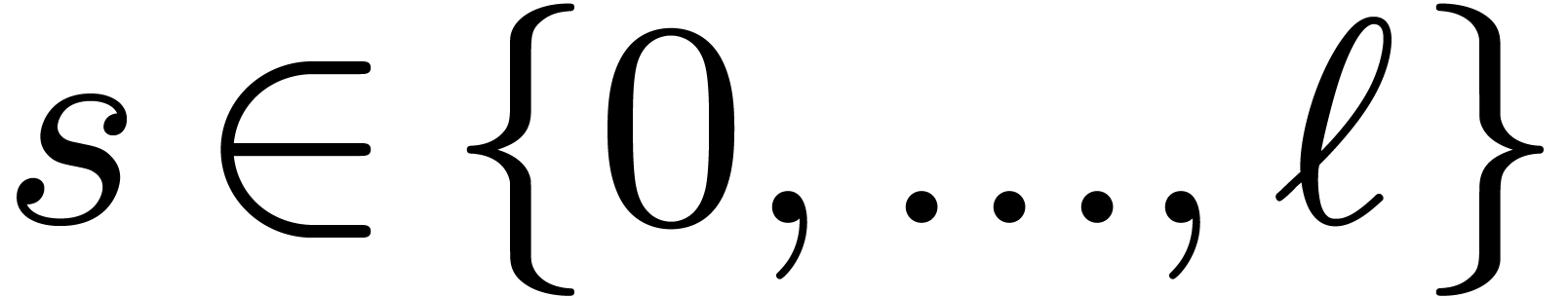 ,
, 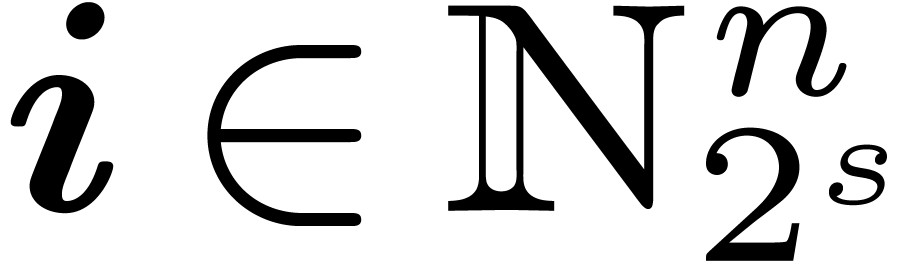 and
and 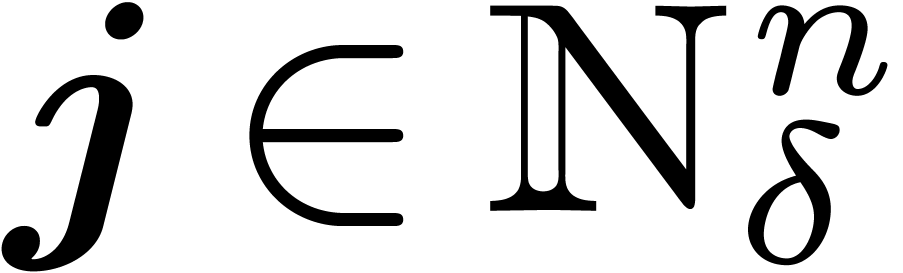 , one has
, one has
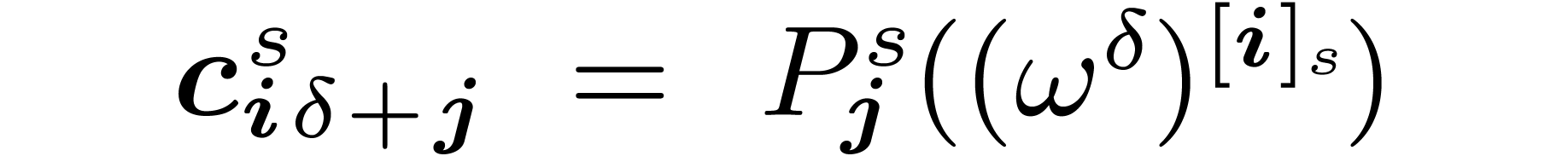 |
(1) |
where 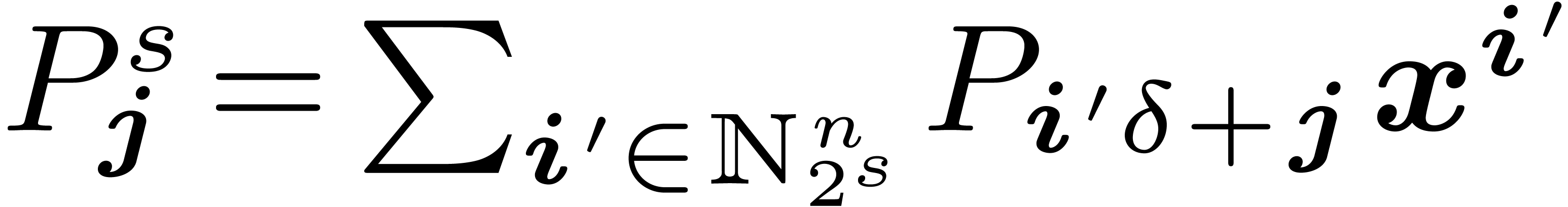 are obtained through an
are obtained through an  -fold decimation of
-fold decimation of 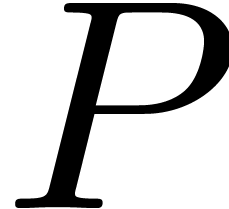 . Equivalently, the coefficients
. Equivalently, the coefficients 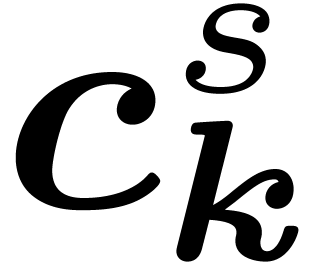 satisfy
satisfy
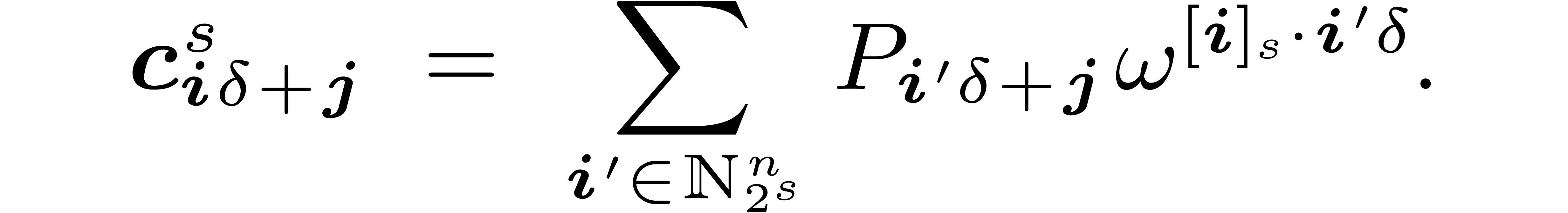 |
(2) |
Thus, 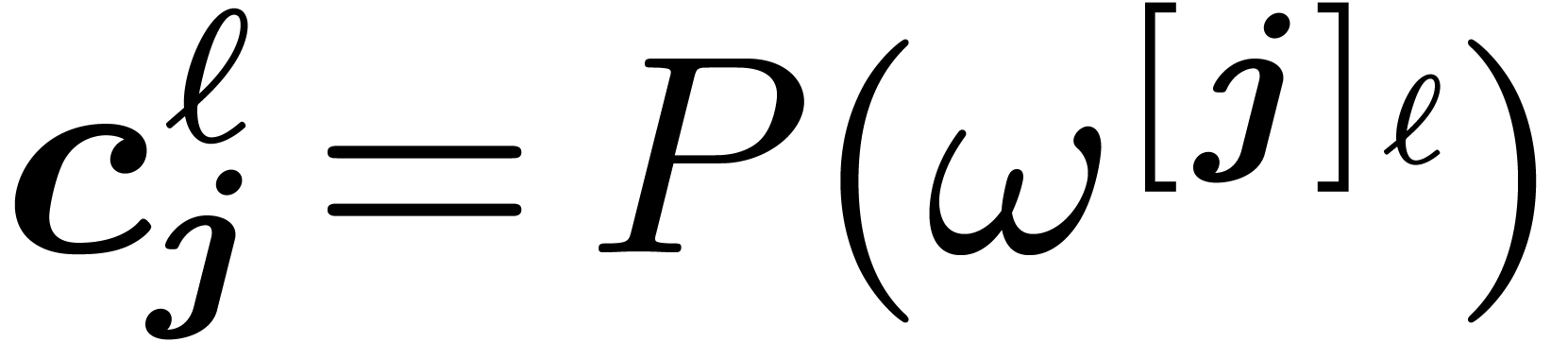 yields
yields 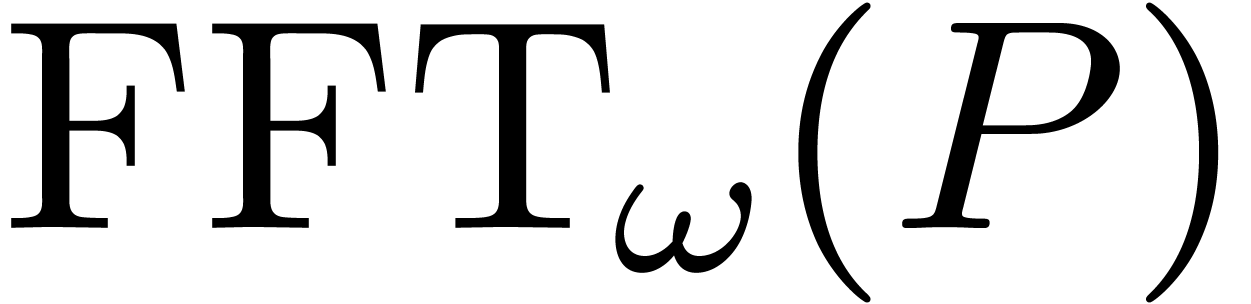 in bit
reversed order.
in bit
reversed order.
For the concrete computation of the coefficients 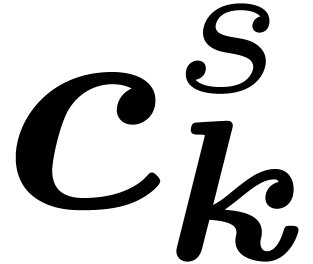 at stage
at stage  from the coefficients
from the coefficients 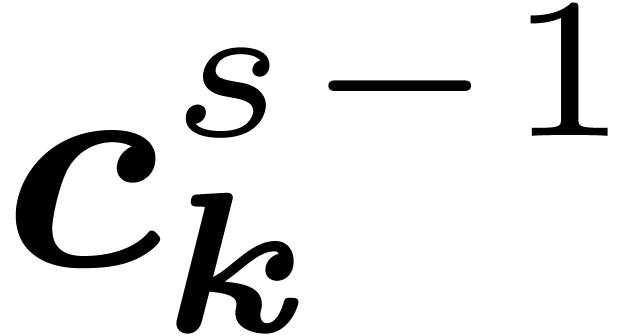 at stage
at stage  , we use
, we use 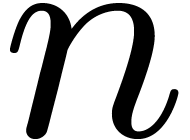 so called “elementary transforms” with respect
to each of the variables
so called “elementary transforms” with respect
to each of the variables  .
For any
.
For any 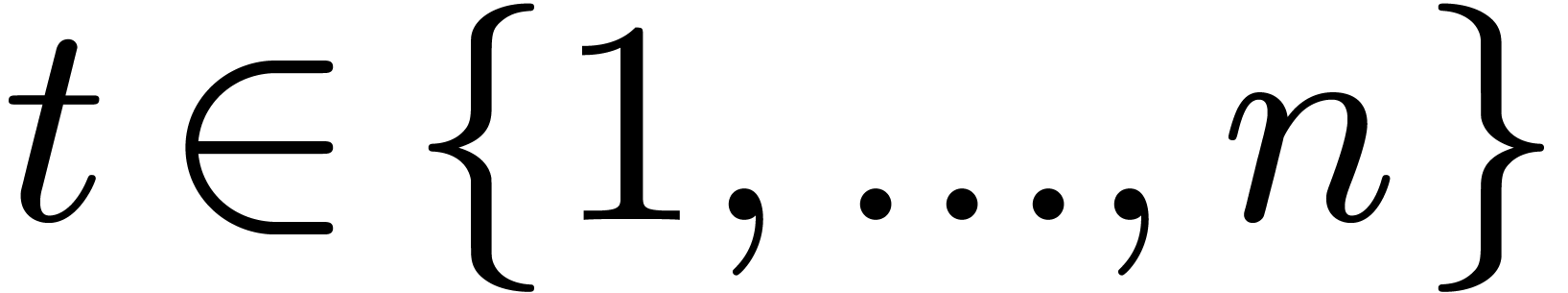 , the coefficients
, the coefficients
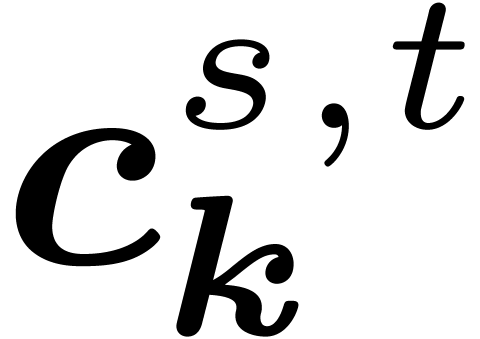 are obtained from the coefficients
are obtained from the coefficients 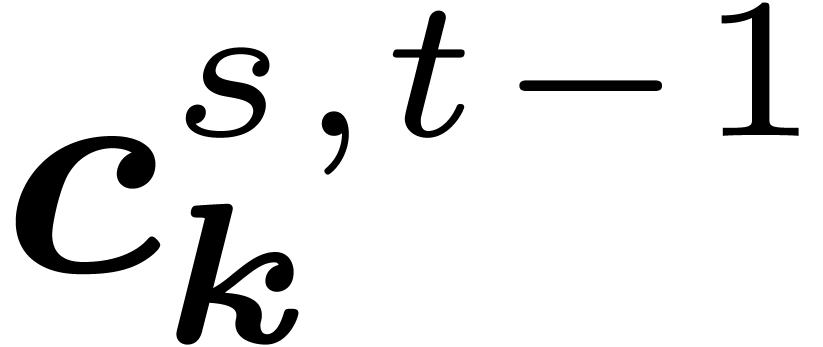 through butterflies of span
through butterflies of span 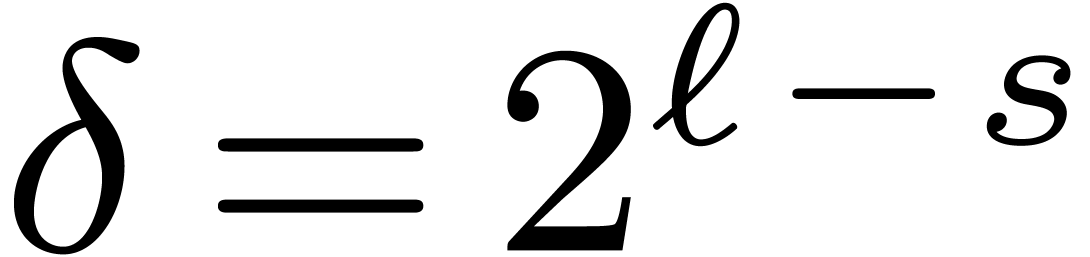 with
respect to the variable
with
respect to the variable 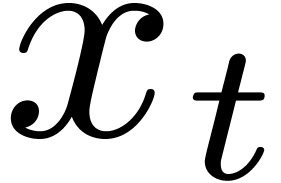 ;
this can be rewritten by means of the formula
;
this can be rewritten by means of the formula
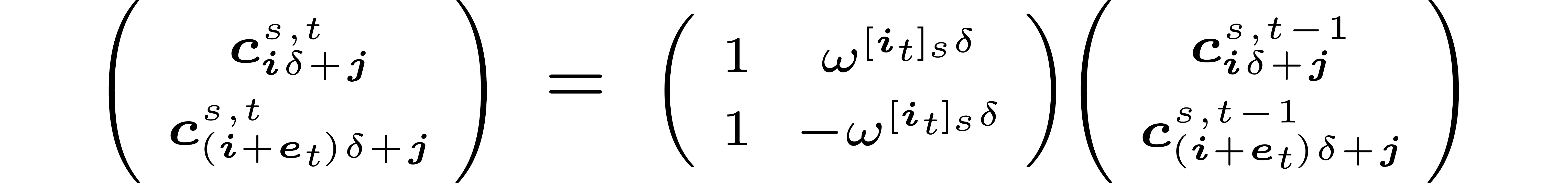 |
(3) |
for any 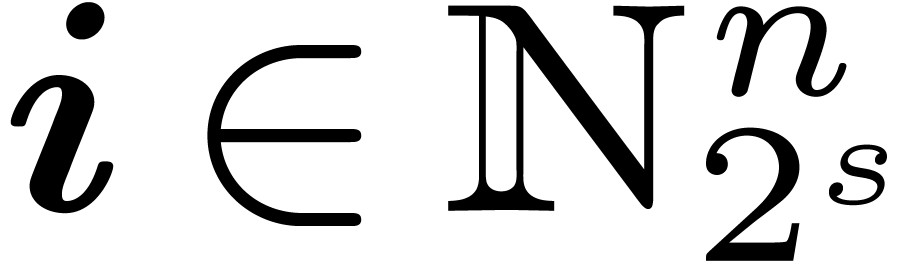 with even
with even 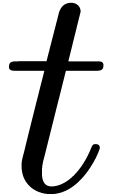 -th
coordinate
-th
coordinate 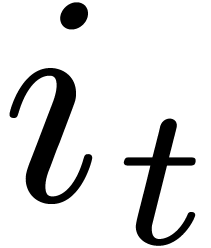 and
and 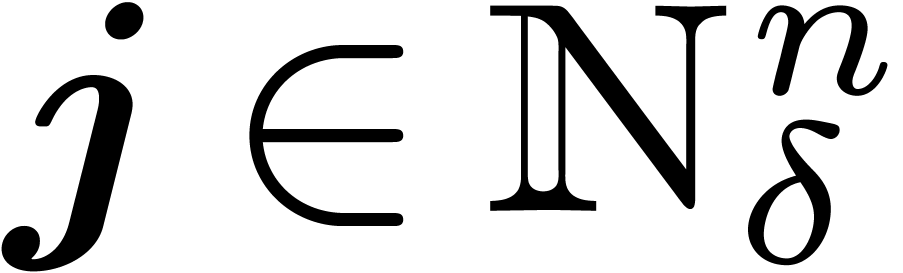 .
Equation (3) can be rewritten more compactly in matrix form
.
Equation (3) can be rewritten more compactly in matrix form
 where
where  is a sparse matrix
in
is a sparse matrix
in  which is naturally indexed by pairs of
multi-indices in
which is naturally indexed by pairs of
multi-indices in 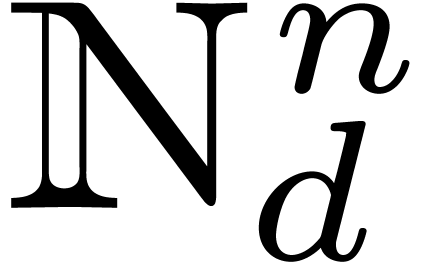 . Setting
. Setting
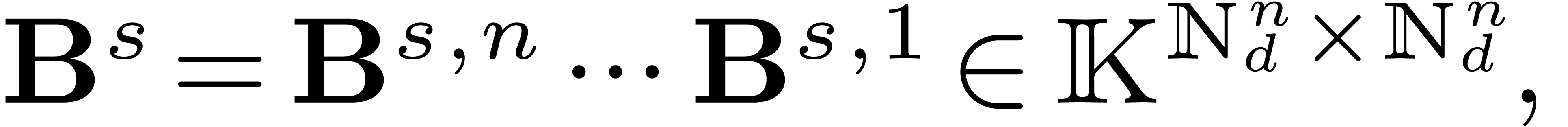 we also obtain a short
formula for
we also obtain a short
formula for 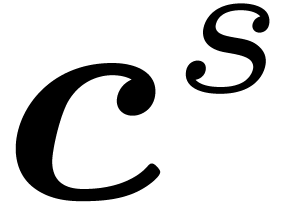 as a function of
as a function of 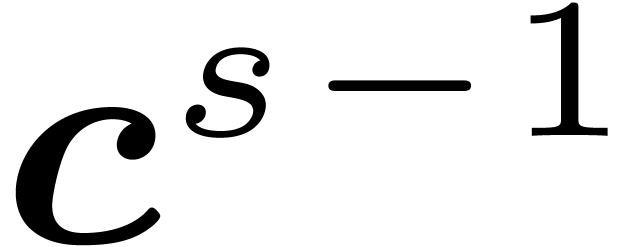 :
:
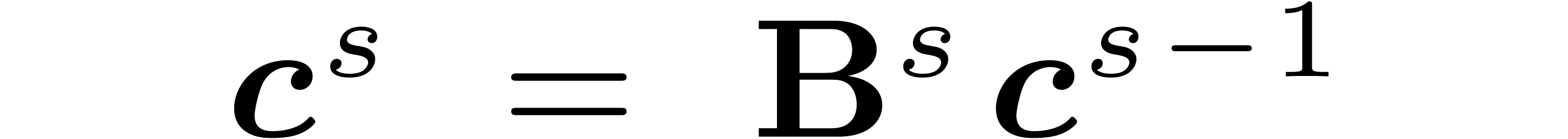 |
(4) |
Remark that the matrices  commute pairwise.
Notice also that each of the rows and columns of
commute pairwise.
Notice also that each of the rows and columns of  has at most
has at most  non zero entries and consequently
those of
non zero entries and consequently
those of 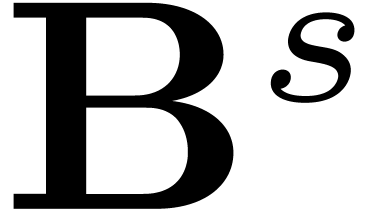 contains at most
contains at most 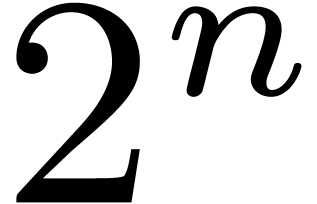 non zero entries. For this reason, we can apply the matrices
non zero entries. For this reason, we can apply the matrices  (resp.
(resp. 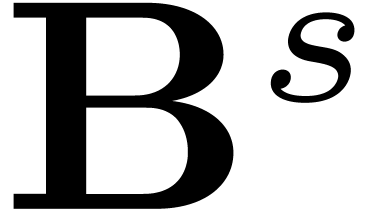 ) within
) within
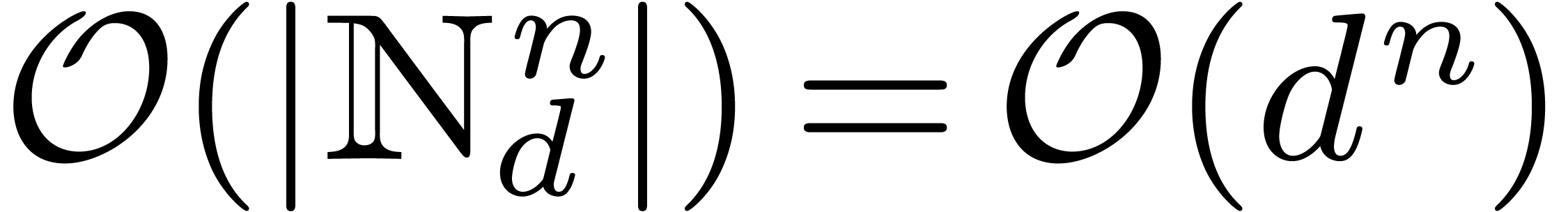 (resp.
(resp. 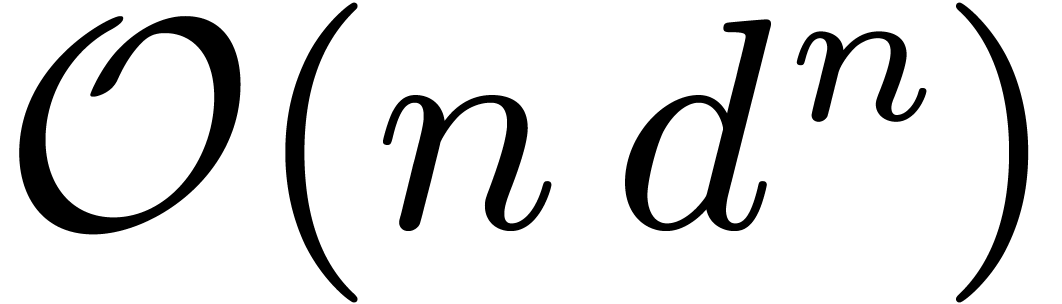 )
operations in
)
operations in  . Finally, the
full
. Finally, the
full 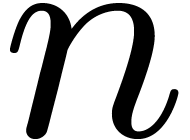 -dimensional FFT of
length
-dimensional FFT of
length 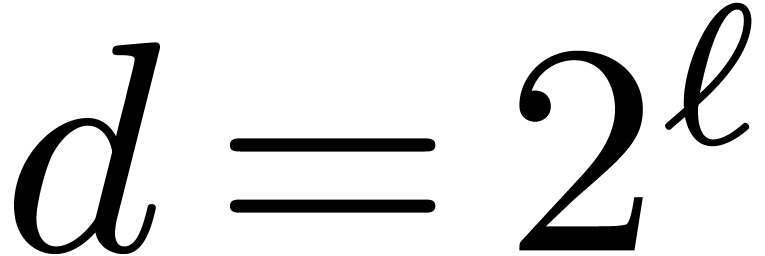 costs
costs 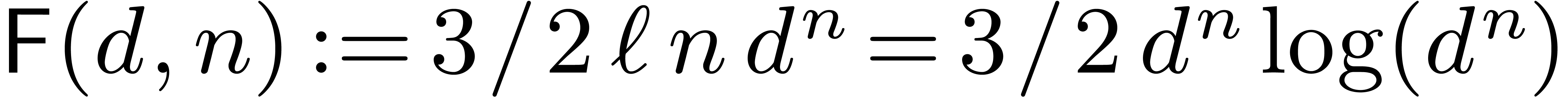 operations
in
operations
in  (see [14, Section 8.2]).
(see [14, Section 8.2]).
Example 1. Let us make these matrices
explicit for polynomials in 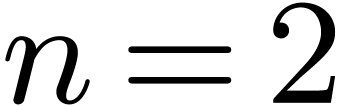 variables and degree
less than
variables and degree
less than  , so that
, so that 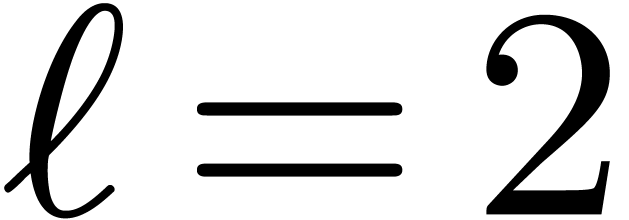 . We start with the first
decimation in
. We start with the first
decimation in 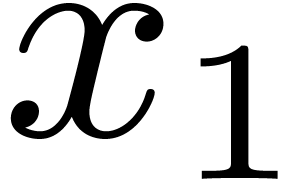 whose butterflies of span
whose butterflies of span  are captured by
are captured by  with
with 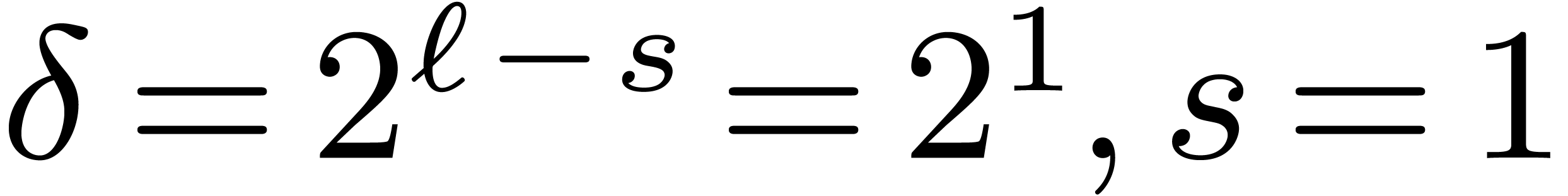 and
and 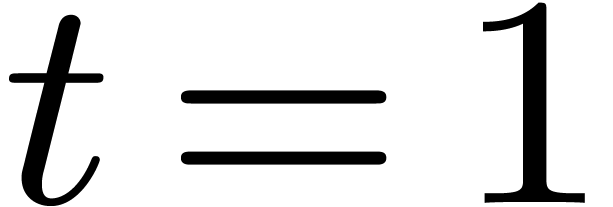 . It
takes as input
. It
takes as input 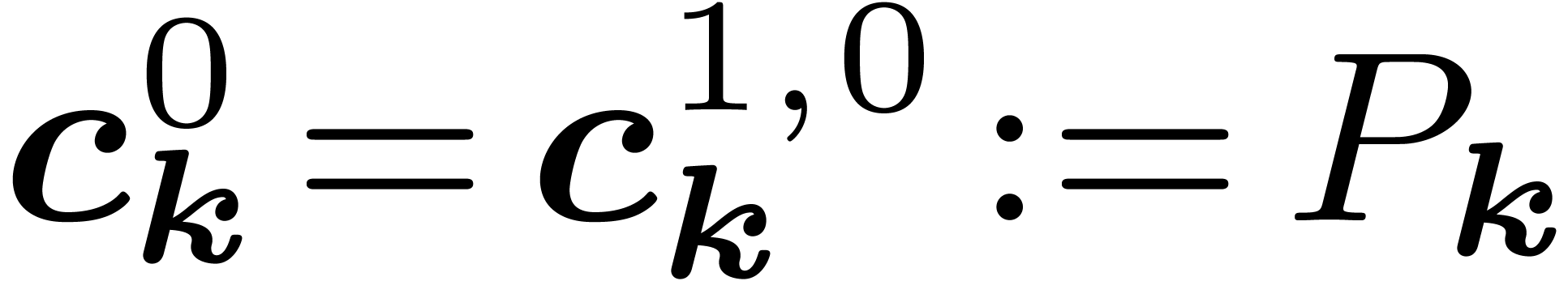 and outputs
and outputs 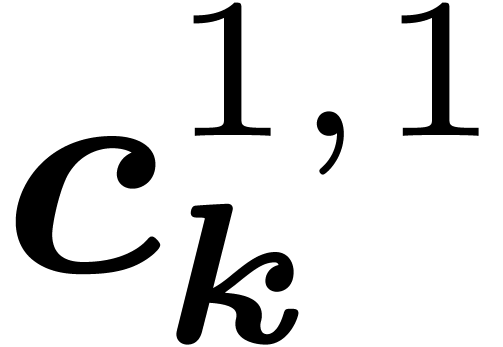 for
for 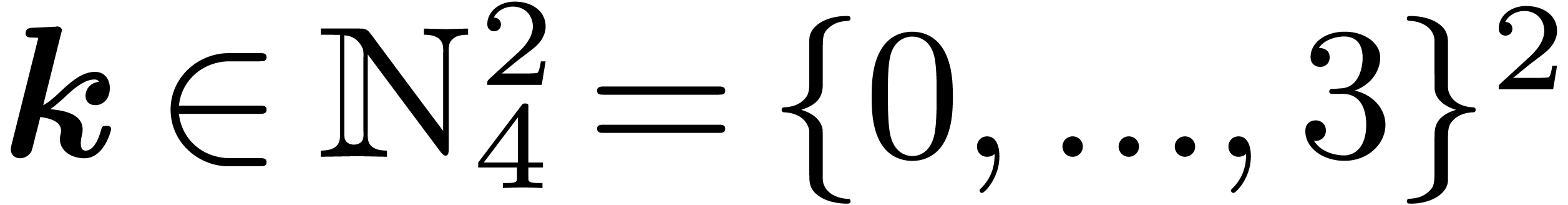 . For any
. For any 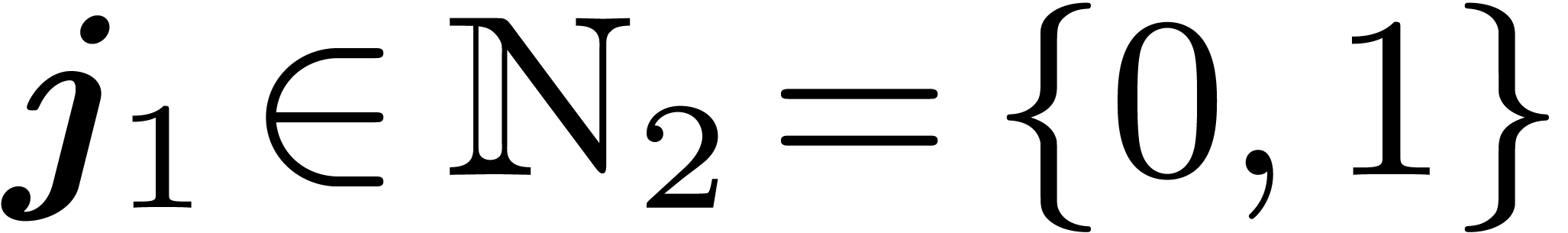 and
and 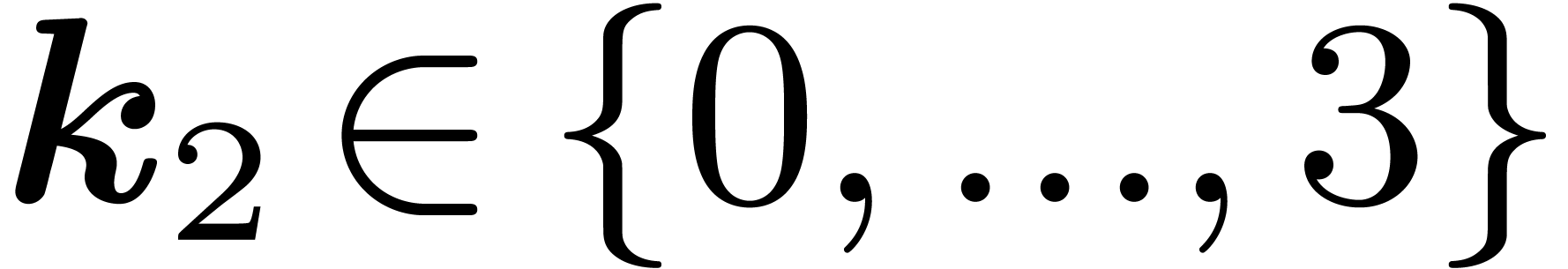 , we let
, we let
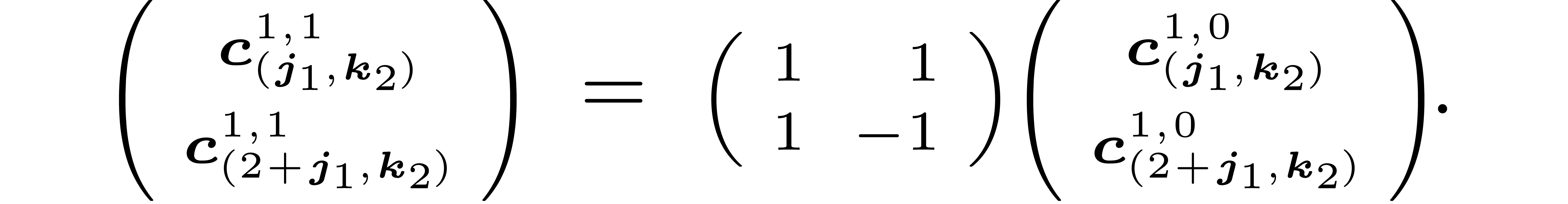
So, 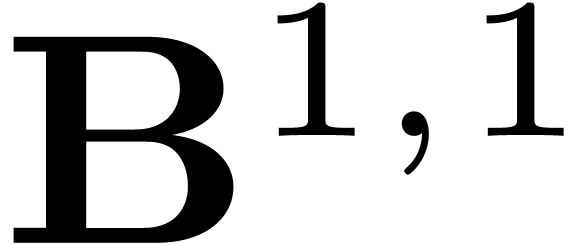 is a 16 by 16 matrix, which is made of
diagonal blocks of
is a 16 by 16 matrix, which is made of
diagonal blocks of 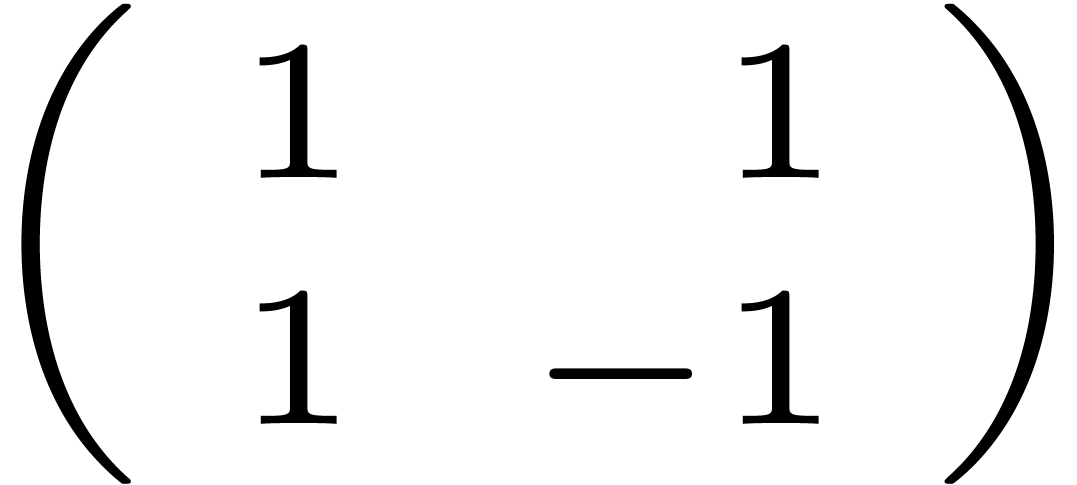 in a suitable basis. The
decimation in
in a suitable basis. The
decimation in 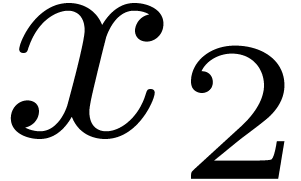 during stage
during stage 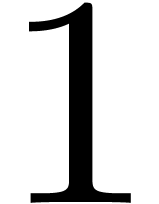 is similar :
is similar :
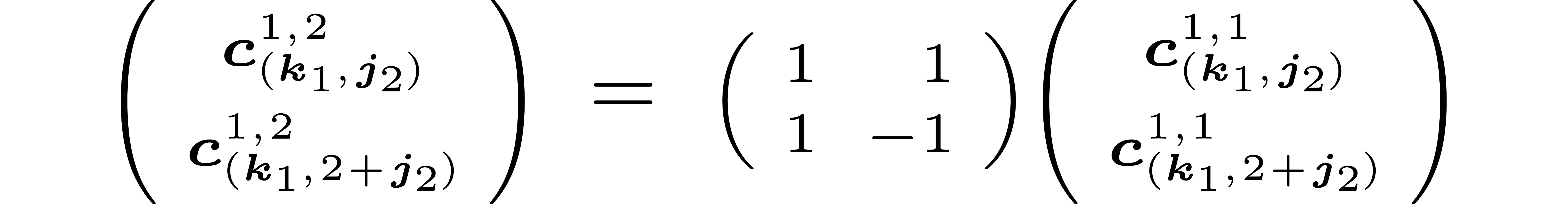
for 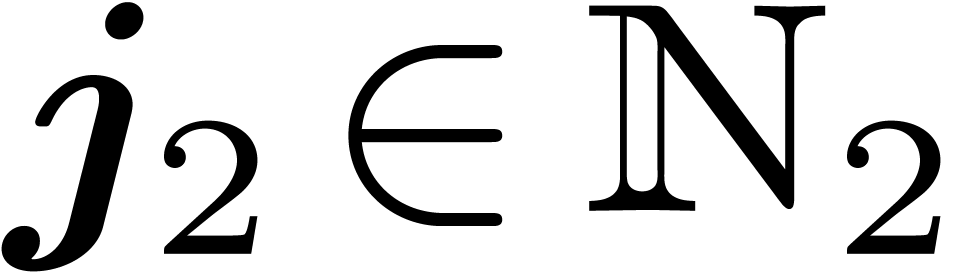 and
and  .
Consequently,
.
Consequently, 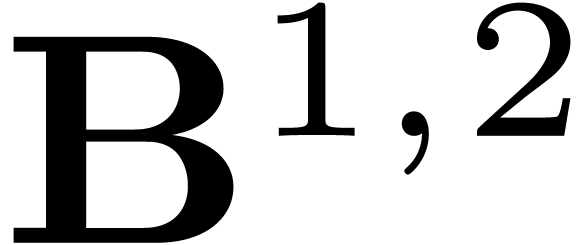 is made of diagonal blocks
is made of diagonal blocks 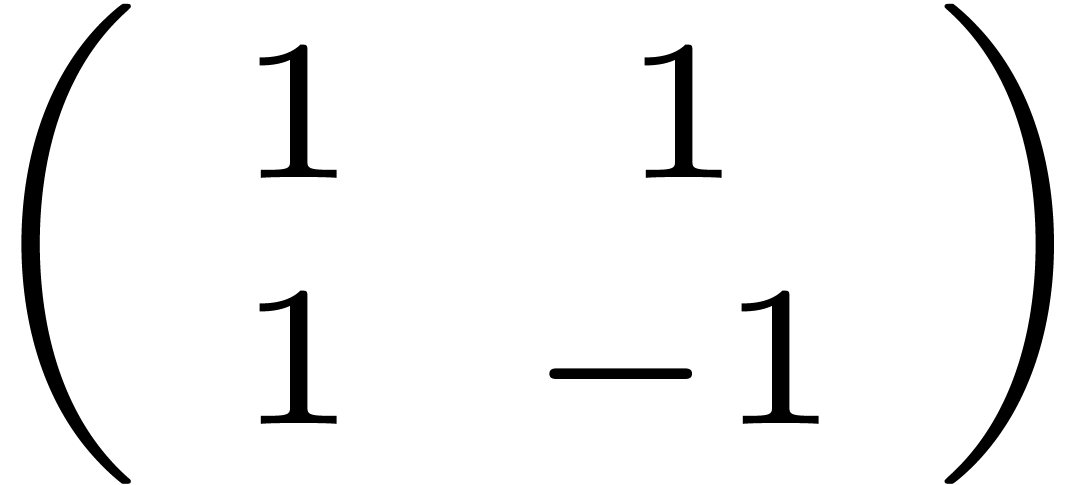 (in another basis than
(in another basis than 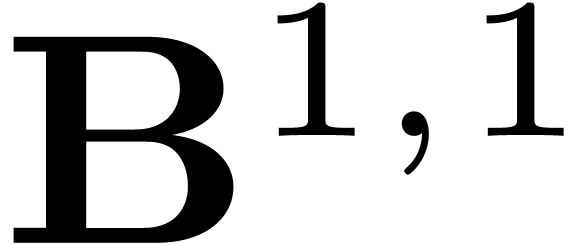 ).
Their product
).
Their product 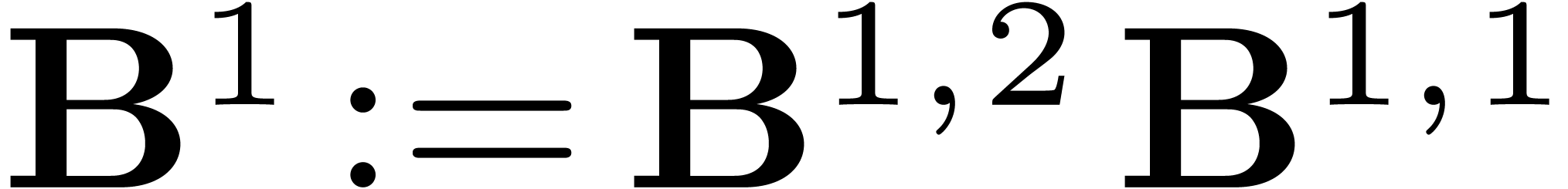 corresponds to the operations
corresponds to the operations
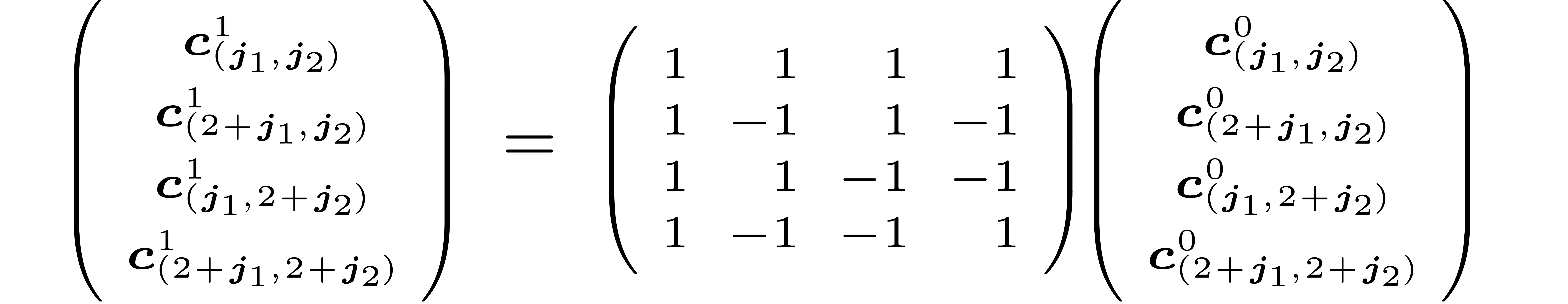
for 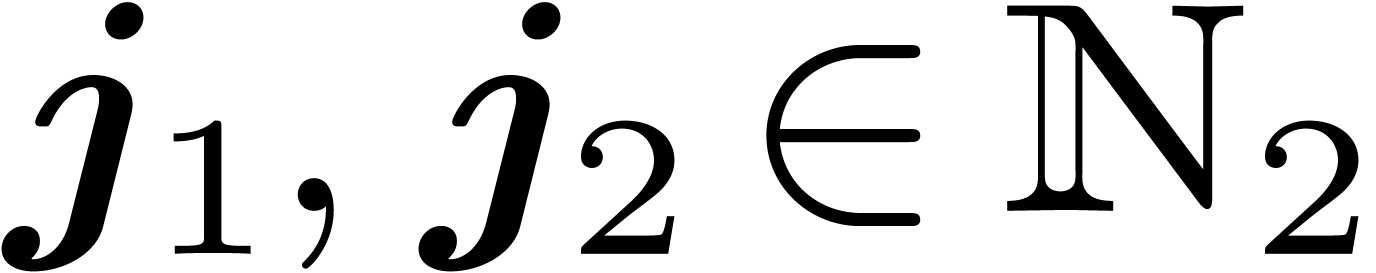 . Thus
. Thus 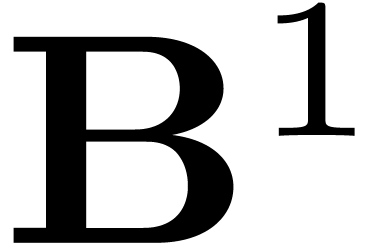 is made of such 4 by 4 matrices on the diagonal (in yet another basis).
Note that in general, the matrices
is made of such 4 by 4 matrices on the diagonal (in yet another basis).
Note that in general, the matrices  and
and 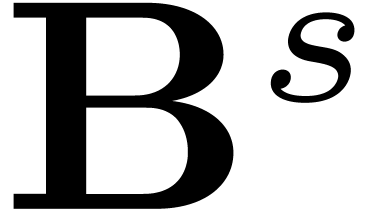 are still made of diagonal blocks, but these blocks vary
along the diagonal.
are still made of diagonal blocks, but these blocks vary
along the diagonal.
We can sum it all up in the two following algorithms.
Algorithm FFT
Input: 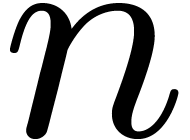 ,
degree ,
degree 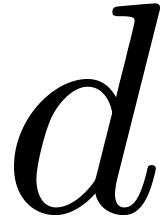 , ,  and coefficients and coefficients 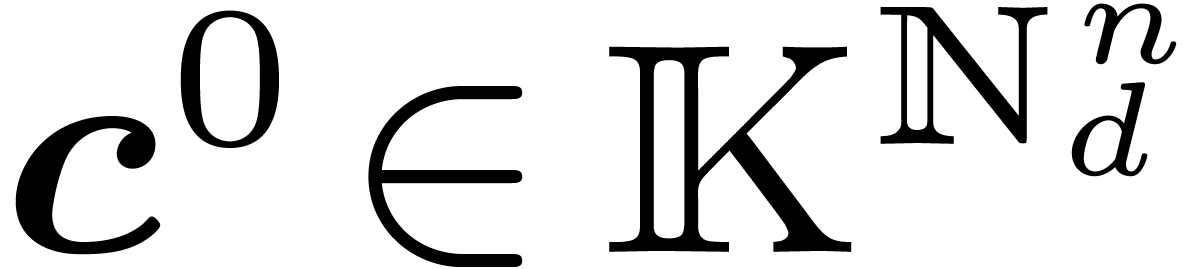 of of 
Output: coefficients 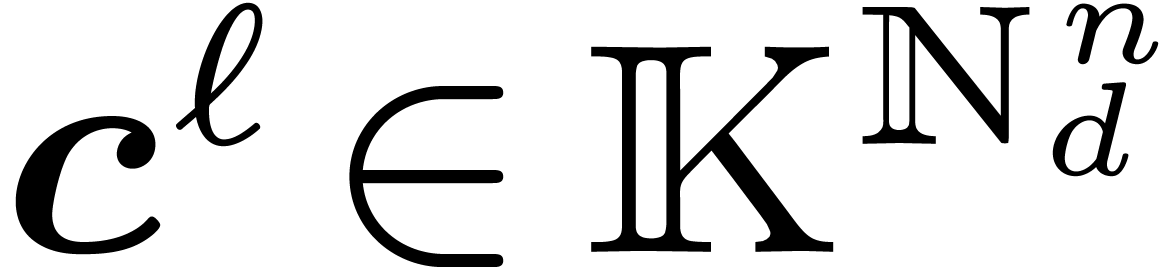 in bit reversed order
in bit reversed order
|
For 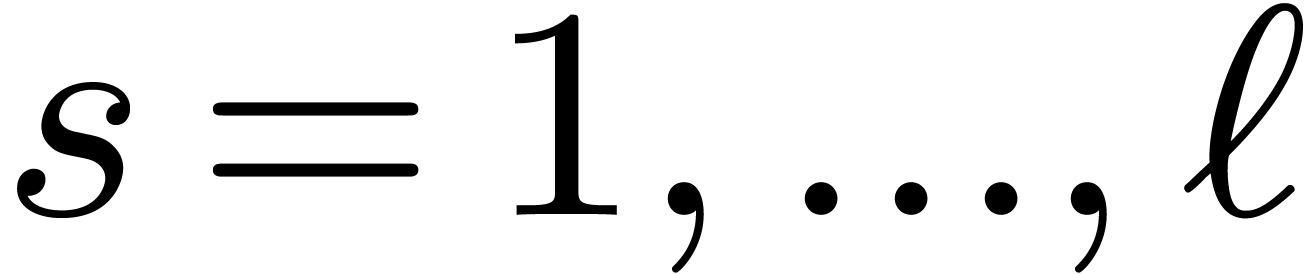 do
//stage 
For 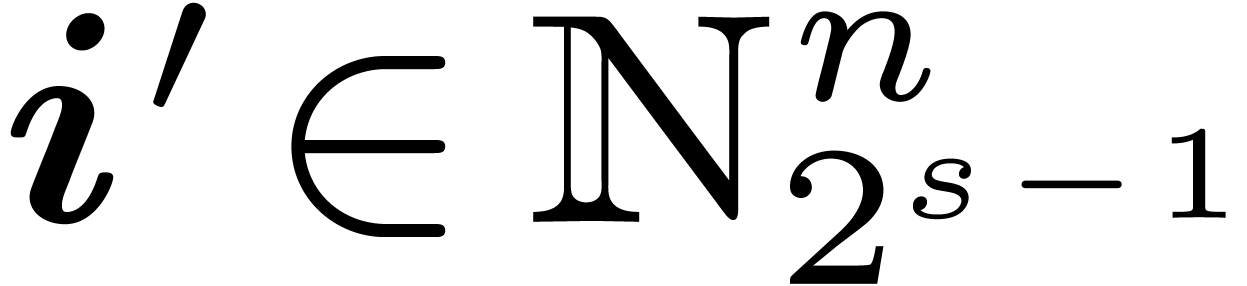 , ,  do
//pick a butterfly
For 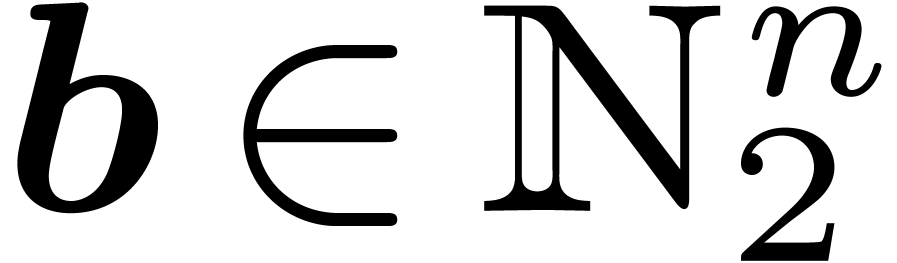 do do 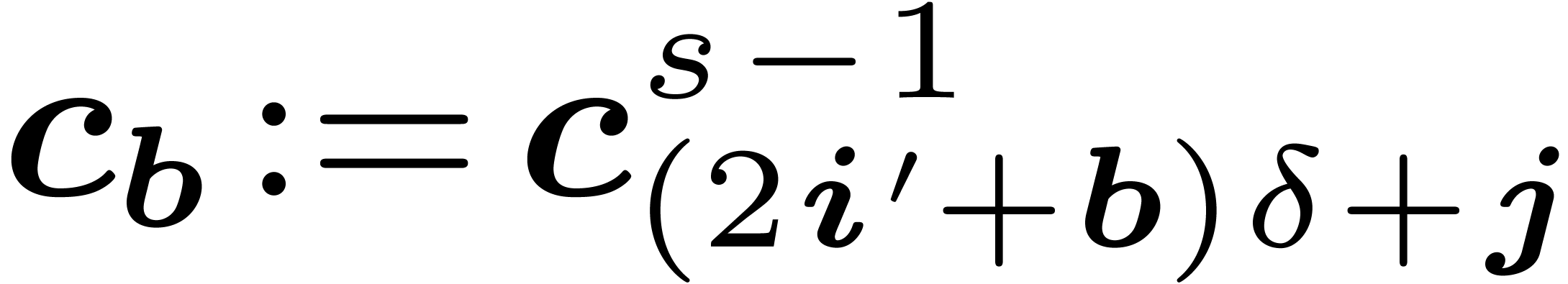
For 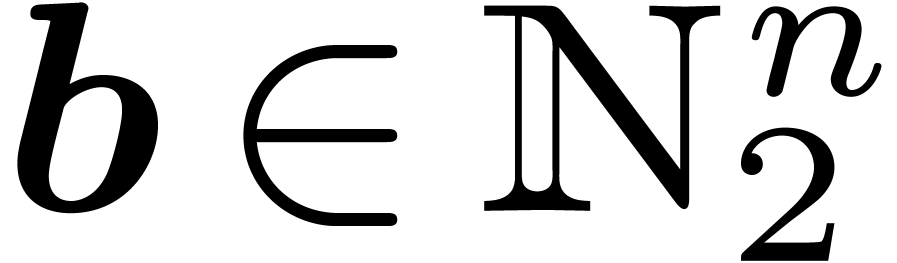 do do 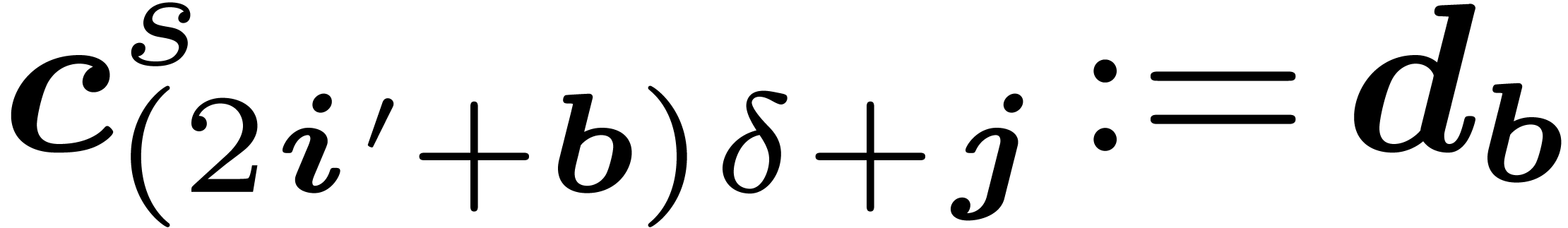
Return 
|
In the last section, we will also use the ring isomorphism
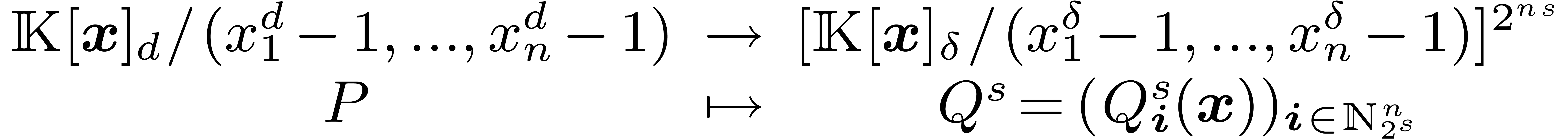
with 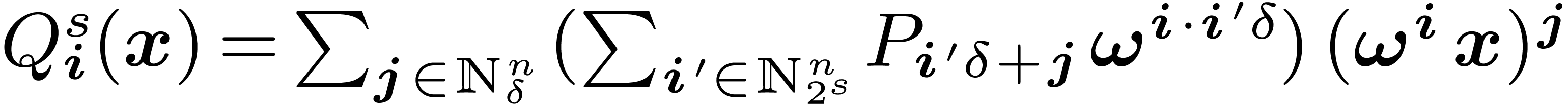 for
for  ,
and
,
and 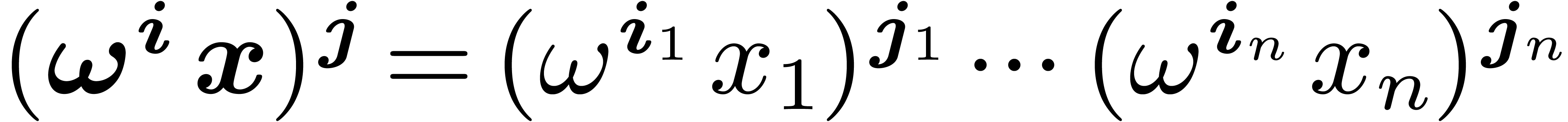 . These polynomials
generalize the decomposition of a univariate polynomials
. These polynomials
generalize the decomposition of a univariate polynomials  into
into  and
and  . We could obtain them through a decimation in
frequency, but it is enough to remark that we can reconstruct them from
the coefficients
. We could obtain them through a decimation in
frequency, but it is enough to remark that we can reconstruct them from
the coefficients 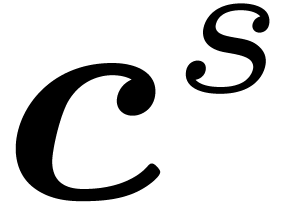 thanks to the formula
thanks to the formula
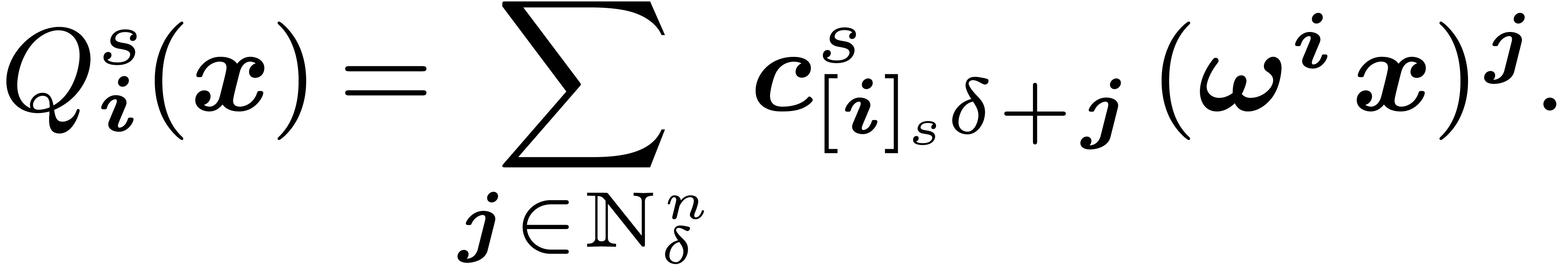 |
(5) |
3.The symmetric FFT
In this section, we let 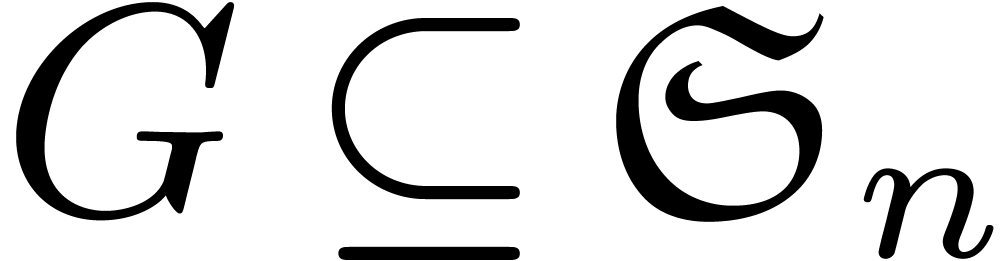 be a permutation group.
The group
be a permutation group.
The group  acts on the polynomials
acts on the polynomials  via the map
via the map
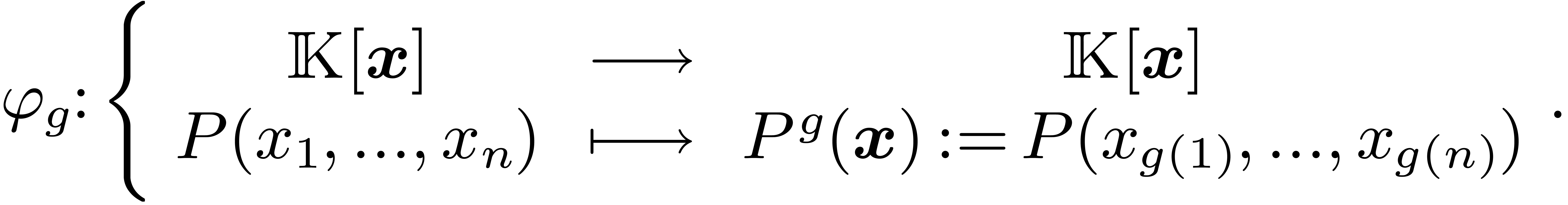
We denote by 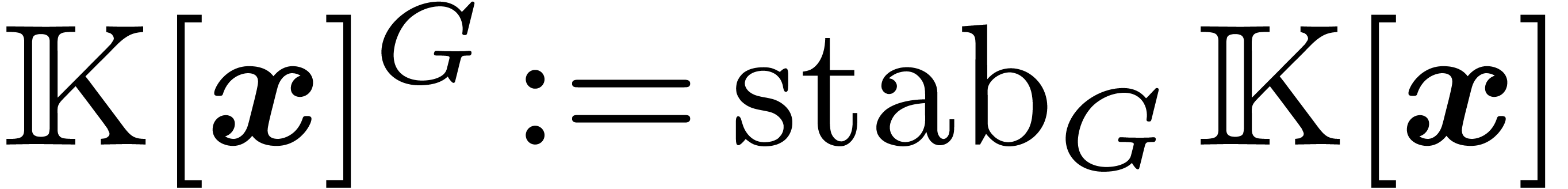 the set of polynomials invariant
under the action of
the set of polynomials invariant
under the action of  . Our
main result here is that one can save a factor (roughly)
. Our
main result here is that one can save a factor (roughly) 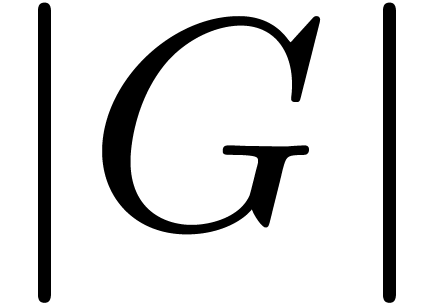 when computing the FFT of an invariant polynomial. Our
approach is in the same spirit as the one in [1], where
similar statements on the savings induced by (very general) symmetries
can be found. However, we are not aware of published results similar to
Theorem 7 below.
when computing the FFT of an invariant polynomial. Our
approach is in the same spirit as the one in [1], where
similar statements on the savings induced by (very general) symmetries
can be found. However, we are not aware of published results similar to
Theorem 7 below.
3.1The bivariate case
Let 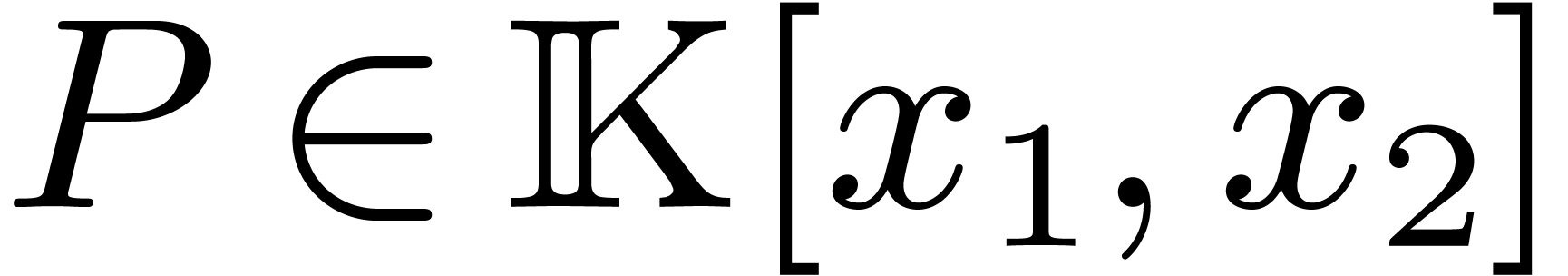 be a symmetric bivariate polynomial of
partial degrees less than
be a symmetric bivariate polynomial of
partial degrees less than 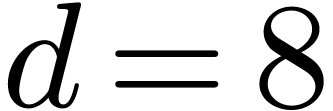 ,
so that
,
so that 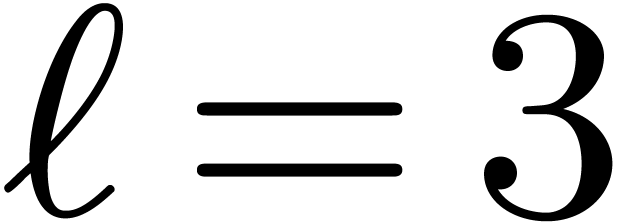 ; let also
; let also 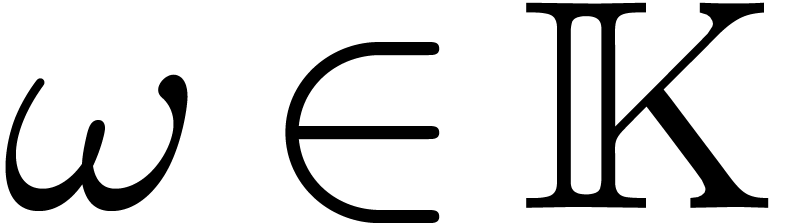 be a primitive eighth root of unity. We detail on this
easy example the methods used to exploit the symmetries to decrease the
cost of the FFT.
be a primitive eighth root of unity. We detail on this
easy example the methods used to exploit the symmetries to decrease the
cost of the FFT.
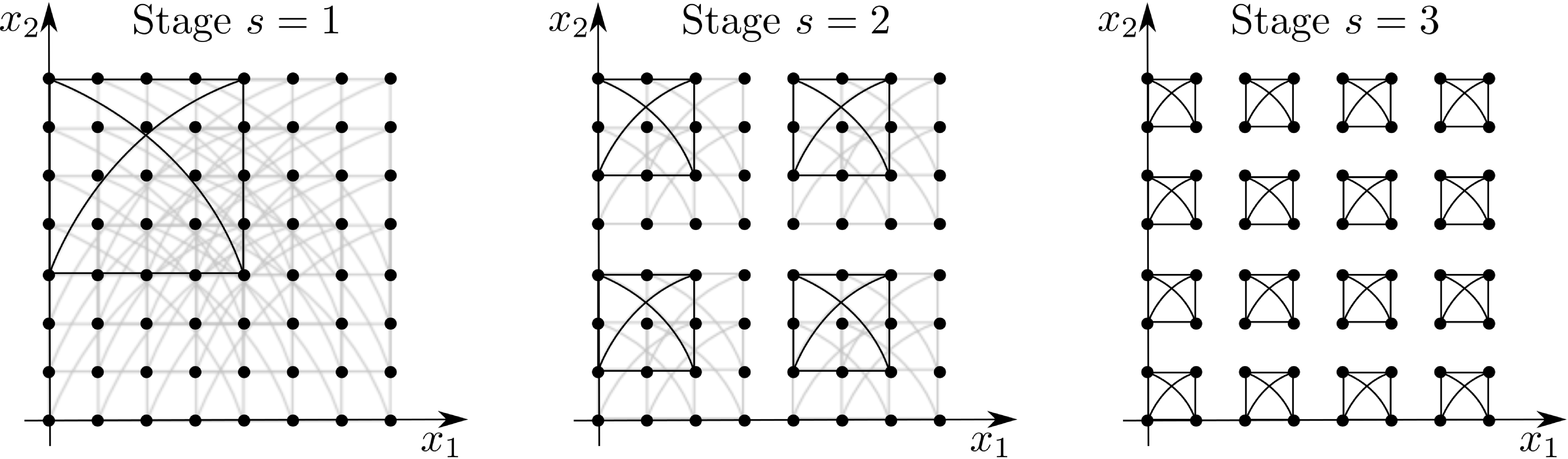
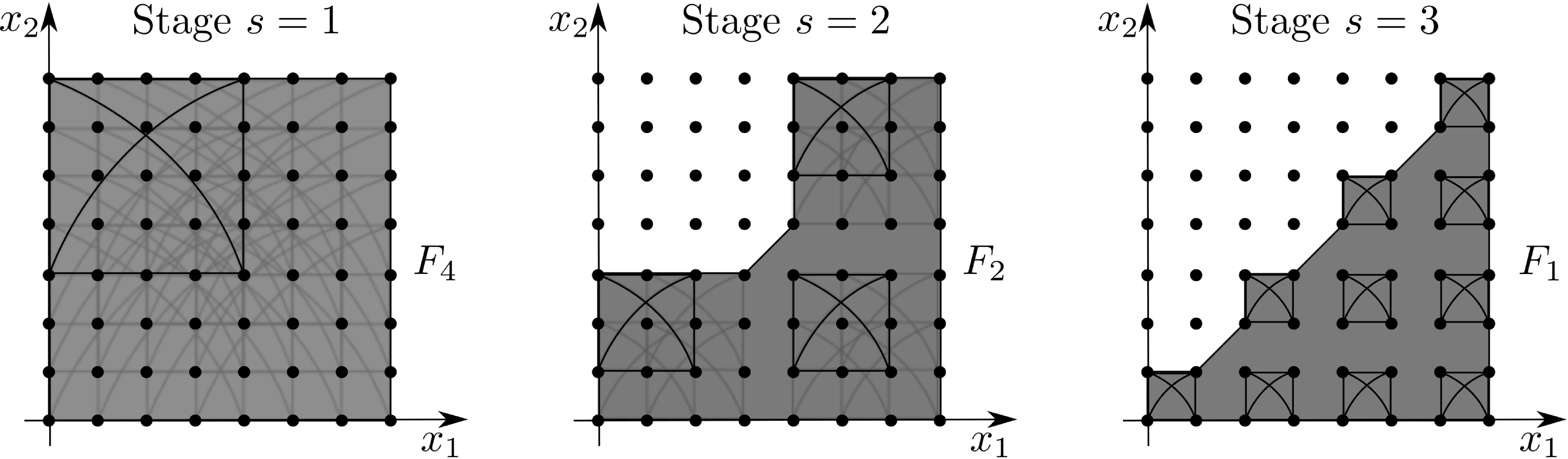
The coefficients of 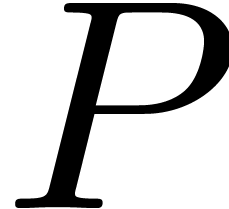 are placed on a
are placed on a  grid. The bivariate classical FFT consists in the
application of butterflies of size
grid. The bivariate classical FFT consists in the
application of butterflies of size 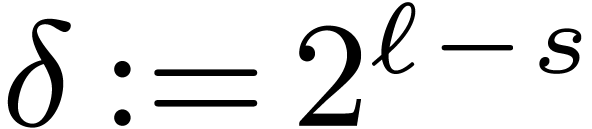 for
for  from
from 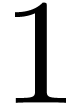 to
to  , as in Figure 1. When some butterflies
overlap, we draw only the shades of all but one of them. The result of
stage
, as in Figure 1. When some butterflies
overlap, we draw only the shades of all but one of them. The result of
stage  is the set of evaluations
is the set of evaluations 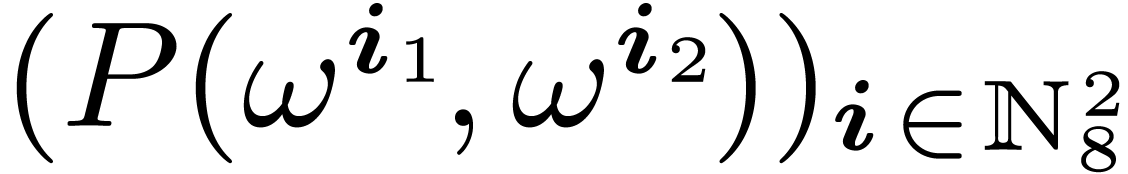 in bit reversed order.
in bit reversed order.
 |
|
Figure 1. Classical bivariate FFT
|
We will remark below that each stage  preserves
the symmetry of the input. In particular, since our polynomial
preserves
the symmetry of the input. In particular, since our polynomial 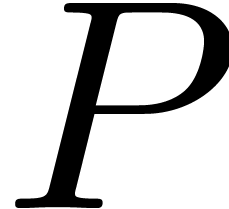 is symmetric, the coefficients
is symmetric, the coefficients 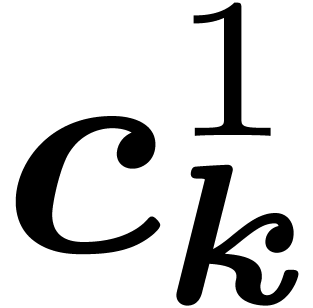 at
stage
at
stage 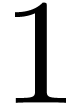 are symmetric too, so we only need to
compute the coefficients
are symmetric too, so we only need to
compute the coefficients 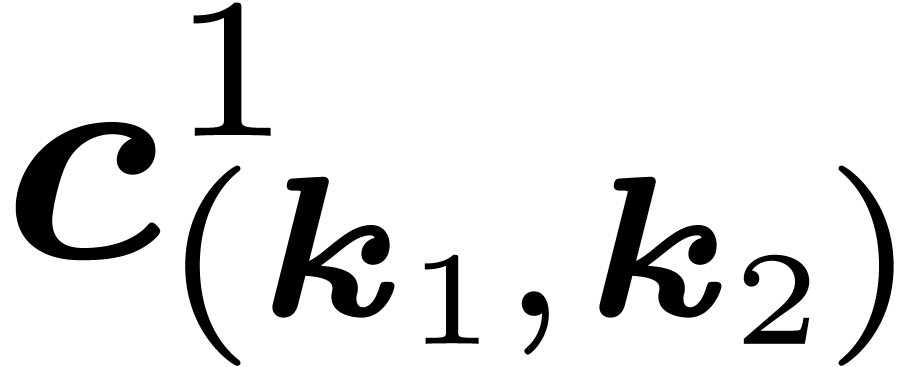 for
for 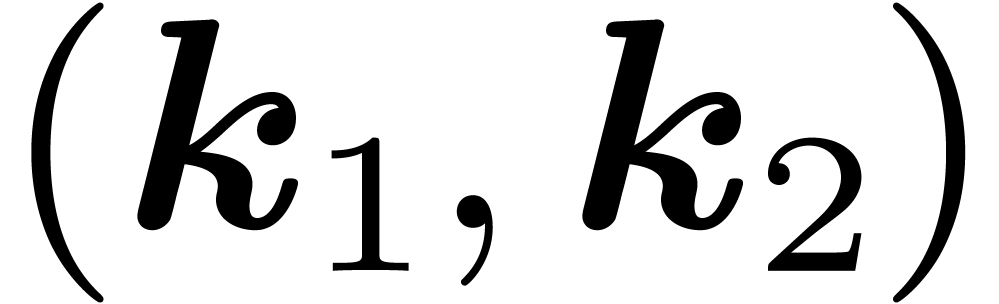 in the fundamental domain (sometimes called asymmetric unit)
in the fundamental domain (sometimes called asymmetric unit)
 . We choose to compute at
stage
. We choose to compute at
stage  only the butterflies which involves at
least an element of
only the butterflies which involves at
least an element of  ; the set
of indices that are included in a butterfly of span
; the set
of indices that are included in a butterfly of span 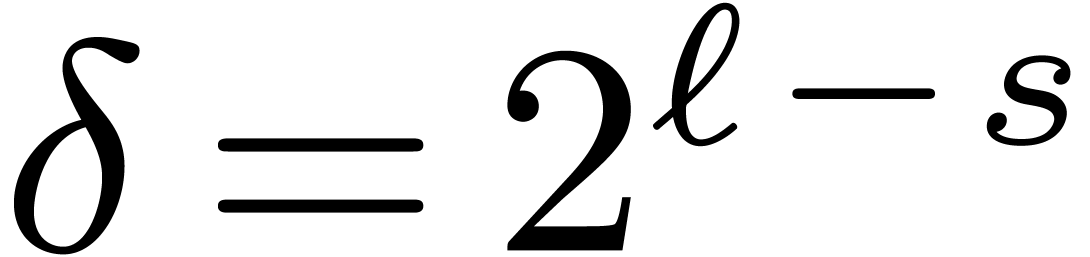 that meets
that meets  will be called the extension
will be called the extension  of
of  .
.
 |
|
Figure 2. Symmetric bivariate FFT
|
Every butterfly of stage  meets the fundamental
domain, so we do not save anything there. However, we save
meets the fundamental
domain, so we do not save anything there. However, we save 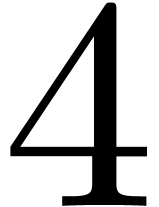 out of
out of 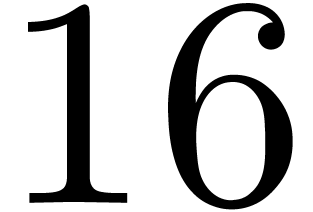 butterflies at stage
butterflies at stage  and
and  out of
out of 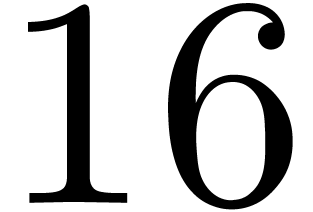 butterflies at the third stage. Asymptotically in
butterflies at the third stage. Asymptotically in 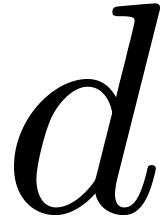 , we gain a factor two in the number of arithmetic
operations in
, we gain a factor two in the number of arithmetic
operations in  compared to the classical FFT;
this corresponds to the order of the group.
compared to the classical FFT;
this corresponds to the order of the group.
3.2Notation
The group  also acts on
also acts on 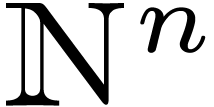 with
with 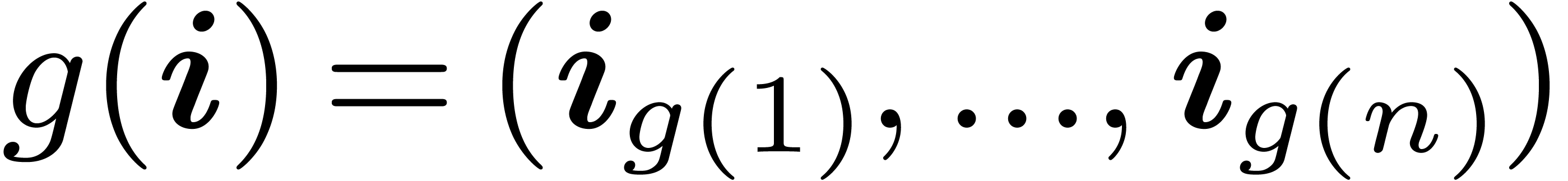 for any
for any 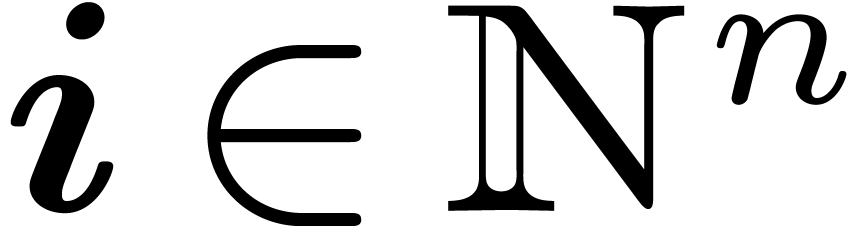 .
This action is consistent with the action on polynomials since
.
This action is consistent with the action on polynomials since 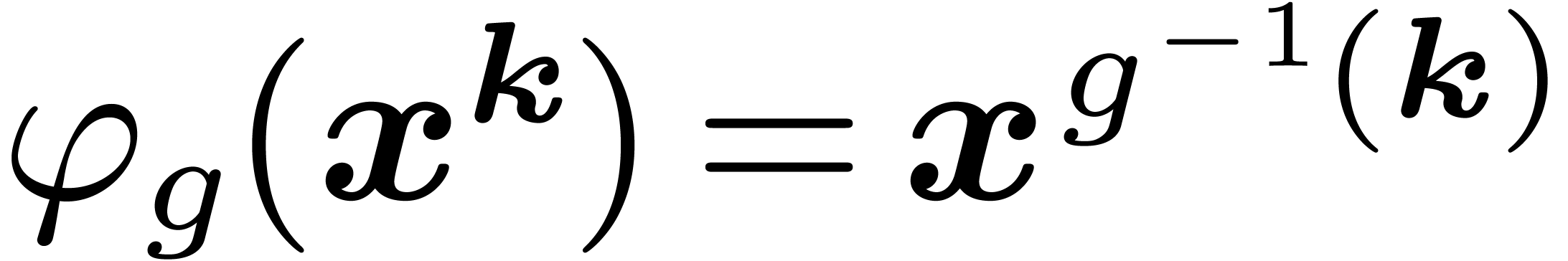 .
.
Because  acts on polynomials, it acts on the
vector of its coefficients. More generally, if
acts on polynomials, it acts on the
vector of its coefficients. More generally, if 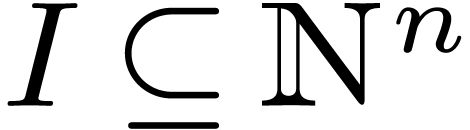 and
and  , we denote by
, we denote by  the vector defined by
the vector defined by 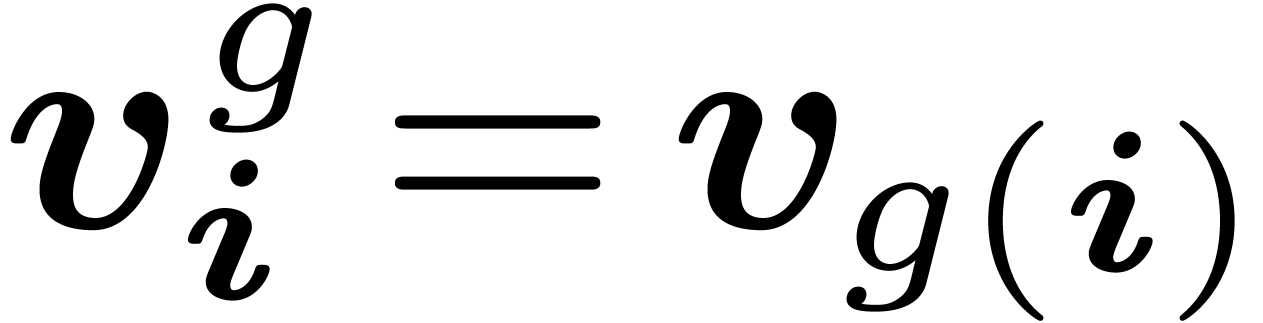 for all
for all
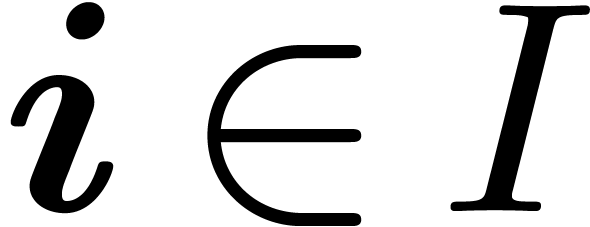 . If
. If 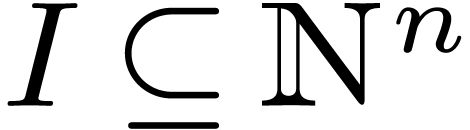 is stable by
is stable by  , i.e.
, i.e.
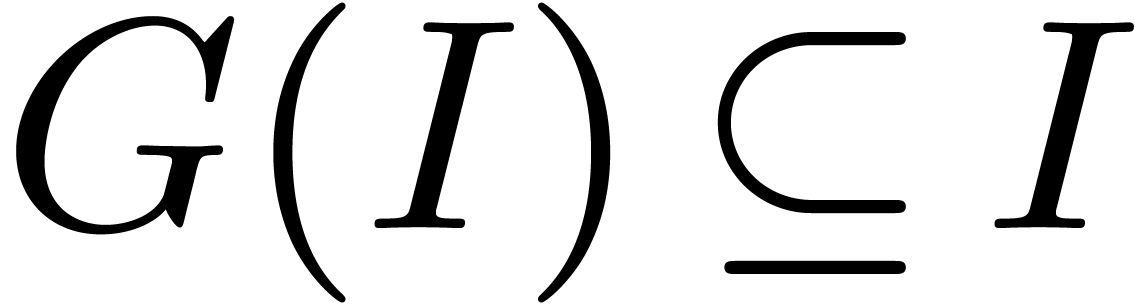 , we define the set of
invariant vectors
, we define the set of
invariant vectors 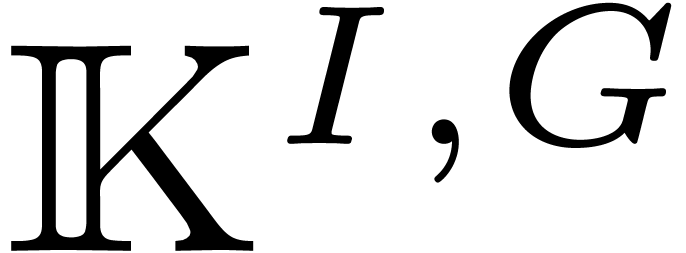 by
by 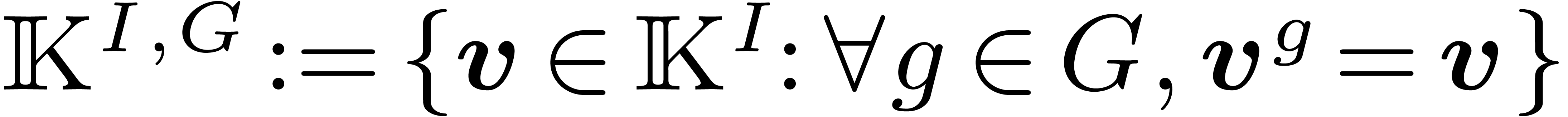 .
.
For any two sets 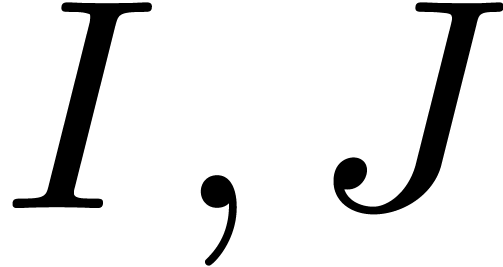 satisfying
satisfying 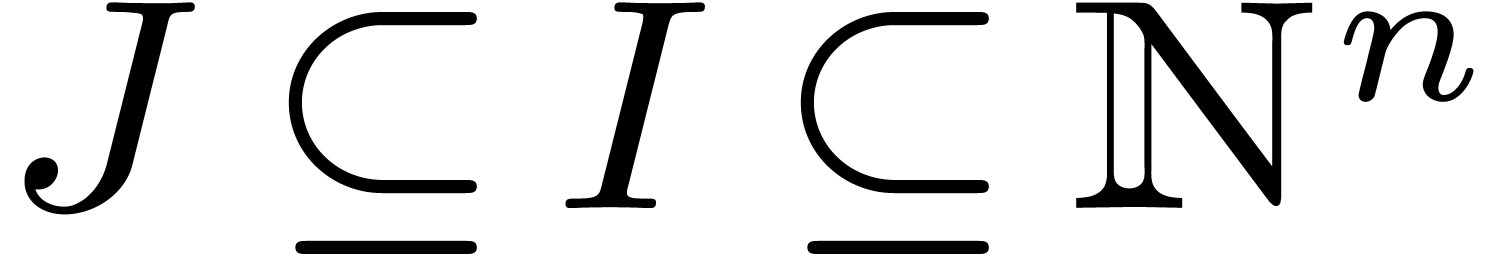 , we define the restriction
, we define the restriction 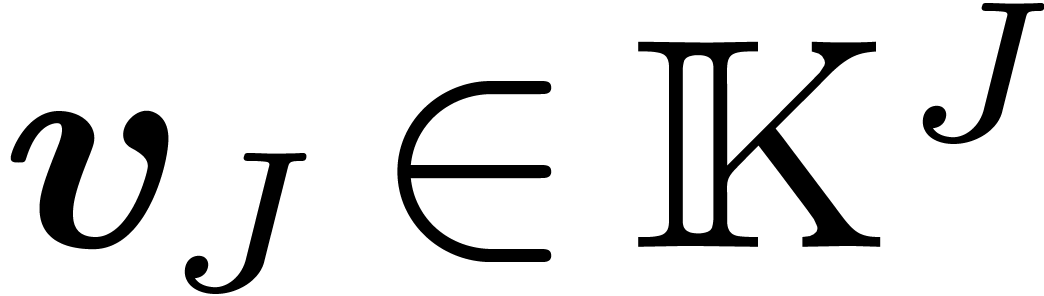 of
of 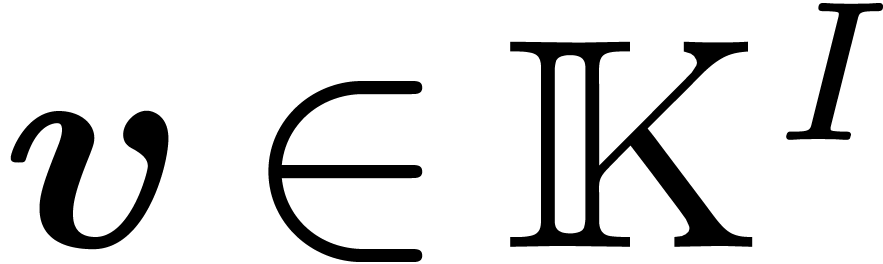 by
by 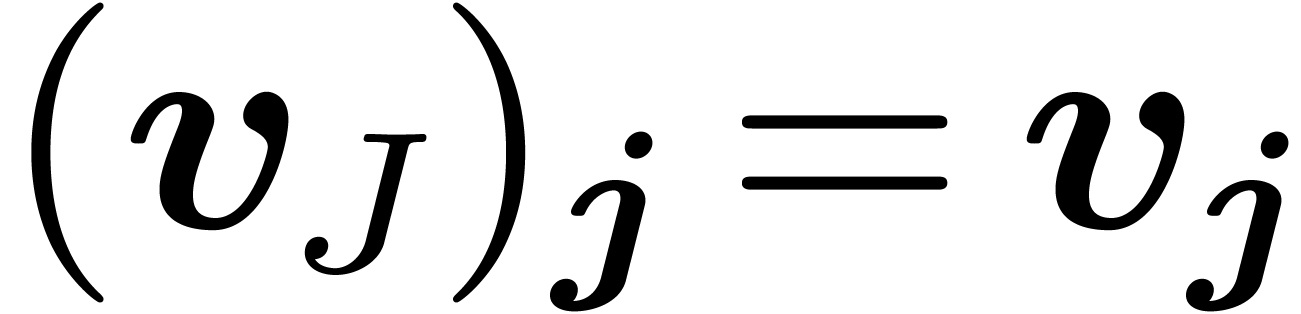 for all
for all 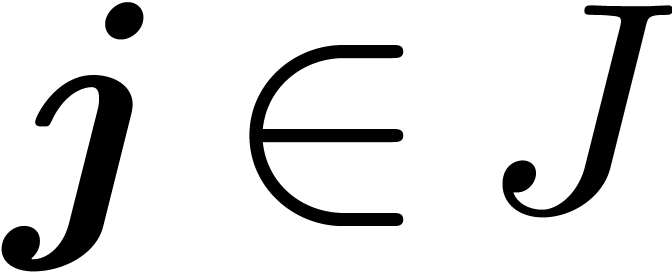 . Recall the definition of the
lexicographical order
. Recall the definition of the
lexicographical order 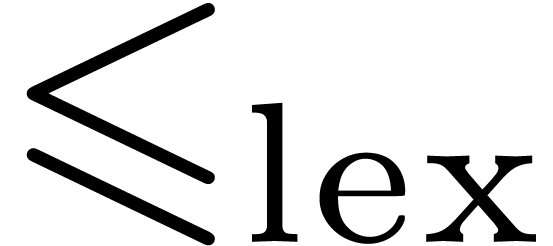 : for all
: for all 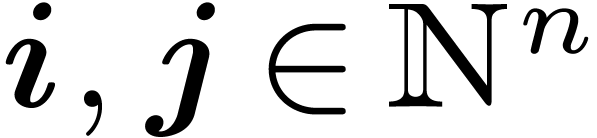 ,
, 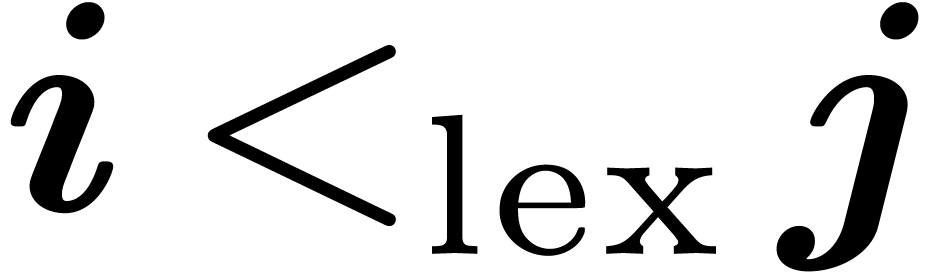 if there exists
if there exists  such that
such that 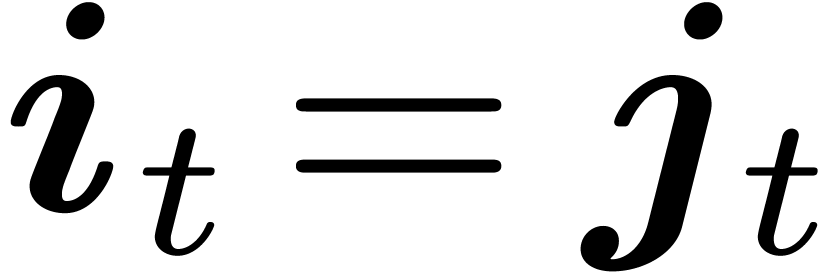 for any
for any 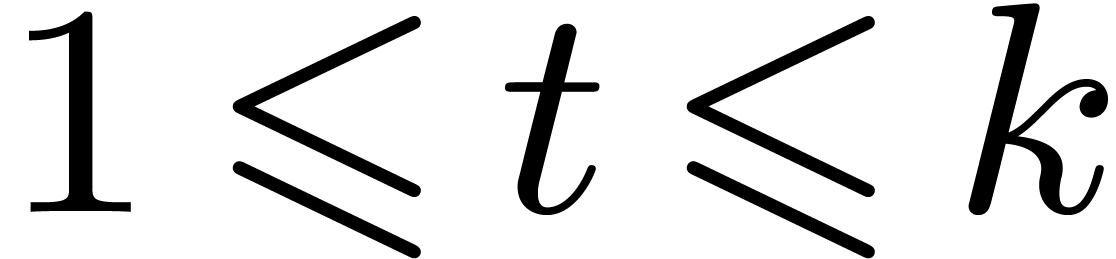 and
and  . Finally
for any subset
. Finally
for any subset 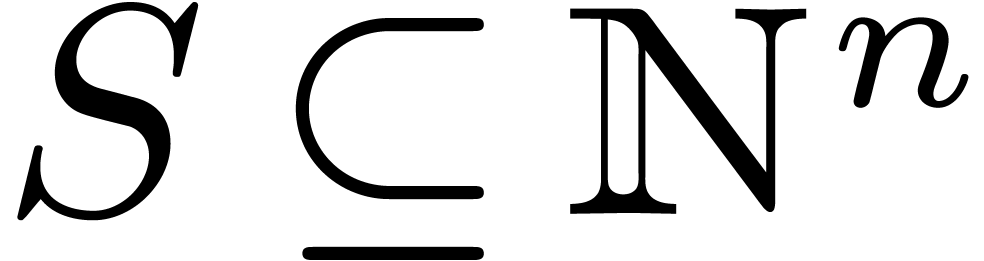 stable by
stable by  , we define a fundamental domain
, we define a fundamental domain  of the action of
of the action of  on
on  by
by
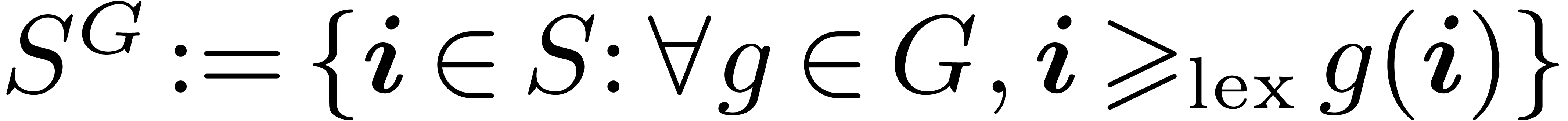 together with the projection
together with the projection 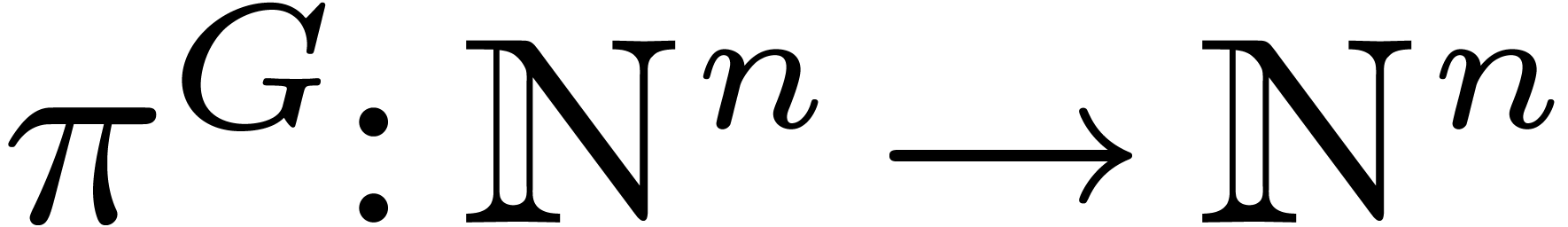 such as
such as 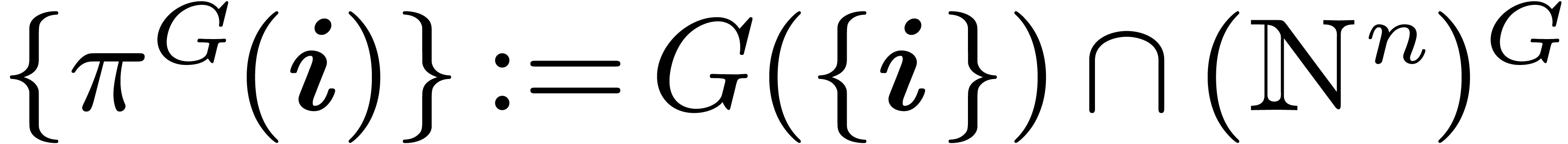 .
.
3.3Fundamental domains
Let 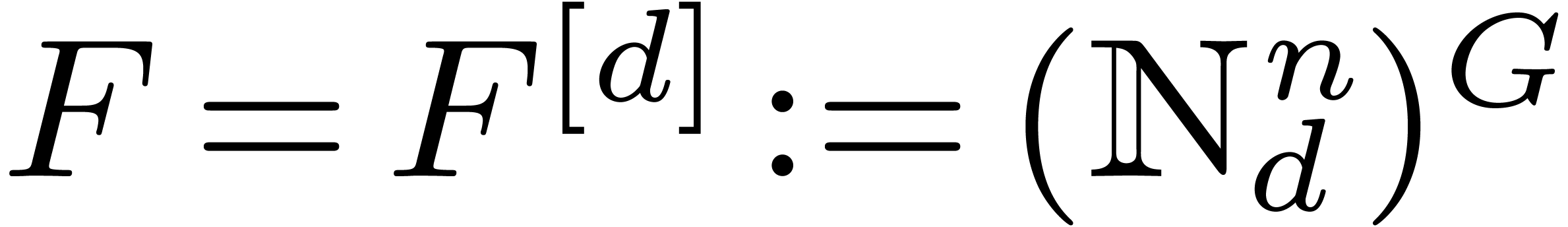 be the fundamental domain associated to the
action of
be the fundamental domain associated to the
action of  on
on 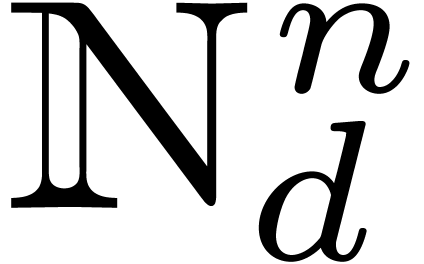 .
Any
.
Any  -symmetric vector
-symmetric vector  can be reconstructed from its restriction
can be reconstructed from its restriction 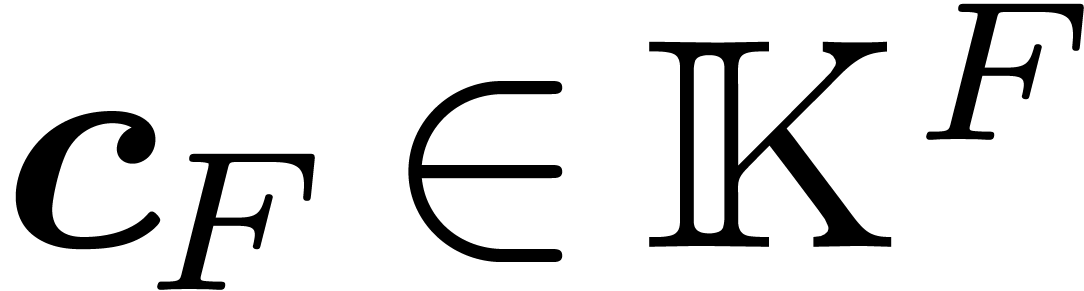 using the formula
using the formula  .
As it turns out, the in-place FFT algorithm from Section 2.2
admits the important property that the coefficients at all stage are
still
.
As it turns out, the in-place FFT algorithm from Section 2.2
admits the important property that the coefficients at all stage are
still  -symmetric.
-symmetric.
Lemma 2. Let
 and the vectors
and the vectors 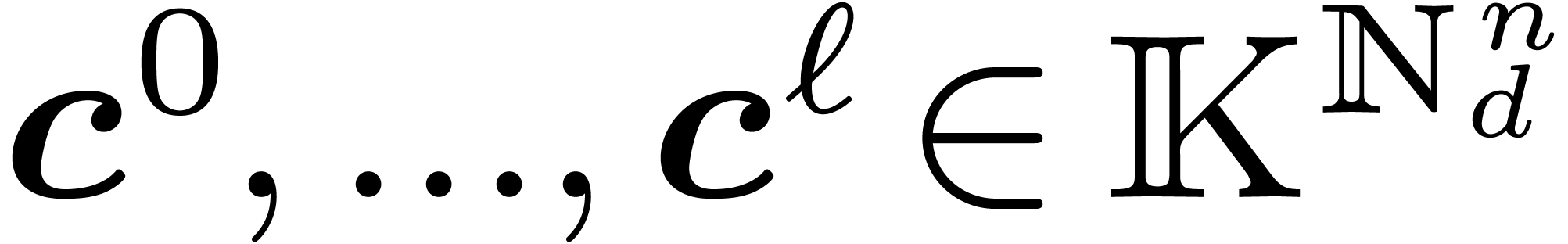 be as in
Section 2.2. Then if
be as in
Section 2.2. Then if 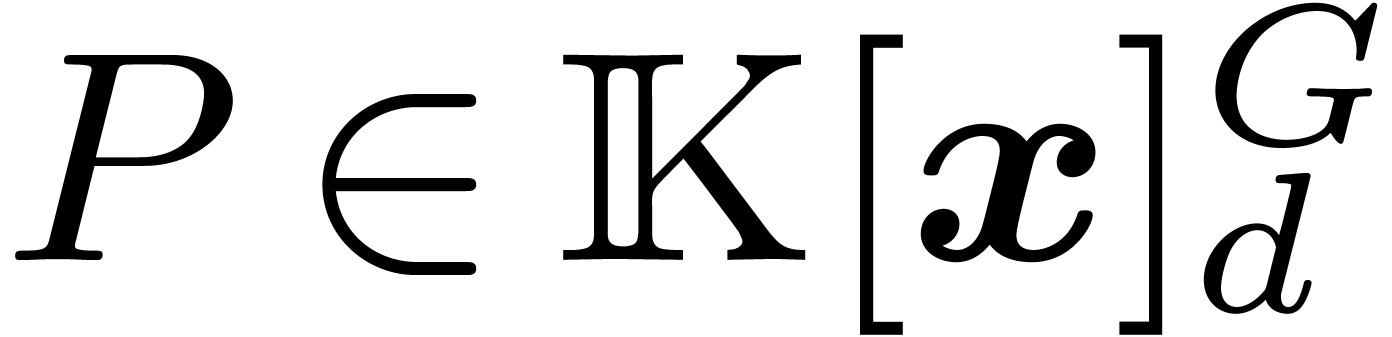 ,
,
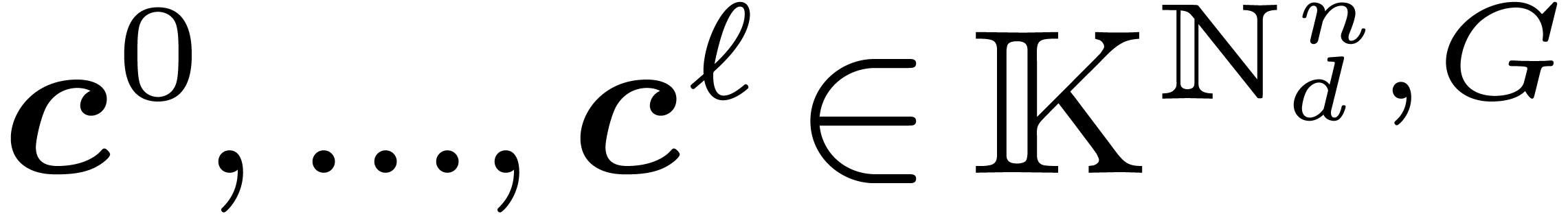 .
.
Proof. Given 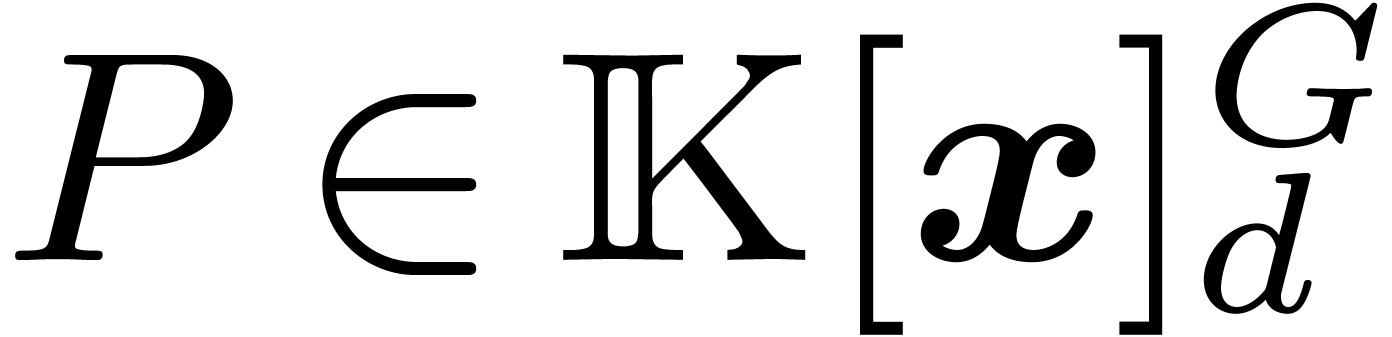 ,
,
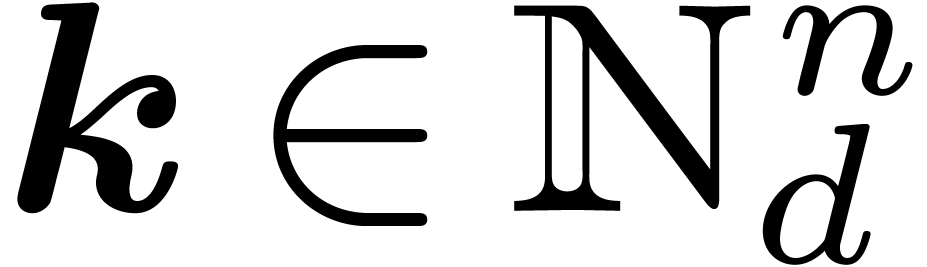 and
and 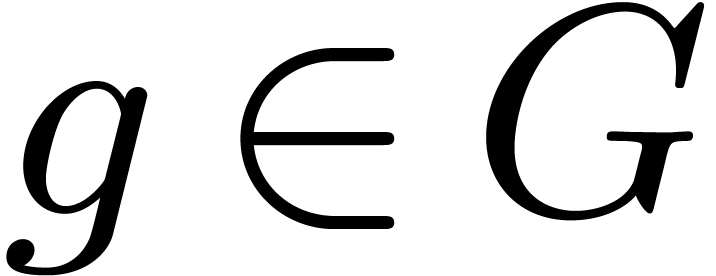 ,
we clearly have
,
we clearly have 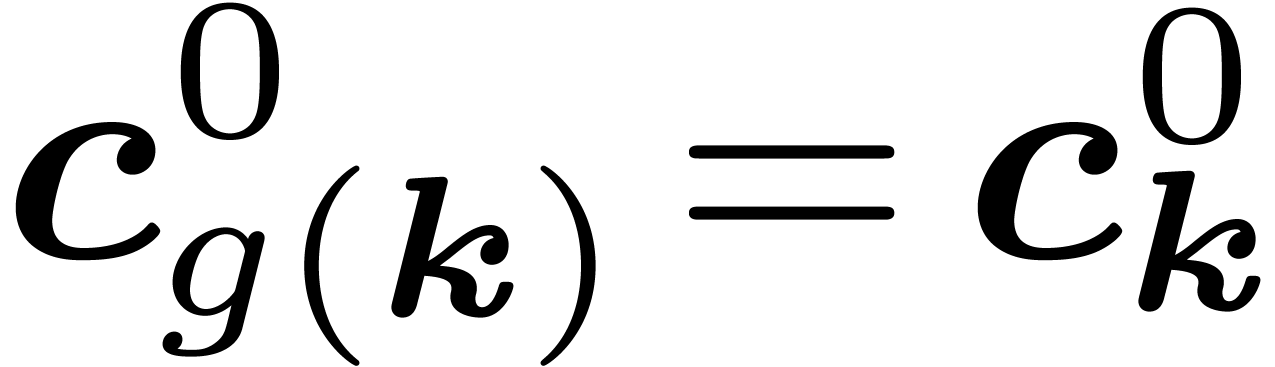 . For any
. For any
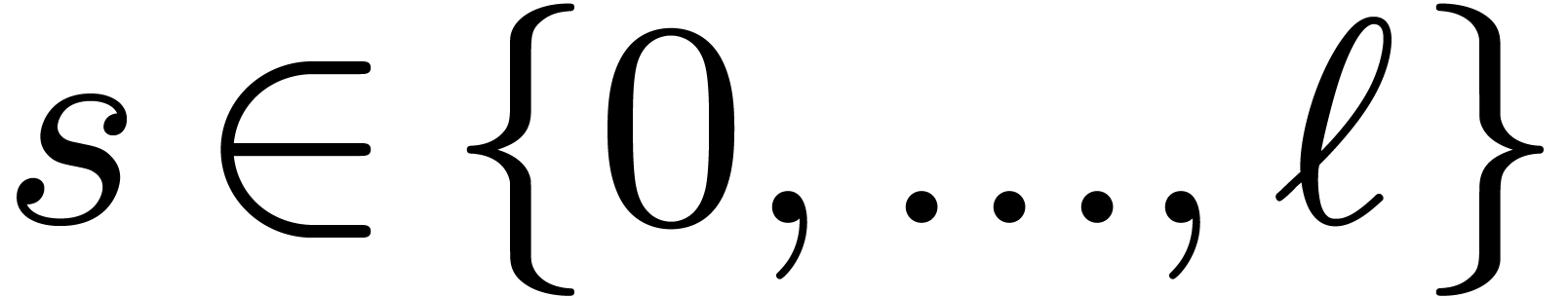 ,
,  ,
,  and
and 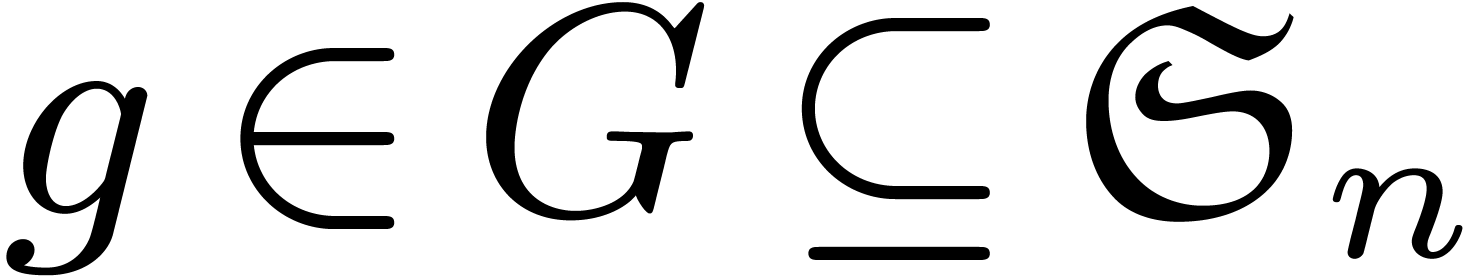 , we also notice that
, we also notice that
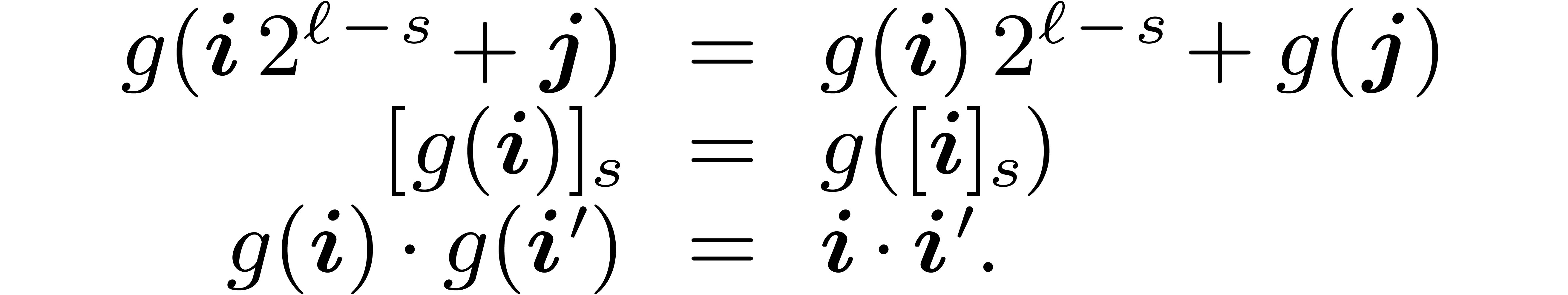
Hence, using Equation (2), we get
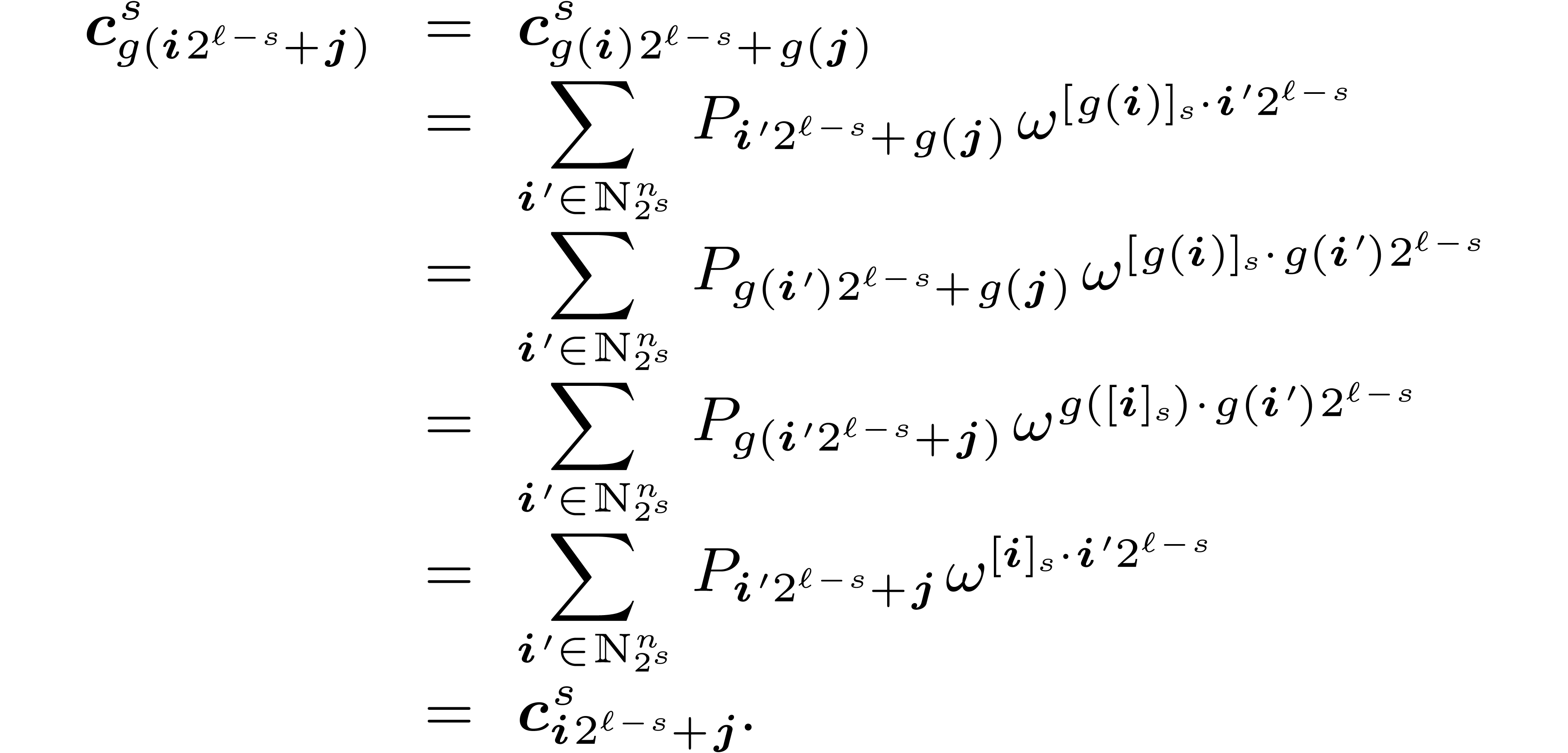
This lemma implies that for the computation of the FFT of a  -symmetric polynomial
-symmetric polynomial 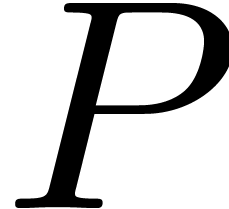 , it suffices to compute the projections
, it suffices to compute the projections  .
.
In order to apply formula (4) for the computation of 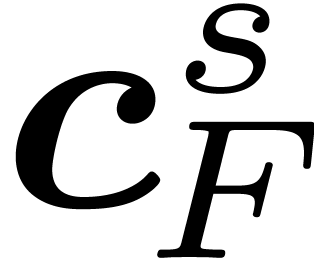 as a function of
as a function of 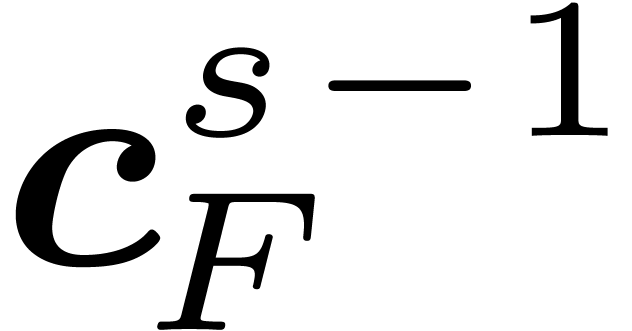 ,
it is not necessary to completely reconstruct
,
it is not necessary to completely reconstruct 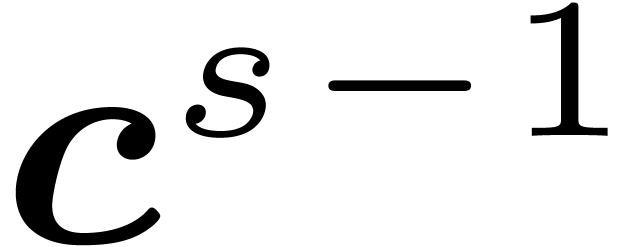 , due to the sparsity of the matrix
, due to the sparsity of the matrix 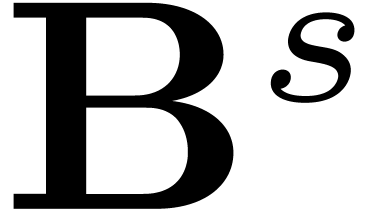 . Instead, we define the
. Instead, we define the  -expansion of the set
-expansion of the set 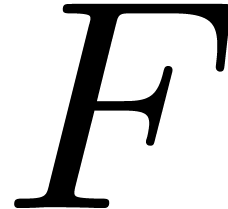 by
by
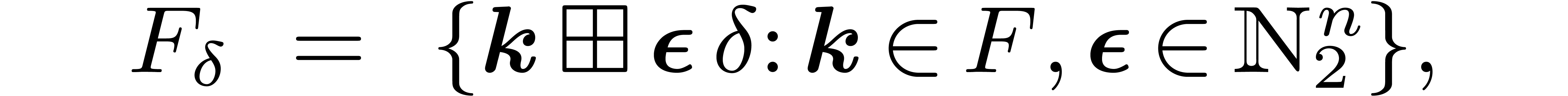
where  stands for the “bitwise exclusive
or” of
stands for the “bitwise exclusive
or” of  and
and  .
For any
.
For any 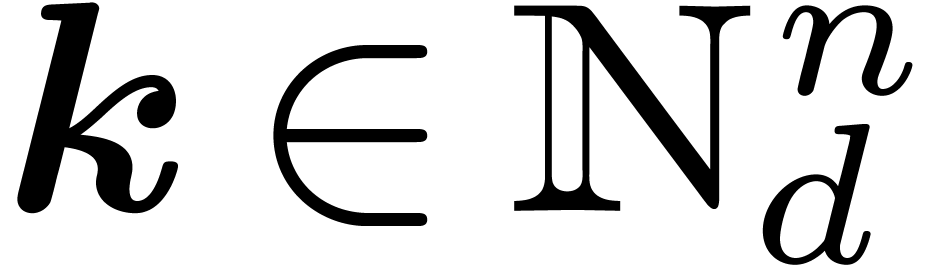 , the set
, the set 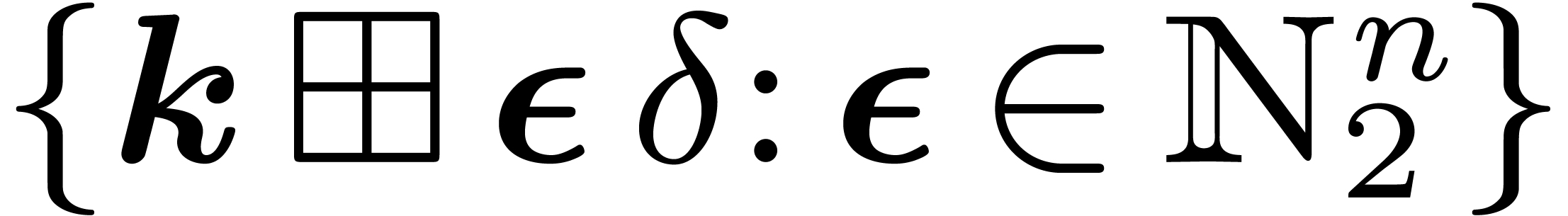 describes the vertices of the butterfly of span
describes the vertices of the butterfly of span  that includes the point
that includes the point  .
Thus,
.
Thus,  is indeed the set of indices of
is indeed the set of indices of  that are involved in the computation of
that are involved in the computation of 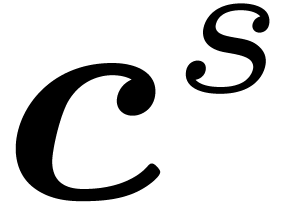 via the formula
via the formula 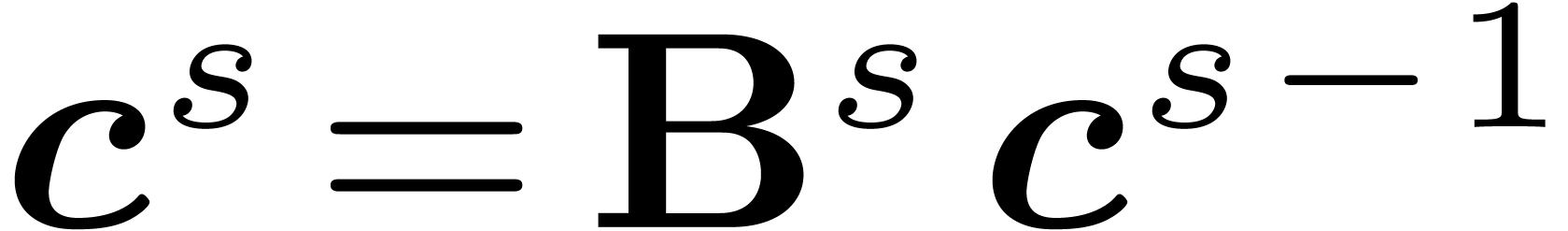 .
.
Lemma 3. For
any 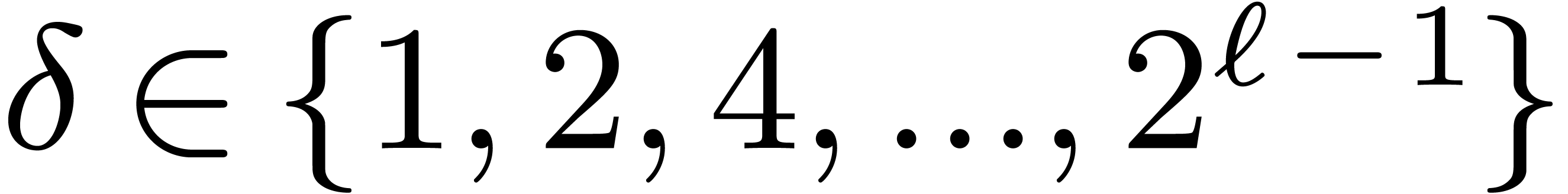 , let
, let
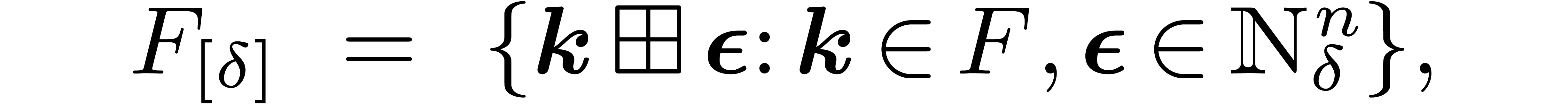
so that 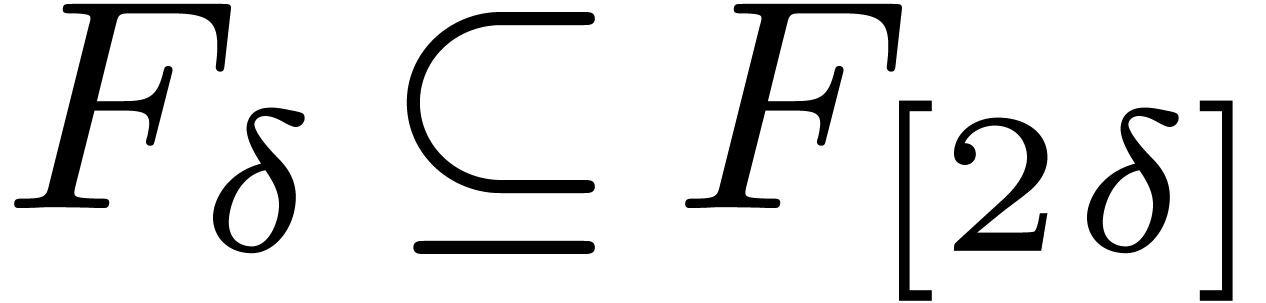 . Then we have
. Then we have
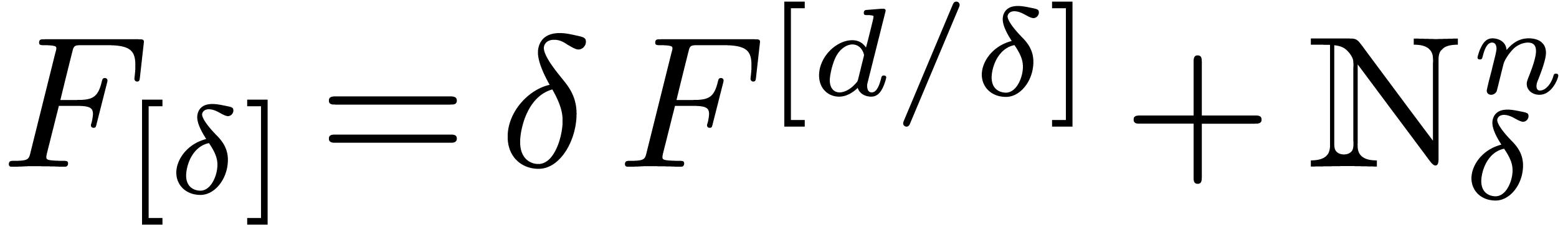 .
.
Proof. Assume that 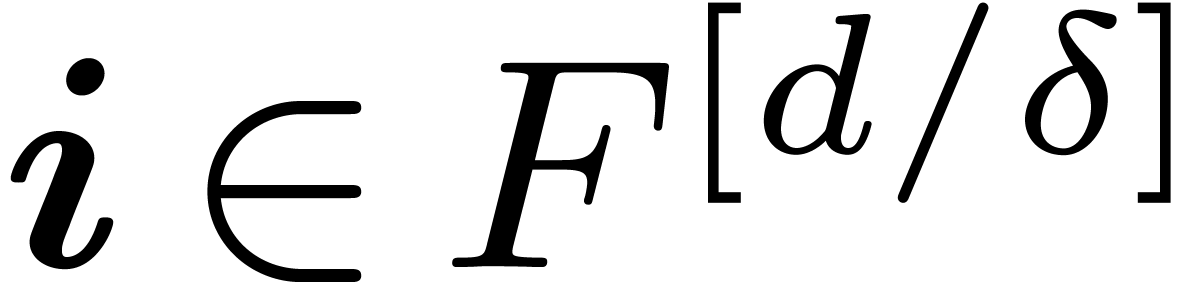 .
Then clearly,
.
Then clearly,  , whence
, whence 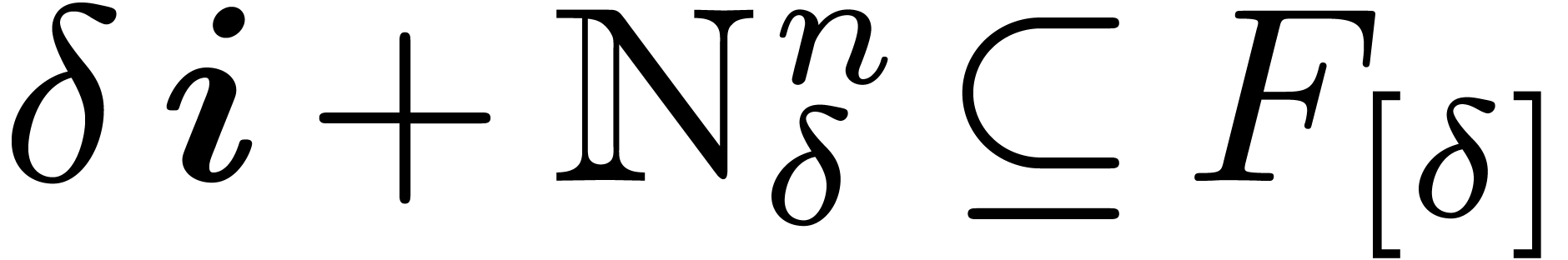 . Conversely, if
. Conversely, if 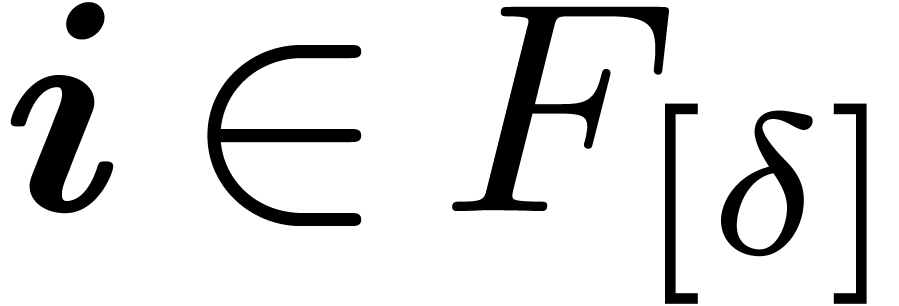 , then there exists a
, then there exists a  with
with  and
and  .
Let
.
Let  . For any
. For any 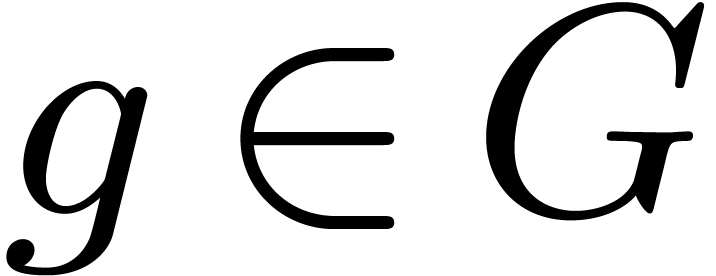 , we have
, we have 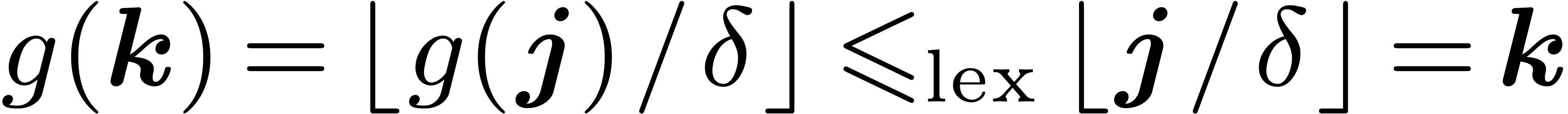 .
Consequently,
.
Consequently,  , whence
, whence 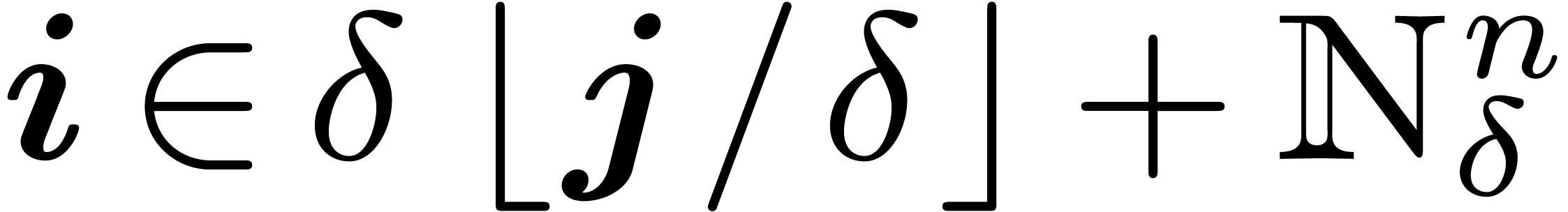 .
.
For the proof of the next lemma, for 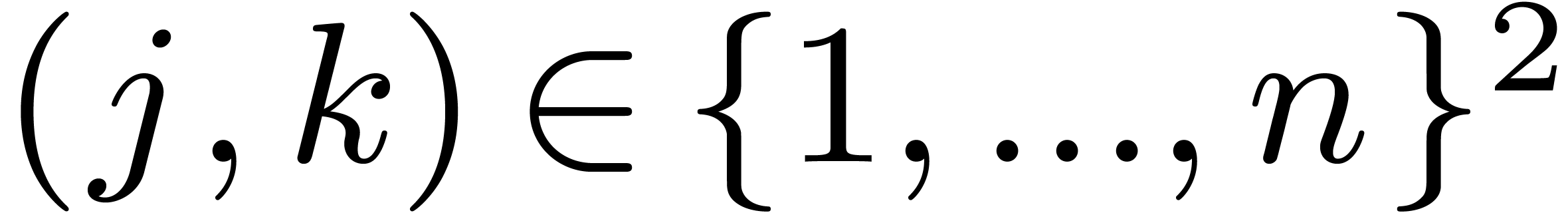 ,
define
,
define 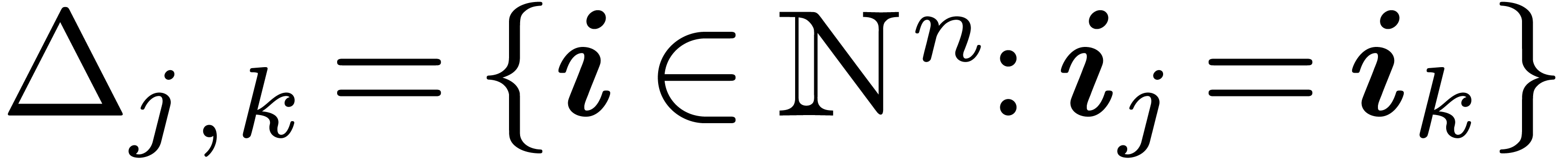 and
and 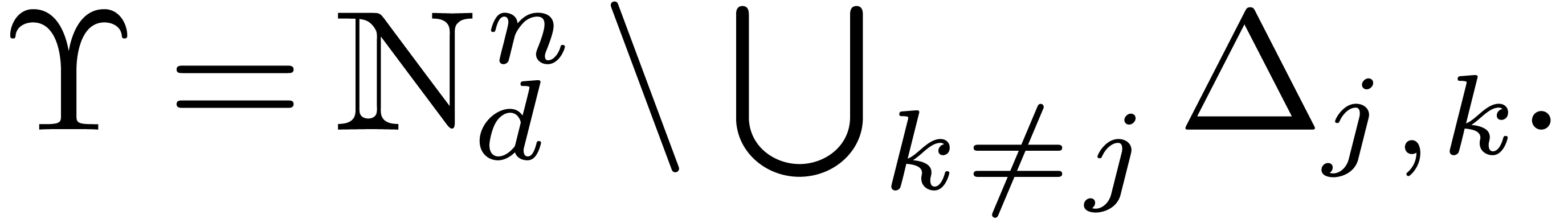
Lemma 4. There
exists a constant  (depending on
(depending on 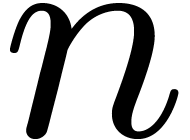 ) such that
) such that
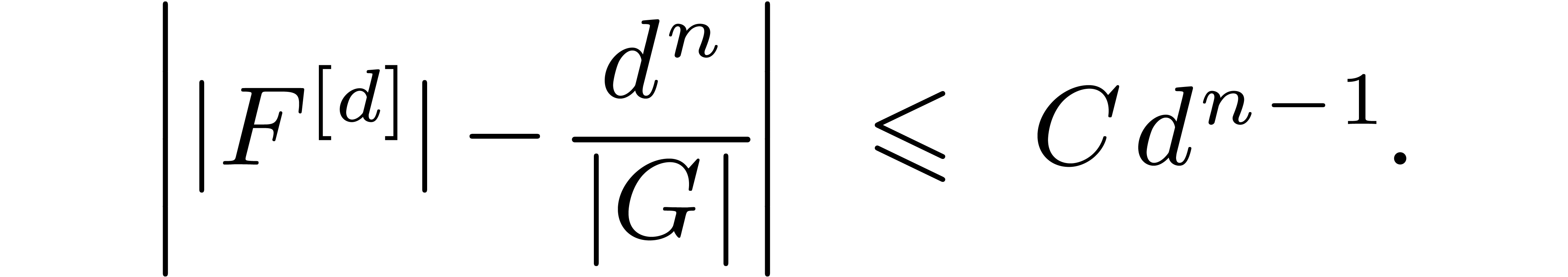
Proof. With the notation above, we have
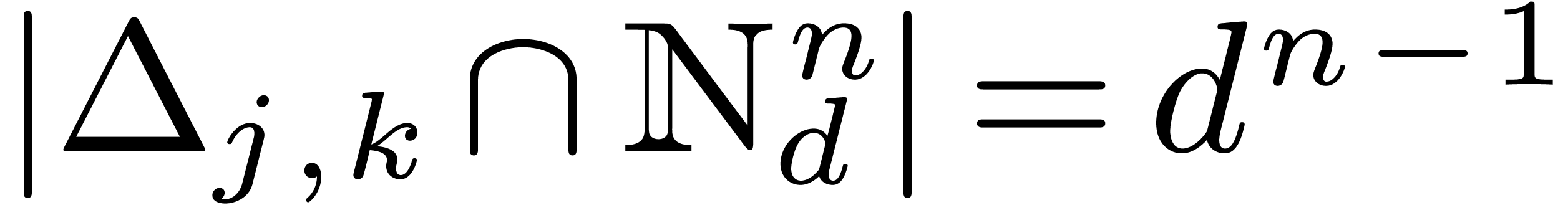 .
. Taking
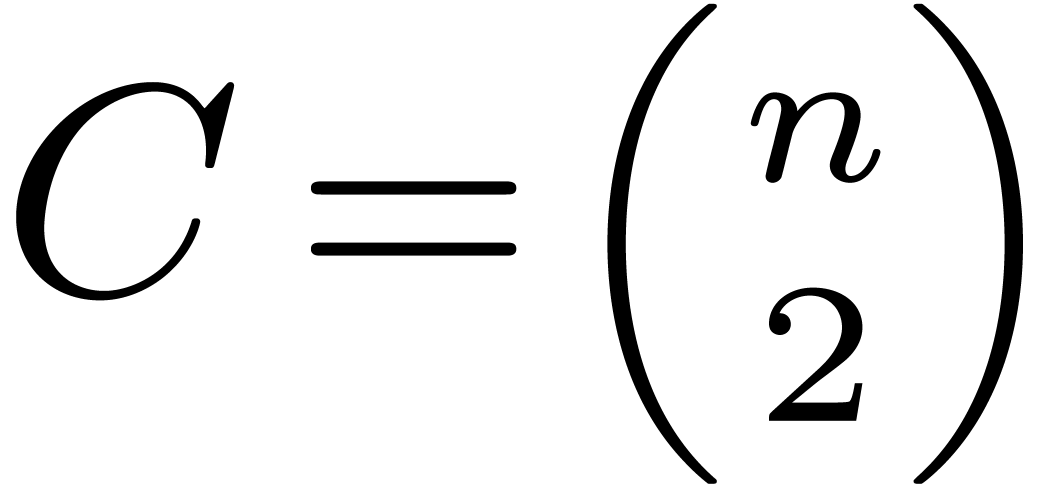 ,
, it follows that
 .
.
On the other hand, the orbit of any element in

under

contains exactly
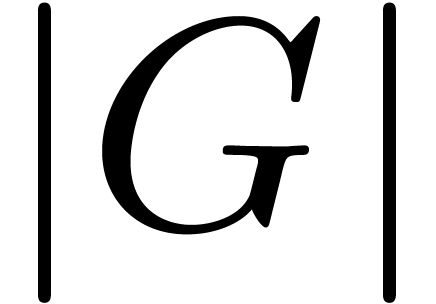
elements and one element in
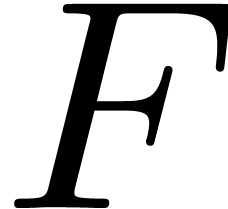 .
.
In other words,
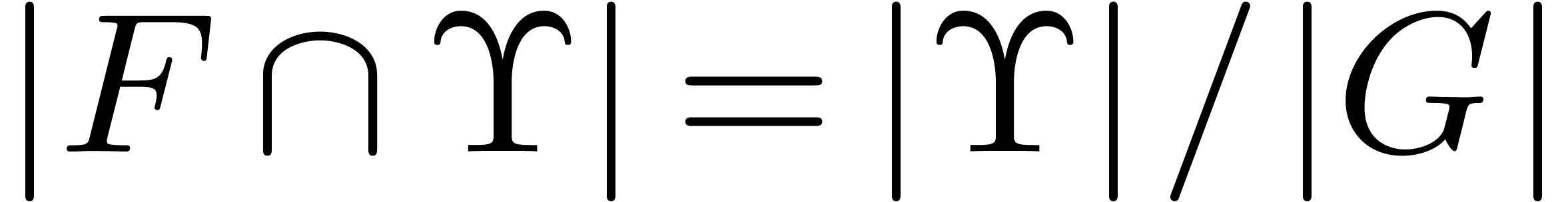
and so
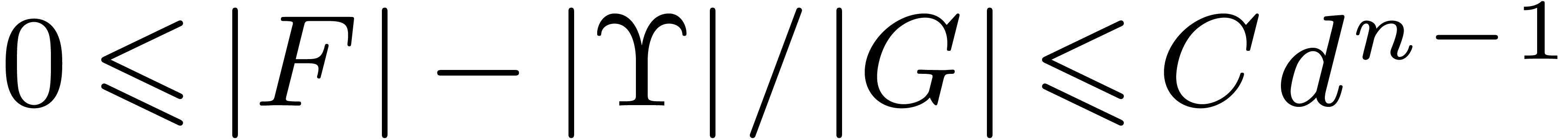 .
. Finally,
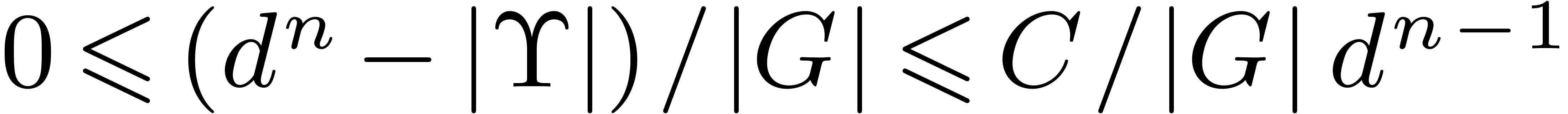
which implies
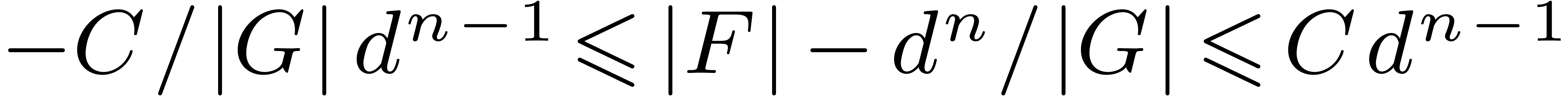 .
.
3.4The symmetric FFT
Let 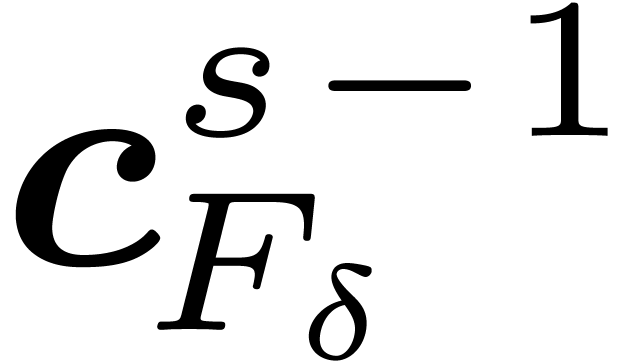 be the restriction of
be the restriction of 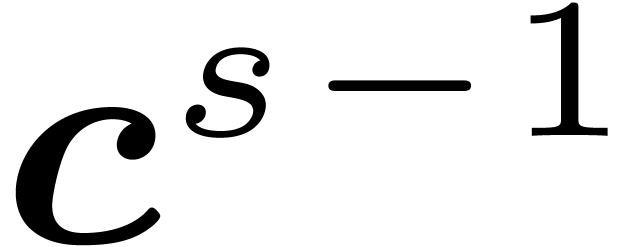 to
to 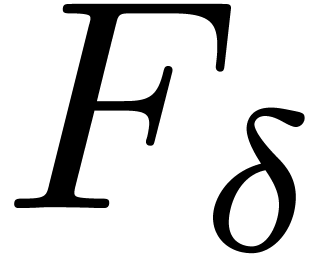 and notice that
and notice that  is
stable under
is
stable under 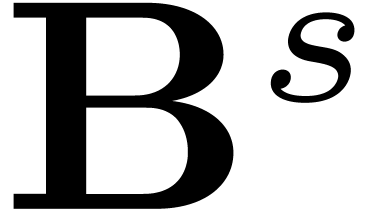 , i.e.
, i.e.
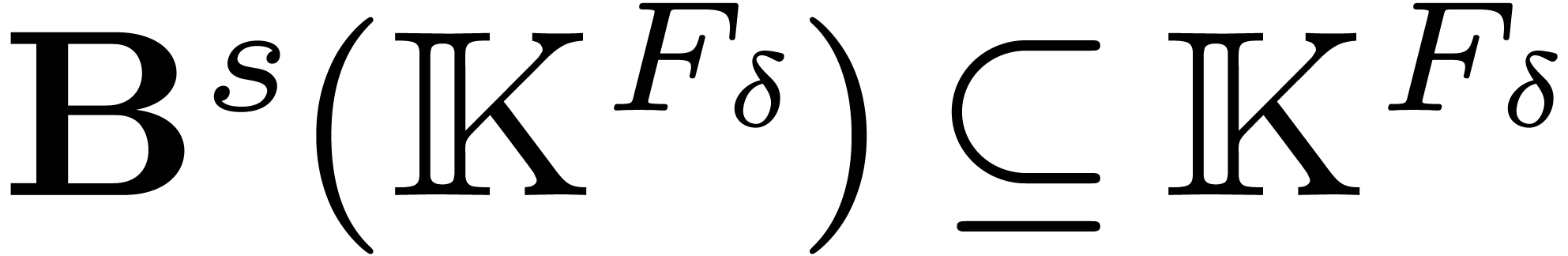 . Therefore the restriction
. Therefore the restriction
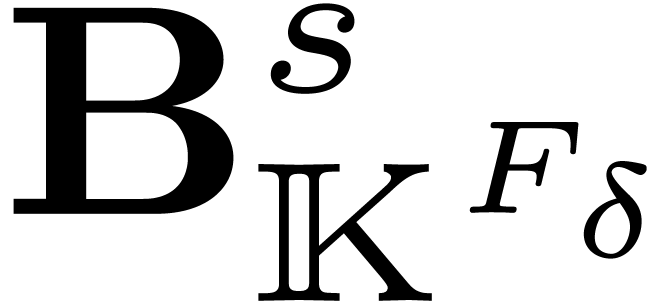 of the map
of the map 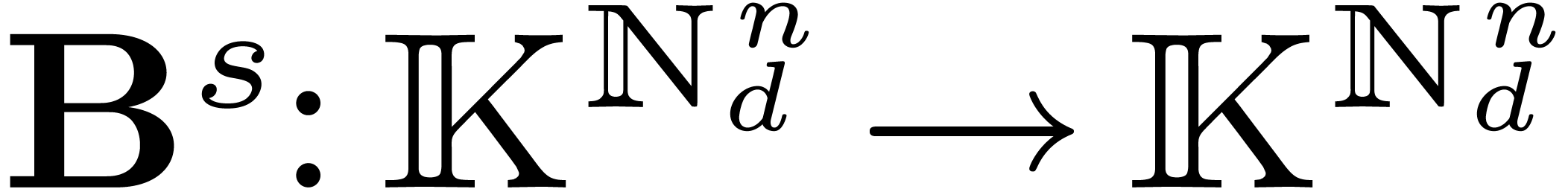 to vectors in
to vectors in
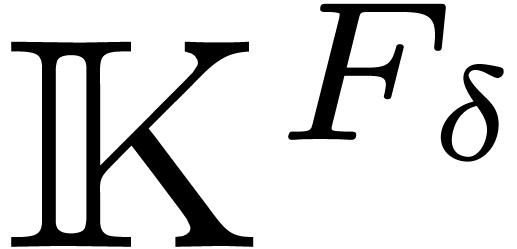 is a
is a  -algebra
morphism from
-algebra
morphism from 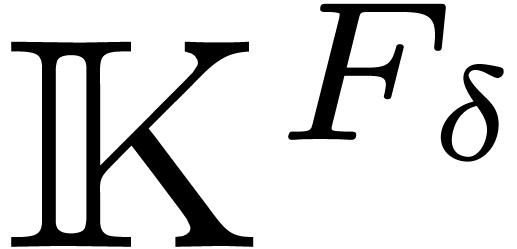 to
to 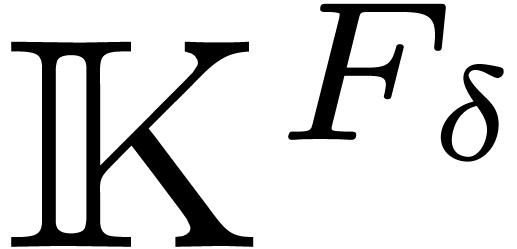 .
By construction, we now have
.
By construction, we now have 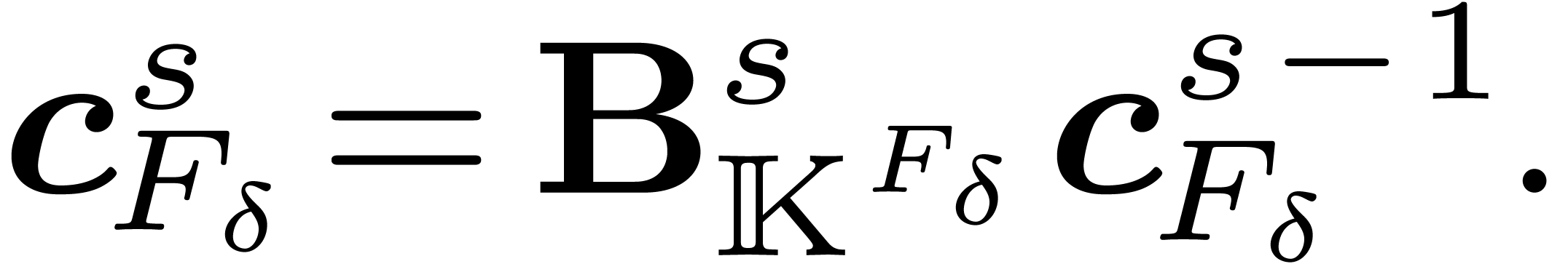 This allows us to
compute
This allows us to
compute 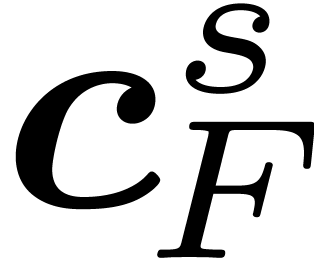 as a function of
as a function of 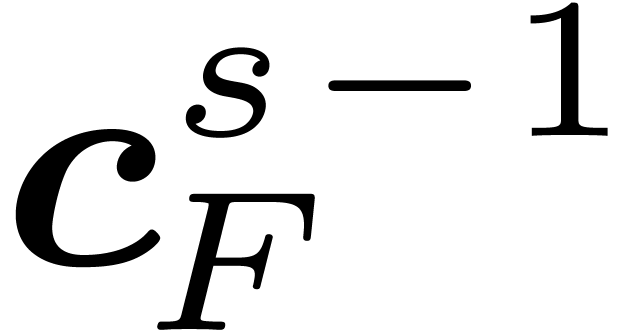 using
using
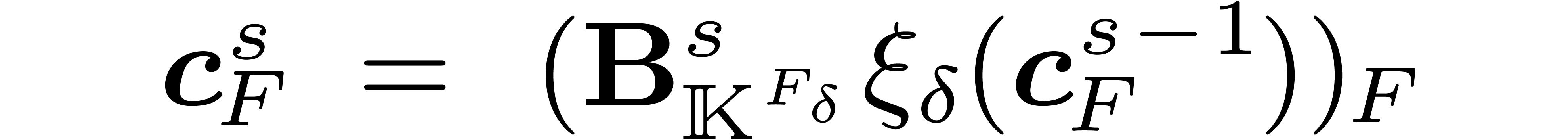 |
(6) |
where 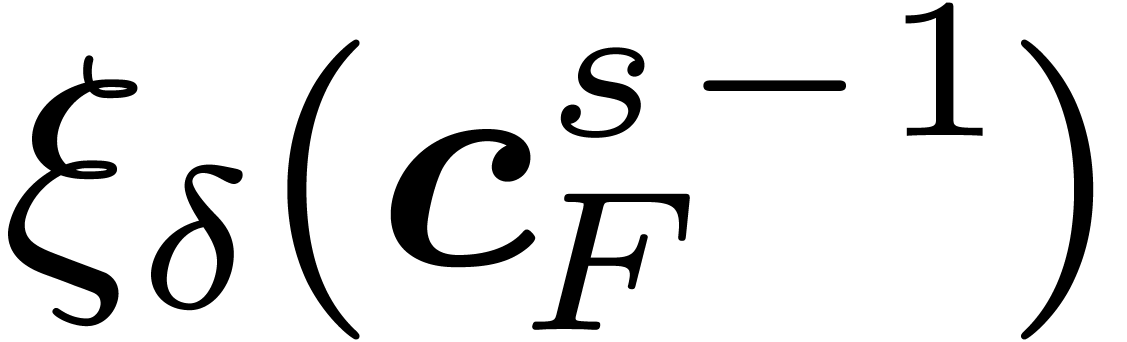 denotes the
denotes the  -expansion
-expansion
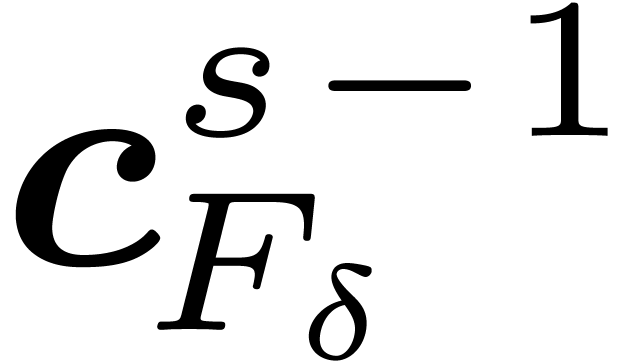 of
of 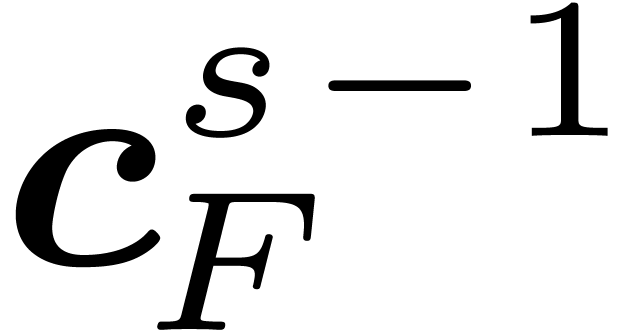 .
.
Remark 5. We could have saved a few more
operations by only computing the coefficients 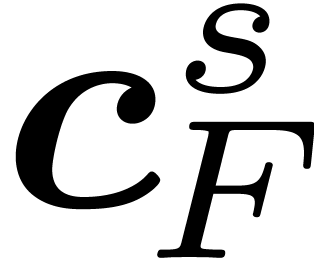 . To do so, we would have performed just the
operations of a butterfly corresponding to vertices inside
. To do so, we would have performed just the
operations of a butterfly corresponding to vertices inside 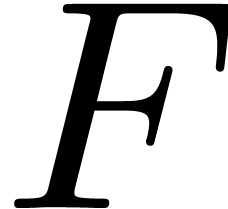 . However, the potential gain of complexity is
only linear in the numbers of monomials
. However, the potential gain of complexity is
only linear in the numbers of monomials 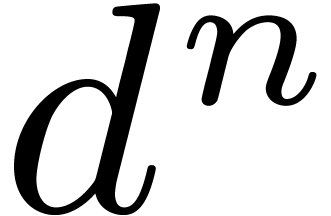 .
.
The formula (6) yields a straightforward way to compute the
direct FFT of a  -symmetric
polynomial:
-symmetric
polynomial:
Remark 6. The main challenge for an actual
implementation of our algorithms consists in finding a way to iterate on
sets like  without too much overhead. We give a
hint on how to iterate over
without too much overhead. We give a
hint on how to iterate over  in Lemma 8
(see also [22] for similar considerations).
in Lemma 8
(see also [22] for similar considerations).
The inverse FFT can be computed classically by unrolling the loops in
the inverse order and inverting the operations of the butterflies. The
main result of this section is then the following theorem, where 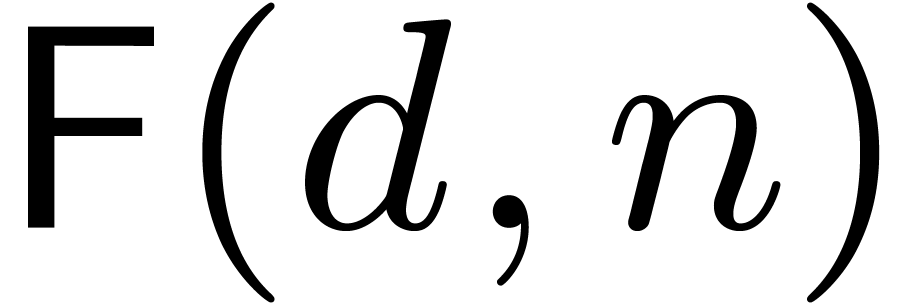 denotes the cost of a full
denotes the cost of a full 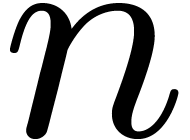 -dimensional FFT of multi-degree
-dimensional FFT of multi-degree 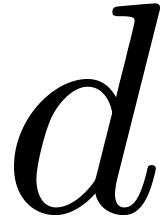 .
.
Theorem 7. For
fixed 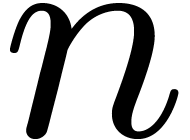 and
and  ,
and for
,
and for 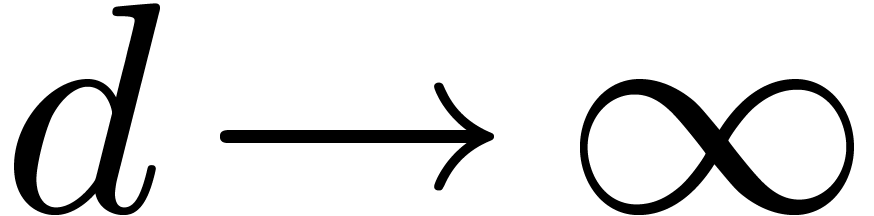 , the direct
(resp. inverse) symmetric FFT can be computed in time
, the direct
(resp. inverse) symmetric FFT can be computed in time
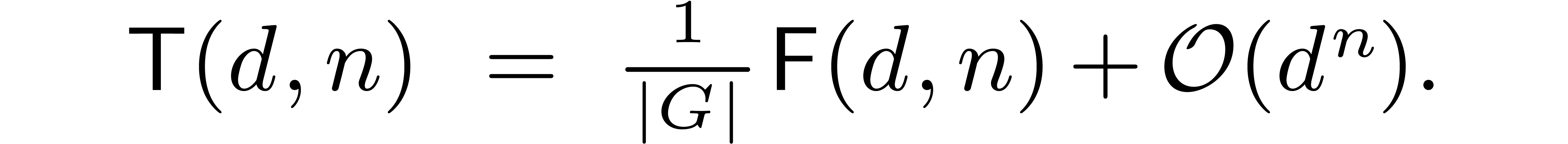
Proof. At stage  of the
computation, the ratio between the computation of
of the
computation, the ratio between the computation of 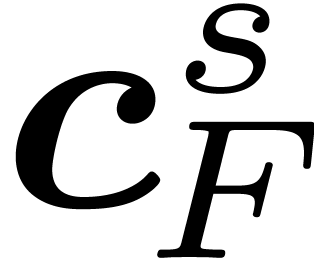 as a function of
as a function of 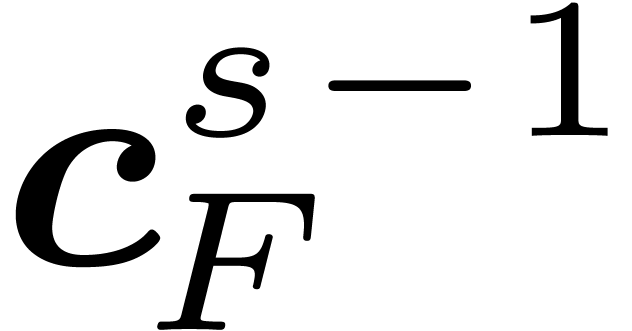 and
and 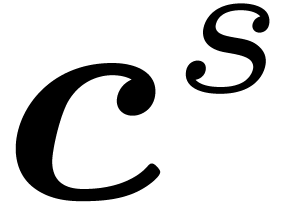 as
a function of
as
a function of 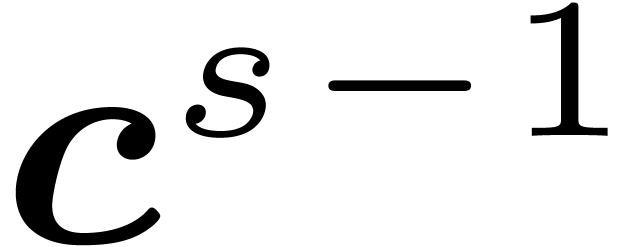 is
is 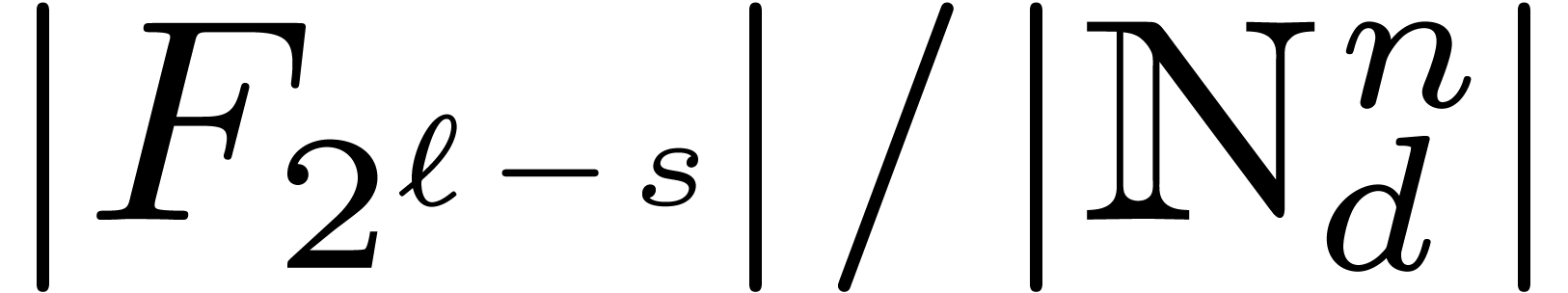 ,
so that
,
so that
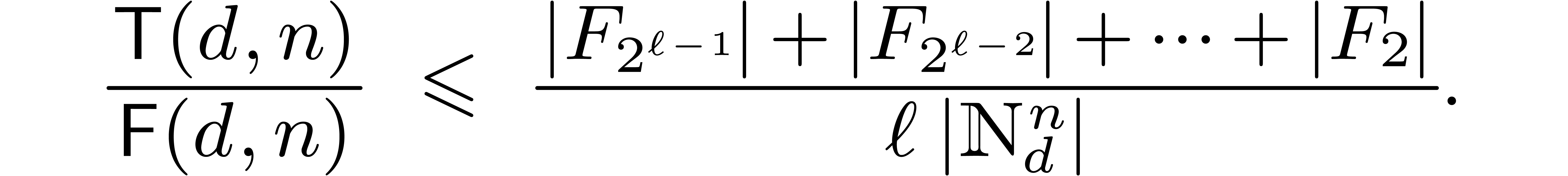
Lemmas 3 and 4 thus imply
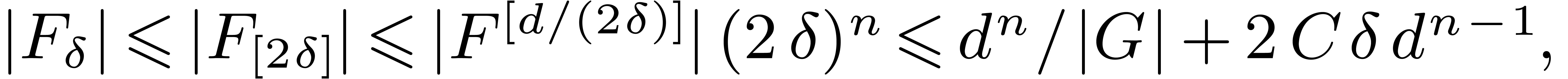
whence
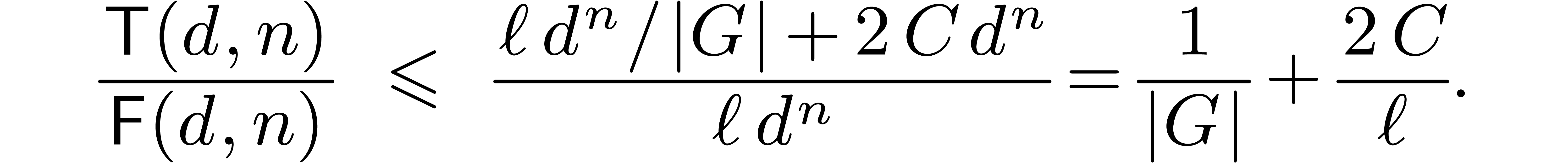
The result follows for
 .
.
Finally, the following lemma gives a description of an
“open” subset of 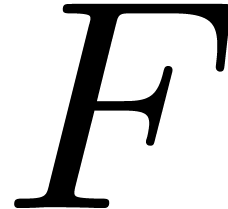 ,
characterized only by simple inequalities. Although we do not describe
implementation questions in detail here, we point out that this simple
characterization would naturally be used in order to iterate over the
sets
,
characterized only by simple inequalities. Although we do not describe
implementation questions in detail here, we point out that this simple
characterization would naturally be used in order to iterate over the
sets 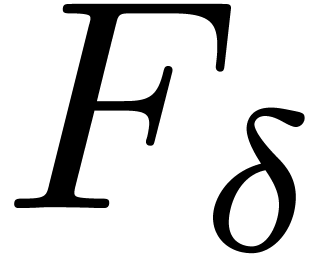 , possibly using
tree-based techniques as in [17].
, possibly using
tree-based techniques as in [17].
Lemma 8. Let
 be the set of
be the set of 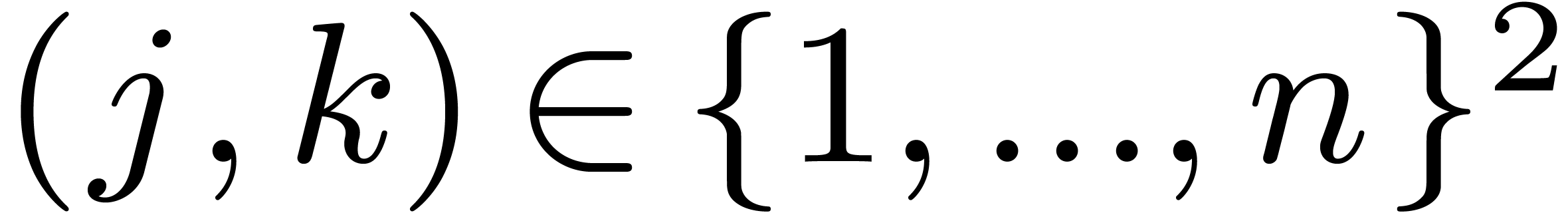 such that
such that
 and
and 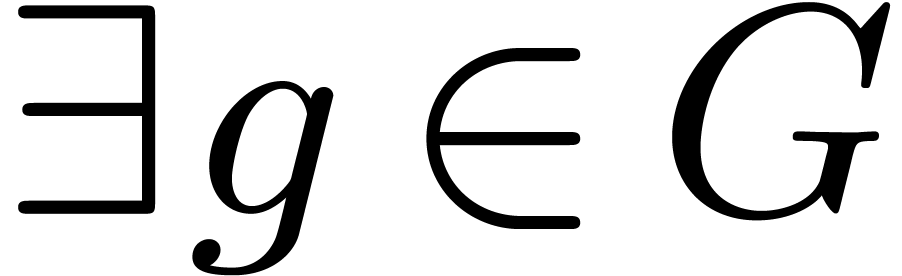 such that
such that 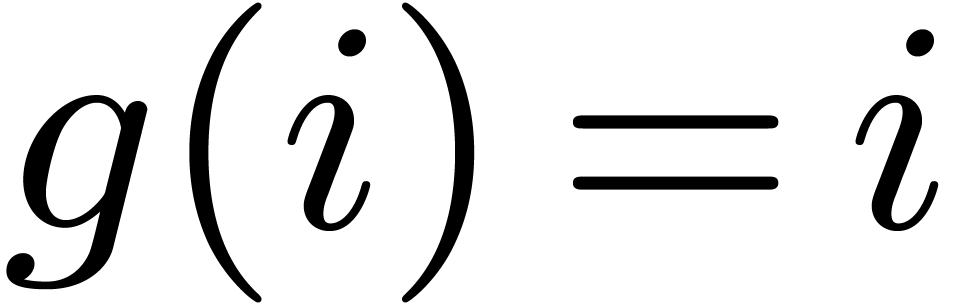 for
for 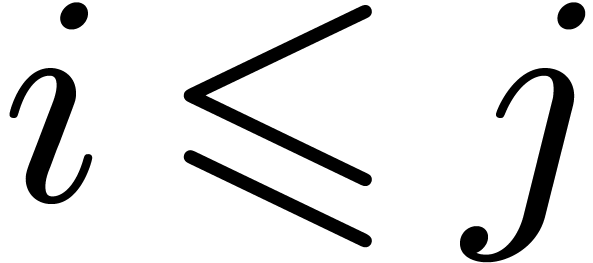 and
and 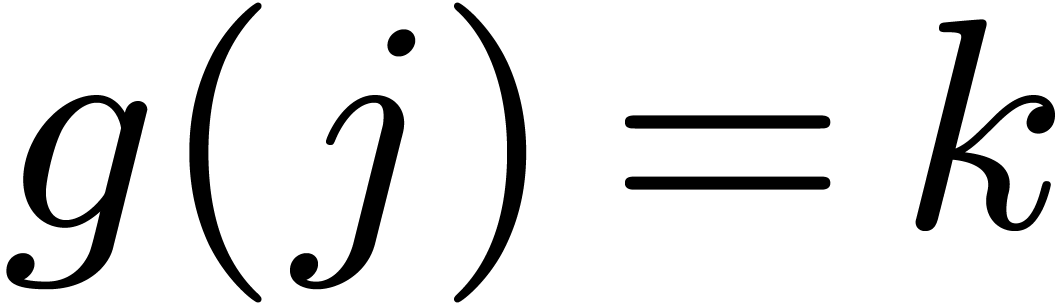 . For
. For 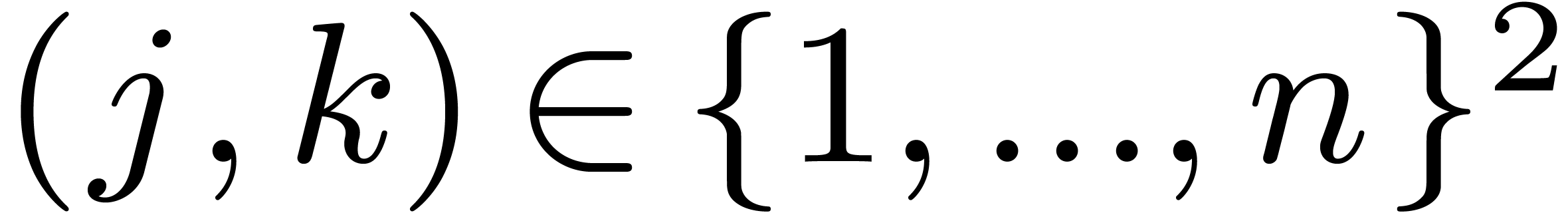 ,
define
,
define 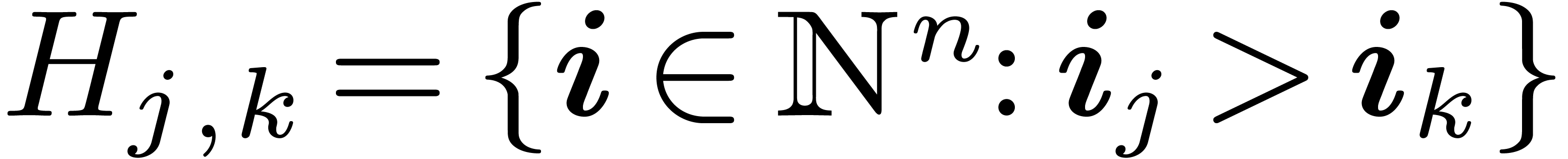 . Then
. Then
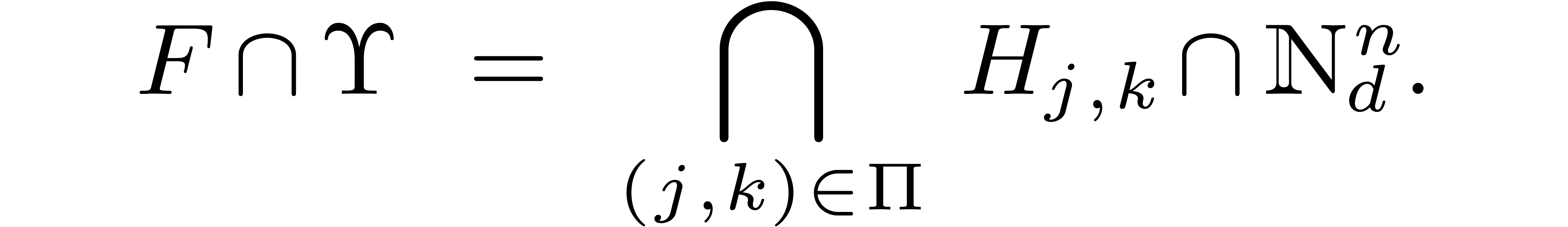
Proof. Assume that
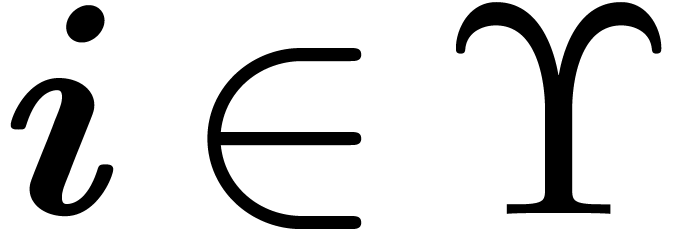
does
not lie in
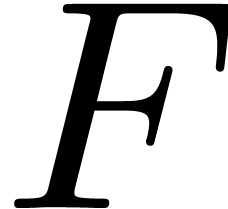 .
. Then
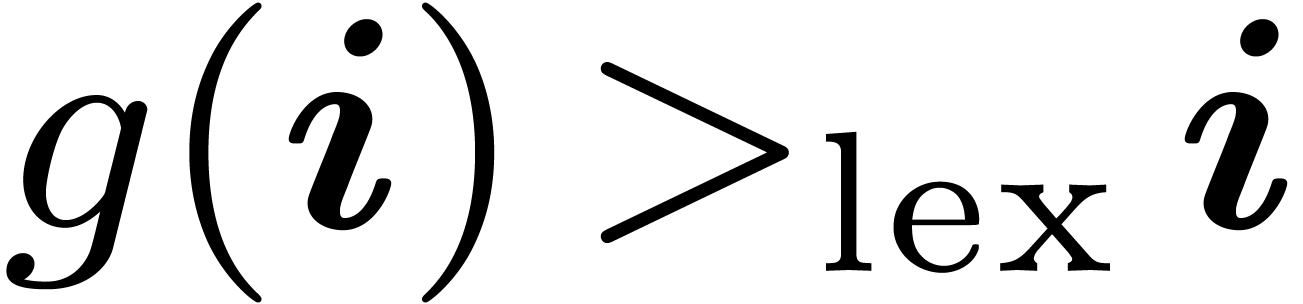
for some
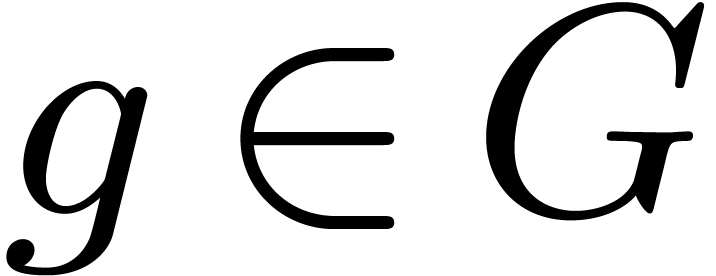 .
. Let
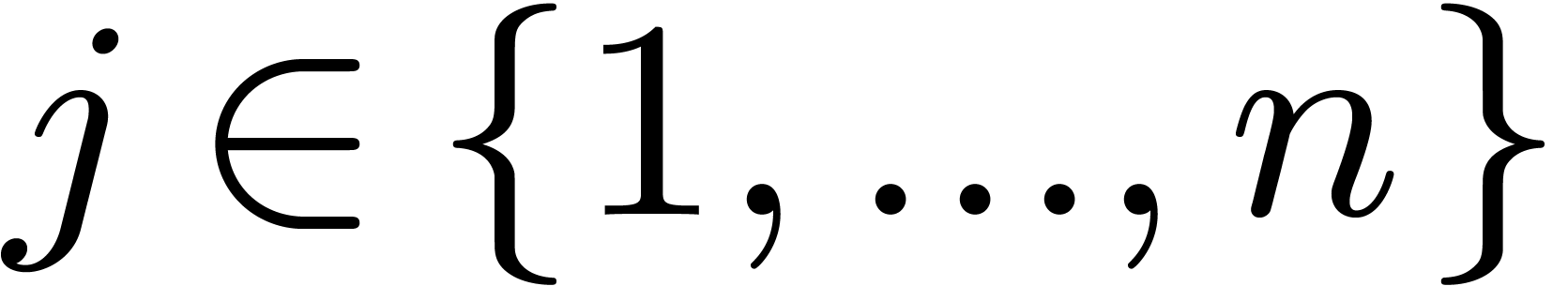
be minimal with
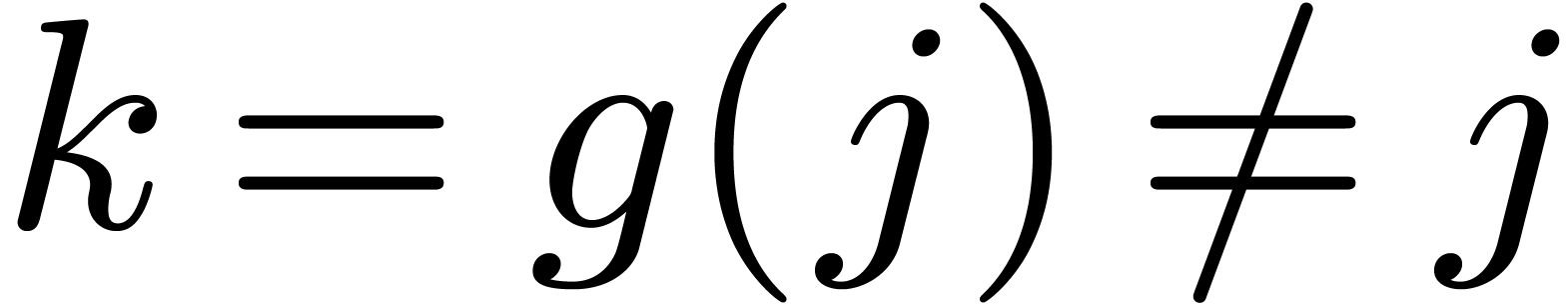 ,
,
whence
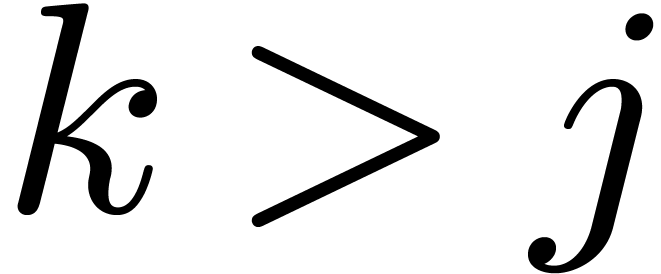
and
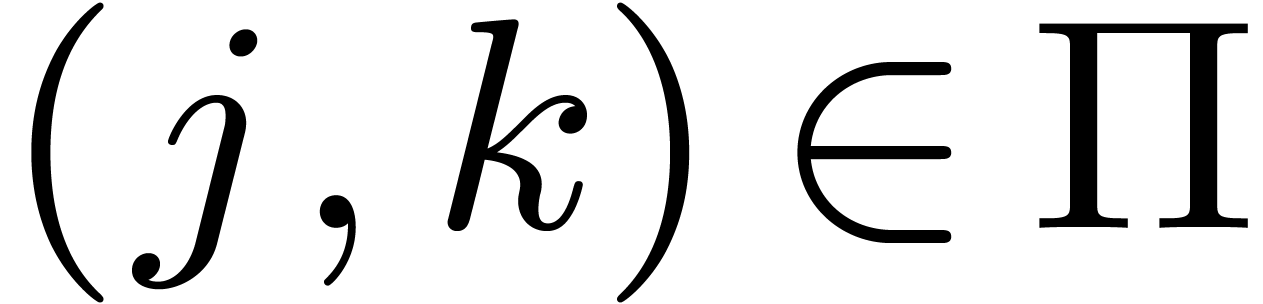 .
.
Since
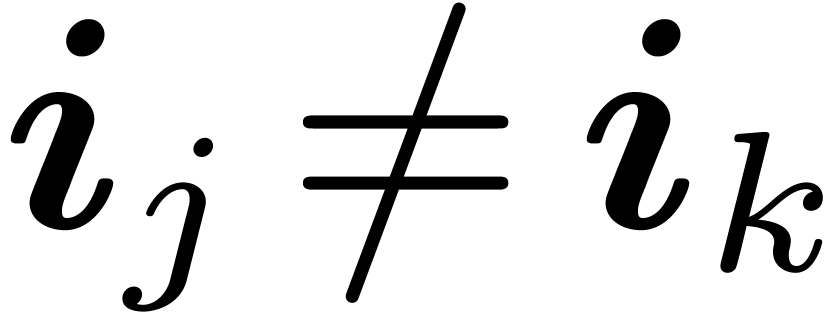 ,
, it follows that
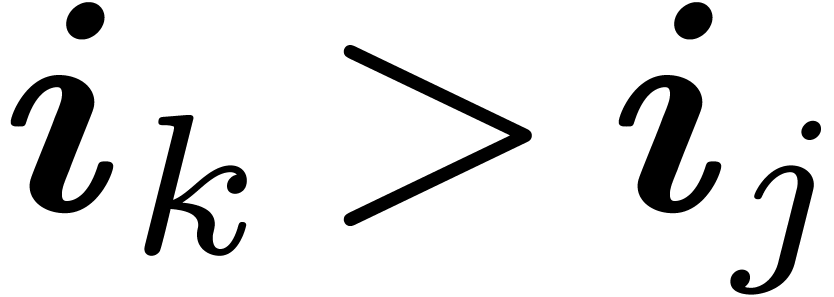 ,
, so
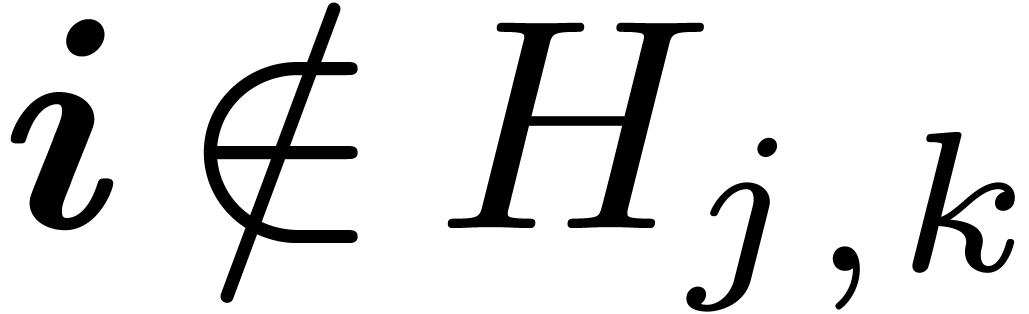 .
.
Inversely, assume that
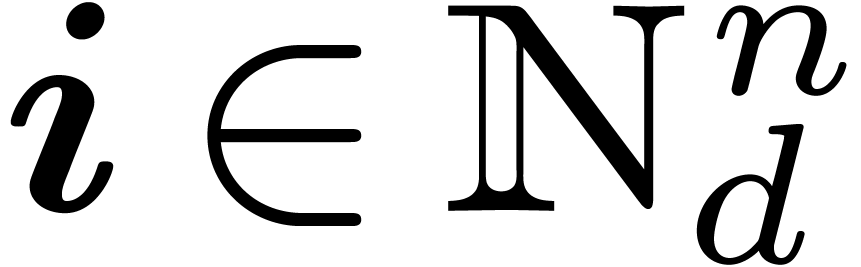
does not lie in
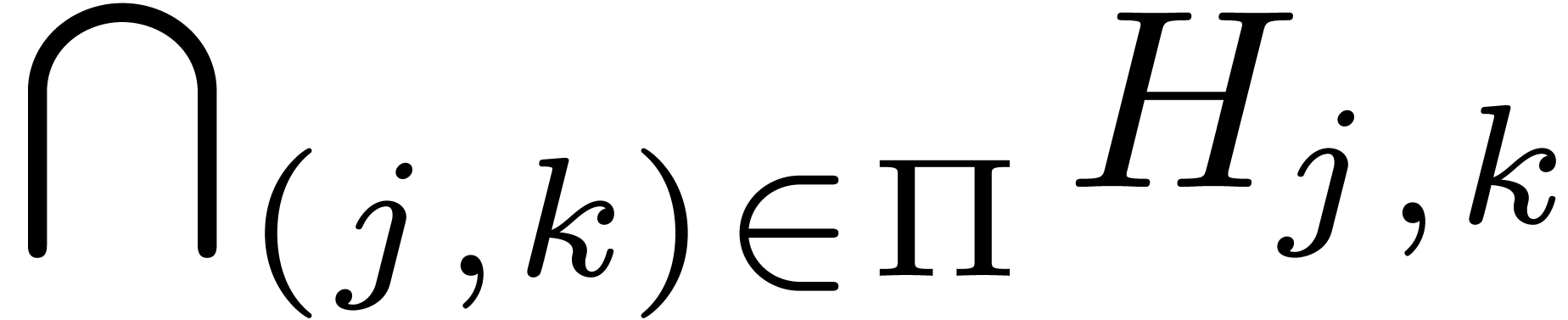 ,
, so that there exists
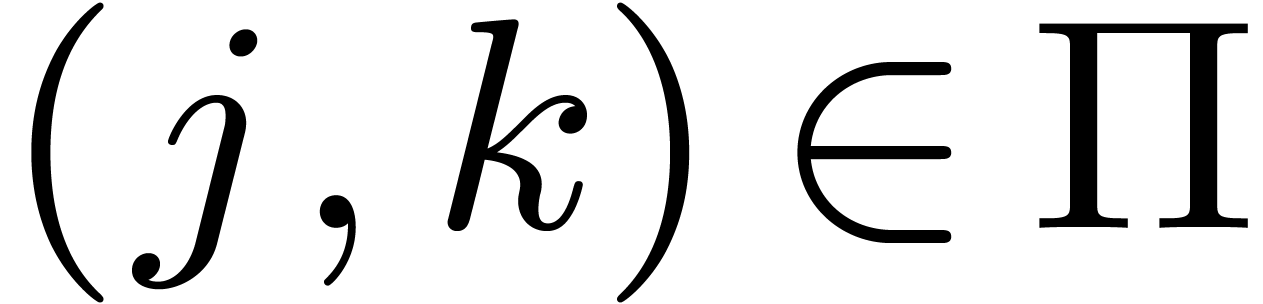
with
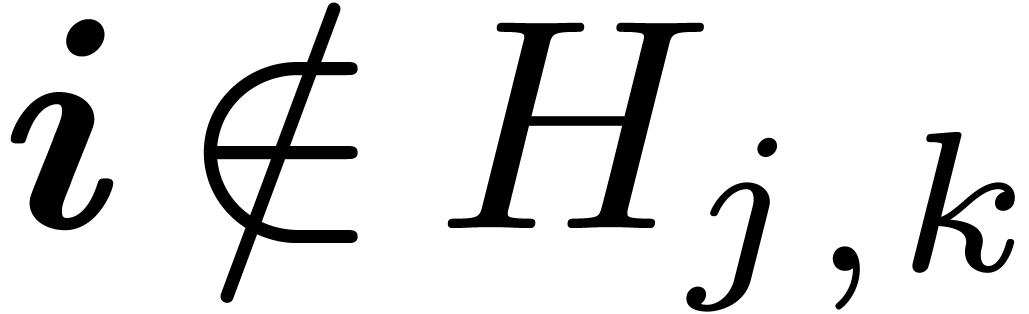 .
. Let
be such that
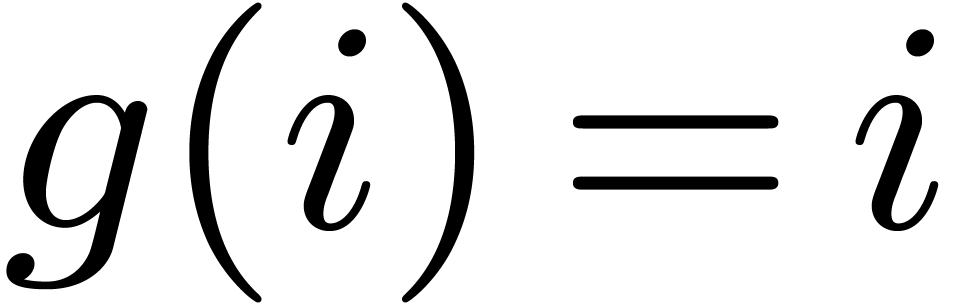
for

and
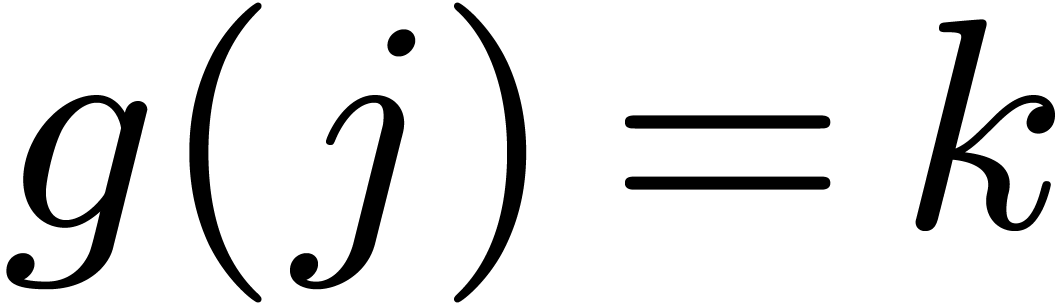 .
. Then,
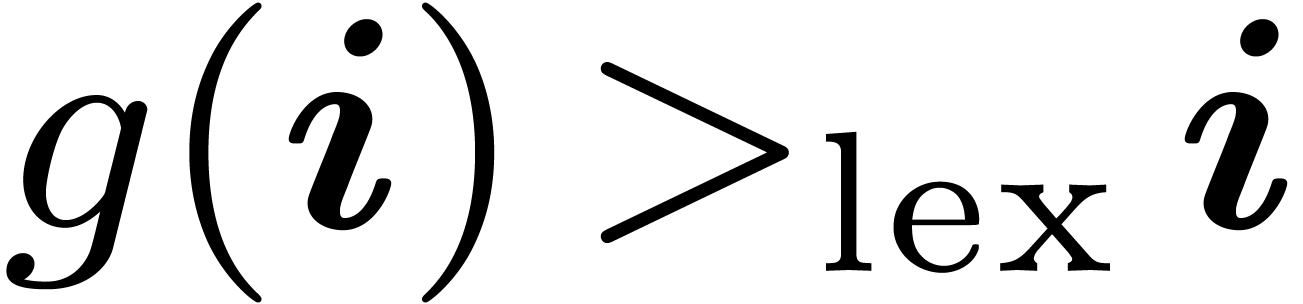 .
.
4.The lattice FFT
In this section, we deal with polynomials supported on lattices; our
main result is an algorithm for the multiplication of such polynomials
using Fourier transforms.
The first subsection introduces the main objects we will need (a lattice
 and its dual
and its dual  );
then, we will give an algorithm, based on Smith normal form computation,
for the FFT on what we will call a basic domain, and we will
finally deduce a multiplication algorithm for the general case.
);
then, we will give an algorithm, based on Smith normal form computation,
for the FFT on what we will call a basic domain, and we will
finally deduce a multiplication algorithm for the general case.
The techniques we use, based on Smith normal form computation, can be
found in several papers, originating from [13]; in
particular, the results in Section 4.2 are essentially in
[33] (in a more general form).
4.1Lattice polynomials
Assume that  admits a primitive
admits a primitive 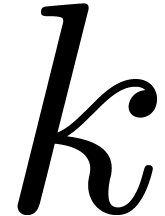 th root of unity for any order
th root of unity for any order  , which we will denote by
, which we will denote by 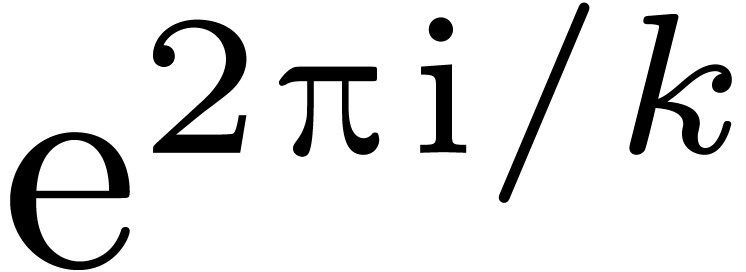 . Let
. Let  be a free
be a free  -submodule of
-submodule of 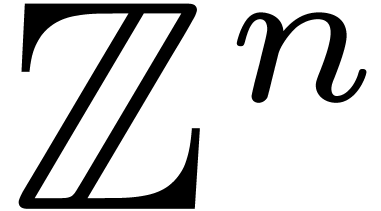 of rank
of rank 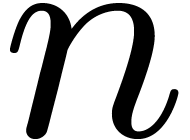 , generated by the
vectors
, generated by the
vectors 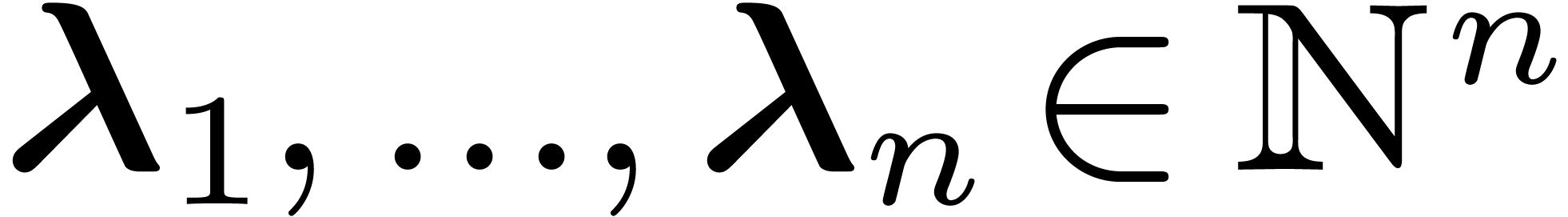 . Then
. Then

is a subring of 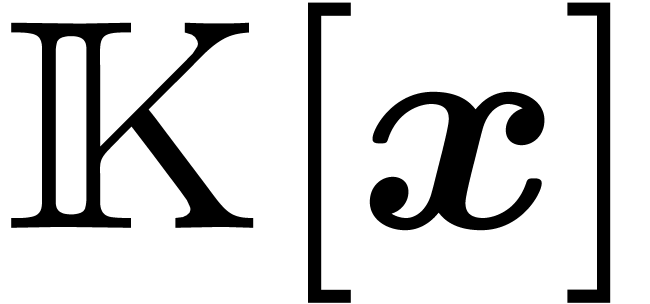 , and we will
call elements of
, and we will
call elements of 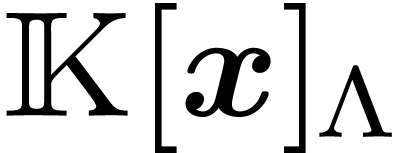 lattice polynomials.
First, we show that these polynomials are the invariant polynomial ring
for a diagonal matrix group.
lattice polynomials.
First, we show that these polynomials are the invariant polynomial ring
for a diagonal matrix group.
The set  acts on
acts on 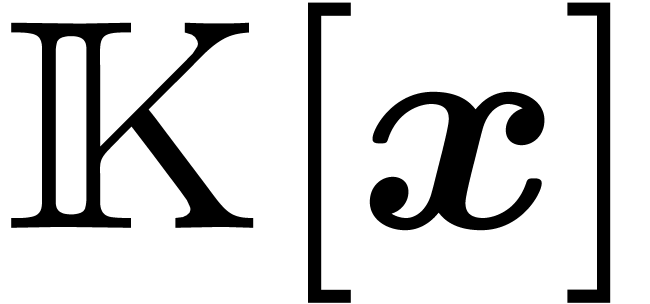 via, for any
via, for any  , the
isomorphism
, the
isomorphism  of
of  given by
given by
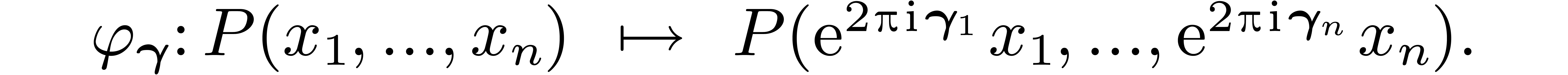
Note that  for any
for any 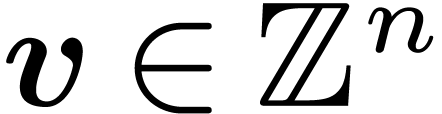 .
The action of
.
The action of  on the monomial
on the monomial  is given by
is given by 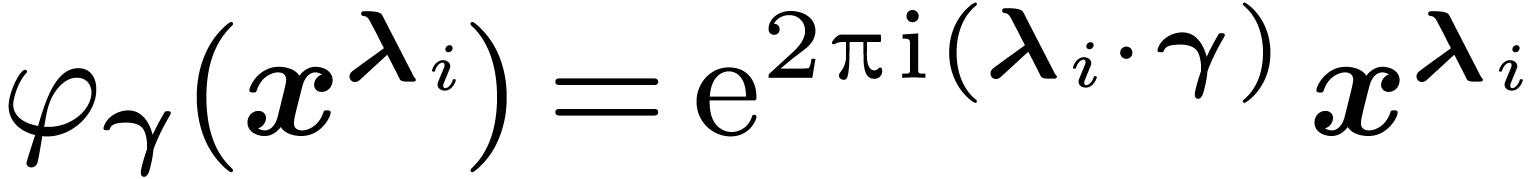 .
.
In particular, all elements of 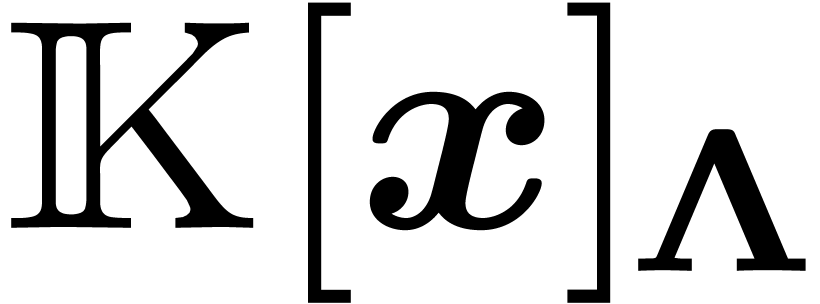 are invariants
under the action of
are invariants
under the action of  if and only if
if and only if
 |
(7) |
where  is the matrix with columns
is the matrix with columns  , that is
, that is 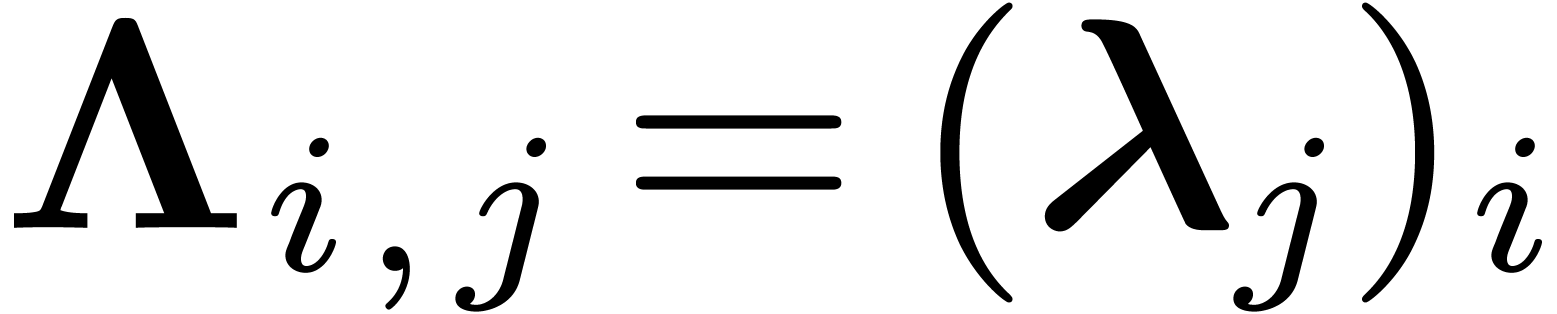 .
Let
.
Let  be the dual (or reciprocal) lattice of
be the dual (or reciprocal) lattice of  , that is the set of all
, that is the set of all 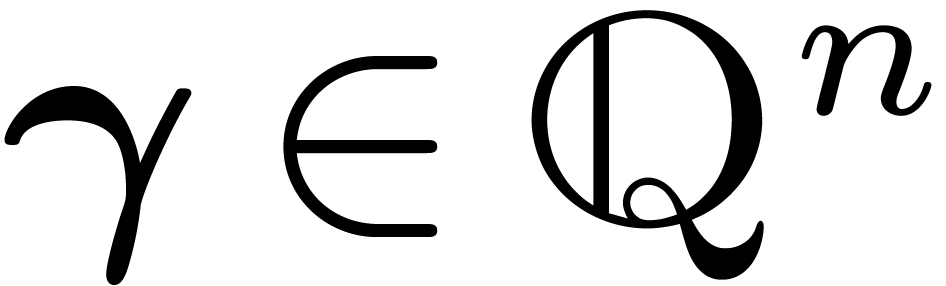 satisfying Equation (7). A basis of
satisfying Equation (7). A basis of  is given by the columns of
is given by the columns of 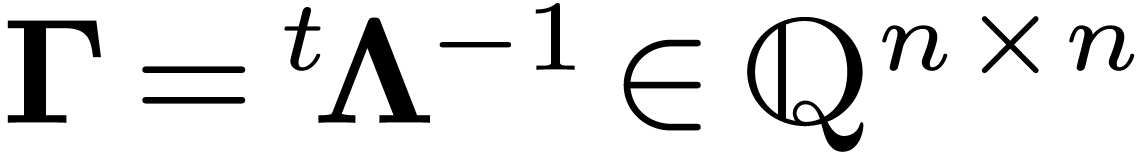 .
.
Let  be the group of actions
be the group of actions  . It is generated by
. It is generated by 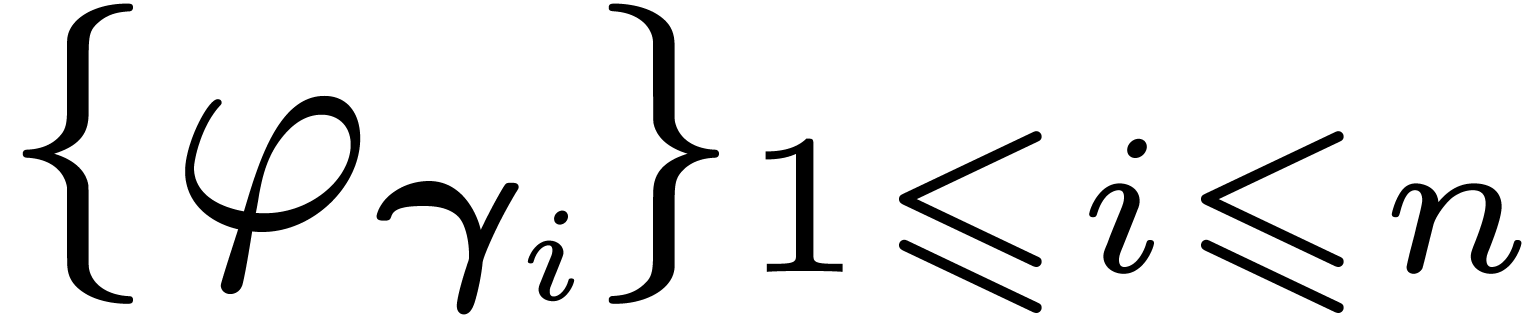 , where
, where 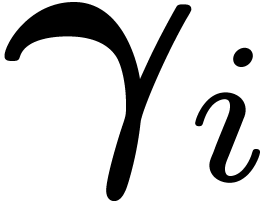 are the columns of
are the columns of
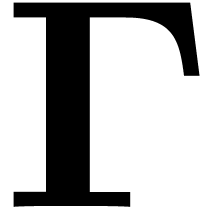 . From Equation (7),
we deduce that
. From Equation (7),
we deduce that  is the diagonal matrix group of
all actions
is the diagonal matrix group of
all actions  which leave
which leave  invariant. Conversely, because monomials are mapped to monomials by
elements of
invariant. Conversely, because monomials are mapped to monomials by
elements of  , the ring of
invariants is spanned by the monomials
, the ring of
invariants is spanned by the monomials  with
with
 , i.e.
, i.e.  belongs to the dual of
belongs to the dual of  .
Since the dual of the dual of a lattice is the lattice itself, we deduce
that
.
Since the dual of the dual of a lattice is the lattice itself, we deduce
that  and
and  .
Note that only
.
Note that only  modulo
modulo 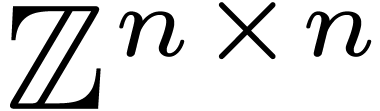 matters to determine the group
matters to determine the group  .
.
Example 9. Consider the lattice  generated by
generated by 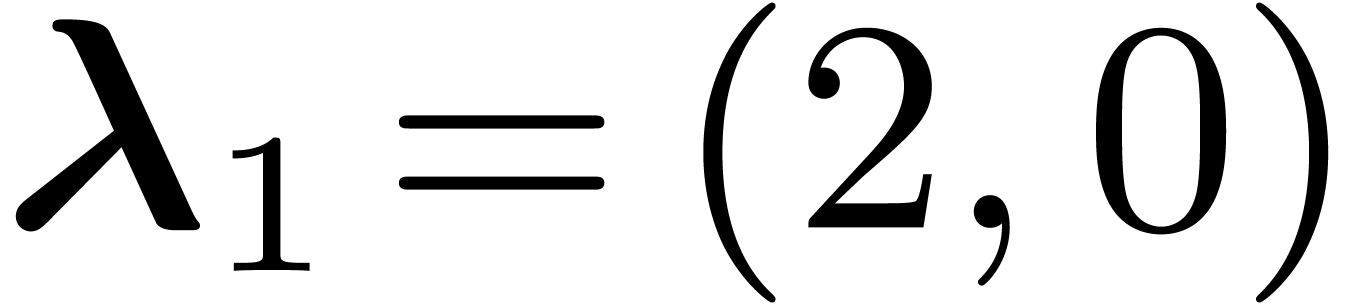 and
and 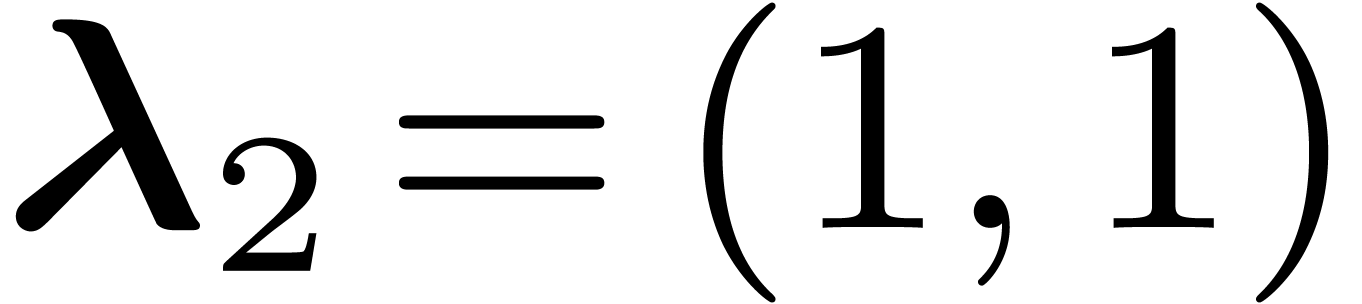 , and let
, and let 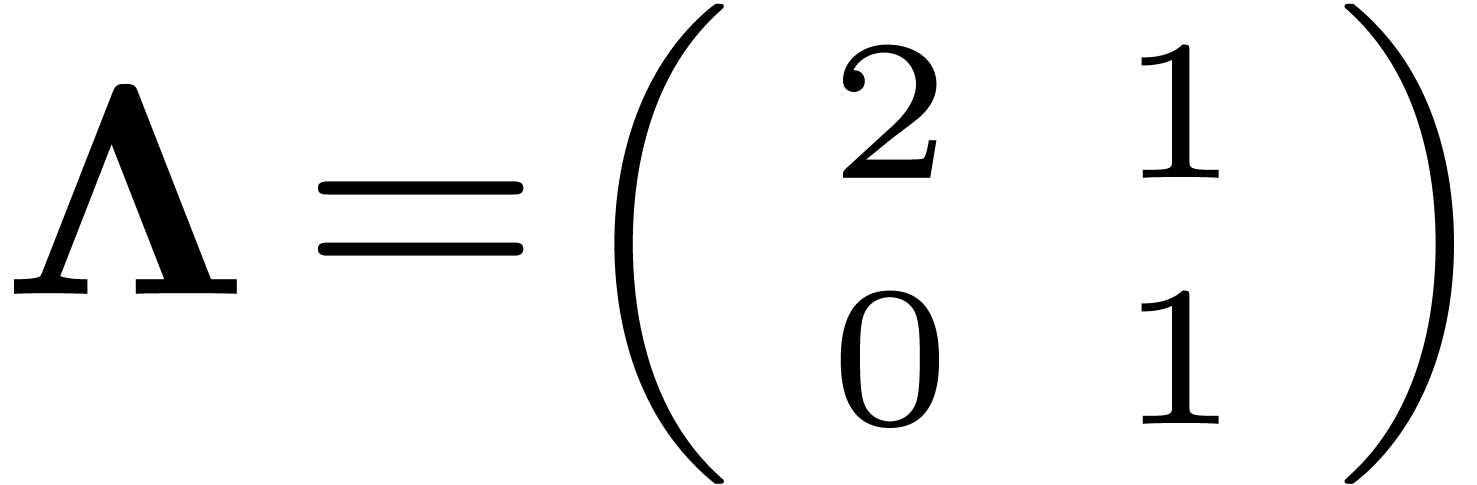 .
The lattice polynomials
.
The lattice polynomials 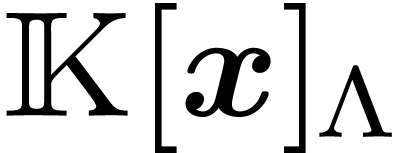 are the polynomials
are the polynomials
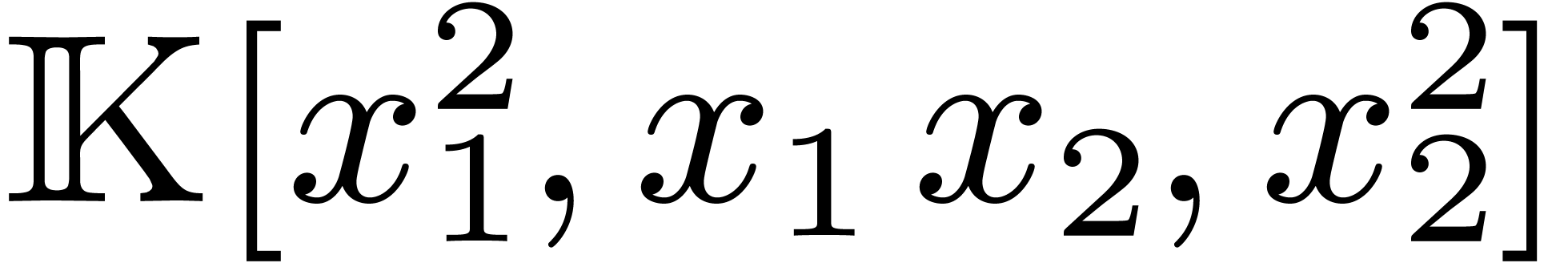 . We have
. We have 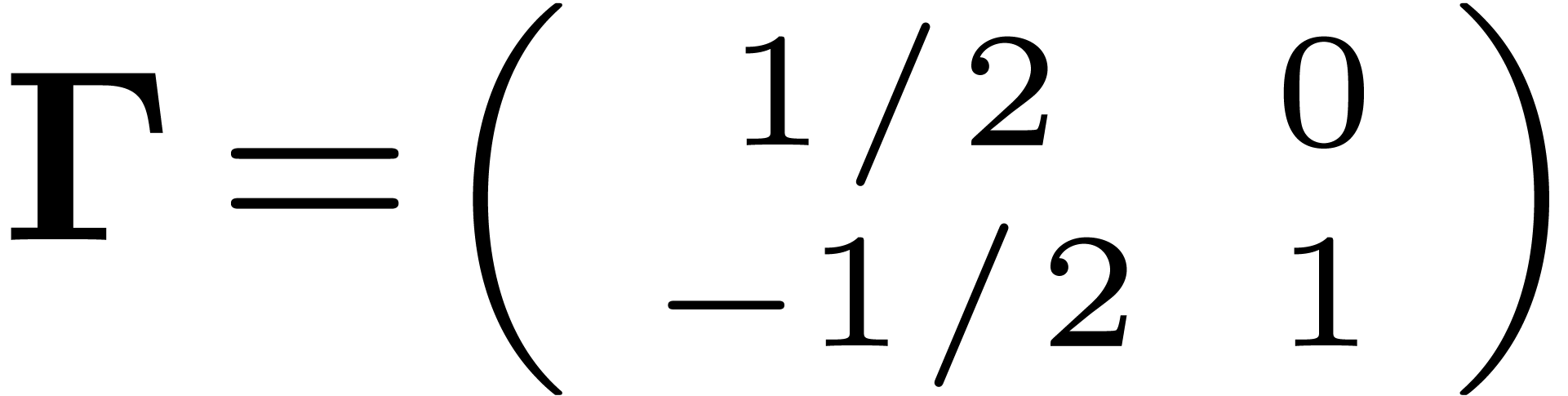 , so
, so  is the group
generated by
is the group
generated by 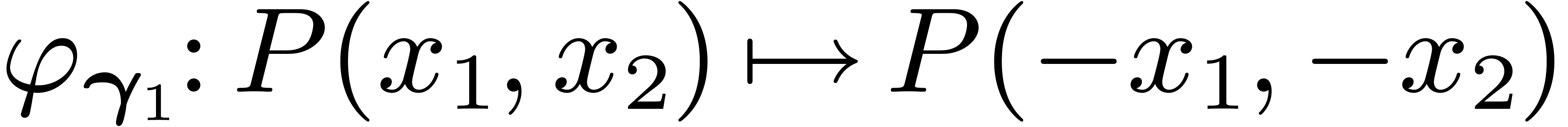 and
and 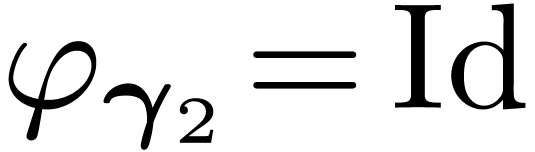 .
The lattice polynomials
.
The lattice polynomials 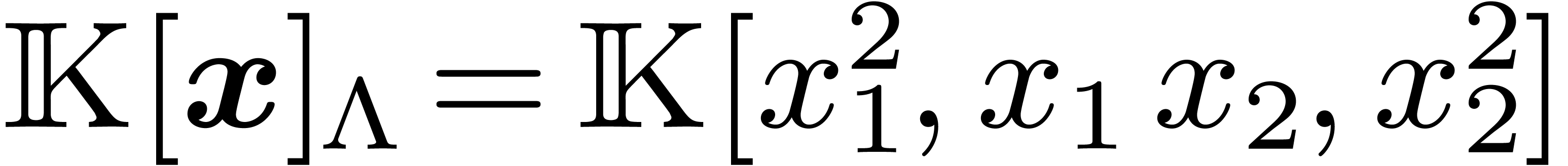 are those polynomials
invariant under the symmetry
are those polynomials
invariant under the symmetry 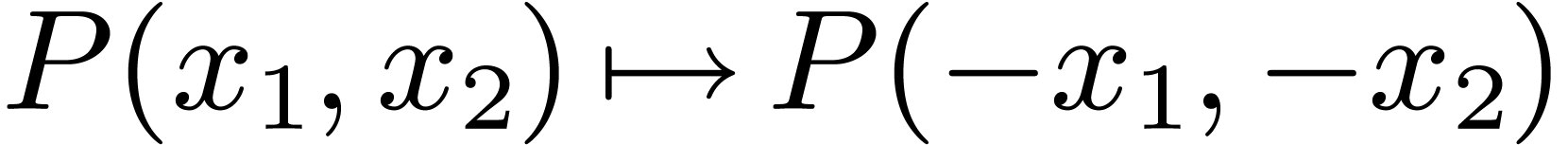 .
.
4.2The lattice FFT on a basic
domain
Given 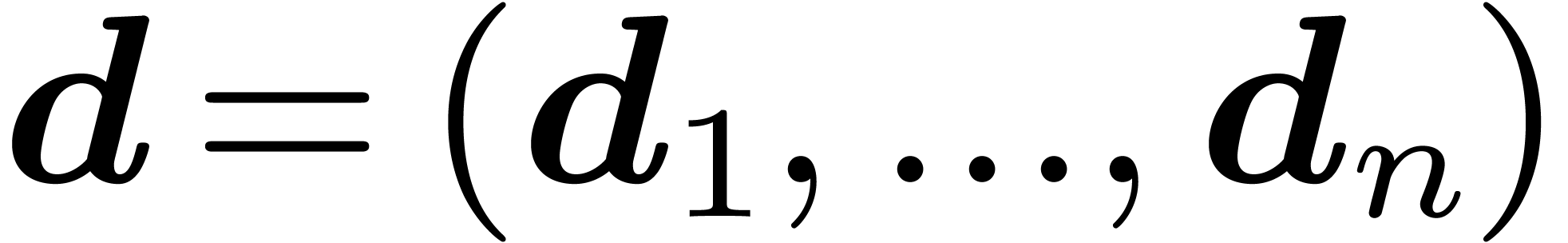 , we define
, we define
For 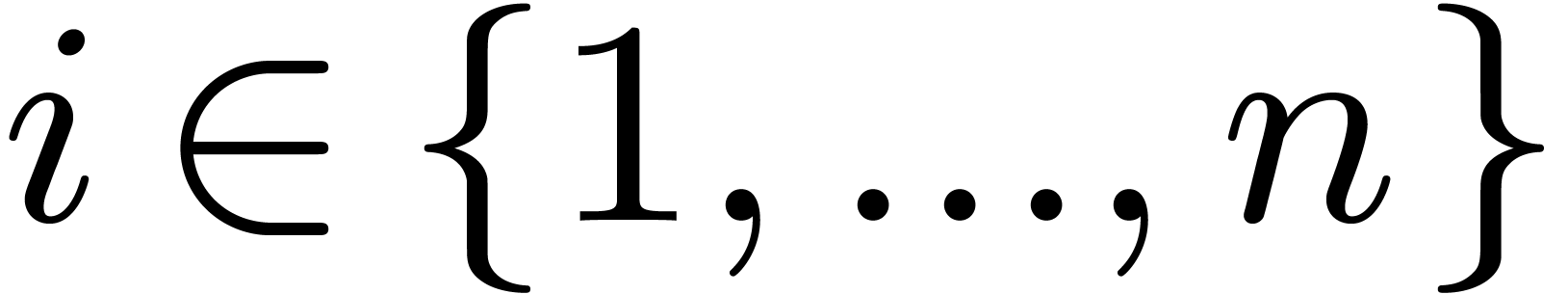 , let
, let  be minimal such that
be minimal such that 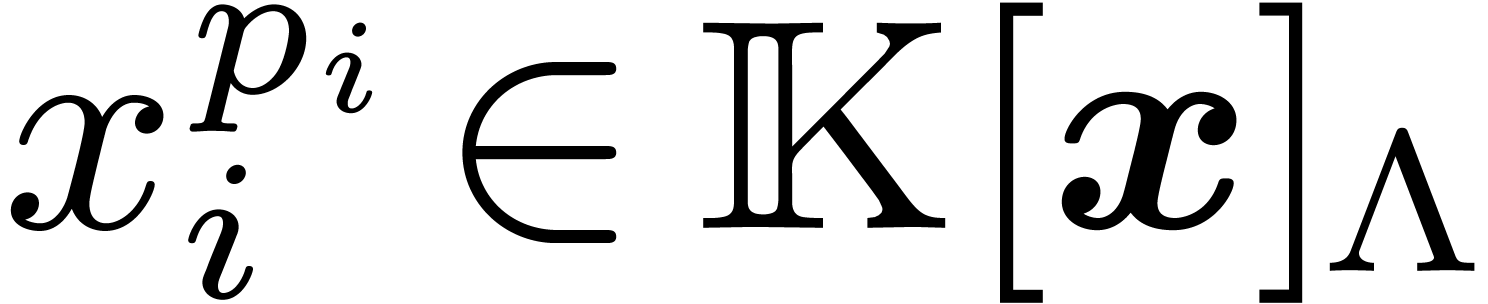 . We
call the block
. We
call the block  a basic domain for
a basic domain for  . In this subsection, we consider
the computation of the FFT at order
. In this subsection, we consider
the computation of the FFT at order  of a
polynomial
of a
polynomial 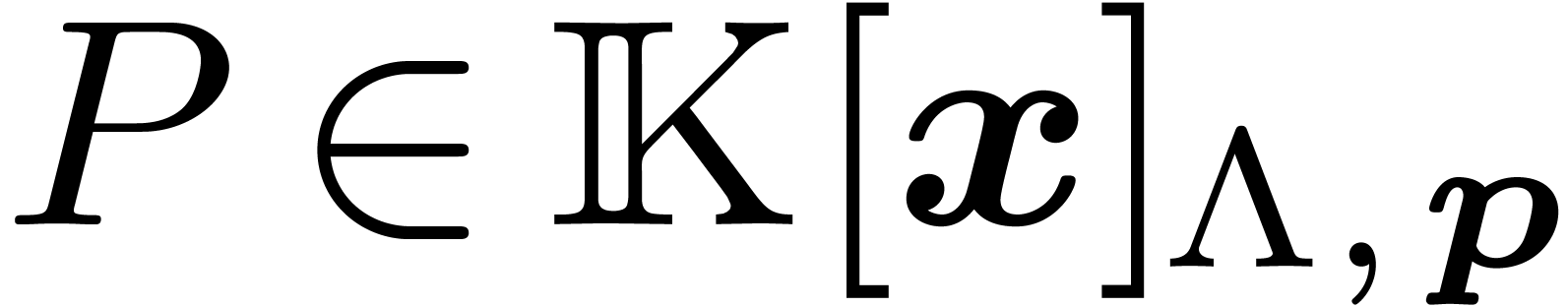 .
.
In what follows, we set 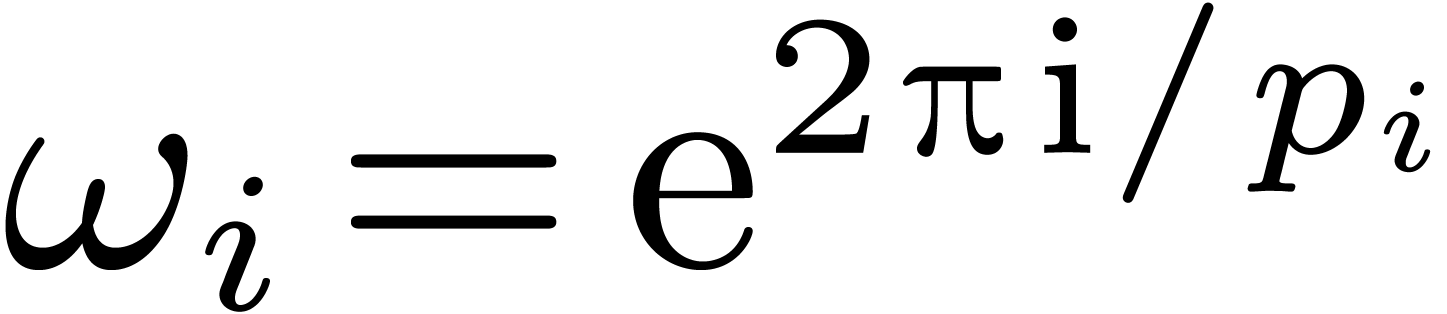 for each
for each 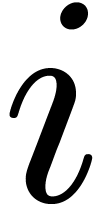 , so that we have to show how to compute the
set of evaluations
, so that we have to show how to compute the
set of evaluations 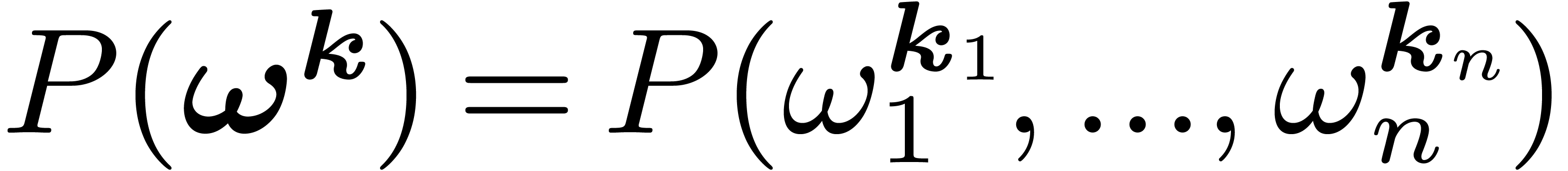 for
for 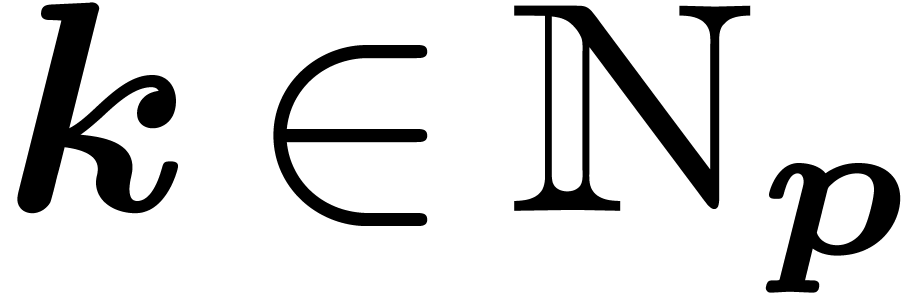 . If we proceeded directly, we would compute more
evaluations that the number of monomials of
. If we proceeded directly, we would compute more
evaluations that the number of monomials of 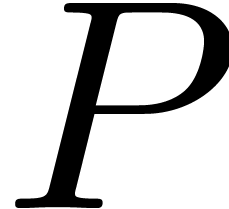 , which is
, which is 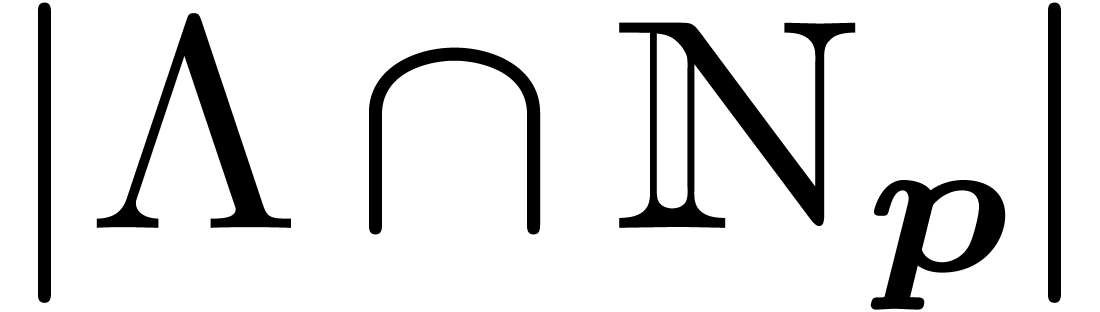 .
We show how to reduce the problem to computing exactly
.
We show how to reduce the problem to computing exactly 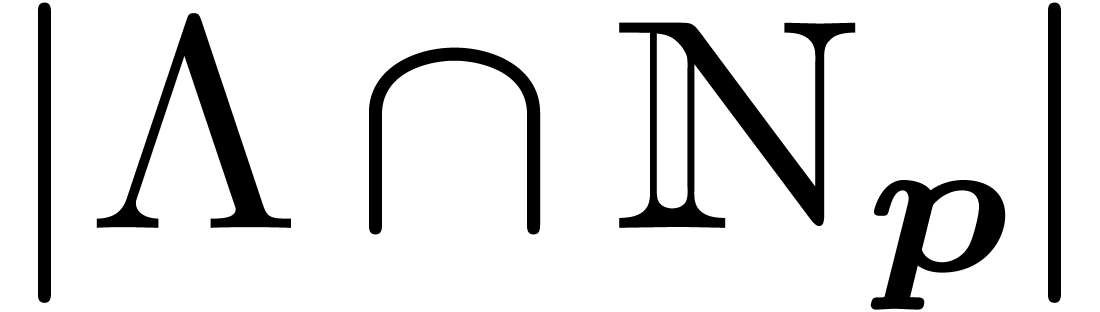 evaluations.
evaluations.
For any  , notice that
, notice that
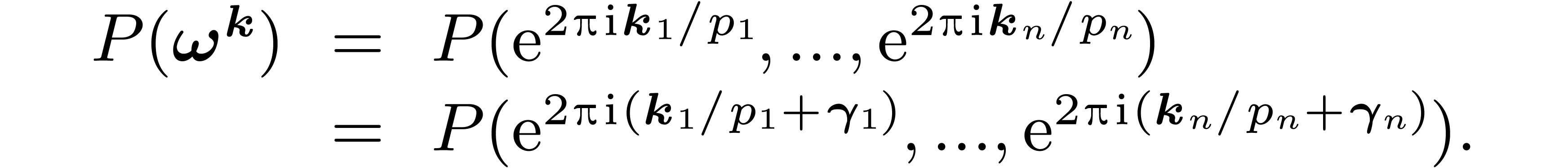
Therefore we would only need to consider the evaluations with
multi-indices in  modulo
modulo  . There are only
. There are only 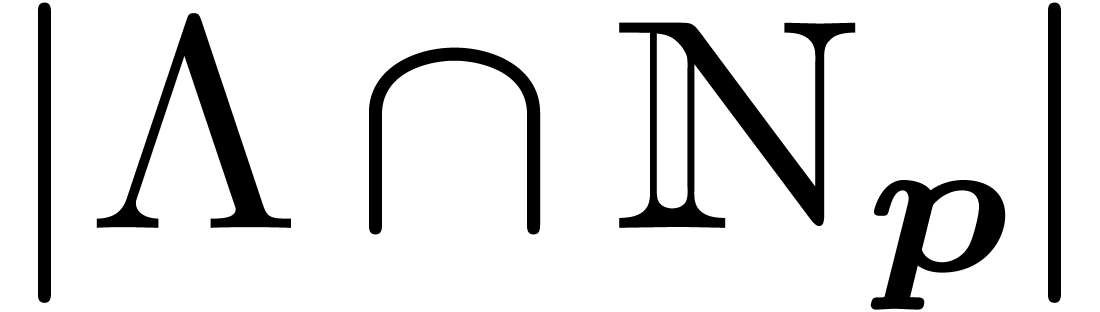 such
evaluations but, as in Section 3.4, we would have to expand
the fundamental domain of evaluations at each stage of the FFT to
compute the butterflies.
such
evaluations but, as in Section 3.4, we would have to expand
the fundamental domain of evaluations at each stage of the FFT to
compute the butterflies.
Instead, we propose a more direct method with no domain expansion. We
show that, regarding the evaluations, polynomials  in
in 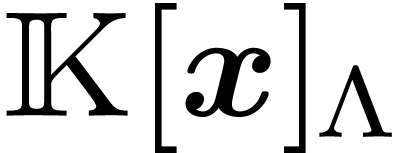 can be written
can be written 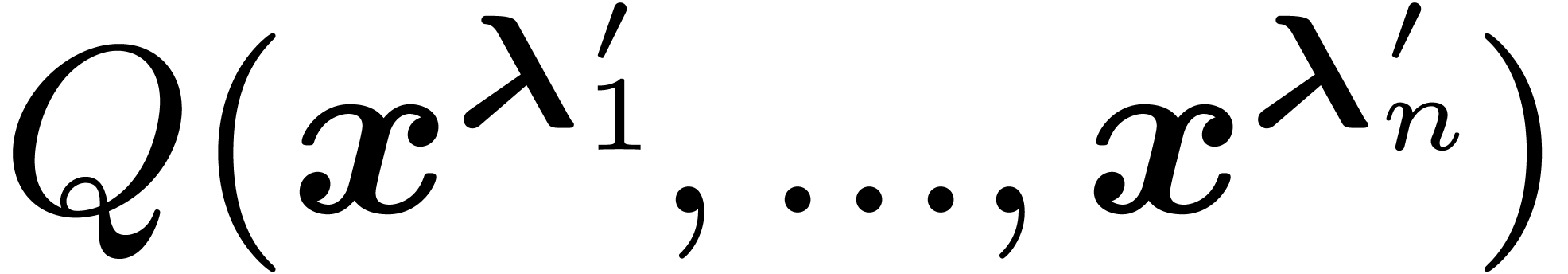 where
where
 is a basis of
is a basis of  and the
evaluation can be done directly in this rewritten form.
and the
evaluation can be done directly in this rewritten form.
We introduce the notation  for the remainder of
for the remainder of
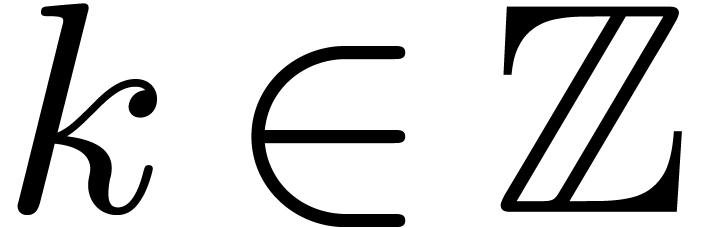 by
by 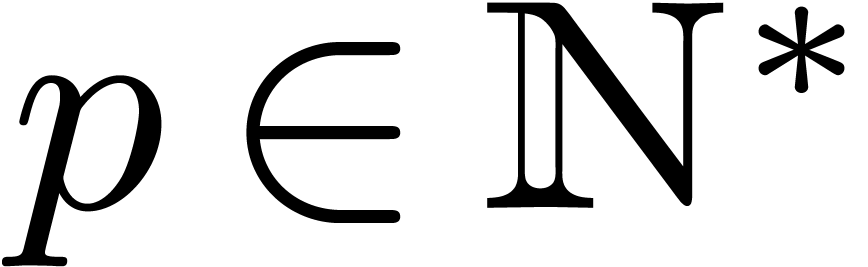 .
If
.
If  and
and 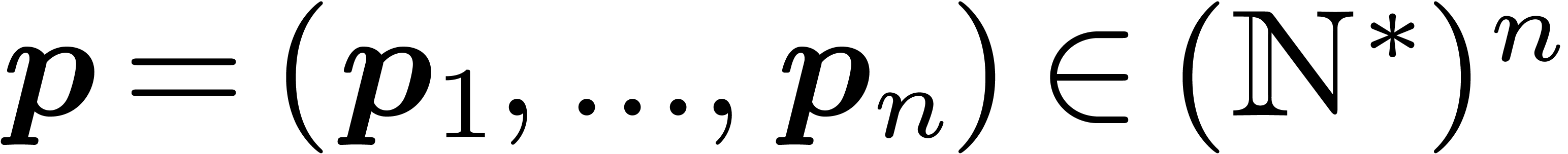 ,
we let
,
we let 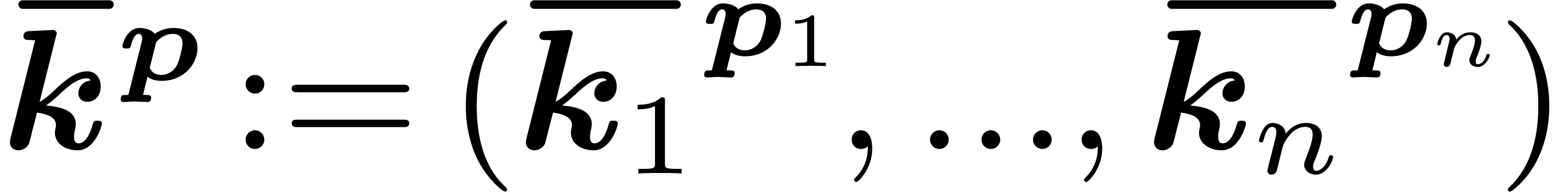 . This notation is
motivated by the remark that
. This notation is
motivated by the remark that 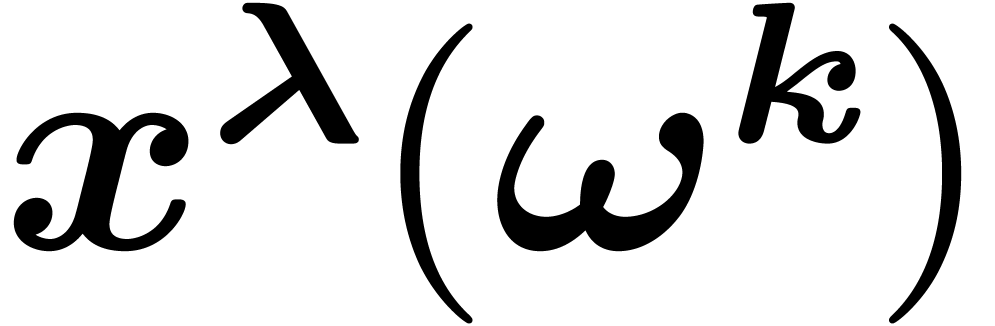 depends only on the
class of
depends only on the
class of  and
and  modulo
modulo
 .
.
Lemma 10. There
exists a basis  of
of  and a
basis
and a
basis  of
of 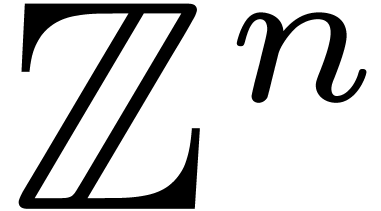 such that
such that
 |
(8) |
where  and the
and the 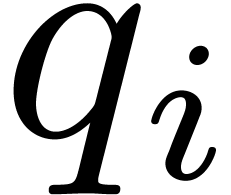 's
are positive integers satisfying
's
are positive integers satisfying  .
.
Proof. Let us consider the lattice of the
exponents of 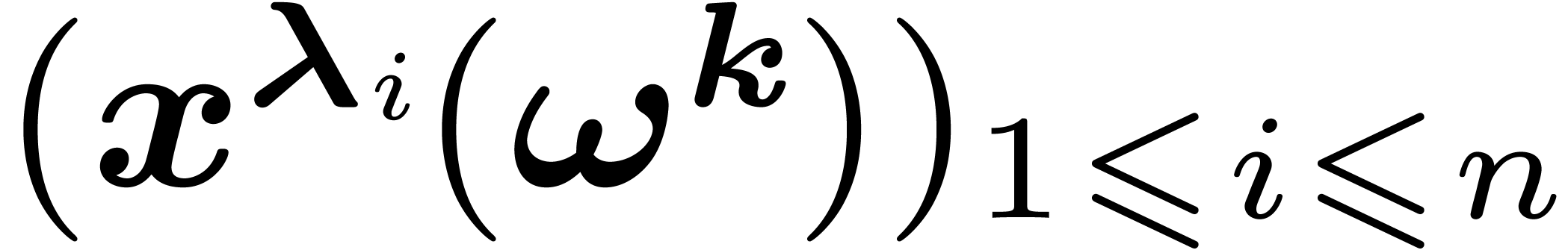 for
for 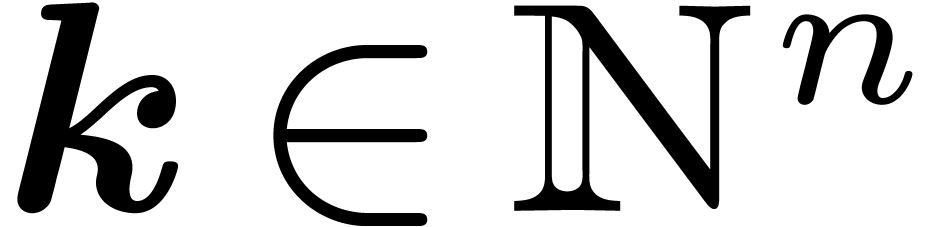 .
If
.
If  , then
, then
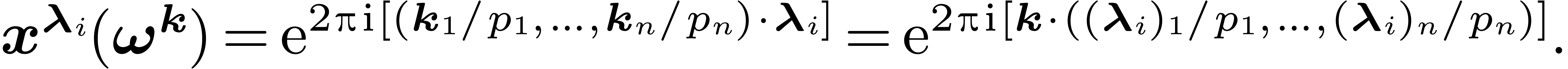
We define the lattice  spanned by the columns of
spanned by the columns of
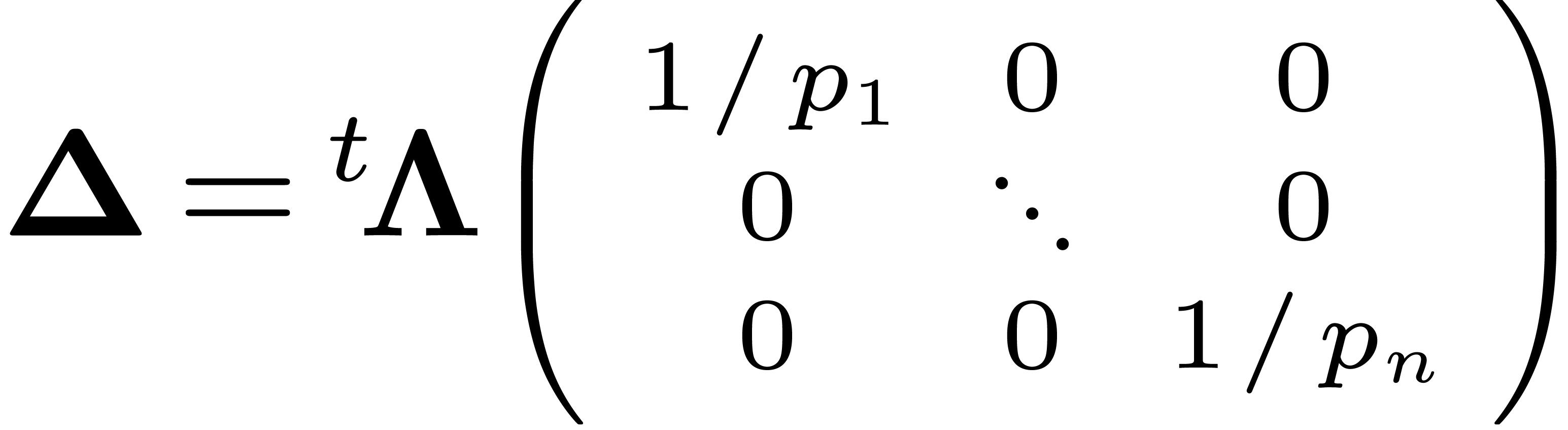 , that is
, that is 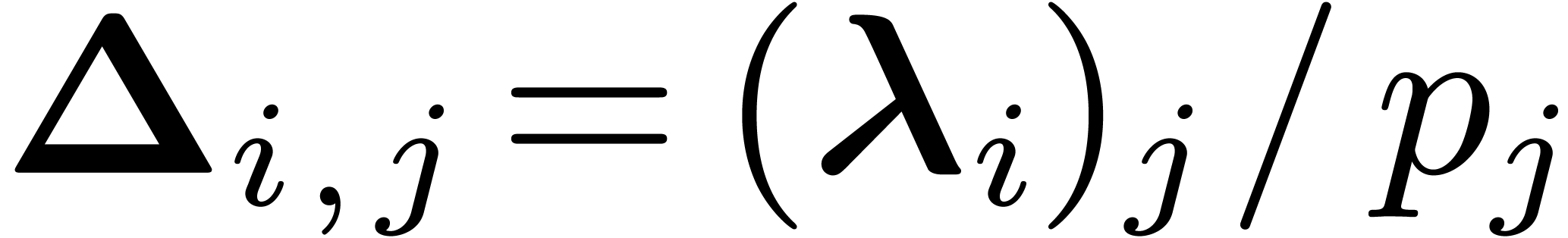 . We want to take the Smith normal form of
. We want to take the Smith normal form of  but the coefficients of
but the coefficients of  are
not necessarily integers. So we multiply the matrix by
are
not necessarily integers. So we multiply the matrix by 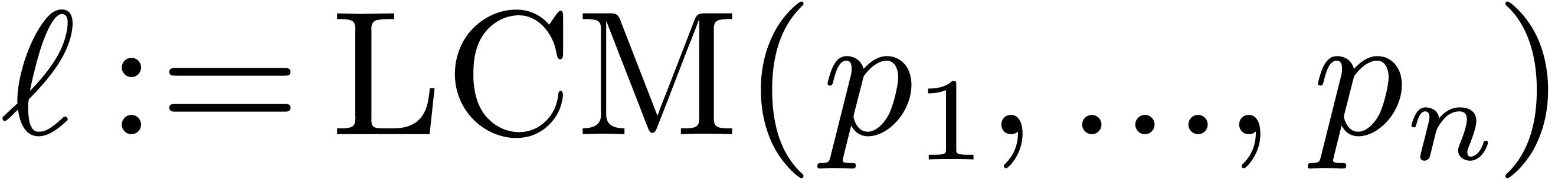 , take the Smith normal form and divide by
, take the Smith normal form and divide by
 . Therefore there exists
. Therefore there exists 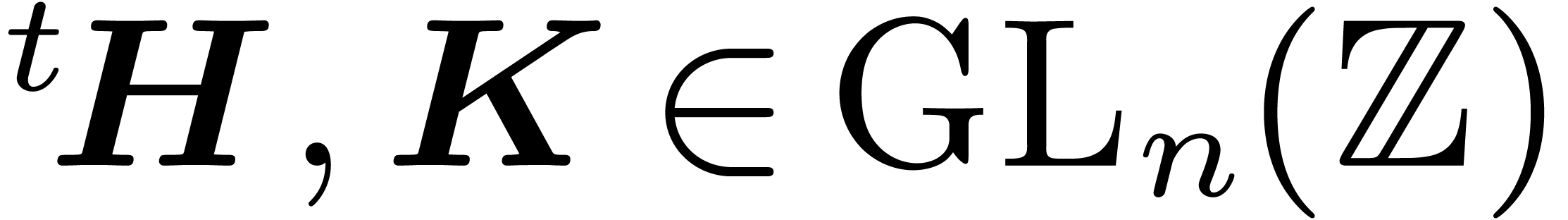 and integers
and integers 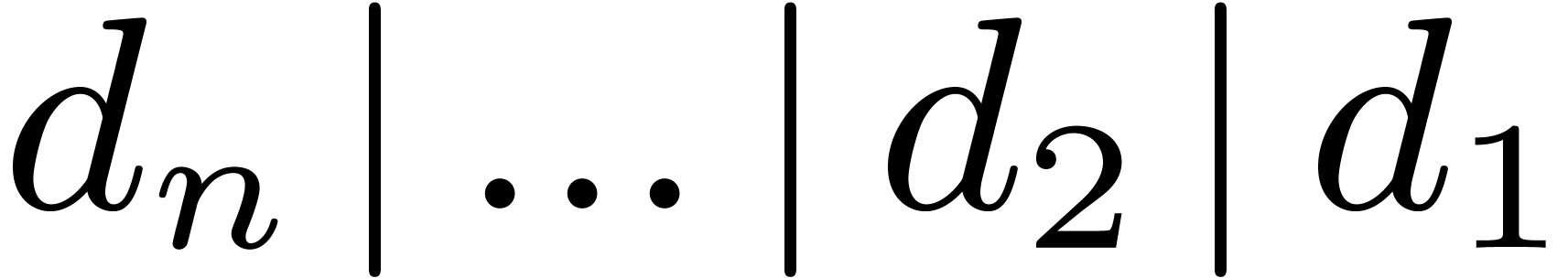 such that
such that
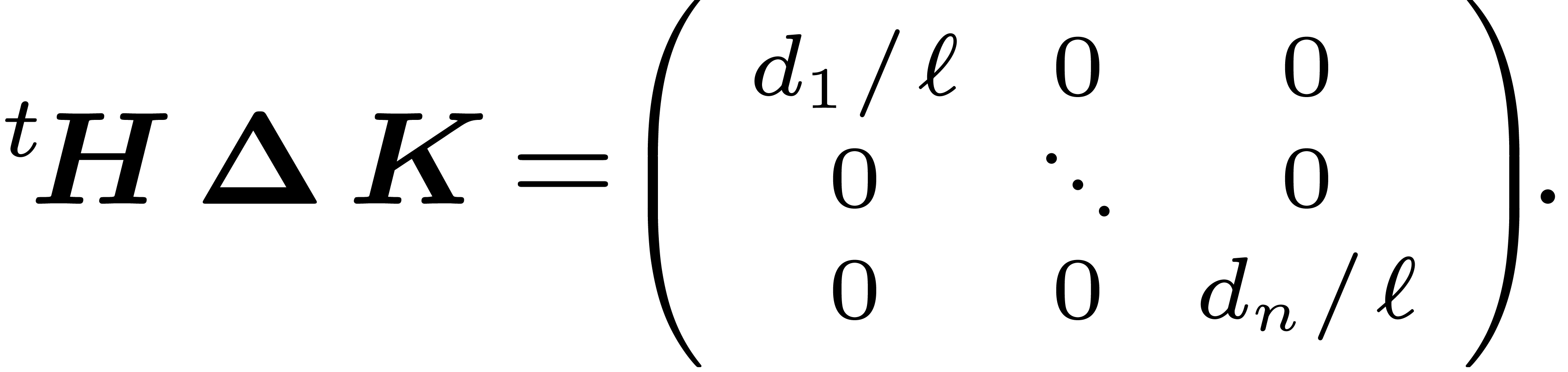 |
(9) |
Let us prove that 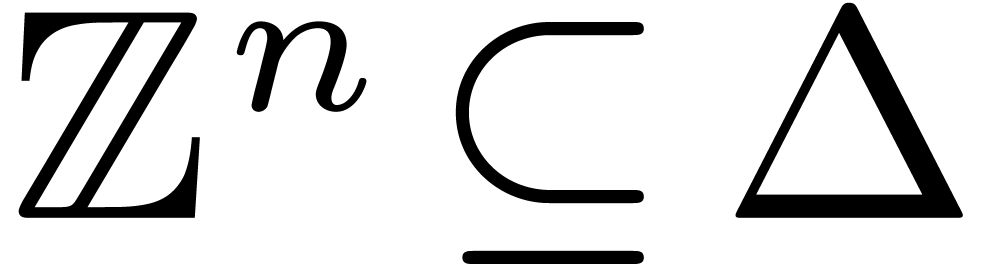 . By
definition of
. By
definition of  , there exists
, there exists
 such that
such that 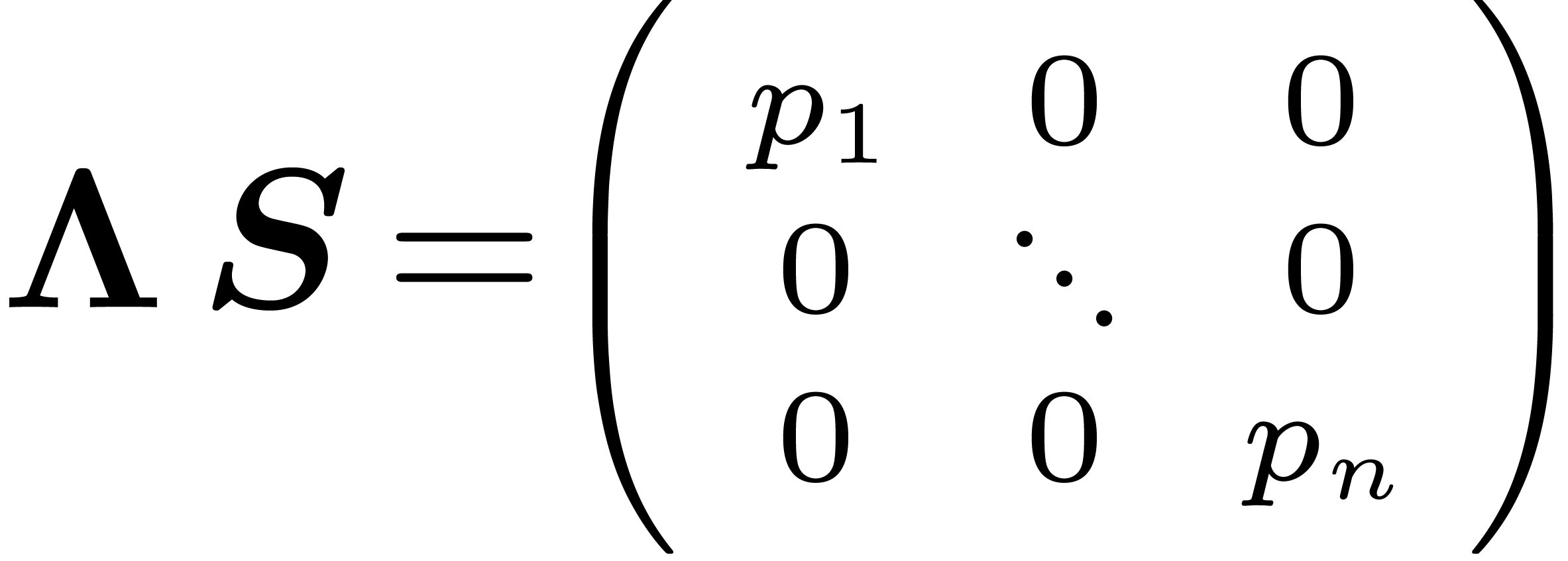 . Thus we have
. Thus we have
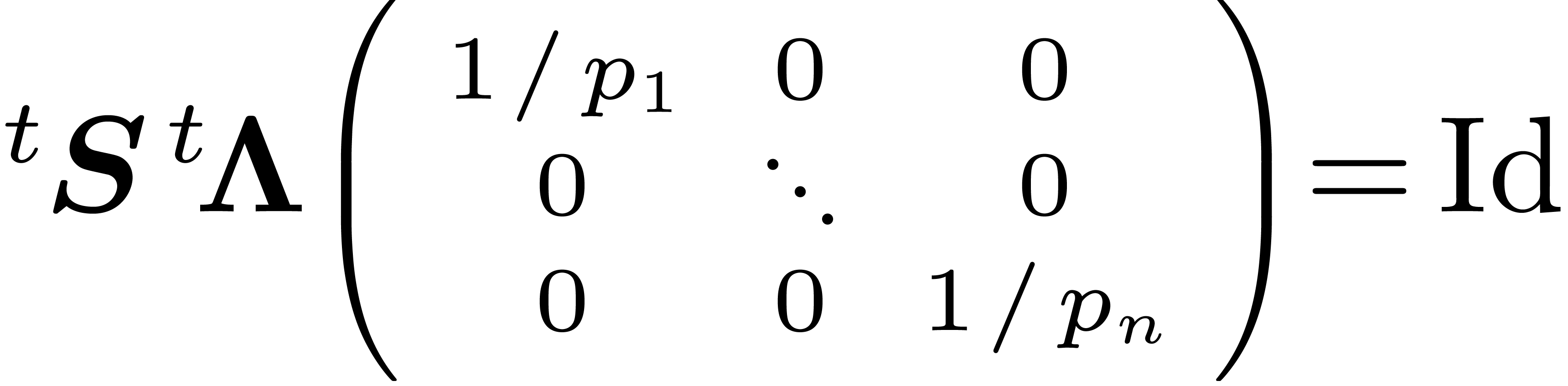 , implying that
, implying that  and our result. Because
and our result. Because  ,
we have
,
we have 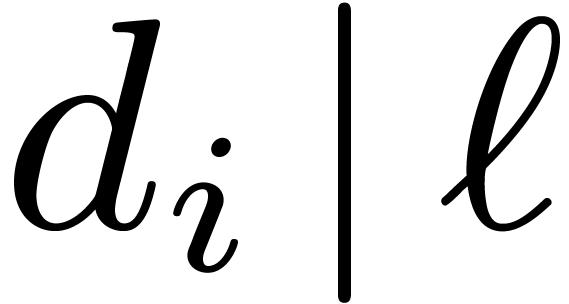 and by setting
and by setting 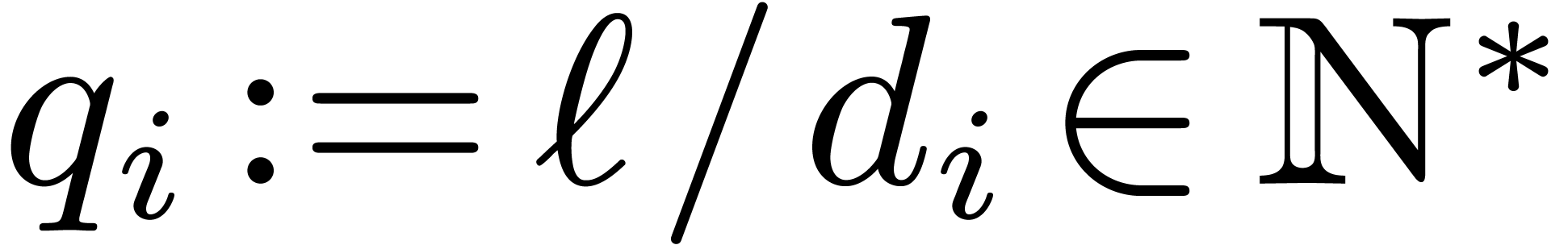 , we get
, we get  .
.
With a geometrical point of view, the equality of Equation (9)
gives the existence of the two required bases. The columns of  give the basis
give the basis  of
of 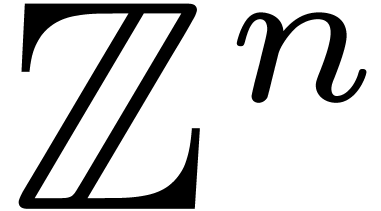 and the columns of
and the columns of 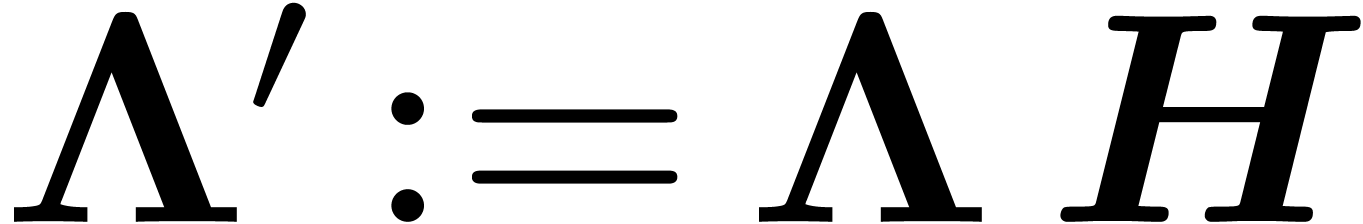 give the basis
give the basis  of
of  . To sum up,
we have
. To sum up,
we have
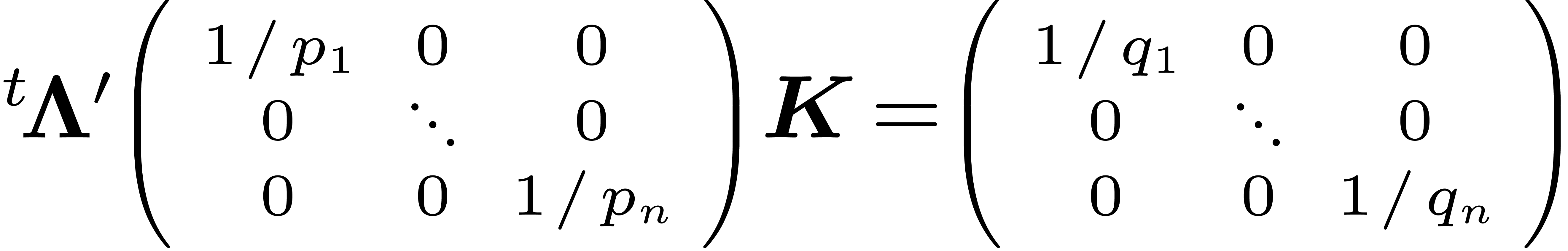 |
(10) |
which is the matricial form of Equation (
8).
Proposition 11. The
following ring morphism 

is well-defined, injective and its image is 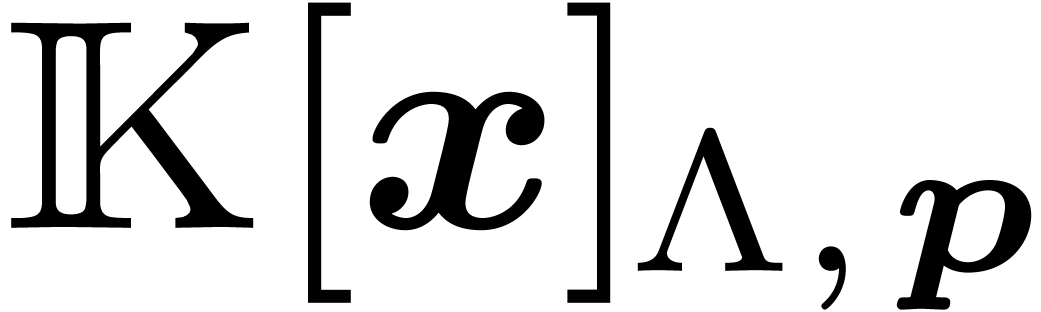 . Moreover, if
. Moreover, if 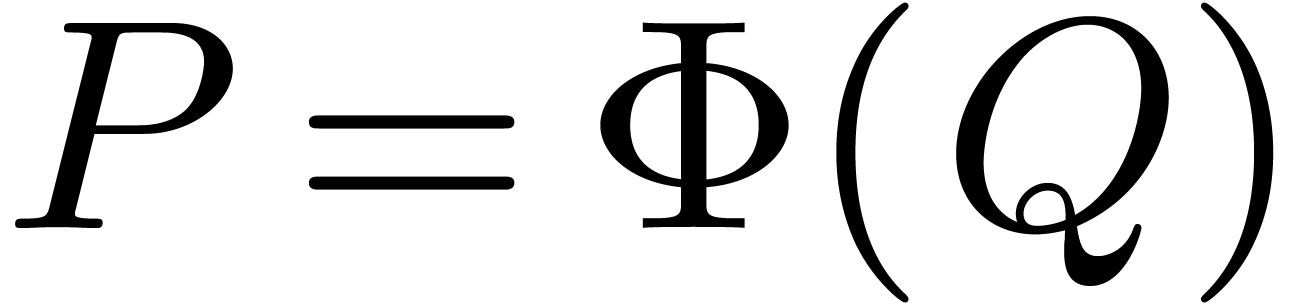 then
then
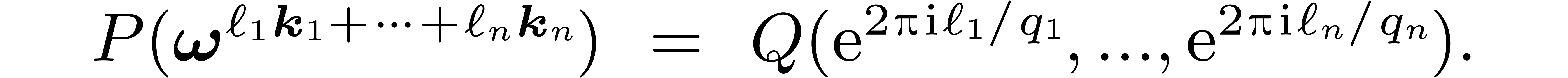 |
(11) |
Proof. First, we prove that  is well defined. For this matter we have to check that
is well defined. For this matter we have to check that 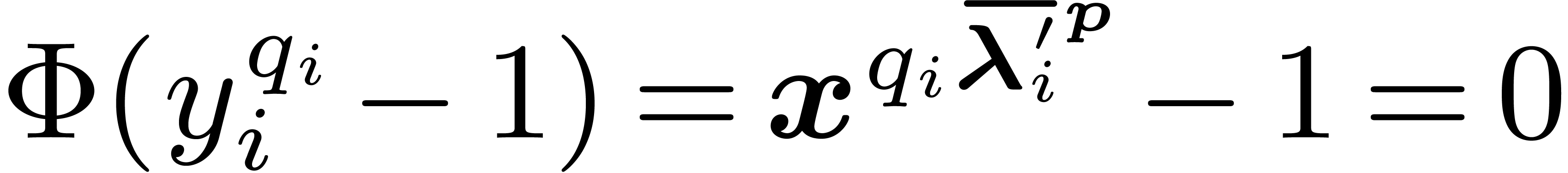 modulo
modulo  . It is sufficient to
prove that
. It is sufficient to
prove that 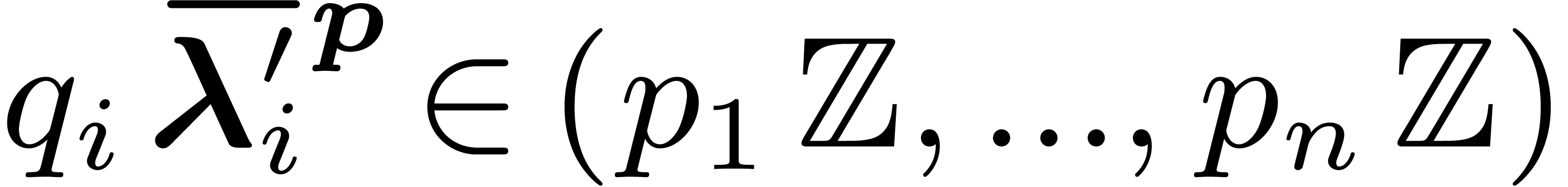 , which follows
from Equation (10).
, which follows
from Equation (10).
Then we prove Equation (11). Let 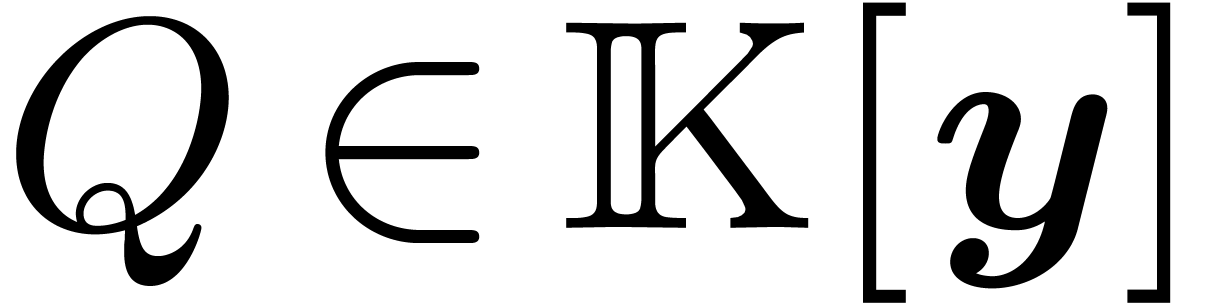 and
and 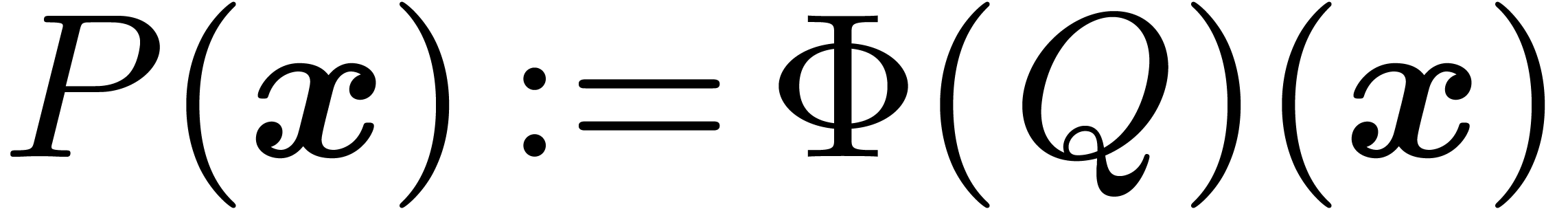 . As a consequence of
Lemma 10, one has
. As a consequence of
Lemma 10, one has
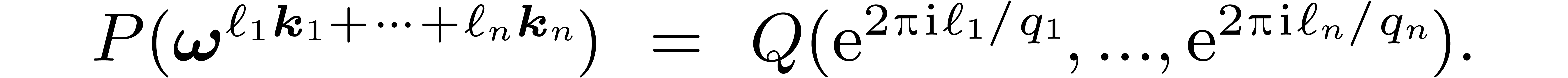
Now, we prove that  is injective. Indeed if
is injective. Indeed if 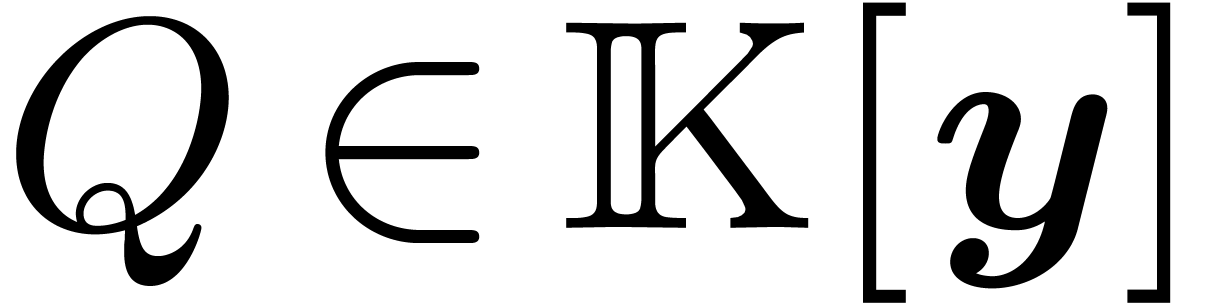 satisfies
satisfies 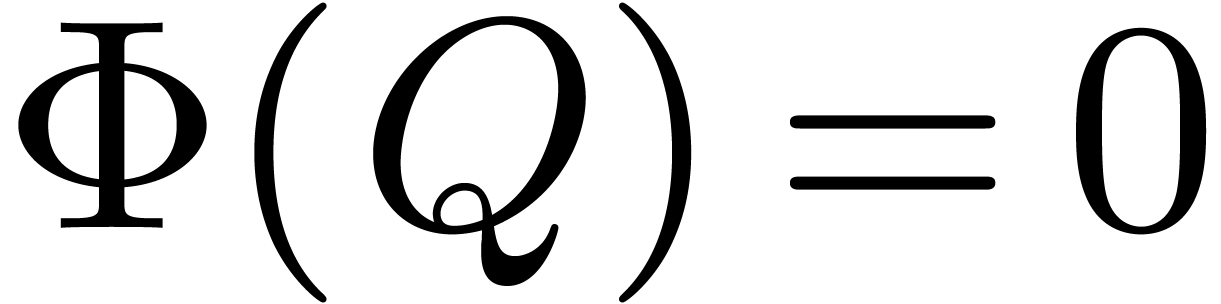 then for all
then for all 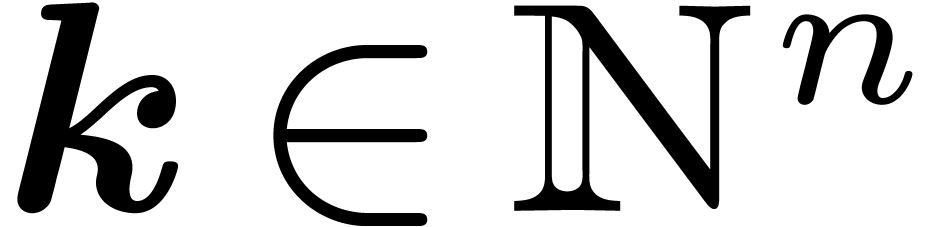 , one has
, one has 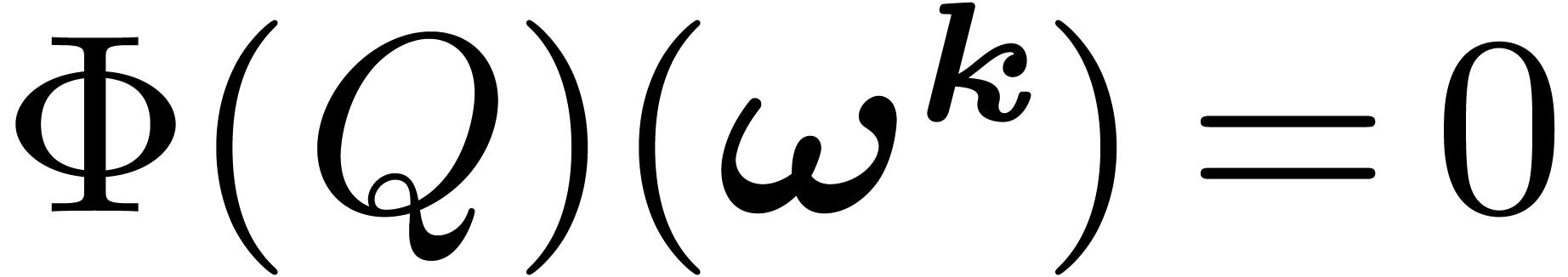 . Using Equation (11), we get that for
all
. Using Equation (11), we get that for
all 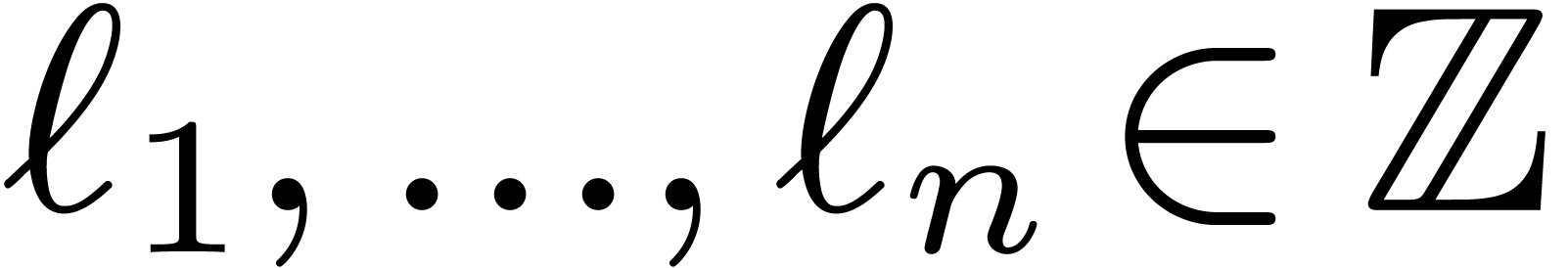 ,
, 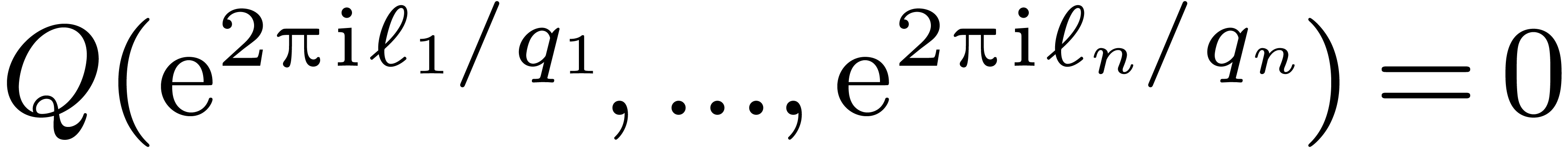 . As a result,
. As a result,  belongs to
the ideal generated by
belongs to
the ideal generated by  .
.
Finally it is trivial to see that the image of

is included in
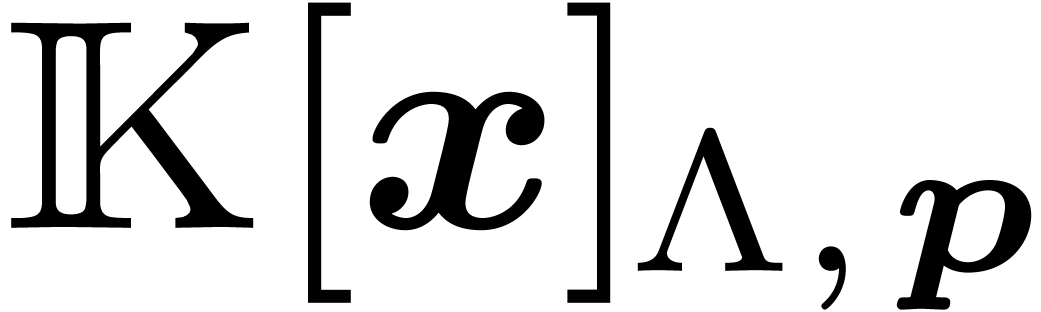 .
.
Reciprocally, let
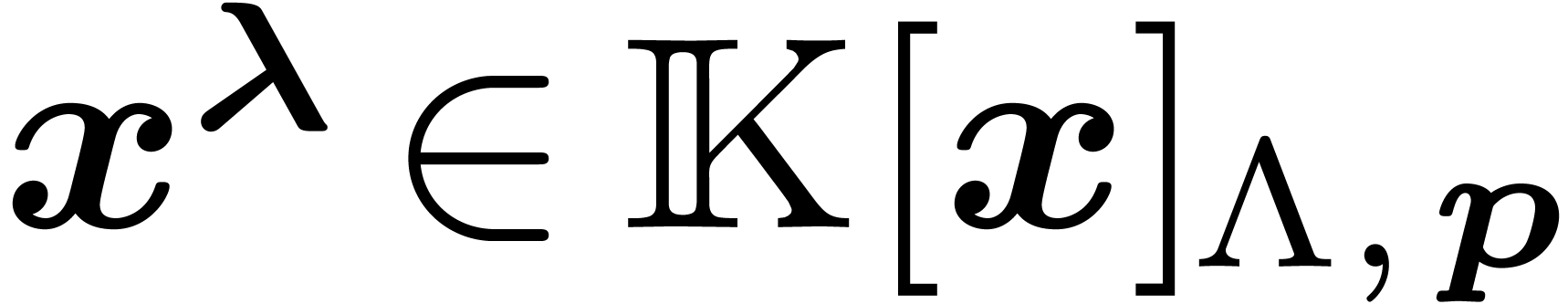 .
. We write
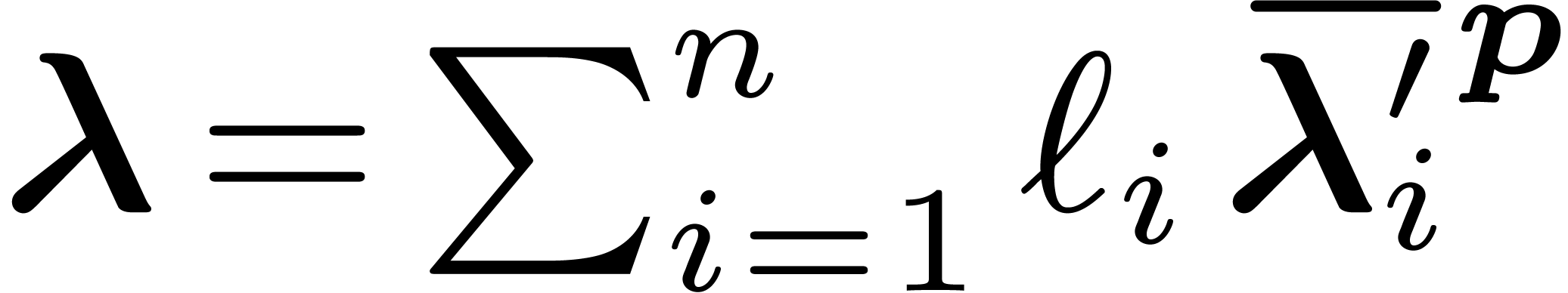
with

and define
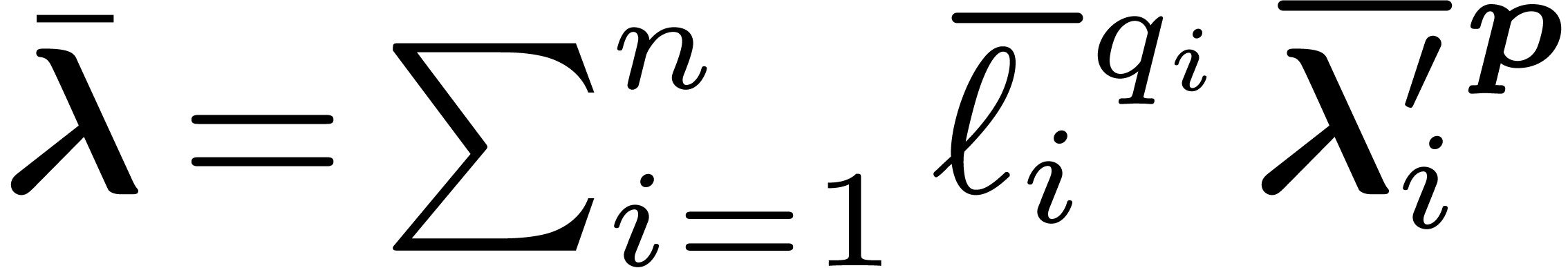 .
. Now because the lattice

is included in
 ,
,
we have that
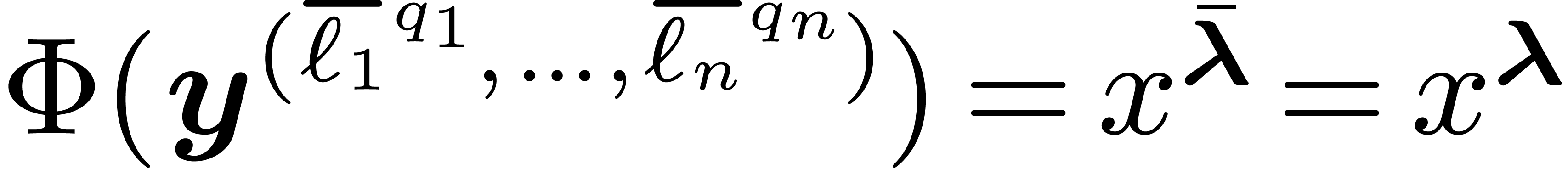
modulo
 .
.
In particular, the FFT of 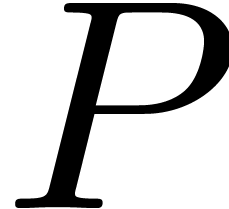 is uniquely determined
by its restriction to evaluations of the form
is uniquely determined
by its restriction to evaluations of the form 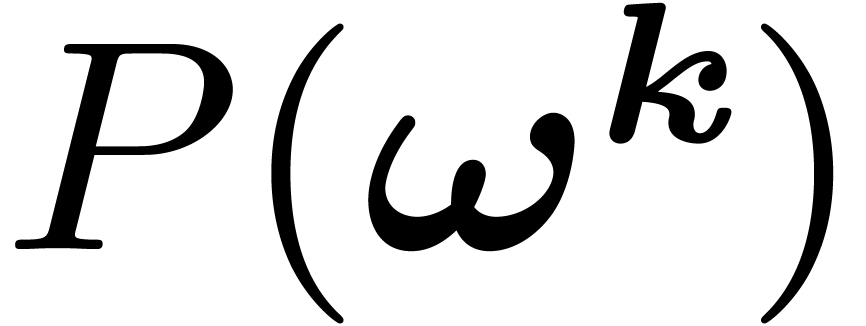 with
with 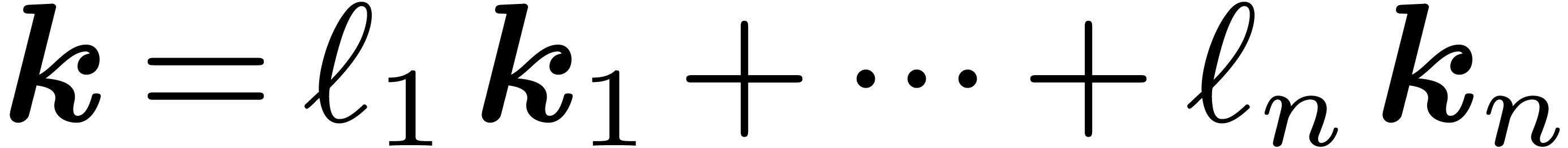 and
and  .
Notice that Proposition 11 implies that the number
.
Notice that Proposition 11 implies that the number  of evaluations equals the numbers
of evaluations equals the numbers 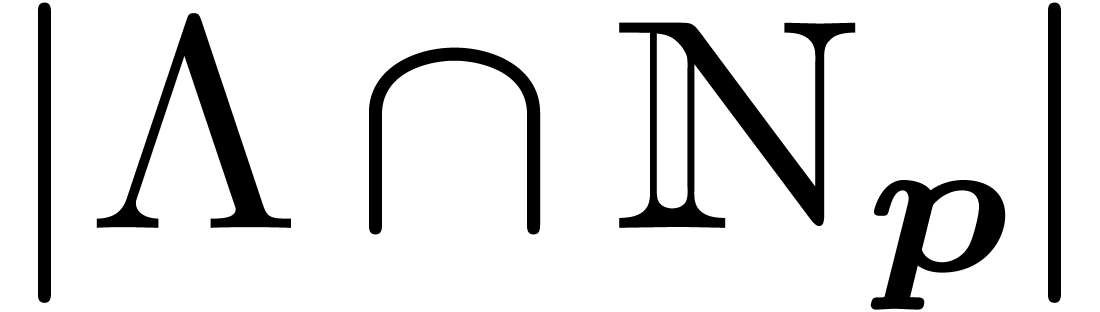 of monomials in
of monomials in 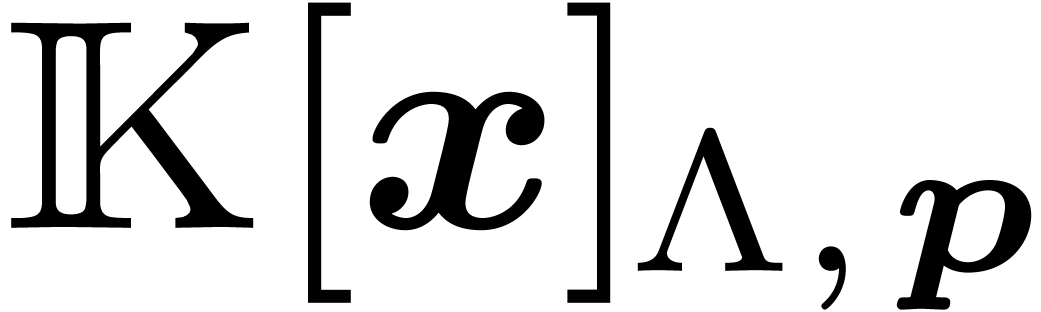 .
.
We define the lattice FFT of 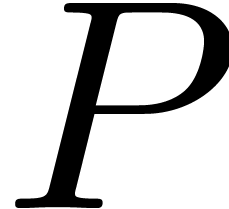 to be the
vector of values
to be the
vector of values 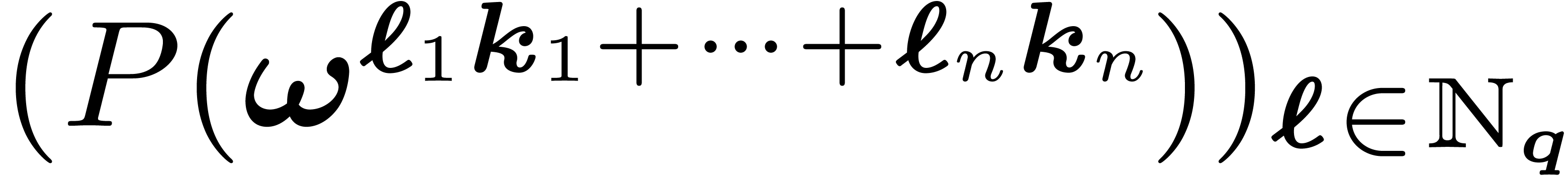 . We have
thus shown that the computation of the lattice FFT of
. We have
thus shown that the computation of the lattice FFT of 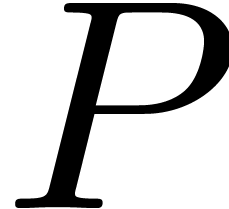 reduces to the computation of an ordinary multivariate FFT of order
reduces to the computation of an ordinary multivariate FFT of order
 .
.
4.3The general lattice FFT multiplication
Assume that 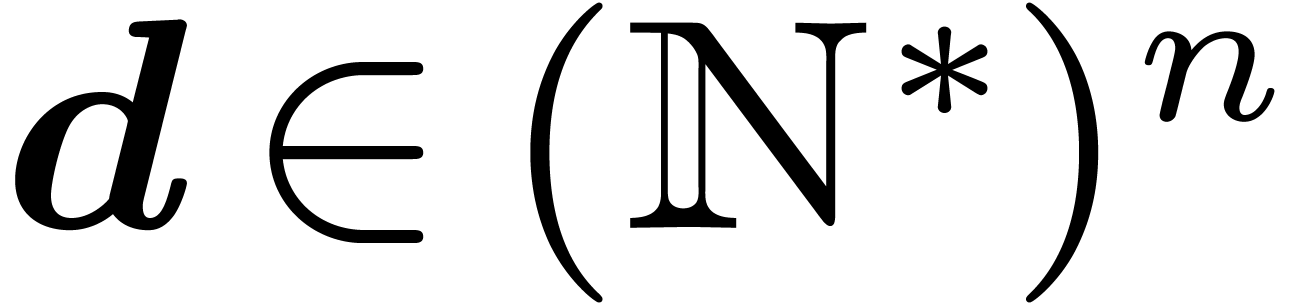 is such that
is such that 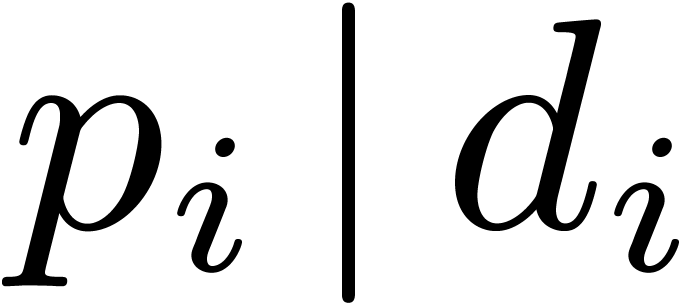 for each
for each 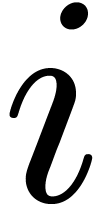 and consider the computation of the FFT
at order
and consider the computation of the FFT
at order  of a lattice polynomial
of a lattice polynomial 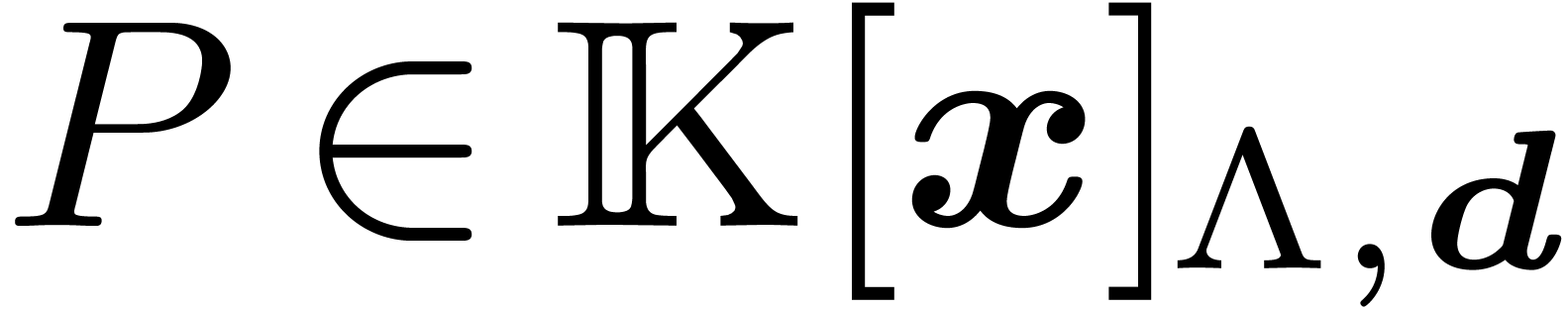 . In practice, one often has
. In practice, one often has 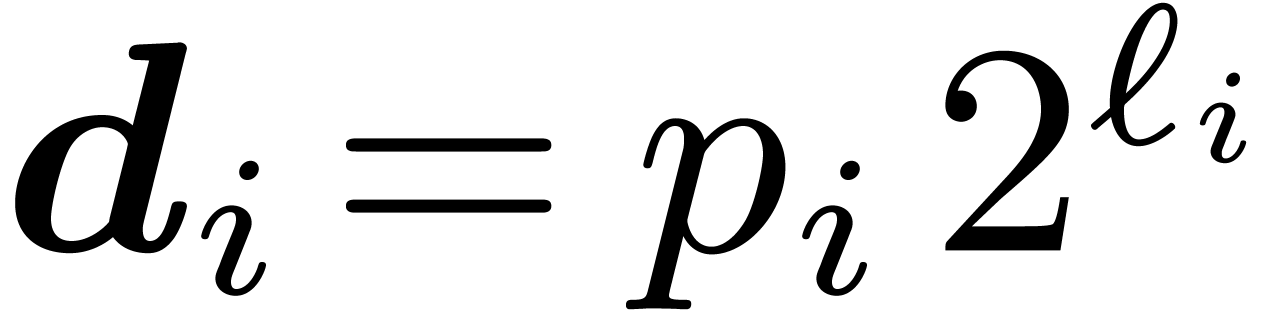 , and this is what we will assume from now on.
For simplicity, we also suppose that
, and this is what we will assume from now on.
For simplicity, we also suppose that  and denote
by
and denote
by 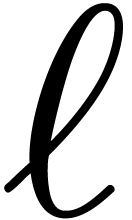 this common value. The results are valid in
general but we would have to do more decimations in some variables than
in others, which would not match the notations of Section 2.
this common value. The results are valid in
general but we would have to do more decimations in some variables than
in others, which would not match the notations of Section 2.
We give here an algorithm for the multiplication of two polynomials
 .
.
We start by doing 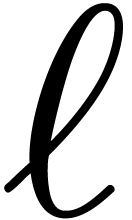 FFT stages. These stages
preserve the lattice
FFT stages. These stages
preserve the lattice  ,
because the butterflies have a span which belongs to
,
because the butterflies have a span which belongs to  . Therefore we compute only the butterflies
whose vertices are in
. Therefore we compute only the butterflies
whose vertices are in  .
.
After these 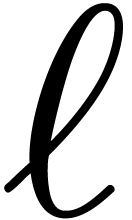 stages, we twist the coefficients
thanks to Formula 5 and obtain the polynomials
stages, we twist the coefficients
thanks to Formula 5 and obtain the polynomials 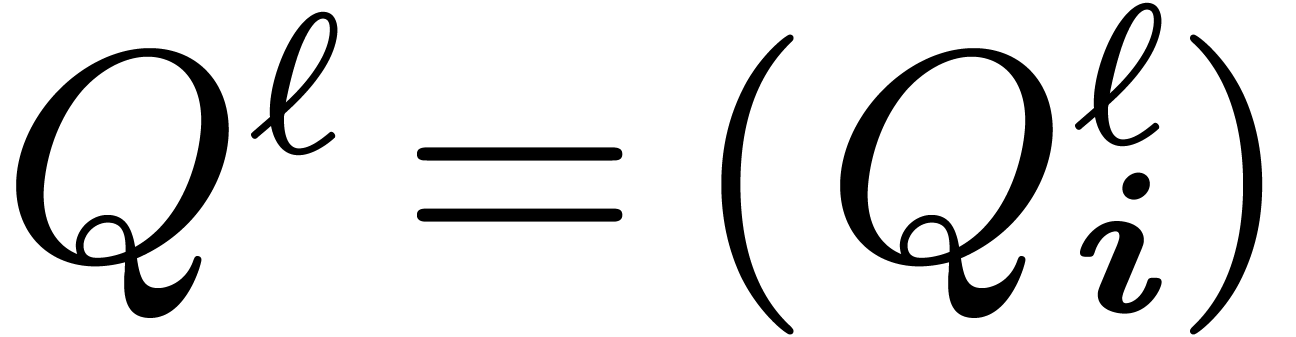 , for
, for 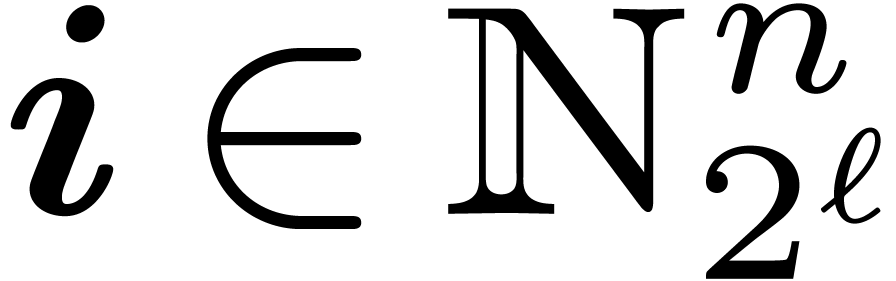 .
As explained in Section 2.2, up to a minor modification
(here, the partial degrees are not all the same), these polynomials
reduce our multiplication to
.
As explained in Section 2.2, up to a minor modification
(here, the partial degrees are not all the same), these polynomials
reduce our multiplication to 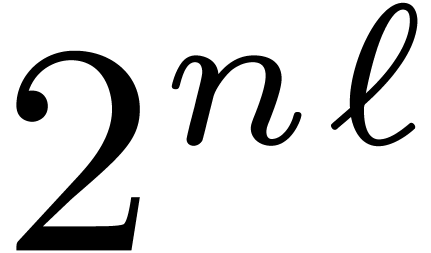 multiplications in
multiplications in
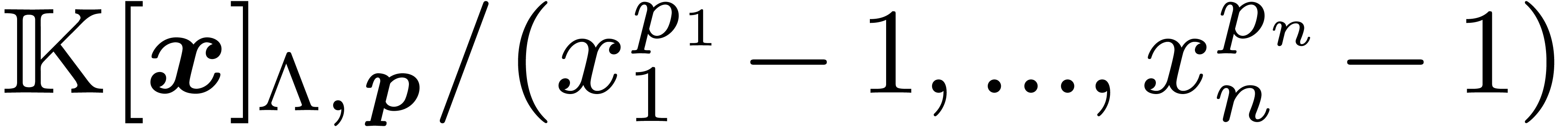 . Thanks to Proposition 11, we are able to perform these latter multiplications as
multiplications in
. Thanks to Proposition 11, we are able to perform these latter multiplications as
multiplications in 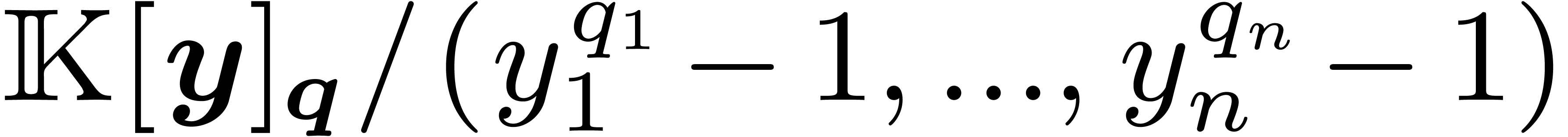 .
.
Algorithm Lattice-partial-FFT
Input:  , ,
 , ,  and coefficients
and coefficients 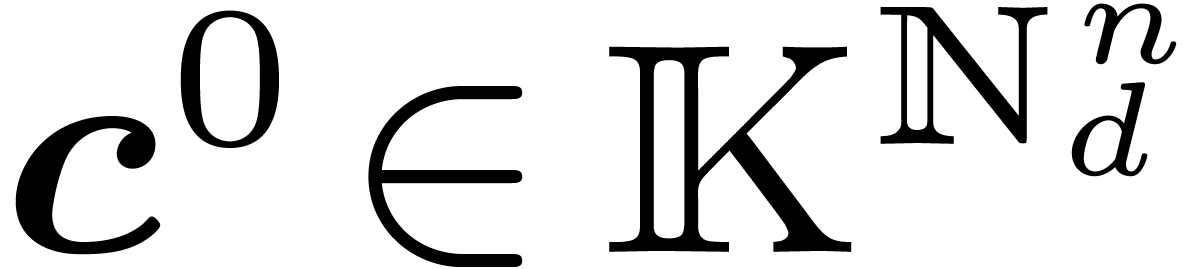 of of 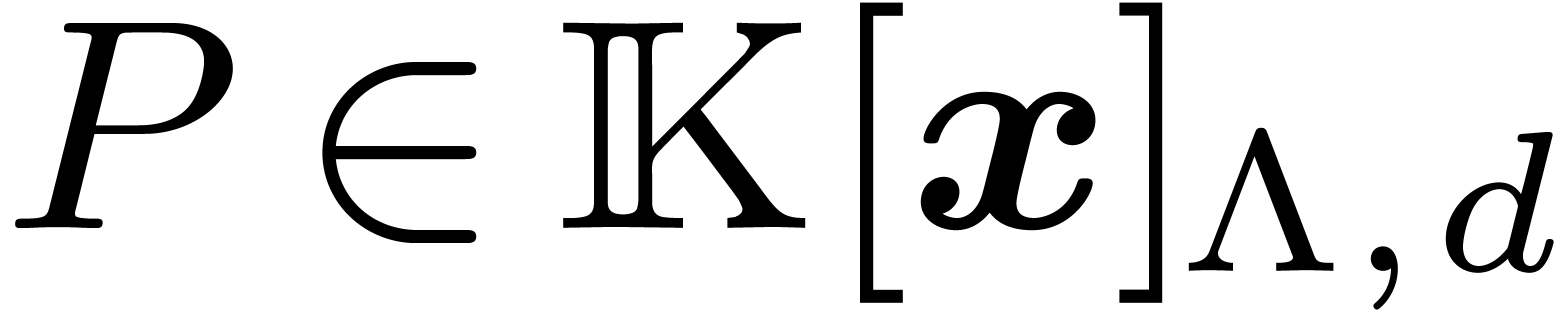
Output: the coefficients  
|
For  do
//  decimation steps in each variable
For 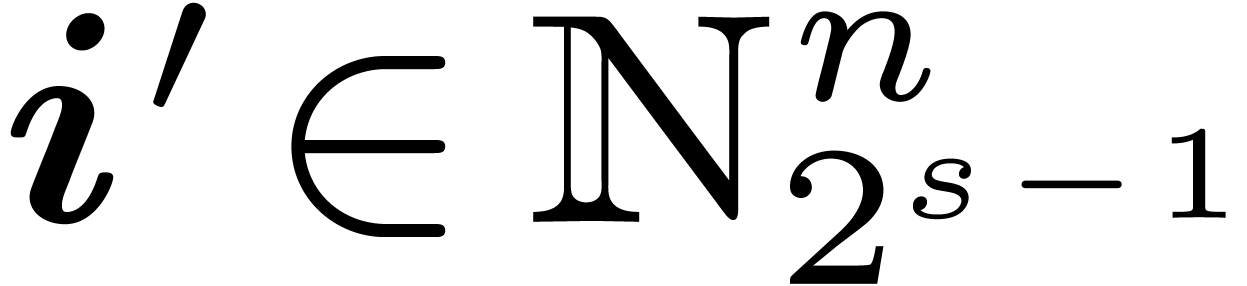 , , 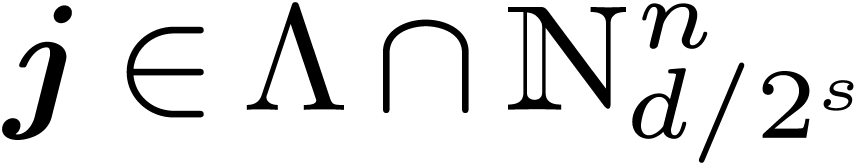 do
//a butterfly in 
For 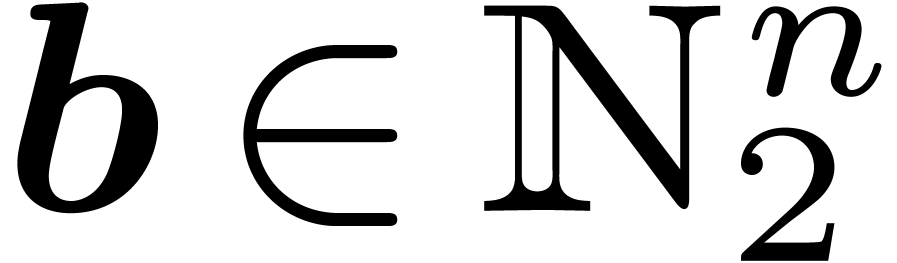 do do 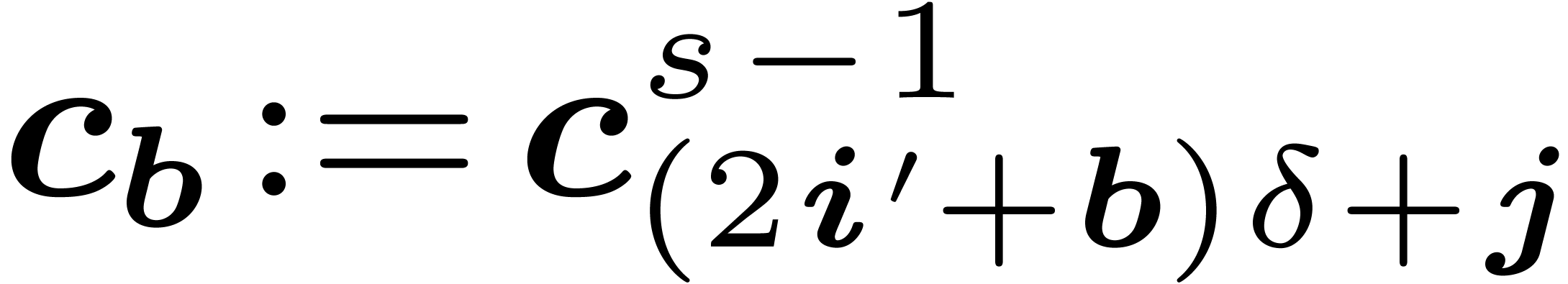
For 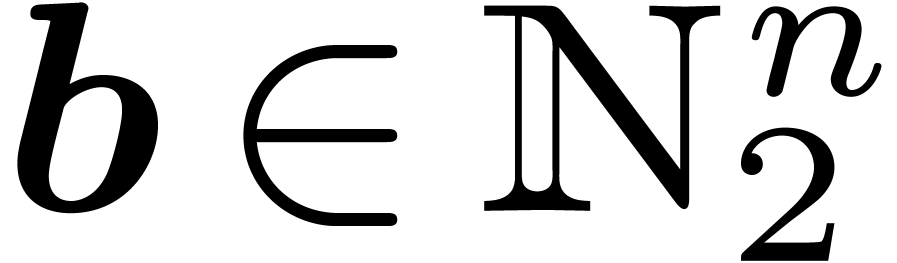 do do 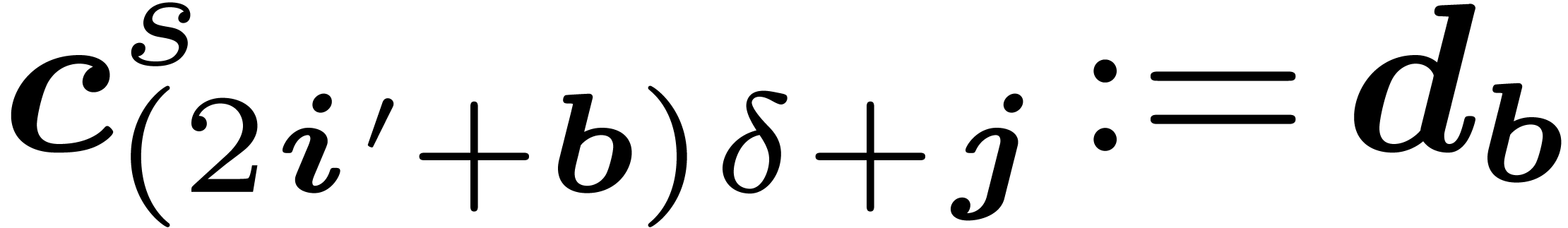
Return 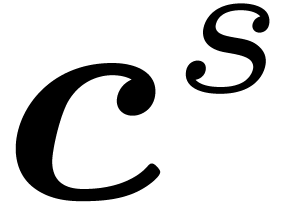
|
As for symmetric polynomials, the inverse algorithm 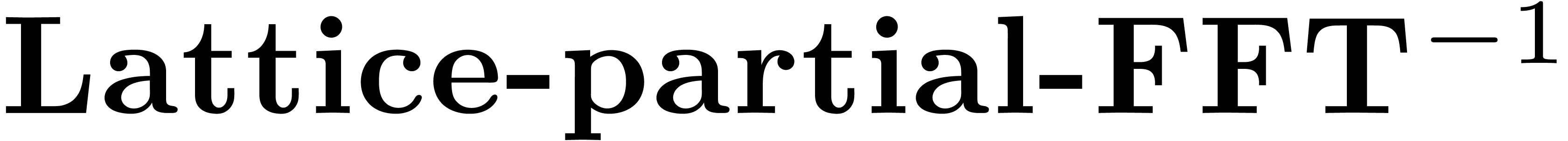 is obtained by reversing the loops and inverting the butterflies of
Lattice-partial-FFT.
is obtained by reversing the loops and inverting the butterflies of
Lattice-partial-FFT.
Let us analyze the cost of this algorithm. It starts with 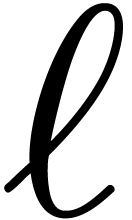 stages of classical
stages of classical 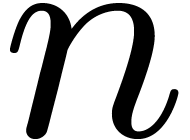 -dimensional
FFT, computing only the butterflies whose vertices are in
-dimensional
FFT, computing only the butterflies whose vertices are in  . This amounts to
. This amounts to  arithmetic operations in
arithmetic operations in  .
The second part is made of the transformations of Equation 5
and Proposition 11. Since we consider that operations with
the lattice
.
The second part is made of the transformations of Equation 5
and Proposition 11. Since we consider that operations with
the lattice  take time
take time 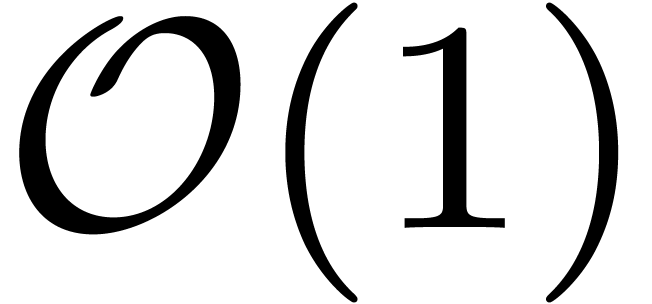 , these transformations take time
, these transformations take time 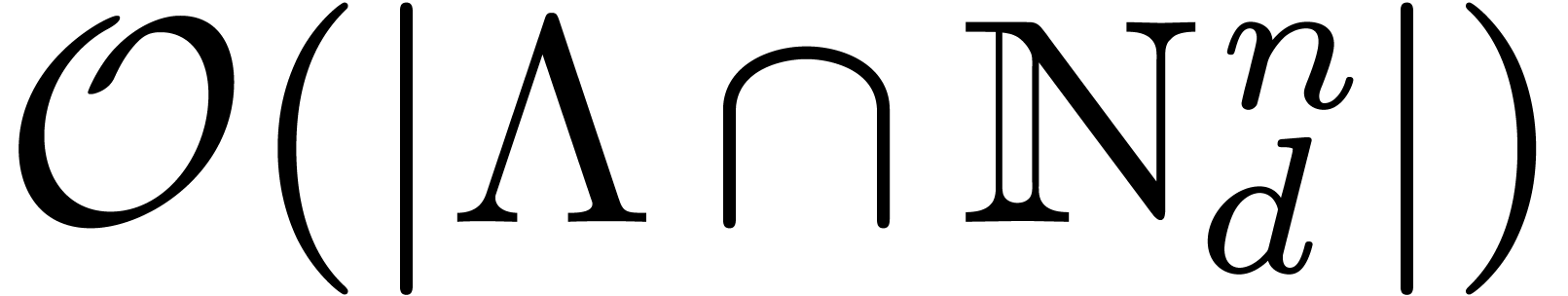 . Finally, the componentwise multiplication of
. Finally, the componentwise multiplication of
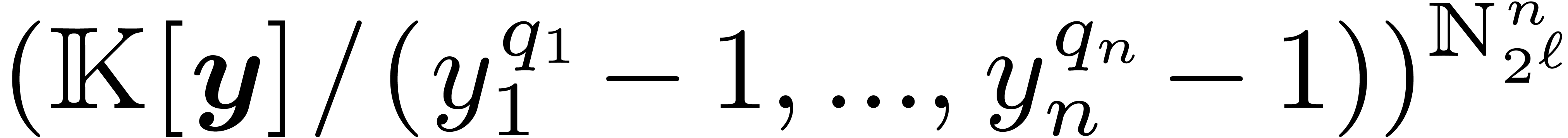 costs
costs 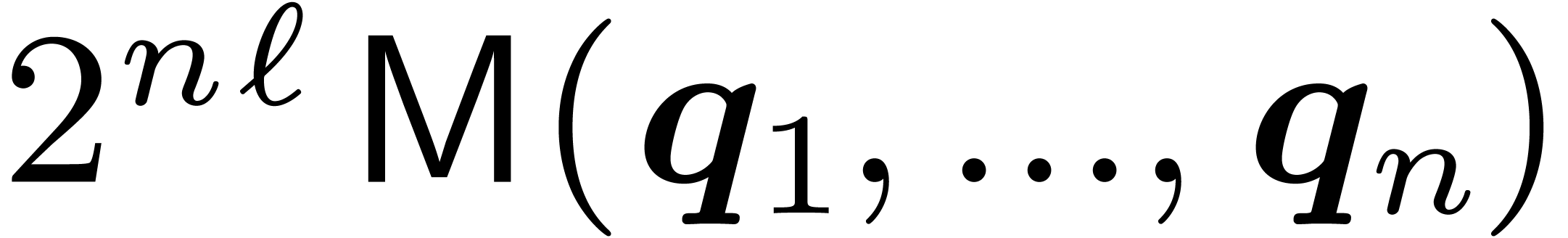 where
where 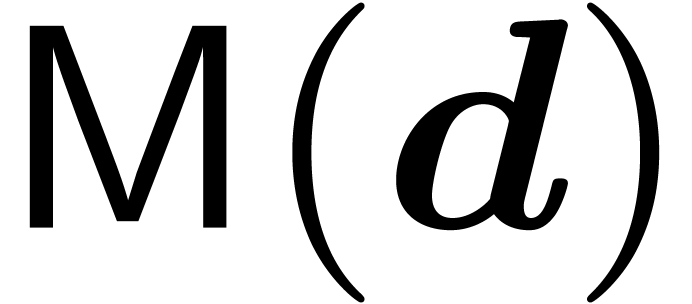 stands for the arithmetic complexity of polynomials
multiplication in
stands for the arithmetic complexity of polynomials
multiplication in 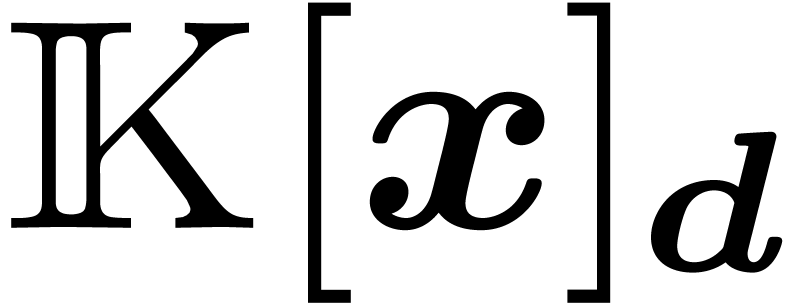 .
Altogether, our multiplication algorithms costs
.
Altogether, our multiplication algorithms costs

By contrast, a symmetry-oblivious approach would consist in doing 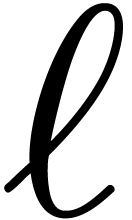 stages of classical
stages of classical 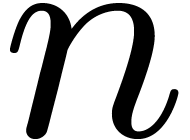 -dimensional
FFT and then
-dimensional
FFT and then 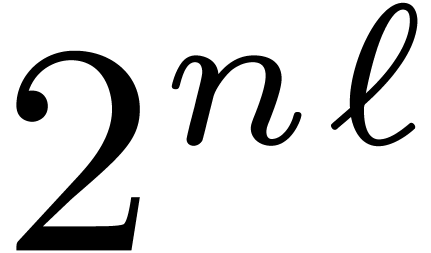 multiplications in
multiplications in 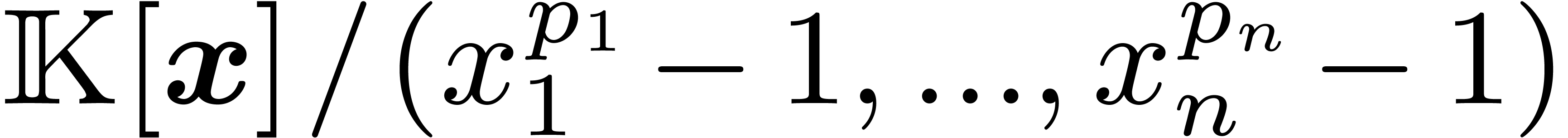 . The cost analysis is similar to the one
before and the classical approach's cost is
. The cost analysis is similar to the one
before and the classical approach's cost is  .
.
The ratio 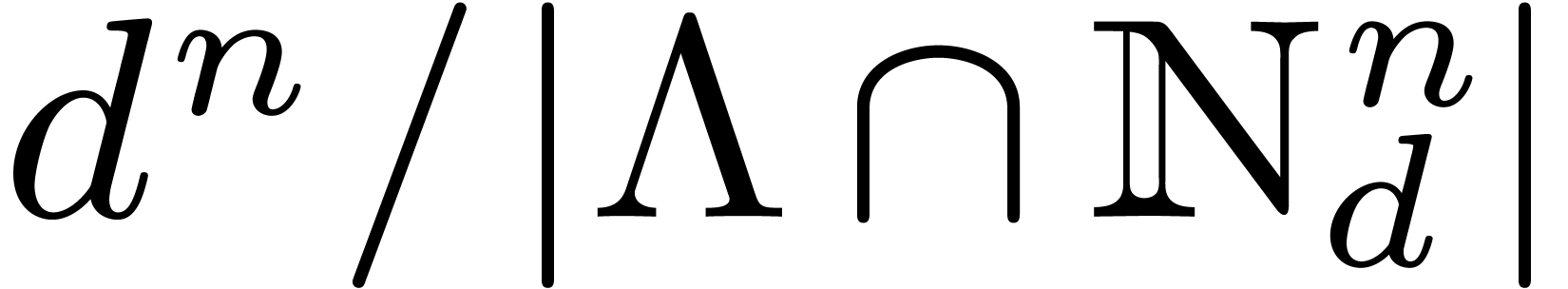 is exactly the volume
is exactly the volume 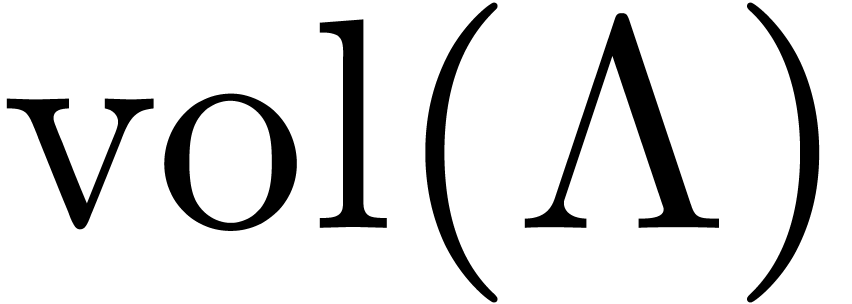 of the lattice, defined by
of the lattice, defined by 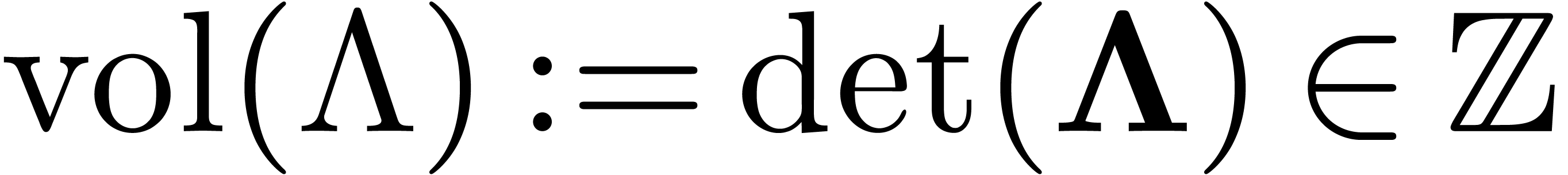 .
Under the superlinearity assumption for the function
.
Under the superlinearity assumption for the function  , we get that
, we get that 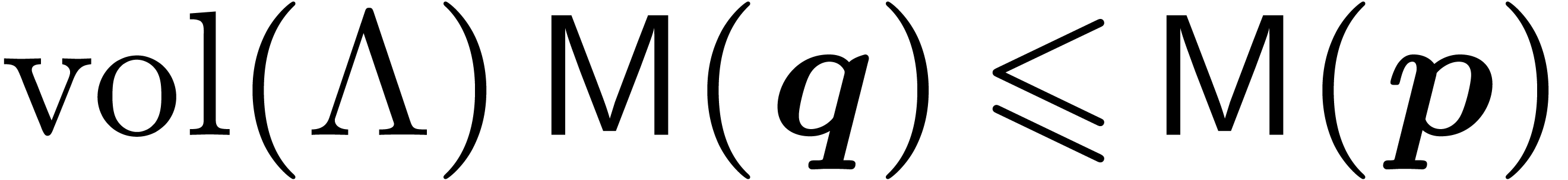 and we
deduce the following theorem.
and we
deduce the following theorem.
Theorem 12. For a fixed
lattice  and
and  ,
the direct (resp. inverse) lattice FFT can be computed in
time
,
the direct (resp. inverse) lattice FFT can be computed in
time
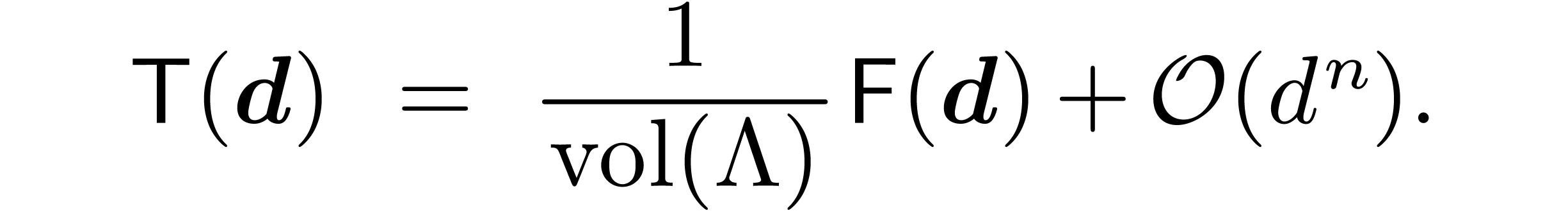
5.The Symmetric TFT
To conclude this paper, we briefly discuss the extensions of the
previous results to the Truncated Fourier Transform (TFT). With the
notation of Section 2, let 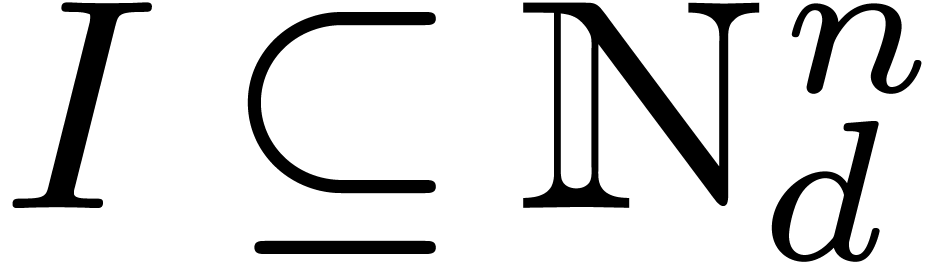 be an
initial segment subset of
be an
initial segment subset of 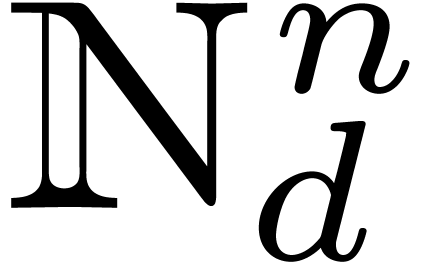 :
for
:
for  , if
, if 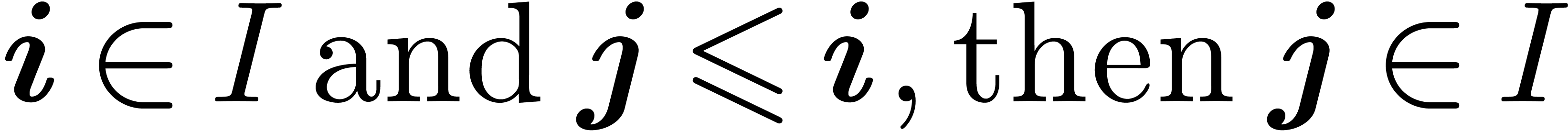 . Given
. Given 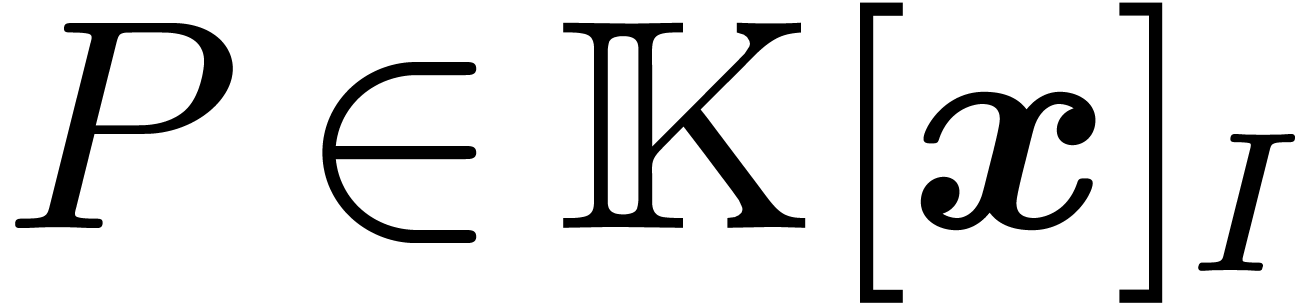 ,
the TFT of
,
the TFT of  is defined to be the vector
is defined to be the vector 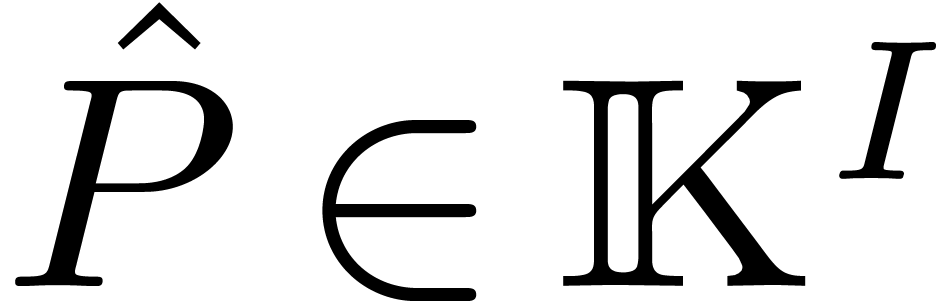 defined by
defined by 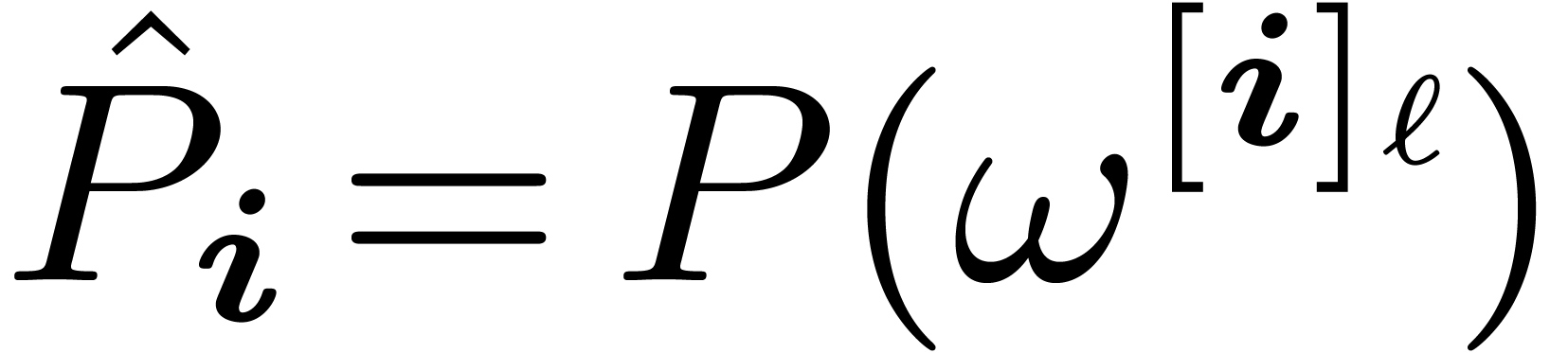 ,
where
,
where  is a root of unity of order
is a root of unity of order 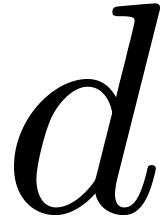 .
.
In [16, 17], van der Hoeven described fast
algorithms for computing the TFT and its inverse. For a fixed dimension
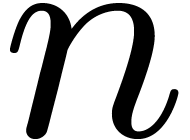 , the cost of these
algorithms is bounded by
, the cost of these
algorithms is bounded by 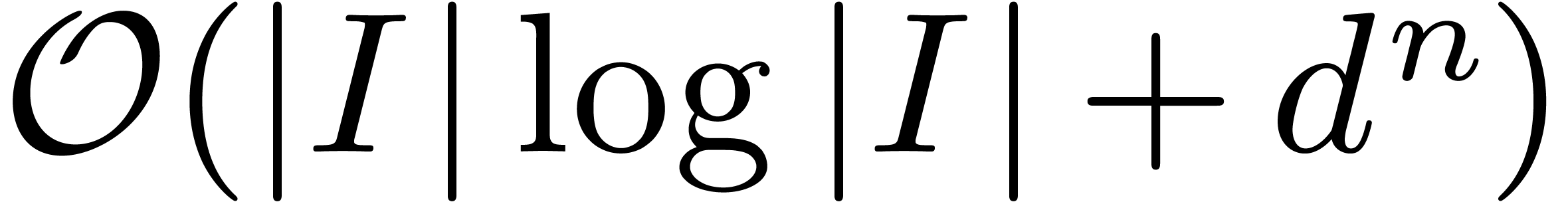 instead of
instead of 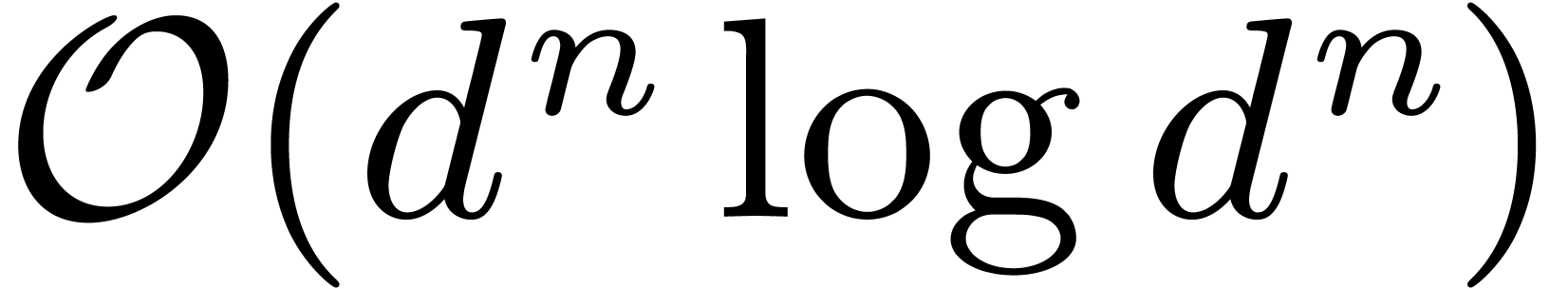 . In this section we will outline how a further
acceleration can be achieved for symmetric polynomials of the types
studied in Sections 3 and 4.
. In this section we will outline how a further
acceleration can be achieved for symmetric polynomials of the types
studied in Sections 3 and 4.
5.1The symmetric TFT
For each 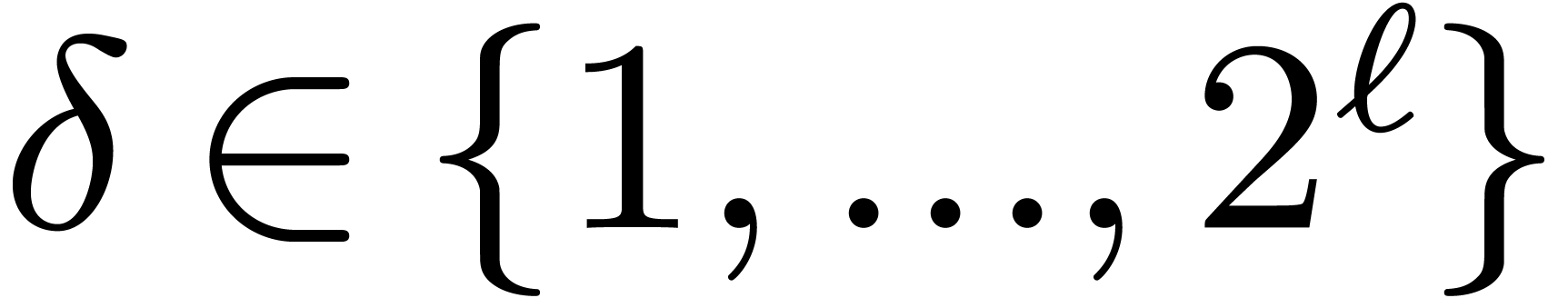 , let
, let 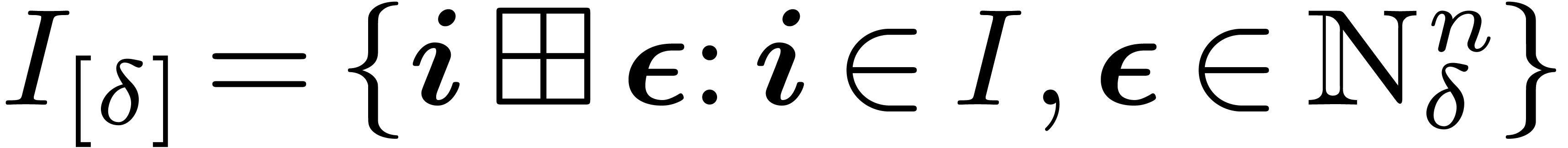 . The entire computation of the TFT and its
inverse can be represented schematically by a graph
. The entire computation of the TFT and its
inverse can be represented schematically by a graph  . The vertices of the graph are pairs
. The vertices of the graph are pairs 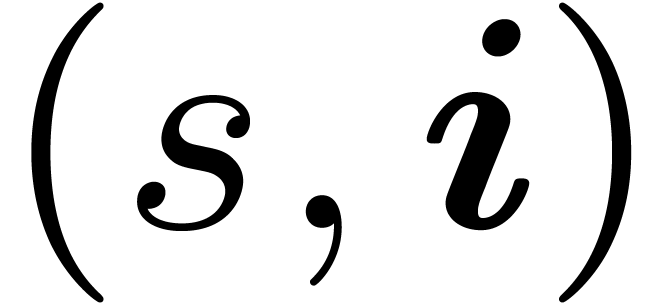 with
with 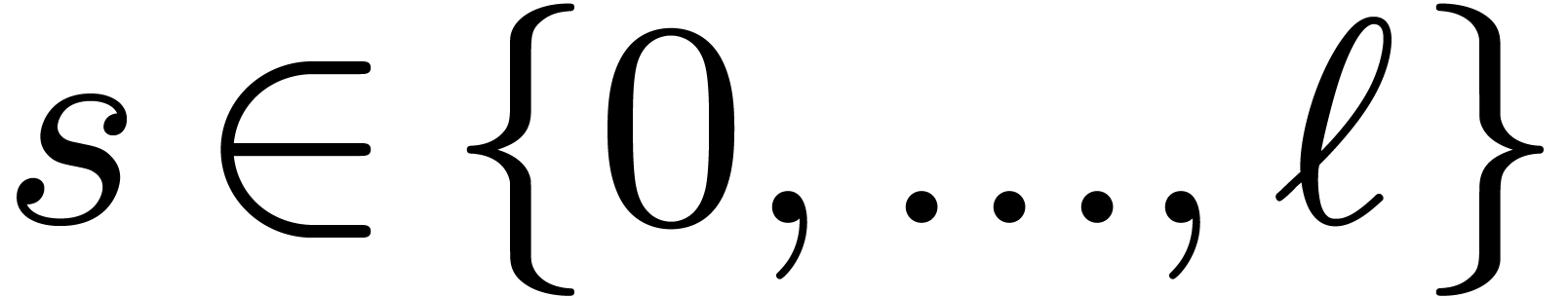 and
and 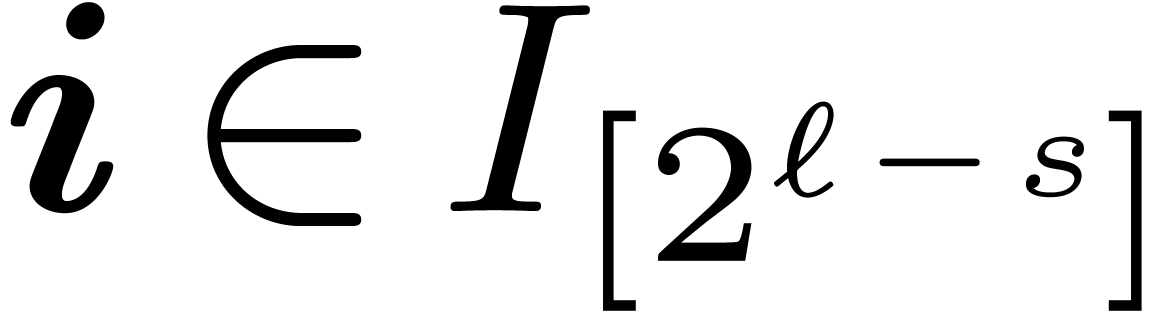 . The edges are between vertices
. The edges are between vertices 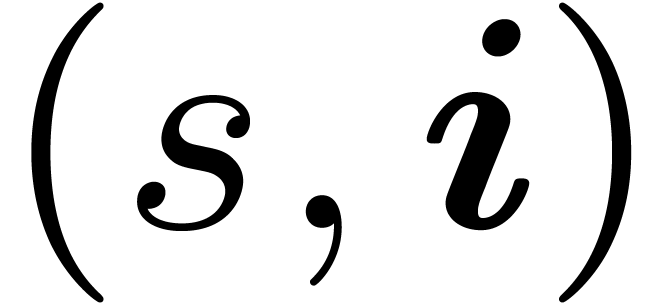 and
and 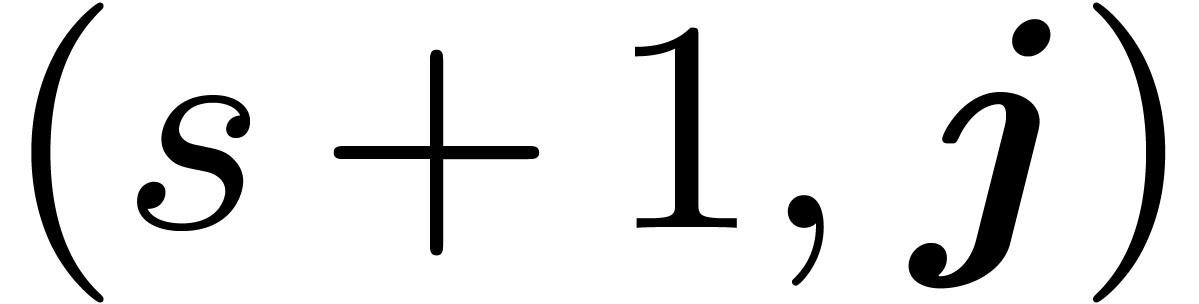 with
with 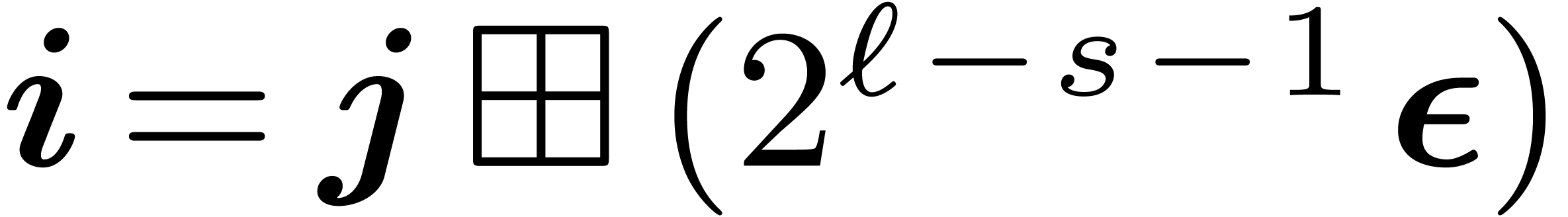 and
and 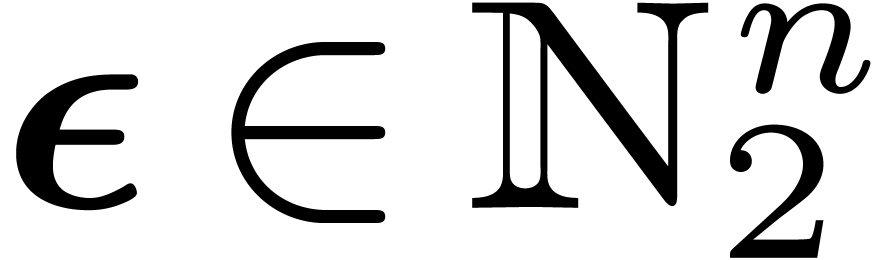 . The edge is labeled by a constant
that we will simply write
. The edge is labeled by a constant
that we will simply write 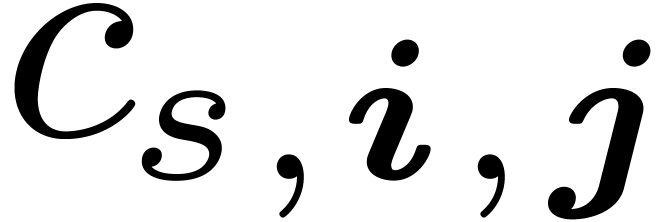 such that
such that
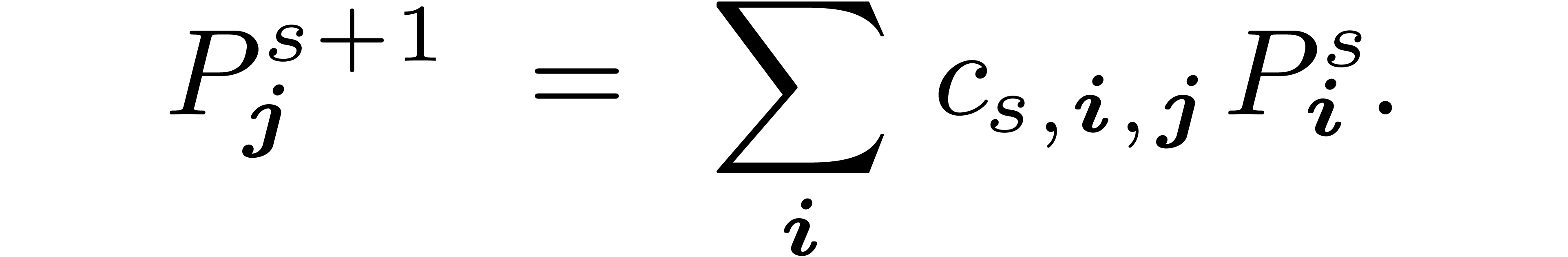 |
(12) |
For a direct TFT, we are given 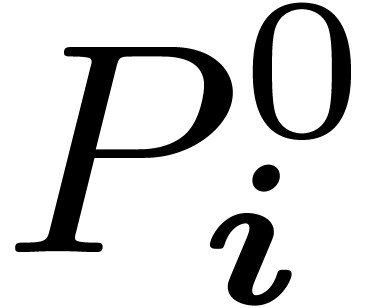 on input and
“fill out” the remaining values
on input and
“fill out” the remaining values 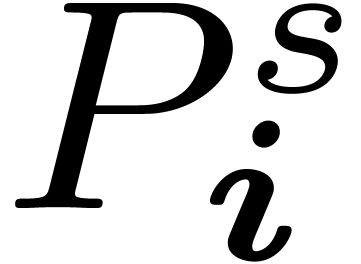 for
increasing values of
for
increasing values of  using (12). In
the case of an inverse TFT, we are given the
using (12). In
the case of an inverse TFT, we are given the 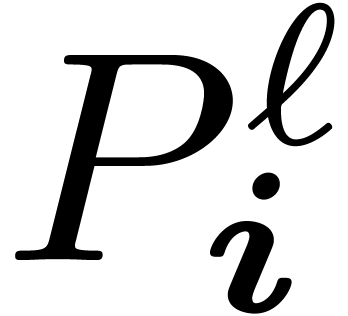 with
with  on input, as well as the coefficients
on input, as well as the coefficients  with
with  . We
next “fill out” the remaining values
. We
next “fill out” the remaining values 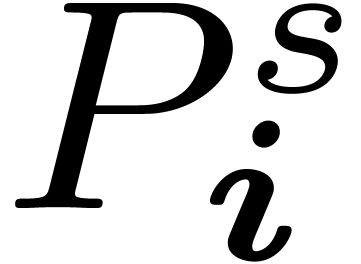 using the special algorithm described in [17].
using the special algorithm described in [17].
Now let  be as in Section 3 and
assume that
be as in Section 3 and
assume that 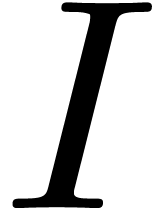 is stable under
is stable under  . Then each of the
. Then each of the 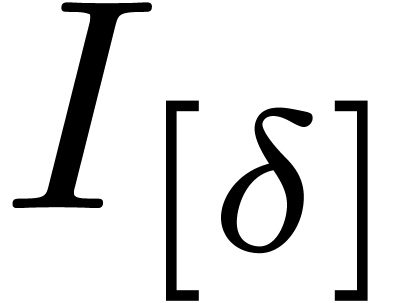 is
also stable under
is
also stable under  .
Furthermore, any
.
Furthermore, any 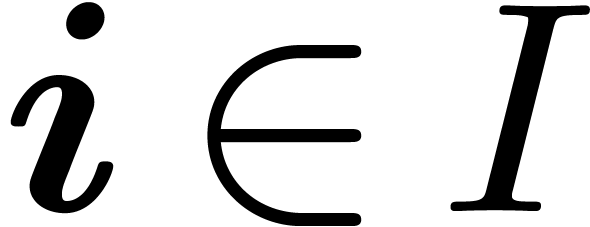 lies in the orbit of some
element of
lies in the orbit of some
element of  under the action of
under the action of  . Let
. Let 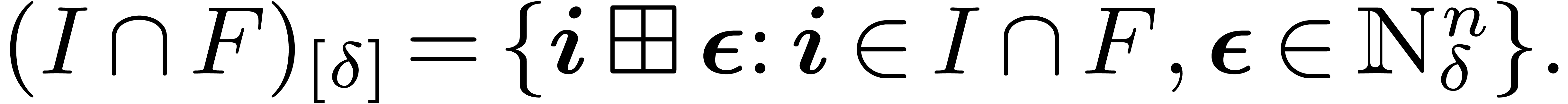 Given a
Given a  -symmetric input polynomial on
input, the idea behind the symmetric TFT is to use the restriction
-symmetric input polynomial on
input, the idea behind the symmetric TFT is to use the restriction 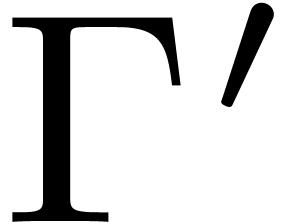 of the above graph
of the above graph  by keeping
only those vertices
by keeping
only those vertices 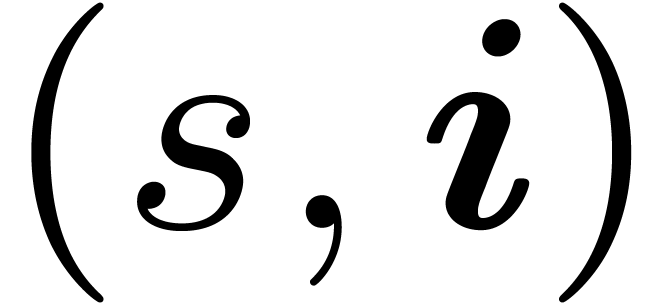 such that
such that 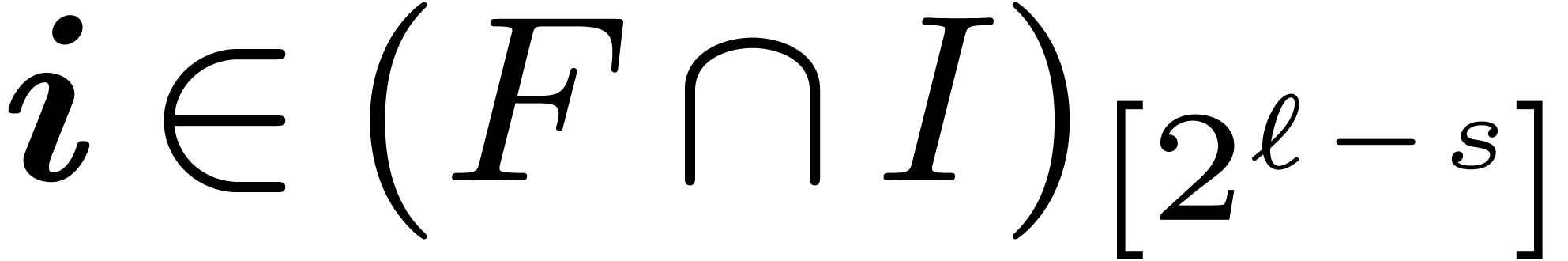 . The symmetric TFT and its inverse can then be
computed by intertwining the above “filling out” process
with steps in which we compute
. The symmetric TFT and its inverse can then be
computed by intertwining the above “filling out” process
with steps in which we compute 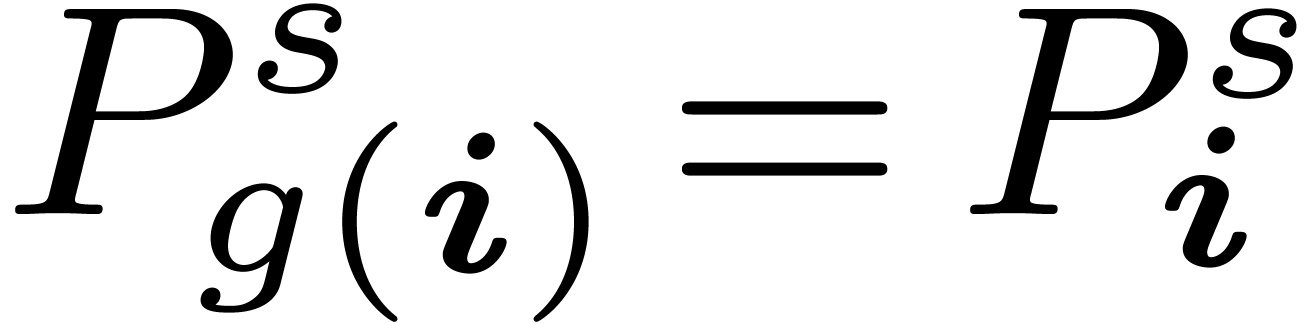 for all
for all 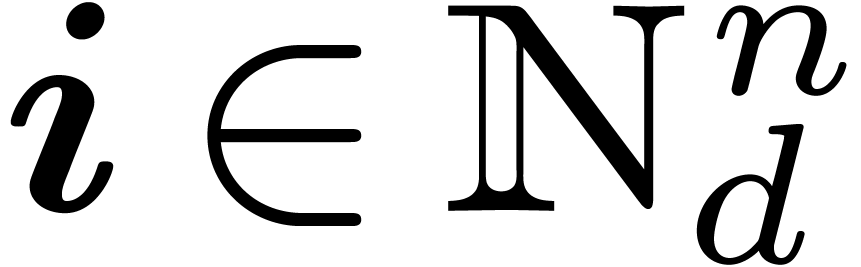 and
and 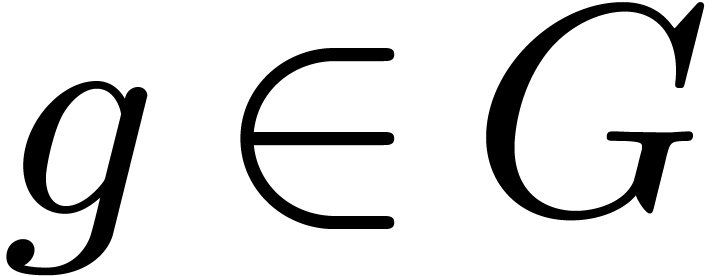 such that
such that 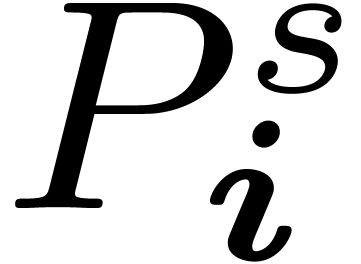 is known but not
is known but not 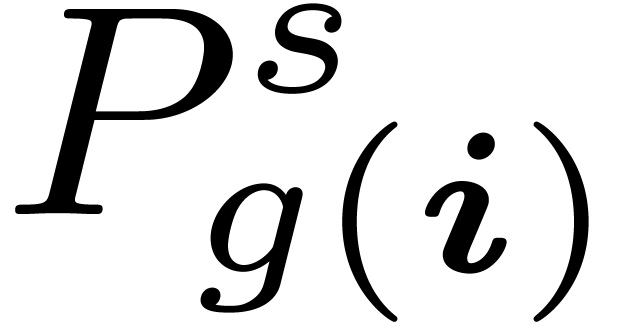 .
.
The computational complexities of the symmetric TFT and its inverse are
both proportional to the size  of
of  . For many initial domains
. For many initial domains  of interest, it can be shown that
of interest, it can be shown that 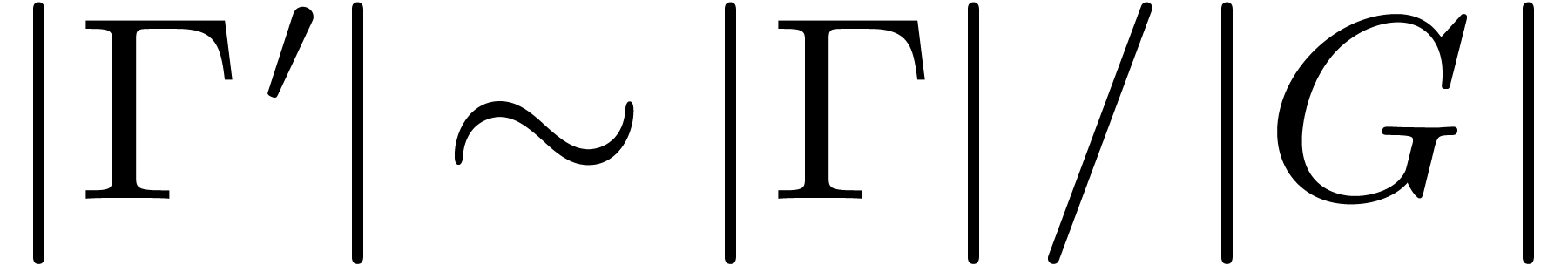 ,
as soon as
,
as soon as 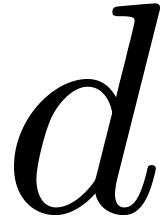 gets large. This is for instance the
case for
gets large. This is for instance the
case for 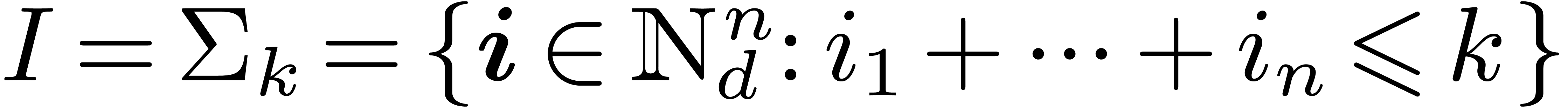 , when
, when 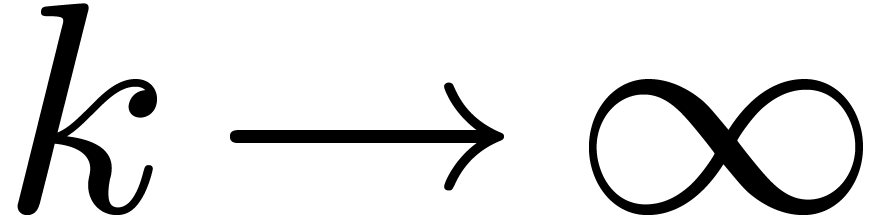 , and where
, and where 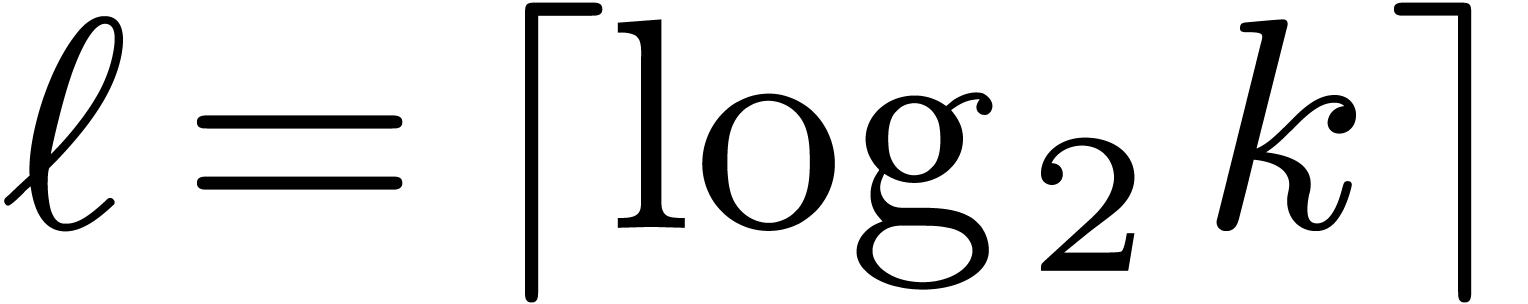 .
Indeed, using similar techniques as in the proof of Theorem 7,
we first show that
.
Indeed, using similar techniques as in the proof of Theorem 7,
we first show that 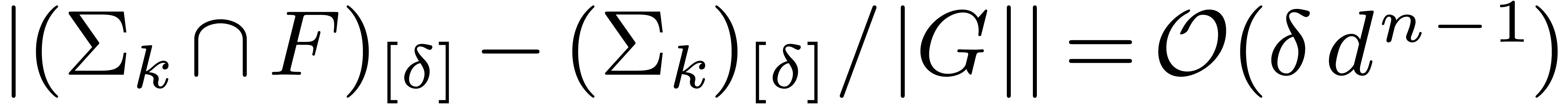 , and then
conclude in a similar way.
, and then
conclude in a similar way.
5.2The lattice TFT
Let us now consider the case of a polynomial 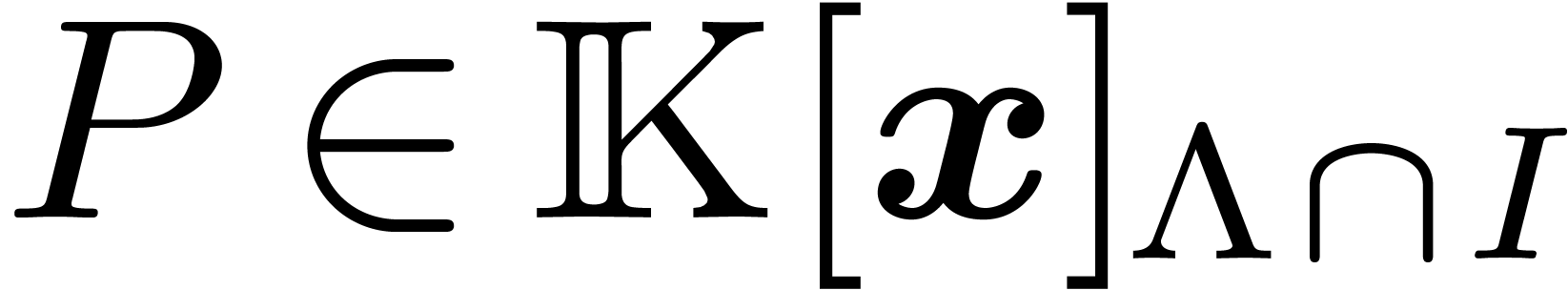 , with
, with  as in Section 4. In order to design a fast “lattice TFT”, the
idea is simply to replace
as in Section 4. In order to design a fast “lattice TFT”, the
idea is simply to replace 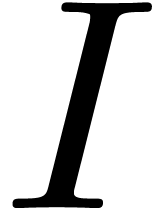 by a slightly larger
set
by a slightly larger
set  which preserves the fundamental domains.
More precisely, with
which preserves the fundamental domains.
More precisely, with  as in Section 4,
we take
as in Section 4,
we take
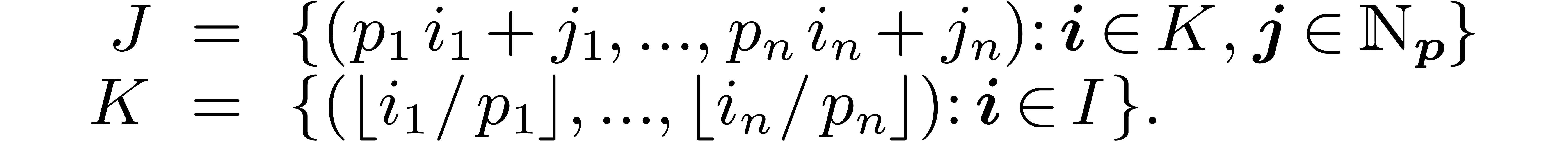
A lattice TFT of order  can then be regarded as
can then be regarded as
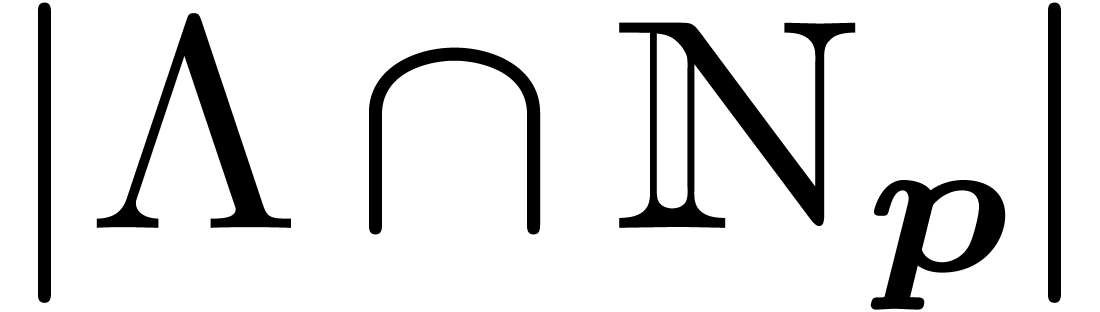 TFTs at order
TFTs at order  and
initial segment
and
initial segment 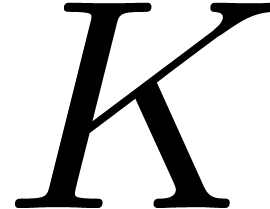 , followed by
, followed by
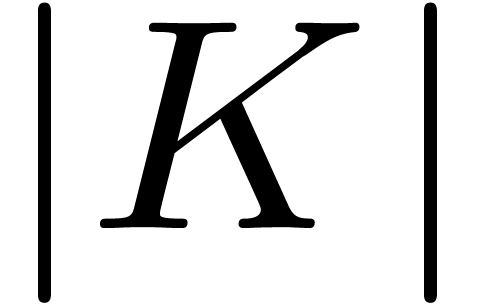 TFTs lattice FFTs on a fundamental domain.
Asymptotically speaking, we thus gain a factor
TFTs lattice FFTs on a fundamental domain.
Asymptotically speaking, we thus gain a factor  with respect to a usual TFT with initial segment
with respect to a usual TFT with initial segment 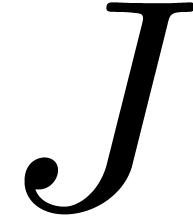 . In the case when
. In the case when 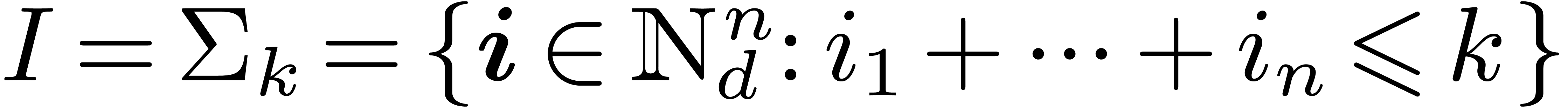 ,
we finally notice that
,
we finally notice that  for
for  .
.
6.conclusion
Let us quickly outline possible generalizations of the results of this
paper.
It seems that the most general kinds of finite groups for which the
techniques in this paper work are finite subgroups  of
of 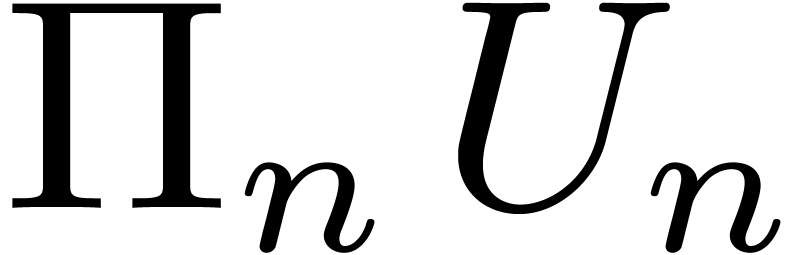 , where
, where 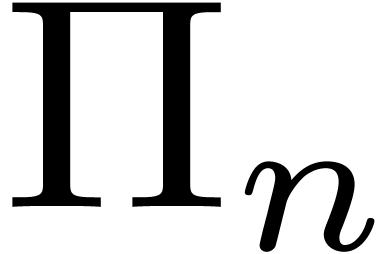 is the group of
is the group of  permutation matrices and
permutation matrices and 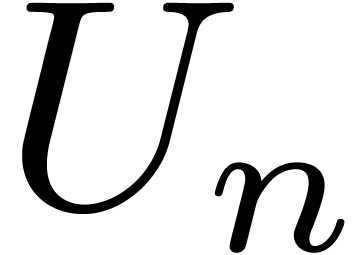 the group of diagonal matrices whose entries are all
roots of unity. Indeed, any such group
the group of diagonal matrices whose entries are all
roots of unity. Indeed, any such group  both acts
on the sets
both acts
on the sets 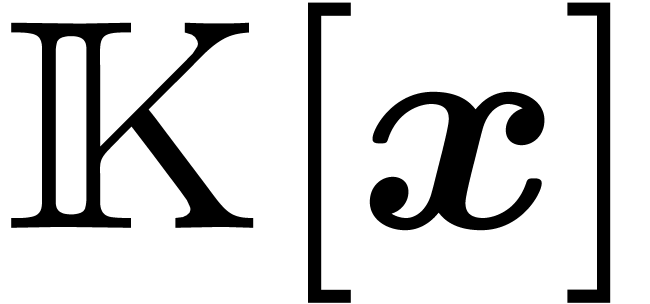 and on the torus
and on the torus  , where
, where 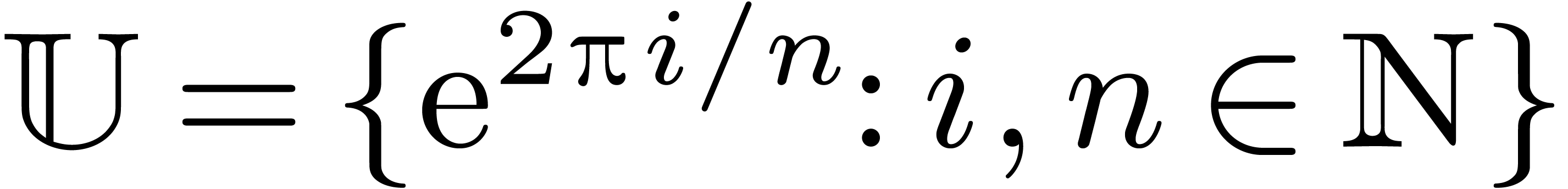 .
Even more generally, the results may still hold for closed algebraic
subgroups
.
Even more generally, the results may still hold for closed algebraic
subgroups  generated by an infinite number of
elements of
generated by an infinite number of
elements of 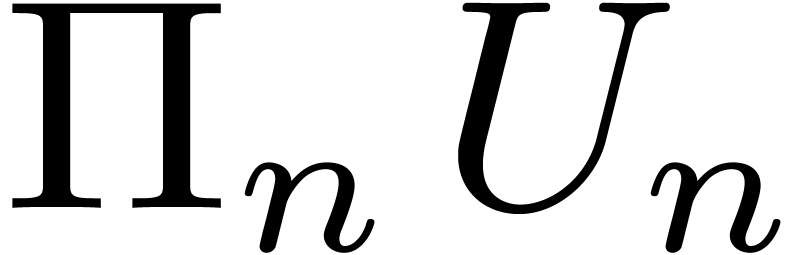 .
.
Many other interesting groups can be obtained as conjugates 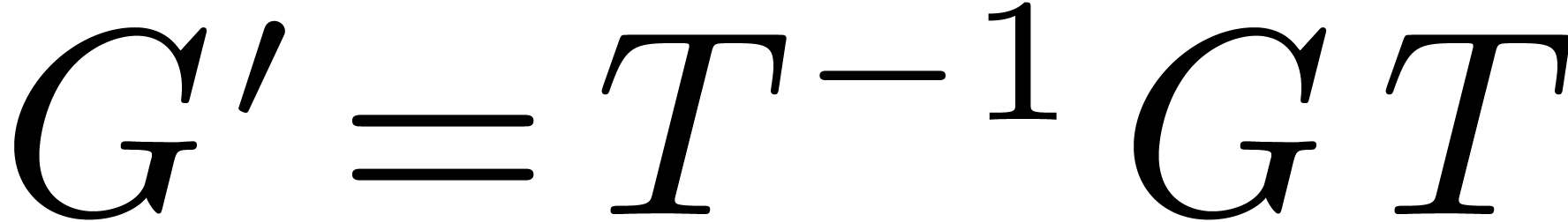 of groups
of groups  of the above kind. For
certain applications, such as the integration of dynamical systems, the
change of coordinates
of the above kind. For
certain applications, such as the integration of dynamical systems, the
change of coordinates  can be done “once
and for all” on the initial differential equations, after which
the results of this paper again apply.
can be done “once
and for all” on the initial differential equations, after which
the results of this paper again apply.
It is classical that the FFT of a polynomial with real coefficients can
be computed twice as fast (roughly speaking) as a polynomial with
complex coefficient. Real polynomials can be considered as symmetric
polynomials for complex conjugation: 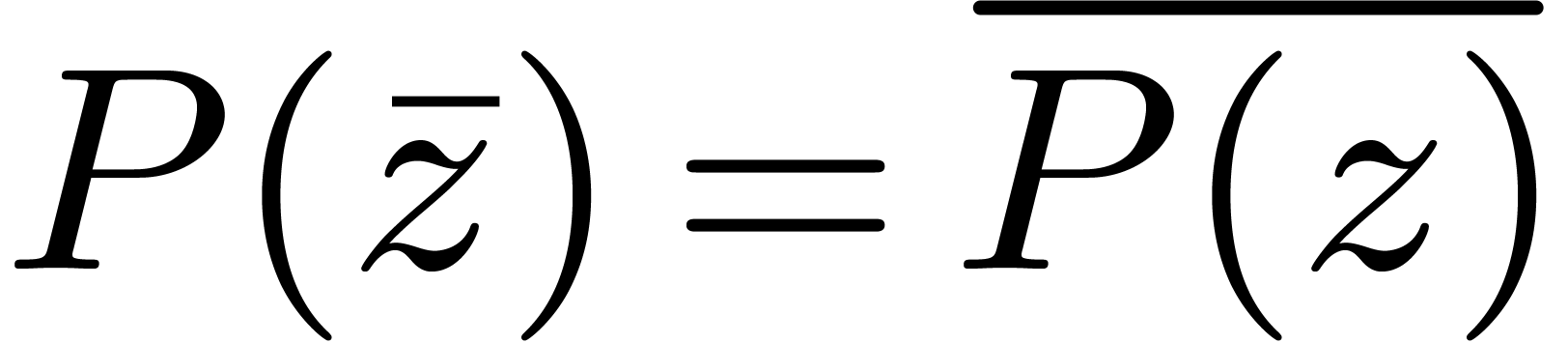 .
Some further extensions of our setting are possible by including this
kind of symmetries.
.
Some further extensions of our setting are possible by including this
kind of symmetries.
On some simple examples, we have verified that the ideas of this paper
generalize to other evaluation-interpolation models for polynomial
multiplication, such as Karatsuba multiplication and Toom-Cook
multiplication.
We intend to study the above generalizations in more detail in a
forthcoming paper.
7.References
-
[1]
-
L. Auslander, J. R. Johnson and R. W. Johnson. An
equivariant Fast Fourier Transform algorithm. Drexel
University Technical Report DU-MCS-96-02, 1996.
-
[2]
-
M. Ben-Or and P. Tiwari. A deterministic algorithm
for sparse multivariate polynomial interpolation. In STOC
'88: Proceedings of the twentieth annual ACM symposium on
Theory of computing, pages 301–309. New York, NY,
USA, 1988. ACM Press.
-
[3]
-
R. Bergmann. The fast Fourier transform and fast
wavelet transform for patterns on the torus. Applied and
Computational Harmonic Analysis, , 2012. In Press.
-
[4]
-
P. Bürgisser, M. Clausen and M. A.
Shokrollahi. Algebraic complexity theory.
Springer-Verlag, 1997.
-
[5]
-
J. Canny, E. Kaltofen and Y. Lakshman. Solving
systems of non-linear polynomial equations faster. In Proc.
ISSAC '89, pages 121–128. Portland, Oregon, A.C.M.,
New York, 1989. ACM Press.
-
[6]
-
D.G. Cantor and E. Kaltofen. On fast multiplication
of polynomials over arbitrary algebras. Acta
Informatica, 28:693–701, 1991.
-
[7]
-
J.W. Cooley and J.W. Tukey. An algorithm for the
machine calculation of complex Fourier series. Math.
Computat., 19:297–301, 1965.
-
[8]
-
S. Czapor, K. Geddes and G. Labahn. Algorithms
for Computer Algebra. Kluwer Academic Publishers, 1992.
-
[9]
-
P. Duhamel and M. Vetterli. Fast Fourier
transforms: a tutorial review and a state of the art.
Signal Process., 19(4):259–299, apr 1990.
-
[10]
-
T. S. Freeman, G. M. Imirzian, E. Kaltofen and Y.
Lakshman. DAGWOOD a system for manipulating polynomials given
bystraight-line programs. ACM Trans. Math. Software,
14:218–240, 1988.
-
[11]
-
S. Garg and É. Schost. Interpolation of
polynomials given by straight-line programs. Theoretical
Computer Science, 410(27-29):2659–2662, 2009.
-
[12]
-
M. Gastineau and J. Laskar. Trip
1.2.26. TRIP Reference manual, IMCCE, 2012.
http://www.imcce.fr/trip/
.
-
[13]
-
A. Guessoum and R. Mersereau. Fast algorithms for
the multidimensional discrete Fourier transform. IEEE
Transactions on Acoustics, Speech and Signal Processing,
34(4):937–943, 1986.
-
[14]
-
J. von zur Gathen and J. Gerhard. Modern
Computer Algebra. Cambridge University Press, 2-nd
edition, 2002.
-
[15]
-
J. van der Hoeven. Relax, but don't be too lazy.
JSC, 34:479–542, 2002.
-
[16]
-
J. van der Hoeven. The truncated Fourier transform
and applications. In J. Gutierrez, editor, Proc. ISSAC
2004, pages 290–296. Univ. of Cantabria, Santander,
Spain, July 4–7 2004.
-
[17]
-
J. van der Hoeven. Notes on the Truncated Fourier
Transform. Technical Report 2005-5, Université
Paris-Sud, Orsay, France, 2005.
-
[18]
-
J. van der Hoeven. Newton's method and FFT trading.
JSC, 45(8):857–878, 2010.
-
[19]
-
J. van der Hoeven and G. Lecerf. On the
bit-complexity of sparse polynomial multiplication. Technical
Report, HAL, 2010. Http://hal.archives-ouvertes.fr/hal-00476223,
accepted for publication in JSC.
-
[20]
-
J. van der Hoeven and G. Lecerf. On the complexity
of blockwise polynomial multiplication. In Proc. ISSAC
'12, pages 211–218. Grenoble, France, July 2012.
-
[21]
-
J. van der Hoeven and É. Schost. Multi-point
evaluation in higher dimensions. Technical Report, HAL, 2010.
Http://hal.archives-ouvertes.fr/hal-00477658,
accepted for publication in AAECC.
-
[22]
-
J. Johnson and X. Xu. Generating symmetric DFTs and
equivariant FFT algorithms. In ISSAC'07, pages
195–202. ACM, 2007.
-
[23]
-
S. C. Johnson. Sparse polynomial arithmetic.
SIGSAM Bull., 8(3):63–71, 1974.
-
[24]
-
E. Kaltofen and Y. N. Lakshman. Improved sparse
multivariate polynomial interpolation algorithms. In ISSAC
'88: Proceedings of the international symposium on Symbolic
and algebraic computation, pages 467–474. Springer
Verlag, 1988.
-
[25]
-
E. Kaltofen, Y. N. Lakshman and J.-M. Wiley.
Modular rational sparse multivariate polynomial interpolation.
In ISSAC '90: Proceedings of the international symposium on
Symbolic and algebraic computation, pages 135–139.
New York, NY, USA, 1990. ACM Press.
-
[26]
-
E. Kaltofen, W. Lee and A. A. Lobo. Early
termination in Ben-Or/Tiwari sparse interpolation and a hybrid
of Zippel's algorithm. In ISSAC '00: Proceedings of the
2000 international symposium on Symbolic and algebraic
computation, pages 192–201. New York, NY, USA, 2000.
ACM Press.
-
[27]
-
A Kudlicki, M. Rowicka and Z. Otwinowski. The
crystallographic Fast Fourier Transform. recursive symmetry
reduction. Acta Cryst., A63:465–480, 2007.
-
[28]
-
Victor Y. Pan. Simple multivariate polynomial
multiplication. JSC, 18(3):183–186, 1994.
-
[29]
-
V. Pan and D. Bini. Polynomial and matrix
computations. Birkhauser, 1994.
-
[30]
-
A. Schönhage and V. Strassen. Schnelle
Multiplikation grosser Zahlen. Computing,
7:281–292, 1971.
-
[31]
-
D. R. Stoutemyer. Which polynomial representation
is best? In Proceedings of the 1984 MACSYMA Users'
Conference: Schenectady, New York, July 23–25, 1984,
pages 221–243. 1984.
-
[32]
-
L. F. Ten Eyck. Crystallographic Fast Fourier
Transform. Acta Cryst., A29:183–191, 1973.
-
[33]
-
A. Vince and X. Zheng. Computing the Discrete
Fourier Transform on a hexagonal lattice. Journal of
Mathematical Imaging and Vision, 28:125–133, 2007.

 . This work has been partly supported
by the
. This work has been partly supported
by the  ,
, and finite groups of diagonal matrices. These cases
are already sufficient to address questions raised e.g. in
celestial mechanics [
and finite groups of diagonal matrices. These cases
are already sufficient to address questions raised e.g. in
celestial mechanics [ with sufficiently many roots of unity; the main objects are polynomials
with sufficiently many roots of unity; the main objects are polynomials
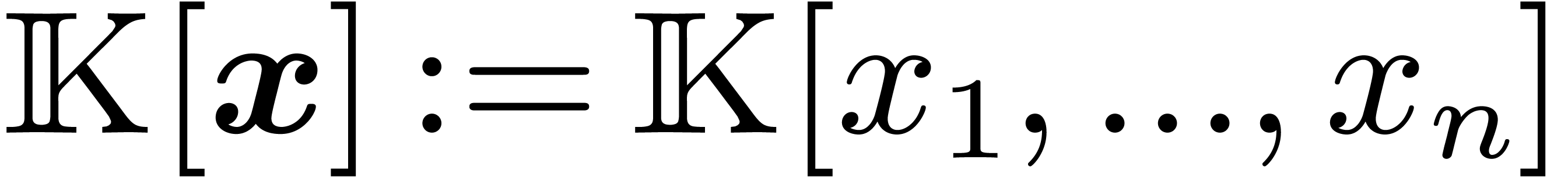 in
in 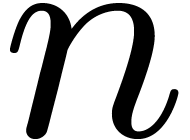 variables over
variables over  and
and 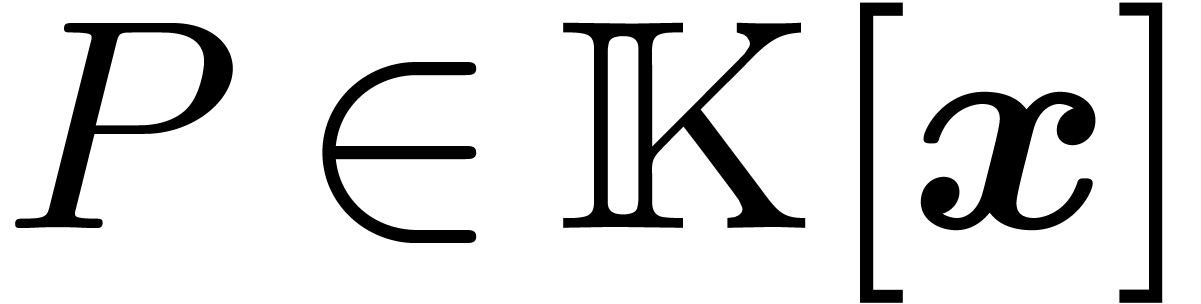 ,
,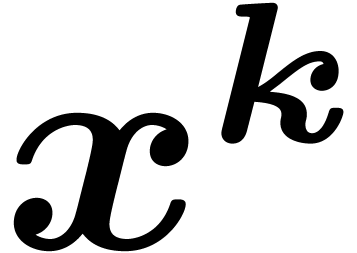 the monomial
the monomial  and by
and by  the coefficient of
the coefficient of  in
in 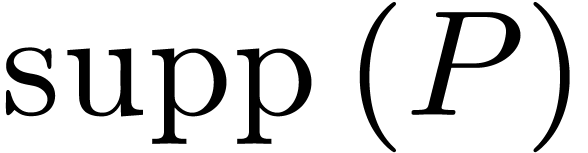 of a
polynomial
of a
polynomial 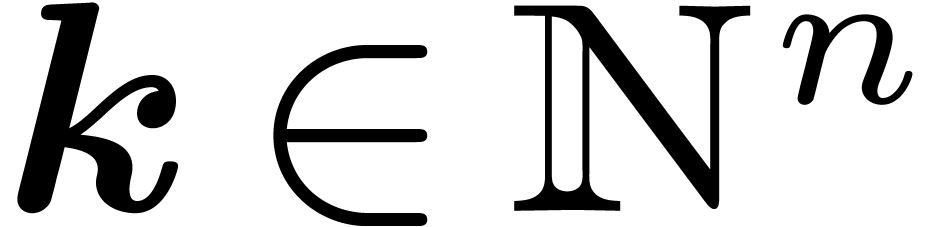 such that
such that 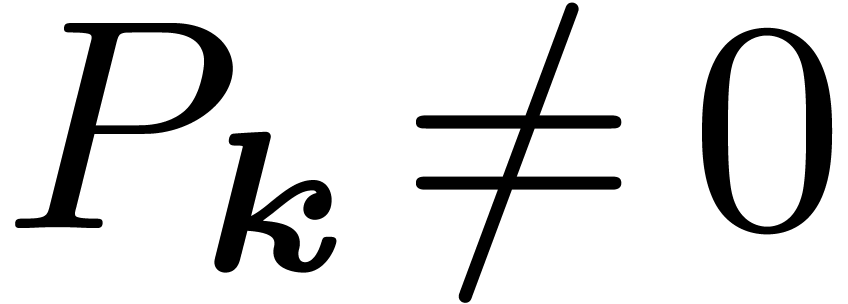 .
.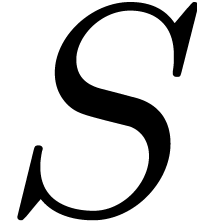 of
of 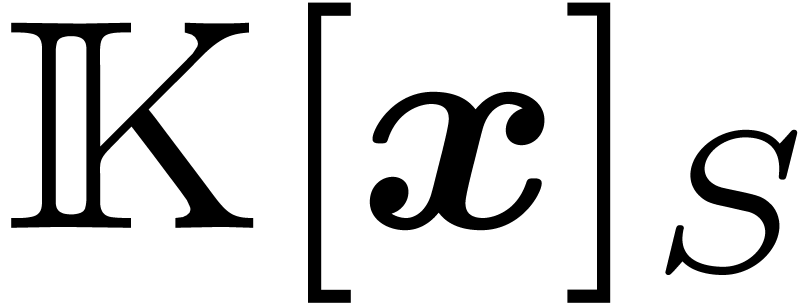 as the polynomials with support
included in
as the polynomials with support
included in  ,
,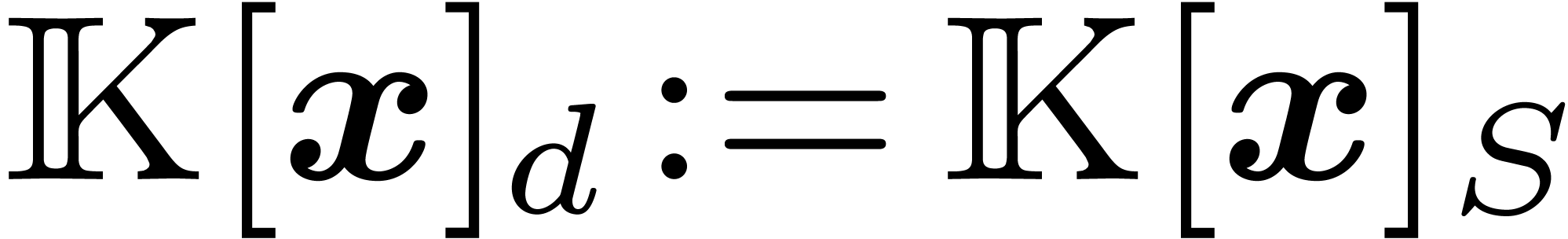 the set of polynomials with partial
degree less than
the set of polynomials with partial
degree less than 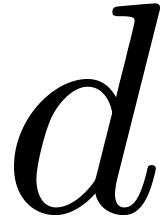 in all variables.
in all variables.
 be a primitive
be a primitive 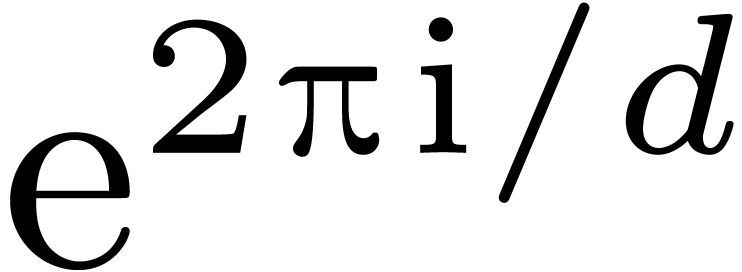 ).
).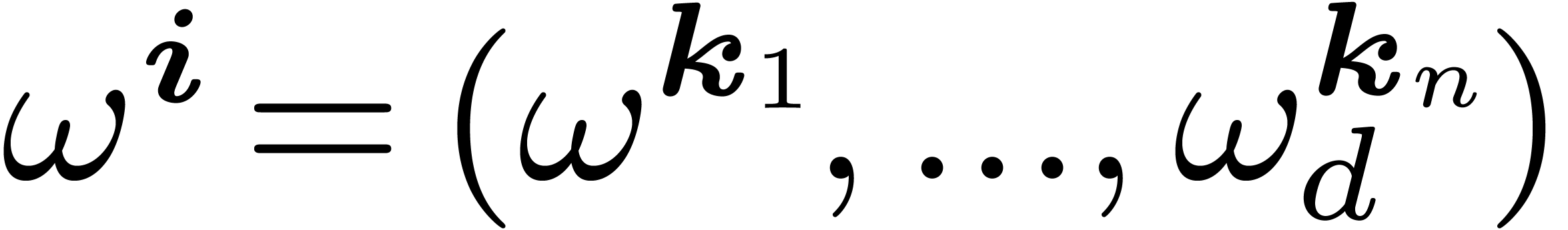 .
.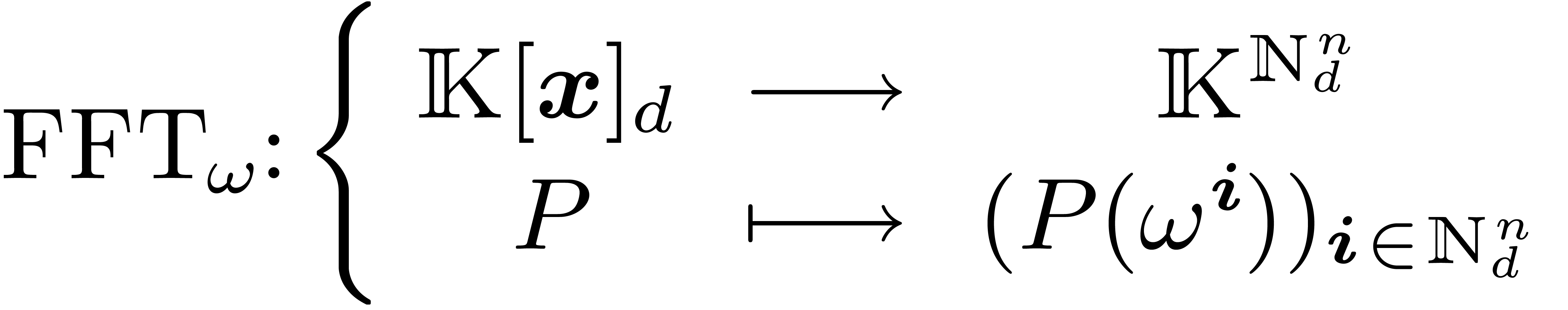
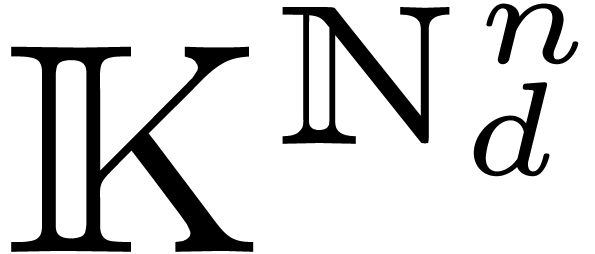 denotes the set of vectors with entries in
denotes the set of vectors with entries in
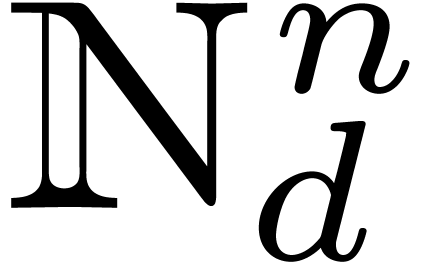 ;
;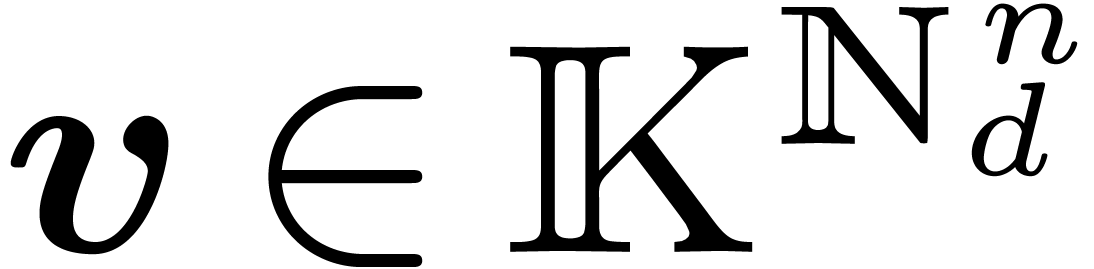 implies that
implies that  for all
for all 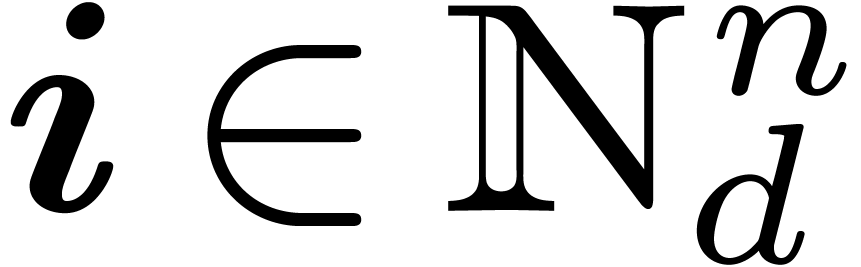 .
.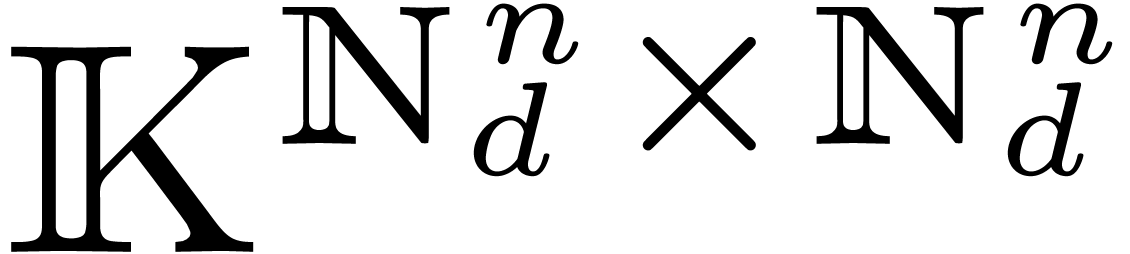 denotes the set of matrices with indices in
denotes the set of matrices with indices in 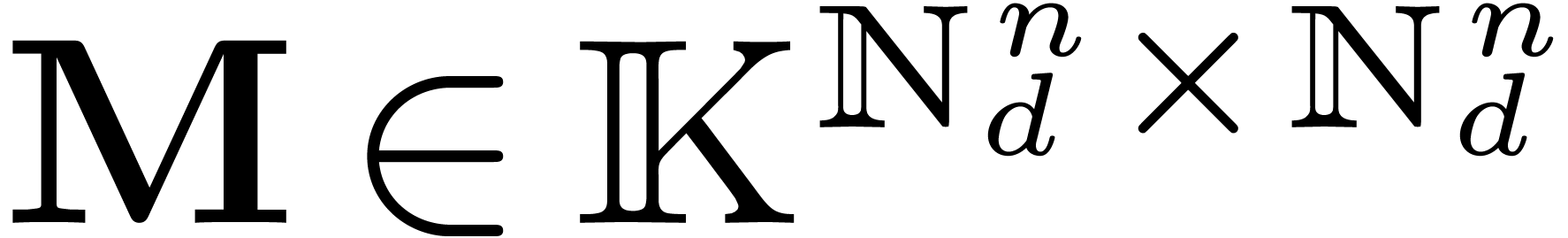 implies that
implies that
 for all
for all  .
.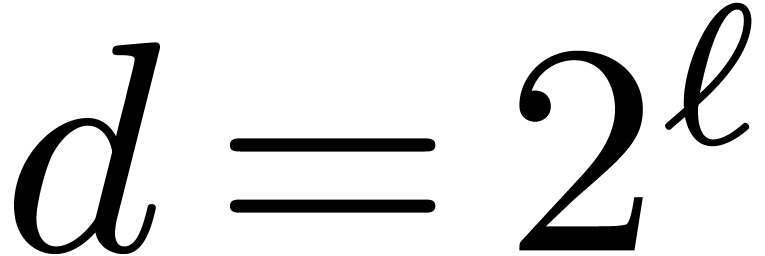 with
with 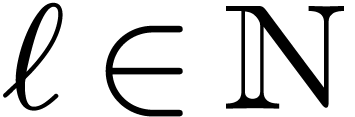 ,
,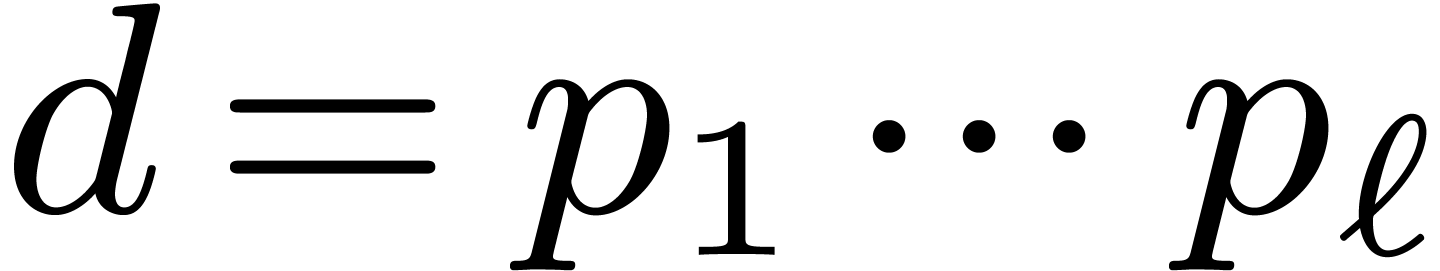 .
.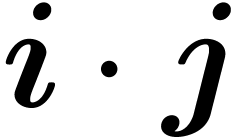 the inner product of two vectors in
the inner product of two vectors in
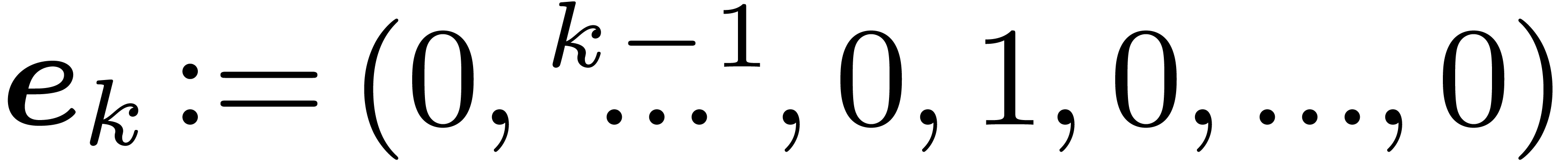 ,
,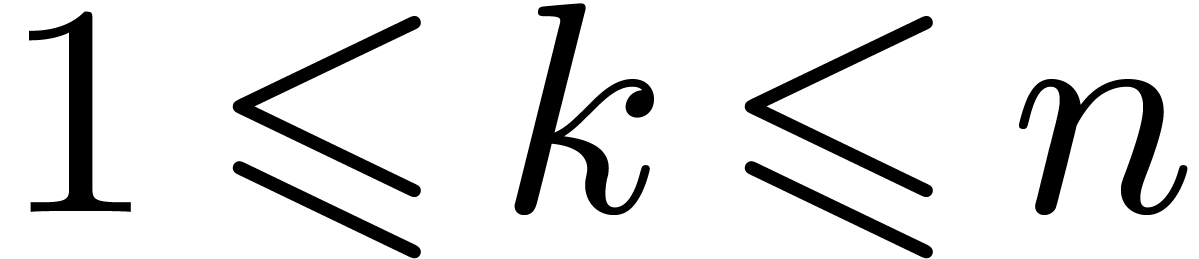 ,
, th
th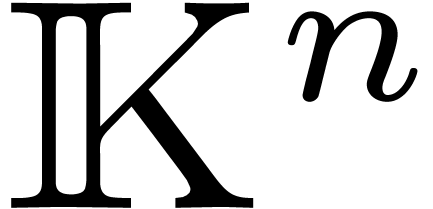 .
.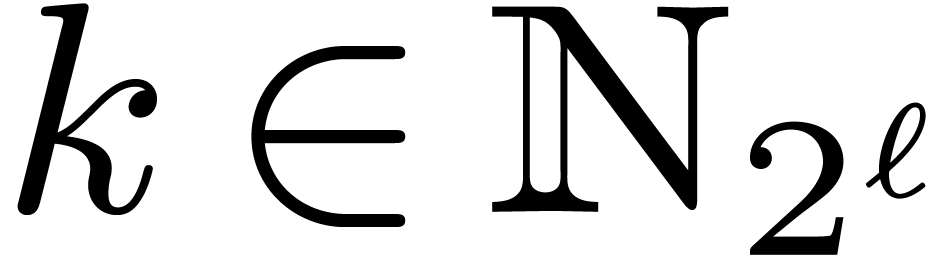 we denote by
we denote by
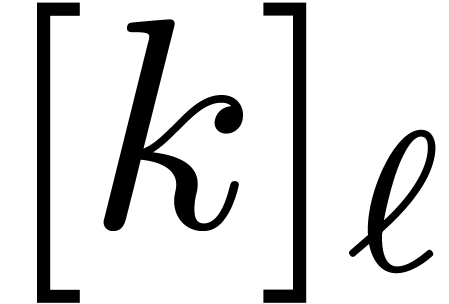 the bit reversal of
the bit reversal of 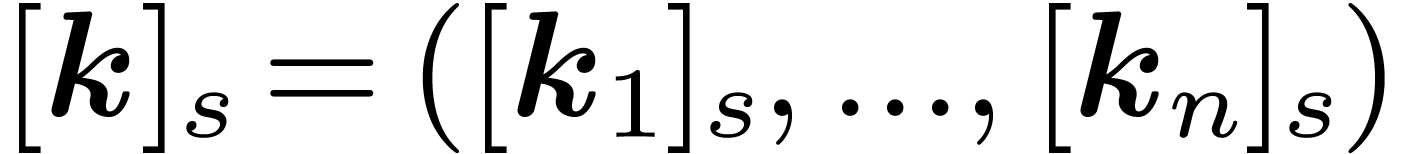 .
. is a
is a 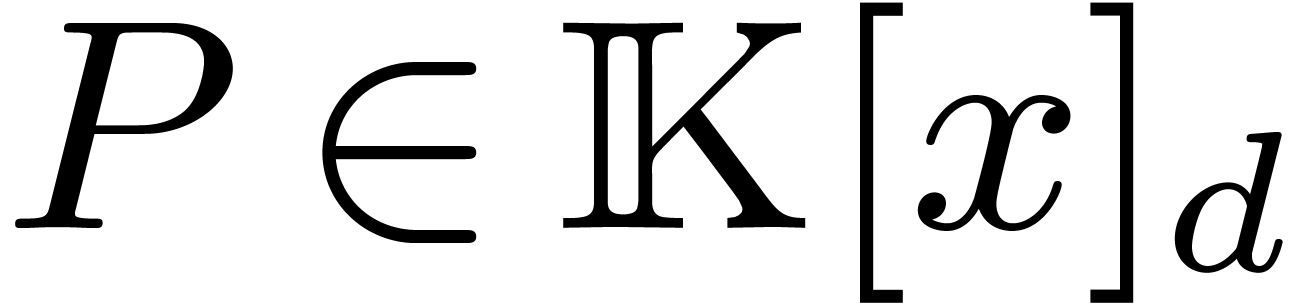 .
. decimations applied to
the variable
decimations applied to
the variable  .
.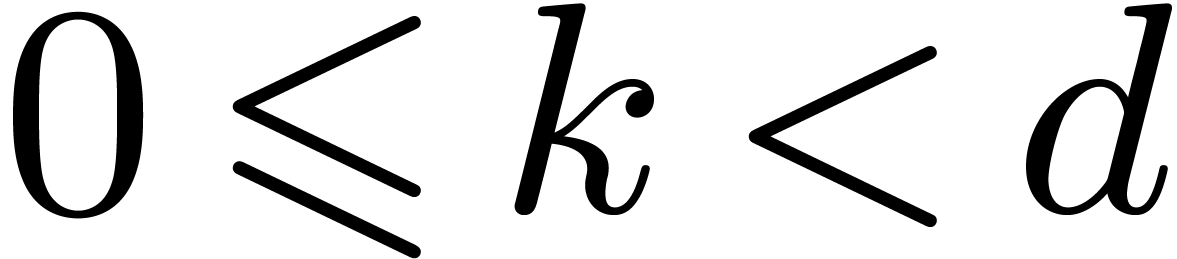 ,
,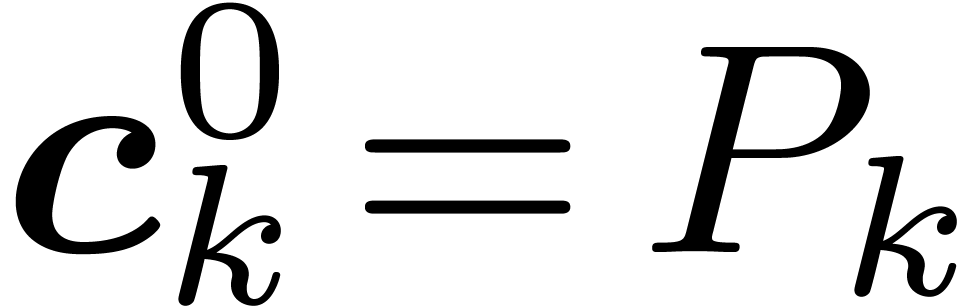 for the input and denote by
for the input and denote by 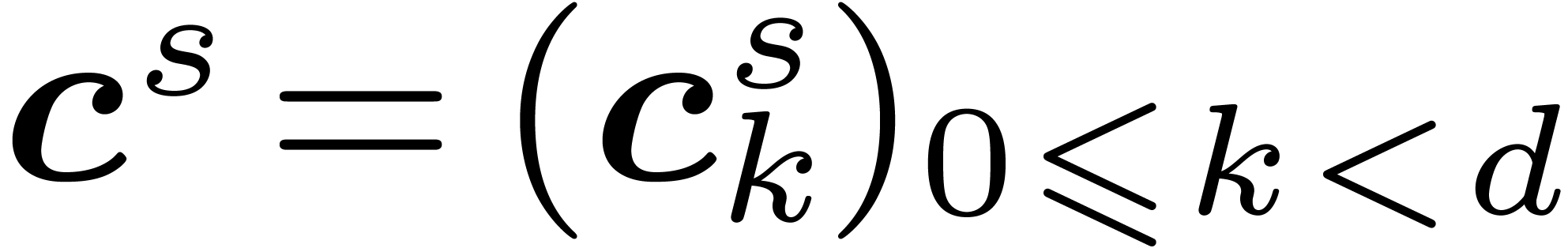 the result after
the result after
 decimation steps, for
decimation steps, for 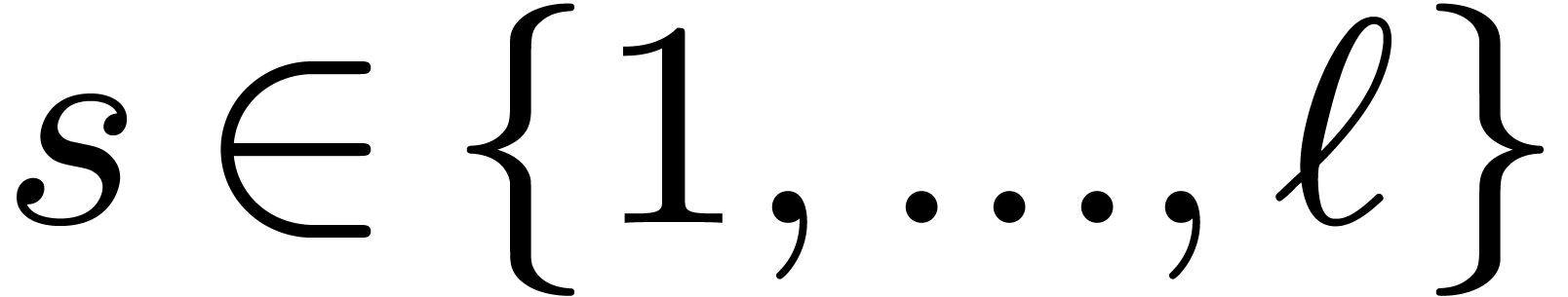 .
.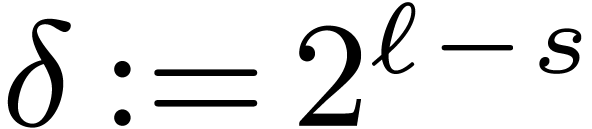 .
.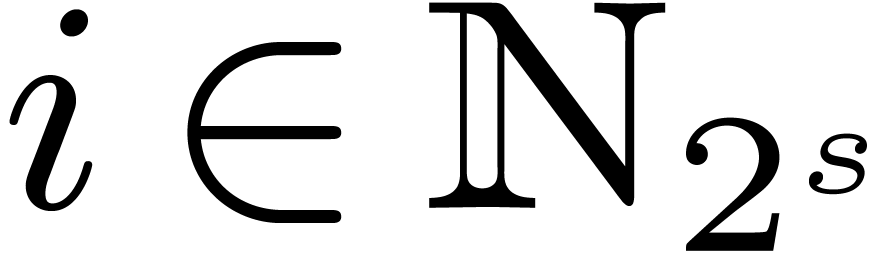 is even and
is even and  belongs
to
belongs
to  then these butterflies are given by
then these butterflies are given by
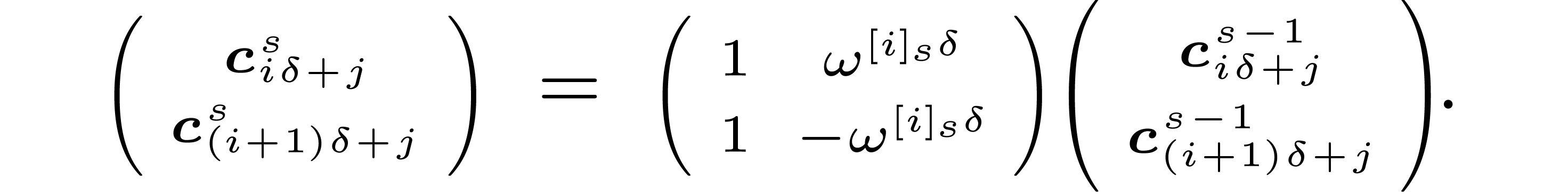
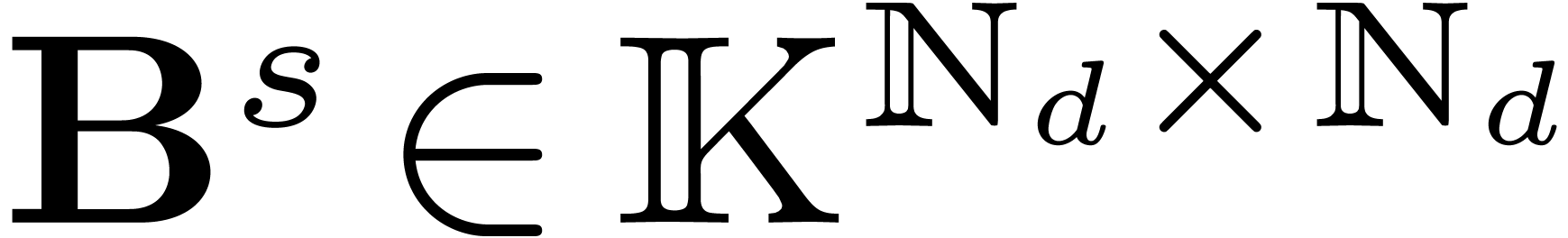 ,
,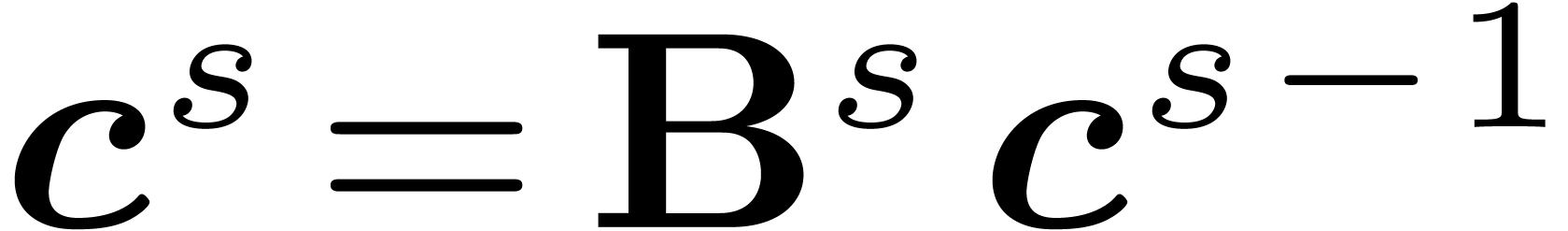 .
.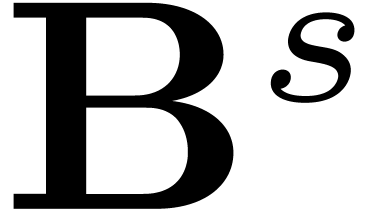 is sparse, with
at most two non-zero coefficients on each row and each column; up to
permutation, it is block-diagonal, with blocks of size 2. After
is sparse, with
at most two non-zero coefficients on each row and each column; up to
permutation, it is block-diagonal, with blocks of size 2. After 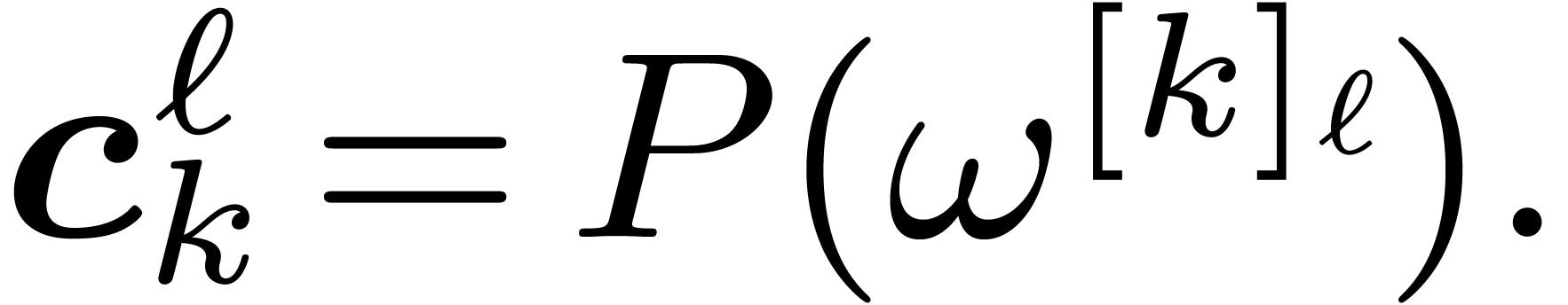
 .
.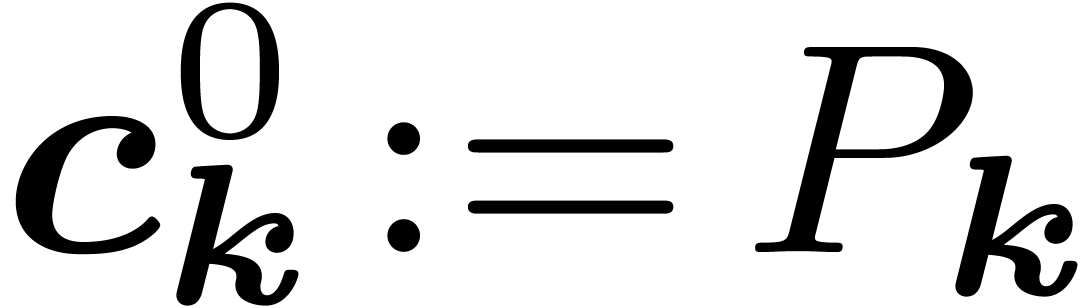 the coefficients of
the input for
the coefficients of
the input for 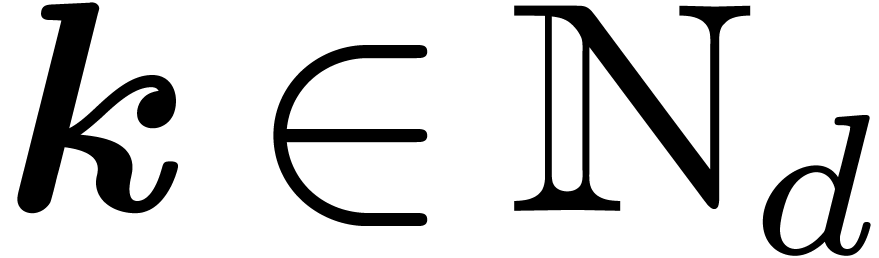 and by
and by 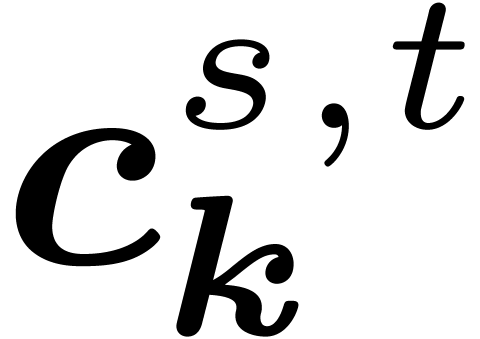 the
coefficients obtained during the
the
coefficients obtained during the  are done, with
are done, with
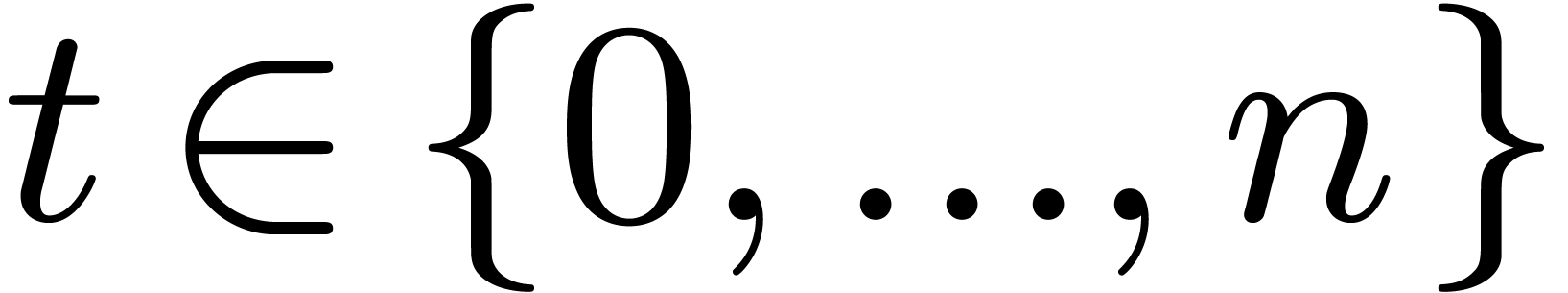 ,
,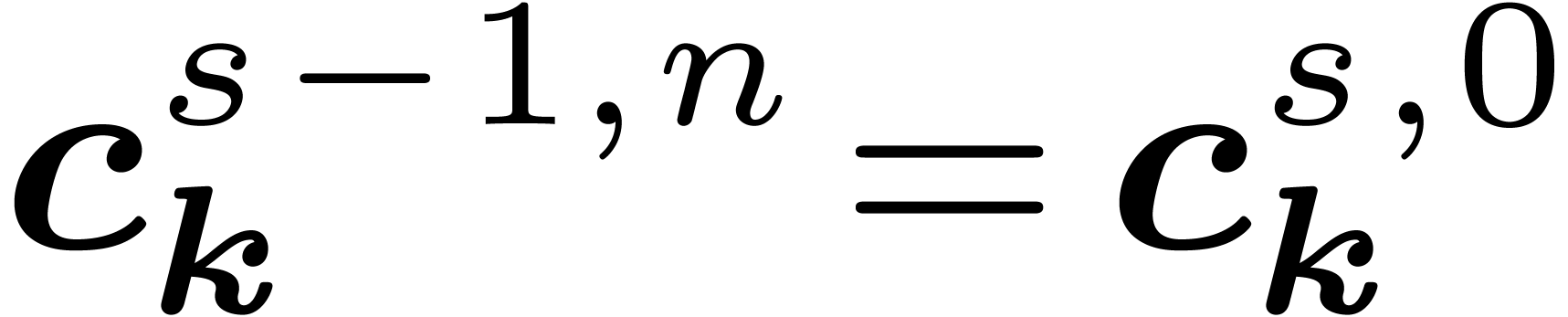 .
.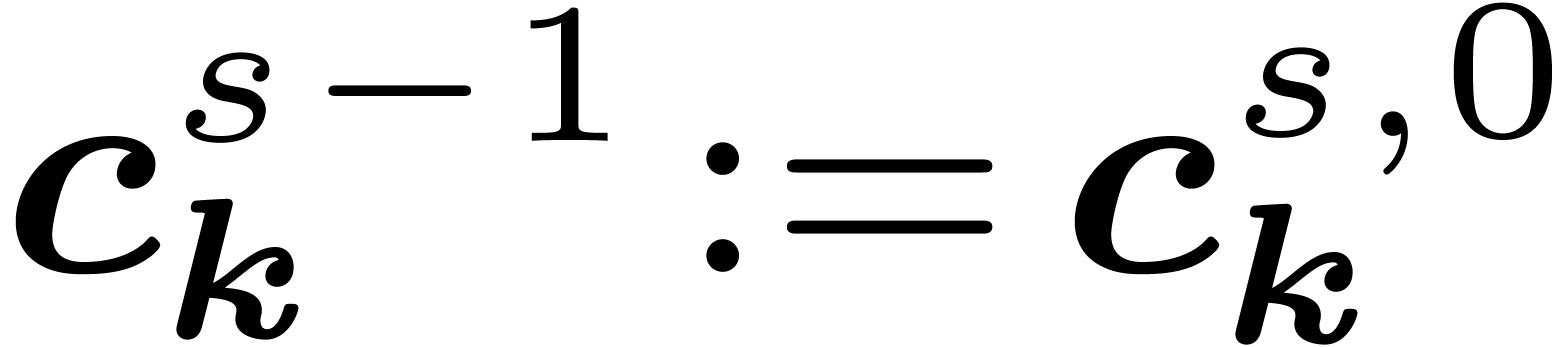 for the coefficients after
for the coefficients after  stages.
stages.
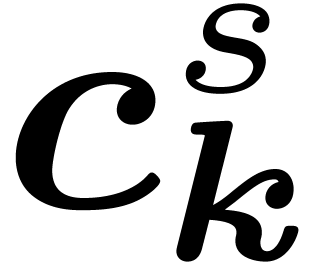 can be seen as
evaluations of intermediate polynomials: for every
can be seen as
evaluations of intermediate polynomials: for every  ,
, and
and 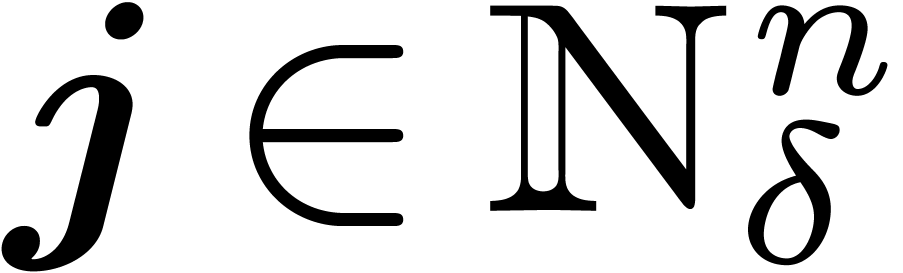 ,
,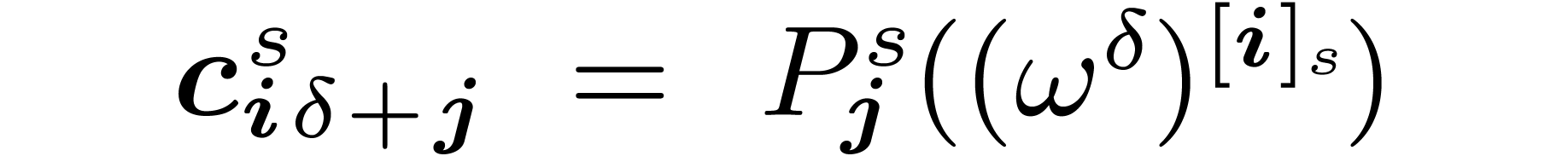
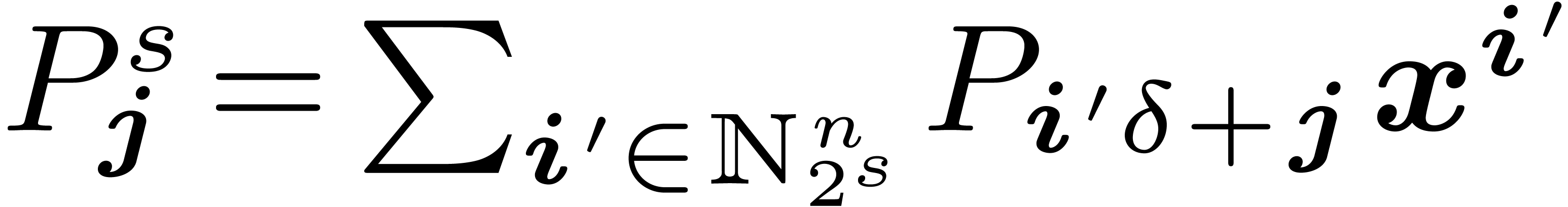 are obtained through an
are obtained through an 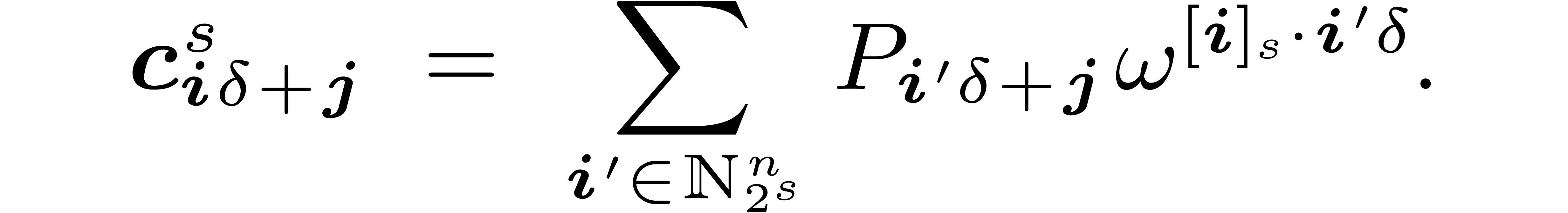
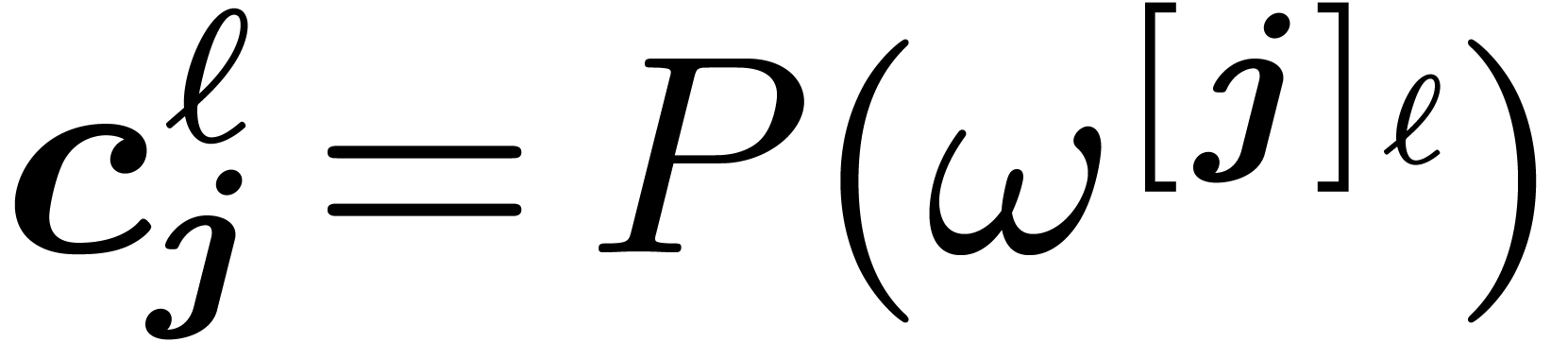 yields
yields 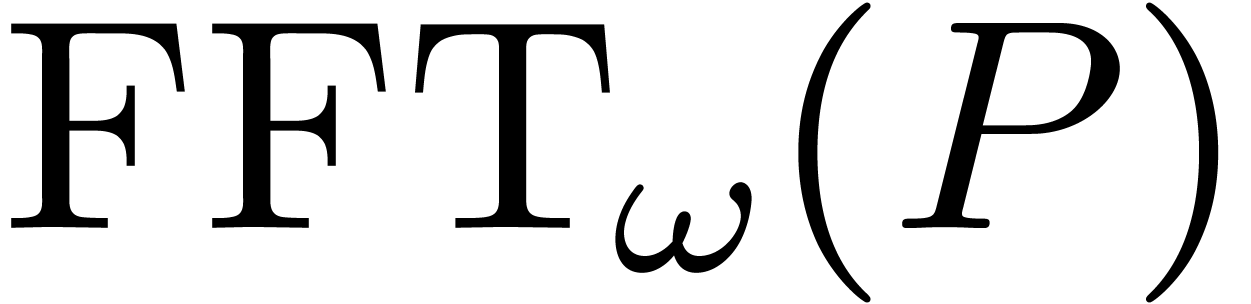 in bit
reversed order.
in bit
reversed order.
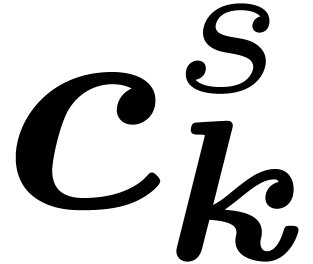 at stage
at stage 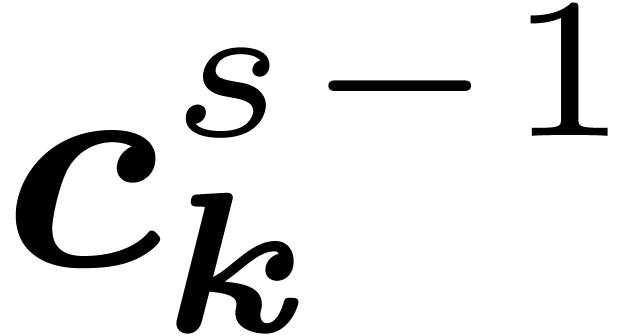 at stage
at stage 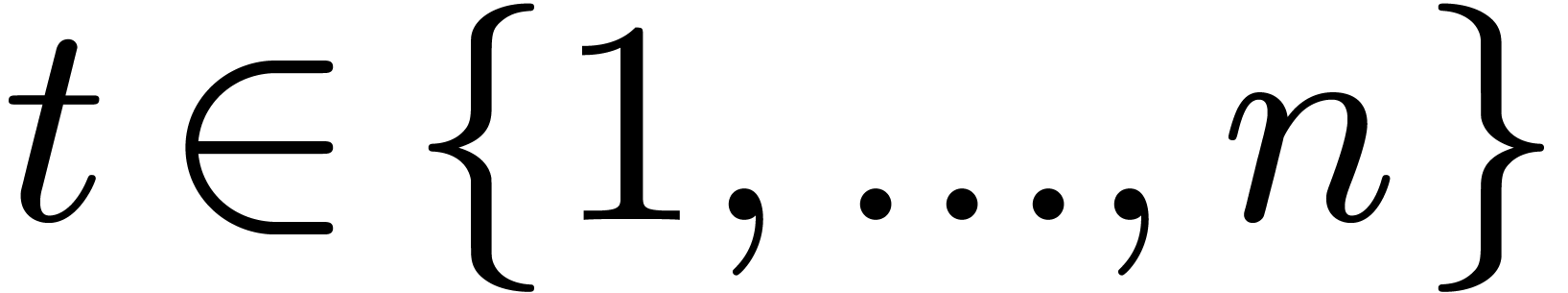 ,
,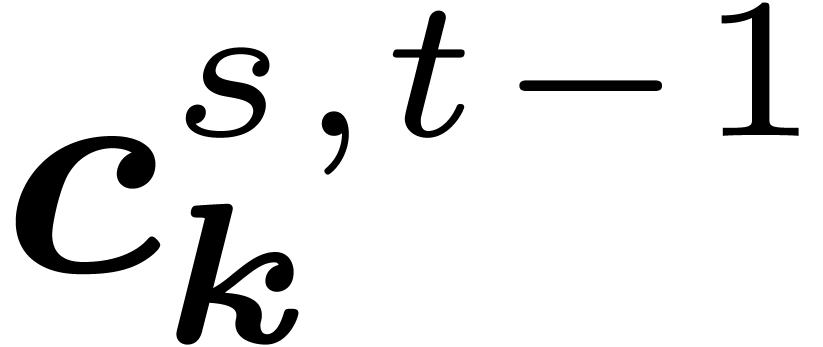 through butterflies of span
through butterflies of span 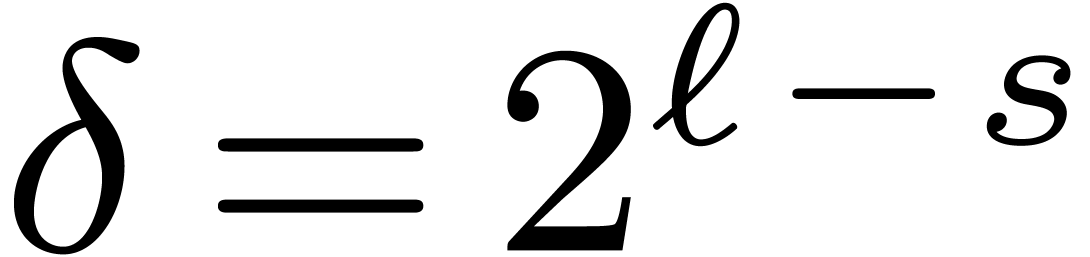 with
respect to the variable
with
respect to the variable 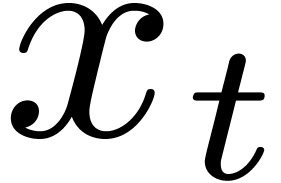 ;
;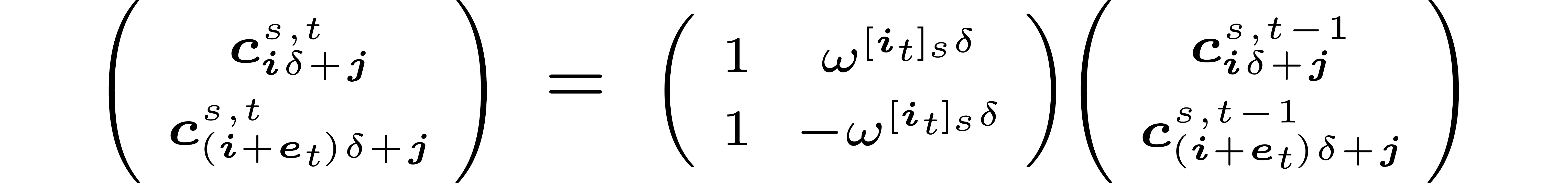
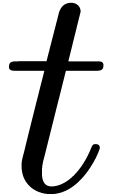 -th
-th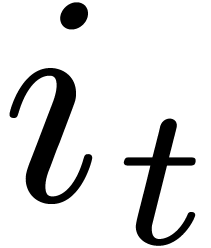 and
and  where
where  is a sparse matrix
in
is a sparse matrix
in 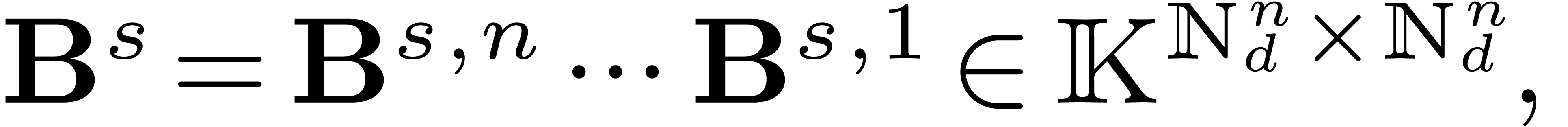 we
we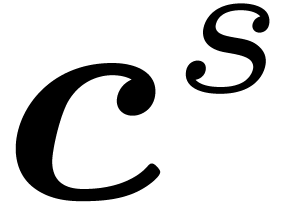 as a function of
as a function of 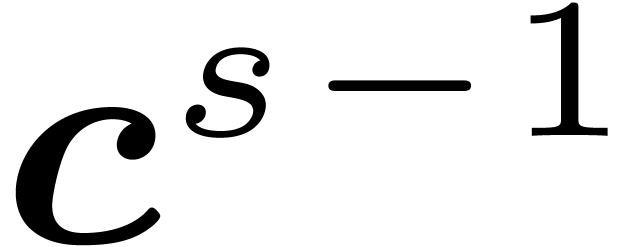 :
: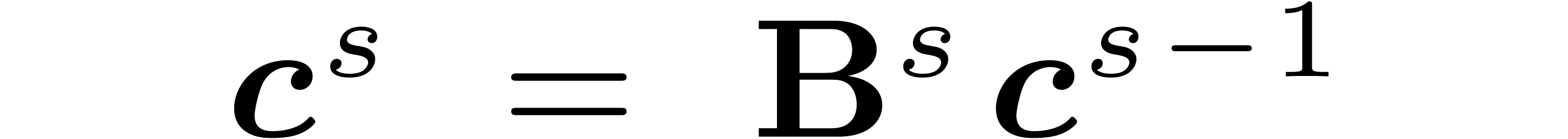
 commute pairwise.
Notice also that each of the rows and columns of
commute pairwise.
Notice also that each of the rows and columns of  has at most
has at most  non zero entries and consequently
those of
non zero entries and consequently
those of 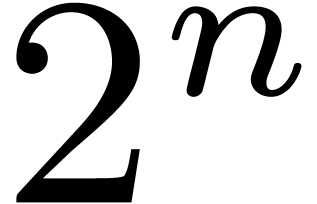 non zero entries. For this reason, we can apply the matrices
non zero entries. For this reason, we can apply the matrices 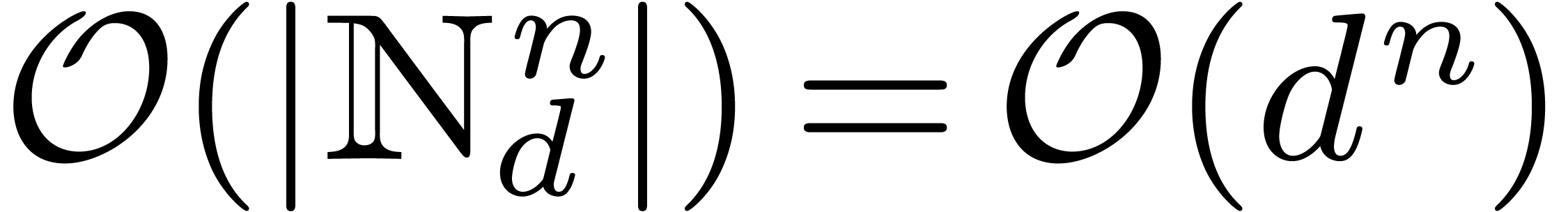 (resp.
(resp. 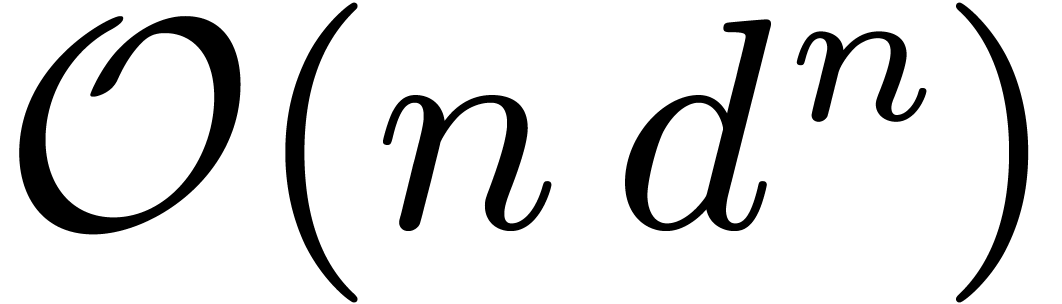 )
)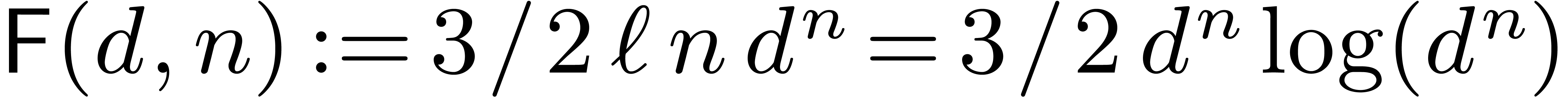 operations
in
operations
in 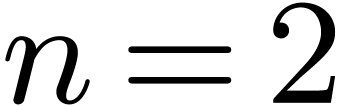 variables and degree
less than
variables and degree
less than  ,
, .
.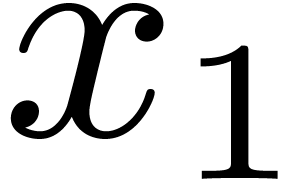 whose butterflies of span
whose butterflies of span  are captured by
are captured by 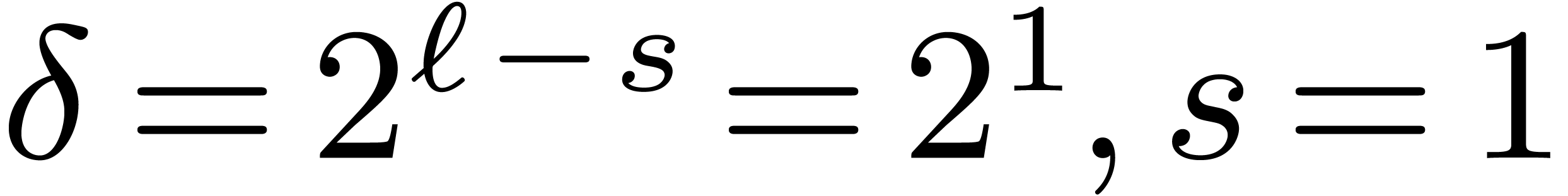 and
and  .
. and outputs
and outputs 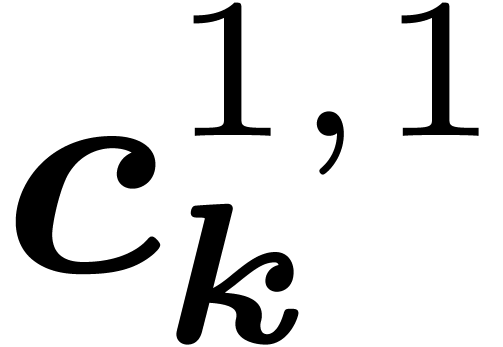 for
for 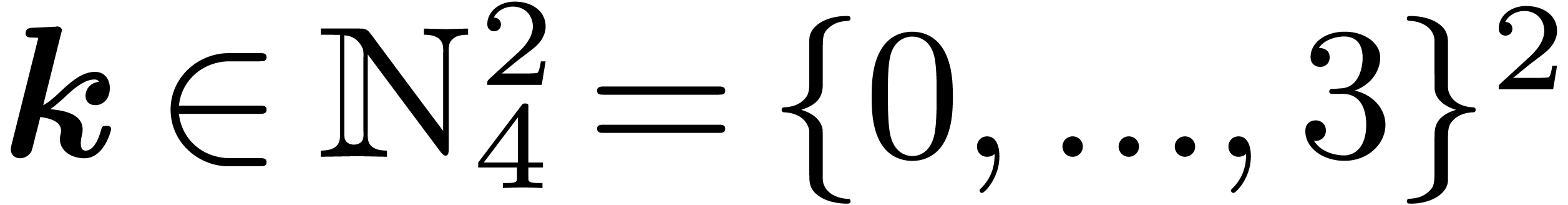 .
.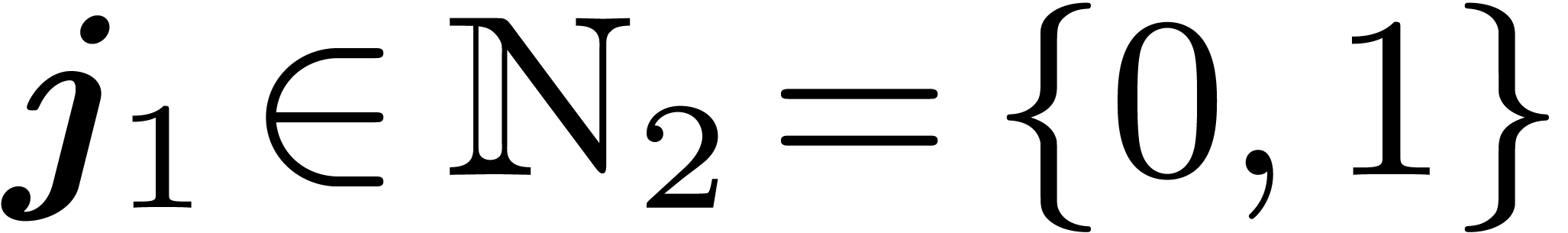 and
and 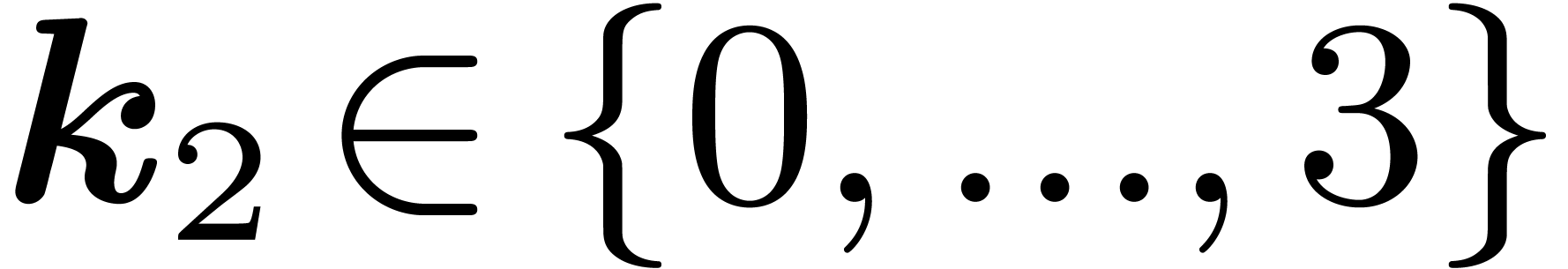 ,
,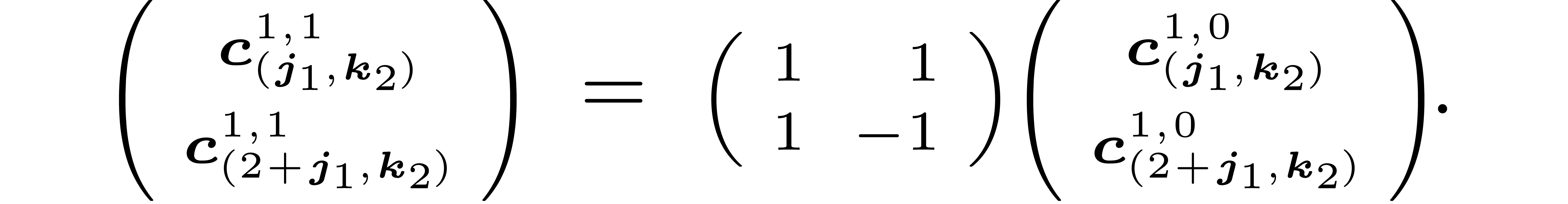
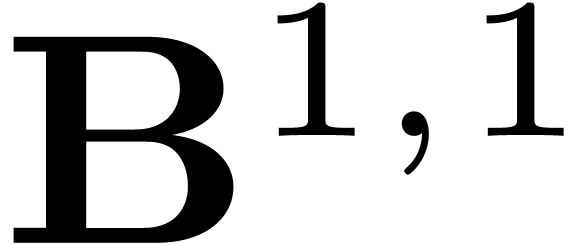 is a 16 by 16 matrix, which is made of
diagonal blocks of
is a 16 by 16 matrix, which is made of
diagonal blocks of 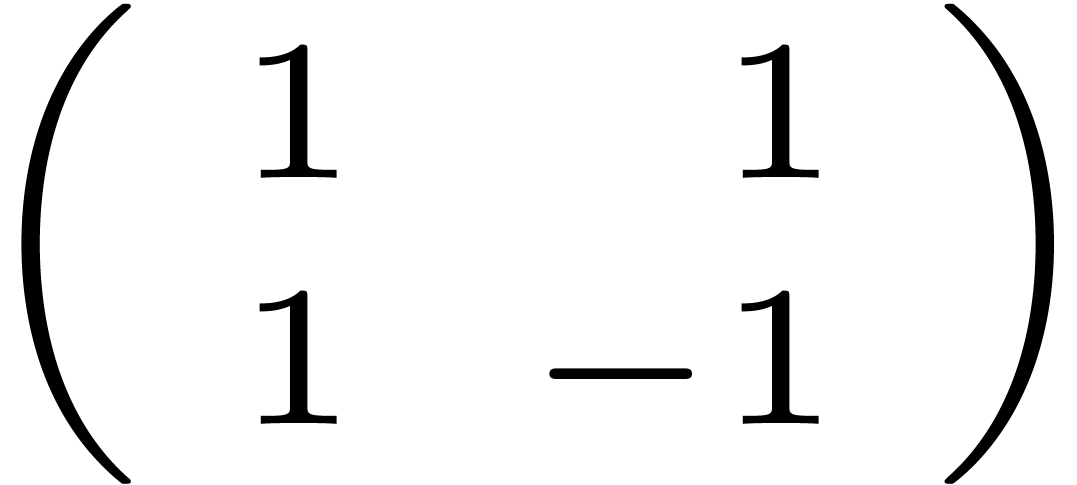 in a suitable basis. The
decimation in
in a suitable basis. The
decimation in  during stage
during stage 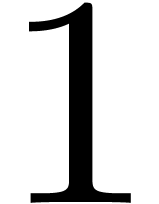 is similar :
is similar :
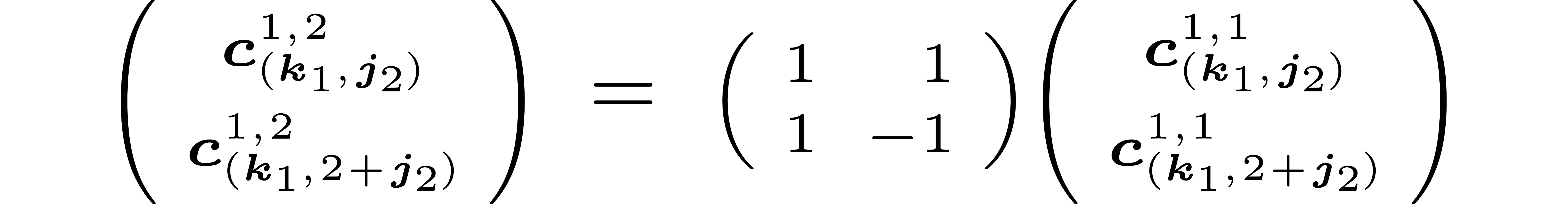
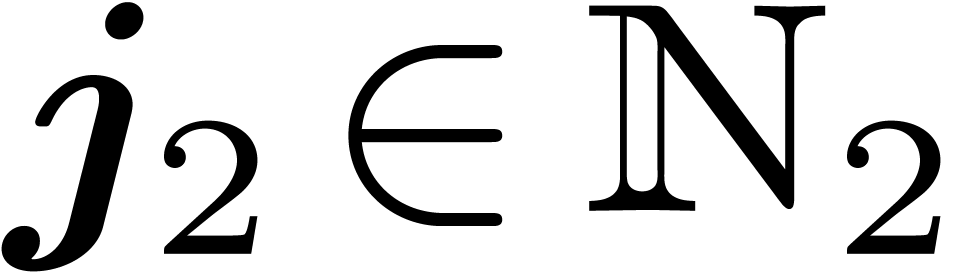 and
and  .
.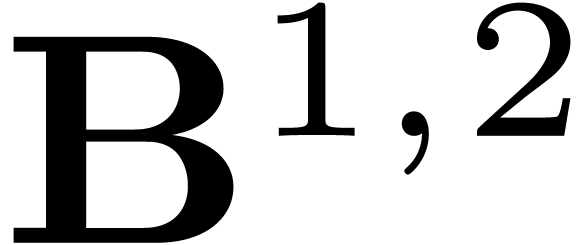 is made of diagonal blocks
is made of diagonal blocks 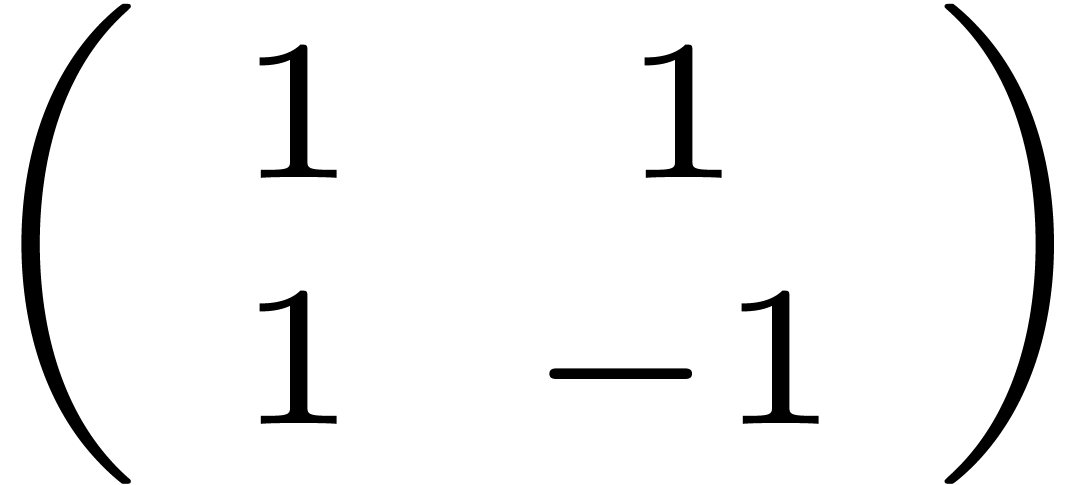 (in another basis than
(in another basis than 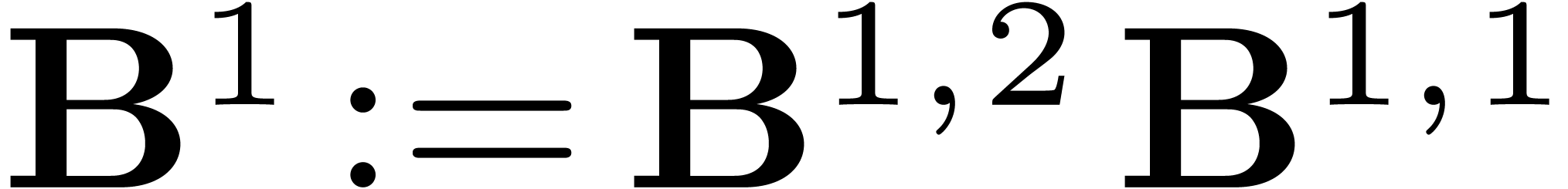 corresponds to the operations
corresponds to the operations
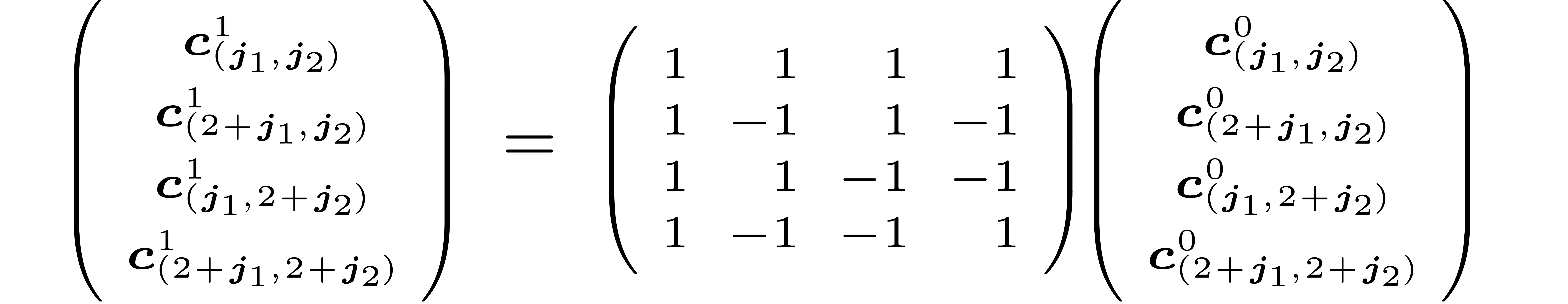
 .
. is made of such 4 by 4 matrices on the diagonal (in yet another basis).
Note that in general, the matrices
is made of such 4 by 4 matrices on the diagonal (in yet another basis).
Note that in general, the matrices 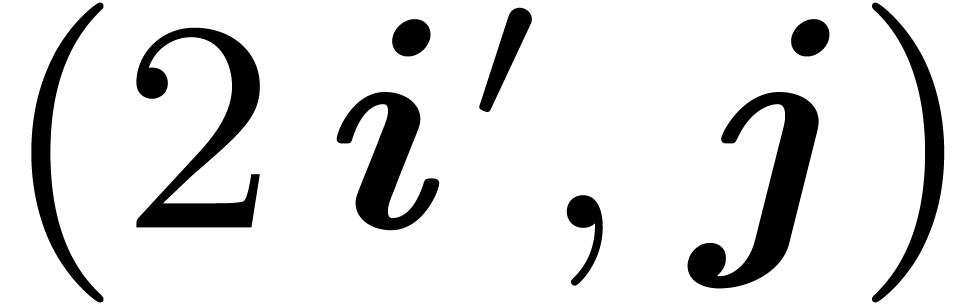 of the butterfly with
of the butterfly with 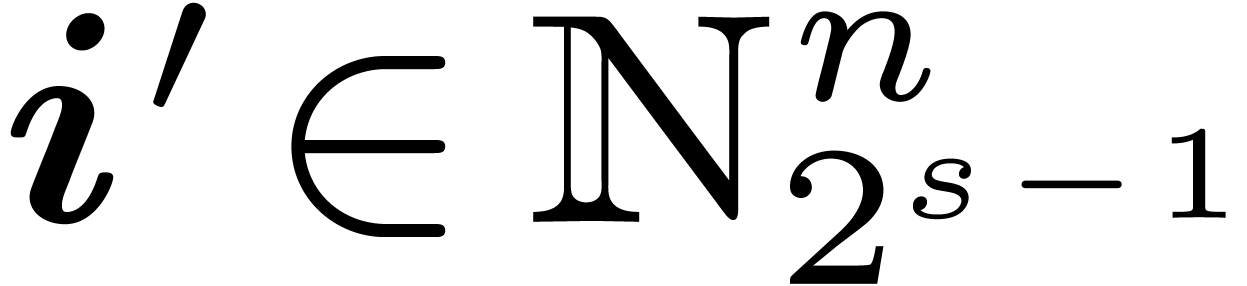 ,
, for
the butterfly (
for
the butterfly (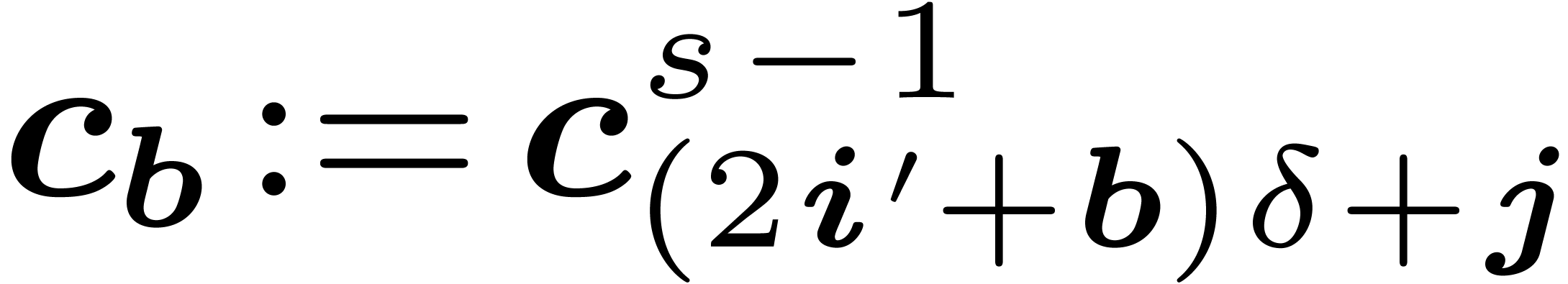 for
for 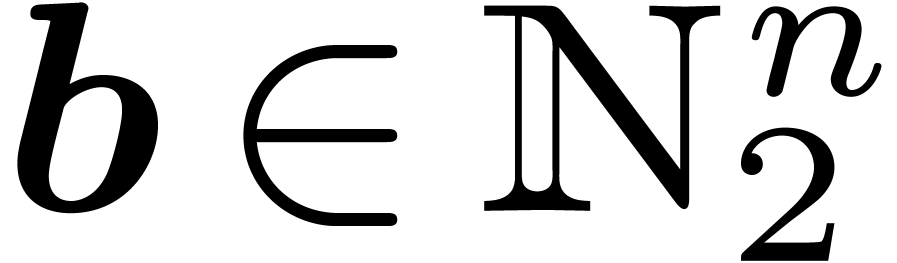 ).
).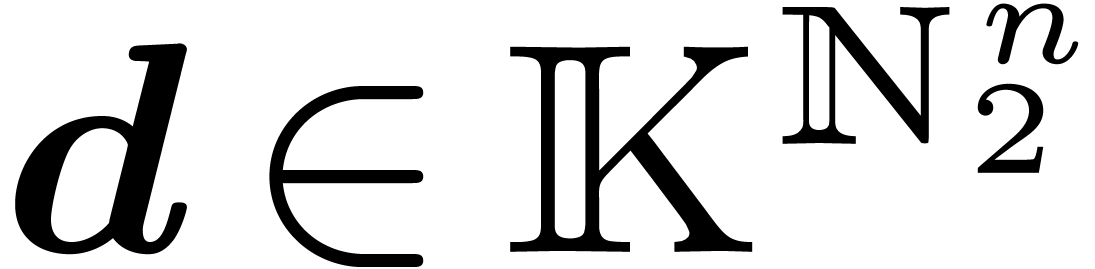
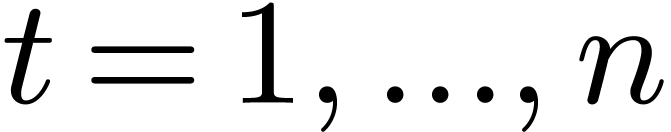 do
do
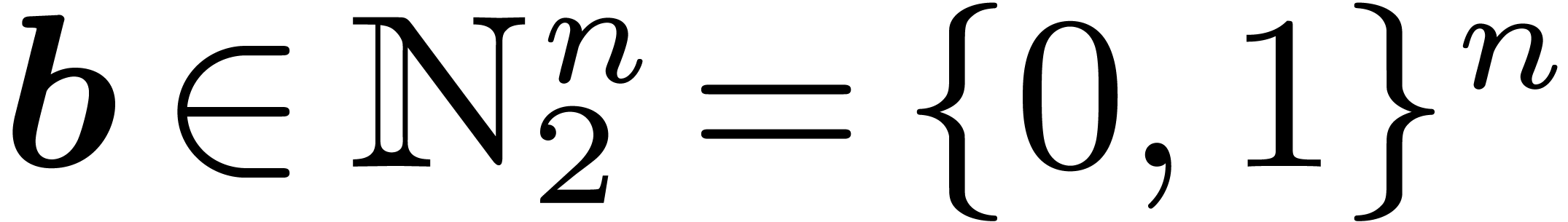 such that
such that 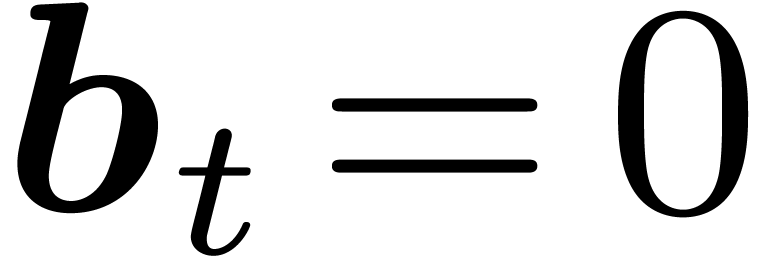 do
do
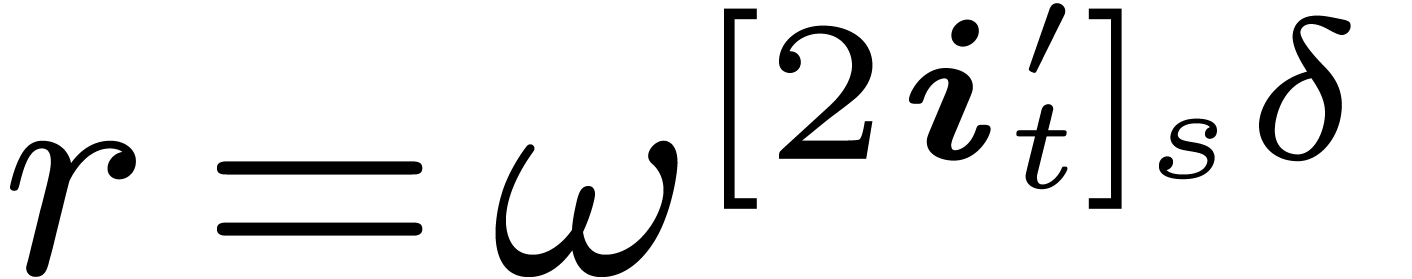
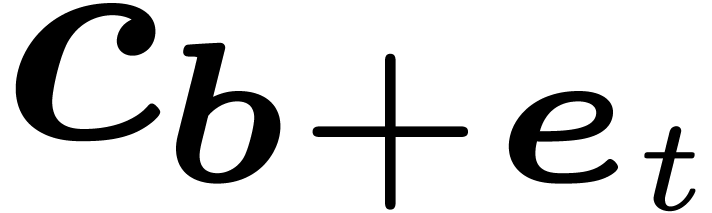
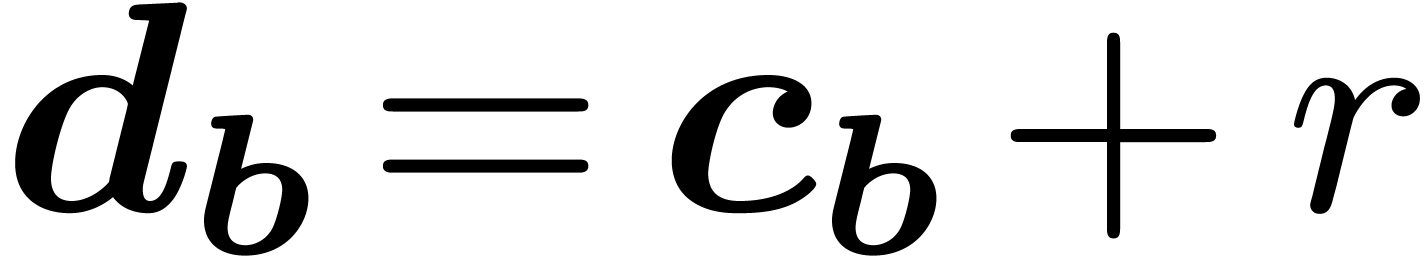
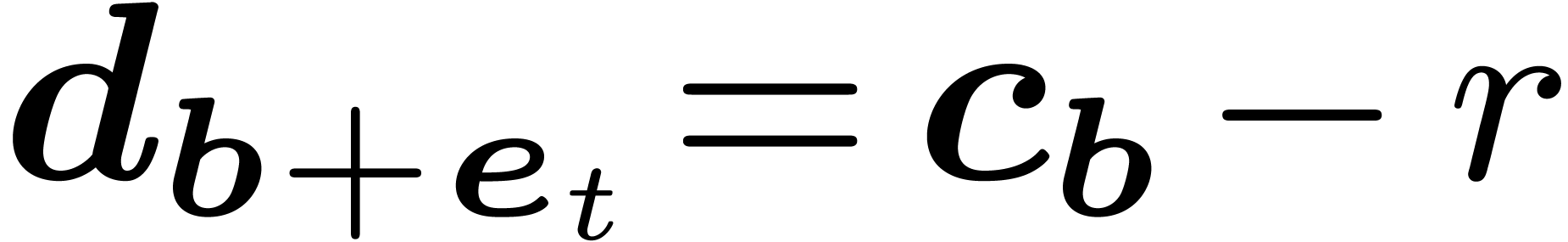
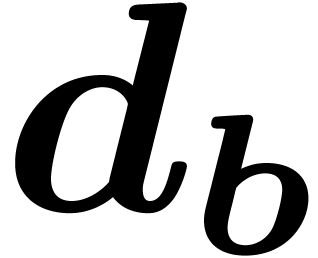
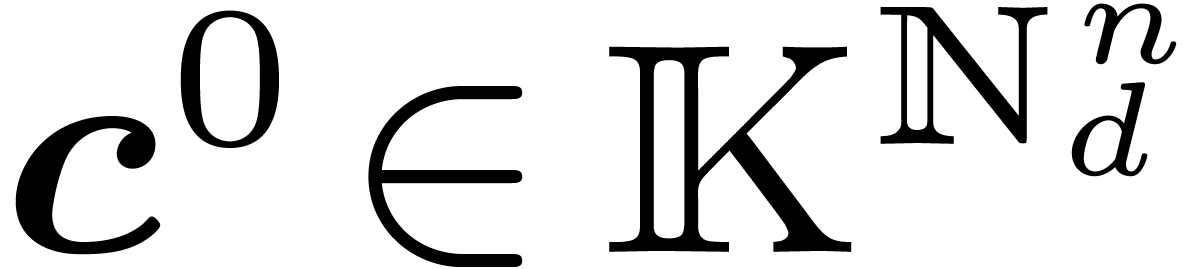 of
of 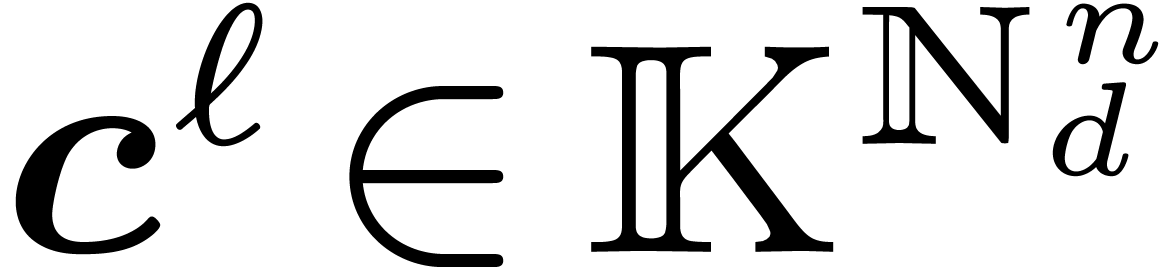 in bit reversed order
in bit reversed order
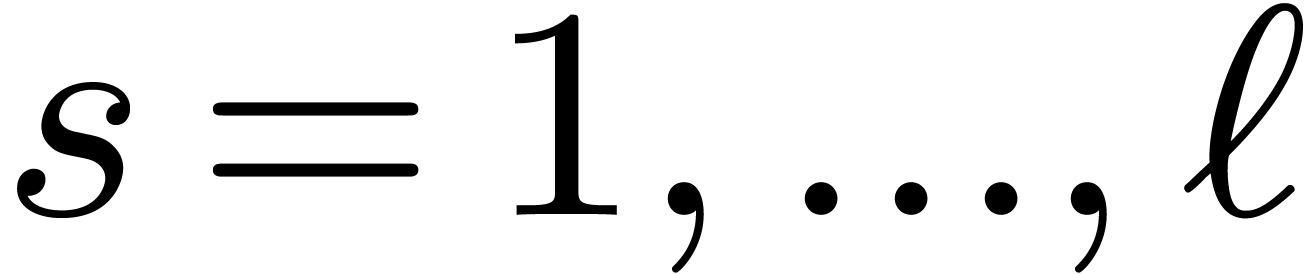 do
do
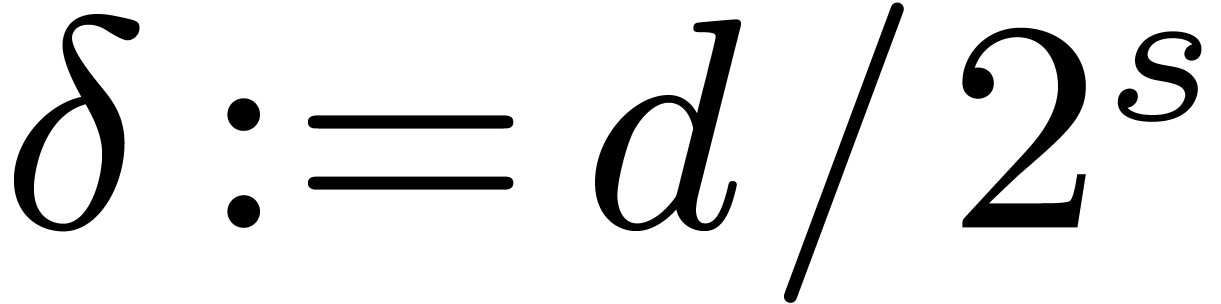
 do
do
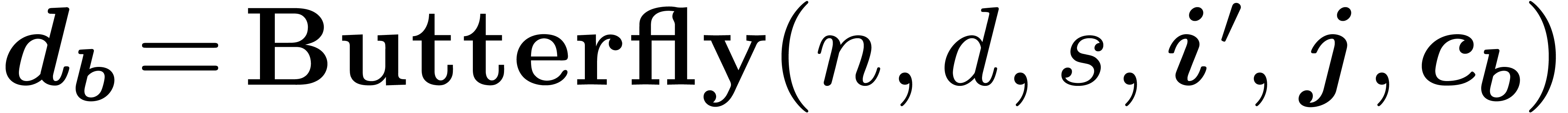
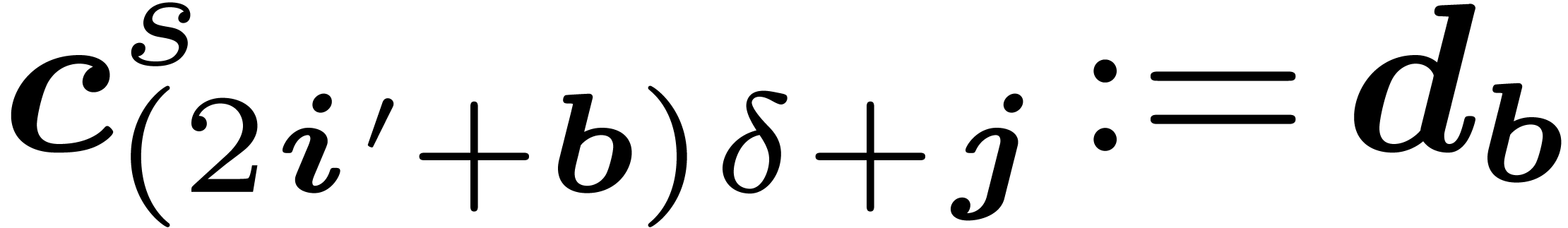
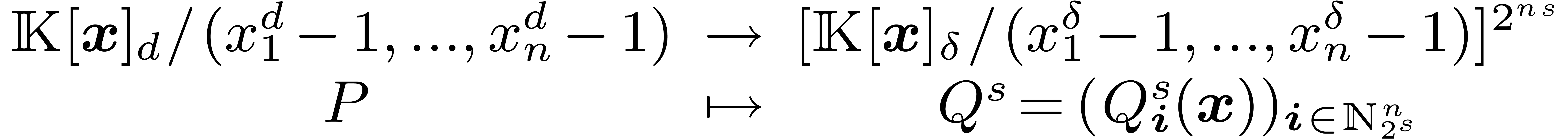
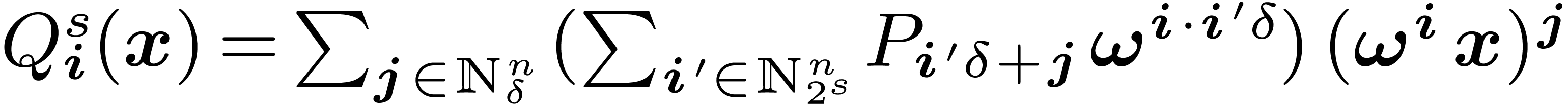 for
for 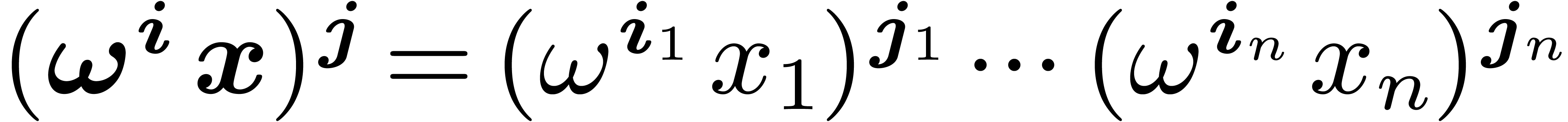 .
.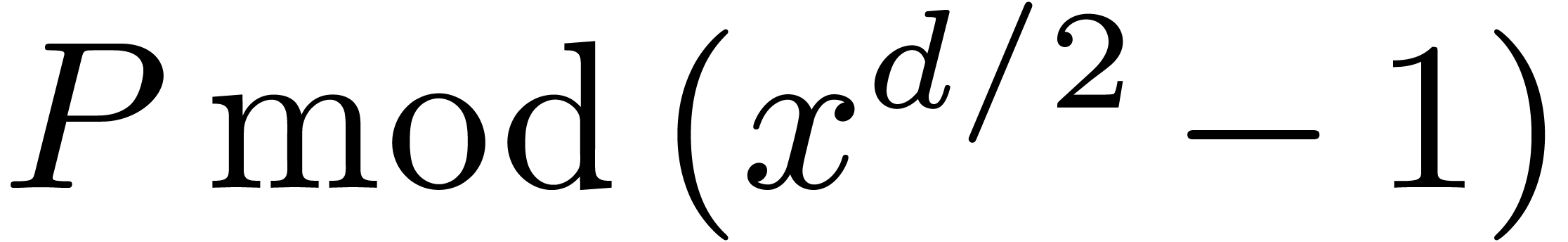 and
and 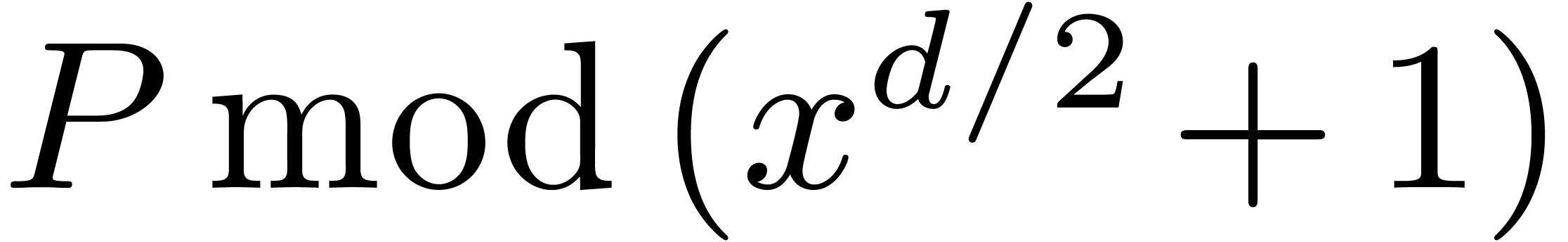 .
.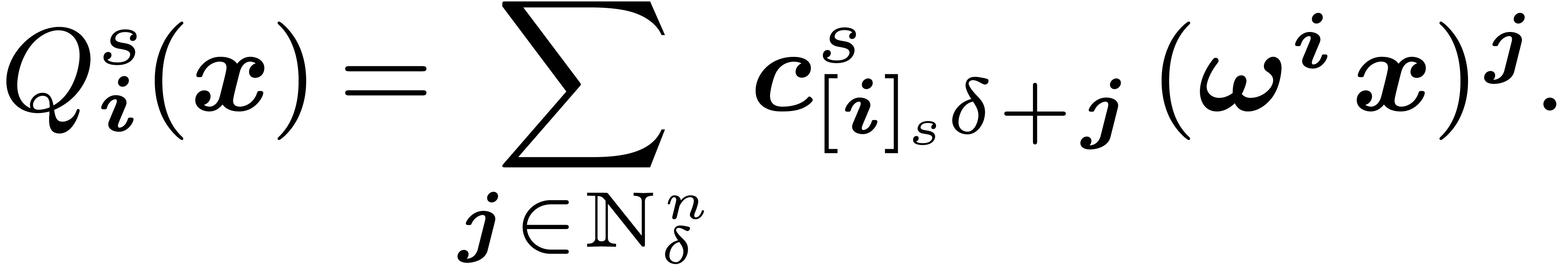
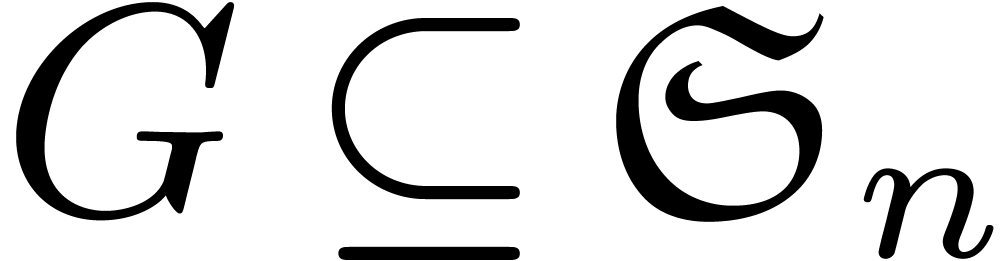 be a permutation group.
The group
be a permutation group.
The group  acts on the polynomials
acts on the polynomials 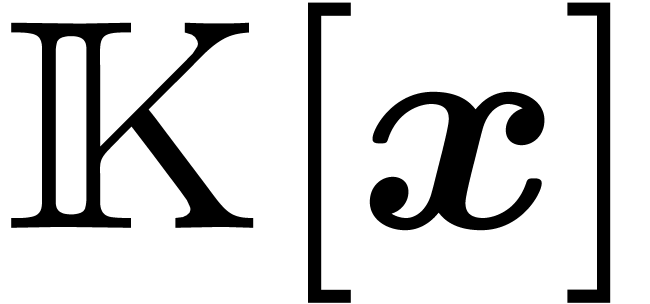 via the map
via the map
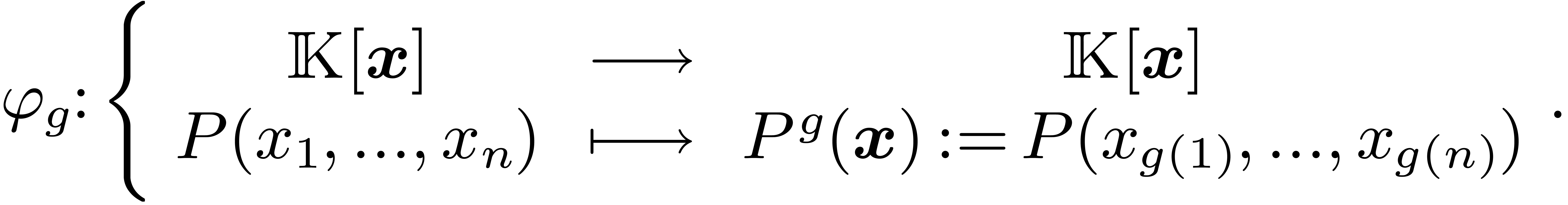
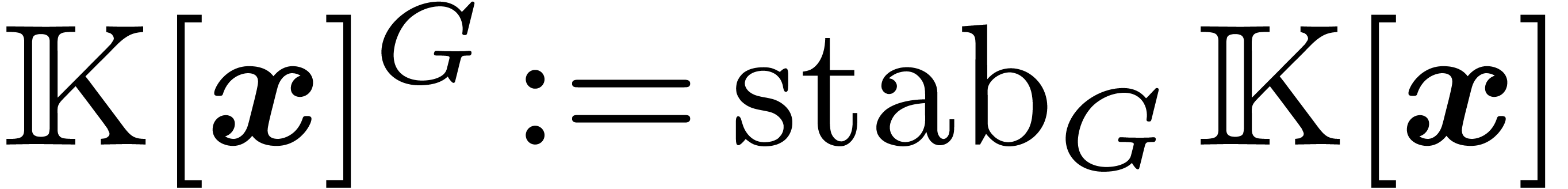 the set of polynomials invariant
under the action of
the set of polynomials invariant
under the action of  when computing the FFT of an invariant polynomial. Our
approach is in the same spirit as the one in [
when computing the FFT of an invariant polynomial. Our
approach is in the same spirit as the one in [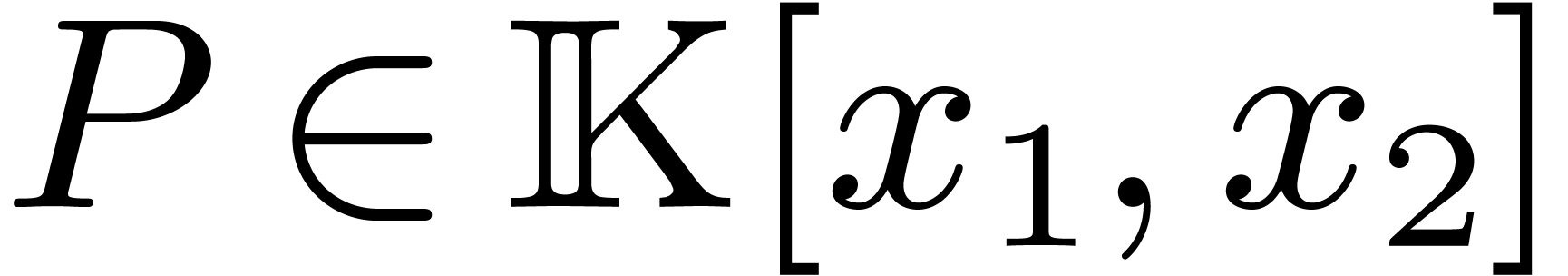 be a symmetric bivariate polynomial of
partial degrees less than
be a symmetric bivariate polynomial of
partial degrees less than 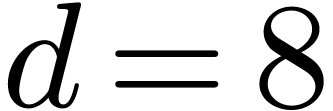 ,
,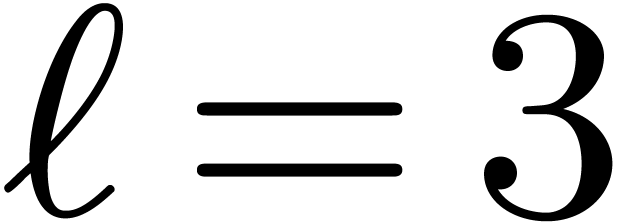 ;
;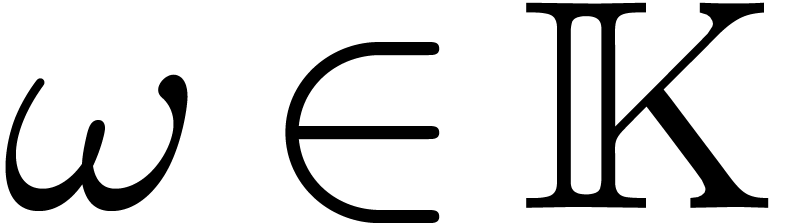 be a primitive eighth root of unity. We detail on this
easy example the methods used to exploit the symmetries to decrease the
cost of the FFT.
be a primitive eighth root of unity. We detail on this
easy example the methods used to exploit the symmetries to decrease the
cost of the FFT.
 grid. The bivariate classical FFT consists in the
application of butterflies of size
grid. The bivariate classical FFT consists in the
application of butterflies of size  to
to  ,
, is the set of evaluations
is the set of evaluations 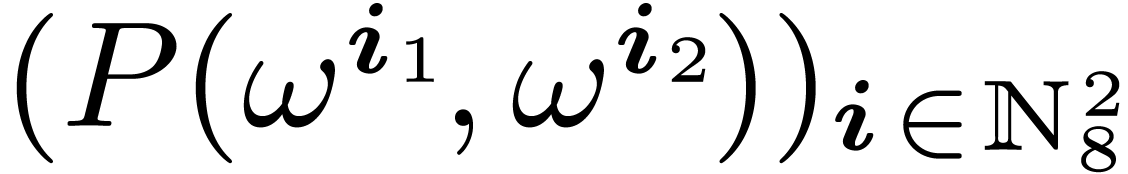 in bit reversed order.
in bit reversed order.

 at
stage
at
stage  for
for 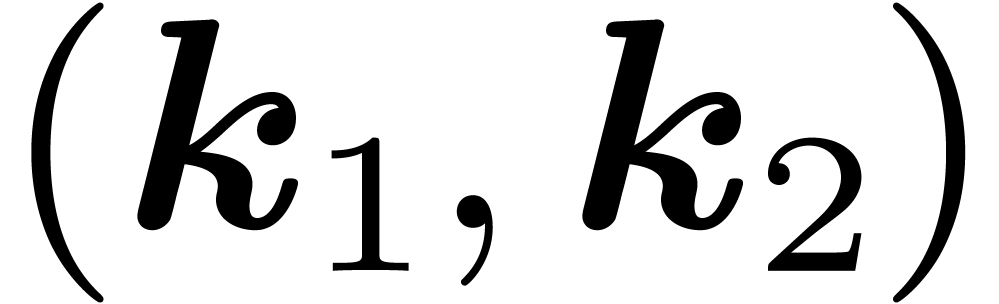 in the fundamental domain (sometimes called asymmetric unit)
in the fundamental domain (sometimes called asymmetric unit)
 .
. ;
; of
of 
 out of
out of  butterflies at stage
butterflies at stage  out of
out of 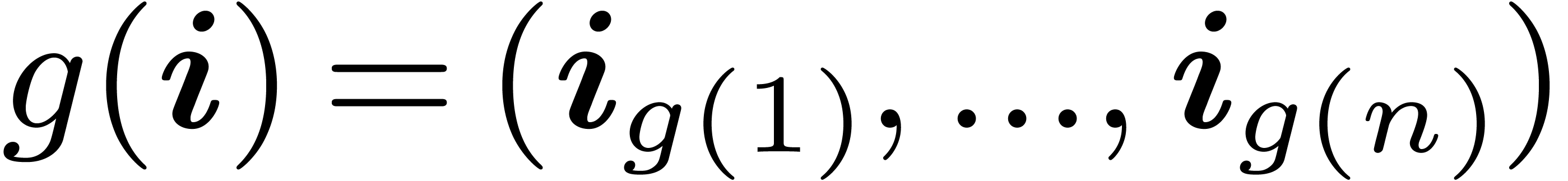 for any
for any 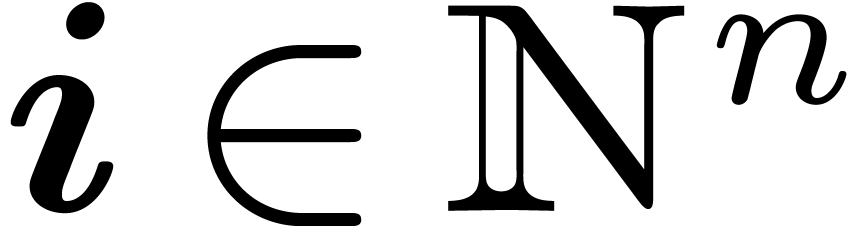 .
.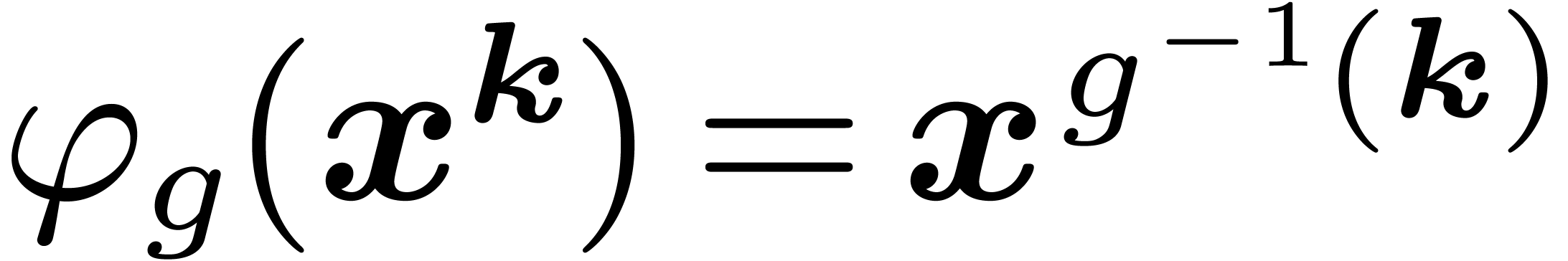 .
.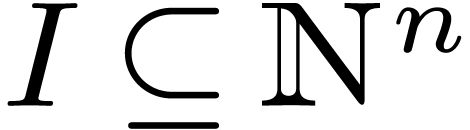 and
and  ,
, the vector defined by
the vector defined by 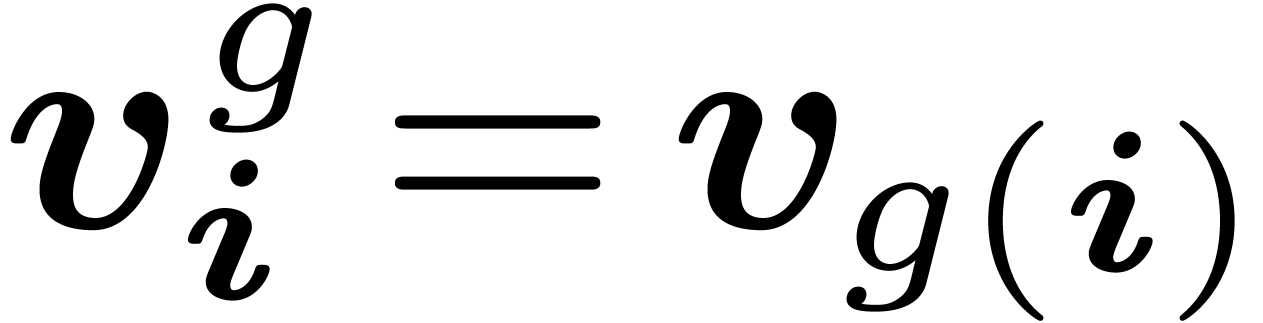 for all
for all
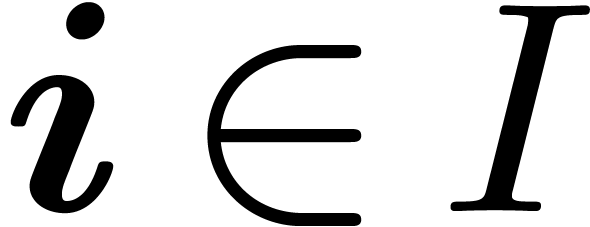 .
.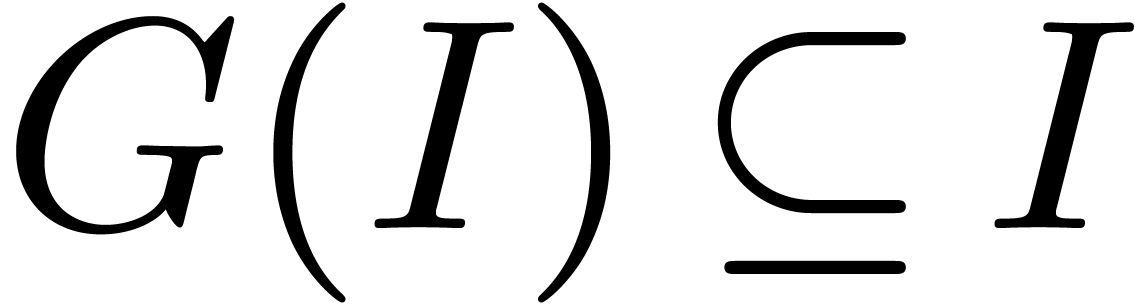 ,
,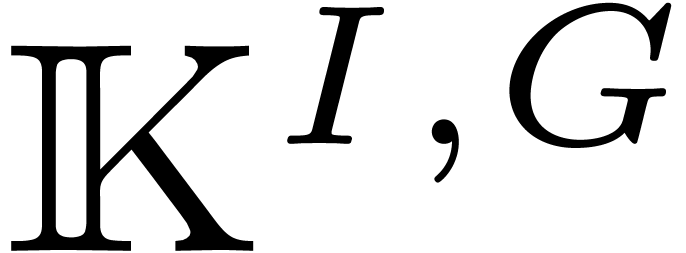 by
by 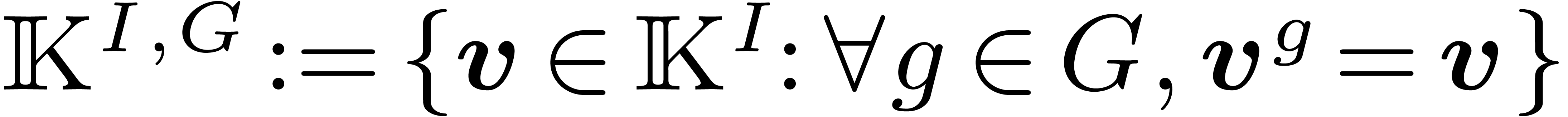 .
.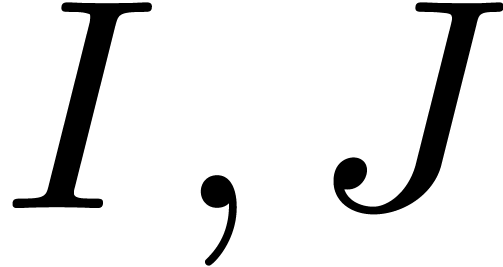 satisfying
satisfying 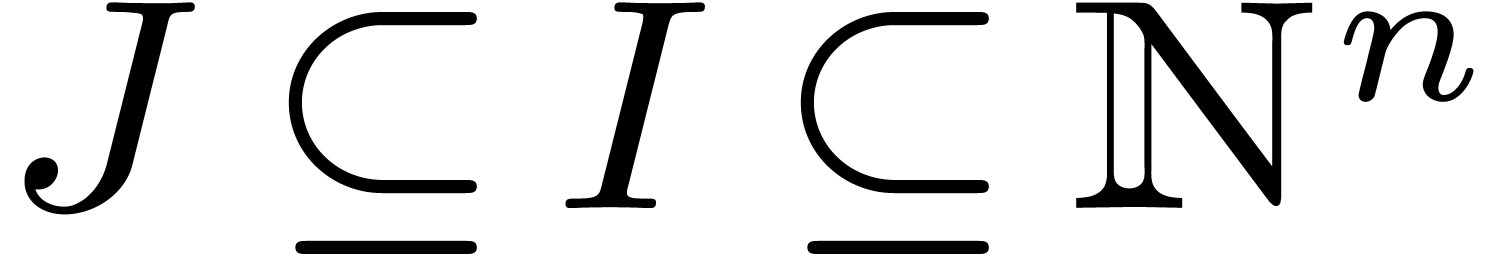 ,
,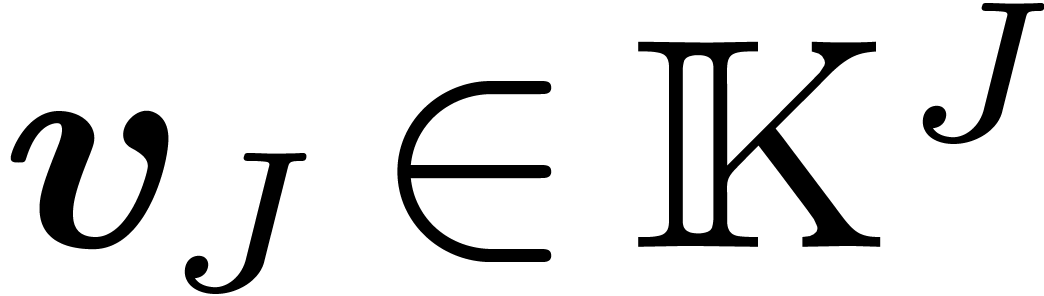 of
of 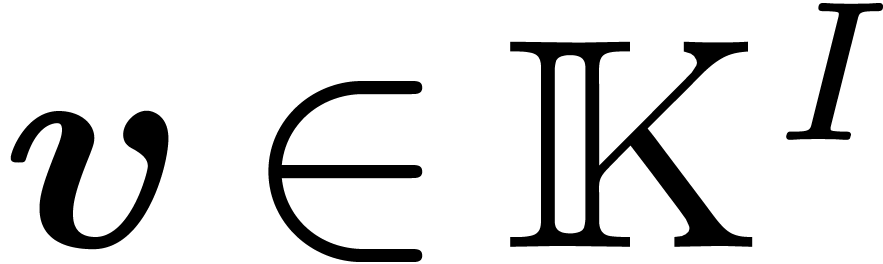 by
by 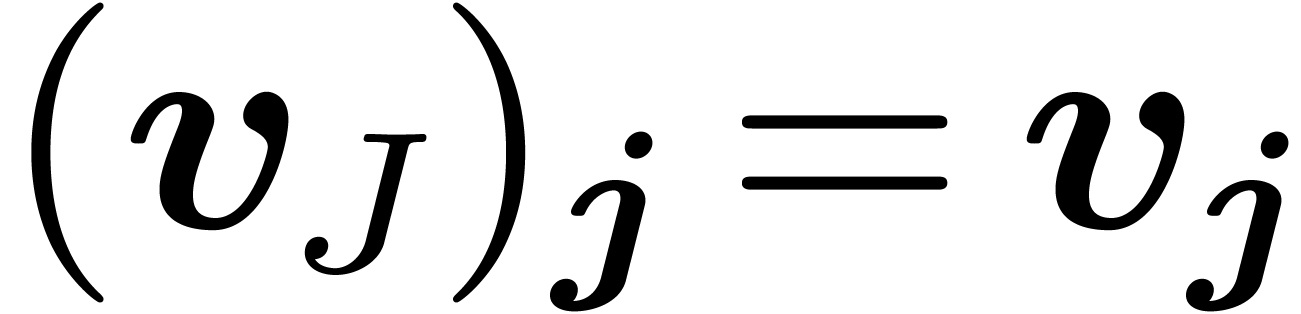 for all
for all  .
.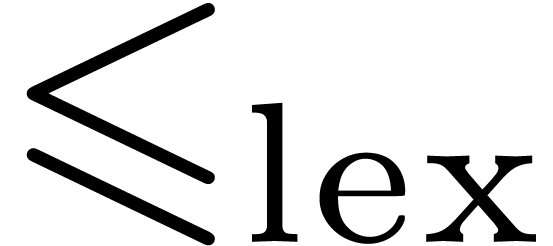 : for all
: for all  ,
,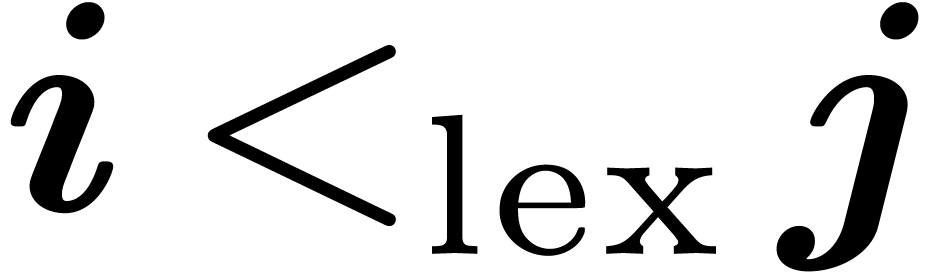 if there exists
if there exists  such that
such that  for any
for any 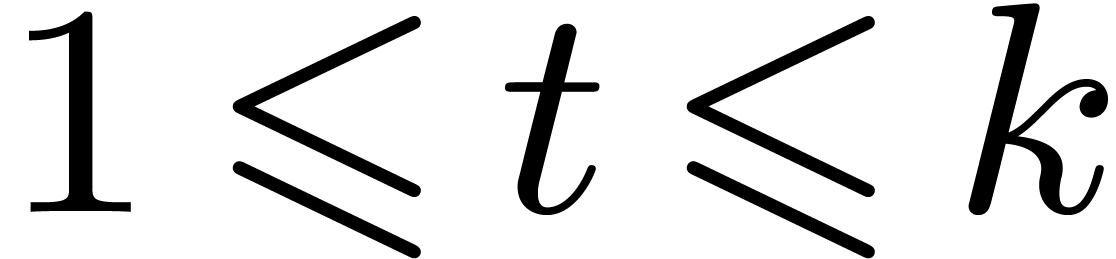 and
and  .
.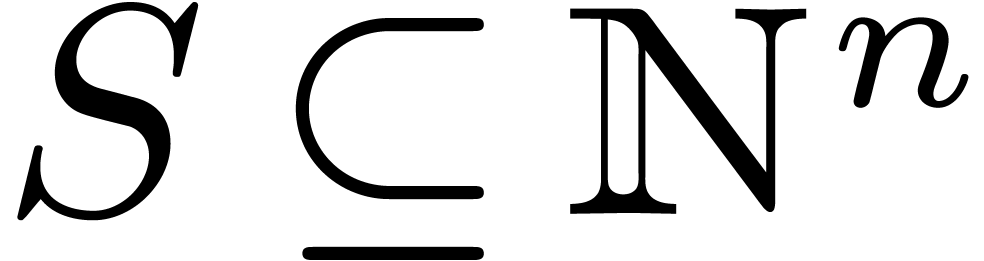 stable by
stable by 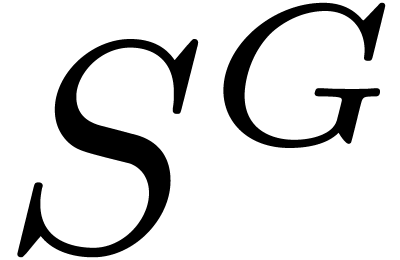 of the action of
of the action of 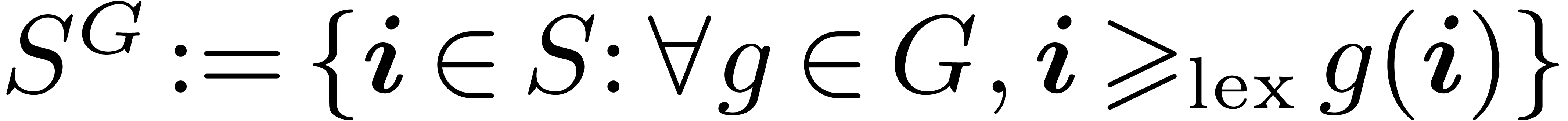 together with the projection
together with the projection 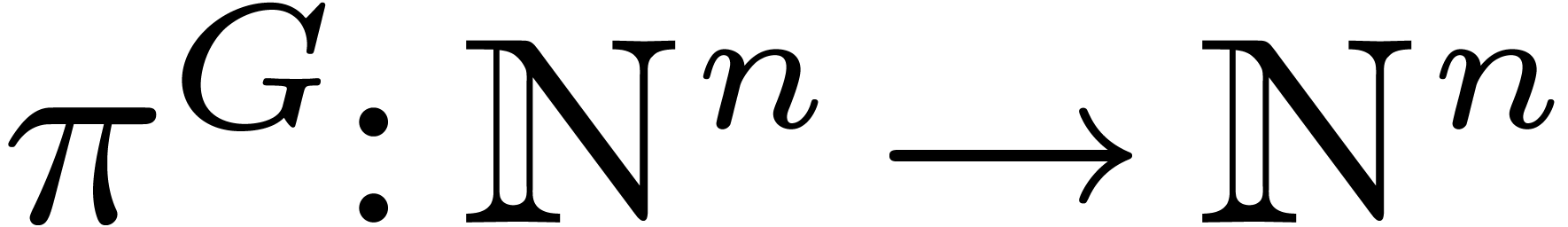 such as
such as 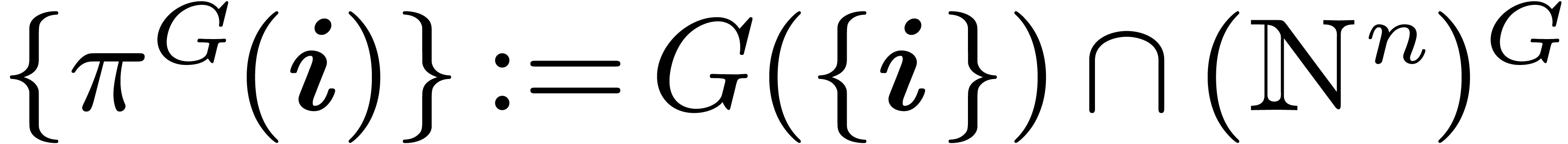 .
.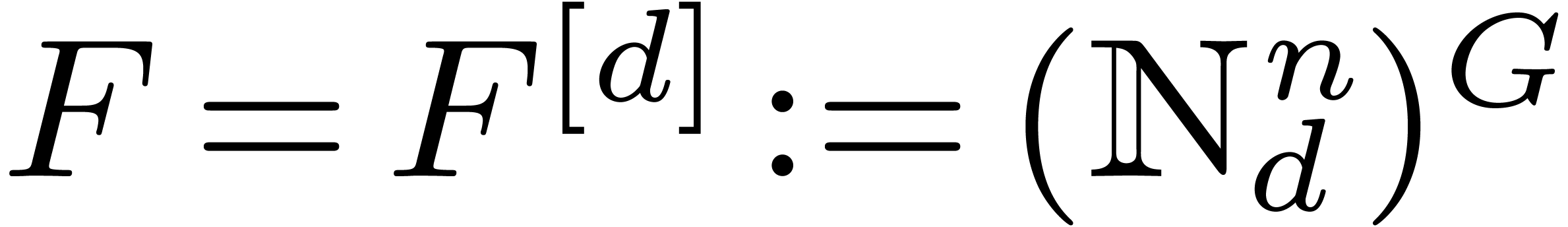 be the fundamental domain associated to the
action of
be the fundamental domain associated to the
action of 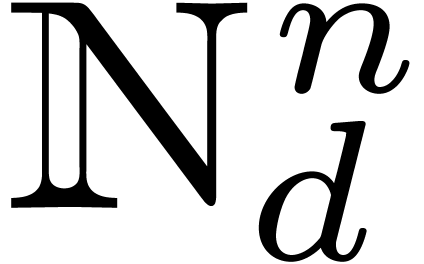 .
. can be reconstructed from its restriction
can be reconstructed from its restriction 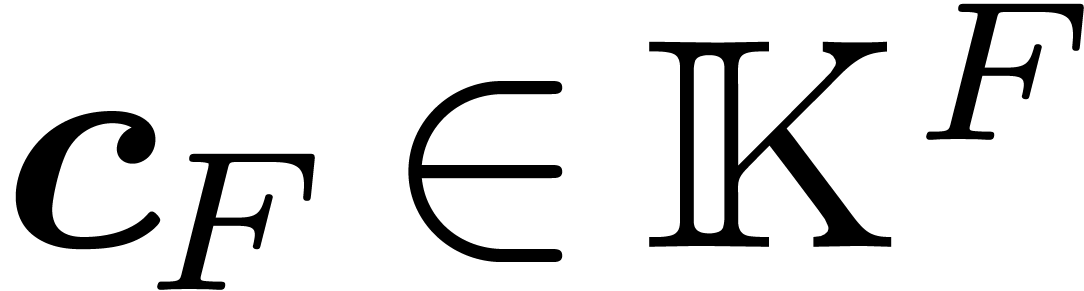 using the formula
using the formula  .
. and the vectors
and the vectors 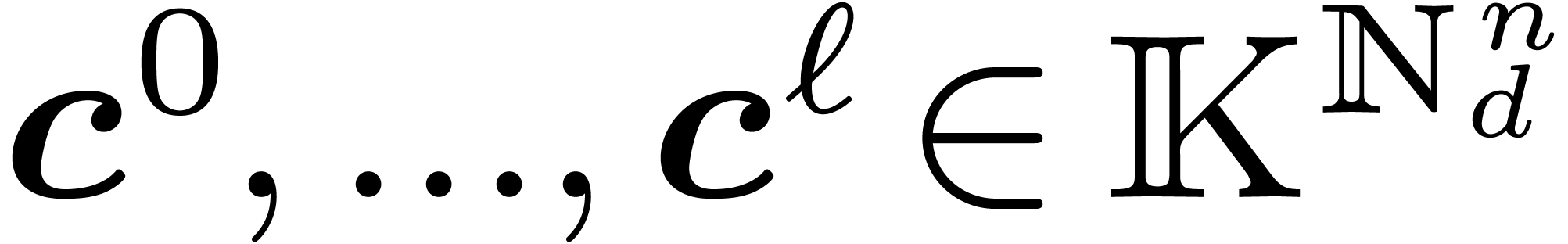 be as in
Section
be as in
Section 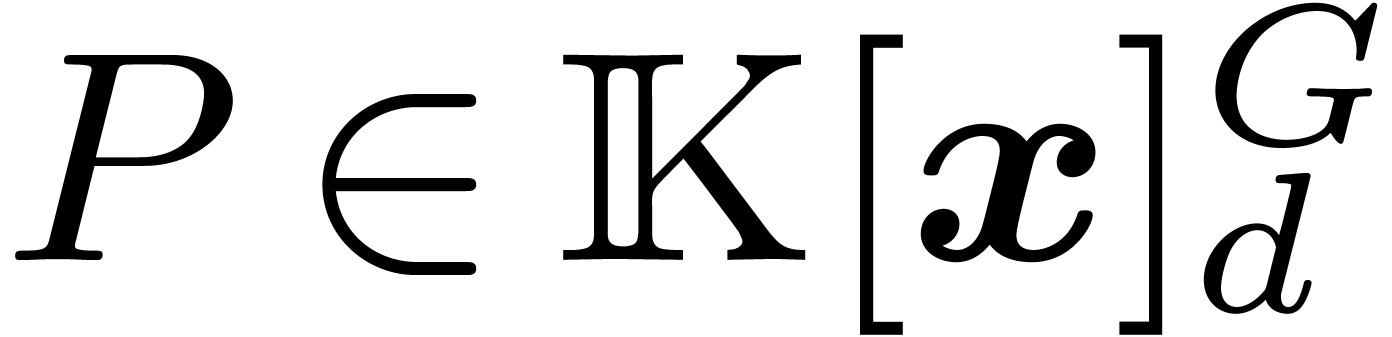 ,
, .
.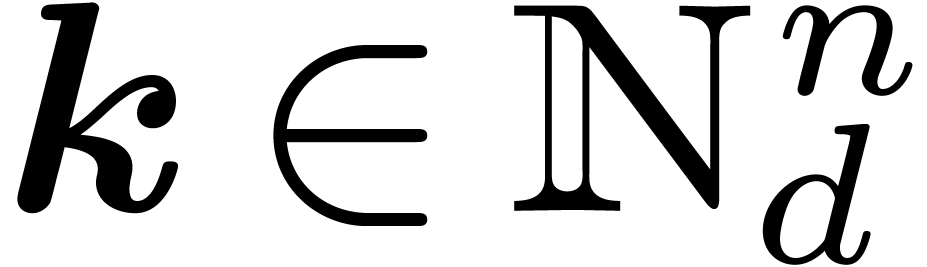 and
and 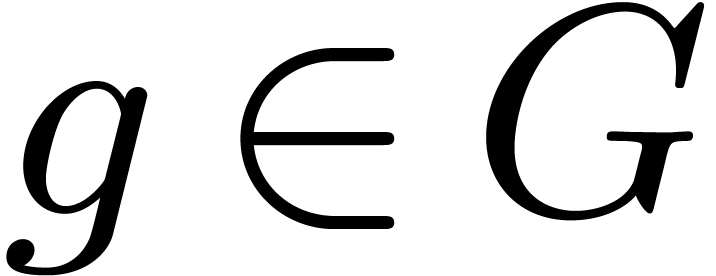 ,
,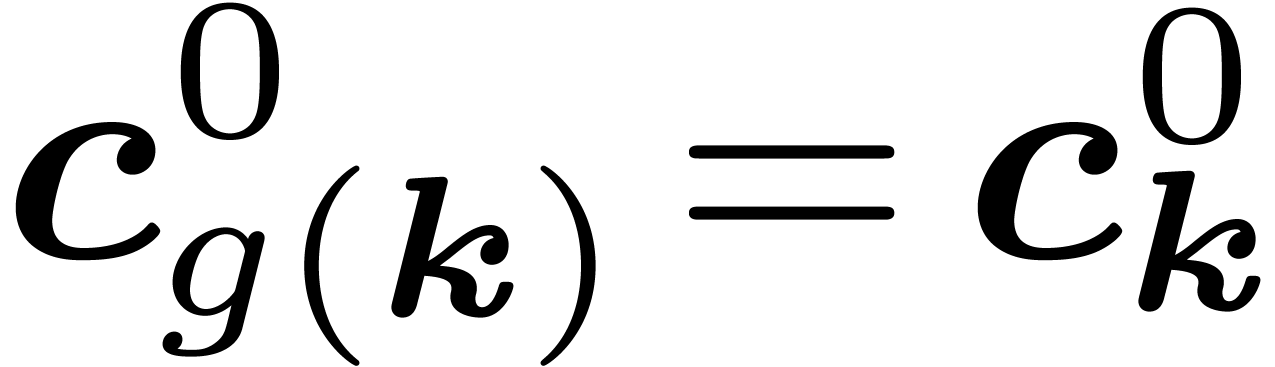 .
. ,
, and
and 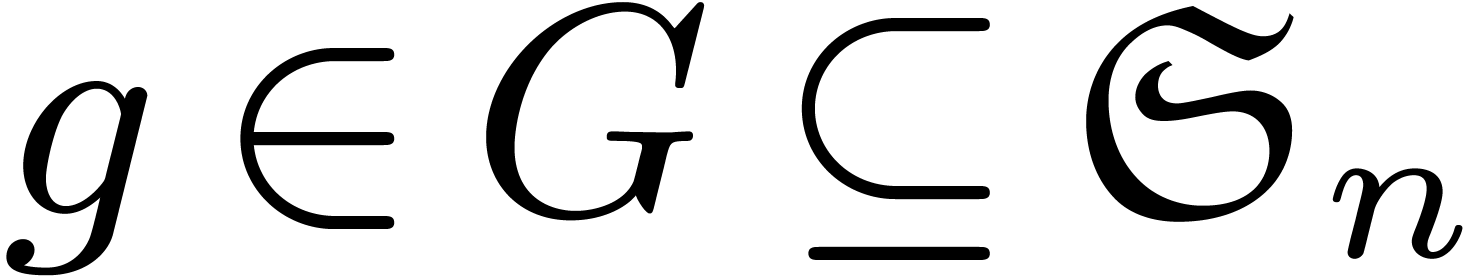 ,
,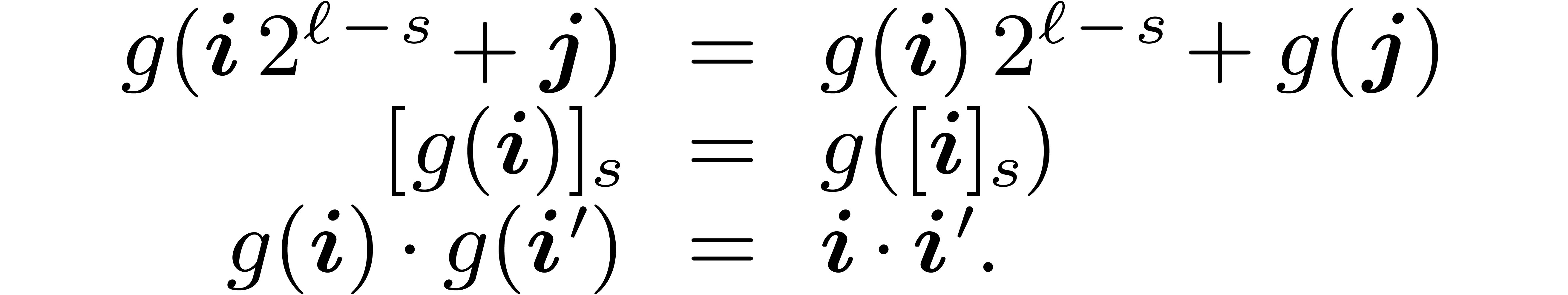
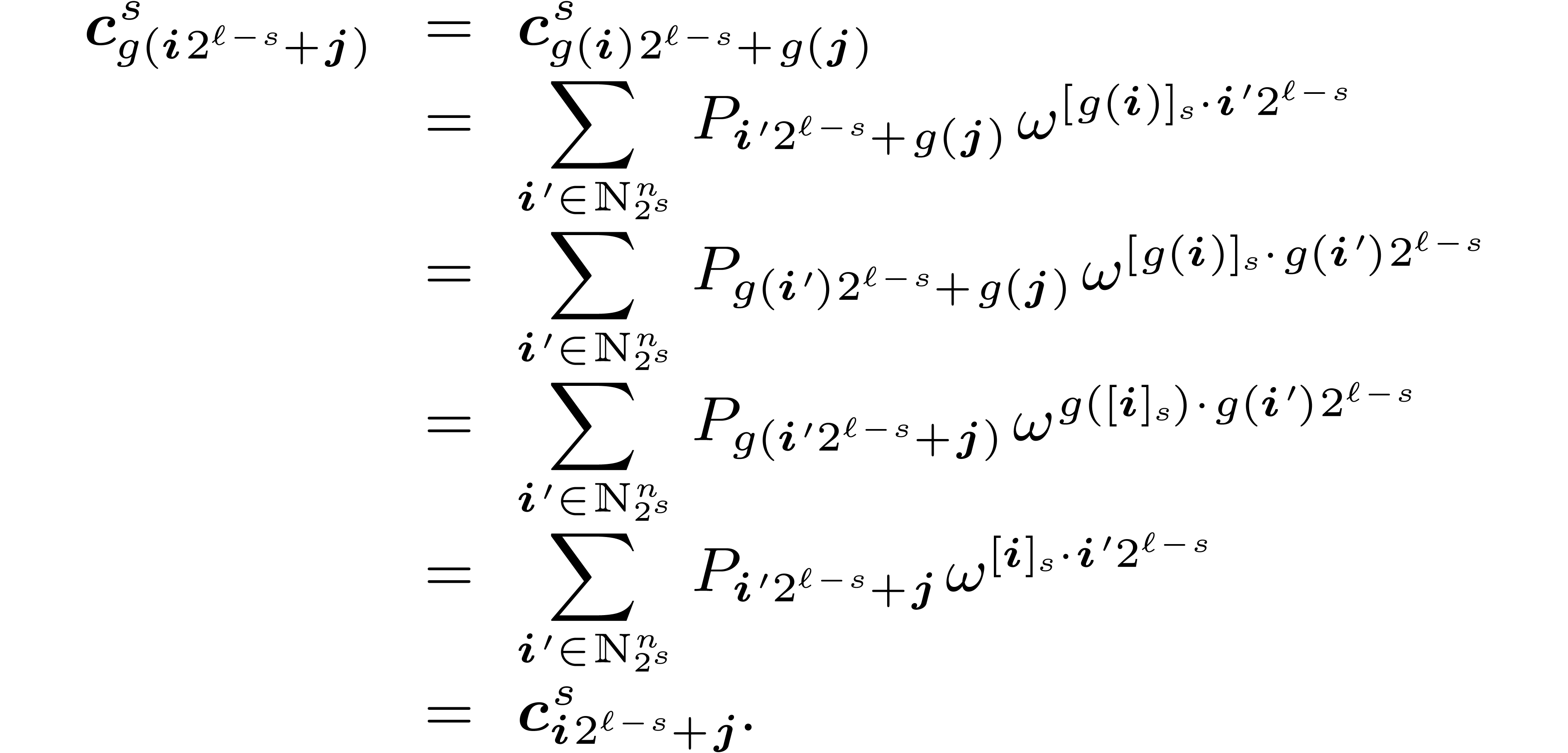
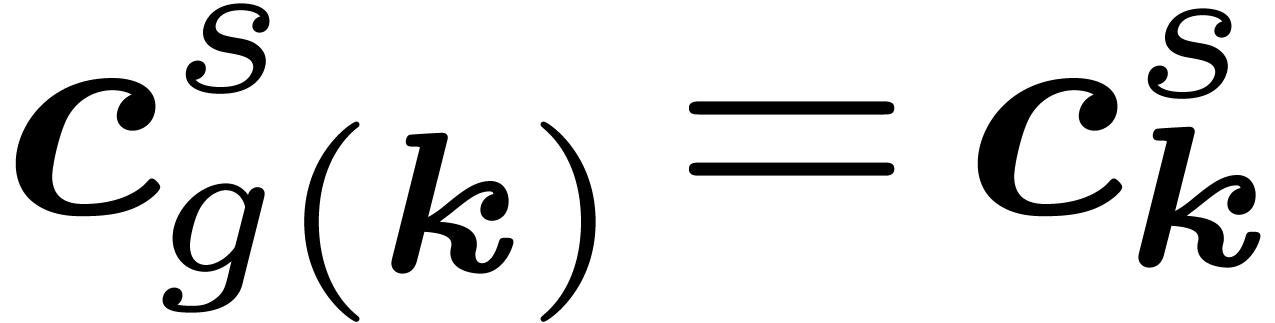 for all
for all 
 .
.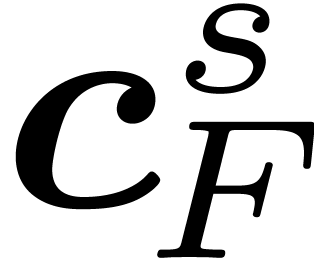 as a function of
as a function of 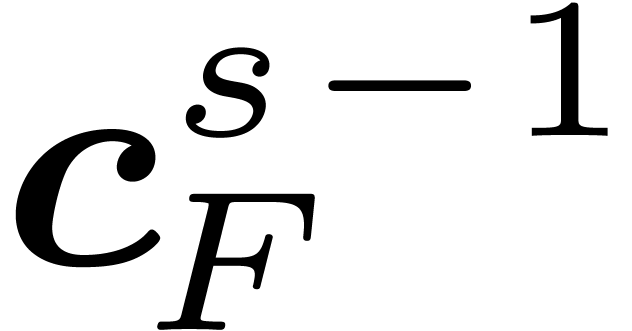 ,
, -expansion
-expansion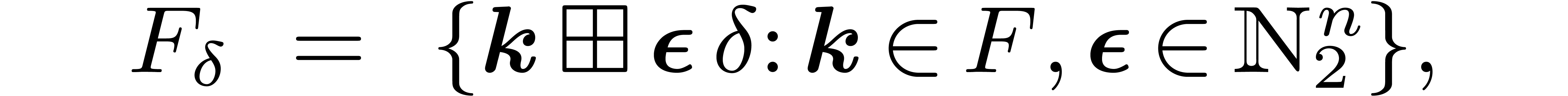
 stands for the “bitwise exclusive
or” of
stands for the “bitwise exclusive
or” of 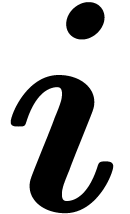 and
and 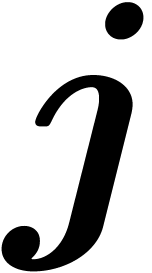 .
.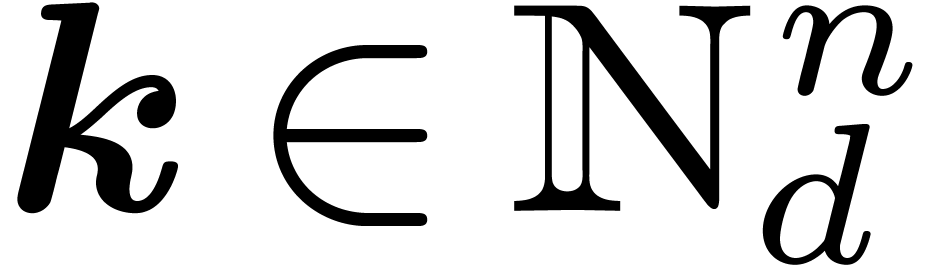 ,
,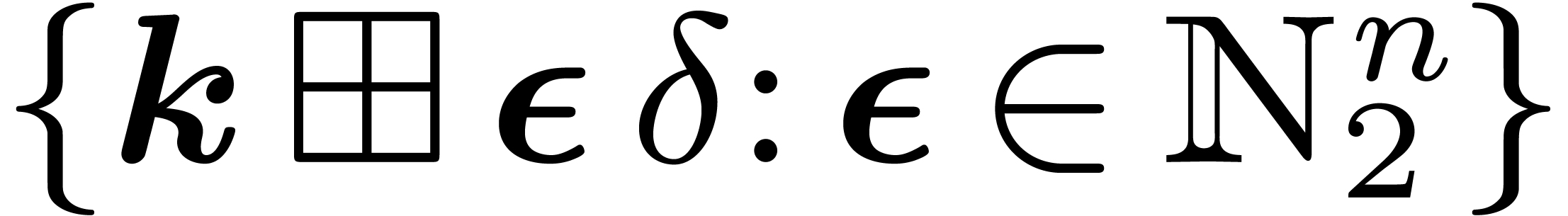 describes the vertices of the butterfly of span
describes the vertices of the butterfly of span  .
.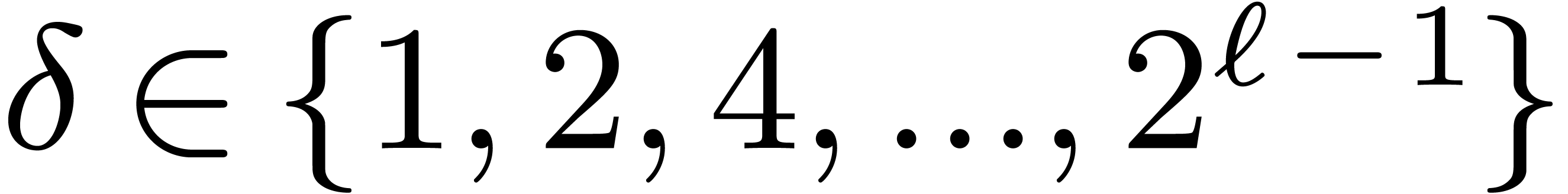 ,
,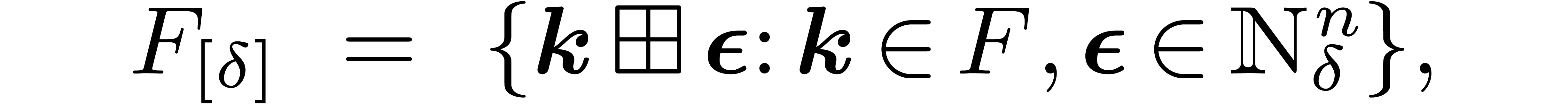
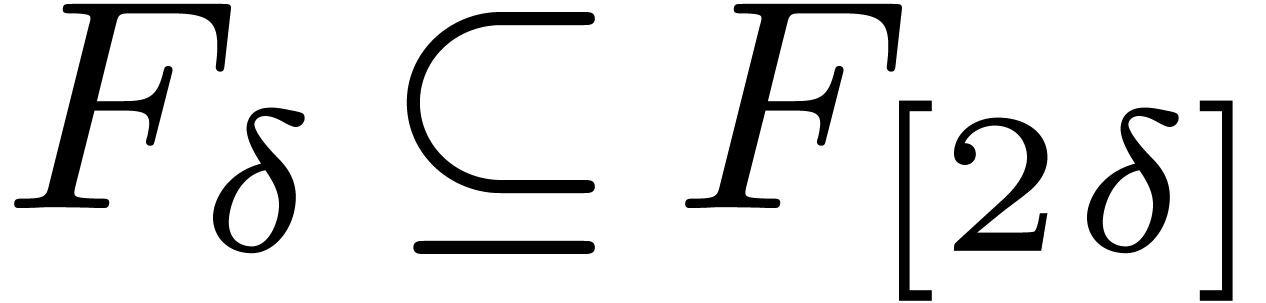 .
.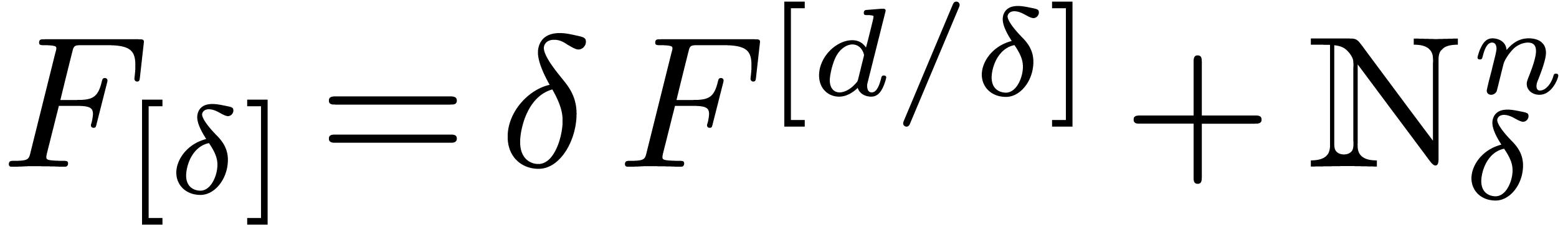 .
. .
. ,
,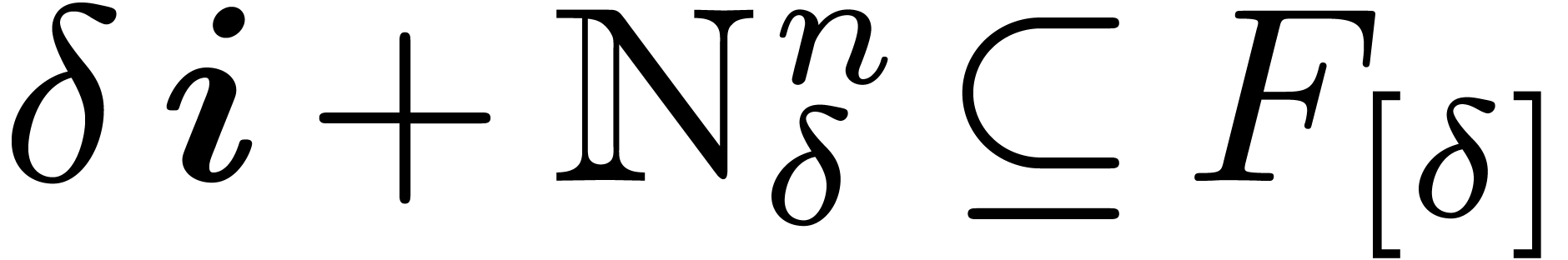 .
.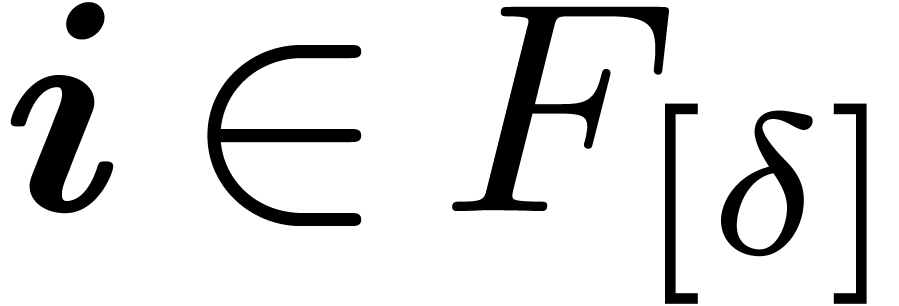 ,
, with
with 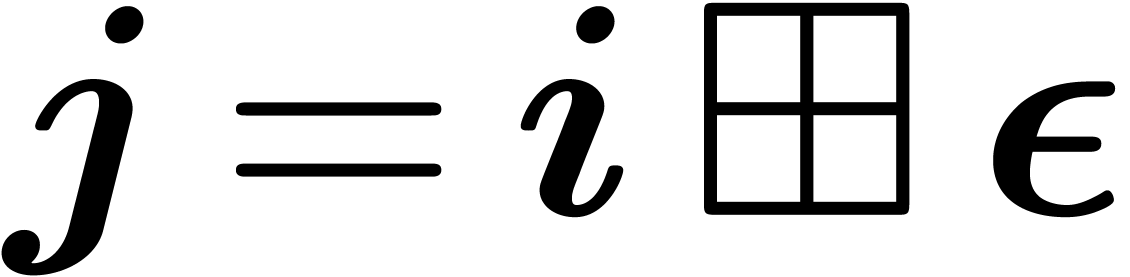 and
and 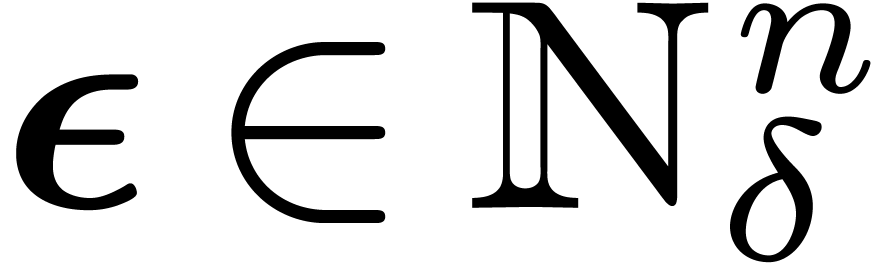 .
.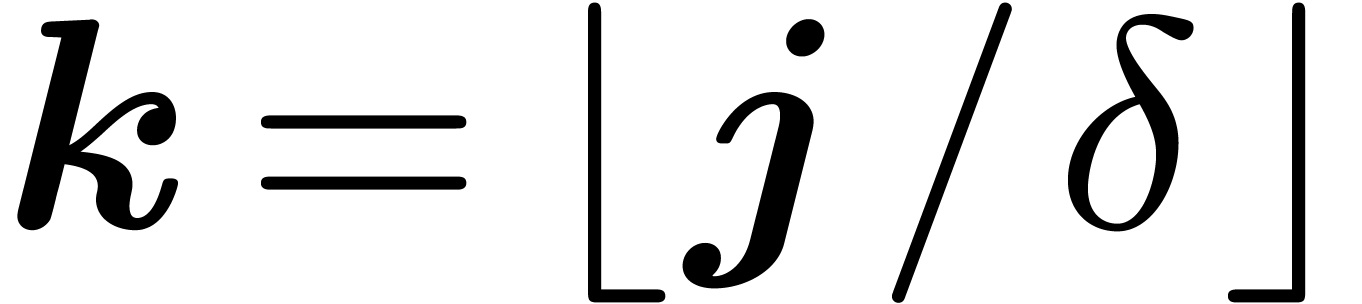 .
.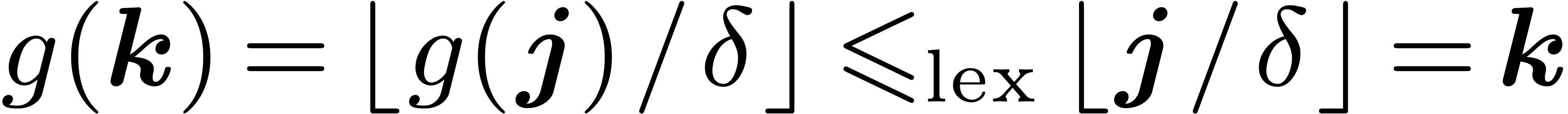 .
. ,
,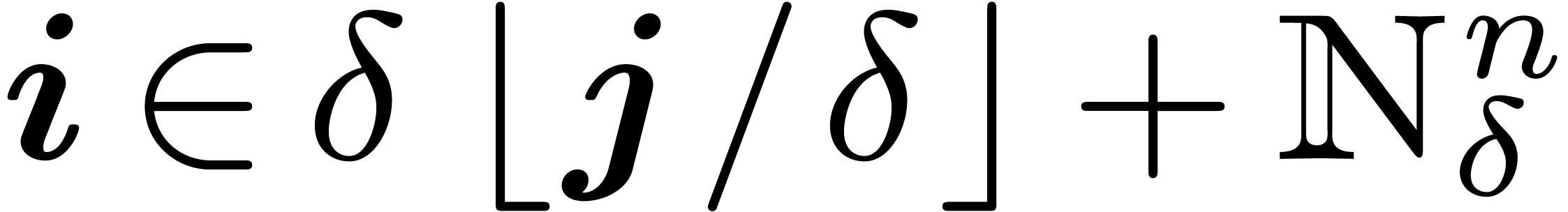 .
.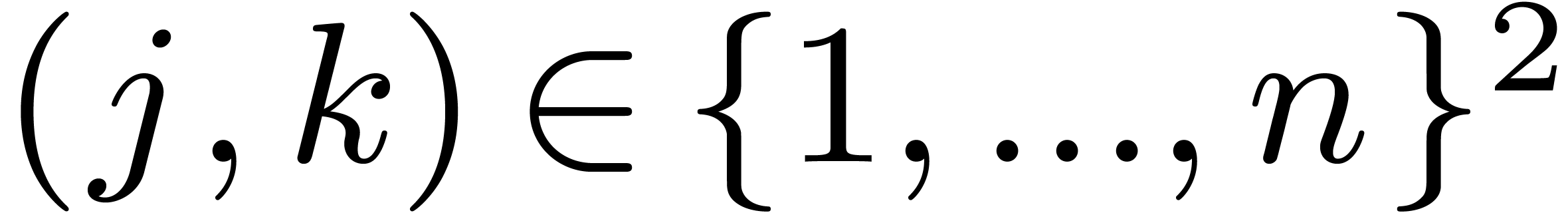 ,
,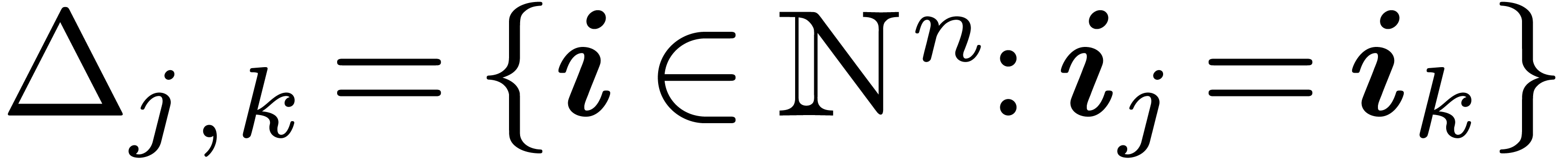 and
and 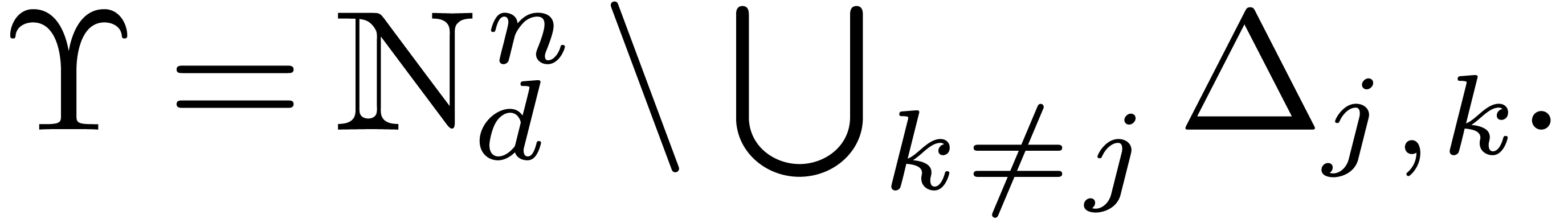
 (depending on
(depending on  )
)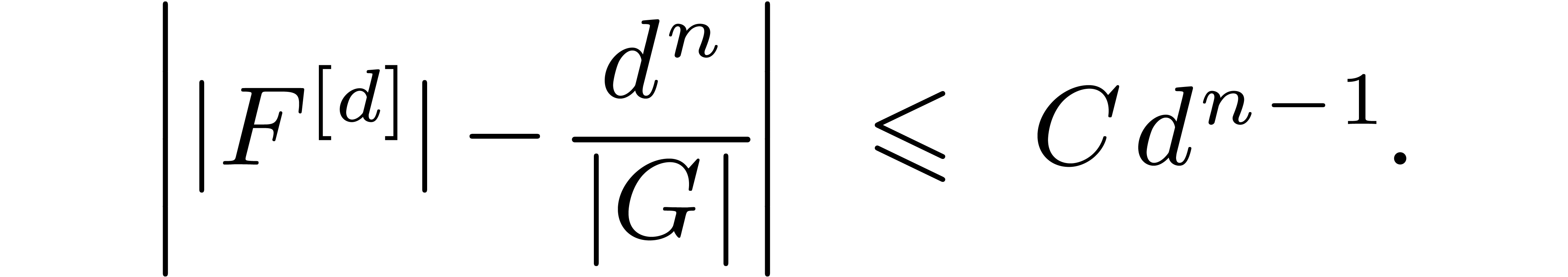
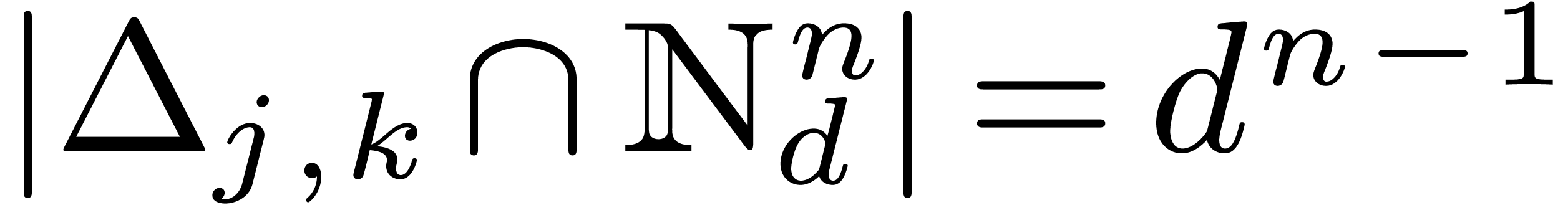 .
.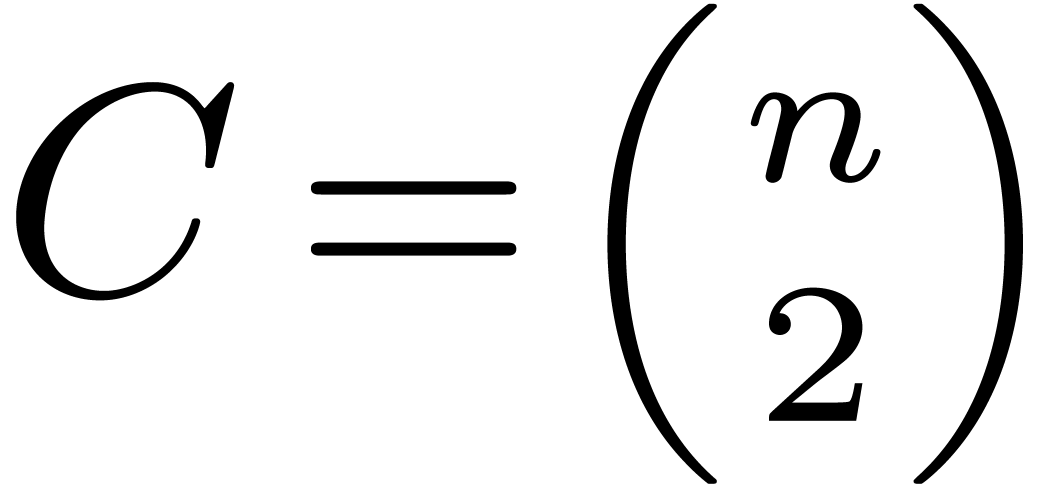 ,
, .
. under
under  contains exactly
contains exactly 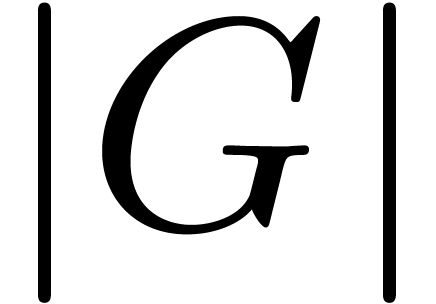 elements and one element in
elements and one element in 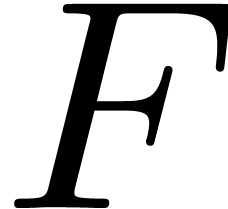 .
.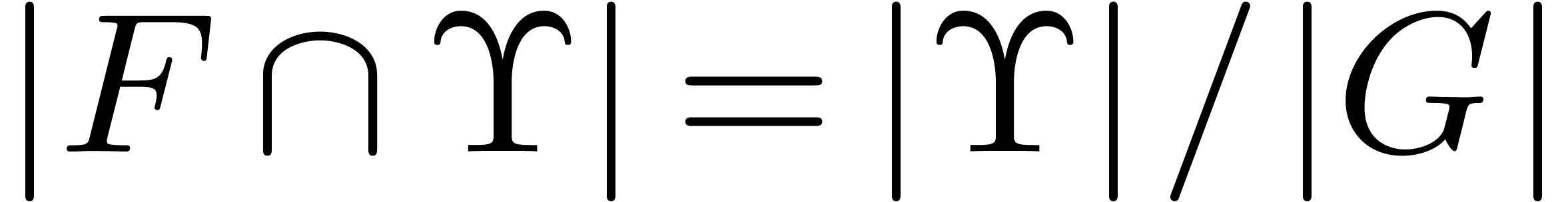 and so
and so 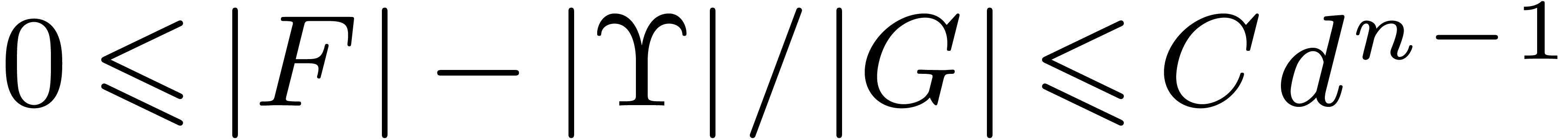 .
.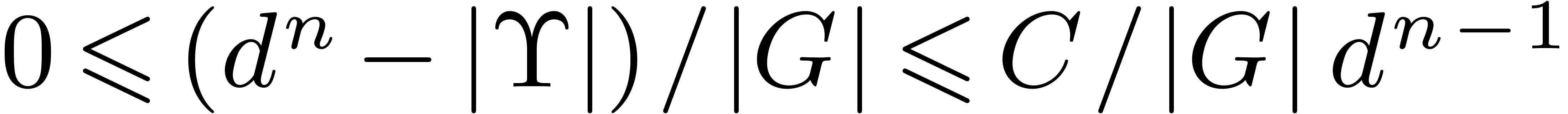 which implies
which implies
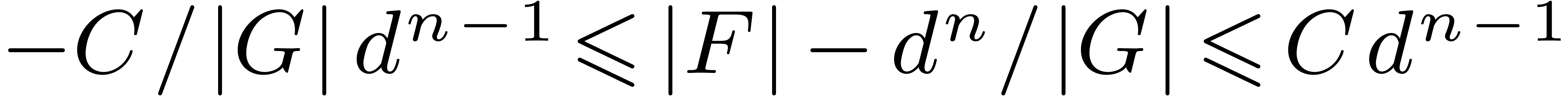 .
.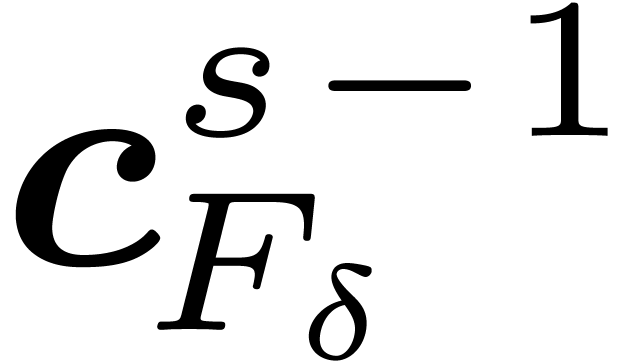 be the restriction of
be the restriction of 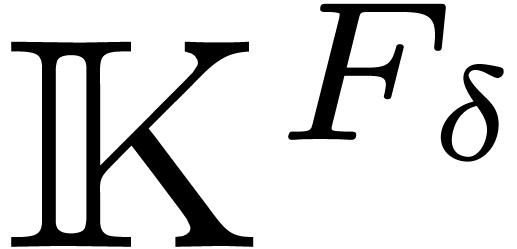 is
stable under
is
stable under 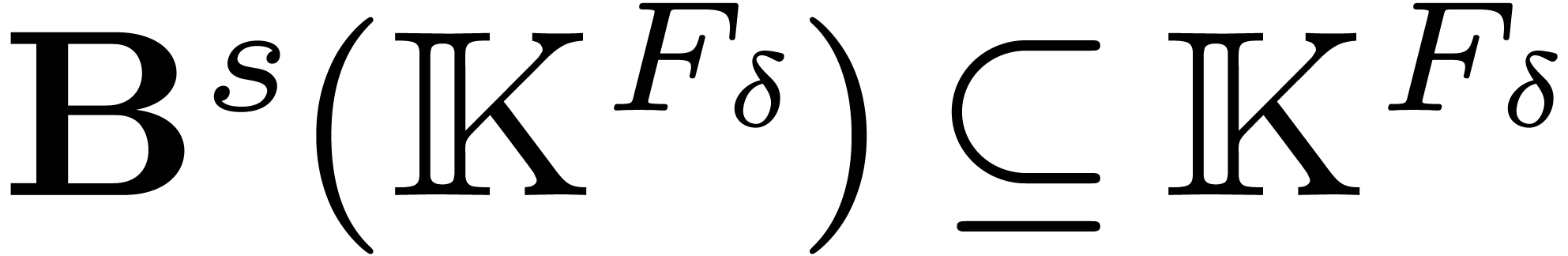 .
.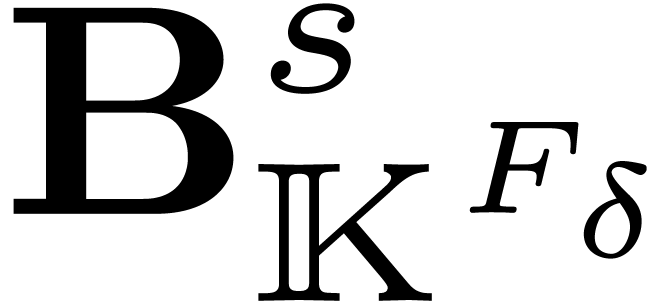 of the map
of the map 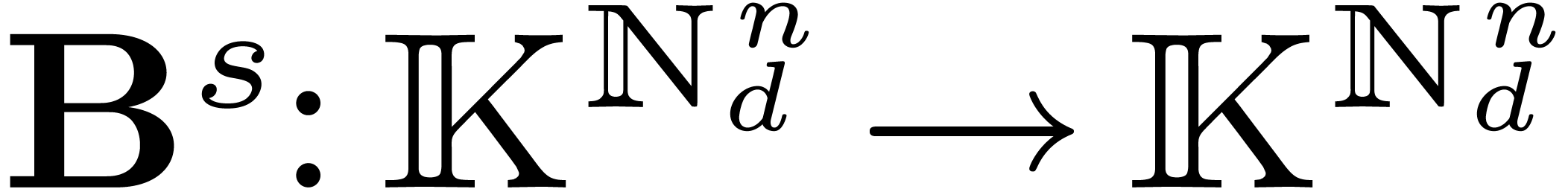 to vectors in
to vectors in
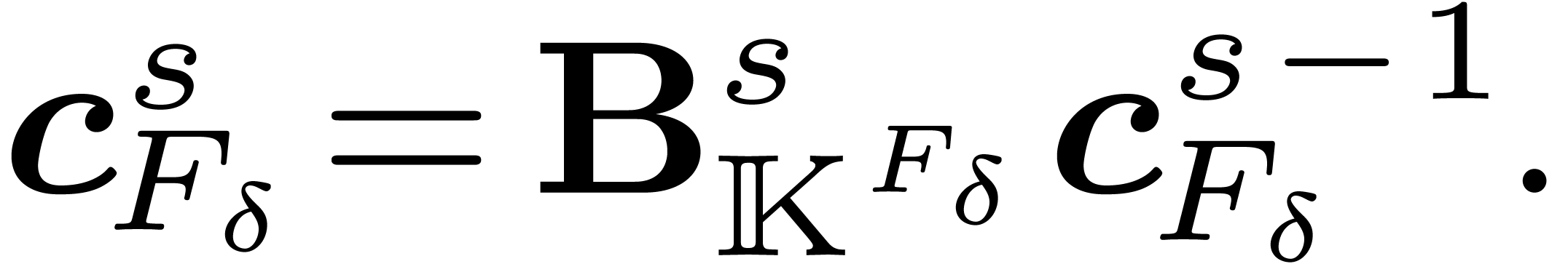 This allows us to
compute
This allows us to
compute 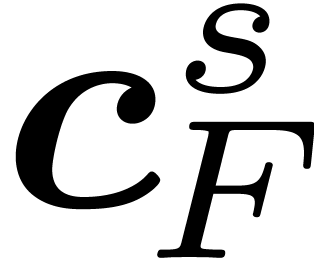 as a function of
as a function of 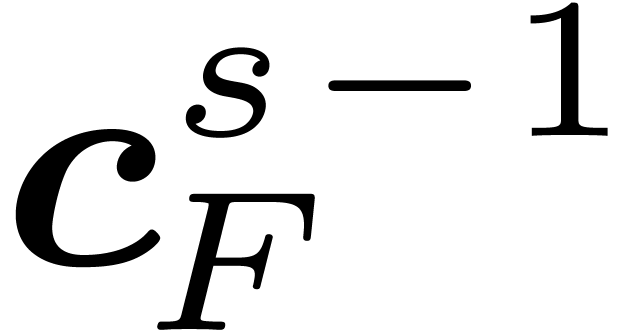 using
using
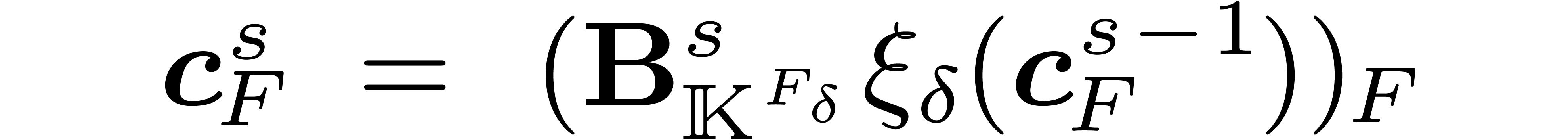
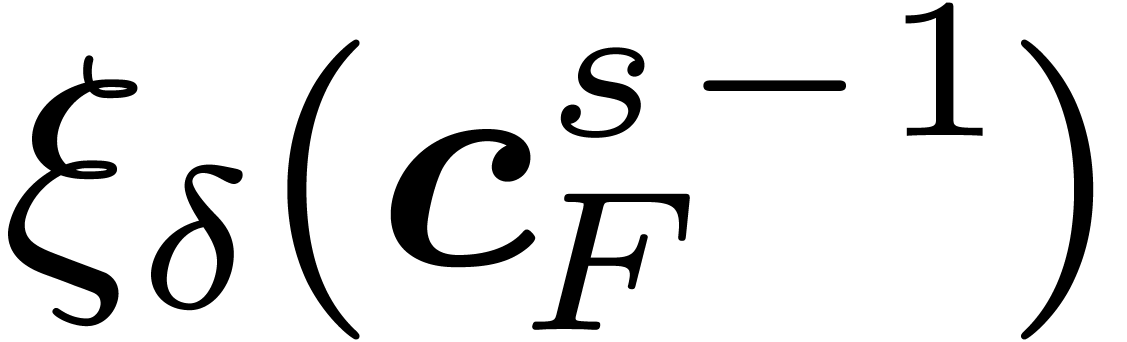 denotes the
denotes the 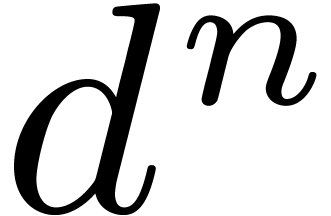 .
.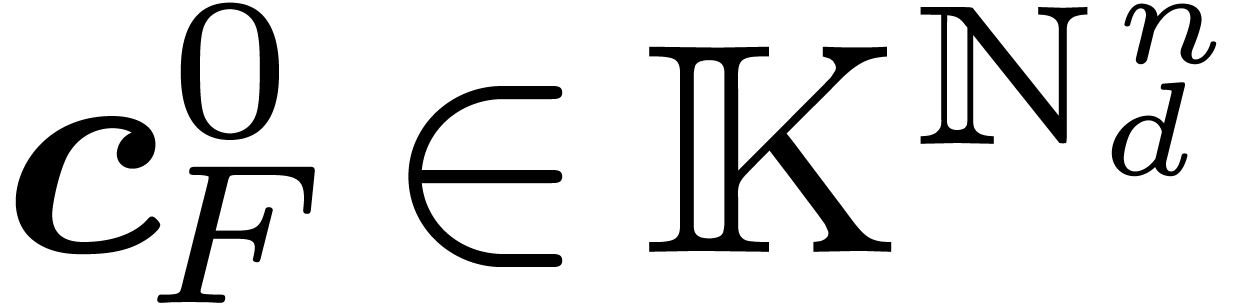 of
of 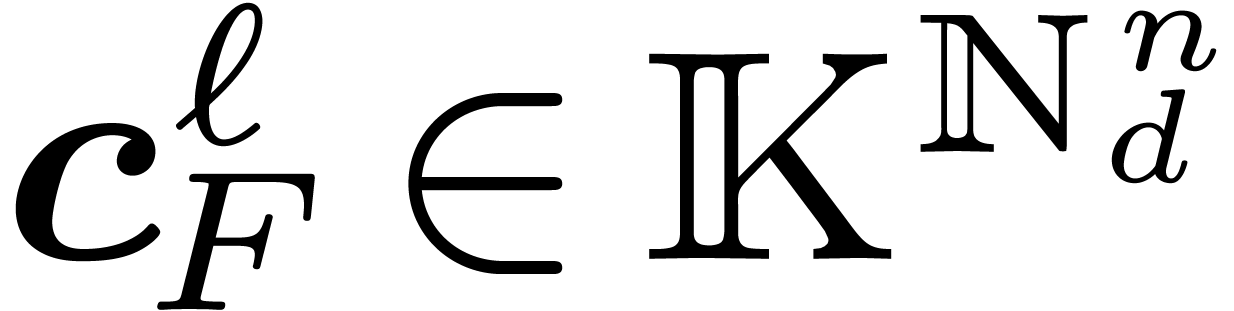 in bit
reversed order
in bit
reversed order
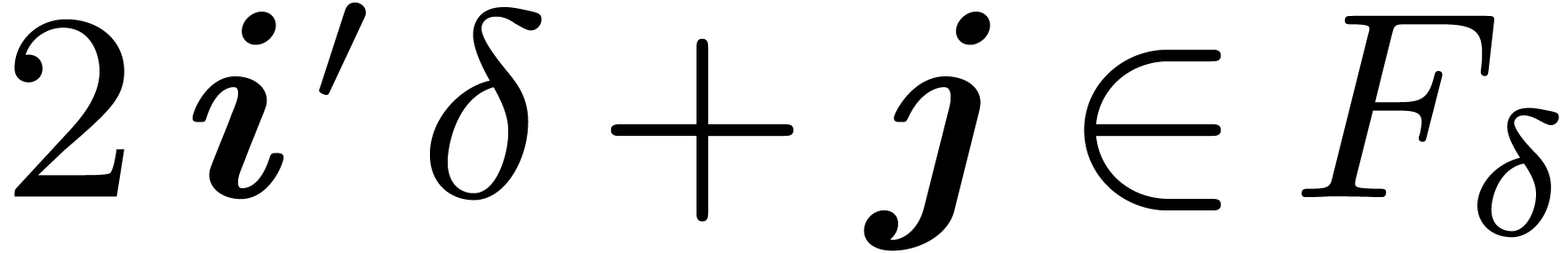 do
do
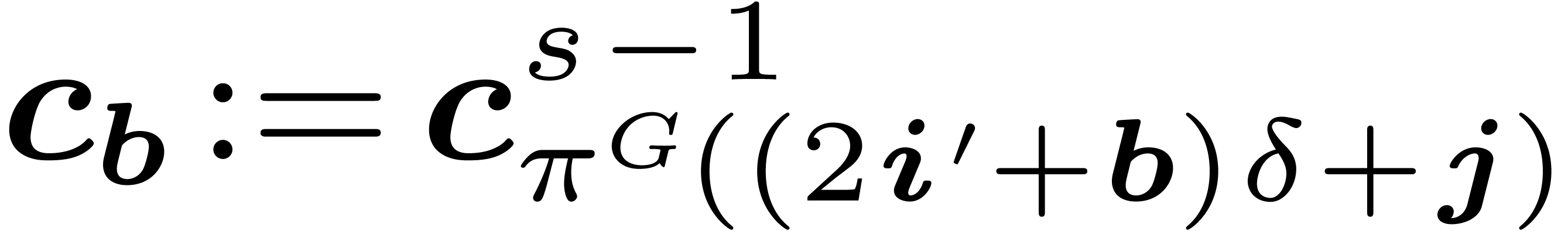
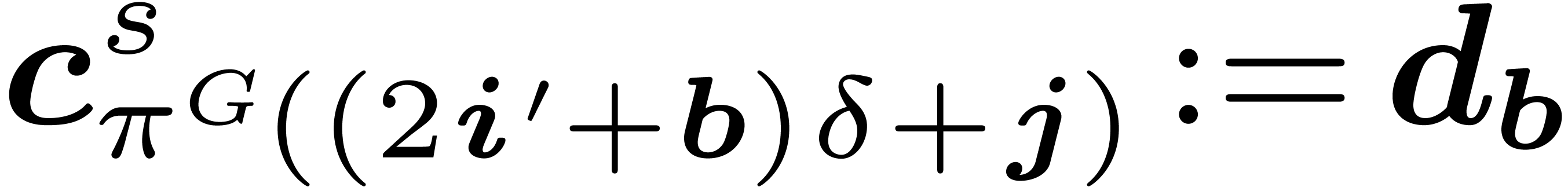
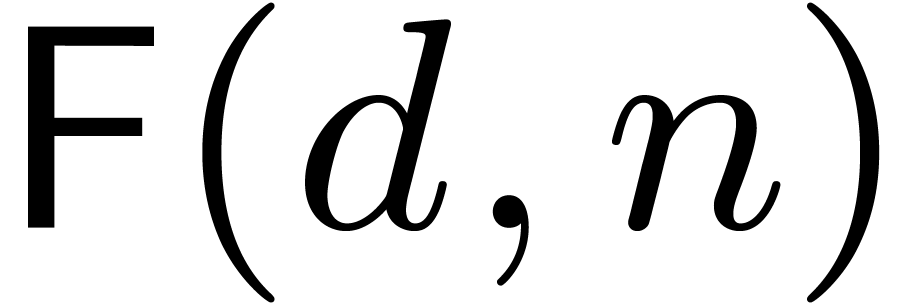 denotes the cost of a full
denotes the cost of a full  ,
,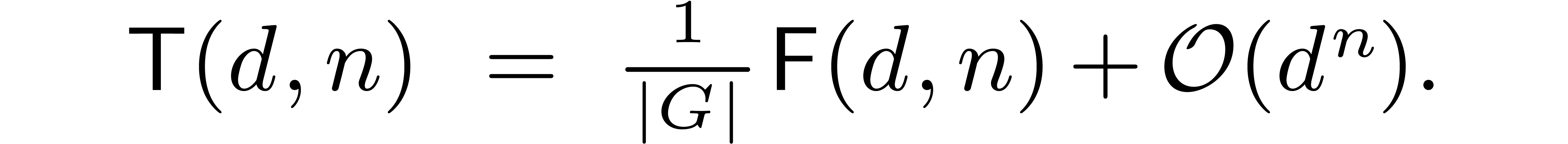
 of the
computation, the ratio between the computation of
of the
computation, the ratio between the computation of  ,
,
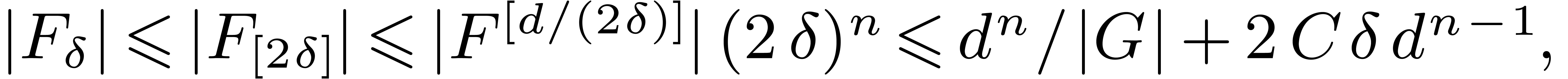
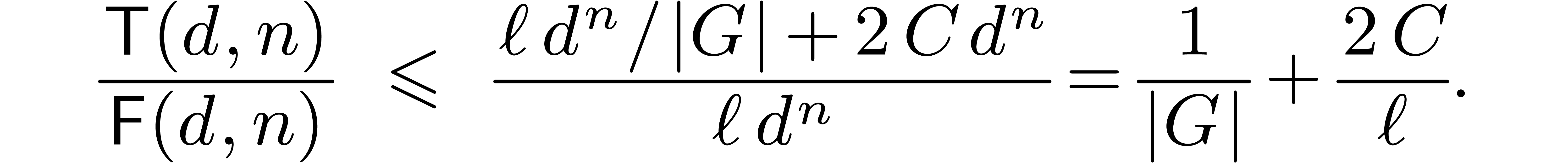
 be the set of
be the set of  and
and 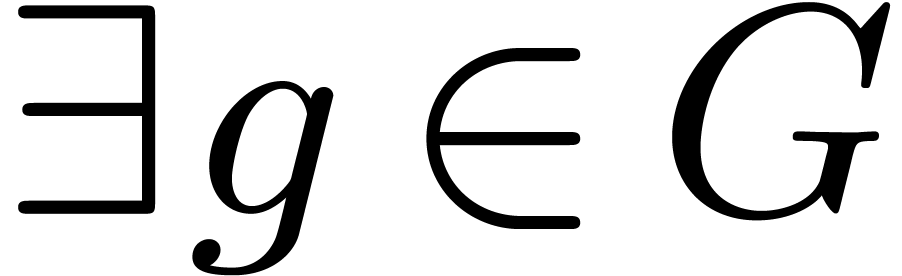 such that
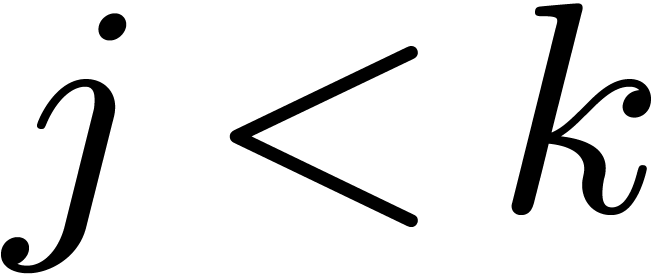
such that 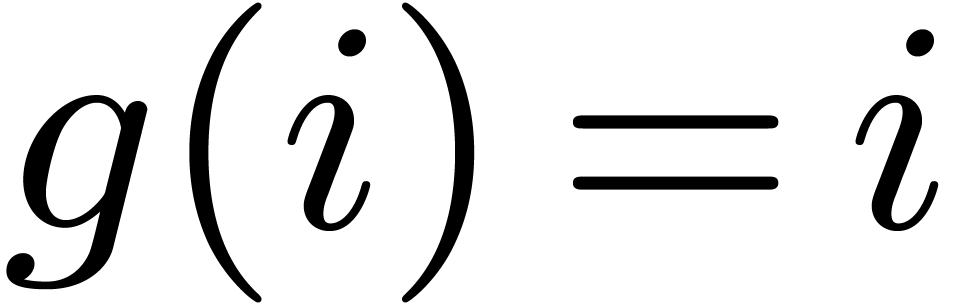 for
for  and
and 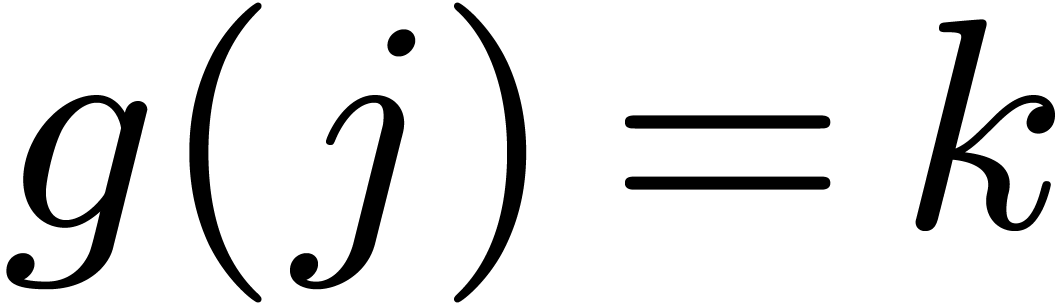 .
.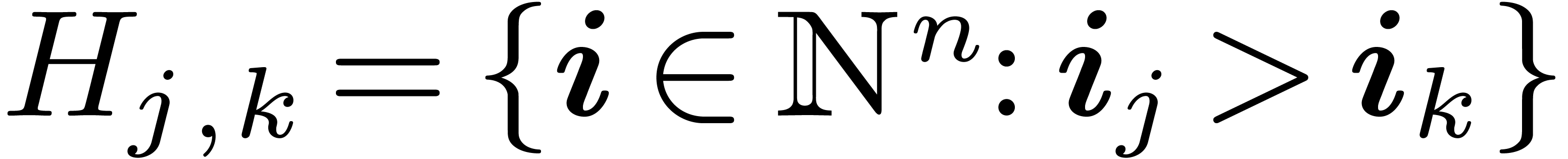 .
.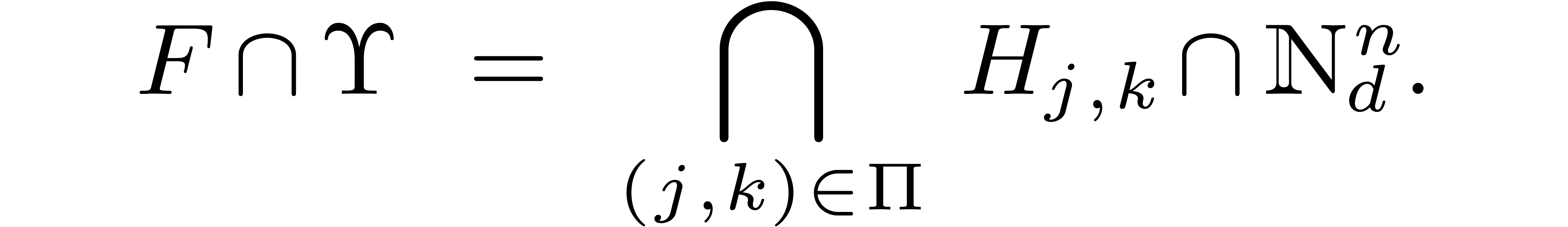
 does
not lie in
does
not lie in 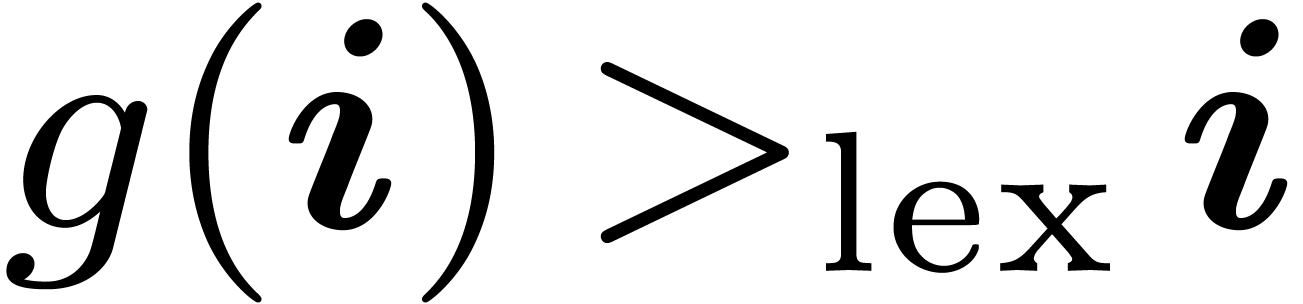 for some
for some 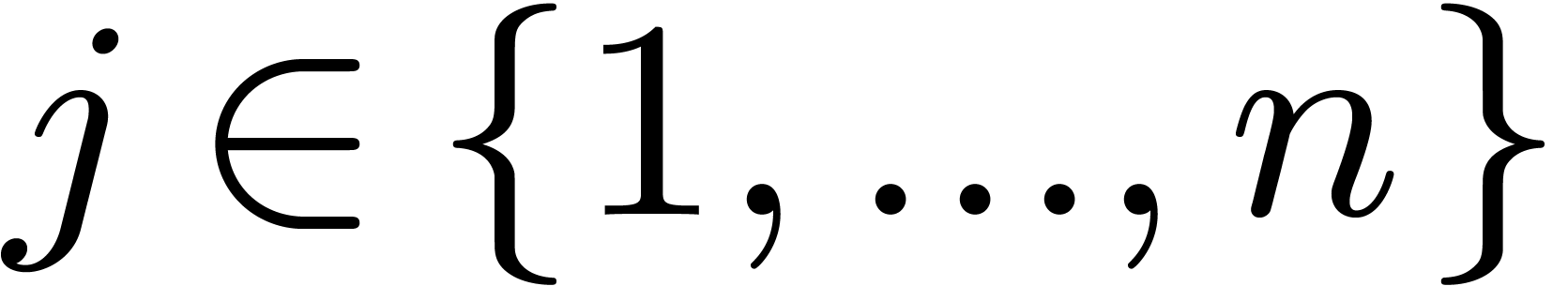 be minimal with
be minimal with 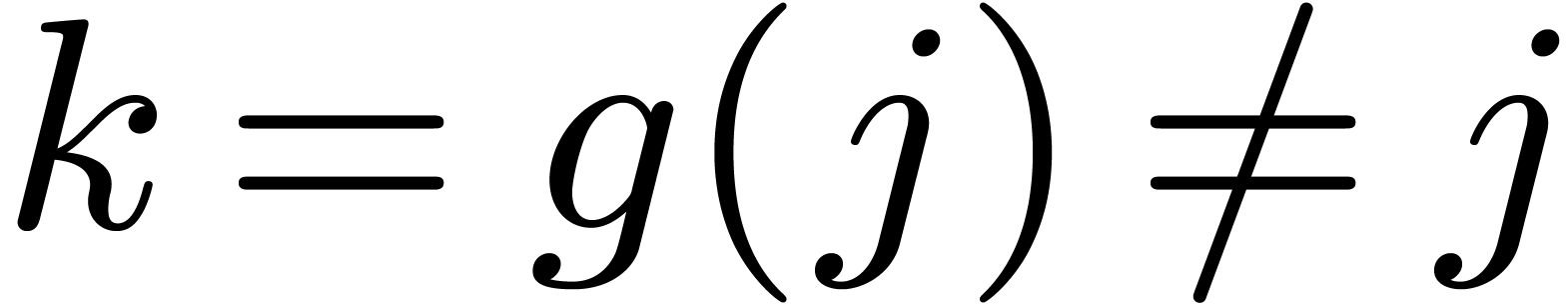 ,
, and
and 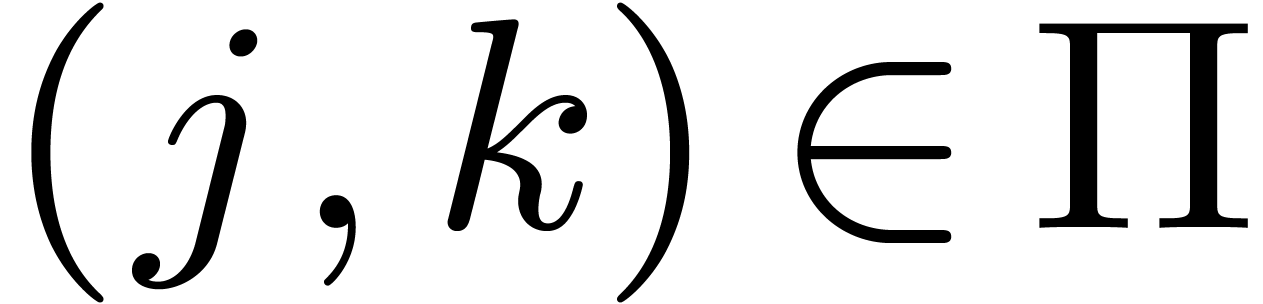 .
.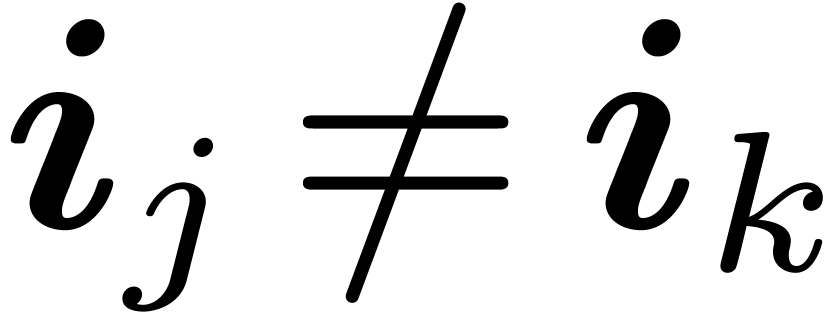 ,
,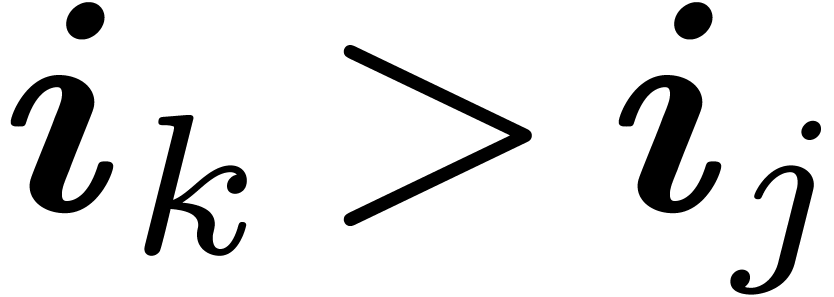 ,
,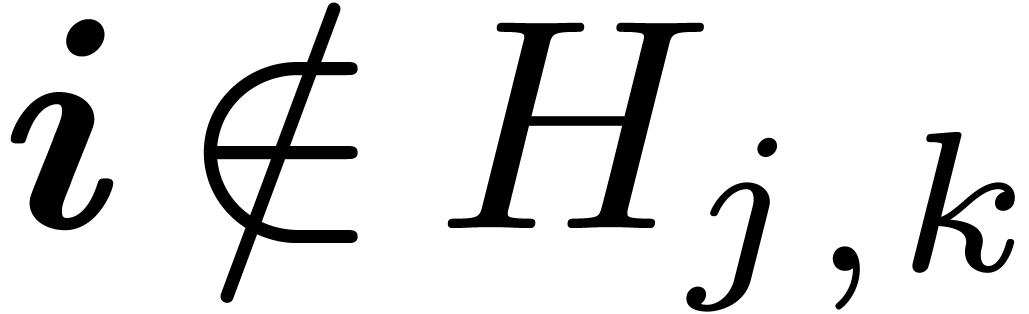 .
.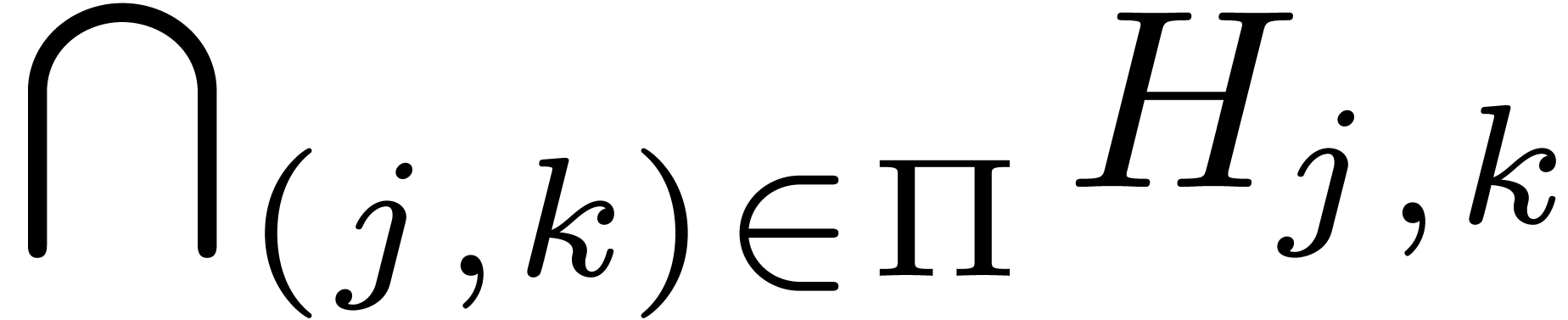 ,
, and its dual
and its dual  );
); ,
,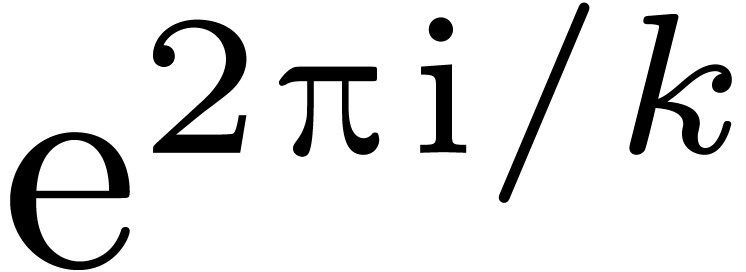 .
. -submodule
-submodule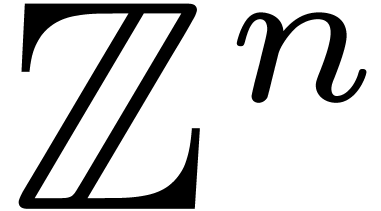 of rank
of rank 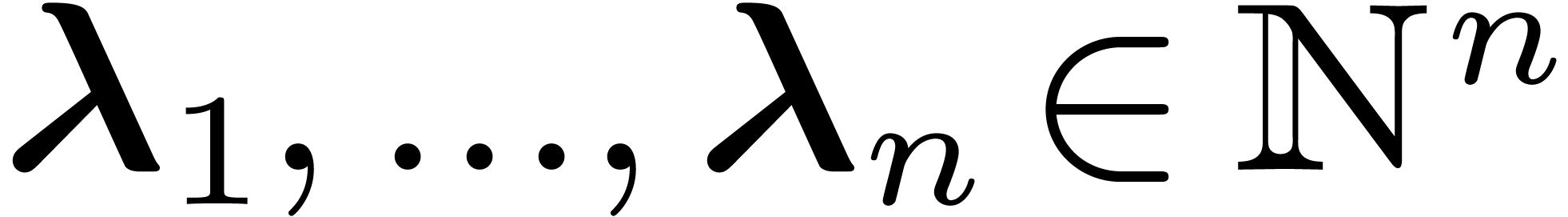 .
.
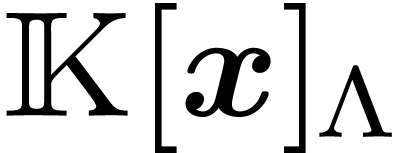 lattice polynomials.
First, we show that these polynomials are the invariant polynomial ring
for a diagonal matrix group.
lattice polynomials.
First, we show that these polynomials are the invariant polynomial ring
for a diagonal matrix group.
 acts on
acts on  ,
, of
of 
 for any
for any 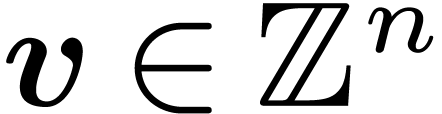 .
.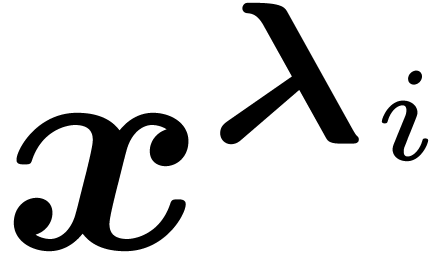 is given by
is given by 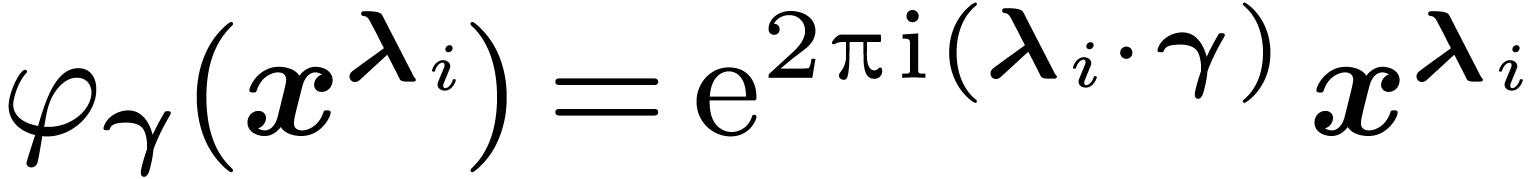 .
.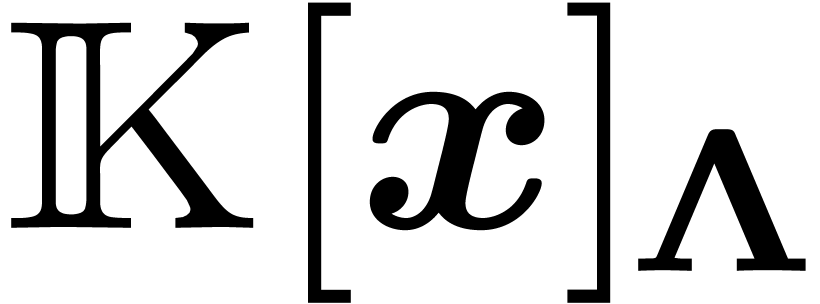 are invariants
under the action of
are invariants
under the action of 
 is the matrix with columns
is the matrix with columns  ,
,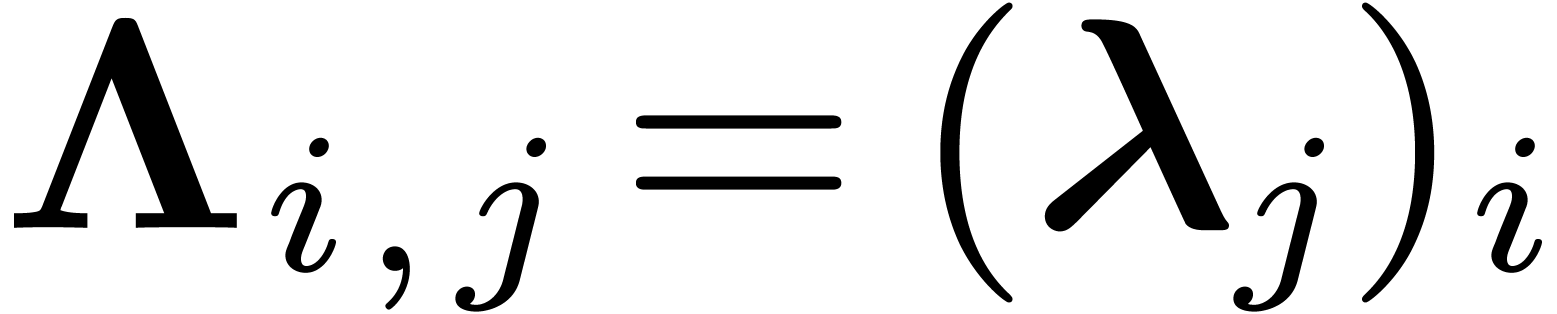 .
.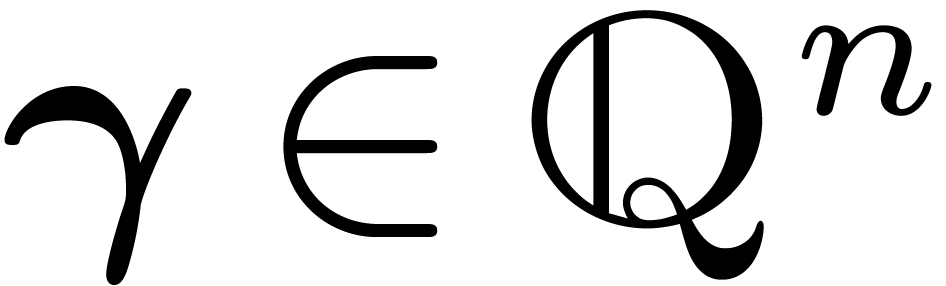 satisfying Equation (
satisfying Equation (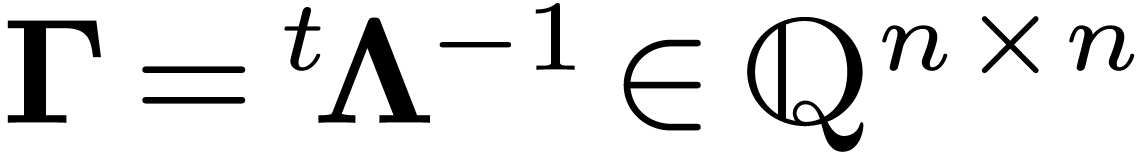 .
. .
. ,
,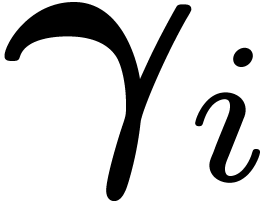 are the columns of
are the columns of
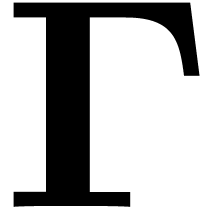 .
.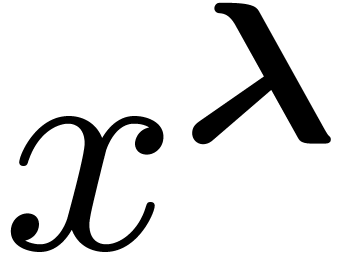 with
with
 ,
, belongs to the dual of
belongs to the dual of  and
and 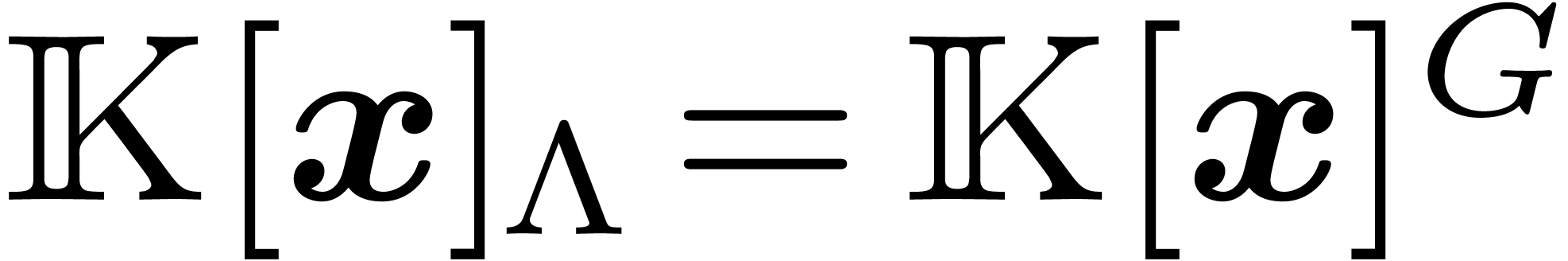 .
.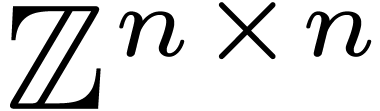 matters to determine the group
matters to determine the group  generated by
generated by 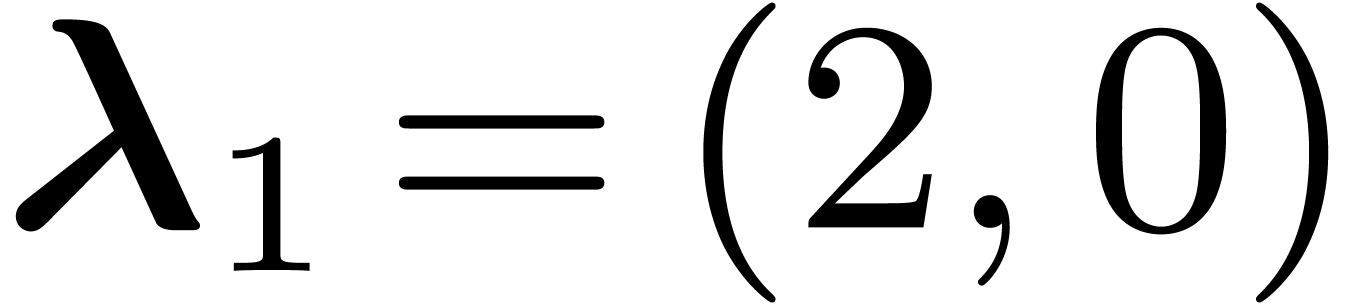 and
and 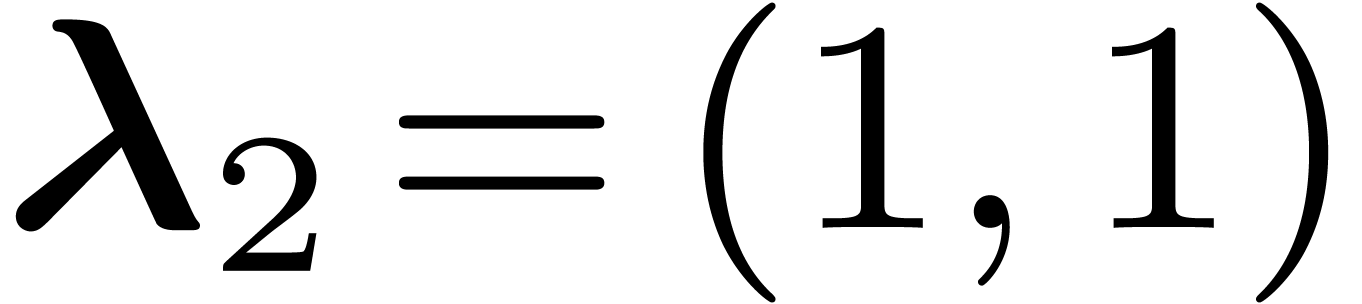 ,
,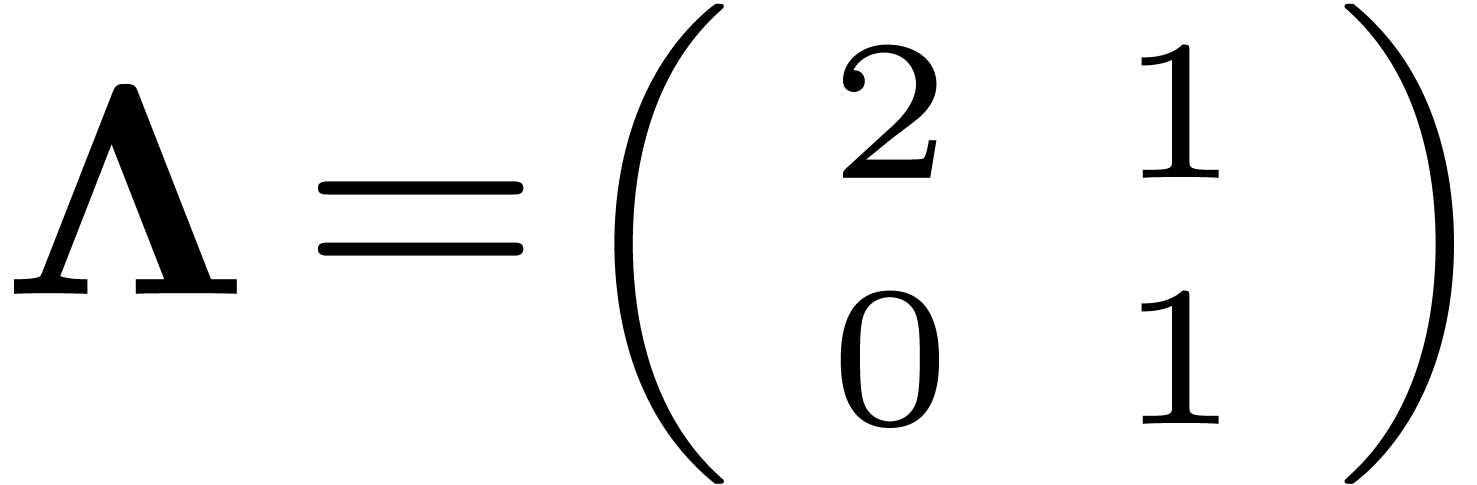 .
.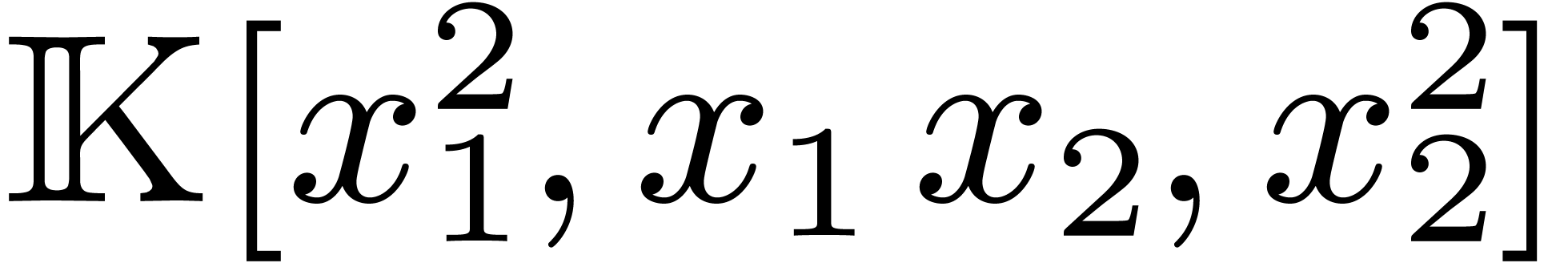 .
.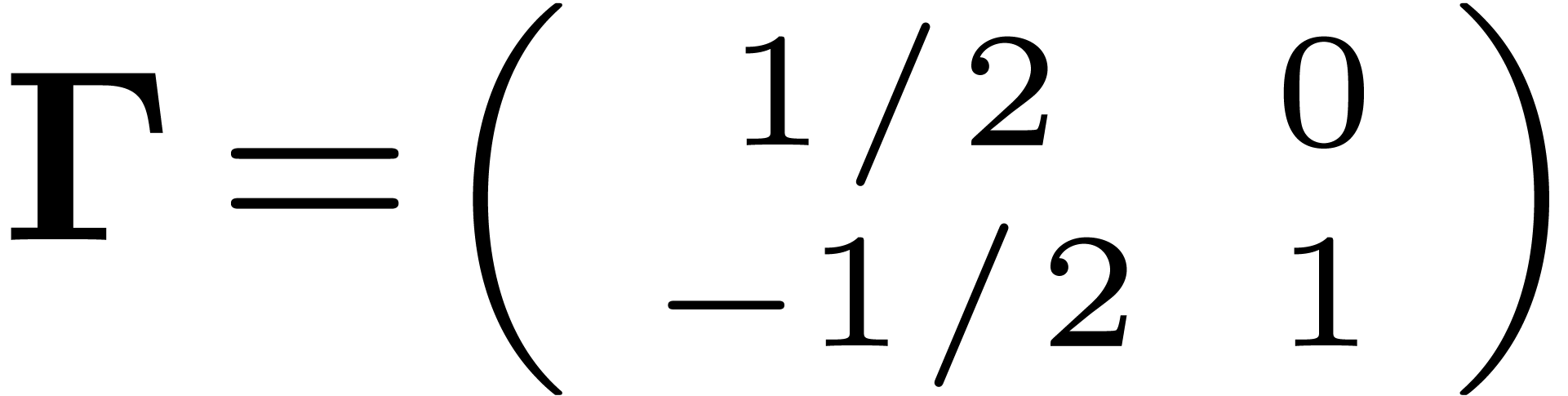 ,
,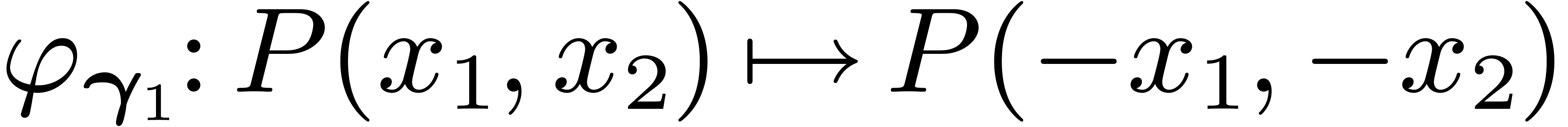 and
and 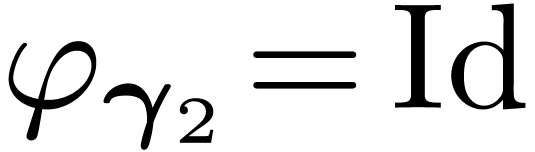 .
.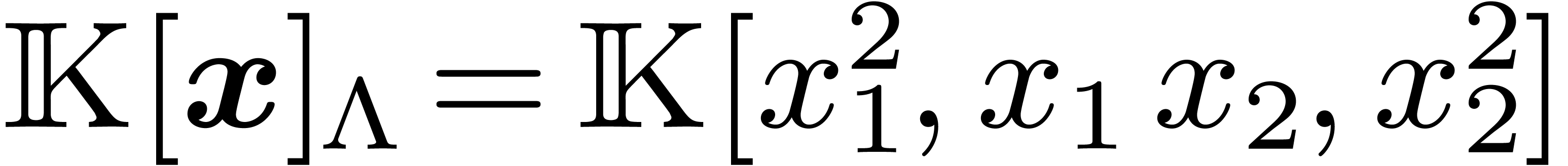 are those polynomials
invariant under the symmetry
are those polynomials
invariant under the symmetry 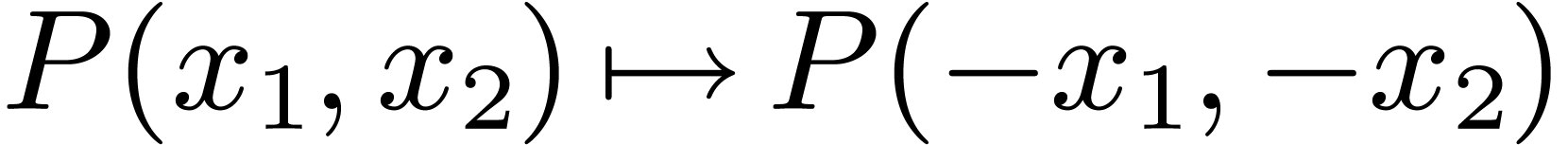 .
. ,
,
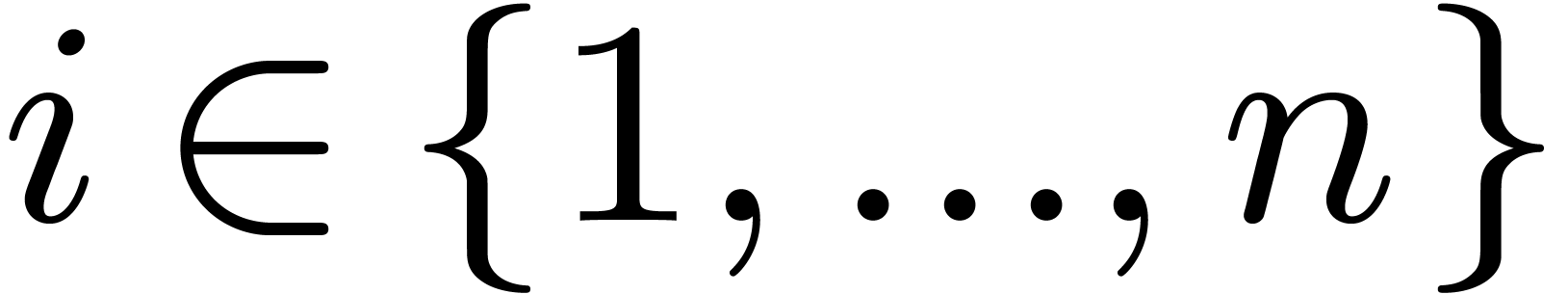 ,
,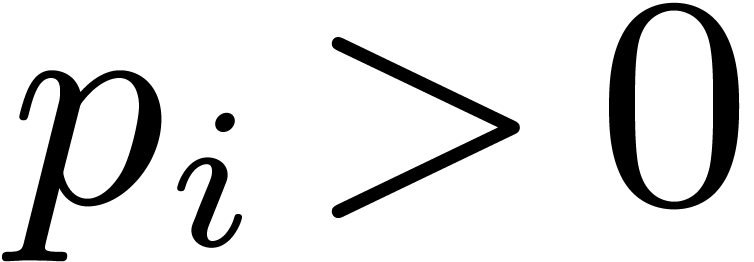 be minimal such that
be minimal such that 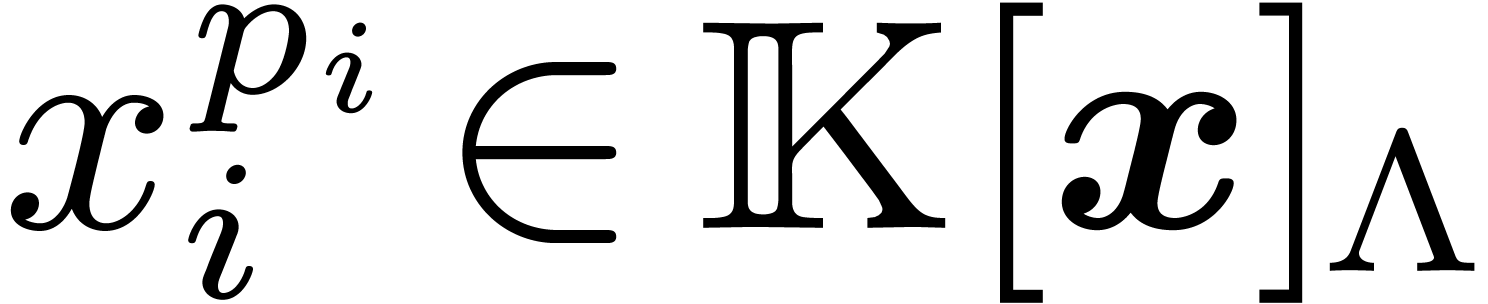 .
.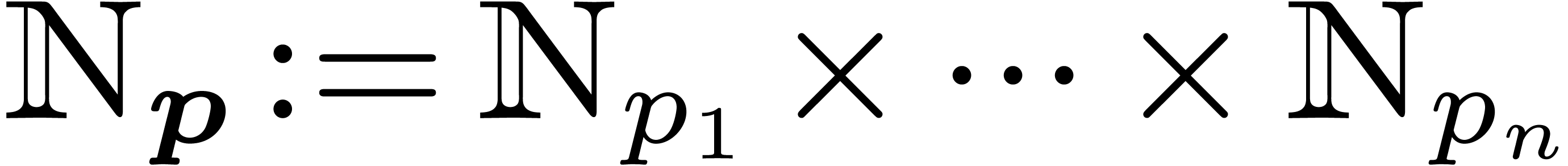 a basic domain for
a basic domain for  of a
polynomial
of a
polynomial 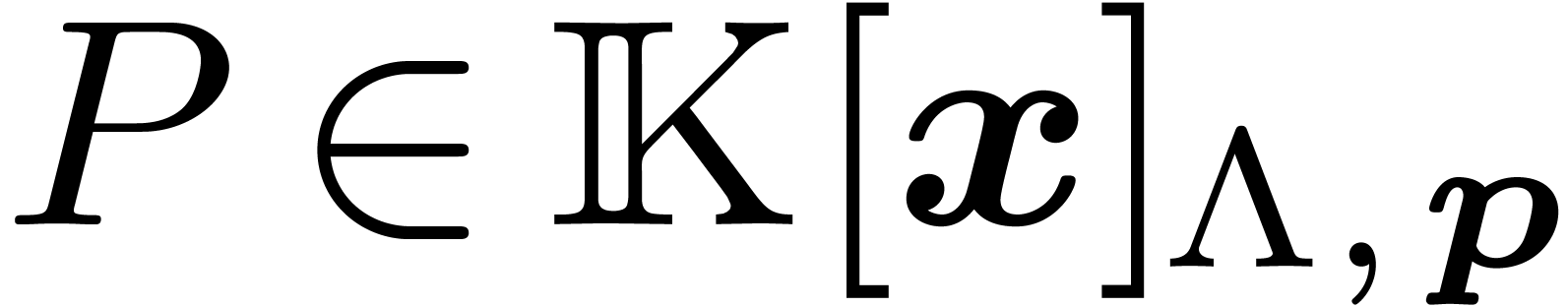 .
.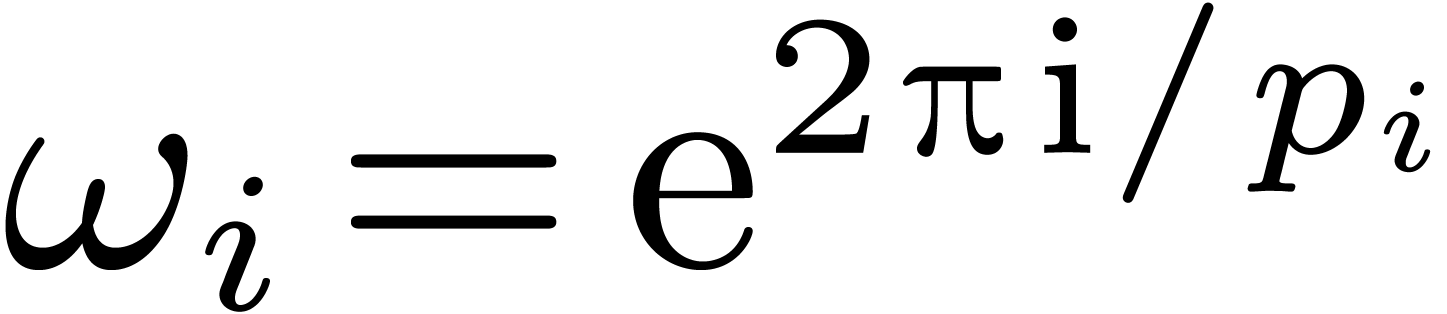 for each
for each  ,
,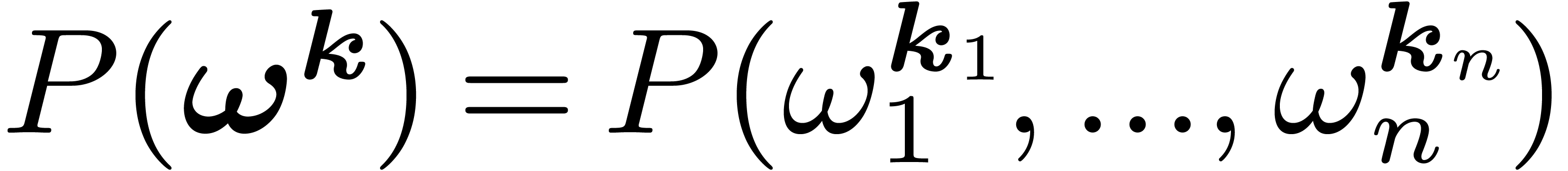 for
for 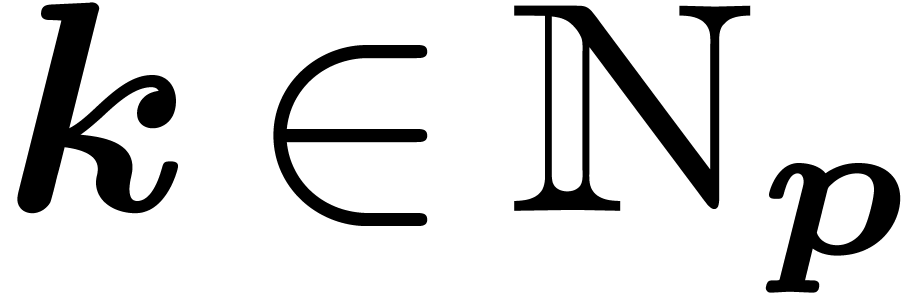 .
.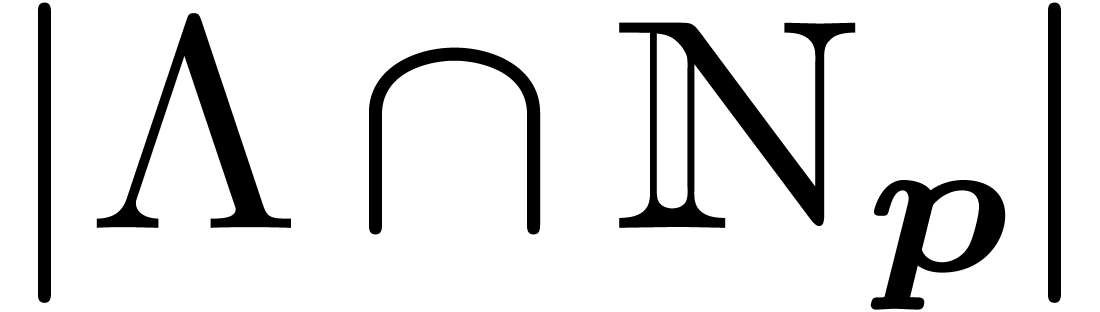 .
. ,
,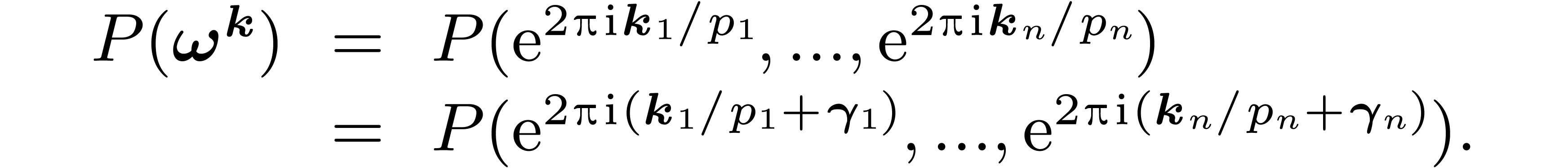
 modulo
modulo  where
where
 is a basis of
is a basis of  for the remainder of
for the remainder of
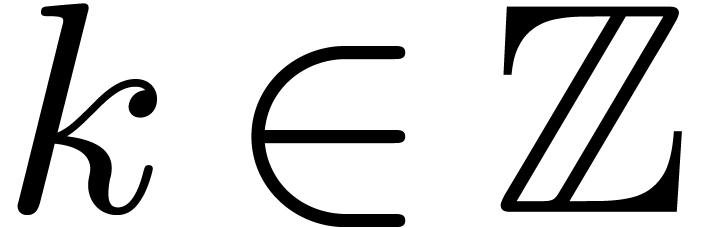 by
by 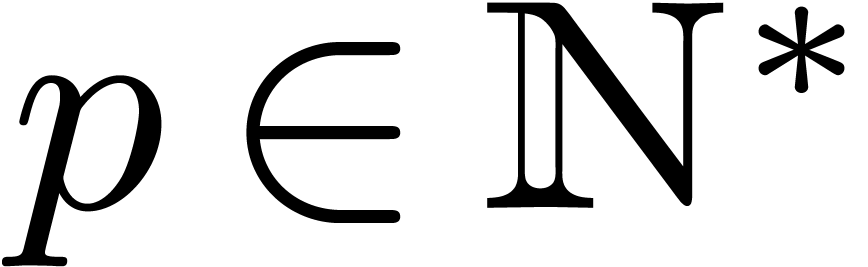 .
. and
and 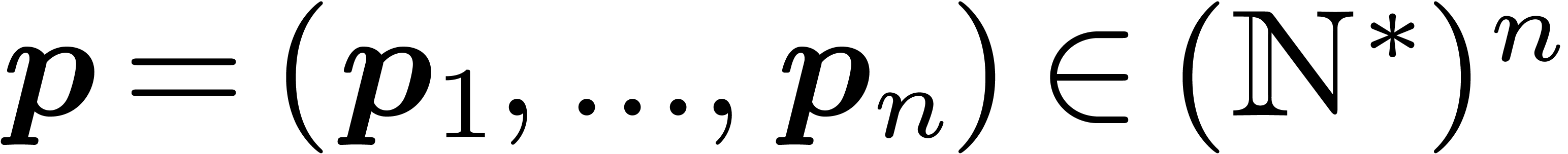 ,
,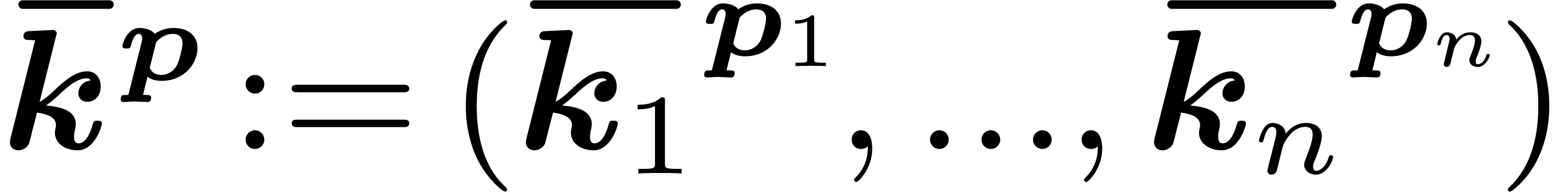 .
.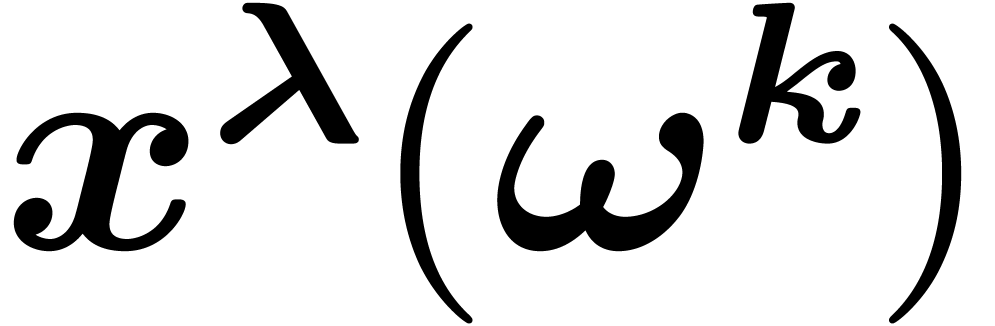 depends only on the
class of
depends only on the
class of  .
. of
of  of
of 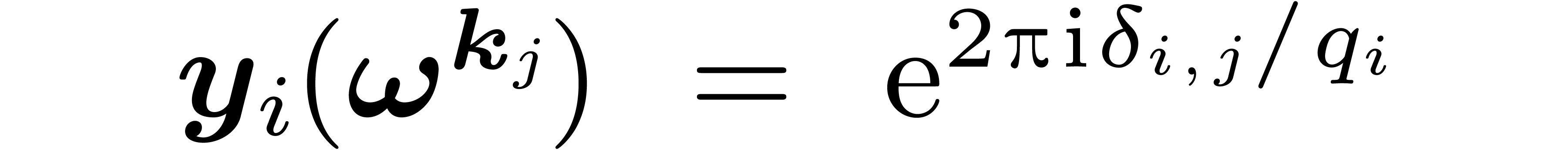
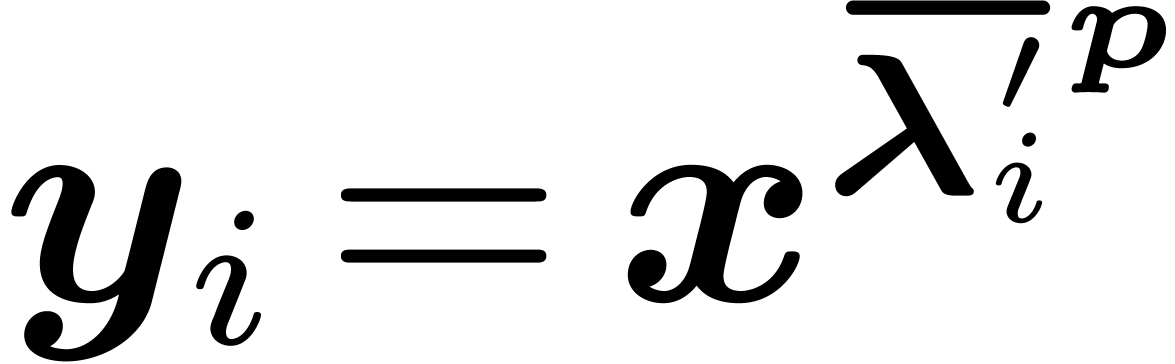 and the
and the 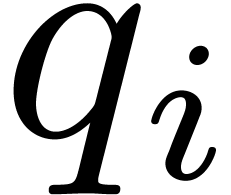 's
's .
.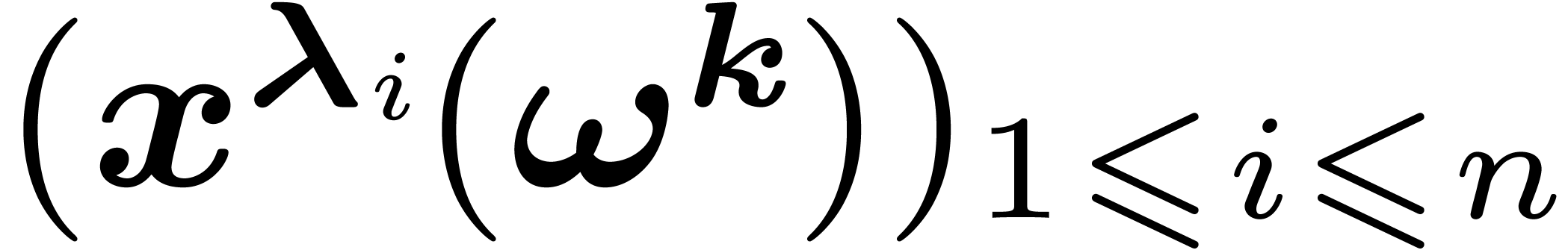 for
for 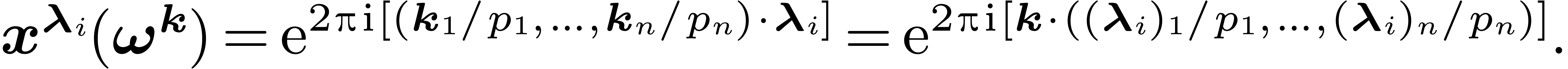
 spanned by the columns of
spanned by the columns of
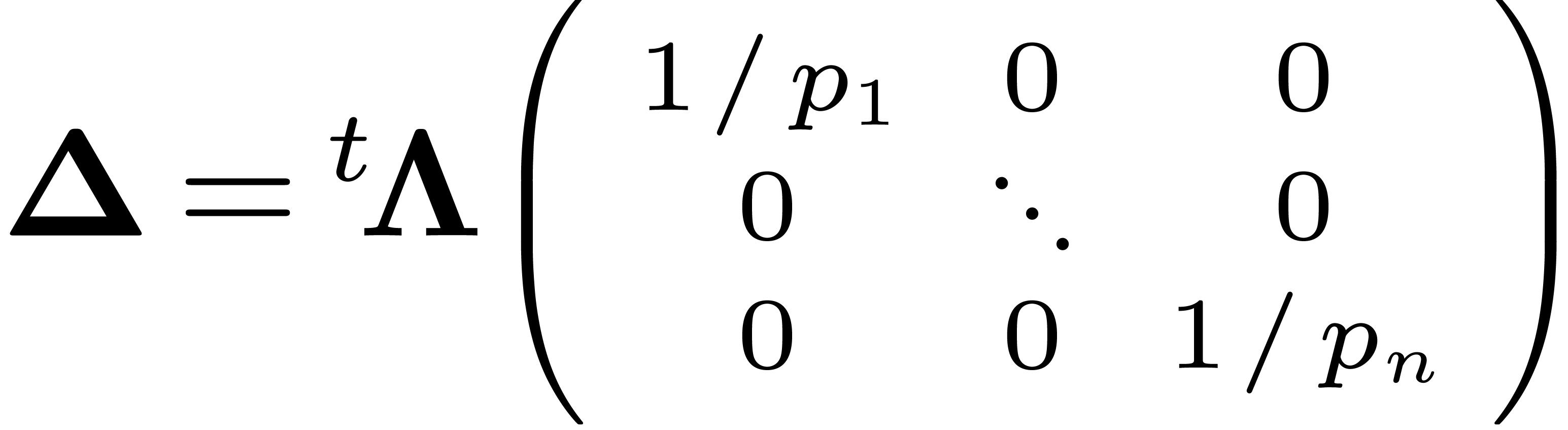 ,
,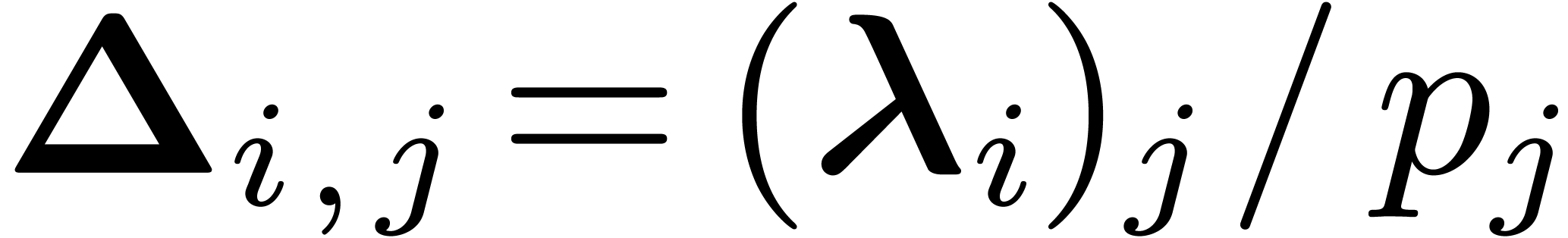 .
. but the coefficients of
but the coefficients of 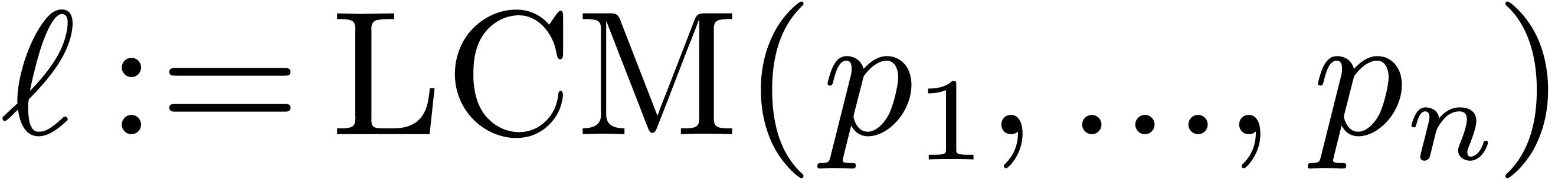 ,
, .
.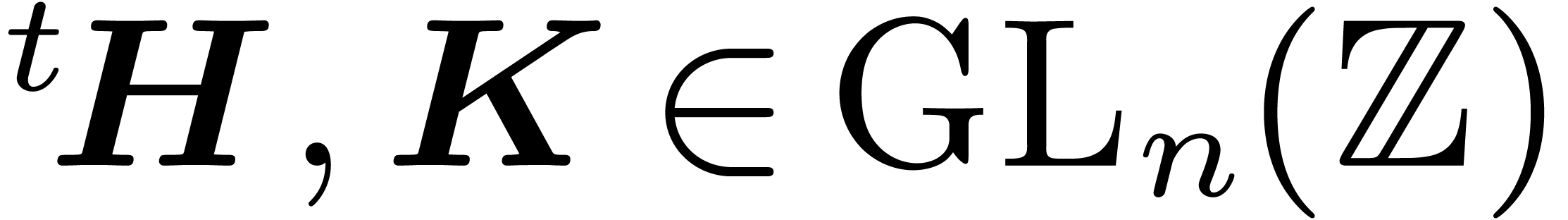 and integers
and integers 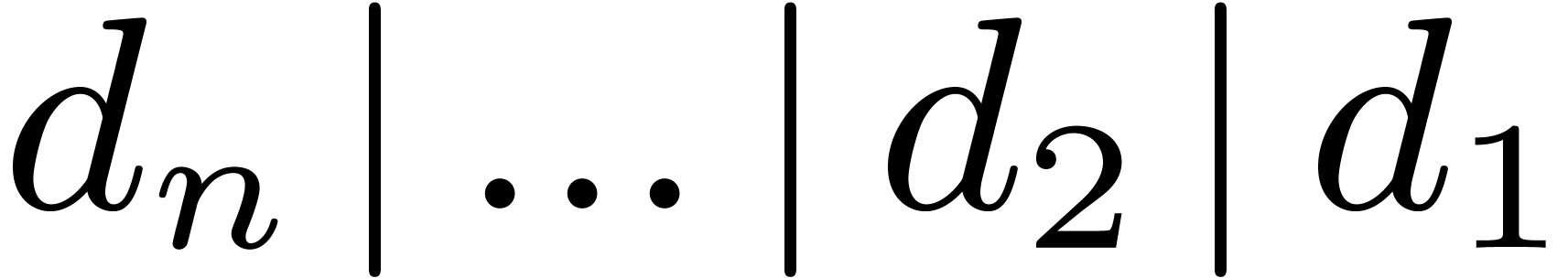 such that
such that
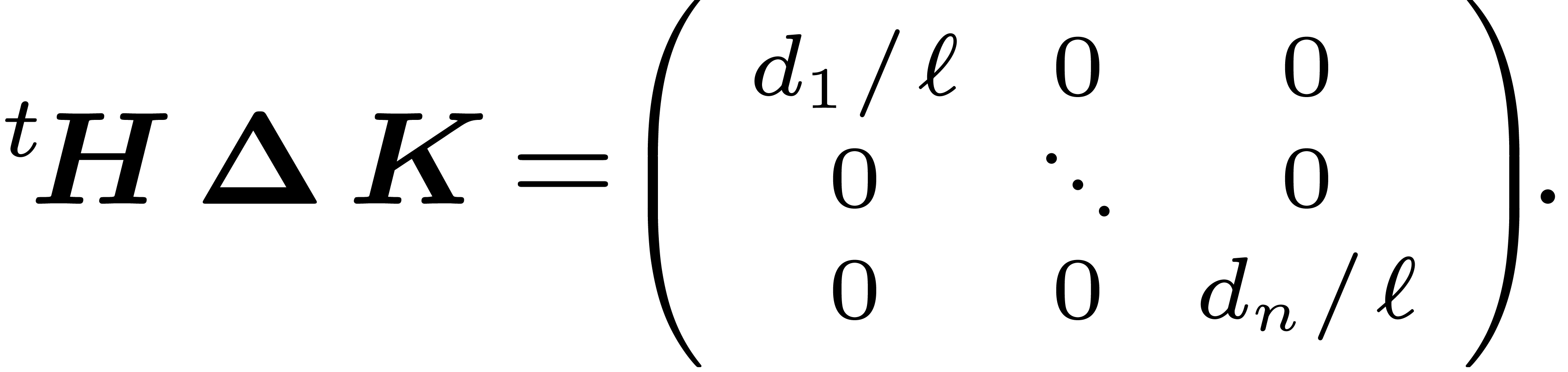
 .
. ,
, such that
such that 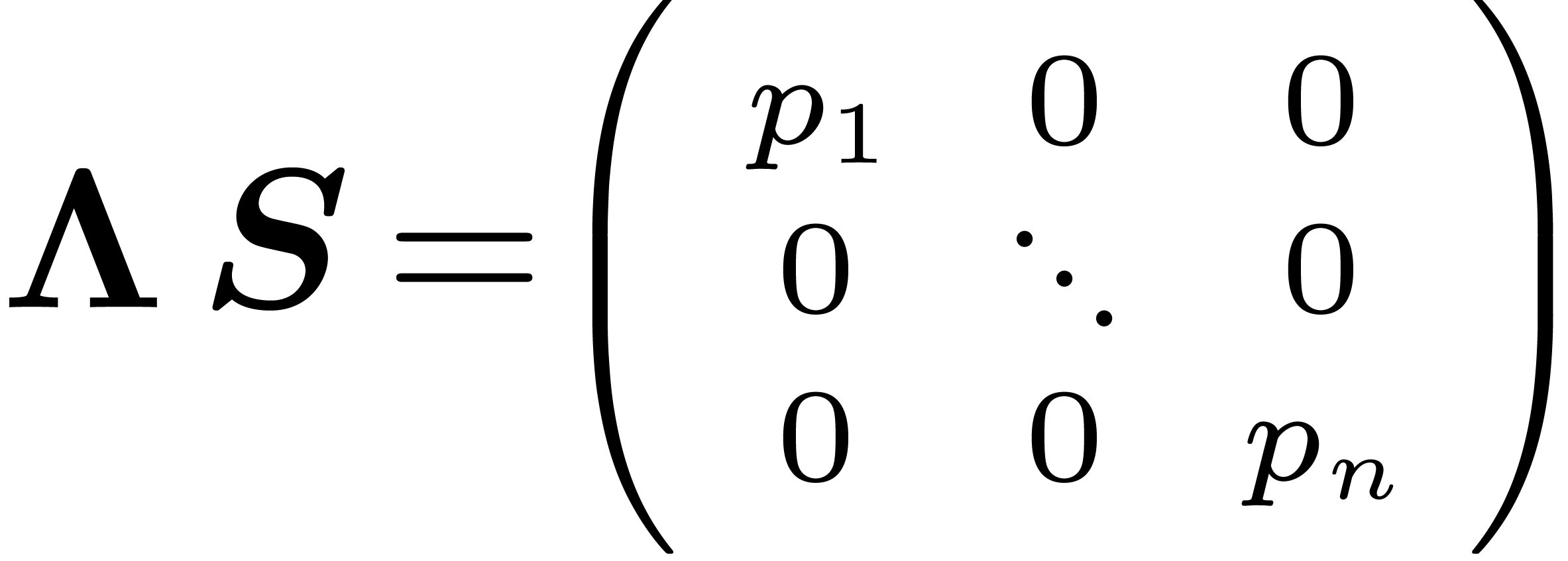 . Thus we have
. Thus we have
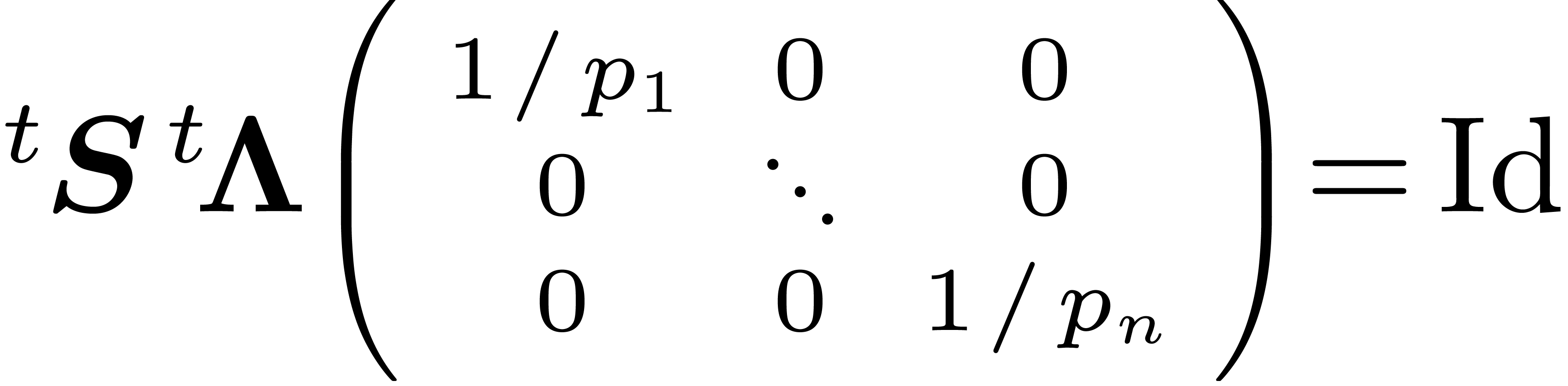 ,
,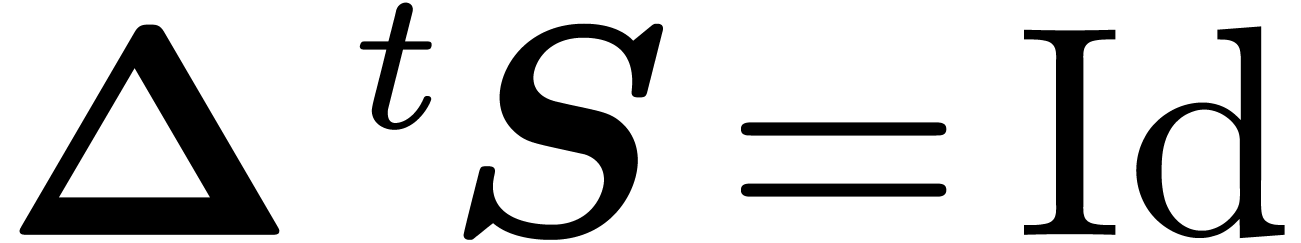 and our result. Because
and our result. Because 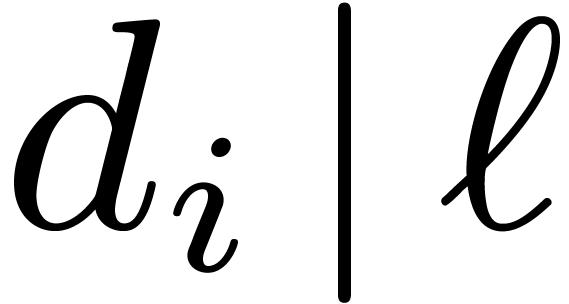 and by setting
and by setting 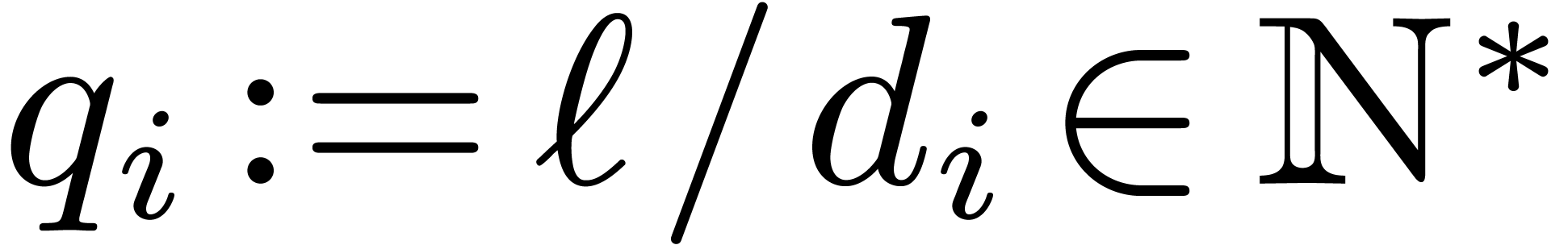 ,
, give the basis
give the basis  give the basis
give the basis 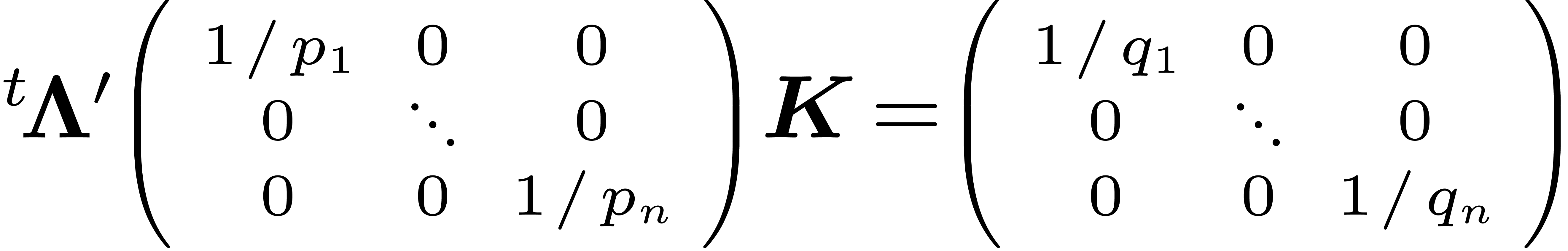


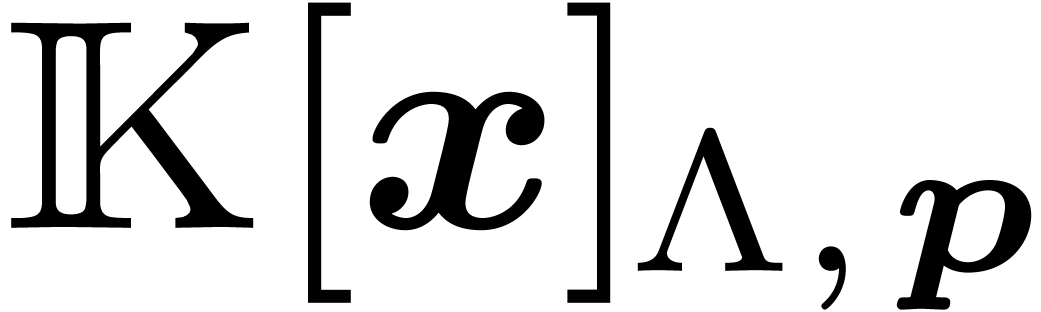 .
.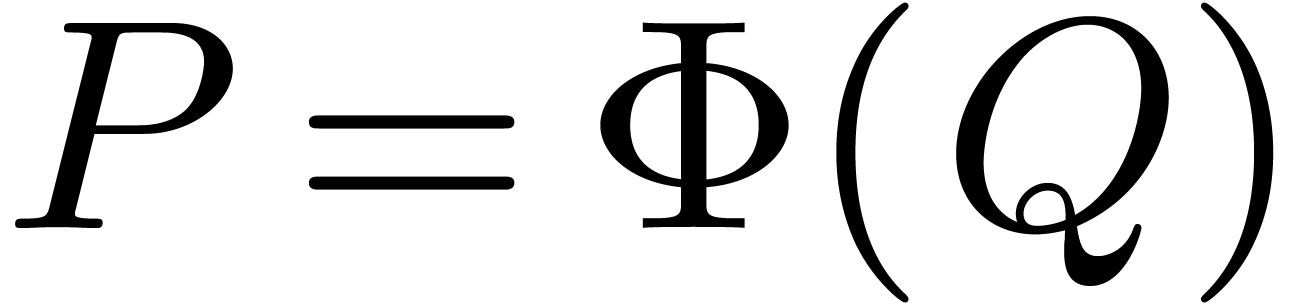 then
then
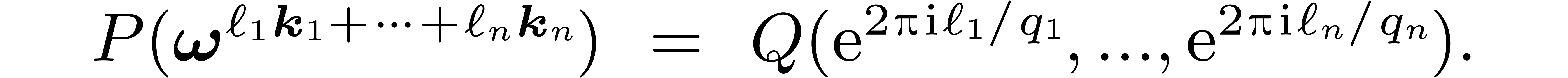
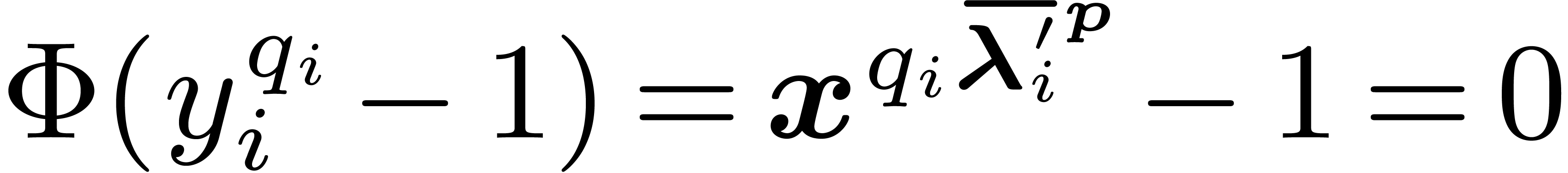 modulo
modulo  .
.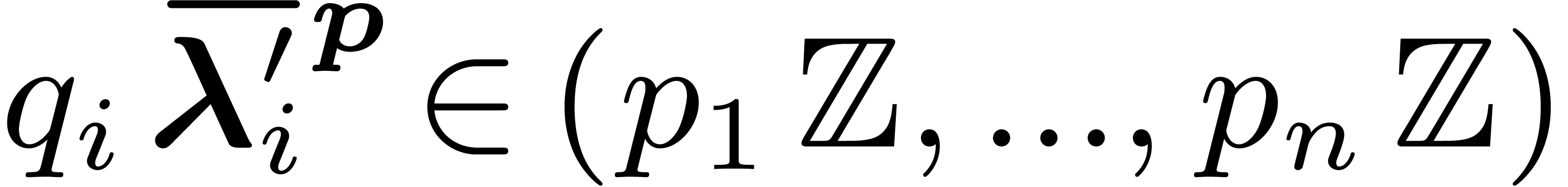 ,
,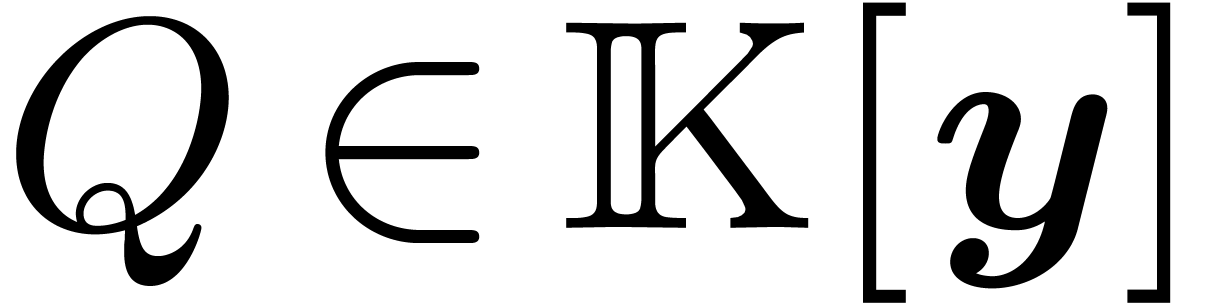 and
and 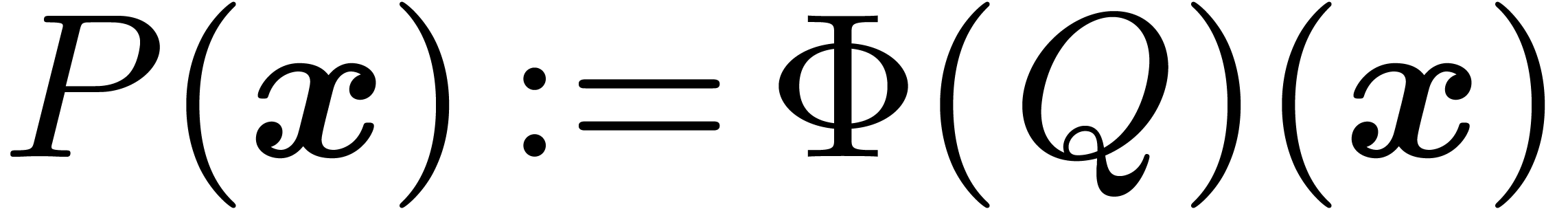 .
.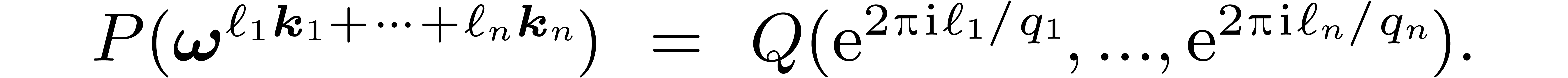
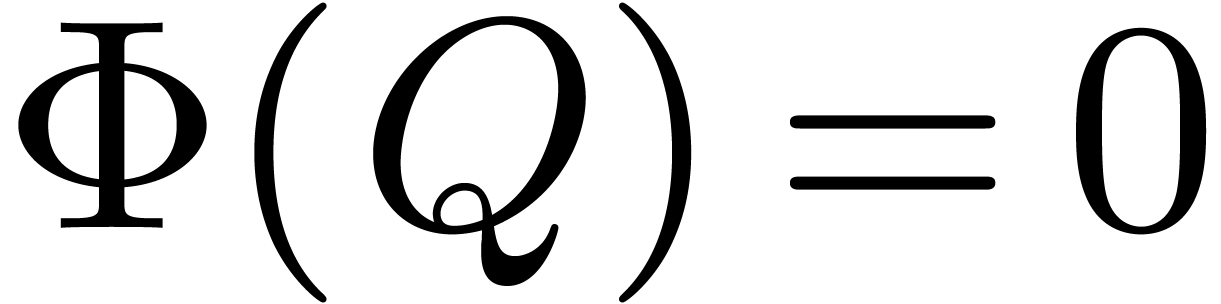 then for all
then for all 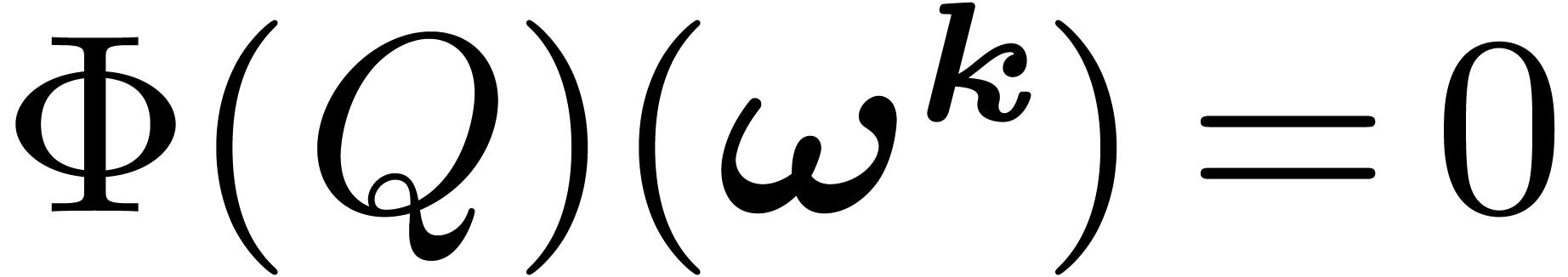 .
. ,
,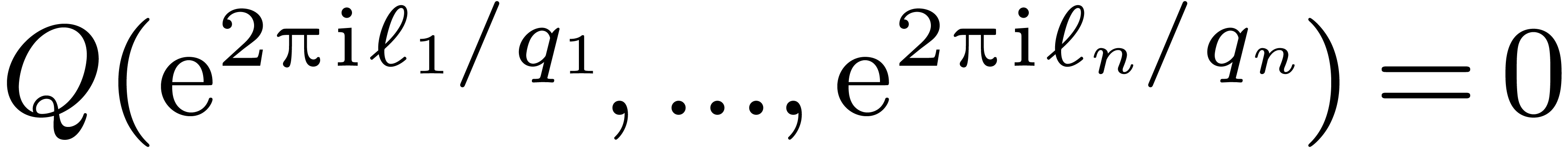 .
. belongs to
the ideal generated by
belongs to
the ideal generated by  .
.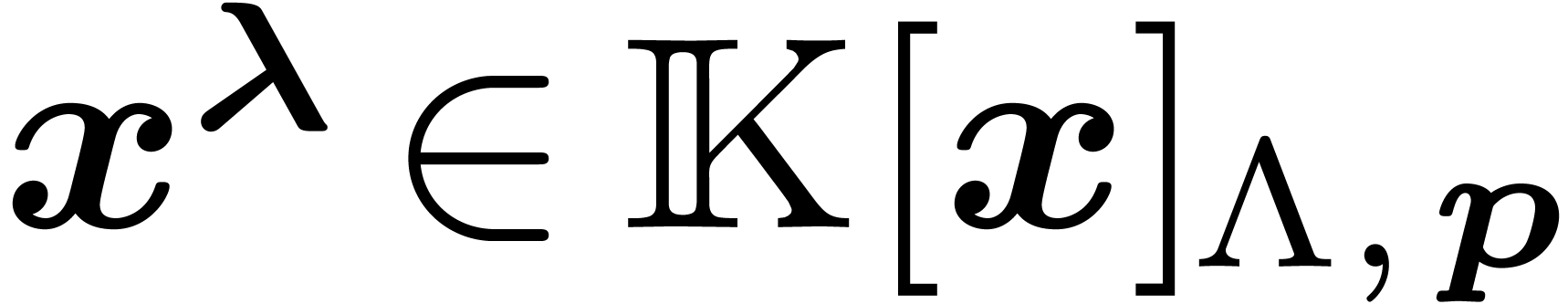 .
.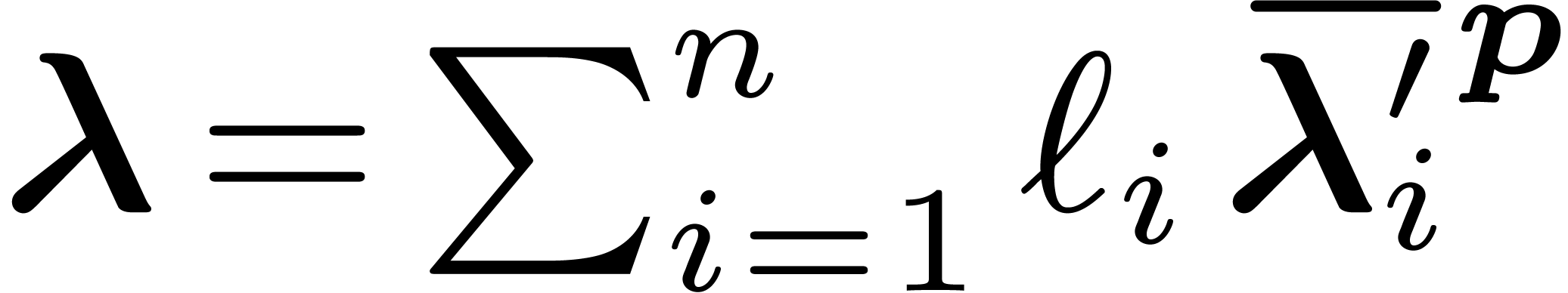 with
with  and define
and define 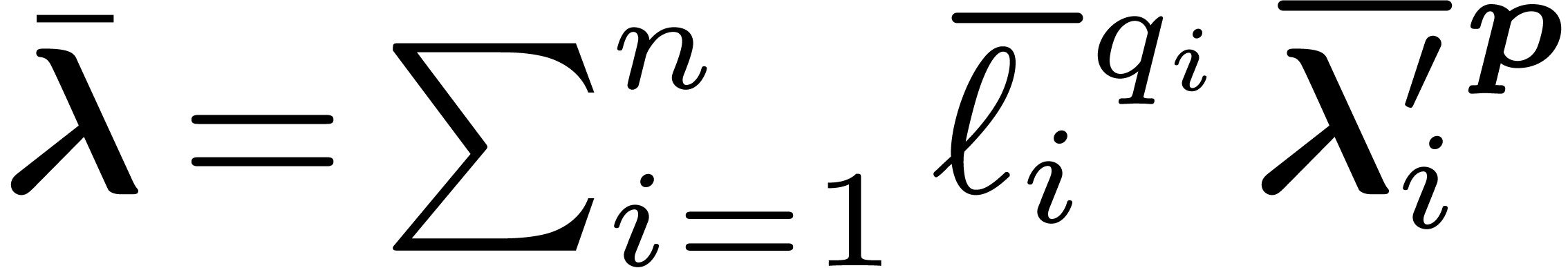 .
. is included in
is included in  ,
,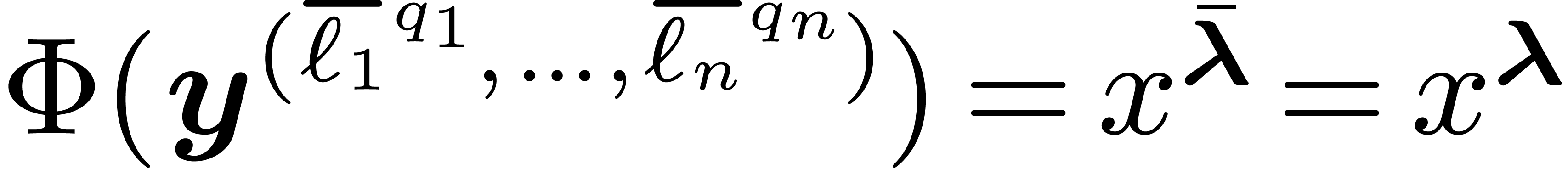 modulo
modulo 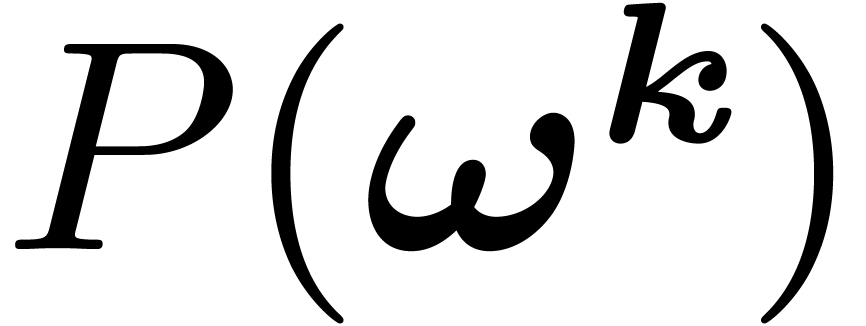 with
with 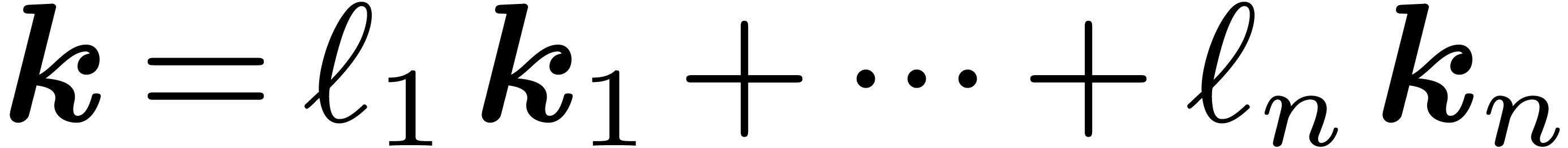 and
and  .
. of evaluations equals the numbers
of evaluations equals the numbers 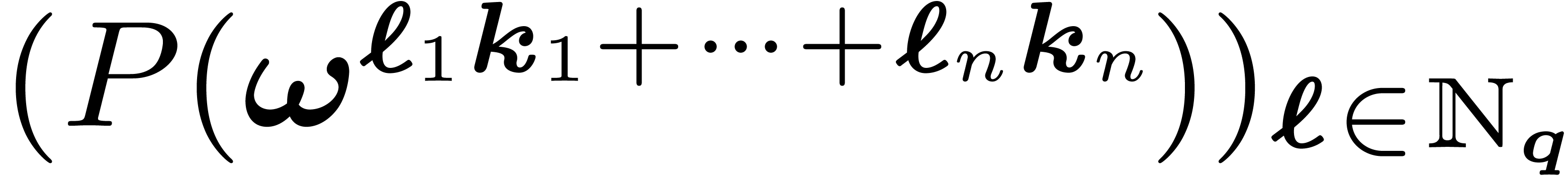 .
. .
.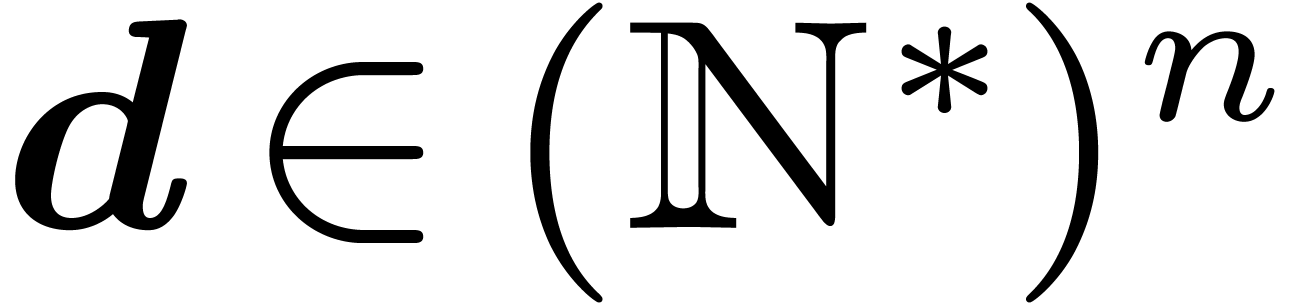 is such that
is such that 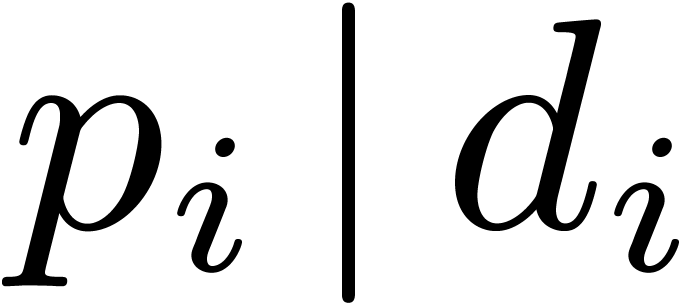 for each
for each  of a lattice polynomial
of a lattice polynomial 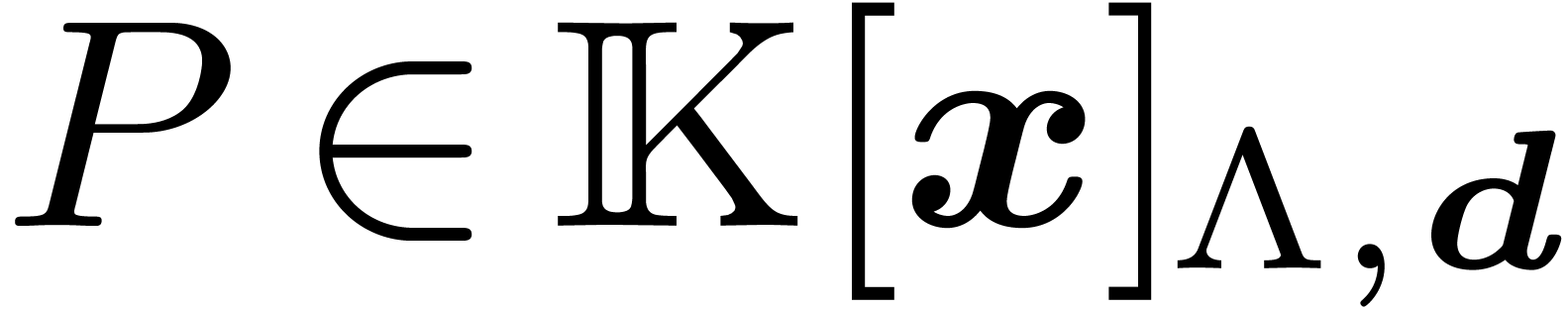 .
.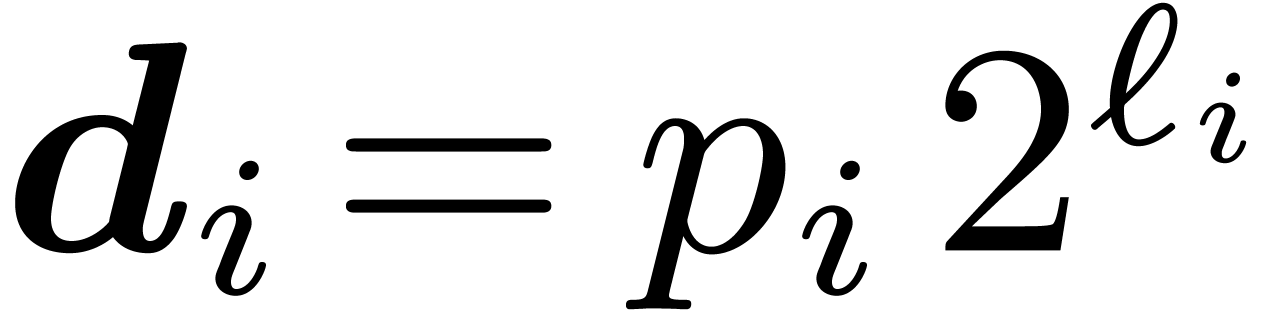 ,
, and denote
by
and denote
by  .
.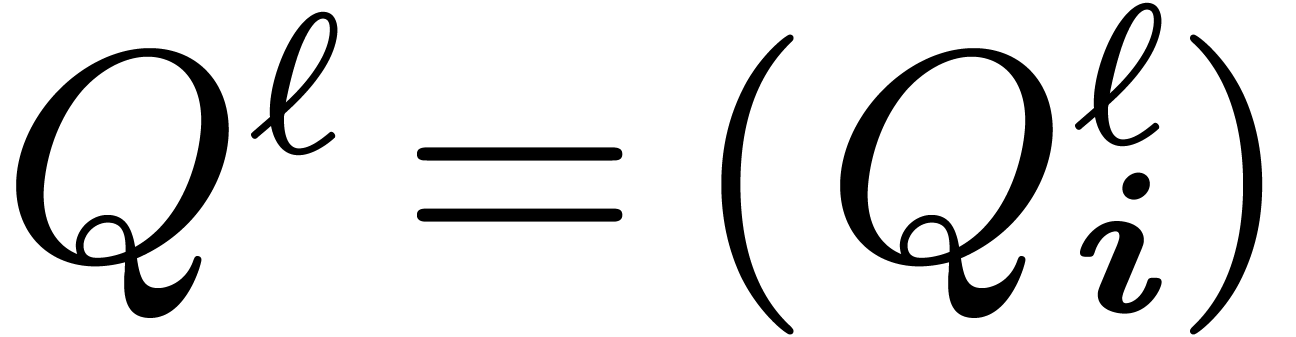 ,
,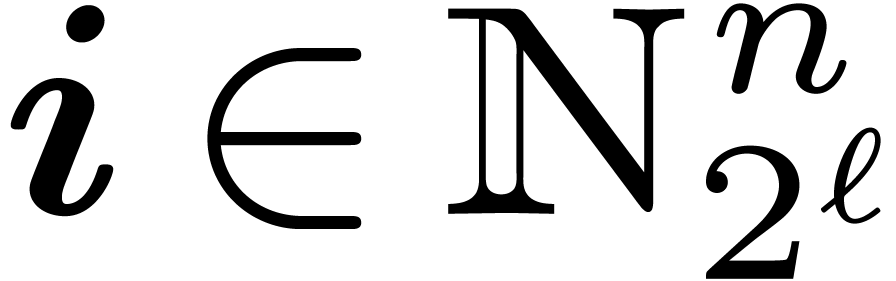 .
.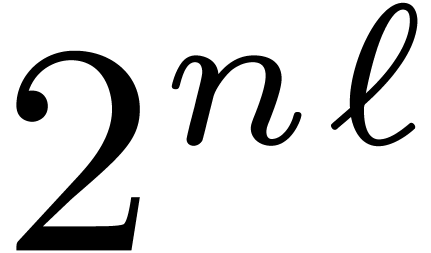 multiplications in
multiplications in
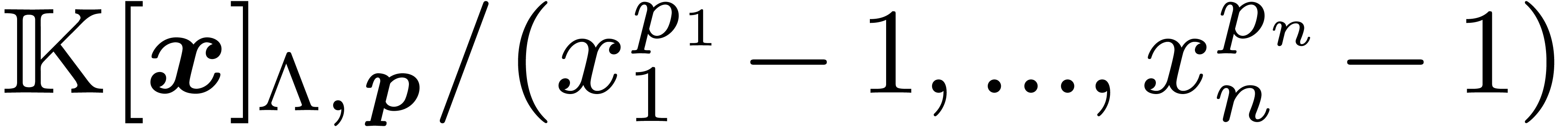 .
.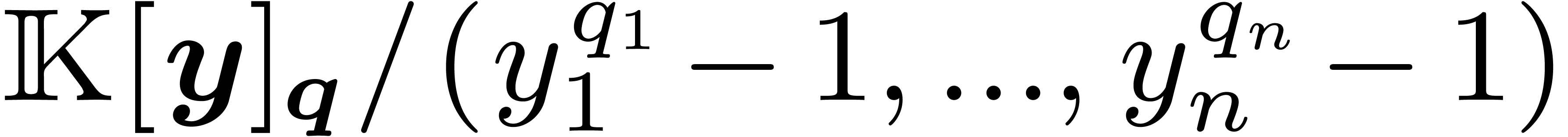 .
.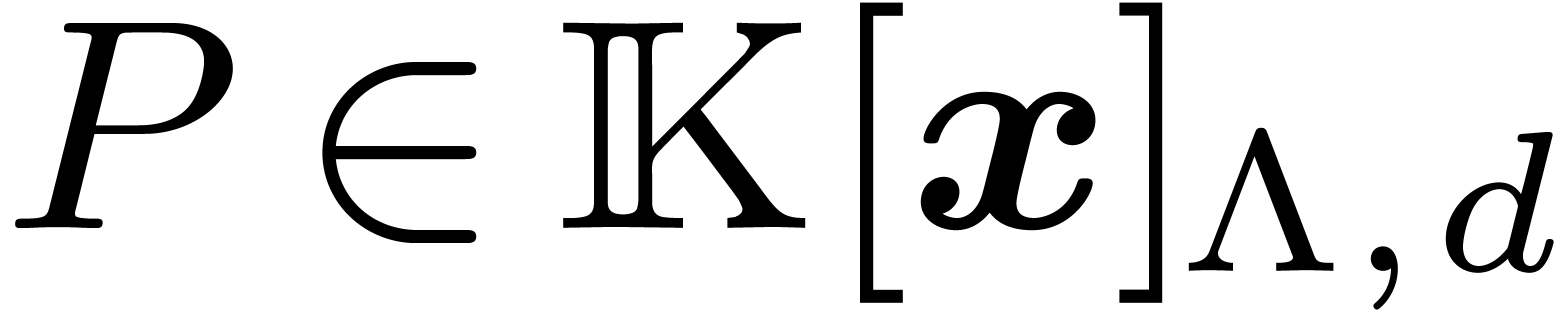
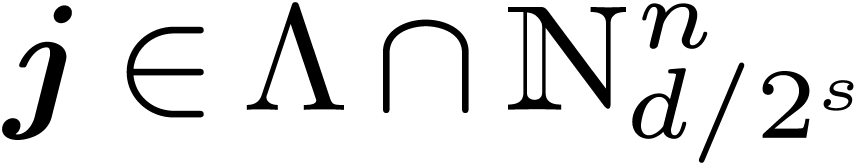 do
do

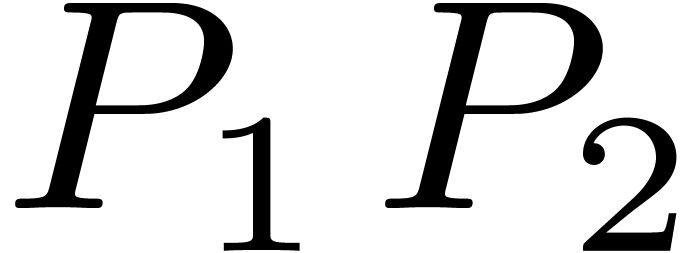
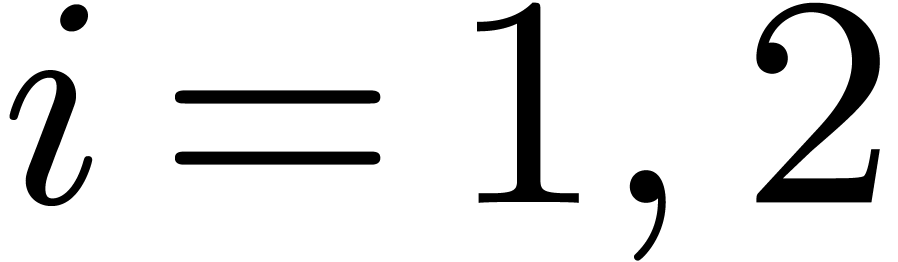 do
do
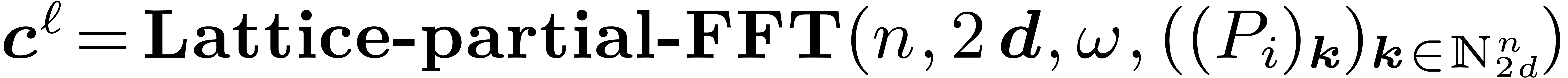
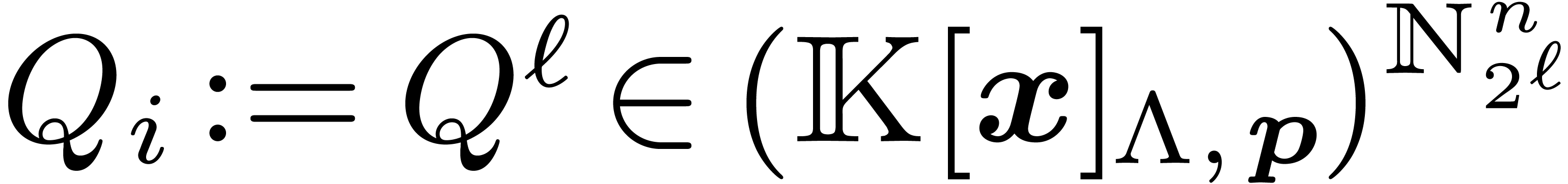 obtained from
obtained from  as a vector of
as a vector of 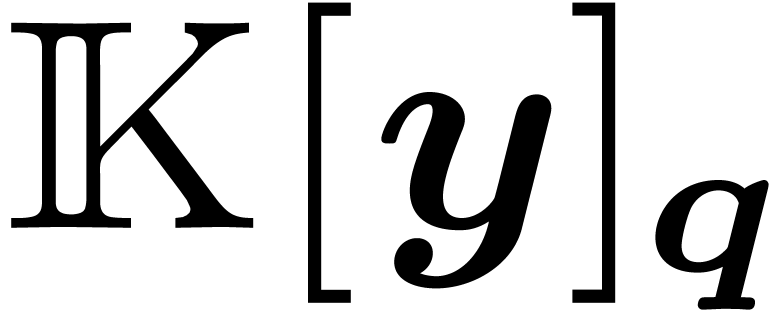 using Proposition
using Proposition  in
in 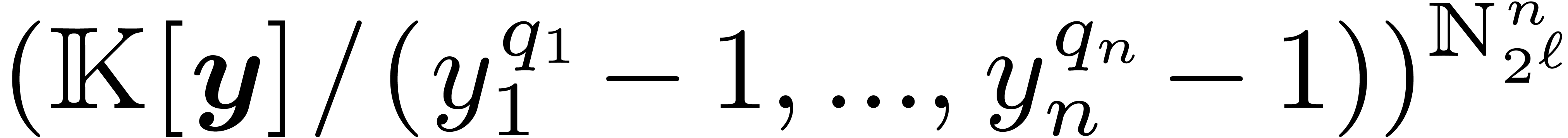
 as a vector of
as a vector of 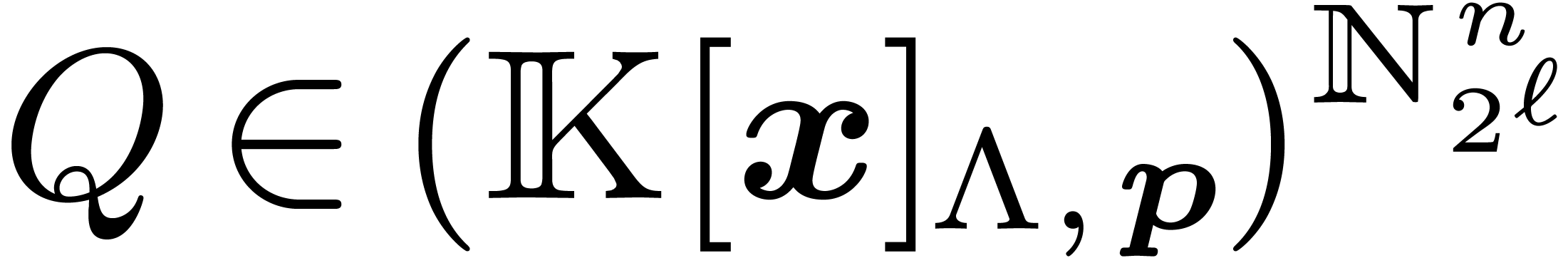
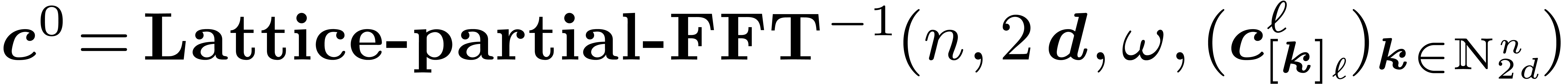
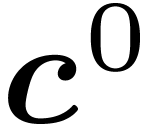
 is obtained by reversing the loops and inverting the butterflies of
Lattice-partial-FFT.
is obtained by reversing the loops and inverting the butterflies of
Lattice-partial-FFT.
 arithmetic operations in
arithmetic operations in 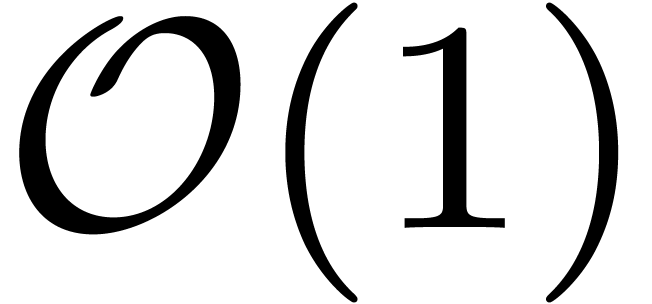 ,
,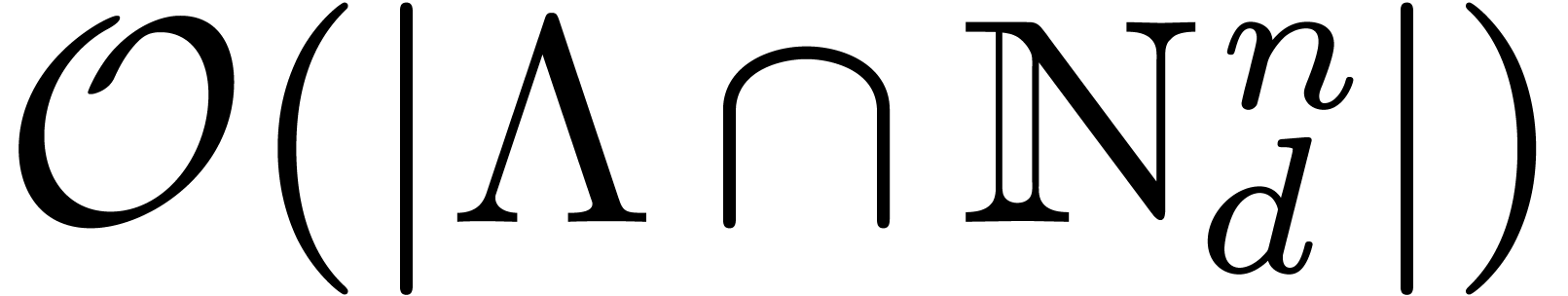 .
.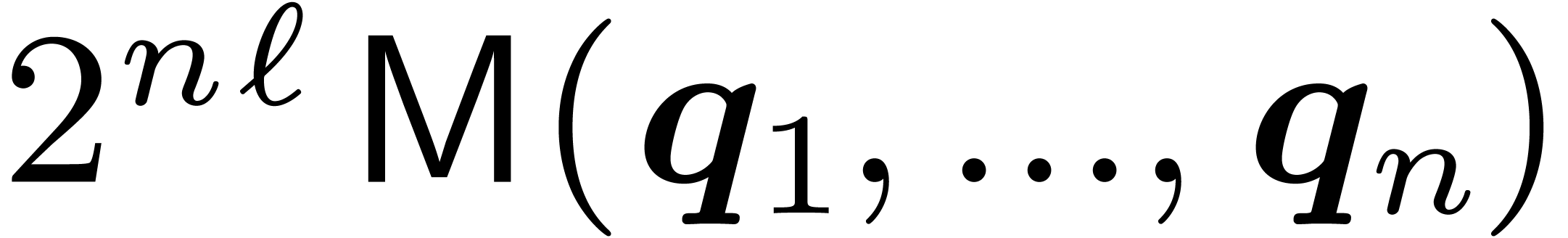 where
where 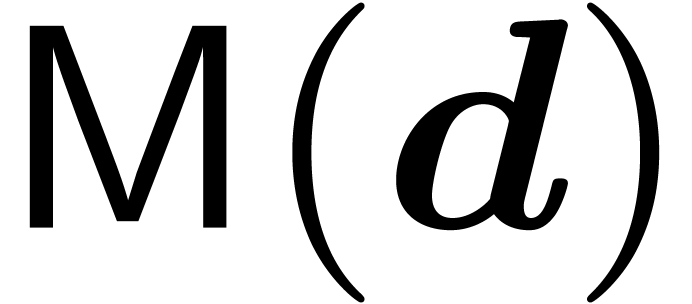 stands for the arithmetic complexity of polynomials
multiplication in
stands for the arithmetic complexity of polynomials
multiplication in 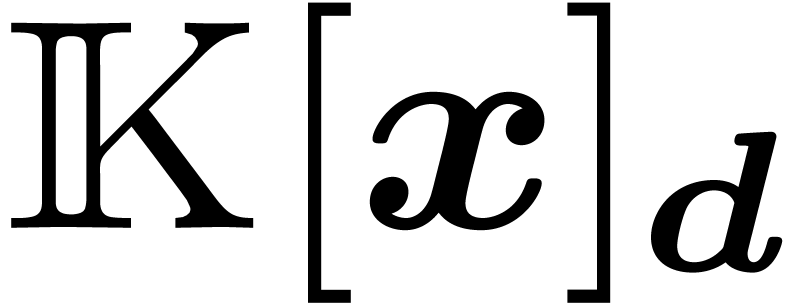 .
.
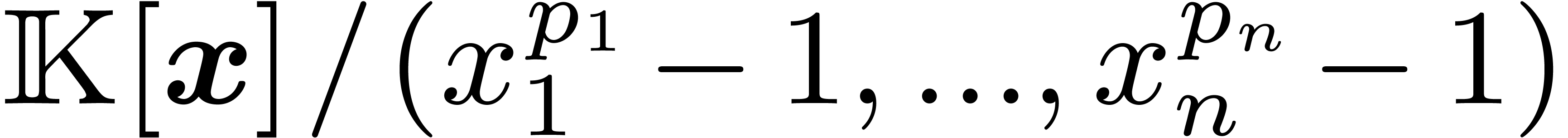 .
. .
.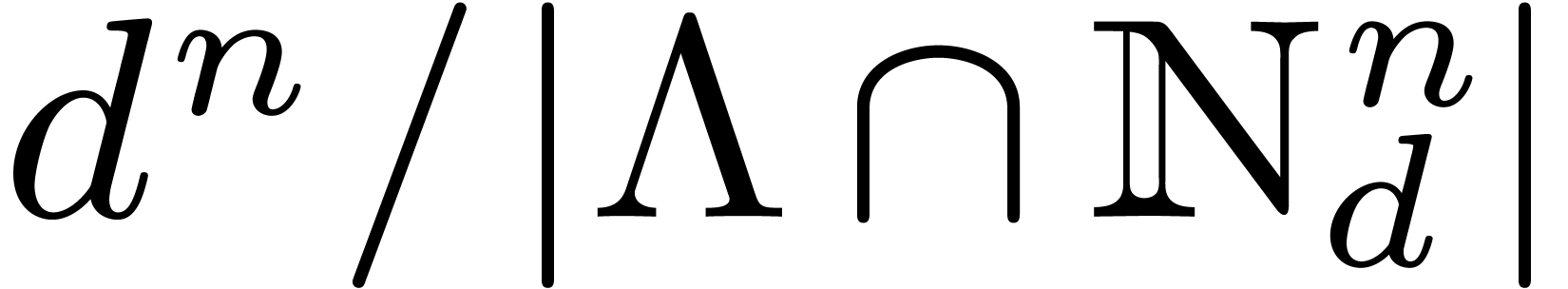 is exactly the volume
is exactly the volume 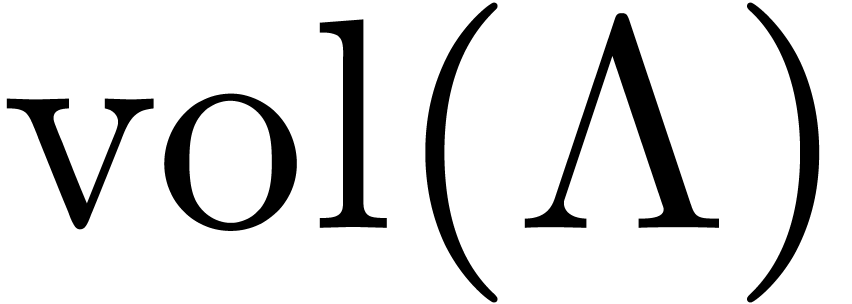 of the lattice, defined by
of the lattice, defined by 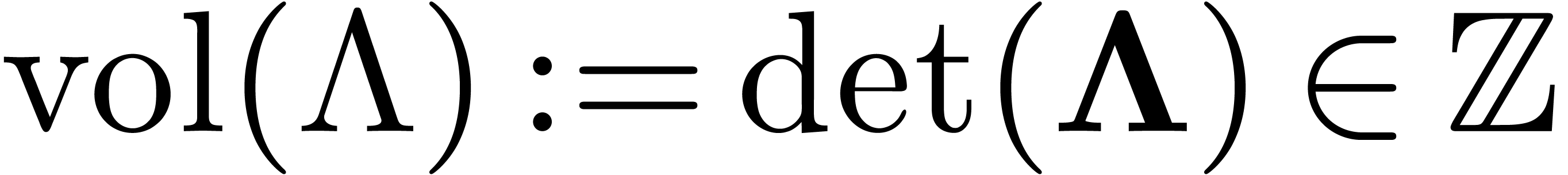 .
. ,
,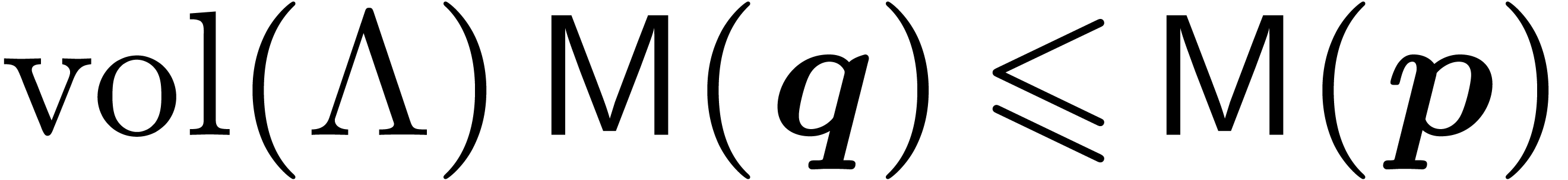 and we
deduce the following theorem.
and we
deduce the following theorem.
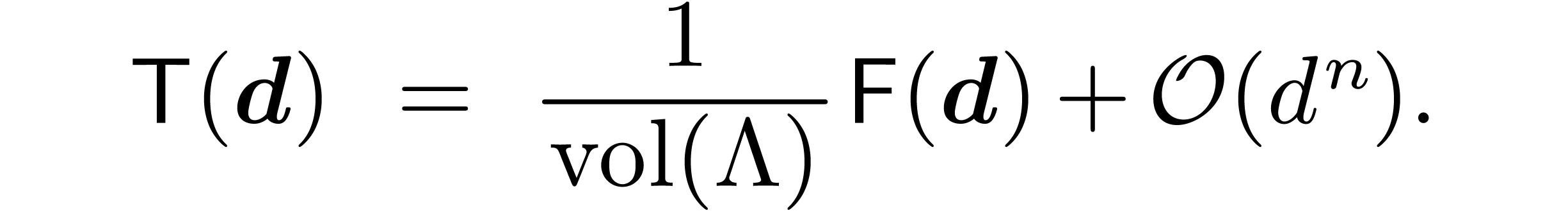
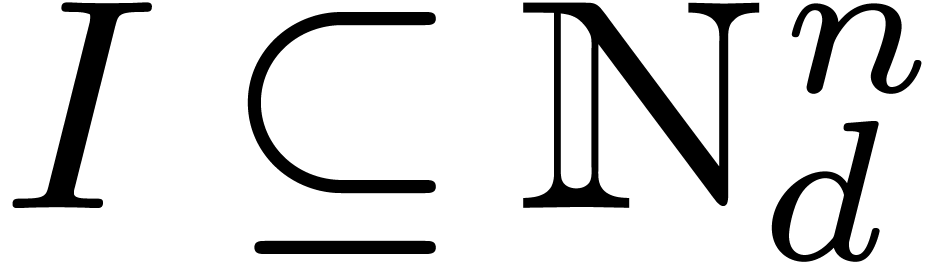 be an
initial segment subset of
be an
initial segment subset of 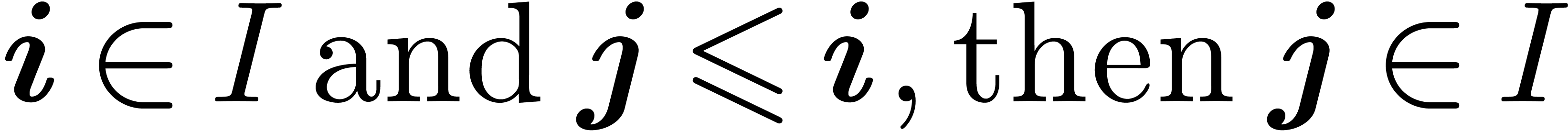 .
.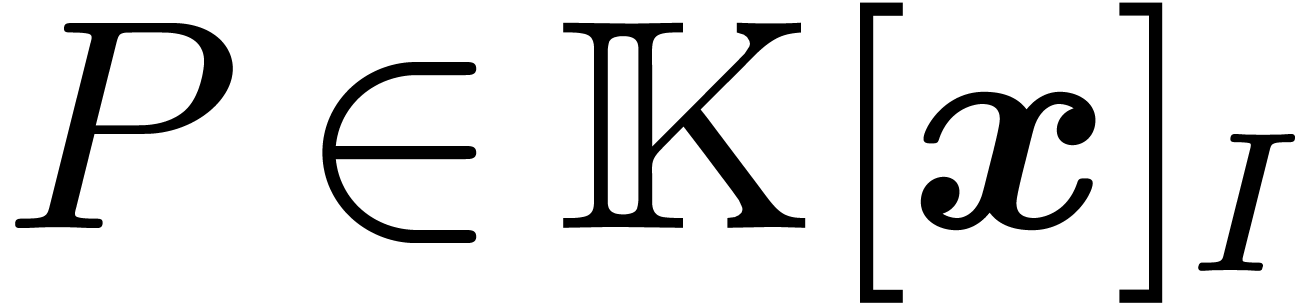 ,
,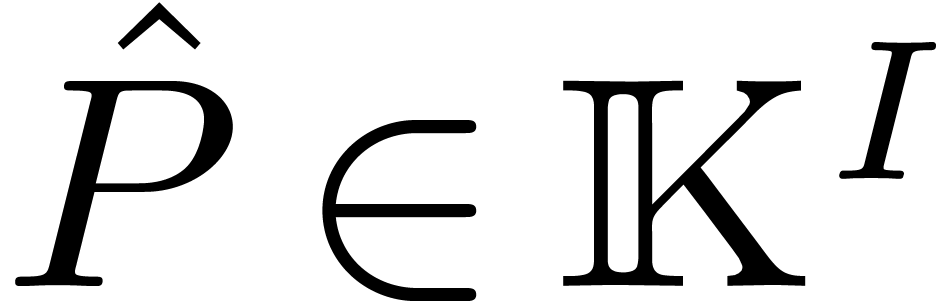 defined by
defined by 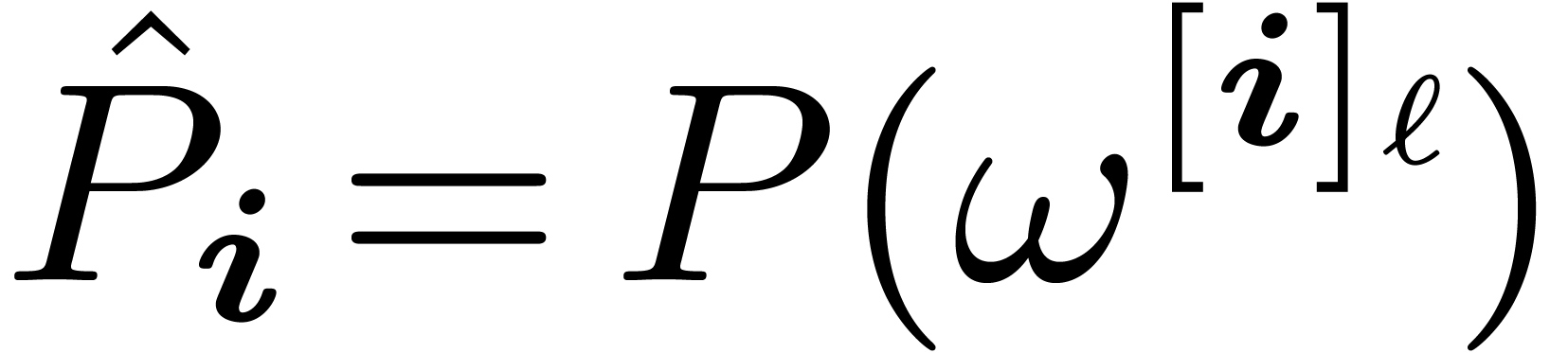 ,
,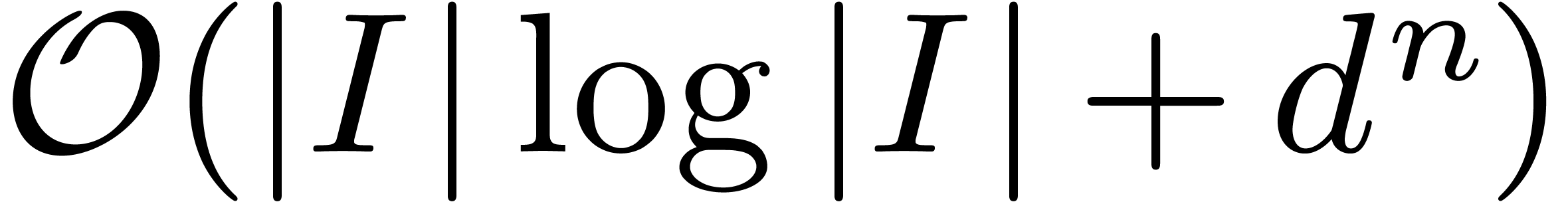 instead of
instead of 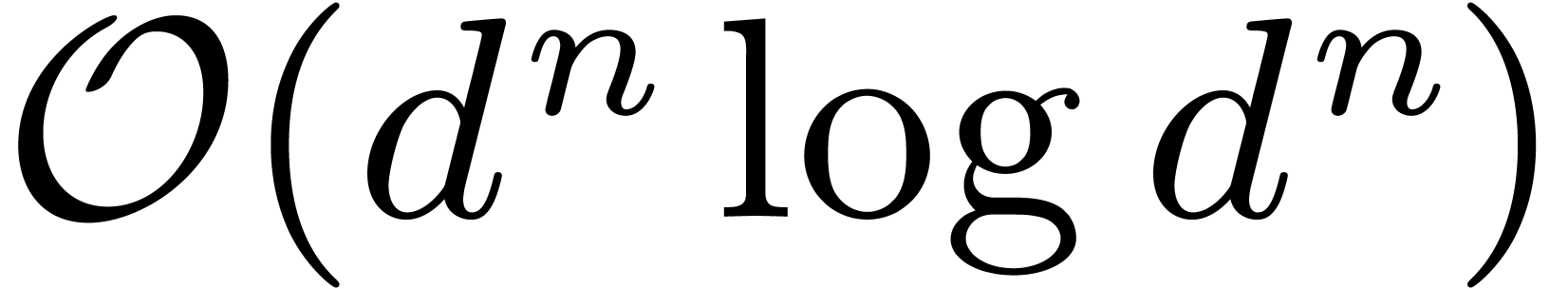 .
.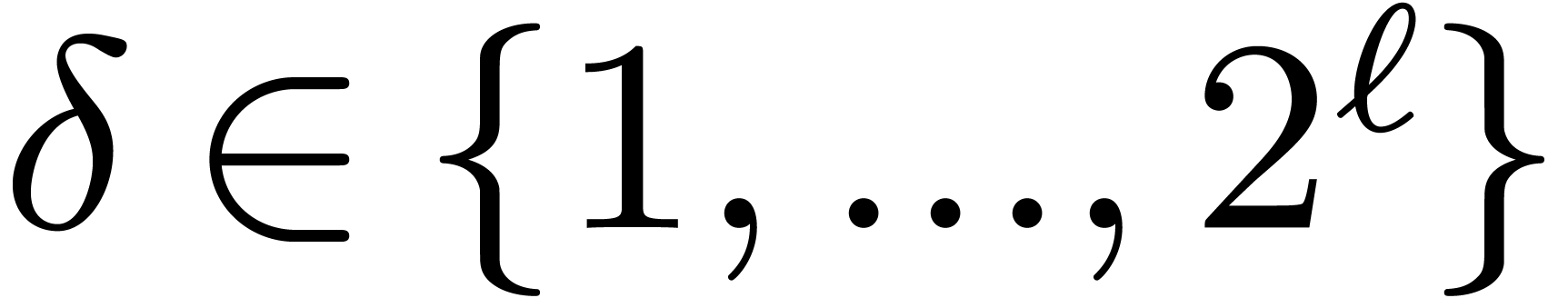 ,
,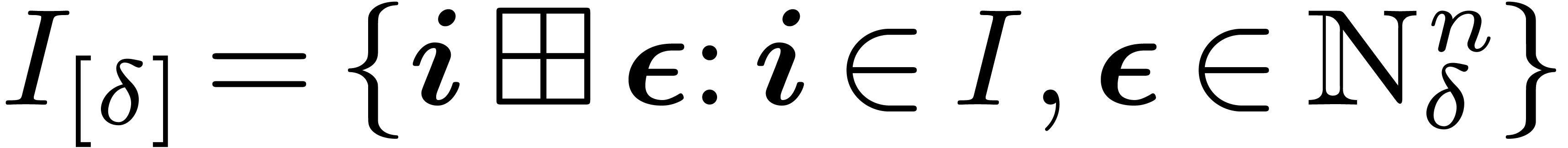 .
.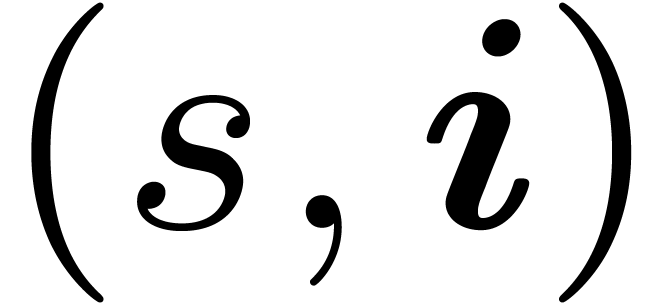 with
with 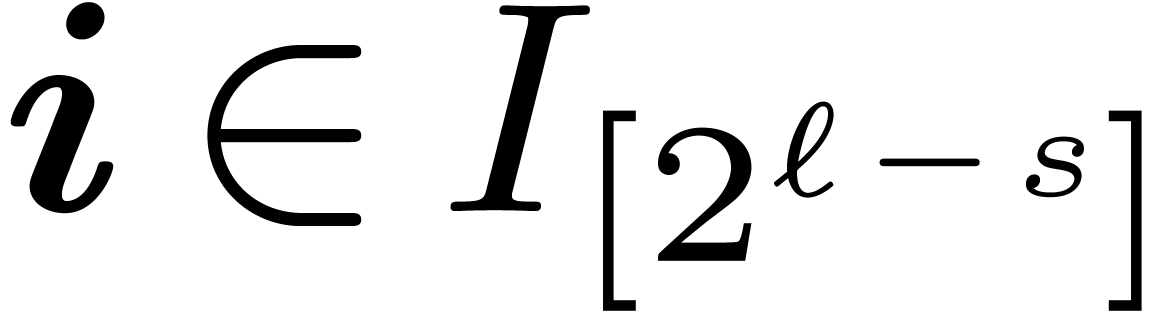 .
.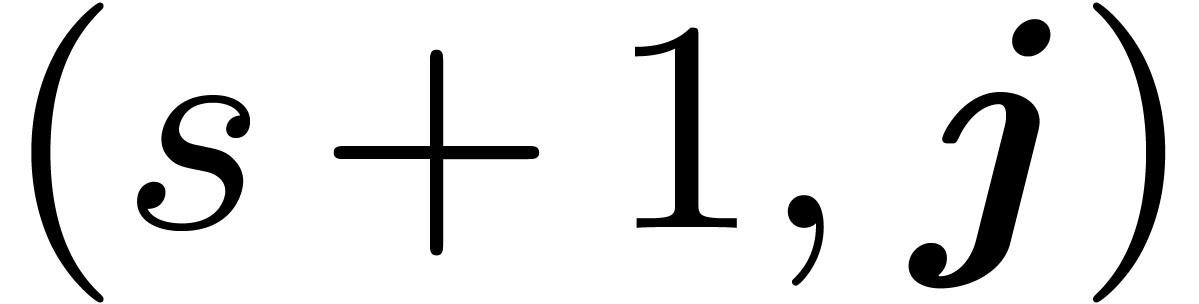 with
with 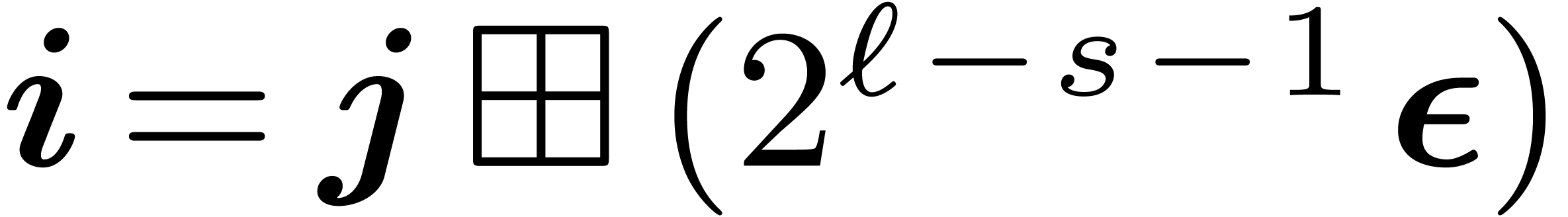 and
and 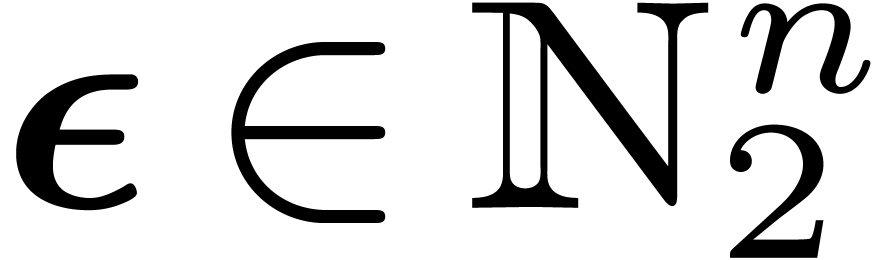 .
.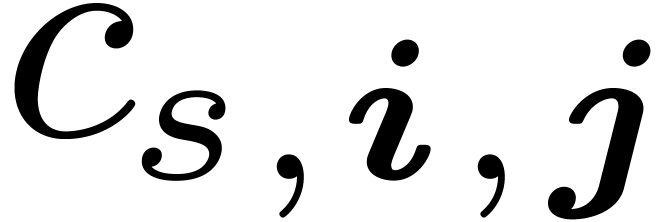 such that
such that
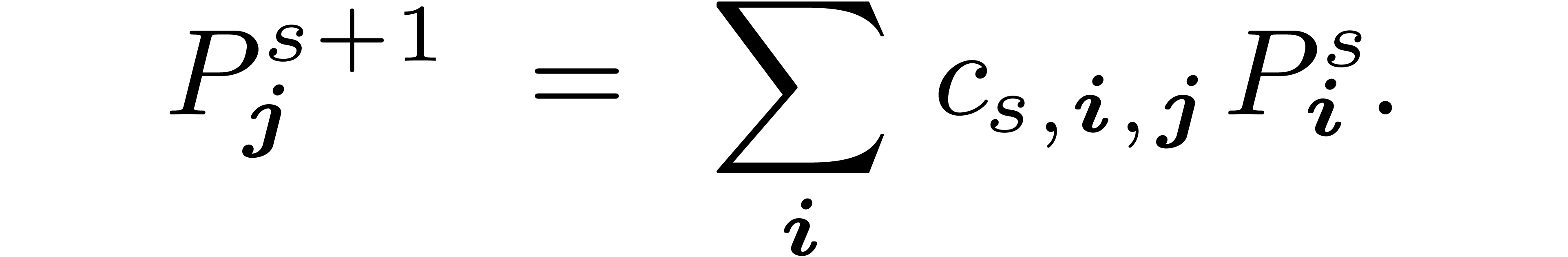
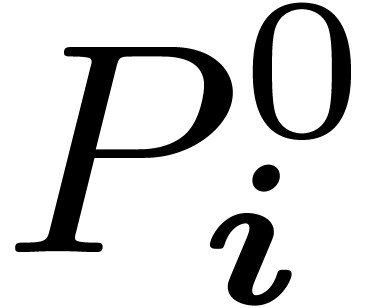 on input and
“fill out” the remaining values
on input and
“fill out” the remaining values 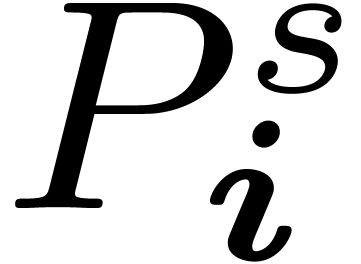 for
increasing values of
for
increasing values of 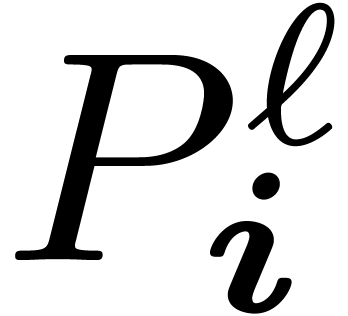 with
with 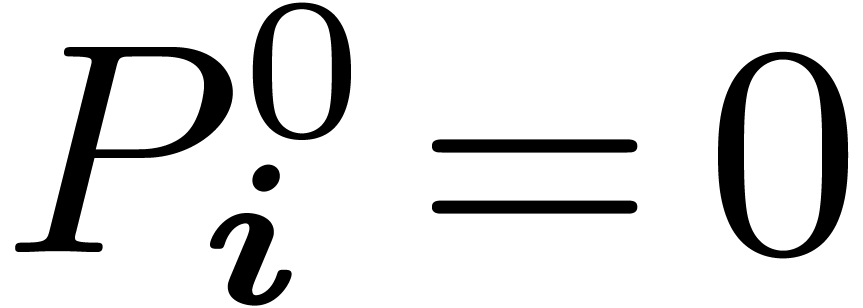 with
with  .
. is stable under
is stable under  is
also stable under
is
also stable under  under the action of
under the action of 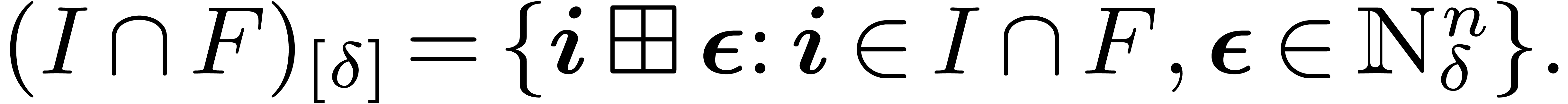 Given a
Given a 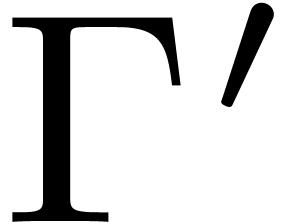 of the above graph
of the above graph 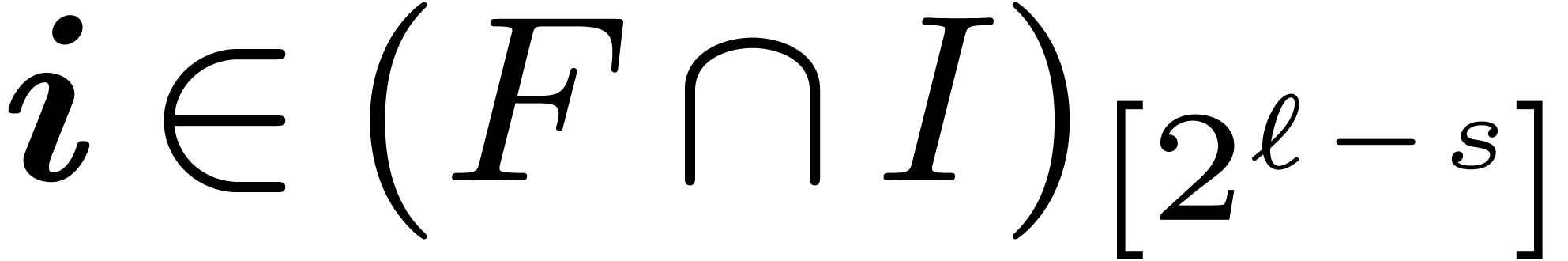 .
.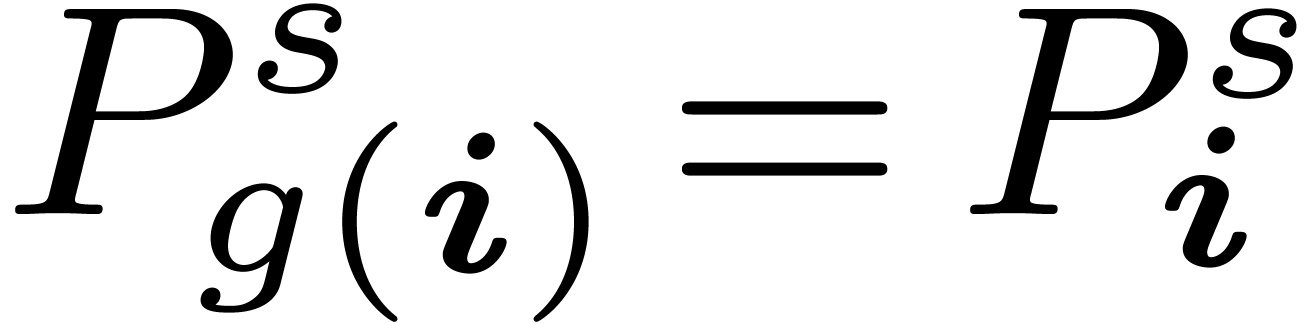 for all
for all 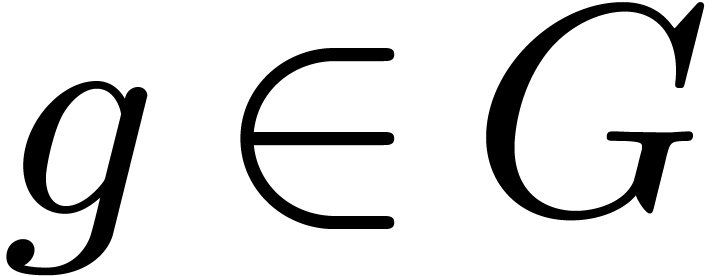 such that
such that 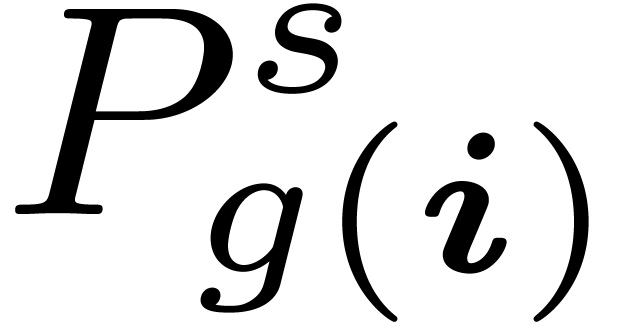 .
. of
of  ,
,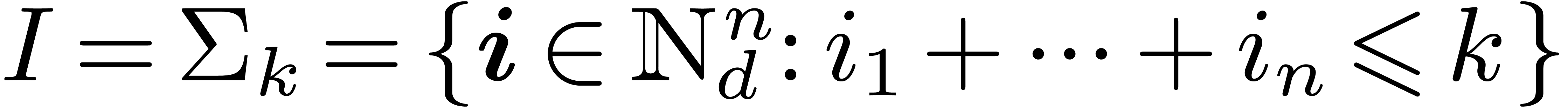 ,
, ,
,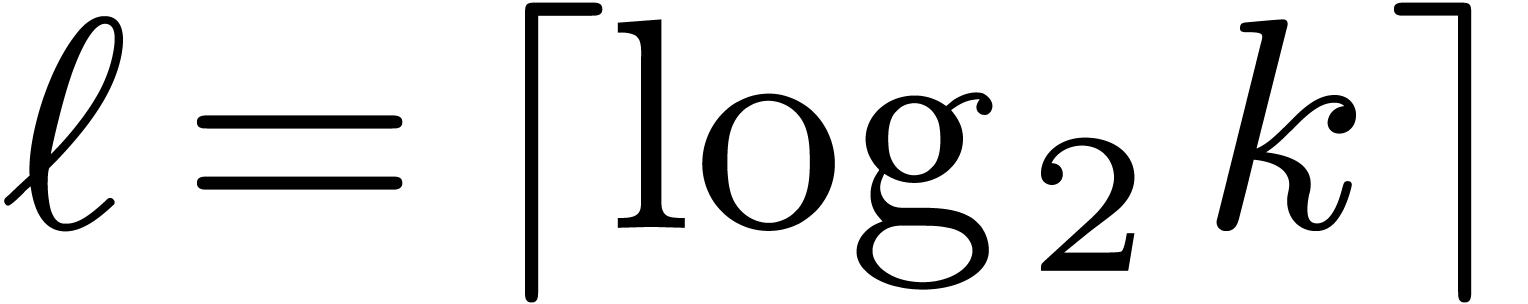 .
.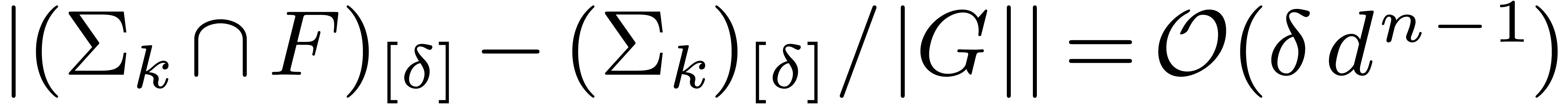 ,
,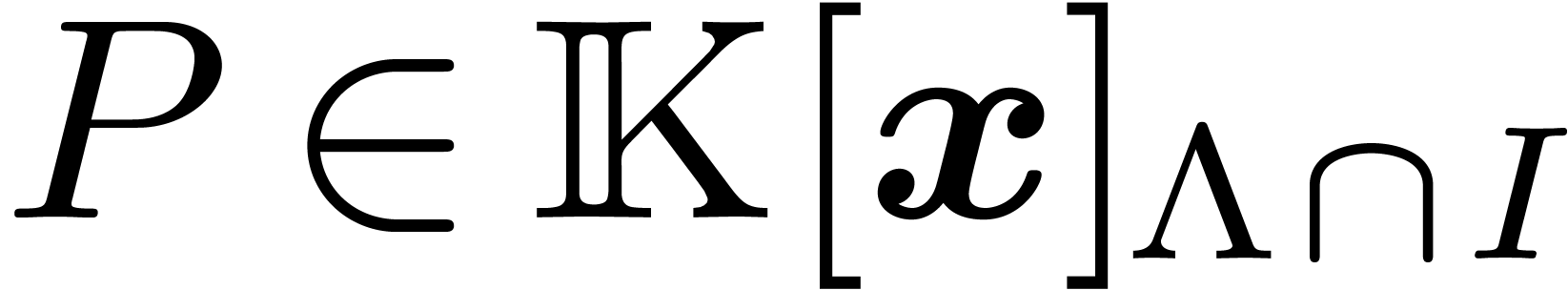 ,
, which preserves the fundamental domains.
More precisely, with
which preserves the fundamental domains.
More precisely, with 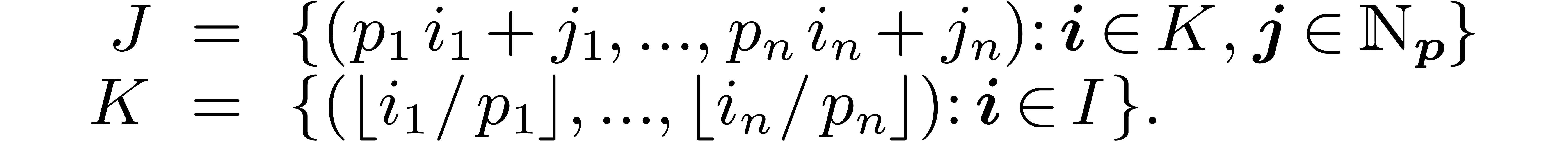
 can then be regarded as
can then be regarded as
 and
initial segment
and
initial segment  ,
, TFTs lattice FFTs on a fundamental domain.
Asymptotically speaking, we thus gain a factor
TFTs lattice FFTs on a fundamental domain.
Asymptotically speaking, we thus gain a factor  with respect to a usual TFT with initial segment
with respect to a usual TFT with initial segment  for
for 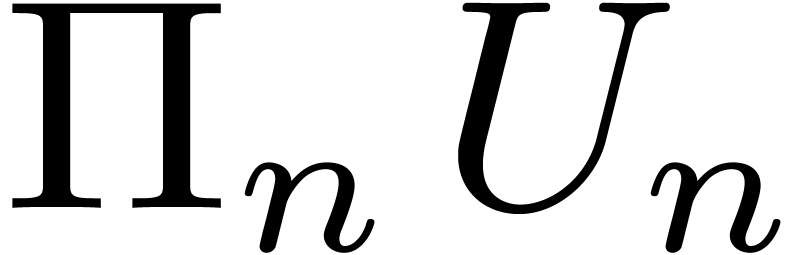 ,
, is the group of
is the group of  permutation matrices and
permutation matrices and  the group of diagonal matrices whose entries are all
roots of unity. Indeed, any such group
the group of diagonal matrices whose entries are all
roots of unity. Indeed, any such group  ,
, .
.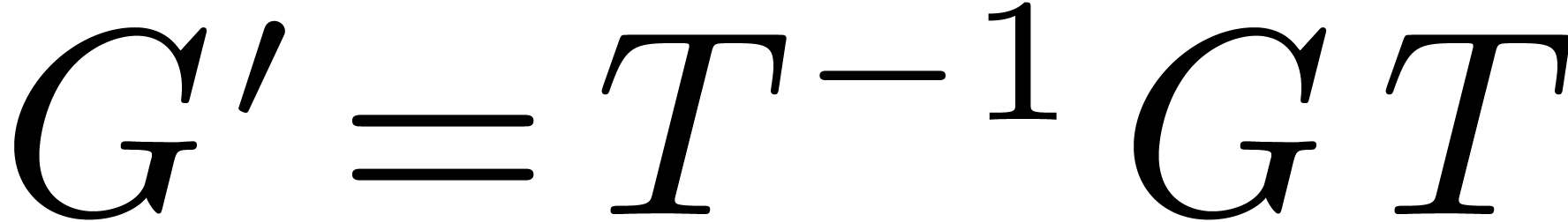 of groups
of groups  can be done “once
and for all” on the initial differential equations, after which
the results of this paper again apply.
can be done “once
and for all” on the initial differential equations, after which
the results of this paper again apply.
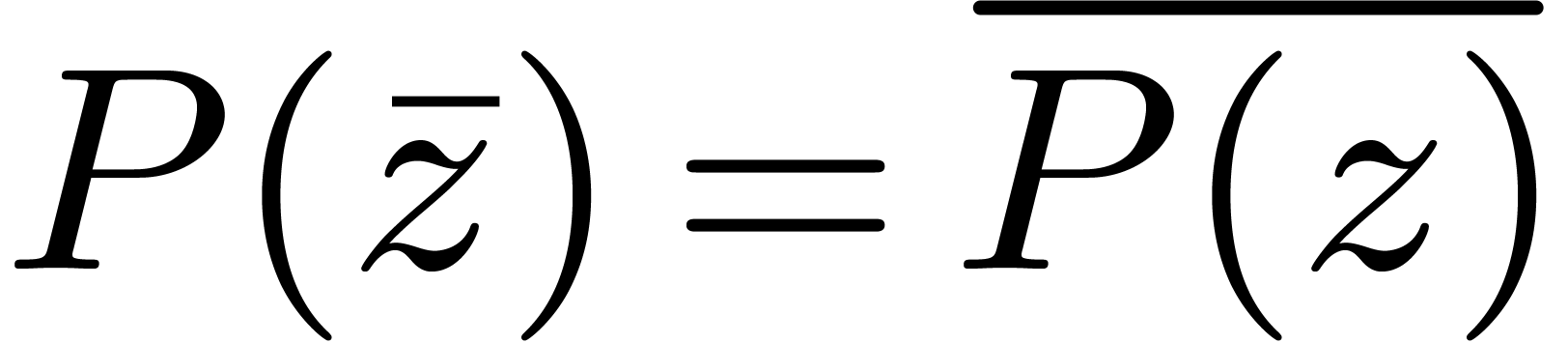 .
.