Preserving syntactic correctness
while editing mathematical formulas |
|
Joris van der Hoevena,
Grégoire Lecerfb, Denis
Rauxc
|
|
Laboratoire d'informatique, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau
|
|
a. Email:
vdhoeven@lix.polytechnique.fr
|
|
b. Email:
lecerf@lix.polytechnique.fr
|
|
c. Web:
raux@lix.polytechnique.fr
|
|
|
GNU TeXmacs is a free software for editing scientific documents
with mathematical formulas, which can also be used as an interface
for many computer algebra systems. We present the design of a new
experimental mathematical editing mode which preserves the
syntactic correctness of formulas during the editing process
(i.e. all formulas can be parsed using a suitable,
sufficiently rich grammar). The main constraint is to remain as
closely as possible to the existing presentation-oriented formula
editor, which has the advantage of being very user friendly.
Keywords: mathematical editing, syntactic
correctness, packrat parsing, TeXmacs
A.M.S. subject classification: 68U15,
68U35, 68N99
|
1.Introduction
Most mathematical formulas in current scientific papers only carry very
poor semantics. For instance, consider the two formulas 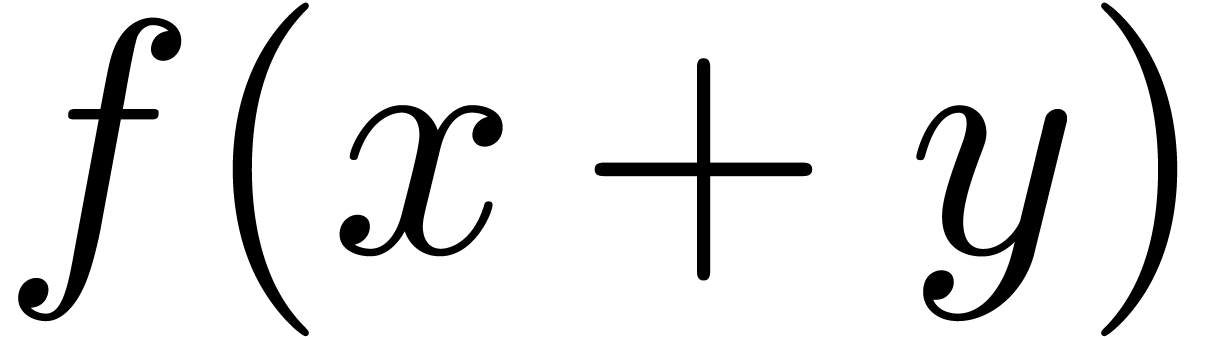 and
and 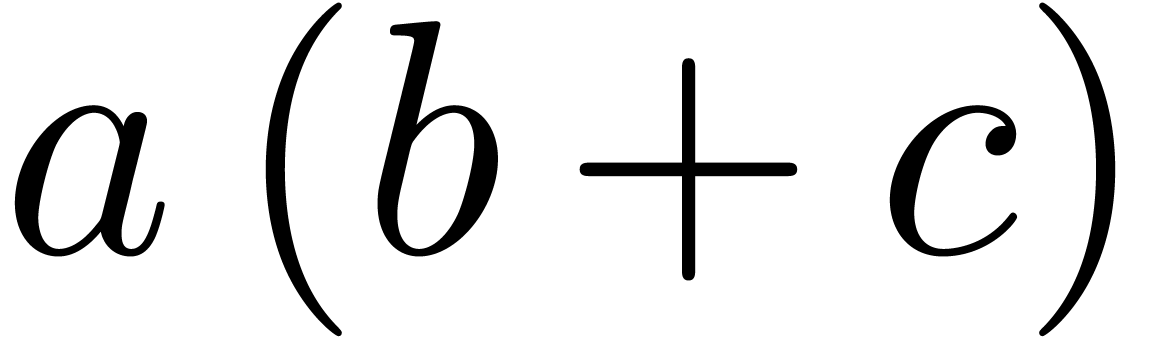 . People typically enter
these formulas using the LaTeX pseudo-code $f(x+y)$ and
$a(b+c)$. Doing so, we do not transmit the important
information that we probably meant to apply
. People typically enter
these formulas using the LaTeX pseudo-code $f(x+y)$ and
$a(b+c)$. Doing so, we do not transmit the important
information that we probably meant to apply 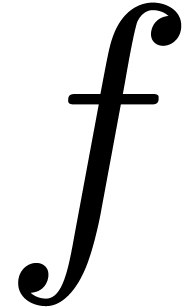 to
to
 in the first formula and to multiply
in the first formula and to multiply  with
with  in the second one. The
problem to automatically recover such information is very hard in
general. For this reason, it would be desirable to have mathematical
authoring tools in which it is easy to write formulas which
systematically carry this type of information.
in the second one. The
problem to automatically recover such information is very hard in
general. For this reason, it would be desirable to have mathematical
authoring tools in which it is easy to write formulas which
systematically carry this type of information.
One important application where semantics matters is computer algebra.
Popular computer algebra systems such as Mathematica
and Maple contain formula editors in which it is
only possible to input formulas which can at least be understood from a
syntactical point of view by the system. However, these systems were not
really designed for writing scientific papers: they only offer a
suboptimal typesetting quality, no advanced document preparation
features, and no support for more informal authoring styles which are
typical for scientific papers.
The GNU TeXmacs editor was designed to be a fully fledged wysiwyg
alternative for TeX/LaTeX, as well as an interface for many computer
algebra systems. The software is free and can be downloaded from http://www.texmacs.org. Although formulas only
carried barely more semantics than LaTeX in old versions of TeXmacs, we
have recently started to integrate more and more semantic editing
features. Let us briefly discuss some of the main ideas behind these
developments; we refer to [7] for more details and
historical references to related work.
First of all, we are only interested in what we like to call
“syntactical semantics”. In the formula  , this means that we wish to capture the fact
that
, this means that we wish to capture the fact
that  is an infix operator with arguments
is an infix operator with arguments  and
and  , but
that we are uninterested in the fact that
, but
that we are uninterested in the fact that  stands
for addition on integers. Such syntactical semantics can be modeled
adequately using a formal grammar. Several other mathematical formula
editors are grammar-based [1–3, 8,
10, 11], and they make use of various kinds of
formal grammars. In TeXmacs, we have opted for so called packrat
grammars [4, 5], which are particularly easy
to implement and customize.
stands
for addition on integers. Such syntactical semantics can be modeled
adequately using a formal grammar. Several other mathematical formula
editors are grammar-based [1–3, 8,
10, 11], and they make use of various kinds of
formal grammars. In TeXmacs, we have opted for so called packrat
grammars [4, 5], which are particularly easy
to implement and customize.
A second question concerns the precise grammar that we should use to
parse formulas in scientific documents. Instead of using different
grammars for various areas with different notations, we were surprised
to emperically find out that a well-designed “universal”
mathematical grammar is actually sufficient for most purposes; new
notations can still be introduced using a suitable macro mechanism.
The last main point concerns the interaction between the editor and the
grammar. So far, we implemented a packrat parser for checking the
correctness of a formula. While editing a formula, its correctness is
indicated using colored boxes. It is also possible to detect and
visualize the scopes of operators through the grammar. In addition to
the parser, we implemented a series of tools which are able to detect
and correct the most common syntactical mistakes and enhance existing
documents with more semantics.
In the present paper, we wish to go one step further and enforce
syntactic correctness throughout the editing process. Ideally speaking,
the following requirements should be met:
-
As far as user input is concerned, there should be no essential
difference between editing formulas with or without the new
mechanism for preserving syntactic correctness. For instance, we do
not wish to force users to provide additional
“annotations” for indicating semantics. It should also
be possible to perform any editing action which makes sense from the
purely visual point of view.
-
The implementation should be as independent as possible from the
actual grammar being used. In other words, we strive for a generic
approach, not one for which specific editing routines are
implemented for each individual grammar symbol.
The main technique that we will use for sticking as close as possible to
the old, presentation oriented editing behaviour is to automatically
insert “transient” markup for enforcing correctness during
the editing process. For instance, when typing X+, TeXmacs will
display
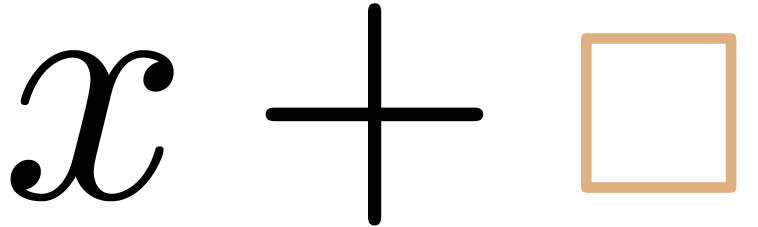
The transient box is used to indicate a missing symbol or subexpression
and will be removed as soon as the user enters the missing part.
The use of transient boxes for missing symbols or subexpressions is
common in other editors [9]. The question which interests
us here is how to automatically insert such markup when needed in a way
that is essentially independent from specific grammars. In this paper,
we work out the following approach which was suggested in [7]:
before and after each editing operation, subject the formula to suitable
“correction” procedures that are only allowed to add or
remove transient markup. Correcting all errors in a general formula is a
very difficult problem, but the power of our approach comes from the
fact that the editing process is incremental: while typing, the user
only introduces small errors—mostly incomplete formulas—,
which are highly localized; we may thus hope to deal with all possible
problems using a small number of “kinds of corrections”.
Obviously, the simplest kinds of corrections are adding or removing a
transient box at the current cursor position. This is indeed sufficient
when typing simple formulas such as 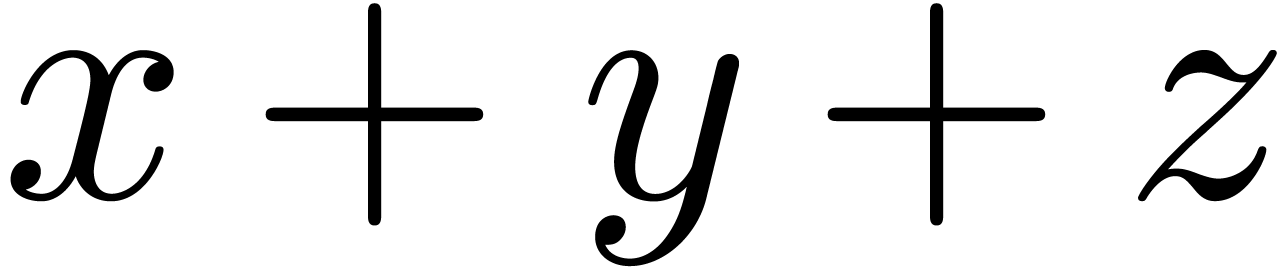 ,
but additional mechanisms are needed in other situations. For instance,
in the formula
,
but additional mechanisms are needed in other situations. For instance,
in the formula  (with the cursor between the
“
(with the cursor between the
“ ” and the
“
” and the
“ ”), entering
another
”), entering
another  results in
results in  (instead of
(instead of  or
or 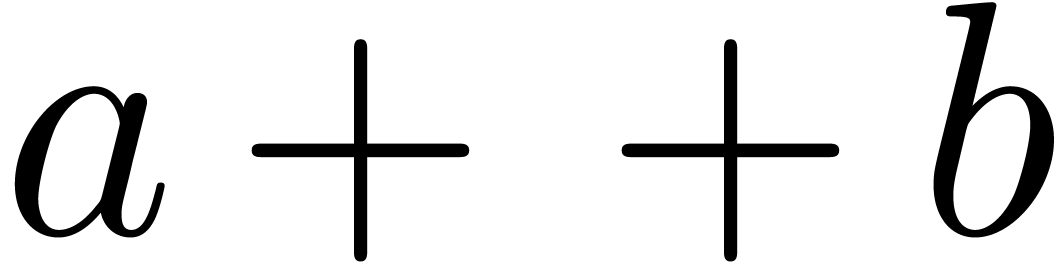 ).
Hitting backspace in the same formula
).
Hitting backspace in the same formula  yields
yields
 ; in this case, the transient
“
; in this case, the transient
“ ” should be
parsed as an infix addition, and not as an ordinary symbol (as was the
case for a transient box).
” should be
parsed as an infix addition, and not as an ordinary symbol (as was the
case for a transient box).
The appropriate corrections are not always so simple. For instance,
consider the quantified expression 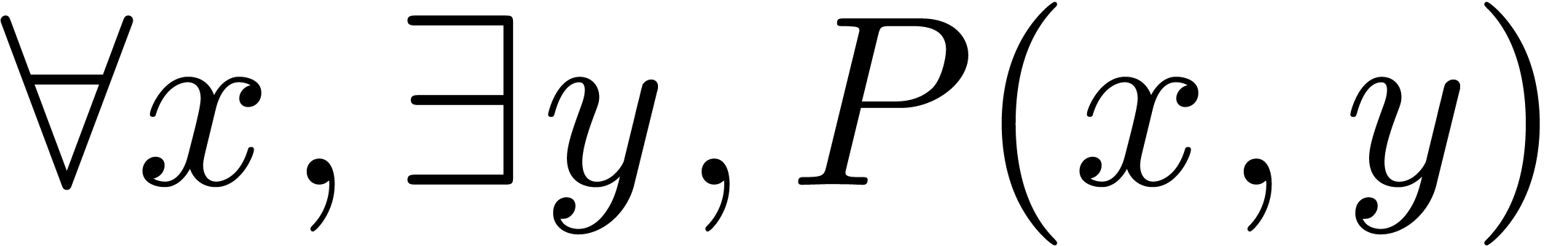 .
Just after we entered the existential quantifier “
.
Just after we entered the existential quantifier “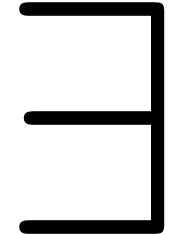 ”, the formula will read
”, the formula will read 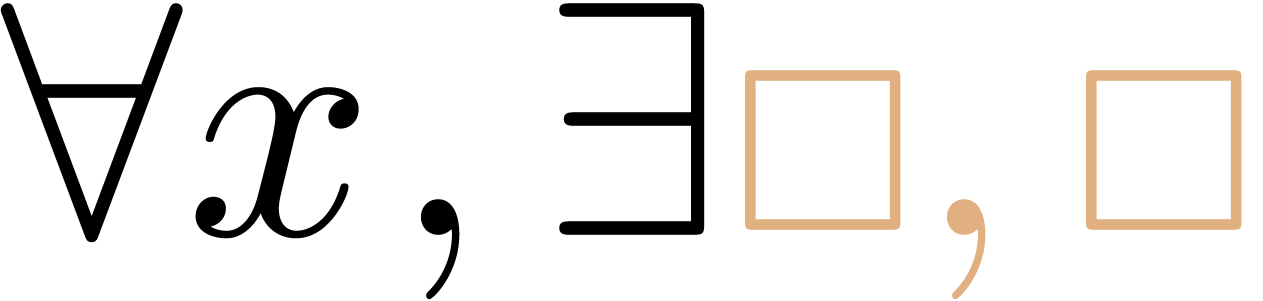 , i.e. it was necessary to add
three transient symbols in order to make the expression syntactically
correct. The fact that our approach should apply to general scientific
documents with mathematical formulas raises several further problems.
For instance, in the formula
, i.e. it was necessary to add
three transient symbols in order to make the expression syntactically
correct. The fact that our approach should apply to general scientific
documents with mathematical formulas raises several further problems.
For instance, in the formula
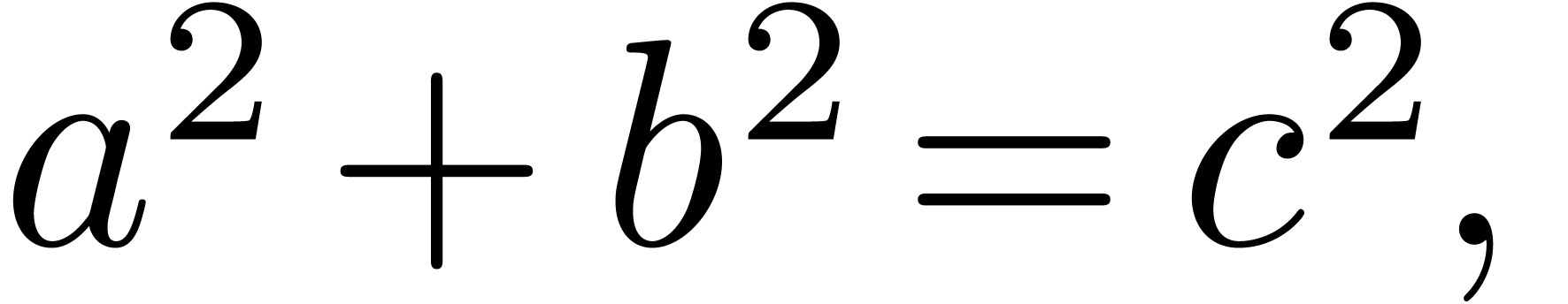
the trailing ponctuation “,” is incorrect from a
mathematical point of view, but needed inside the surrounding English
sentence. Similarly, more work remains to be done on the most convenient
way to include English text inside formulas while maintaining syntactic
correctness.
Yet another difficulty stems from the implementation: one needs to make
sure that the necessary corrections take place after any kind
of editing operation. However, for efficiency reasons, it is important
to only run the correction procedures on small parts of the document.
Inside an existing editor such as TeXmacs, these requirements turn out
to be quite strong, so some trade-offs may be necessary.
In what follows, we report on our first implementation of these ideas
inside TeXmacs. We describe and motivate the current design, discuss
remaining problems, and outline directions for future improvements. Of
course, more user feedback will be necessary in order to make the new
mechanisms suitable for wide-spread use.
2.Survey of formula editing with TeXmacs
In this section, we briefly recall the main design philosophy behind the
TeXmacs formula editor. We start with the description of the original,
purely presentation-oriented mathematical editing mode. We pursue with
the more recent grammar-based editing features, which are presented in
more detail in [7].
2.1.Presentation oriented editing
The original goal behind TeXmacs was to provide a user friendly editor
for mathematical papers with a similar typesetting quality as TeX. The
challenge was to design a real time wysiwyg editor for complex,
structured documents. Some early inspiration came from the idea [1] that graphically oriented math editors achieve the highest
level of user friendliness. For instance, when pressing the right arrow
key, the cursor should move to the right if possible (instead of moving
forward in some abstract document tree, as was the case in some other
existing editors). Early versions of TeXmacs used algorithms for the
cursor movement which achieved this in a systematic way [6],
while still making sure that all possible cursor positions in the
corresponding document tree could be reached.
Another aspect of user friendliness concerned the efficiency of
mathematical input methods. We designed highly efficient (and easy to
memorize) keyboard shortcuts for entering common mathematical symbols,
such as ->
for 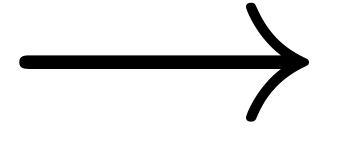 , <= for
, <= for 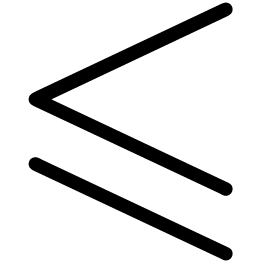 , <⇥/ for
, <⇥/ for 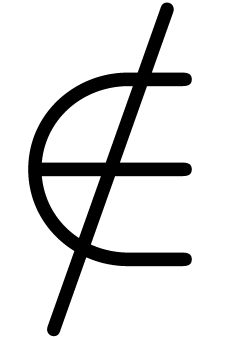 , ⇧R⇧R for
, ⇧R⇧R for  , etc. TeXmacs also implements many
“structured editing operations”, so as to fully exploit the
structure of documents. For instance, adding a row or column to a matrix
can be done by pressing a single key or keyboard combination. Similarly,
it is easy to change a matrix into a determinant or vice versa.
, etc. TeXmacs also implements many
“structured editing operations”, so as to fully exploit the
structure of documents. For instance, adding a row or column to a matrix
can be done by pressing a single key or keyboard combination. Similarly,
it is easy to change a matrix into a determinant or vice versa.
2.2.Grammar-based editing
The next challenge for TeXmacs is to ensure that we can only enter
syntactically correct formulas, while keeping a presentation-oriented
interface, which proved to be most user friendly. The first steps of
this program were made in [7]. Now syntactic correctness is
usually modeled as “parsability against a suitable grammar”.
Before anything else, one should decide on the grammar. In particular,
does a single “universal grammar” suffice, or do we need
many different grammars, depending on the preferred notations of
authors?
For reasons that are explained in detail in [7], we opted
for the development of a universal packrat grammar [4, 5] for parsing all our mathematical formulas. In order to
conserve a sufficient degree of flexibility for the introduction of new
notations, we rely on a combination of two techniques: on the one hand,
TeXmacs comes with a powerful macro language for introducing new markup
elements. On the other hand, we introduced a special construct which
allows a symbol or expression to be behave (i.e. be parsed)
as an arbitrary other symbol or expression. This allows you for instance
to annotate the symbol  to behave as
to behave as  , which implies that
, which implies that 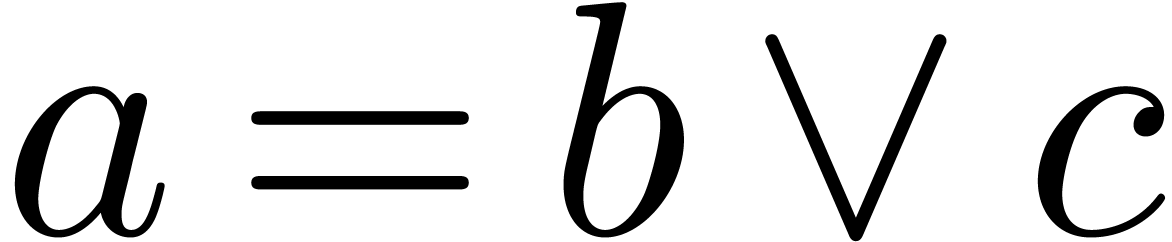 will be parsed as
will be parsed as 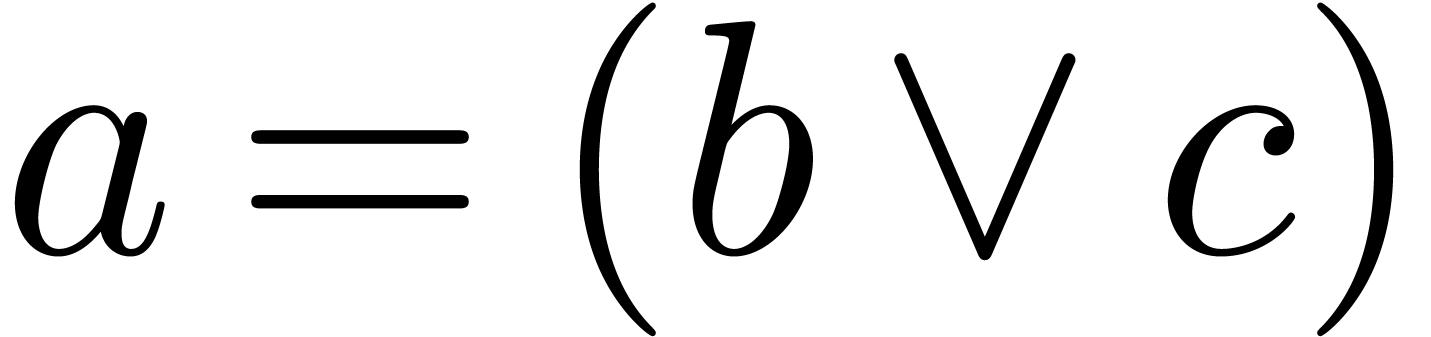 instead of
instead of 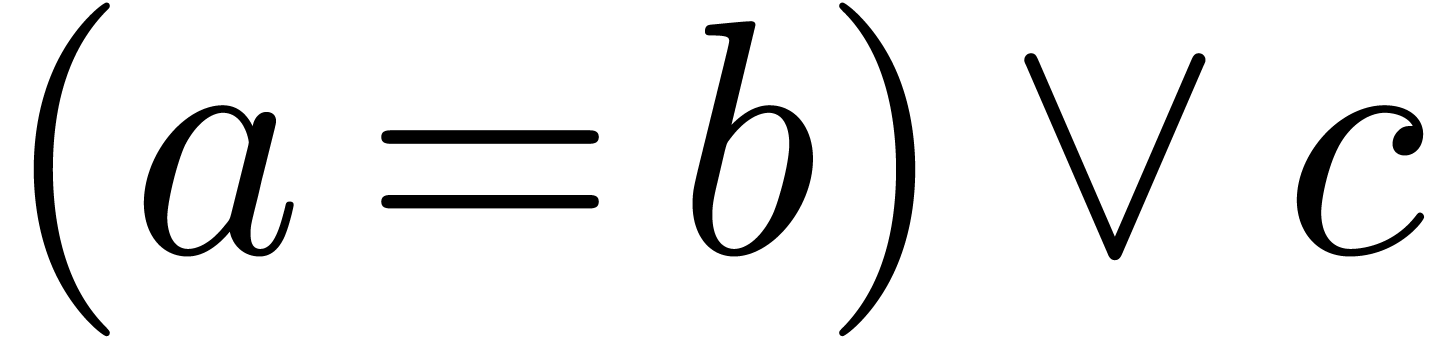 .
.
One of the major difficulties of semantic editing is a clean treatment
of homoglyphs, i.e. symbols with the same
graphical shape, but a different syntactical meaning. The most annoying
homoglyph is the multiplication/function-application ambiguity mentioned
in the introduction. Another good example concerns the wedge product
 and logical conjunction
and logical conjunction 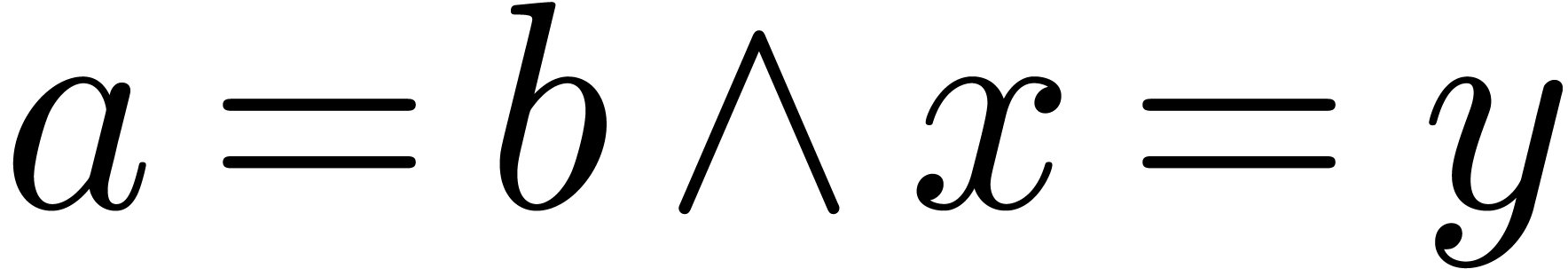 , which admit different binding forces. Fortunately,
there are not that many mathematical homoglyphs; for this reason, we
advocate the introduction of separate symbols for them into the Unicode standard.
, which admit different binding forces. Fortunately,
there are not that many mathematical homoglyphs; for this reason, we
advocate the introduction of separate symbols for them into the Unicode standard.
3.Preservation of correctness
In this section, we describe several strategies that can be used to
preserve the syntactic correctness of formulas under editing operations.
TeXmacs currently implements the “multiple correction
schemes” strategy from Sections 3.2 and 3.3.
The reader may try this implementation by downloading version 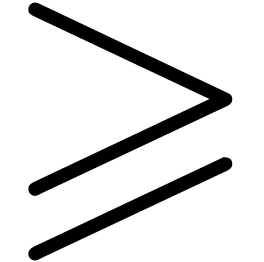 1.99.3 or SVN revision
1.99.3 or SVN revision  9718. The new editing mode is still
experimental and can be enabled inside math mode by clicking on the
9718. The new editing mode is still
experimental and can be enabled inside math mode by clicking on the  icon and checking Semantic
correctness.
icon and checking Semantic
correctness.
3.1.The ideal strategy for preserving
correctness
Ideally speaking, maintaining the syntactic correctness of mathematical
formulas throughout the editing process can be done by
-
Writing a “formula correction” procedure which takes any
(correct or incorrect) formula on input and which inserts or removes
transient markup in order to make it correct.
-
Run the correction procedure on all modified formulas in the
document(s) after every editing operation.
This ideal strategy is simple and robust; it trivially guarantees the
correctness of all formulas throughout the editing process. However, it
does not take into account the specific nature of certain editing
operations. In particular, it does not exploit the locality of many
editing actions.
Example 1. Consider
the strict application of the ideal strategy to the creation of a
subscript in the formula 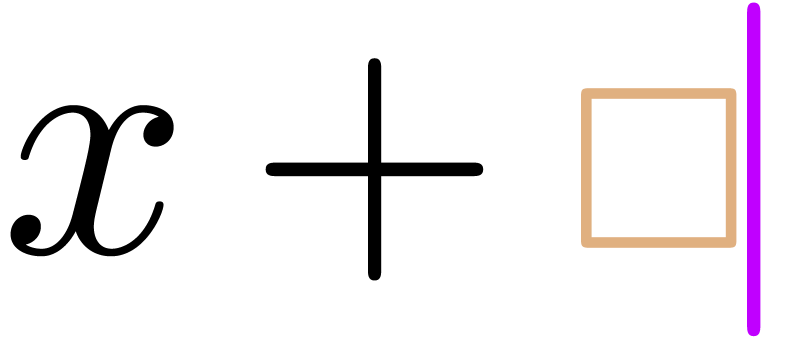 .
Since
.
Since  is a valid symbol, the main editing action
would create an empty subscript for it. We next launch the correction
procedure, which replaces the empty subscript by a transient box,
yielding
is a valid symbol, the main editing action
would create an empty subscript for it. We next launch the correction
procedure, which replaces the empty subscript by a transient box,
yielding 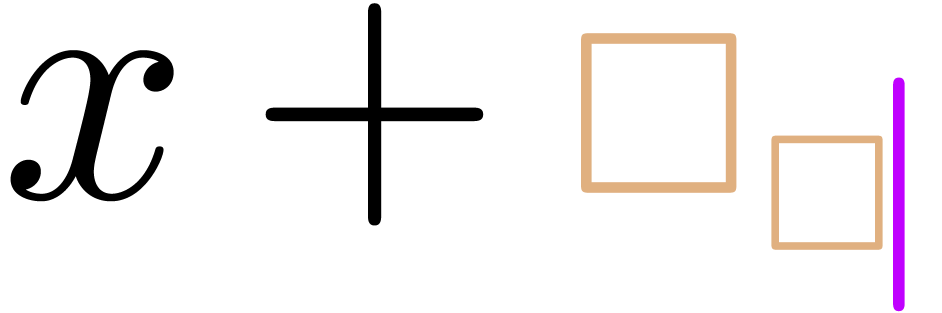 . However, the
. However, the  being transient, the user would rather expect to
endow the “
being transient, the user would rather expect to
endow the “ ”
operator with a subscript: this is indeed what happens in the old
presentation-oriented editing mode when ignoring all transient markup.
In other words, we rather expect to obtain
”
operator with a subscript: this is indeed what happens in the old
presentation-oriented editing mode when ignoring all transient markup.
In other words, we rather expect to obtain 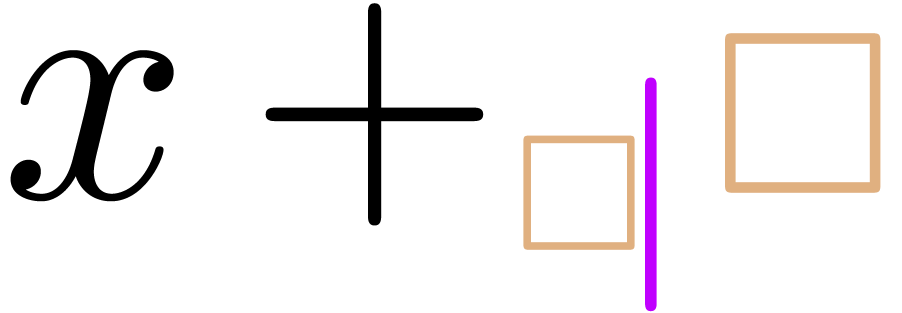 .
.
The above example shows that an indiscriminate global correction
procedure does not provide enough control. In fact, there are usually
many ways to correct a formula by adding or removing transient markup.
In order to determine the “best” solution, one typically
needs to take into account the precise editing operation and the current
cursor position.
Another constraint is that we would like the editor to behave as closely
as possible as the old presentation-oriented editing mode when ignoring
all transient markup. The above example shows that a global correction
procedure does not necessarily respect this constraint. One theoretic
solution to this problem is to remove all transient markup before
performing the editing action and then put it back in when running the
correction procedure. However, this approach may lead to non local
changes in the document for every editing action, which is obviously not
desirable.
Remark 2. For
the above reasons, we have not implemented the correction strategy from
this section yet. The idea nevertheless remains interesting for future
research. Indeed, on the one hand side it raises the interesting
theoretical question of correcting a string so as to make it parsable by
a given (packrat) grammar. From the practical point of view, the ideal
strategy has the important advantage of trivially guaranteeing syntactic
correctness all along. In cases where this is hard to achieve using
other means, it thereby remains a good fallback strategy.
3.2.Multiple correction
schemes
Instead of implementing one global correction procedure, our current
TeXmacs implementation relies on multiple “correction
schemes”. Each correction scheme is allowed to add or remove
transient markup both before and after the actual editing operation. In
other words, it really encapsulates the editing action into a
semantically enhanced editing action. Furthermore, the correction scheme
is allowed to fail (i.e. to produce an incorrect formula at
the end). For this reason, we try multiple correction schemes in a row
(the set of “eligible” schemes depends on the specific
editing action), and stop as soon as we managed to obtain a correct
formula.
In summary, we proceed as follows:
-
Depending on the editing action, determine a list of eligible
correction schemes.
-
Try each eligible correction scheme in the list until we managed to
obtain a correct formula.
-
If none of the correction schemes succeeded, then cancel
the editing action.
For the actual implementation, it is clearly crucial to be able to undo
editing actions whenever necessary, and in a way that is orthogonal to
the usual undo/redo operations in TeXmacs.
Example 3. When
inserting a mathematical symbol, the first correction scheme we try is
the following: first remove all transient markup around the cursor, then
insert the symbol, and finally insert a transient box at the cursor
position (if needed). For instance, typing A+B in an empty
mathematical formula successively yields  ,
,
 ,
,  , and
, and  .
.
Example 4. The
basic correction scheme from the previous example sometimes fails. For
instance, assume that we are in the situation  , and that we add a second “
, and that we add a second “ ”. When applying the basic correction
scheme, we need to correct
”. When applying the basic correction
scheme, we need to correct 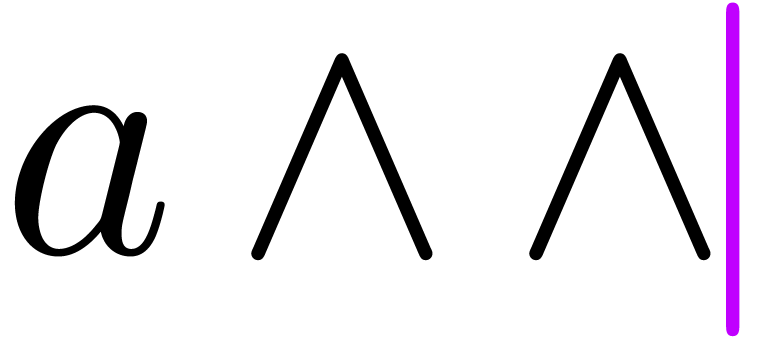 through the insertion
of a single transient box. However, the formula
through the insertion
of a single transient box. However, the formula 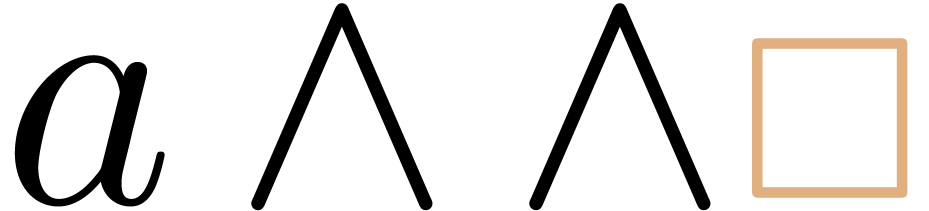 is still incorrect. For this particular case, we therefore use the
following correction scheme: first add a transient box (
is still incorrect. For this particular case, we therefore use the
following correction scheme: first add a transient box (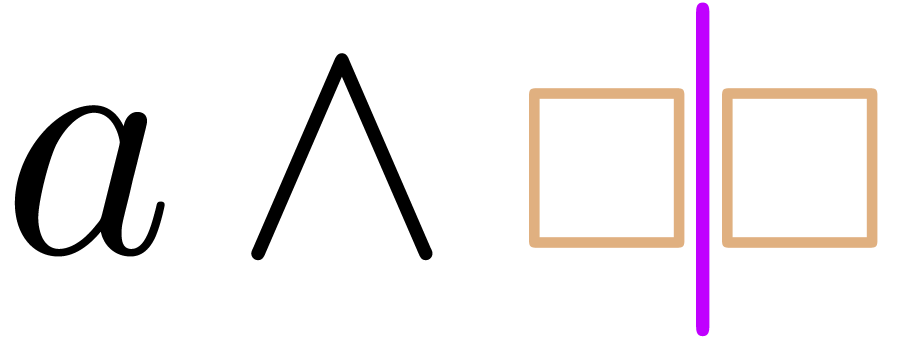 ), then perform the editing action (
), then perform the editing action ( ), and finally correct (nothing
needs to be done at this step).
), and finally correct (nothing
needs to be done at this step).
In Step 3, we simply canceled the editing action if all
correction schemes failed. Several other fallback strategies can be
considered. If we do not aim to maintain correctness at all costs, then
we may apply the editing action without any corrections, and temporarily
tolerate incorrect formulas. We might also implement an unconditionally
successful fallback strategy as in Remark 2; by always
adding such a strategy at the end of our list of eligible correction
schemes, we will never reach Step 3. Yet another idea is to
introduce a correction scheme which annotates subexpressions with exotic
notations in such a way that they become correct.
3.3.Quick survey of some of the
implemented correction schemes
Our approach of using multiple correction schemes allows for
fine-grained control, but also requires an increased amount of manual
labour. Indeed, we both have to cover the complete set of editing
actions, and for each editing action, we have to implement at least one
correction scheme that will succeed in all possible situations.
Fortunately, the most common editing operations fall into four main
categories: insertions and deletions that operate either on selections
or not. Some other operations such as “search and replace”
have not yet been adapted (see also the next section). Ultimately, the
idea would be to provide manual support for the most common operations
and to implement a suitable fallback strategy for the other ones.
3.3.1.Correction schemes for insertions
Let us briefly list how we perform the most prominent correction schemes
for insertions, in absence of active selections. For each of the
schemes, we show the successive states of the formula for a simple
example.
-
The basic scheme from Example 3.
-
“Starting a prime or right script after a transient box”
(e.g. inserting a new subscript in the formula 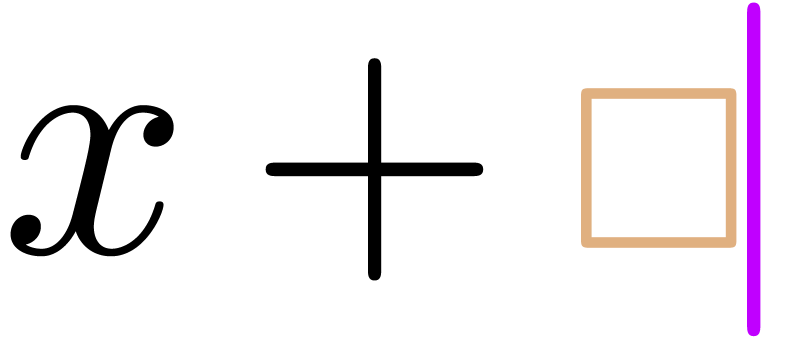 from Example 1): first jump over the
box with the cursor (
from Example 1): first jump over the
box with the cursor ( ),
then perform the action (
),
then perform the action ( ),
and finally add a transient box if necessary (
),
and finally add a transient box if necessary (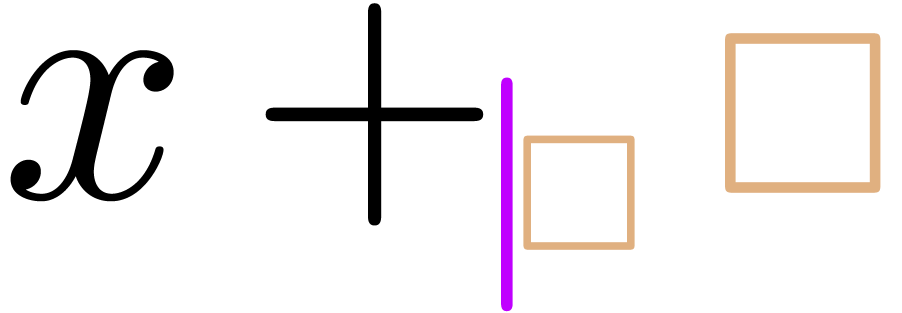 ).
).
-
“Inserting a pure infix operator after a transient box”
(e.g. inserting the infix operator “ ” in
” in 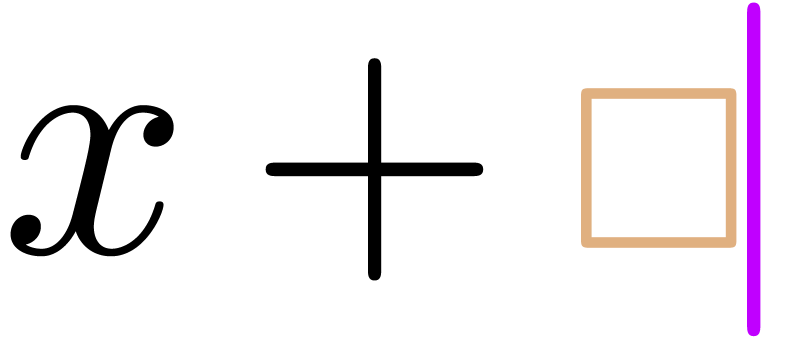 ):
perform the editing action (
):
perform the editing action (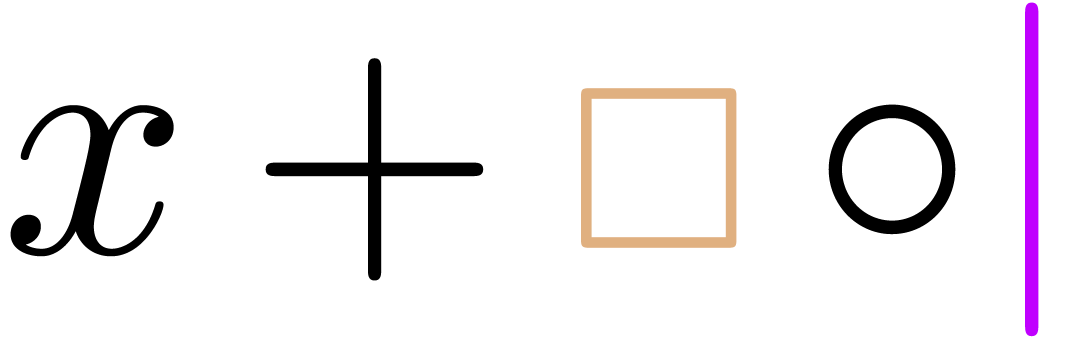 )
and add a transient box if necessary (
)
and add a transient box if necessary (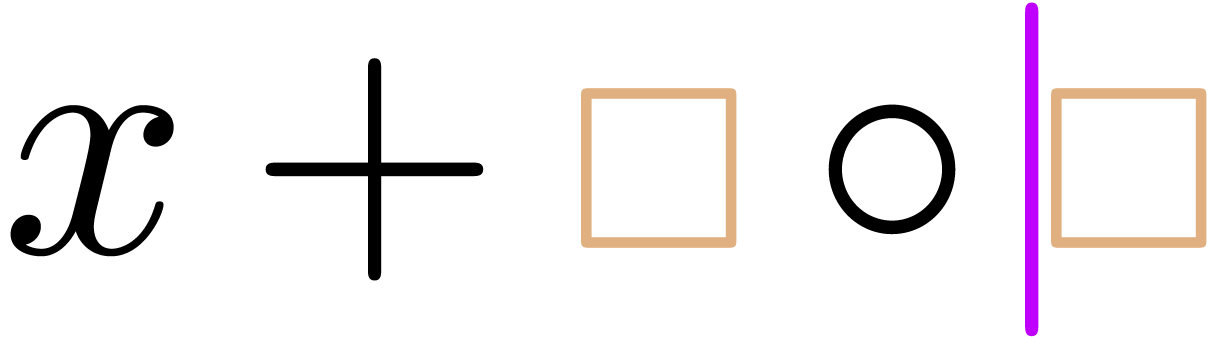 ).
).
-
The scheme from Example 4 for inserting two infix
operators in a row.
-
“Starting an extensible arrow with a script”
(e.g. in the situation  ):
remove all transient markup around the cursor (
):
remove all transient markup around the cursor ( ), perform the operation (
), perform the operation ( ), add a transient box after the arrow
(
), add a transient box after the arrow
( ), as well as a
transient box at the cursor position (
), as well as a
transient box at the cursor position ( ).
).
-
“Insert content after an ordinary symbol” (e.g. entering
 after
after  ):
remove all transient markup around the cursor (
):
remove all transient markup around the cursor ( ), insert a transient “explicit
space” (
), insert a transient “explicit
space” ( ), perform
the editing action (
), perform
the editing action ( ),
insert further transient boxes if needed (
),
insert further transient boxes if needed ( ).
).
-
“Insert content before an ordinary symbol” (e.g.
entering  before
before  ): remove all transient markup around the cursor
(
): remove all transient markup around the cursor
( ), insert a transient
“explicit space” after the cursor (
), insert a transient
“explicit space” after the cursor ( ), perform the editing action (
), perform the editing action (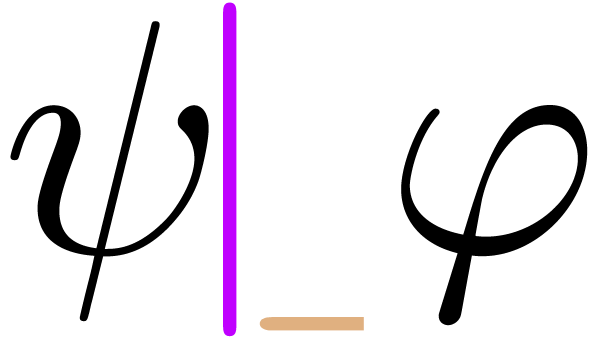 ), insert further transient boxes if needed
(
), insert further transient boxes if needed
( ).
).
-
“Insert content in the middle of an operator”
(e.g. starting a fraction in  ): remove all transient markup around the cursor
(
): remove all transient markup around the cursor
( ), insert transient
“explicit spaces” before and after the cursor (
), insert transient
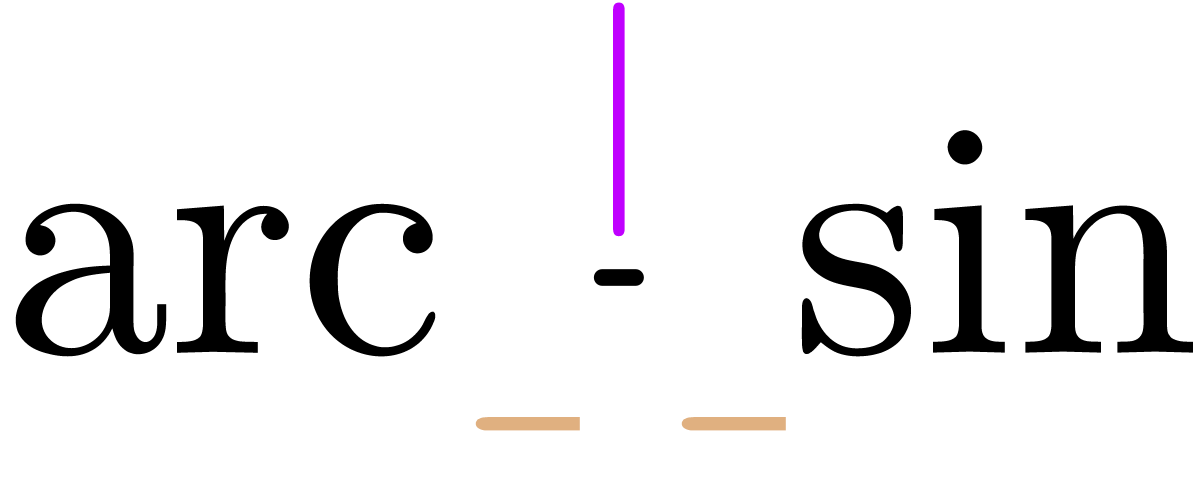
“explicit spaces” before and after the cursor (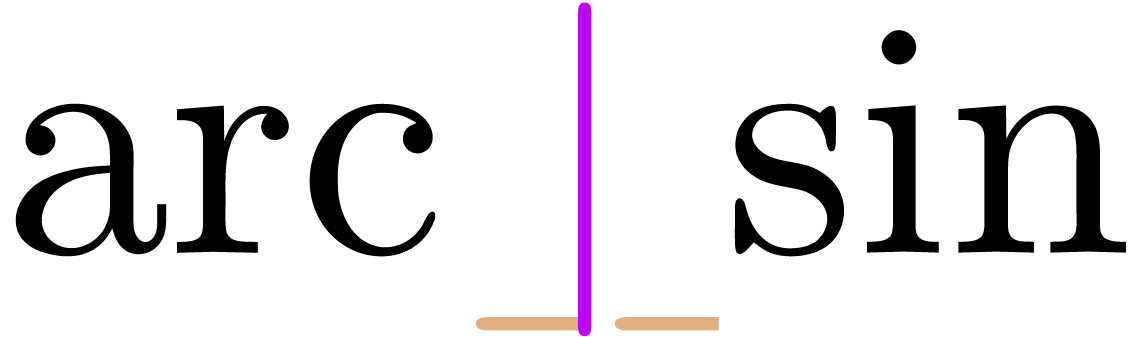 ), perform the editing action
(
), perform the editing action
( ), insert further
transient boxes if needed (
), insert further
transient boxes if needed (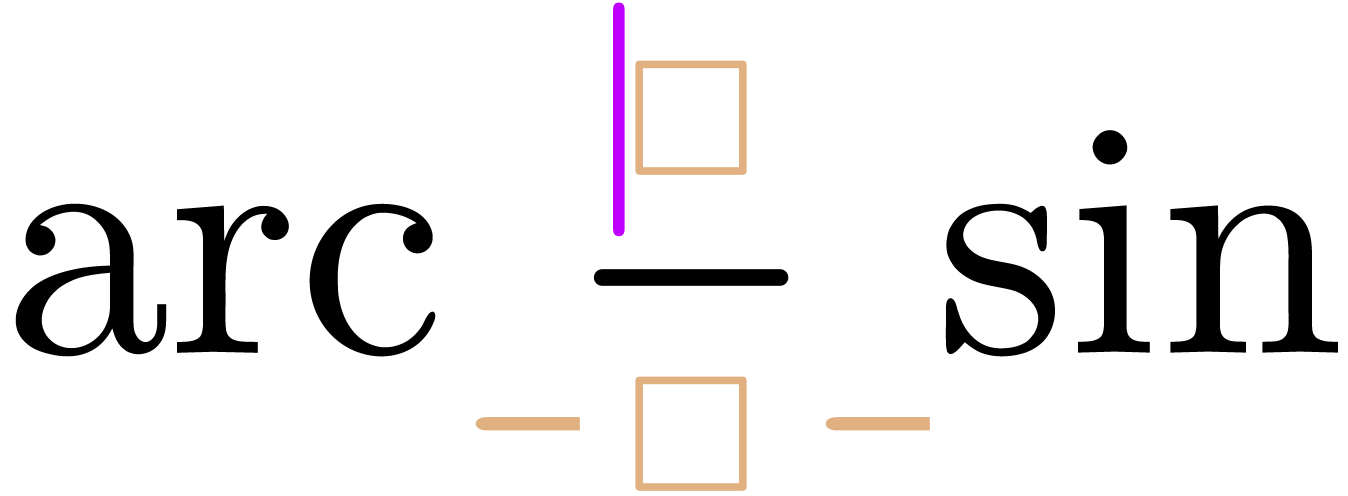 ).
).
The last three schemes also show that it is sometimes necessary to
insert transient markup with different semantics as an ordinary symbol
in order to make the formula correct.
3.3.2.Correction schemes for deletions
For completion, we continue our list of examples with the most prominent
correction schemes for deletions.
-
“The basic deletion scheme if there is transient markup around
the cursor” (e.g. hitting backspace in 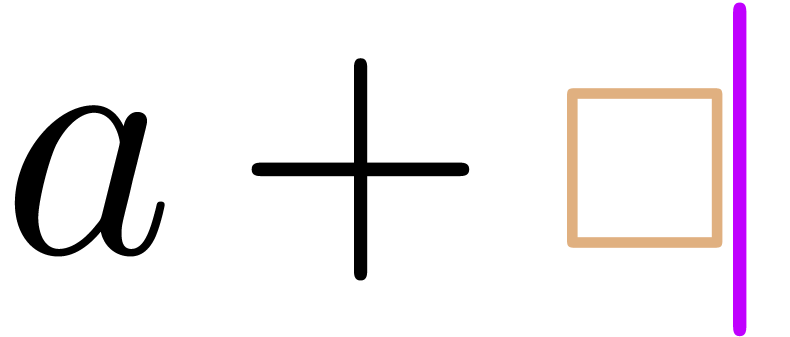 or in
or in 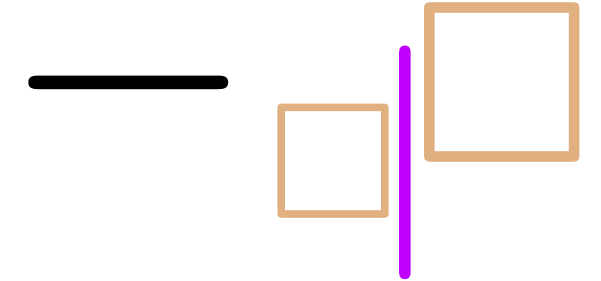 ):
remove the transient markup around the cursor (
):
remove the transient markup around the cursor (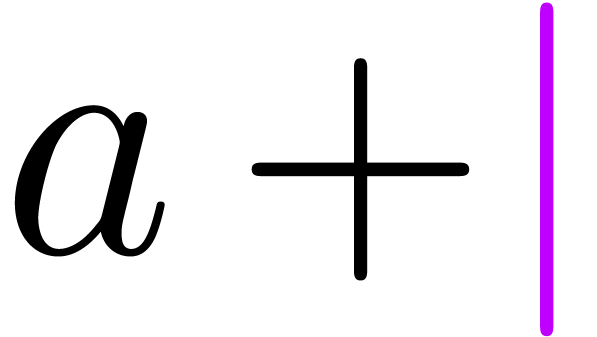 resp.
resp. 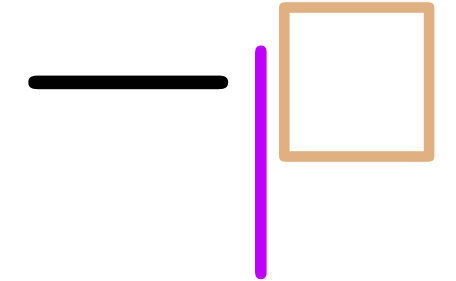 ),
perform the editing action (
),
perform the editing action ( resp.
resp.  ),
again remove all transient markup around the cursor if we deleted
any composite tag (
),
again remove all transient markup around the cursor if we deleted
any composite tag ( resp.
resp.  ), add transient box if needed
(
), add transient box if needed
( resp.
resp.  ).
).
-
“The basic deletion scheme” (e.g. hitting
backspace in  ): remove
transient markup around the cursor (
): remove
transient markup around the cursor ( ),
perform the deletion (
),
perform the deletion (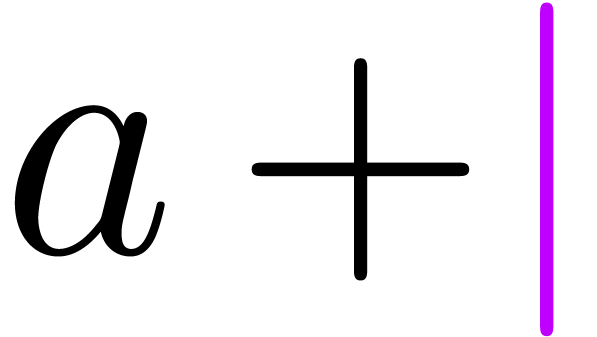 ),
again remove all transient markup around the cursor if we deleted
any composite tag (
),
again remove all transient markup around the cursor if we deleted
any composite tag (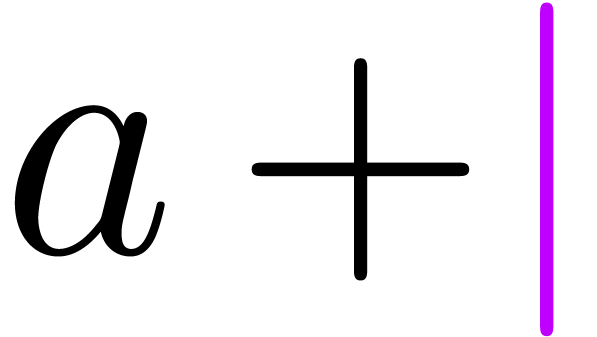 ), add
transient box if needed (
), add
transient box if needed ( ).
).
-
“Removal of actual infix operators” (e.g.
hitting backspace in 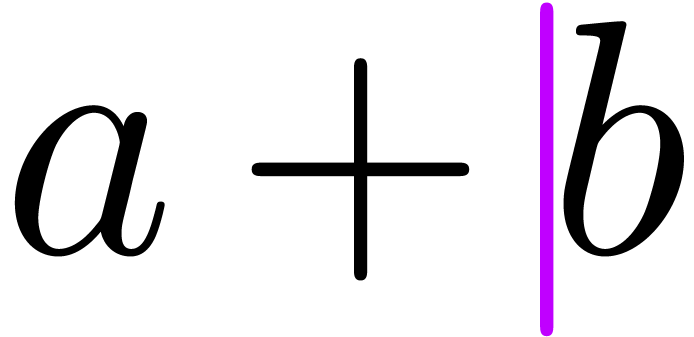 ,
but not in
,
but not in  ):
remove transient markup around the cursor (
):
remove transient markup around the cursor (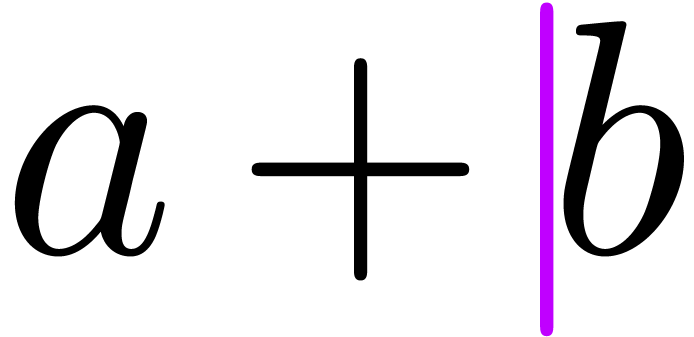 ), perform the deletion
), perform the deletion  , add a transient version of the deleted infix
operator after the cursor (
, add a transient version of the deleted infix
operator after the cursor ( ),
add transient boxes around the cursor if needed (
),
add transient boxes around the cursor if needed ( ).
).
-
“Need to jump over cursor before deletion”
(e.g. hitting backspace in  ): jump over the cursor (
): jump over the cursor (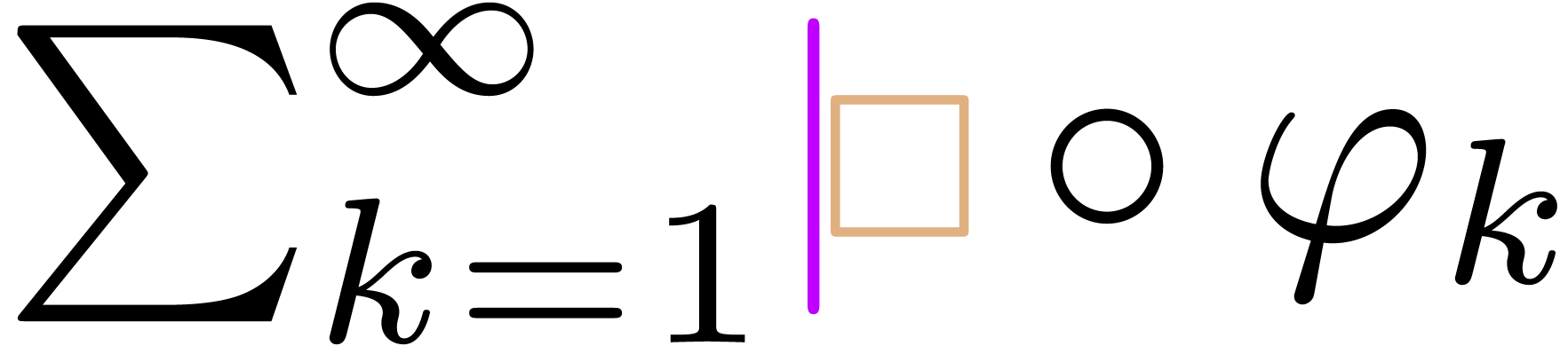 ), perform the “deletion” (
), perform the “deletion” (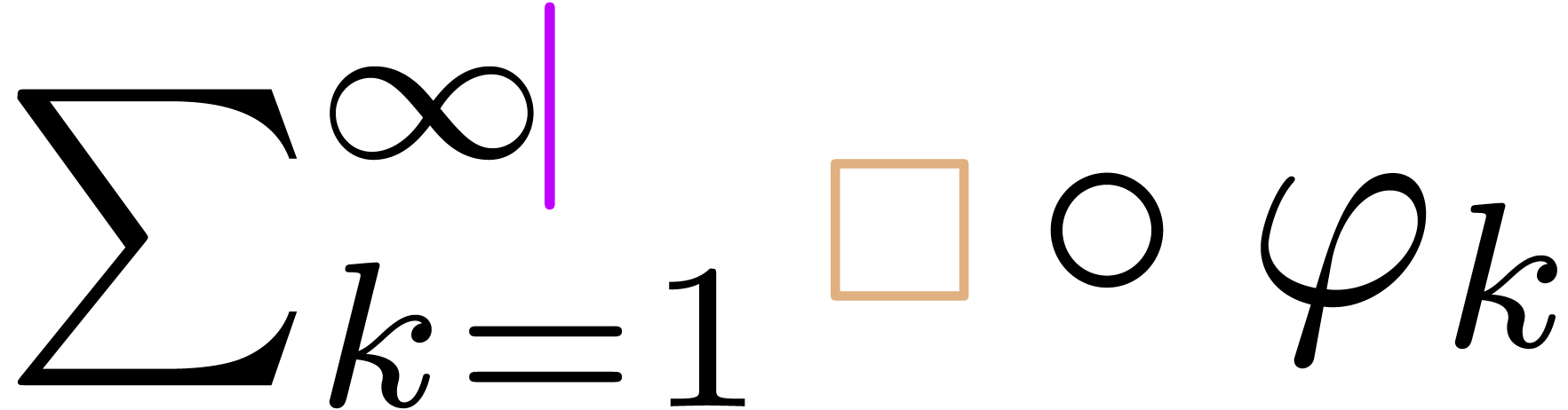 ), add transient boxes around
the cursor if needed (
), add transient boxes around
the cursor if needed (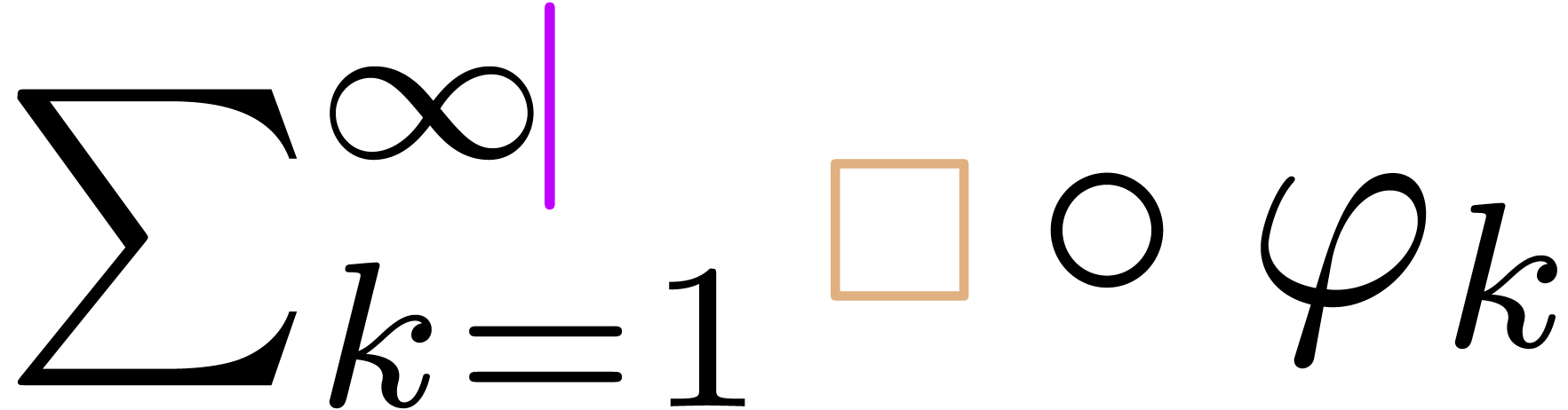 ).
).
These examples show that the correction schemes have to be implemented
with quite a lot of care. This is due to the fact that it is convenient
to design the schemes to apply with the right level of generality
(e.g. not only to the deletion of symbols for the basic
schemes, but also to the deletion of more complex structures, such as
subscripts, fractions, etc.).
4.Problematic cases and challenges
Several problems arose during the implementation of the new semantic
mathematical editing mode which preserves syntactic correctness. Some of
them were more or less expected and have been solved; others require
more work and further experimentation. So far, all problematic cases
that we encountered fall into two categories:
-
The incorrect treatment of special syntactic forms (and informal
content in particular).
-
Complex editing operations (such as search and replace) that require
special attention.
In this section, we will survey the most interesting issues that came up
and highlight some of the remaining challenges.
4.1.Informal content inside formulas
One difficulty with mathematical formulas in scientific papers with
respect to formulas in, say, computer algebra systems, is that they may
contain ponctuation, decorations, typesetting directives, or explicative
text. For instance, consider the following formula:
This formula concentrates three difficulties:
-
We used a trailing punctuation period “.” to finish the
formula.
-
Since the formula does not fit on a single line, we used an
“equation array” to manually break it into two rows. The
cells of the underlying table should not be regarded as separate
formulas (in which case the empty lower left cell would be
incorrect), but rather be concatenated from left to right and from
top to bottom.
-
The formula involves English text “and” and
“almost everywhere”. The word “and” has the
same semantics as the “ ”
operator, whereas “almost everywhere” should be
interpreted as a “postfix quantification”.
”
operator, whereas “almost everywhere” should be
interpreted as a “postfix quantification”.
The best approach to these problems is to introduce suitable annotation
markup which describes the semantics of informal content of this kind.
For instance, we might introduce a tag “punctuation” for
annotating the trailing period, and which would be ignored by the
parser. Alternatively, one might use a special symbol “punctuation
period in math mode”. In a similar spirit, AMS-LaTeX provides
special environments (split, align, gather, etc.) for typesetting large formulas
while preserving some of the intended semantics. TeXmacs also contains a
general purpose tag “syntax”, which may be used to parse an
expression according to the rules of another specified expression. This
allows us for instance to parse the word “and” in the same
way as the infix operator “ ”.
However, we have no “postfix quantification” rule in our
grammar yet. More generally, the design of a complete DTD for informal
annotations is an interesting challenge.
”.
However, we have no “postfix quantification” rule in our
grammar yet. More generally, the design of a complete DTD for informal
annotations is an interesting challenge.
Assuming suitable markup, the design of user friendly ways to perform
the necessary annotations is another matter. Trailing periods are so
common that we actually would like to enter them simply by pressing
..
There are two approaches to this problem. Our current solution is to
adapt the grammar for displayed formulas so as to accept trailing
punctuation (which also means that we do not need any special annotation
semantics). A better solution would be to “requalify”
symbols whenever needed. For instance, in the formula
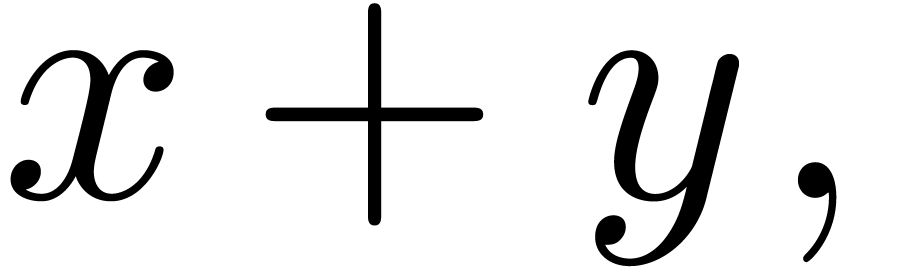
the trailing comma would be interpreted by default as a
“punctuation symbol”. However, as soon as we add a new
character  to the line, we remove the annotation
markup and requalify the comma to become a separator.
to the line, we remove the annotation
markup and requalify the comma to become a separator.
Of course, for arbitrarily complex informal text (such as the
“almost everywhere” example), it will be hard to completely
avoid user feedback on how to insert the necessary annotations.
Nevertheless, some of the most common words (“and”,
“or”, “iff”, etc.) might be
annotated automatically.
4.2.Special syntactic constructs
One obvious drawback of our strategy to manually design the necessary
correction schemes is completeness: every additional mathematical
notation potentially requires one or more new correction schemes.
Fortunately, most mathematical notations are quite simple, so this
disadvantage is not as bad as it might seem. General purpose scientific
papers nevertheless involve far more special syntactic constructs than,
say, computer algebra input. Let us illustrate some typical issues that
occur on the hand of a few somewhat unorthodox constructs.
-
The “universal grammar” from [7] contains
special rules for decorated operators (as in 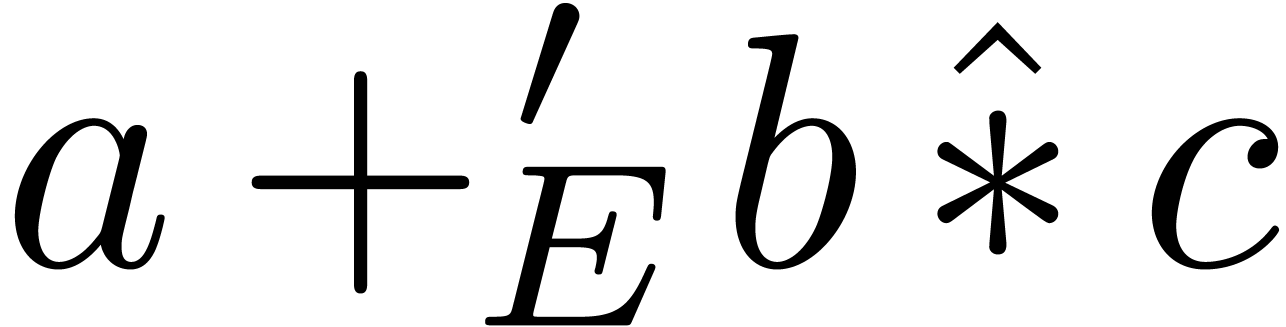 ) and big operators (as in
) and big operators (as in 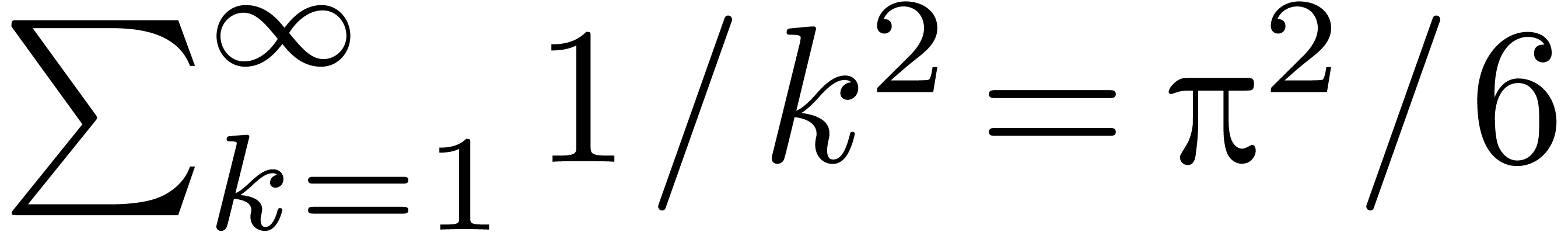 ). The usual correction schemes are mostly
sufficient for editing this kind of formulas. One example of a
remaining problem is entering
). The usual correction schemes are mostly
sufficient for editing this kind of formulas. One example of a
remaining problem is entering 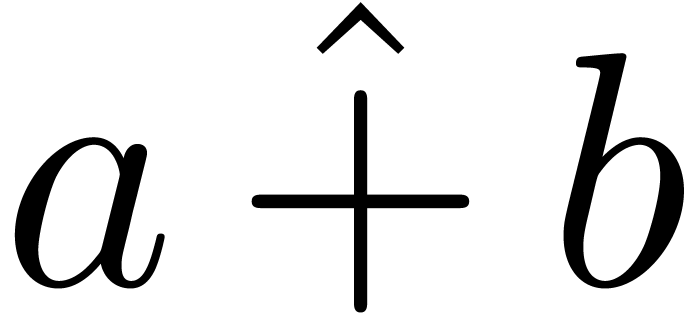 .
In the old, presentation-oriented editing mode, we would type A⌥^+→B
(insert
.
In the old, presentation-oriented editing mode, we would type A⌥^+→B
(insert  , start an empty
hat, enter
, start an empty
hat, enter  , move out of
the hat, insert
, move out of
the hat, insert 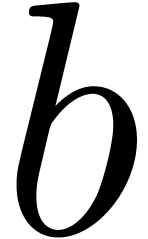 ).
However, in the new semantic mode, this successively yields
).
However, in the new semantic mode, this successively yields  ,
, 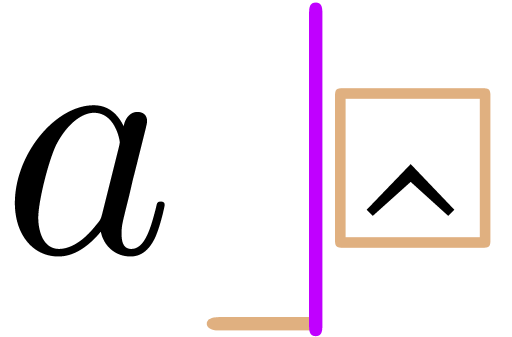 ,
,
 ,
, 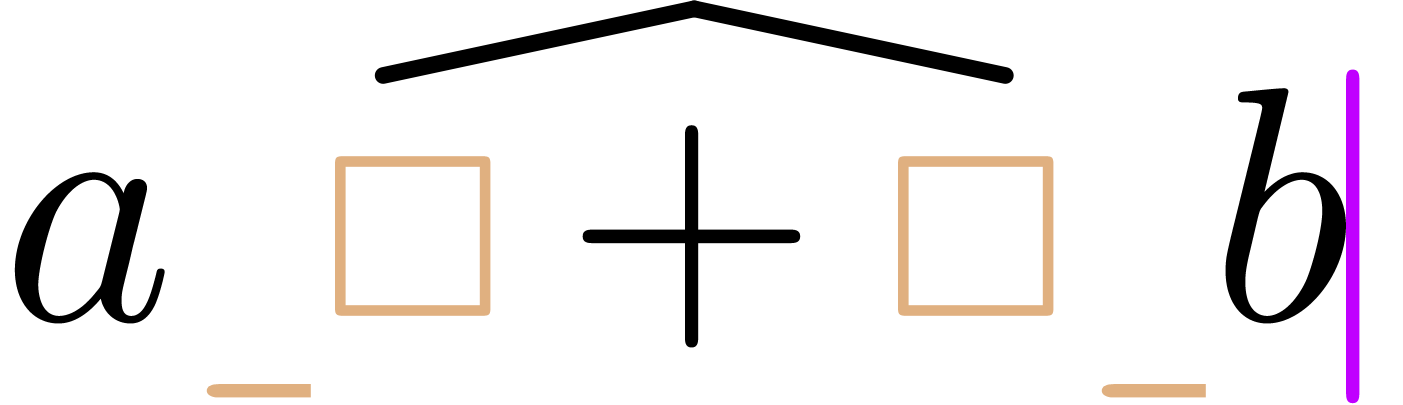 ; a new correction scheme should be designed to
treat this case more smoothly. Notice that an alternative way to
enter
; a new correction scheme should be designed to
treat this case more smoothly. Notice that an alternative way to
enter  is to first type
is to first type  , then select “
, then select “ ”, and finally insert a hat.
”, and finally insert a hat.
-
The “universal grammar” from [7] also
contains a few rules that are uncommon in programming languages, but
crucial for general purpose mathematical texts. For instance, the
formula 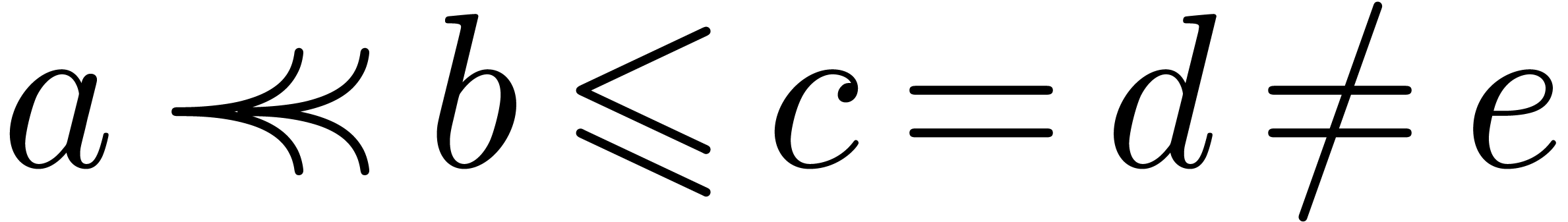 is interpreted as
is interpreted as  , and the formula
, and the formula 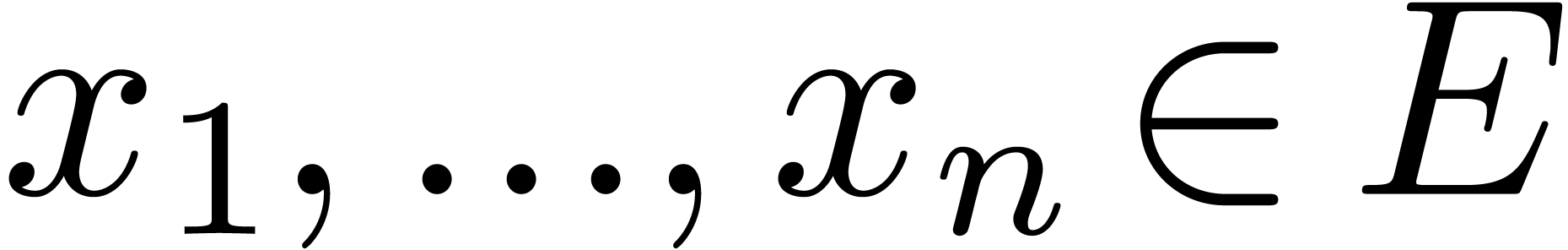 as
as  . Less common is
. Less common is  ; what is the correct
semantics? Fortunately, these special rules do not require any
special correction schemes.
; what is the correct
semantics? Fortunately, these special rules do not require any
special correction schemes.
-
Different authors use wildly varying notations for quantified
expressions:
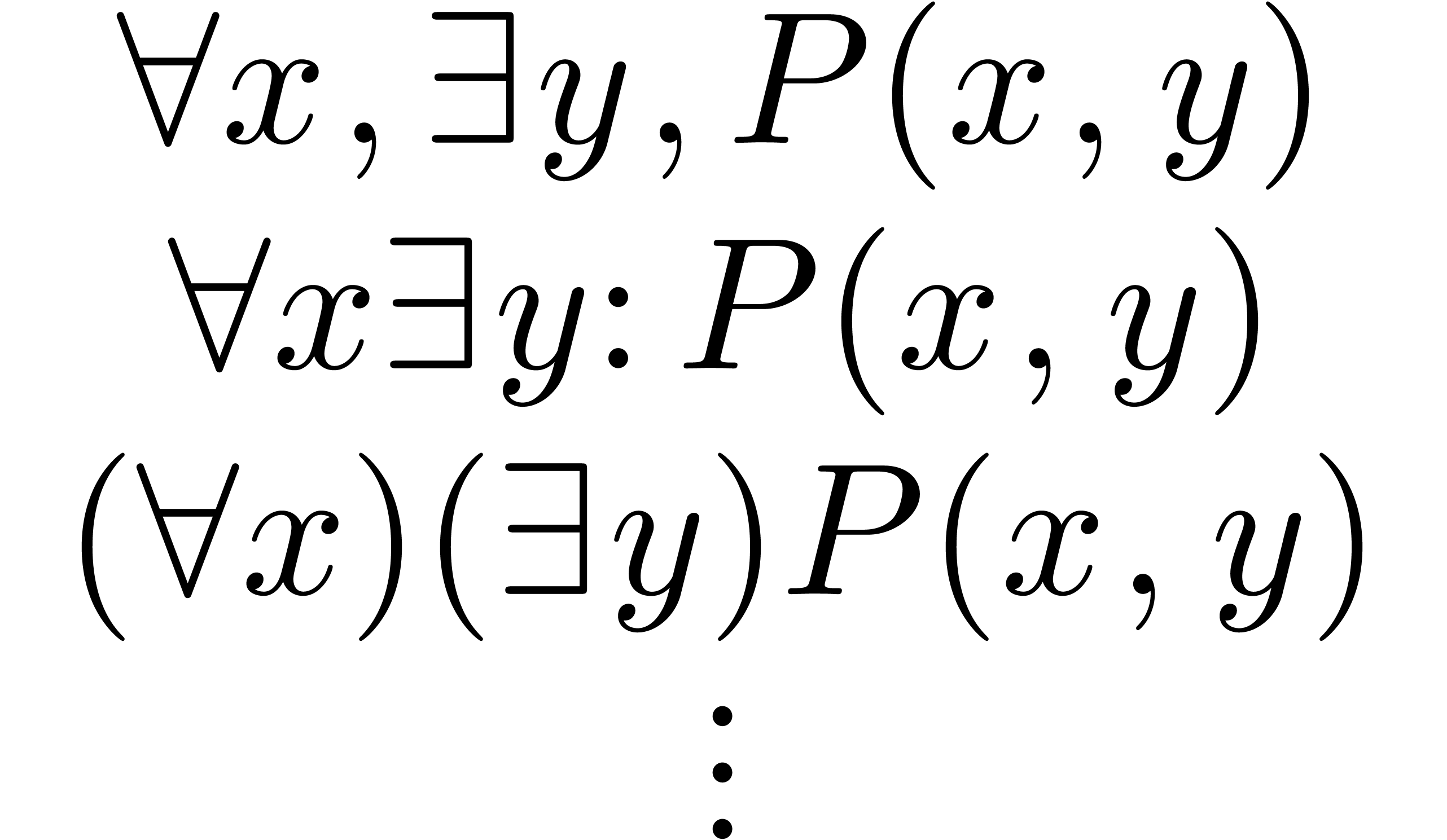
We already noticed in the introduction that it is “nice”
to correct 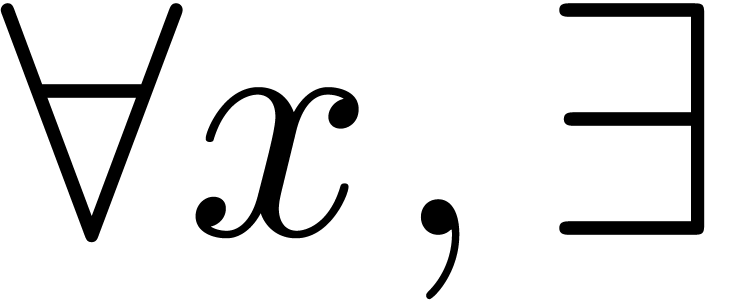 into
into 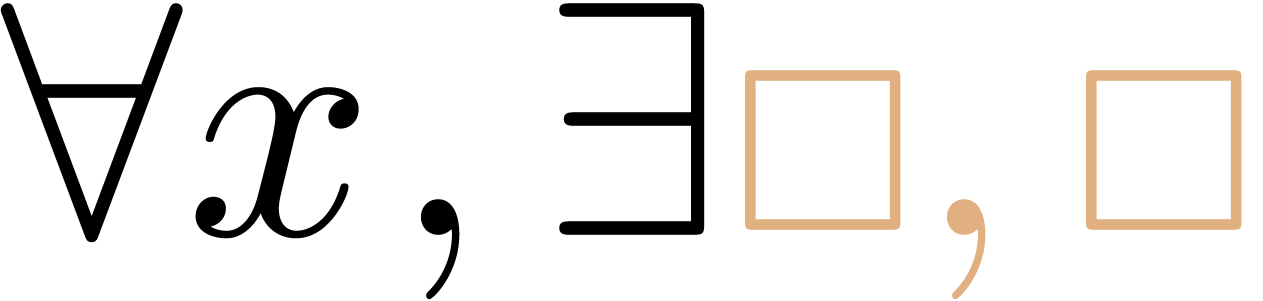 . However,
. However,  might be
corrected just as well as
might be
corrected just as well as  or as
or as 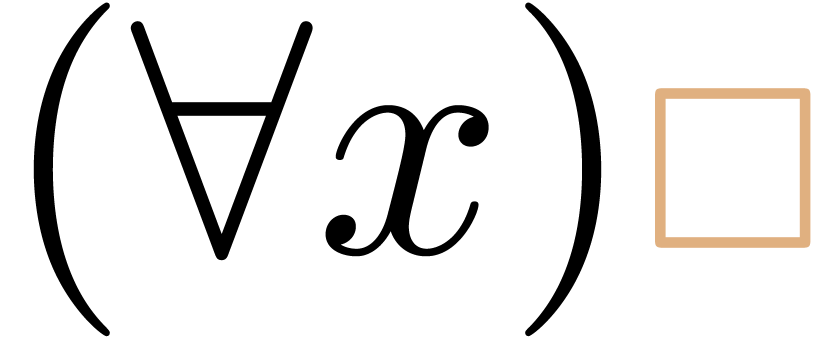 , depending on the author's preferred
style. Our present solution to this kind of ambiguities is to
further relax our grammar, by considering
, depending on the author's preferred
style. Our present solution to this kind of ambiguities is to
further relax our grammar, by considering 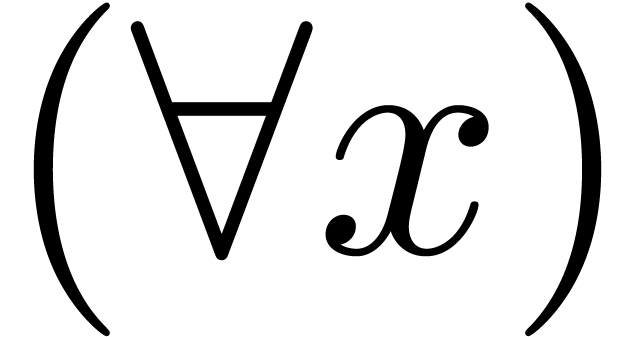 to
be a correct expression.
to
be a correct expression.
-
One of the advantages of the new correctness-preserving editing mode
is that missing expressions are clearly indicated to the user. When
entering a  matrix
matrix 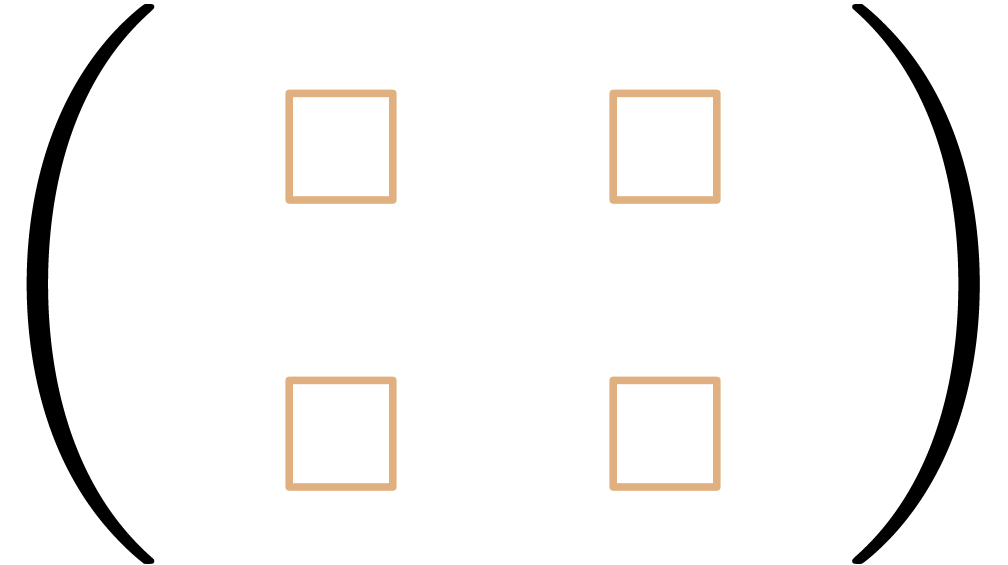 in
a computer algebra system, this is indeed quite pleasant. But in the
example
in
a computer algebra system, this is indeed quite pleasant. But in the
example
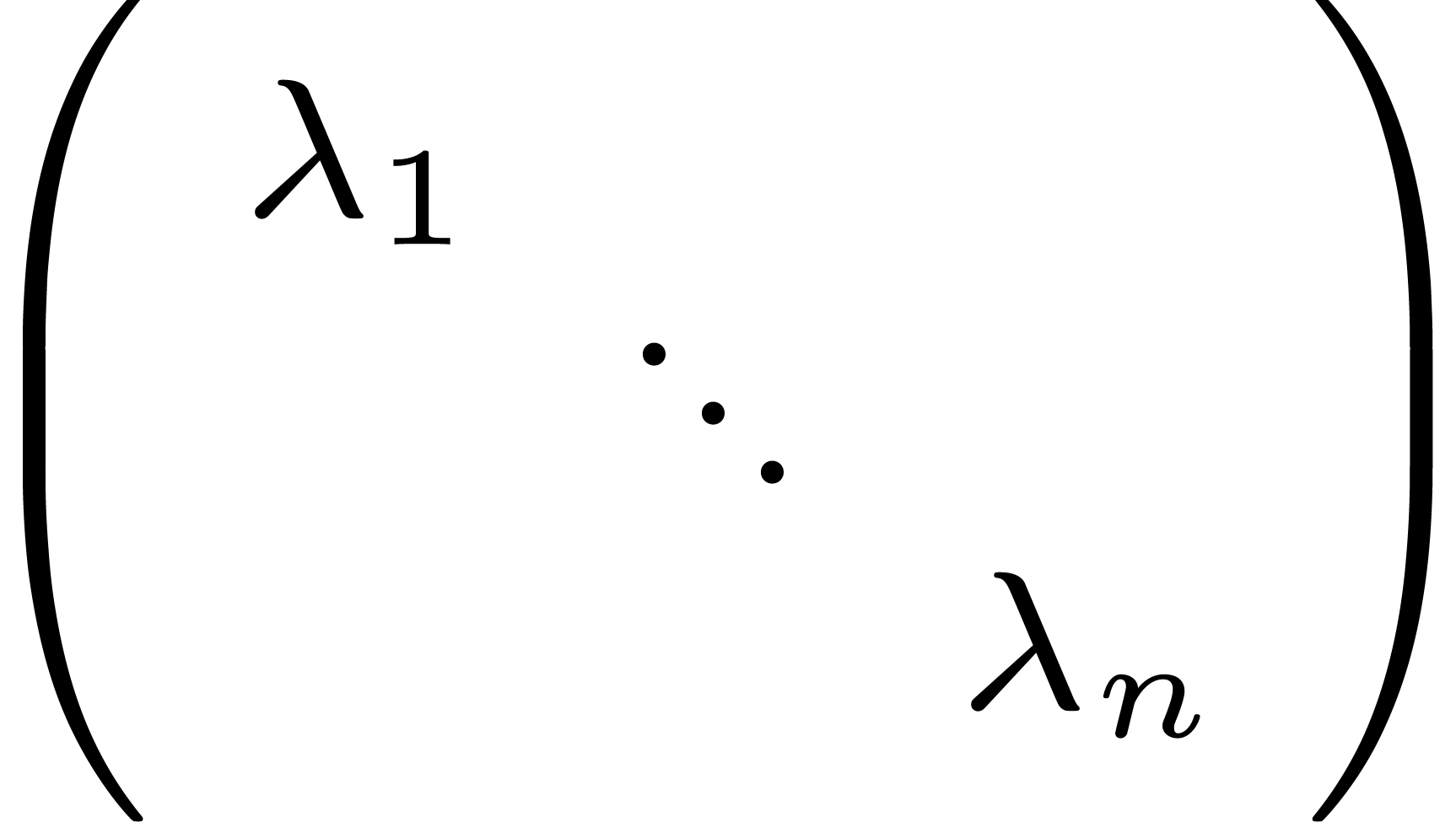
of a diagonal matrix, this also forces users to manually fill out
six of the cells with “invisible zeros”. Our present
solution is therefore to only require tables cells to be explicitly
entered inside computer algebra sessions.
-
The “universal grammar” from [7] also
contains a few rules for “personal use”. In particular,
inside subscripts, we allow for notations such as  and
and 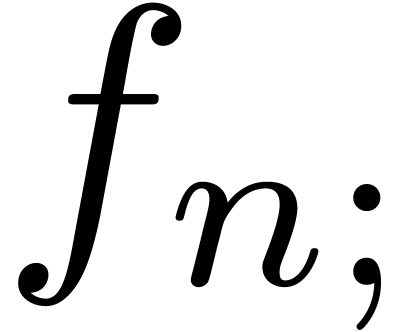 . Here
. Here  has the semantics of “post-multiplication”
with
has the semantics of “post-multiplication”
with  . Given a power
series
. Given a power
series 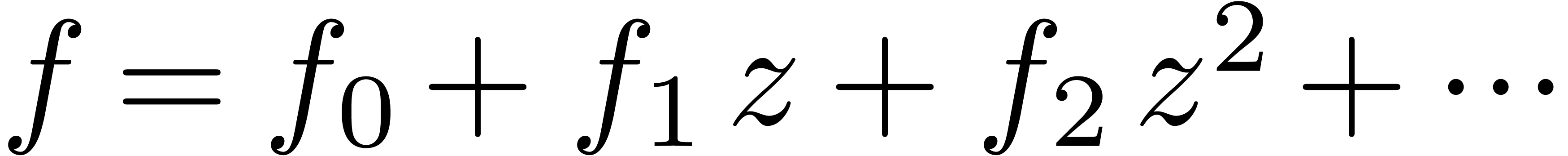 , the notation
, the notation
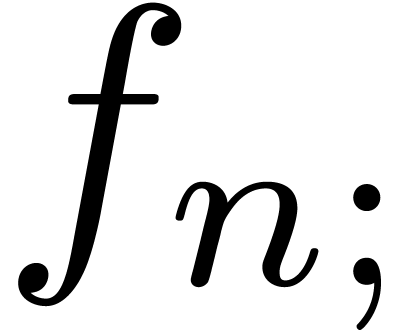 stands for
stands for 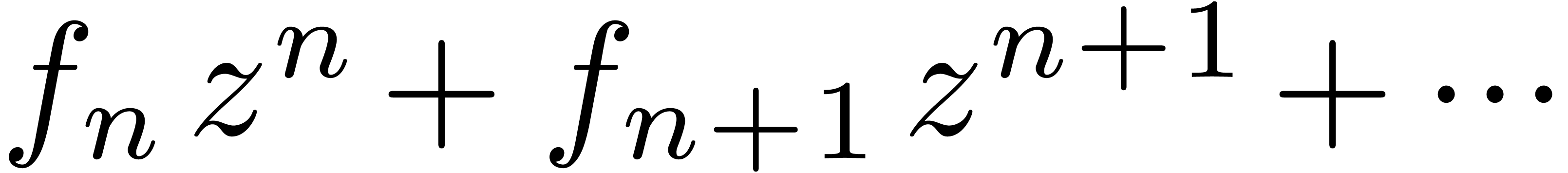 .
Now we are facing a dilemma: on the one hand, we are fond of these
notations, which do not harm anyone. On the other hand, some users
might want to be constrained to input something behind the
“;” in
.
Now we are facing a dilemma: on the one hand, we are fond of these
notations, which do not harm anyone. On the other hand, some users
might want to be constrained to input something behind the
“;” in 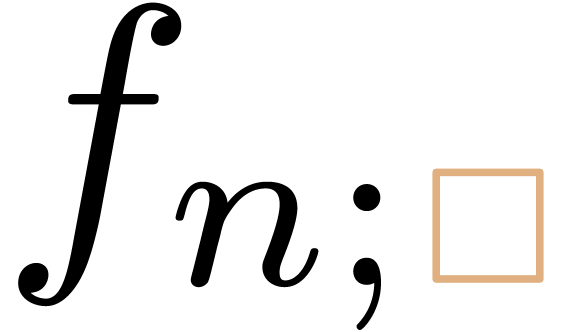 . One
solution would be to depart from the idea from [7] to
promote using a “universal grammar”. Instead, we might
provide special style packages for specific notations. Another
approach is to introduce suitable prefix and postfix homoglyphs of
. One
solution would be to depart from the idea from [7] to
promote using a “universal grammar”. Instead, we might
provide special style packages for specific notations. Another
approach is to introduce suitable prefix and postfix homoglyphs of
 and
and  ,
together with simple keyboard shortcuts for entering them.
,
together with simple keyboard shortcuts for entering them.
4.3.Special editing operations and markup
Let us finally investigate to which extent existing editing operations
have to be adapted to the new, more semantic editing mode. We will start
with a few issues that are already dealt with and then turn our
attention to the remaining challenges.
-
TeXmacs provides a special “\-style” input method for
people who already know LaTeX. For instance, one may enter  by typing \ALPHA↩, or
start a fraction by typing \FRAC↩. The
fact that a wide variety of editing actions can be triggered in this
way required us to implement special correction schemes for this
input method.
by typing \ALPHA↩, or
start a fraction by typing \FRAC↩. The
fact that a wide variety of editing actions can be triggered in this
way required us to implement special correction schemes for this
input method.
-
The main TeXmacs input method for mathematical symbols is
particularly powerful and intuitive. For instance, one may enter
 and
and  by typing ->
resp. <=.
However, this facility requires a lot of control over the
undo-mechanism: when typing a shortcut ->, TeXmacs
“forgets” the incomplete keystroke - and treats
the shortcut ->
as an atomic operation. In other words, typing -> and
pressing “undo” will remove the entire arrow and not
leave any
by typing ->
resp. <=.
However, this facility requires a lot of control over the
undo-mechanism: when typing a shortcut ->, TeXmacs
“forgets” the incomplete keystroke - and treats
the shortcut ->
as an atomic operation. In other words, typing -> and
pressing “undo” will remove the entire arrow and not
leave any  . Now remember
from Section 3.2 that trying several correction schemes
in succession also makes use of the undo-mechanism inside TeXmacs.
Trying corrections while entering shortcuts such as ->
necessitates the mechanism to work in a nested way. We had to
further tweak our implementation so as to make that possible.
. Now remember
from Section 3.2 that trying several correction schemes
in succession also makes use of the undo-mechanism inside TeXmacs.
Trying corrections while entering shortcuts such as ->
necessitates the mechanism to work in a nested way. We had to
further tweak our implementation so as to make that possible.
-
Certain editing operations such as “save the current selection
as an image” have side-effects that cannot be undone.
Additional care is needed when implementing correction schemes for
such operations. Fortunately, such operations usually do not need to
be corrected.
-
One interesting editing action which is not necessarily local is
“search and replace”. Global editing actions of this
kind are harder to support since the corresponding correction
schemes need to track all modifications made throughout the
document, and less indication is provided by the local context which
corrections to choose in case of ambiguities. The “search and
replace” operation also raises the question whether adapting
the operation to a semantic context actually involves more than
corrections via the addition or removal of transient
markup: if we replace 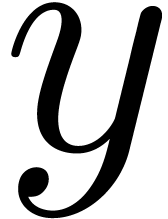 by
by  in
in  , do we expect to
obtain
, do we expect to
obtain 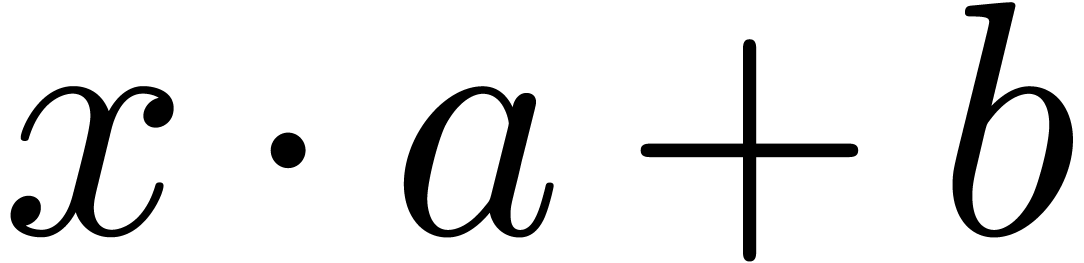 or
or 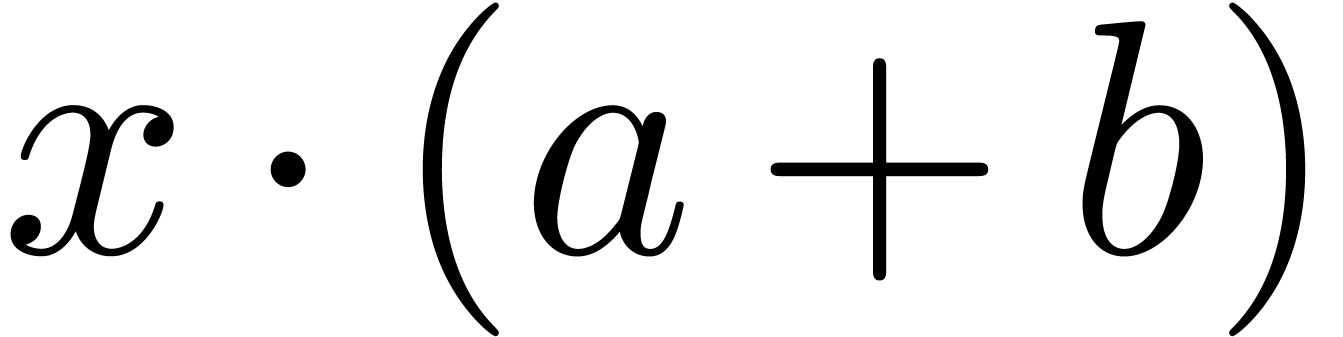 ?
?
-
For some editing operations, it is not always clear what their
semantic counterparts should be. One good example concerns the
facility to compute and inspect the structured differences between
two versions of a document. When applied to the formulas 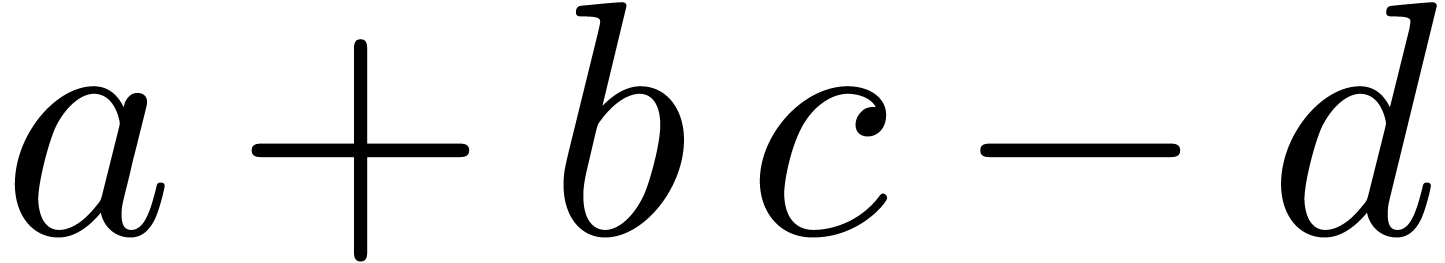 and
and 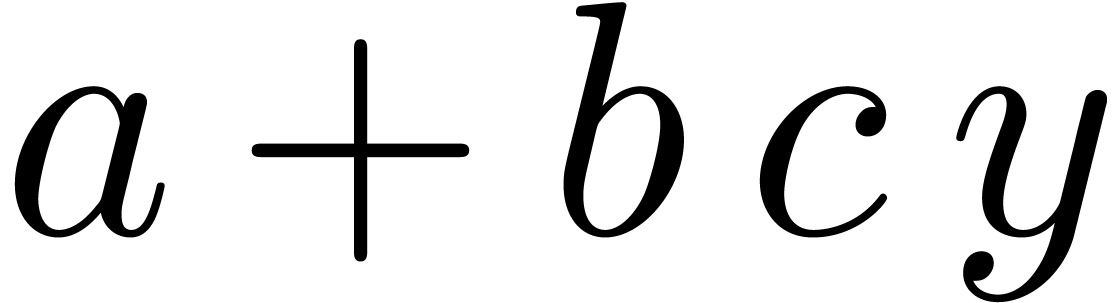 , the
differences are indicated using red and green colors:
, the
differences are indicated using red and green colors:  . How should we parse this formula? Both
. How should we parse this formula? Both
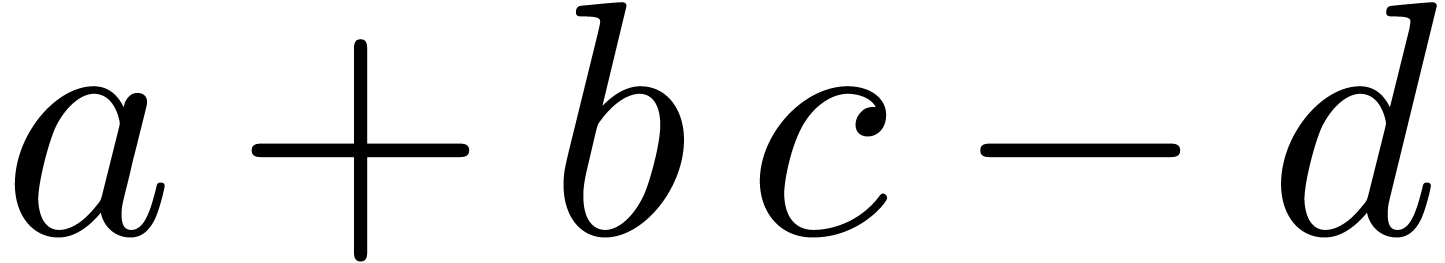 and
and 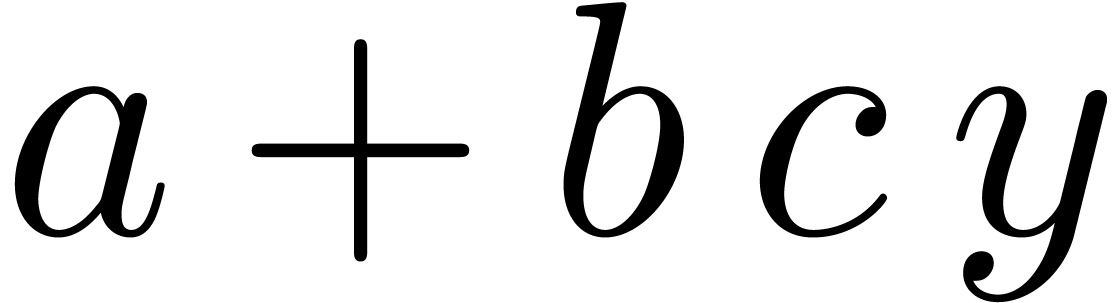 do make sense,
but not
do make sense,
but not 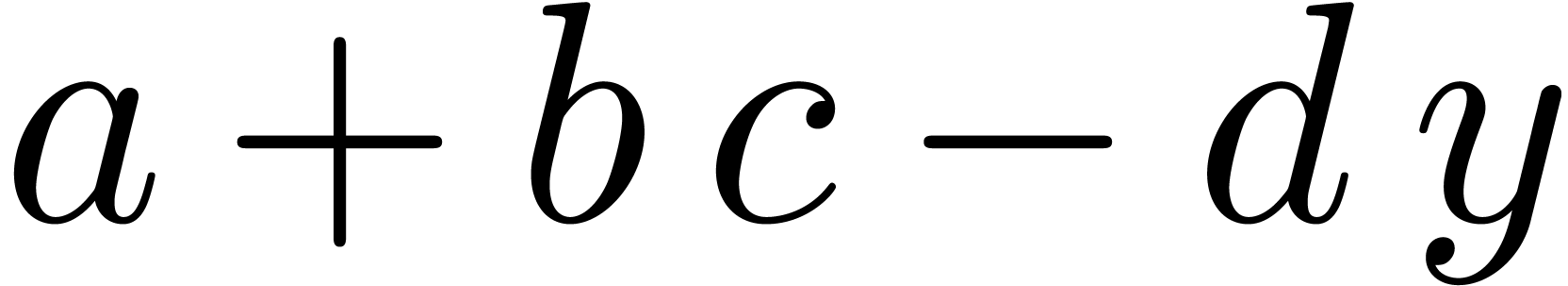 . It is not clear
to us yet how the editor should behave in this situation.
. It is not clear
to us yet how the editor should behave in this situation.
Bibliography
-
[1]
-
O. Arsac, S. Dalmas, and M. Gaëtano. The design
of a customizable component to display and edit formulas. In
ACM Proceedings of the 1999 International Symposium on
Symbolic and Algebraic Computation, July 28–31, pages
283–290. 1999.
-
[2]
-
Y. Bertot. The CtCoq system: design and architecture.
Formal Aspects of Computing, 11(3):225–243, 1999.
-
[3]
-
P. Borras, D. Clement, Th. Despeyroux, J. Incerpi, G.
Kahn, B. Lang, and V. Pascual. Centaur: the system. SIGSOFT
Softw. Eng. Notes, 13(5):14–24, 1988.
-
[4]
-
B. Ford. Packrat parsing: a practical linear-time
algorithm with backtracking. Master's thesis, Massachusetts
Institute of Technology, September 2002.
-
[5]
-
B. Ford. Packrat parsing: simple, powerful, lazy,
linear time. In Proceedings of the seventh ACM SIGPLAN
international conference on Functional programming, ICFP
'02, pages 36–47. New York, NY, USA, 2002. ACM Press.
-
[6]
-
J. van der Hoeven. GNU TeXmacs: a free, structured,
wysiwyg and technical text editor. In Daniel Filipo, editor,
Le document au XXI-ième siècle, volume
39–40, pages 39–50. Metz, 14–17 mai 2001.
Actes du congrès GUTenberg.
-
[7]
-
J. van der Hoeven. Towards semantic mathematical
editing. J. Symbolic Comput., 71:1–46, 2015.
-
[8]
-
N. Kajler. Environnement graphique
distribué pour le calcul formel. PhD thesis,
Université de Nice-Sophia Antipolis, 1993.
-
[9]
-
L. Padovani and R. Solmi. An investigation on the
dynamics of direct-manipulation editors for mathematics. In A.
Asperti, G. Bancerek, and A. Trybulec, editors, Mathematical
Knowledge Management, volume 3119 of Lect. Notes Comp.
Sci., pages 302–316. Springer Berlin Heidelberg, 2004.
-
[10]
-
N. M. Soiffer. The Design of a User Interface for
Computer Algebra Systems. PhD thesis, University of
California at Berkeley, 1991.
-
[11]
-
L. Théry, Y. Bertot, and G. Kahn. Real theorem
provers deserve real user-interfaces. SIGSOFT Softw. Eng.
Notes, 17(5):120–129, nov 1992.
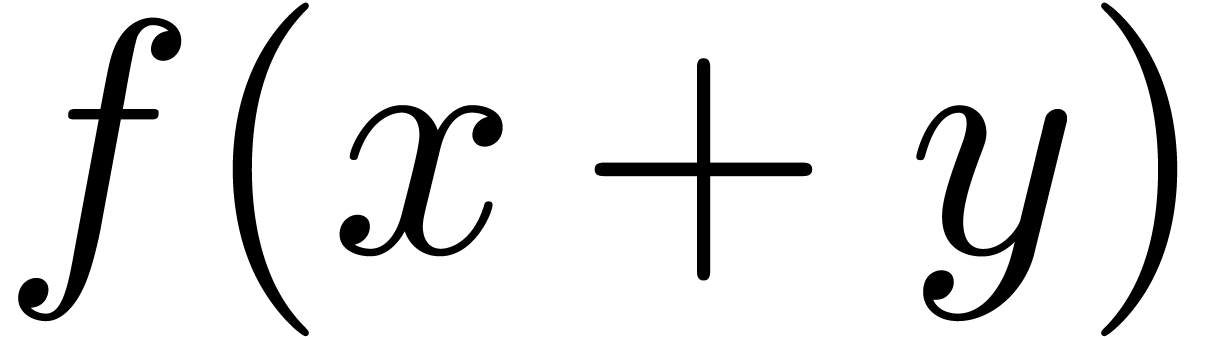 and
and 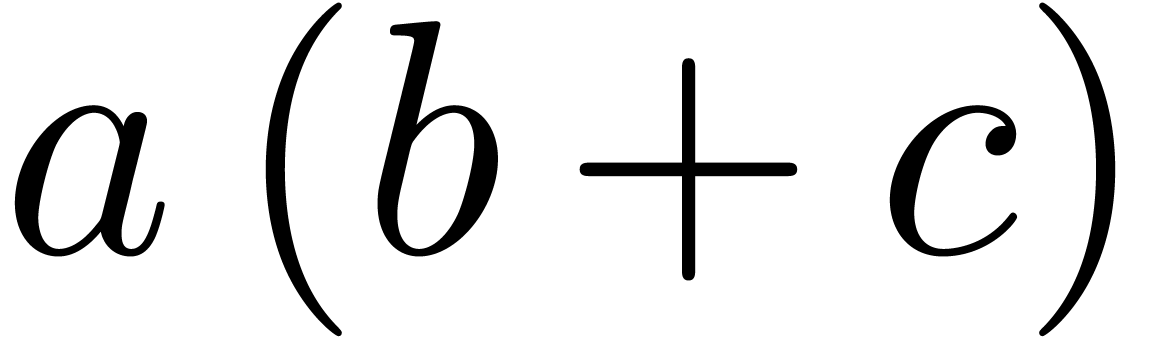 . People typically enter
these formulas using the LaTeX pseudo-code $f(x+y)$ and
$a(b+c)$. Doing so, we do not transmit the important
information that we probably meant to apply
. People typically enter
these formulas using the LaTeX pseudo-code $f(x+y)$ and
$a(b+c)$. Doing so, we do not transmit the important
information that we probably meant to apply  to
to
 in the first formula and to multiply
in the first formula and to multiply  with
with  in the second one. The
problem to automatically recover such information is very hard in
general. For this reason, it would be desirable to have mathematical
authoring tools in which it is easy to write formulas which
systematically carry this type of information.
in the second one. The
problem to automatically recover such information is very hard in
general. For this reason, it would be desirable to have mathematical
authoring tools in which it is easy to write formulas which
systematically carry this type of information.
 ,
, is an infix operator with arguments
is an infix operator with arguments  and
and  ,
,
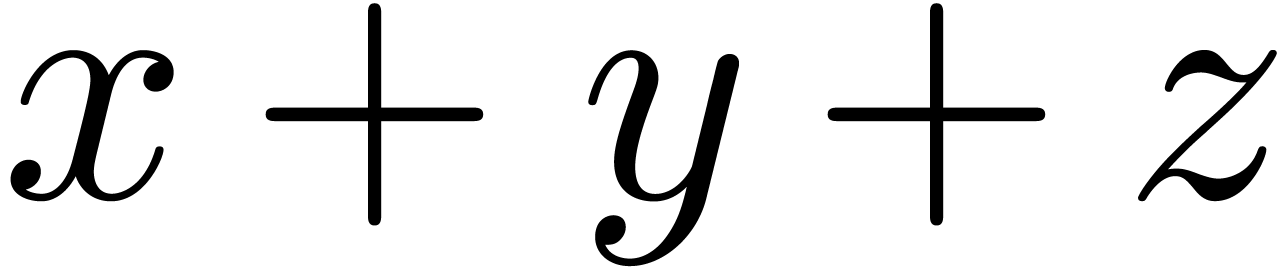 ,
, (with the cursor between the
“
(with the cursor between the
“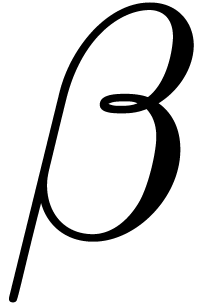 ”),
”), (instead of
(instead of 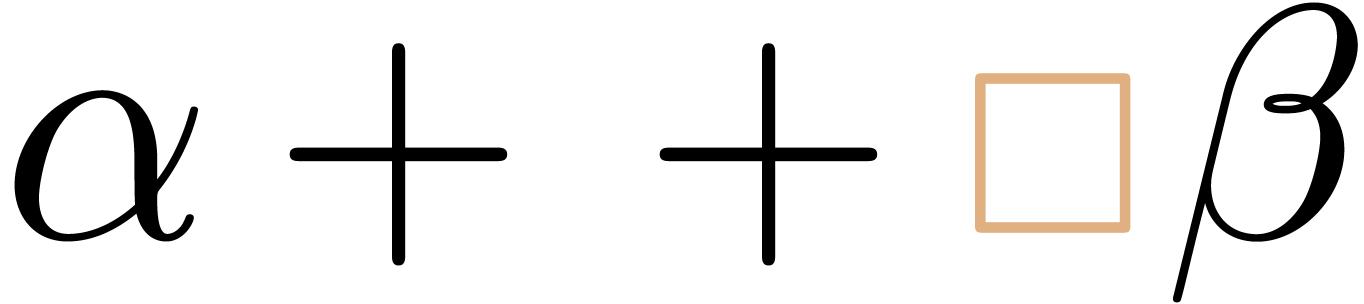 or
or 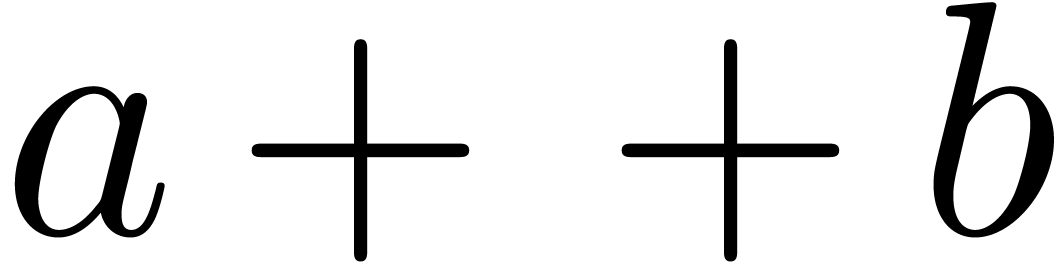 ).
). ;
;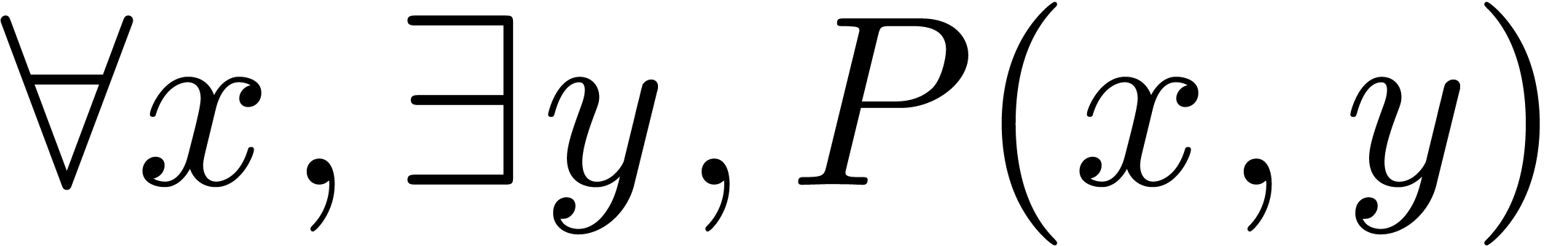 .
.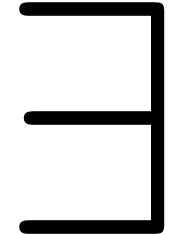 ”,
”,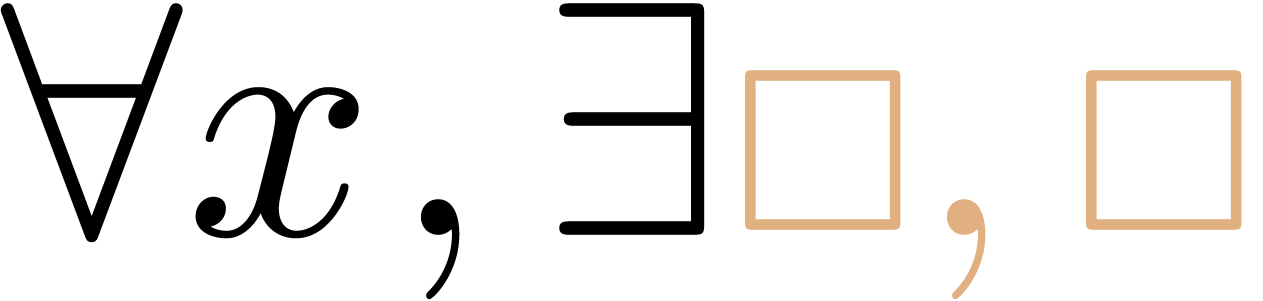 ,
,
 ,
, ,
, ,
, ,
, to behave as
to behave as 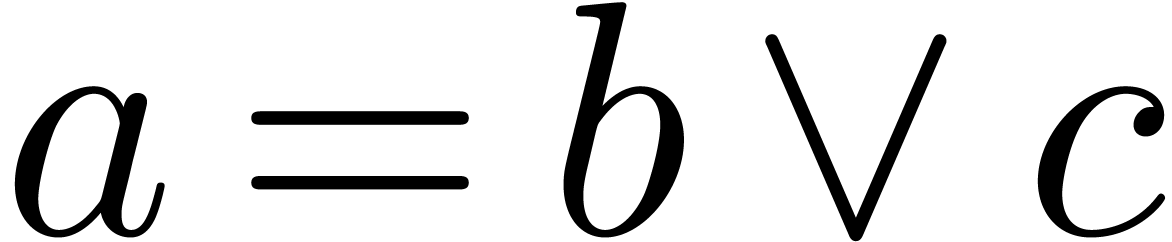 will be parsed as
will be parsed as 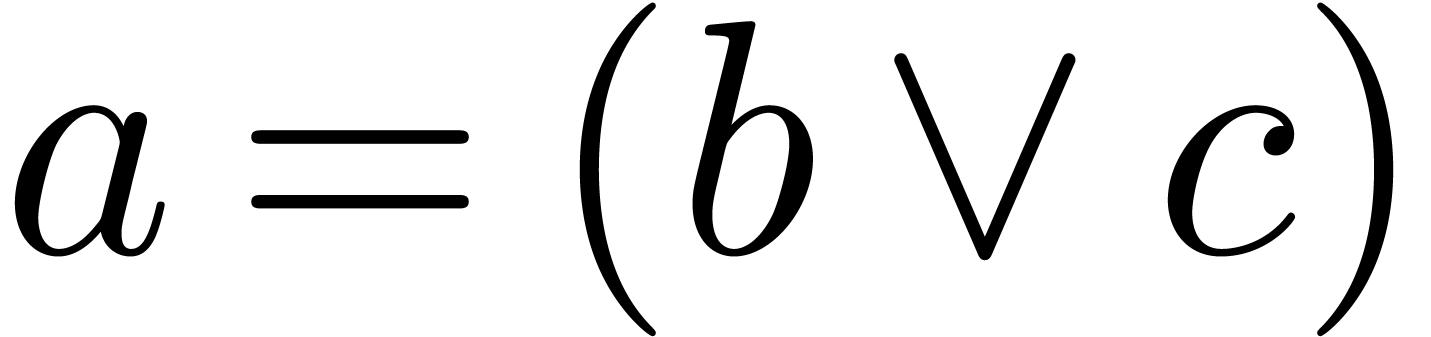 instead of
instead of 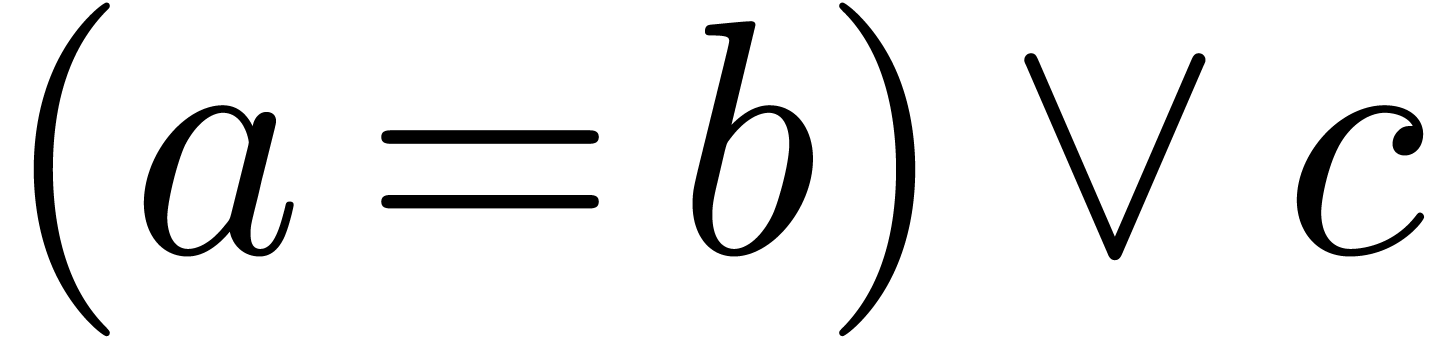 .
. and logical conjunction
and logical conjunction 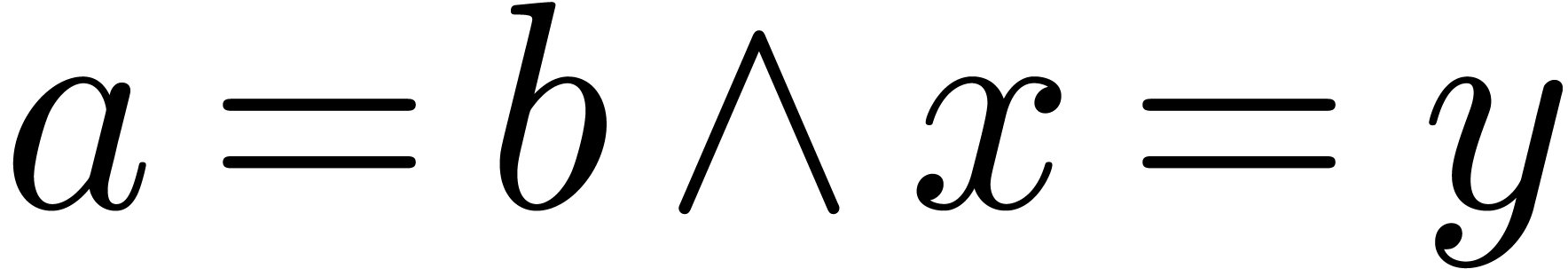 ,
, 1.99.3
1.99.3 .
. is a valid symbol, the main editing action
would create an empty subscript for it. We next launch the correction
procedure, which replaces the empty subscript by a transient box,
yielding
is a valid symbol, the main editing action
would create an empty subscript for it. We next launch the correction
procedure, which replaces the empty subscript by a transient box,
yielding 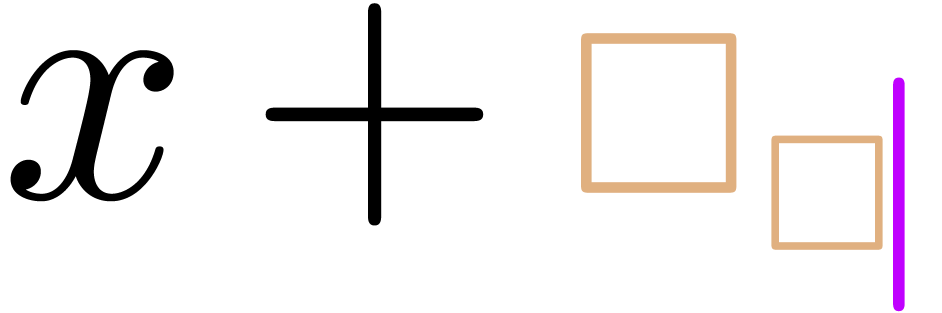 .
. ”
”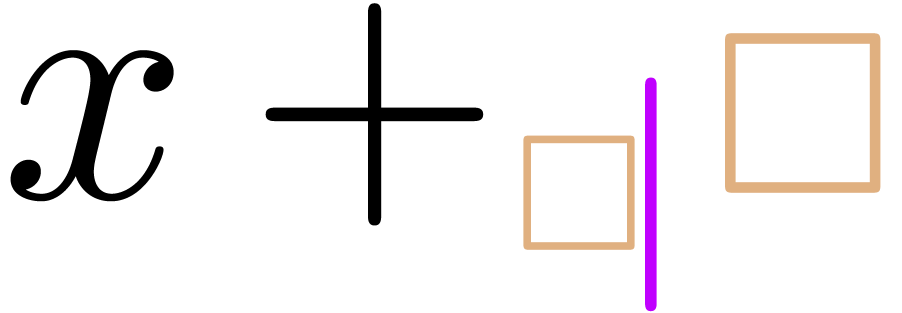 .
. ,
, ,
, ,
, .
. ,
, ”.
”.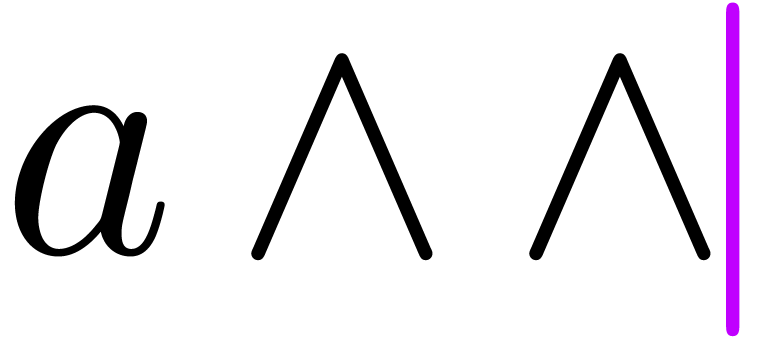 through the insertion
of a single transient box. However, the formula
through the insertion
of a single transient box. However, the formula 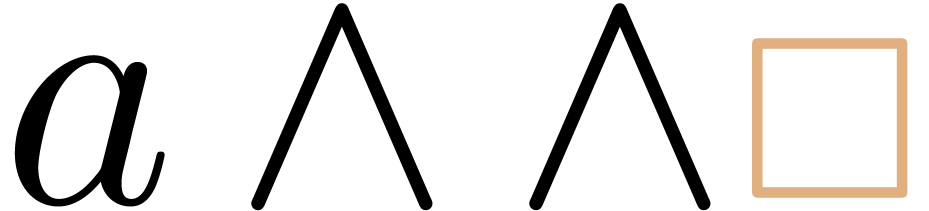 is still incorrect. For this particular case, we therefore use the
following correction scheme: first add a transient box (
is still incorrect. For this particular case, we therefore use the
following correction scheme: first add a transient box (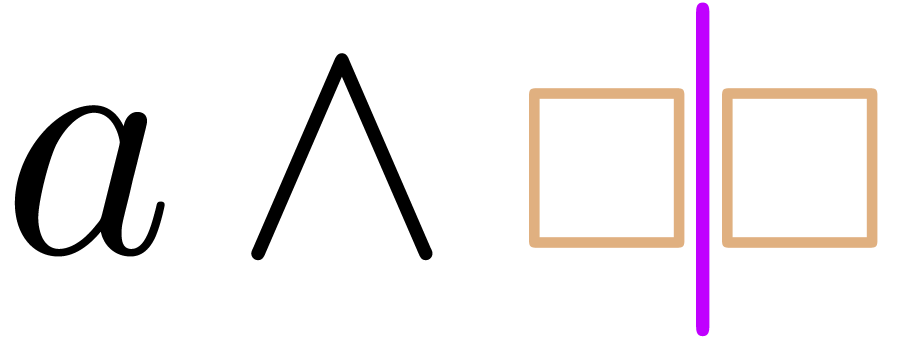 ),
), ),
),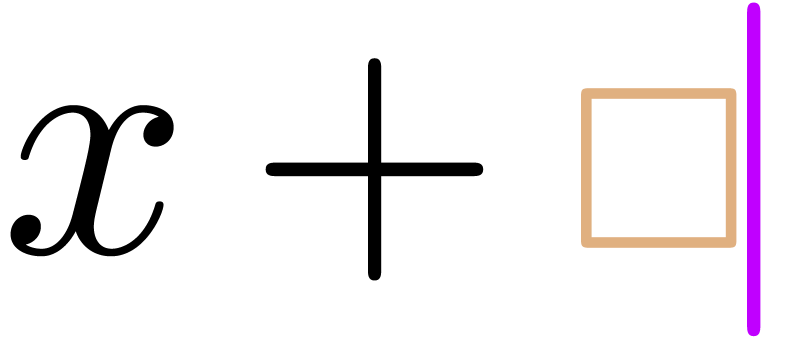 from Example
from Example  ),
), ),
), ).
). ”
”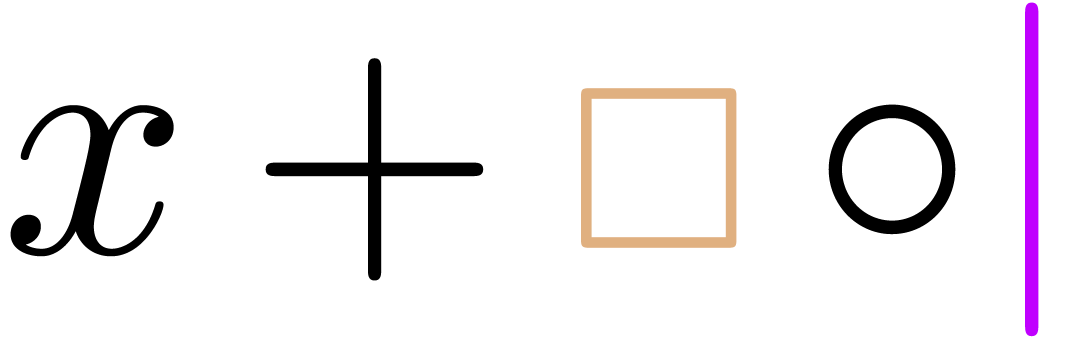 )
)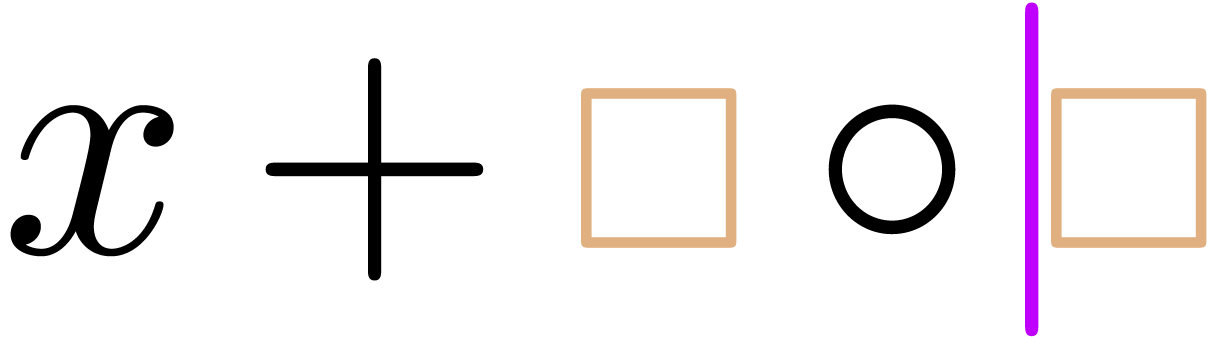 ).
). ):
): ),
), ),
), ).
).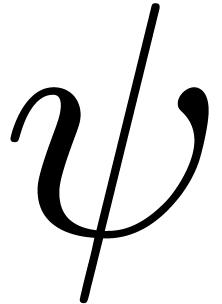 after
after  ):
): ),
), ),
), ):
): ),
), ),
), ):
): ),
), ),
), ).
).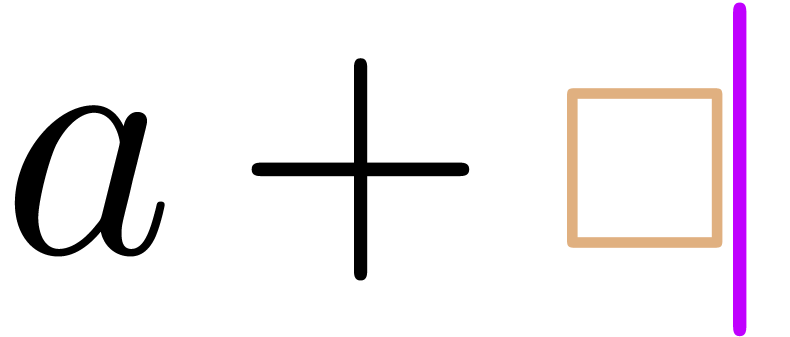 or in
or in  ):
):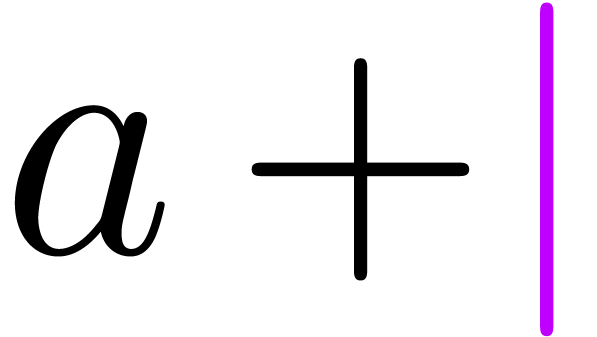 resp.
resp.  ),
), ),
), ),
), ).
).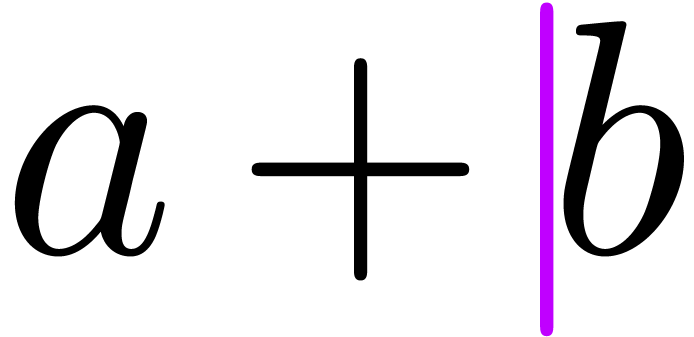 ,
, ):
): ,
, ),
), ):
): ),
),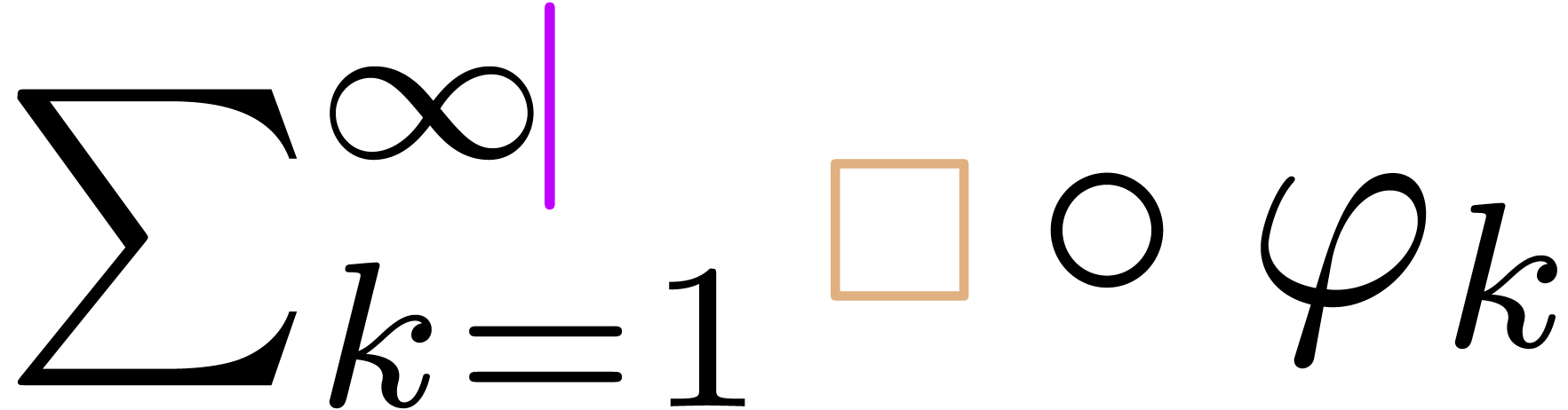 ),
),
 ”
”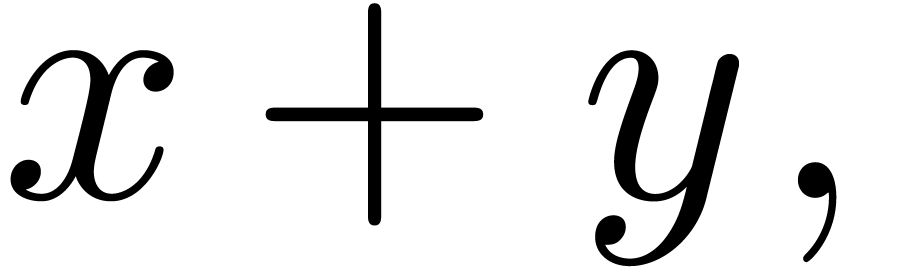
 to the line, we remove the annotation
markup and requalify the comma to become a separator.
to the line, we remove the annotation
markup and requalify the comma to become a separator.
 )
) ).
). .
.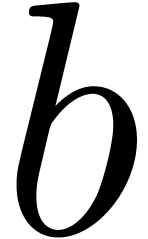 ).
). ,
, ,
,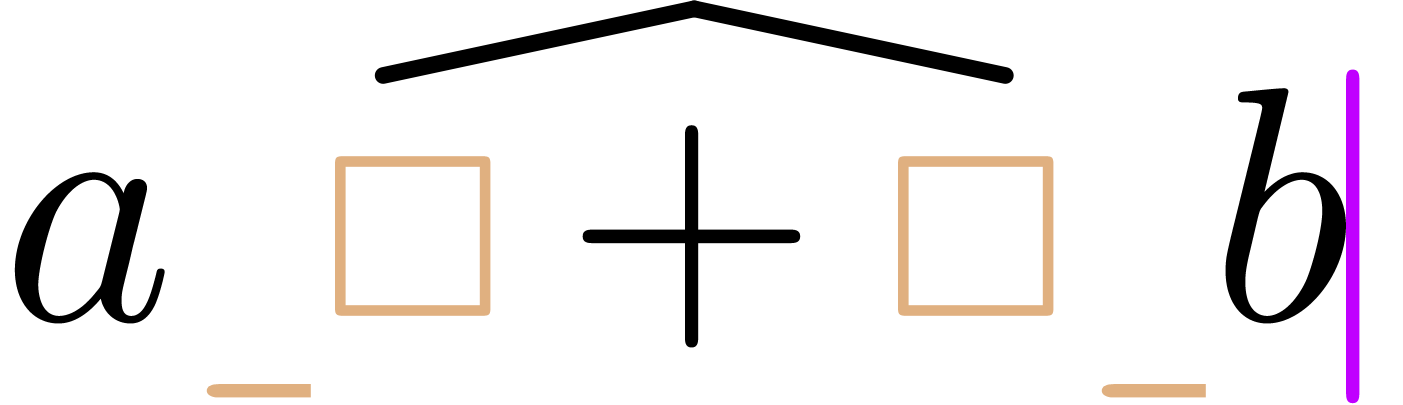 ;
; ,
, is interpreted as
is interpreted as  ,
, as
as  .
.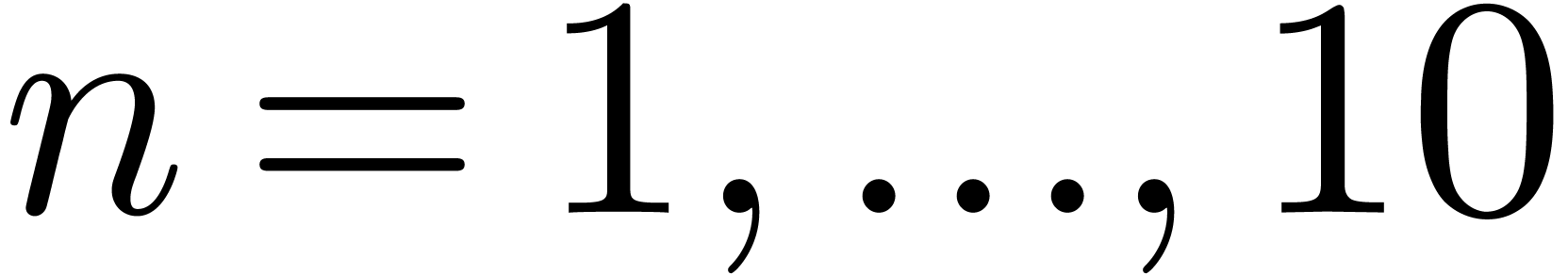 ;
;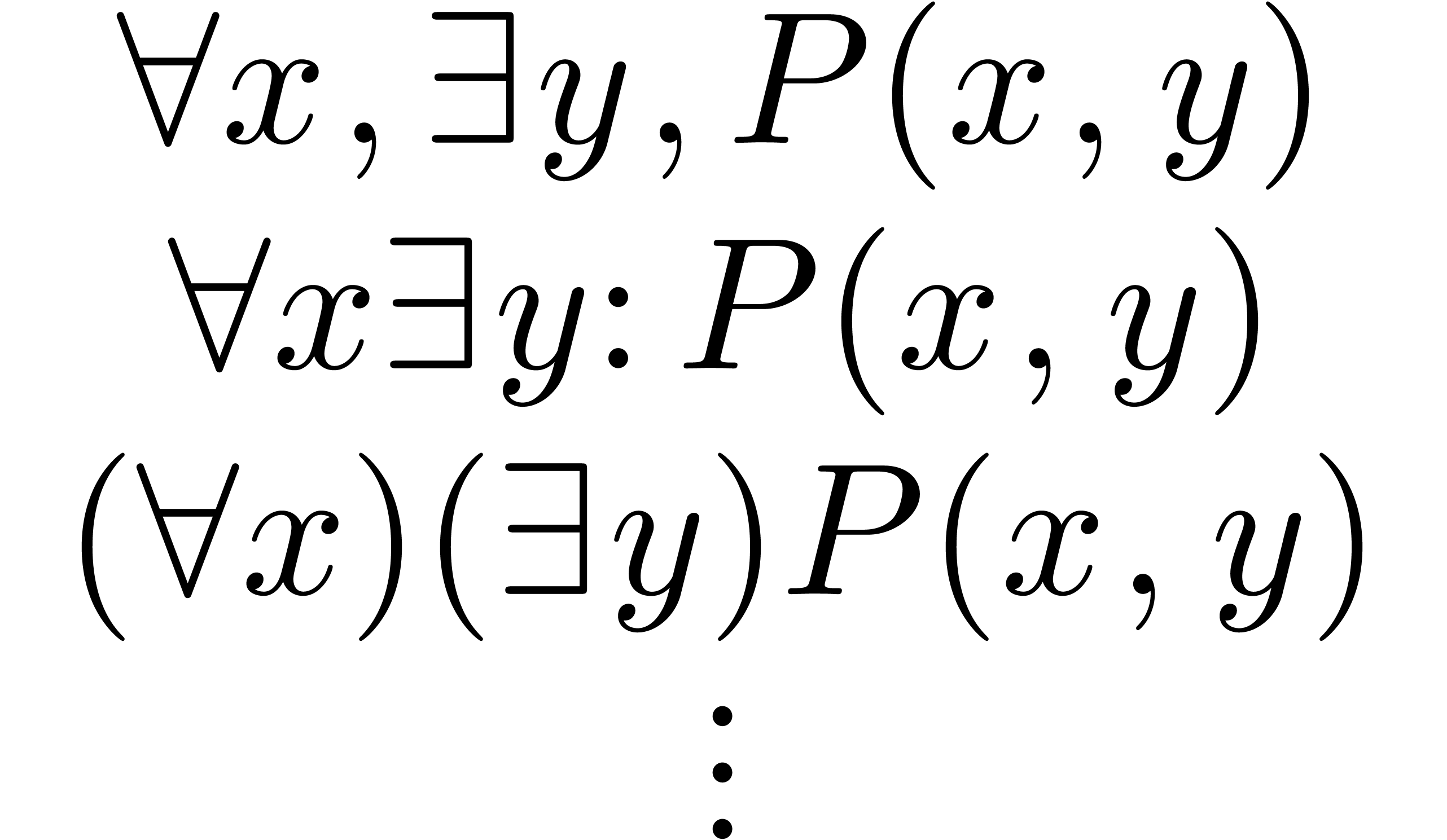
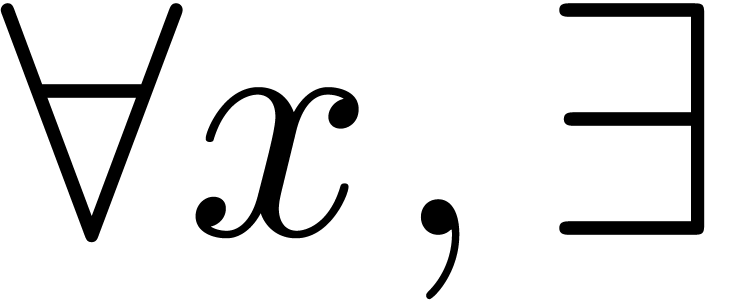 into
into 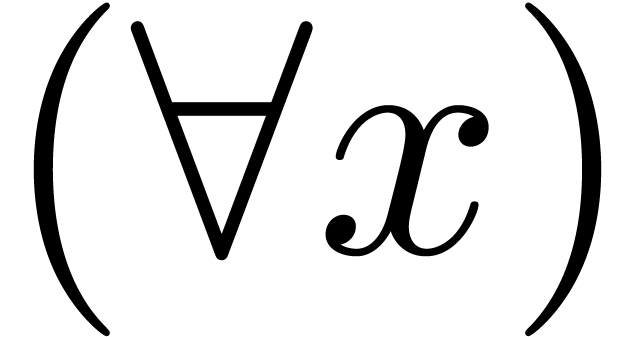 might be
corrected just as well as
might be
corrected just as well as 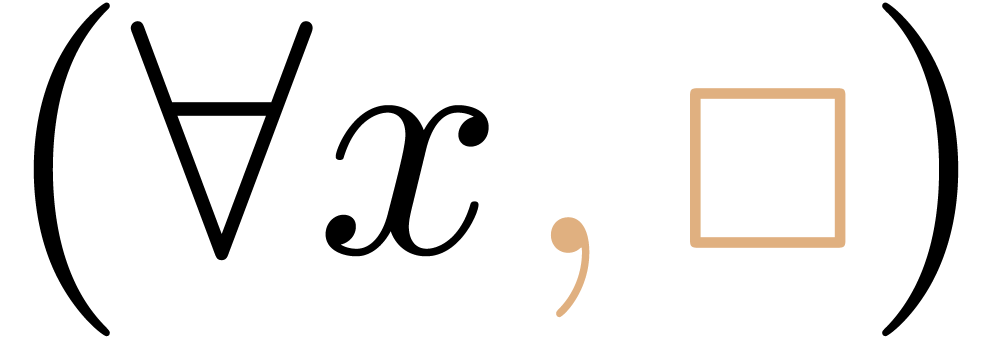 or as
or as 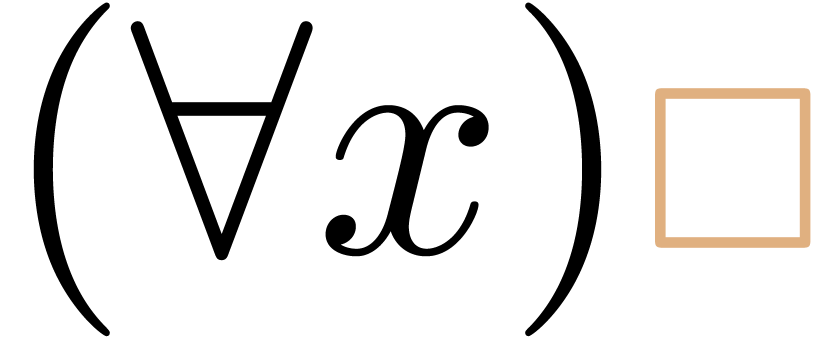 ,
, matrix
matrix  in
a computer algebra system, this is indeed quite pleasant. But in the
example
in
a computer algebra system, this is indeed quite pleasant. But in the
example
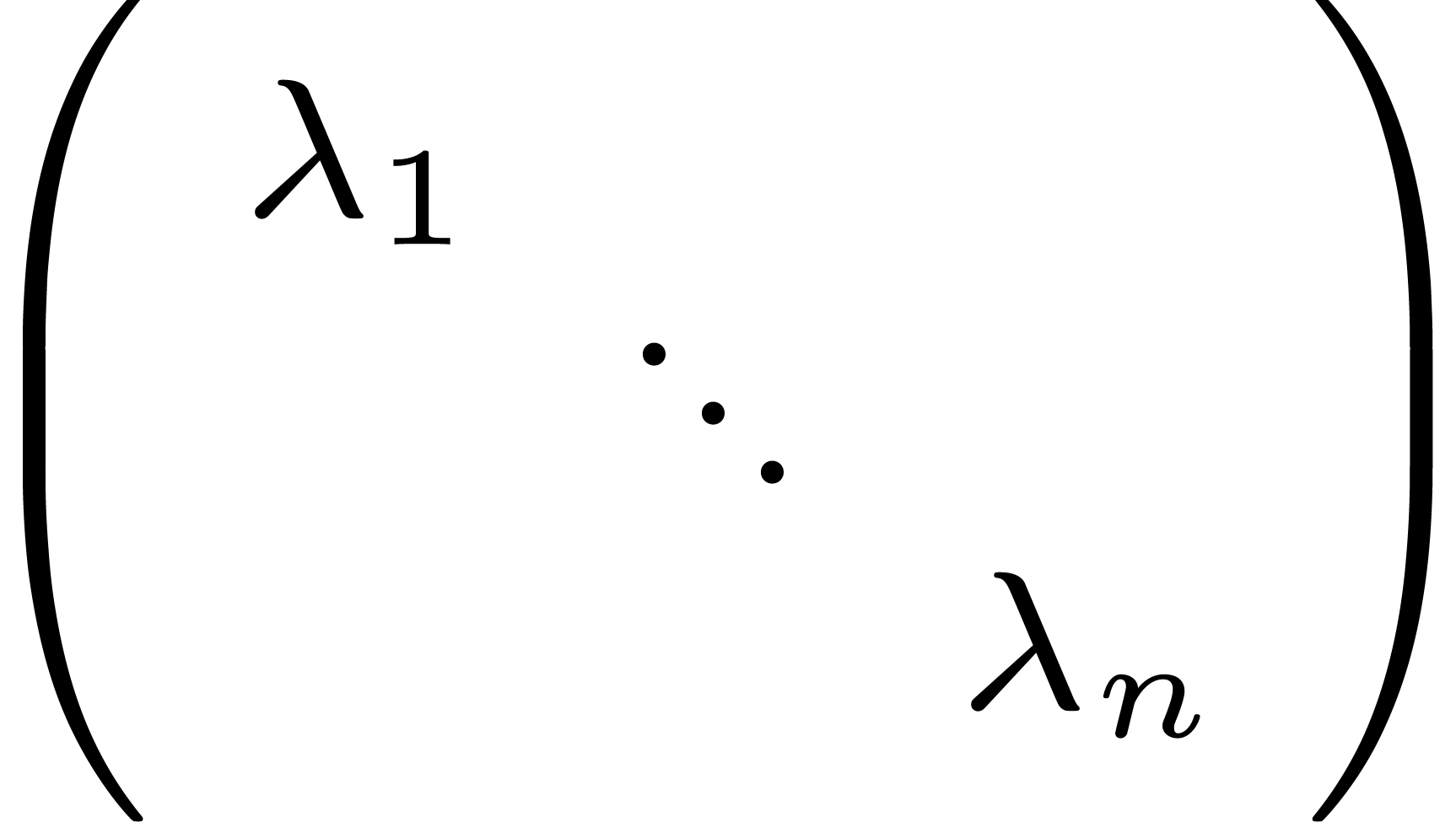
 and
and 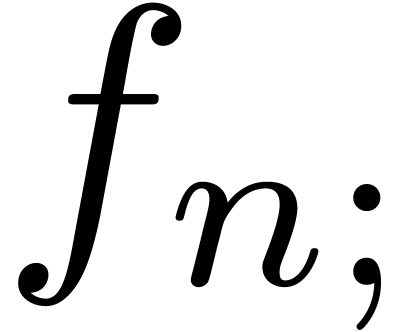 .
.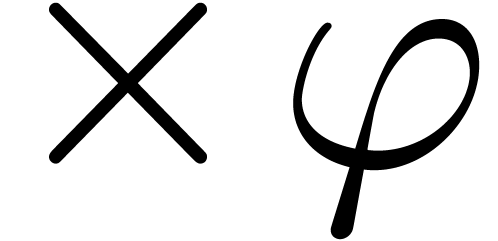 has the semantics of “post-multiplication”
with
has the semantics of “post-multiplication”
with  .
.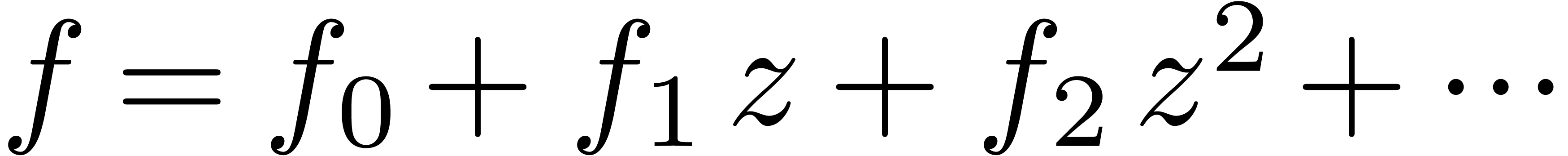 ,
,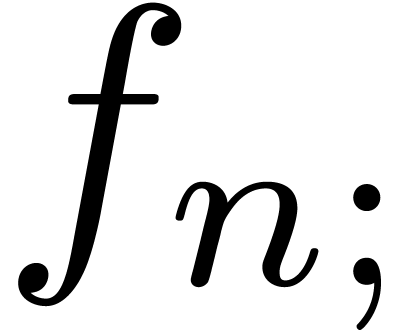 stands for
stands for 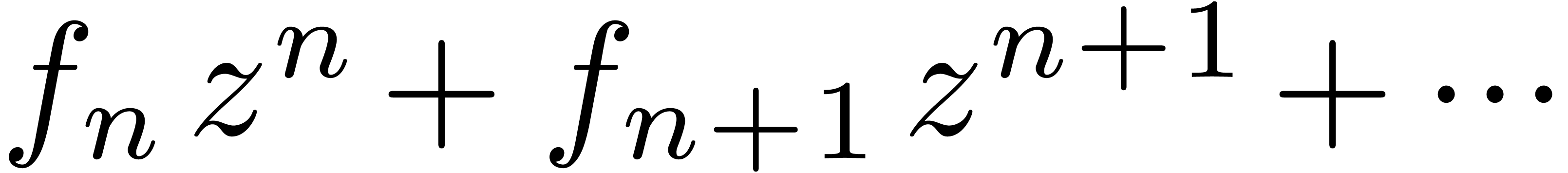 .
.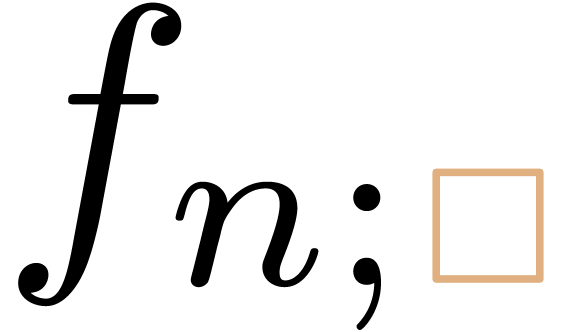 .
. and
and  ,
, by typing
by typing 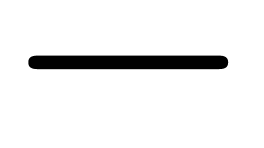 .
.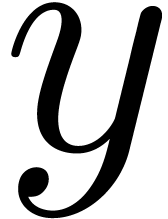 by
by  ,
,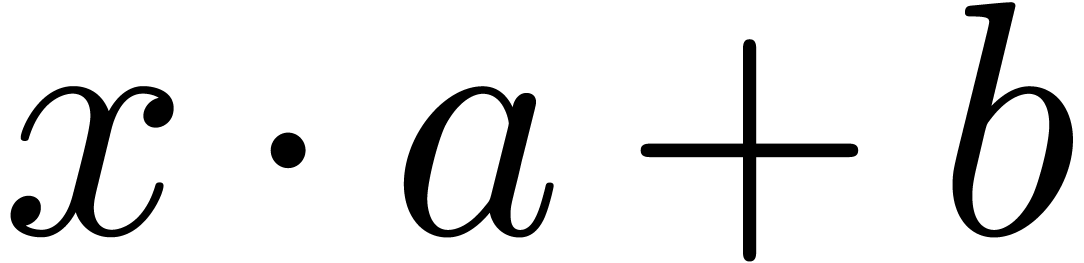 or
or 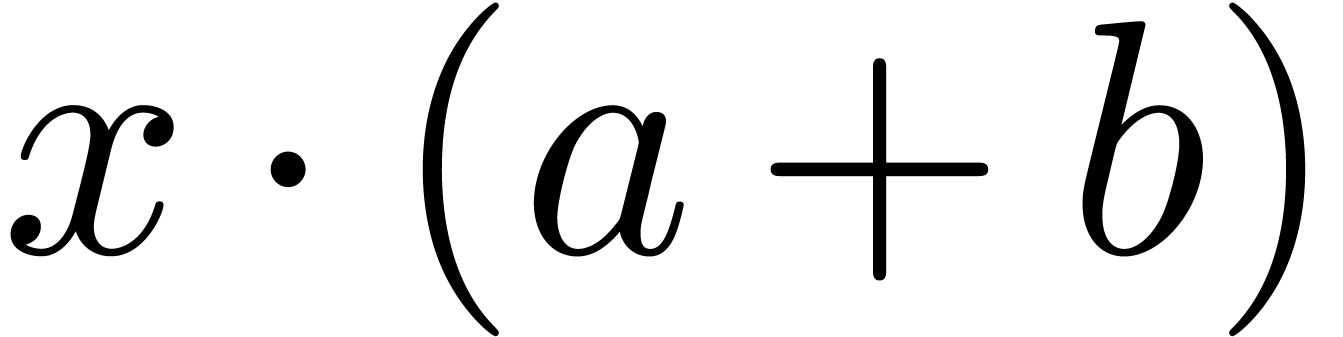 ?
?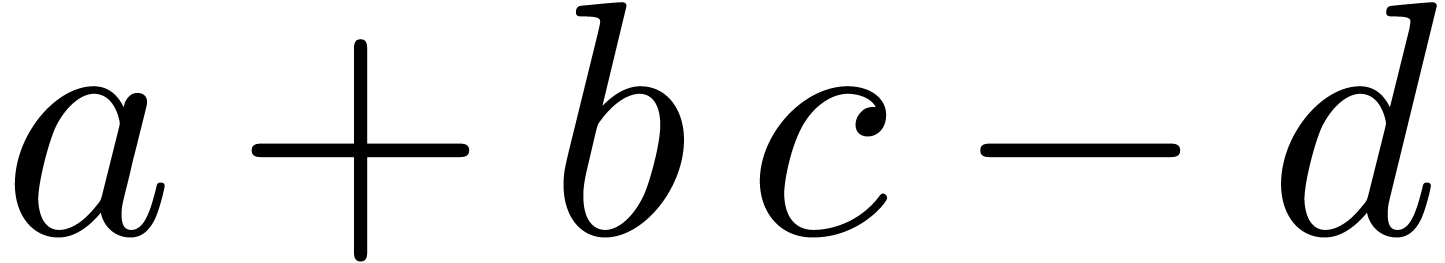 and
and 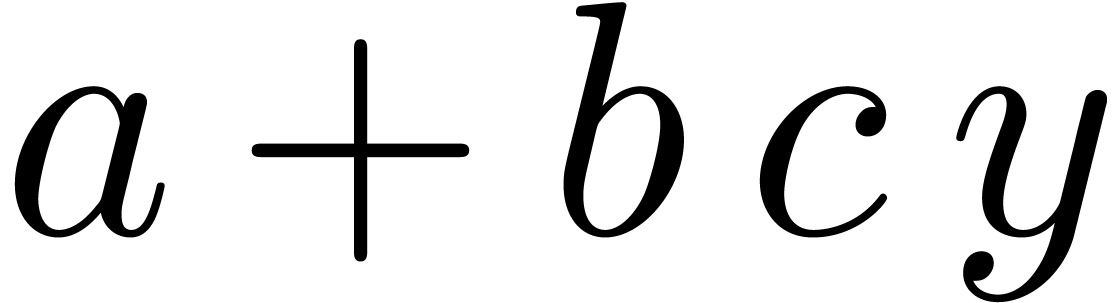 ,
, .
.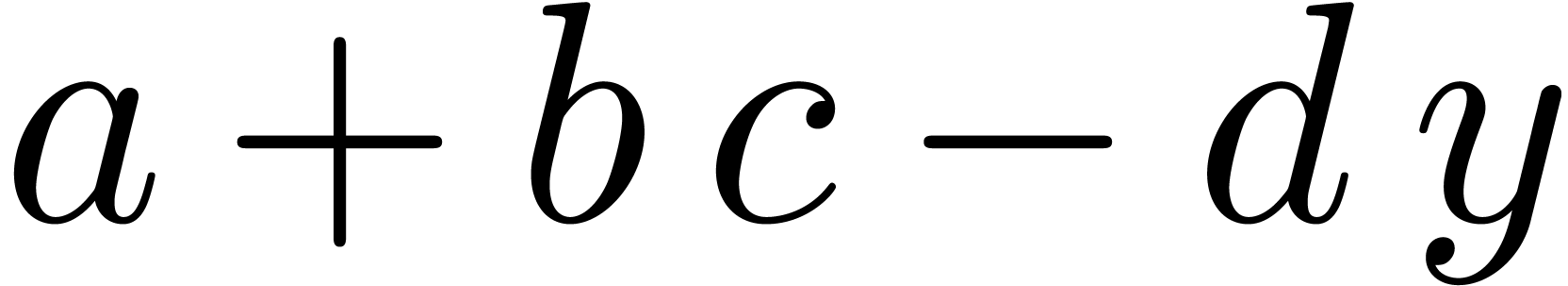 .
.