 be an effective field of characteristic zero
and
be an effective field of characteristic zero
and 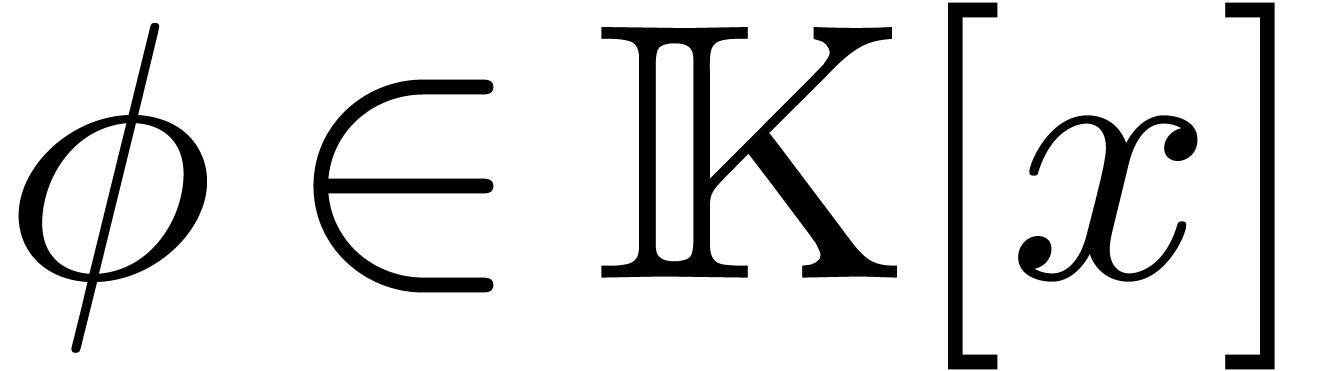 a non-zero polynomial. Consider the system
of differential equations
a non-zero polynomial. Consider the system
of differential equations
|
The class of reduction-based algorithms was introduced recently as a new approach towards creative telescoping. Starting with Hermite reduction of rational functions, various reductions have been introduced for increasingly large classes of holonomic functions. In this paper we show how to construct reductions for general holonomic functions, in the purely differential setting.
I.1.2 Algebraic algorithms |
Let  be an effective field of characteristic zero
and
be an effective field of characteristic zero
and 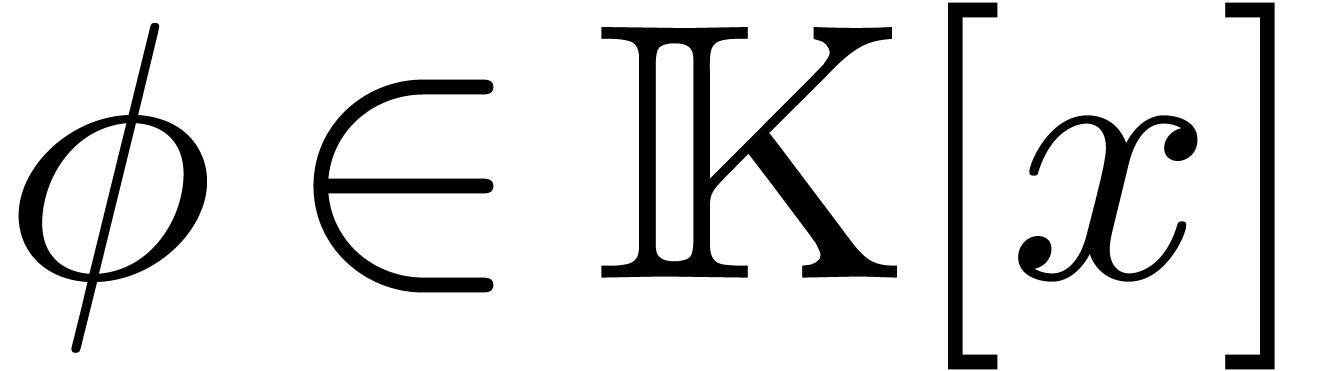 a non-zero polynomial. Consider the system
of differential equations
a non-zero polynomial. Consider the system
of differential equations
where 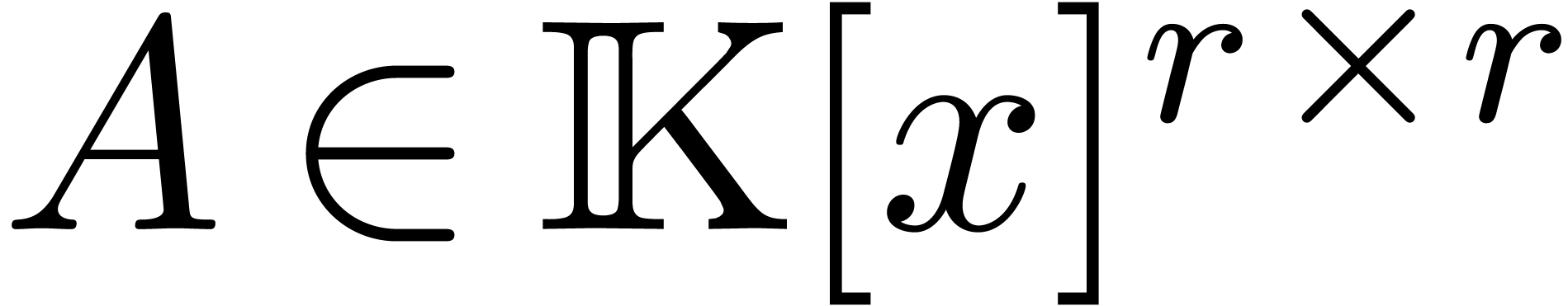 is an
is an  matrix with
entries in
matrix with
entries in 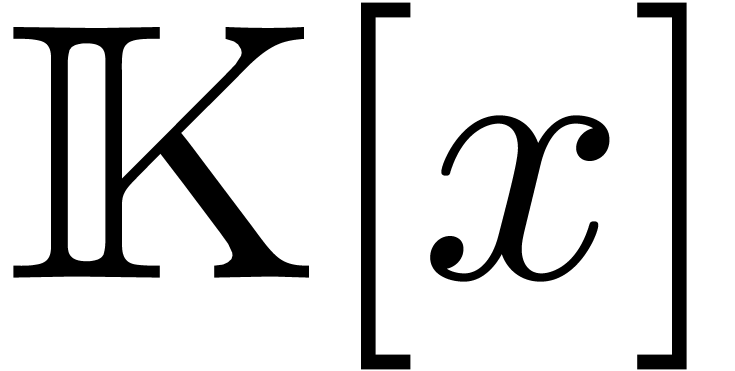 and
and 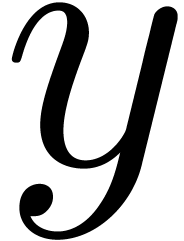 is a
column vector of
is a
column vector of 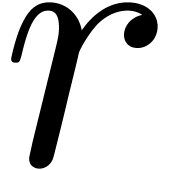 unknown functions. Notice that
any system of differential equations
unknown functions. Notice that
any system of differential equations 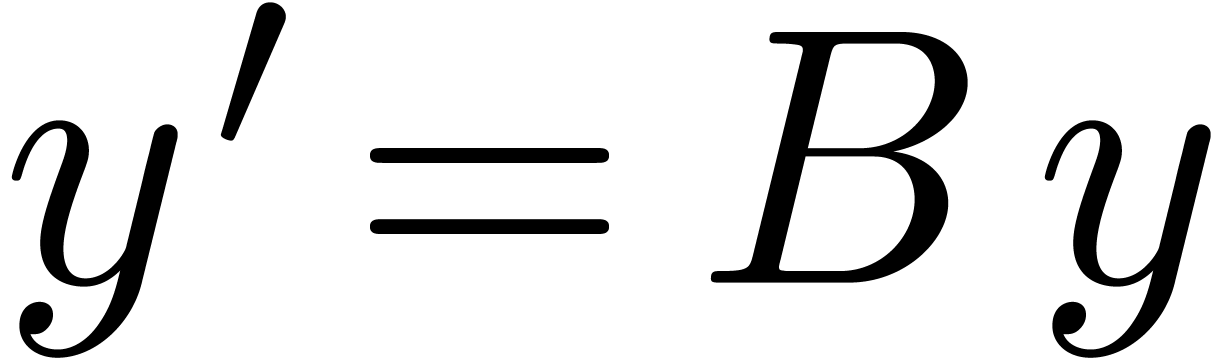 with
with 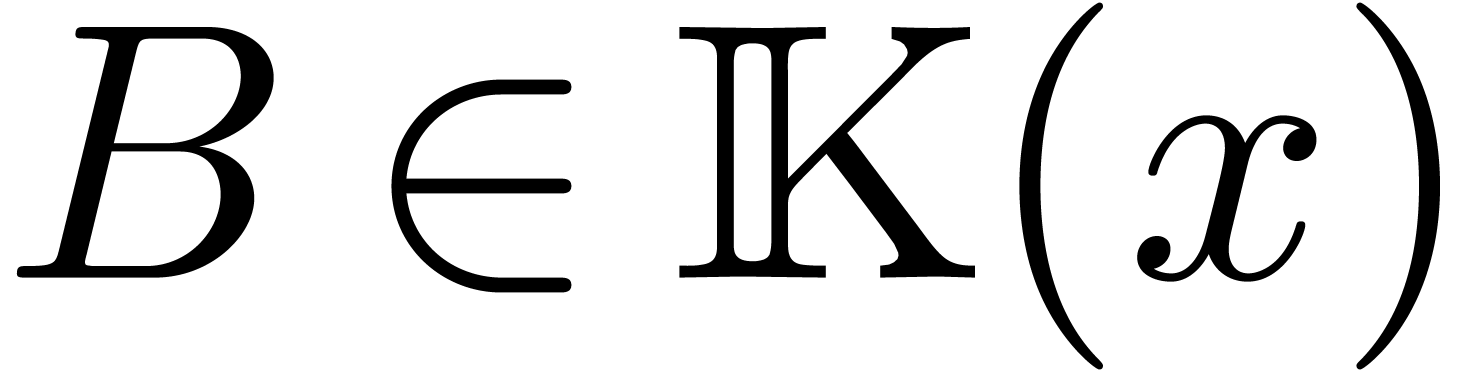 can be rewritten in this form by taking
can be rewritten in this form by taking 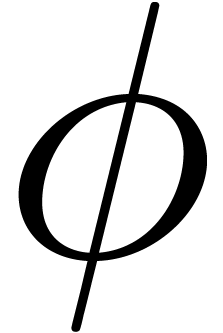 to be a multiple of all denominators.
to be a multiple of all denominators.
Let 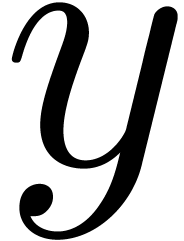 be a formal solution to (1) and
consider the
be a formal solution to (1) and
consider the 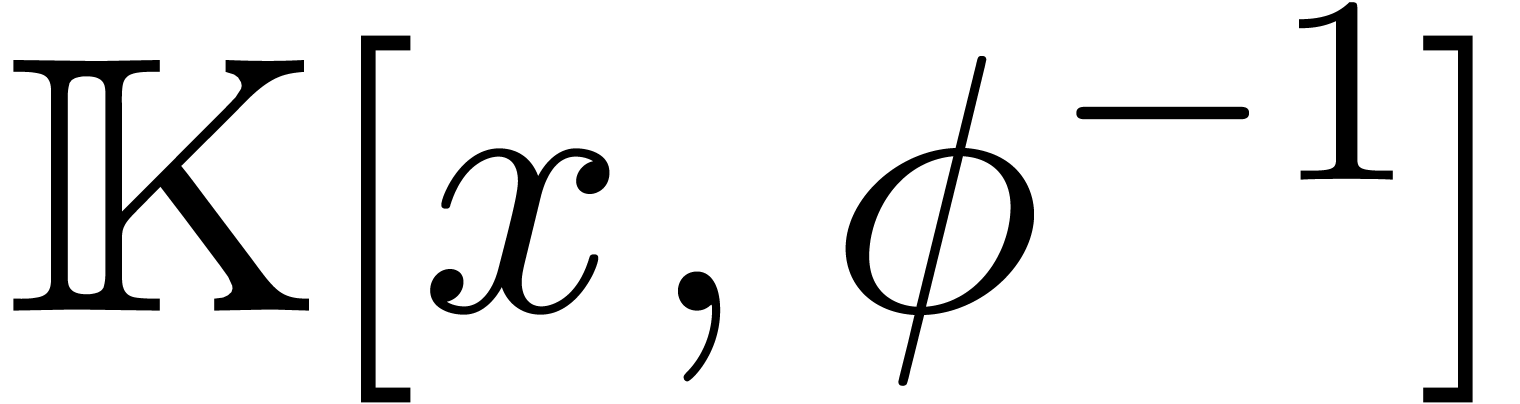 -module
-module  of linear combinations
of linear combinations 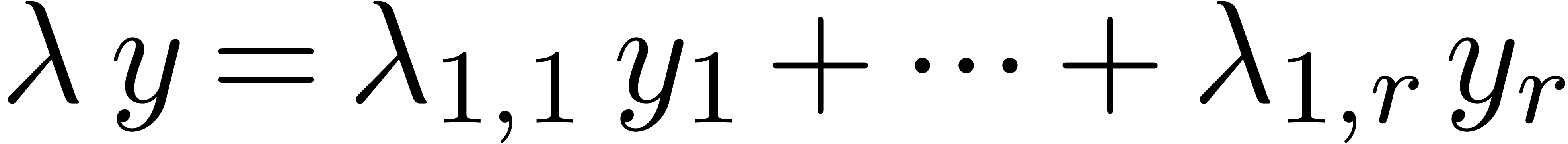 where
where
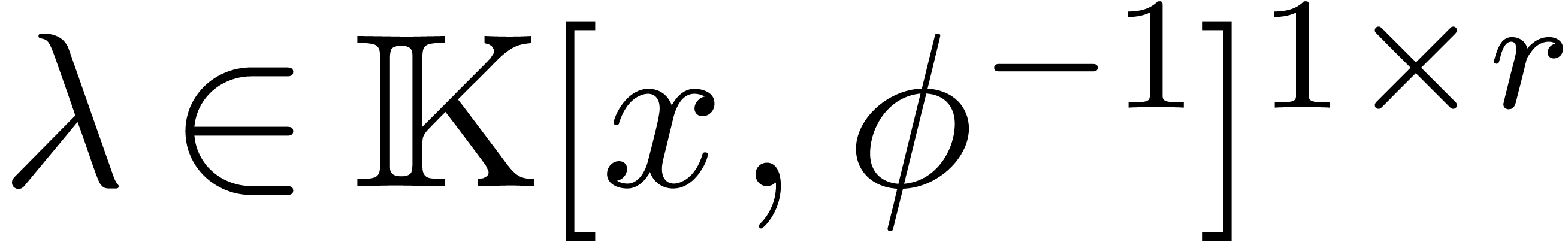 is a row vector. Then
is a row vector. Then  has the natural structure of a D-module for the derivation
has the natural structure of a D-module for the derivation  defined by
defined by 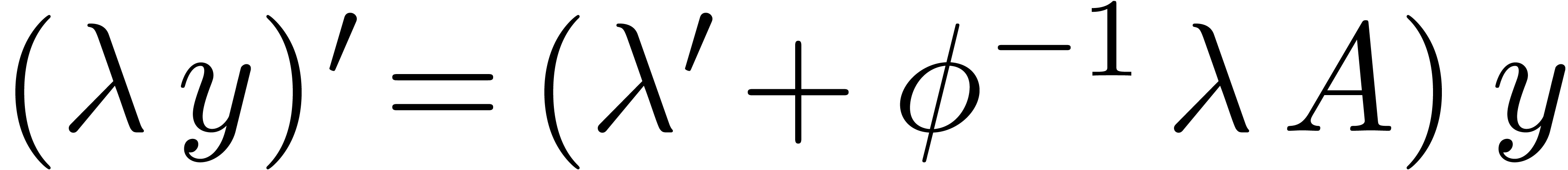 . A
. A
 -linear mapping
-linear mapping 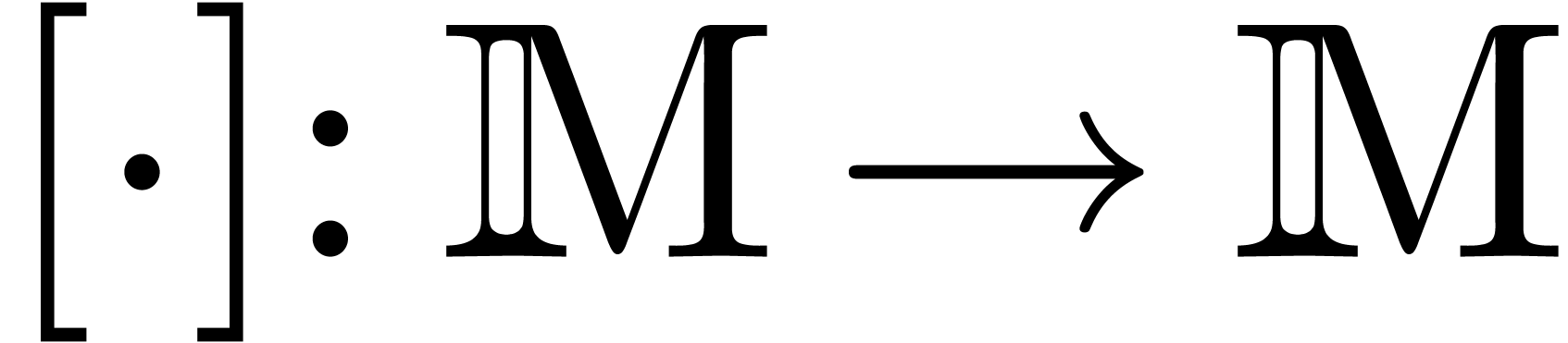 is said to be a reduction if
is said to be a reduction if 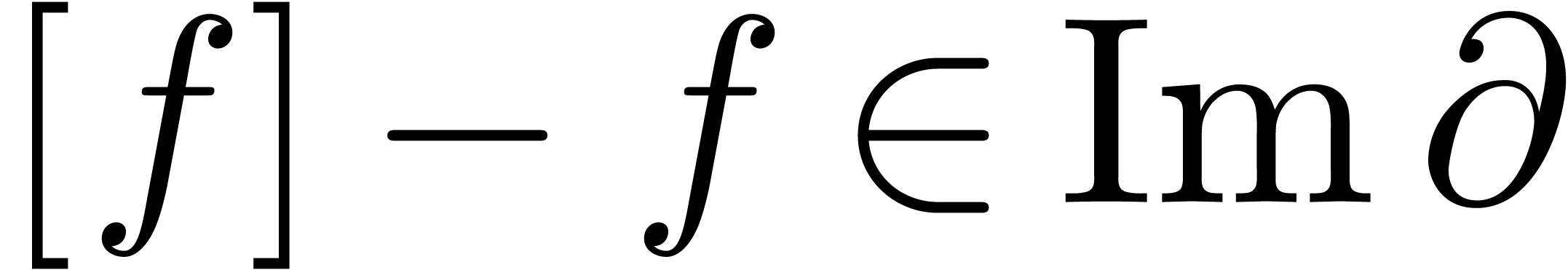 for all
for all 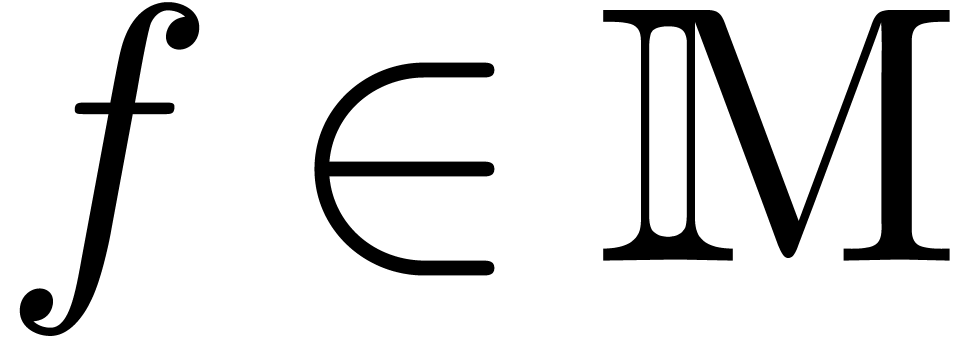 . Such a reduction is
said to be confined if its image is a finite dimensional
subspace of
. Such a reduction is
said to be confined if its image is a finite dimensional
subspace of  and normal if
and normal if 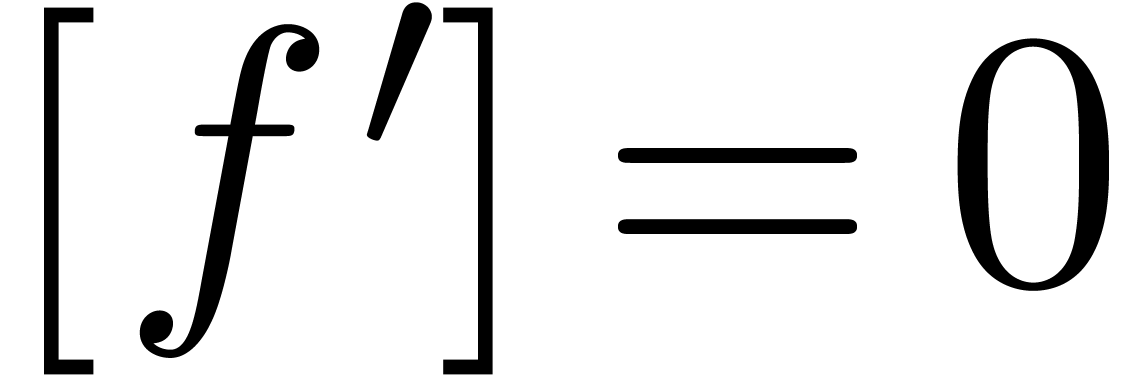 for all
for all 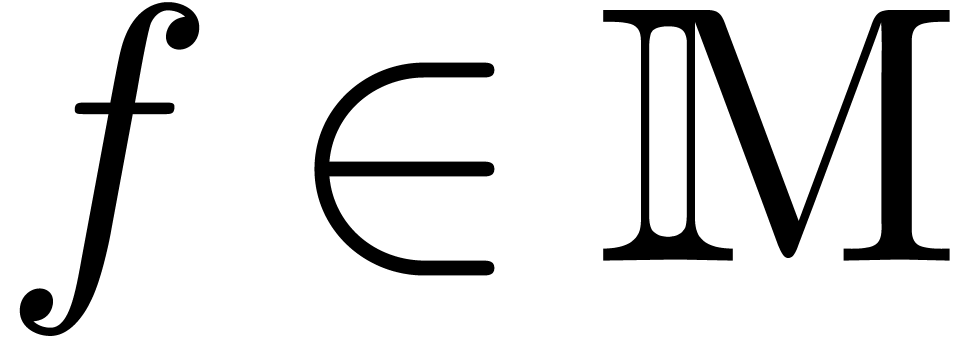 .
.
In this paper, we will show how to construct confined reductions. Such
reductions are interesting for their application to creative telescoping
[13, 7], as we briefly recall in section 2. The first reduction of this kind is Hermite reduction [2, 4], in which case 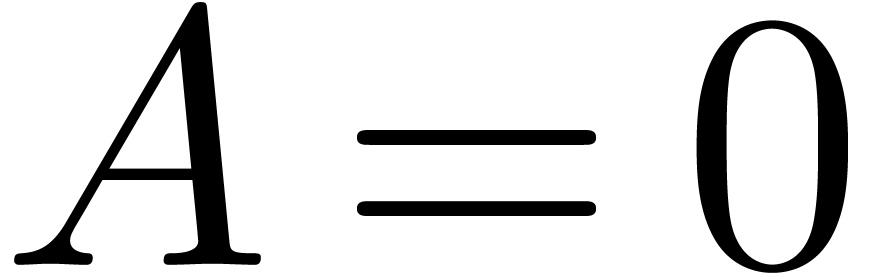 . The existence of normal confined reductions has
been shown in increasingly general cases [12, 6]
and most noticeably for Fuchsian differential equations [5].
We refer to [4, 9] for more details and the
application to creative telescoping.
. The existence of normal confined reductions has
been shown in increasingly general cases [12, 6]
and most noticeably for Fuchsian differential equations [5].
We refer to [4, 9] for more details and the
application to creative telescoping.
Our construction of confined reductions proceeds in two stages. In
section 4, we first focus on the 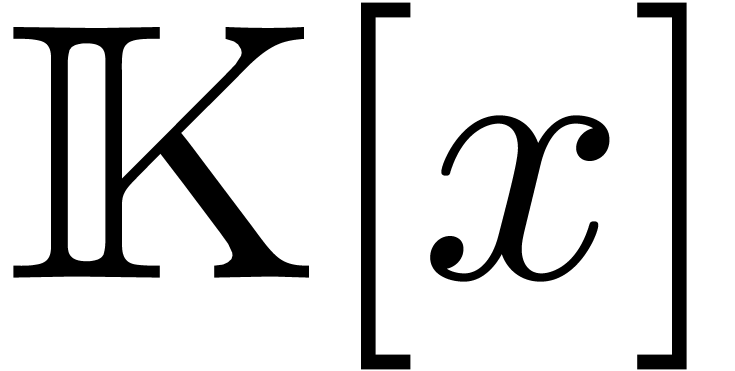 -submodule
-submodule  of
of  of linear combinations
of linear combinations  with
with 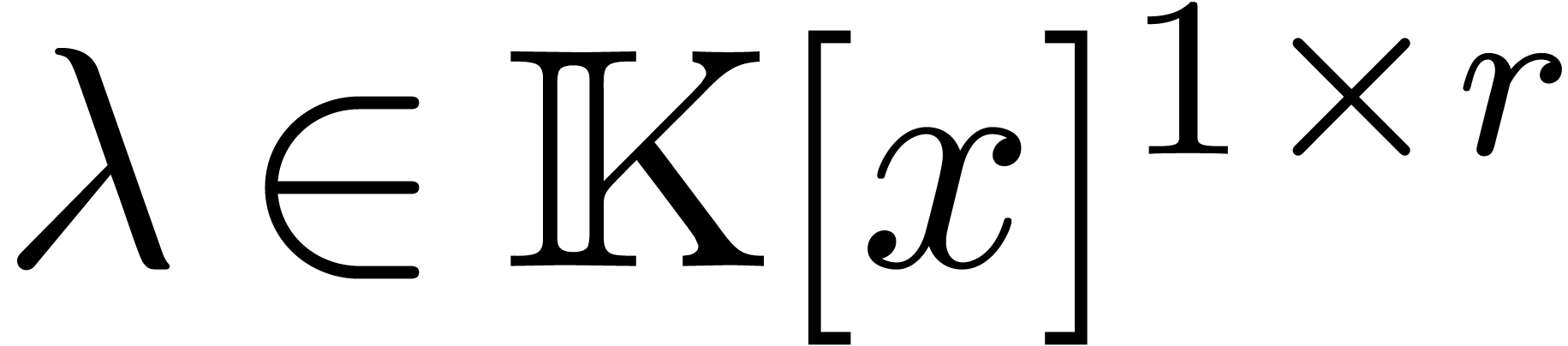 . We will construct a
. We will construct a  -linear head reduction
-linear head reduction 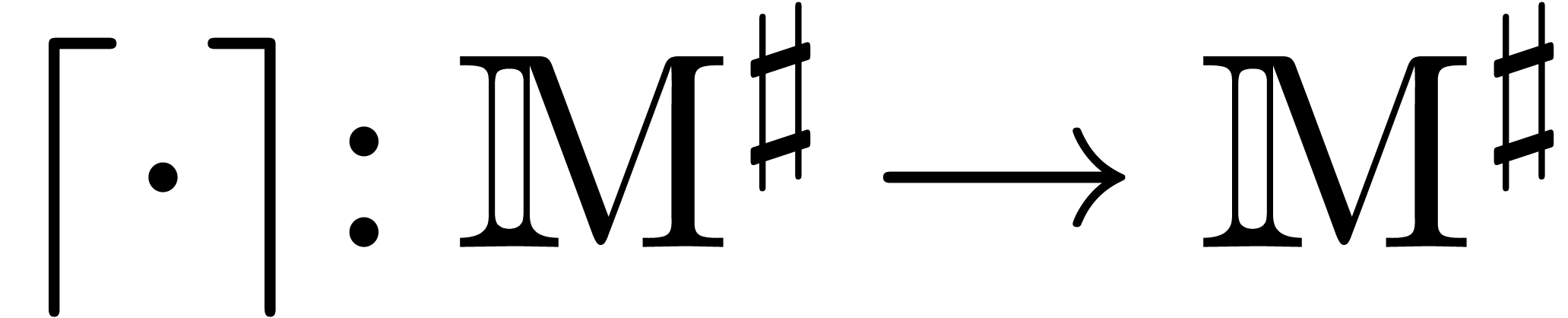 such that
such that 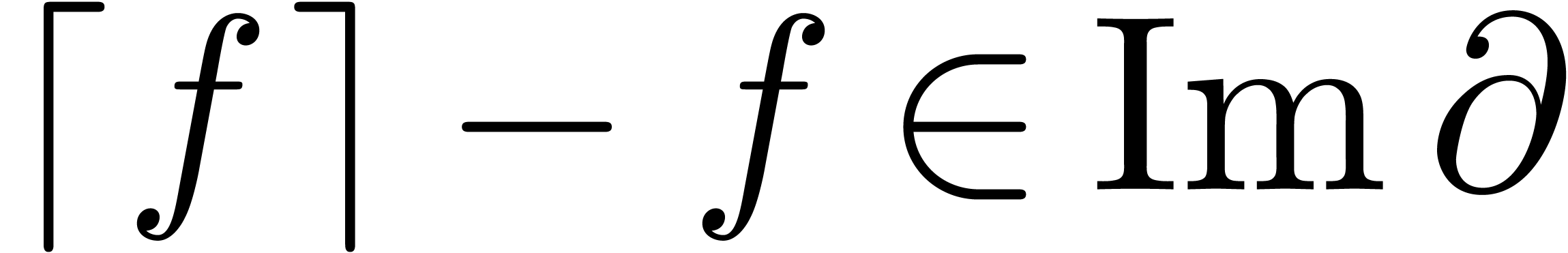 and
and 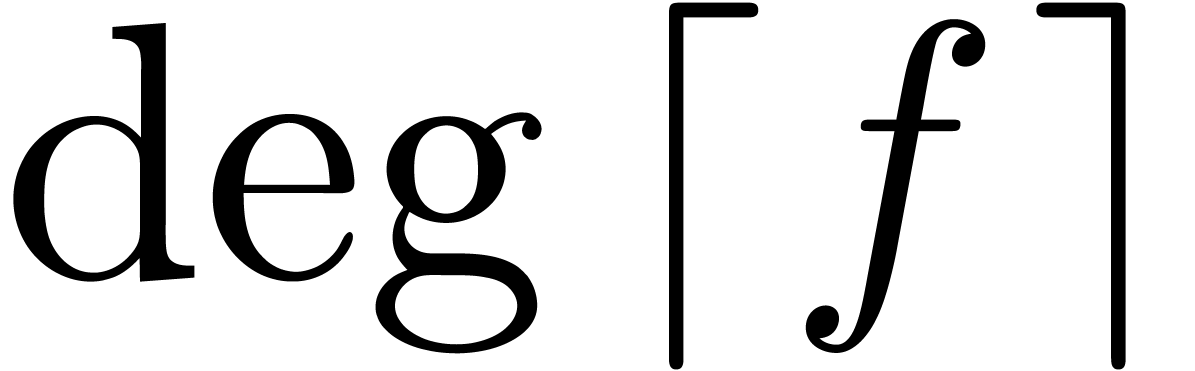 is bounded from above for all
is bounded from above for all 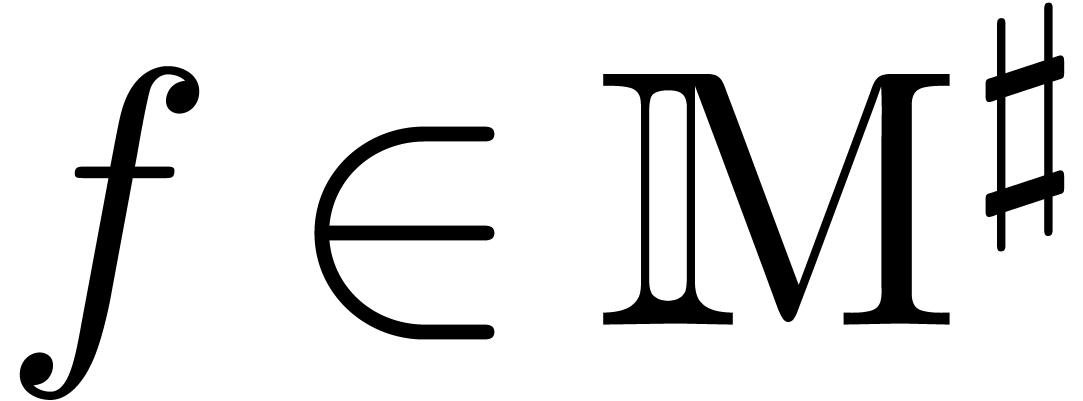 .
Here we understand that
.
Here we understand that 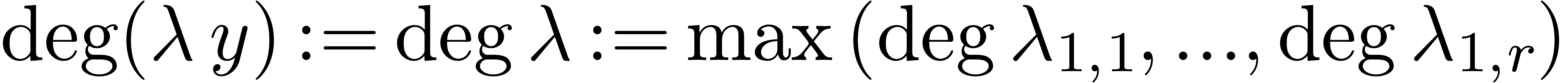 for all
for all 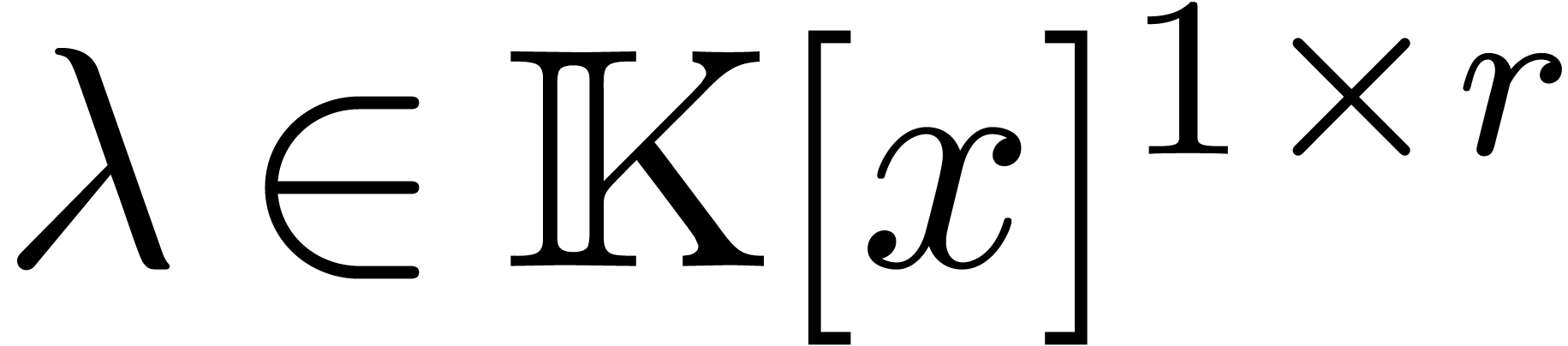 . The construction uses a variant of Gaussian
elimination that will be described in section 3.
. The construction uses a variant of Gaussian
elimination that will be described in section 3.
The head reduction may also be regarded as a way to reduce the valuation
of 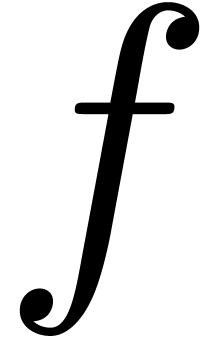 in
in 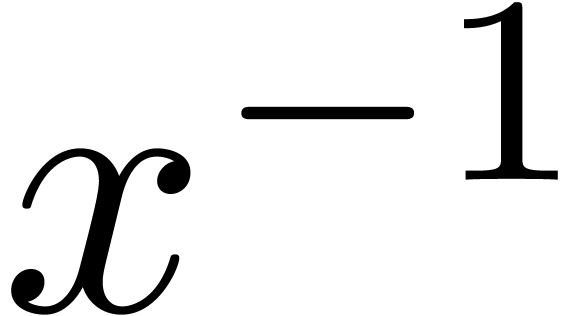 ,
at the point at infinity. In section 5 we turn to tail
reductions, with the aim to reduce the valuation of
,
at the point at infinity. In section 5 we turn to tail
reductions, with the aim to reduce the valuation of  at all other points in
at all other points in  and its algebraic closure
and its algebraic closure
 . This is essentially similar
to head reduction via a change of variables, while allowing
ourselves to work in algebraic extensions of
. This is essentially similar
to head reduction via a change of variables, while allowing
ourselves to work in algebraic extensions of  .
.
In the last section 7, we show how to glue the head
reduction and the tail reductions at each of the roots of  together into a global confined reduction on
together into a global confined reduction on  . Using straightforward linear algebra and
suitable valuation bounds, one can further turn this reduction into a
normal one, as will be shown in detail in section 7.2.
. Using straightforward linear algebra and
suitable valuation bounds, one can further turn this reduction into a
normal one, as will be shown in detail in section 7.2.
The valuation bounds that are required in section 7.2 are
proved in section 6. In this section we also prove degree
and valuation bounds for so called head and tail choppers. The existence
of head and tail choppers whose size is polynomial in the size of the
original equation makes it possible to derive polynomial bounds for the
complexity of creative telescoping: this follows from polynomial bounds
for the dimension of 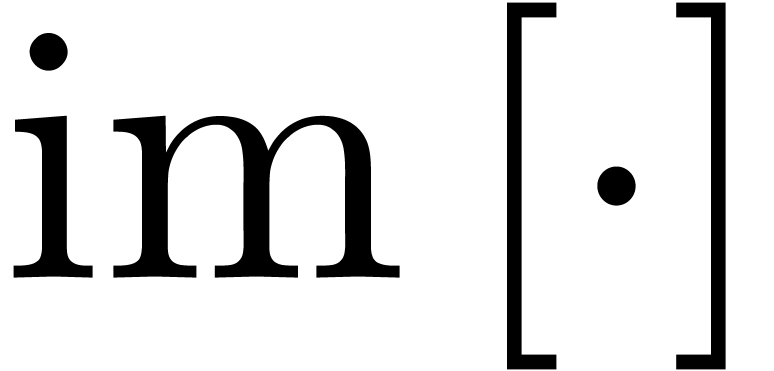 and for the reduction of an
elements in
and for the reduction of an
elements in  . We intend to
work out the details in a forthcoming paper.
. We intend to
work out the details in a forthcoming paper.
Let  be an effective subfield of
be an effective subfield of  and let
and let 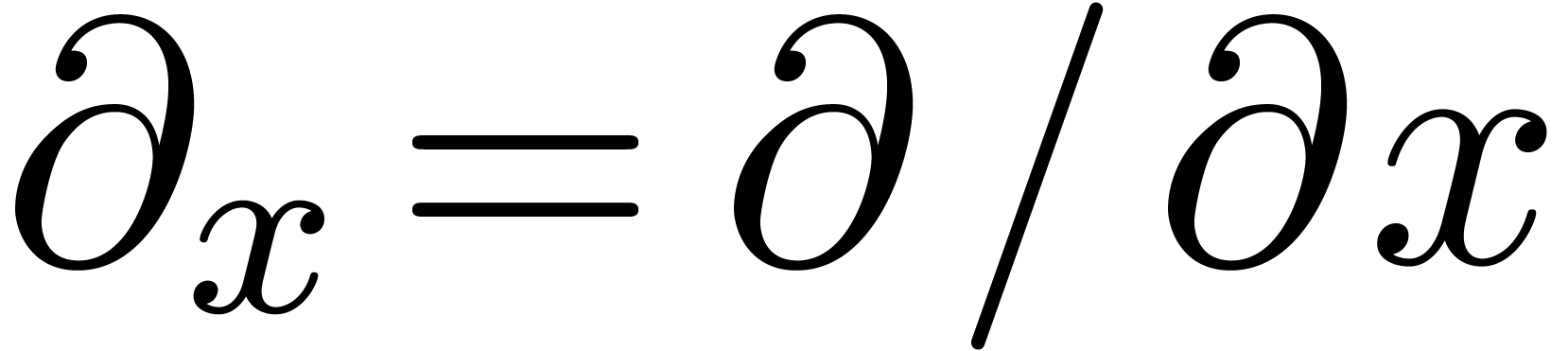 and
and 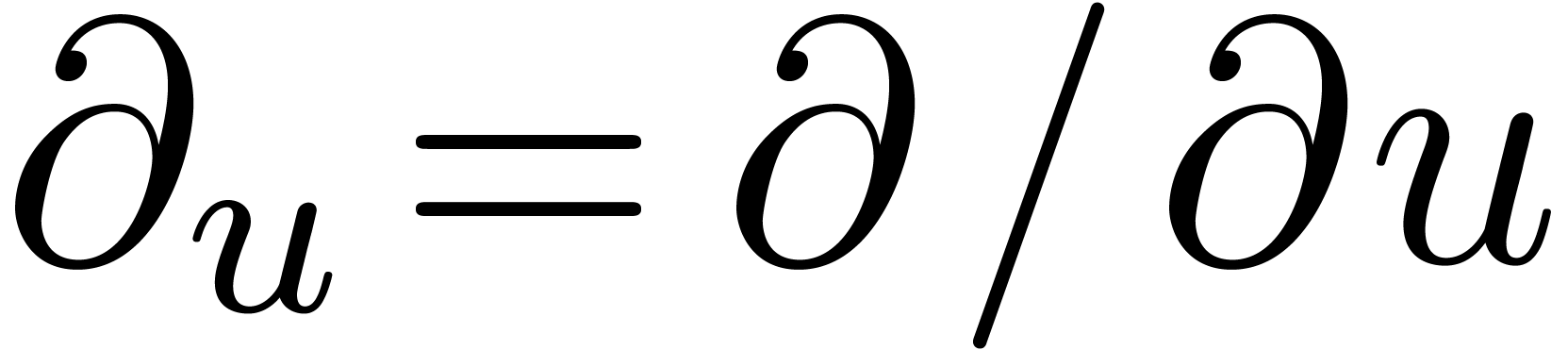 denote the
partial derivations with respect to
denote the
partial derivations with respect to  and
and  . Consider a system of differential
equations
. Consider a system of differential
equations
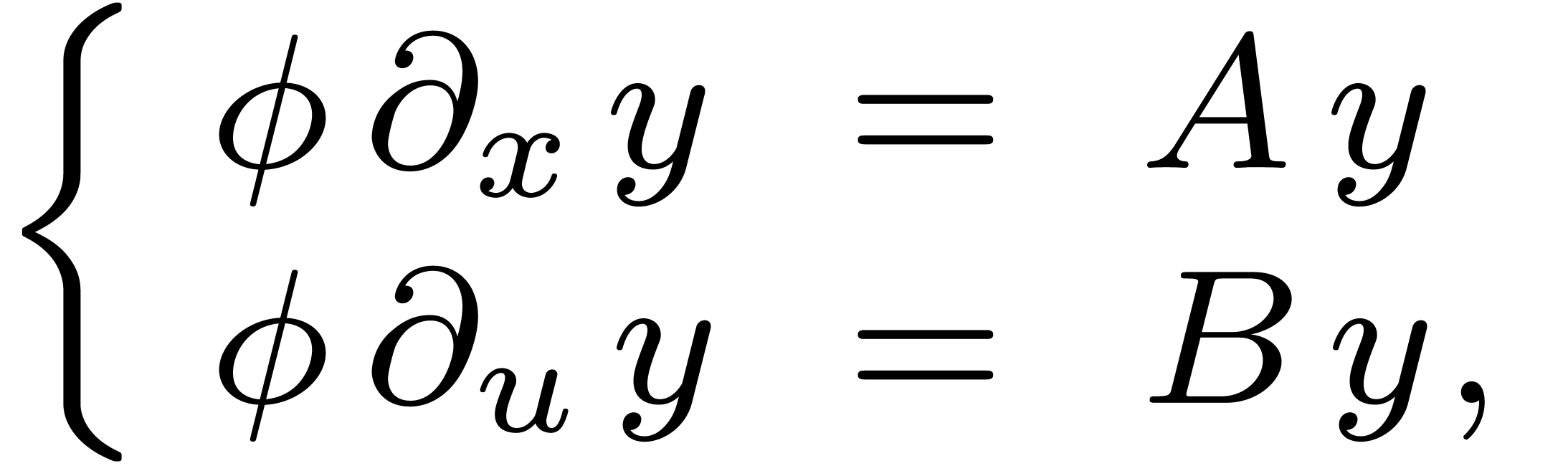 |
(2) |
where 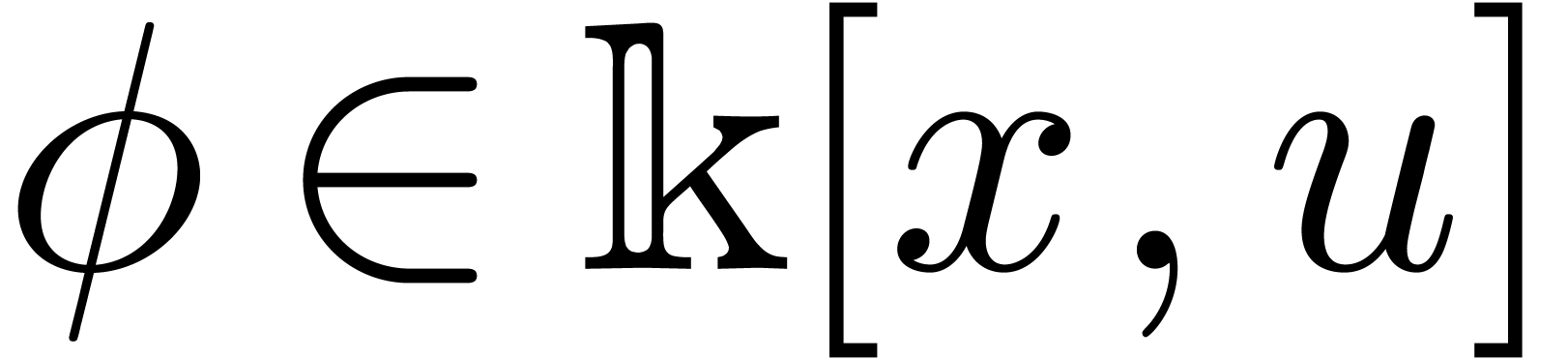 is non-zero and
is non-zero and 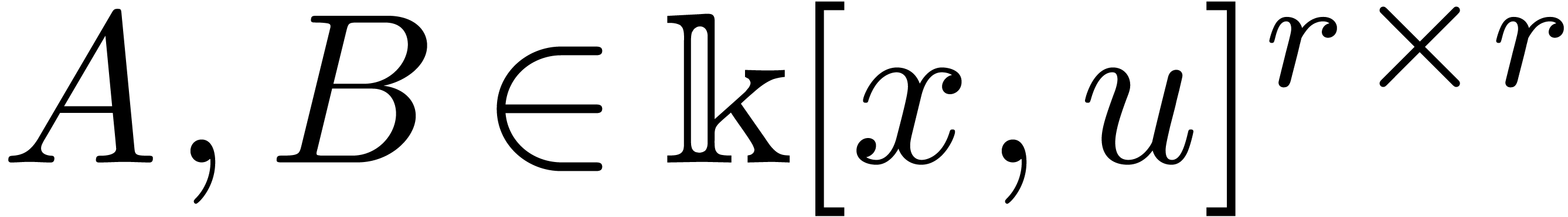 are such that
are such that
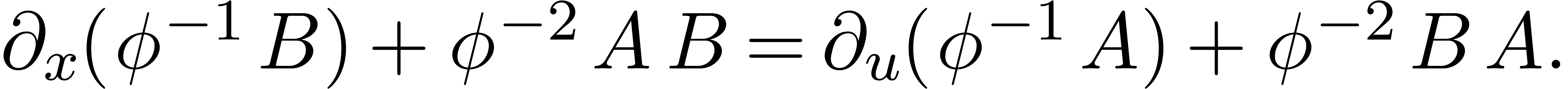
Setting 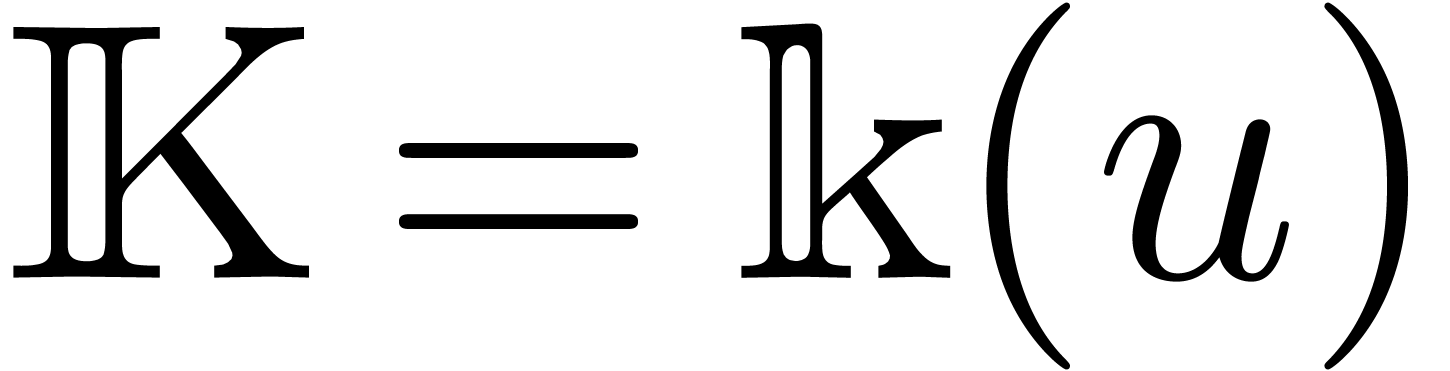 , the first part of
(2) then becomes of the form (1). Notice that
any bivariate holonomic function is an entry of a solution to a system
of the form (2).
, the first part of
(2) then becomes of the form (1). Notice that
any bivariate holonomic function is an entry of a solution to a system
of the form (2).
Let 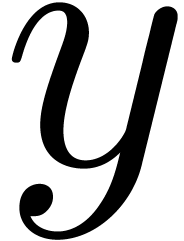 be a complex analytic solution of the above
system of equations and let
be a complex analytic solution of the above
system of equations and let  be the
be the 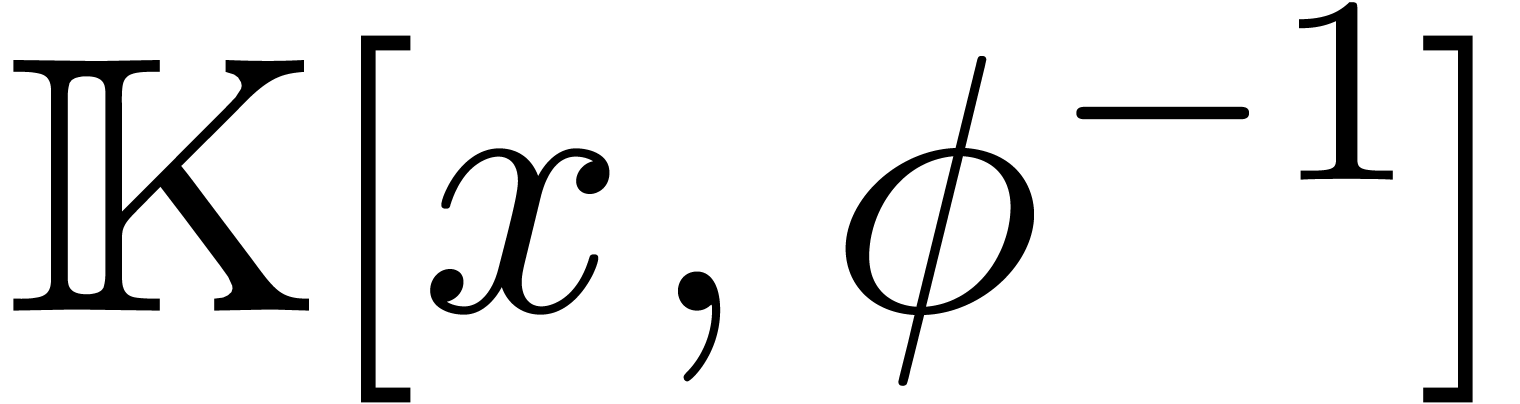 -module generated by the entries of
-module generated by the entries of 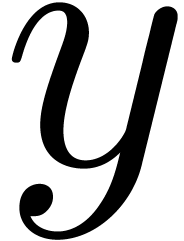 . Notice that
. Notice that  is stable under both
is stable under both 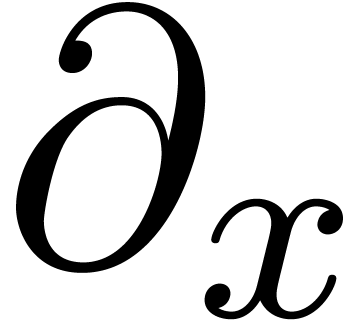 and
and 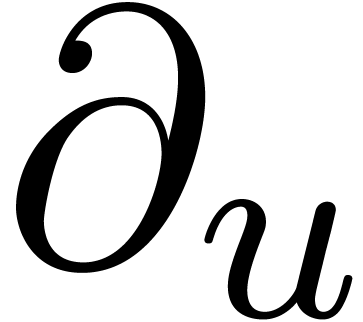 . For any
. For any  with
with  and any non-singular contour
and any non-singular contour  in
in
 between two points
between two points 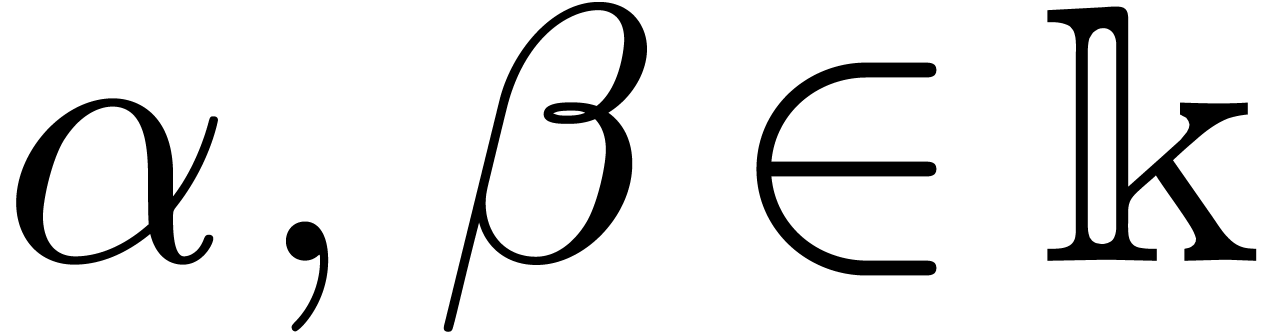 ,
we may consider the integral
,
we may consider the integral
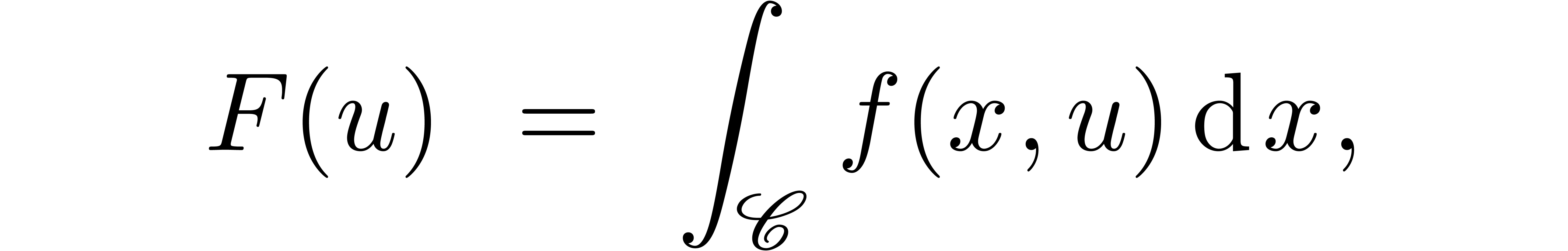
which defines a function in the single variable  . It is natural to ask under which conditions
. It is natural to ask under which conditions  is a holonomic function and how to compute a
differential operator
is a holonomic function and how to compute a
differential operator  with
with 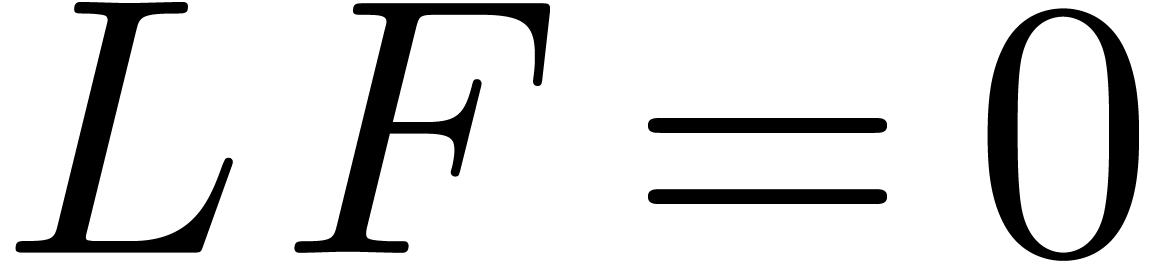 .
.
The idea of creative telescoping is to compute a differential
operator 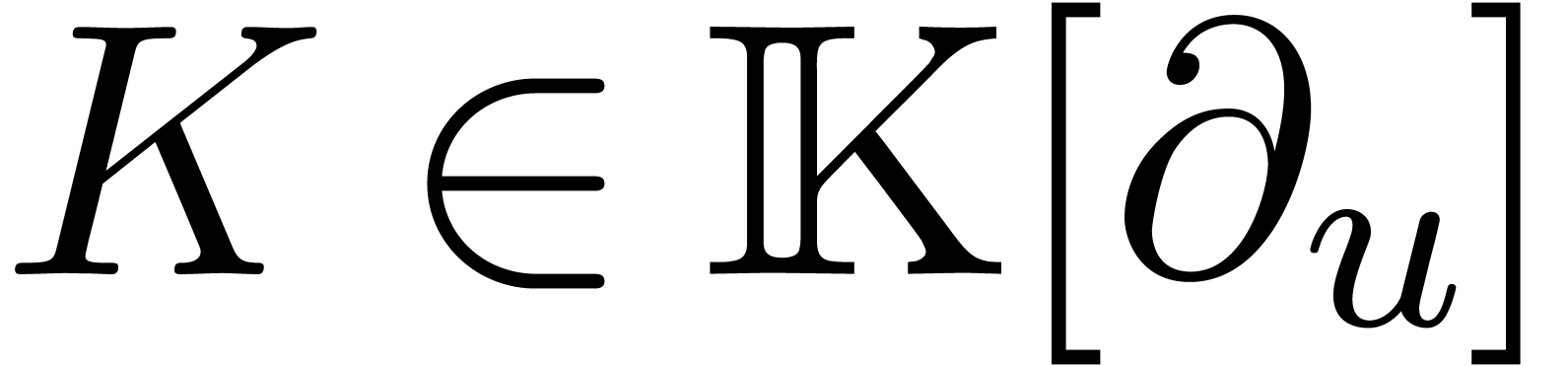 and a function
and a function 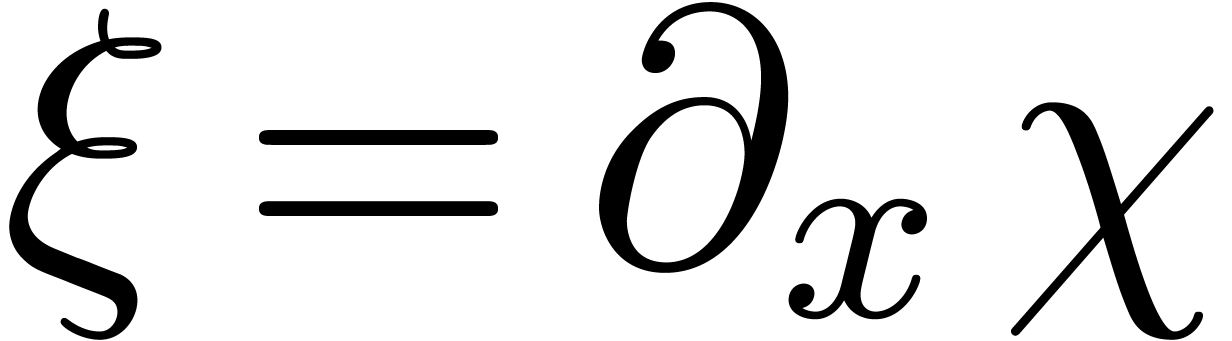 with
with 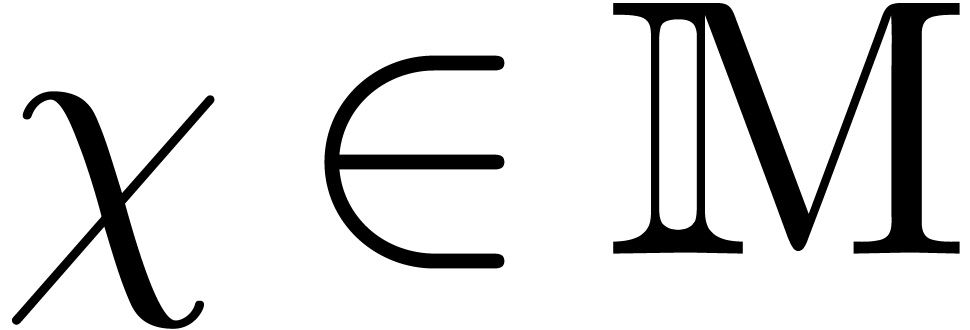 such that
such that
Integrating over  , we then
obtain
, we then
obtain
If the contour  has the property that
has the property that 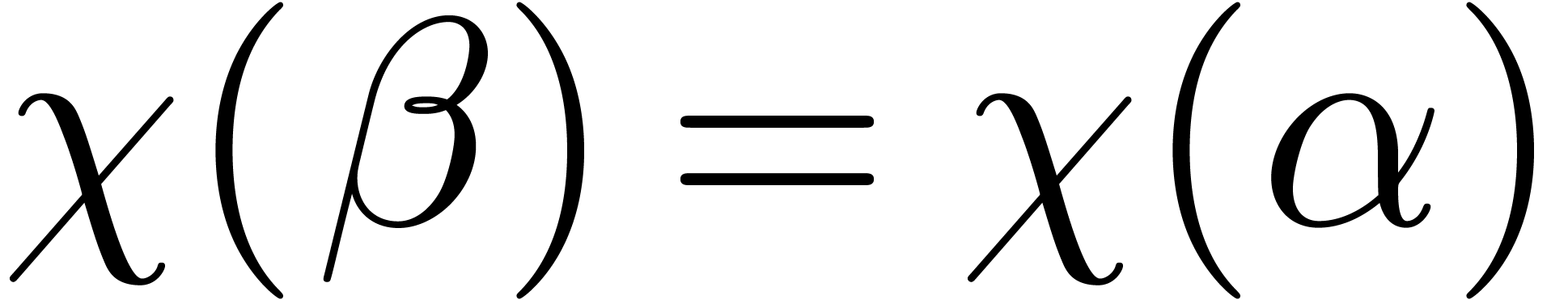 for all
for all 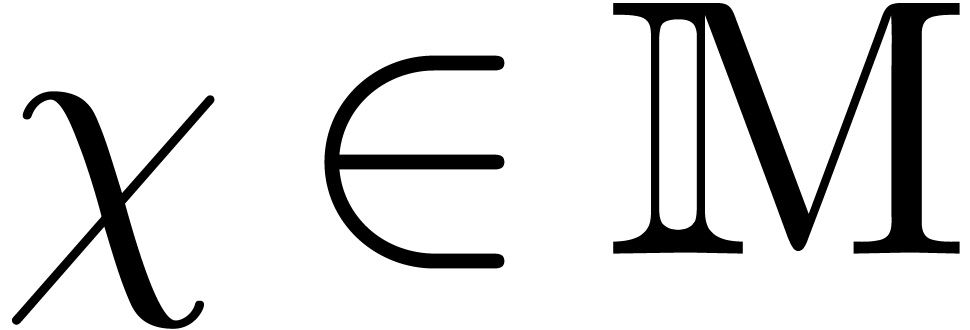 (where the equality is
allowed to hold at the limit if necessary), then
(where the equality is
allowed to hold at the limit if necessary), then 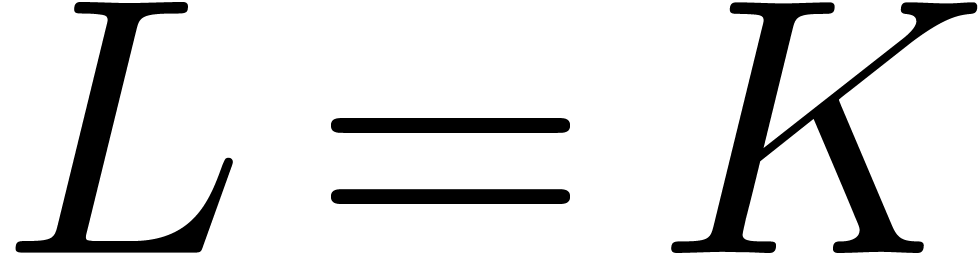 yields the desired annihilator with
yields the desired annihilator with 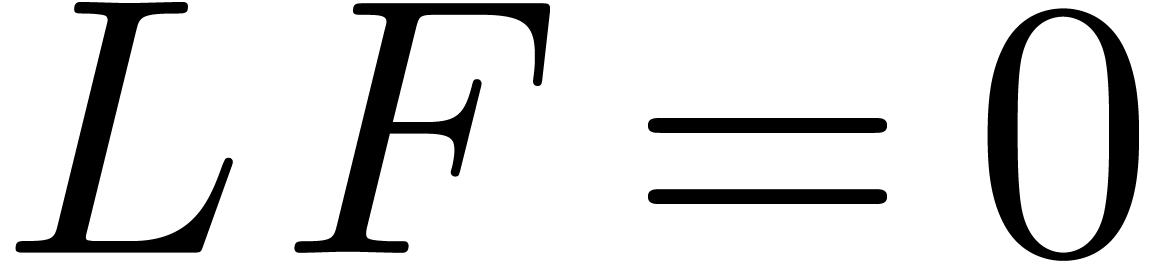 .
In general, we need to multiply
.
In general, we need to multiply 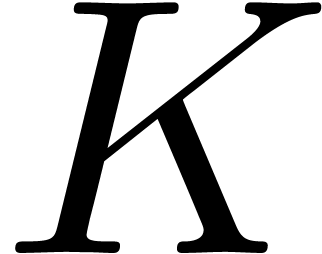 on the left with
an annihilator of
on the left with
an annihilator of  .
.
Now assume that we have a computable confined reduction 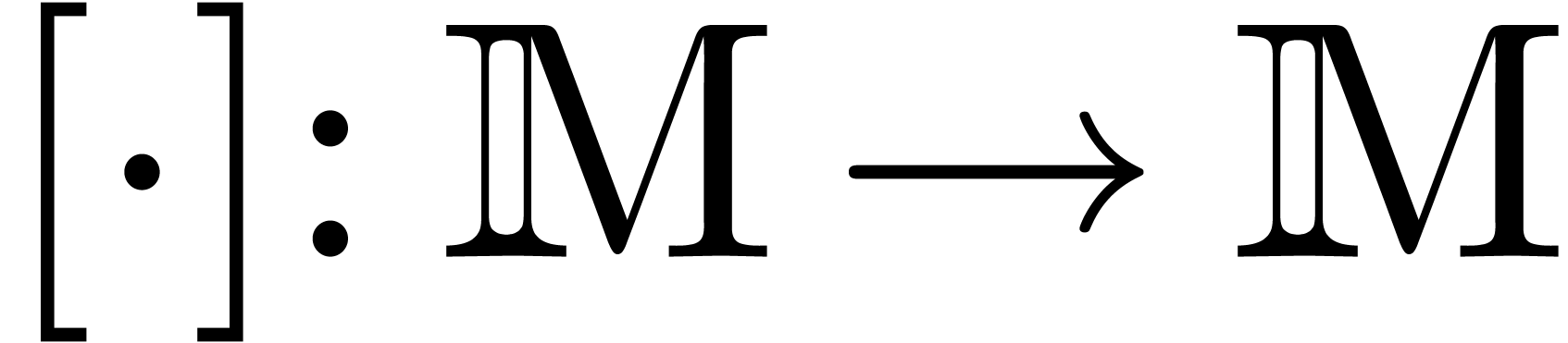 . Then the functions in the sequence
. Then the functions in the sequence 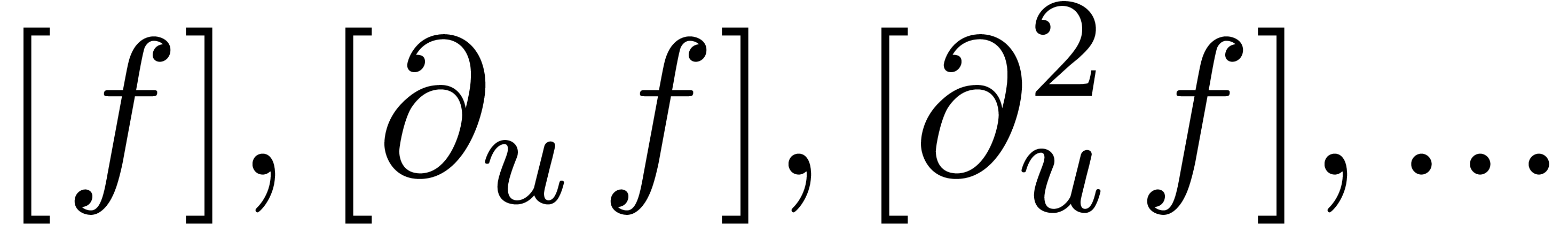 can all be computed and they belong to a finite
dimensional
can all be computed and they belong to a finite
dimensional  -vector space
-vector space
 . Using linear algebra, that
means that we can compute a relation
. Using linear algebra, that
means that we can compute a relation
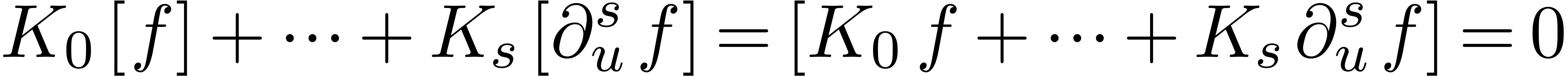 |
(4) |
with 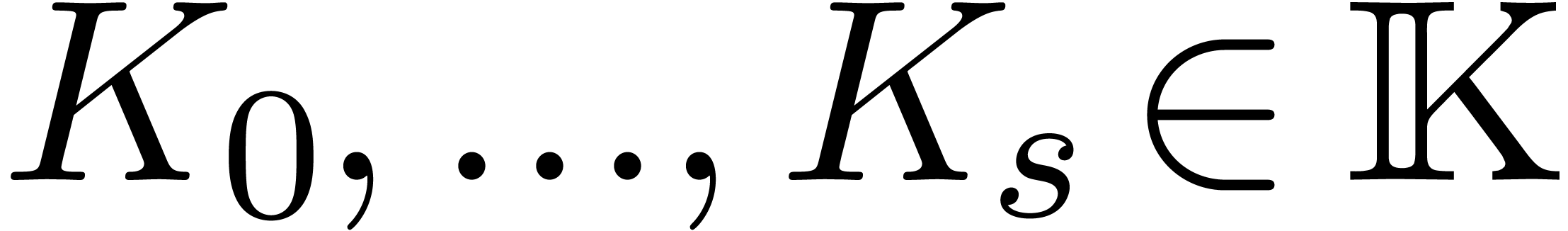 . Taking
. Taking
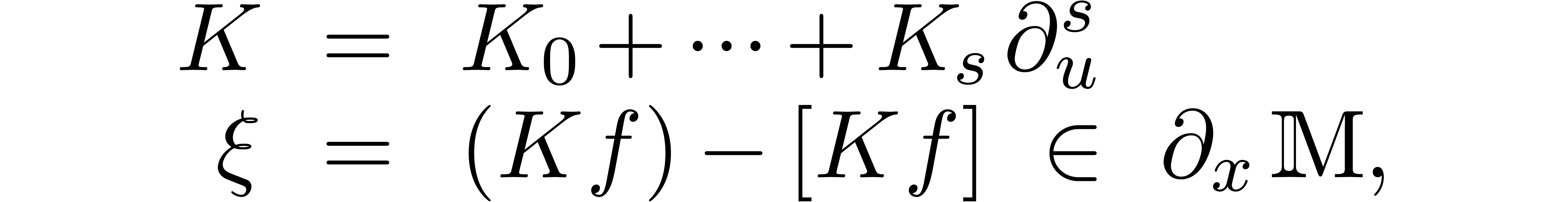
we thus obtain (3). If the relation (4) has
minimal order  and the reduction
and the reduction  is normal, then it can be shown [9] that there exist no
relations of the form (3) of order lower than
is normal, then it can be shown [9] that there exist no
relations of the form (3) of order lower than  .
.
Let 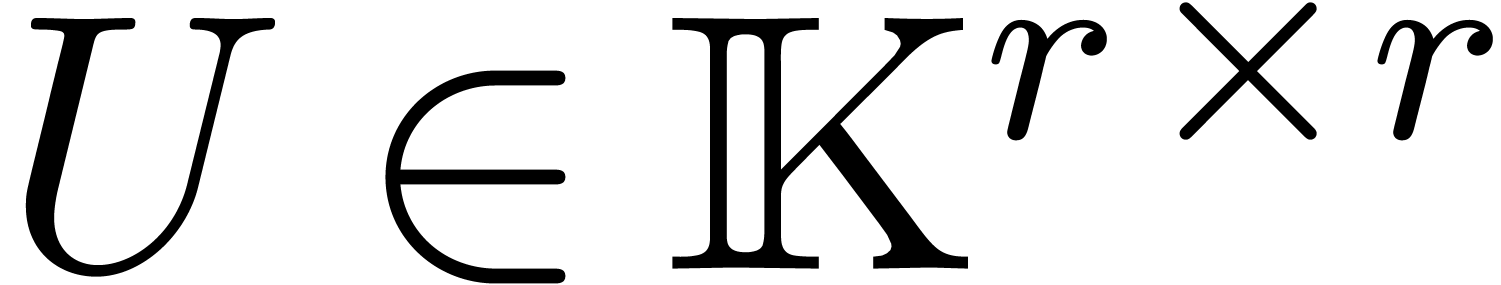 be a matrix and denote the
be a matrix and denote the  -th row of
-th row of  by
by 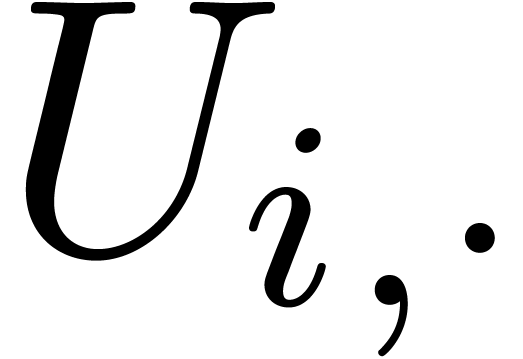 . Assuming that
. Assuming that 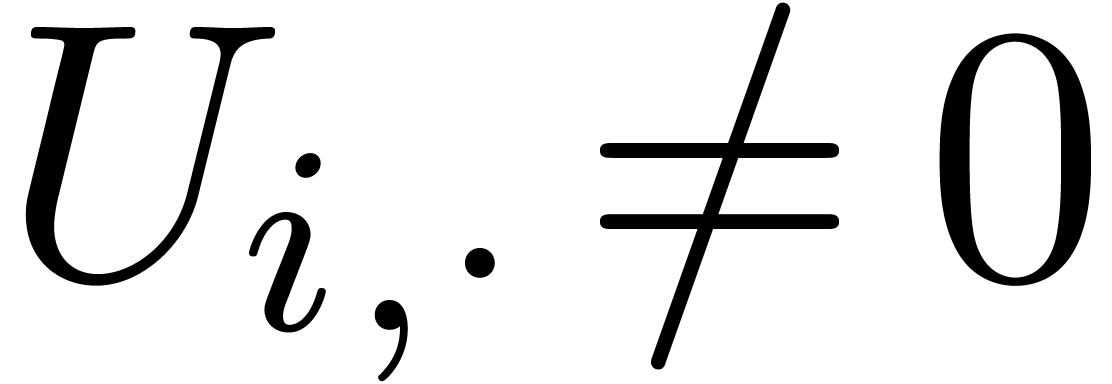 , its leading index
, its leading index  is the smallest index
is the smallest index  with
with  . We say that
. We say that  is in
row swept form if there exists a
is in
row swept form if there exists a 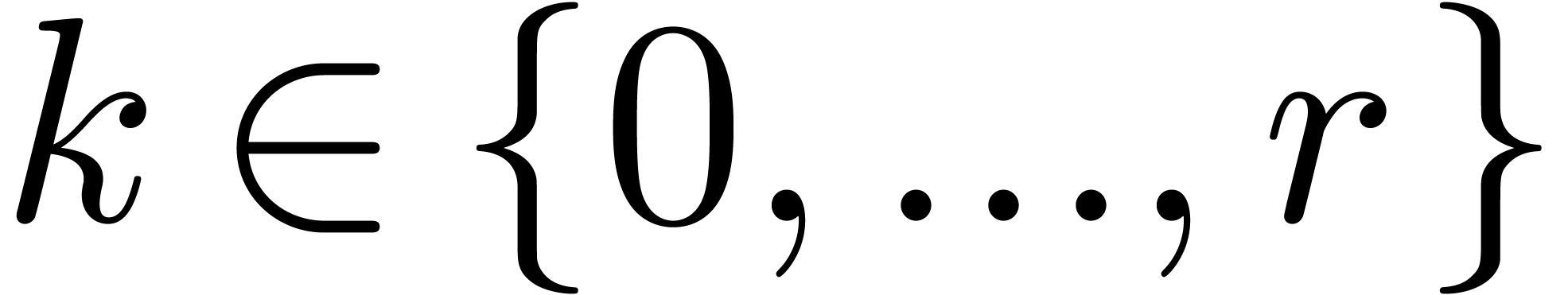 such
that
such
that 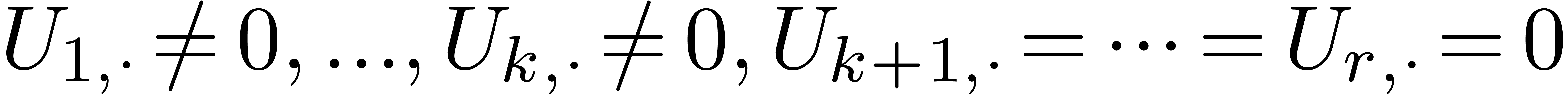 and
and 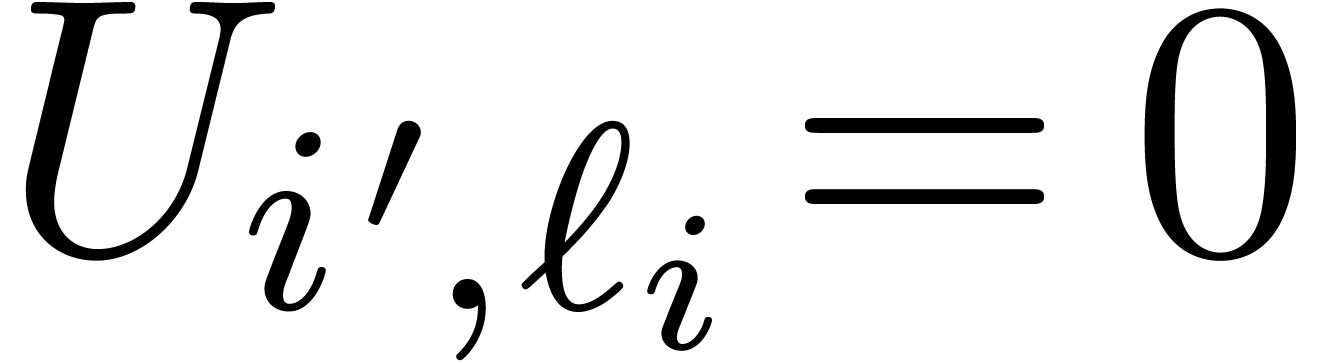 for all
for all 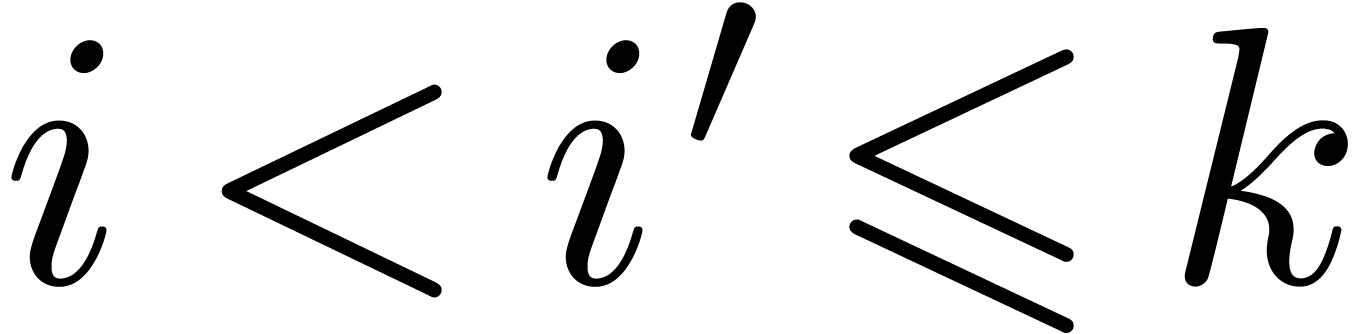 . Notice that
. Notice that  has rank
has rank  in this case.
in this case.
An invertible matrix  such that
such that  is in row swept form will be called a row sweaper for
is in row swept form will be called a row sweaper for  . We may compute such a matrix
. We may compute such a matrix  using the routine RowSweaper below,
which is really a variant of Gaussian elimination. Whenever we apply
this routine to a matrix
using the routine RowSweaper below,
which is really a variant of Gaussian elimination. Whenever we apply
this routine to a matrix  such that the truncated
matrix
such that the truncated
matrix  with rows
with rows 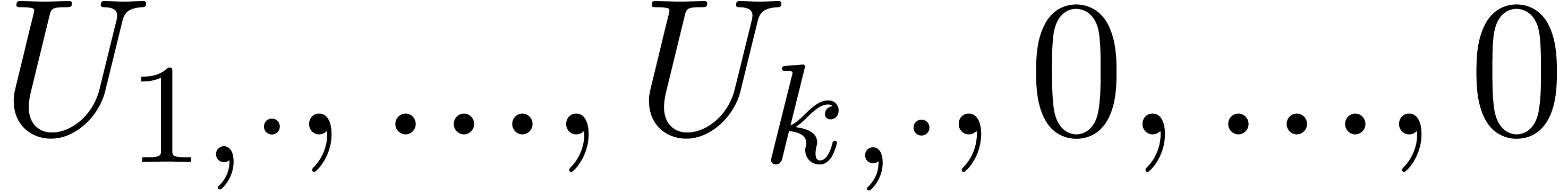 is in
row swept form, we notice that these first
is in
row swept form, we notice that these first 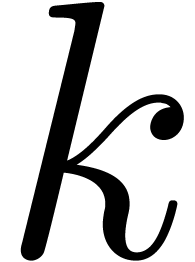 rows
are left invariant by the row sweaping process. In other words, the
returned row sweaper
rows
are left invariant by the row sweaping process. In other words, the
returned row sweaper 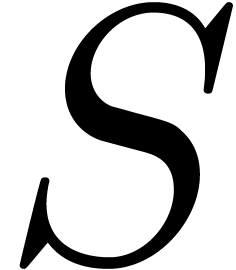 is of the form
is of the form 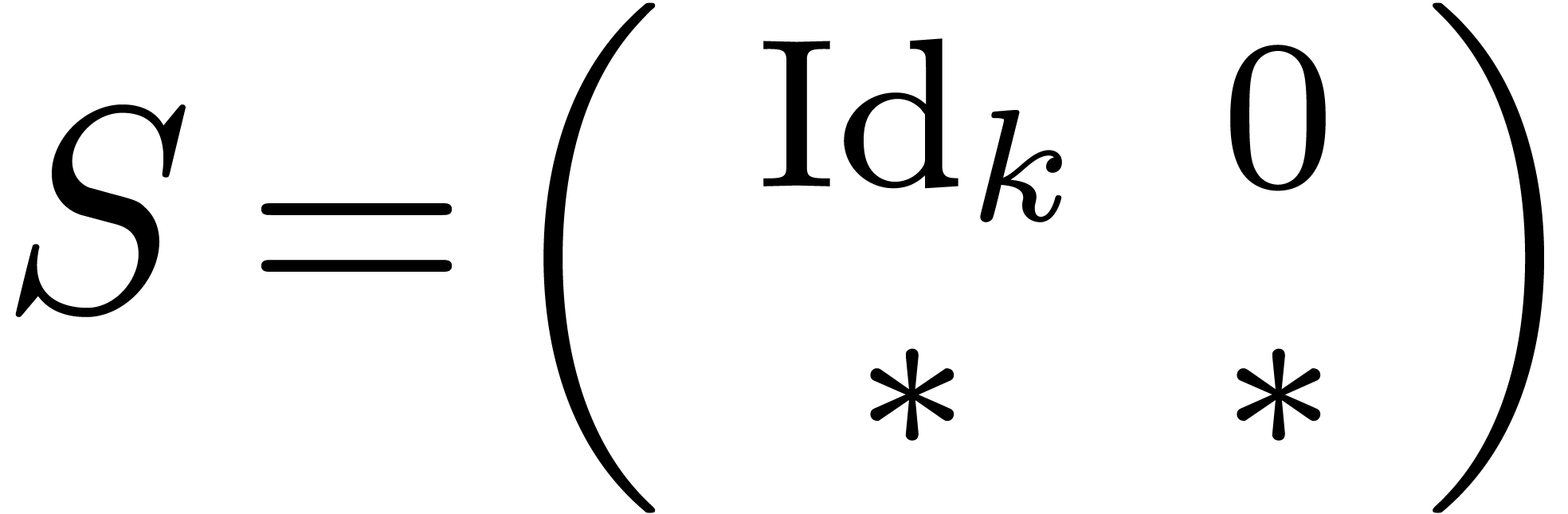 . If, in addition, the matrix
. If, in addition, the matrix  has rank
has rank 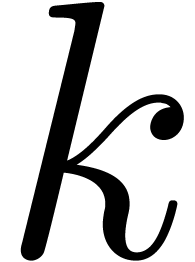 , then
, then  is of the form
is of the form 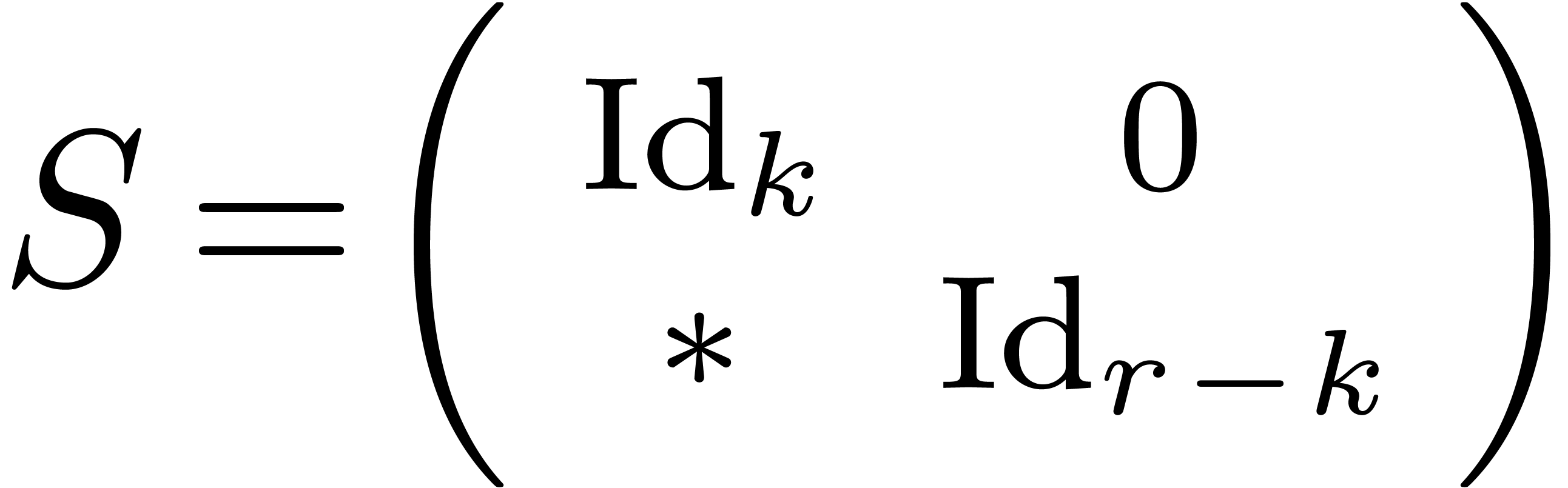 .
.
Algorithm RowSweaper |
for
if
Let
Swap the
for
return |
Let 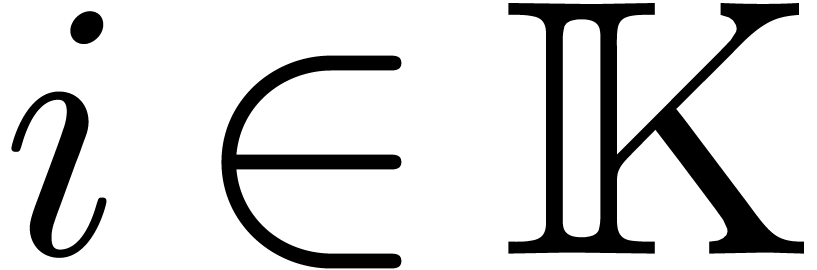 and
and 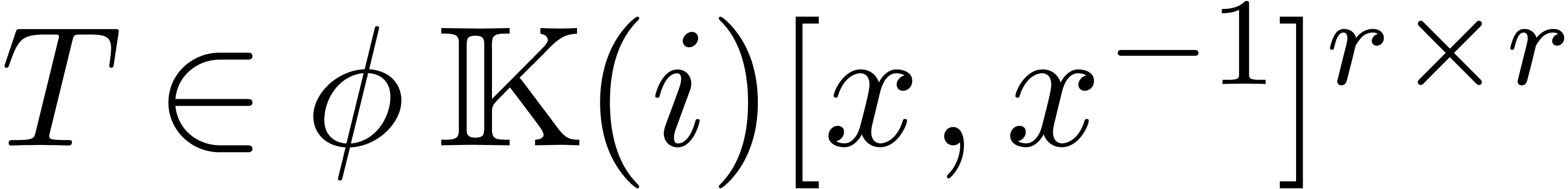 .
We may regard
.
We may regard  as a Laurent polynomial with
matrix coefficients
as a Laurent polynomial with
matrix coefficients 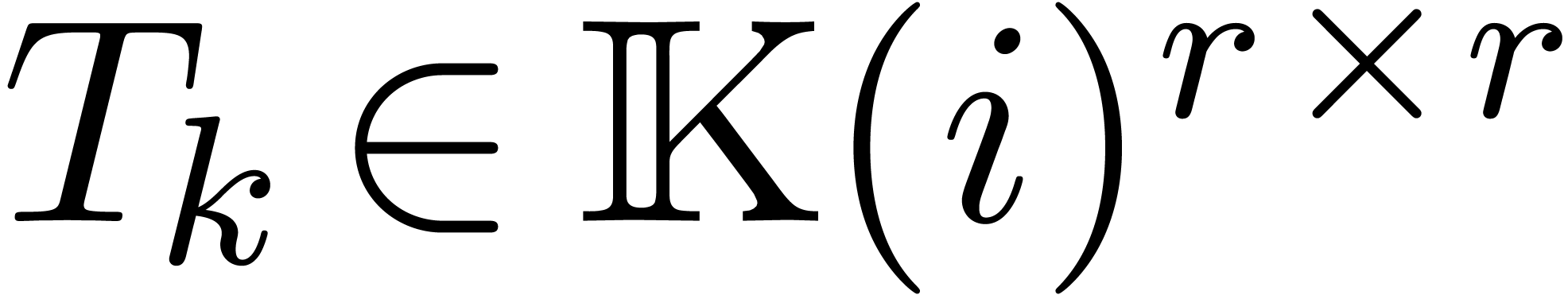 :
:
If 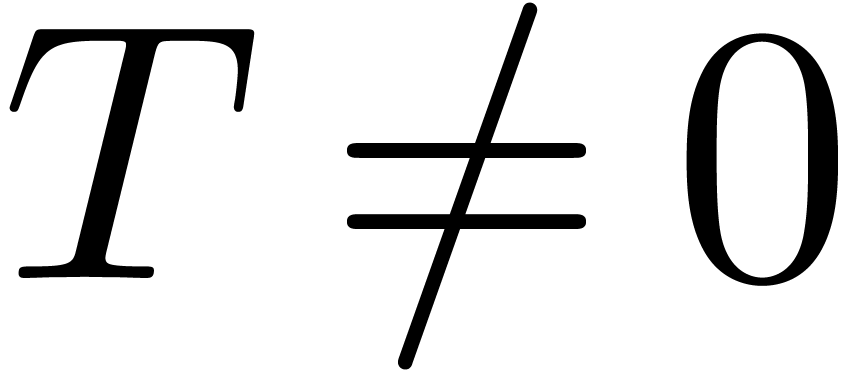 , then we denote
, then we denote 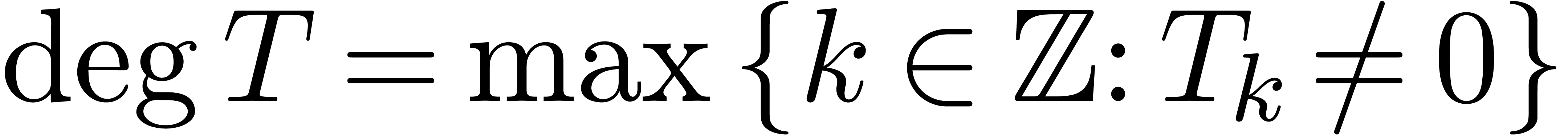 and
and 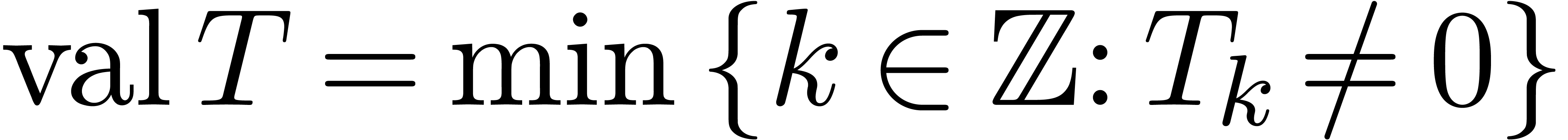 . For any
. For any
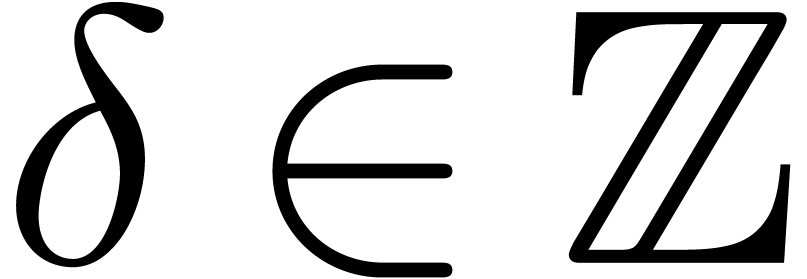 , we also denote
, we also denote 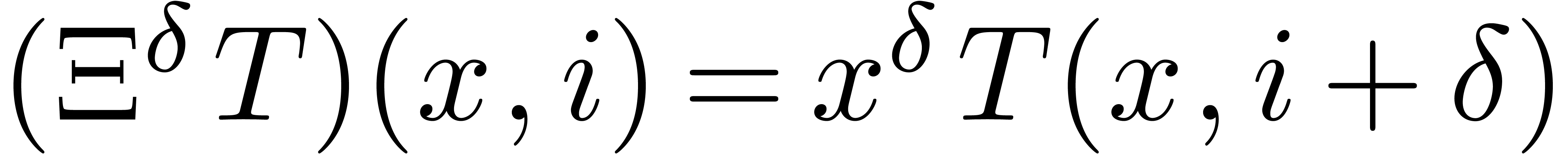 . Setting
. Setting
the equation (1) implies
for any constant matrix 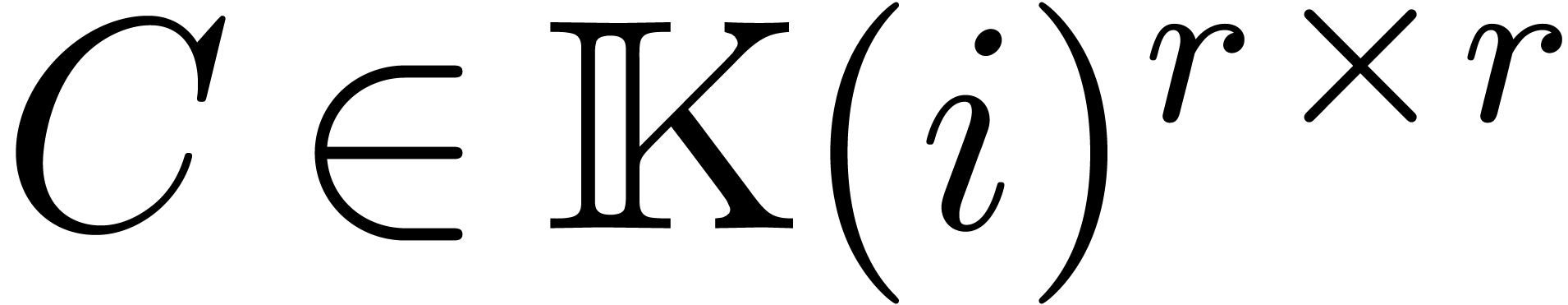 . The
matrix
. The
matrix  can also be regarded as a Laurent
polynomial with matrix coefficients
can also be regarded as a Laurent
polynomial with matrix coefficients 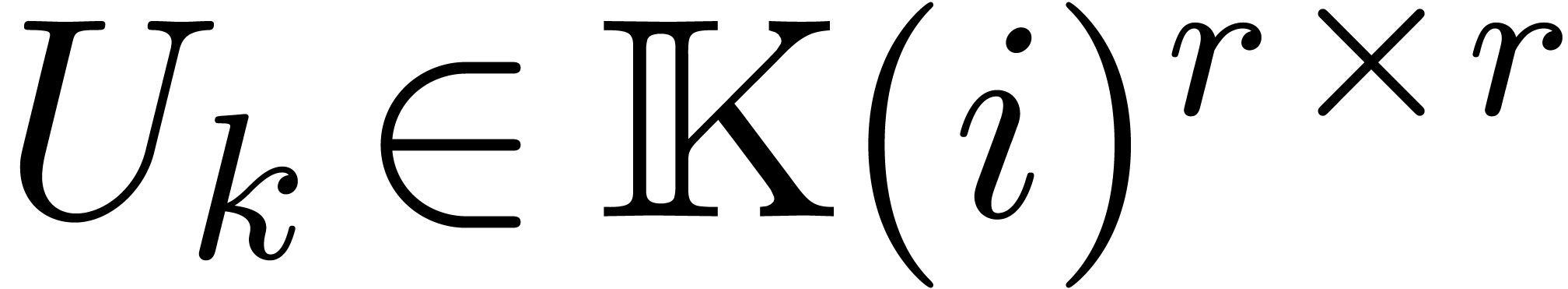 .
We say that
.
We say that  is a head chopper for (1) if
is a head chopper for (1) if  is an invertible matrix.
is an invertible matrix.
Proof. Setting 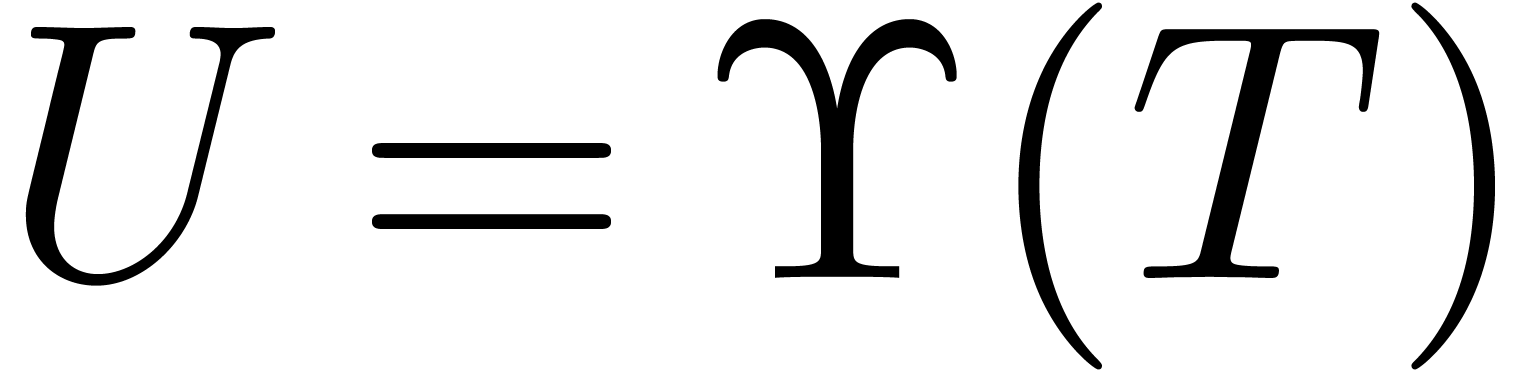 ,
,
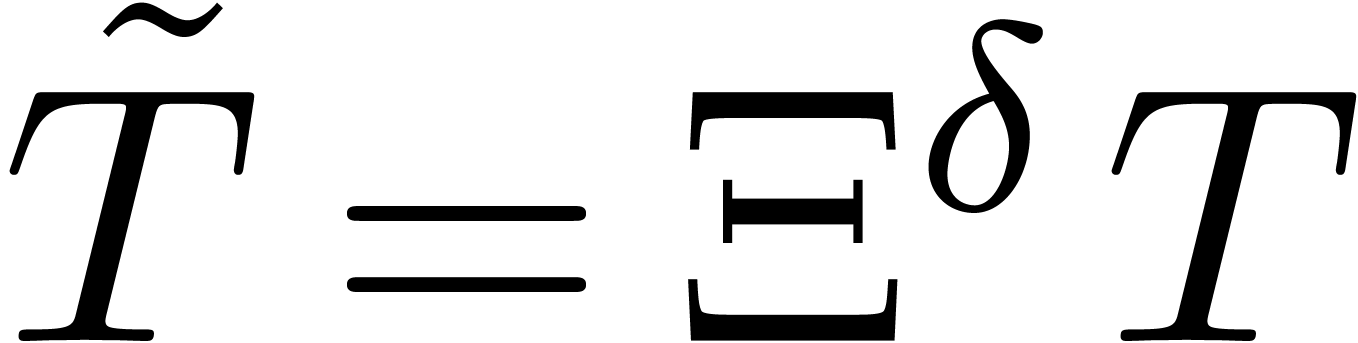 and
and 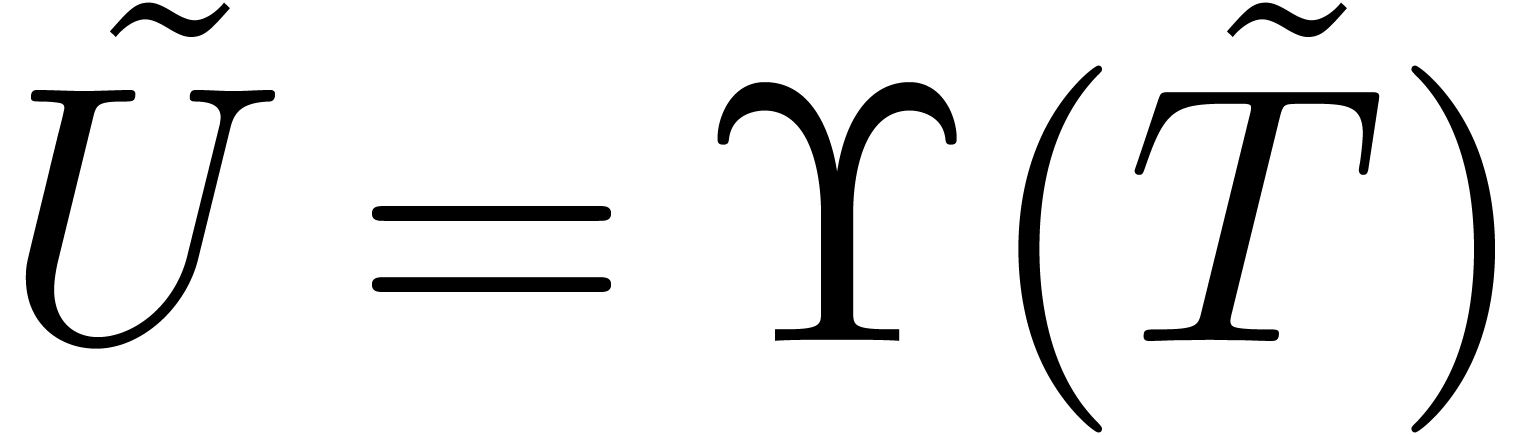 ,
we have
,
we have
In other words, 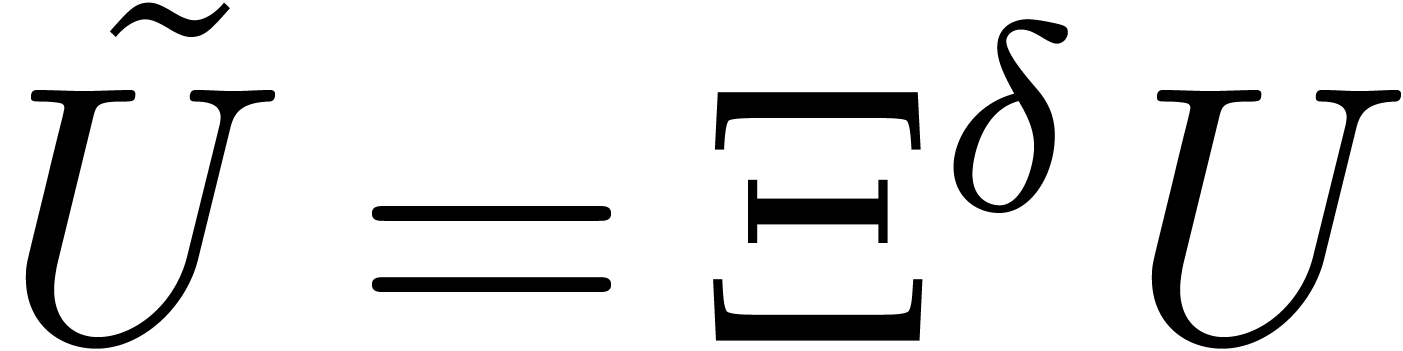 .□
.□
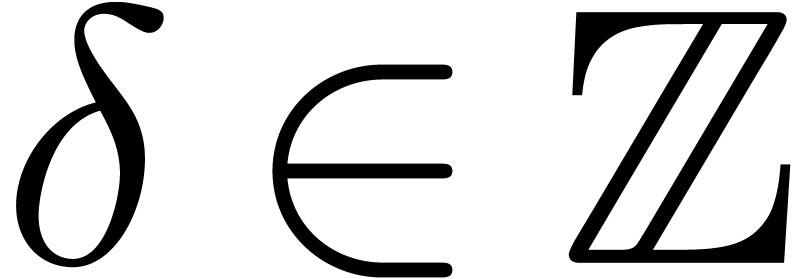 and that
and that  is invertible. Then
is invertible. Then
Proof. Assume that  is a
head chopper for (1). Setting
is a
head chopper for (1). Setting 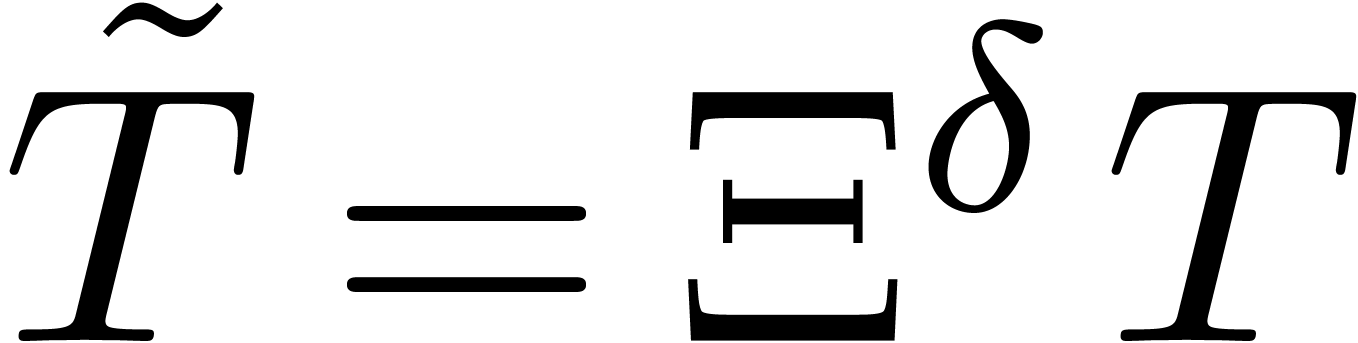 and
and
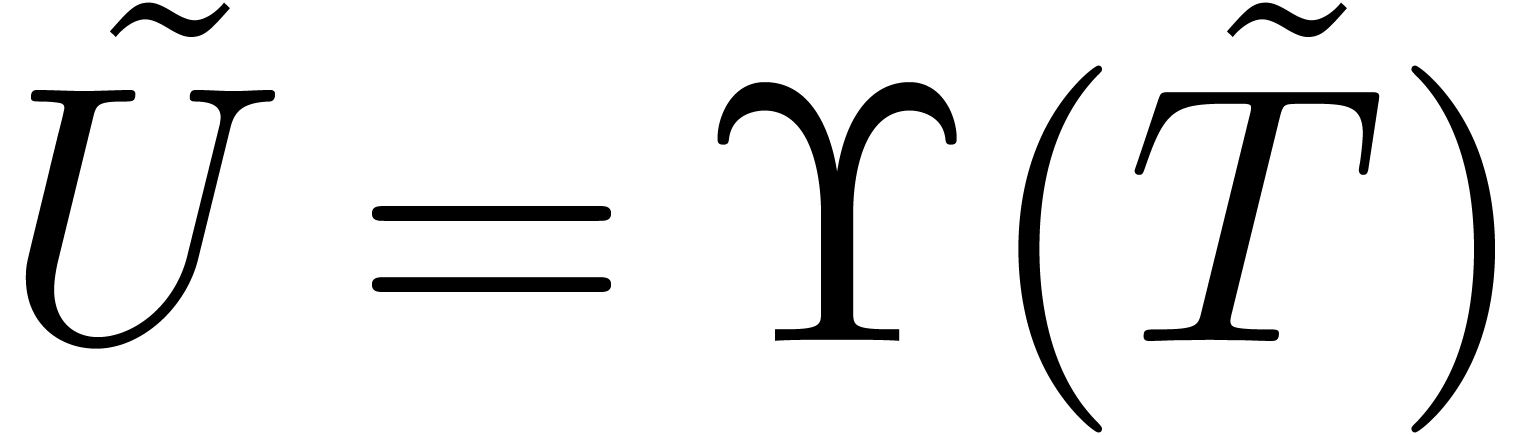 , we have
, we have 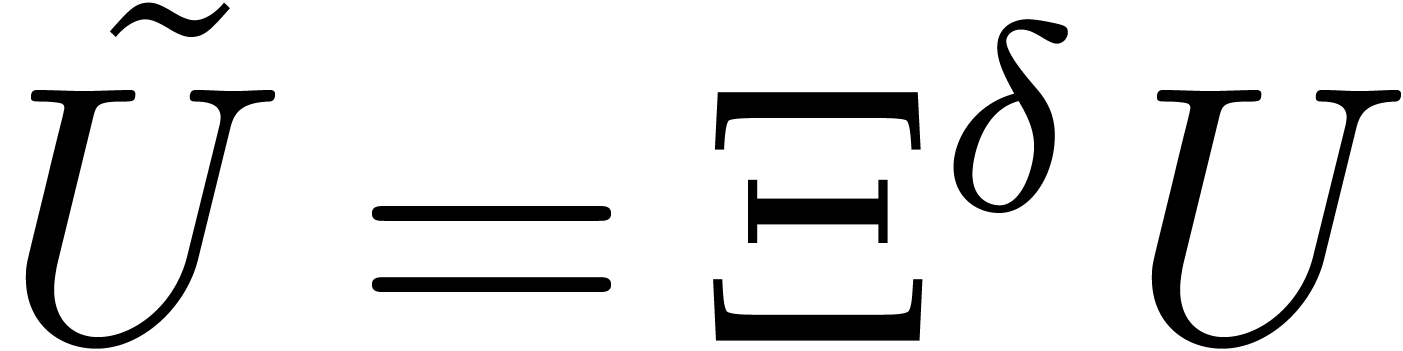 and
and 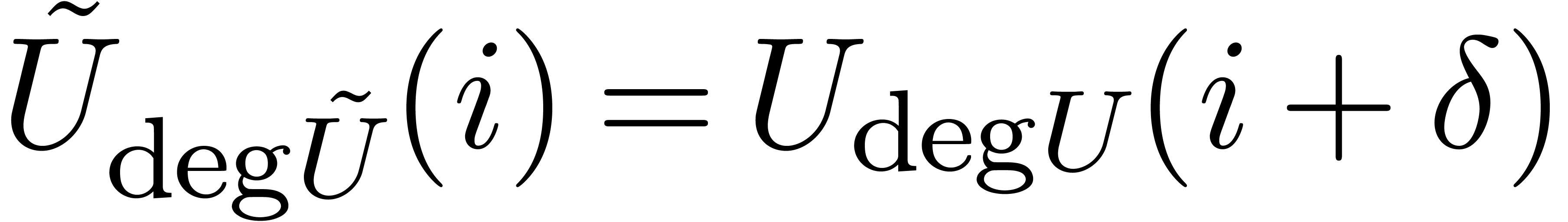 is invertible. Similarly, setting
is invertible. Similarly, setting 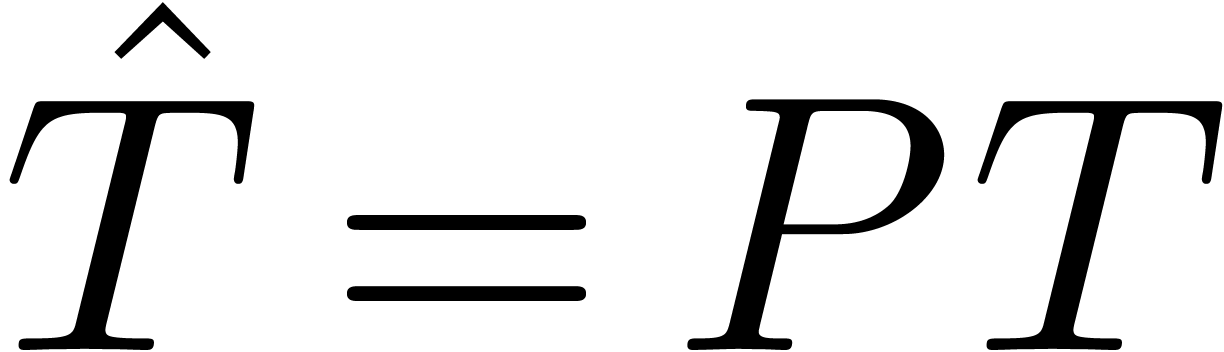 and
and 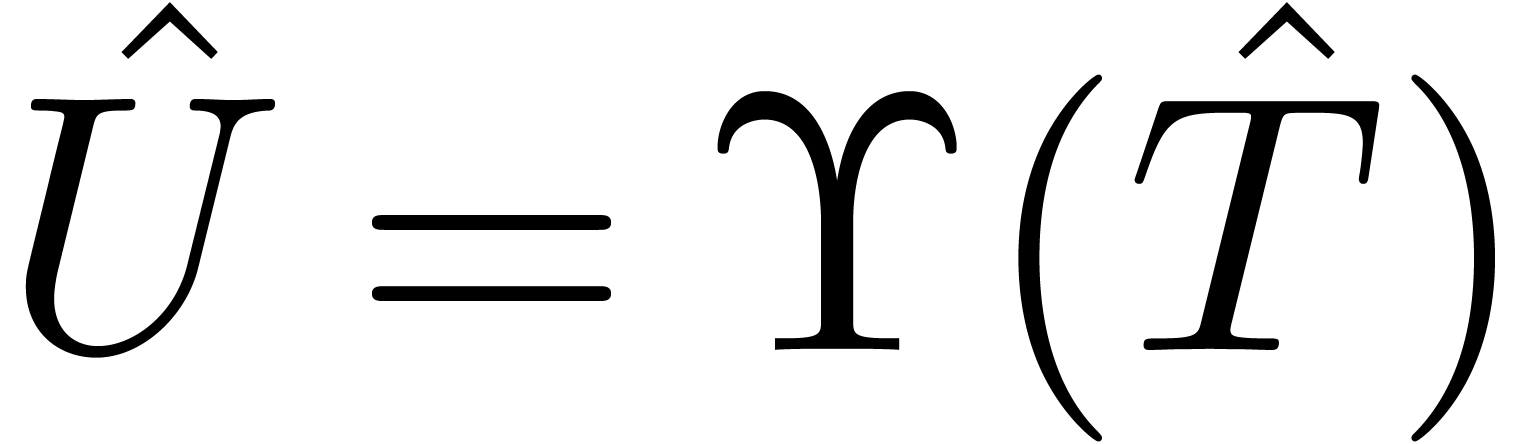 , we have
, we have
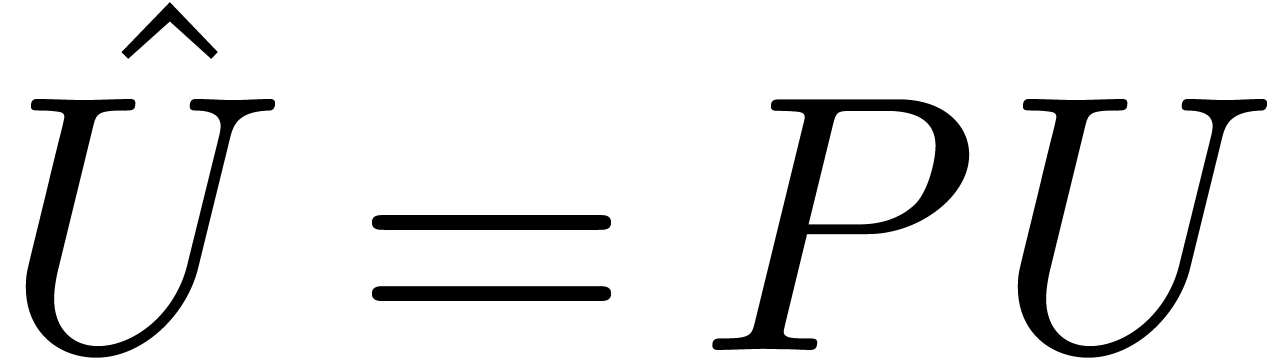 , whence
, whence 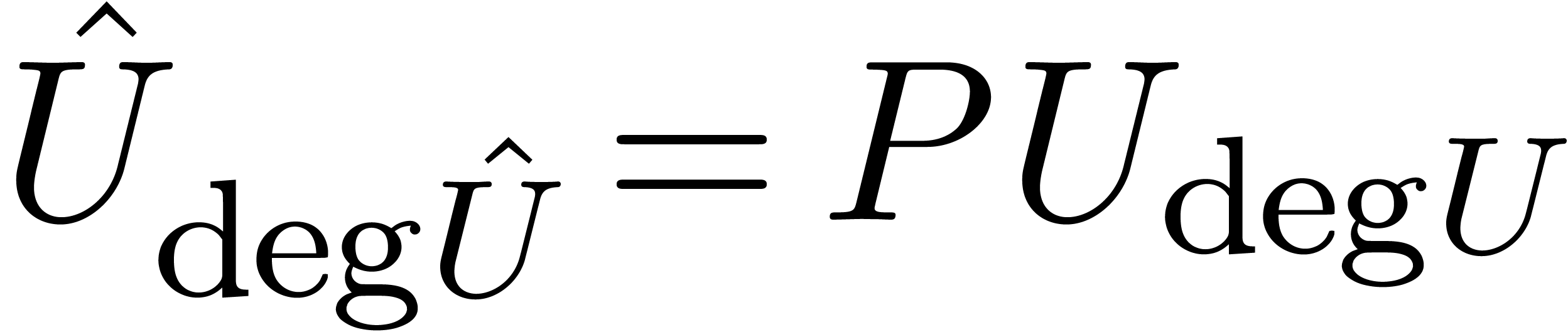 is invertible. The opposite directions follow by taking
is invertible. The opposite directions follow by taking 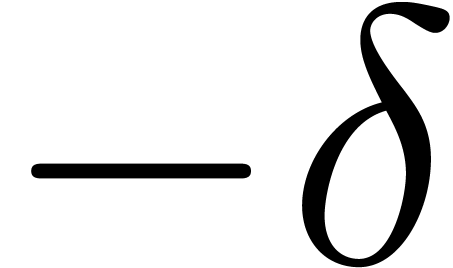 and
and 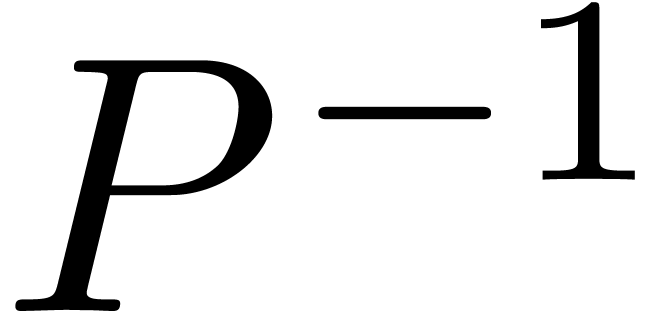 in the roles of
in the roles of  and
and
 .□
.□
Notice that the equations (5–7) and
Proposition 1 generalize to the case when 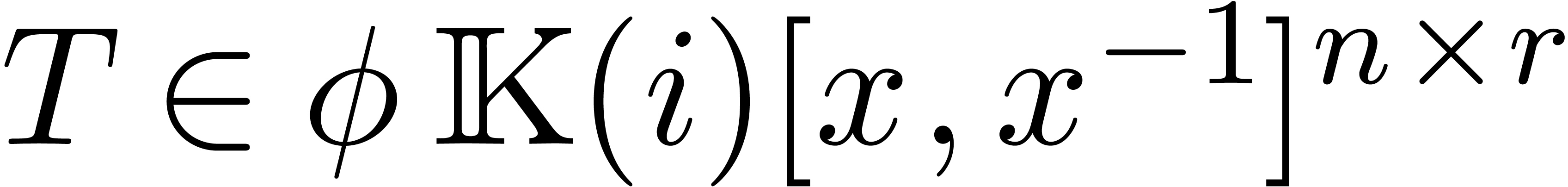 for some arbitrary
for some arbitrary  . Notice
also that
. Notice
also that  , where
, where 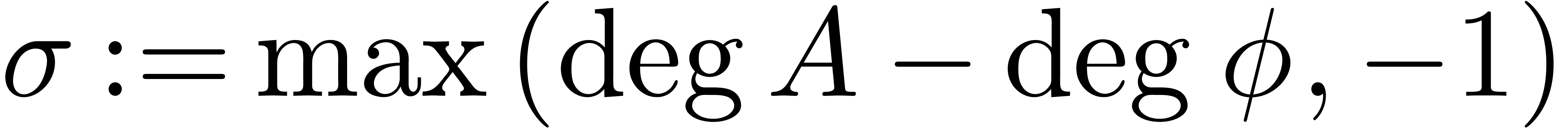 . Given
. Given 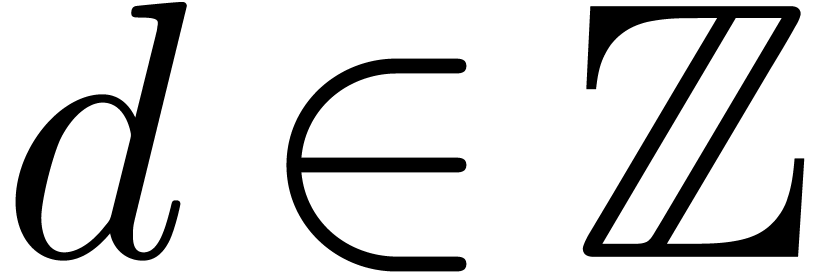 and
and
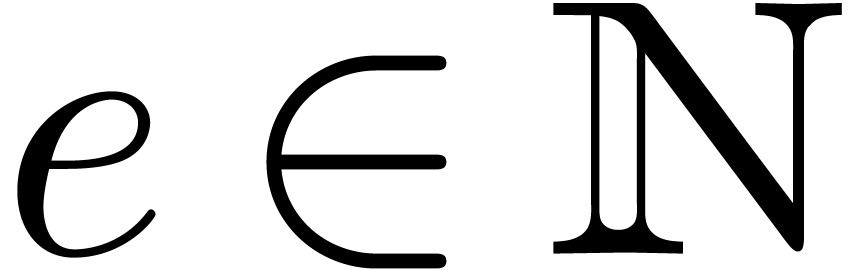 , let
, let
It is easy to see that both  and
and  are
are 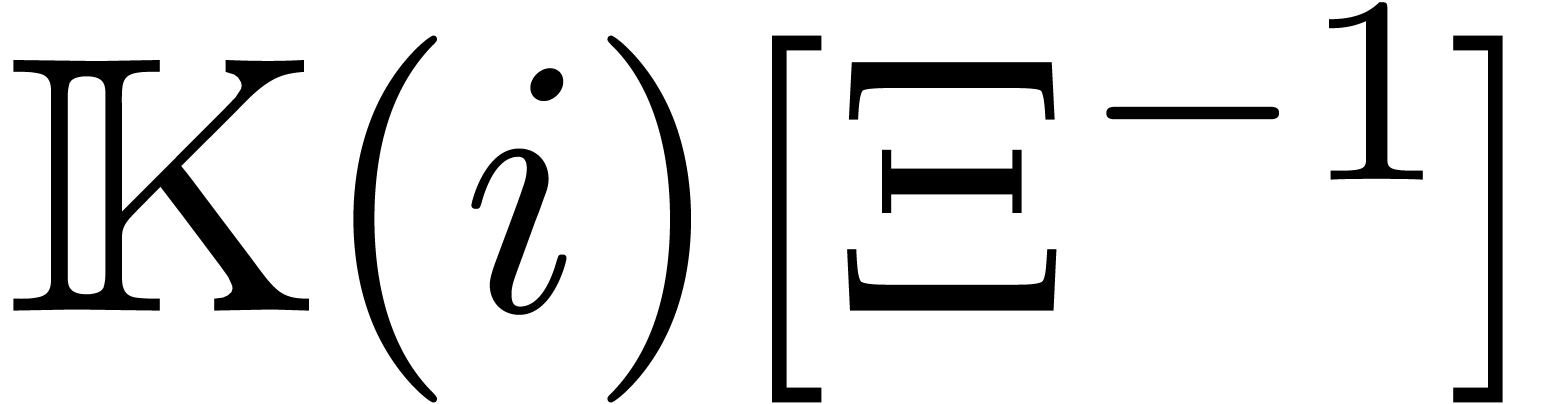 -modules.
-modules.
Now consider a matrix 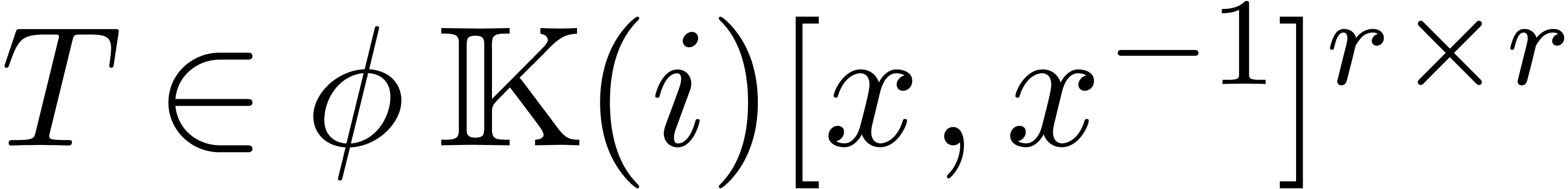 with rows
with rows  ordered by increasing degree
ordered by increasing degree  .
Let
.
Let 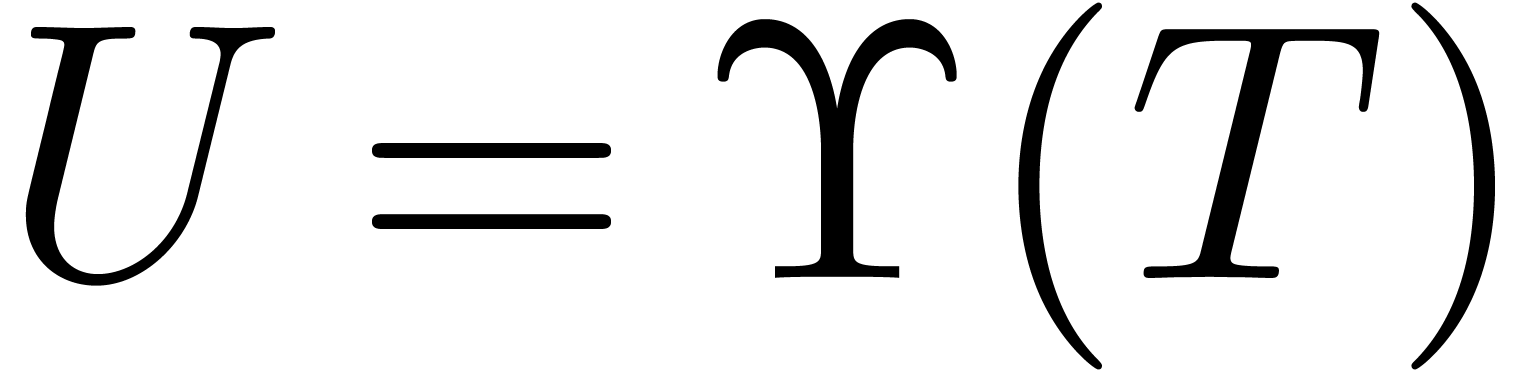 , let
, let 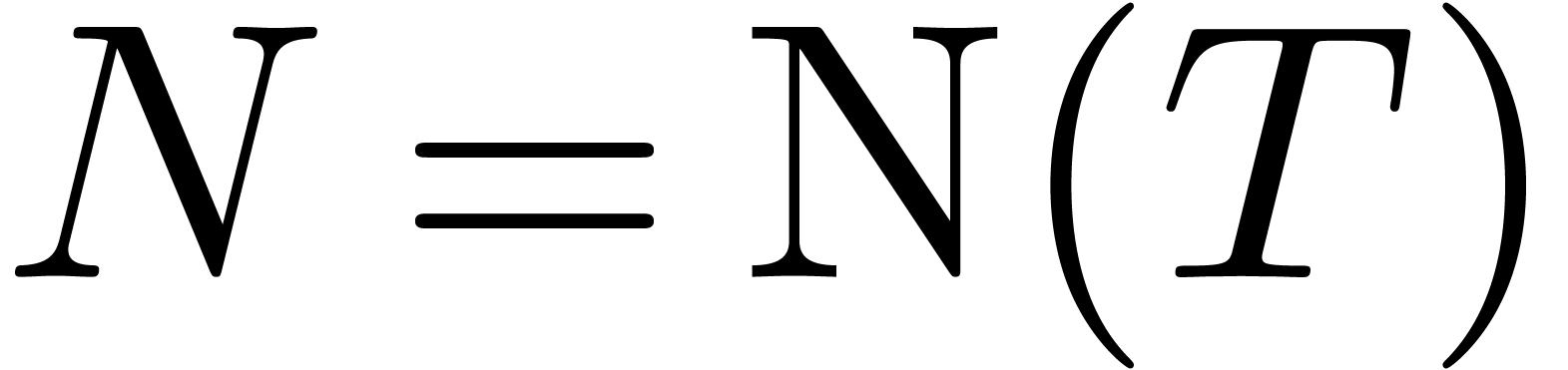 be the matrix with rows
be the matrix with rows  , and
let
, and
let 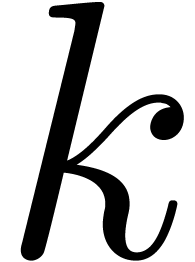 be maximal such that
be maximal such that 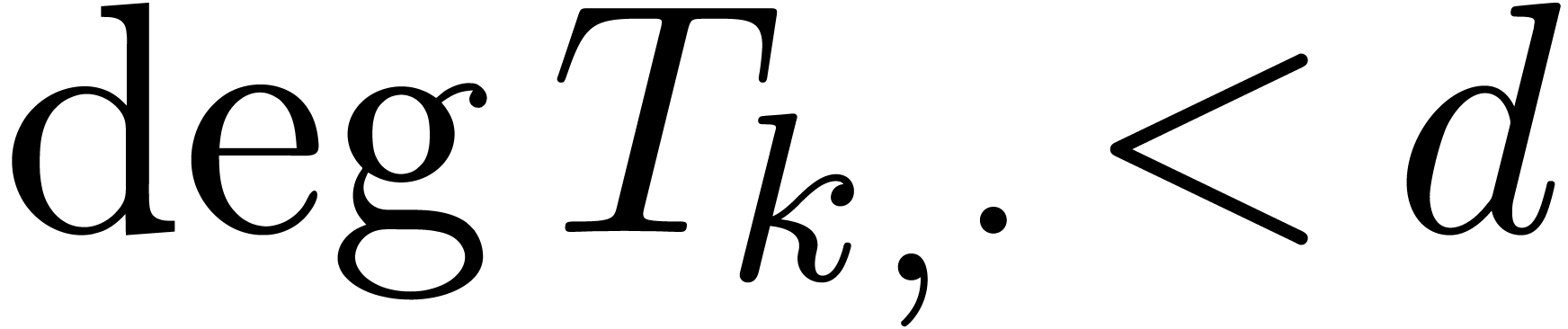 . We say that
. We say that  is a
is a 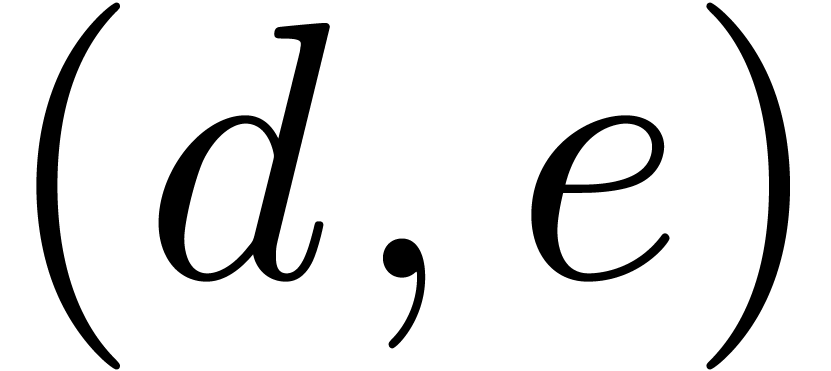 -head annihilator for (1) if the following conditions are satisfied:
-head annihilator for (1) if the following conditions are satisfied:
The rows of  form a basis for the
form a basis for the 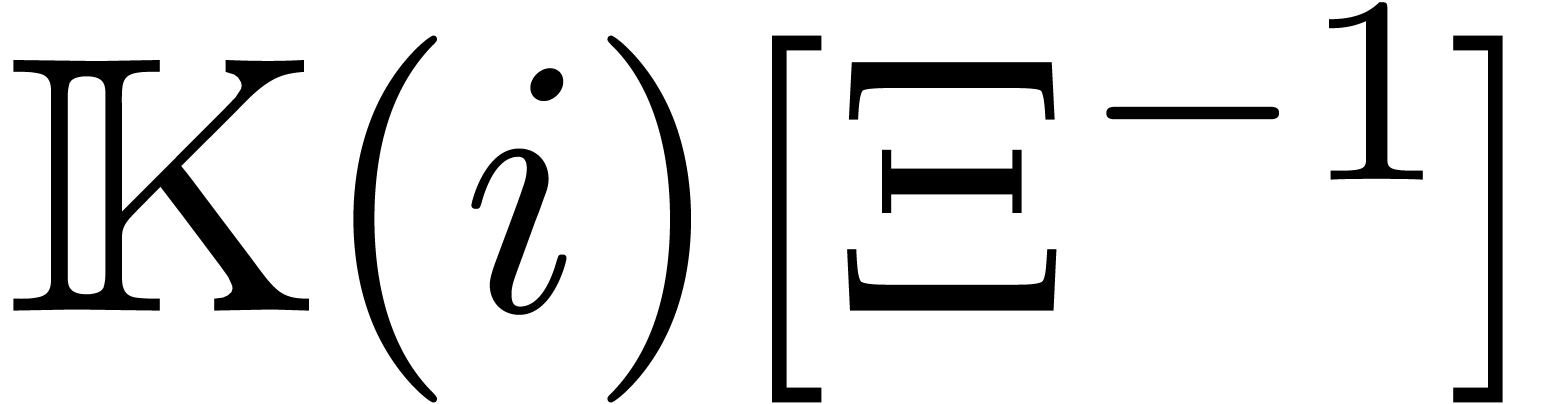 -module
-module  ;
;
The matrix 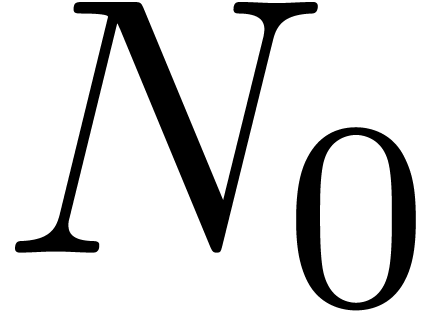 is invertible;
is invertible;
The first 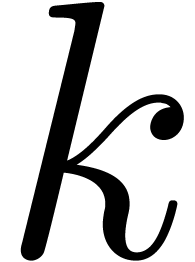 rows of
rows of 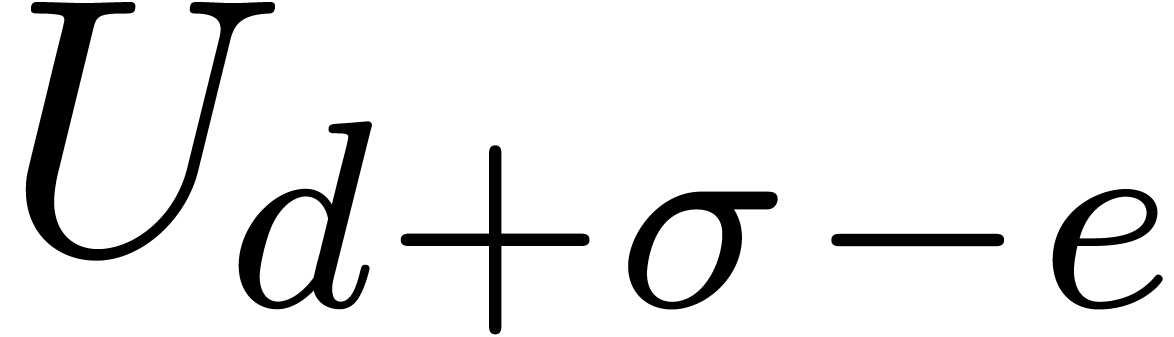 are
are 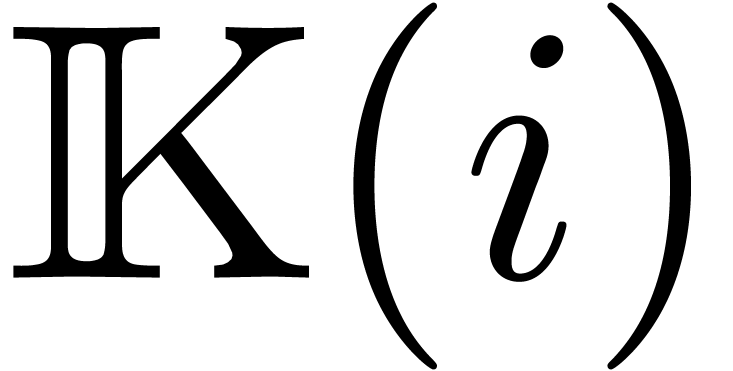 -linearly
independent.
-linearly
independent.
The matrix 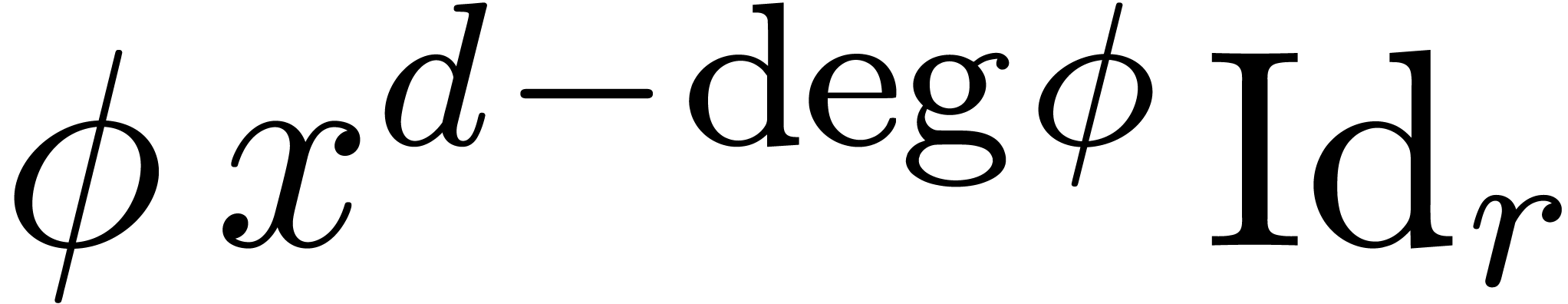 is obviously a
is obviously a 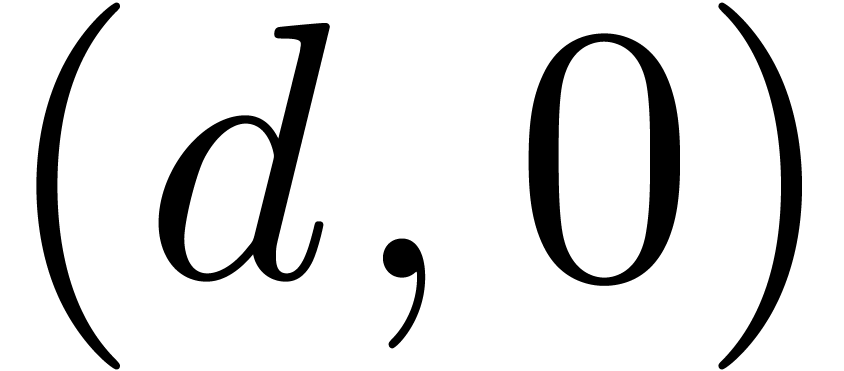 -head annihilator. If
-head annihilator. If 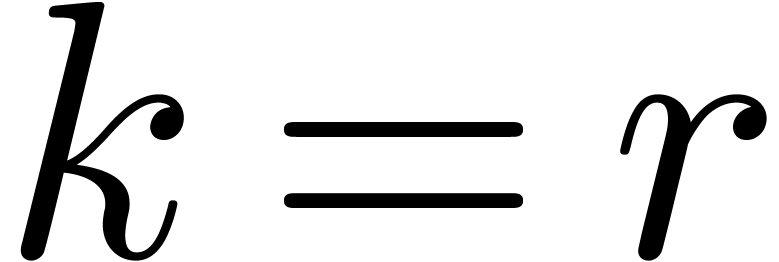 ,
then we notice that HA3 implies that
,
then we notice that HA3 implies that  is a head chopper for (1). The following proposition is
also easily checked:
is a head chopper for (1). The following proposition is
also easily checked:
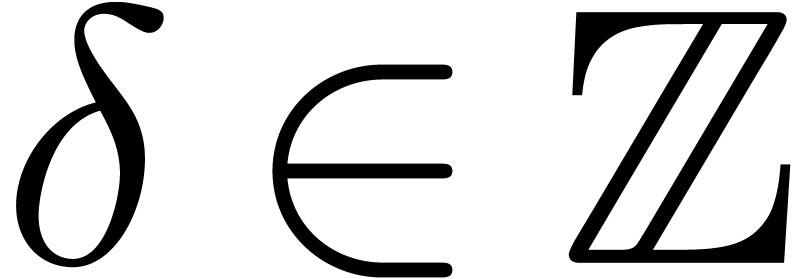 , we
have
, we
have
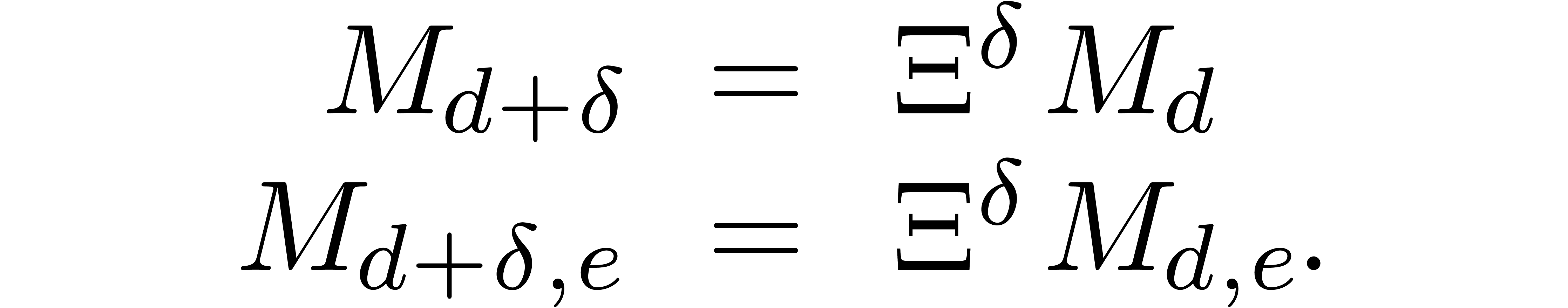
 is a
is a 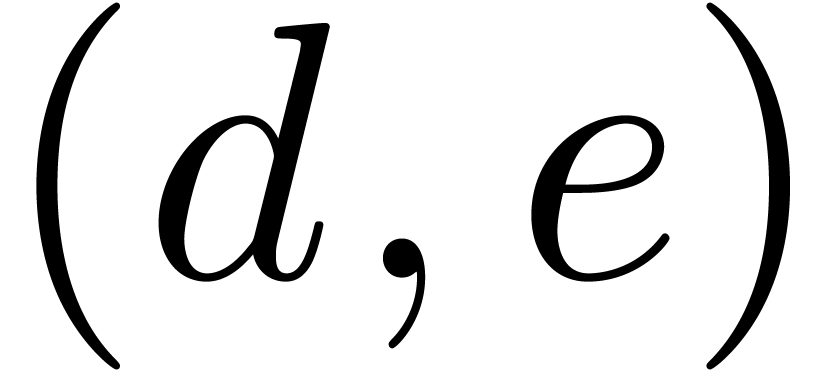 -head
annihilator if and only if
-head
annihilator if and only if 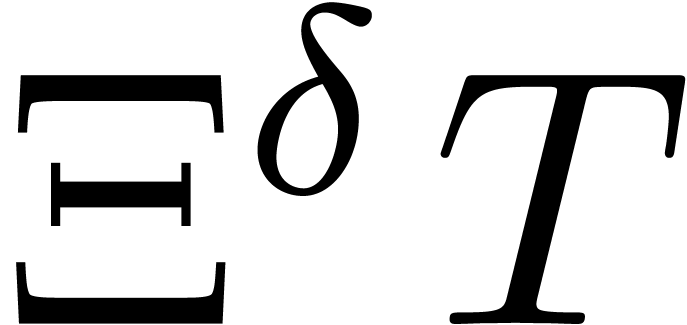 is a
is a 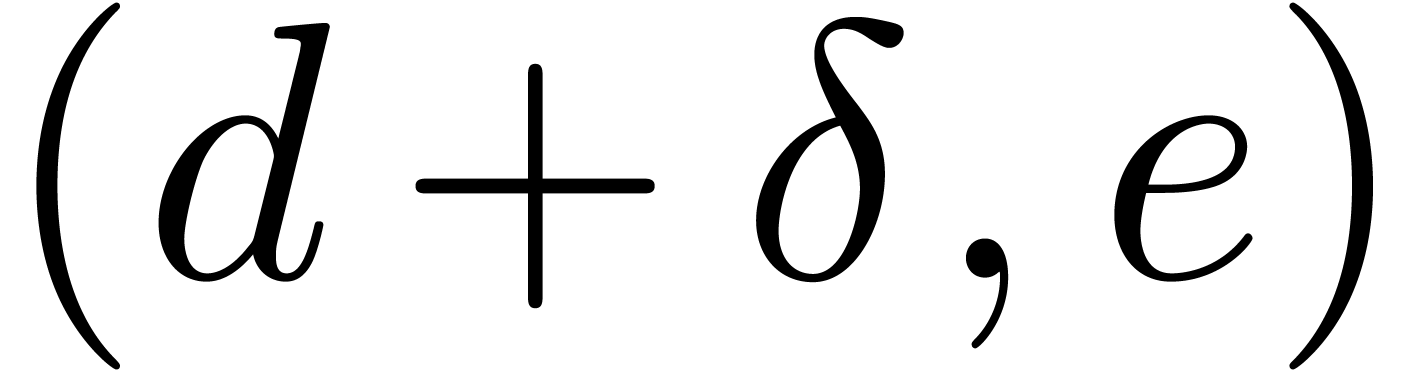 -head annihilator.
-head annihilator.
 be a
be a 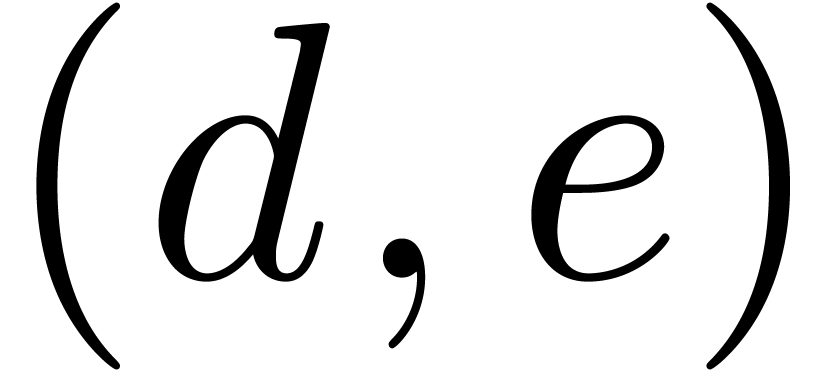 -head annihilator for
-head annihilator for  and
and  be as in
be as in
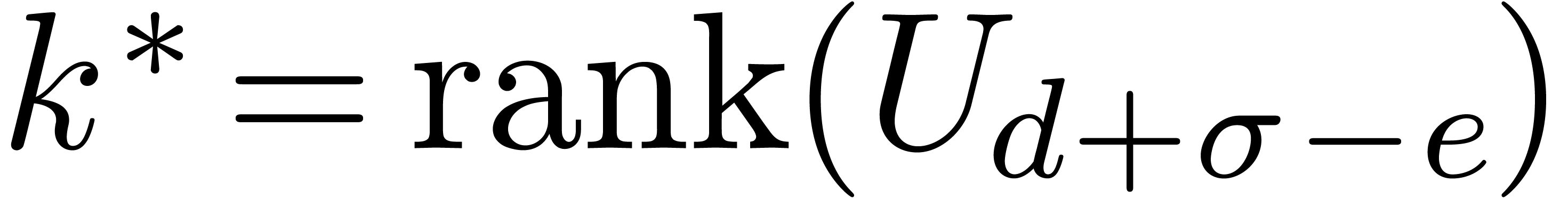 . Then there
exists an invertible matrix
. Then there
exists an invertible matrix 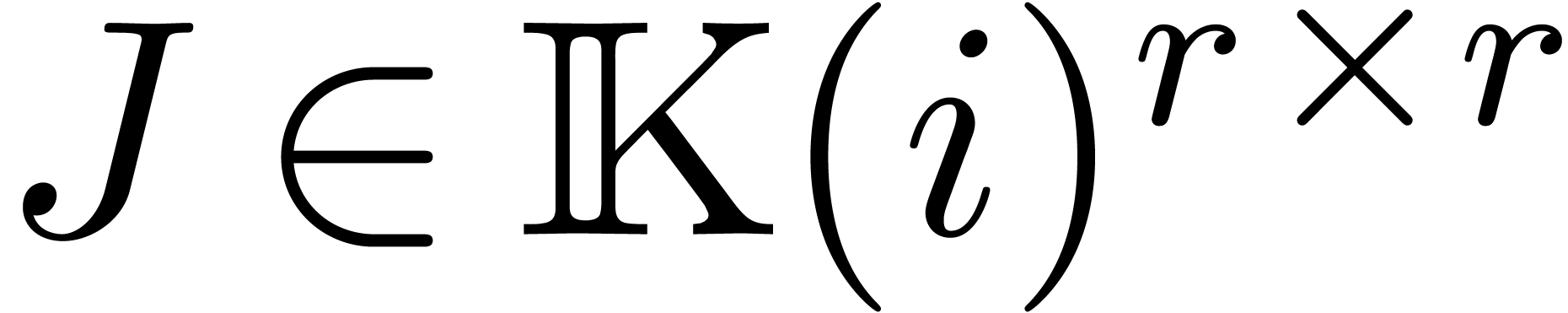 of the form
of the form 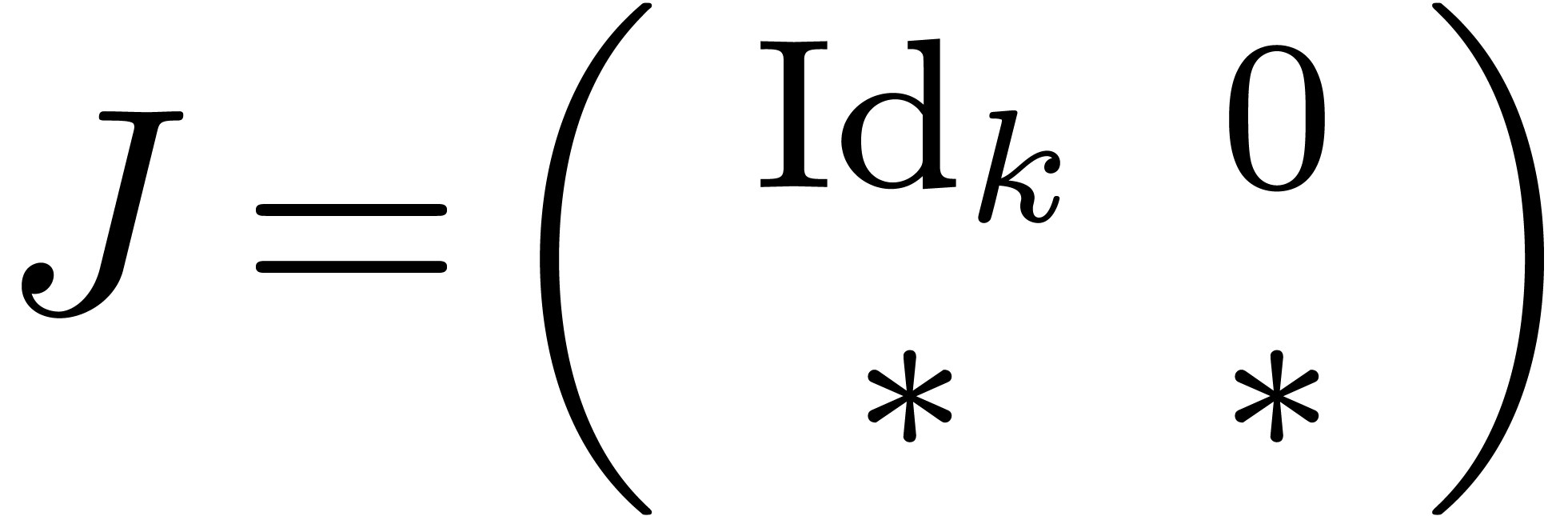 such that the last
such that the last 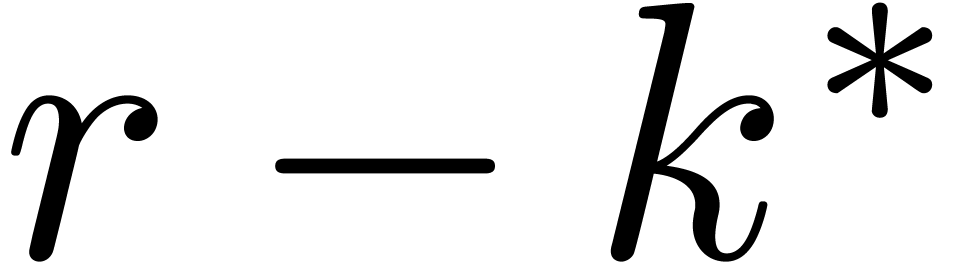 rows of
rows of
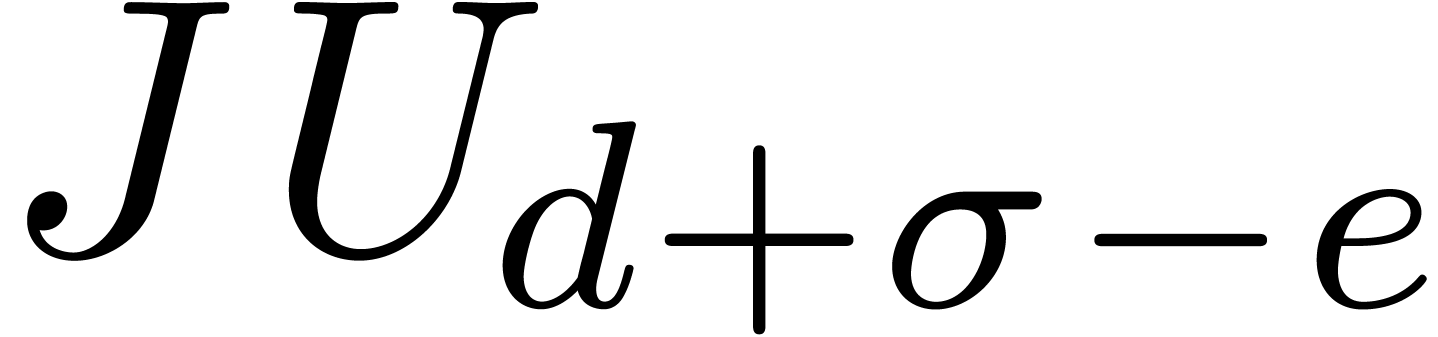 vanish and such that
vanish and such that  is a
is a 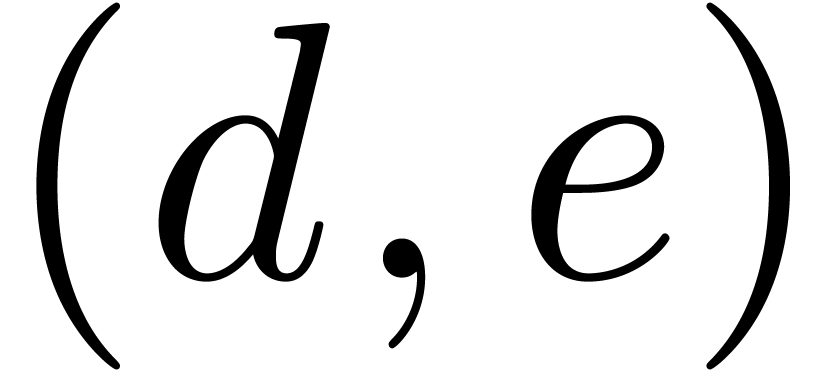 -head annihilator for
-head annihilator for
Proof. Let 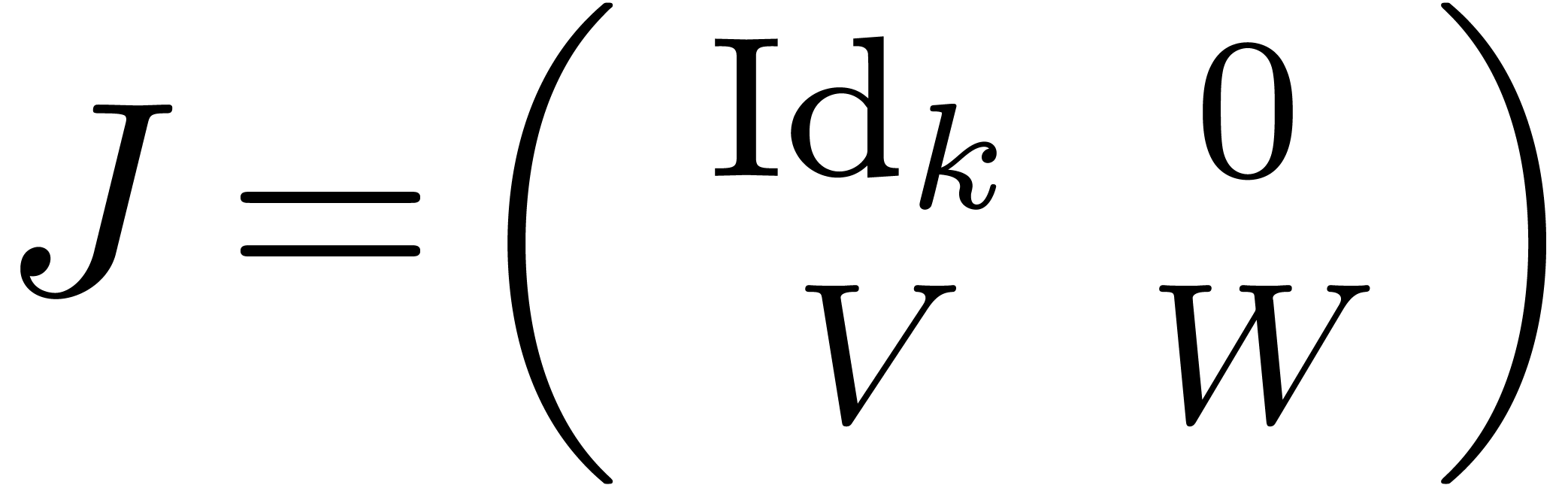 be the row
sweaper for
be the row
sweaper for 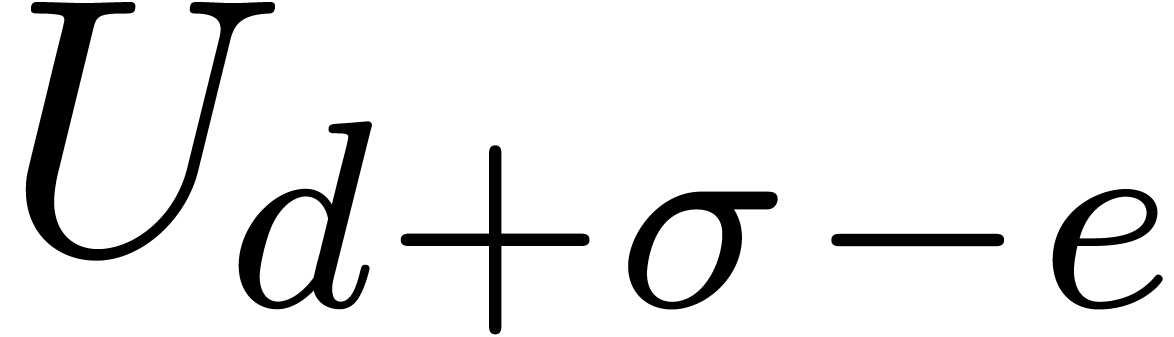 as computed by the algorithm
RowSweaper from section 3. By
construction,
as computed by the algorithm
RowSweaper from section 3. By
construction, 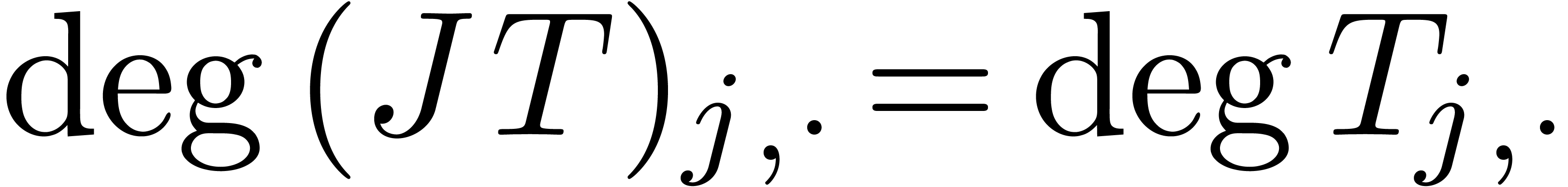 for all
for all 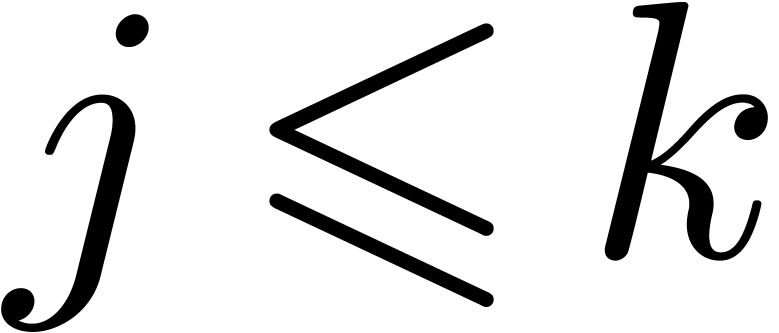 . We claim that
. We claim that 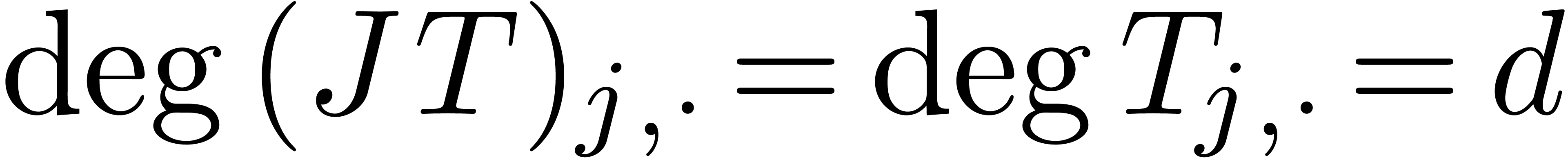 for all
for all
 . Indeed, if
. Indeed, if 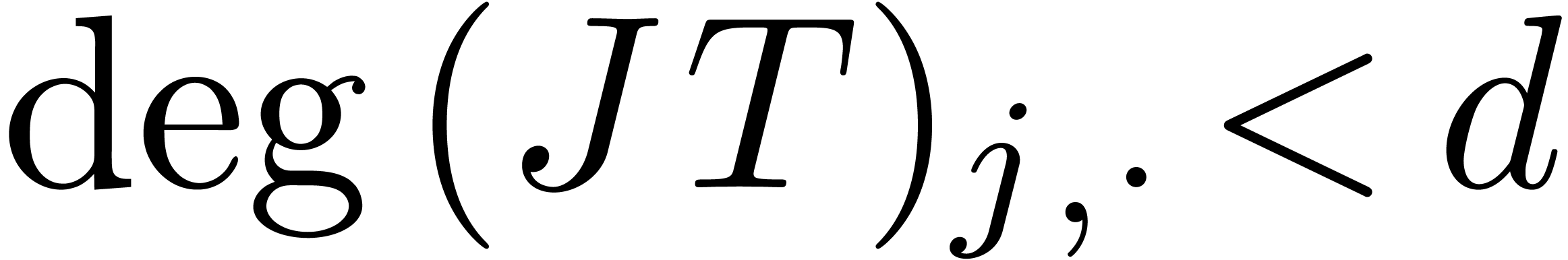 , then this would imply that
, then this would imply that 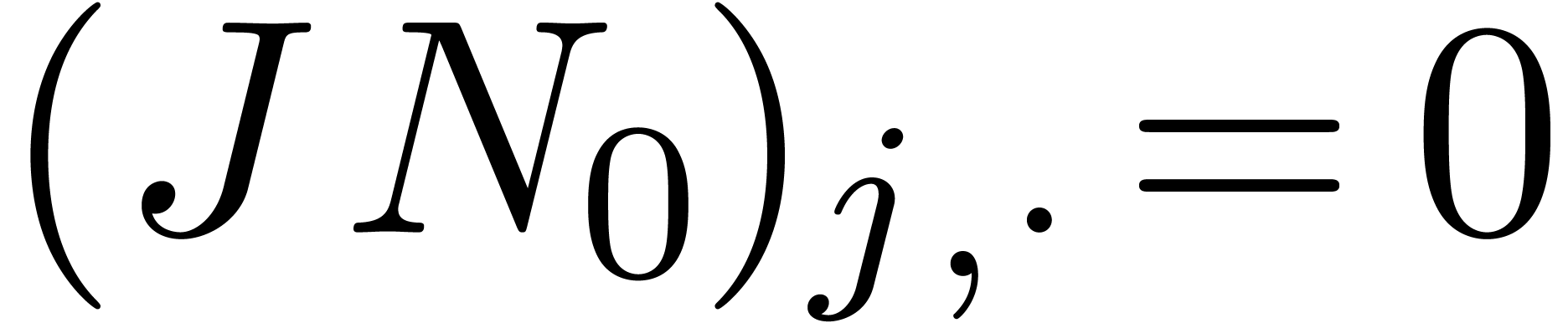 , which contradicts HA2. From
our claim, it follows that
, which contradicts HA2. From
our claim, it follows that  and
and 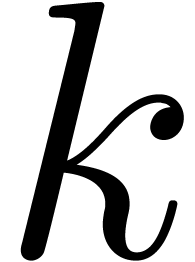 is maximal with the property that
is maximal with the property that 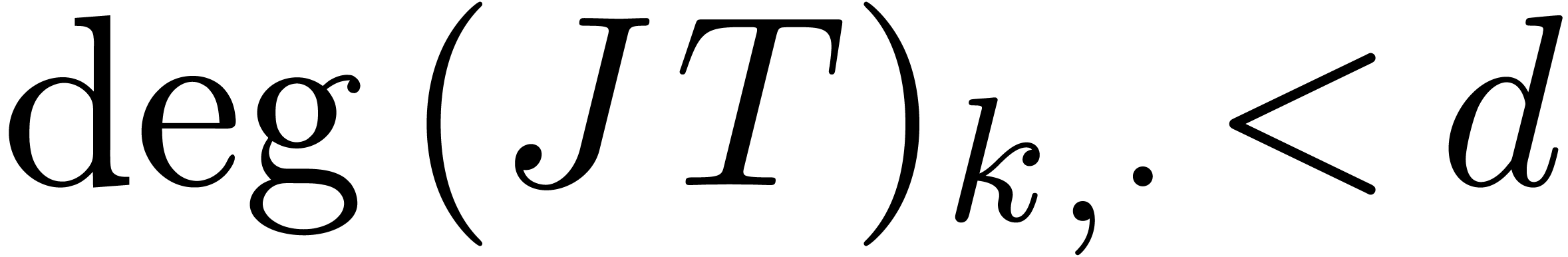 .
Since the first
.
Since the first 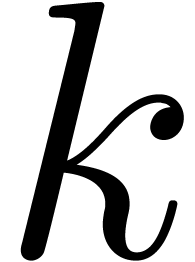 rows of
rows of  and
and 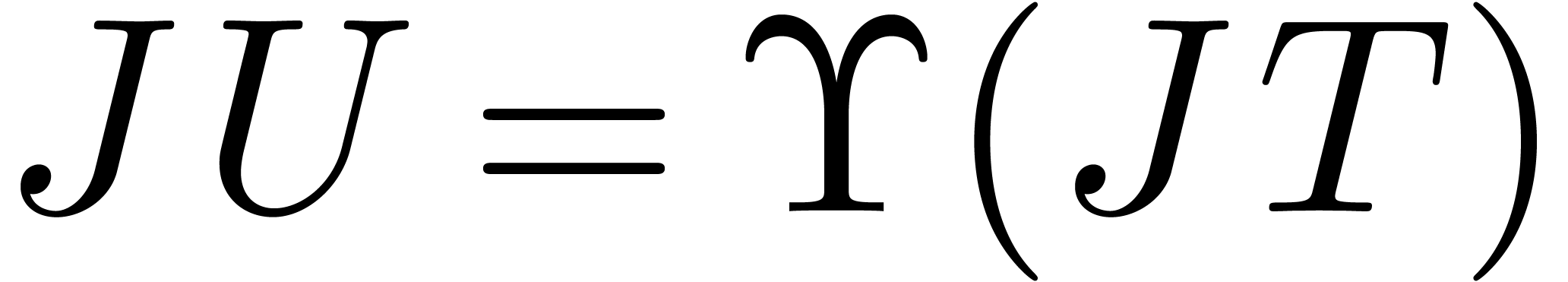 coincide, the first
coincide, the first 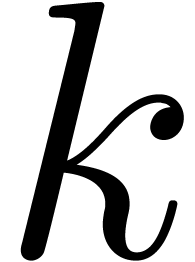 rows of
rows of 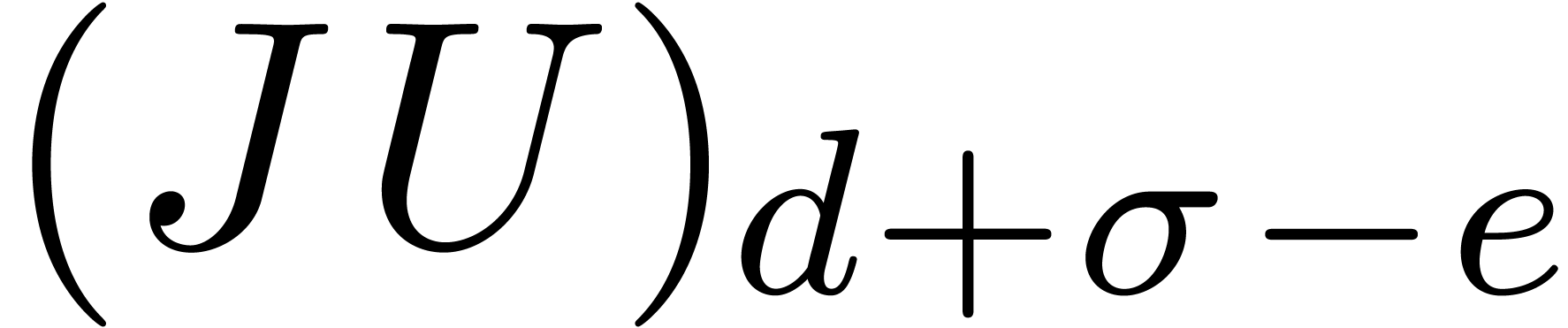 are
are 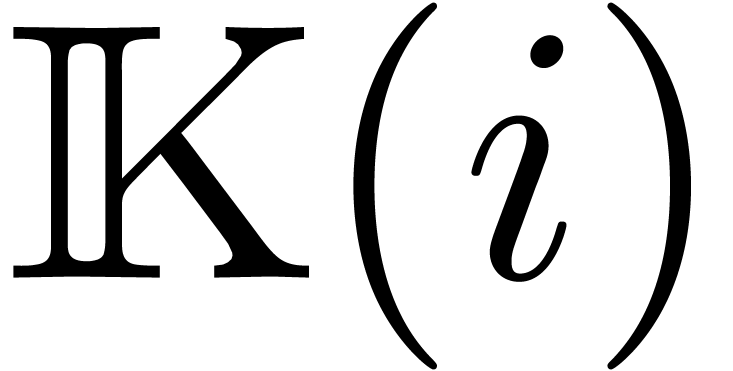 -linearly
independent. This shows that HA3 is satisfied for
-linearly
independent. This shows that HA3 is satisfied for  . As to HA2, let
. As to HA2, let
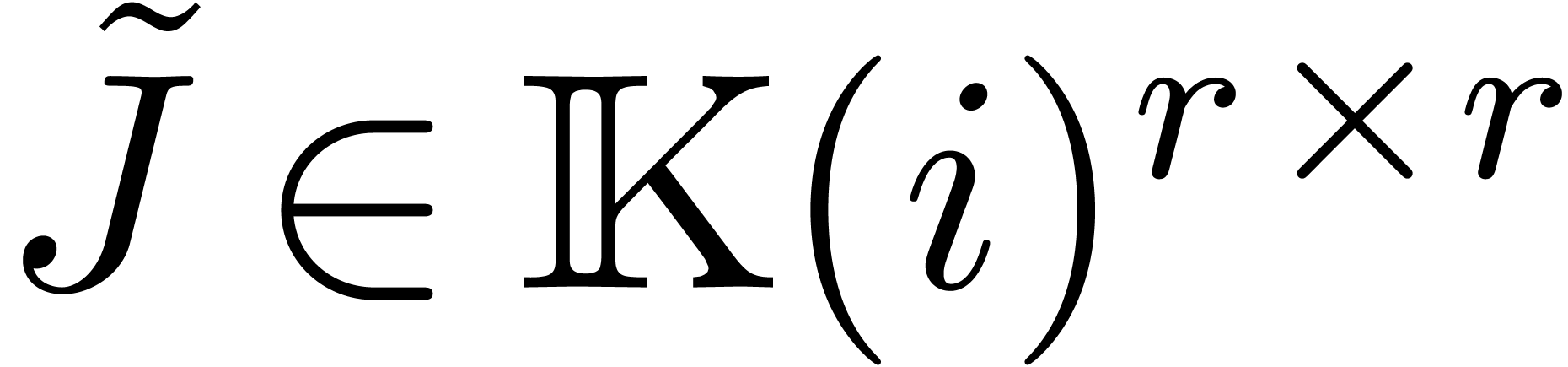 be the invertible matrix with
be the invertible matrix with 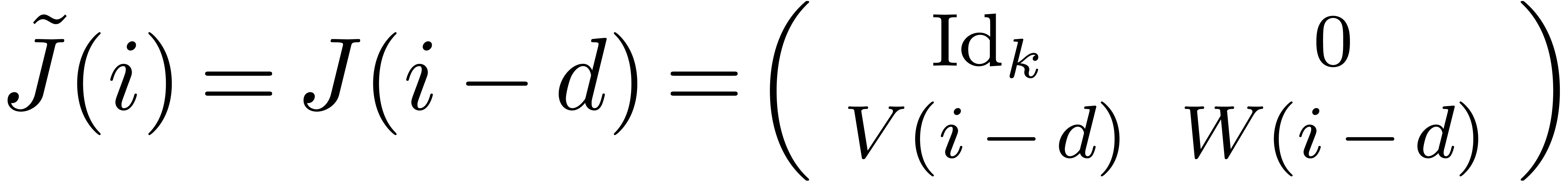 . Then we notice that
. Then we notice that 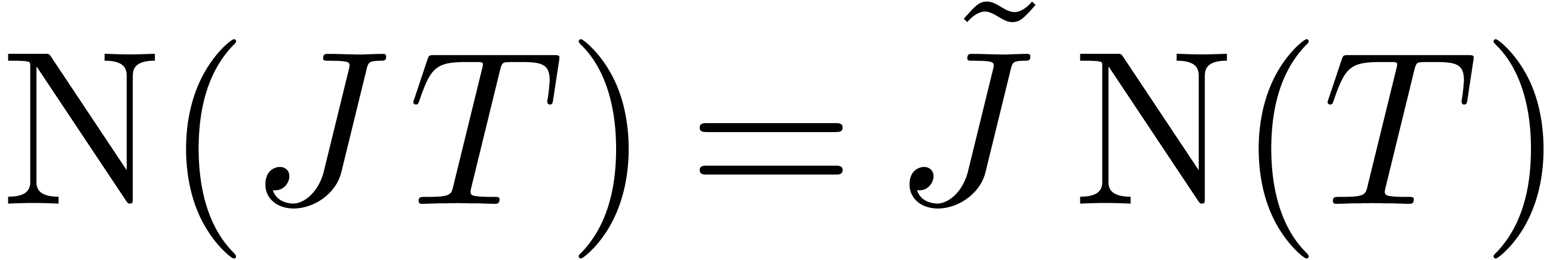 , whence
, whence 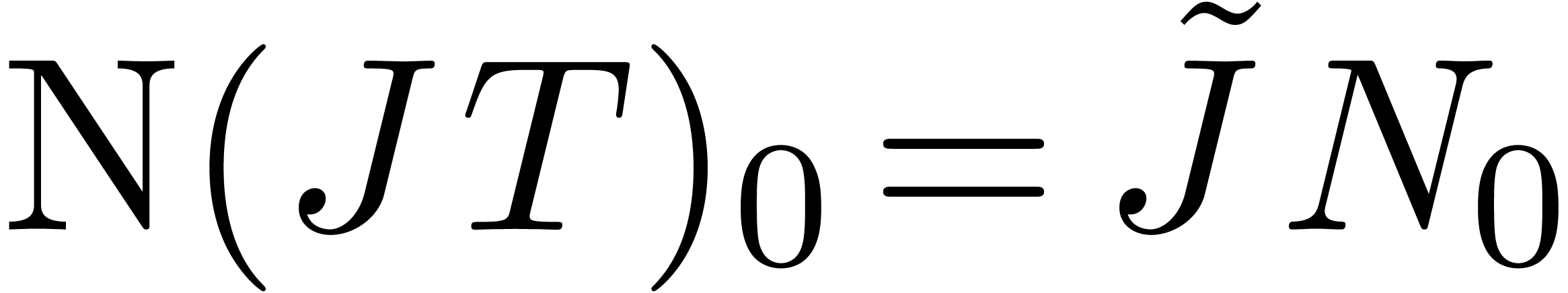 is invertible. The
rows of
is invertible. The
rows of  clearly form a basis for
clearly form a basis for  , since
, since 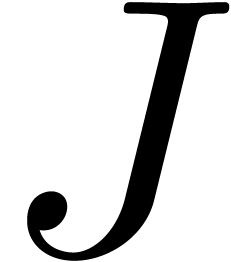 is
invertible.□
is
invertible.□
 be a
be a 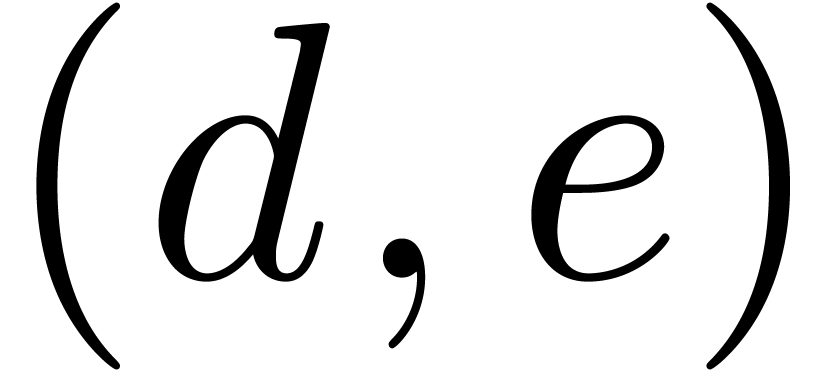 -head annihilator for
-head annihilator for 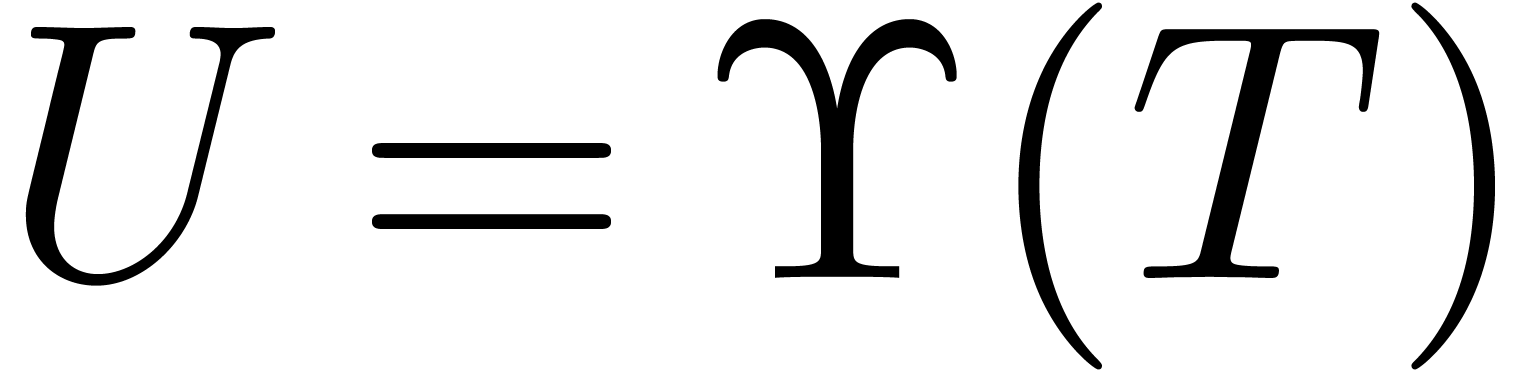 , let
, let 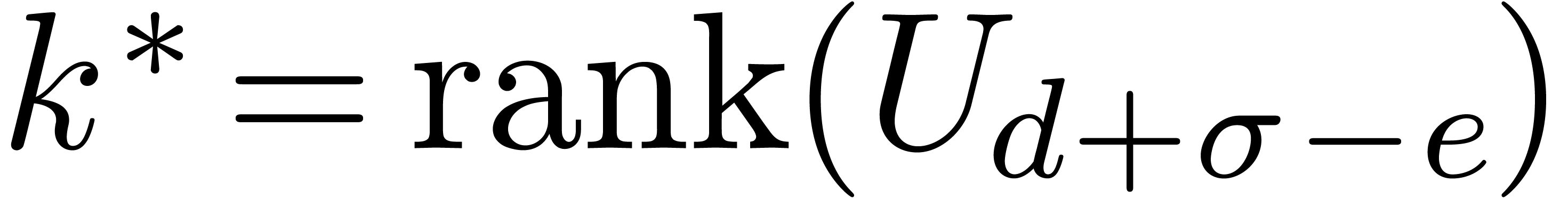 , and assume that the last
, and assume that the last 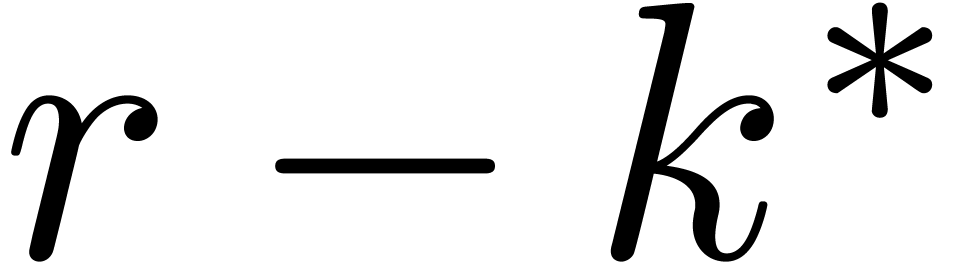 rows of
rows of 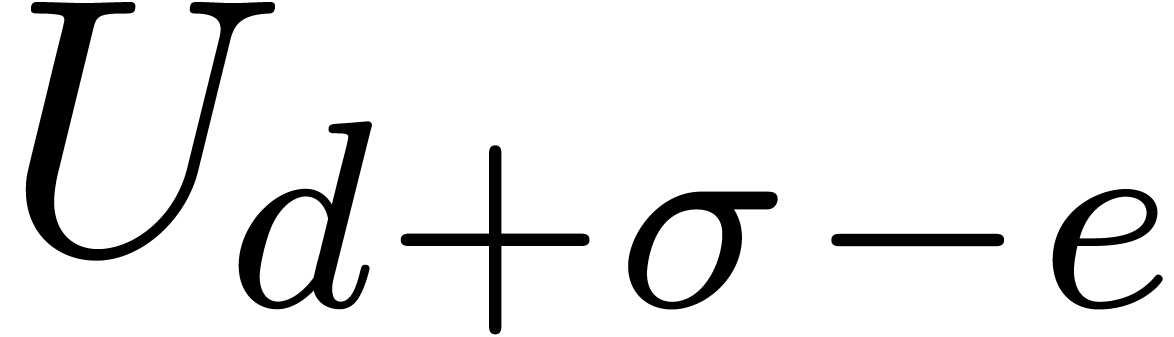 vanish. Let
vanish. Let  be
the matrix with rows
be
the matrix with rows 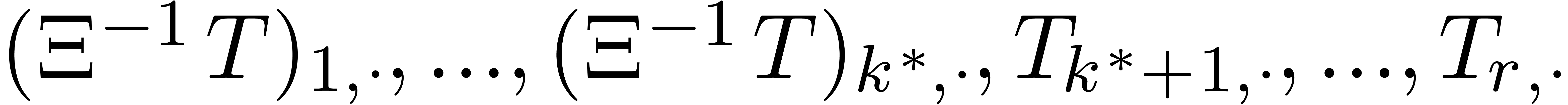 . Then
. Then
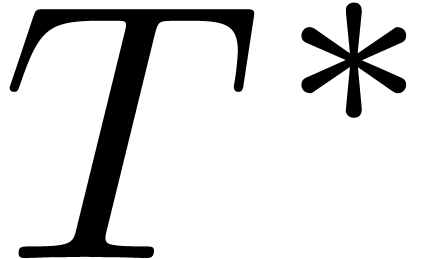 is a
is a  -head
annihilator for
-head
annihilator for
Proof. We have  for all
for all
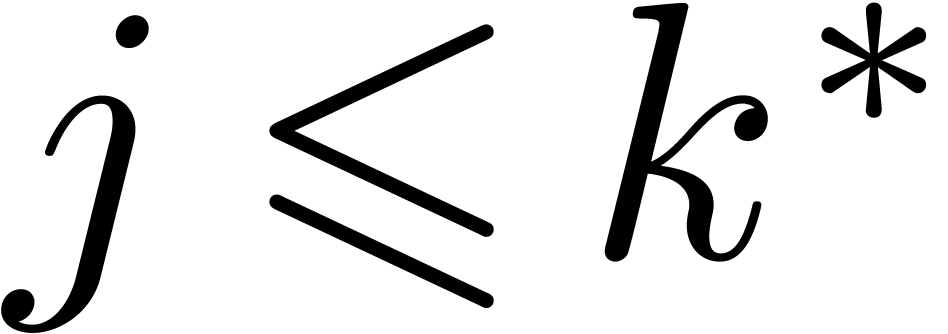 and
and 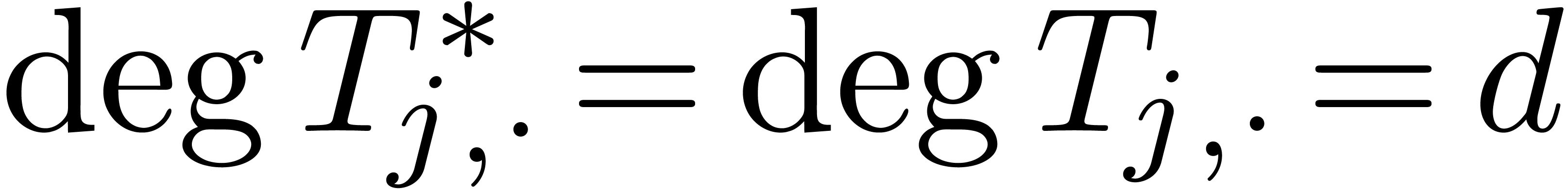 for all
for all 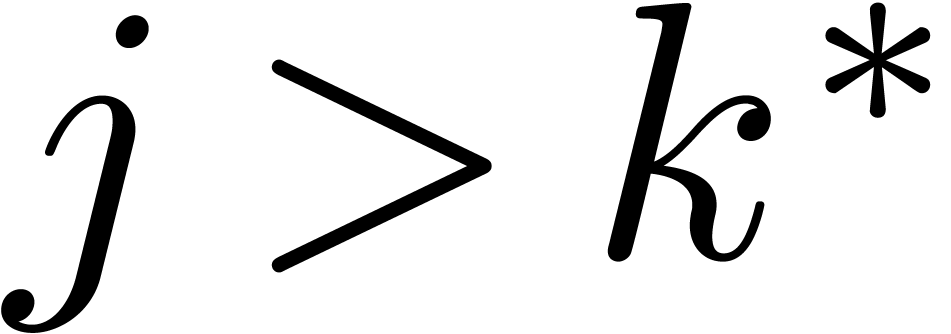 . In particular, we have
. In particular, we have  and
and  is maximal with the property that
is maximal with the property that 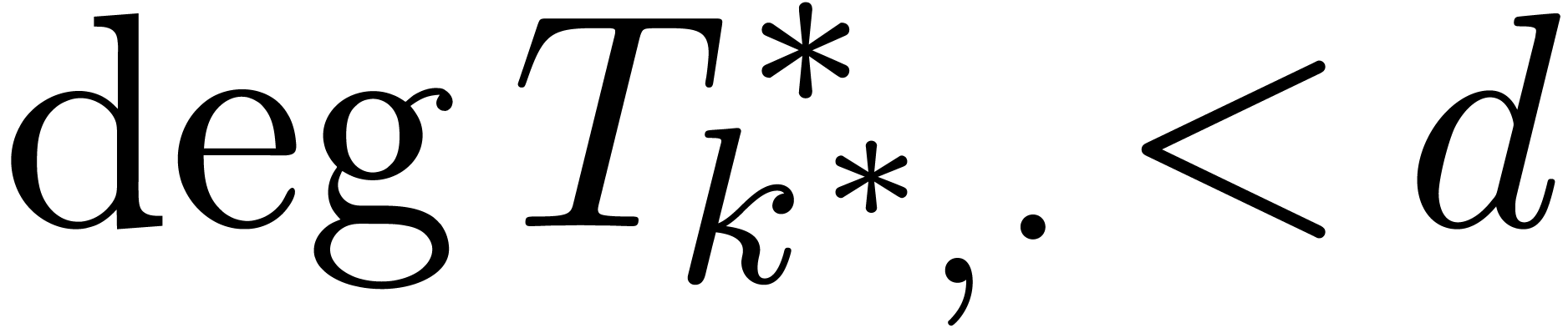 . Setting
. Setting 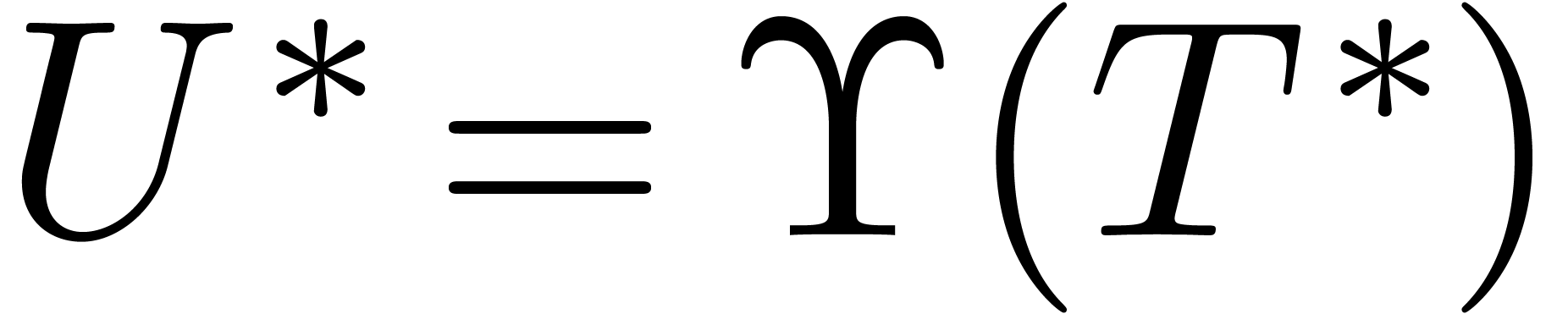 , we also observe that
, we also observe that 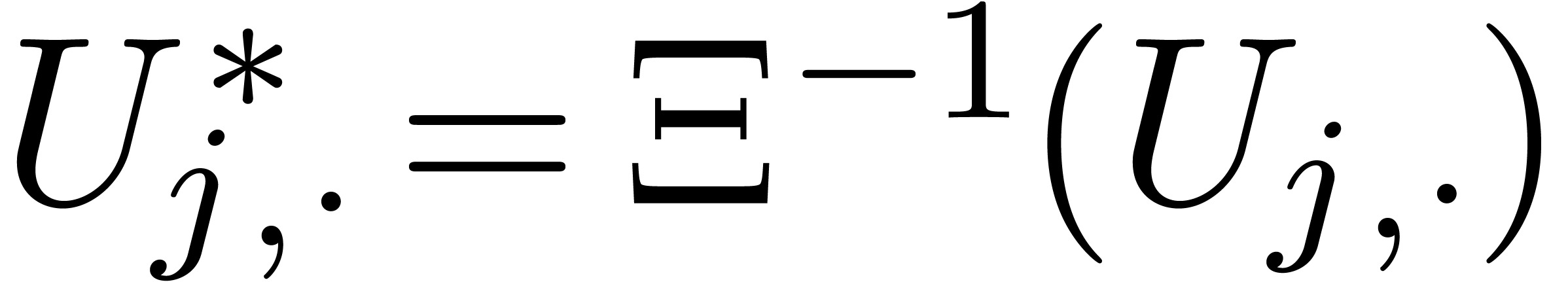 for
all
for
all 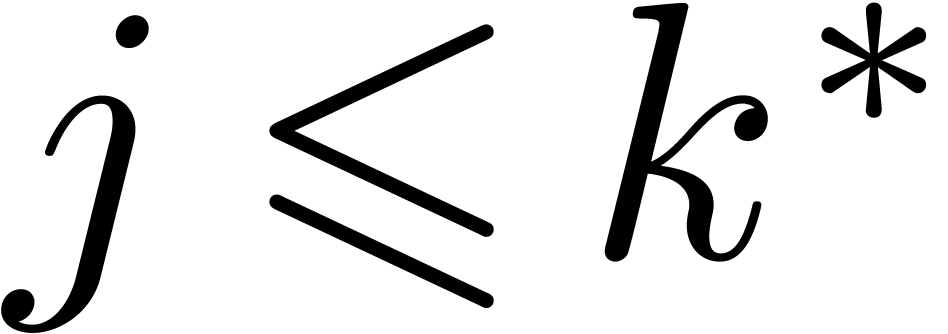 . Since
. Since 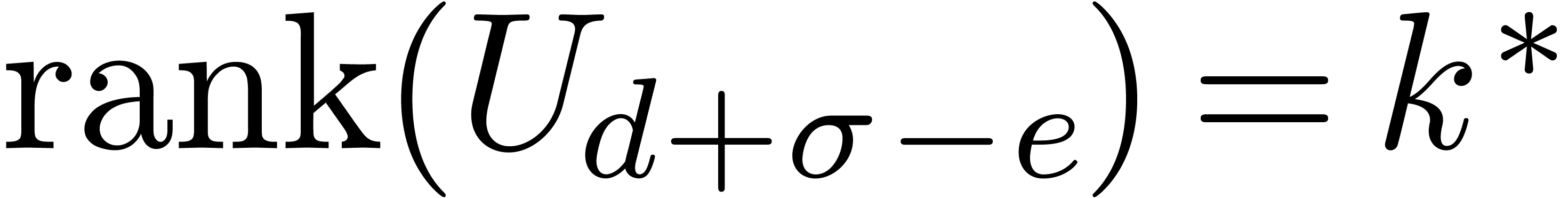 and the last
and the last 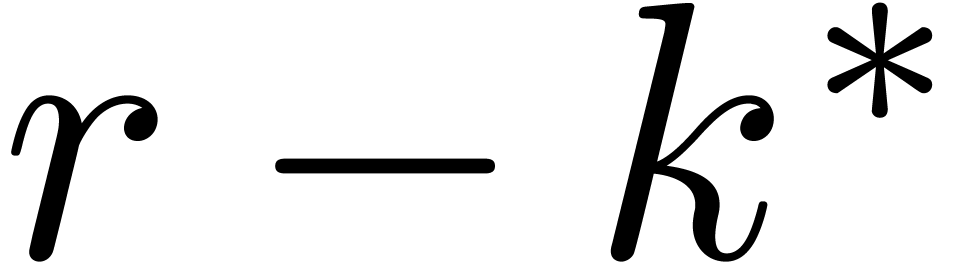 rows of
rows of 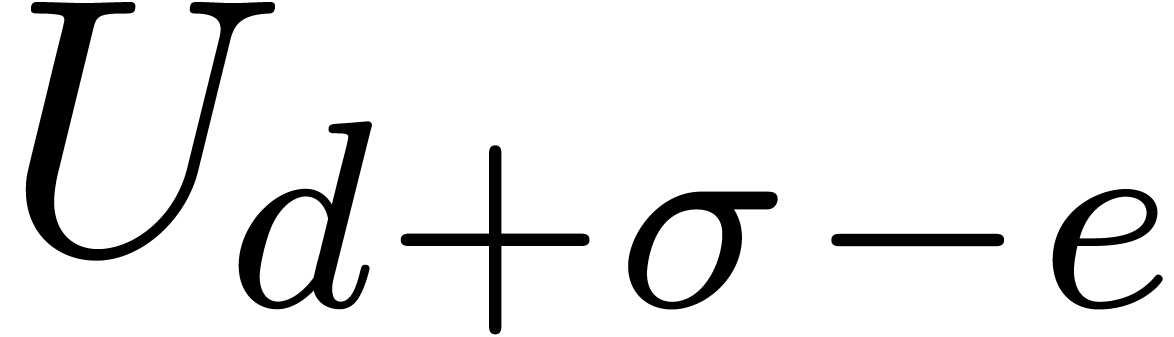 vanish, the first
vanish, the first 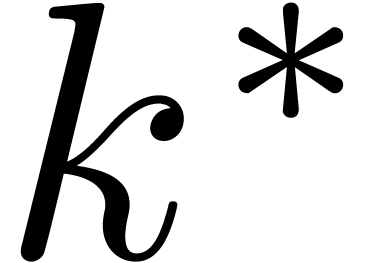 rows of both
rows of both 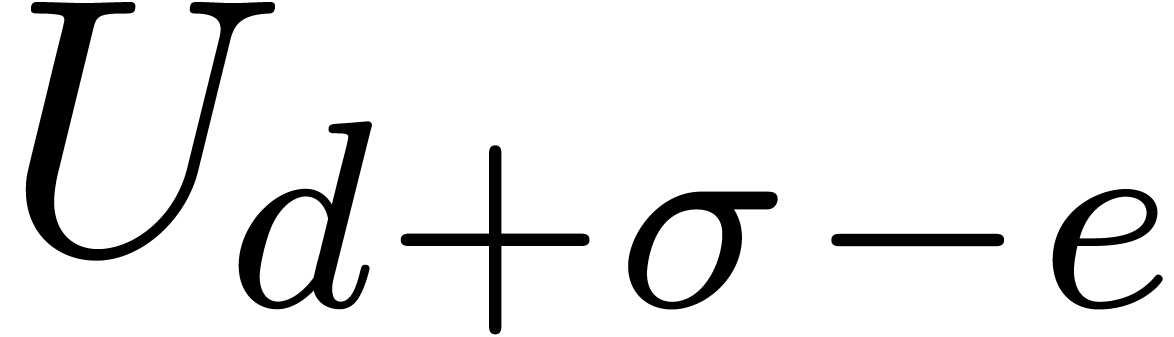 and
and 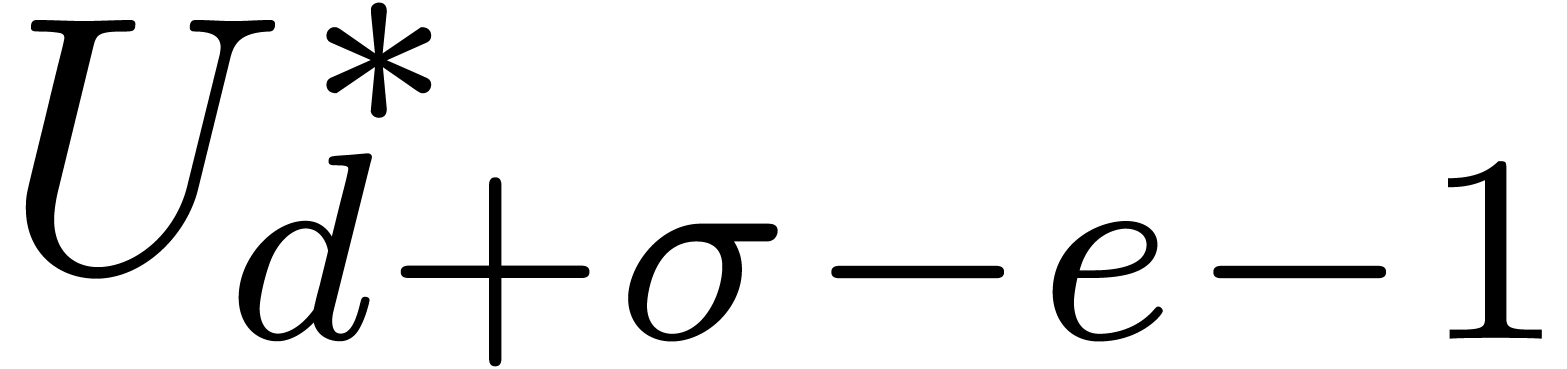 are
are  -linearly
independent. In other words, HA3 is satisfied for
-linearly
independent. In other words, HA3 is satisfied for  . As to HA2, we
observe that
. As to HA2, we
observe that 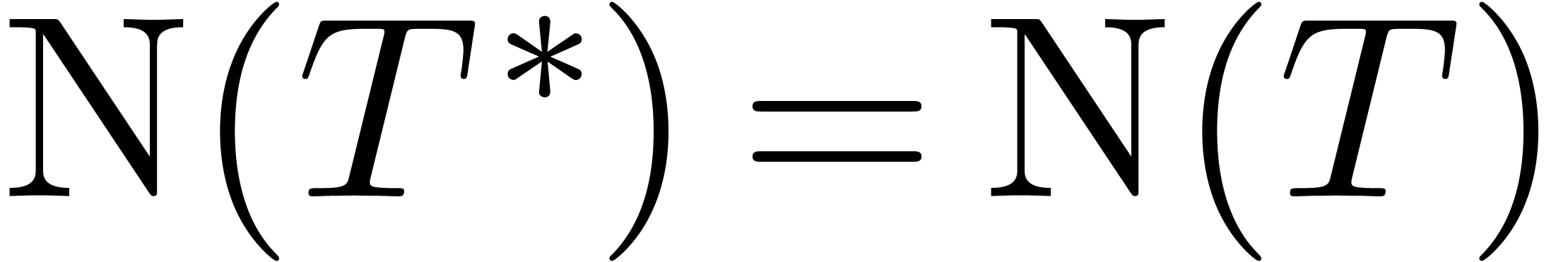 , whence
, whence 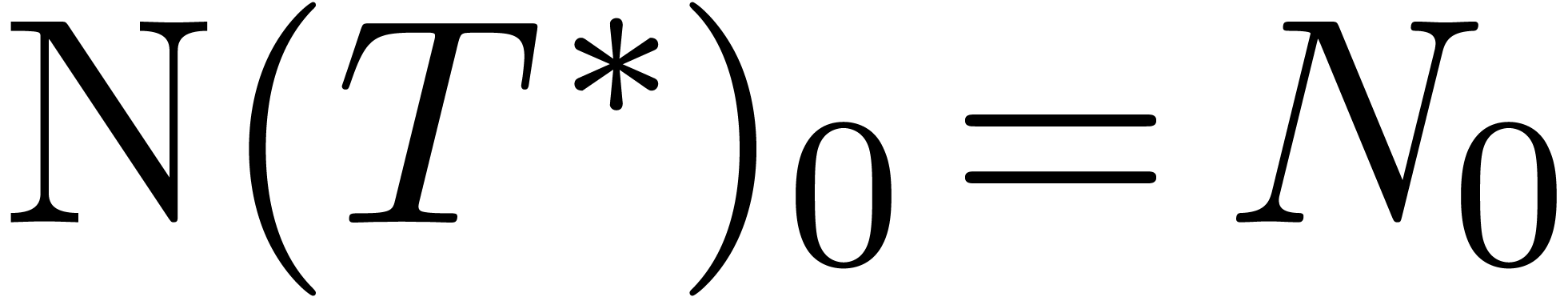 is invertible.
is invertible.
Let us finally show that 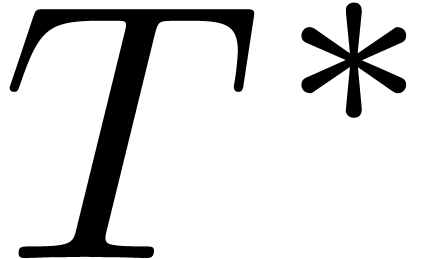 forms a basis for the
forms a basis for the
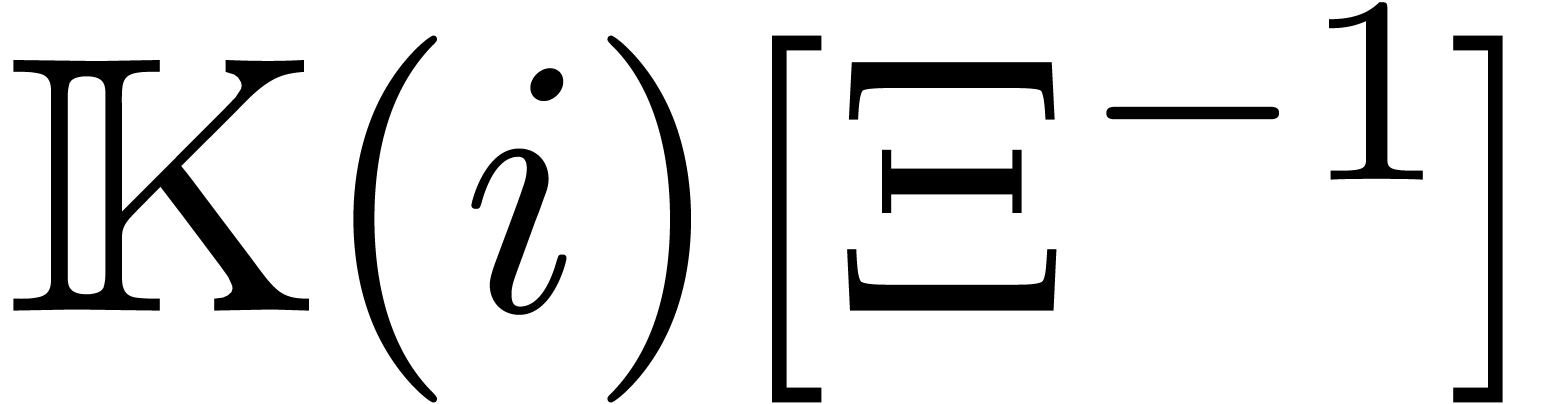 -module
-module 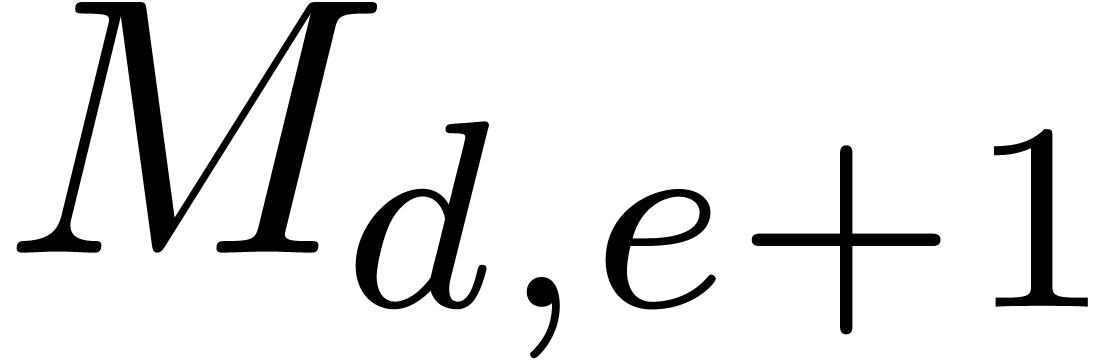 . So let
. So let 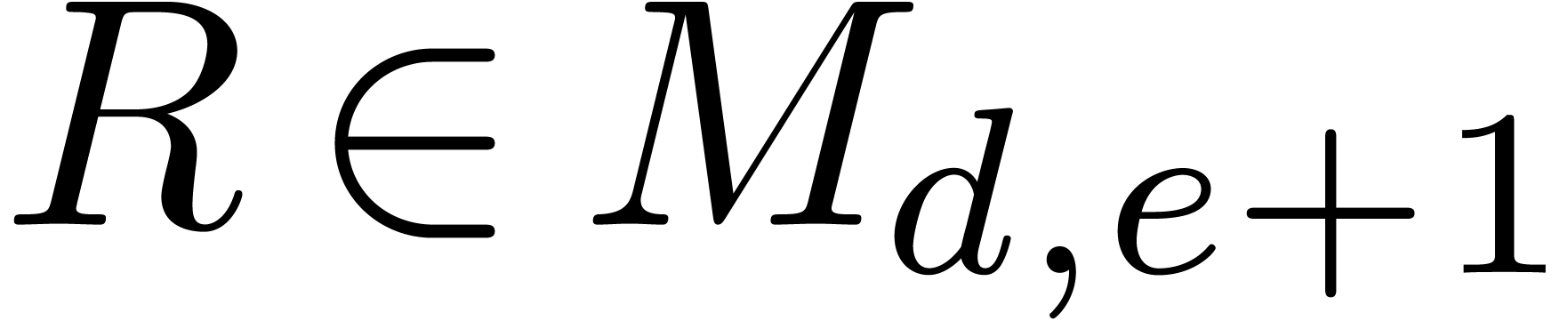 .
Then
.
Then 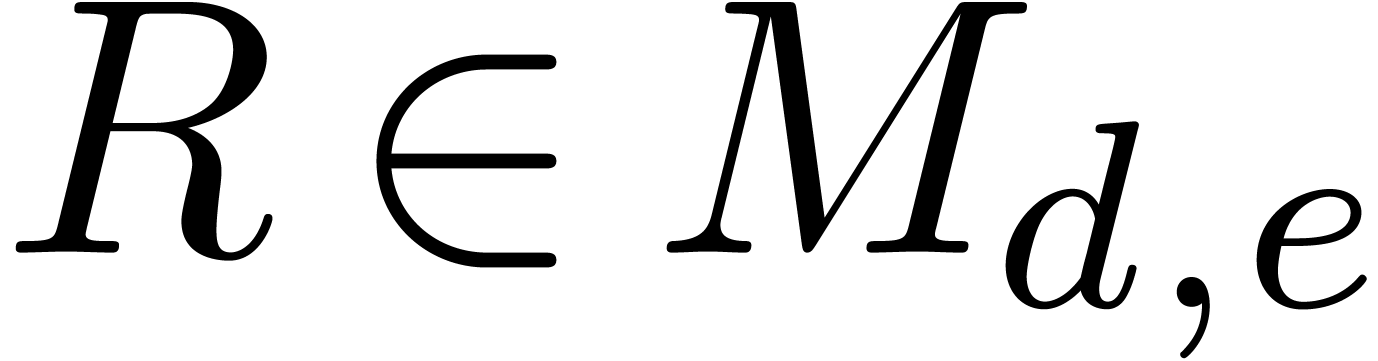 , so
, so  for some row matrix
for some row matrix 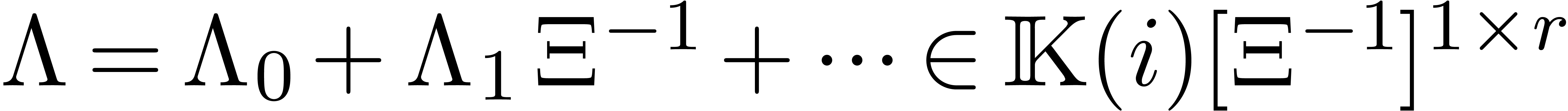 . Setting
. Setting
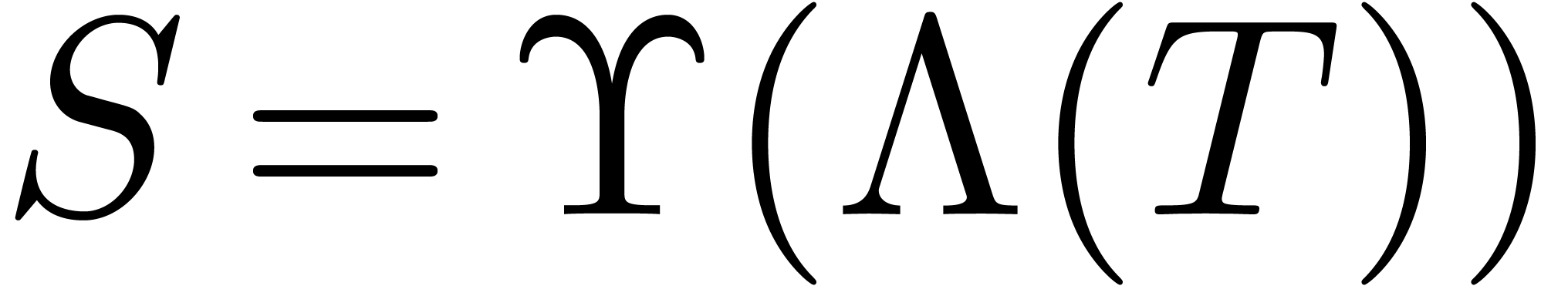 , we have
, we have  , whence
, whence 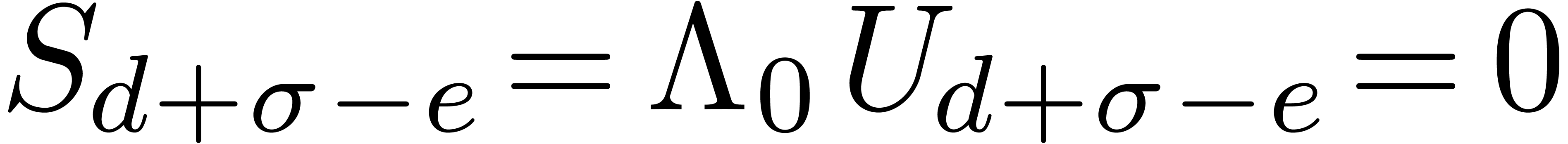 .
Since the first
.
Since the first 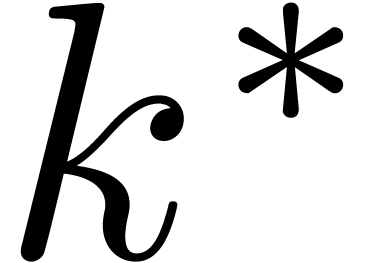 rows of
rows of 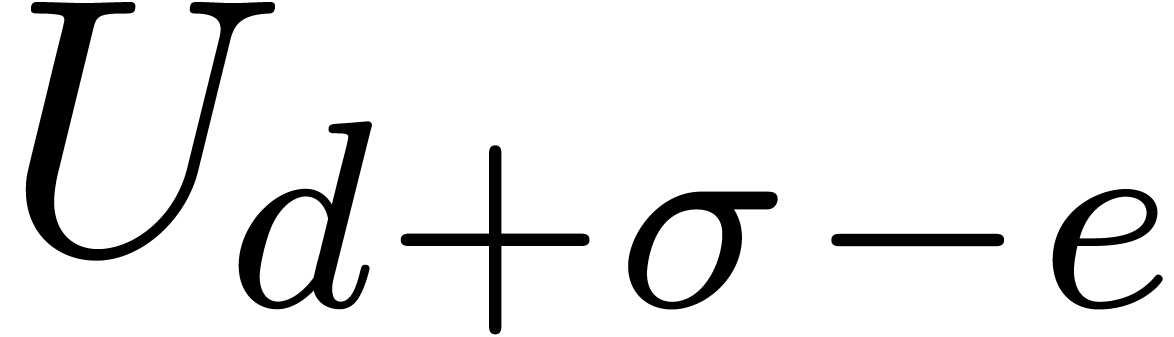 are
are 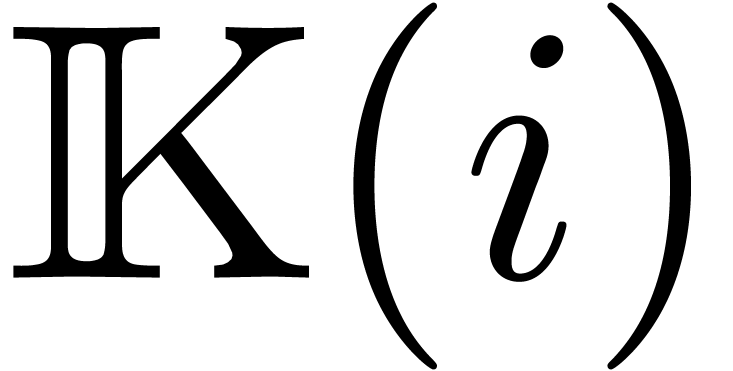 -linearly independent and
the last
-linearly independent and
the last 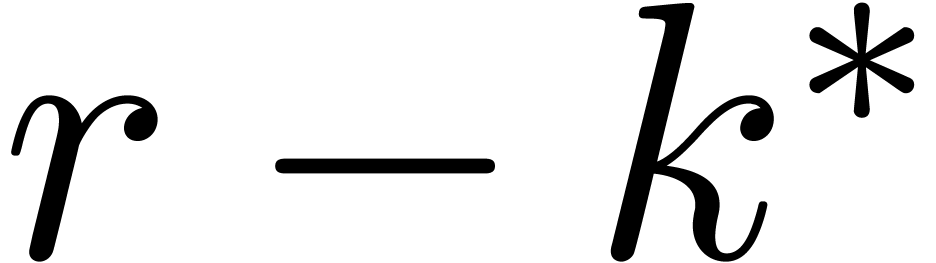 rows of
rows of 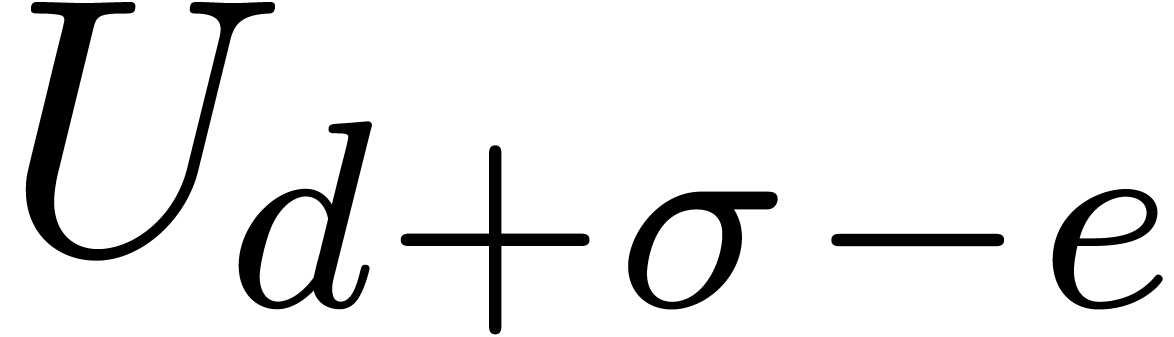 vanish,
we get
vanish,
we get 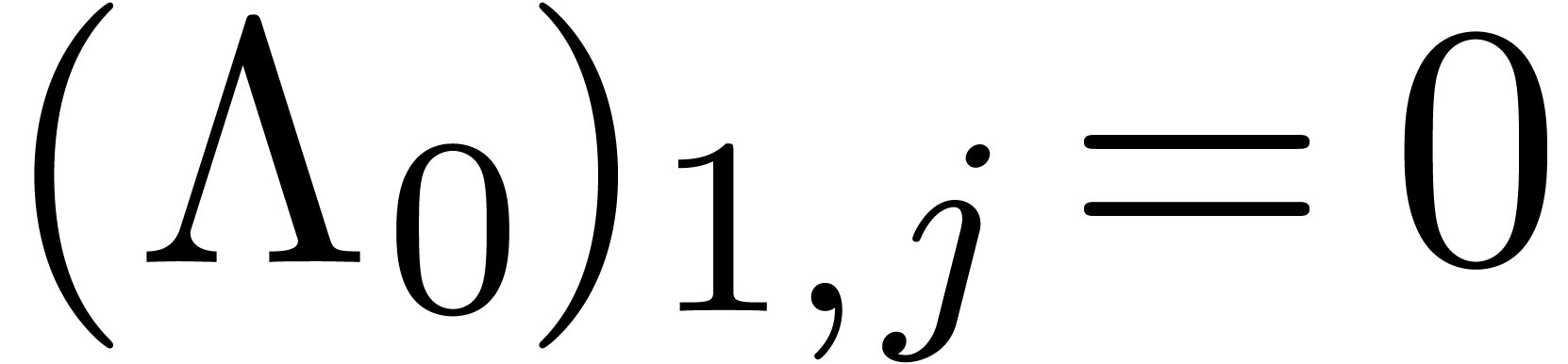 for all
for all 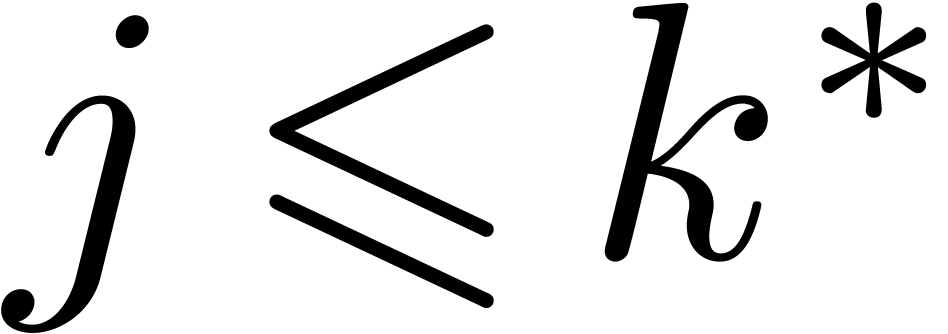 .
Let
.
Let  be the row vector with
be the row vector with 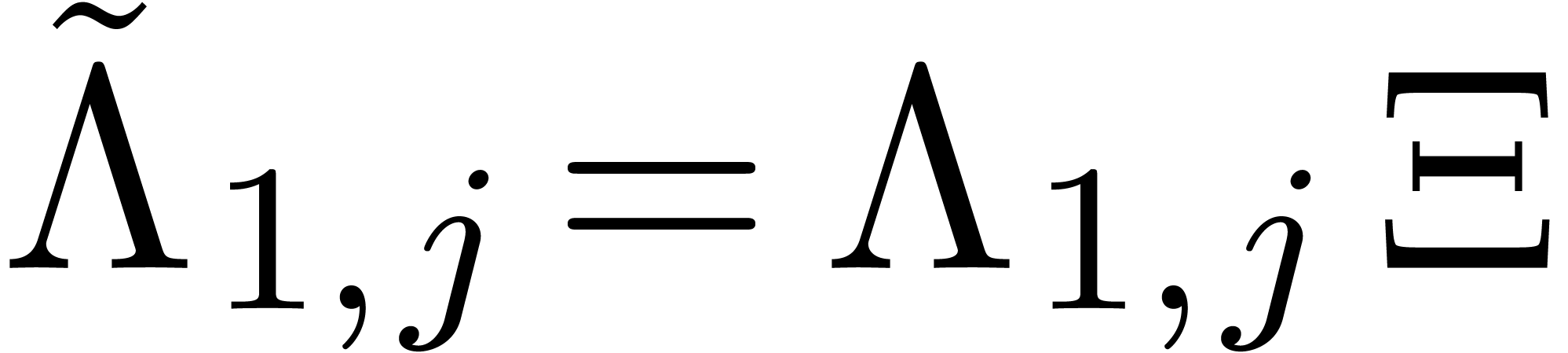 for
for 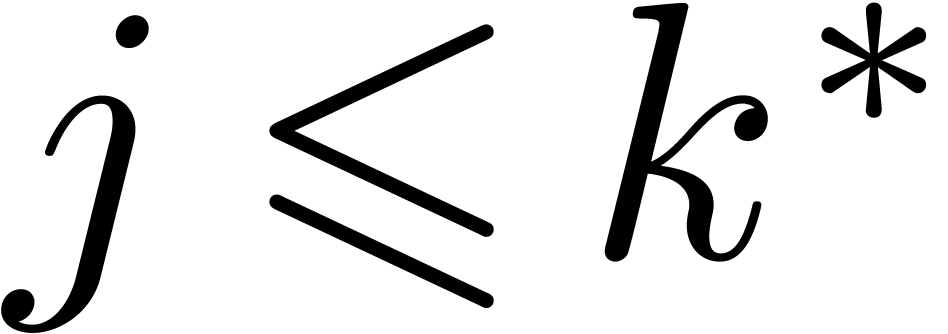 and
and 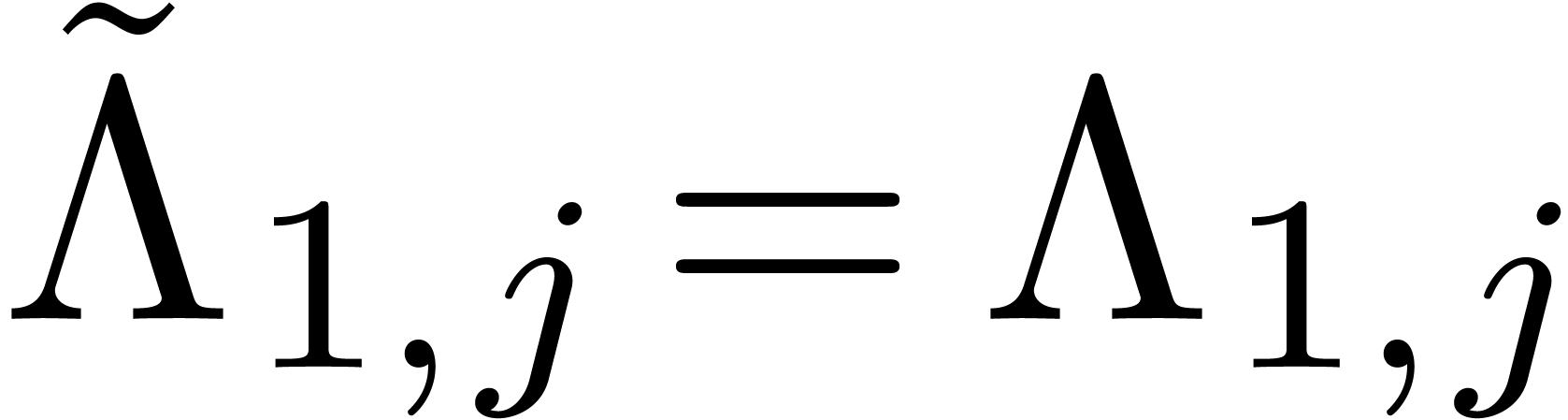 for
for 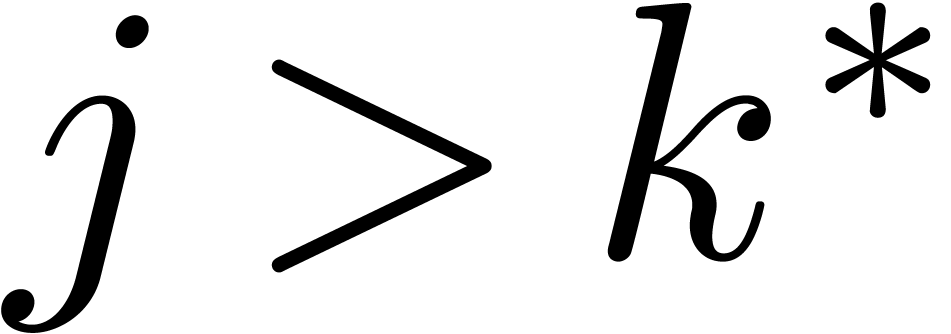 . By what precedes, we have
. By what precedes, we have 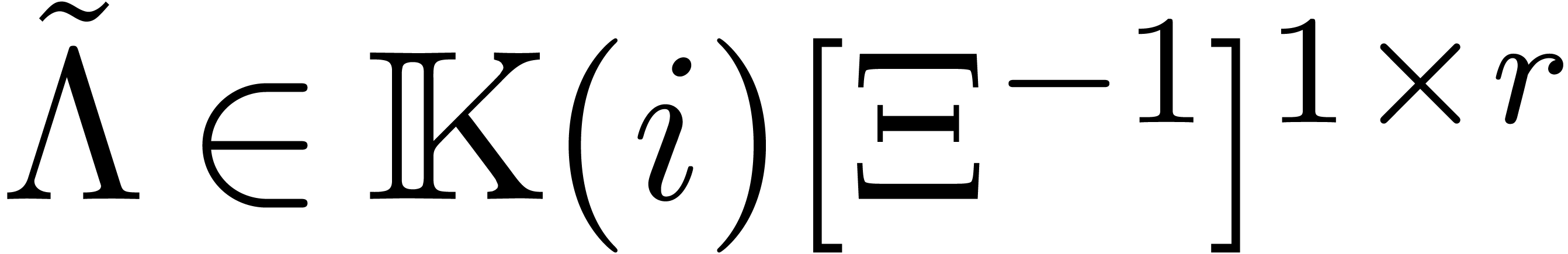 and
and  . Now we have
. Now we have 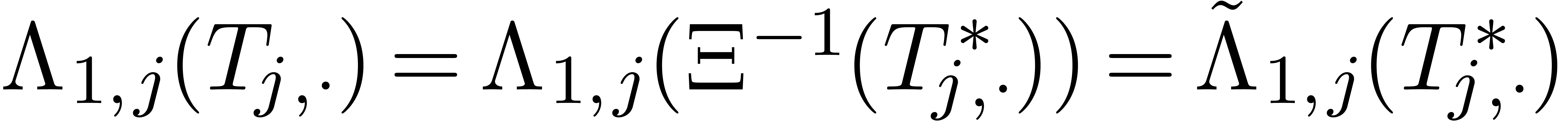 for
for 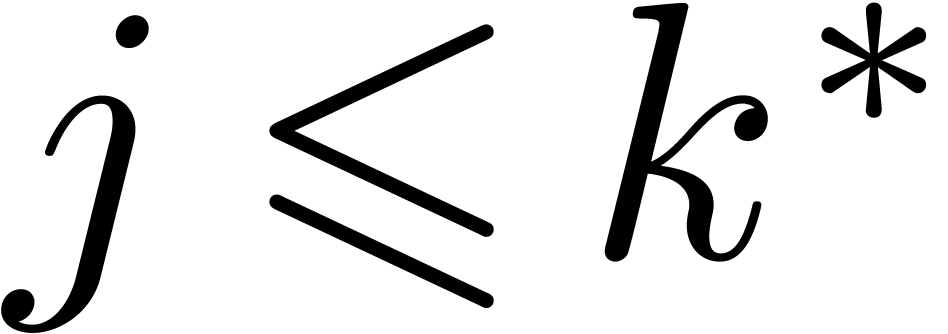 and
and 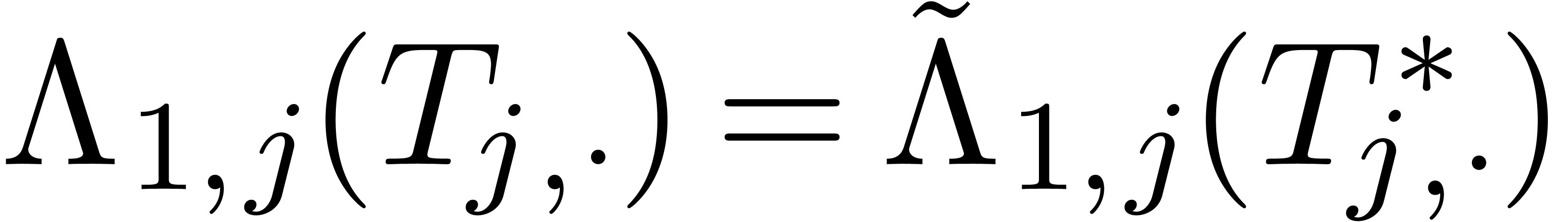 for
for 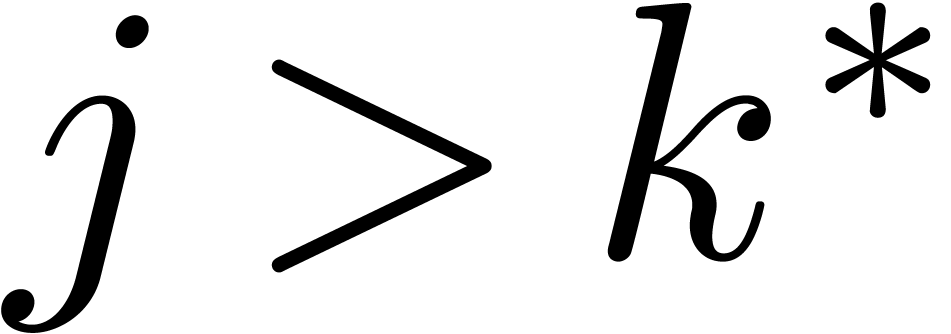 . In other words,
. In other words, 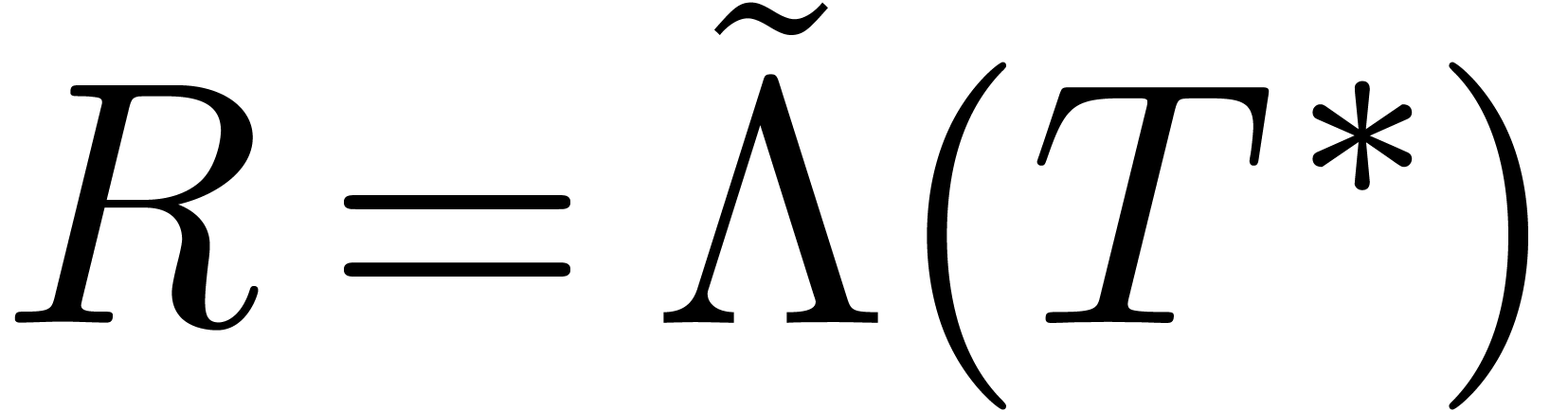 , as desired.□
, as desired.□
Propositions 4 and 5 allow us to compute 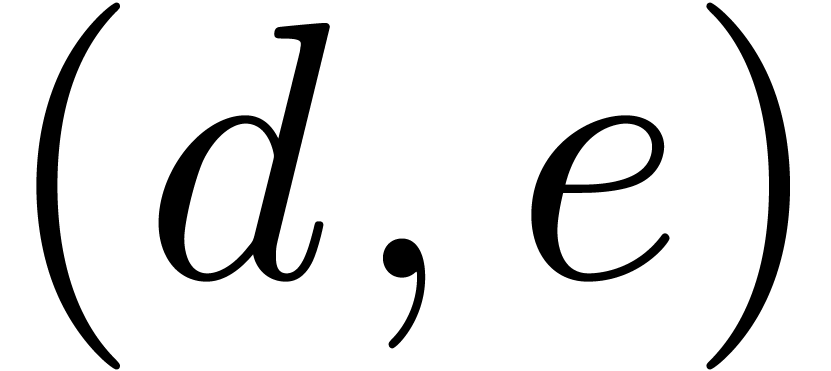 -head annihilators for (1)
with arbitrarily large
-head annihilators for (1)
with arbitrarily large  .
Assuming that we have
.
Assuming that we have 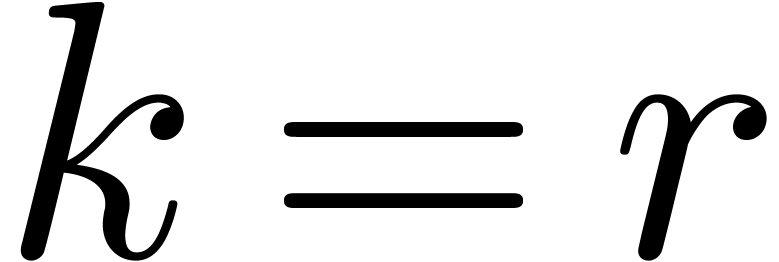 in HA3
for sufficiently large
in HA3
for sufficiently large  , this
yields the following algorithm for the computation of a head chopper for
(1):
, this
yields the following algorithm for the computation of a head chopper for
(1):
Algorithm HeadChopper |
repeat
if
|
 . Consider
the value of
. Consider
the value of  at the beginning of the loop and
after
at the beginning of the loop and
after  iterations. Then
iterations. Then  is a
is a 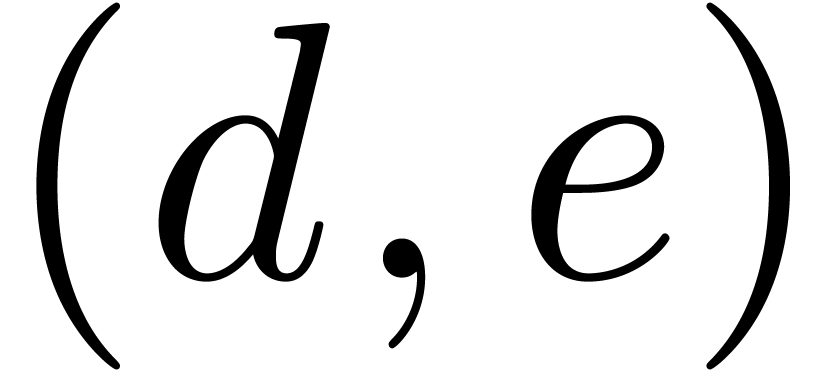 -head annihilator.
-head annihilator.
Proof. We first observe that 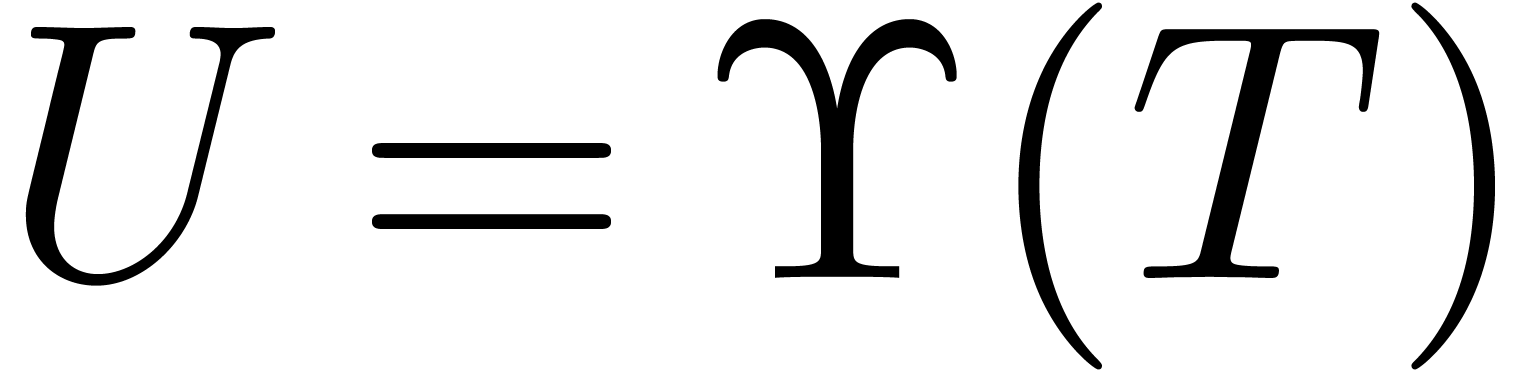 throughout the algorithm. Let us now prove the proposition by induction
over
throughout the algorithm. Let us now prove the proposition by induction
over  . The proposition
clearly holds for
. The proposition
clearly holds for 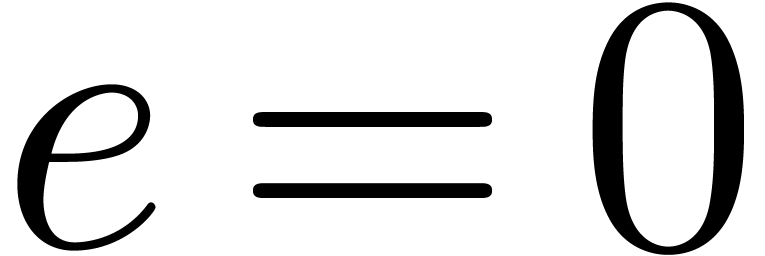 . Assuming
that the proposition holds for a given
. Assuming
that the proposition holds for a given  ,
let us show that it again holds at the next iteration. Consider the
values of
,
let us show that it again holds at the next iteration. Consider the
values of  and
and  at the
beginning of the loop and after
at the
beginning of the loop and after  iterations. Let
iterations. Let
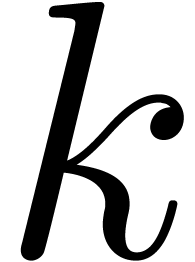 be maximal such that
be maximal such that  . From the induction hypothesis, it follows that the
first
. From the induction hypothesis, it follows that the
first 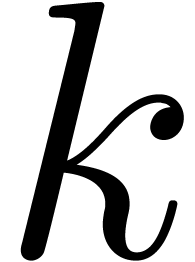 rows of
rows of  are
are 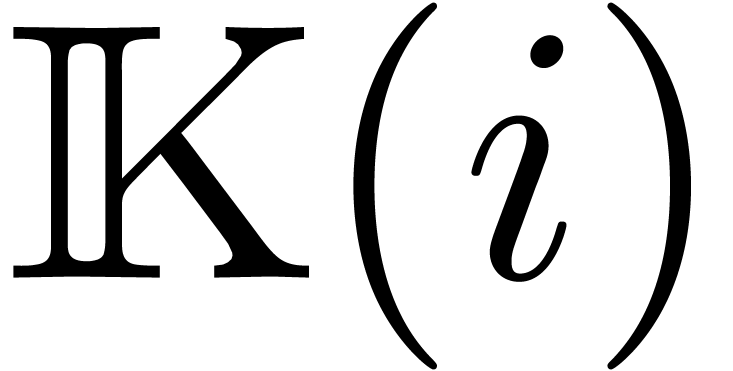 -linearly independent, whence the
matrix
-linearly independent, whence the
matrix 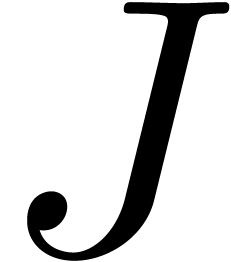 is of the form
is of the form 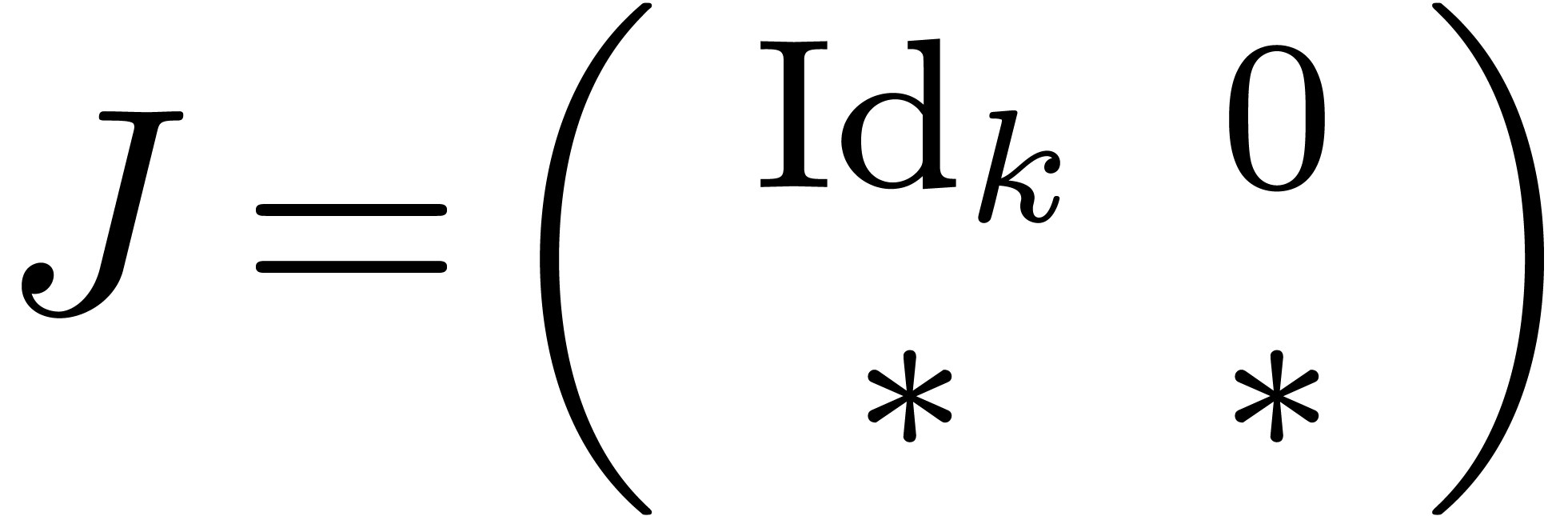 . Now Proposition 4 implies that
. Now Proposition 4 implies that  is still a
is still a  -head
annihilator. Since the last
-head
annihilator. Since the last 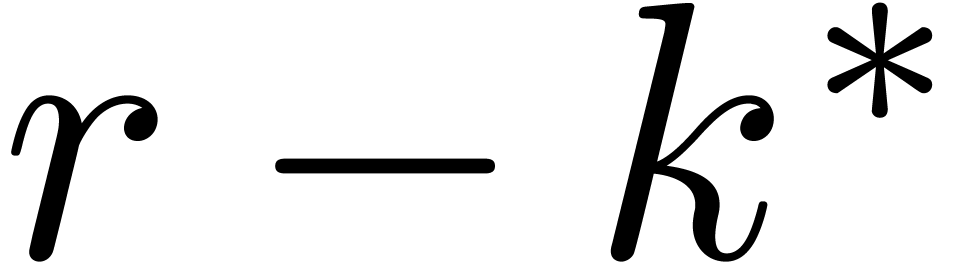 rows of
rows of 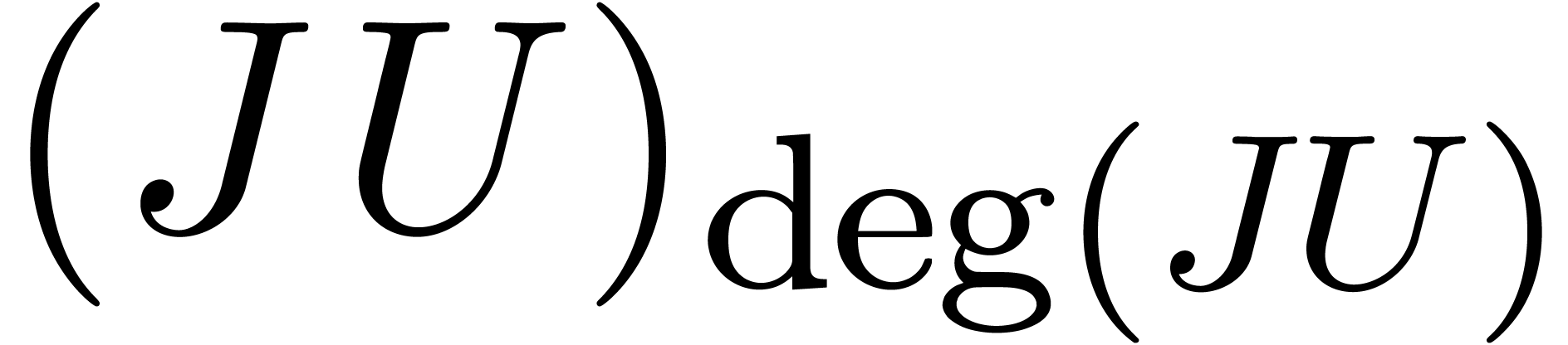 vanish, Proposition 5 also implies that
vanish, Proposition 5 also implies that 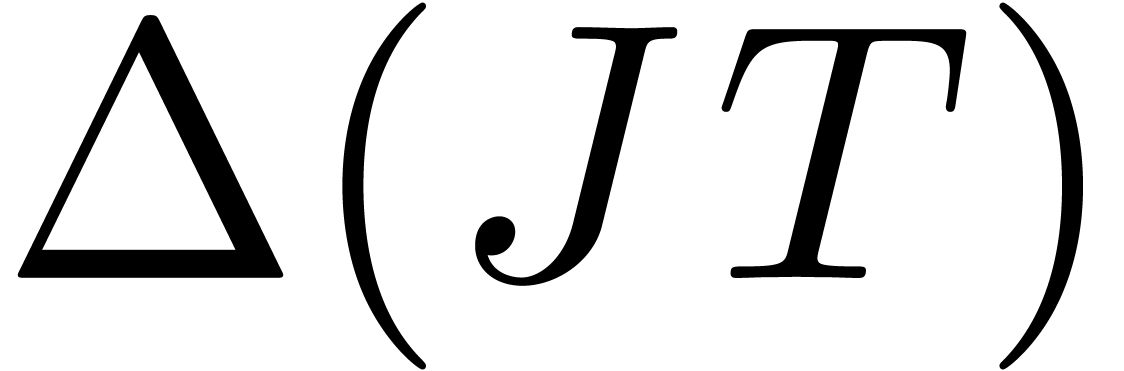 is a
is a 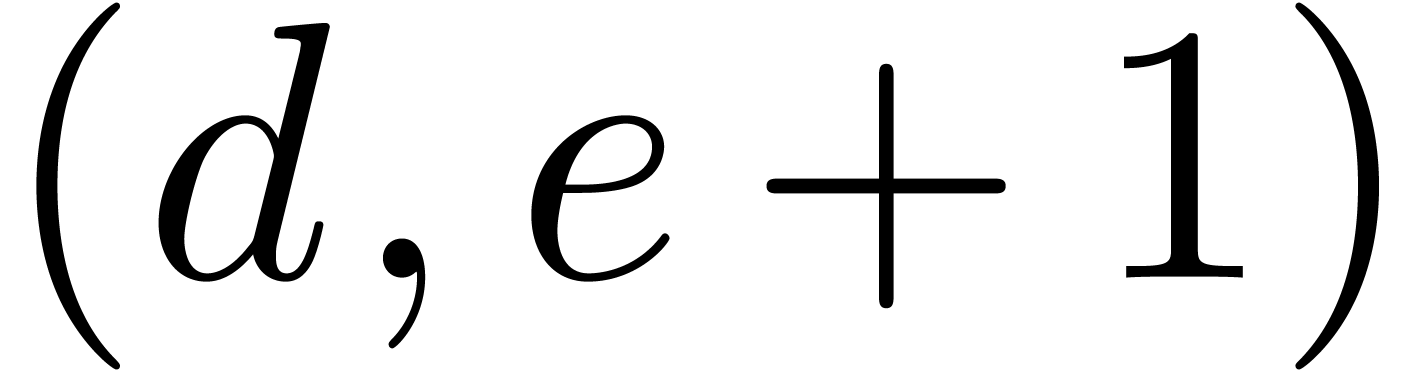 -head
annihilator. This completes the induction. Notice also that
-head
annihilator. This completes the induction. Notice also that 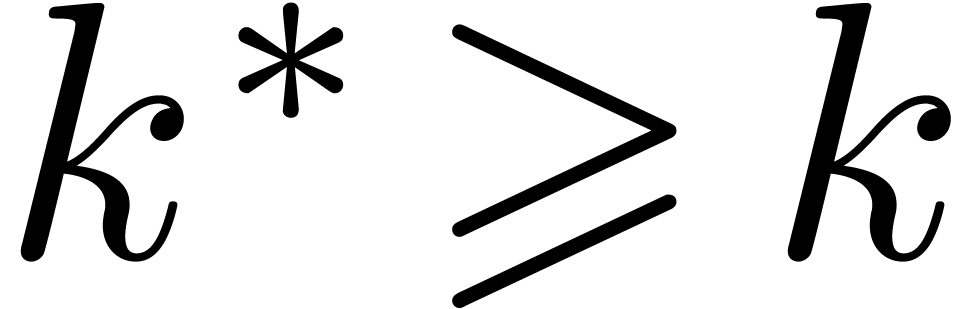 is maximal with the property that
is maximal with the property that 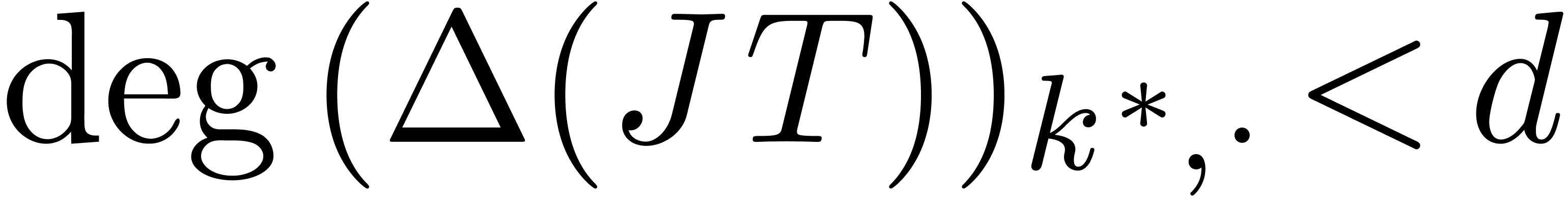 .□
.□
 with
with  . In
particular,
. In
particular, 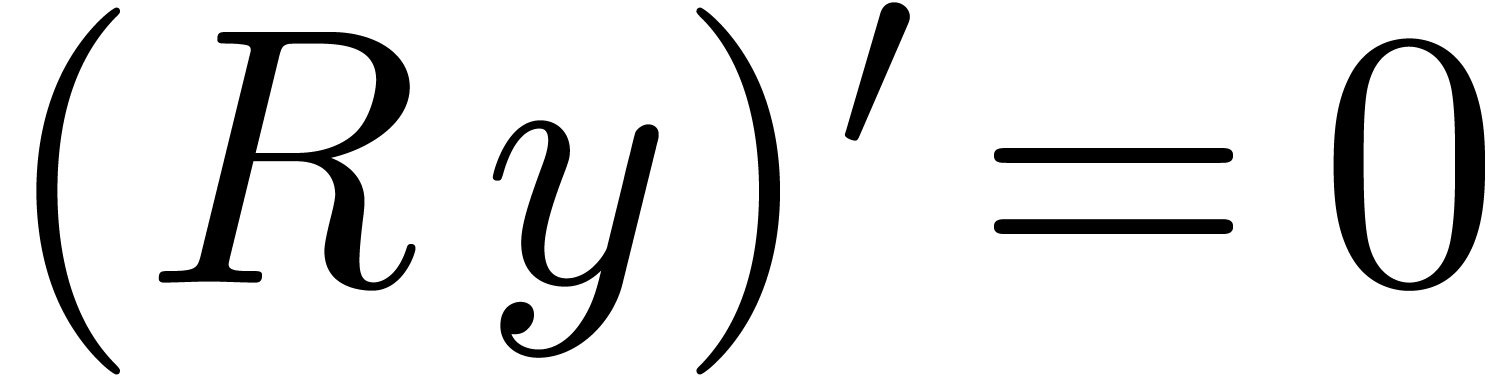 .
.
Proof. Assume that 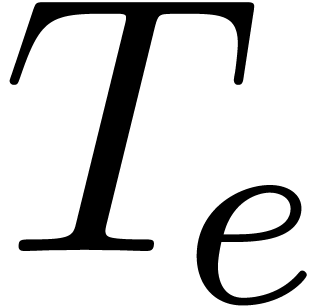 be the value of
be the value of  at the beginning of the main loop after
at the beginning of the main loop after  iterations. Also let
iterations. Also let  and
and 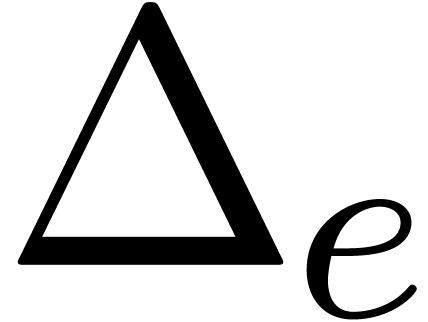 be the values of
be the values of 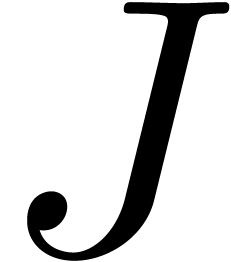 and
and  as computed during the
as computed during the  -th
iteration.
-th
iteration.
Let  be maximal such that
be maximal such that 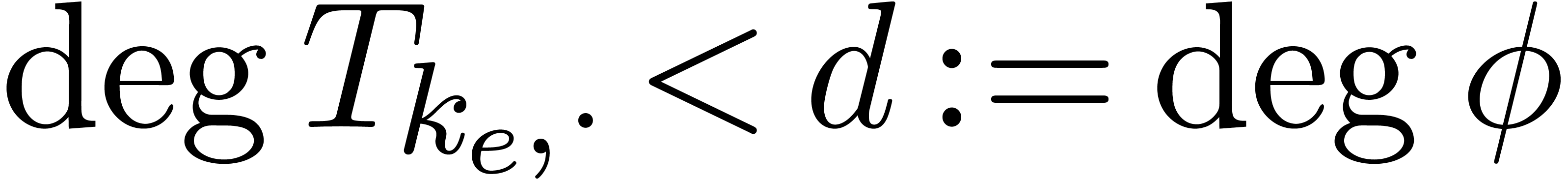 . Using the observation made at the end of the above
proof, we have
. Using the observation made at the end of the above
proof, we have 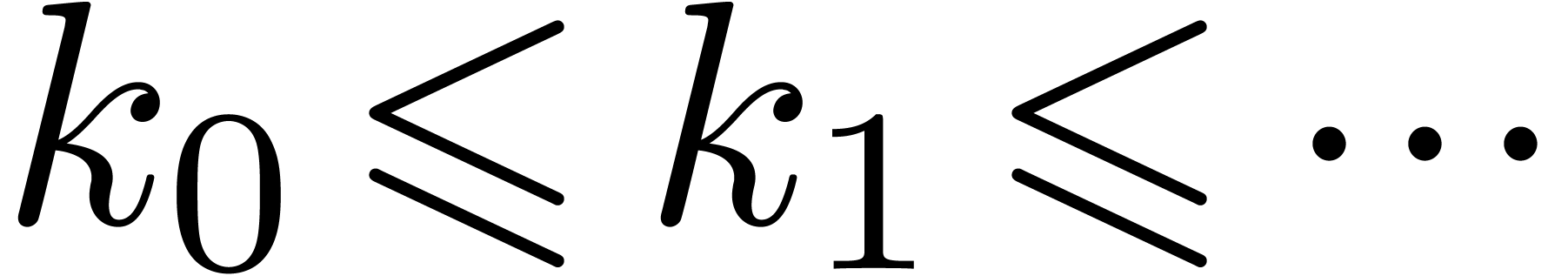 , so there
exist an index
, so there
exist an index  and
and 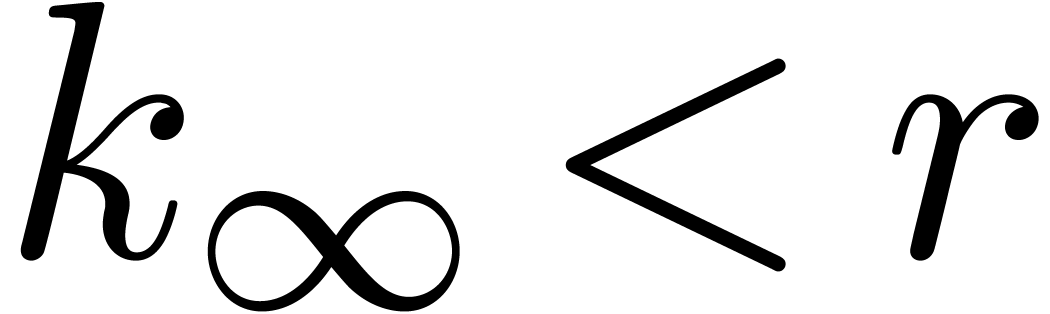 with
with
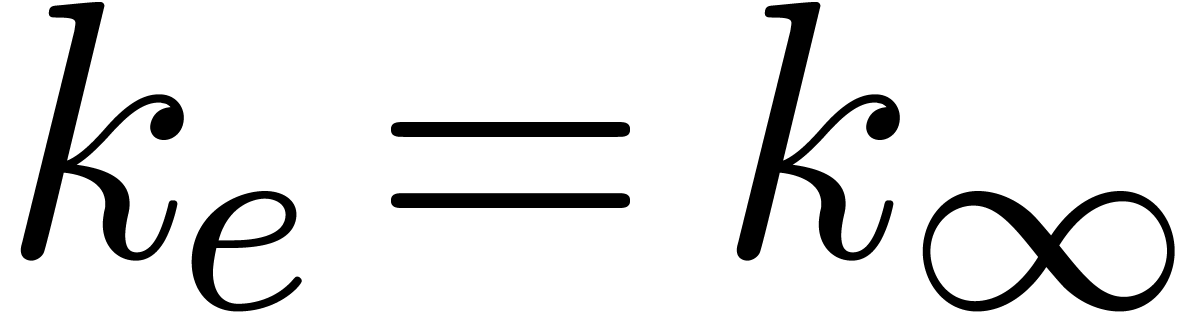 for all
for all 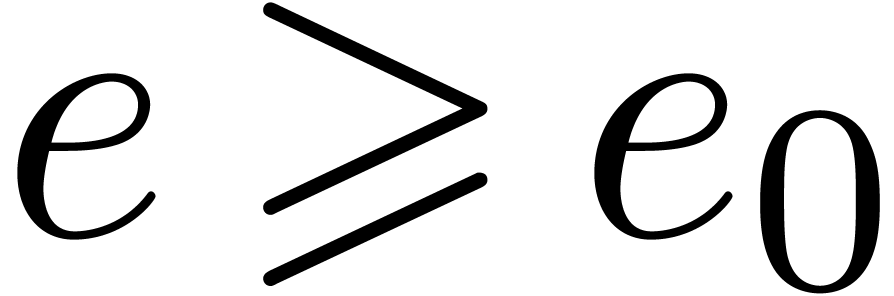 .
Furthermore,
.
Furthermore,
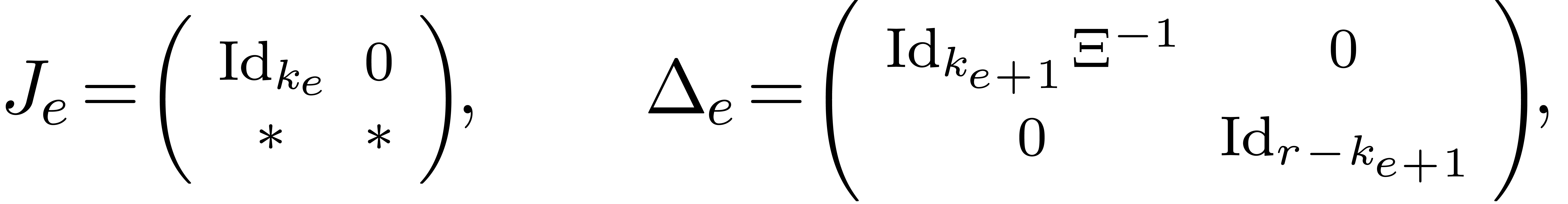
and

Moreover, for  , the row
sweaper
, the row
sweaper  is even of the form
is even of the form
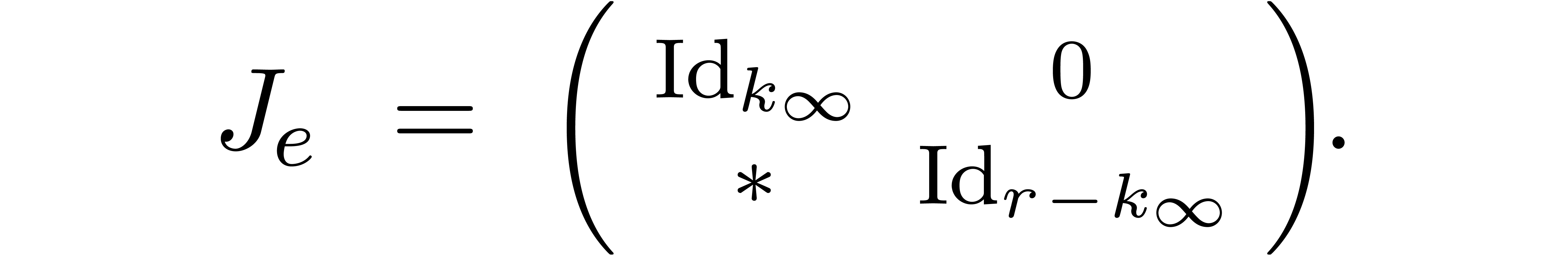
By induction on 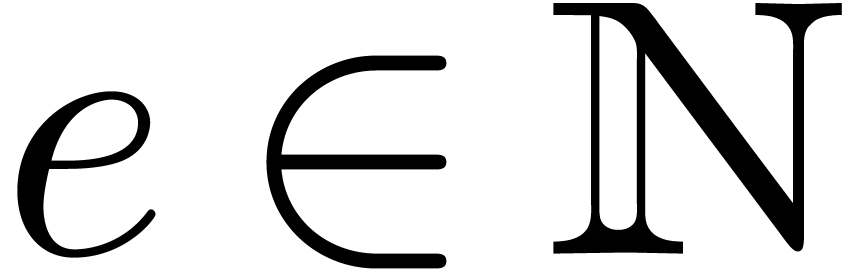 , we observe
that
, we observe
that 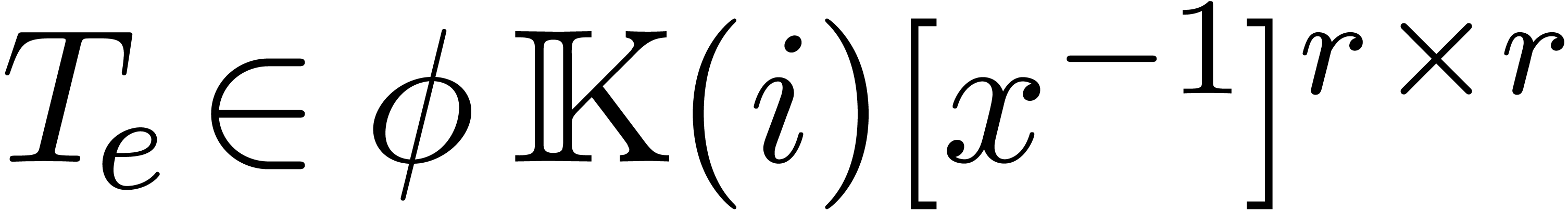 . For
. For  , we also have
, we also have 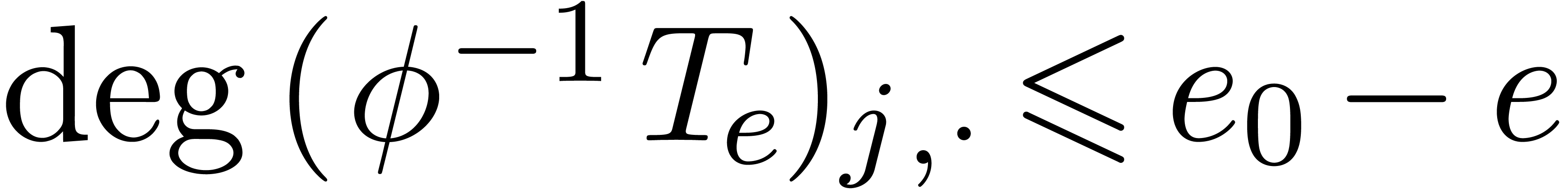 for all
for all
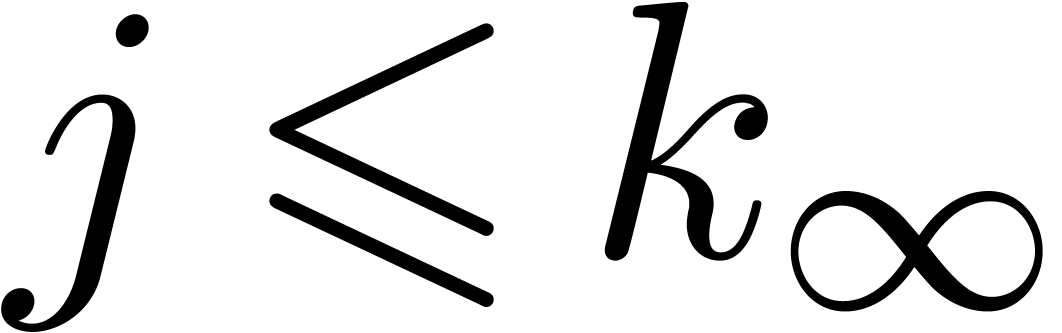 , again by induction.
Consequently,
, again by induction.
Consequently, 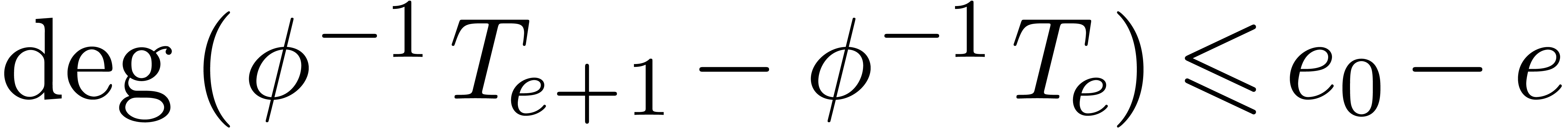 for all
for all  , which means that the sequence
, which means that the sequence 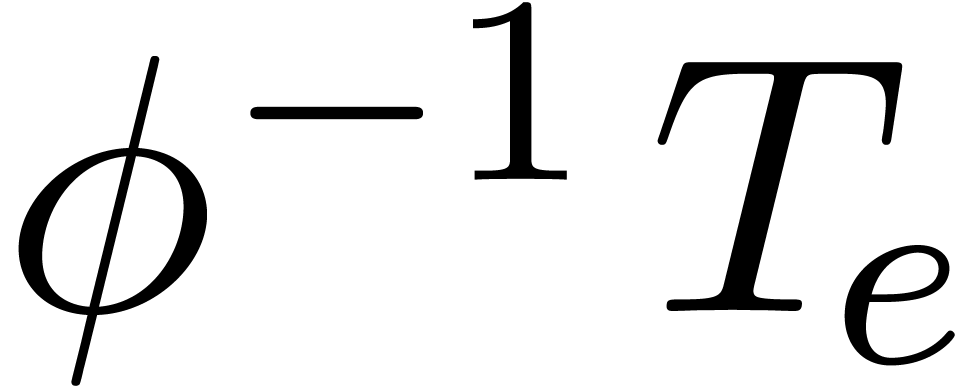 converges to a limit
converges to a limit 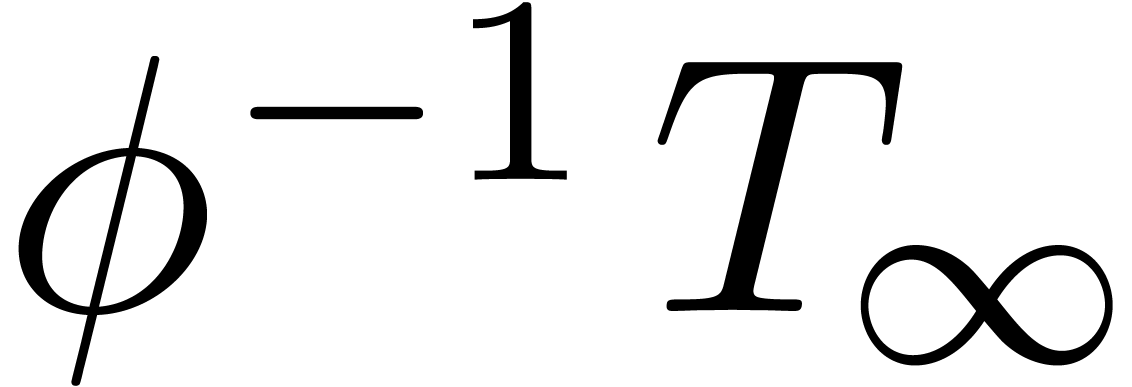 in
in 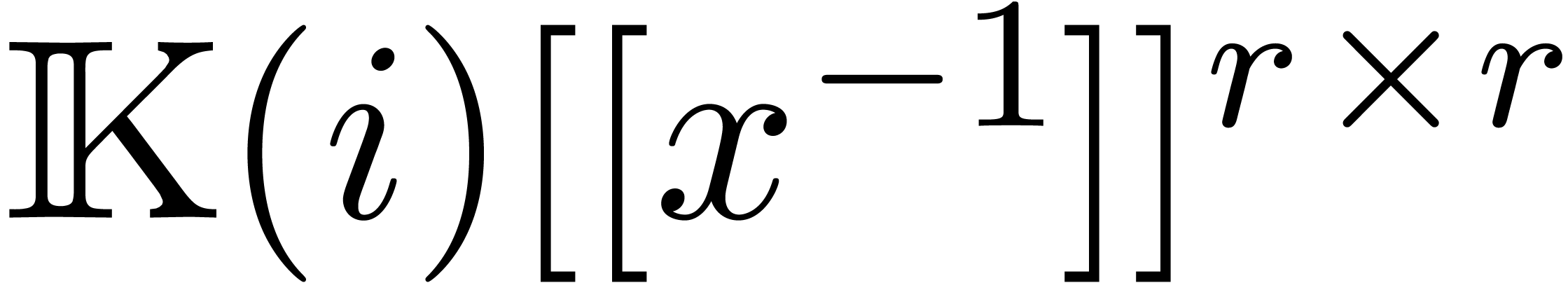 . By construction, the first
. By construction, the first 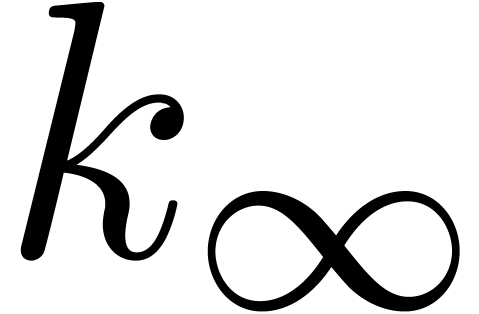 rows of
rows of  are zero, its last
are zero, its last 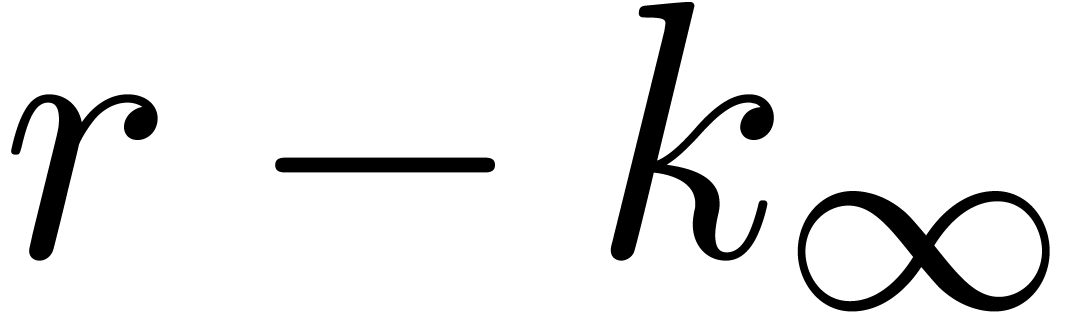 rows have rank
rows have rank 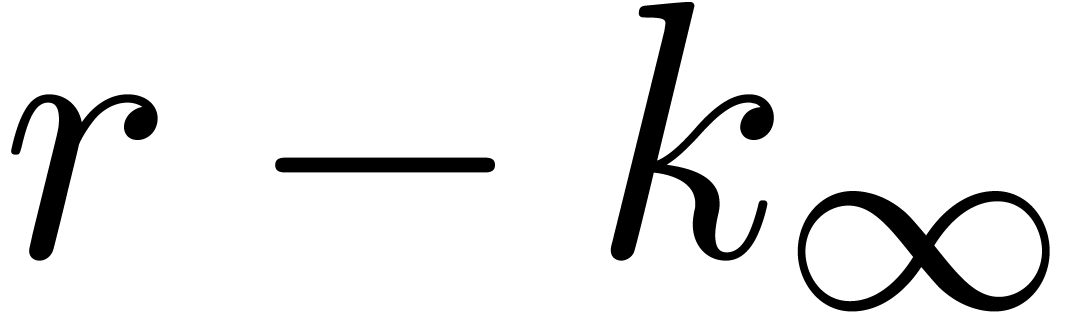 , and
, and 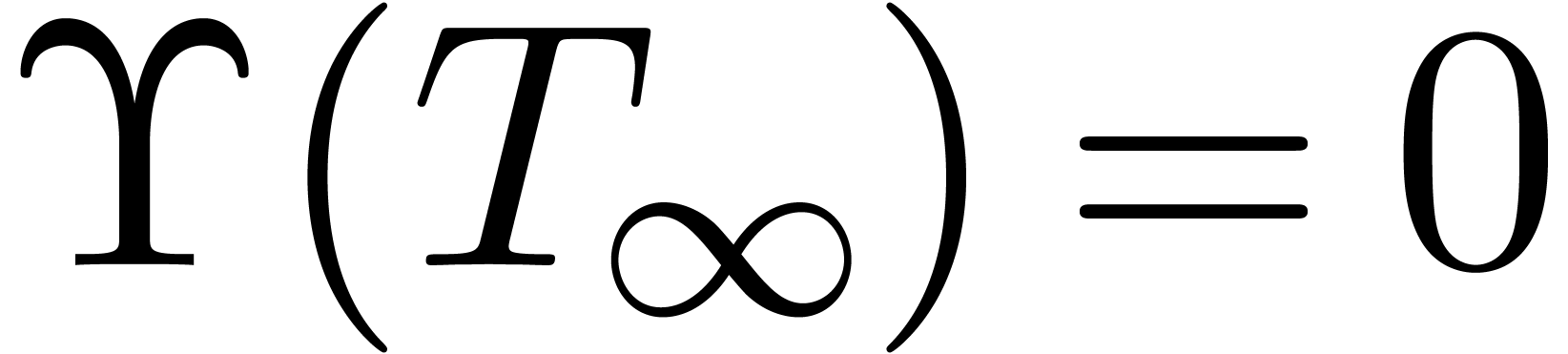 . We conclude by taking
. We conclude by taking 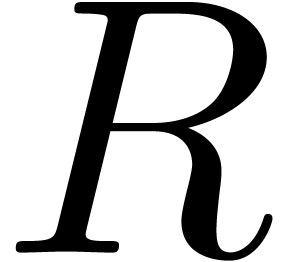 to be the last row of
to be the last row of 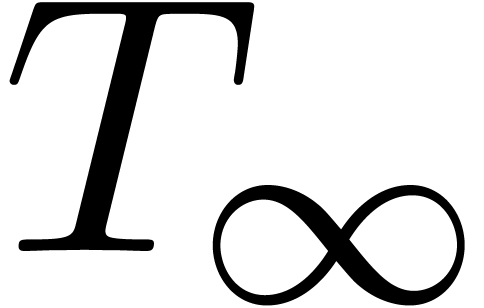 .□
.□
Proof. We already observed that 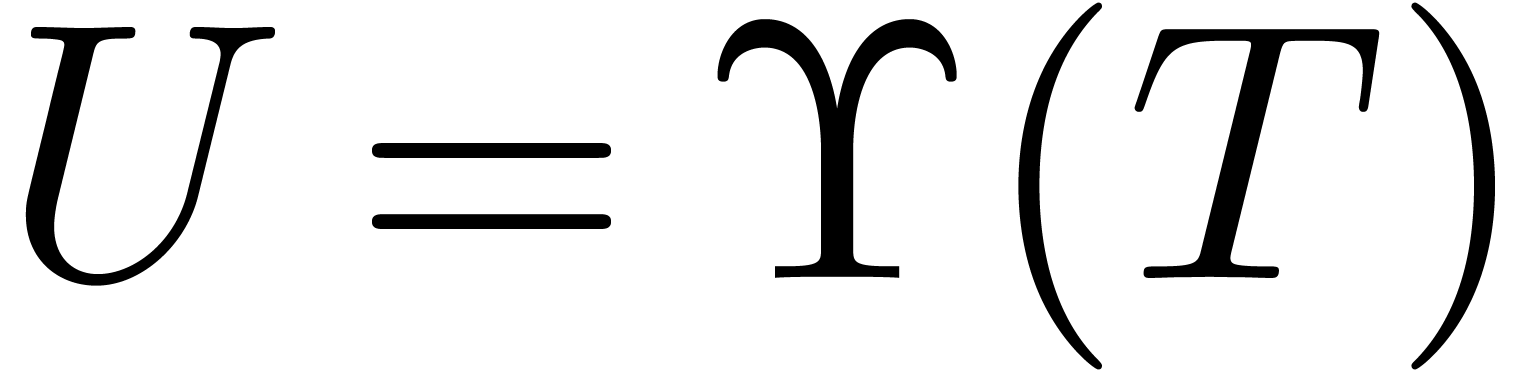 throughout the algorithm. If the algorithm terminates, then it follows
that
throughout the algorithm. If the algorithm terminates, then it follows
that  is indeed a head chopper for (1).
Assume for contradiction that the algorithm does not terminate and let
is indeed a head chopper for (1).
Assume for contradiction that the algorithm does not terminate and let
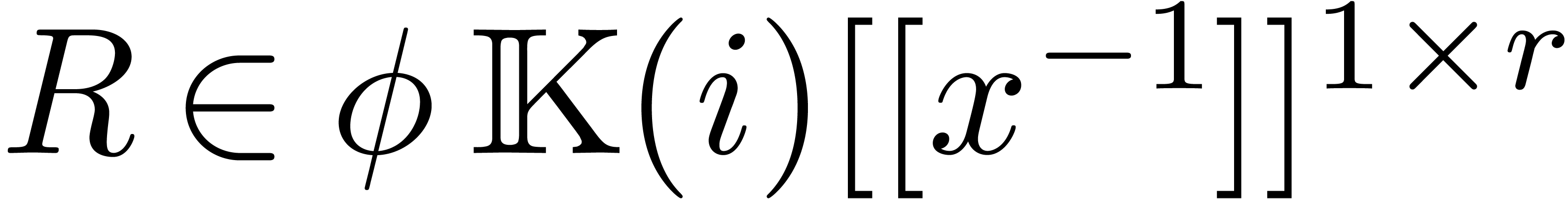 be such that
be such that 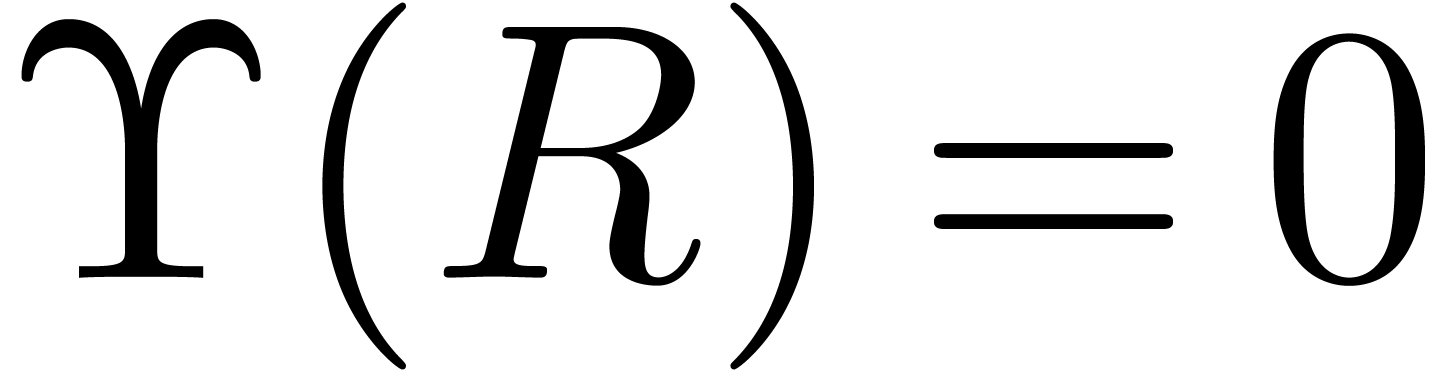 .
Let
.
Let 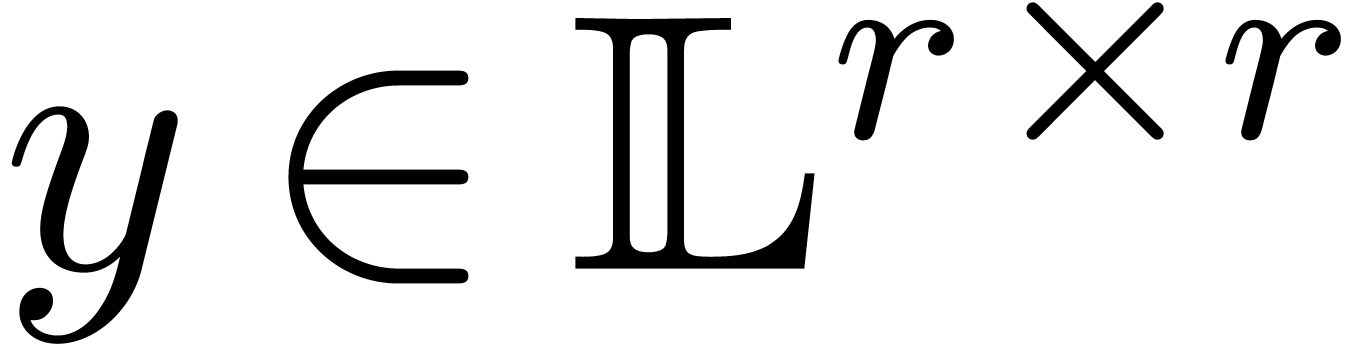 be a fundamental system of solutions to the
equation
be a fundamental system of solutions to the
equation  is some differential field extension of
is some differential field extension of 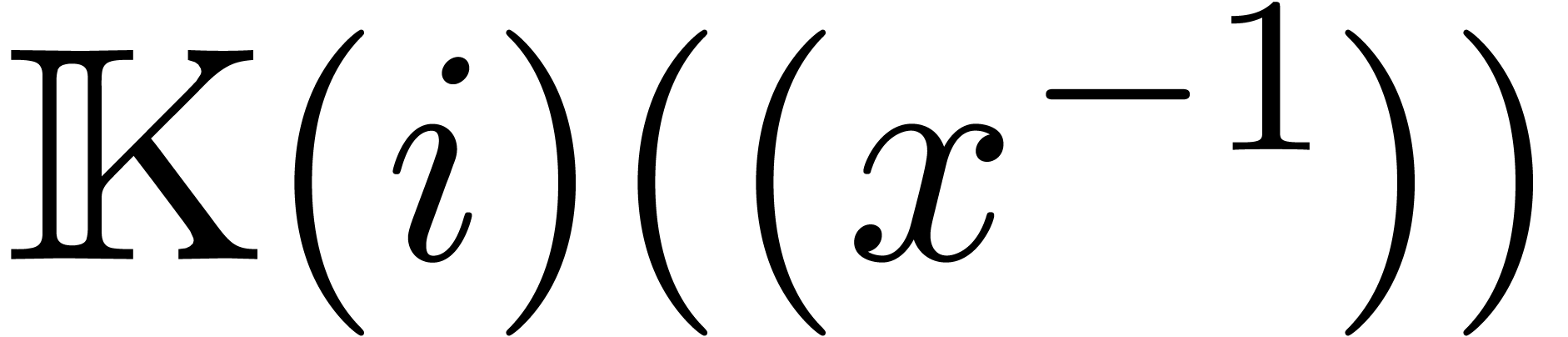 with
constant field
with
constant field 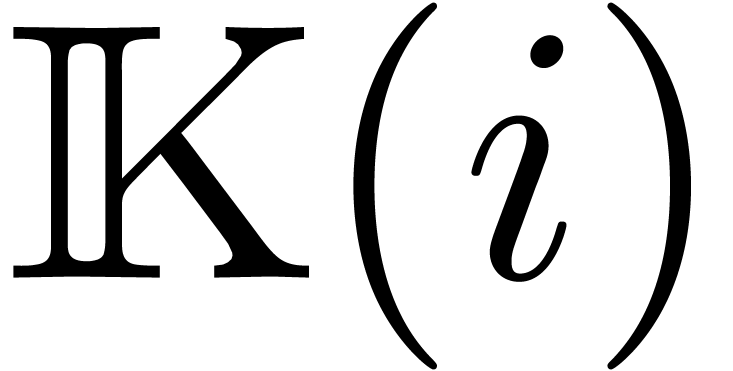 . From
. From 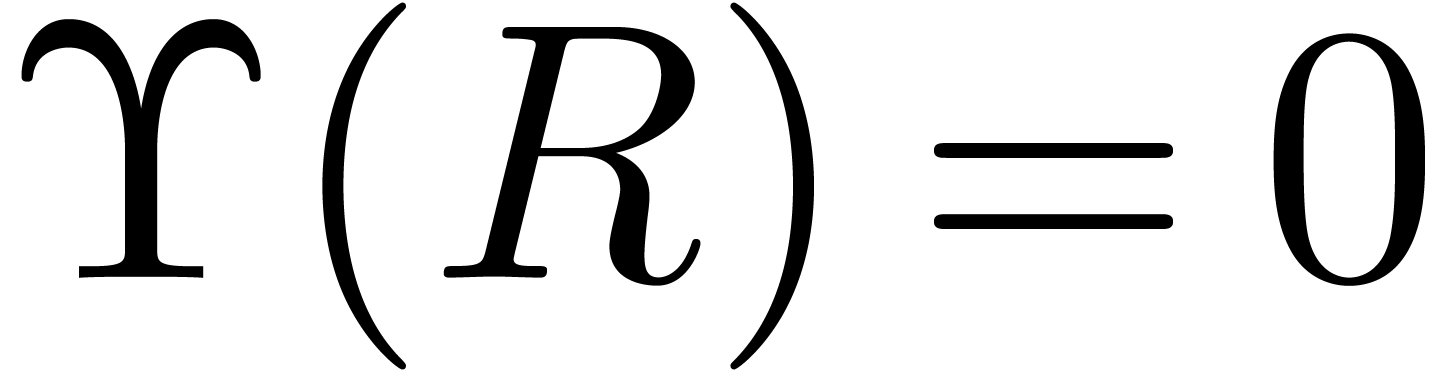 we deduce that
we deduce that 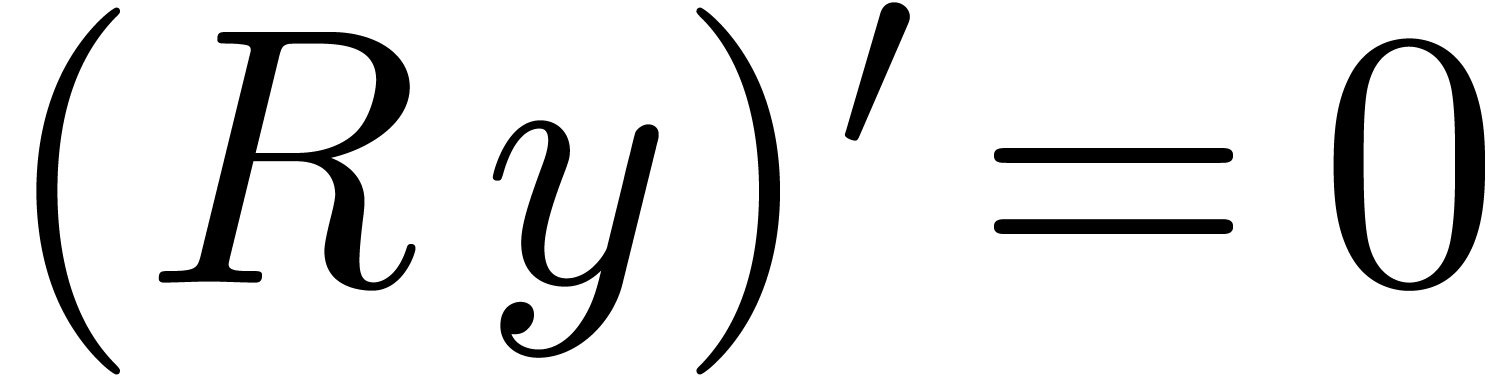 ,
whence
,
whence 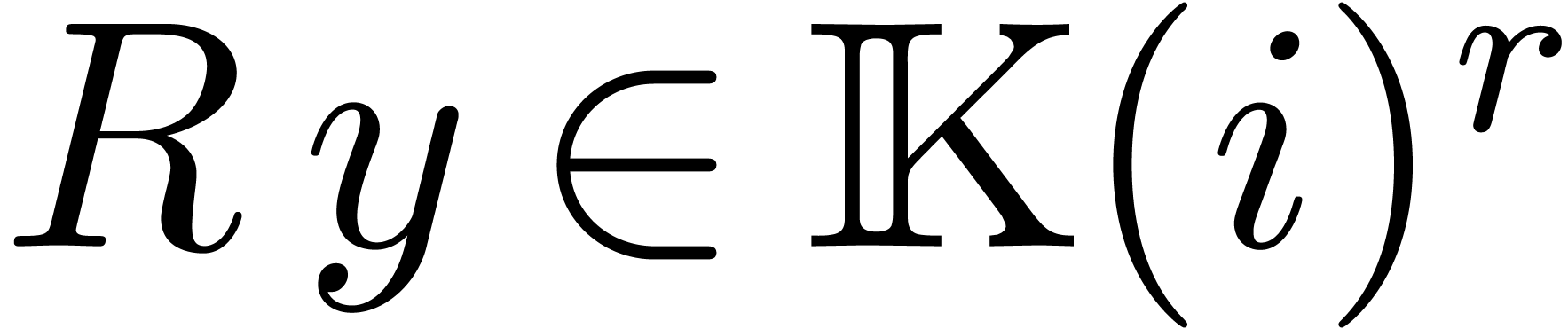 . More generally,
. More generally, 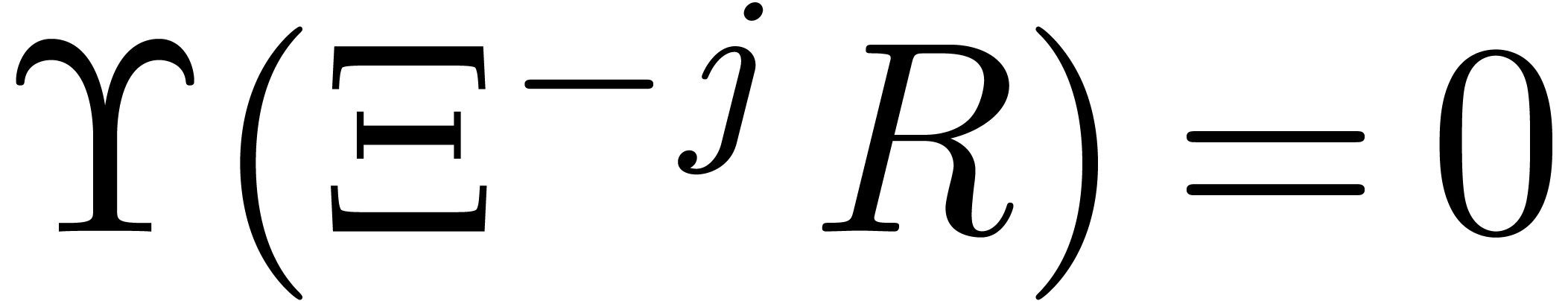 whence
whence 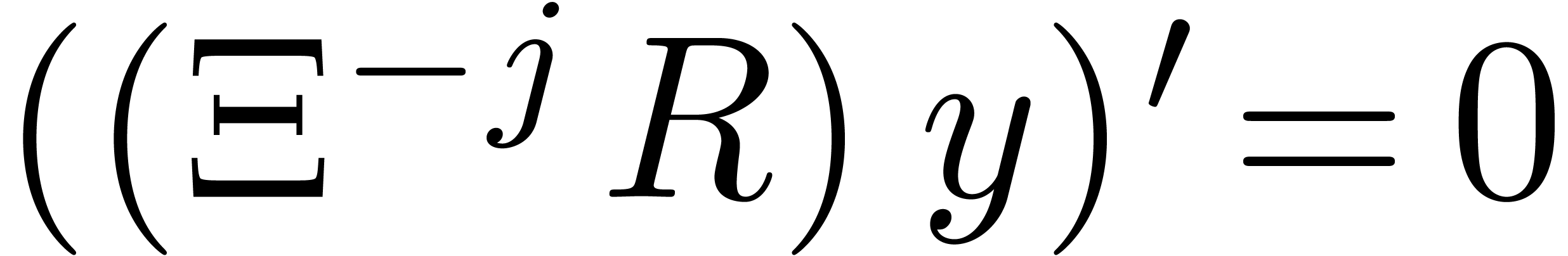 and
and 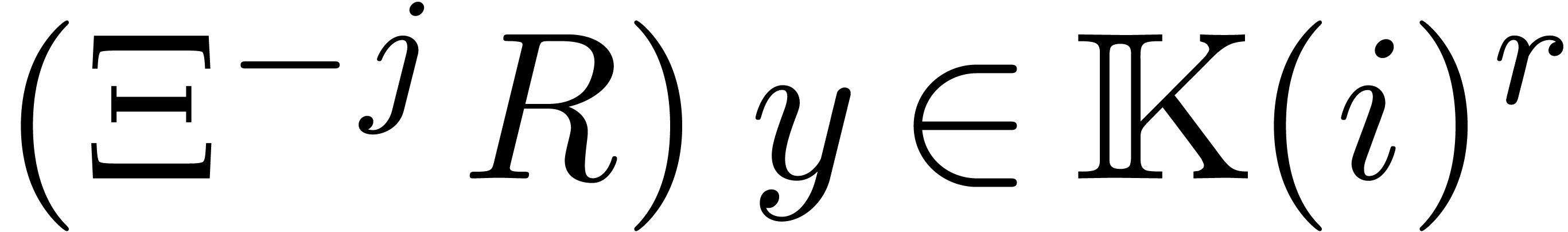 for all
for all  . Since the space
. Since the space
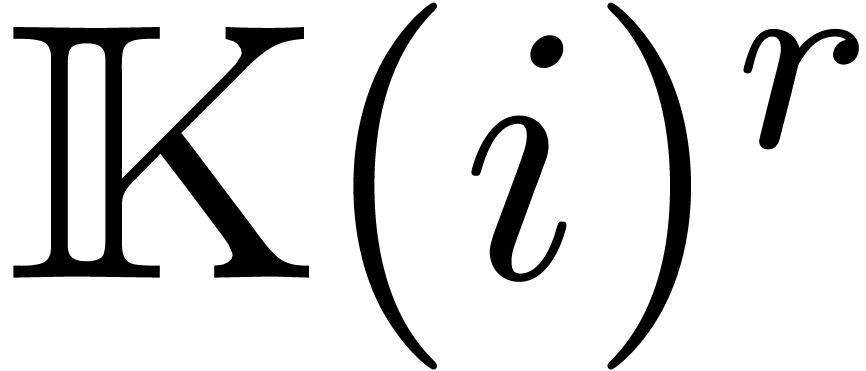 has dimension
has dimension  over
over 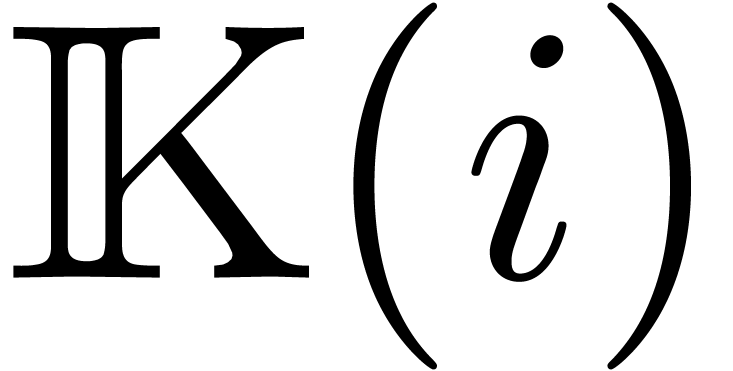 , it follows that there exists a
polynomial
, it follows that there exists a
polynomial 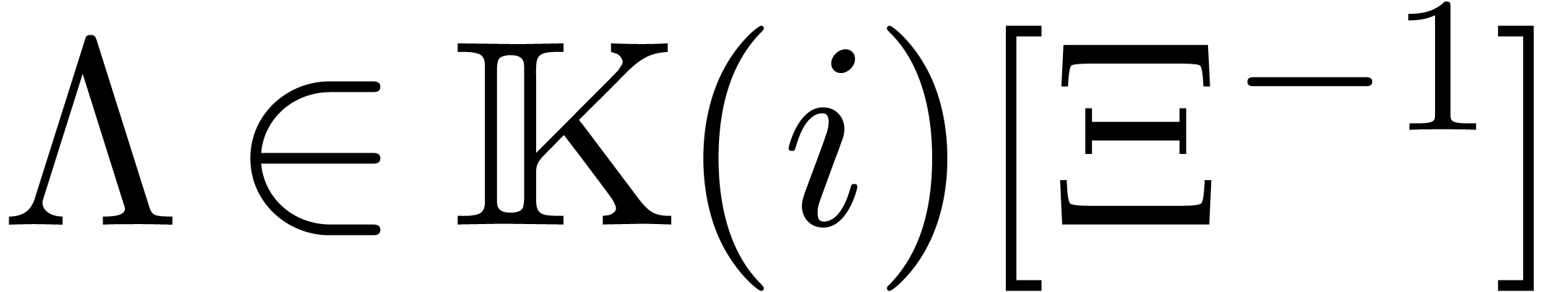 of degree at most
of degree at most 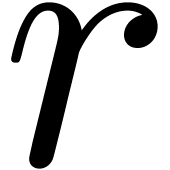 in
in 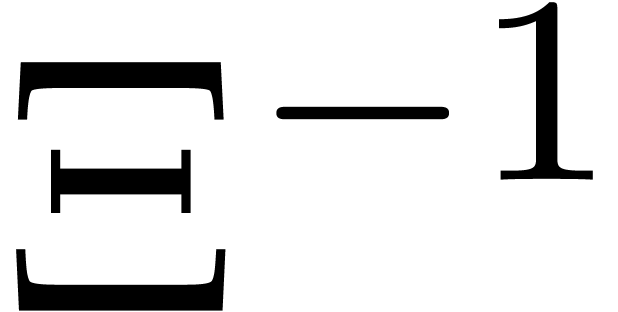 such that
such that 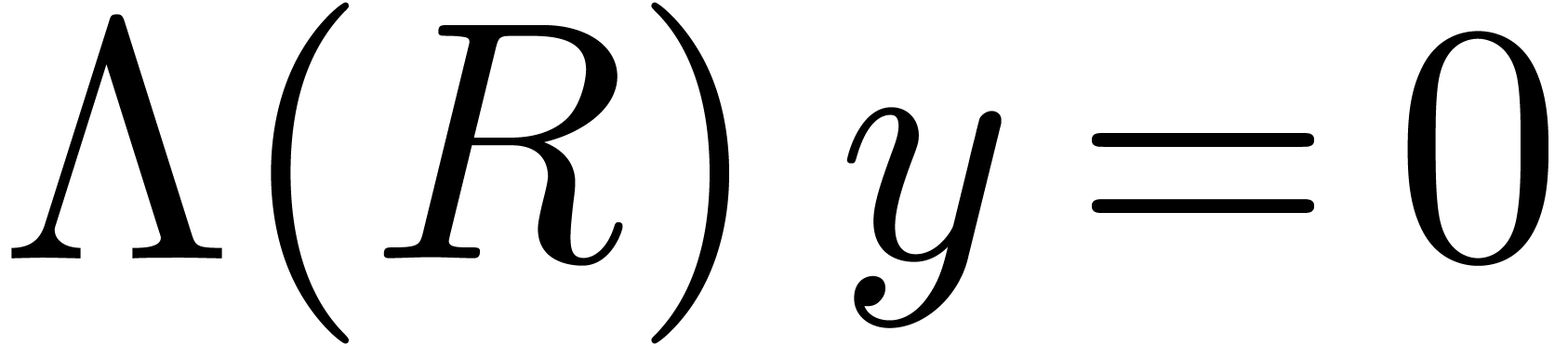 and
and 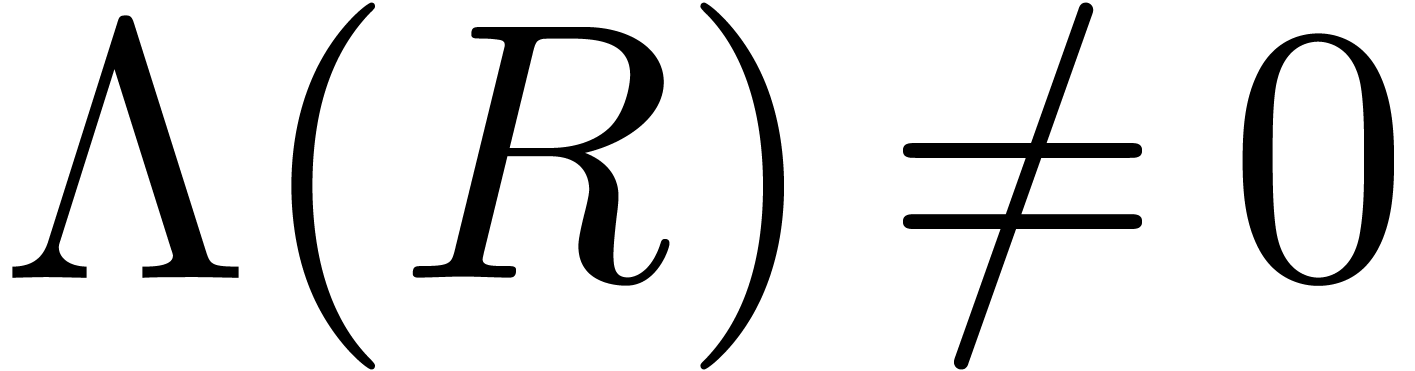 . Since
. Since  is
a fundamental system of solutions, we have
is
a fundamental system of solutions, we have 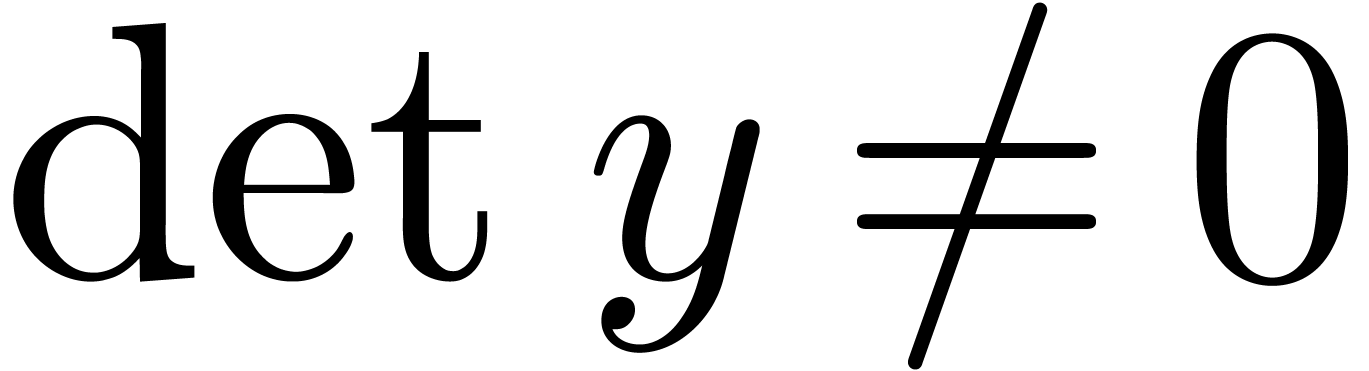 .
This contradicts the existence of an element
.
This contradicts the existence of an element 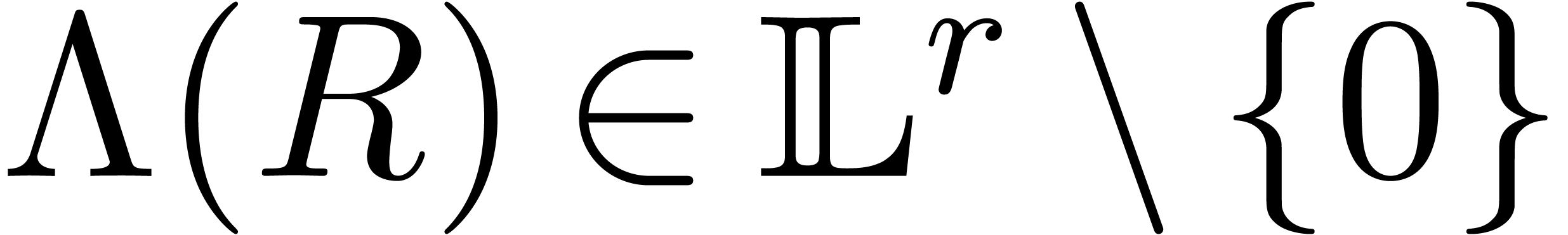 with
with 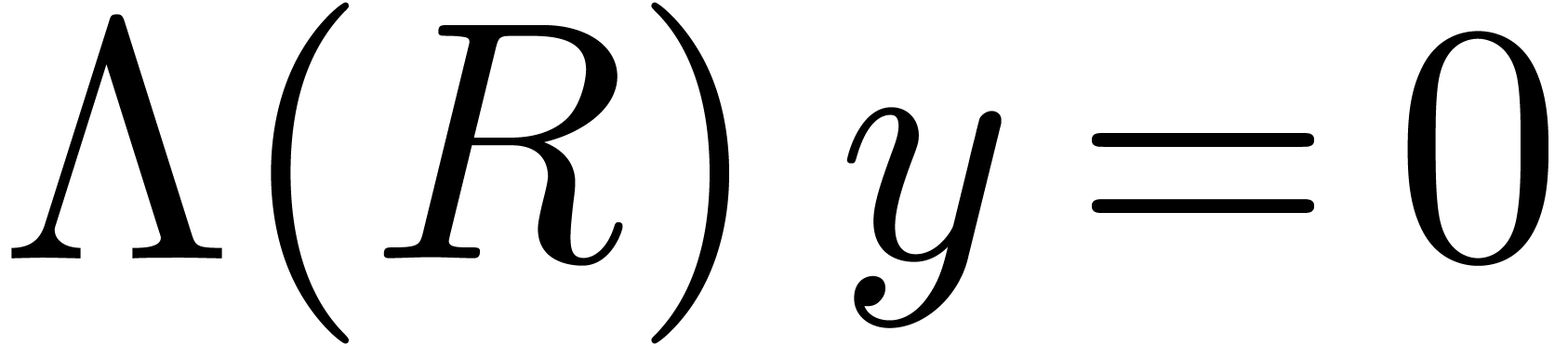 .□
.□
Let  be a head chopper for (1).
Replacing
be a head chopper for (1).
Replacing  by
by 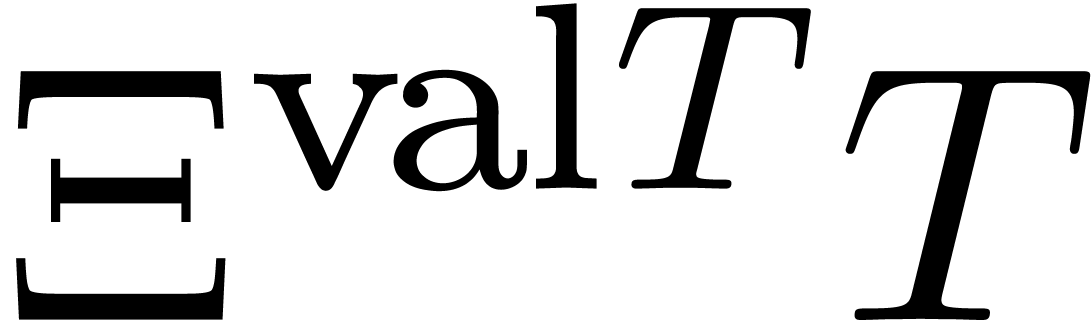 if
necessary, we may assume without loss of generality that
if
necessary, we may assume without loss of generality that 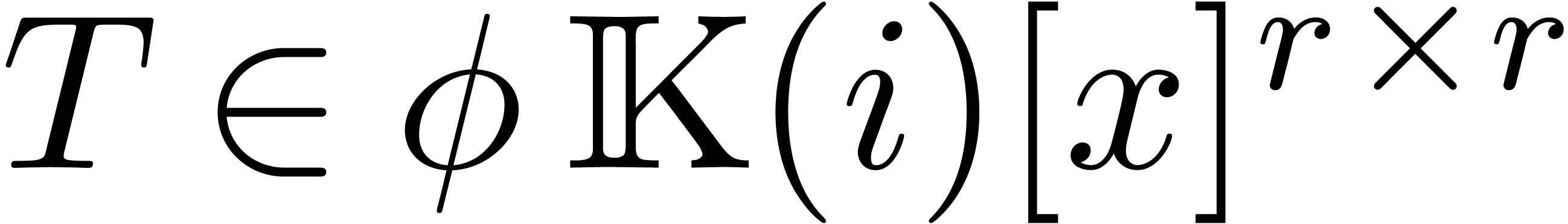 and
and 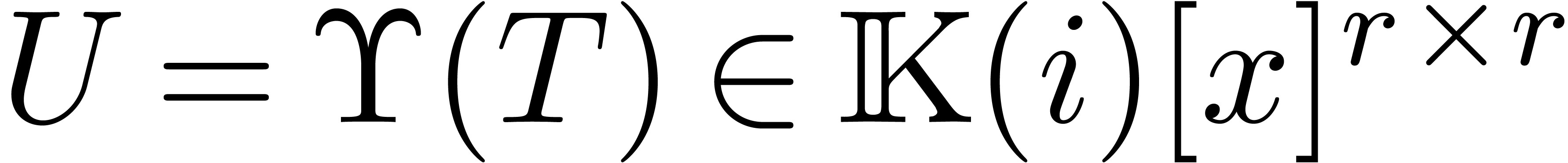 . Let
. Let  . Writing
. Writing 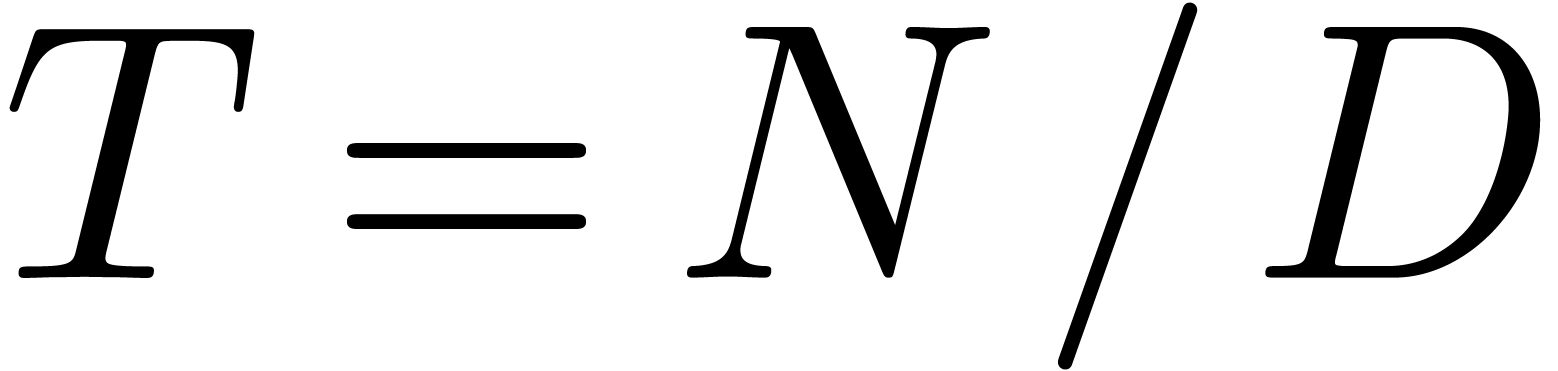 with
with  and
and 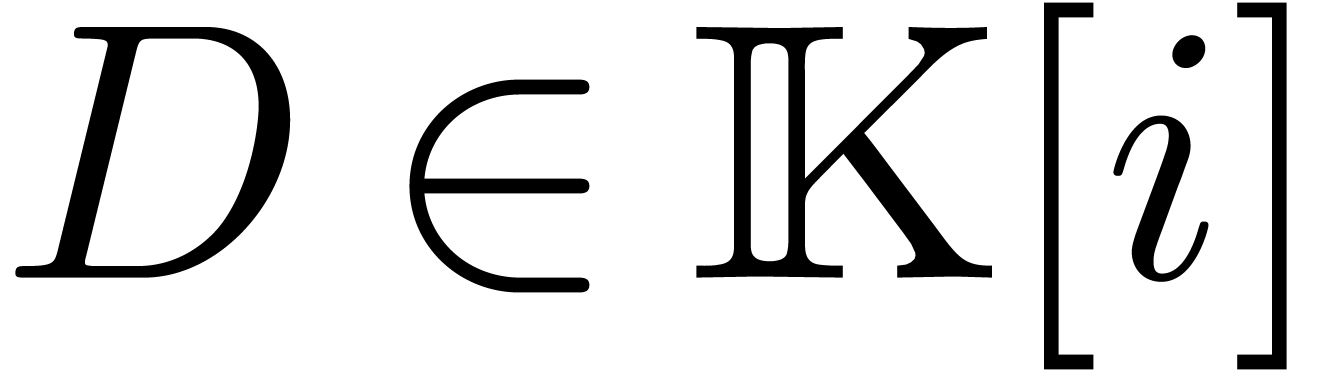 ,
let
,
let  to be the set of exceptional
indices
to be the set of exceptional
indices 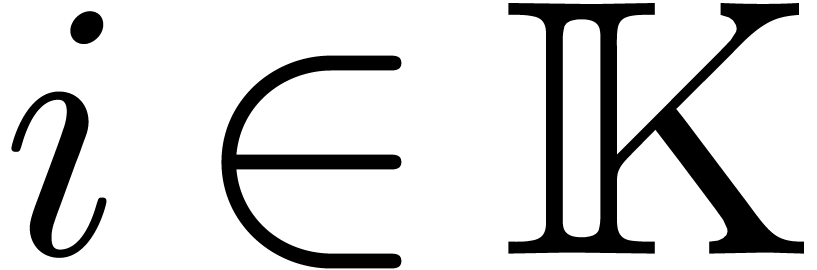 for which
for which 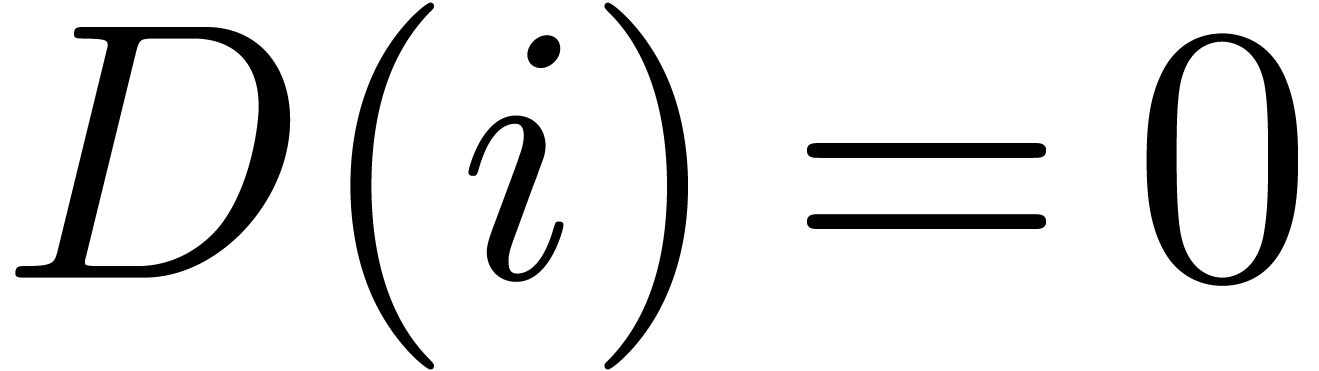 or
or 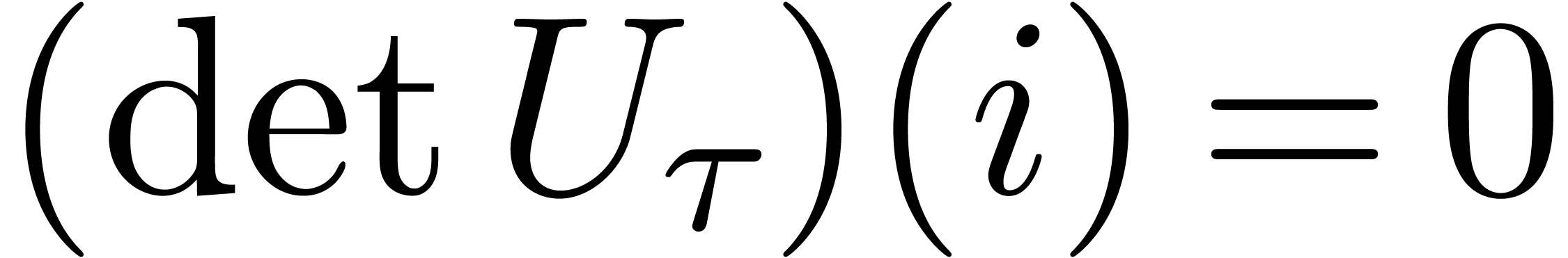 . For any
. For any 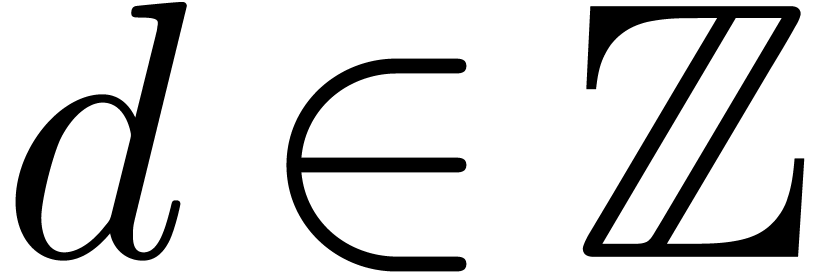 , let
, let
If 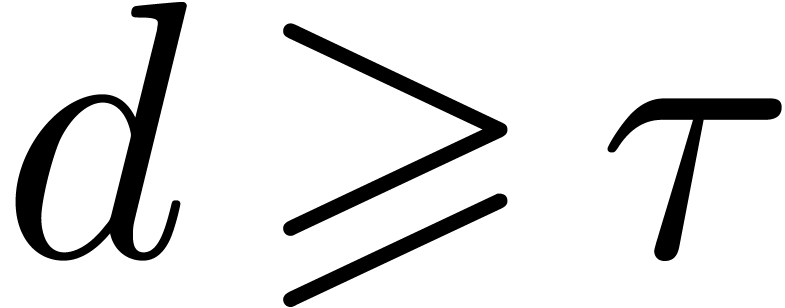 and
and 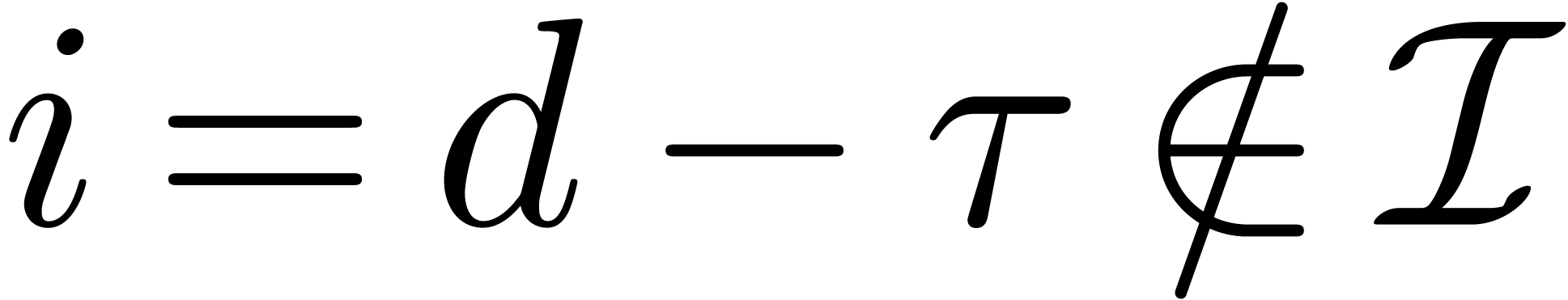 ,
then the matrix
,
then the matrix 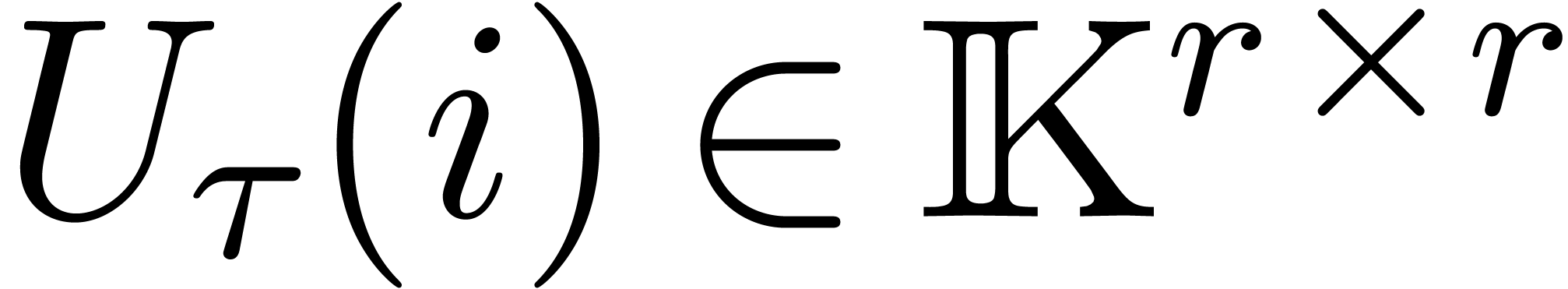 is invertible. We define the
is invertible. We define the
 -linear mapping
-linear mapping 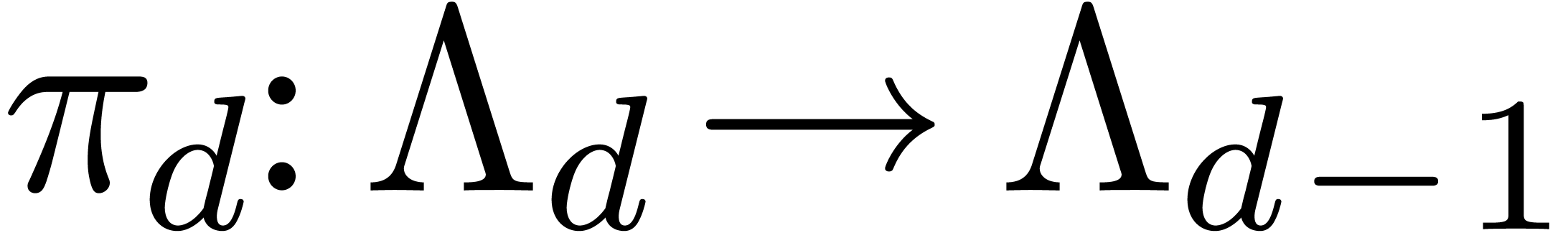 by
by
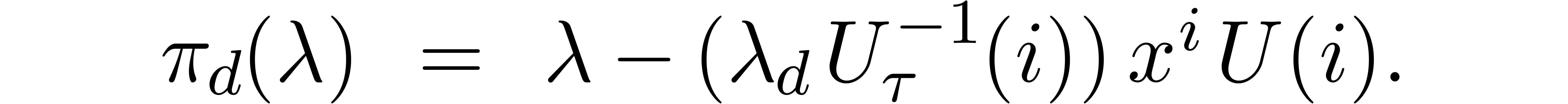
We indeed have  , since
, since 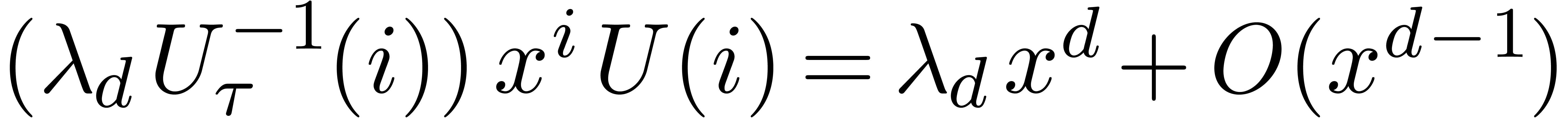 . The mapping
. The mapping 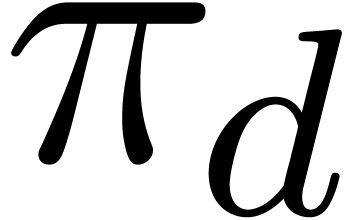 also induces a mapping
also induces a mapping 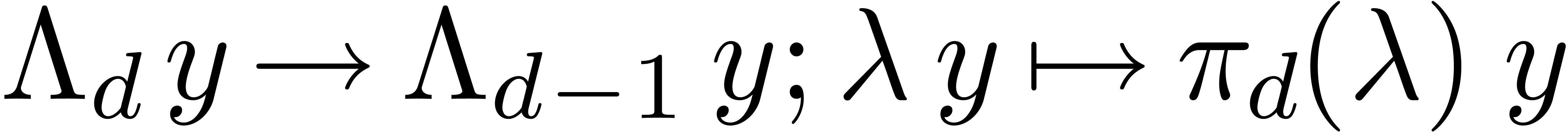 that we will still denote
by
that we will still denote
by 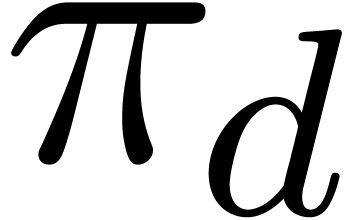 . Setting
. Setting 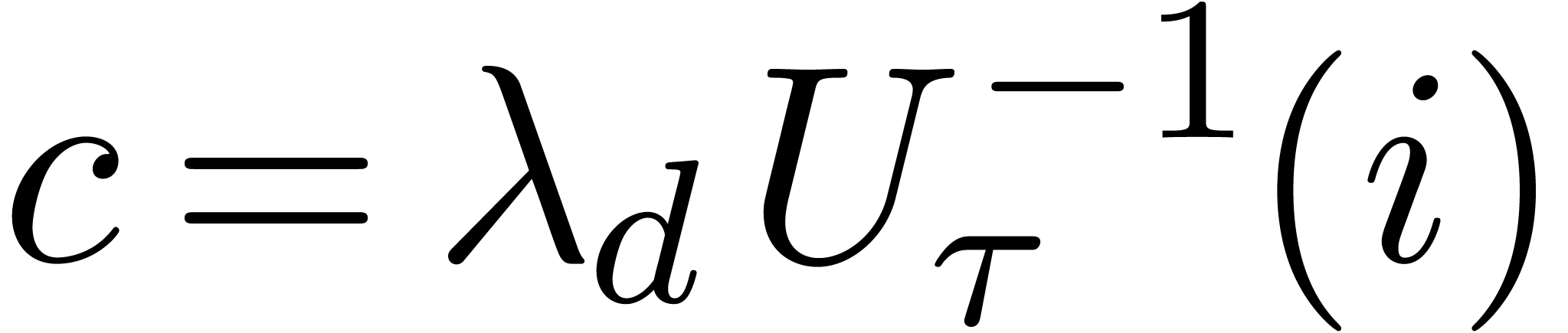 , the relation (7) yields
, the relation (7) yields
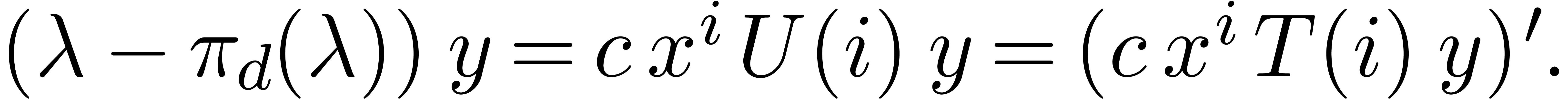
This shows that the mapping 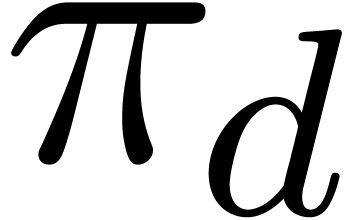 is a reduction. If
is a reduction. If
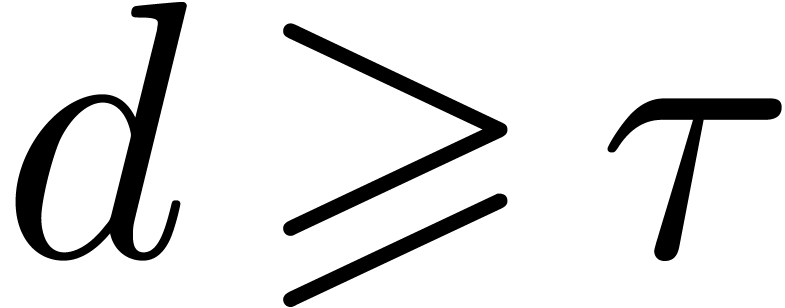 and
and 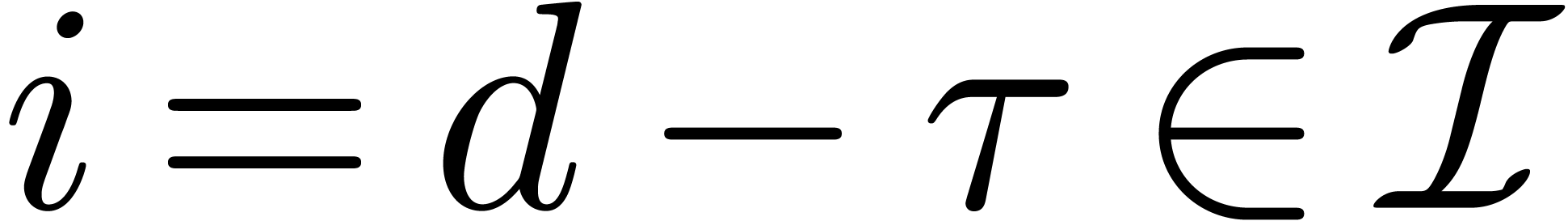 ,
then we have
,
then we have 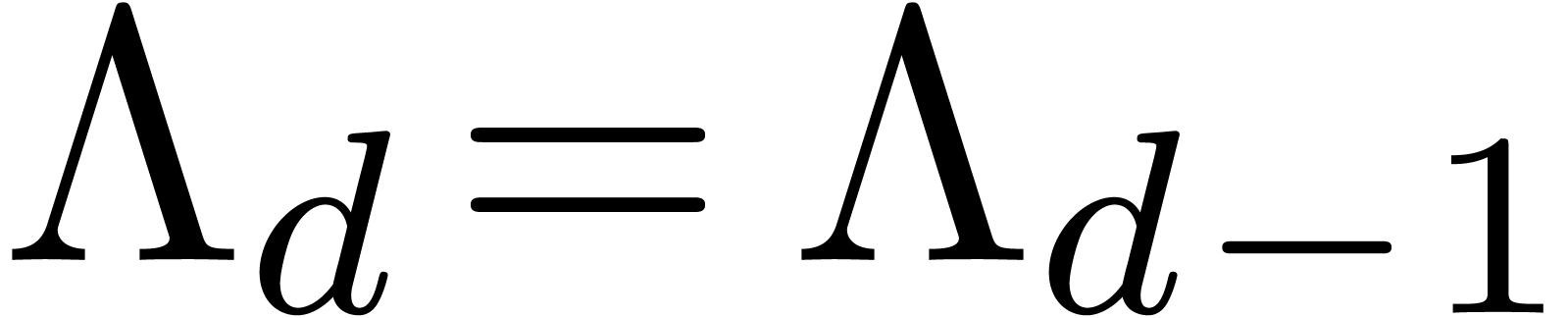 and the identity map
and the identity map 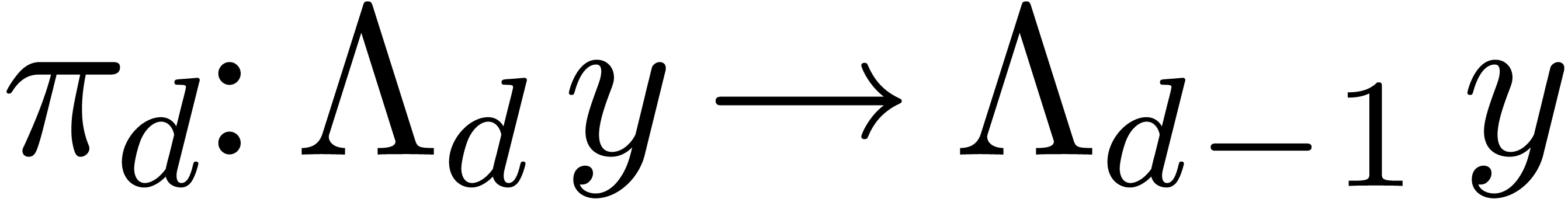 is clearly a reduction as well.
is clearly a reduction as well.
Since compositions of reductions are again reductions, we also obtain a
reduction 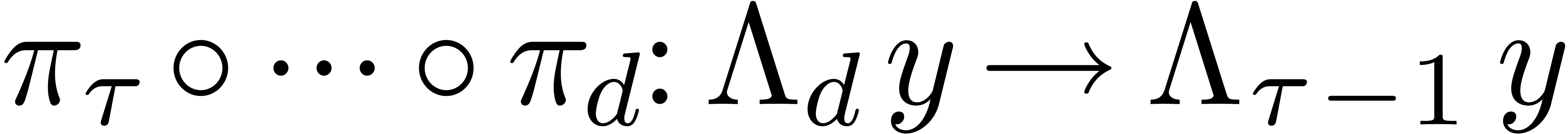 for each
for each  .
Now let
.
Now let 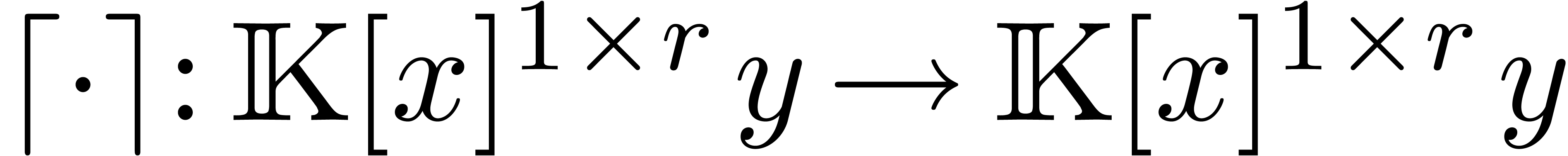 be the unique mapping with
be the unique mapping with  for all
for all  and
and  . Then
. Then  is clearly a
reduction as well and it has a finite dimensional image
is clearly a
reduction as well and it has a finite dimensional image  . For any
. For any 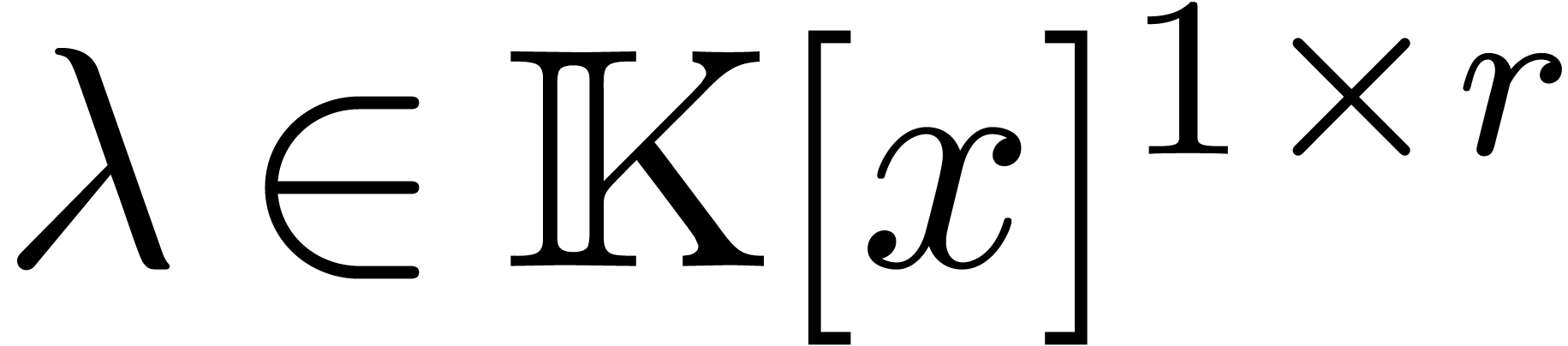 ,
we call
,
we call 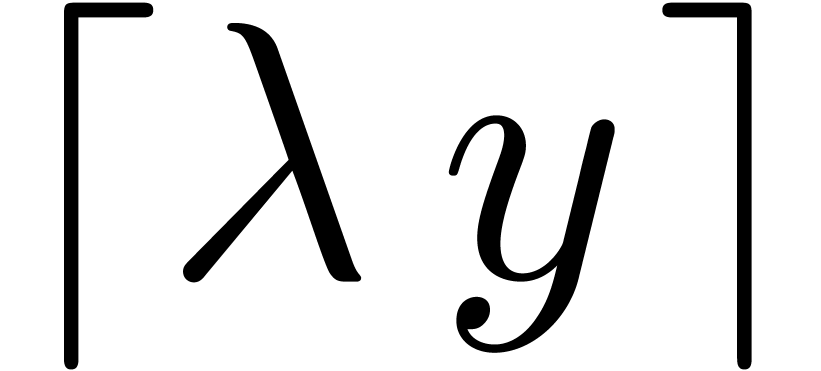 the head reduction of
the head reduction of 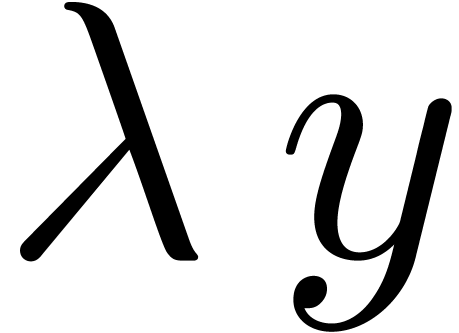 . The following straightforward
algorithm allows us to compute head reductions:
. The following straightforward
algorithm allows us to compute head reductions:
Algorithm HeadReduce |
repeat
if
Let
|
Remark  with
with 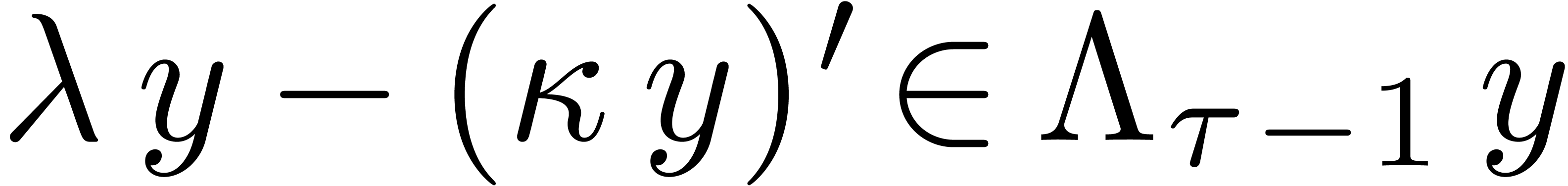 . Indeed, it suffices to start with
. Indeed, it suffices to start with 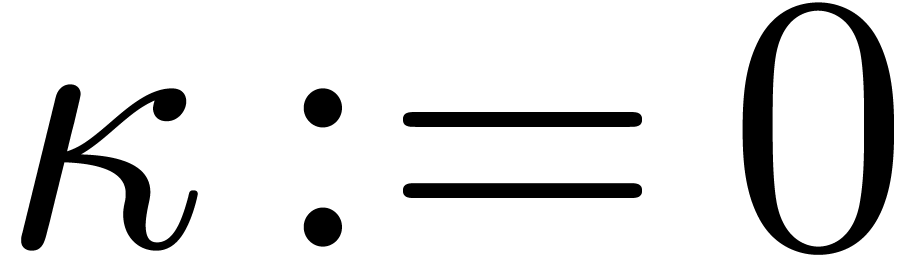 and accumulate
and accumulate 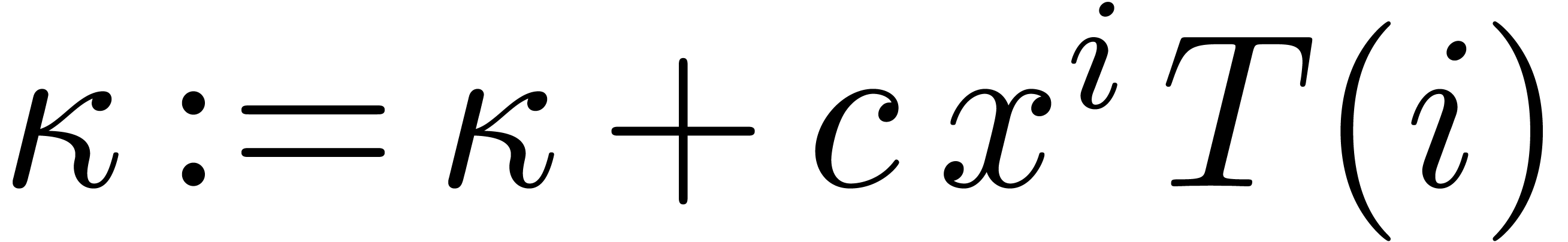 at the end of the
main loop.
at the end of the
main loop.
Remark  can be computed more efficiently in a relaxed
manner [10].
can be computed more efficiently in a relaxed
manner [10].
Remark 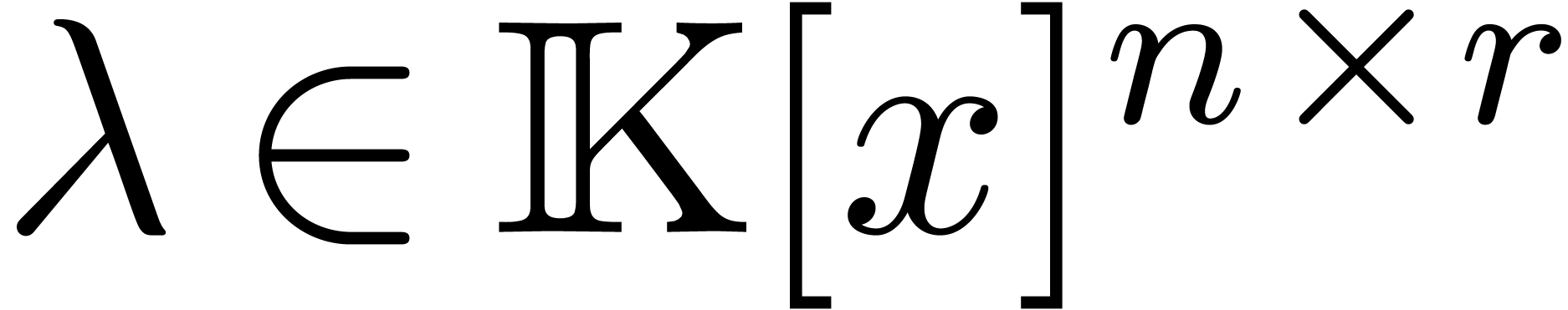 with an arbitrary number of rows
with an arbitrary number of rows 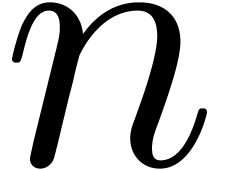 .
This allows for the simultaneous head reduction of several elements in
.
This allows for the simultaneous head reduction of several elements in
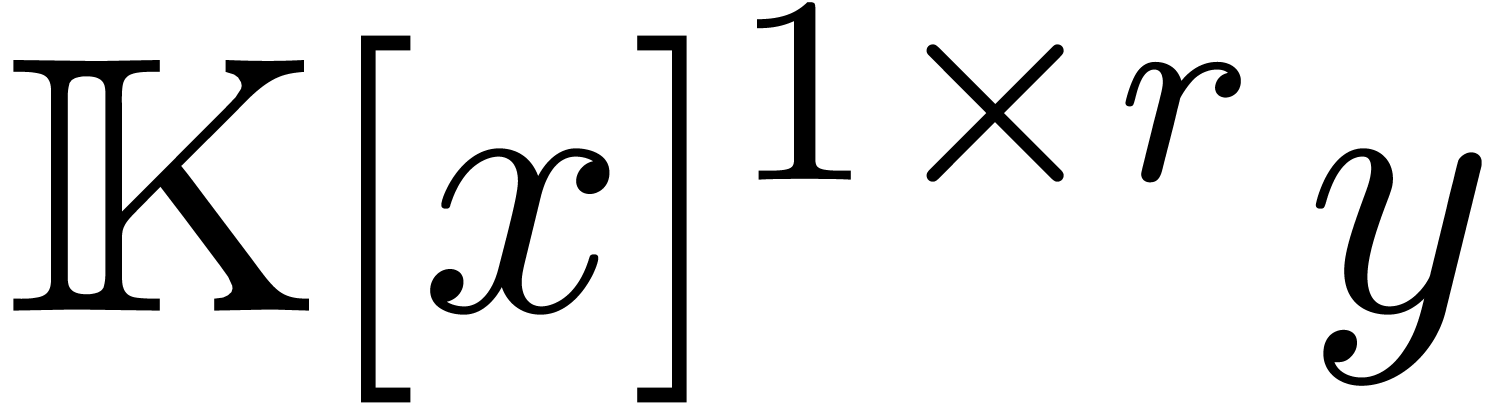 , something that might be
interesting for the application to creative telescoping.
, something that might be
interesting for the application to creative telescoping.
Head reduction essentially allows us to reduce the valuation in 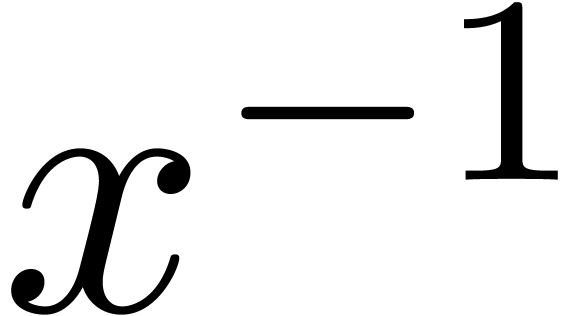 of elements in
of elements in  via
the subtraction of elements in
via
the subtraction of elements in  .
Tail reduction aims at reducing the valuation in
.
Tail reduction aims at reducing the valuation in 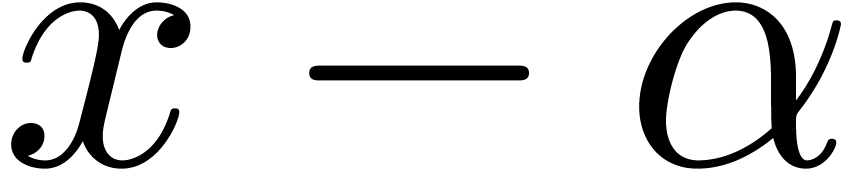 in a similar way for any
in a similar way for any  in the algebraic
closure
in the algebraic
closure  of
of  .
More precisely, let
.
More precisely, let 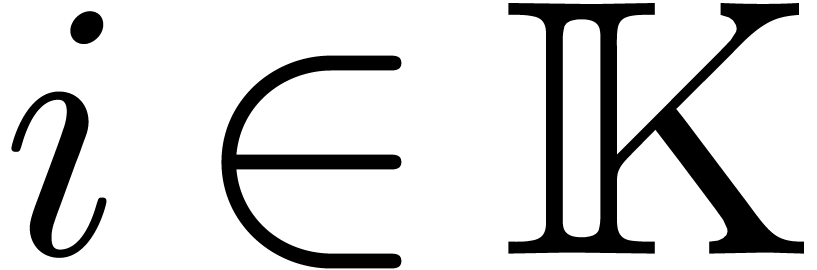 ,
, 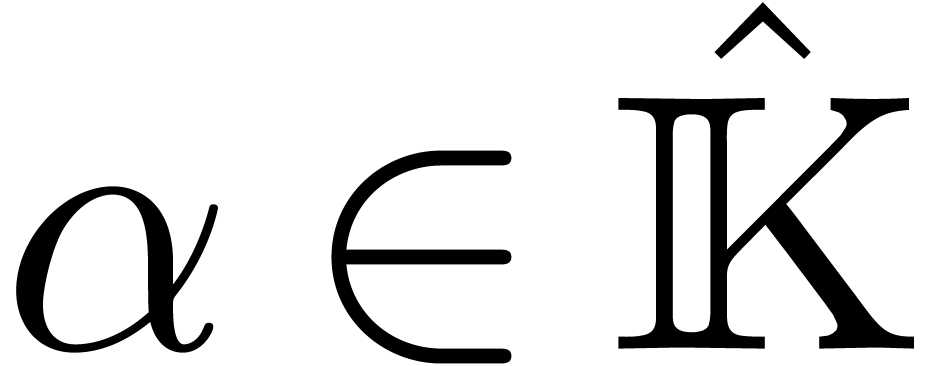 and
and 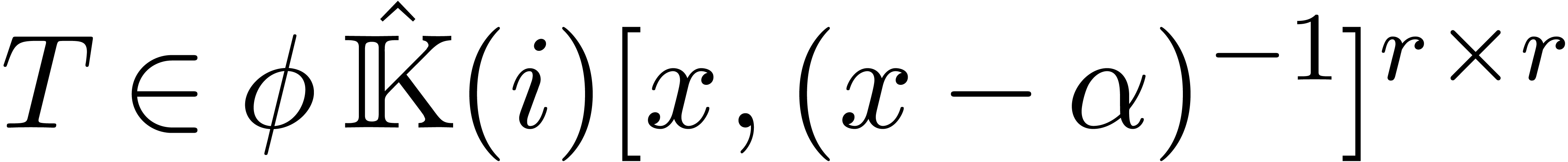 . We
may regard
. We
may regard  as a Laurent polynomial in
as a Laurent polynomial in  with matrix coefficients
with matrix coefficients 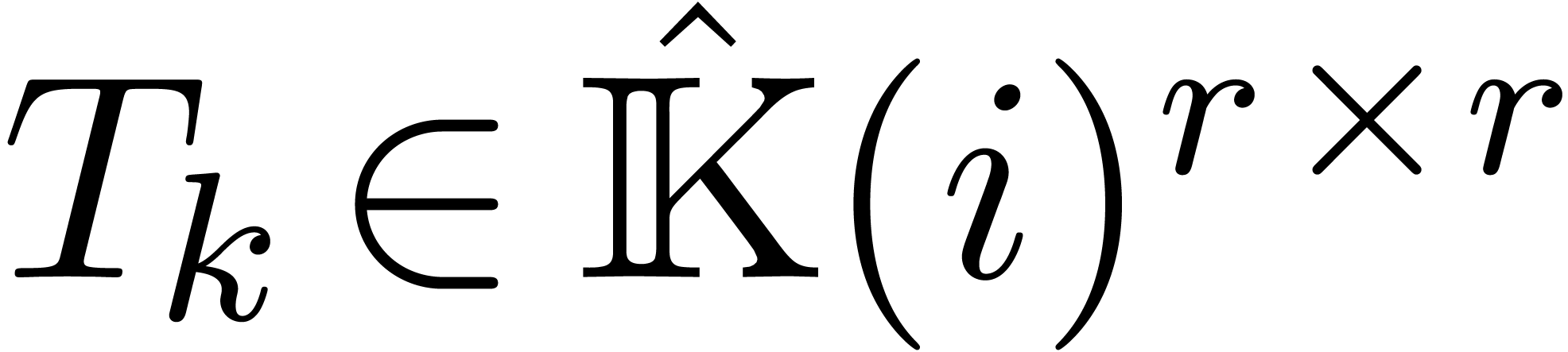 :
:
If 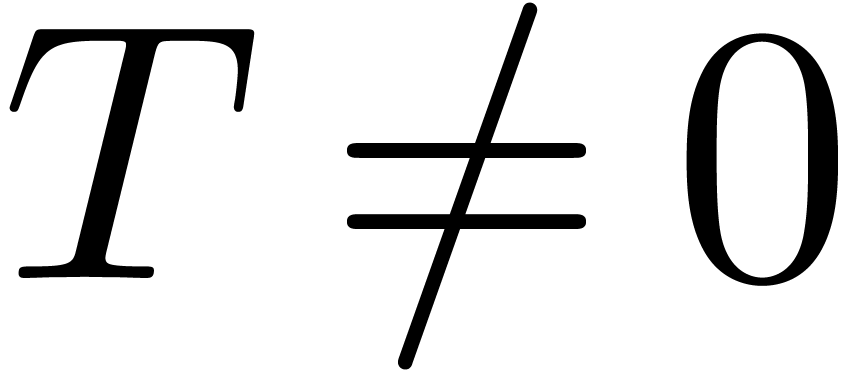 , then we denote its
valuation in
, then we denote its
valuation in  by
by 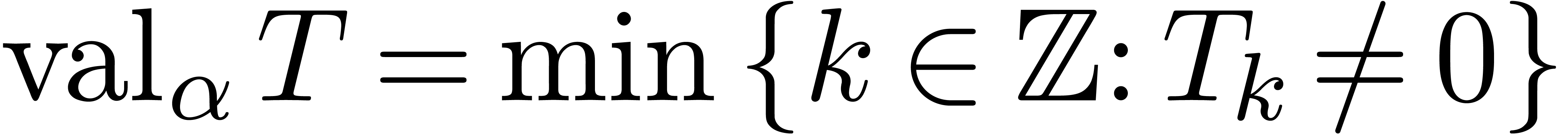 .
Setting
.
Setting
the equation (1) implies
for any matrix 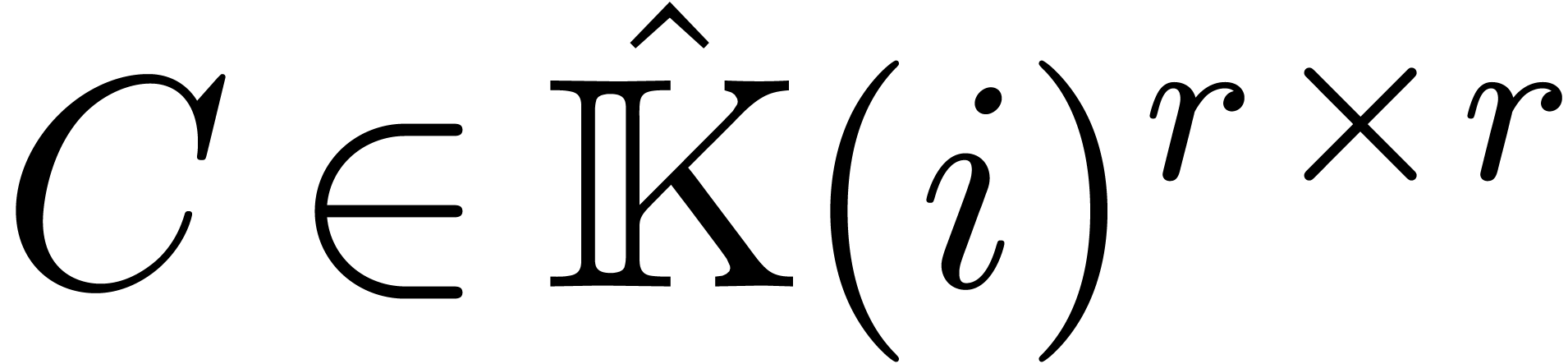 . The matrix
. The matrix
 can also be regarded as a Laurent polynomial
with matrix coefficients
can also be regarded as a Laurent polynomial
with matrix coefficients 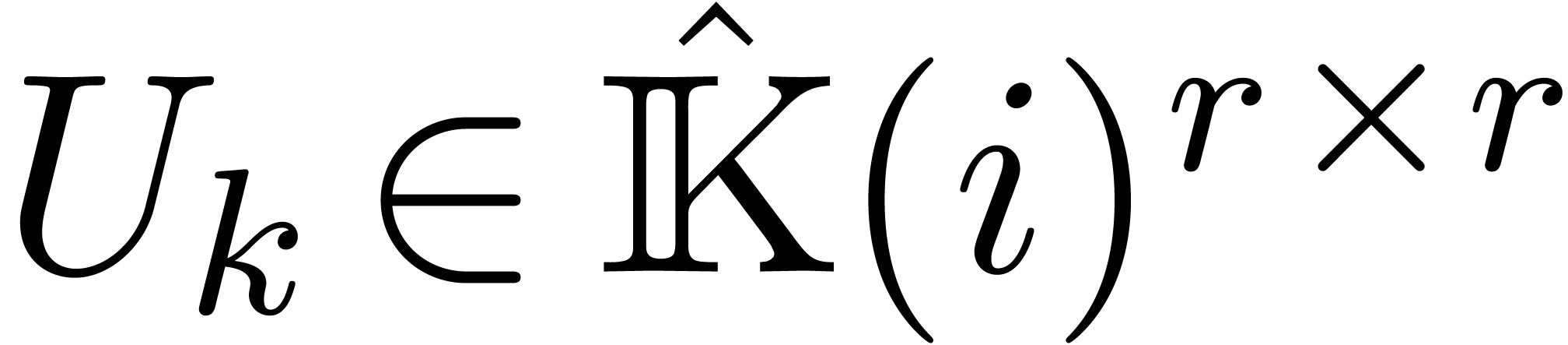 . We
say that
. We
say that  is a tail chopper at
is a tail chopper at  for (1) if
for (1) if  is an
invertible matrix. In fact, it suffices to consider tail choppers at the
origin:
is an
invertible matrix. In fact, it suffices to consider tail choppers at the
origin:
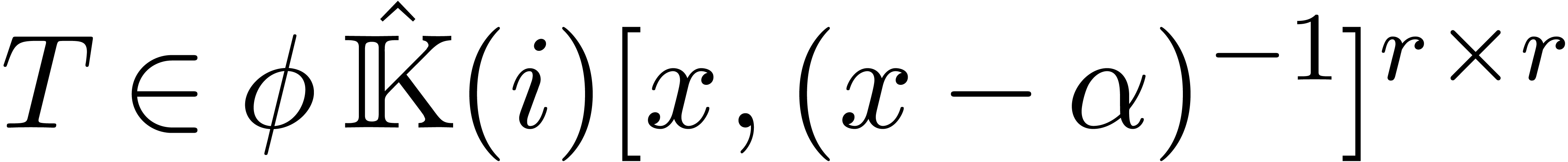 , where
, where 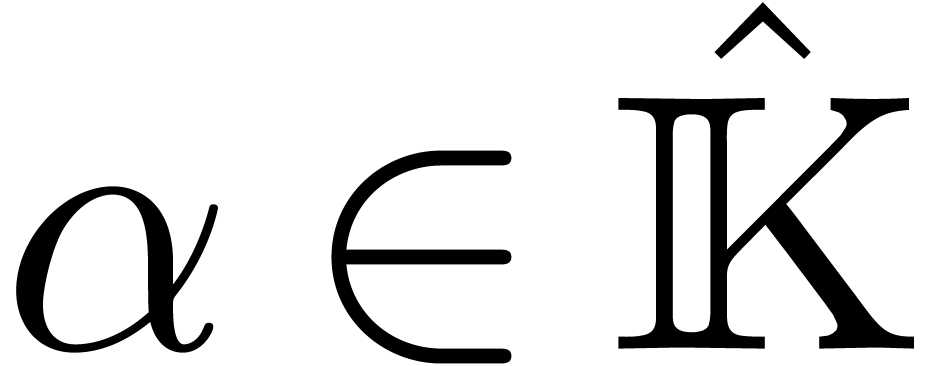 . Define
. Define 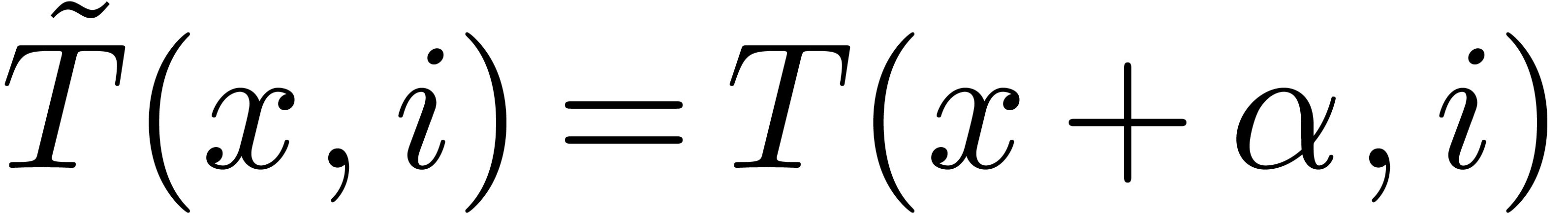 ,
,
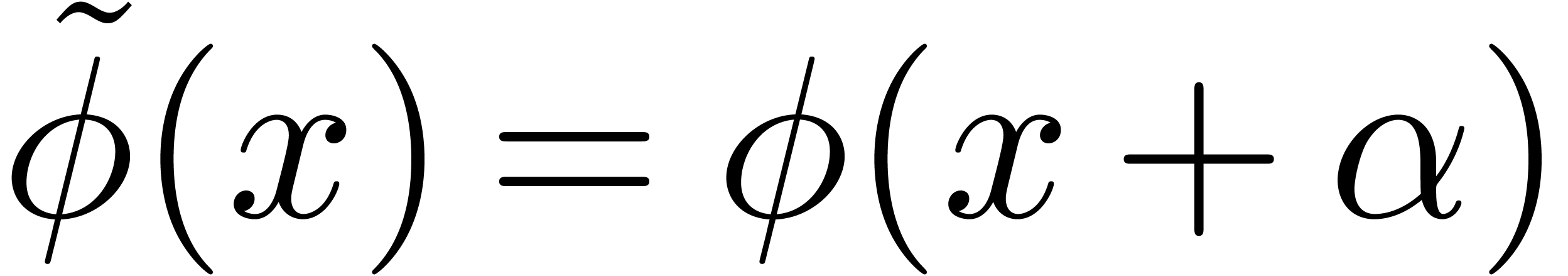 and
and 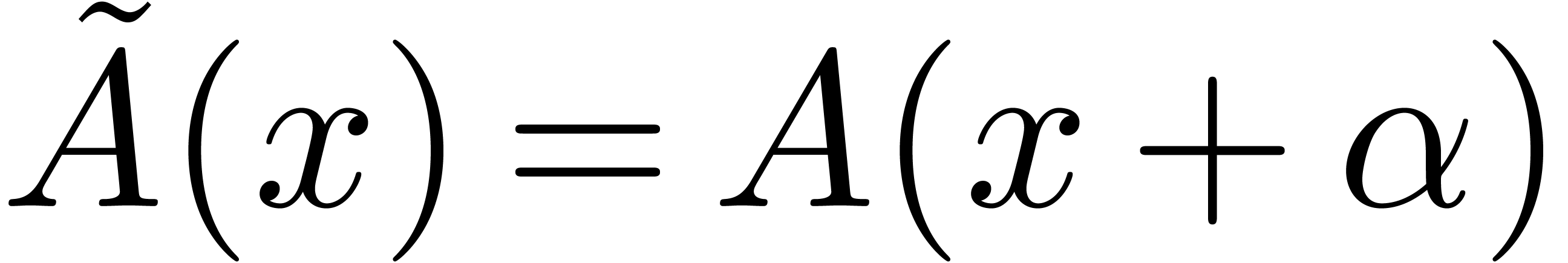 .
Then
.
Then  is a tail chopper at
is a tail chopper at  for
for  is a tail chopper at
is a tail chopper at 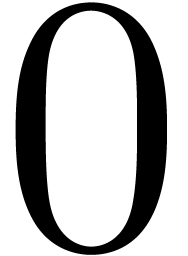 for
for 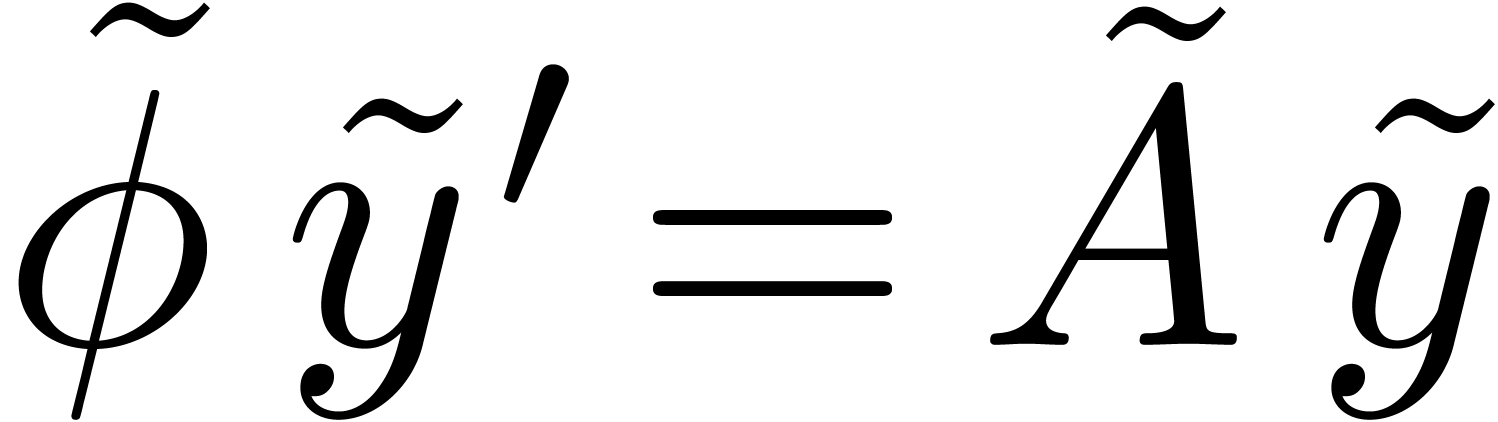 .
.
Proof. Setting 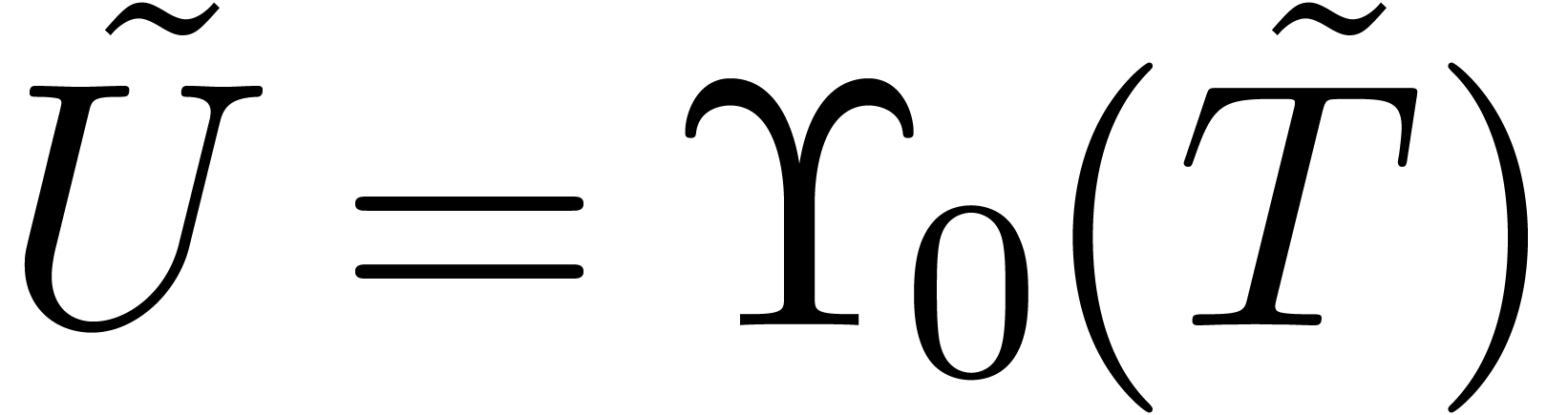 ,
we have
,
we have 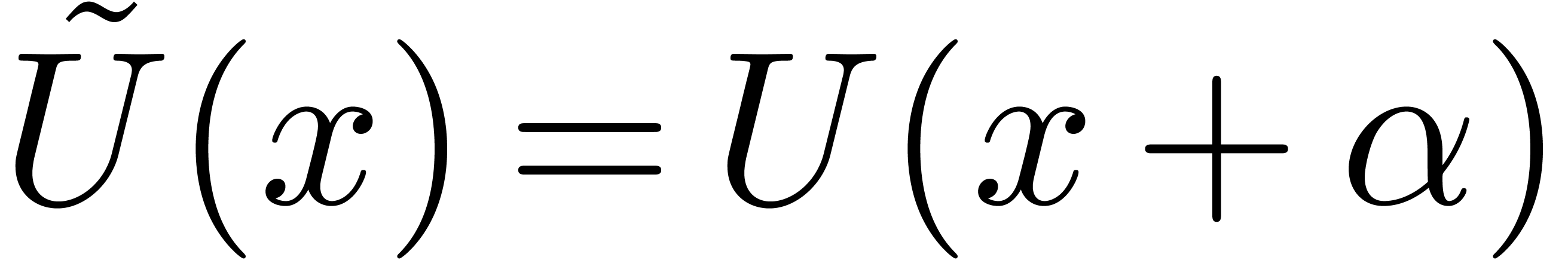 . Consequently,
. Consequently,  and
and 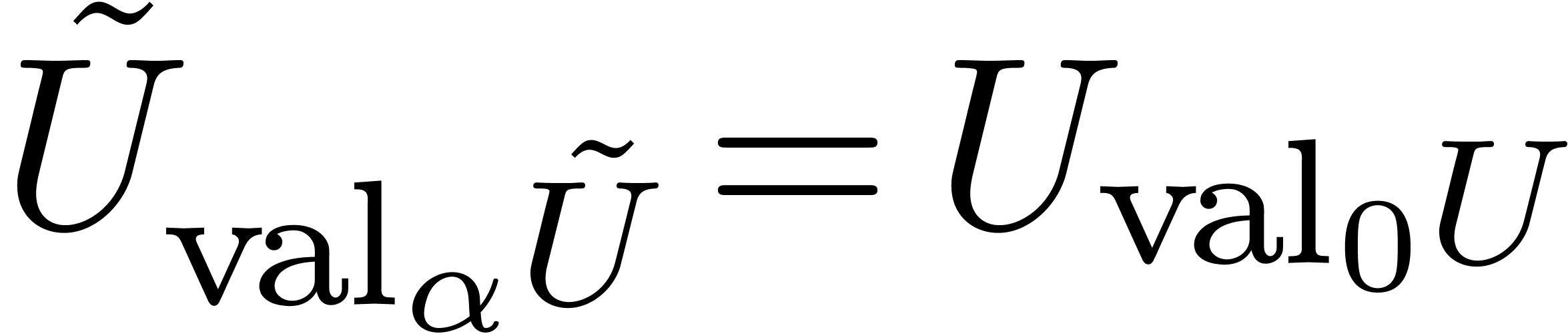 .□
.□
There is also a direct link between head choppers and tail choppers at
 via the change of variables
via the change of variables 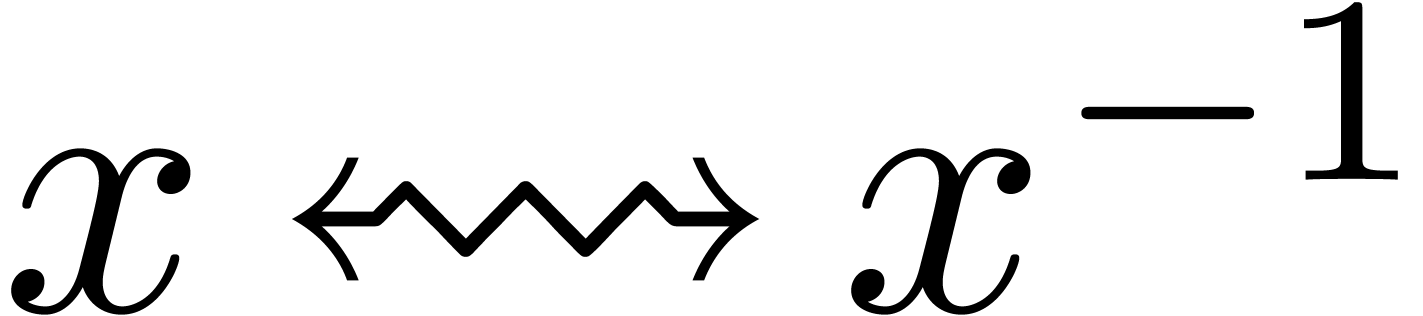 .
.
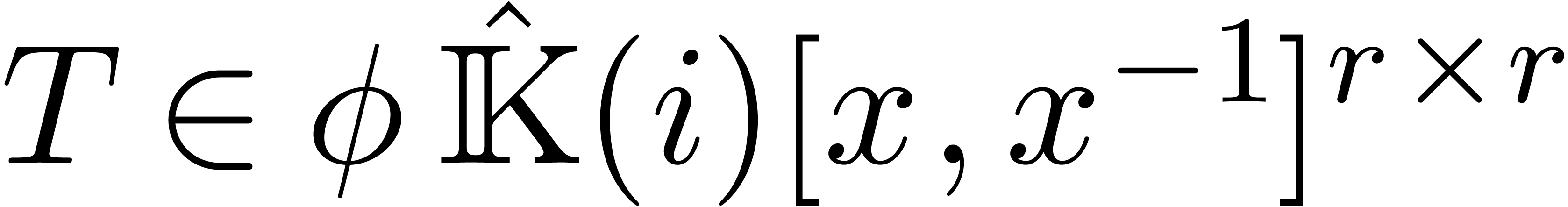 . Setting
. Setting 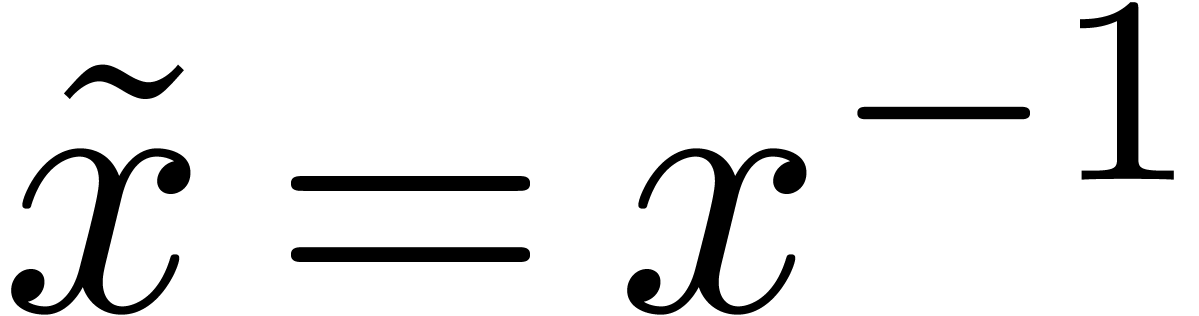 , we define
, we define 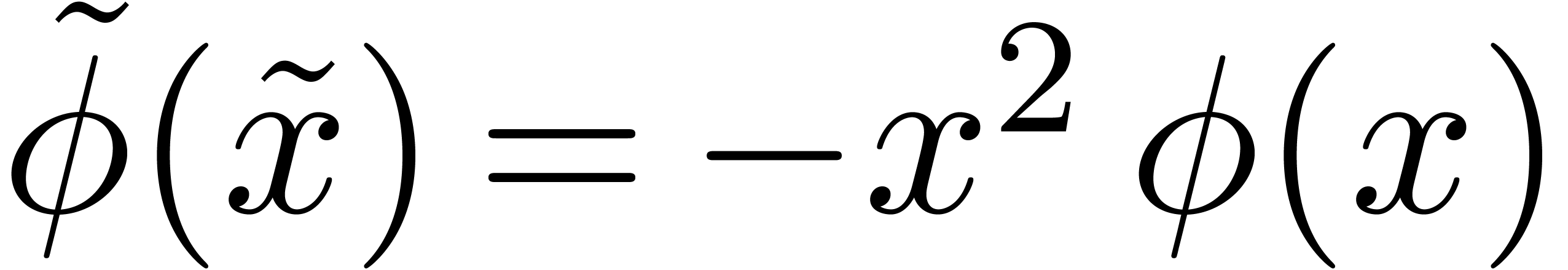 ,
,
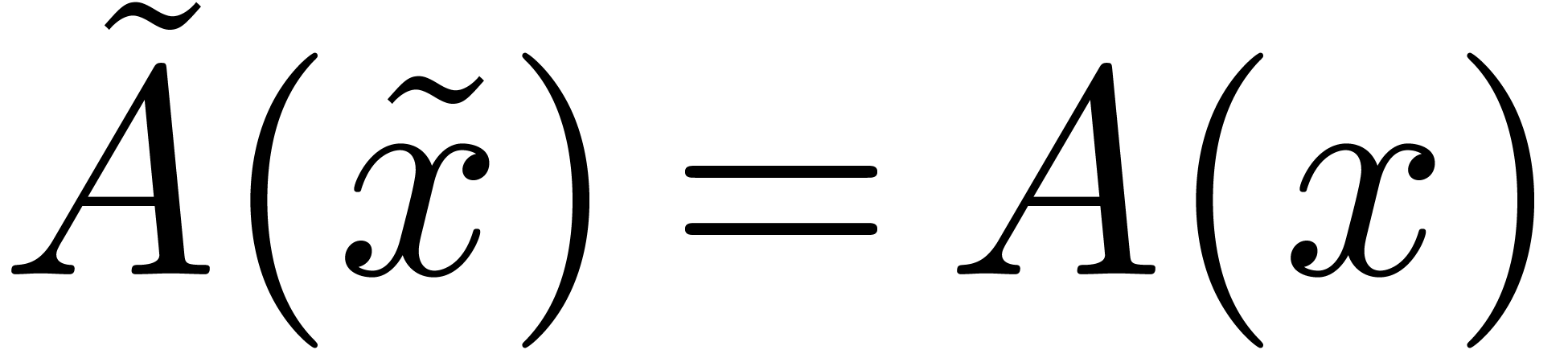 and
and  .
Then
.
Then  is a tail chopper at
is a tail chopper at  for
for  is a head chopper for
is a head chopper for 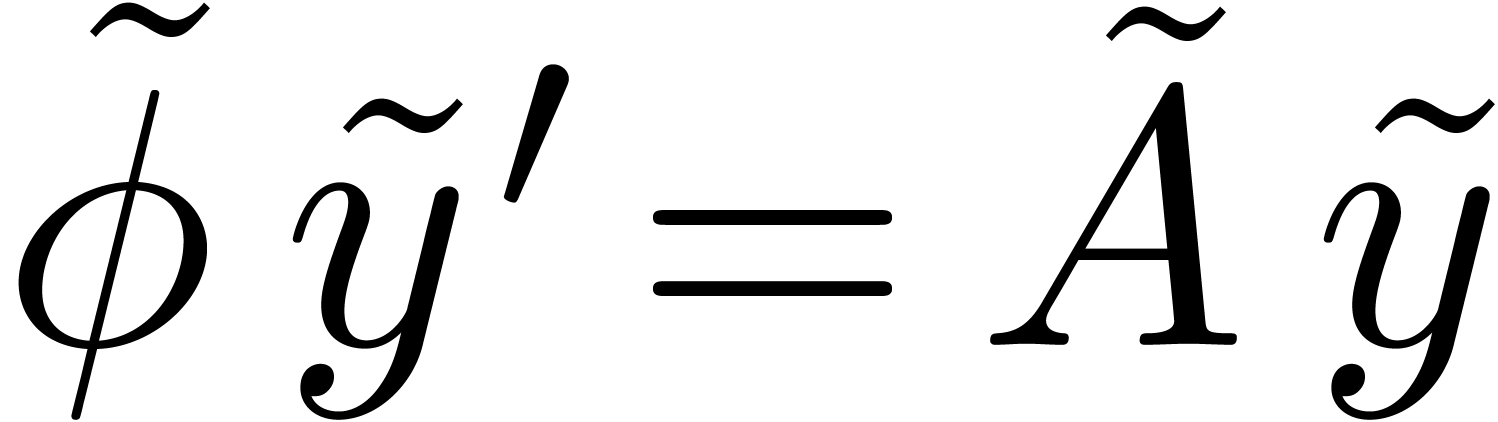 .
.
Proof. Setting  ,
we have
,
we have
Consequently, 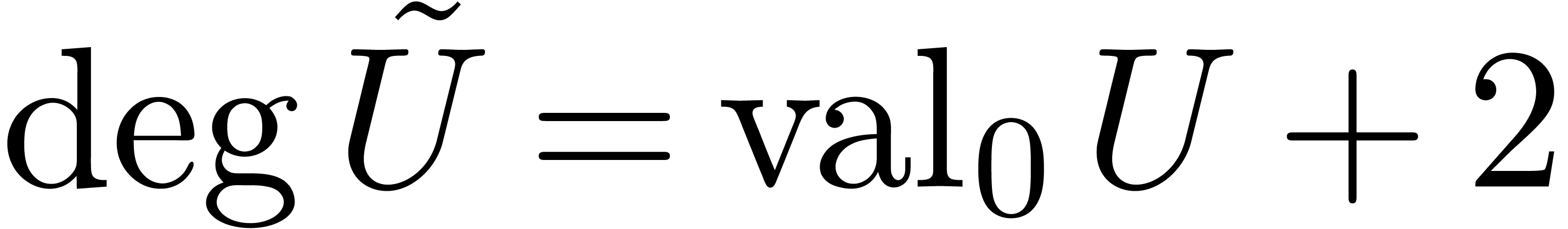 and
and 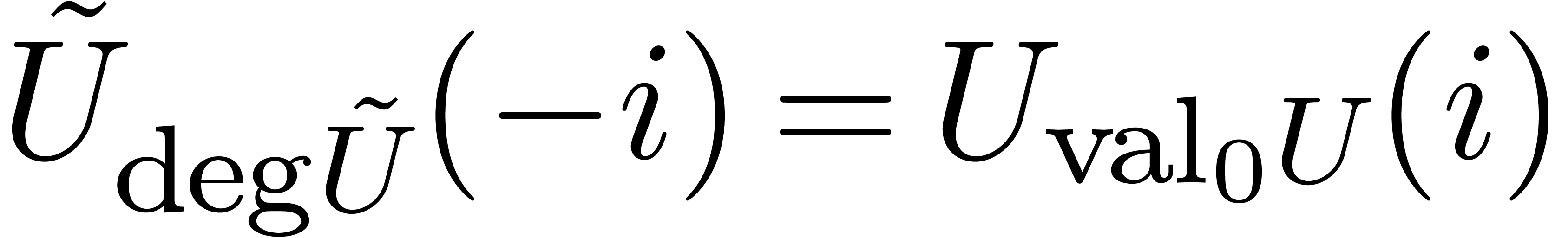 .□
.□
Finally, the matrix 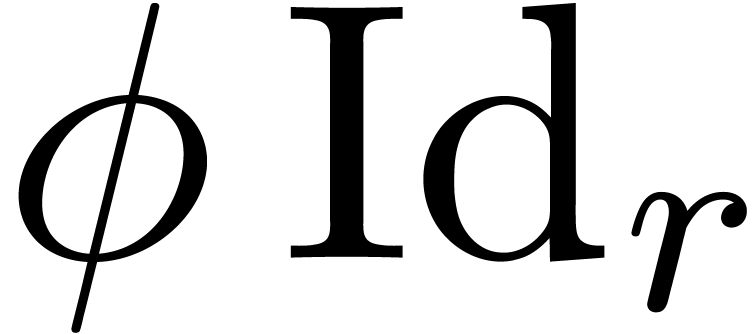 is a tail chopper at almost
all points
is a tail chopper at almost
all points  :
:
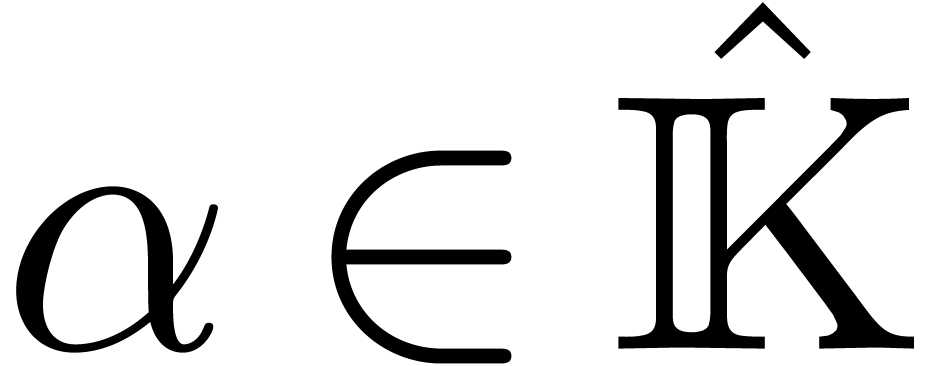 be such that
be such that 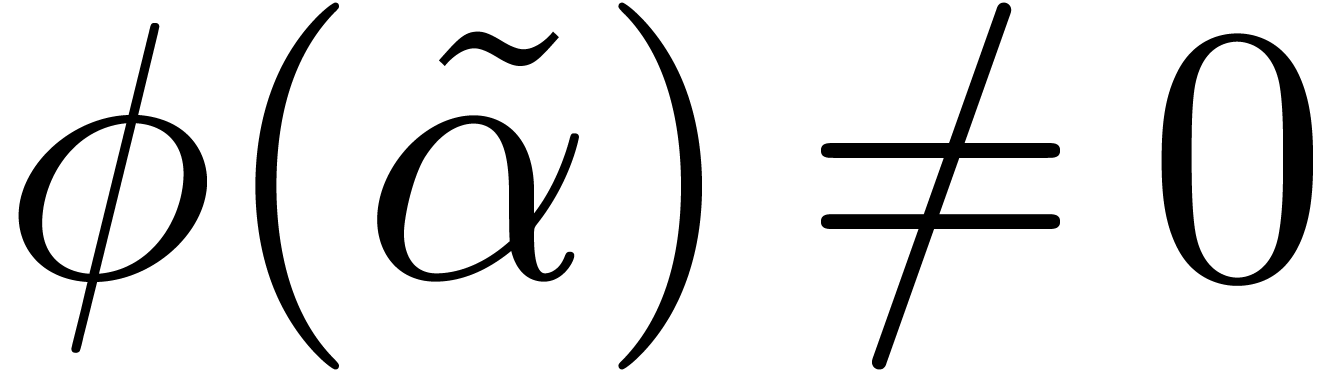 .
Then
.
Then 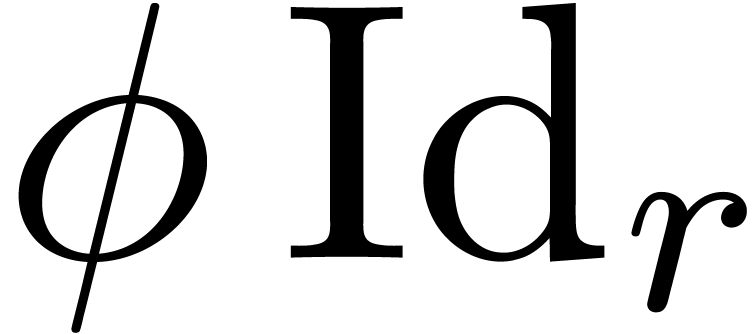 is a tail chopper for
is a tail chopper for  .
.
Proof. If 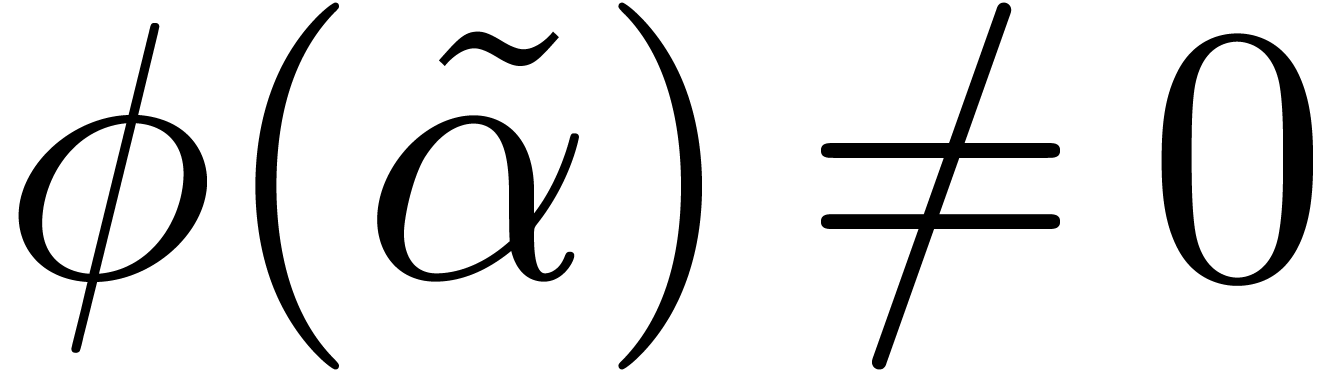 and
and 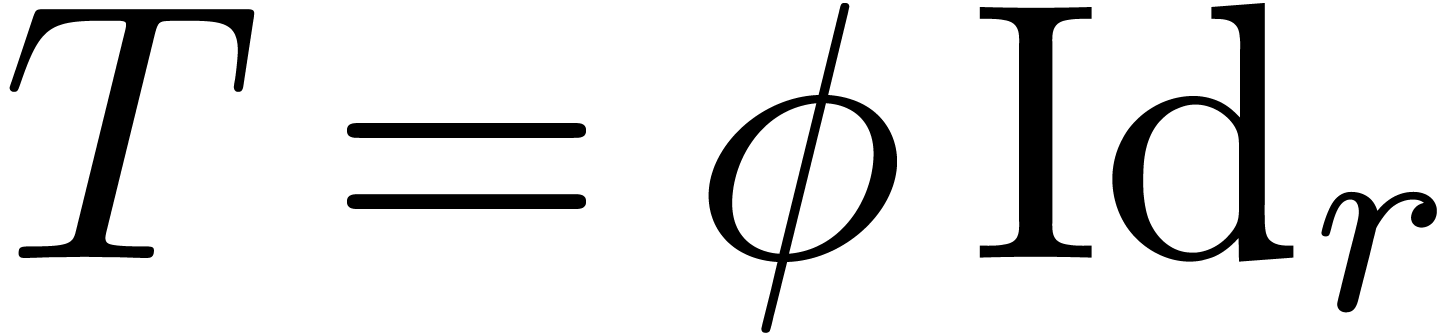 , then (9) becomes
, then (9) becomes
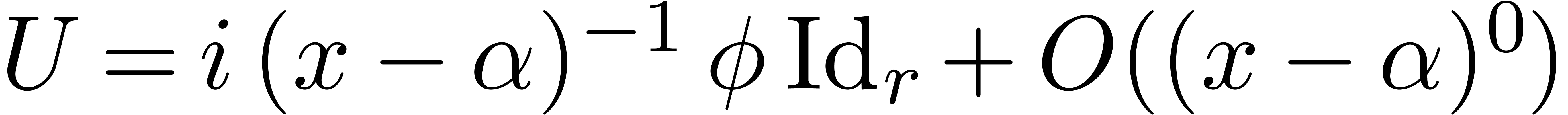 for
for  .
In particular,
.
In particular, 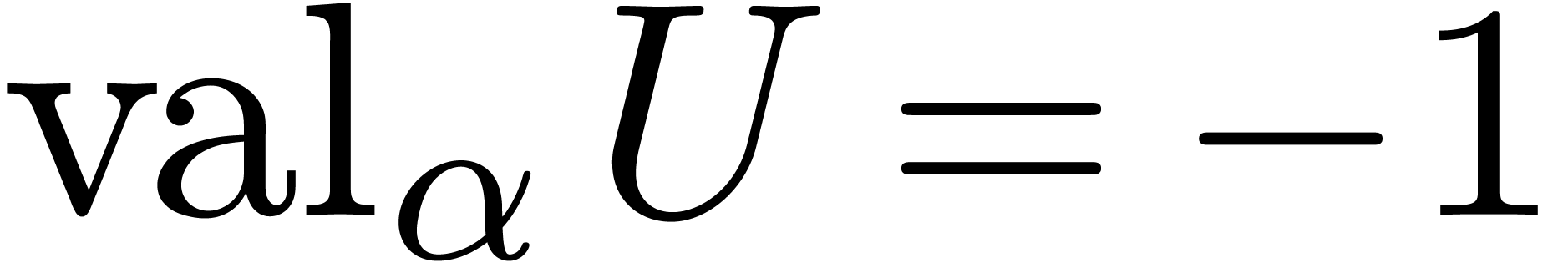 and
and 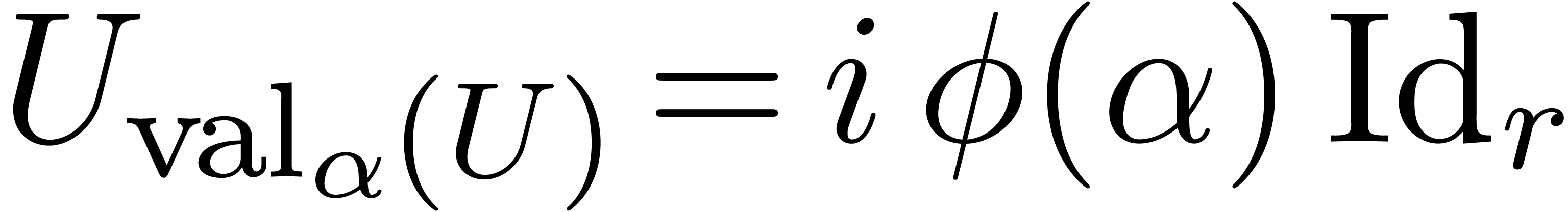 is
invertible in
is
invertible in 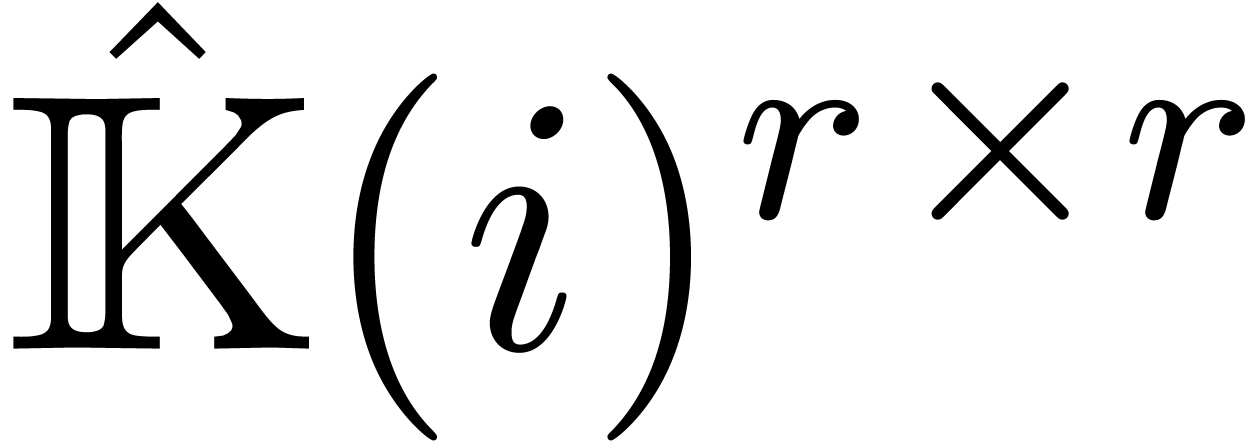 .□
.□
Now consider a monic square-free polynomial 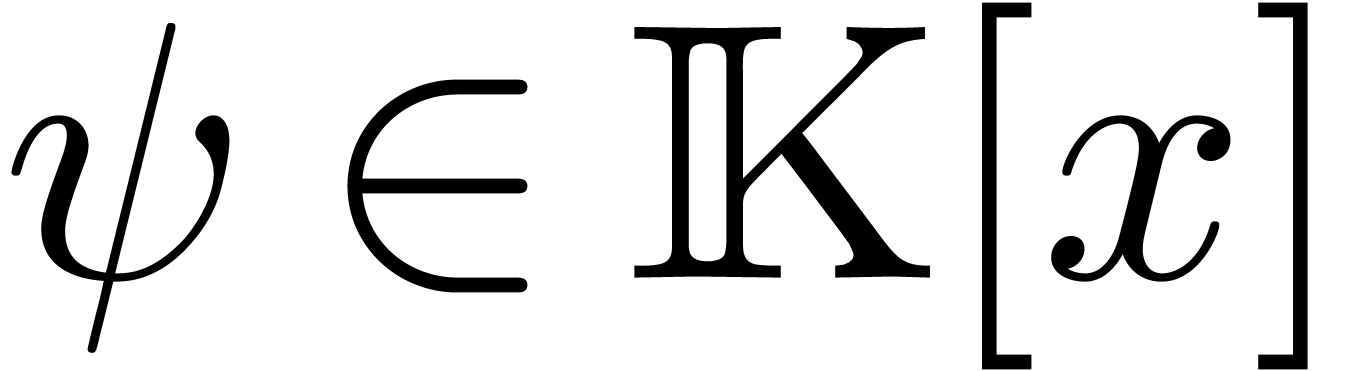 and
assume that we wish to compute a tail chopper for (1) at a
root
and
assume that we wish to compute a tail chopper for (1) at a
root  of
of 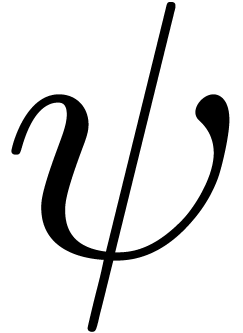 in
in  . First of all, we have to decide how to
conduct computations in
. First of all, we have to decide how to
conduct computations in  . If
. If
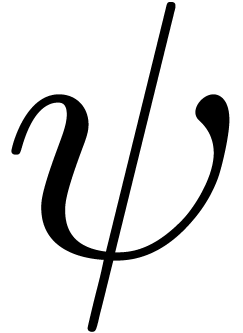 is irreducible, then we may simply work in the
field
is irreducible, then we may simply work in the
field 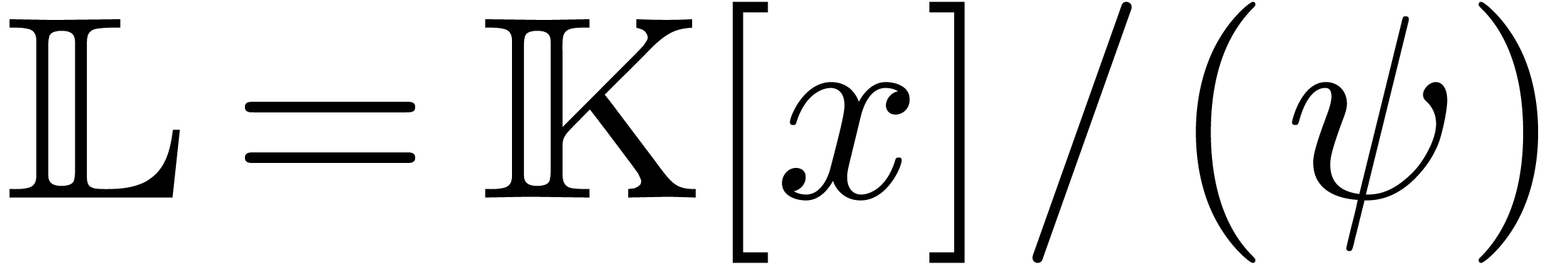 instead of
instead of  and
take
and
take  to be the residue class of
to be the residue class of  , so that
, so that  becomes a
generic formal root of
becomes a
generic formal root of 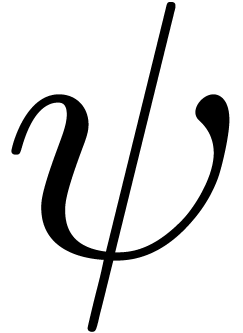 . In
general, factoring
. In
general, factoring 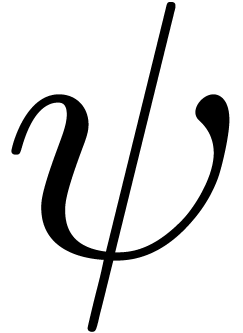 over
over  may be hard, so we cannot assume
may be hard, so we cannot assume 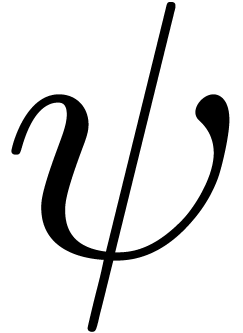 to be
irreducible. Instead, we rely on the well known technique of dynamic
evaluation [8].
to be
irreducible. Instead, we rely on the well known technique of dynamic
evaluation [8].
For convenience of the reader, let us recall that dynamic evaluation
amounts to performing all computations as if 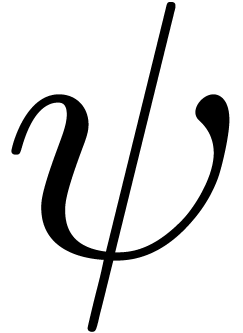 were irreducible and
were irreducible and 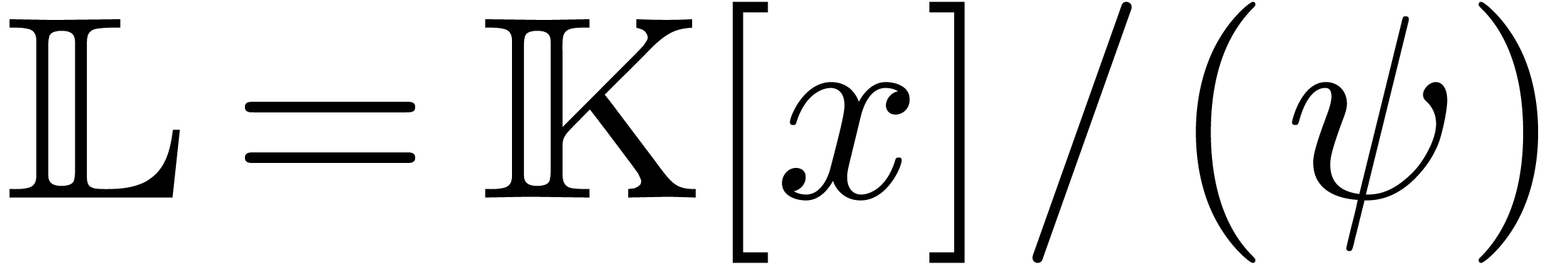 were a field with an
algorithm for division. Whenever we wish to divide by a non-zero element
were a field with an
algorithm for division. Whenever we wish to divide by a non-zero element
 (with
(with 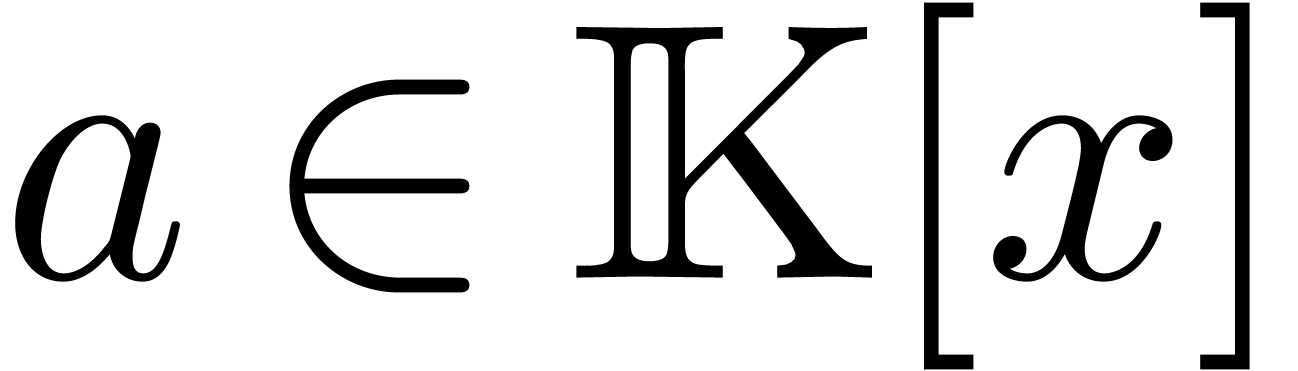 )
that is not invertible, then
)
that is not invertible, then 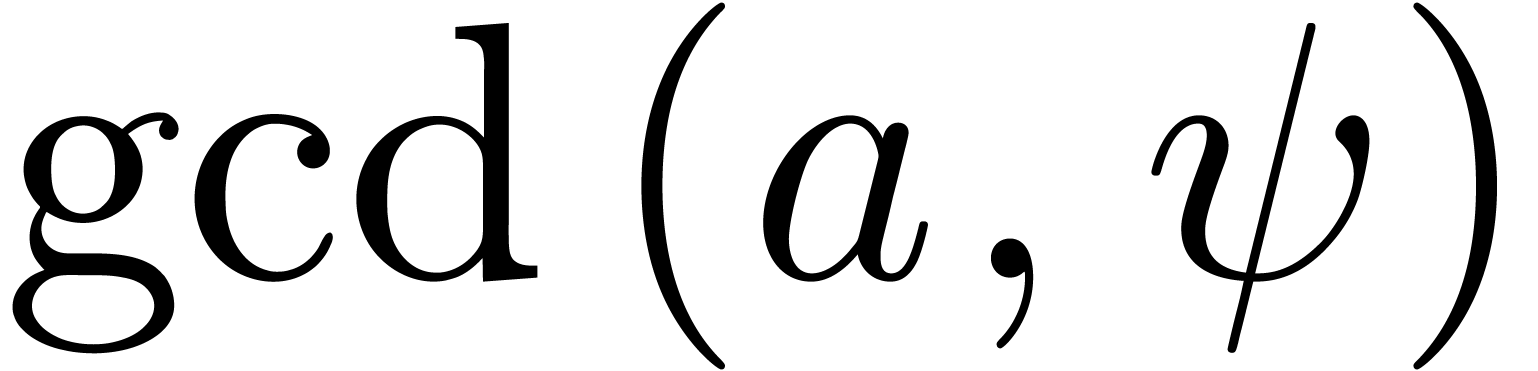 provides us with a
non trivial factor of
provides us with a
non trivial factor of 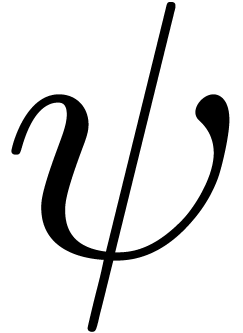 . In
that case, we launch an exception and redo all computations with
. In
that case, we launch an exception and redo all computations with 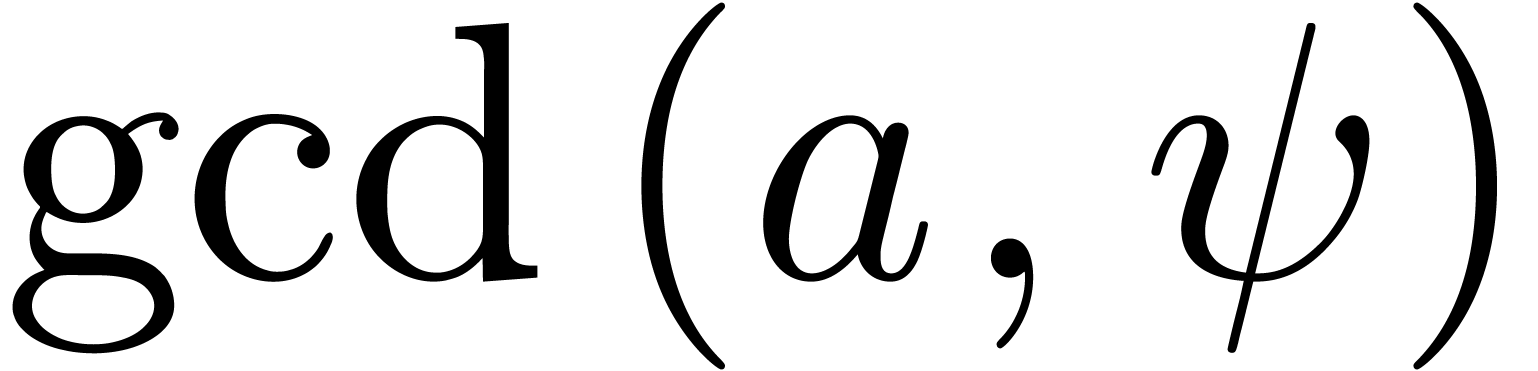 or
or 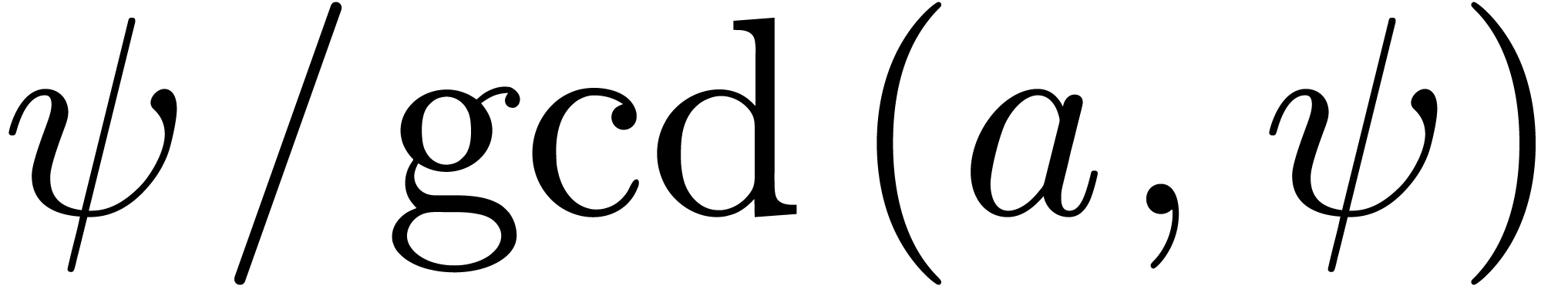 in the role of
in the role of 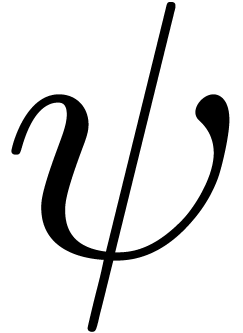 .
.
So let 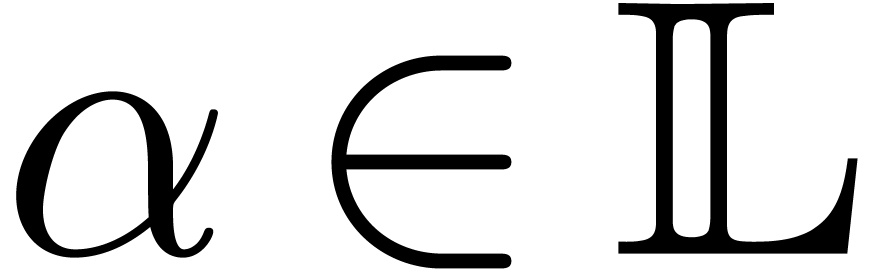 be a formal root of
be a formal root of 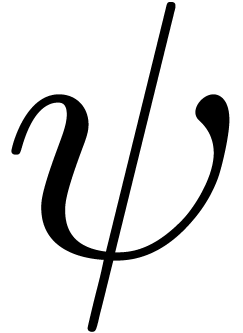 and define
and define  ,
,  ,
, 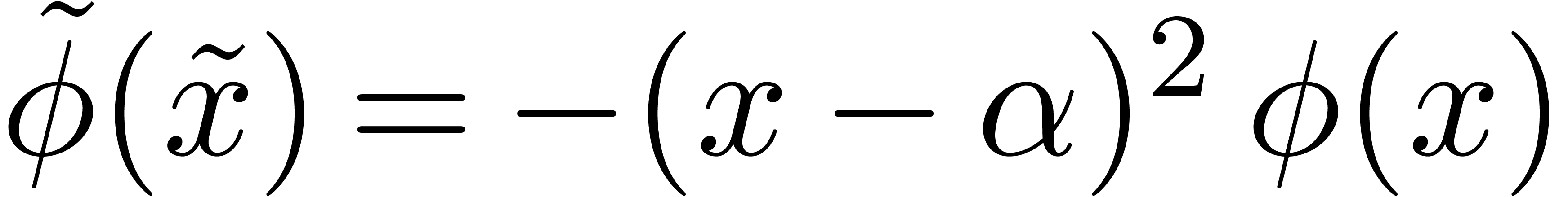 and
and 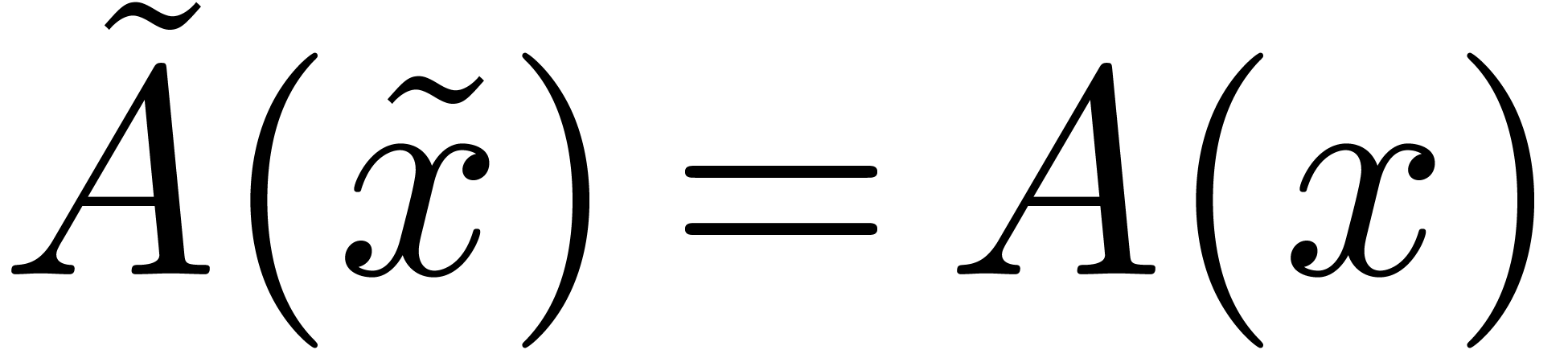 . Let
. Let 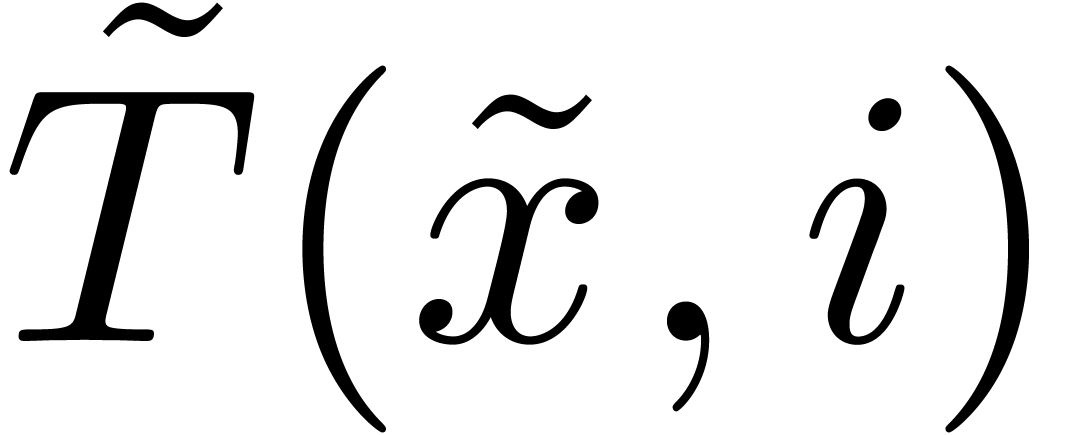 be a head chopper
for the equation
be a head chopper
for the equation 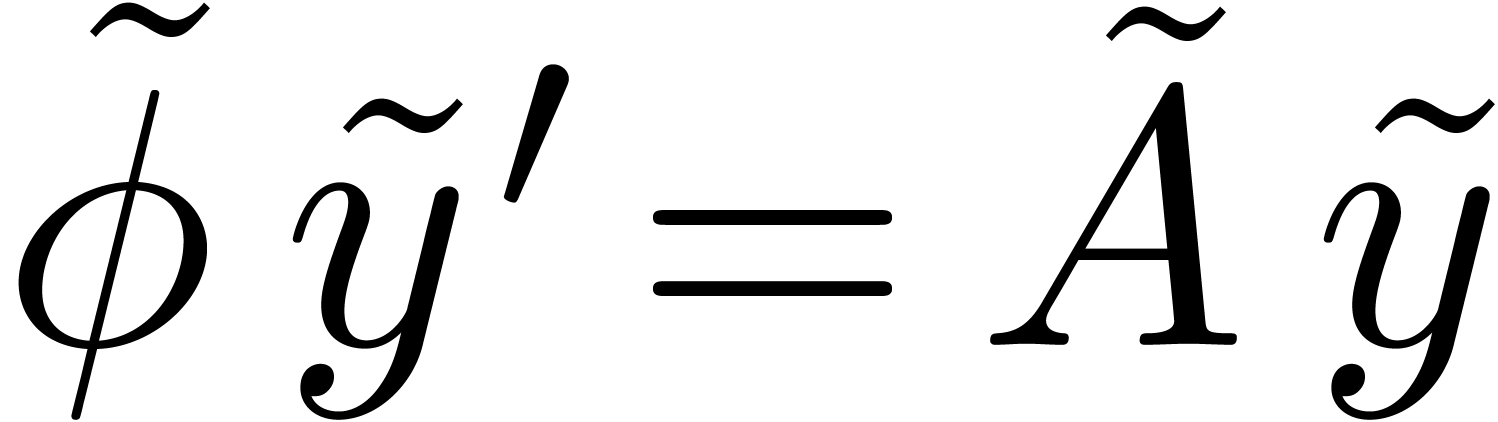 , as
computed using the algorithm from section 4.3. Then
, as
computed using the algorithm from section 4.3. Then 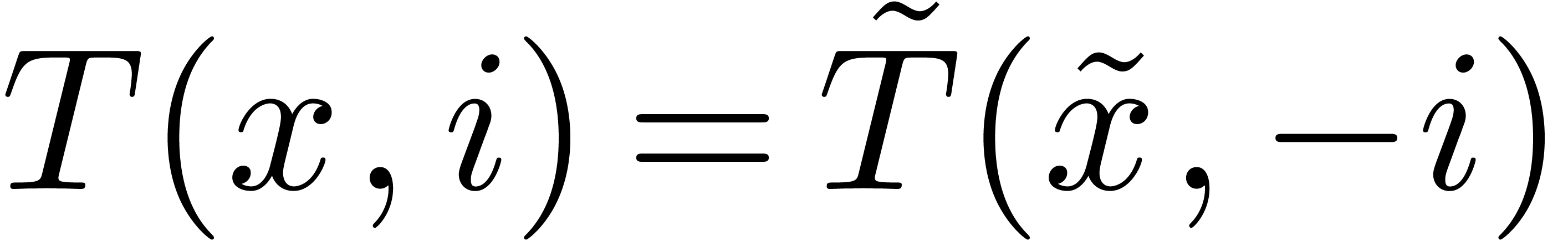 is a tail chopper at
is a tail chopper at  by
Lemmas 13 and 14.
by
Lemmas 13 and 14.
Let  be a tail chopper for (1) at
be a tail chopper for (1) at
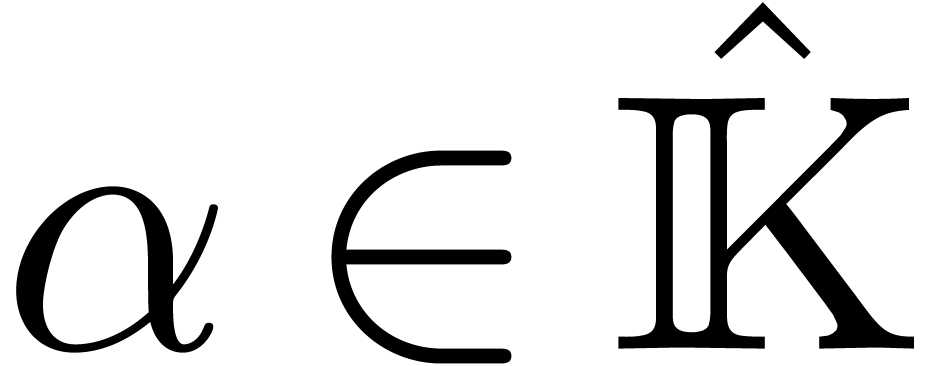 . Let
. Let 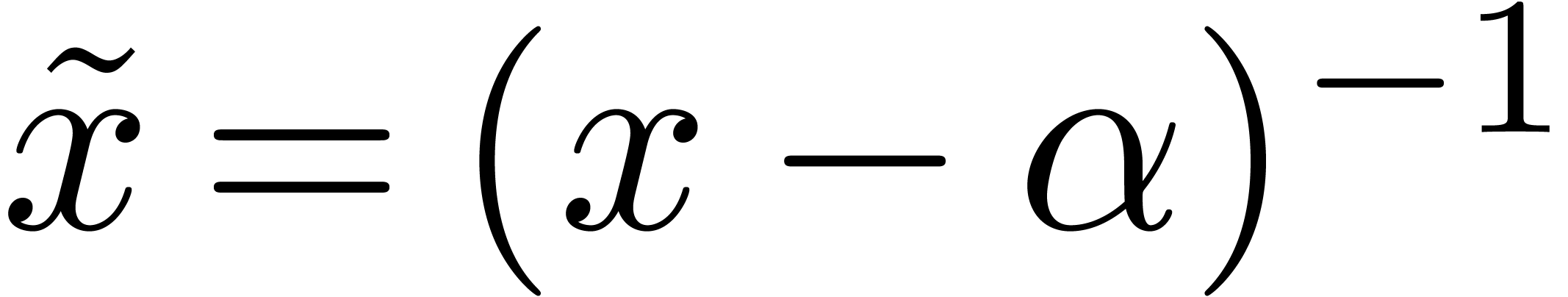 ,
, 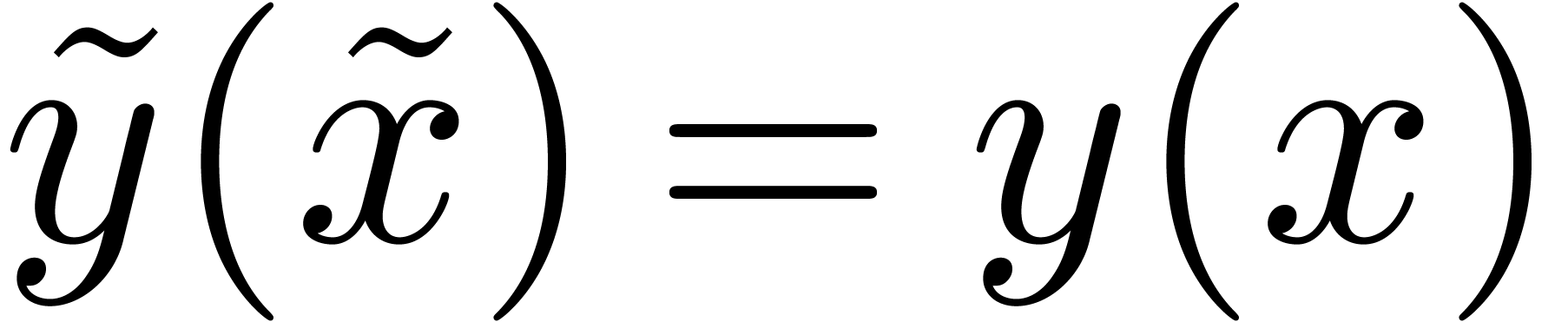 ,
, 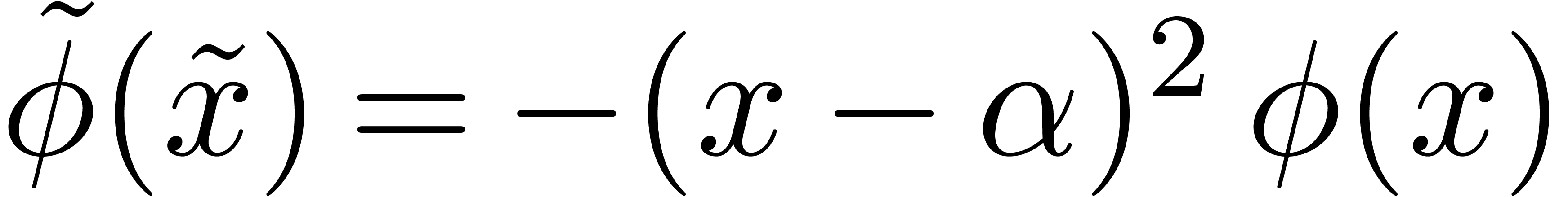 and
and 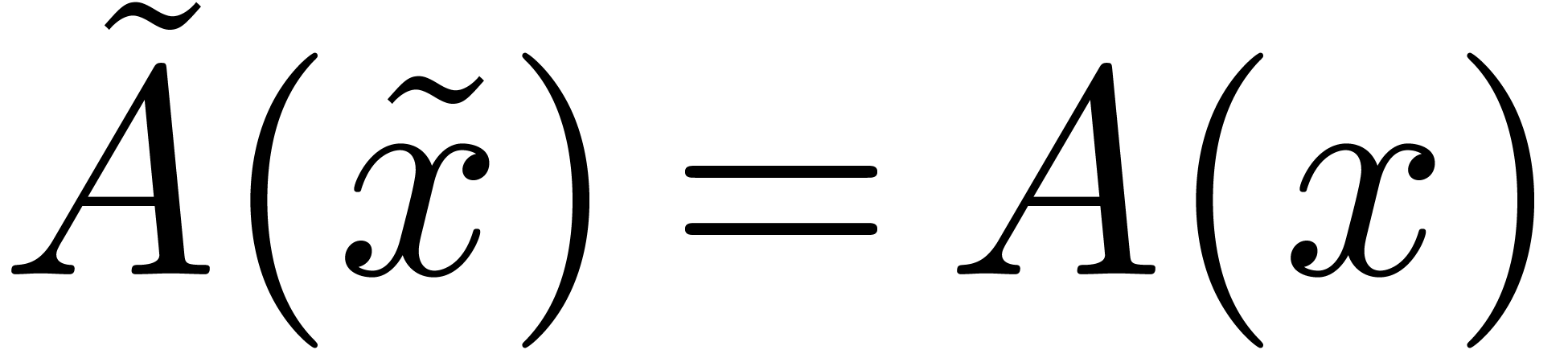 be as above, so that
be as above, so that
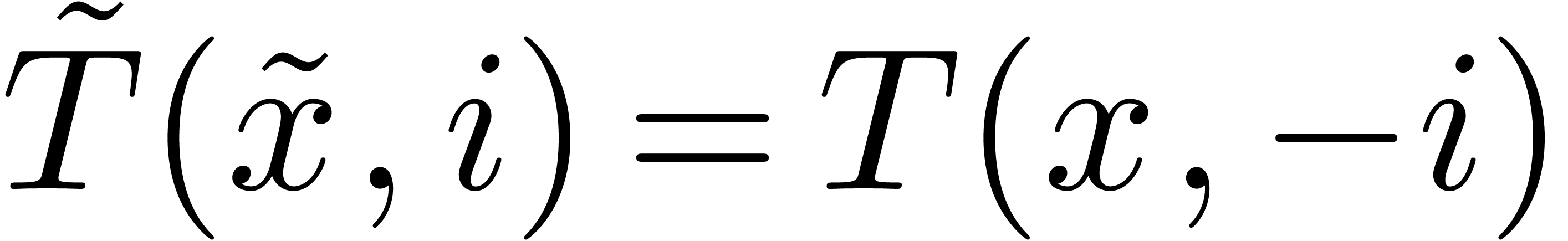 , is a head chopper for the
equation
, is a head chopper for the
equation 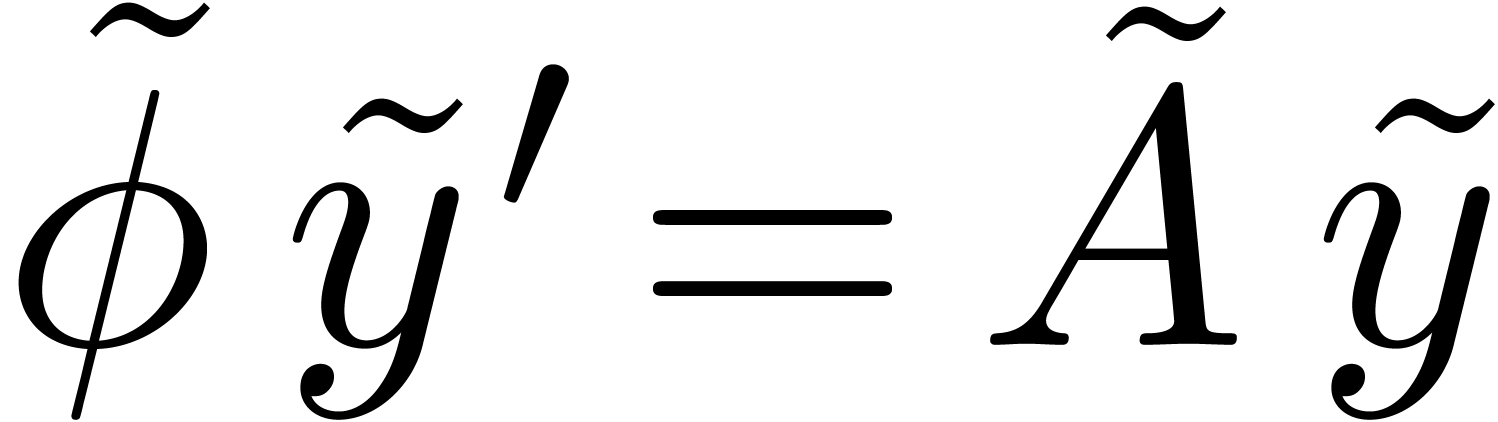 . In particular,
rewriting linear combinations
. In particular,
rewriting linear combinations  with
with 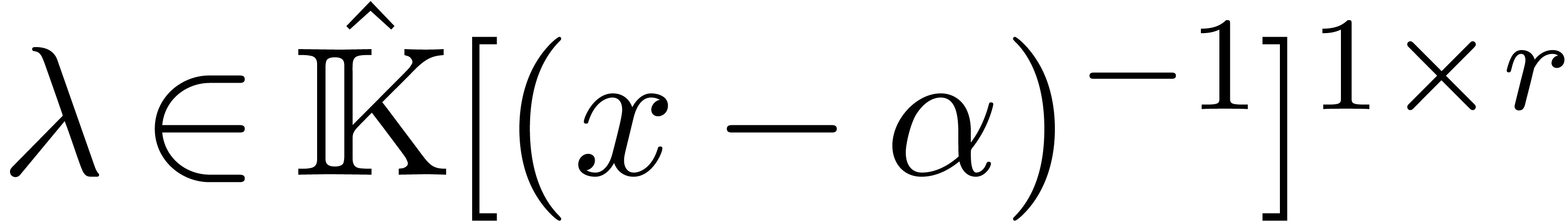 as linear combinations
as linear combinations  with
with 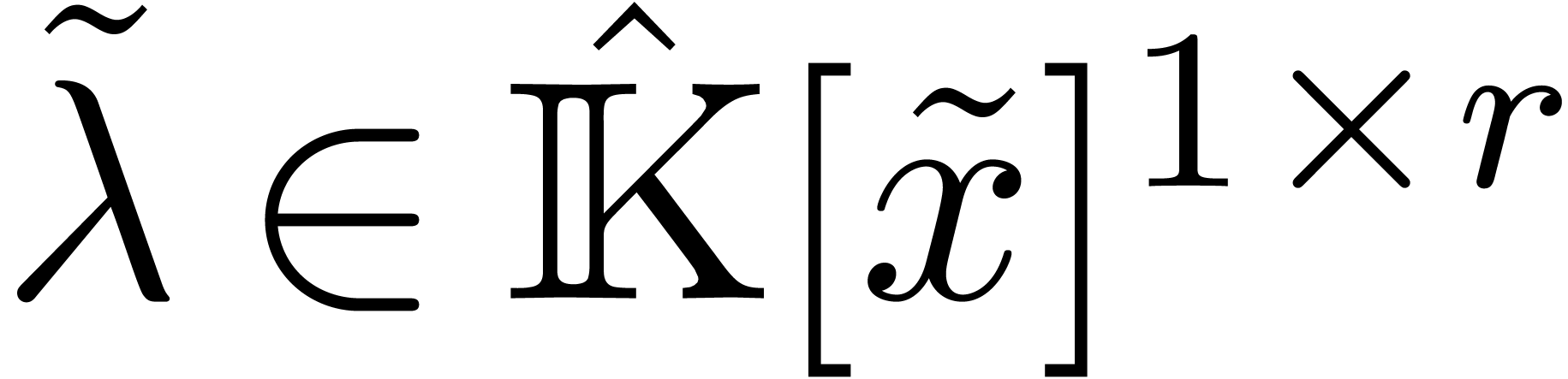 , we may head reduce
, we may head reduce  as described in section 4.4. Let
as described in section 4.4. Let 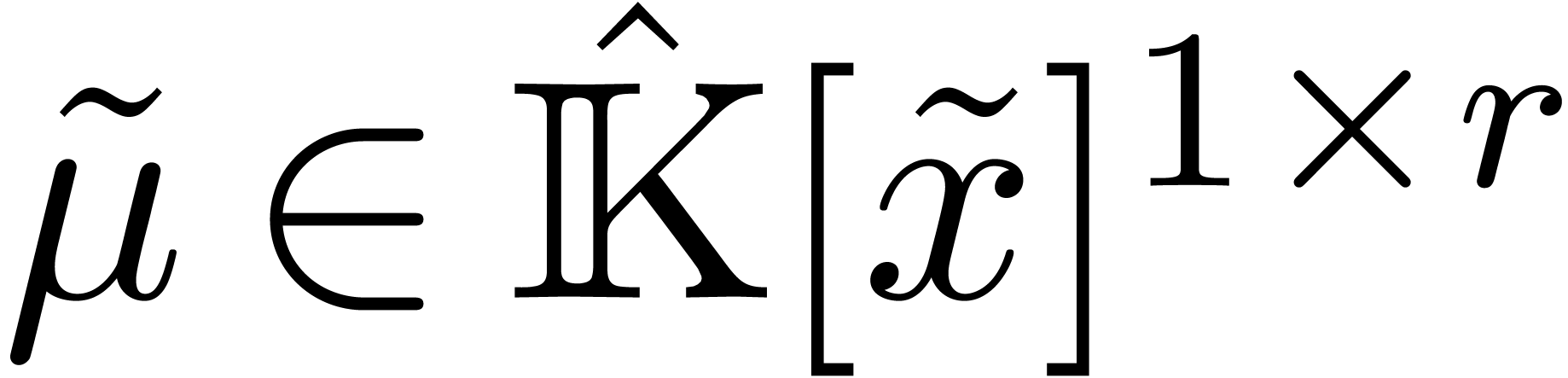 be such that
be such that  .
Then we may rewrite
.
Then we may rewrite  as an element
as an element  of
of 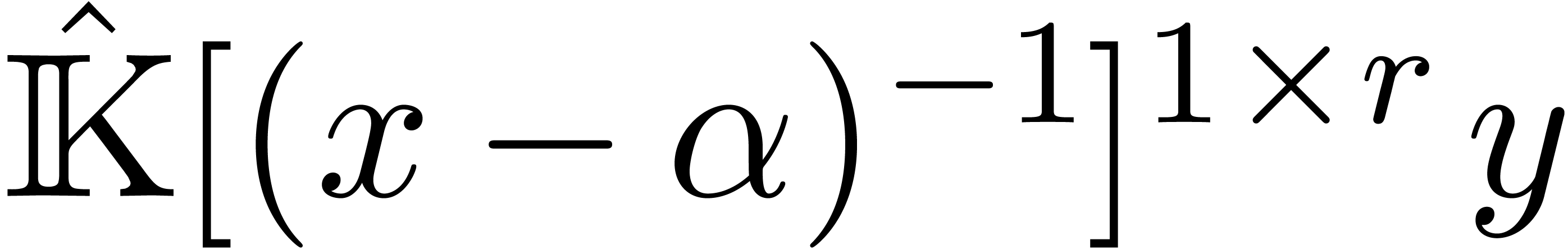 . We call
. We call
 the tail reduction of
the tail reduction of  at
at  and write
and write 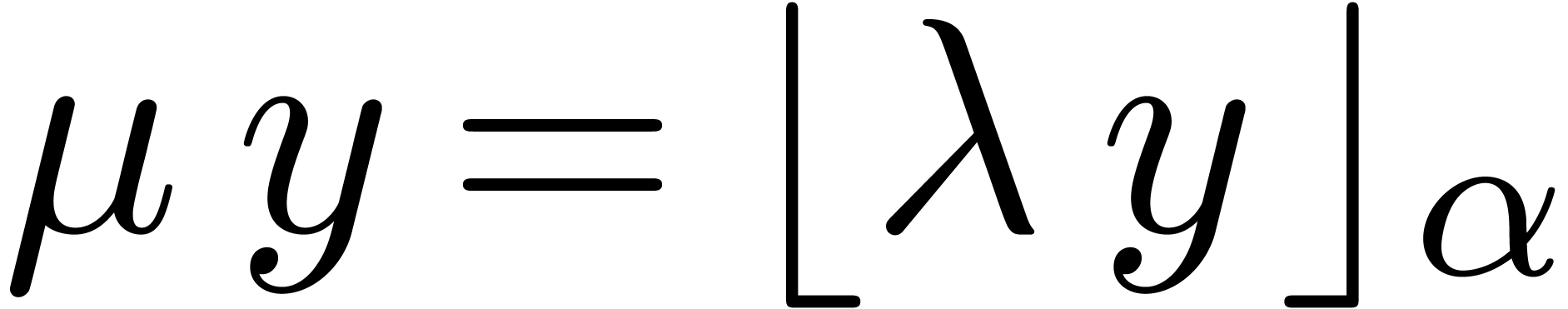 .
.
Let  be the finite set of exceptional indices for
the above head reduction and
be the finite set of exceptional indices for
the above head reduction and 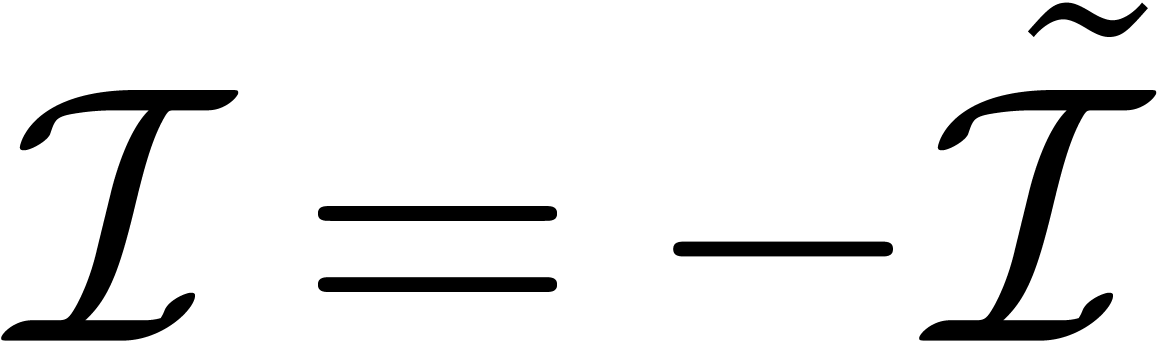 .
Setting
.
Setting 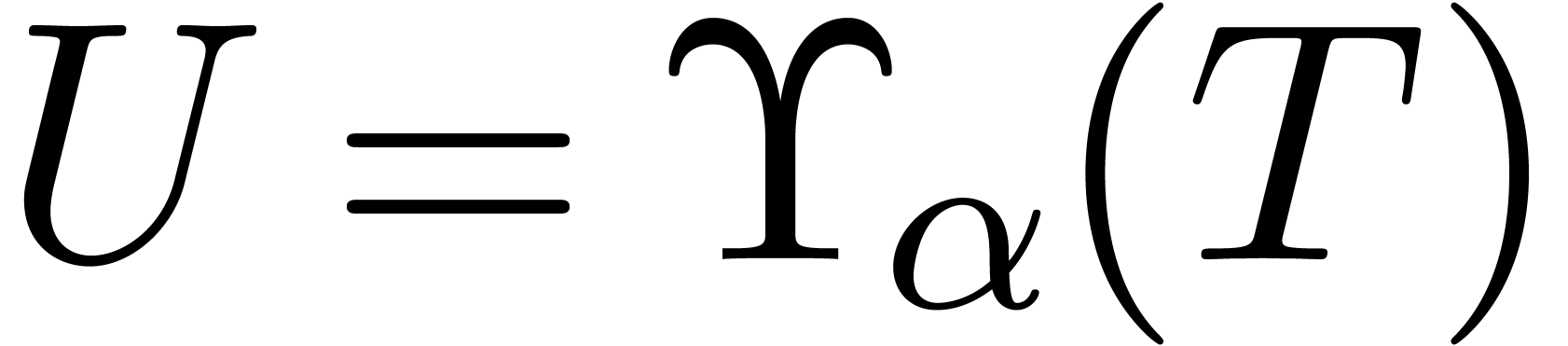 and
and 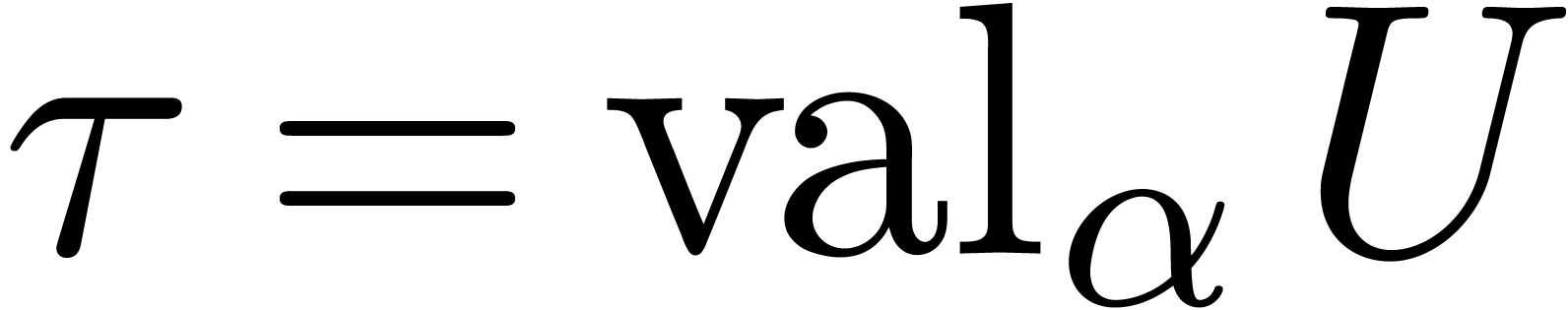 ,
it can be checked that the following algorithm computes the tail
reduction at
,
it can be checked that the following algorithm computes the tail
reduction at  :
:
Algorithm TailReduce |
repeat
if
Let
|
In the particular case when
 |
(11) |
for some operator 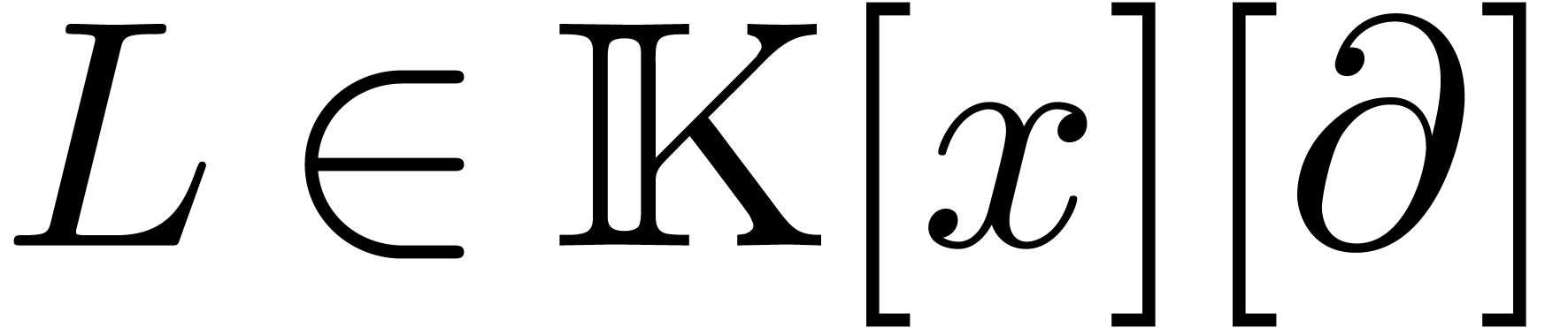 of order
of order 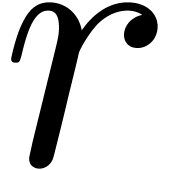 , the system (1) is equivalent to
, the system (1) is equivalent to
Given a general system (1), there always exists an element
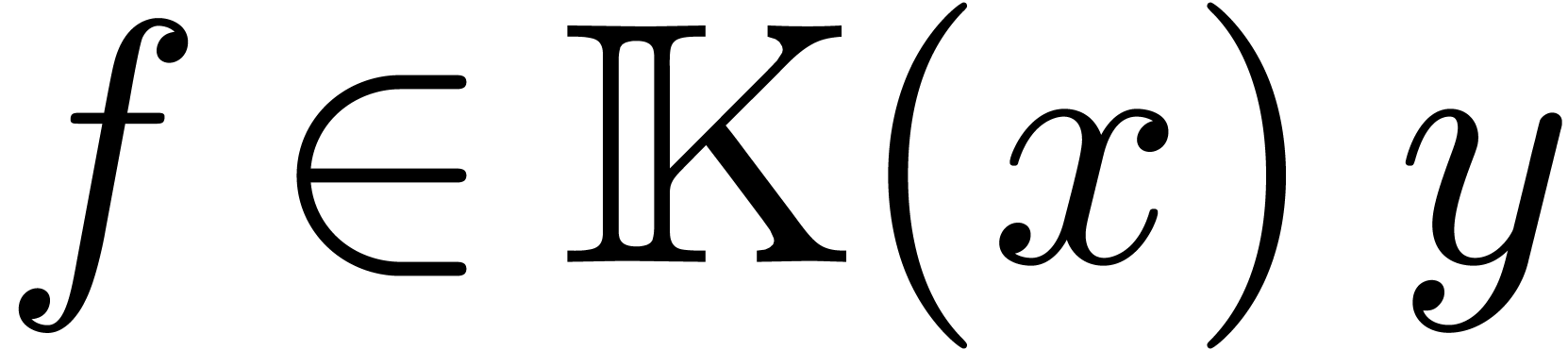 such that
such that 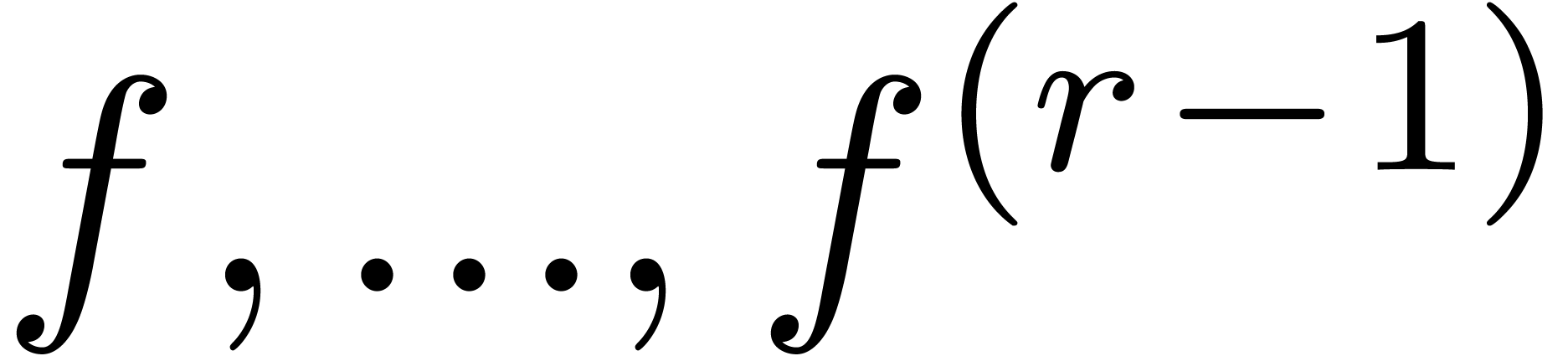 are
are 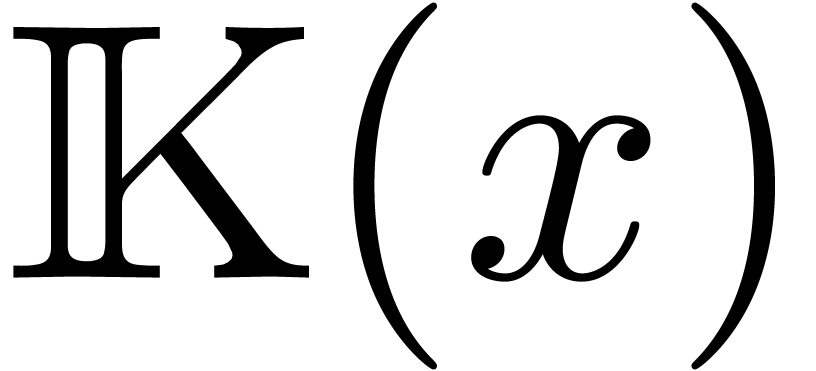 -linearly independent. Such an
element
-linearly independent. Such an
element  is called a cyclic vector and,
with respect to the basis
is called a cyclic vector and,
with respect to the basis 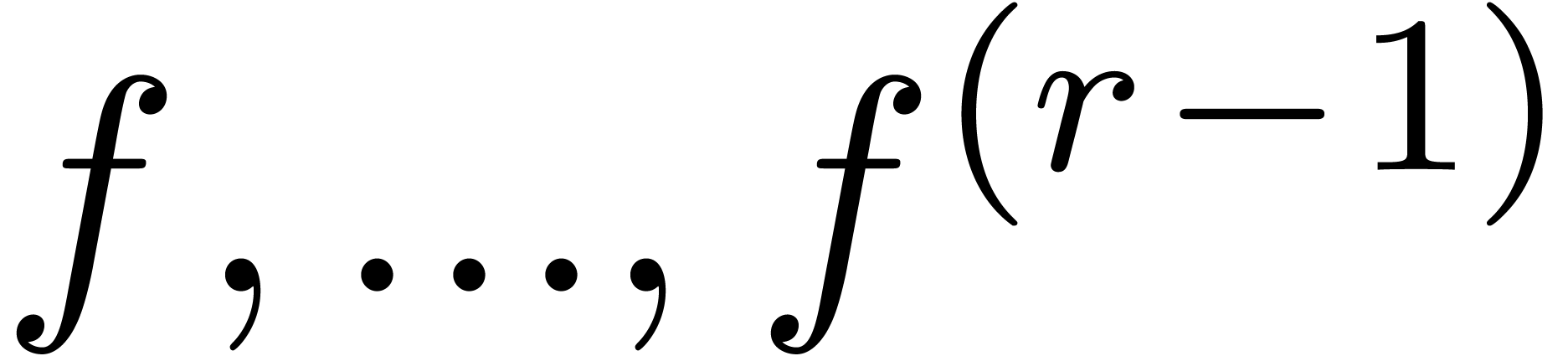 of
of  , the equation (1) transforms into
an equation of the form (12). For efficient algorithms to
compute cyclic vectors, we refer to [3].
, the equation (1) transforms into
an equation of the form (12). For efficient algorithms to
compute cyclic vectors, we refer to [3].
In the remainder of this section, we focus on systems (1)
that are equivalent to (12), with  ,
,  and
and  as in (11).
as in (11).
Let us start with a quick review of some well known results about the
asymptotic behaviour of solutions to (12) when  . We define
. We define
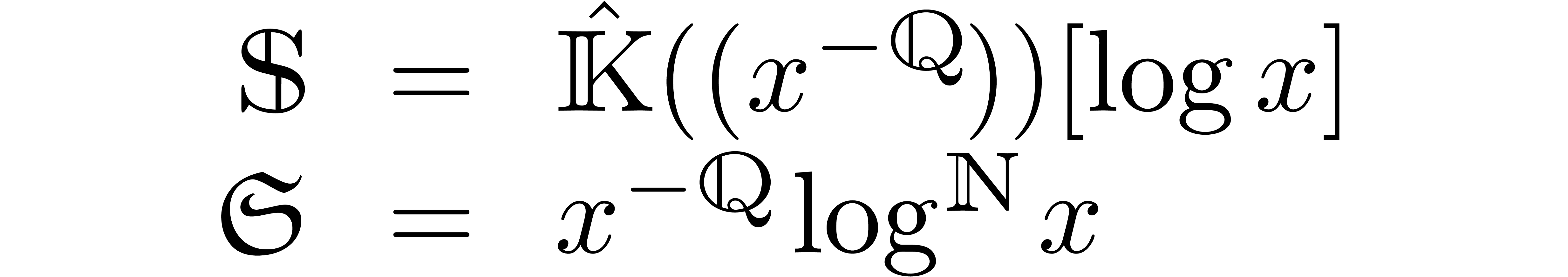
to be the set of polynomials in 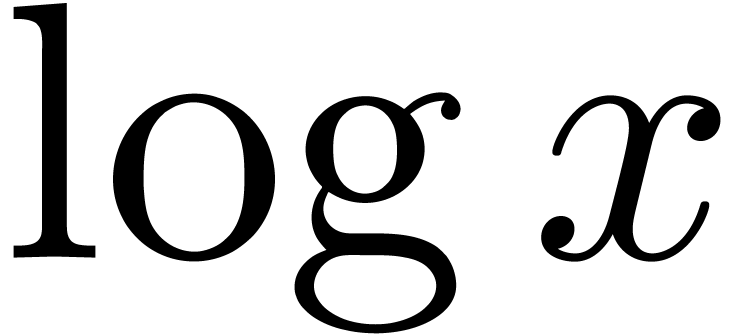 whose
coefficients are Puiseux series in
whose
coefficients are Puiseux series in 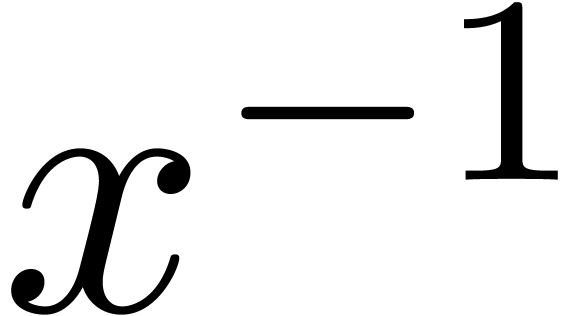 ,
together with the corresponding set of monomials. The set
,
together with the corresponding set of monomials. The set  is asymptotically ordered by
is asymptotically ordered by

and elements  of
of  can be
written as series
can be
written as series 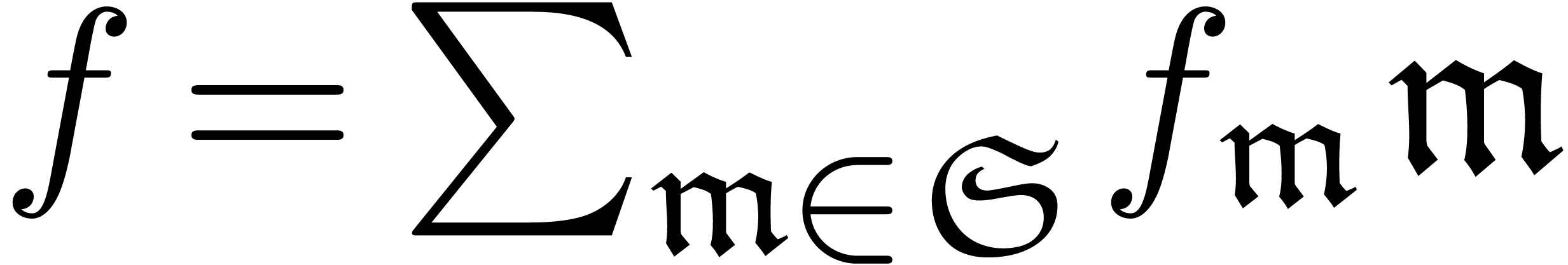 with
with 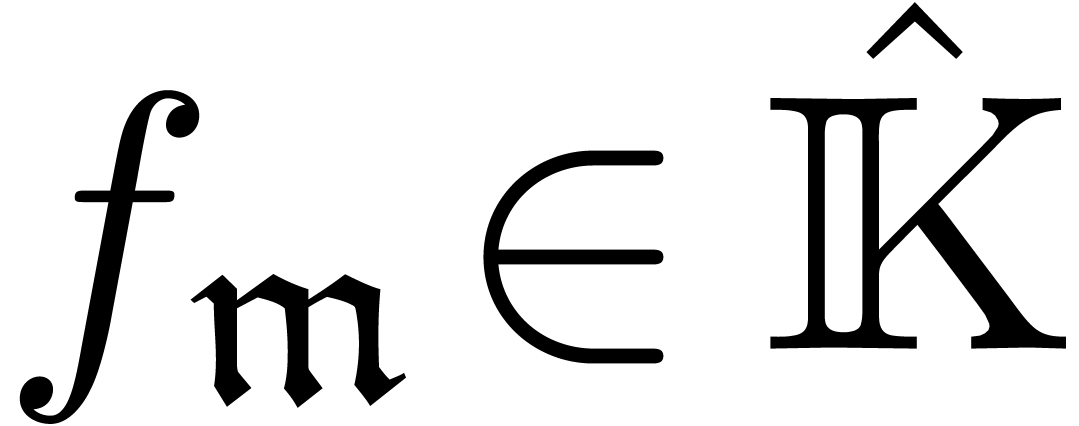 . We call
. We call  the
support of
the
support of  . If
. If
 , then the maximal element
, then the maximal element
 of the support is called the dominant
monomial of
of the support is called the dominant
monomial of  .
.
We may also regard elements  of
of  as series
as series 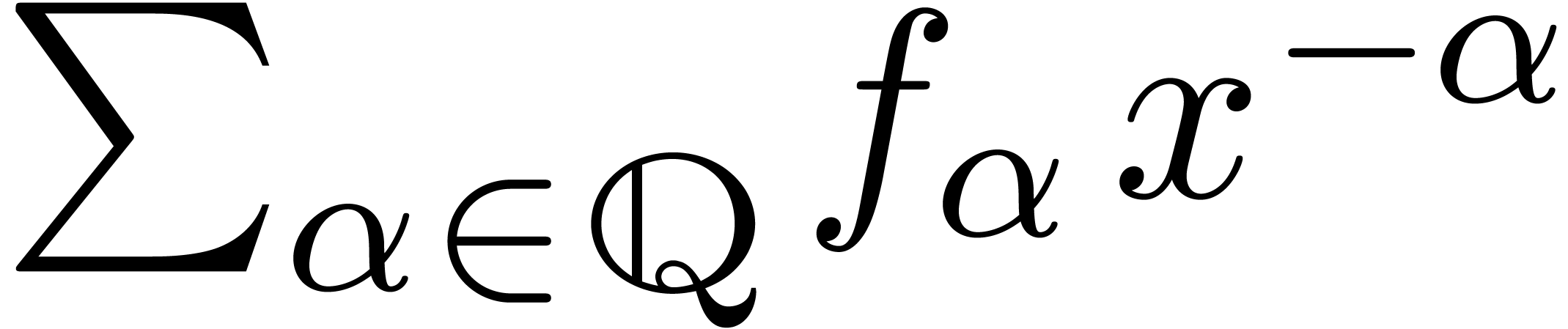 in
in 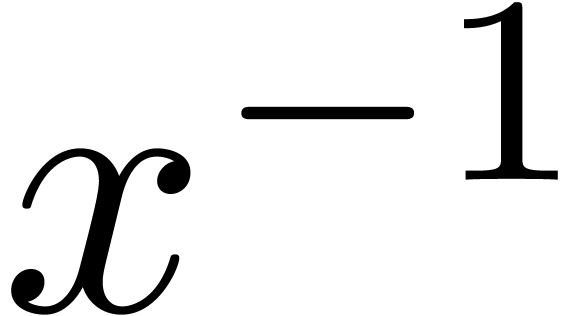 with
coefficients in
with
coefficients in 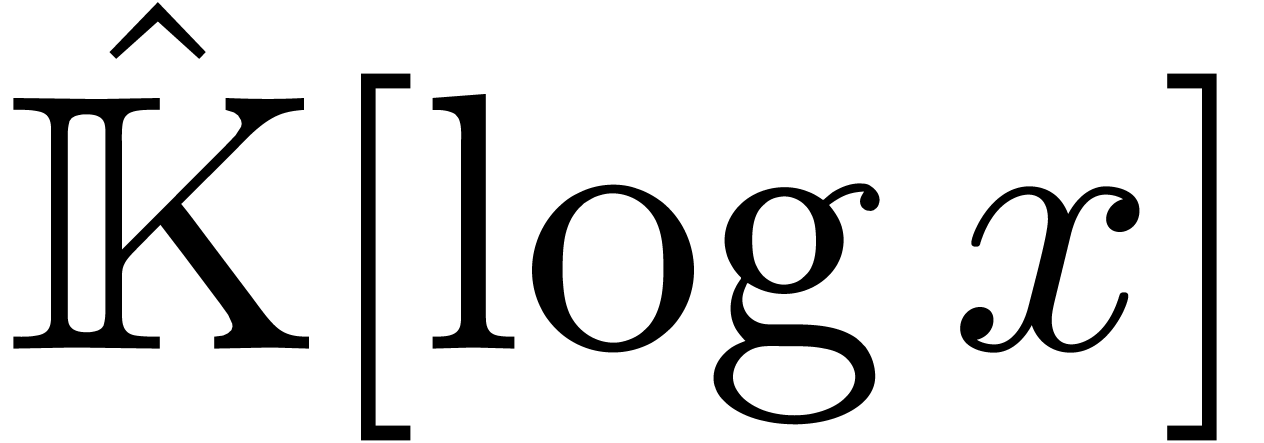 . If
. If 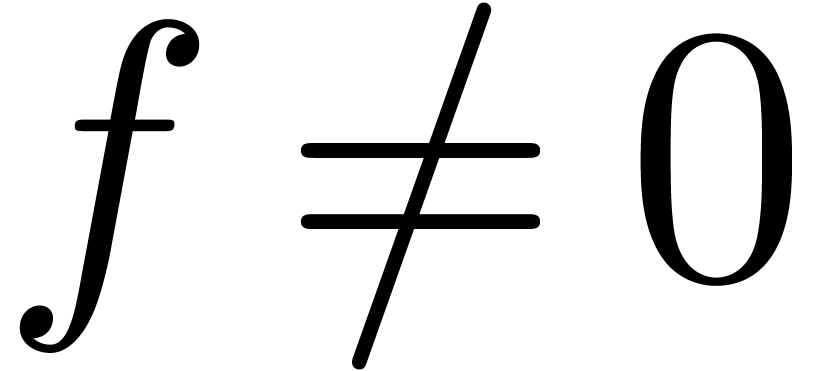 , then we denote by
, then we denote by 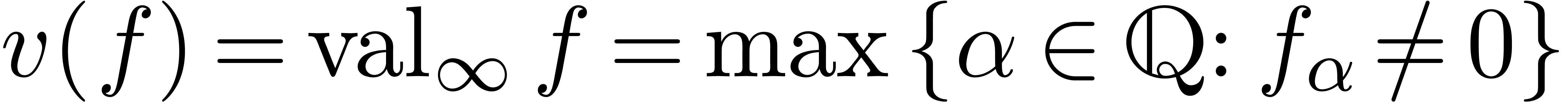 the corresponding valuation of
the corresponding valuation of 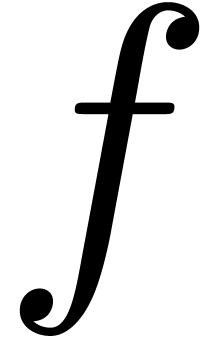 in
in
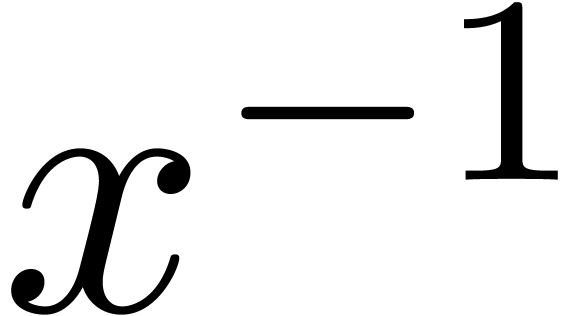 . Notice that we have
. Notice that we have 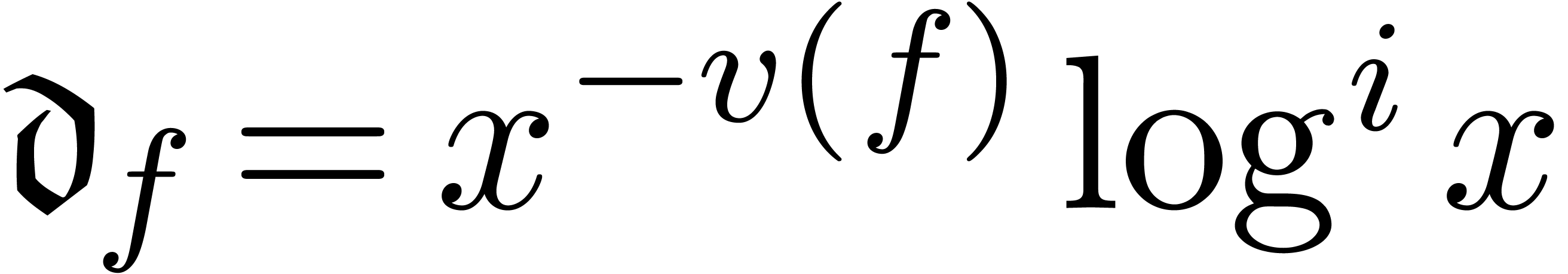 for some
for some 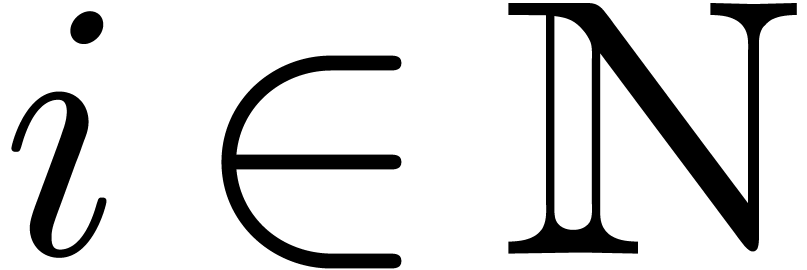 .
.
Let 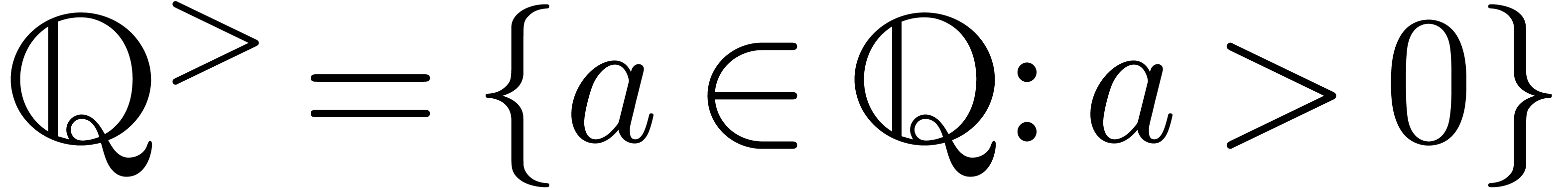 . We write
. We write  for the set of finite
for the set of finite  -linear
combinations of elements of
-linear
combinations of elements of  .
The sets
.
The sets 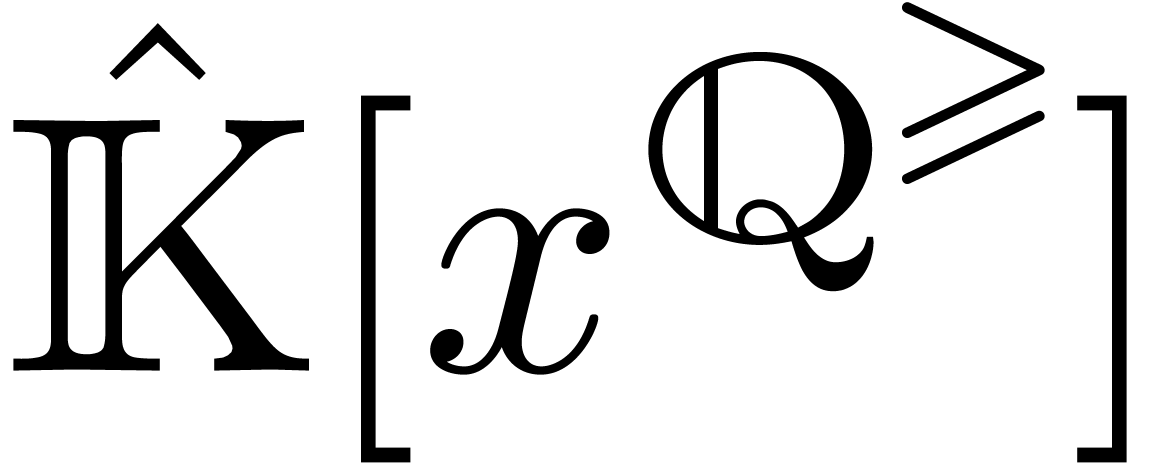 and
and 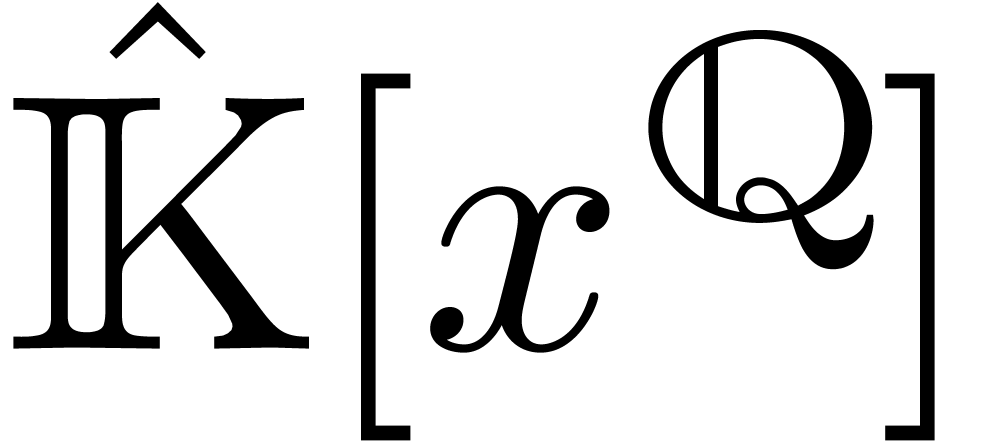 are defined
likewise. Consider the formal exponential monomial group
are defined
likewise. Consider the formal exponential monomial group
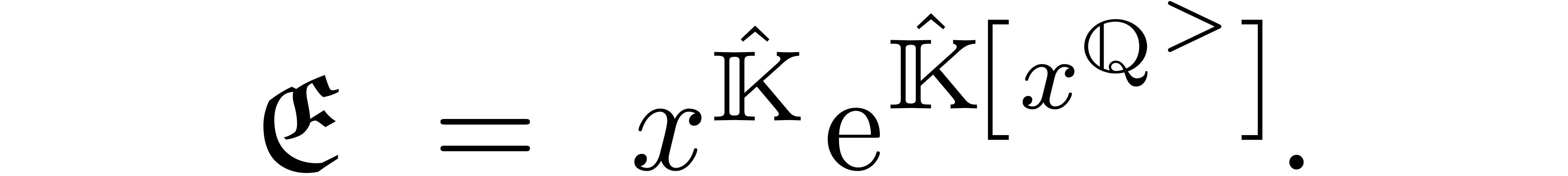
It is well known [1, 11] that the equation (12) admits a basis  of formal solutions
of the form
of formal solutions
of the form
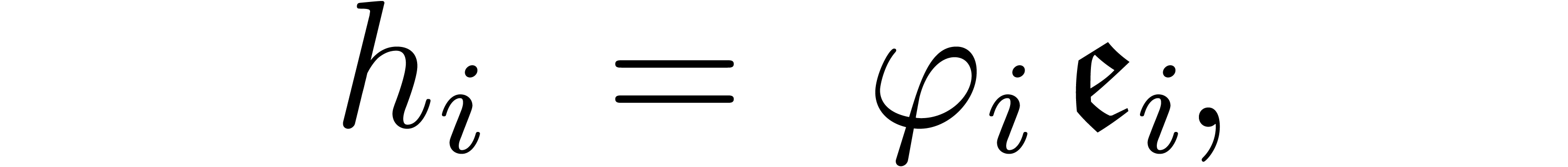
with 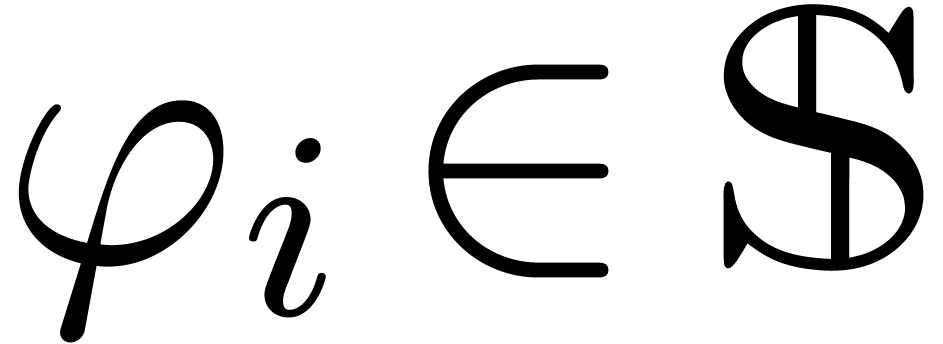 ,
,  and such that the monomials
and such that the monomials  are pairwise
distinct. We will write
are pairwise
distinct. We will write
Notice that this result generalizes to the case when  via a straightforward change of variables
via a straightforward change of variables 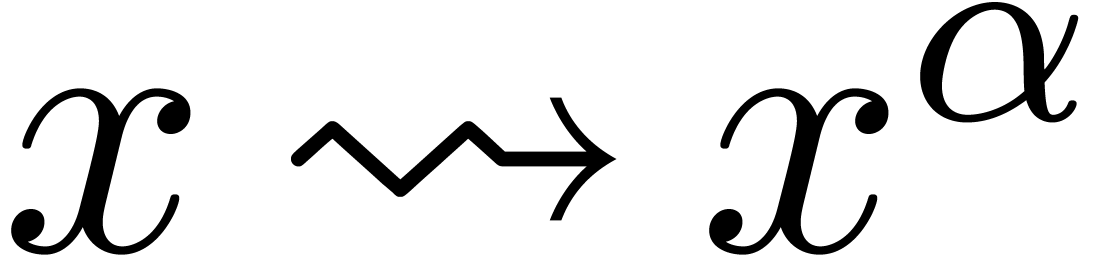 with
with 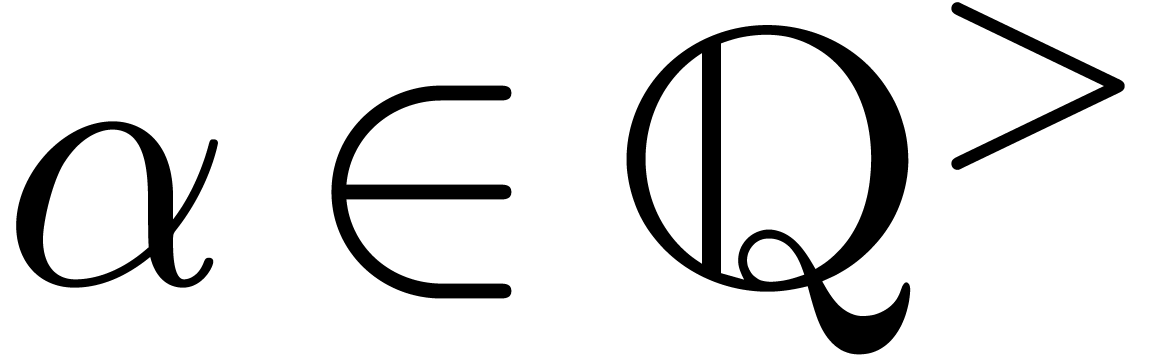 .
.
Let us now consider a linear differential operator 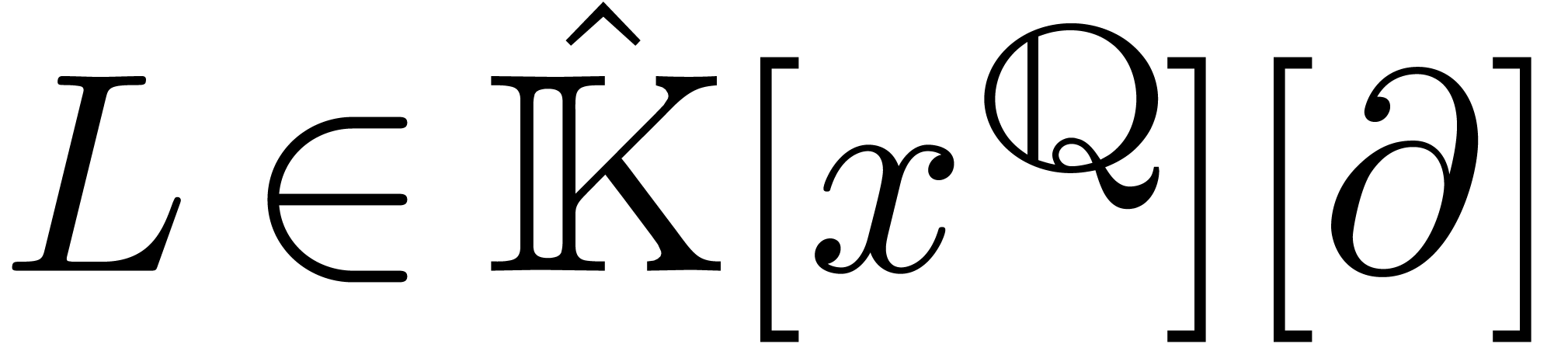 . Such an operator can also be expanded with
respect to
. Such an operator can also be expanded with
respect to 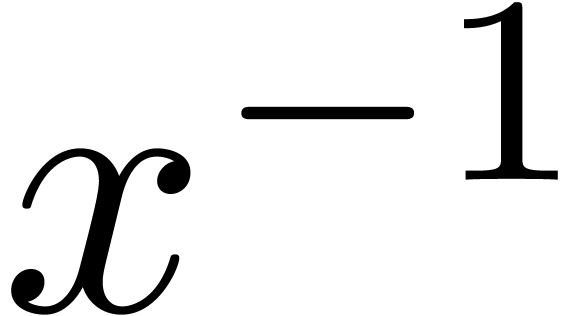 ; we denote by
; we denote by
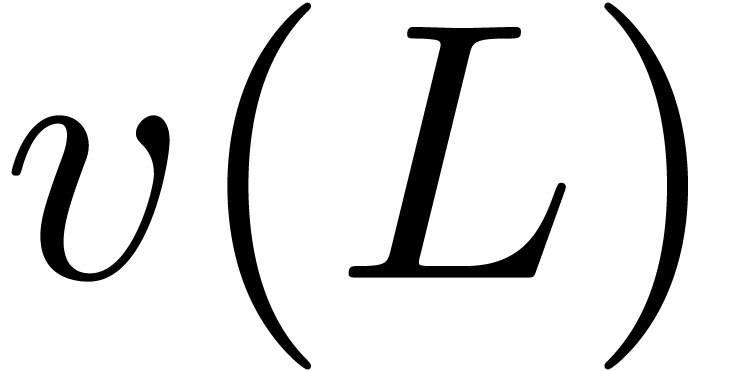 the valuation of
the valuation of  in
in 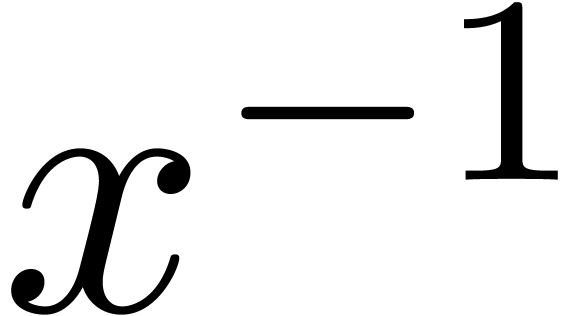 and by
and by  the coefficient of
the coefficient of
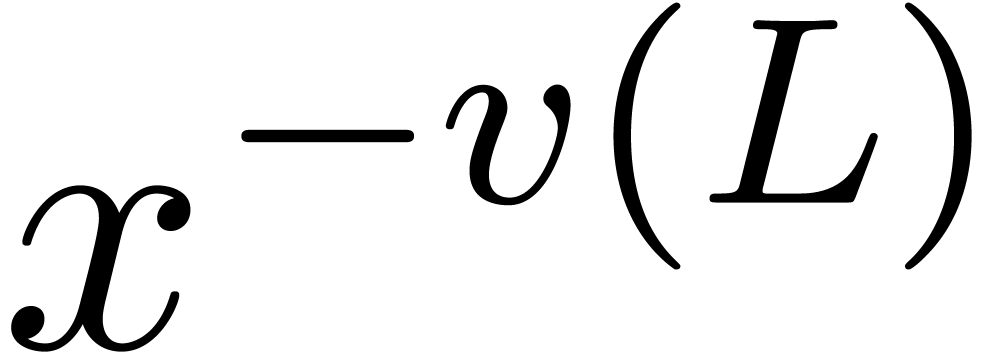 in this expansion.
in this expansion.
From the valuative point of view it is more convenient to work with
linear differential operators 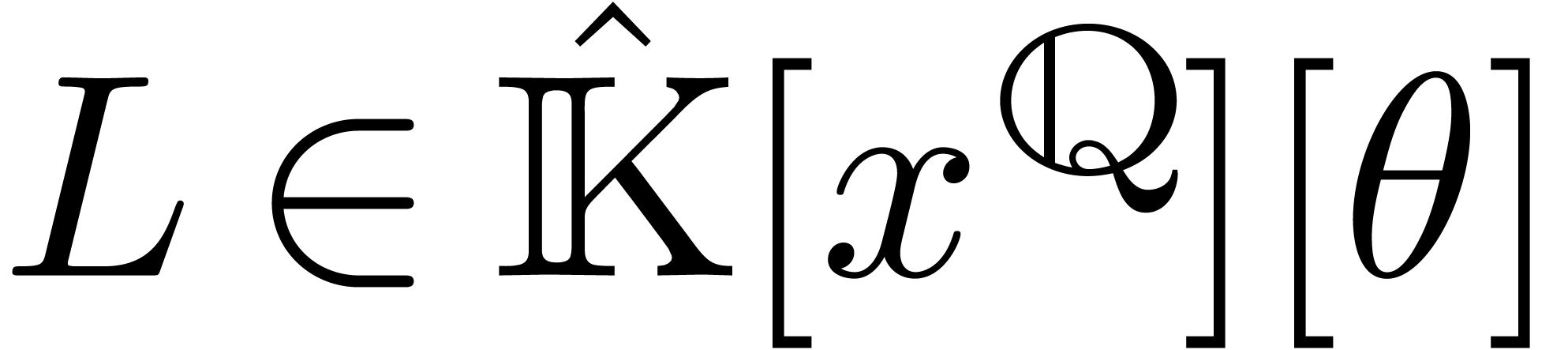 ,
where
,
where 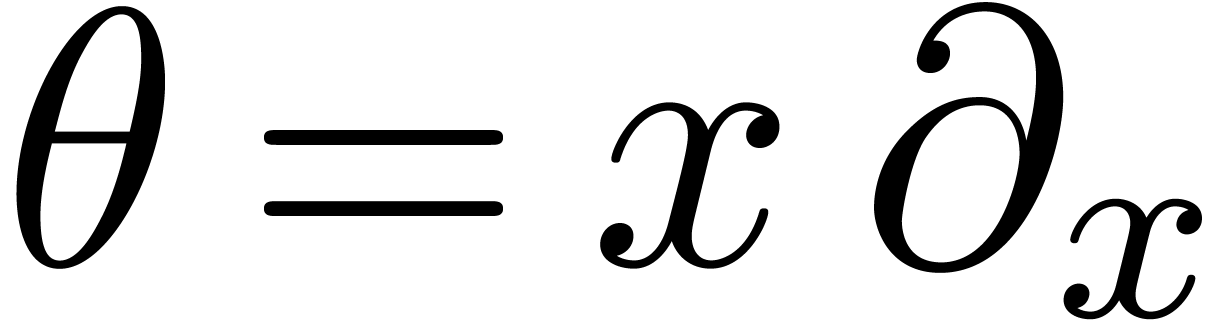 is the Euler derivation. Such operators
can be expanded with respect to
is the Euler derivation. Such operators
can be expanded with respect to  in a similar way
and
in a similar way
and  and
and 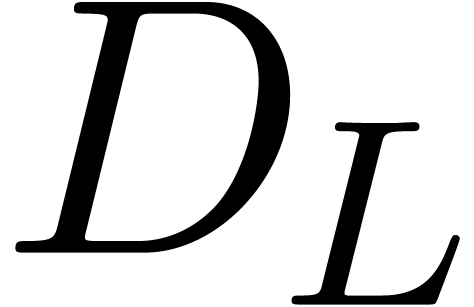 are defined as
above.
are defined as
above.
For 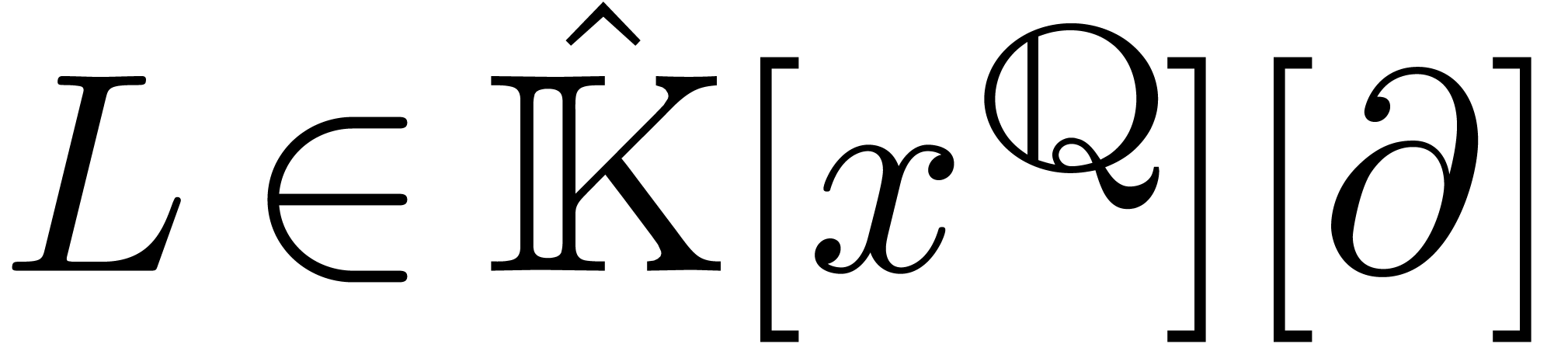 , let
, let 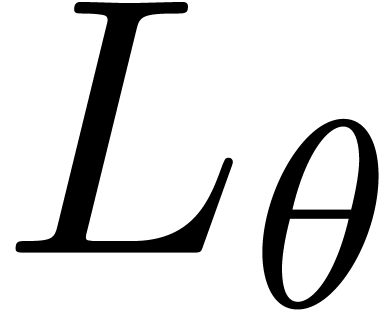 be the corresponding operator in
be the corresponding operator in 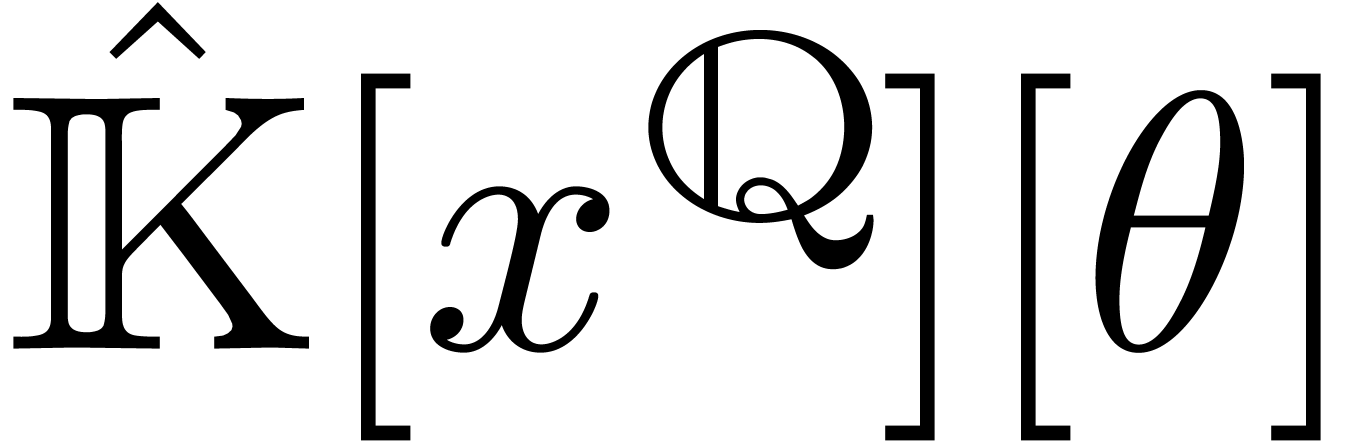 .
If
.
If  has order
has order 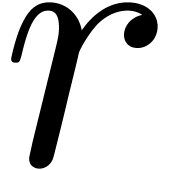 ,
then
,
then
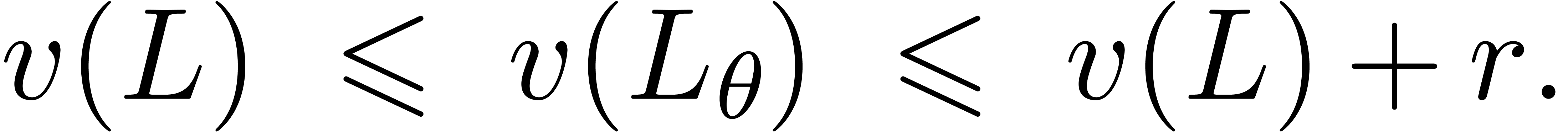
For 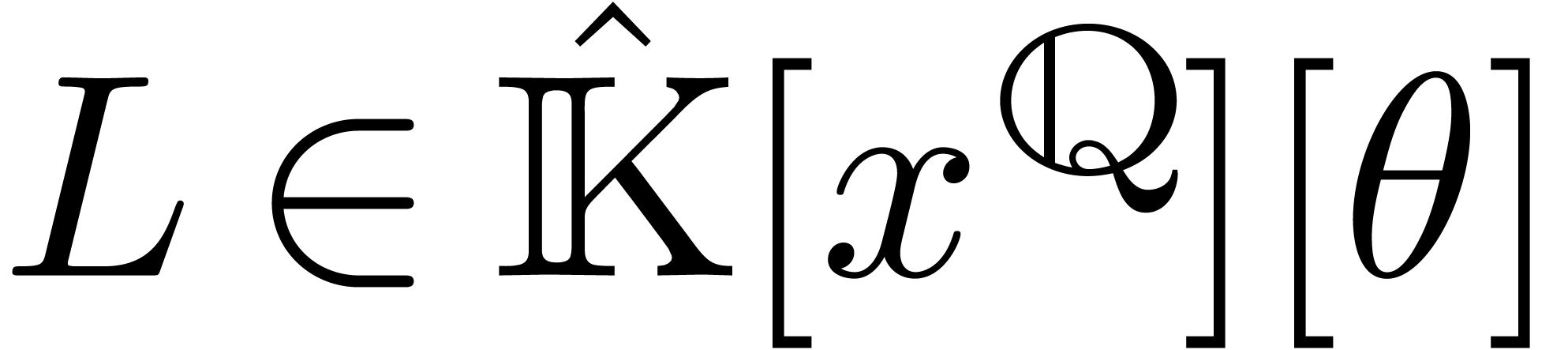 , let
, let  be the corresponding operator in
be the corresponding operator in 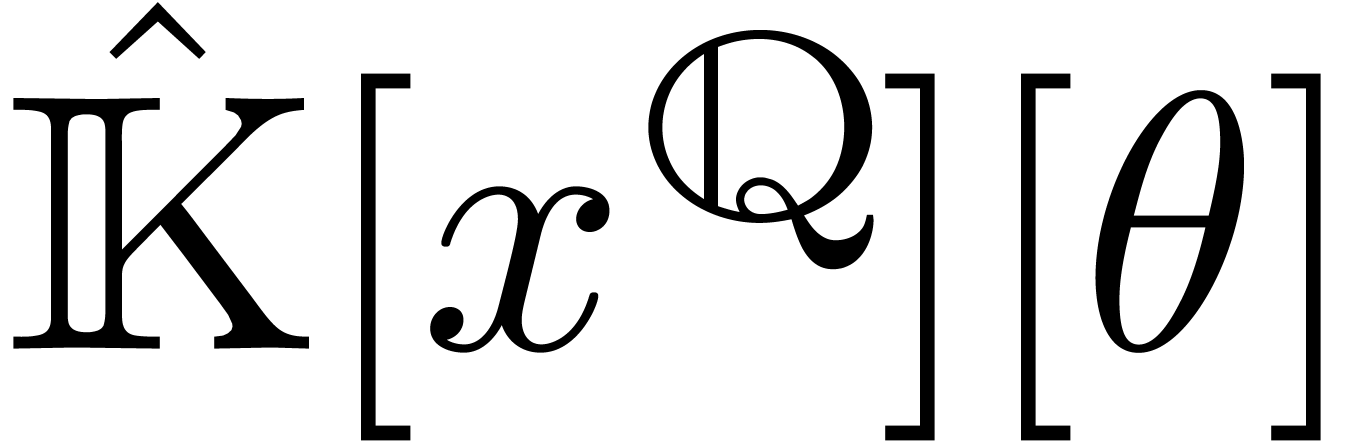 .
If
.
If  has order
has order  ,
then
,
then
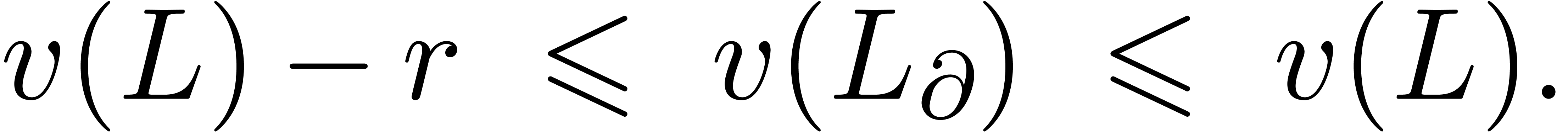
Given 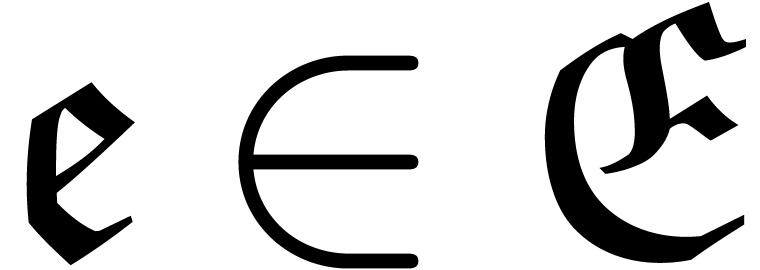 , we notice that its
logarithmic Euler derivative
, we notice that its
logarithmic Euler derivative 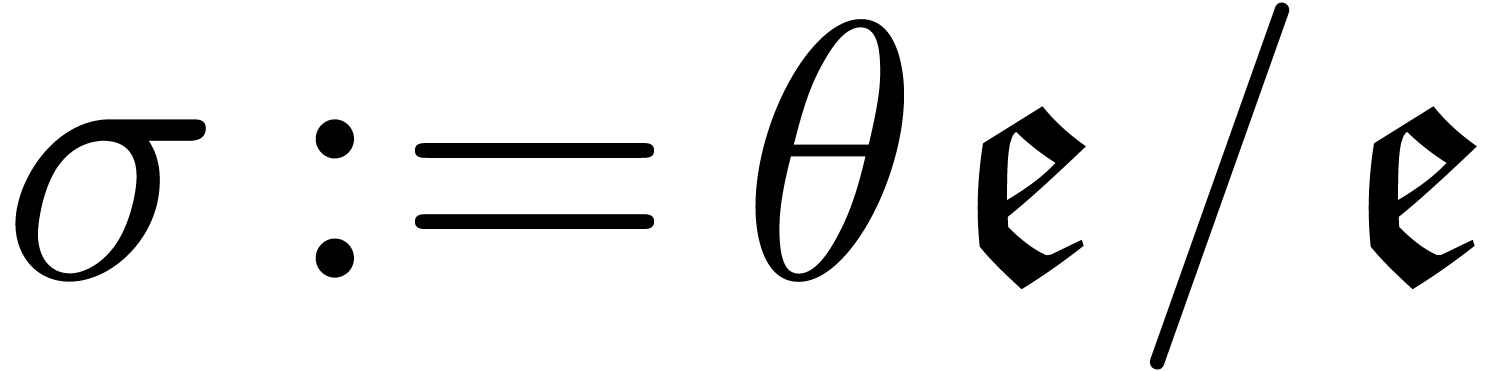 belongs to
belongs to 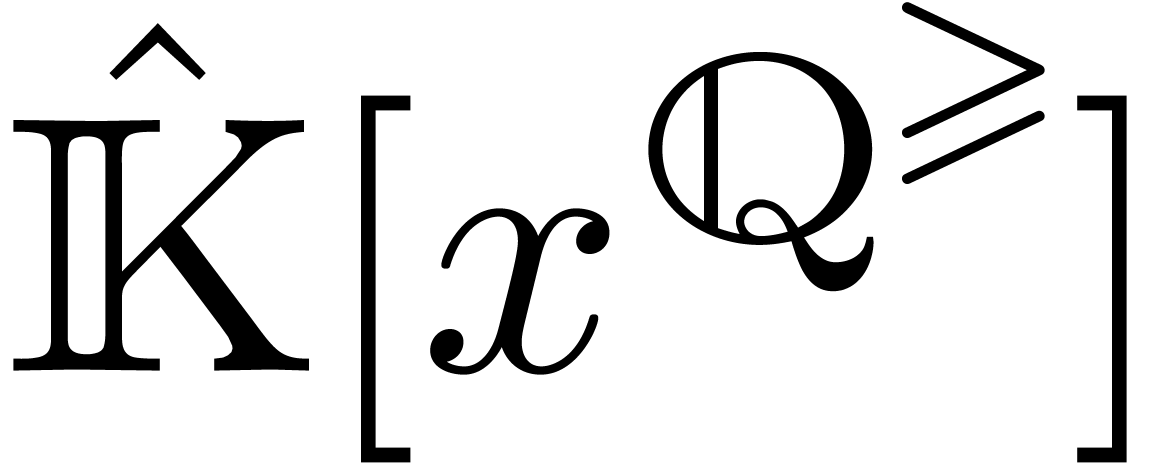 . Let
. Let 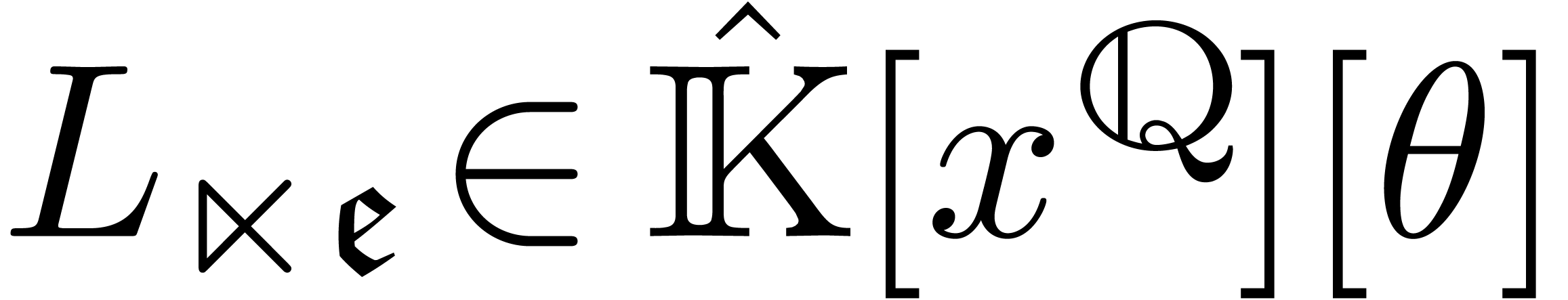 be
the operator obtained from
be
the operator obtained from  by substituting
by substituting  for
for  . Then
. Then
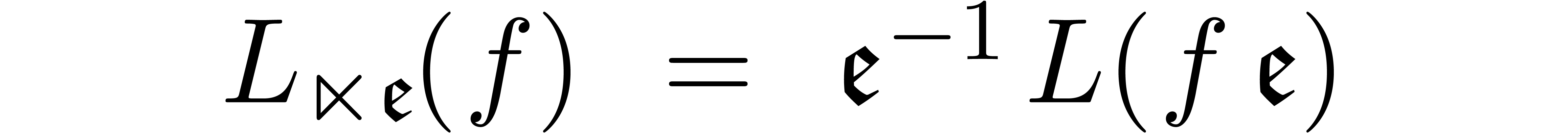
for all  . If
. If 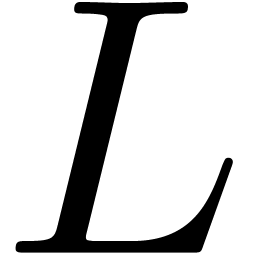 has order
has order 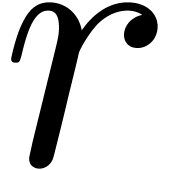 , then
, then
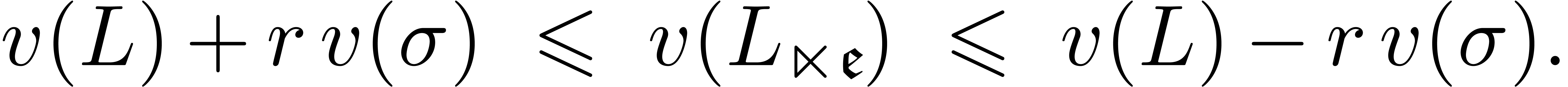
We call 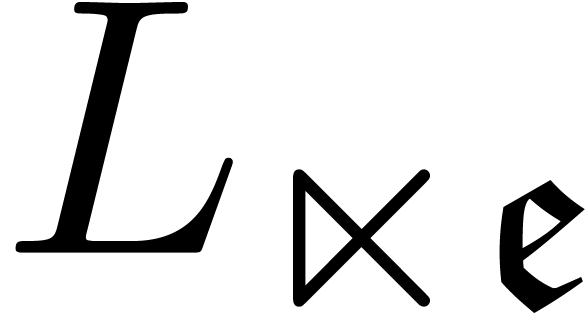 the twist of
the twist of  by
by  .
.
Now consider an operator 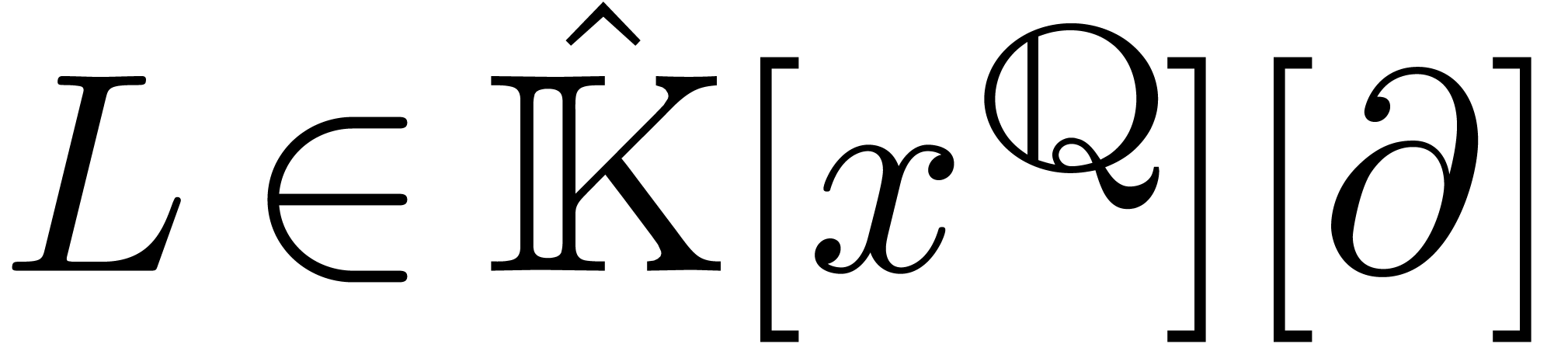 and
and  . If
. If 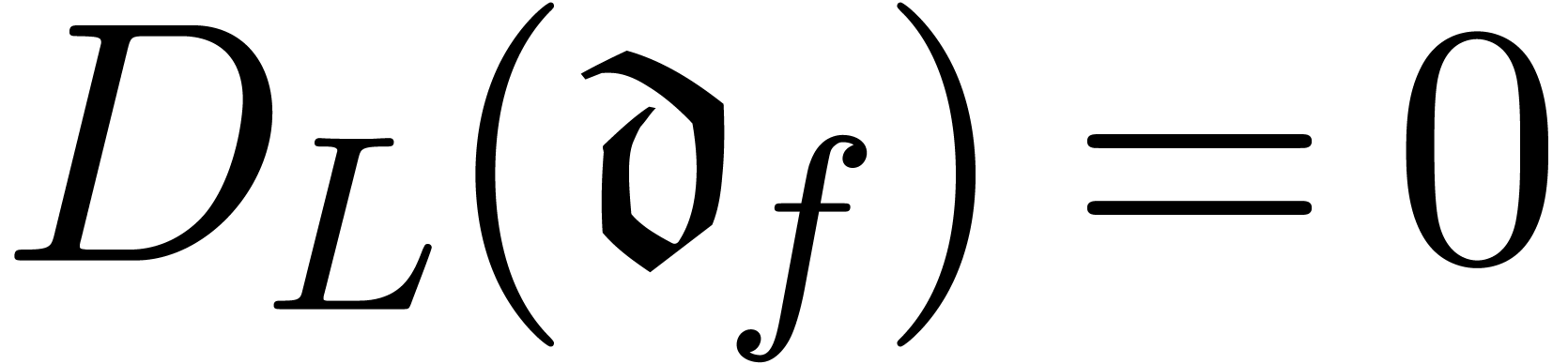 ,
then it can be shown that
,
then it can be shown that 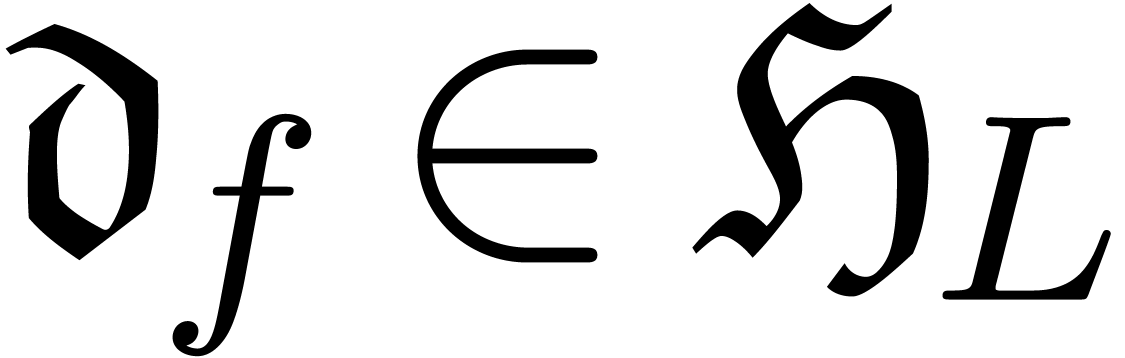 .
Otherwise,
.
Otherwise, 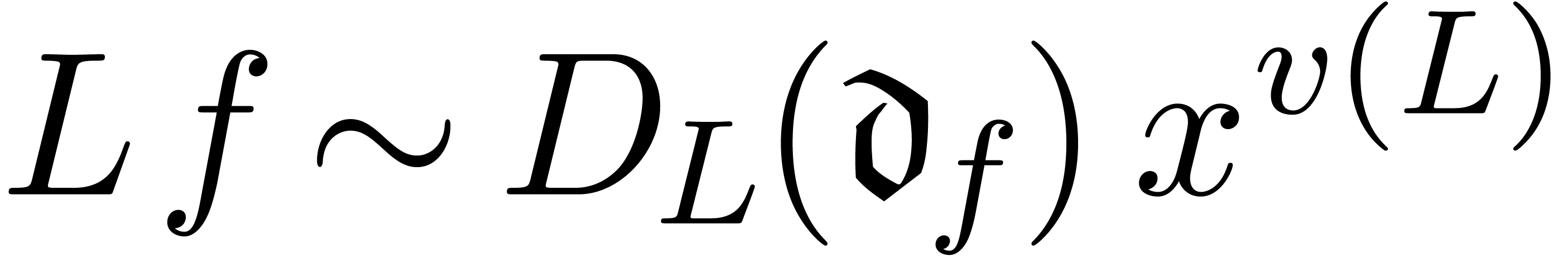 , whence
, whence 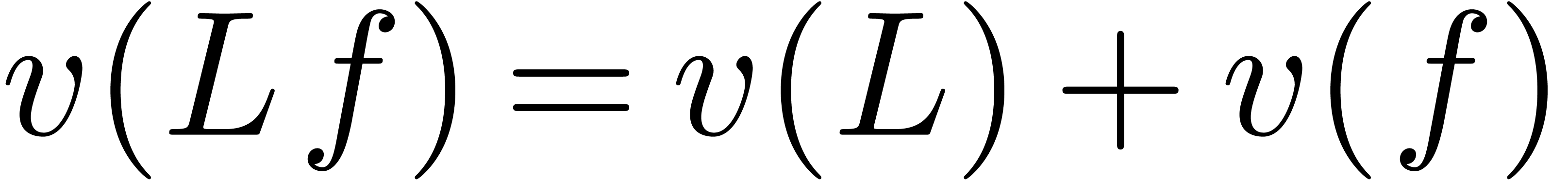 . In other words,
. In other words,
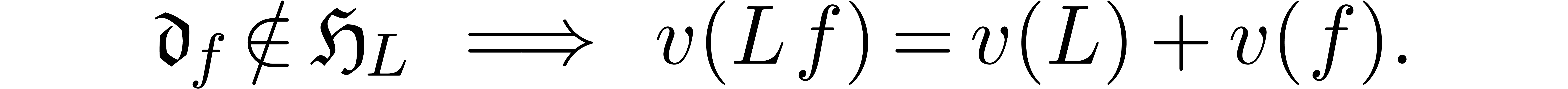
More generally, if  and
and 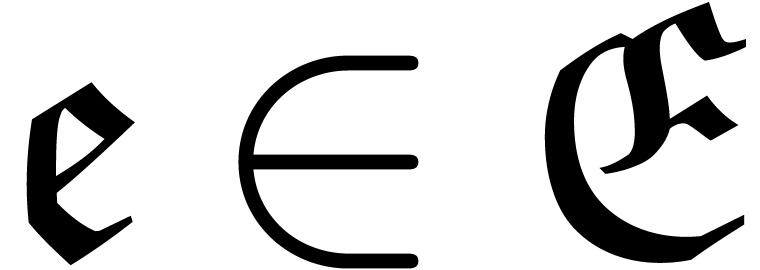 , then
, then
Let

If 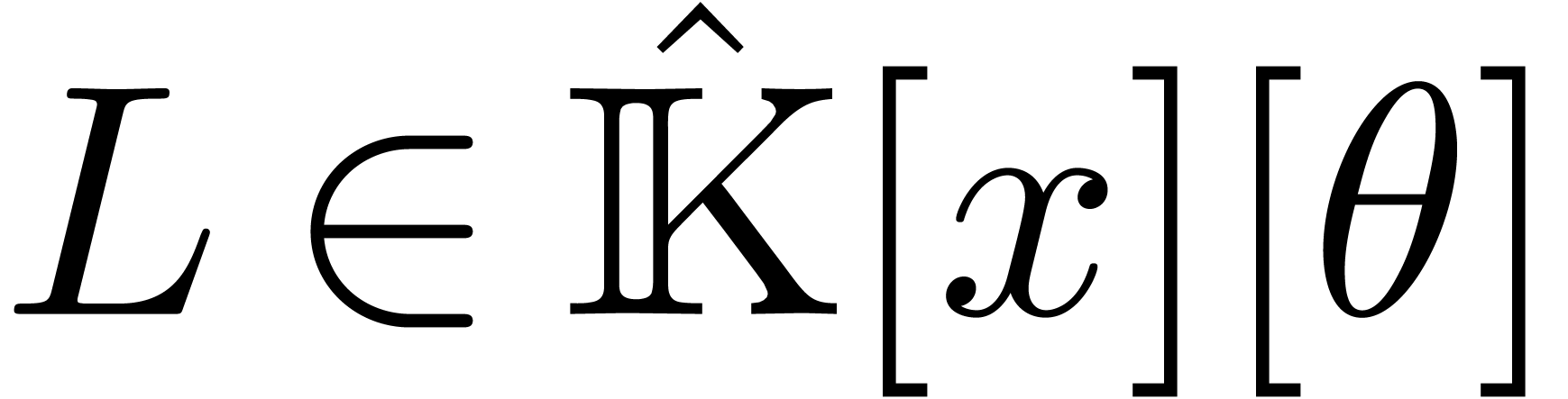 , then it can be shown
using the Newton polygon method that
, then it can be shown
using the Newton polygon method that 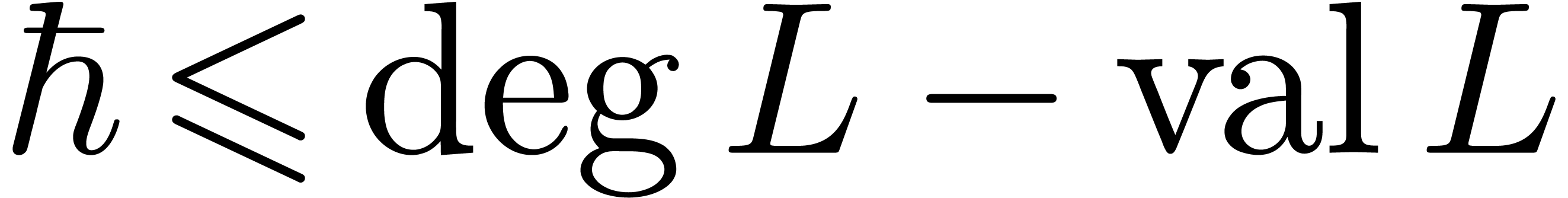 .
.
Let 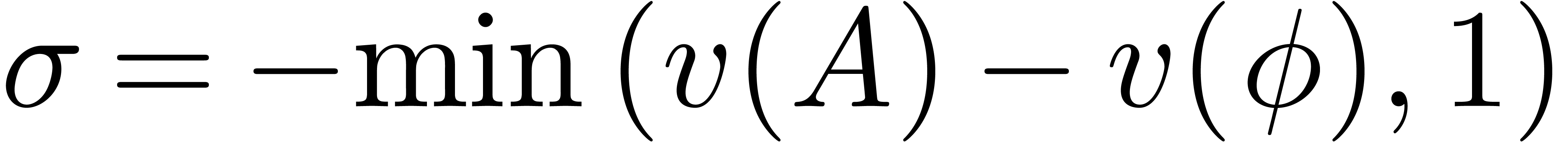 and notice that
and notice that 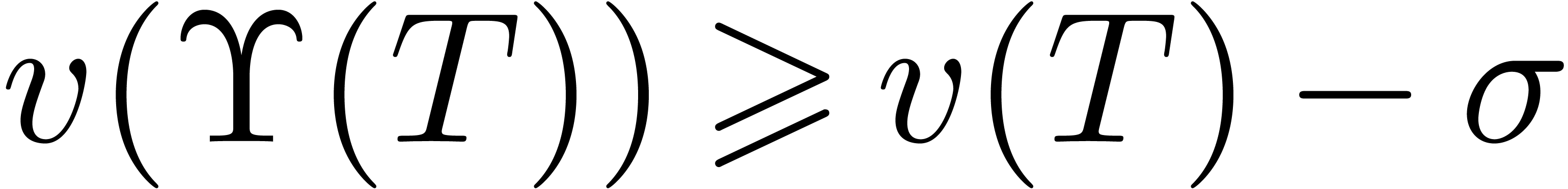 for
all
for
all 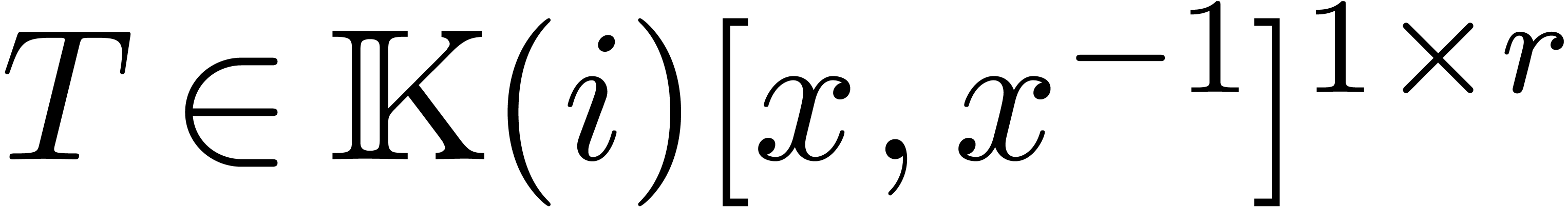 .
.
Proof. Let  be a
transcendental constant over
be a
transcendental constant over  with
with 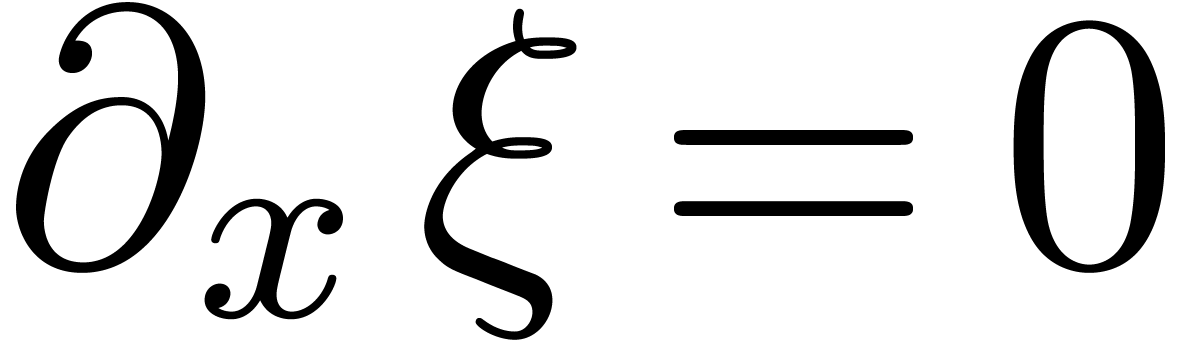 and let
and let 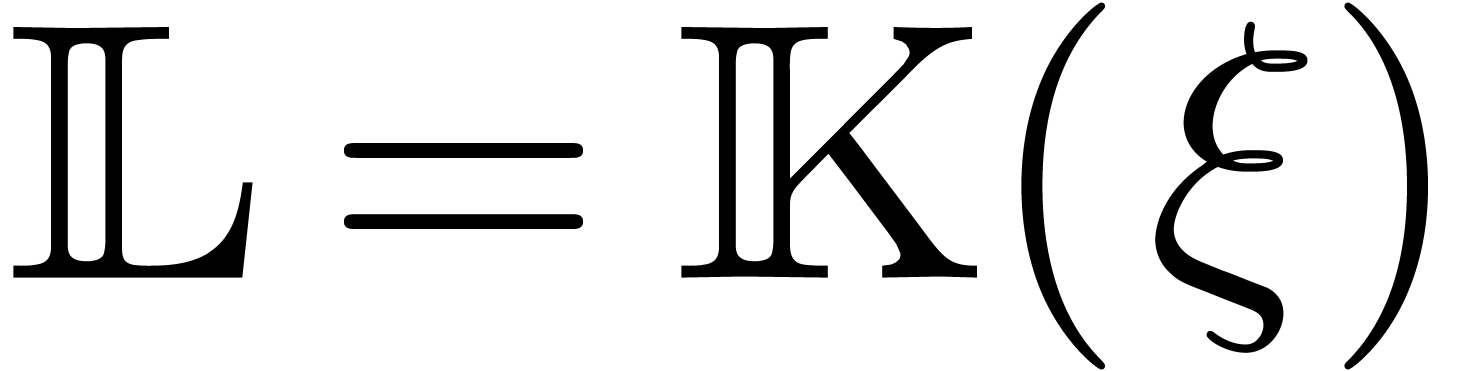 . Then
. Then
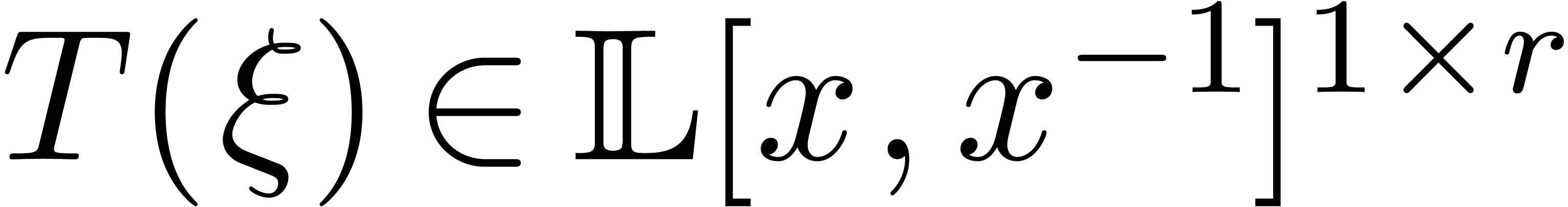 satisfies
satisfies 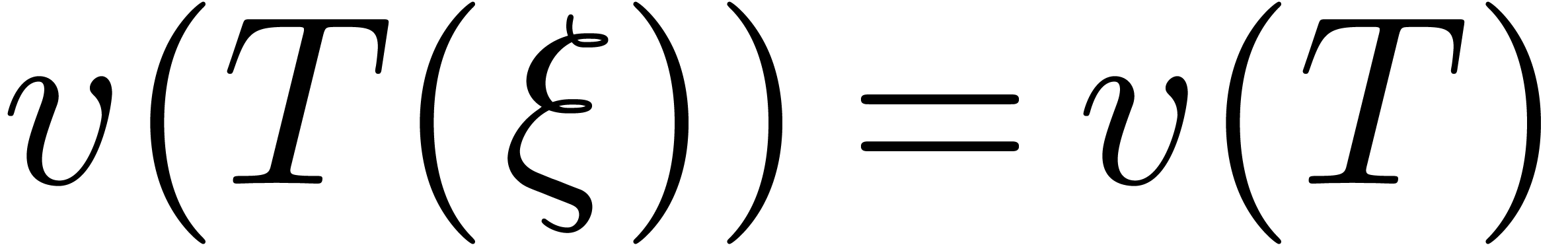 ,
,
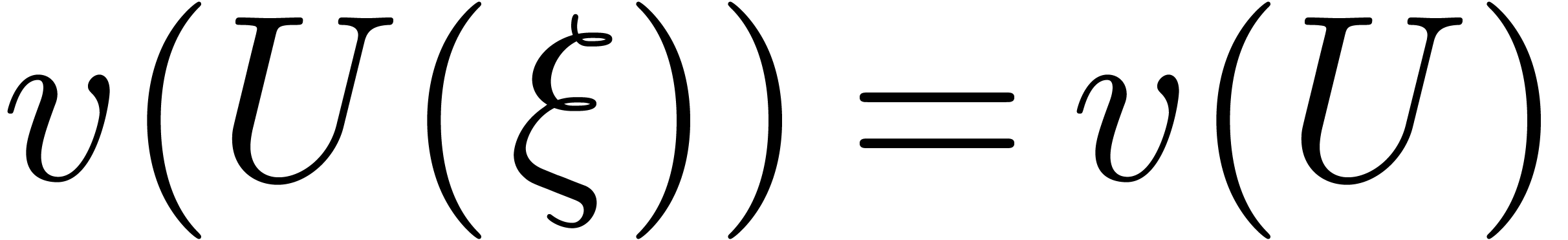 , and
, and
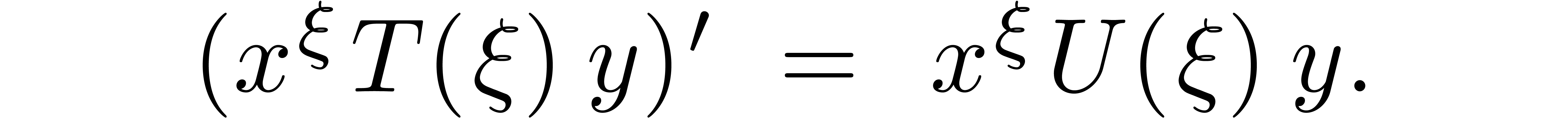
We may rewrite 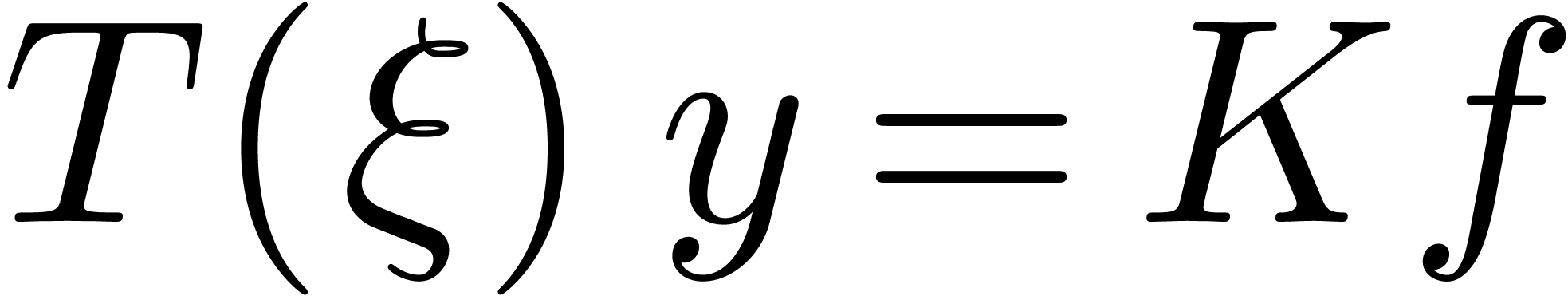 for the linear differential
operator
for the linear differential
operator 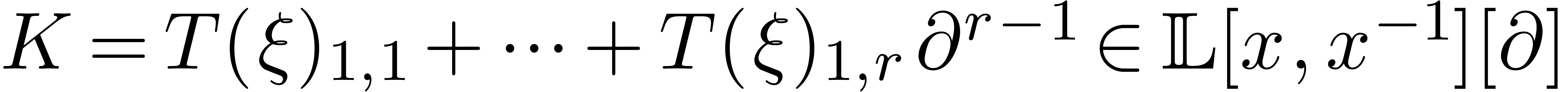 . Notice that
. Notice that 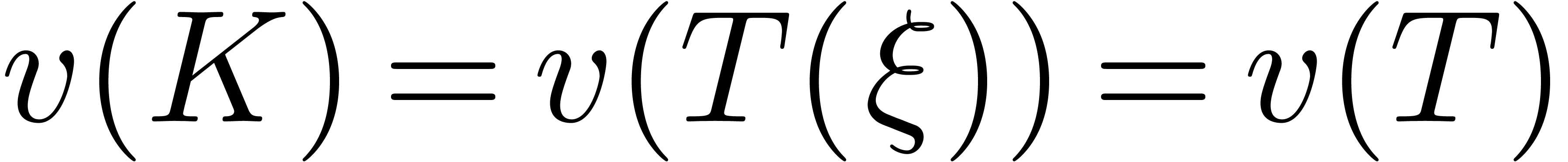 . Similarly, we may rewrite
. Similarly, we may rewrite 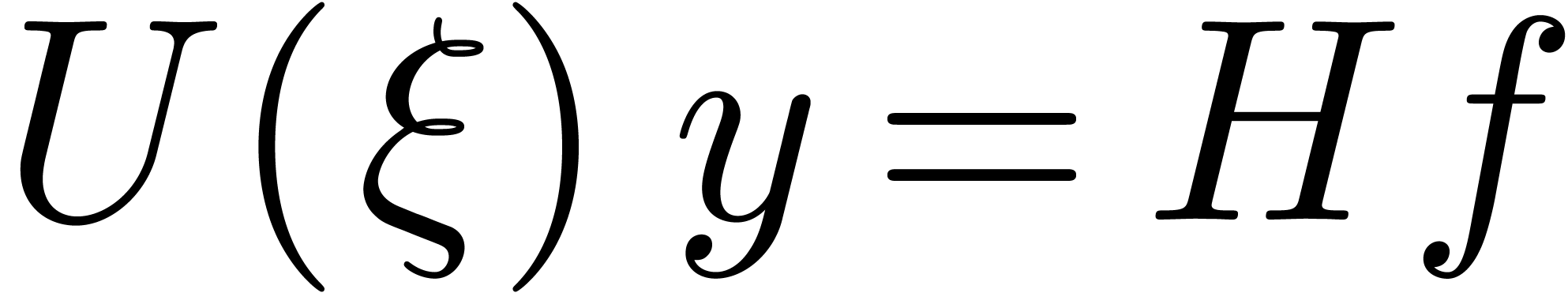 for some operator
for some operator 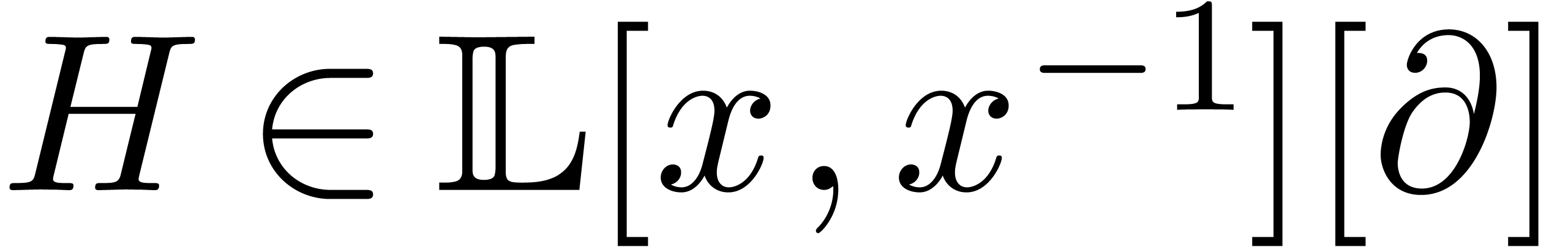 with
with 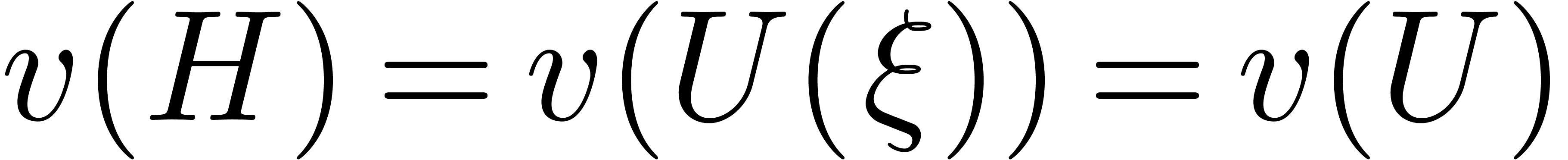 .
.
Let 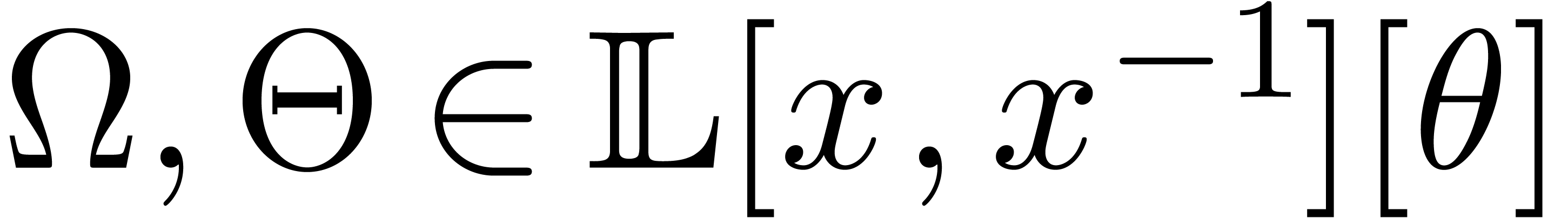 be the operators given by
be the operators given by 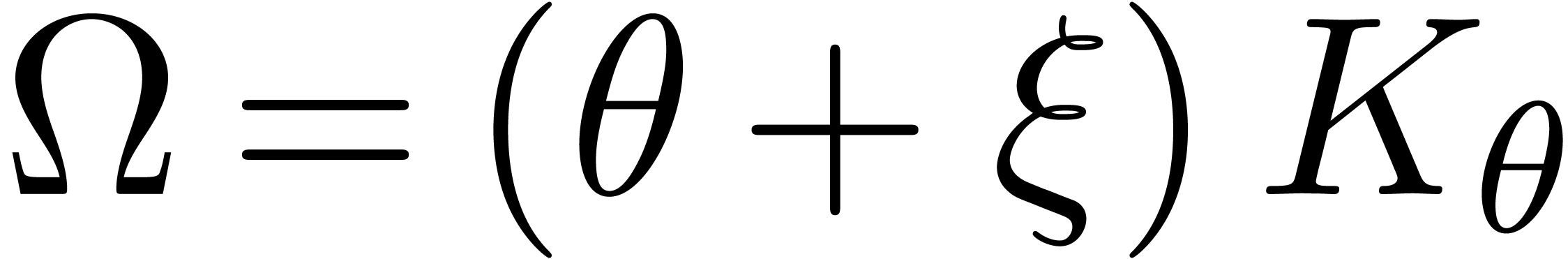 and
and 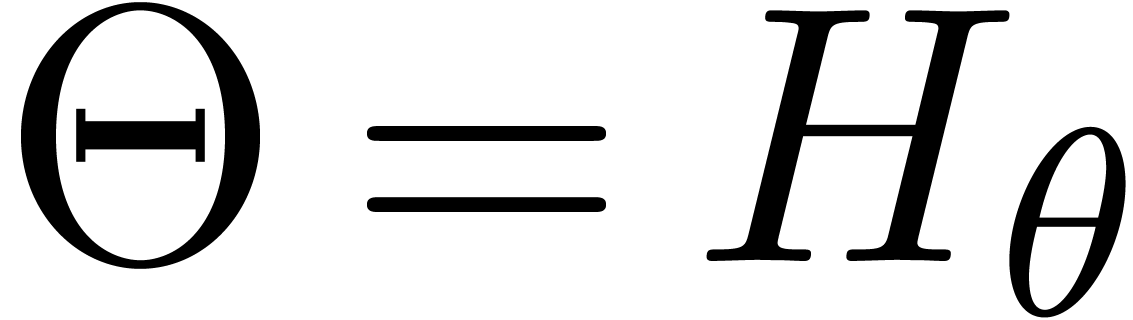 , so that
, so that 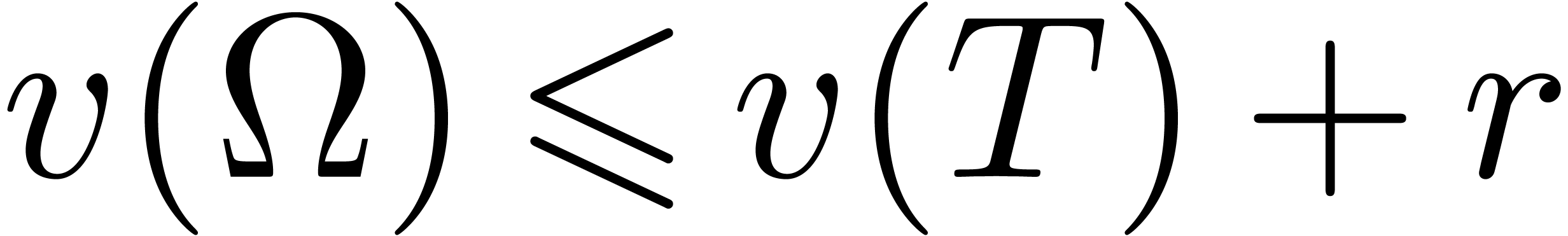 and
and  . By
construction,
. By
construction,
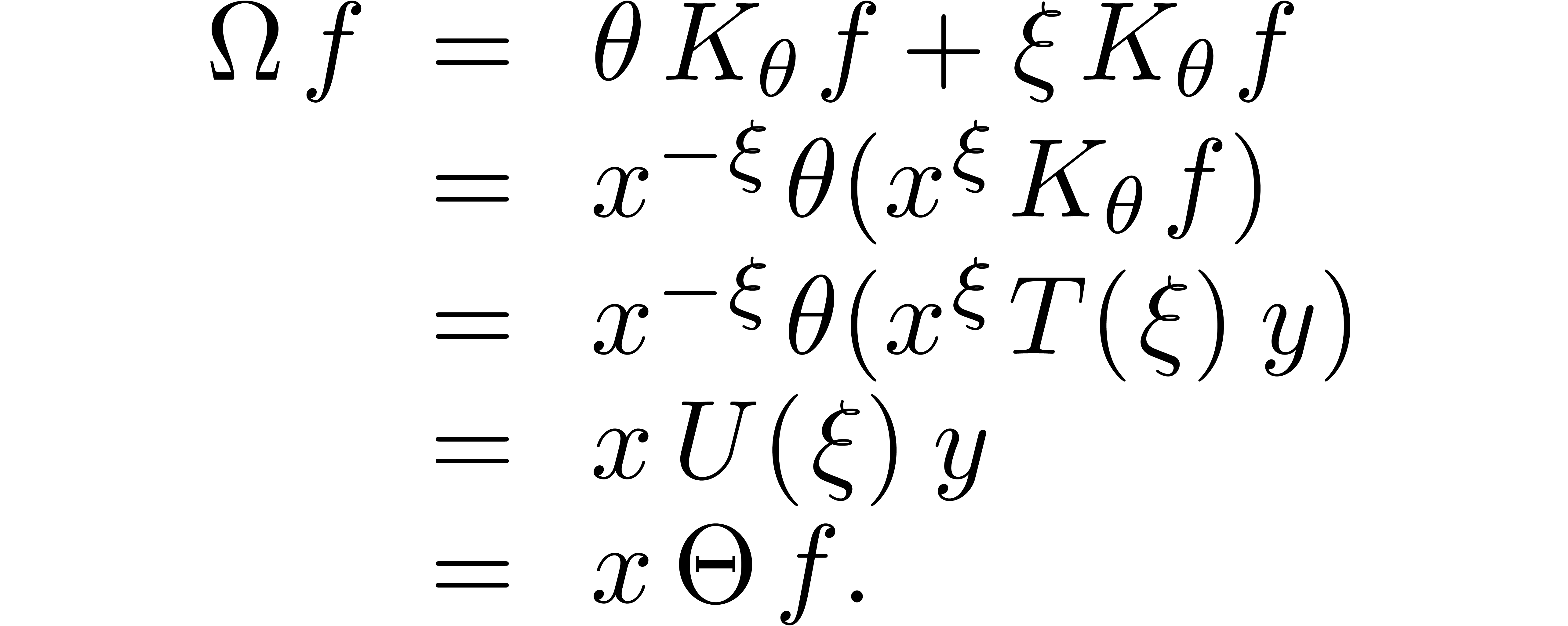
Since  has order at most
has order at most  , there exists a monomial
, there exists a monomial 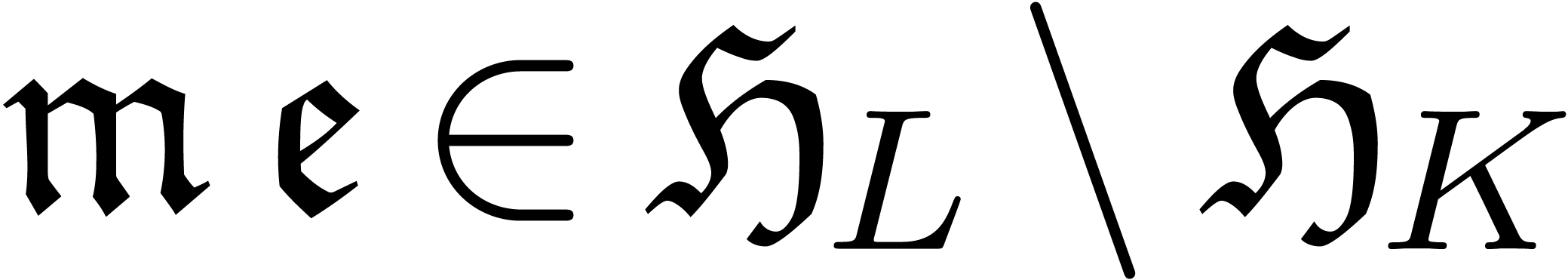 with
with  and
and  .
Now the solutions of
.
Now the solutions of 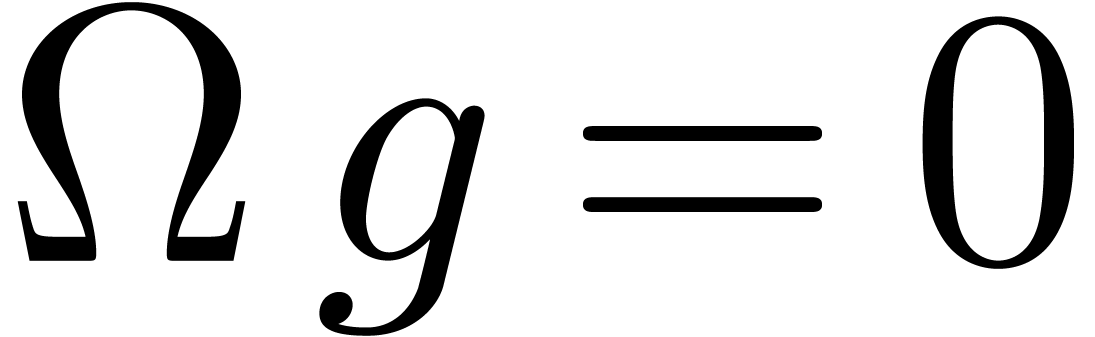 are spanned by the
solutions to
are spanned by the
solutions to 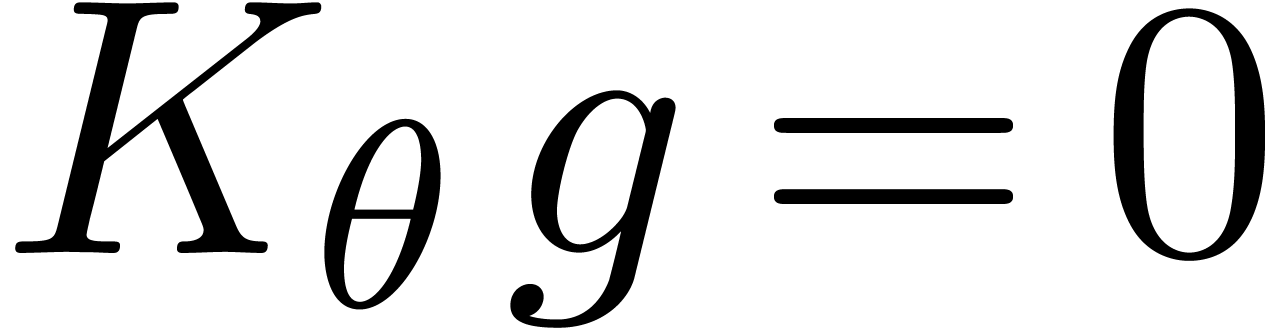 and any particular solution to the
inhomogeneous equation
and any particular solution to the
inhomogeneous equation 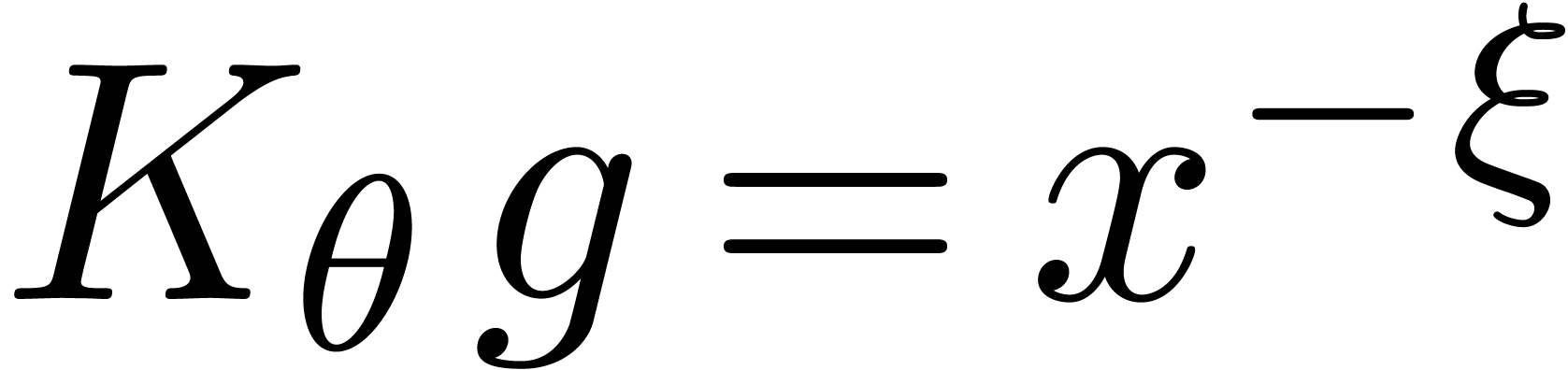 . In
[11, Chapter 7] it is shown that the latter equation admits
a so called distinguished solution
. In
[11, Chapter 7] it is shown that the latter equation admits
a so called distinguished solution 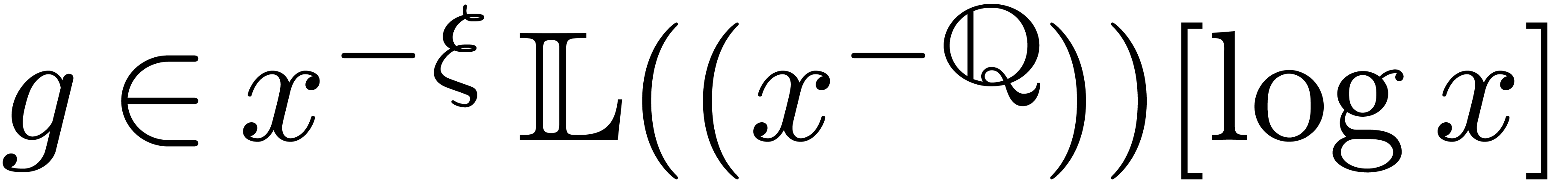 with
with 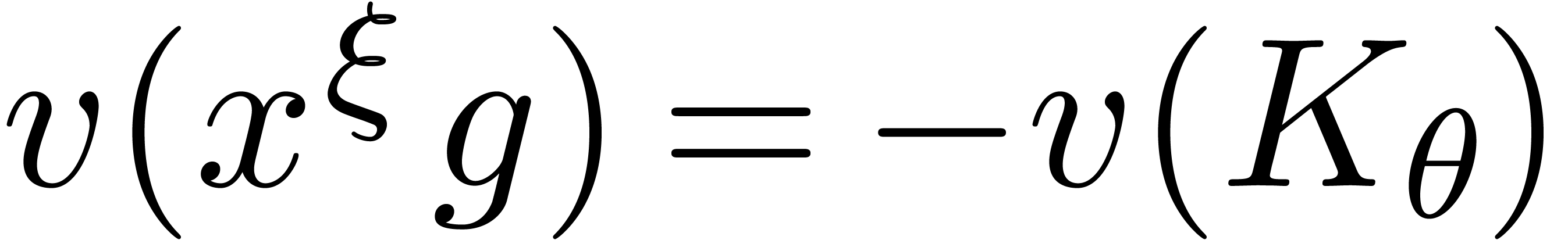 and
and 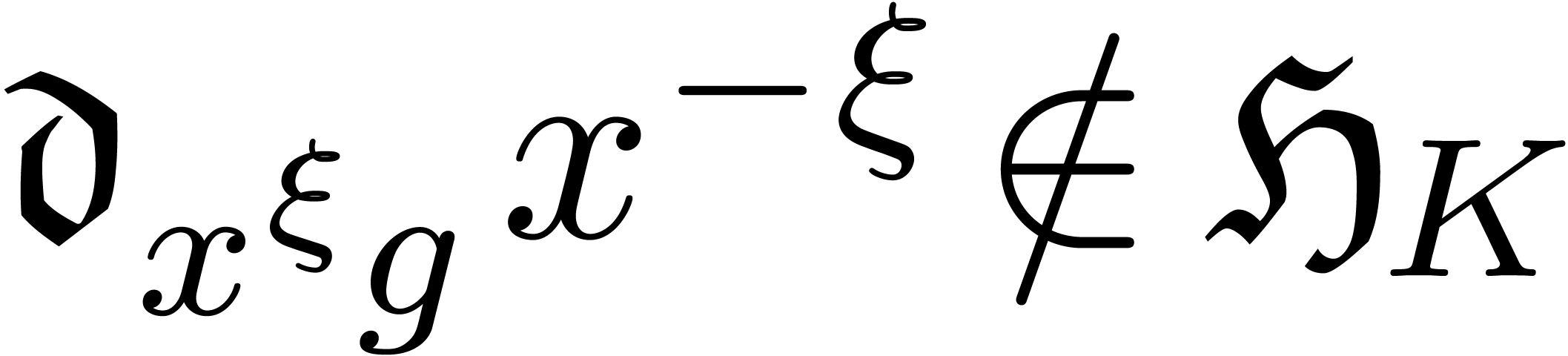 .
Since
.
Since  is transcendental over
is transcendental over  , it follows that
, it follows that 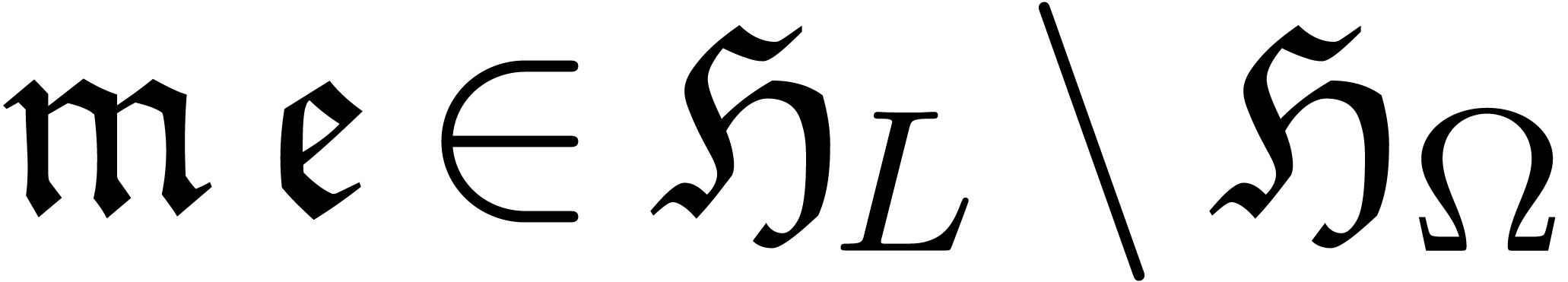 .
Let
.
Let  be a solution to
be a solution to  with
with  . Then
. Then  satisfies
satisfies
whereas
(The last equality follows from (13) and the fact that
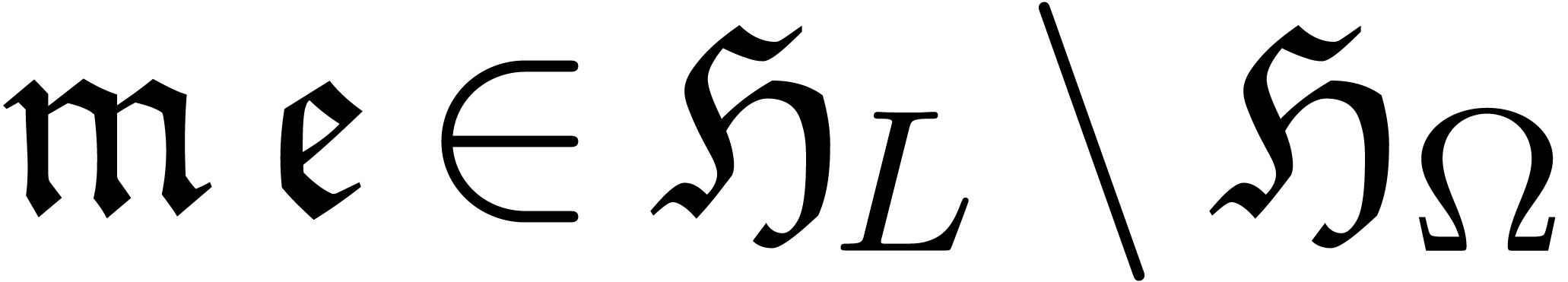 .) Now
.) Now 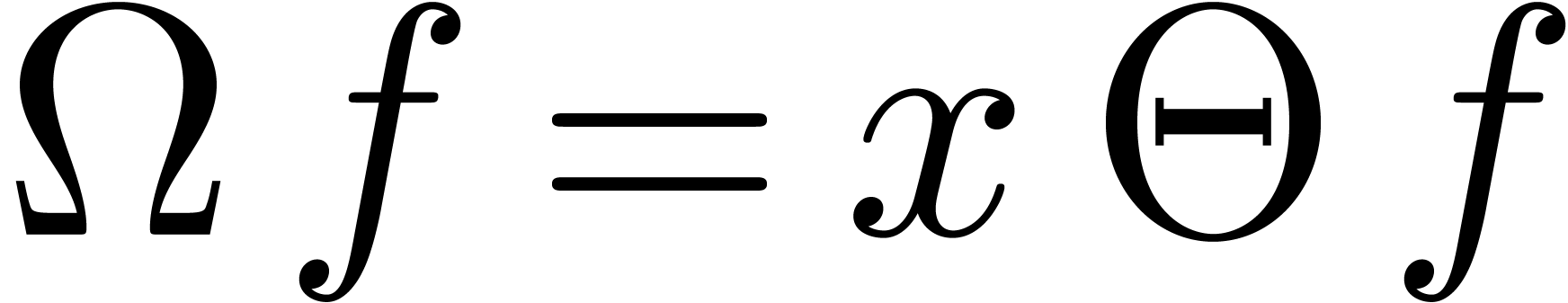 implies
implies
whence
We already noticed before that 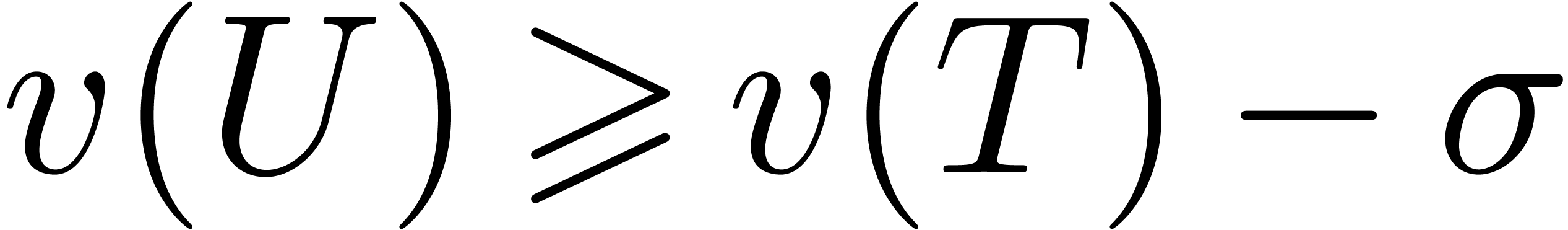 .□
.□
We notice that our definition of  coincides with
the one from section 4.2, since the degree in
coincides with
the one from section 4.2, since the degree in  coincides with the opposite of the valuation in
coincides with the opposite of the valuation in 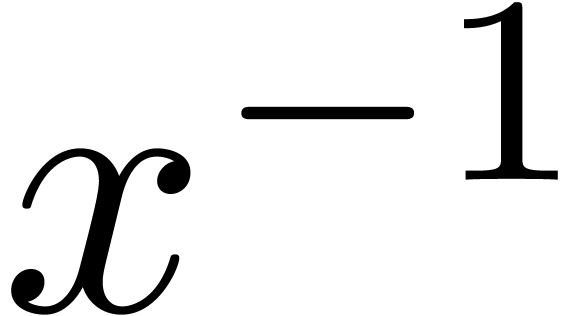 . Theorem 16
immediately yields a bound for the number
. Theorem 16
immediately yields a bound for the number  of
iterations that are necessary in HeadChopper in order
to obtain a head chopper. More precisely:
of
iterations that are necessary in HeadChopper in order
to obtain a head chopper. More precisely:
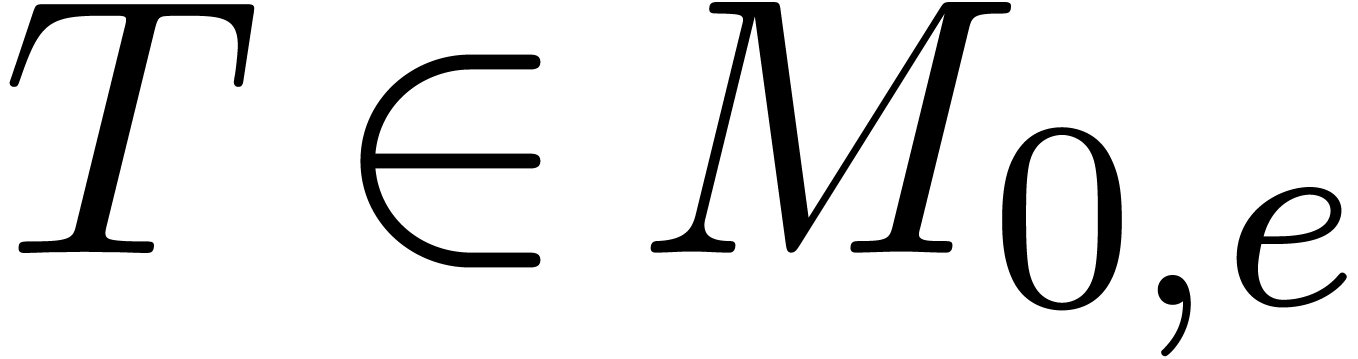 for
for  .
.
Proof. Let  be the head
chopper as computed by HeadChopper and let
be the head
chopper as computed by HeadChopper and let 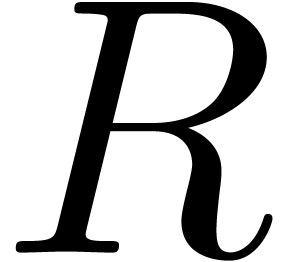 be its last row. Then
be its last row. Then 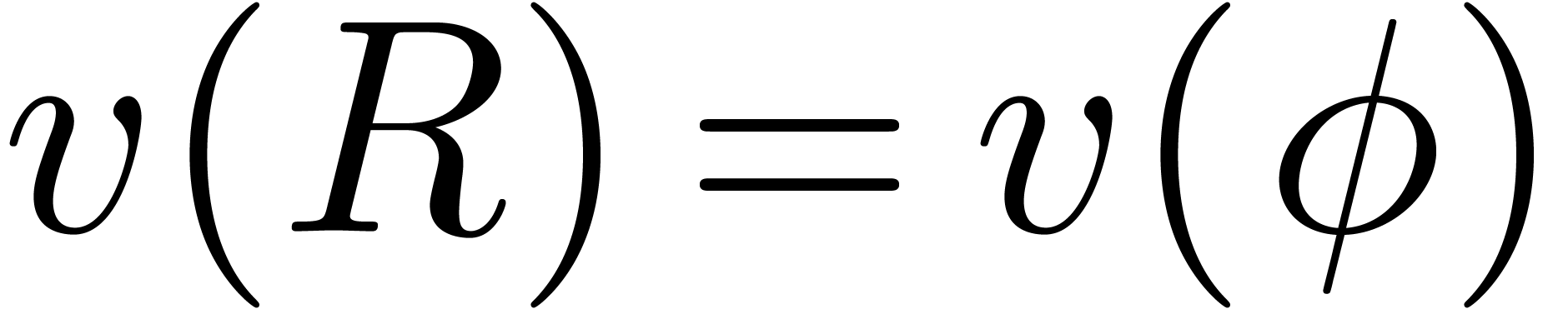 and
and 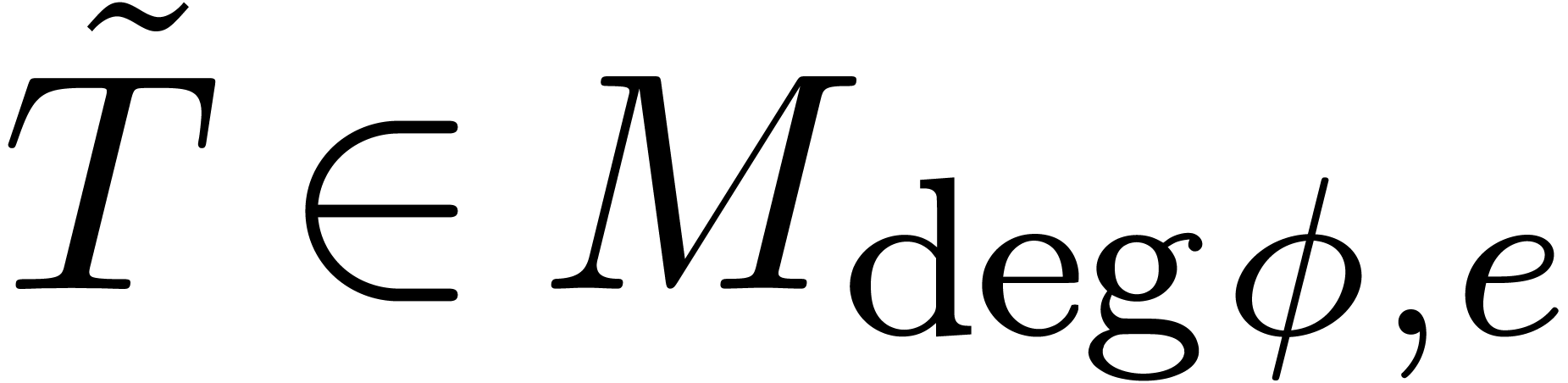 where
where 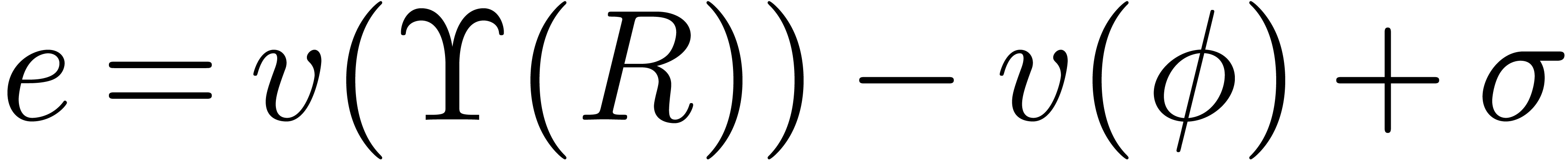 .
Now the theorem implies
.
Now the theorem implies 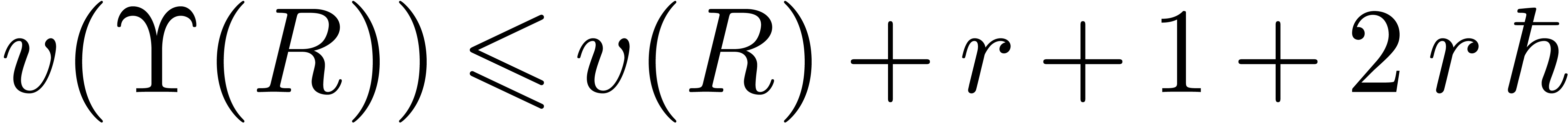 ,
whence
,
whence  . We conclude that
. We conclude that
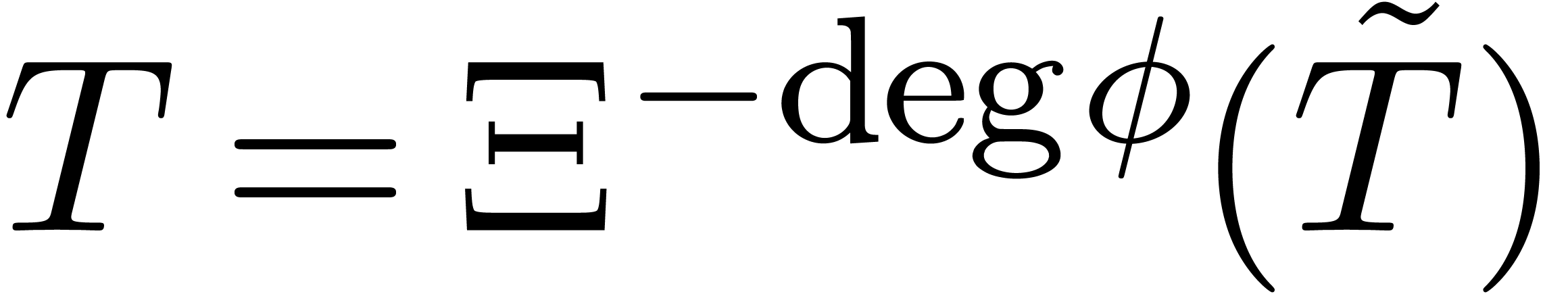 is a head chopper in
is a head chopper in 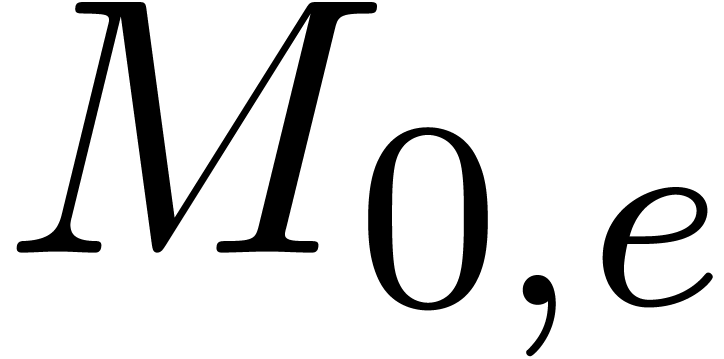 .□
.□
Let  ,
,  , and let
, and let 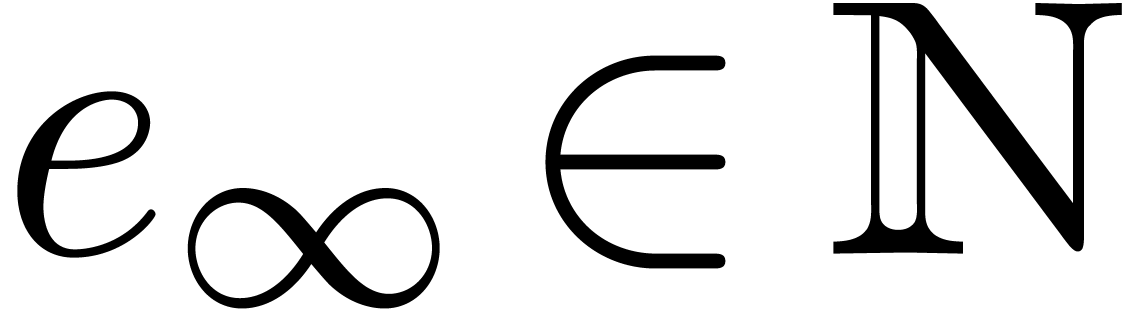 be the smallest
number for which there exists a head chopper
be the smallest
number for which there exists a head chopper  with
with
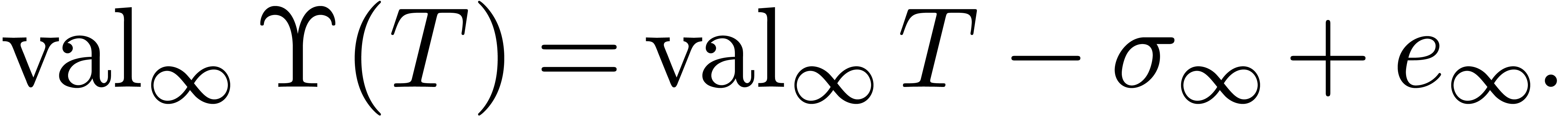 |
(14) |
We will call 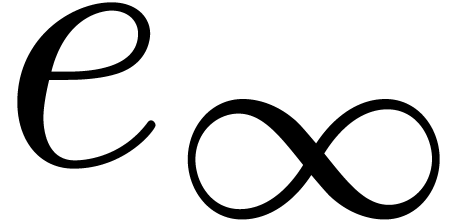 the defect of (1)
at infinity. Collarary 17 shows that
the defect of (1)
at infinity. Collarary 17 shows that 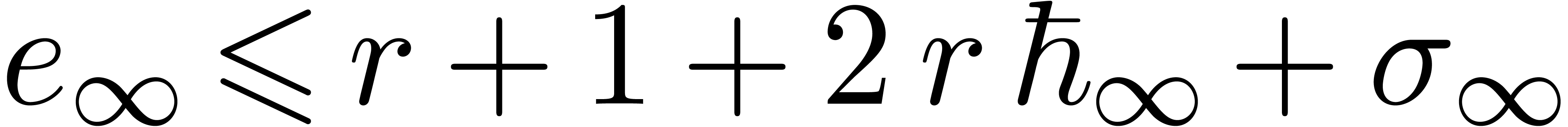 . In a similar way, given
. In a similar way, given 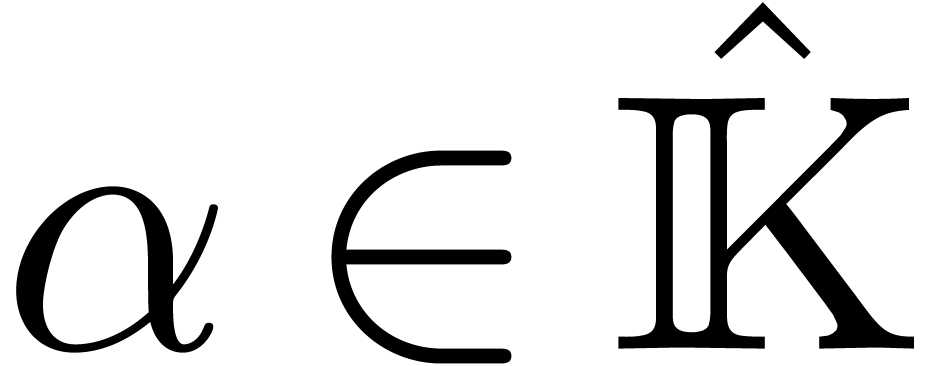 , let
, let 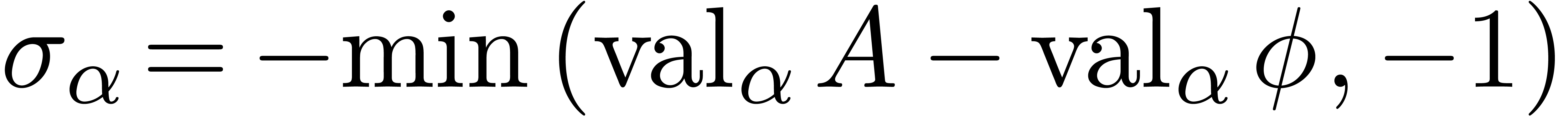 and let
and let  be the smallest number for which there exists a tail
chopper
be the smallest number for which there exists a tail
chopper  with
with
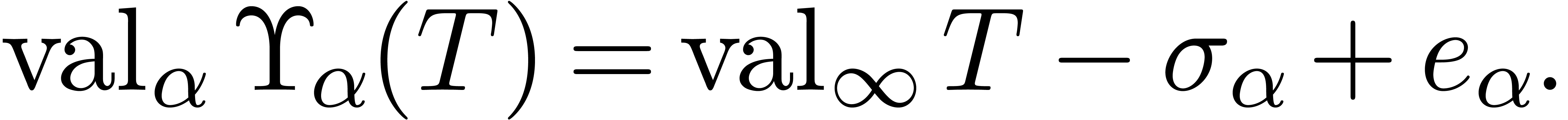 |
(15) |
We call 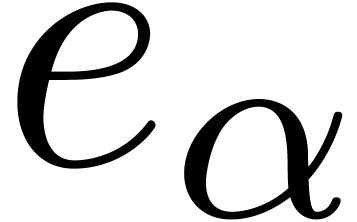 the defect of (1)
at
the defect of (1)
at  . Defining
. Defining 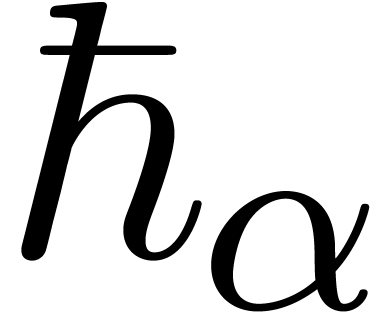 in a similar way as
in a similar way as 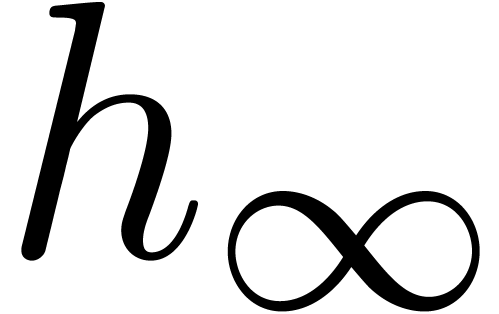 ,
but at the point
,
but at the point 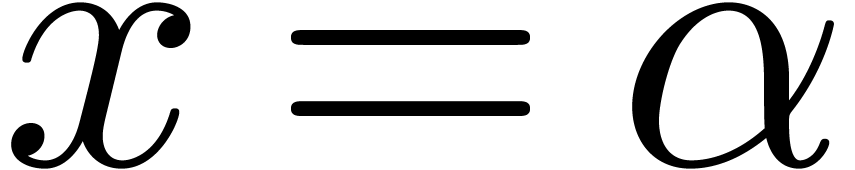 , one has
, one has
 .
.

Let  and
and 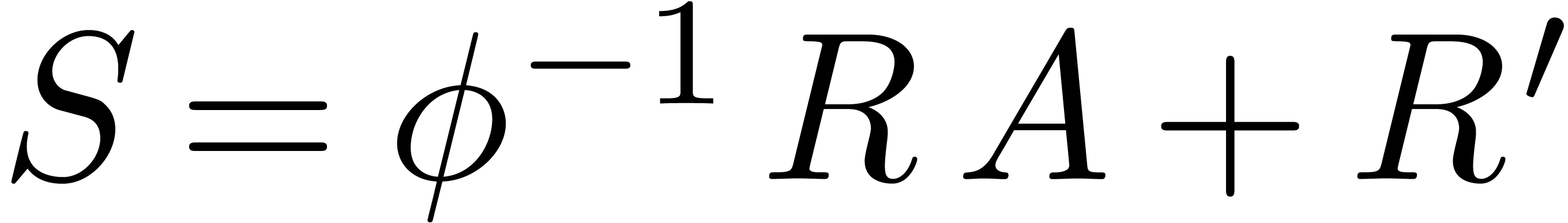 ,
so that
,
so that 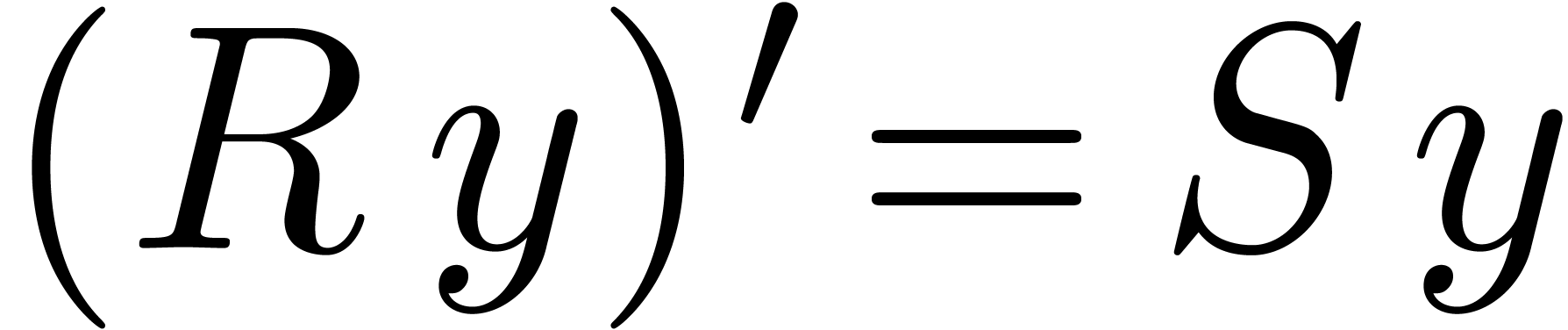 . Let
. Let 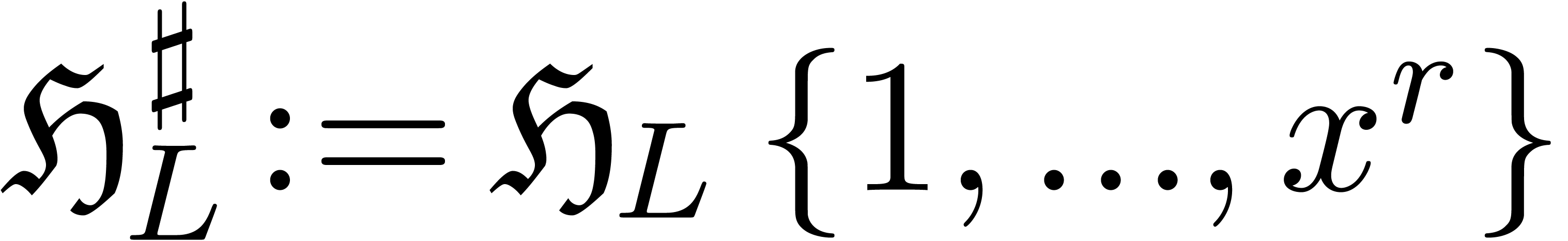 . The proof technique from Theorem 16
can also be used for studying
. The proof technique from Theorem 16
can also be used for studying 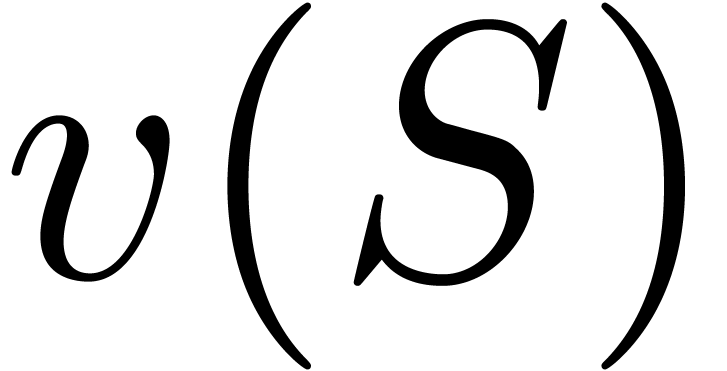 as a function of
as a function of
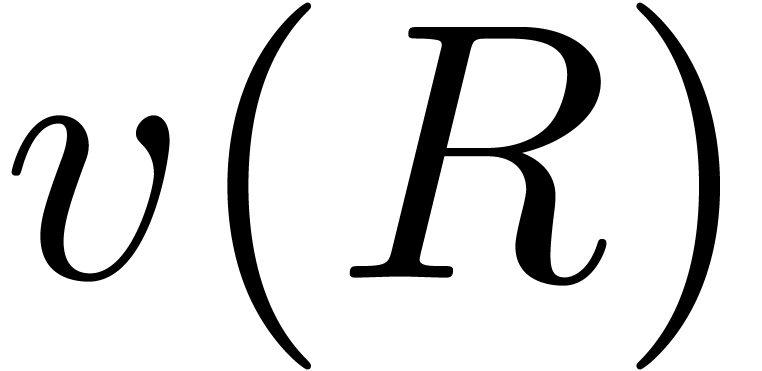 :
:
Proof. Let 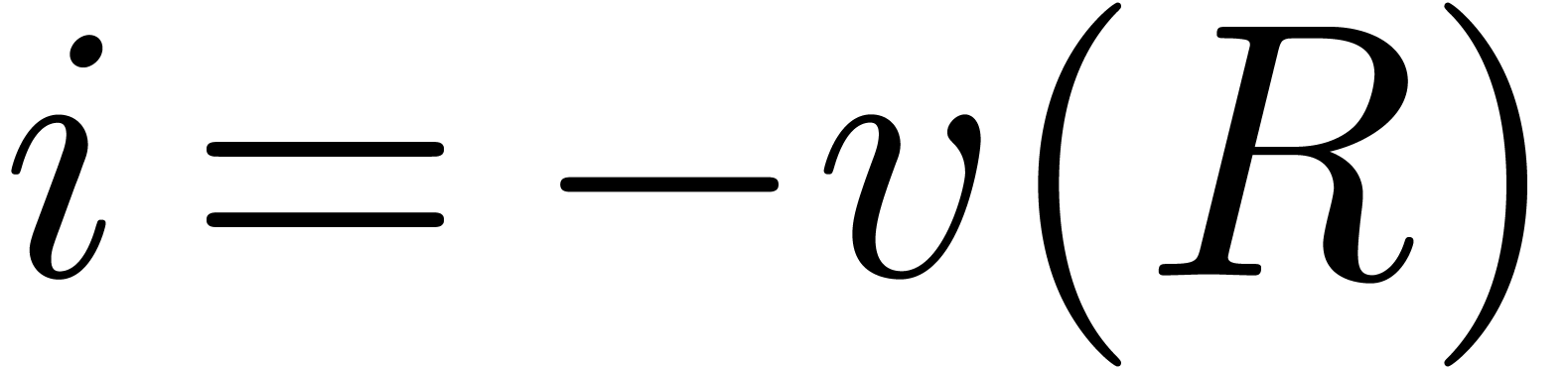 and rewrite
and rewrite
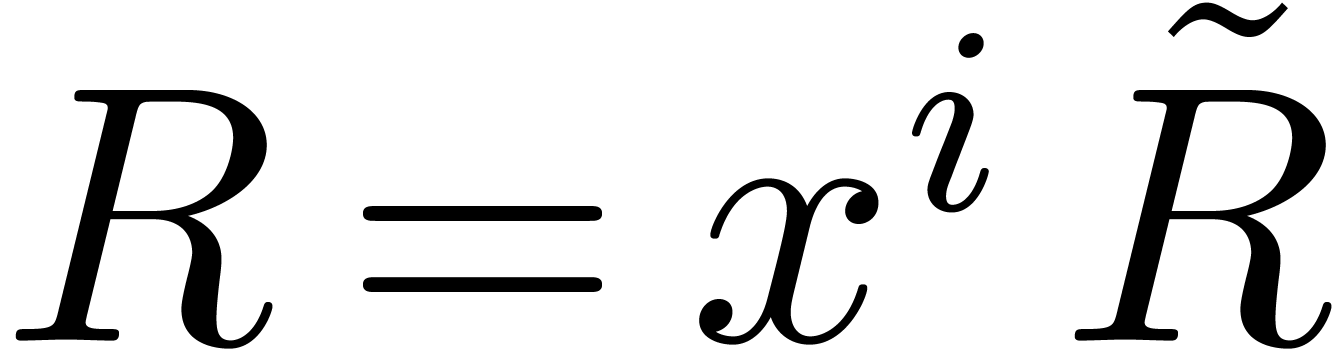 and
and 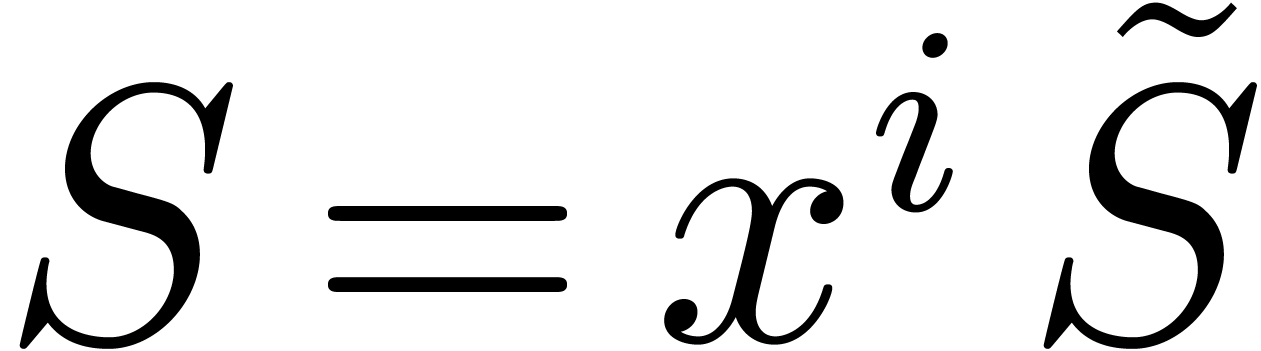 with
with 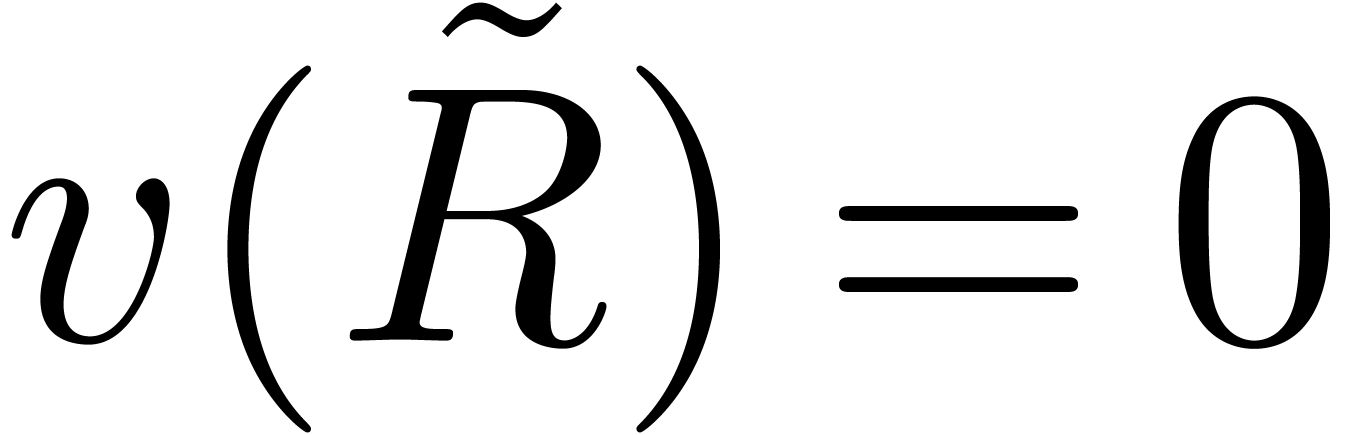 . Then we have
. Then we have
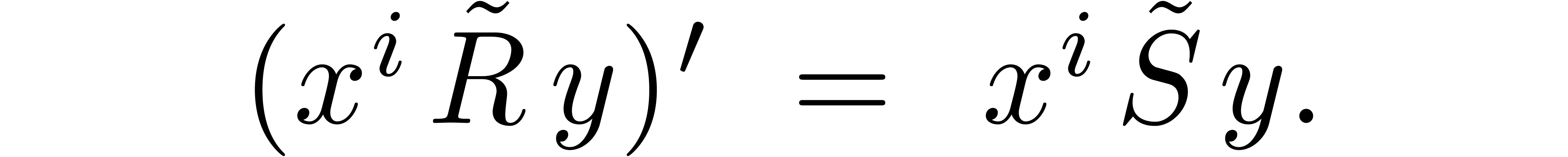
We may rewrite 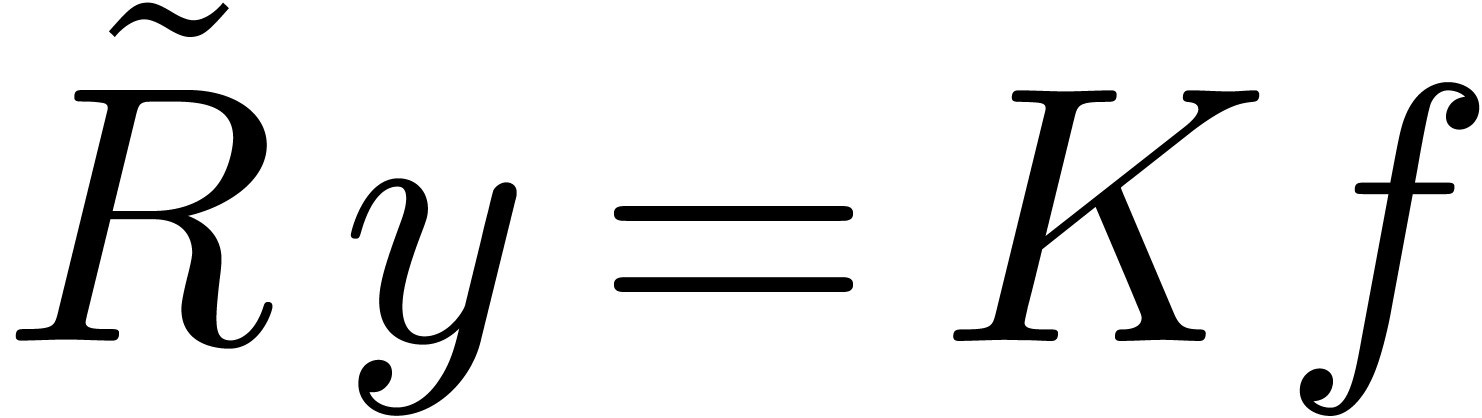 and
and 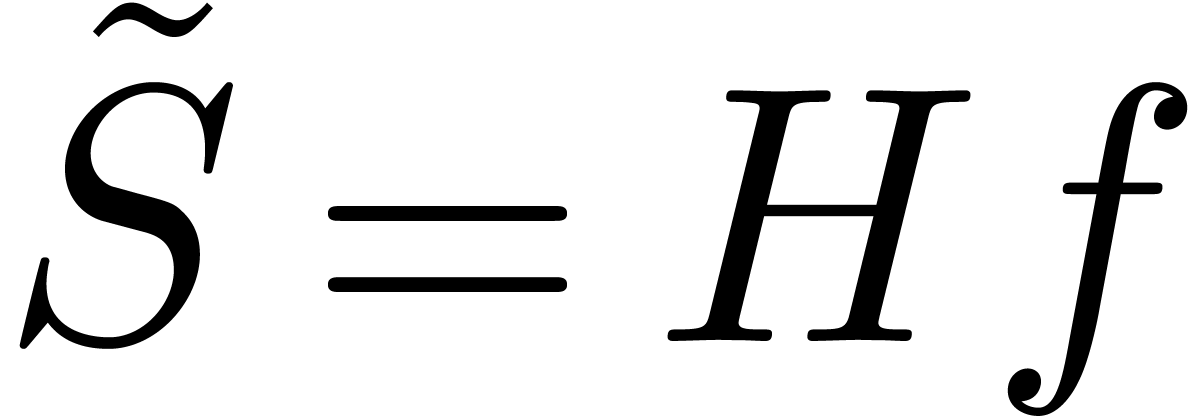 for
some
for
some 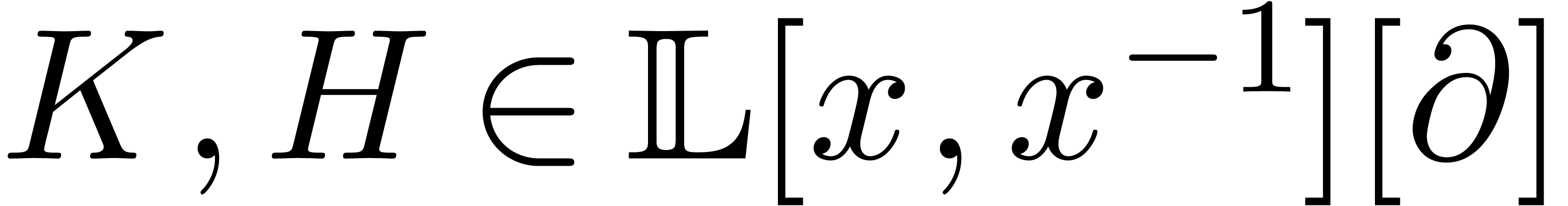 with
with 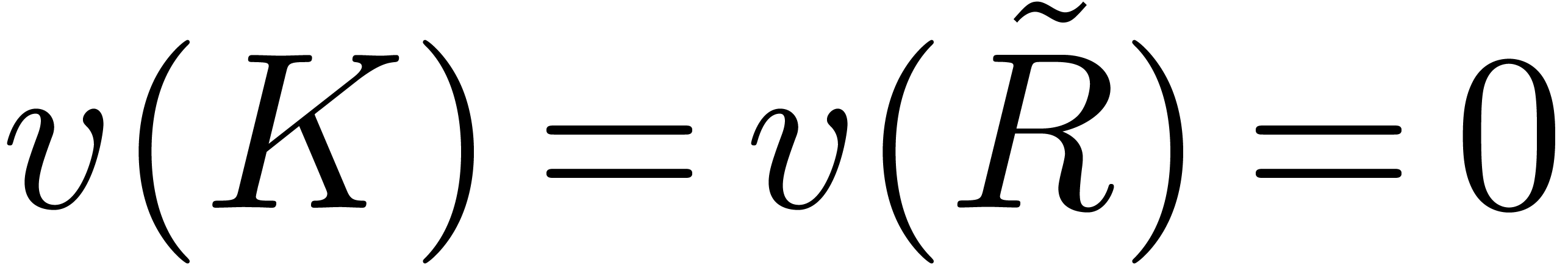 and
and 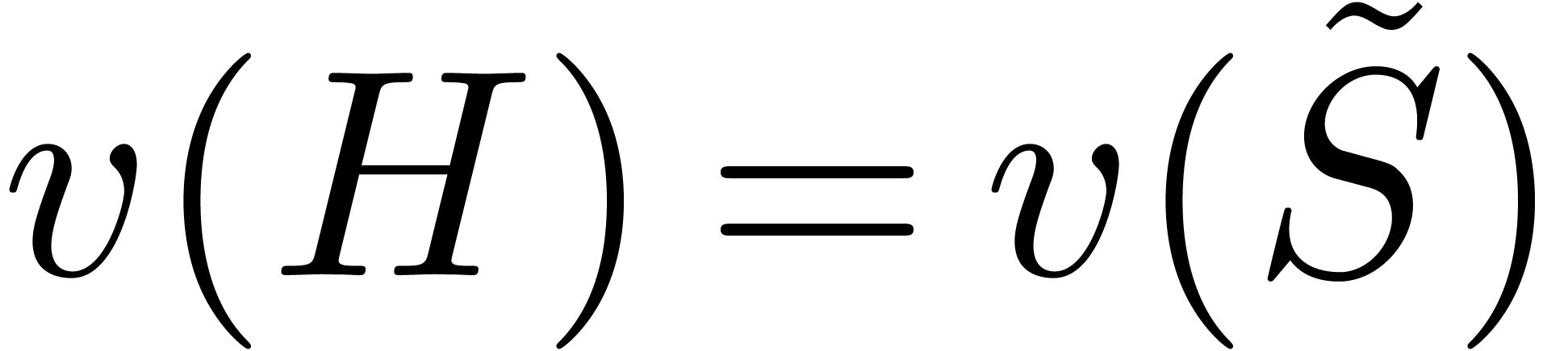 . Let
. Let 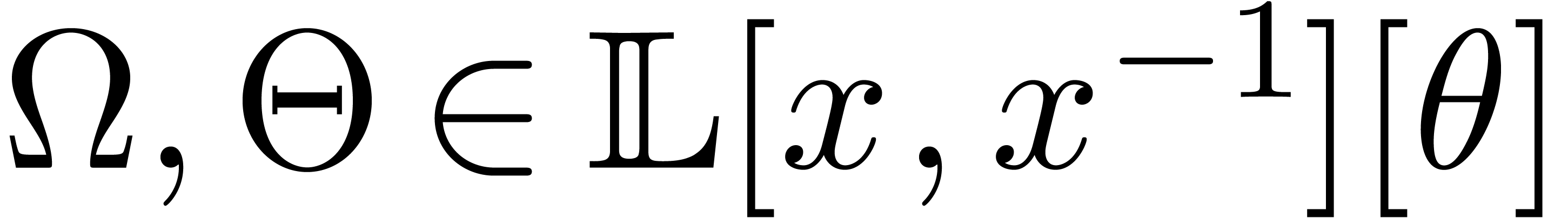 be
the operators given by
be
the operators given by 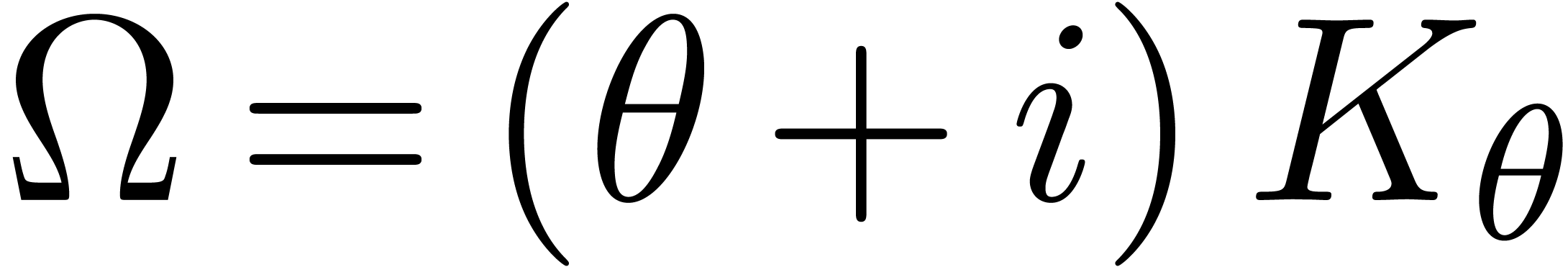 and
and 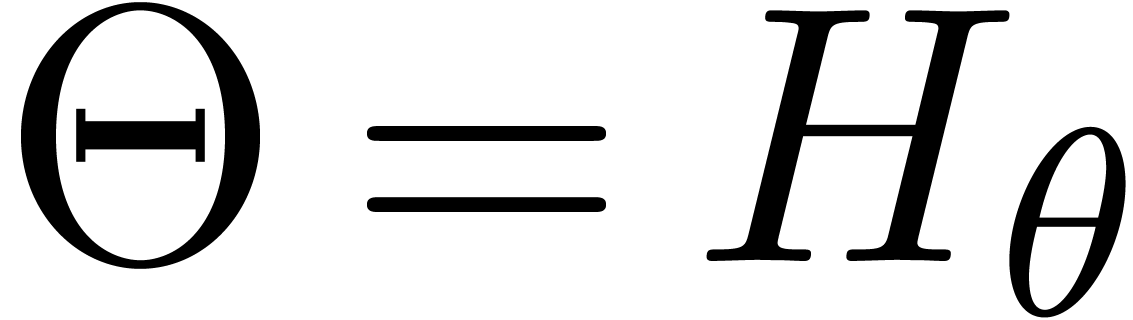 , so that
, so that 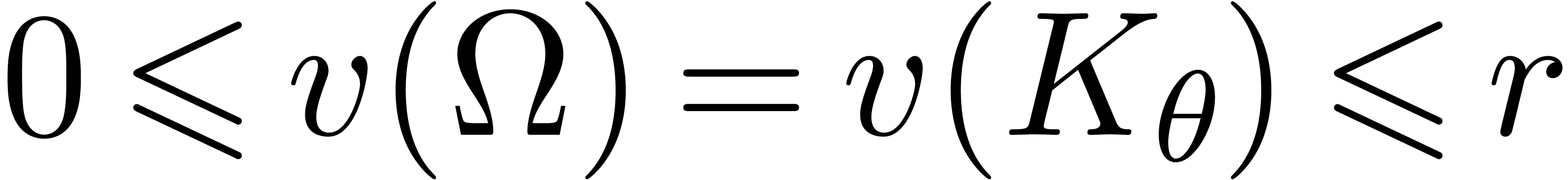 and
and  . In a similar way as in the proof
of Theorem 16, we deduce that
. In a similar way as in the proof
of Theorem 16, we deduce that
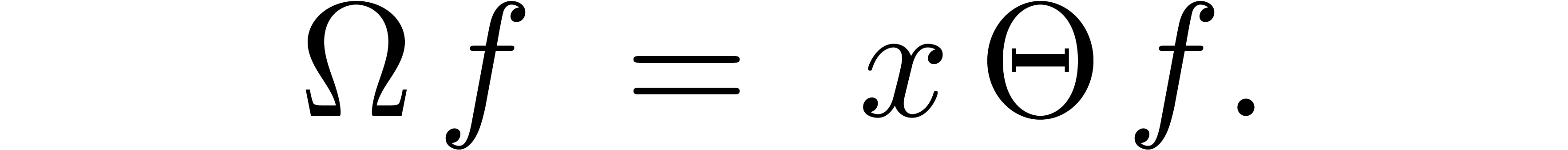
Since  has order at most
has order at most  , there exists a monomial
, there exists a monomial 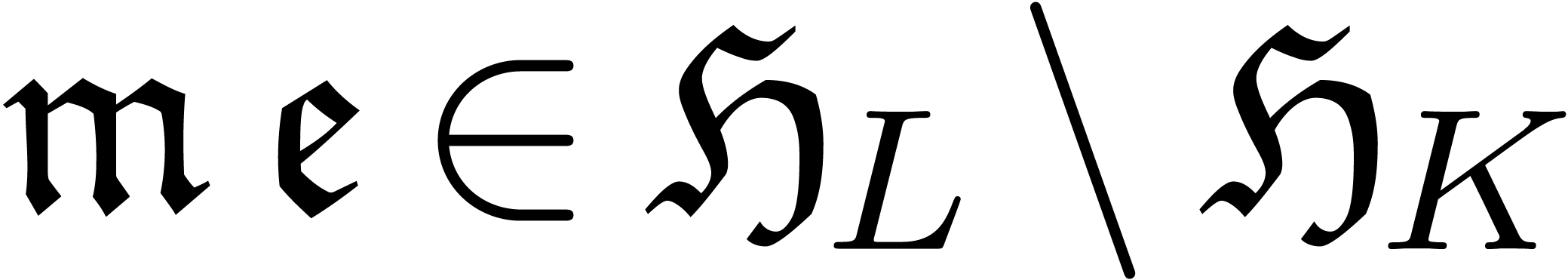 with
with  and
and  .
The distinguised solution to the equation
.
The distinguised solution to the equation 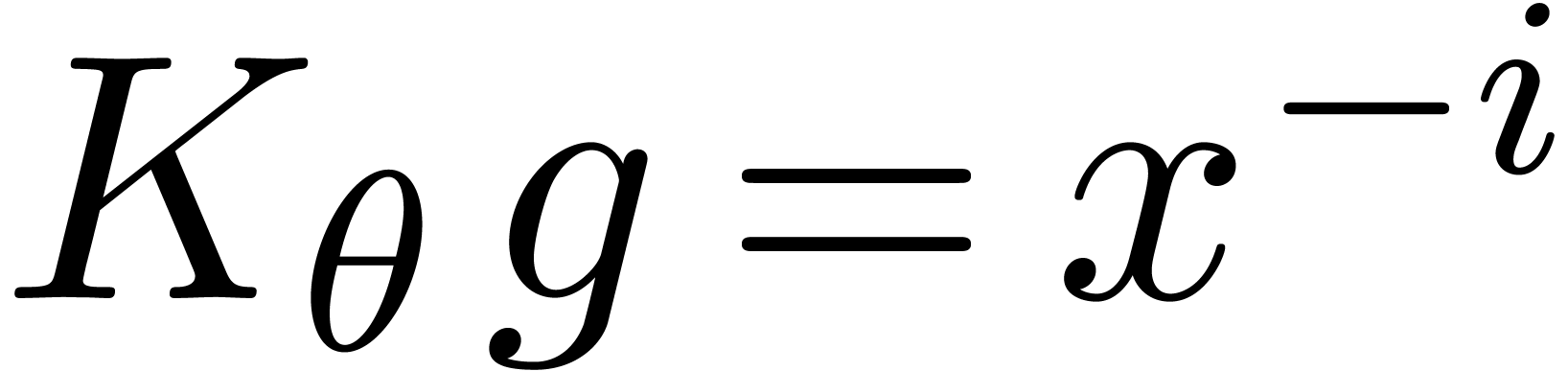 with
with
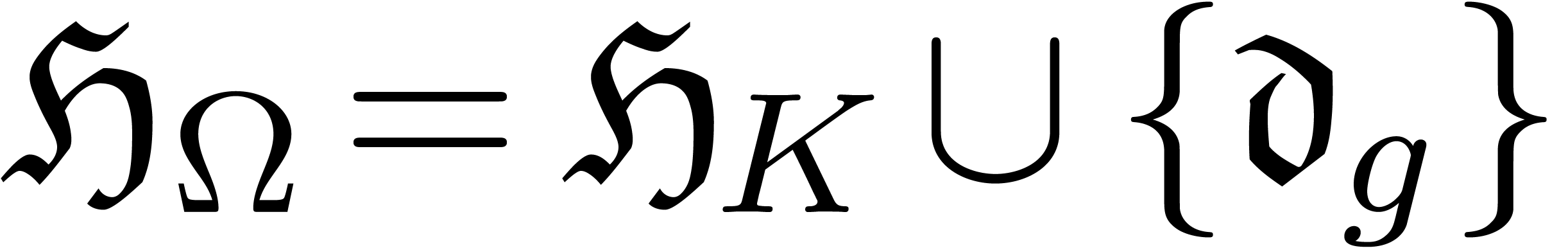 has valuation
has valuation 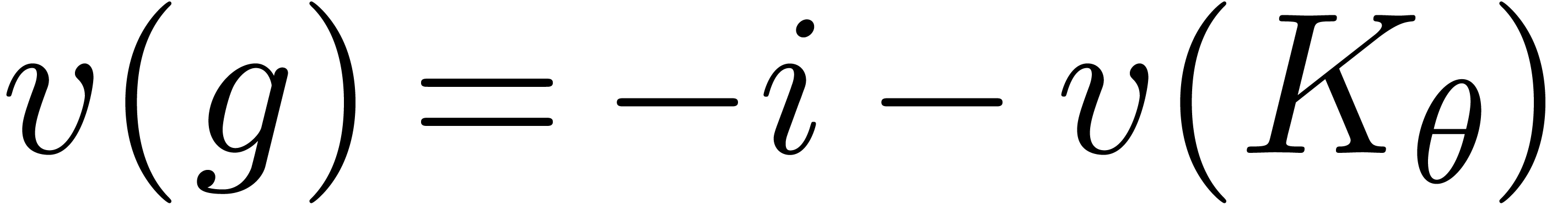 ,
so that
,
so that 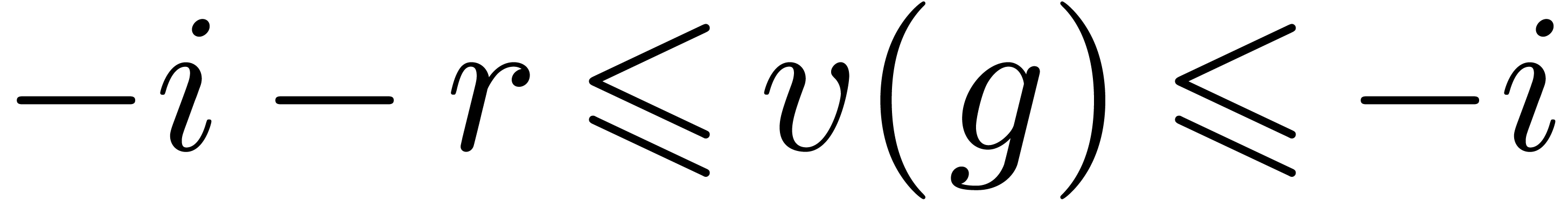 . Since
. Since 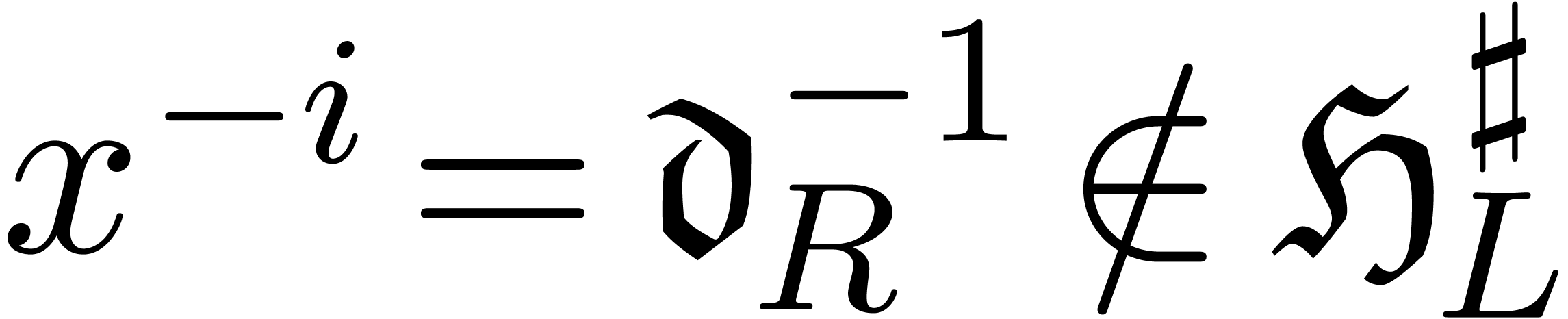 , it follows that
, it follows that 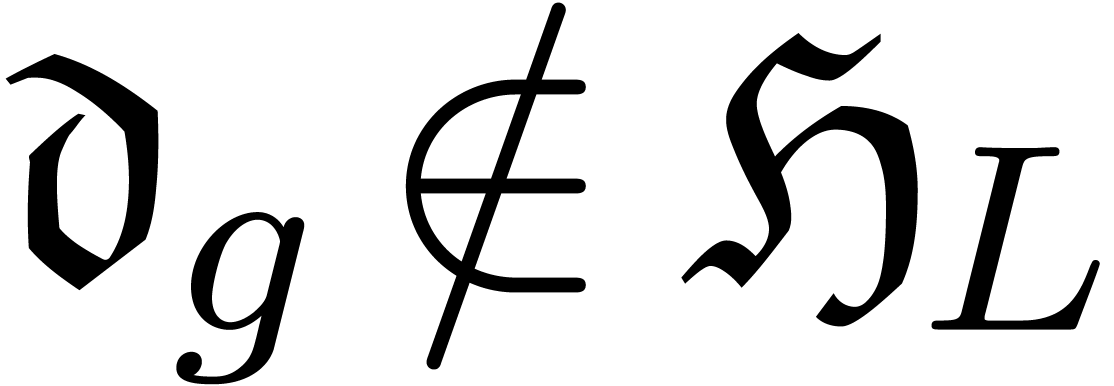 ,
whence
,
whence  . In a similar way as
in the proof of Theorem 16, we obtain
. In a similar way as
in the proof of Theorem 16, we obtain

whence
The inequality 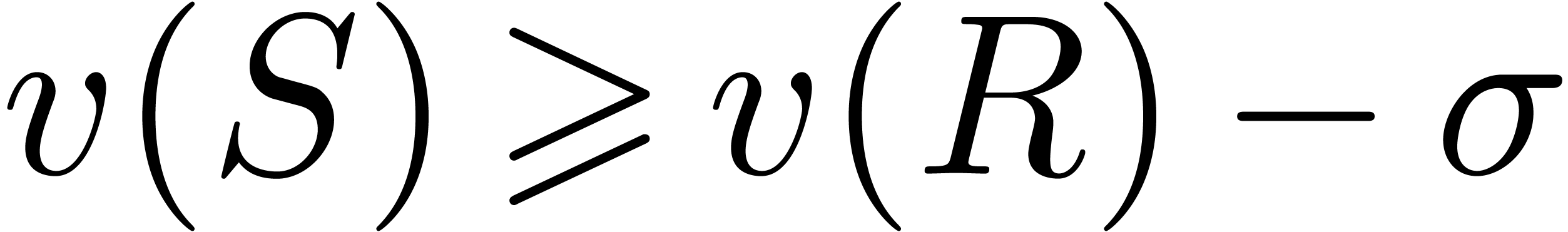 in the other direction is
straightforward.□
in the other direction is
straightforward.□
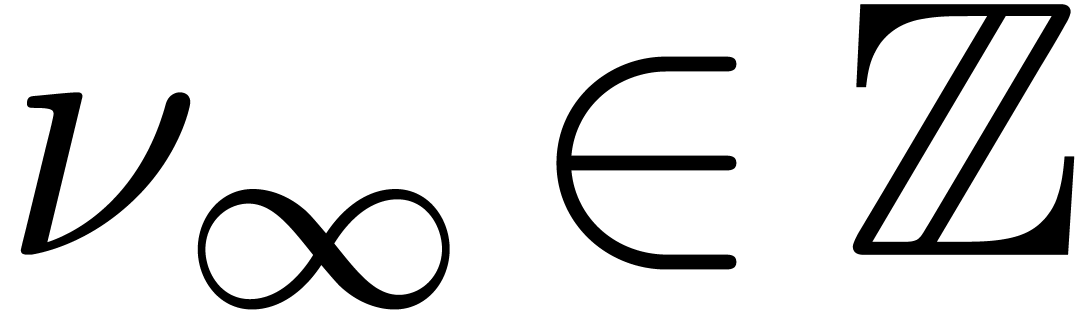 such that for all
such that for all 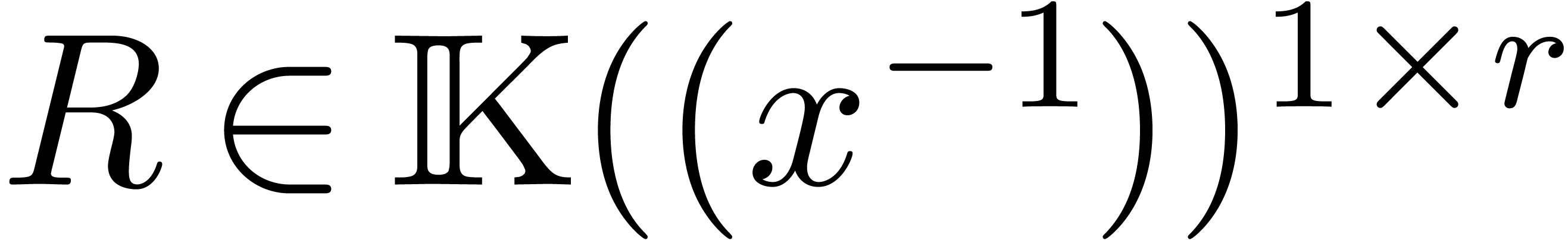 and
and 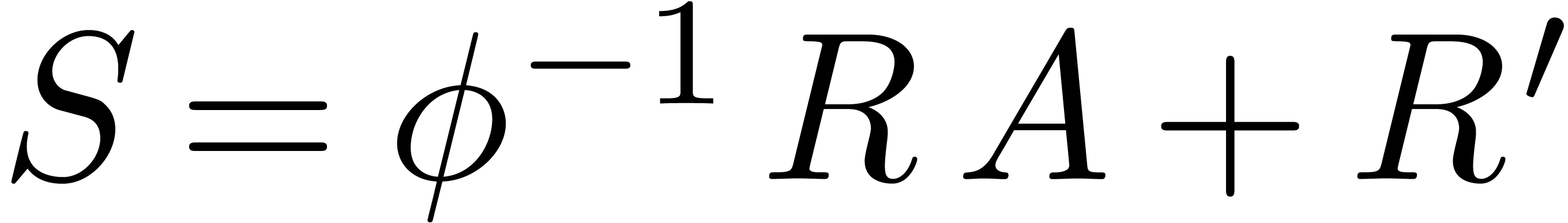 with
with 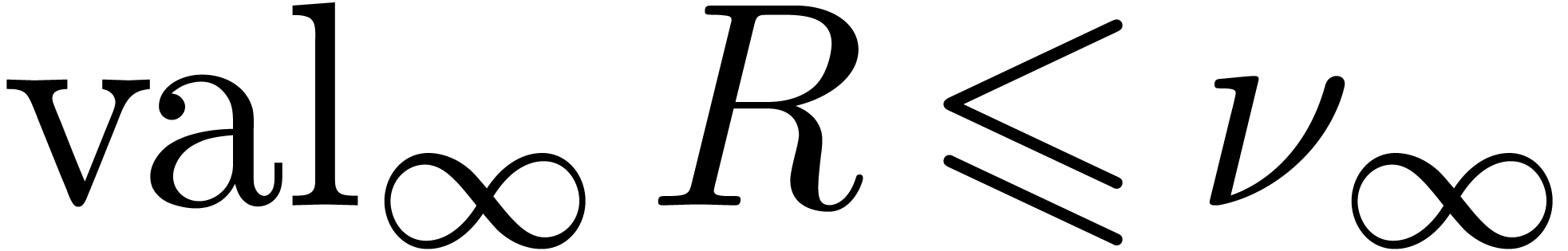 , we have
, we have
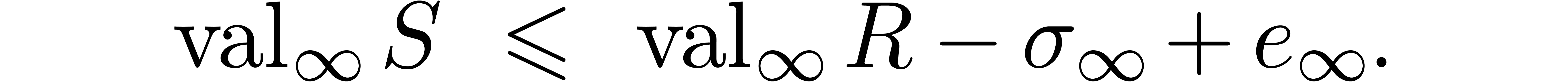
Proof. Let  be a head
chopper for (1) such that
be a head
chopper for (1) such that 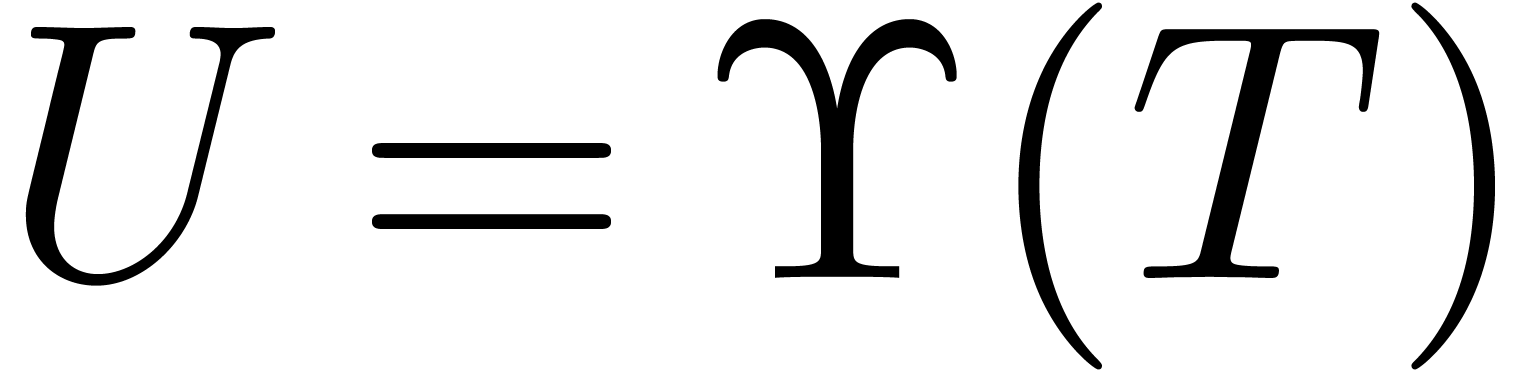 satisfies
satisfies
 . Let
. Let  be sufficiently small such that
be sufficiently small such that 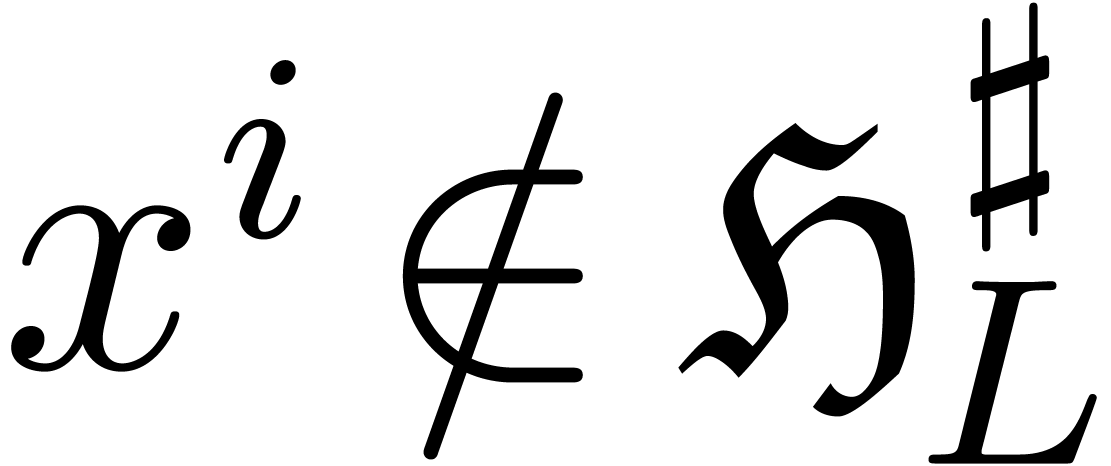 and
and 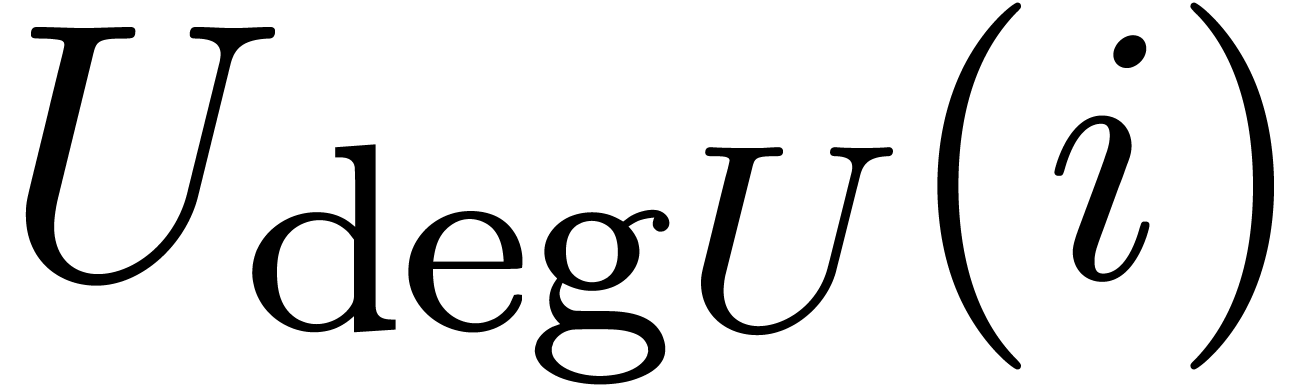 is defined and invertible for all
is defined and invertible for all 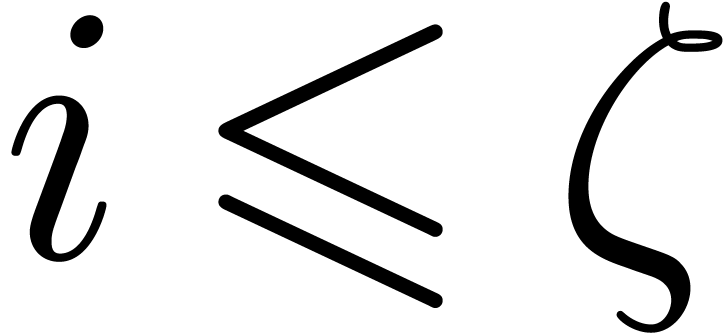 . We take
. We take 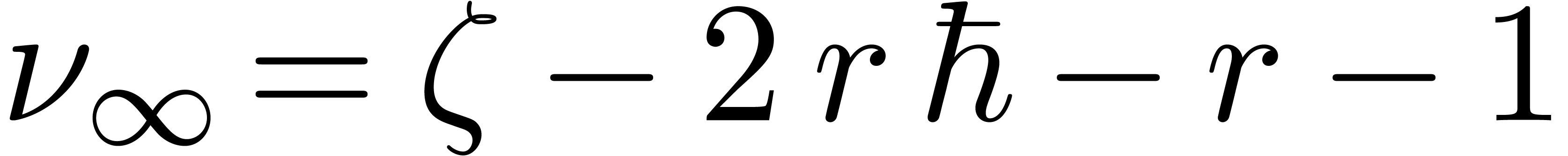 .
.
Assume for contradiction that 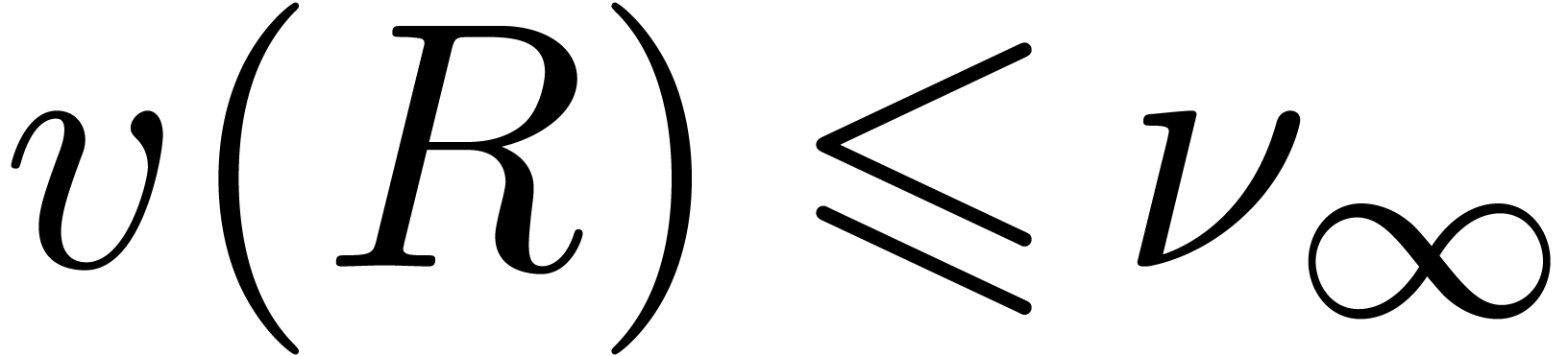 and
and 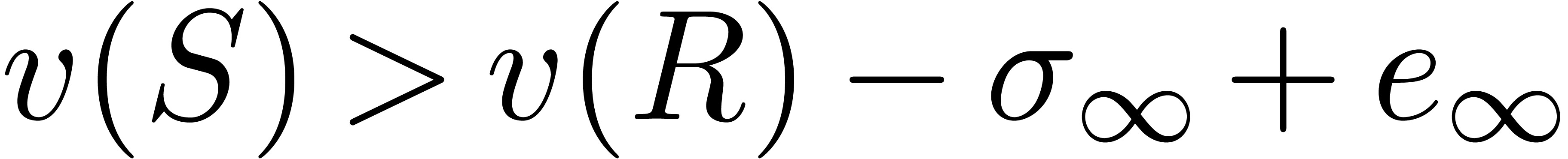 . Let
. Let  and
and  be such that
be such that  and
and 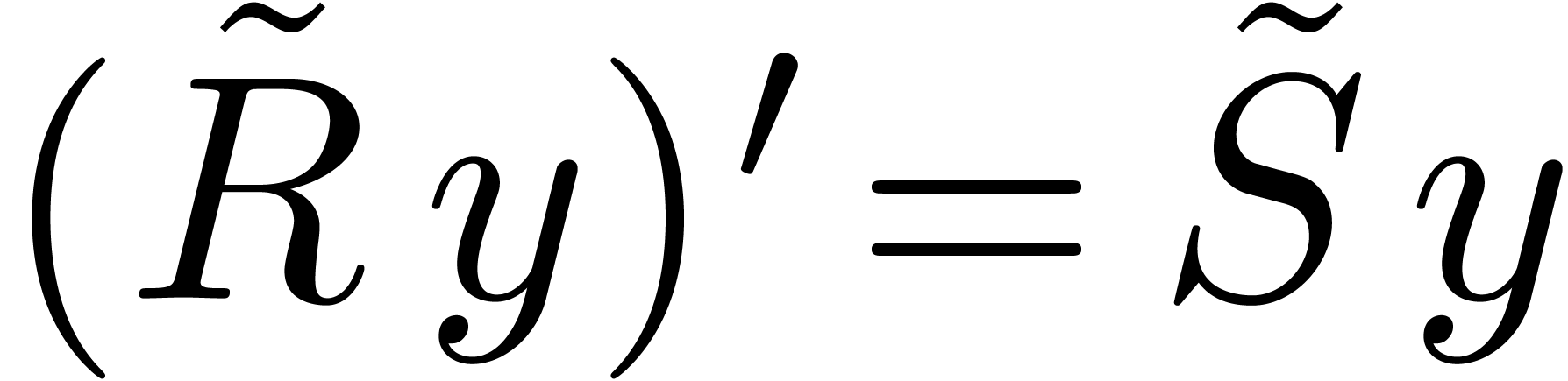 . By construction,
. By construction, 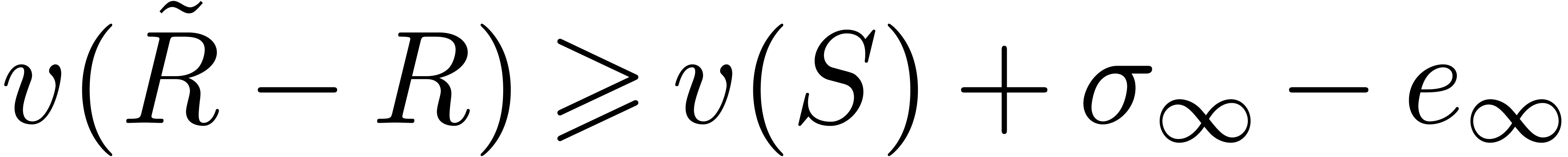 , whence
, whence 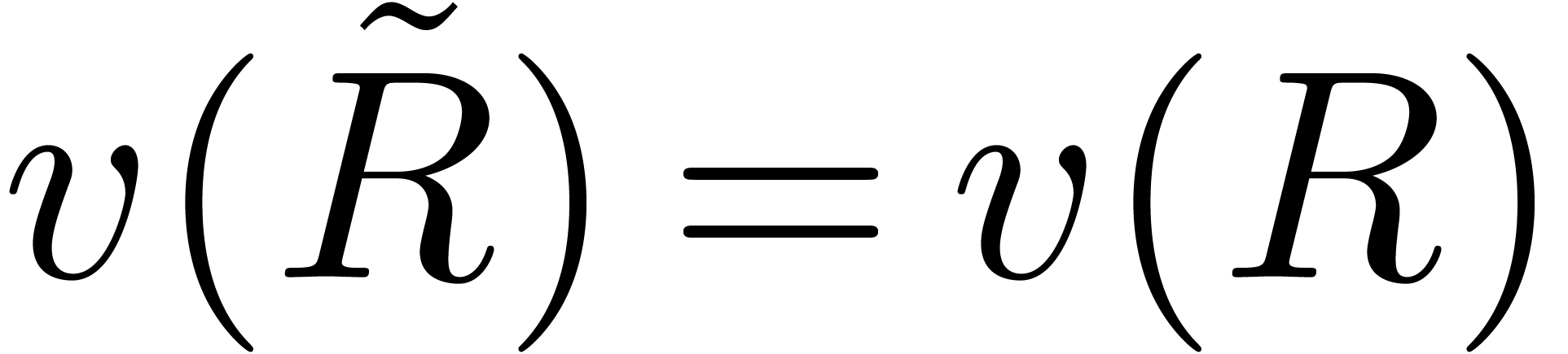 ,
and
,
and 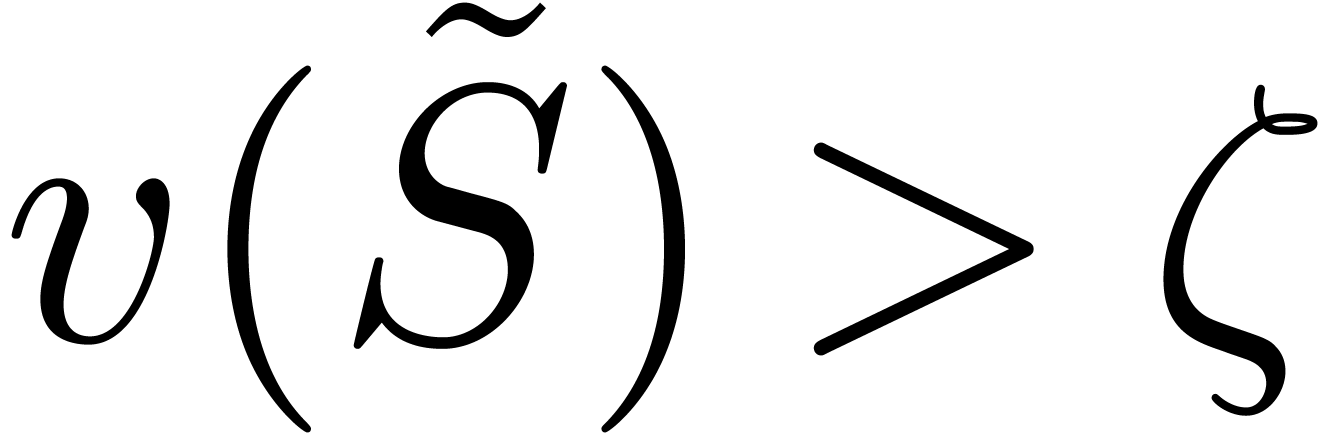 . But then
. But then  . This contradicts Theorem 18,
since
. This contradicts Theorem 18,
since 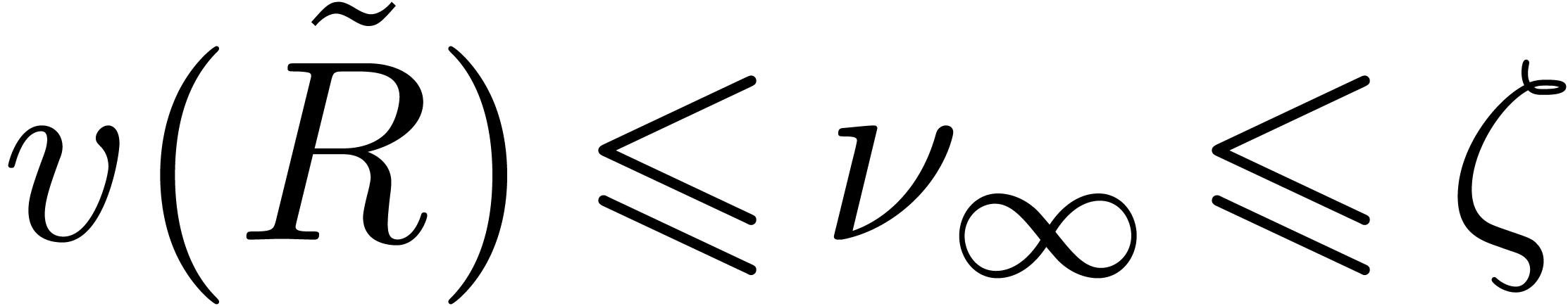 implies
implies 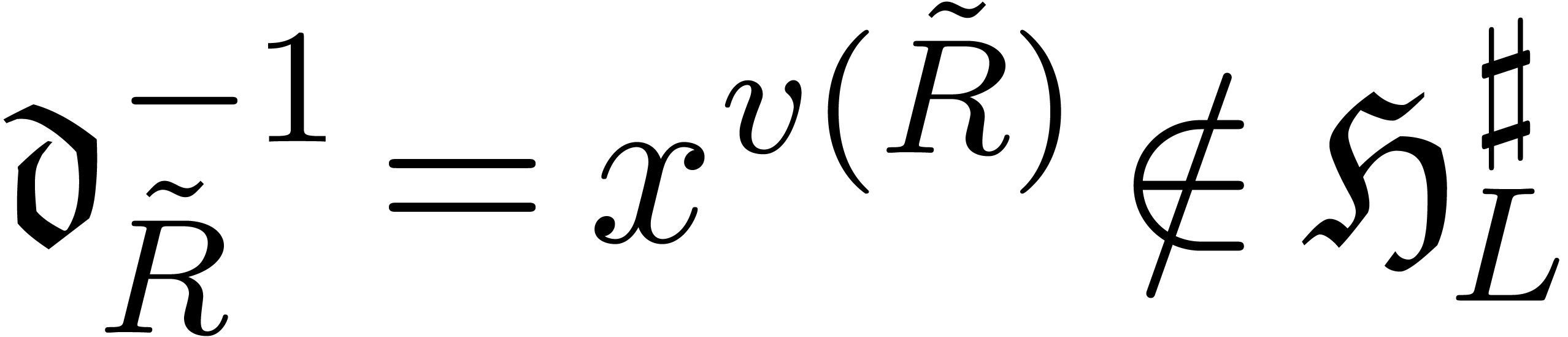 .□
.□
 , we can
compute an integer
, we can
compute an integer  such that for all
such that for all 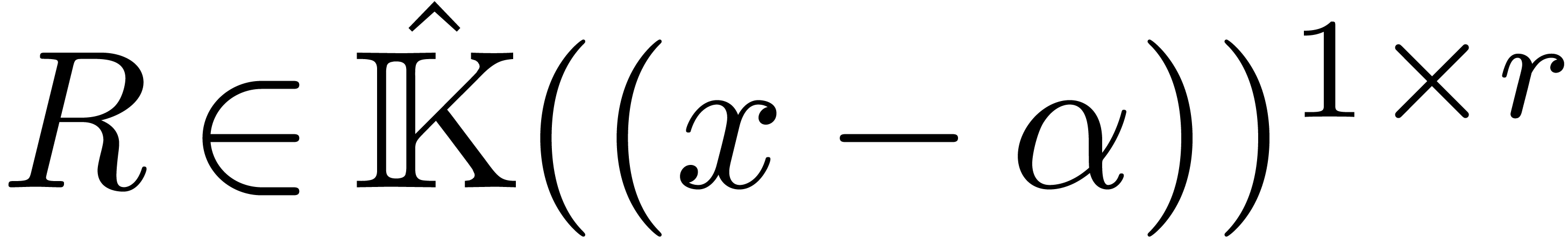 and
and 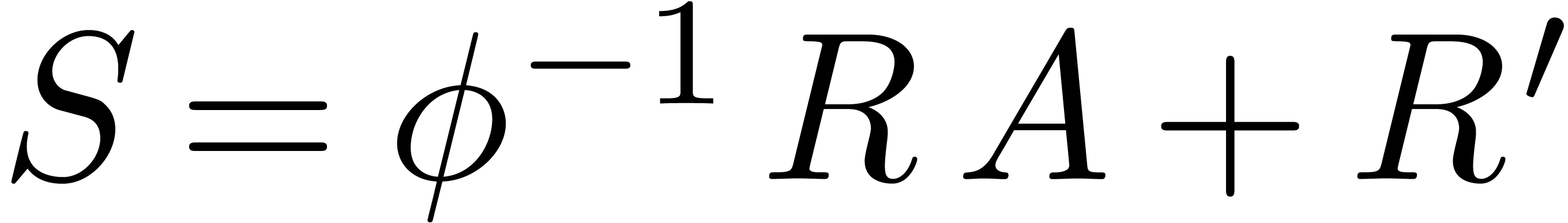 with
with 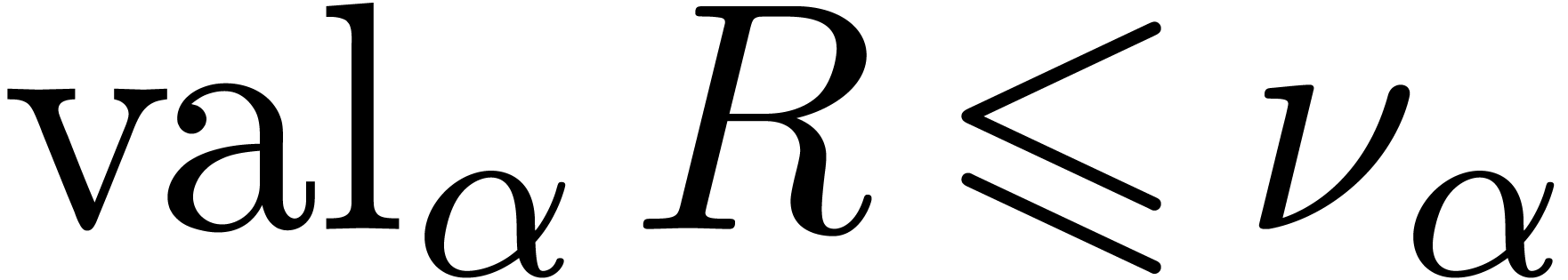 , we have
, we have
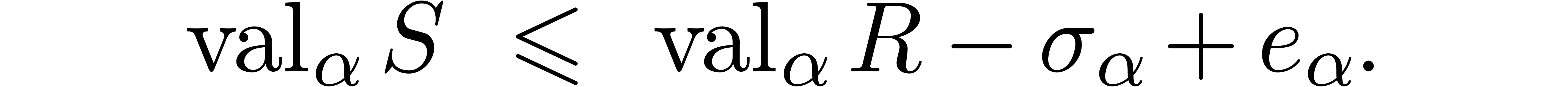
Proof. Follows from the previous proposition via a change of variables.□
Let us now study how head and tail reductions can be glued together into
a global confined reduction on 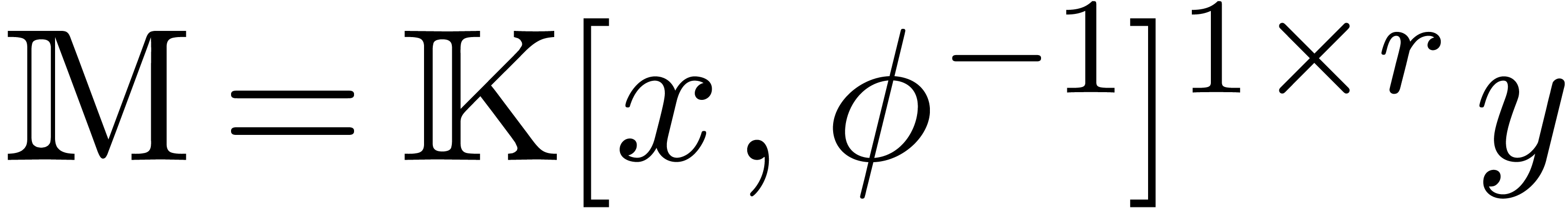 .
More generally, we consider the case when
.
More generally, we consider the case when 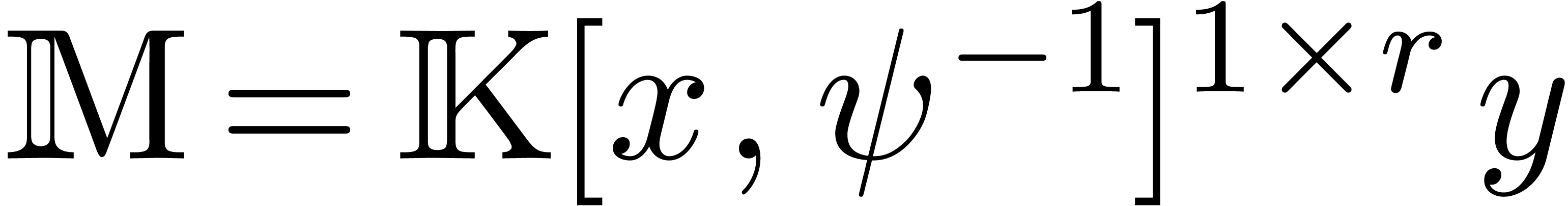 ,
where
,
where 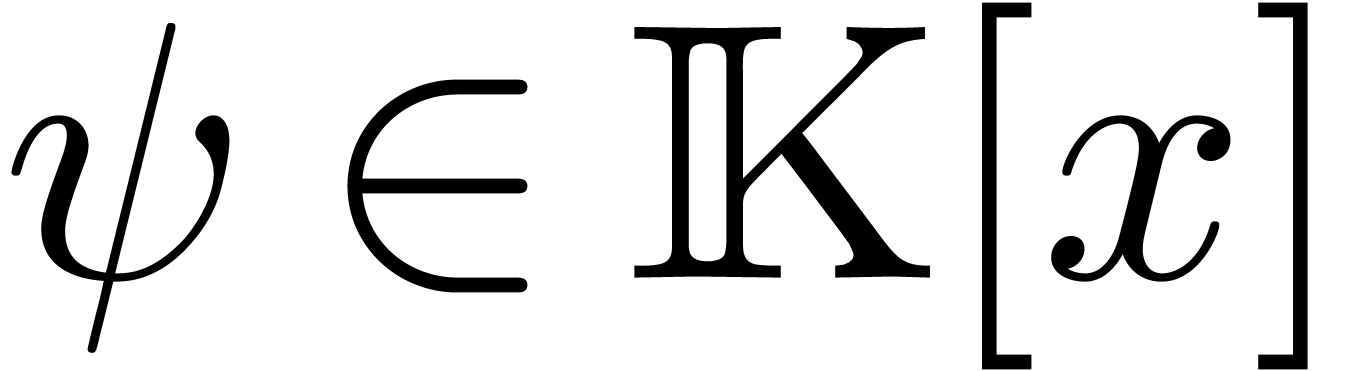 is a monic square-free polynomial such
that
is a monic square-free polynomial such
that  divides
divides 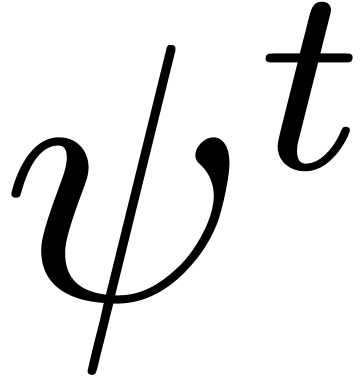 for some
for some
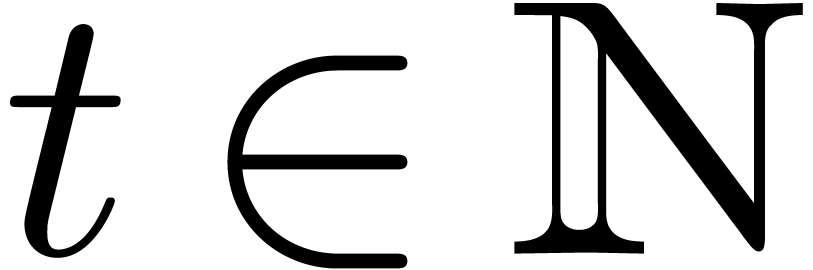 .
.
We assume that we have computed a head chopper for (1) and
tail choppers 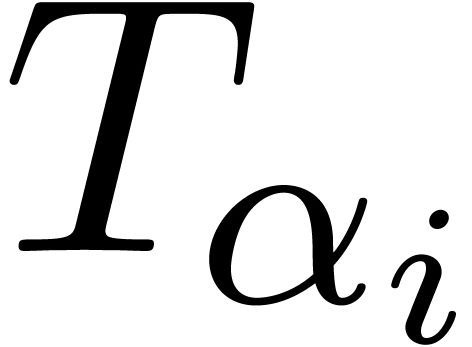 for (1) at each the
roots
for (1) at each the
roots  of
of 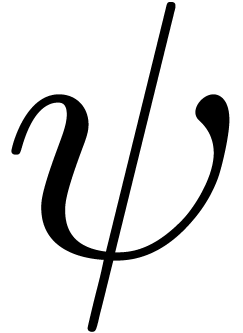 in
in  . In particular, we may compute the
corresponding head and tail reductions. Given an element
. In particular, we may compute the
corresponding head and tail reductions. Given an element  of the Galois group of
of the Galois group of  over
over  , we may also assume without loss
of generality that the tail choppers were chosen such that
, we may also assume without loss
of generality that the tail choppers were chosen such that 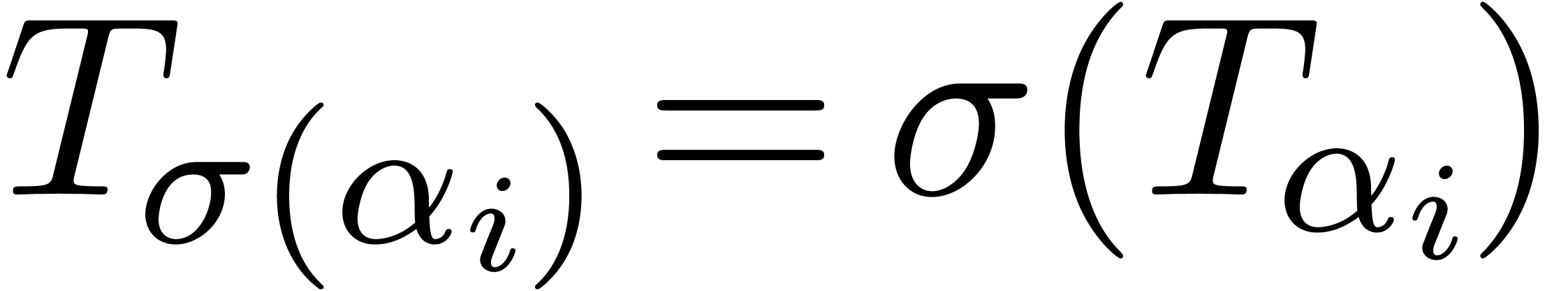 for all
for all  .
.
Partial fraction decomposition yields  -linear
mappings
-linear
mappings
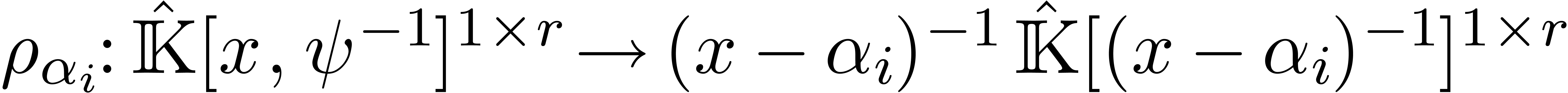
and
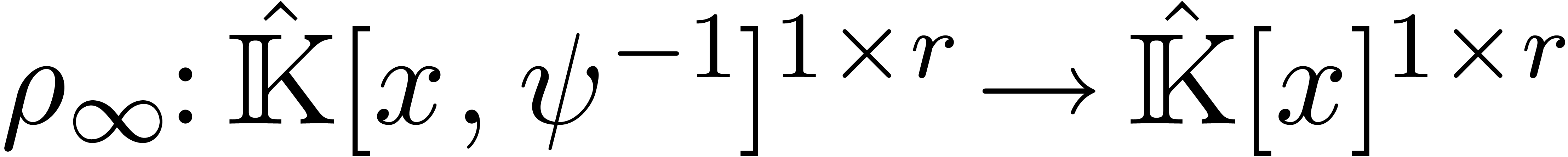
with
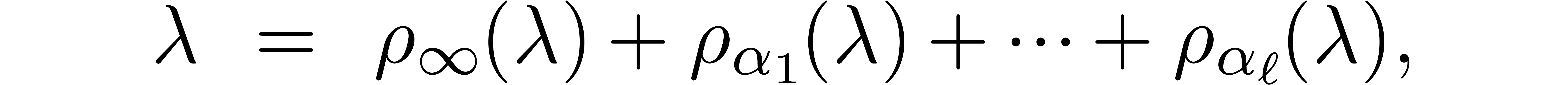
for all 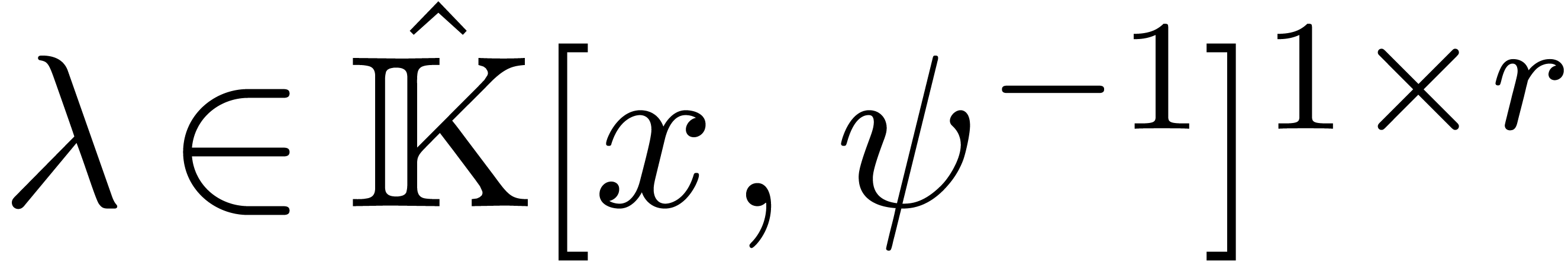 . This allows us to
define a global reduction
. This allows us to
define a global reduction 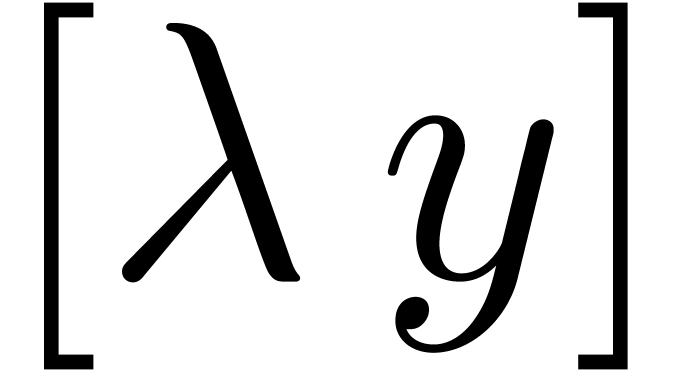 of
of 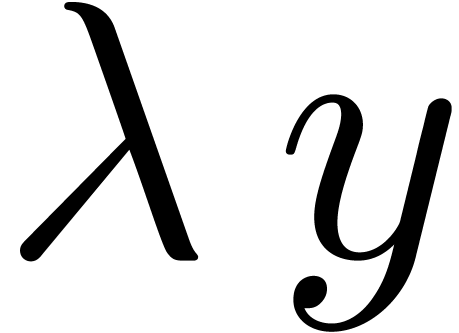 by
by
By our assumption that the tail choppers were chosen in a way that is
compatible with the action of the Galois group, we have 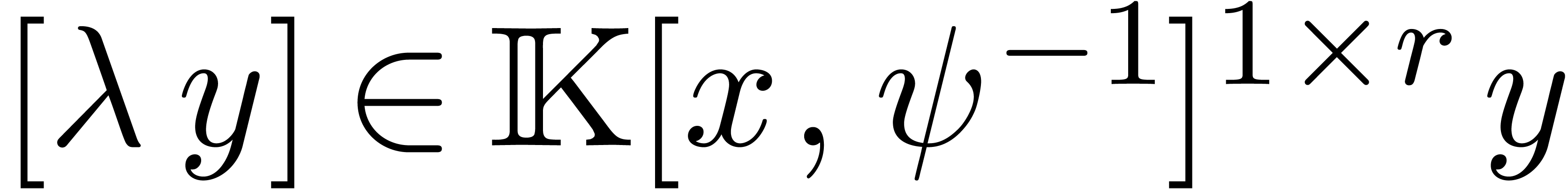 whenever
whenever 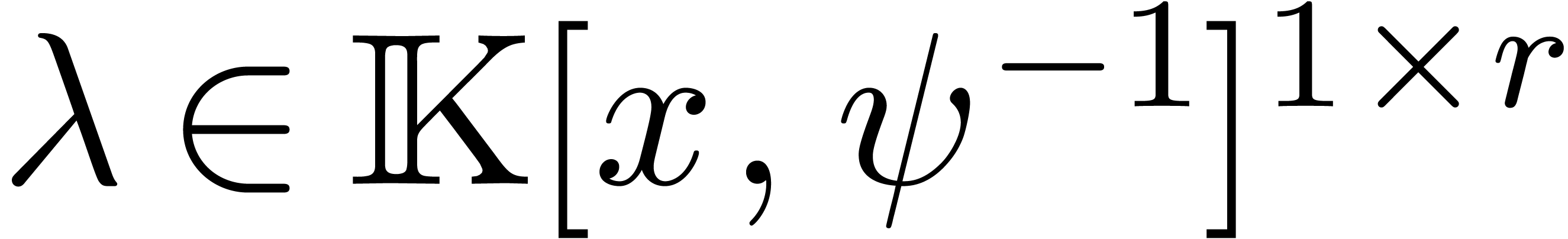 . Furthermore, the
restriction of the reduction on
. Furthermore, the
restriction of the reduction on 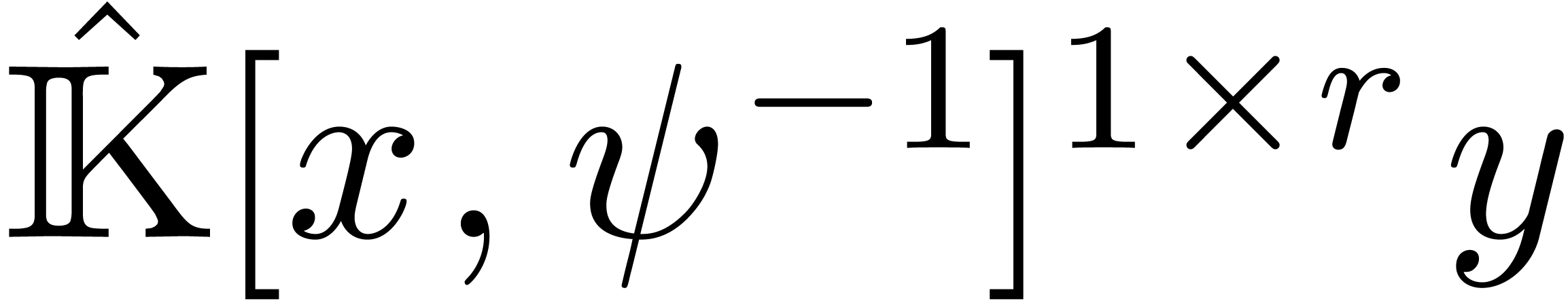 to
to 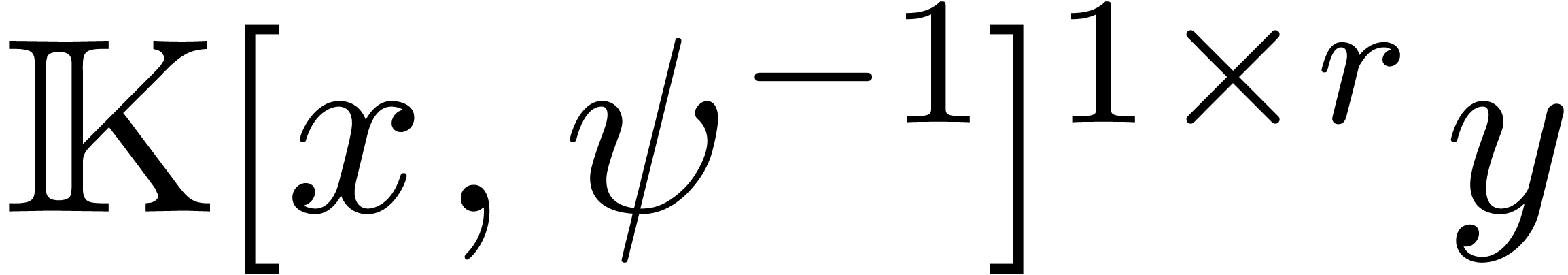 is still a reduction.
is still a reduction.
Remark
Given the confined reduction 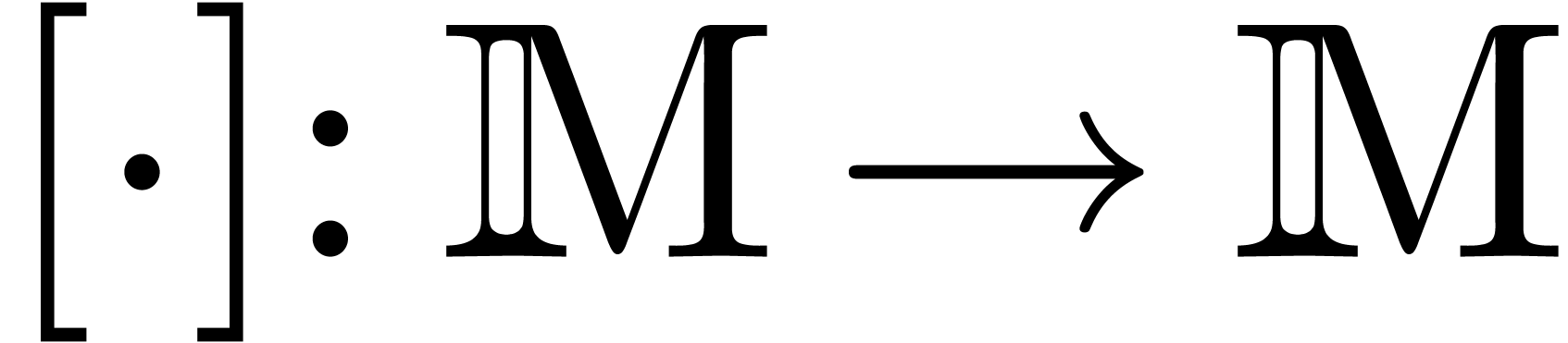 from section 7.1, let us show how to construct a normal confined reduction
from section 7.1, let us show how to construct a normal confined reduction
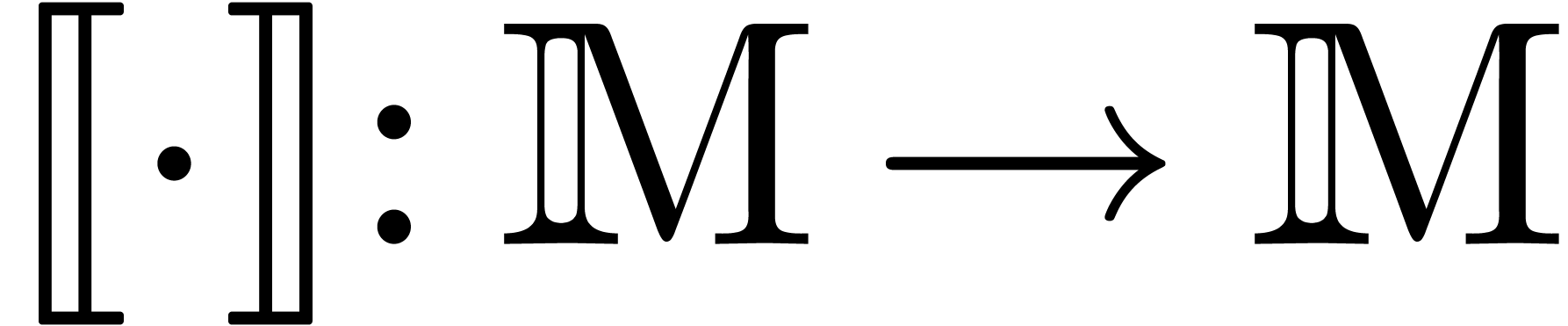 . For each
. For each 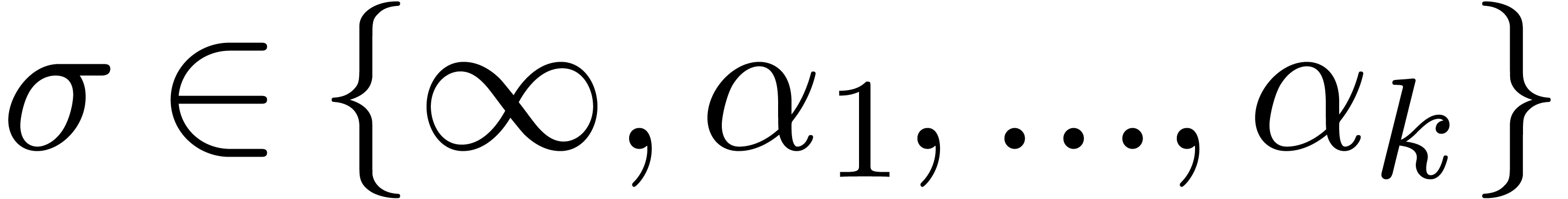 , assume that we have computed constants
, assume that we have computed constants 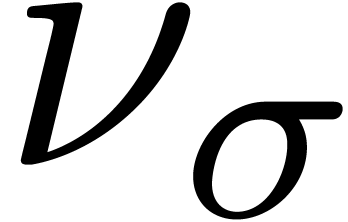 and
and 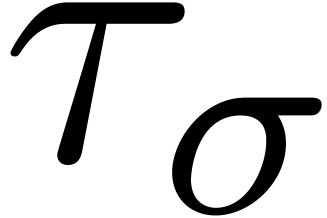 with the property that
for all
with the property that
for all  with
with  and
and  , we have
, we have 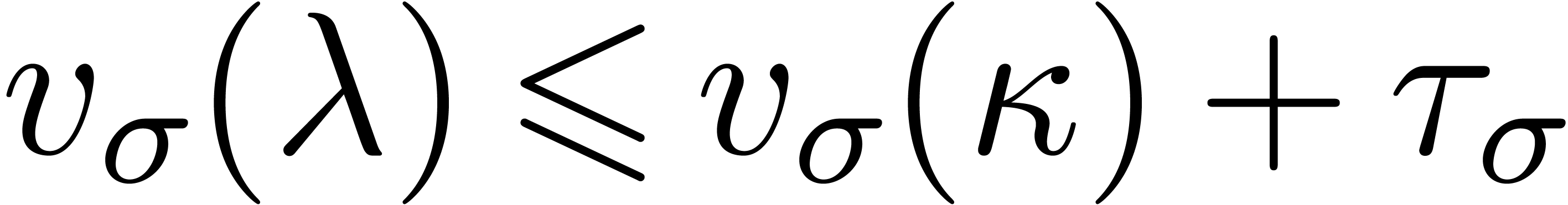 .
.
Consider the finite dimensional  -vector
space
-vector
space 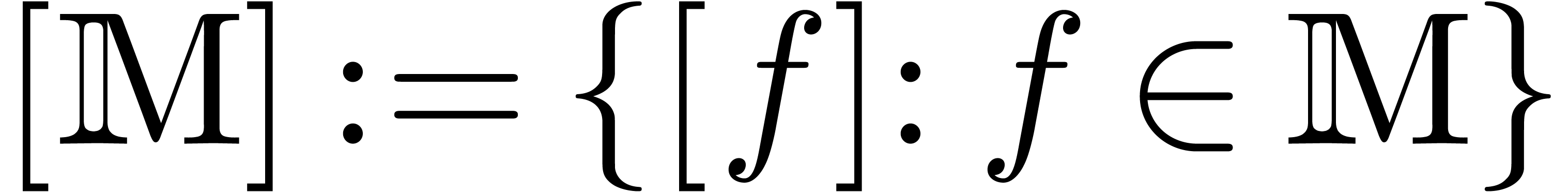 and let
and let  for all
for all
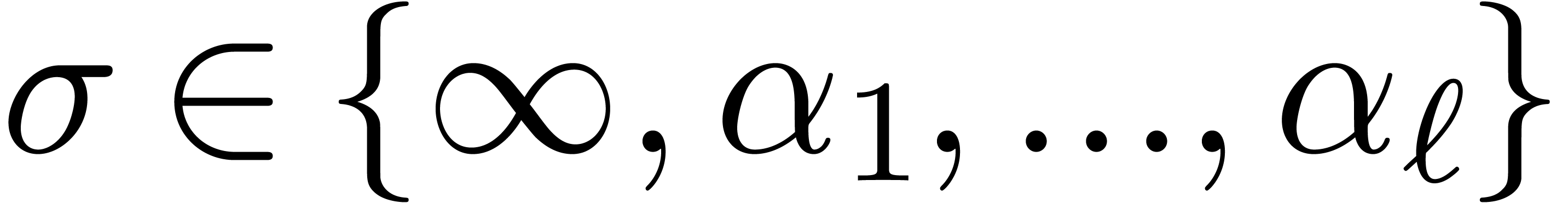 . Let
. Let  be the
be the  -subvector space of
-subvector space of
 of all
of all 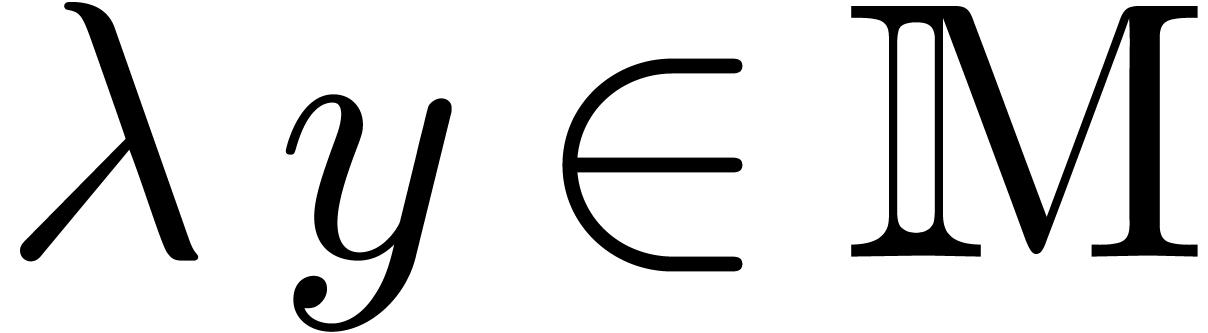 with
with 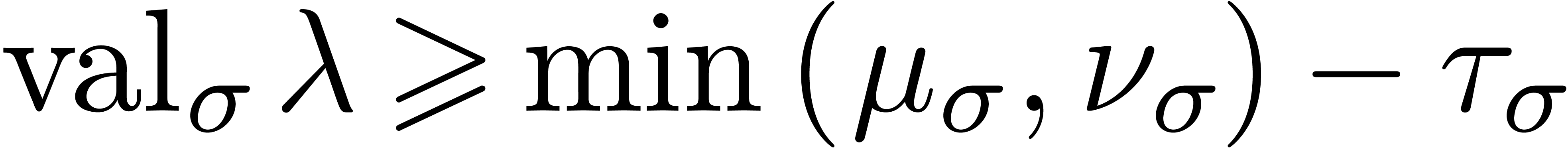 for all
for all 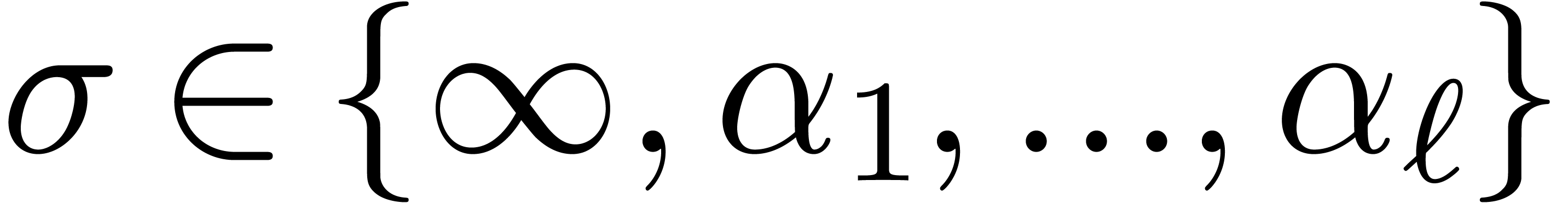 . This
space is finite dimensional and our assumptions imply that we cannot
have
. This
space is finite dimensional and our assumptions imply that we cannot
have 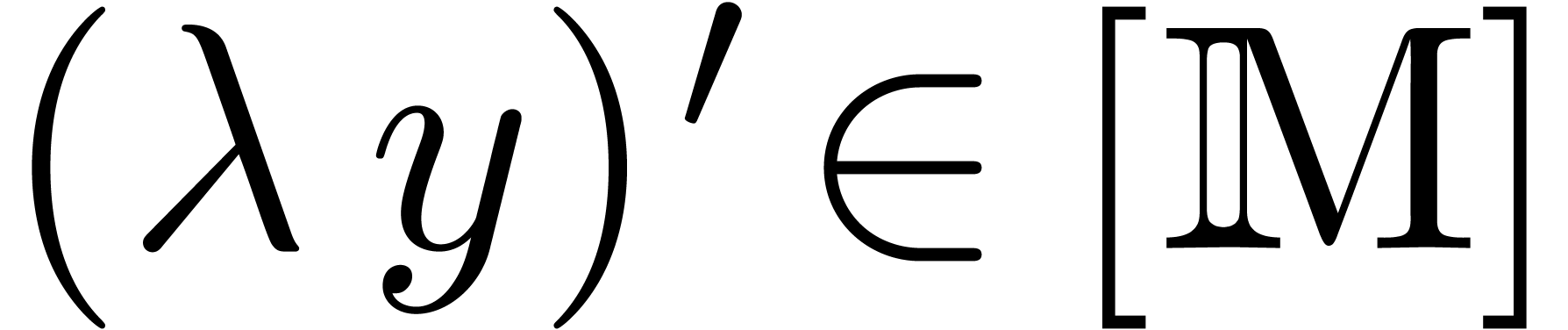 for
for 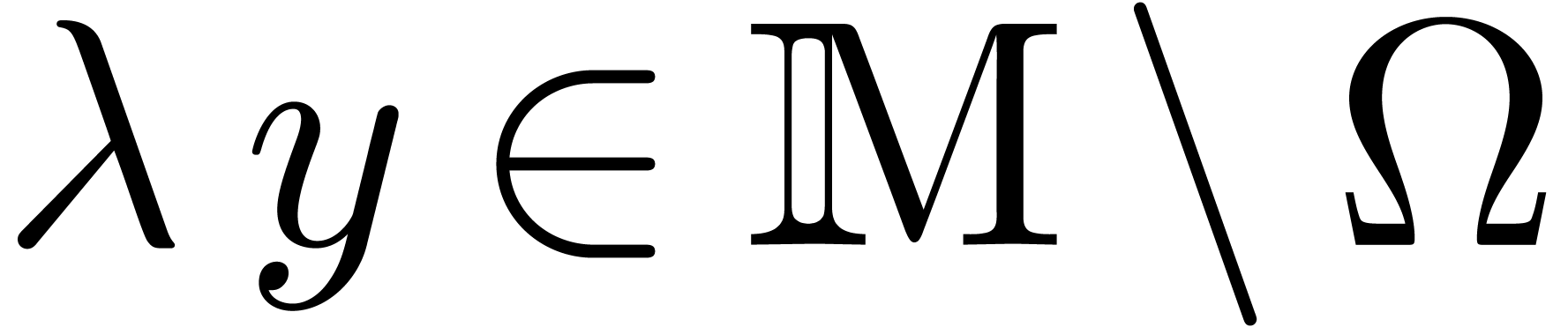 .
In other words, for any
.
In other words, for any 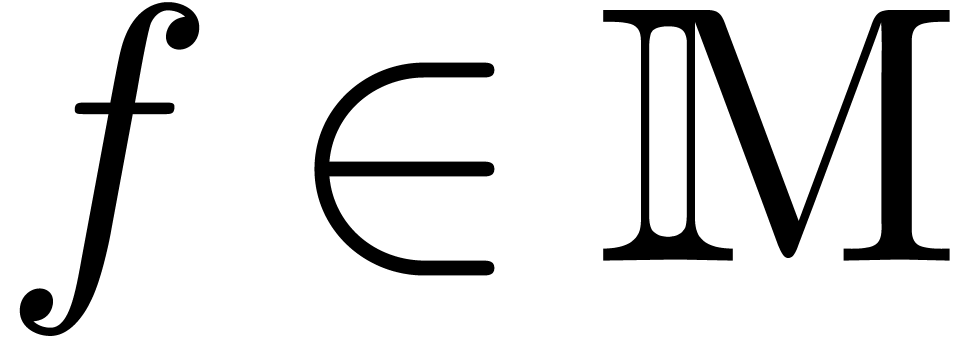 with
with 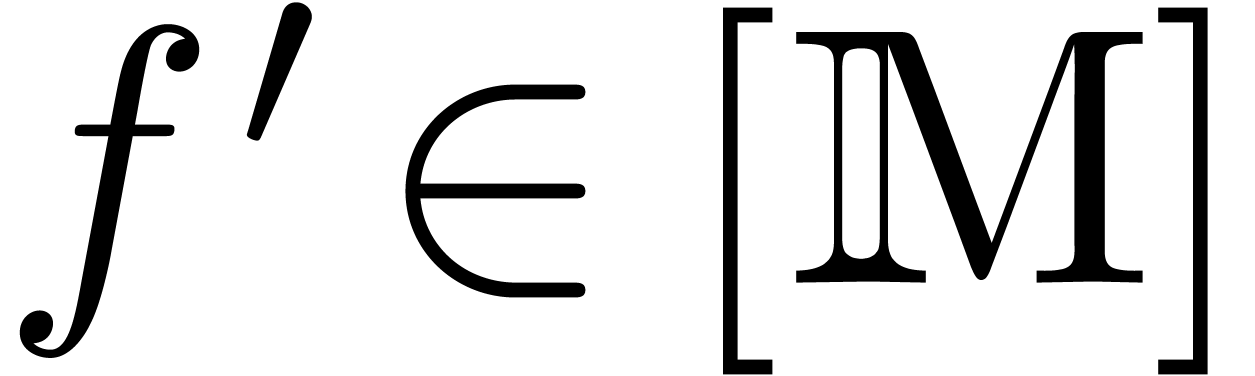 , we have
, we have  .
.
Now let 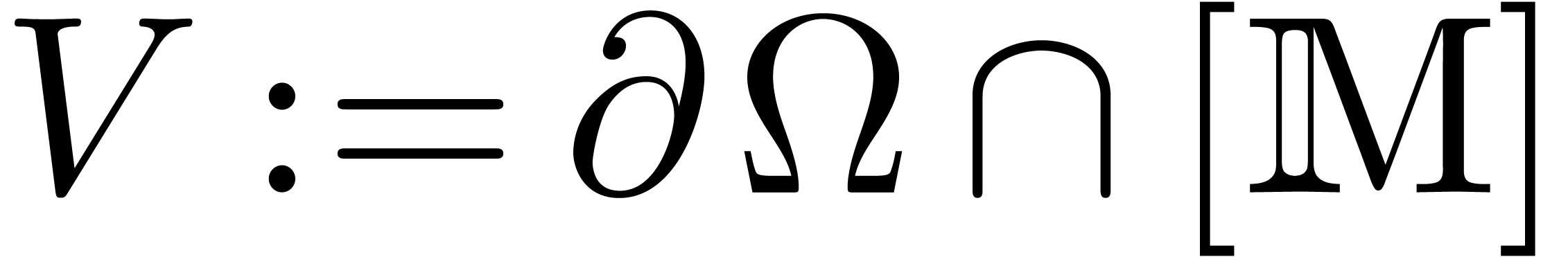 and let
and let  be a
supplement of
be a
supplement of  in
in  so that
so that
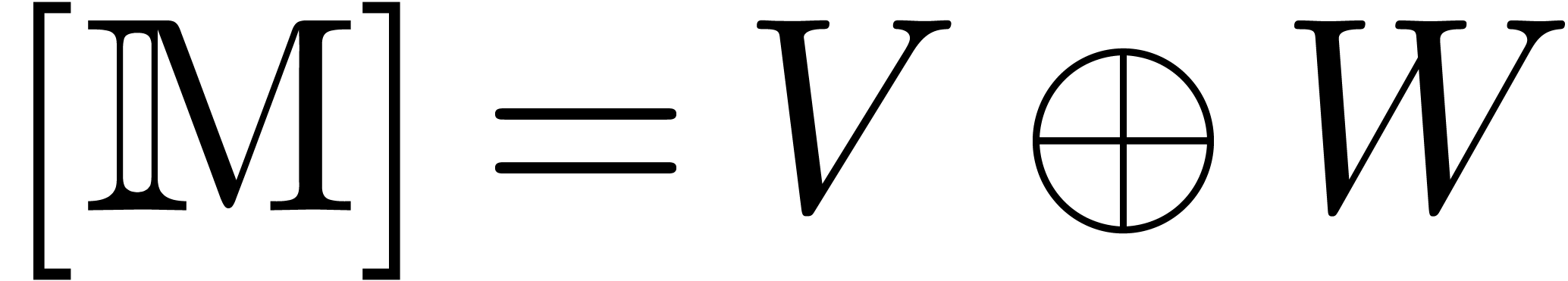 . We may compute bases of
. We may compute bases of
 and
and 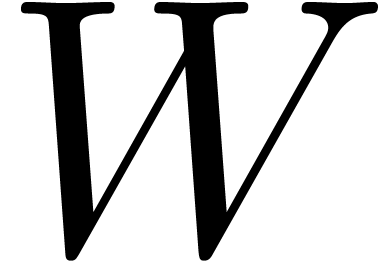 using
straightforward linear algebra. The canonical
using
straightforward linear algebra. The canonical  -linear projections
-linear projections 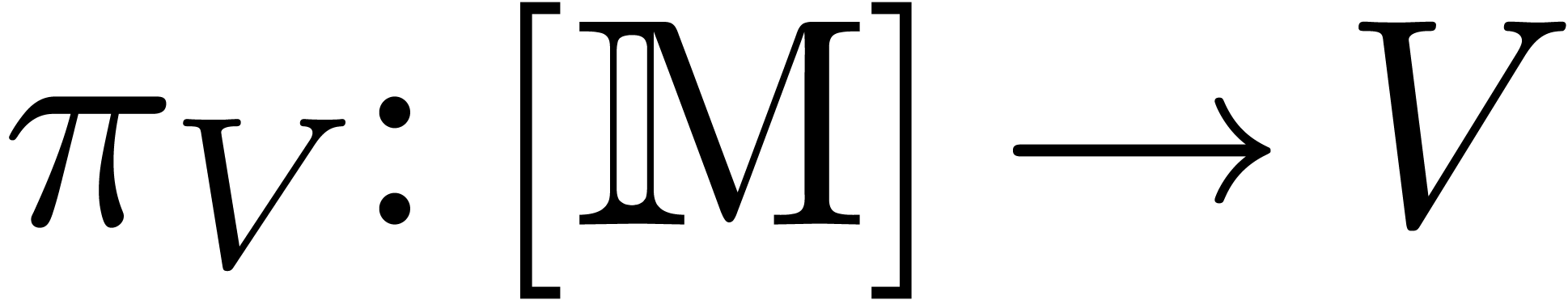 and
and 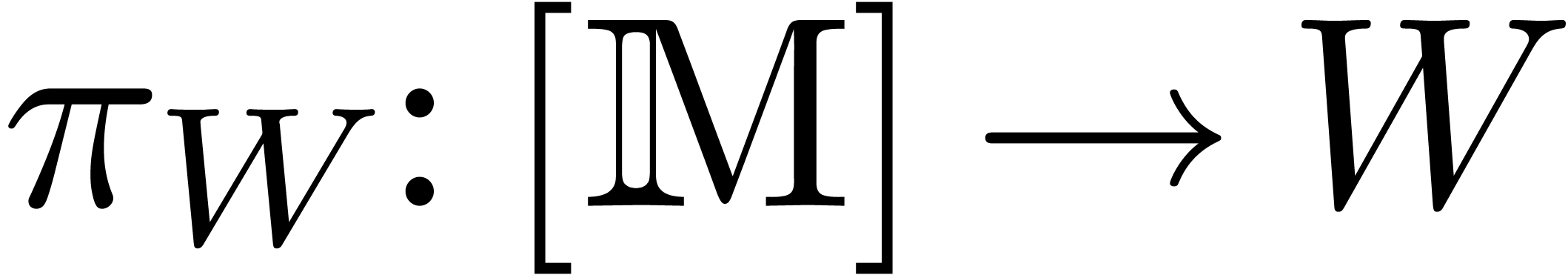 with
with 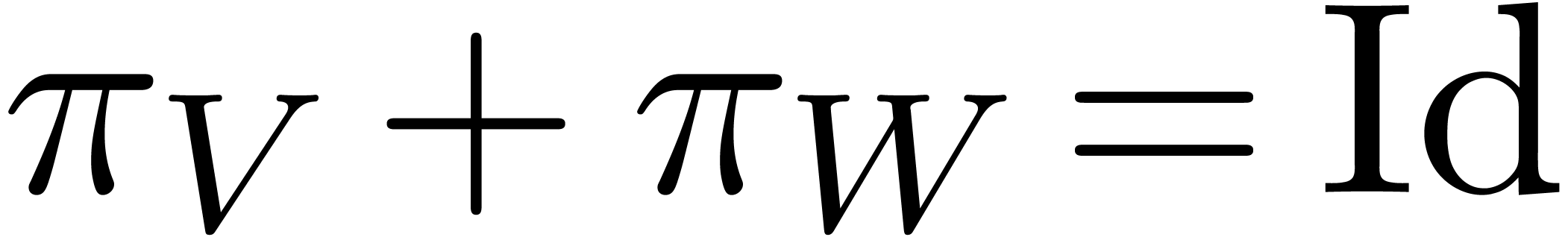 are also computable. We
claim that we may take
are also computable. We
claim that we may take 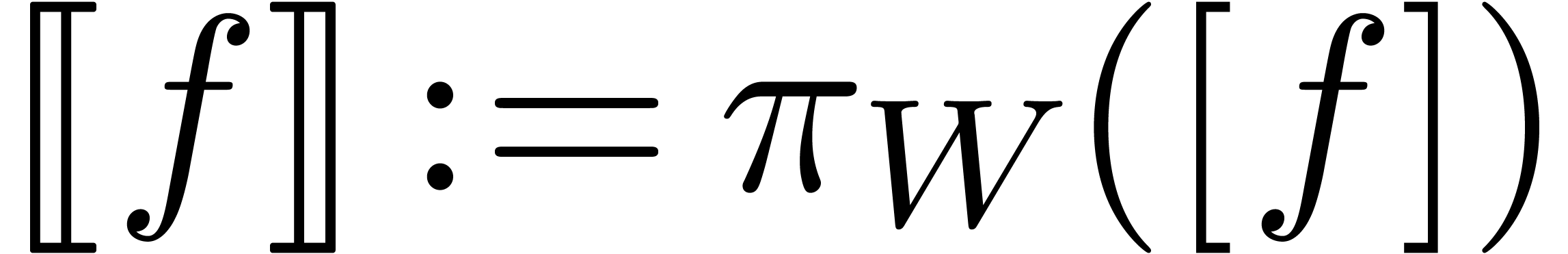 for every
for every 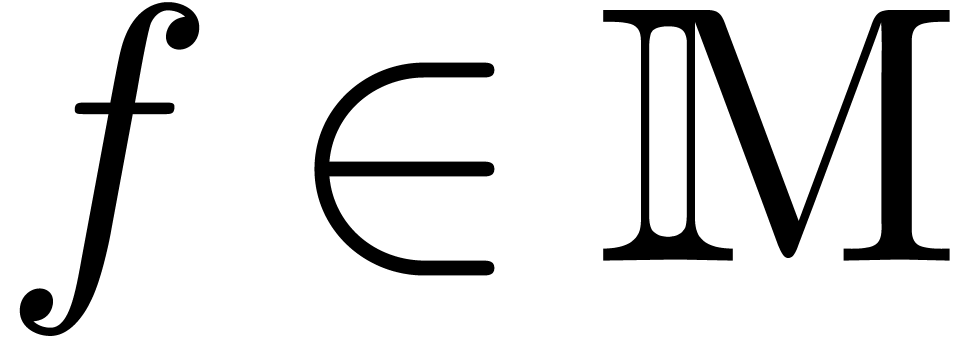 .
.
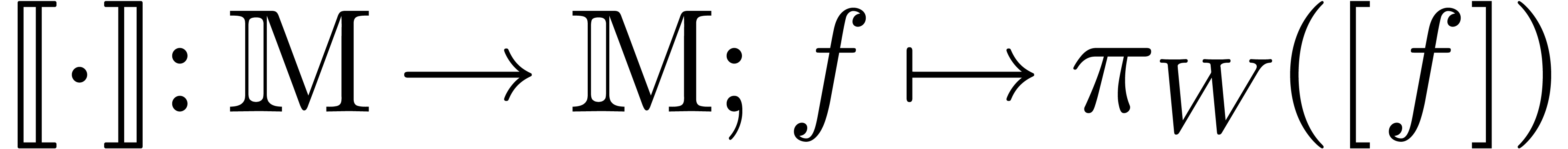 defines a computable
normal confined reduction on
defines a computable
normal confined reduction on  .
.
Proof. The mapping  is
clearly a computable confined reduction on
is
clearly a computable confined reduction on  .
It remains to be shown that
.
It remains to be shown that 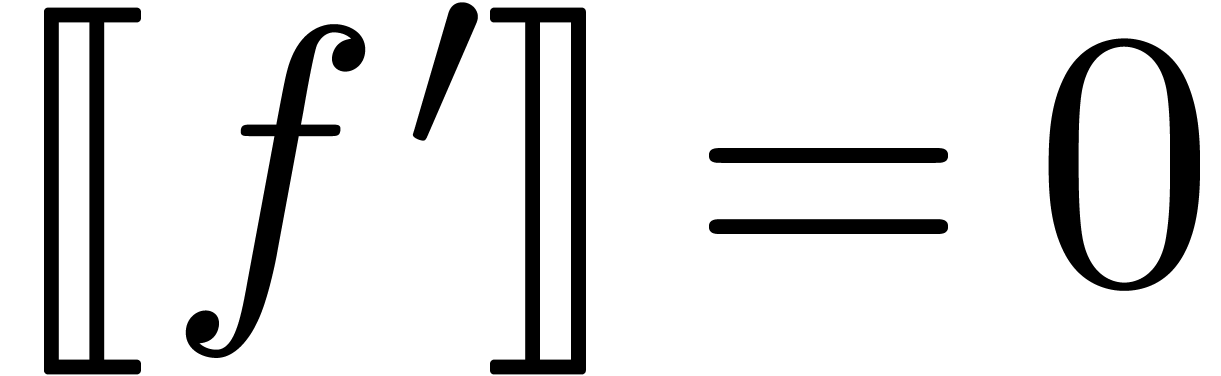 for all
for all  . Now
. Now 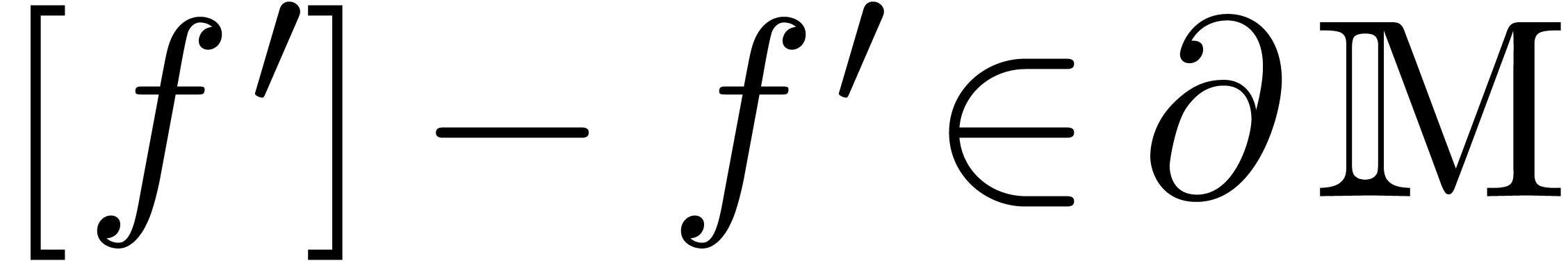 ,
so
,
so 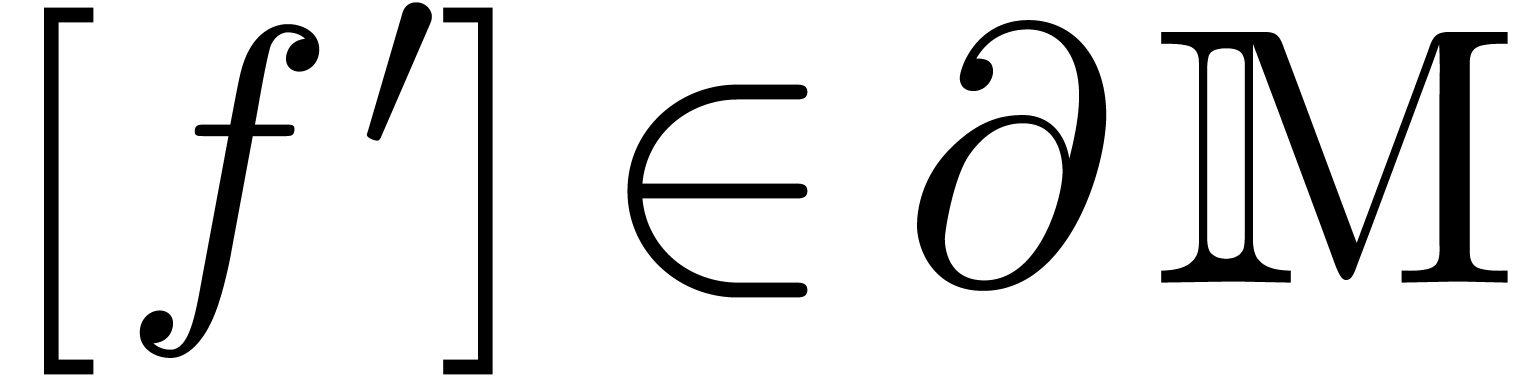 and there exists a
and there exists a 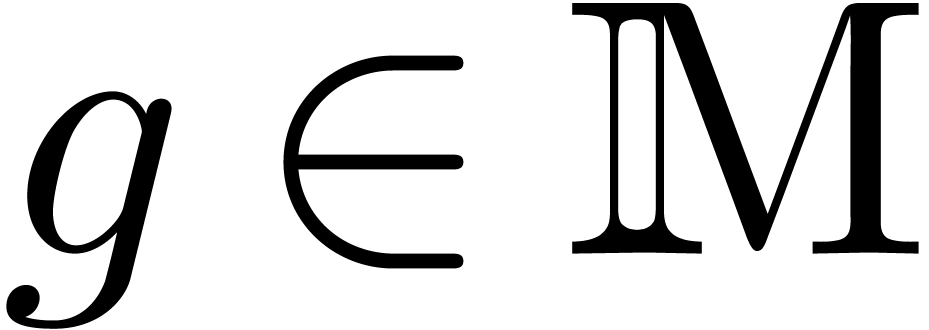 with
with 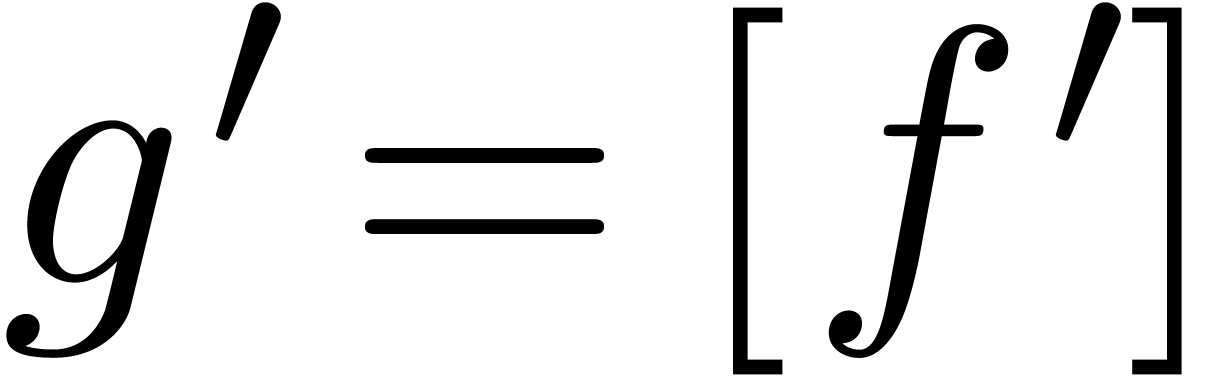 . Since
. Since 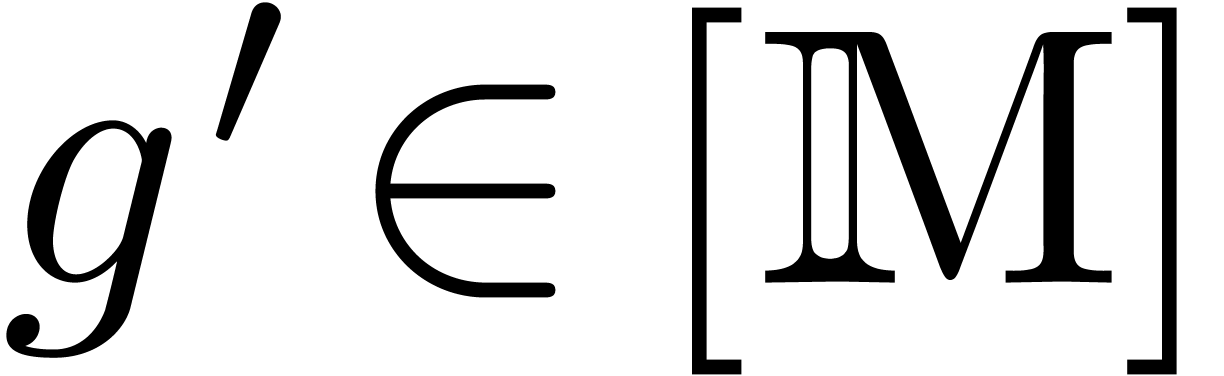 , it follows that
, it follows that 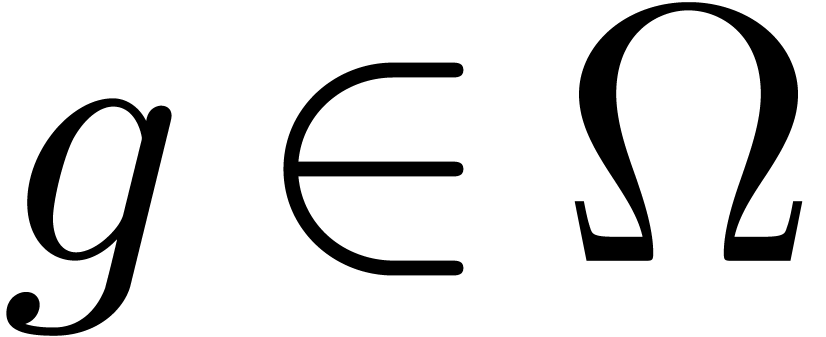 and
and
 . In other words,
. In other words,  and
and  .□
.□
Acknowledgments. We would like to thank Pierre Lairez for a helpful remark on an earlier version of this paper.
G.D. Birkhoff. Singular points of ordinary differential equations. Trans. Am. Math. Soc., 10:436–470, 1909.
A. Bostan, F. Chen, S. Chyzak, and Z. Li. Complexity of creative telescoping for bivariate rational functions. In Proc. ISSAC '12, pages 203–210. New York, NY, USA, 2010. ACM.
A. Bostan, F. Chyzak, and É. de Panafieu. Complexity estimates for two uncoupling algorithms. In Proc. ISSAC 2013, ISSAC '13, pages 85–92. New York, NY, USA, 2013. ACM.
S. Chen. Some applications of differential-difference algebra to creative telescoping. PhD thesis, École Polytechnique, 2011.
S. Chen, M. van Hoeij, M. Kauers, and C. Koutschan. Reduction-based creative telescoping for Fuchsian D-finite functions. Technical Report, ArXiv, 2016. http://arxiv.org/abs/1611.07421.
S. Chen, M. Kauers, and C. Koutschan. Reduction-based creative telescoping for algebraic functions. In Proc. ISSAC '16, pages 175–182. New York, NY, USA, 2016. ACM.
F. Chyzak. The ABC of Creative Telescoping — Algorithms, Bounds, Complexity. Habilitation, École polytechnique, 2014.
J. Della Dora, C. Dicrescenzo, and D. Duval. A new method for computing in algebraic number fields. In G. Goos and J. Hartmanis, editors, Eurocal'85 (2), volume 174 of Lect. Notes in Comp. Science, pages 321–326. Springer, 1985.
L. Dumont. Efficient algorithms for the symbolic computation of some contour integrals depending on one parameter. PhD thesis, École Polytechnique, 2016.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Transseries and real differential algebra, volume 1888 of Lecture Notes in Mathematics. Springer-Verlag, 2006.
P. Lairez. Periods of rational integrals: algorithms and applications. PhD thesis, École polytechnique, Nov 2014.
D. Zeilberger. The method of creative telescoping. JSC, 11(3):195–204, 1991.