Uniformly fast evaluation of
holonomic functions |
|
Laboratoire d'informatique, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau
|
|
|
In a series of previous articles, we have given efficient
algorithms for the evaluation of holonomic functions over the
algebraic numbers and for the computation of their limits at
singularities. The focus of these articles was mainly on the
efficient evaluation at a fixed point. In the present note, we
will show that there exist uniformly efficient algorithms for
evaluating holonomic functions. The main technical difficulty is
to maintain uniform efficiency near irregular singularities. We
will introduce a variant of accelerato-summation for this purpose
that we call “expedito-summation”.
Keywords: holonomic function, special
function, fast evaluation, accelero-summation, expedito-summation
A.M.S. subject classification: 33-04,
30-04, 40-04, 33F05, 33E30, 40G10, 30B40
|
1.Introduction
Statement of the problem and the main result
Let  be a subfield of
be a subfield of  . A holonomic function over
. A holonomic function over  is a solution
is a solution  to a linear
differential equation
to a linear
differential equation 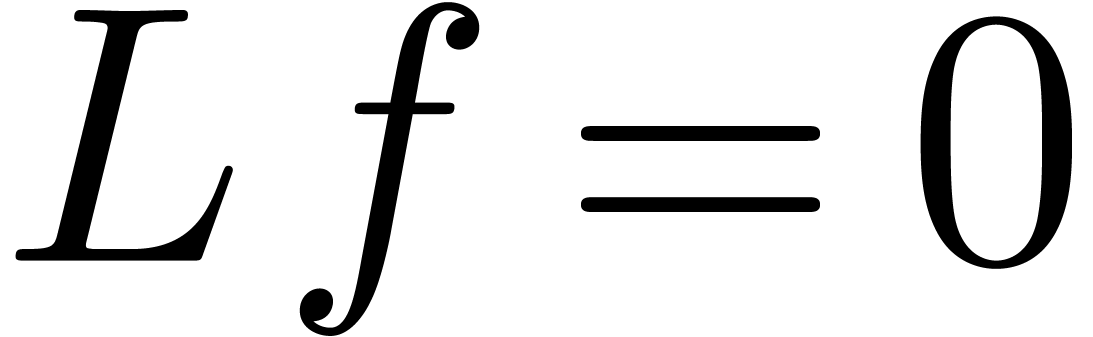 , where
, where
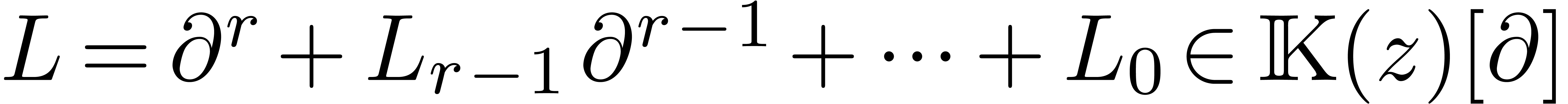 is a monic linear differential operator of order
is a monic linear differential operator of order
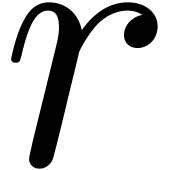 . Many classical special
functions, such as
. Many classical special
functions, such as  ,
, 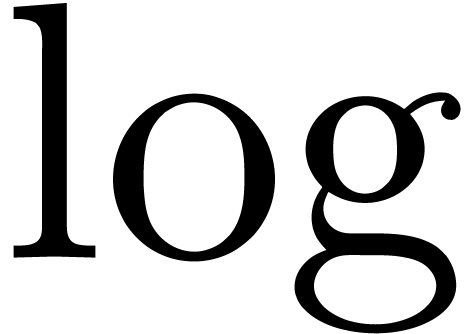 ,
,  ,
,
 ,
,  , hypergeometric functions, Bessel functions, the
Airy function, etc. are holonomic. Moreover, the class of
holonomic functions is stable under many operations, such as addition,
multiplication, differentiation, integration and postcomposition with
algebraic functions.
, hypergeometric functions, Bessel functions, the
Airy function, etc. are holonomic. Moreover, the class of
holonomic functions is stable under many operations, such as addition,
multiplication, differentiation, integration and postcomposition with
algebraic functions.
In the sequel, and unless stated otherwise, we will assume that  is the field of algebraic numbers. The only
singularities of a holonomic function
is the field of algebraic numbers. The only
singularities of a holonomic function  as above
can occur at the poles of the rational functions
as above
can occur at the poles of the rational functions  ; let
; let  denote the finite set
of these poles. We will say that
denote the finite set
of these poles. We will say that  has initial
conditions in
has initial
conditions in  if
if  for a certain non-singular point
for a certain non-singular point  .
In this paper, we are interested in the design of efficient algorithms
for the numeric evaluation of such a function
.
In this paper, we are interested in the design of efficient algorithms
for the numeric evaluation of such a function  , with a particular focus on high precision and
uniform efficiency as a function of the argument
, with a particular focus on high precision and
uniform efficiency as a function of the argument  .
.
For a fixed non singular evaluation point, say  , an efficient general purpose algorithm was first
given by the Chudnovsky brothers [3]. More precisely, in
the case when
, an efficient general purpose algorithm was first
given by the Chudnovsky brothers [3]. More precisely, in
the case when 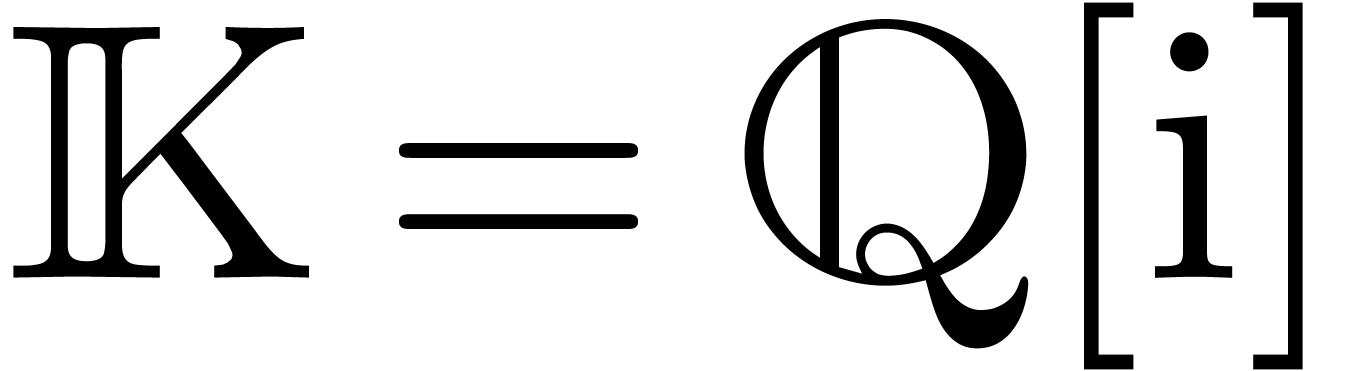 , they proved
that an
, they proved
that an 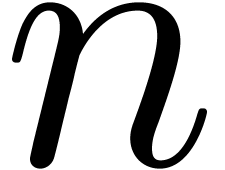 -bit approximation of
-bit approximation of
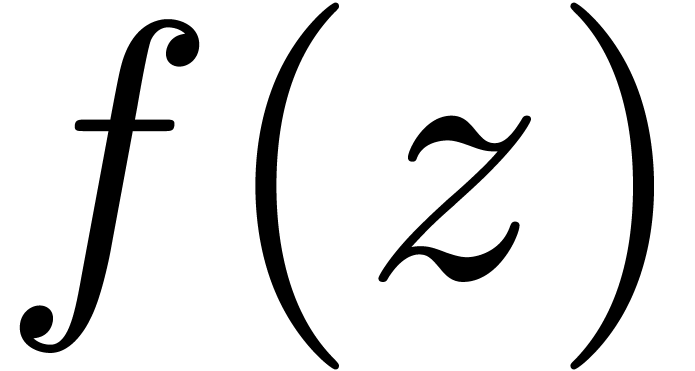 can be computed in time
can be computed in time 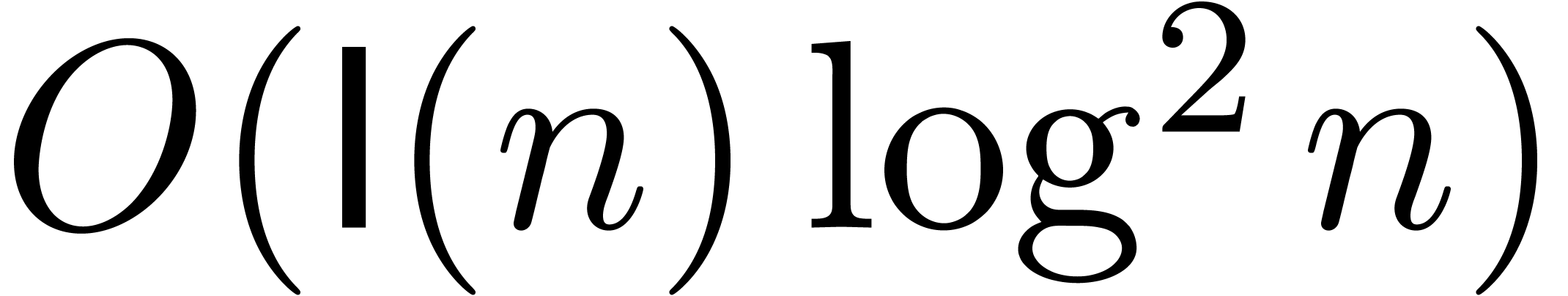 . Here
. Here 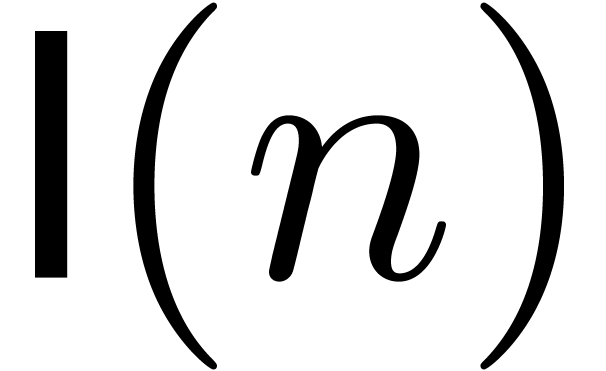 stands for a
complexity bound for integer multiplication and it has recently been
proved that one may take
stands for a
complexity bound for integer multiplication and it has recently been
proved that one may take 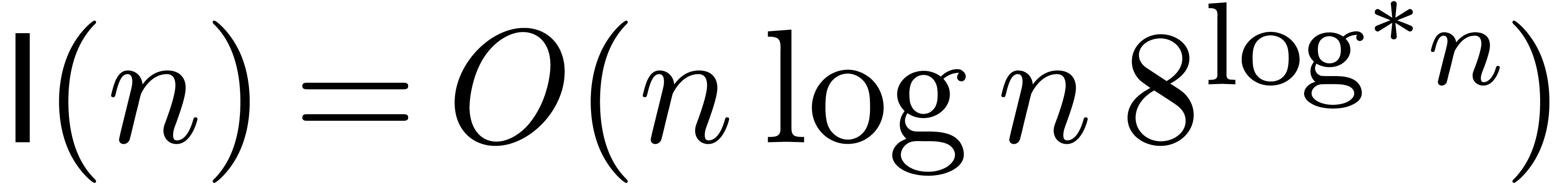 ,
where
,
where  . The
Chudnovsky–Chudnovsky algorithm was rediscovered in [7]
and generalized to the case when
. The
Chudnovsky–Chudnovsky algorithm was rediscovered in [7]
and generalized to the case when  is the field of
algebraic numbers. An early precursor and further variants can be found
in [2, 10, 6].
is the field of
algebraic numbers. An early precursor and further variants can be found
in [2, 10, 6].
In order to design uniformly efficient evaluation algorithms, it is
crucial to control the efficiency when  approaches one of the singularities in
approaches one of the singularities in  .
Actually, one first question concerns the computation of the limit of a
holonomic function at a singularity if this limit exists. This was first
done in [8] for so called regular singularities (achieving
the same complexity bound as for non singular points), and in [9]
for irregular singularities (in which case we showed that
.
Actually, one first question concerns the computation of the limit of a
holonomic function at a singularity if this limit exists. This was first
done in [8] for so called regular singularities (achieving
the same complexity bound as for non singular points), and in [9]
for irregular singularities (in which case we showed that 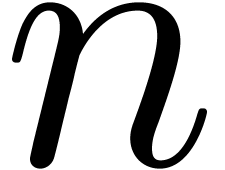 -bit approximations of limits can be computed
in time
-bit approximations of limits can be computed
in time 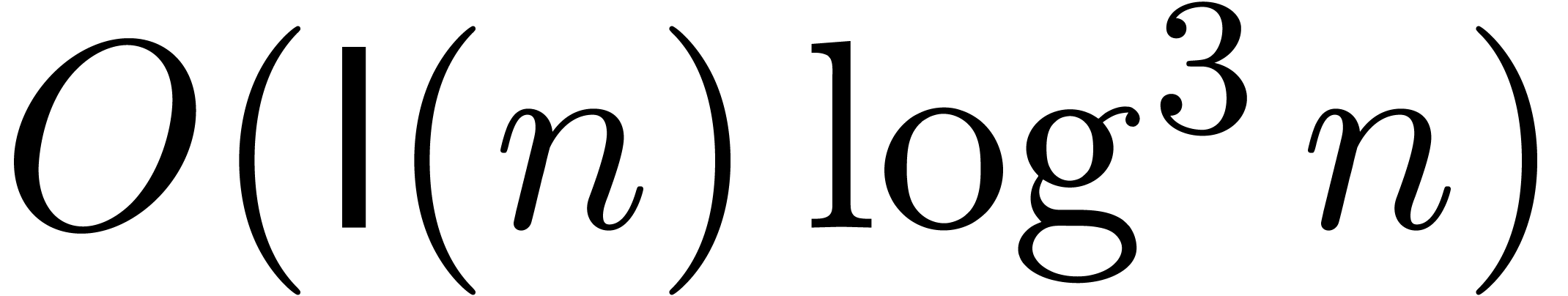 ). We refer to [8, 9] for the definitions of the concepts of
regular and irregular singularities.
). We refer to [8, 9] for the definitions of the concepts of
regular and irregular singularities.
The main aim of this paper is to achieve the same kind of complexity
bounds uniformly in  . Such
bounds need to be stated with a lot of care. First of all, a holonomic
function such as
. Such
bounds need to be stated with a lot of care. First of all, a holonomic
function such as 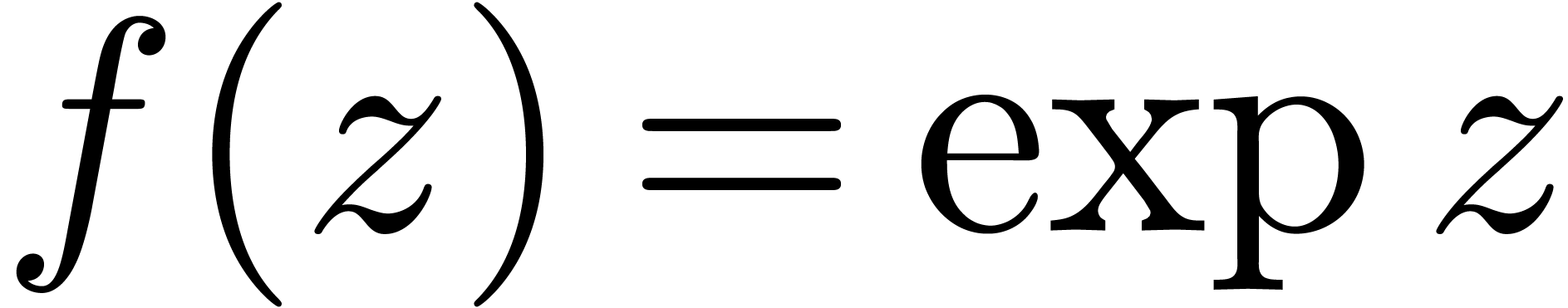 grows exponentially fast at
infinity: given the
grows exponentially fast at
infinity: given the 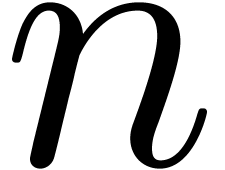 -bit
number
-bit
number 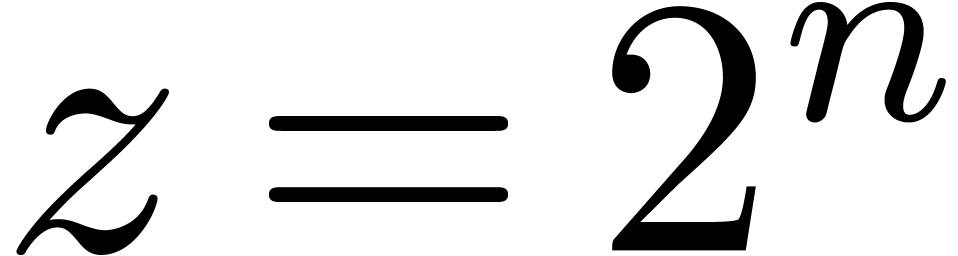 , one needs
, one needs 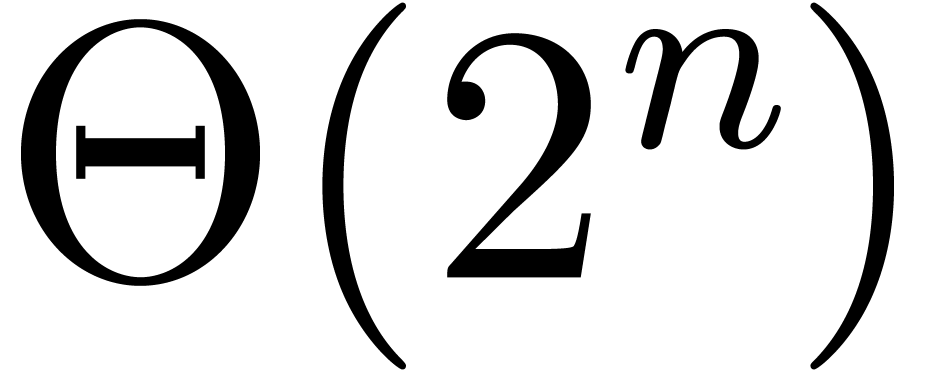 bits to merely write down the closest integer
approximation
bits to merely write down the closest integer
approximation 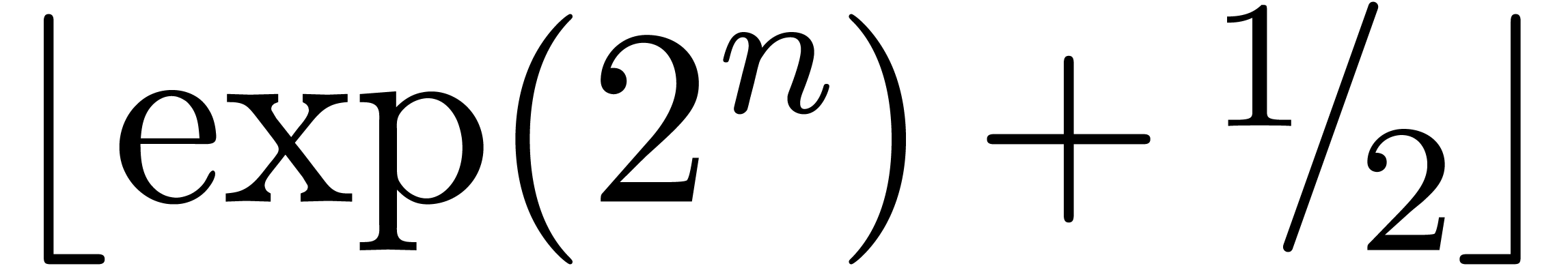 of
of 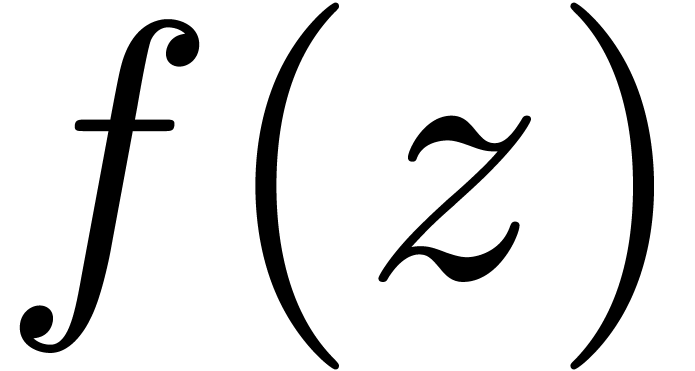 .
Using floating point approximations for both
.
Using floating point approximations for both  and
and
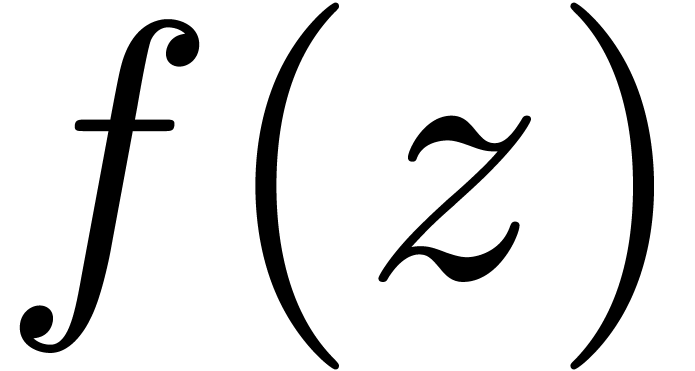 does not help, since a similar explosion then
occurs for the exponent. But we may hope for a good uniform complexity
bound if we use fixed point approximations for
does not help, since a similar explosion then
occurs for the exponent. But we may hope for a good uniform complexity
bound if we use fixed point approximations for  and floating point approximations for
and floating point approximations for 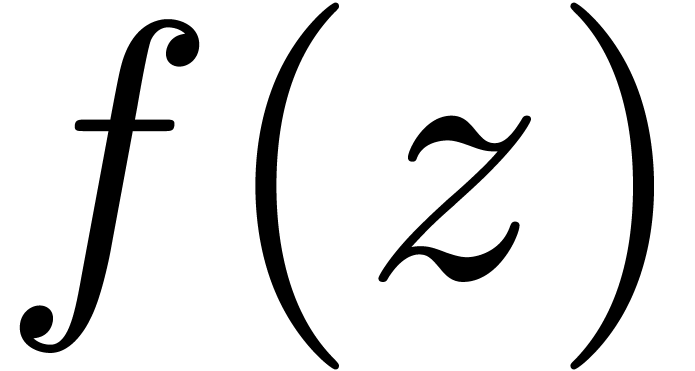 .
.
Another complication is due to the number zero, which should be regarded
as a singularity when using floating point representations: it is
difficult to compute accurate floating point approximations for 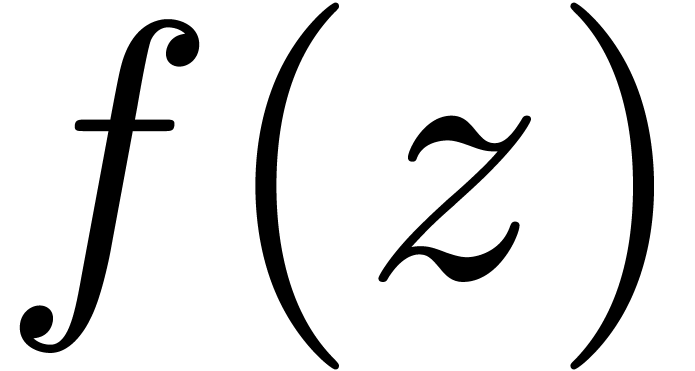 if
if  is close to a zero of
is close to a zero of
 . Predicting the exact
locations of zeros of holonomic functions is a notoriously difficult
problem. Even the basic question to decide whether
. Predicting the exact
locations of zeros of holonomic functions is a notoriously difficult
problem. Even the basic question to decide whether 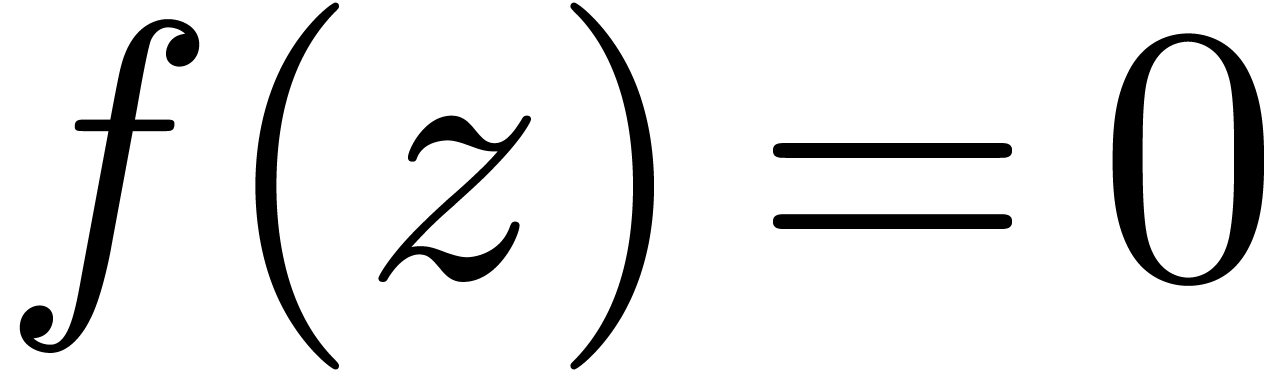 for
for  admits no algorithmic answer for the moment.
Nevertheless, the number
admits no algorithmic answer for the moment.
Nevertheless, the number  is often the
approximation of some other complex number with a precision of
is often the
approximation of some other complex number with a precision of 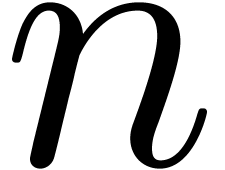 binary digits behind the dot. In that case, it is natural
to consider the more general evaluation of
binary digits behind the dot. In that case, it is natural
to consider the more general evaluation of  on
the ball
on
the ball 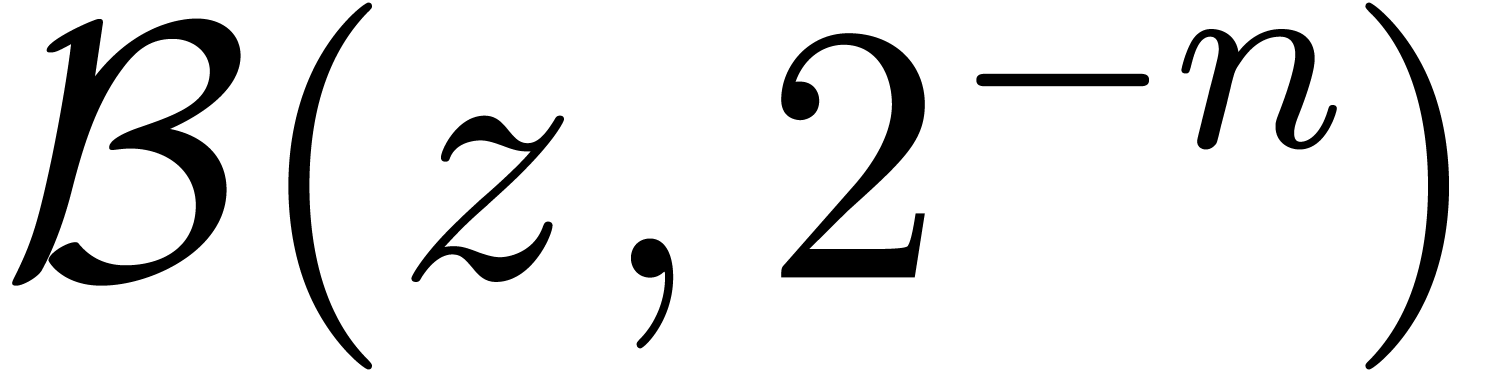 with center
with center  and
radius
and
radius  , and to require that
, and to require that
 admits no zeros on this ball.
admits no zeros on this ball.
We are almost in a position to state the main result of this paper. Let
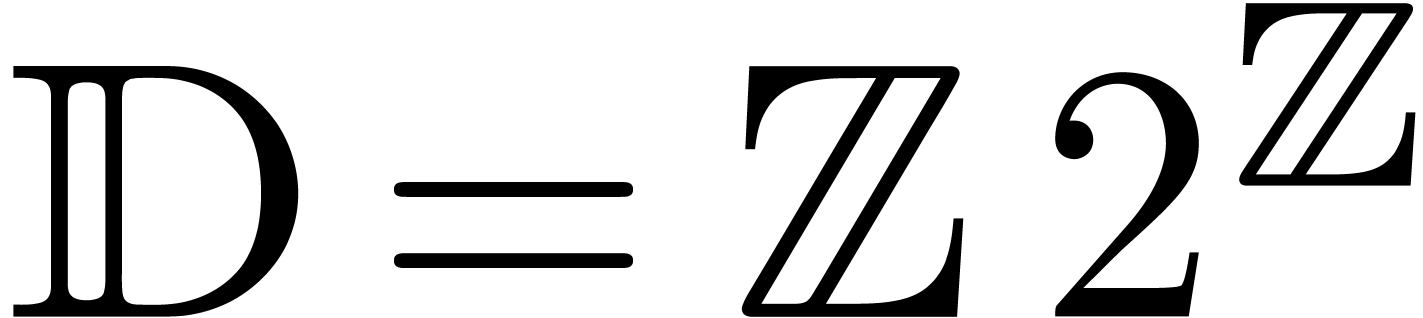 be the set of dyadic numbers. Given
be the set of dyadic numbers. Given
 , we denote by
, we denote by 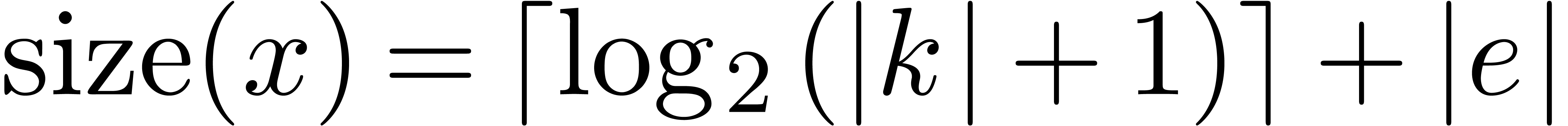 the bitsize of
the bitsize of  .
Given
.
Given 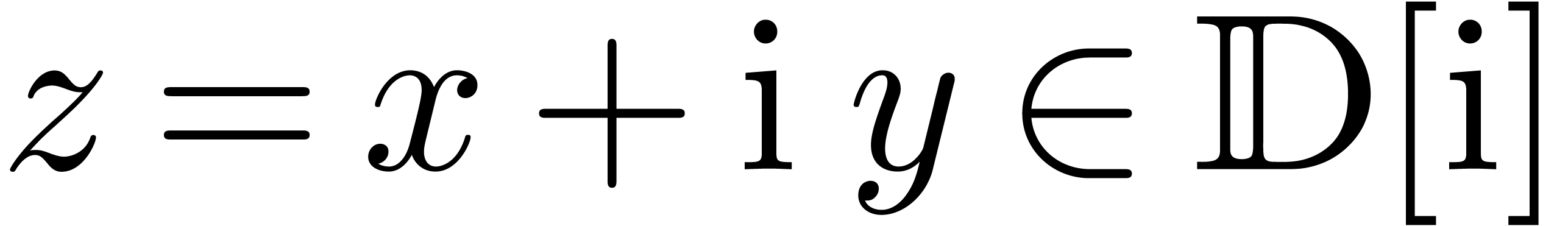 , we also denote
, we also denote 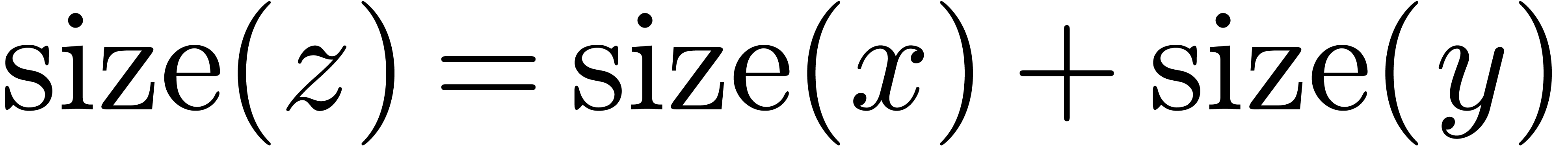 . The set
. The set  of floating point numbers is defined in the same way as
of floating point numbers is defined in the same way as  , but the exponent of a floating
point numbers
, but the exponent of a floating
point numbers 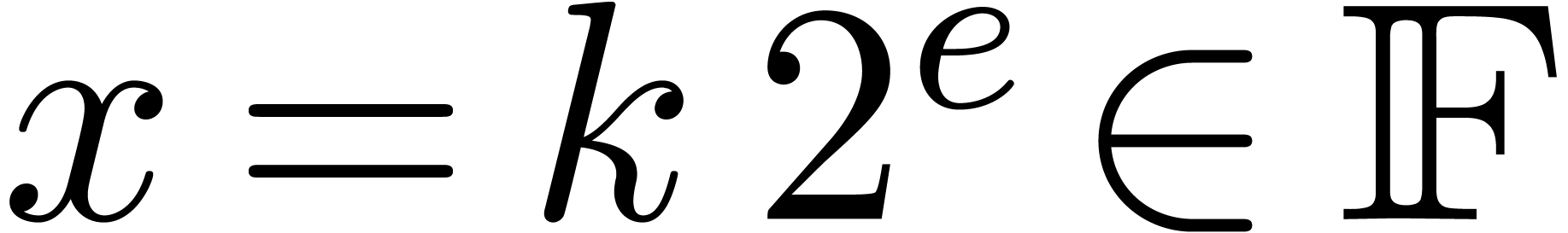 is represented in binary notation,
so that the bitsize of
is represented in binary notation,
so that the bitsize of  is now fiven by
is now fiven by 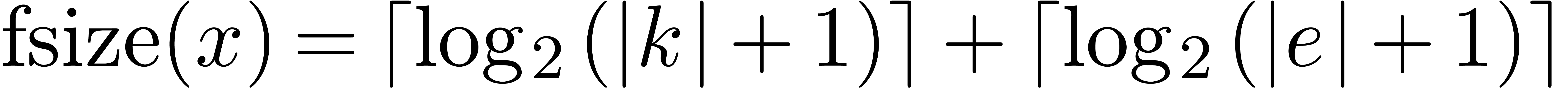 .
.
Let  be the point at which we specified the
initial conditions of
be the point at which we specified the
initial conditions of  . We
define
. We
define  to be the open subset of
to be the open subset of  of all points
of all points  such that the straightline segment
such that the straightline segment
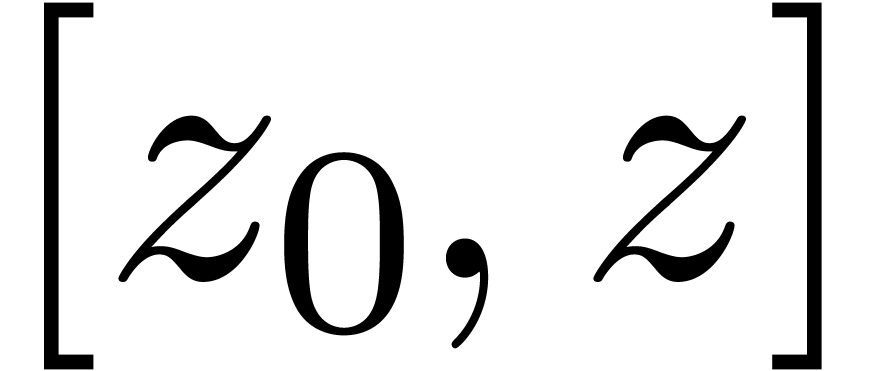 from
from 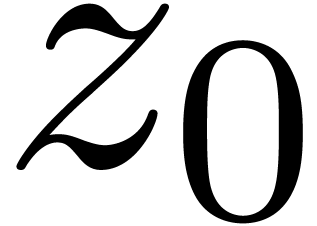 to
to  does not intersect
does not intersect  . We take
. We take
 to be the unique solution of
to be the unique solution of 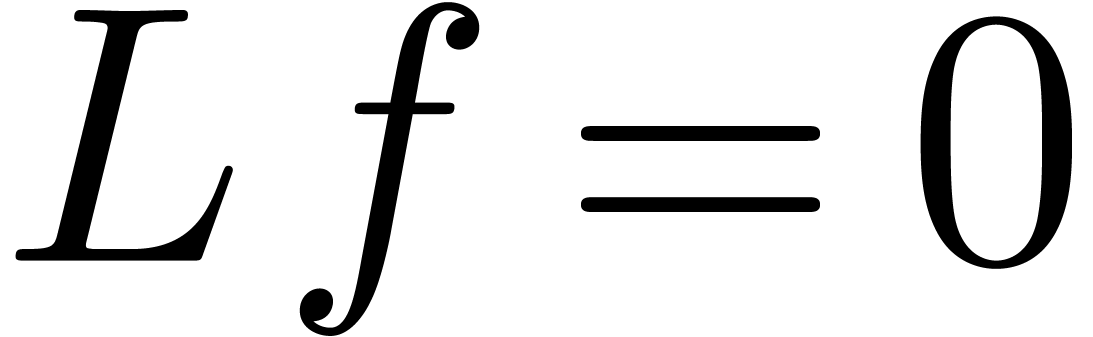 on
on  that matches the prescribed initial
conditions at
that matches the prescribed initial
conditions at 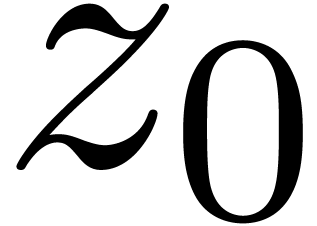 . Let
. Let  denote the set of zeros of
denote the set of zeros of  .
The main theorem of this paper is the following.
.
The main theorem of this paper is the following.
Proof strategy
As long as  remains in a compact subset
remains in a compact subset 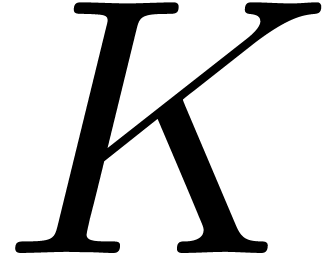 of
of  in Theorem 1, the
conclusion essentially follows from the existing complexity bounds in
[3, 7]; using a refinement [11]
of the complexity analysis from [7], one even obtains the
stronger complexity bound
in Theorem 1, the
conclusion essentially follows from the existing complexity bounds in
[3, 7]; using a refinement [11]
of the complexity analysis from [7], one even obtains the
stronger complexity bound 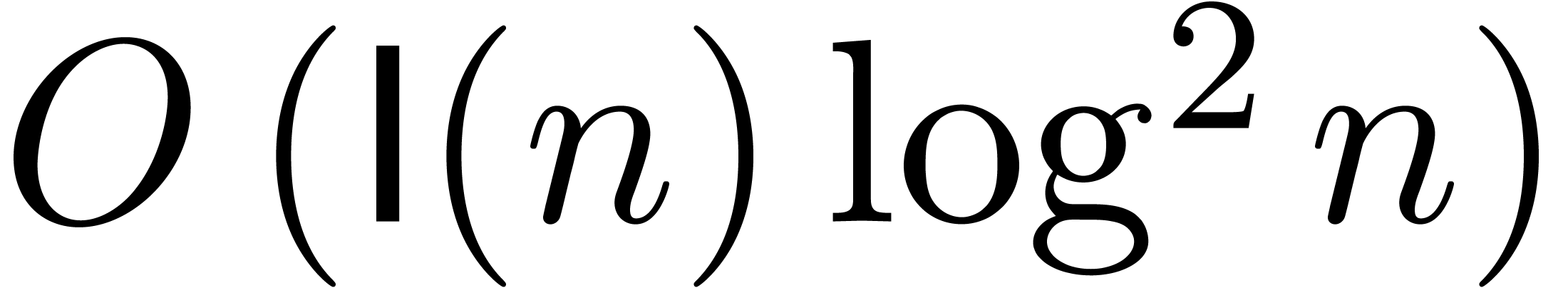 for the evaluation of
for the evaluation of
 . Using the techniques from
[8], these complexity bounds generalize to subsets
. Using the techniques from
[8], these complexity bounds generalize to subsets  of
of  , where
, where
 is a compact set that contains none of the
irregular singularities of
is a compact set that contains none of the
irregular singularities of  .
If the point at infinity is a regular singularity, then the bound also
applies on subsets
.
If the point at infinity is a regular singularity, then the bound also
applies on subsets  for sufficiently large
for sufficiently large 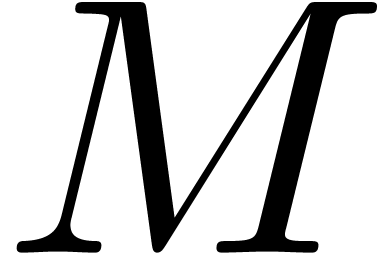 , modulo the change of coordinates
, modulo the change of coordinates
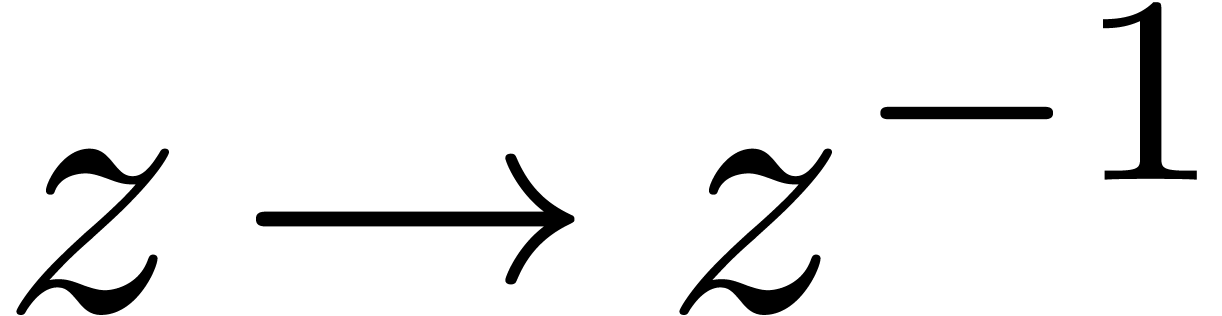 .
.
The above discussion shows that the proof of Theorem 1
involves two main difficulties: controlling the complexity near
irregular singularities and controlling the complexity of evaluating
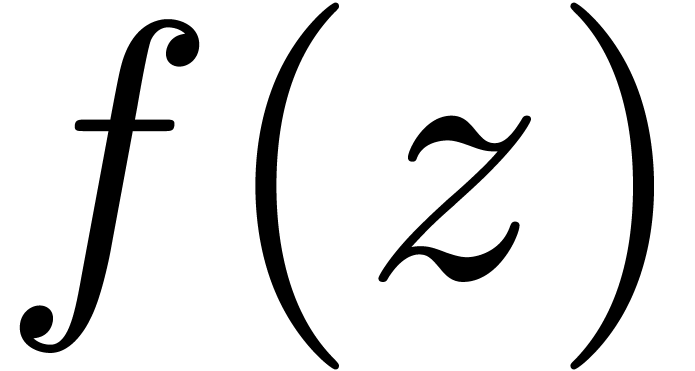 near zeros of
near zeros of  .
For the first task, we will adapt the technique of accelero-summation
from [9]. For the second task, we rely on the idea that
.
For the first task, we will adapt the technique of accelero-summation
from [9]. For the second task, we rely on the idea that
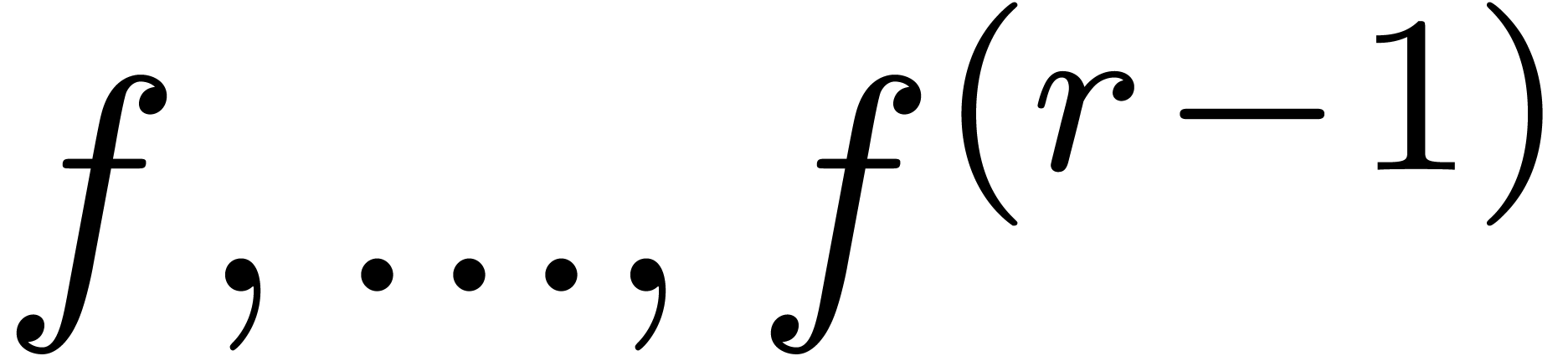 can never simultaneously become “smaller
than expected”. A precise statement will be presented in Section
4; this statement can be regarded as a quantitative version
of the well-known property that
can never simultaneously become “smaller
than expected”. A precise statement will be presented in Section
4; this statement can be regarded as a quantitative version
of the well-known property that 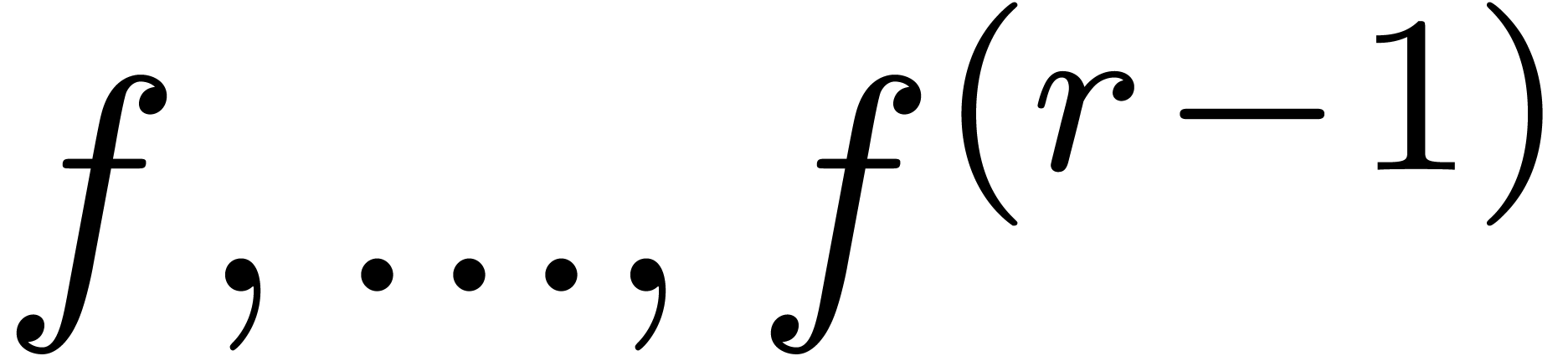 cannot vanish
simultaneously unless
cannot vanish
simultaneously unless  vanishes itself.
vanishes itself.
Let us return to the evaluation of  near an
irregular singulary, say
near an
irregular singulary, say  . At
the origin, it is well-known that
. At
the origin, it is well-known that 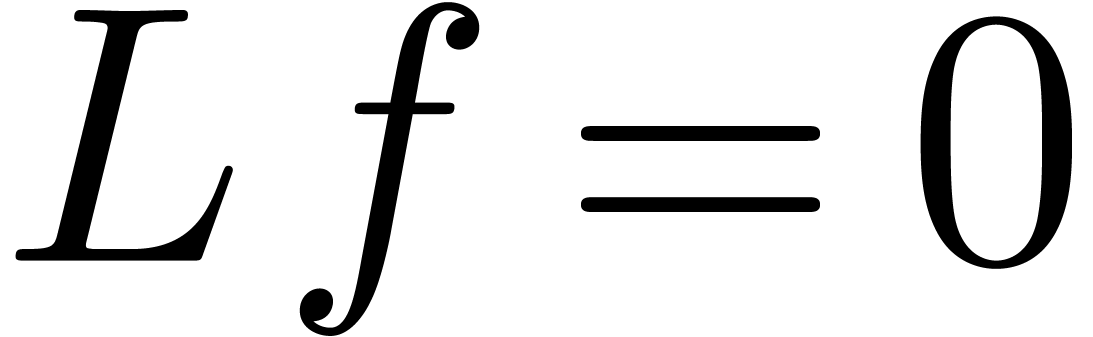 admits a basis
of formal solution of the form
admits a basis
of formal solution of the form
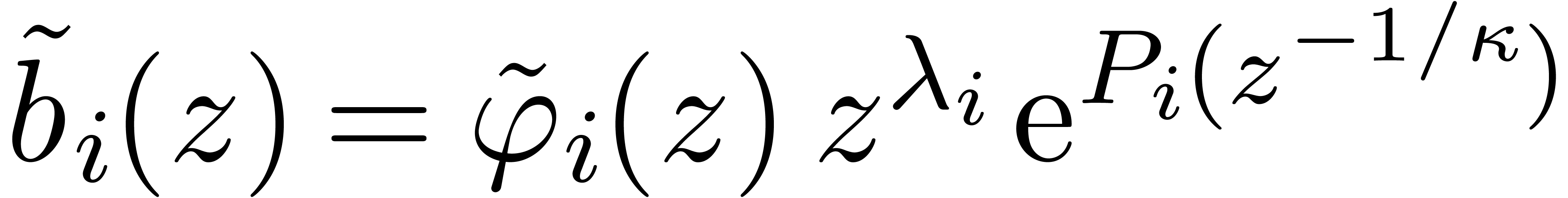
for 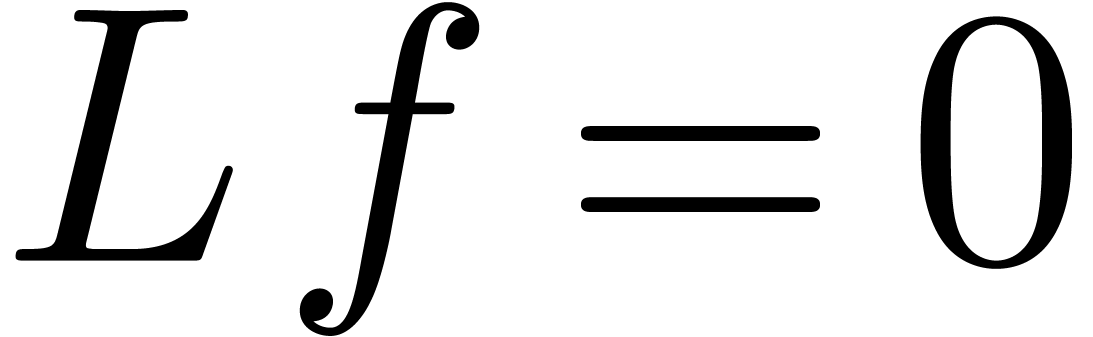 , where
, where 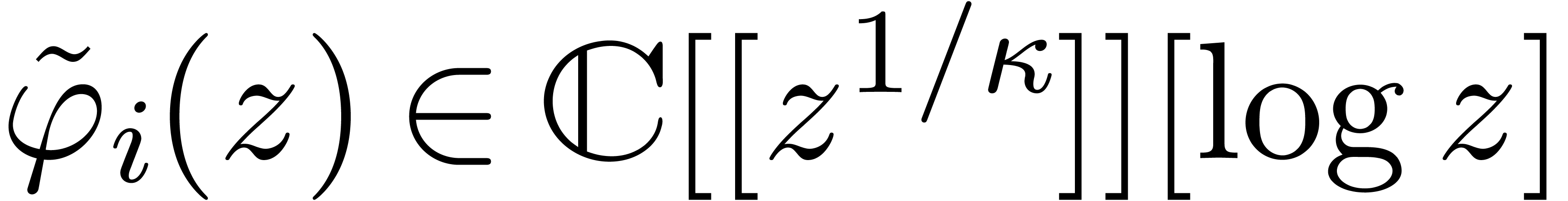 ,
,  ,
,
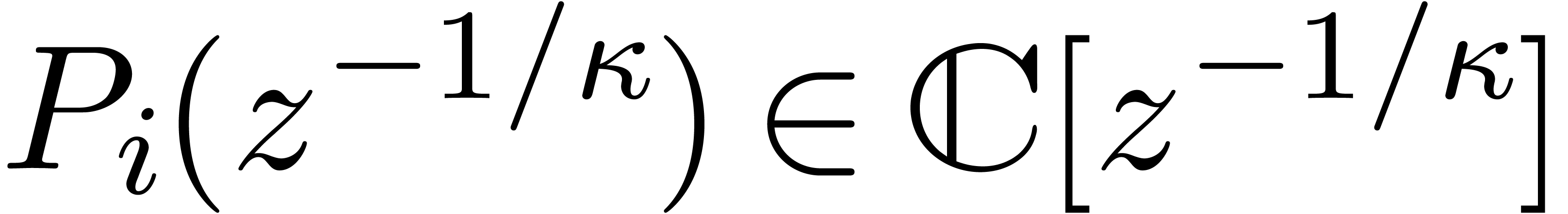 ,
, 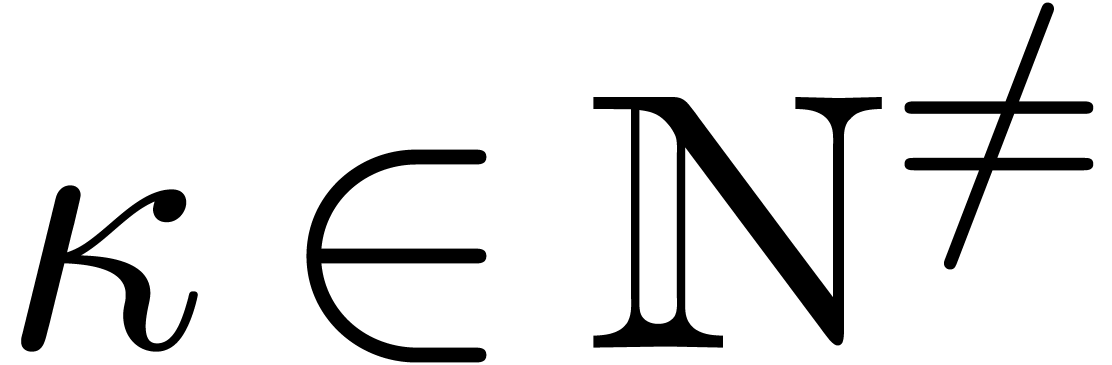 , and where
, and where 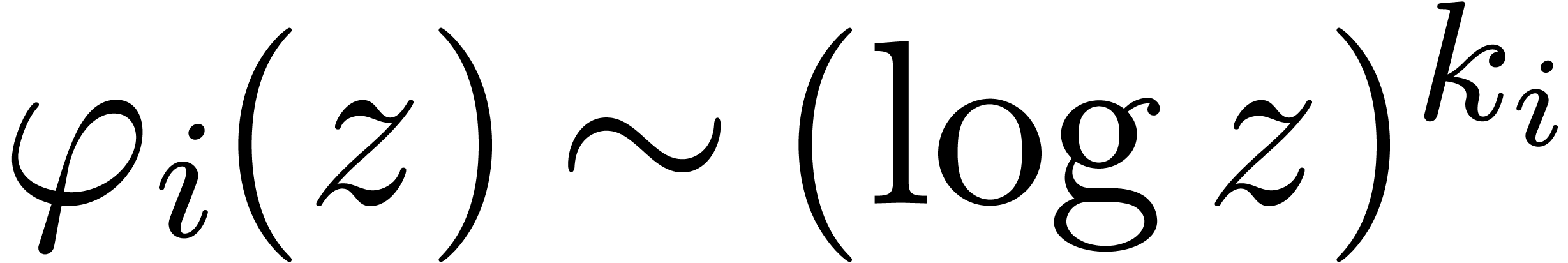 for some
for some  . In [9], it is shown
that the series
. In [9], it is shown
that the series 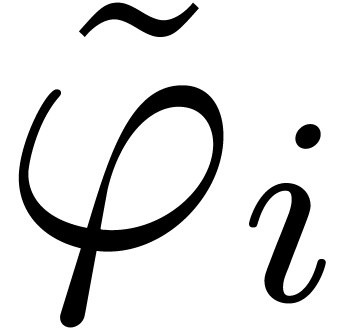 are accelero-summable and that
we can associate actual functions
are accelero-summable and that
we can associate actual functions 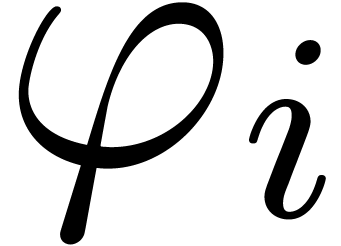 to them that
are defined on sectors of the form
to them that
are defined on sectors of the form
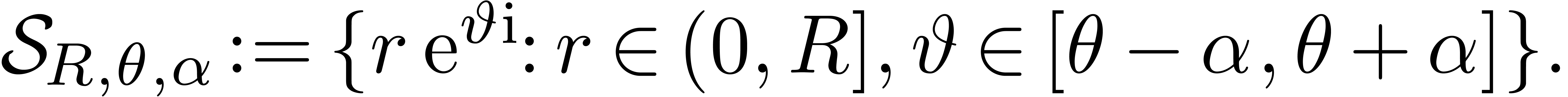
Moreover, a finite number of these sectors can be made to cover a
punctured neighbourhood of the origin. One crucual step toward the
design of an efficient evaluation algorithm for  on such a sector is to deal with the special case when
on such a sector is to deal with the special case when 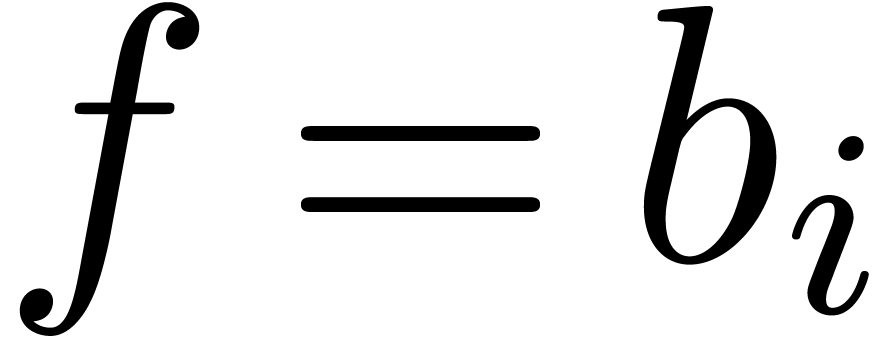 for some
for some 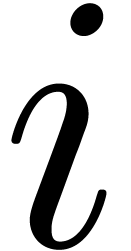 , which further
reduces to the case when
, which further
reduces to the case when 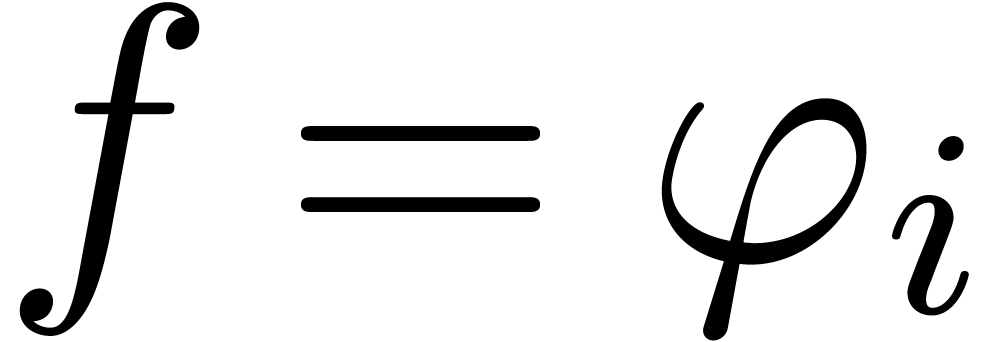 .
.
In the remainder of this paper, we will assume that the reader is
familiar with [9] and the notations that we used there. For
simplicity, we will also restrict to accelerations and Laplace
transforms such that we integrate on the positive real axis. Using a
change of variables  for a suitable
for a suitable 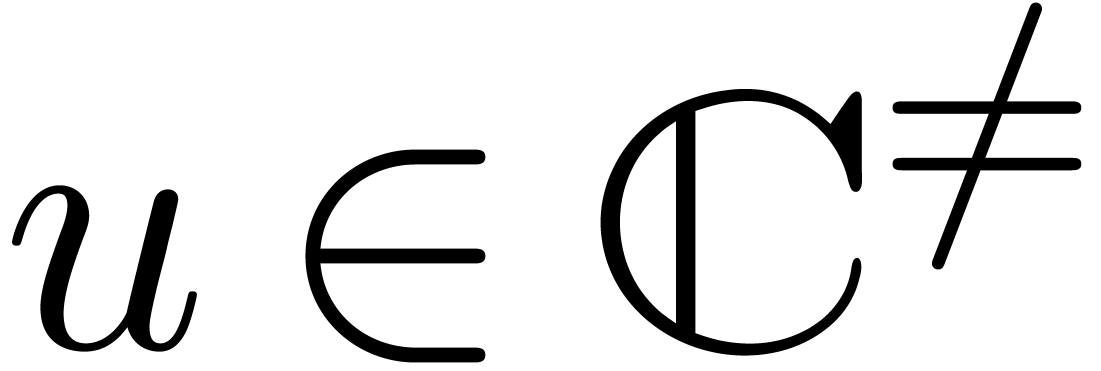 , this entails no loss of generality. More
precisely, we assume that we are in the following situation. The
function
, this entails no loss of generality. More
precisely, we assume that we are in the following situation. The
function  is the result
is the result
of an accelero-summation process with critical times  ,
,  ,
and all integrals taken on the positive real axis. The accelero-sum
,
and all integrals taken on the positive real axis. The accelero-sum  is defined in some sector
is defined in some sector
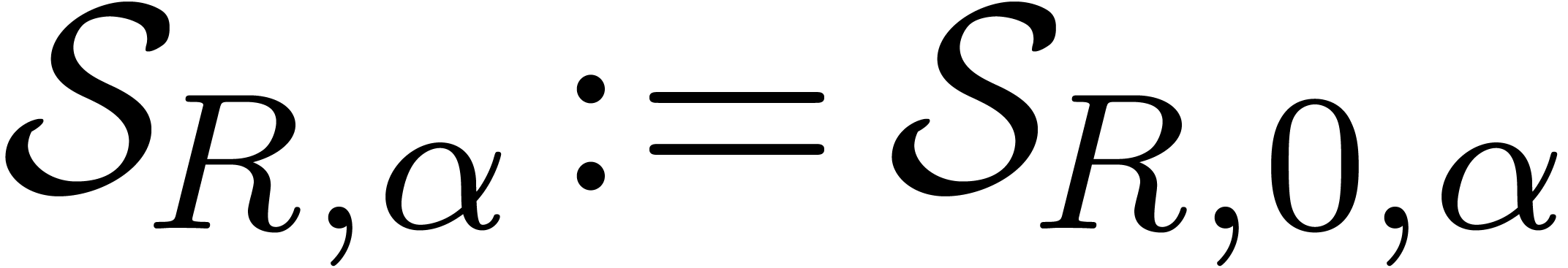
for any  with
with  .
.
For any fixed 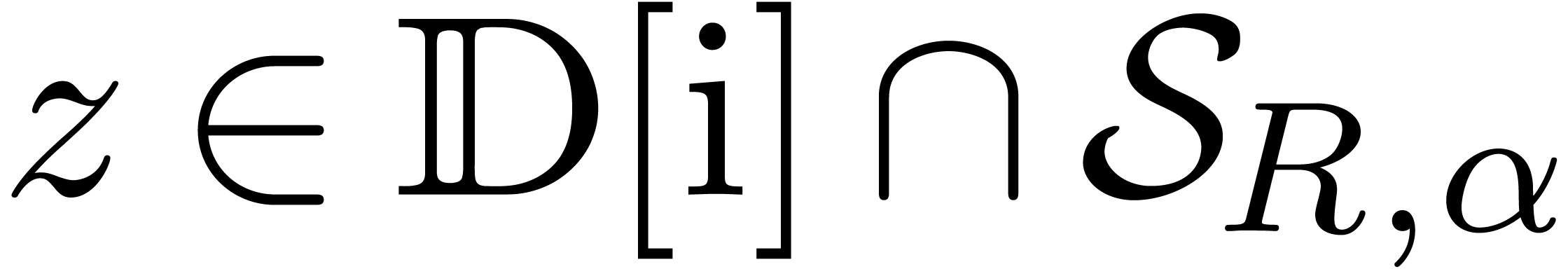 , the
accelero-summation process from [9] provides us with an
algorithm to compute
, the
accelero-summation process from [9] provides us with an
algorithm to compute  digits of
digits of 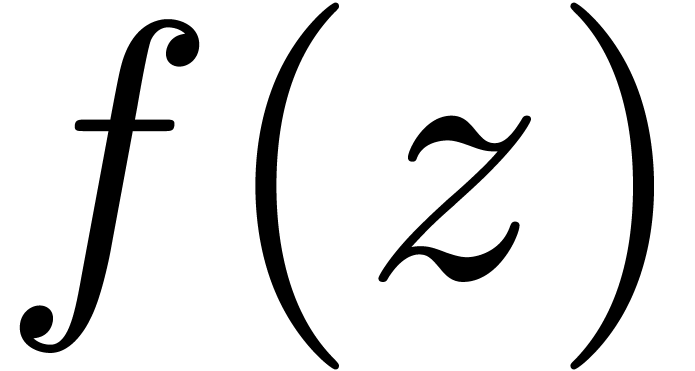 in time
in time 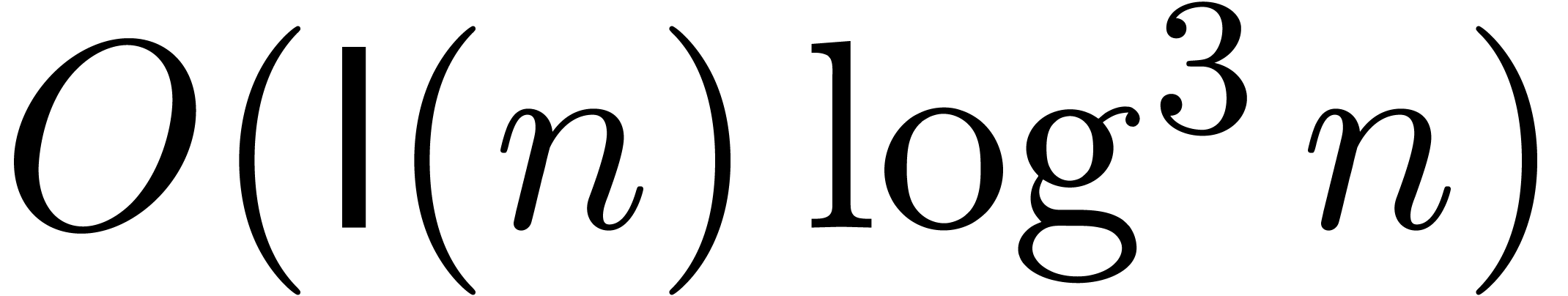 . In Section 3.1,
we will show that this complexity is uniform in
. In Section 3.1,
we will show that this complexity is uniform in  , provided that
, provided that 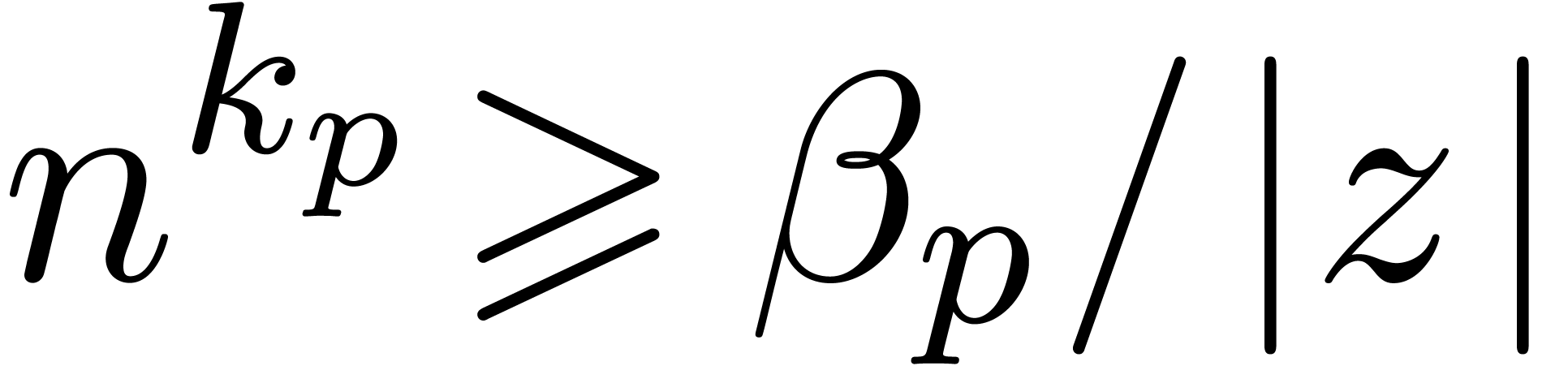 for some
computable constant
for some
computable constant 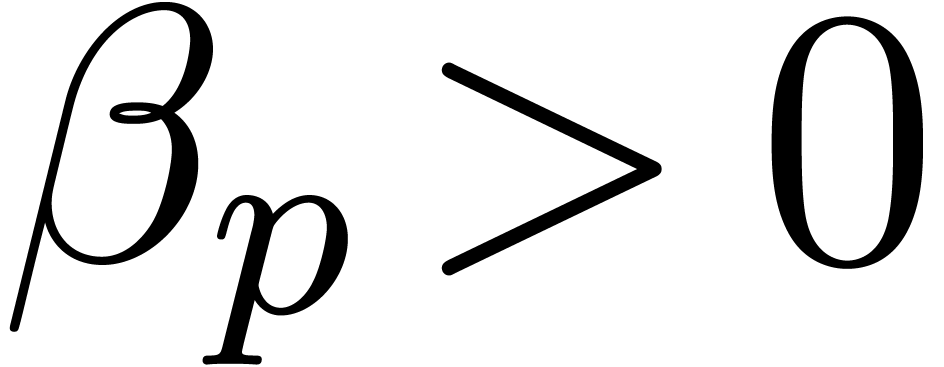 . In
other words: accelero-summation is a good numerical scheme under the
condition that we really need a lot of digits. In [9], we
also showed that the technique of “summation until the least
term” [12] allows to compute
. In
other words: accelero-summation is a good numerical scheme under the
condition that we really need a lot of digits. In [9], we
also showed that the technique of “summation until the least
term” [12] allows to compute 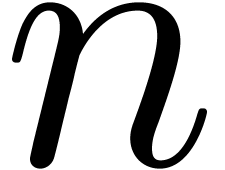 digits of
digits of 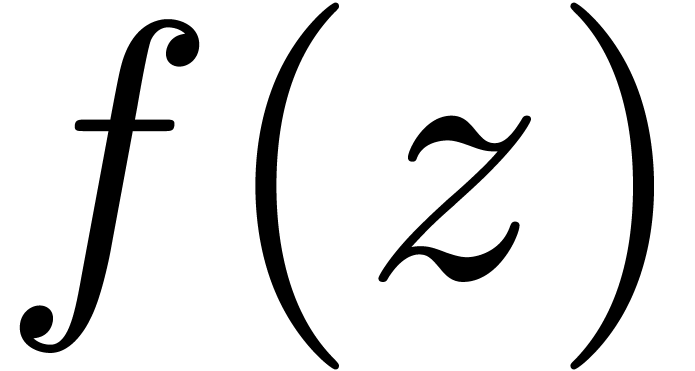 in time
in time 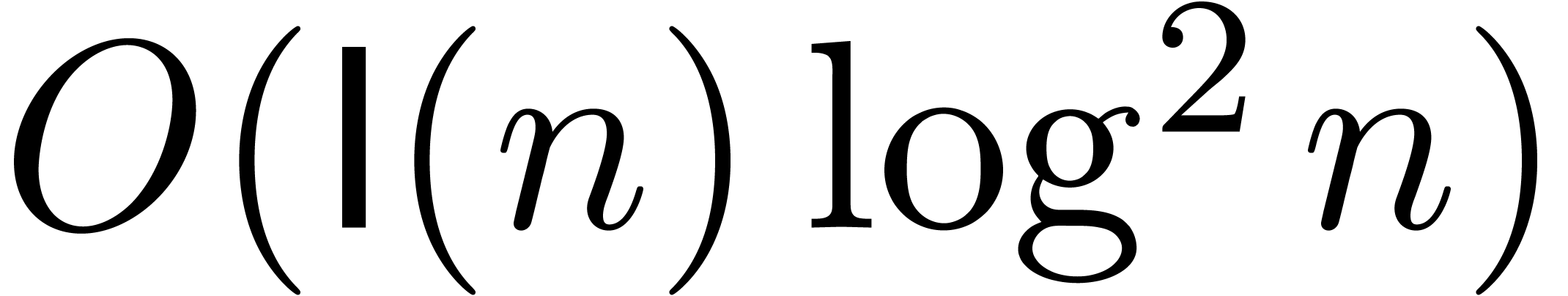 ,
provided that
,
provided that 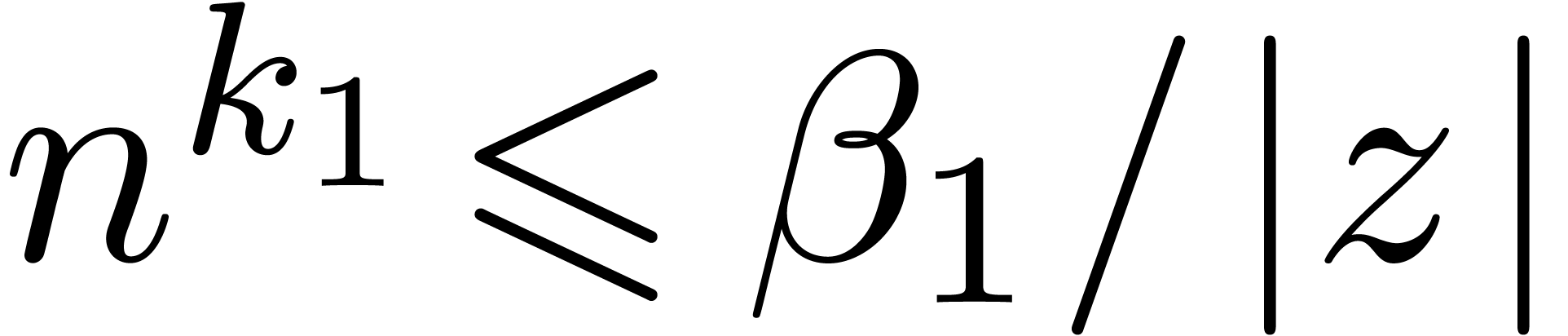 for some computable constant
for some computable constant 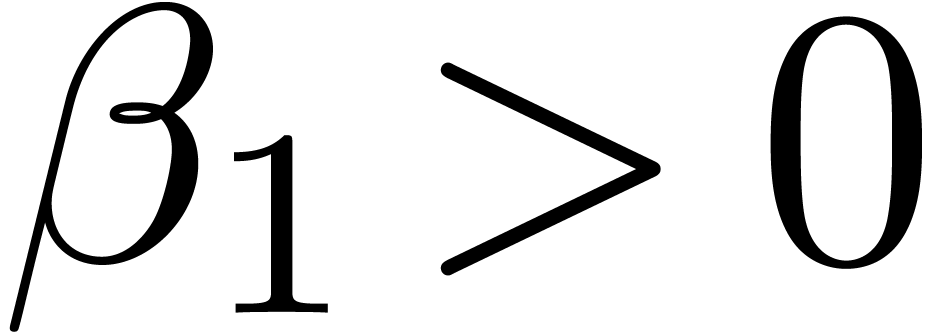 . This complexity bound is also
uniform in
. This complexity bound is also
uniform in  .
.
The above uniform complexity bounds still leave a gap for precisions
 between
between  and
and 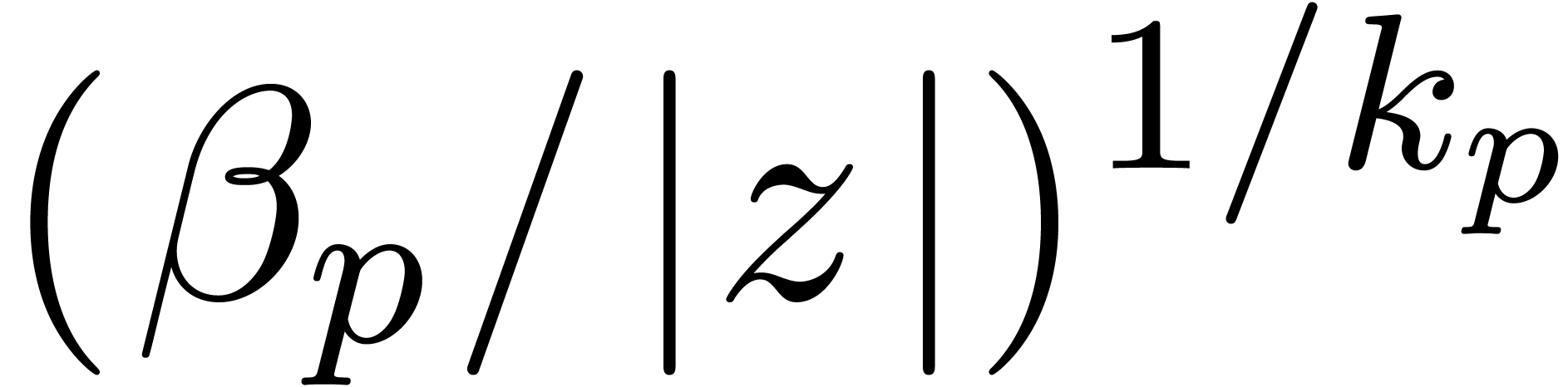 . In order to fill this gap, we introduce the
technique of expedito-summation in Section 2. Roughly
speaking, we perform the accelero-summation process until some critical
time
. In order to fill this gap, we introduce the
technique of expedito-summation in Section 2. Roughly
speaking, we perform the accelero-summation process until some critical
time 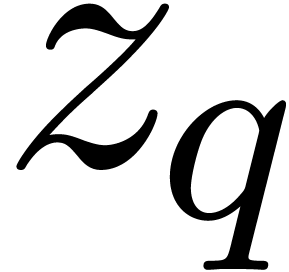 with
with 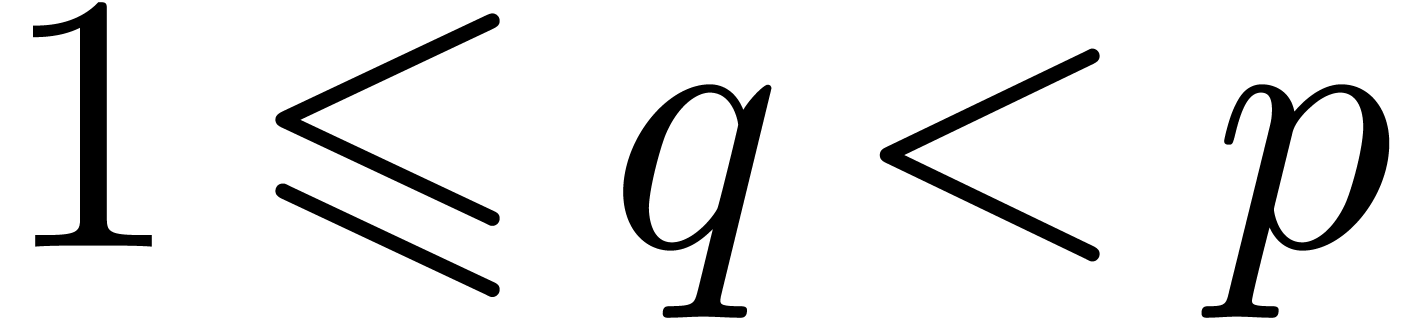 and then
“expedite” the process by directly taking a truncated
Laplace transform with respect to
and then
“expedite” the process by directly taking a truncated
Laplace transform with respect to 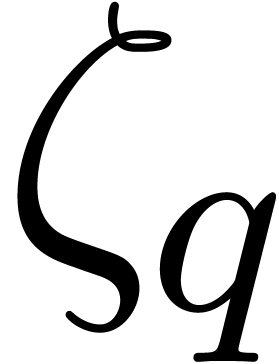 .
We will show in Section 3.3 that there exist computable
constants
.
We will show in Section 3.3 that there exist computable
constants 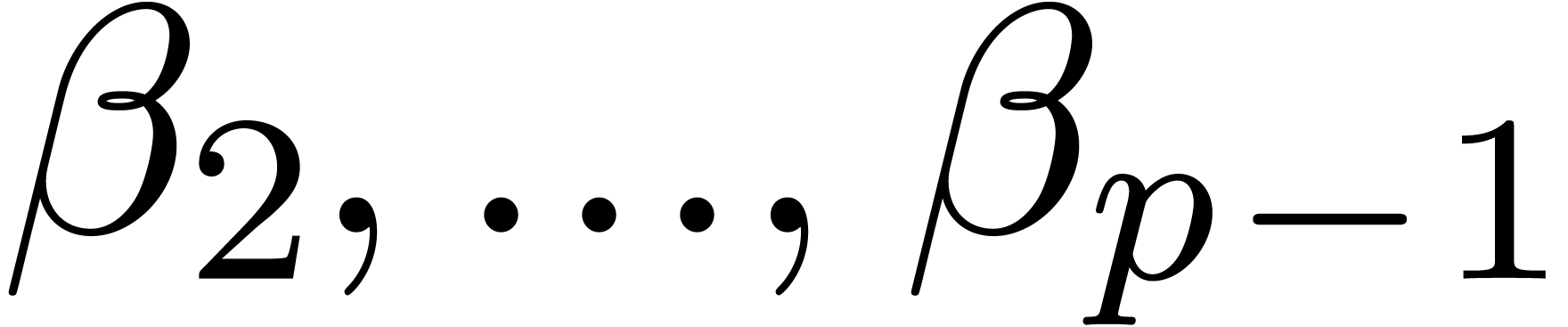 such that expedito-summation until the
critical time
such that expedito-summation until the
critical time 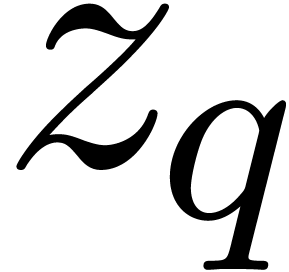 allows us compute
allows us compute 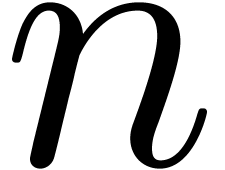 digits of
digits of 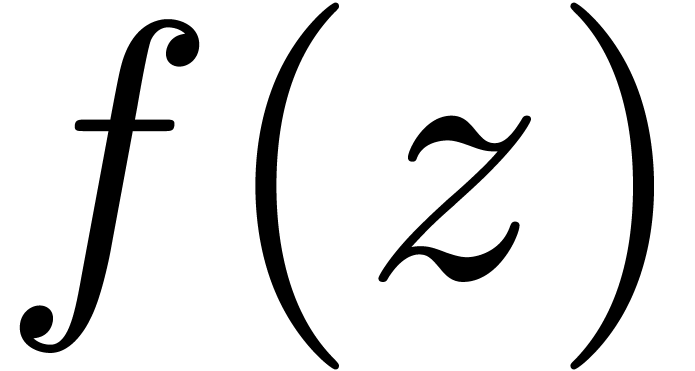 in time
in time 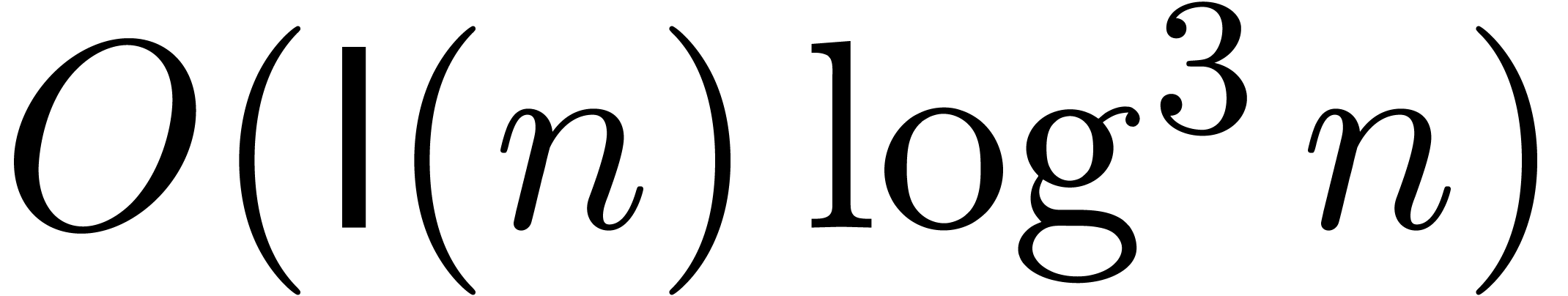 ,
uniformly in
,
uniformly in  provided that
provided that 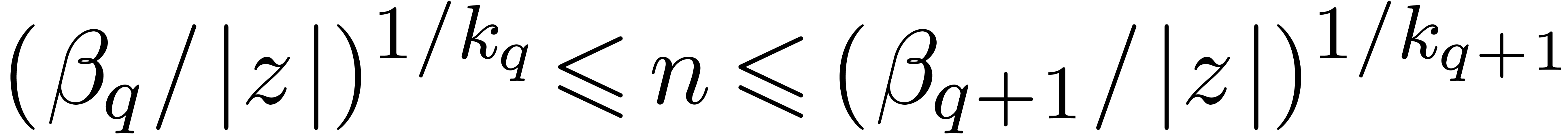 .
.
Notational conventions
This paper should be regarded as a supplement to [9]. For
this reason, and as we already stressed before, we will freely use
concepts and notations from that paper. In this area it also frequently
happens that there exist algorithms to explicitly compute various
constants involved in error bounds, but that the precise values of these
constants are irrelevant. In [9], we strived to make all
error bounds as explicit as possible, but in this paper we will simply
denote strictly positive constants of this kind by  . In analysis, the habit to write
. In analysis, the habit to write 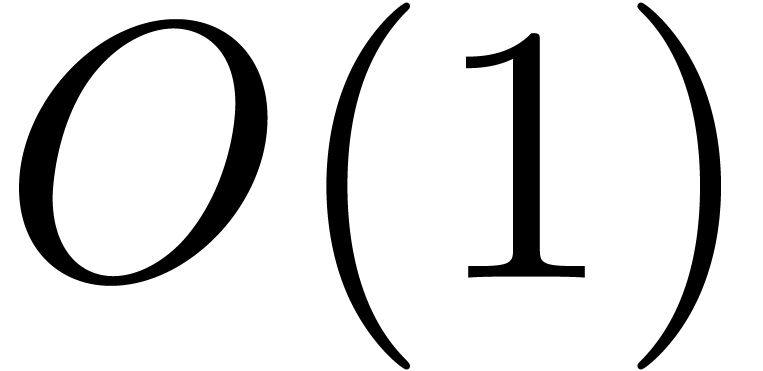 for “some bounded function” is somewhat
analoguous. For instance, given a real function
for “some bounded function” is somewhat
analoguous. For instance, given a real function  and a constant
and a constant 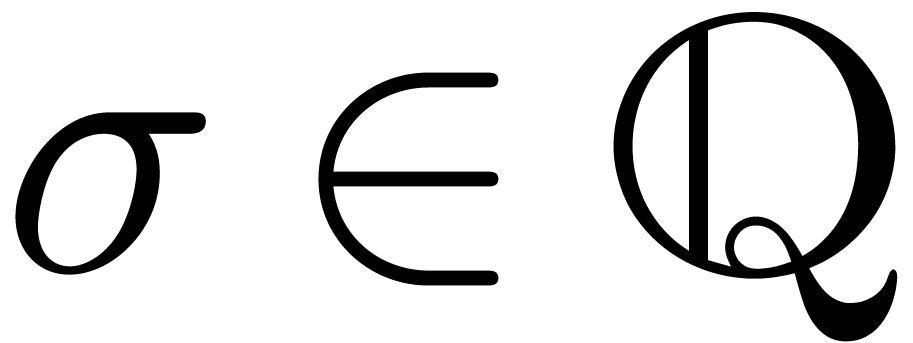 , saying that
, saying that

for all 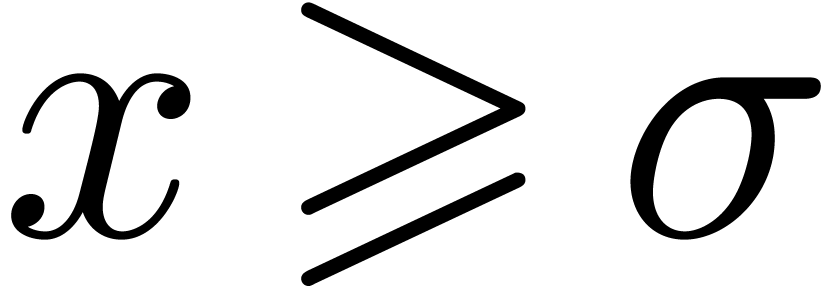 means that we can compute an explicit
exponential bound for
means that we can compute an explicit
exponential bound for 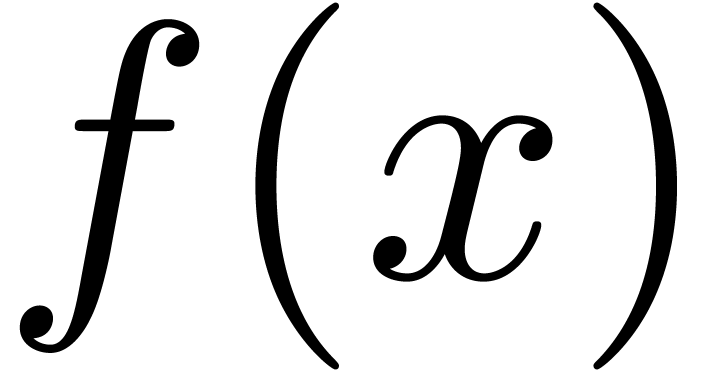 on the interval
on the interval 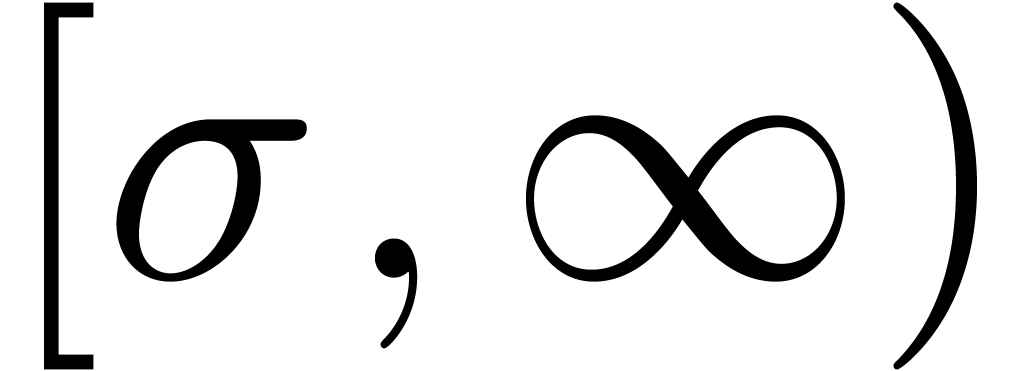 .
.
Acknowledgments. We wish to like Grégoire
Lecerf for some helpful remarks.
2.Expedito-summation
Throughout this and the next section, we make the following assumptions:
2.1.Introduction to expedito-summation
In [9], we provided a detailed analysis of two summation
methods of 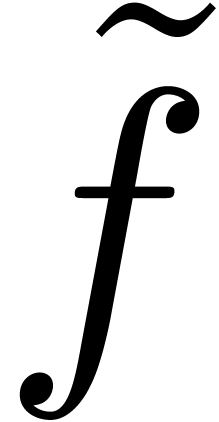 . The usual
accelero-summation process associates the accelero-sum
. The usual
accelero-summation process associates the accelero-sum 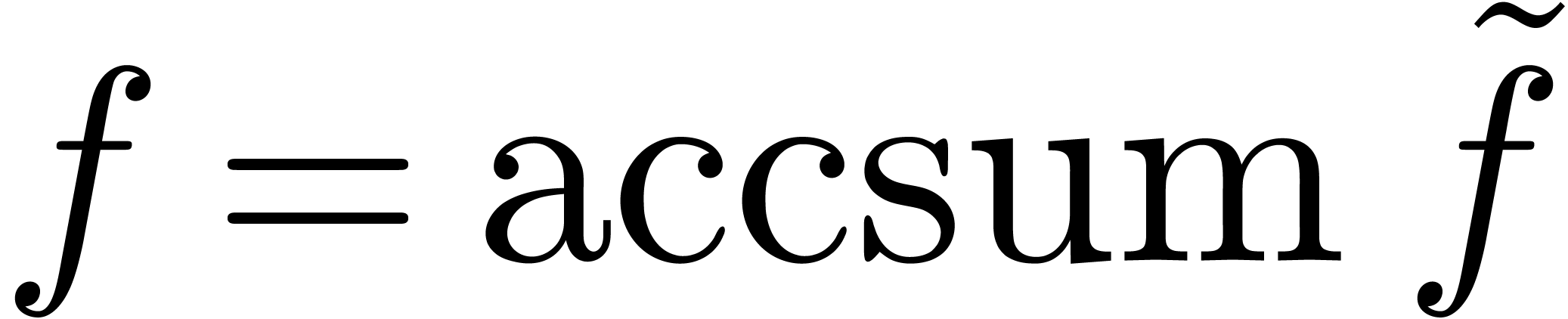 to
to 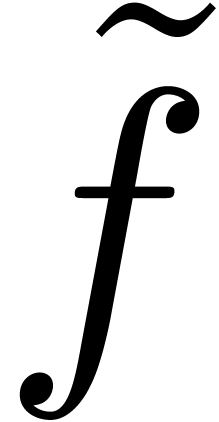 using
using
In the appendix, we also considered “summation up to the least
term”: given 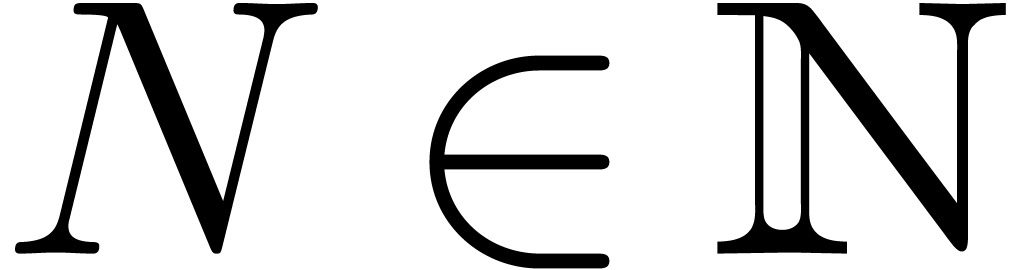 , one may
approximate
, one may
approximate  by
by 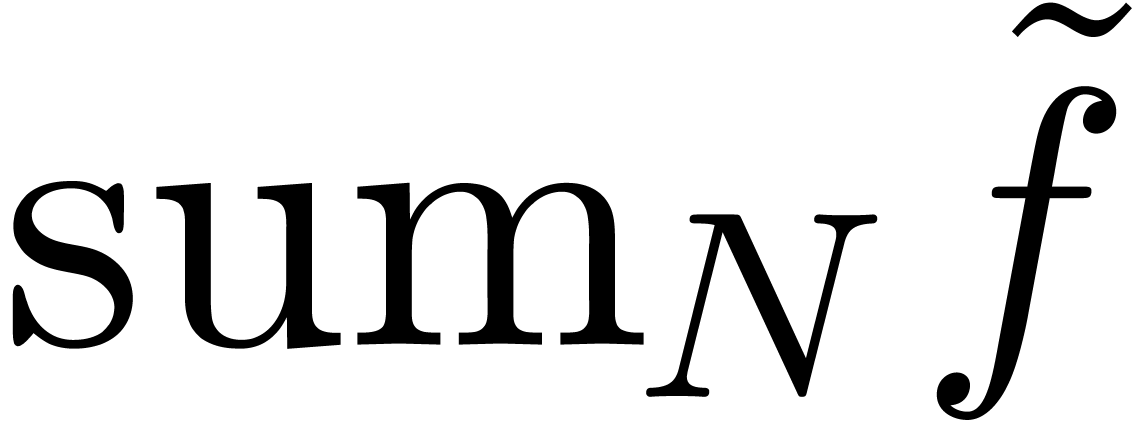 ,
where
,
where
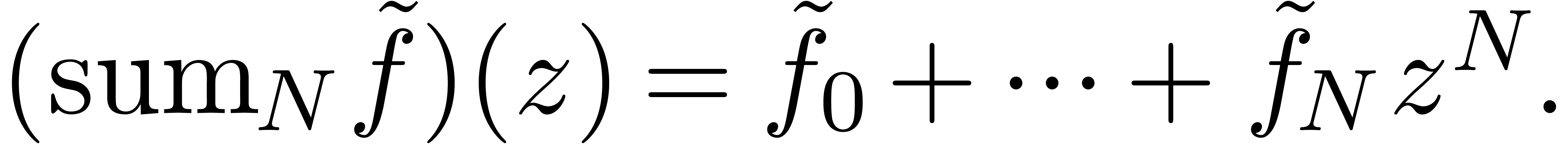
Taking 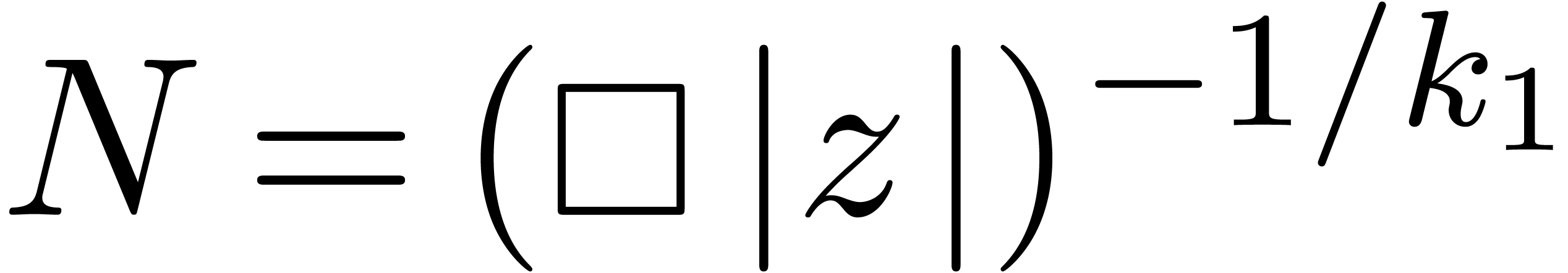 , we proved that
, we proved that
for all 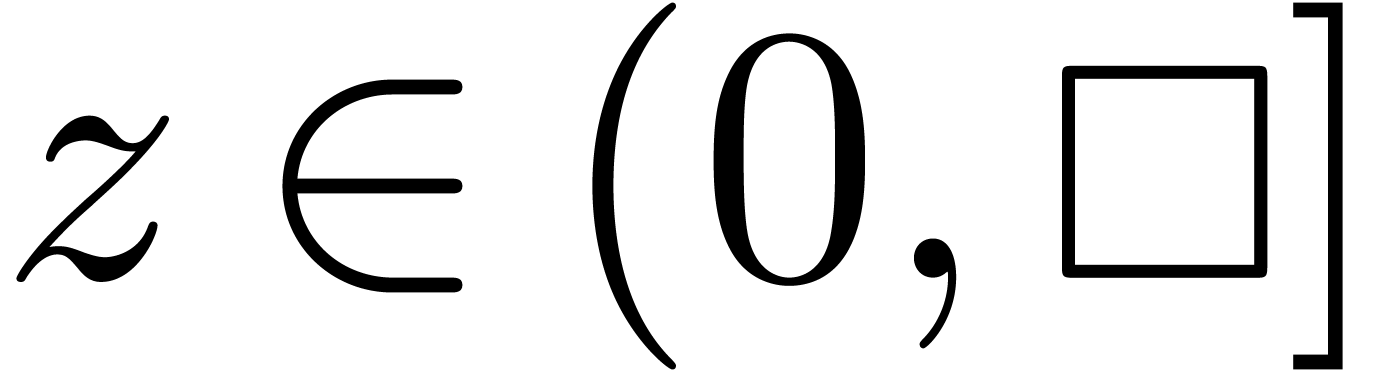 .
.
Summation up to the least term completely shortcuts the whole
accelero-summation process. It provides approximations of a precision
that correspond to stopping the accelero-summation process at the first
singularity for the first critical time. It is natural to consider more
general shortcuts, where we perform the usual accelero-summation process
up till a given critical time 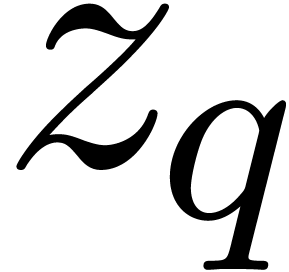 and then
“expedite” the remainer of the process by directly
performing a truncated Laplace transform on
and then
“expedite” the remainer of the process by directly
performing a truncated Laplace transform on 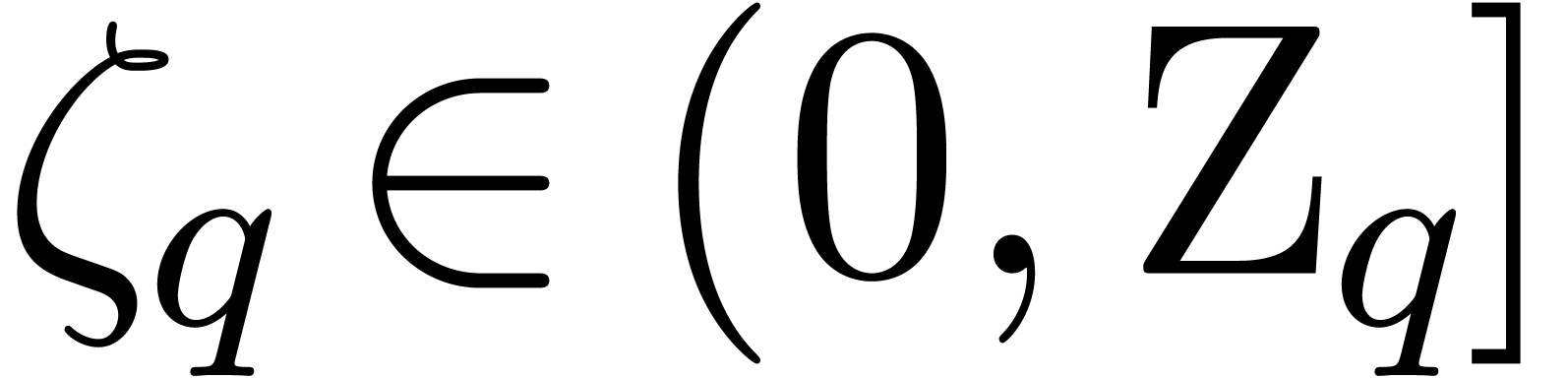 for
a suitable
for
a suitable 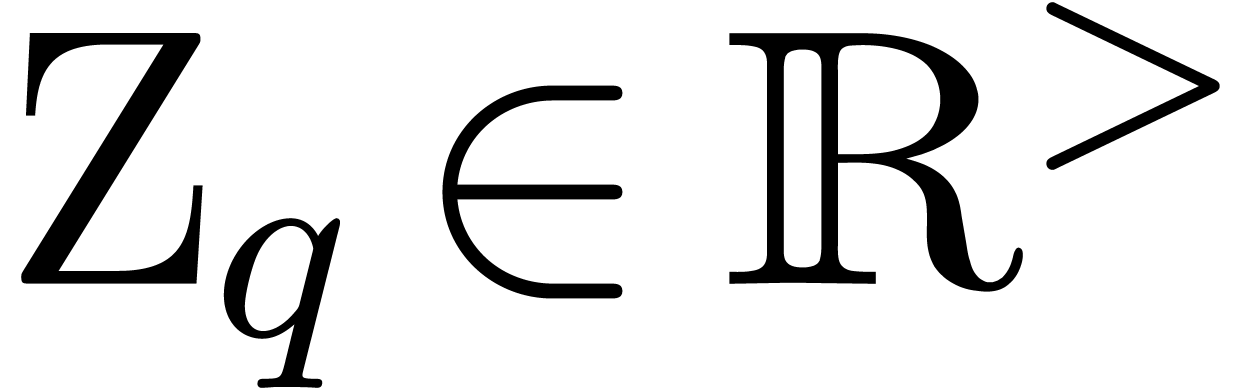 . More precisely,
given
. More precisely,
given  and
and 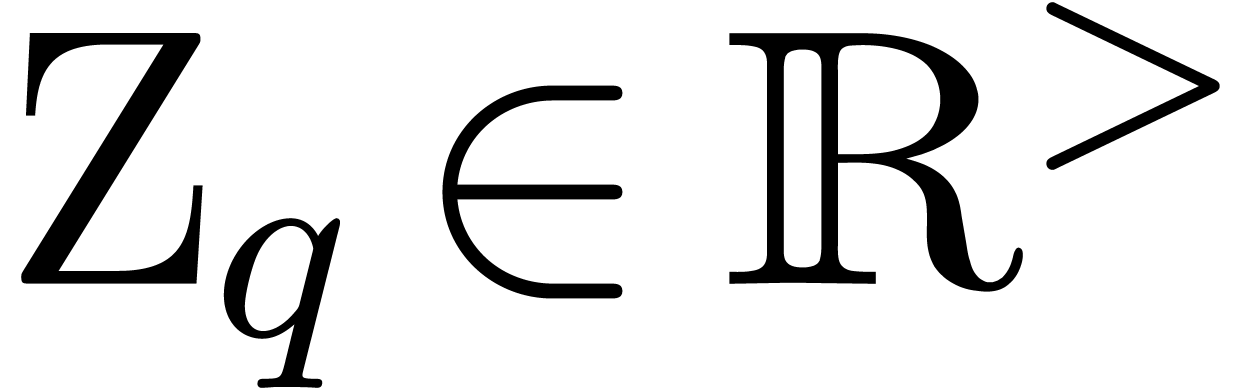 ,
we define
,
we define
Here  denotes the contour from
denotes the contour from 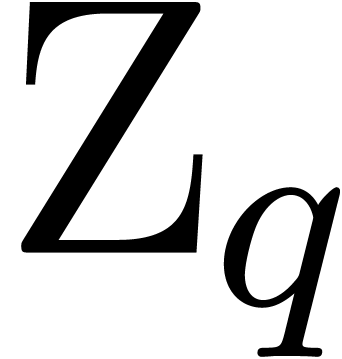 to
to  , turning around
, turning around  and then back from
and then back from  to
to 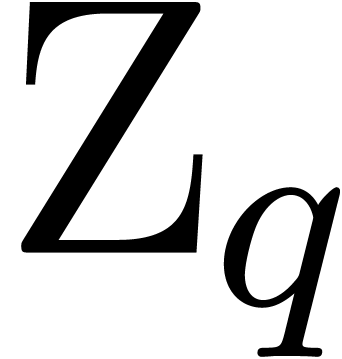 .
.
As for summation to the least term, it is natural to chose 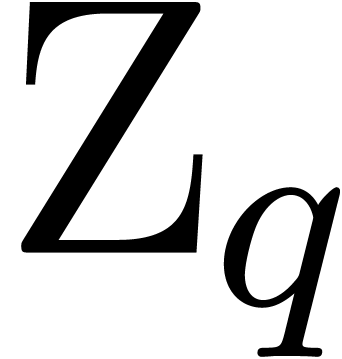 such that
such that  is minimal. Since
is minimal. Since  satisfies a bound of the form
satisfies a bound of the form

at infinity, this means that we should take  , where
, where
Our main aim is to prove the error bound
for 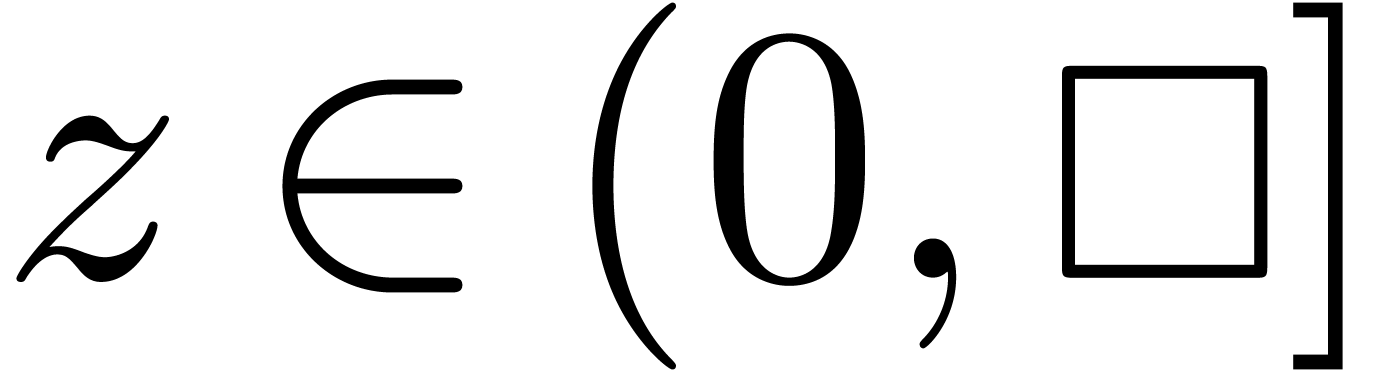 . When taking
. When taking  , this bound further simplifies to
, this bound further simplifies to
2.2.The expedited approximation
The truncated Laplace transform
Let
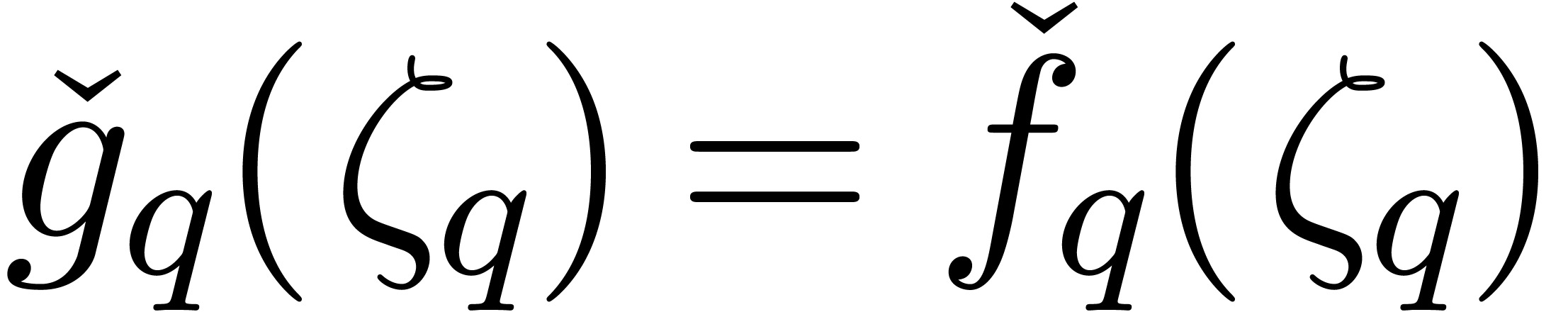
for
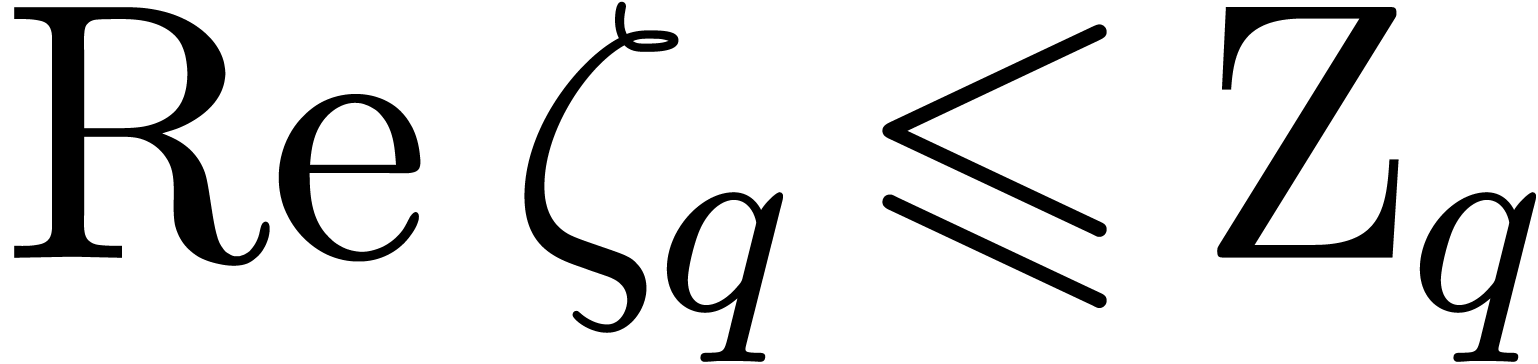
and
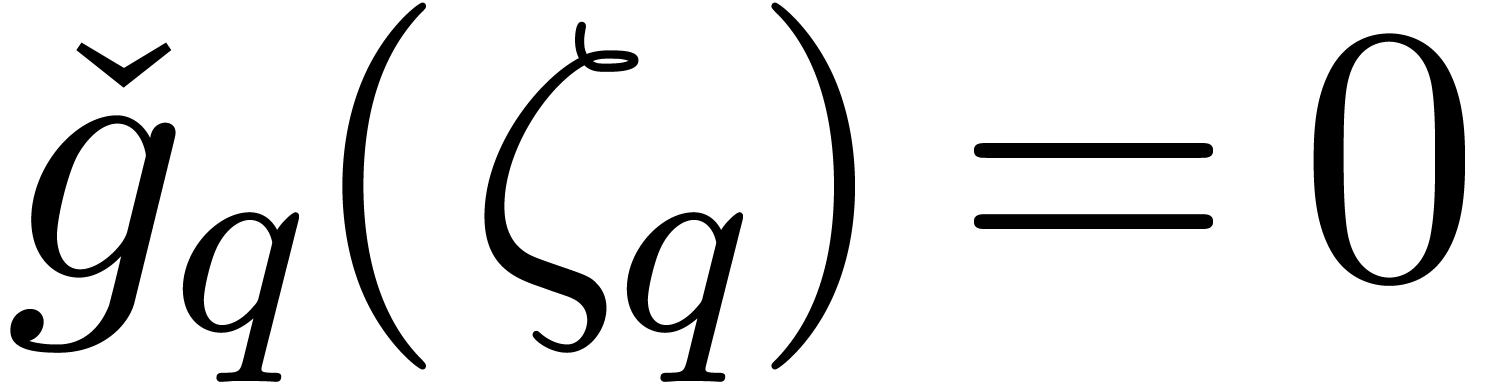
for
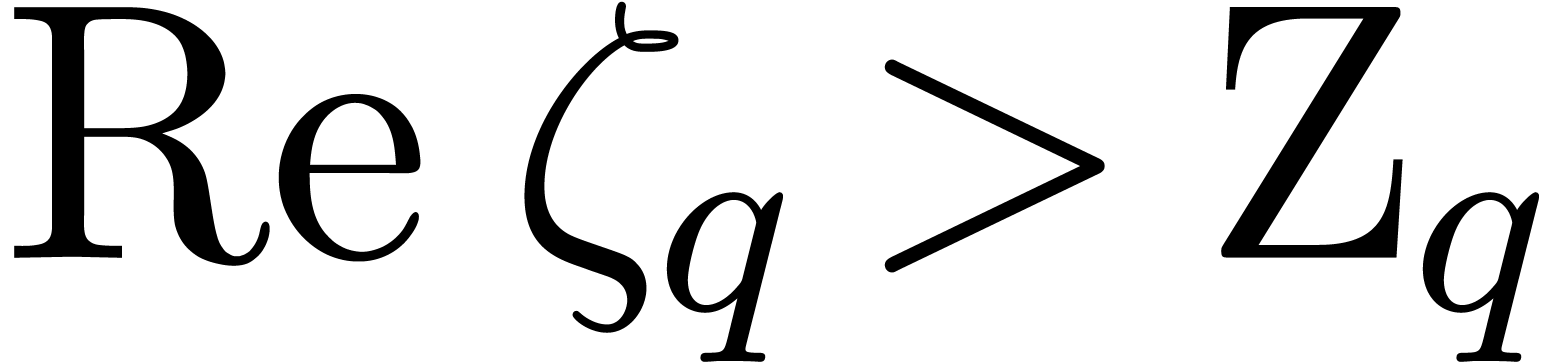 ,
, so that
Since we know how to compute a bound for  on the
contour
on the
contour 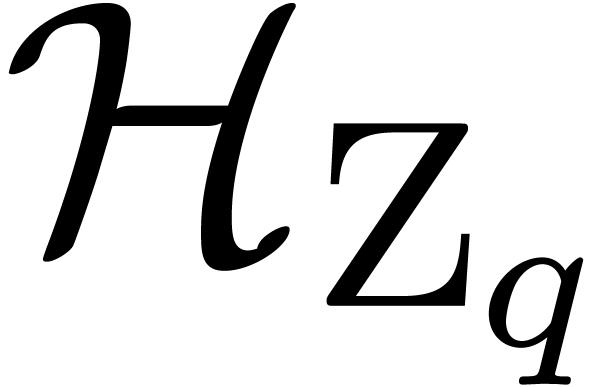 , we may compute an
explicit bound of the form
, we may compute an
explicit bound of the form
 |
(1) |
for 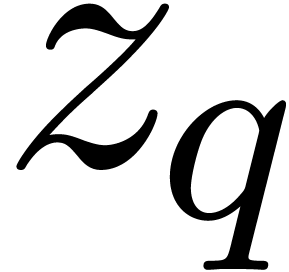 on a small positive sector near zero.
on a small positive sector near zero.
Borel transforms of  at other critical
times
at other critical
times
For
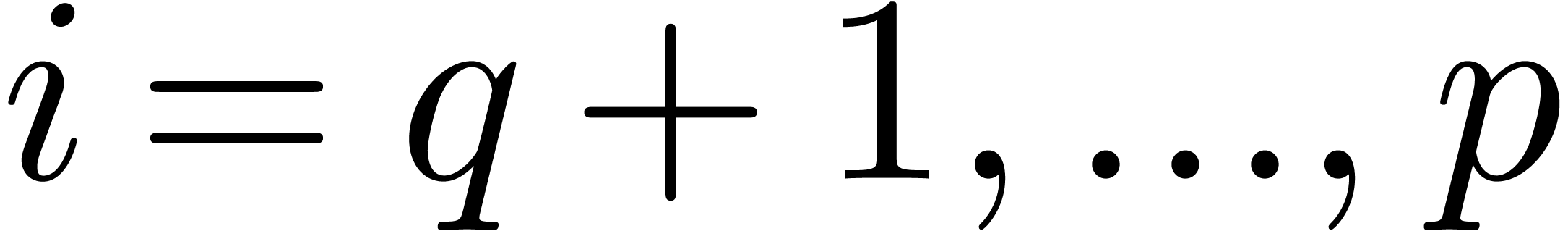 ,
, we define
where
We may also represent 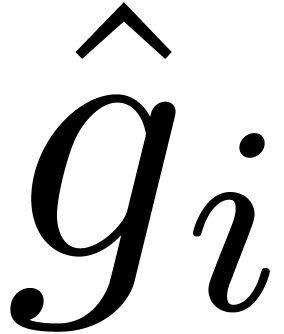 as the analytic Borel
transform of
as the analytic Borel
transform of 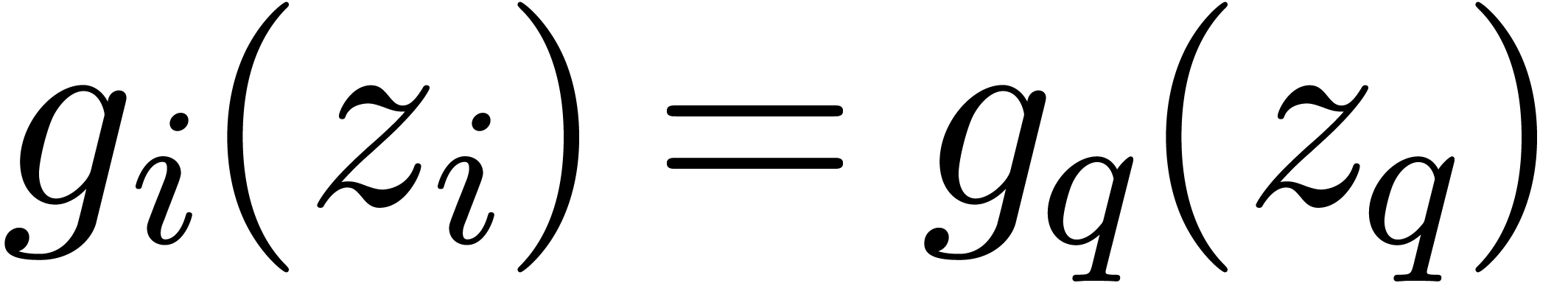 with respect to
with respect to 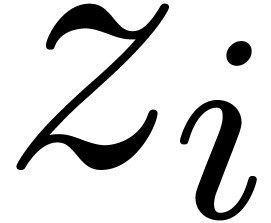 . Using the bound (1), this allows
us to compute a bound
. Using the bound (1), this allows
us to compute a bound
 |
(2) |
for 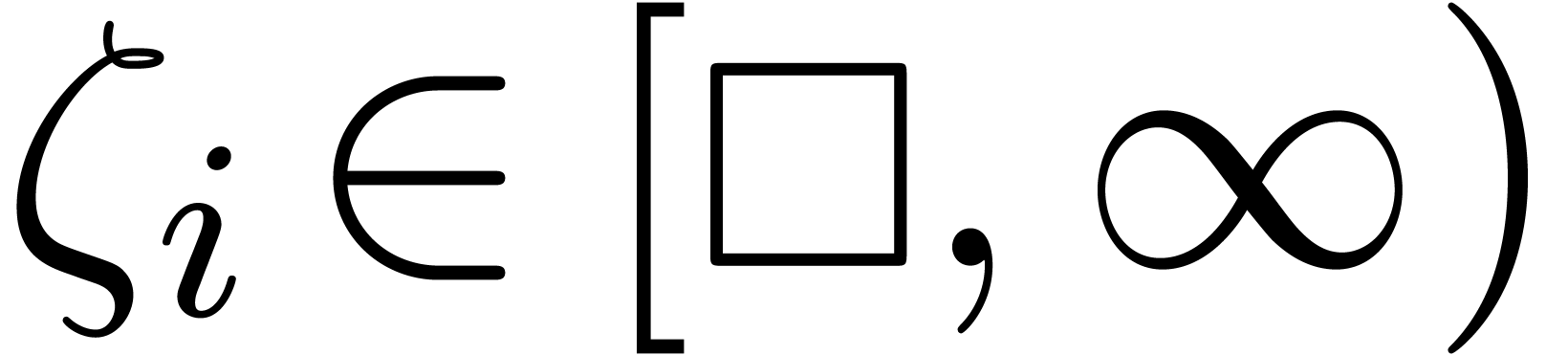 .
.
The difference between  and
and 
Let
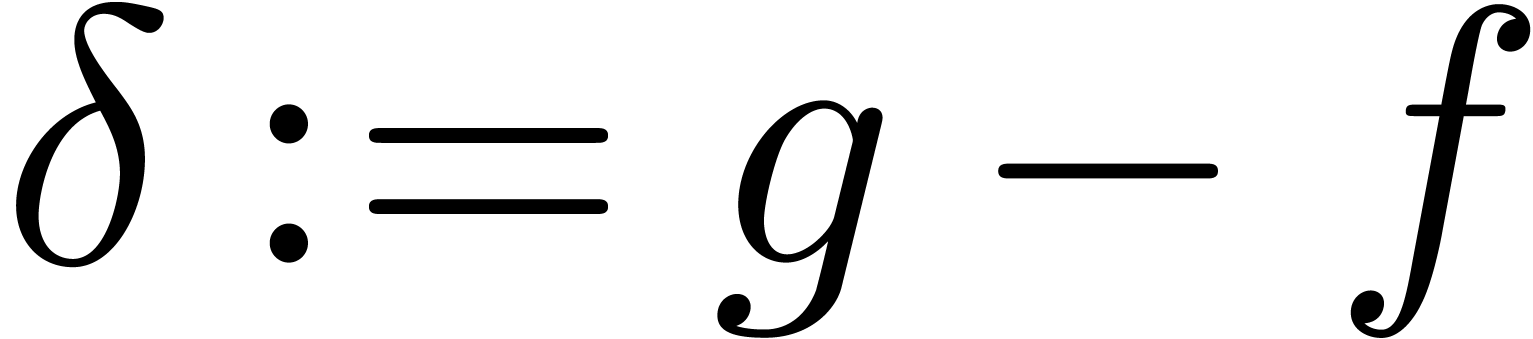 .
. For
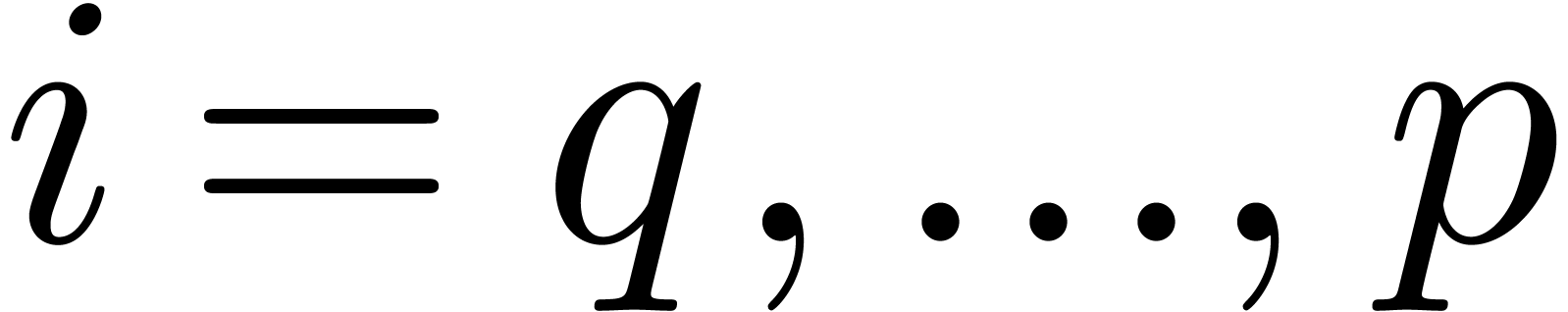 ,
, we also define
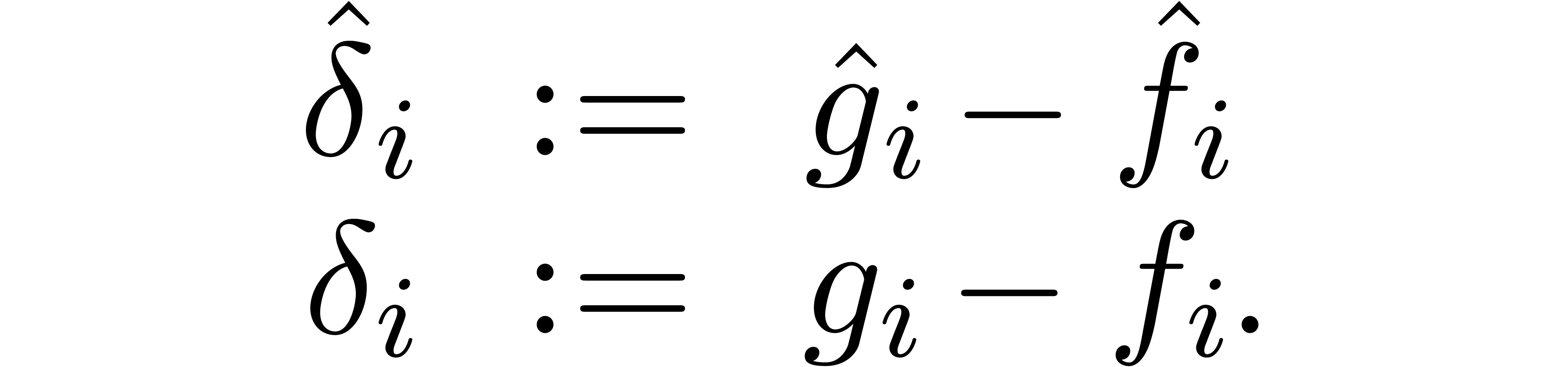
For 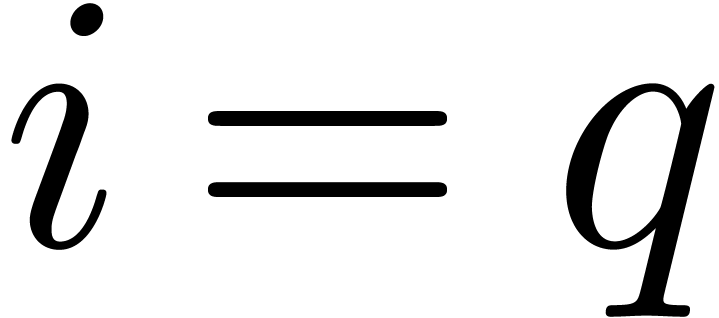 , and setting
, and setting 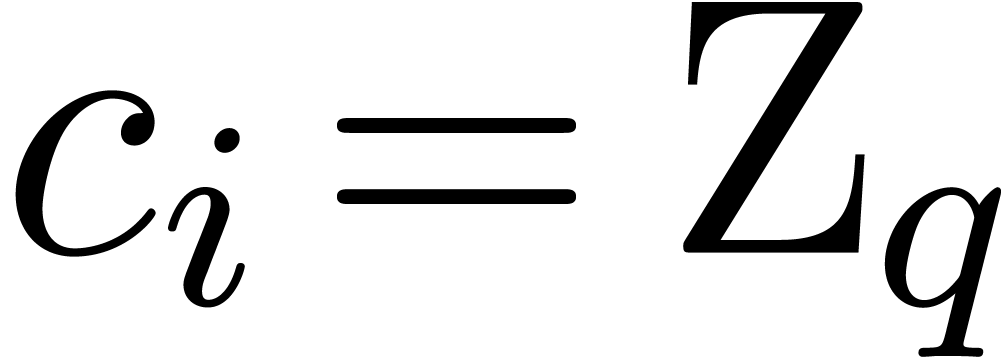 , we thus have
, we thus have
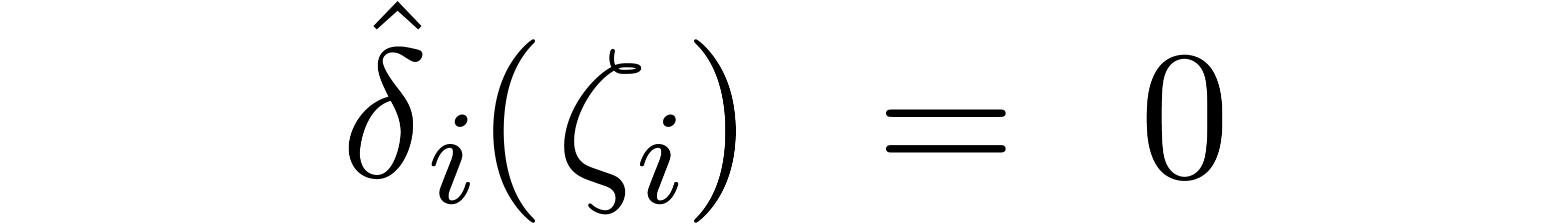
for 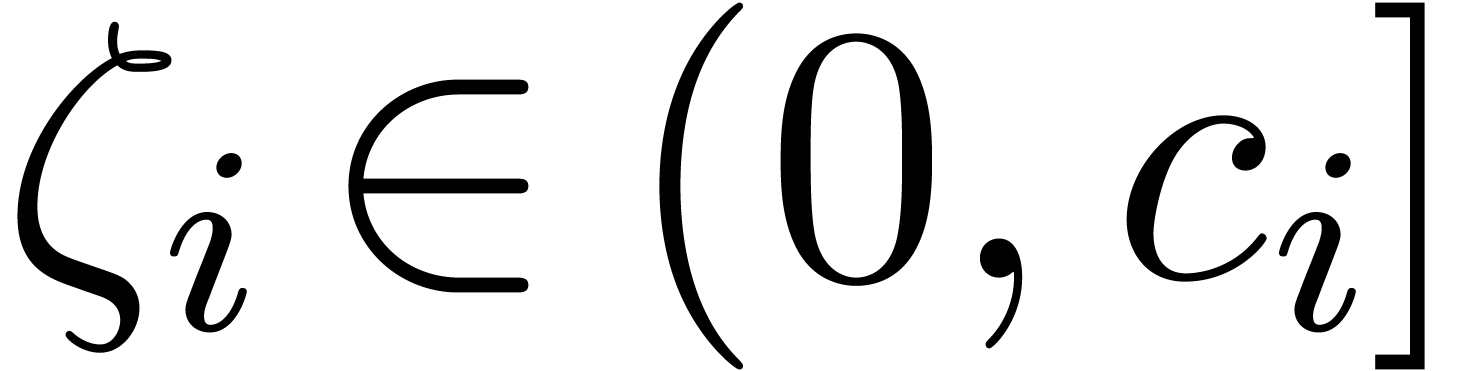 . One major topic of this
section will be to compute bounds at the origin for
. One major topic of this
section will be to compute bounds at the origin for 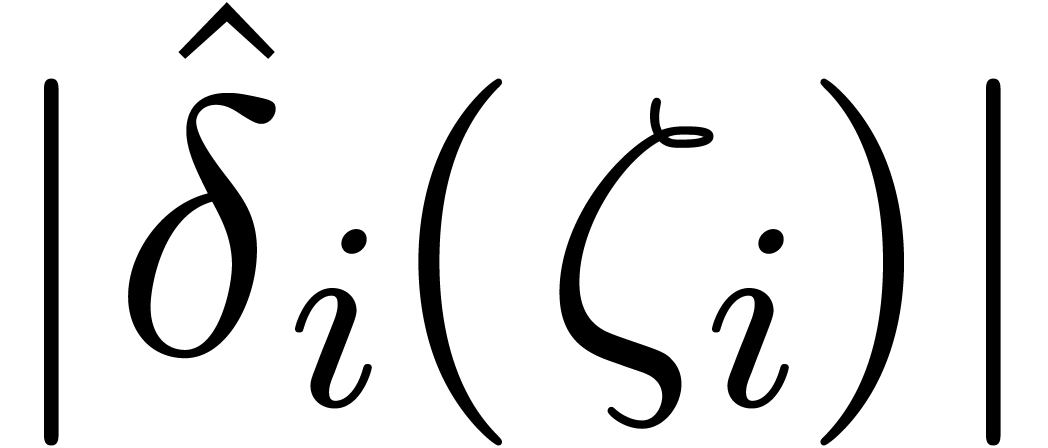 and
and 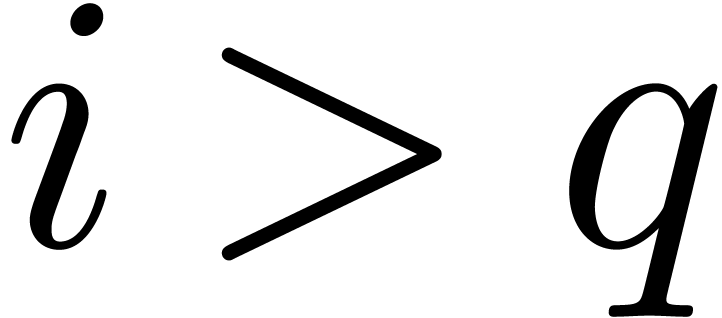 .
.
Behaviour of the 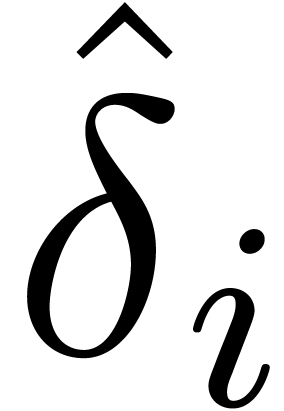 at infinity
at infinity
Let
 .
. Combining the bound
(
2) with the superexponential bound for
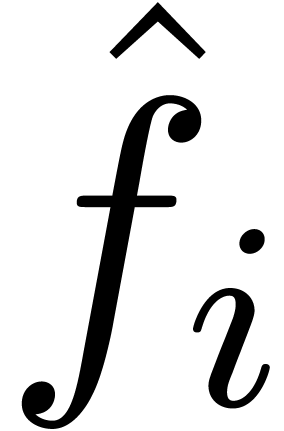 ,
, as provided by the accelero-summation
process, we may compute a bound
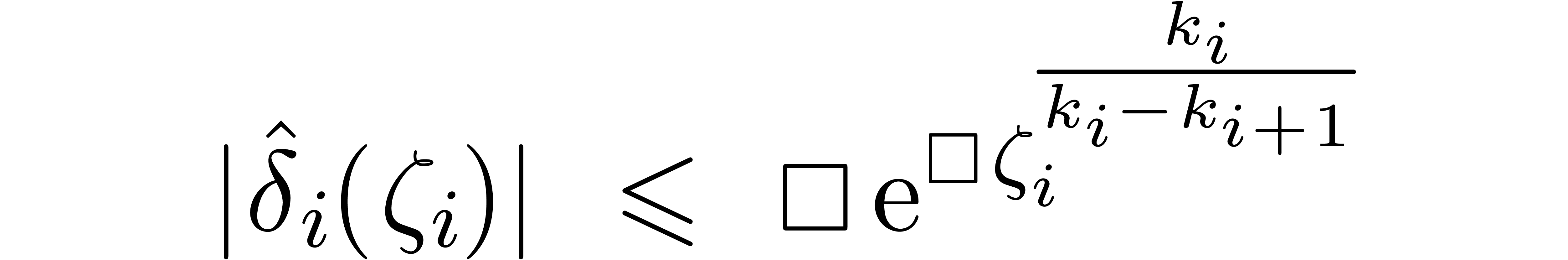 |
(3) |
for  . Notice that we may also
compute a bound
. Notice that we may also
compute a bound
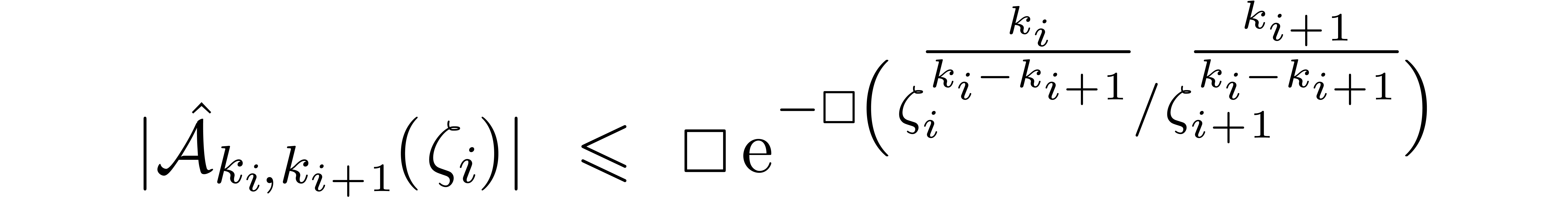 |
(4) |
for  and
and 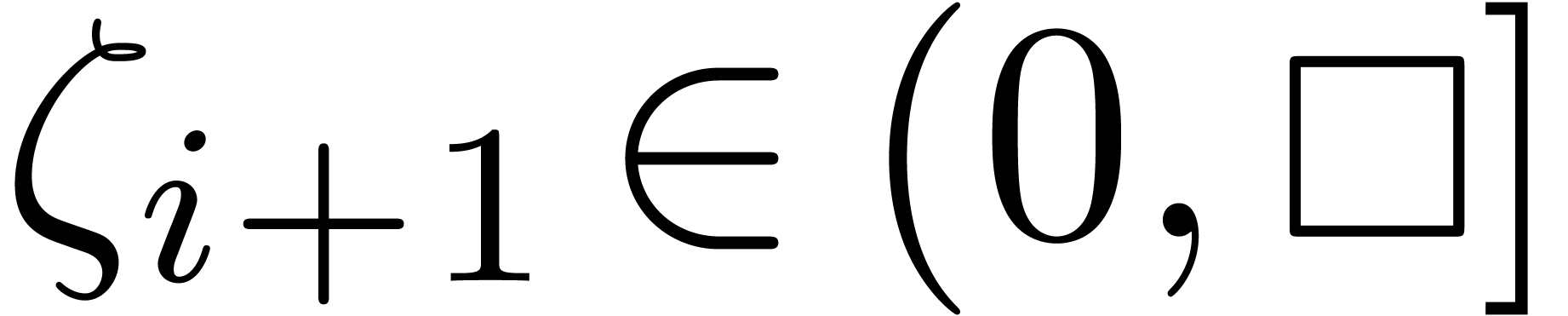 .
.
Majorants for specific accelerates and Laplace transforms
The following bounds will be useful for proving precise error
estimates for the
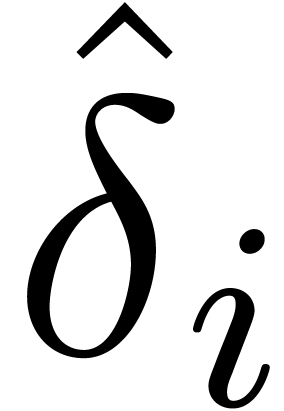
and
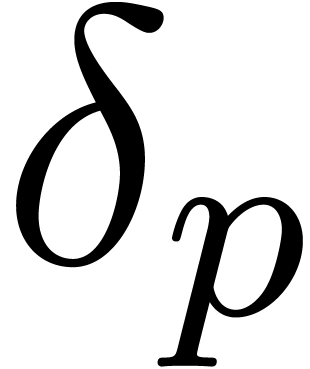 .
. The proofs are a routine application of the
saddle point technique.
2.3.The first acceleration
Proof. We have
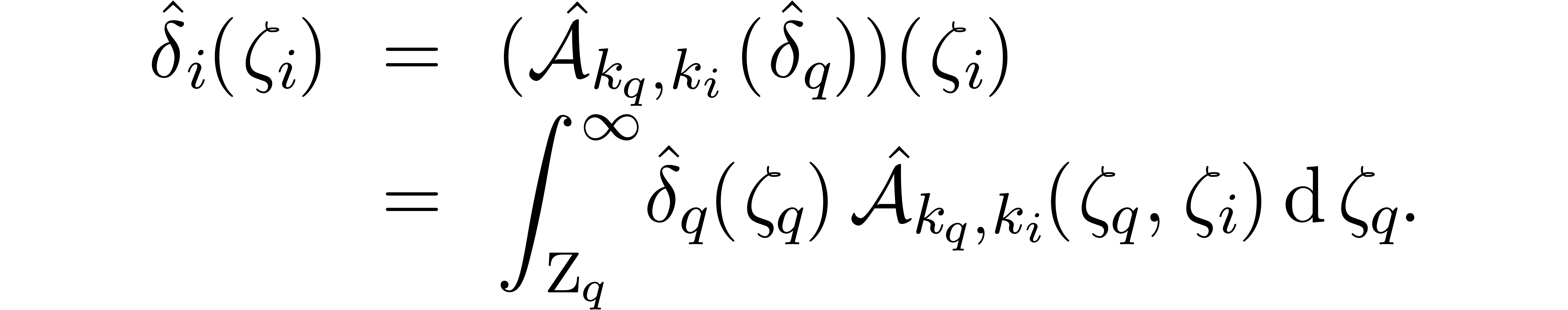
Using (3) and (4), it follows that
on an interval 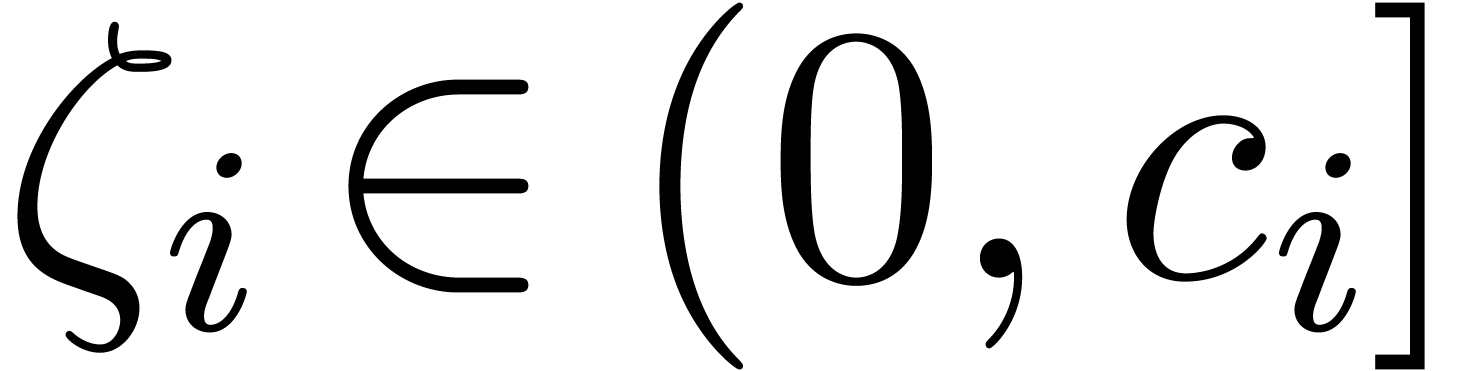 for some computable
for some computable 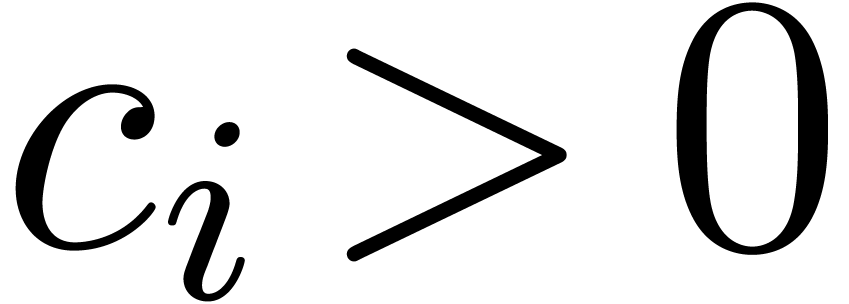 .
.
2.4.Subsequent accelerations
Lemma 4. For
each 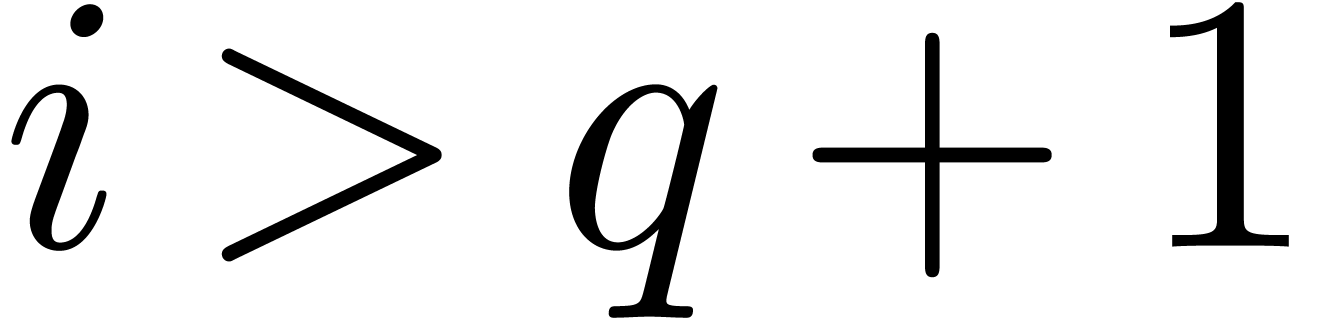 , we can compute a
constant
, we can compute a
constant  , together with a
bound
, together with a
bound
for 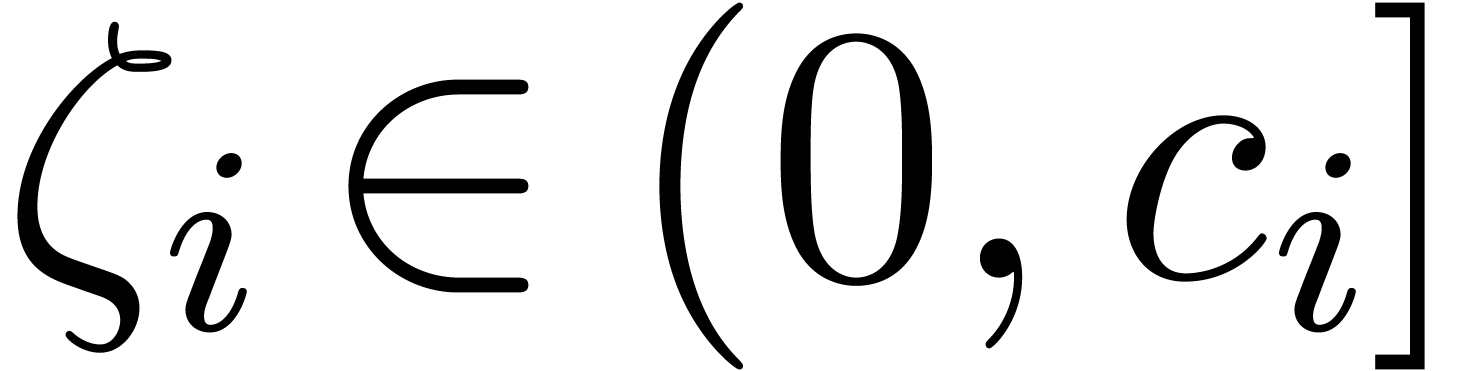 .
.
Proof. We will prove the lemma by induction over
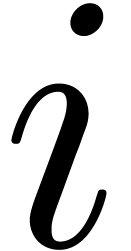 . We have
. We have
where
If 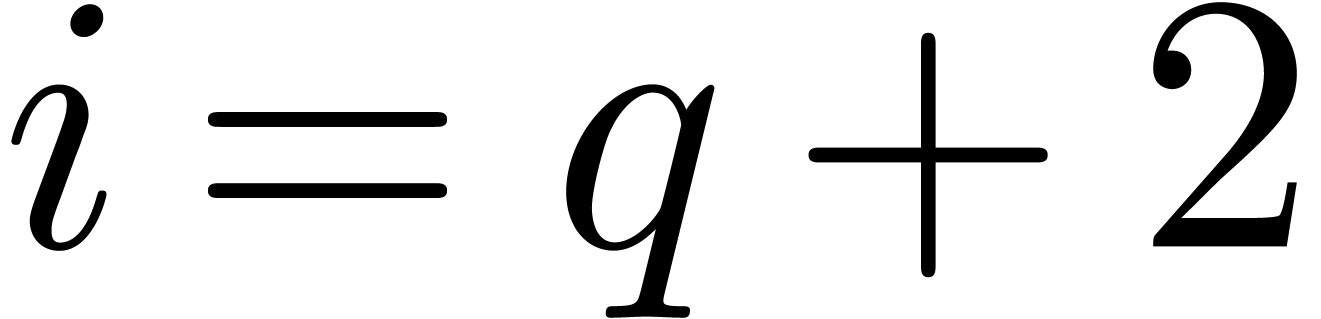 , then Lemma 3
yields a bound
, then Lemma 3
yields a bound
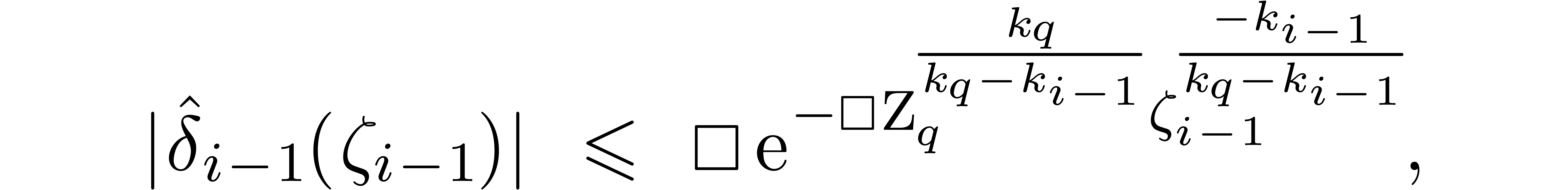
for 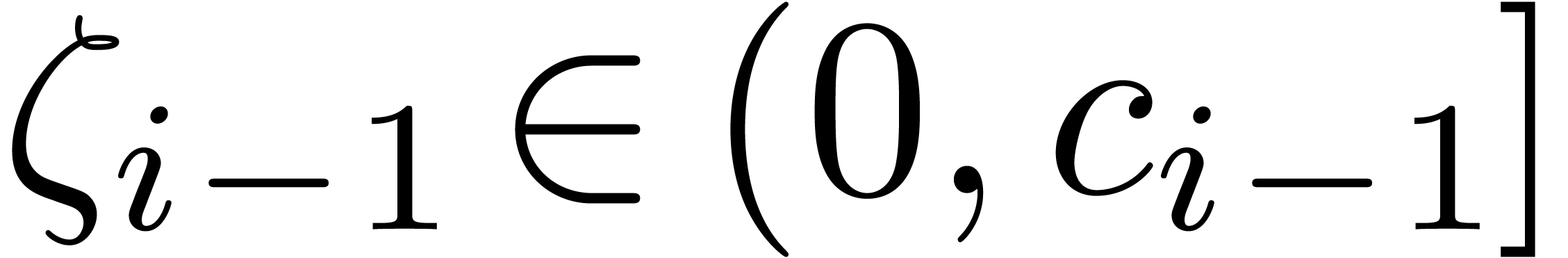 . For
. For 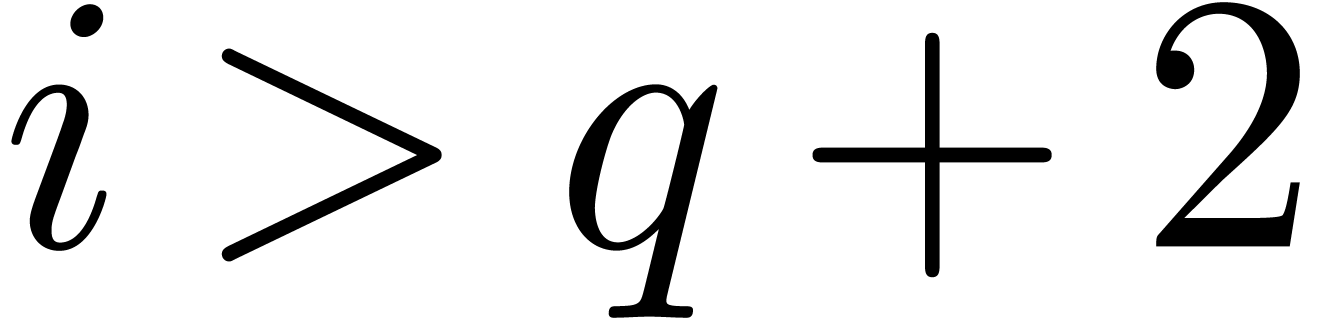 , the induction hypothesis yields the bound
, the induction hypothesis yields the bound
for 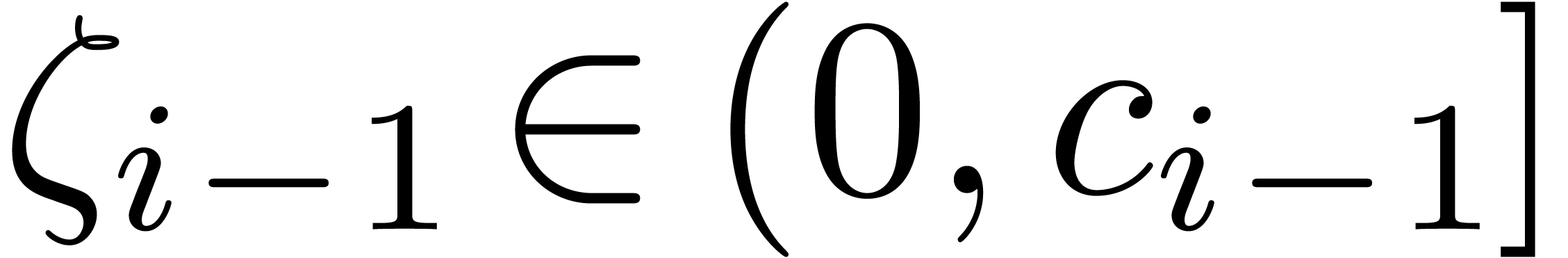 . Now, in view of (6), we may compute a suffiently small
. Now, in view of (6), we may compute a suffiently small  such that
such that
for all 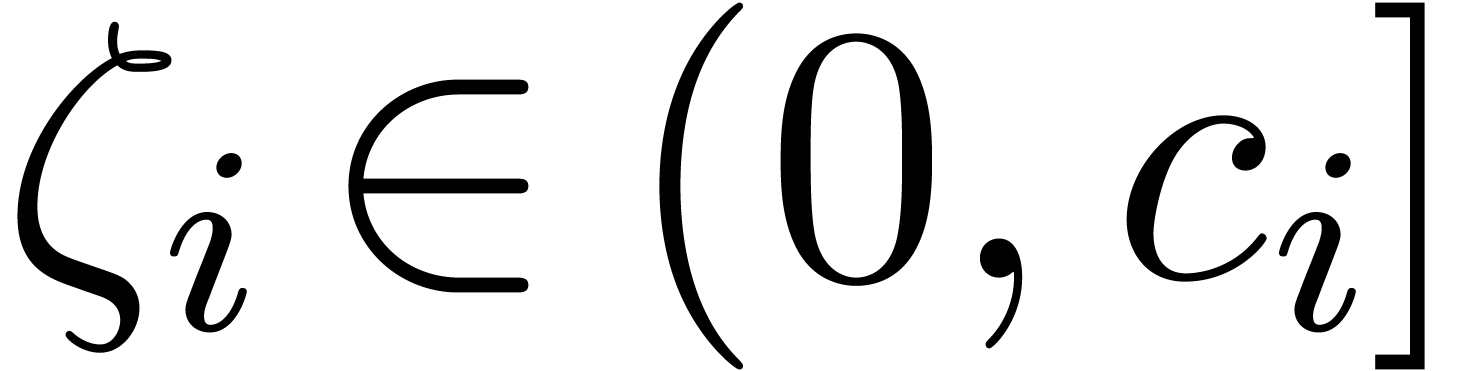 . If
. If 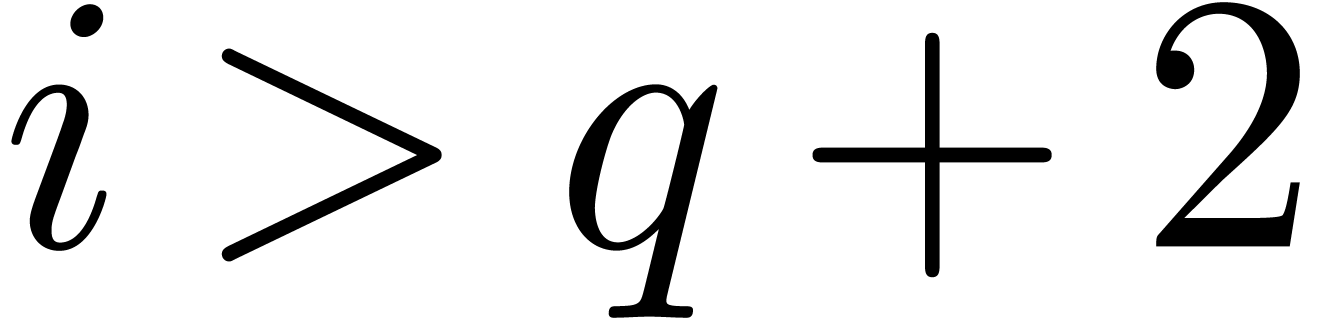 , then a similar computation yields
, then a similar computation yields
for all 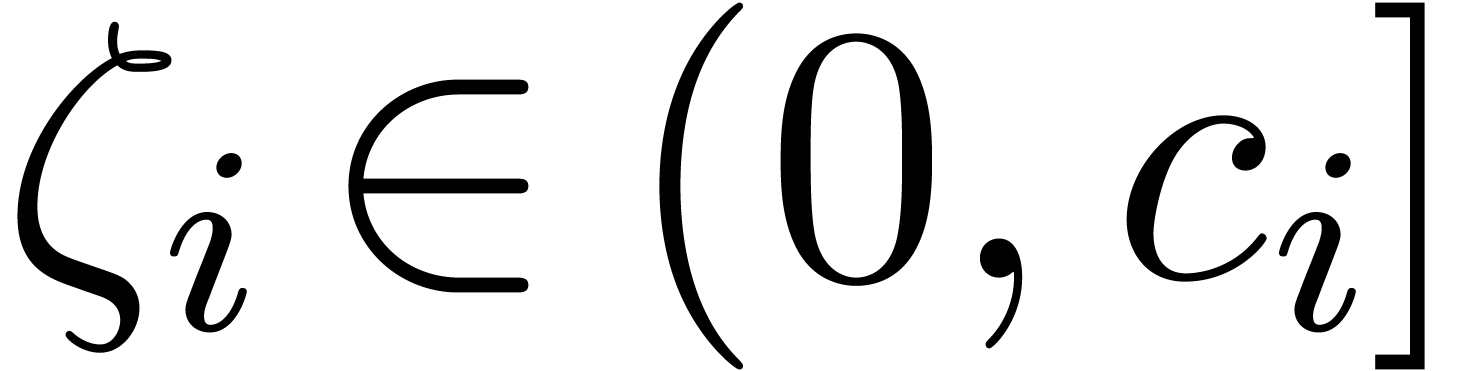 , modulo a decrease
of
, modulo a decrease
of 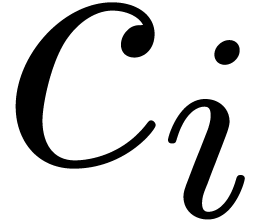 if necessary. Putting these bounds together,
we obtain
if necessary. Putting these bounds together,
we obtain
for 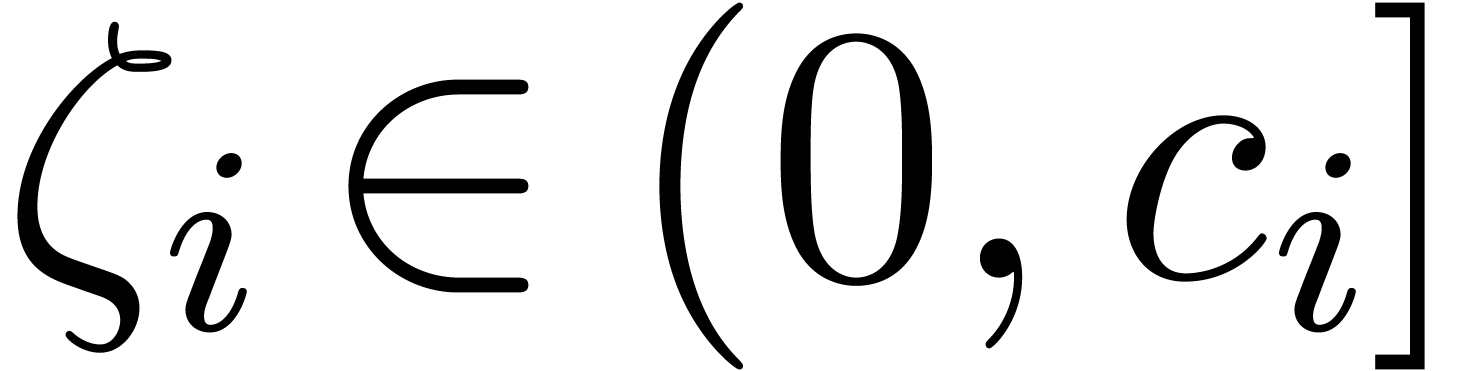 . Using (3)
and (4), we may also compute a bound
. Using (3)
and (4), we may also compute a bound
for 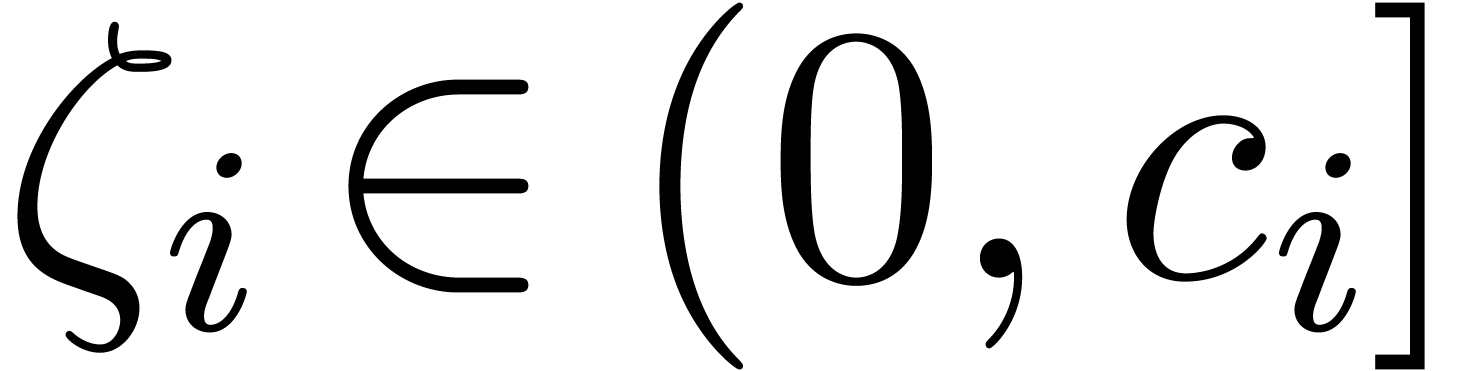 , modulo a further
decrease of
, modulo a further
decrease of 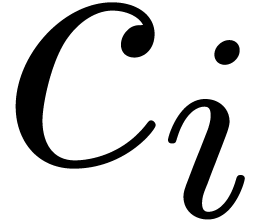 if necessary, and where we used the
fact that
if necessary, and where we used the
fact that 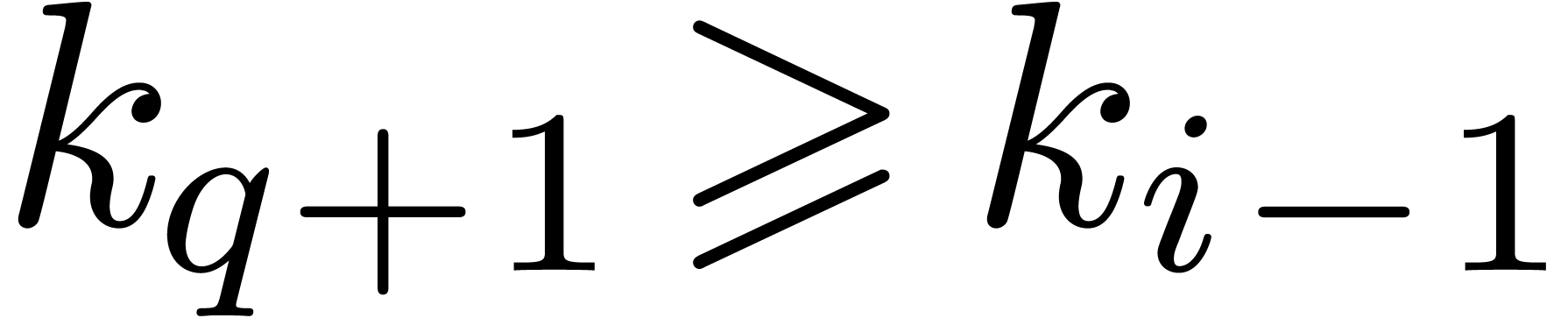 . Combining the
bounds for
. Combining the
bounds for 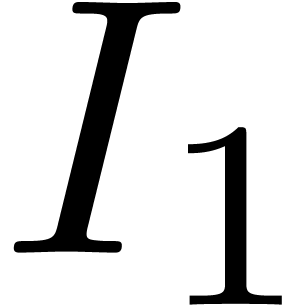 and
and 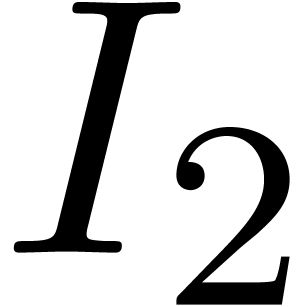 ,
the result follows.
,
the result follows.
2.5.The final Laplace transform
Lemma 5. For
any aperture  , we can
compute a
, we can
compute a  and a bound
and a bound
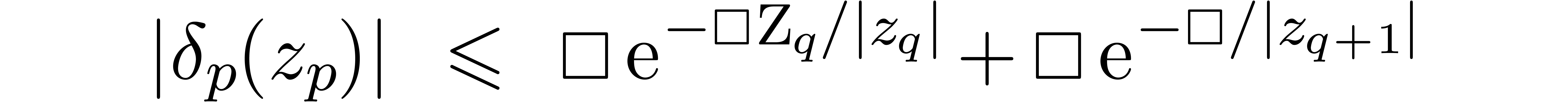
for all 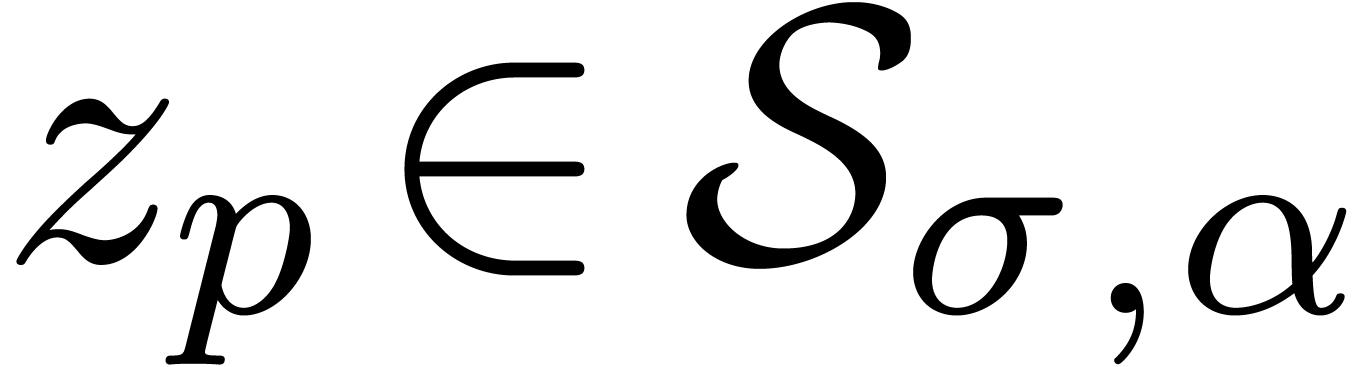 .
.
Proof. We have
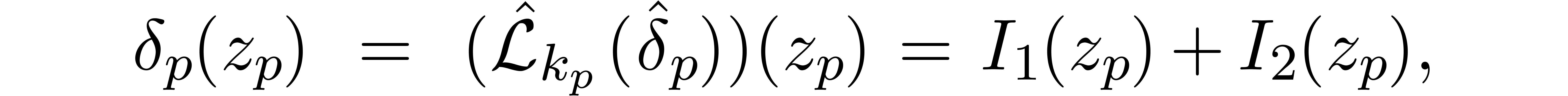
where
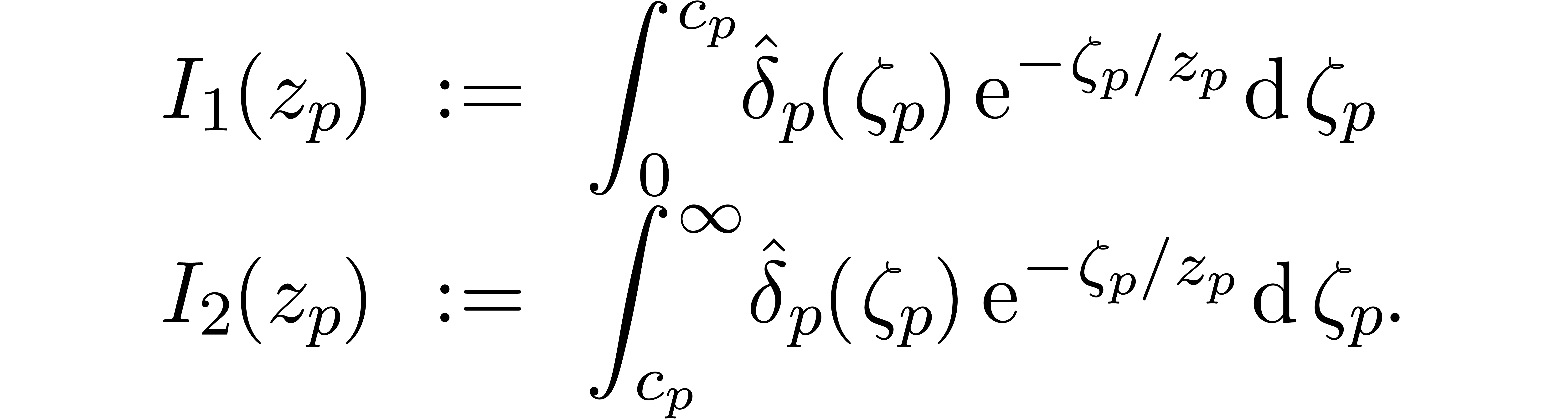
Using Lemma 4 and (5), we can compute  and a bound
and a bound
for 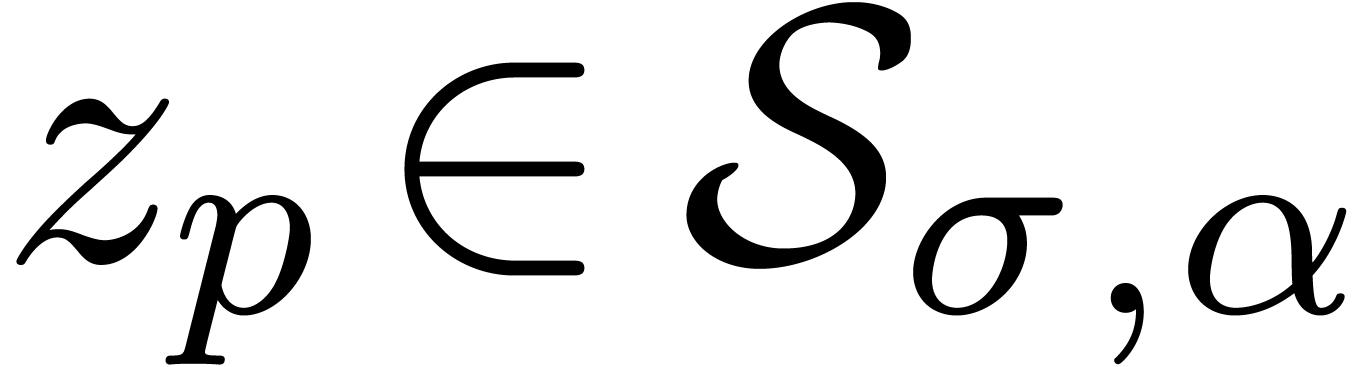 . Using (2)
and the exponential bound for
. Using (2)
and the exponential bound for 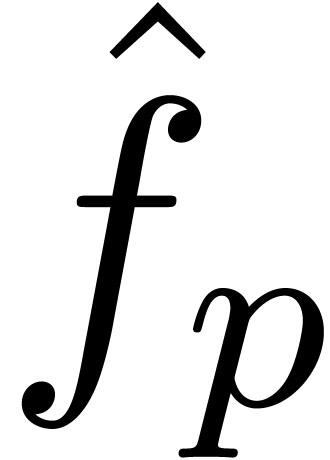 as provided by the
accelero-summation process, we may also compute a bound
as provided by the
accelero-summation process, we may also compute a bound

for 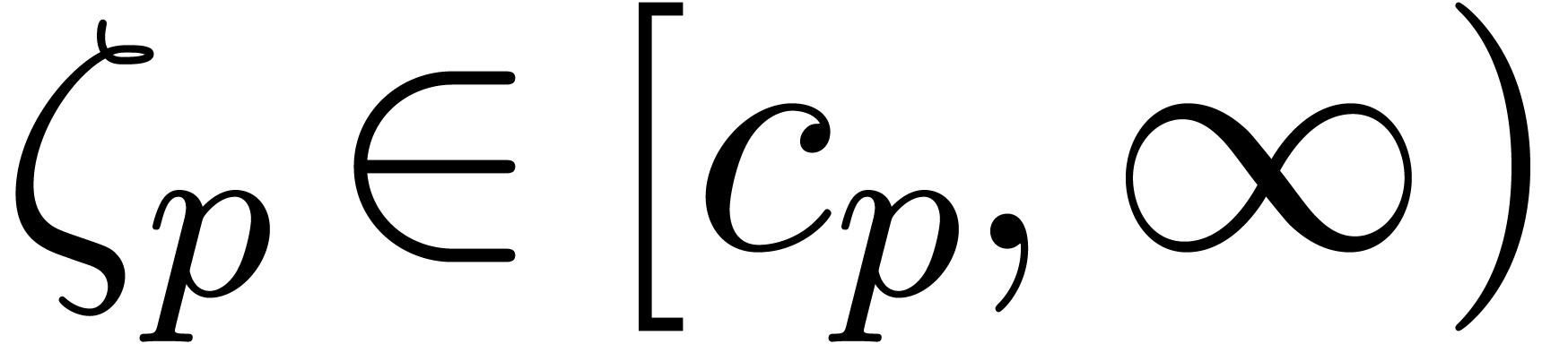 . Modulo a further
increase of
. Modulo a further
increase of  if necessary, this allows us to
compute a bound
if necessary, this allows us to
compute a bound
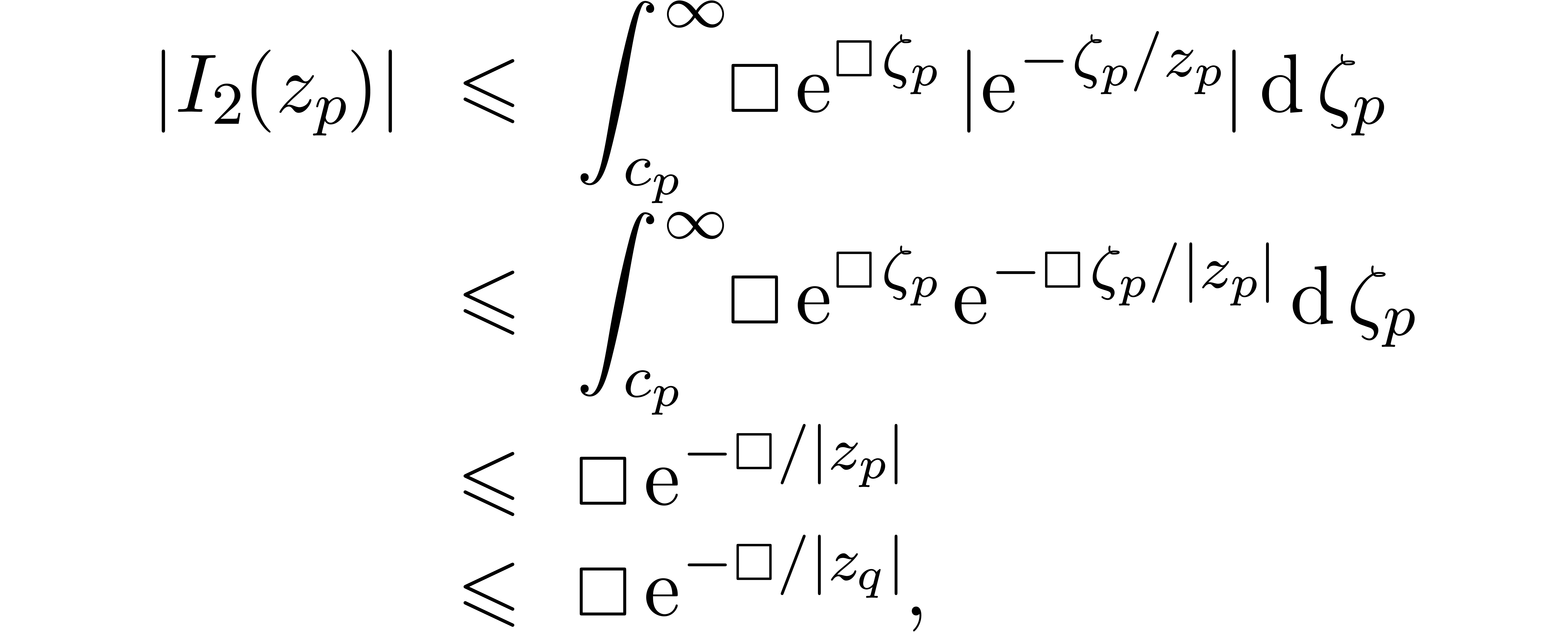
for  . Adding up the bounds
for
. Adding up the bounds
for 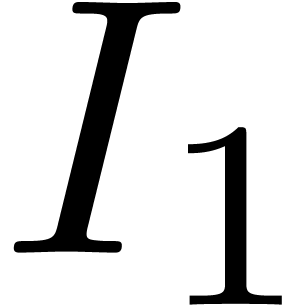 and
and 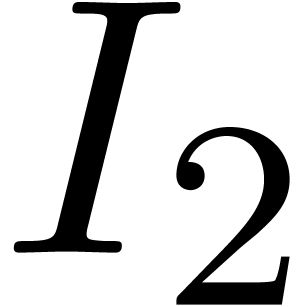 ,
the results follows.
,
the results follows.
Corollary 6. For any aperture 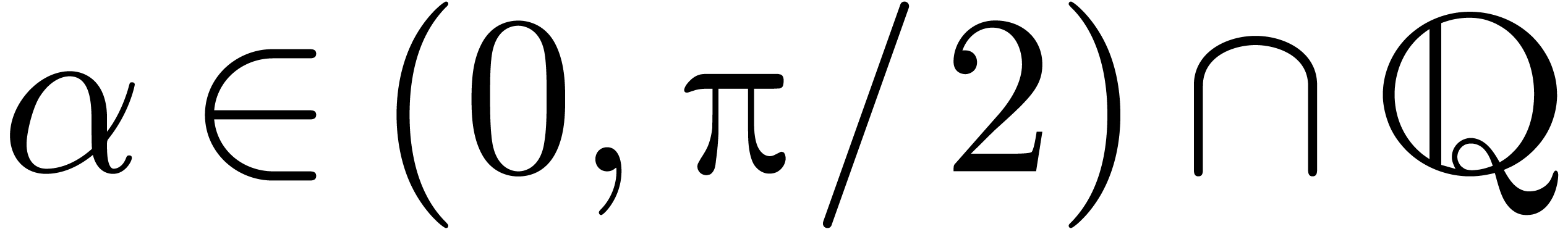 ,
and assuming that
,
and assuming that
we can compute a  and a bound
and a bound

for all 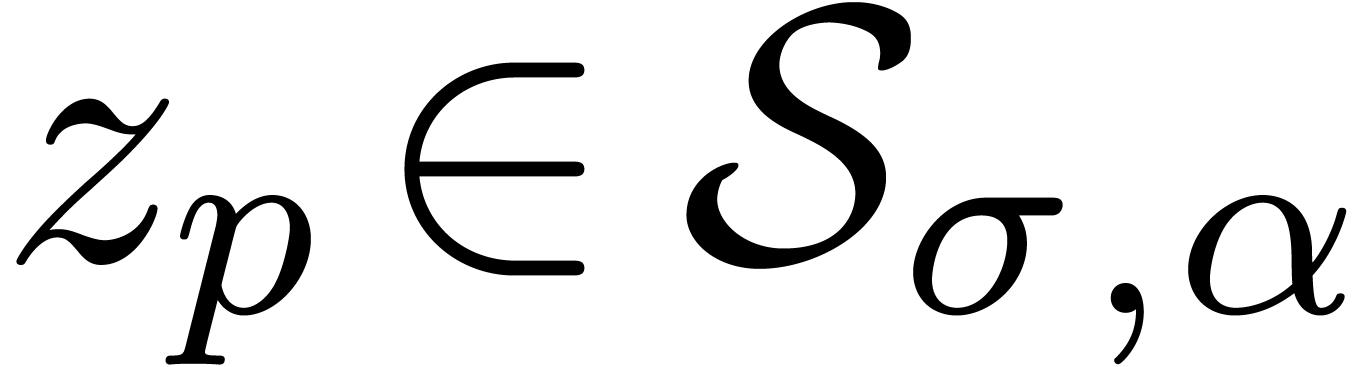 .
.
Proof. This directly follows from the fact that
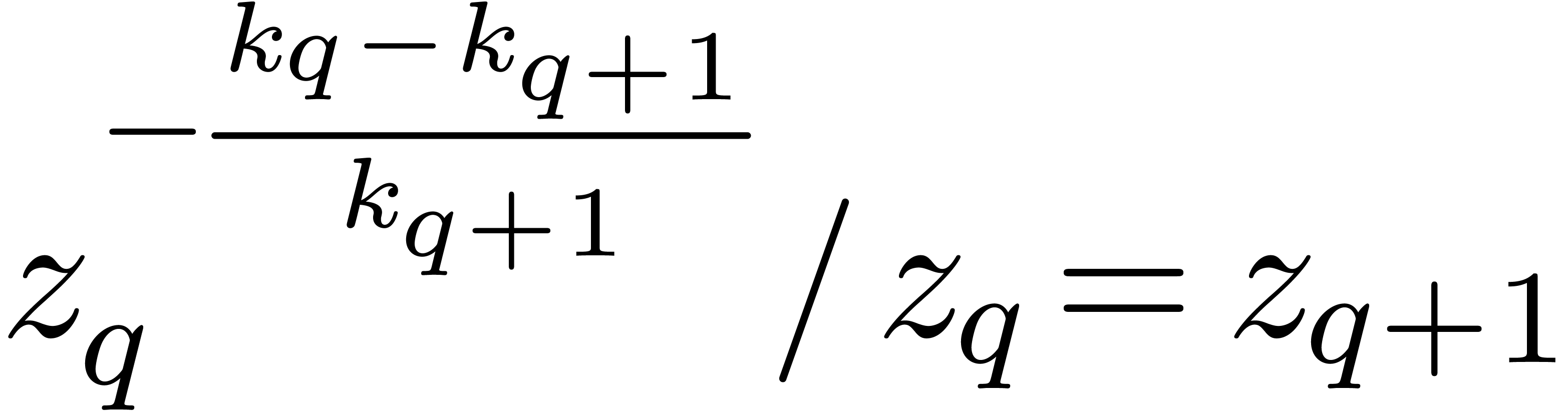 .
.
3.Uniform complexity on local sectors
3.1.Uniform complexity of
accelero-summation
Proof. Recall that we may compute an exponential
bound

for  at infinity. For
at infinity. For  and
and
 , this yields a bound
, this yields a bound
We now wish to compute 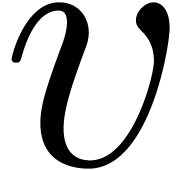 by approximating the
truncated Laplace integral
by approximating the
truncated Laplace integral
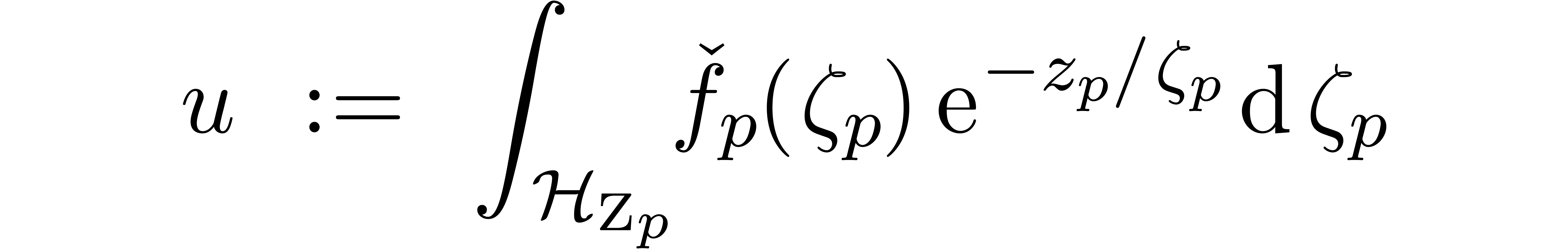 |
(7) |
with precision 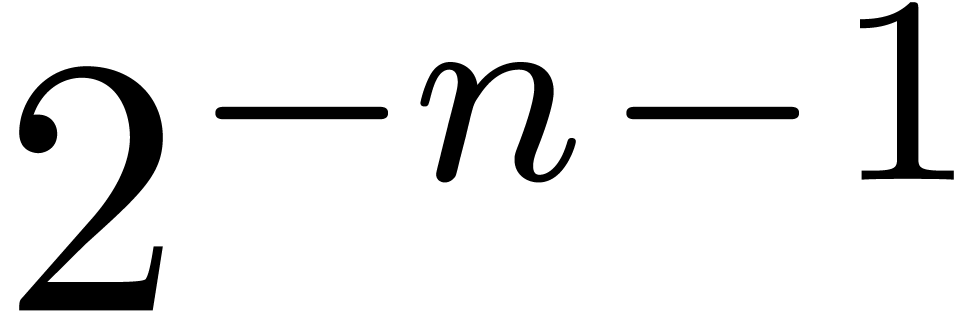 ,
i.e.
,
i.e. 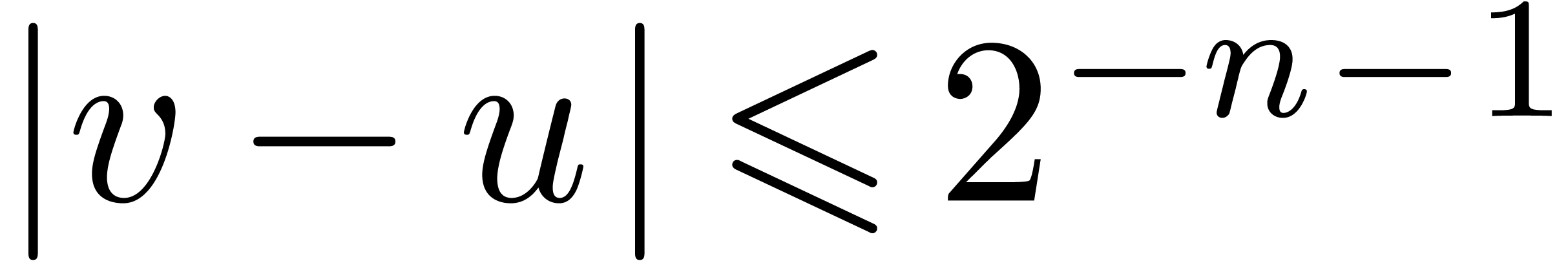 and
and  .
.
Let us first consider the case when the bitsize of 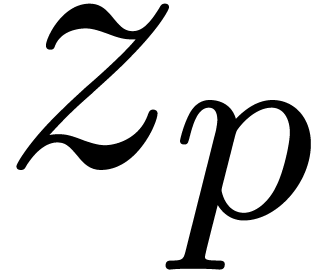 is bounded by
is bounded by 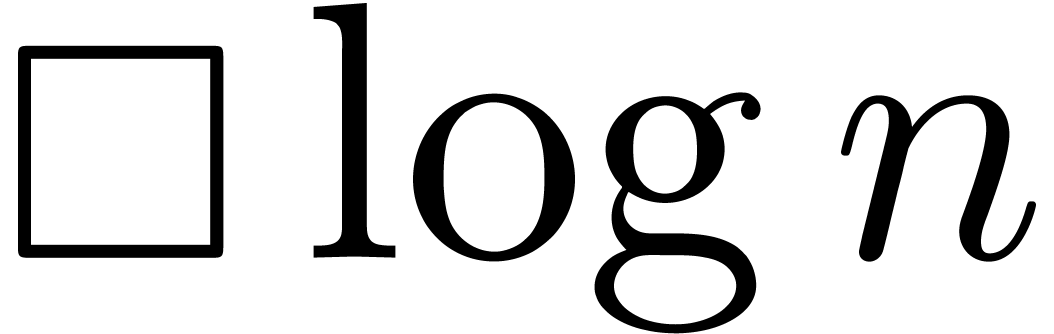 . Under the
assumption that
. Under the
assumption that 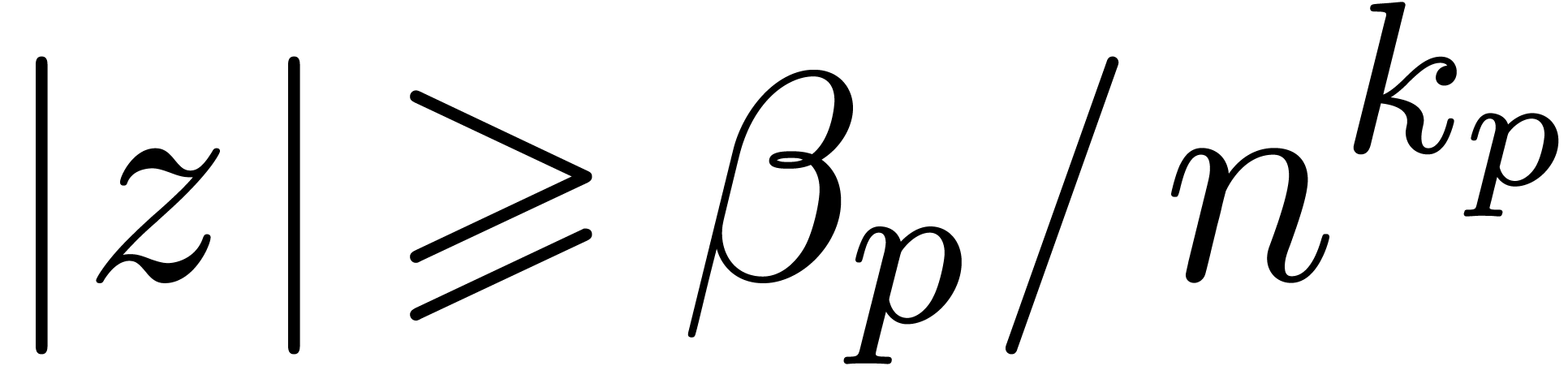 , we observe
that
, we observe
that 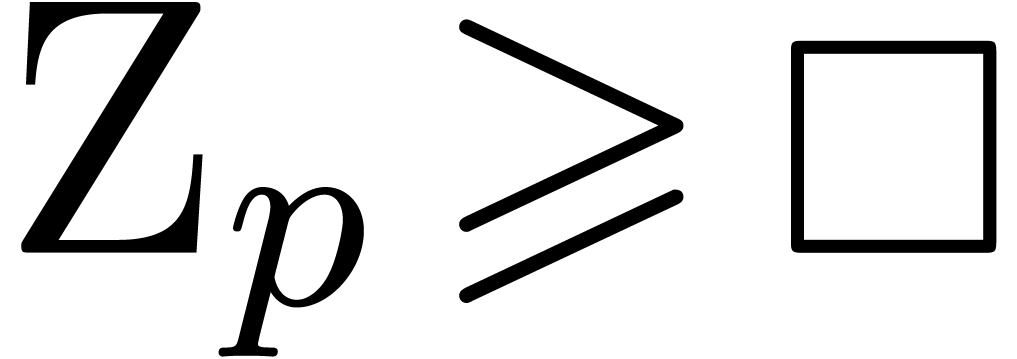 . This implies that we
can chose the contour
. This implies that we
can chose the contour 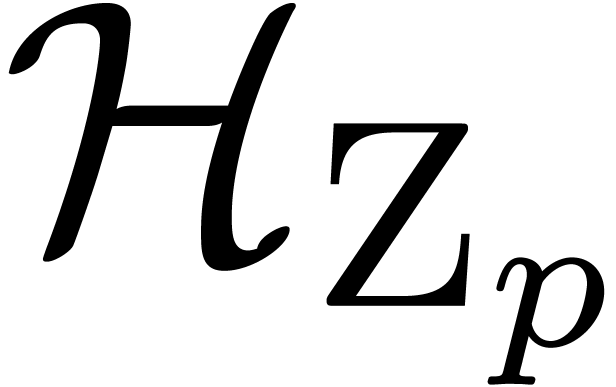 to use a circle of fixed
radius around the origin (which does not depend on
to use a circle of fixed
radius around the origin (which does not depend on 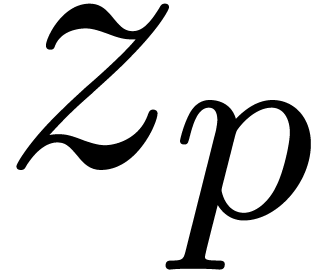 ). We next evaluate (7) using the
algorithm from [9, Section 6]. Our hypothesis that
). We next evaluate (7) using the
algorithm from [9, Section 6]. Our hypothesis that 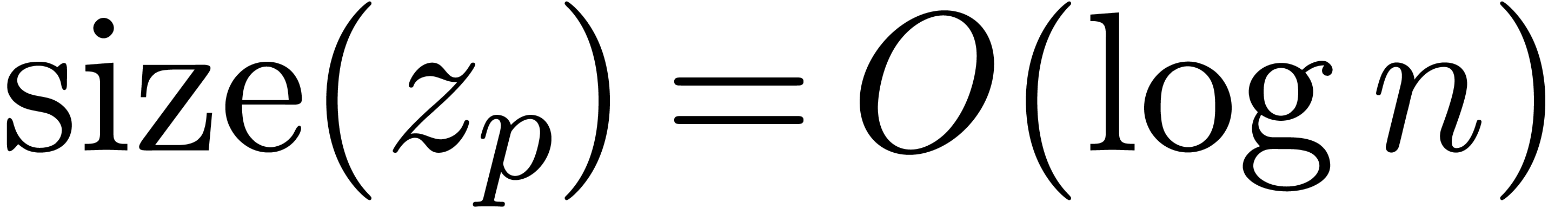 implies that the primitive of
implies that the primitive of 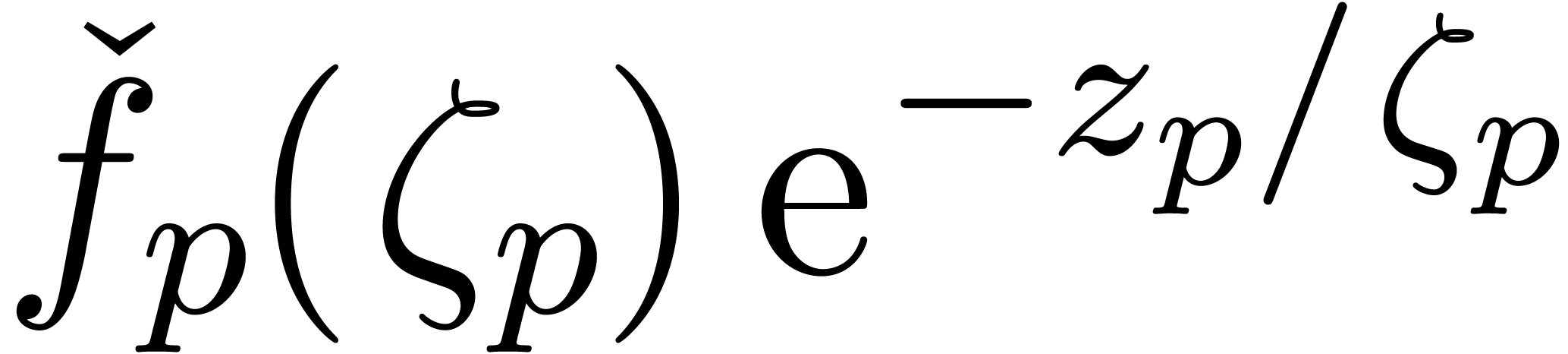 satisfies a holonomic equation of size
satisfies a holonomic equation of size 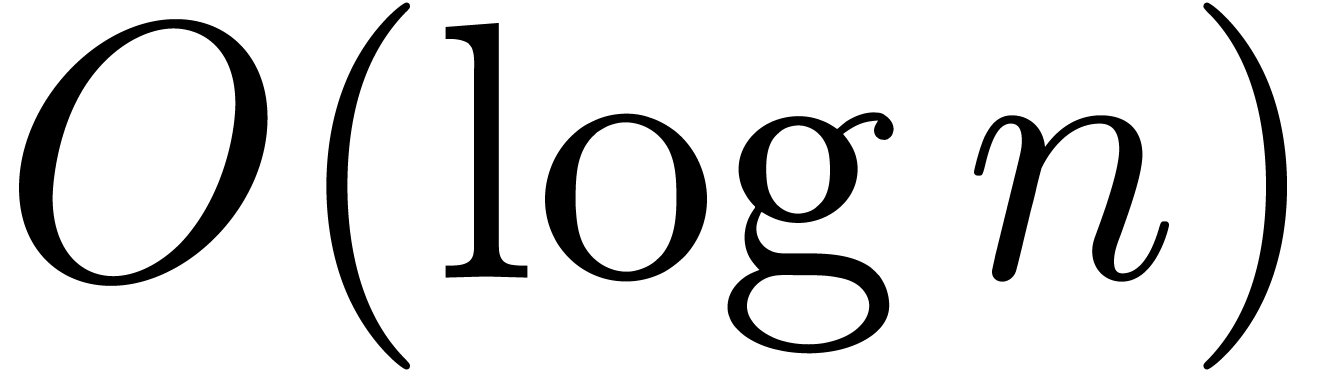 ,
uniformly in
,
uniformly in 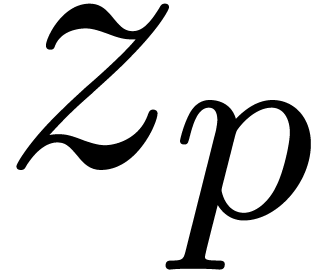 . Consequently,
it can be checked that the complexity bound from [9] holds
uniformly in
. Consequently,
it can be checked that the complexity bound from [9] holds
uniformly in 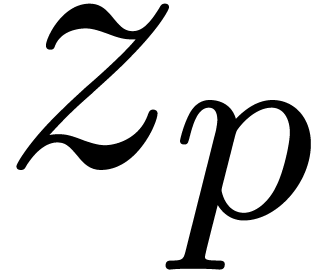 . This means
that the required
. This means
that the required 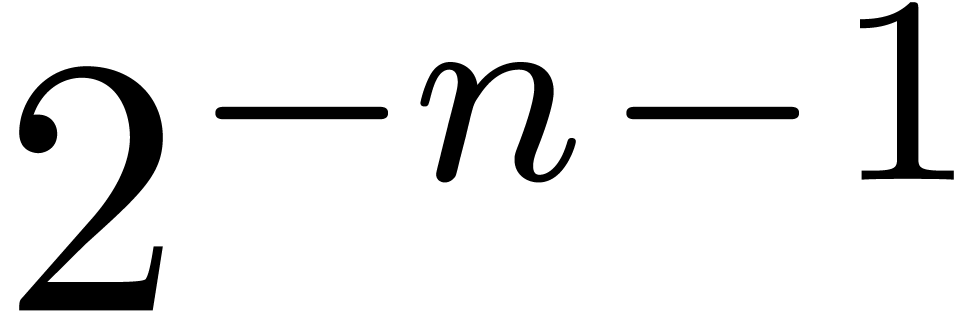 -approximation
-approximation
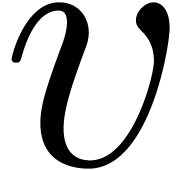 of
of  can be computed in
time
can be computed in
time 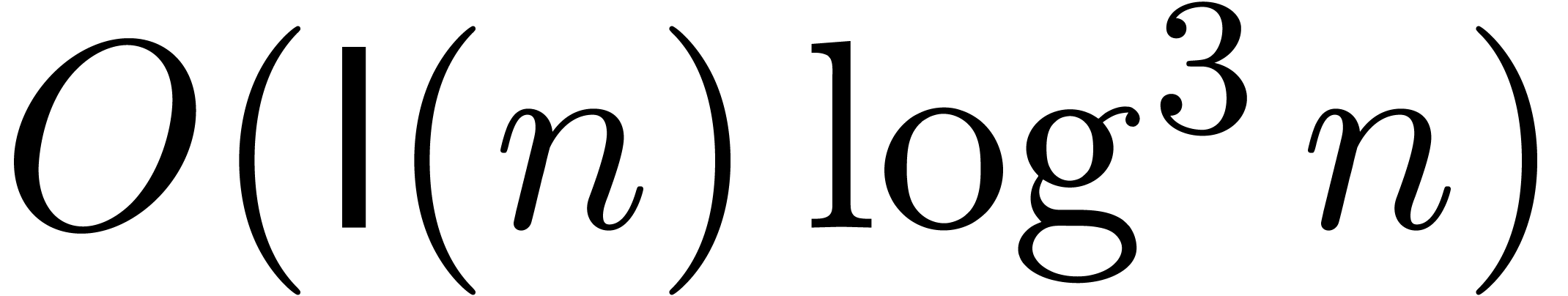 , uniformly in
, uniformly in 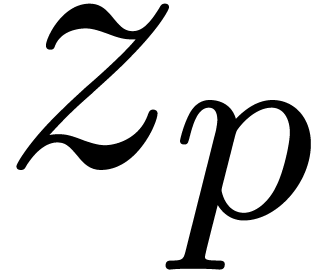 .
.
For general  , we approximate
, we approximate
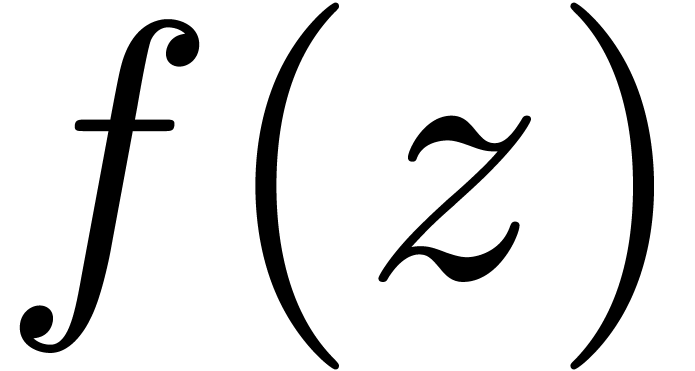 in two steps. Let
in two steps. Let 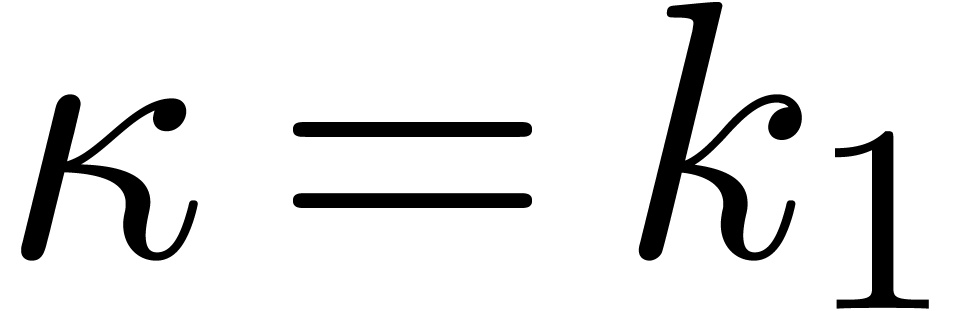 be the
growth rate of the linear differential equation satisfied by
be the
growth rate of the linear differential equation satisfied by 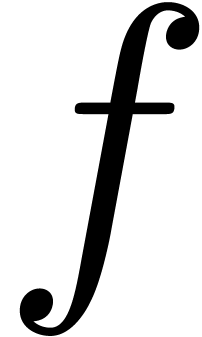 at the origin. In [9, Theorem 5.2], we showed
that in the sector
at the origin. In [9, Theorem 5.2], we showed
that in the sector 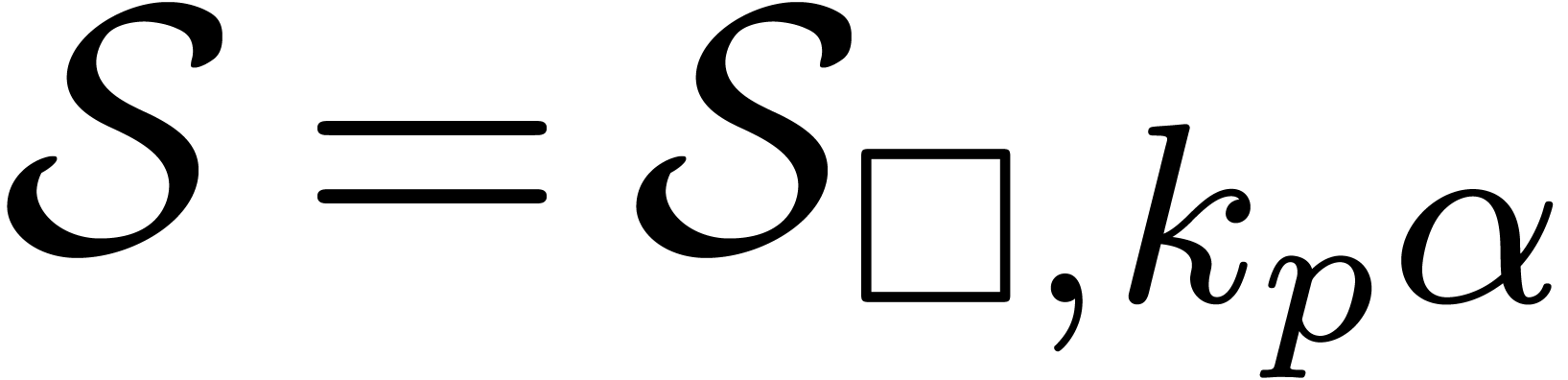 , we have
the following bound for the transition matrix on a straightline path
, we have
the following bound for the transition matrix on a straightline path
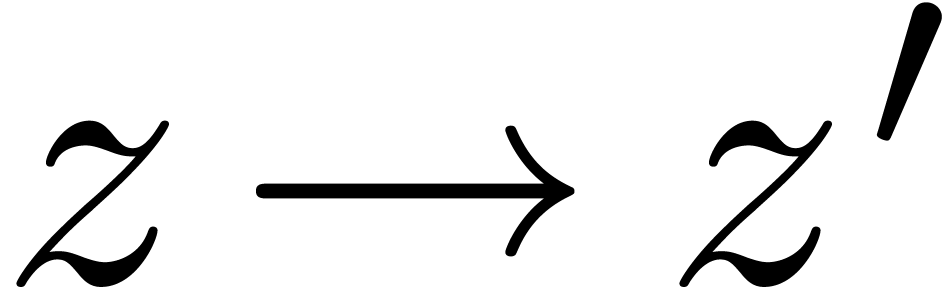 in
in  :
:

For  , it follows that
, it follows that
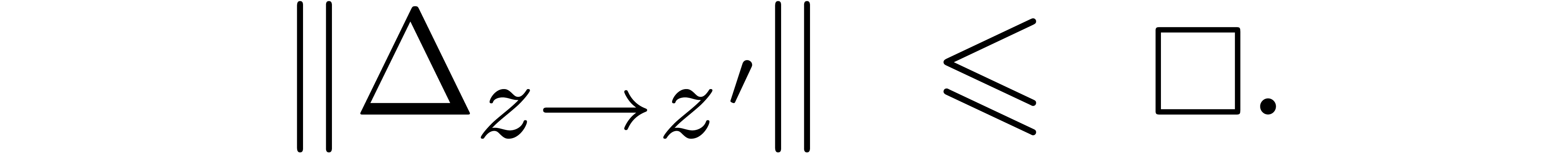 |
(8) |
Now let 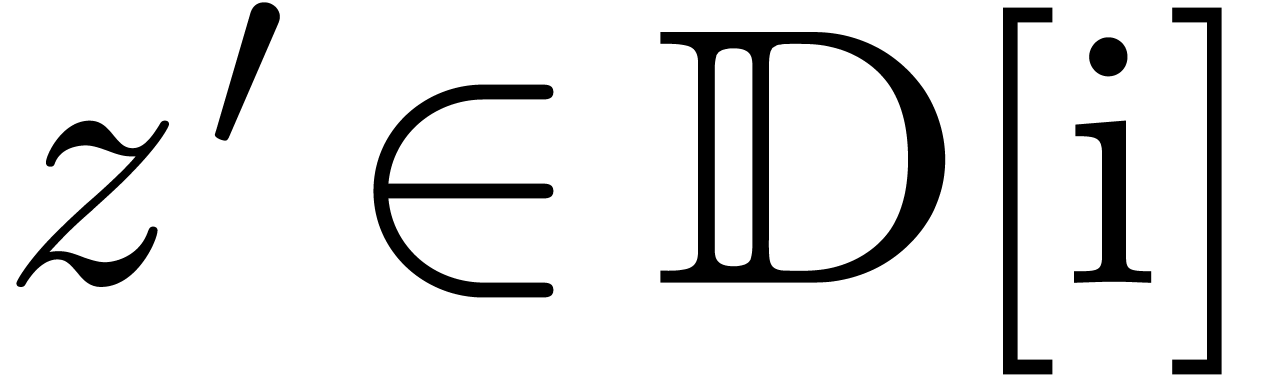 be an approximation of
be an approximation of  with
with  and
and  .
By what precedes, we may compute
.
By what precedes, we may compute 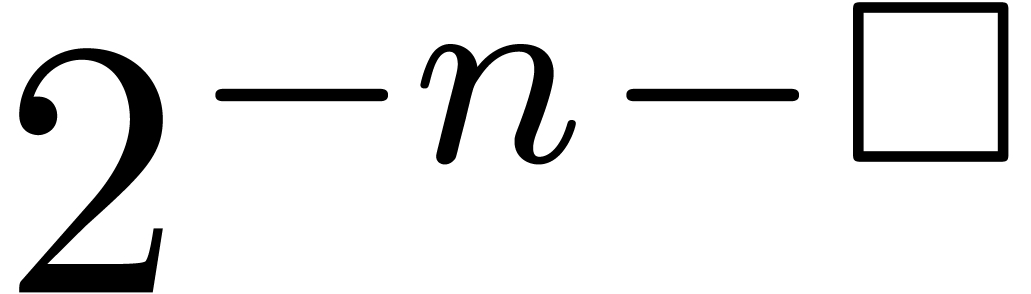 -approximations
of
-approximations
of 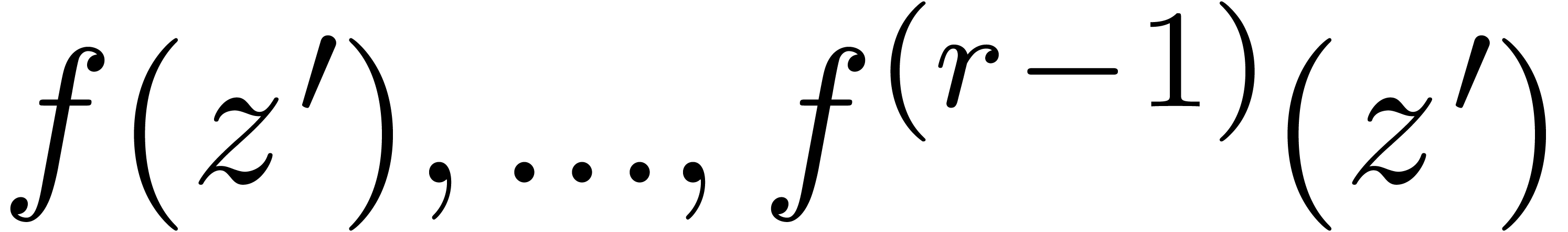 in time
in time 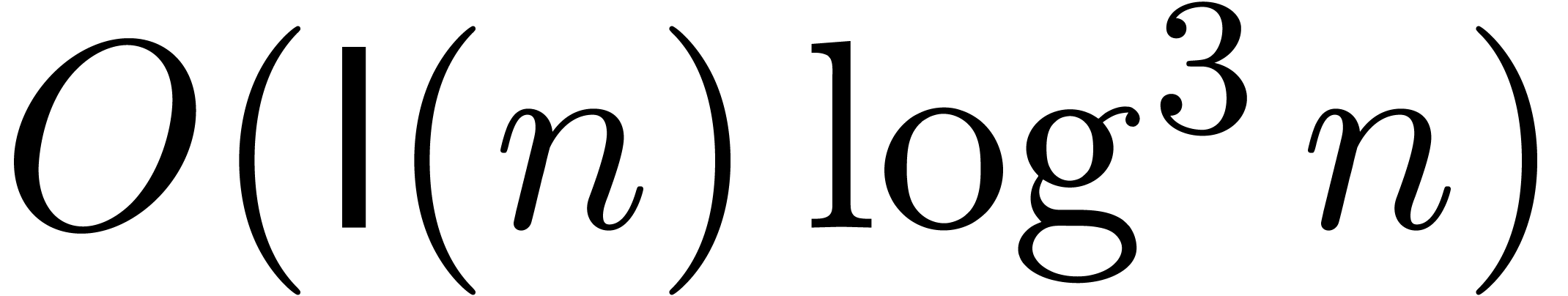 ,
uniformly in
,
uniformly in  . Using the
usual “bitburst” algorithm from [3, 7,
11], together with (8), it follows that we may
compute a
. Using the
usual “bitburst” algorithm from [3, 7,
11], together with (8), it follows that we may
compute a  -approximation of
-approximation of
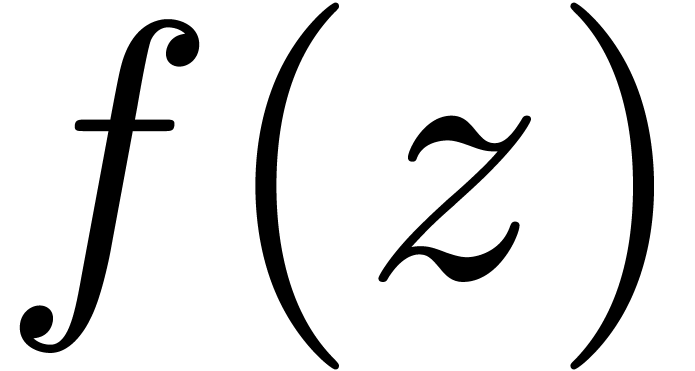 using an additional time of
using an additional time of 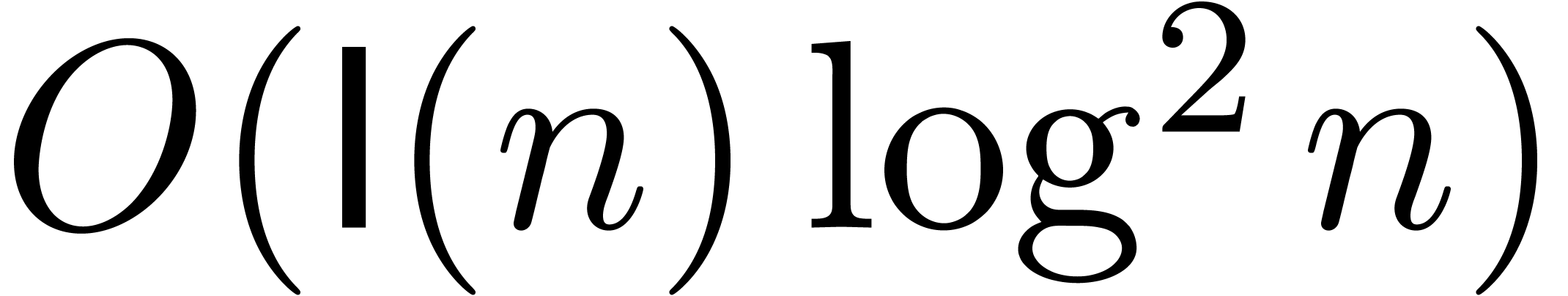 , uniformly in
, uniformly in  .
Adding up these complexity bounds, the result follows.
.
Adding up these complexity bounds, the result follows.
3.2.Uniform complexity of summation until the
least term
Proof. Direct consequence of [9,
Theorem A.1].
3.3.Uniform complexity of
expedito-summation
Proof. Our hypothesis on  implies that
implies that
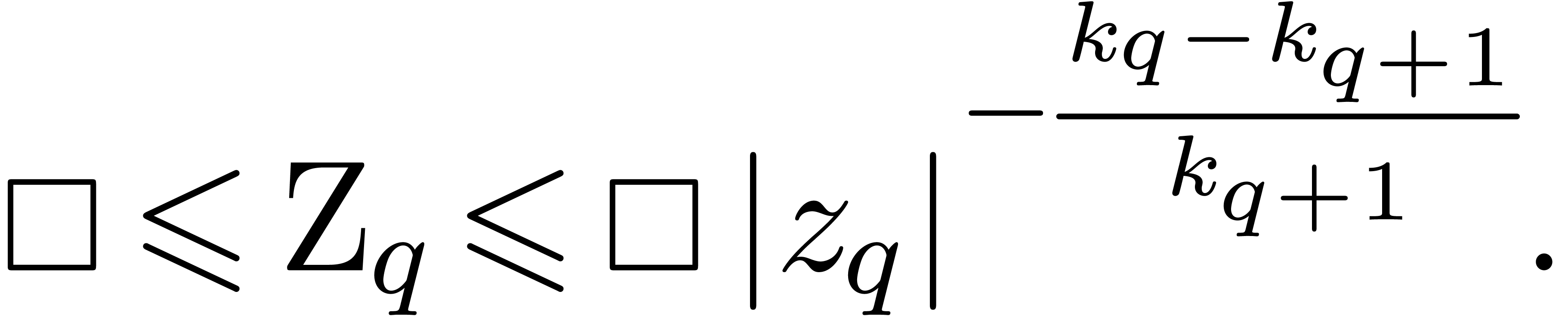
By Corollary 6, it follows that for all 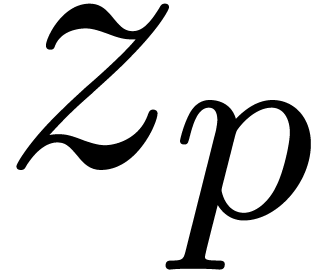 with
with 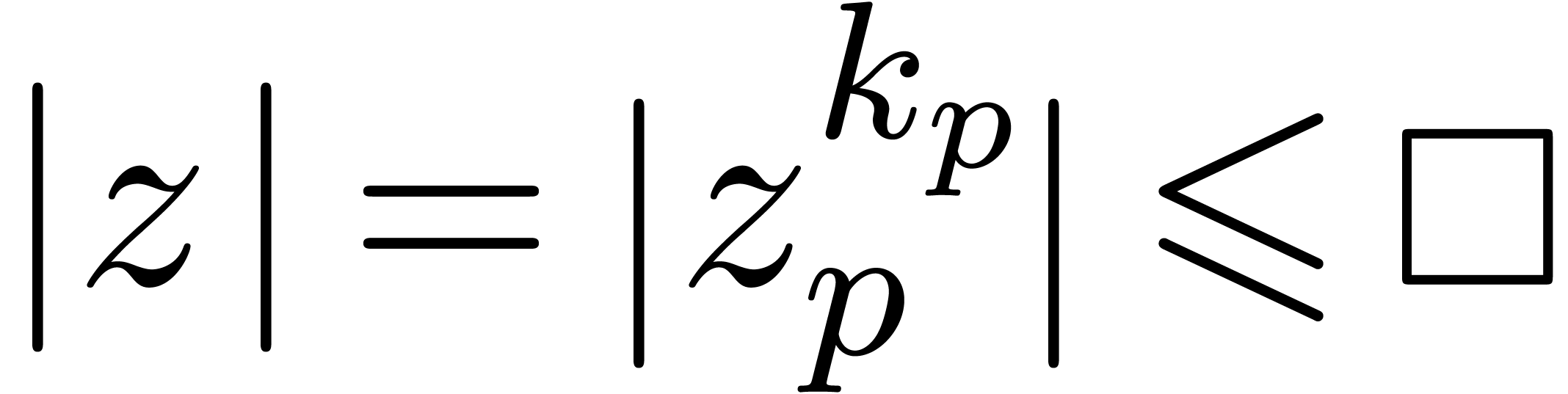 and
and 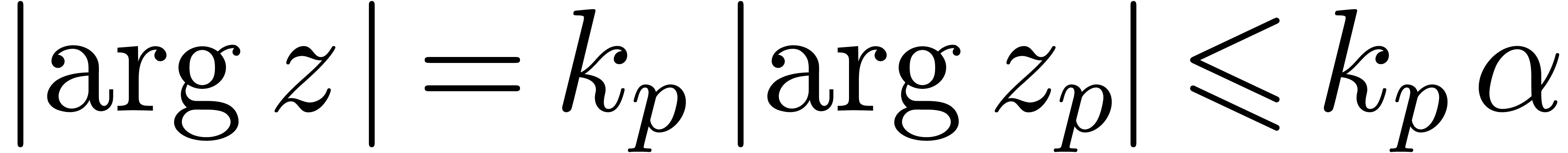 ,
we have
,
we have
For any suitable point 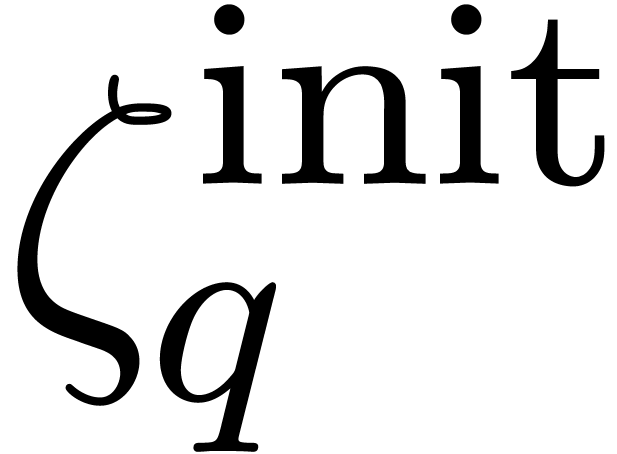 close to the origin and
close to the origin and
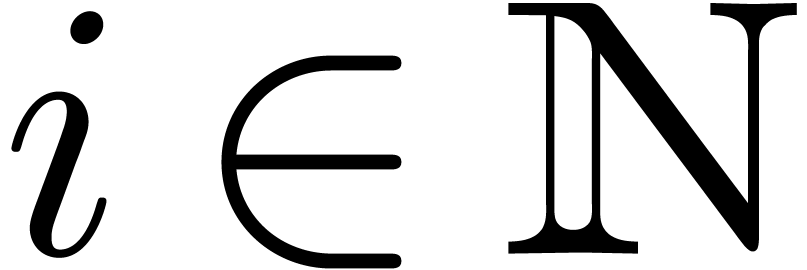 , we have shown in [9]
how to compute
, we have shown in [9]
how to compute  decimal digits of
decimal digits of 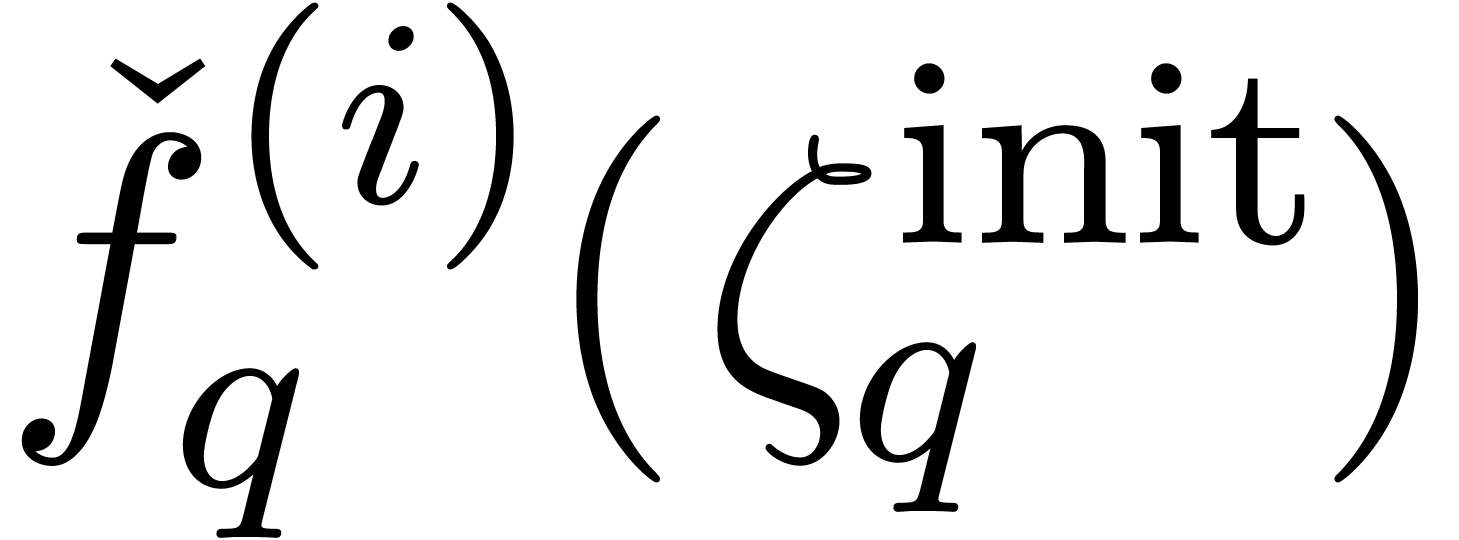 in time
in time 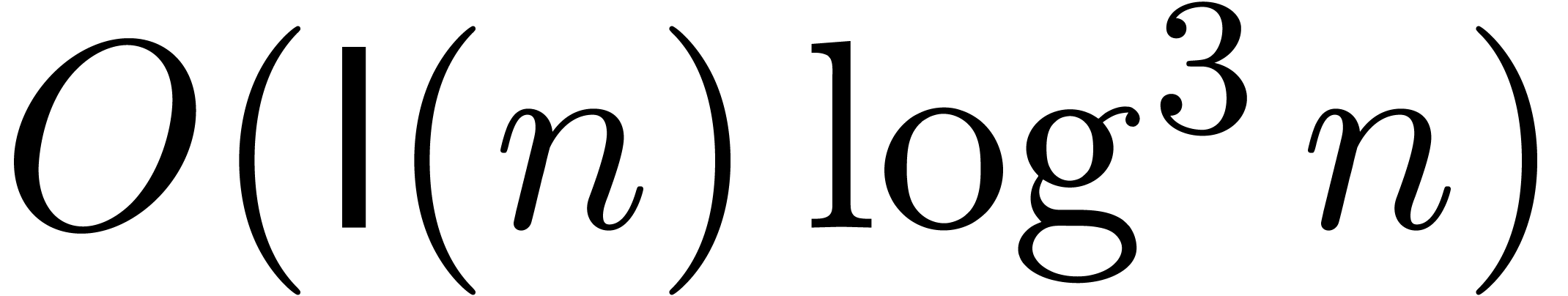 . This
provides us with the required initial conditions for the analytic
continuation of the integrant of the truncated Laplace integral
. This
provides us with the required initial conditions for the analytic
continuation of the integrant of the truncated Laplace integral
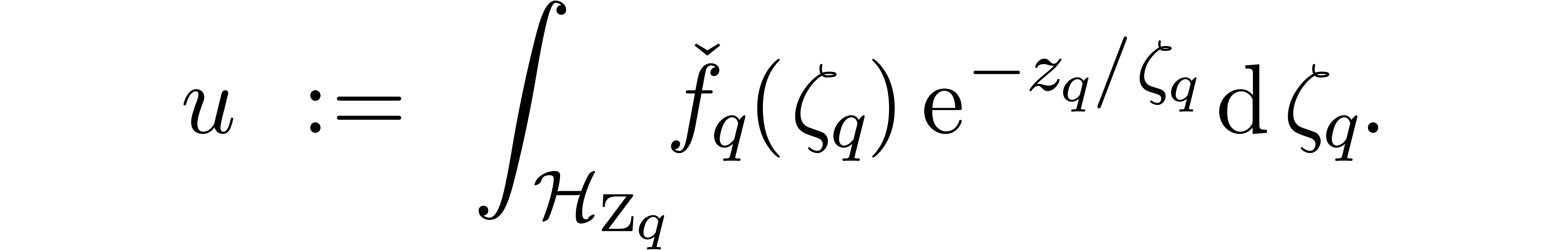
In a similar way as in the proof of Proposition 7, we may
therefore approximate  to precision
to precision 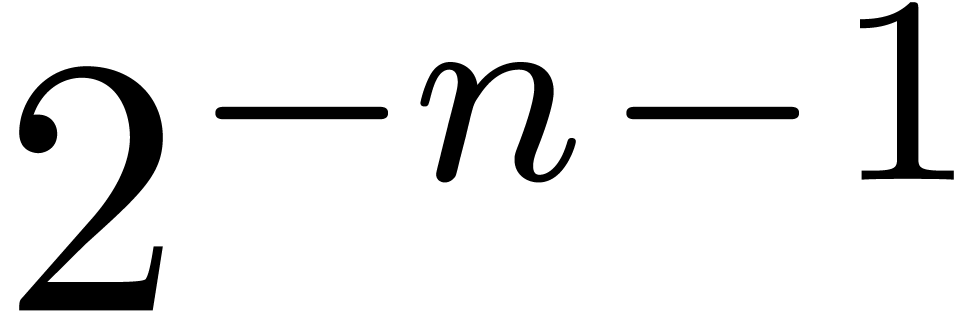 in time
in time 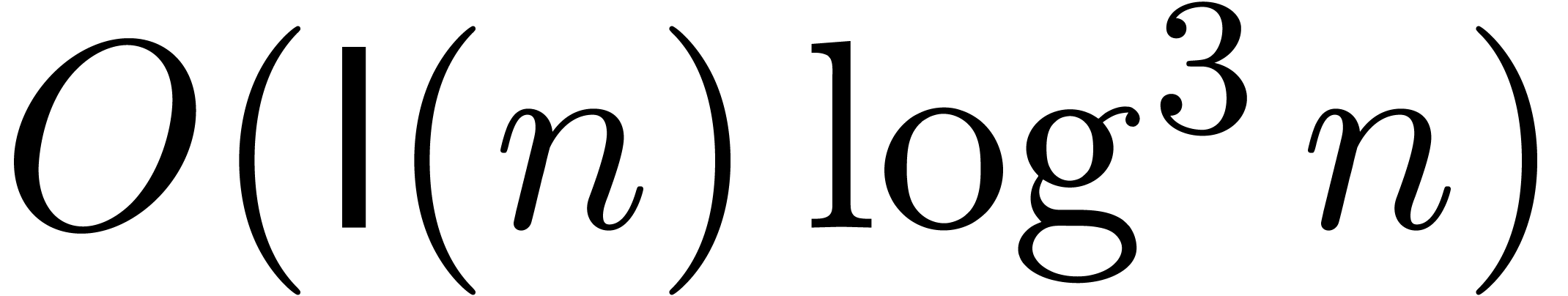 , where
the complexity bound is uniform in
, where
the complexity bound is uniform in  under our
conditions.
under our
conditions.
3.4.The combined local strategy
Putting Propositions 7, 8 and 9
together, we obtain:
Proof. Let 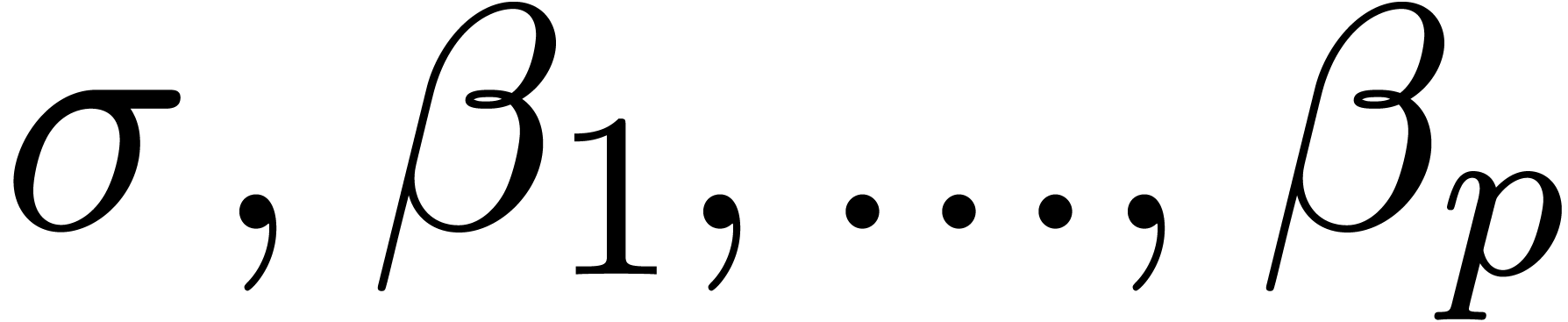 be as in
Propositions 8, 9 and 7. For any
be as in
Propositions 8, 9 and 7. For any
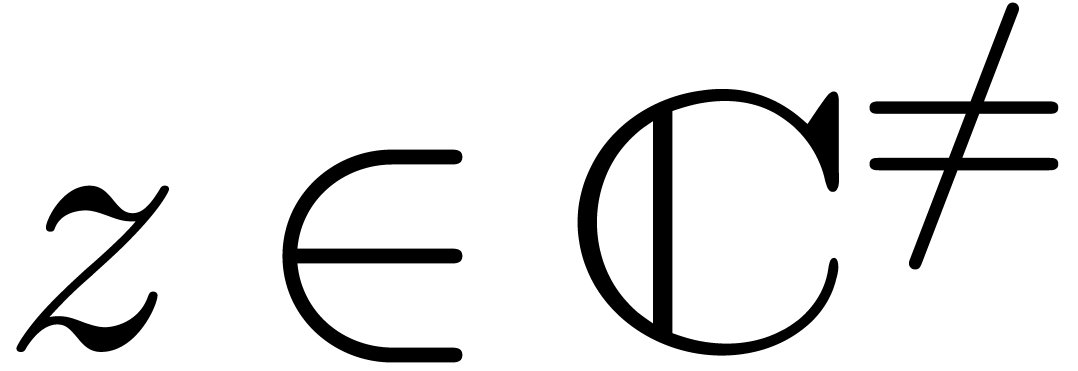 with
with 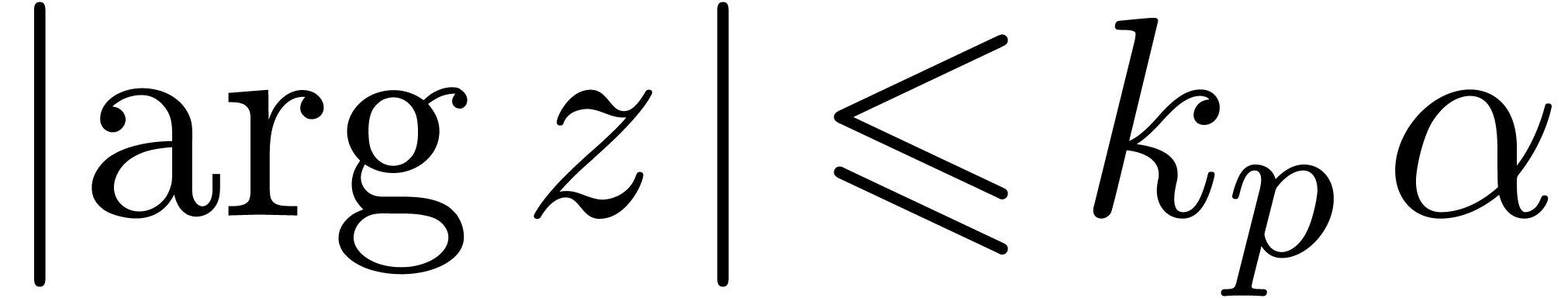 and
and 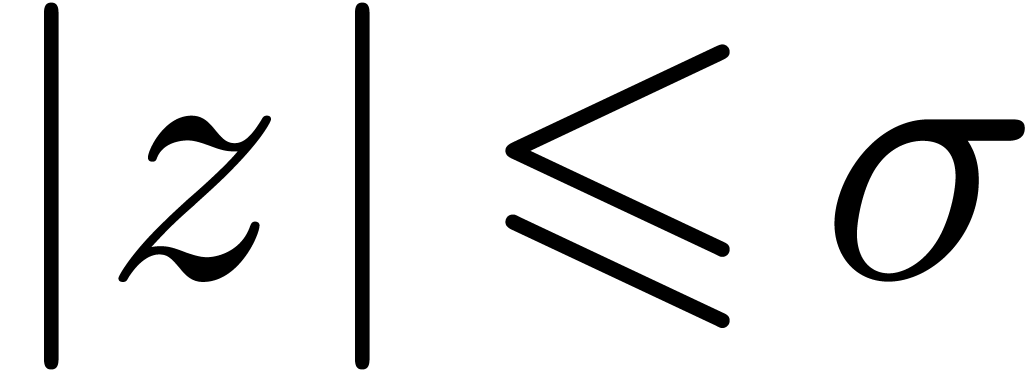 , at least one of the following three
statements holds:
, at least one of the following three
statements holds:
-
We have 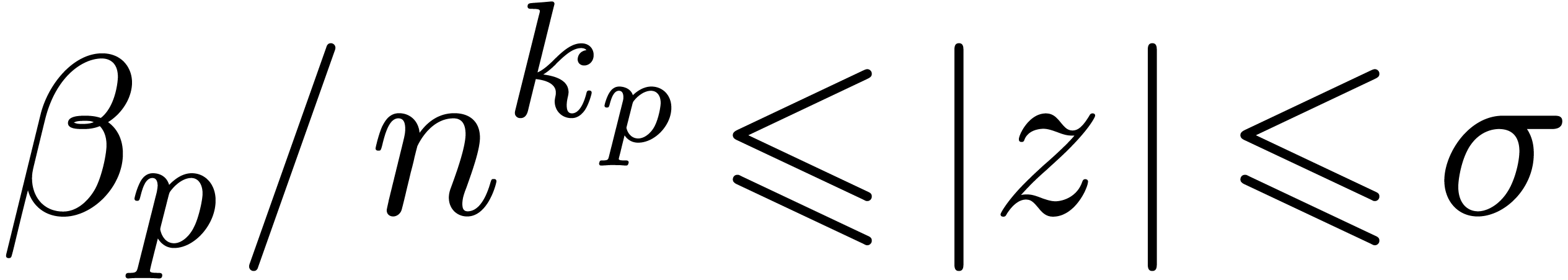 .
.
-
We have 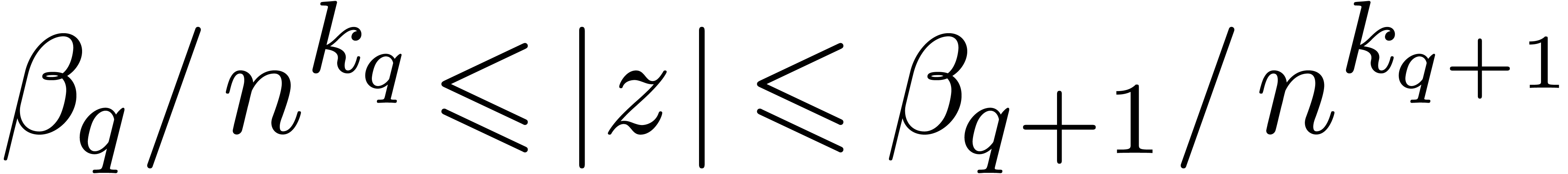 for some
for some  .
.
-
We have 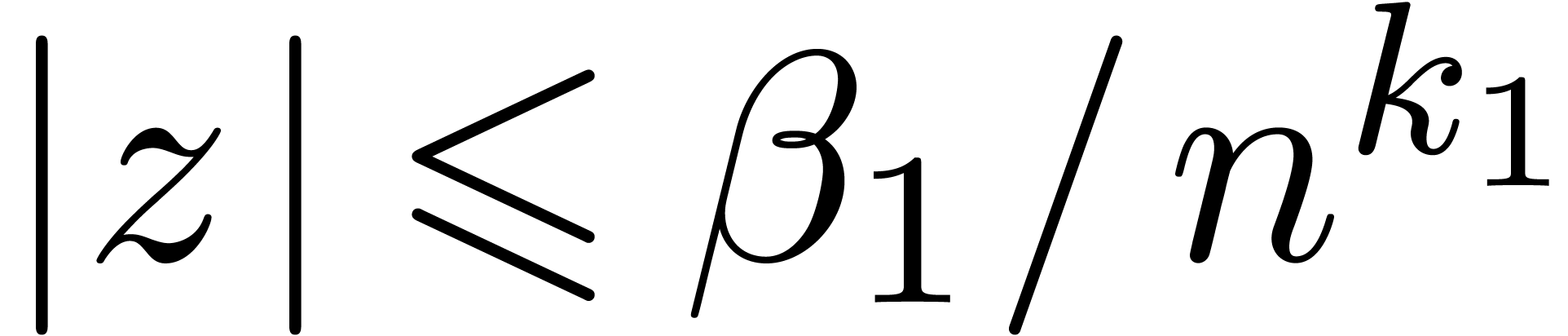 .
.
In these cases we respectively apply Proposition 7, 9 or 8 in order to obtain the desired
result.
4.Globally efficient
evaluation
4.1.Local analysis of cancellations
Assume that 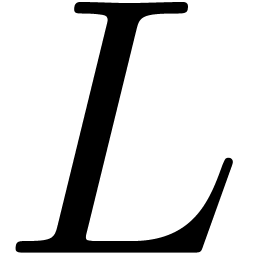 is singular at the origin. Then for
some
is singular at the origin. Then for
some  , there exists a basis
of formal solutions of the form
, there exists a basis
of formal solutions of the form
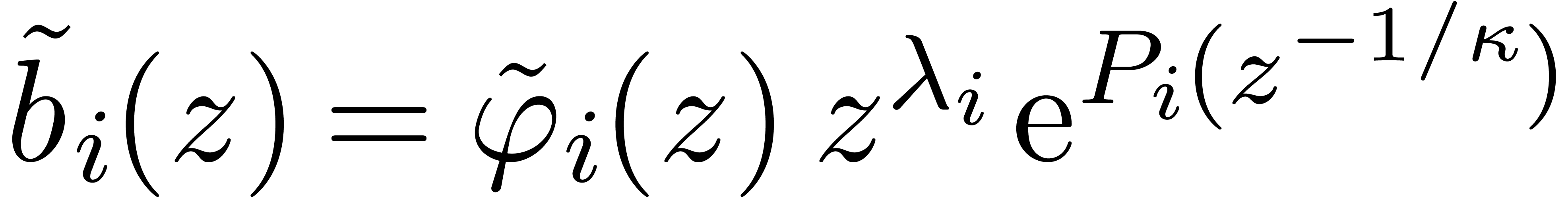 |
(9) |
for 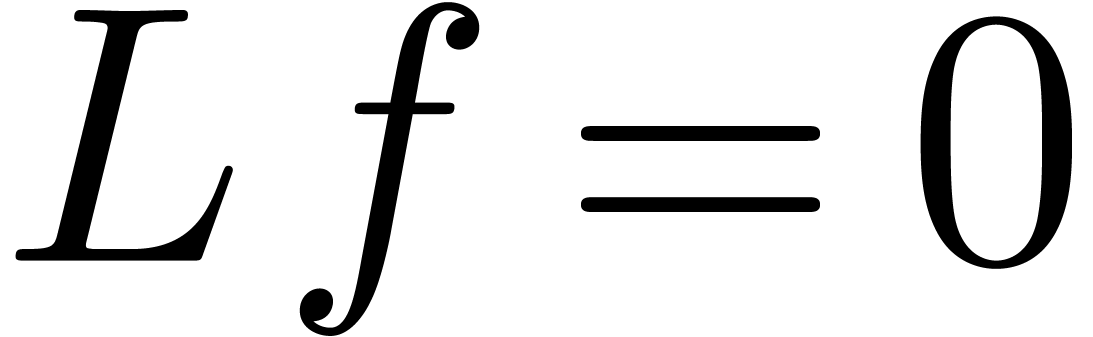 , where
, where 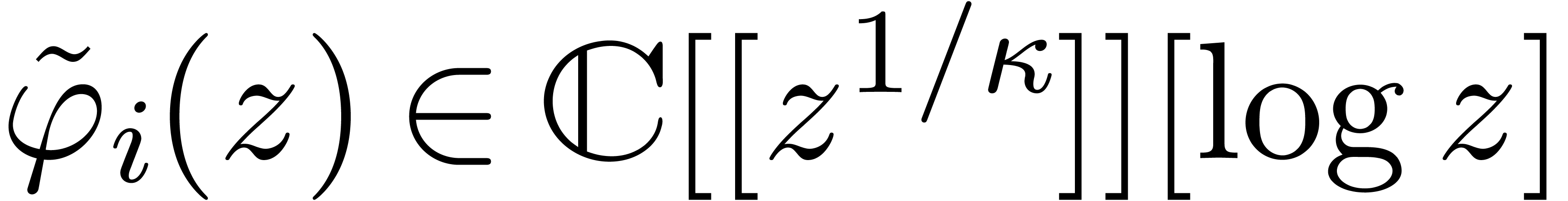 ,
,  ,
,
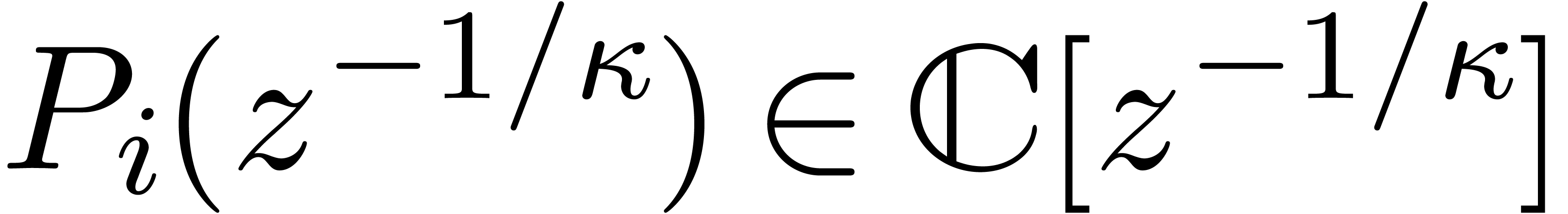 , and where
, and where 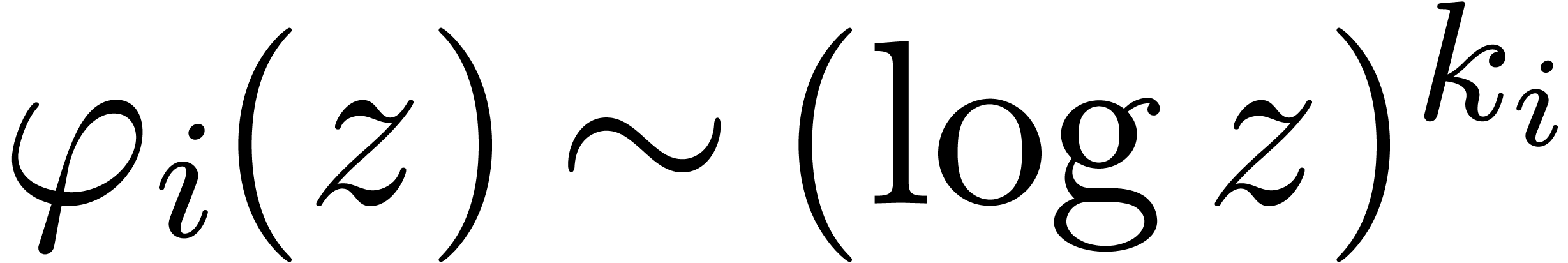 for some
for some  . Moreover, each
. Moreover, each
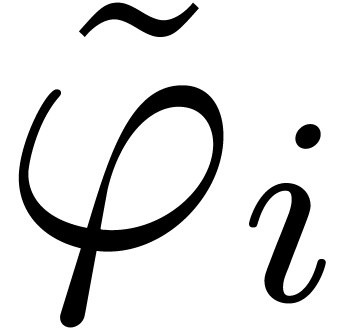 belongs to the subset
belongs to the subset  of
of
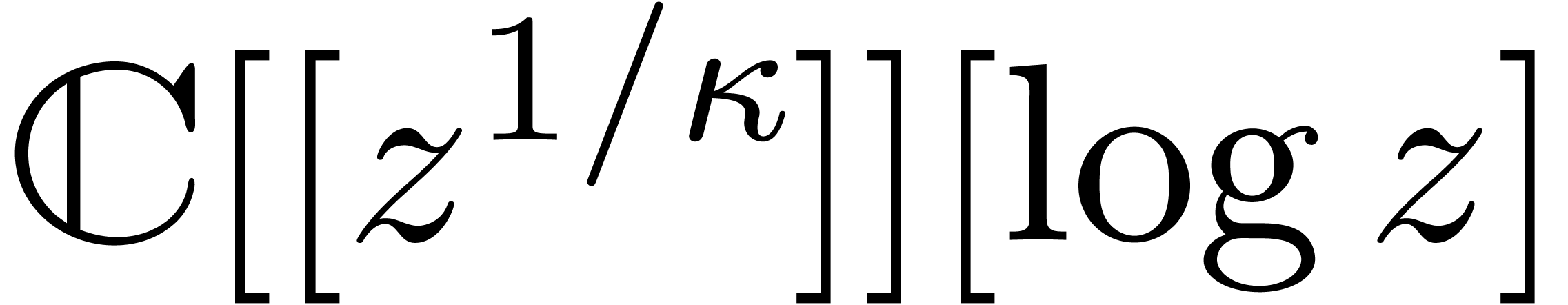 accelero-summable series.
accelero-summable series.
For each fixed accelero-summation scheme, there exist 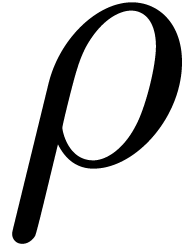 ,
, 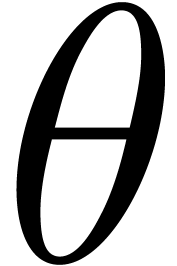 and
and  such that the
such that the 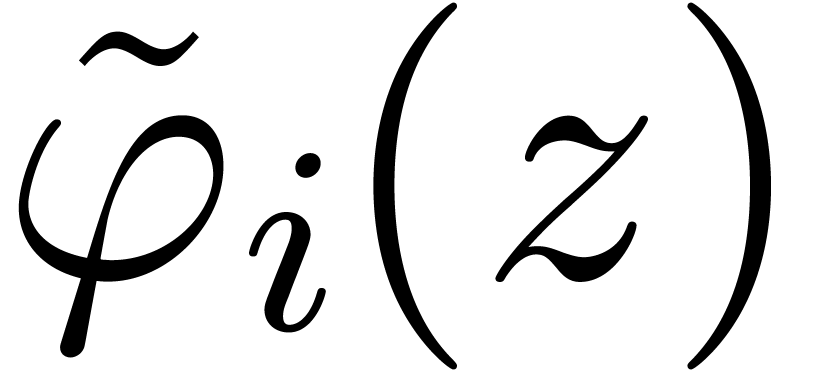 and
and 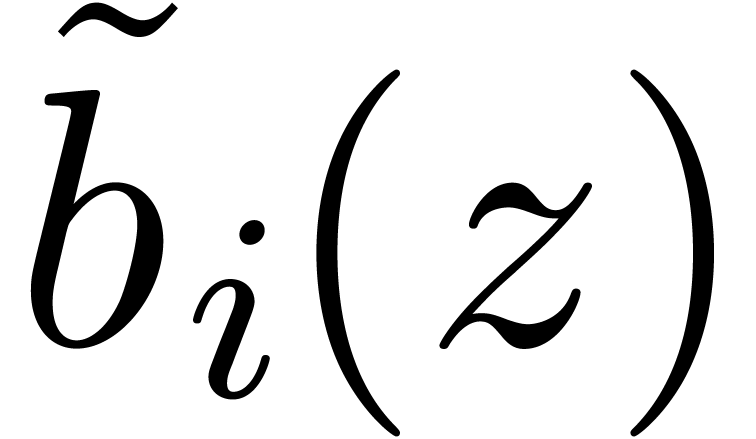 give
rise to analytic functions
give
rise to analytic functions 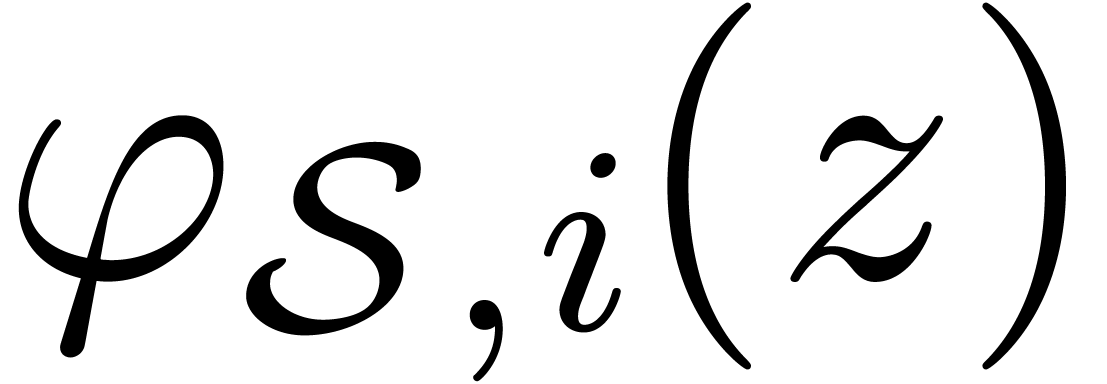 and
and 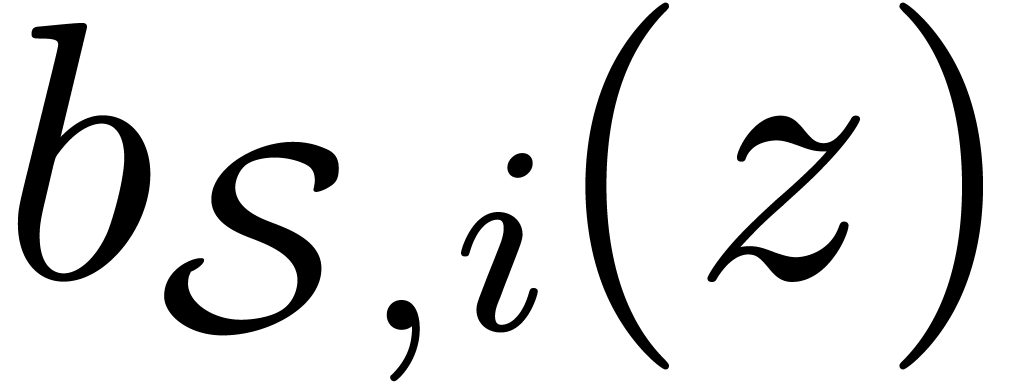 on the sector
on the sector  . A sector
. A sector  for which this happens is said to be
admissible. Moreover, there exist a finite number of admissible
sectors
for which this happens is said to be
admissible. Moreover, there exist a finite number of admissible
sectors  with
with  whose
interiors cover a small neighbourhood of
whose
interiors cover a small neighbourhood of  .
We will call this an admissible cover.
.
We will call this an admissible cover.
Let  be one of the sectors in an admissible cover
and let
be one of the sectors in an admissible cover
and let 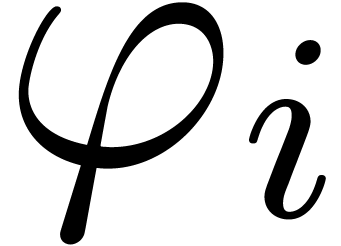 and
and 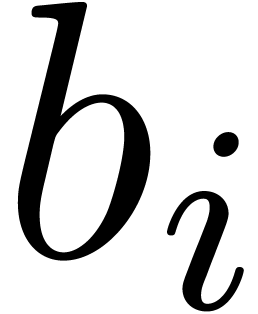 denote the
accelero-sums of
denote the
accelero-sums of 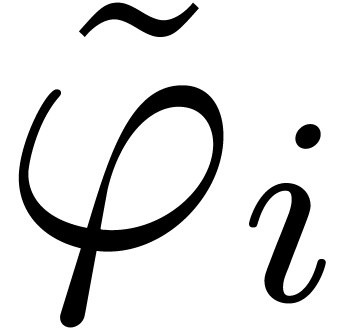 and
and 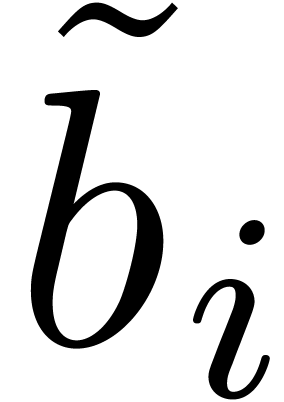 on
this sector. For each
on
this sector. For each 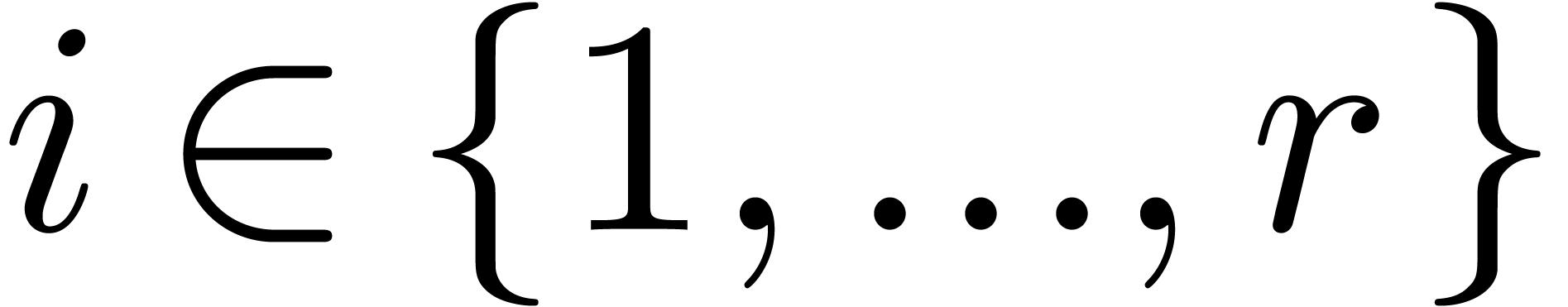 , let
, let
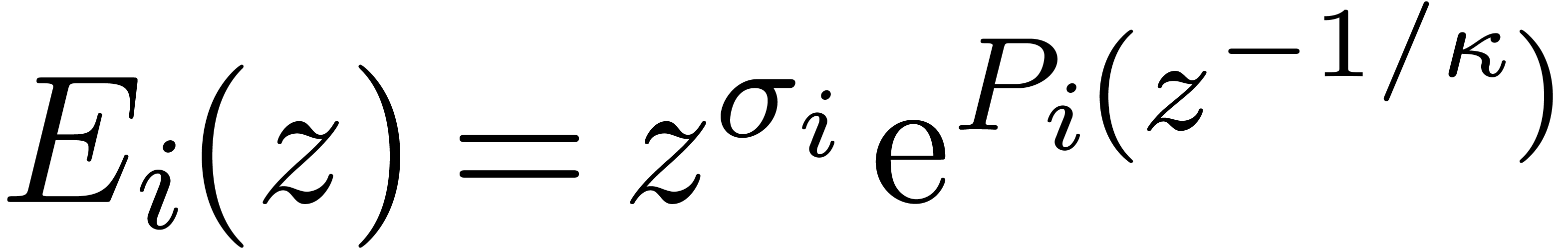 . Let
. Let  denote the subset of all
denote the subset of all 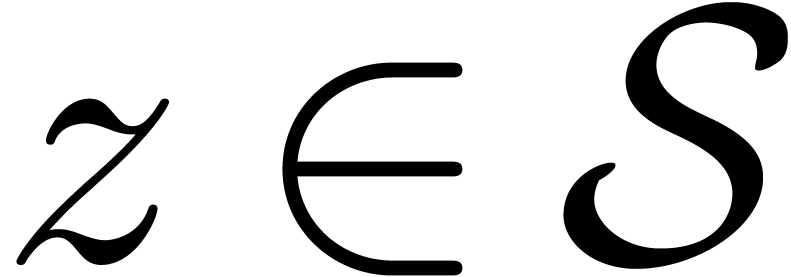 such that
such that
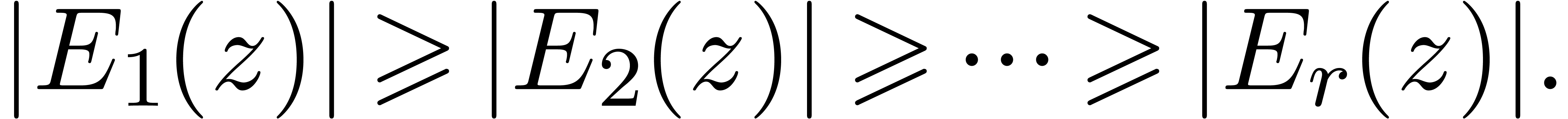
More generally, given a permutation  of
of  , let
, let  denote the subset of all
denote the subset of all 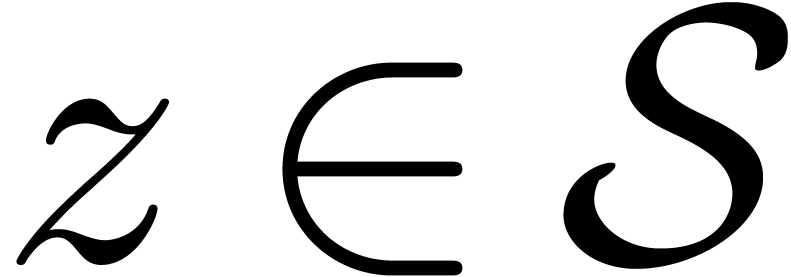 with
with

Clearly,  .
.
Let 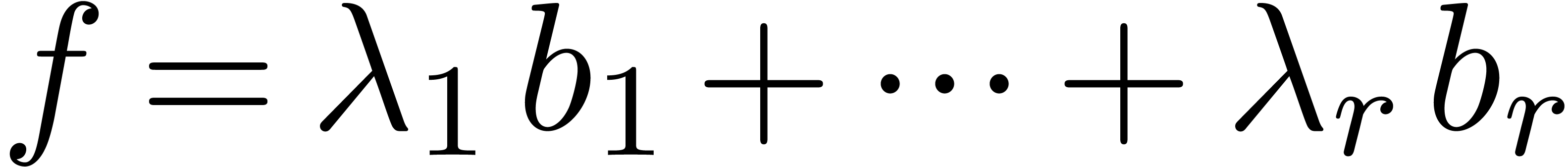 be a non zero solution to
be a non zero solution to 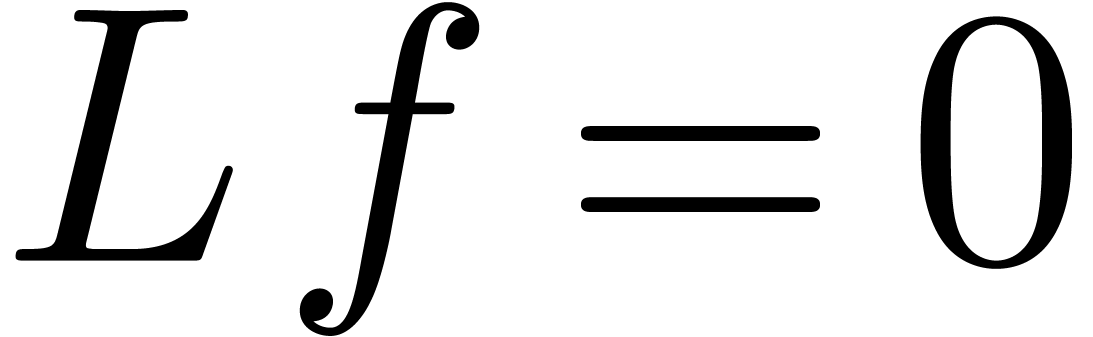 on
on  and let
and let  be the column
vectors with entries
be the column
vectors with entries  .
Although
.
Although  can vanish on
can vanish on  due to cancellations among the terms
due to cancellations among the terms 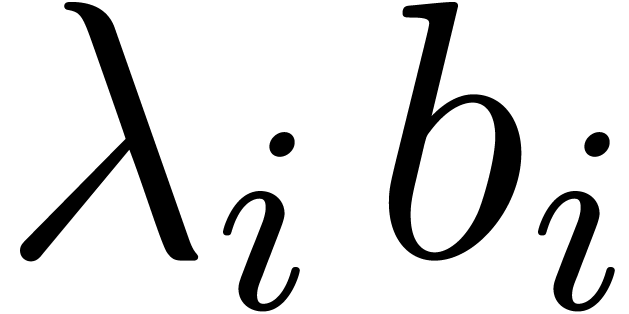 and
and 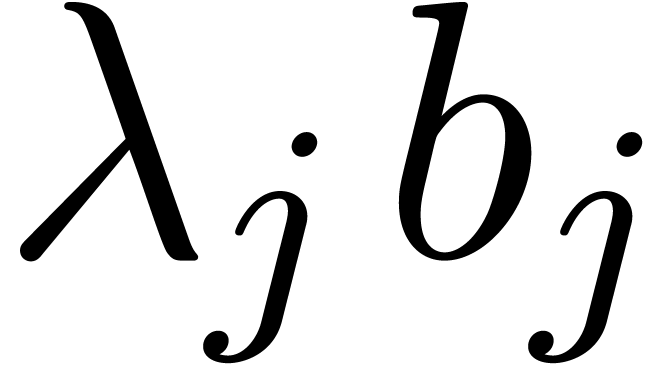 , the vector
, the vector  cannot vanish unless
cannot vanish unless 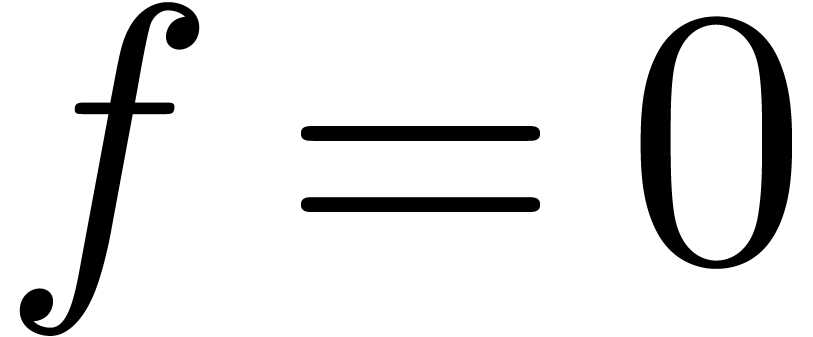 . We
will now prove a stronger version of this observation by showing that
the sup-norm
. We
will now prove a stronger version of this observation by showing that
the sup-norm  of
of  cannot
become much smaller than
cannot
become much smaller than 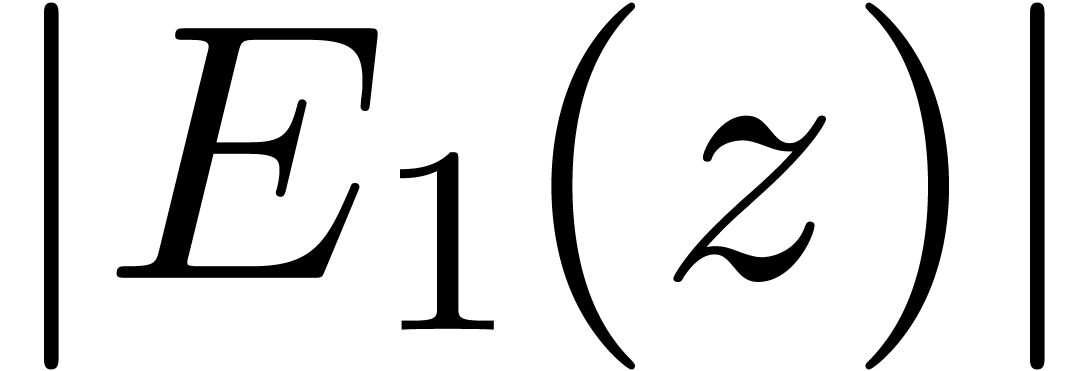 .
.
Theorem 11. There exist constants 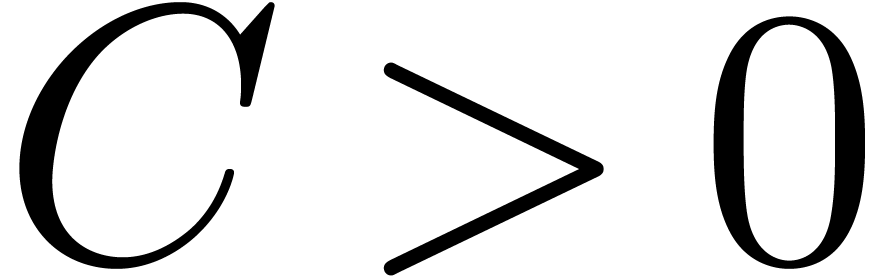 and
and 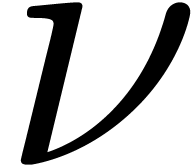 such that
such that

for all 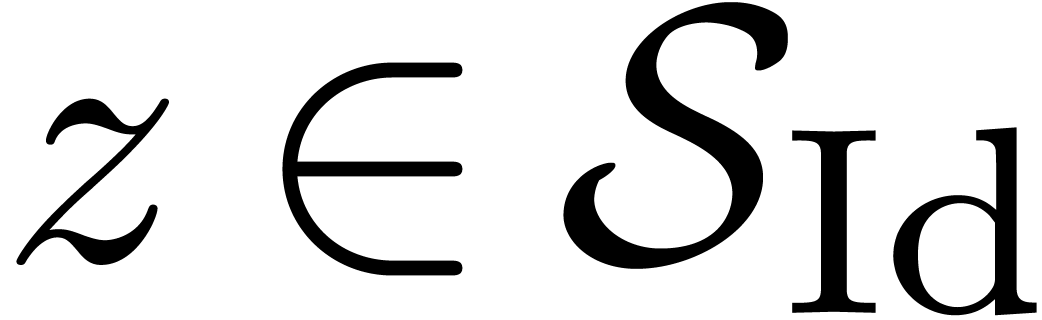 .
.
Proof. Without loss of generality, we may assume
that 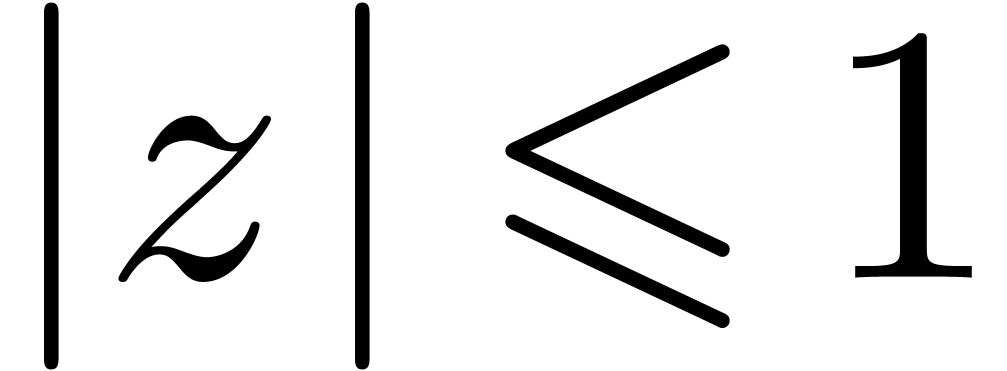 . For each
. For each 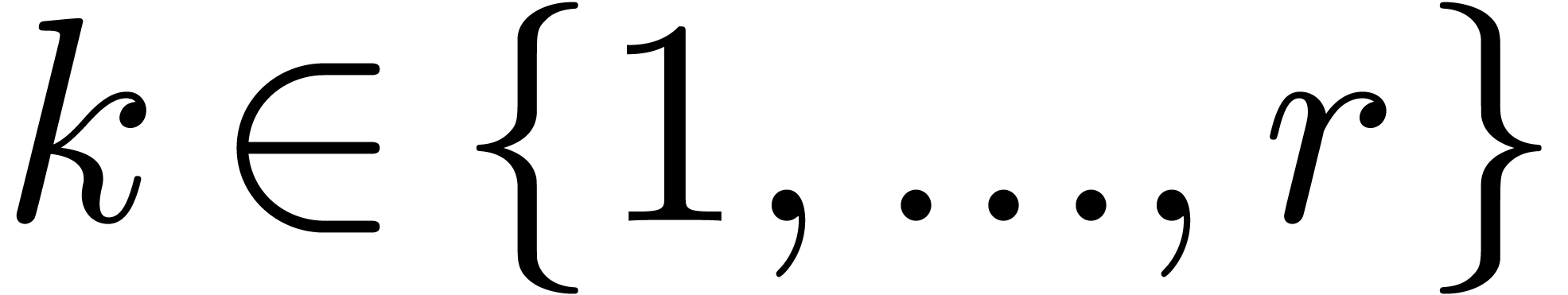 , let
, let 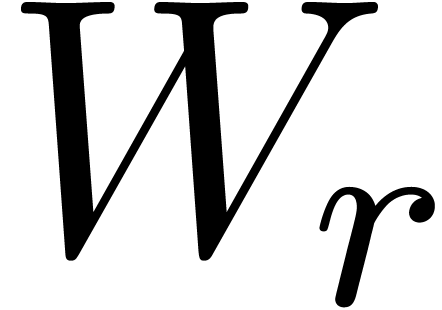 be the Wronskian
matrix
be the Wronskian
matrix
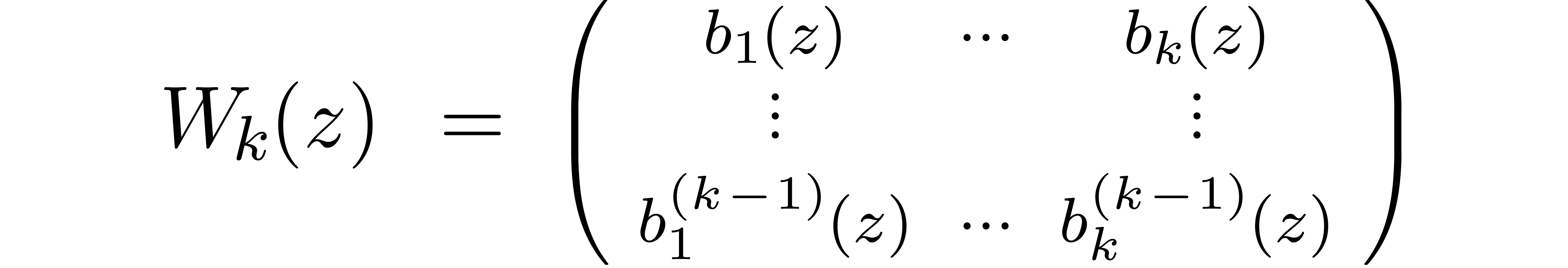
We may decompose

where
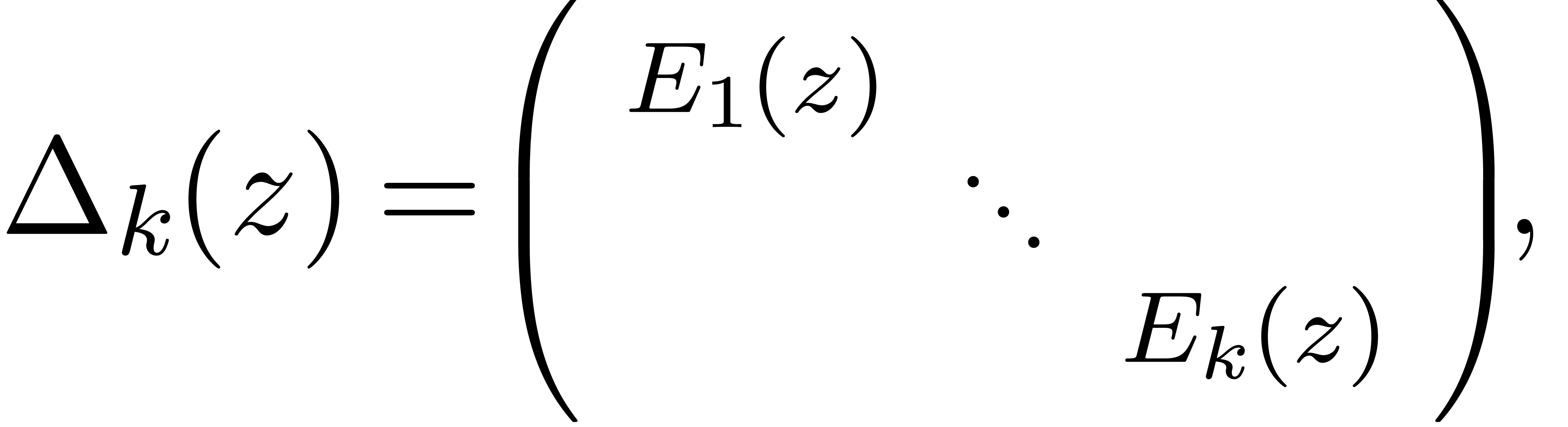
and where the entries of  are in
are in 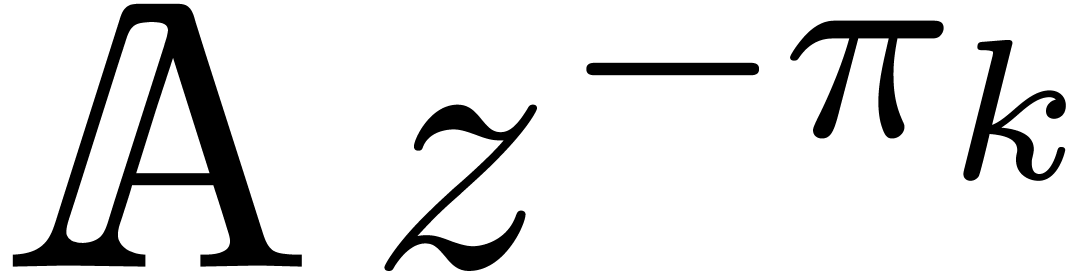 for some
for some  that only depends on the degrees of
that only depends on the degrees of
 . It follows that
. It follows that
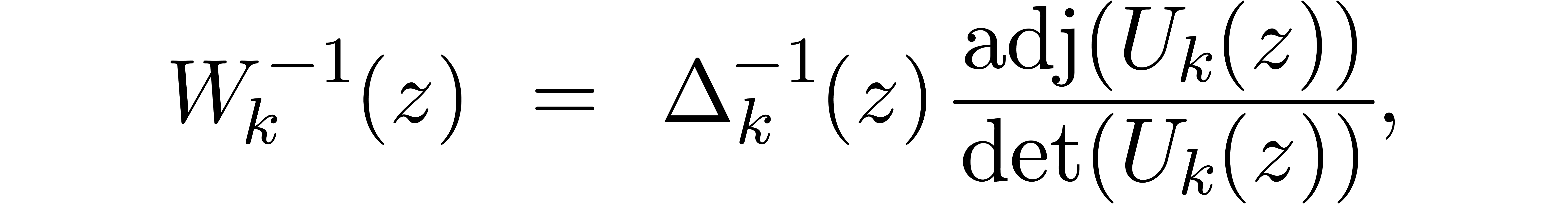
where 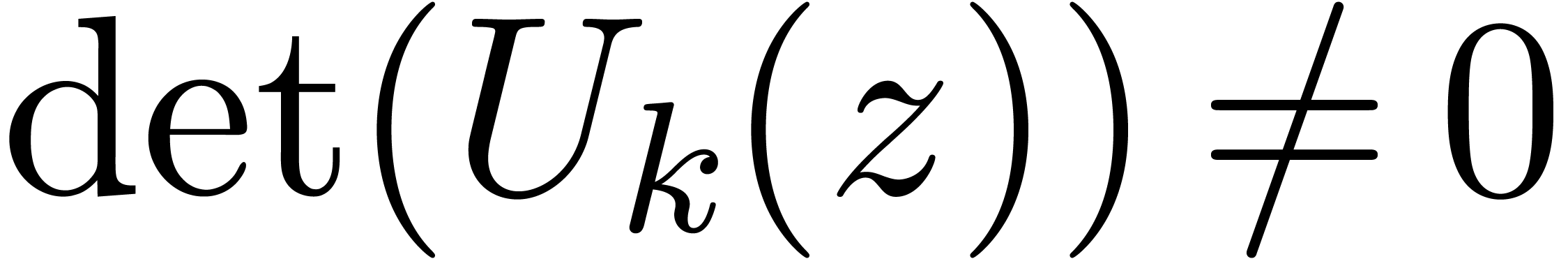 by the linear independence of
by the linear independence of  . Now
. Now  and the entries
of
and the entries
of  are all elements of
are all elements of 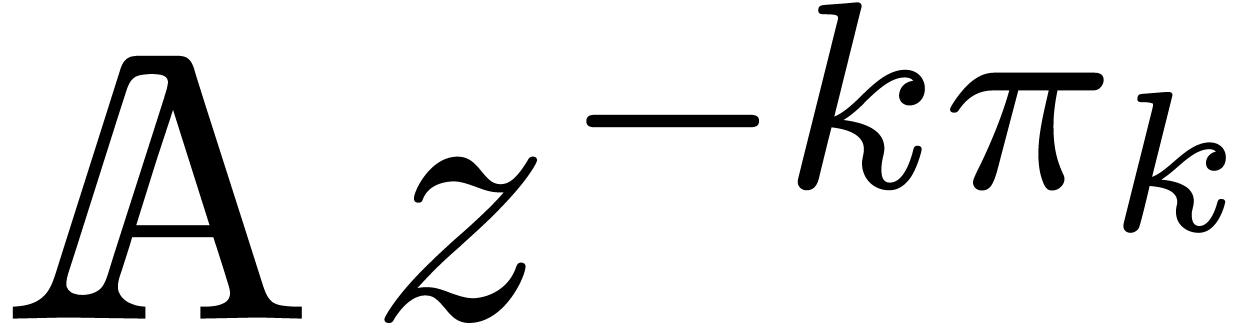 . It follows that there exists a constant
. It follows that there exists a constant  such that
such that 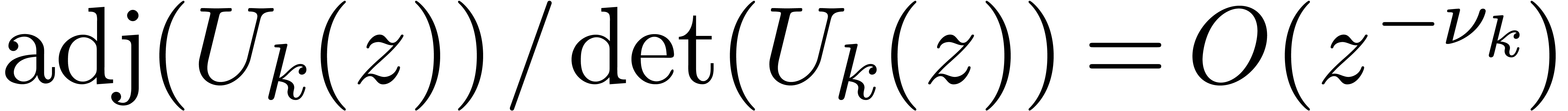 for all
for all 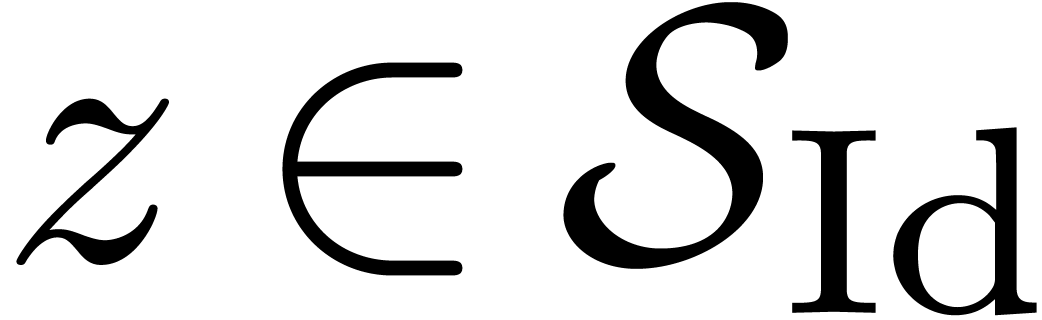 .
.
Now consider our fixed linear combination 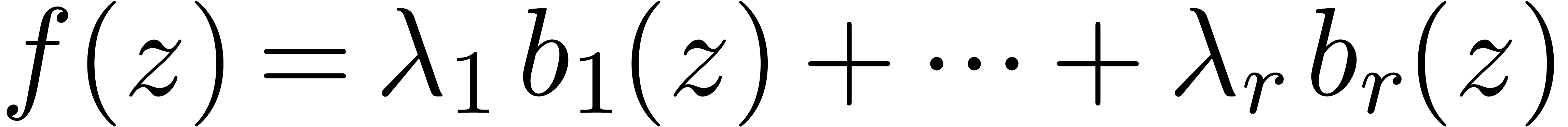 and
let
and
let
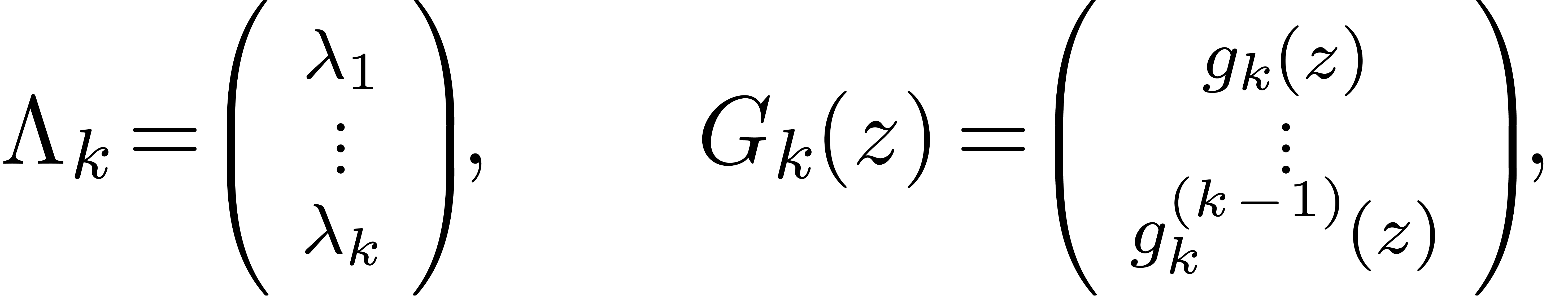
where 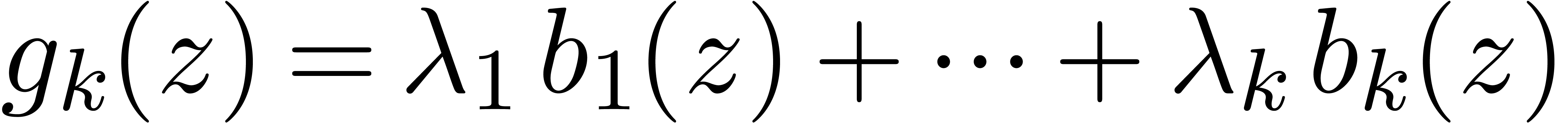 , so that
, so that 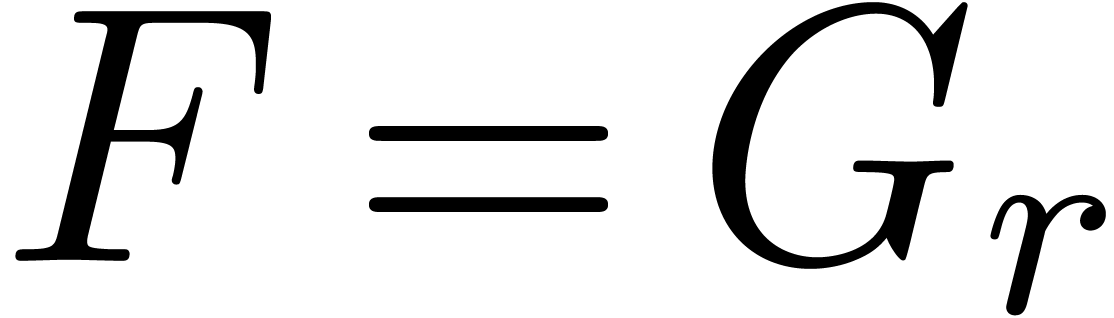 and
and 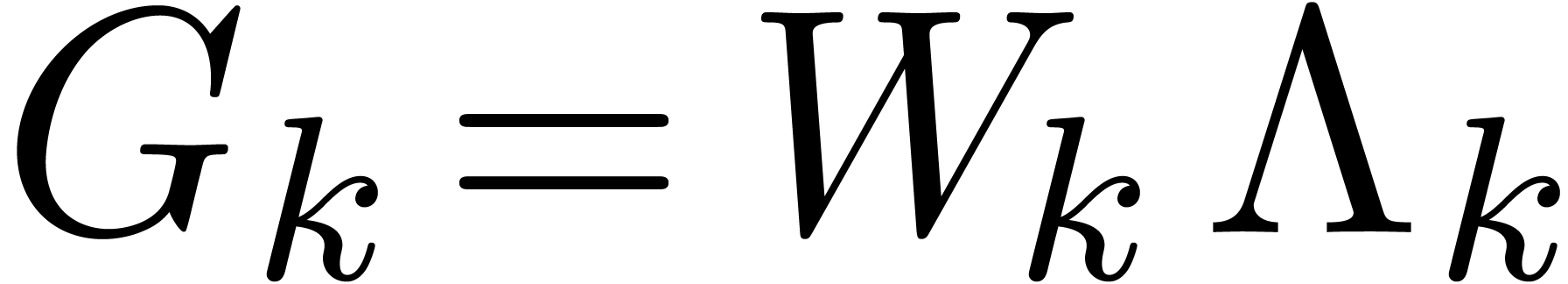 . Also let
. Also let
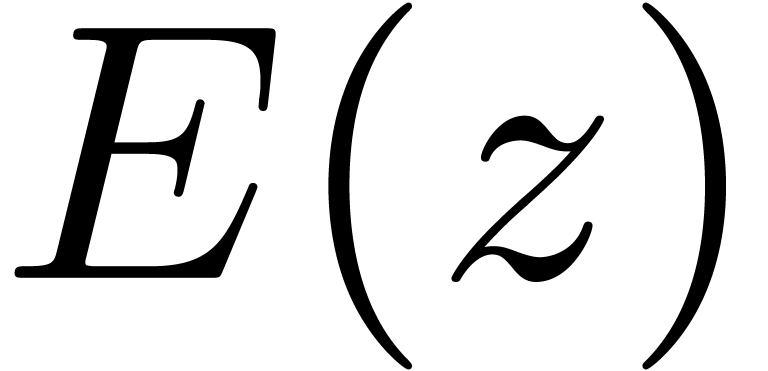 be the column vector with entries
be the column vector with entries  . For the sup-norm on vectors, the above
discussion shows that
. For the sup-norm on vectors, the above
discussion shows that
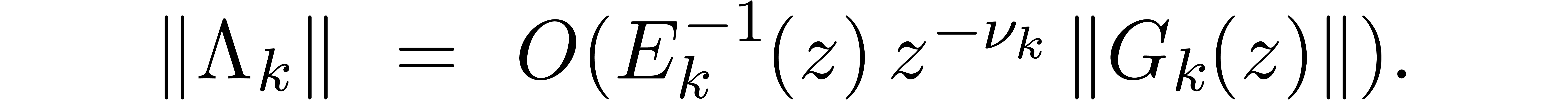
For some fixed constant 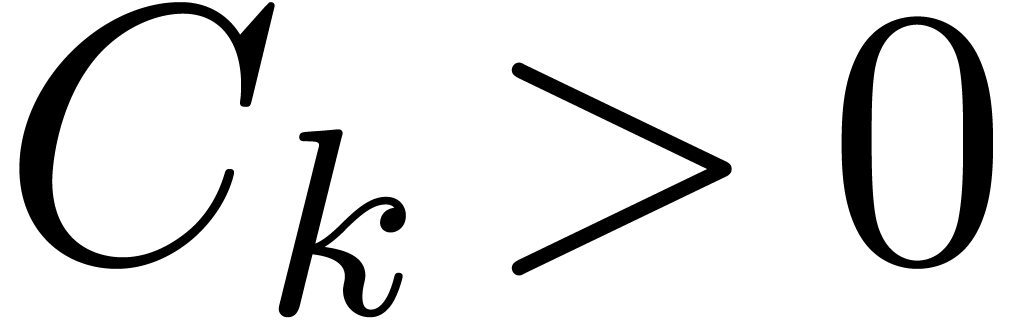 ,
this means that
,
this means that
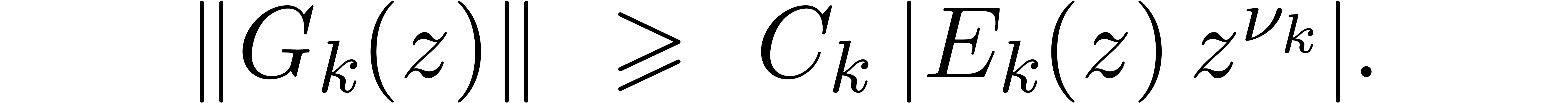 |
(10) |
There also exist constants 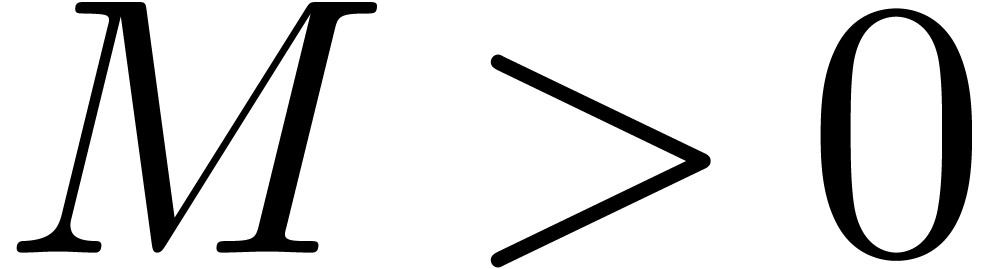 and
and 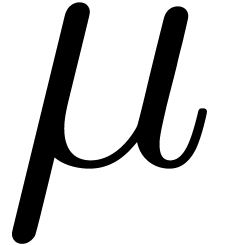 such that for all
such that for all 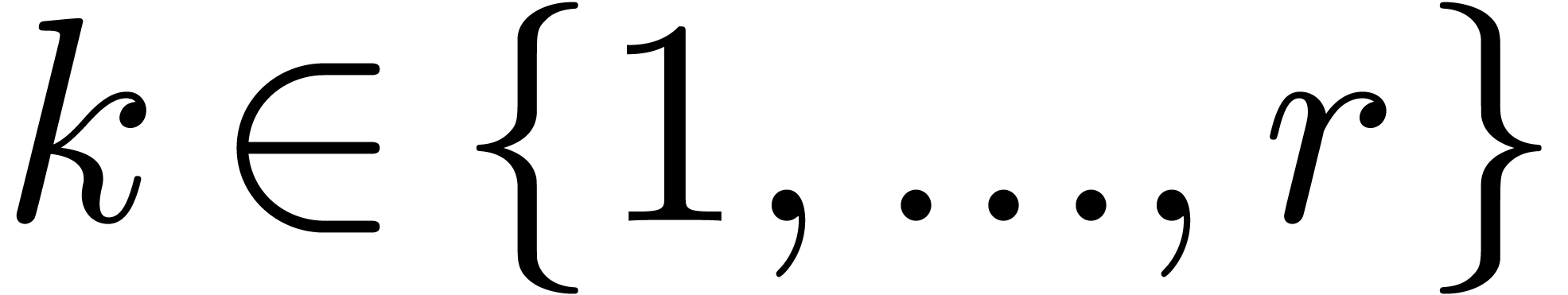 and
and  ,
,
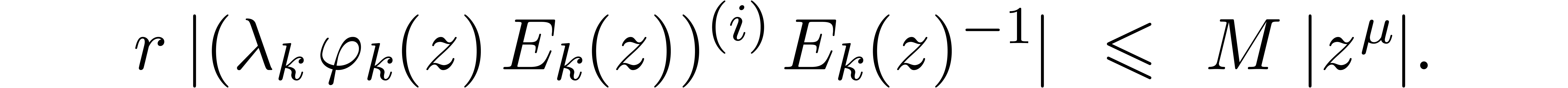 |
(11) |
Now we may partition  into
into  subsets
subsets  as follows. By induction over
as follows. By induction over  , we define
, we define 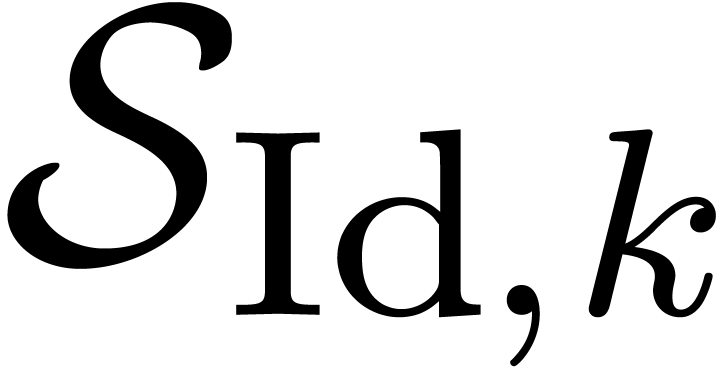 to be the subset of all
to be the subset of all 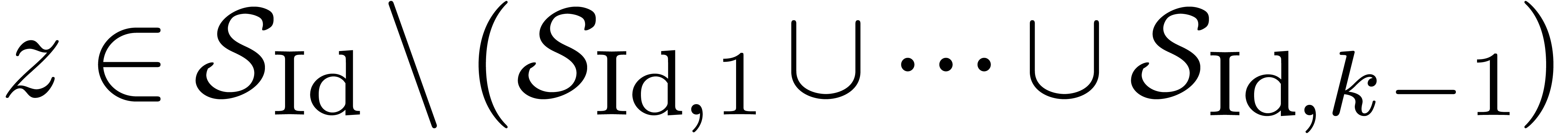 such that
such that
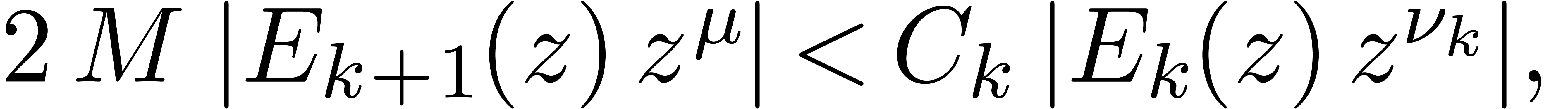
where we understand that 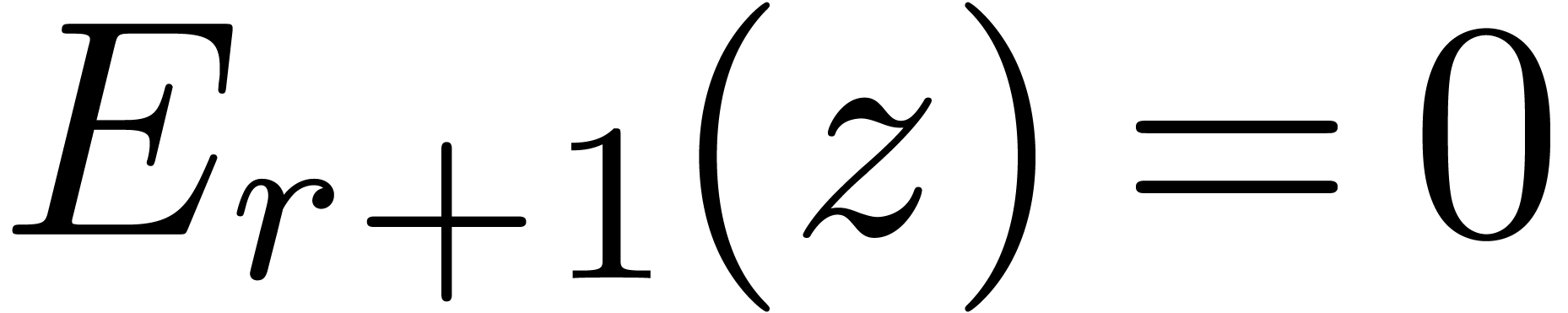 . If
. If
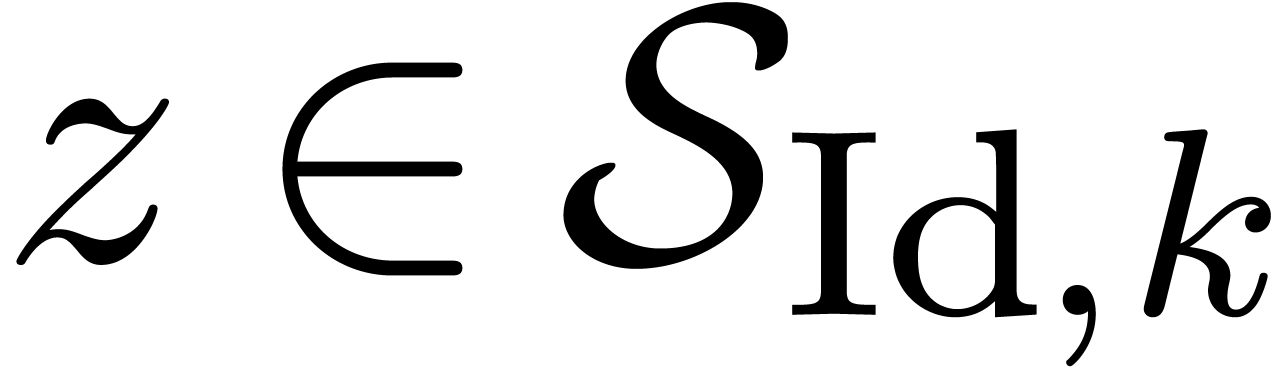 , then it follows that
, then it follows that
Still for 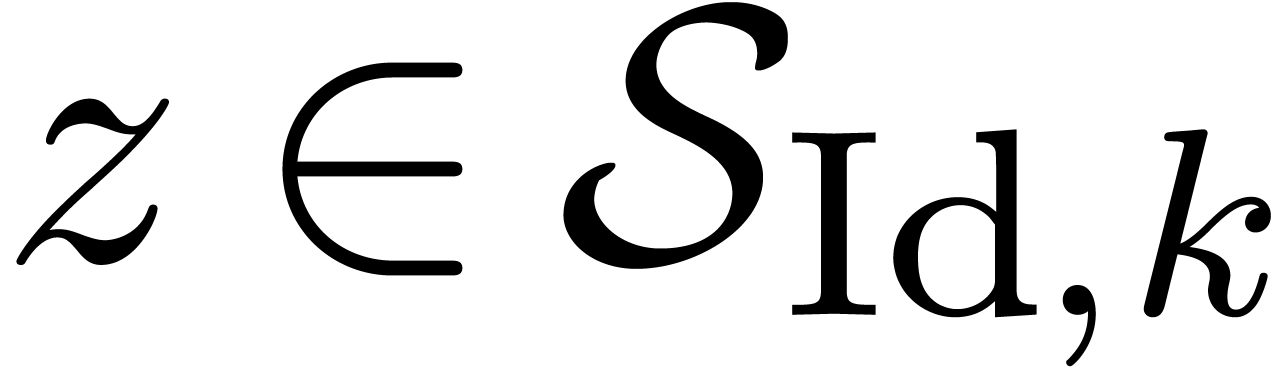 , the relation (10) also implies the existence of an
, the relation (10) also implies the existence of an 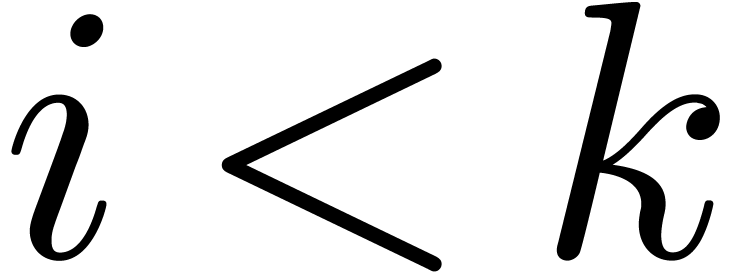 such that
such that

Using (11), it follows that
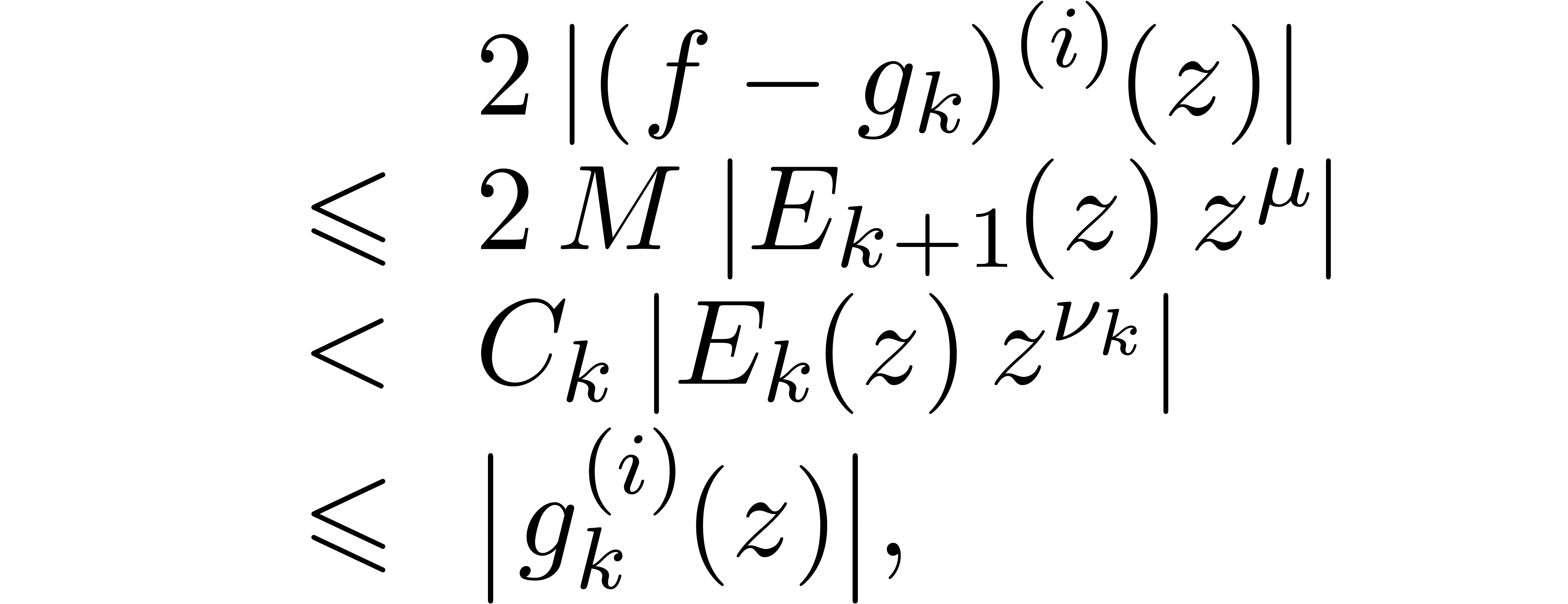
whence
We conclude that  for
for 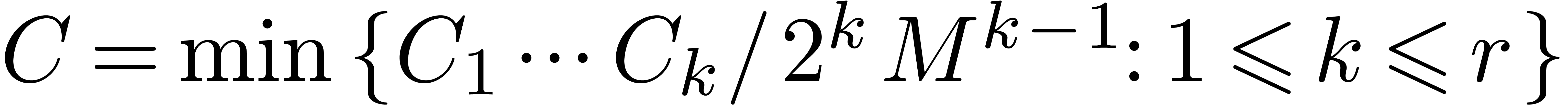 and
and
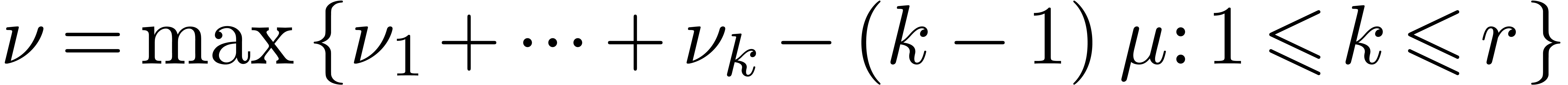 , using our assumption that
, using our assumption that
 .
.
Remark 12. It is plausible
that a bound for 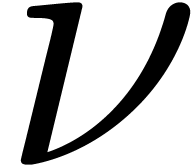 can be stated in terms of
can be stated in terms of 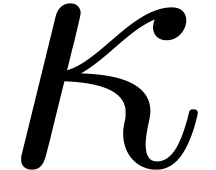 and the degrees of
and the degrees of  .
We have not pursued this line of thought any further since any constant
.
We have not pursued this line of thought any further since any constant
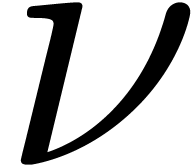 will do for our purposes.
will do for our purposes.
4.2.Existence of zeros on disks
Consider the power series expansion 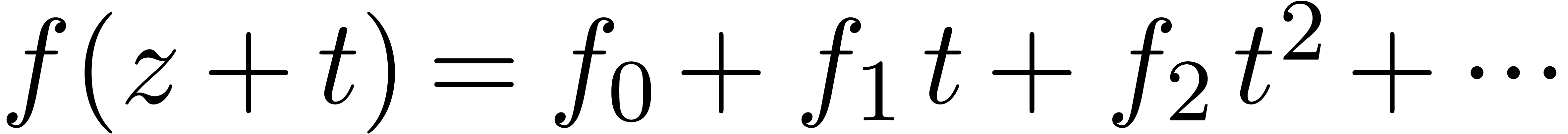 of
of  at
at  . For each
. For each
 , let
, let  be the vector with entries
be the vector with entries 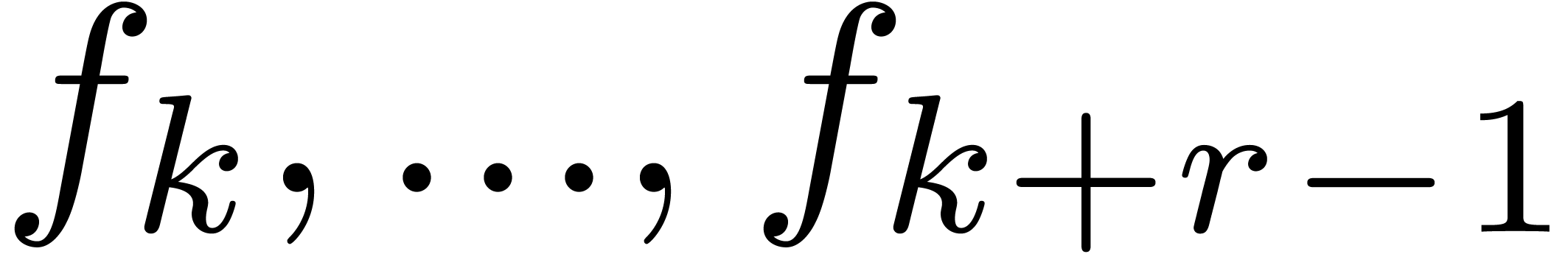 .
Theorem 11 provides us with a uniform lower bound for
.
Theorem 11 provides us with a uniform lower bound for  in terms of
in terms of  .
We also have the following upper bound for the remaining coefficients.
.
We also have the following upper bound for the remaining coefficients.
Proof. Since 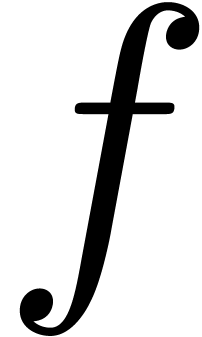 is
holonomic, there exists a matrix
is
holonomic, there exists a matrix 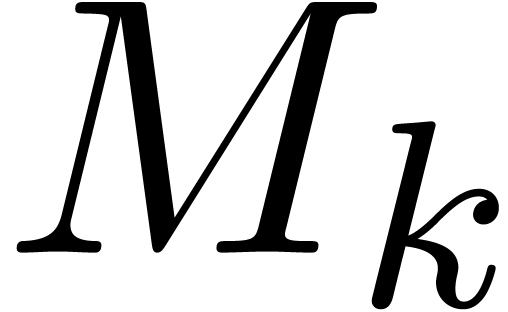 with
coefficients in
with
coefficients in 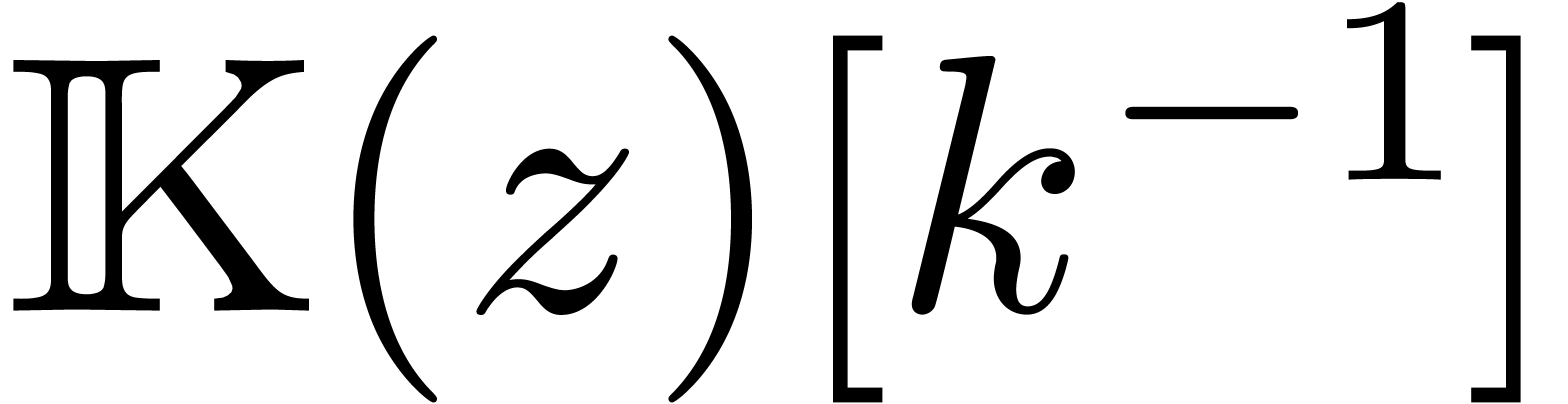 such that
such that
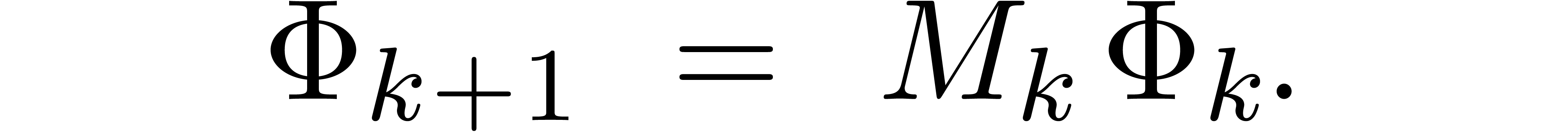
Consequently, there exists a uniform majorant equation for 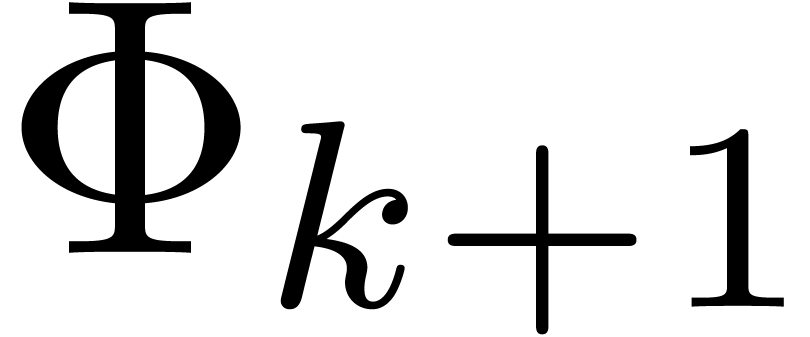 of the form
of the form
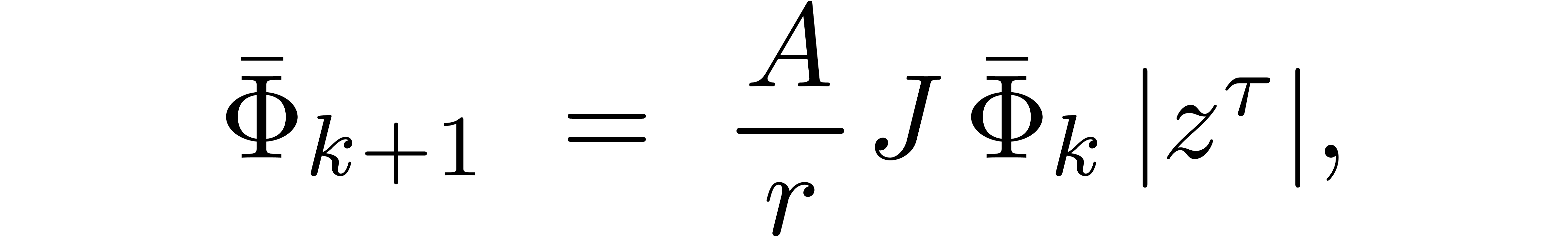
for suitable constants 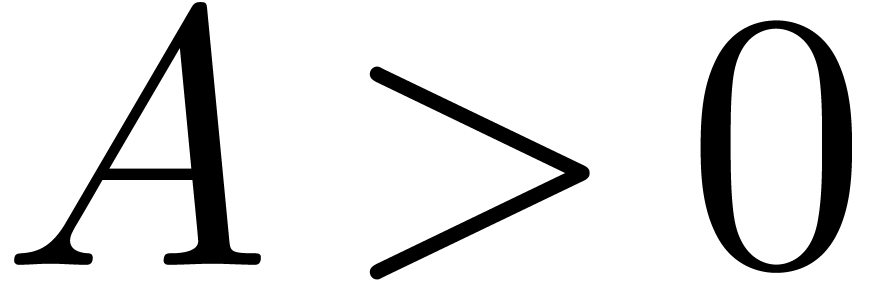 and
and  , and where
, and where  denotes the
denotes the
 matrix whose coefficients are all one. Taking
matrix whose coefficients are all one. Taking
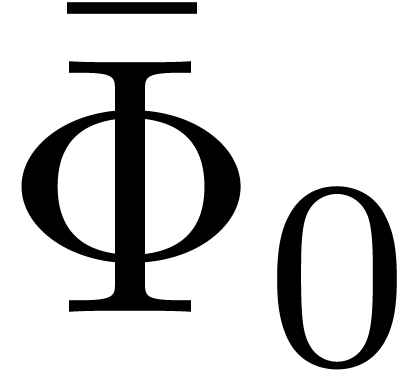 to be the vector with entries
to be the vector with entries  , it follows that
, it follows that 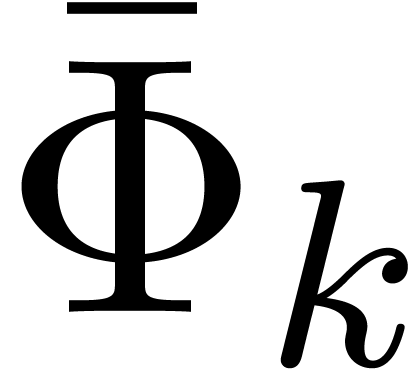 is
the vector with entries
is
the vector with entries  . By
construction
. By
construction 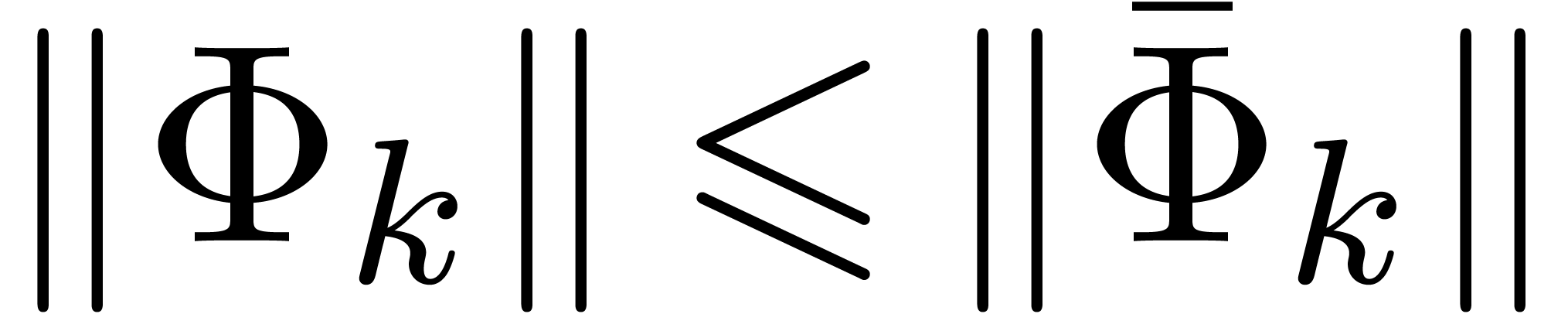 .
.
Proof. Let 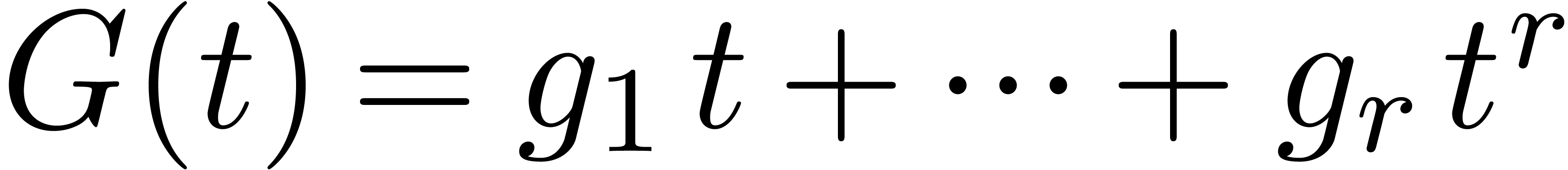 .
We may factor
.
We may factor 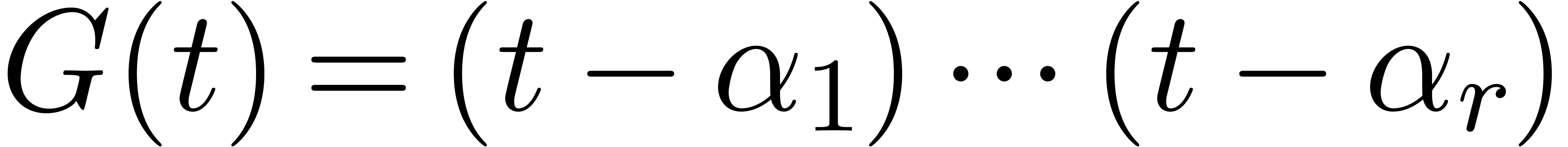 with
with 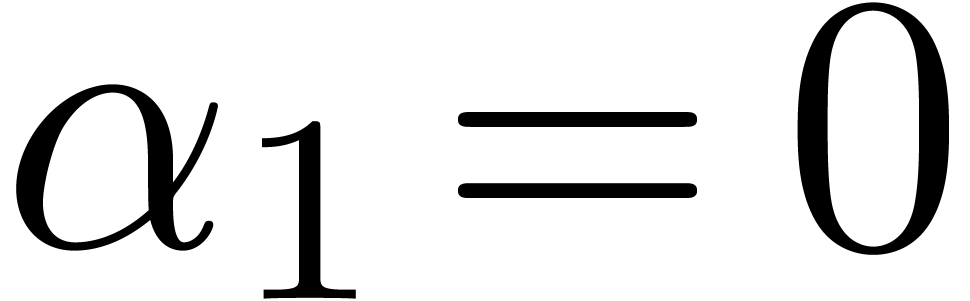 .
Let
.
Let 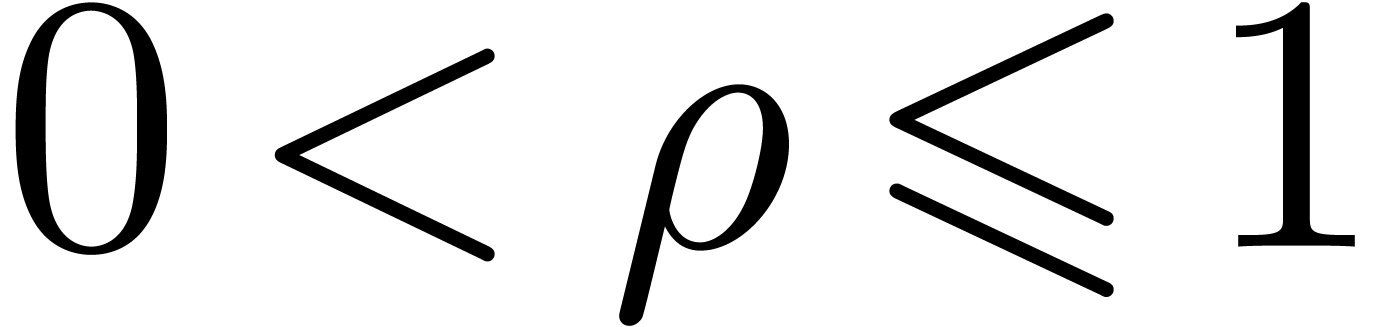 be such that
be such that 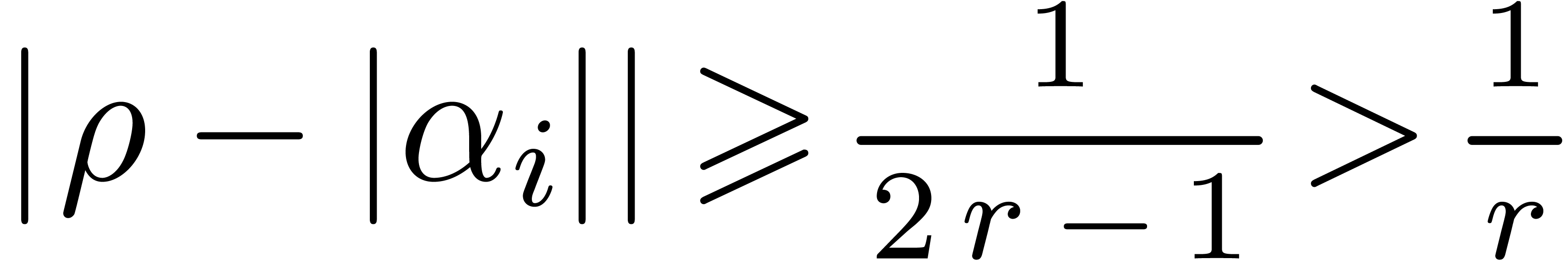 for all
for all
 . Then we have
. Then we have  for all
for all  with
with 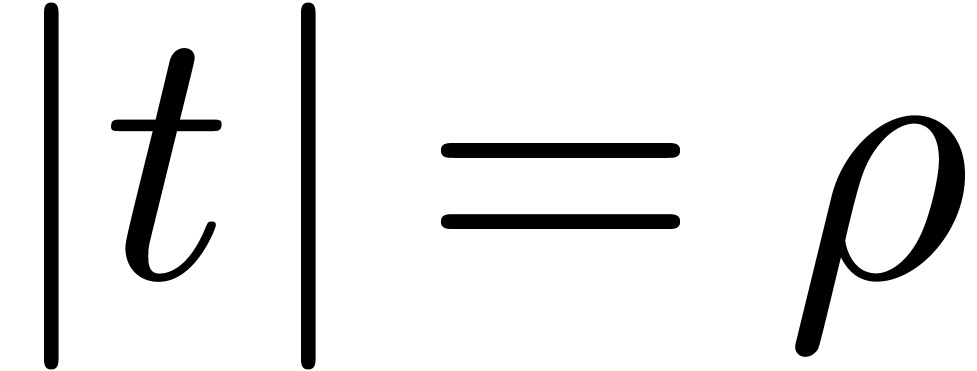 , whence
, whence 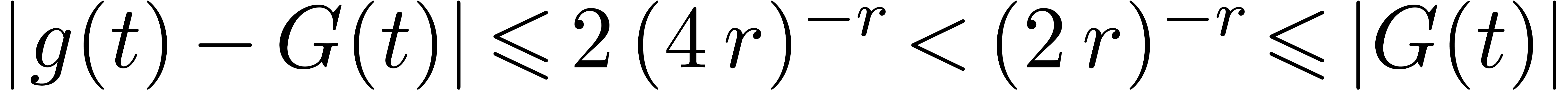 .
By Rouché's theorem, it follows that
.
By Rouché's theorem, it follows that  and
and
 admit the same number of zeros in
admit the same number of zeros in 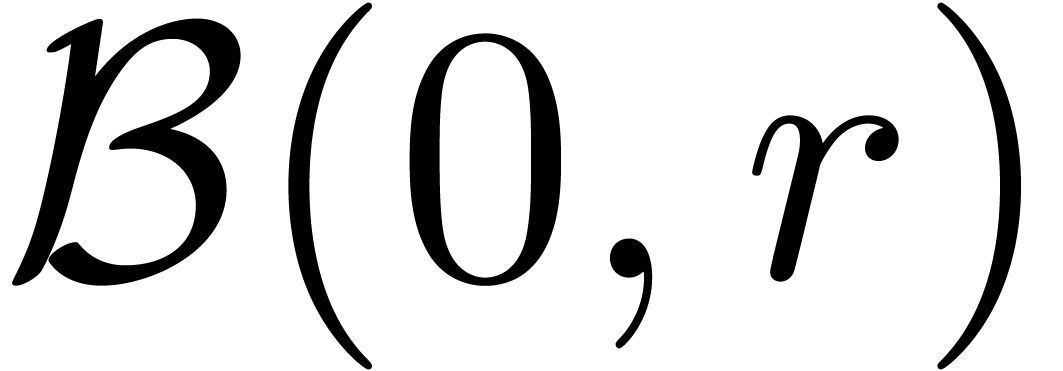 . Hence
. Hence  admits at least
one zero inside
admits at least
one zero inside  .
.
Proof. Let  and
and 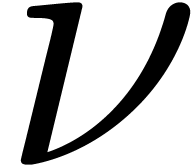 be as in Theorem 11 and
be as in Theorem 11 and 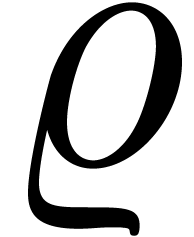 ,
,  and
and  as in Lemma 13. Take
as in Lemma 13. Take  .
We thus have
.
We thus have 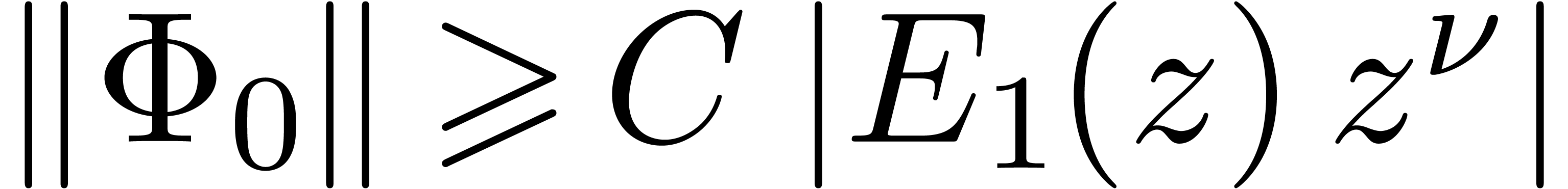 and
and 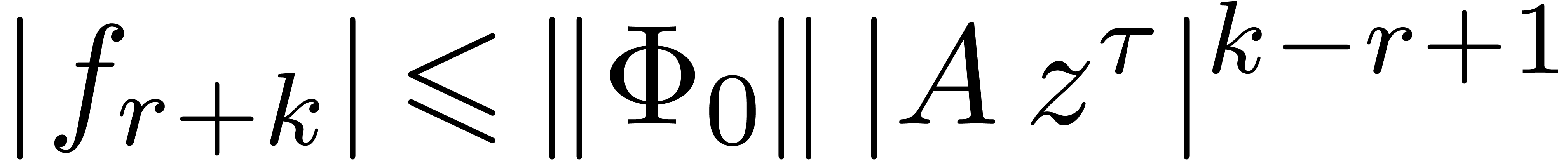 for all
for all
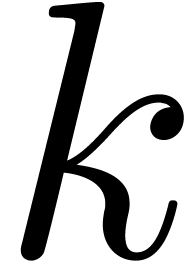 . Let
. Let 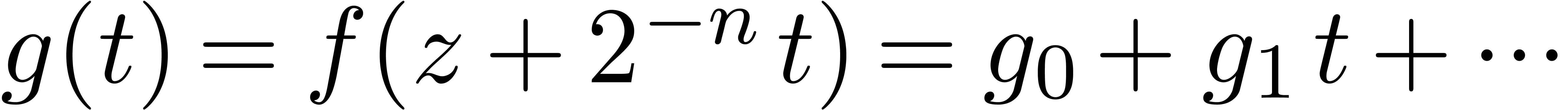 . Then it follows that
. Then it follows that 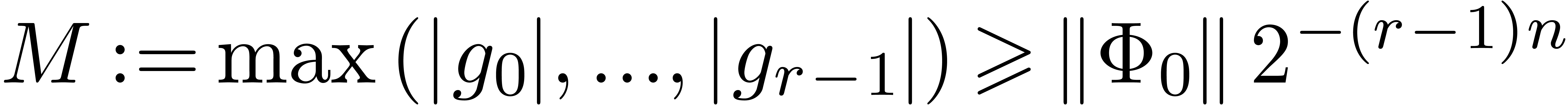 and
and
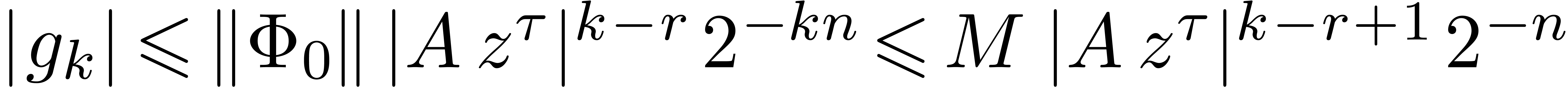 for
for 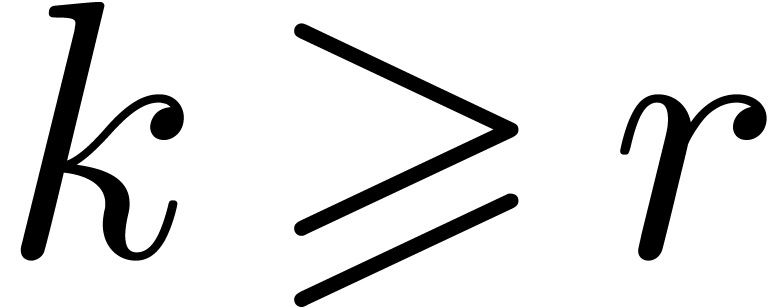 .
Assuming that
.
Assuming that 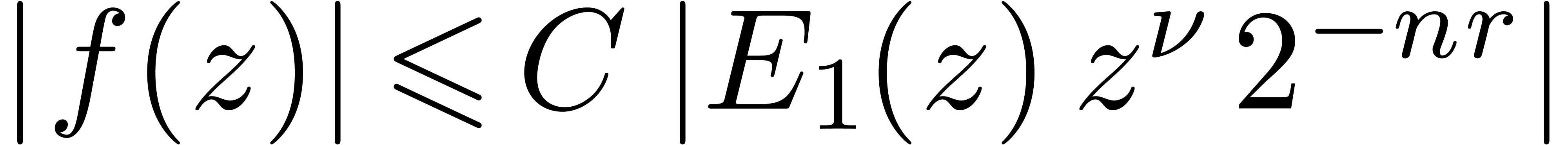 , we also
obtain
, we also
obtain 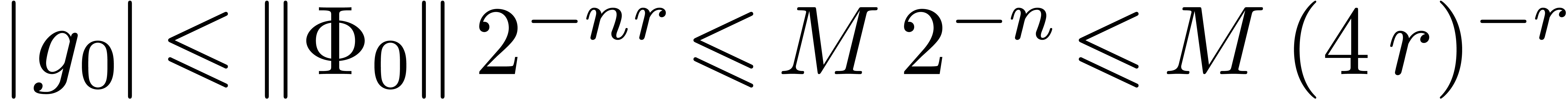 . Decreasing
. Decreasing 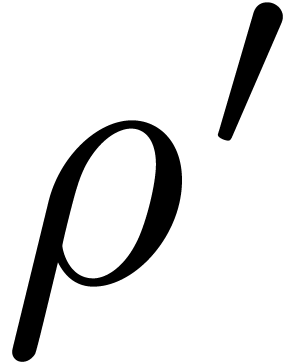 if necessary, we may arrange ourselves so that
if necessary, we may arrange ourselves so that 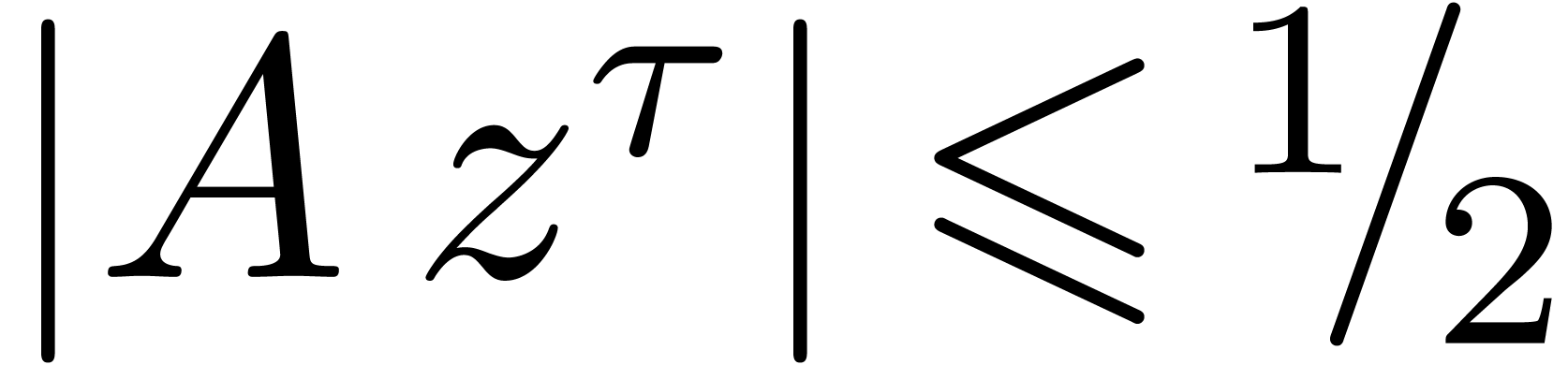 . Consequently,
. Consequently, 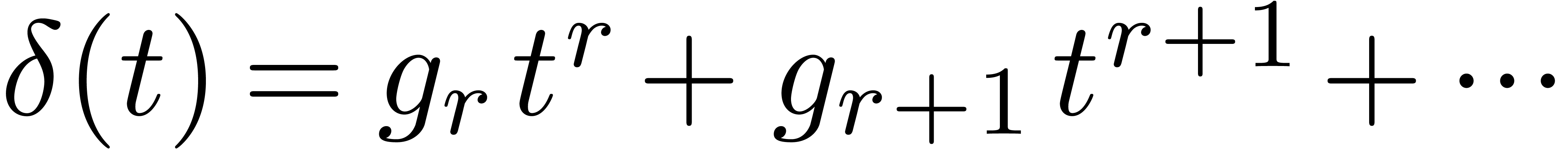 satisfies
satisfies 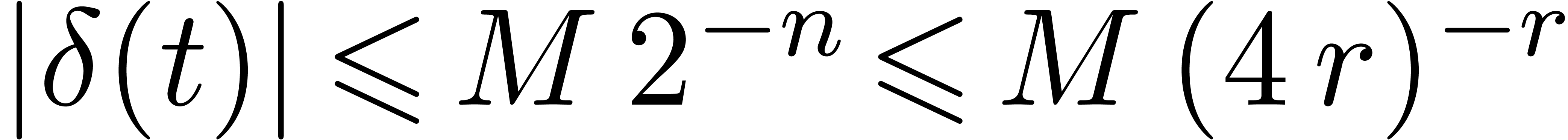 for
for 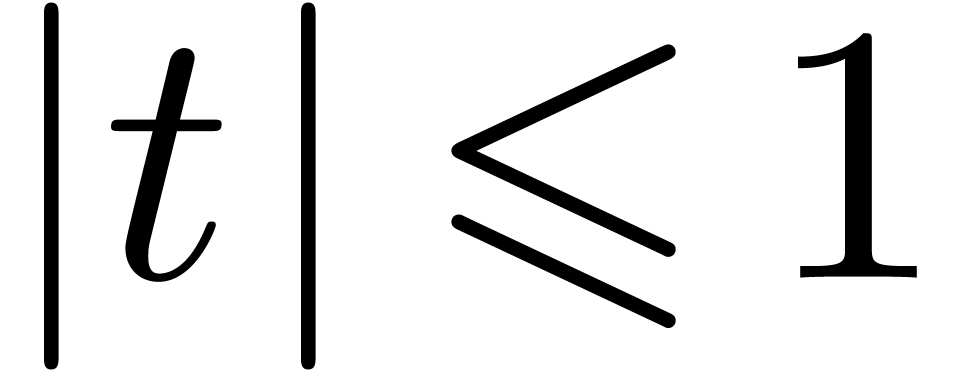 .
We now conclude by Lemma 14.
.
We now conclude by Lemma 14.
4.3.Global uniform complexity bounds
We are now in a position to prove our main theorem. We start with
proving the uniform bound on “super-admissible” sectors near
singularities. Here the sector 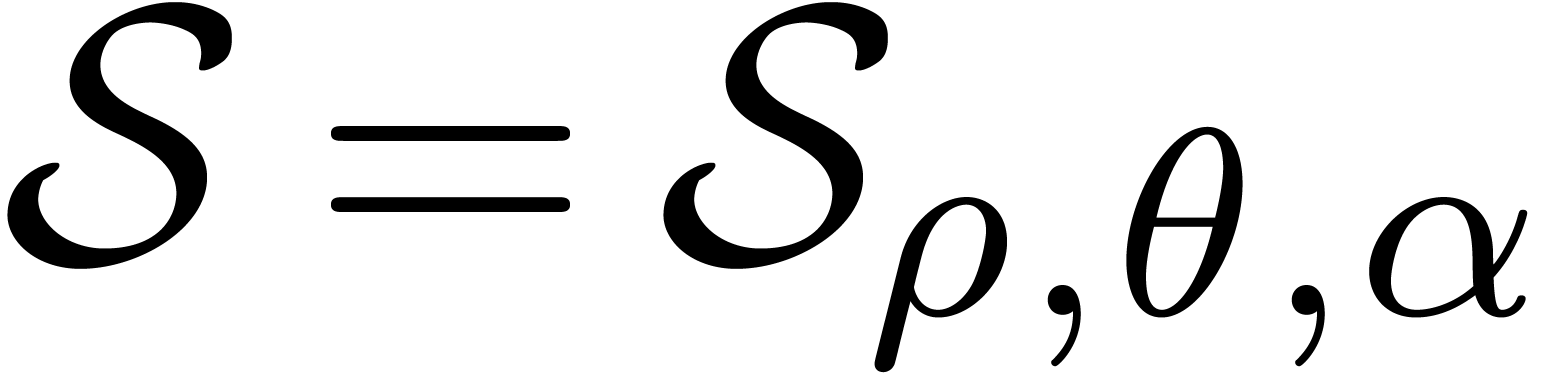 is said to be
super-admissible if we may take
is said to be
super-admissible if we may take 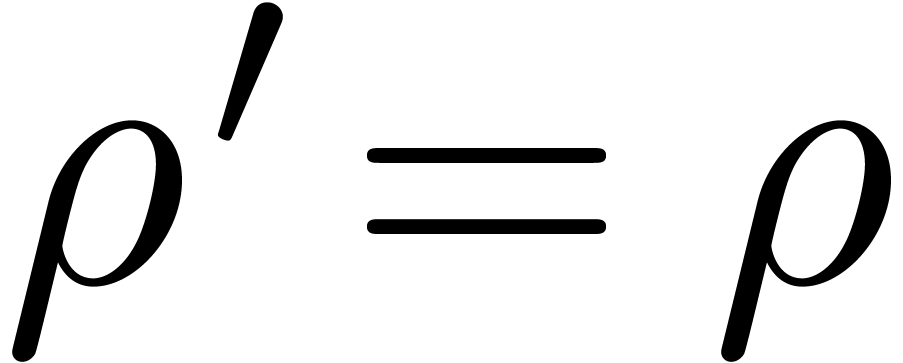 in
Lemma 15, as well as in the analoguous statement on
in
Lemma 15, as well as in the analoguous statement on 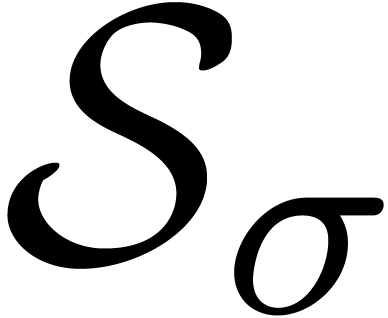 for each permutation
for each permutation  of
of  . Given
. Given  and
and
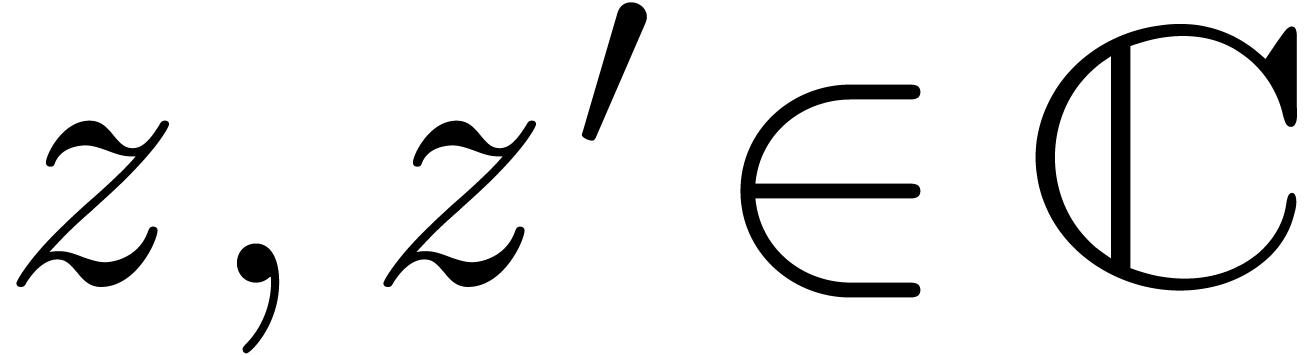 with
with 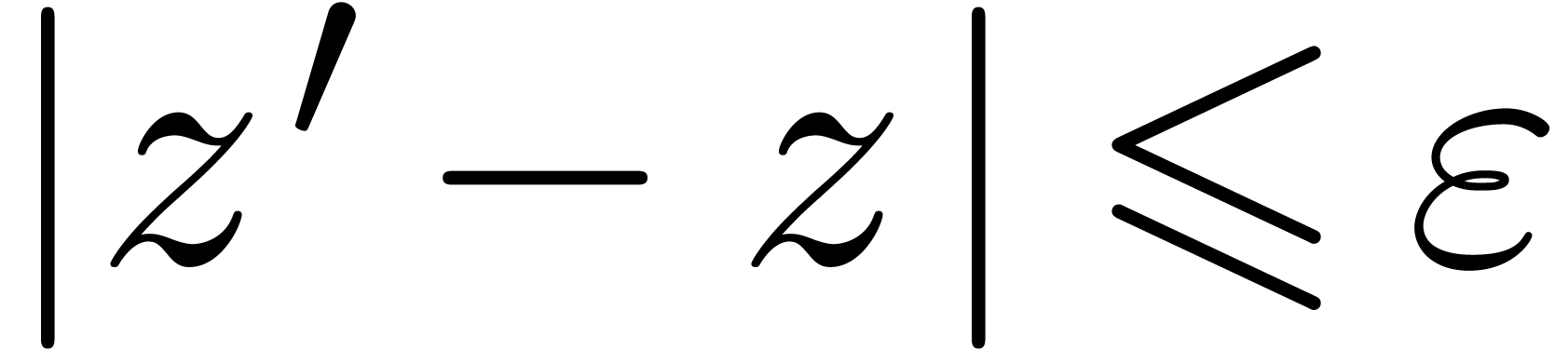 ,
we will say that
,
we will say that 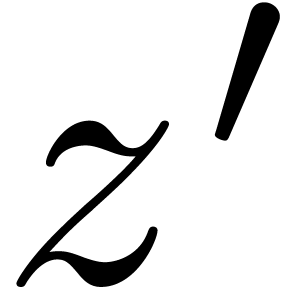 is an
is an  -approximation of
-approximation of  .
.
Proof. Let 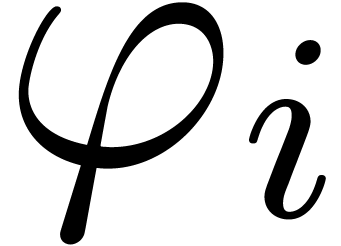 and
and 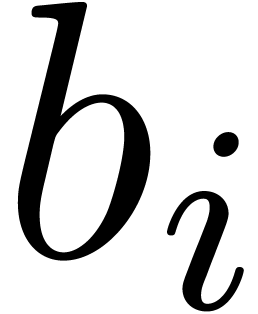 denote the accelero-sums of
denote the accelero-sums of 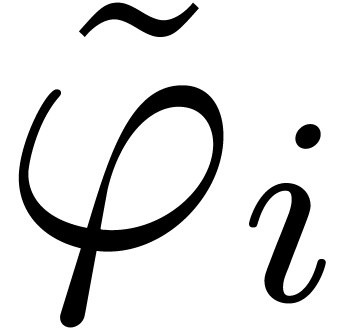 and
and
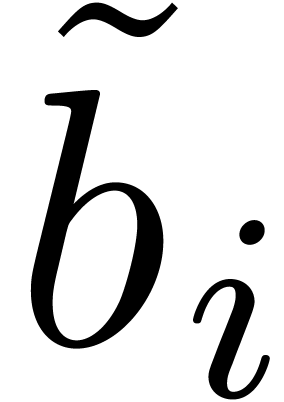 on
on  .
By Theorem 10, we may compute
.
By Theorem 10, we may compute  -approximations
of the evaluations
-approximations
of the evaluations 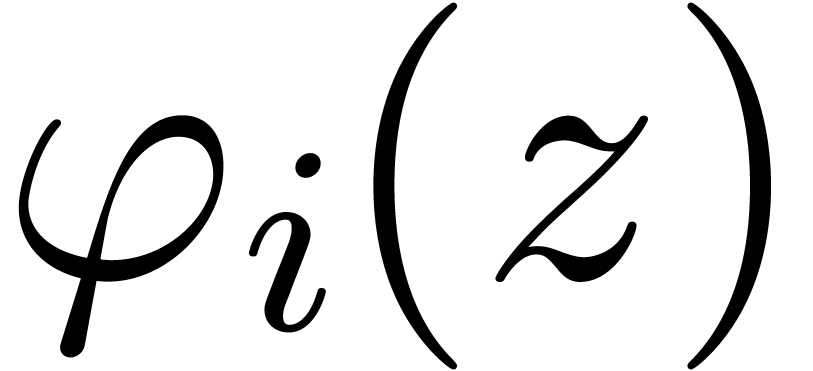 in time
in time 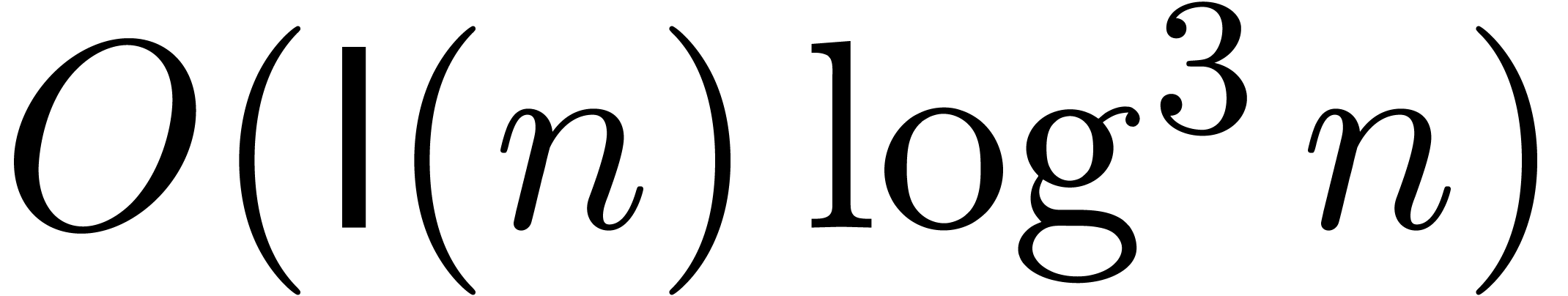 , uniformly for
, uniformly for 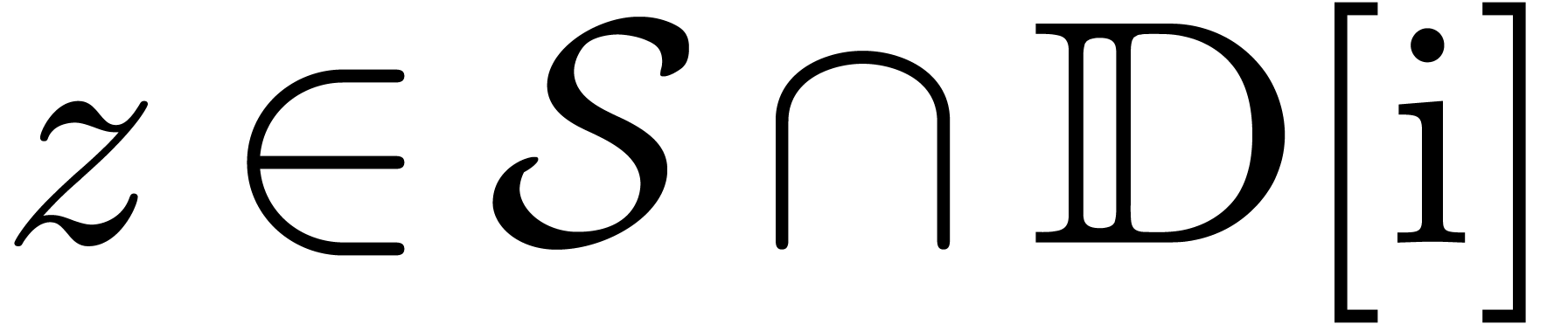 .
In particular, the constants
.
In particular, the constants  with
with 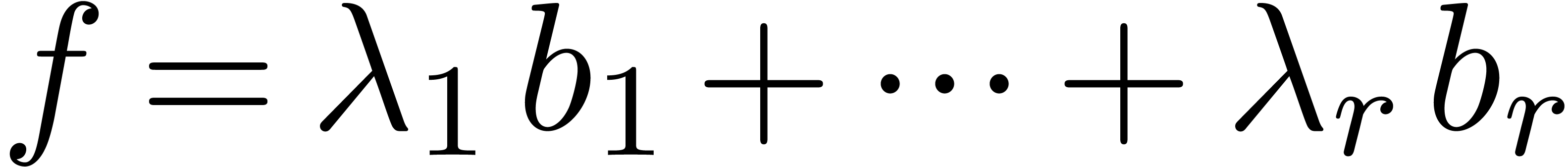 can be evaluated with a precision of
can be evaluated with a precision of 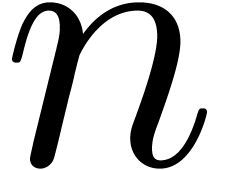 bits in time
bits in time 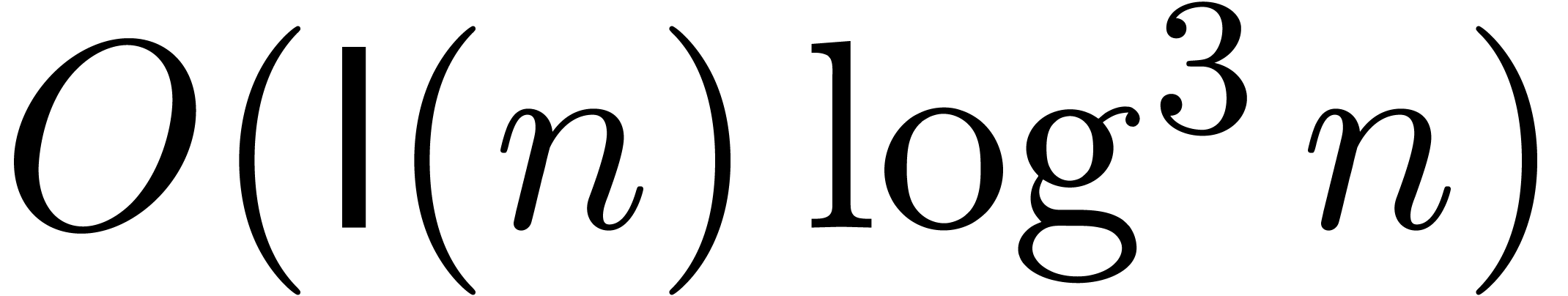 .
.
For a given 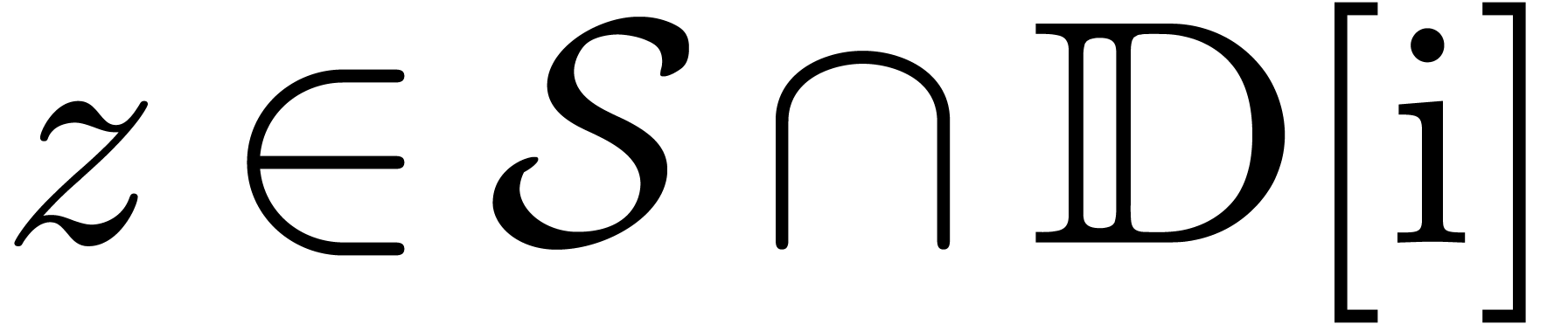 , we first
determine a permutation
, we first
determine a permutation  such that
such that 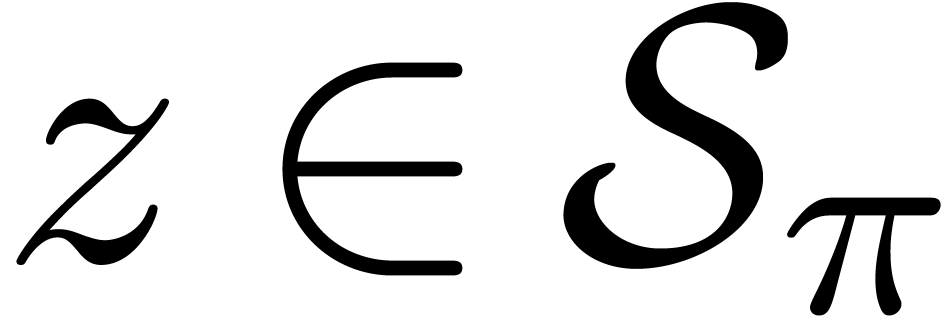 . Modulo a permutation of the basis elements
. Modulo a permutation of the basis elements
 , we may assume without loss
of generality that
, we may assume without loss
of generality that  . In order
to evaluate
. In order
to evaluate  at
at  ,
we perform tentative evaluations at increasing bit precisions
,
we perform tentative evaluations at increasing bit precisions  until the desired approximation with a relative precision
of
until the desired approximation with a relative precision
of  bits is found. For the tentative evaluations,
we proceed as follows:
bits is found. For the tentative evaluations,
we proceed as follows:
If the 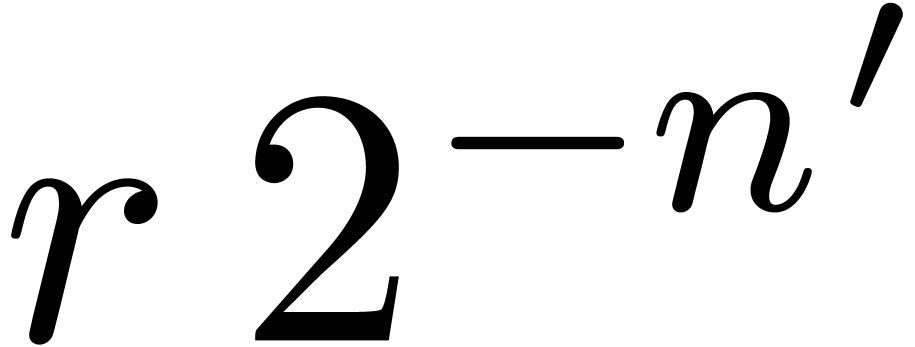 -approximation of
-approximation of 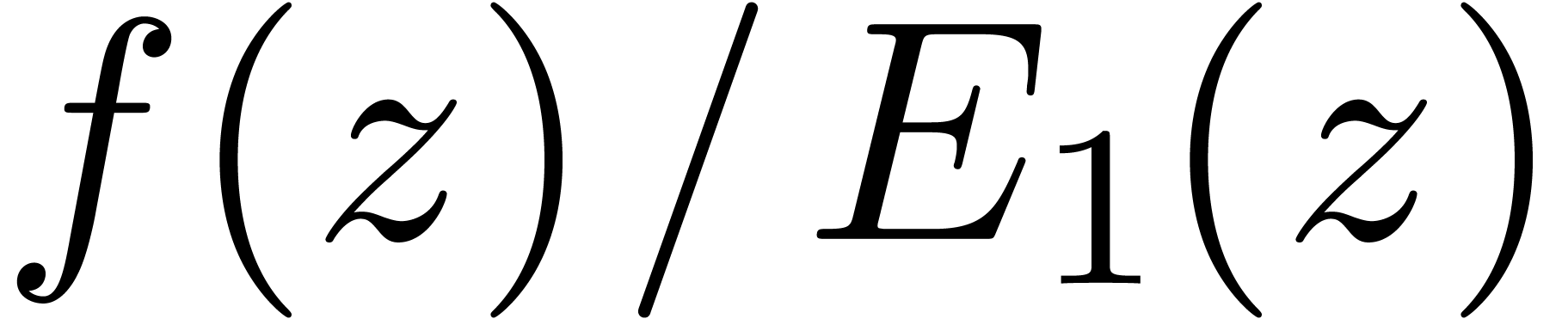 has a relative precision of at least
has a relative precision of at least  bits, then we obtain
bits, then we obtain 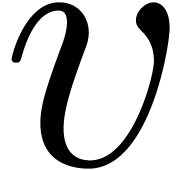 using one final
multiplication with a floating point approximation of
using one final
multiplication with a floating point approximation of 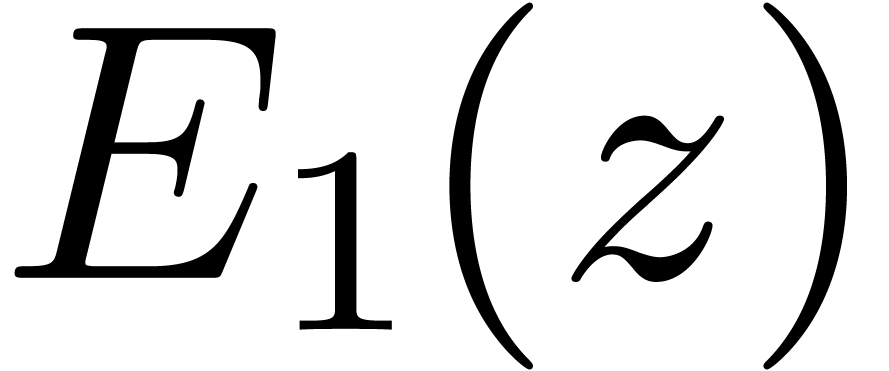 . If
. If 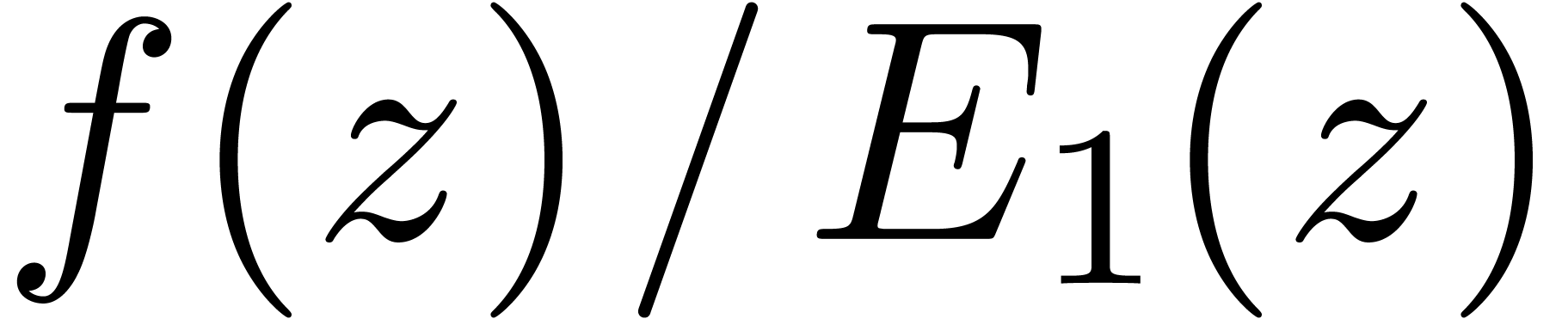 has a smaller
relative precision, then we set
has a smaller
relative precision, then we set 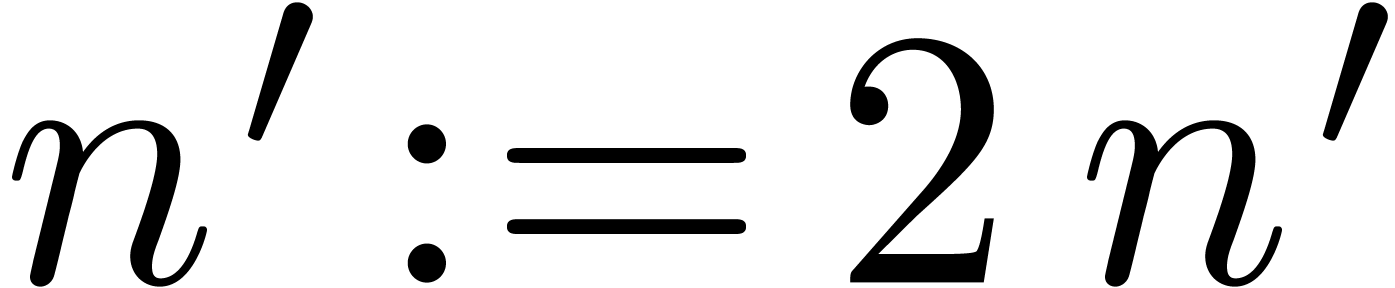 and keep
iterating.
and keep
iterating.
Now whenever both 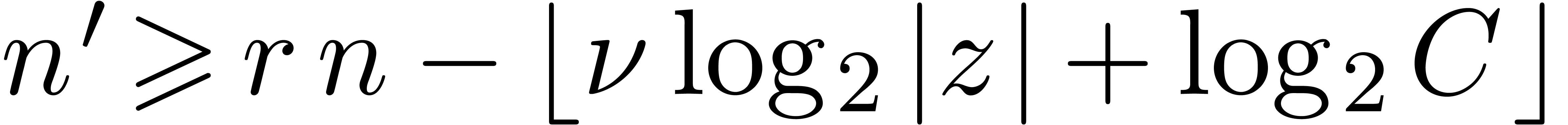 and
and 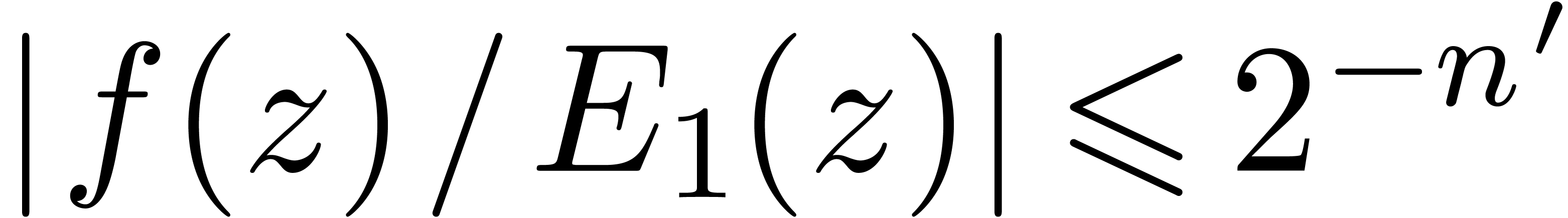 , Lemma 15 implies that
, Lemma 15 implies that 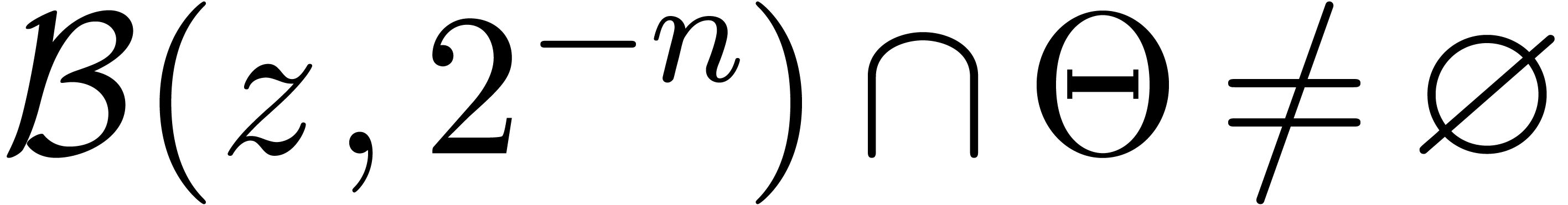 . In other words, the iteration will stop
whenever
. In other words, the iteration will stop
whenever  . Since
. Since 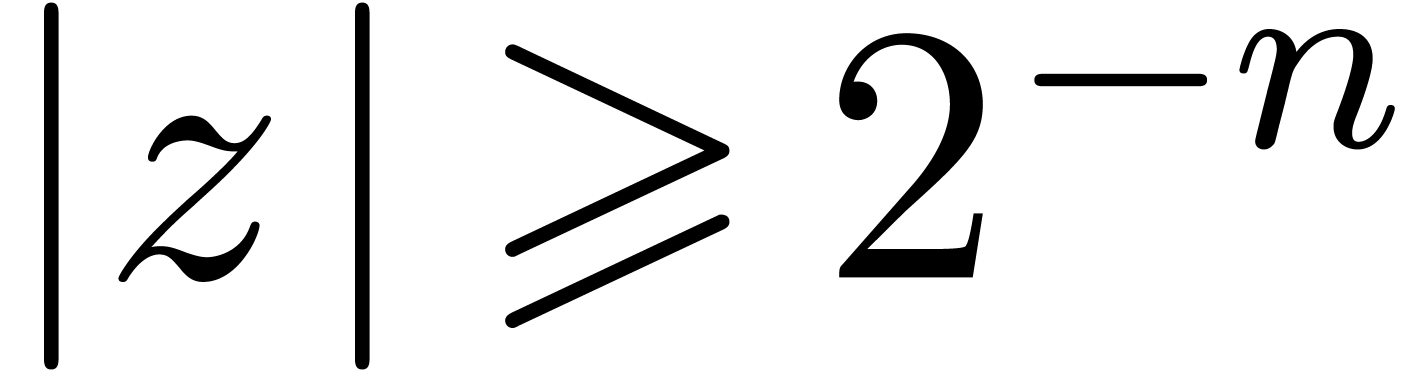 , this happens for
, this happens for 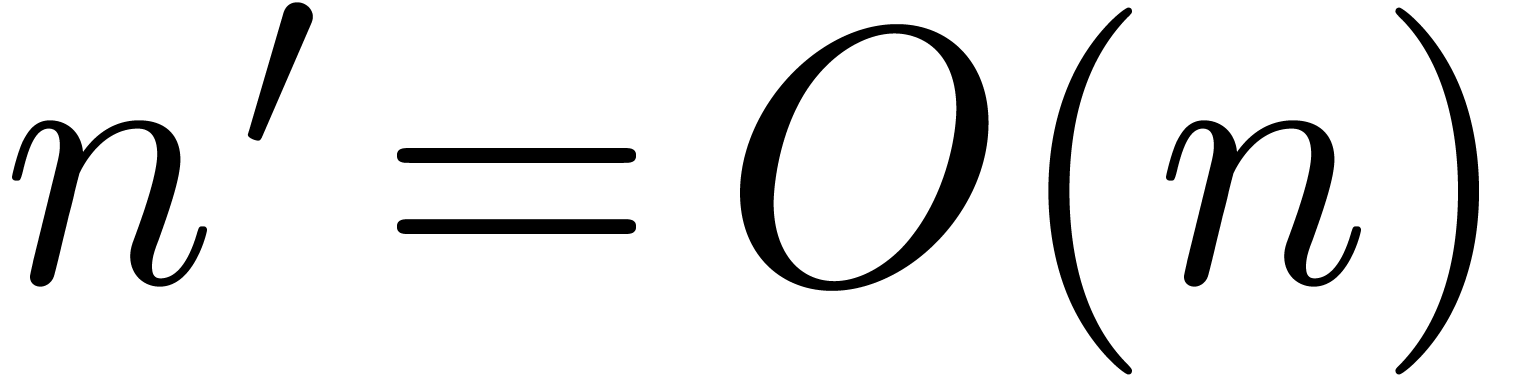 . Since we double
. Since we double 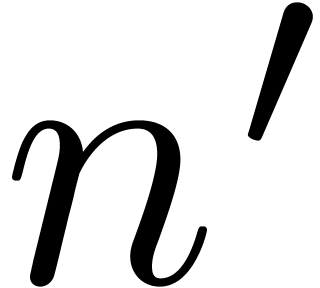 at every
iteration, the total running time is dominated by the running time of
the last tentative evaluation at precision
at every
iteration, the total running time is dominated by the running time of
the last tentative evaluation at precision 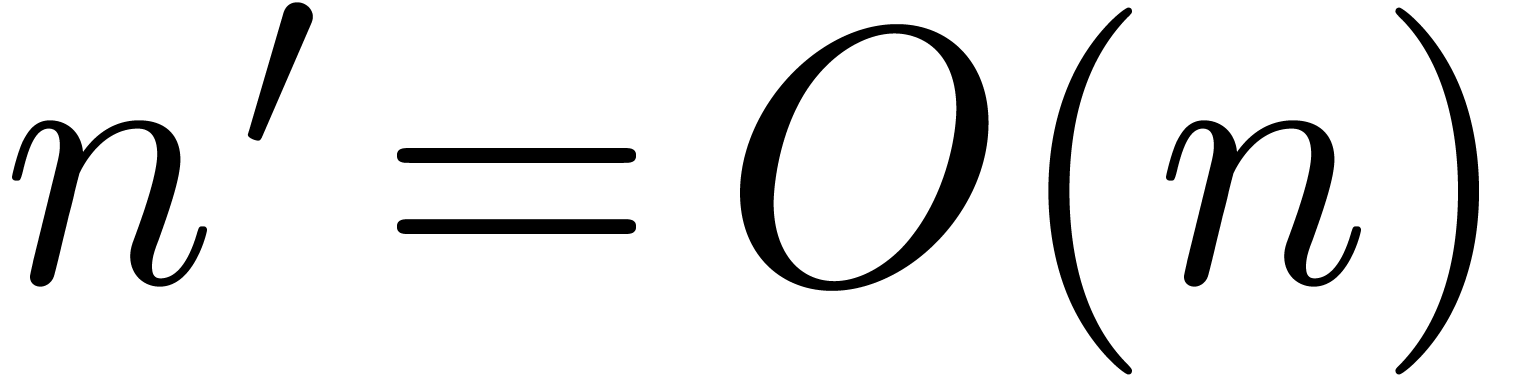 .
The most expensive step of this tentative evaluation is the computation
of the
.
The most expensive step of this tentative evaluation is the computation
of the 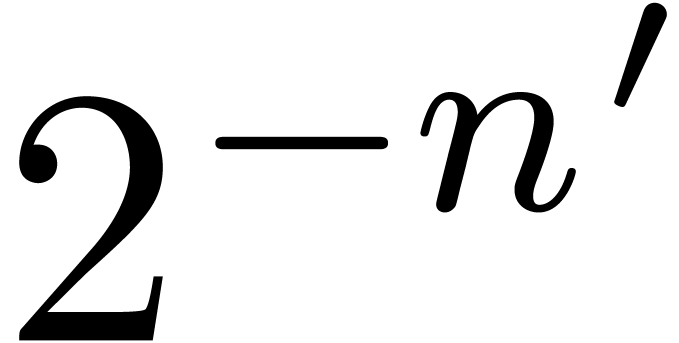 -approximations of
-approximations of
 . By Theorem 10,
this can be done in time
. By Theorem 10,
this can be done in time 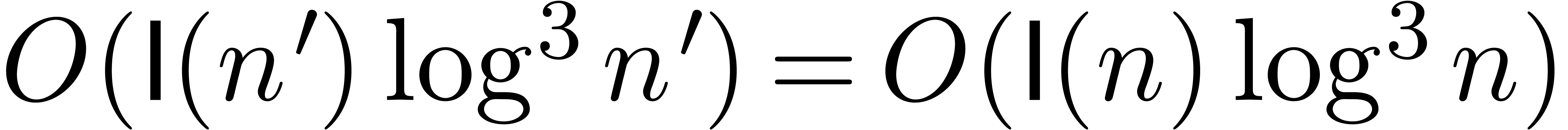 ,
uniformly in
,
uniformly in  .
.
Proof of Theorem 1. Let 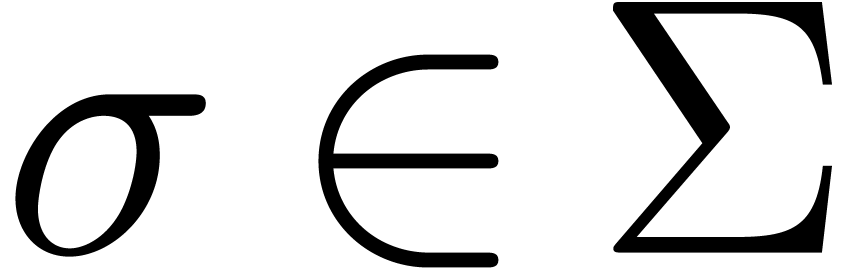 be one of the singularities and let
be one of the singularities and let  be an admissible ball cover in the neighbourhood of
be an admissible ball cover in the neighbourhood of  . For each admissible sector
. For each admissible sector 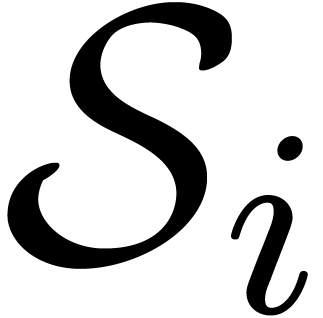 and each connected component
and each connected component 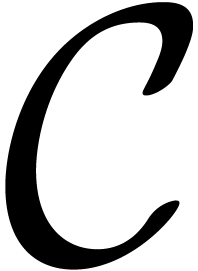 of
of  (there are at most two such connected components), we also arbitrarily
pick a point
(there are at most two such connected components), we also arbitrarily
pick a point 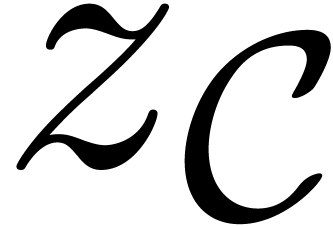 in
in 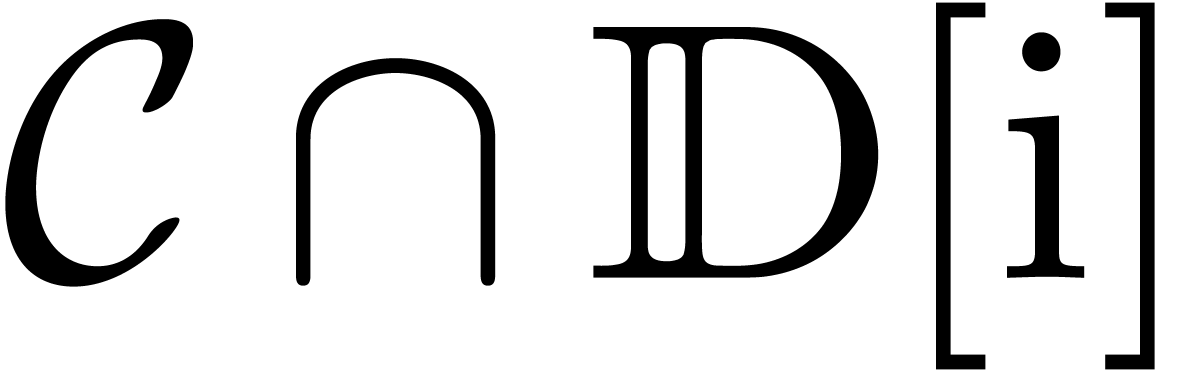 .
We may compute
.
We may compute  -approximations
for
-approximations
for 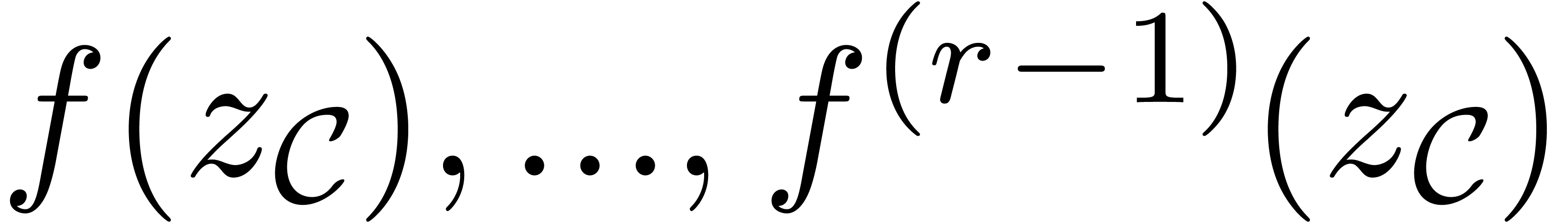 in time
in time 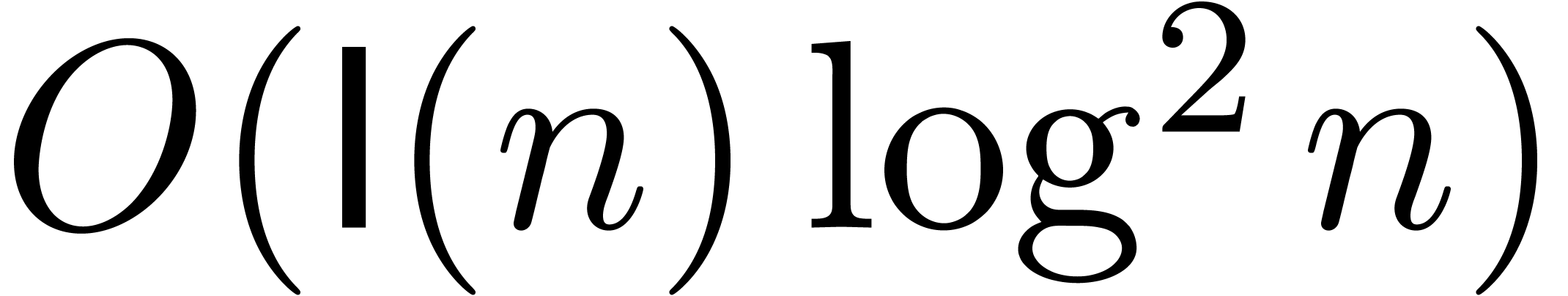 .
These values may be used as initial conditions for
.
These values may be used as initial conditions for 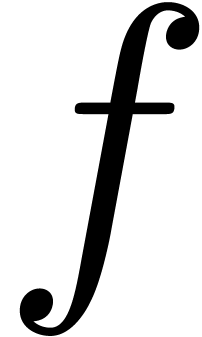 on
on 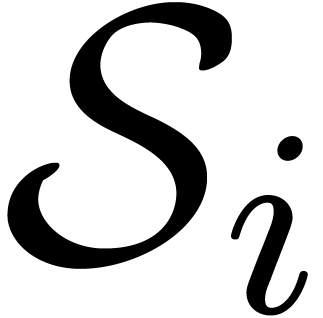 .
.
For  sufficiently close to
sufficiently close to  , we use the following algorithm for the evaluation
of
, we use the following algorithm for the evaluation
of  . Among the sectors
. Among the sectors 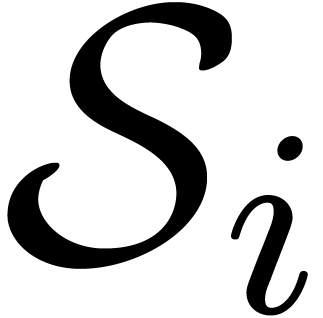 that contain
that contain  ,
we pick the one for which
,
we pick the one for which 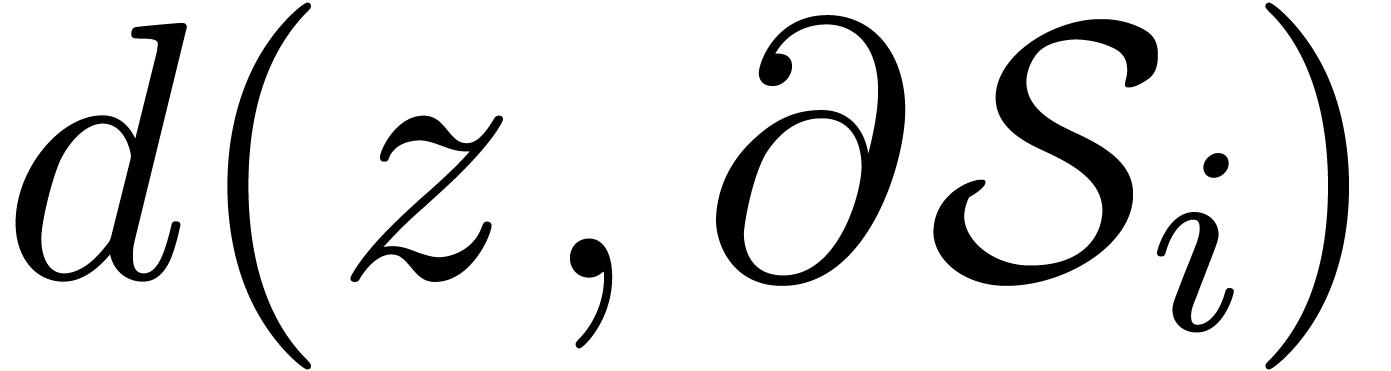 is maximal. In
particular,
is maximal. In
particular, 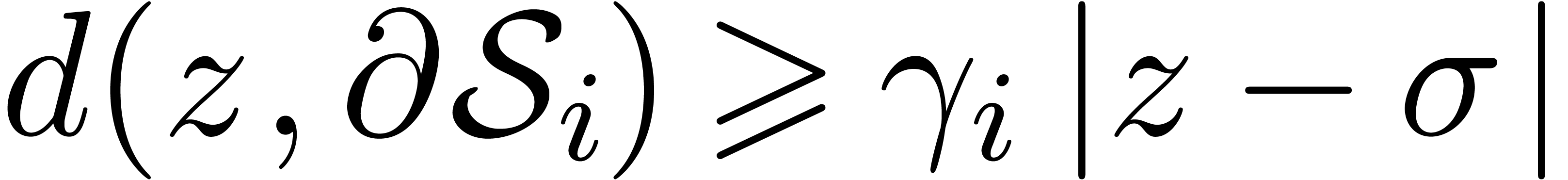 for some fixed constant
for some fixed constant 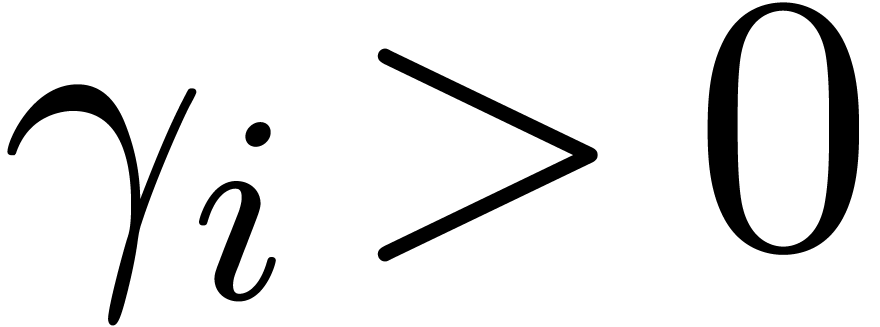 . Let
. Let 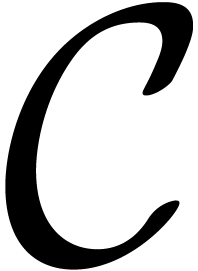 be the connected
component of of
be the connected
component of of  that contains
that contains  . We now evaluate
. We now evaluate 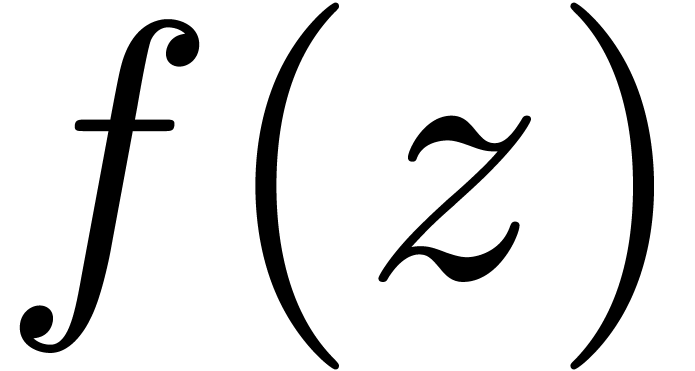 using
the algorithm from Lemma 16, by using the initial
conditions for
using
the algorithm from Lemma 16, by using the initial
conditions for  at
at  .
Applying Lemma 16 on each of the sectors
.
Applying Lemma 16 on each of the sectors  , we obtain a constant
, we obtain a constant  such that
such that  can be approximated with a relative
precision of
can be approximated with a relative
precision of  bits in time
bits in time 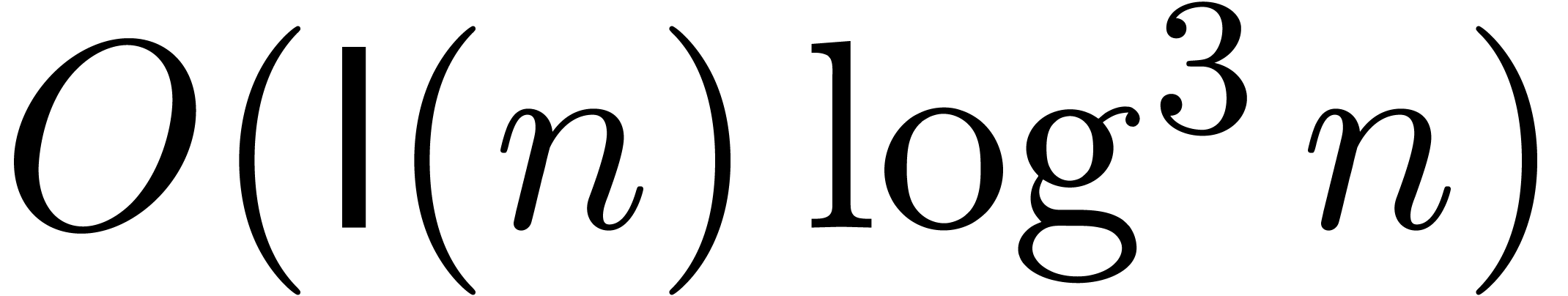 , uniformly in
, uniformly in 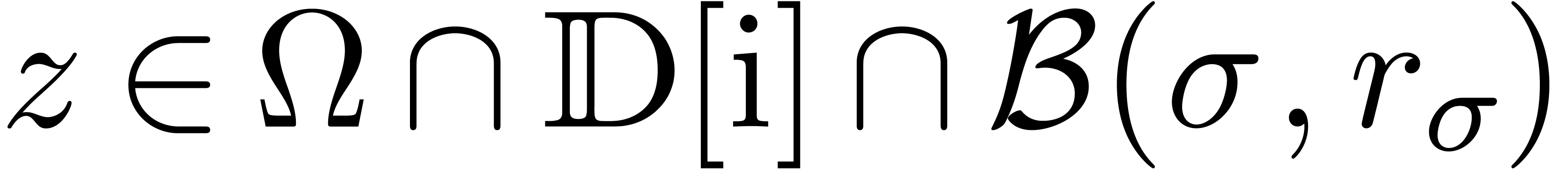 ,
provided that
,
provided that 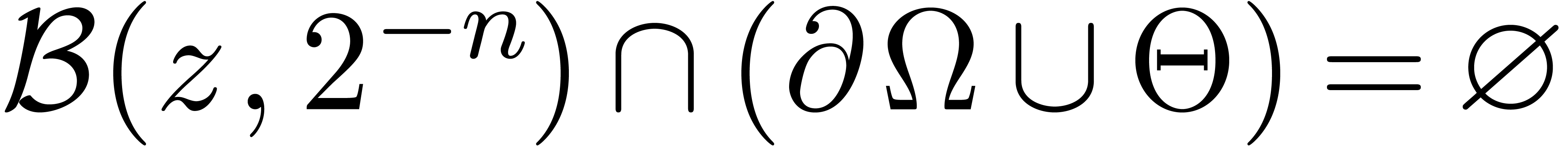 .
.
Considering the change of variables 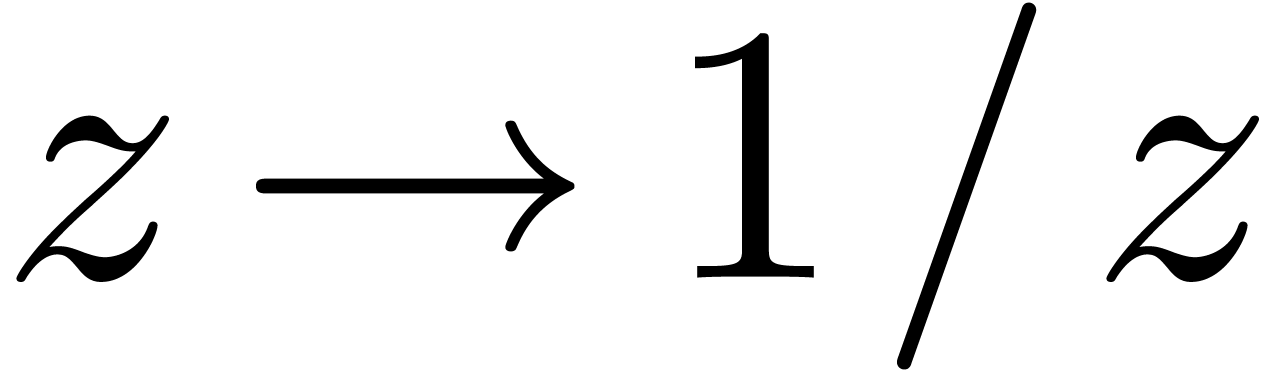 ,
one may prove in a similar way that, for some sufficiently large
,
one may prove in a similar way that, for some sufficiently large 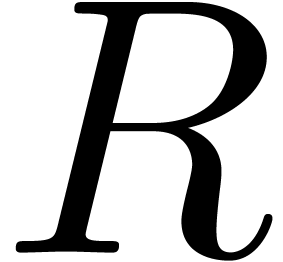 , we can approximate
, we can approximate 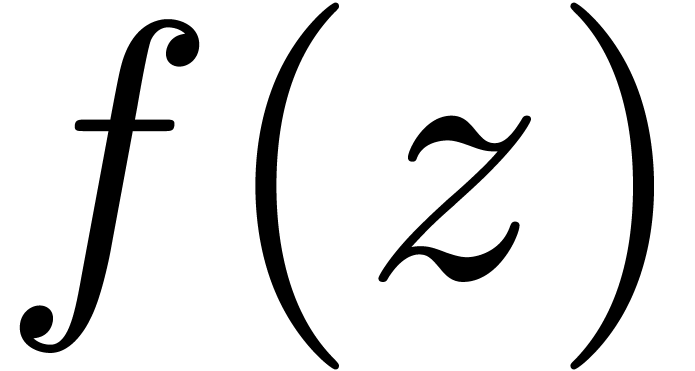 with a relative precision of
with a relative precision of 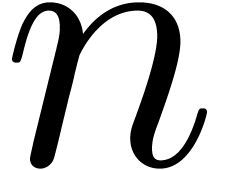 bits
in time
bits
in time 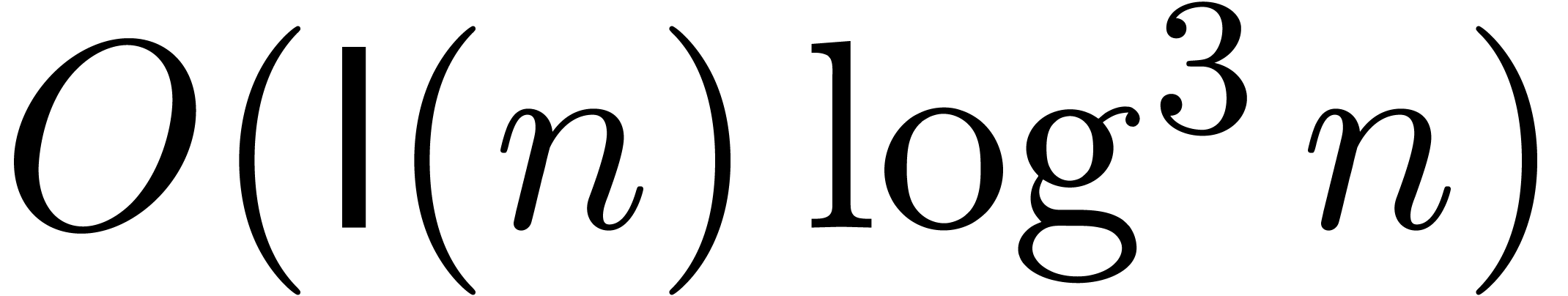 , uniformly in
, uniformly in  , provided that
, provided that 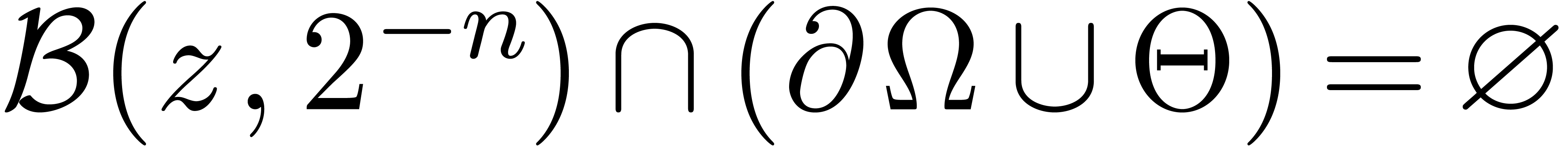 .
.
Let 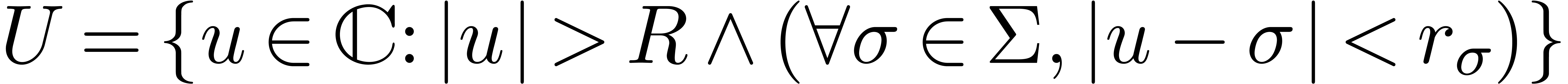 . The complement
. The complement 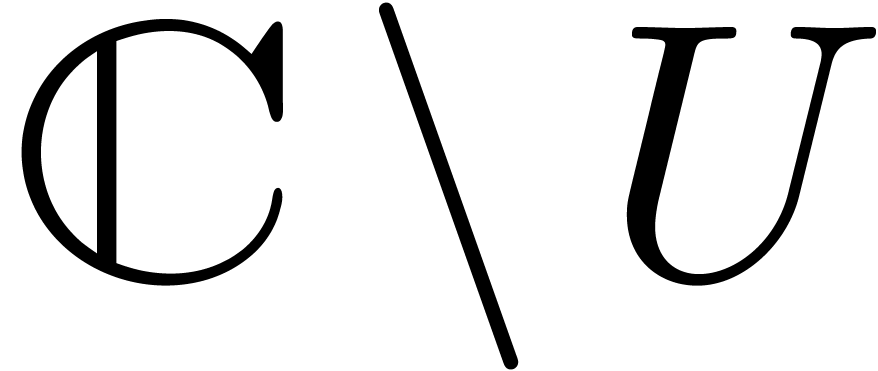 is a compact set that contains none of the
singularities of
is a compact set that contains none of the
singularities of 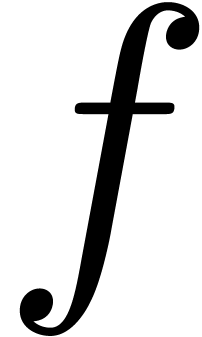 . Using the
complexity bounds from [7], it follows that a
. Using the
complexity bounds from [7], it follows that a  -approximation for
-approximation for 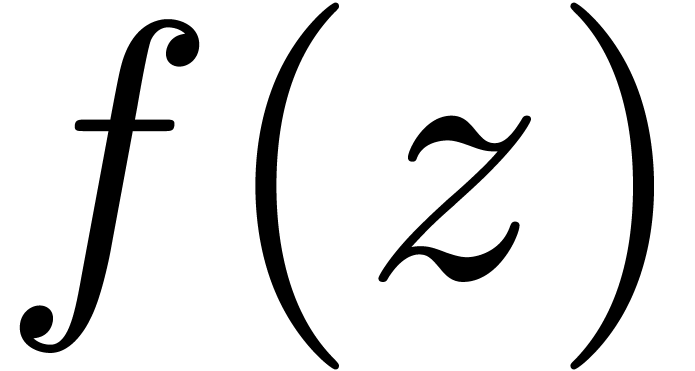 can
be computed in time
can
be computed in time 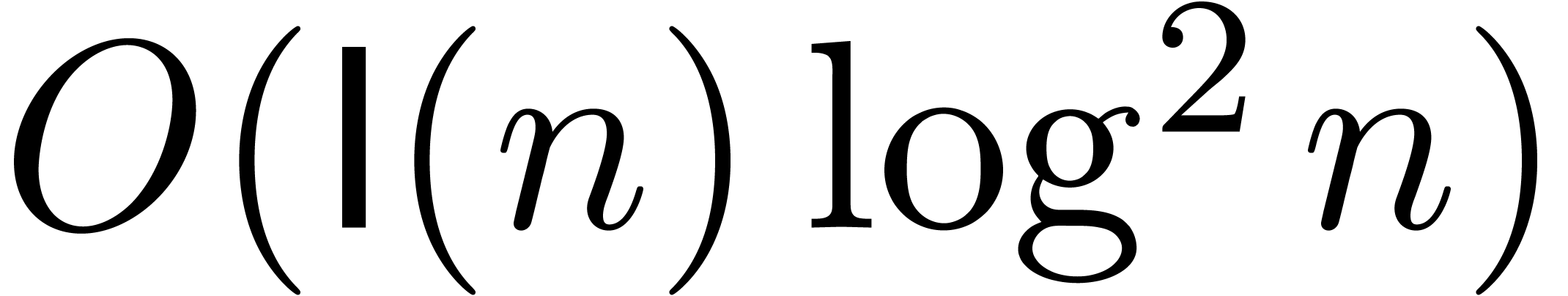 ,
uniformly in
,
uniformly in 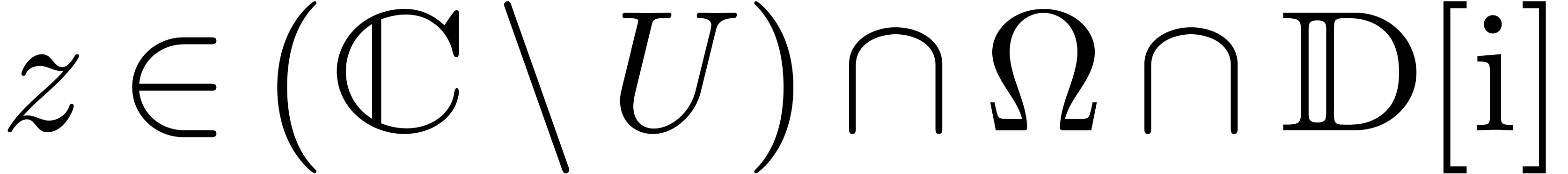 . Now
. Now 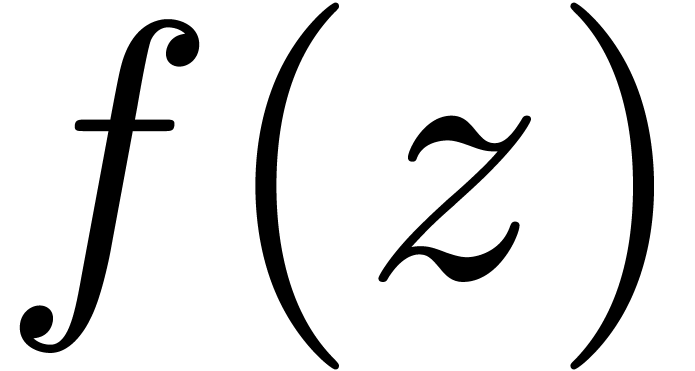 admits only a finite number of zeros on
admits only a finite number of zeros on 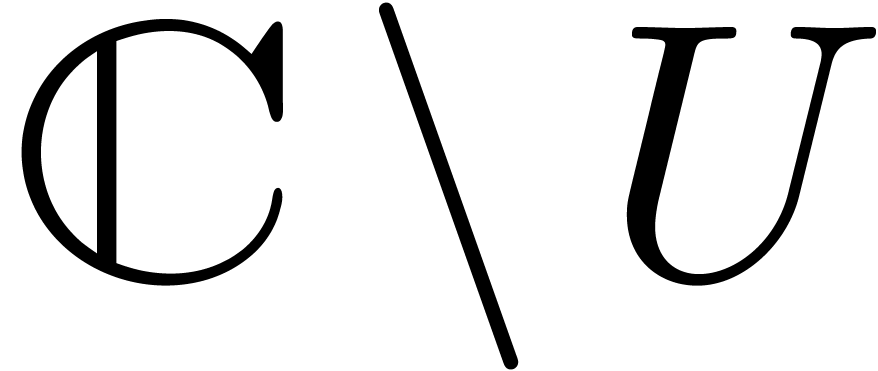 and each zero has multiplicity at most
and each zero has multiplicity at most  .
Considering the local power series expansions around any of these zeros
.
Considering the local power series expansions around any of these zeros
 , we observe that
, we observe that 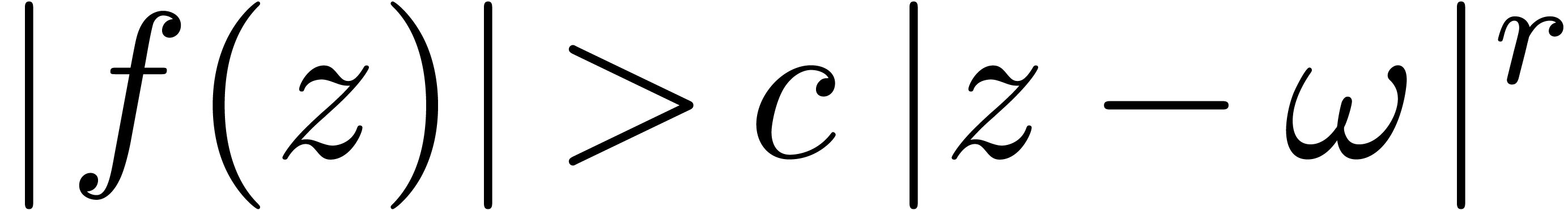 for some computable contant
for some computable contant  and
and
 sufficiently close to
sufficiently close to  . Provided that
. Provided that 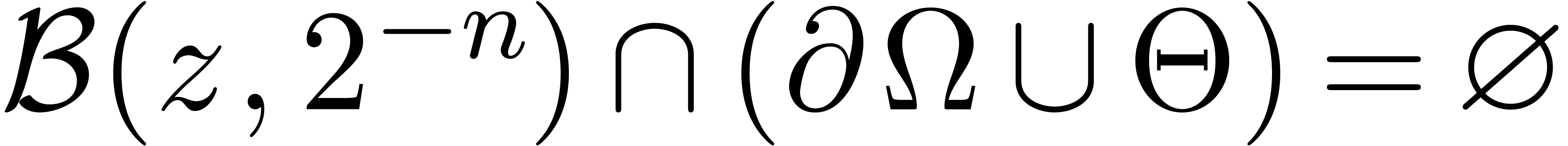 ,
this implies that we can also compute an approximation for
,
this implies that we can also compute an approximation for 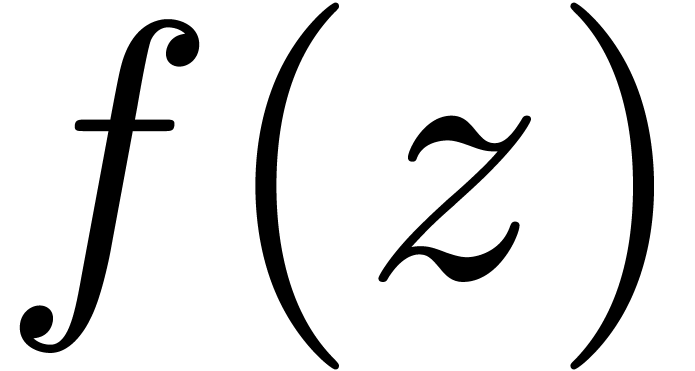 with a relative precision of
with a relative precision of 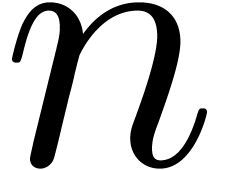 bits
in time
bits
in time  , uniformly for
, uniformly for  .
.
5.Further thoughts and challenges
There are several directions in which the results of this paper can be
extended or made more precise.
More general constants
In our main Theorem
1, we assumed that

is the field of algebraic numbers. Following the Chudnovsky's [
3], and using the baby-step-giant-step technique, one may
replace

with more general effective subfield
of

whose elements can be approximated fast.
More precisely, if for any constants

in

we can compute a
 -approximation
-approximation
of

in time
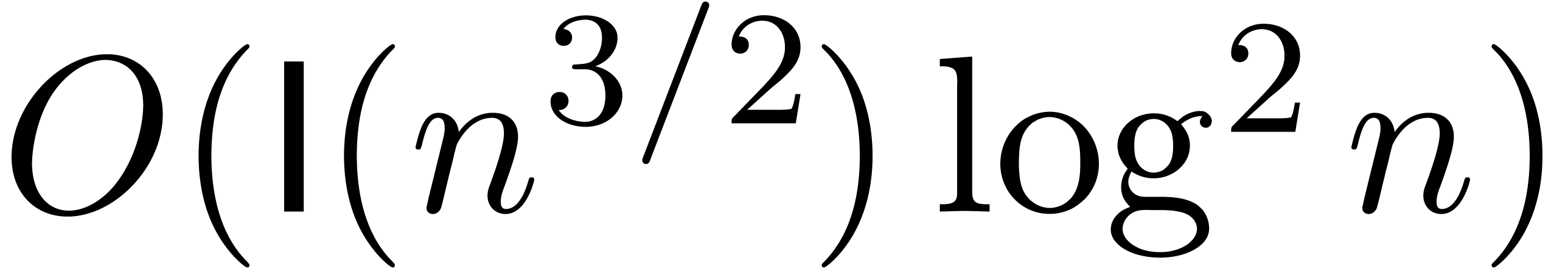 ,
,
then Theorem
1 still holds, but one should replace the
uniform complexity bound
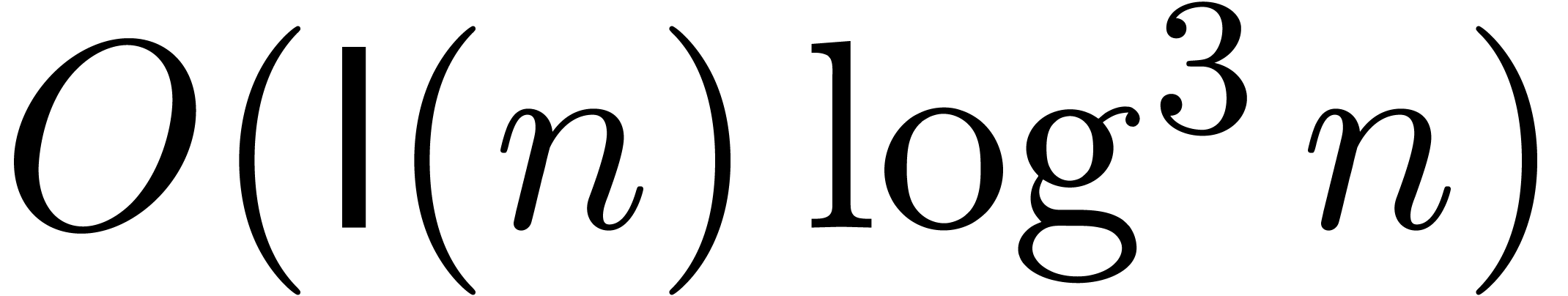
by
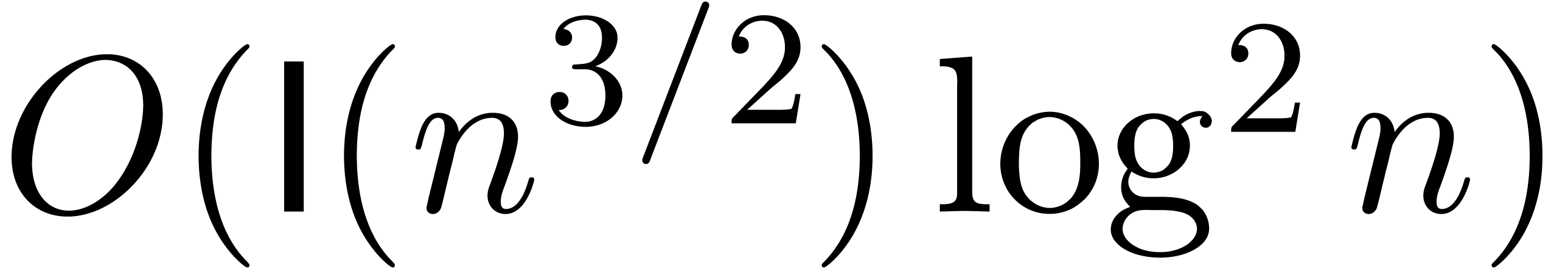 .
.
Riemann surfaces
In this paper, we used

for the domain of our
holonomic function
 .
. Of
course,

is really defined on the covering
space of
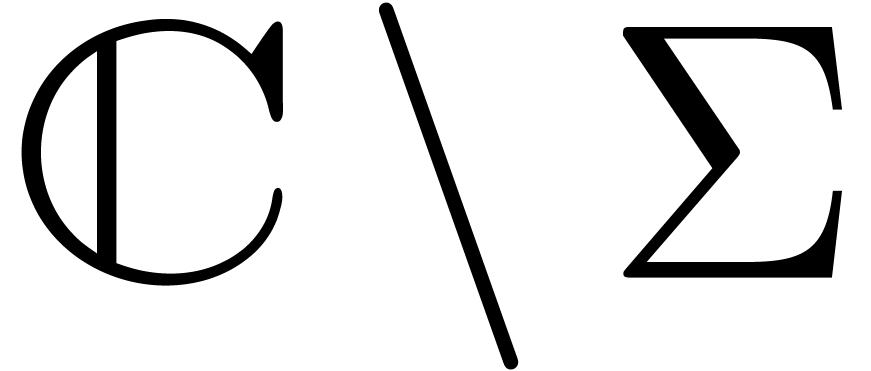
which is a Riemann surface. Points on
this Riemann surface can be represented by broken line paths as in [
7,
8,
9]. By using a suitable size
function for broken line paths with vertices in
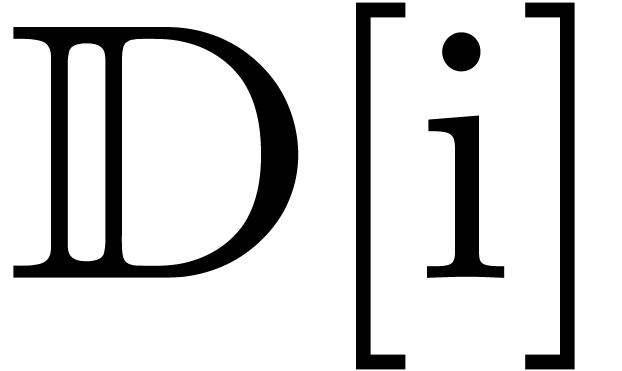 ,
, one may extend Theorem
1 to the
evaluation of

at points above
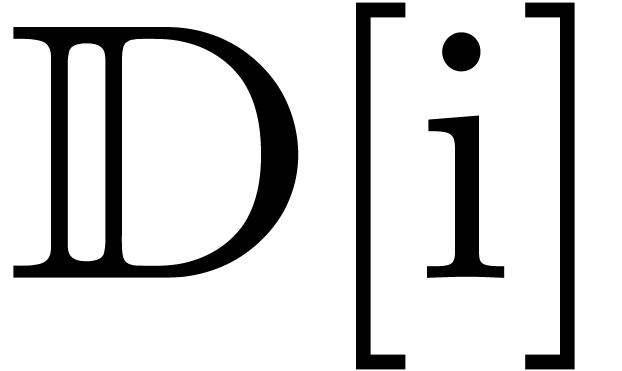
on this Riemann surface.
Fast approximation of zeros
Given a sufficiently good approximation
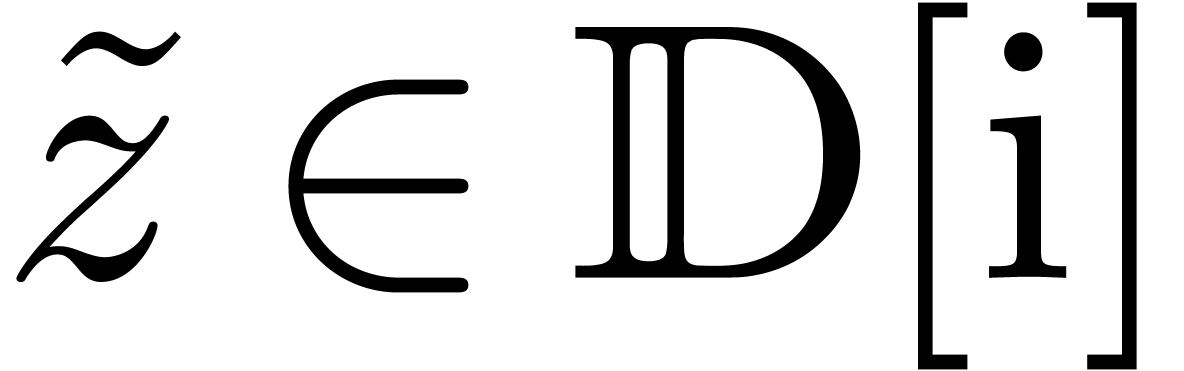
of a
zero

of

of
multiplicity
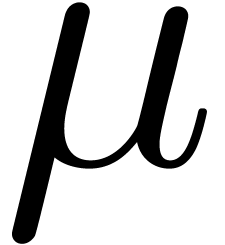
(we must have
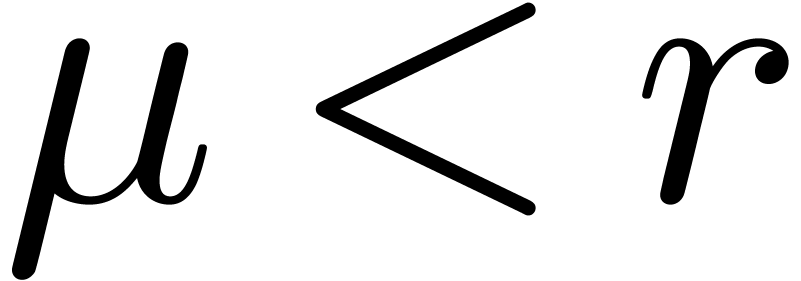 ),
), we may use Newton method's
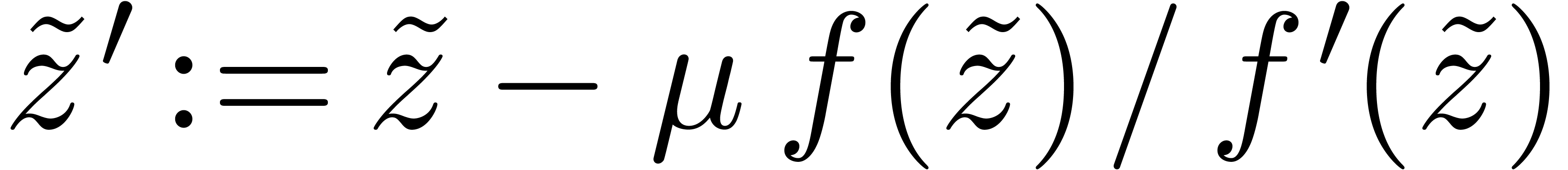
to compute a better approximation
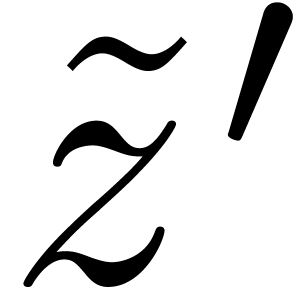 .
. Since the evaluations of

and
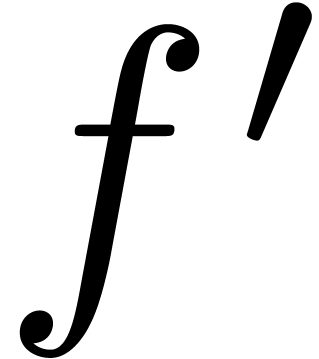
can be done with good uniform complexity,
this should make it possible to compute a
 -approximation
-approximation of

in time
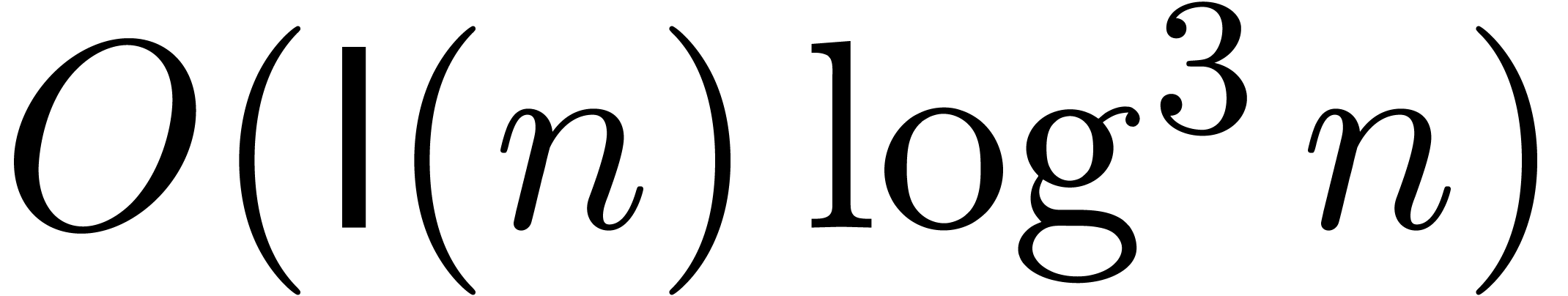 ,
, uniformly in
under suitable conditions. It would be a useful
contribution to prove a more precise statement of this kind.
Ball evaluations
In this paper, we assumed that the points

where we evaluate

are exactly known. An
interesting question concerns the efficient computation of high
quality ball lifts
of
 .
. In that case, the evaluation point

is replaced by an explicit ball
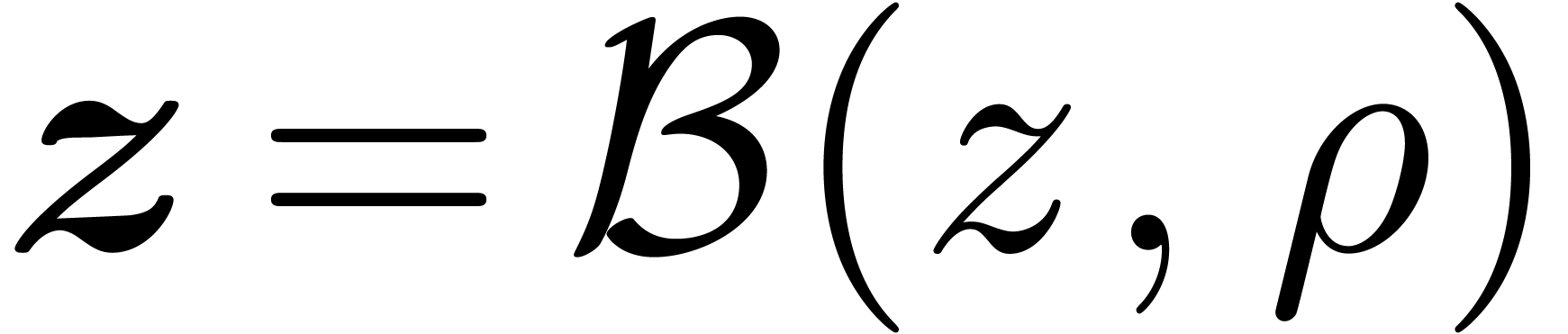
with
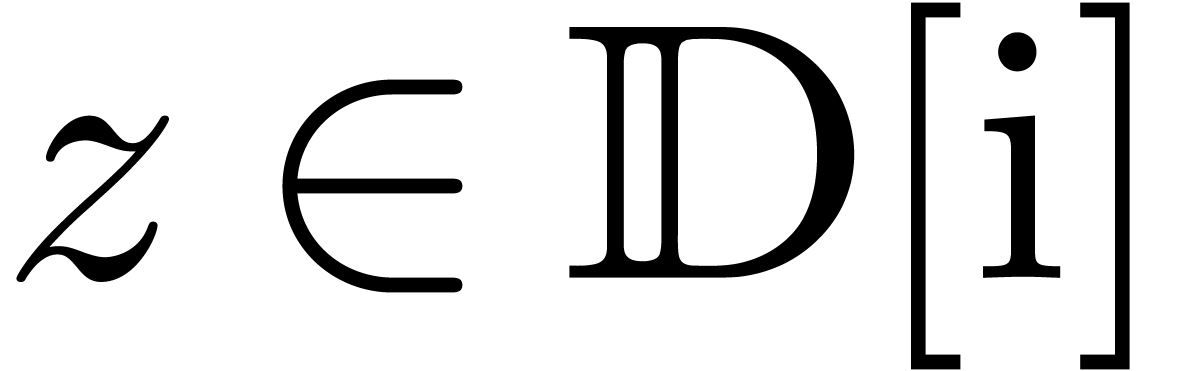
and
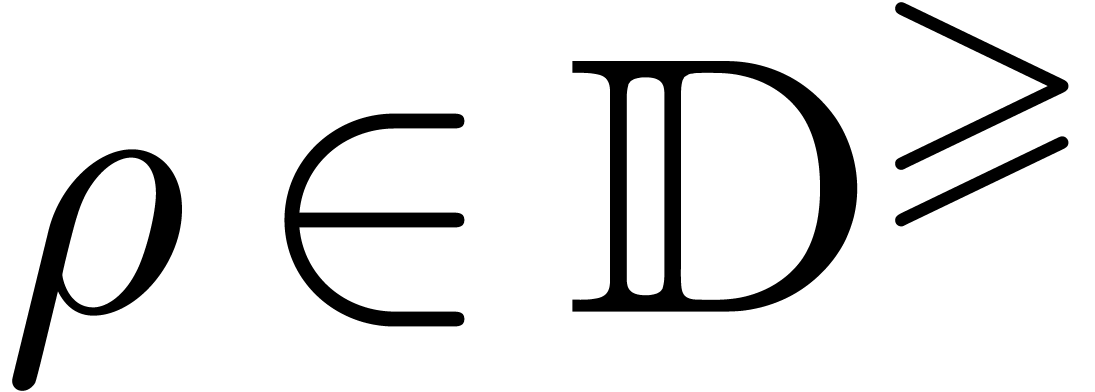 ,
,
and the evaluation
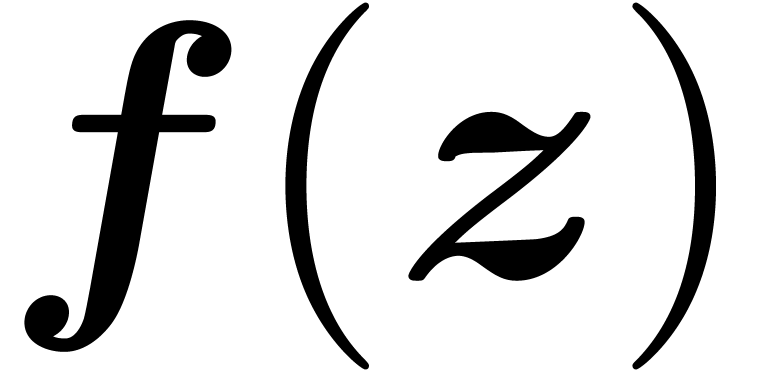
should be a similar ball
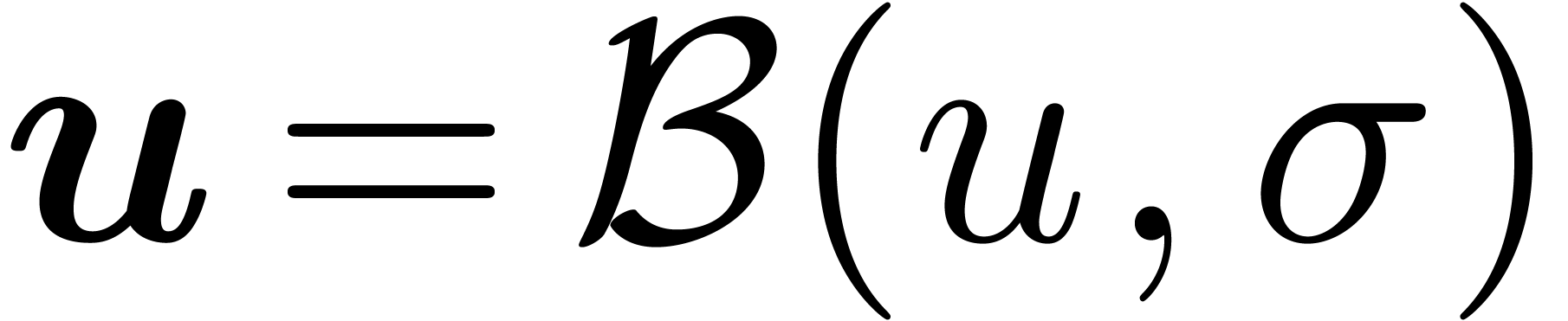
with the property that
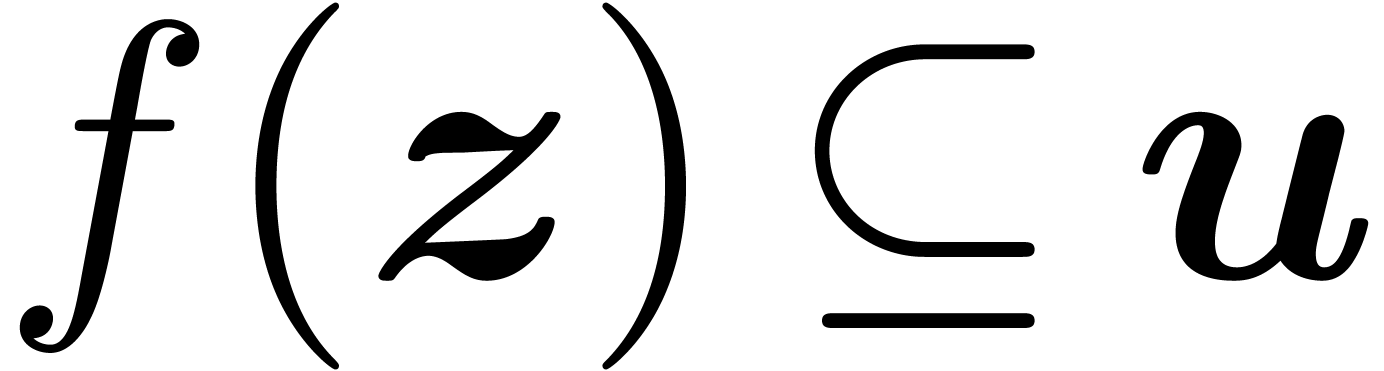
and
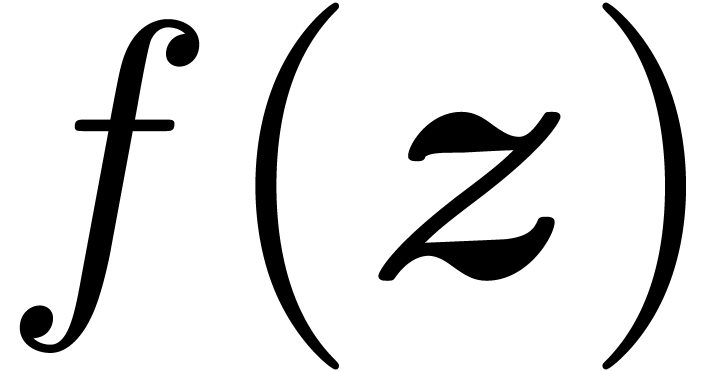
contains two points with distance at least
 .
. It would be worthwhile to
extend Theorem
1 to this kind of arithmetic.
Multi-summation
When introducing the theory of accelero-summability [
4,
5], Écalle also described a variant which only
relies on the evaluation of iterated Laplace integrals (instead of the
more general accelerations). This idea was further developed by Balser
[
1] who rebaptized it under the term
“multi-summation”. It is quite plausible that [
9]
and the present paper can be adapted to this setting.
Bibliography
-
[1]
-
W. Balser. From divergent power series to analytic
functions. Theory and application of multisummable power
series, volume 1582 of Lect. Notes in Math.
Springer-Verlag, Berlin, 1994.
-
[2]
-
R. P. Brent. The complexity of multiprecision
arithmetic. In Complexity of Computational problem
solving, 1976.
-
[3]
-
D. V. Chudnovsky and G. V. Chudnovsky. Computer
algebra in the service of mathematical physics and number theory
(Computers in mathematics, Stanford, CA, 1986). In Lect.
Notes in Pure and Applied Math., volume 125, pages
109–232, New-York, 1990. Dekker.
-
[4]
-
J. Écalle. L'accélération des
fonctions résurgentes (survol). Unpublished manuscript,
1987.
-
[5]
-
J. Écalle. Introduction aux fonctions
analysables et preuve constructive de la conjecture de
Dulac. Hermann, collection: Actualités
mathématiques, 1992.
-
[6]
-
B. Haible and T. Papanikolaou. Fast
multiple-precision evaluation of elementary functions. Technical
Report TI-7/97, Universität Darmstadt, 1997.
-
[7]
-
J. van der Hoeven. Fast evaluation of holonomic
functions. TCS, 210:199–215, 1999.
-
[8]
-
J. van der Hoeven. Fast evaluation of holonomic
functions near and in singularities. JSC,
31:717–743, 2001.
-
[9]
-
J. van der Hoeven. Efficient accelero-summation of
holonomic functions. JSC, 42(4):389–428, 2007.
-
[10]
-
E. A. Karatsuba. Fast evaluation of Bessel functions.
Integral Transforms and Special Functions,
1(4):269–276, 1993.
-
[11]
-
Marc Mezzarobba. Autour de l'évaluation
numérique des fonctions D-finies. PhD thesis,
École polytechnique, 2011.
-
[12]
-
H. Poincaré. Sur les intégrales
irrégulières des équations
linéaires. Acta Math., 8:295–344, 1886.
 be a subfield of
be a subfield of  . A holonomic function over
. A holonomic function over  is a solution
is a solution  to a linear
differential equation
to a linear
differential equation 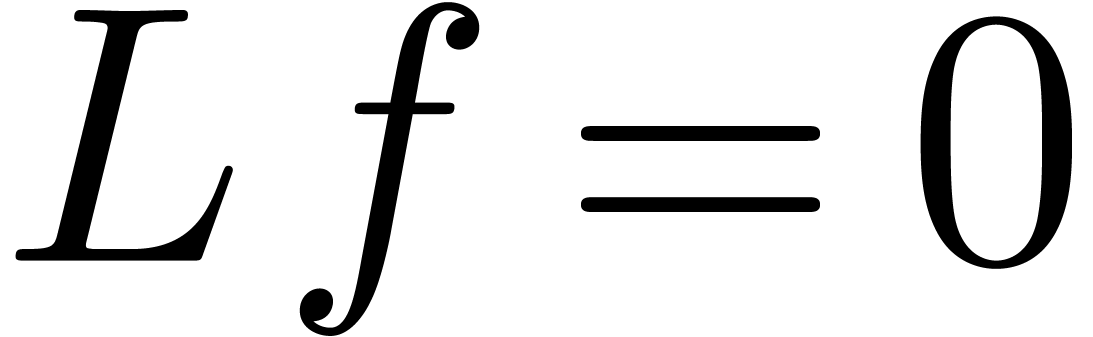 , where
, where
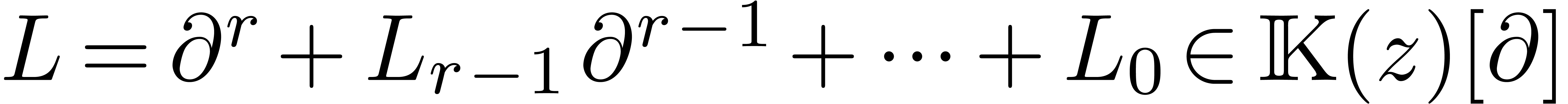 is a monic linear differential operator of order
is a monic linear differential operator of order
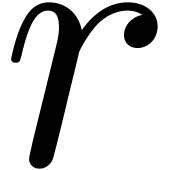 . Many classical special
functions, such as
. Many classical special
functions, such as 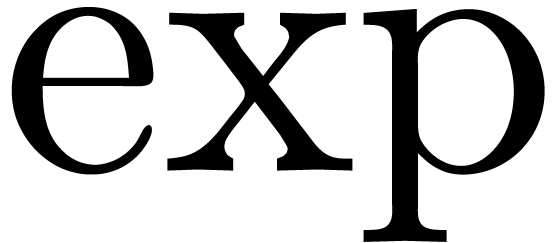 ,
, 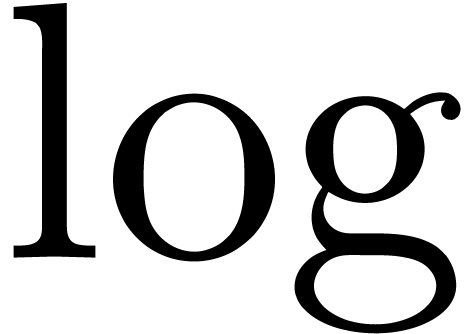 ,
,  ,
,
 ,
,  , hypergeometric functions, Bessel functions, the
Airy function, etc. are holonomic. Moreover, the class of
holonomic functions is stable under many operations, such as addition,
multiplication, differentiation, integration and postcomposition with
algebraic functions.
, hypergeometric functions, Bessel functions, the
Airy function, etc. are holonomic. Moreover, the class of
holonomic functions is stable under many operations, such as addition,
multiplication, differentiation, integration and postcomposition with
algebraic functions.
 ;
; denote the finite set
of these poles. We will say that
denote the finite set
of these poles. We will say that 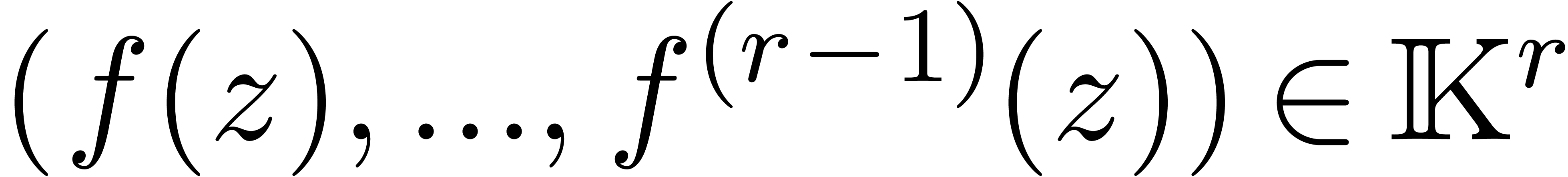 for a certain non-singular point
for a certain non-singular point  .
. .
.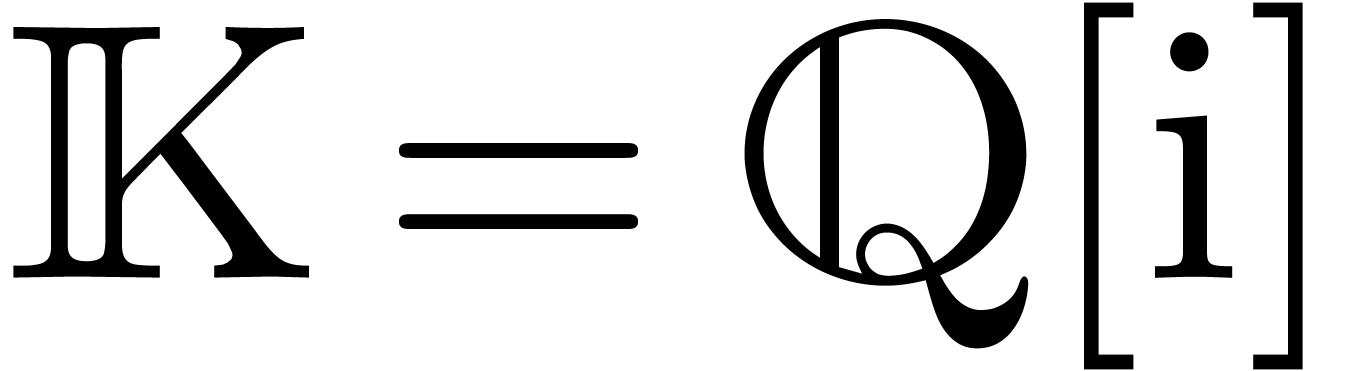 ,
,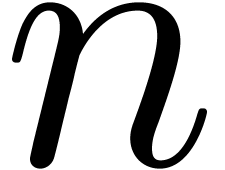 -bit
-bit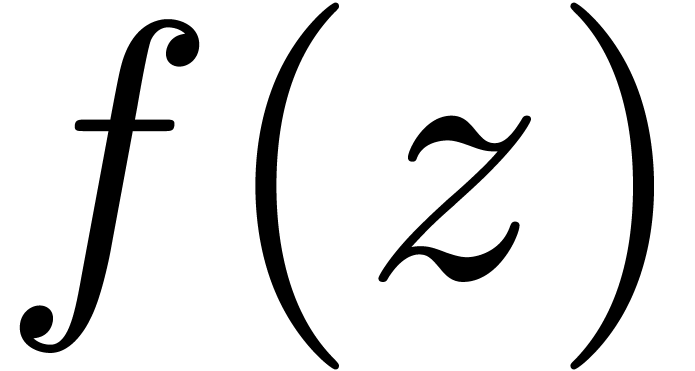 can be computed in time
can be computed in time 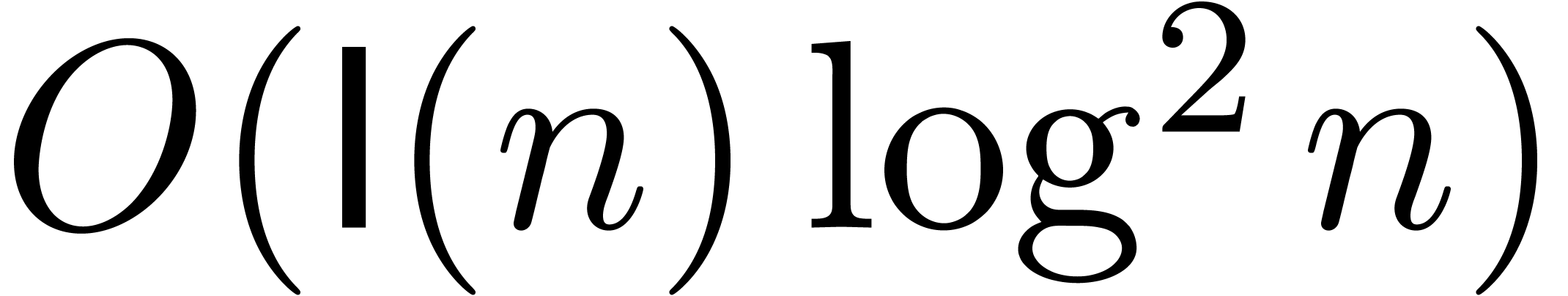 .
.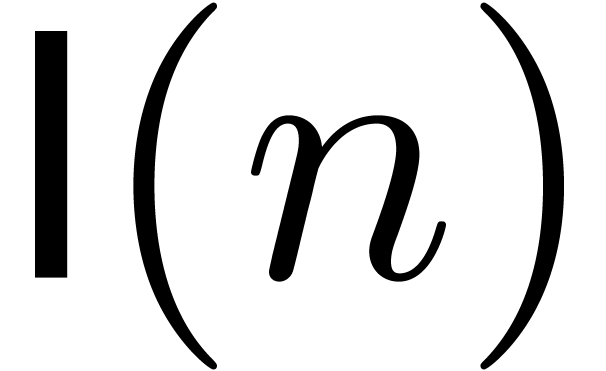 stands for a
complexity bound for integer multiplication and it has recently been
proved that one may take
stands for a
complexity bound for integer multiplication and it has recently been
proved that one may take 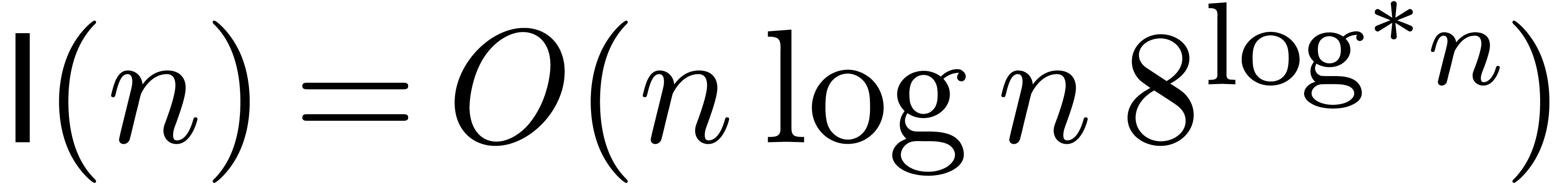 ,
,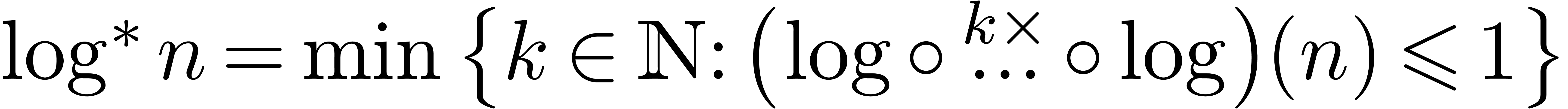 .
.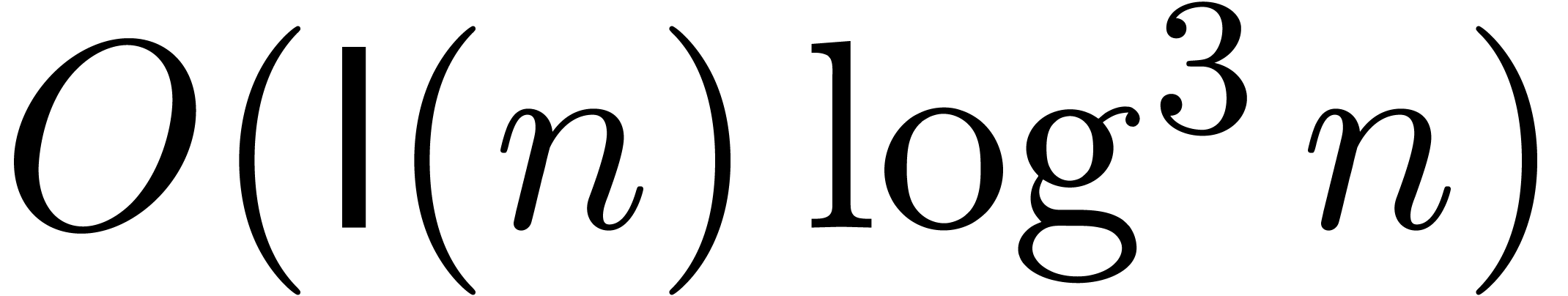 ).
).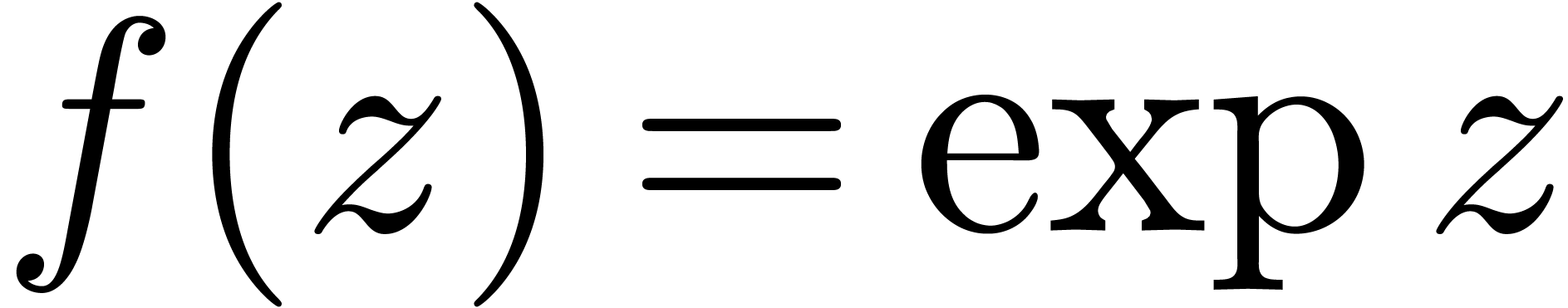 grows exponentially fast at
infinity: given the
grows exponentially fast at
infinity: given the 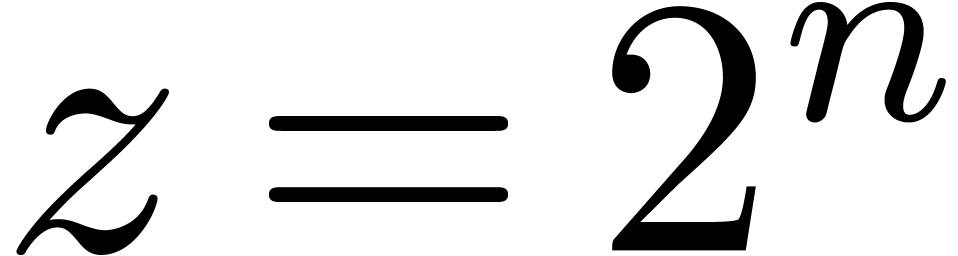 ,
,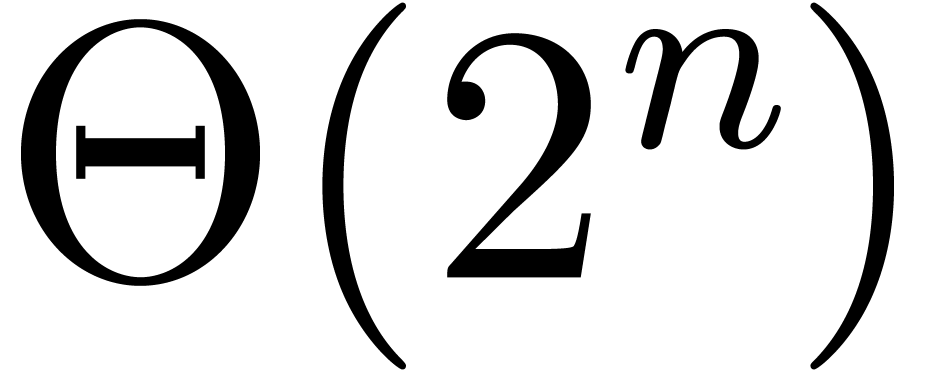 bits to merely write down the closest integer
approximation
bits to merely write down the closest integer
approximation 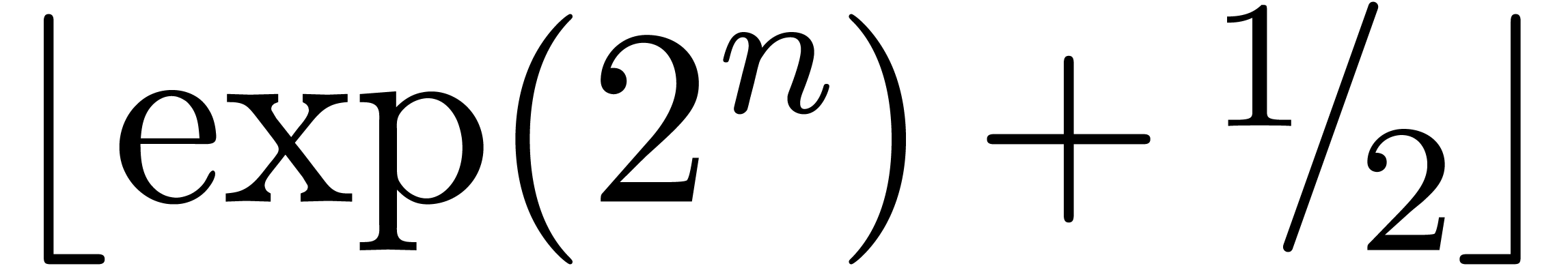 of
of 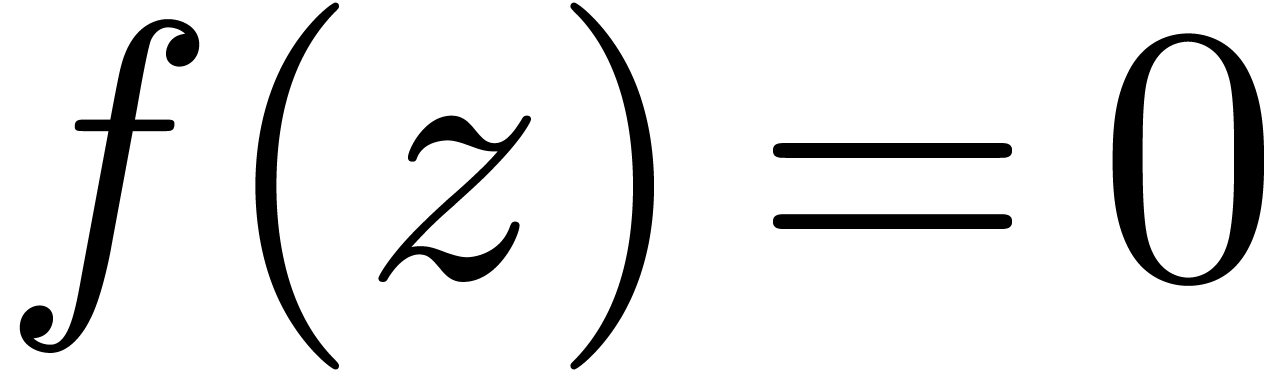 for
for 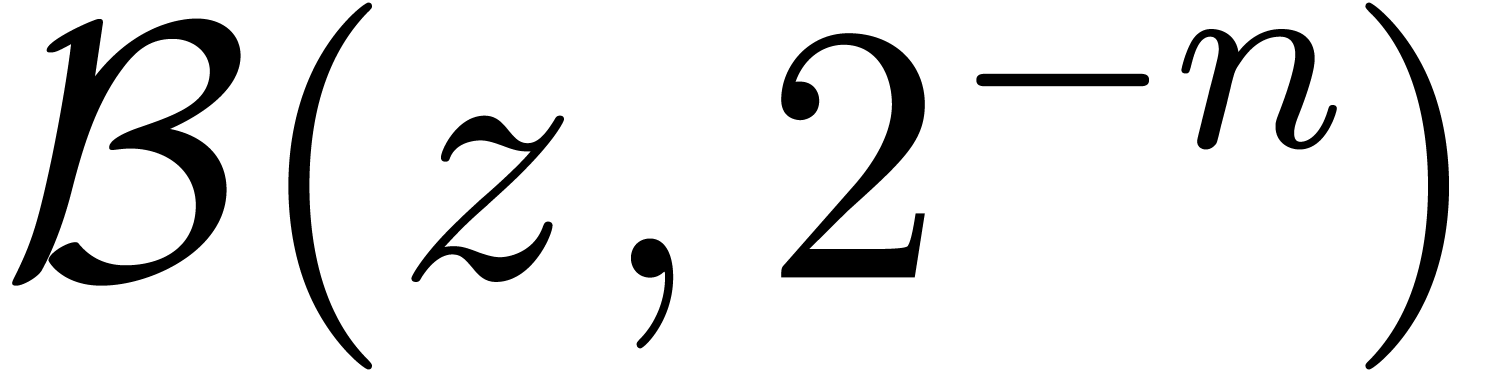 with center
with center  ,
,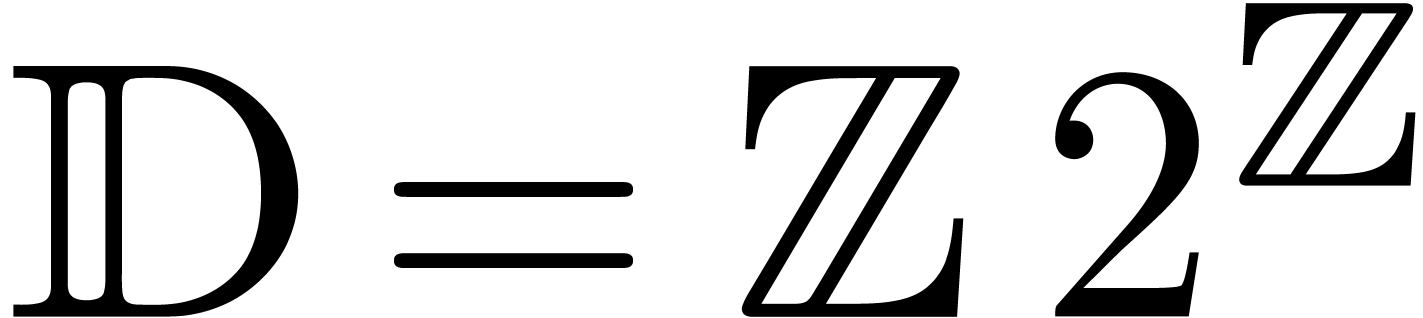 be the set of dyadic numbers. Given
be the set of dyadic numbers. Given
 ,
,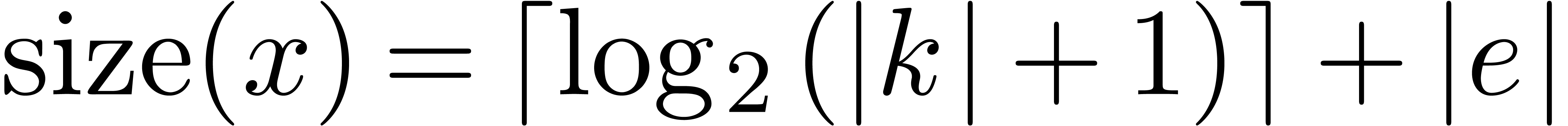 the bitsize of
the bitsize of  .
.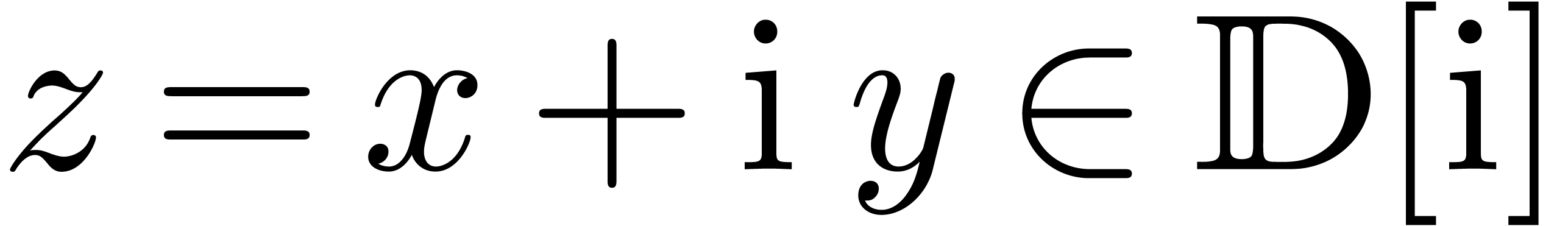 ,
,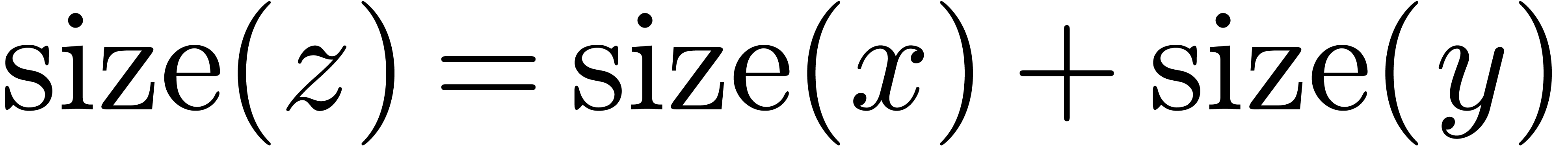 .
.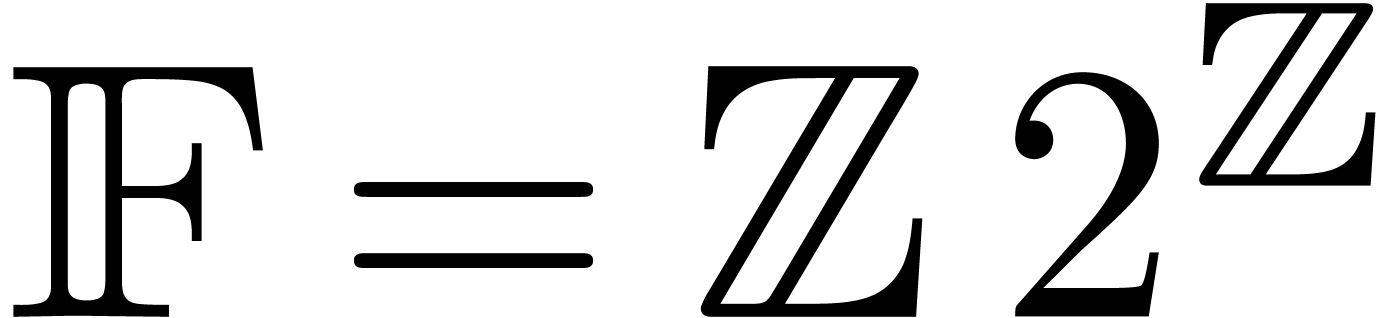 of floating point numbers is defined in the same way as
of floating point numbers is defined in the same way as  ,
,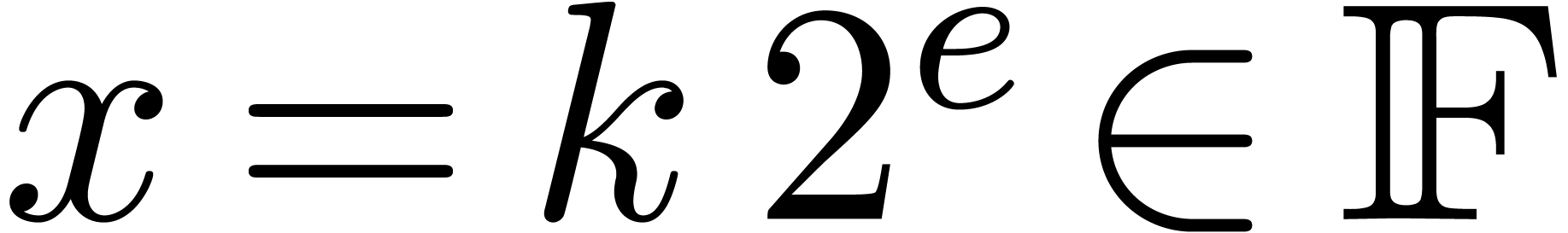 is represented in binary notation,
so that the bitsize of
is represented in binary notation,
so that the bitsize of 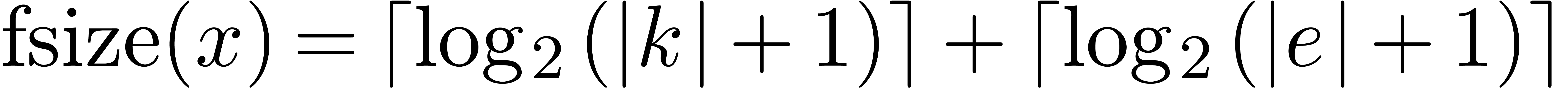 .
. be the point at which we specified the
initial conditions of
be the point at which we specified the
initial conditions of  to be the open subset of
to be the open subset of 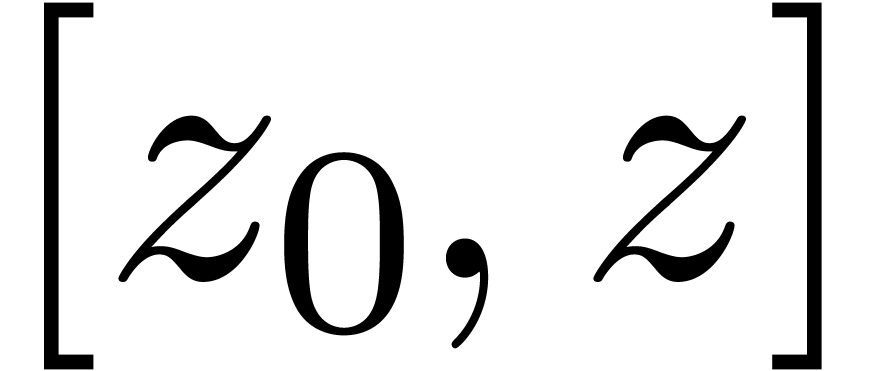 from
from  to
to  denote the set of zeros of
denote the set of zeros of 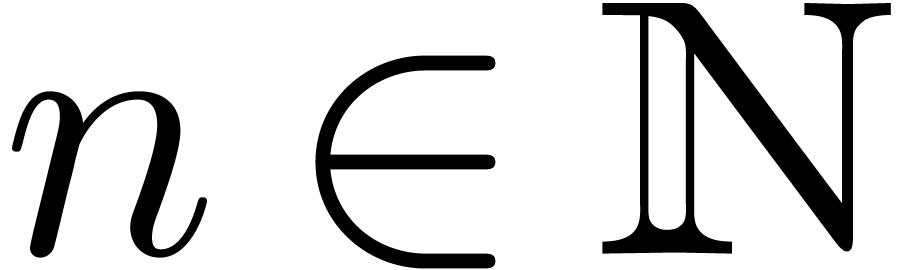 and
and 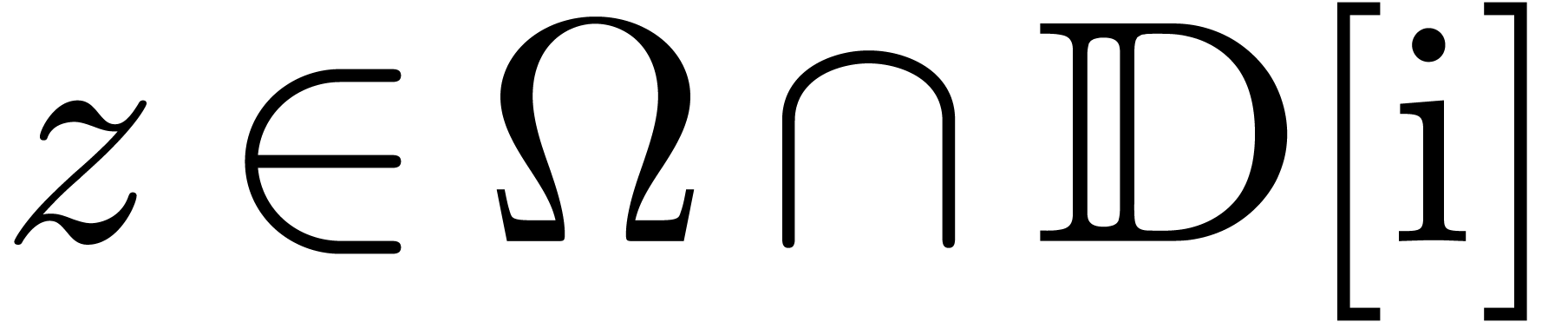 with
with  and
and  on input and that computes
on input and that computes 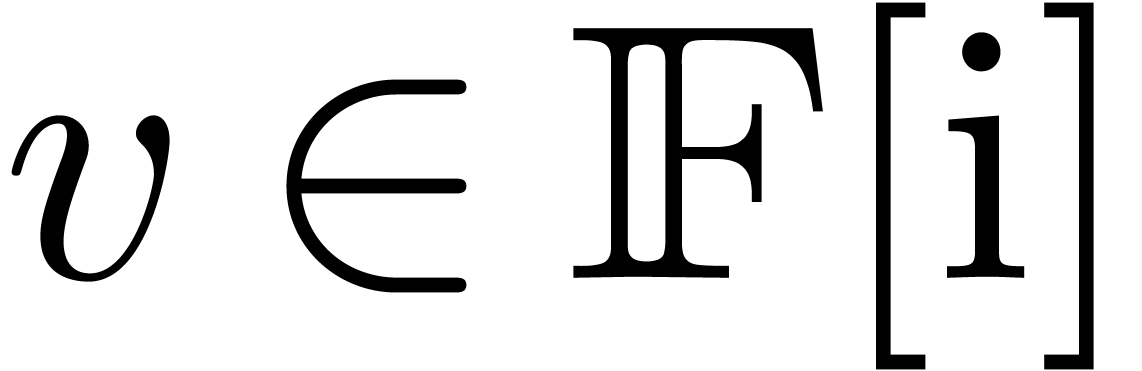 on
output with
on
output with 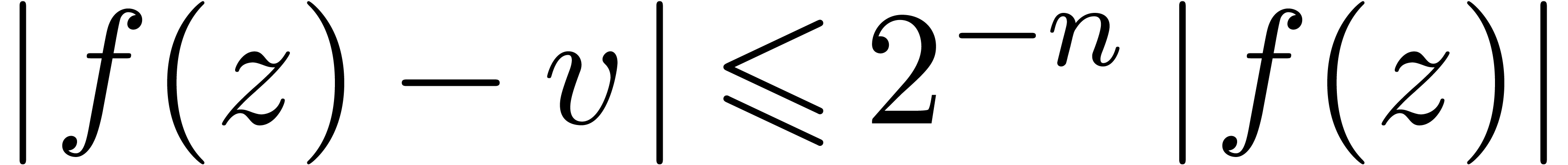 .
. .
.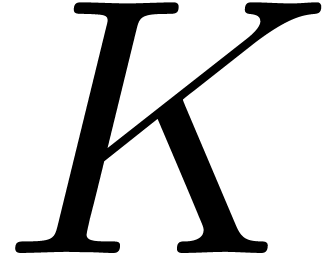 of
of 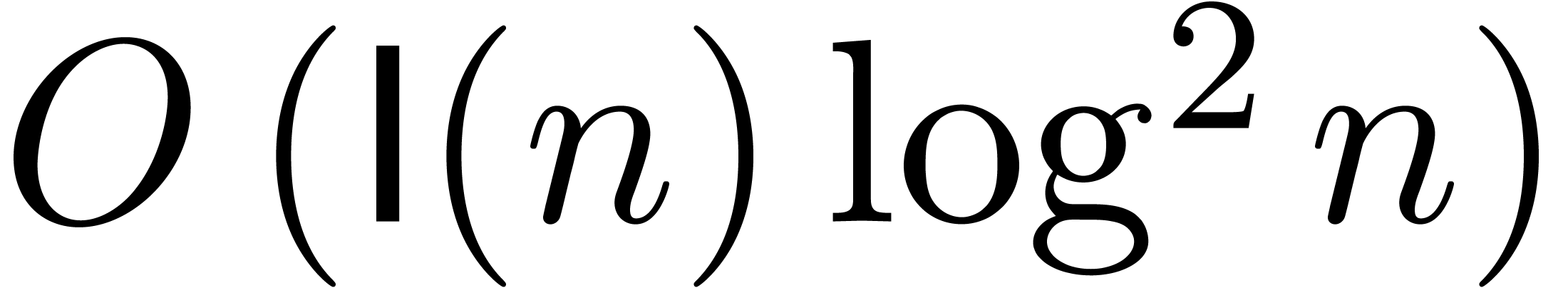 for the evaluation of
for the evaluation of
 of
of  for sufficiently large
for sufficiently large  ,
,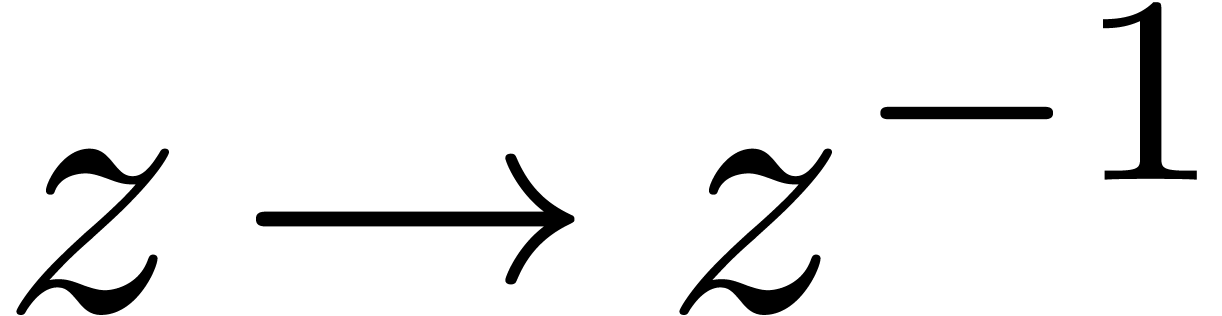 .
.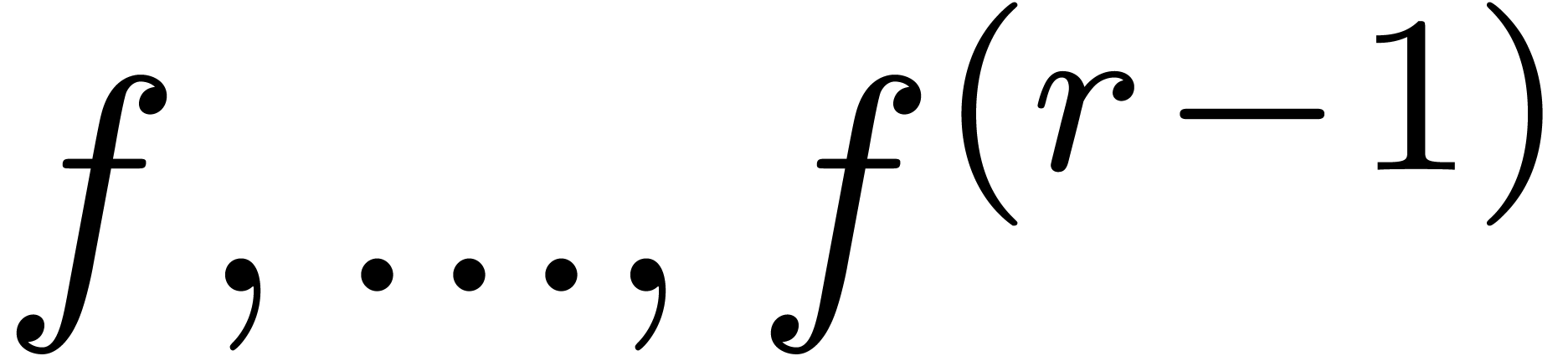 can never simultaneously become “smaller
than expected”. A precise statement will be presented in Section
can never simultaneously become “smaller
than expected”. A precise statement will be presented in Section
 .
.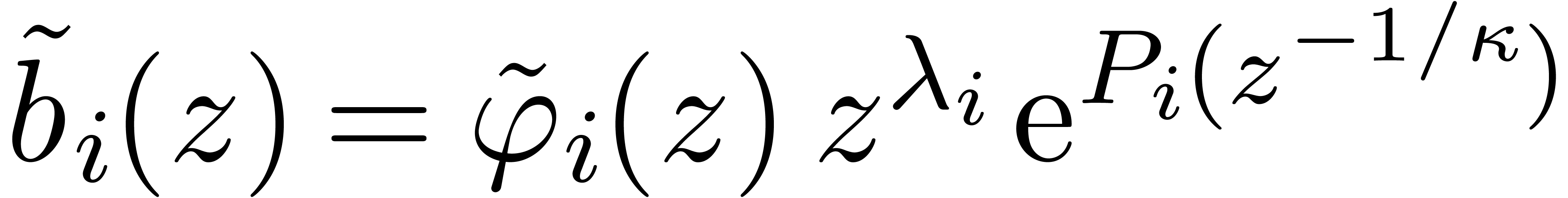
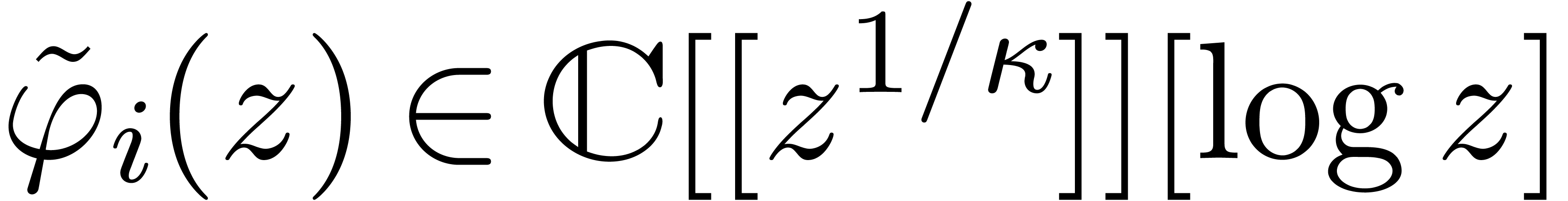 ,
, ,
,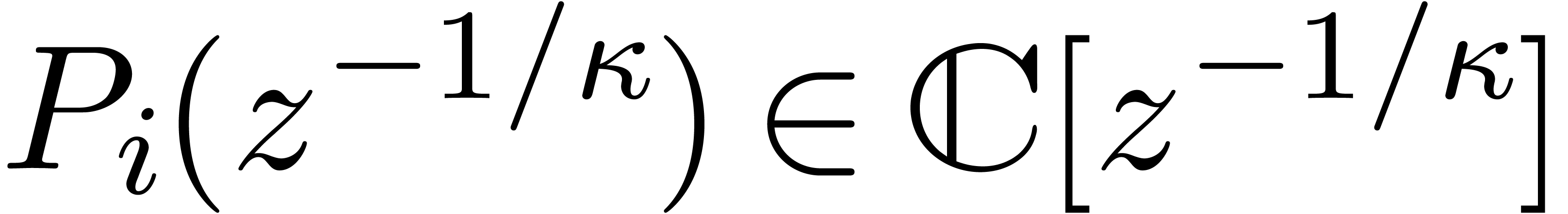 ,
, ,
,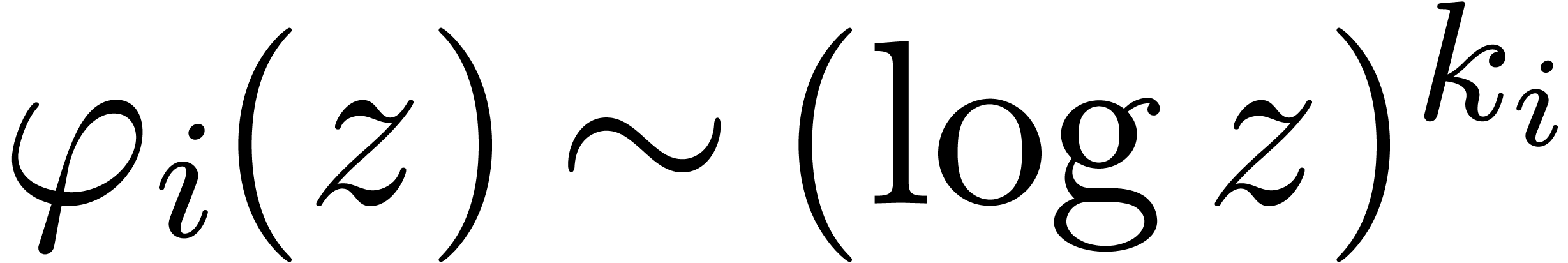 for some
for some  .
.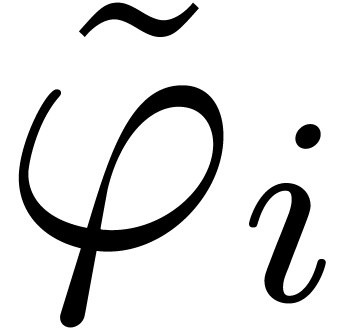 are accelero-summable and that
we can associate actual functions
are accelero-summable and that
we can associate actual functions 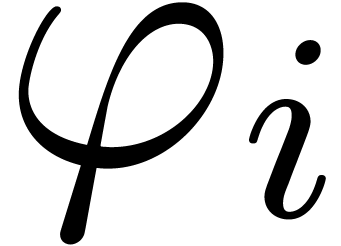 to them that
are defined on sectors of the form
to them that
are defined on sectors of the form
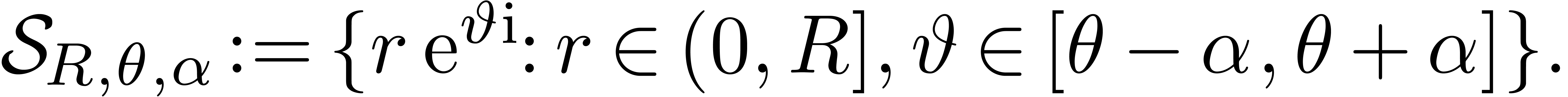
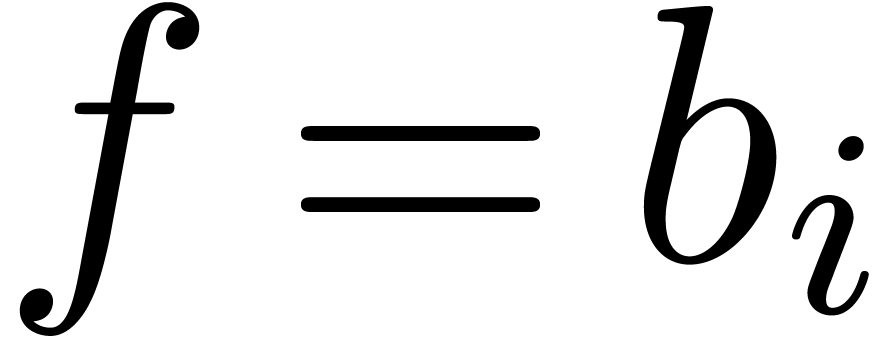 for some
for some 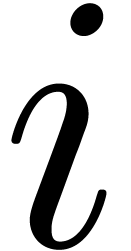 ,
,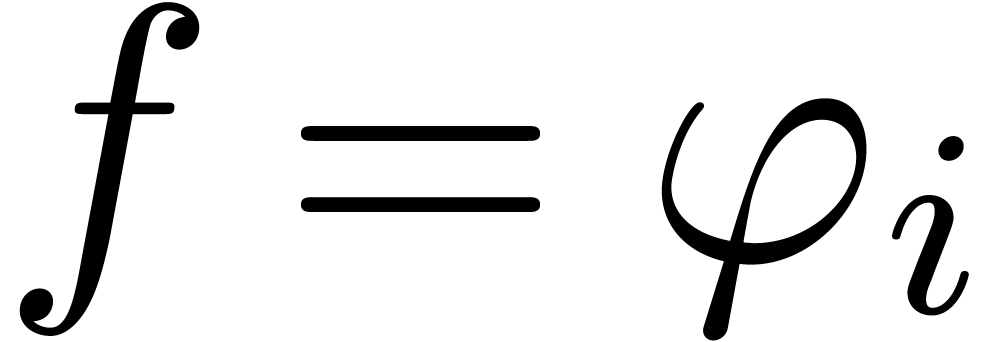 .
. for a suitable
for a suitable  ,
,
 ,
, ,
,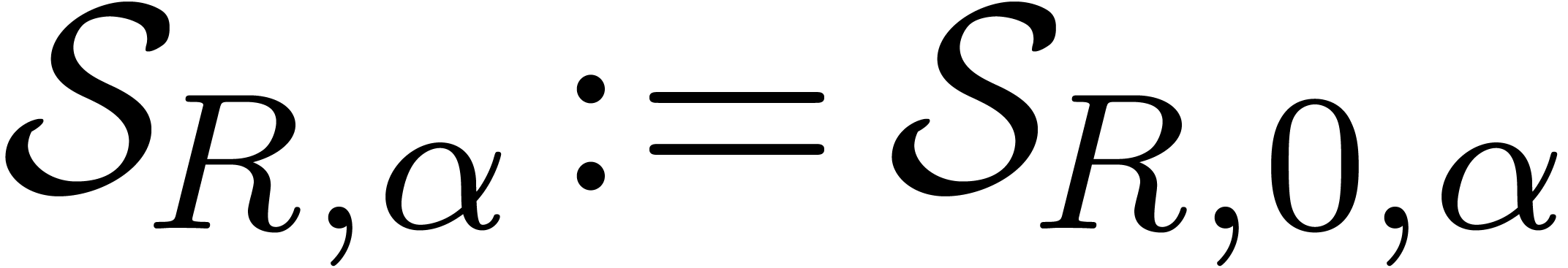
 with
with  .
.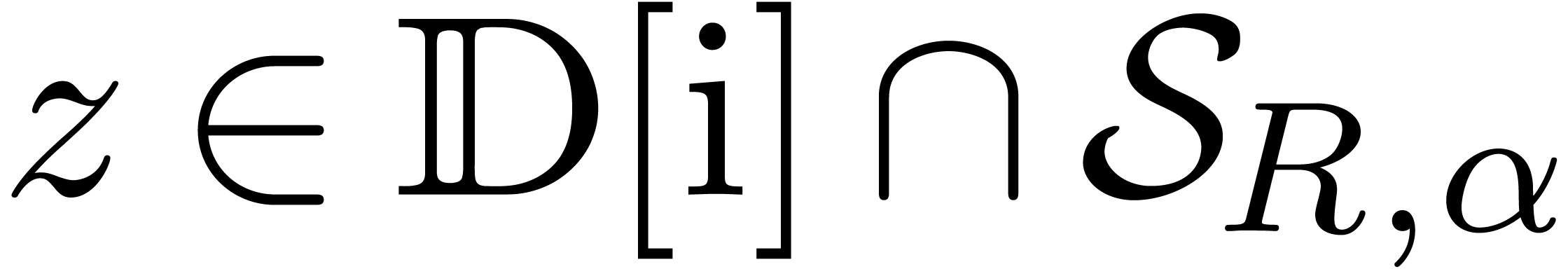 ,
,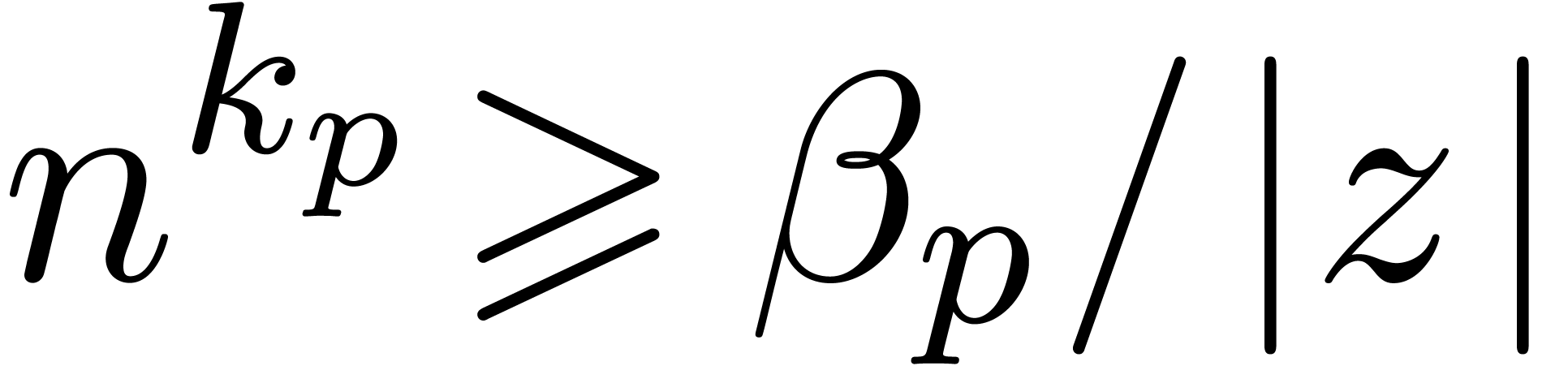 for some
computable constant
for some
computable constant 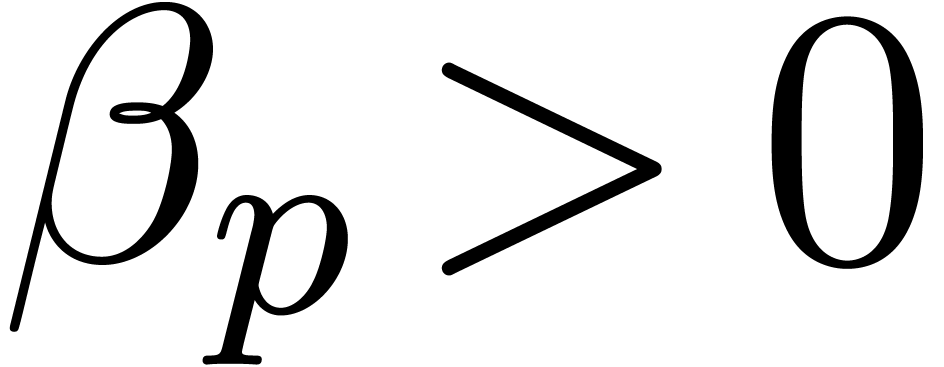 .
.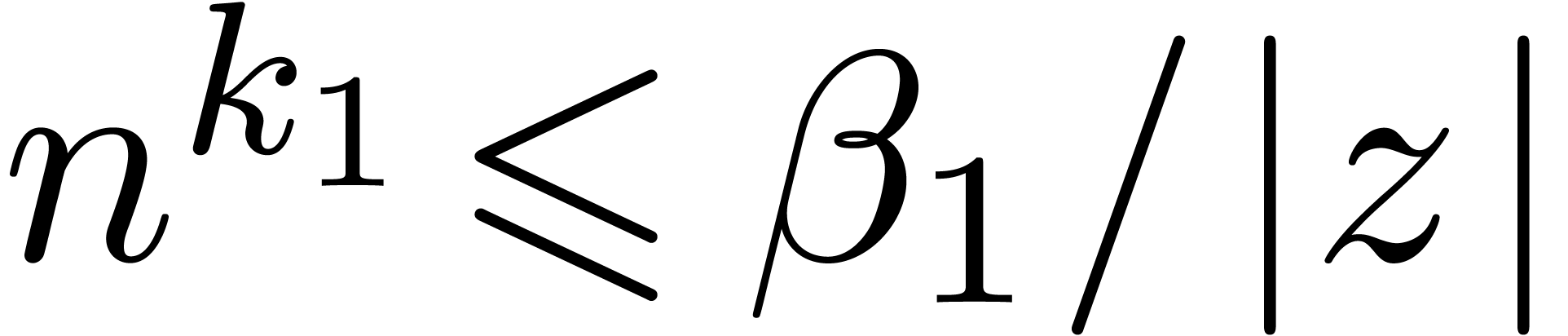 for some computable constant
for some computable constant 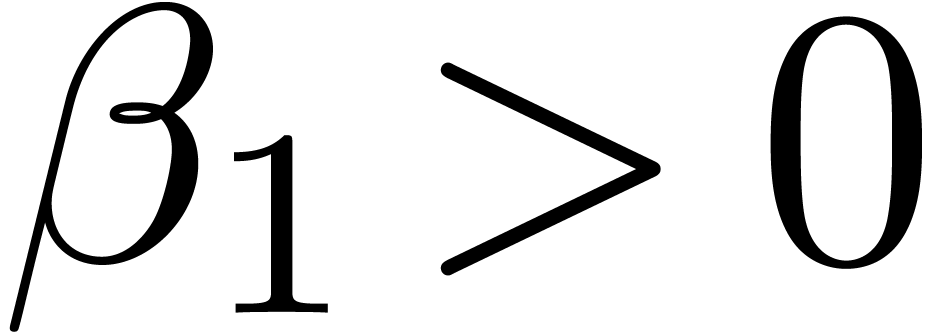 .
. and
and 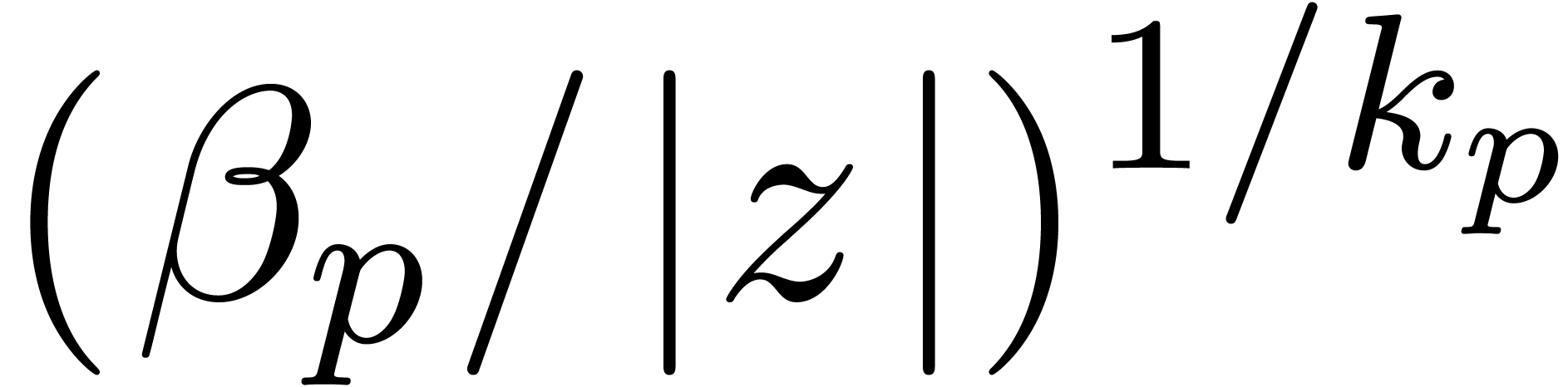 .
.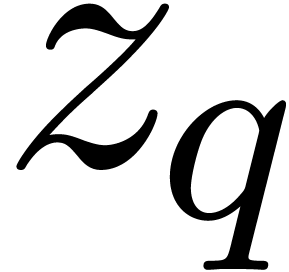 with
with 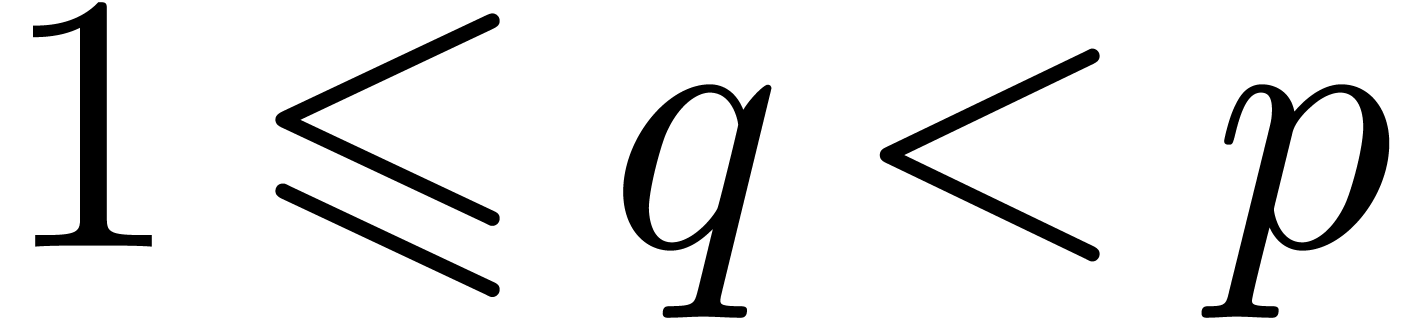 and then
“expedite” the process by directly taking a truncated
Laplace transform with respect to
and then
“expedite” the process by directly taking a truncated
Laplace transform with respect to 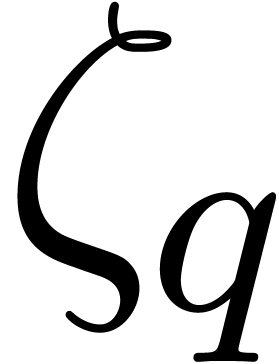 .
.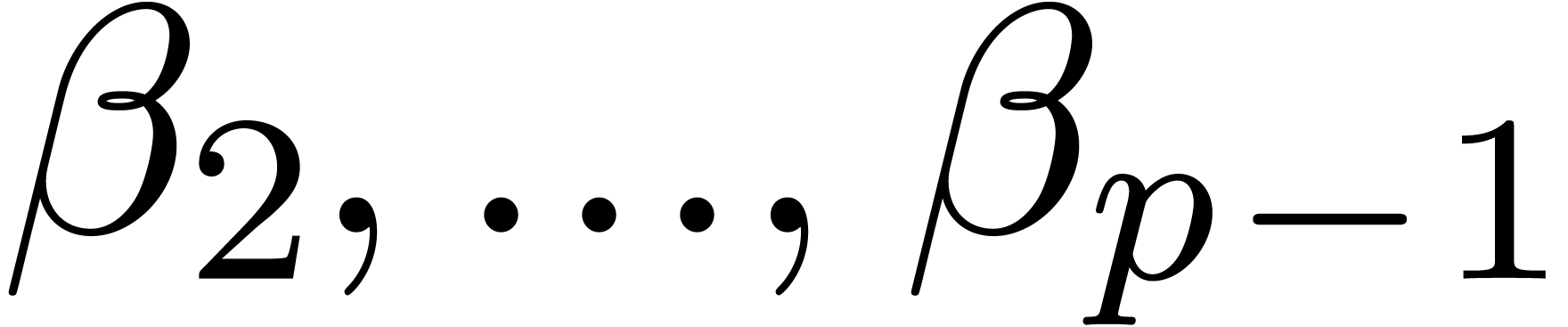 such that expedito-summation until the
critical time
such that expedito-summation until the
critical time 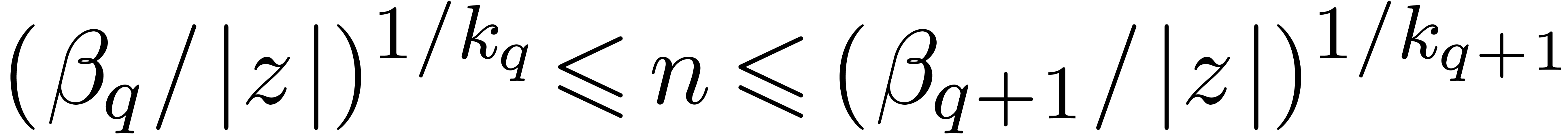 .
. .
.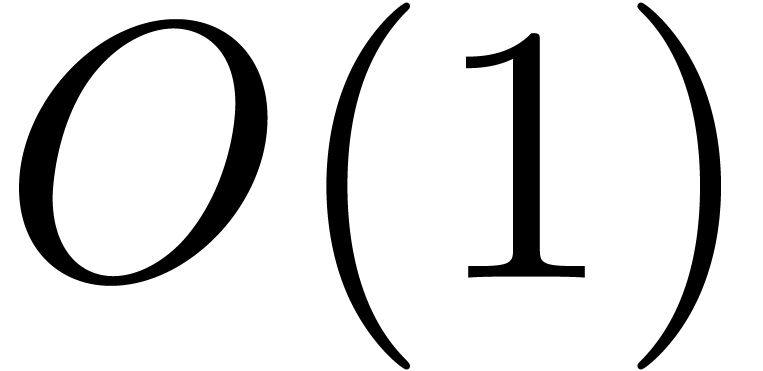 for “some bounded function” is somewhat
analoguous. For instance, given a real function
for “some bounded function” is somewhat
analoguous. For instance, given a real function 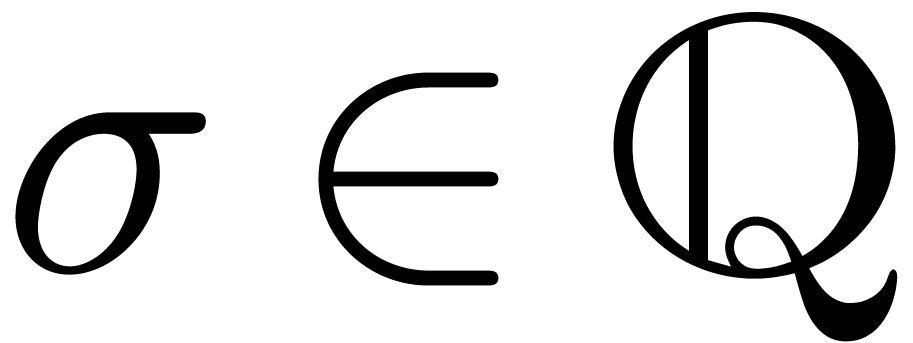 ,
,
 means that we can compute an explicit
exponential bound for
means that we can compute an explicit
exponential bound for 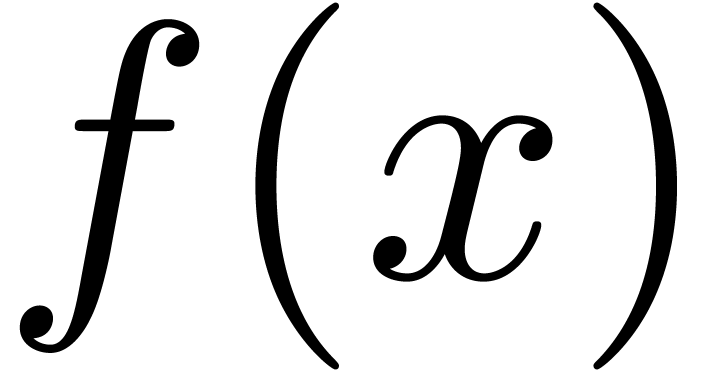 on the interval
on the interval 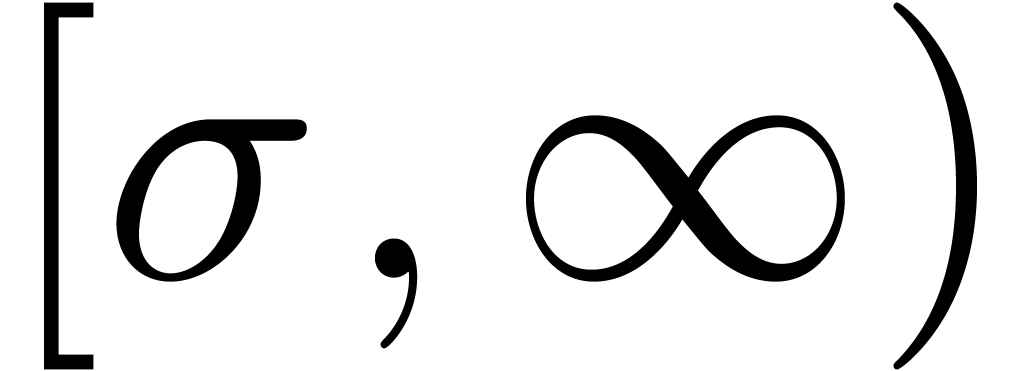 .
.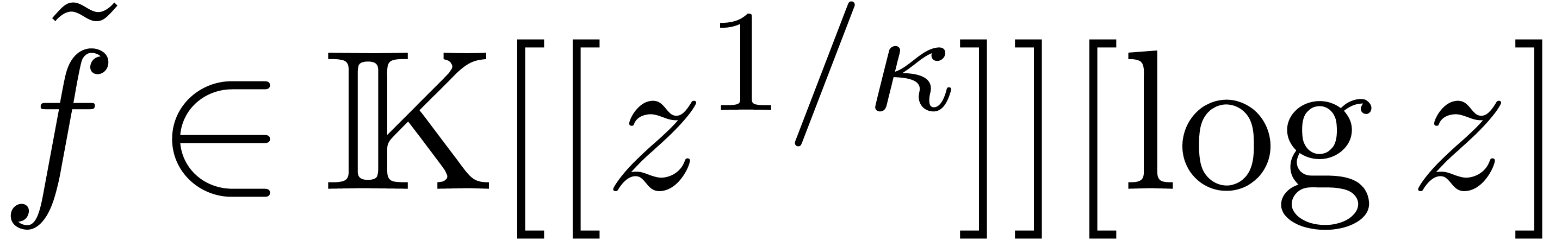 with
with 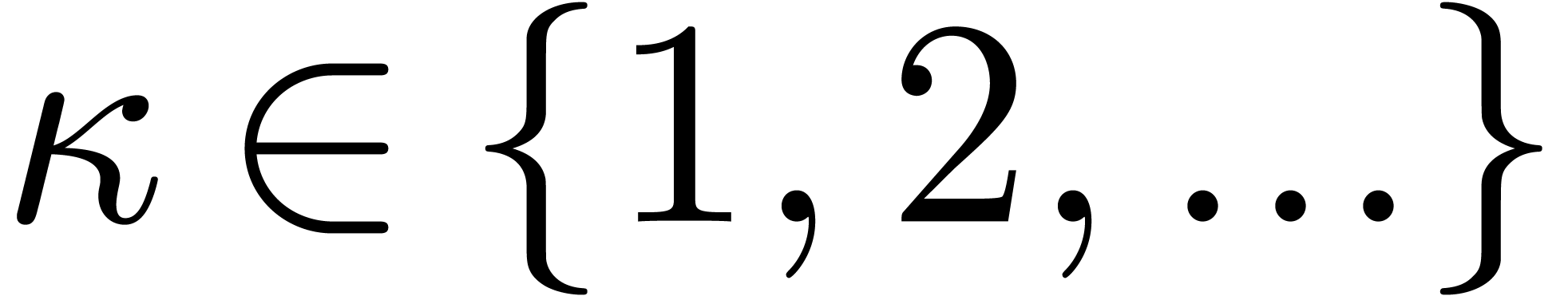 is a formal
solution to
is a formal
solution to 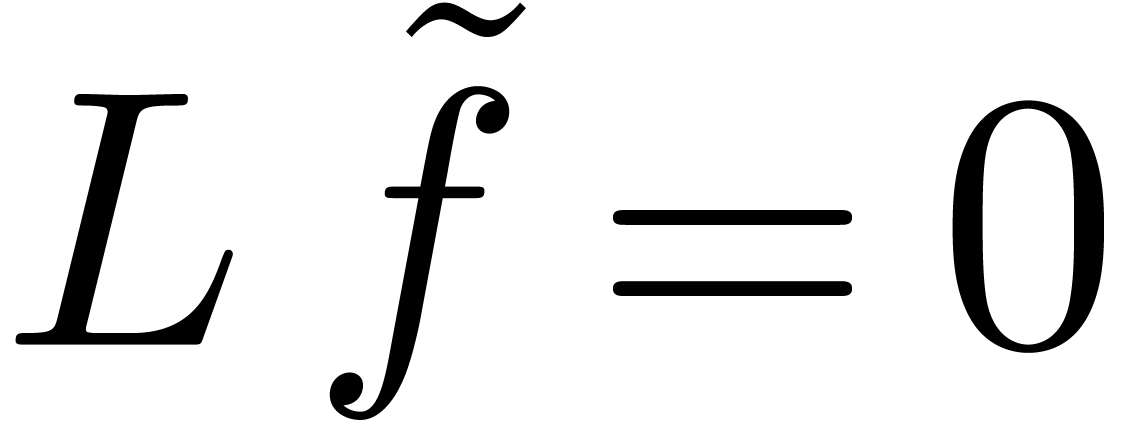 .
. is accelero-summable with critical times
is accelero-summable with critical times
 at the various critical times admit no
singularities on the positive real axis.
at the various critical times admit no
singularities on the positive real axis.
 to
to 
 ,
, by
by 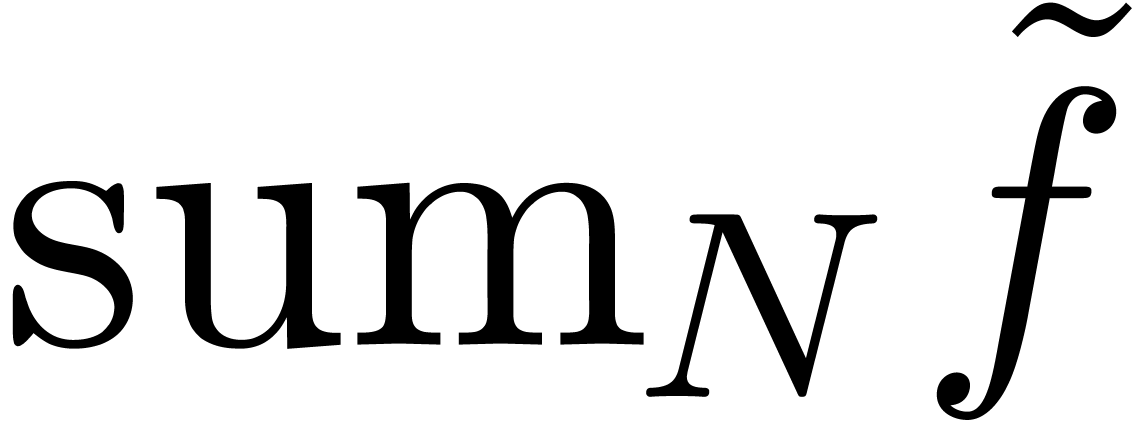 ,
,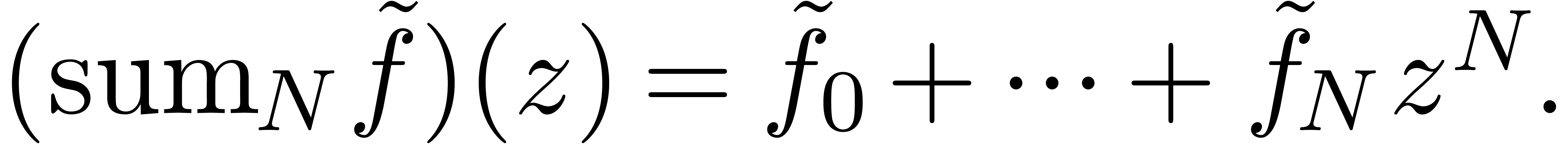
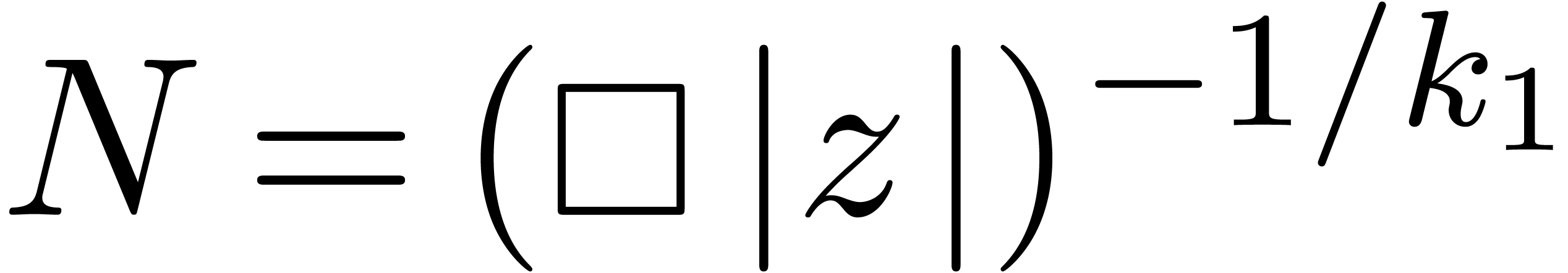 ,
,
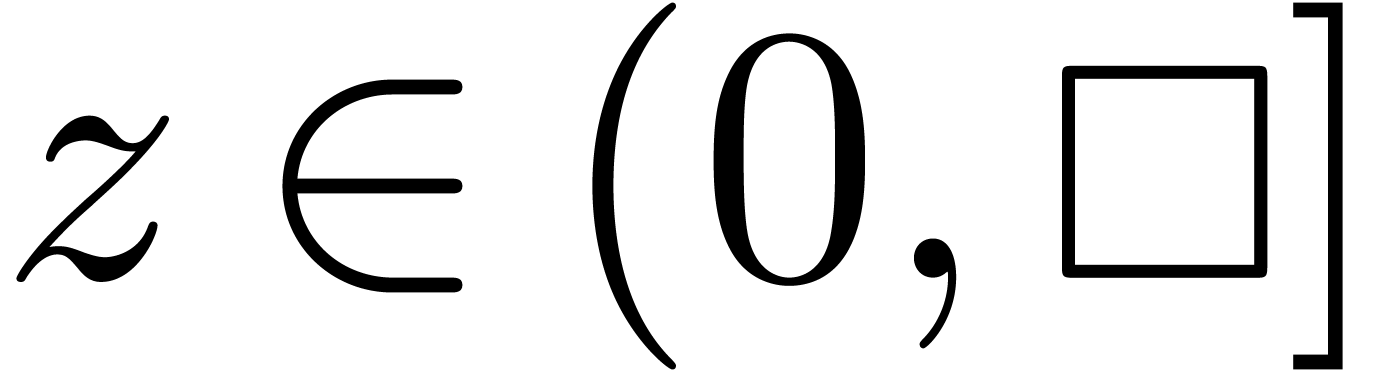 .
.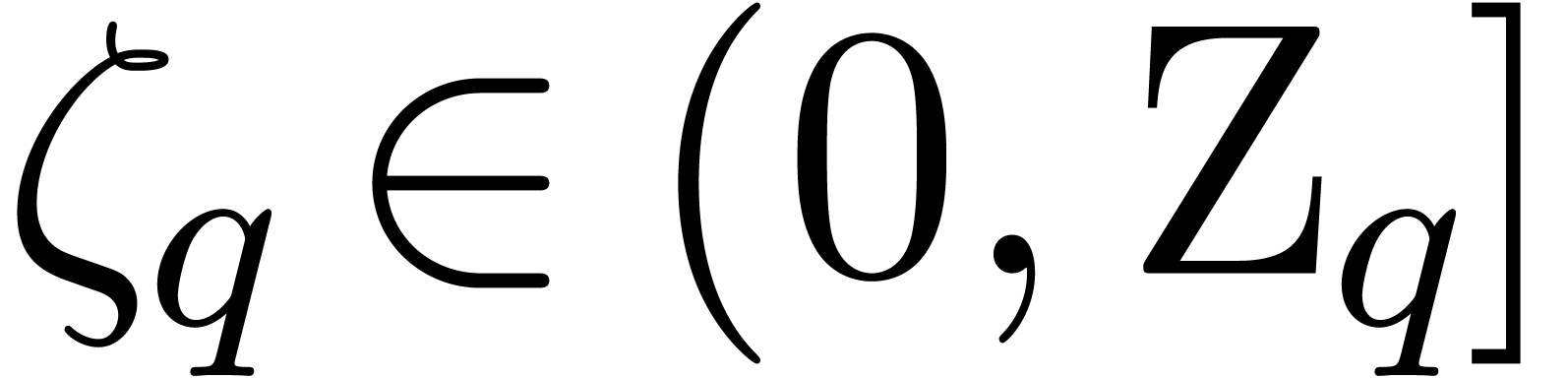 for
a suitable
for
a suitable 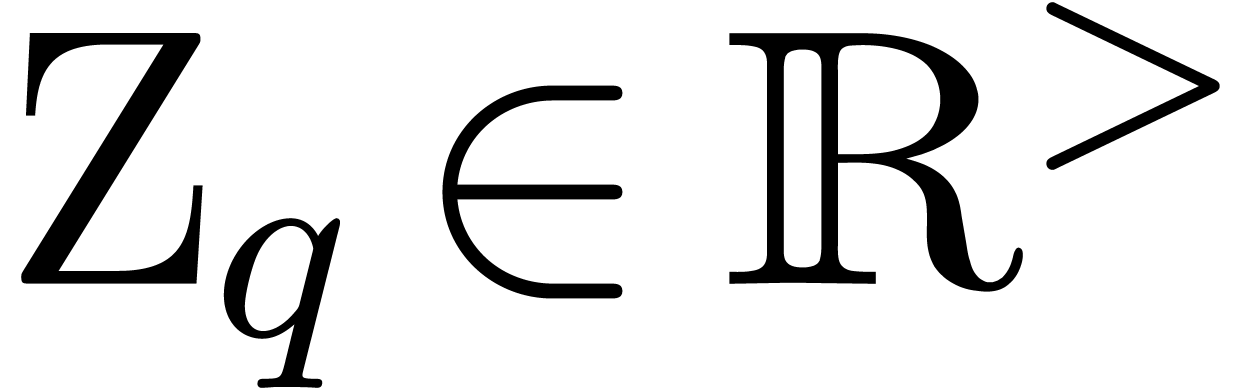 .
. and
and 
 denotes the contour from
denotes the contour from  to
to  ,
, and then back from
and then back from  to
to 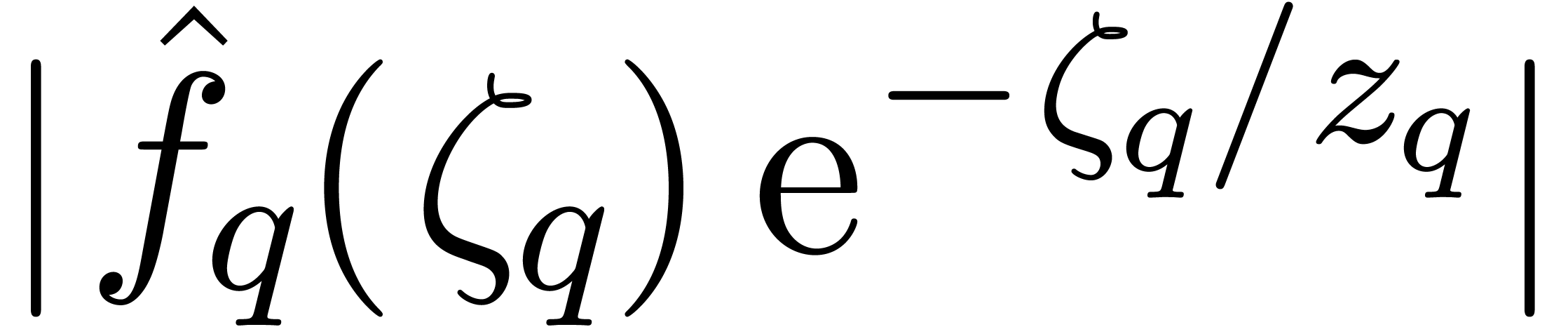 is minimal. Since
is minimal. Since  satisfies a bound of the form
satisfies a bound of the form

 ,
,
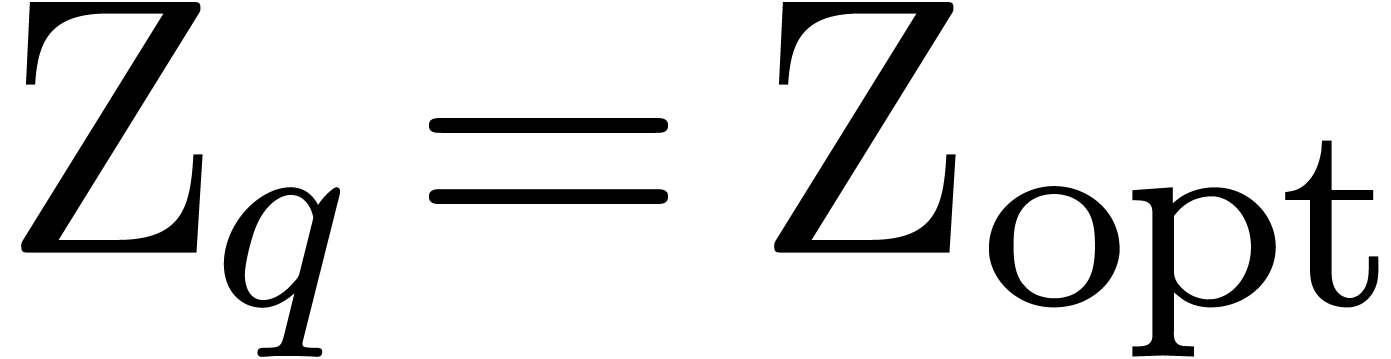 ,
,
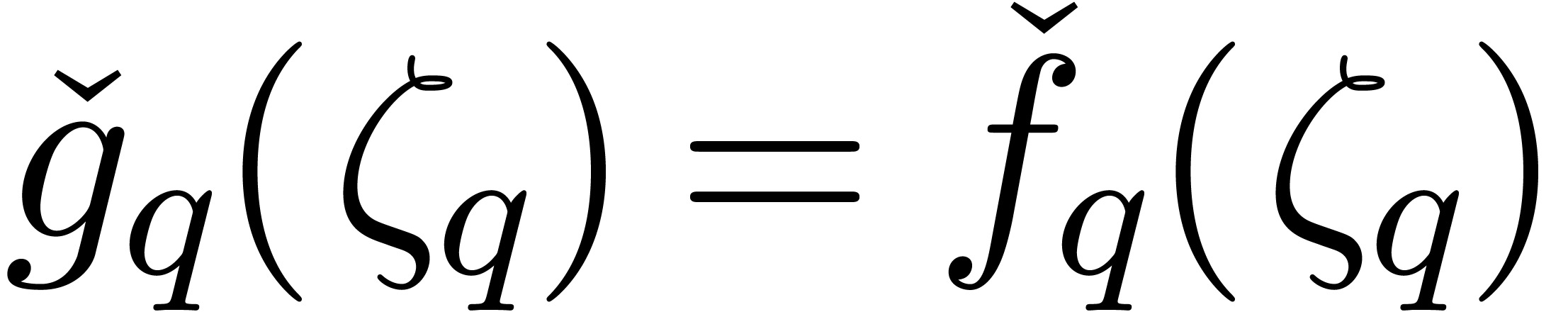 for
for 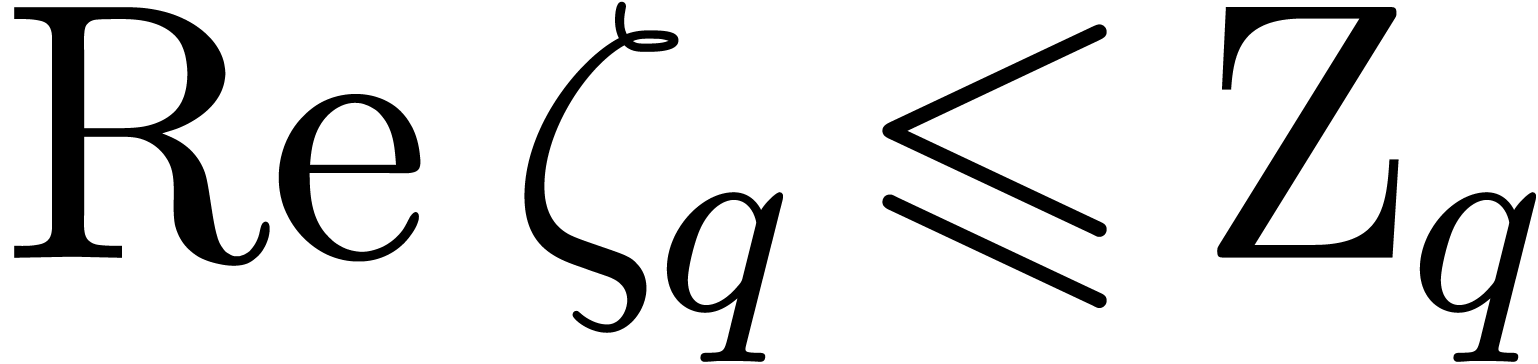 and
and 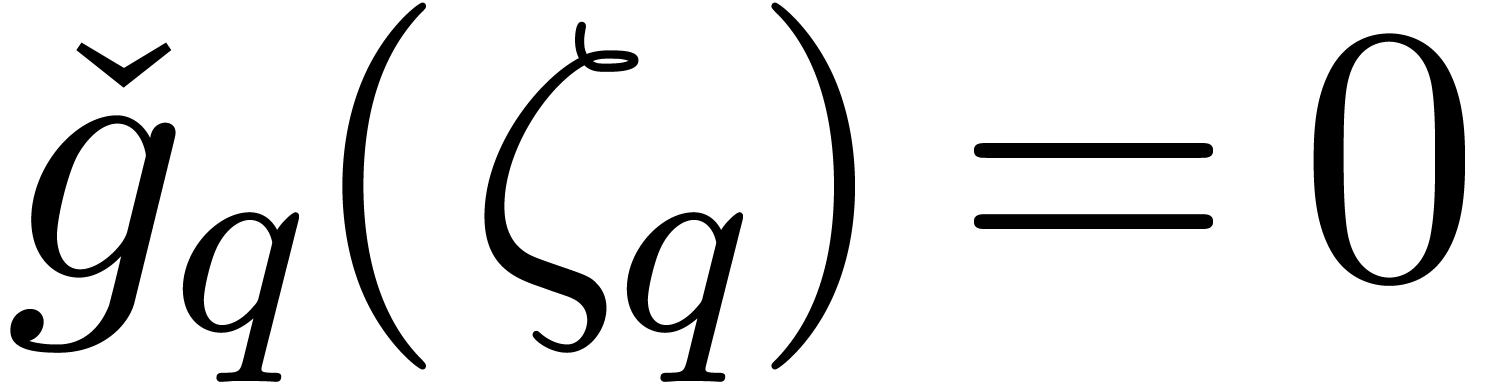 for
for 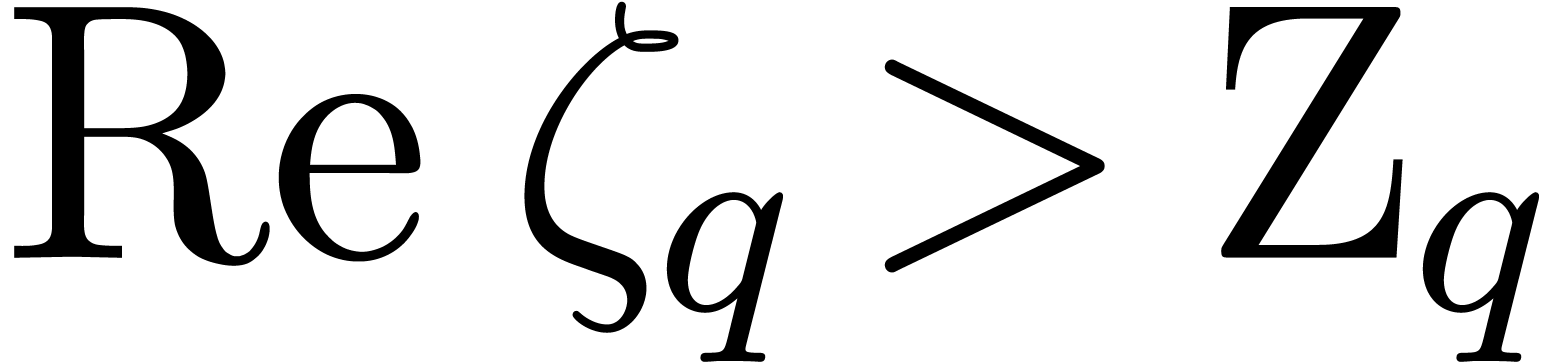 ,
,
 on the
contour
on the
contour 
 at other critical
times
at other critical
times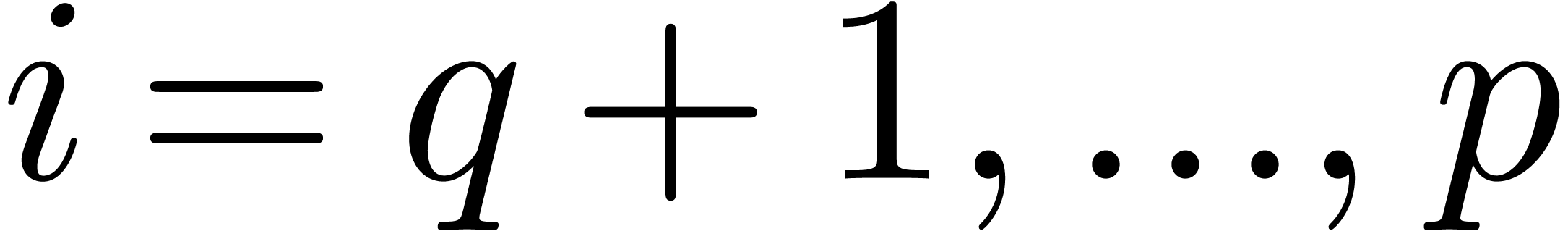 ,
,
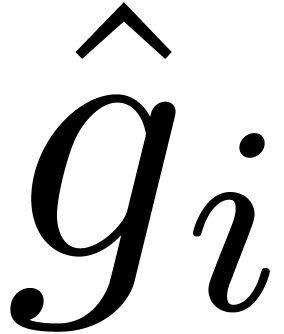 as the analytic Borel
transform of
as the analytic Borel
transform of 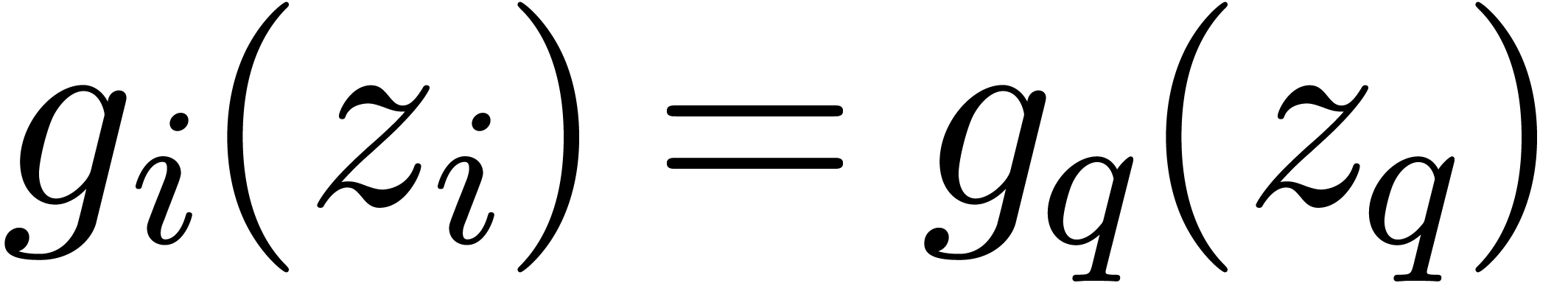 with respect to
with respect to 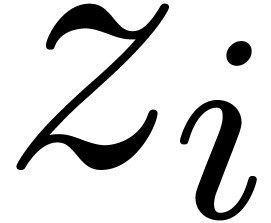 .
.
 .
.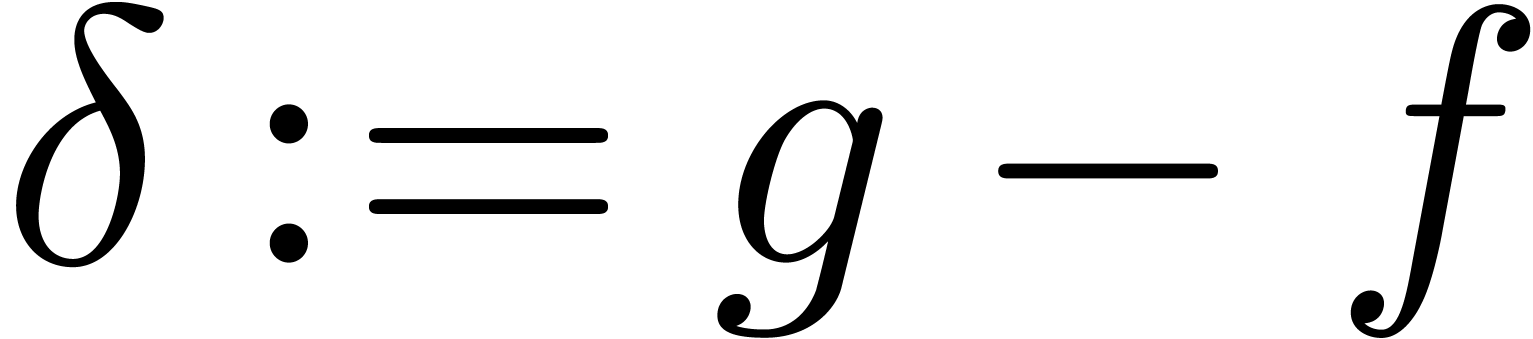 .
. ,
,
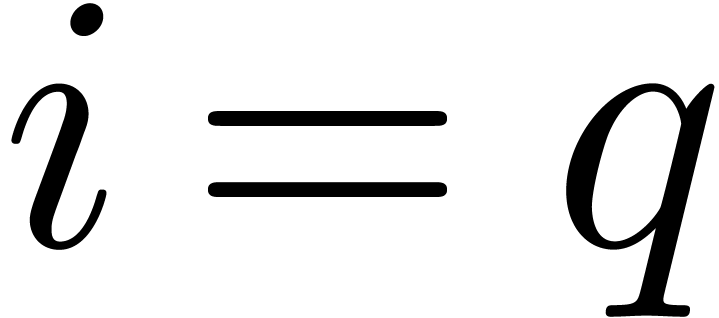 ,
,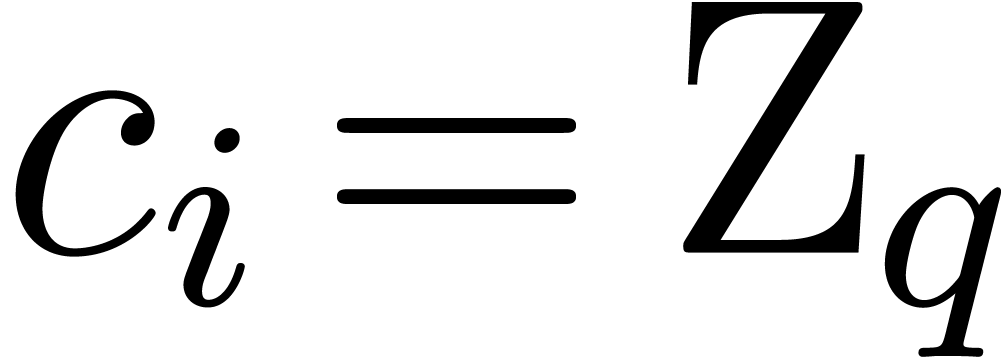 ,
,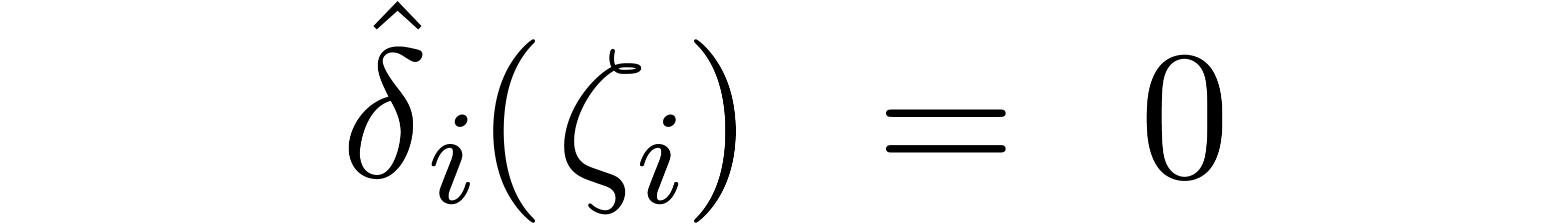
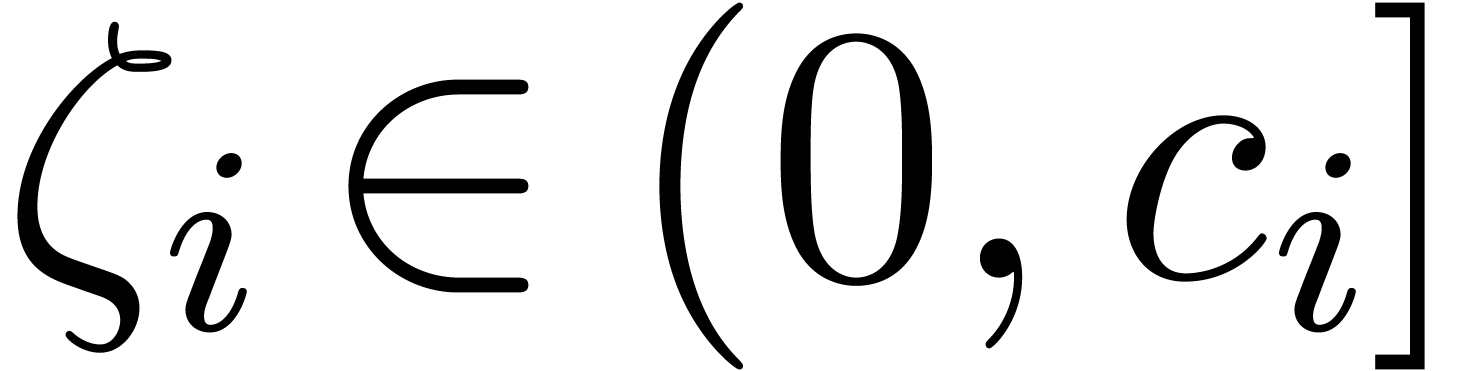 .
.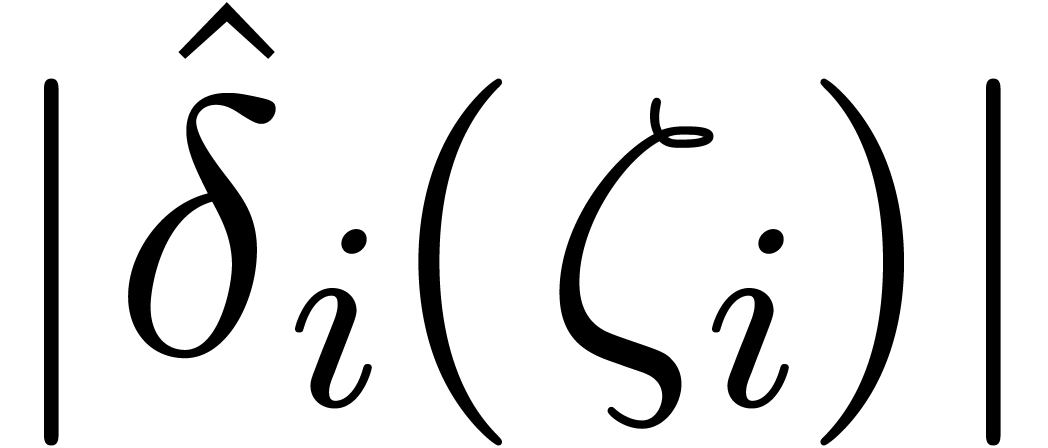 and
and  .
.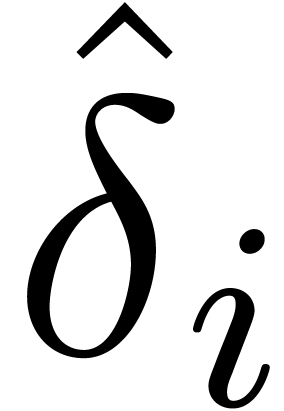 at infinity
at infinity .
.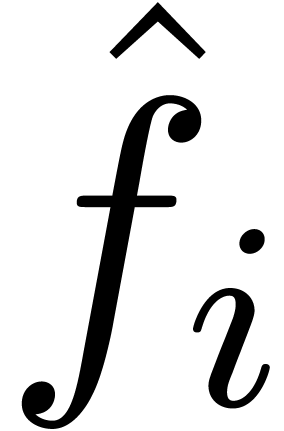 ,
,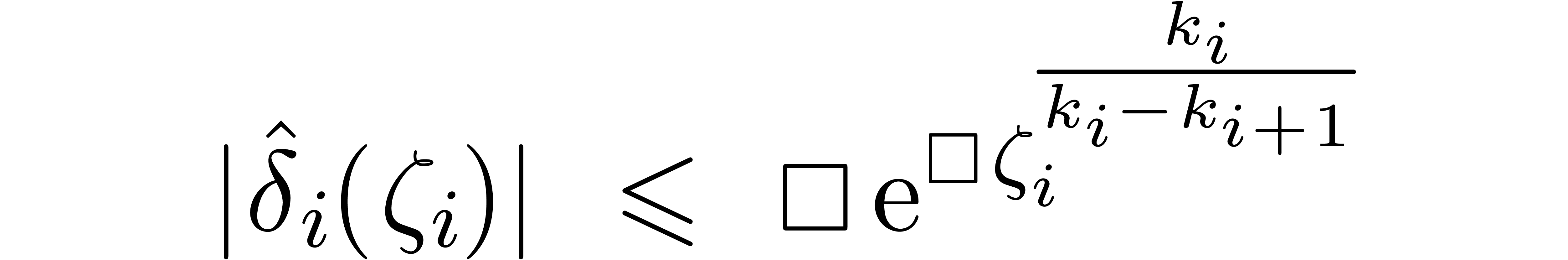
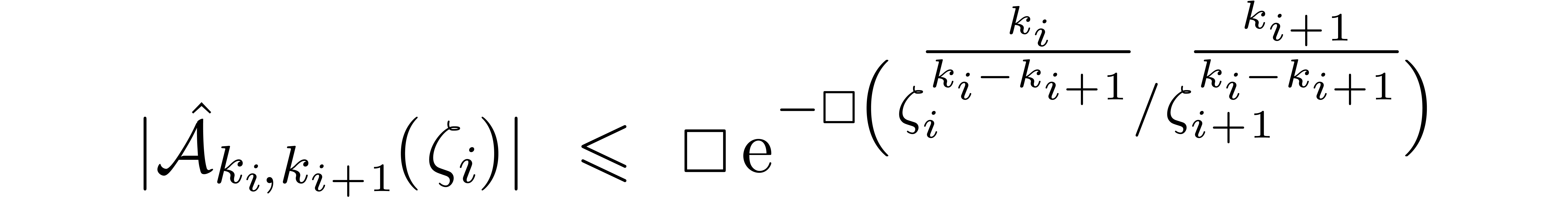
 .
. .
.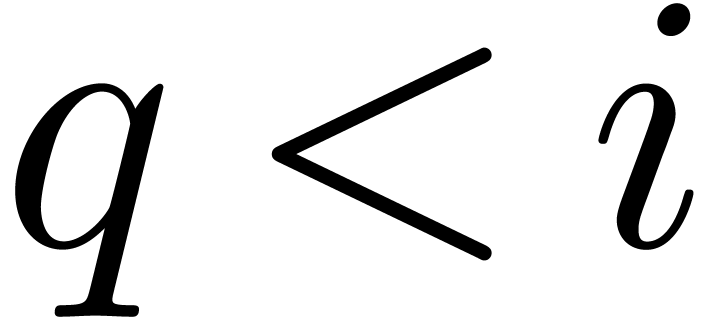 .
.
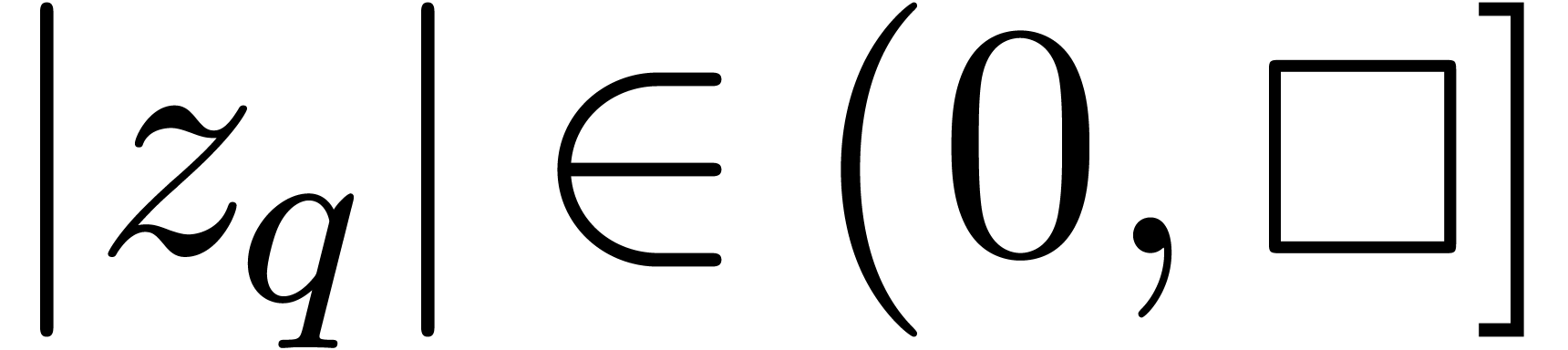 .
.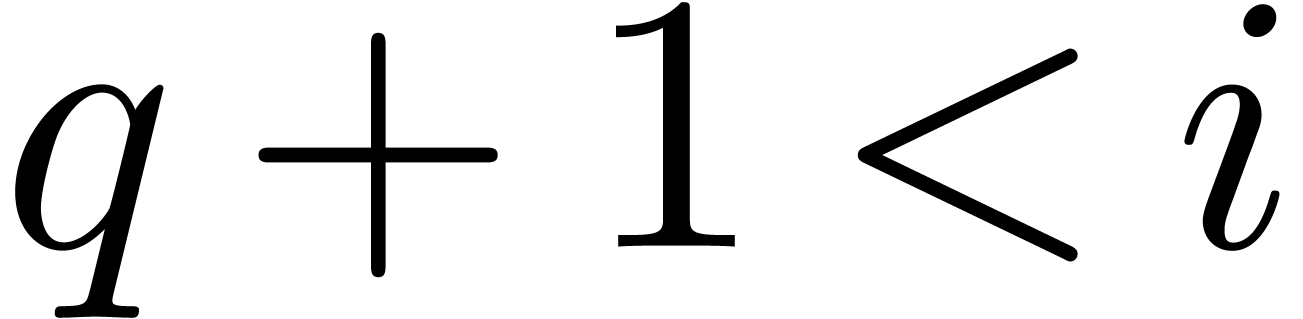 ,
,
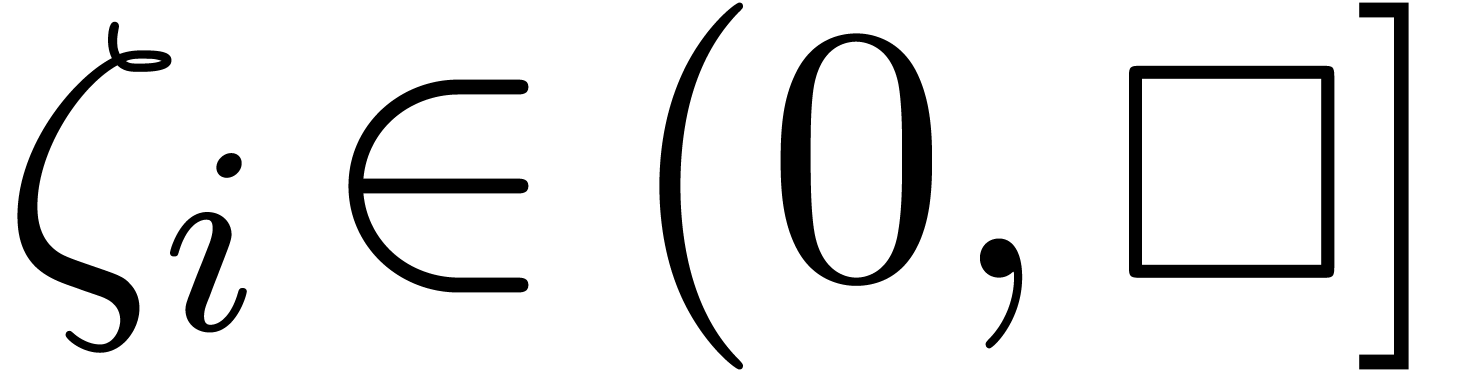 .
.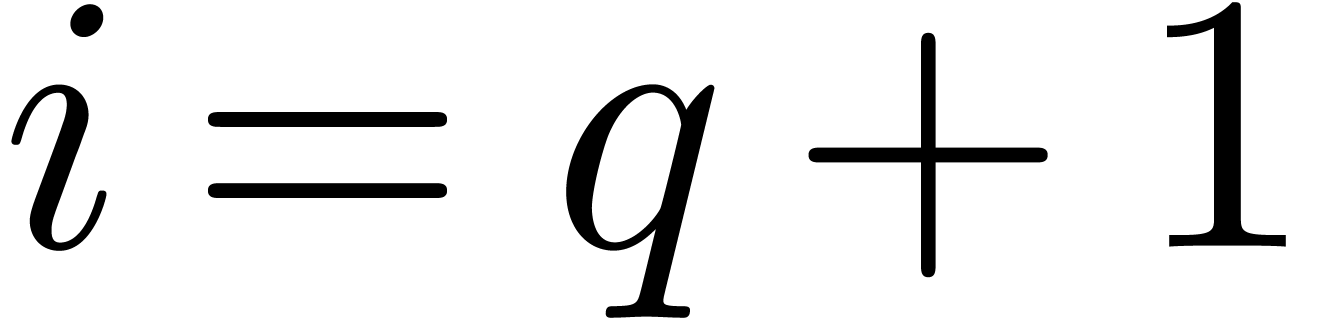 .
. such that, for
such that, for 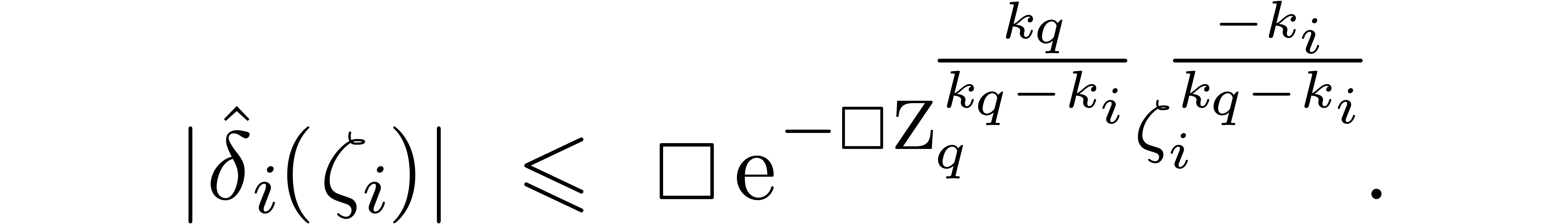
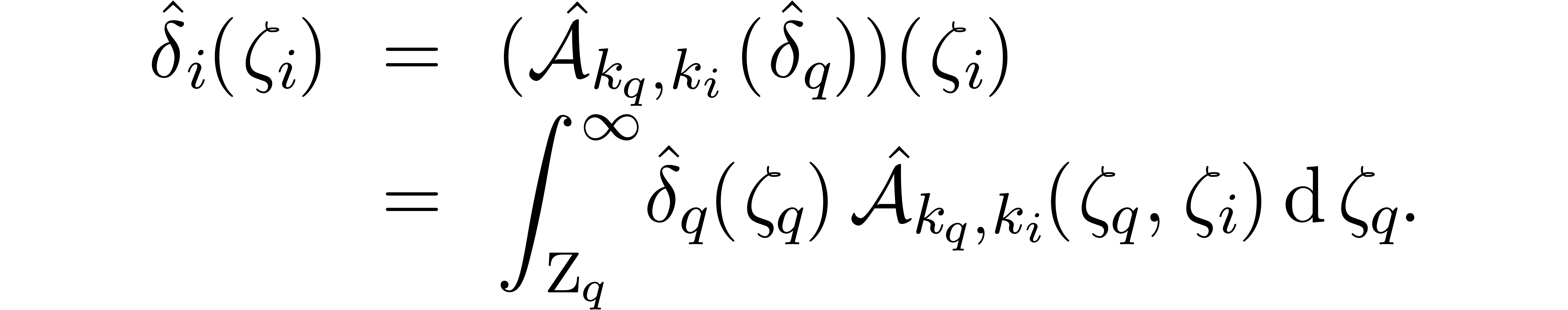

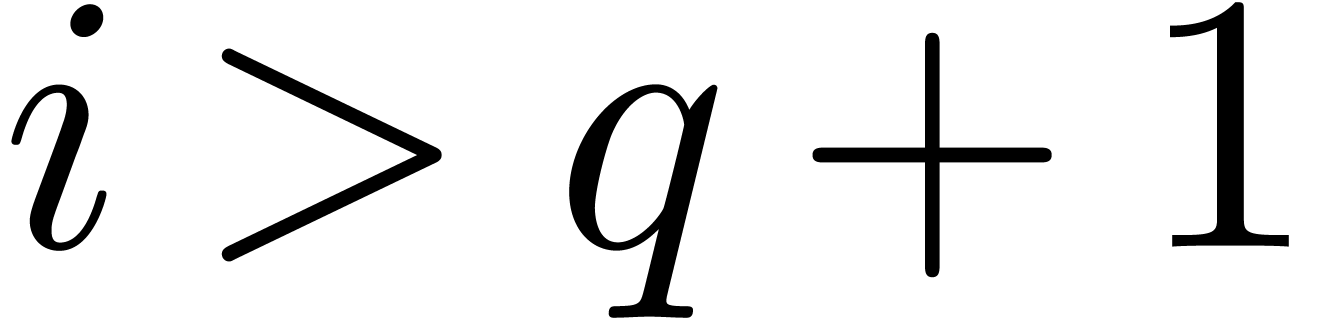 ,
,
 .
.
 ,
,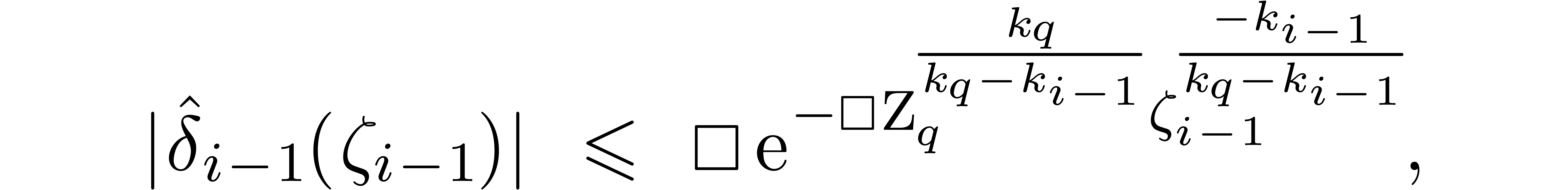
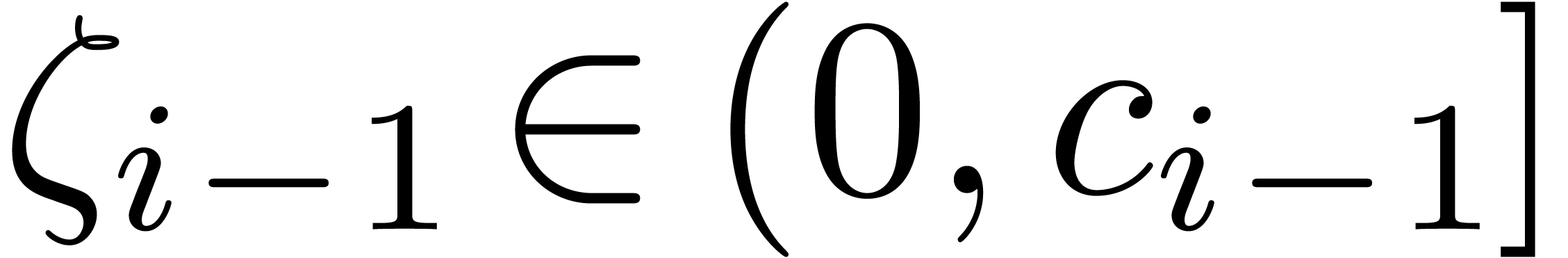 .
.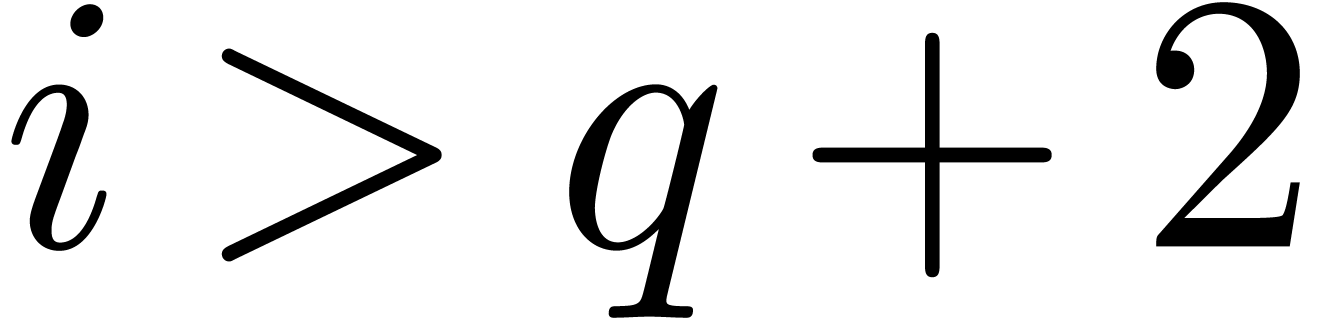 ,
,
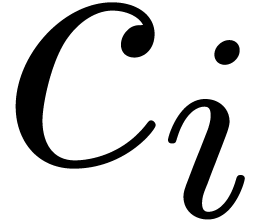 if necessary. Putting these bounds together,
we obtain
if necessary. Putting these bounds together,
we obtain
 .
.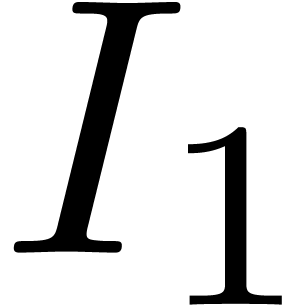 and
and 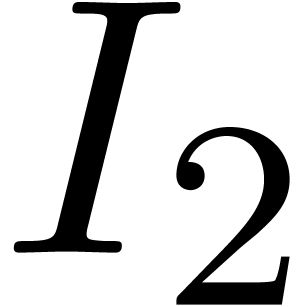 ,
,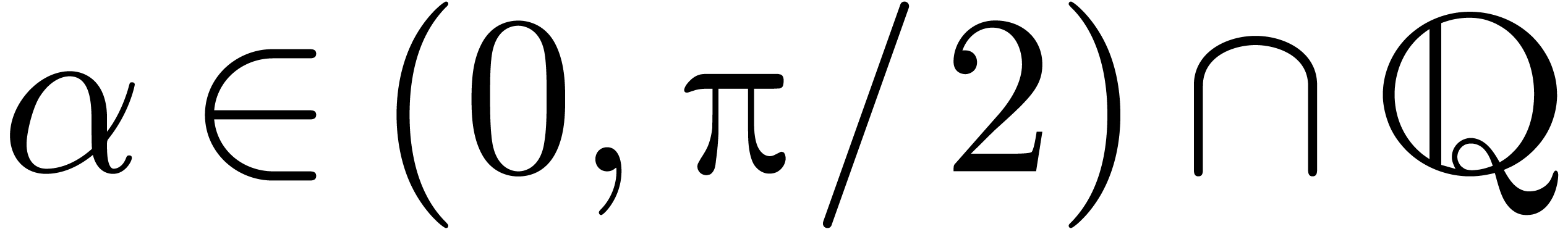 ,
, and a bound
and a bound
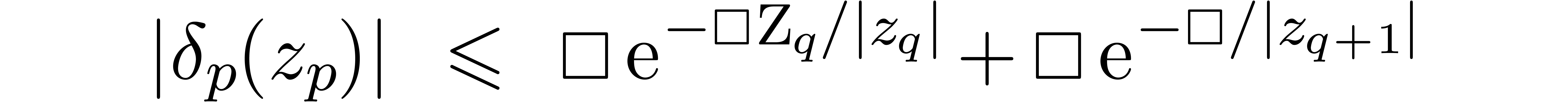
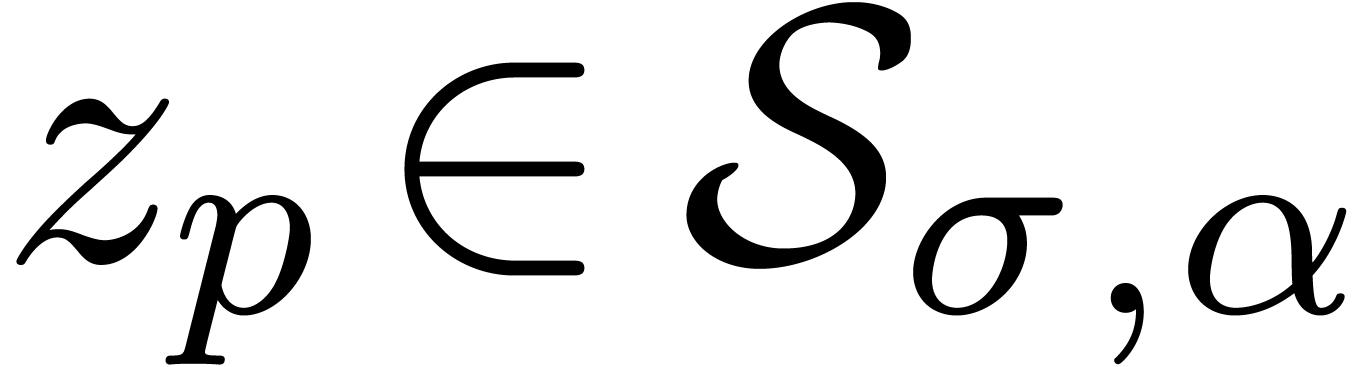 .
.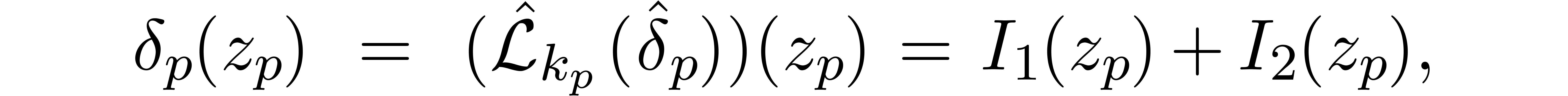
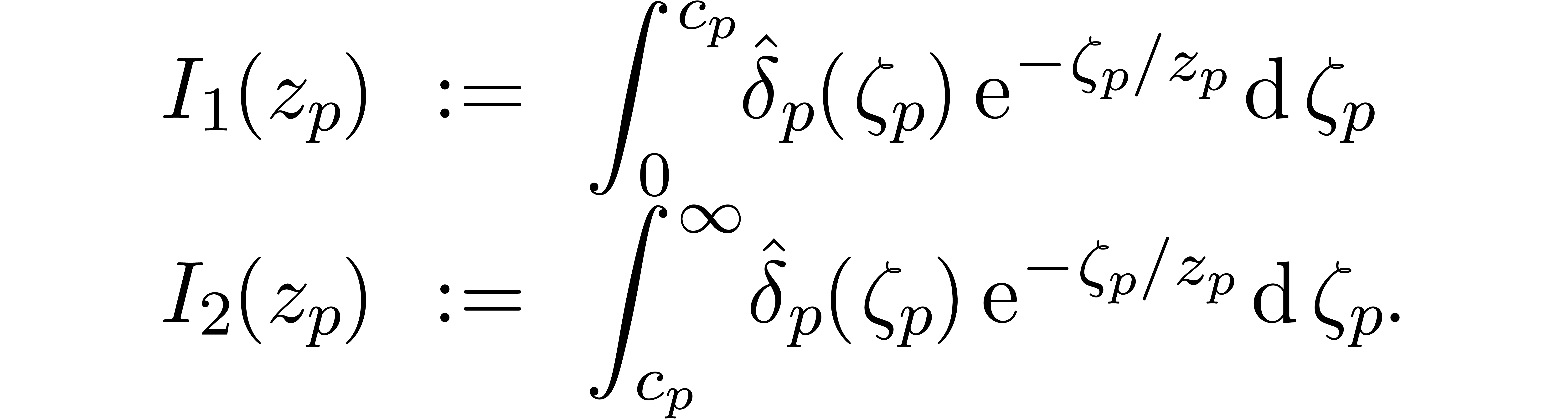
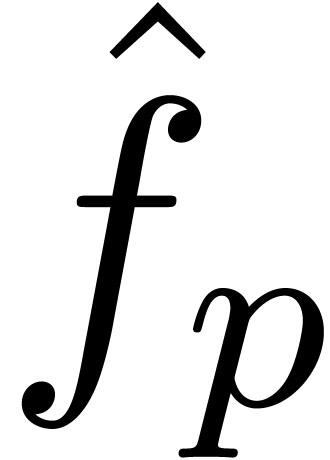 as provided by the
accelero-summation process, we may also compute a bound
as provided by the
accelero-summation process, we may also compute a bound

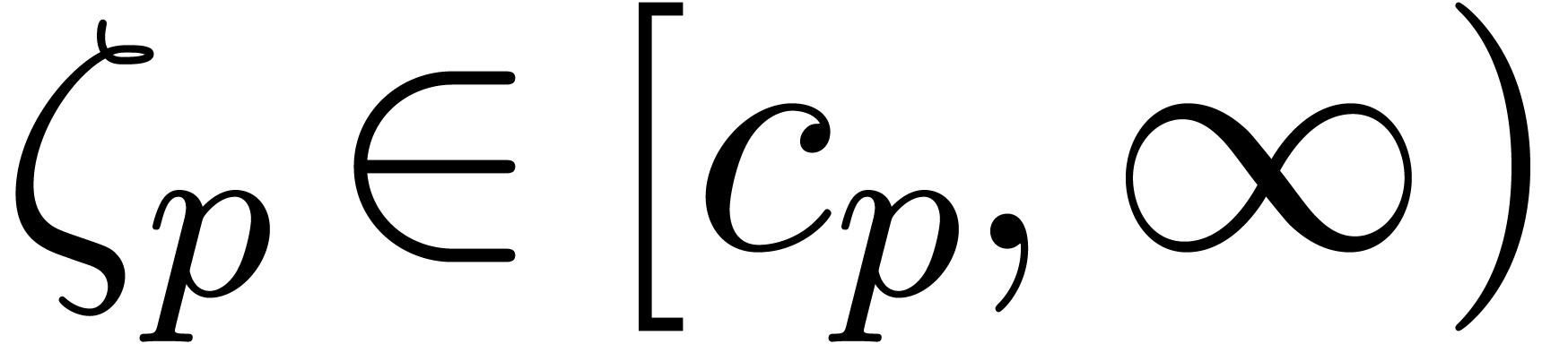 .
. if necessary, this allows us to
compute a bound
if necessary, this allows us to
compute a bound
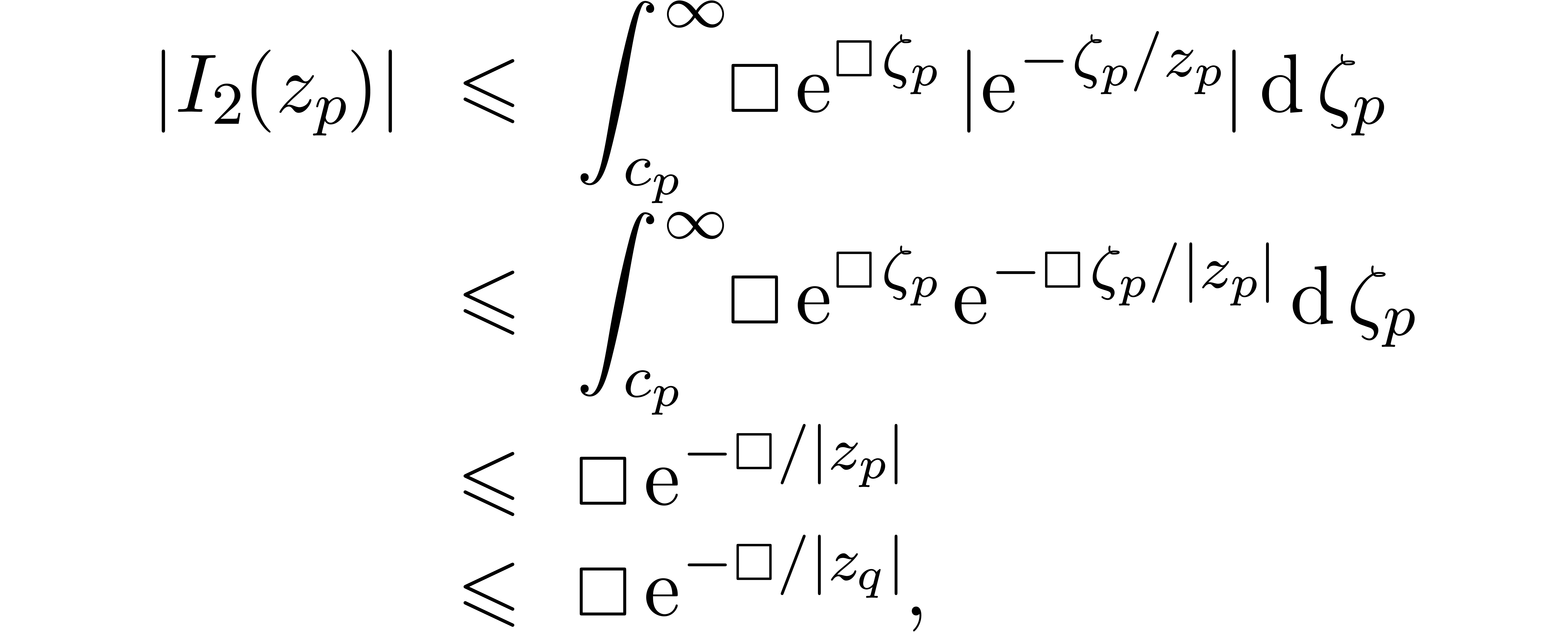
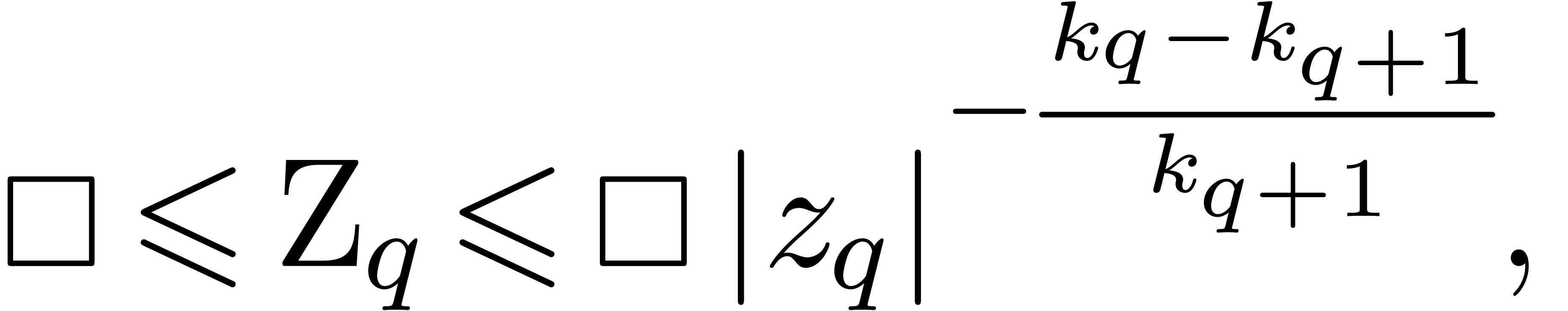

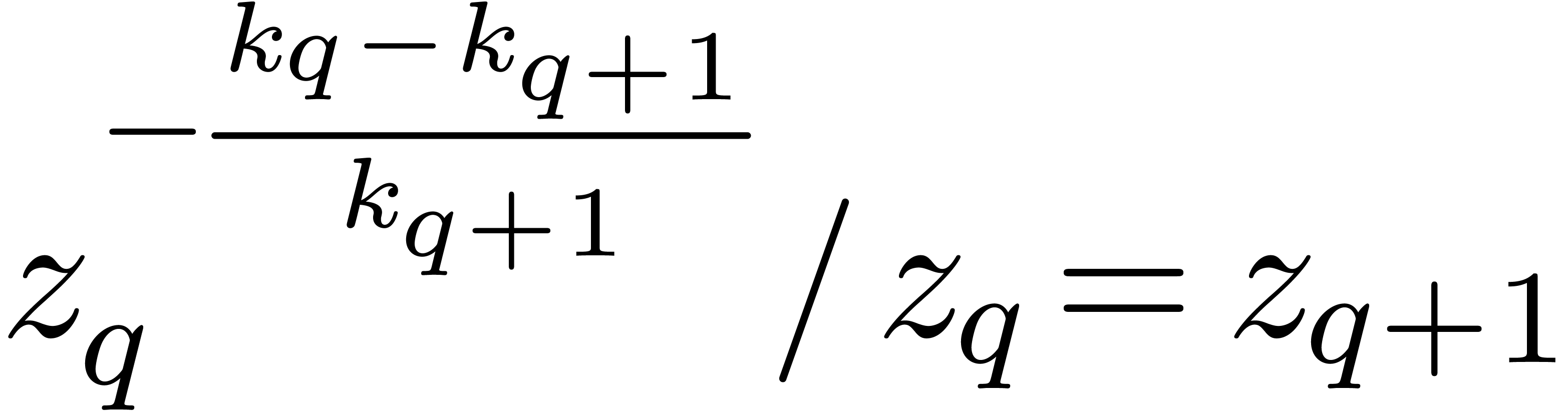 .
. be a fixed aperture
and let
be a fixed aperture
and let  .
.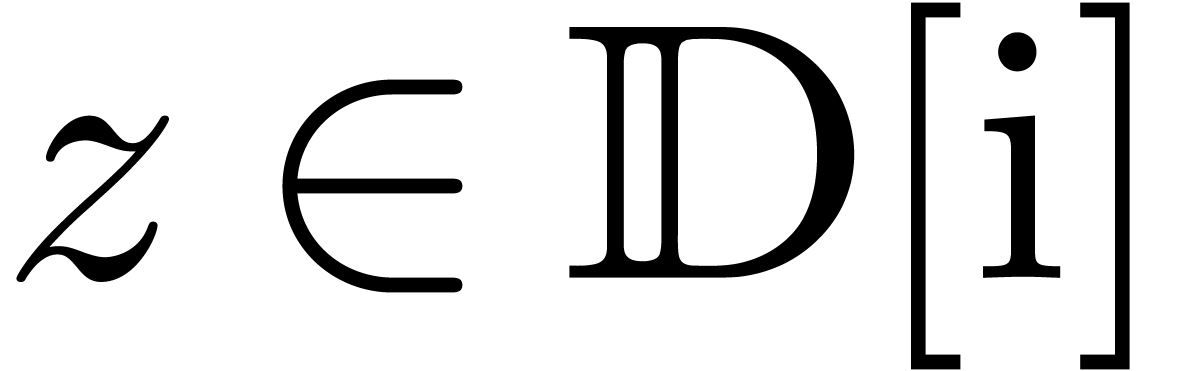 and
and 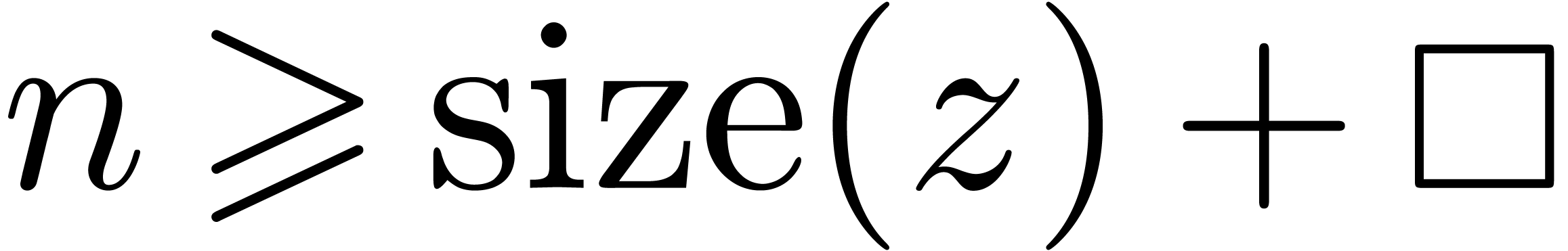 with
with
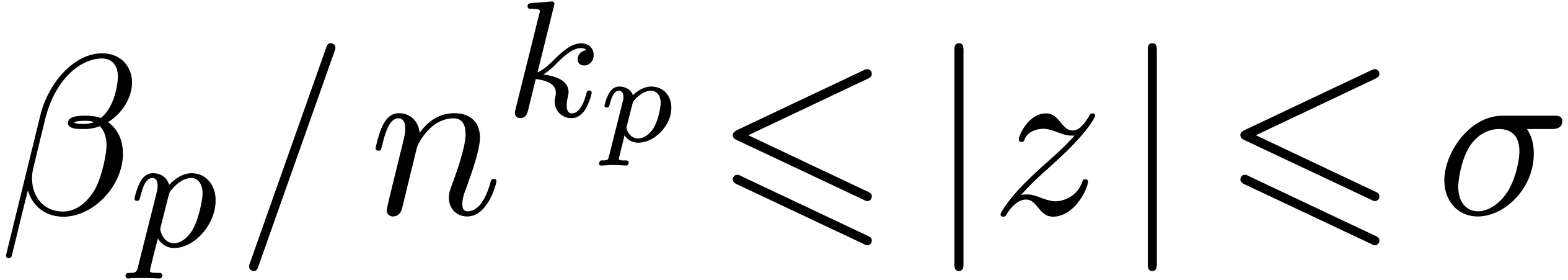
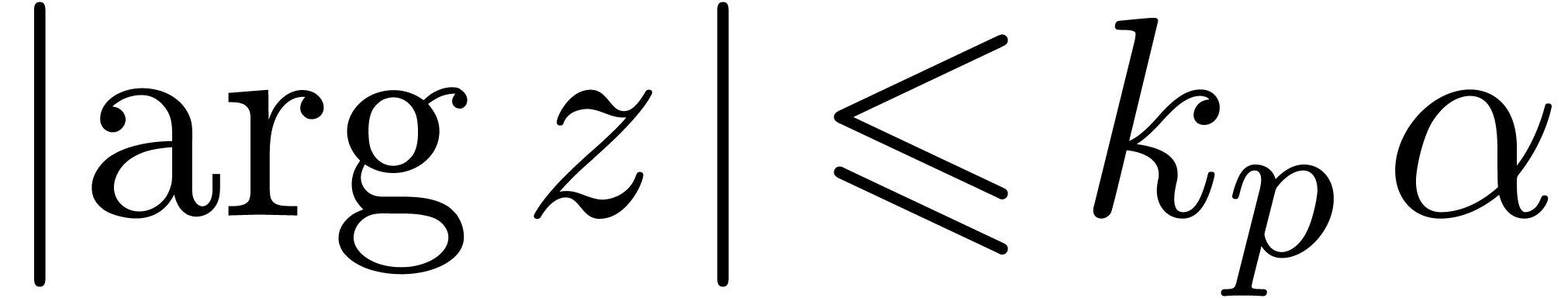 ,
,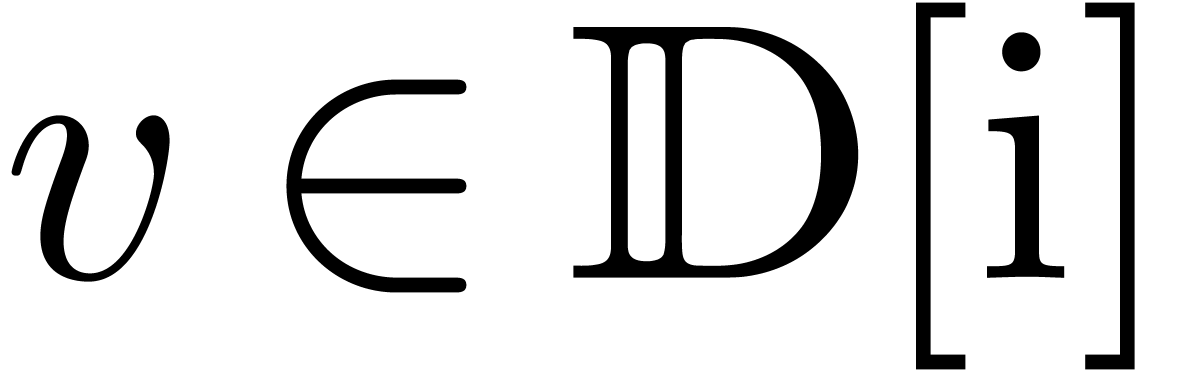 with
with  in
time
in
time 
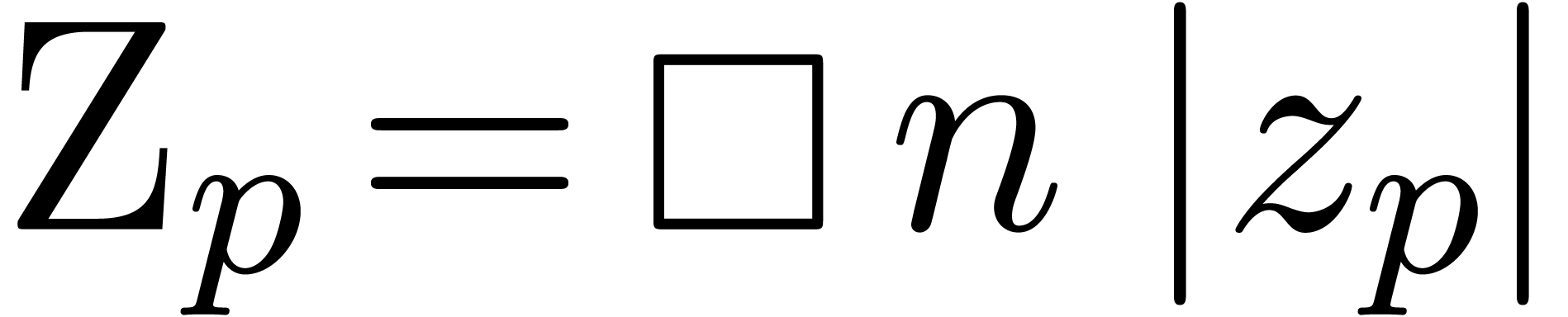 and
and
 ,
,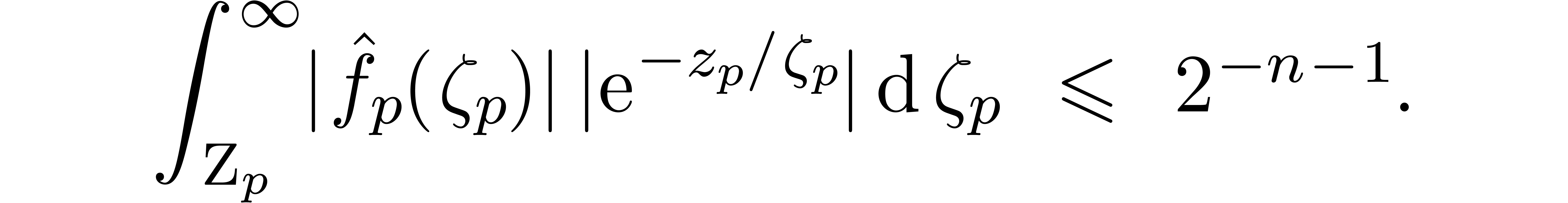
 by approximating the
truncated Laplace integral
by approximating the
truncated Laplace integral
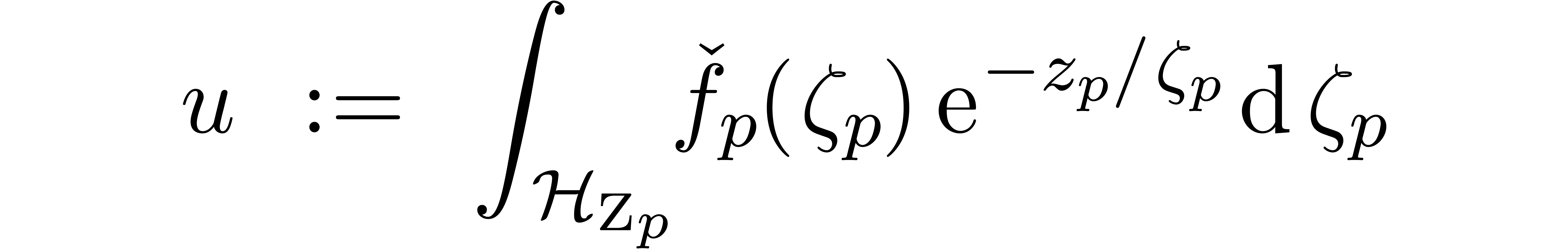
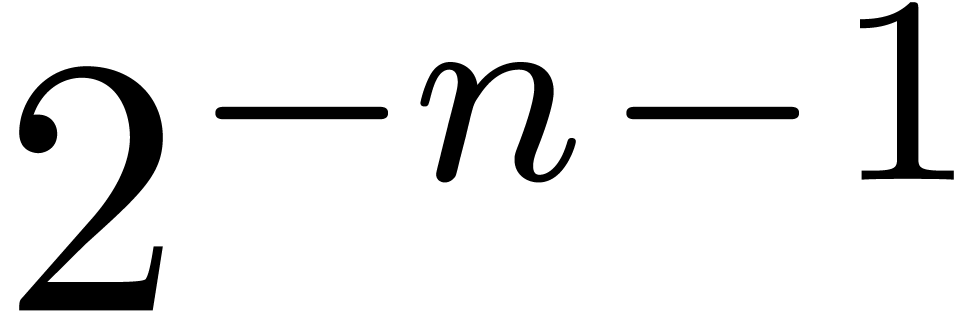 ,
,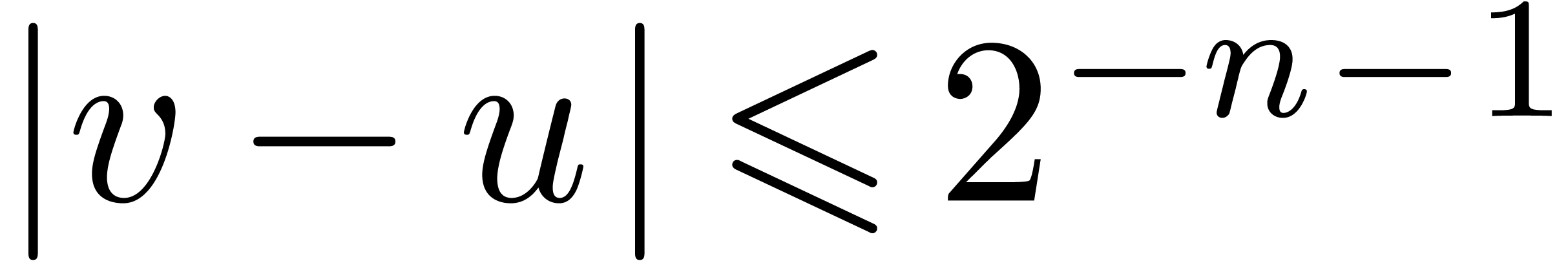 and
and  is bounded by
is bounded by 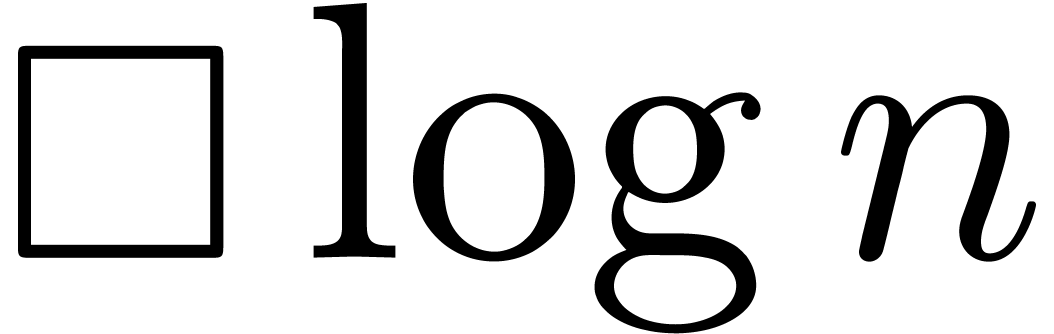 .
.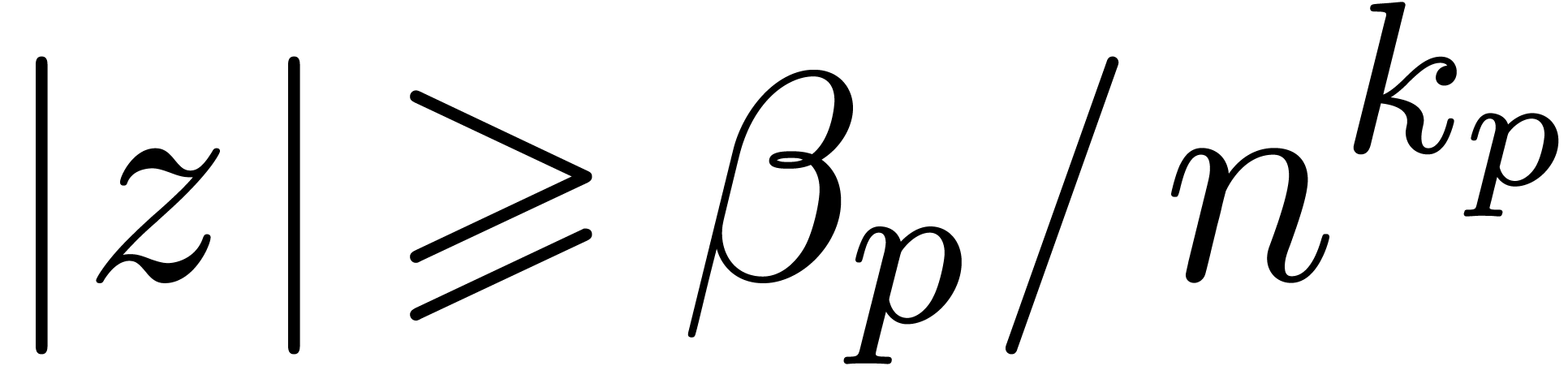 ,
,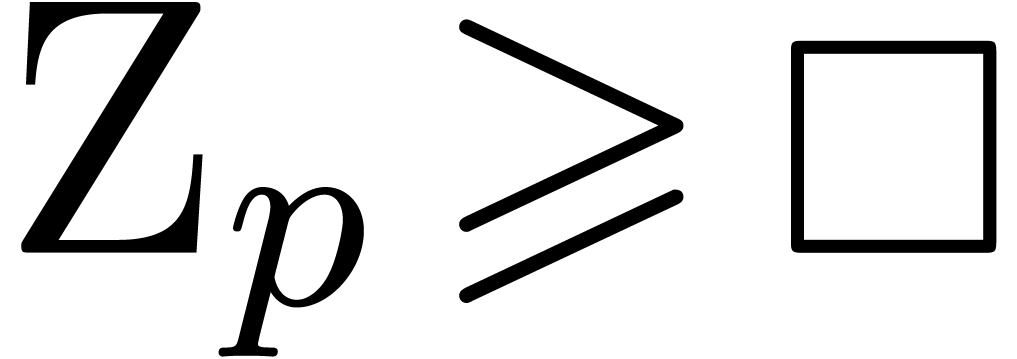 .
.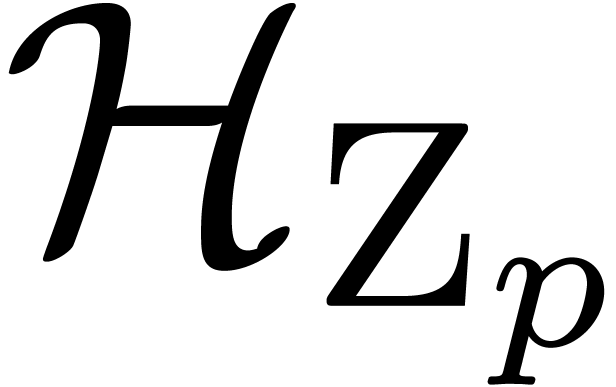 to use a circle of fixed
radius around the origin (which does not depend on
to use a circle of fixed
radius around the origin (which does not depend on 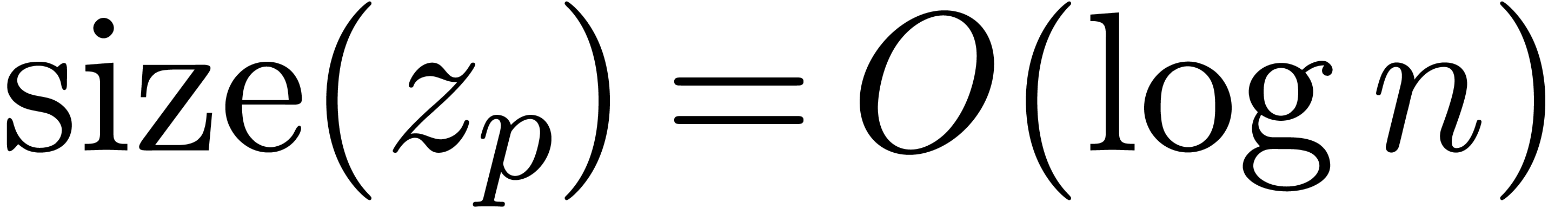 implies that the primitive of
implies that the primitive of 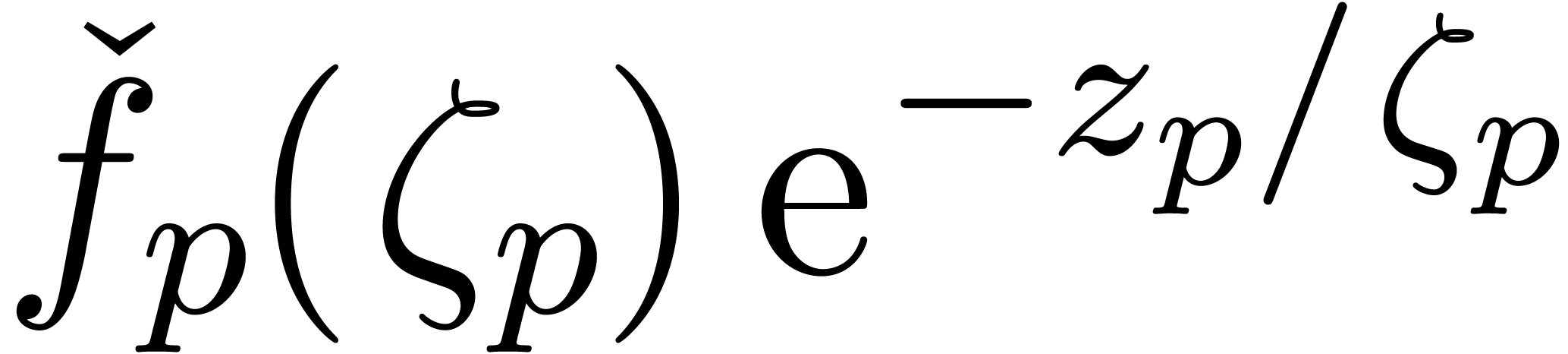 satisfies a holonomic equation of size
satisfies a holonomic equation of size 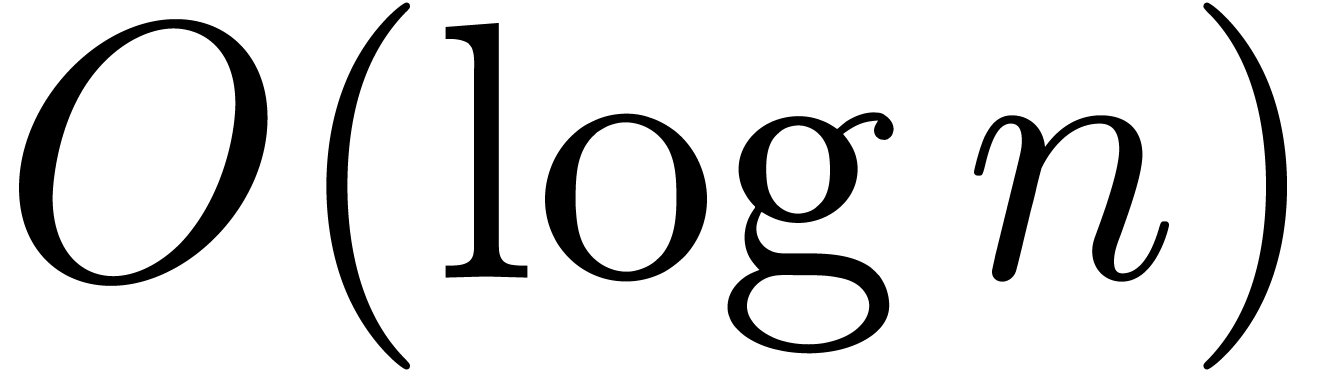 ,
, can be computed in
time
can be computed in
time  be the
growth rate of the linear differential equation satisfied by
be the
growth rate of the linear differential equation satisfied by  at the origin. In [
at the origin. In [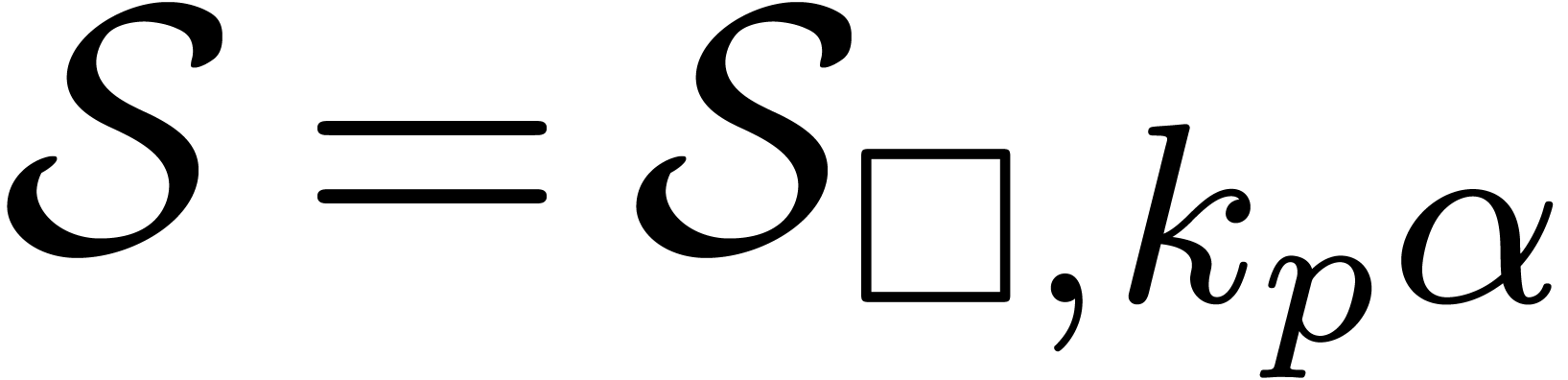 ,
, in
in  :
:
 ,
,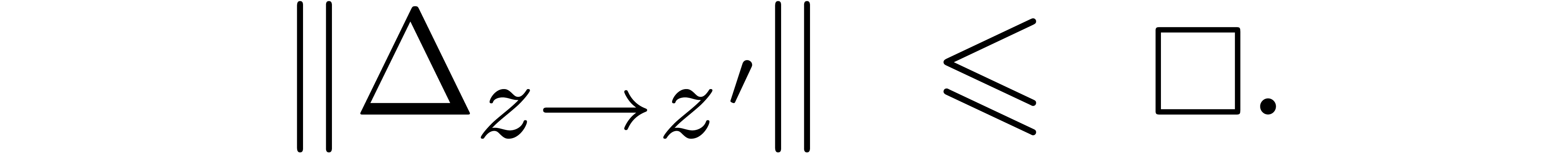
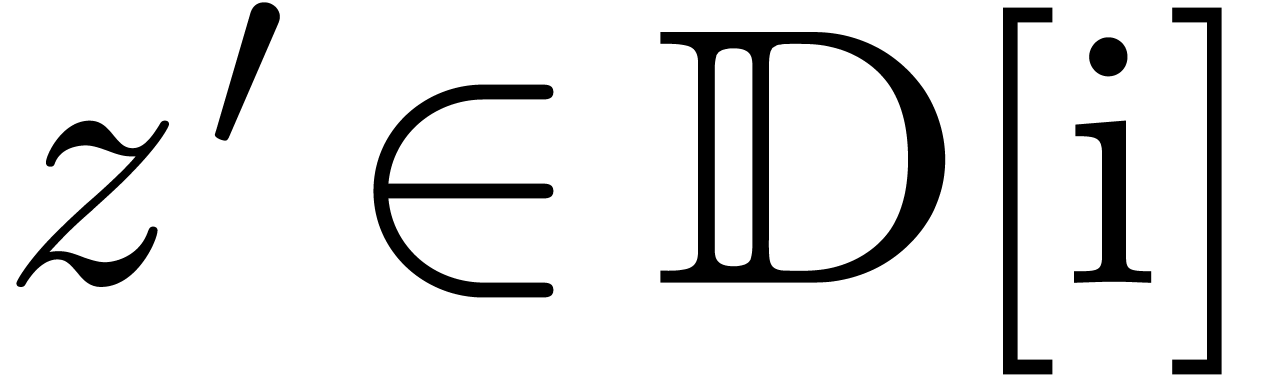 be an approximation of
be an approximation of  .
.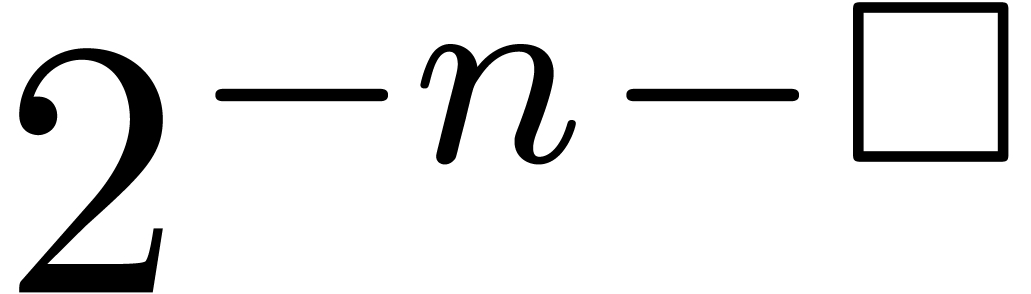 -approximations
-approximations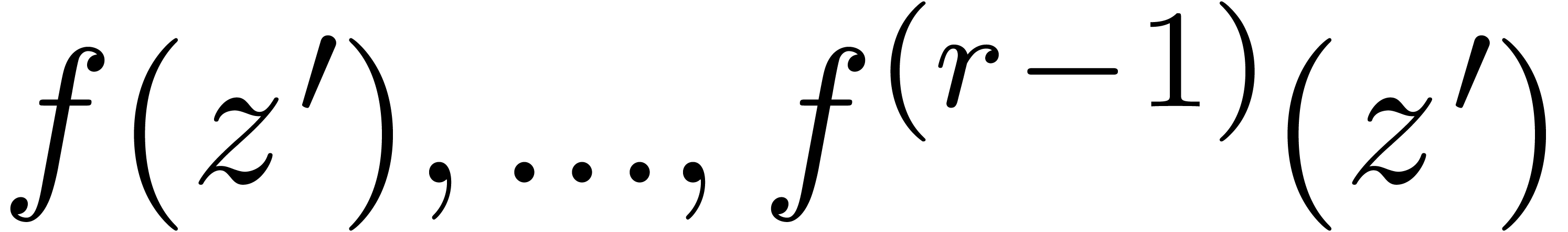 in time
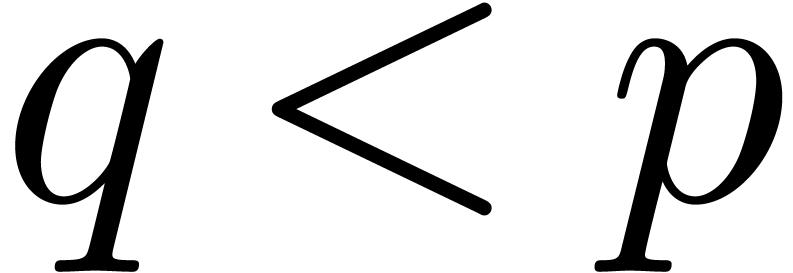
in time  such that
such that
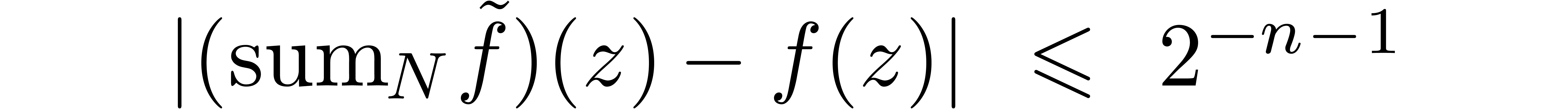
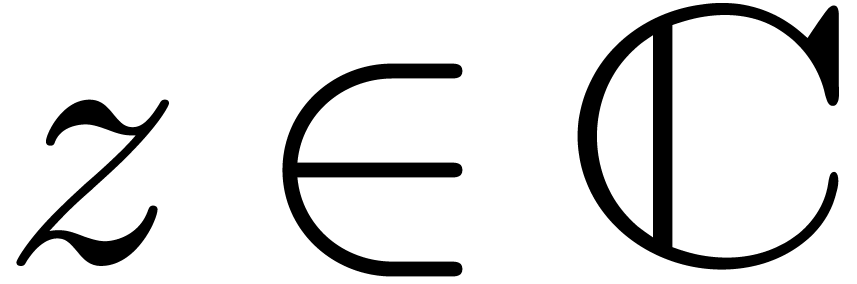 ,
,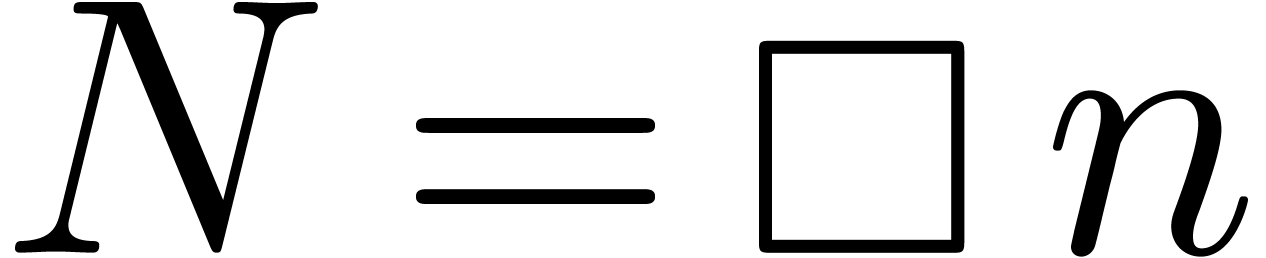 with
with
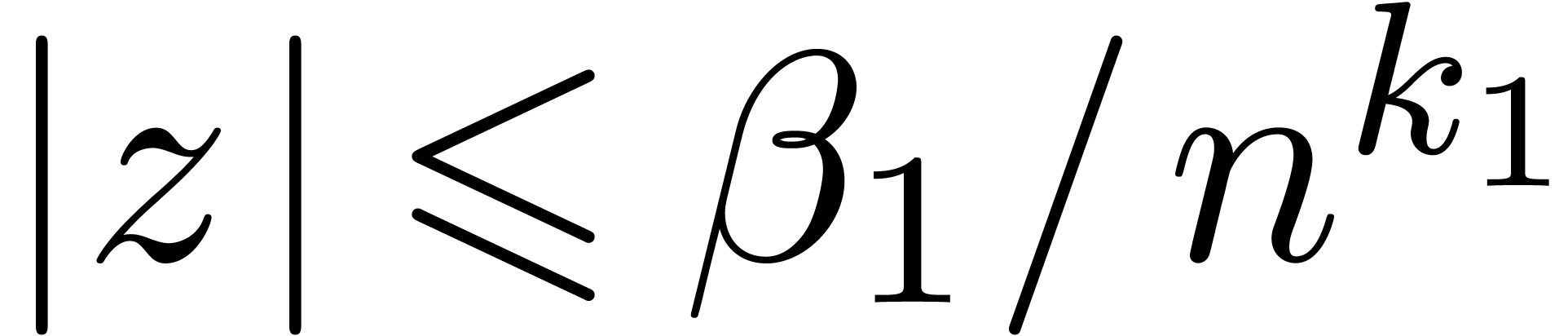
 ,
,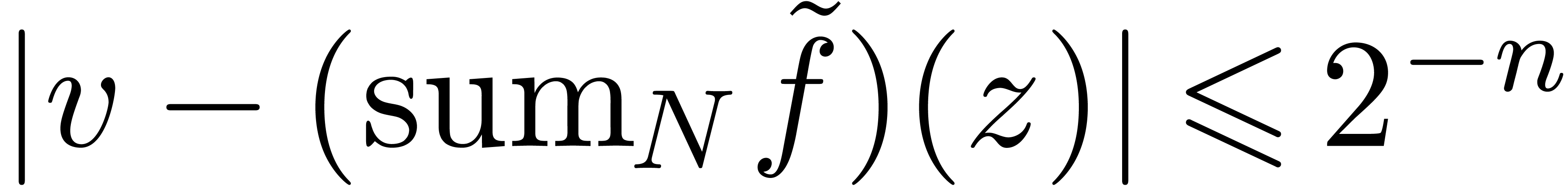 in time
in time 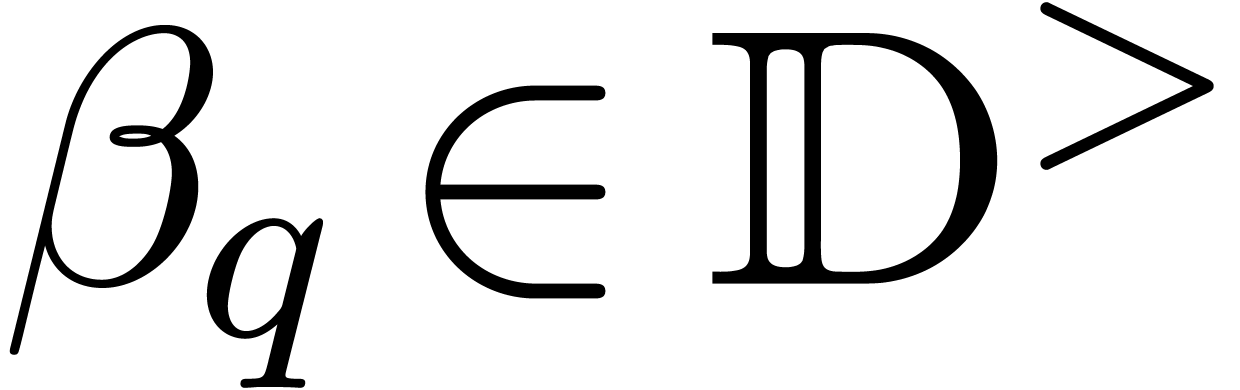 ,
, .
.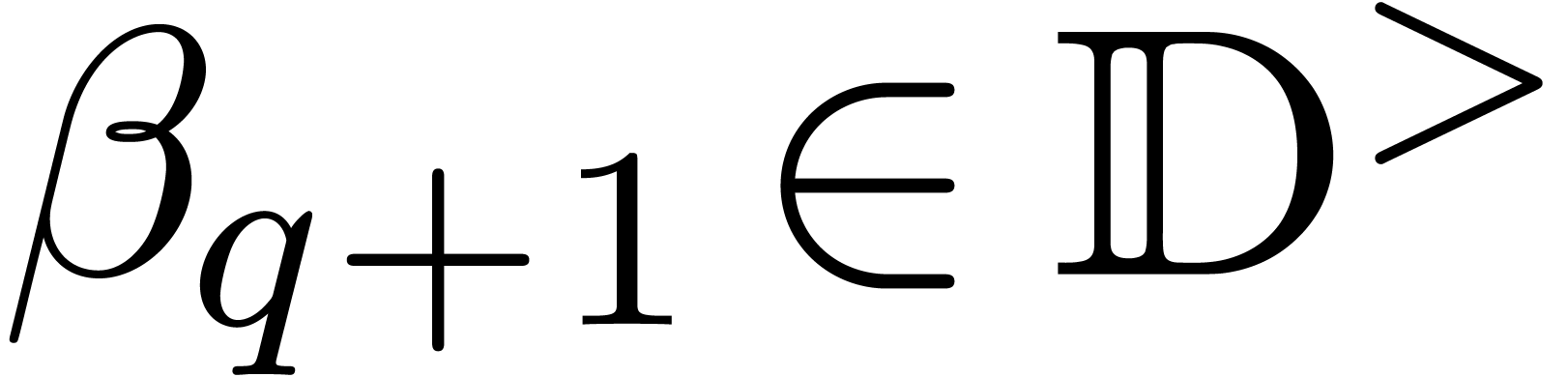 such that
such that
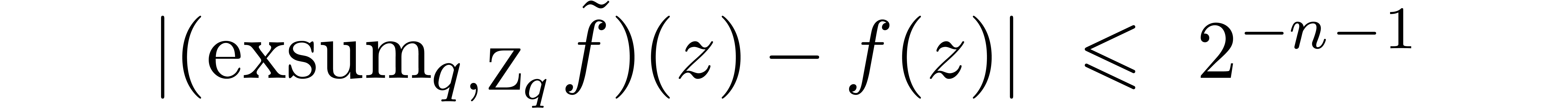
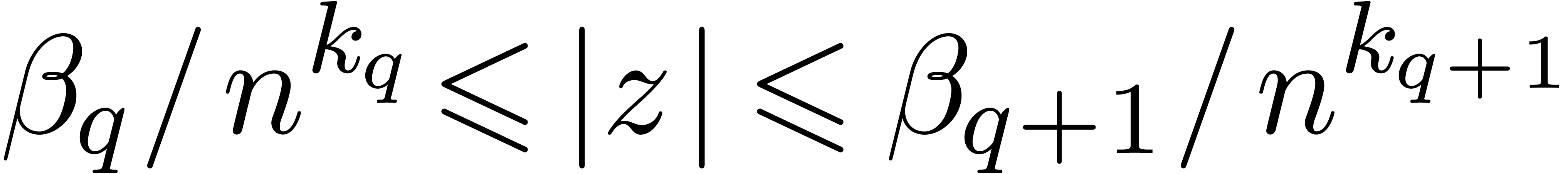

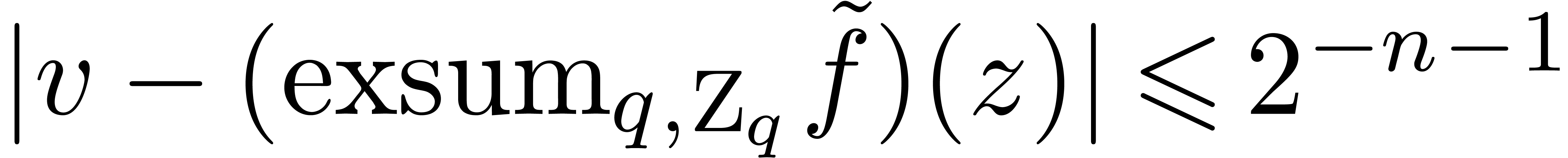 in time
in time  implies that
implies that
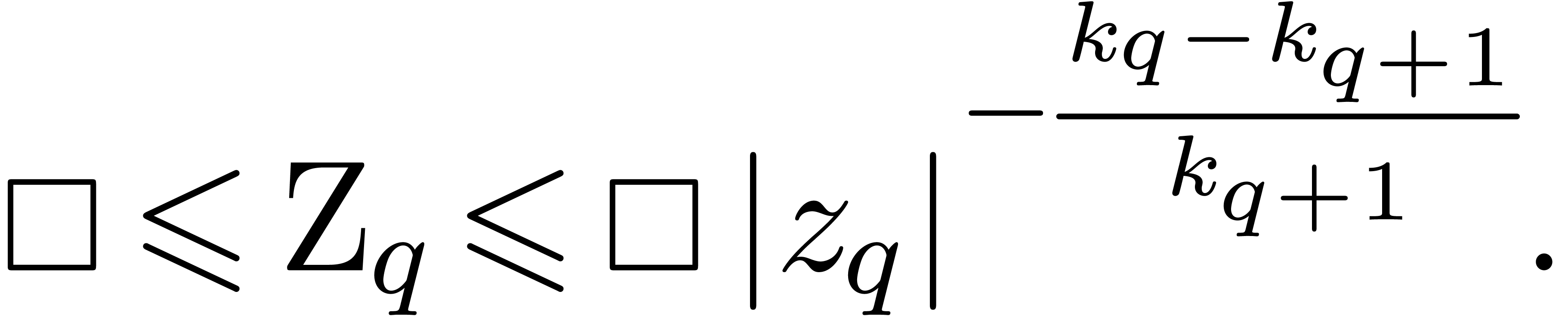
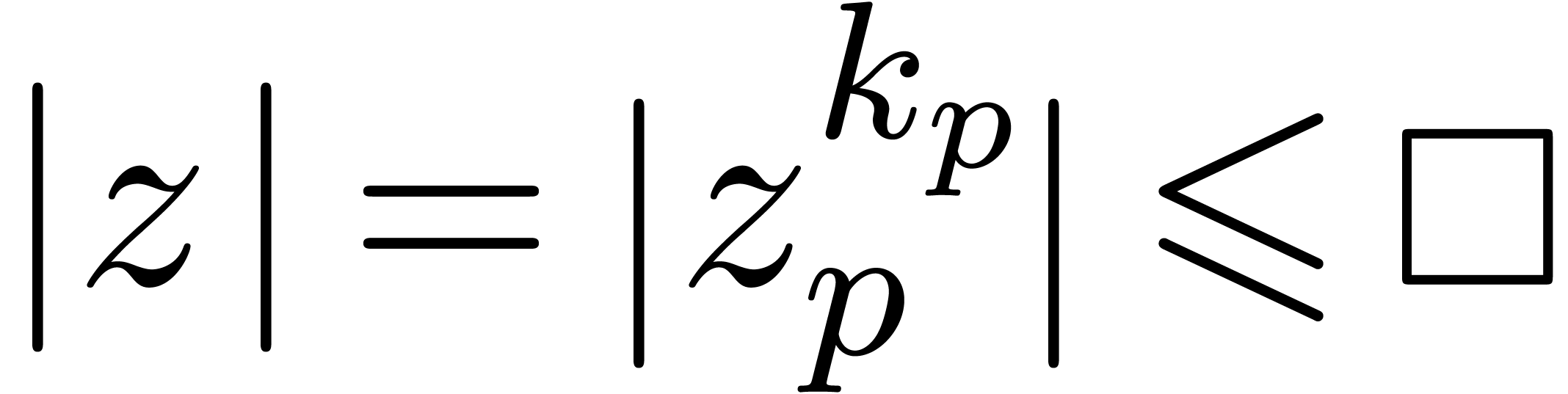 and
and 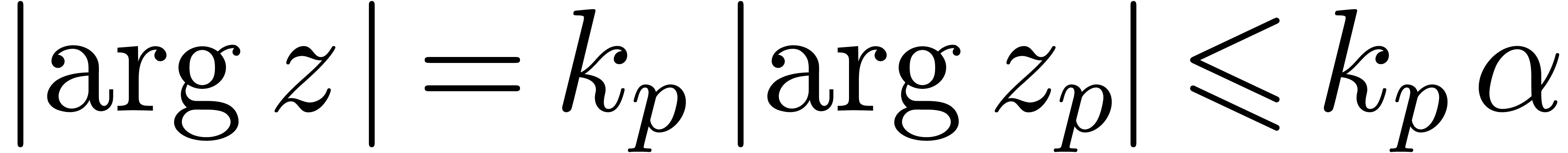 ,
,
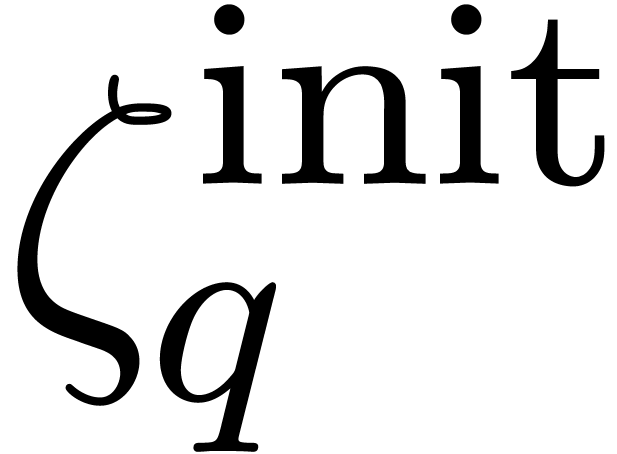 close to the origin and
close to the origin and
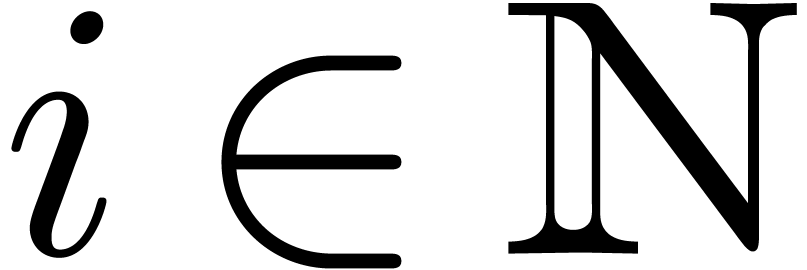 ,
,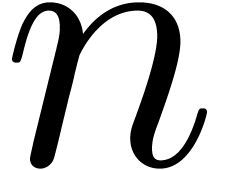 decimal digits of
decimal digits of 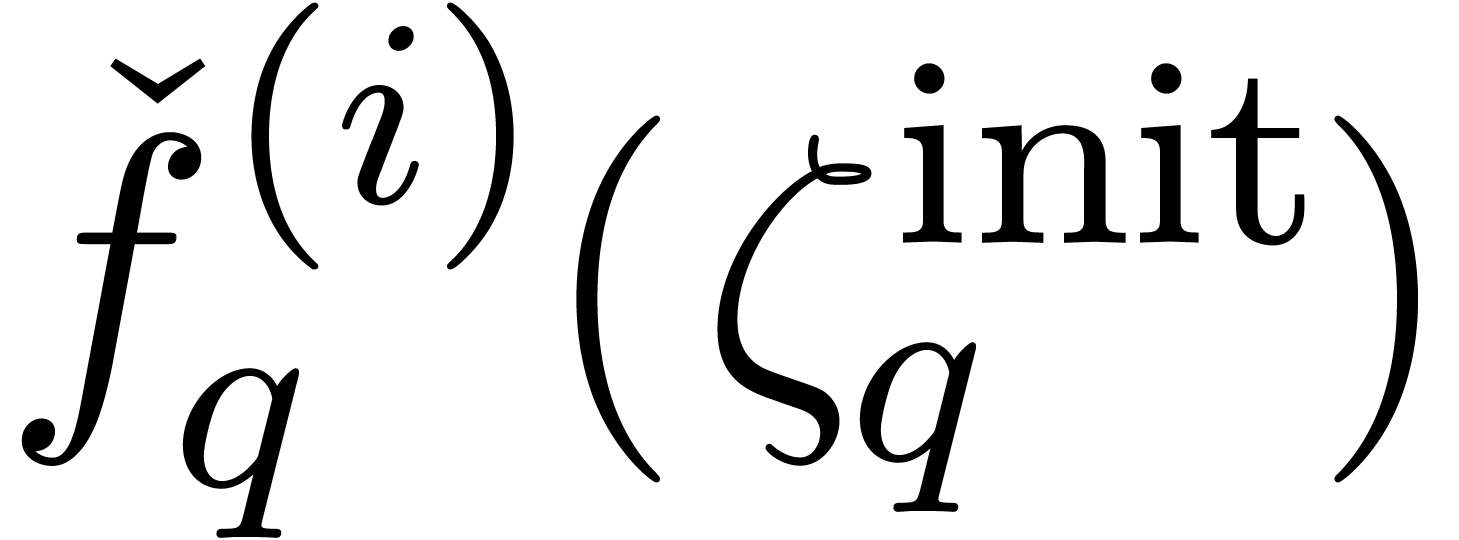 in time
in time 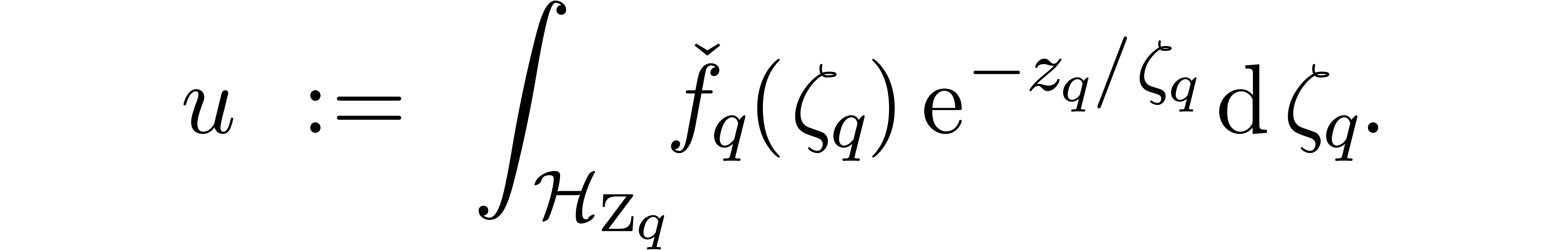
 with the following
property. Given
with the following
property. Given  and
and  ,
,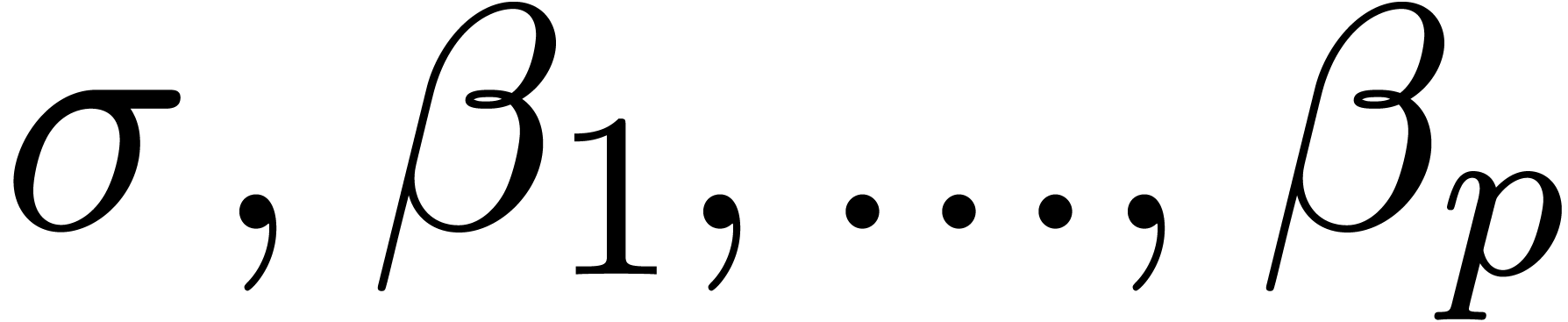 be as in
Propositions
be as in
Propositions 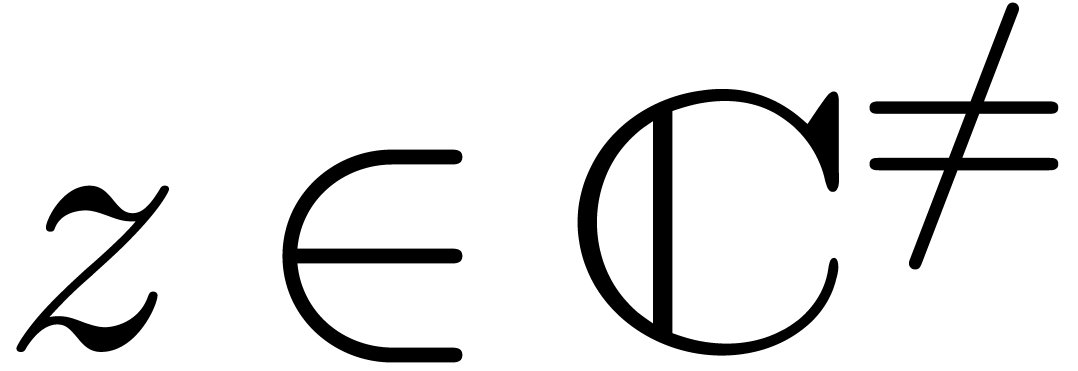 with
with 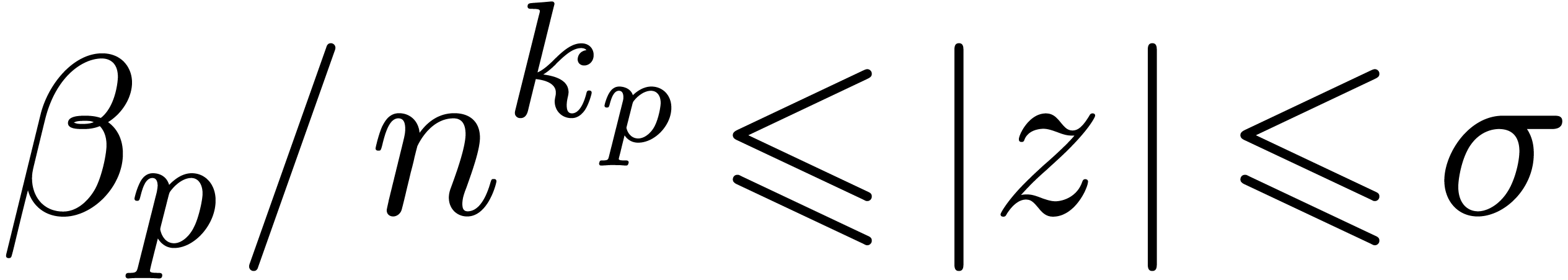 .
.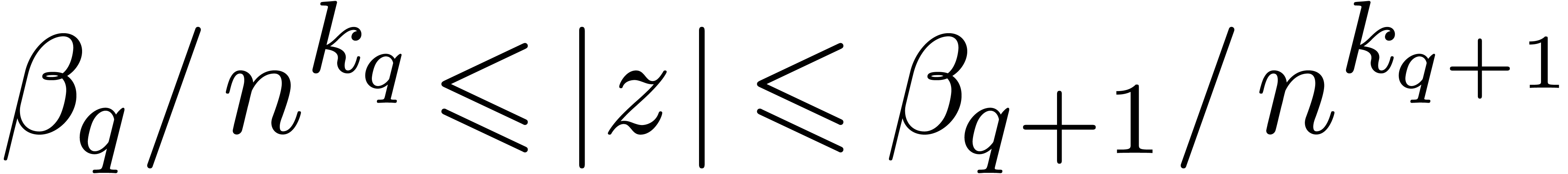 for some
for some 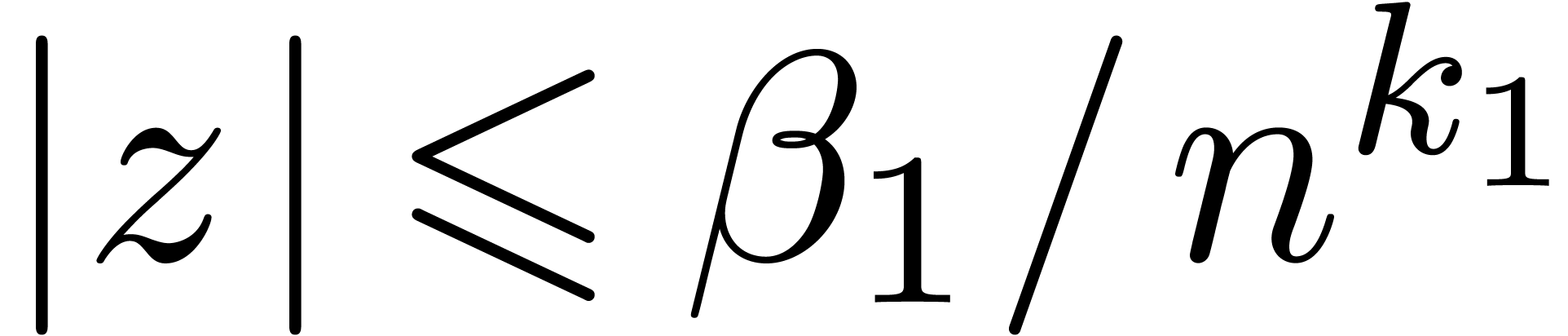 .
. is singular at the origin. Then for
some
is singular at the origin. Then for
some 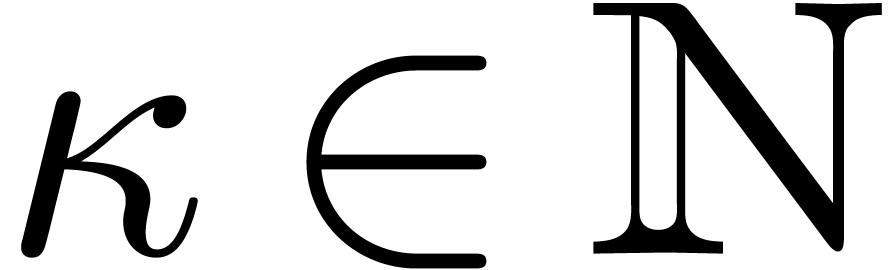 ,
,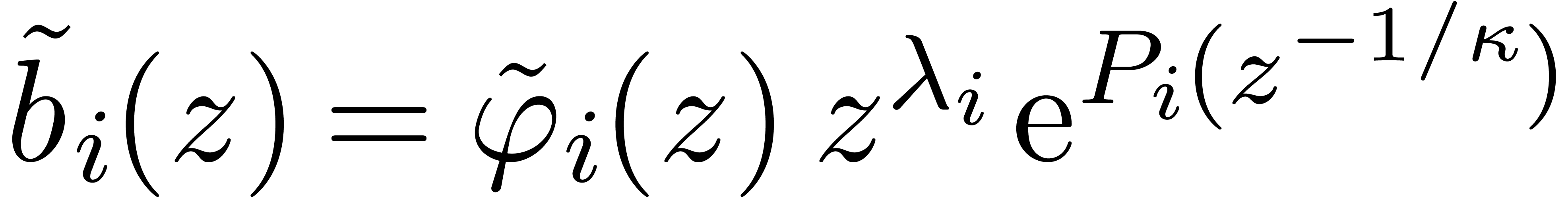
 of
of
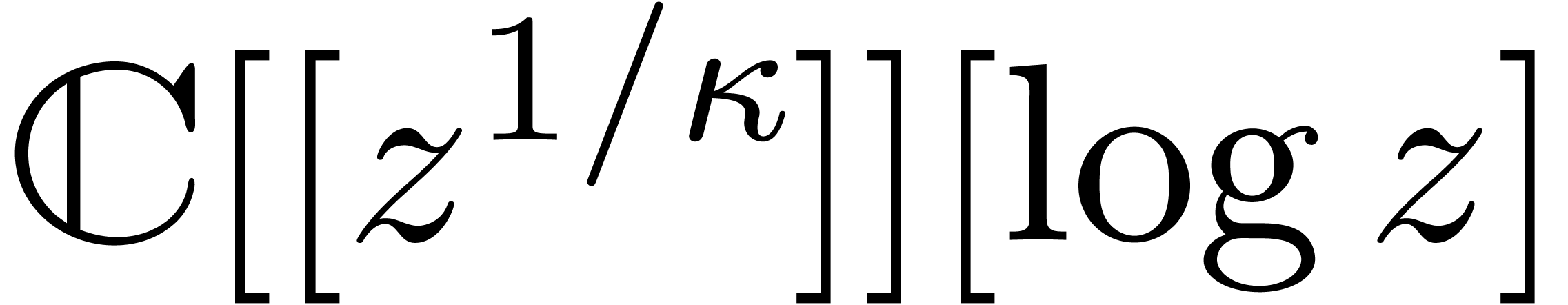 accelero-summable series.
accelero-summable series.
 ,
, and
and  such that the
such that the 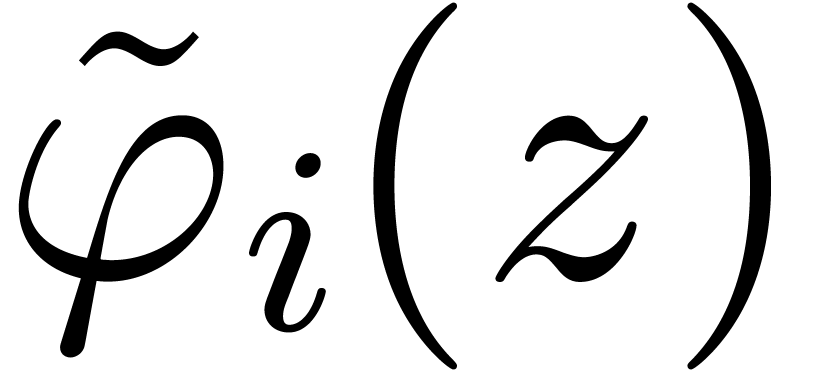 and
and 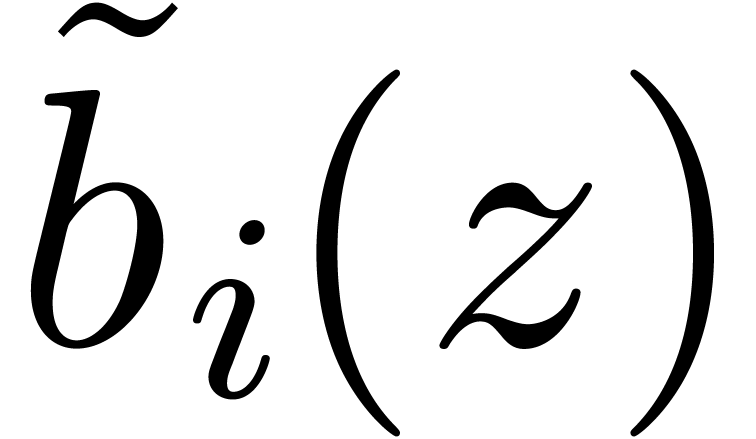 give
rise to analytic functions
give
rise to analytic functions 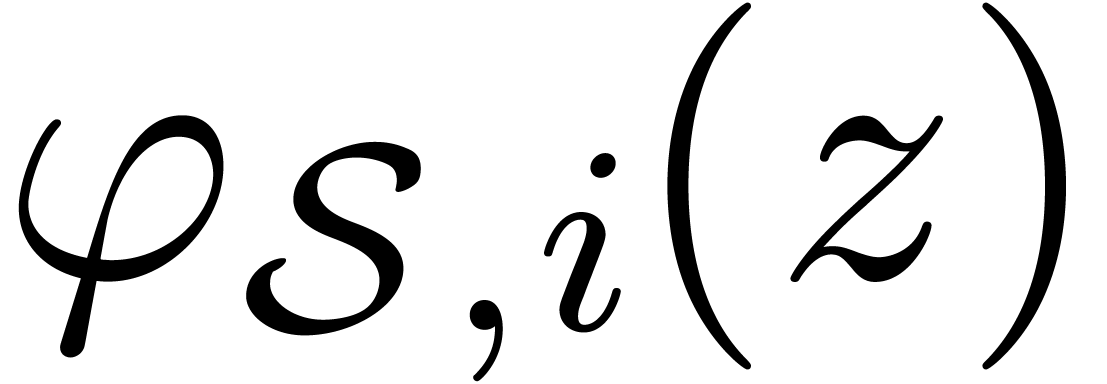 and
and 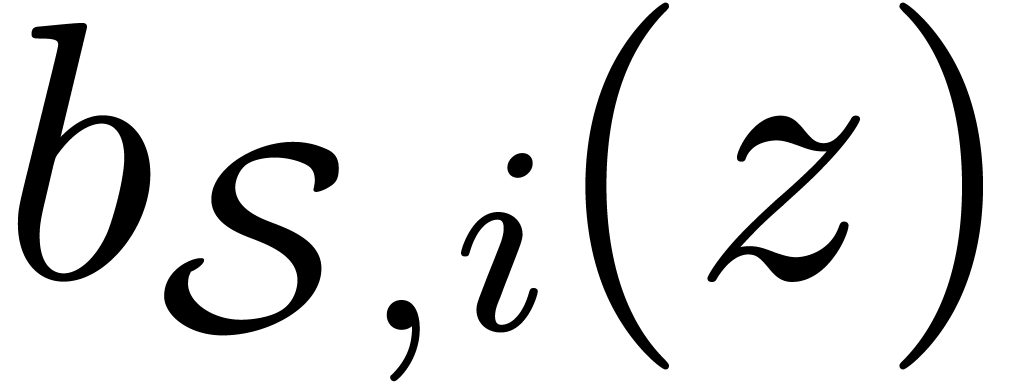 on the sector
on the sector 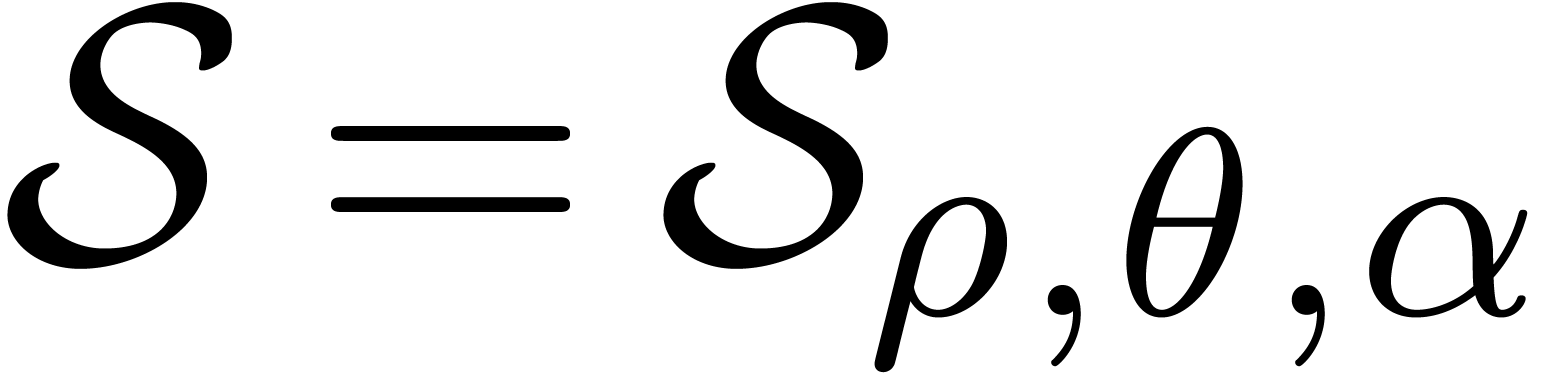 .
. for which this happens is said to be
admissible. Moreover, there exist a finite number of admissible
sectors
for which this happens is said to be
admissible. Moreover, there exist a finite number of admissible
sectors  with
with 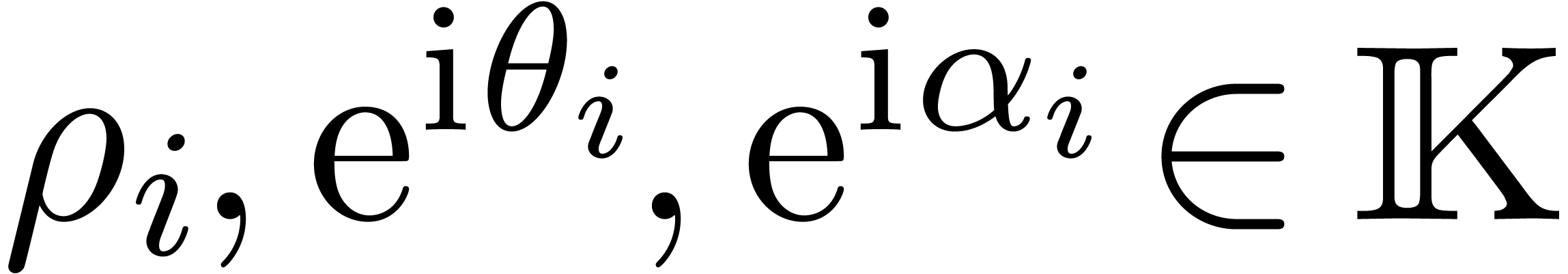 whose
interiors cover a small neighbourhood of
whose
interiors cover a small neighbourhood of 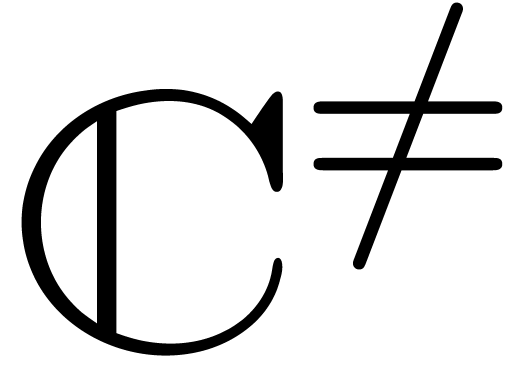 .
.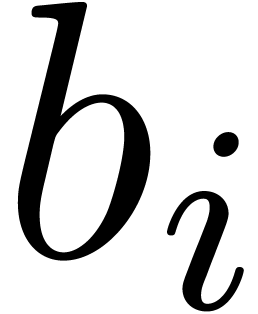 denote the
accelero-sums of
denote the
accelero-sums of 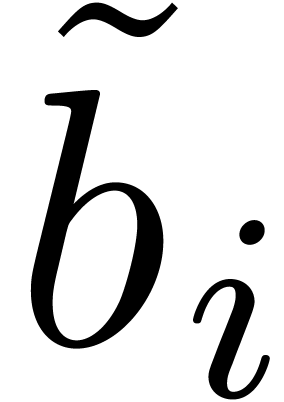 on
this sector. For each
on
this sector. For each 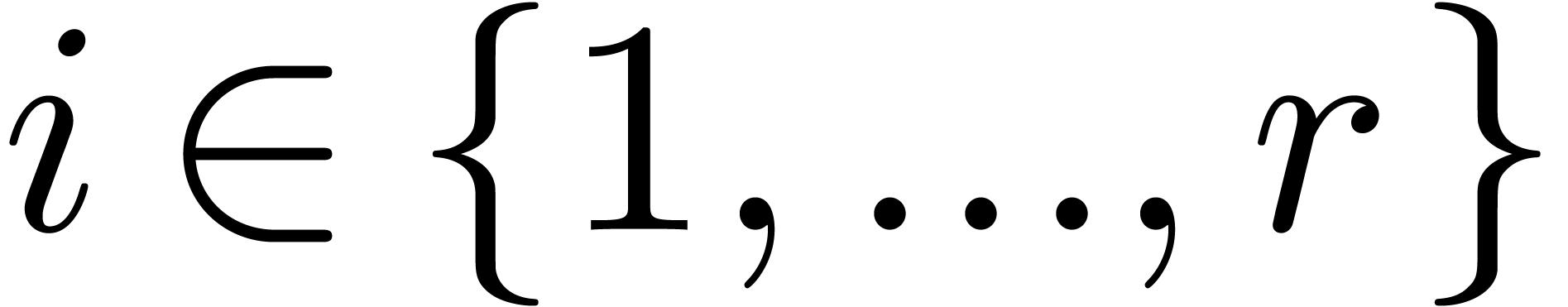 ,
,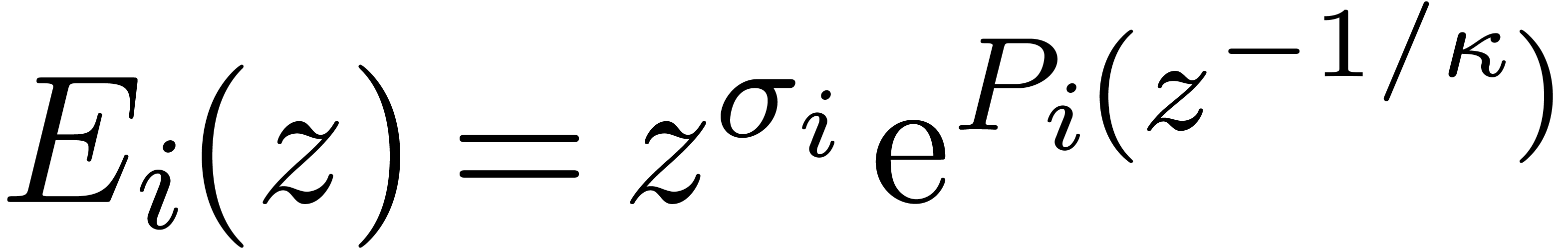 .
. denote the subset of all
denote the subset of all 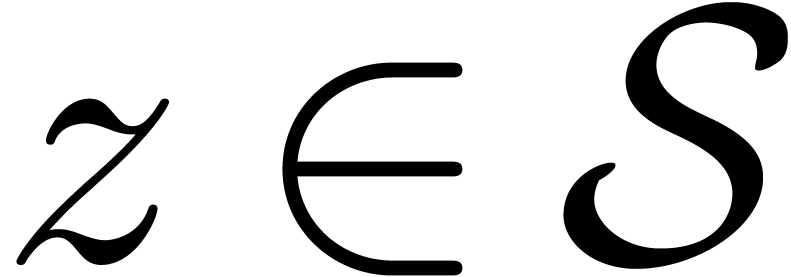 such that
such that
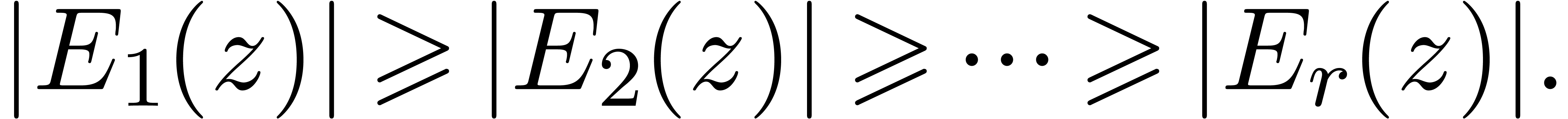
 of
of  ,
, denote the subset of all
denote the subset of all 
 .
. be a non zero solution to
be a non zero solution to  be the column
vectors with entries
be the column
vectors with entries  .
. and
and  ,
,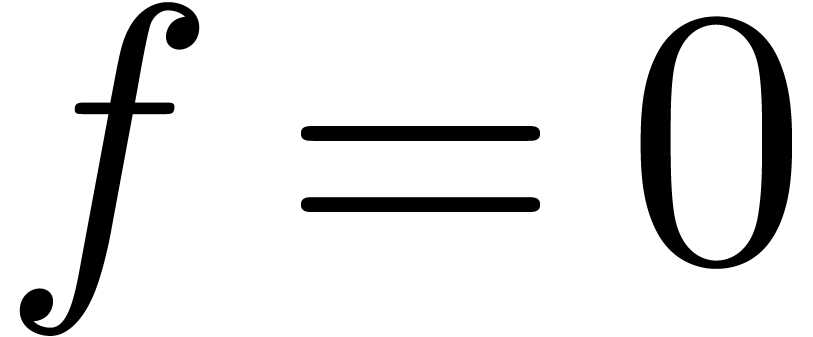 .
. of
of 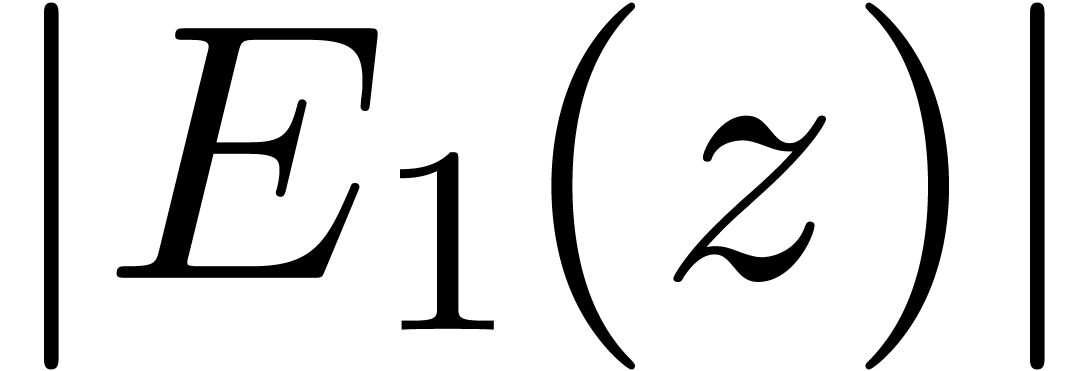 .
.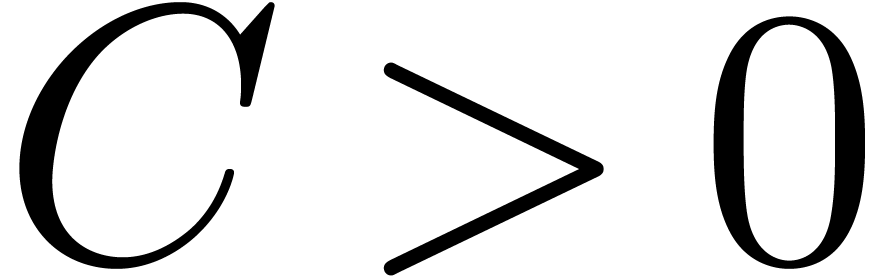 and
and 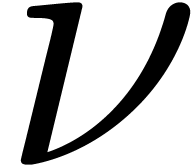 such that
such that

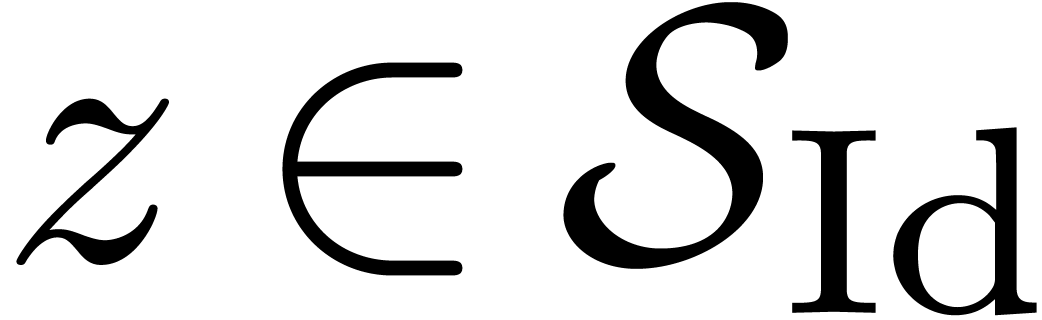 .
. .
.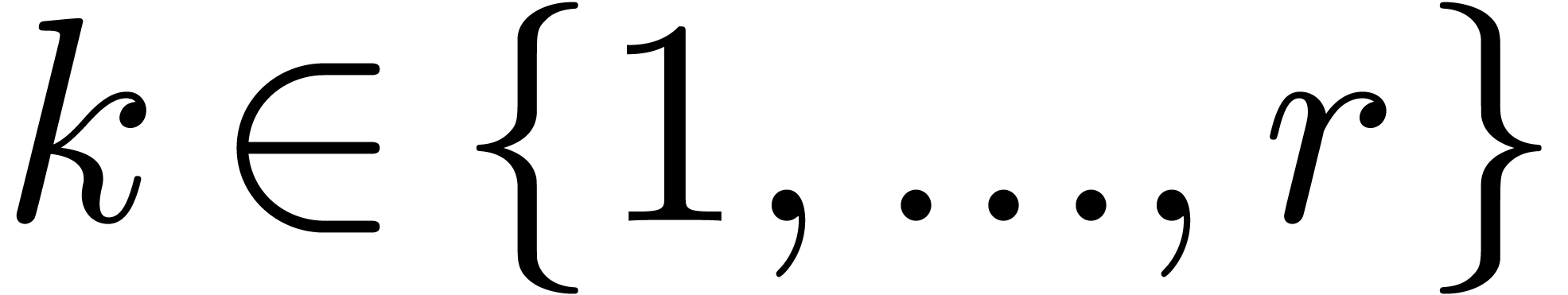 ,
, be the Wronskian
matrix
be the Wronskian
matrix
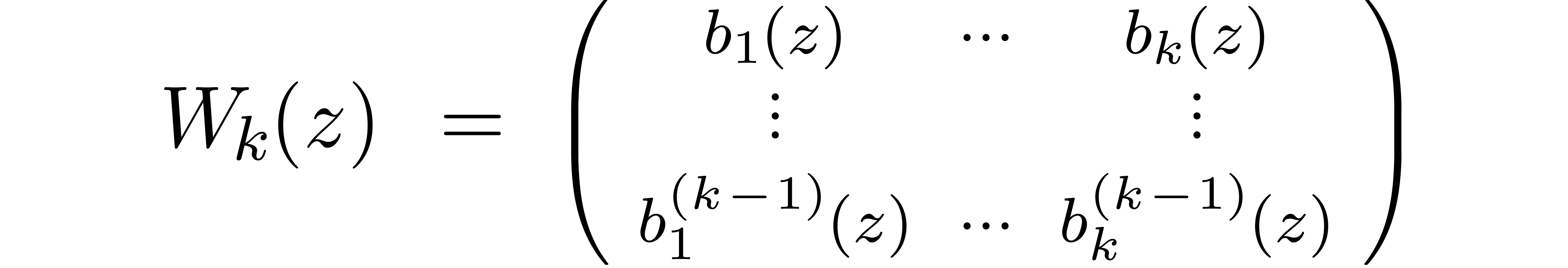

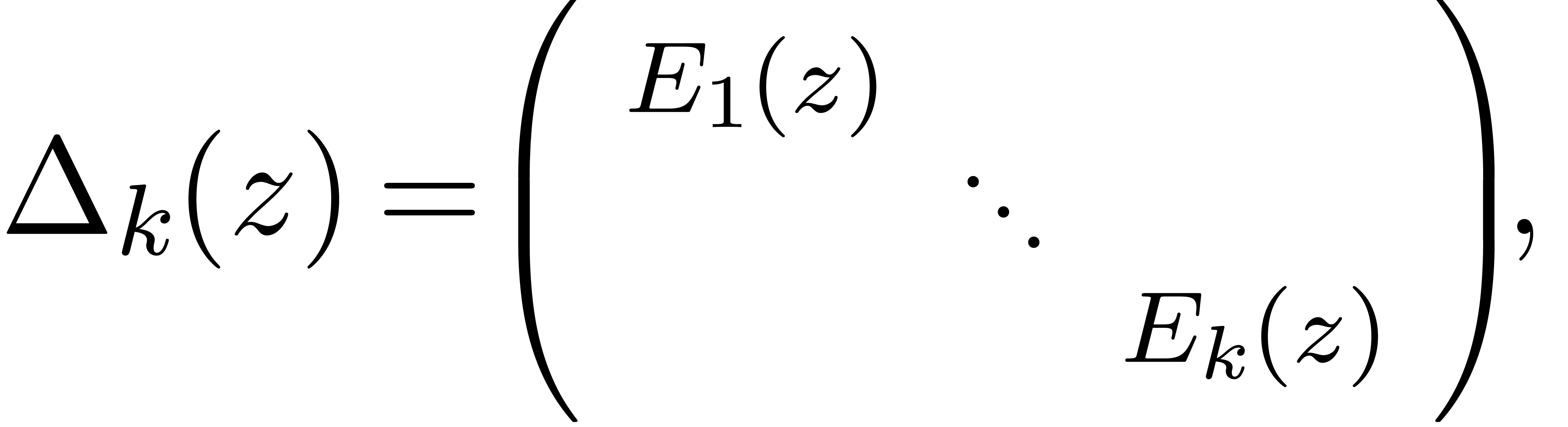
 are in
are in 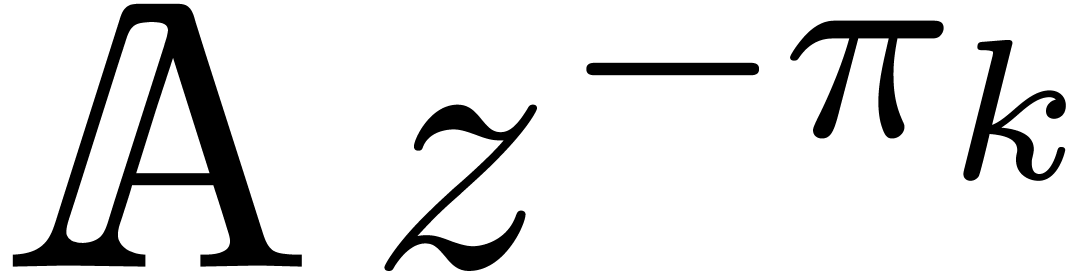 for some
for some  that only depends on the degrees of
that only depends on the degrees of
 .
.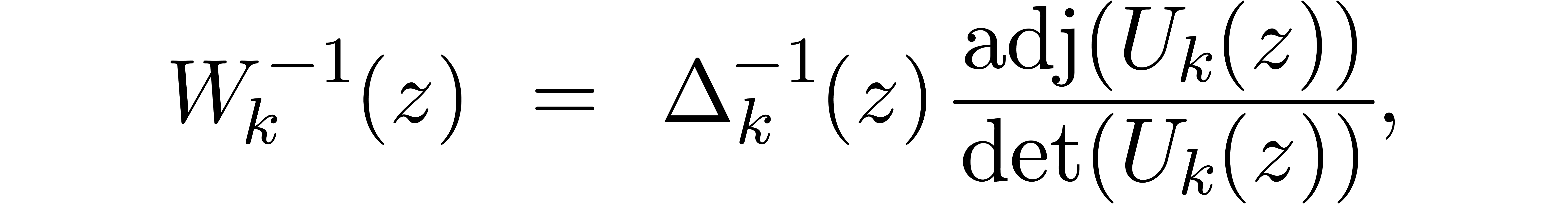
 by the linear independence of
by the linear independence of  .
. and the entries
of
and the entries
of  are all elements of
are all elements of 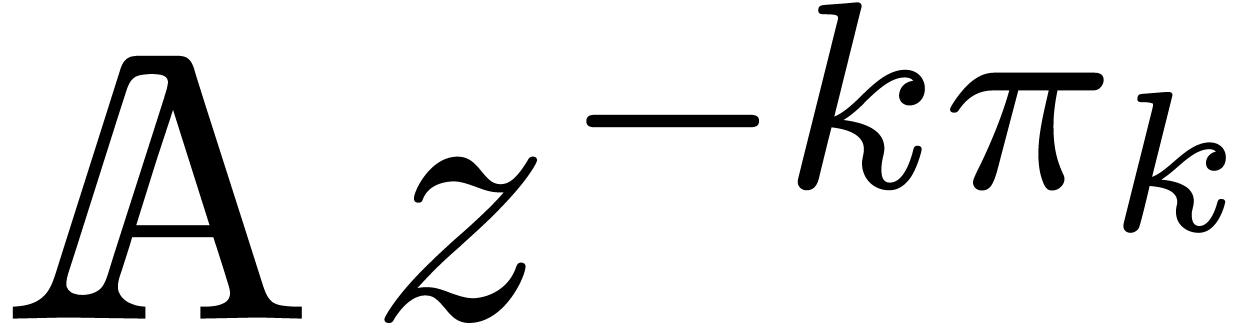 .
. such that
such that 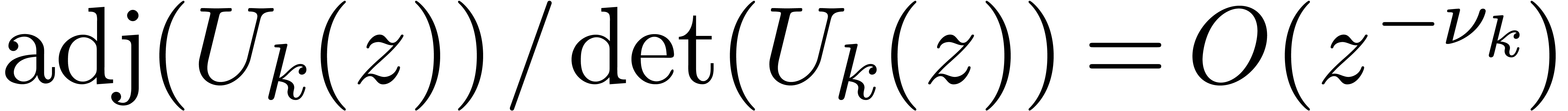 for all
for all 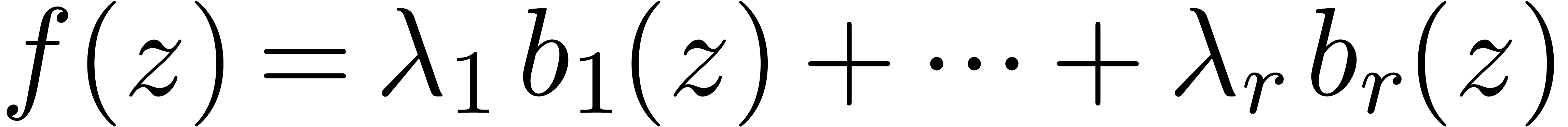 and
let
and
let
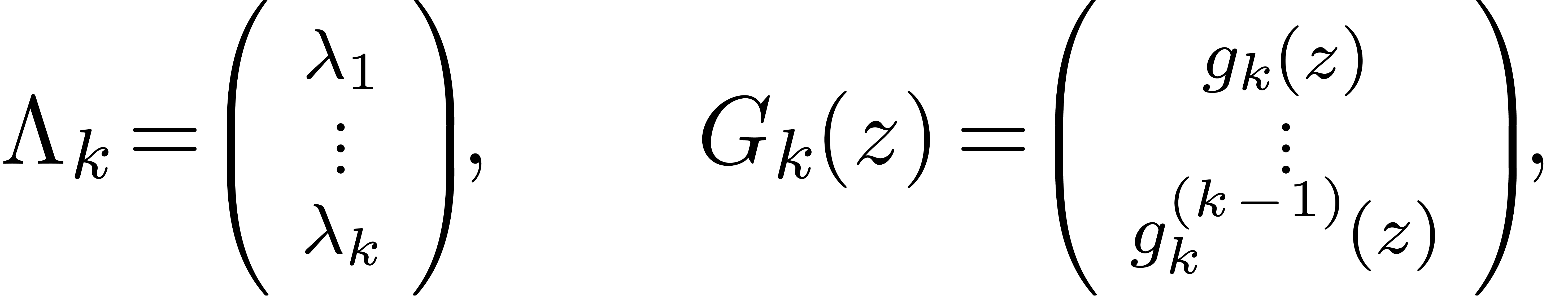
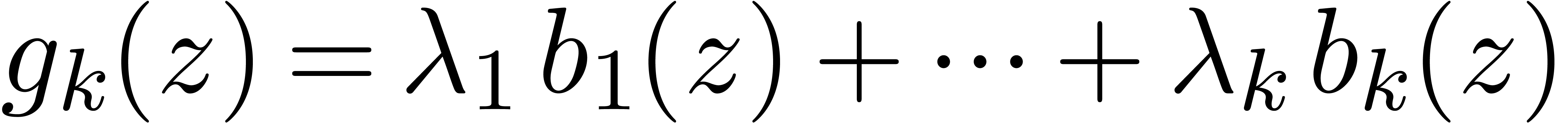 ,
,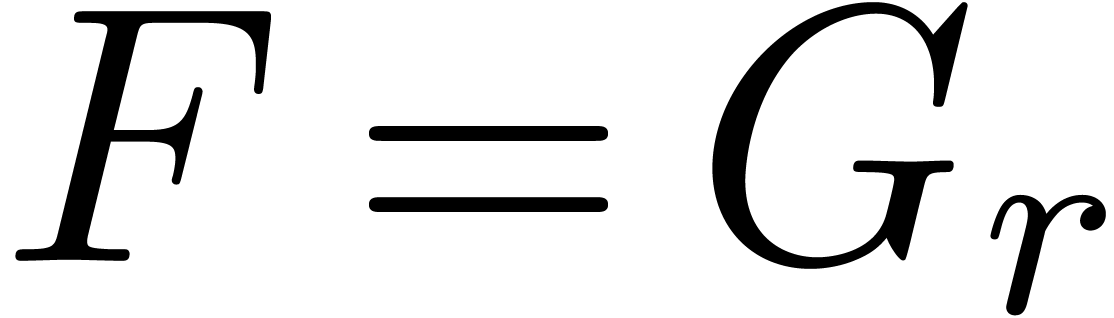 and
and 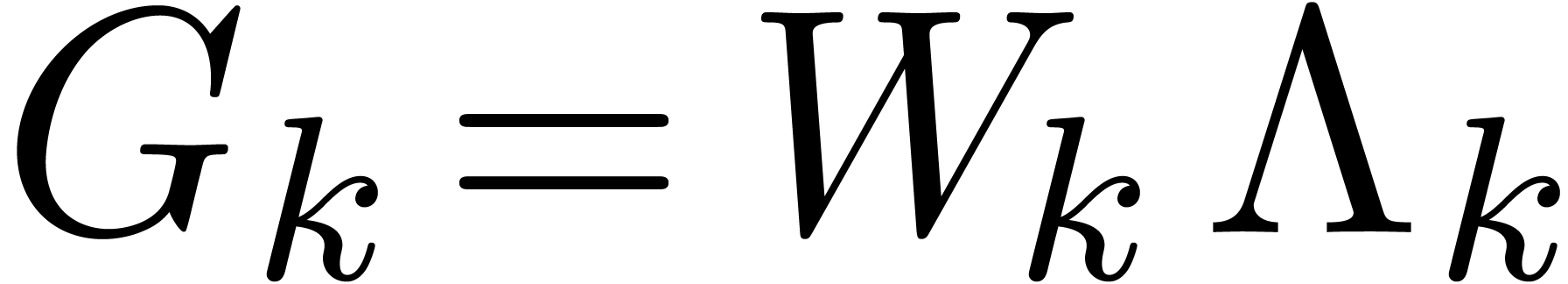 .
.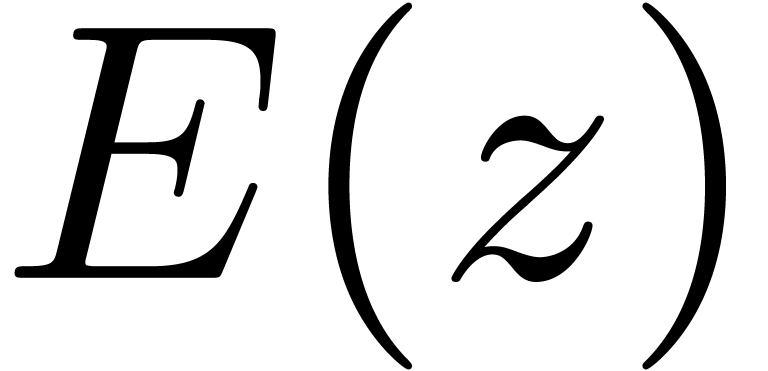 be the column vector with entries
be the column vector with entries  .
.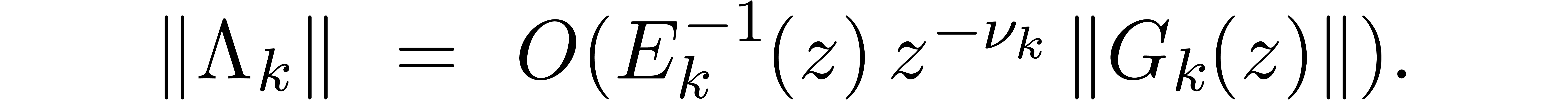
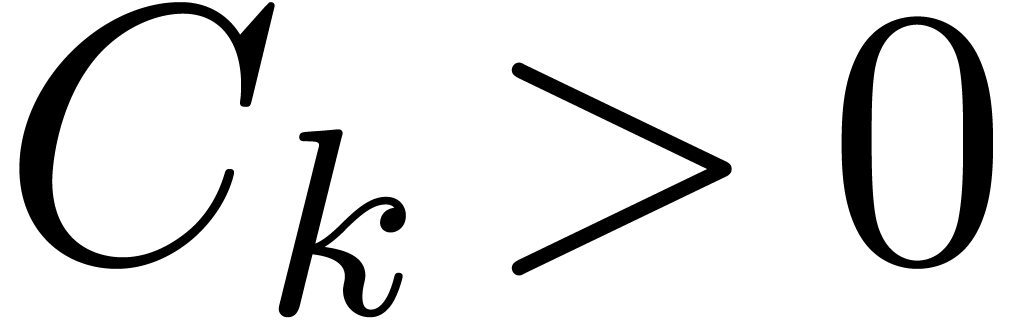 ,
,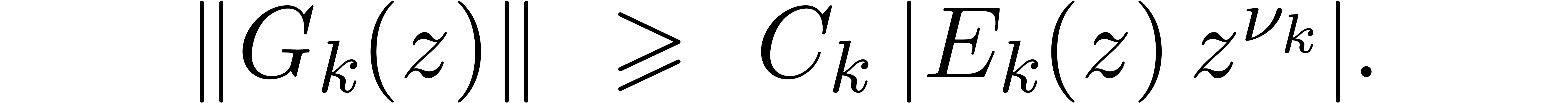
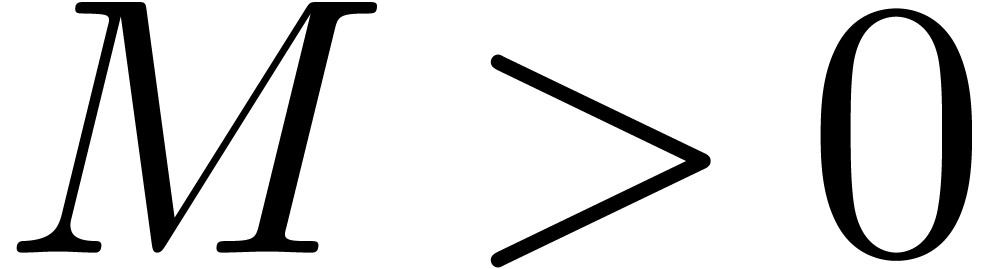 and
and  such that for all
such that for all  ,
,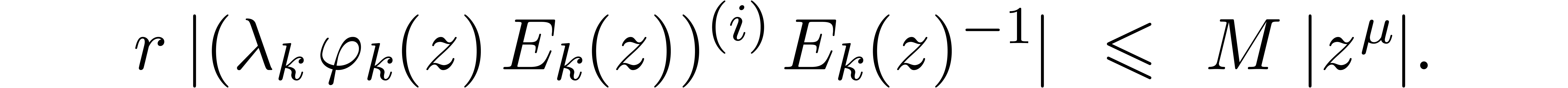
 subsets
subsets  as follows. By induction over
as follows. By induction over  ,
,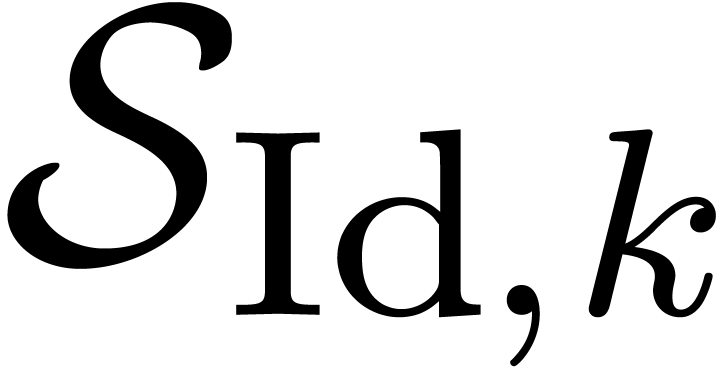 to be the subset of all
to be the subset of all 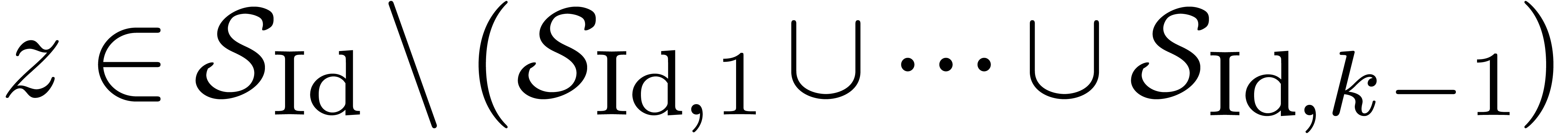 such that
such that
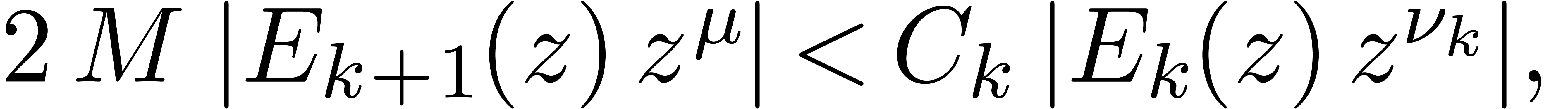
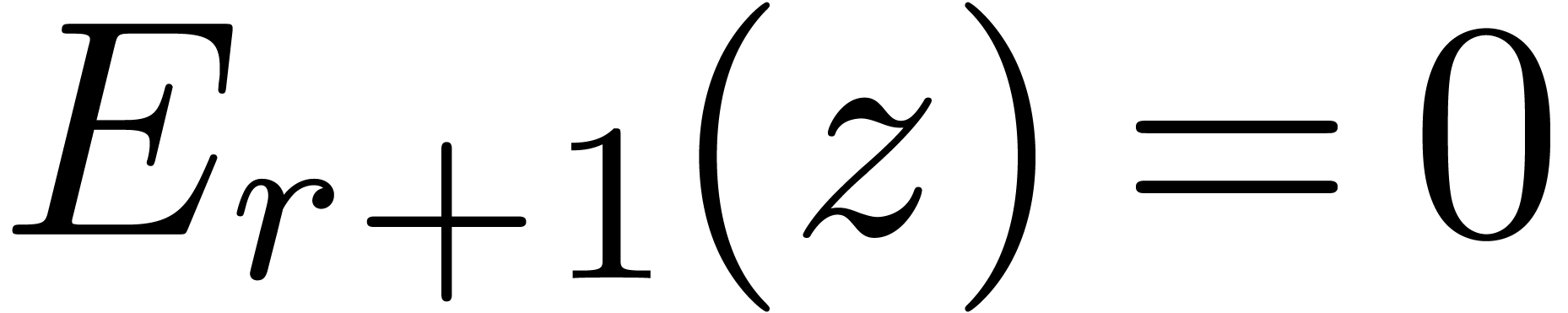 .
.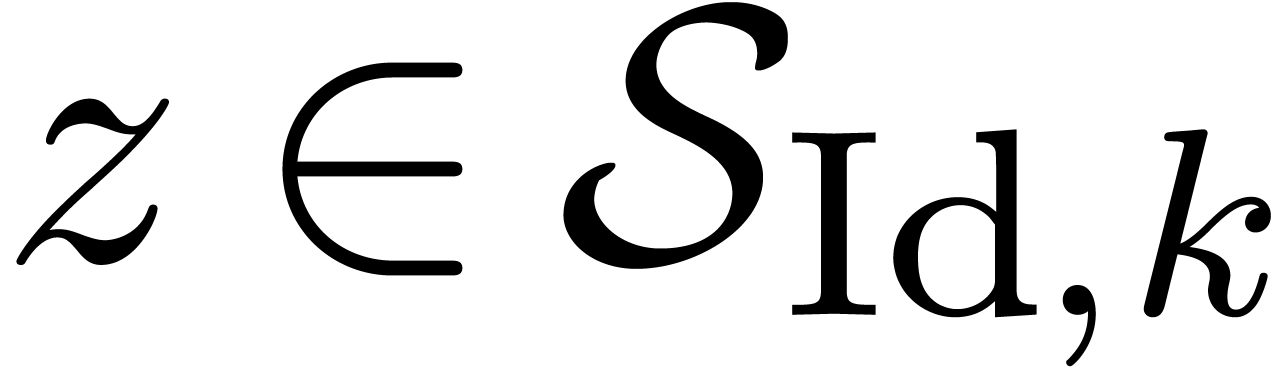 ,
,
 such that
such that

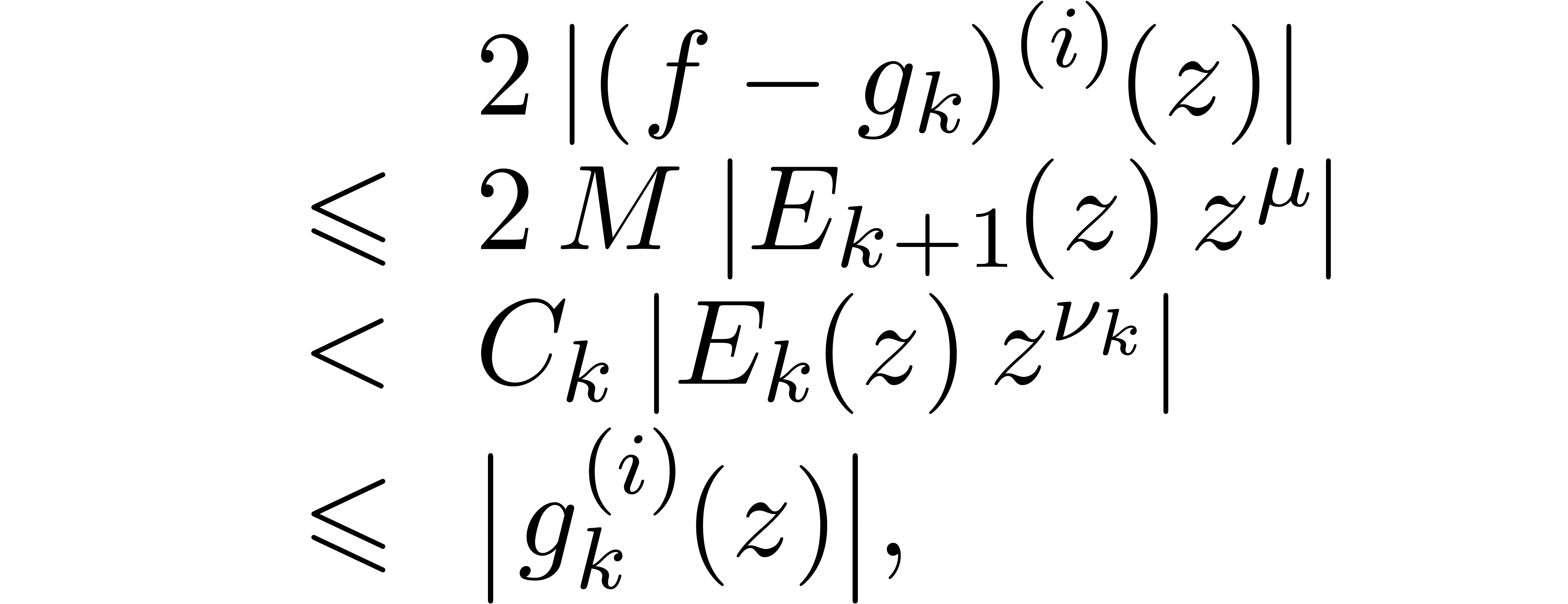
 for
for 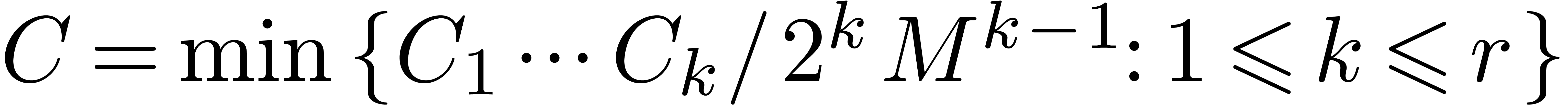 and
and
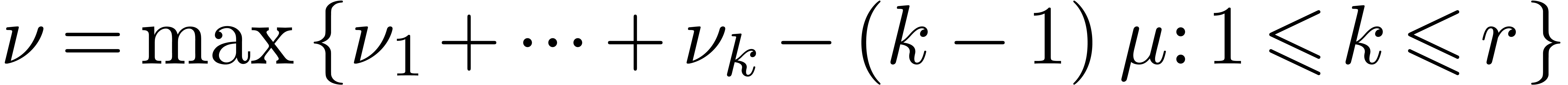 ,
, and the degrees of
and the degrees of  .
.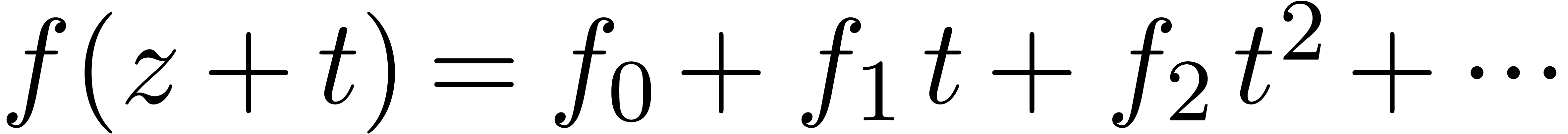 of
of 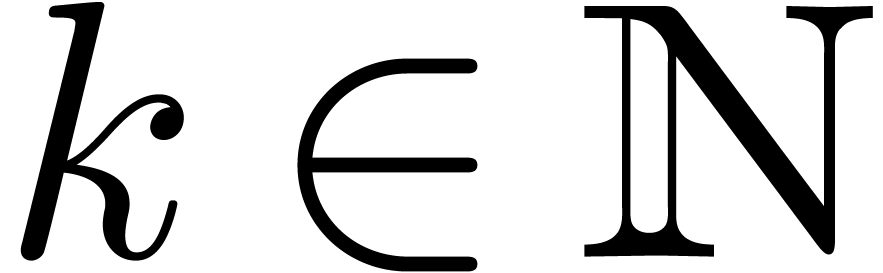 ,
, be the vector with entries
be the vector with entries  .
. in terms of
in terms of  .
. ,
,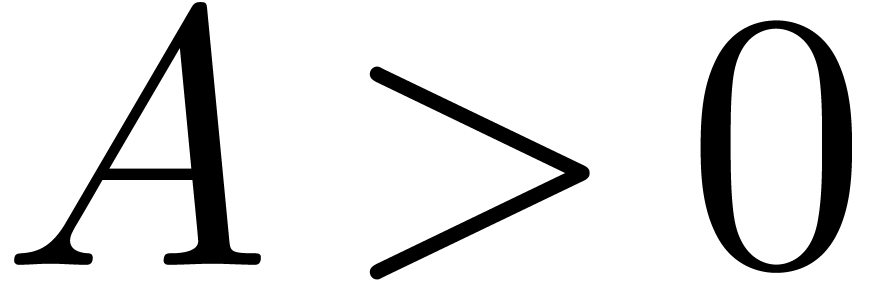 and
and 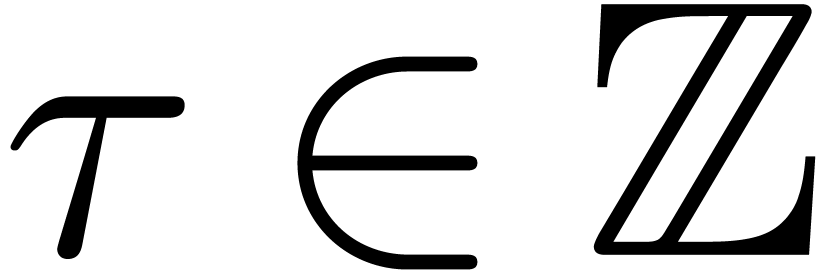 such that
such that


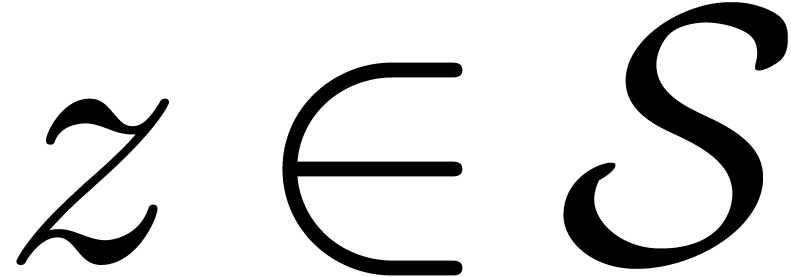 with
with 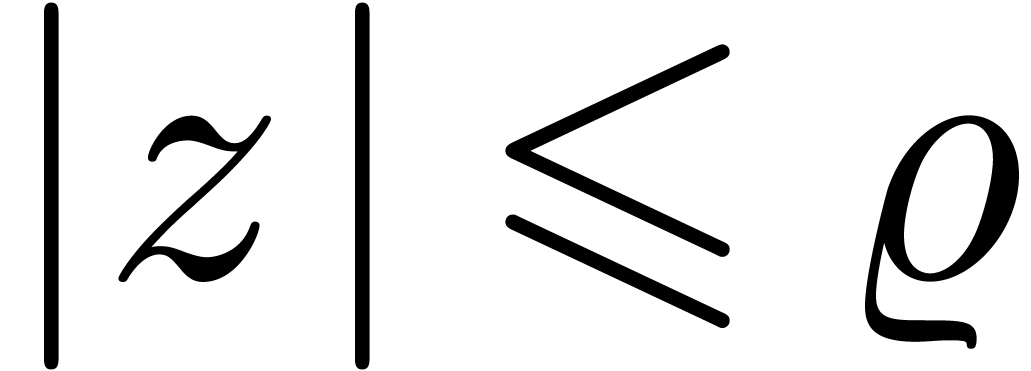 .
.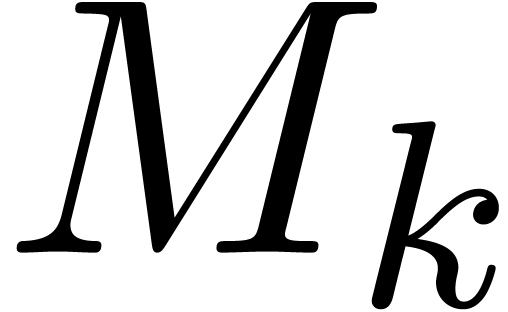 with
coefficients in
with
coefficients in 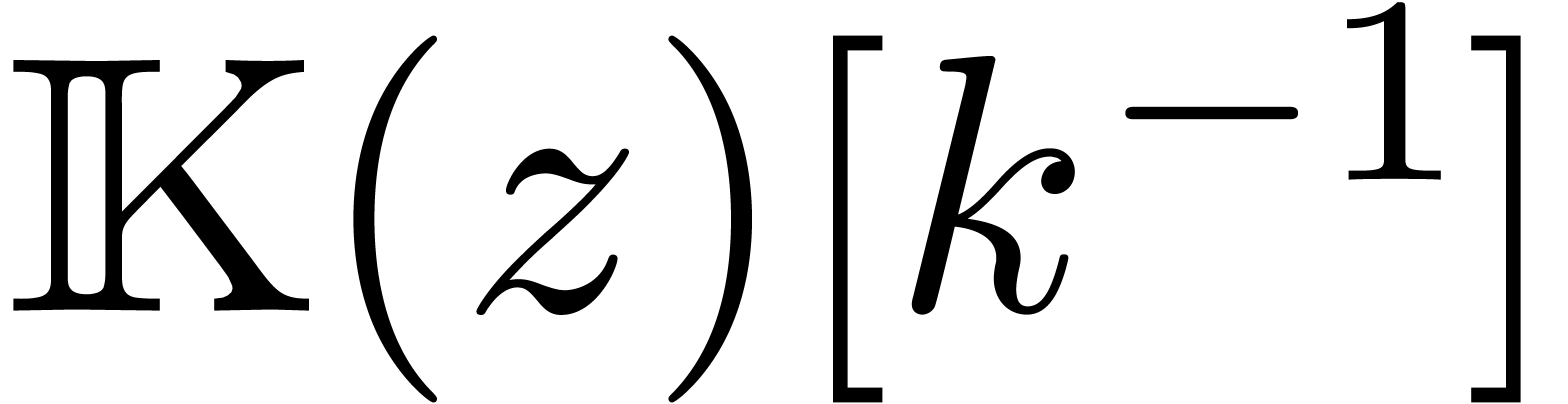 such that
such that
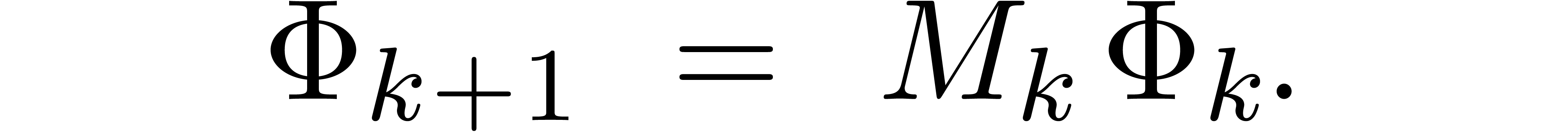
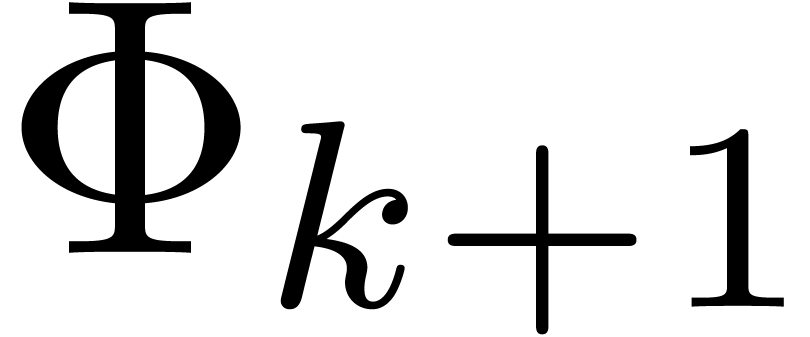 of the form
of the form
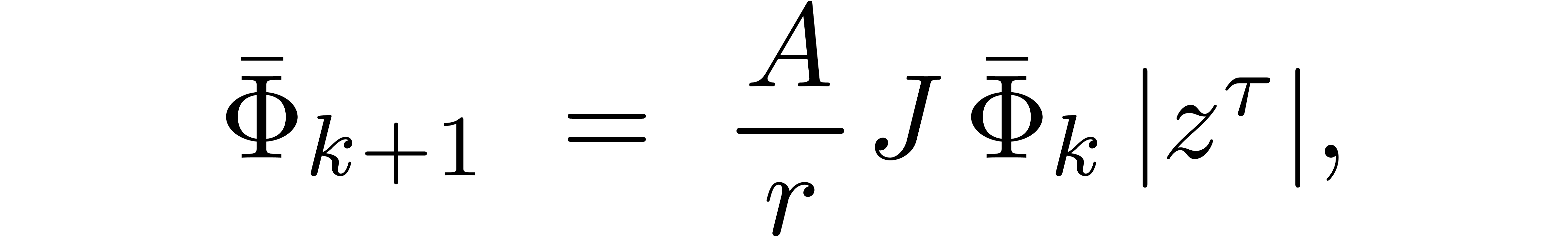
 denotes the
denotes the
 matrix whose coefficients are all one. Taking
matrix whose coefficients are all one. Taking
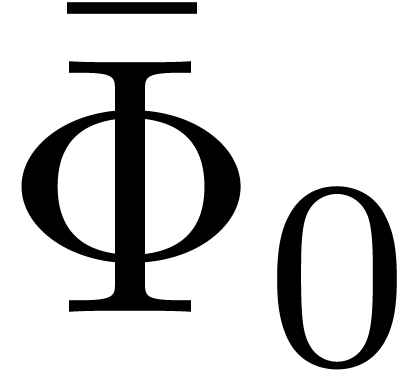 to be the vector with entries
to be the vector with entries  ,
,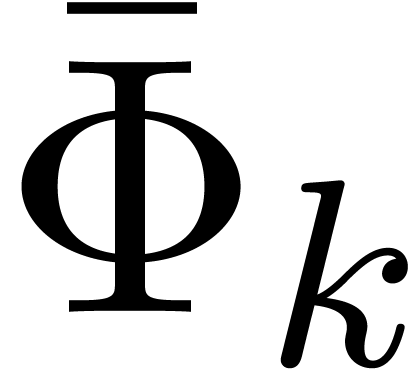 is
the vector with entries
is
the vector with entries  .
. .
.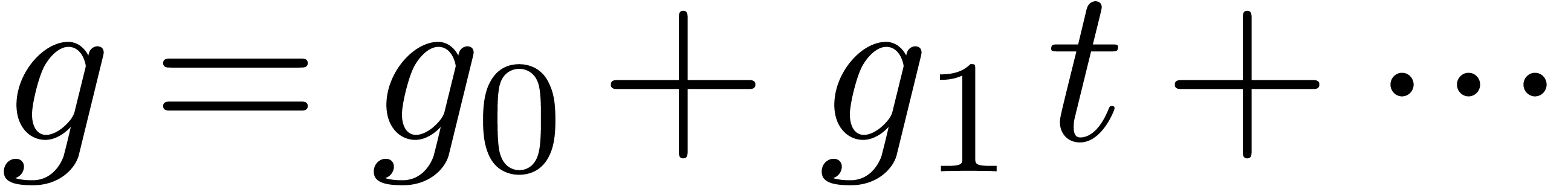 be an analytic function on the unit disk
be an analytic function on the unit disk 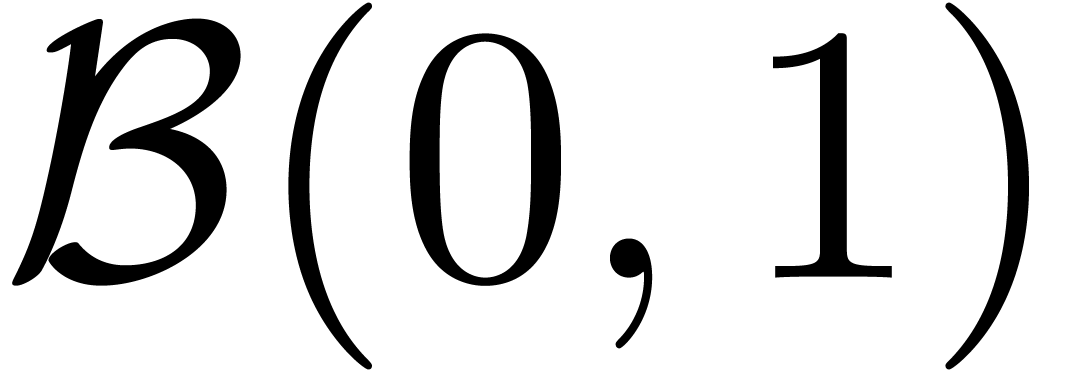 such that
such that 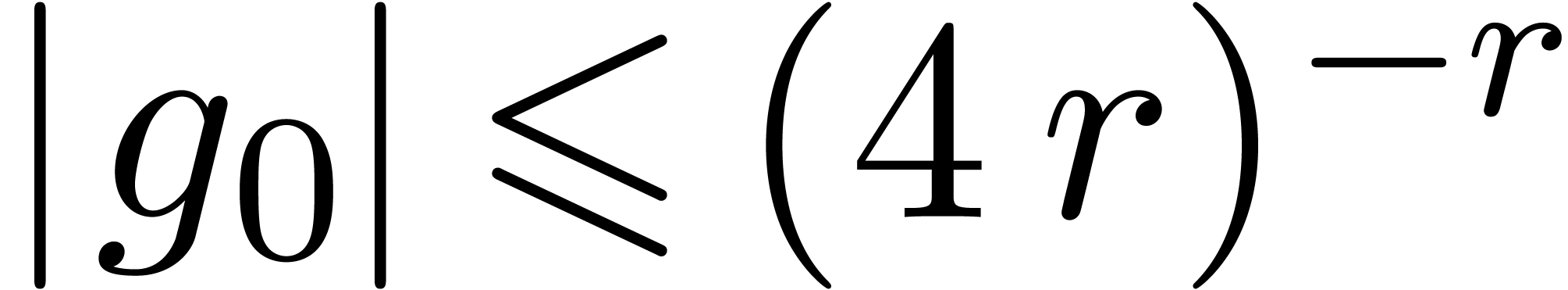 ,
, and
and 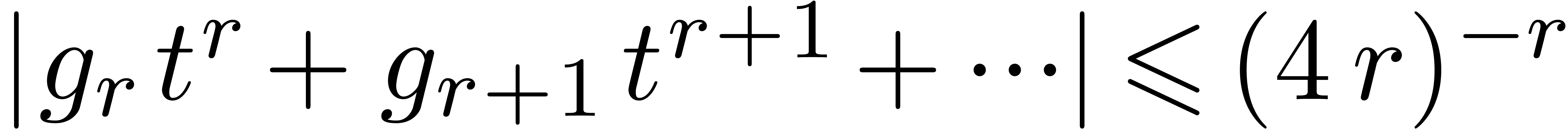 on
on  admits a root
on
admits a root
on 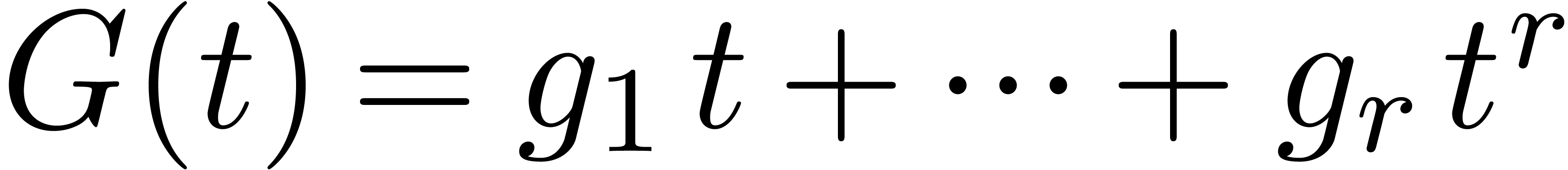 .
.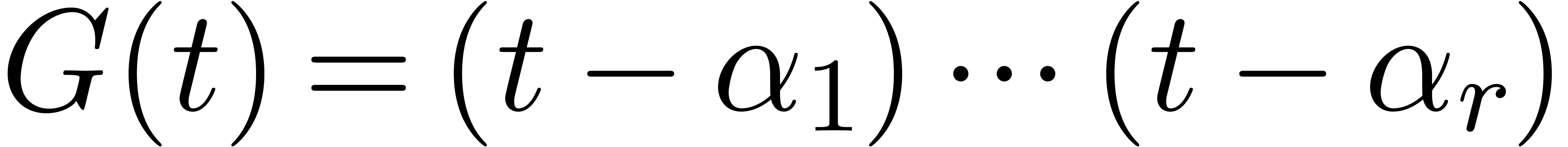 with
with 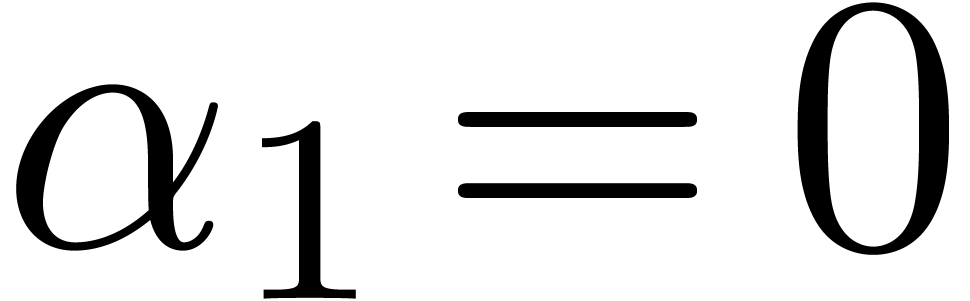 .
.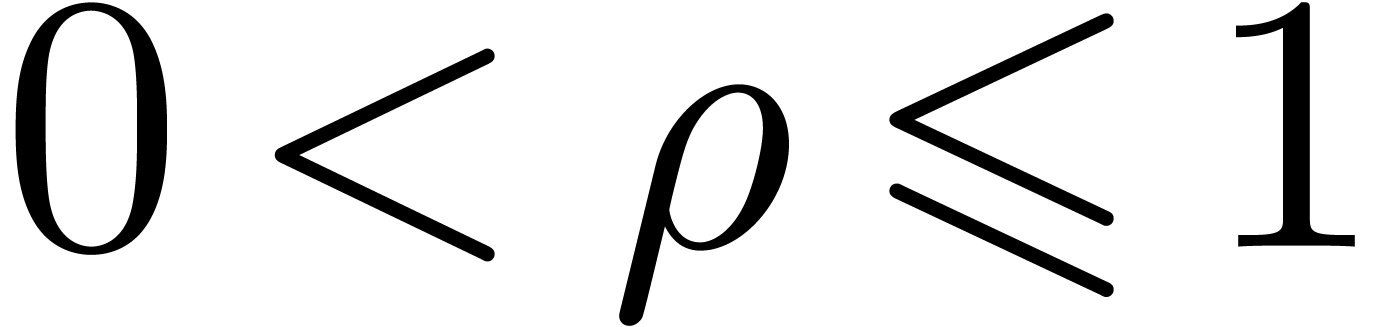 be such that
be such that 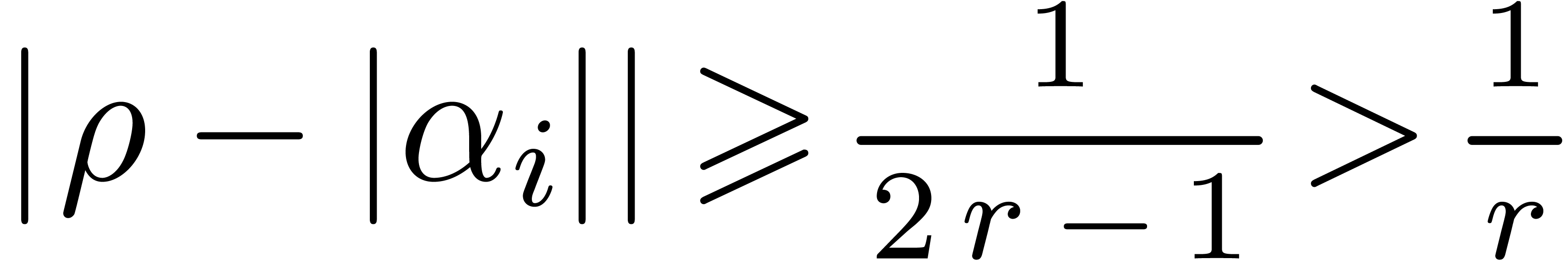 for all
for all
 for all
for all 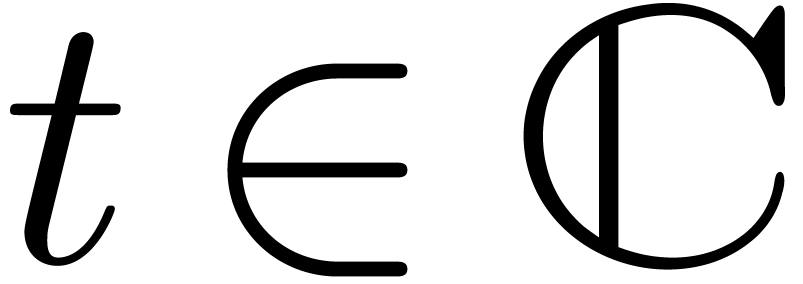 with
with 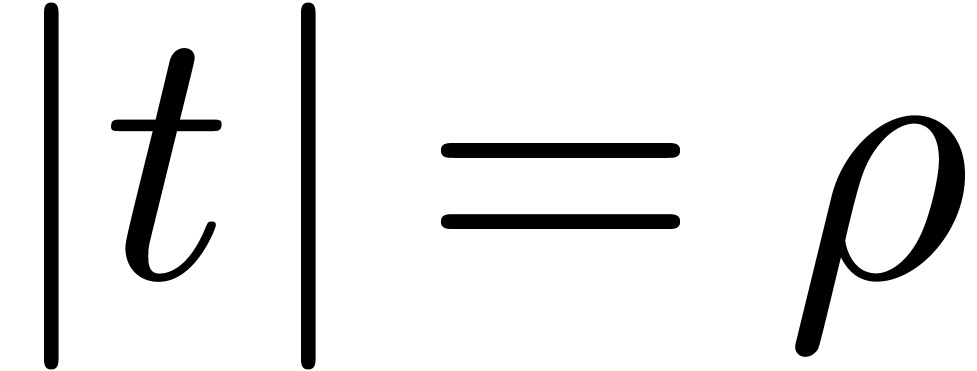 ,
,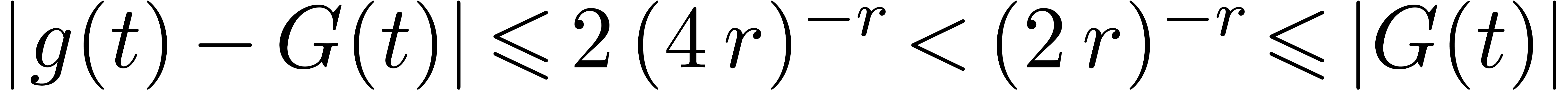 .
. admit the same number of zeros in
admit the same number of zeros in 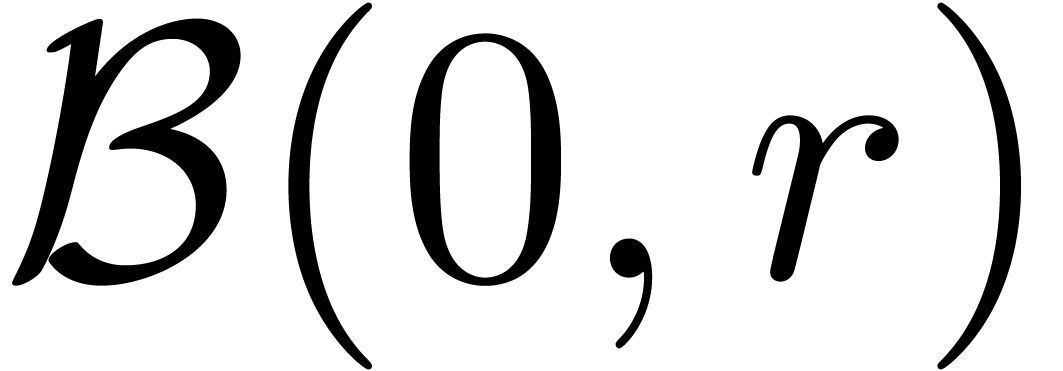 .
. .
.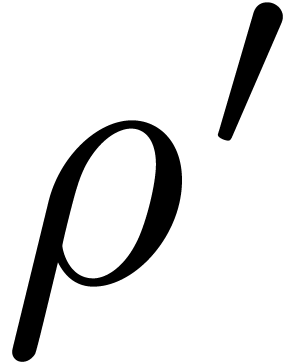 ,
, and
and 
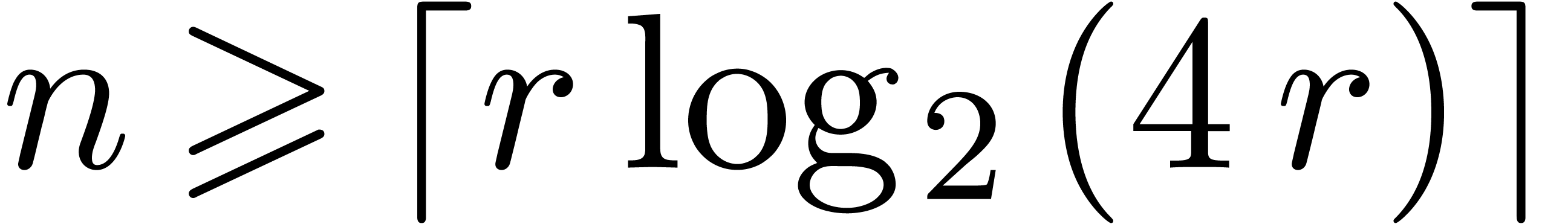 and
and 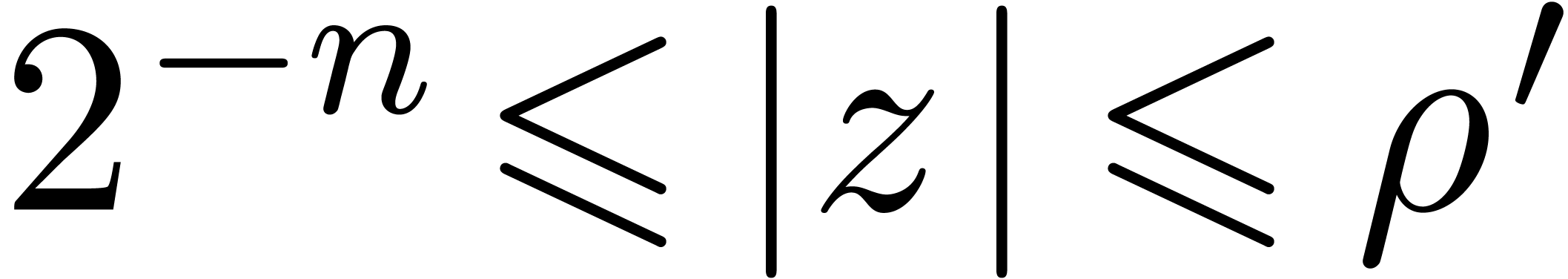 .
.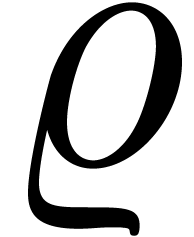 ,
, and
and  as in Lemma
as in Lemma  .
.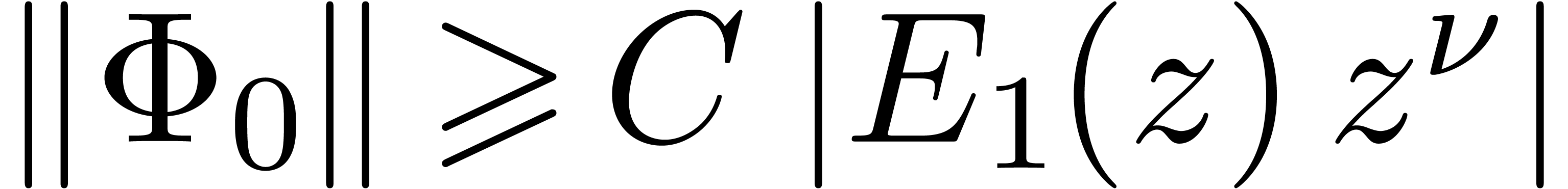 and
and 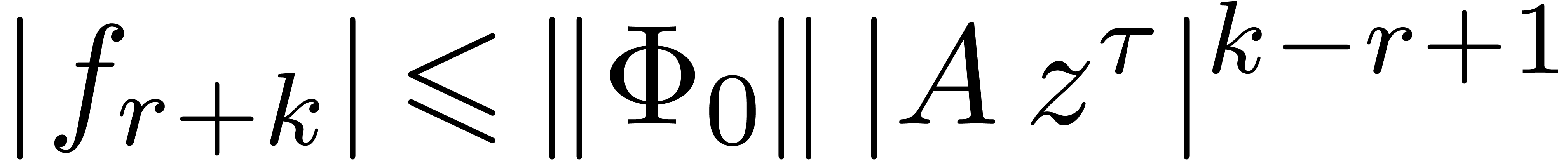 for all
for all
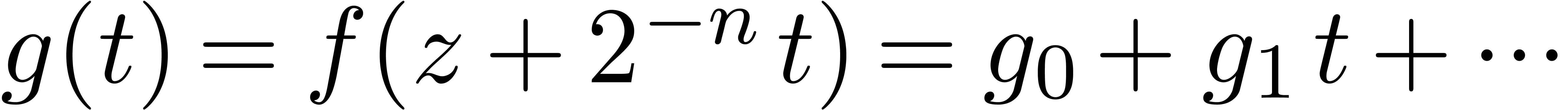 .
.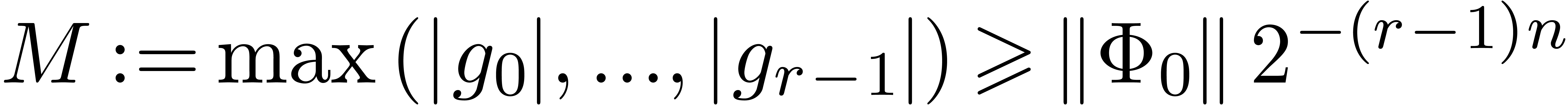 and
and
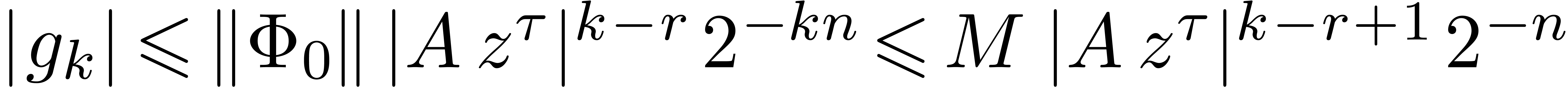 for
for  .
.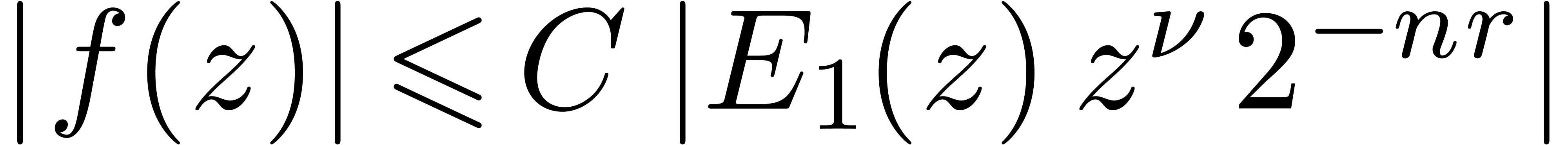 ,
,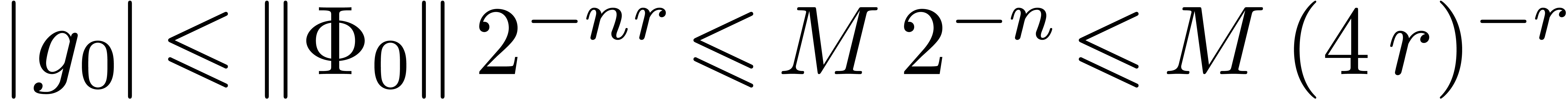 .
.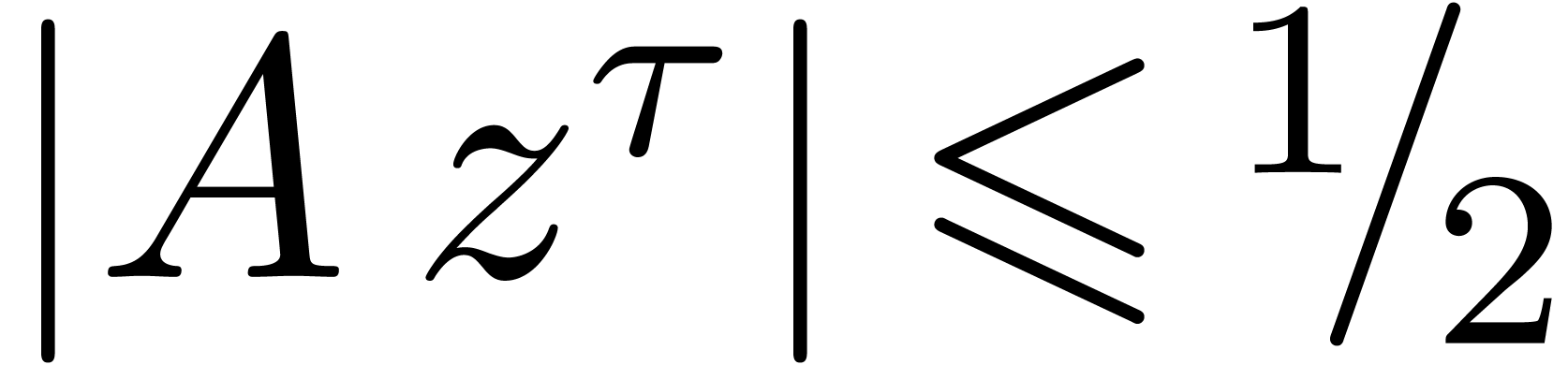 .
.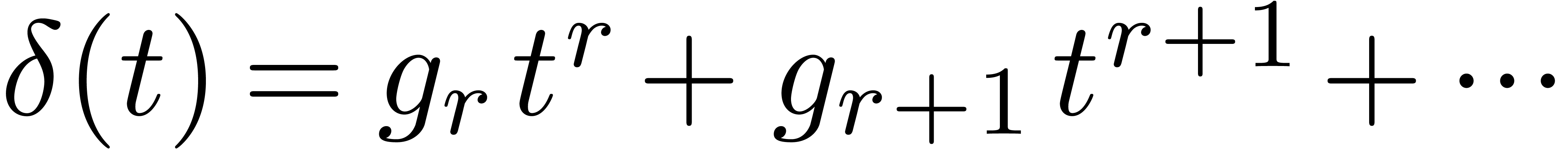 satisfies
satisfies 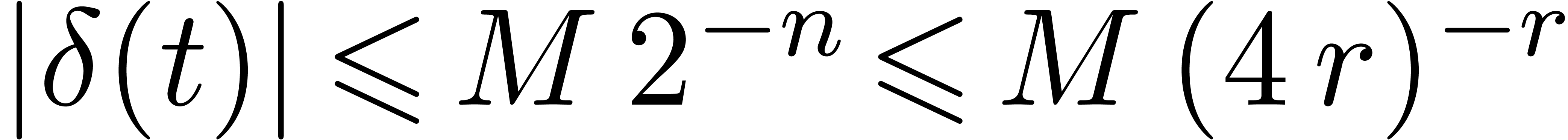 for
for  .
.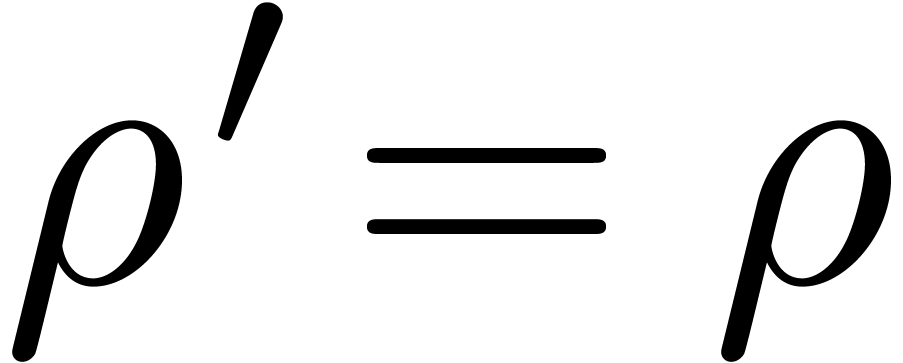 in
Lemma
in
Lemma 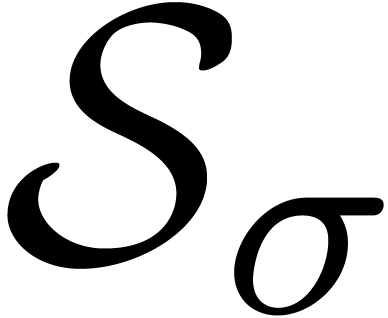 for each permutation
for each permutation  of
of 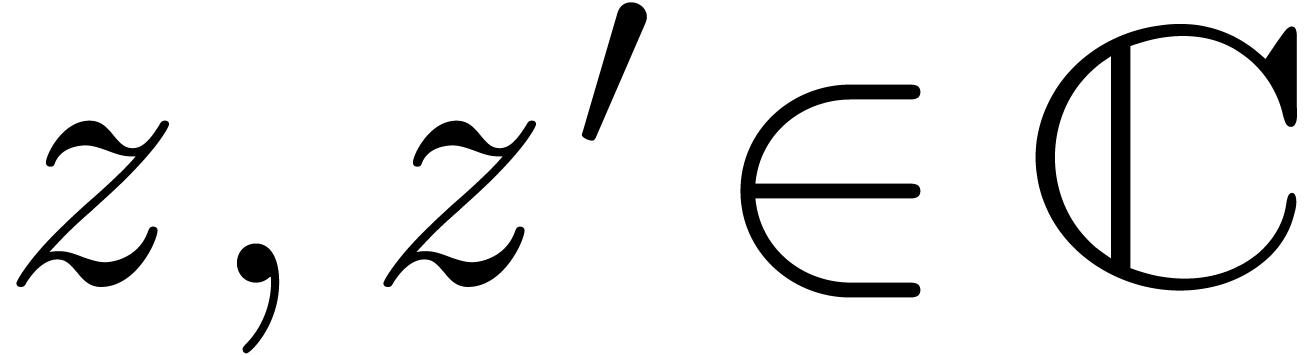 with
with 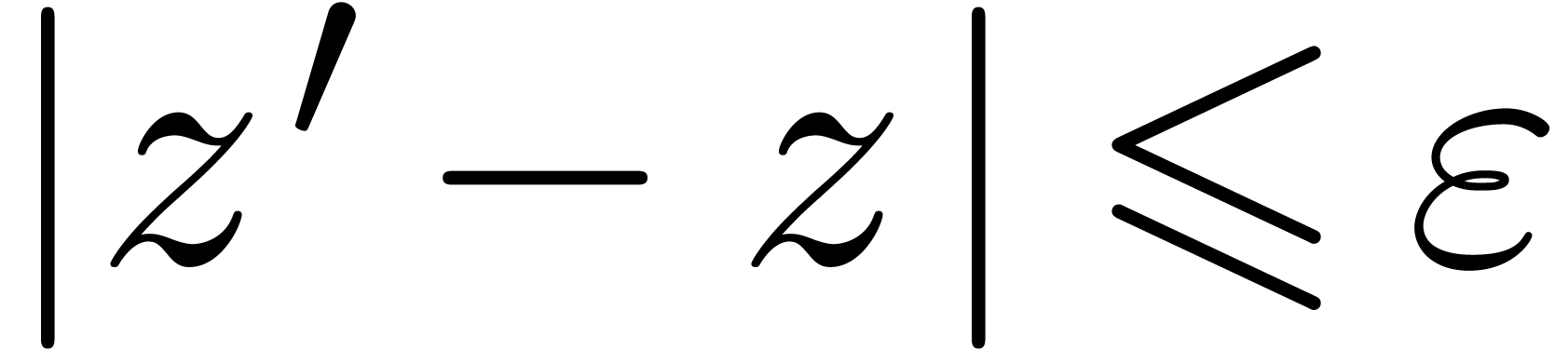 ,
, is an
is an  is a singularity for
is a singularity for  and that
and that 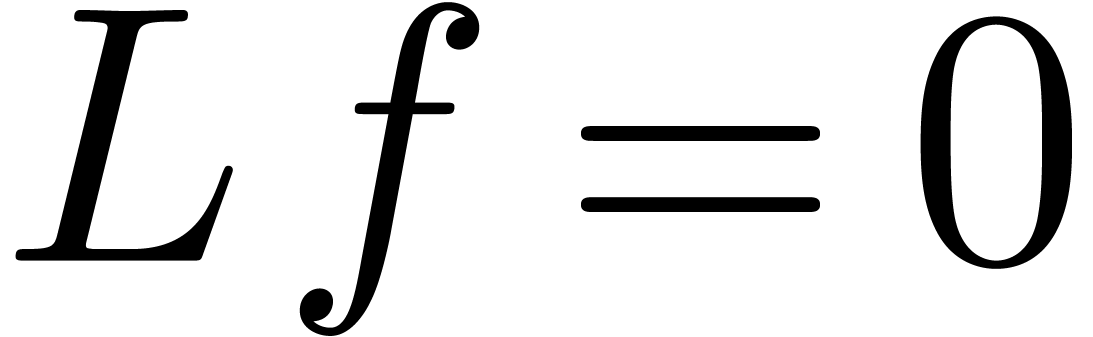 on a super-admissible sector
on a super-admissible sector  .
.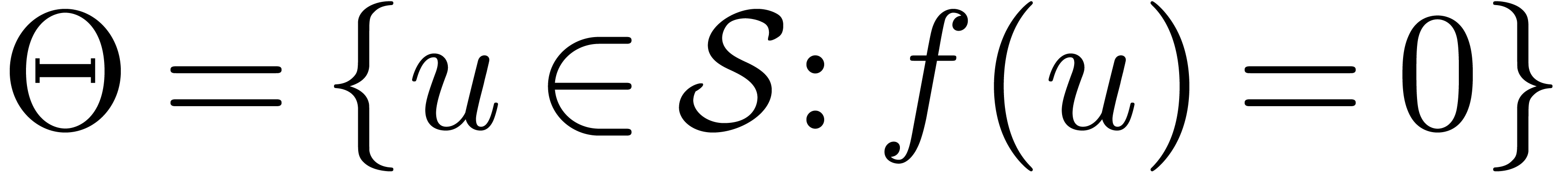 .
.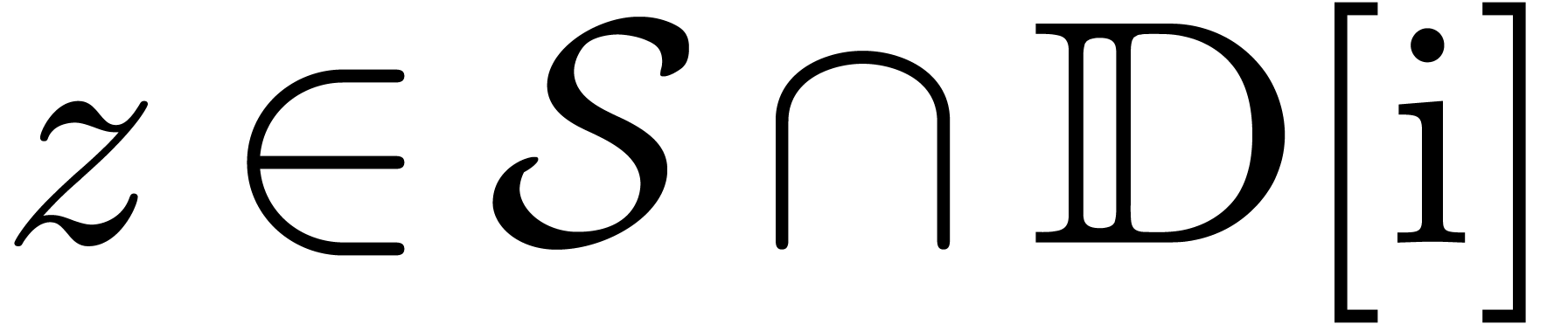 with
with 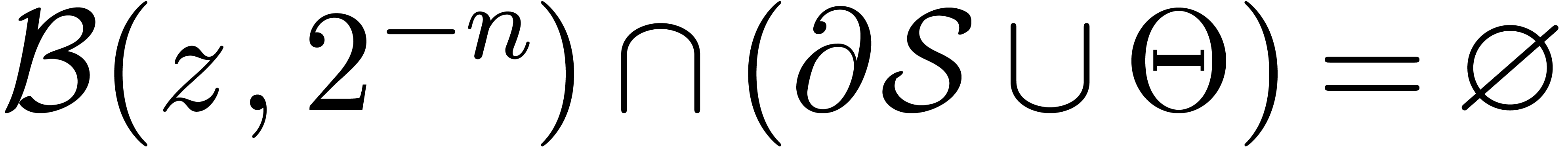 and
and 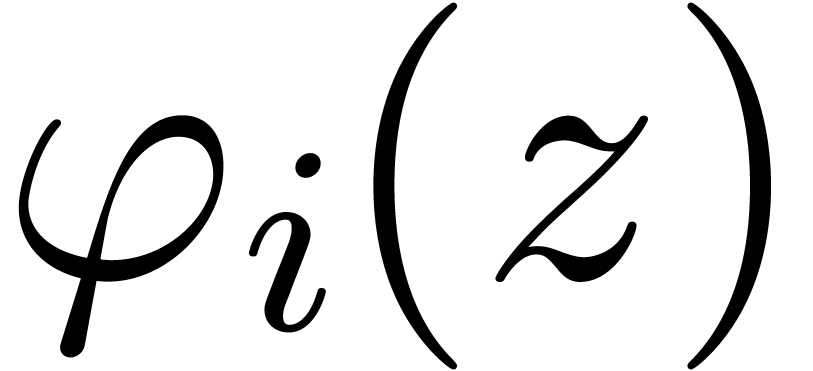 in time
in time  with
with  such that
such that 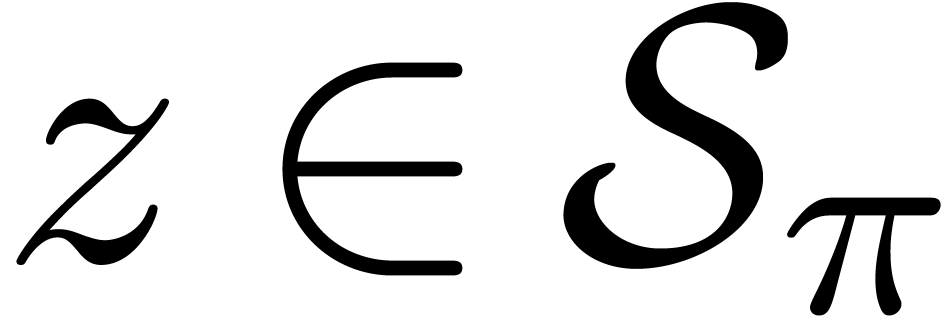 .
.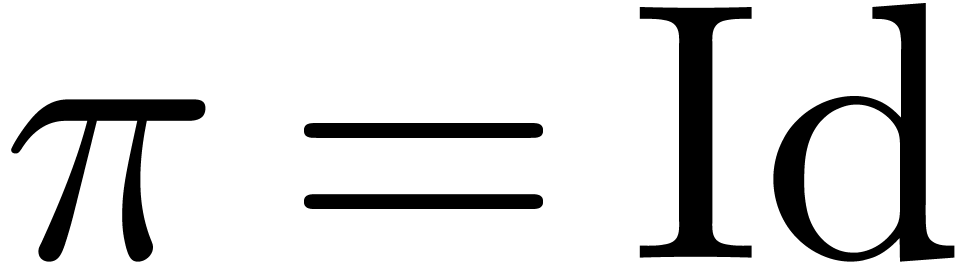 .
. until the desired approximation with a relative precision
of
until the desired approximation with a relative precision
of  -approximations
-approximations .
.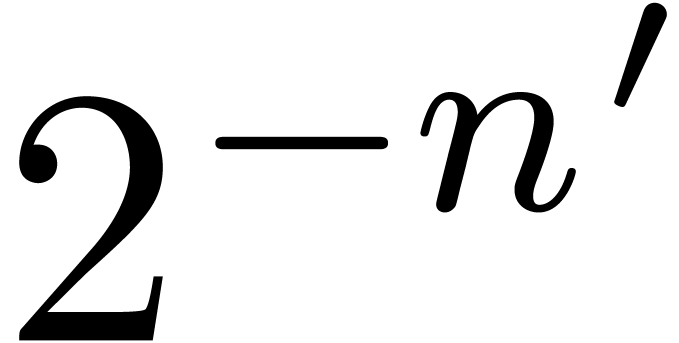 -approximations
-approximations .
.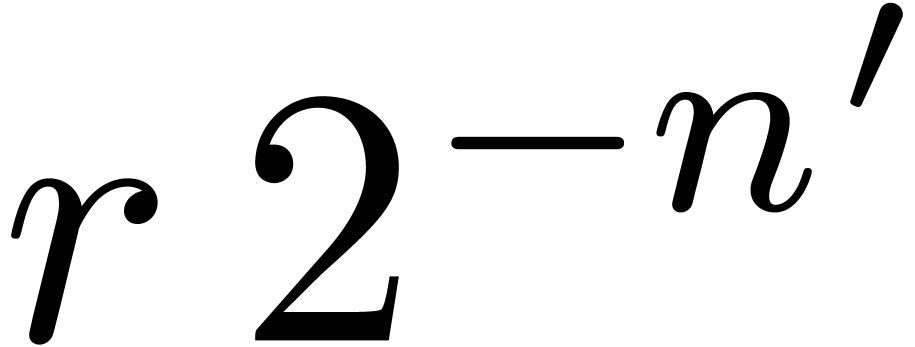 -approximation
-approximation .
. bits, then we obtain
bits, then we obtain  .
.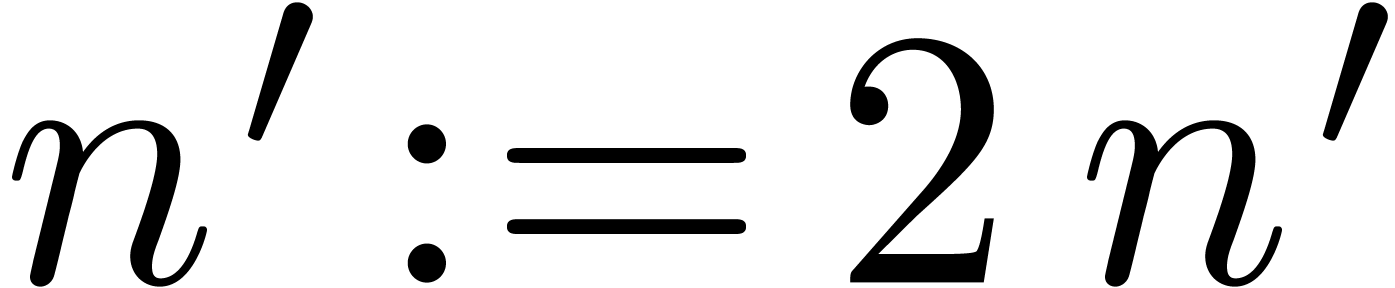 and keep
iterating.
and keep
iterating.
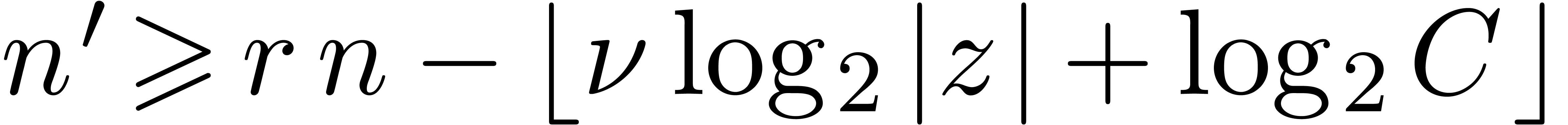 and
and 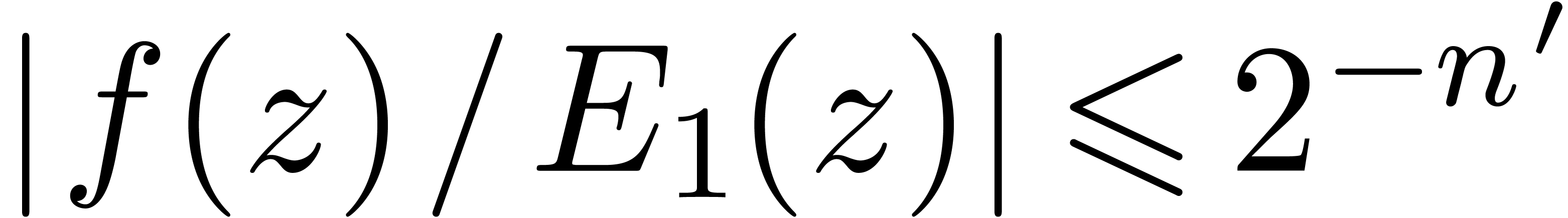 ,
,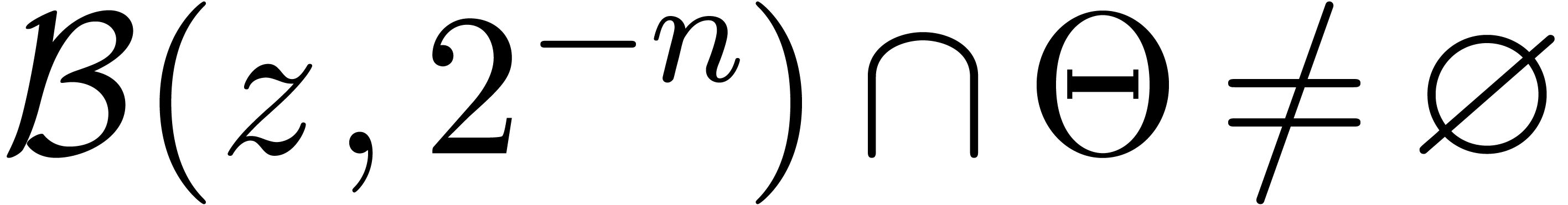 .
. .
.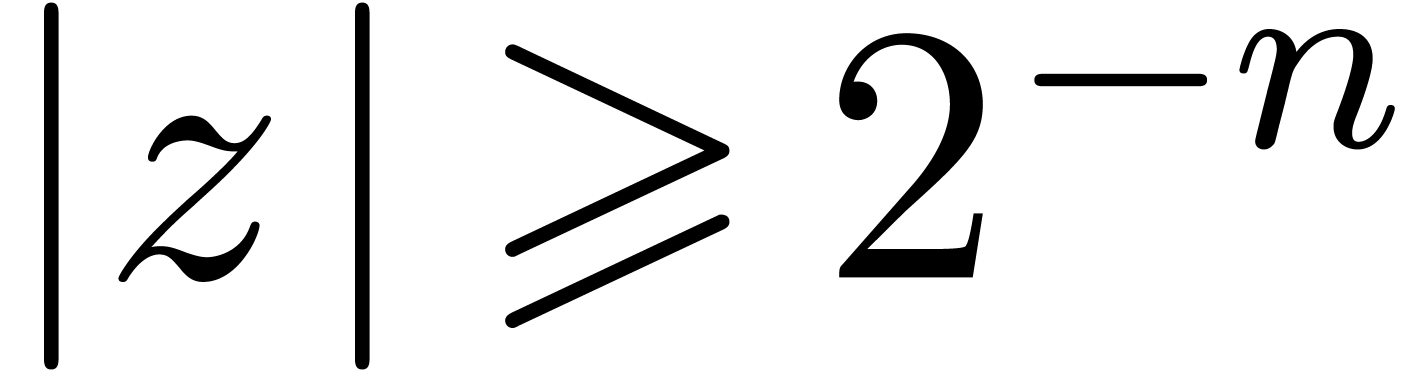 ,
,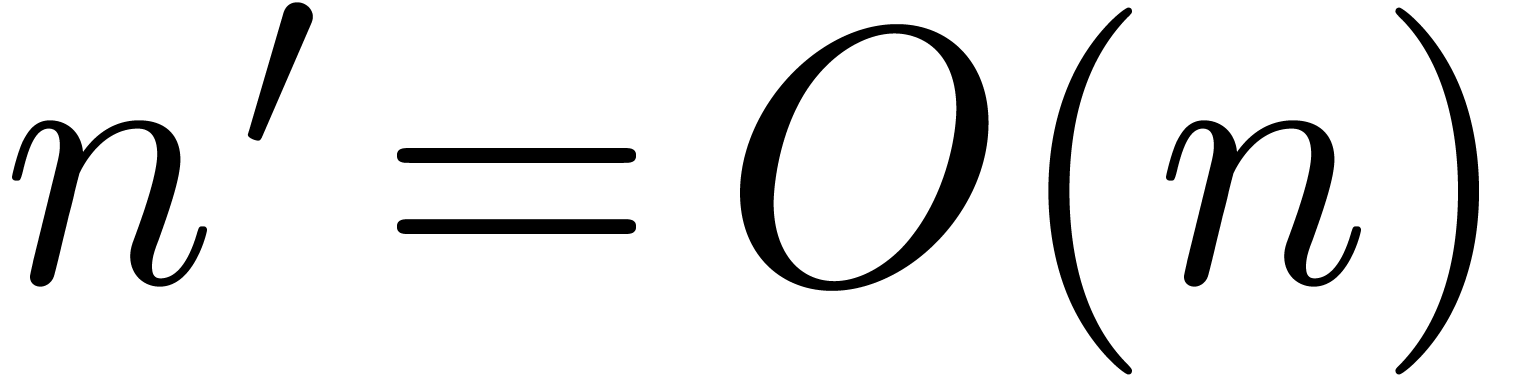 .
. at every
iteration, the total running time is dominated by the running time of
the last tentative evaluation at precision
at every
iteration, the total running time is dominated by the running time of
the last tentative evaluation at precision 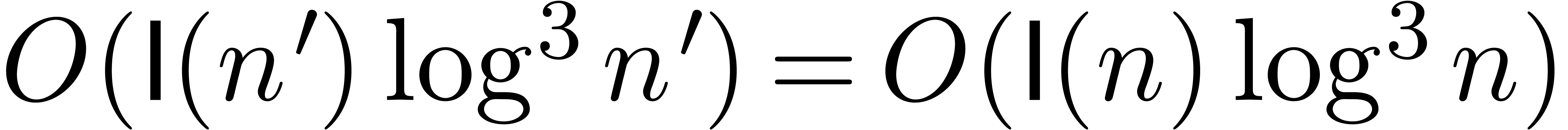 ,
,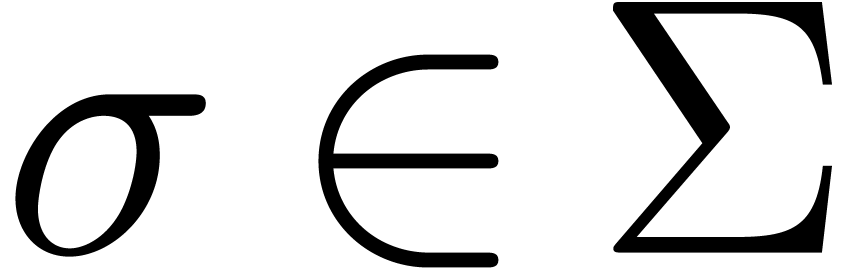 be one of the singularities and let
be one of the singularities and let  be an admissible ball cover in the neighbourhood of
be an admissible ball cover in the neighbourhood of 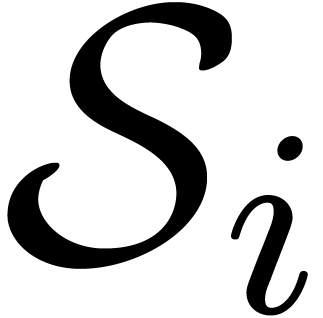 and each connected component
and each connected component 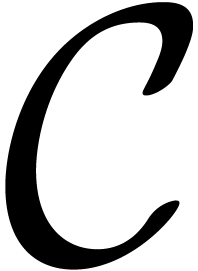 of
of  (there are at most two such connected components), we also arbitrarily
pick a point
(there are at most two such connected components), we also arbitrarily
pick a point 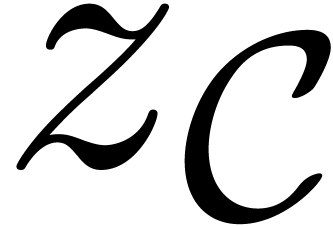 in
in 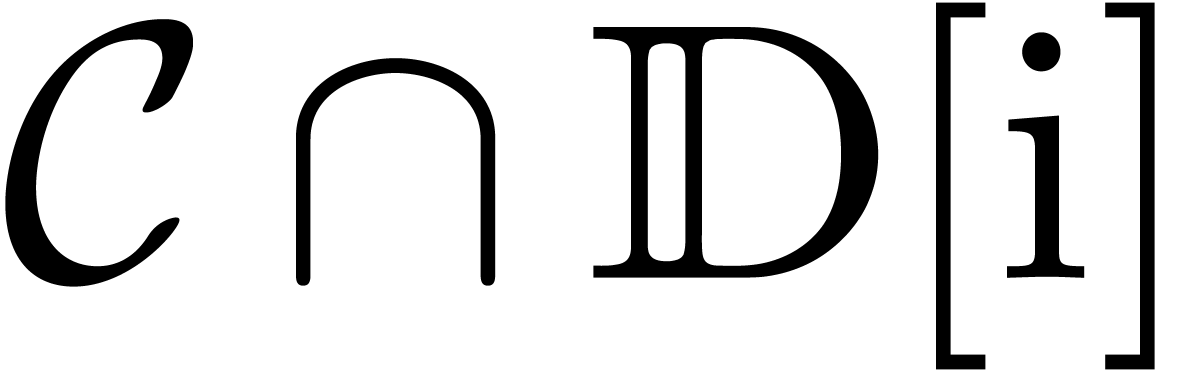 .
.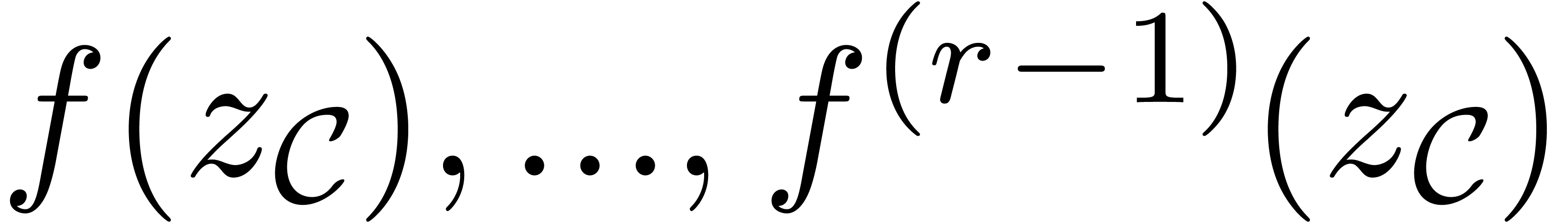 in time
in time 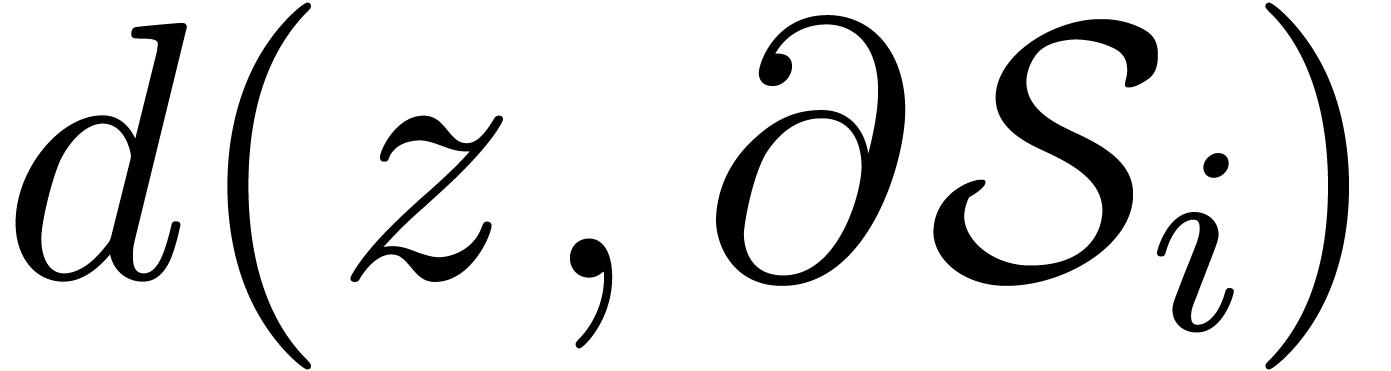 is maximal. In
particular,
is maximal. In
particular, 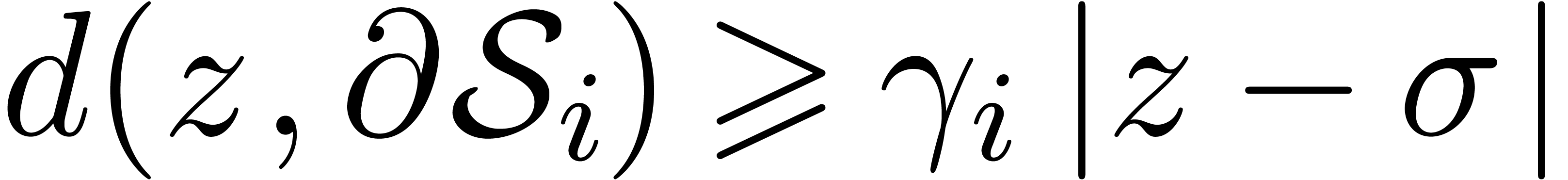 for some fixed constant
for some fixed constant  .
.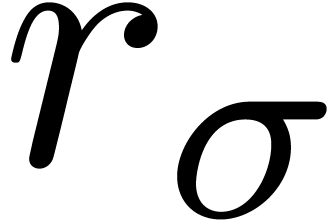 such that
such that 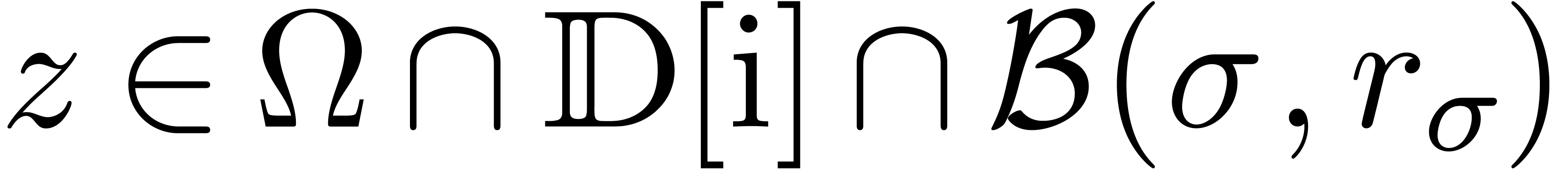 ,
,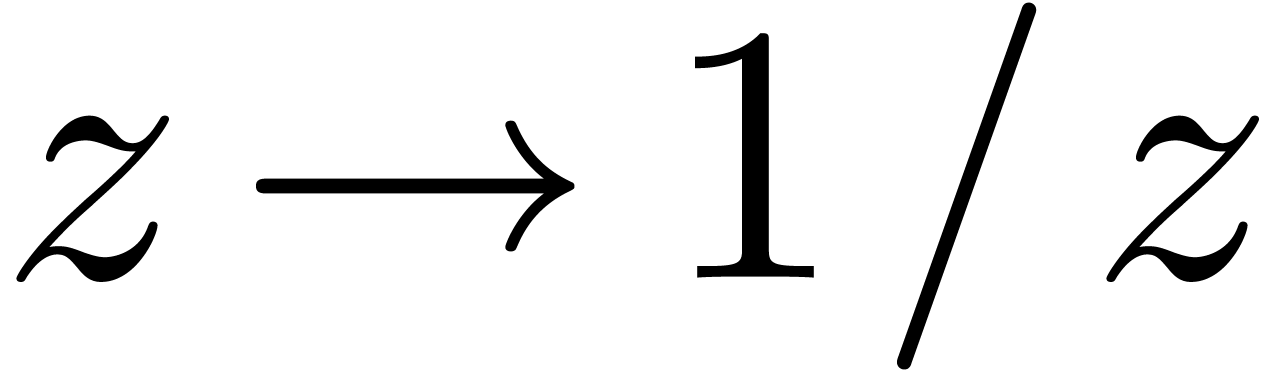 ,
, ,
,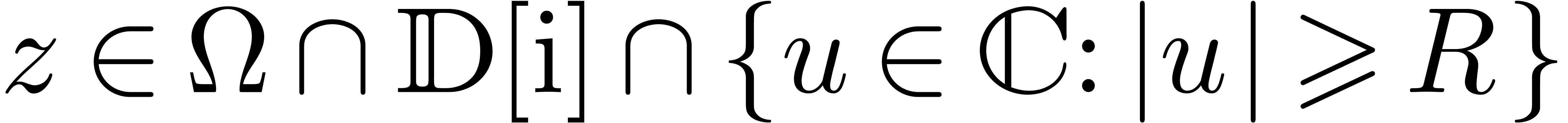 ,
,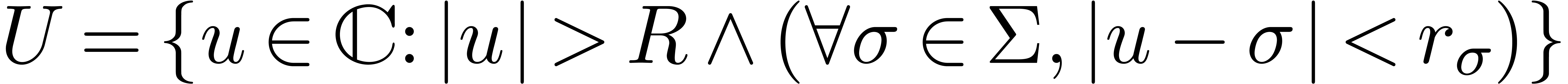 .
.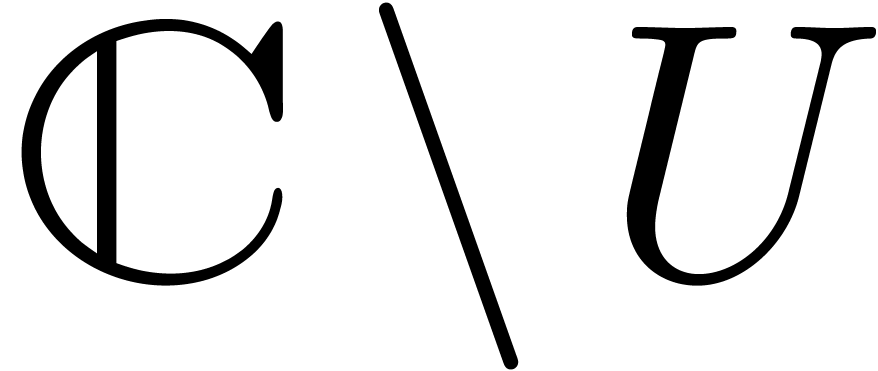 is a compact set that contains none of the
singularities of
is a compact set that contains none of the
singularities of 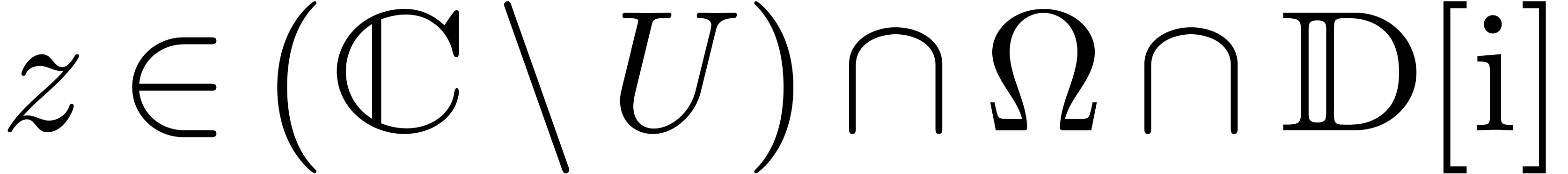 .
. .
. ,
,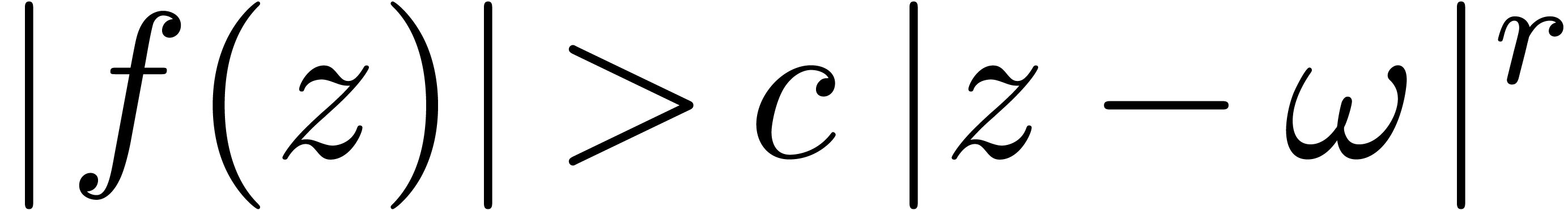 for some computable contant
for some computable contant  and
and
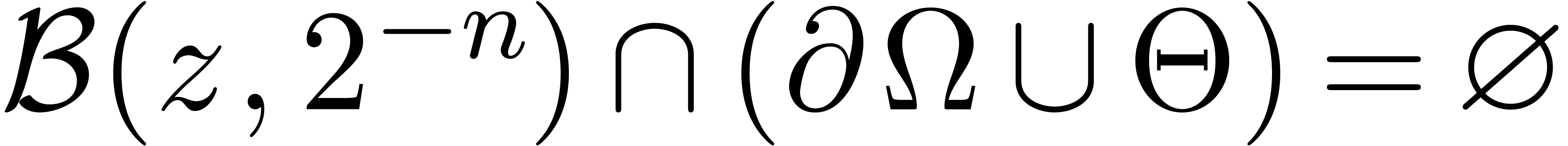 ,
,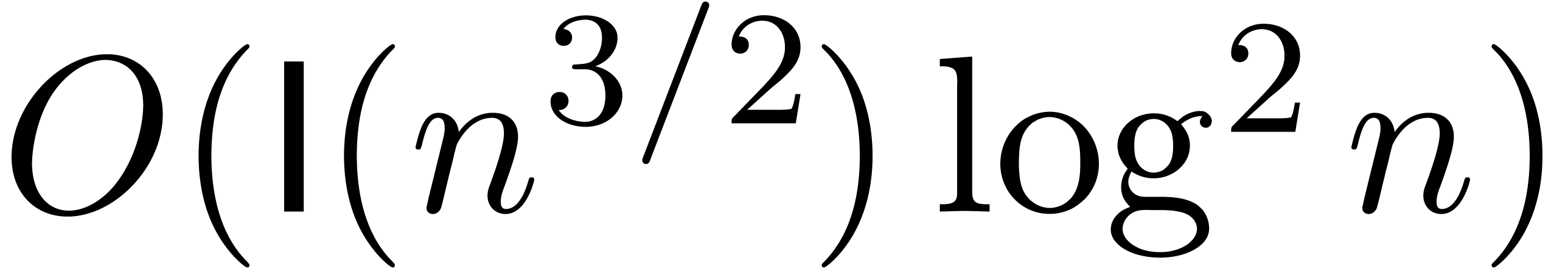 ,
,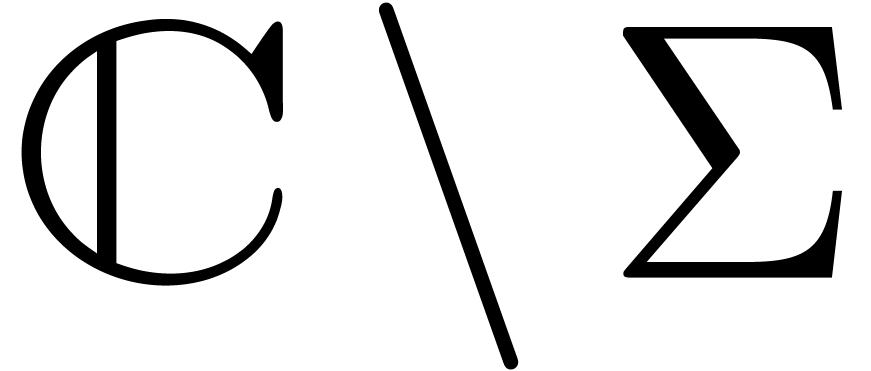 which is a Riemann surface. Points on
this Riemann surface can be represented by broken line paths as in [
which is a Riemann surface. Points on
this Riemann surface can be represented by broken line paths as in [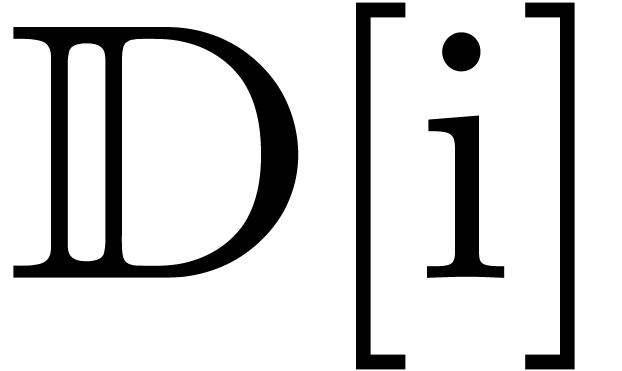 ,
,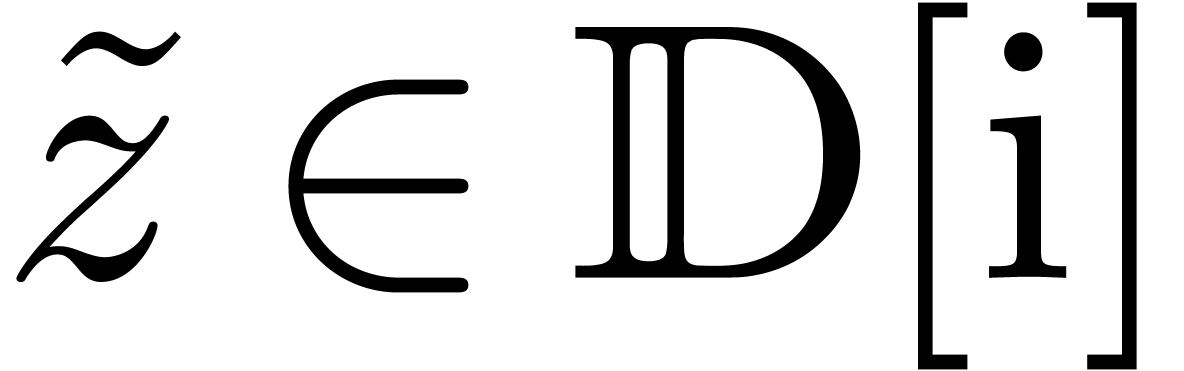 of a
zero
of a
zero 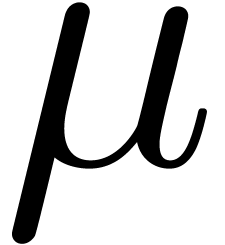 (we must have
(we must have  ),
),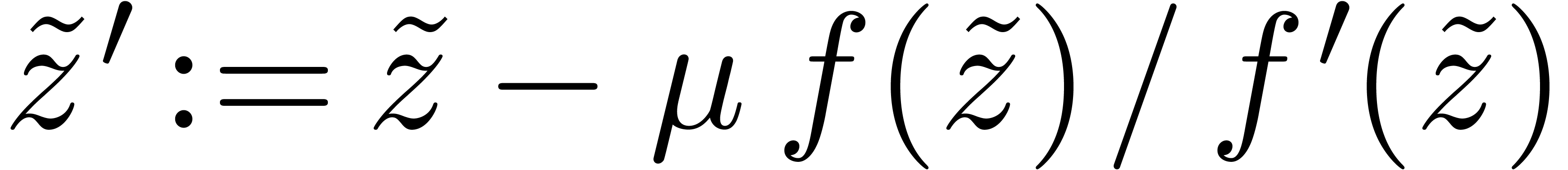 to compute a better approximation
to compute a better approximation  .
. can be done with good uniform complexity,
this should make it possible to compute a
can be done with good uniform complexity,
this should make it possible to compute a  under suitable conditions. It would be a useful
contribution to prove a more precise statement of this kind.
under suitable conditions. It would be a useful
contribution to prove a more precise statement of this kind.
 of
of 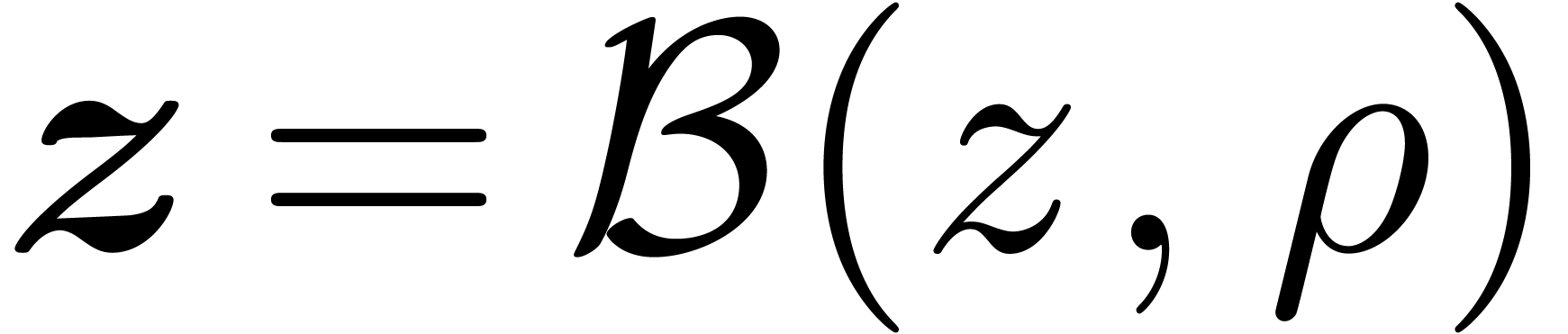 with
with 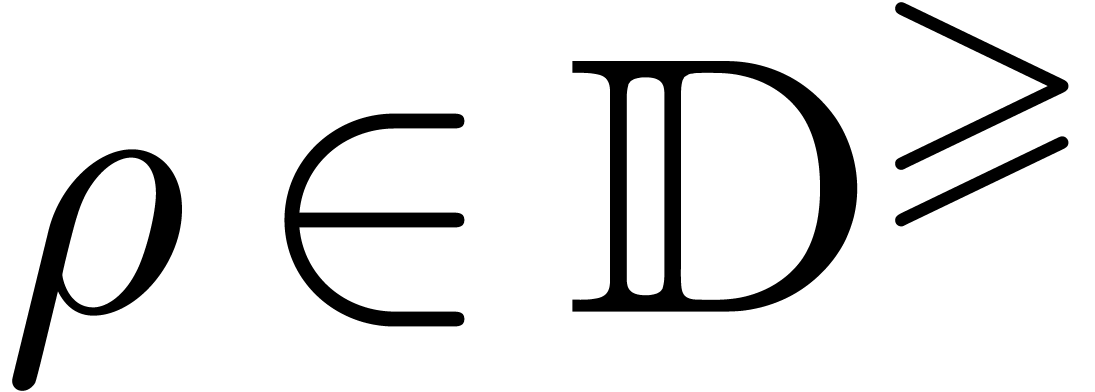 ,
,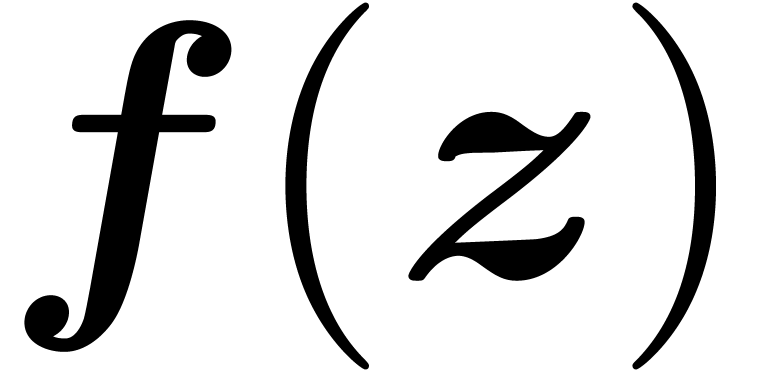 should be a similar ball
should be a similar ball
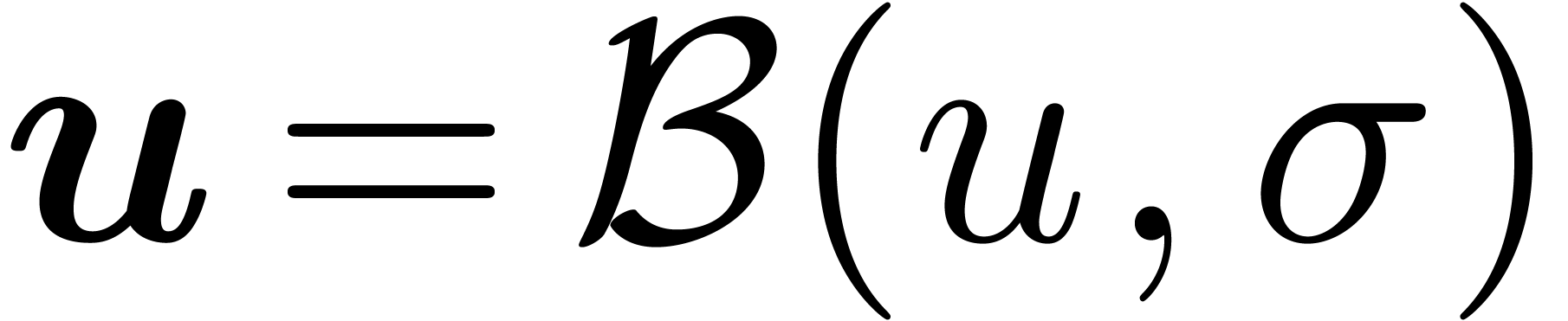 with the property that
with the property that 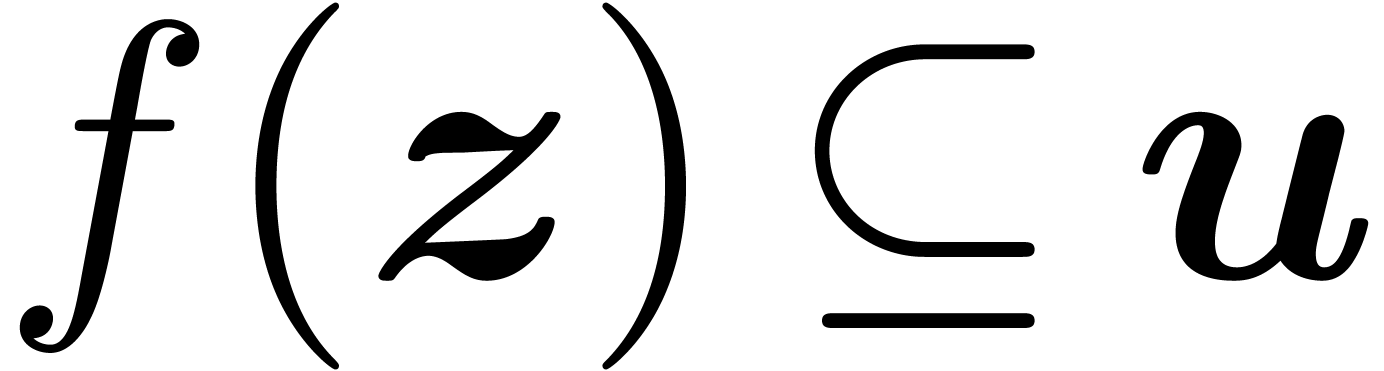 and
and 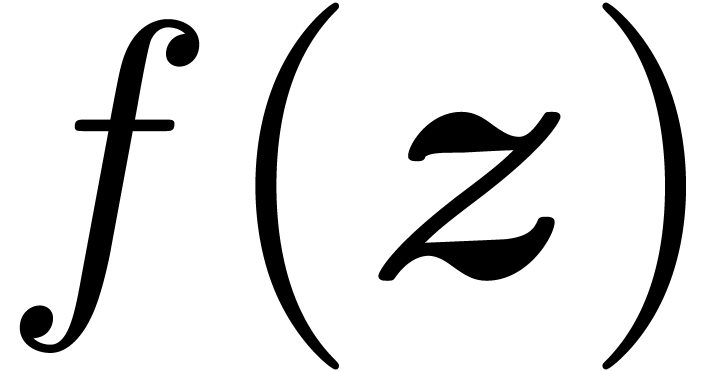 contains two points with distance at least
contains two points with distance at least