Fast amortized multi-point
evaluation  |
|
| March 14, 2020 |
|
 . This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
. This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
 . This article has
been written using GNU TeXmacs [18].
. This article has
been written using GNU TeXmacs [18].
The efficient evaluation of multivariate polynomials at many points is an important operation for polynomial system solving. Kedlaya and Umans have recently devised a theoretically efficient algorithm for this task when the coefficients are integers or when they lie in a finite field. In this paper, we assume that the set of points where we need to evaluate is fixed and “sufficiently generic”. Under these restrictions, we present a quasi-optimal algorithm for multi-point evaluation over general fields. We also present a quasi-optimal algorithm for the opposite interpolation task. |
Let  be an effective field, so that we have
algorithms for the field operations. Given a polynomial
be an effective field, so that we have
algorithms for the field operations. Given a polynomial 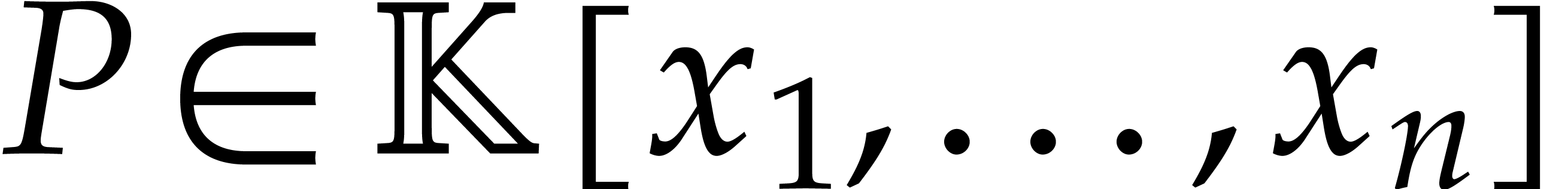 and a tuple
and a tuple 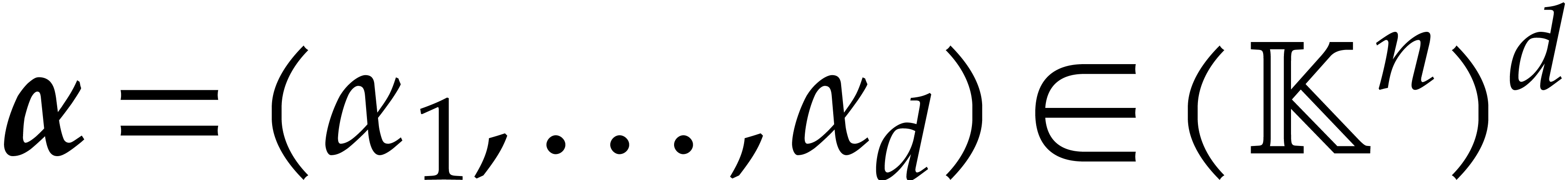 of points, the computation of
of points, the computation of 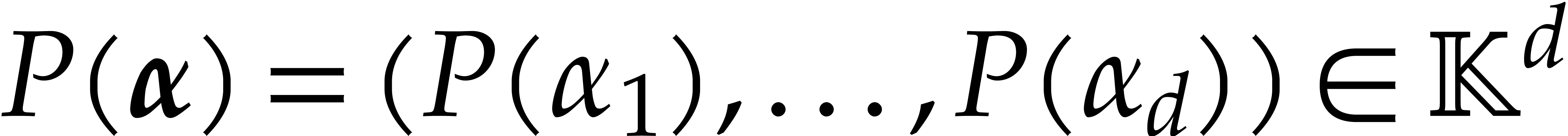 is called the problem of multi-point
evaluation. The converse problem is called interpolation
and takes a candidate support of
is called the problem of multi-point
evaluation. The converse problem is called interpolation
and takes a candidate support of  as input.
as input.
This problem naturally relates to several areas of applied algebra, including polynomial system solving, since we may use it to verify whether all points in a given set are solutions to a system of polynomial equations. In [16], it has even be shown that efficient algorithms for multi-point evaluation lead to efficient algorithms for polynomial system solving. As an other more specific application, bivariate polynomial evaluation intervenes in computing generator matrices of geometric error correcting codes [20].
An important particular case of interpolation concerns polynomials with prescribed supports and that vanish at a given set of points. This happens in list decoding algorithms for Reed–Solomon error correcting codes; see recent complexity bounds in [7]. In the bivariate case, this task also occurs in the Brill–Noether strategy for computing Riemann–Roch spaces; see recent advances in [2]. Further applications can be found in [24].
In the univariate case when 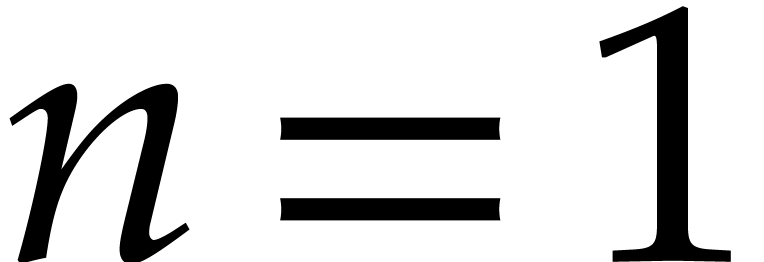 ,
it is well known that one may use so-called “remainder
trees” to compute multi-point evaluations in quasi-optimal time
[3, 9, 23]. More precisely, if
,
it is well known that one may use so-called “remainder
trees” to compute multi-point evaluations in quasi-optimal time
[3, 9, 23]. More precisely, if
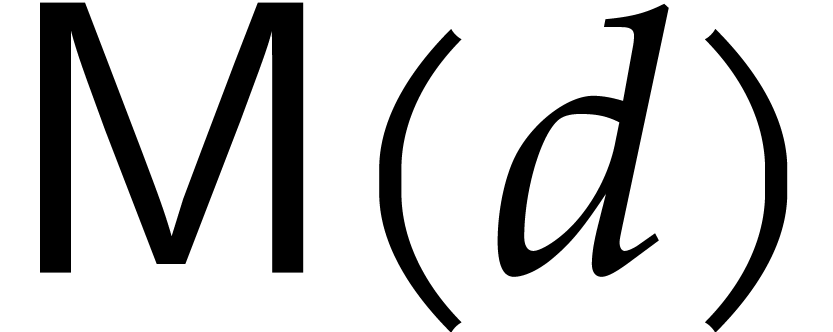 stands for the cost to multiply two univariate
polynomials of degree
stands for the cost to multiply two univariate
polynomials of degree 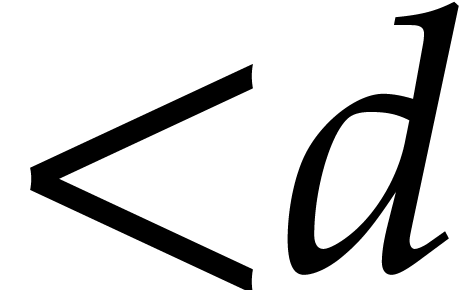 (in terms of the number of
field operations in
(in terms of the number of
field operations in  ), then
the multi-point evaluation of a polynomial of degree
), then
the multi-point evaluation of a polynomial of degree 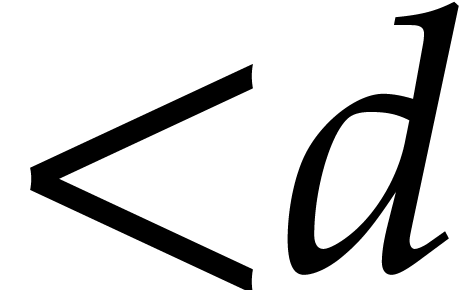 at
at  points can be computed in time
points can be computed in time 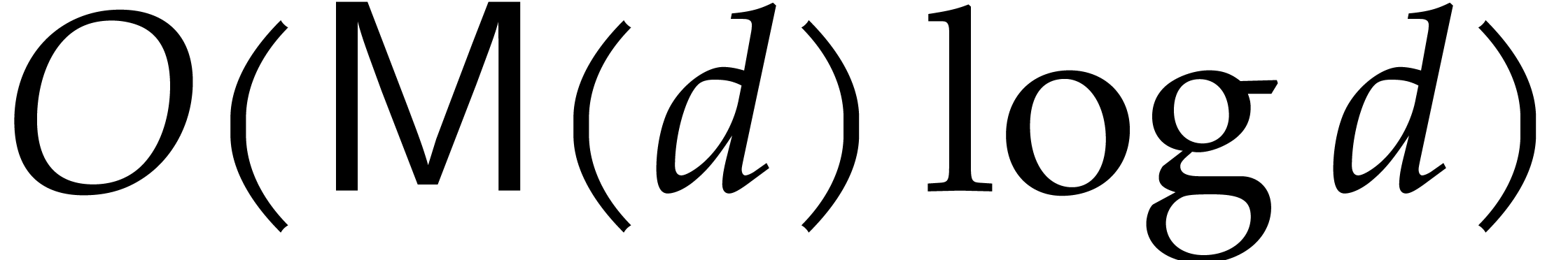 . A similar complexity bound holds for the
opposite operation of interpolation. The constants hidden in
the latter “
. A similar complexity bound holds for the
opposite operation of interpolation. The constants hidden in
the latter “ ”
have been studied in [5]. Recently, and under suitable
technical assumptions, it has been shown that the cost of univariate
multi-point evaluation (and interpolation) drops to
”
have been studied in [5]. Recently, and under suitable
technical assumptions, it has been shown that the cost of univariate
multi-point evaluation (and interpolation) drops to 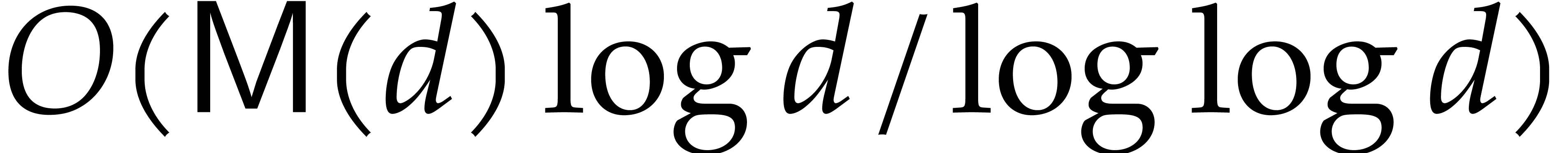 if the set of evaluation points is fixed [13]. In this
case, we do not count the cost of certain precomputations that only
depend on the evaluation points and not on the polynomials to evaluate.
We may also speak about the “amortized cost” of multi-point
evaluation.
if the set of evaluation points is fixed [13]. In this
case, we do not count the cost of certain precomputations that only
depend on the evaluation points and not on the polynomials to evaluate.
We may also speak about the “amortized cost” of multi-point
evaluation.
In the multivariate case when  ,
no quasi-optimal algorithms are currently known for multi-point
evaluation. From a theoretical point of view, the best bit-complexity
bounds are due to Kedlaya and Umans, in the special cases when the
coefficients of our polynomials are modular integers or when they lie in
a finite field [19]. They also related the problem to other
important operations such as modular composition and power projection.
Their results have recently been refined in [17]. Over
general fields and for
,
no quasi-optimal algorithms are currently known for multi-point
evaluation. From a theoretical point of view, the best bit-complexity
bounds are due to Kedlaya and Umans, in the special cases when the
coefficients of our polynomials are modular integers or when they lie in
a finite field [19]. They also related the problem to other
important operations such as modular composition and power projection.
Their results have recently been refined in [17]. Over
general fields and for 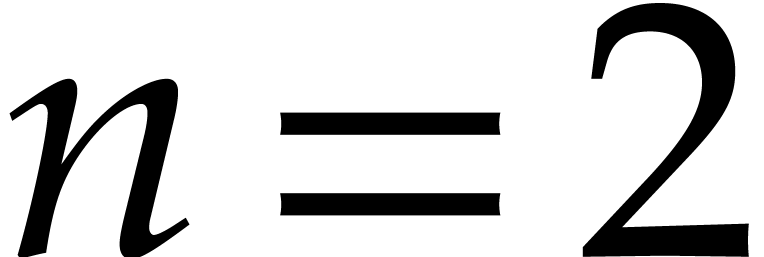 , the
best known bound is
, the
best known bound is 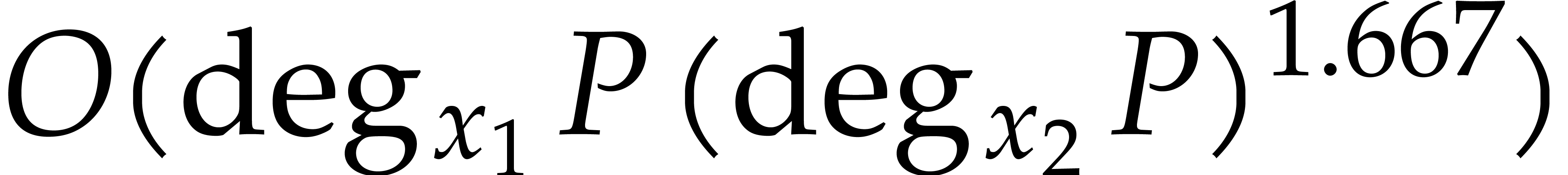 ; due to
Nüsken and Ziegler [26].
; due to
Nüsken and Ziegler [26].
The multivariate interpolation problem turns out to be more intricate
than evaluation, and fewer efficient algorithms are known. Using naive
linear algebra, one may design polynomial time algorithms, but with
costs that are higher than quadratic in  .
To our knowledge no interpolation method has been designed in the vein
of the Kedlaya–Umans evaluation algorithms. Several methods are
surveyed in [10] for instance, but, here, we will focus on
symbolic approaches and their asymptotical complexity bounds.
.
To our knowledge no interpolation method has been designed in the vein
of the Kedlaya–Umans evaluation algorithms. Several methods are
surveyed in [10] for instance, but, here, we will focus on
symbolic approaches and their asymptotical complexity bounds.
Concerning the computation of polynomials that vanish at a given set of
points, with suitable constraints on the supports, early methods can be
found in [1, 22, 24]:
Gröbner bases of the ideal made of these polynomials are obtained
with cost at least cubic in  .
After a generic change of coordinates the lexicographic basis satisfies
the “shape lemma” and it can be computed in softly linear
time by means of univariate interpolations. In other words, our set of
points is the solution set of a system
.
After a generic change of coordinates the lexicographic basis satisfies
the “shape lemma” and it can be computed in softly linear
time by means of univariate interpolations. In other words, our set of
points is the solution set of a system 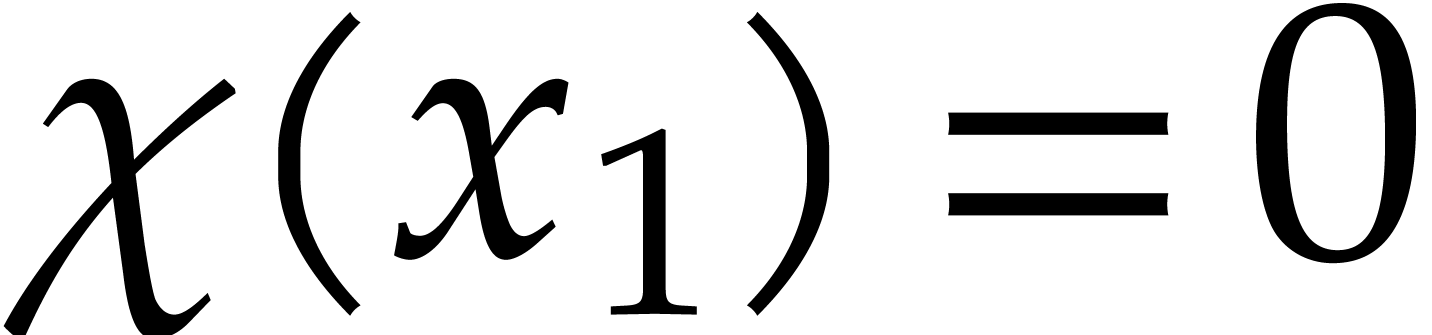 and
and 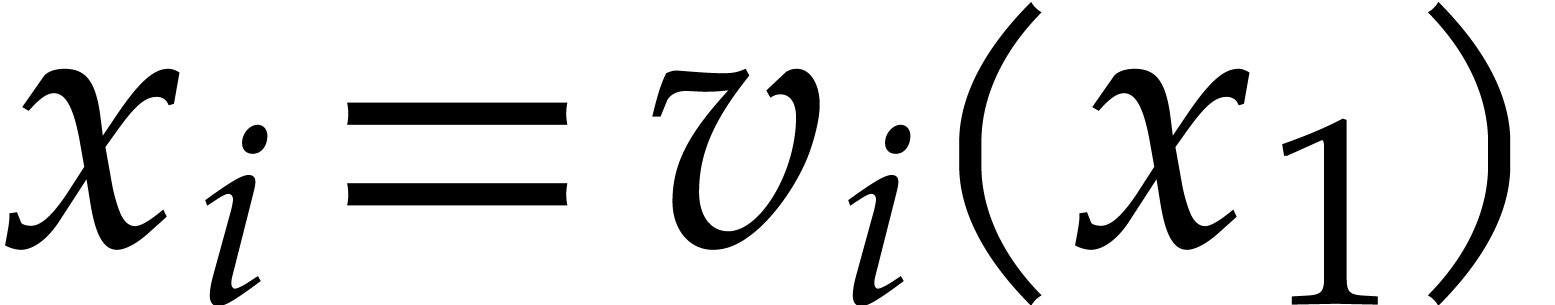 for
for 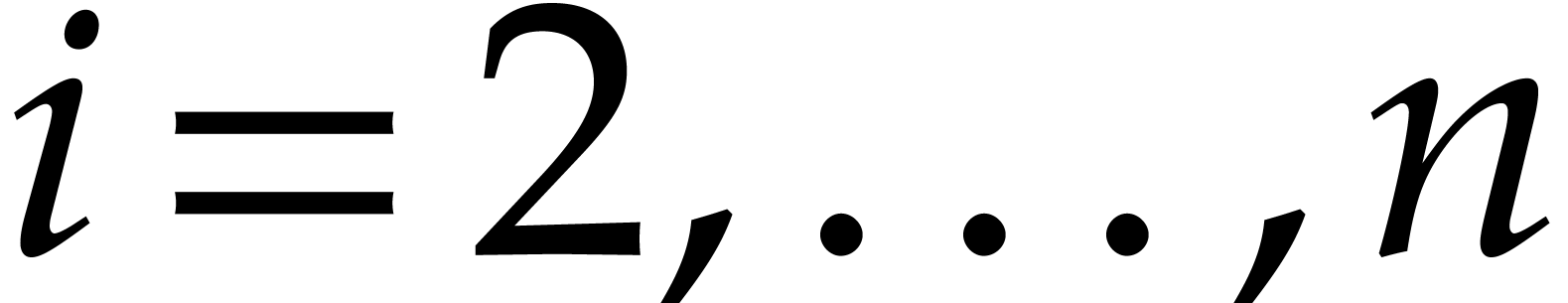 ,
where
,
where 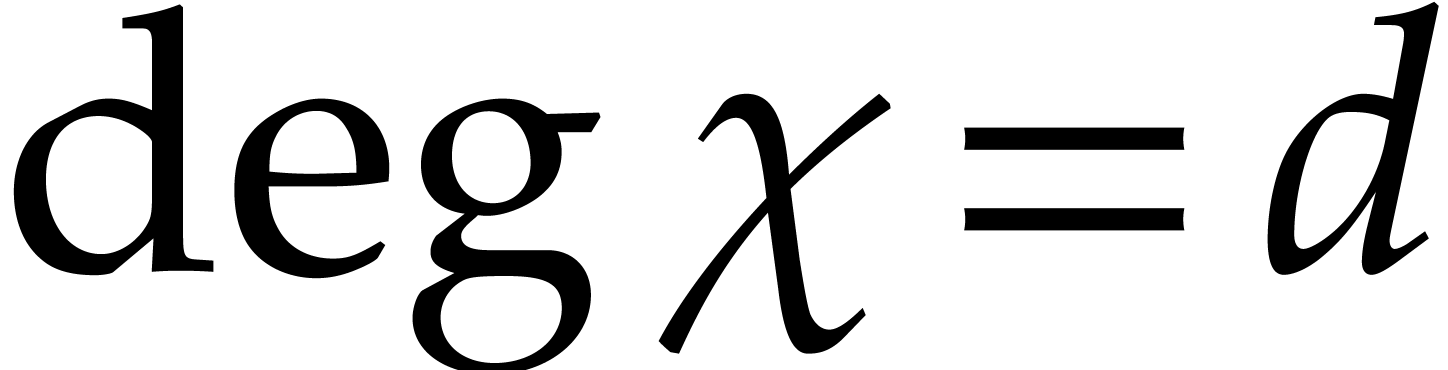 and
and 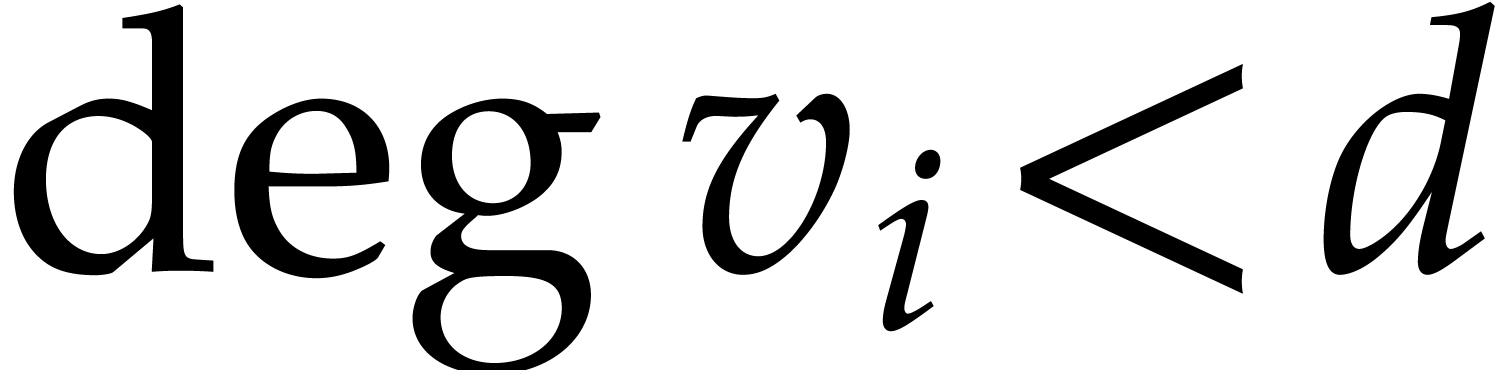 .
From
.
From  and the
and the 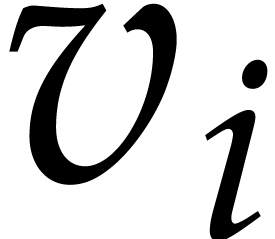 ,
a Gröbner basis for any other monomial ordering can be recovered
with
,
a Gröbner basis for any other monomial ordering can be recovered
with 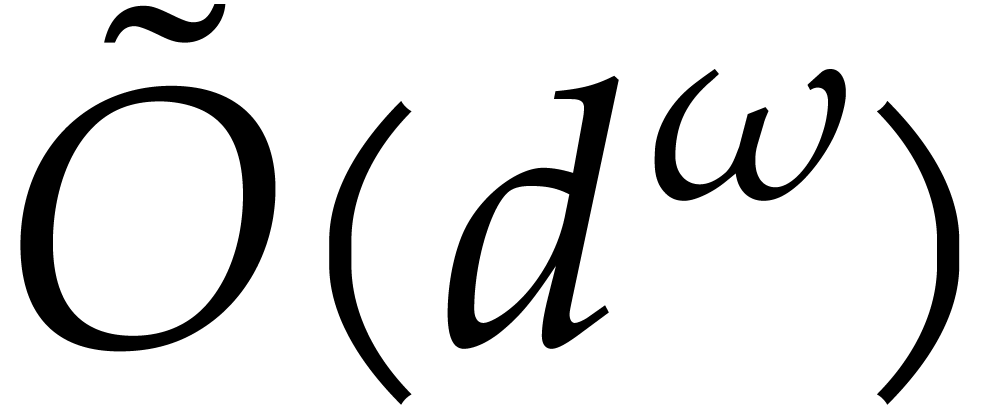 field operations thanks to the algorithm
designed in [8].
field operations thanks to the algorithm
designed in [8].
In the bivariate case, with generic coordinates, from the latter
univariate parametrization, and given 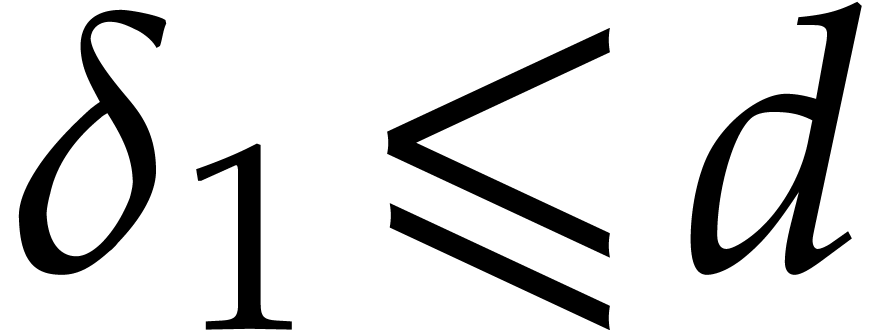 ,
we may compute a basis of the
,
we may compute a basis of the 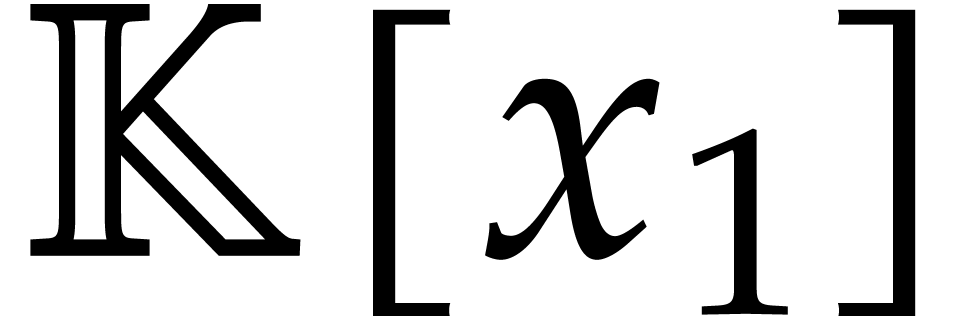 -module
of polynomials of degree
-module
of polynomials of degree 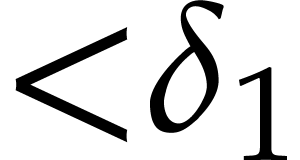 in
in 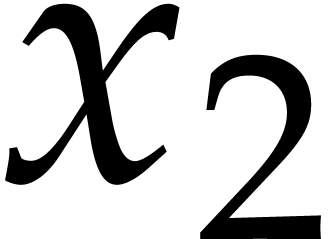 that vanish at
that vanish at  . Indeed this
reduces to computing a basis of the kernel of the map
. Indeed this
reduces to computing a basis of the kernel of the map
This kernel is a free 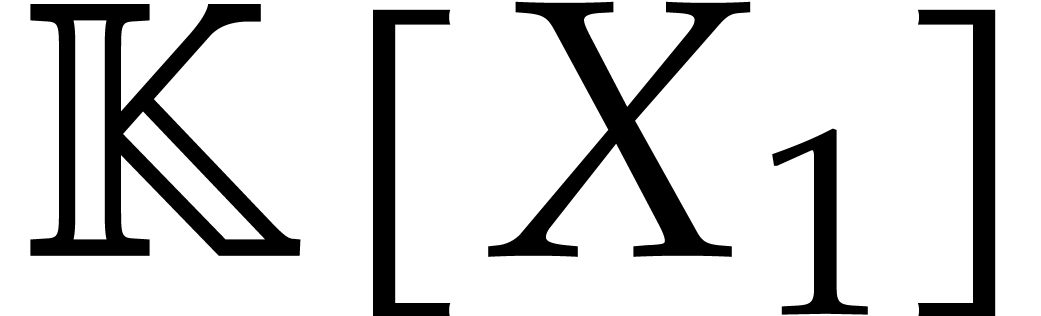 -module
of rank
-module
of rank 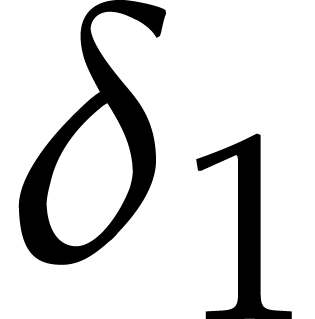 . The basis in Popov
form can be computed with
. The basis in Popov
form can be computed with 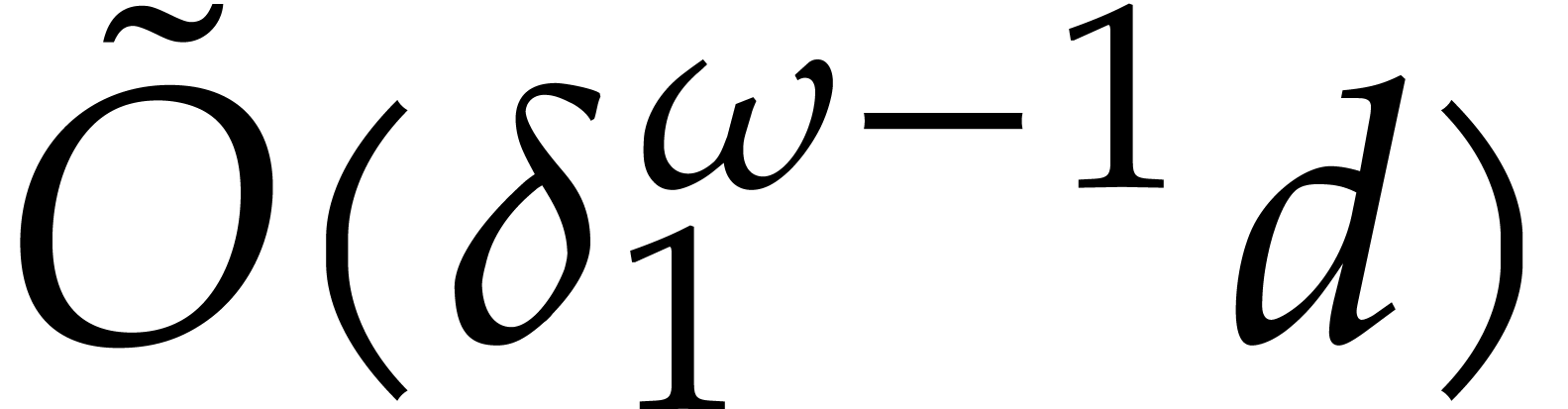 operations in
operations in  ; this complexity bound is due to
Neiger [25]. Taking
; this complexity bound is due to
Neiger [25]. Taking 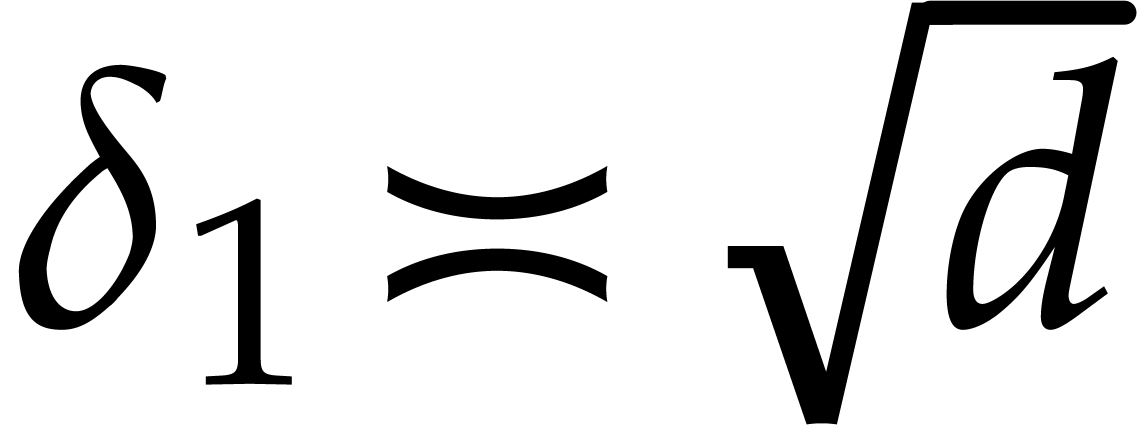 ,
the latter cost rewrites
,
the latter cost rewrites 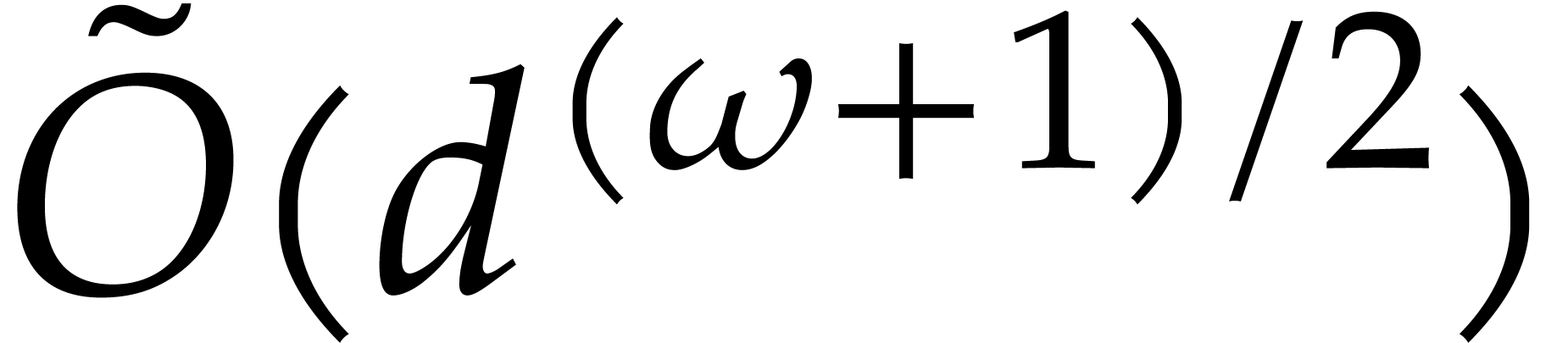 .
The bivariate interpolation problem can be solved with the same kind of
complexity bound by means of linear algebra algorithms that exploit
displacement ranks [4].
.
The bivariate interpolation problem can be solved with the same kind of
complexity bound by means of linear algebra algorithms that exploit
displacement ranks [4].
In a more general setting, one may consider evaluation at “multisets of points” in the sense that values of polynomials and of certain of its derivatives are involved. The converse problem is usually called Hermite interpolation, so values for the polynomial and its derivative are prescribed. We will not address these extended problems in the present paper.
In this paper, we turn our attention to the amortized cost of
multivariate multi-point evaluation. Given a “sufficiently
generic” tuple  of evaluation points, we
first construct a suitable “evaluation tree” that is similar
to the remainder trees from the univariate case. After this
precomputation, we next show how to evaluate polynomials at
of evaluation points, we
first construct a suitable “evaluation tree” that is similar
to the remainder trees from the univariate case. After this
precomputation, we next show how to evaluate polynomials at  in quasi-optimal time. For instance, for a fixed dimension
in quasi-optimal time. For instance, for a fixed dimension
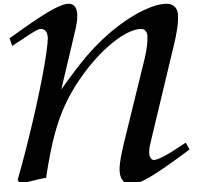 , a sufficiently large base
field
, a sufficiently large base
field  , and a polynomial
, and a polynomial 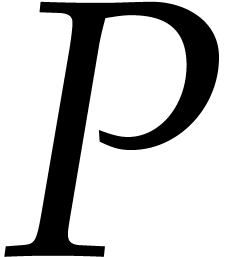 of partial degrees
of partial degrees 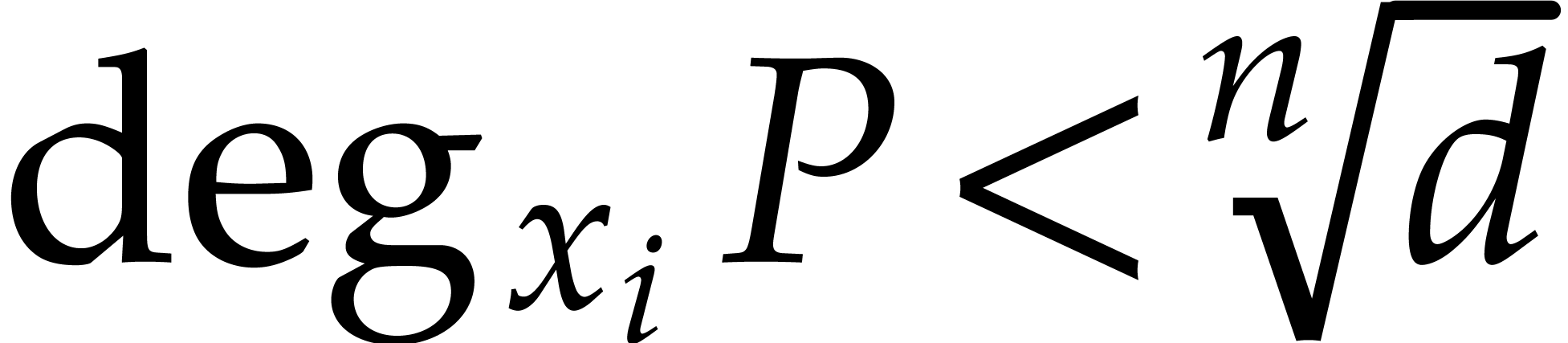 for
for  , we show how to compute
, we show how to compute 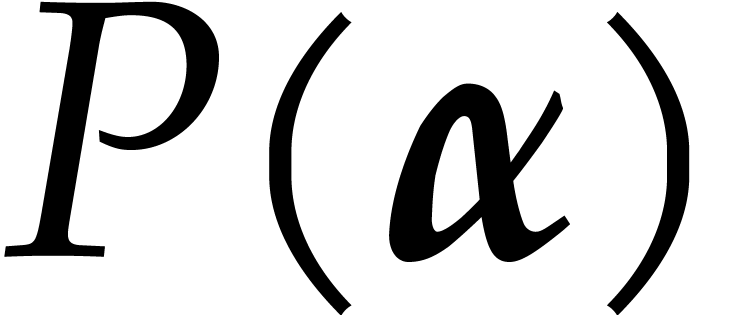 in time
in time 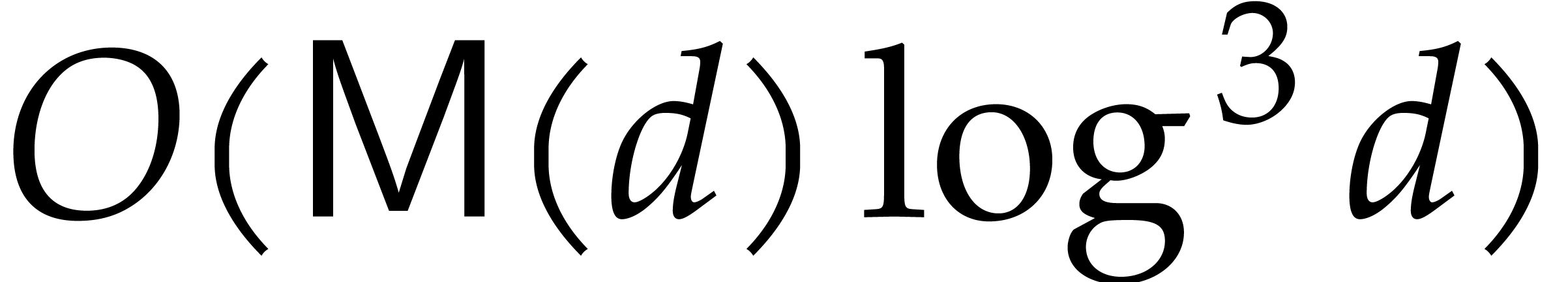 . We
also show how to do the opposite operation of interpolation with a
similar complexity. It can be shown that the “constant
factors” in the big-Oh hide a factorial dependence in
. We
also show how to do the opposite operation of interpolation with a
similar complexity. It can be shown that the “constant
factors” in the big-Oh hide a factorial dependence in 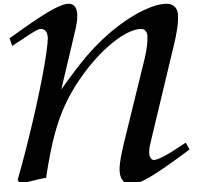 .
.
Our algorithms rely on suitable genericity hypotheses that ensure the
existence of Gröbner bases of a specific shape for the vanishing
ideal  at the evaluation points. This will be
detailed in section 3. Another key ingredient is an
algorithm from [14] for the relaxed reduction of
polynomials with respect to such Gröbner bases or more general sets
of polynomials. In this paper, all reductions will be done with respect
to so-called “axial bases”, which provide sufficiently good
approximations of the actual Gröbner bases of
at the evaluation points. This will be
detailed in section 3. Another key ingredient is an
algorithm from [14] for the relaxed reduction of
polynomials with respect to such Gröbner bases or more general sets
of polynomials. In this paper, all reductions will be done with respect
to so-called “axial bases”, which provide sufficiently good
approximations of the actual Gröbner bases of  . This will be detailed in section 4.
. This will be detailed in section 4.
Having an efficient algorithm for reducing polynomials with respect to
 , we may use it as a
generalization of Euclidean division. In sections 5 and 6, this allows us to generalize the remainder tree technique
to higher dimensions, and establish our complexity bounds for amortized
multi-point evaluation and interpolation. It is also noteworthy that the
necessary precomputations can be done using linear algebra in time
, we may use it as a
generalization of Euclidean division. In sections 5 and 6, this allows us to generalize the remainder tree technique
to higher dimensions, and establish our complexity bounds for amortized
multi-point evaluation and interpolation. It is also noteworthy that the
necessary precomputations can be done using linear algebra in time 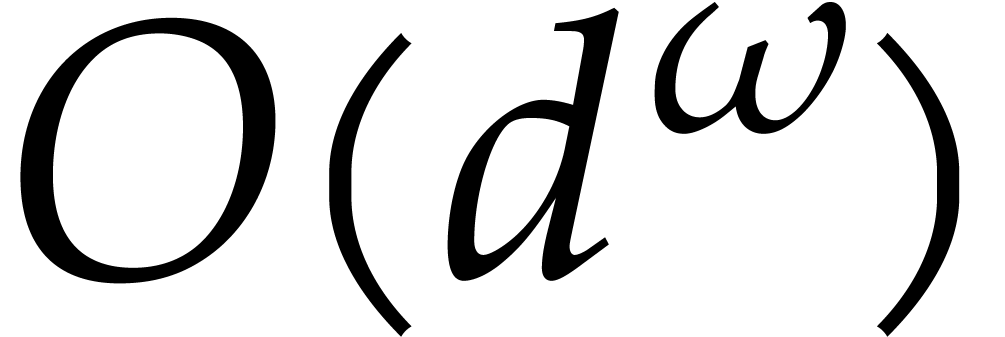 , where
, where 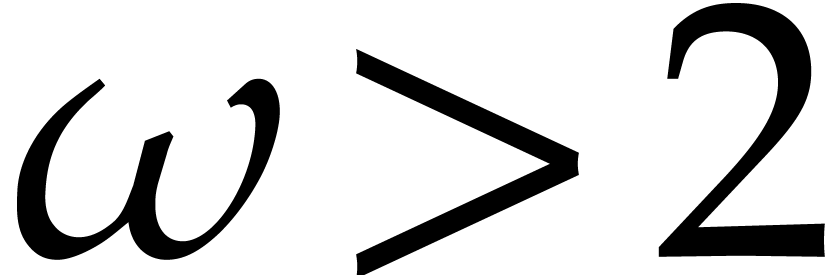 is
a feasible exponent for matrix multiplication.
is
a feasible exponent for matrix multiplication.
When comparing our new amortized bound 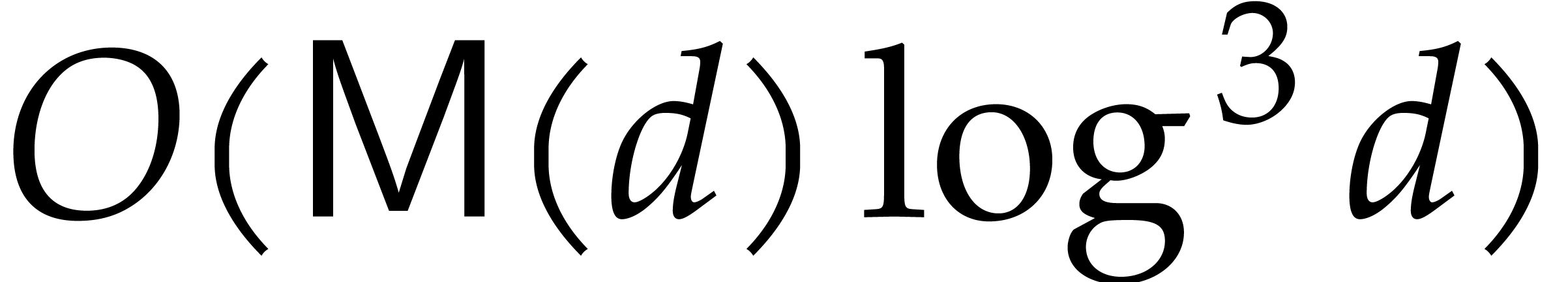 with the
traditional bound
with the
traditional bound 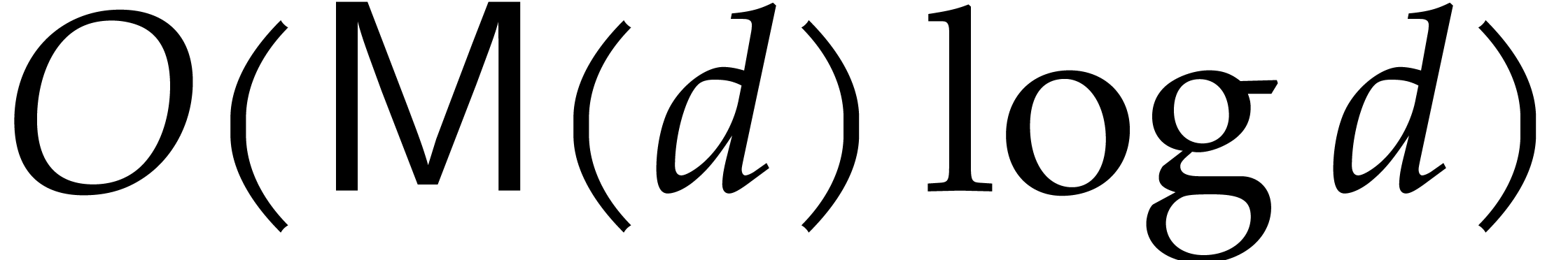 in the univariate case, we
note that we lose a factor
in the univariate case, we
note that we lose a factor 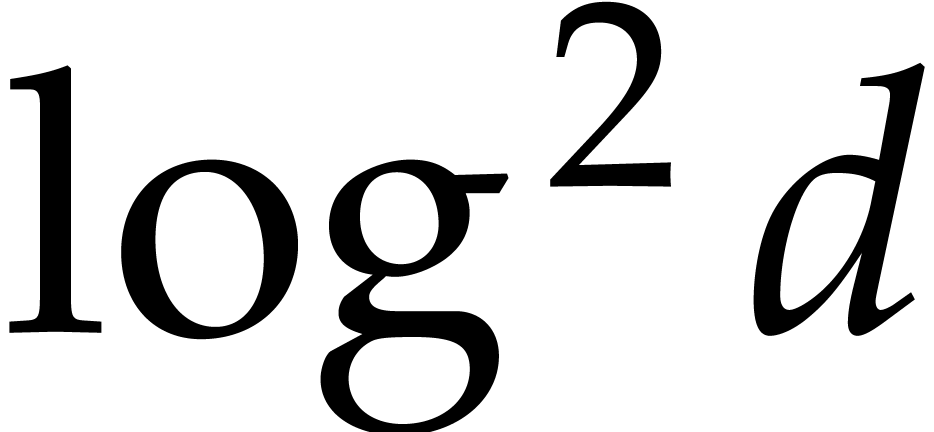 .
This is due to the fact that we rely on relaxed computations for our
polynomial reductions. With a bit of work, a factor
.
This is due to the fact that we rely on relaxed computations for our
polynomial reductions. With a bit of work, a factor 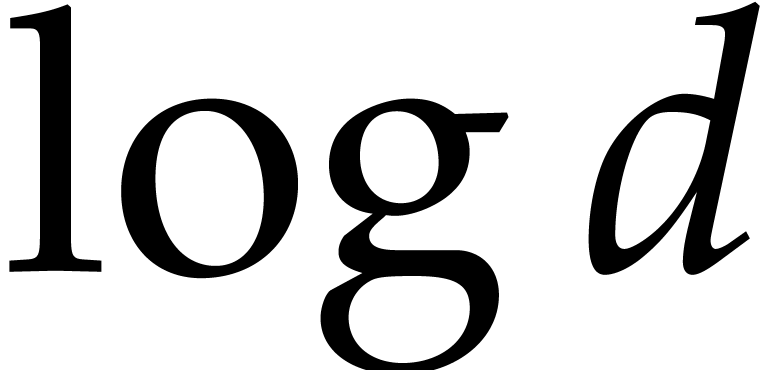 might be removed by exploiting the fact that our polynomials are not
really sparse, so that we may take
might be removed by exploiting the fact that our polynomials are not
really sparse, so that we may take 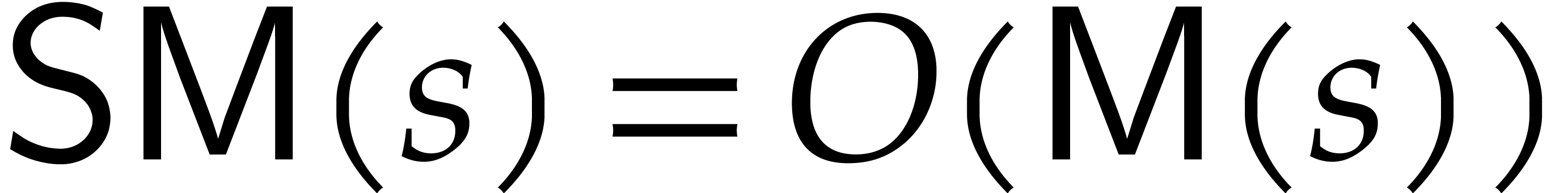 in the proof
of Theorem 6 (under our assumption that
in the proof
of Theorem 6 (under our assumption that 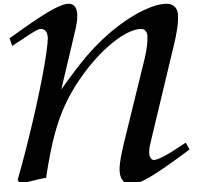 is fixed and with the notation
is fixed and with the notation  defined in [14]). It is plausible that the second logarithmic factor can
be further reduced using techniques from [12] or a clever
Newton iteration.
defined in [14]). It is plausible that the second logarithmic factor can
be further reduced using techniques from [12] or a clever
Newton iteration.
Our genericity assumptions can also be weakened significantly: with the
notations from section 4, it is essentially sufficient to
assume that 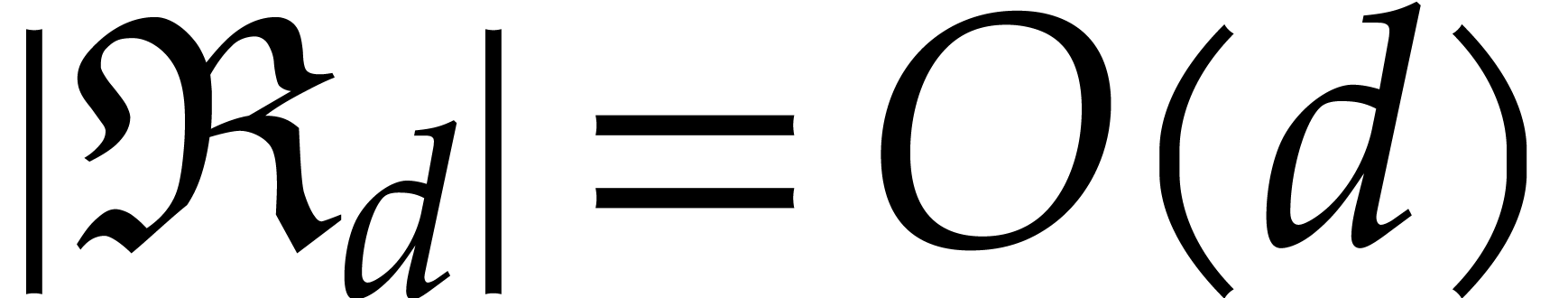 . Another
interesting question is whether the cost
. Another
interesting question is whether the cost 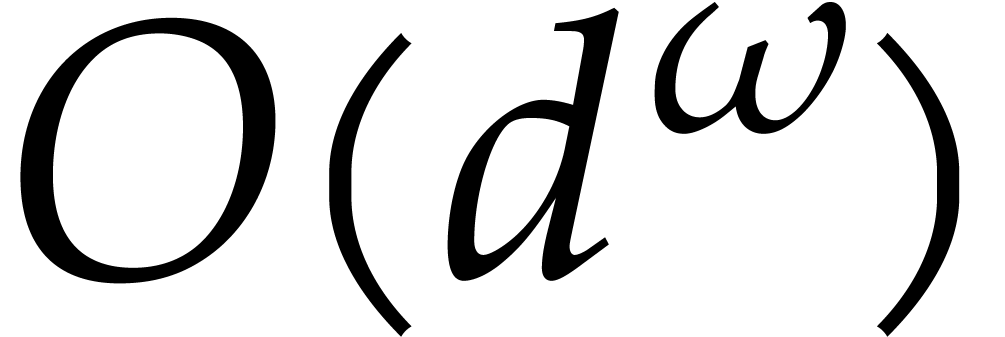 of the
precomputations can be lowered. Under additional genericity assumptions,
this is indeed possible when
of the
precomputations can be lowered. Under additional genericity assumptions,
this is indeed possible when 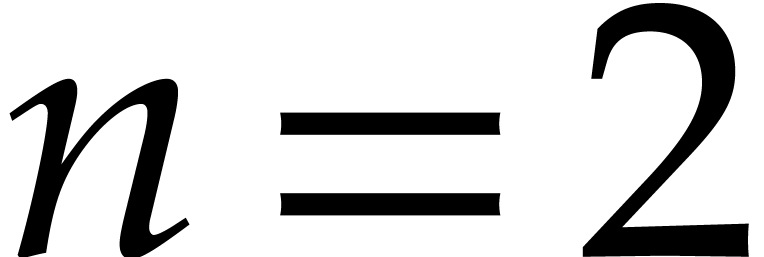 :
using the probabilistic algorithm of type Las Vegas from [4],
the precomputations take an expected number of
:
using the probabilistic algorithm of type Las Vegas from [4],
the precomputations take an expected number of 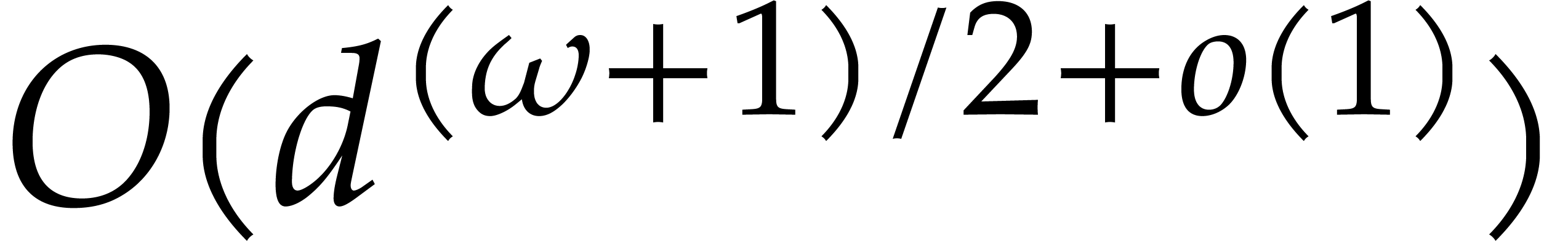 field operations.
field operations.
For complexity analyses, we will only consider algebraic complexity
models (such as computation trees). In other words we will simply count
numbers of arithmetic operations and zero-tests in  .
.
Throughout this paper, we assume 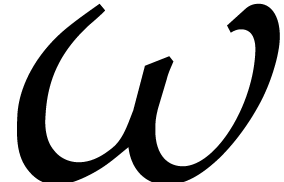 to be a
feasible exponent for matrix multiplication with
to be a
feasible exponent for matrix multiplication with 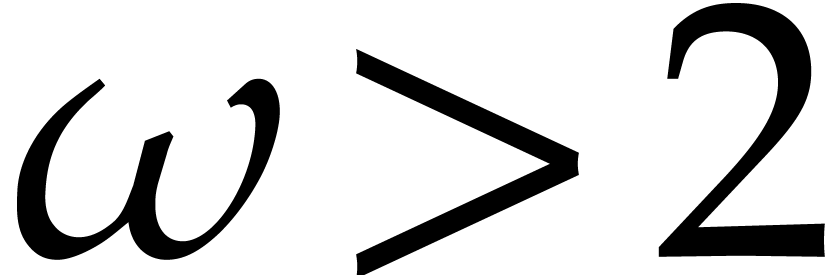 . This means that two
. This means that two  matrices in
matrices in 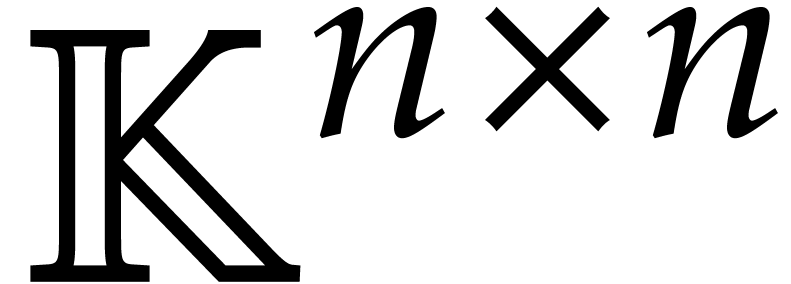 can be multiplied in time
can be multiplied in time 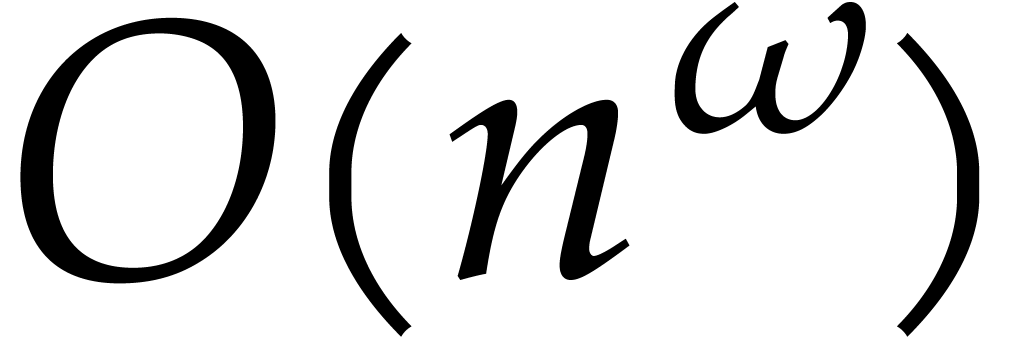 . Le Gall has shown in [21]
that one may take
. Le Gall has shown in [21]
that one may take 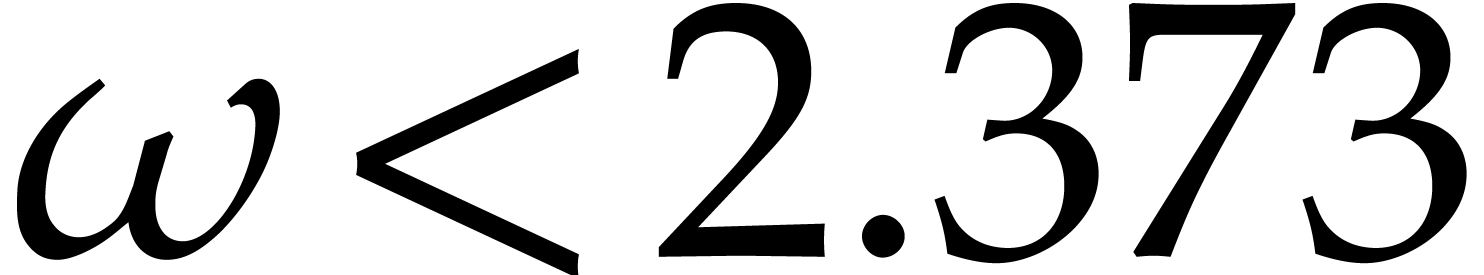 .
.
We denote by 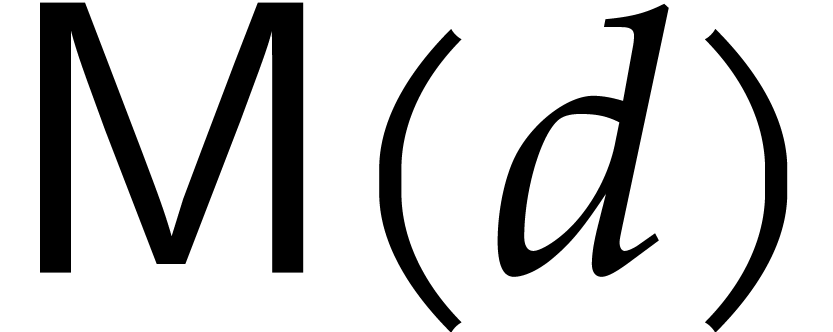 the time that is needed to compute
a product
the time that is needed to compute
a product  of two polynomials
of two polynomials 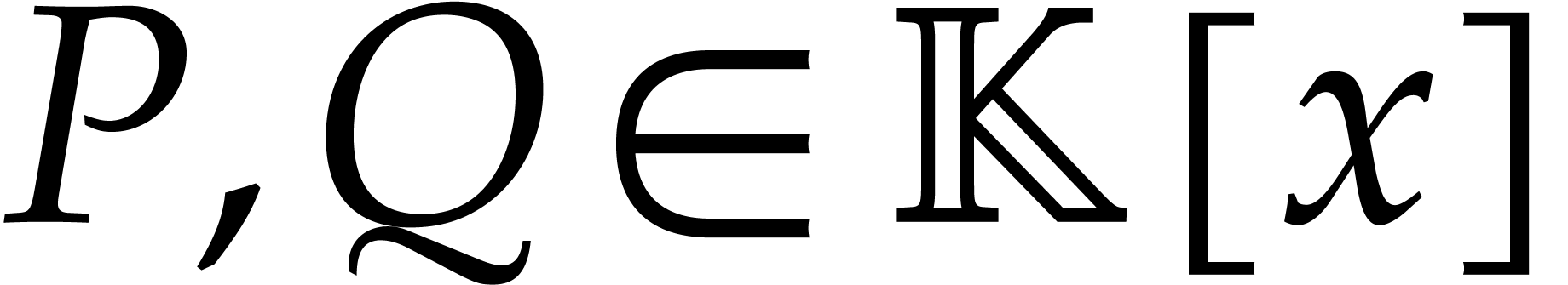 of degree
of degree  . We make the usual
assumption that
. We make the usual
assumption that 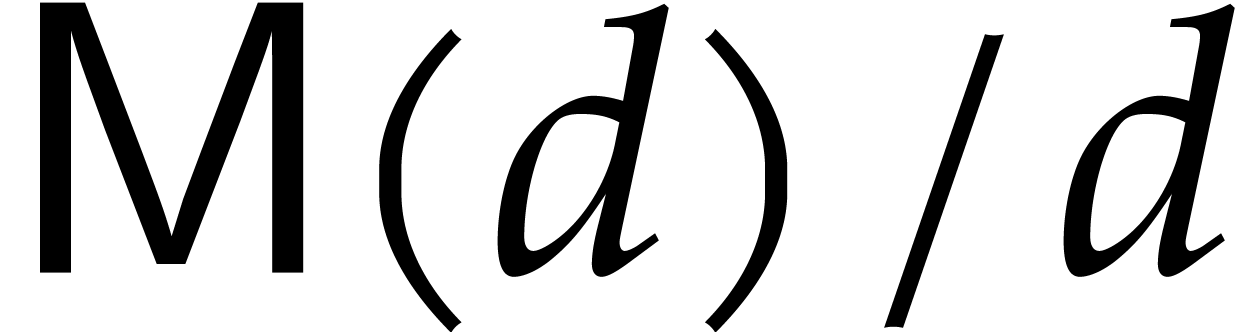 is non-decreasing as a function
of
is non-decreasing as a function
of  . It is also convenient to
assume that
. It is also convenient to
assume that  for
for 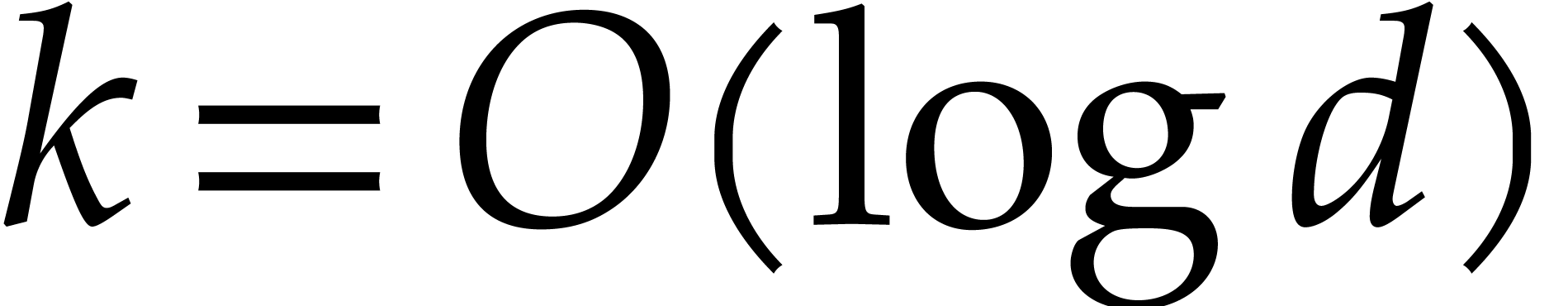 .
Using a variant of Schönhage–Strassen's algorithm [6,
28, 29], it is well known that
.
Using a variant of Schönhage–Strassen's algorithm [6,
28, 29], it is well known that 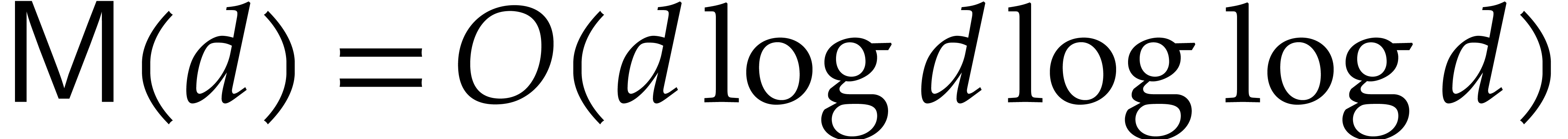 . If we restrict our attention to fields
. If we restrict our attention to fields  of positive characteristic, then we may take
of positive characteristic, then we may take 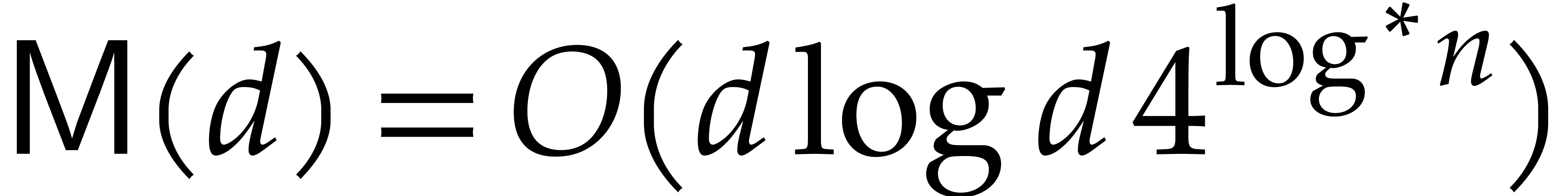 [11].
[11].
In order to use the extended multivariate reduction algorithms from [14], sparse polynomial arithmetic is needed. A sparse
representation of a polynomial 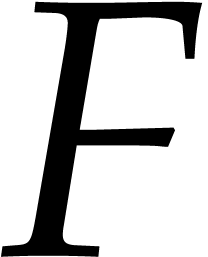 in
in  is a data structure that stores the set of the non-zero
terms of
is a data structure that stores the set of the non-zero
terms of  . Each such term is
a pair made of a coefficient and a degree vector. In an algebraic
complexity model the bit size of the exponents counts for free, so the
relevant size of such a polynomial is the cardinality of its support.
. Each such term is
a pair made of a coefficient and a degree vector. In an algebraic
complexity model the bit size of the exponents counts for free, so the
relevant size of such a polynomial is the cardinality of its support.
Consider two polynomials  and
and  of
of  in sparse representation. An extensive
literature exists on the general problem of multiplying
in sparse representation. An extensive
literature exists on the general problem of multiplying  and
and  ; see [27]
for a recent survey. For the purposes of this paper, a superset
; see [27]
for a recent survey. For the purposes of this paper, a superset  for the support of
for the support of  will
always be known. Then we define
will
always be known. Then we define 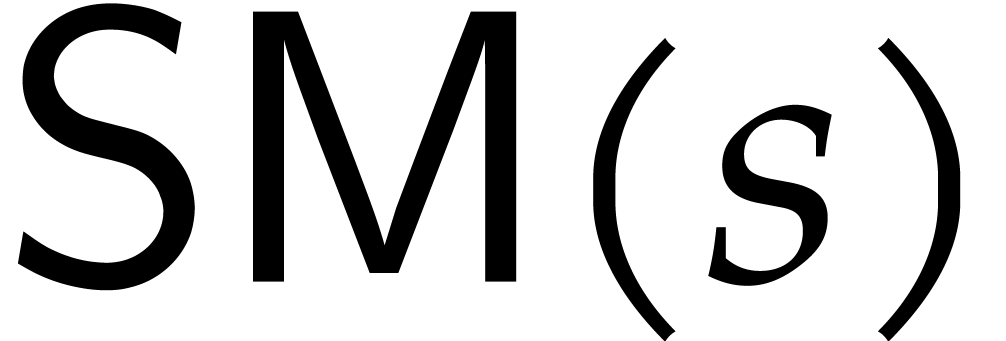 to be the cost
to compute
to be the cost
to compute  , where
, where  is the maximum of the sizes of such a superset
is the maximum of the sizes of such a superset  and the supports of
and the supports of  and
and  . Under suitable assumptions, the
following proposition will allow us to take
. Under suitable assumptions, the
following proposition will allow us to take 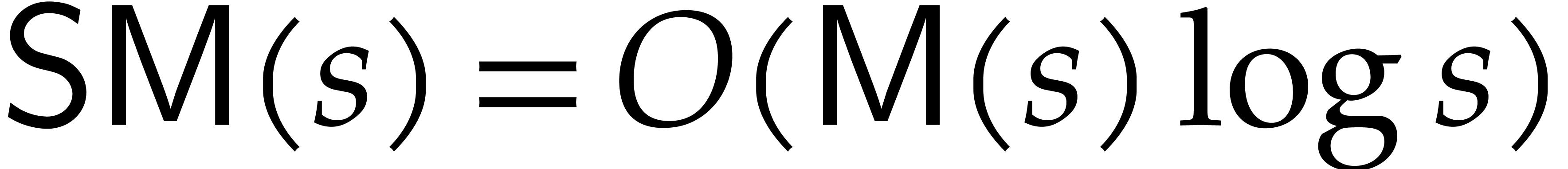 in
our multivariate evaluation and interpolation algorithms.
in
our multivariate evaluation and interpolation algorithms.
 be positive integers
and let
be positive integers
and let  in
in  be of
multiplicative order at least
be of
multiplicative order at least  .
.
The set  made of the products
made of the products 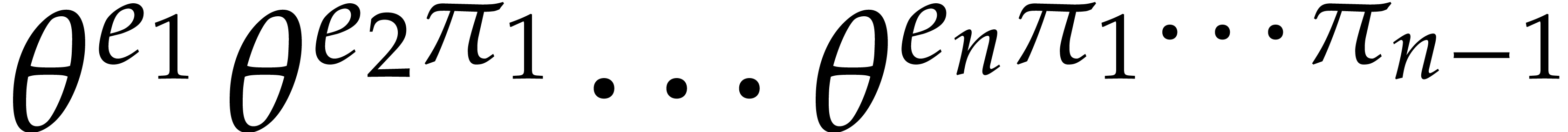 for
for 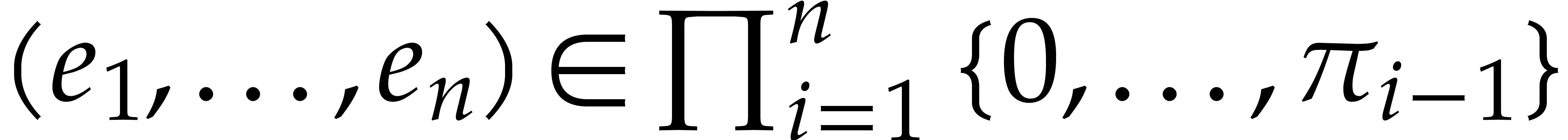 can be computed using
can be computed using
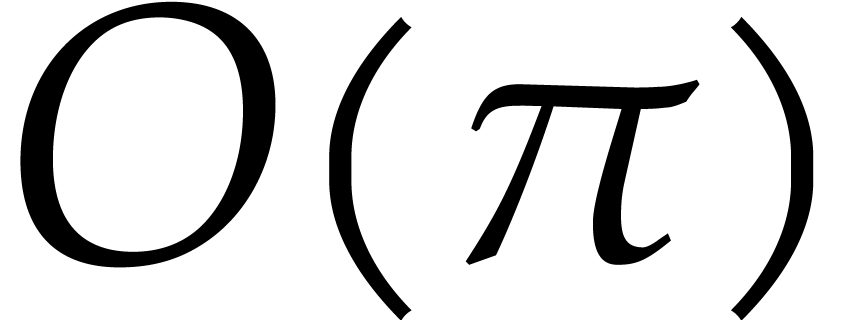 operations in
operations in  .
.
Let 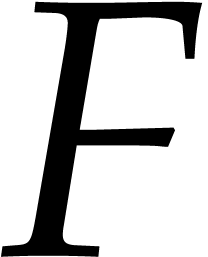 and
and  be in
be in
 , in sparse
representation, and let
, in sparse
representation, and let  be a superset of
the support of
be a superset of
the support of 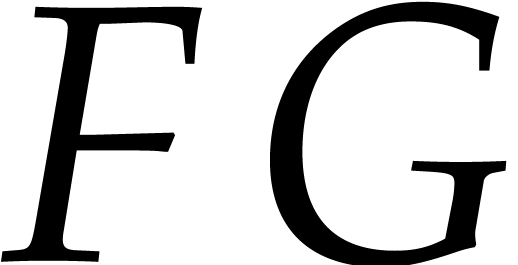 .
Assume that
.
Assume that 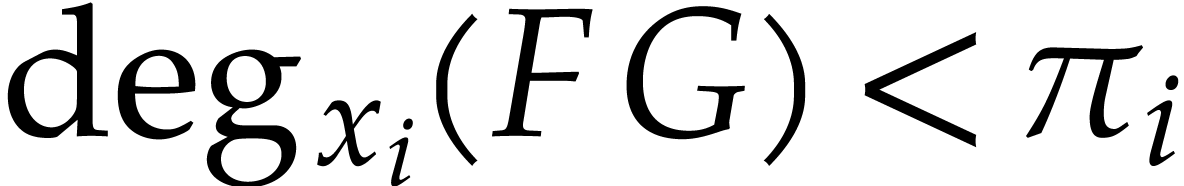 for
for  , and that
, and that  has been
precomputed. Then the product
has been
precomputed. Then the product  can be
computed using
can be
computed using 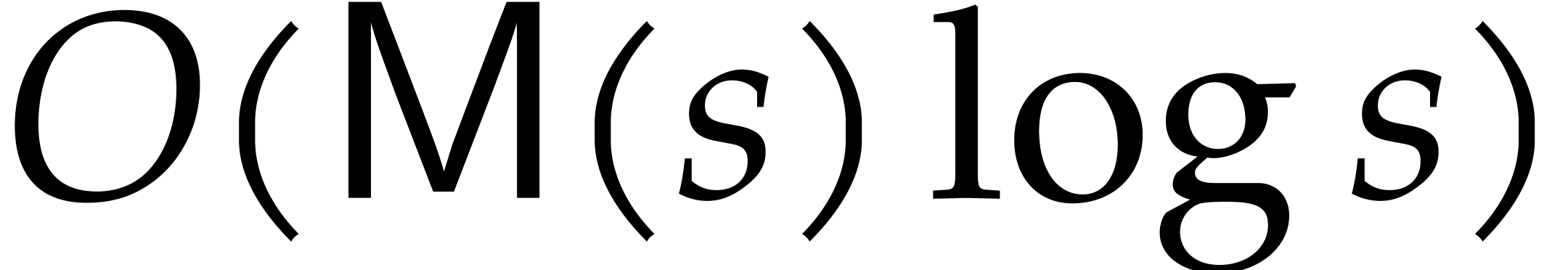 operations in
operations in  , where
, where  denotes the maximum of the sizes of
denotes the maximum of the sizes of  and
the supports of
and
the supports of  and
and  .
.
Proof. The first statement is straightforward.
The second one is simply adapted from [15, Proposition
6].
Computing an element of sufficiently large multiplicative order depends
on the ground field  . In
characteristic zero, any integer different from
. In
characteristic zero, any integer different from 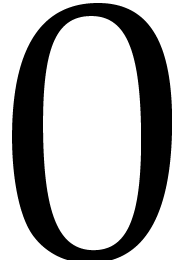 and
and 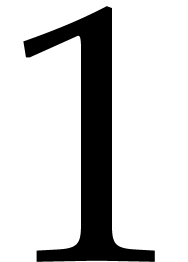 will do. For finite fields
will do. For finite fields 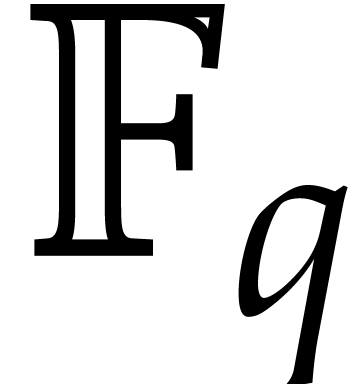 of characteristic
of characteristic  , working
in an algebraic extension
, working
in an algebraic extension 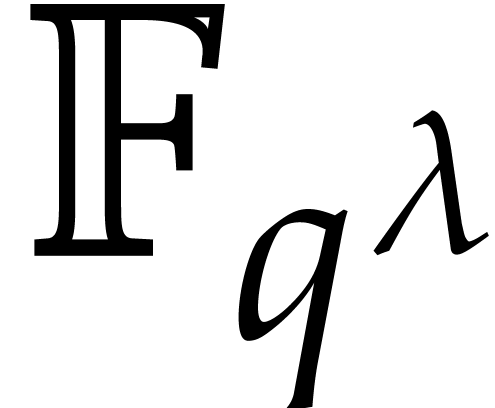 yields elements of
order up to
yields elements of
order up to 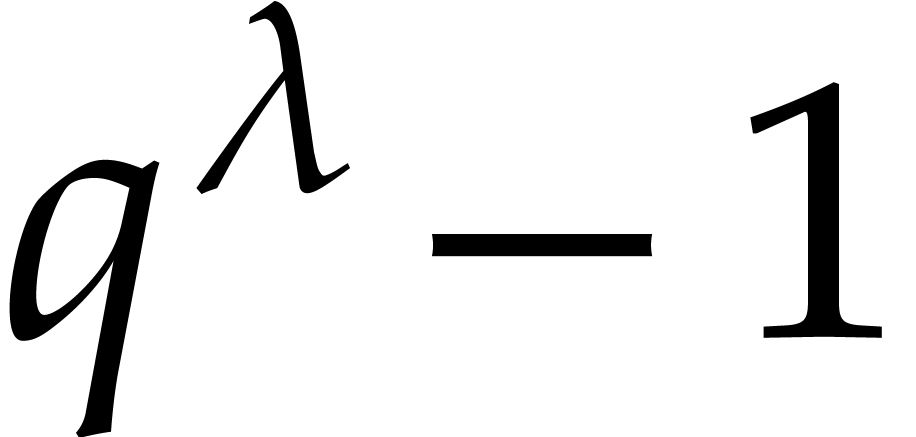 . In the context
of Proposition 1, we may take
. In the context
of Proposition 1, we may take 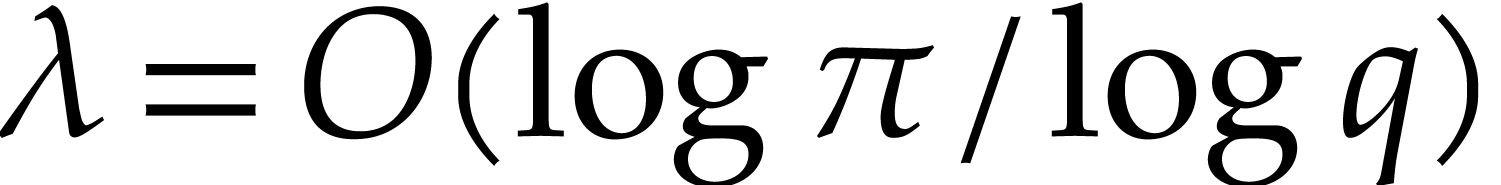 .
In infinite fields
.
In infinite fields  of positive charactersitic
of positive charactersitic
 , elements of arbitrarily
large orders exist, but they may be hard to access without prior
knowledge. However, this is mostly a theoretical problem: in practice,
we usually either know a transcendental element of infinite order or a
way to construct arbitrarily large finite fields inside
, elements of arbitrarily
large orders exist, but they may be hard to access without prior
knowledge. However, this is mostly a theoretical problem: in practice,
we usually either know a transcendental element of infinite order or a
way to construct arbitrarily large finite fields inside  .
.
For variables 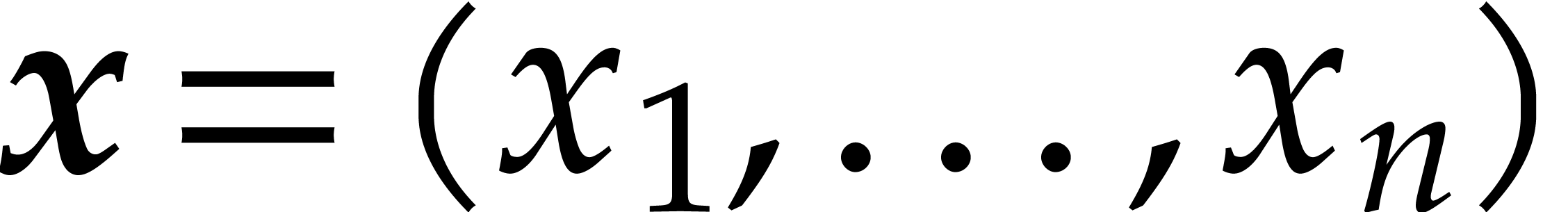 and exponents
and exponents  , we define
, we define 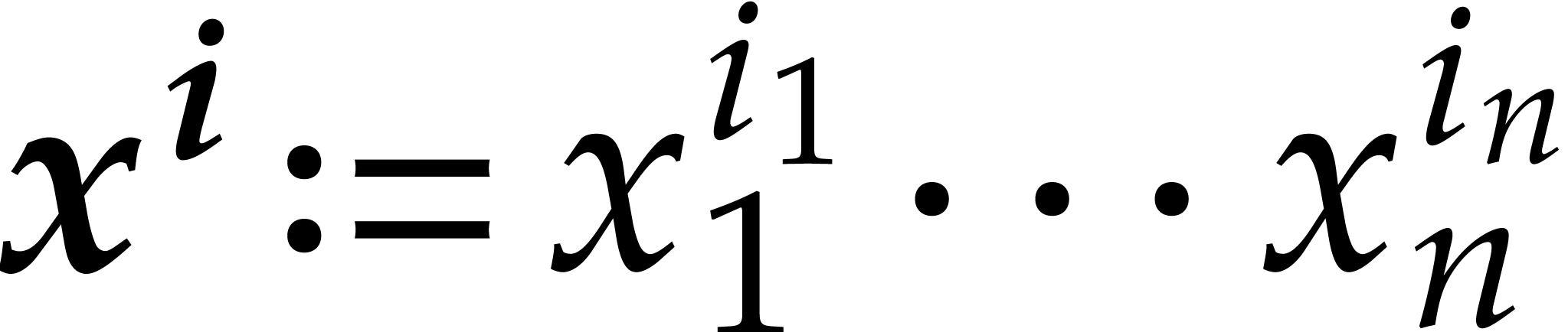 ,
,
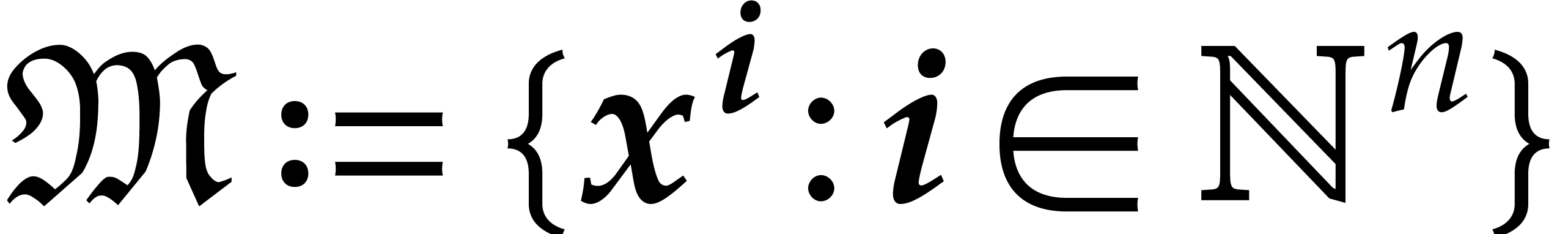 , and
, and 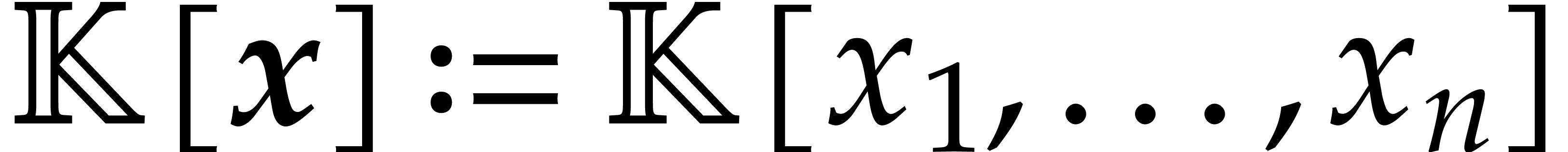 . The monoid
. The monoid  comes with a
natural partial ordering
comes with a
natural partial ordering 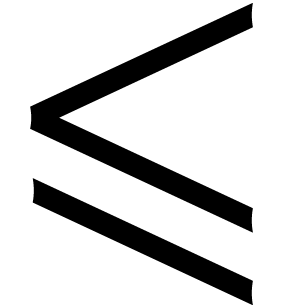 that is defined by
that is defined by
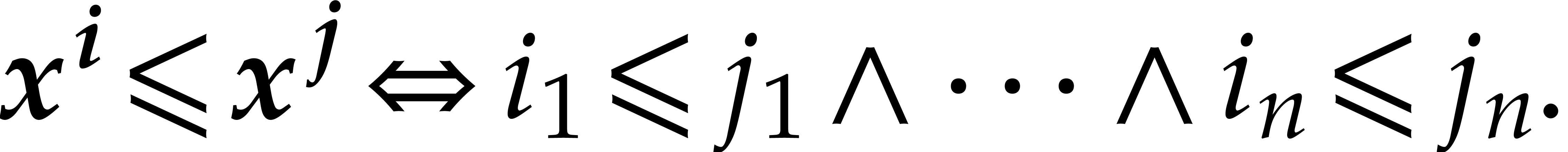
We also assume that we fixed a total admissible ordering  on
on  that extends
that extends 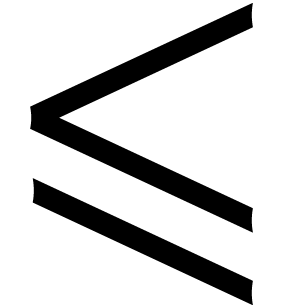 and which turns
and which turns  into a totally ordered monoid.
Given a polynomial
into a totally ordered monoid.
Given a polynomial
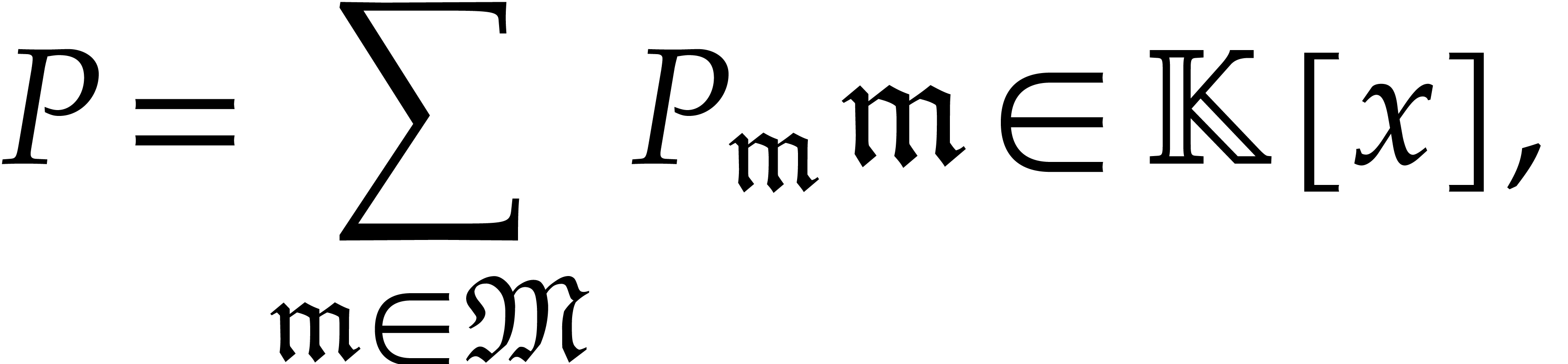
we call 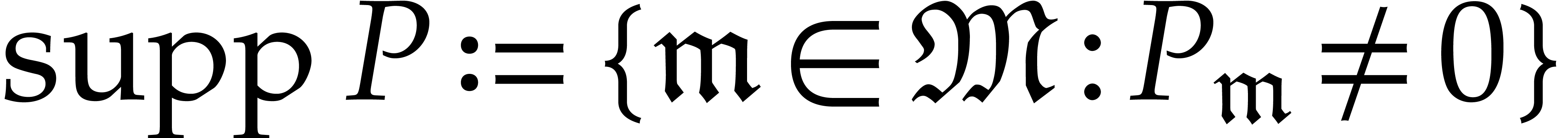 its support. If
its support. If 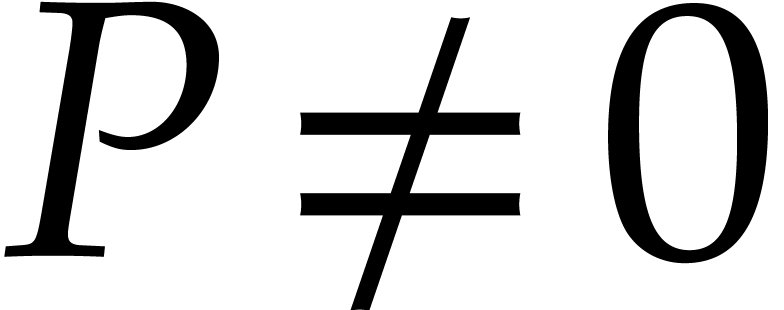 , then we define
, then we define
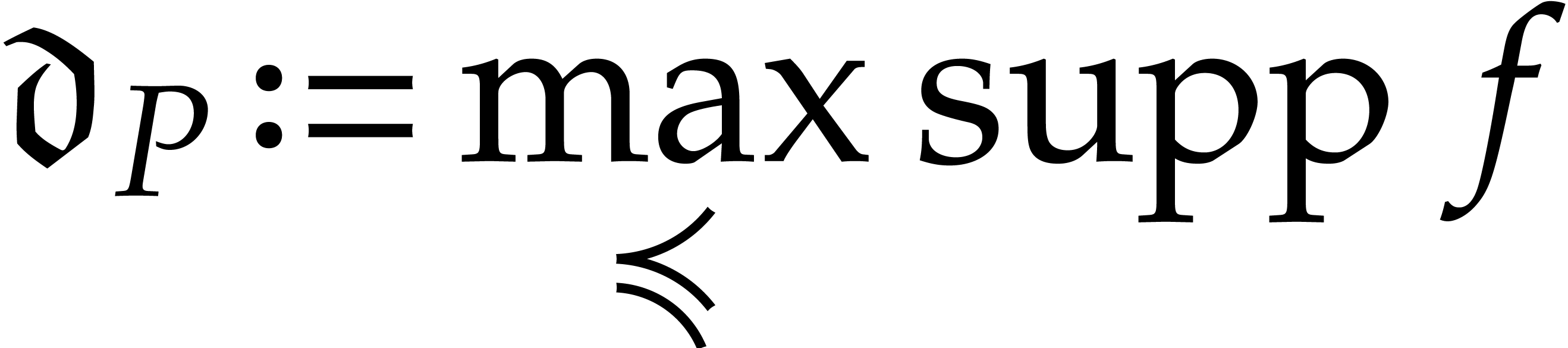
to be the dominant monomial of 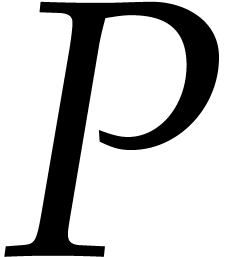 .
.
Let 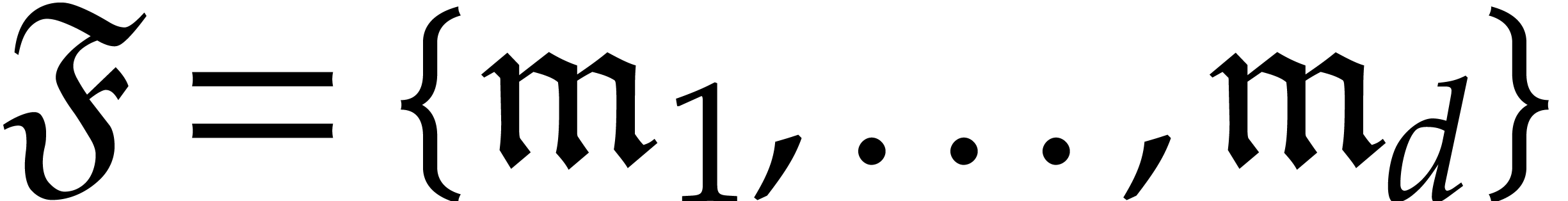 be a finite set of monomials. Given a
polynomial
be a finite set of monomials. Given a
polynomial 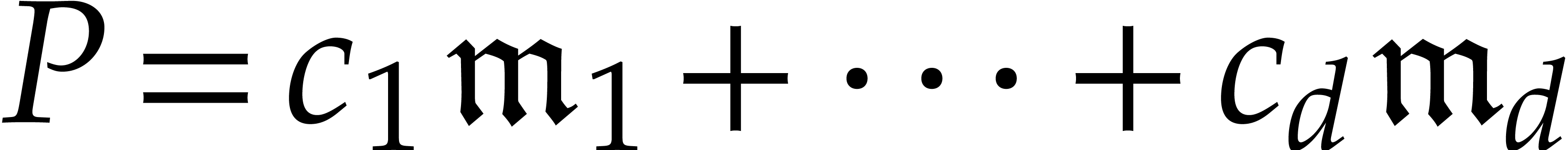 and a finite tuple of points
and a finite tuple of points 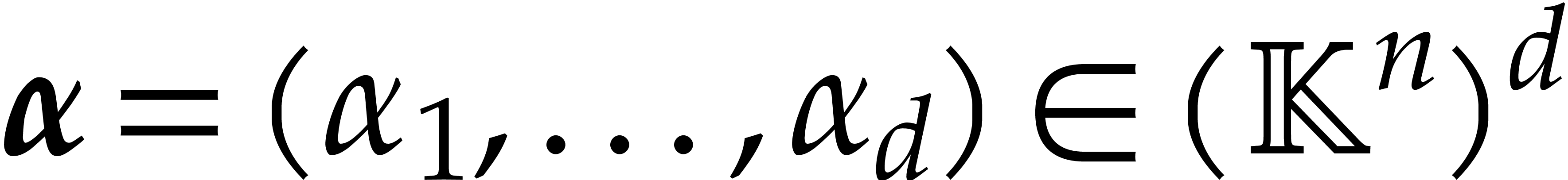 , we have
, we have
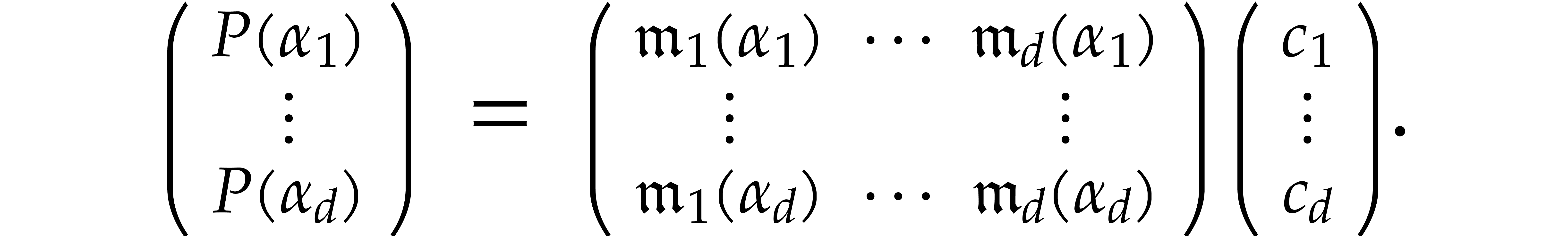
The set of tuples of points for which the matrix
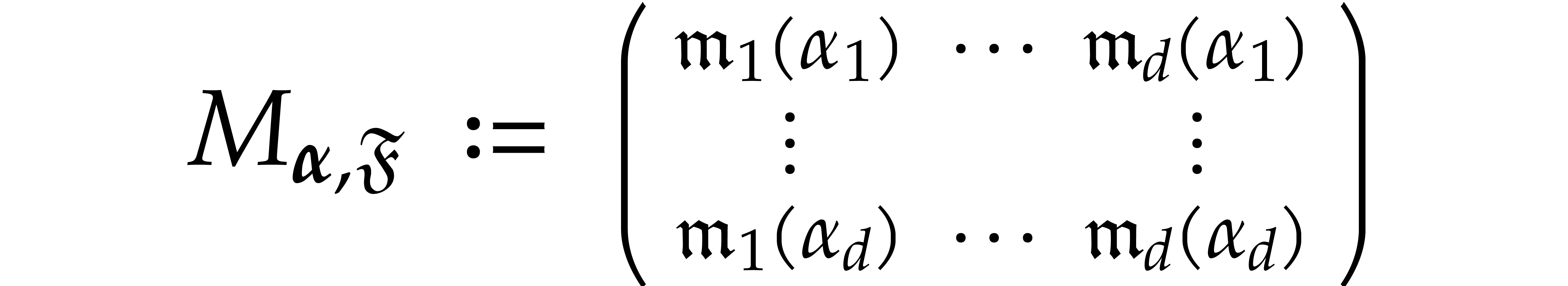
is non-invertible forms a proper Zariski closed subset of 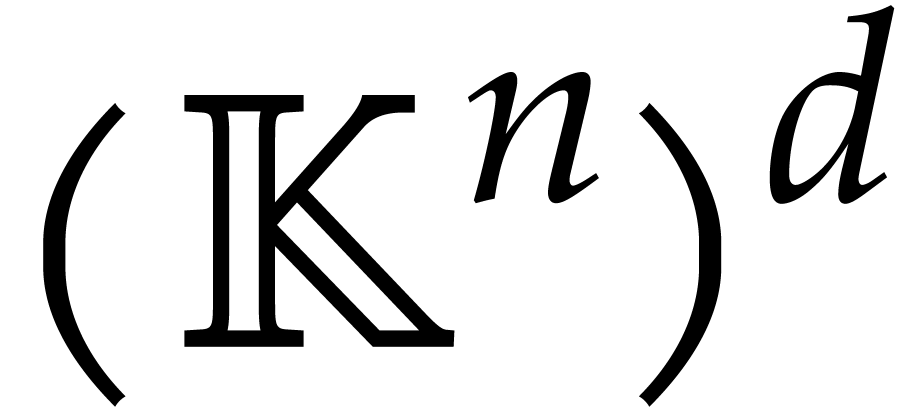 . If
. If  is algebraically
closed, then its open complement is actually non-empty:
is algebraically
closed, then its open complement is actually non-empty:
 is algebraically closed. Then there
exists a tuple of points
is algebraically closed. Then there
exists a tuple of points 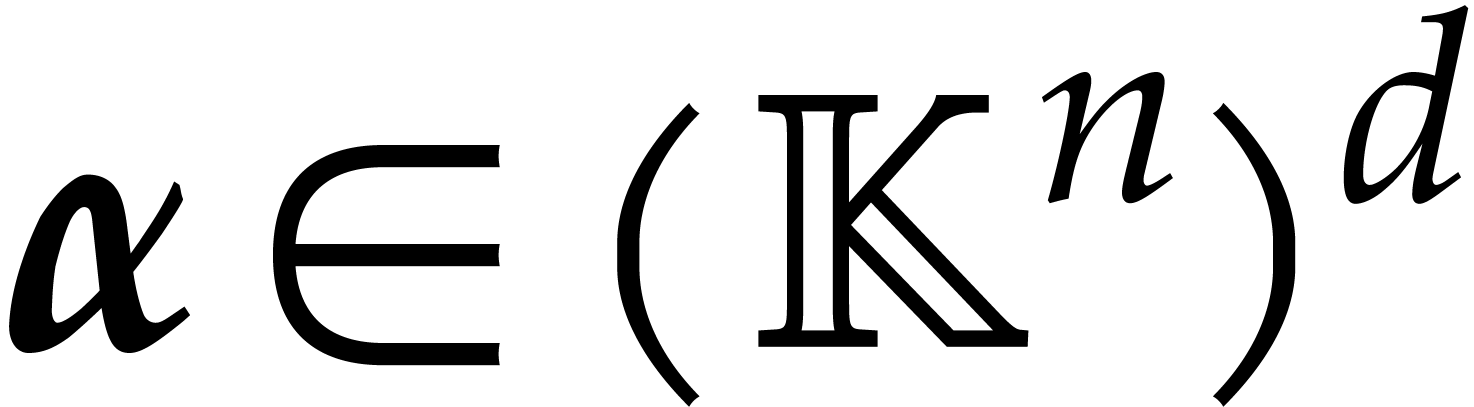 for which
for which 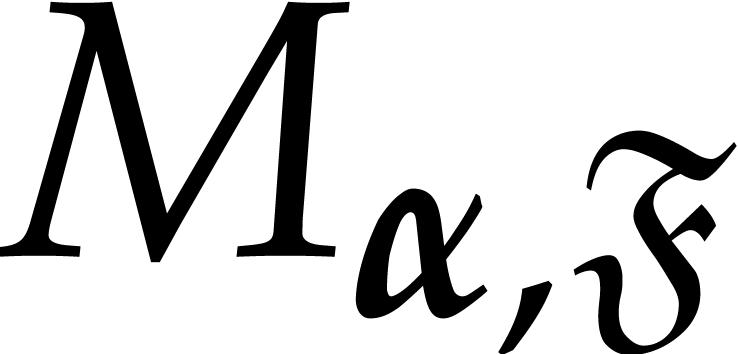 is invertible.
is invertible.
Proof. Let  be a point
such that
be a point
such that  are pairwise distinct; such a point
are pairwise distinct; such a point
 exists since
exists since  is
algebraically closed. Now take
is
algebraically closed. Now take 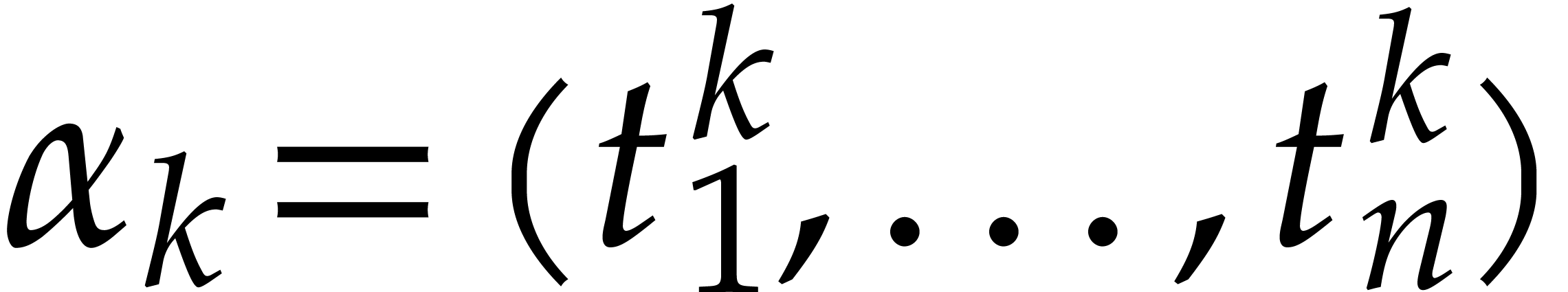 for
for 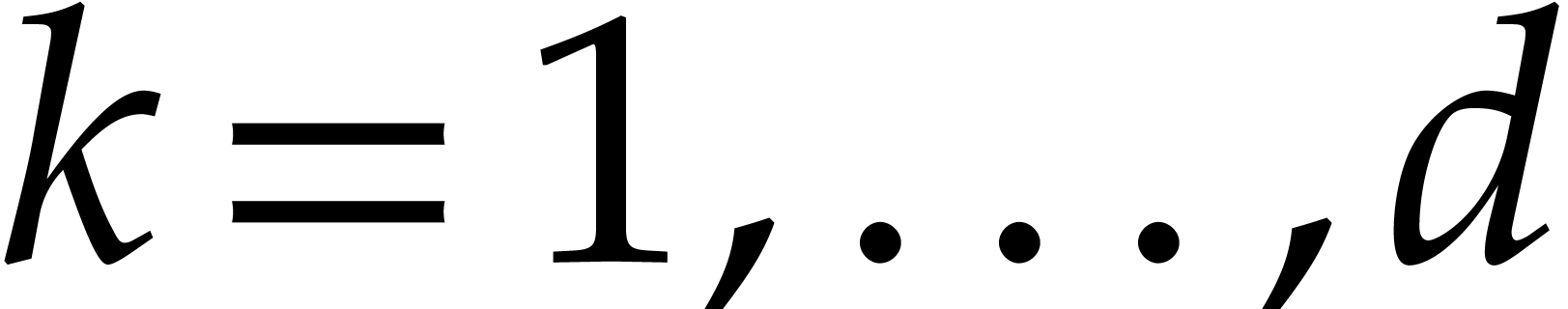 . Then have
. Then have
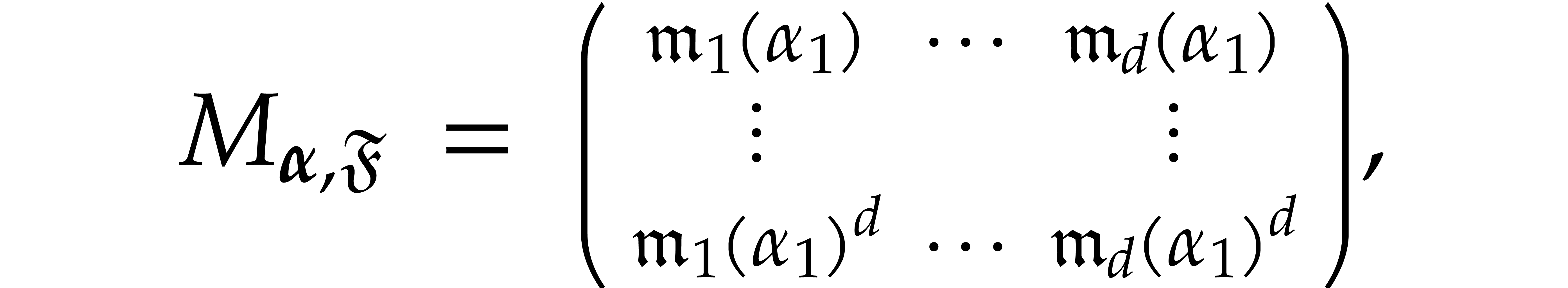
whence 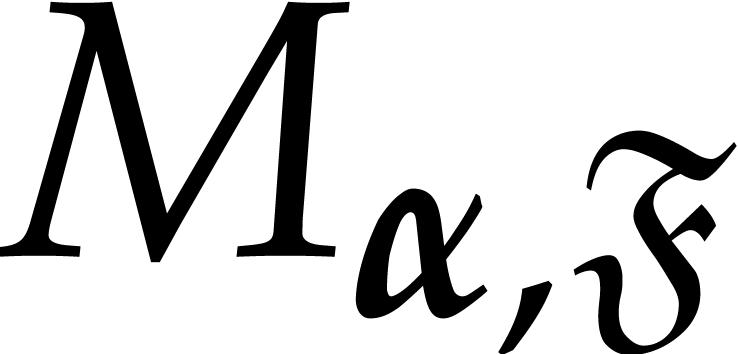 is an invertible Vandermonde matrix.
is an invertible Vandermonde matrix.
The lemma shows that 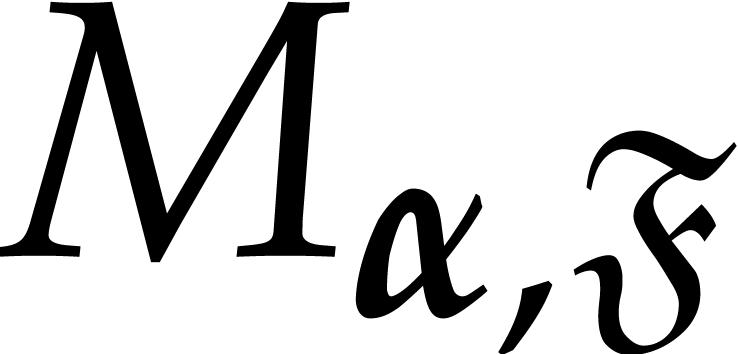 is invertible for a
“generic” tuple of points
is invertible for a
“generic” tuple of points 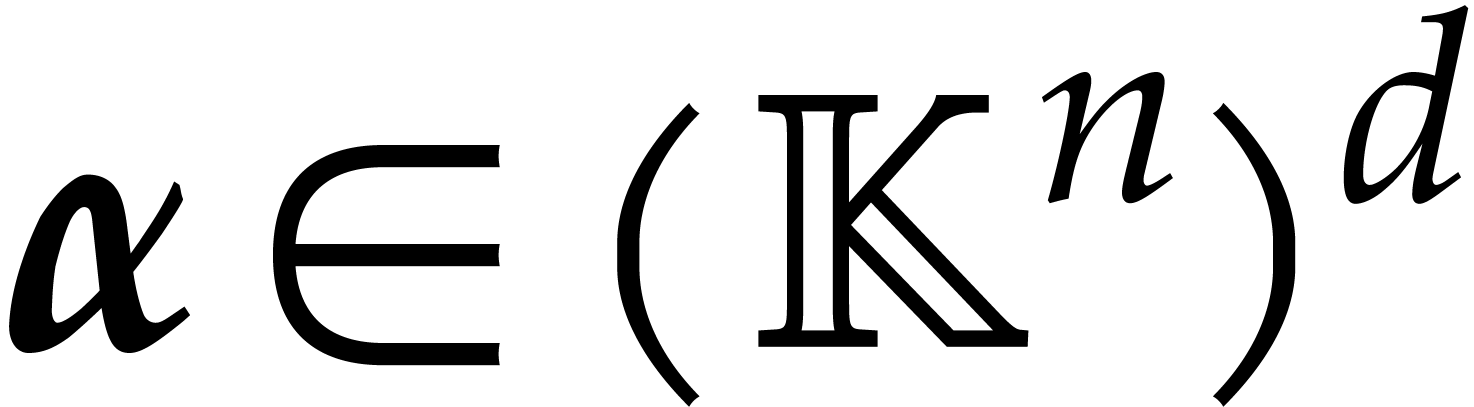 .
Assume from now on that this is indeed the case and let us write
.
Assume from now on that this is indeed the case and let us write  for the ideal of polynomials
for the ideal of polynomials  such that
such that 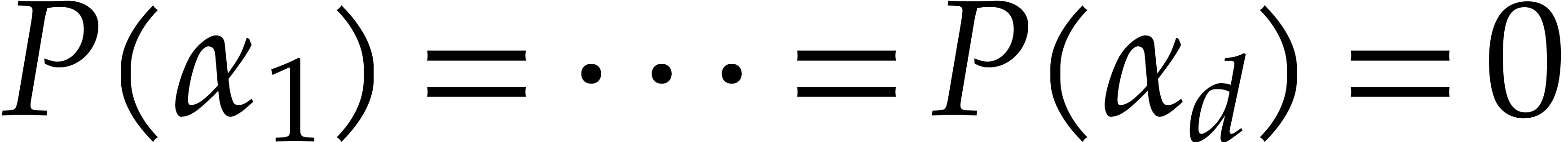 . For any other
monomial
. For any other
monomial  and
and  ,
we have
,
we have
whence  if and only if
if and only if
This shows that  form a basis for the quotient
algebra
form a basis for the quotient
algebra 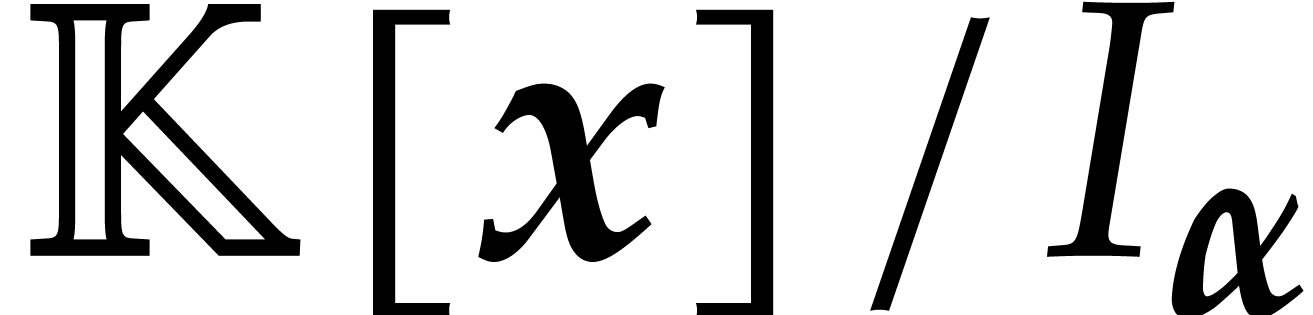 and it provides us with a formula to
express
and it provides us with a formula to
express 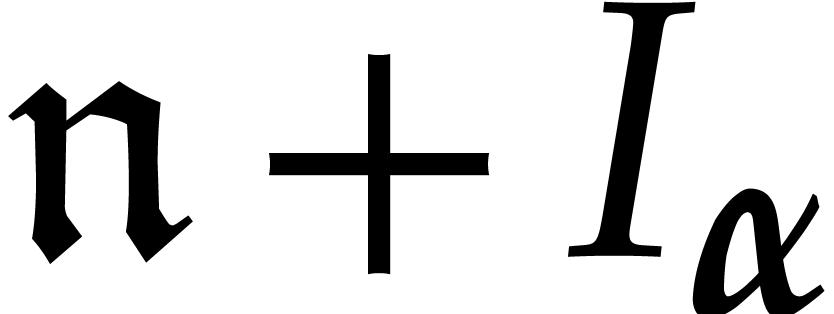 in terms of these basis elements.
in terms of these basis elements.
Let  be such that
be such that  is the
set of
is the
set of  smallest elements of
smallest elements of  for each
for each  and with respect to the total ordering
and with respect to the total ordering
 . We define
. We define  to be the set of smallest elements of the complement
to be the set of smallest elements of the complement  for
for  . By Dickson's lemma,
this set is finite and it forms an antichain for
. By Dickson's lemma,
this set is finite and it forms an antichain for  . Let
. Let 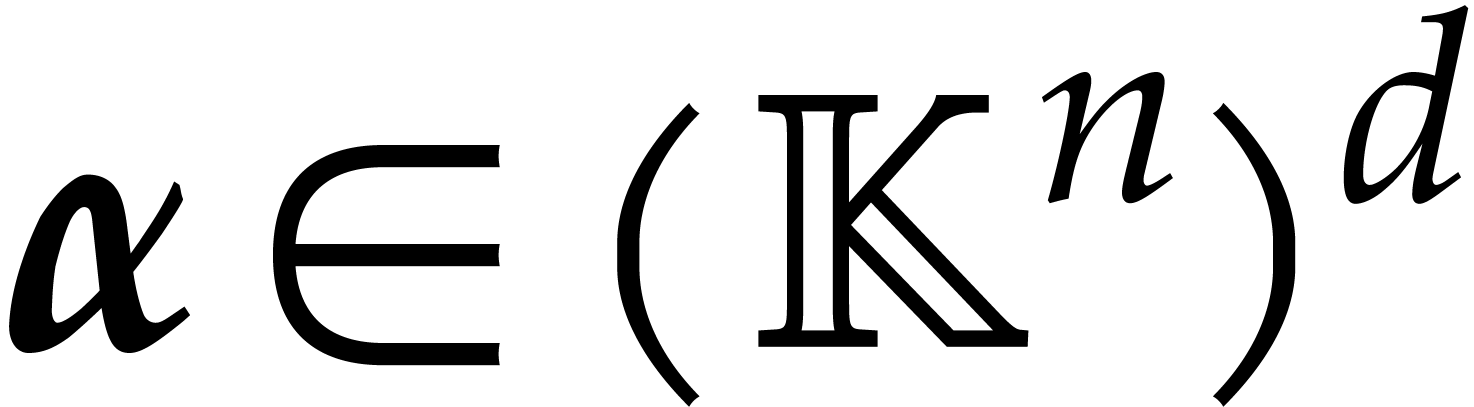 be a generic tuple of
points in the sense that
be a generic tuple of
points in the sense that 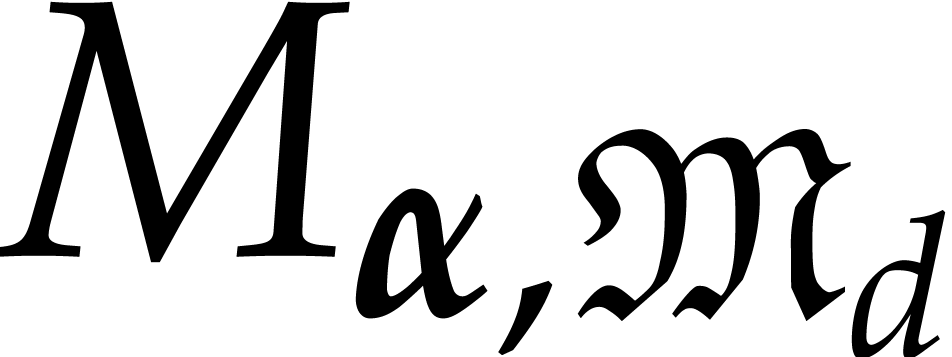 is invertible.
is invertible.
where  satisfy
satisfy 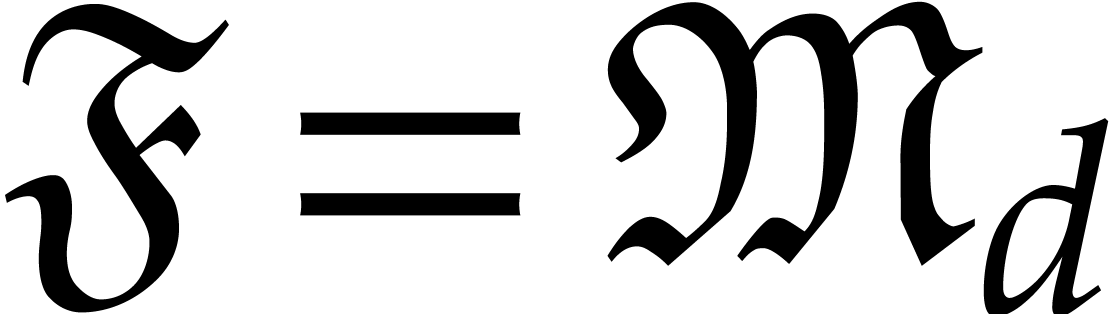 .
Then
.
Then 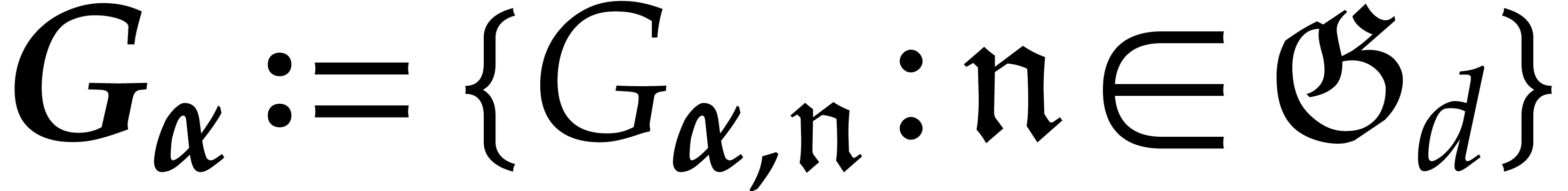 forms the reduced Gröbner basis of
forms the reduced Gröbner basis of
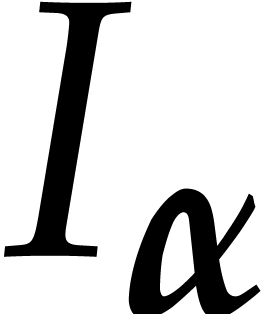 with respect to
with respect to  .
.
Proof. Let  be the set of
dominant monomials of non-zero elements of
be the set of
dominant monomials of non-zero elements of 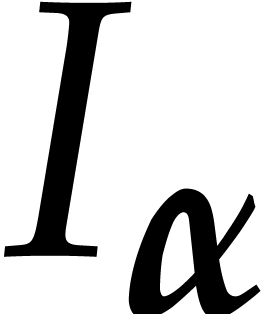 .
Given
.
Given 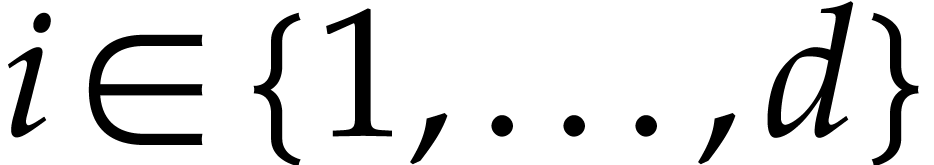 , we have
, we have  : otherwise,
: otherwise, 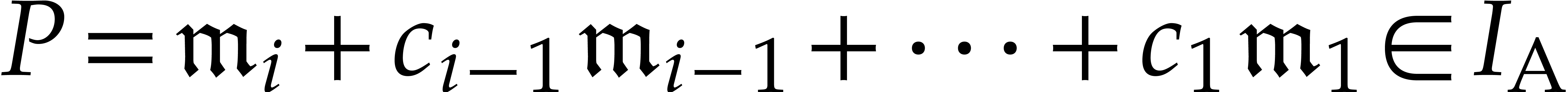 for
certain
for
certain 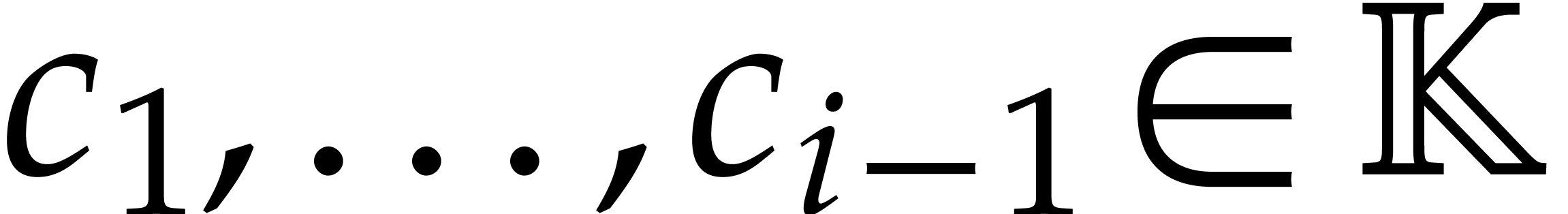 , which is impossible
since
, which is impossible
since 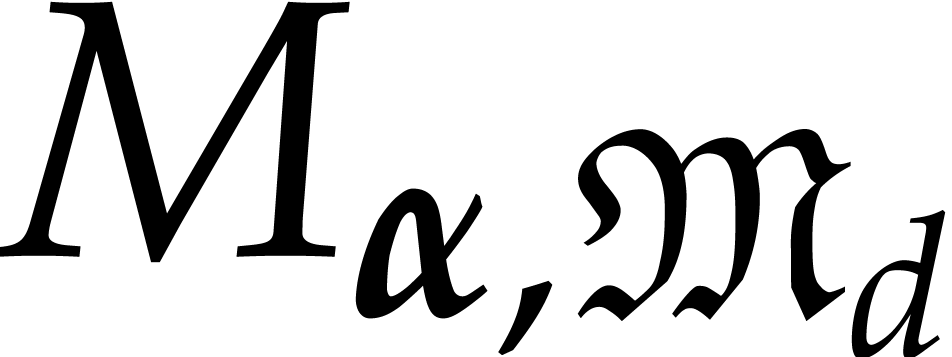 is invertible. Conversely,
is invertible. Conversely,  for all
for all 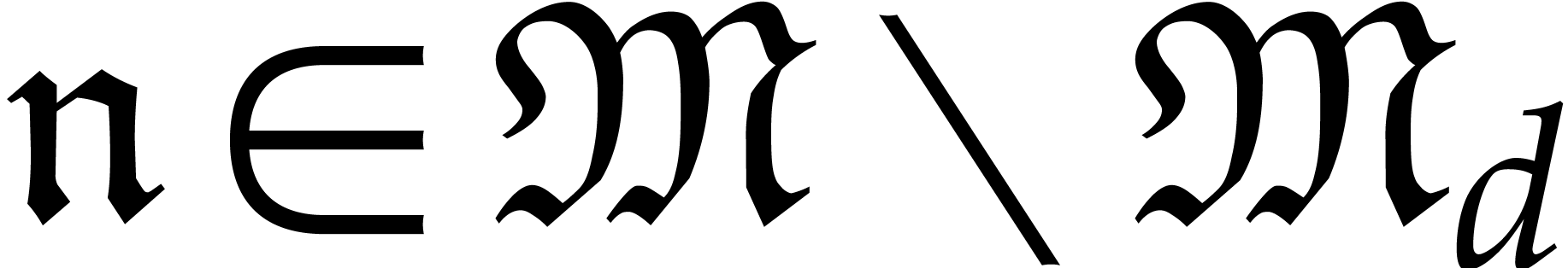 , whence
, whence 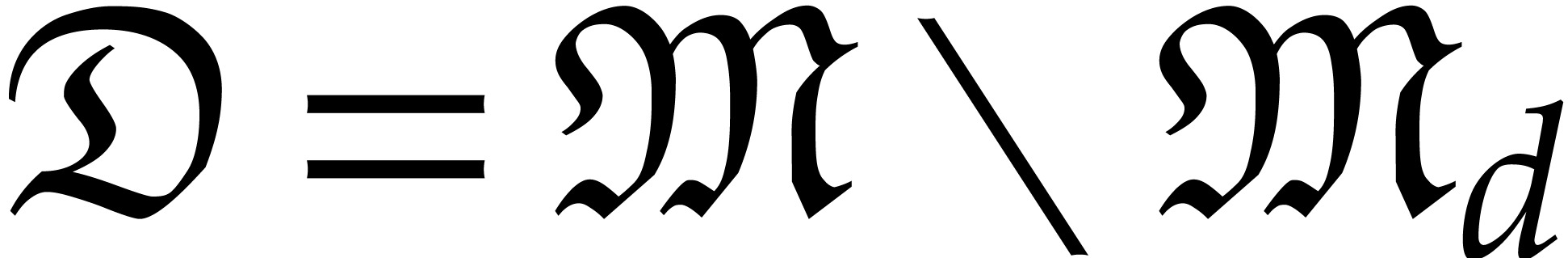 .
.
Now it is well known that  is a finite segment of
is a finite segment of
 for
for  and that each
minimal element
and that each
minimal element  corresponds to exactly one
polynomial
corresponds to exactly one
polynomial  in the reduced Gröbner basis
with dominant monomial
in the reduced Gröbner basis
with dominant monomial 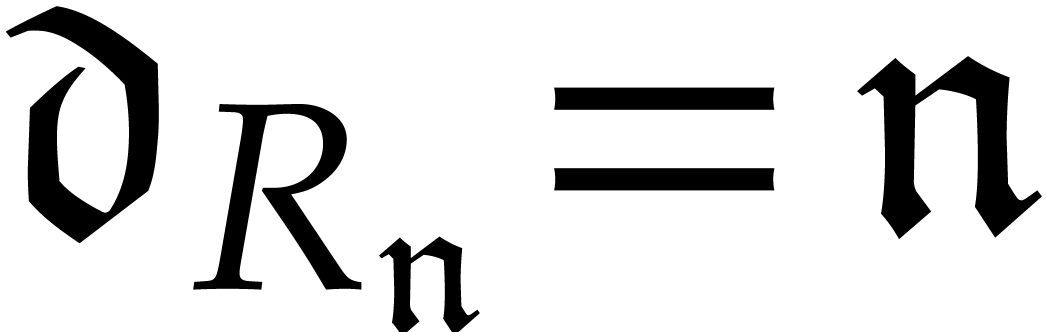 . Now
such a reduced polynomial is by definition of the form
. Now
such a reduced polynomial is by definition of the form 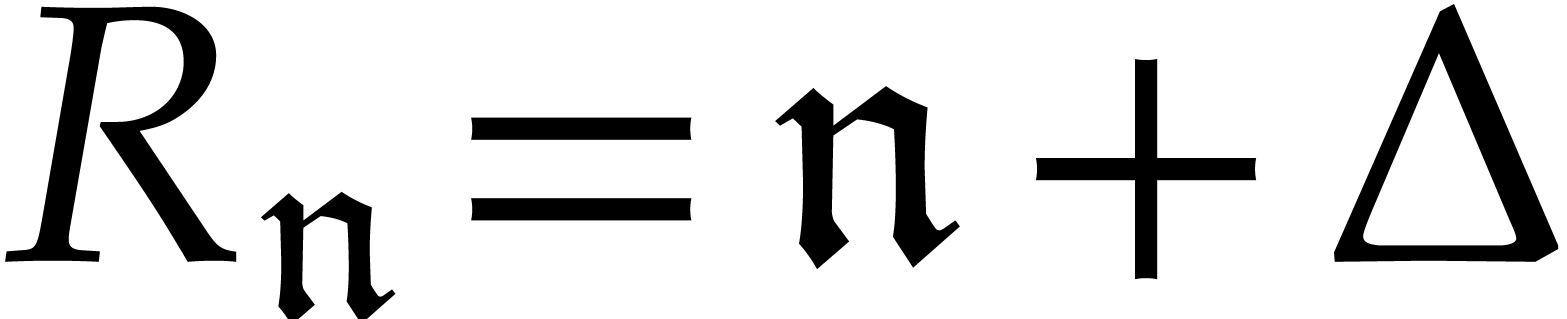 with
with 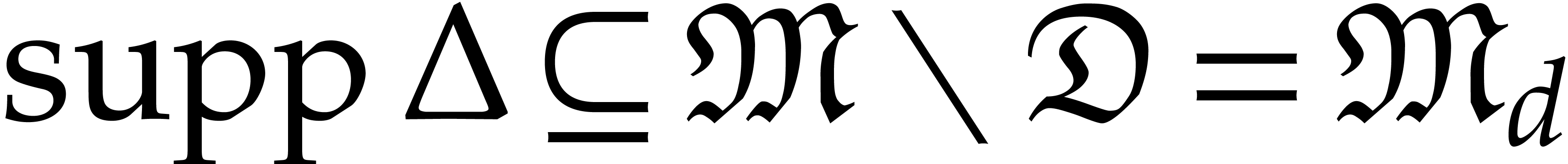 . But
. But 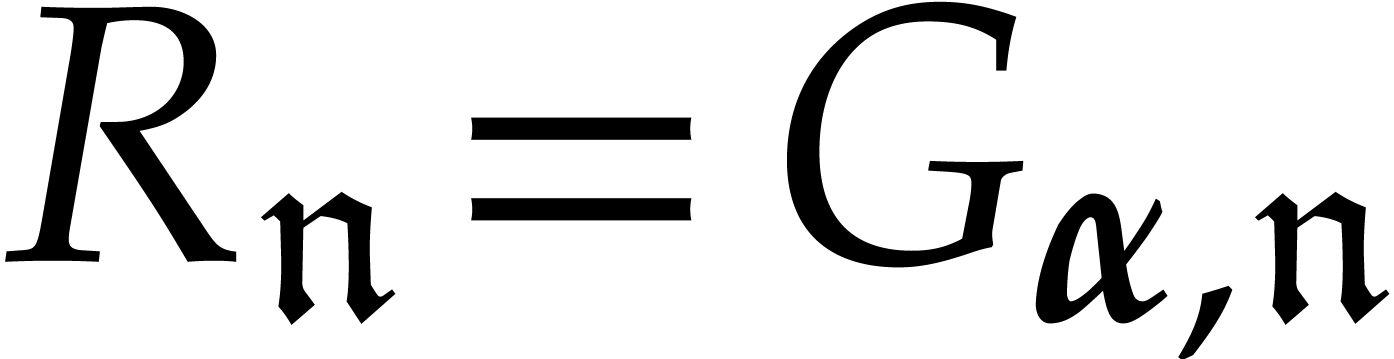 of that form.
of that form.
Example  be a graded ordering for
be a graded ordering for  .
For any
.
For any 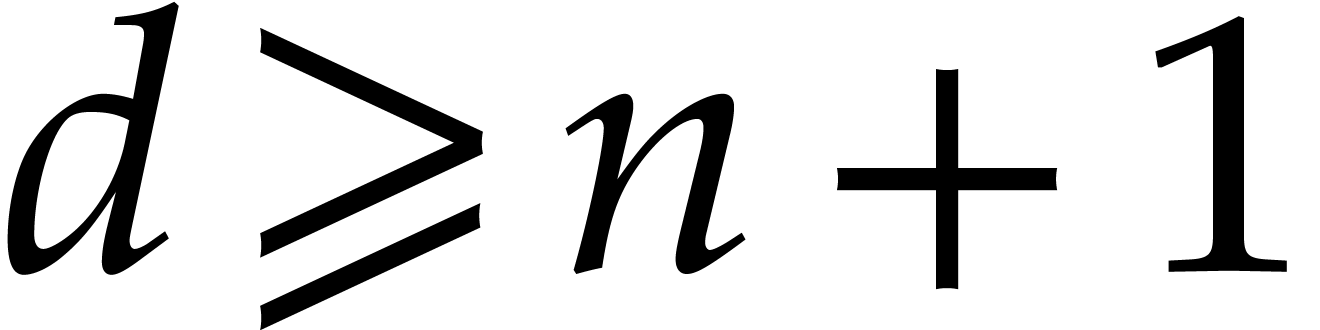 , we have
, we have 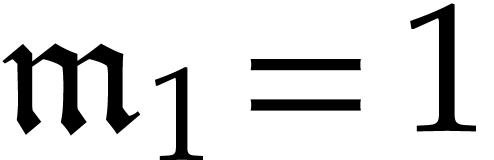 and
and 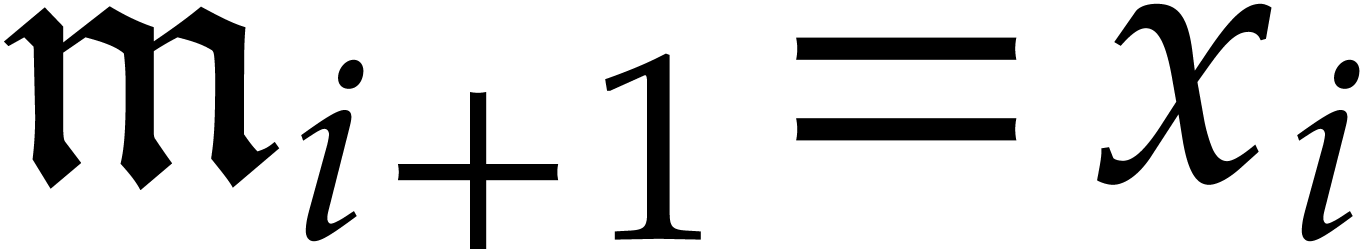 for
for  . The
. The  -th
column of
-th
column of 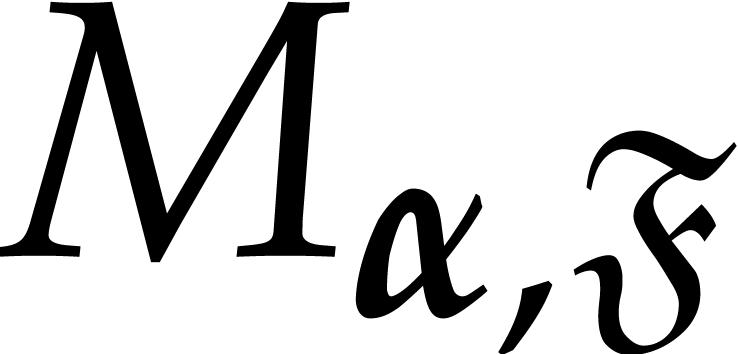 contains the
contains the  -th coordinates of the points of
-th coordinates of the points of  . If these columns are not linearly independent
then
. If these columns are not linearly independent
then 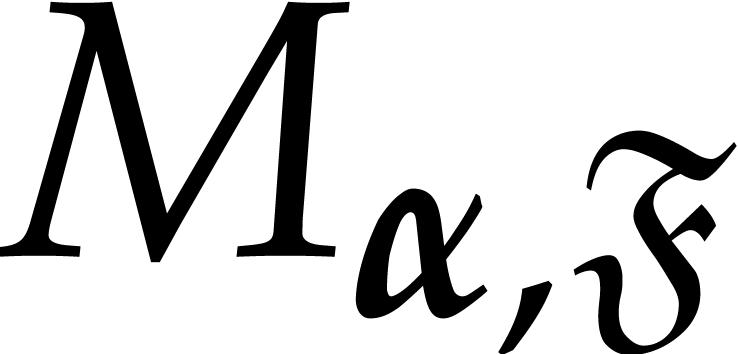 is not invertible. If
is not invertible. If  is any
is any  invertible matrix over
invertible matrix over  , and if
, and if 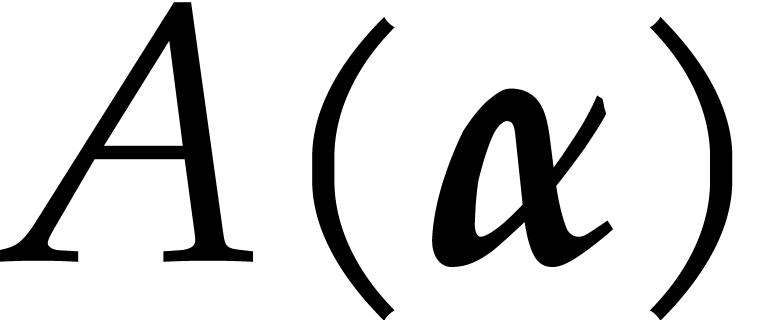 denotes
denotes  then the columns from
then the columns from 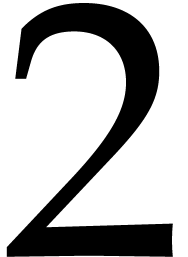 to
to  of
of  are linearly dependent, so
are linearly dependent, so
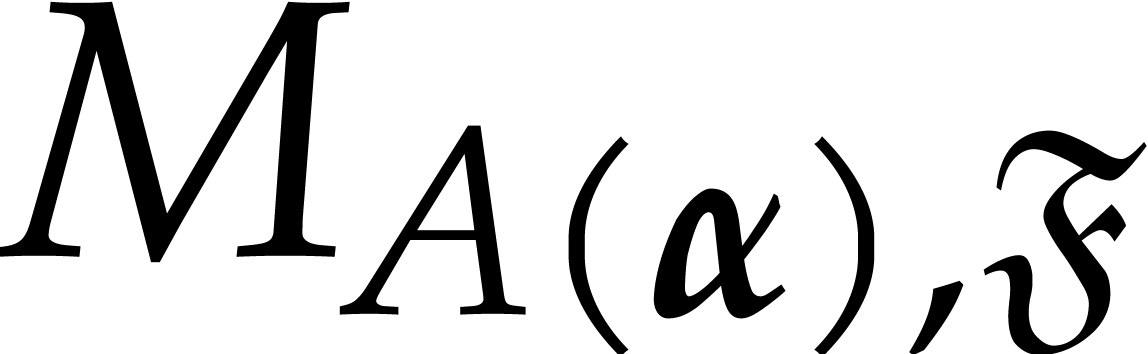 is not invertible. This example illustrates that
the genericity of a tuple of points
is not invertible. This example illustrates that
the genericity of a tuple of points 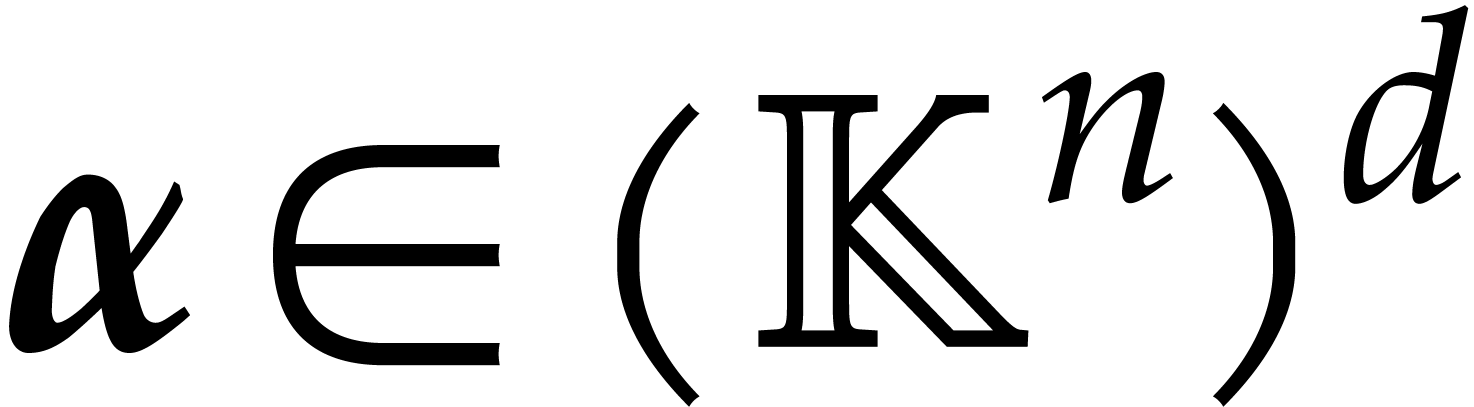 cannot be
necessarily recovered after a linear change of the coordinates.
cannot be
necessarily recovered after a linear change of the coordinates.
Let  be as in the previous section, with a total
admissible ordering
be as in the previous section, with a total
admissible ordering  , and let
, and let
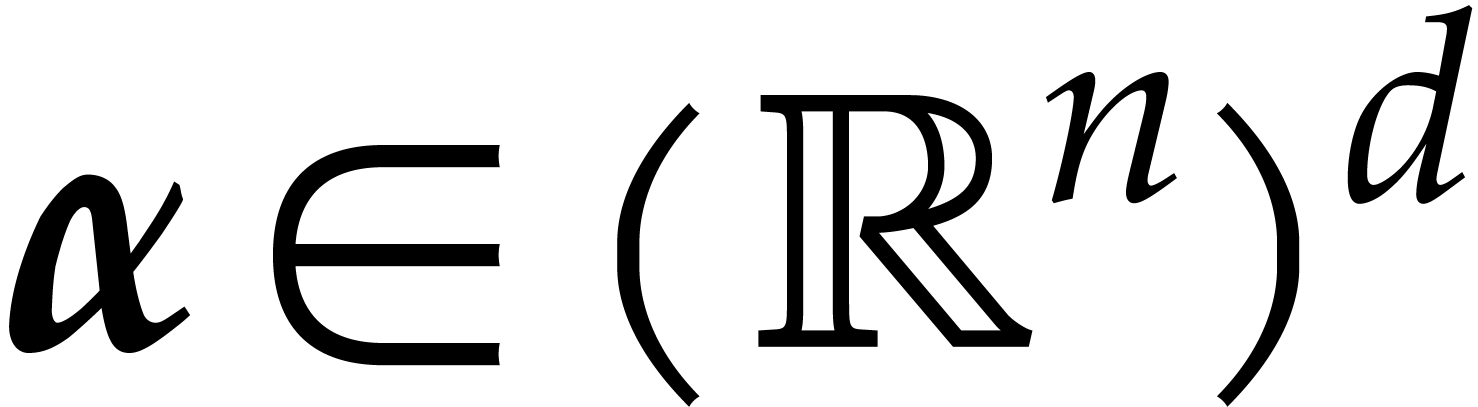 be a generic tuple of points. We need a way to
efficiently reduce polynomials
be a generic tuple of points. We need a way to
efficiently reduce polynomials  with respect to
the Gröbner basis
with respect to
the Gröbner basis 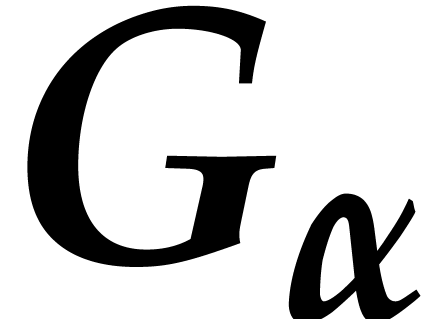 .
Since the entire Gröbner basis can be voluminous to store, we will
only reduce with respect to a special subset
.
Since the entire Gröbner basis can be voluminous to store, we will
only reduce with respect to a special subset  of
“axial” basis elements. This also requires us to work with
respect to a weighted total degree ordering
of
“axial” basis elements. This also requires us to work with
respect to a weighted total degree ordering  .
.
For 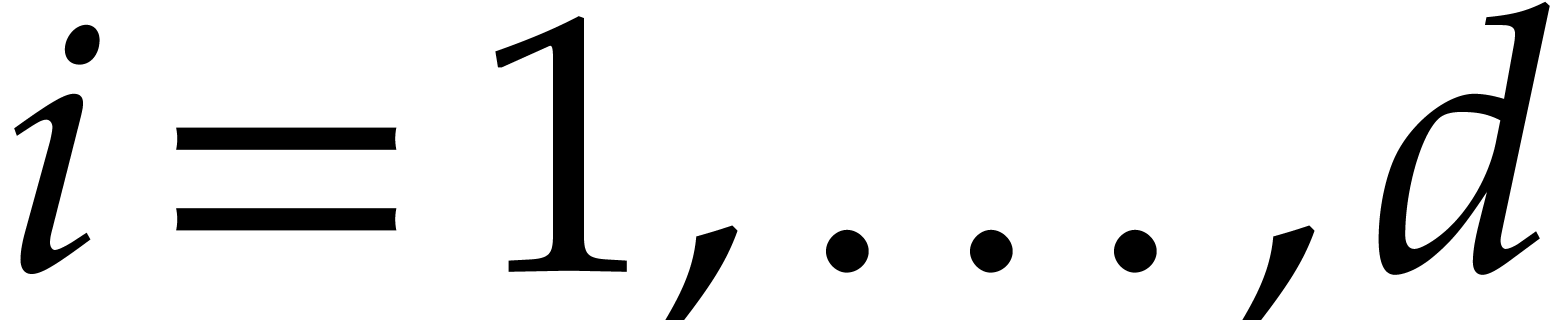 , we define
, we define
so that 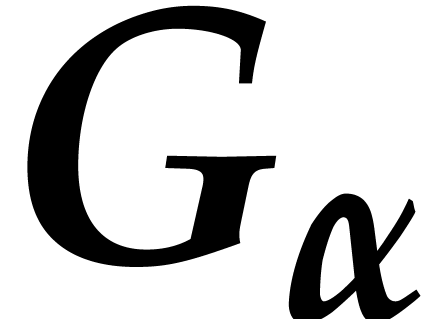 contains a unique element
contains a unique element 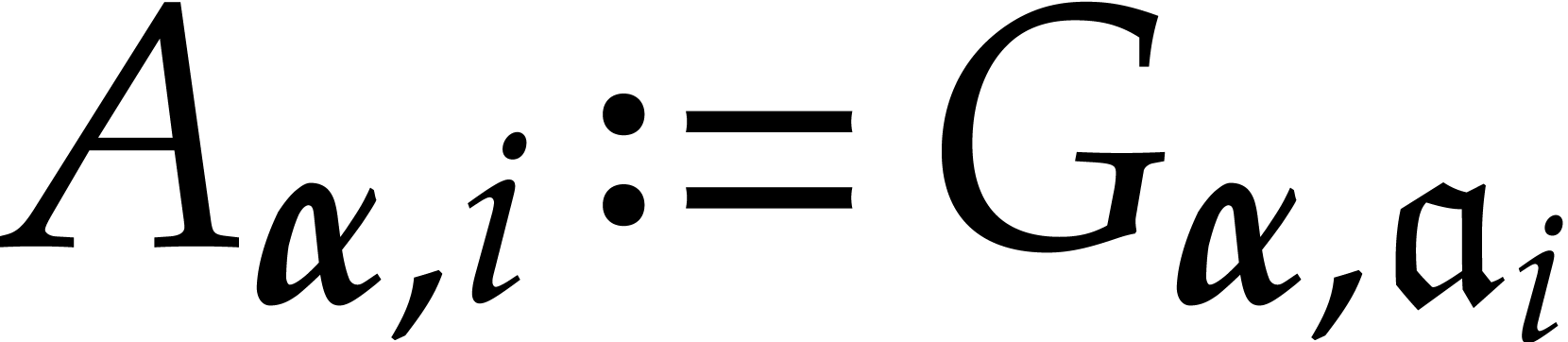 with dominant monomial
with dominant monomial 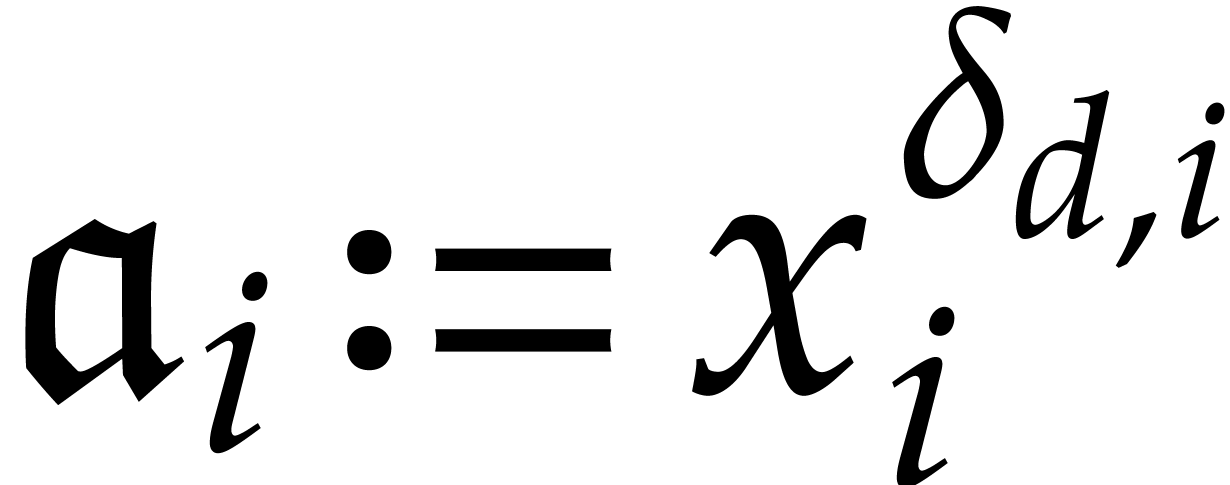 .
We define
.
We define 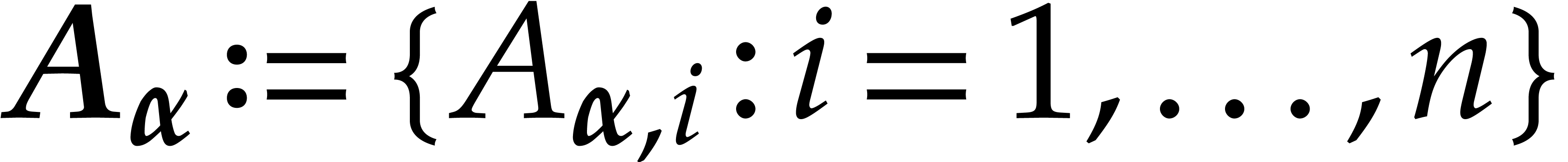 to be the axial basis of
to be the axial basis of
 . Although this set is not a
“basis” of
. Although this set is not a
“basis” of 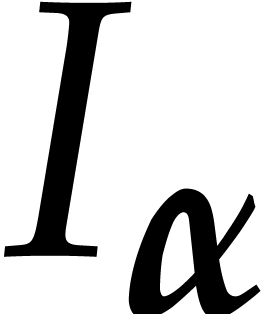 , it
forms a sufficiently good approximation of
, it
forms a sufficiently good approximation of 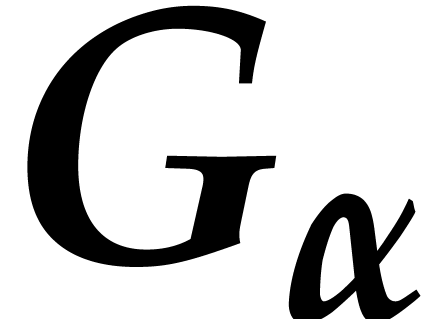 for
the purposes of this paper. We define
for
the purposes of this paper. We define
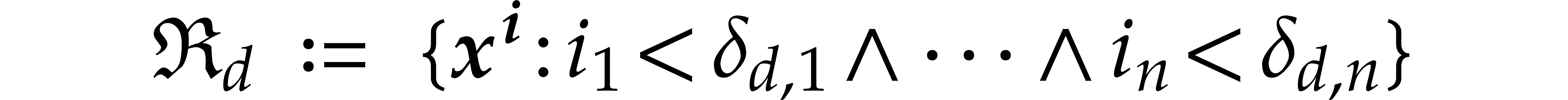
to be the set of monomials that are not divisible by any of the
monomials  . We also define
. We also define
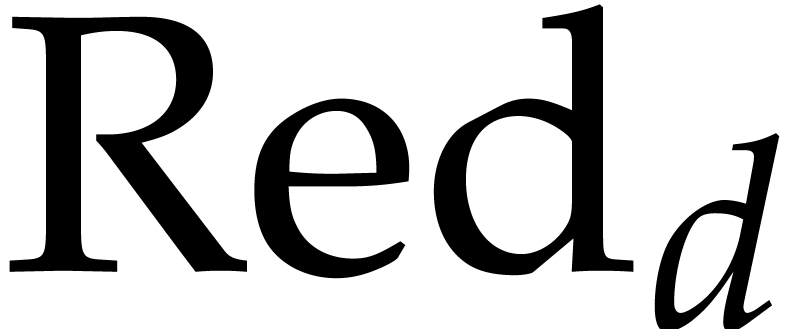 to be the
to be the  -vector
spaced spanned by the elements of
-vector
spaced spanned by the elements of 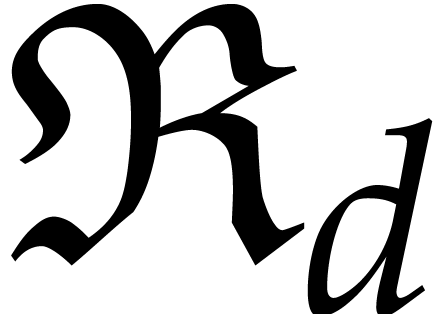 .
.
In all what follows, we assume that the ordering is graded by a weighted
total degree. This means that there exist positive real weights 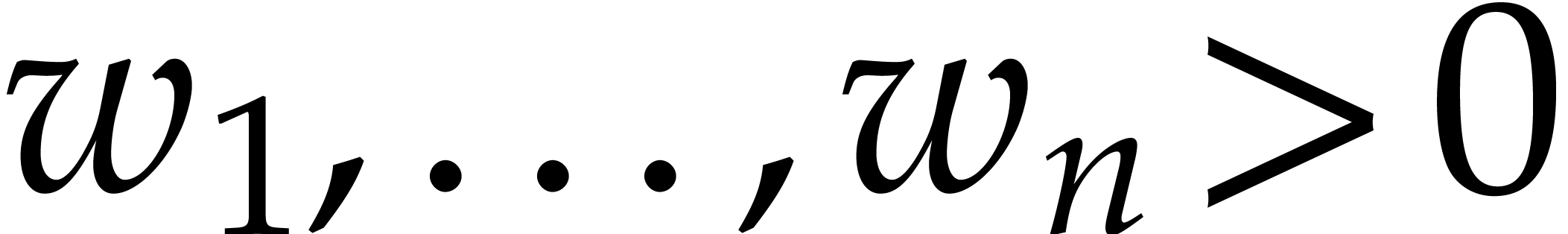 such that for all
such that for all 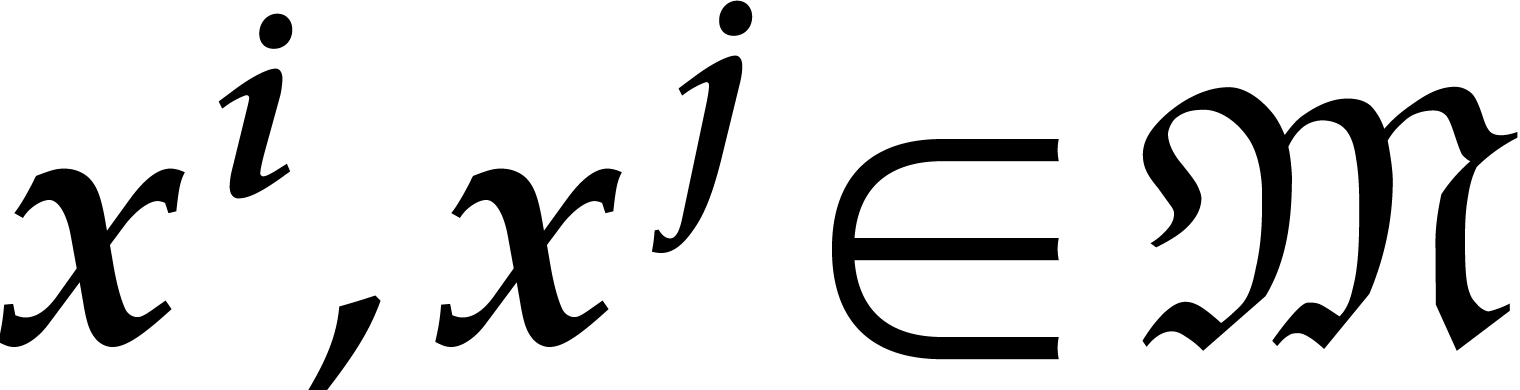 ,
we have
,
we have
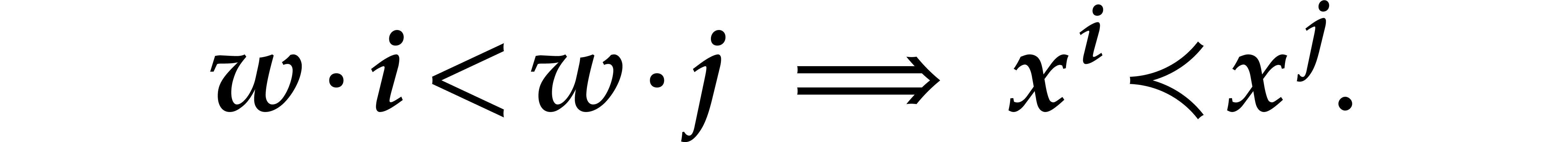
Here 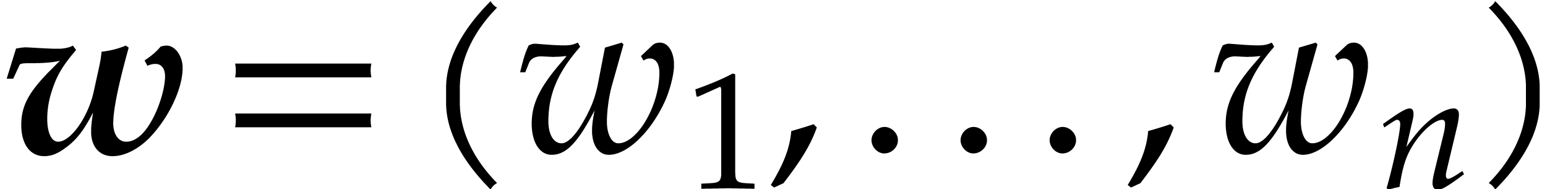 and “
and “ ”
stands for the dot product:
”
stands for the dot product: 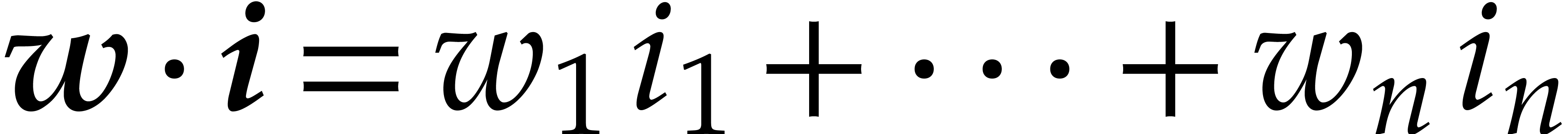 .
Let
.
Let
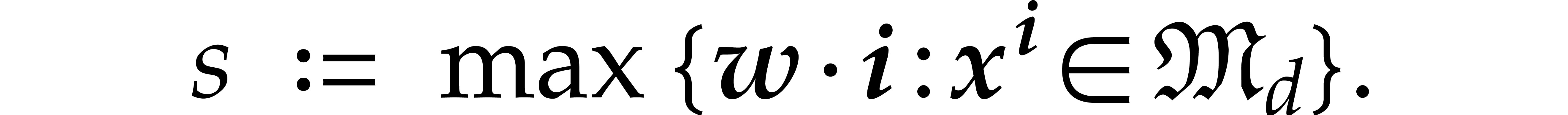
Then
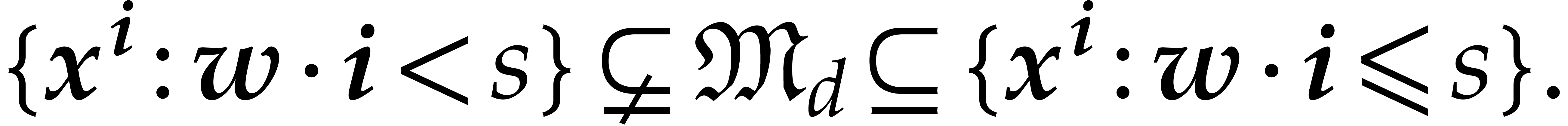
Geometrically speaking, the exponents  with
with 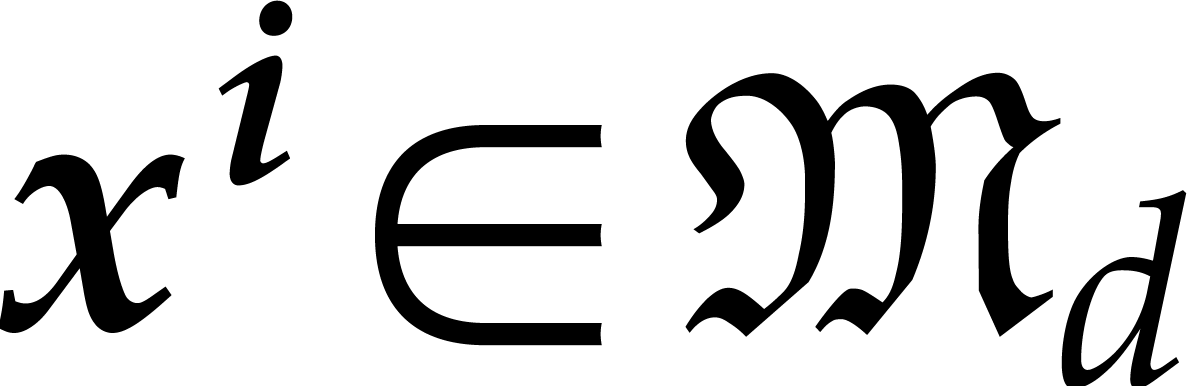 correspond to lattice points inside or on the
boundary of the simplex with vertices
correspond to lattice points inside or on the
boundary of the simplex with vertices  ,
,
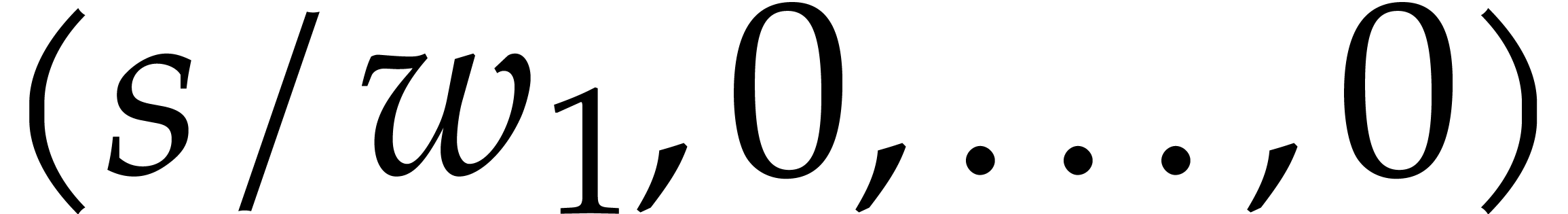 ,
, 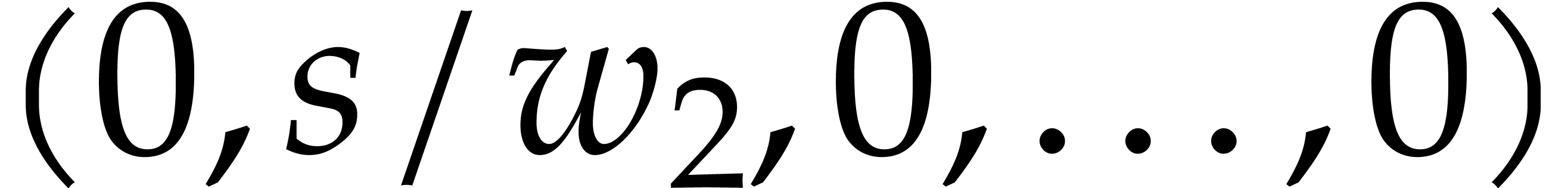 ,
,  ,
, 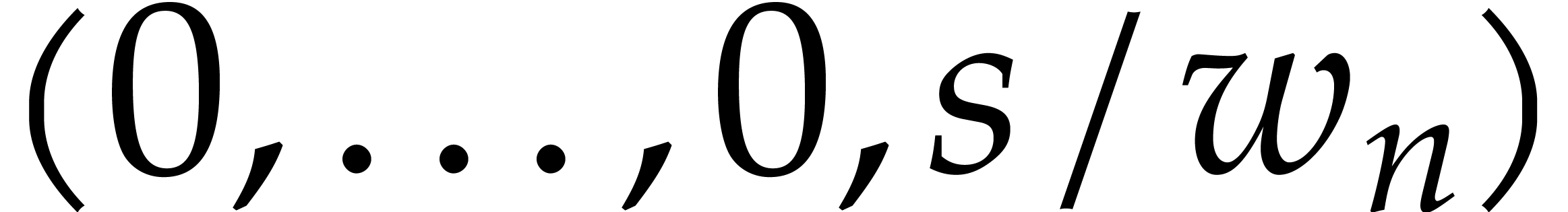 . For fixed
. For fixed 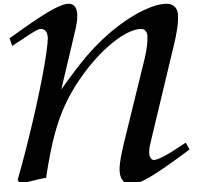 and large
and large  (whence
(whence 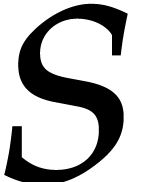 ),
it follows that
),
it follows that
where  stands for the cardinality of
stands for the cardinality of  . In the remainder of this paper, we assume
that
. In the remainder of this paper, we assume
that 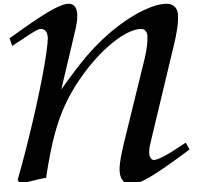 and
and  have been fixed
once and for all. Our asymptotic complexity estimates hold for large
have been fixed
once and for all. Our asymptotic complexity estimates hold for large
 and under this assumption.
and under this assumption.
Remark 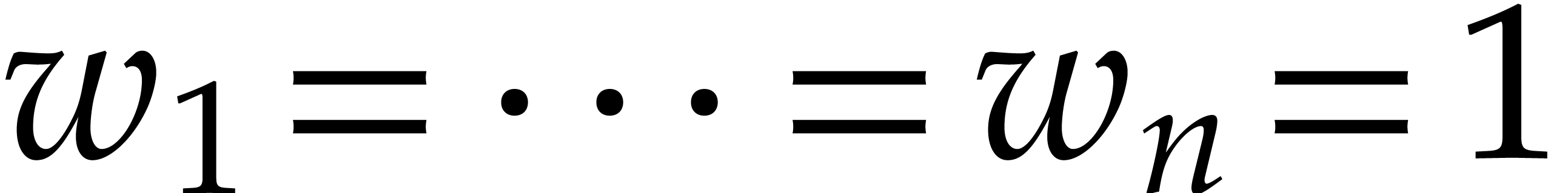 , then one may take
, then one may take  to
be the usual graded reverse lexicographic ordering. In that case, the
to
be the usual graded reverse lexicographic ordering. In that case, the
 are of the same order of magnitude and
are of the same order of magnitude and  is approximately a hypercube. Considering general weights
gives us more flexibility in the choice of
is approximately a hypercube. Considering general weights
gives us more flexibility in the choice of  and
allows us to deal with more general hyperrectangular supports.
and
allows us to deal with more general hyperrectangular supports.
Given a polynomial  , an
extended reduction of
, an
extended reduction of 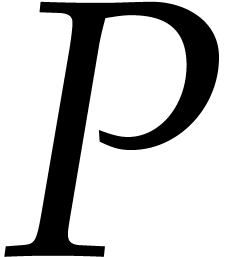 with respect to
with respect to
 is a relation
is a relation
with 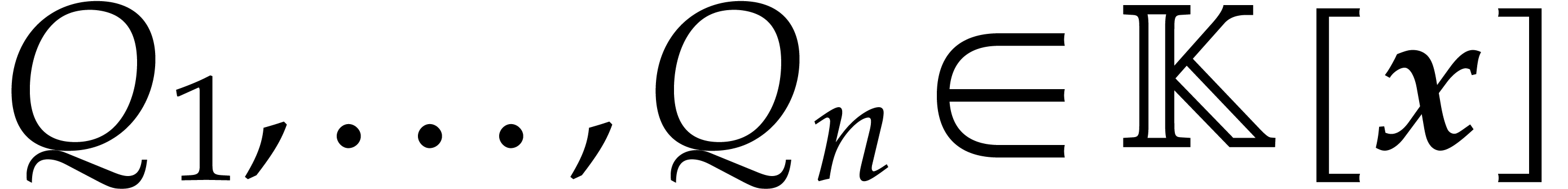 and
and 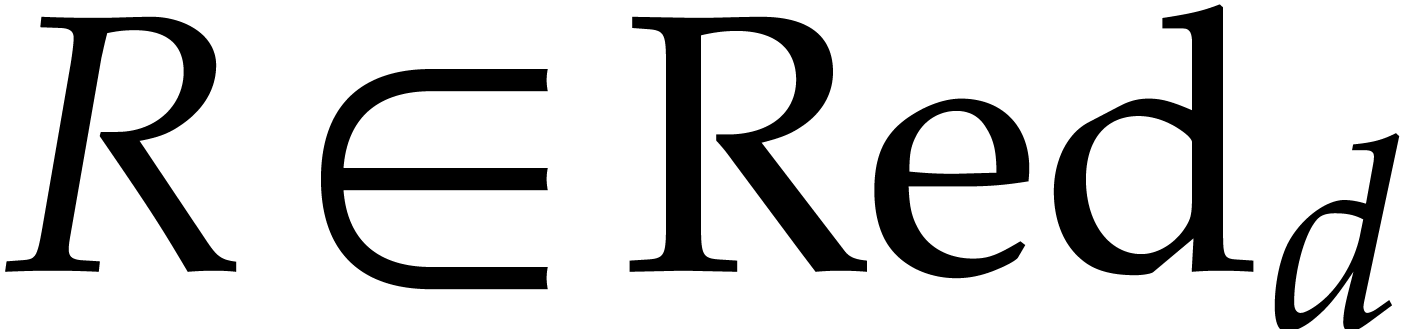 .
Extended reductions are computed by reducing
.
Extended reductions are computed by reducing 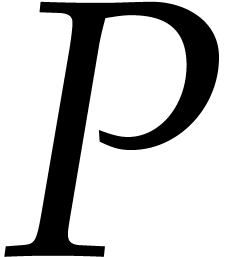 with respect to
with respect to 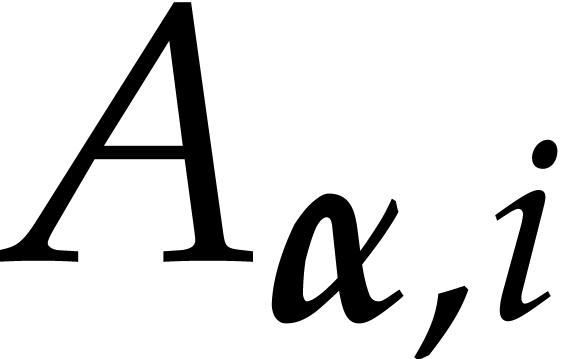 as long as there exists an index
as long as there exists an index
 for which
for which 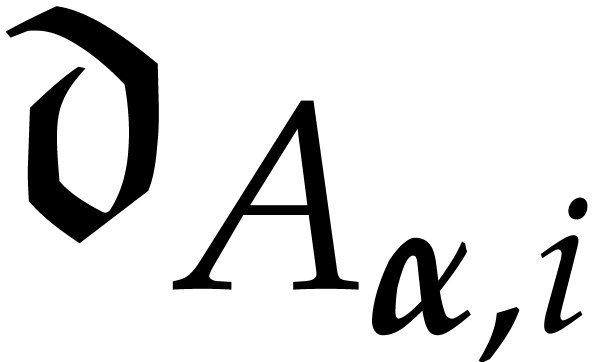 divides
divides  . There are many ways to compute
extended reductions of
. There are many ways to compute
extended reductions of  depending on the way we
chose the index
depending on the way we
chose the index  in case of multiple options. If
we always privilege the lowest possible index
in case of multiple options. If
we always privilege the lowest possible index  , then the process is deterministic and we call
, then the process is deterministic and we call
 with respect to
with respect to  . In that case, we define
. In that case, we define  and call it the remainder of
and call it the remainder of 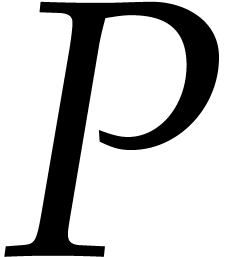 with
respect to
with
respect to  . Using relaxed
evaluation, this remainder can be computed efficiently:
. Using relaxed
evaluation, this remainder can be computed efficiently:
 be integers, let
be integers, let  , and let
, and let  be such
that
be such
that 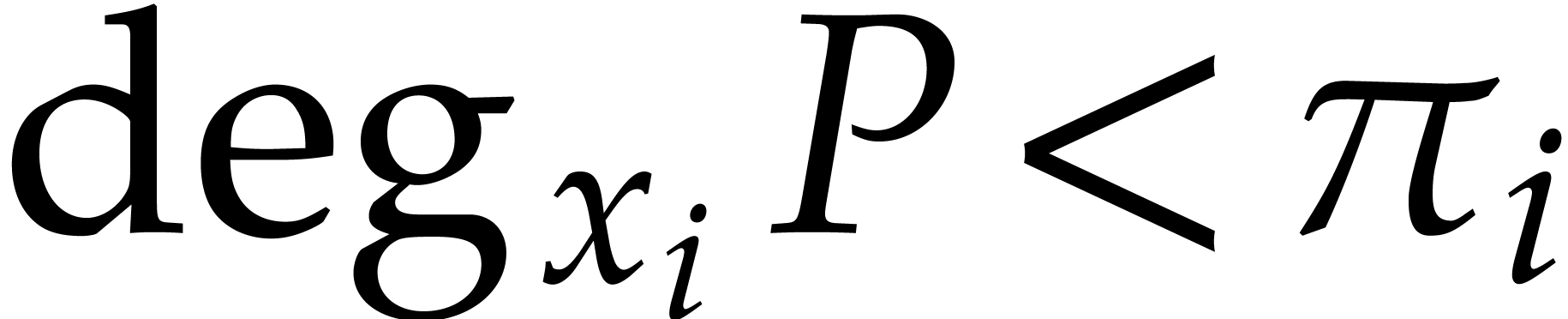 for
for  .
Then an extended reduction
.
Then an extended reduction
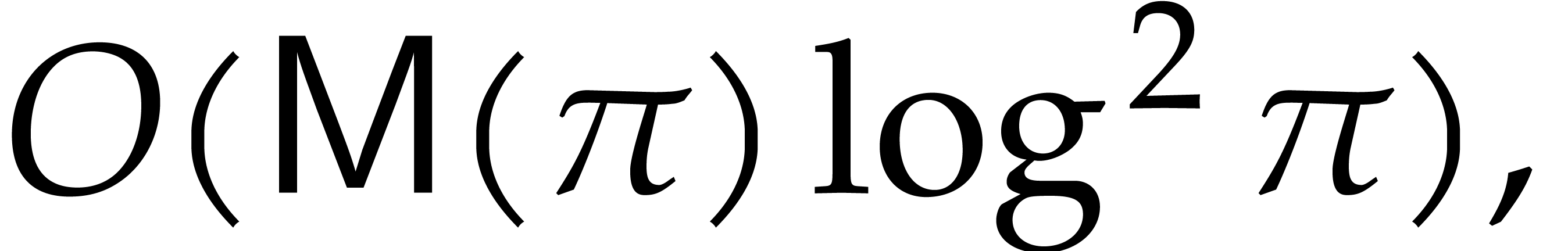
whenever an element of multiplicative order 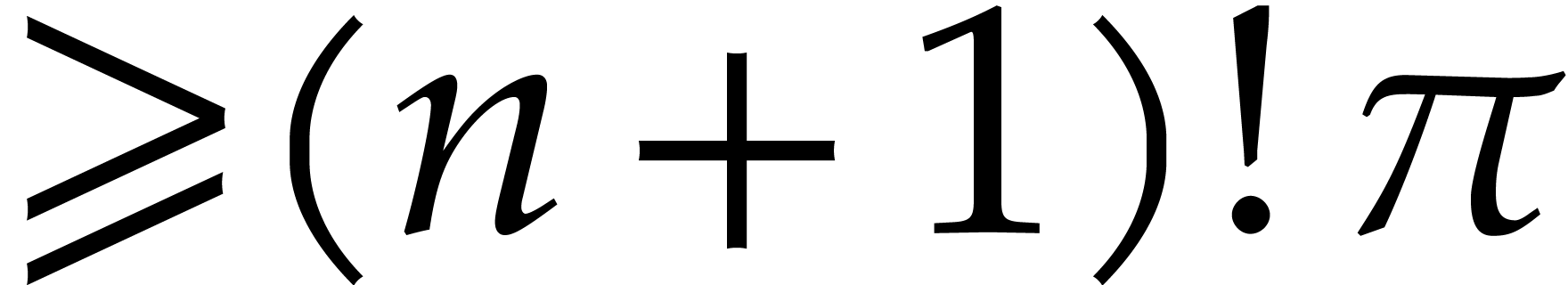 is given in
is given in  .
.
Proof. Without loss of generality, we may assume that

We use the reduction algorithm from [14] with the reduction
strategy that always reduces with respect to the axial element 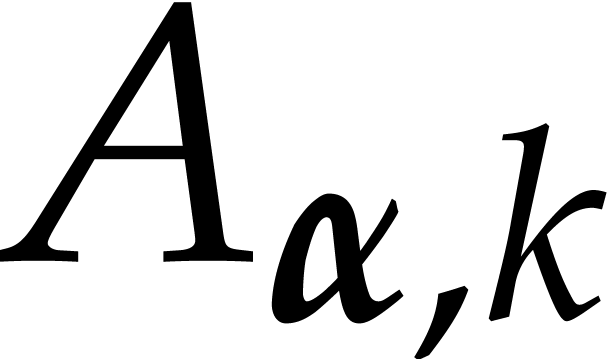 for which
for which 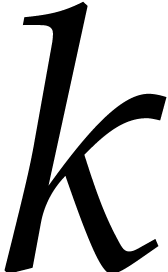 is minimal. Then we
claim that the supports of the successive reductions of
is minimal. Then we
claim that the supports of the successive reductions of 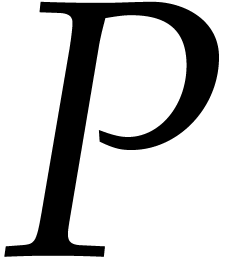 are all contained in the set
are all contained in the set
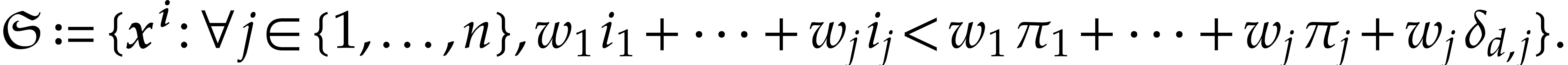
Indeed, let  , let
, let 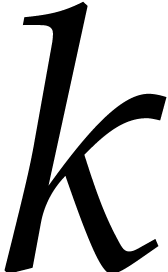 be minimal such that
be minimal such that 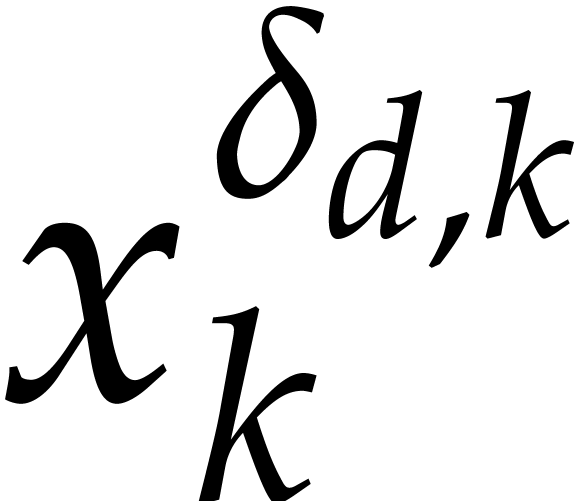 divides
divides 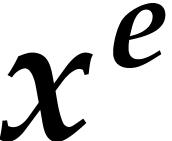 , and consider a monimial
, and consider a monimial 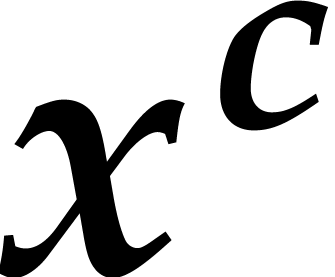 in the support of
in the support of 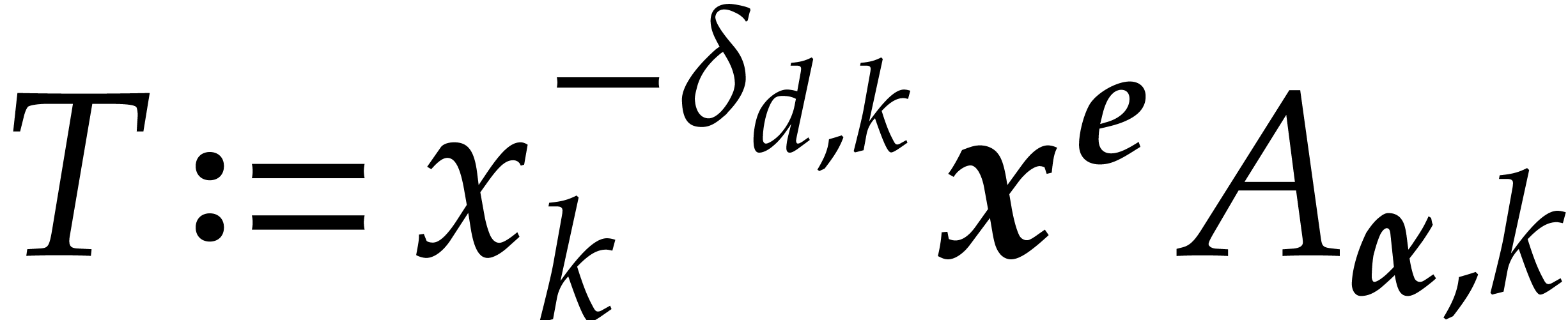 .
It suffices to show that
.
It suffices to show that  .
Let
.
Let 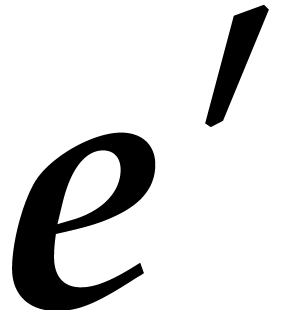 be such that
be such that 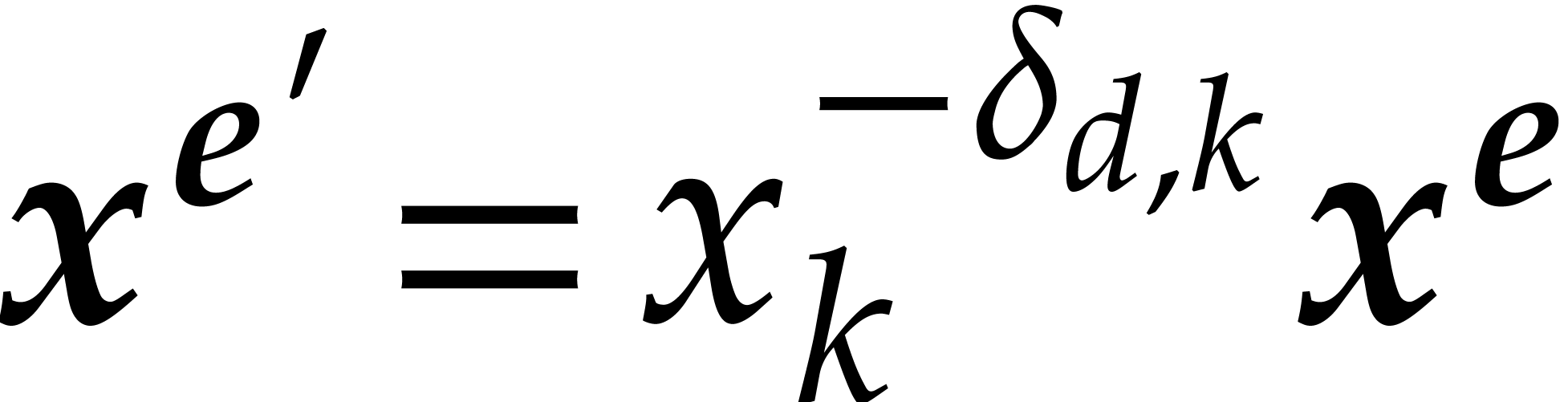 .
For
.
For  , the relations
, the relations  and
and 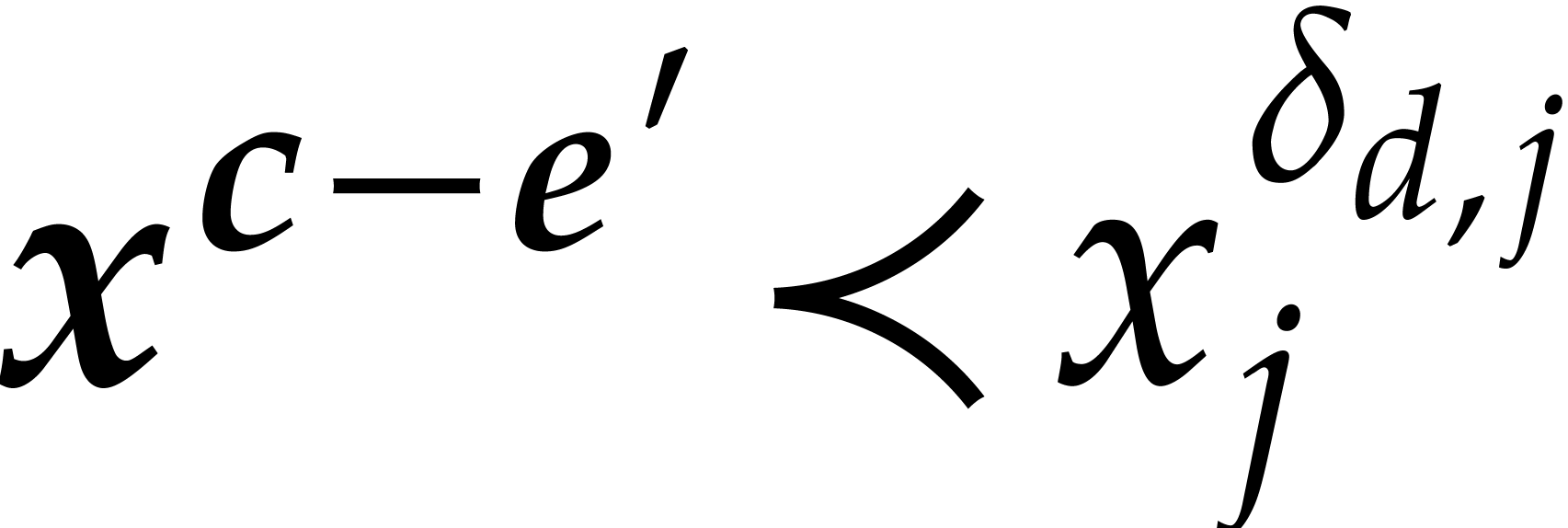 imply
imply
Now 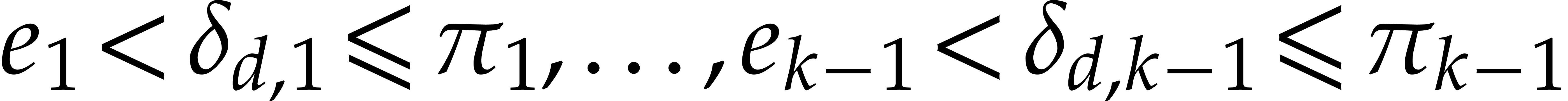 , whence
, whence
For 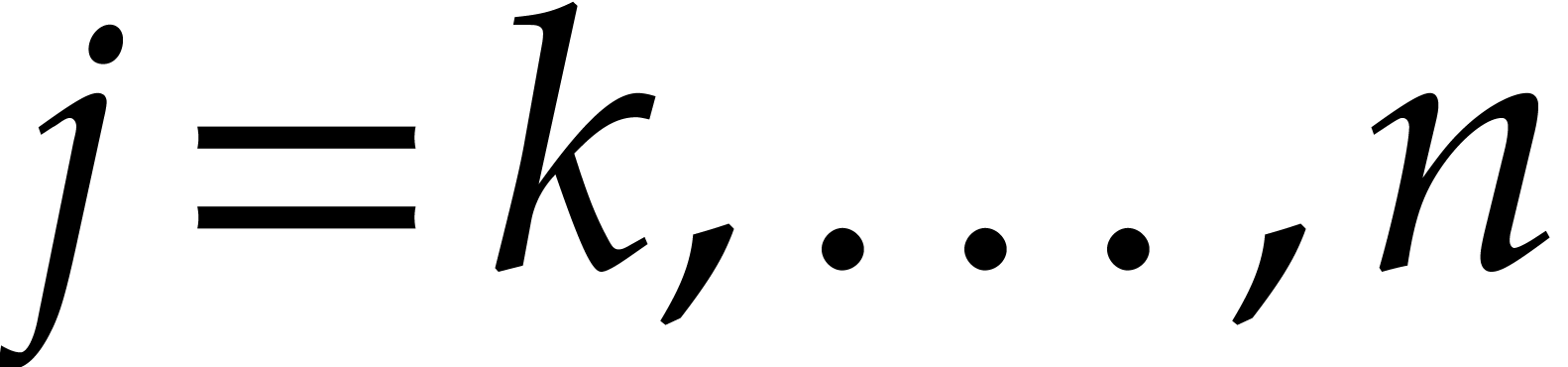 , we directly have
, we directly have
Having shown our claim, we next observe that 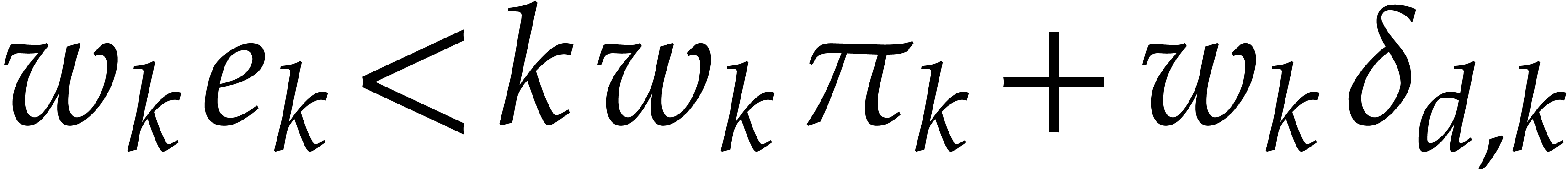 for
all
for
all  and
and 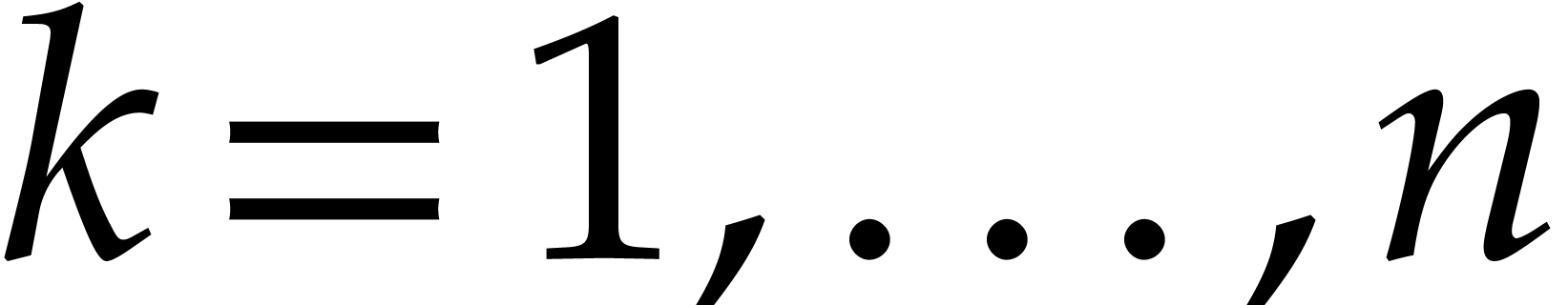 ,
whence
,
whence 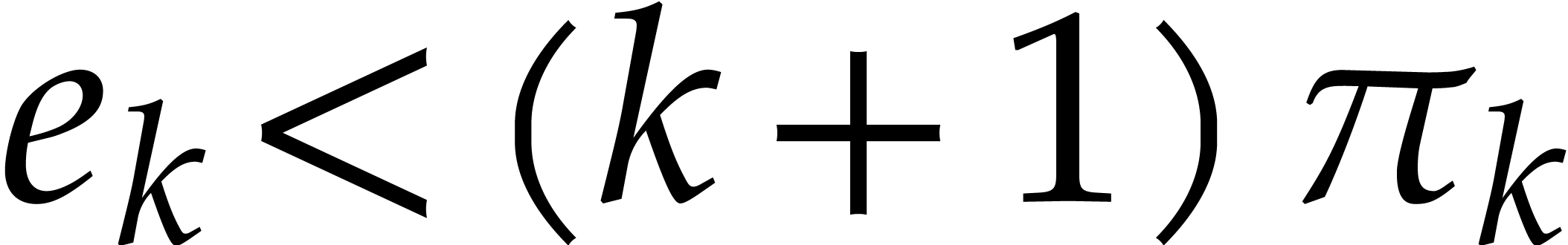 and
and 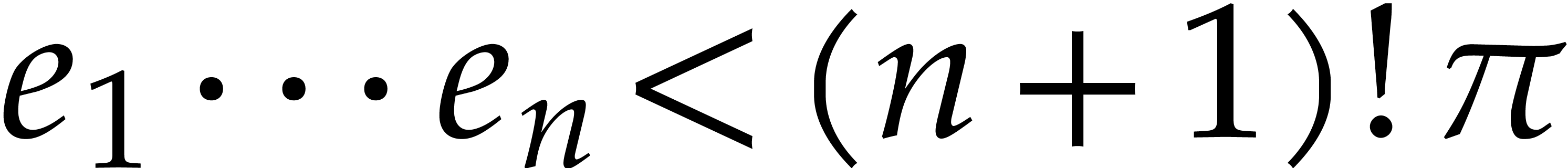 .
In particular, the size of the support of the
.
In particular, the size of the support of the 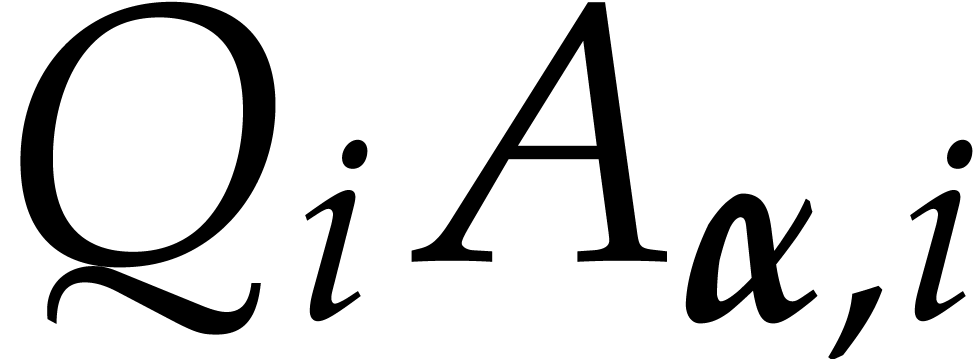 and
and  in the extended reduction
in the extended reduction 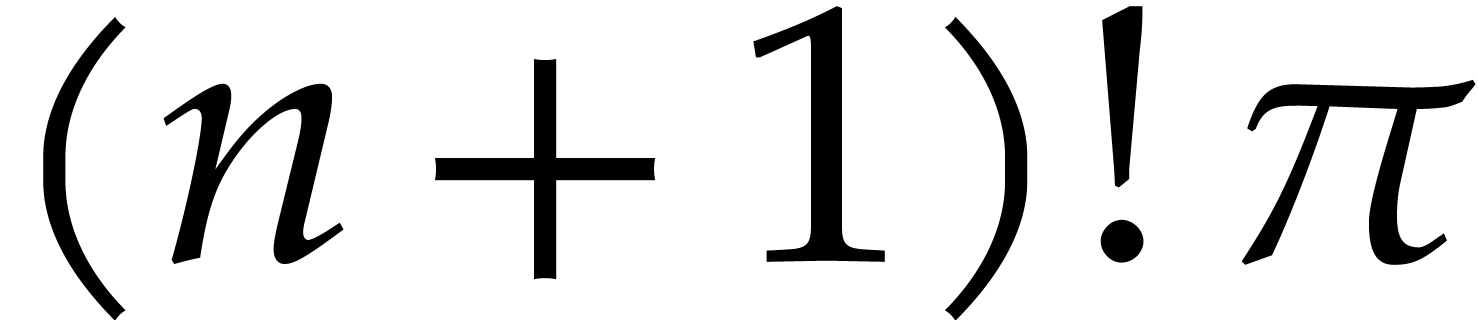 .
The theorem now becomes a consequence of [14, Theorem 4]
and Proposition 1, by taking
.
The theorem now becomes a consequence of [14, Theorem 4]
and Proposition 1, by taking 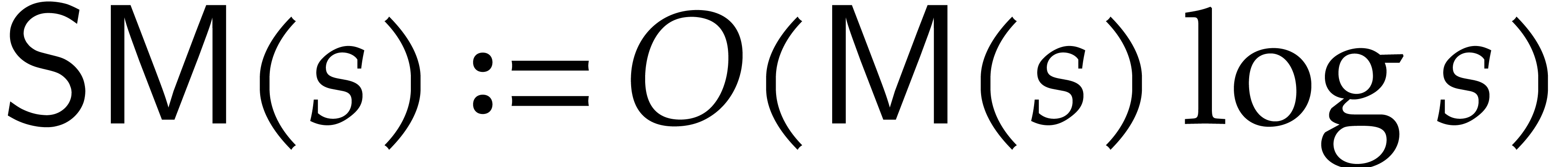 .
.
Remark  is the finite field
is the finite field 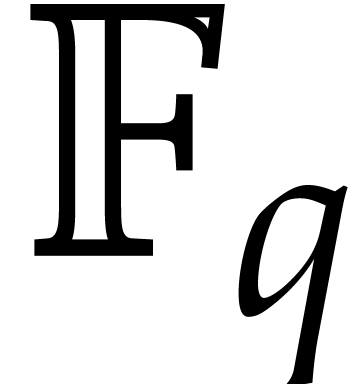 and
if
and
if 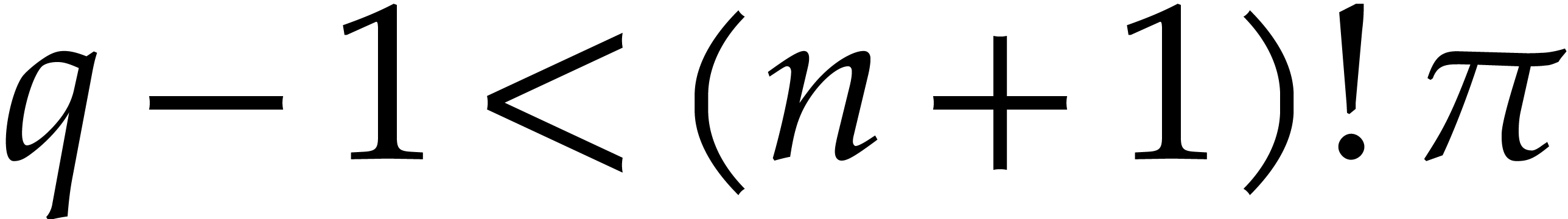 , then we can apply
Theorem 6 over an algebraic extension
, then we can apply
Theorem 6 over an algebraic extension 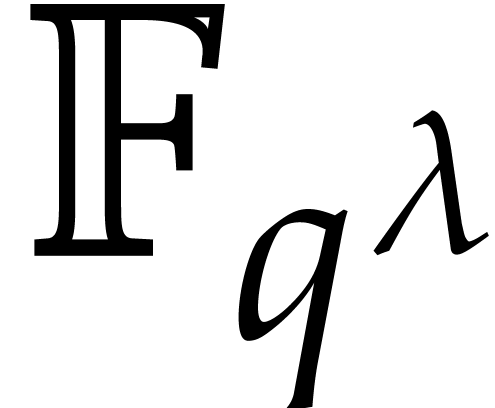 of degree
of degree
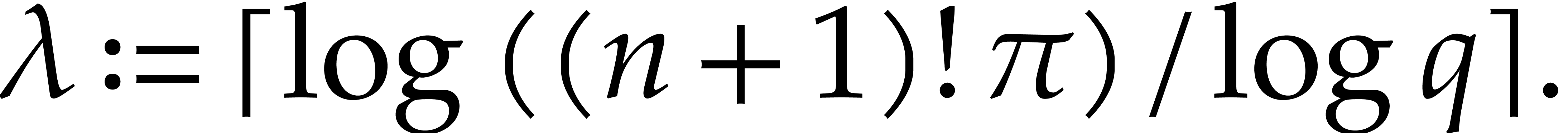
Constructing this extension can be done using 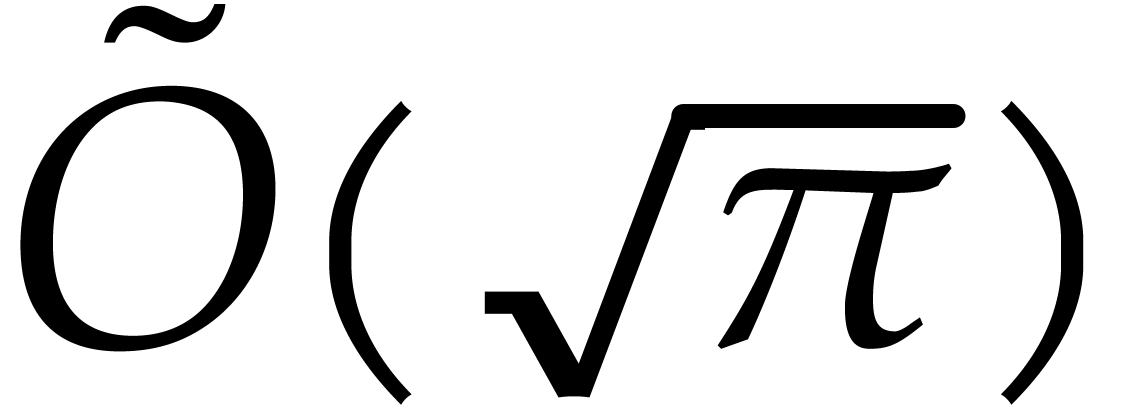 operations in
operations in  by [30, Theorem 3.2].
The primitive root of
by [30, Theorem 3.2].
The primitive root of 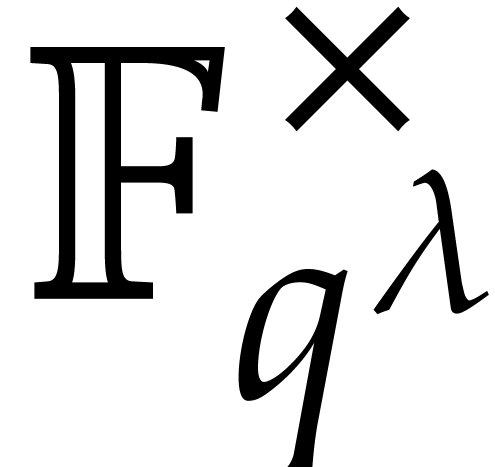 can be obtained in
negligible expected time using a probabilistic algorithm of Las Vegas
type. Then the complexity bound in Theorem 6 becomes
can be obtained in
negligible expected time using a probabilistic algorithm of Las Vegas
type. Then the complexity bound in Theorem 6 becomes
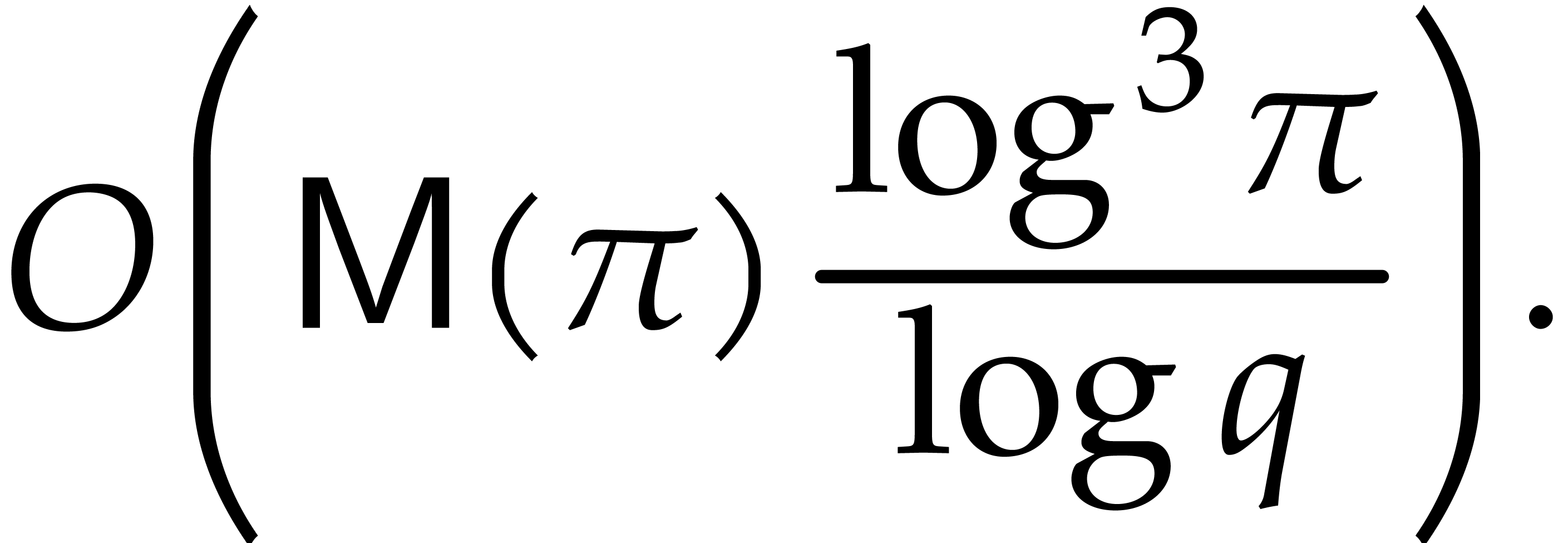
The fast algorithms for multi-point evaluation of univariate polynomials
make use of the technique of remainder trees [3,
9, 23]. For instance, the remainder tree for
four points 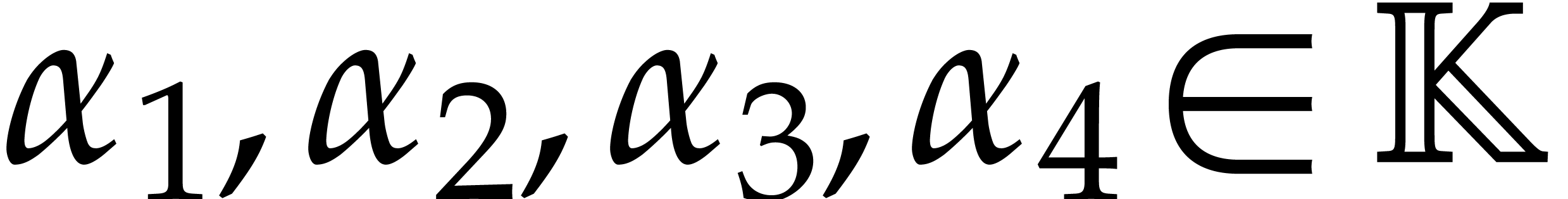 is the labeled binary tree given by
is the labeled binary tree given by
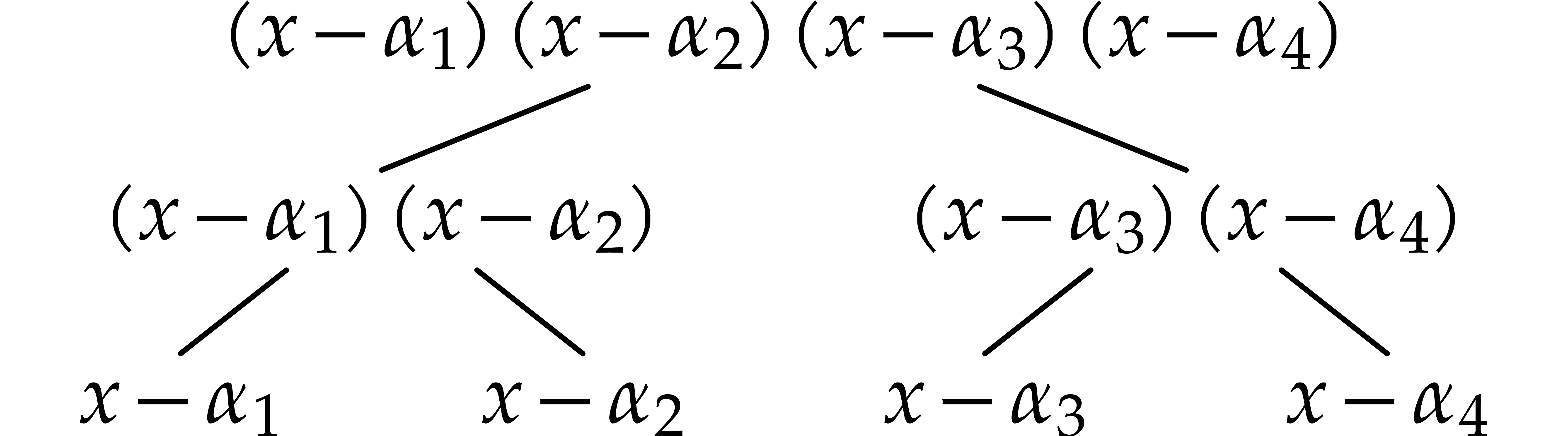 |
(4) |
Given a polynomial  to evaluate at these four
points, we compute the remainders of
to evaluate at these four
points, we compute the remainders of 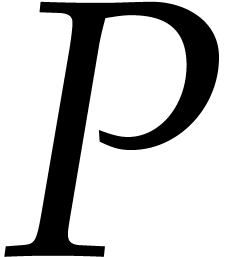 with
respect to each of the polynomials at the nodes, in a top-down fashion.
For instance, the value at
with
respect to each of the polynomials at the nodes, in a top-down fashion.
For instance, the value at 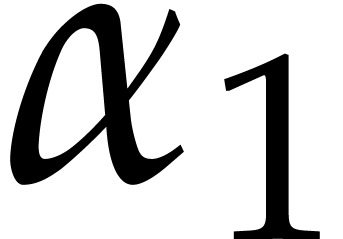 is obtained as
is obtained as
Using Theorem 6, we may use a similar technique for
multivariate polynomials and points 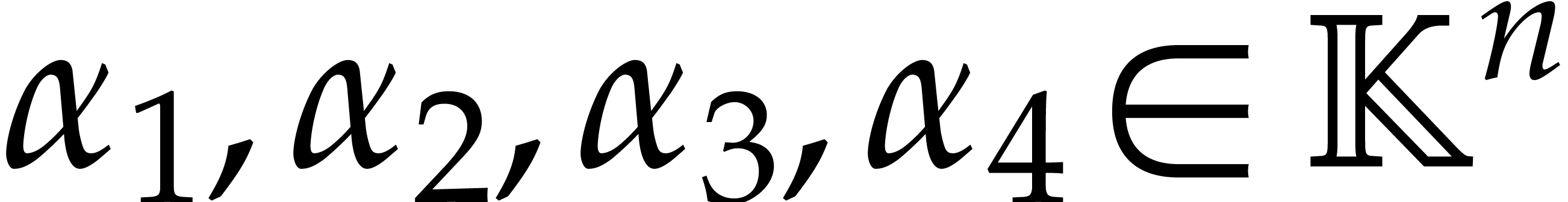 :
we replace each polynomial
:
we replace each polynomial  by the axial basis
by the axial basis
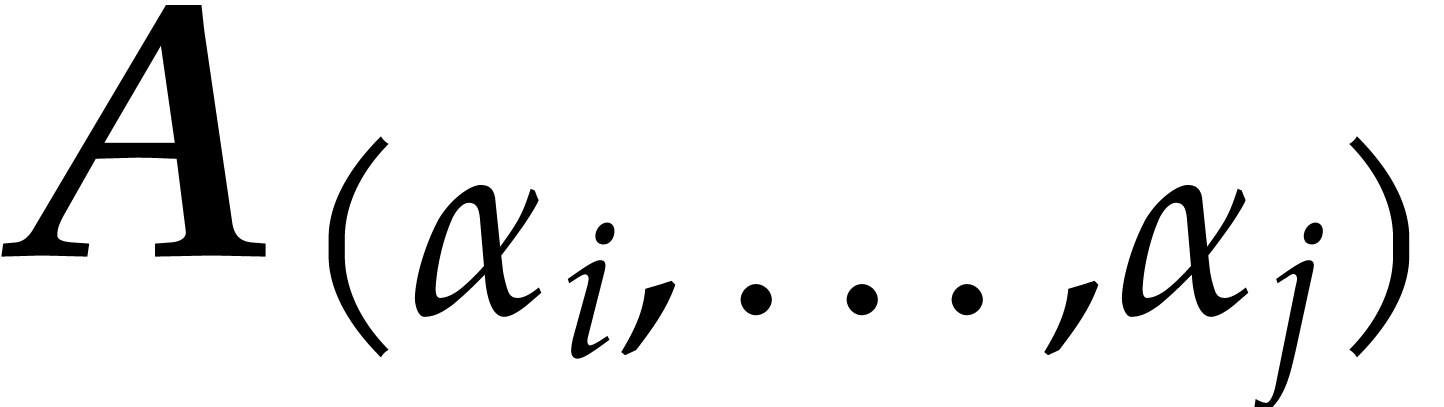 :
:
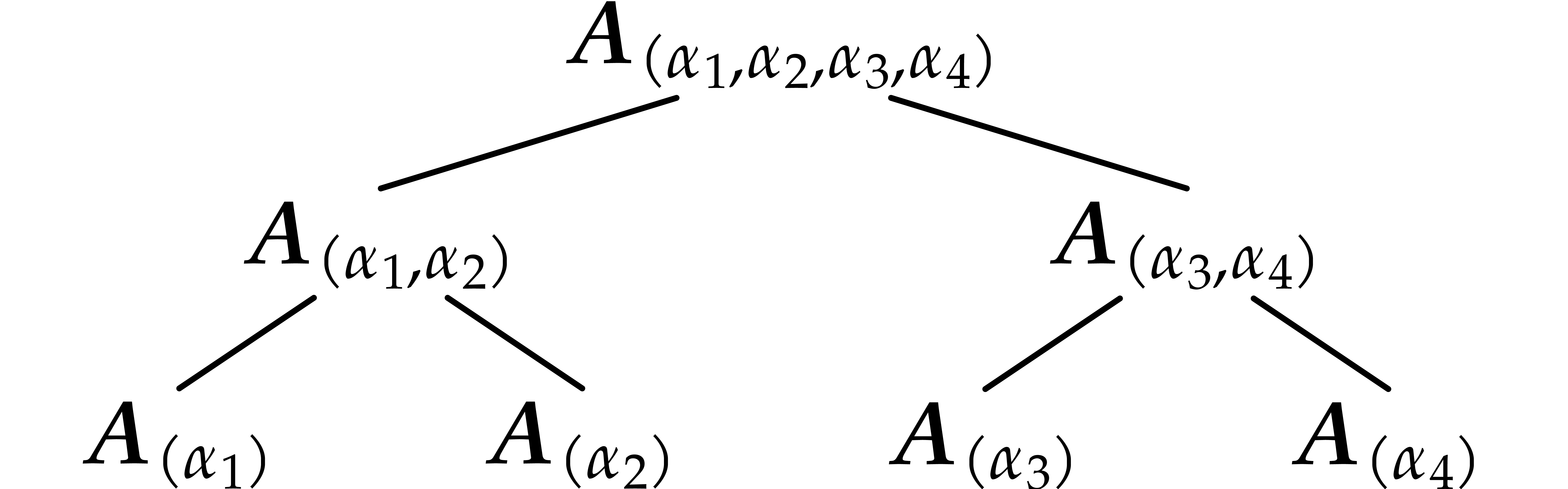 |
(5) |
We may then compute the evaluation of 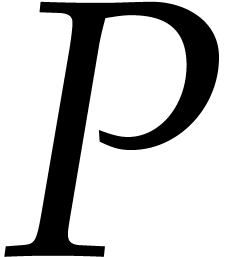 at
at 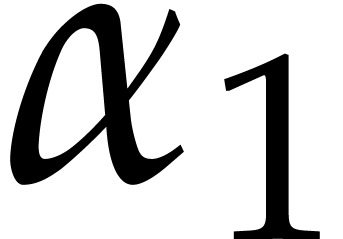 using
using
We will call
In order to specify our general algorithms for multi-point evaluation
and the computation of evaluation trees, it is convenient to introduce a
few more notations. Given a vector 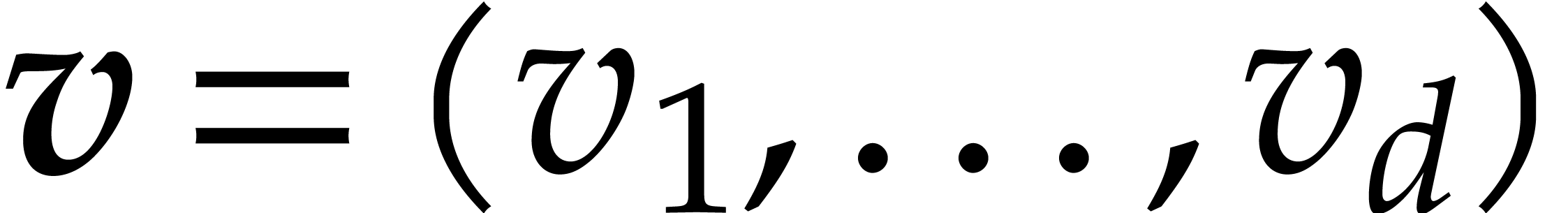 ,
we will write
,
we will write
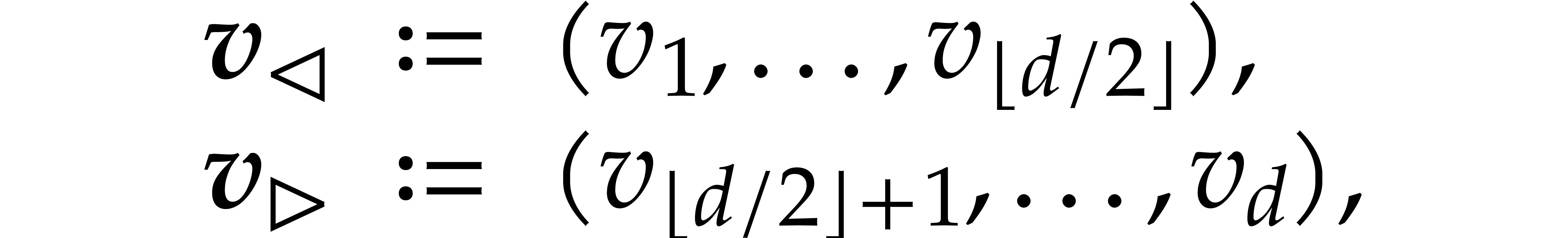
where  represents the largest integer smaller or
equal to
represents the largest integer smaller or
equal to  . The least integer
larger or equal to
. The least integer
larger or equal to  is written
is written  .
.
Given vectors 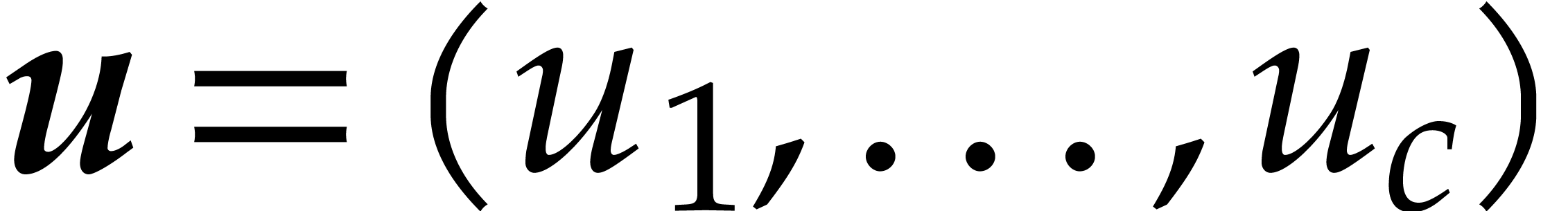 and
and 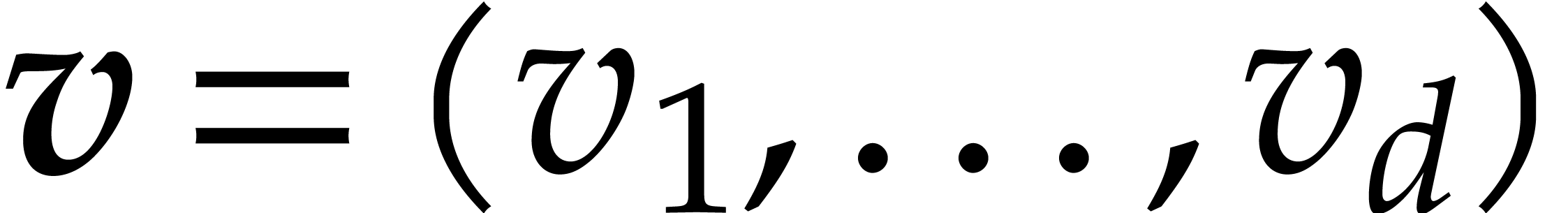 ,
we also write
,
we also write

for their concatenation. Given 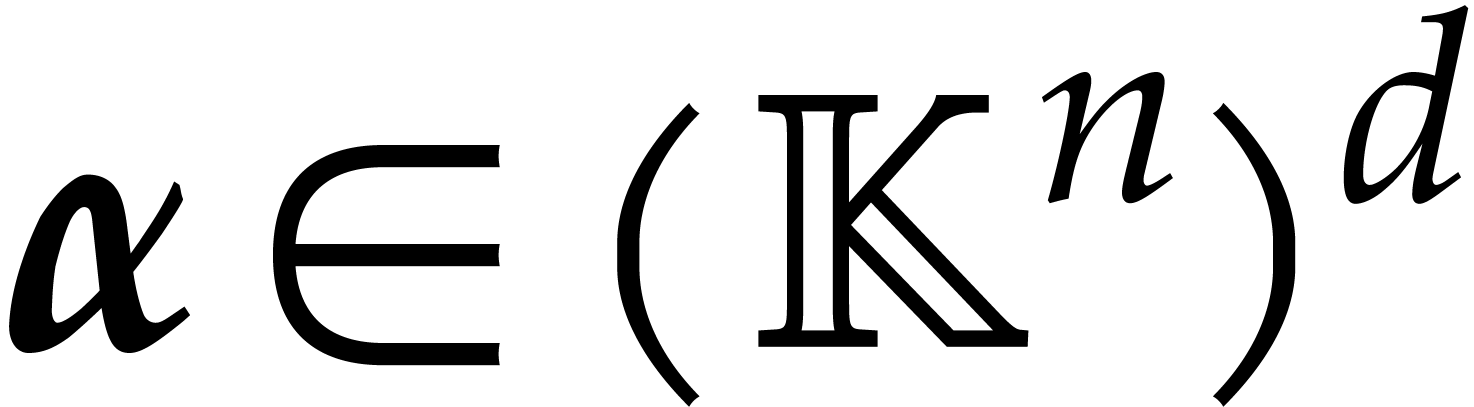 ,
we may use the following recursive algorithm to compute the evaluation
tree for
,
we may use the following recursive algorithm to compute the evaluation
tree for  :
:
Algorithm EvalTree(
Input: a vector of points
Output: an evaluation tree for |
Compute the axial basis
If
Let
Return the tree with root labeled by |
We regard the computation of an evaluation tree as a precomputation.
Given an evaluation tree  for
for  , we may efficiently evaluate polynomials
, we may efficiently evaluate polynomials  at all points
at all points  using the
following algorithm:
using the
following algorithm:
Algorithm Eval(
Input: a polynomial
Output: the vector |
Let
Let
If
Let
Return |
The algorithms  and
and  actually work for arbitrary point vectors
actually work for arbitrary point vectors 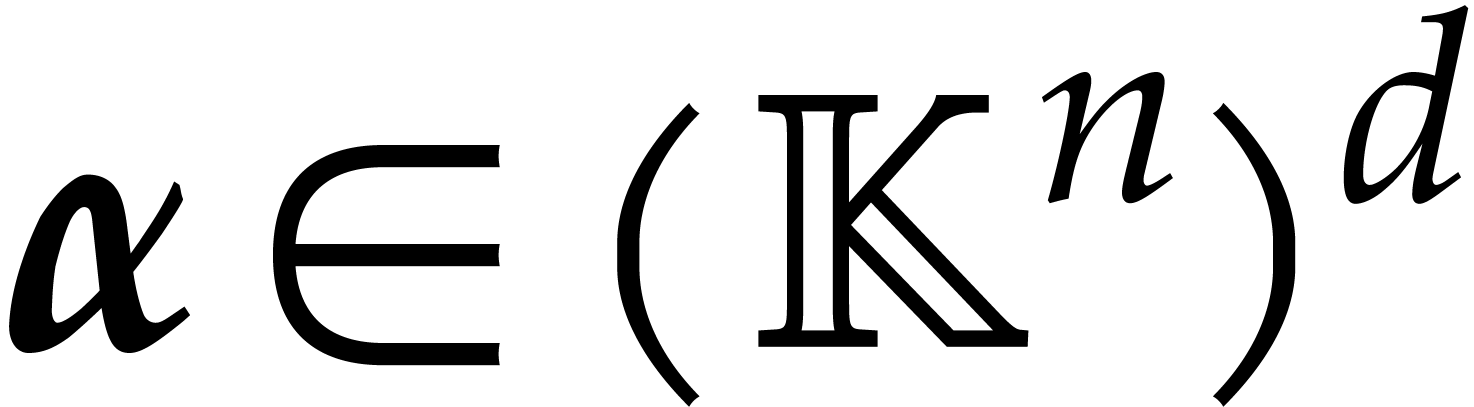 :
it suffices to use a general purpose algorithm to compute Gröbner
bases for the ideals
:
it suffices to use a general purpose algorithm to compute Gröbner
bases for the ideals 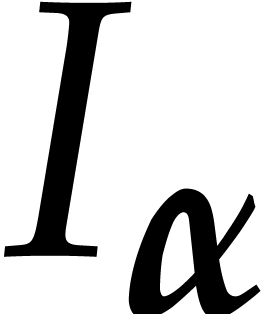 , from
which we can then extract the required axial bases. We say that
, from
which we can then extract the required axial bases. We say that  is hereditarily generic if
is hereditarily generic if 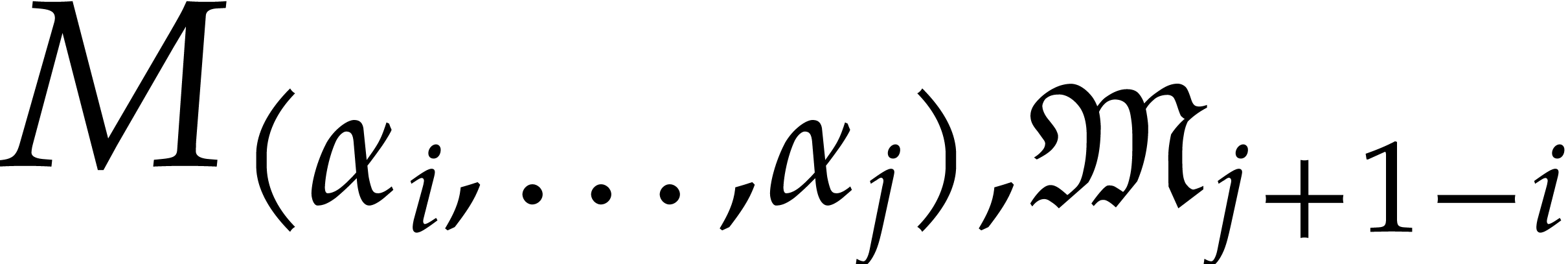 is invertible for all
is invertible for all 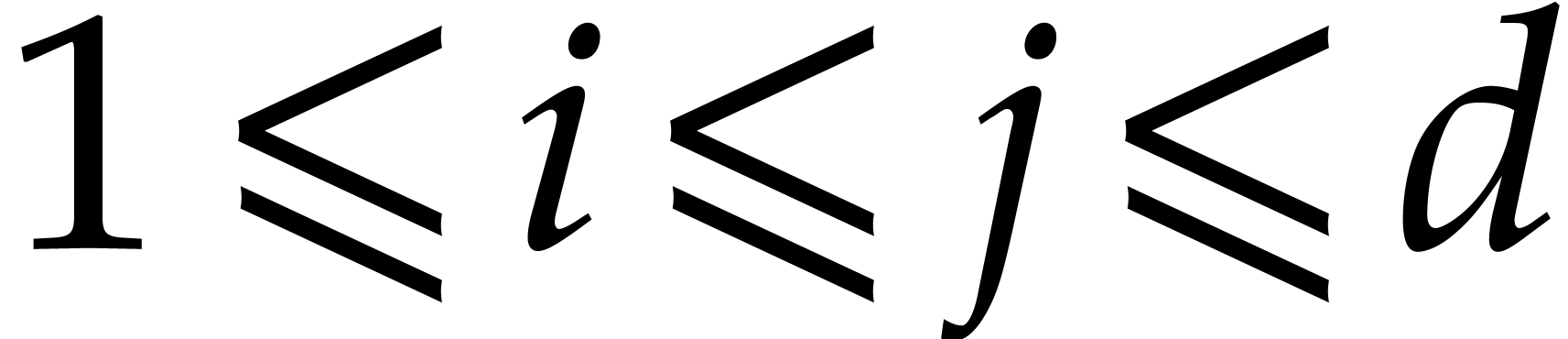 . In
that case, each of the required axial bases during recursive calls can
be computed using Proposition 3.
. In
that case, each of the required axial bases during recursive calls can
be computed using Proposition 3.
 and
and  are correct. Let
are correct. Let  with
with 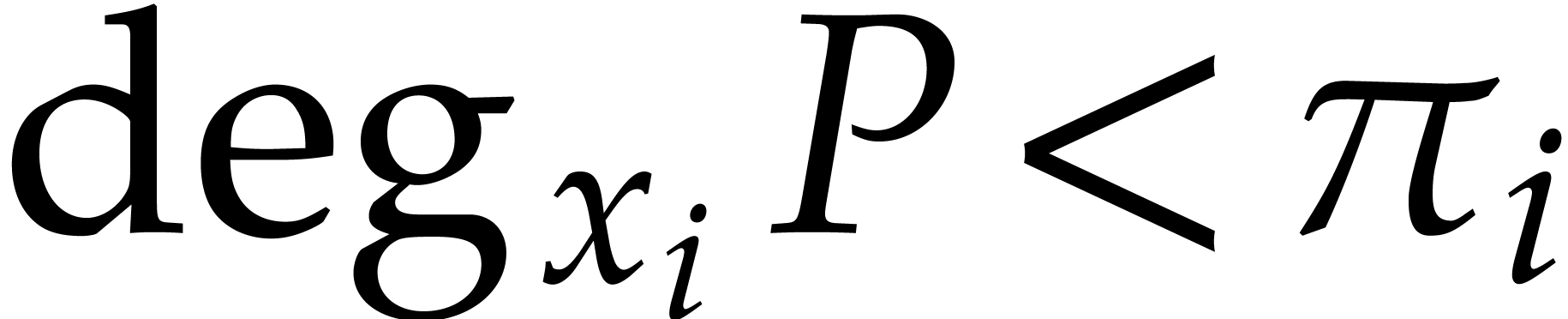 and
and 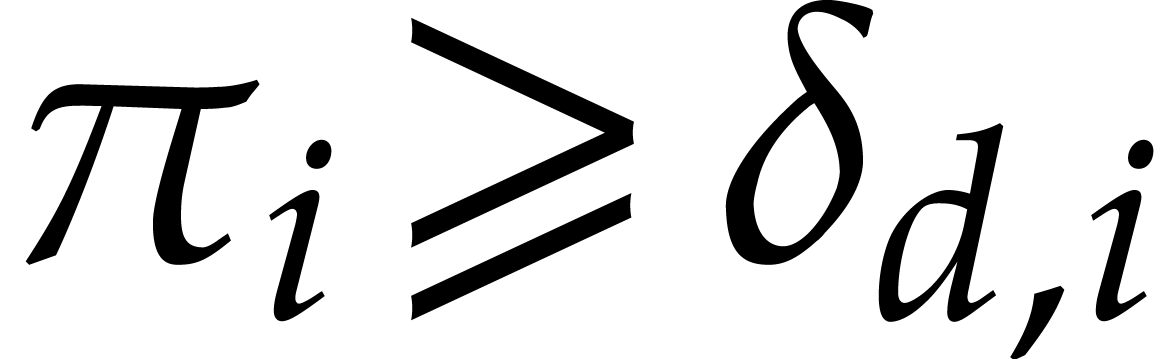 for
for  ,
and
,
and  . If
. If  is hereditarily generic, then the running times of
is hereditarily generic, then the running times of  and
and  are respectively bounded by
are respectively bounded by
whenever an element of multiplicative order 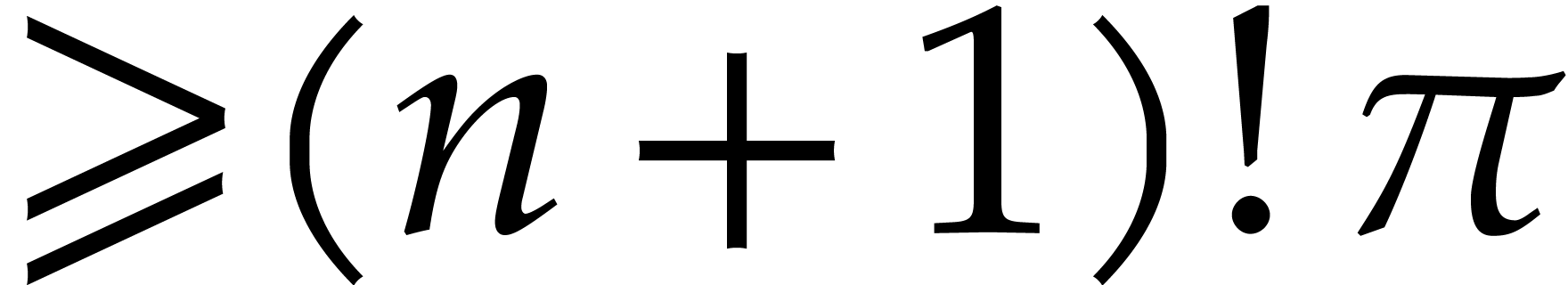 is given in
is given in  .
.
Proof. By induction on  , the algorithms
, the algorithms  and
and  are clearly correct. Using Proposition 3
and linear algebra, we see that the computation of
are clearly correct. Using Proposition 3
and linear algebra, we see that the computation of  in the first step of
in the first step of  can be done in time
can be done in time 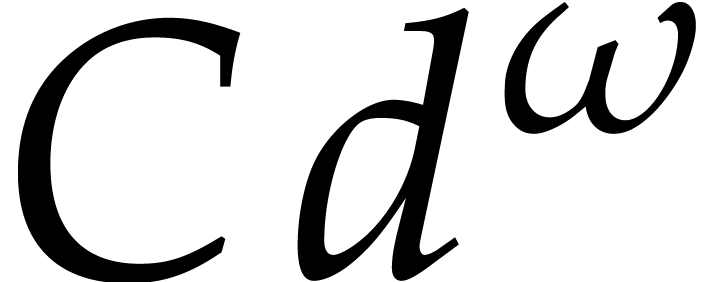 , for some constant
, for some constant  . The running time
. The running time  therefore satisfies
therefore satisfies
By induction on  , this yields
, this yields
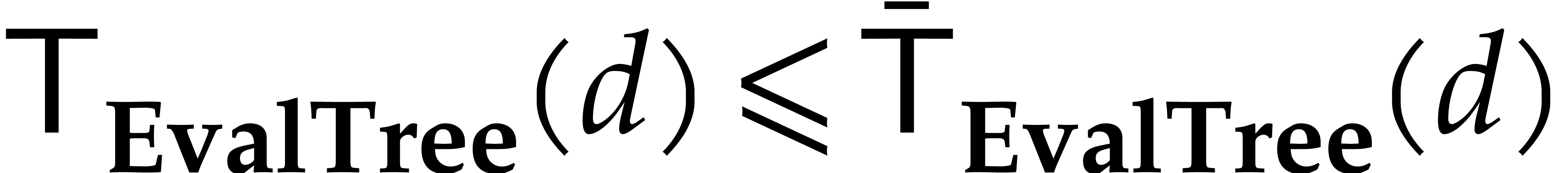 , where
, where
Again using induction on  , we
also note that
, we
also note that  is increasing. It follows that
is increasing. It follows that
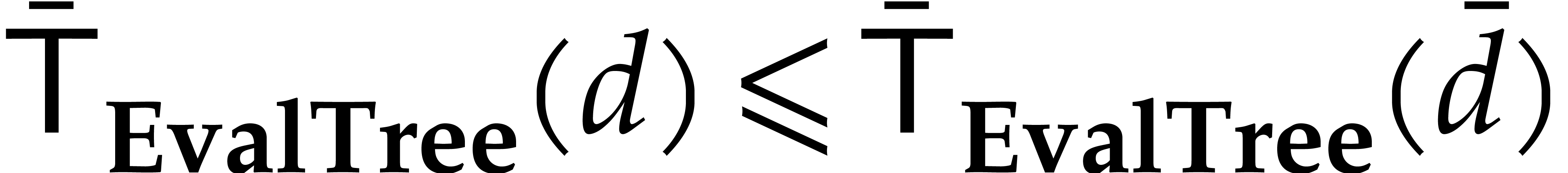 for
for 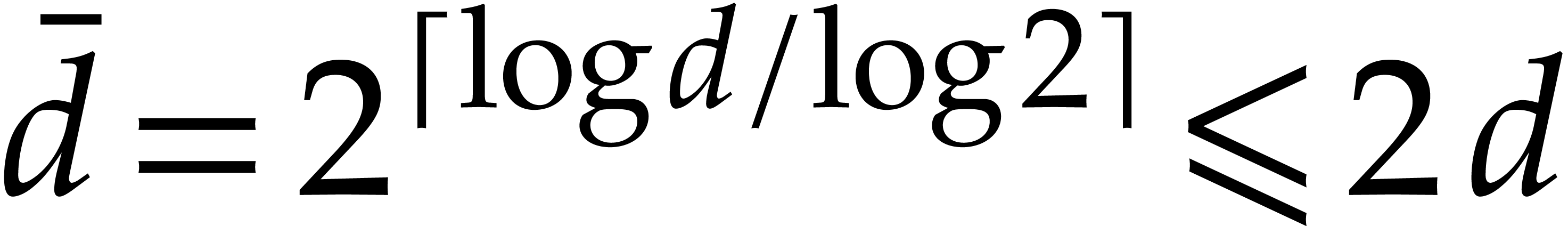 .
Unrolling the equation
.
Unrolling the equation
we find
As to the running time  of
of  , we recall that
, we recall that  ,
whence
,
whence 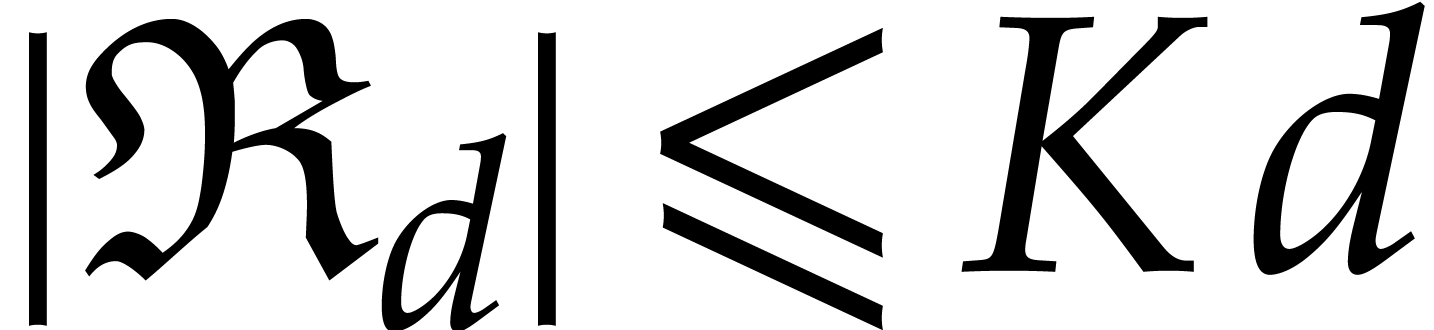 for some constant
for some constant  that depends on
that depends on 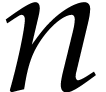 . Theorem 6 also implies the existence of a constant
. Theorem 6 also implies the existence of a constant  such that
such that
Modulo a further increase of  ,
the first and third relation may be combined such as to replace the
third relation by
,
the first and third relation may be combined such as to replace the
third relation by
By unrolling the latter inequality in a similar way as above for powers
of two, we obtain 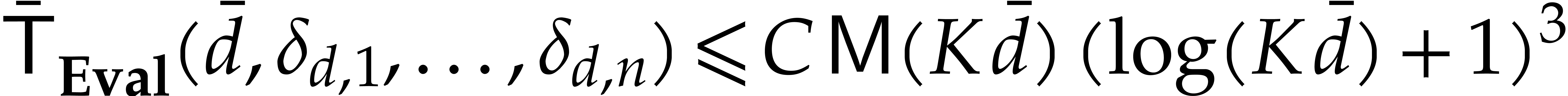 , while
using our assumption that
, while
using our assumption that 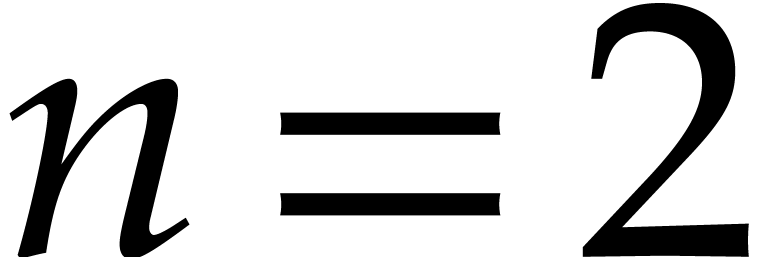 is
non-decreasing.
is
non-decreasing.
Remark 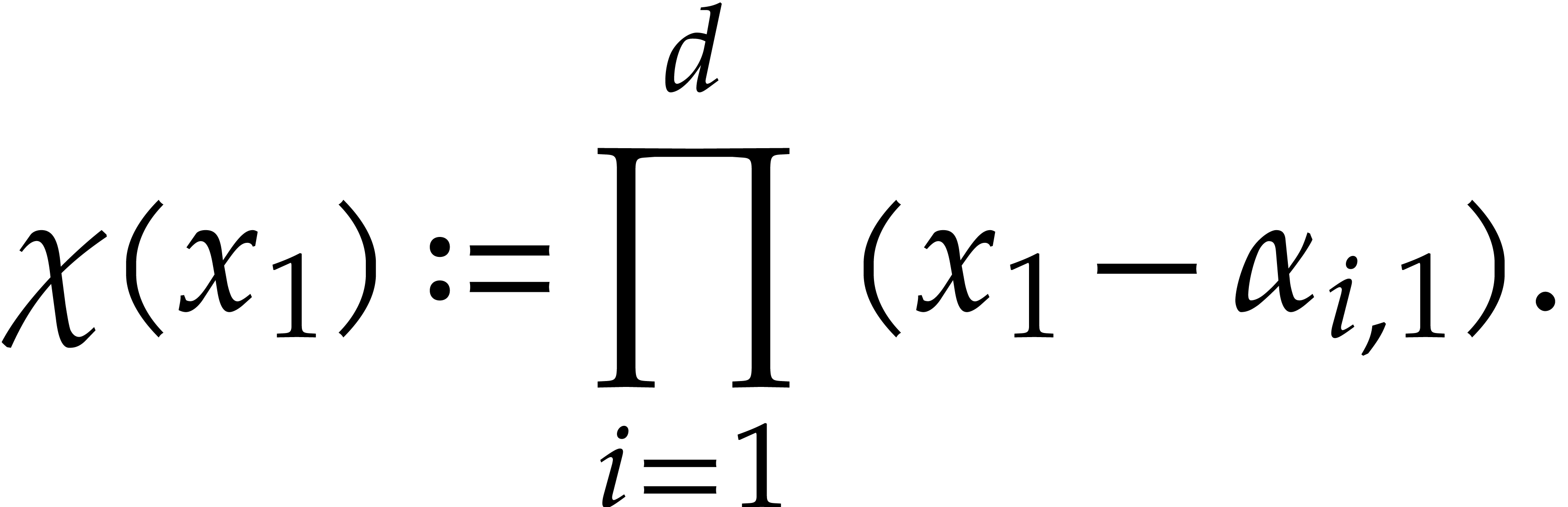 and the first coordinates of the evaluation points are
pairwise distinct, then precomputations can be handled more efficiently
as follows. The annihilating polynomial takes
and the first coordinates of the evaluation points are
pairwise distinct, then precomputations can be handled more efficiently
as follows. The annihilating polynomial takes 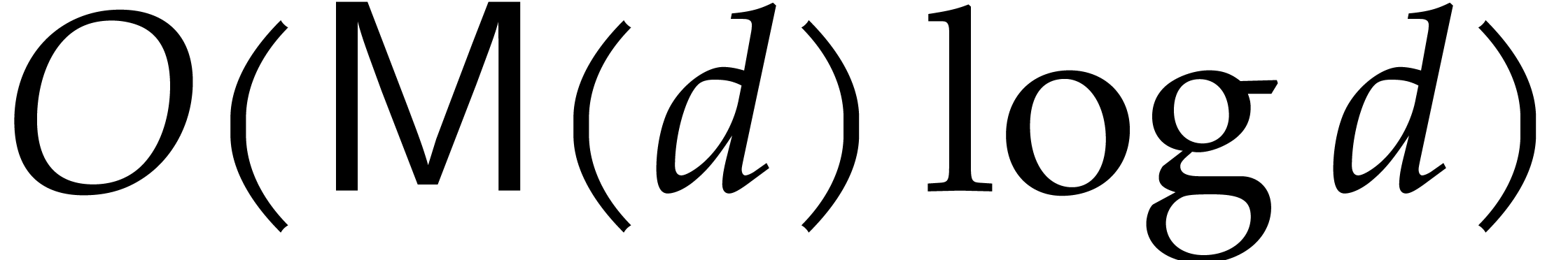 operations in
operations in  , using the
formula
, using the
formula
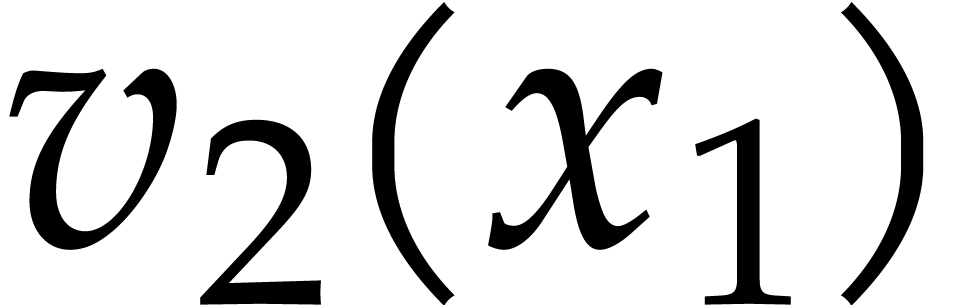
With a similar cost we can also interpolate the polynomial 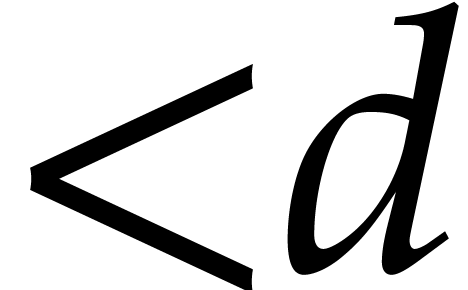 of degree
of degree  satisfying
satisfying 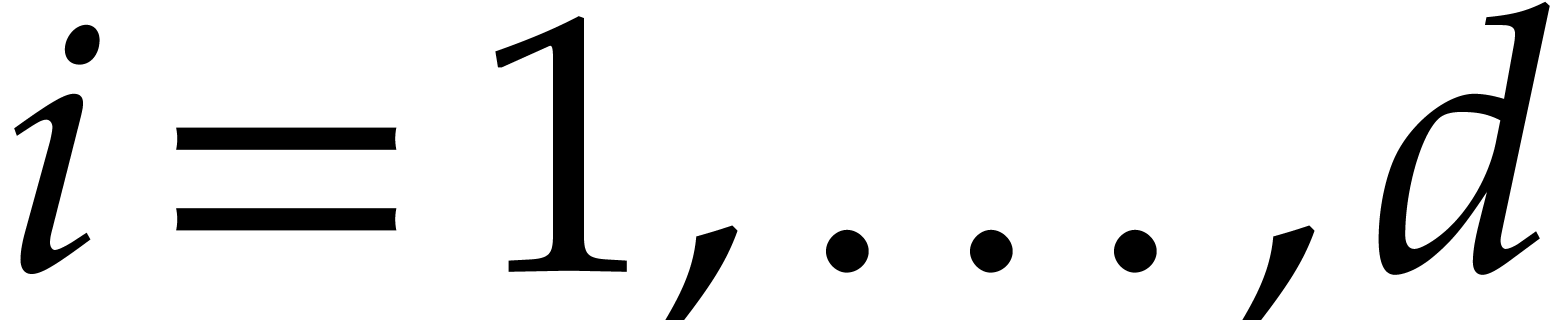 for
for 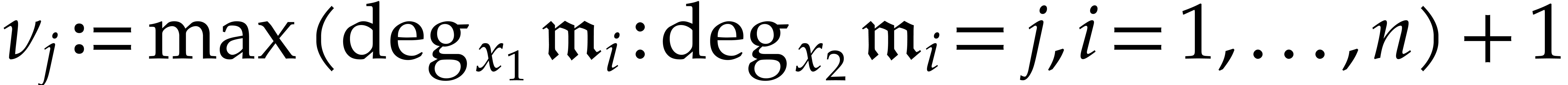 .
.
Setting  for
for 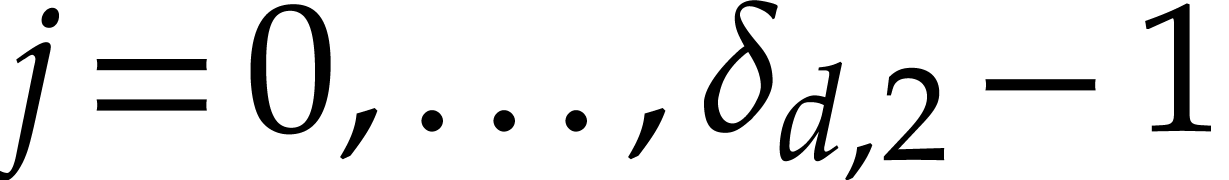 ,
we note that
,
we note that  . Determining
the coordinates of
. Determining
the coordinates of  in the basis
in the basis 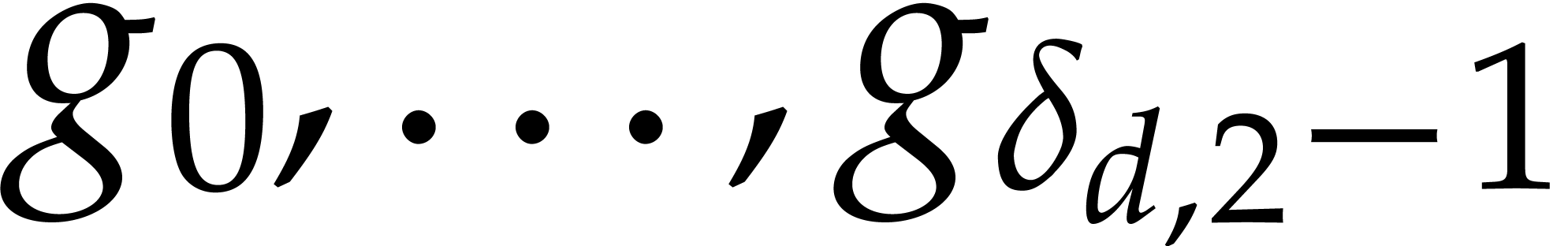 of the quotient ring of
of the quotient ring of  reduces to computing
polynomials
reduces to computing
polynomials 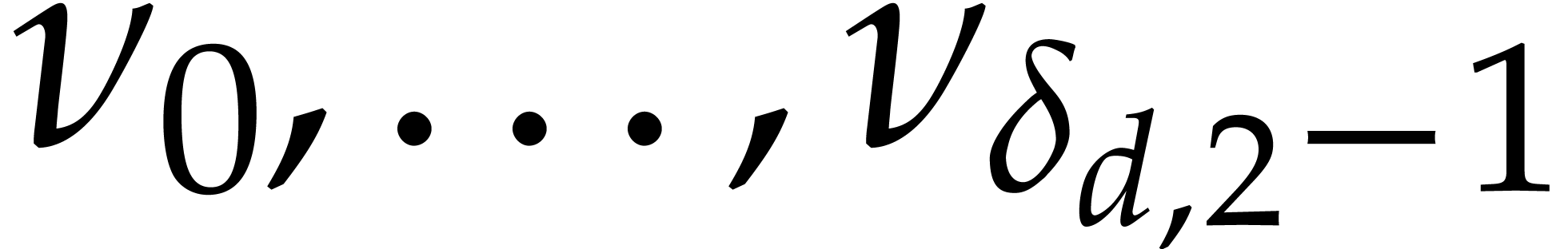 in
in 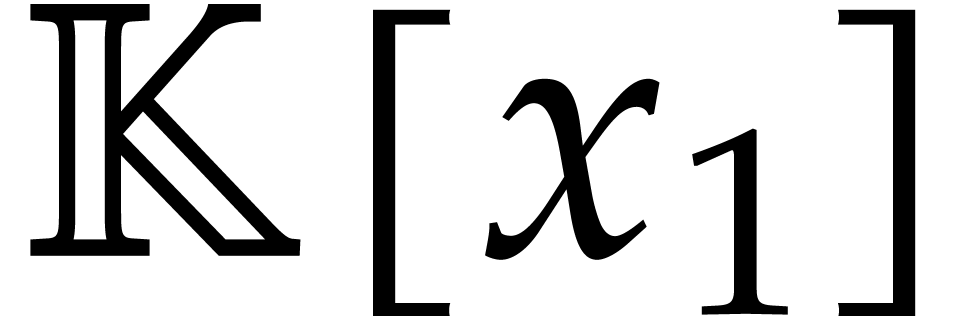 of
respective degree less than
of
respective degree less than  and a scalar
and a scalar  such that
such that
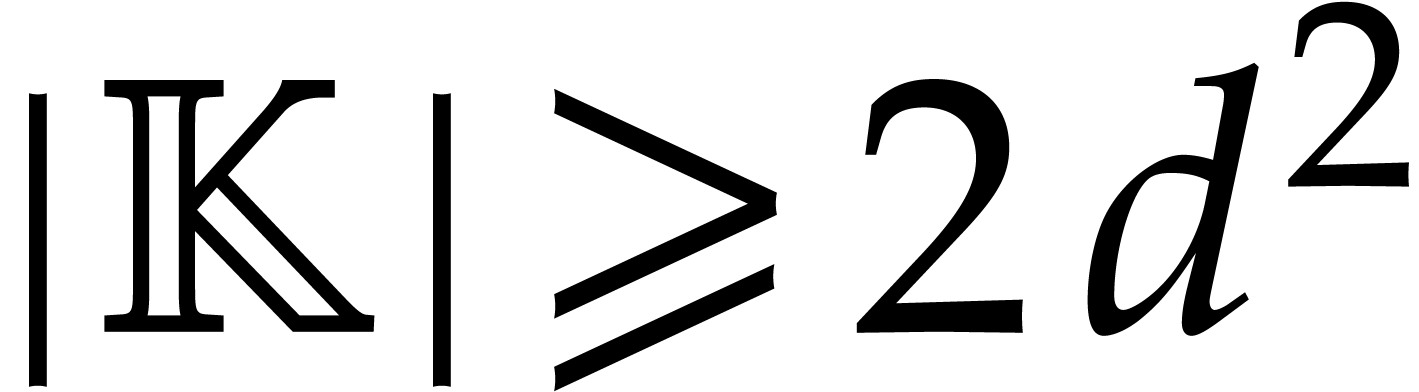
Assuming that 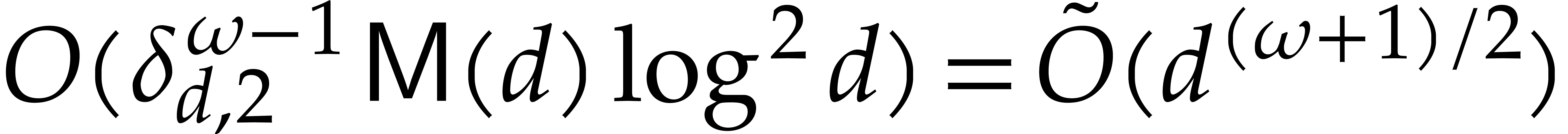 , a non-trivial
solution can be computed in expected time
, a non-trivial
solution can be computed in expected time  using
the probabilistic algorithm of Las Vegas type underlying [4,
Corollary 1]. Since
using
the probabilistic algorithm of Las Vegas type underlying [4,
Corollary 1]. Since 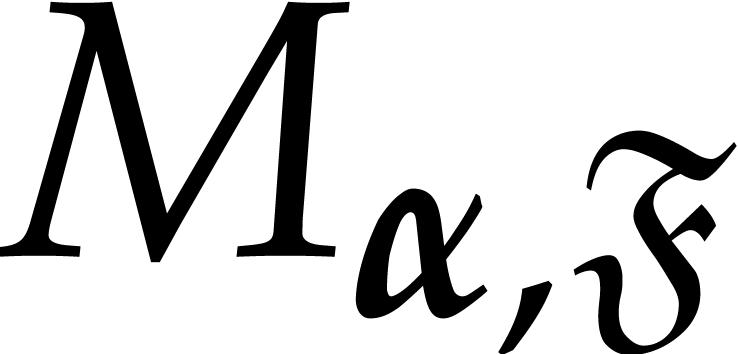 is invertible, the value
found for
is invertible, the value
found for 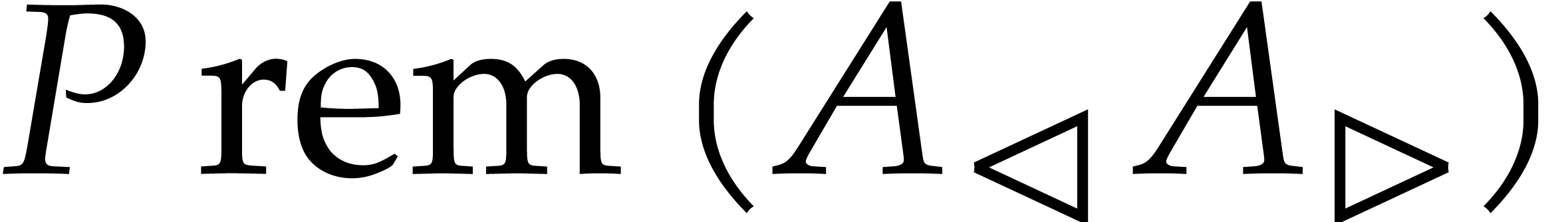 cannot be zero, and we obtain the
solution of
cannot be zero, and we obtain the
solution of
In the univariate case, the technique of remainder trees can also be
used to efficiently reconstruct a polynomial  from its values at
from its values at  distinct points
distinct points  . This basically amounts to reversing the
evaluation process, while using the Chinese remainder theorem to
reconstruct
. This basically amounts to reversing the
evaluation process, while using the Chinese remainder theorem to
reconstruct 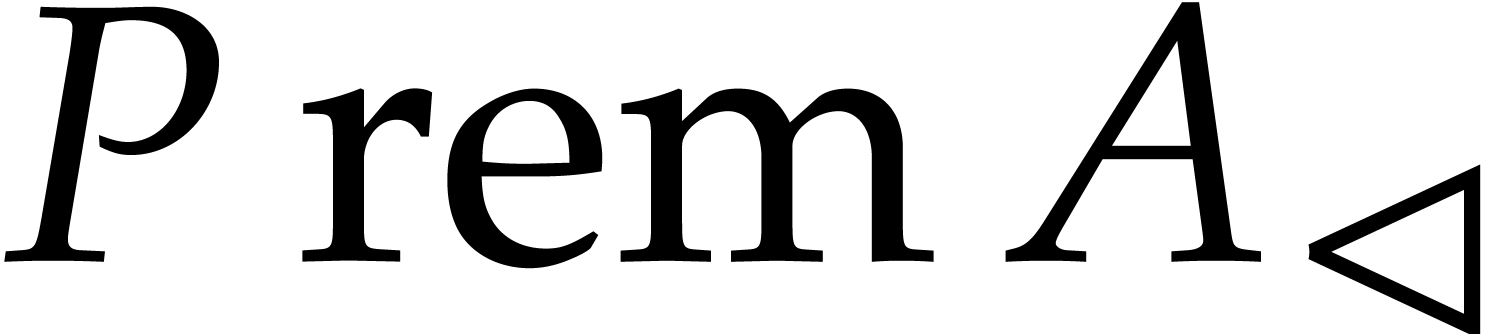 from
from 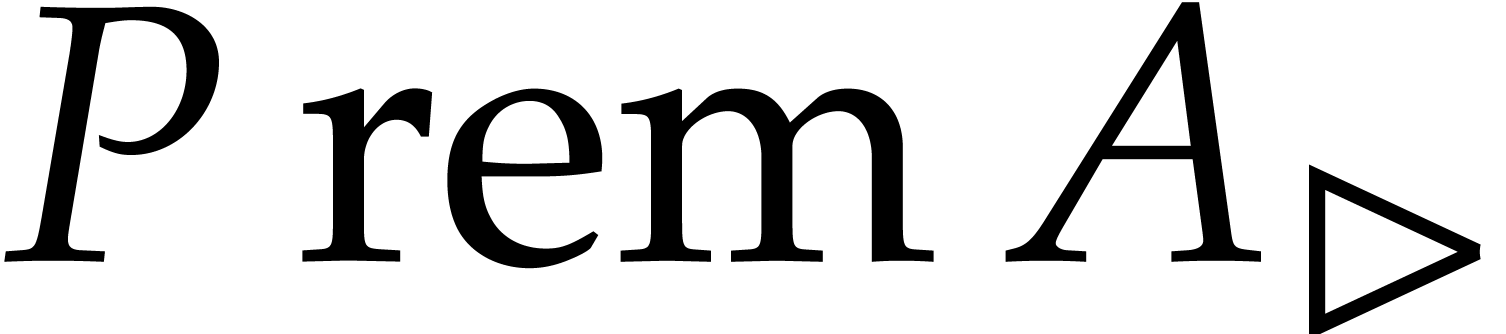 and
and
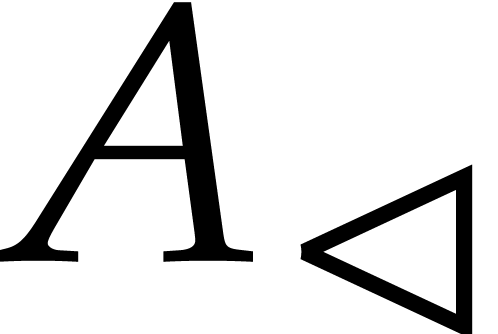 for coprime polynomials
for coprime polynomials 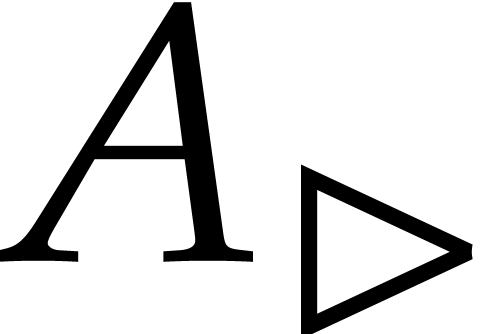 and
and 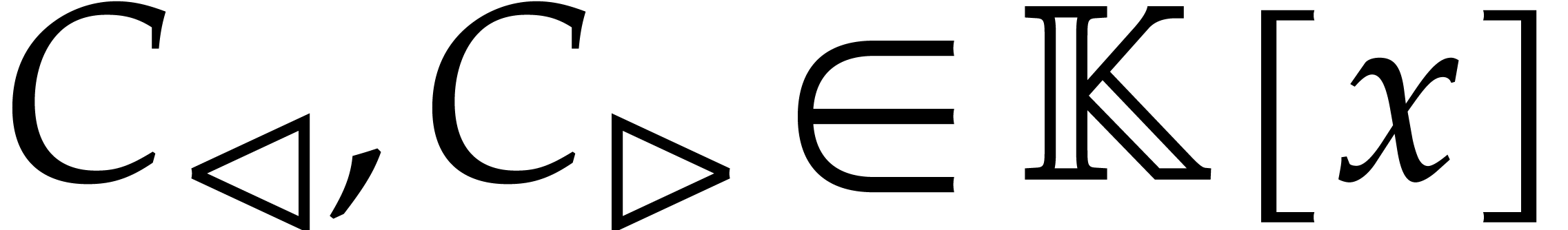 . For such
reconstructions using the Chinese remainder theorem, it is useful to
precompute the “cofactors”
. For such
reconstructions using the Chinese remainder theorem, it is useful to
precompute the “cofactors” 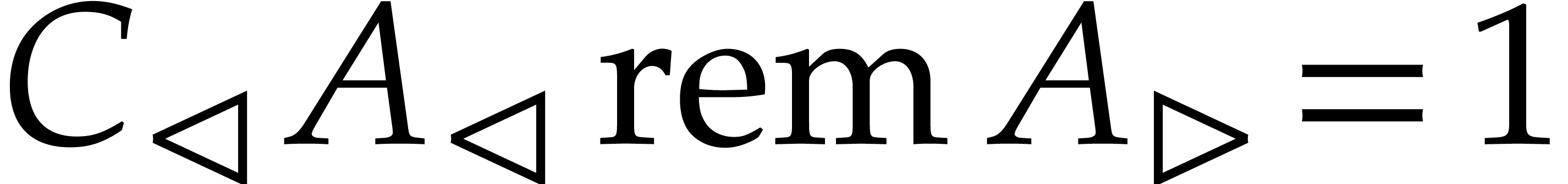 with
with
 ,
,  ,
,  , and
, and
 , after which
, after which
These cofactors are typically stored in an upgraded version of the remainder tree.
In our multivariate setting, a similar idea works, modulo some
additional precautions when computing the cofactors. The cofactors are
most easily constructed via their evaluations. Indeed, consider
a tuple of points 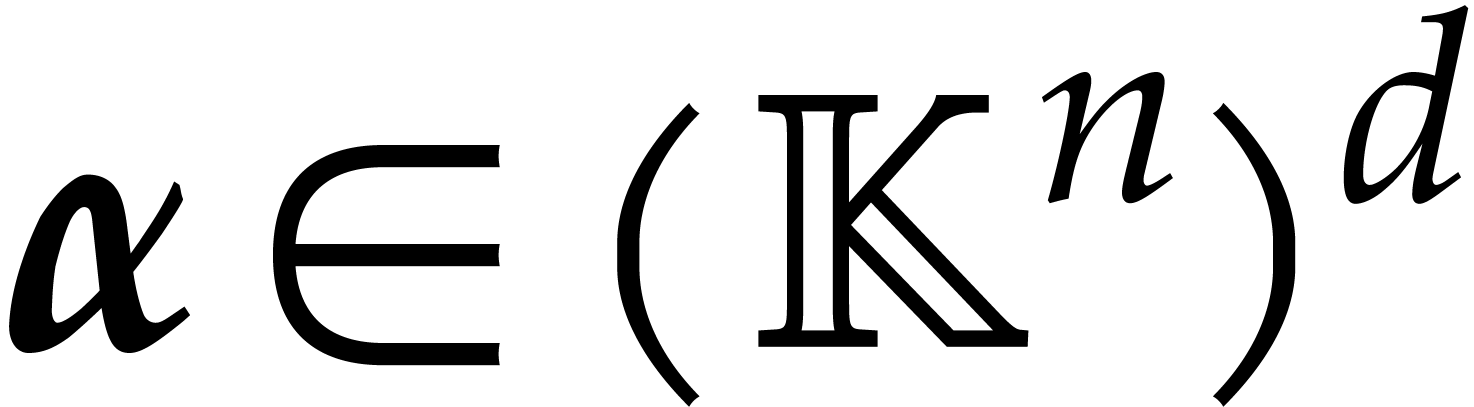 with
with  and its decomposition
and its decomposition 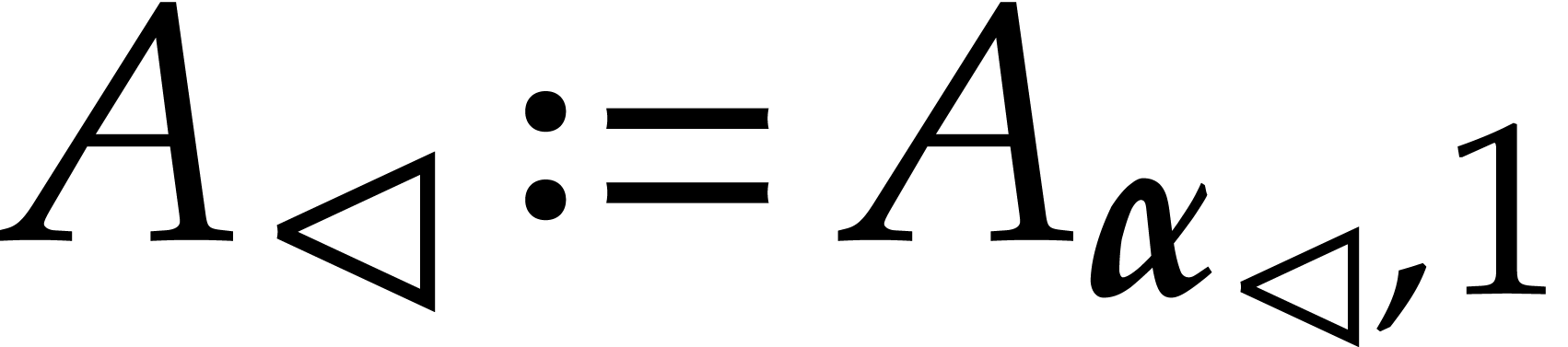 . Then
the first element
. Then
the first element 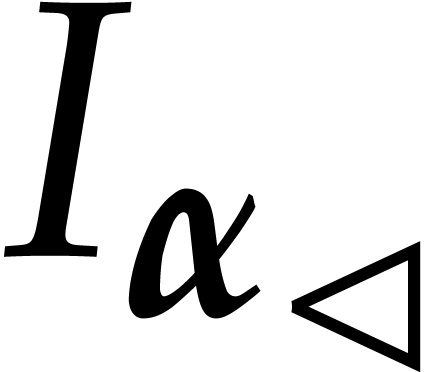 of the axial basis of
of the axial basis of 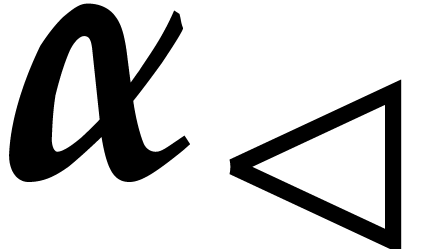 certainly vanishes at
certainly vanishes at 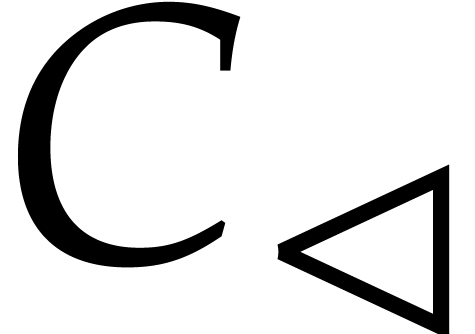 and we
wish to let it play the same role as
and we
wish to let it play the same role as 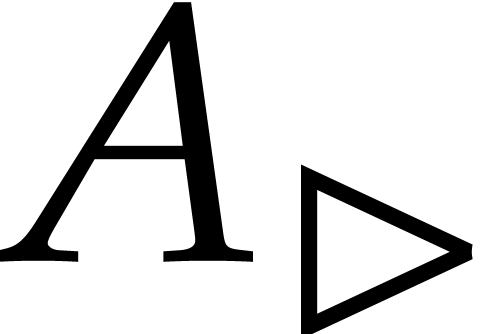 above. The
corresponding cofactor
above. The
corresponding cofactor  should satisfy
should satisfy  , so we may compute it through
interpolation from its evaluation
, so we may compute it through
interpolation from its evaluation 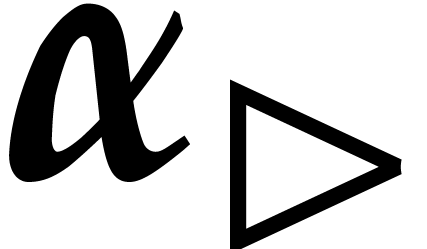 at
at 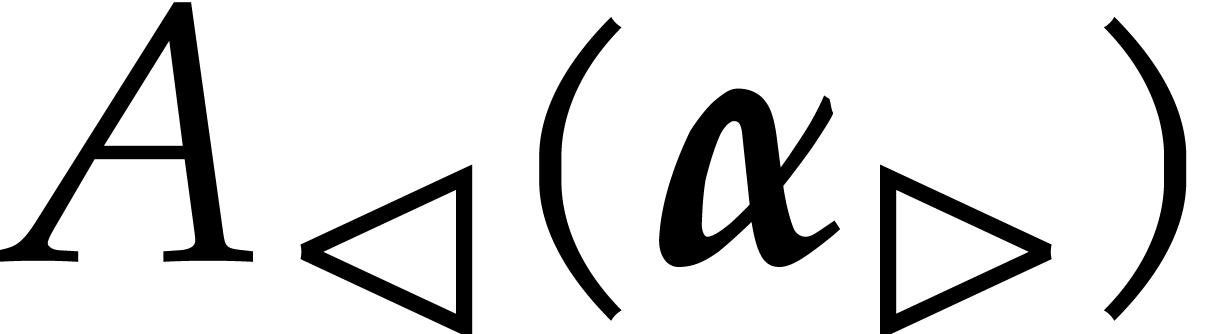 . However, this requires
. However, this requires 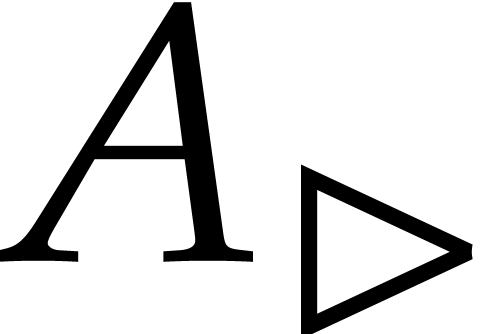 not to vanish at any of the entries of
not to vanish at any of the entries of 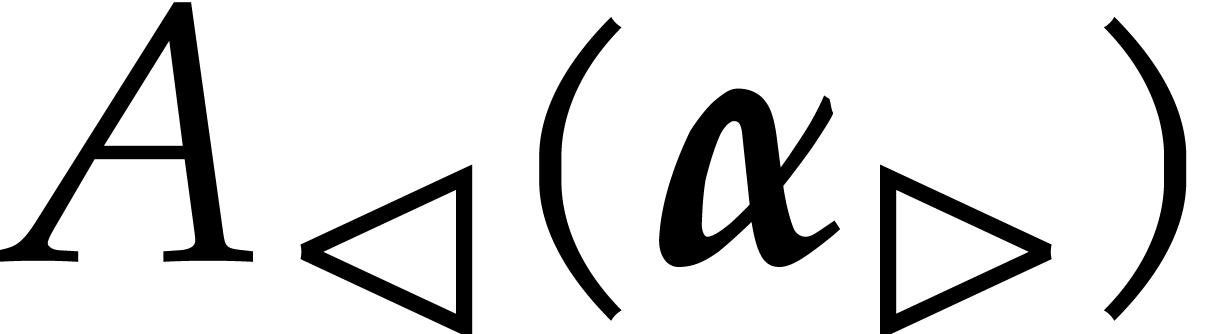 . Now the set of tuples of points
. Now the set of tuples of points 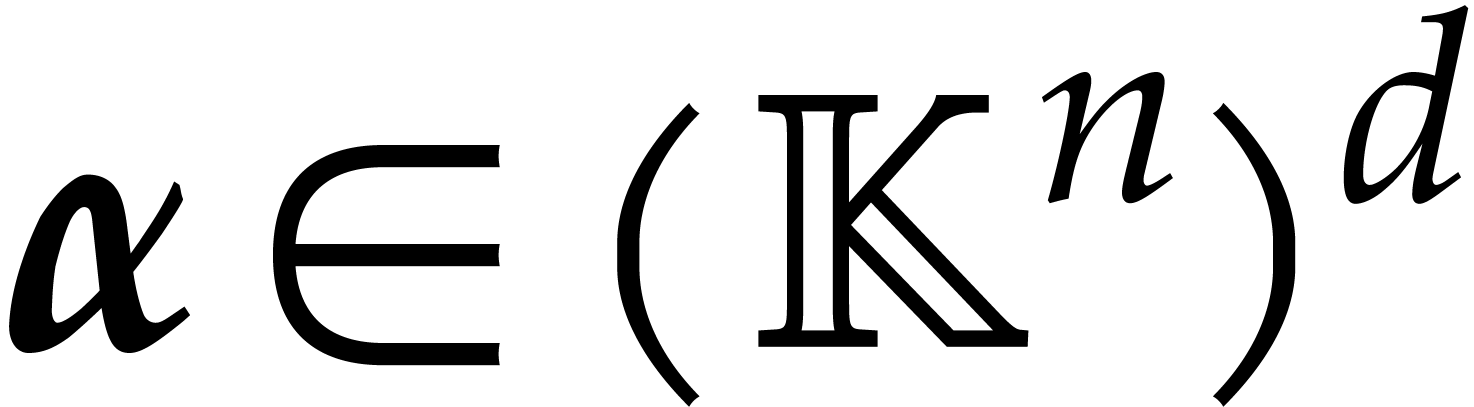 for which one of the entries of
for which one of the entries of 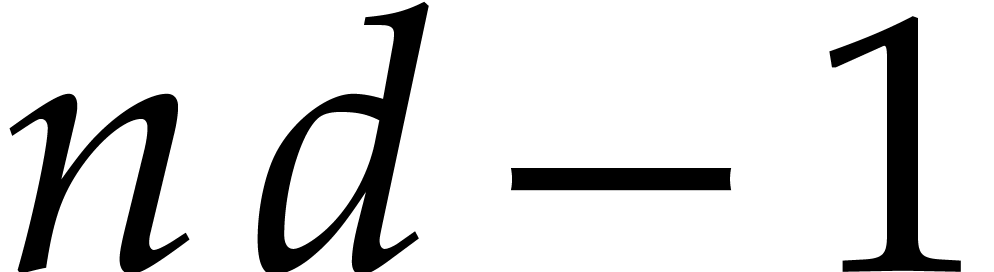 vanishes forms a Zariski closed subset of dimension
vanishes forms a Zariski closed subset of dimension 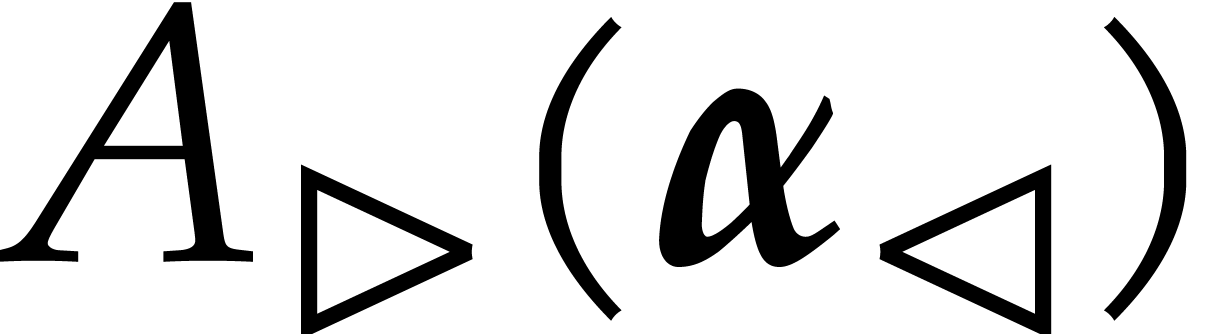 ; for a “generic” tuple of points,
both
; for a “generic” tuple of points,
both 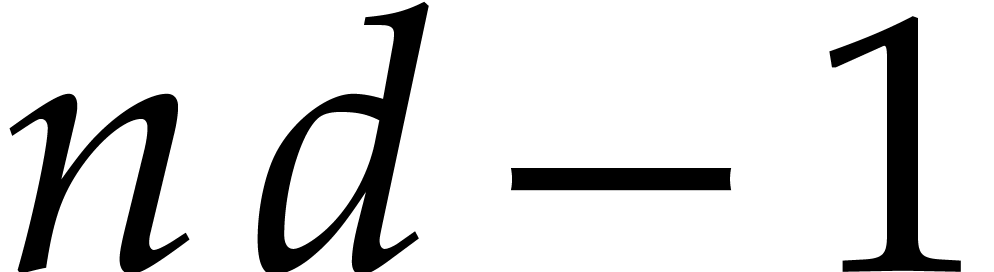 and
and 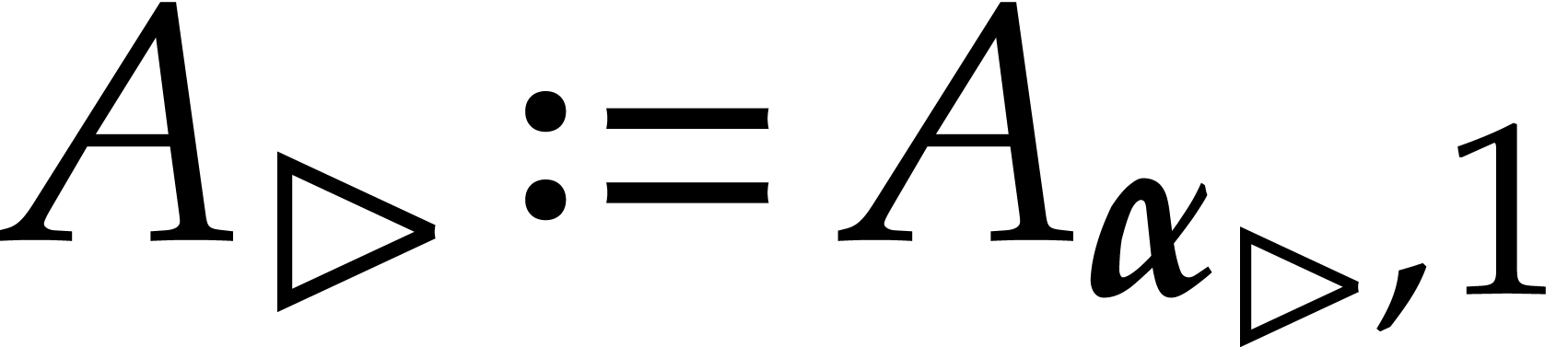 (where
(where  ) are therefore invertible. Given
) are therefore invertible. Given
 , this allows us to
reconstruct
, this allows us to
reconstruct 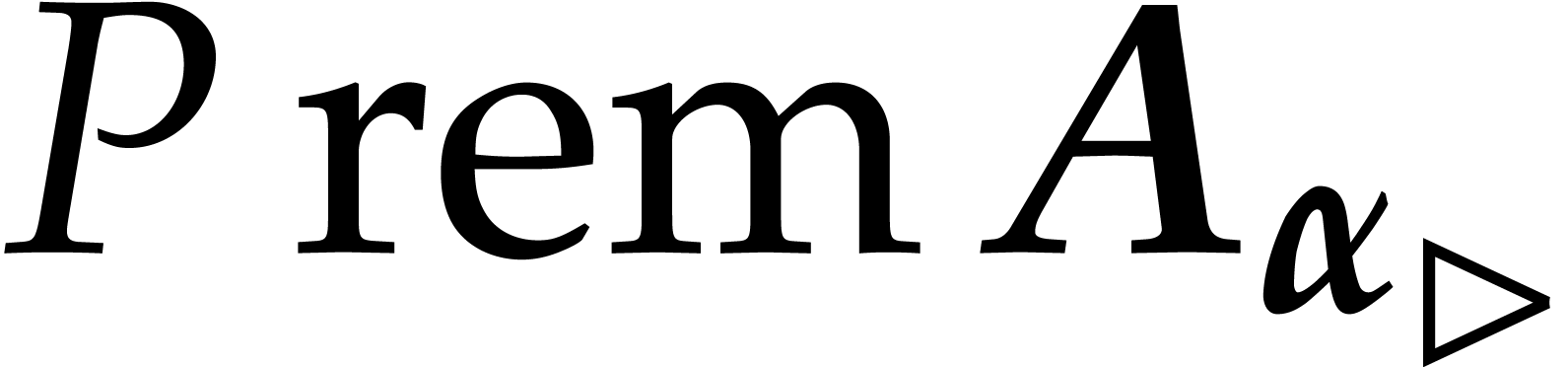 from
from 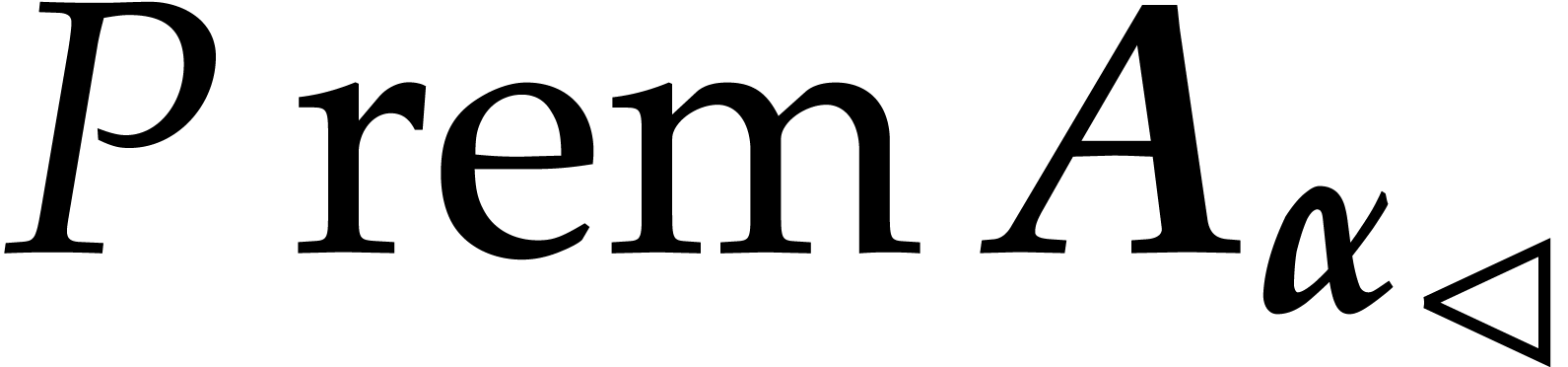 and
and
 using
using
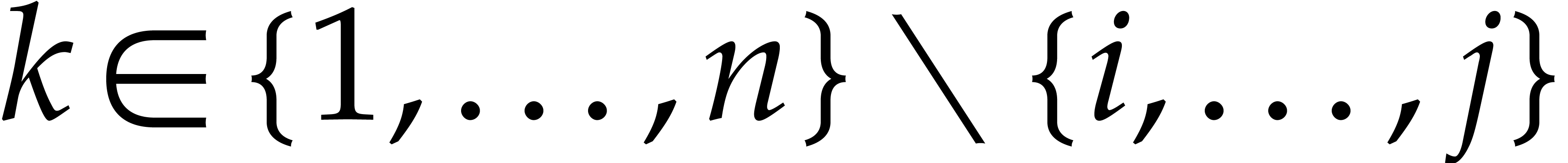
More generally, we define  to be
super-generic if it is hereditarily generic and, for all
to be
super-generic if it is hereditarily generic and, for all 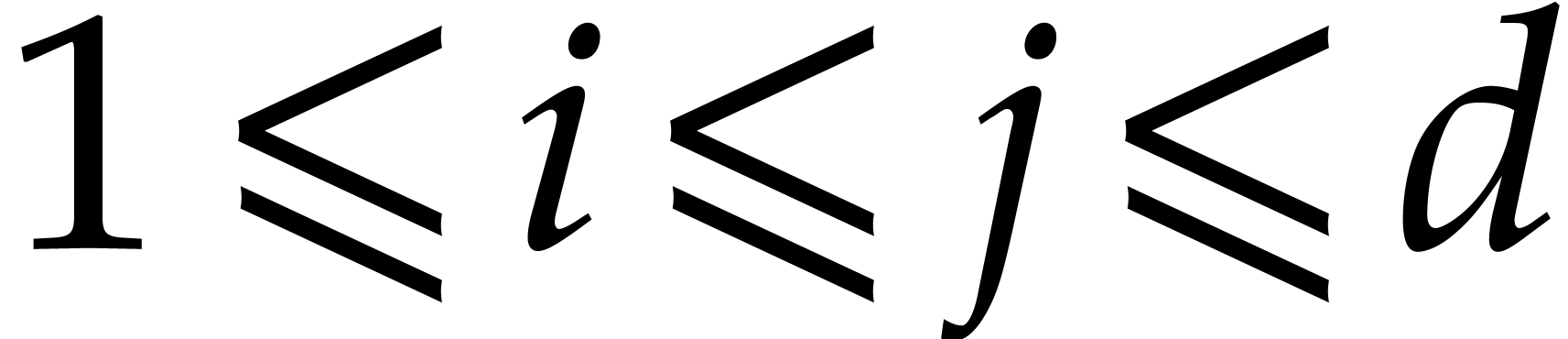 and
and 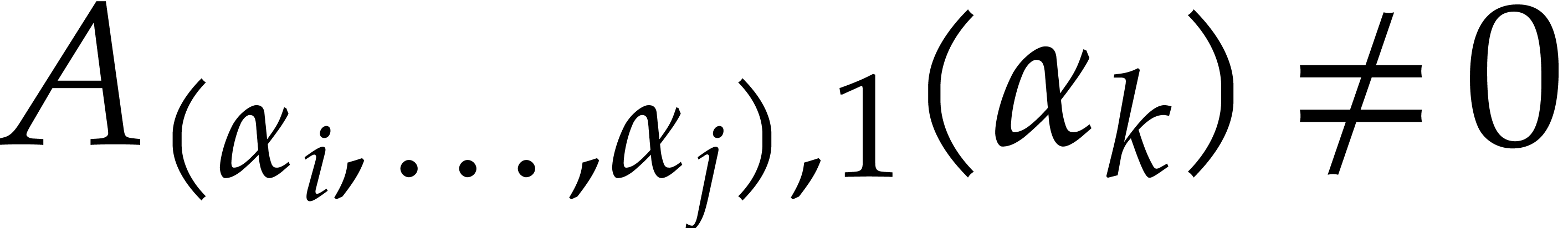 , we
have
, we
have  .
.
Let us now detail the interpolation algorithm that was summarized and explained above. Similarly to the case of multi-point evaluation, it relies on the construction of an interpolation tree, which contains the required cofactors. Contrary to before, the construction of this tree recursively involves interpolations (in order to reconstruct the cofactors from their evaluations).
Algorithm IpolTree(
Input: an evaluation tree
Output: an interpolation tree |
If
Let
Recursively apply the algorithm to the children
Let
Compute
Compute
Return the tree with root labeled by |
Algorithm Ipol(
Input:
Output: |
If
Let
Let
Let
Let
Return |
 and
and 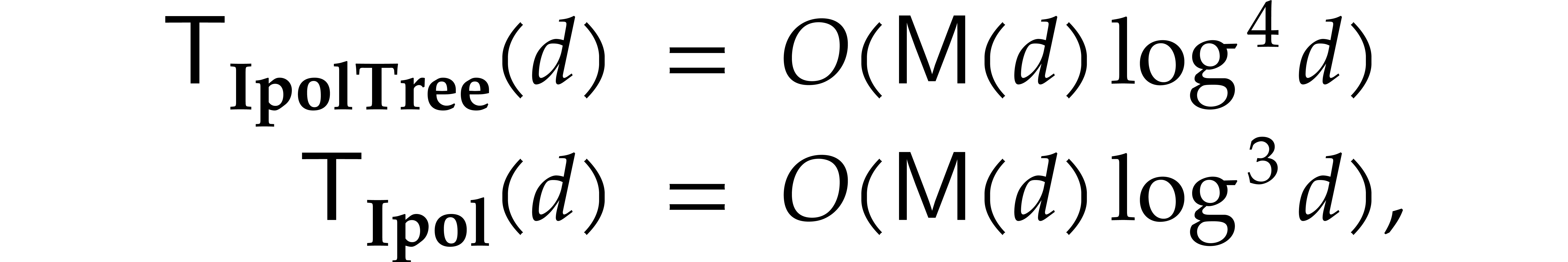 are correct. If
are correct. If  is super generic, then the
running times of
is super generic, then the
running times of  and
and 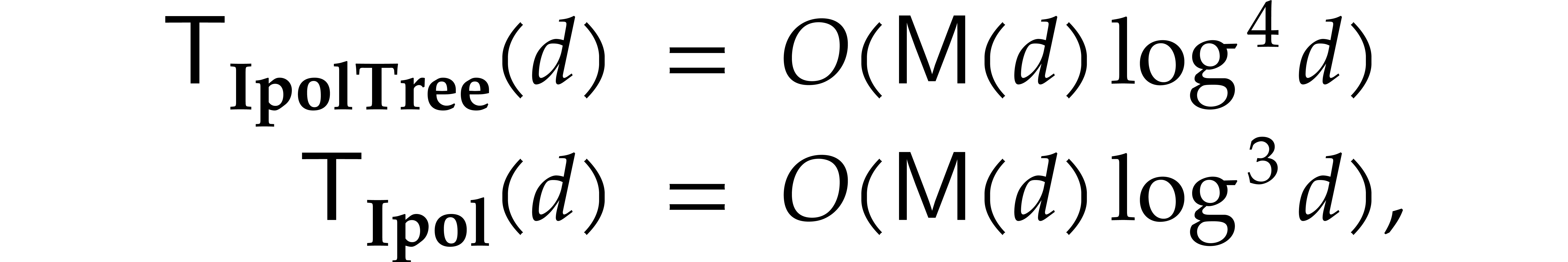 are respectively bounded by
are respectively bounded by
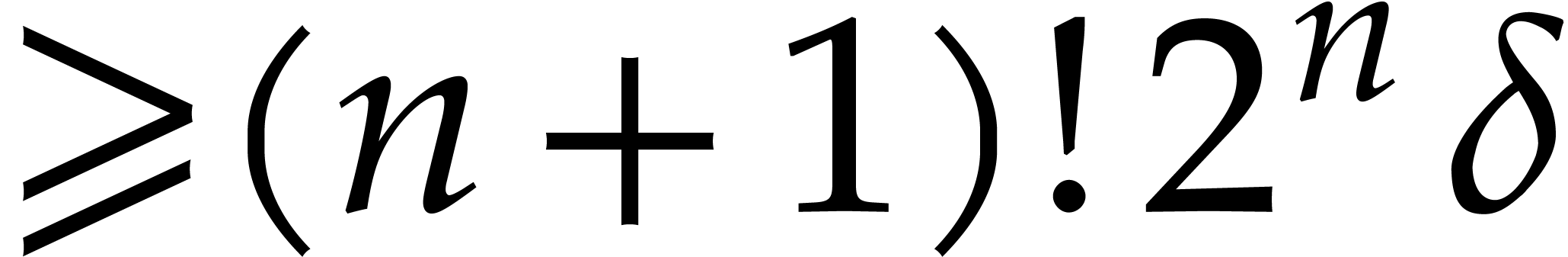
whenever an element of multiplicative order 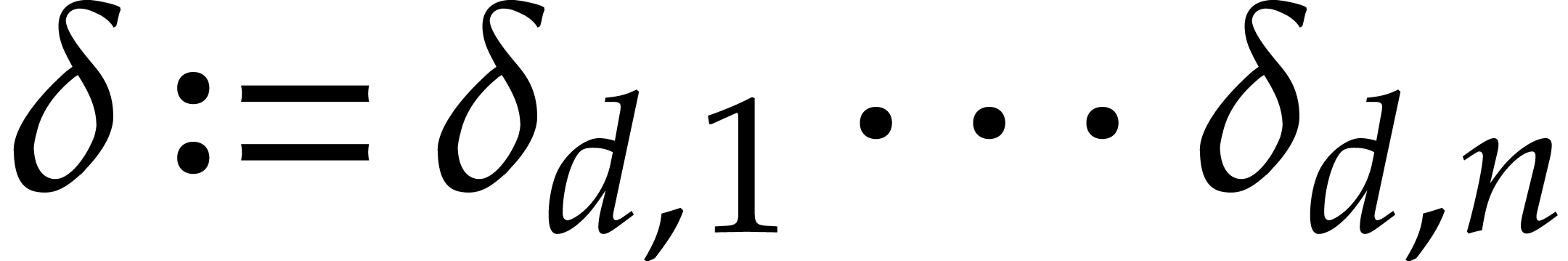 is given in
is given in  , where
, where 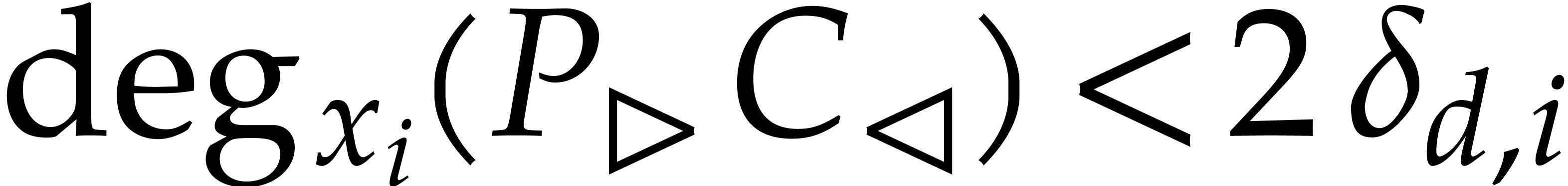 .
.
Proof. By induction on  , the algorithms
, the algorithms  and
and 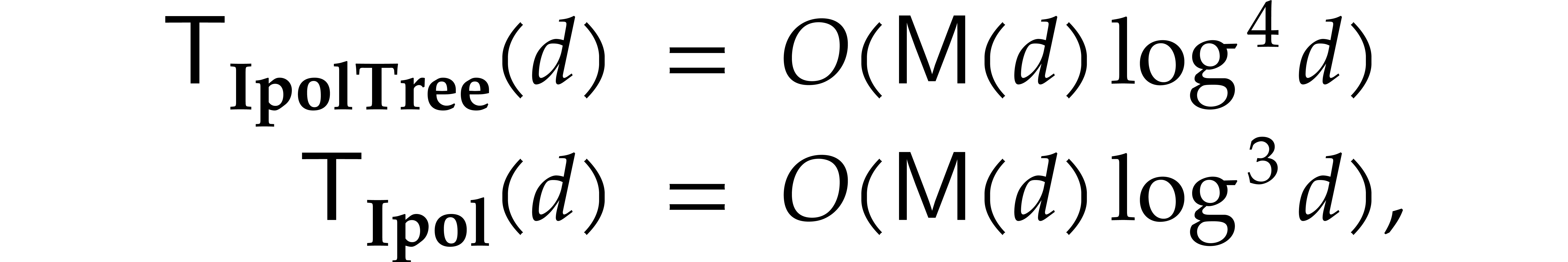 are clearly correct. Let us start with the complexity
bound for
are clearly correct. Let us start with the complexity
bound for 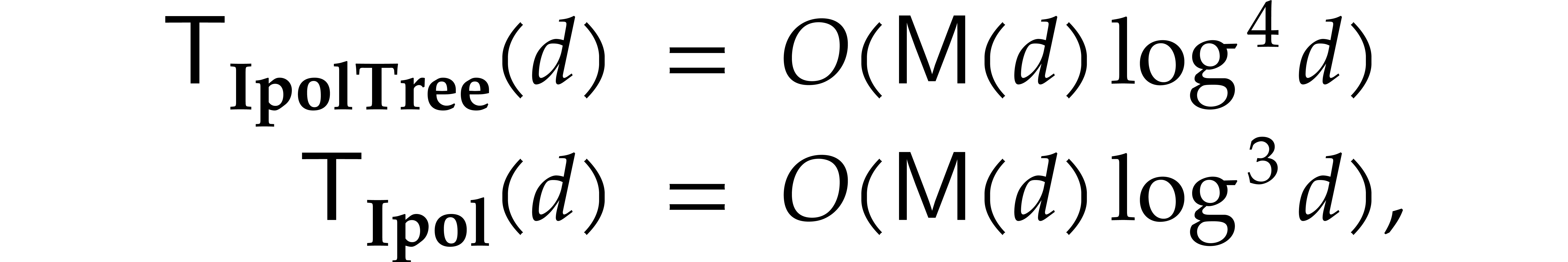 . We have
. We have 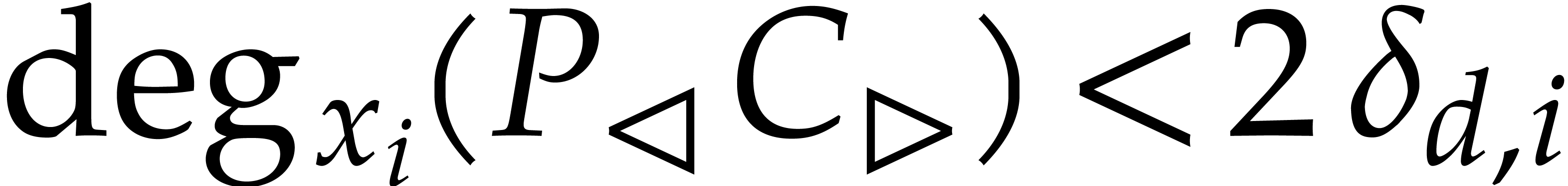 ,
, 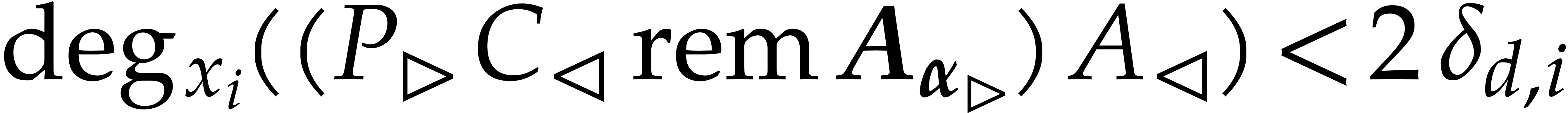 ,
,
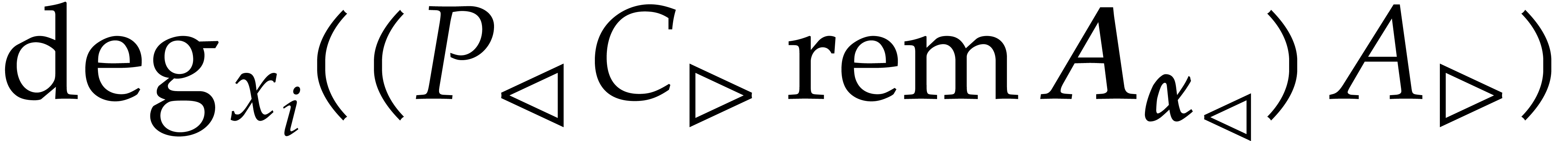 , and
, and 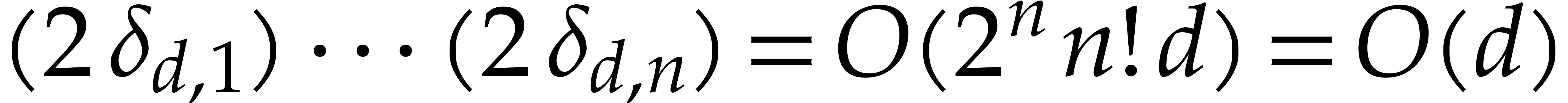 , for
, for  ,
where
,
where  . Theorem 6
therefore implies the existence of constants
. Theorem 6
therefore implies the existence of constants  and
and
 with
with
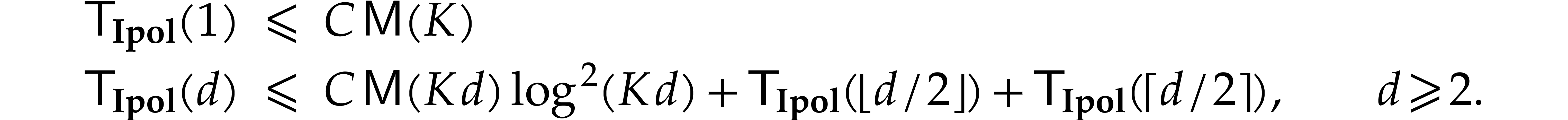
By unrolling the latter inequality in a similar way as in the proof of
Theorem 8 for powers of two, we obtain  , while using our assumption that
, while using our assumption that 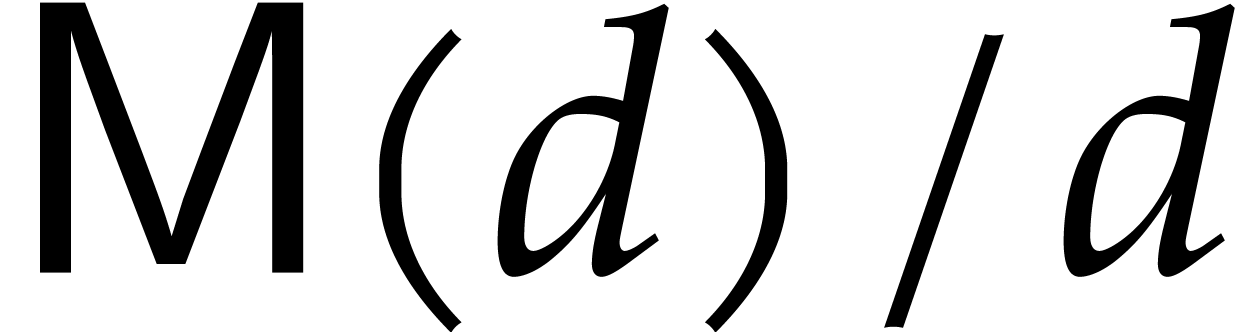 non-decreasing.
non-decreasing.
As to the construction of the interpolation tree, Theorem 6,
together with the bound for  of Theorem 8,
and
of Theorem 8,
and  imply the existence of other constants
imply the existence of other constants  and
and  with
with
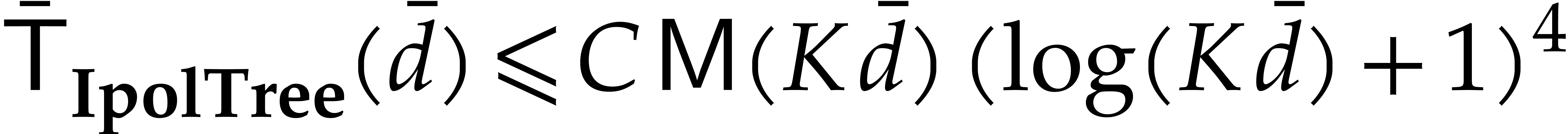
Unrolling the latter inequality yields 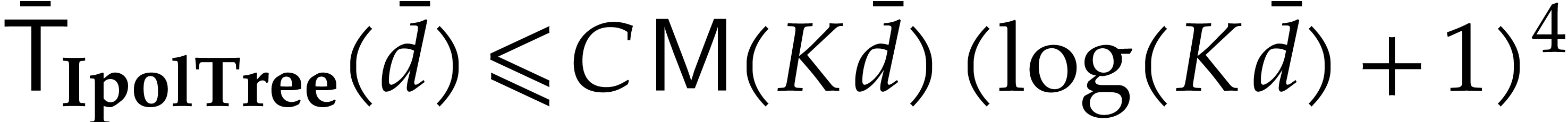 .
.
J. Abbott, A. Bigatti, M. Kreuzer, and L. Robbiano. Computing ideals of points. J. Symbolic Comput., 30(4):341–356, 2000.
S. Abelard, A. Couvreur, and G. Lecerf. Sub-quadratic time for Riemann–Roch spaces. The case of smooth divisors over nodal plane projective curves. Technical Report, HAL, 2020. https://hal.archives-ouvertes.fr/hal-02477371.
A. Borodin and R. T. Moenck. Fast modular transforms. J. Comput. System Sci., 8:366–386, 1974.
A. Bostan, C.-P. Jeannerod, and É. Schost. Solving structured linear systems with large displacement rank. Theor. Comput. Sci., 407(1):155–181, 2008.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, ISSAC '03, pages 37–44. New York, NY, USA, 2003. ACM.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Inform., 28:693–701, 1991.
M. F. I. Chowdhury, C. Jeannerod, V. Neiger, É. Schost, and G. Villard. Faster algorithms for multivariate interpolation with multiplicities and simultaneous polynomial approximations. IEEE Trans. Inf. Theory, 61(5):2370–2387, 2015.
J.-C. Faugère, P. Gaudry, L. Huot, and G. Renault. Sub-cubic change of ordering for Gröbner basis: a probabilistic approach. In Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, ISSAC '14, pages 170–177. New York, NY, USA, 2014. ACM.
C. M. Fiduccia. Polynomial evaluation via the division algorithm: the fast Fourier transform revisited. In Proceedings of the Fourth Annual ACM Symposium on Theory of Computing, STOC '72, pages 88–93. New York, NY, USA, 1972. ACM.
M. Gasca and T. Sauer. Polynomial interpolation in several variables. Adv. Comput. Math., 12(4):377, 2000.
D. Harvey and J. van der Hoeven. Faster polynomial multiplication over finite fields using cyclotomic coefficient rings. J. Complexity, 54:101404, 2019.
J. van der Hoeven. Faster relaxed multiplication. In Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, ISSAC '14, pages 405–412. New York, NY, USA, 2014. ACM.
J. van der Hoeven. Faster Chinese remaindering. Technical Report, CNRS & École polytechnique, 2016. http://hal.archives-ouvertes.fr/hal-01403810.
J. van der Hoeven. On the complexity of multivariate polynomial division. In I. S. Kotsireas and E. Martínez-Moro, editors, Applications of Computer Algebra. Kalamata, Greece, July 20–23, 2015, volume 198 of Springer Proceedings in Mathematics & Statistics, pages 447–458. Cham, 2017. Springer International Publishing.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial multiplication. J. Symbolic Comput., 50:227–254, 2013.
J. van der Hoeven and G. Lecerf. On the complexity exponent of polynomial system solving. Technical Report, HAL, 2018. http://hal.archives-ouvertes.fr/hal-01848572.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. Complexity, 56:101405, 2020.
J. van der Hoeven et al. GNU TeXmacs. http://www.texmacs.org, 1998.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J.Comput., 40(6):1767–1802, 2011.
D. Le Brigand and J.-J. Risler. Algorithme de Brill–Noether et codes de Goppa. Bulletin de la société mathématique de France, 116(2):231–253, 1988.
F. Le Gall. Powers of tensors and fast matrix multiplication. In K. Nabeshima, editor, Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, ISSAC '14, pages 296–303. New York, NY, USA, 2014. ACM.
M. G. Marinari, H. M. Möller, and T. Mora. Gröbner bases of ideals defined by functionals with an application to ideals of projective points. Appl. Algebra Eng. Commun. Comput., 4(2):103–145, 1993.
R. T. Moenck and A. Borodin. Fast modular transforms via division. In 13th Annual Symposium on Switching and Automata Theory, pages 90–96. USA, 1972. IEEE.
H. M. Möller and B. Buchberger. The construction of multivariate polynomials with preassigned zeros. In J. Calmet, editor, Computer Algebra. EUROCAM '82, European Computer Algebra Conference. Marseille, France 5–7 April 1982, volume 144 of Lect. Notes Comput. Sci., pages 24–31. Berlin, Heidelberg, 1982. Springer Berlin Heidelberg.
V. Neiger. Fast computation of shifted Popov forms of polynomial matrices via systems of modular polynomial equations. In Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '16, pages 365–372. New York, NY, USA, 2016. ACM.
M. Nüsken and M. Ziegler. Fast multipoint evaluation of bivariate polynomials. In S. Albers and T. Radzik, editors, Algorithms – ESA 2004. 12th Annual European Symposium, Bergen, Norway, September 14-17, 2004, volume 3221 of Lect. Notes Comput. Sci., pages 544–555. Springer Berlin Heidelberg, 2004.
D. S. Roche. What can (and can't) we do with sparse polynomials? In C. Arreche, editor, ISSAC '18: Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, pages 25–30. ACM Press, 2018.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Infor., 7:395–398, 1977.
A. Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
V. Shoup. New algorithms for finding irreducible polynomials over finite fields. Math. Comp., 54(189):435–447, 1990.