Amortized bivariate multi-point
evaluation  |
|
| May 11, 2021 |
|
 . This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
. This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
 . This article has
been written using GNU TeXmacs [10].
. This article has
been written using GNU TeXmacs [10].
The evaluation of a polynomial at several points is called the problem of multi-point evaluation. Sometimes, the set of evaluation points is fixed and several polynomials need to be evaluated at this set of points. Efficient algorithms for this kind of “amortized” multi-point evaluation were recently developed for the special case when the set of evaluation points is sufficiently generic. In this paper, we design a new algorithm for arbitrary sets of points, while restricting ourselves to bivariate polynomials. |
Let  be an effective field, so that we have
algorithms for the field operations. Given a polynomial
be an effective field, so that we have
algorithms for the field operations. Given a polynomial 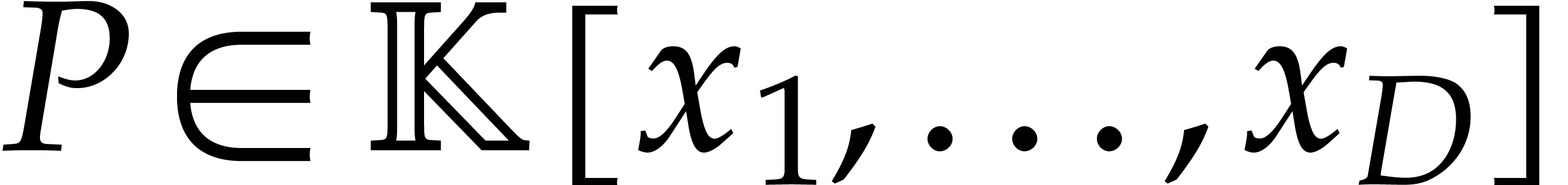 and a tuple
and a tuple 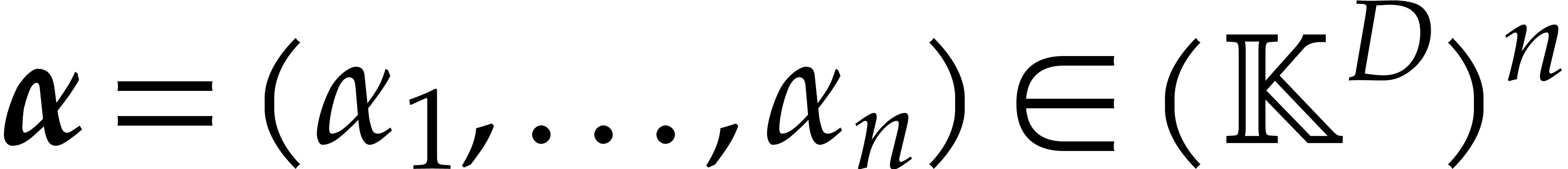 of points, the computation of
of points, the computation of  is called the problem of multi-point
evaluation. The converse problem is called interpolation
and takes a candidate support of
is called the problem of multi-point
evaluation. The converse problem is called interpolation
and takes a candidate support of 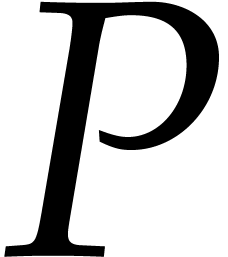 as input.
as input.
These problems naturally occur in several areas of applied algebra. When solving a polynomial system, multi-point evaluation can for instance be used to check whether all points in a given set are indeed solutions of the system. In [14], we have shown that fast algorithms for multi-point evaluation actually lead to efficient algorithms for polynomial system solving. The more specific problem of bivariate multi-point evaluation appears for example in the computation of generator matrices of algebraic geometry error correcting codes [18].
The general problem of multivariate multi-point evaluation is
notoriously hard. If 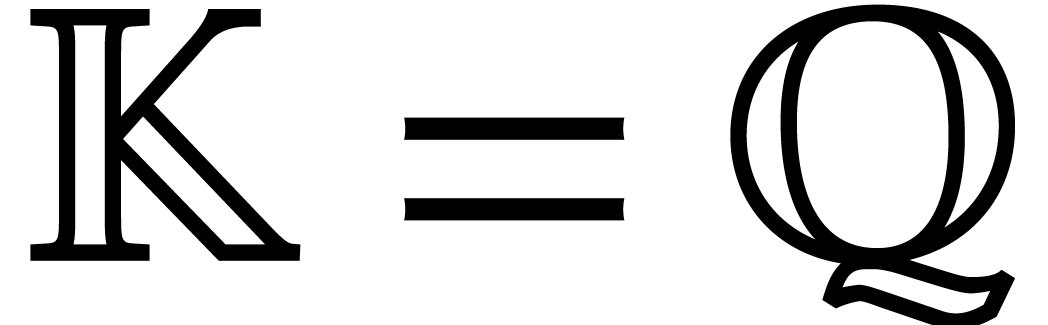 or
or  is a field of finite characteristic, then theoretical algorithms of
Kedlaya and Umans [17] achieve a complexity exponent
is a field of finite characteristic, then theoretical algorithms of
Kedlaya and Umans [17] achieve a complexity exponent  , where
, where 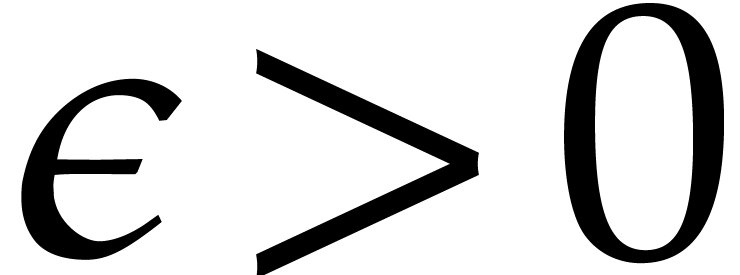 represents a constant that can be taken arbitrarily close to zero.
Unfortunately, to our best knowledge, these algorithms do not seem
suitable for practical purposes [13, Conclusion].
represents a constant that can be taken arbitrarily close to zero.
Unfortunately, to our best knowledge, these algorithms do not seem
suitable for practical purposes [13, Conclusion].
The best known bound for 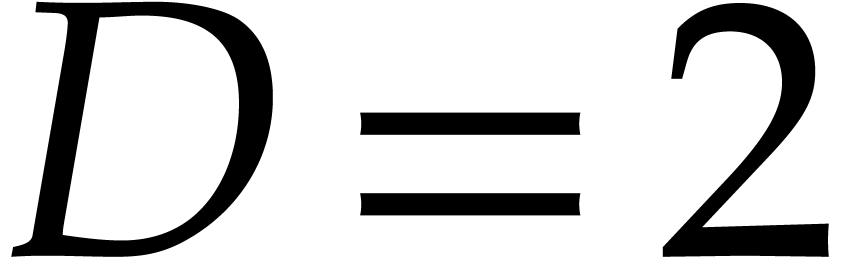 over general fields is
due to Nüsken and Ziegler [22]: the evaluation of
over general fields is
due to Nüsken and Ziegler [22]: the evaluation of 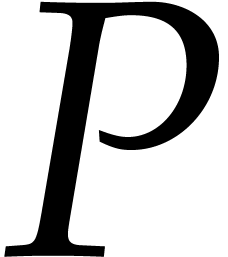 at
at 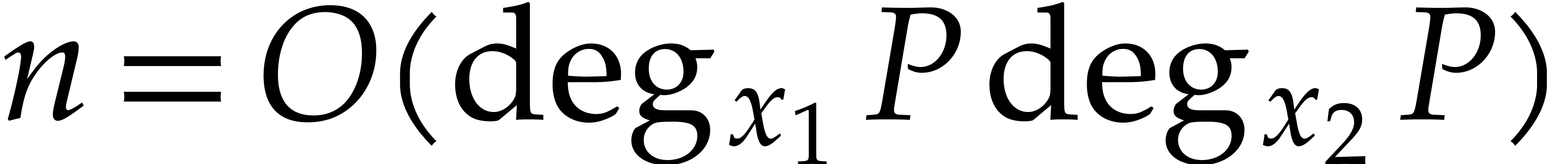 points can be done with
points can be done with
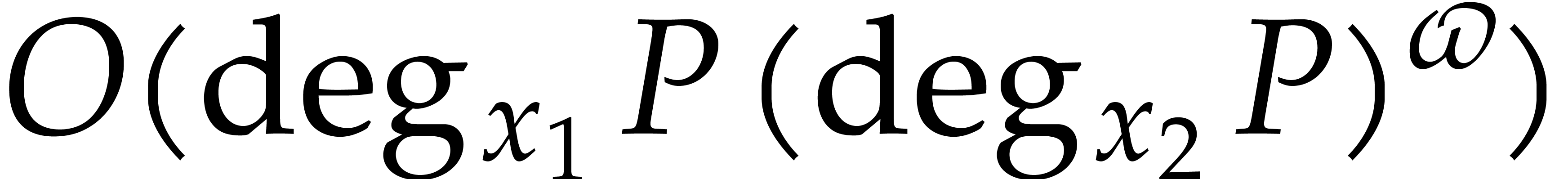 operations in
operations in  .
This bound is based on the Paterson–Stockmeyer technique for
modular composition [23]. Here, the constant
.
This bound is based on the Paterson–Stockmeyer technique for
modular composition [23]. Here, the constant 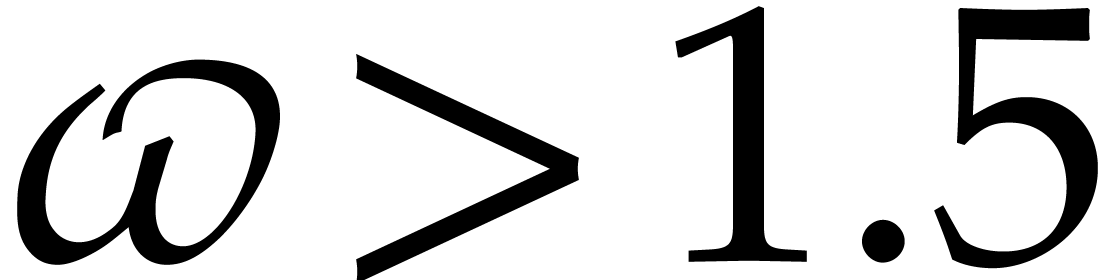 is a real value such that the product of a
is a real value such that the product of a 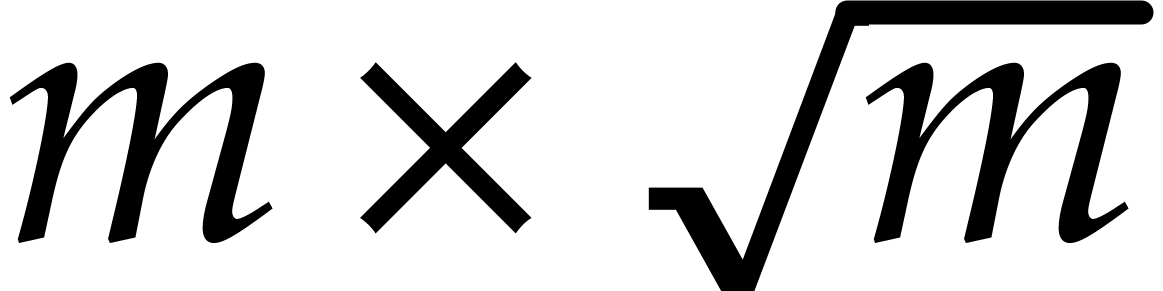 matrix by a
matrix by a  matrix takes
matrix takes 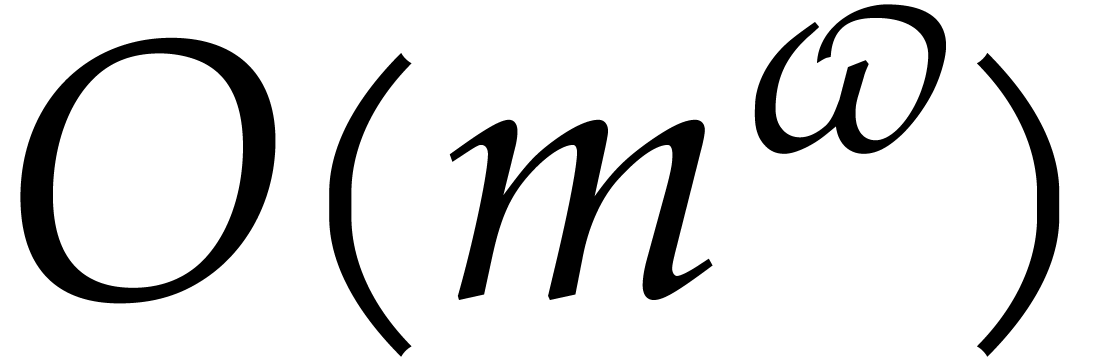 operations; one may take
operations; one may take 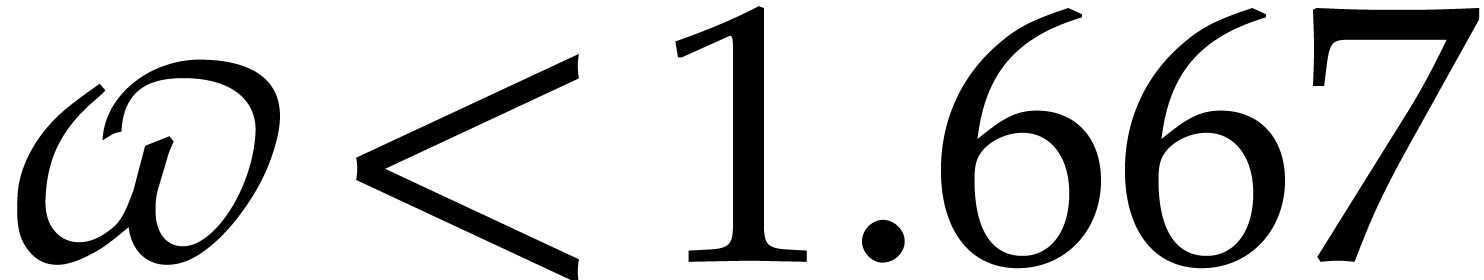 ;
see [16, Theorem 10.1]. We further cite [15]
for an efficient algorithm in the case of special sets of points
;
see [16, Theorem 10.1]. We further cite [15]
for an efficient algorithm in the case of special sets of points  .
.
Last year, new softly linear algorithms have been proposed for
multi-point evaluation and interpolation in the case when  is a fixed generic tuple of points [12, 20]. These algorithms are amortized in the sense that
potentially expensive precomputations as a function of
is a fixed generic tuple of points [12, 20]. These algorithms are amortized in the sense that
potentially expensive precomputations as a function of  are allowed. When the dimension
are allowed. When the dimension 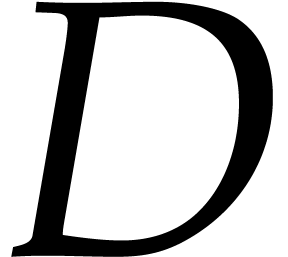 is arbitrary but
fixed, the algorithms from [12] take softly linear time:
they generalize the classical univariate “divide and
conquer” approach, as presented for instance in [6,
chapter 10]. The results in [20] are restricted to the case
is arbitrary but
fixed, the algorithms from [12] take softly linear time:
they generalize the classical univariate “divide and
conquer” approach, as presented for instance in [6,
chapter 10]. The results in [20] are restricted to the case
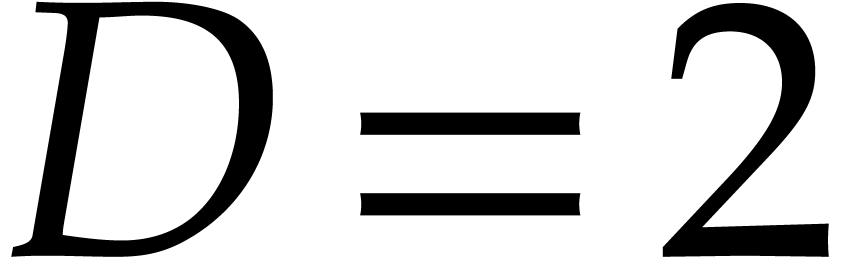 . They take into account the
partial degrees of
. They take into account the
partial degrees of 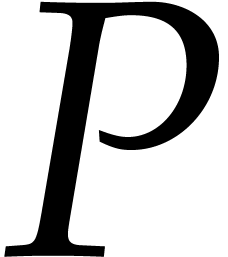 and are based on changes of
polynomial bases that are similar to the ones of [11,
section 6.2].
and are based on changes of
polynomial bases that are similar to the ones of [11,
section 6.2].
In the present paper, we turn our attention to arbitrary (i.e.
possibly non-generic) tuples of evaluation points  , while restricting ourselves to the bivariate case
, while restricting ourselves to the bivariate case
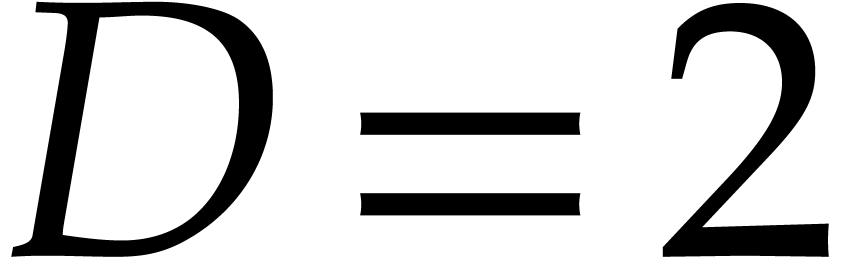 and
and 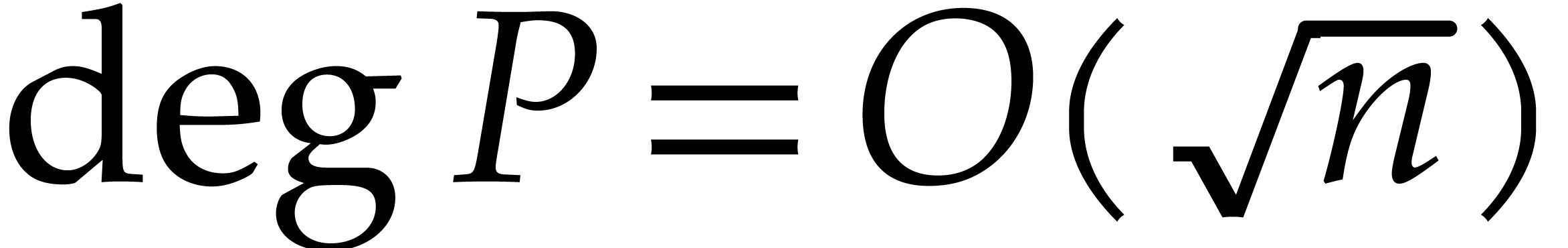 .
Combining ideas from [12] and [20], we present
a new softly linear algorithm for amortized multi-point evaluation. For
the sake of simplicity, we have not optimized all constant factors
involved in the cost analysis of our new algorithm, so our complexity
bound is mostly of theoretical interest for the moment. The opposite
task of interpolation is more subtle: since interpolants of total degree
.
Combining ideas from [12] and [20], we present
a new softly linear algorithm for amortized multi-point evaluation. For
the sake of simplicity, we have not optimized all constant factors
involved in the cost analysis of our new algorithm, so our complexity
bound is mostly of theoretical interest for the moment. The opposite
task of interpolation is more subtle: since interpolants of total degree
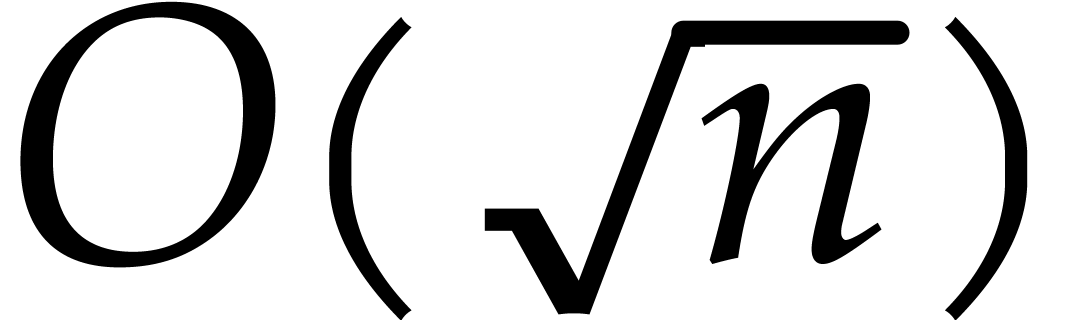 do not necessarily exist, the very problem needs
to be stated with additional care. For this reason, we do not
investigate interpolation in this paper.
do not necessarily exist, the very problem needs
to be stated with additional care. For this reason, we do not
investigate interpolation in this paper.
Our bivariate multi-point evaluation makes use of polynomial arithmetic with respect to weighted graded monomial orderings. This section is devoted to the costs of products and divisions in this context.
For complexity analyses, we will only consider algebraic complexity
models like computation trees [3], for which elements in
 are freely at our disposal. The time complexity
simply measures the number of arithmetic operations and zero-tests in
are freely at our disposal. The time complexity
simply measures the number of arithmetic operations and zero-tests in
 .
.
We denote by 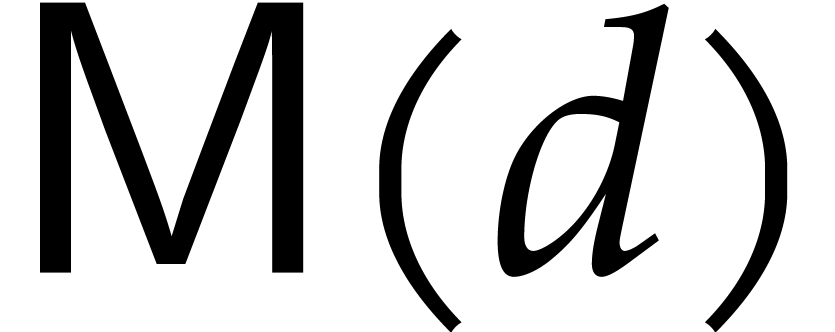 the time that is needed to compute
a product
the time that is needed to compute
a product  of two polynomials
of two polynomials 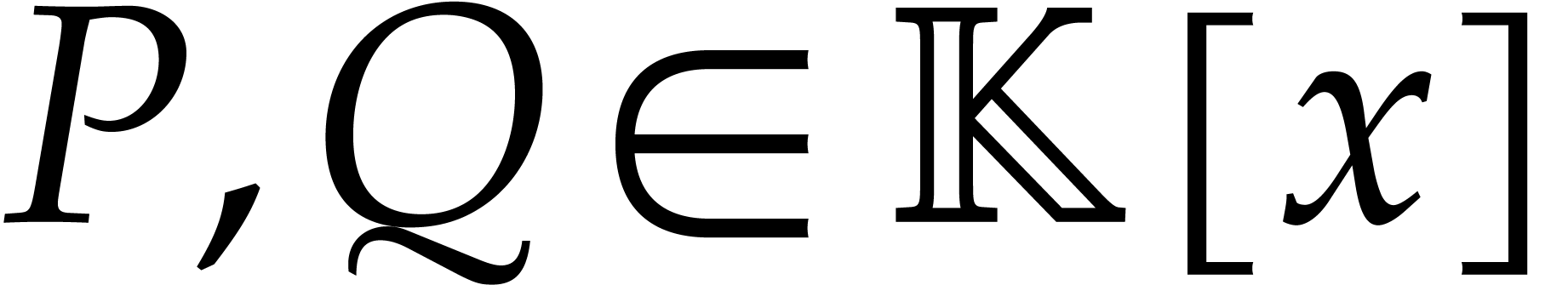 of degree
of degree 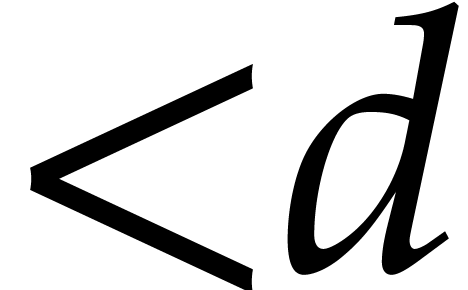 . We make the usual
assumptions that
. We make the usual
assumptions that 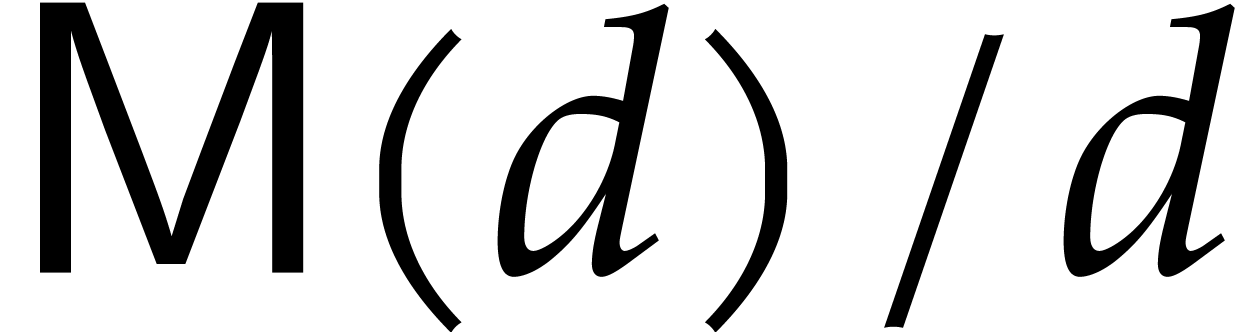 is non-decreasing as a function
of
is non-decreasing as a function
of  . Using a variant of the
Schönhage–Strassen algorithm [4], it is well
known that we may take
. Using a variant of the
Schönhage–Strassen algorithm [4], it is well
known that we may take 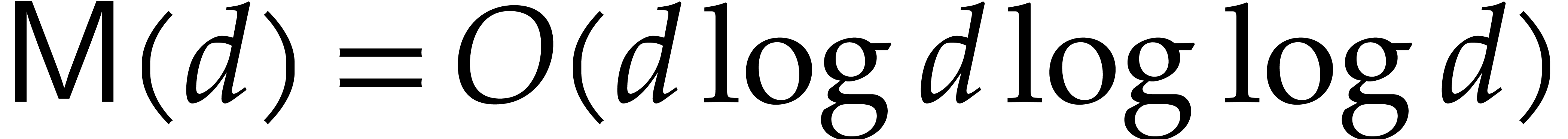 . If
we restrict our attention to fields
. If
we restrict our attention to fields  of positive
characteristic, then we may even take
of positive
characteristic, then we may even take 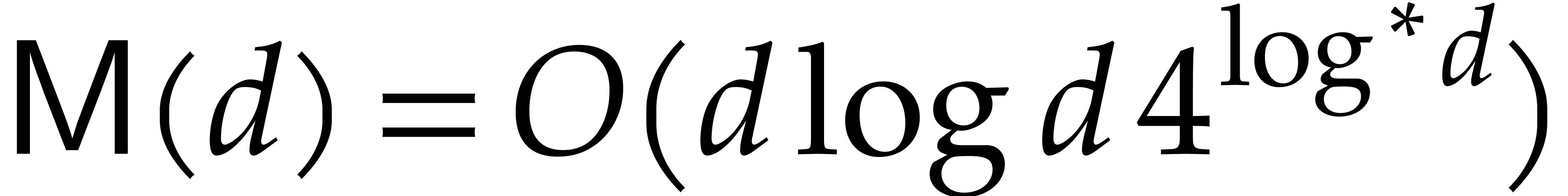 [7].
[7].
General monomial orderings, that are suitable for Gröbner basis computations, have been classified in [24]. For the purpose of this paper, we focus on the following specific family of bivariate monomial orderings.
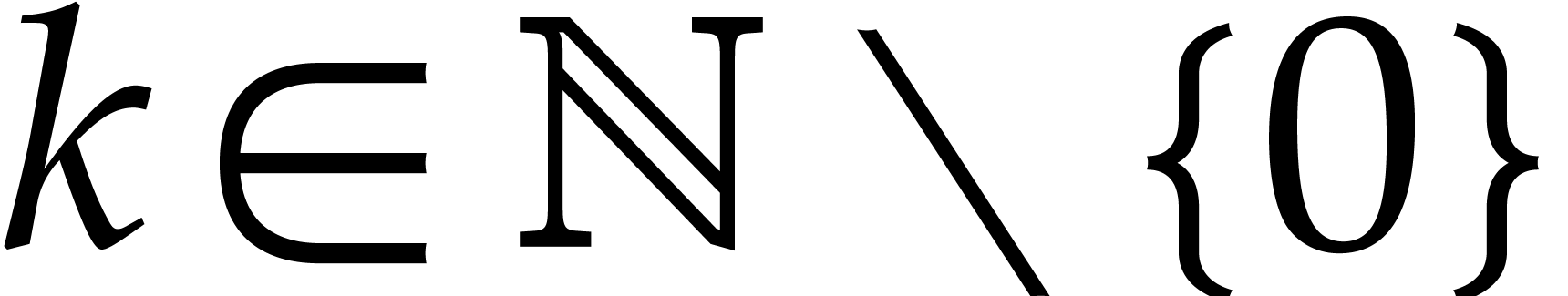 . We define
the
. We define
the 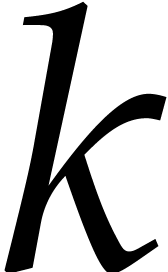 -degree
of a monomial
-degree
of a monomial 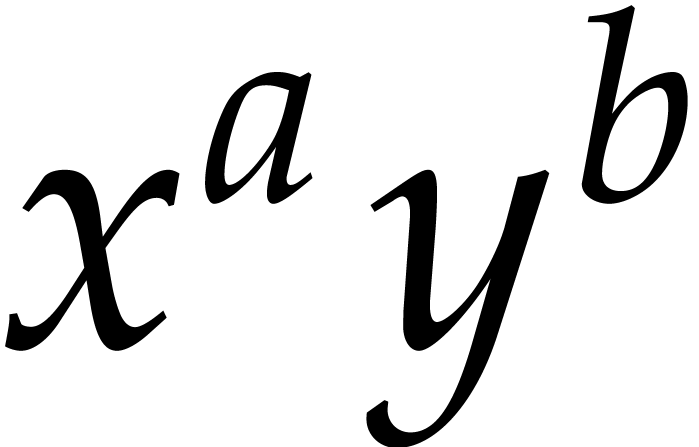 with
with 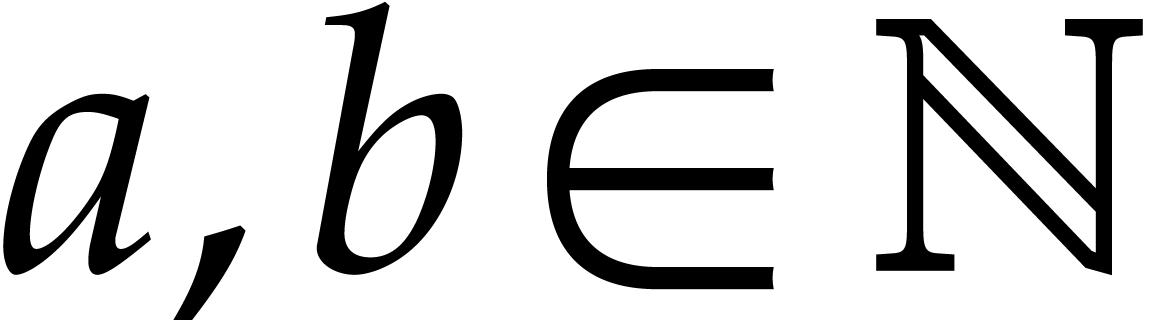 by
by
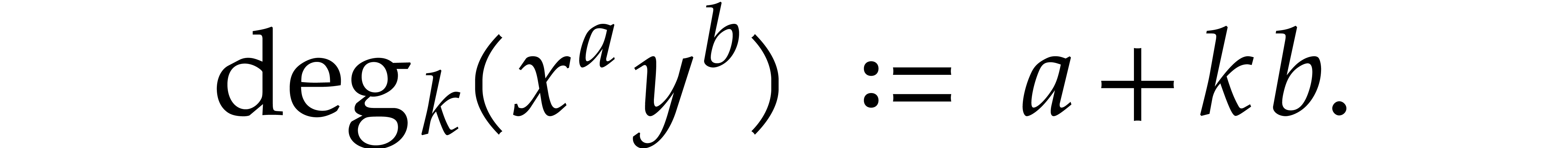
We define the 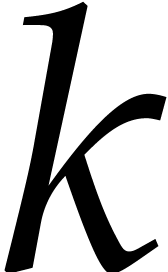 -ordering
to be the monomial ordering
-ordering
to be the monomial ordering  such that
such that
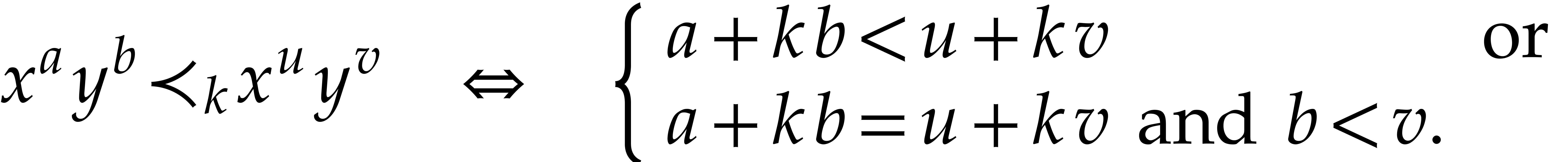
Let us mention that the idea of using such kinds of families of monomial orderings in the design of fast algorithms for bivariate polynomials previously appeared in [11].
Consider the product  of two non-zero bivariate
polynomials
of two non-zero bivariate
polynomials  and the obvious bound
and the obvious bound
for the number of terms of  .
Then it is well known that Kronecker substitution allows for the
computation of the product
.
Then it is well known that Kronecker substitution allows for the
computation of the product  using
using 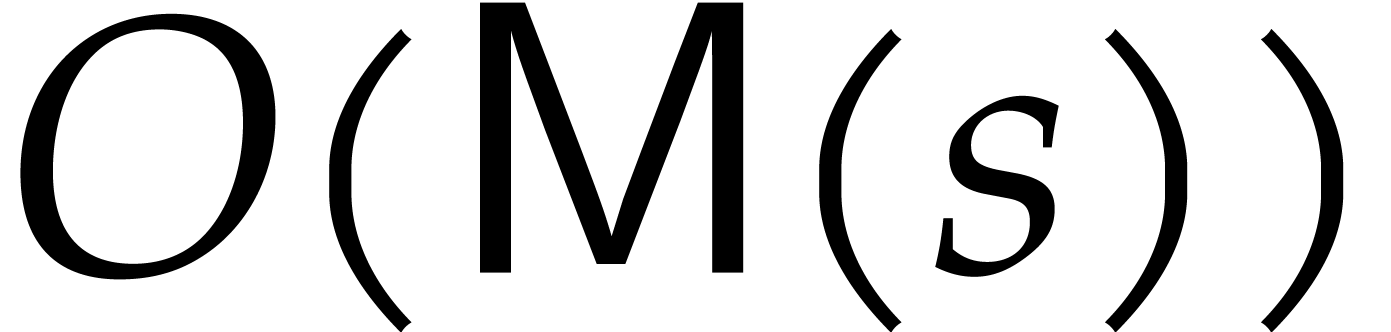 operations in
operations in  ;
see [6, Corollary 8.27], for instance.
;
see [6, Corollary 8.27], for instance.
Writing 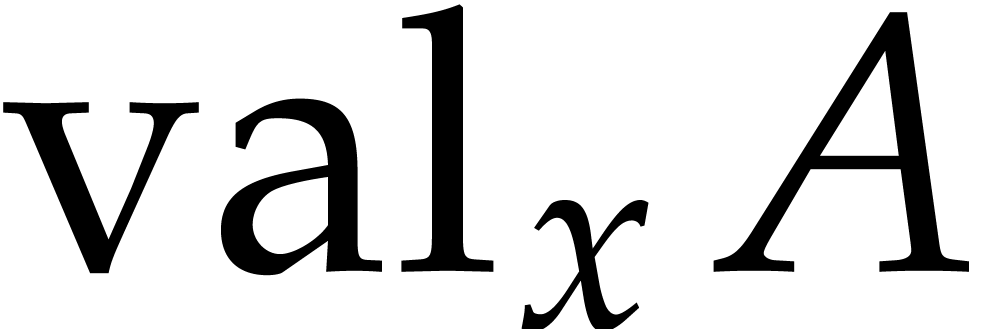 for the valuation of
for the valuation of  in
in  , the number of non-zero
terms of
, the number of non-zero
terms of  is more accurately bounded by
is more accurately bounded by
Via the appropriate multiplications and divisions by powers of  , we observe that
, we observe that  can be computed using
can be computed using 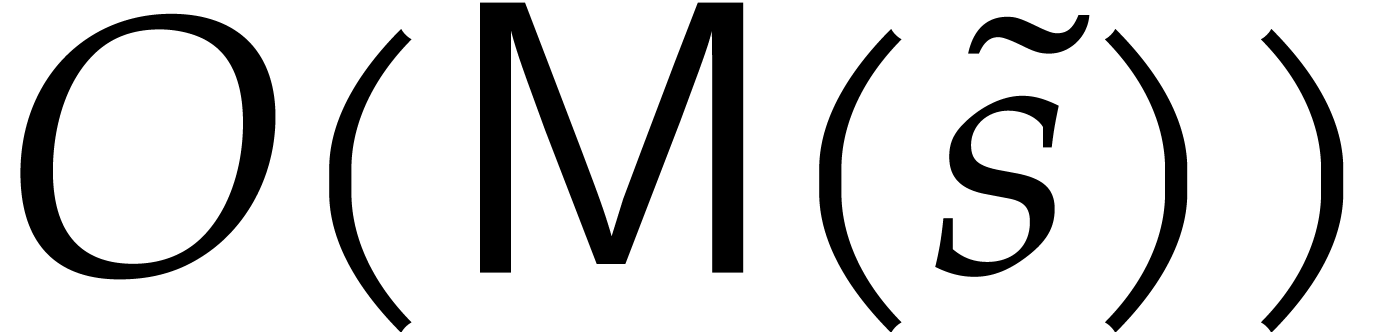 operations in
operations in  .
.
Let us next show that a similar bound holds for slices of polynomials
that are dense with respect to the 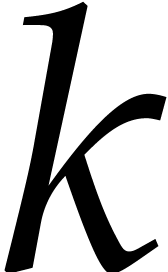 -ordering.
More precisely, let
-ordering.
More precisely, let 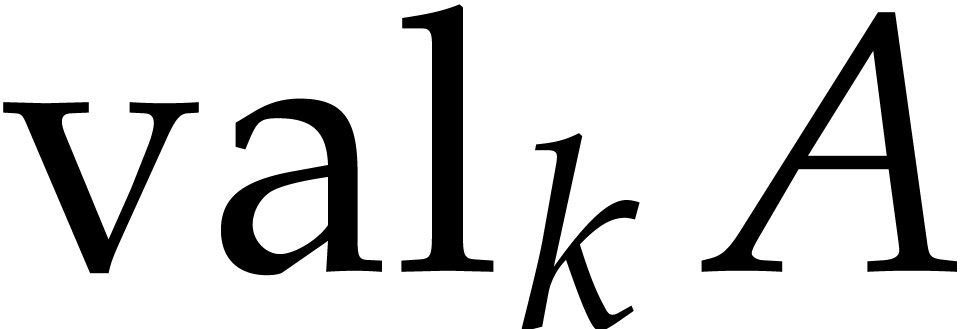 denote the minimum of
denote the minimum of 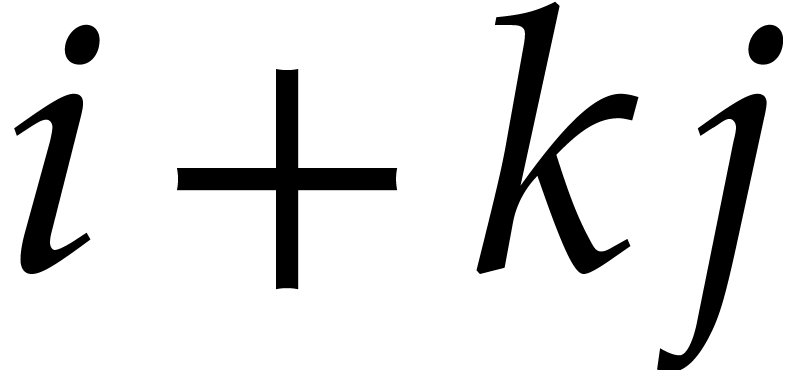 over the monomials
over the monomials 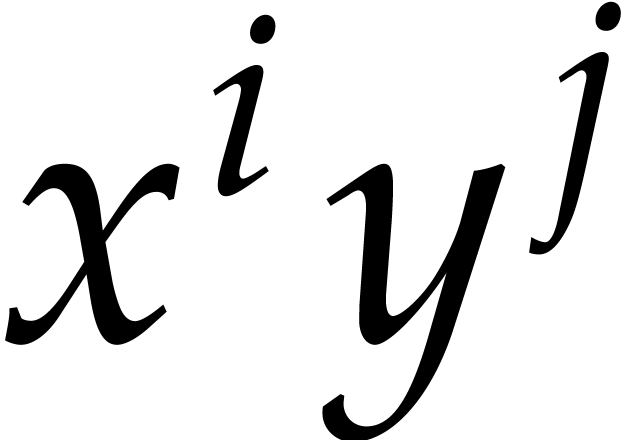 occurring
in
occurring
in  . By convention we set
. By convention we set
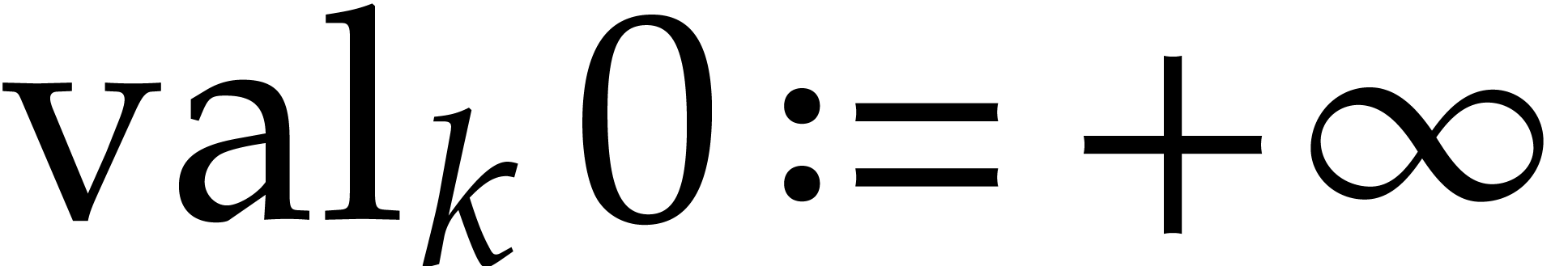 .
.
Proof. From the monomial identity
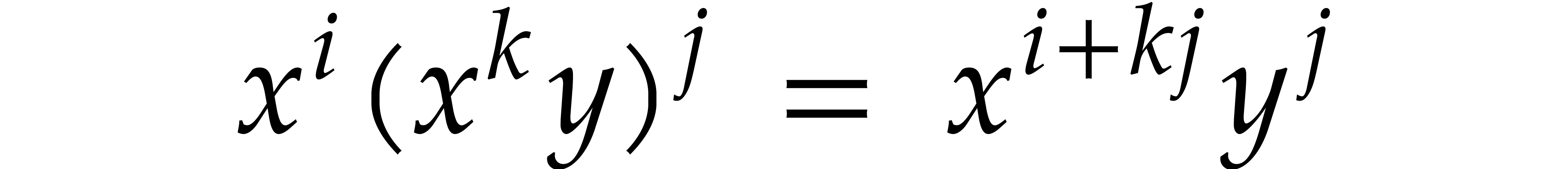
we observe that the monomials of 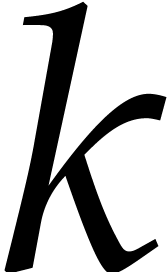 -degree
-degree
 are in one-to-one correspondence with the
monomials of degree
are in one-to-one correspondence with the
monomials of degree  in
in  and degree in
and degree in 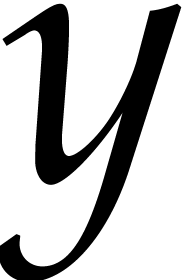 in
in 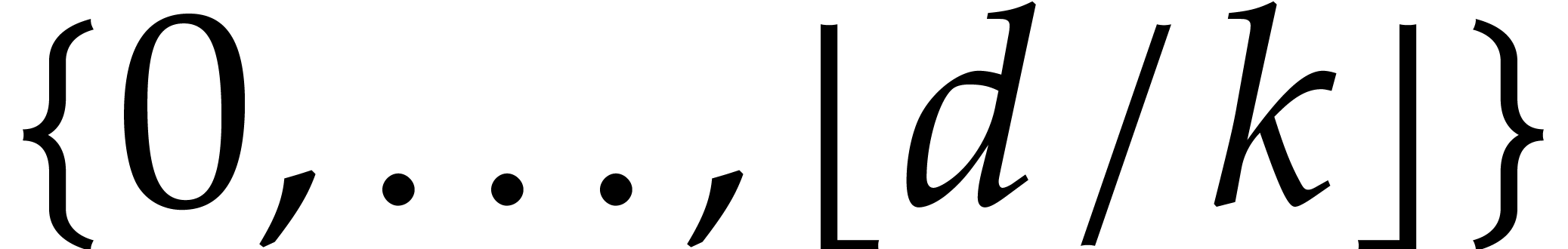 .
It also follows that the number of terms of a non-zero polynomial
.
It also follows that the number of terms of a non-zero polynomial  is bounded by
is bounded by
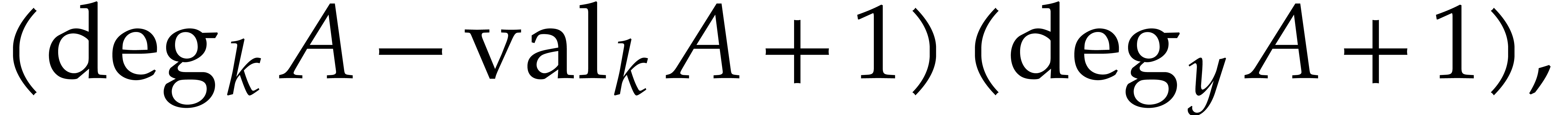
and that
In addition, the number of non-zero terms in the product  is bounded by
is bounded by 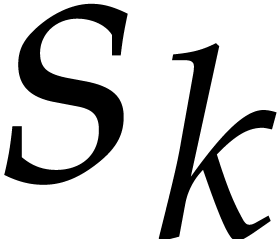 .
So it suffices to compute
.
So it suffices to compute  via the
formula
via the
formula
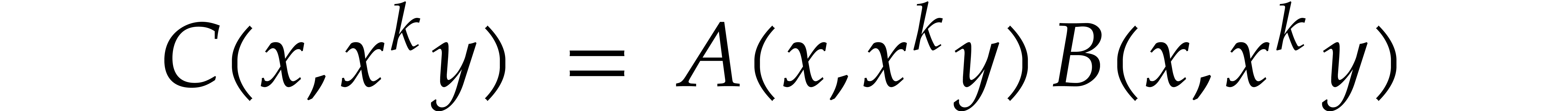
in order to obtain the claimed complexity bound.
Let 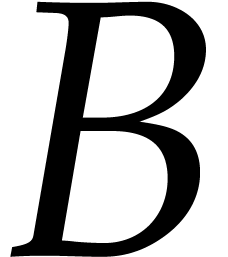 be a polynomial in
be a polynomial in 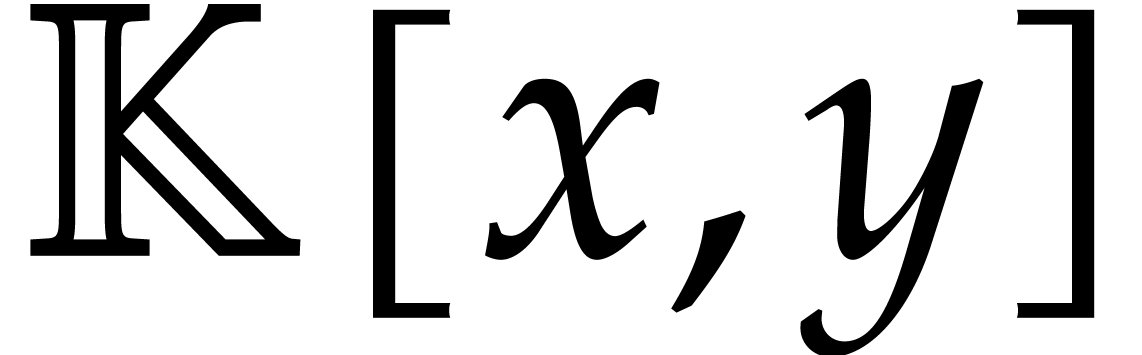 of
of 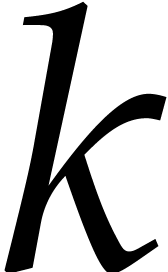 -degree
-degree  and of leading monomial written
and of leading monomial written 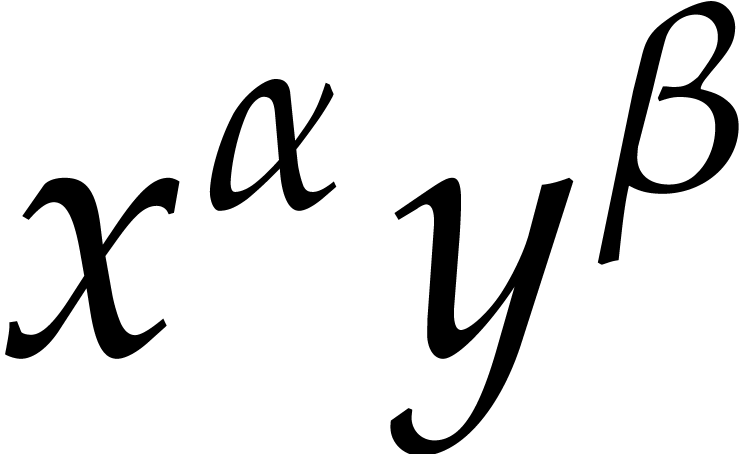 .
Without loss of generality we may assume that the coefficient of this
monomial is
.
Without loss of generality we may assume that the coefficient of this
monomial is 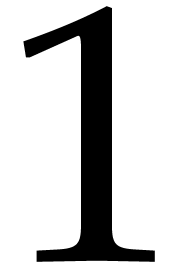 . We examine the
cost of the division of
. We examine the
cost of the division of  of
of 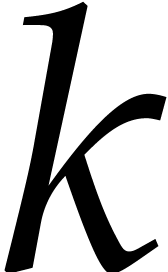 -degree
-degree  by
by 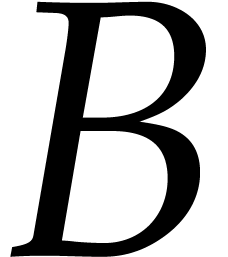 with respect to
with respect to  :
:
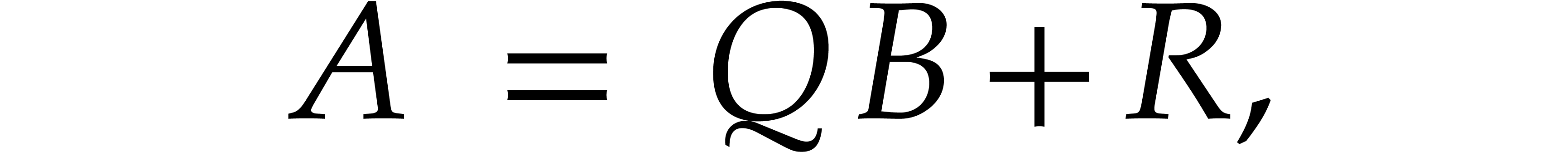
where 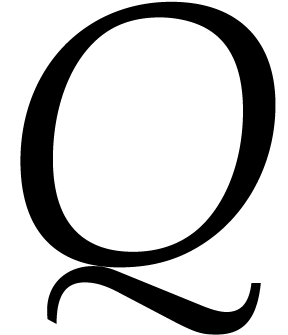 and
and 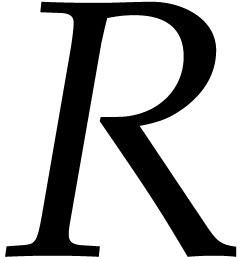 are in
are in 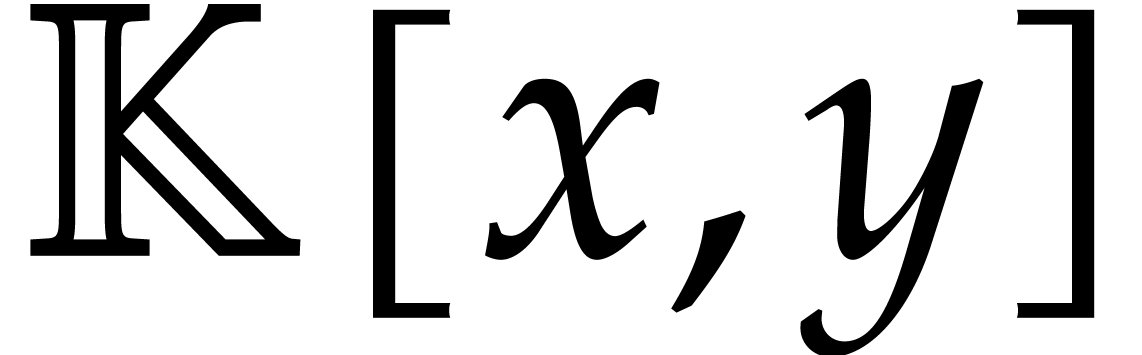 , and such that no monomial in
, and such that no monomial in 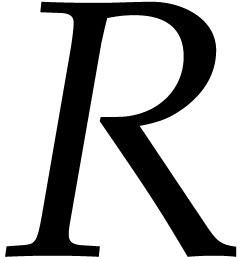 is divisible by
is divisible by 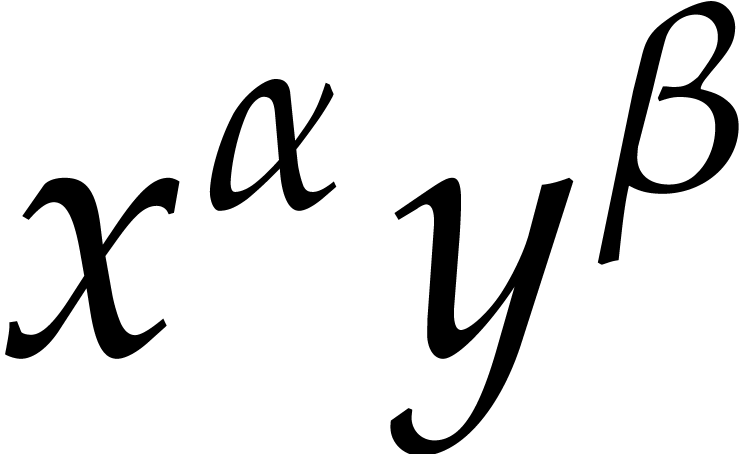 .
Such a division does exist: this is a usual fact from the theory of
Gröbner bases. In this context, a polynomial
.
Such a division does exist: this is a usual fact from the theory of
Gröbner bases. In this context, a polynomial  is said to be reduced with respect to
is said to be reduced with respect to 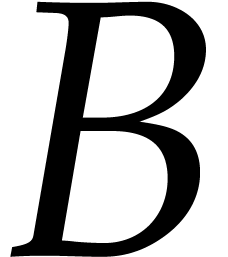 when none of its terms is divisible by
when none of its terms is divisible by 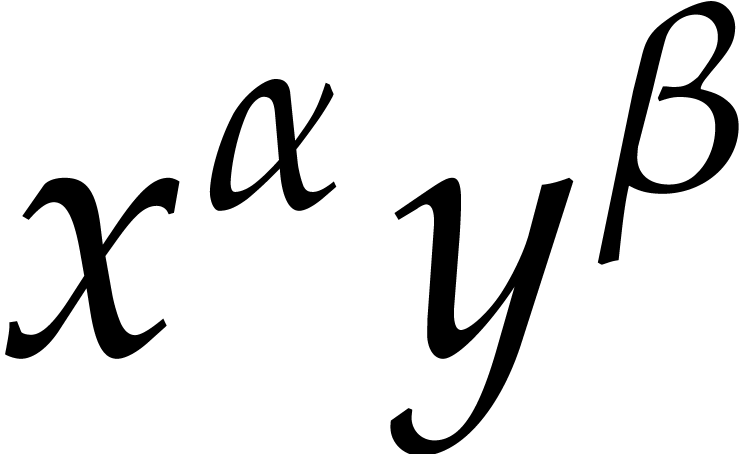 .
.
If 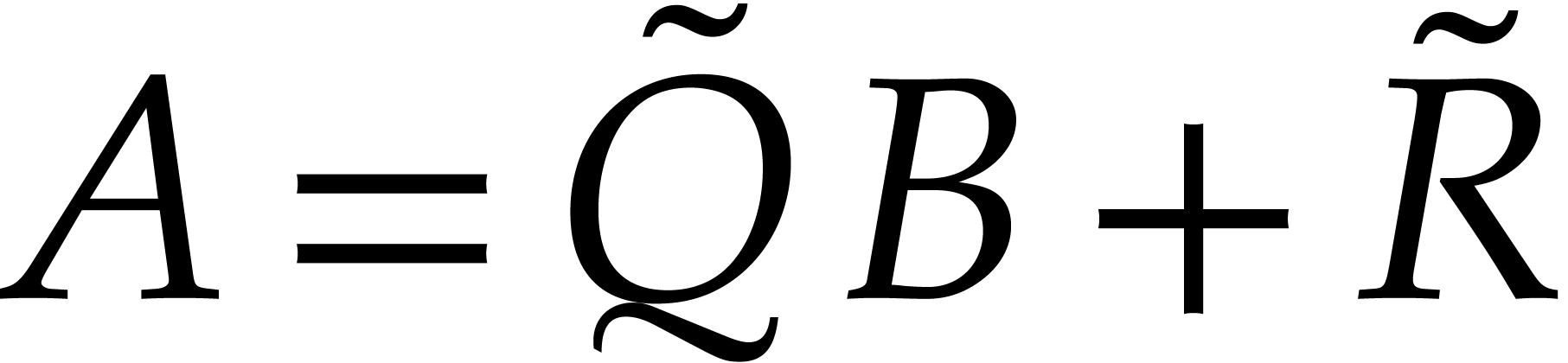 for polynomials
for polynomials  and
and
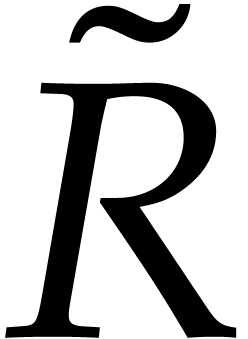 such that
such that 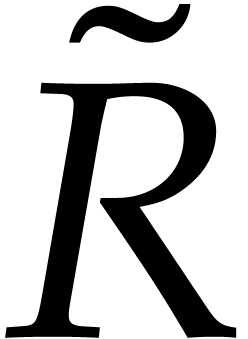 is reduced
with respect to
is reduced
with respect to 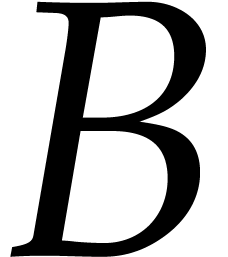 , then
, then 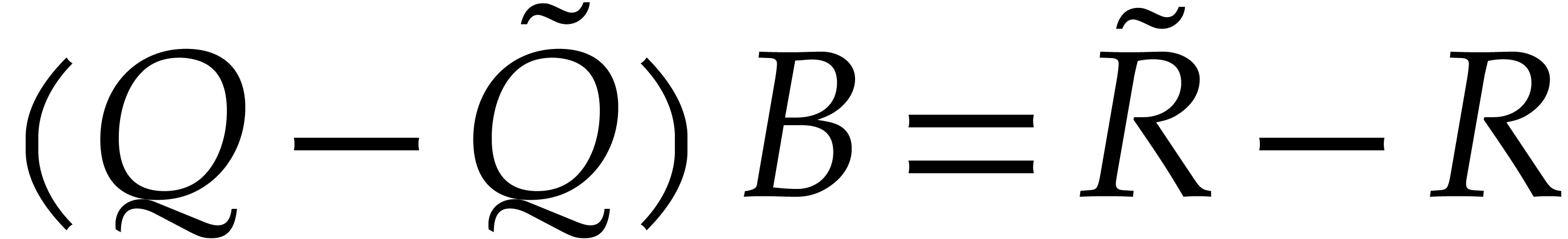 , so
, so  and
and
 . In other words,
. In other words,  and
and  are unique, so we may write
are unique, so we may write
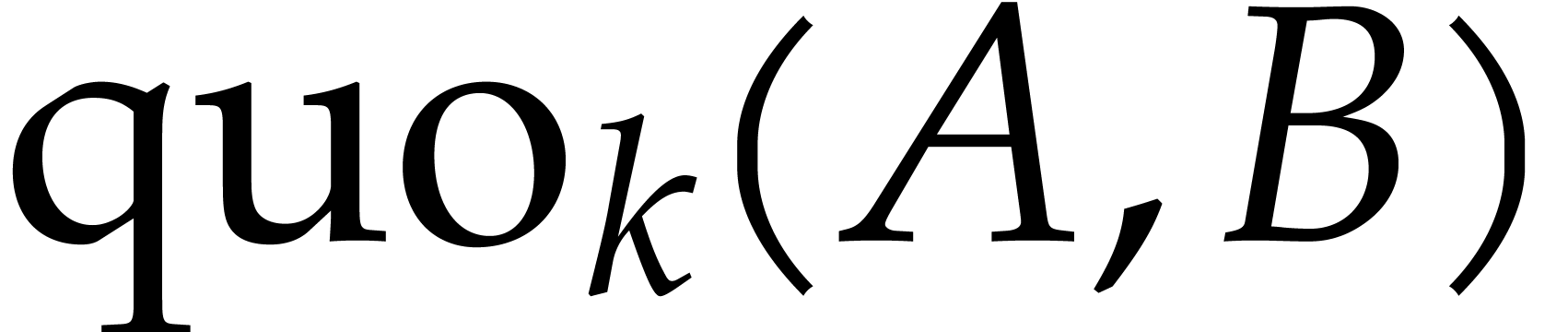 for the quotient
for the quotient  of
of  by
by  with respect to
with respect to
 .
.
In the remainder of this section, we assume that  has been fixed once and for all. Given
has been fixed once and for all. Given 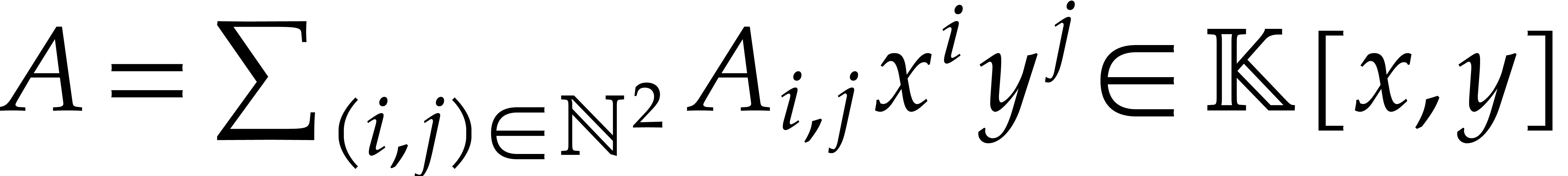 ,
we define
,
we define

The naive division algorithm proceeds as follows: if  has a term
has a term 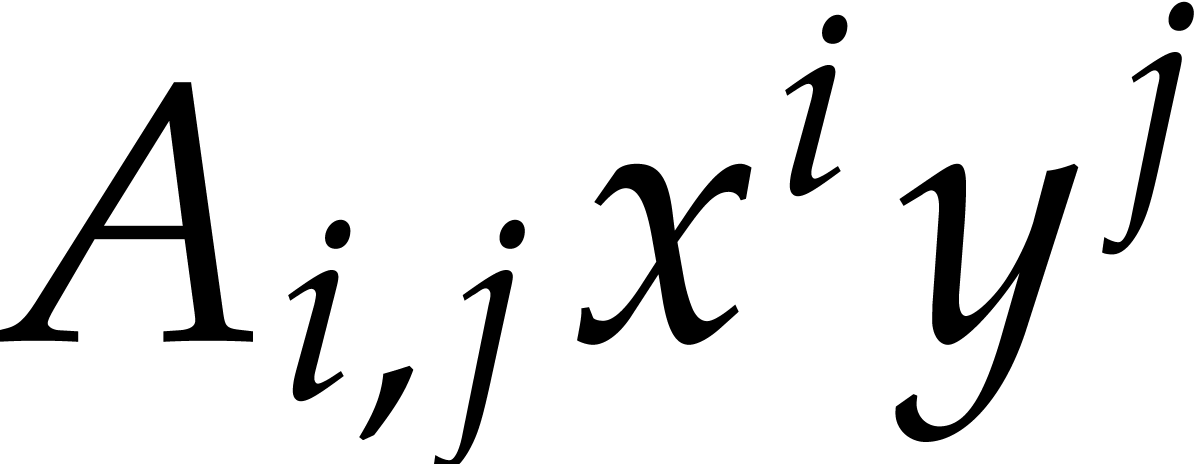 that is divisible by
that is divisible by 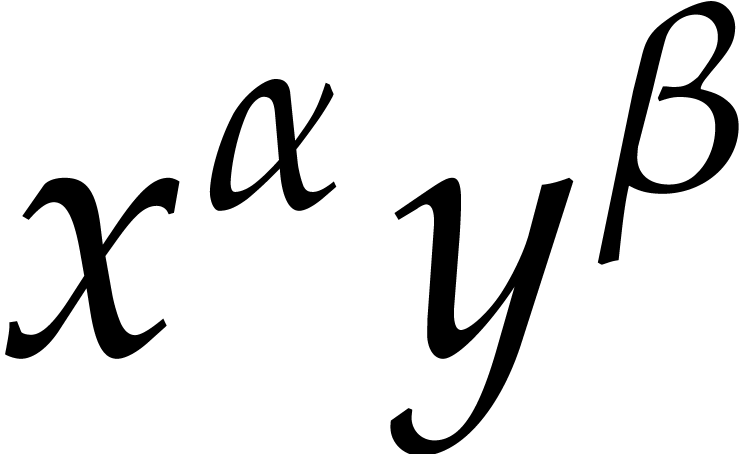 , then we pick a maximal such term for
, then we pick a maximal such term for  and compute
and compute
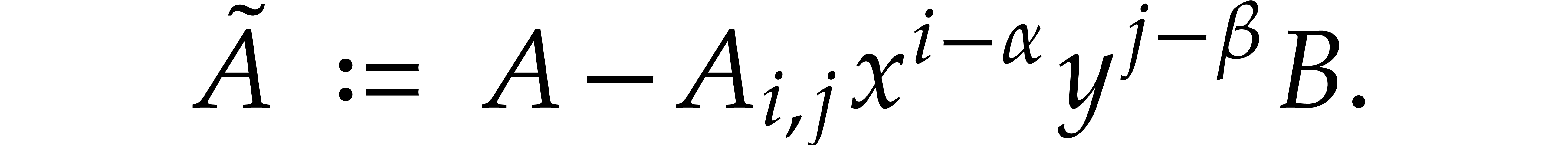
Then 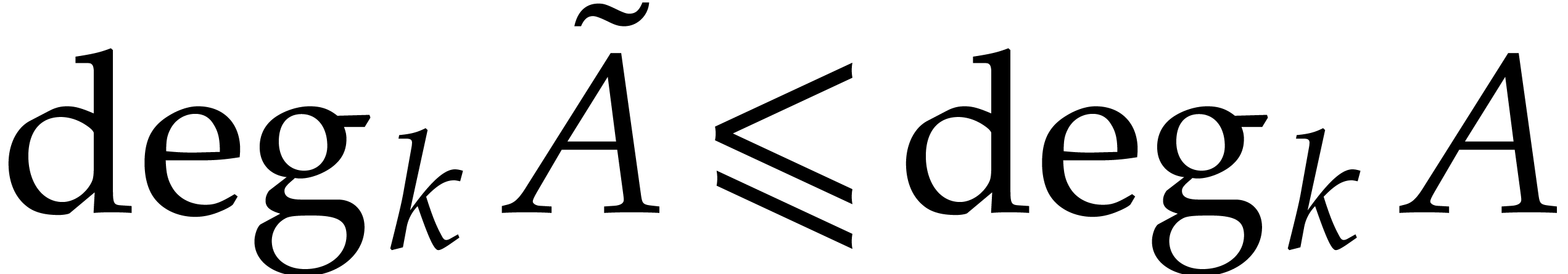 and the largest term of
and the largest term of  that is divisible by
that is divisible by 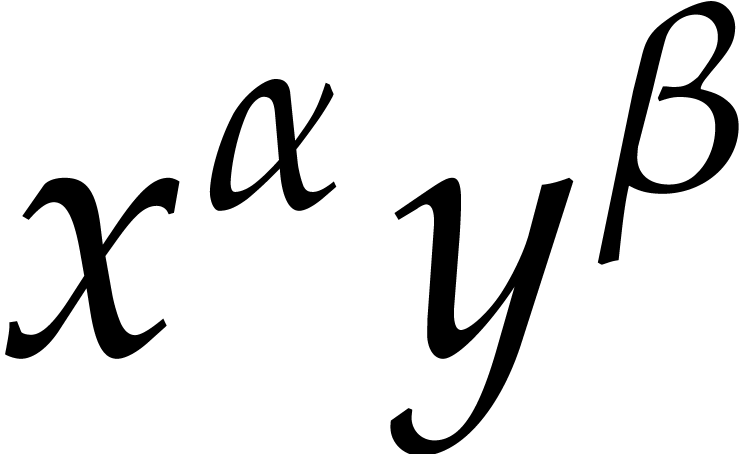 is strictly less than
is strictly less than 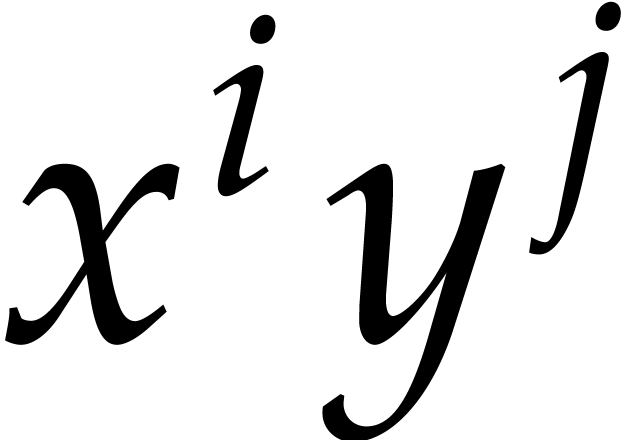 for
for  . This
division step is repeated for
. This
division step is repeated for  and for its
successive reductions, until
and for its
successive reductions, until  and
and  are found.
are found.
During this naive division process, we note that  only depends on
only depends on 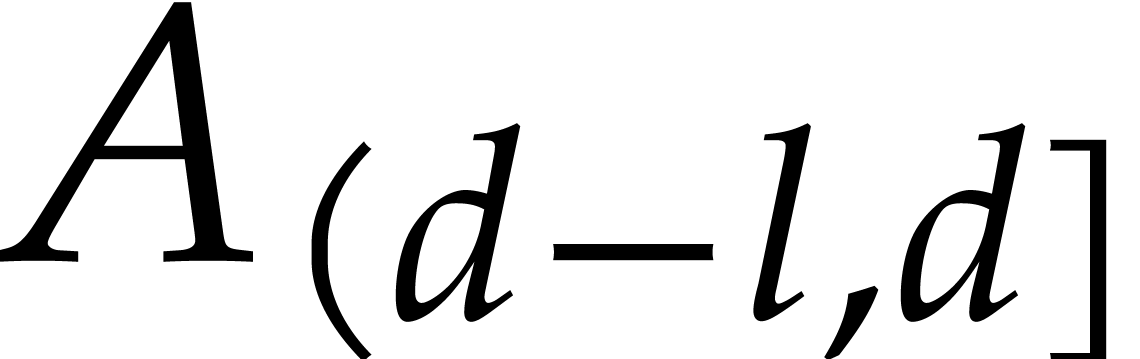 and
and 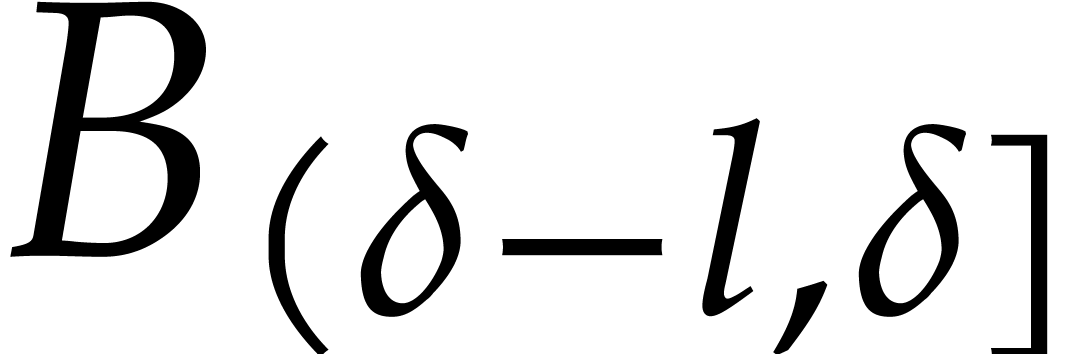 , for
, for 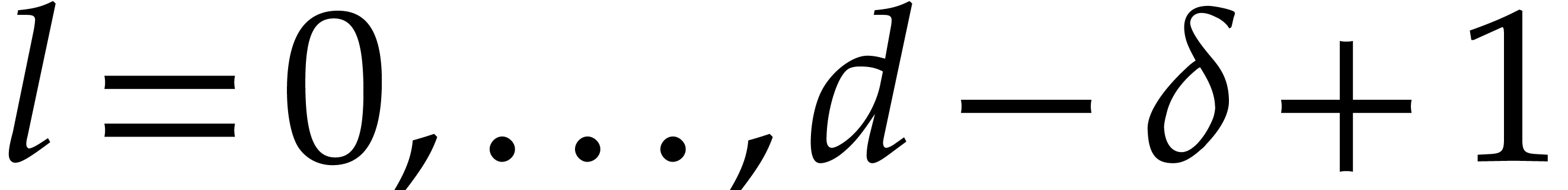 .
When
.
When 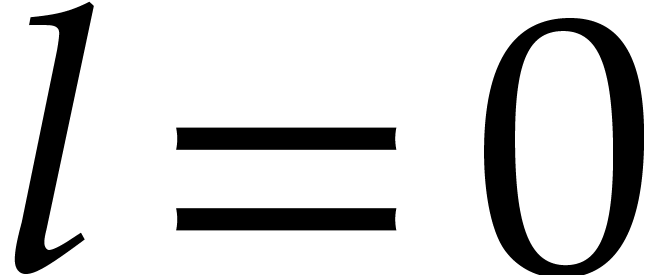 nothing needs to be computed. Let us now
describe a more efficient way to handle the case
nothing needs to be computed. Let us now
describe a more efficient way to handle the case 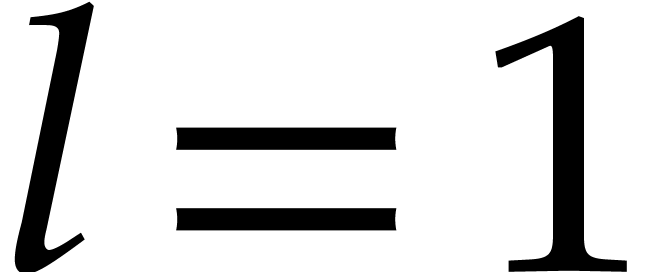 , when we need to compute the quasi-homogeneous
component of
, when we need to compute the quasi-homogeneous
component of 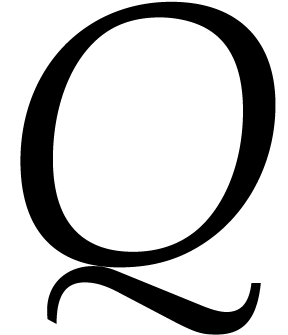 of maximal
of maximal 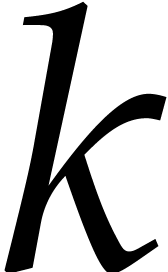 -degree
-degree  :
:
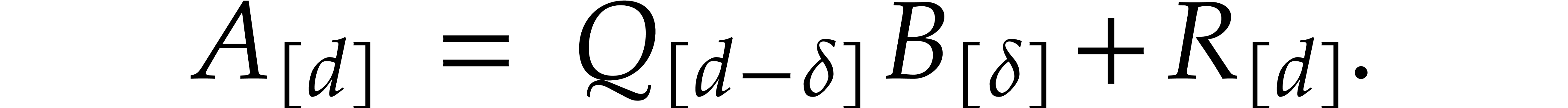
Proof. We first decompose
and note that  is reduced with respect to
is reduced with respect to 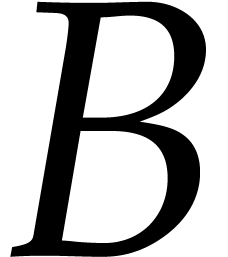 . In particular, the division of
. In particular, the division of
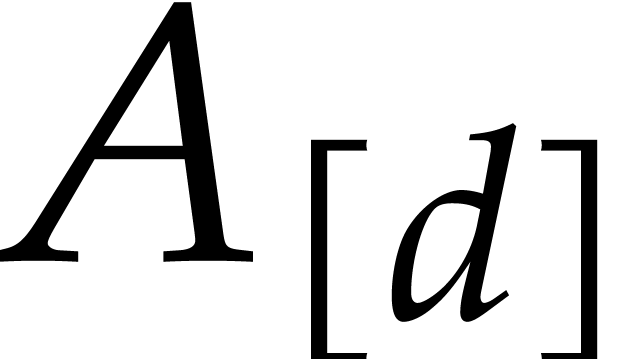 by
by 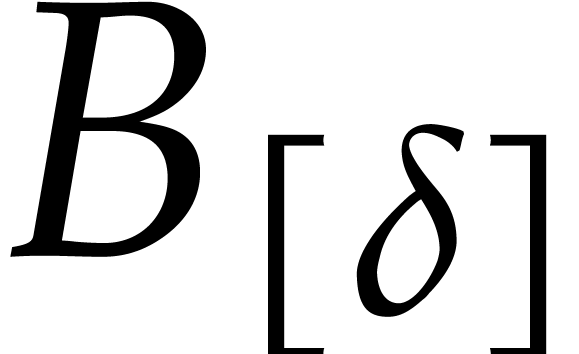 yields the same
quotient as the division of
yields the same
quotient as the division of  by
by 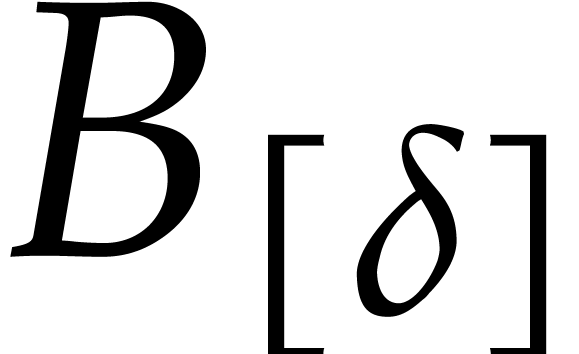 , so
, so
for some quasi-homogeneous polynomial  of
of 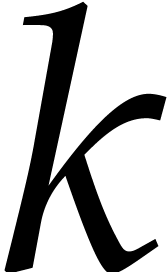 -degree
-degree  with
with 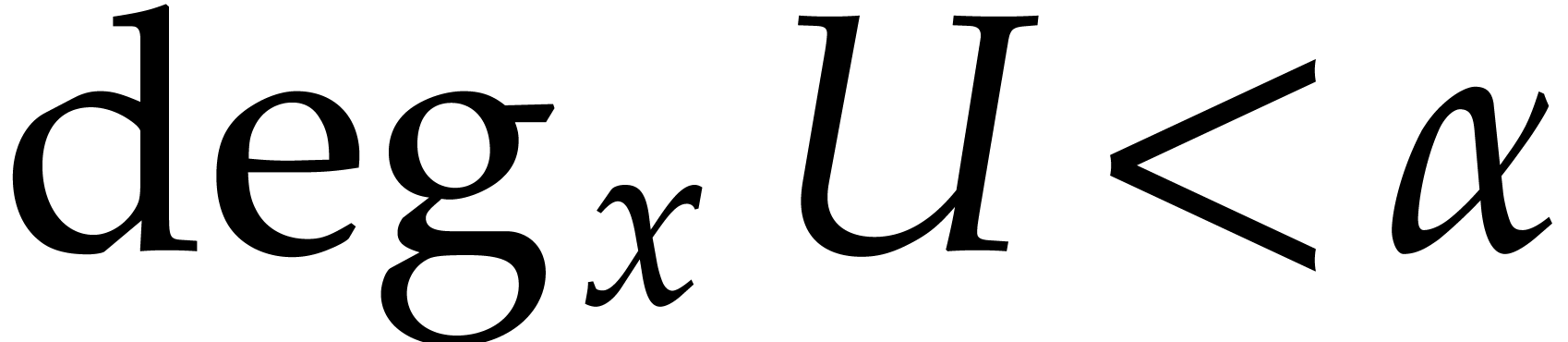 . Dehomogenization of
the relation (1) yields
. Dehomogenization of
the relation (1) yields
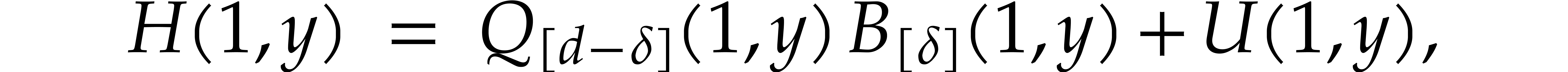
with 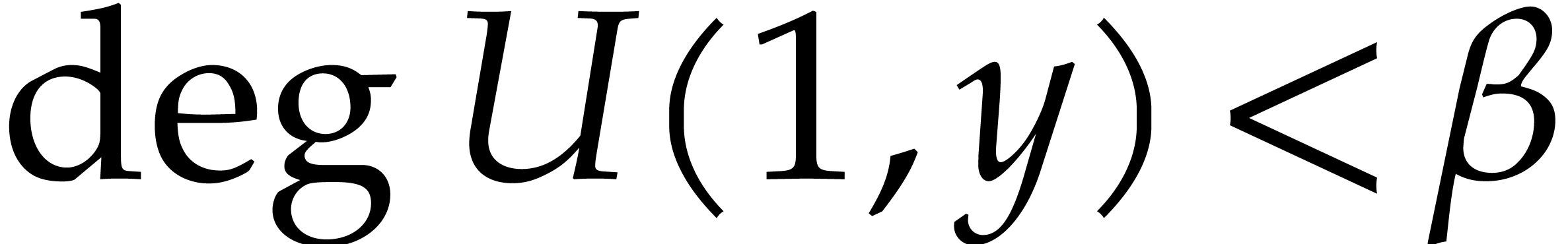 . Consequently, the
computation of
. Consequently, the
computation of 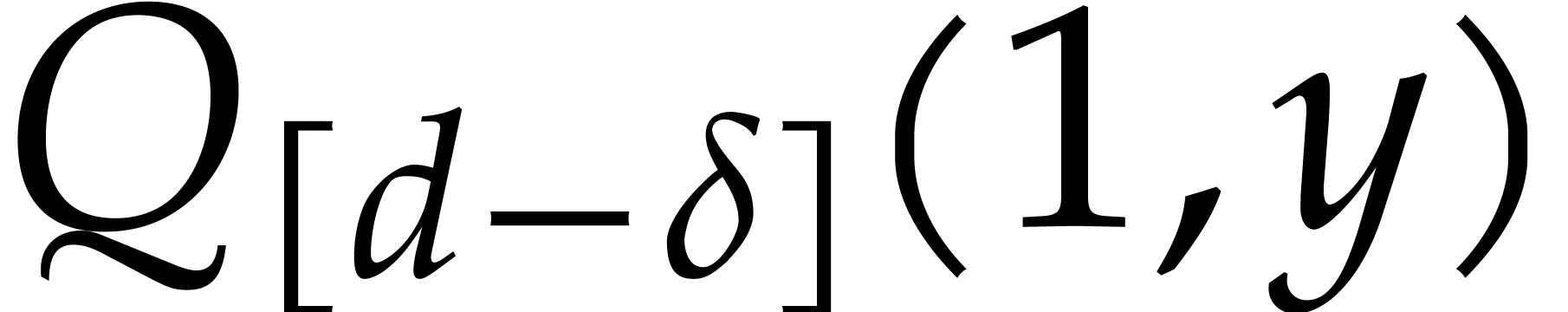 and
and 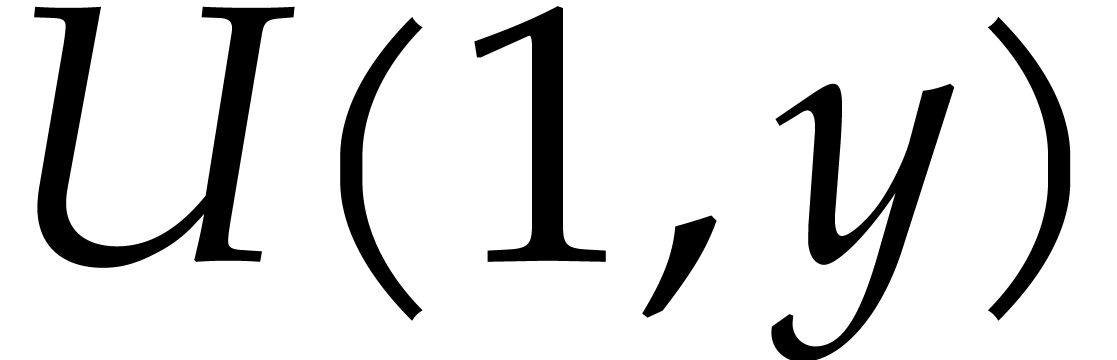 takes
takes
 operations in
operations in  ,
using a fast algorithm for Euclidean division in
,
using a fast algorithm for Euclidean division in 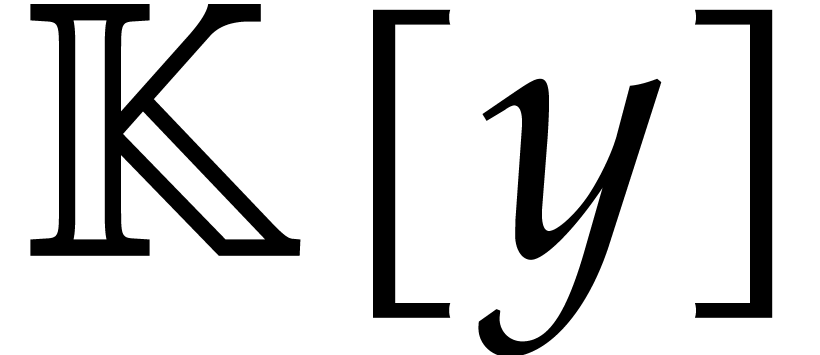 ; see [6, chapter 9] or [8],
for instance.
; see [6, chapter 9] or [8],
for instance.
For higher values of 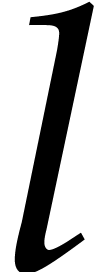 , the
following “divide and conquer” division algorithm is more
efficient than the naive algorithm:
, the
following “divide and conquer” division algorithm is more
efficient than the naive algorithm:
Algorithm |
|
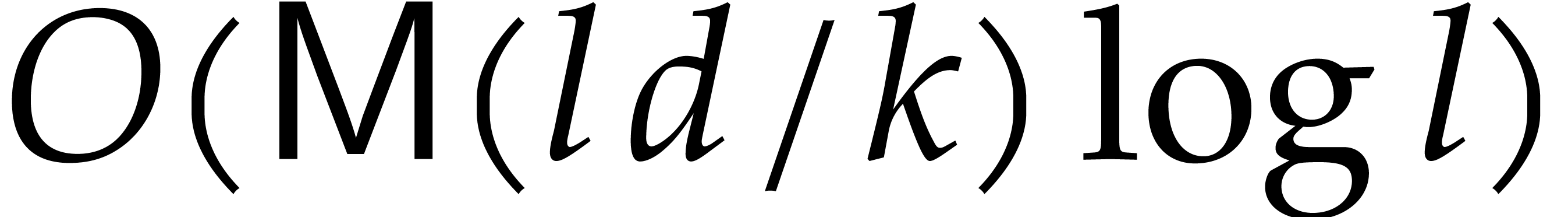 operations in
operations in  .
.
Proof. Let us prove the correctness by induction
on 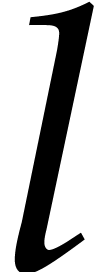 . If
. If  , then
, then  and the result
of the algorithm is correct. If
and the result
of the algorithm is correct. If 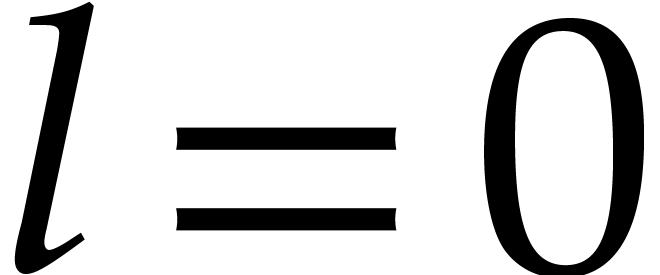 ,
then
,
then 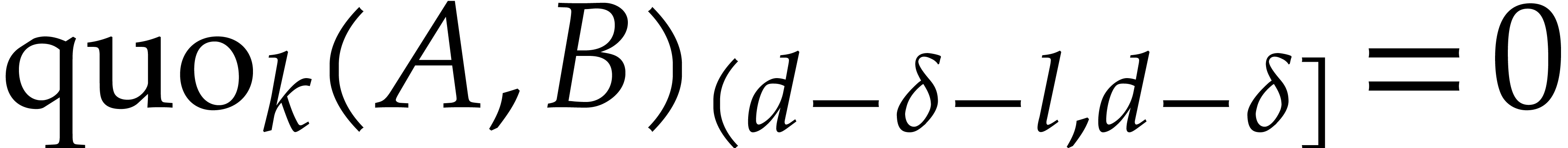 and the result is also correct. The case
and the result is also correct. The case
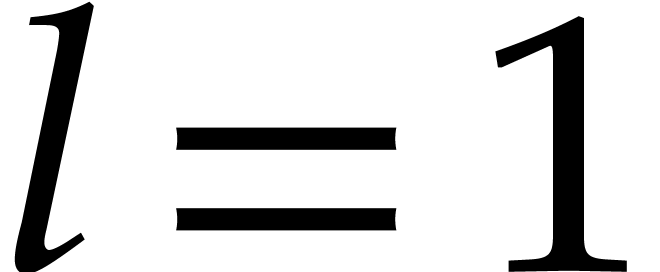 has been treated in Lemma 3.
has been treated in Lemma 3.
Now assume that 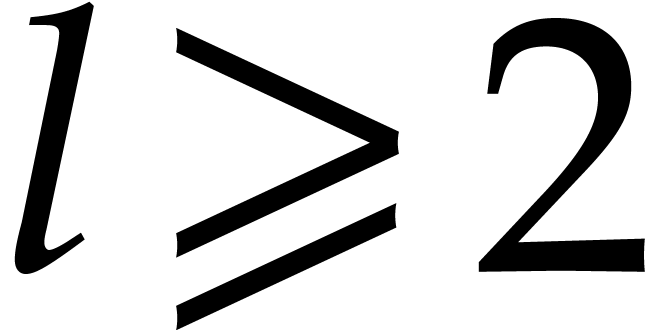 and
and 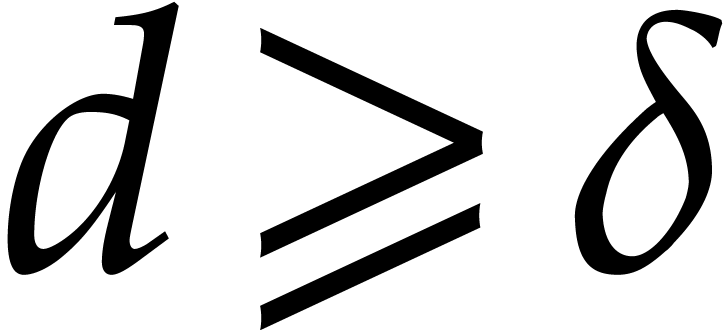 , so
, so 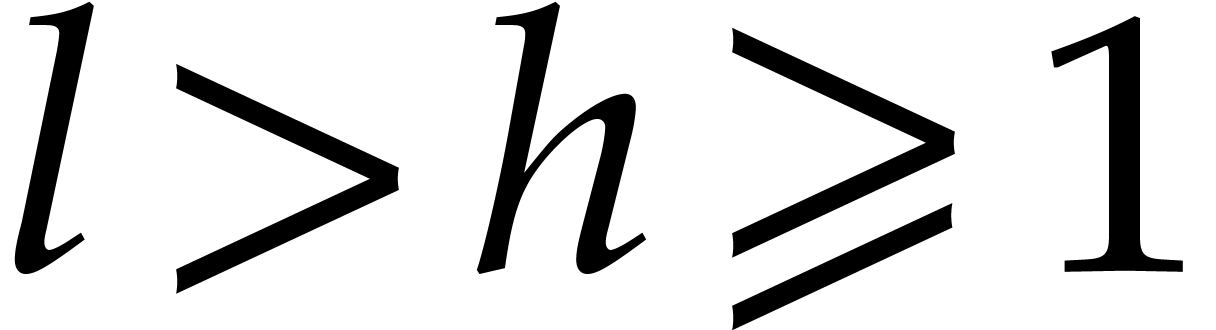 .
The induction hypothesis implies that
.
The induction hypothesis implies that 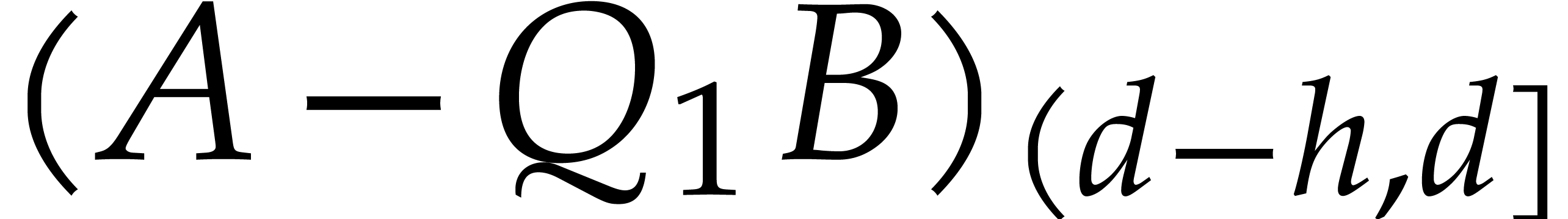 is reduced
with respect to
is reduced
with respect to 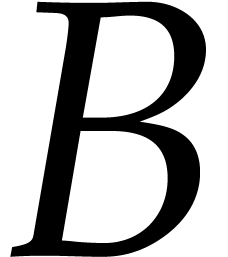 and that
and that 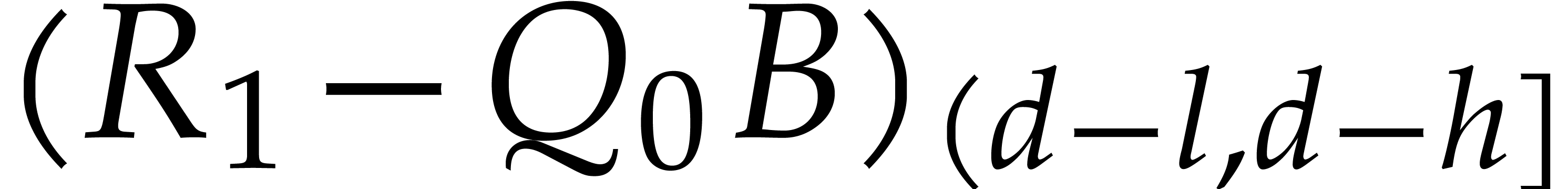 is reduced with respect to
is reduced with respect to  .
After noting that
.
After noting that
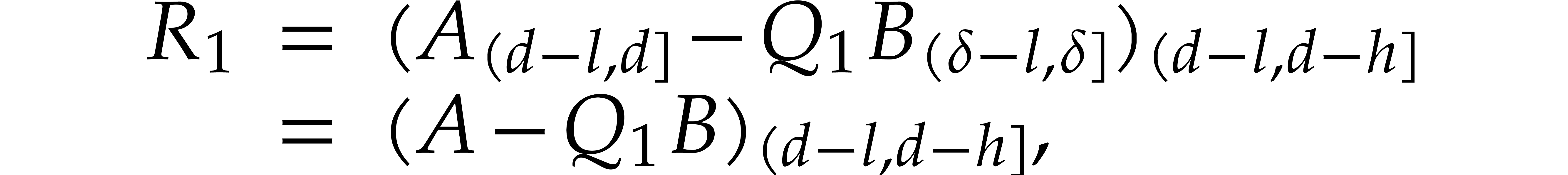
we verify that
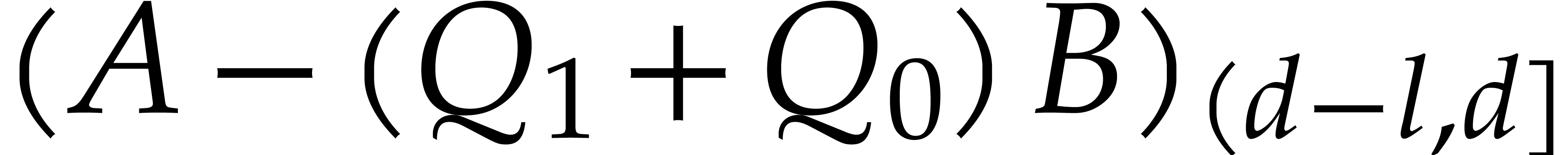 |
 |
 |
|
 |
 |
||
 |
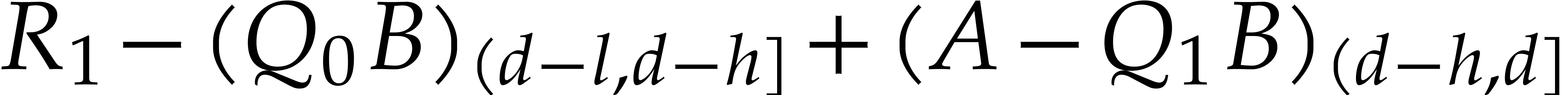 |
(since degk(Q0*B)⩽d-h) | |
 |
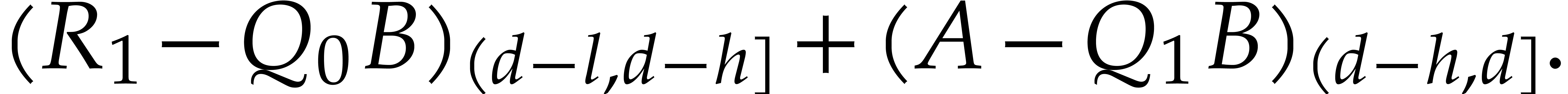 |
Consequently, 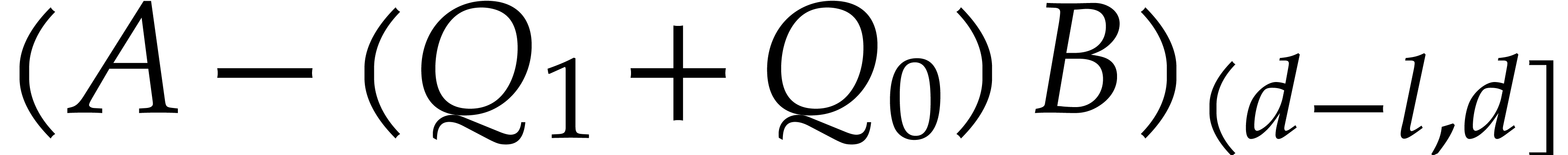 is reduced with respect to
is reduced with respect to 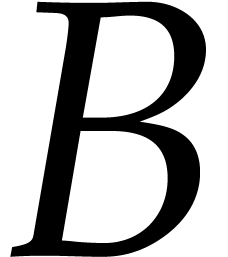 , whence
, whence

This completes the induction and our correctness proof.
Concerning the complexity, step 2 takes 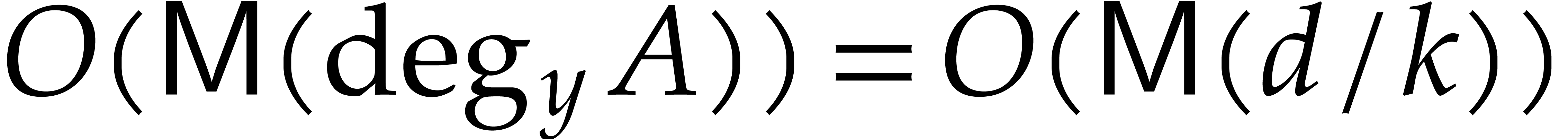 operations in
operations in  , by Lemma 3. In step 5, the computation of
, by Lemma 3. In step 5, the computation of 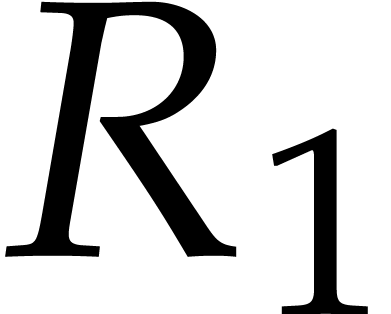 takes
takes
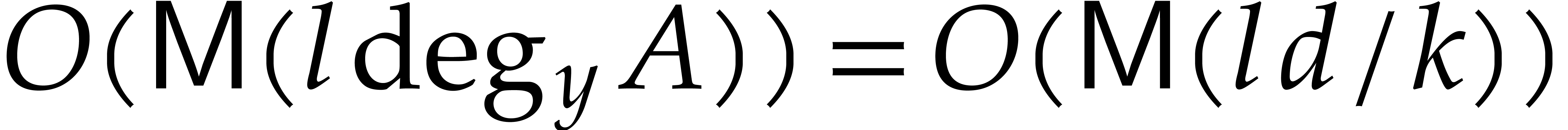 operations in
operations in  ,
by Lemma 2.
,
by Lemma 2.
Let 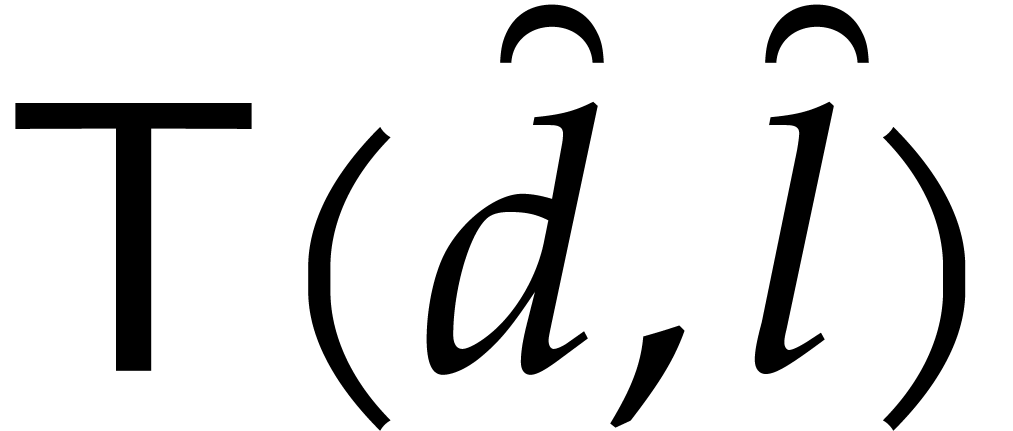 stand for the maximum of the costs of
Algorithm 1 for
stand for the maximum of the costs of
Algorithm 1 for 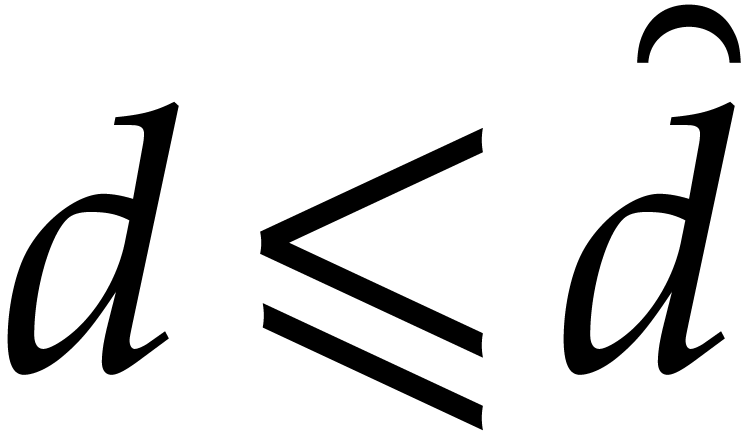 and
and 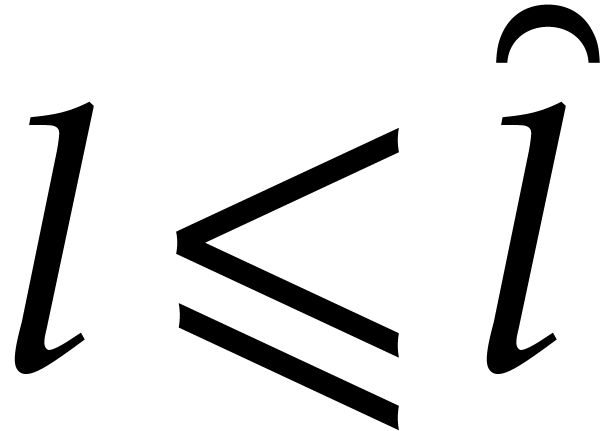 . We have shown that
. We have shown that 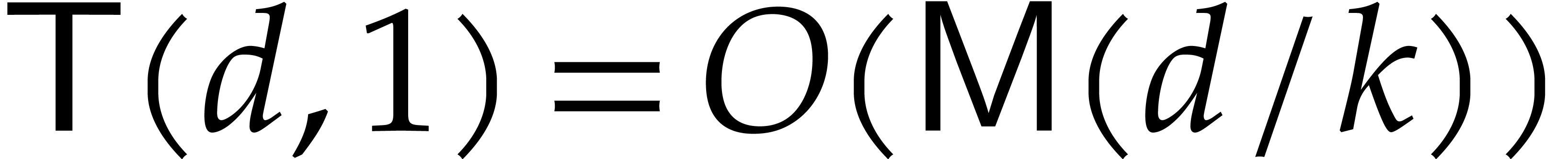 and that
and that
Unrolling this inequality, we obtain the claimed complexity bound.
 be of
be of 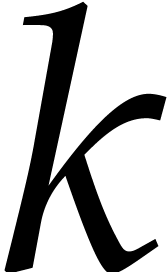 -degree
-degree 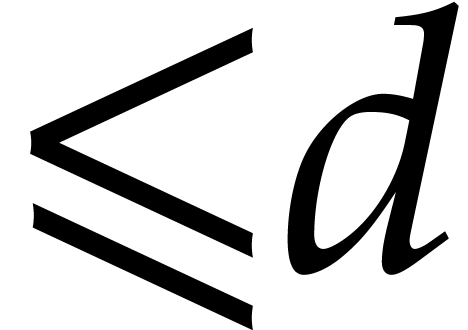 .
The remainder in the division of
.
The remainder in the division of  by
by  with respect to
with respect to  can be computed
using
can be computed
using 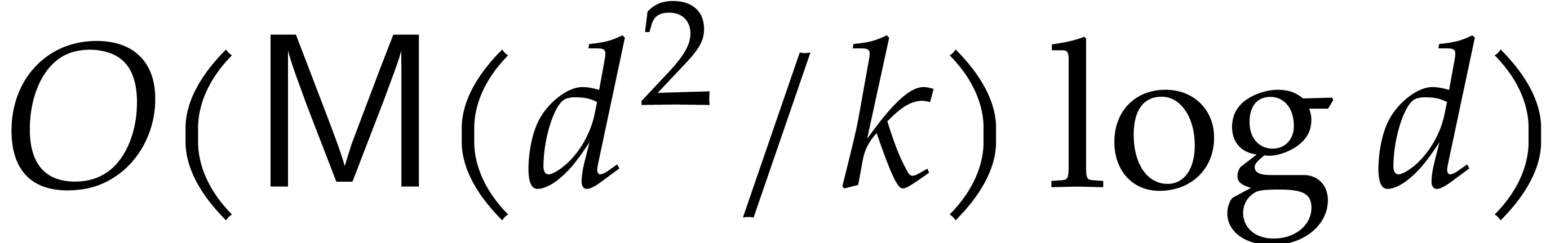 operations in
operations in  .
.
Proof. By Proposition 4, the
computation of 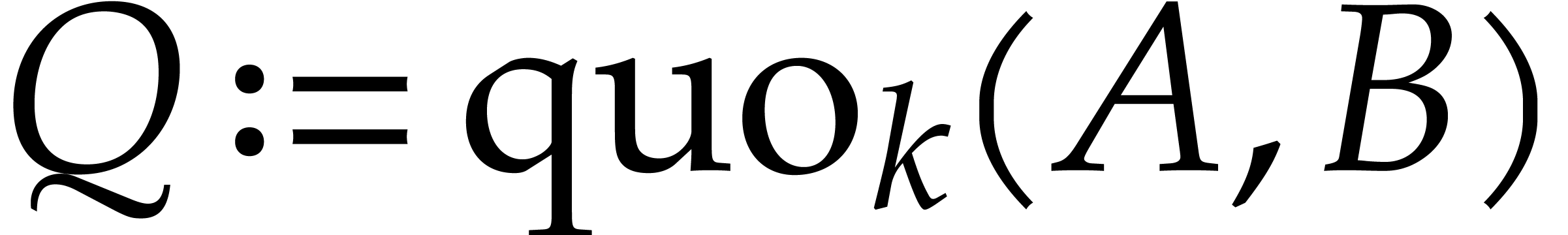 takes
takes 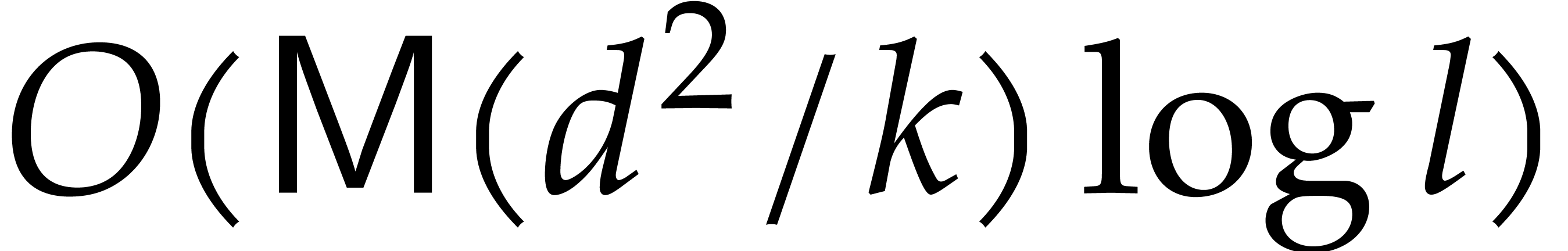 operations in
operations in  . The
computation of the corresponding remainder
. The
computation of the corresponding remainder 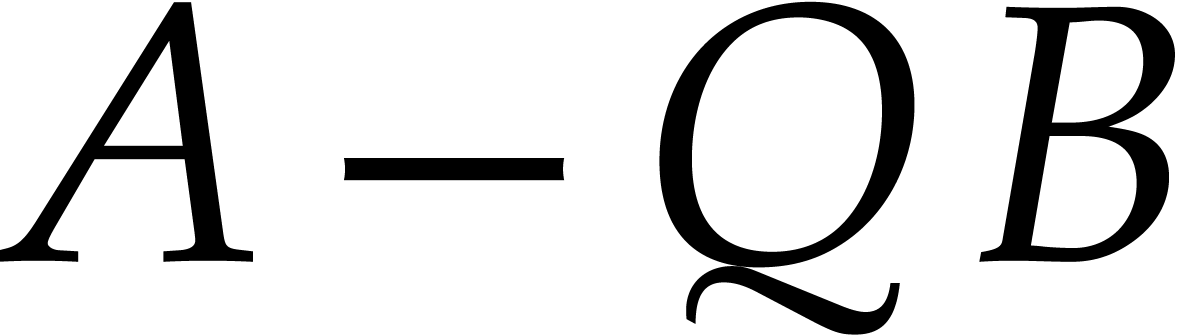 takes
takes
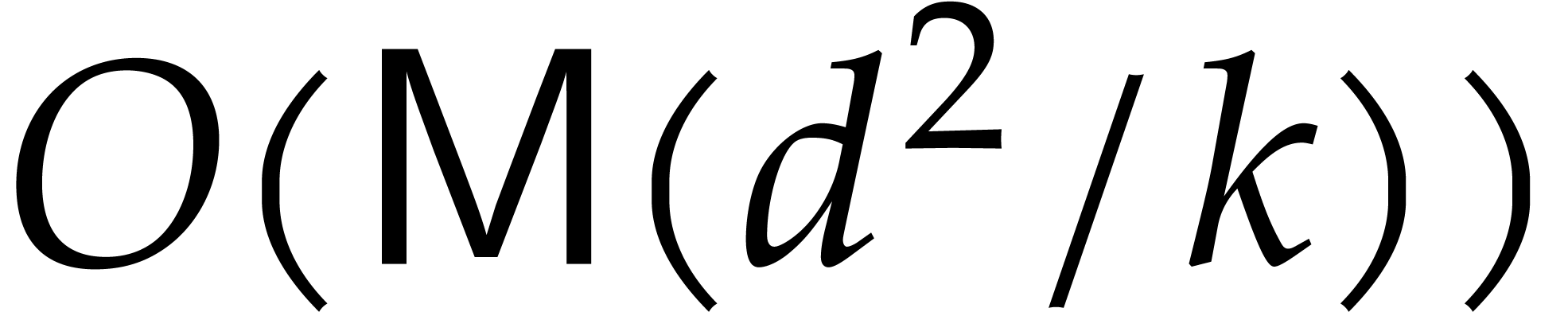 further operations in
further operations in  by
Lemma 2.
by
Lemma 2.
Remark 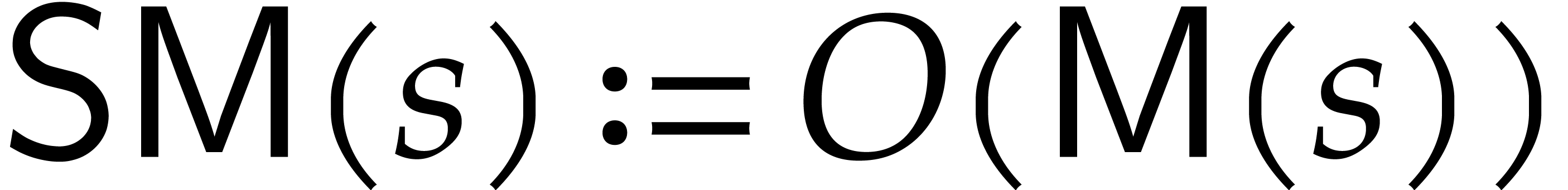 for the cost of sparse
polynomial products of size
for the cost of sparse
polynomial products of size 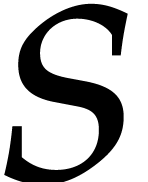 .
This cost is warranted mutatis mutandis by the observation that
all sparse bivariate polynomial products occurring within the algorithm
underlying [9, Theorem 4] are either univariate products or
products of slices of polynomials that are dense with respect to the
.
This cost is warranted mutatis mutandis by the observation that
all sparse bivariate polynomial products occurring within the algorithm
underlying [9, Theorem 4] are either univariate products or
products of slices of polynomials that are dense with respect to the
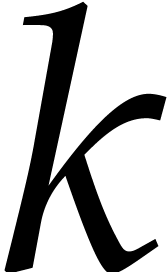 -ordering. We have seen in
section 2.3 how to compute such products efficiently.
-ordering. We have seen in
section 2.3 how to compute such products efficiently.
Let 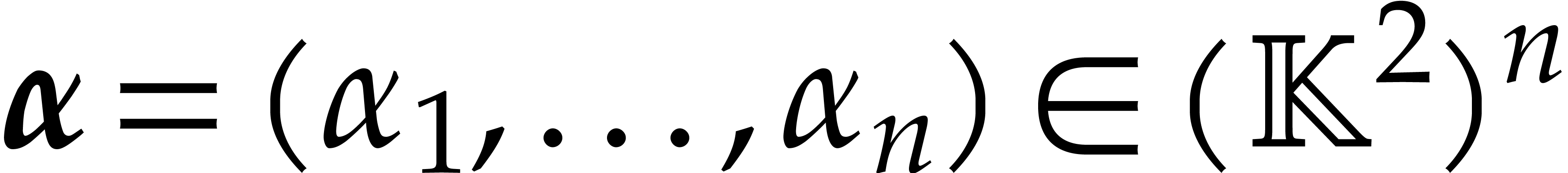 be a tuple of pairwise distinct points. We
define the vanishing ideal for
be a tuple of pairwise distinct points. We
define the vanishing ideal for  by
by
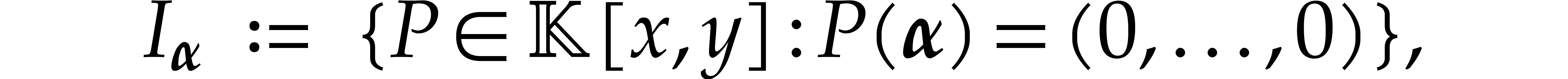
where we recall that 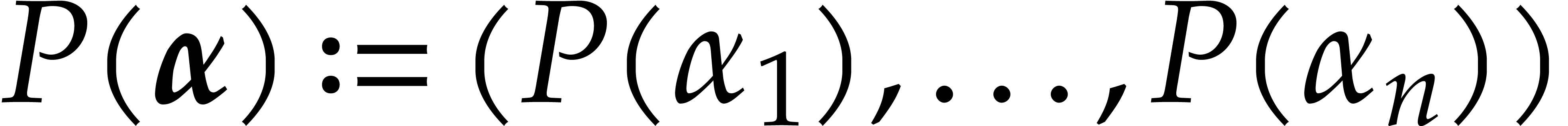 .
.
A monic polynomial  is said to be axial
if its leading monomial with respect to
is said to be axial
if its leading monomial with respect to  is of
the form
is of
the form 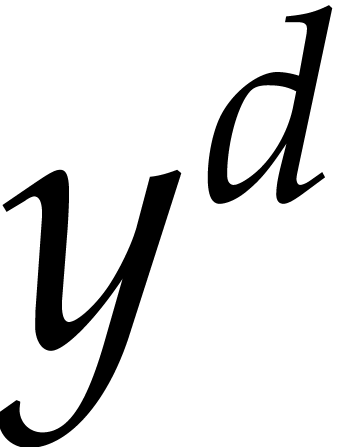 . The goal of this
section is to prove the existence of such a polynomial modulo a
sufficiently generic change of variables of the form
. The goal of this
section is to prove the existence of such a polynomial modulo a
sufficiently generic change of variables of the form
This change of variables transforms  into a new
tuple
into a new
tuple 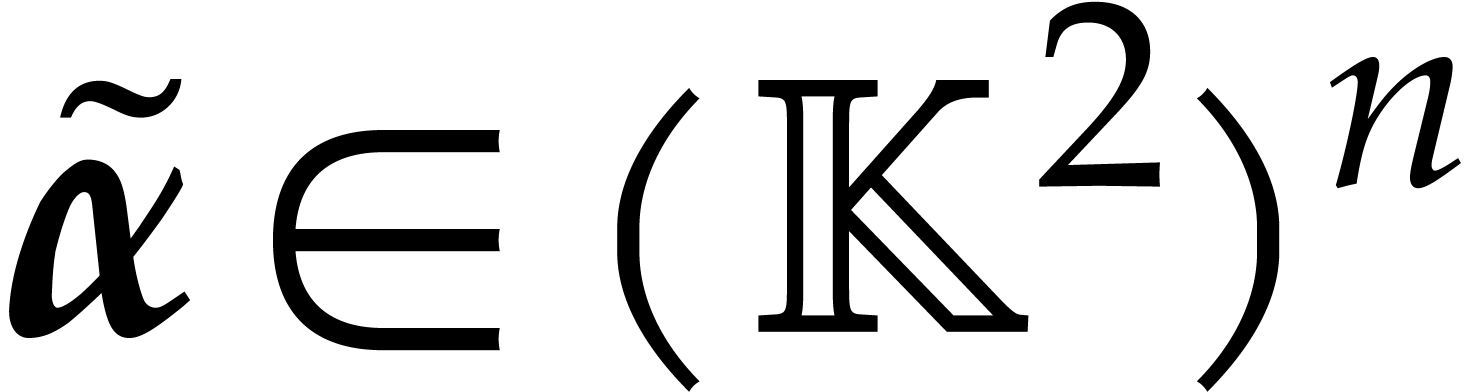 with
with
and the ideal  into
into
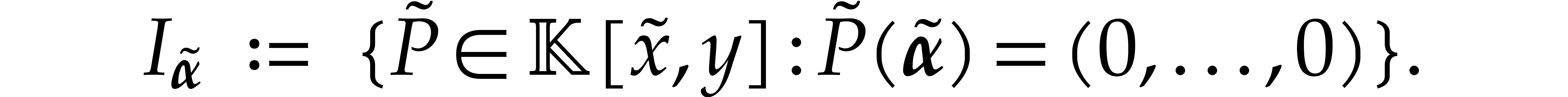
For any degree  , we define
, we define

Given a polynomial 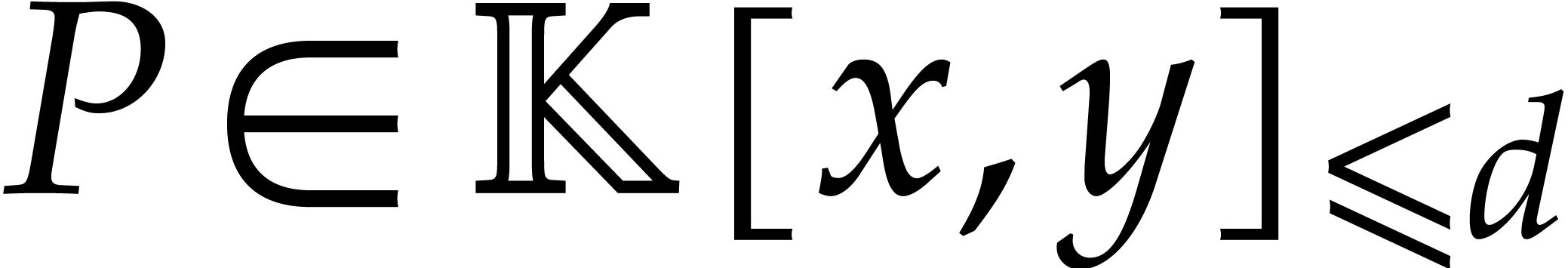 such that
such that 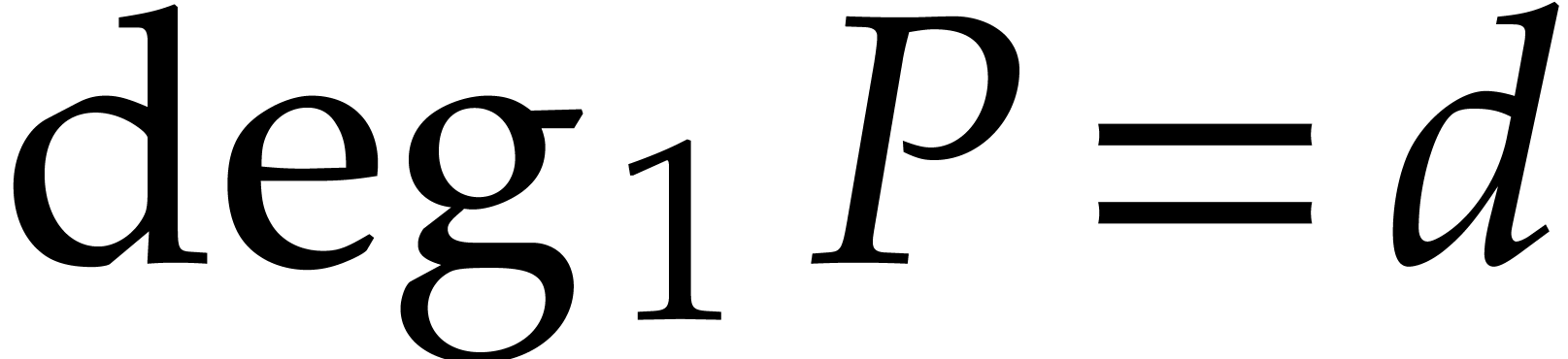 we may decompose
we may decompose
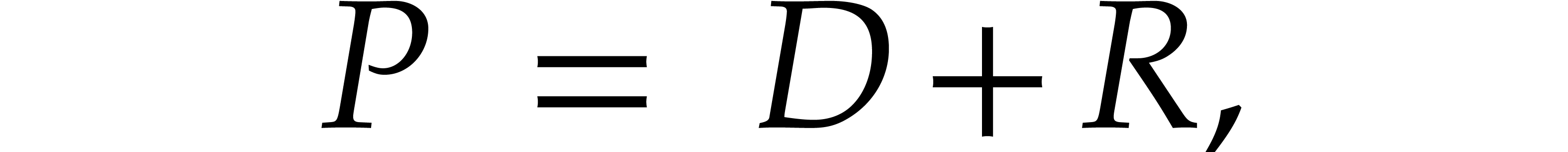
where 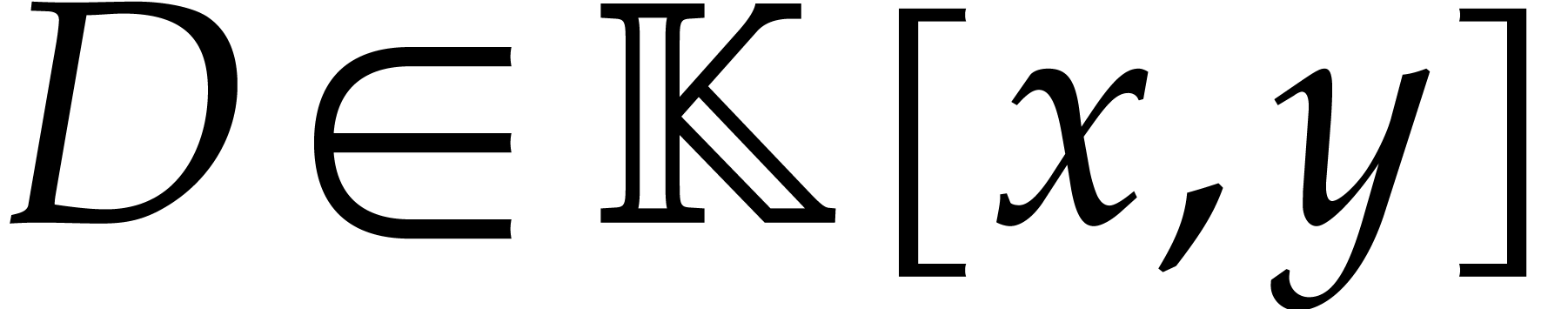 is homogeneous of degree
is homogeneous of degree  and
and 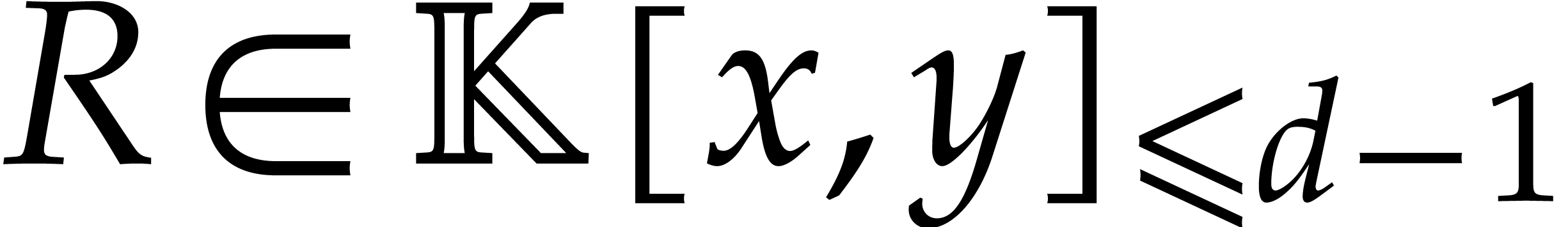 . The change of variables
(2) transforms
. The change of variables
(2) transforms 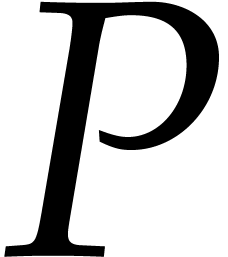 into
into
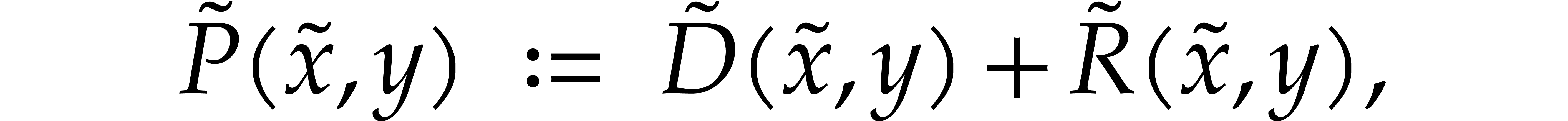
where
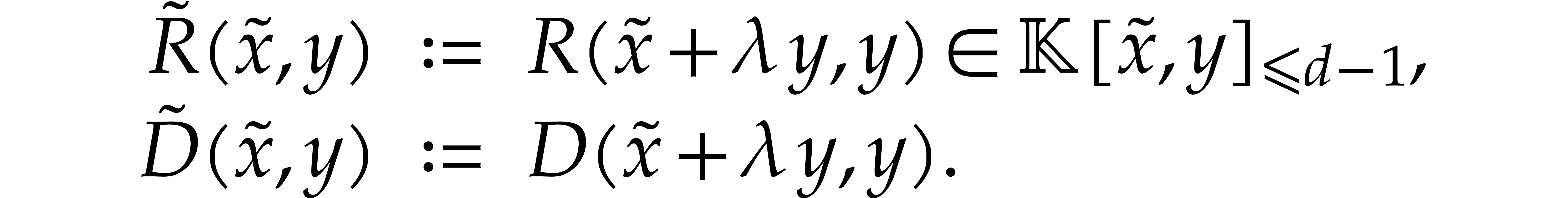
The coefficient of the monomial 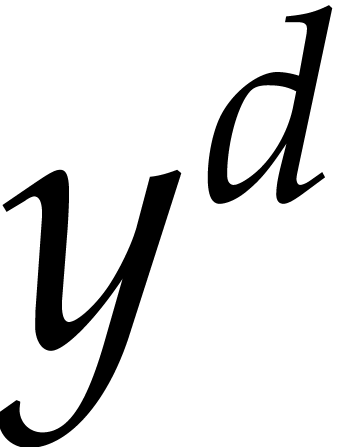 in
in 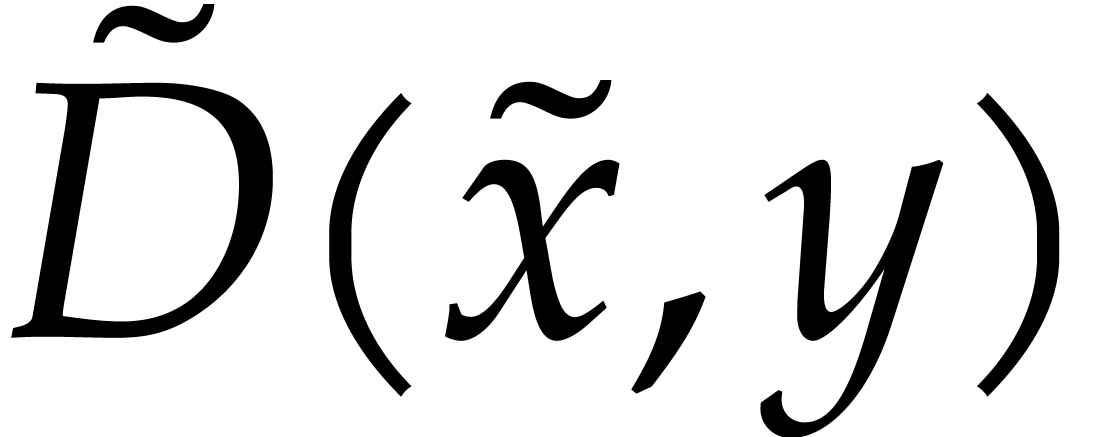 is
is 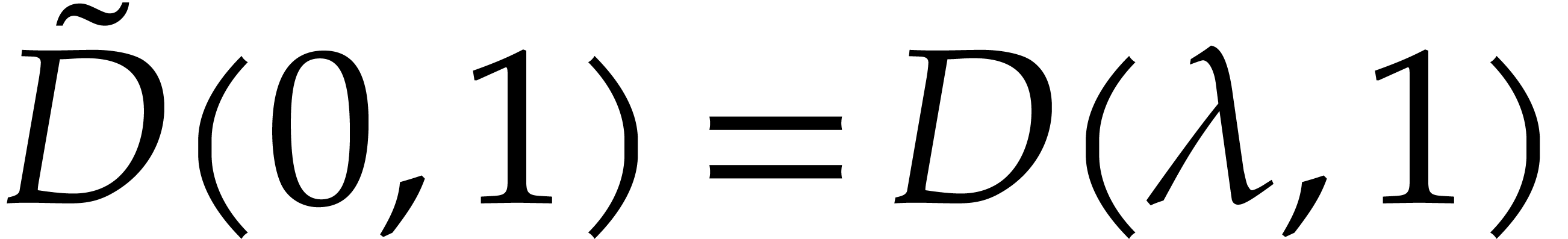 .
.
The  -vector space
-vector space 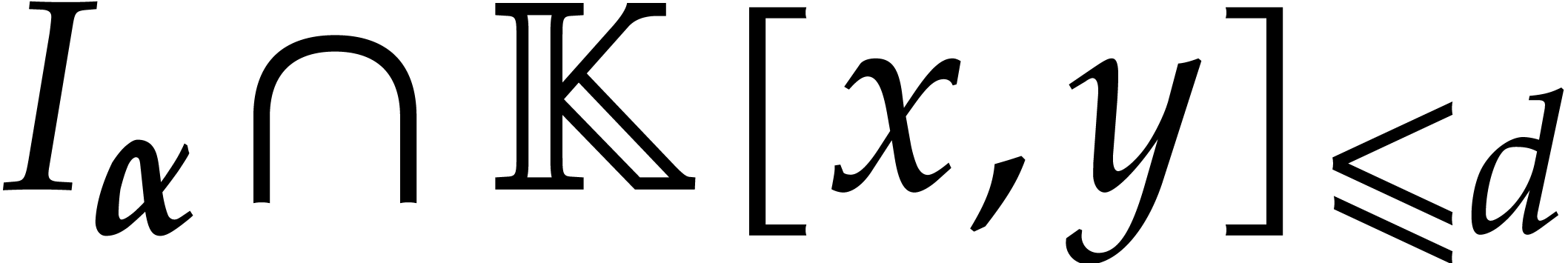 is the solution set of a linear system consisting of
is the solution set of a linear system consisting of  equations and
equations and 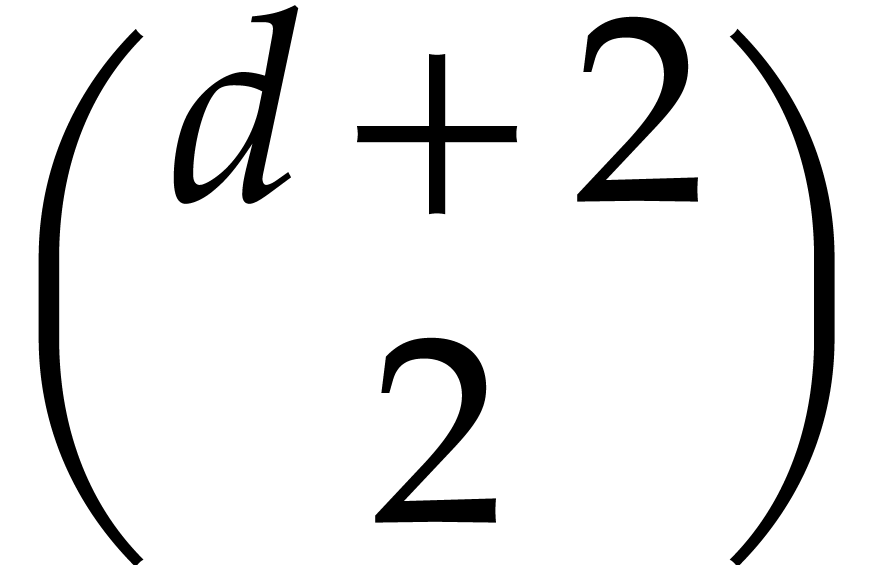 unknowns, that
are the unknown coefficients of a polynomial in
unknowns, that
are the unknown coefficients of a polynomial in 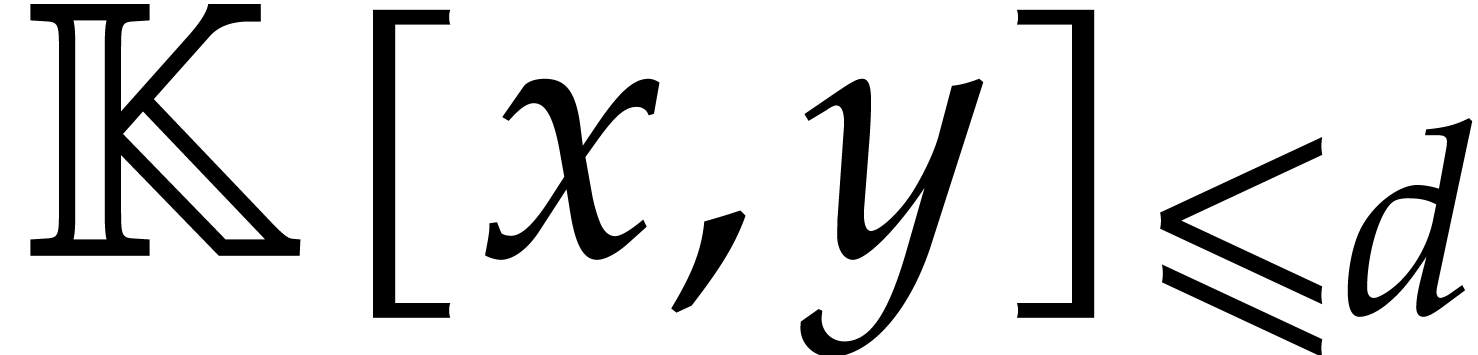 . Such a system admits a non-zero solution whenever
. Such a system admits a non-zero solution whenever
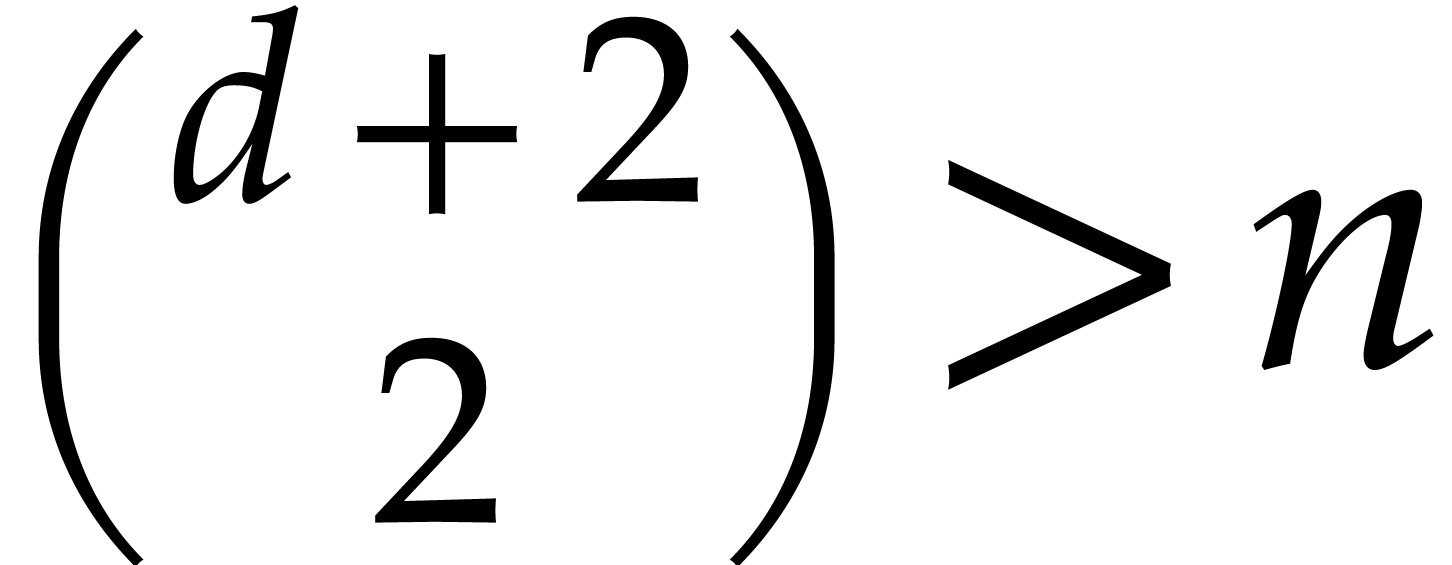 . Now assume that
. Now assume that 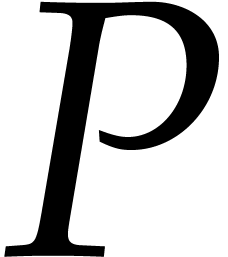 is a non-zero element of
is a non-zero element of 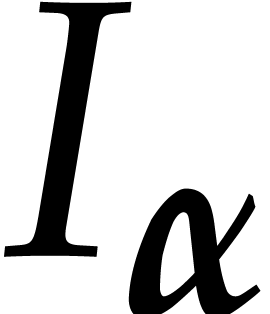 of
minimal total degree
of
minimal total degree  and let
and let  denote the set of roots of
denote the set of roots of 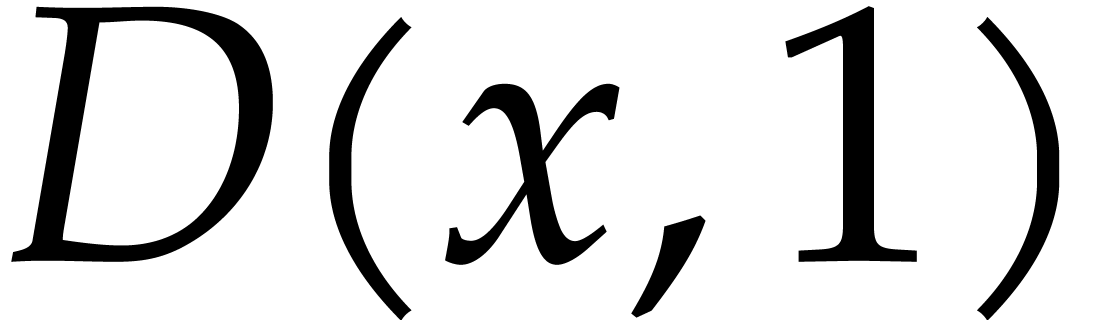 in
in  . Since
. Since  is minimal we
have
is minimal we
have
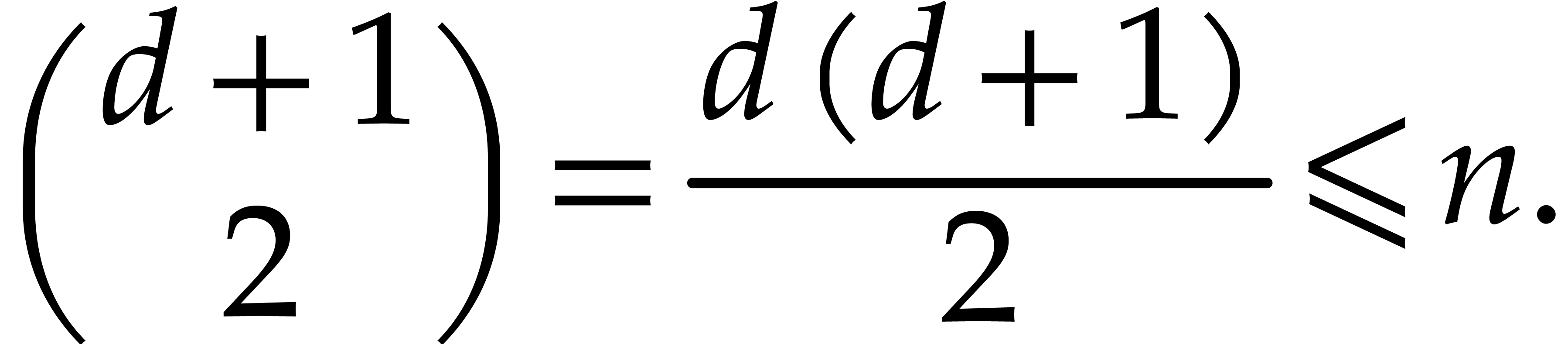
that implies
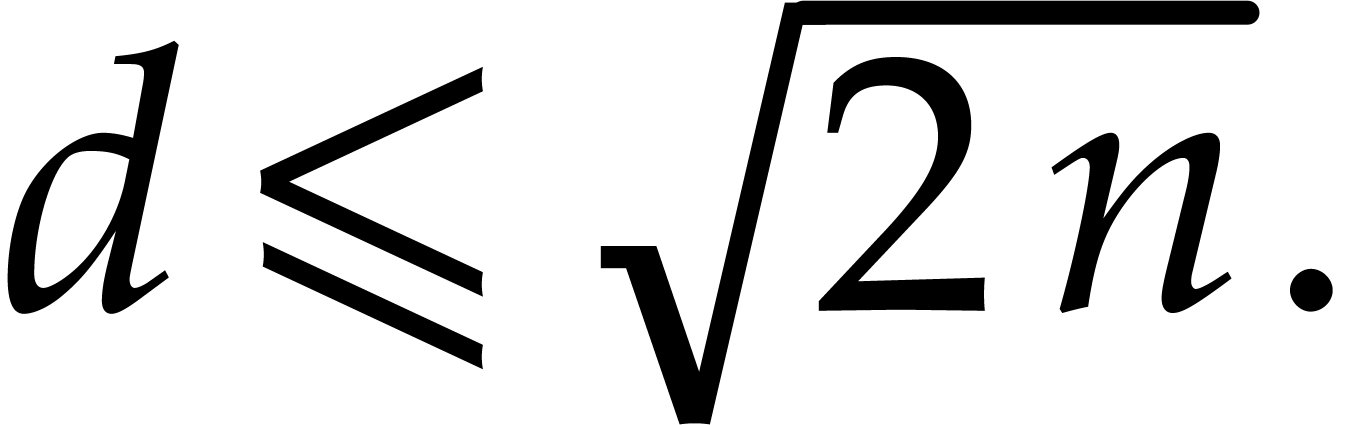 |
(4) |
On the other hand, we have 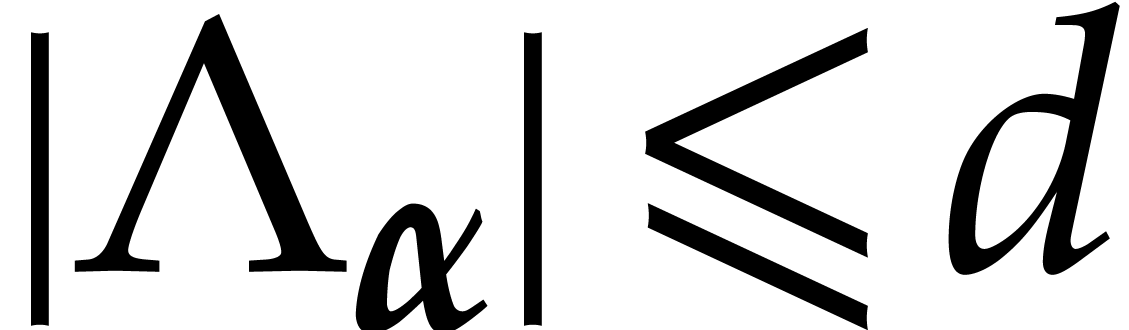 .
And if
.
And if 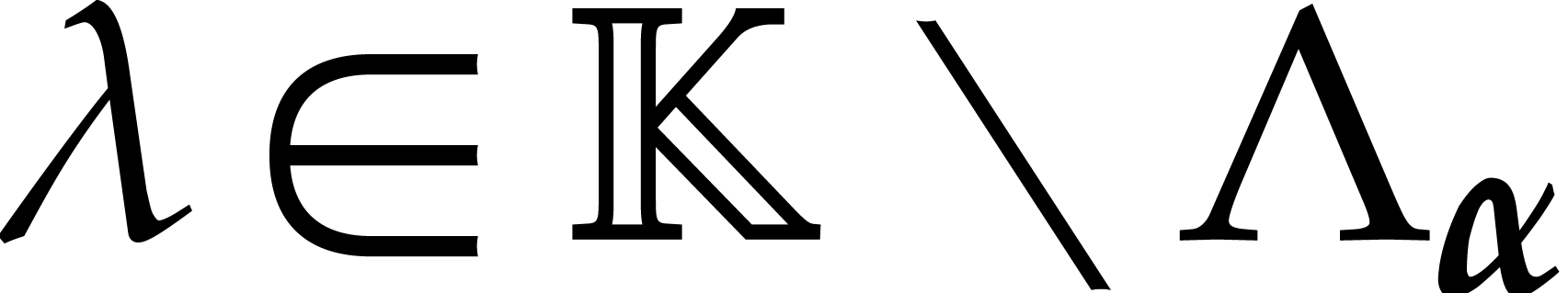 , then
, then  is the leading monomial of
is the leading monomial of  for
for
 . Assuming that
. Assuming that  , this proves the existence of an axial
polynomial
, this proves the existence of an axial
polynomial 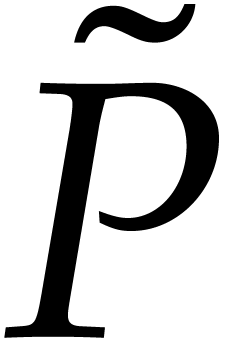 of degree
of degree  after a suitable change of variables of the form (2).
after a suitable change of variables of the form (2).
We say that  is in general position if
there exists a polynomial of minimal degree in
is in general position if
there exists a polynomial of minimal degree in 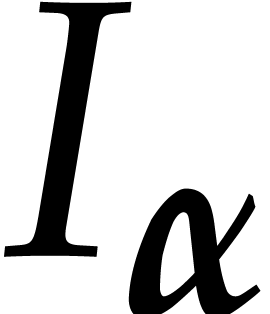 that is axial.
that is axial.
Let 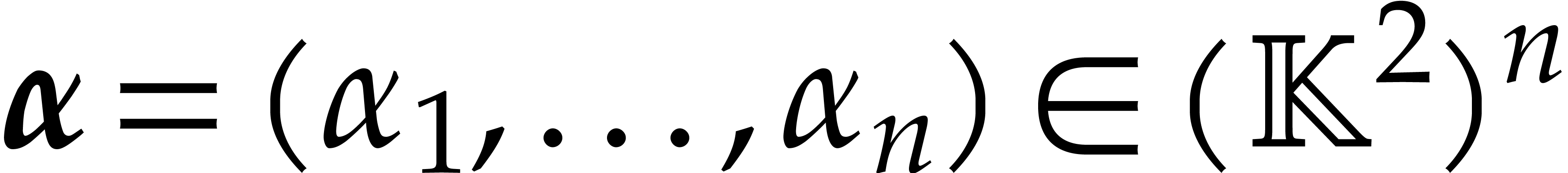 be a tuple of points in general position, as
defined in the previous section. In this section, we describe a process
for reducing a polynomial
be a tuple of points in general position, as
defined in the previous section. In this section, we describe a process
for reducing a polynomial 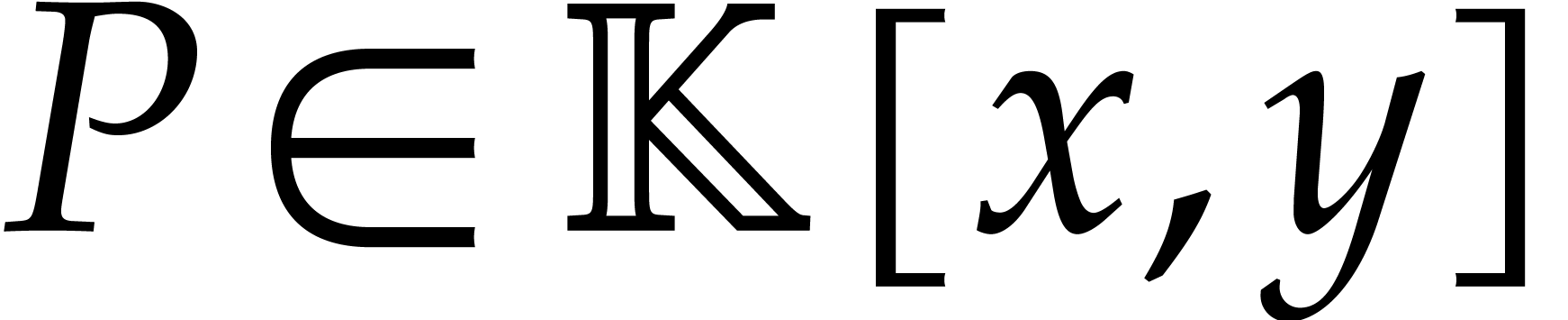 modulo
modulo 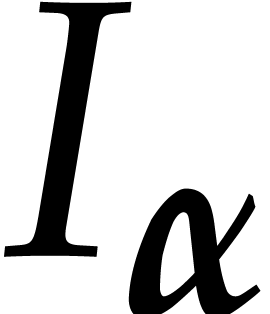 . The reduction of
. The reduction of 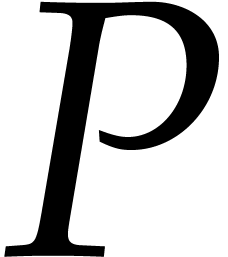 is a
polynomial whose support is controlled in a way that will be made
precise.
is a
polynomial whose support is controlled in a way that will be made
precise.
Since  is assumed to be in general position,
thanks to
is assumed to be in general position,
thanks to 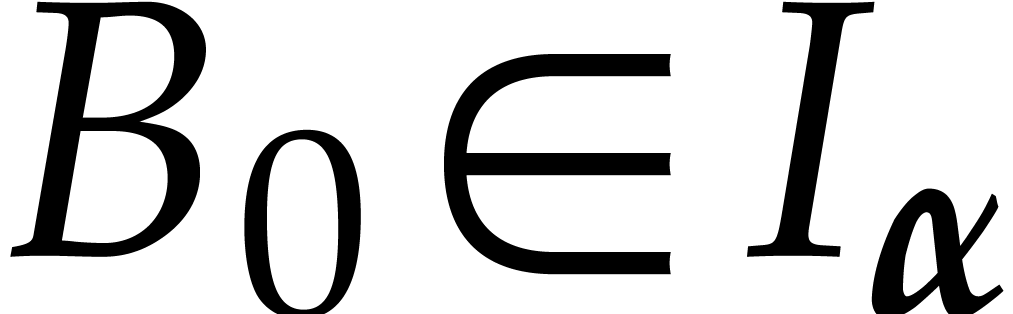 for
for  of
degree
of
degree
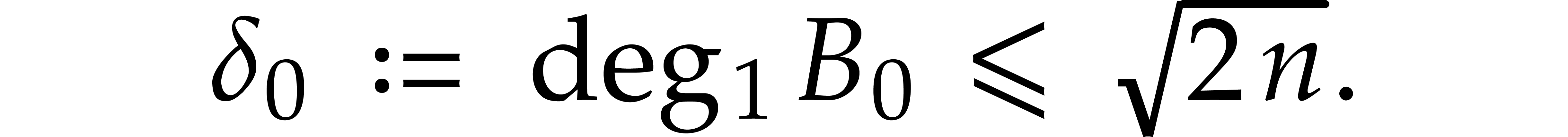
For  , let
, let 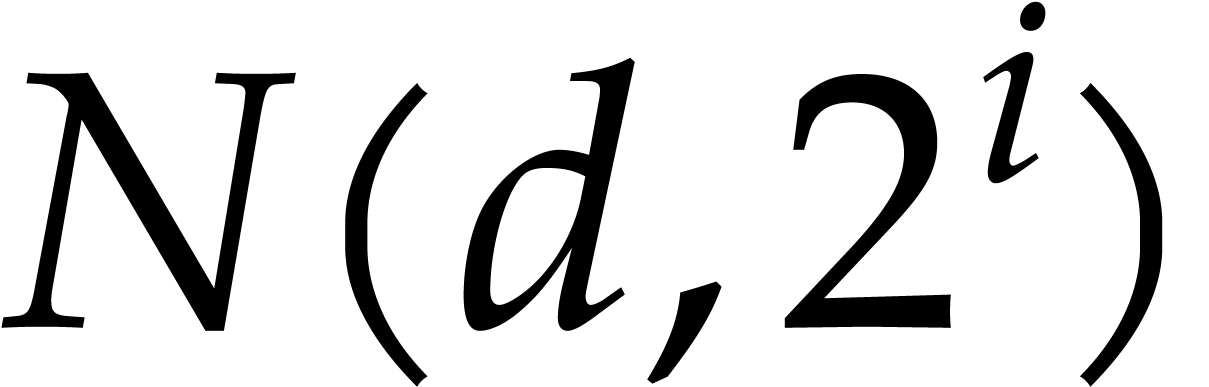 denote the number of monomials of
denote the number of monomials of 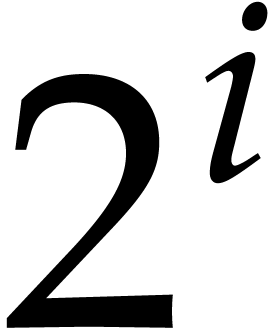 -degree
-degree
 . We have
. We have
The  -vector space of the
polynomials in
-vector space of the
polynomials in 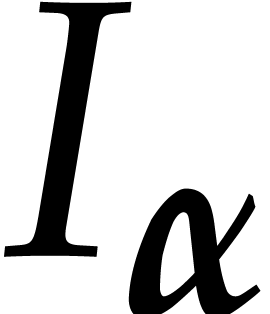 with
with 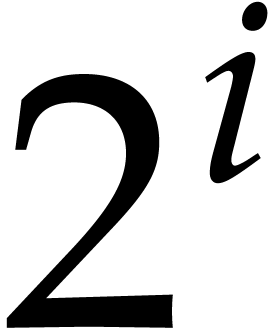 -degree
-degree  is the solution set
of a linear system consisting of
is the solution set
of a linear system consisting of 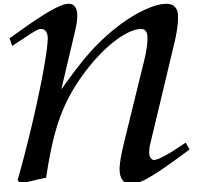 equations and
equations and
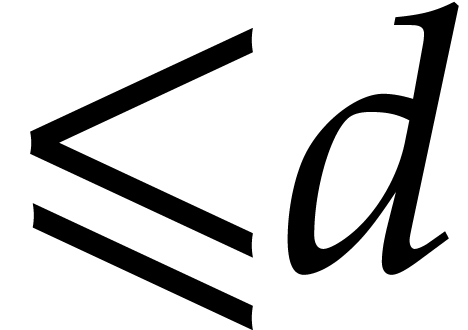
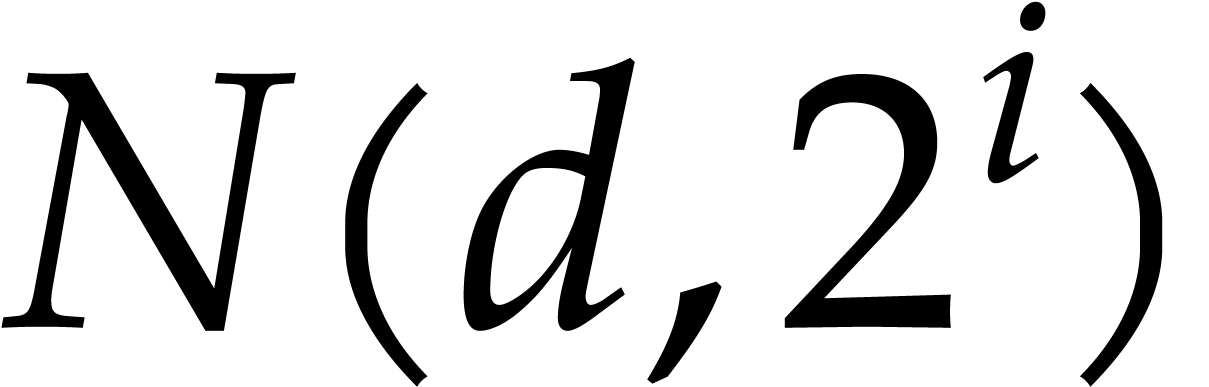 unknowns. Consequently, if
unknowns. Consequently, if 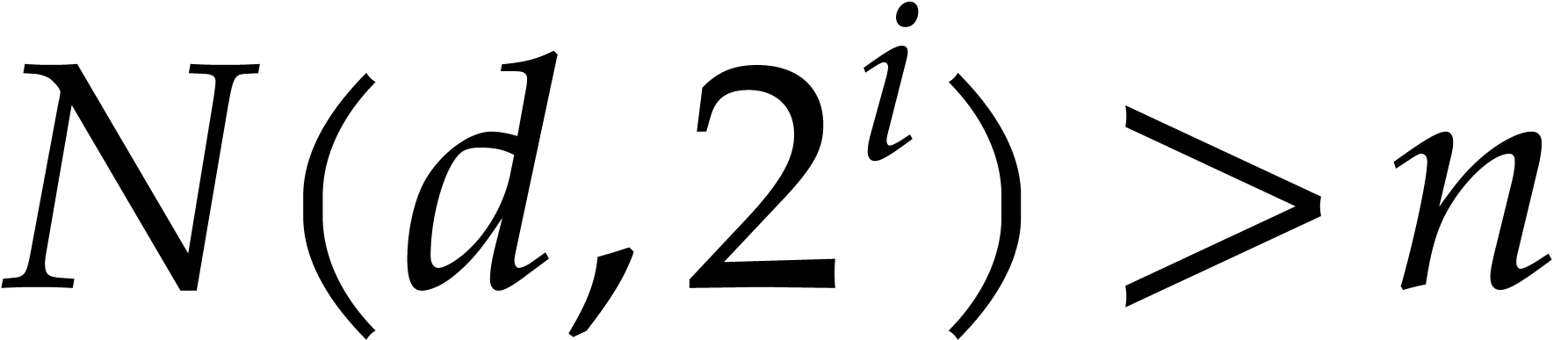 , then there exists a non-zero polynomial in
, then there exists a non-zero polynomial in
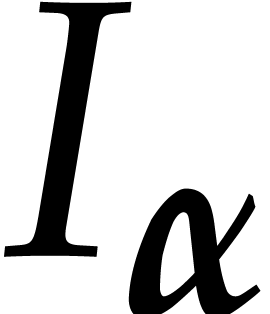 of
of 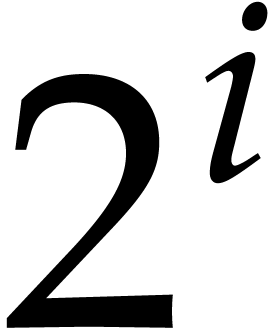 -degree
-degree
 . Let
. Let  be a monic polynomial whose leading monomial is minimal for
be a monic polynomial whose leading monomial is minimal for 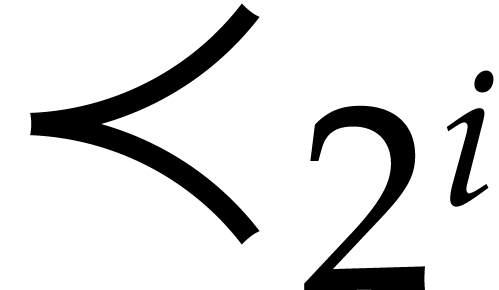 and set
and set

We may precompute 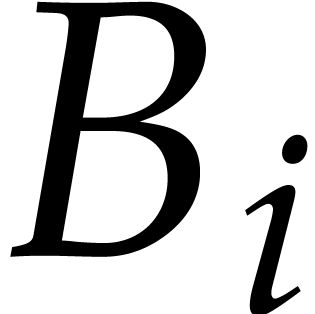 ,
e.g. by extracting it from a Gröbner basis for
,
e.g. by extracting it from a Gröbner basis for 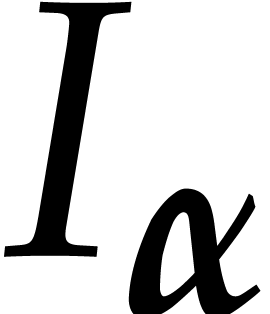 with respect to
with respect to 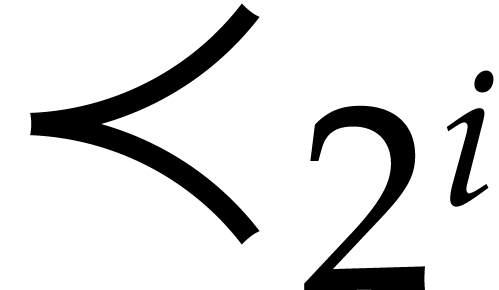 .
By the minimality of the
.
By the minimality of the 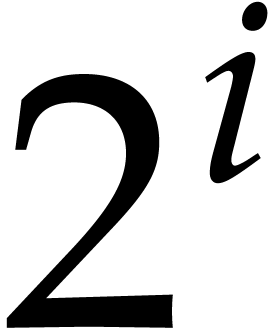 -degree
-degree
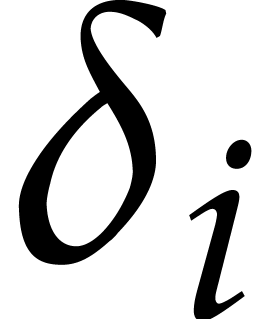 of
of 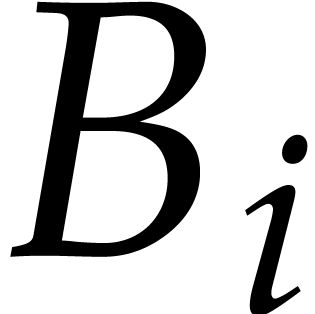 ,
we have
,
we have
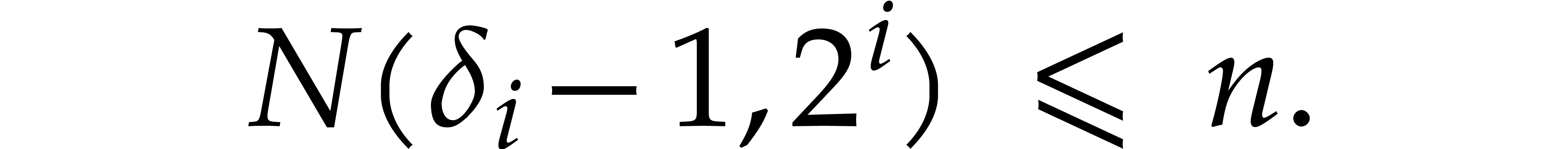
Now write 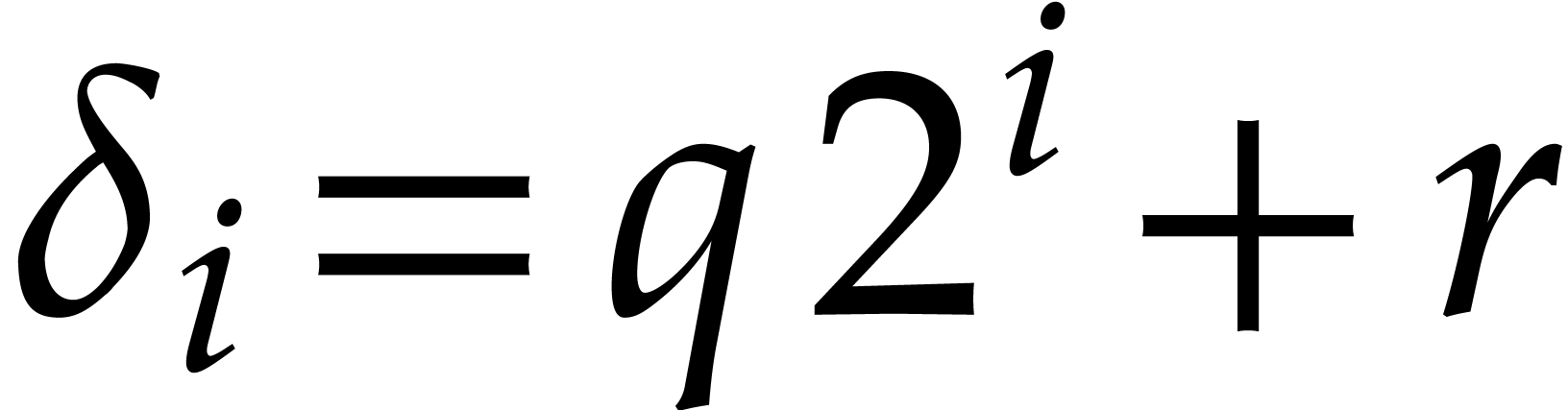 with
with 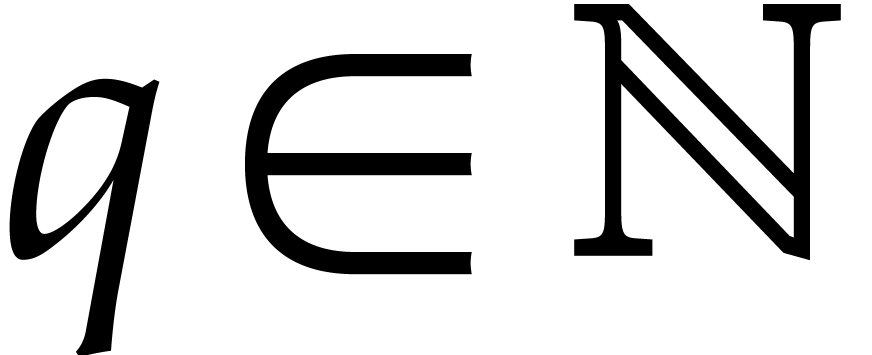 and
and  . Then
. Then
Consequently, 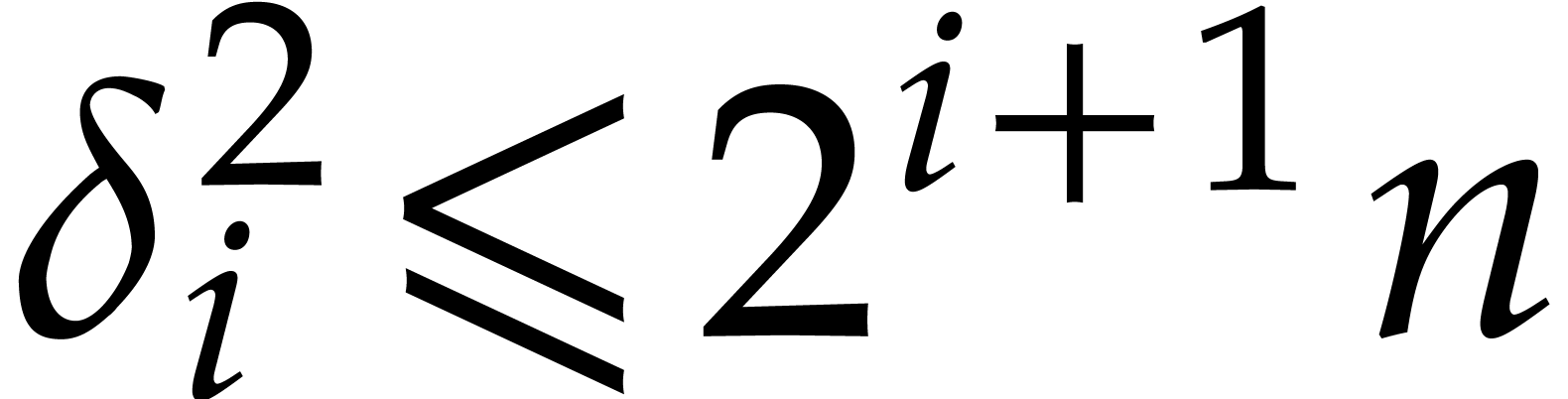 and
and
We let 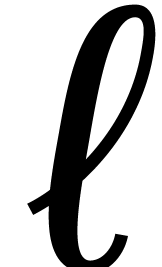 be the smallest integer such that
be the smallest integer such that 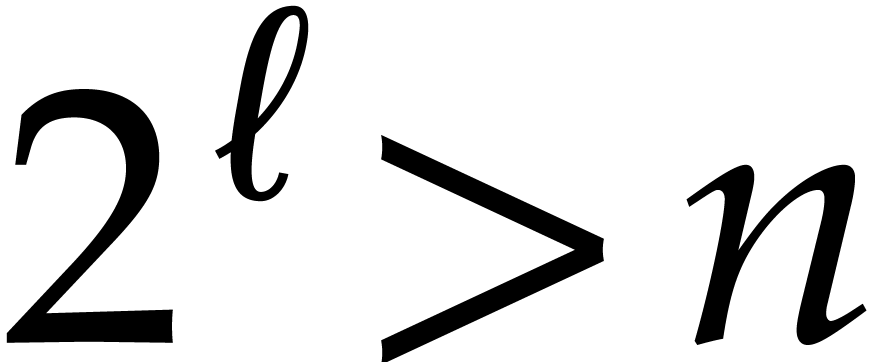 , hence
, hence
and 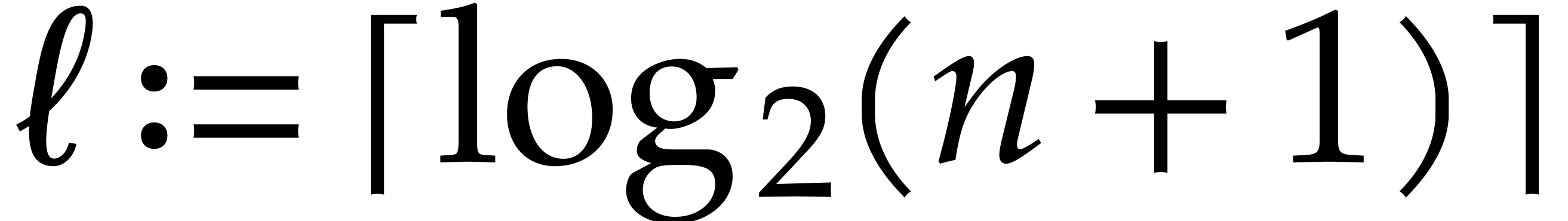 . There exists a monic
non-zero polynomial
. There exists a monic
non-zero polynomial 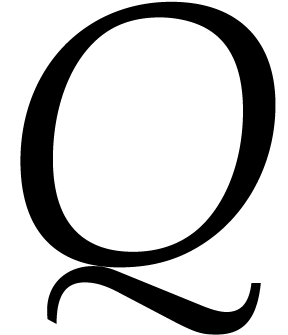 in
in 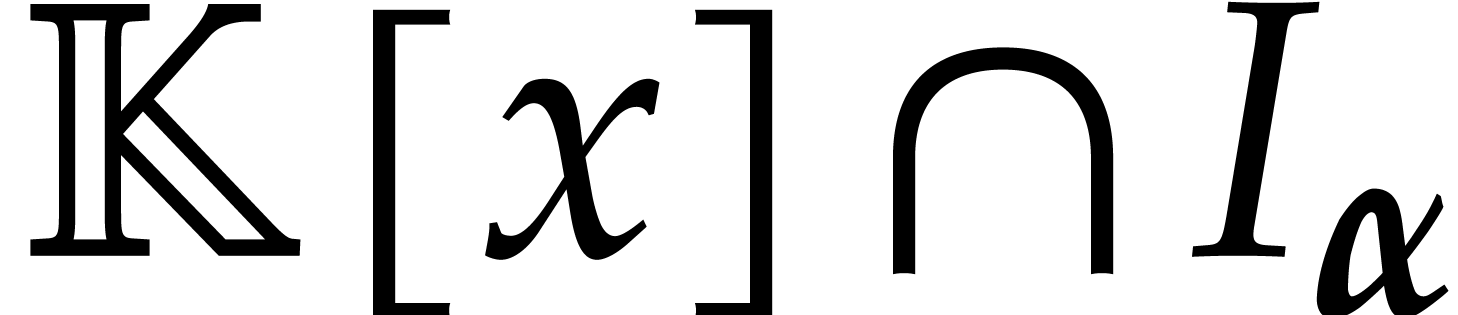 of minimal degree
of minimal degree 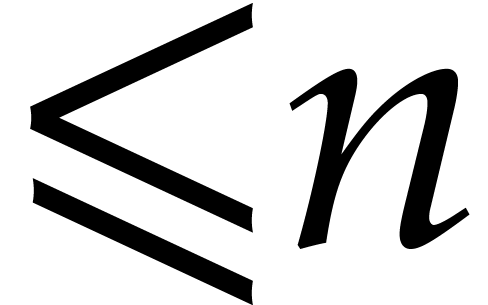 . Since
. Since
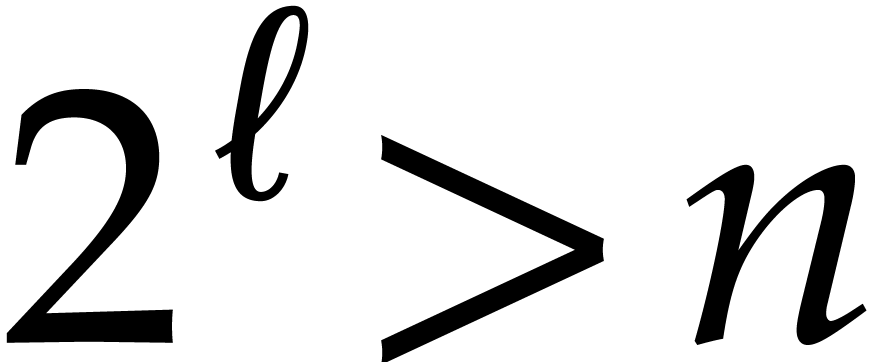 , we may take
, we may take 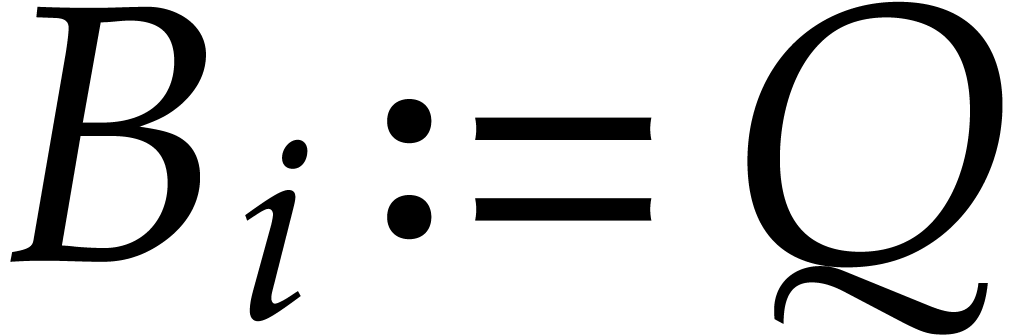 for
for  . We call
. We call
 a heterogeneous basis for
a heterogeneous basis for  . We further define
. We further define
Note that 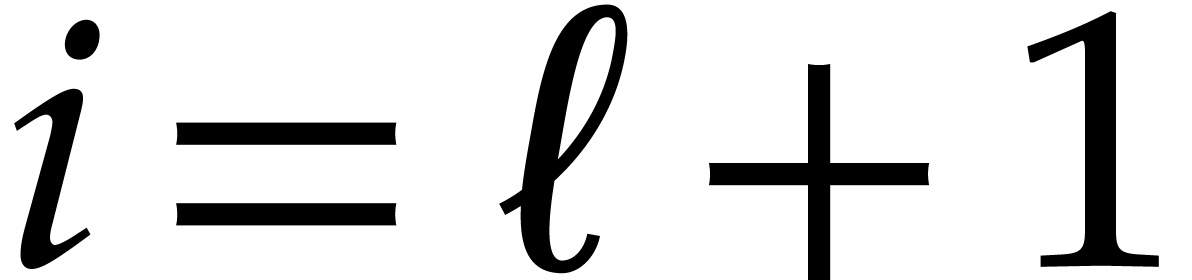 is the first integer such that the
upper bound (7) is zero, although
is the first integer such that the
upper bound (7) is zero, although 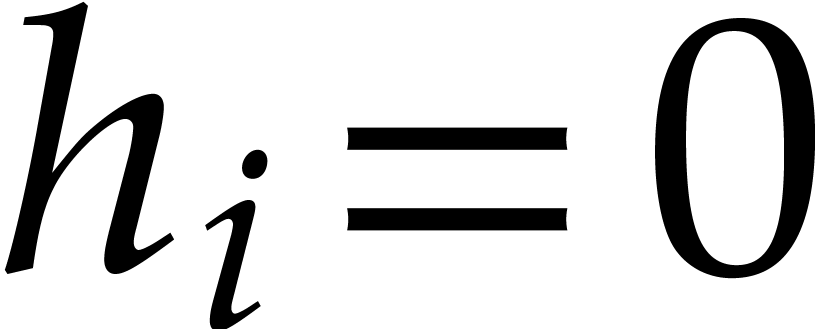 holds even for
holds even for 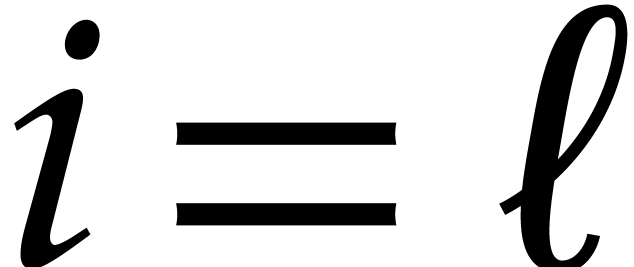 .
.
Remark. If the  are
pairwise distinct and if the cardinality of
are
pairwise distinct and if the cardinality of  is
sufficiently large, then, after a sufficiently generic linear change of
coordinates, a Gröbner basis for
is
sufficiently large, then, after a sufficiently generic linear change of
coordinates, a Gröbner basis for  with
respect to the lexicographic ordering induced by
with
respect to the lexicographic ordering induced by  can be computed in softly linear time: see [22, section 6],
for instance. Then, a Gröbner basis for
can be computed in softly linear time: see [22, section 6],
for instance. Then, a Gröbner basis for 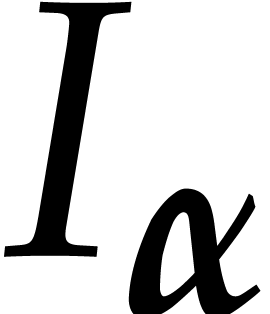 with respect to
with respect to 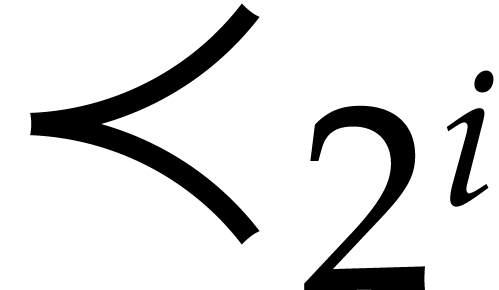 can be deduced with
can be deduced with 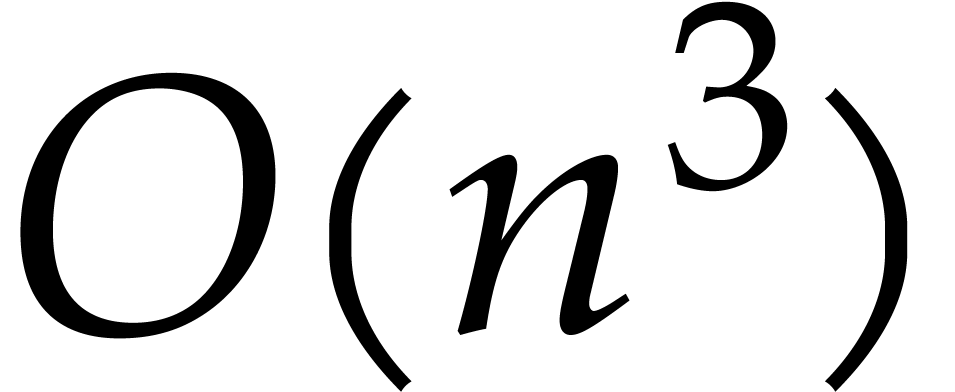 operations in
operations in  thanks to the FGLM
algorithm [5]. This bound has recently been lowered to
thanks to the FGLM
algorithm [5]. This bound has recently been lowered to 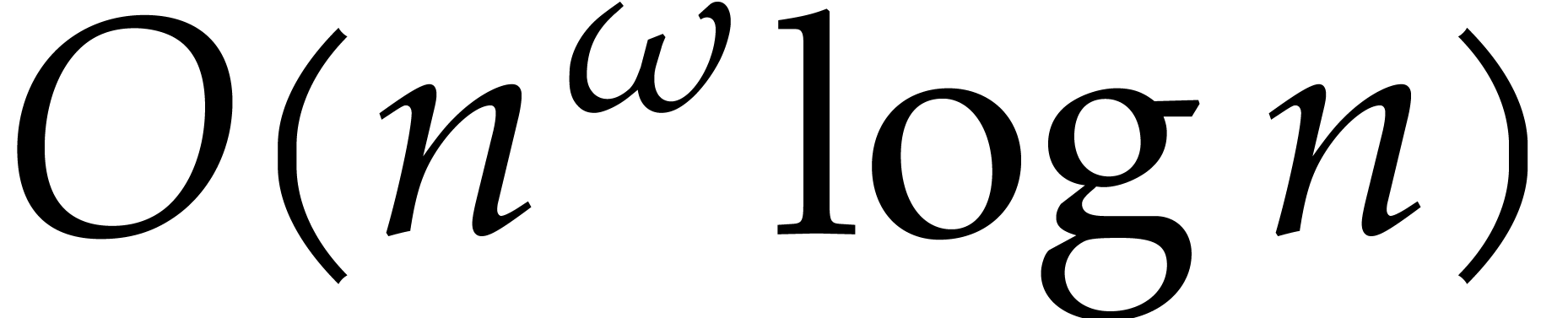 in [21, Theorem 1.7, Example 1.3], where
in [21, Theorem 1.7, Example 1.3], where
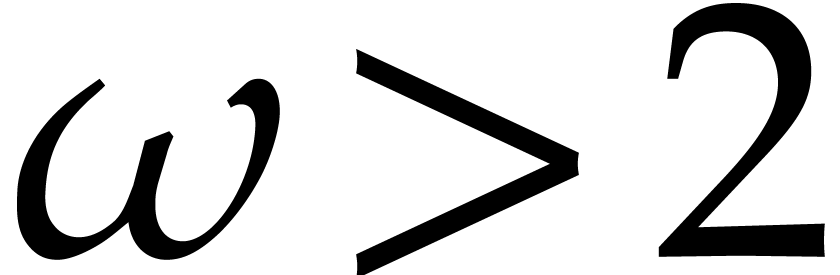 is a feasible exponent for matrix
multiplication.
is a feasible exponent for matrix
multiplication.
Given 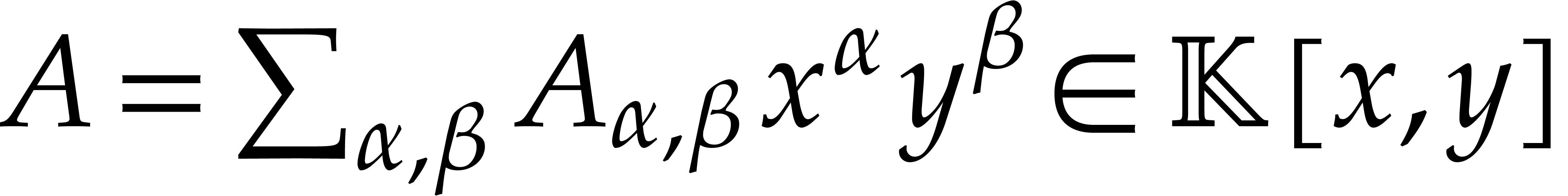 and
and 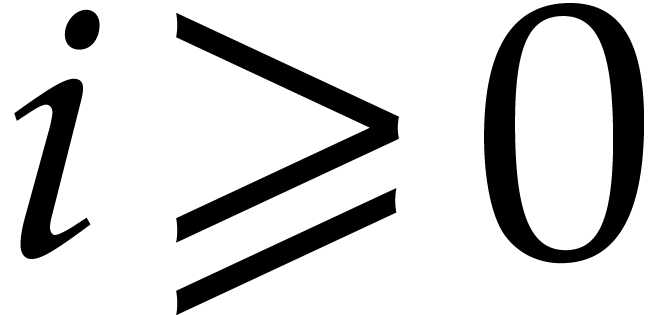 ,
we may use the division procedure from section 2.4 to
reduce
,
we may use the division procedure from section 2.4 to
reduce  with respect to
with respect to 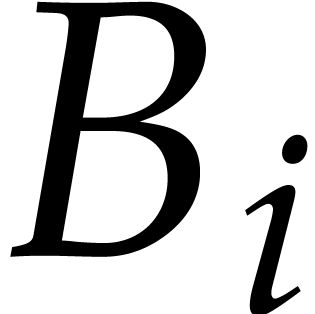 . This yields a relation
. This yields a relation
where 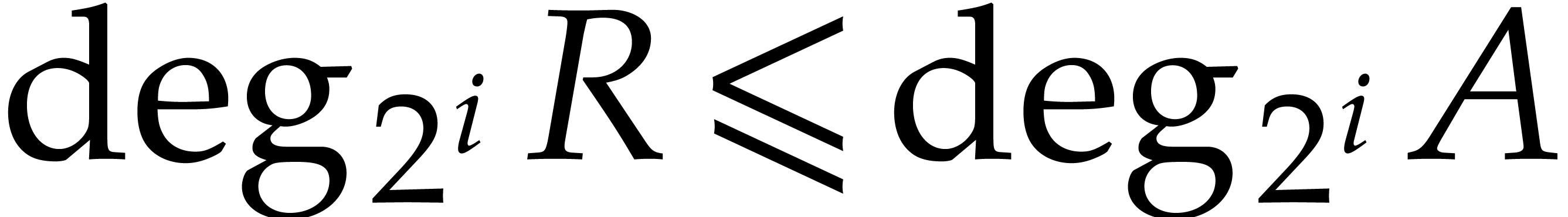 and such that none of the monomials in the
support of
and such that none of the monomials in the
support of 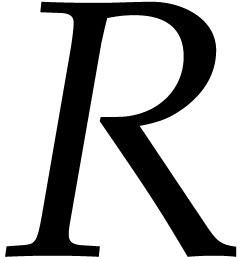 is divisible by the leading monomial
of
is divisible by the leading monomial
of 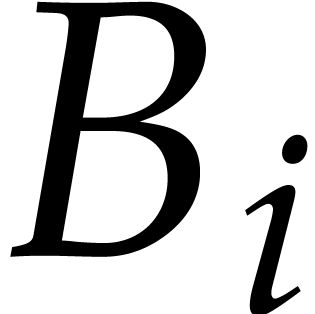 . We write
. We write 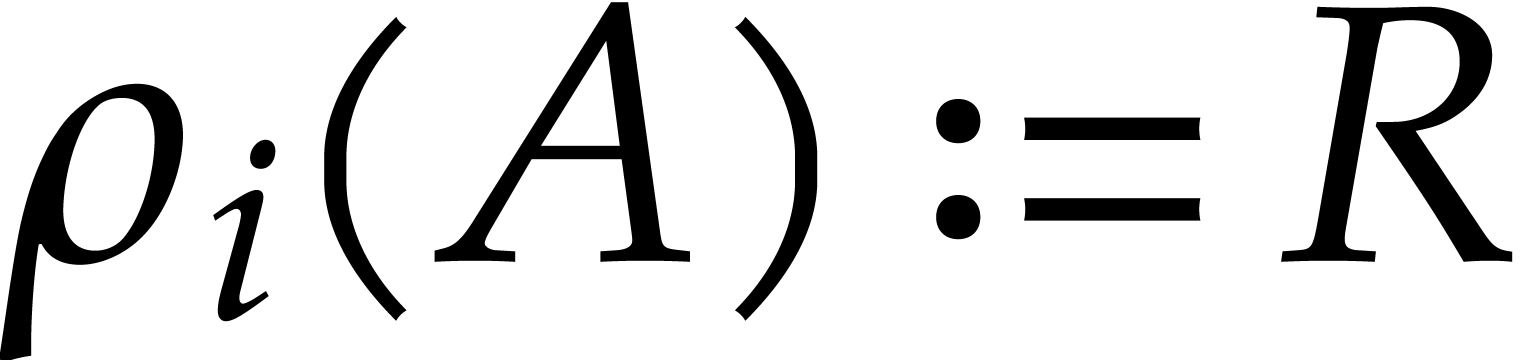 and recall that
and recall that 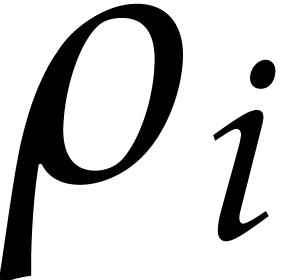 is a
is a  -linear map.
-linear map.
We also define the projections 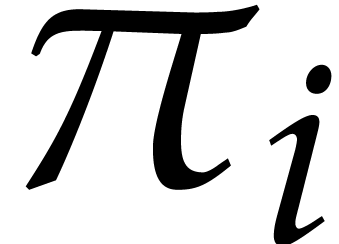 and
and 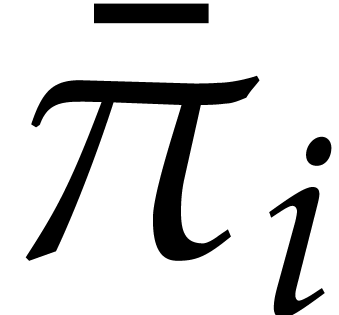 by
by
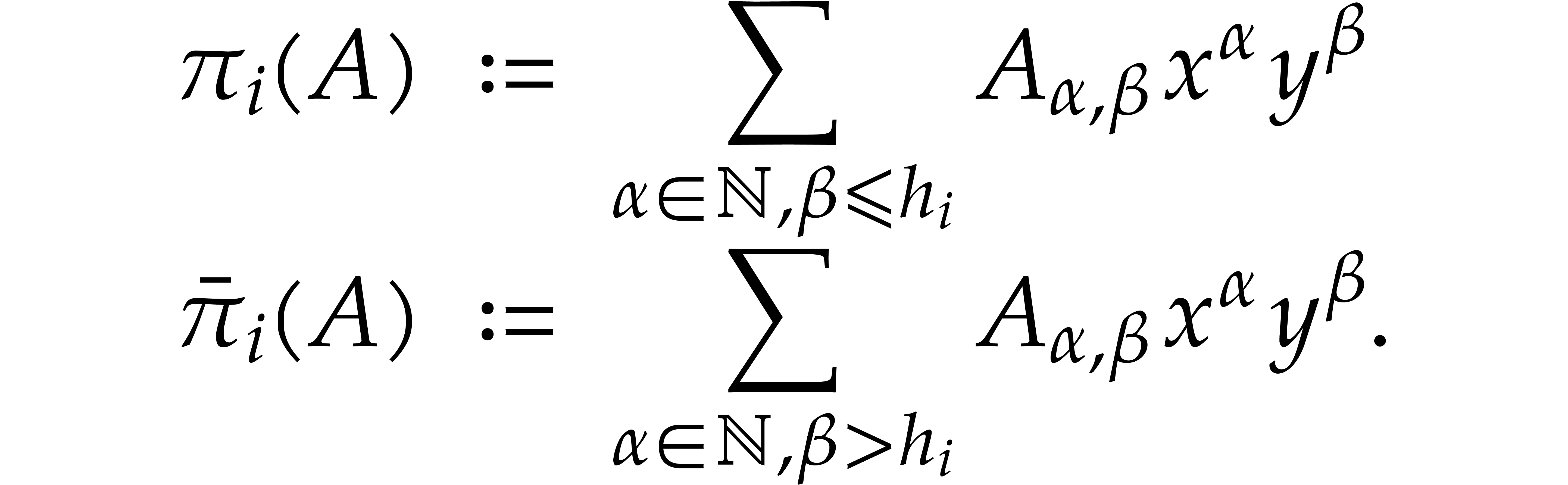
For 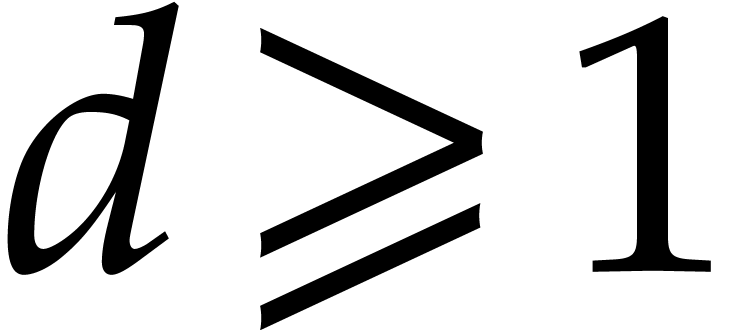 , we let
, we let 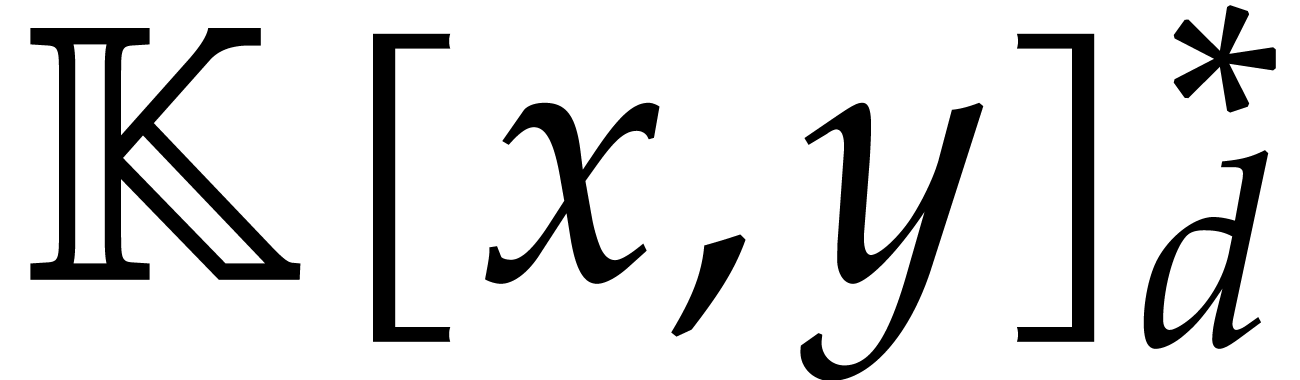 denote the set of tuples of polynomials
denote the set of tuples of polynomials 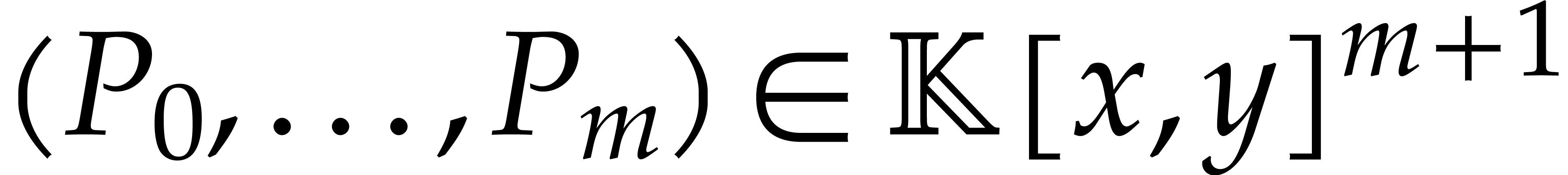 such
that
such
that
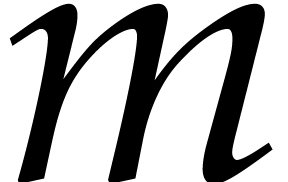 is the first integer such that
is the first integer such that 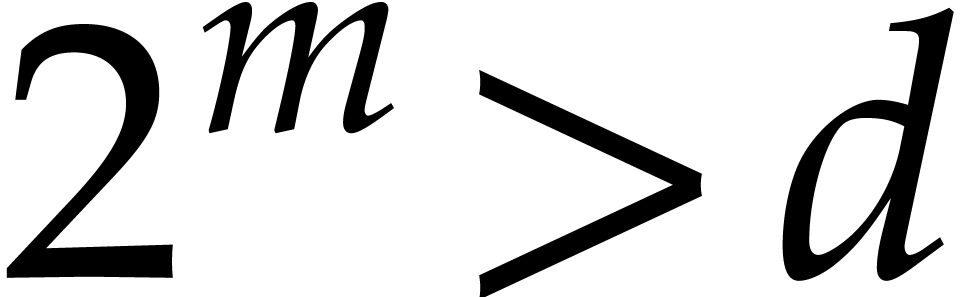 ,
,
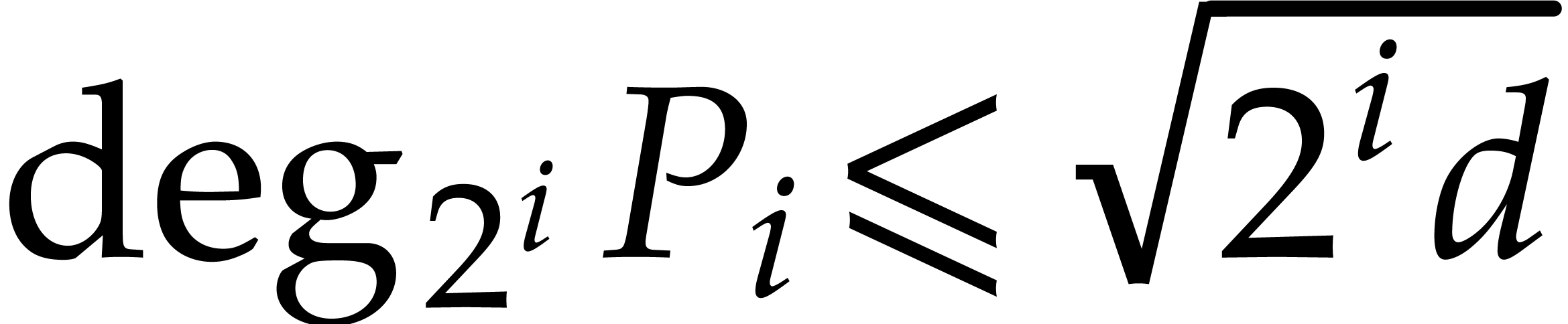 , for
, for 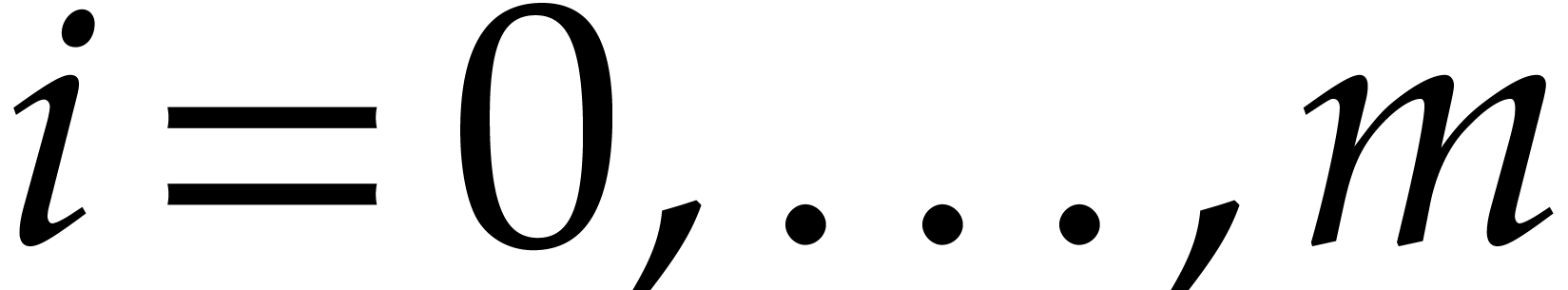 .
.
Intuitively speaking, such a tuple will represent a sum 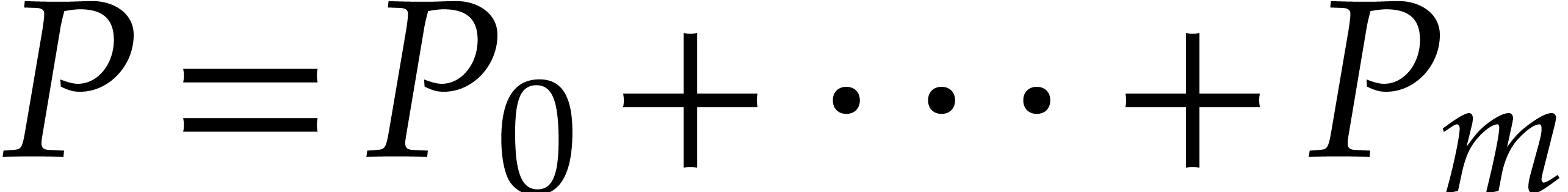 modulo
modulo  . Note that
. Note that 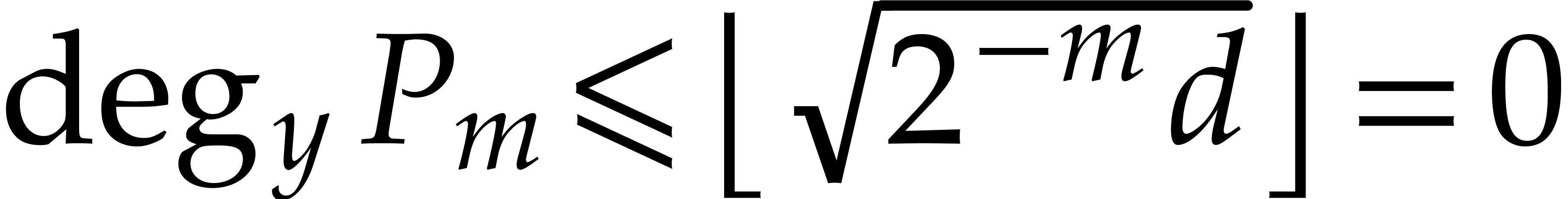 , so
, so 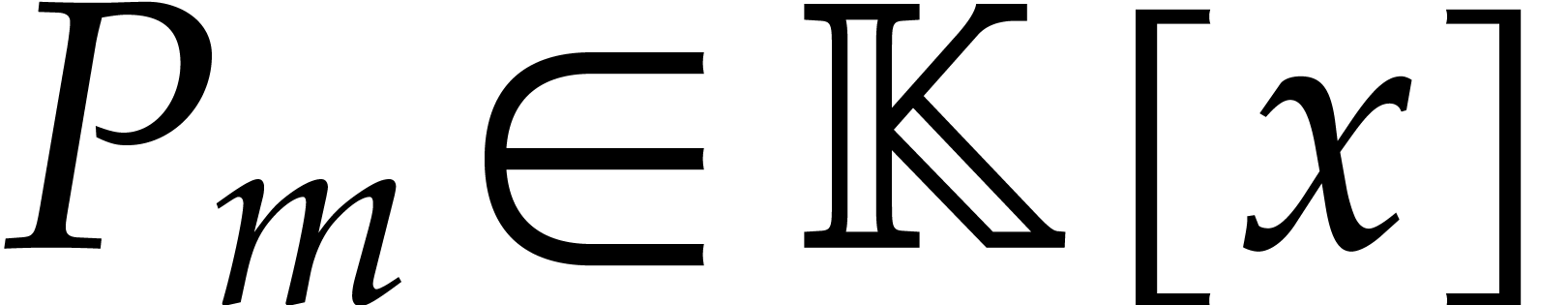 .
.
Given 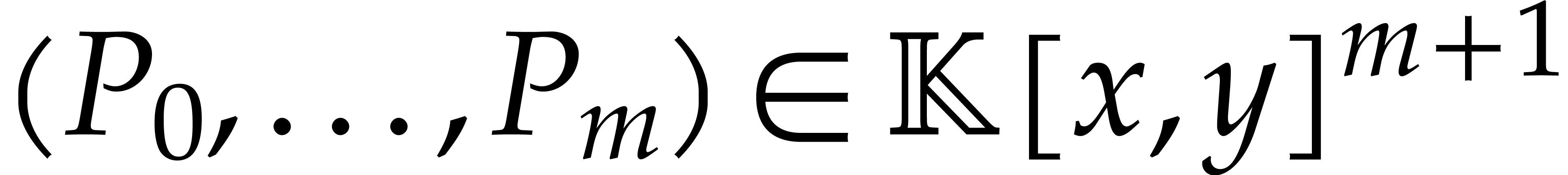 , we define three new
sequences of polynomials by
, we define three new
sequences of polynomials by
Proof. We first note that  and
and
Let us prove the degree bounds by induction on  . For
. For 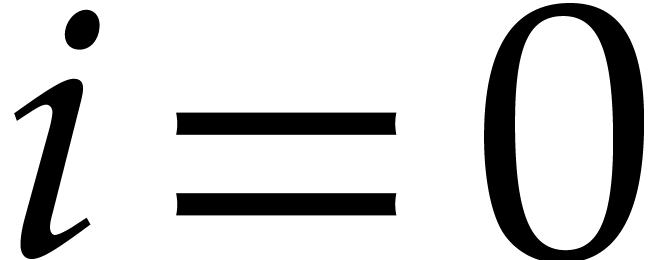 ,
we have
,
we have
by using 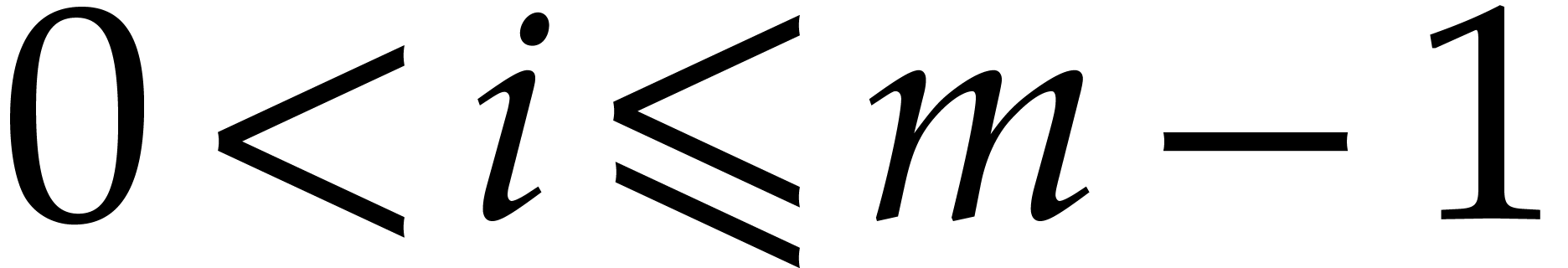 and that
the bounds of the lemma hold for all smaller
and that
the bounds of the lemma hold for all smaller  . Since
. Since  ,
the induction hypothesis yields
,
the induction hypothesis yields
Using
 |
 |
Assume that 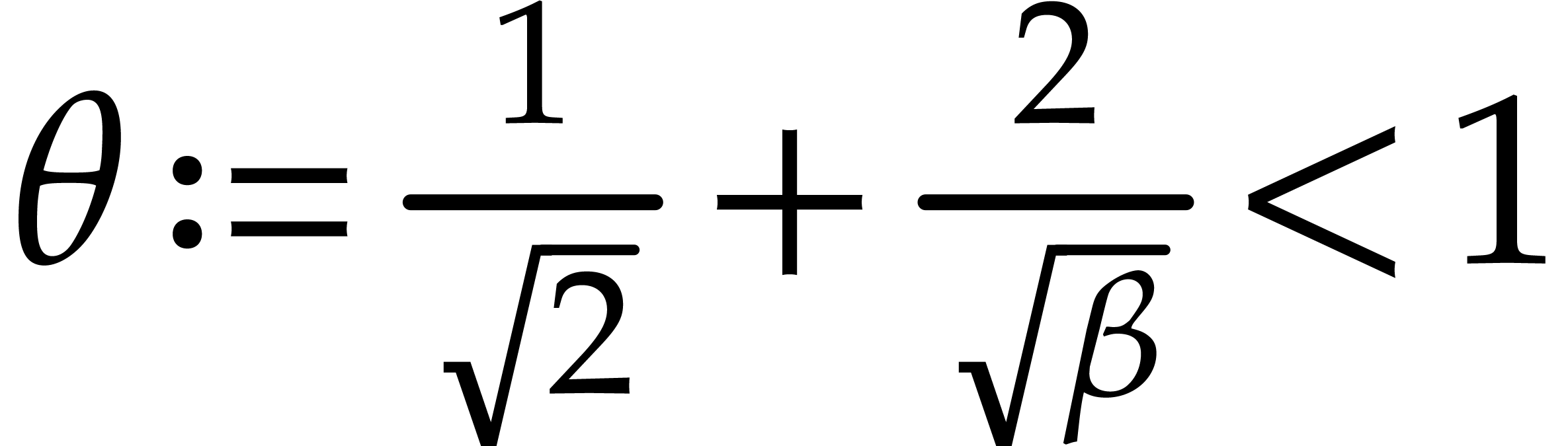 , let
, let  , and let
, and let 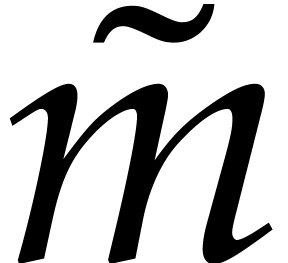 be the first integer such that
be the first integer such that 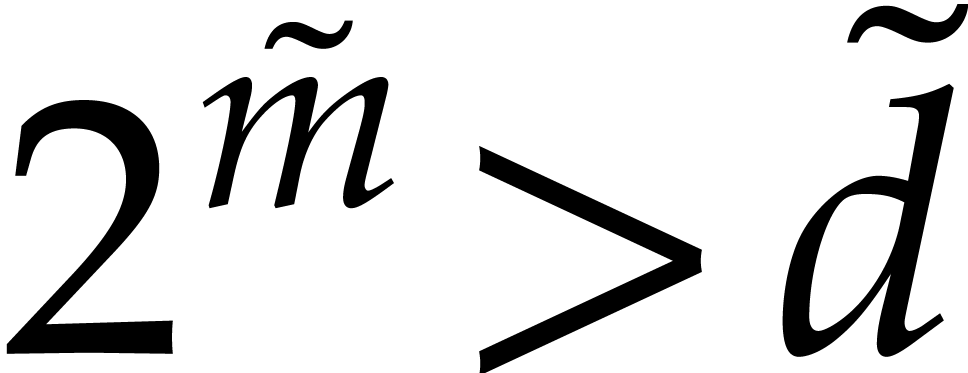 .
If
.
If 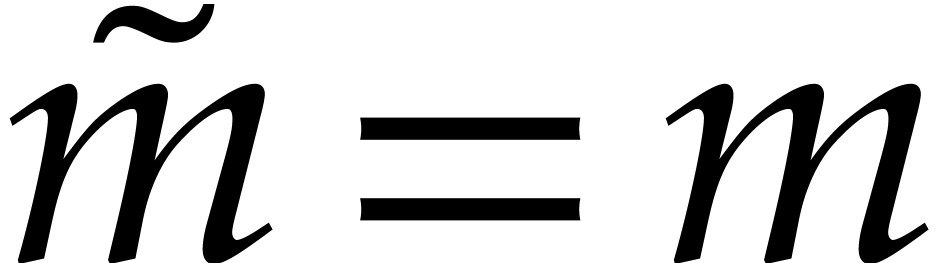 , then
, then
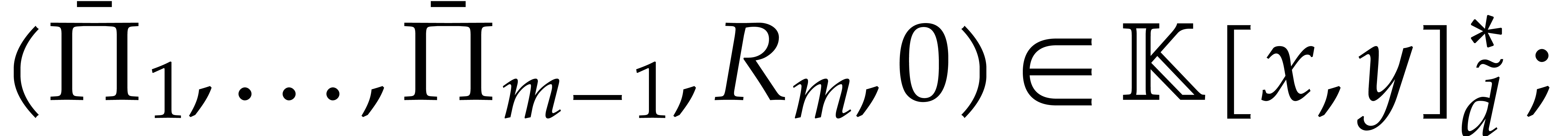
otherwise, 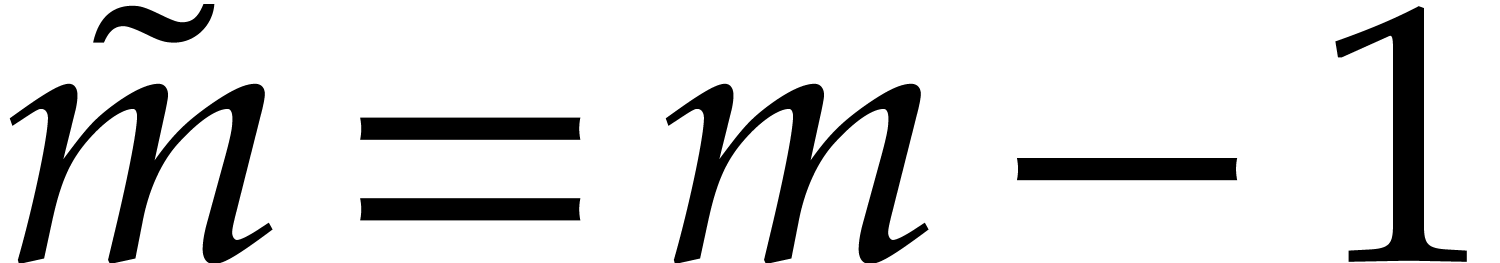 and
and
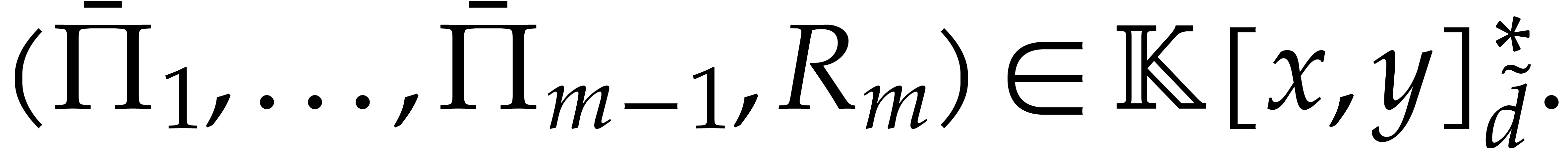
Proof. By construction, we have
whence
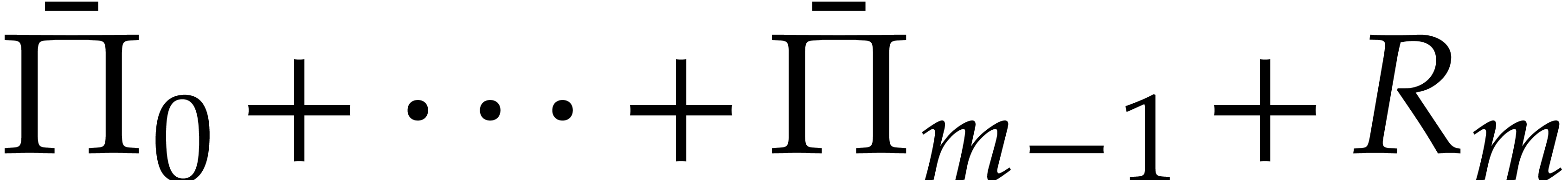 |
 |
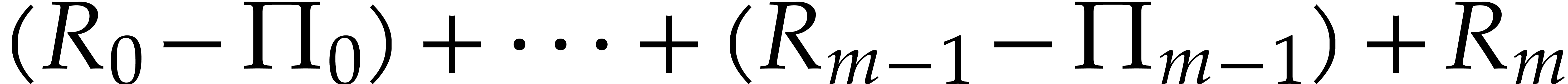 |
|
 |
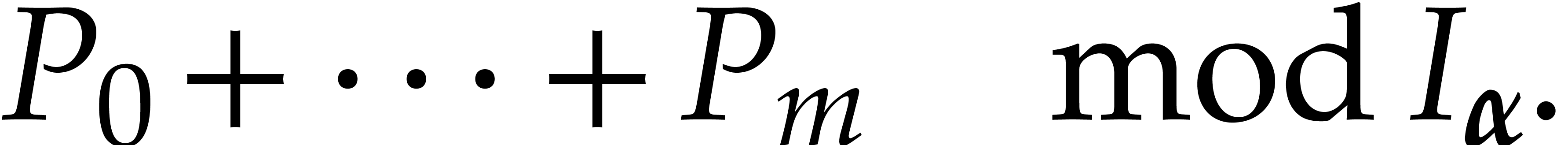 |
Since 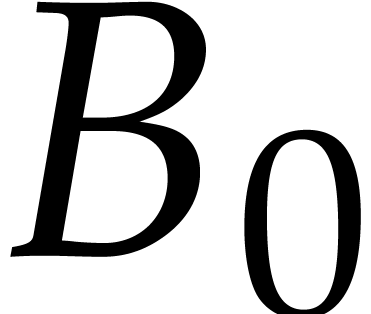 is axial, we have
is axial, we have 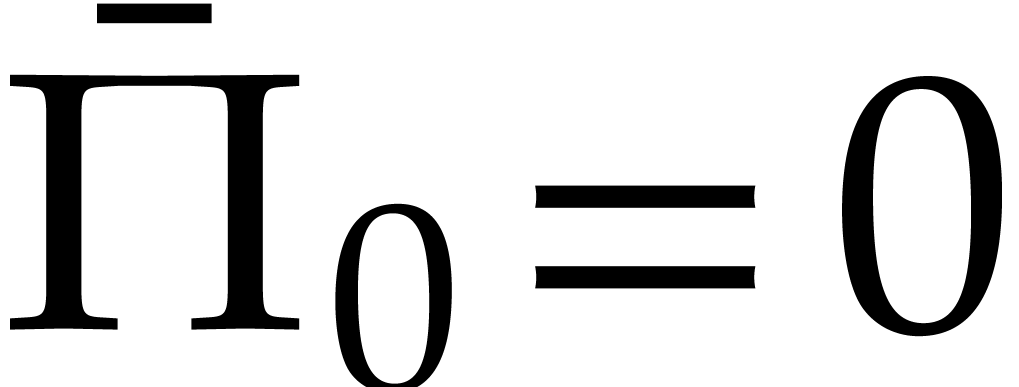 , which entails
, which entails
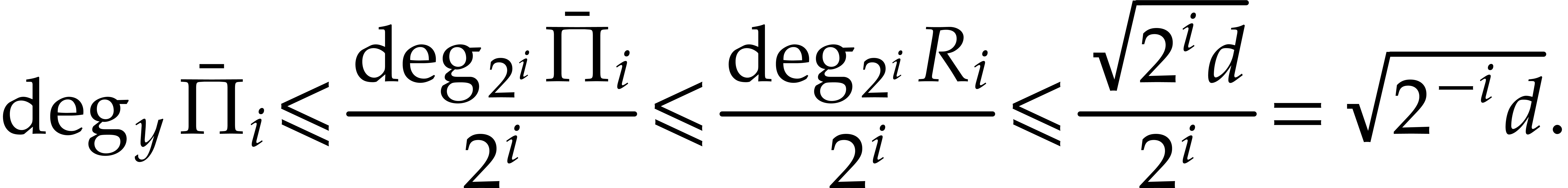 |
(11) |
Now 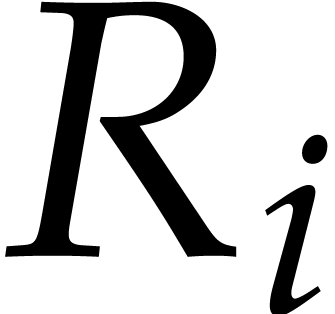 contains no monomial that is divisible by
the leading monomial of
contains no monomial that is divisible by
the leading monomial of 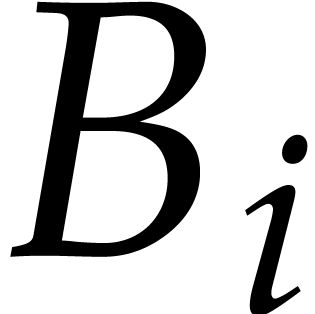 for
for 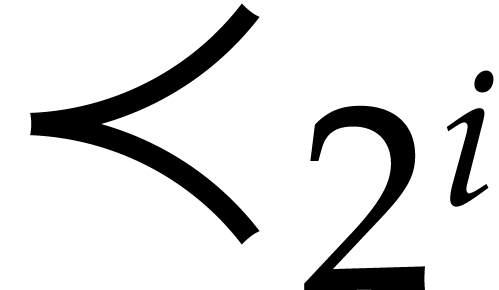 and
and 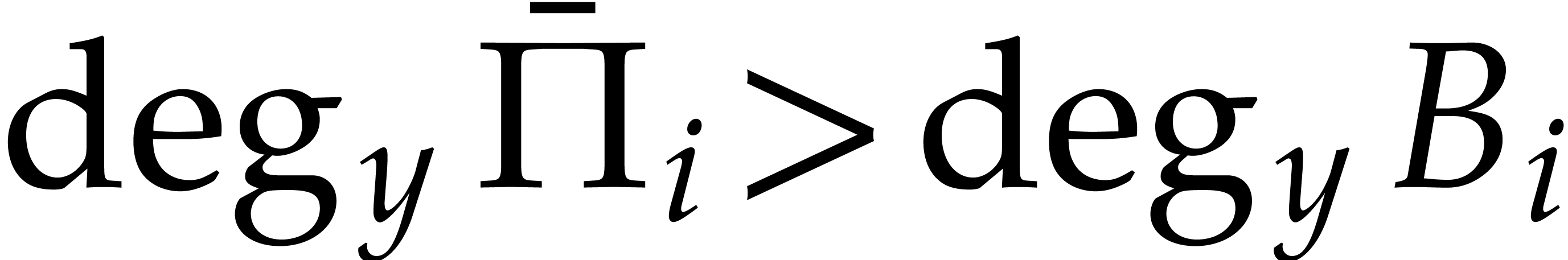 . Using
. Using
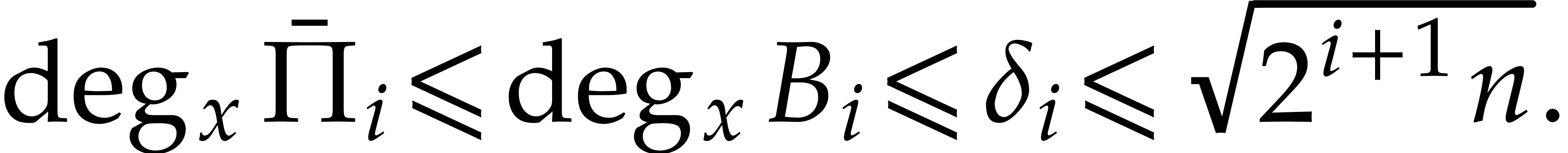 |
(12) |
Consequently, for  ,
inequalities
,
inequalities 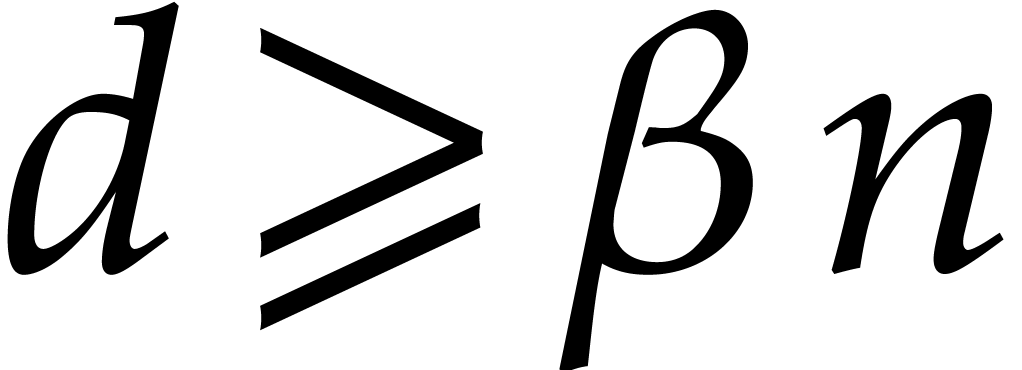 ,
lead to
,
lead to
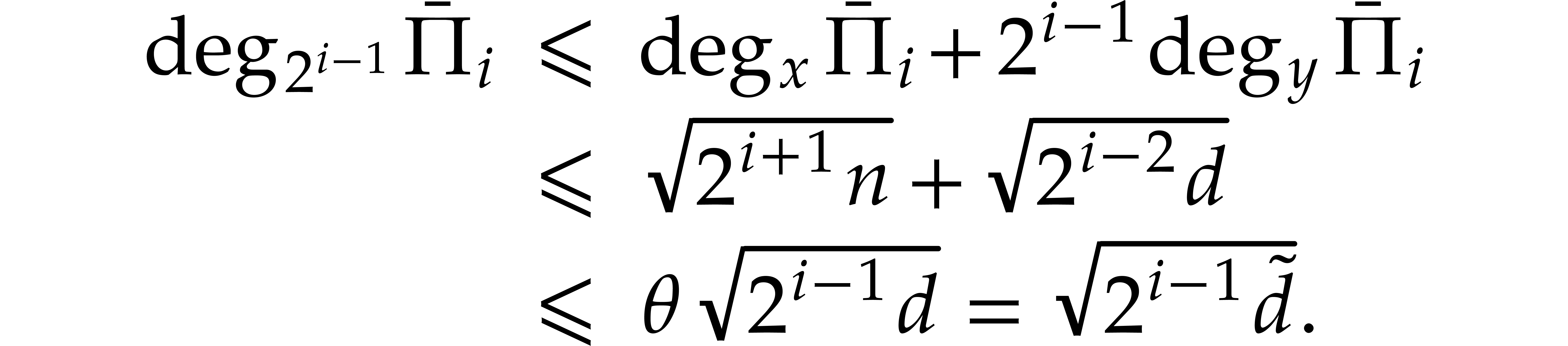
From 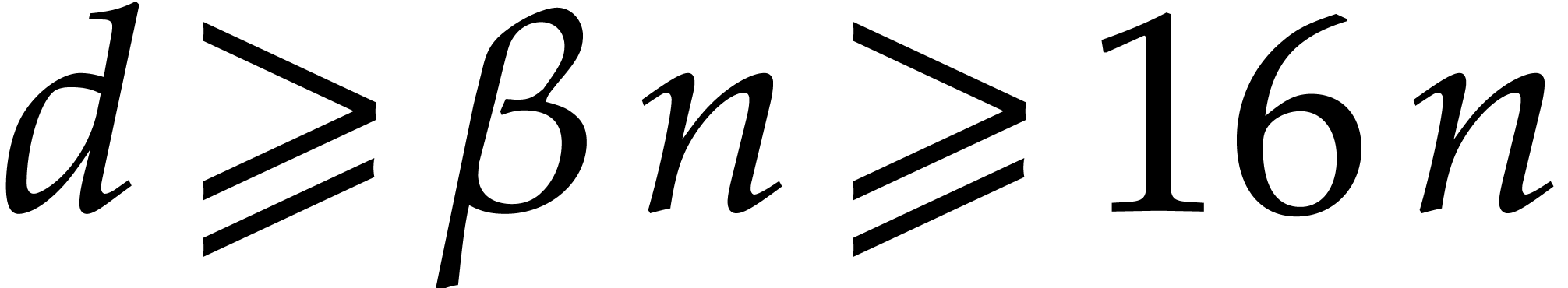 and
and 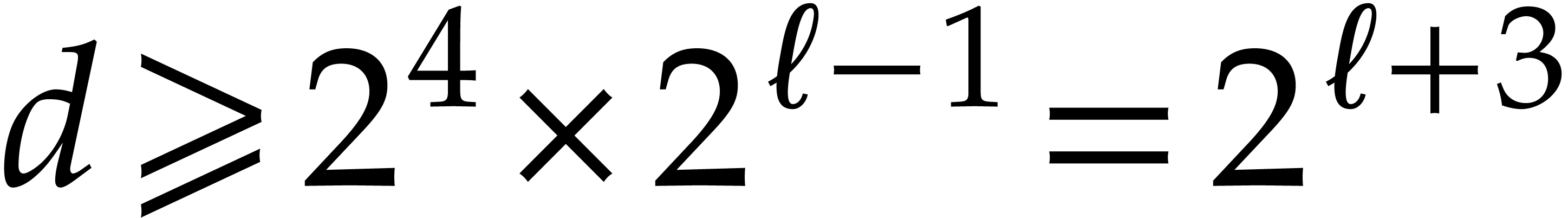 , whence
, whence 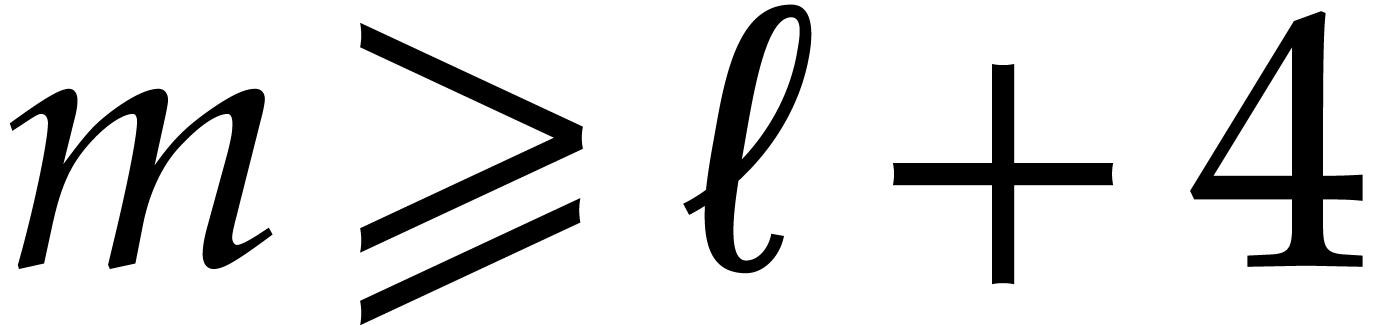 . If follows that
. If follows that
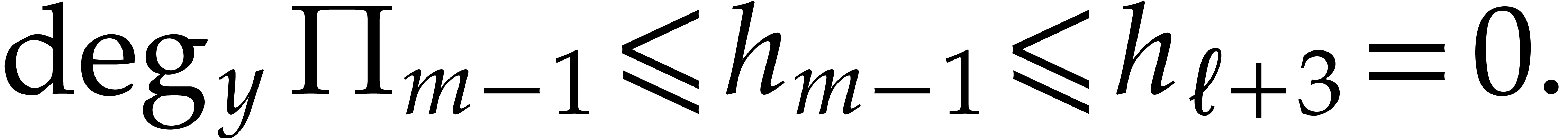
From 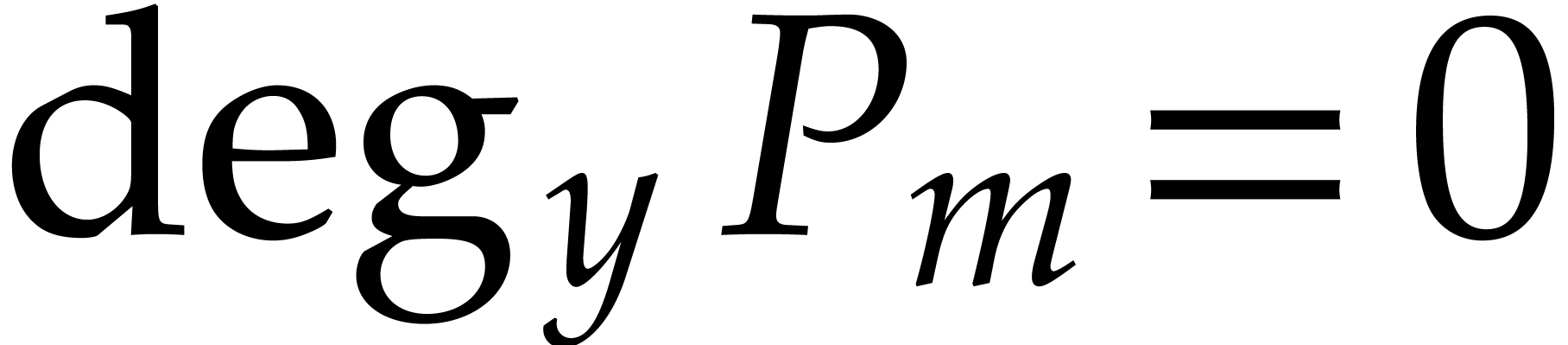 , we thus obtain
, we thus obtain 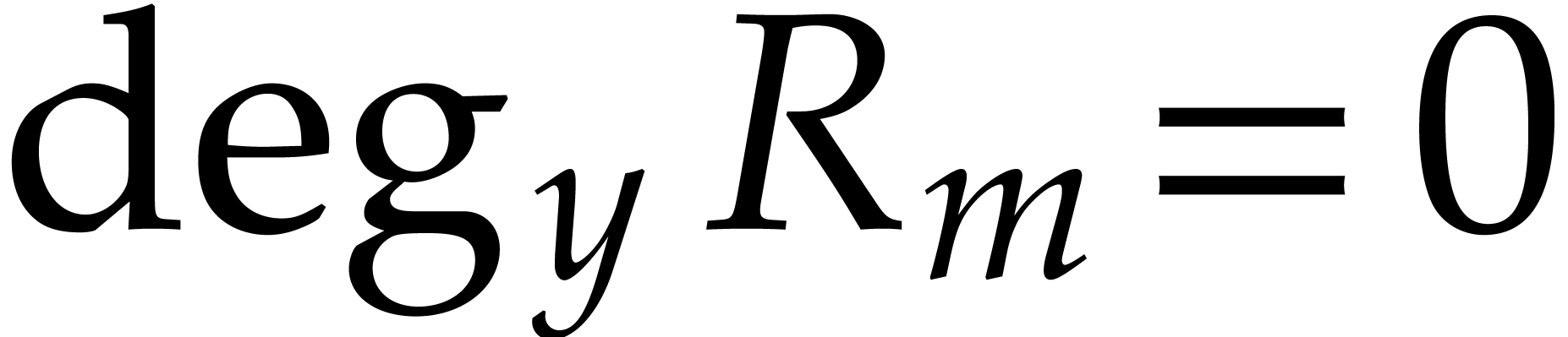 . Since
. Since 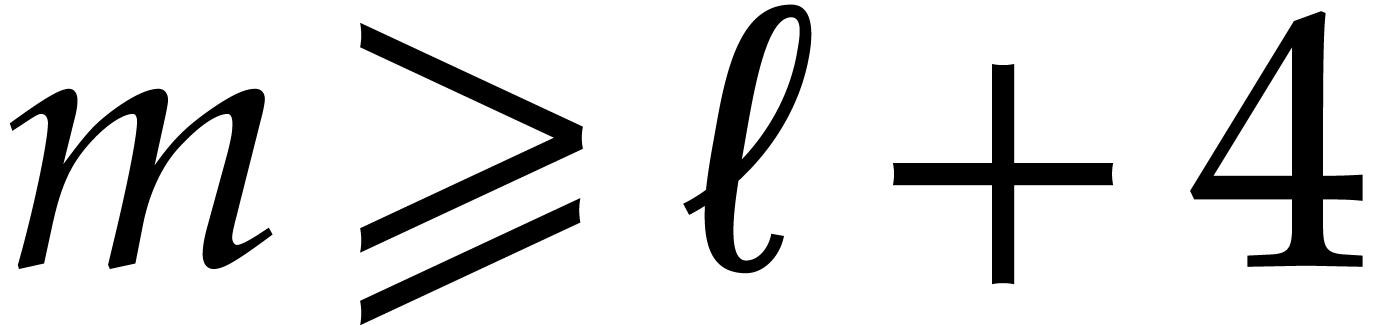 , the polynomial
, the polynomial 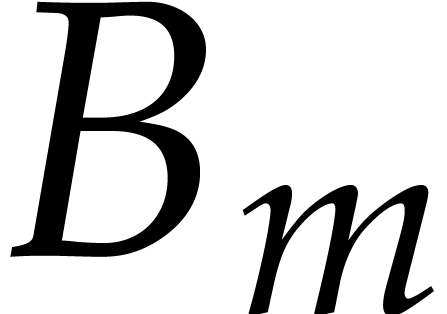 belongs to
belongs to
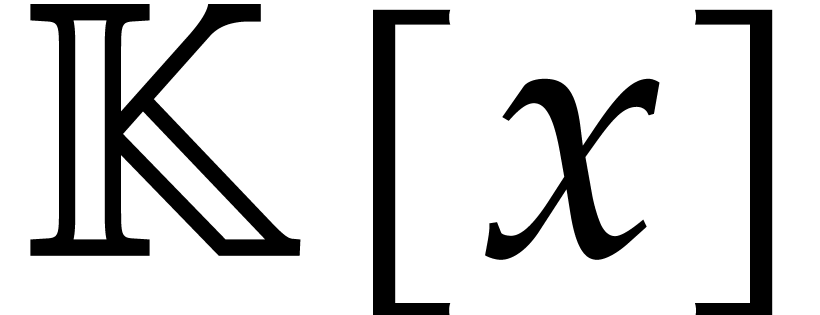 and has degree
and has degree 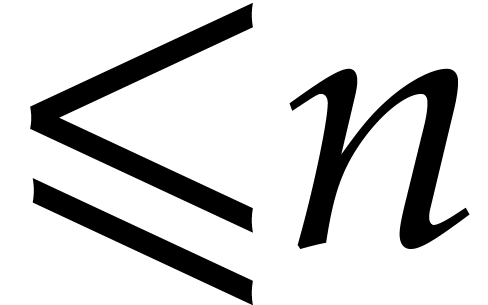 .
It follows that
.
It follows that 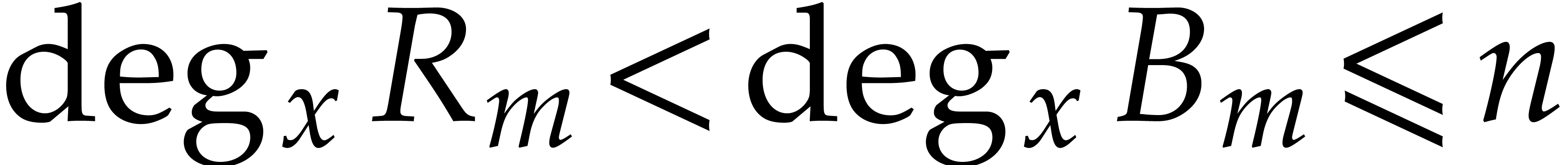 .
.
Since 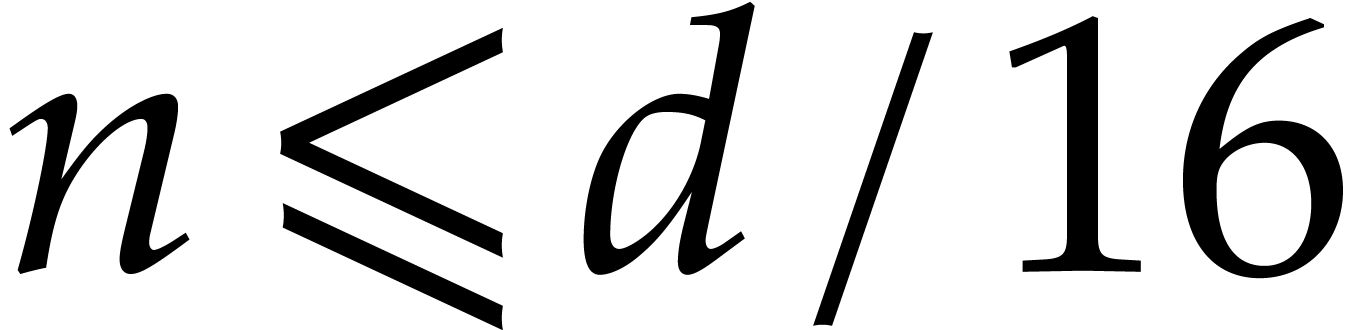 and
and 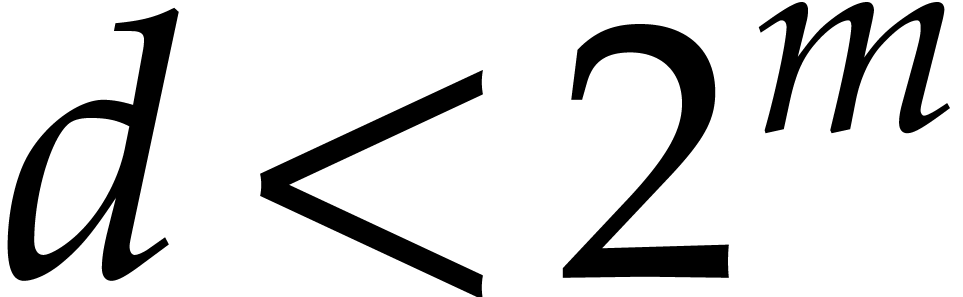 ,
we further deduce
,
we further deduce
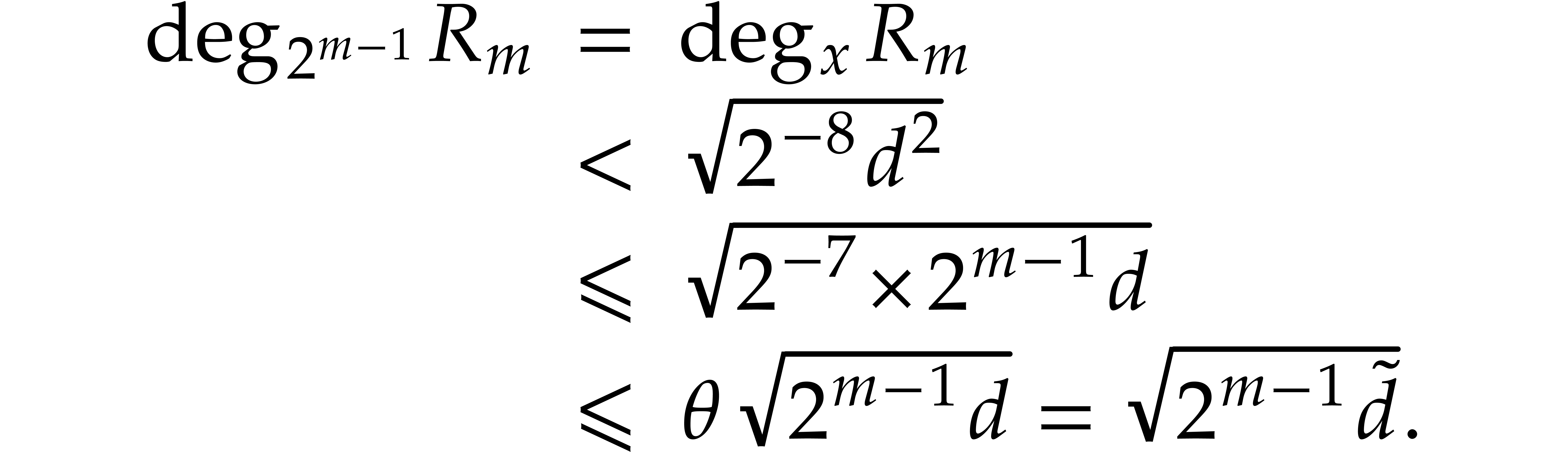
Finally 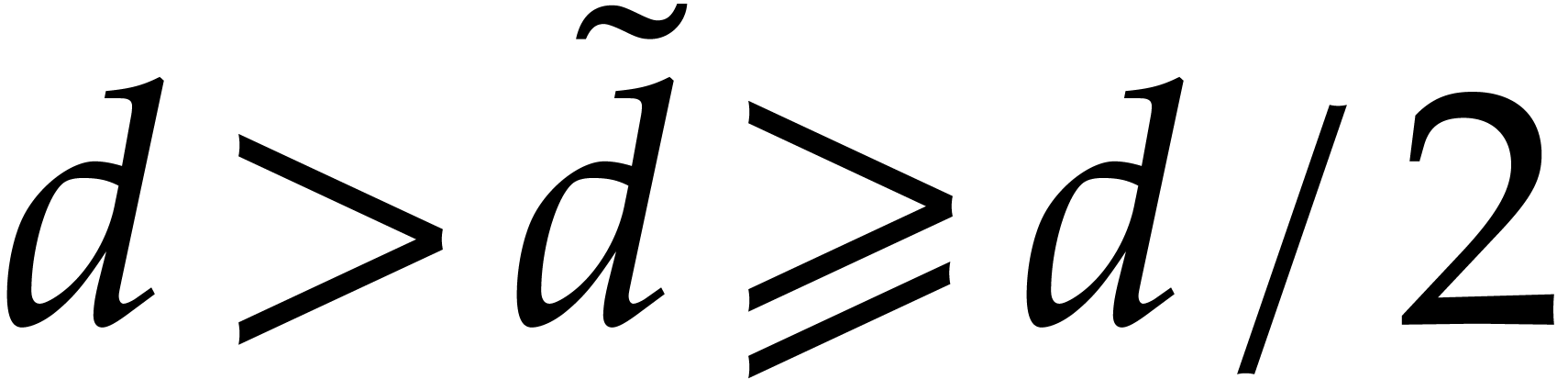 and
and  imply
imply 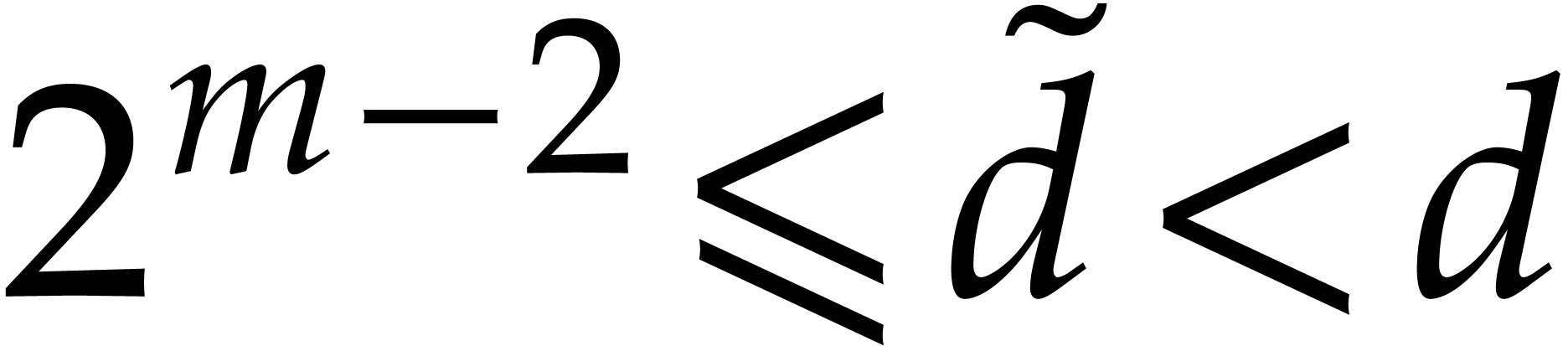 , whence
, whence 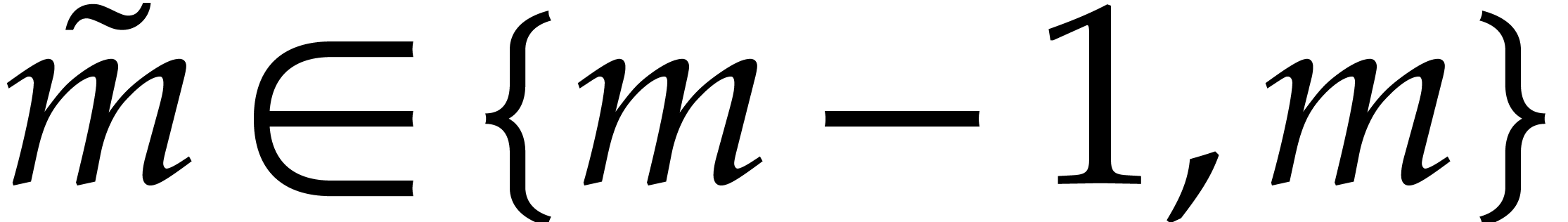 .
.
We call the tuple 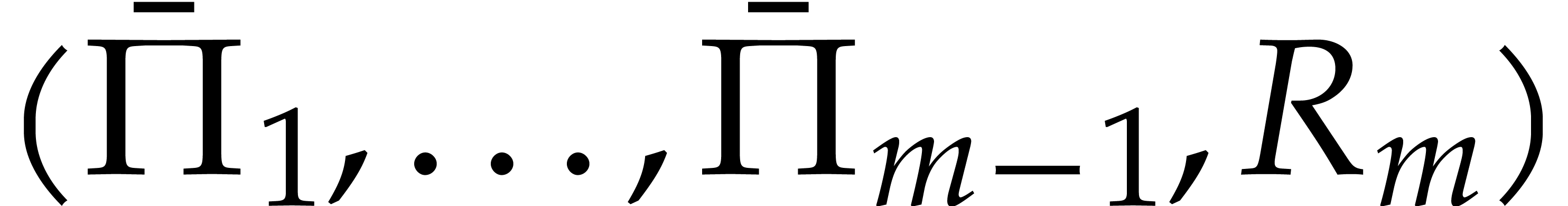 the reduction of
the reduction of  with respect to
with respect to  .
.
 with respect to
with respect to  takes
takes
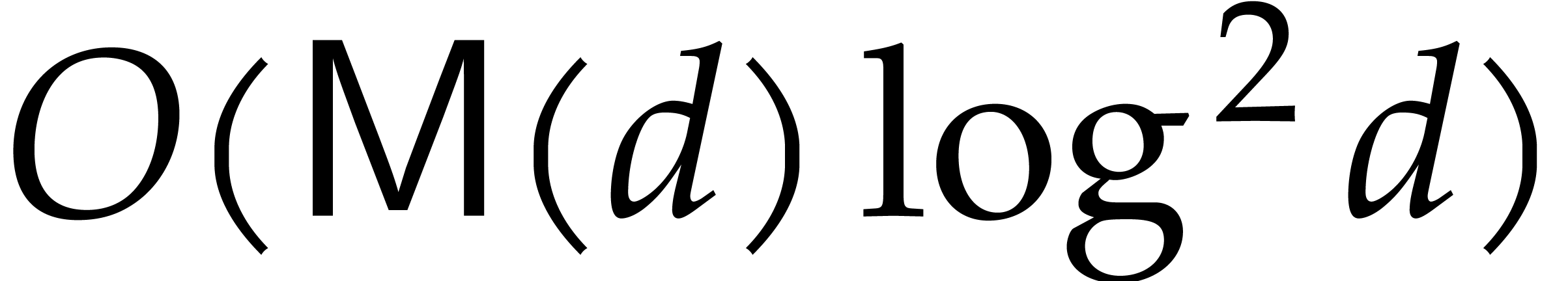 operations in
operations in  .
.
Proof. First note that 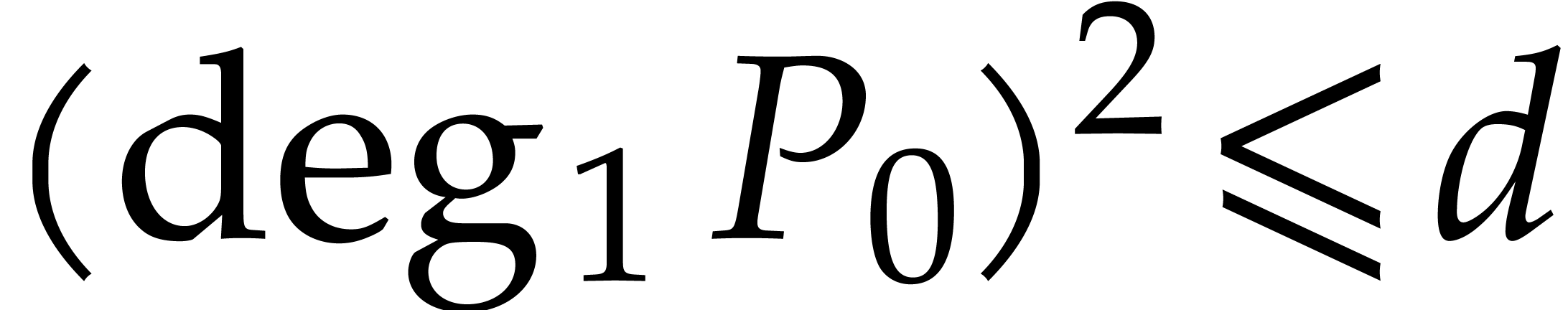 and
and 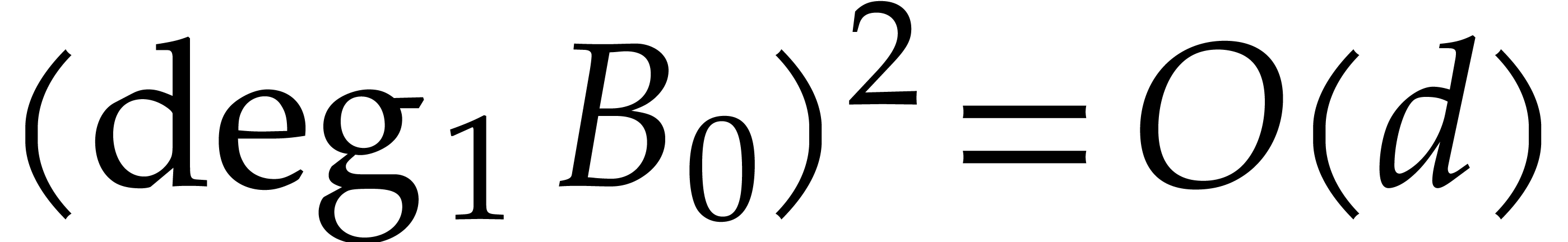 . By Corollary 5,
the computation of
. By Corollary 5,
the computation of 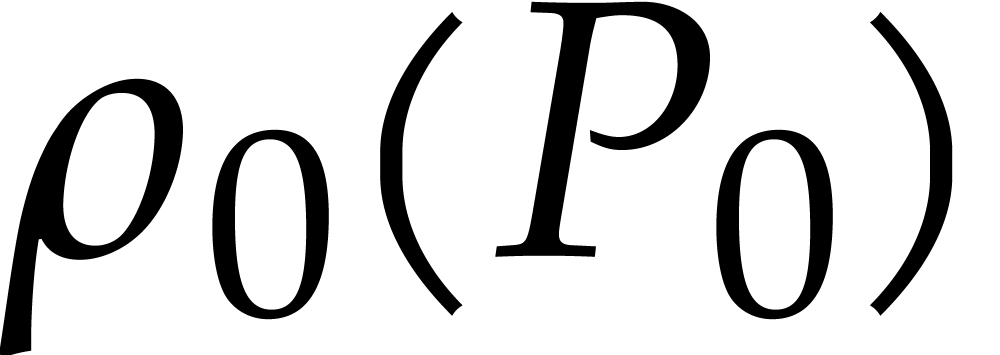 therefore takes
therefore takes 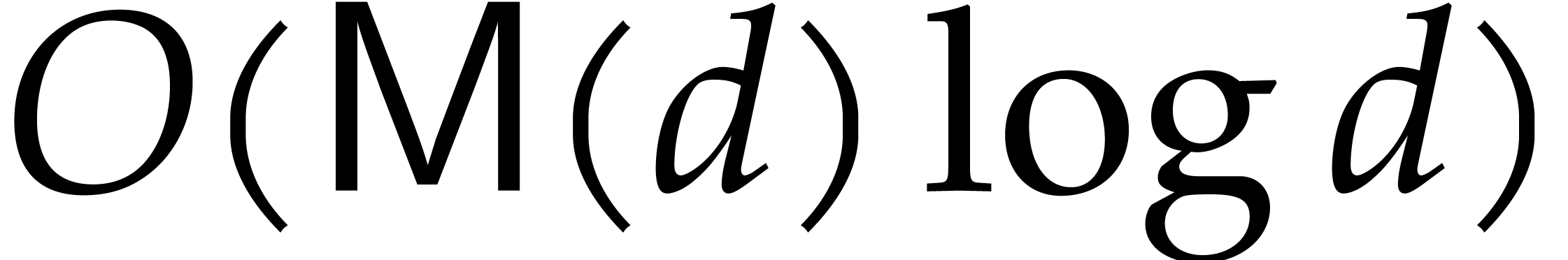 operations in
operations in  .
For
.
For 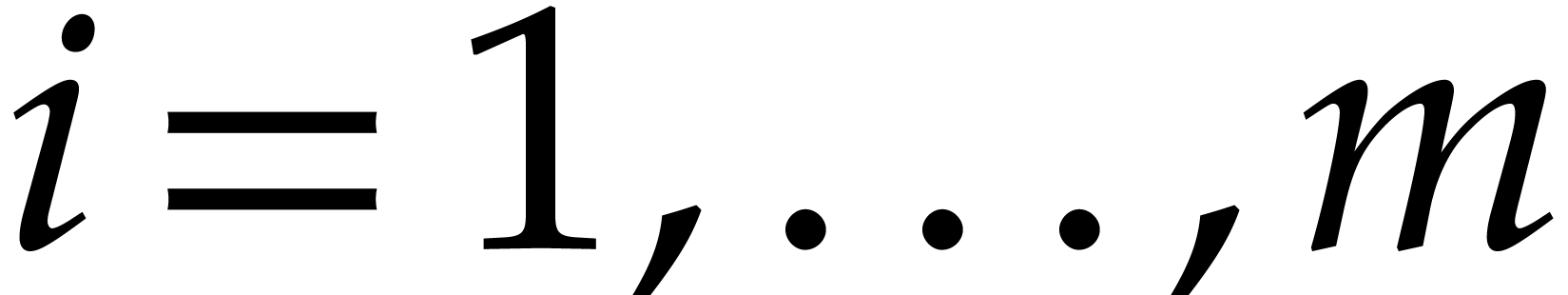 , Lemma 7
and
, Lemma 7
and
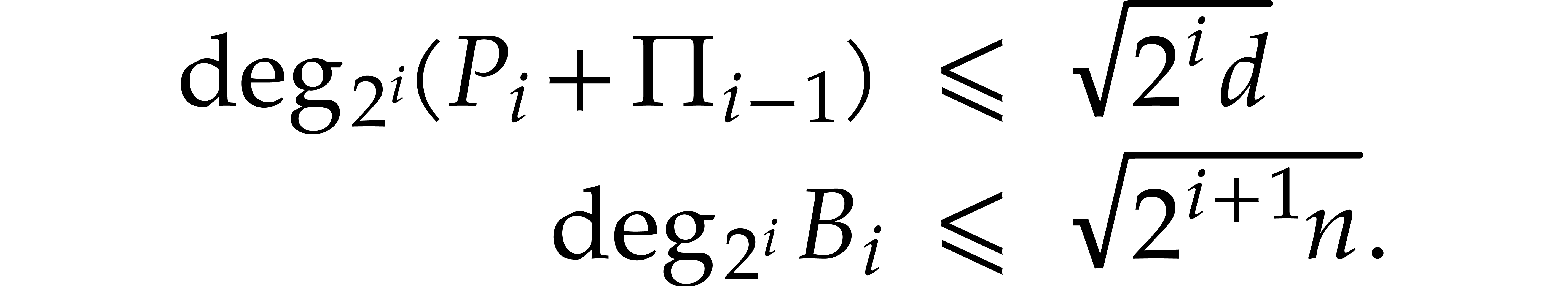
By Corollary 5, we deduce that the computation of 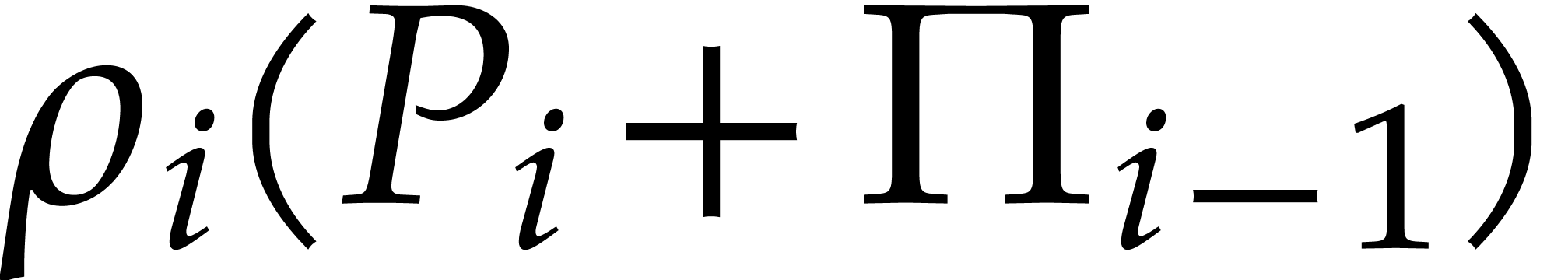 takes
takes
operations in  . Summing the
costs to compute
. Summing the
costs to compute 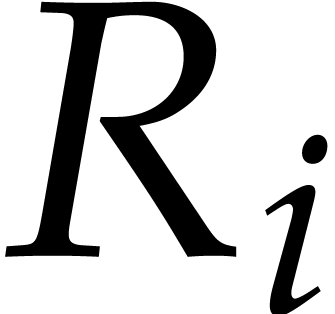 for
for 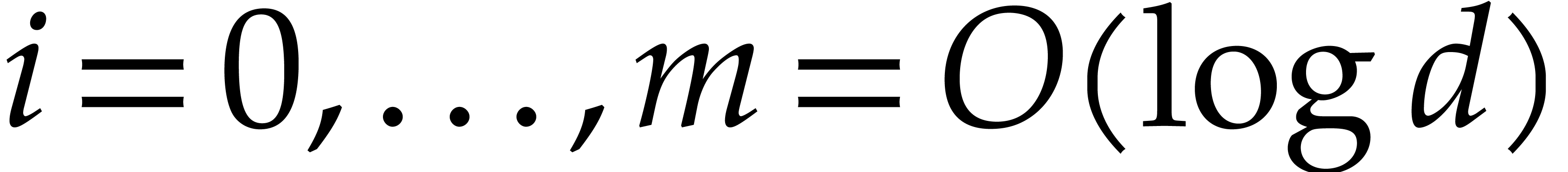 , we obtain the claimed bound.
, we obtain the claimed bound.
Proof. We set 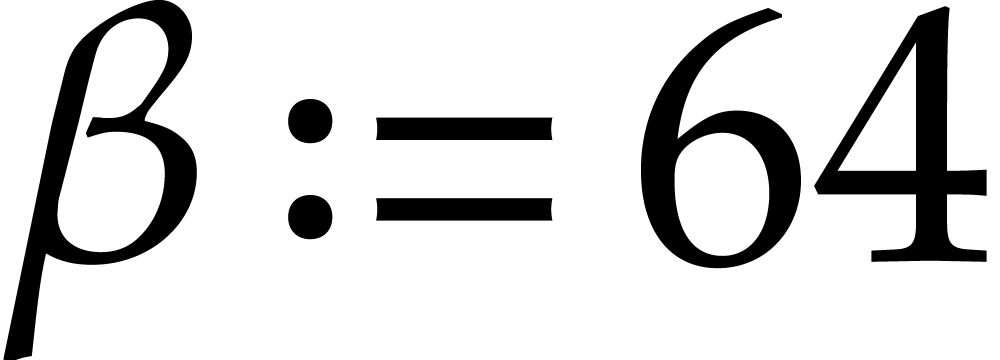 ,
so that
,
so that 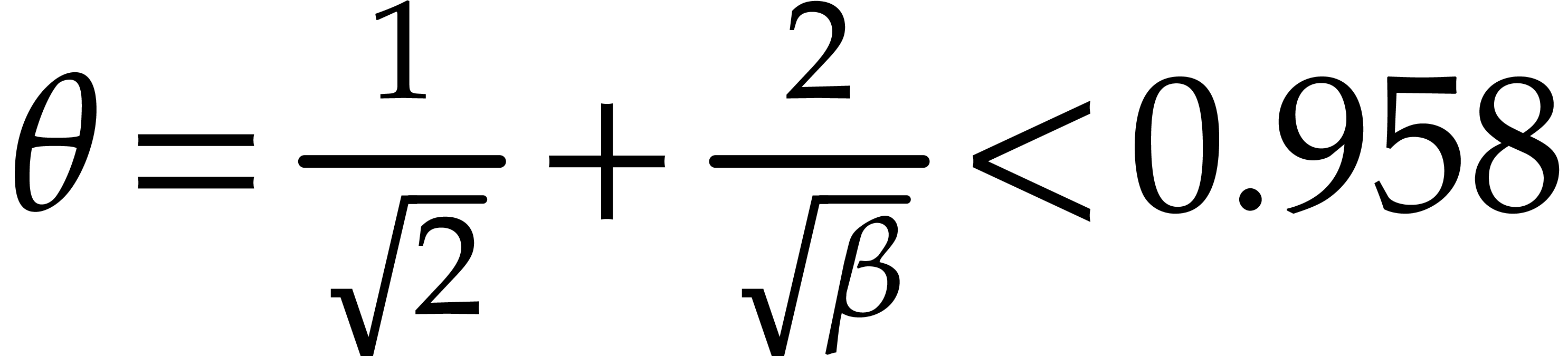 . We set
. We set 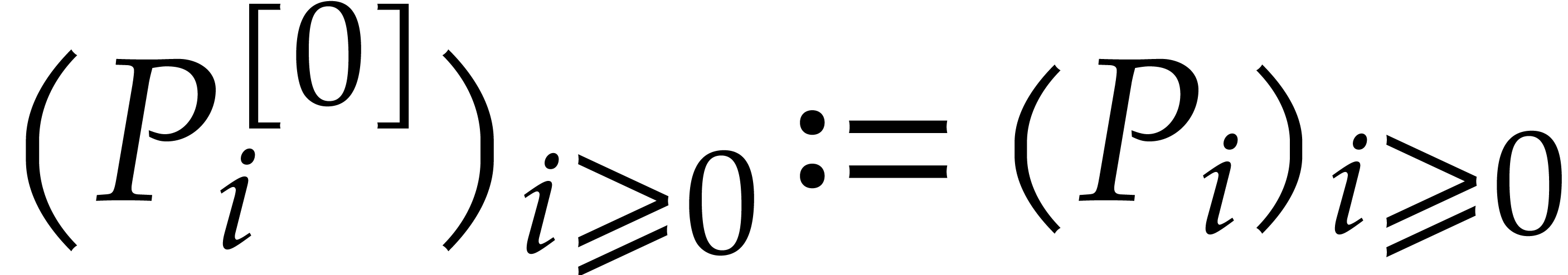 and define
and define 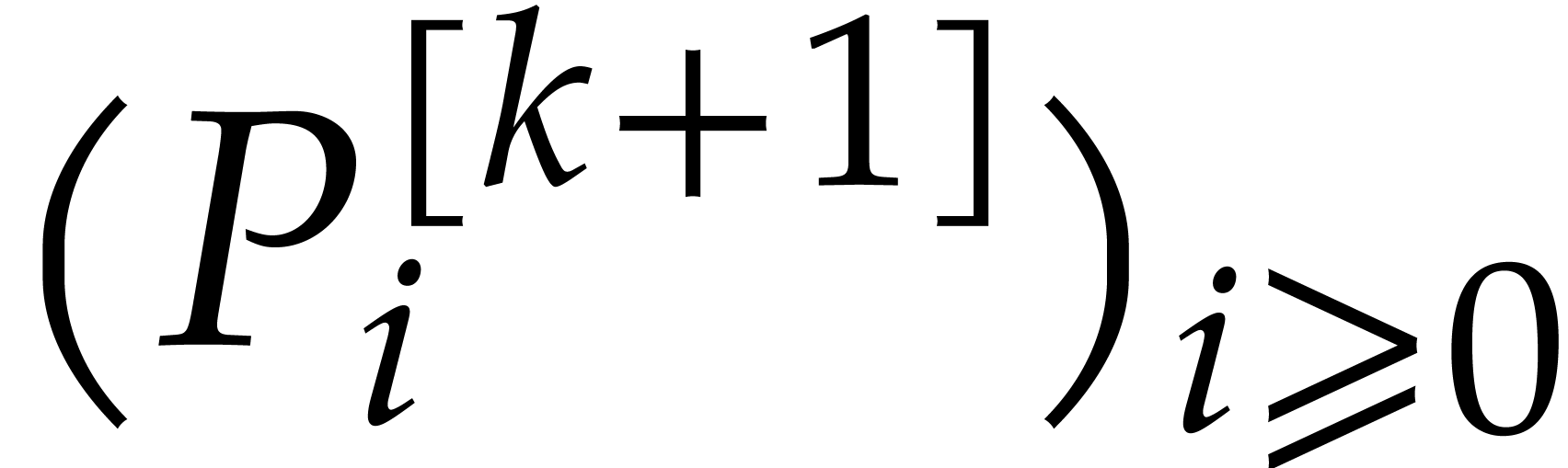 recursively as the
reduction of
recursively as the
reduction of 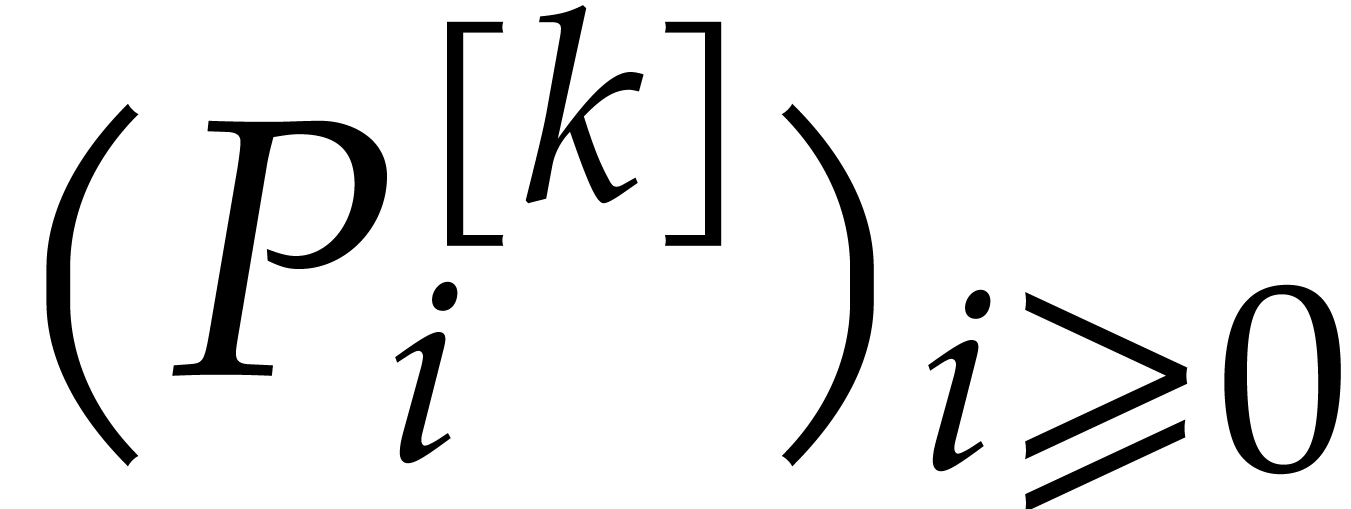 with respect to
with respect to  , for
, for 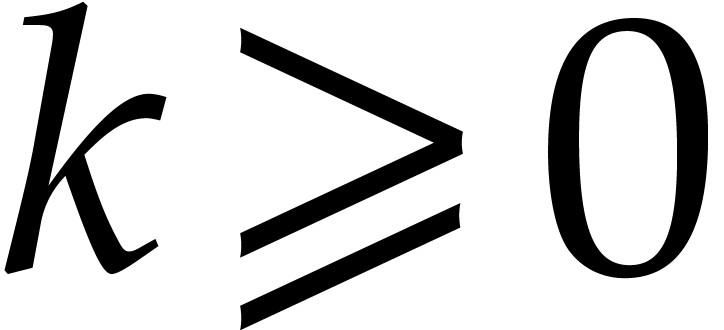 .
The integer
.
The integer 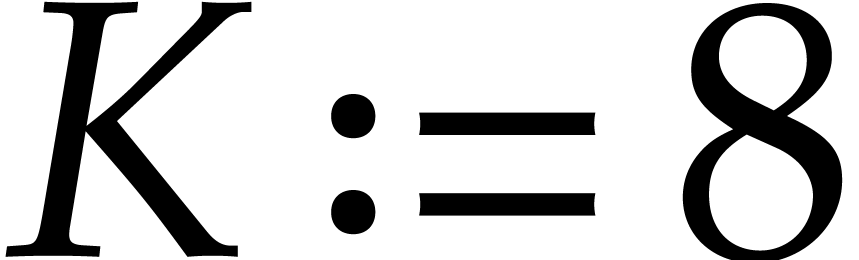 is the first integer such that
is the first integer such that
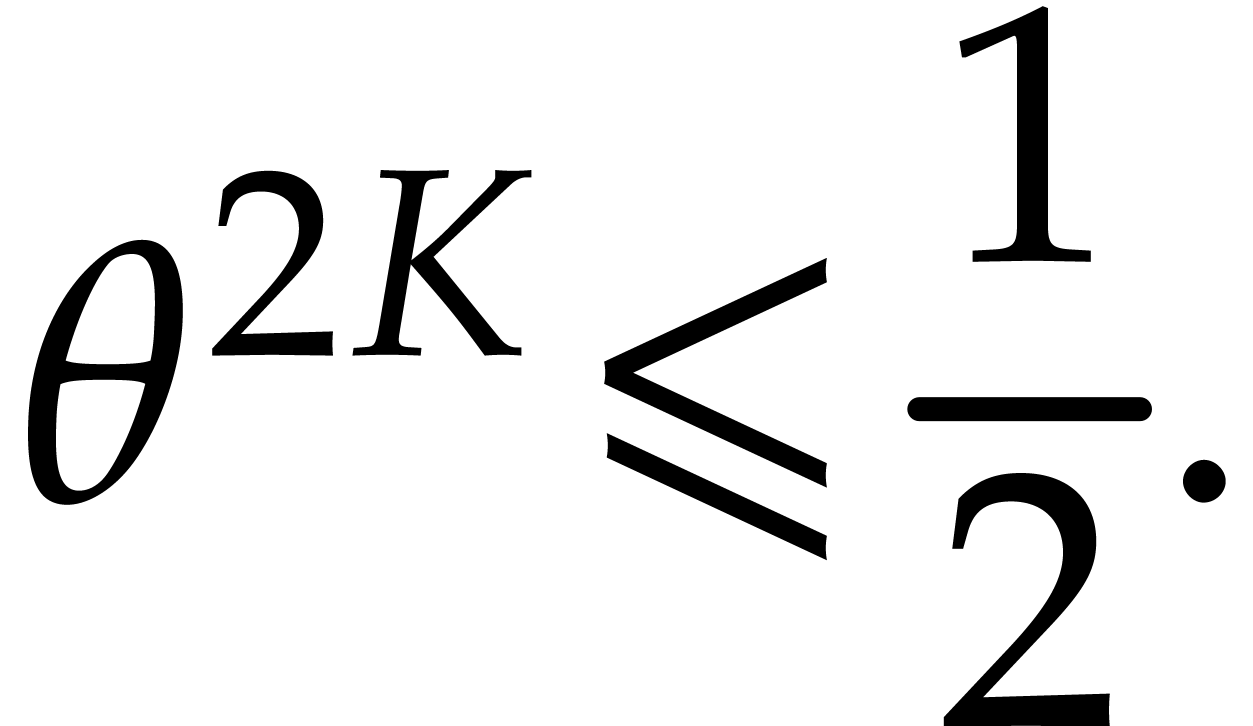
We finally take 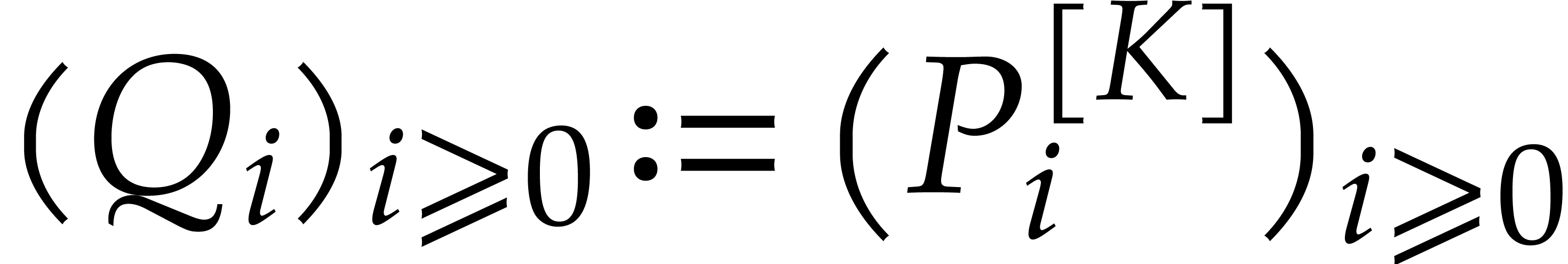 . Lemma 8 implies that
. Lemma 8 implies that 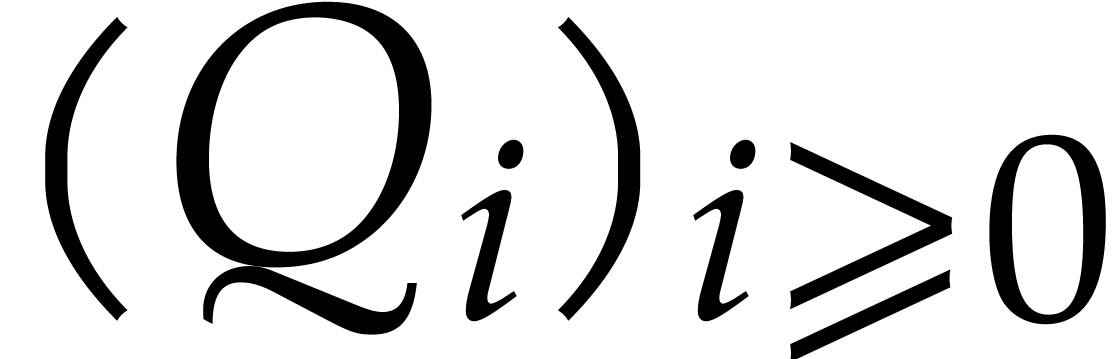 belongs to
belongs to 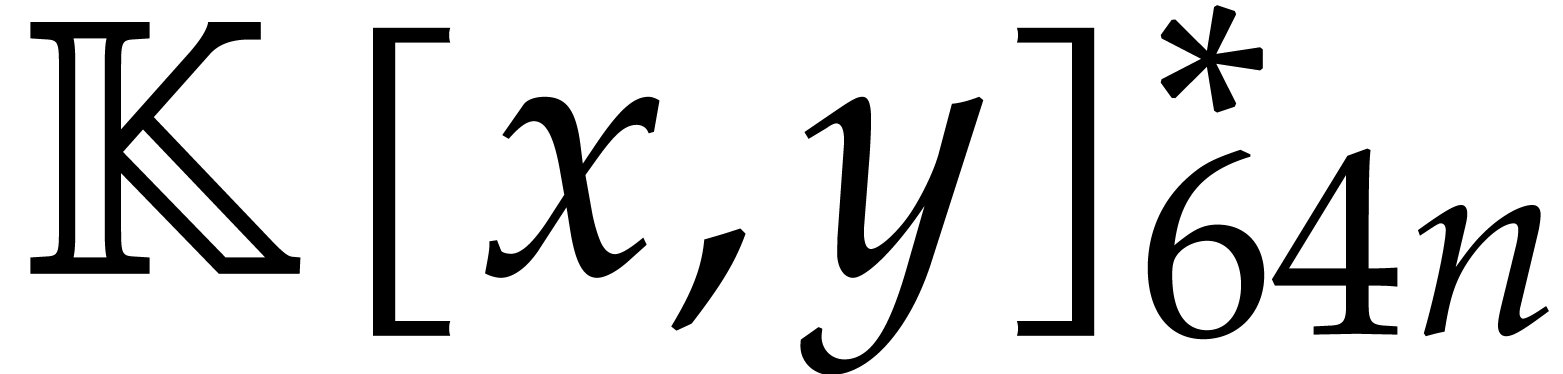 . The complexity bound follows from Lemma 9.
. The complexity bound follows from Lemma 9.
Let 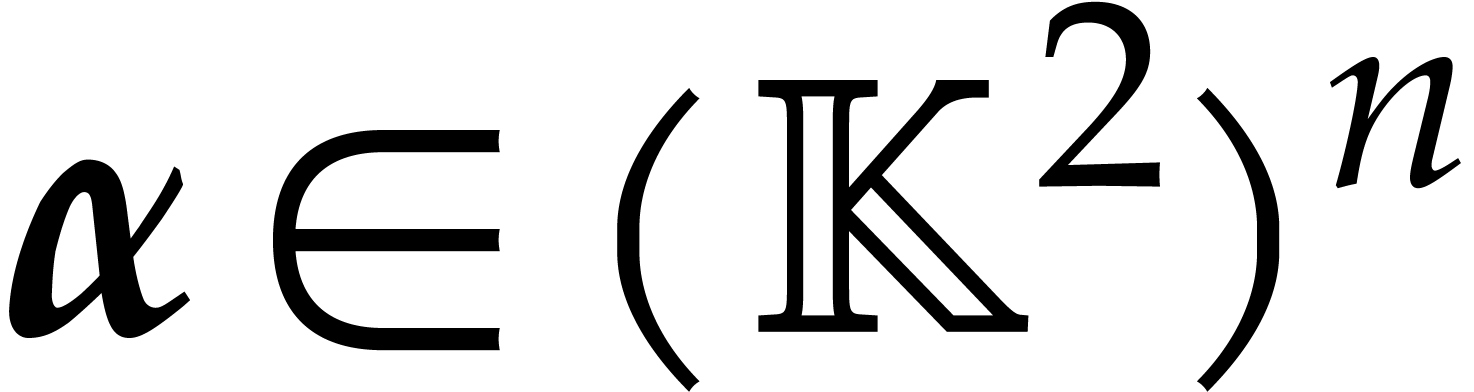 be a tuple of pairwise distinct points and
consider the problem of fast multi-point evaluation of a polynomial
be a tuple of pairwise distinct points and
consider the problem of fast multi-point evaluation of a polynomial 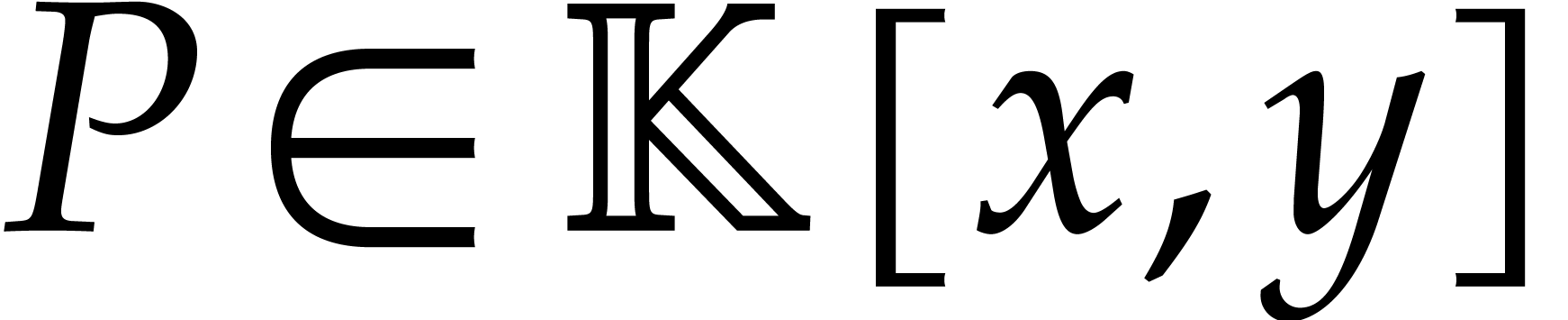 of total degree
of total degree 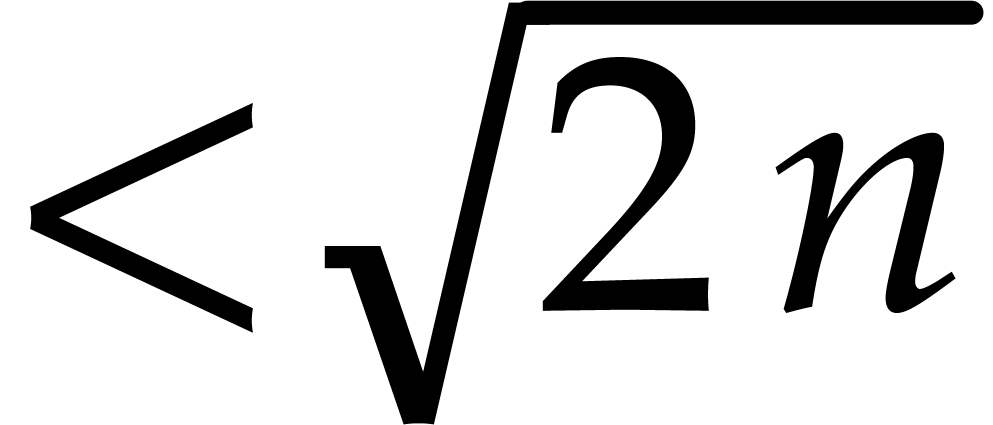 at
at  . For simplicity of the exposition,
it is convenient to first consider the case when
. For simplicity of the exposition,
it is convenient to first consider the case when 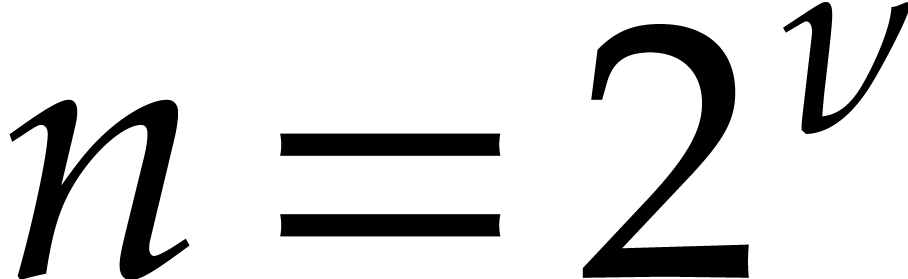 is a power of two and
is a power of two and  is in general position.
The core of our method is based on the usual “divide and
conquer” paradigm.
is in general position.
The core of our method is based on the usual “divide and
conquer” paradigm.
We say that  is in recursive general
position if
is in recursive general
position if  is in general position and if
is in general position and if
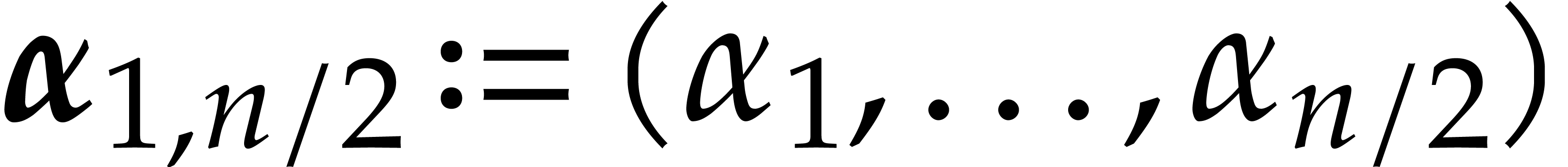 and
and 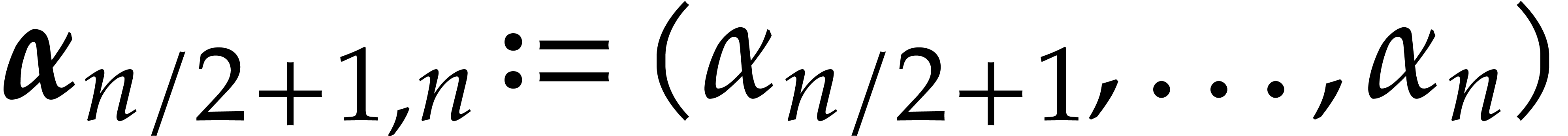 are in recursive
general position. An empty sequence is in recursive general position.
With the notation of section 3 a recursive general position
is ensured if the cardinality of
are in recursive
general position. An empty sequence is in recursive general position.
With the notation of section 3 a recursive general position
is ensured if the cardinality of  is strictly
larger that
is strictly
larger that 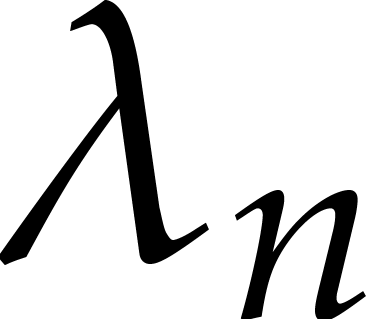 that is recursively defined by
that is recursively defined by
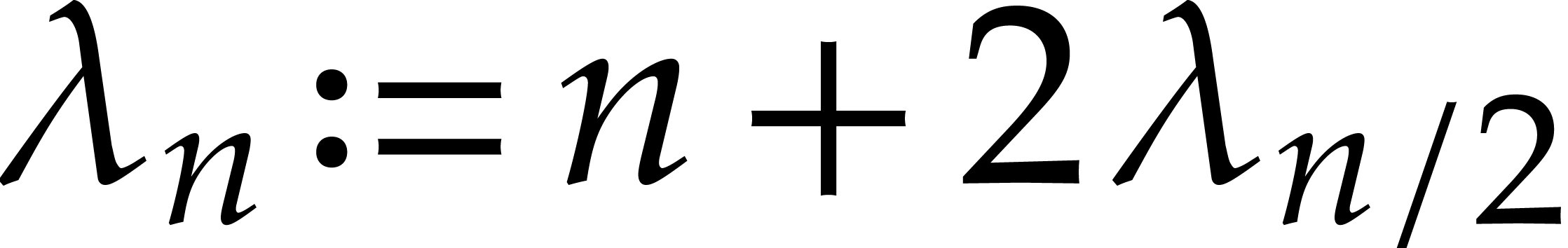
for  and with
and with 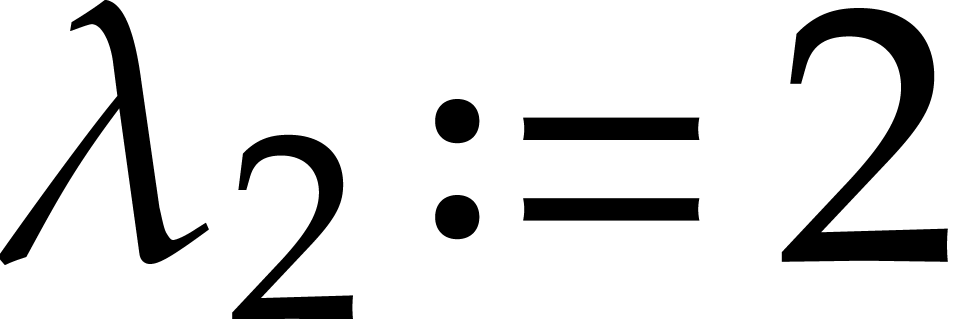 .
Consequently
.
Consequently 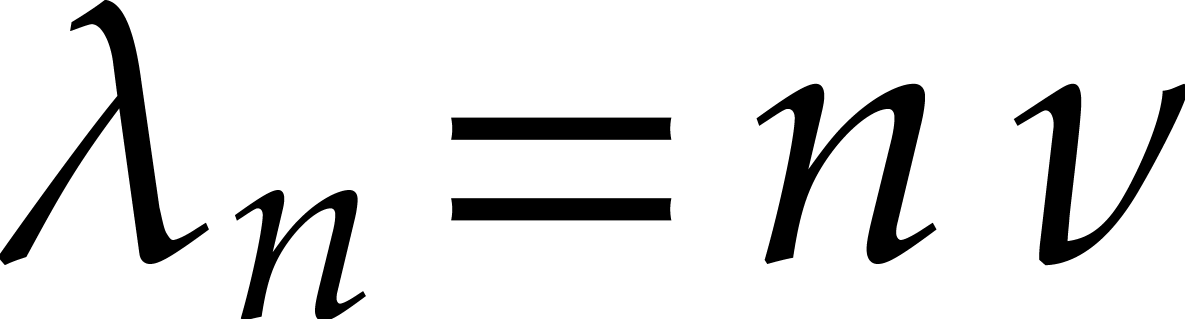 . Whenever
. Whenever  , we know from section 3
that we can reduce to the case where
, we know from section 3
that we can reduce to the case where  is in
recursive general position. In this case, we can compute a recursive
heterogeneous basis, that is made of a heterogeneous basis for
is in
recursive general position. In this case, we can compute a recursive
heterogeneous basis, that is made of a heterogeneous basis for  and recursive heterogeneous bases for
and recursive heterogeneous bases for 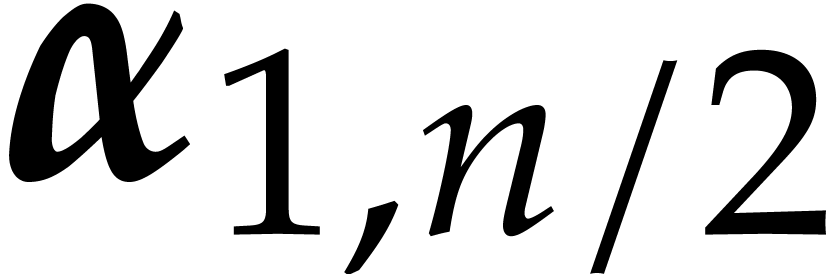 and
and 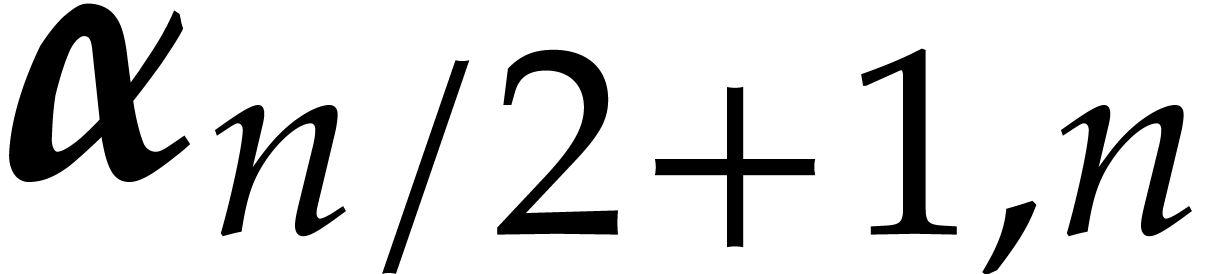 .
.
Algorithm |
|
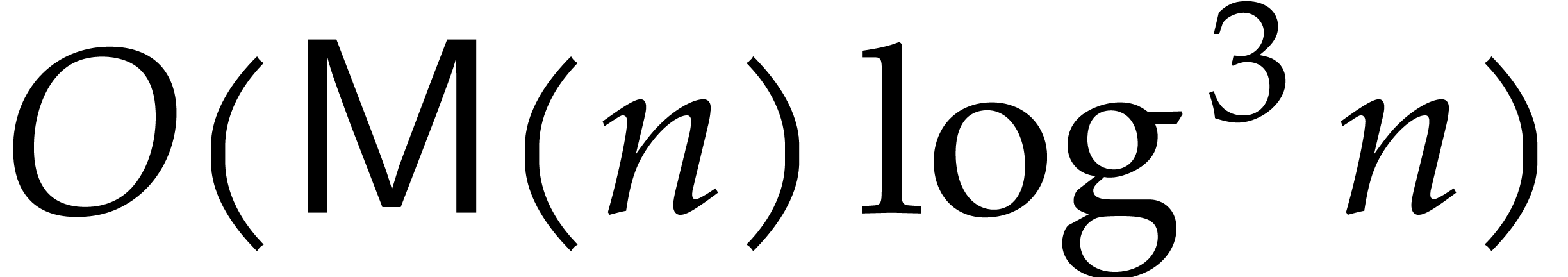 .
.
Proof. The algorithm is clearly correct if 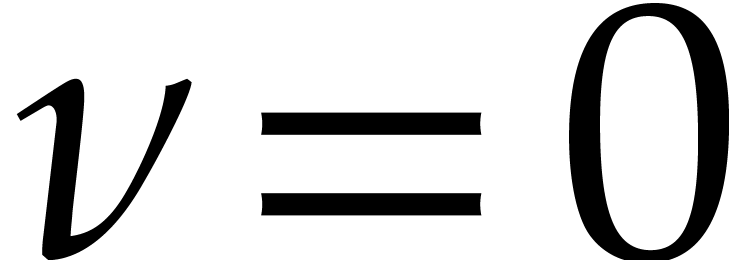 . If
. If 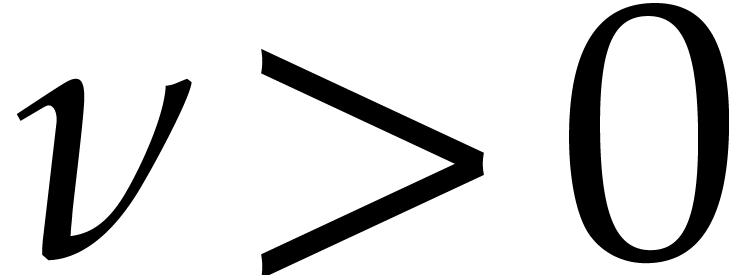 ,
then we first observe that both
,
then we first observe that both 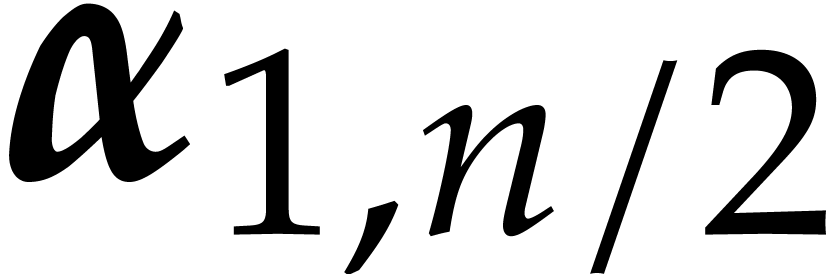 and
and 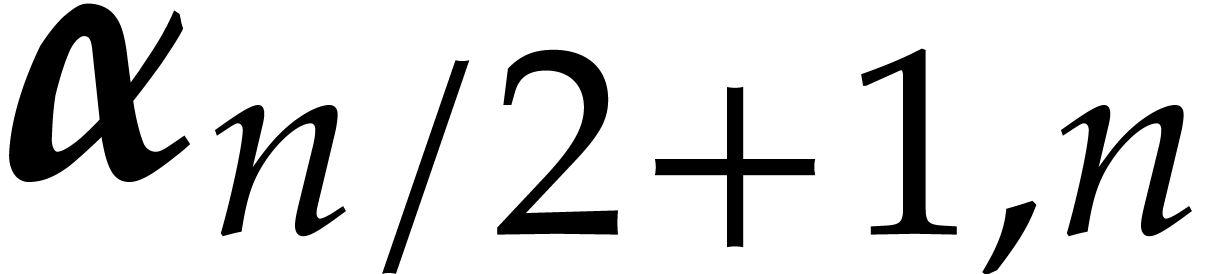 are in recursive general position by definition.
Furthermore, Proposition 10 ensures that
are in recursive general position by definition.
Furthermore, Proposition 10 ensures that
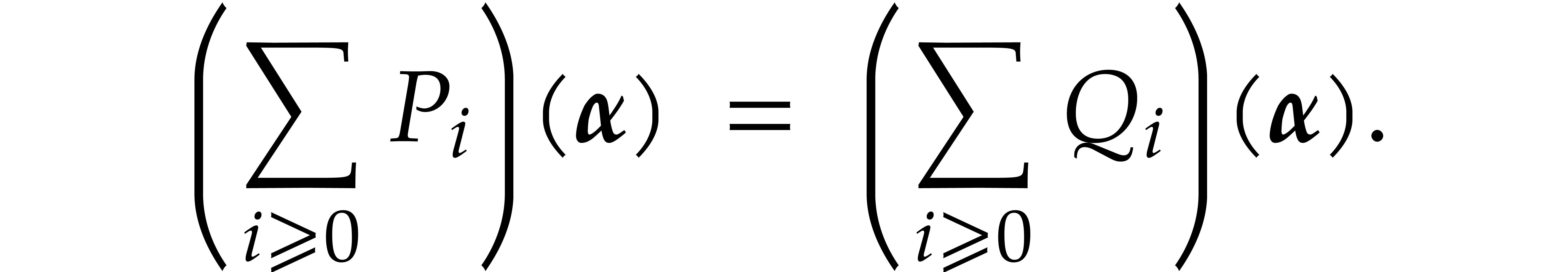
The concatenation of the results of the recursive applications of the algorithm therefore yields the correct result.
As to the complexity bound, the cost of step 2 is bounded by 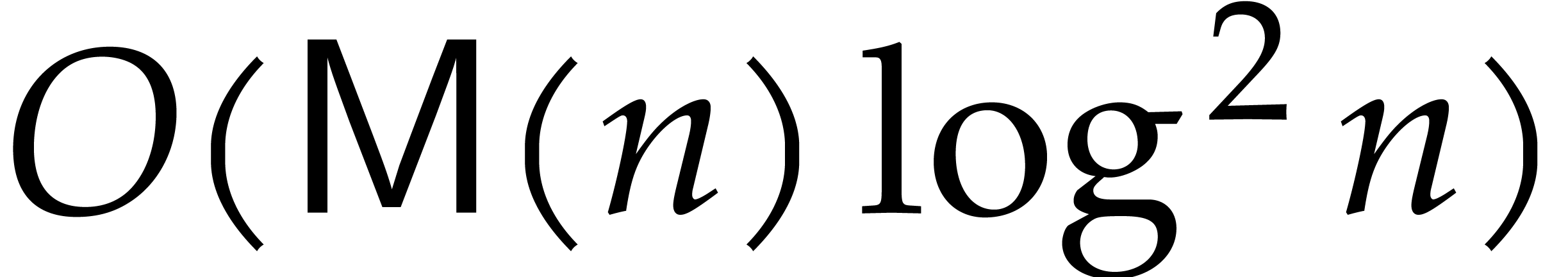 according to Proposition 10. Hence, the total
execution time
according to Proposition 10. Hence, the total
execution time 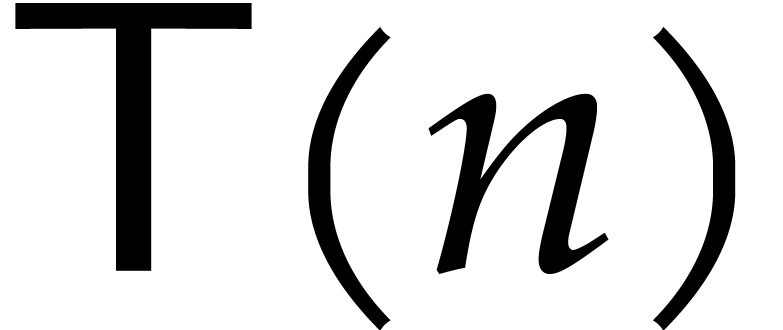 satisfies
satisfies
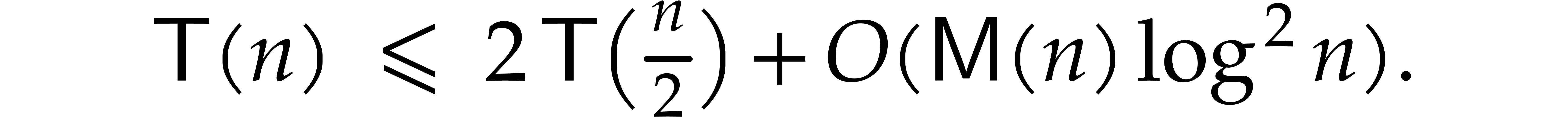
The desired complexity bound follows by unrolling this recurrence
inequality.
 and
and 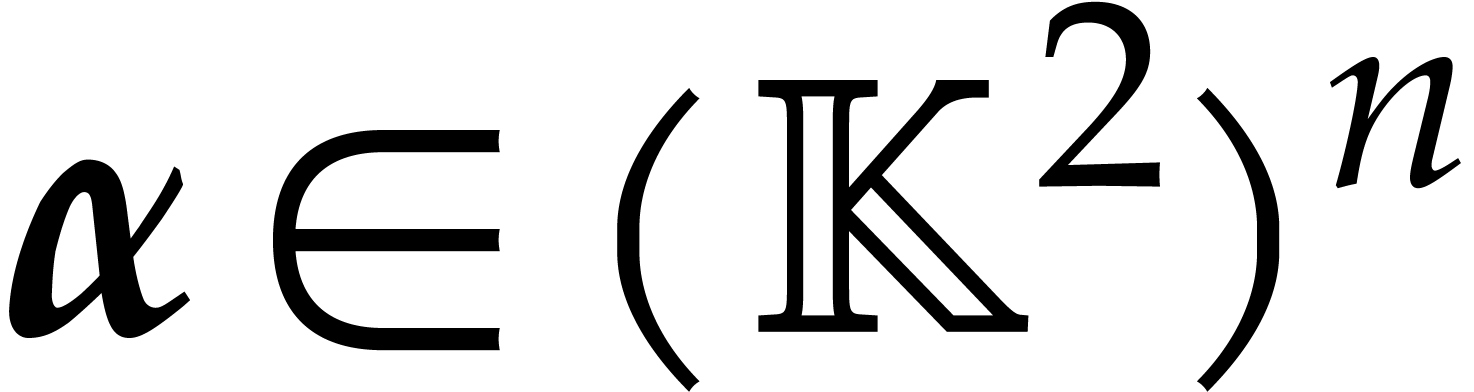 , where
, where 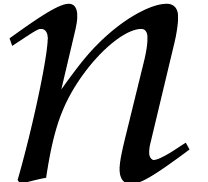 is not necessarily a power of two. Modulo
precomputations that only depend on
is not necessarily a power of two. Modulo
precomputations that only depend on  and
and  , we can evaluate any polynomial
in
, we can evaluate any polynomial
in 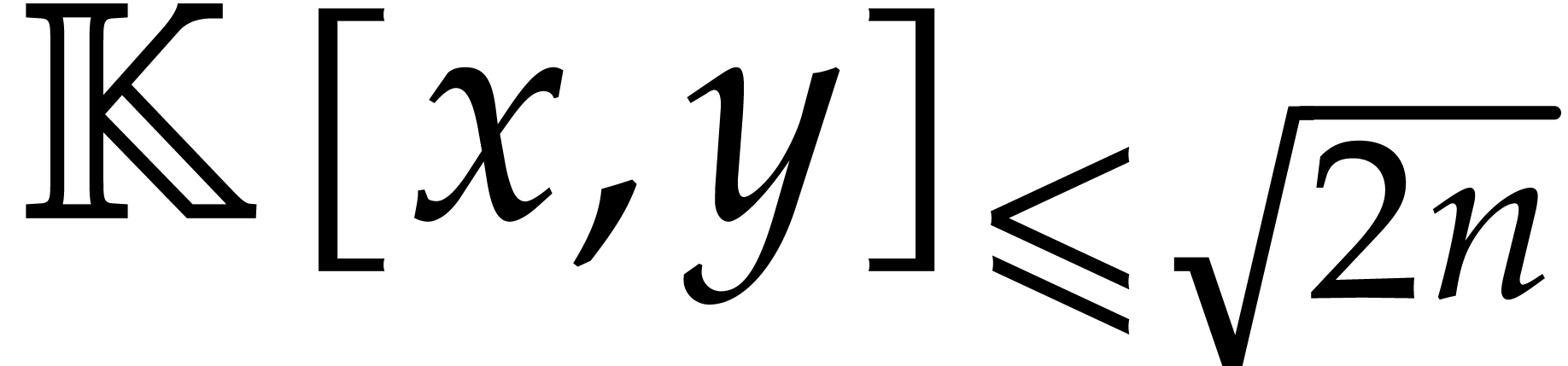 at
at  in time
in time 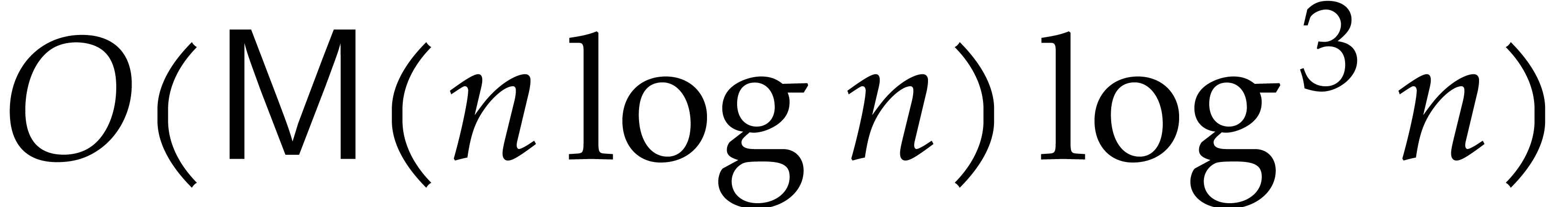 .
.
Proof. Modulo the repetition of at most  more points, we may assume without loss of generality
that
more points, we may assume without loss of generality
that 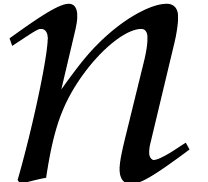 is a power of two
is a power of two 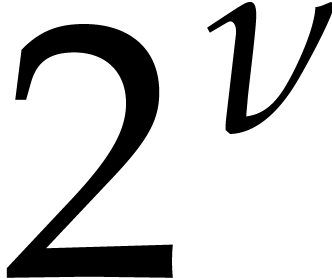 .
.
If  is finite then we build an algebraic
extension
is finite then we build an algebraic
extension  of
of  of degree
of degree
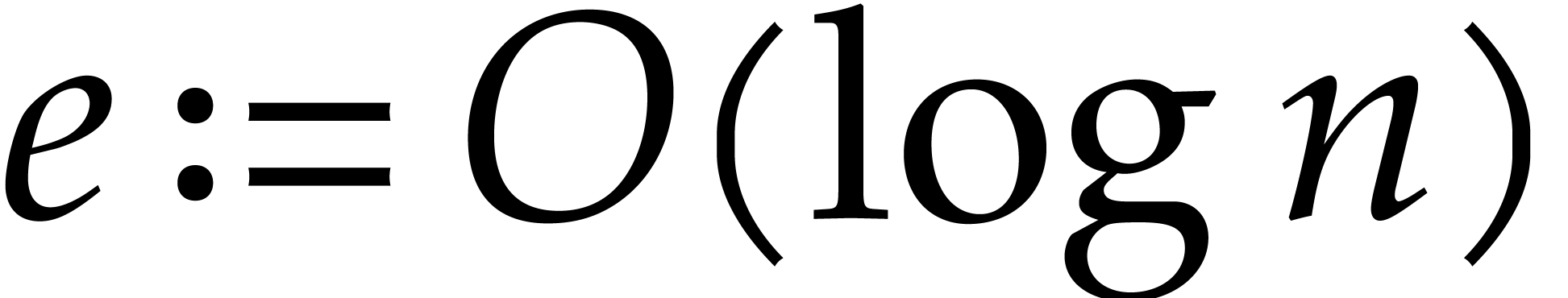 , so that
, so that  . Multiplying two polynomials in
. Multiplying two polynomials in 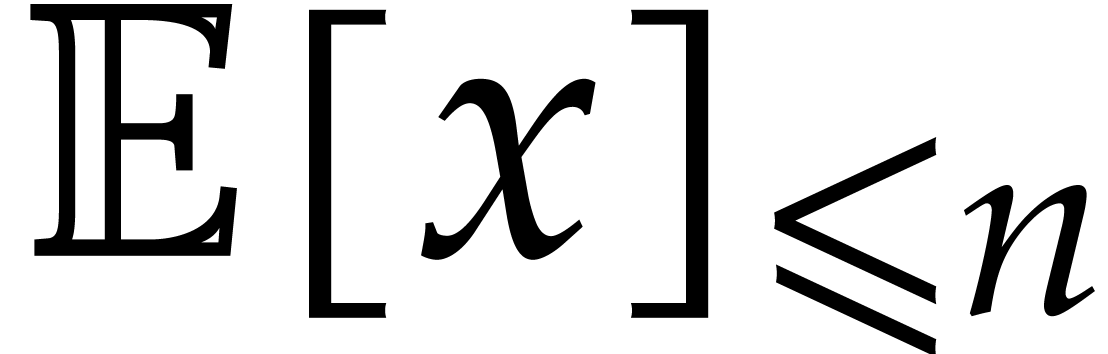 takes
takes

operations in  . Consequently,
up to introducing an extra
. Consequently,
up to introducing an extra 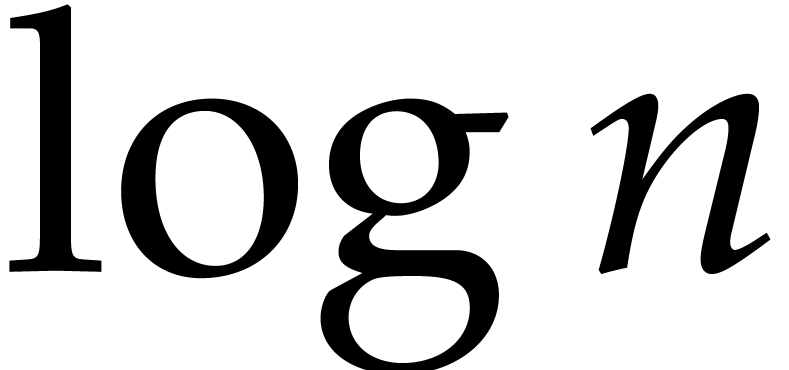 factor in our
complexity bounds, we may assume that
factor in our
complexity bounds, we may assume that  .
.
Modulo a change of variables (2) from section 3,
we may then assume that  ,
defined in
,
defined in
Given 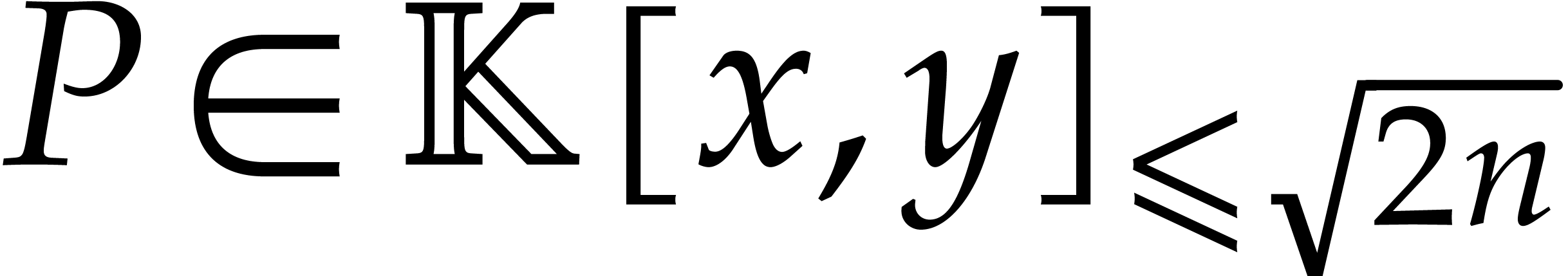 , we claim that we may
compute
, we claim that we may
compute 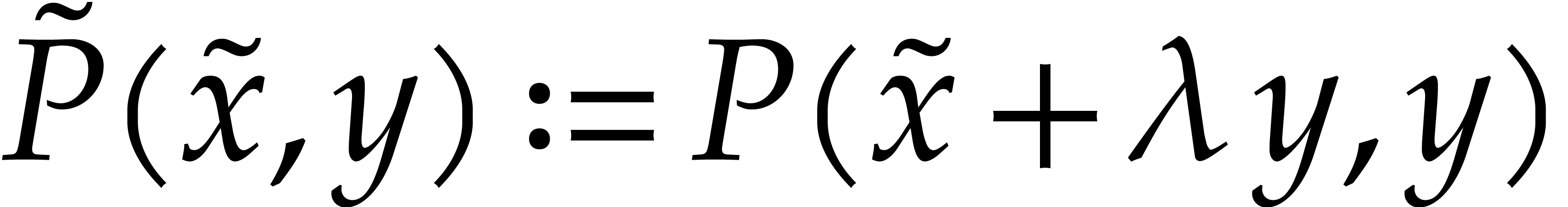 using
using 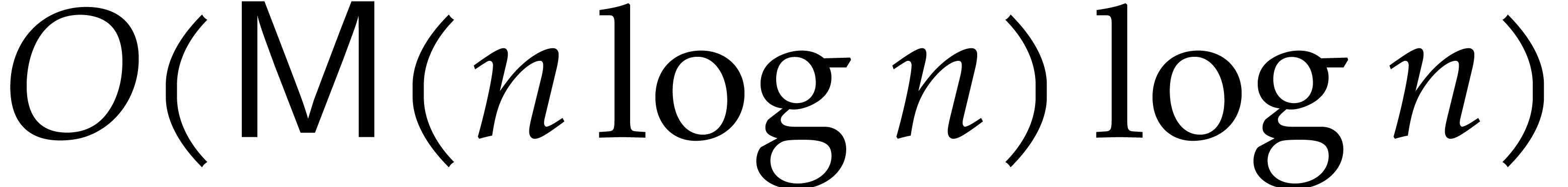 operations
in
operations
in  . Indeed, we first
decompose
. Indeed, we first
decompose
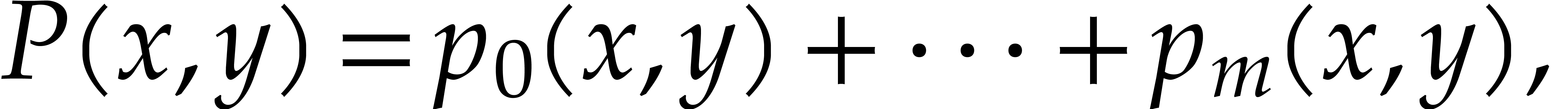
where 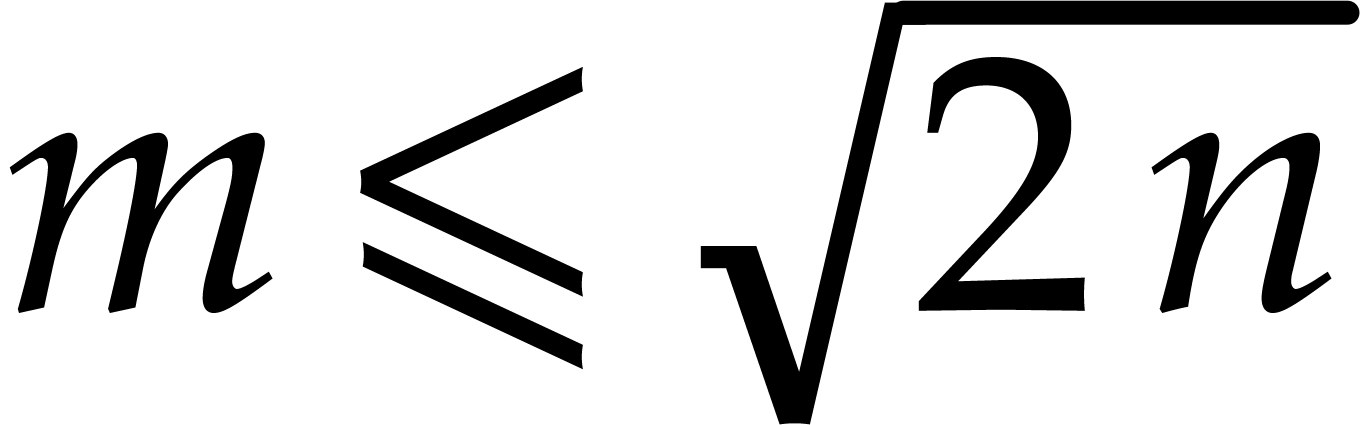 and each
and each 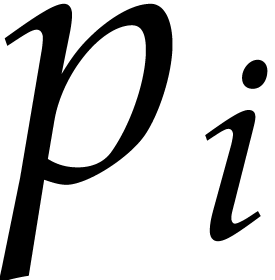 is zero
or homogenous of degree
is zero
or homogenous of degree  .
Computing
.
Computing 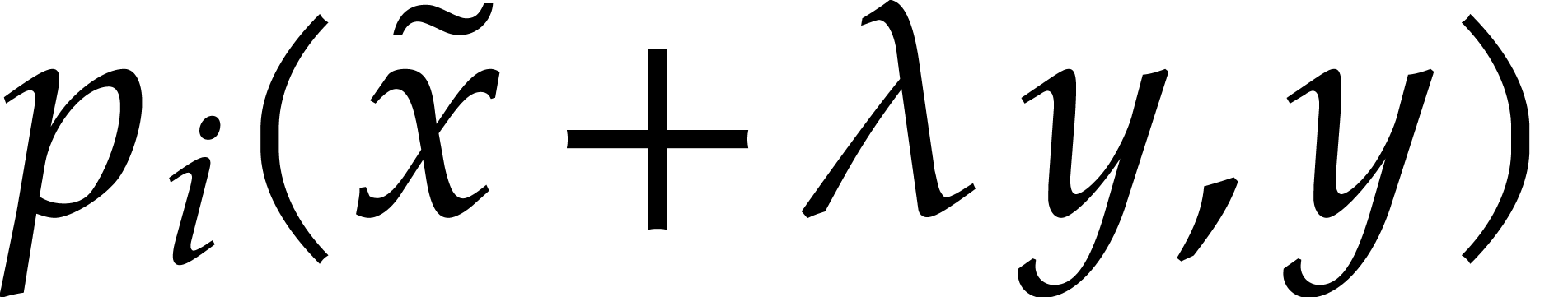 then reduces to computing
then reduces to computing 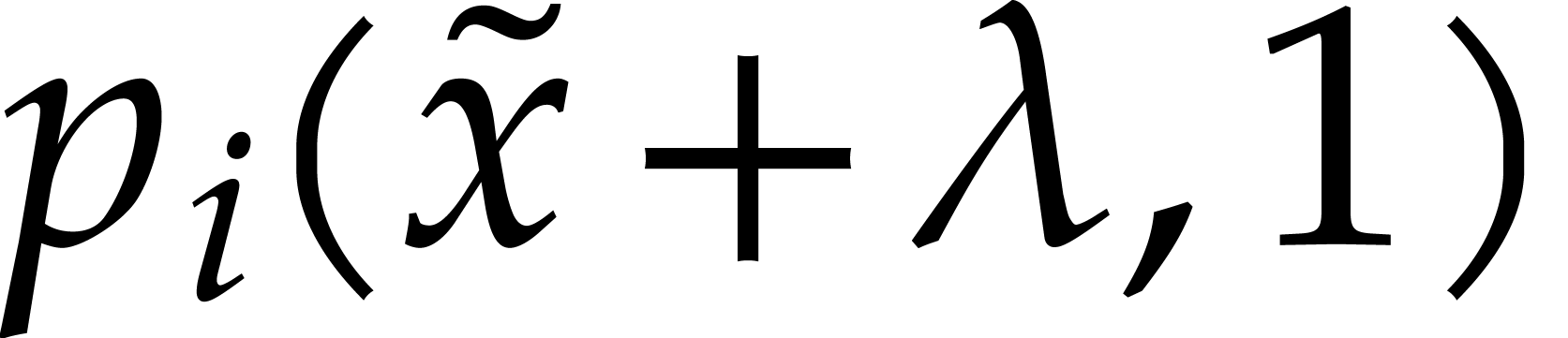 . This corresponds in turn to a univariate
Taylor shift, which takes
. This corresponds in turn to a univariate
Taylor shift, which takes 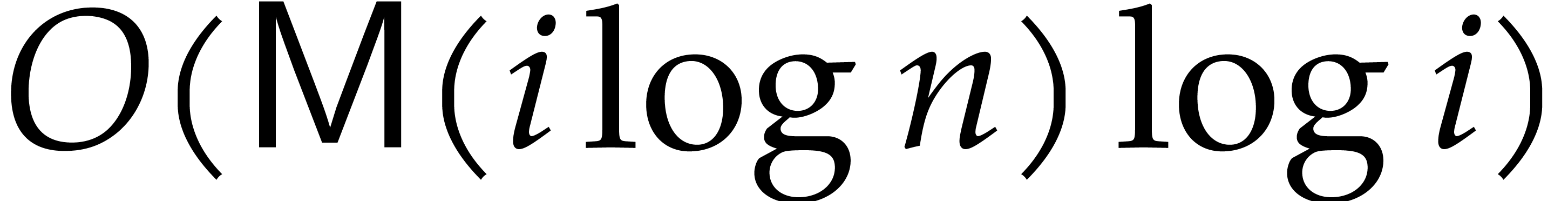 operations in
operations in  ; see [1, Lemma 7],
for instance. Finally, we apply Theorem 11 to
; see [1, Lemma 7],
for instance. Finally, we apply Theorem 11 to 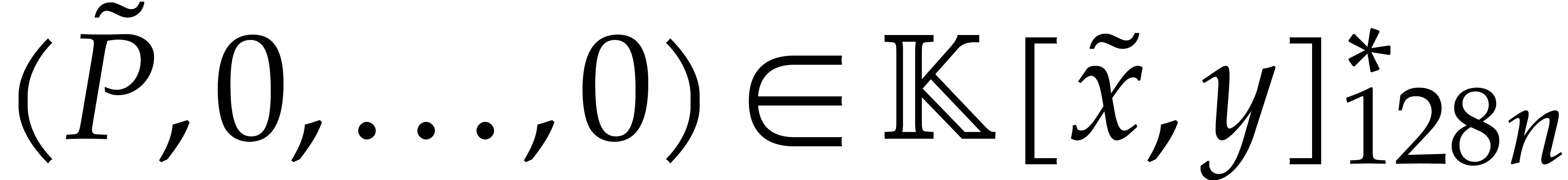 and
and  .
.
We have designed a softly linear time algorithm for bivariate
multi-point evaluation, modulo precomputations that only depend on the
evaluation points. This result raises several new questions. First, it
would be useful to optimize the constant factors involved in the cost
analysis, and study the efficiency of practical implementations. Second,
one may investigate extensions of Corollary 12 that take
into account the partial degrees of the input polynomial,
e.g. by applying Theorem 11 to inputs of the
form 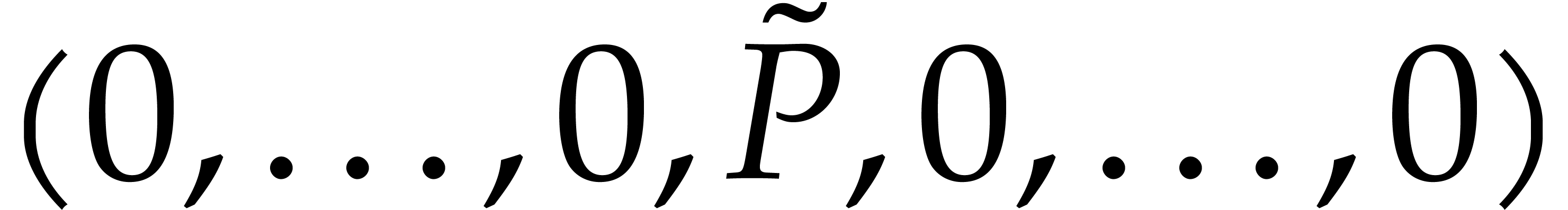 . A final challenge
concerns the possibility to perform all precomputations in sub-quadratic
time. For this, one might use techniques from [2, 19],
as in [12]. The problem of achieving an almost linear cost
appears to be even harder.
. A final challenge
concerns the possibility to perform all precomputations in sub-quadratic
time. For this, one might use techniques from [2, 19],
as in [12]. The problem of achieving an almost linear cost
appears to be even harder.
J. Berthomieu, G. Lecerf, and G. Quintin. Polynomial root finding over local rings and application to error correcting codes. Appl. Alg. Eng. Comm. Comp., 24(6):413–443, 2013.
A. Bostan, C.-P. Jeannerod, and É. Schost. Solving structured linear systems with large displacement rank. Theor. Comput. Sci., 407(1):155–181, 2008.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic Complexity Theory, volume 315 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, 1997.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Inform., 28:693–701, 1991.
J.-C. Faugère, P. Gianni, D. Lazard, and T. Mora. Efficient computation of zero-dimensional Gröbner bases by change of ordering. J. Symbolic Comput., 16(4):329–344, 1993.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2nd edition, 2002.
D. Harvey and J. van der Hoeven. Faster polynomial multiplication over finite fields using cyclotomic coefficient rings. J. Complexity, 54:101404, 2019.
J. van der Hoeven. Newton's method and FFT trading. J. Symbolic Comput., 45(8):857–878, 2010.
J. van der Hoeven. On the complexity of multivariate polynomial division. In I. S. Kotsireas and E. Martínez-Moro, editors, Applications of Computer Algebra. Kalamata, Greece, July 20–23, 2015, volume 198 of Springer Proceedings in Mathematics & Statistics, pages 447–458. Cham, 2017. Springer International Publishing.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and R. Larrieu. Fast reduction of bivariate polynomials with respect to sufficiently regular Gröbner bases. In C. Arreche, editor, Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '18, pages 199–206. New York, NY, USA, 2018. ACM.
J. van der Hoeven and G. Lecerf. Fast amortized multi-point evaluation. Technical Report, HAL, 2020. https://hal.archives-ouvertes.fr/hal-02508529.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. Complexity, 56:101405, 2020.
J. van der Hoeven and G. Lecerf. On the complexity exponent of polynomial system solving. Found. Comput. Math., 21:1–57, 2021.
J. van der Hoeven and É. Schost. Multi-point evaluation in higher dimensions. Appl. Alg. Eng. Comm. Comp., 24(1):37–52, 2013.
X. Huang and V. Y. Pan. Fast rectangular matrix multiplication and applications. J. Complexity, 14(2):257–299, 1998.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
D. Le Brigand and J.-J. Risler. Algorithme de Brill–Noether et codes de Goppa. Bulletin de la société mathématique de France, 116(2):231–253, 1988.
V. Neiger. Fast computation of shifted Popov forms of polynomial matrices via systems of modular polynomial equations. In Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '16, pages 365–372. New York, NY, USA, 2016. ACM.
V. Neiger, J. Rosenkilde, and G. Solomatov. Generic bivariate multi-point evaluation, interpolation and modular composition with precomputation. In A. Mantzaflaris, editor, Proceedings of the 45th International Symposium on Symbolic and Algebraic Computation, ISSAC '20, pages 388–395. New York, NY, USA, 2020. ACM.
V. Neiger and É. Schost. Computing syzygies in finite dimension using fast linear algebra. J. Complexity, 60:101502, 2020.
M. Nüsken and M. Ziegler. Fast multipoint evaluation of bivariate polynomials. In S. Albers and T. Radzik, editors, Algorithms – ESA 2004. 12th Annual European Symposium, Bergen, Norway, September 14-17, 2004, volume 3221 of Lect. Notes Comput. Sci., pages 544–555. Springer Berlin Heidelberg, 2004.
M. S. Paterson and L. J. Stockmeyer. On the number of nonscalar multiplications necessary to evaluate polynomials. SIAM J. Comput., 2(1):60–66, 1973.
L. Robbiano. Term orderings on the polynomial ring. In B. F. Caviness, editor, EUROCAL '85. European Conference on Computer Algebra. Linz, Austria, April 1-3, 1985. Proceedings. Volume 2: Research Contributions, volume 204 of Lect. Notes Comput. Sci., pages 513–517. Springer-Verlag Berlin Heidelberg, 1985.