Dendromorphic functions  |
|
| Draft version, August 22, 2025 |
|
 . This work has
been supported by an ERC-2023-ADG grant for the ODELIX project
(number 101142171).
. This work has
been supported by an ERC-2023-ADG grant for the ODELIX project
(number 101142171).
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
 . This article has
been written using GNU TeXmacs [3].
. This article has
been written using GNU TeXmacs [3].
We study analytic properties of the Picard-Vessiot closure of
|
Let  be a differential field of characteristic
zero whose field of constants is algebraically closed. We say that
be a differential field of characteristic
zero whose field of constants is algebraically closed. We say that  is Picard-Vessiot closed if any differential
equation
is Picard-Vessiot closed if any differential
equation
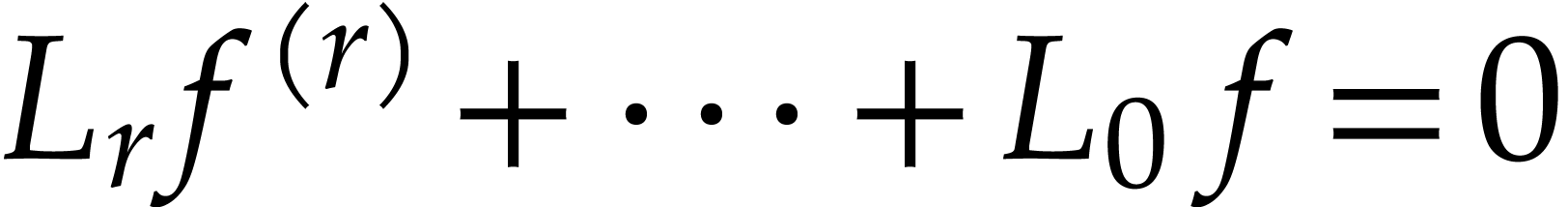
with 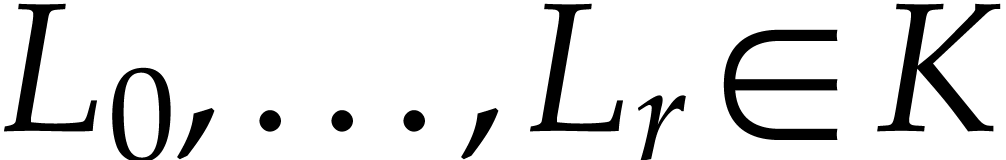 and
and 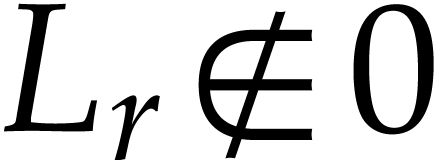 has a
fundamental system of
has a
fundamental system of  linearly independent
solutions over the constant field of
linearly independent
solutions over the constant field of  .
For any differential field
.
For any differential field  ,
and up to isomorphism, there exists a smallest Picard-Vessiot closed
extension
,
and up to isomorphism, there exists a smallest Picard-Vessiot closed
extension 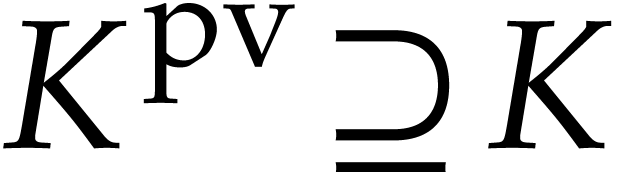 that contains
that contains  and that has the same constant field as
and that has the same constant field as  .
We refer to [7] for the algebraic theory of Picard-Vessiot
extensions. In [4], elements of
.
We refer to [7] for the algebraic theory of Picard-Vessiot
extensions. In [4], elements of 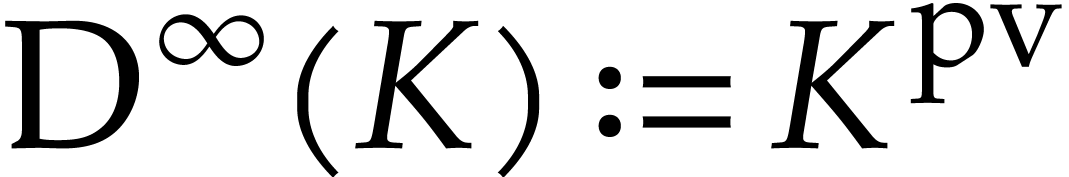 are
called differentially definable functions and algorithms are presented
to compute with such functions.
are
called differentially definable functions and algorithms are presented
to compute with such functions.
Seidenberg's embedding theorem states that any countably generated
differential field can be embedded into a field of meromorphic functions
on some domain [9, 6]. However, this domain
can be quite small. If 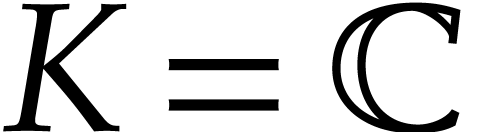 or
or 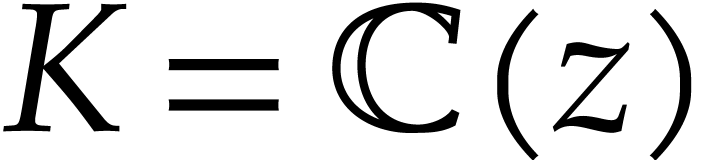 , then the main goal of this note is to show that
elements of
, then the main goal of this note is to show that
elements of 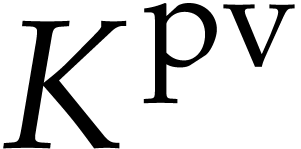 can be materialized as analytic
functions on suitable, much larger, Riemann surfaces and to investigate
analytic properties of these functions.
can be materialized as analytic
functions on suitable, much larger, Riemann surfaces and to investigate
analytic properties of these functions.
We first explore the kind of Riemann surfaces on which elements of 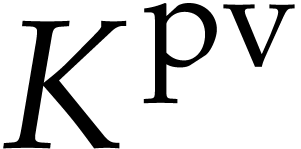 are defined. Intuitively, the only singularities that
can occur are isolated ones, or accumulation points of isolated
singularities, or accumulation points of accumulation points of isolated
singularities, and so on. This leads to the notion of “recursive
discrete ramifications” that will be formally defined in section
2. For simplicity, we will restrict our attention to simply
connected Riemann surfaces, but we note that it should not be hard to
extend the theory to arbitrary connected Riemann surfaces.
are defined. Intuitively, the only singularities that
can occur are isolated ones, or accumulation points of isolated
singularities, or accumulation points of accumulation points of isolated
singularities, and so on. This leads to the notion of “recursive
discrete ramifications” that will be formally defined in section
2. For simplicity, we will restrict our attention to simply
connected Riemann surfaces, but we note that it should not be hard to
extend the theory to arbitrary connected Riemann surfaces.
Let  be a simply connected Riemann surface. The
recursively discretely ramified Riemann surfaces above
be a simply connected Riemann surface. The
recursively discretely ramified Riemann surfaces above  give rise to an inductive system of analytic function spaces on these
surfaces. The inductive limit
give rise to an inductive system of analytic function spaces on these
surfaces. The inductive limit 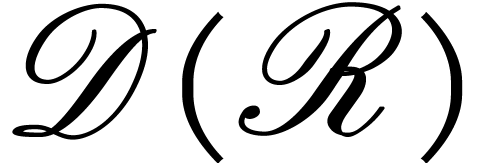 of these spaces is
the space of dendromorphic functions on
of these spaces is
the space of dendromorphic functions on  . If
. If  ,
then we will show in section 3 that
,
then we will show in section 3 that 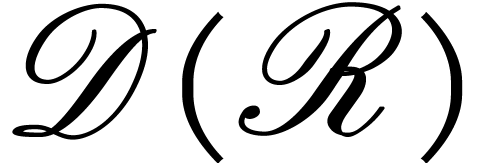 is a Picard-Vessiot closed field. In particular,
is a Picard-Vessiot closed field. In particular, 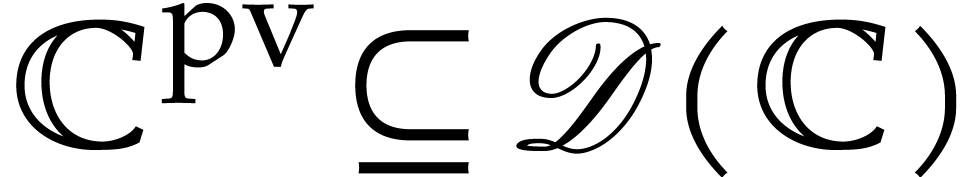 .
.
In section 4, we will derive some consequences of the fact
that the only singularities of dendromorphic functions arise as
recursive accumulation points of isolated singularities. In particular,
such singularities cannot give rise to natural boundaries in a strong
sense. As a corollary, we shall see that the generating series of the
number of partitions of an integer does not belong to  . This answers open question 4 from [1].
. This answers open question 4 from [1].
The set 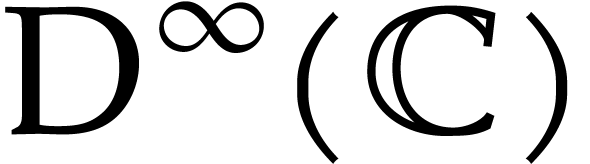 is closed under composition [4].
In section 5, we shall show that this also holds for
is closed under composition [4].
In section 5, we shall show that this also holds for 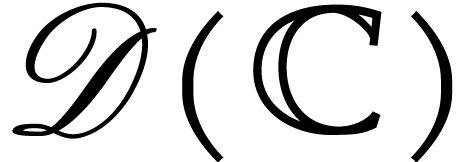 and a suitable class of “boundaryless”
functions. We no not know whether
and a suitable class of “boundaryless”
functions. We no not know whether 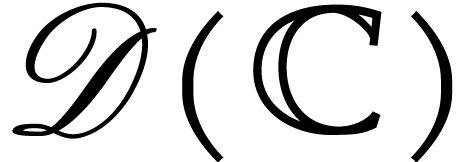 is closed
under functional inversion. Weierstrass
is closed
under functional inversion. Weierstrass  functions are examples of differentially algebraic dendromorphic
functions that are not in
functions are examples of differentially algebraic dendromorphic
functions that are not in 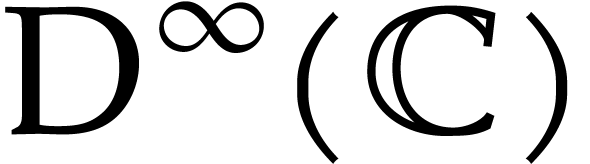 .
.
Acknowledgments. We are grateful to Gleb Pogudin for his helpful comments on a first version of this note.
Let  be a connected Riemann surface. A
Riemann surface above
be a connected Riemann surface. A
Riemann surface above  is a pair
is a pair 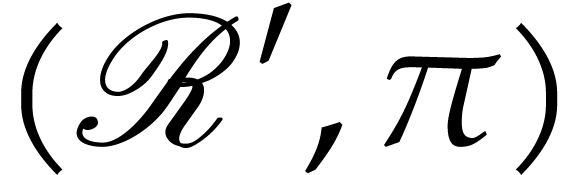 , where
, where 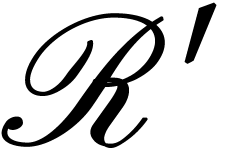 is
another Riemann surface
is
another Riemann surface 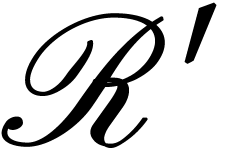 and
and 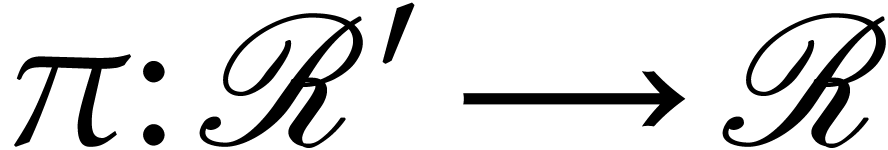 a holomorphic covering: for every
a holomorphic covering: for every  ,
there exists an open neighborhood
,
there exists an open neighborhood  and a
countable set
and a
countable set 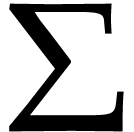 such that
such that 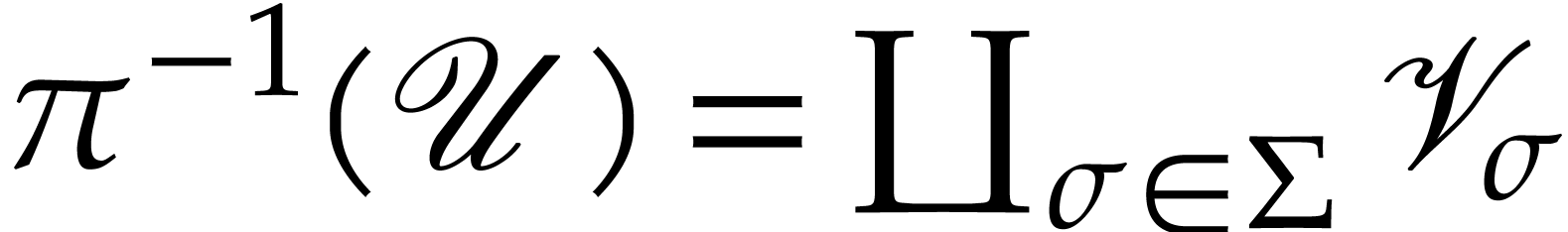 and
and 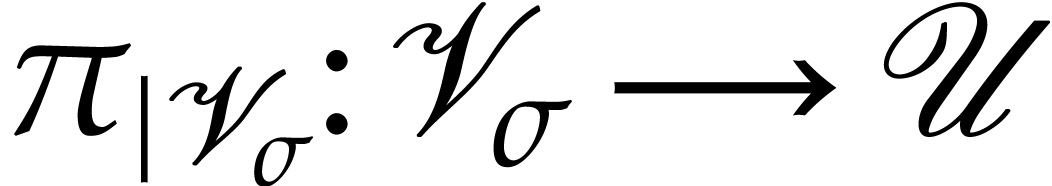 is a homeomorphism for every
is a homeomorphism for every 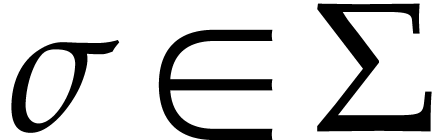 .
.
We recall that there exists a Riemann surface 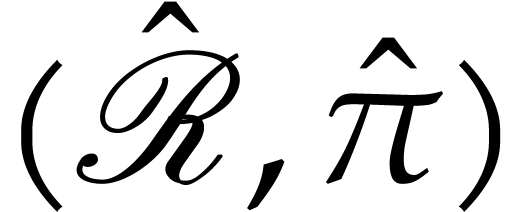 above
above  with the property that for any other
Riemann surface
with the property that for any other
Riemann surface 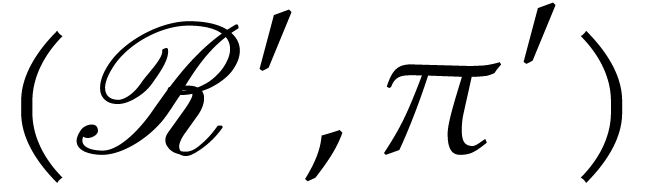 above
above  , there exists a unique
, there exists a unique 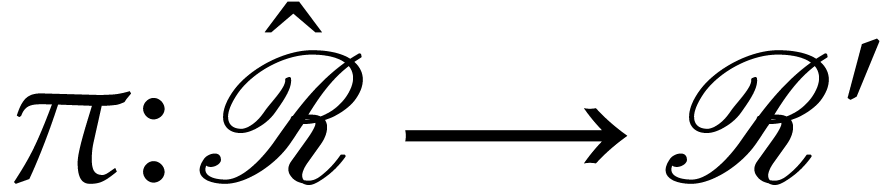 with
with
 and such that
and such that 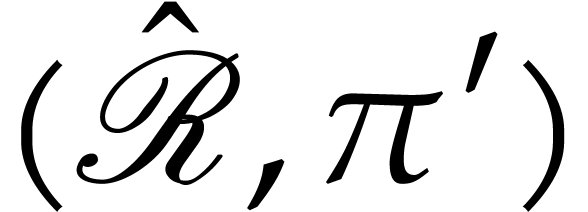 is a
Riemann surface above
is a
Riemann surface above 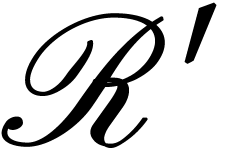 . In
particular, if
. In
particular, if 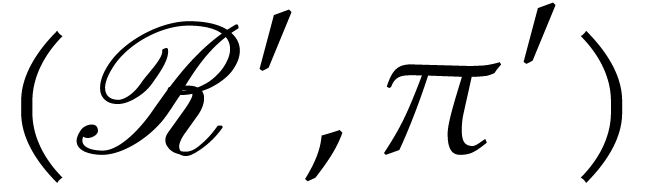 has the same universal property
as
has the same universal property
as 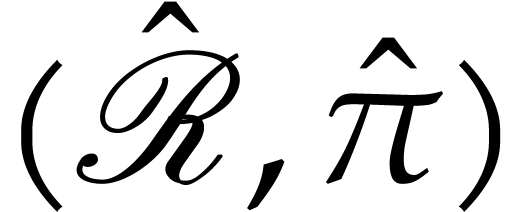 , then
, then 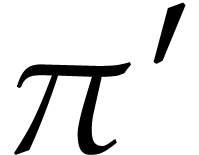 is a homeomorphism. In other words, the space
is a homeomorphism. In other words, the space 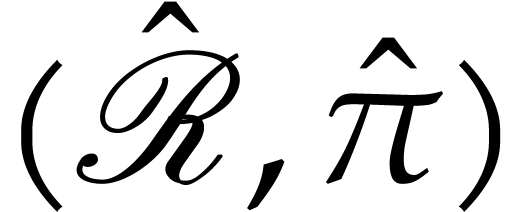 is
unique up to such a homeomorphism and we call it the covering
space of
is
unique up to such a homeomorphism and we call it the covering
space of  . We also
recall that the covering space of
. We also
recall that the covering space of  is
is 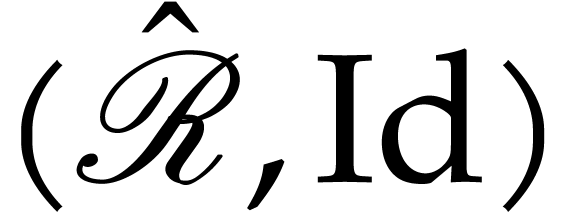 .
.
Assume now that  is a simply connected Riemann
surface and consider a discrete subset
is a simply connected Riemann
surface and consider a discrete subset  ,
i.e. every
,
i.e. every  has an open neighborhood
has an open neighborhood
 with
with  .
Let
.
Let 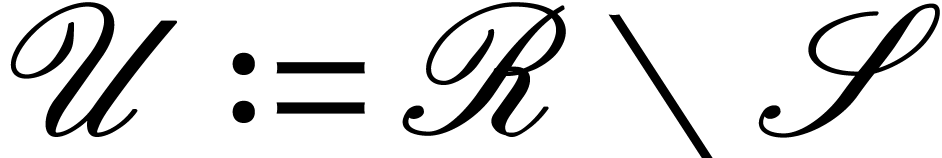 and consider the covering space
and consider the covering space 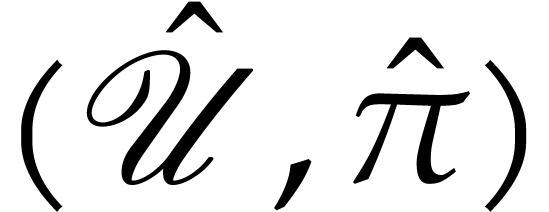 of
of  . We define
. We define
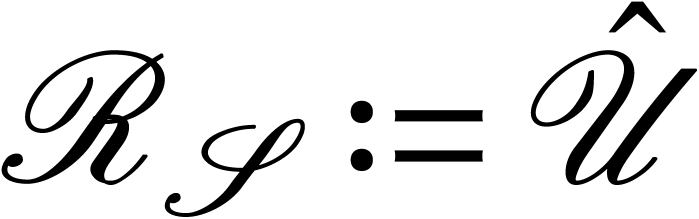 and
and 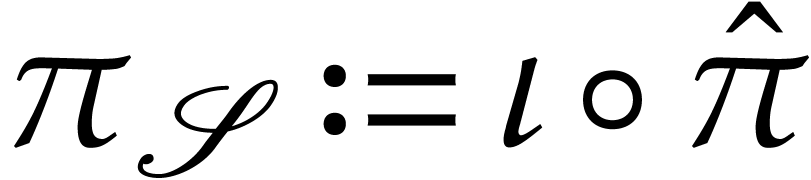 ,
where
,
where 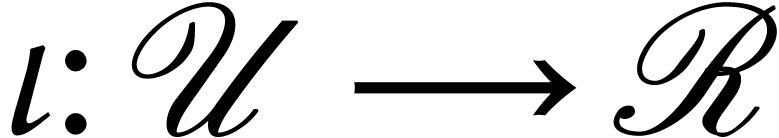 is the inclusion map, and call
is the inclusion map, and call 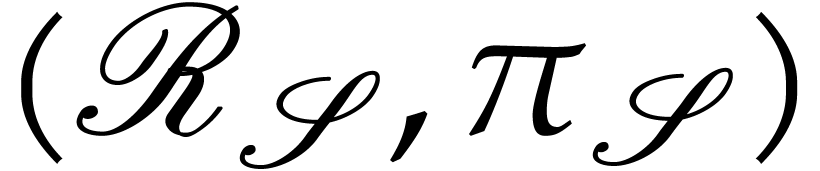 a discrete ramification of
a discrete ramification of  . We will also say that the map
. We will also say that the map 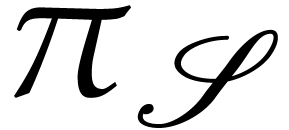 is a discrete ramification.
is a discrete ramification.
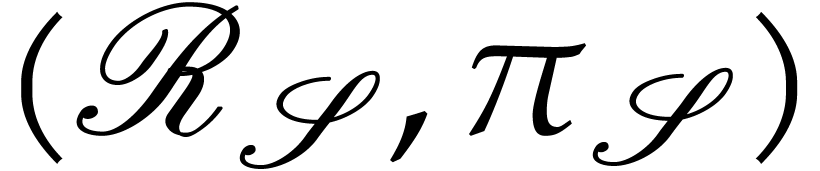 and
and 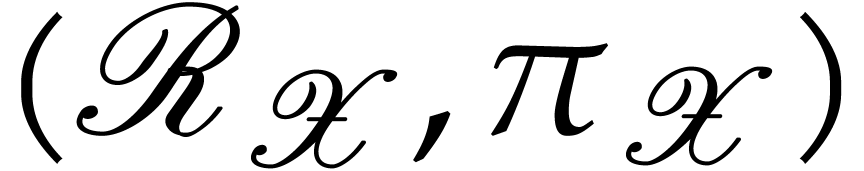 of
of  . Let
. Let 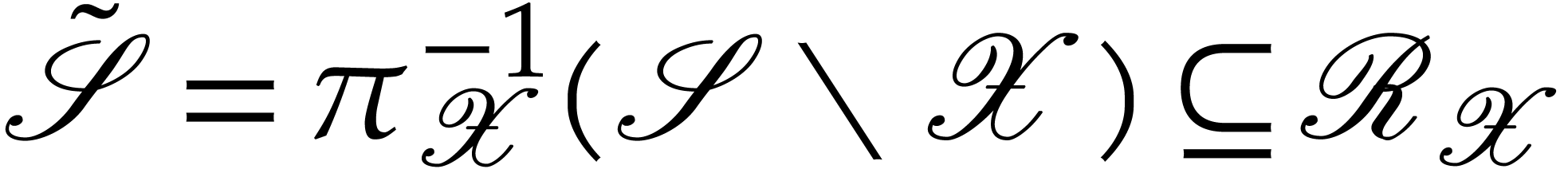 and
and 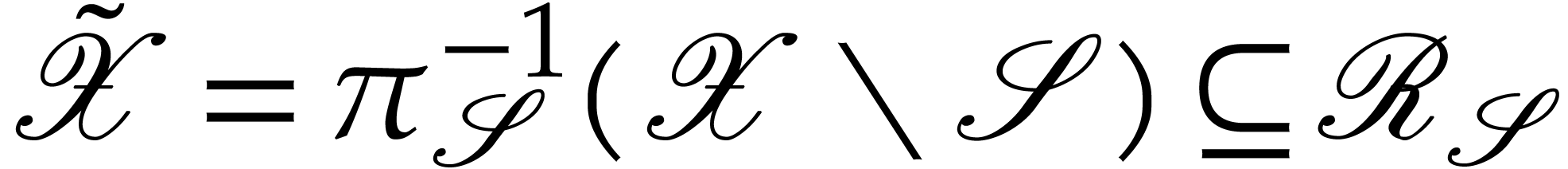 .
Then
.
Then 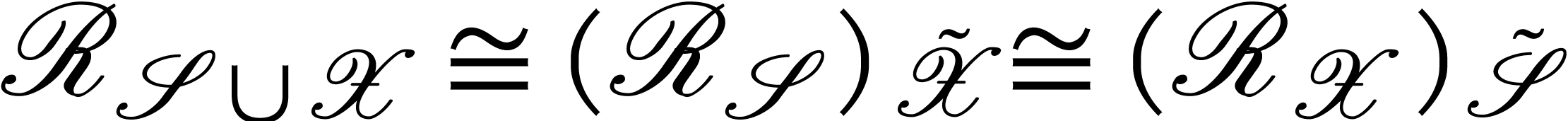 and, after identification of
and, after identification of 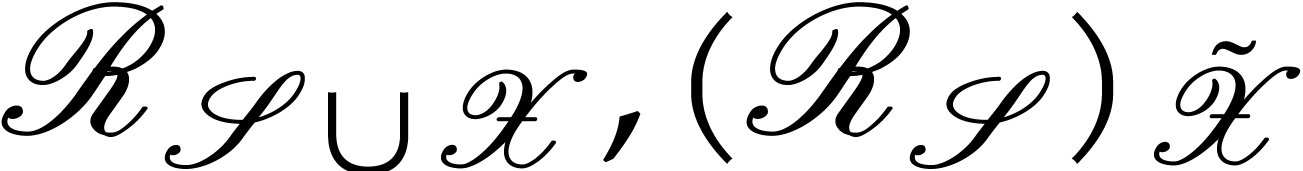 , and
, and 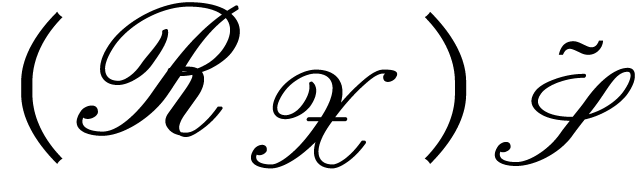 via these
isomorphisms, the following diagram commutes
via these
isomorphisms, the following diagram commutes
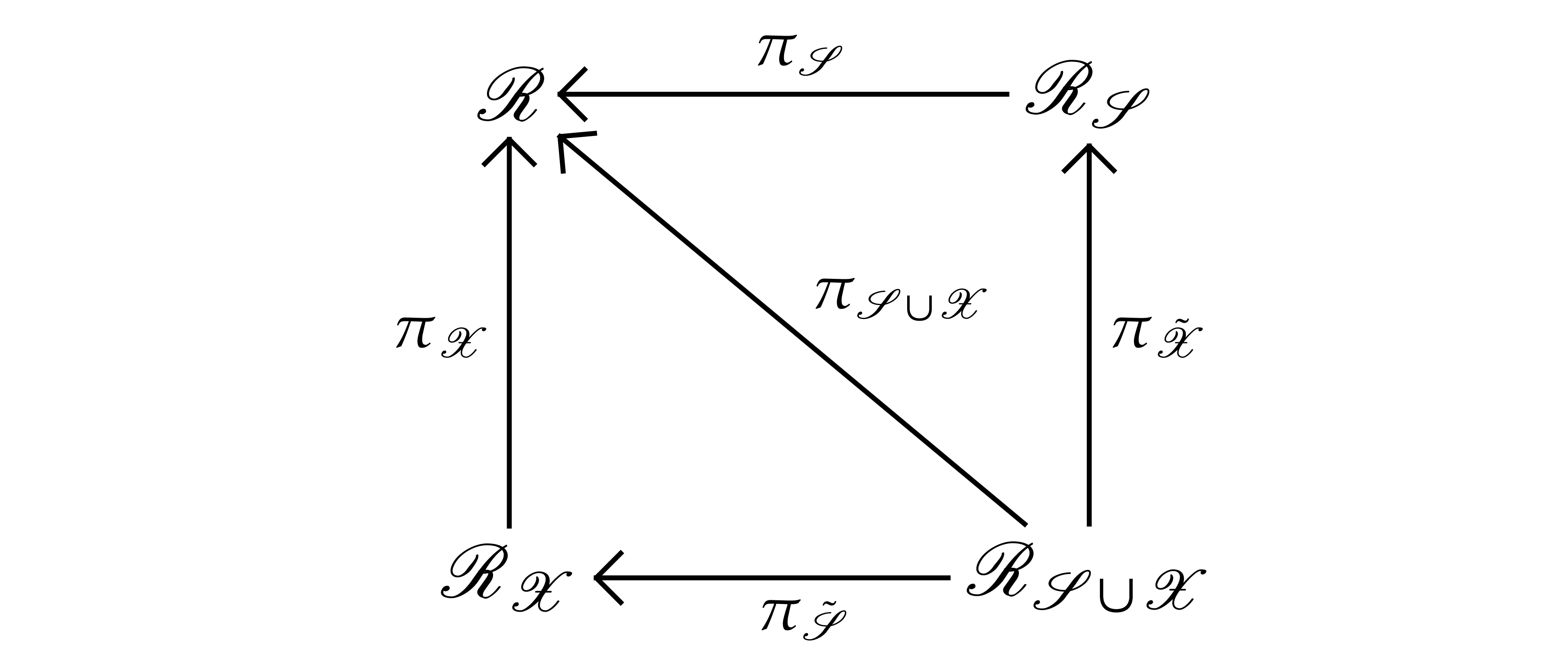
Proof. Since 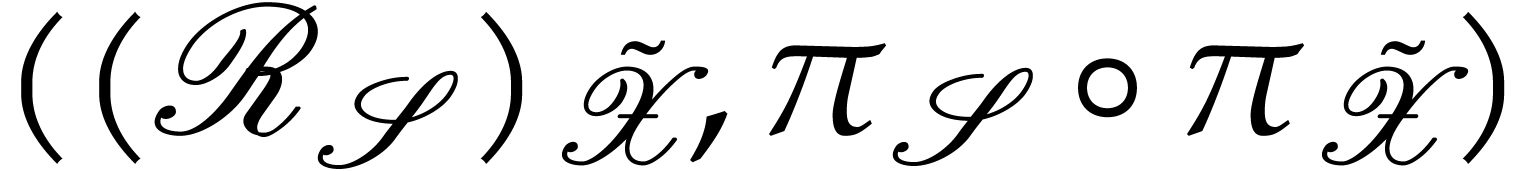 is a
Riemann surface above
is a
Riemann surface above  , there
exists a unique
, there
exists a unique 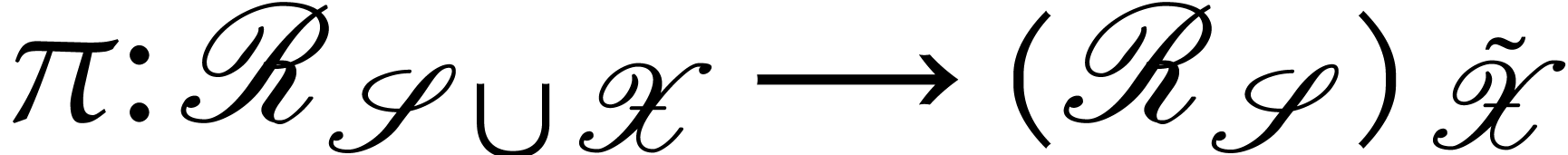 with
with 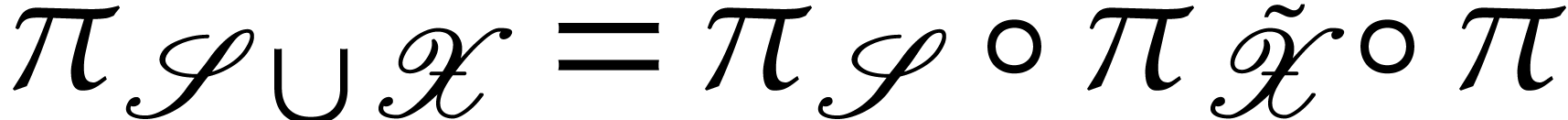 . Conversely,
. Conversely, 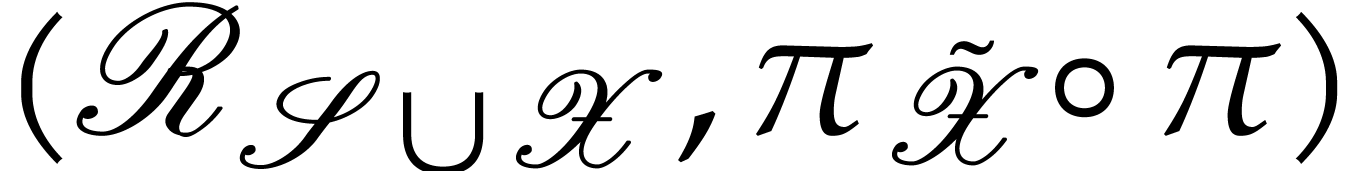 is a Riemann
surface above
is a Riemann
surface above  , so there
exists a unique
, so there
exists a unique 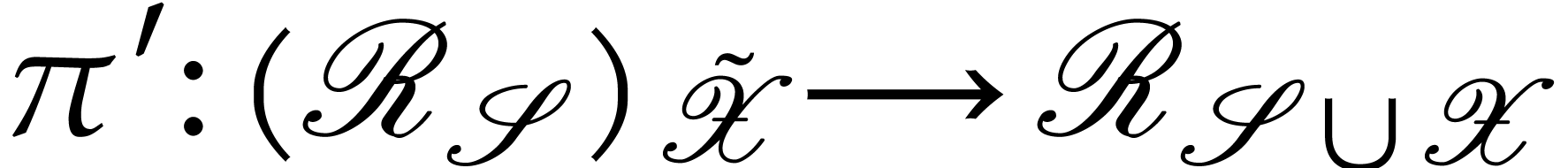 with
with 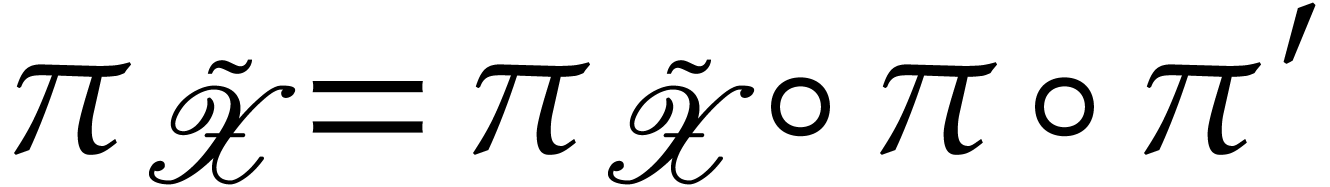 . Next
. Next 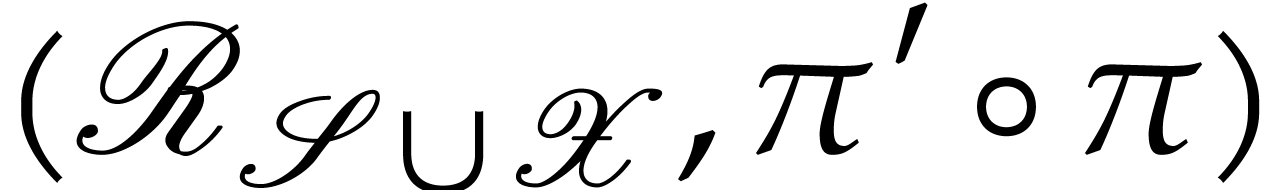 is a Riemann surface
above
is a Riemann surface
above  , so there exists a
unique map
, so there exists a
unique map  with
with  .
This shows that
.
This shows that 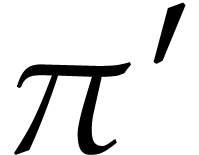 and
and  are
mutual inverses and
are
mutual inverses and 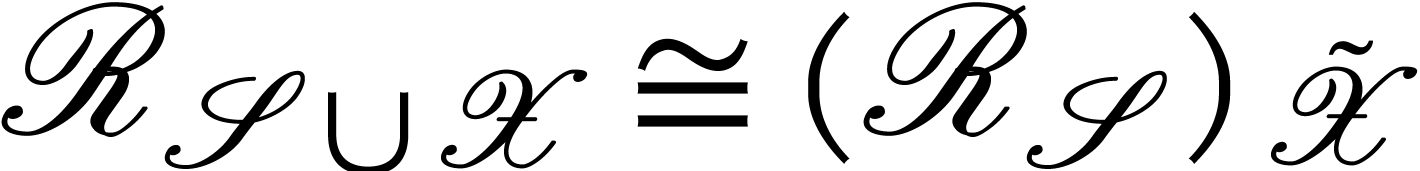 .
Identifying
.
Identifying  and
and  via this
isomorphism, we have
via this
isomorphism, we have 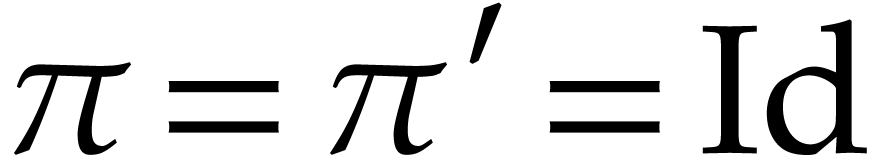 and we already showed above
that
and we already showed above
that 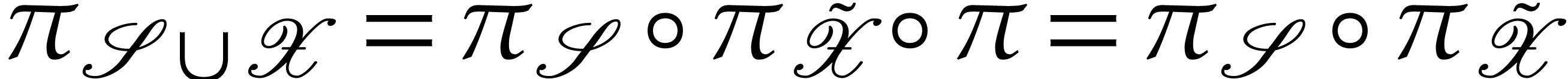 . We conclude that the
top triangle in the above diagram commutes. The isomorphism
. We conclude that the
top triangle in the above diagram commutes. The isomorphism 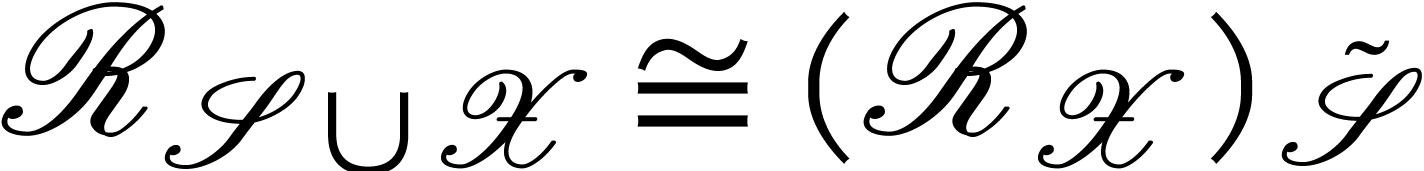 and the commutation of the bottom triangle are proved
similarly.
and the commutation of the bottom triangle are proved
similarly.
Now consider a sequence 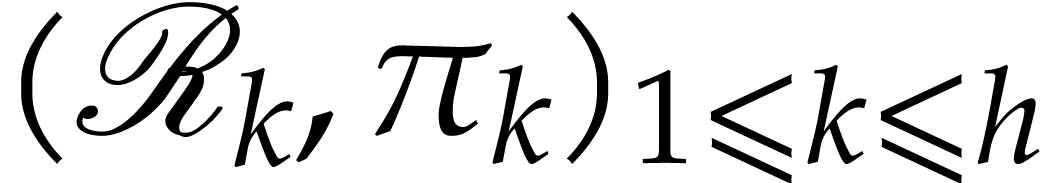 with
with 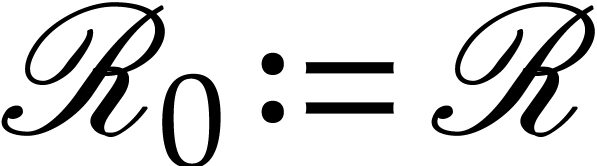 and
and 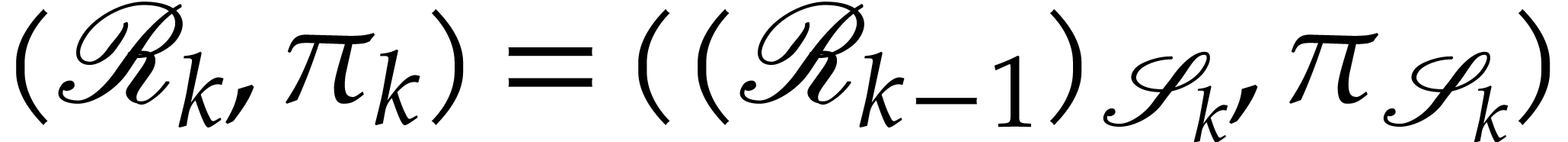 for
for 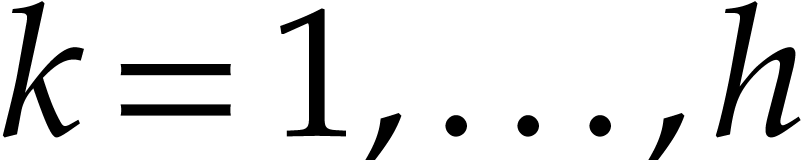 ,
where
,
where  is a discrete subset of
is a discrete subset of 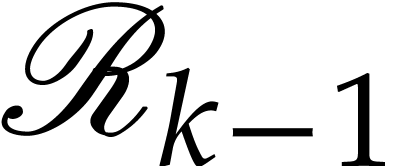 . Then we call
. Then we call 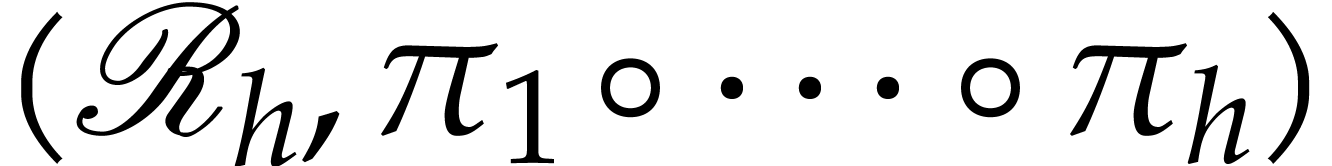 a
recursive discrete ramification of
a
recursive discrete ramification of  of
height
of
height 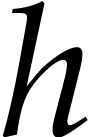 . We will also say
that the map
. We will also say
that the map  is a recursive discrete
ramification. If
is a recursive discrete
ramification. If 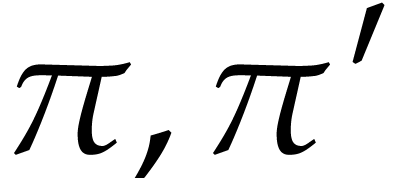 are two recursive discrete
ramifications, then we will say that
are two recursive discrete
ramifications, then we will say that 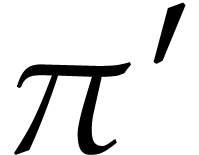 lies
over
lies
over  if there exists a recursive discrete
ramification
if there exists a recursive discrete
ramification 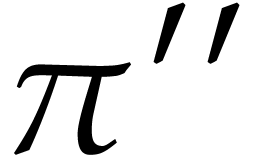 with
with  .
.
 and
and 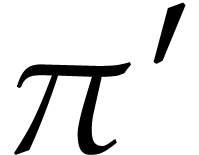 of respective heights
of respective heights  and
and
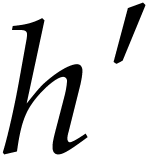 , there exists a recursive
discrete ramification
, there exists a recursive
discrete ramification 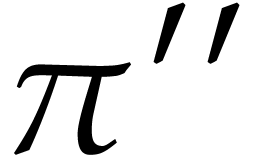 of height
of height  that lies above both
that lies above both  and
and 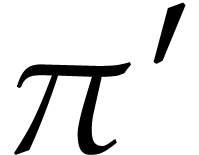 .
.
Proof. Setting 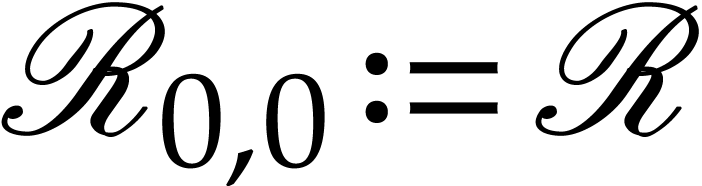 ,
there exist sequences of discrete ramifications
,
there exist sequences of discrete ramifications

whose compositions are  and
and 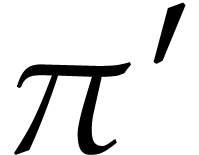 , respectively. Using
, respectively. Using 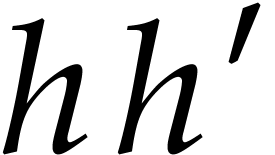 applications of Lemma 1, we can extend these sequences into
a commutative diagram
applications of Lemma 1, we can extend these sequences into
a commutative diagram
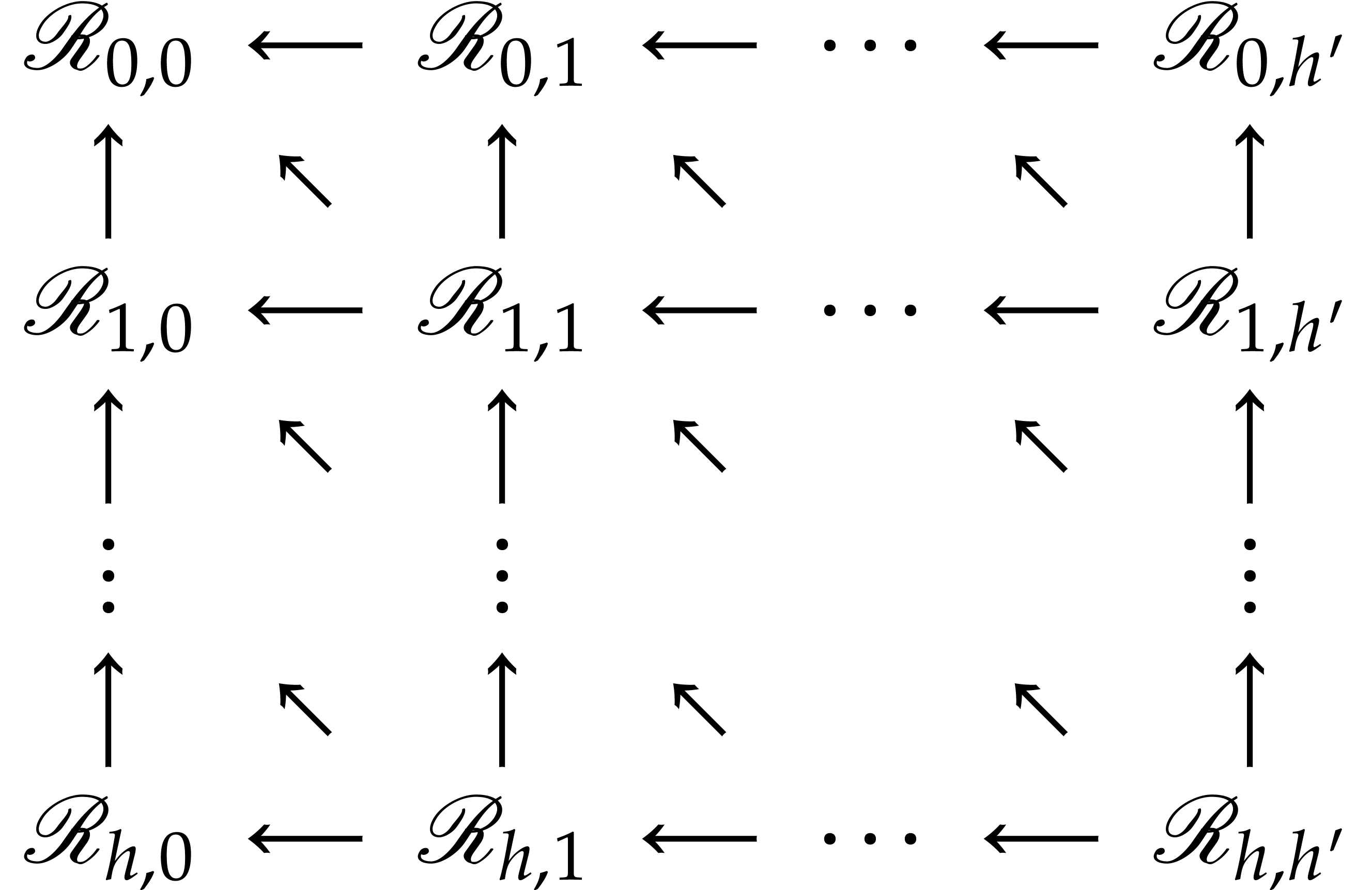
where all the arrows are discrete ramifications. The composite map  is the desired recursive ramification
is the desired recursive ramification 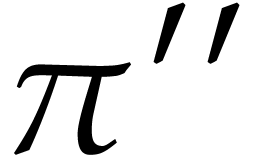 . Since we can obtain it by following
. Since we can obtain it by following 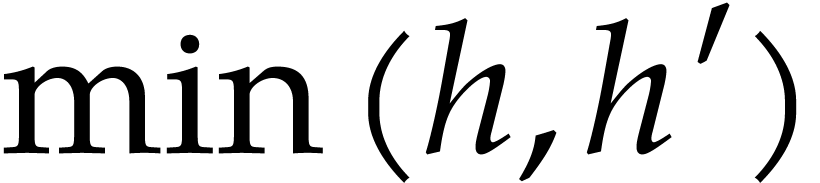 diagonal arrows and
diagonal arrows and 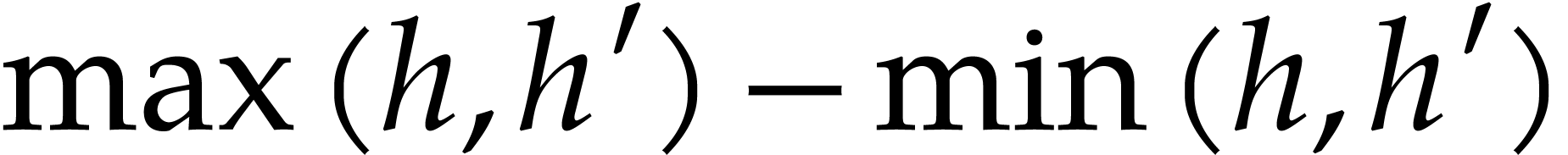 horizontal or
vertical arrows, the height of
horizontal or
vertical arrows, the height of 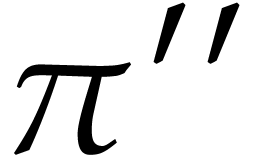 is
is 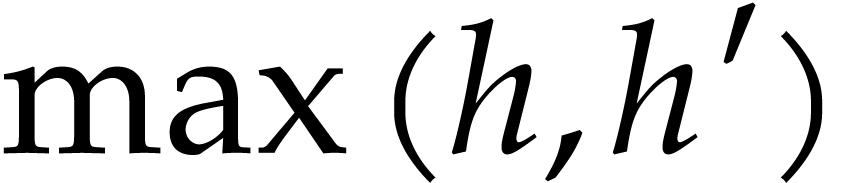 , as claimed.
, as claimed.
Given a simply connected Riemann surface  ,
let
,
let 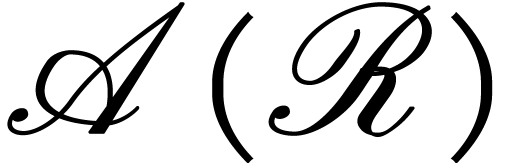 denote the space of analytic functions on
denote the space of analytic functions on
 . For any discrete
ramification
. For any discrete
ramification 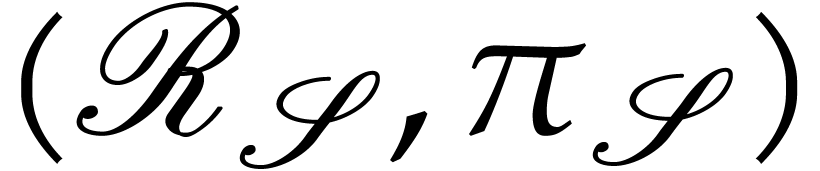 , we have a
natural injection of
, we have a
natural injection of 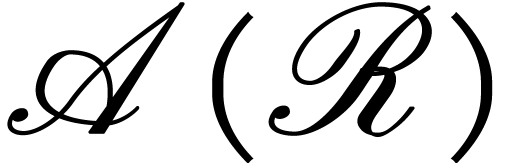 into
into 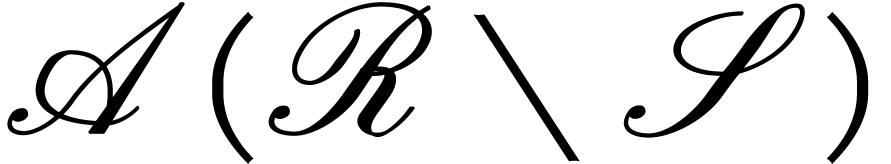 into
into 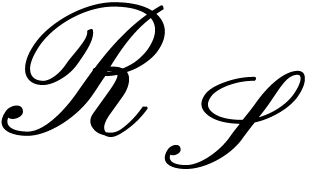 . Consequently, any
recursive discrete ramification
. Consequently, any
recursive discrete ramification 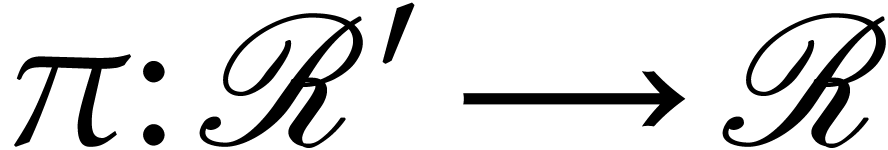 induces a
natural injection
induces a
natural injection  . By Lemma
2, we know that these injections form an inductive system.
We denote the inductive limit of these injections by
. By Lemma
2, we know that these injections form an inductive system.
We denote the inductive limit of these injections by 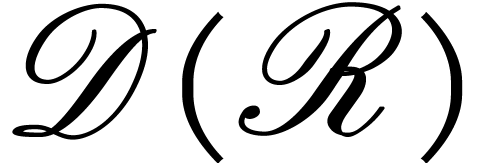 and call the elements of
and call the elements of 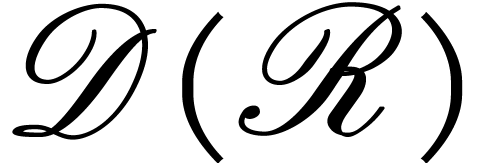 dendromorphic
functions on
dendromorphic
functions on  .
.
Any dendromorphic function can concretely be represented as an analytic
function 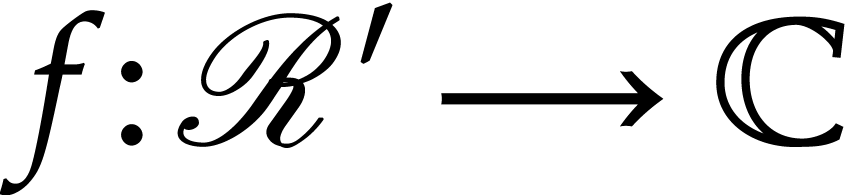 for some recursive discrete
ramification
for some recursive discrete
ramification 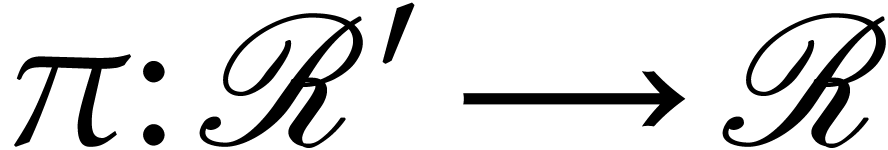 . Now consider
two such representations
. Now consider
two such representations 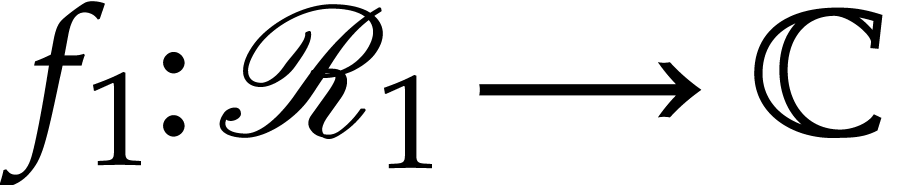 and
and 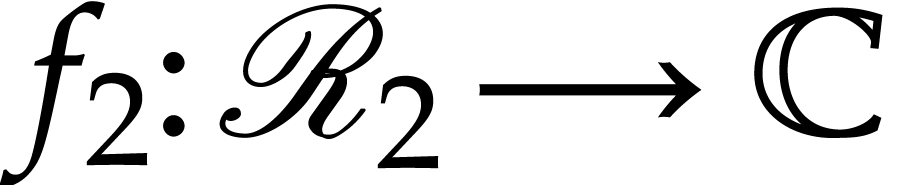 for recursive discrete ramifications
for recursive discrete ramifications 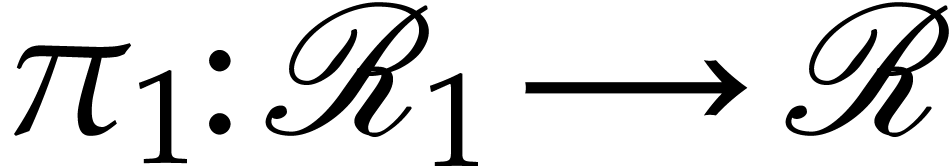 and
and 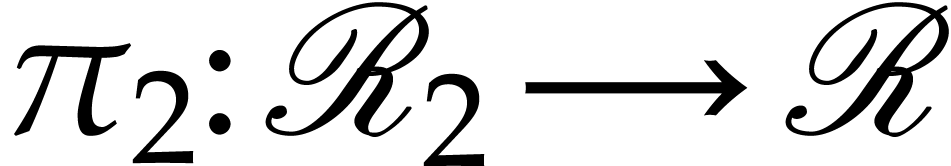 . Let
. Let 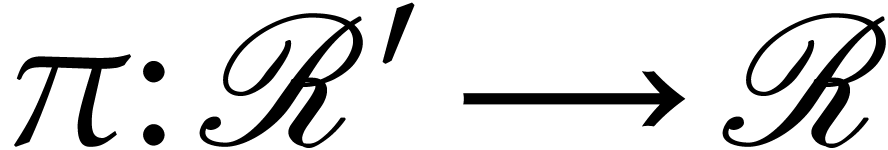 be a
recursive discrete ramification over both
be a
recursive discrete ramification over both 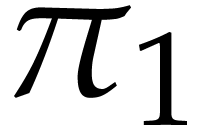 and
and
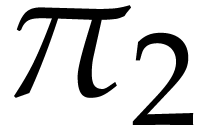 , and let
, and let 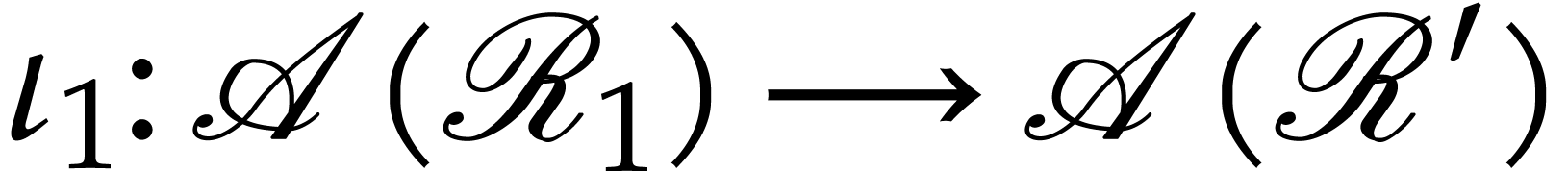 and
and 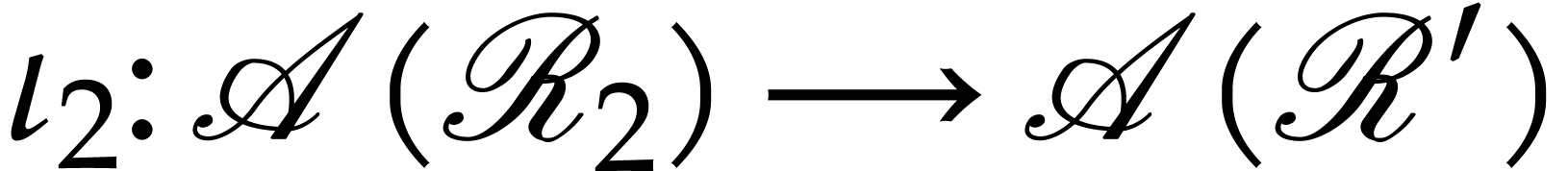 be the natural induced injections as above.
Then
be the natural induced injections as above.
Then 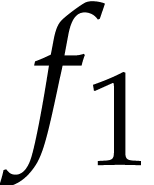 and
and 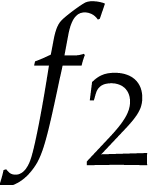 represent the
same dendromorphic function whenever
represent the
same dendromorphic function whenever 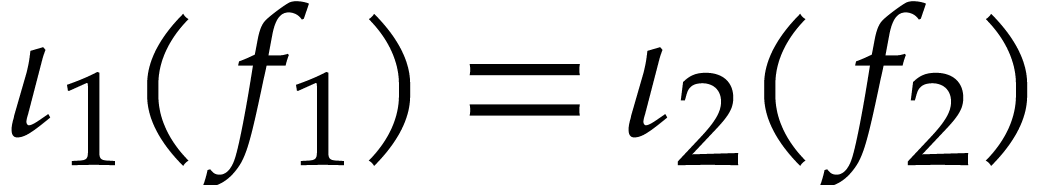 .
.
 be a simply connected open subset of
be a simply connected open subset of  . Then the space
. Then the space 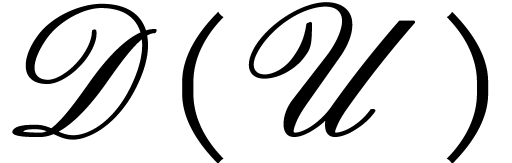 is a Picard-Vessiot closed field.
is a Picard-Vessiot closed field.
Proof. The space 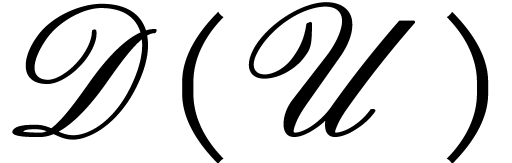 is
clearly a differential ring, since it is the inductive limit of
differential rings
is
clearly a differential ring, since it is the inductive limit of
differential rings 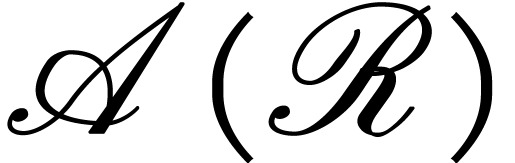 . Consider
a non-zero dendromorphic function, represented by an analytic function
. Consider
a non-zero dendromorphic function, represented by an analytic function
 . Then the set
. Then the set  of points where
of points where 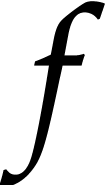 vanishes is
discrete, so
vanishes is
discrete, so 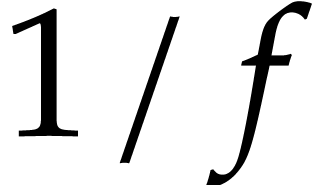 is defined on
is defined on  , and
, and  .
Since
.
Since 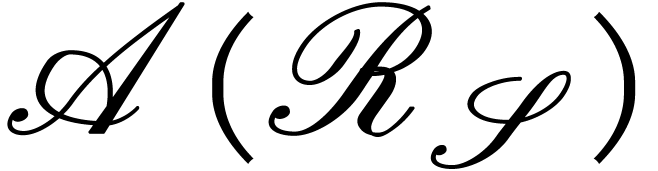 embeds into
embeds into 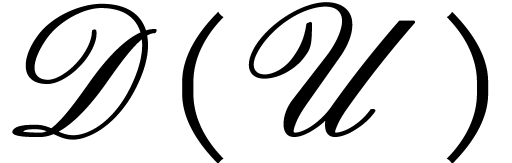 ,
this shows that
,
this shows that 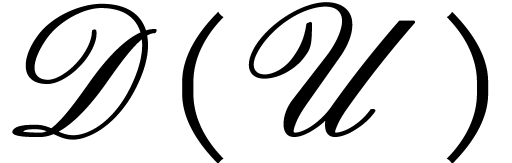 is a field. Let us next consider
a differential equation
is a field. Let us next consider
a differential equation
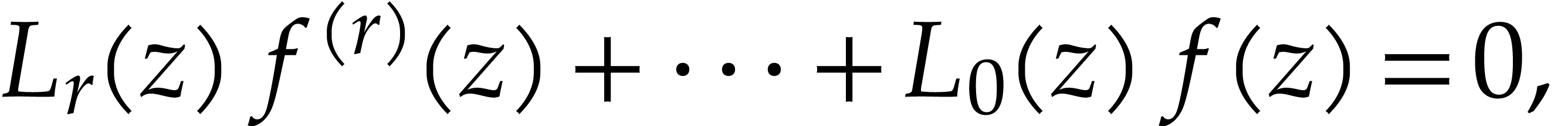 |
(1) |
where 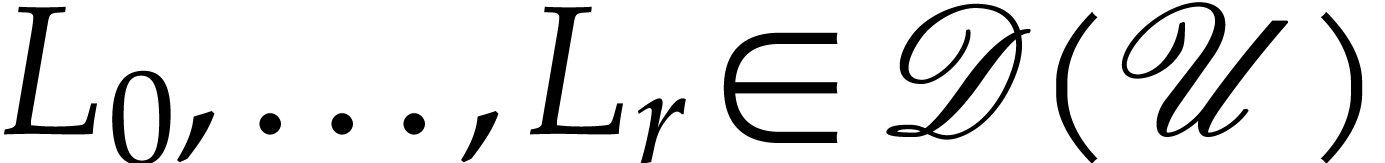 with
with 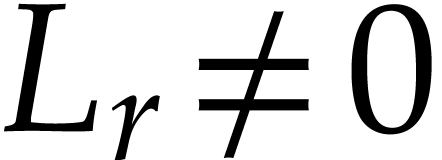 .
By Lemma 2, we may represent
.
By Lemma 2, we may represent  by
analytic functions in
by
analytic functions in  for some recursive
discrete ramification
for some recursive
discrete ramification  . The
set
. The
set  of points where
of points where 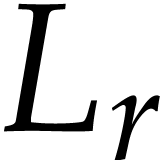 vanishes is discrete and it is classical that any solution of (1)
at a point
vanishes is discrete and it is classical that any solution of (1)
at a point  can be analytically continued along
any path on
can be analytically continued along
any path on  that avoids
that avoids  . Doing this for a fundamental system of solutions
at
. Doing this for a fundamental system of solutions
at  , we obtain a fundamental
system of solutions
, we obtain a fundamental
system of solutions  . We
conclude that
. We
conclude that 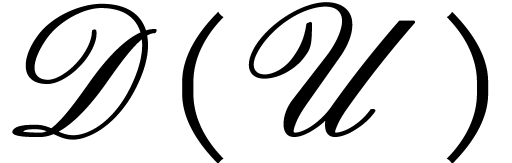 is Picard-Vessiot closed.
is Picard-Vessiot closed.
Let  be a simply connected open subset of
be a simply connected open subset of  and consider a dendromorphic function
and consider a dendromorphic function 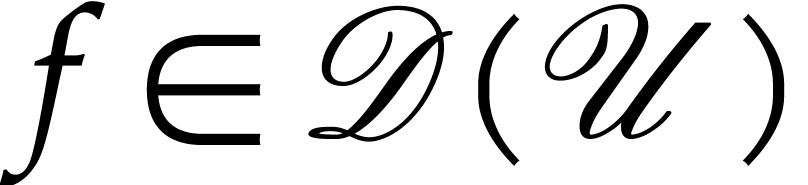 . We say that
. We say that 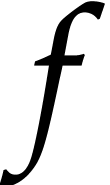 is
boundaryless if the following property holds for every
representation
is
boundaryless if the following property holds for every
representation  , where
, where 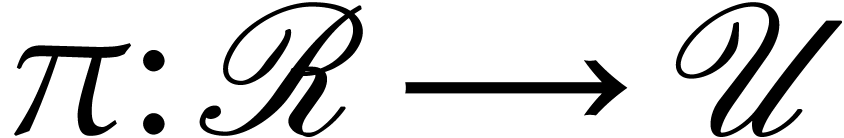 is a recursive discrete ramification: given a
continuous path
is a recursive discrete ramification: given a
continuous path 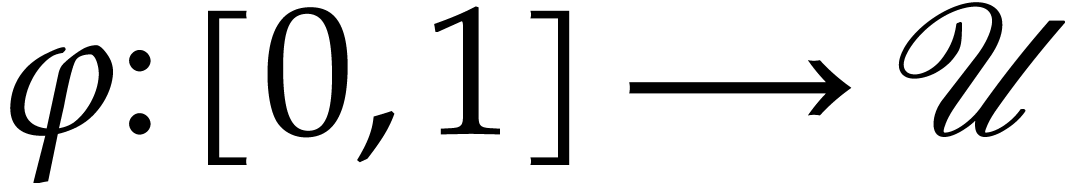 with
with 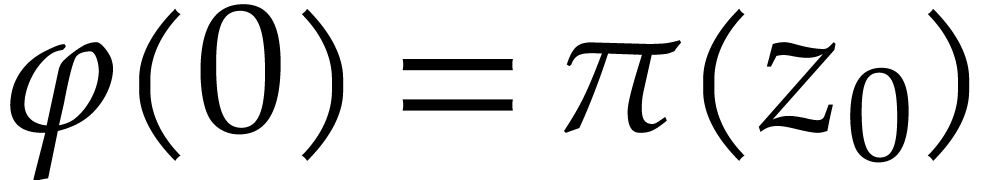 for
some
for
some  and
and  ,
there exists a continuous path
,
there exists a continuous path 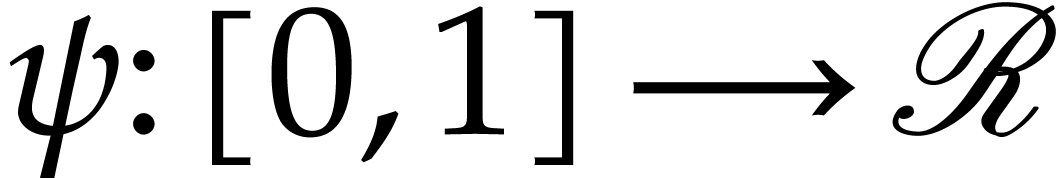 with
with 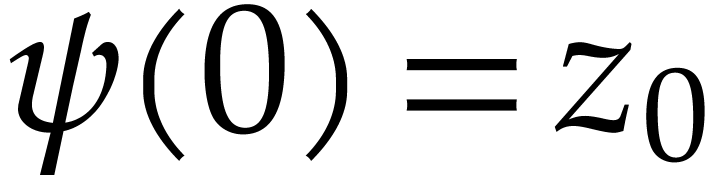 and
and
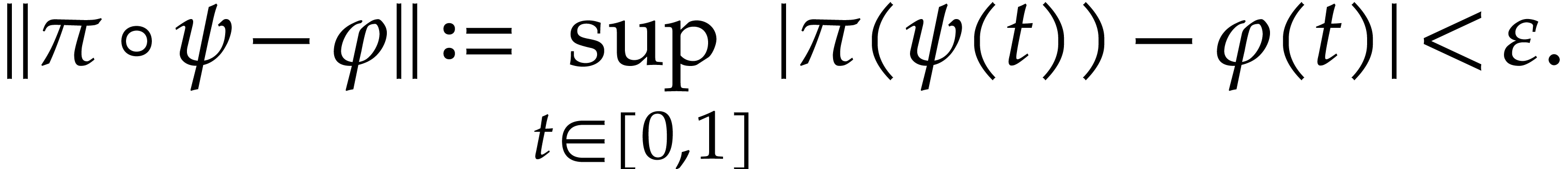
Proof. With  ,
,
 ,
,  , and
, and  as in the above
definition of boundaryless, there exist discrete ramifications
as in the above
definition of boundaryless, there exist discrete ramifications  with
with  ,
, 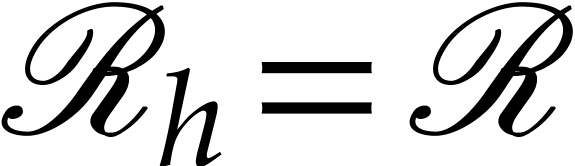 , and
, and  .
We proceed by induction over
.
We proceed by induction over 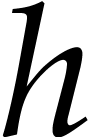 .
The result is clear for
.
The result is clear for 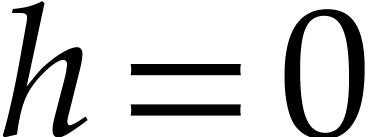 , so
assume that
, so
assume that 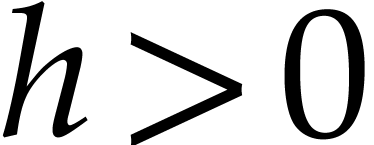 and let
and let  . The induction hypothesis implies the existence of
a continuous path
. The induction hypothesis implies the existence of
a continuous path 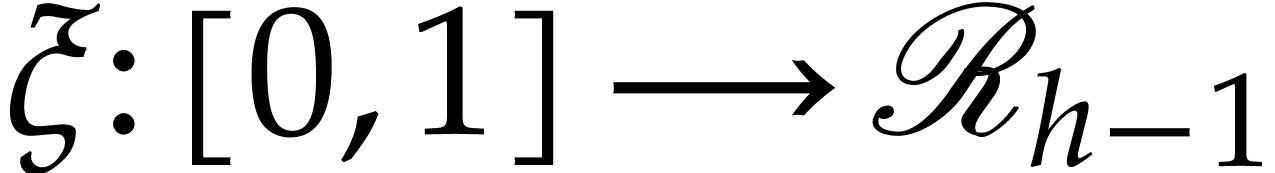 with
with 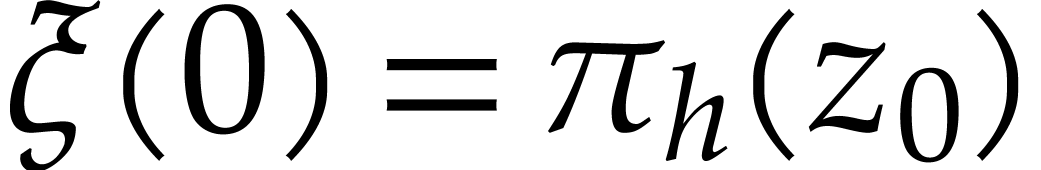 and
and 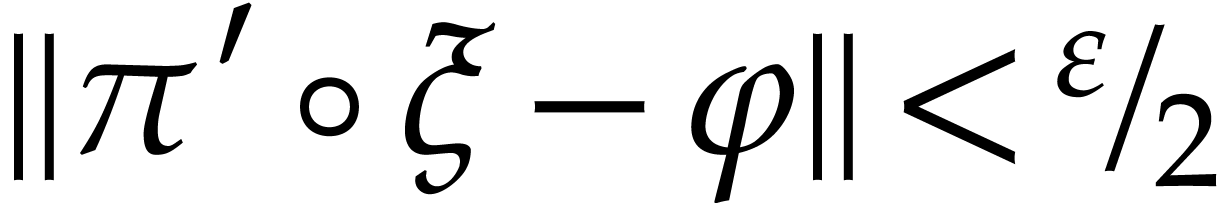 . Let
. Let  be the discrete subset of
be the discrete subset of 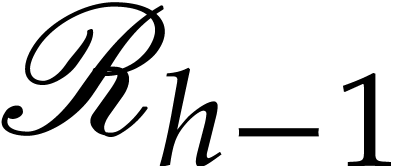 such that
such that 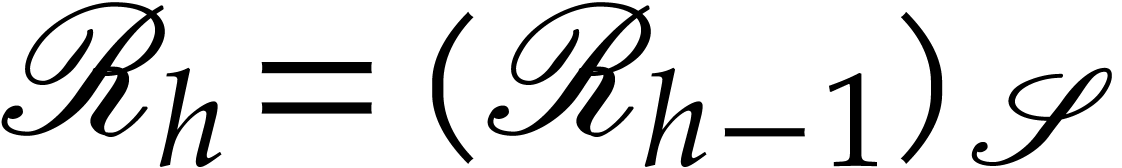 .
.
Since 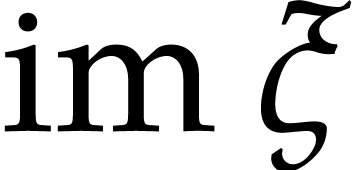 is compact, there exists an
is compact, there exists an 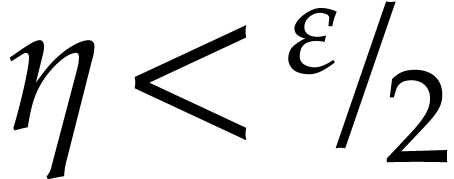 such that for every
such that for every 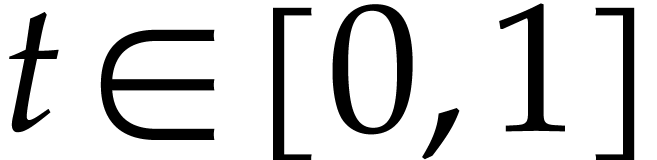 ,
the closed ball
,
the closed ball 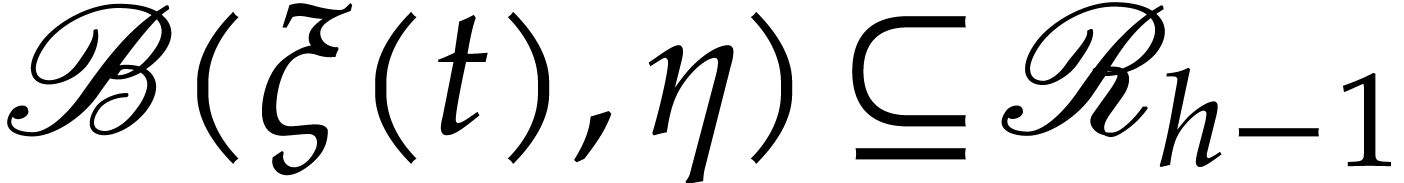 with center
with center 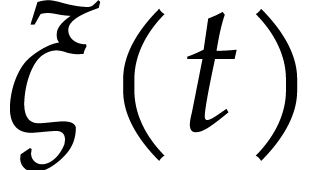 and radius
and radius 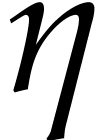 is an isomorphic lift of the ball
is an isomorphic lift of the ball
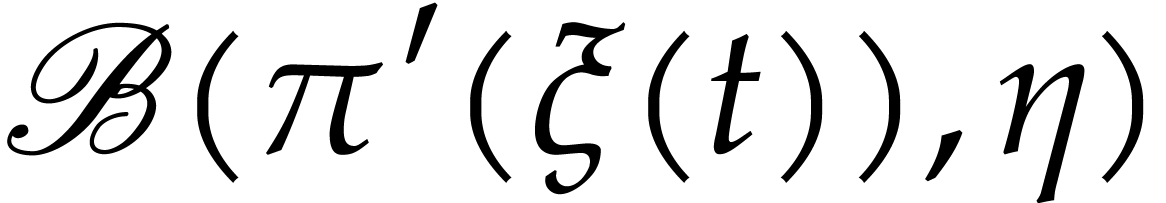 . Then the thickened image
. Then the thickened image
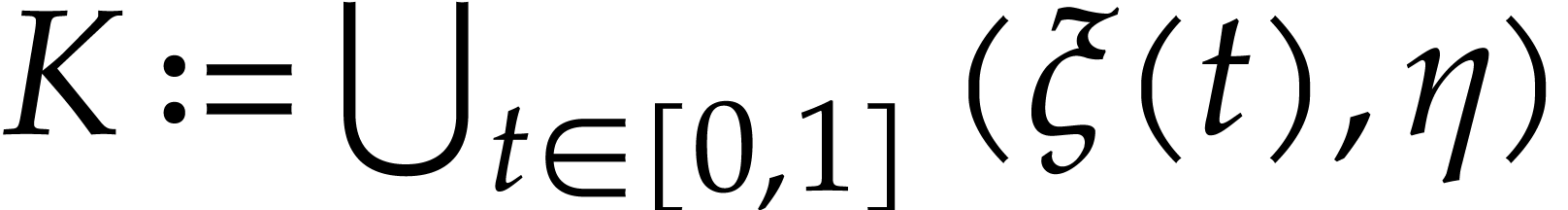 of
of  is also compact, so
the set
is also compact, so
the set  is finite, since
is finite, since  is discrete. Modulo taking a smaller
is discrete. Modulo taking a smaller 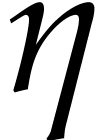 ,
we may therefore assume that
,
we may therefore assume that 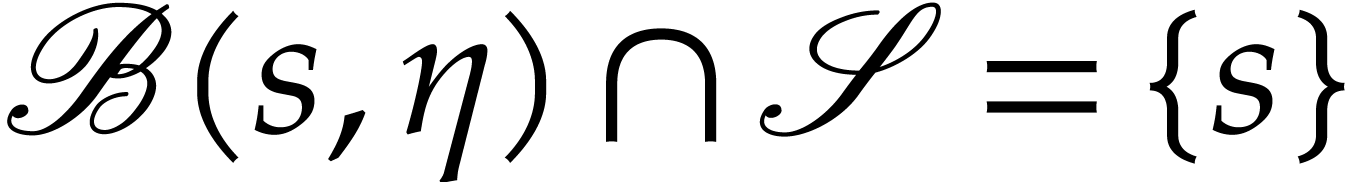 and
and 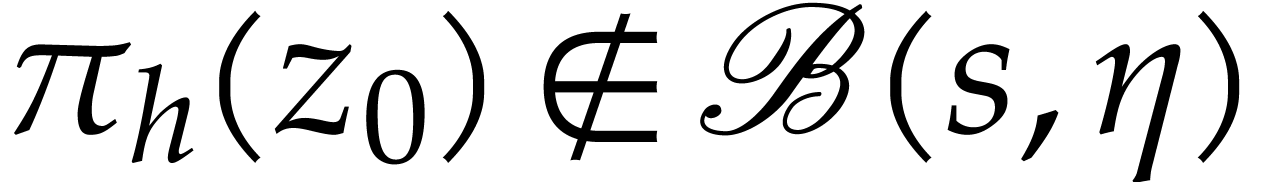 for all
for all  , and
that
, and
that 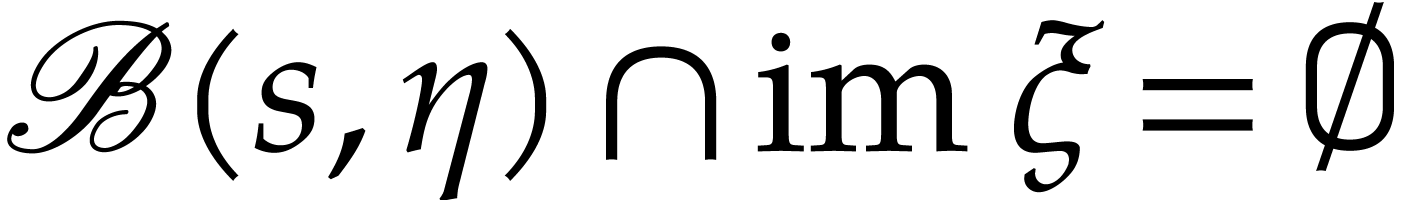 whenever
whenever 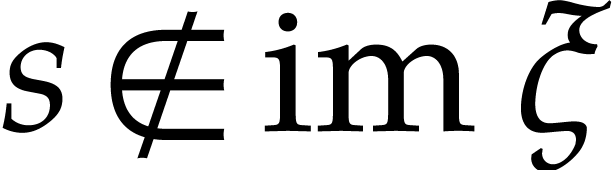 .
.
Let  be the values of
be the values of 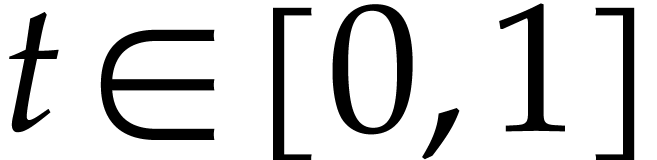 for
which
for
which  . For some sufficiently
small
. For some sufficiently
small 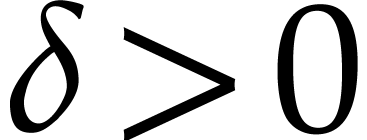 with
with 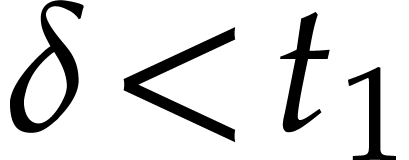 ,
the intervals
,
the intervals 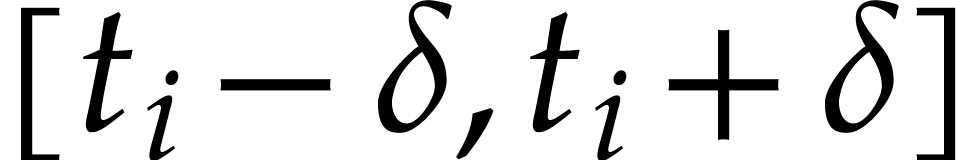 are pairwise disjoint and
are pairwise disjoint and 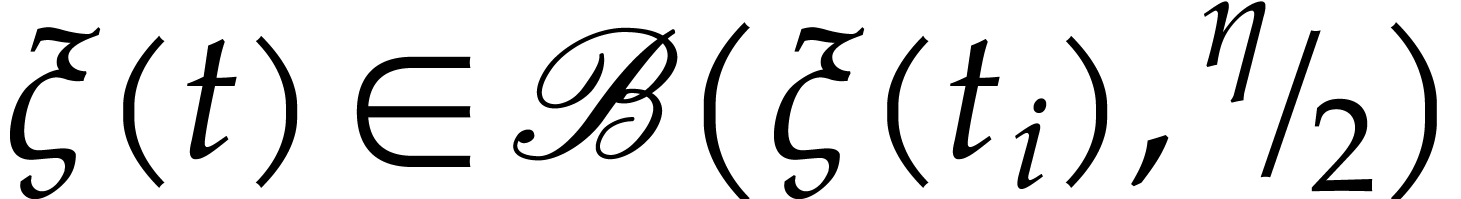 whenever
whenever 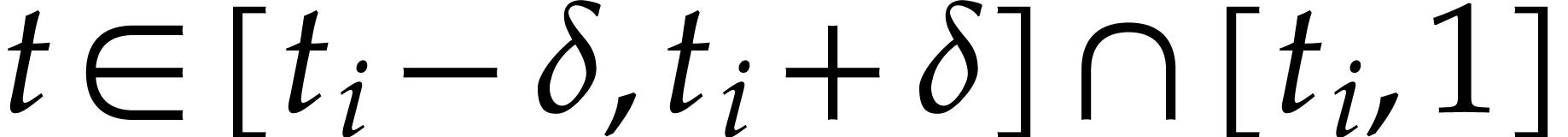 .
Now consider any path
.
Now consider any path 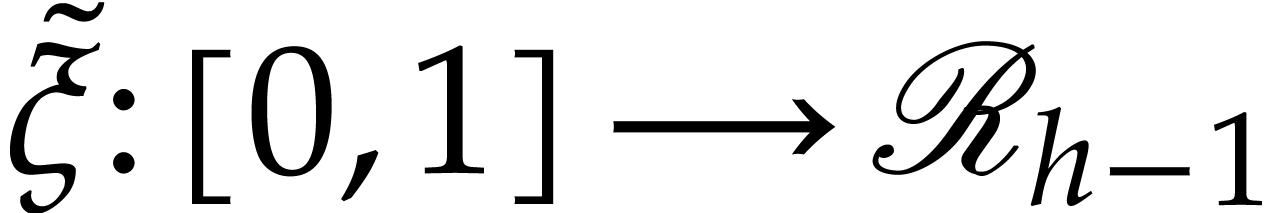 with the following
properties:
with the following
properties:
If 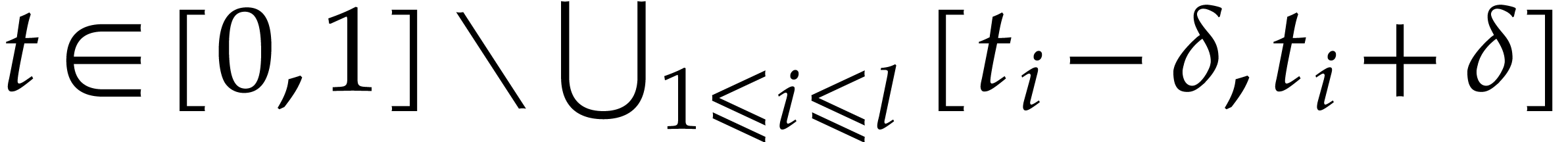 , then
, then 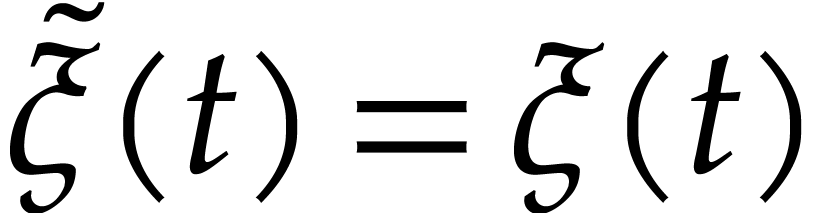 .
.
If  , then
, then  restricted to
restricted to 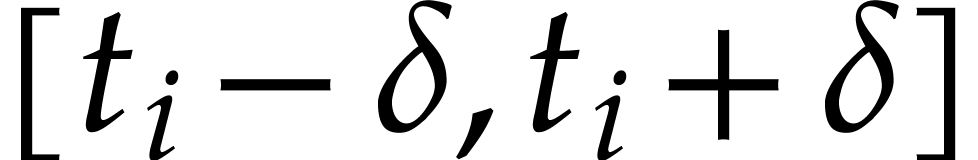 is any path from
is any path from
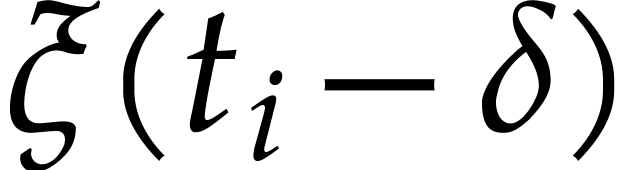 to
to 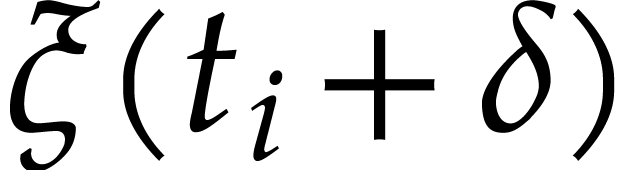 inside the
punctured disk
inside the
punctured disk 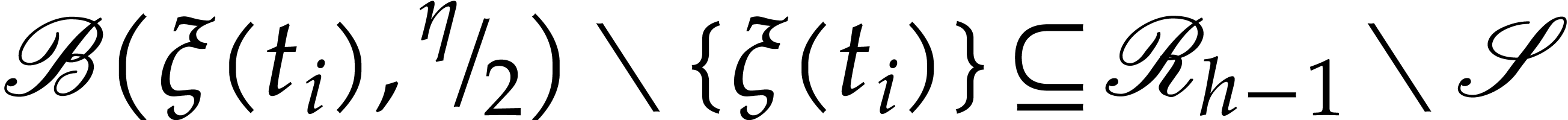 .
.
If  , then
, then 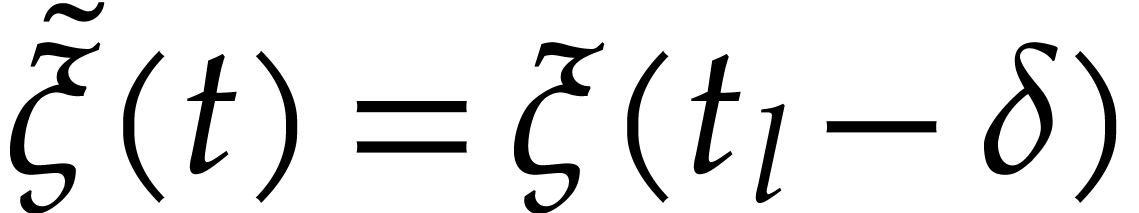 for all
for all 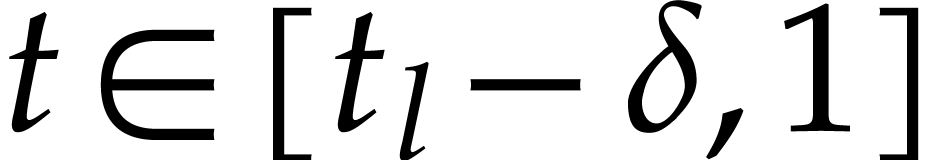 .
.
By construction, we have 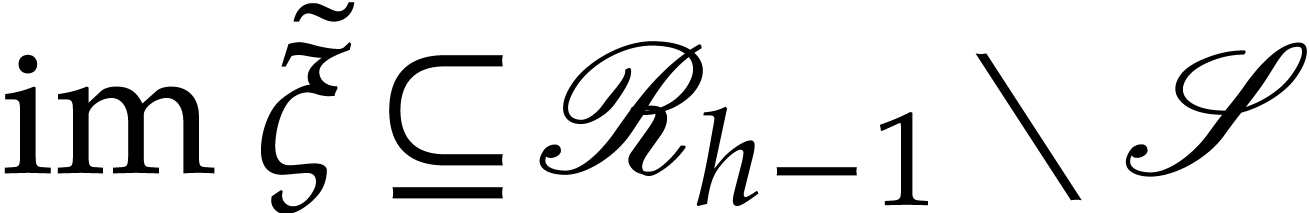 ,
,
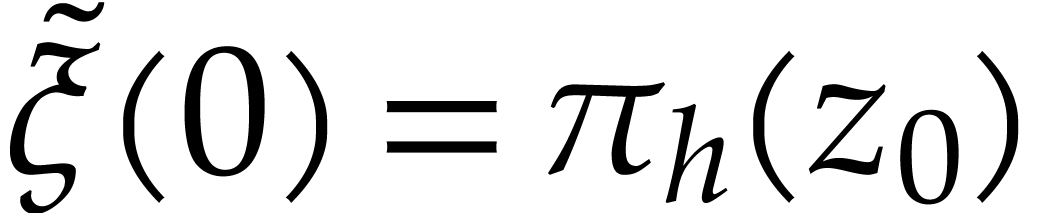 and
and 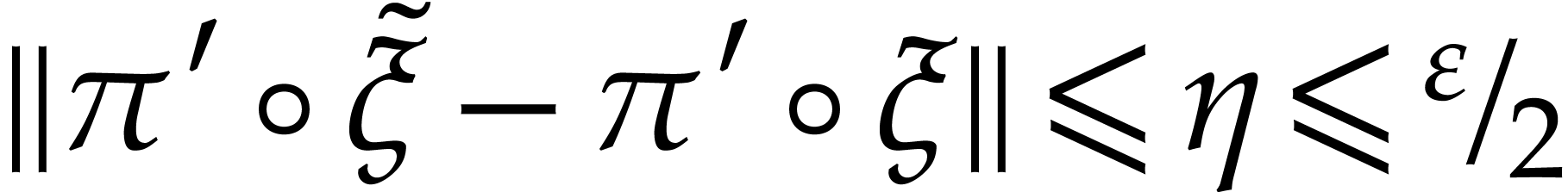 .
Consequently, there exists a unique lift
.
Consequently, there exists a unique lift 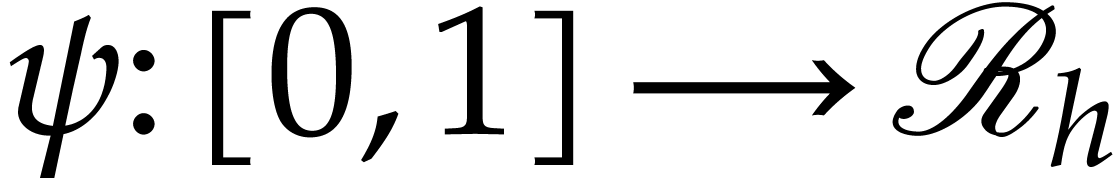 with
with
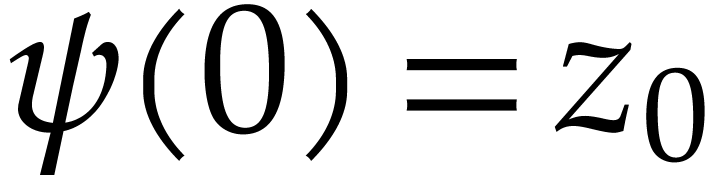 and
and 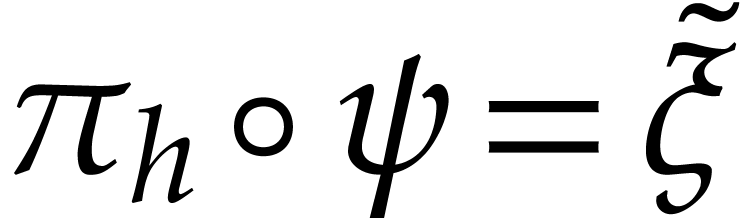 .
This lift satisfies
.
This lift satisfies 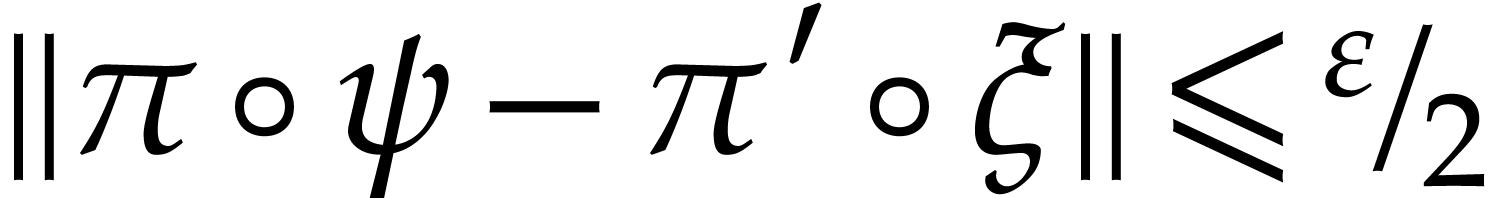 and
and  .
.
Recall that the generating function for the number 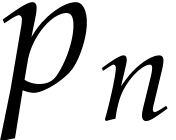 of partitions of an integer
of partitions of an integer 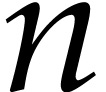 is given by the
explicit formula
is given by the
explicit formula
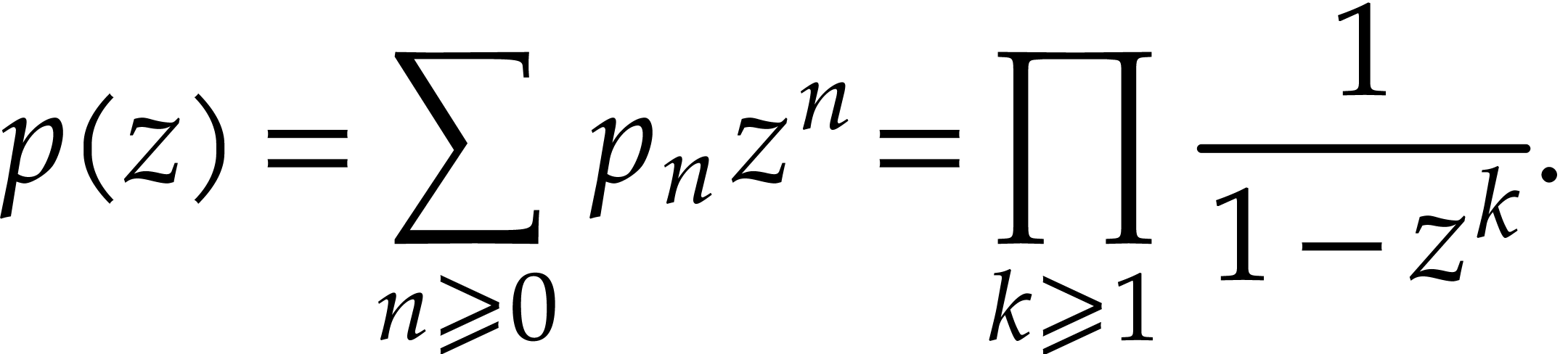 |
(2) |
It is well known [10, 5] that 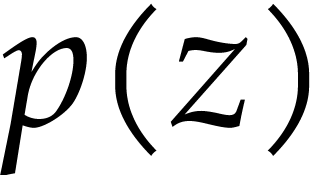 has a natural boundary on the unit circle and that it satisfies an
algebraic differential over
has a natural boundary on the unit circle and that it satisfies an
algebraic differential over  .
Consequently, if
.
Consequently, if  contains the closed unit disk,
then
contains the closed unit disk,
then 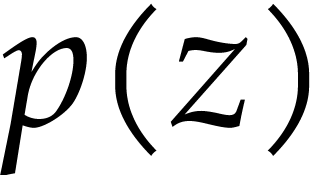 cannot be boundaryless above
cannot be boundaryless above  .
.
 contains the closed unit disk, then the
function
contains the closed unit disk, then the
function 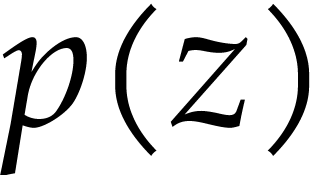 from
from  .
.
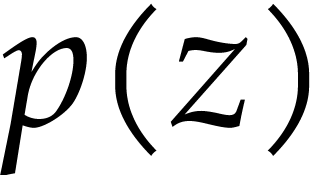 does not belong to
does not belong to 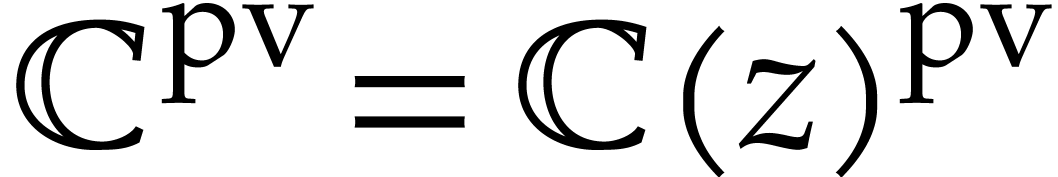 .
.
Given a simply connected Riemann surface, we say that a local analytic
function 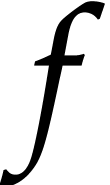 defined at
defined at  is
dendromorphic on
is
dendromorphic on  if it lifts and
extends into an analytic function on
if it lifts and
extends into an analytic function on 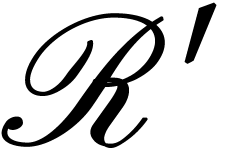 for some
recursive discrete ramification
for some
recursive discrete ramification 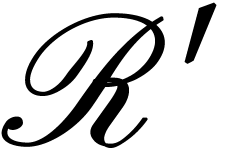 of
of  .
.
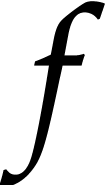 and
and 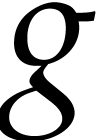 be two local
analytic functions above
be two local
analytic functions above 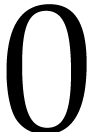 ,
which are both dendromorphic. If
,
which are both dendromorphic. If 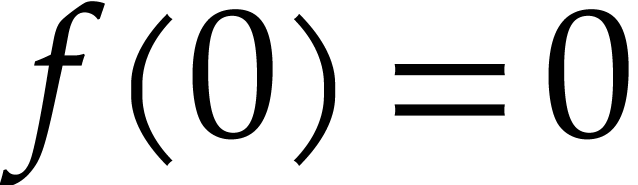 (after the
natural identification of
(after the
natural identification of 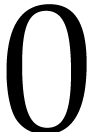 with its lift), then
with its lift), then
 is dendromorphic.
is dendromorphic.
Proof. The result is clear if 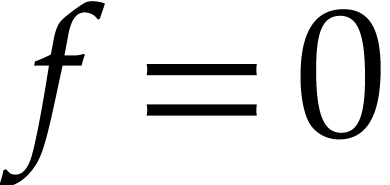 , so assume that
, so assume that 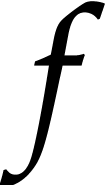 is
non-constant. There exist sequences of discrete ramifications
is
non-constant. There exist sequences of discrete ramifications

of  and distinguished points
and distinguished points 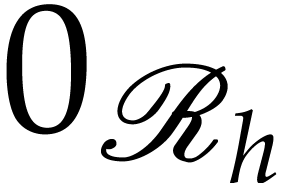 and
and 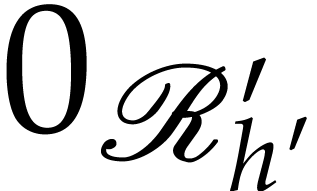 above
above 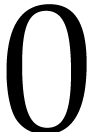 that we
identify with
that we
identify with 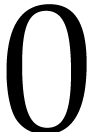 , such that the
local functions
, such that the
local functions 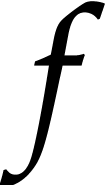 and
and 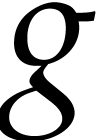 extend analytically to
extend analytically to  and
and 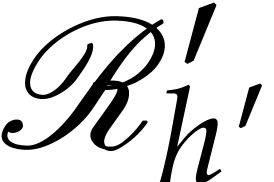 , respectively. Let us show how to extend the
first sequence of discrete ramifications into a sequence
, respectively. Let us show how to extend the
first sequence of discrete ramifications into a sequence
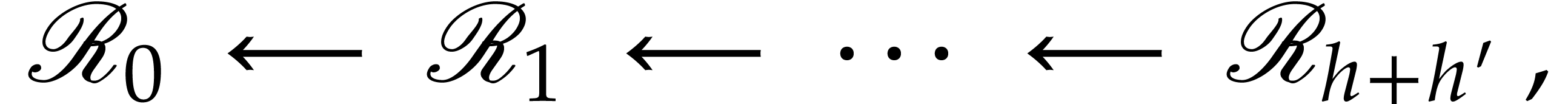
where 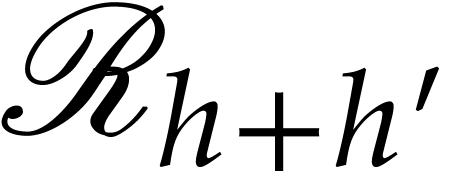 again comes with a distinguished lift of
again comes with a distinguished lift of
 , and such that
, and such that 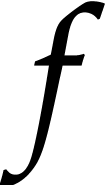 can be lifted into an analytic map
can be lifted into an analytic map 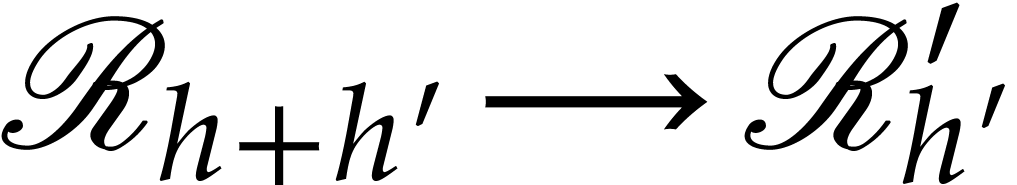 that we will also denote by
that we will also denote by 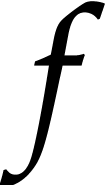 .
Consequently, the composition
.
Consequently, the composition  will be naturally
defined on
will be naturally
defined on 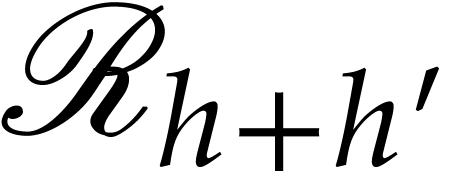 .
.
We proceed by induction and note that the inductive property is
trivially satisfied if 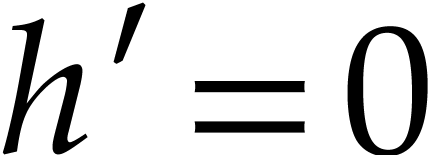 . So
assume that
. So
assume that 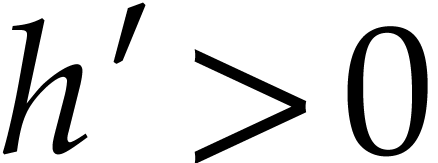 and that
and that 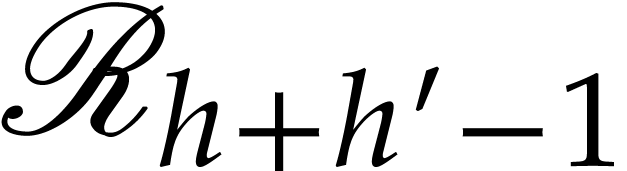 has
been constructed. Let
has
been constructed. Let 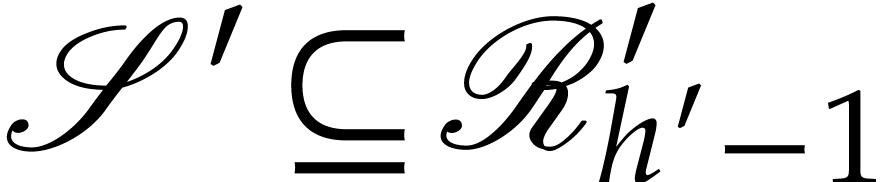 be such that
be such that  . By the induction hypothesis, we may regard
. By the induction hypothesis, we may regard
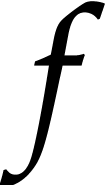 as an analytic function from
as an analytic function from 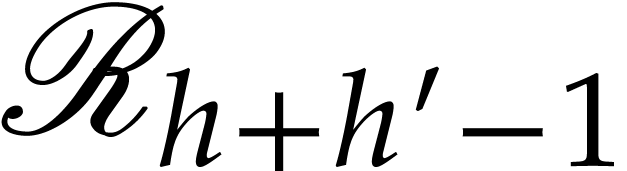 into
into 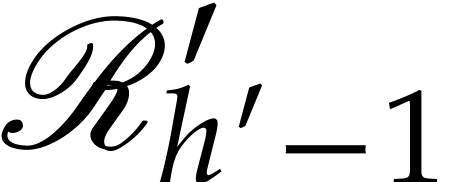 . Since
. Since 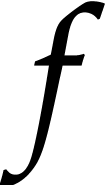 is non-constant, the set
is non-constant, the set 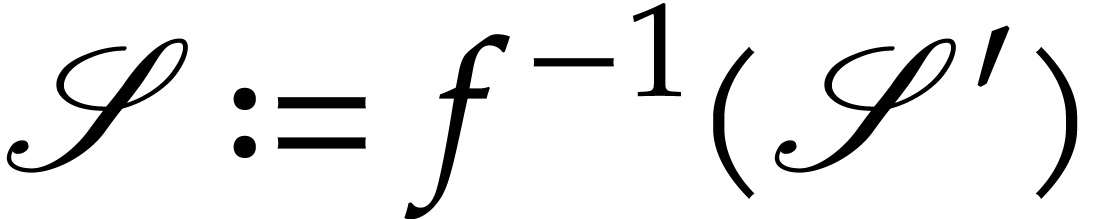 is discrete. We take
is discrete. We take
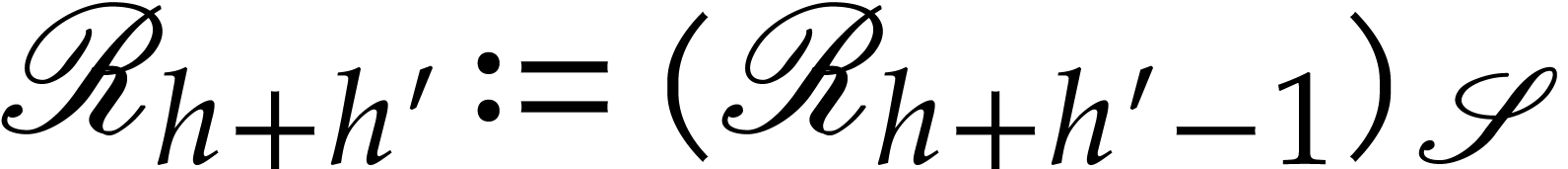 and also pick any lift
and also pick any lift 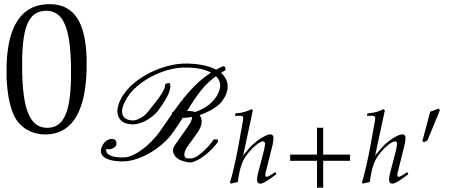 of
of 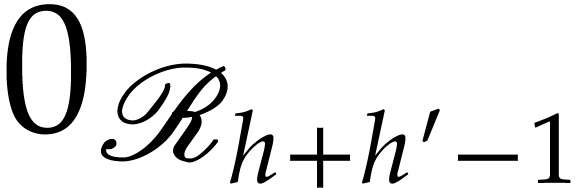 to be our distinguished point above zero. By
our choice of
to be our distinguished point above zero. By
our choice of  , the function
, the function
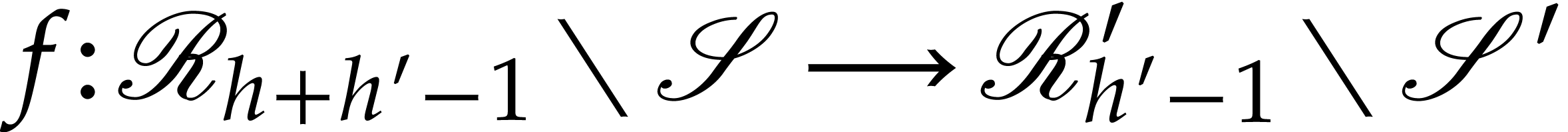 has a unique lift
has a unique lift 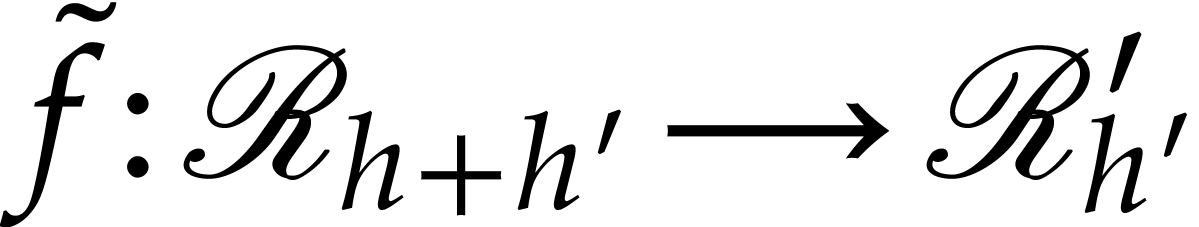 with
with
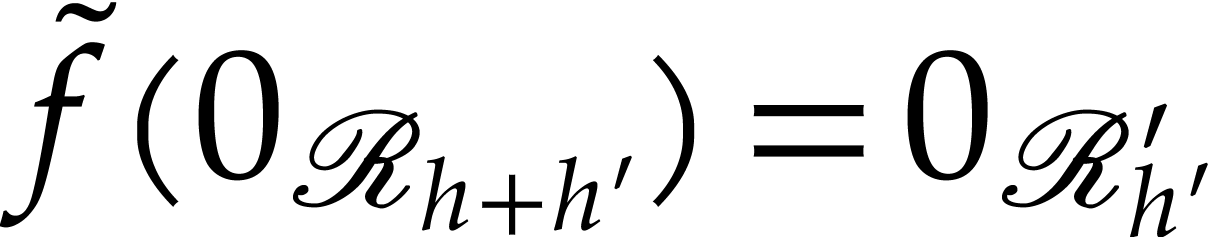 . This completes our
inductive construction of
. This completes our
inductive construction of 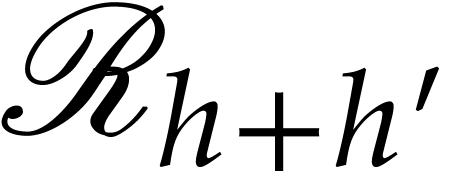 and thereby also the
proof.
and thereby also the
proof.
We say that a local analytic function 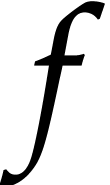 defined at
defined at
 is boundaryless above an open set
is boundaryless above an open set  if for every path
if for every path 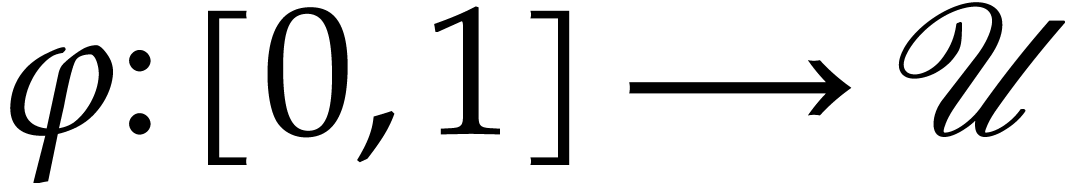 with
with 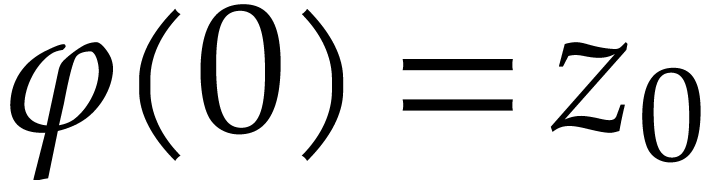 and every
and every  ,
there exists a path
,
there exists a path 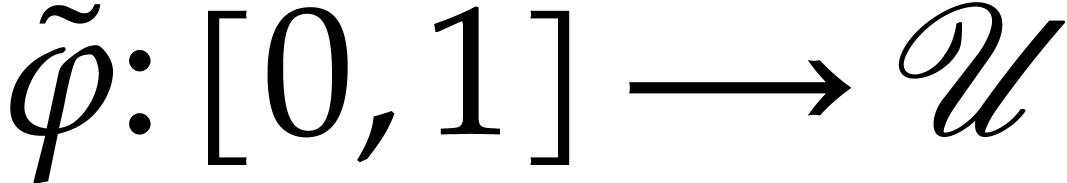 with
with 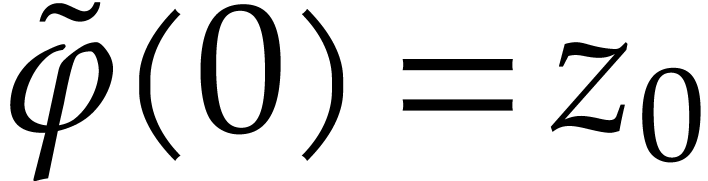 and
and 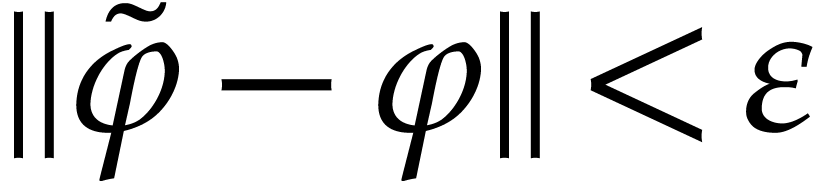 , such that
, such that 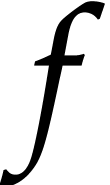 can be continued analytically along
can be continued analytically along  . We simply say that
. We simply say that 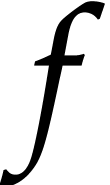 is
boundaryless if it is boundaryless above
is
boundaryless if it is boundaryless above  .
.
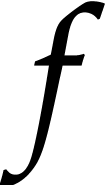 and
and 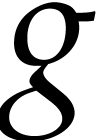 be two local
analytic functions at
be two local
analytic functions at 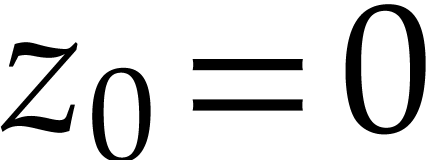 ,
which are both boundaryless. If
,
which are both boundaryless. If 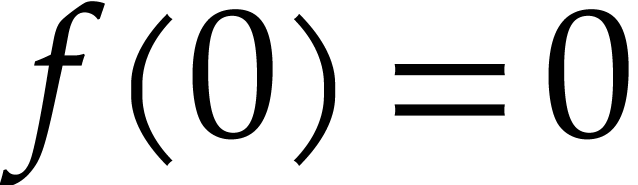 (after the
natural identification of
(after the
natural identification of 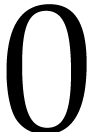 with its lift), then
with its lift), then
 is again boundaryless.
is again boundaryless.
Proof. The result is clear if 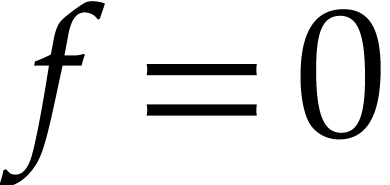 , so assume that
, so assume that 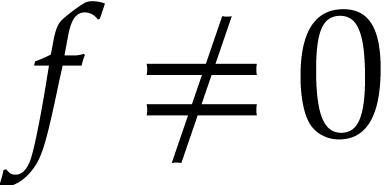 .
Modulo replacing
.
Modulo replacing 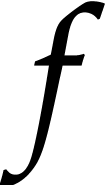 by
by 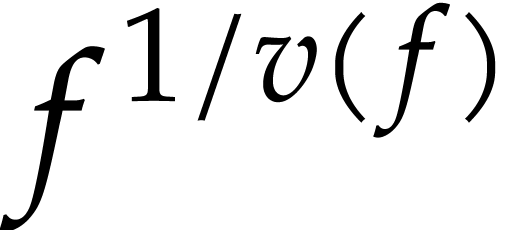 , where
, where 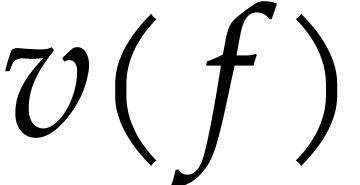 is the valuation of
is the valuation of
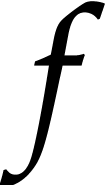 at zero, we may assume without loss of
generality that
at zero, we may assume without loss of
generality that 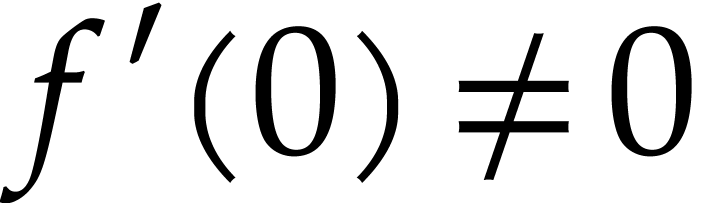 .
.
Let  and consider a path
and consider a path 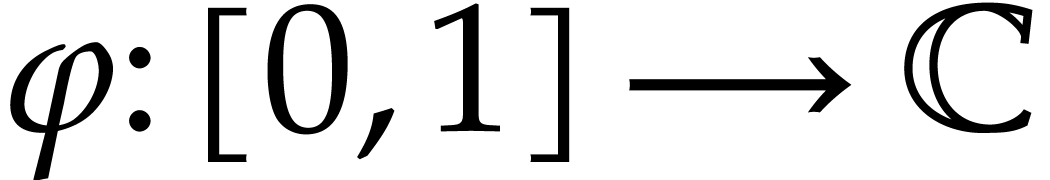 with
with 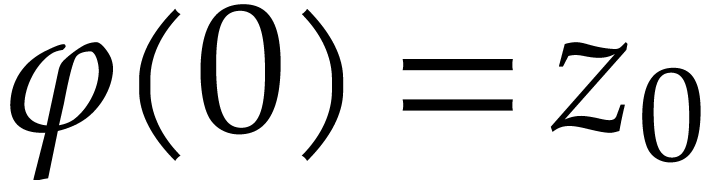 . Since
. Since 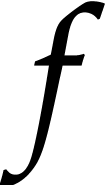 is boundaryless, there exists a path
is boundaryless, there exists a path 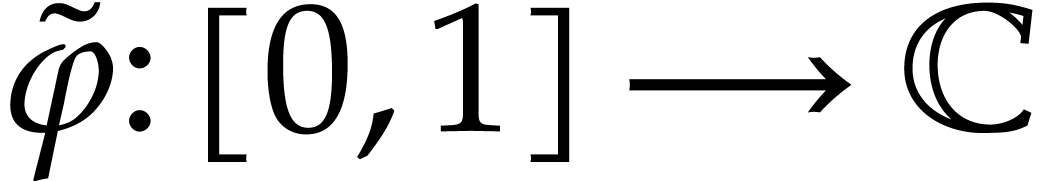 with
with 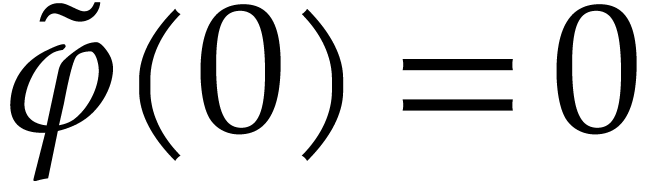 and
and  , such
that
, such
that  is defined on
is defined on 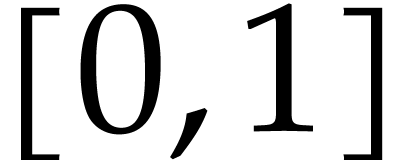 .
Since the image of
.
Since the image of  is compact, it contains only
a finite number of zeros of
is compact, it contains only
a finite number of zeros of 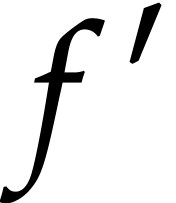 .
By applying Theorem 4 to
.
By applying Theorem 4 to 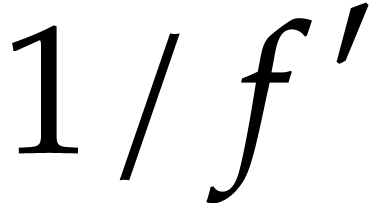 ,
we may also arrange that
,
we may also arrange that 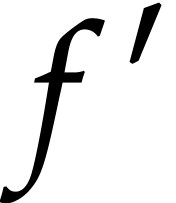 does not vanish on
does not vanish on
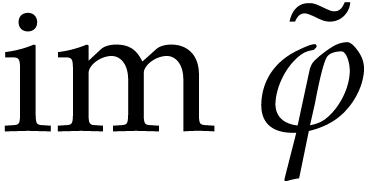 . Consequently, the local
functional inverse
. Consequently, the local
functional inverse 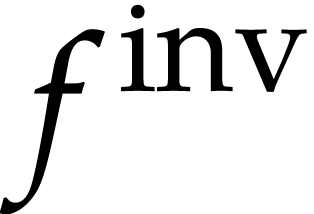 of
of 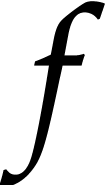 at
zero can be continued analytically on
at
zero can be continued analytically on 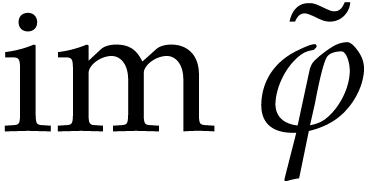 .
Let
.
Let  with
with 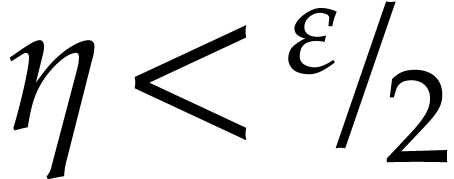 be such that
be such that
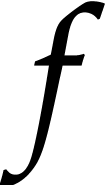 is defined on the compact set
is defined on the compact set
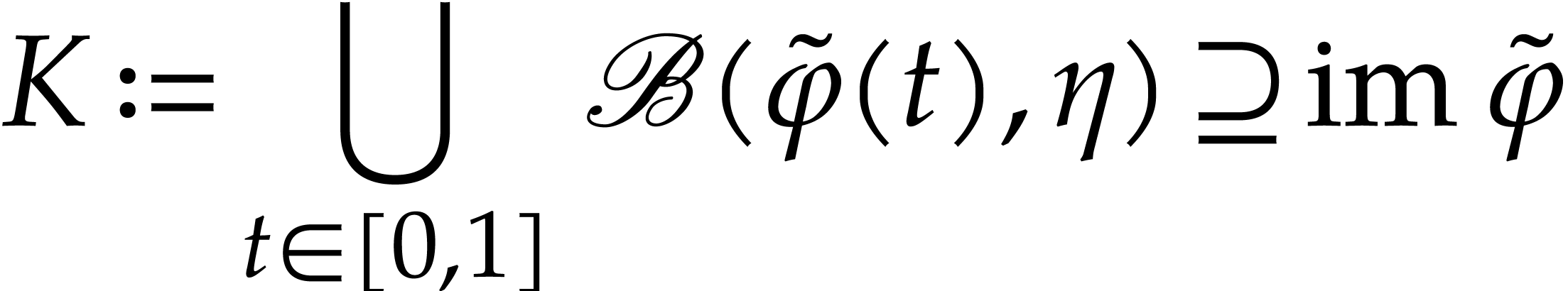
and such that 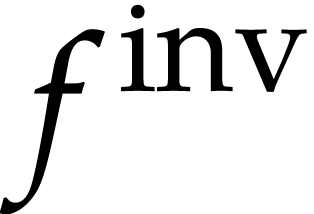 is defined on
is defined on 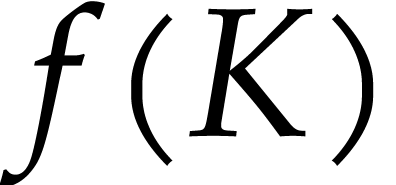 . Let
. Let
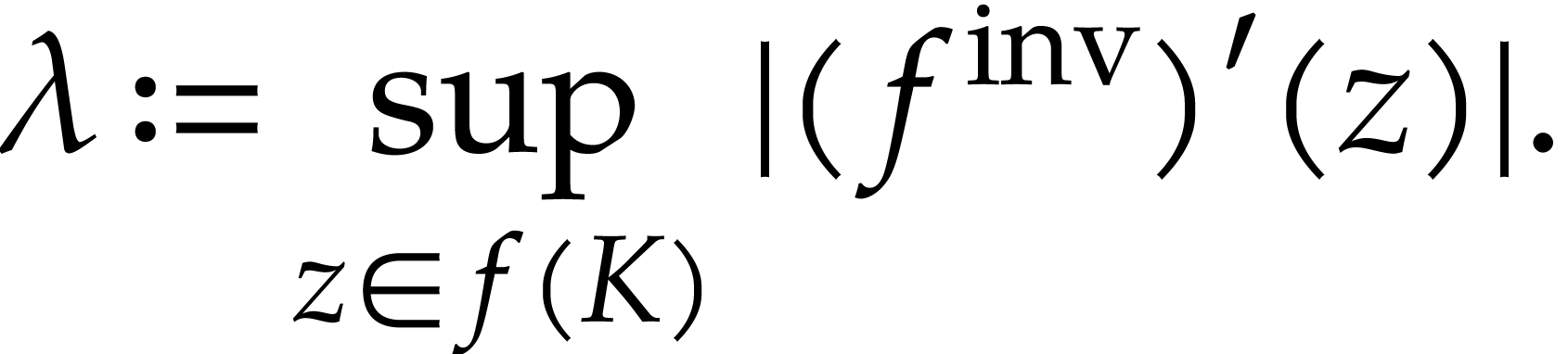
Since  is boundaryless, there exists a path
is boundaryless, there exists a path 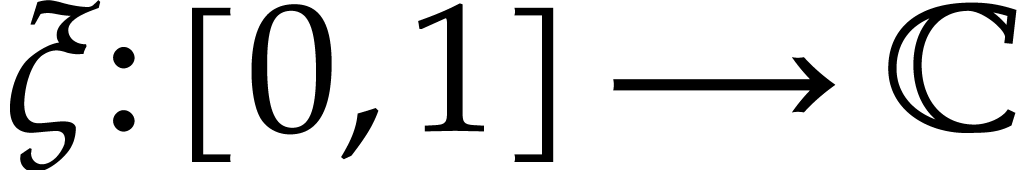 with
with 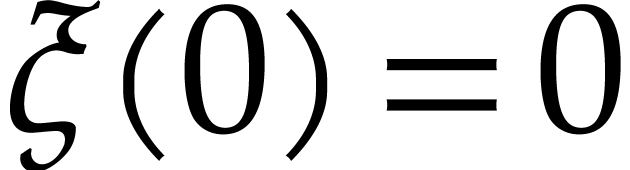 and
and 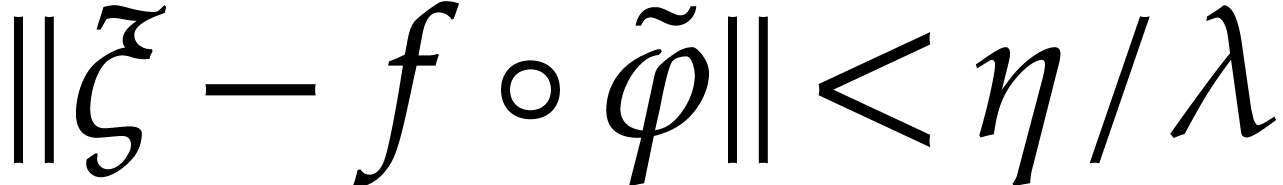 , such that
, such that 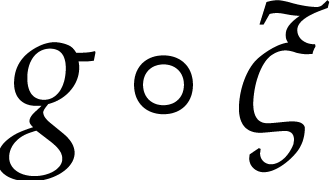 is defined
on
is defined
on 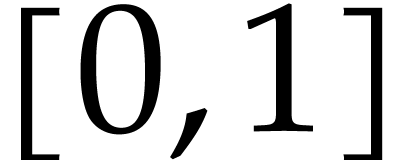 . But then
. But then 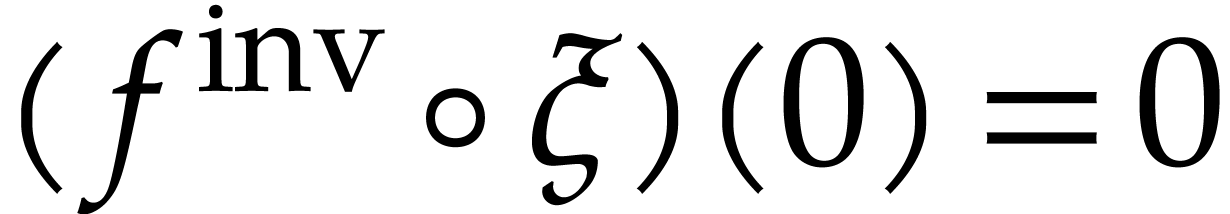 ,
, 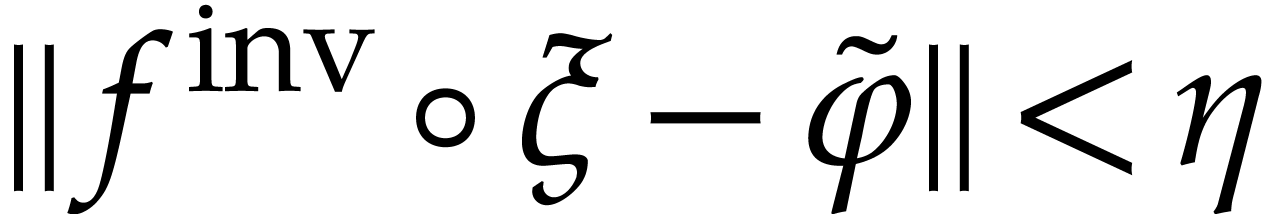 ,
and
,
and 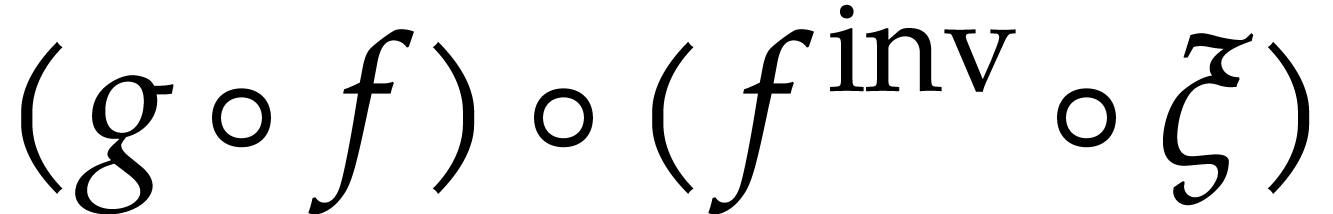 is defined on
is defined on 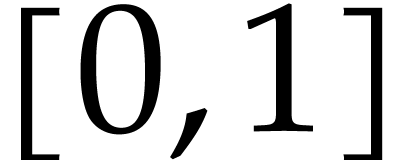 .
We finally observe that
.
We finally observe that 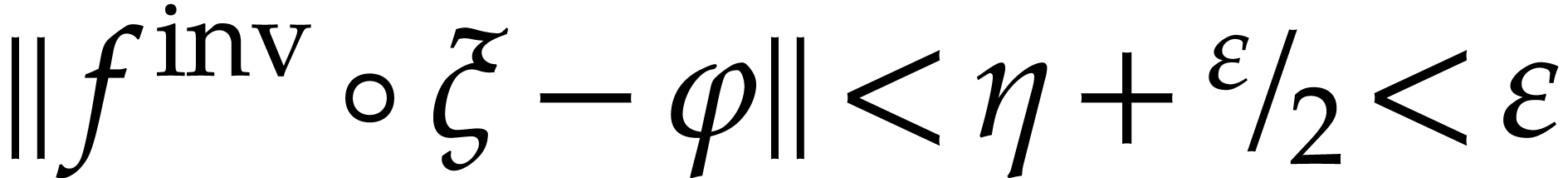 .
.
It would be interesting to know whether 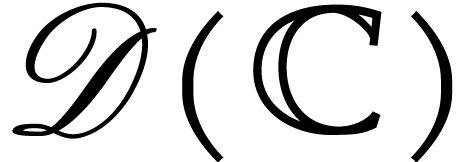 is also
closed under functional inversion. The functional inverse of any entire
function is easily seen to be in
is also
closed under functional inversion. The functional inverse of any entire
function is easily seen to be in 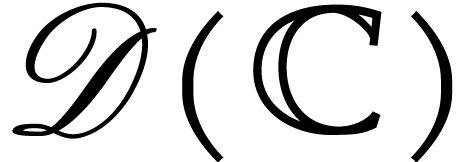 .
Any Weierstrass elliptic function
.
Any Weierstrass elliptic function  is also in
is also in
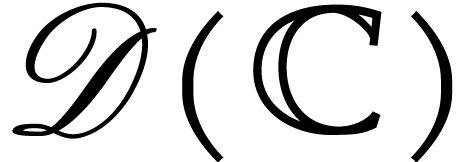 , since it is meromorphic on
, since it is meromorphic on
 . The function
. The function  is not holonomic, but it is the functional inverse of a
holonomic function. In fact,
is not holonomic, but it is the functional inverse of a
holonomic function. In fact,  is differentially
algebraic, but not in
is differentially
algebraic, but not in  . This
is due to the fact that
. This
is due to the fact that  embeds into any
differentially valued field and Picard-Vessiot closed field
embeds into any
differentially valued field and Picard-Vessiot closed field  of complex transseries from [2], but such a
field
of complex transseries from [2], but such a
field  never contains
never contains  (see also [8, Example 9]).
(see also [8, Example 9]).
The functional inverse of 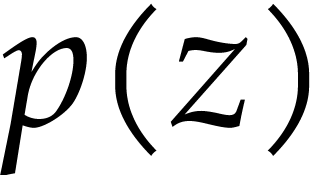 from (2)
might be a candidate for a dendromorphic function
from (2)
might be a candidate for a dendromorphic function 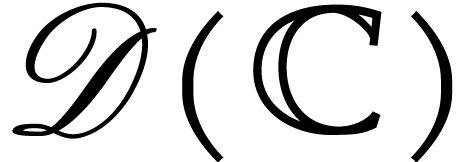 whose functional inverse is not. We expect this functional inverse to
have a very dendromorphic-like structure, although it might necessitate
a non-finite number of discrete ramifications in the required global
sense. Variations on the concept of dendromorphic functions might
therefore be another topic for further investigations.
whose functional inverse is not. We expect this functional inverse to
have a very dendromorphic-like structure, although it might necessitate
a non-finite number of discrete ramifications in the required global
sense. Variations on the concept of dendromorphic functions might
therefore be another topic for further investigations.
A. Bostan and A. Jiménez-Pastor. On the exponential generating function of labelled trees. Comptes Rendus. Mathématique, 358(9-10):1005–1009, 2020.
J. van der Hoeven. Complex transseries solutions to algebraic differential equations. Technical Report 2001-34, Univ. d'Orsay, 2001.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
A. Jiménez-Pastor, V. Pillwein, and M. F.
Singer. Some structural results on 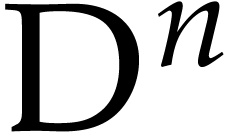 -finite
functions. Advances in Applied Mathematics, 117, 2020.
Article ID 102027 (29 pages).
-finite
functions. Advances in Applied Mathematics, 117, 2020.
Article ID 102027 (29 pages).
A. M. Mian and S. Chowla. The differential equations satisfied by certain functions. J. of the Indian Math. Soc., New Series, 8:27–28, 1944.
D. Pavlov, G. Pogudin, and Yu. P. Razmyslov. From algebra to analysis: new proofs of theorems by Ritt and Seidenberg. Proc. Amer. Math. Soc., 150:5085–5095, 2022.
M. van der Put and M. Singer. Galois Theory of Linear Differential Equations, volume 328 of Grundlehren der mathematischen Wissenschaften. Springer, 2003.
M. Rosenlicht. Differential valuations. Pacific J. Math., 86:301–319, 1980.
A. Seidenberg. Abstract differential algebra and the analytic case. Proc. of the A.M.S., 9(1):159–164, 1958.
G. Szegö. Über die Randwerte einer analytischen Funktion. Mathematische Annalen, 84(3):232–244, 1921.