A zero test for  -algebraic
power series -algebraic
power series |
|
| May 11, 2021 |
|
 . This article has
been written using GNU TeXmacs [7].
. This article has
been written using GNU TeXmacs [7].
One fundamental problem in symbolic computation is zero testing of expressions that involve special functions. Several such zero tests have been designed for the case when such special functions satisfy algebraic differential equations or linear difference equations. In this paper, we present an algorithm for the case of power series solutions to certain non-linear difference equations.
|
How far can we push exact computations with symbolic mathematical expressions? Starting from polynomial arithmetic, efficient algorithms have been developed for computing with expressions that involve increasingly elaborate algebraic and transcendental functions. The central problem for such computations is to decide whether two expressions represent the same mathematical function or constant. This problem in turn reduces to testing whether a given expression represents zero.
One popular traditional approach for zero testing is based on
“structure theorems”. For instance, given a function 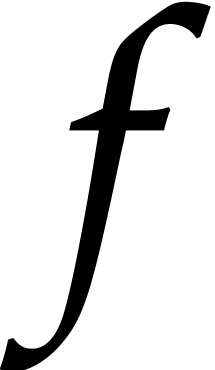 that is built up using algebraic functions,
exponentiation, and logarithm, we may test whether
that is built up using algebraic functions,
exponentiation, and logarithm, we may test whether 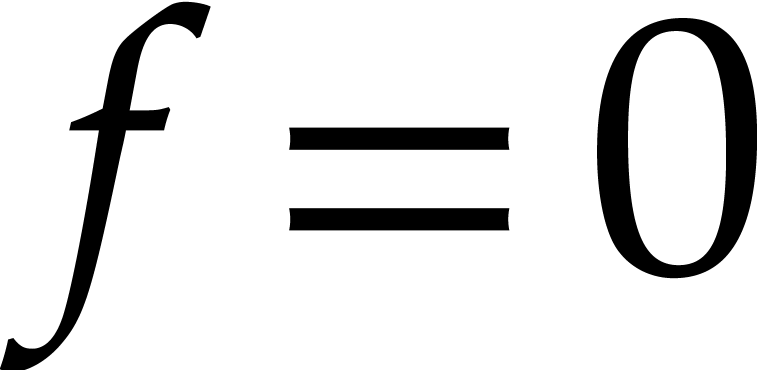 using the Risch structure theorem [10]. Zeilberger's
holonomic systems approach [12] is another popular tool for
proving equalities, in the restricted setting of solutions to linear
differential and difference equations. A powerful theoretical approach
for computations with power series solutions to non-linear differential
equations was proposed by Denef and Lipshitz in [2, 3]. Several more practical alternative algorithms have also
been developed for that purpose [11, 9, 4, 6].
using the Risch structure theorem [10]. Zeilberger's
holonomic systems approach [12] is another popular tool for
proving equalities, in the restricted setting of solutions to linear
differential and difference equations. A powerful theoretical approach
for computations with power series solutions to non-linear differential
equations was proposed by Denef and Lipshitz in [2, 3]. Several more practical alternative algorithms have also
been developed for that purpose [11, 9, 4, 6].
In this paper, we study the zero testing problem for solutions of non-linear difference equations. For such equations there are two prominent solution spaces: power series and sequences. In the latter case, there exists a zero-test for a large class of non-linear algebraic difference equations [8]. We will consider the power series case.
In order to state our main result, we need to introduce a few notions. A
power series domain is a  -algebra
-algebra
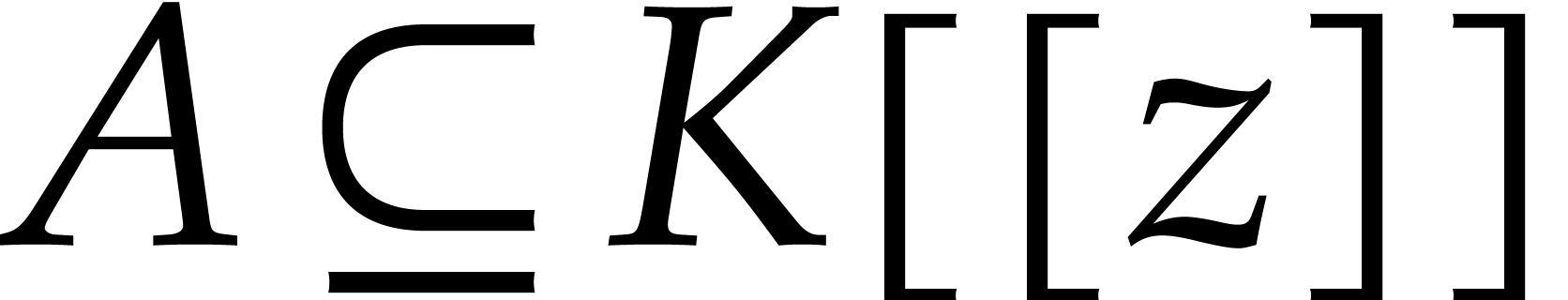 with
with  and such that
and such that  is closed under division whenever defined. We say
that
is closed under division whenever defined. We say
that  is a
is a  -difference
power series domain if it is also closed under the difference
operator
-difference
power series domain if it is also closed under the difference
operator  for some fixed
for some fixed 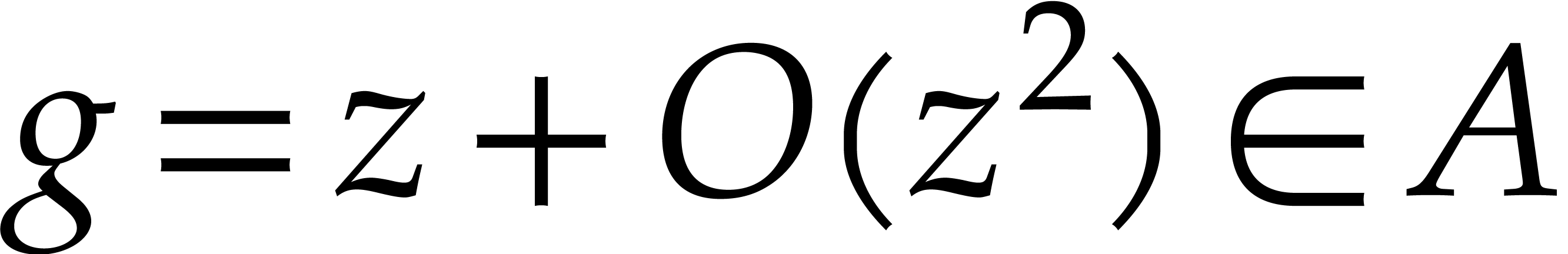 . Note that the standard shift operator
. Note that the standard shift operator 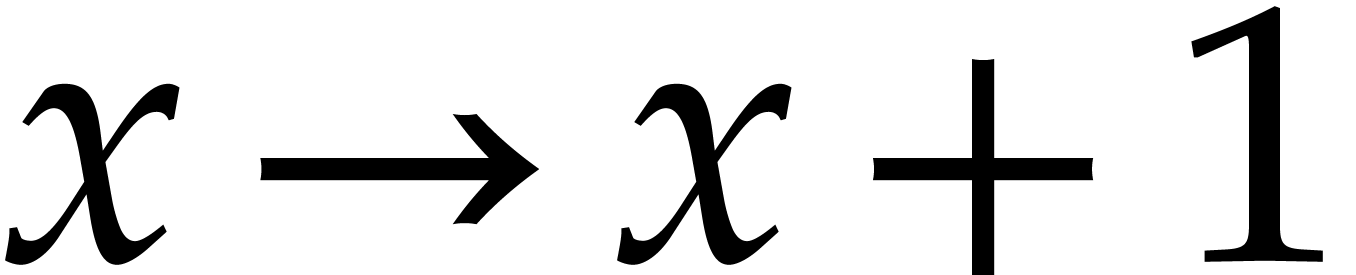 is of this form if one considers the power series
expansion at infinity, that is,
is of this form if one considers the power series
expansion at infinity, that is, 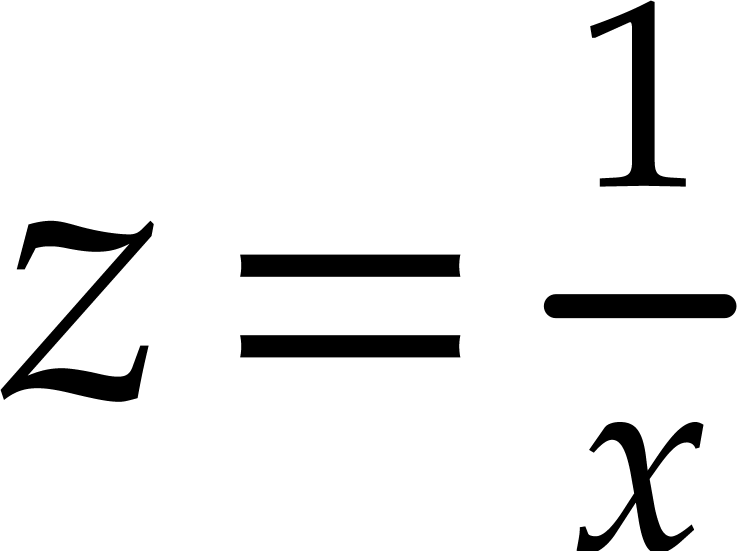 (see Example 1). Finally,
(see Example 1). Finally,  is said to be
effective if all these operations can be carried out through
algorithms. Now assume that we are given a power series solution
is said to be
effective if all these operations can be carried out through
algorithms. Now assume that we are given a power series solution 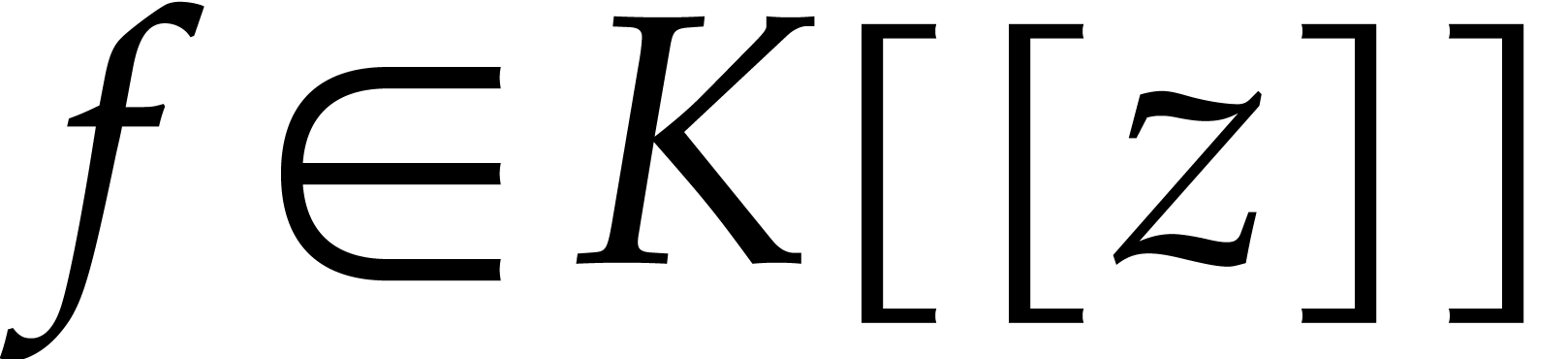 to the equation
to the equation
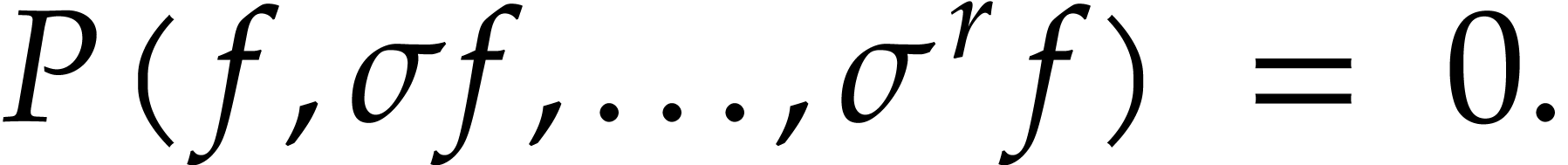 |
(1) |
for some non-trivial polynomial 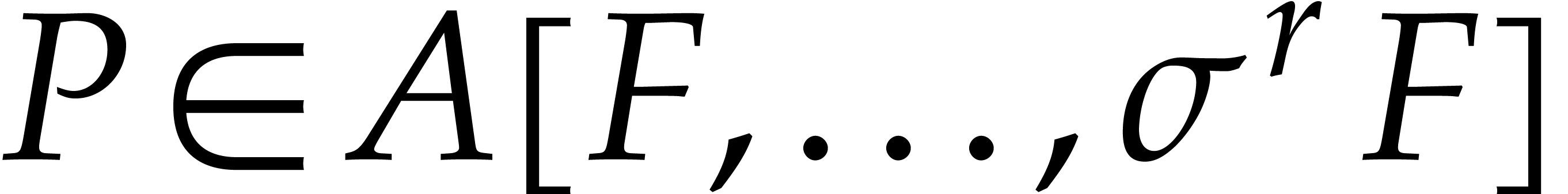 .
Such a power series
.
Such a power series  is said to be
is said to be  -algebraic over
-algebraic over  .
A typical example is the power series part of Stirling's asymptotic
expansion for the
.
A typical example is the power series part of Stirling's asymptotic
expansion for the  -function:
see section 6.1. Our main result (see section 5)
is a zero-test for elements in
-function:
see section 6.1. Our main result (see section 5)
is a zero-test for elements in 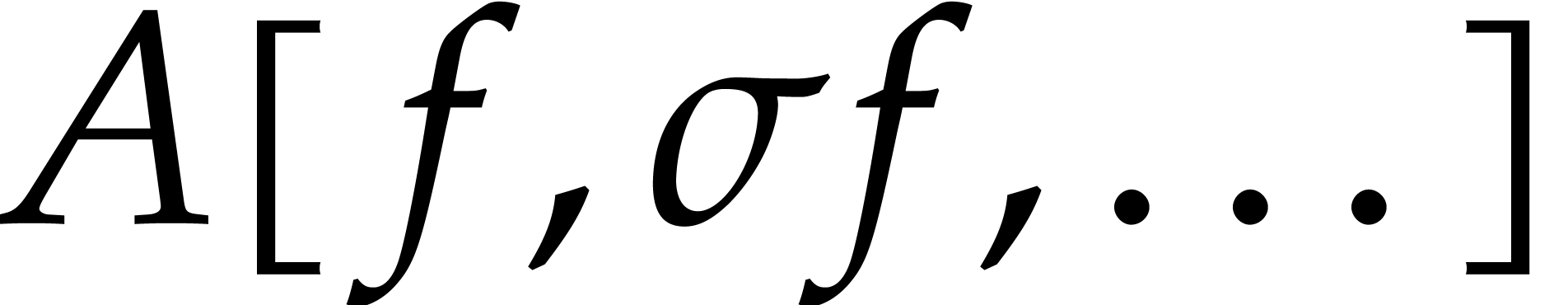 under assumption
under assumption
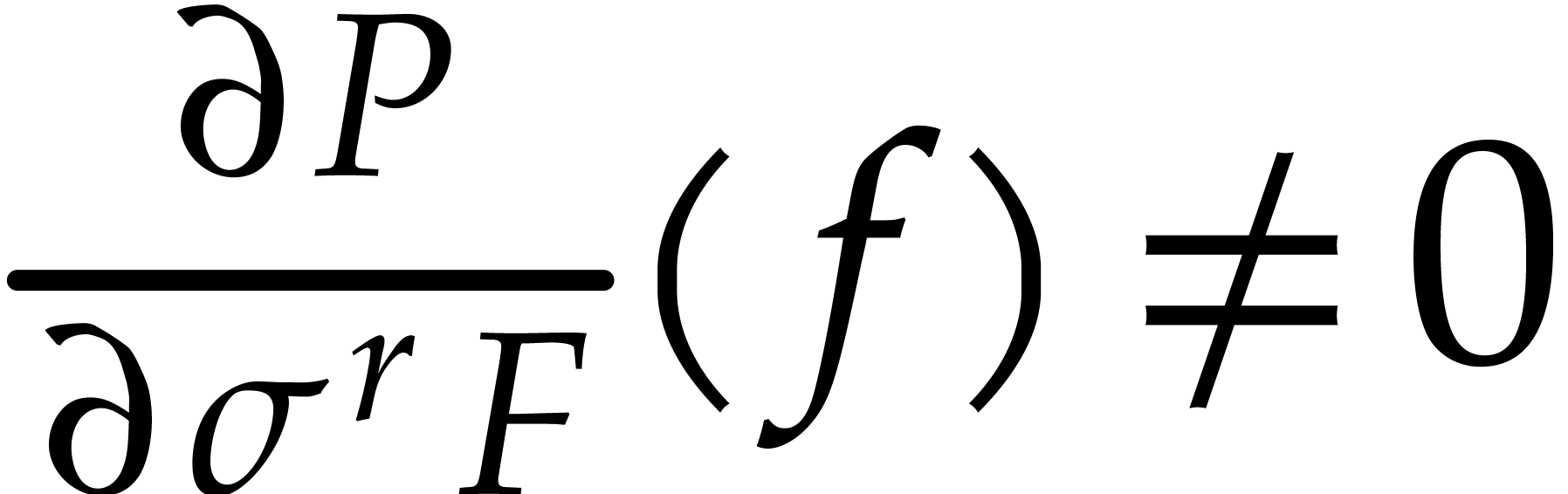 (note that this assumption can be forced by
differentiating
(note that this assumption can be forced by
differentiating  a finite number of times). In
particular, this implies that
a finite number of times). In
particular, this implies that  is again an
effective
is again an
effective  -difference power
series domain.
-difference power
series domain.
A similar type of zero-test was designed in [4, 6]
for the case when the difference operator  is
replaced by differentiation with respect to
is
replaced by differentiation with respect to  . We show that this approach can indeed be
transposed, but there are a few subtleties. The algorithm in the
differential case exploits the fact that a prime univariate differential
ideal is defined by a single differential equation. In the present
setting, the main difficulty is that this is not longer the case in
difference algebra, so we have to work with a system of compatible
difference equations (called a coherent autoreduced chain). One of the
key ingredients of our algorithm, Proposition 6, is an
existence result for a power series solution to such a system of
difference equations.
. We show that this approach can indeed be
transposed, but there are a few subtleties. The algorithm in the
differential case exploits the fact that a prime univariate differential
ideal is defined by a single differential equation. In the present
setting, the main difficulty is that this is not longer the case in
difference algebra, so we have to work with a system of compatible
difference equations (called a coherent autoreduced chain). One of the
key ingredients of our algorithm, Proposition 6, is an
existence result for a power series solution to such a system of
difference equations.
Another feature of our algorithm is that it integrates an optimization
of [6] over [4]: in order to test whether 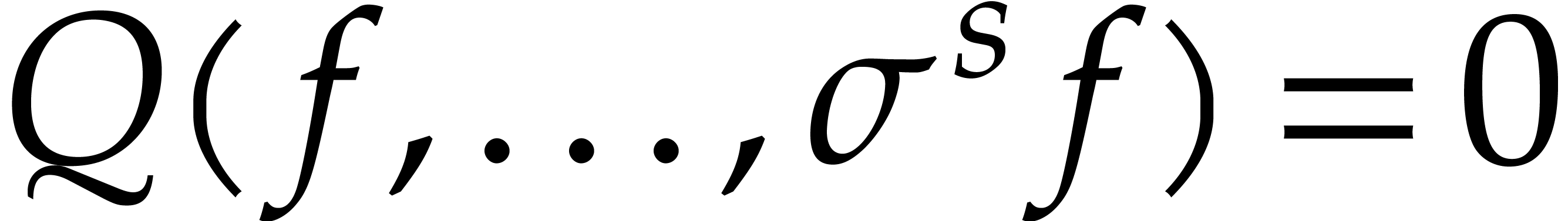 for some
for some 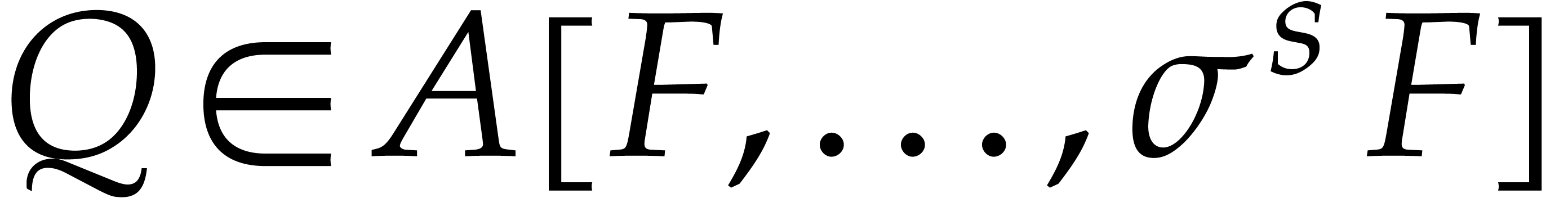 ,
the number of coefficients of
,
the number of coefficients of 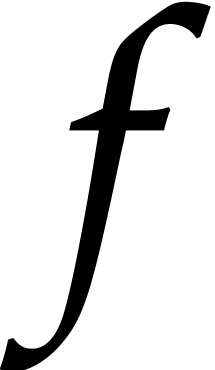 that we need to
evaluate only depends on
that we need to
evaluate only depends on  and
and 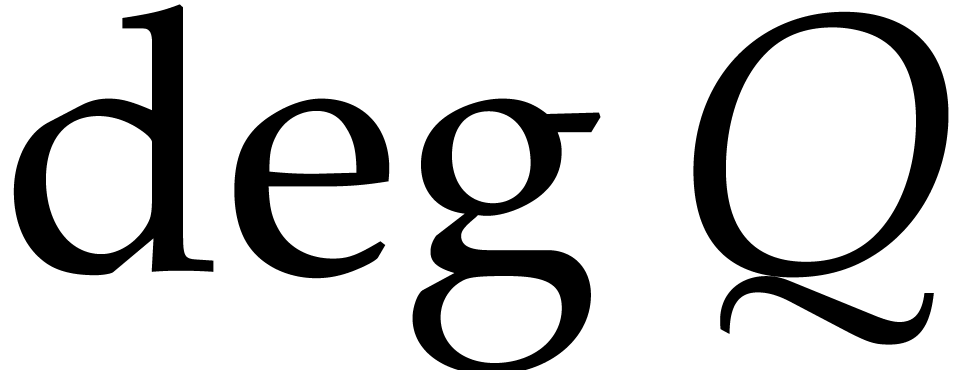 , but not on the individual coefficients of
, but not on the individual coefficients of
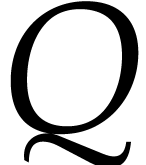 .
.
A proof-of-concept implementation of the algorithm in Julia based on the OSCAR computer algebra system is available at https://github.com/pogudingleb/DifferenceZeroTest.
Let us start with some notions from difference algebra. Let  be a field of characteristic zero. A
be a field of characteristic zero. A  -difference algebra is a
-difference algebra is a  -algebra
-algebra  together with
an injective morphism
together with
an injective morphism 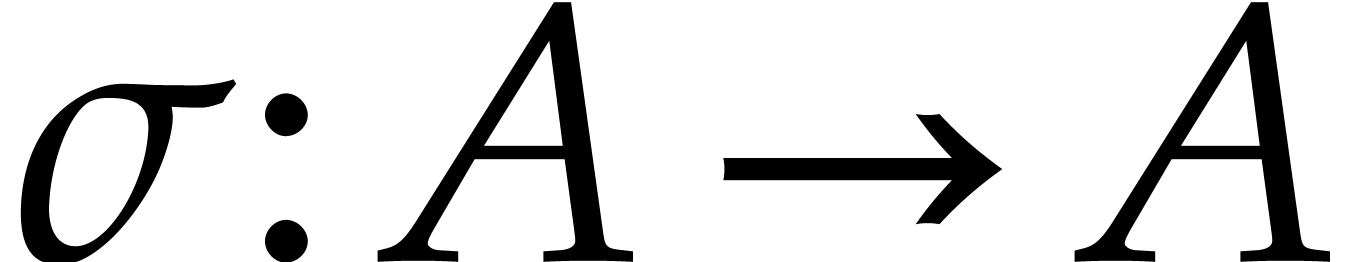 of
of  -algebras. In what follows, we will always assume
that
-algebras. In what follows, we will always assume
that  is also an integral domain.
is also an integral domain.
Given an indeterminate 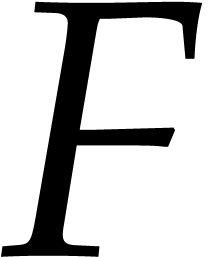 , we
denote by
, we
denote by  the difference ring of difference
polynomials in
the difference ring of difference
polynomials in 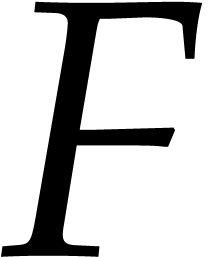 and by
and by  its fraction field. The algebraic variables
its fraction field. The algebraic variables 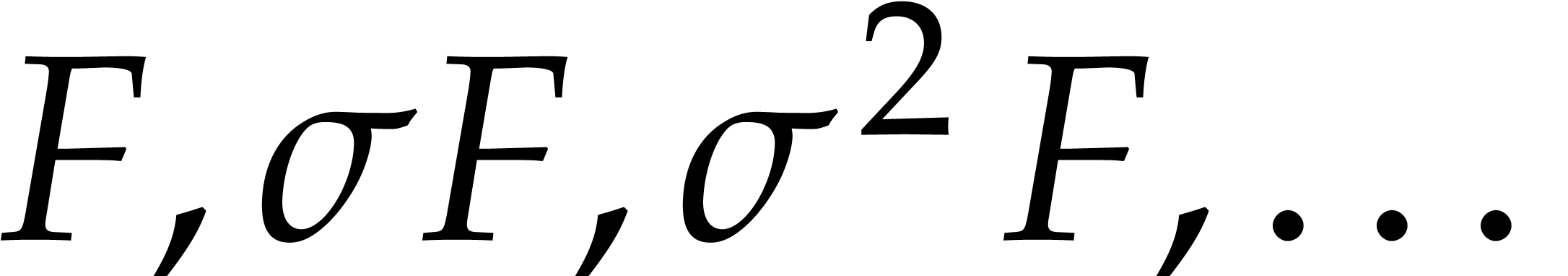 are
naturally ordered by
are
naturally ordered by 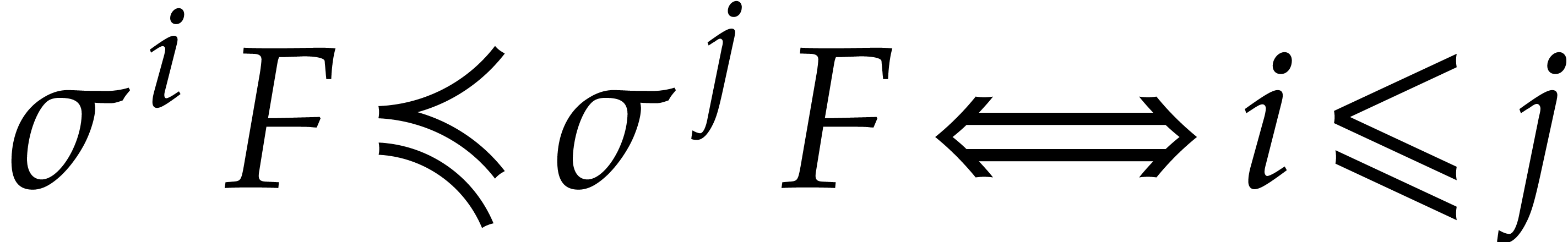 .
.
For a difference polynomial  ,
the leader
,
the leader  of
of  is the largest variable
is the largest variable 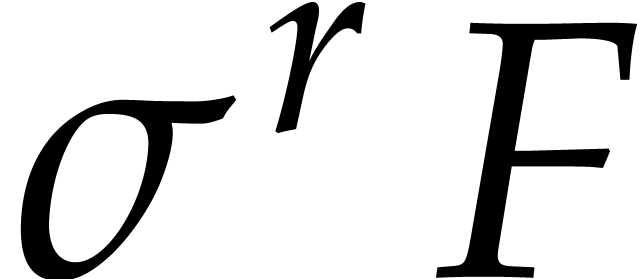 that occurs in
that occurs in  , and we set
, and we set 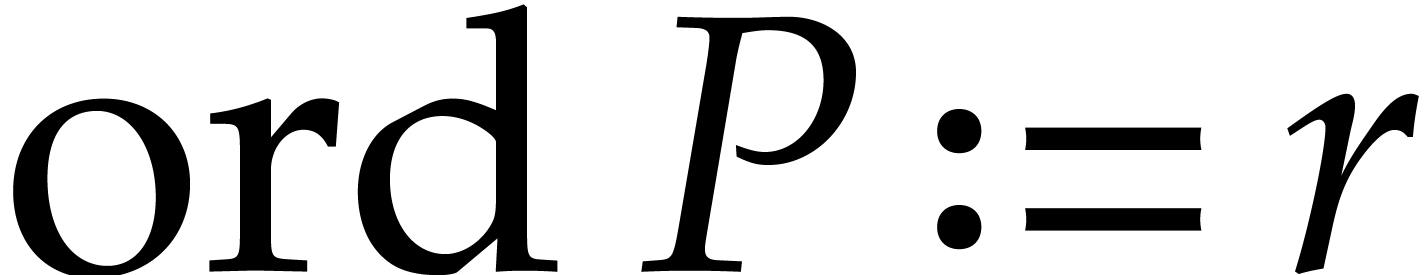 . We write
. We write 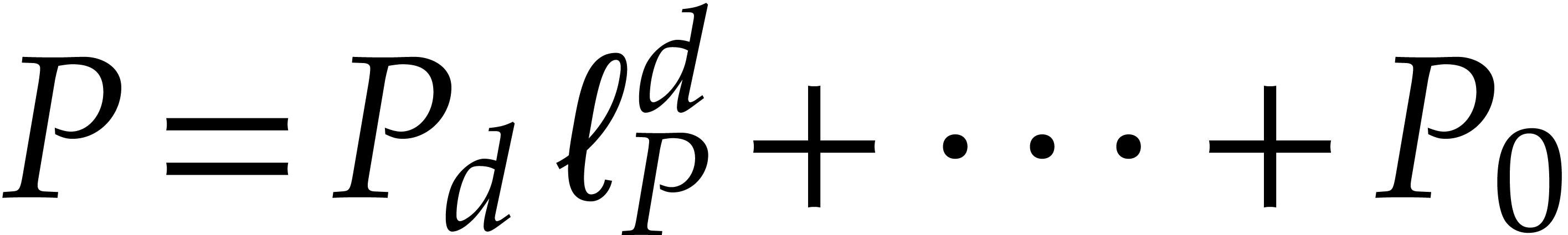 with
with 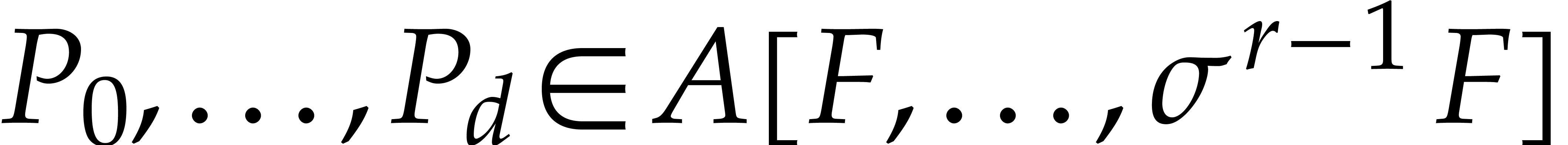 and
and 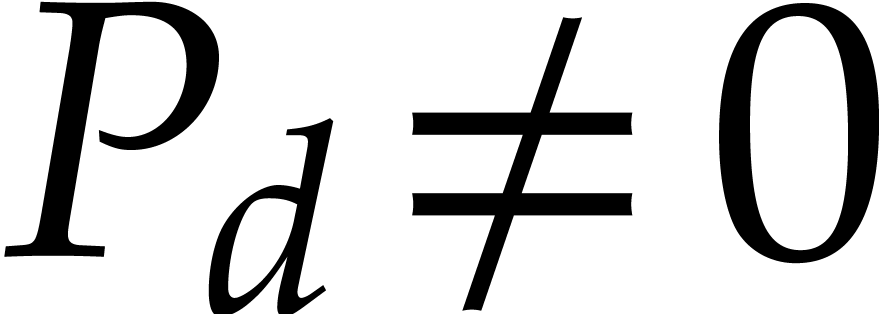 and define:
and define:
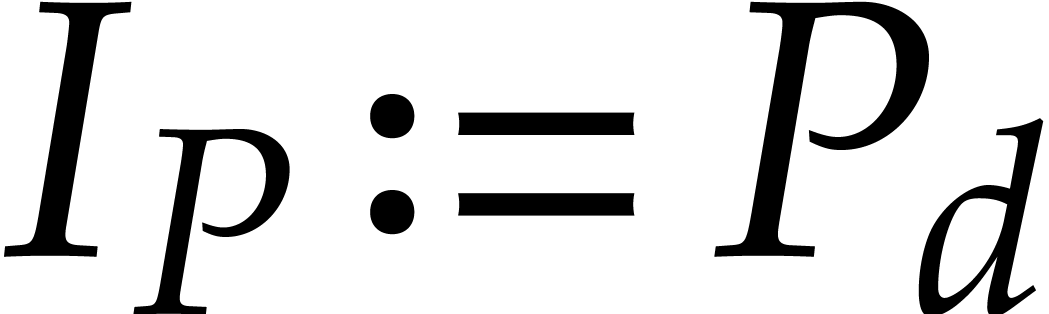 , the initial of
, the initial of
 ;
;
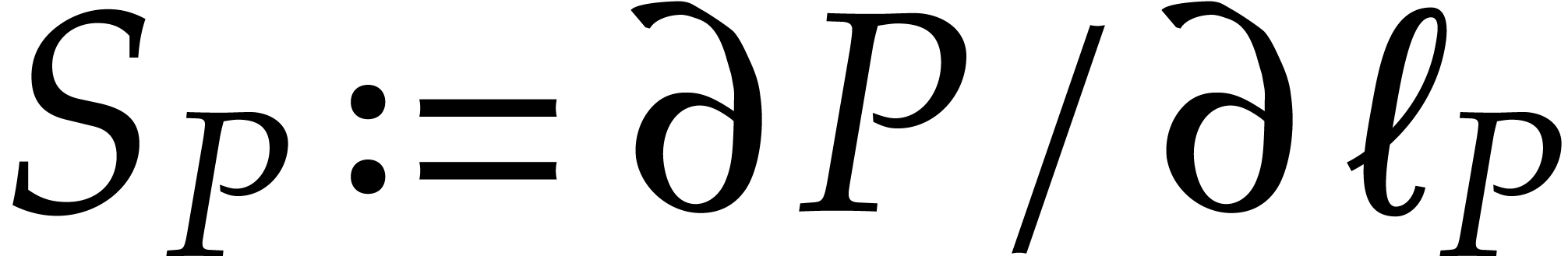 , the separant
of P;
, the separant
of P;
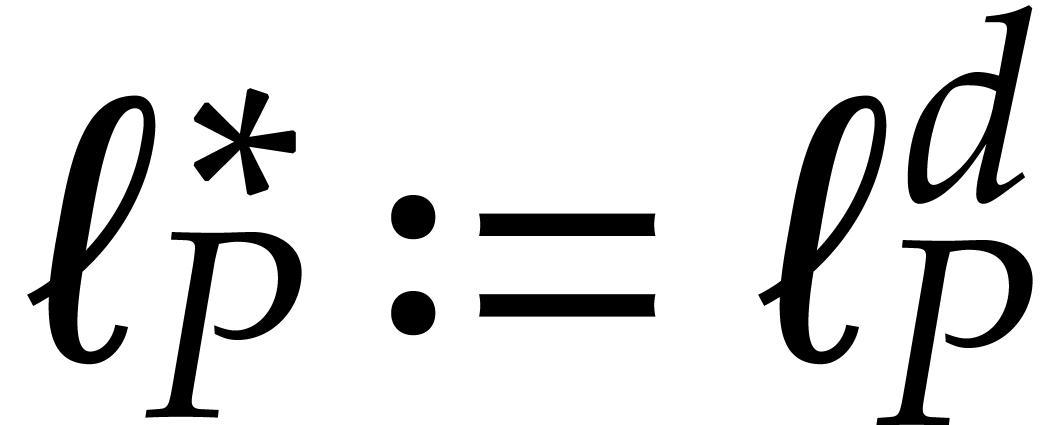 , the extended
leader of
, the extended
leader of  ;
;
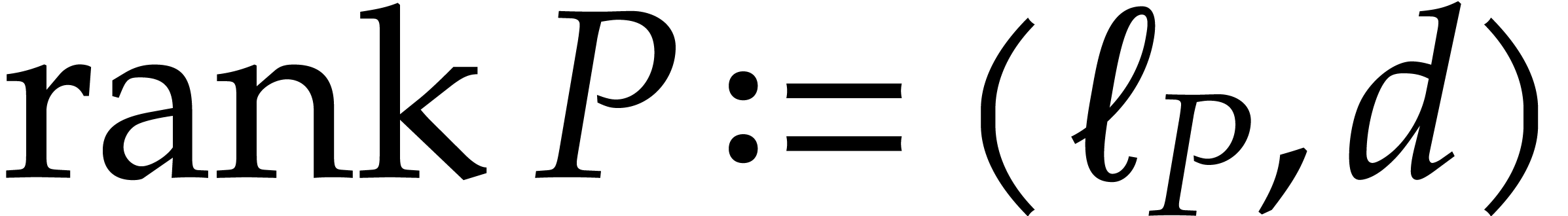 , the Ritt rank
of
, the Ritt rank
of  .
.
It is convenient to further extend the definition of Ritt rank by
setting 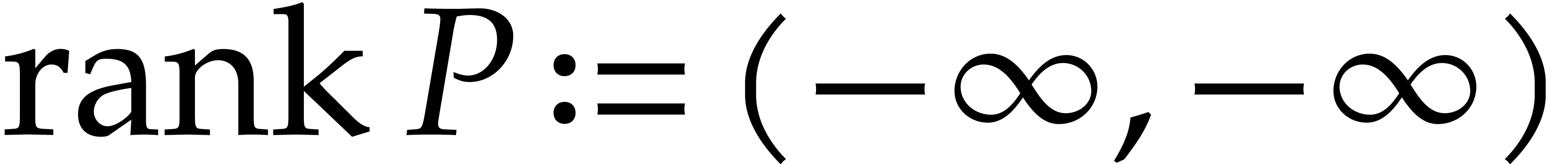 for polynomials
for polynomials 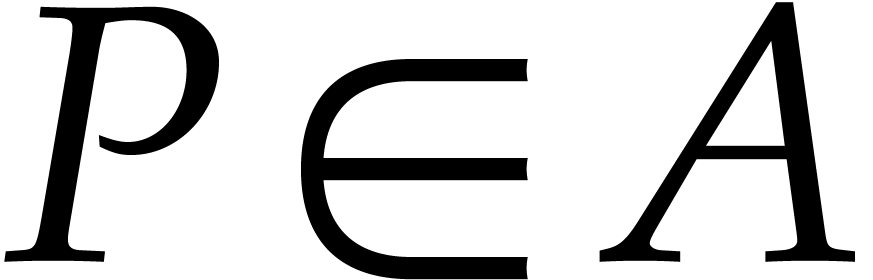 . We finally define a total ordering
. We finally define a total ordering 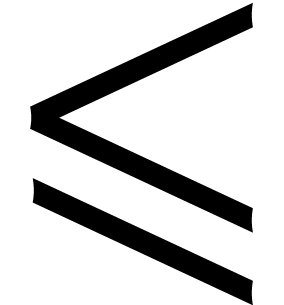 and a partial ordering
and a partial ordering  on Ritt
ranks by
on Ritt
ranks by
A list of difference polynomials  such that
such that  is called a chain.
is called a chain.
Given 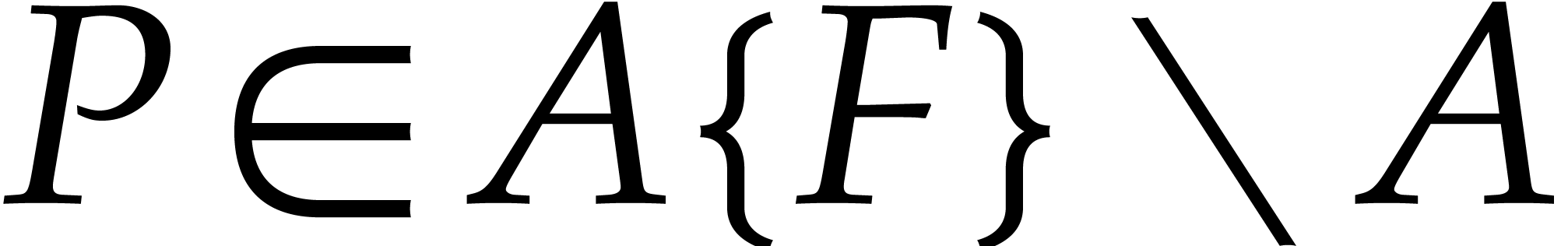 , we say that
, we say that  is
is 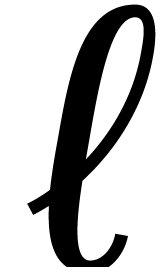 -reducible
with respect to a chain
-reducible
with respect to a chain  if there exists an
if there exists an  with
with  . For
. For
 such that
such that  ,
we define the
,
we define the 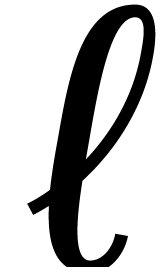 -remainder
of
-remainder
of  with respect to
with respect to 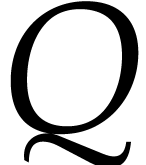 denoted by
denoted by  as follows:
as follows:
If  is not
is not 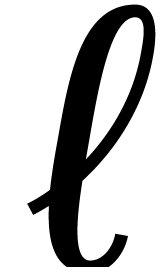 -reducible
with respect to
-reducible
with respect to 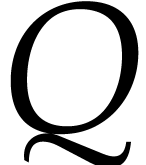 , we set
, we set
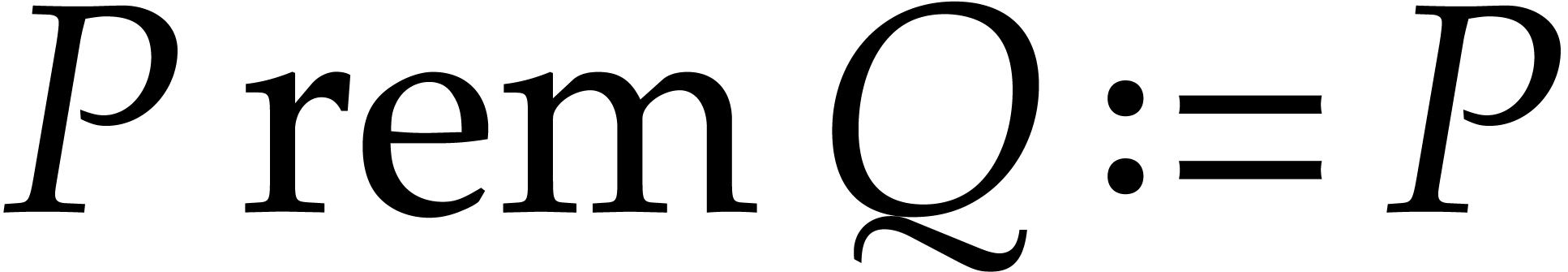 ;
;
Let 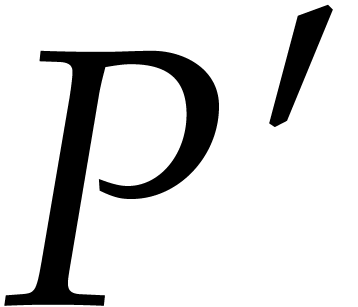 be the remainder of the Euclidean
pseudo-division of
be the remainder of the Euclidean
pseudo-division of  by
by 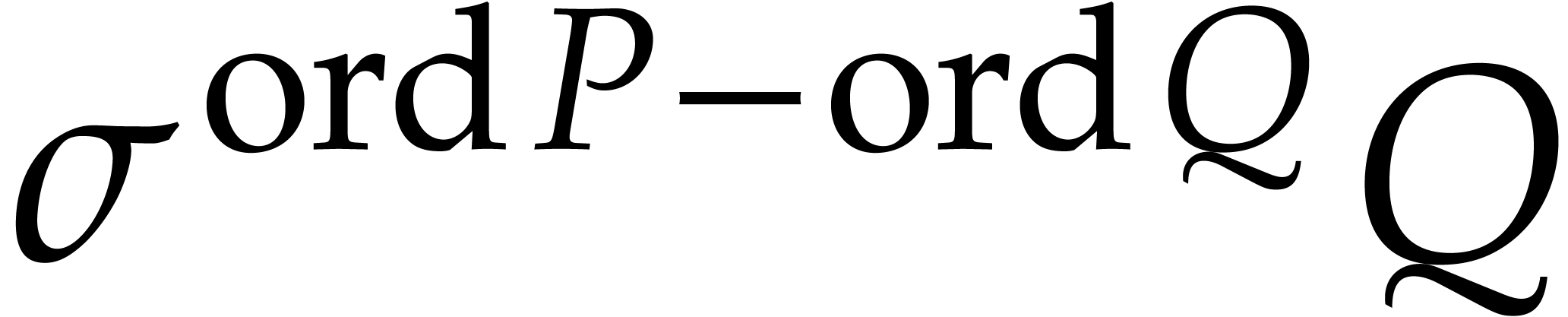 as univariate polynomials in
as univariate polynomials in 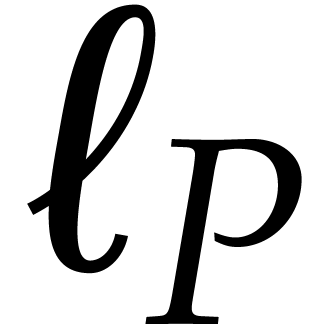 .
We set
.
We set 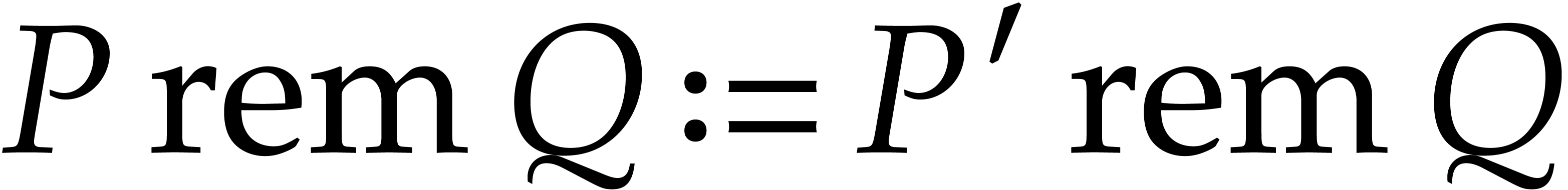 .
.
For a chain 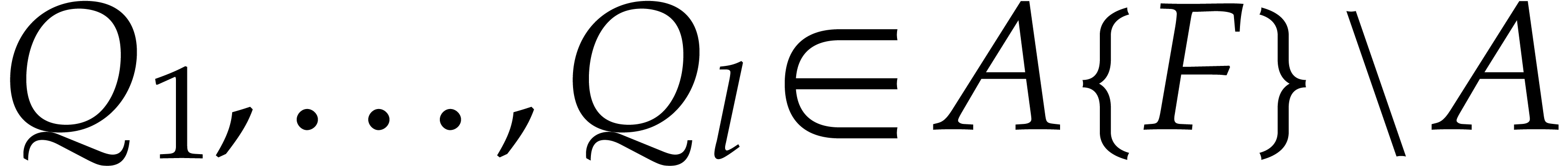 , we define
, we define

If 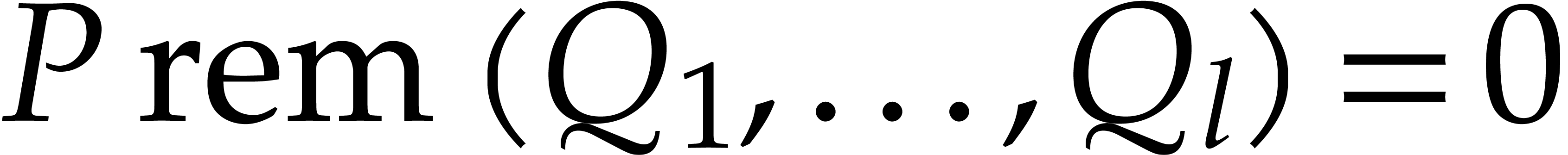 , we say that
, we say that  is
is  -reduced
to zero with respect to
-reduced
to zero with respect to  .
.
Let us now consider 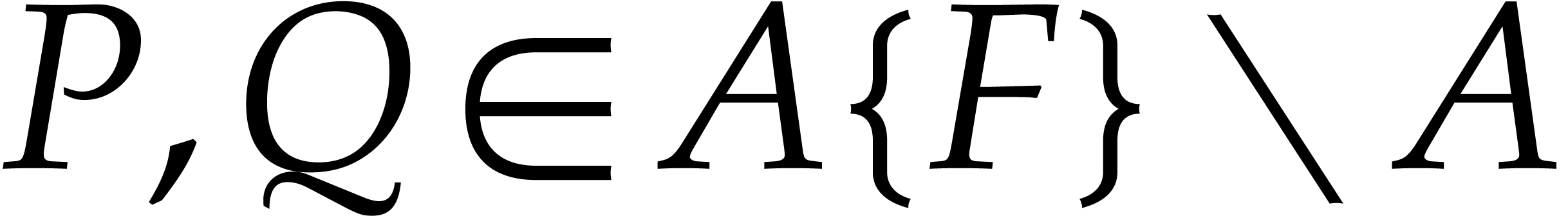 such that
such that  and
and  are incomparable for
are incomparable for  . So either
. So either  and
and  , or
, or  and
and 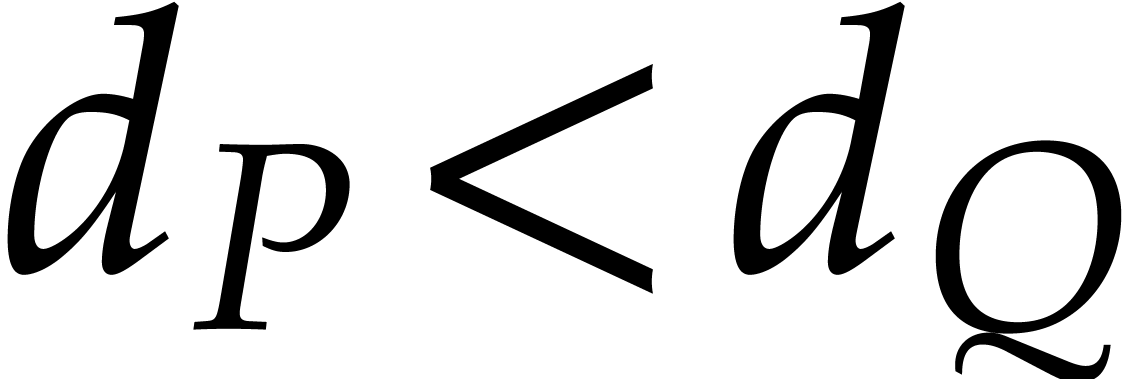 . If
. If 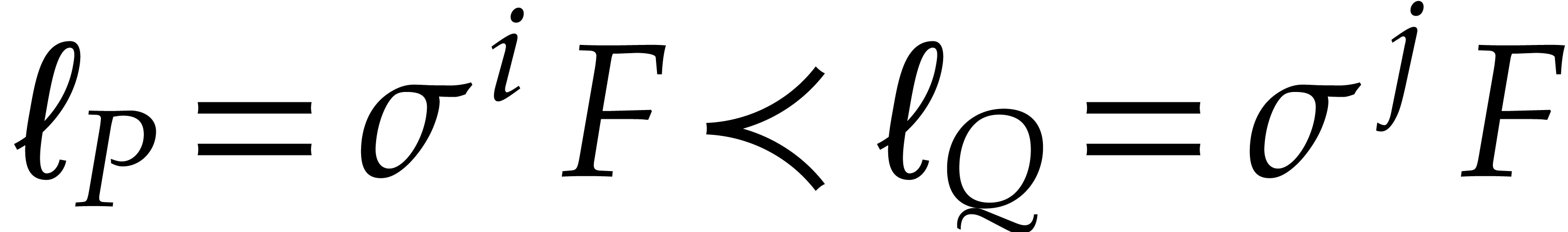 ,
then we define the
,
then we define the  -polynomial
of
-polynomial
of  and
and  by
by
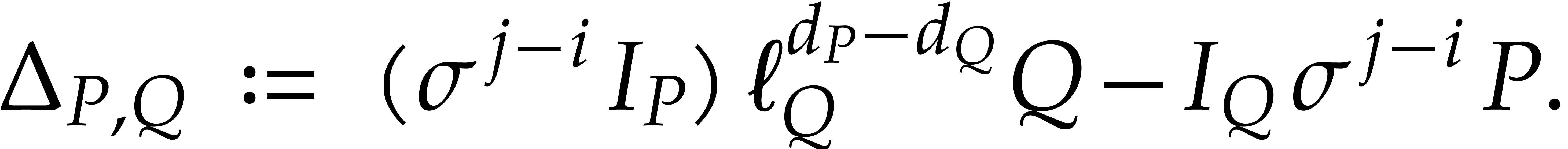
If  , then we define
, then we define 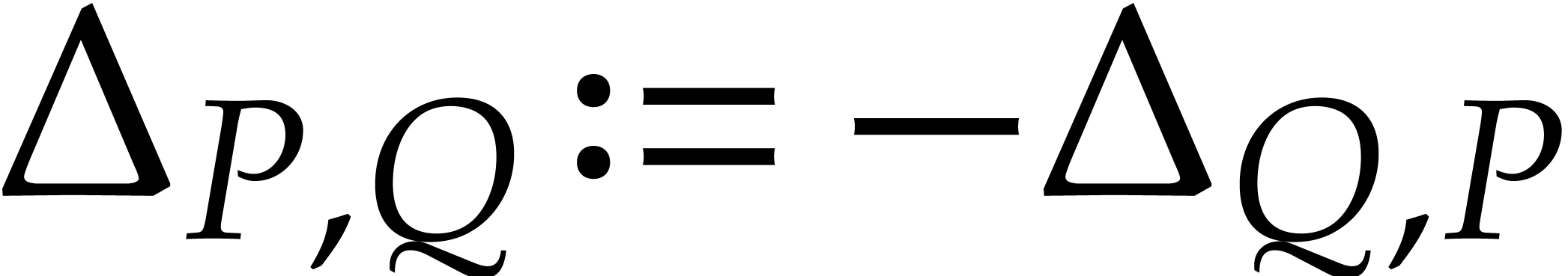 .
.
We say that the chain  is
is 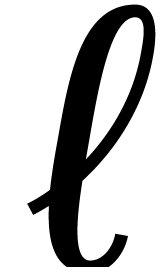 -autoreduced if
-autoreduced if 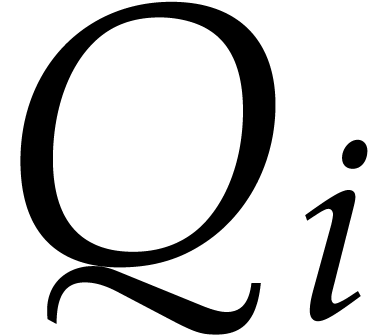 is
is
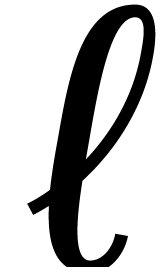 -reduced with respect to
-reduced with respect to 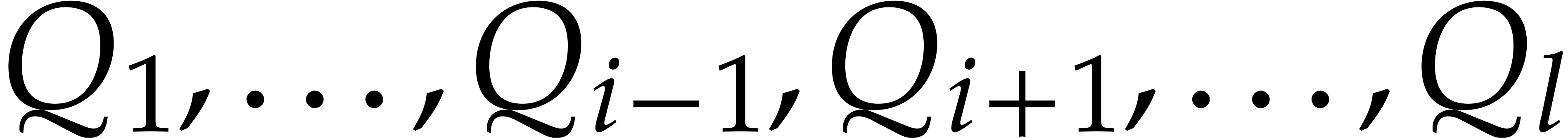 for each
for each  .
We say that
.
We say that  is coherent if
is coherent if 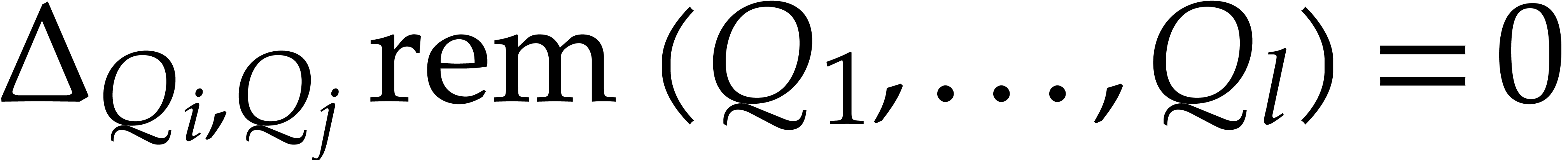 for all
for all 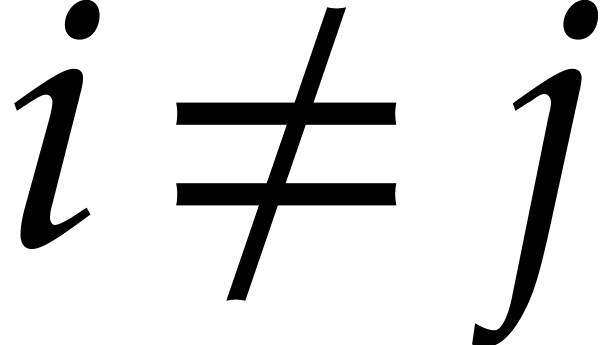 such that
such that 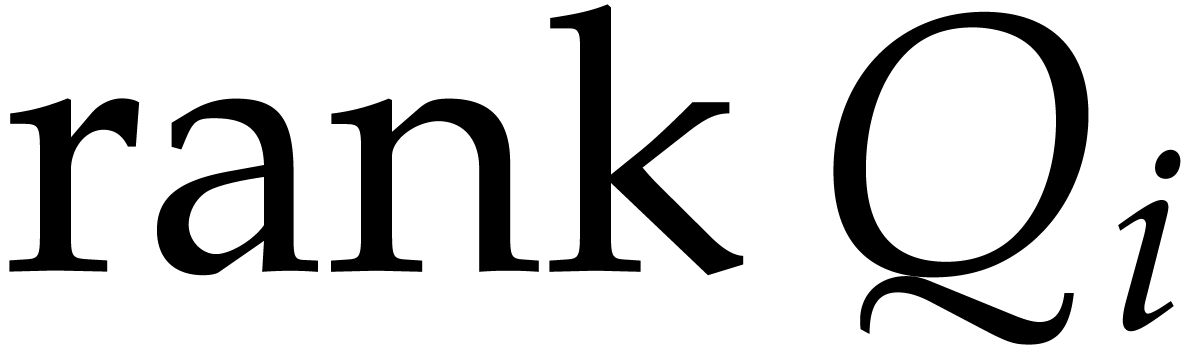 and
and 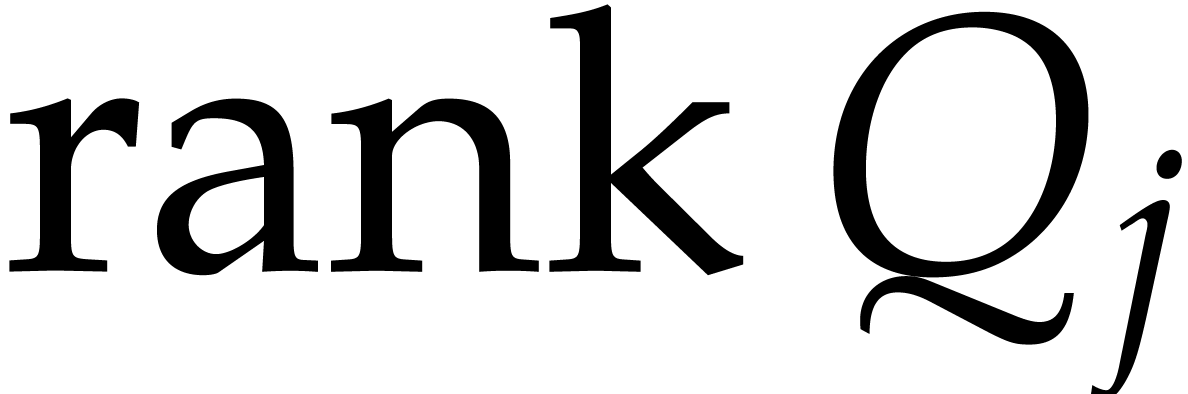 are incomparable for
are incomparable for  .
.
Consider a power series 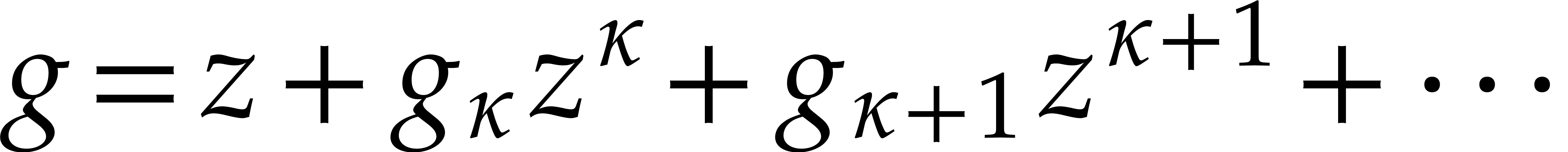 with
with 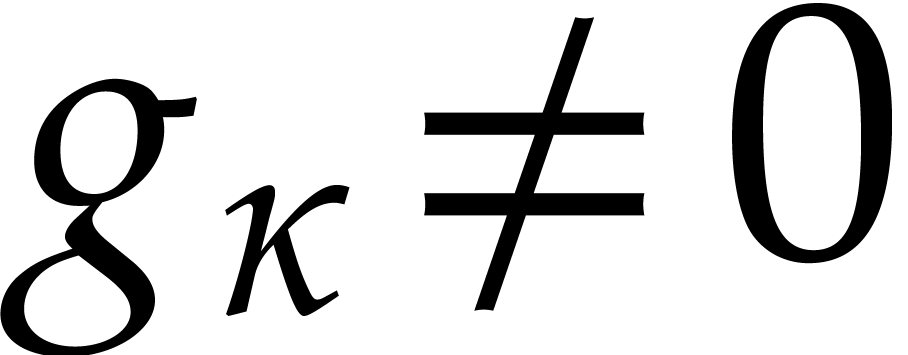 and
and  . Then we may define an
injective homomorphism
. Then we may define an
injective homomorphism 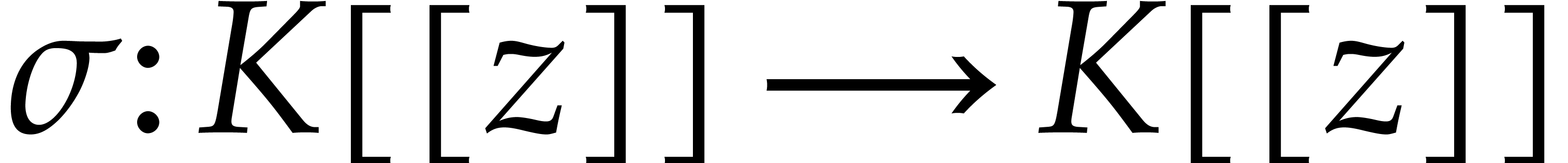 of
of  -algebras by
-algebras by
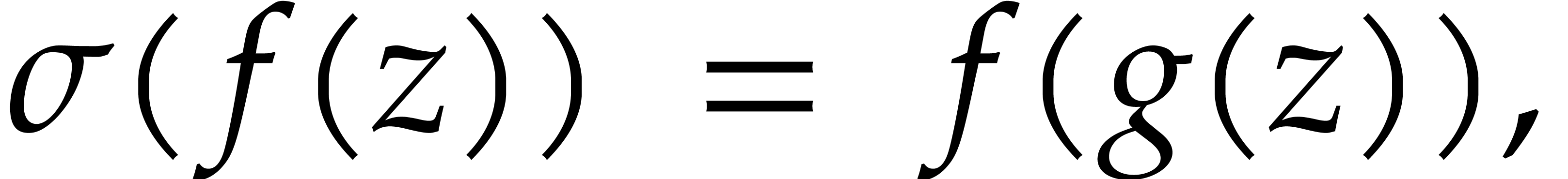
so 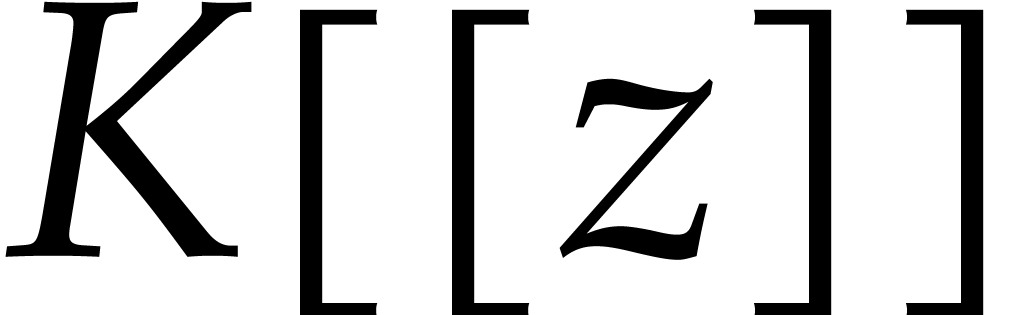 is a difference
is a difference  -algebra
with respect to the mapping
-algebra
with respect to the mapping  .
From now on, we will assume that
.
From now on, we will assume that  is a difference
subalgebra of
is a difference
subalgebra of 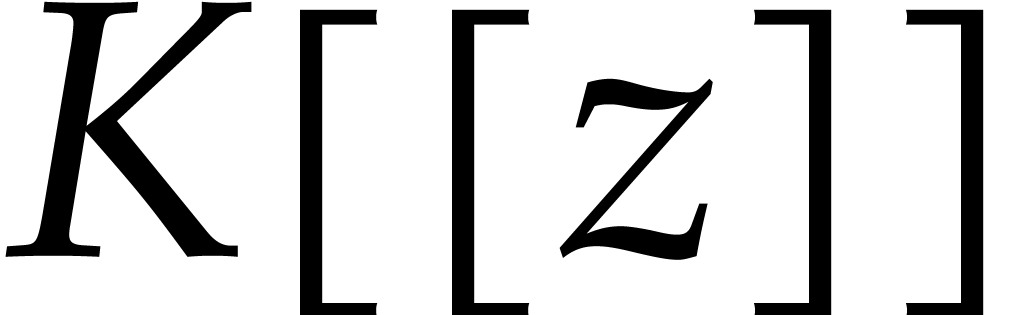 for
for  (in
particular,
(in
particular,  is closed under
is closed under  ). In addition, we assume that
). In addition, we assume that 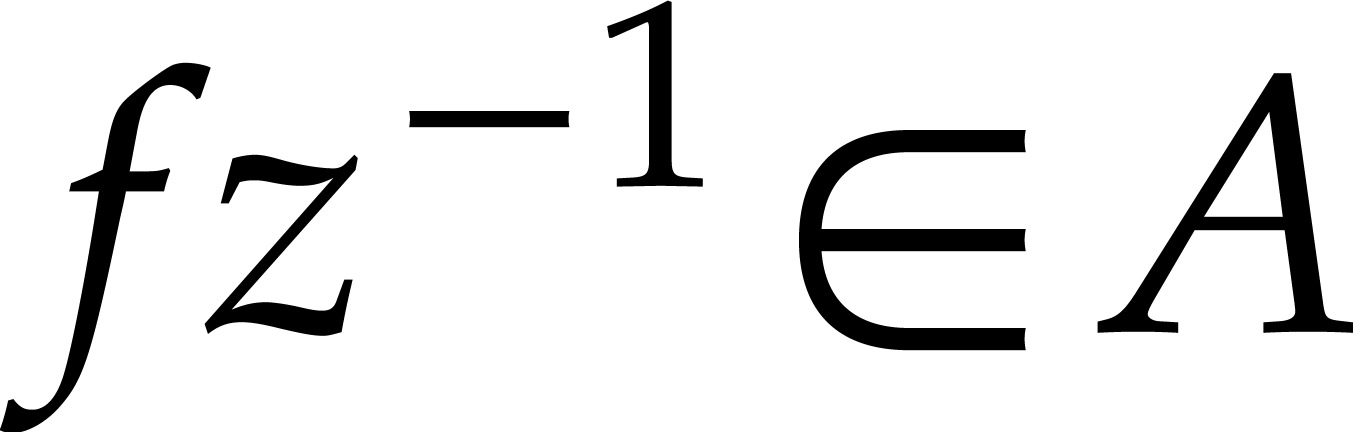 whenever
whenever 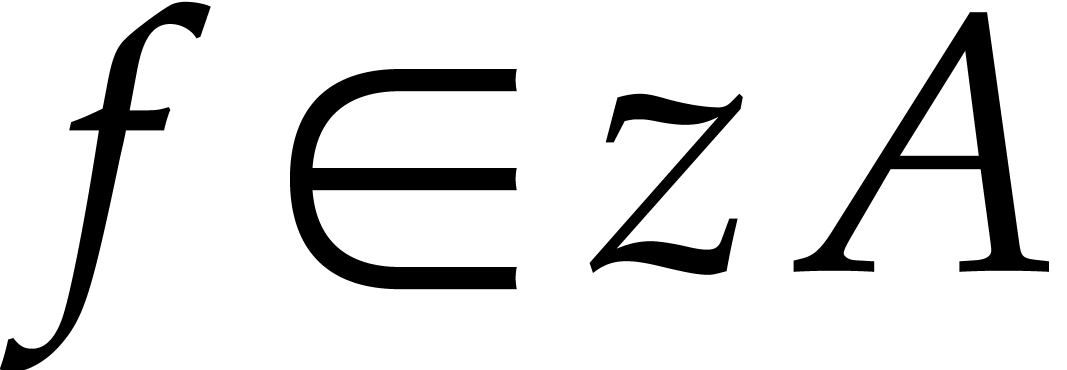 . This allows us to
define a second operator
. This allows us to
define a second operator
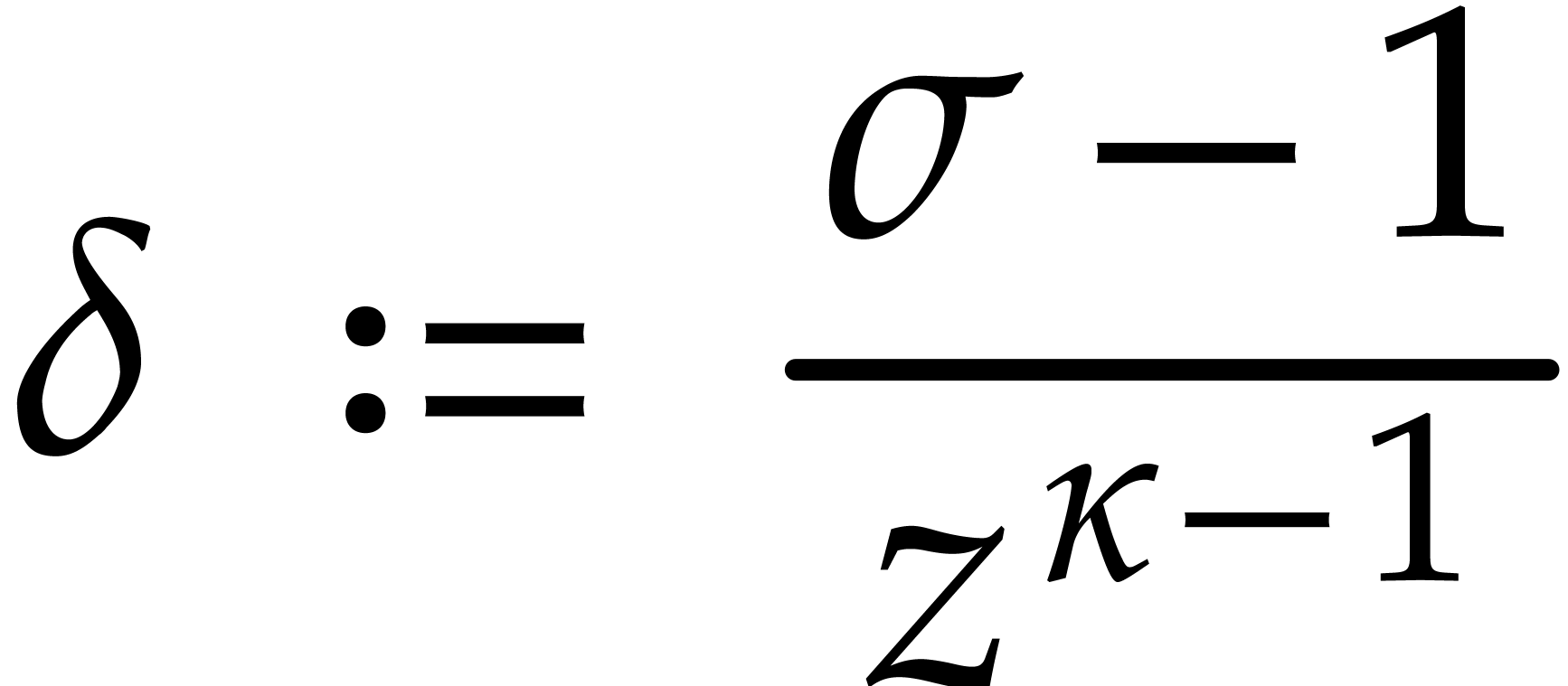
on  and we note that any operator in
and we note that any operator in 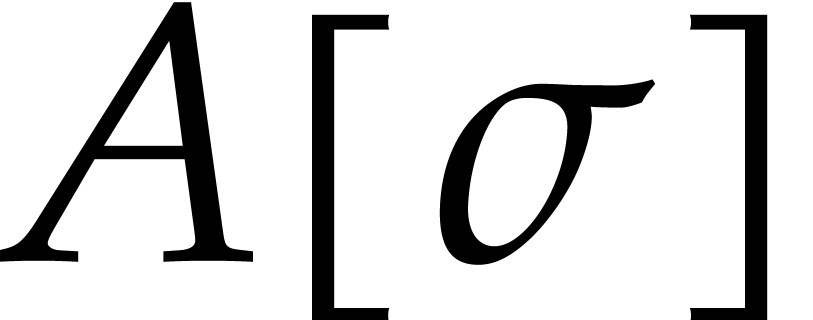 can be rewritten as an operator in
can be rewritten as an operator in 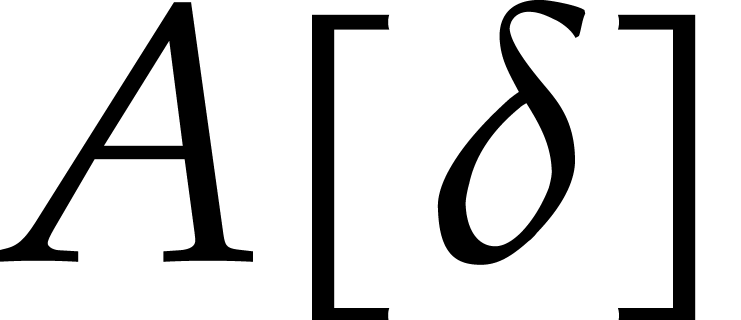 by substituting
by substituting  for
for  .
.
Example  ,
the shift operator
,
the shift operator  can be regarded as an
injective homomorphism of
can be regarded as an
injective homomorphism of 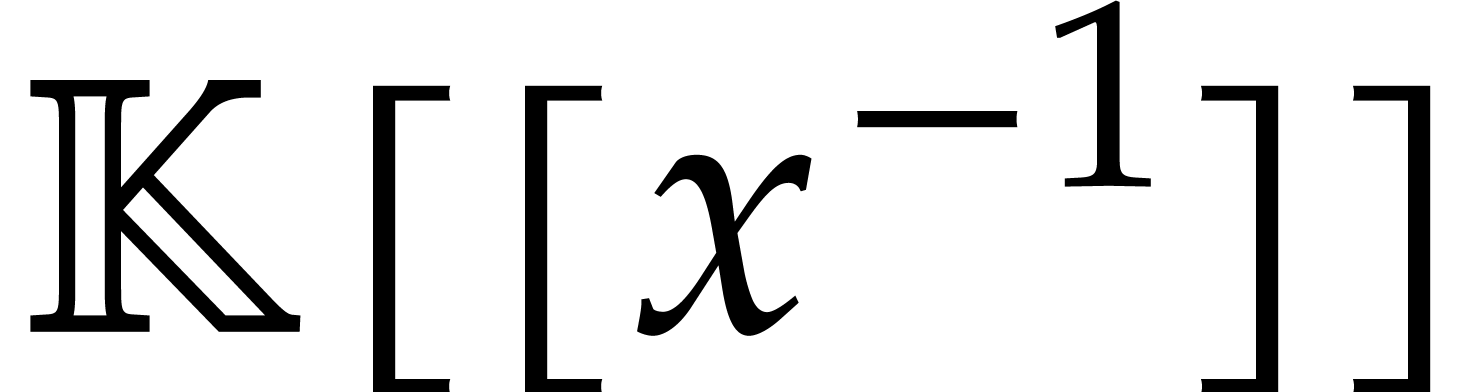 into itself. Setting
into itself. Setting
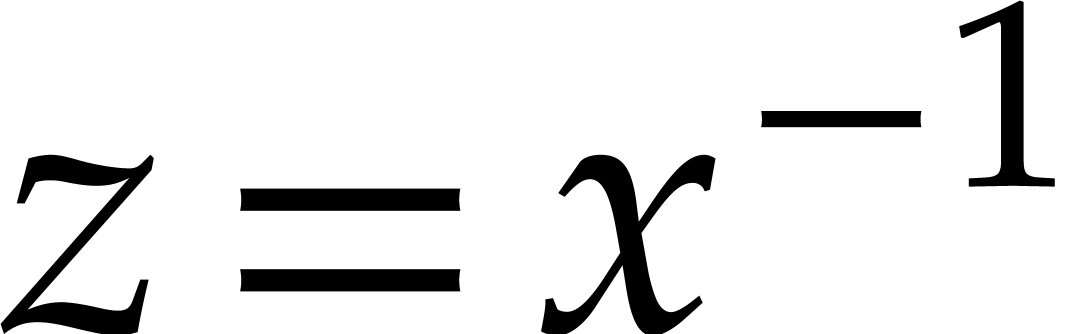 , this operator corresponds
to the operator
, this operator corresponds
to the operator  on
on 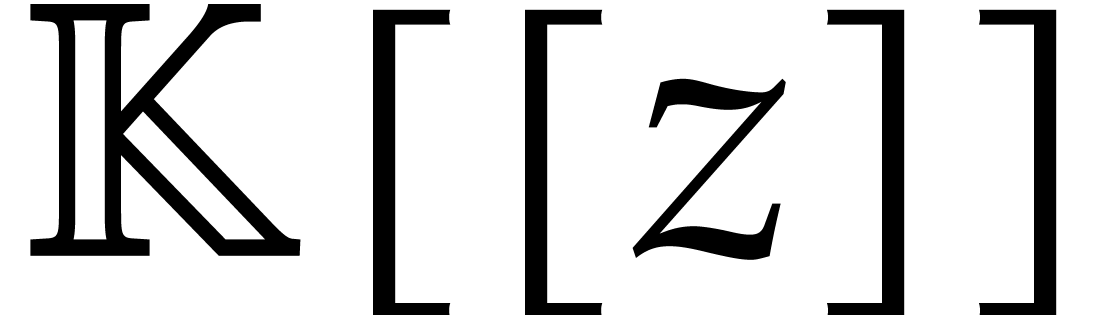 .
.
The corresponding operator  in this case will be
in this case will be
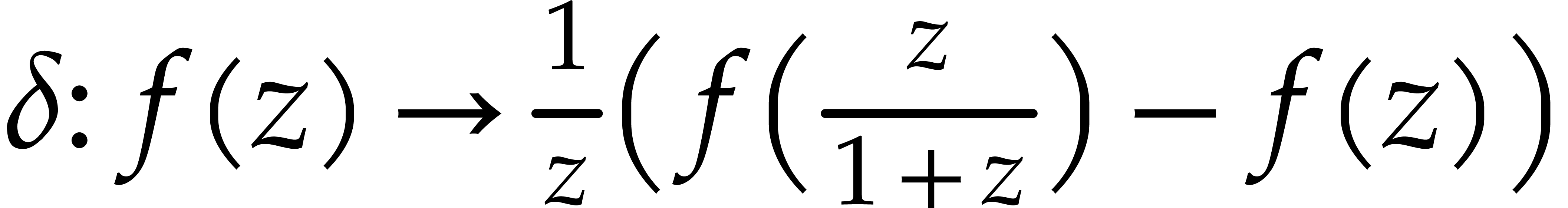 . The conversion between
. The conversion between 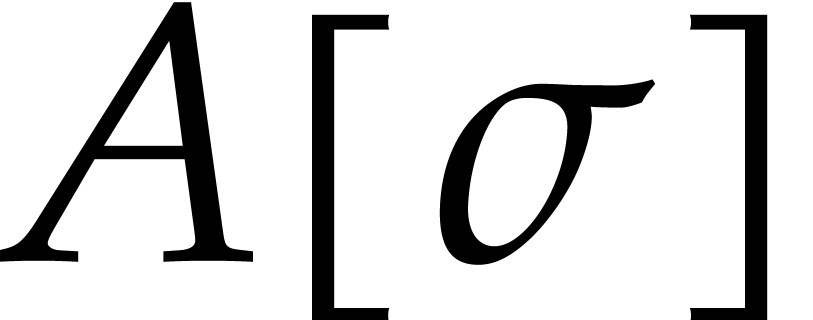 and
and 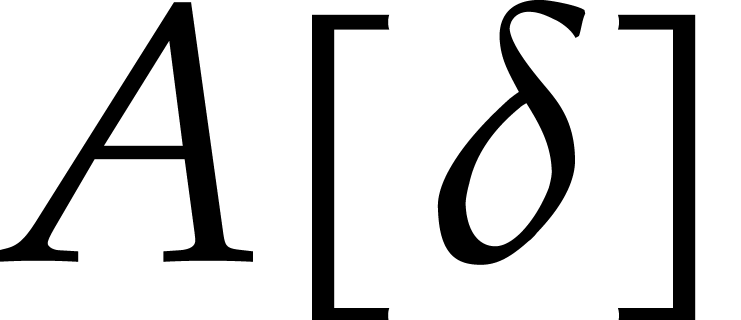 can be performed by
formulas
can be performed by
formulas
For example, the operator 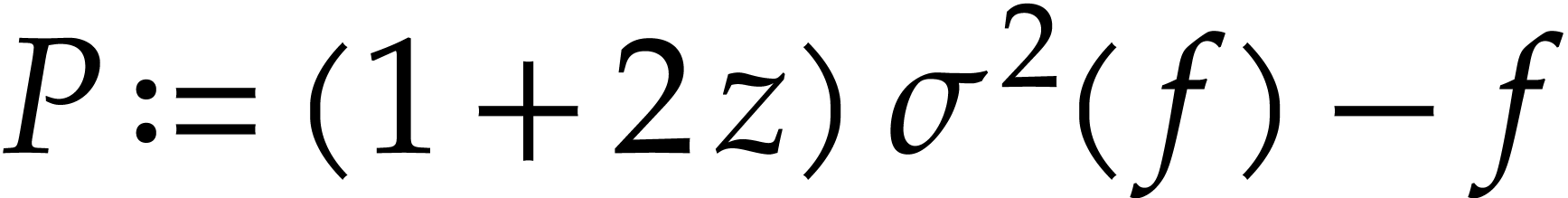 can be written as
can be written as
Given  , we will denote by
, we will denote by
 its valuation in
its valuation in  .
We extend this valuation to difference polynomials in
.
We extend this valuation to difference polynomials in 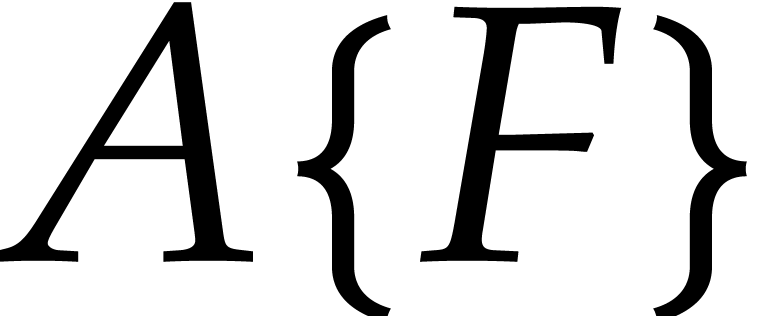 so that
so that 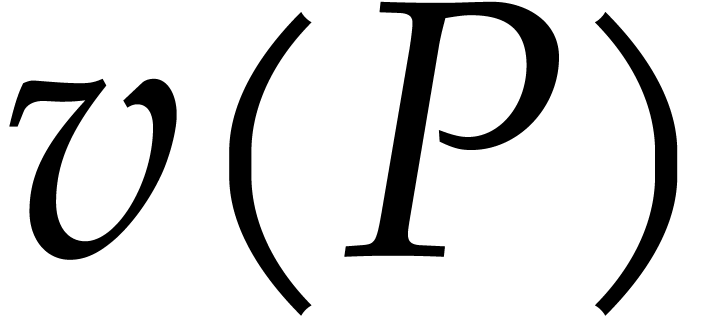 is the minimum of the valuation of the
non-zero coefficients of
is the minimum of the valuation of the
non-zero coefficients of  if
if 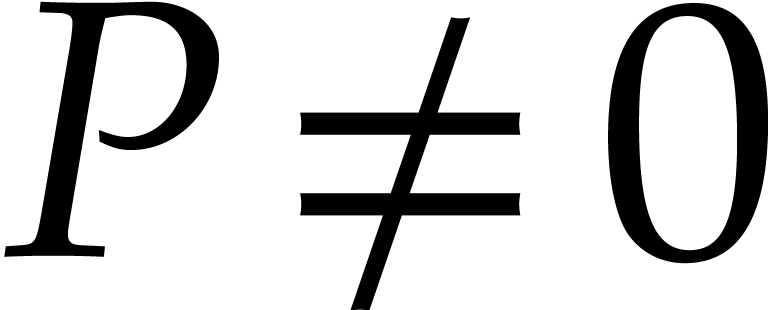 and
and  otherwise. The advantage of using the
operator
otherwise. The advantage of using the
operator  instead of
instead of  is
that
is
that 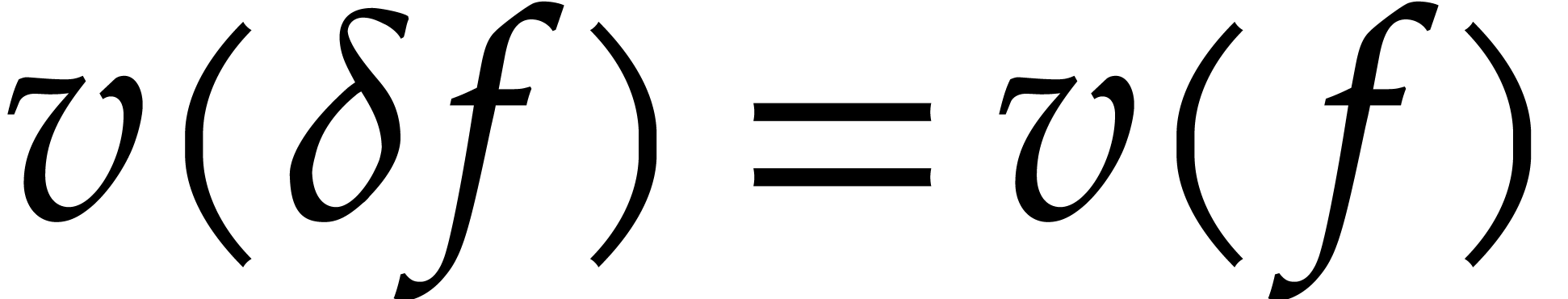 for all
for all 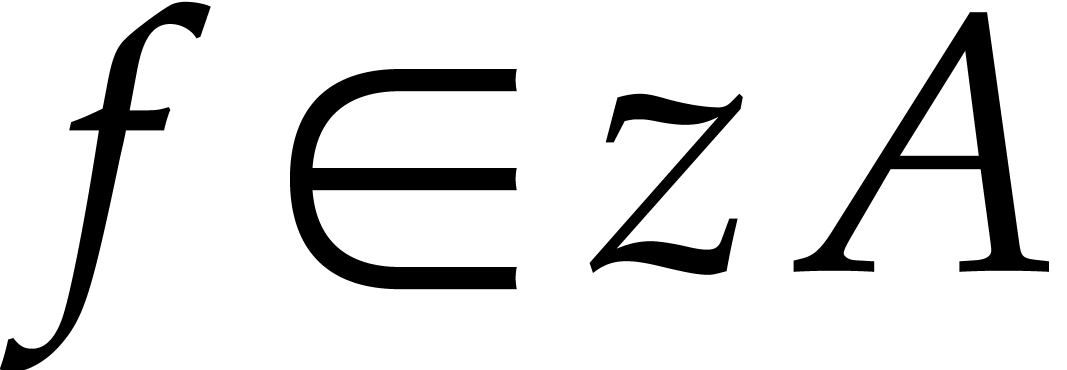 .
More generally, assume that
.
More generally, assume that 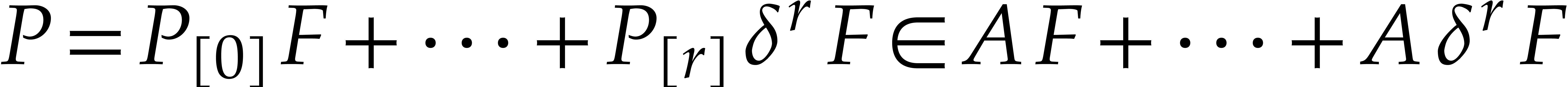 is a linear
difference polynomial of order
is a linear
difference polynomial of order 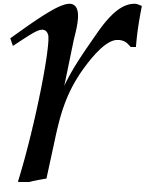 .
For each
.
For each 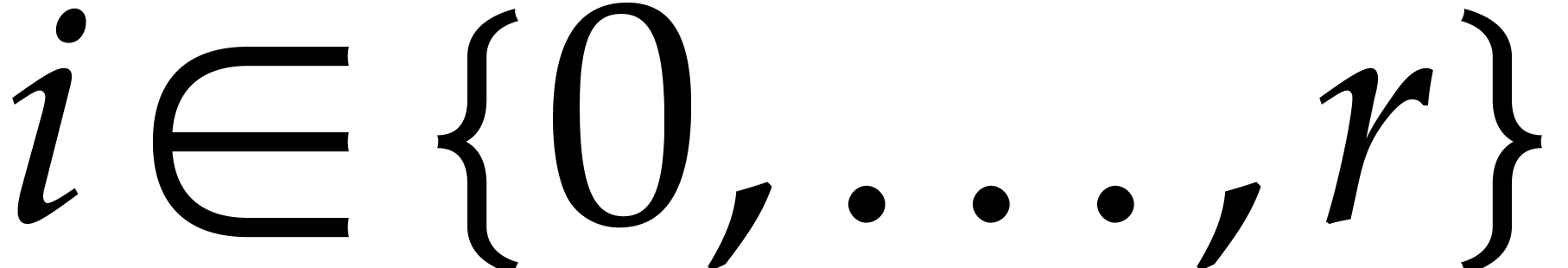 , we have
, we have  . Let
. Let 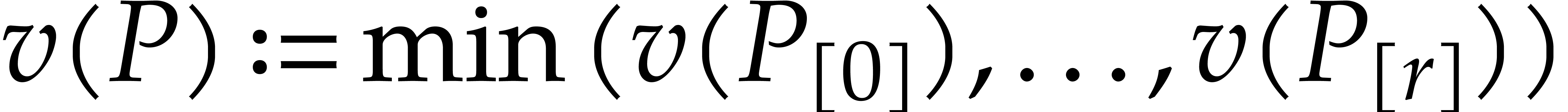 .
Then, for any
.
Then, for any 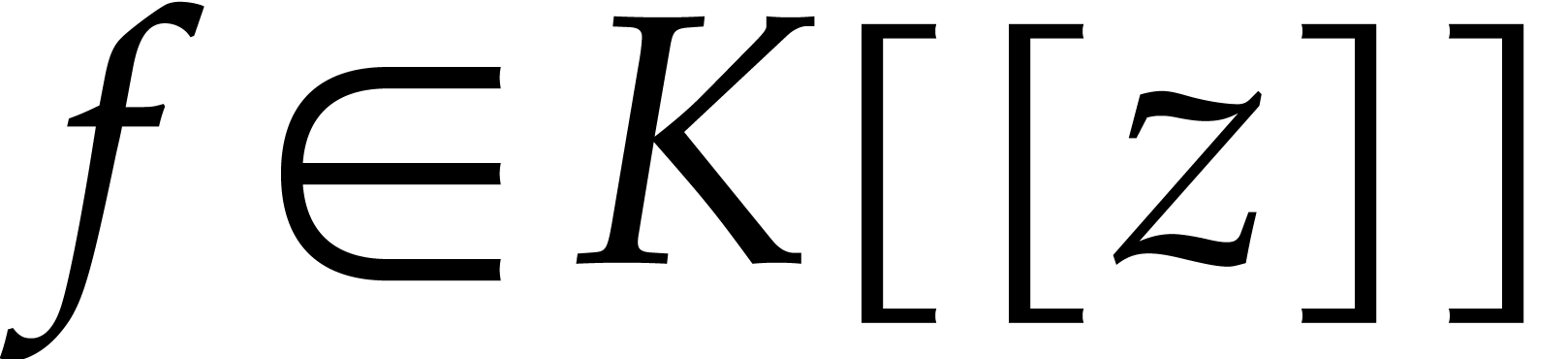 , we have
, we have

Furthermore, the coefficient in front of 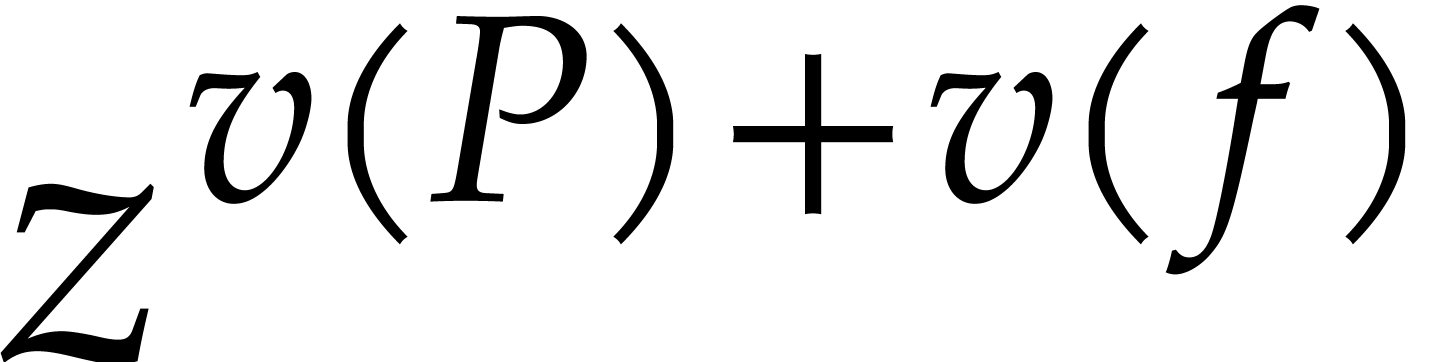 in
in 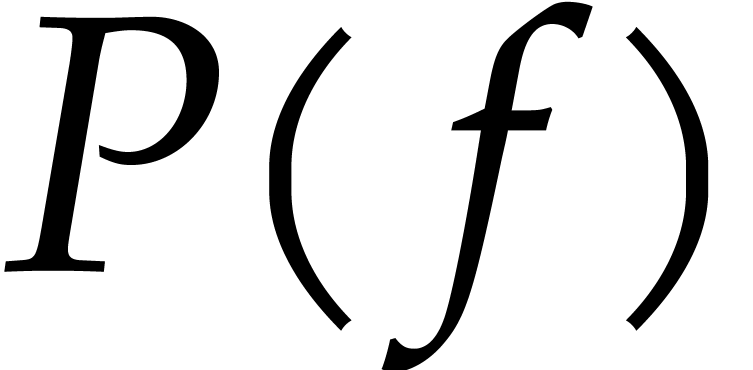 can be written as
can be written as
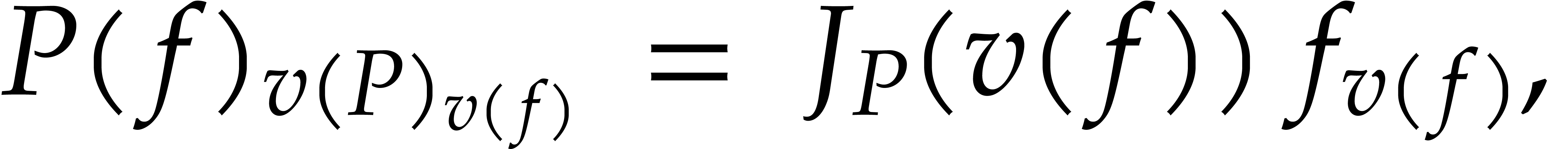 |
(2) |
where 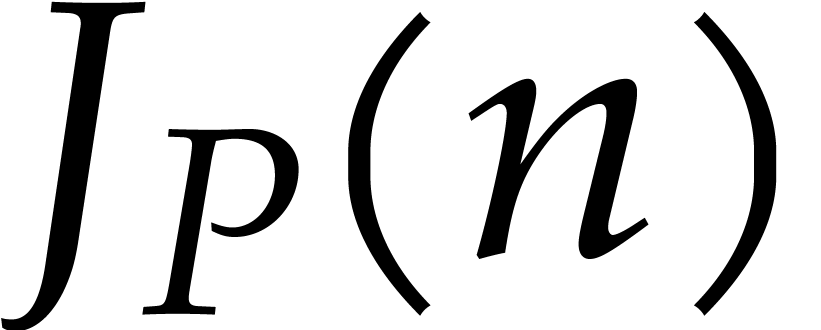 is the indicial polynomial of
is the indicial polynomial of
 defined by
defined by
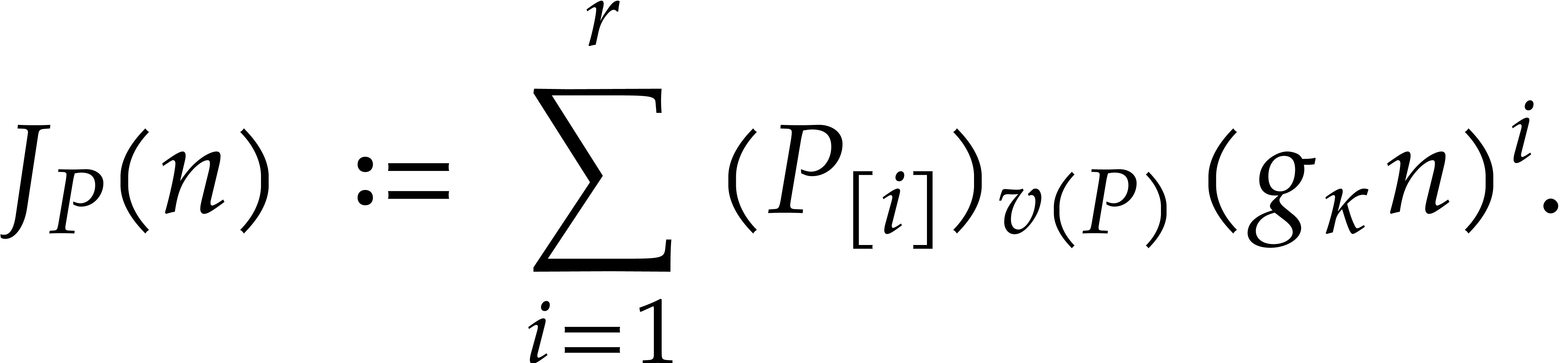
In particular, whenever 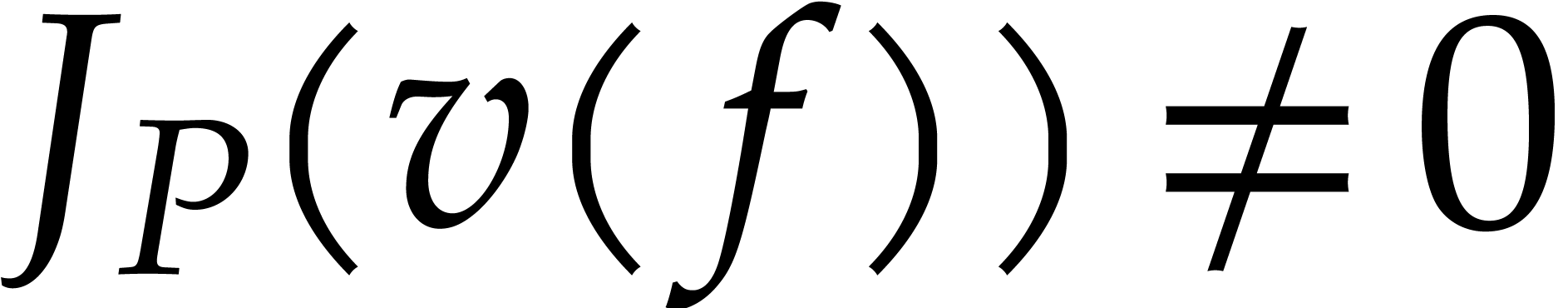 , we
have
, we
have 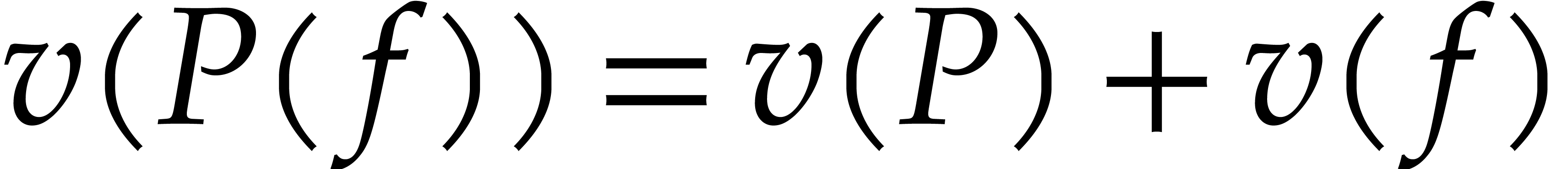 , so
, so  does not vanish at
does not vanish at  . We will
denote by
. We will
denote by 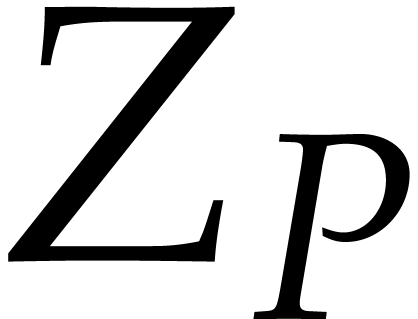 the largest root of
the largest root of 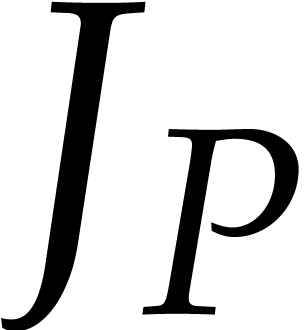 in
in  , while taking
, while taking 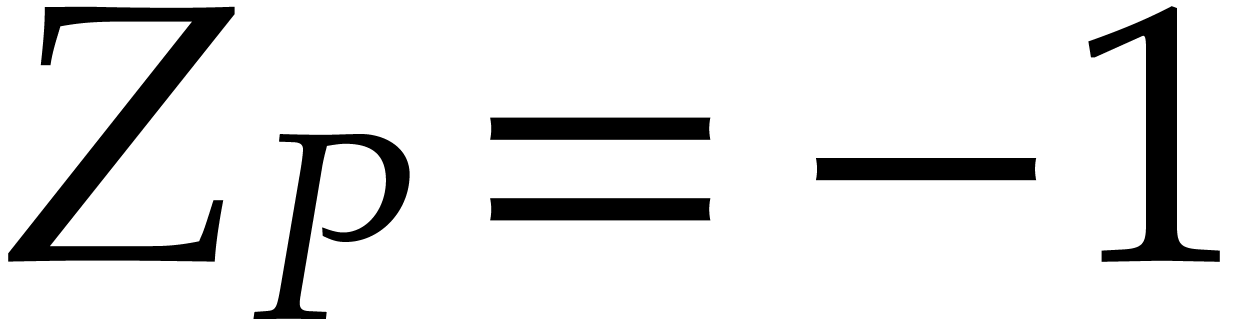 if no such
root exists. This number will be an upper bound for the valuation of a
power series solutions of
if no such
root exists. This number will be an upper bound for the valuation of a
power series solutions of 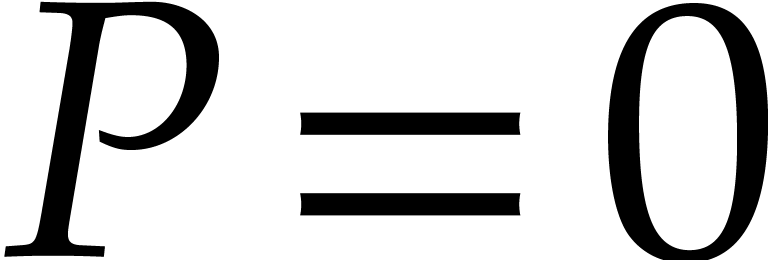 .
.
Example  from Example 1. We have
from Example 1. We have 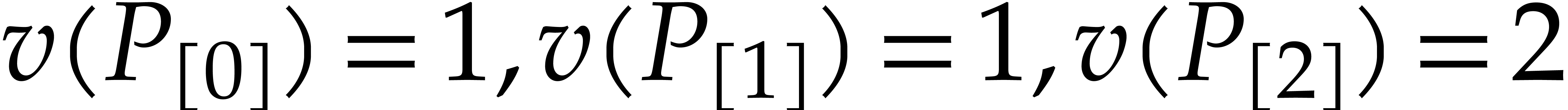 ,
so
,
so 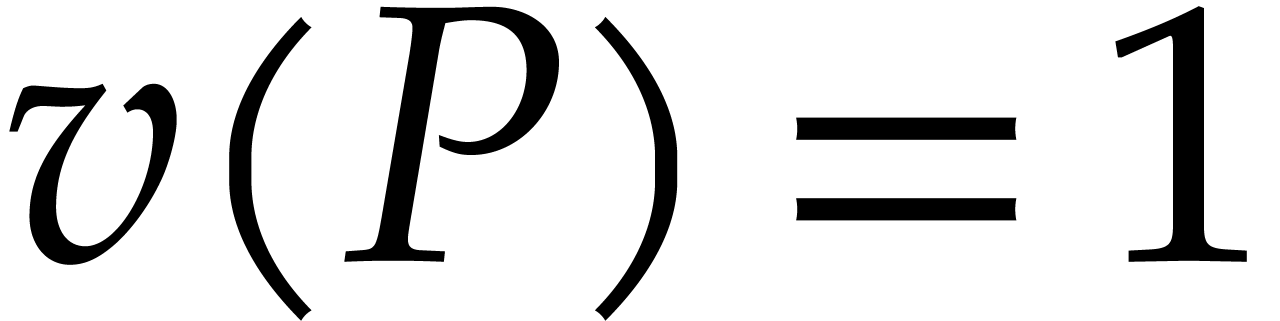 . Then the indicial
polynomial will be
. Then the indicial
polynomial will be 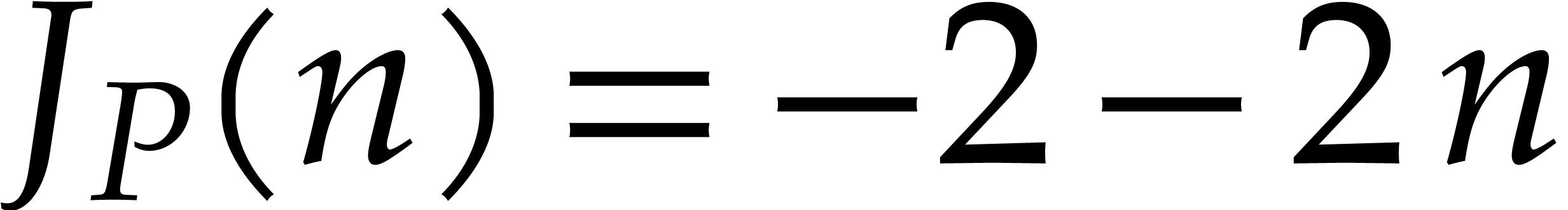 , so we
have
, so we
have 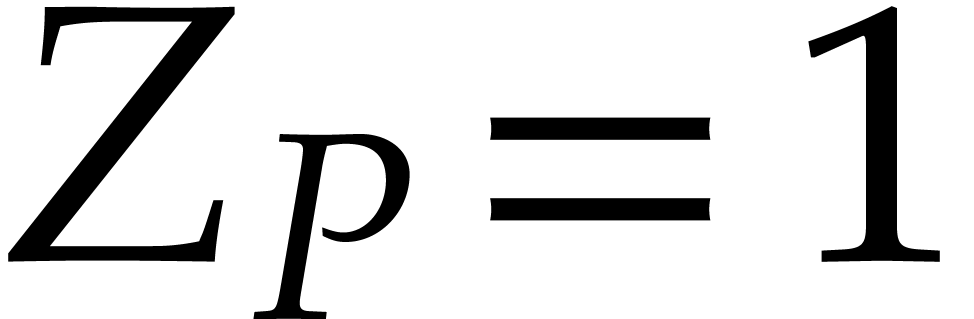 . This implies that the
valuation of every power series solution of
. This implies that the
valuation of every power series solution of 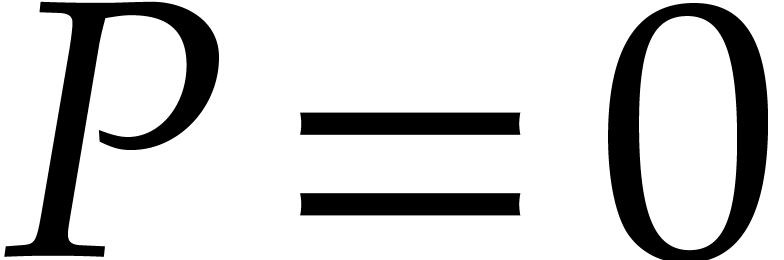 must
be equal to one. Note that there is a solution
must
be equal to one. Note that there is a solution 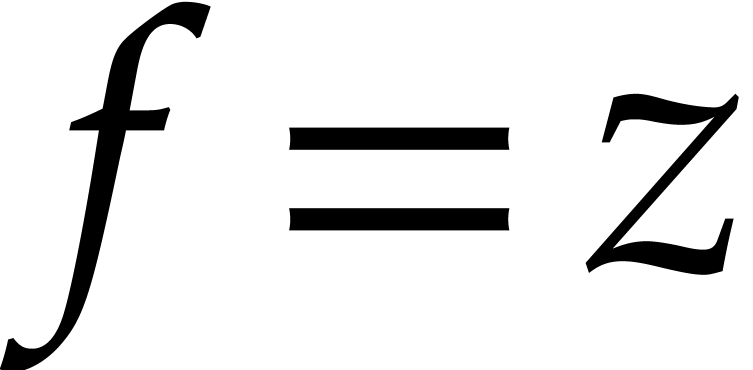 with
with 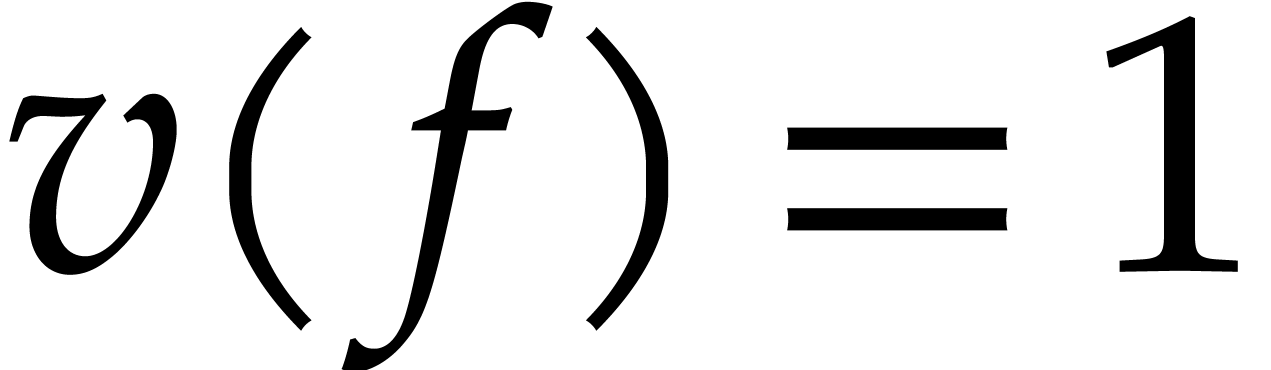 .
.
Given a general difference polynomial  and a
“point”
and a
“point” 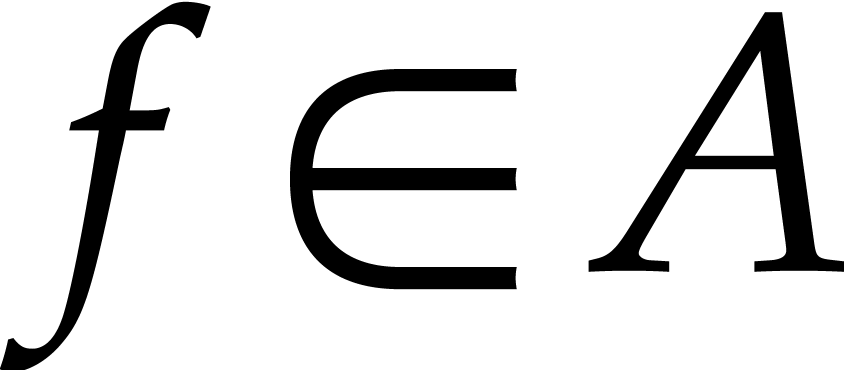 , the
unique difference polynomial
, the
unique difference polynomial  such that
such that
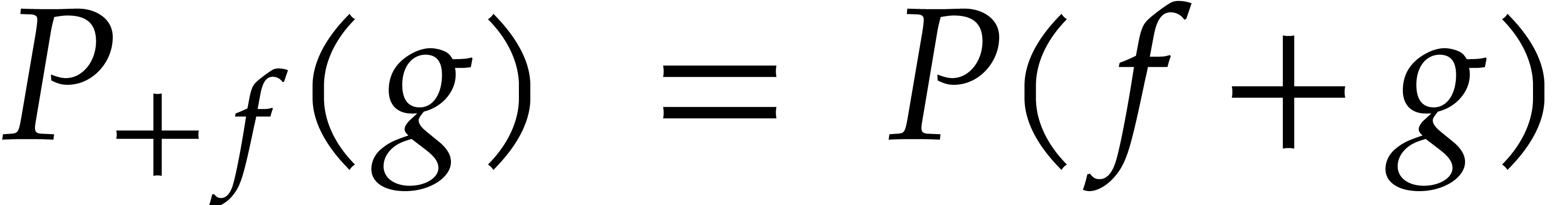
for all  is called the additive
conjugate of
is called the additive
conjugate of  by
by  . This transformation can be thought as shifting the
“origin” to
. This transformation can be thought as shifting the
“origin” to  .
.
For every difference polynomial  and
and  , we define
, we define  to be the
homogeneous component of degree
to be the
homogeneous component of degree  in
in  . If
. If  has total degree
has total degree
 , then
, then 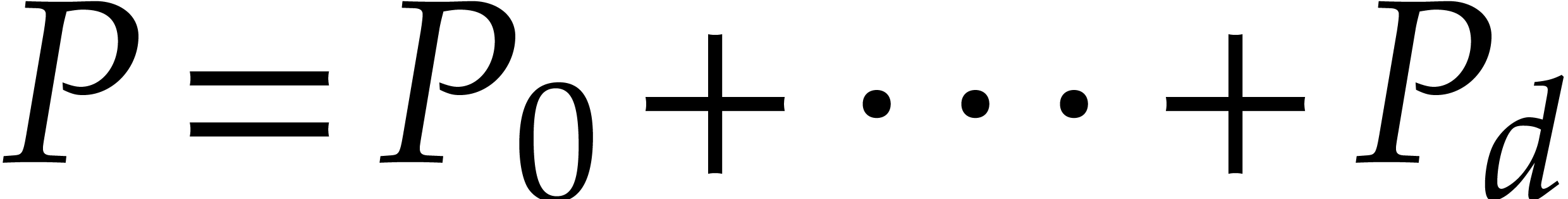 is the decomposition of
is the decomposition of  into homogeneous parts.
Given
into homogeneous parts.
Given  , we will use
, we will use 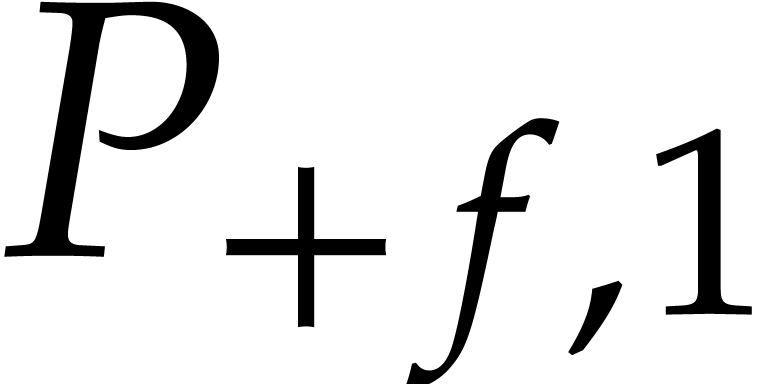 as an abbreviation for
as an abbreviation for 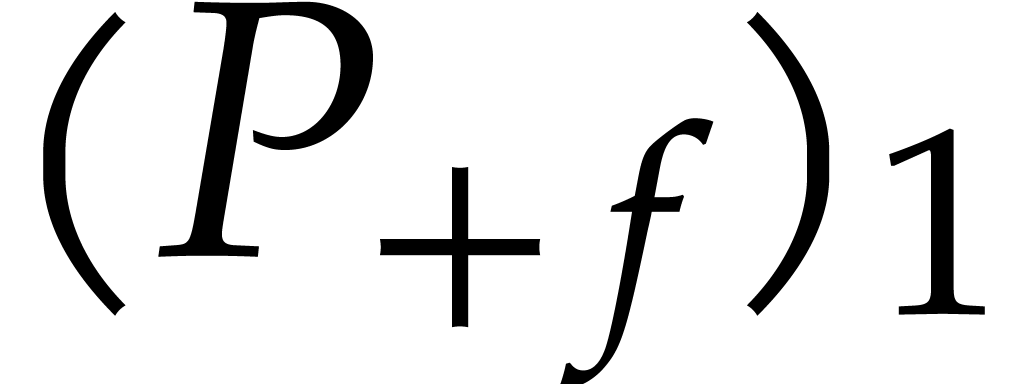 .
.
In order to ensure the existence of solutions to certain difference
equations, it is convenient to also consider logarithmic power series
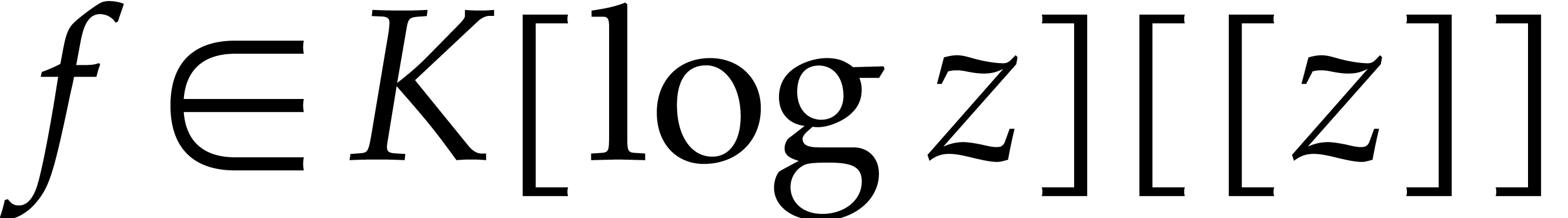 . Such series can still be
considered as power series
. Such series can still be
considered as power series  in
in  and we will still denote by
and we will still denote by 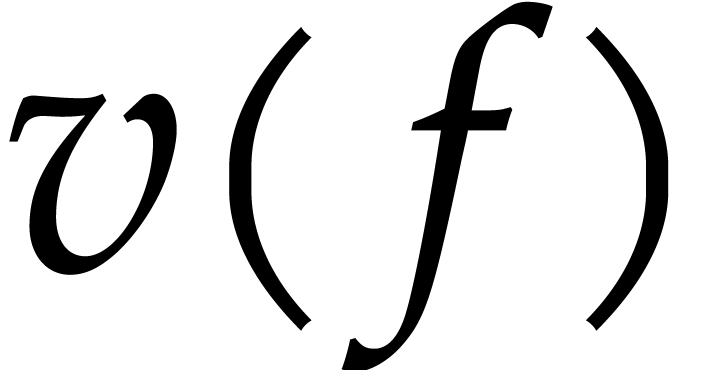 the valuation of
the valuation of
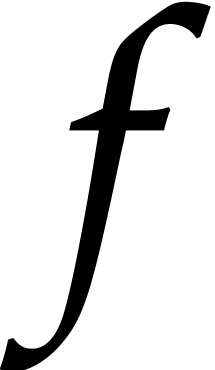 in
in  .
The coefficients
.
The coefficients 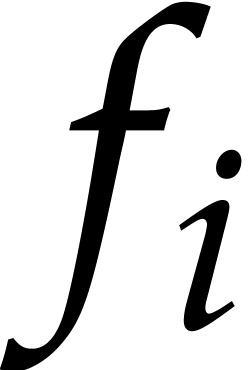 are polynomials in
are polynomials in  , and we will write
, and we will write 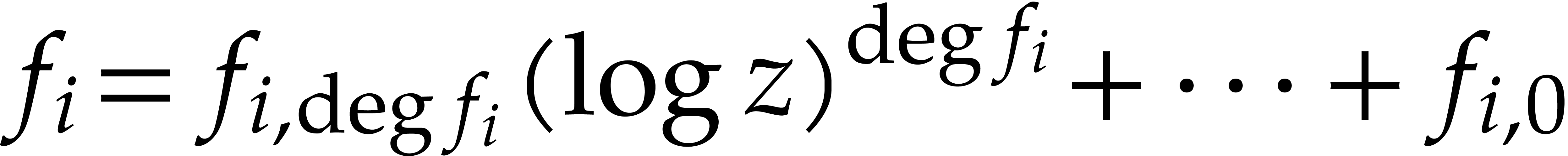 . Note that, for every
. Note that, for every 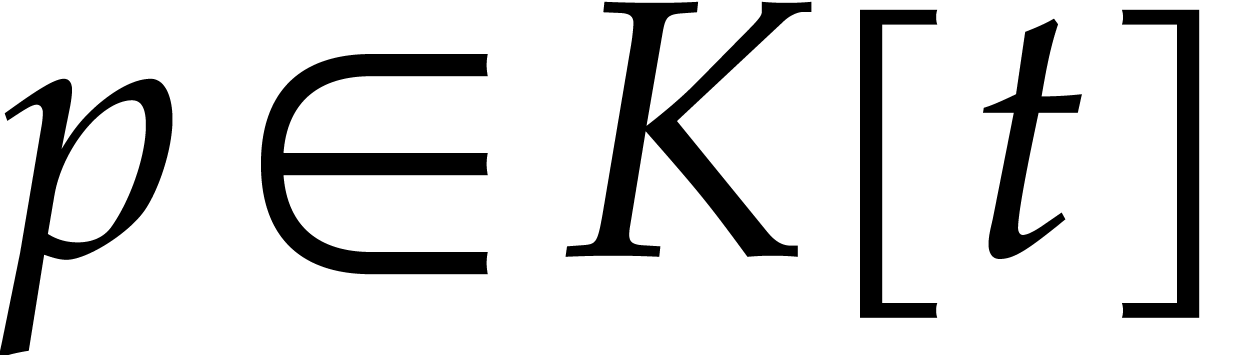 and
and
 , we have
, we have
This allows us to generalize (2) to the case when 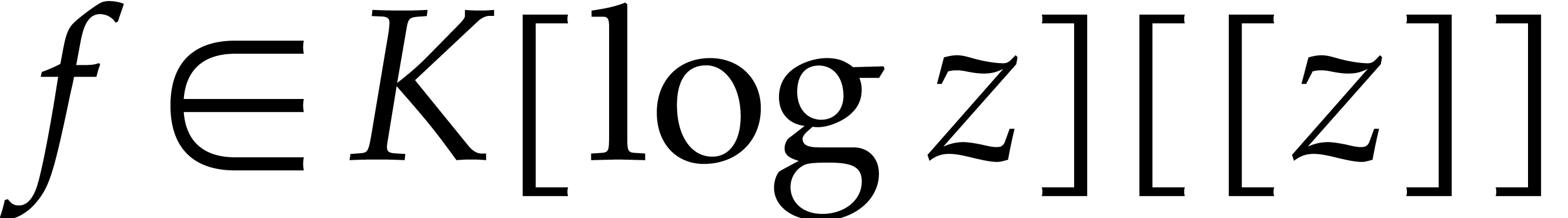 and
and 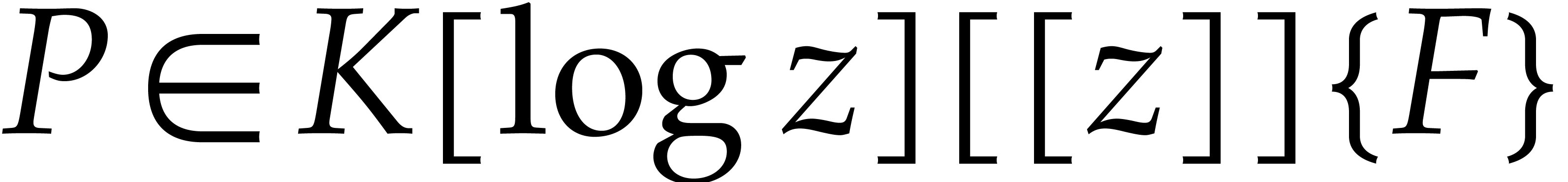 is a homogeneous linear
differential polynomial:
is a homogeneous linear
differential polynomial:
 |
(3) |
where  acts on
acts on 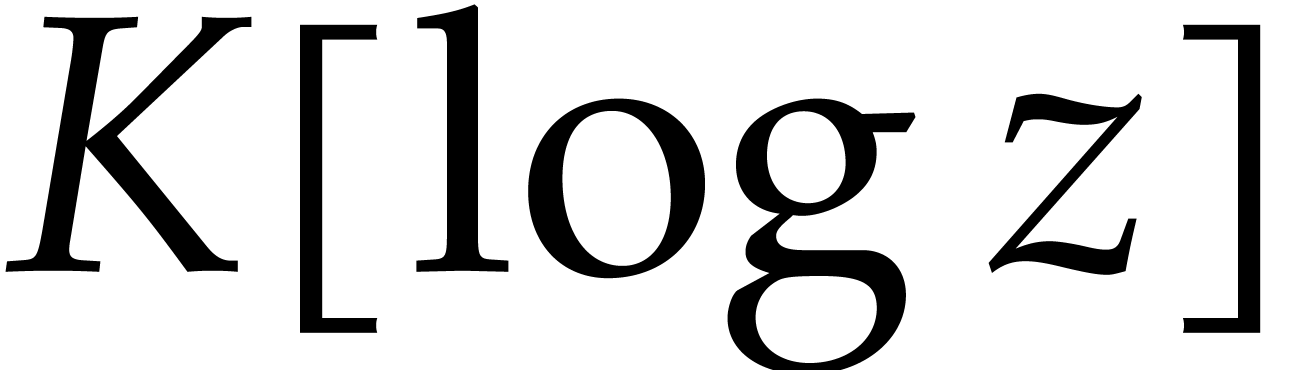 as the
derivation with respect to
as the
derivation with respect to 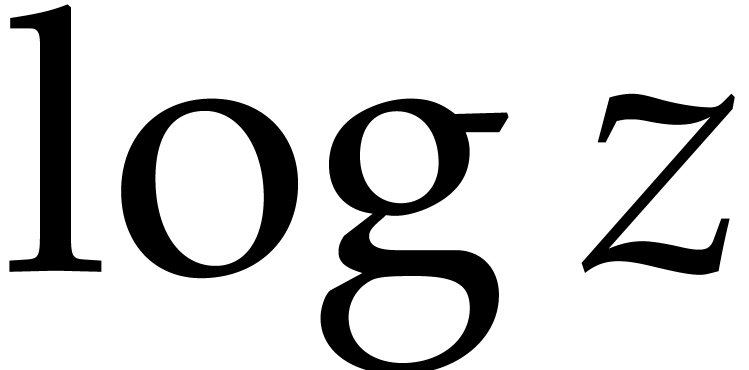 .
.
 -algebraic
power series
-algebraic
power series -algebraic power series
-algebraic power series
Let  be a field of characteristic zero. Let
be a field of characteristic zero. Let 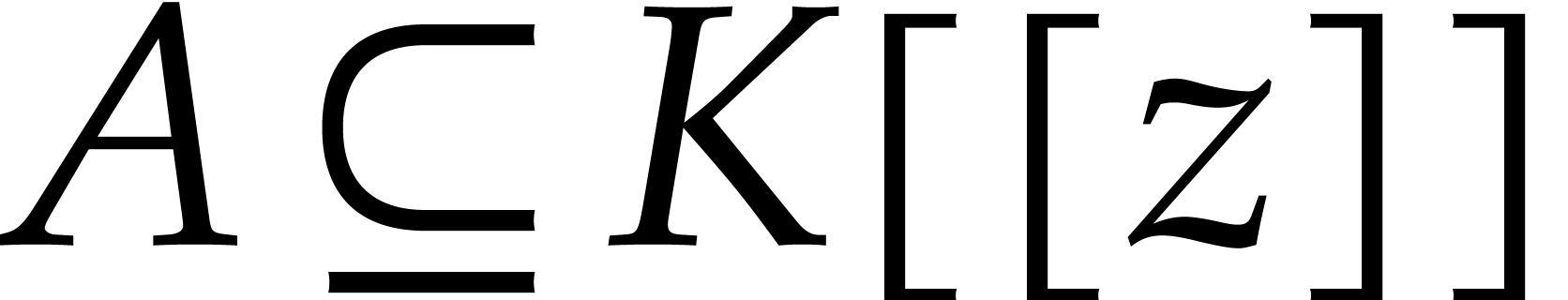 be a
be a  -difference
-difference  -subalgebra of
-subalgebra of
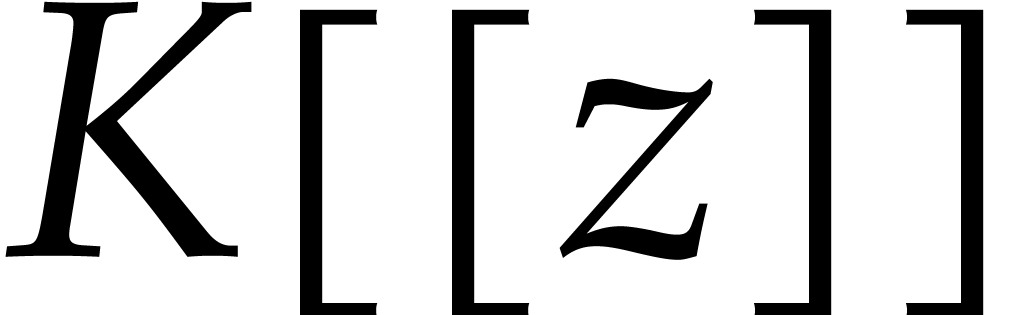 with corresponding shift operator
with corresponding shift operator  . Assume furthermore that, for all
. Assume furthermore that, for all 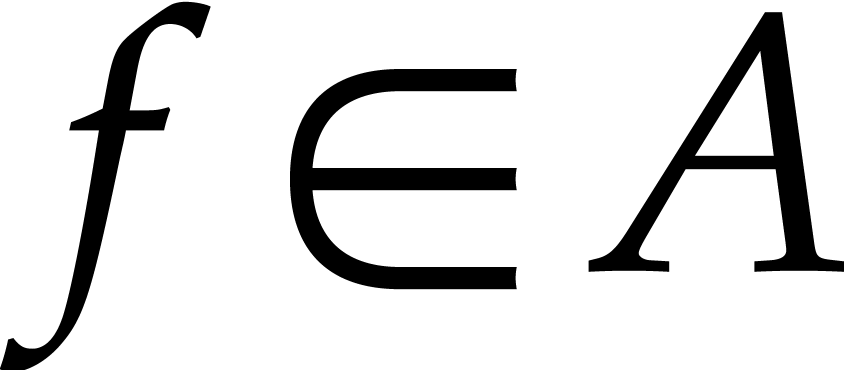 and
and 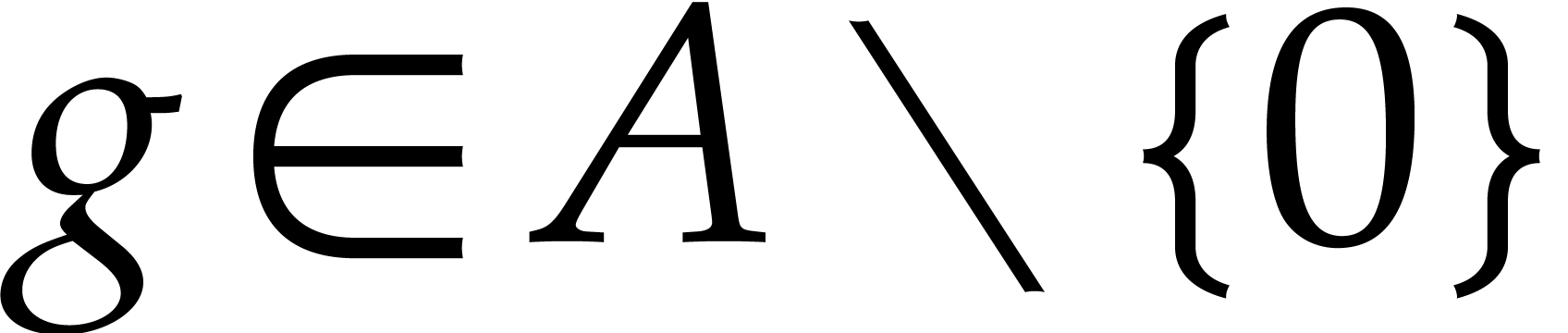 such that
such that 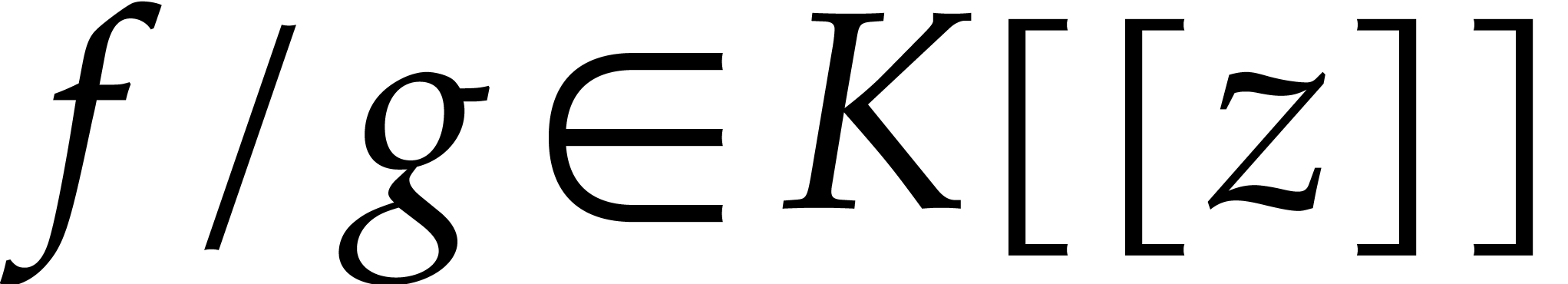 , we have
, we have 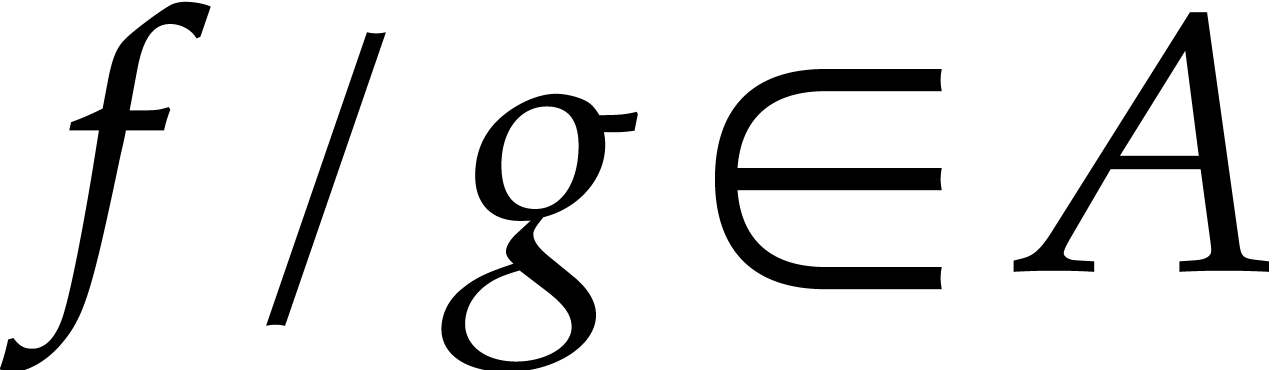 .
We call such an algebra
.
We call such an algebra  a
a  -difference power series domain. A series
-difference power series domain. A series
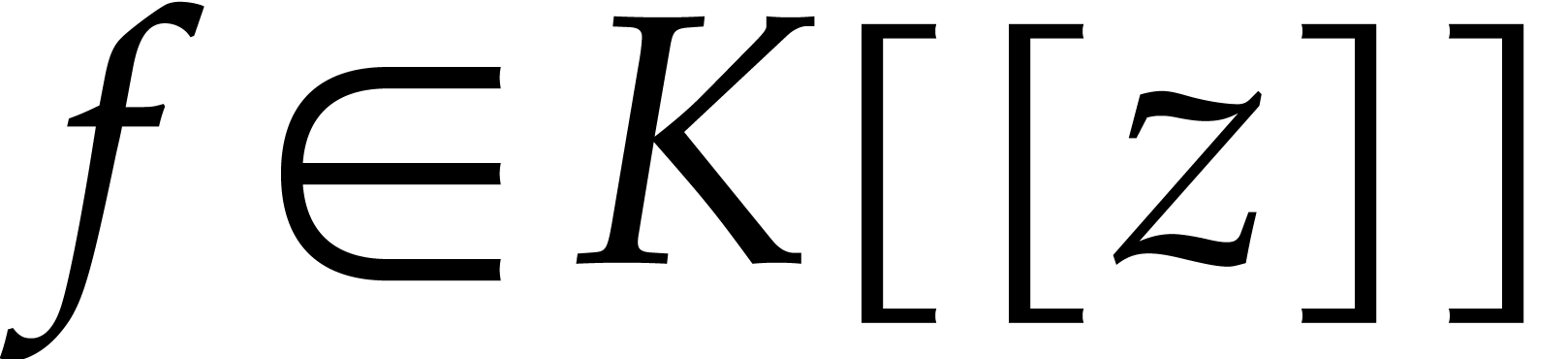 is said to be
is said to be  -algebraic
over
-algebraic
over  if it satisfies a non-trivial difference
equation
if it satisfies a non-trivial difference
equation 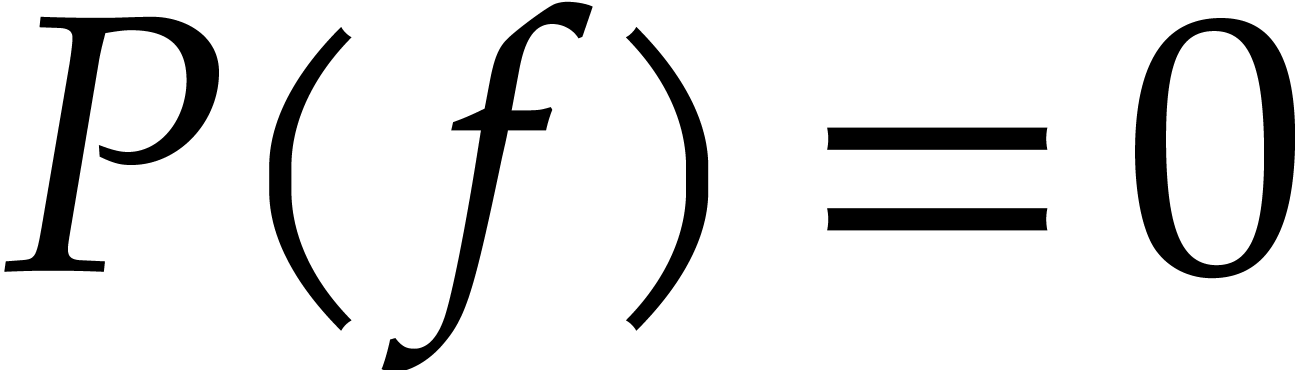 with
with 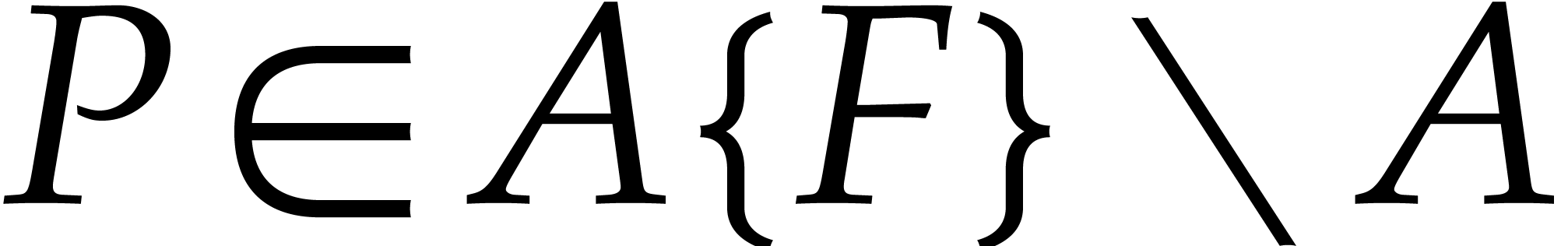 .
.
Assume now that  is an effective power series
domain. The most obvious way to effectively represent a
is an effective power series
domain. The most obvious way to effectively represent a  -algebraic power series over
-algebraic power series over  is to represent it by a pair
is to represent it by a pair 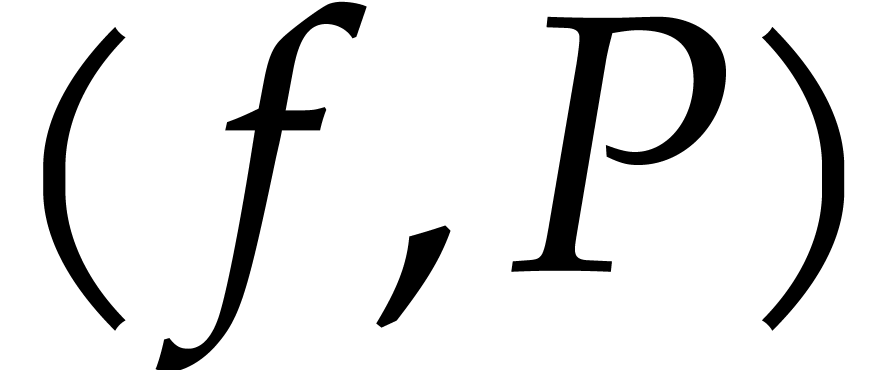 where
where 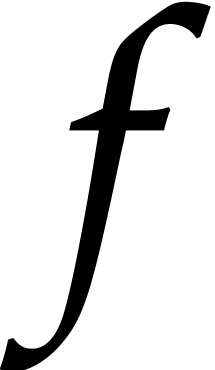 is a computable series and
is a computable series and  a
non-trivial annihilator with
a
non-trivial annihilator with 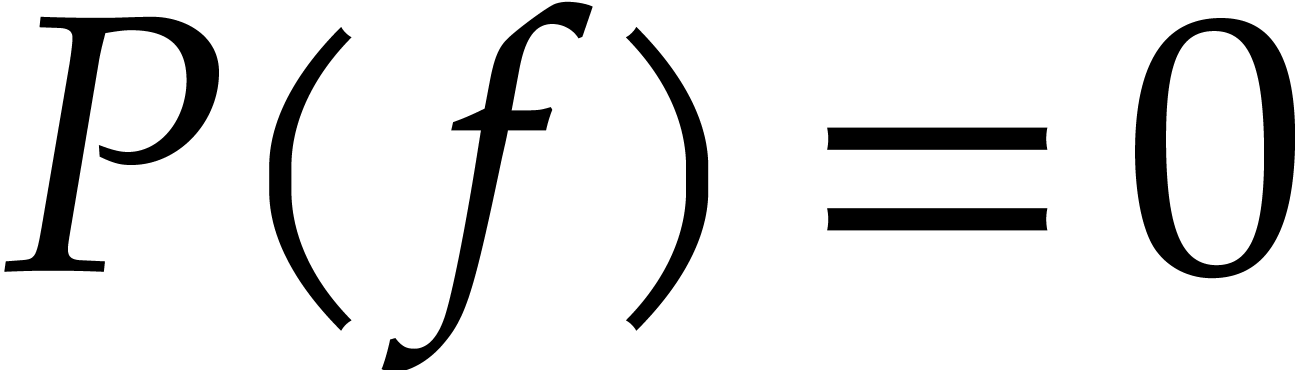 .
We say that the annihilator
.
We say that the annihilator  is
non-degenerate if
is
non-degenerate if 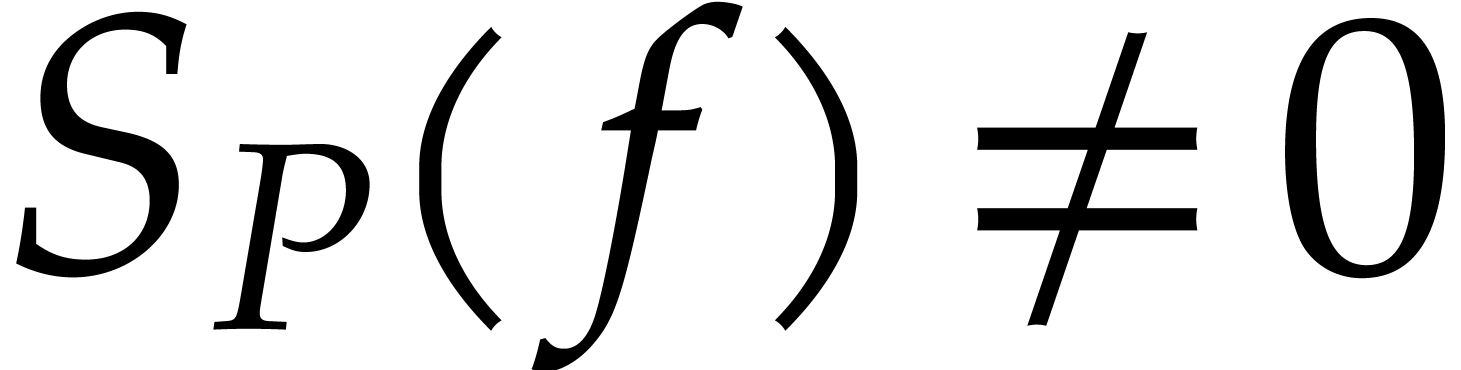 .
.
Let 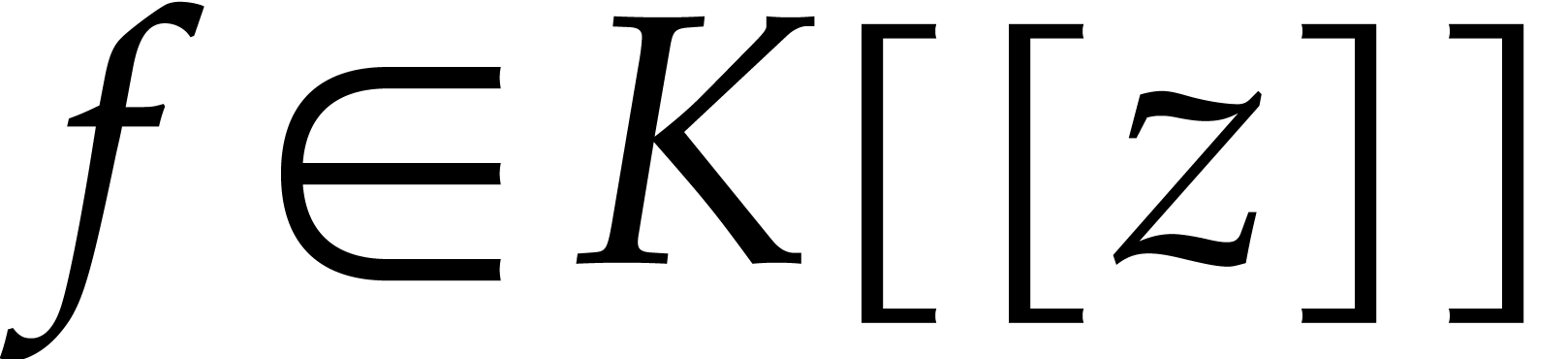 be
be  -algebraic
over
-algebraic
over  with annihilator
with annihilator 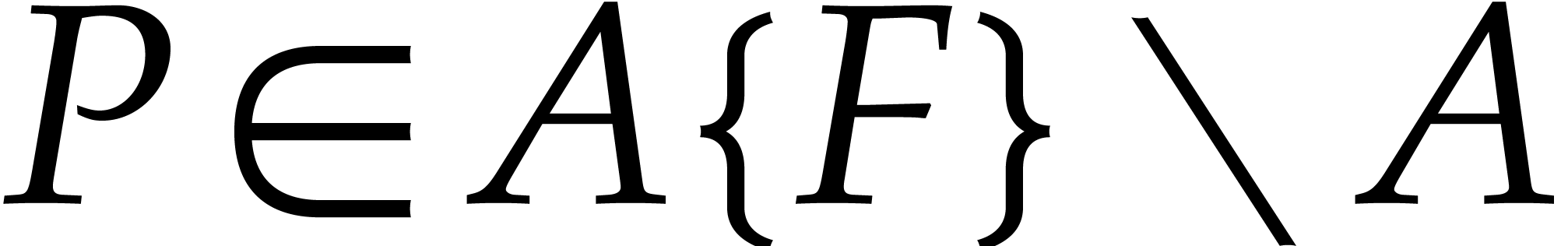 . Assume that there exists a number
. Assume that there exists a number 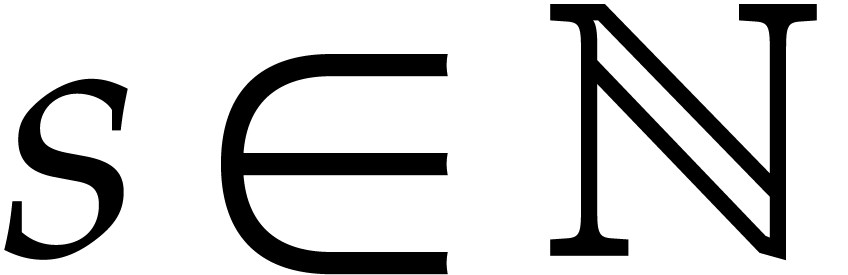 such that for any
such that for any  with
with 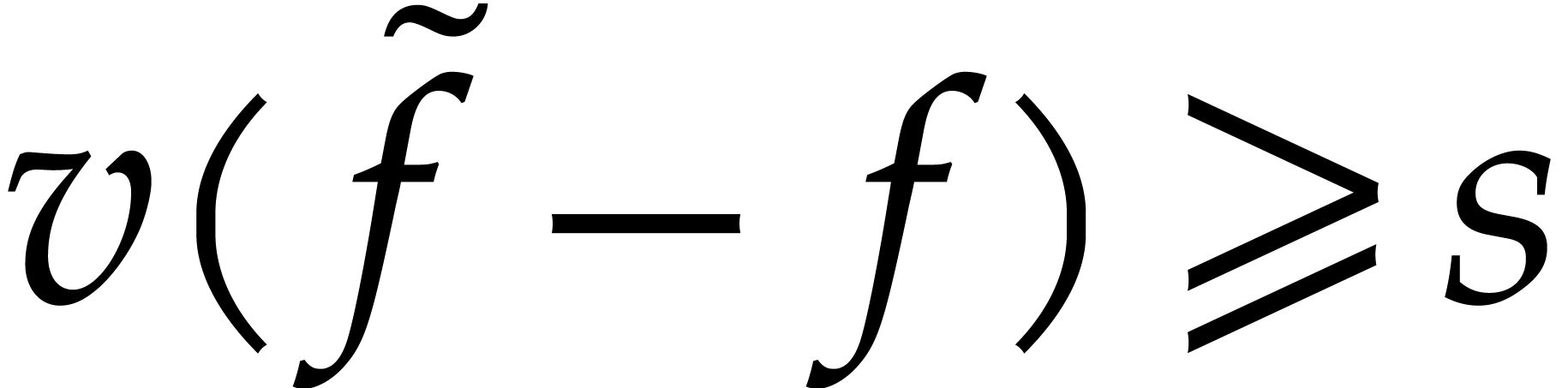 , we have
, we have 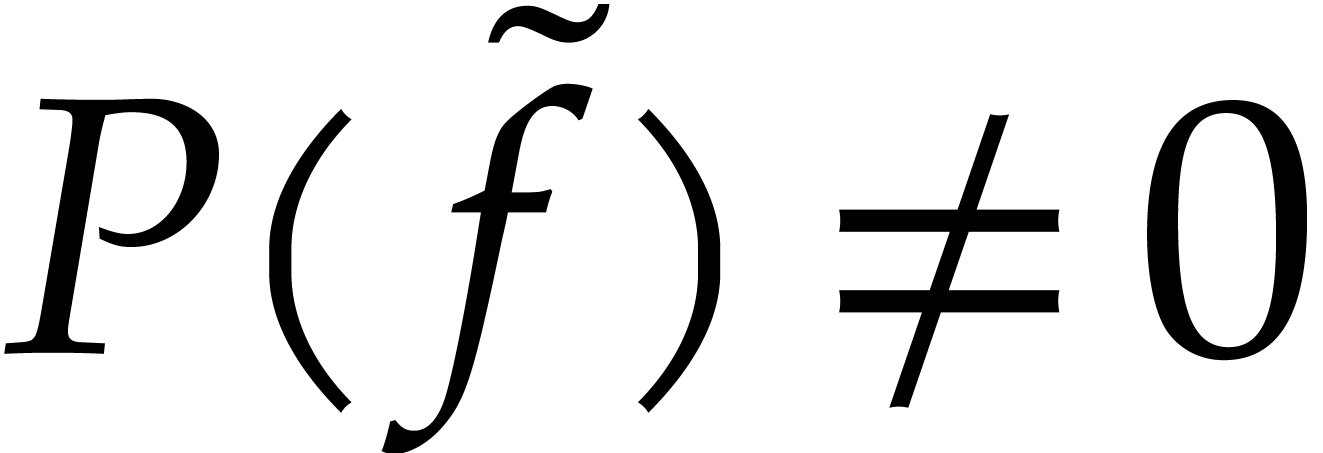 .
Then we define
.
Then we define 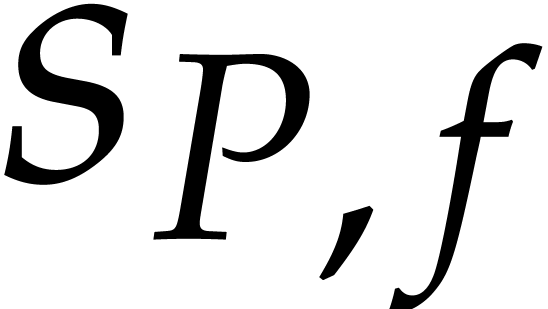 to be the smallest such number
to be the smallest such number
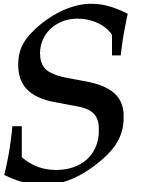 and call it the root separation of
and call it the root separation of  at
at 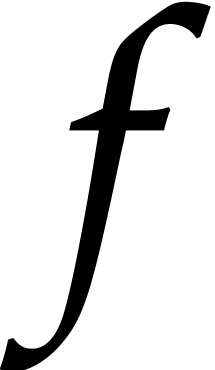 . It
corresponds to the number of initial conditions that should be known in
order to determine
. It
corresponds to the number of initial conditions that should be known in
order to determine 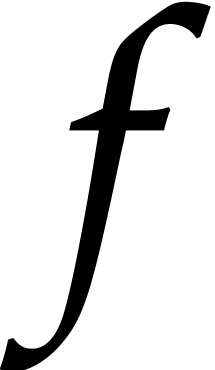 in a unique way as a root of
in a unique way as a root of
 .
.
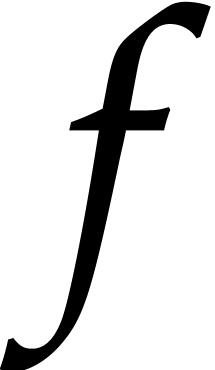 is
is  -algebraic over
-algebraic over  with a non-degenerate annihilator
with a non-degenerate annihilator  .
Then the following root separation bound holds:
.
Then the following root separation bound holds:
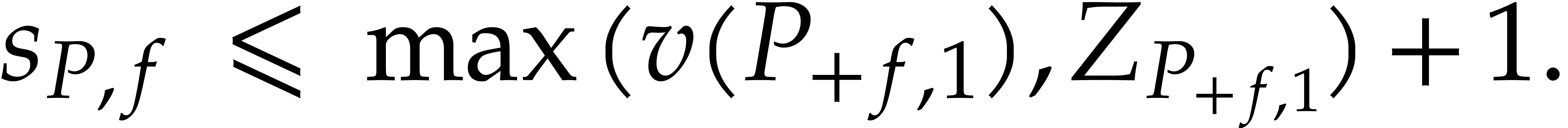 |
(4) |
Proof. Since 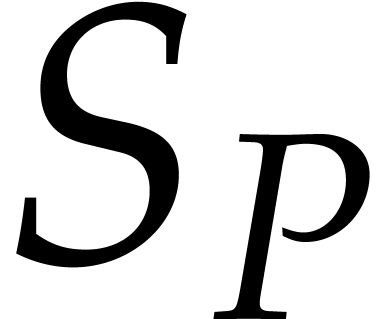 does not
vanish at
does not
vanish at 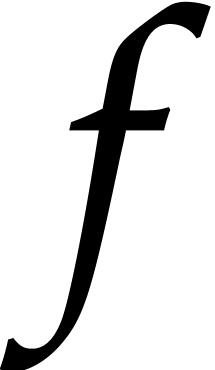 , we have
, we have 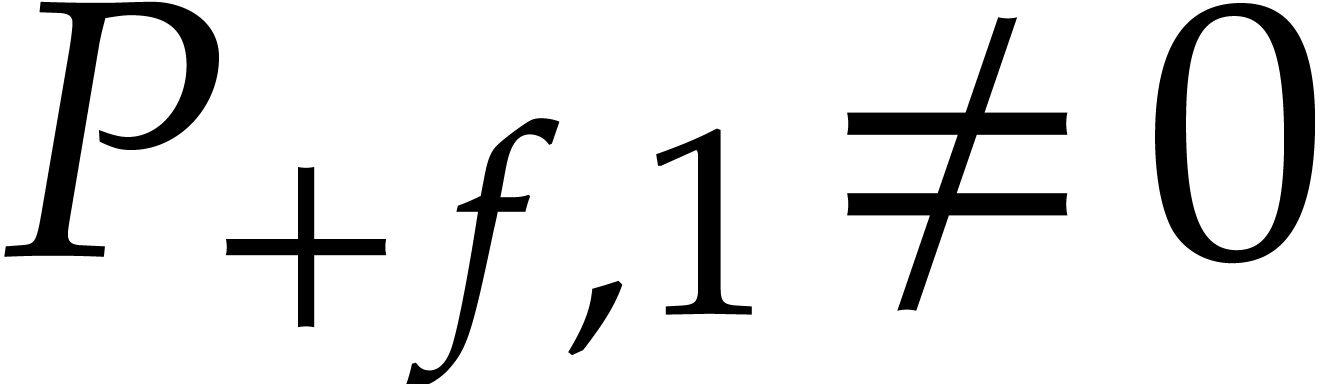 . Let
. Let 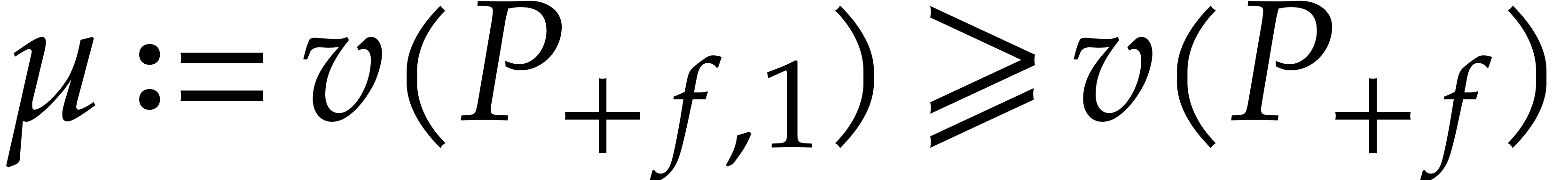 .
Given
.
Given 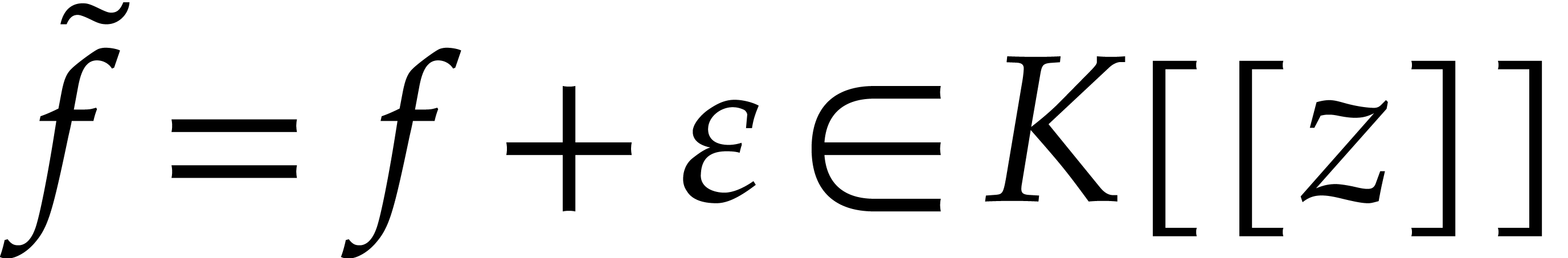 with
with 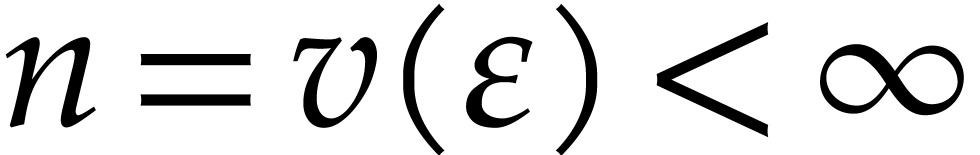 ,
we have
,
we have
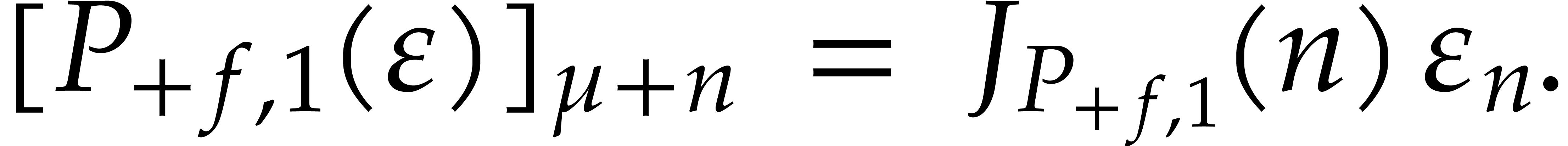 |
(5) |
Now assume that 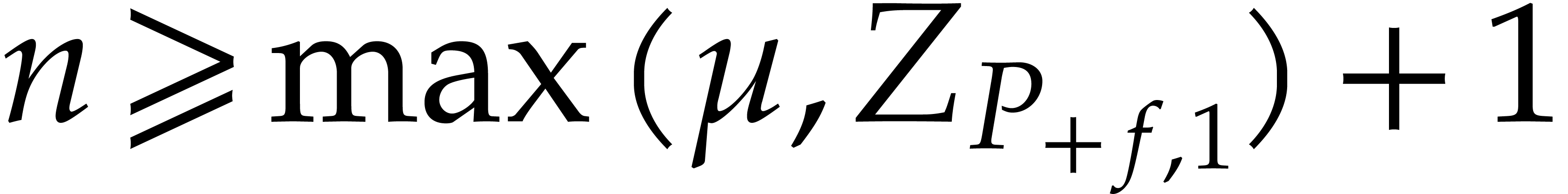 . Then
. Then

whence
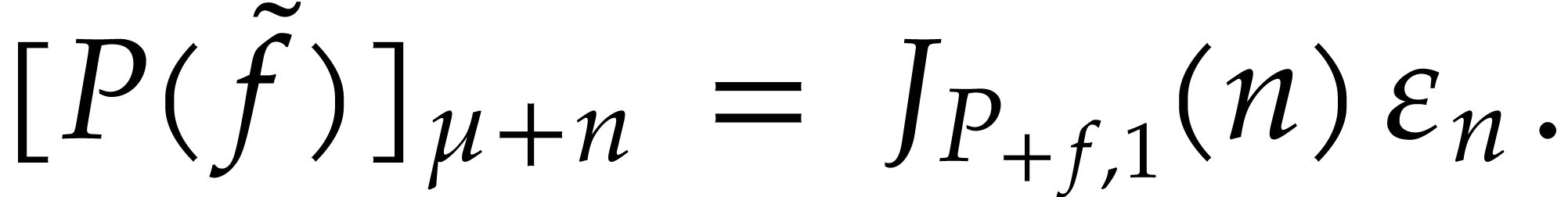
Since 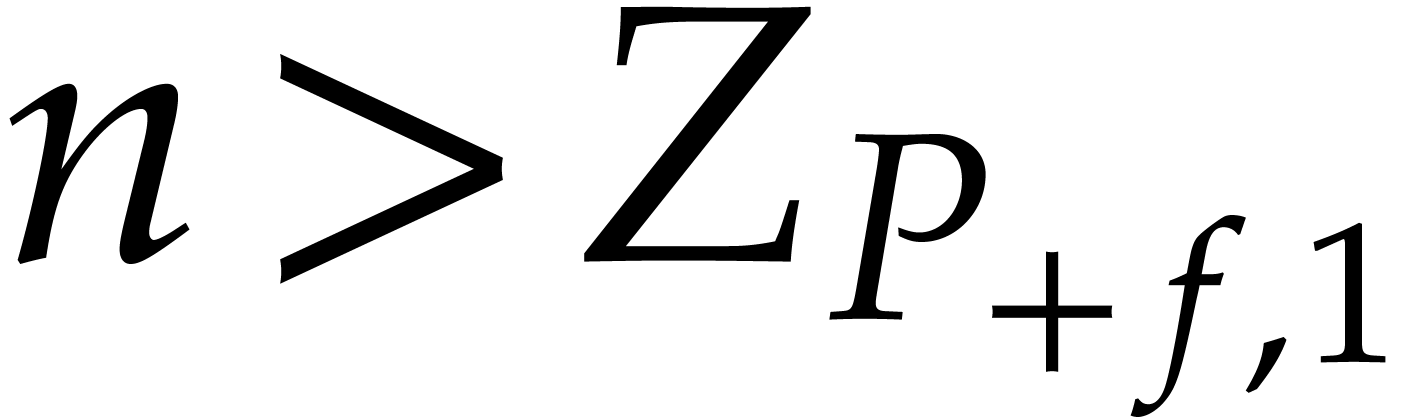 , we also get
, we also get 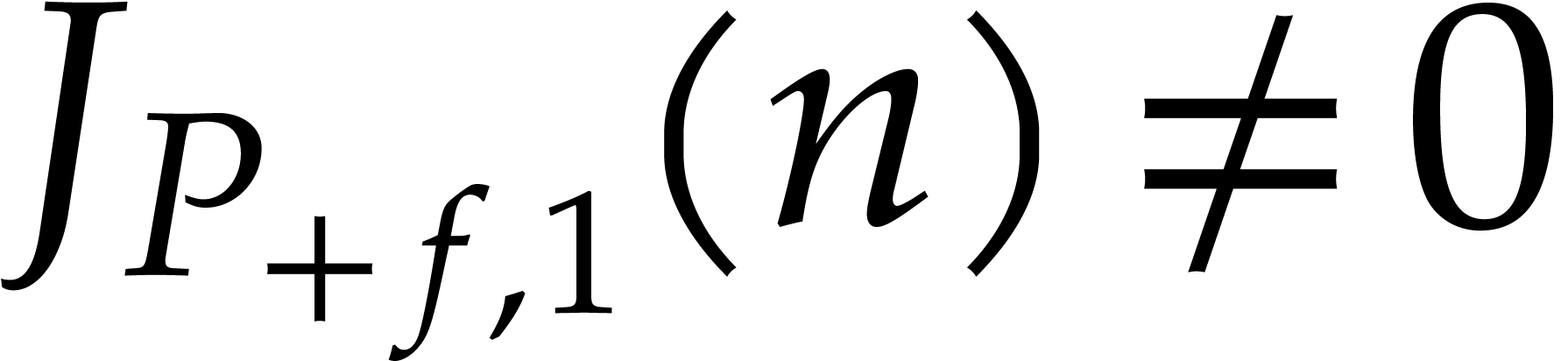 , which entails
, which entails 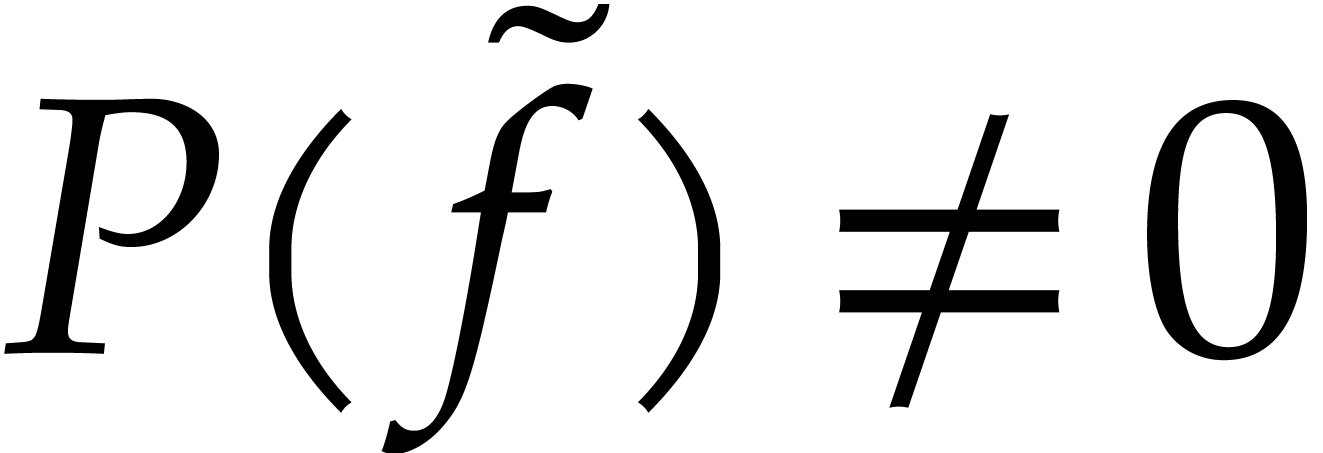 .
.
What we will really need is a stronger version of Proposition 3
that also takes care of logarithmic power series solutions. Assume that
there exists a number 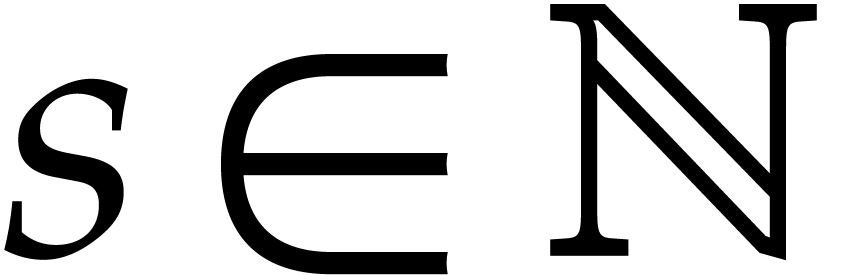 such that for any
such that for any 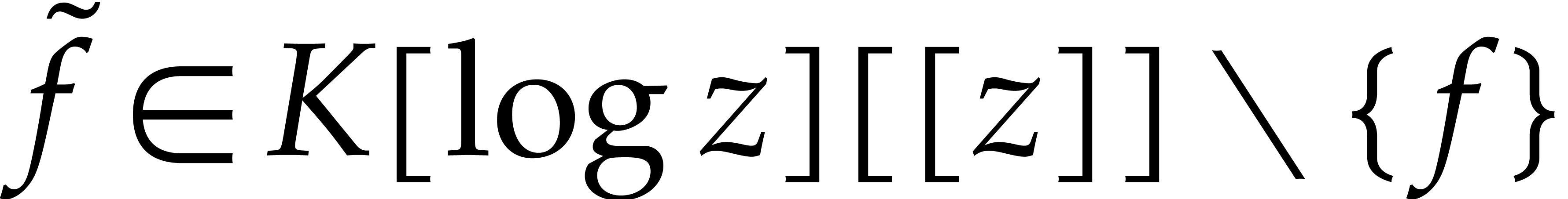 with
with 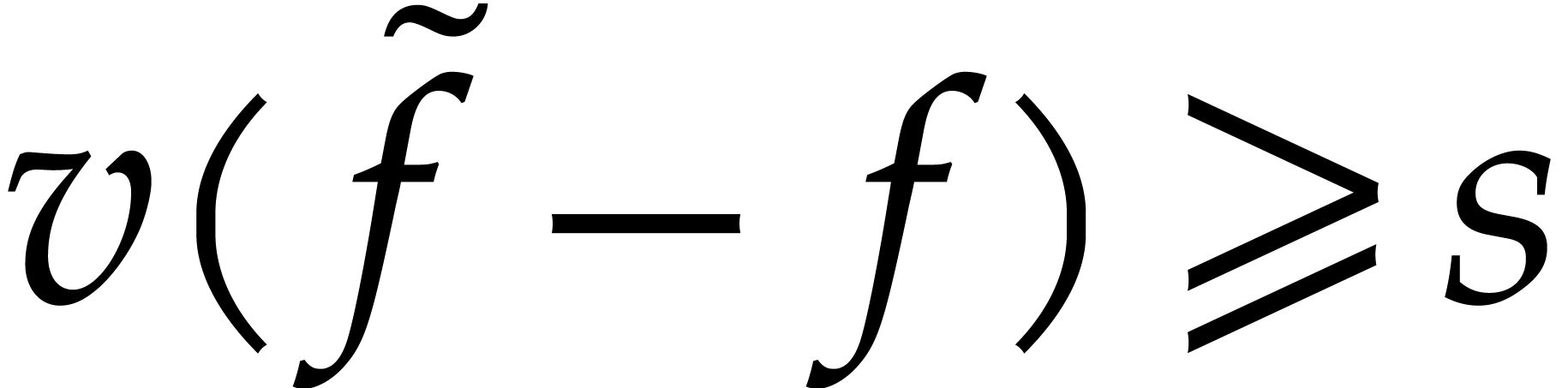 , we
have
, we
have 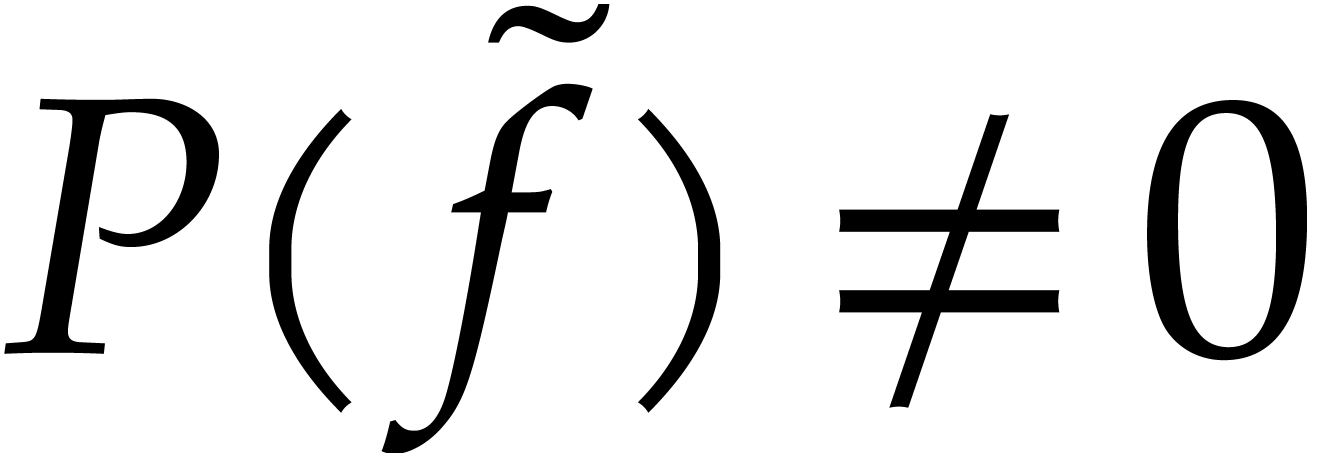 . Then we define
. Then we define 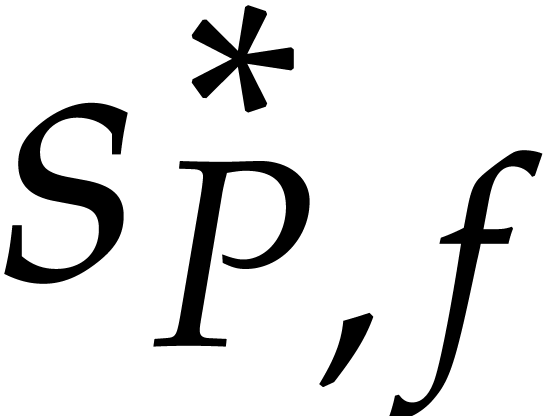 to be the smallest such number
to be the smallest such number  and call it the strong root separation of
and call it the strong root separation of  at
at 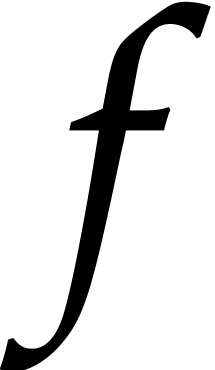 .
.
 is
is  -algebraic over
-algebraic over  with non-degenerate annihilator
with non-degenerate annihilator 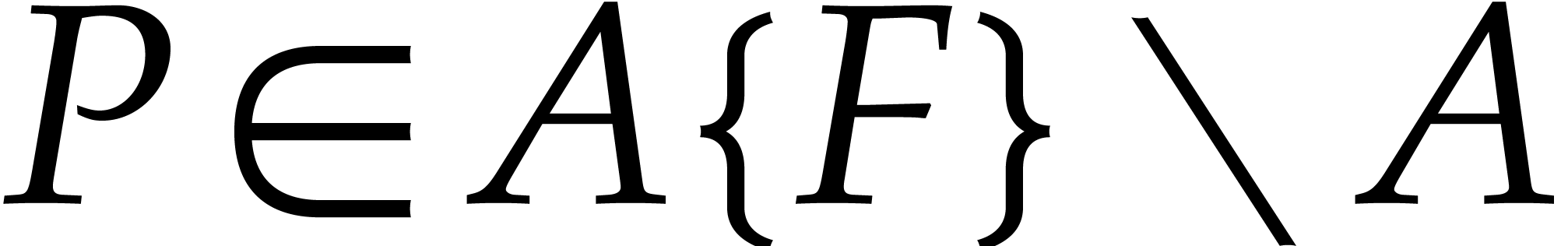 .
Then the following strong root separation bound holds:
.
Then the following strong root separation bound holds:
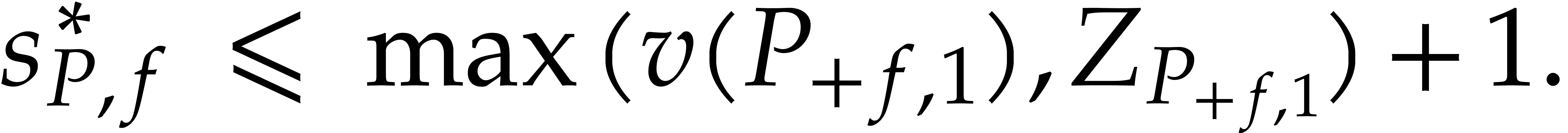 |
(6) |
Proof. The proof is similar to the proof of
Proposition 3 with the following change. Writing 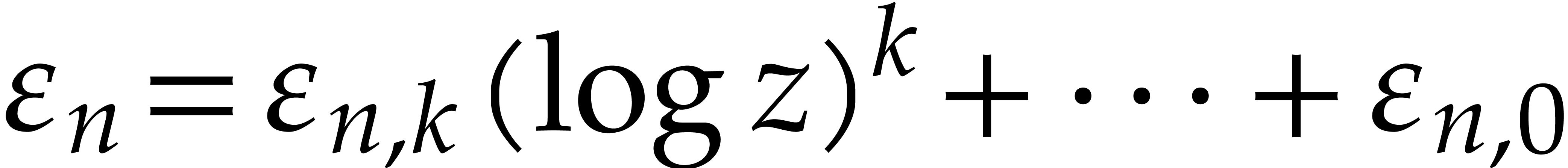 with
with 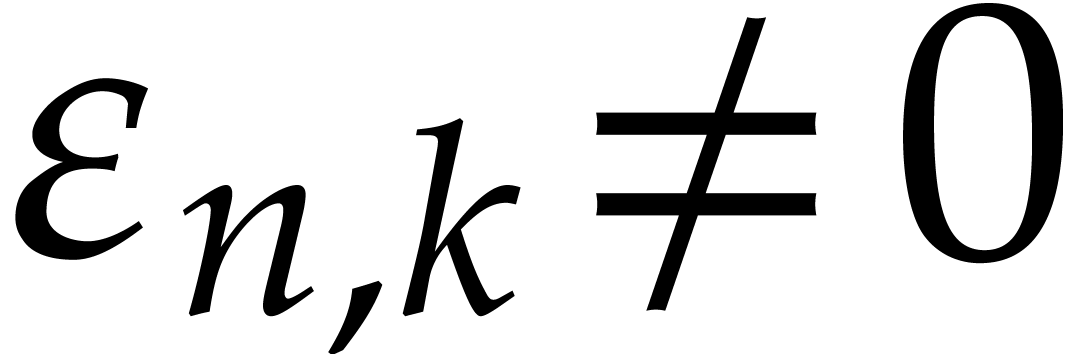 , we now
have
, we now
have
 |
(7) |
instead of (5), and where 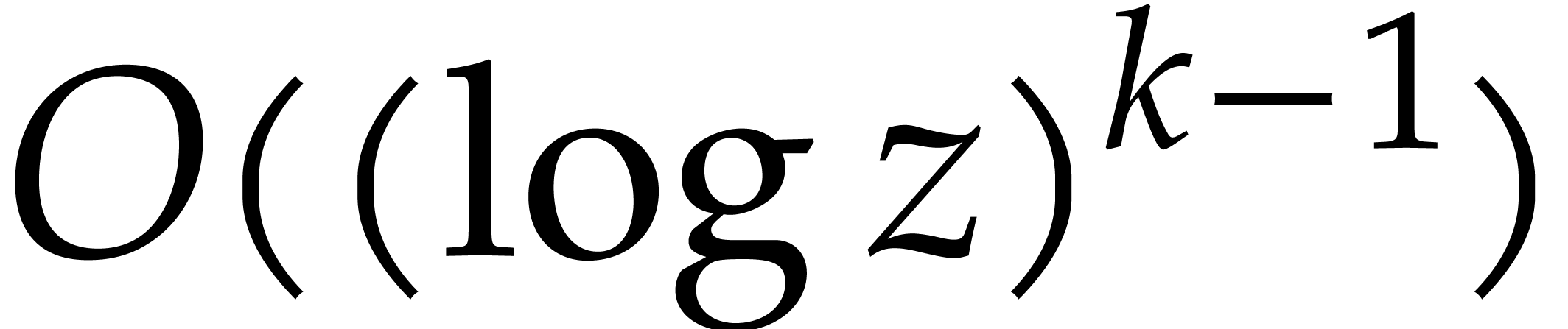 stands
for a polynomial of degree at most
stands
for a polynomial of degree at most  in
in 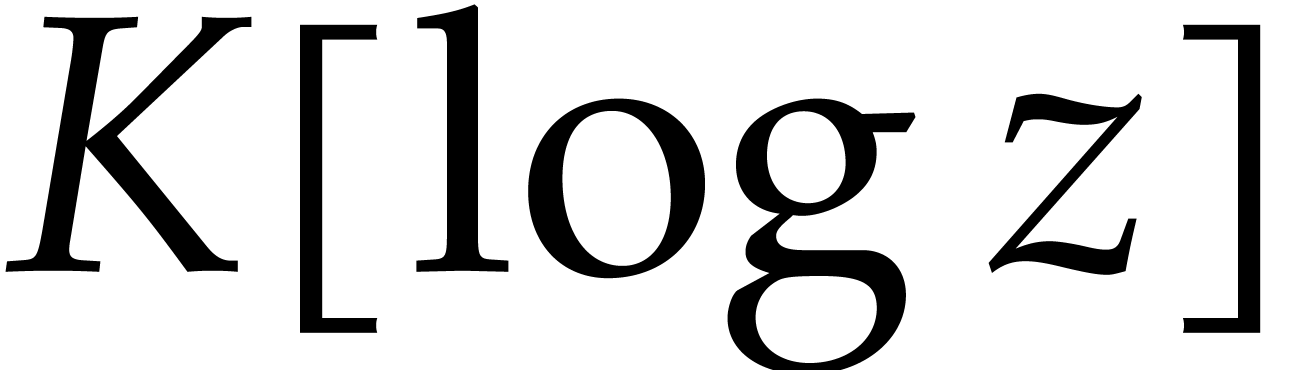 .
.
Note that in the both propositions above, the non-degeneracy of the
annihilator implies that 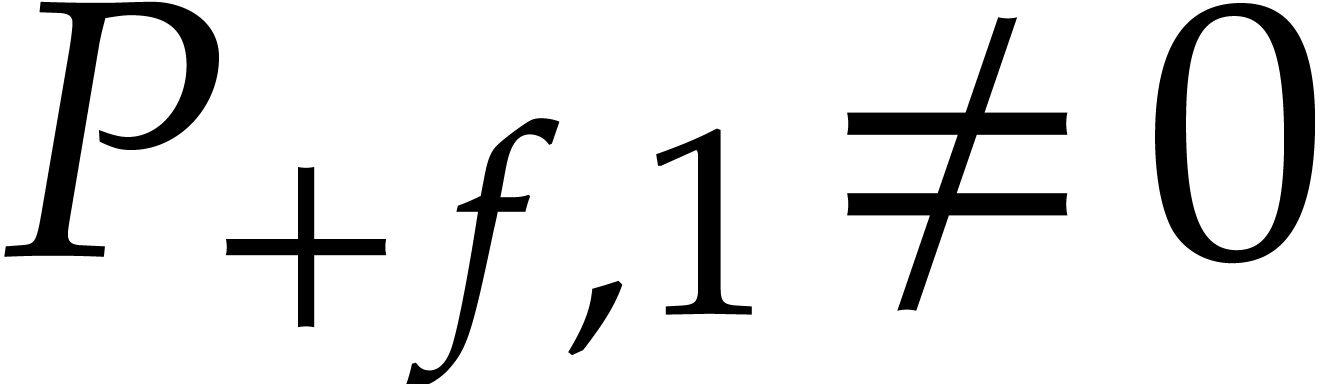 , so
the provided bounds are always finite.
, so
the provided bounds are always finite.
The following proposition also provides us with a partial converse of Proposition 4.
Proof. 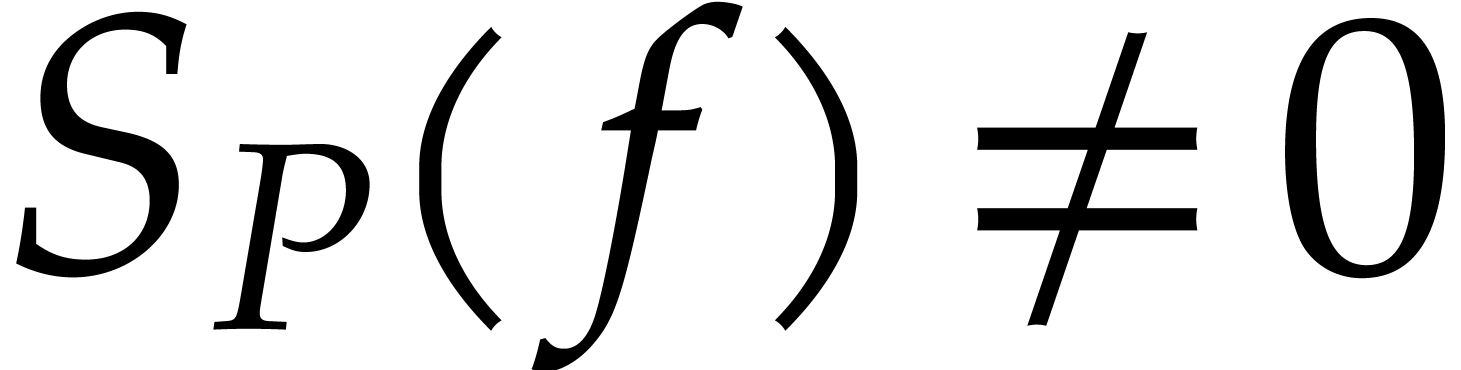 implies that
implies that
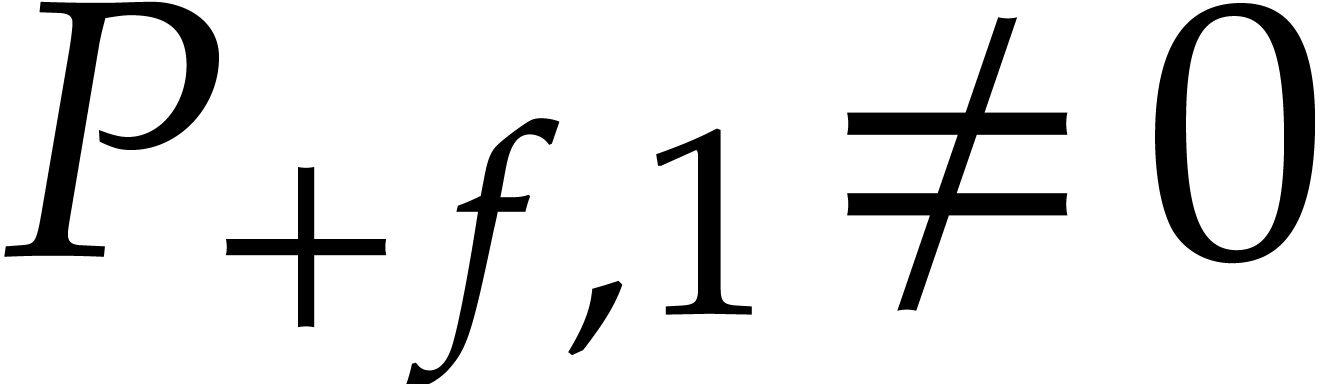 . Let
. Let 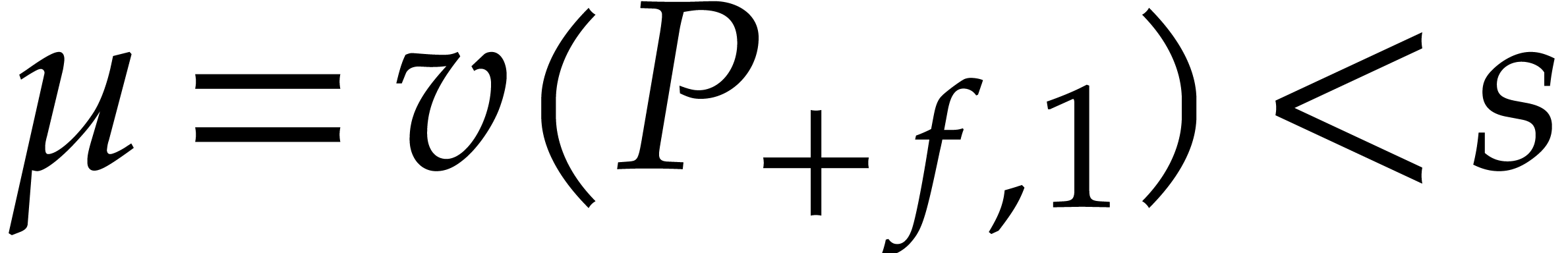 . We have to show the existence of a unique series
. We have to show the existence of a unique series
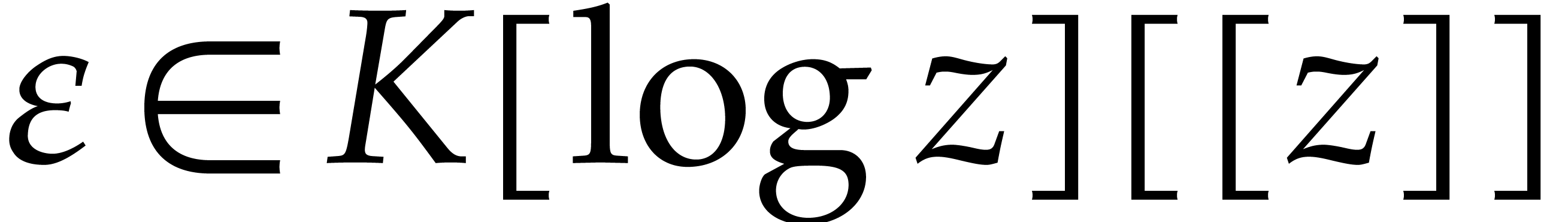 with
with 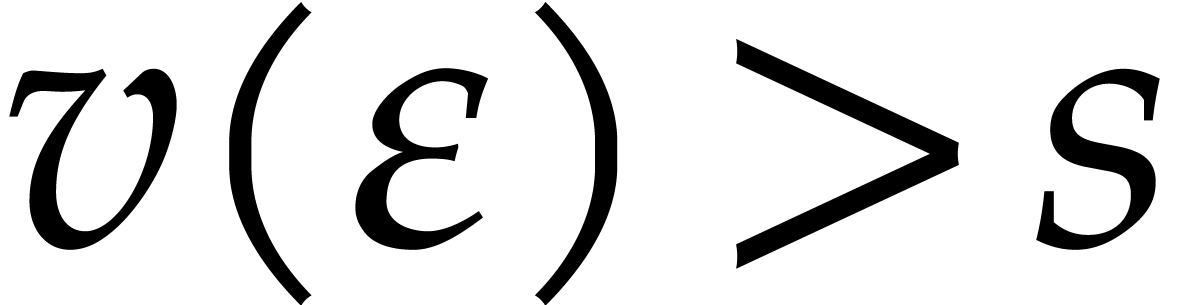 and
and 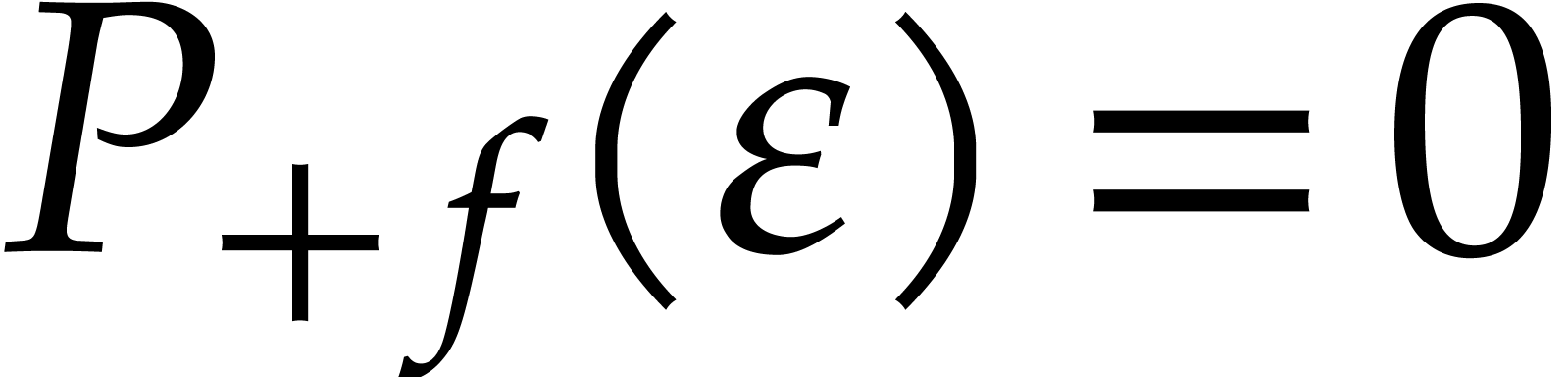 . We may decompose
. We may decompose
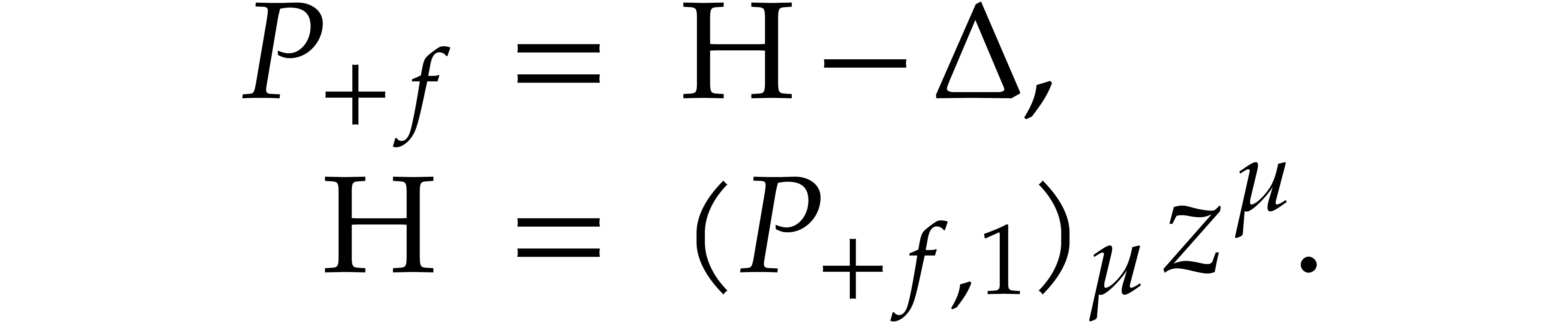
Extracting the coefficient of 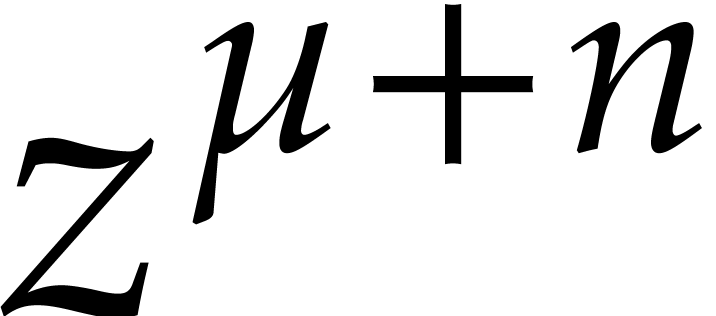 in the relation
in the relation
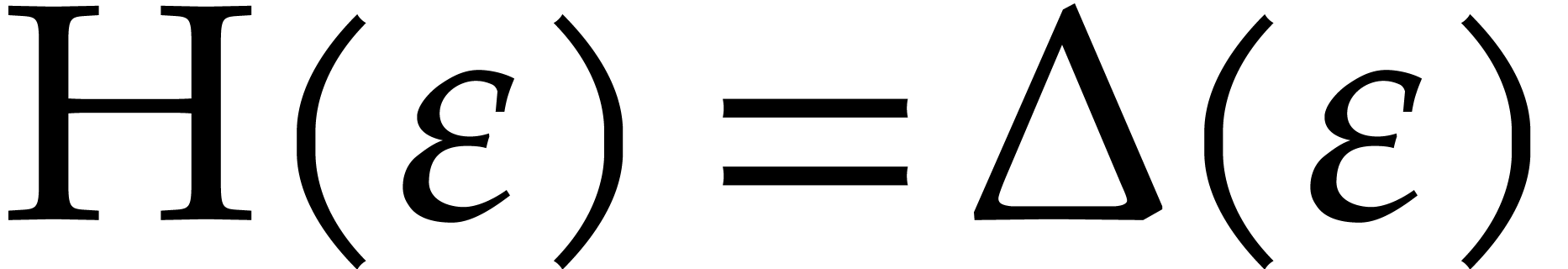 now yields (similarly to (3))
now yields (similarly to (3))
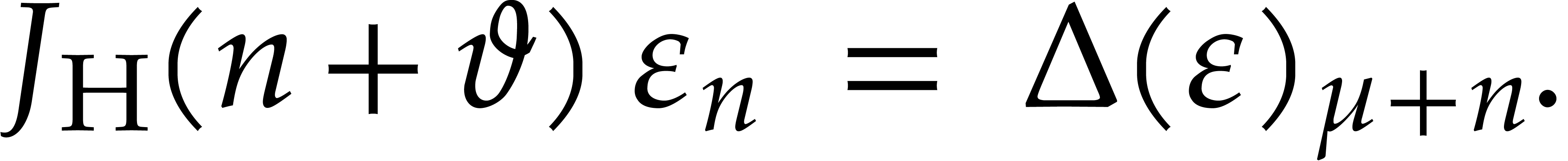 |
(8) |
For all  , the right hand side
, the right hand side
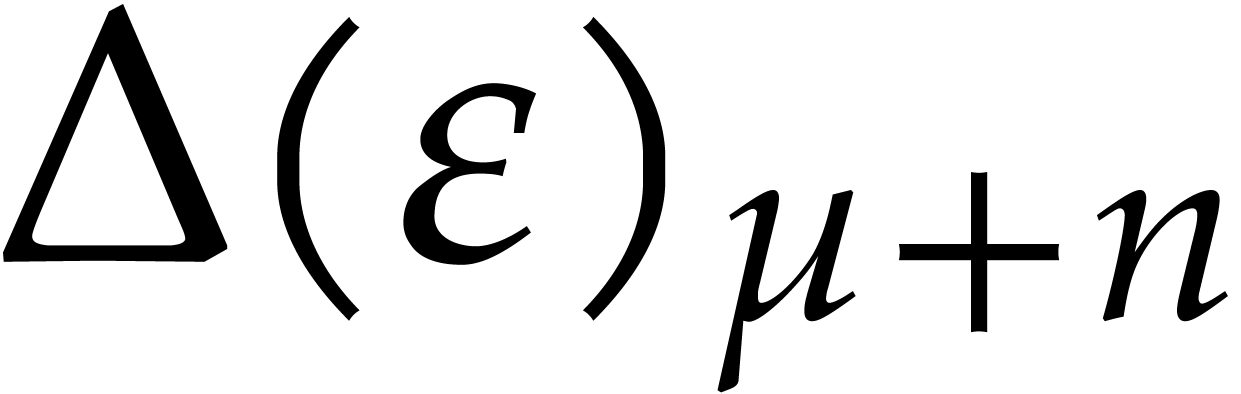 only depends on
only depends on  ,
and
,
and 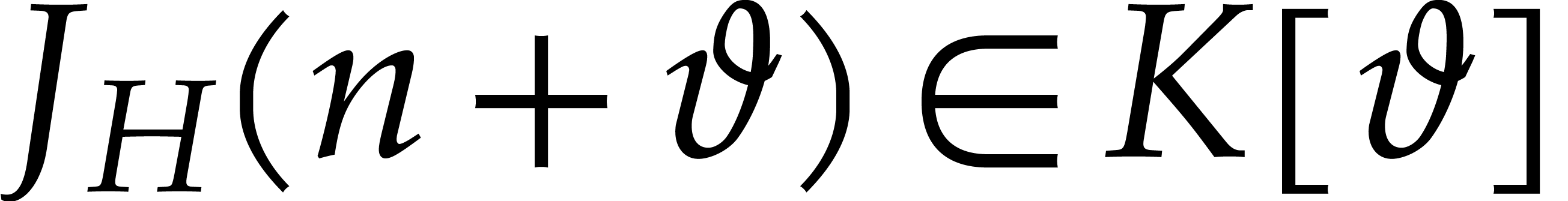 is a non-zero differential operator with
is a non-zero differential operator with
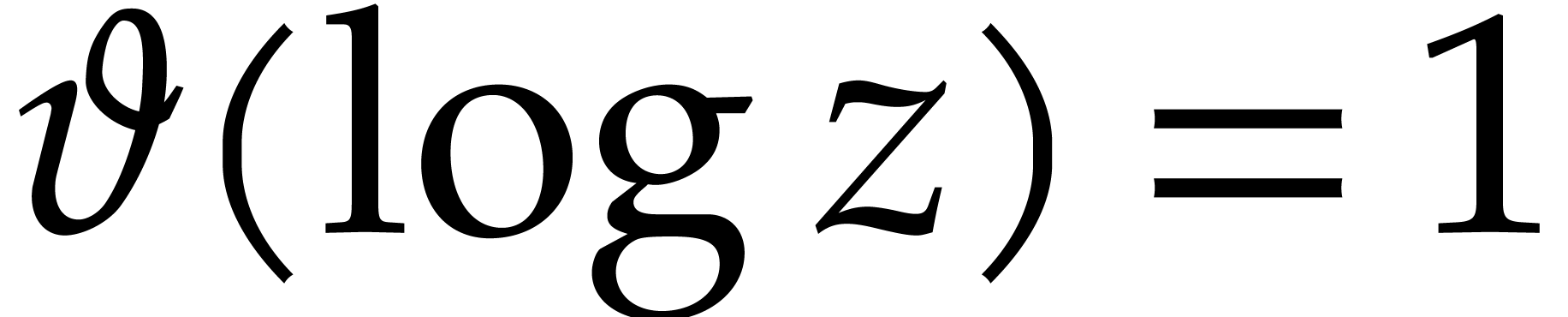 . Then [6,
Proposition 1] implies that the equation
. Then [6,
Proposition 1] implies that the equation 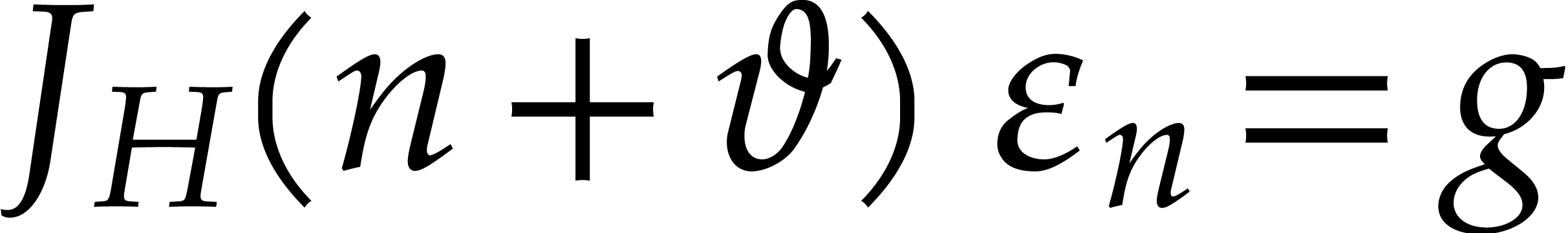 has a
solution in
has a
solution in 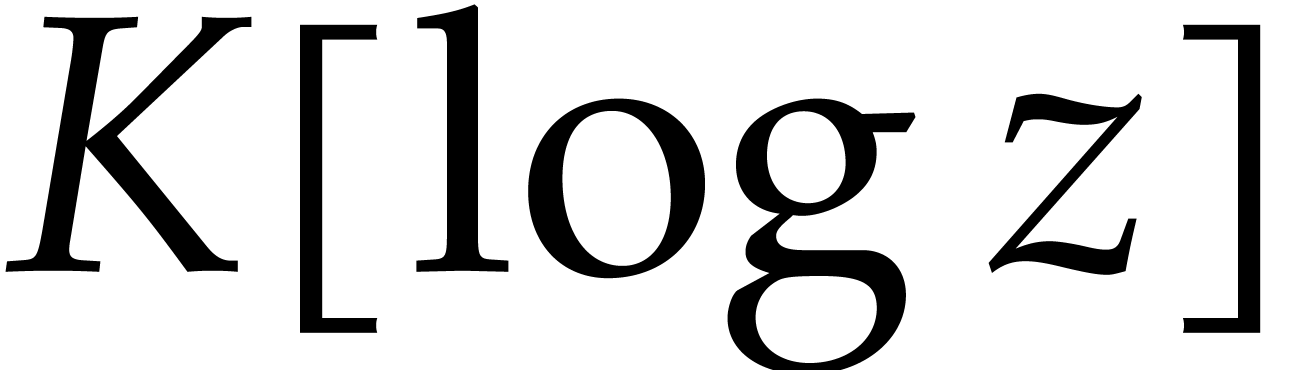 for any
for any 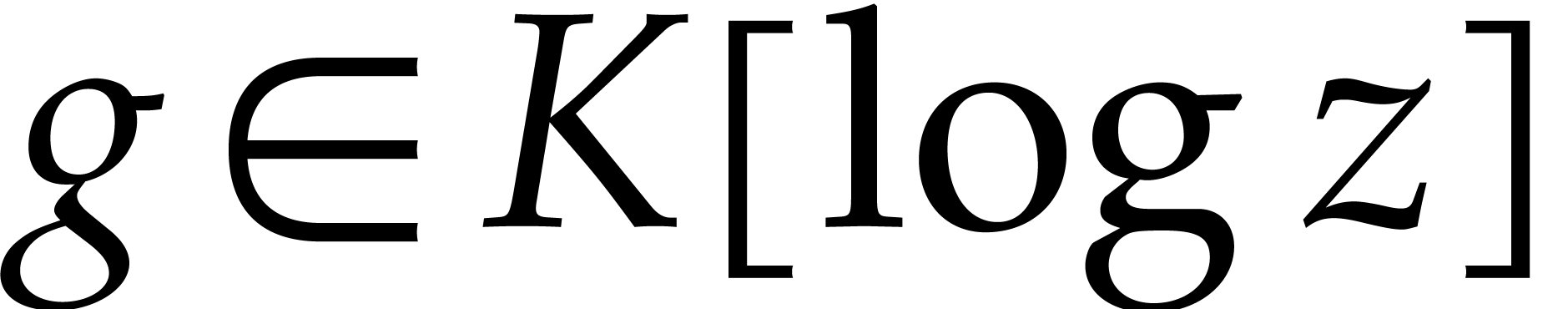 . Therefore, there exists a solution
. Therefore, there exists a solution  to the equation
to the equation 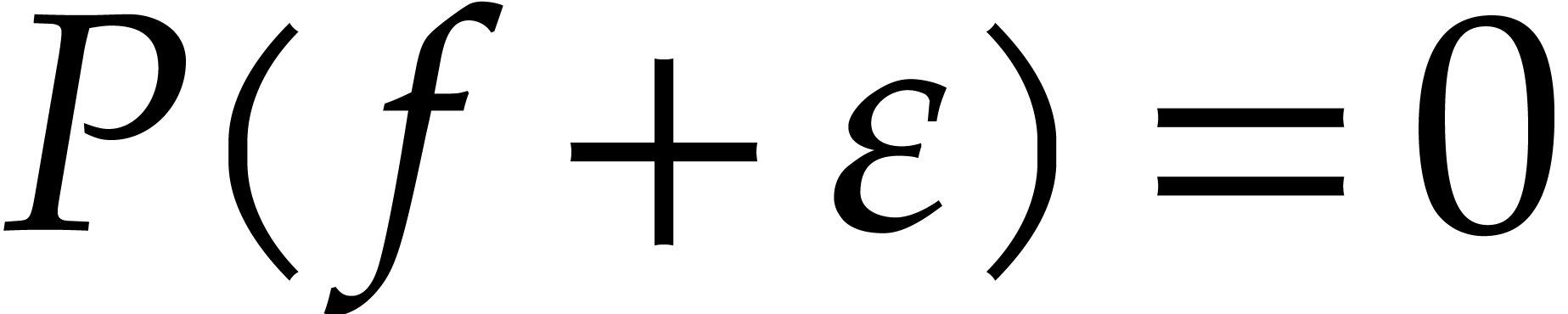 .
.
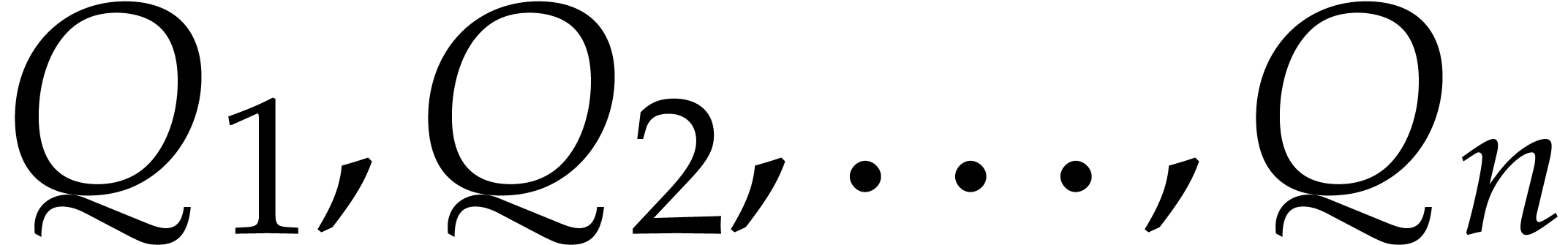 be a coherent
be a coherent 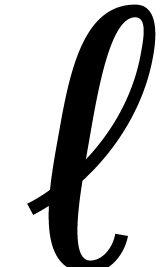 -autoreduced chain in
-autoreduced chain in 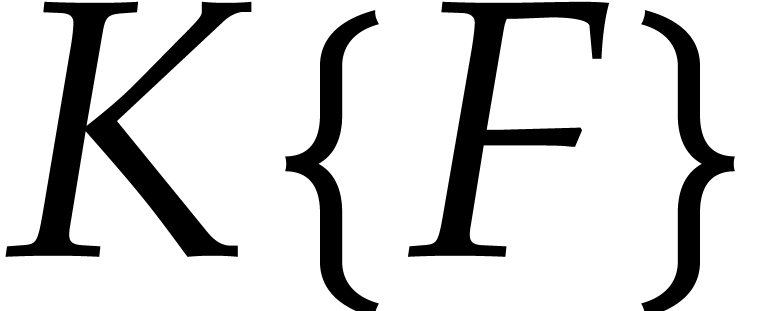 . For every
. For every 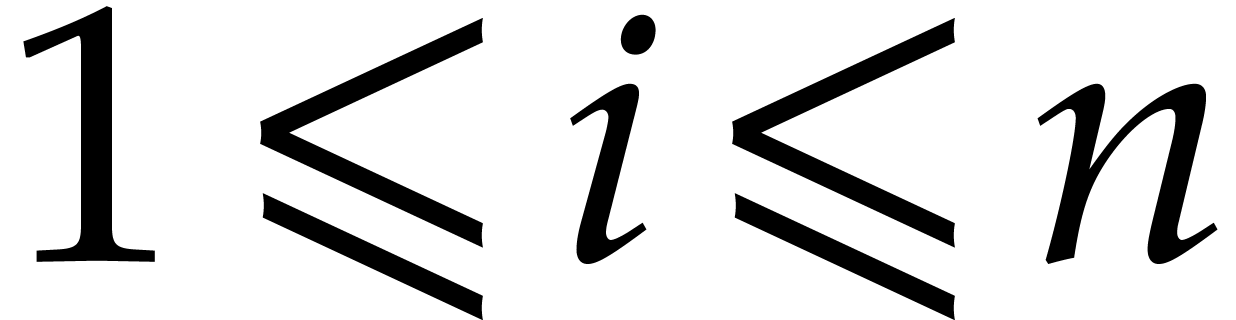 , denote
, denote  and
and 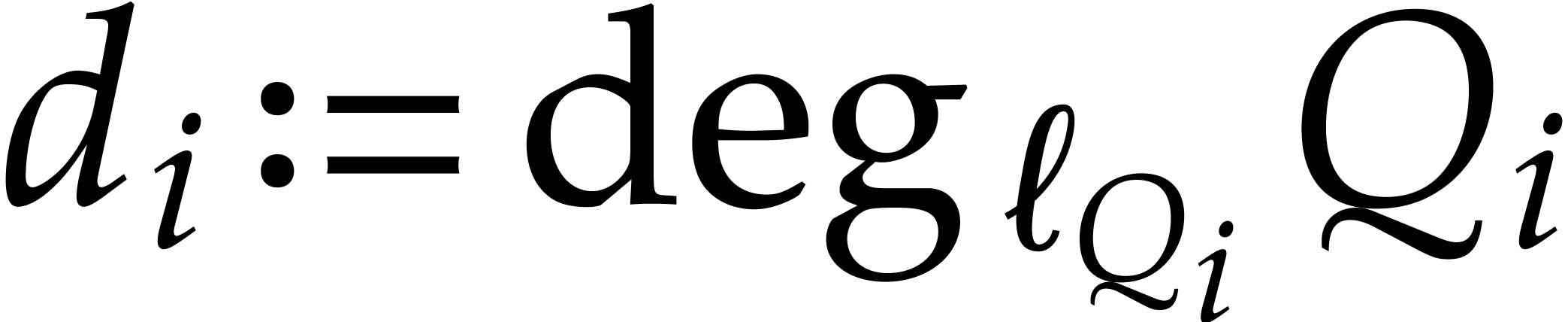 , and assume
, and assume 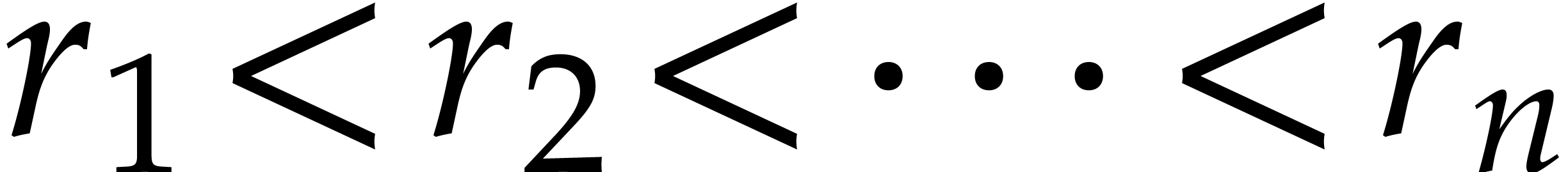 . Let
. Let 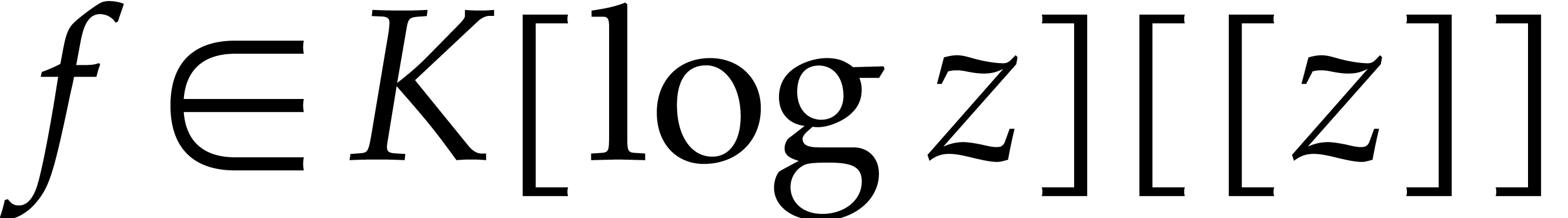 be a
logarithmic power series and let
be a
logarithmic power series and let 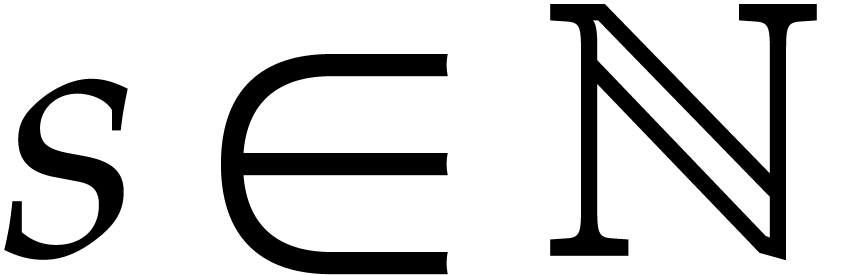 be such
that
be such
that
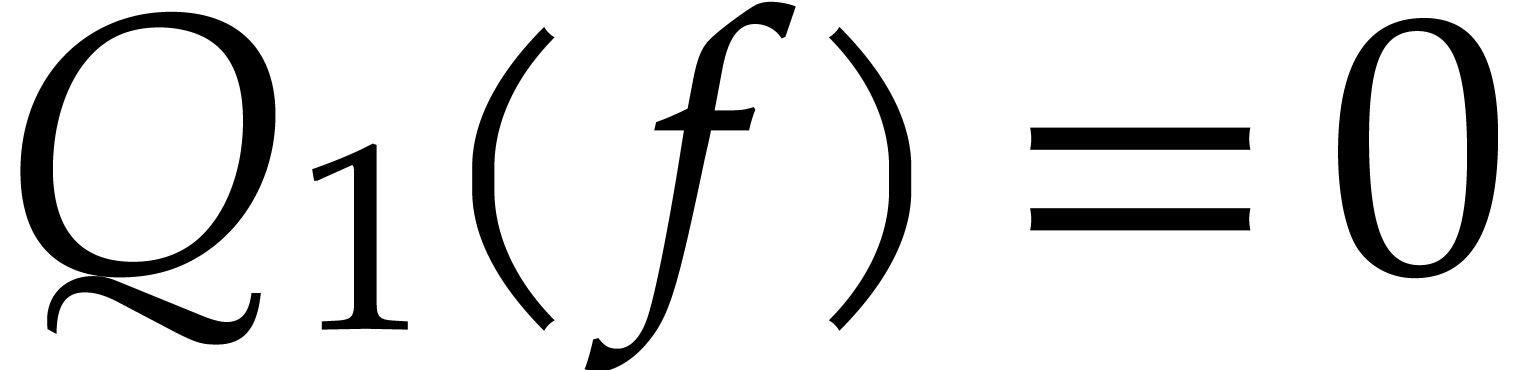 ;
;
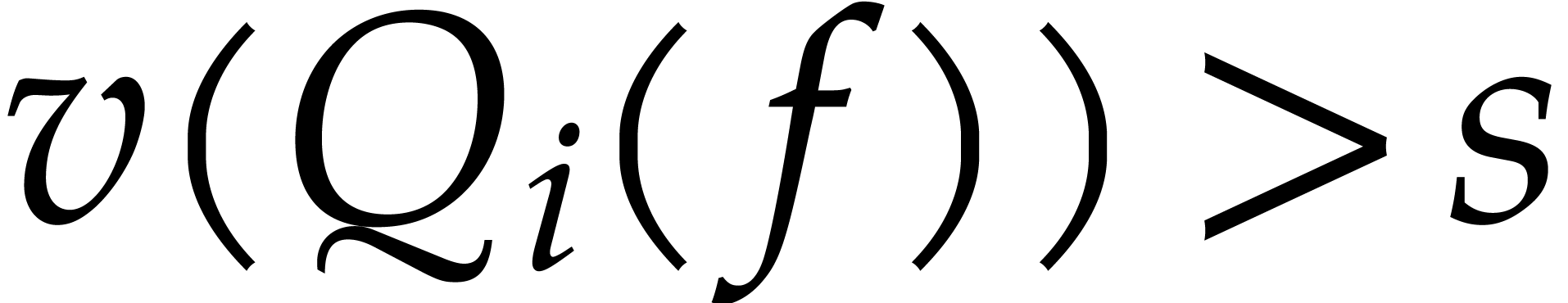 , for
, for 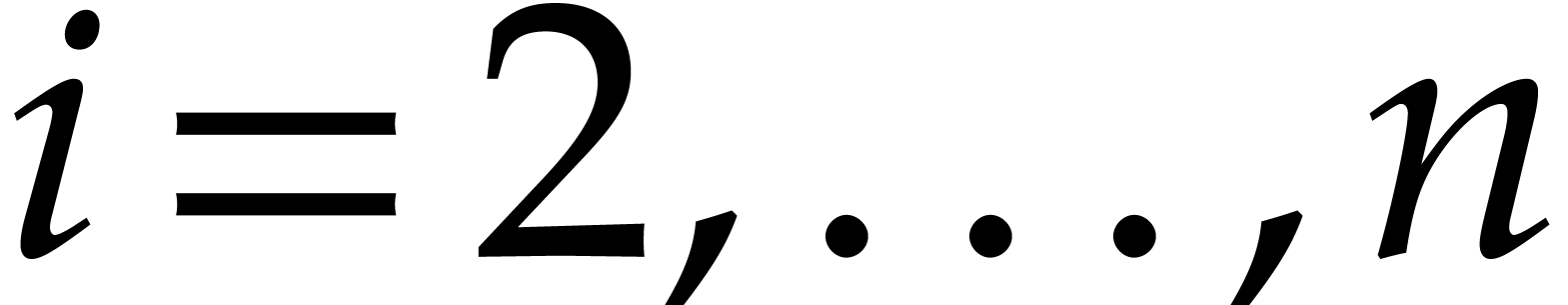 ;
;
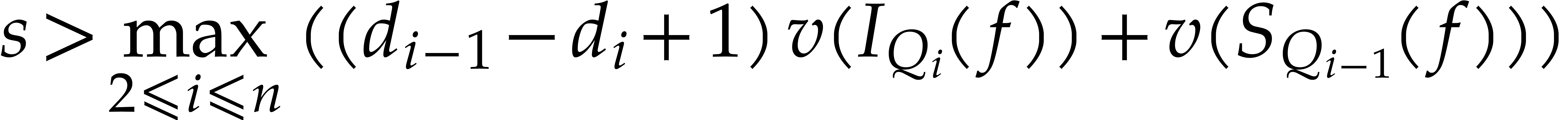 .
.
Then 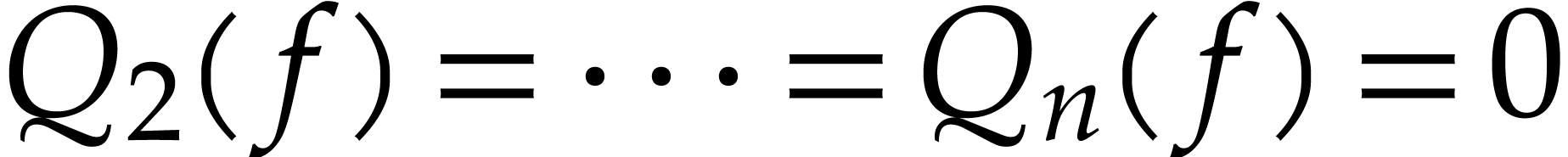 .
.
Proof. Let us prove by induction that 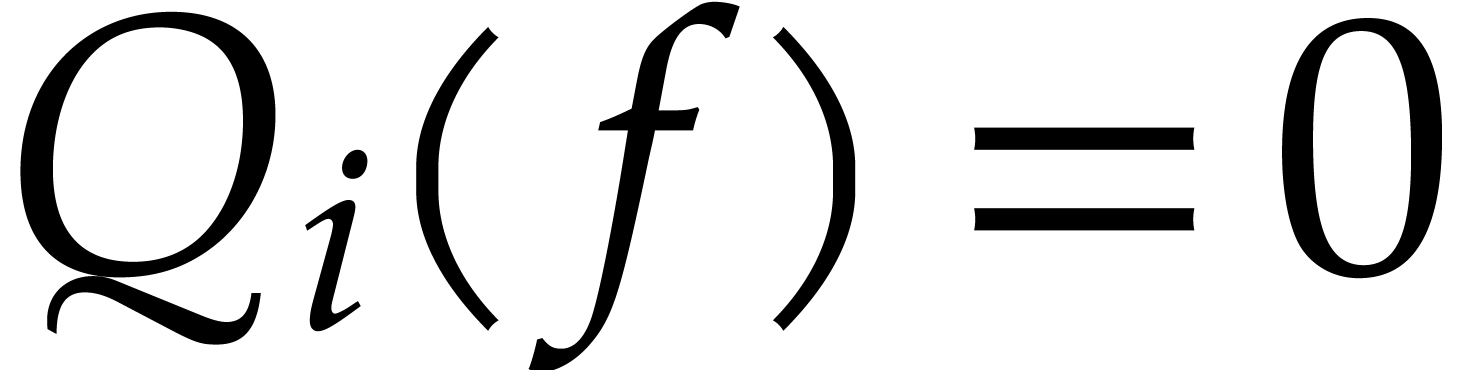 for
for 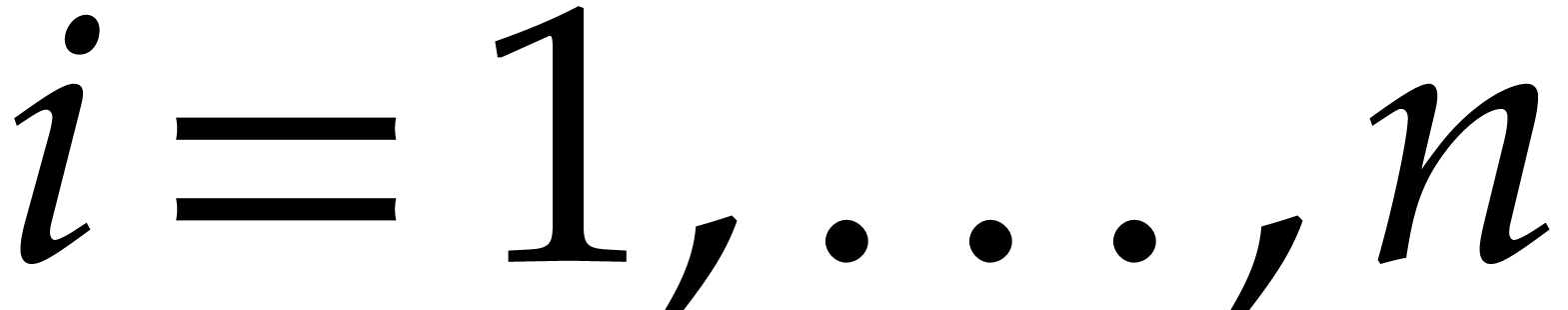 . The base
case
. The base
case 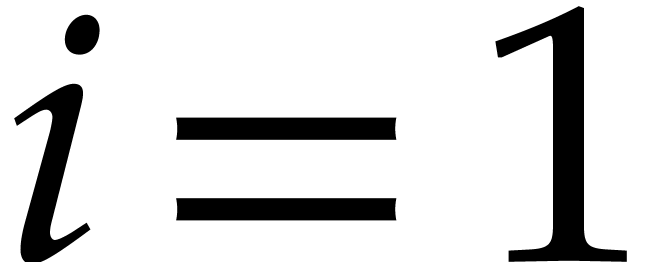 is already given. Assume that
is already given. Assume that 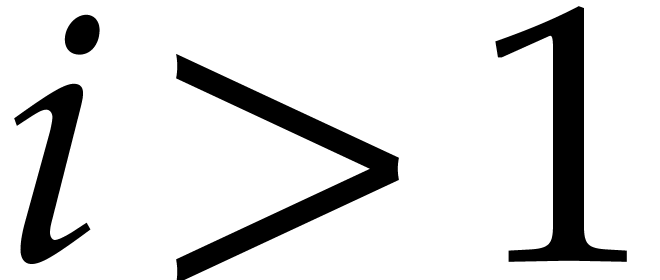 . Since
. Since  is
is  -autoreduced, the
-autoreduced, the 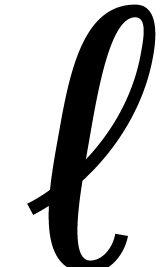 -reduction
of
-reduction
of 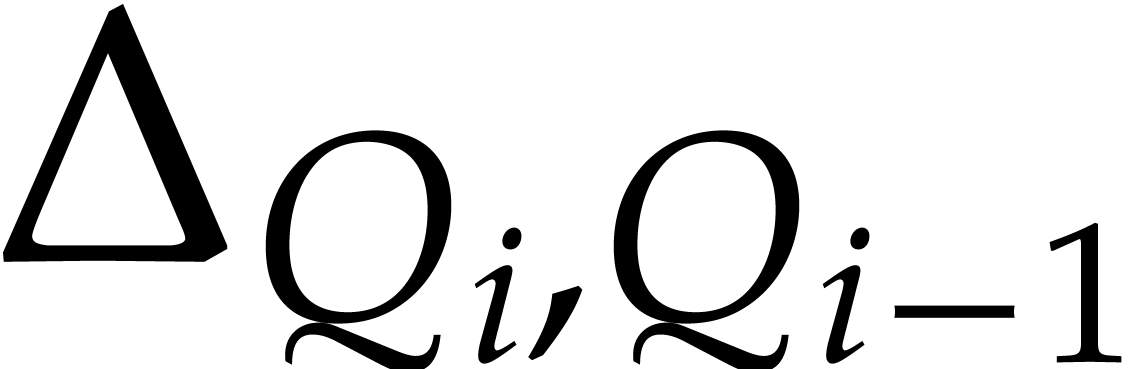 with respect to
with respect to  vanishes. Since the leader of
vanishes. Since the leader of 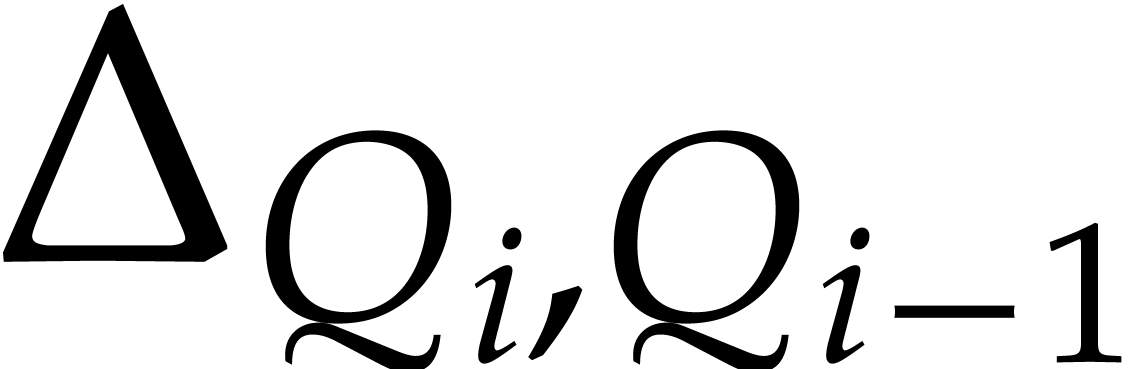 is at most
is at most  , the polynomial
, the polynomial 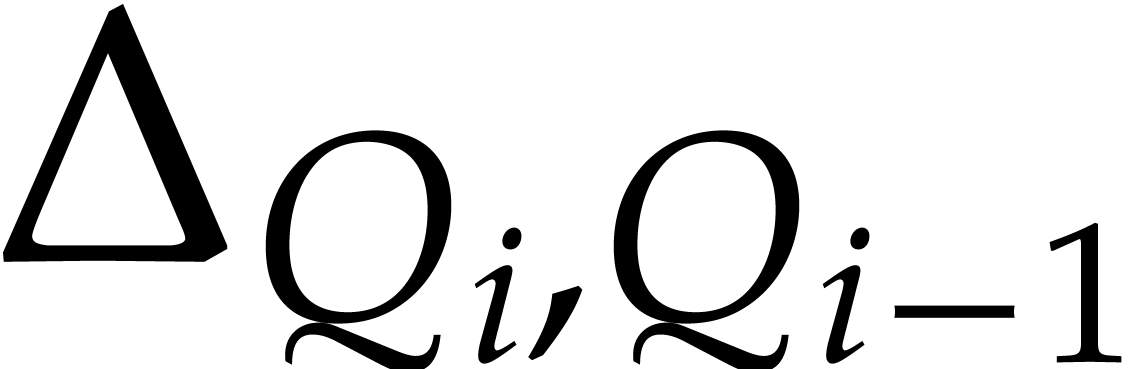 also
also 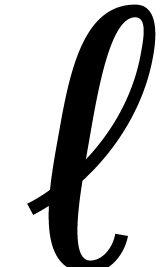 -reduces to zero with
respect to
-reduces to zero with
respect to  . Setting
. Setting 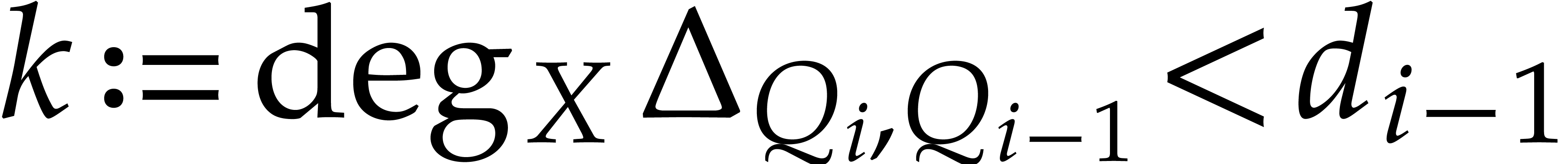 , the
, the 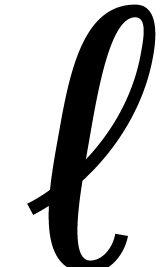 -reduction
of
-reduction
of 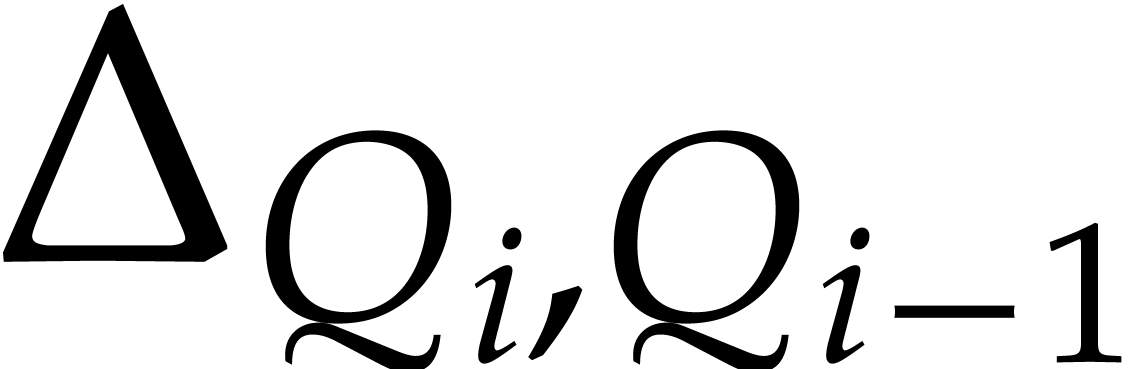 with respect to
with respect to 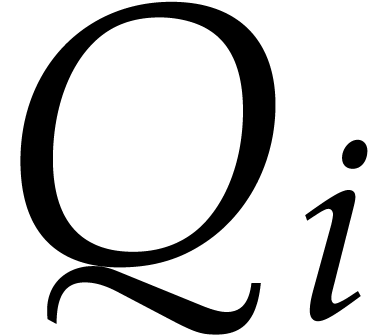 therefore yields a relation
therefore yields a relation
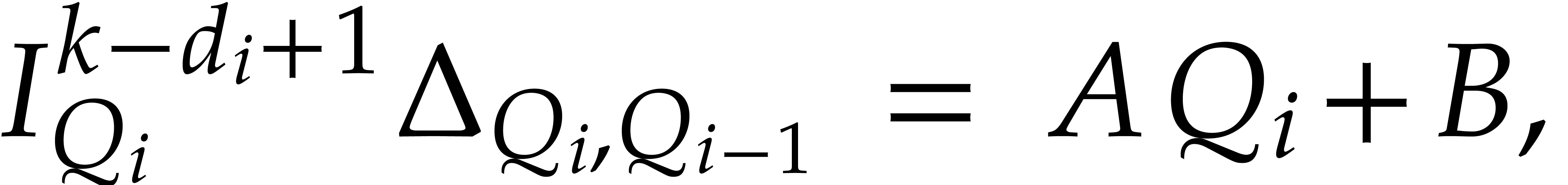
where 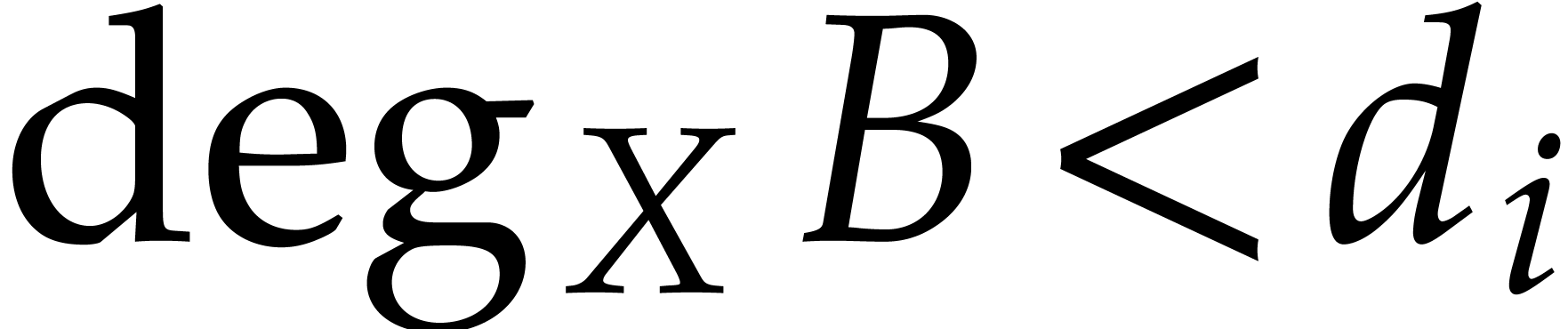 and the
and the 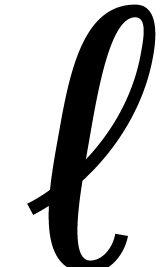 -reduction
of
-reduction
of 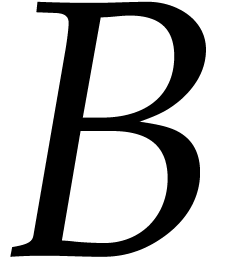 with respect to
with respect to  is
zero. Since
is
zero. Since  and
and 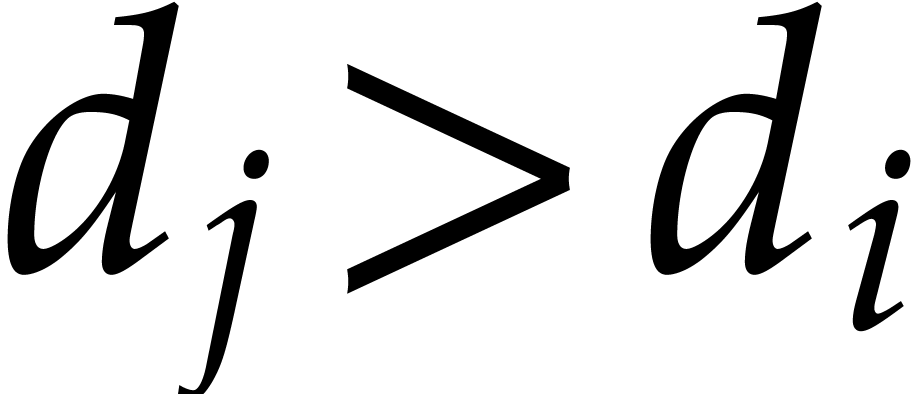 for all
for all
 , we actually must have
, we actually must have 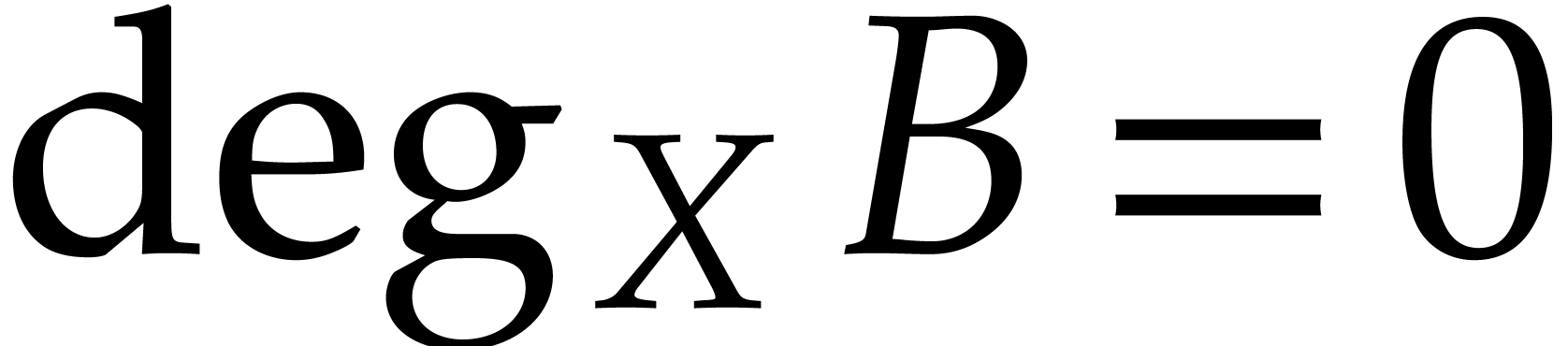 . Writing
. Writing 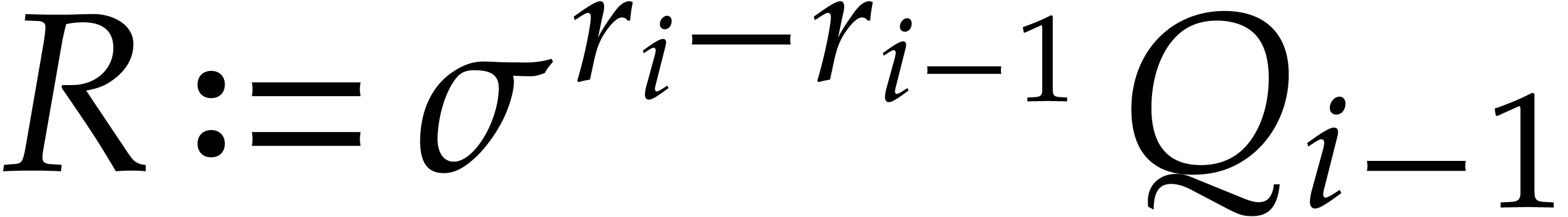 , so that
, so that
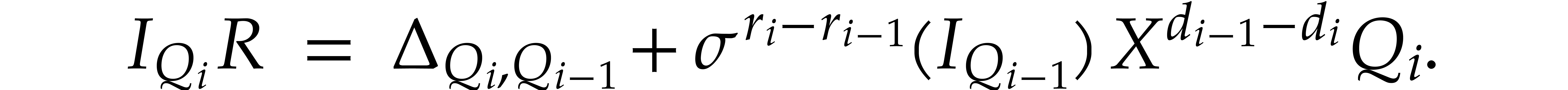
we have
This yields a new relation of the form
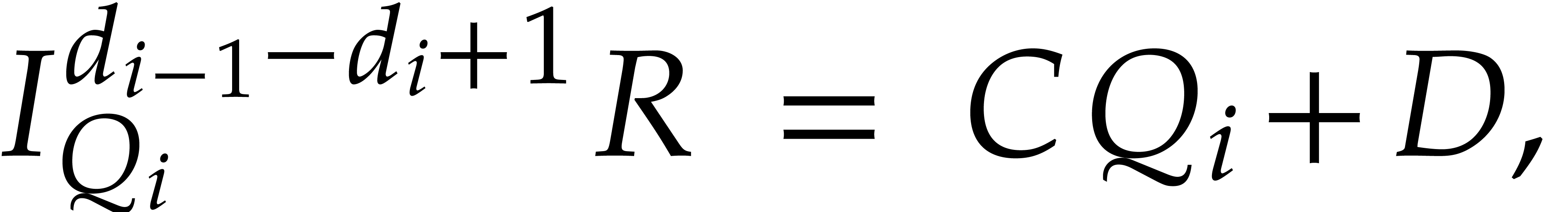 |
(9) |
where 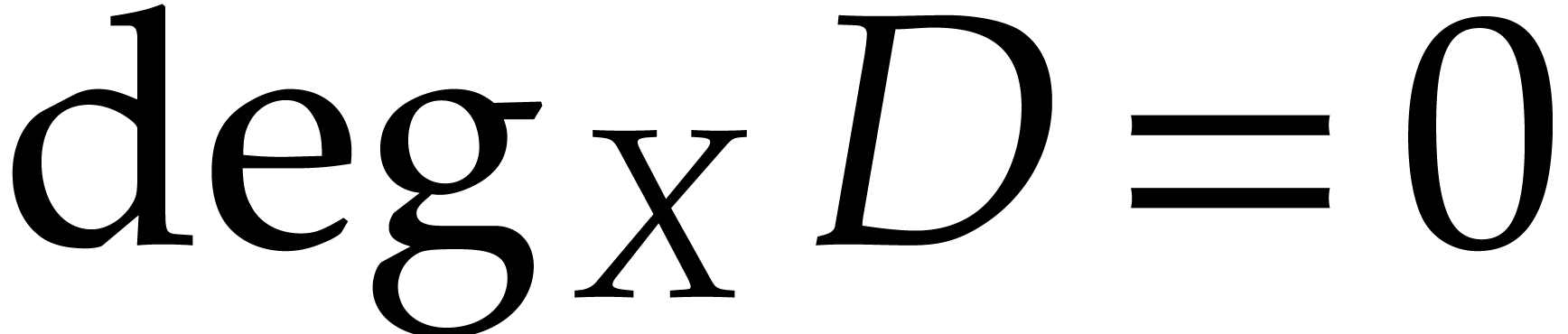 . Differentiating this
relation with respect to
. Differentiating this
relation with respect to  yields
yields
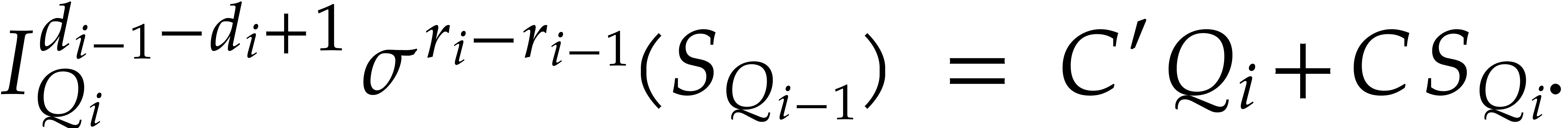
Now we evaluate this relation at  and compute the
valuations of both sides. This yields
and compute the
valuations of both sides. This yields
Since 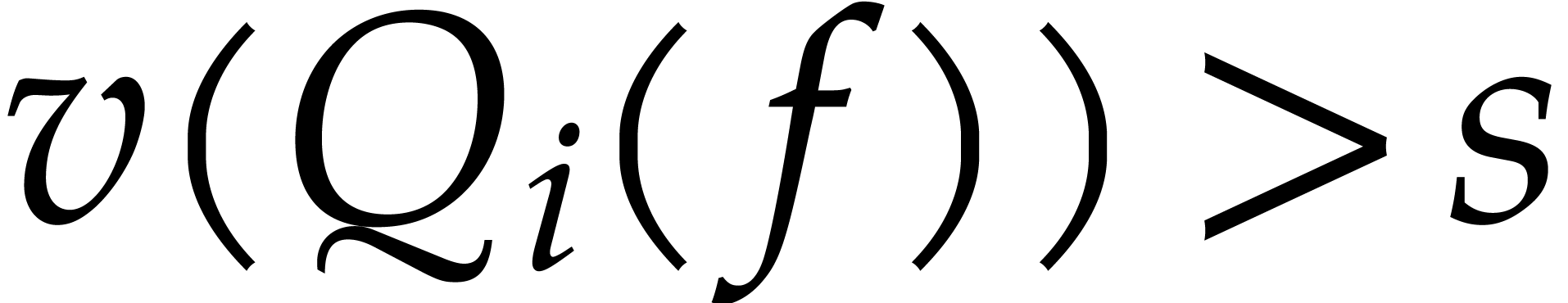 , we deduce
, we deduce 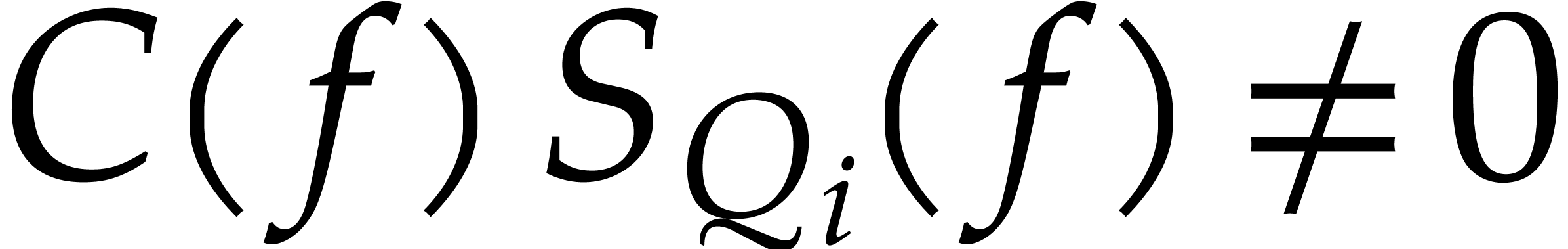 , whence
, whence 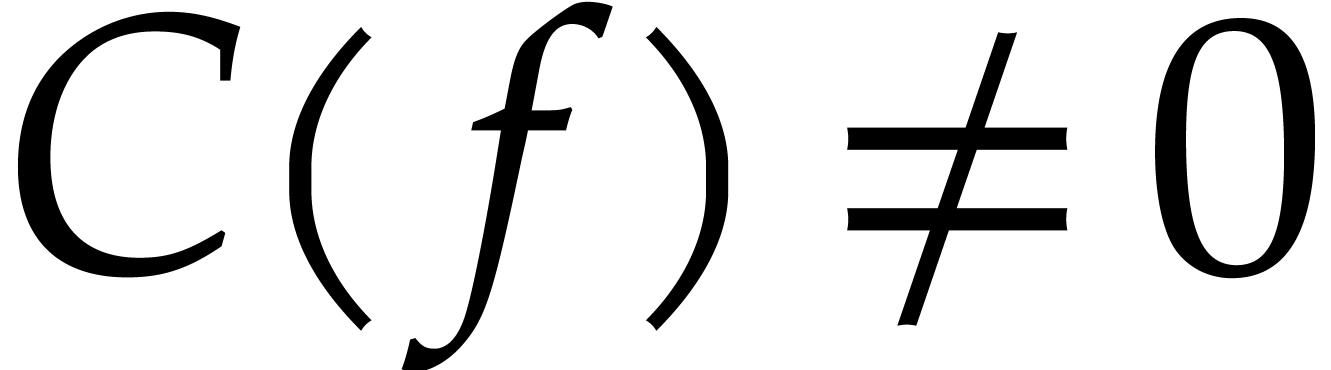 . Since the
. Since the 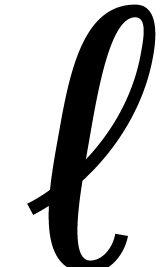 -reduction
of
-reduction
of 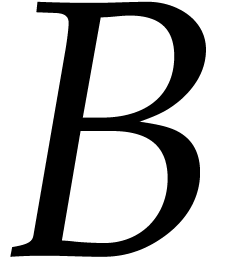 with respect to
with respect to 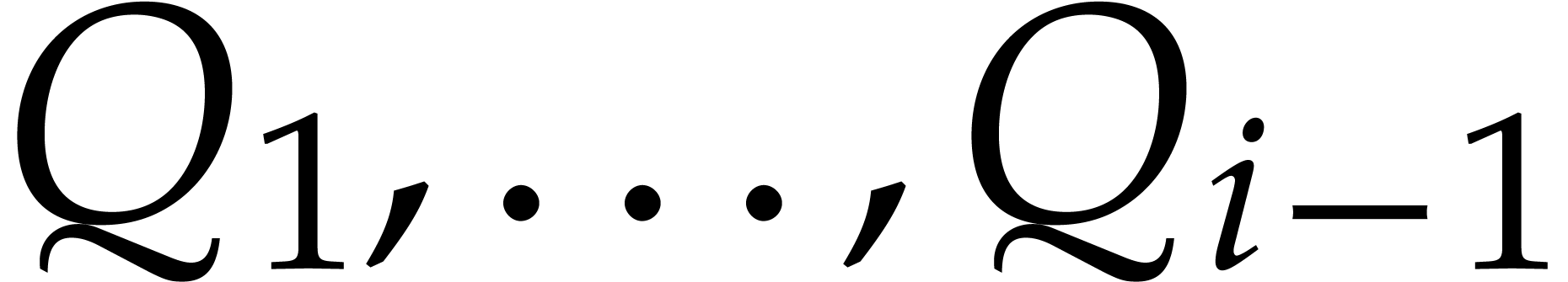 vanishes and
vanishes and 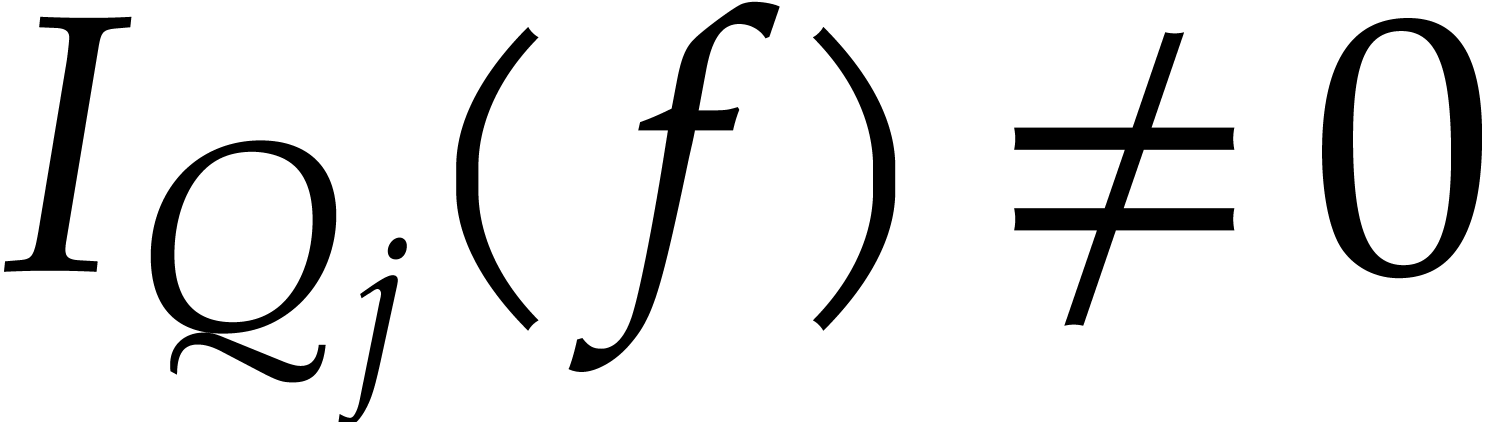 for all
for all  , we have
, we have 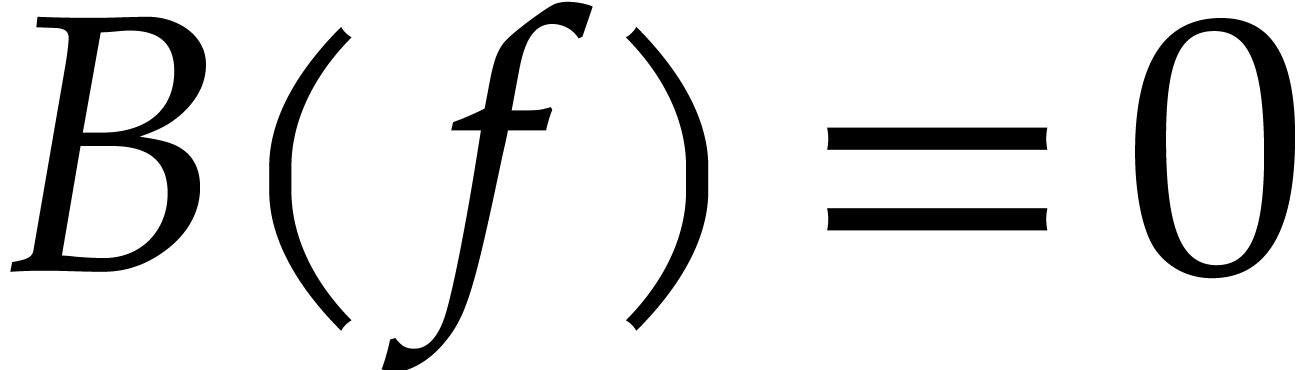 and
and 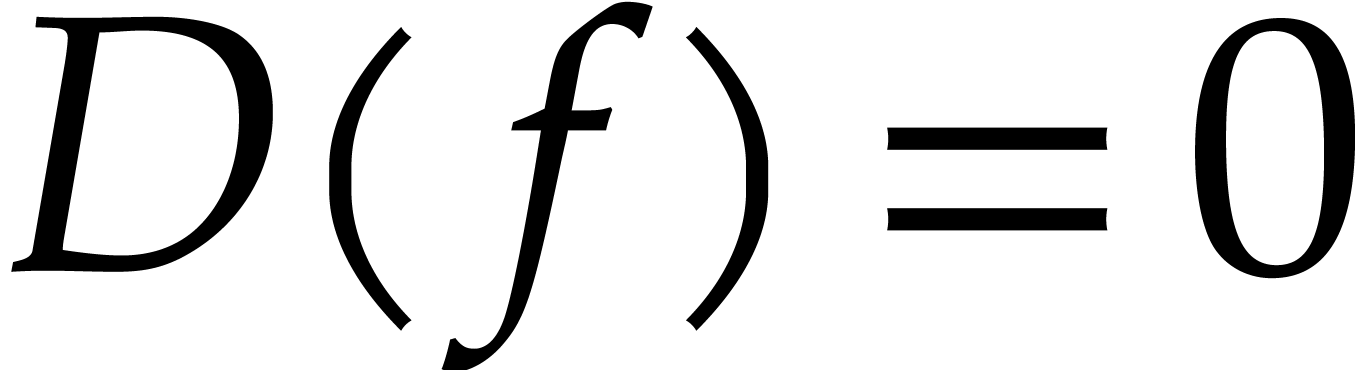 . Evaluating (9) at
. Evaluating (9) at 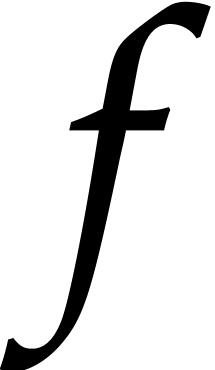 , we conclude that
, we conclude that 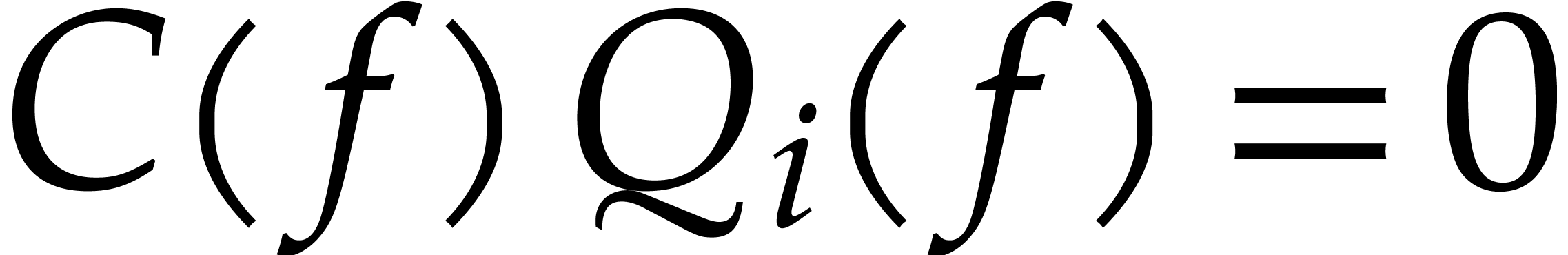 and
therefore
and
therefore 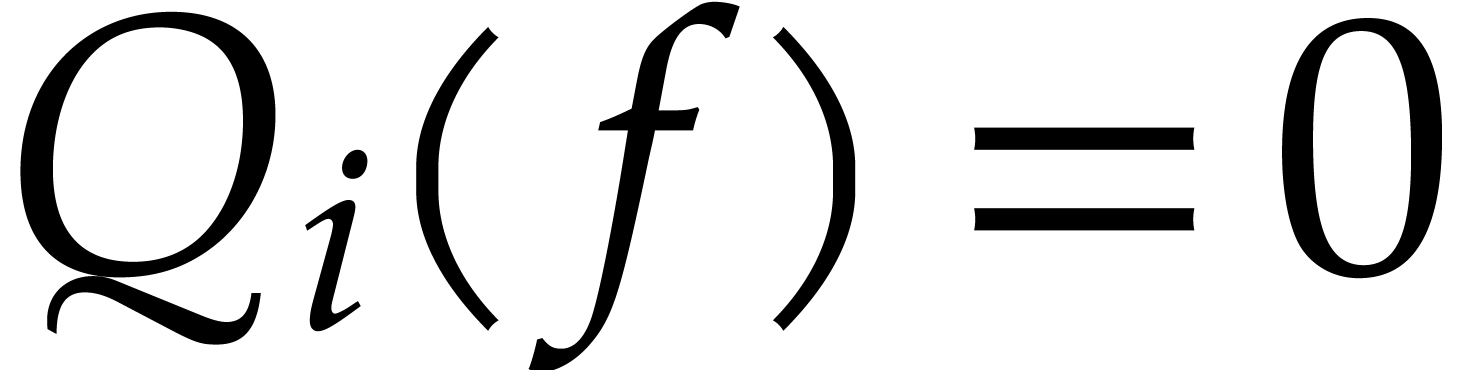 .
.
We say that  is effective if its
elements can be represented effectively and if all field operations can
be carried out by algorithms. We call
is effective if its
elements can be represented effectively and if all field operations can
be carried out by algorithms. We call  an
effective diophantine field if all positive integer roots of
polynomials over
an
effective diophantine field if all positive integer roots of
polynomials over  can be determined by an
algorithm. In particular, this means that
can be determined by an
algorithm. In particular, this means that  has an
effective zero test, i.e. there exists an algorithm which
takes an element
has an
effective zero test, i.e. there exists an algorithm which
takes an element  of
of  on
input and which returns true if
on
input and which returns true if 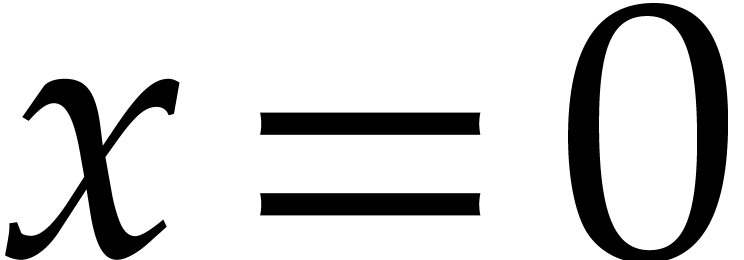 and false otherwise.
and false otherwise.
A power series 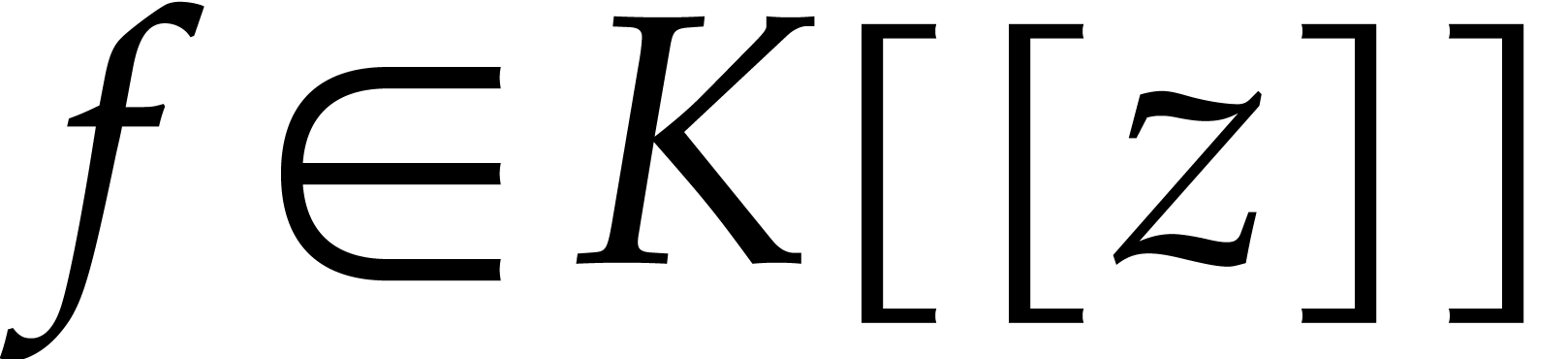 is said to be
computable, if there exists an algorithm for computing
is said to be
computable, if there exists an algorithm for computing 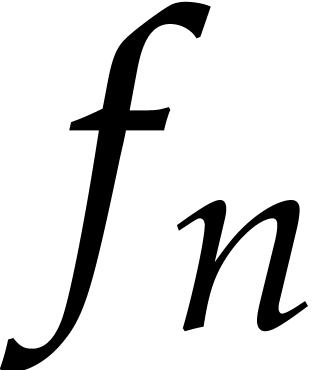 as a function of
as a function of  .
The power series domain
.
The power series domain  is said to be
effective, if its elements are all effective power series and
if the difference
is said to be
effective, if its elements are all effective power series and
if the difference  -algebra
operations can be carried out by algorithms. We notice that the
difference
-algebra
operations can be carried out by algorithms. We notice that the
difference  -algebra
-algebra 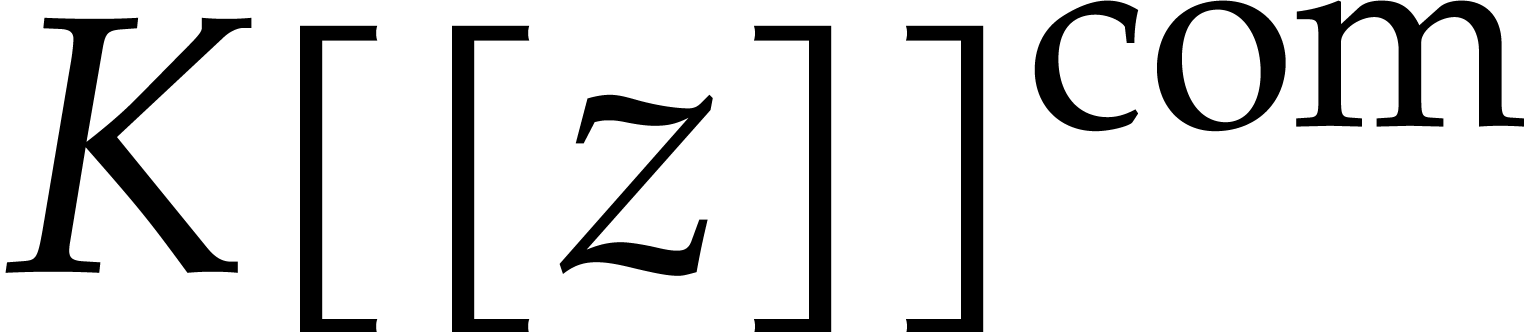 of all computable series is effective, although it does
not have an effective zero test.
of all computable series is effective, although it does
not have an effective zero test.
Assume now that we are given an effective power series domain  with an effective zero test over an effective diophantine
field
with an effective zero test over an effective diophantine
field  . Assume also that we
are given an effective
. Assume also that we
are given an effective  -algebraic
power series
-algebraic
power series 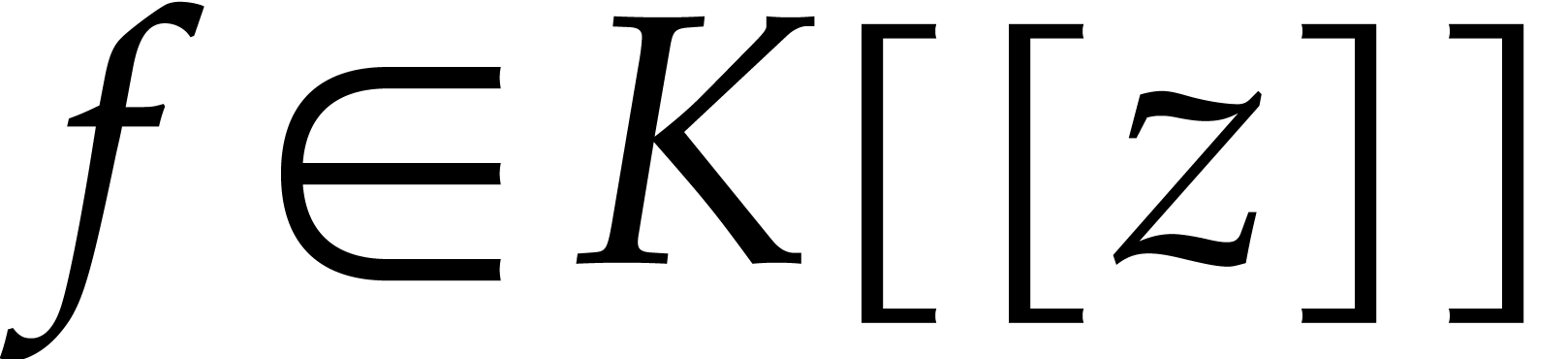 and an annihilator
and an annihilator 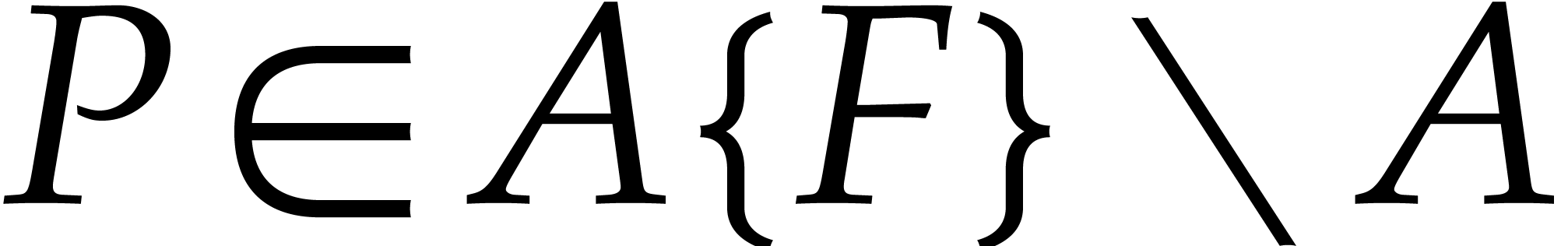 for
for 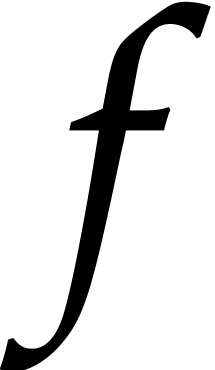 . Assume finally that the
annihilator
. Assume finally that the
annihilator  is non-degenerate, that is,
is non-degenerate, that is, 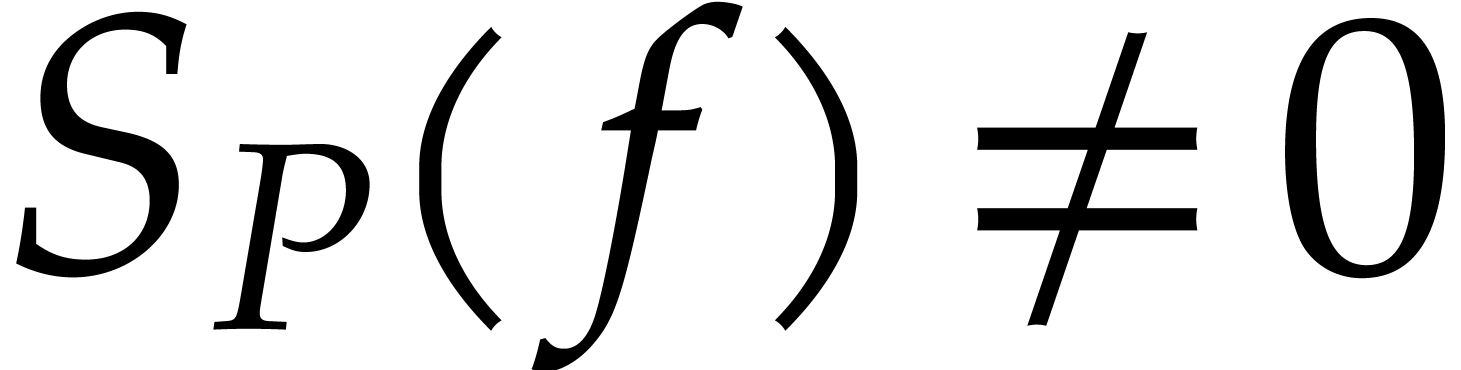 . In this case,
. In this case, 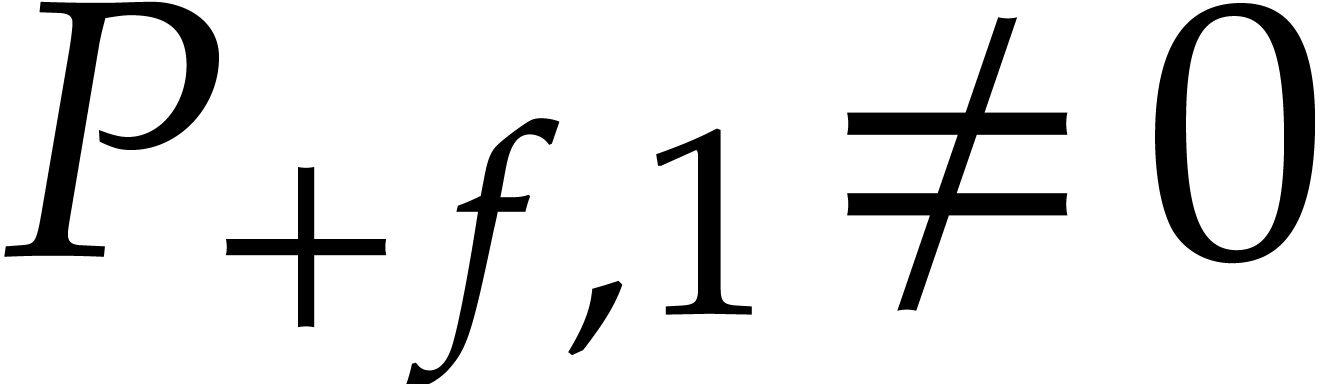 , so we may compute
, so we may compute 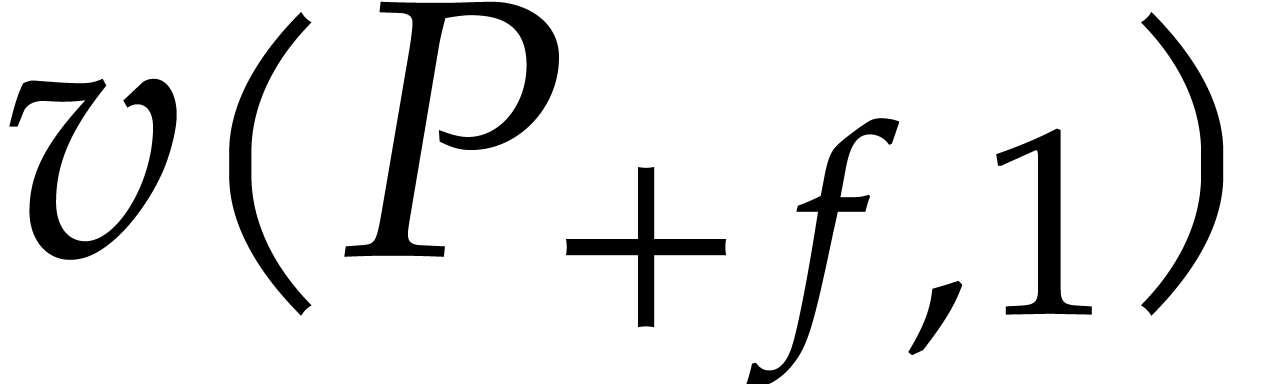 and
and
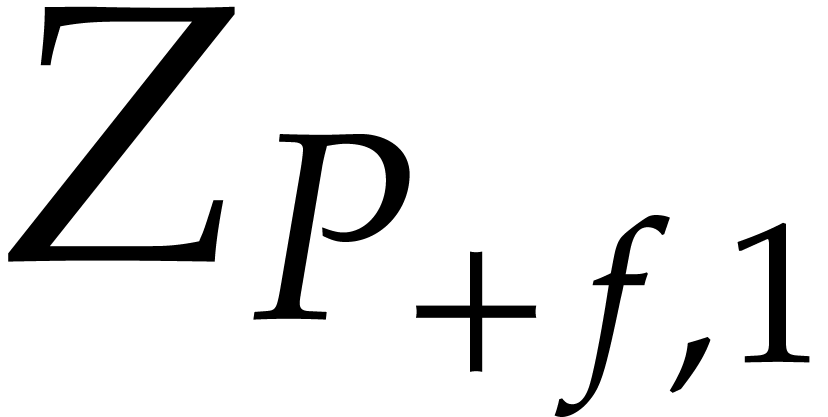 by expanding the power series coefficients of
by expanding the power series coefficients of
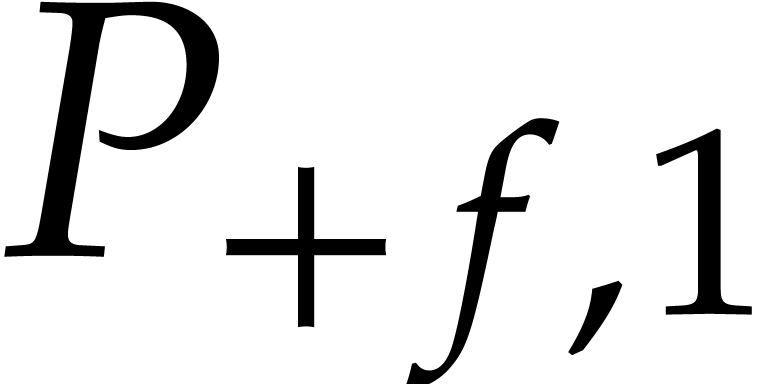 . In other words, the bound
(4) from Proposition 3 provides us with an
effective upper bound for
. In other words, the bound
(4) from Proposition 3 provides us with an
effective upper bound for 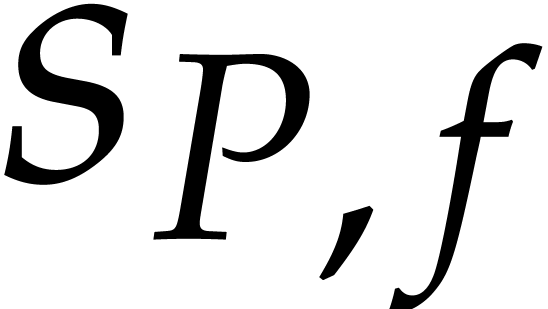 .
Proposition 4 also yields an upper bound for
.
Proposition 4 also yields an upper bound for 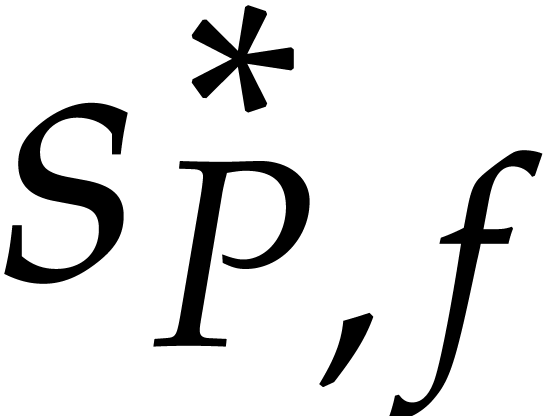 .
.
Given difference polynomials 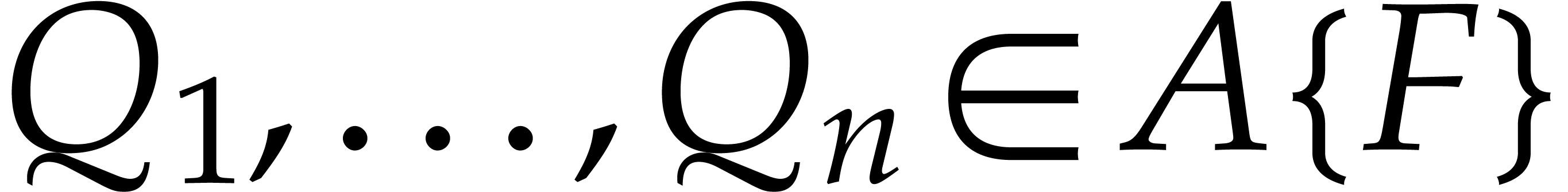 ,
we will now give an algorithm ZeroTest for testing
whether
,
we will now give an algorithm ZeroTest for testing
whether  simultaneously vanish at
simultaneously vanish at 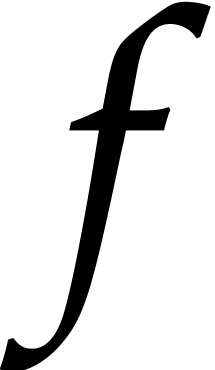 . In particular, this will show that the
. In particular, this will show that the  -algebra
-algebra 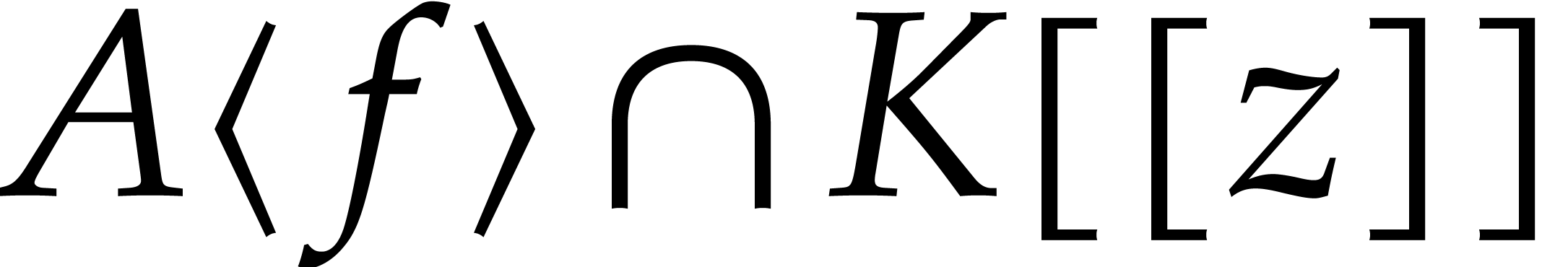 is
again an effective power series domain.
is
again an effective power series domain.
Algorithm ZeroTest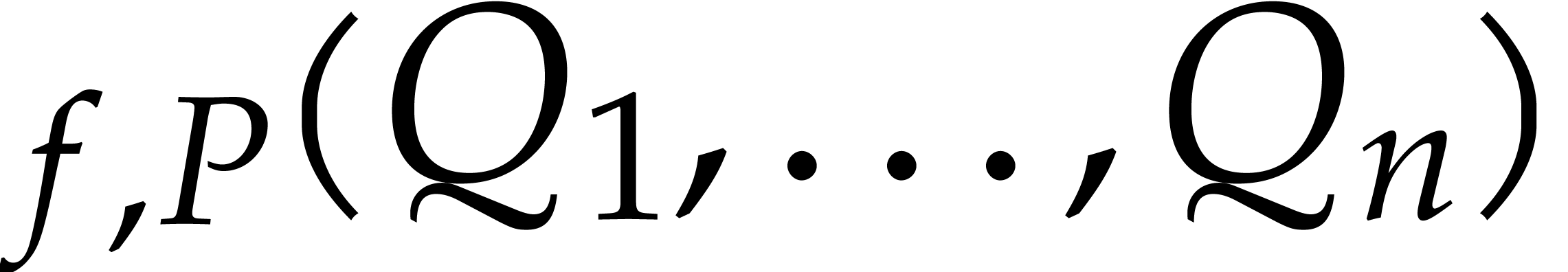
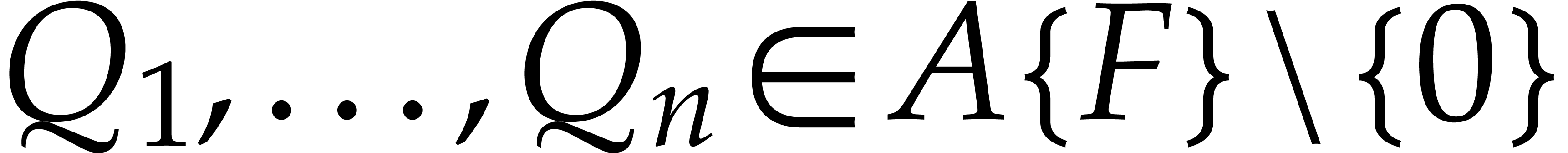
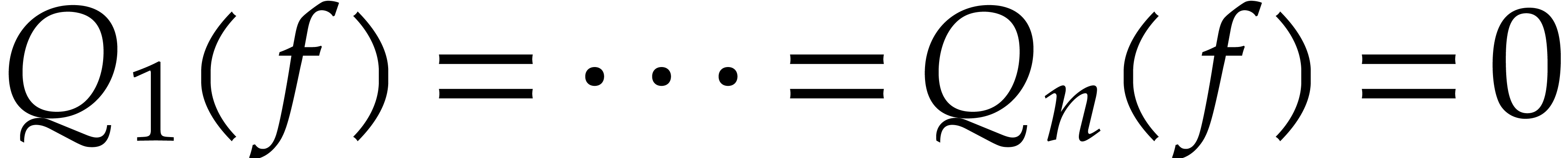 and
and  otherwise
otherwise
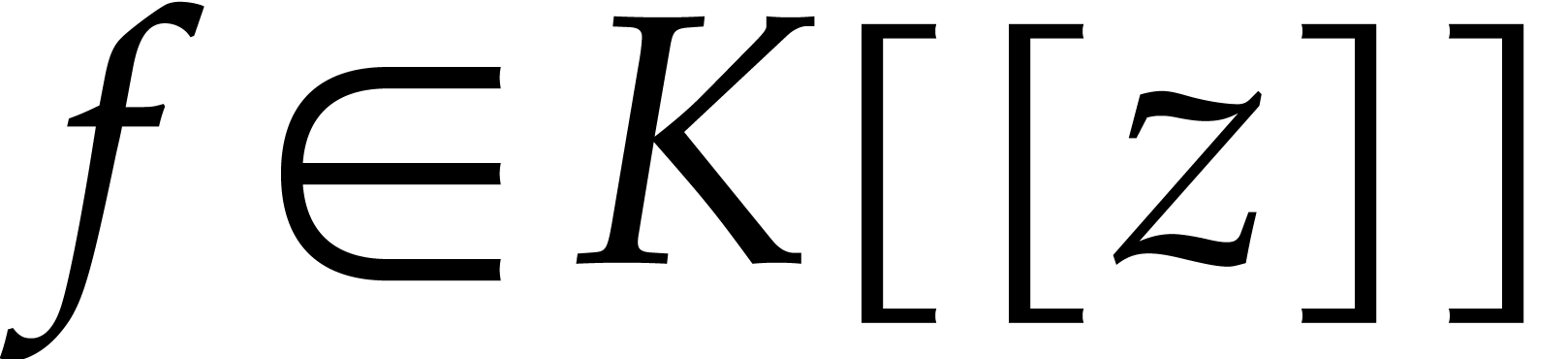 with non-degenerate annihilator
with non-degenerate annihilator 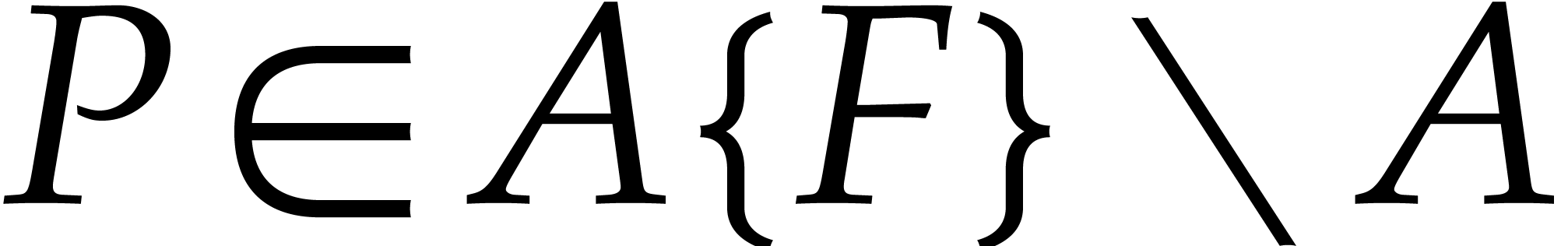
| 1 |
If |
| 2 |
Let |
| 3 |
For |
| 4 |
|
| 5 |
If |
| 6 |
If |
| 7 |
Expand |
| 8 |
If this coefficient
comes from one of the |
| 9 |
For |
| 10 |
If |
| 11 |
For |
| 12 |
If |
| 13 |
Let |
| 14 |
Let |
| 15 |
Return the result of the test |
Remark 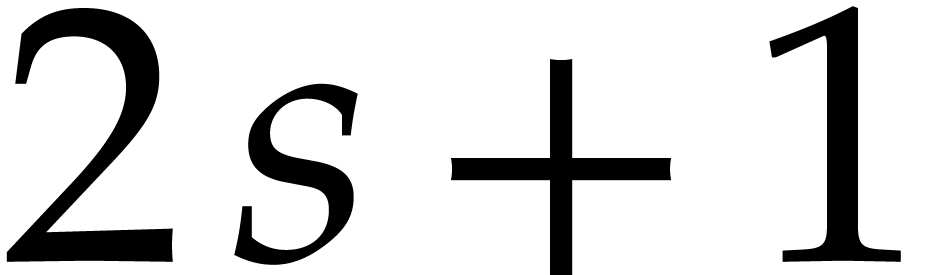 coefficients of the series
coefficients of the series  .
Such power series expansions can be done efficiently using relaxed power
series arithmetic [5].
.
Such power series expansions can be done efficiently using relaxed power
series arithmetic [5].
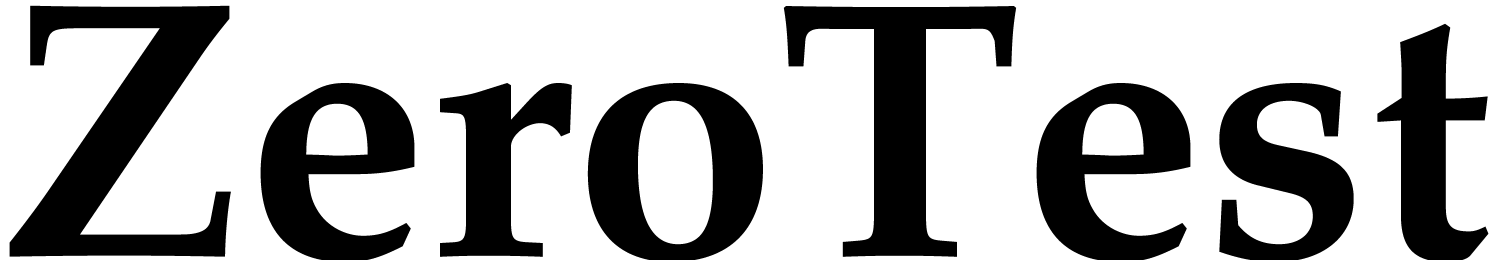 is correct and terminates.
is correct and terminates.
Proof. Let us first prove that the algorithm
always terminates. To each input  ,
we assign the tuple with the Ritt ranks of
,
we assign the tuple with the Ritt ranks of  .
We order such tuples lexicographically, and this ordering is
well-founded. Then the assigned tuple strictly decreases for this
ordering during any recursive call. This shows that our algorithm always
terminates.
.
We order such tuples lexicographically, and this ordering is
well-founded. Then the assigned tuple strictly decreases for this
ordering during any recursive call. This shows that our algorithm always
terminates.
In step 1, note that we assumed that 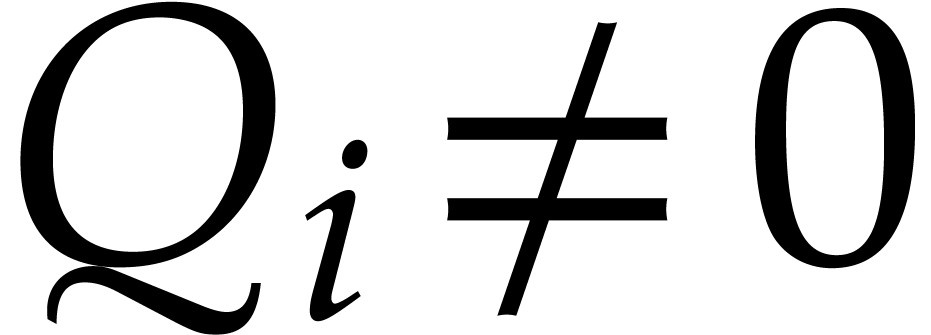 as an
element of
as an
element of 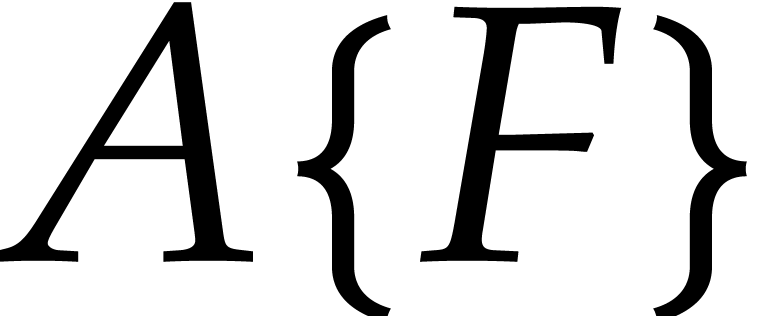 for all
for all  .
So if
.
So if  , then we indeed have
, then we indeed have
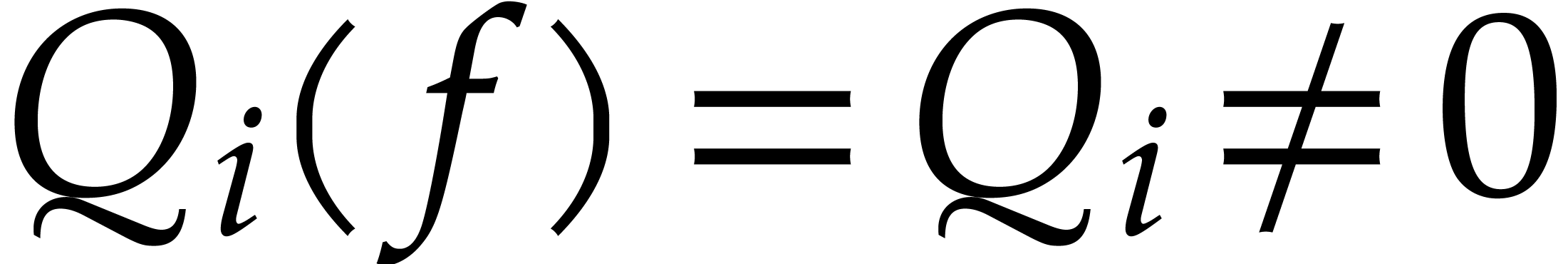 . The correctness of the
algorithm is also clear if we return during one of the steps 6, 8, 10,
or 12.
. The correctness of the
algorithm is also clear if we return during one of the steps 6, 8, 10,
or 12.
Assume now that we reach step 15. By construction, this means that 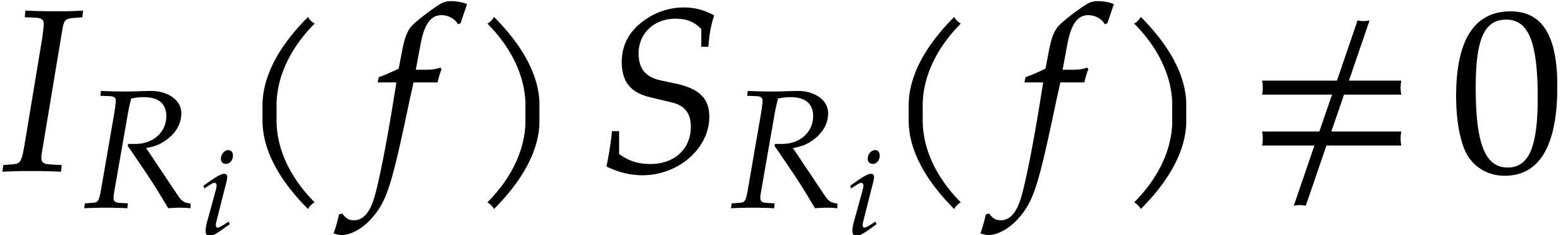 for every
for every 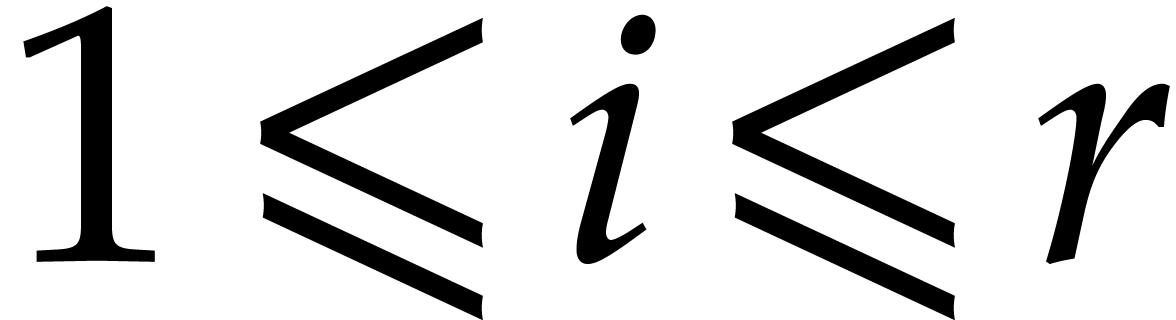 and
and 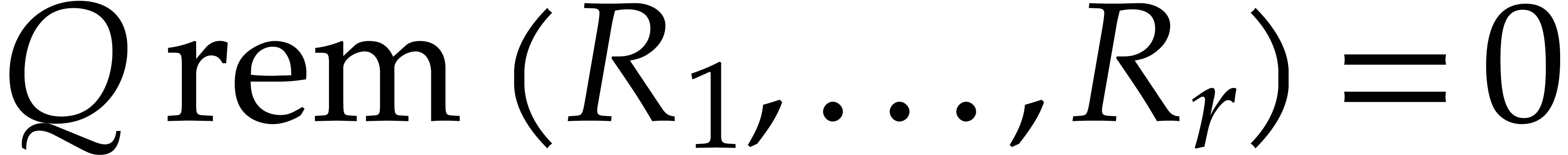 for every
for every  .
Furthermore, since we passed step 11, the chain
.
Furthermore, since we passed step 11, the chain  is both coherent and
is both coherent and 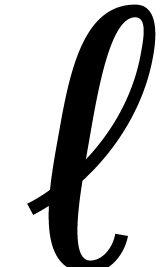 -autoreduced.
-autoreduced.
Applying Proposition 5, we obtain a unique logarithmic
power series 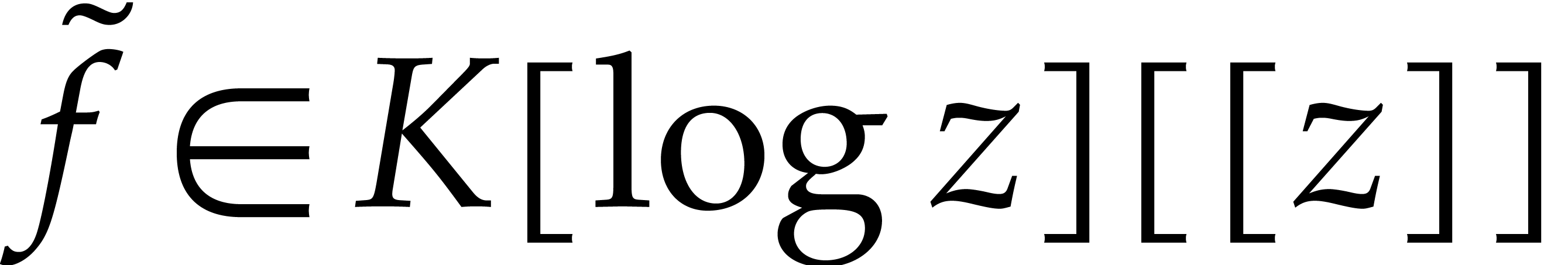 with
with 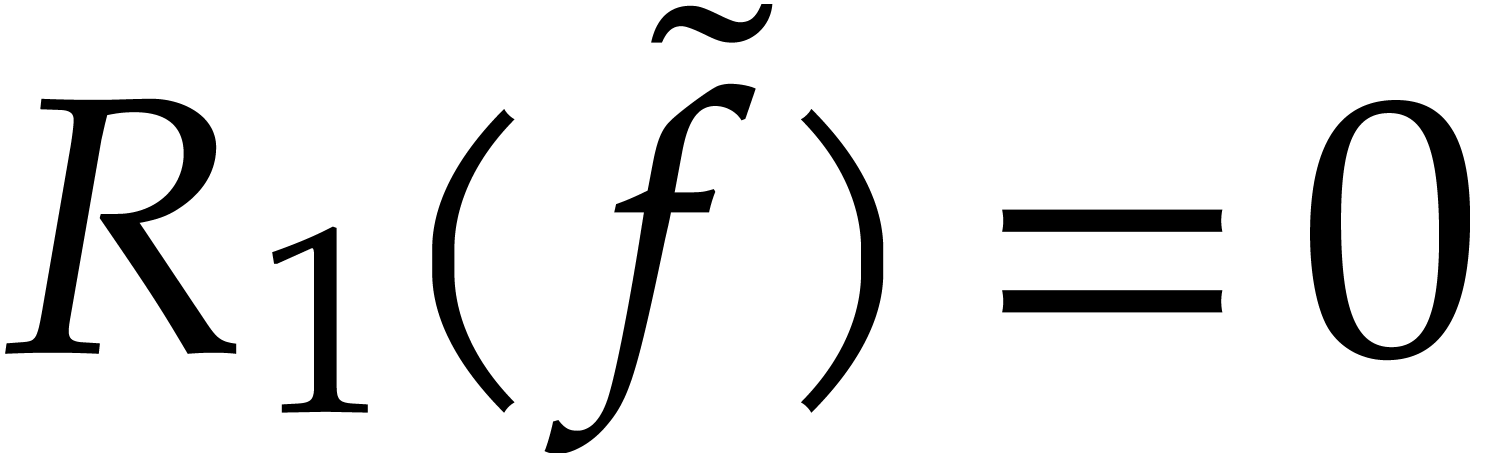 and
and
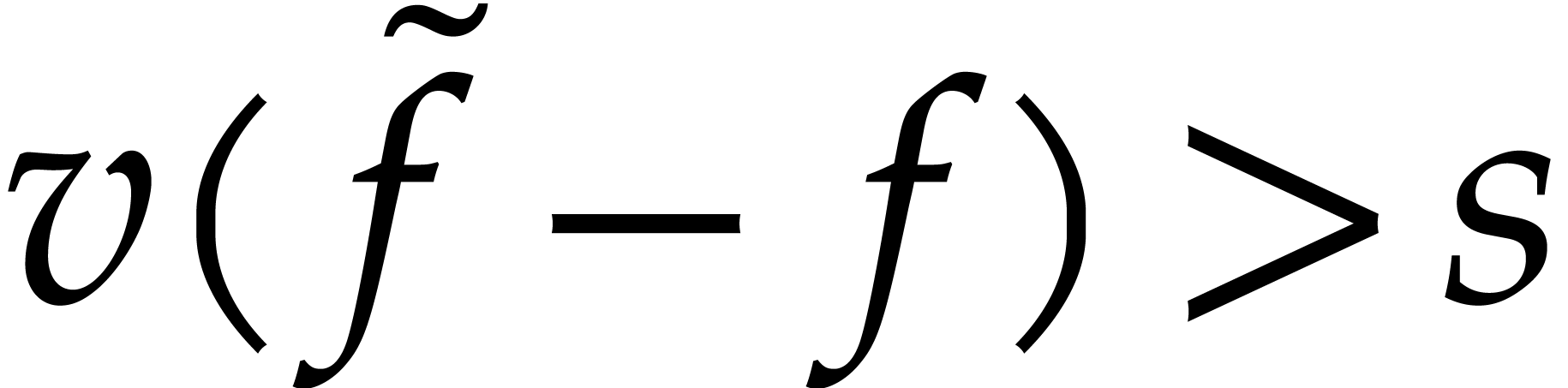 . Since
. Since 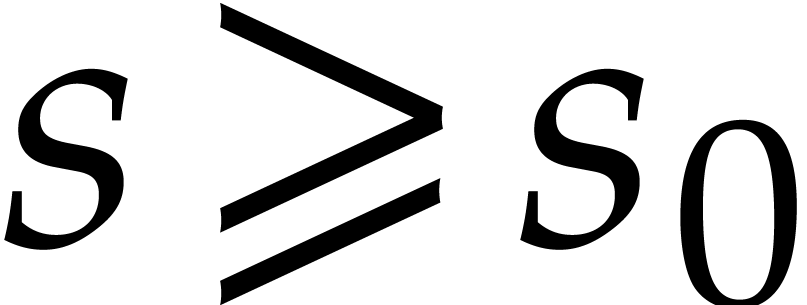 , Proposition 6 implies that
, Proposition 6 implies that 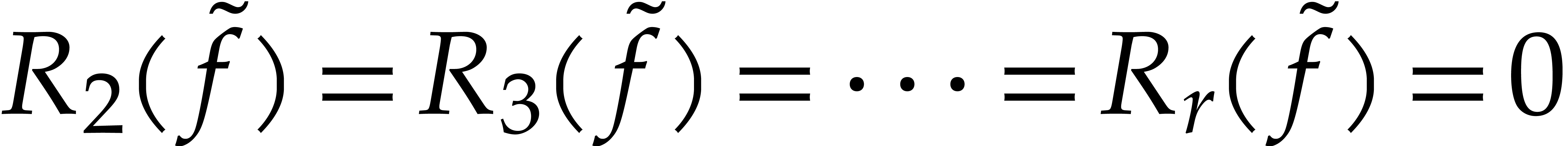 . Since each of
. Since each of  is
is 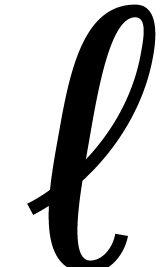 -reducible to zero with
respect to
-reducible to zero with
respect to  and none of the initials of
and none of the initials of  vanishes at
vanishes at 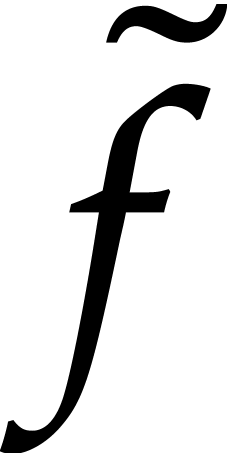 ,
we deduce that
,
we deduce that 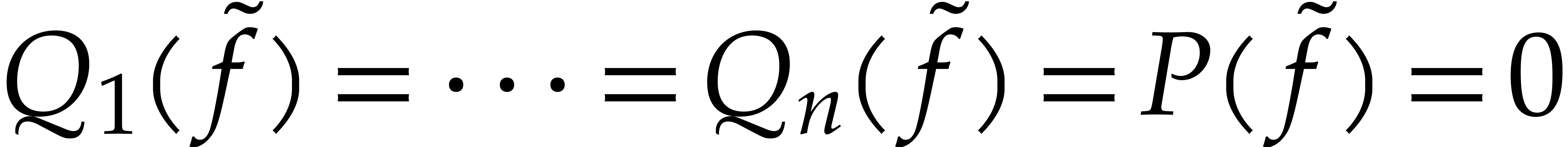 . Proposition
4 applied to
. Proposition
4 applied to 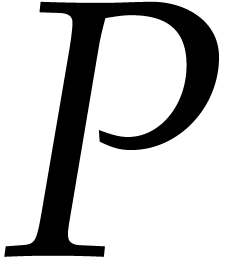 and its roots
and its roots 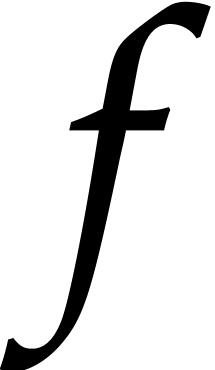 and
and 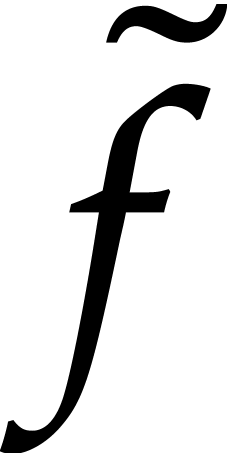 implies that
implies that  whenever the test succeeds, so the returned result is
correct.
whenever the test succeeds, so the returned result is
correct.
Remark  depends on parameters
depends on parameters  in
in
 (when using the technique of dynamic evaluation
[1] for examining the finite number of branches that can
occur depending on algebraic conditions on the parameters). The original
equation
(when using the technique of dynamic evaluation
[1] for examining the finite number of branches that can
occur depending on algebraic conditions on the parameters). The original
equation 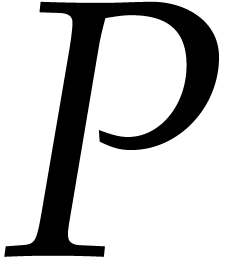 may also depend on parameters, as long
as we have a uniform bound for
may also depend on parameters, as long
as we have a uniform bound for 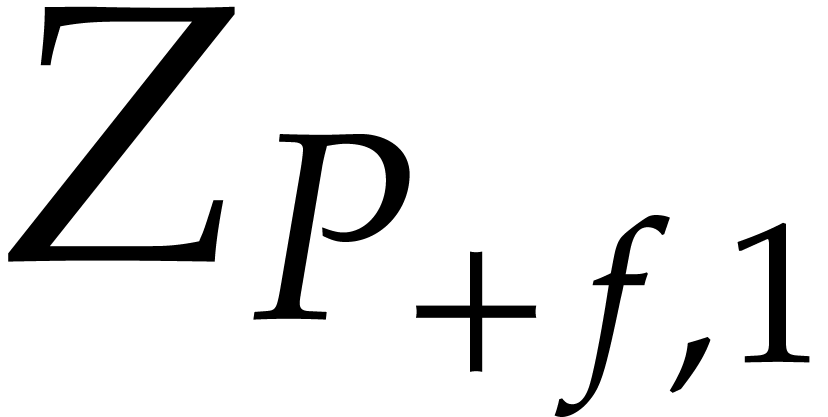 .
.
Consider Stirling's series
Rewritten in terms of 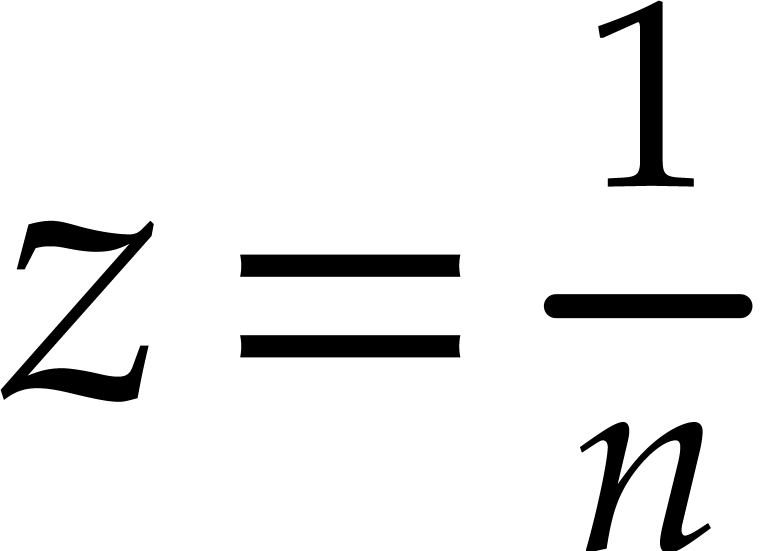 , the
rightmost series
, the
rightmost series  satisfies
satisfies
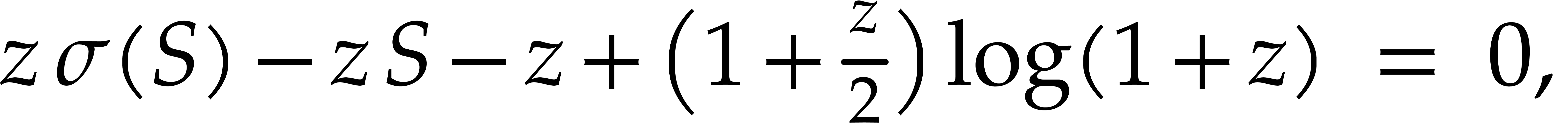
where 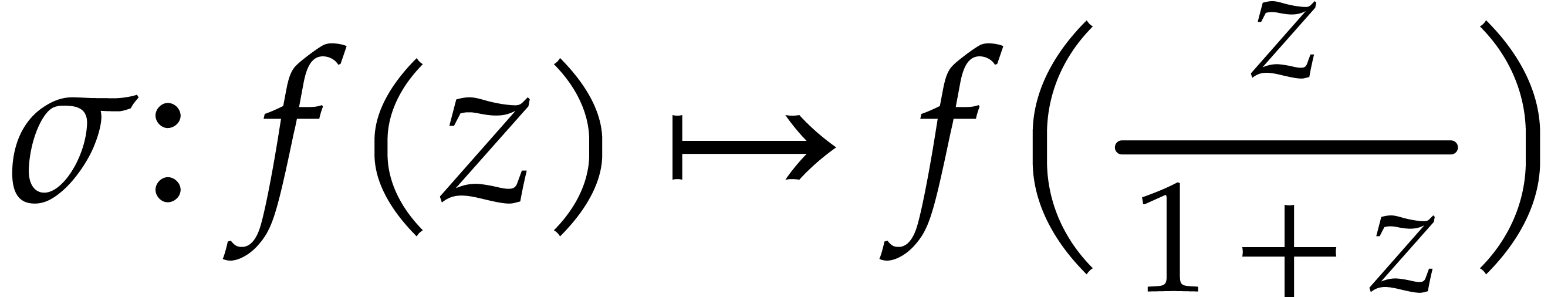 . The coefficients of
this difference equation belong to
. The coefficients of
this difference equation belong to
where we note that 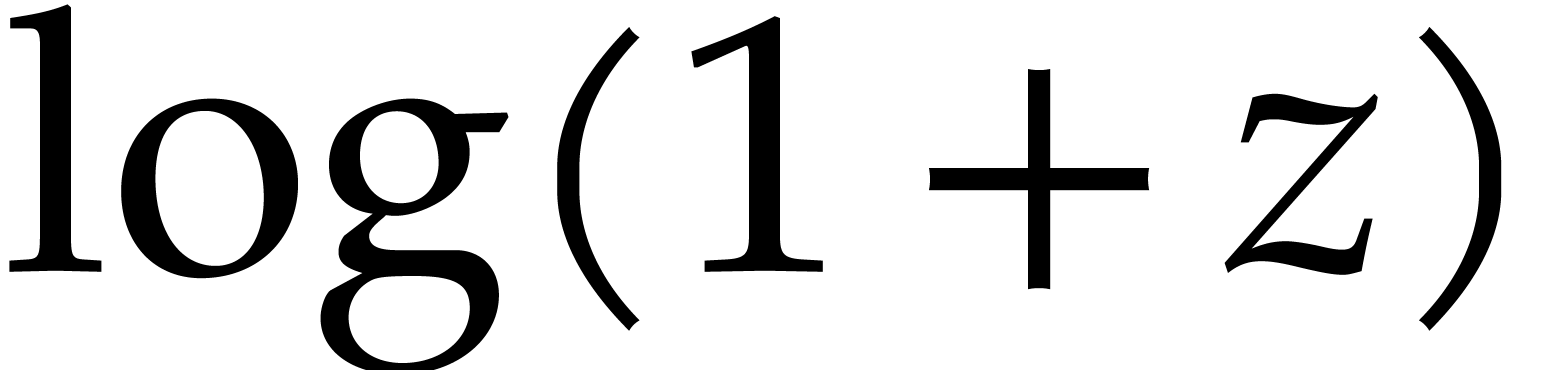 is
is  -transcendental over
-transcendental over 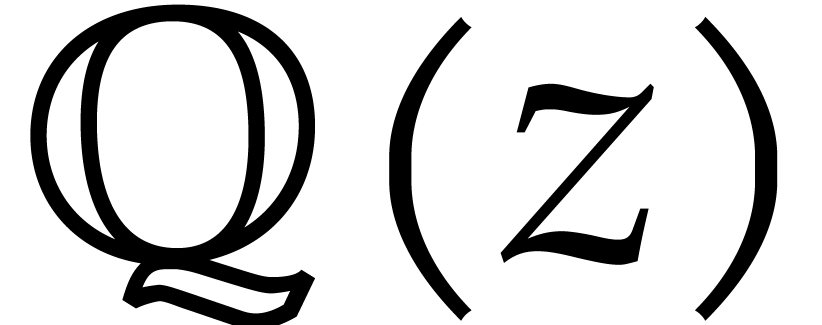 .
In particular,
.
In particular,  comes with a natural zero test
and our algorithm yields a zero test for
comes with a natural zero test
and our algorithm yields a zero test for 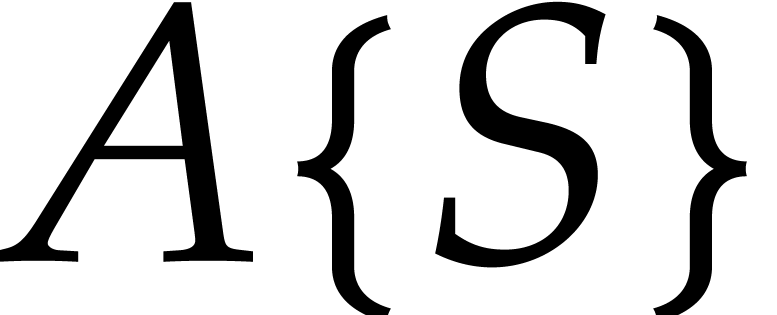 .
.
One can perform the same computations for functions of the form 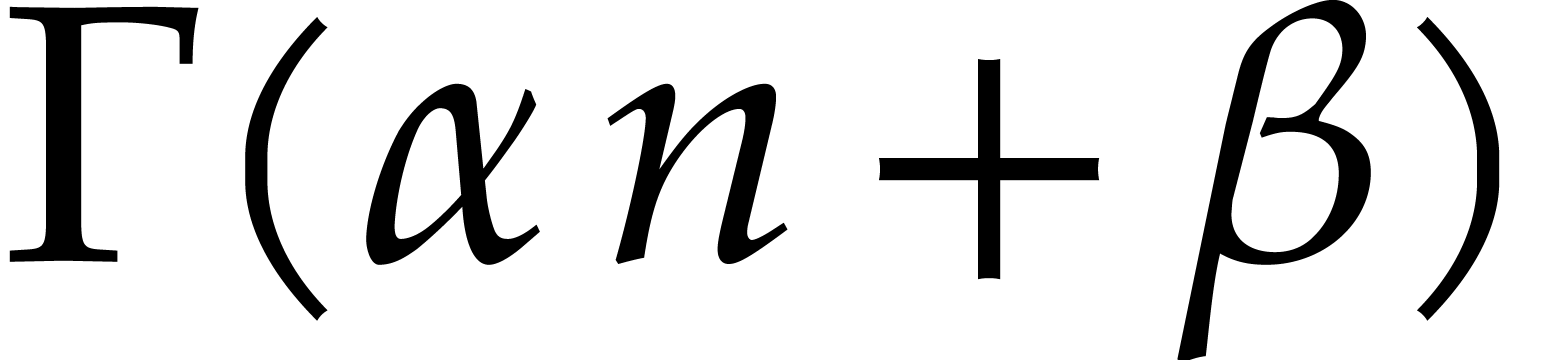 . Having a zero test for
expressions involving the corresponding Stirling series can be used to
prove identities for the gamma function, for example, to formally
establish the Legendre duplication formula:
. Having a zero test for
expressions involving the corresponding Stirling series can be used to
prove identities for the gamma function, for example, to formally
establish the Legendre duplication formula:
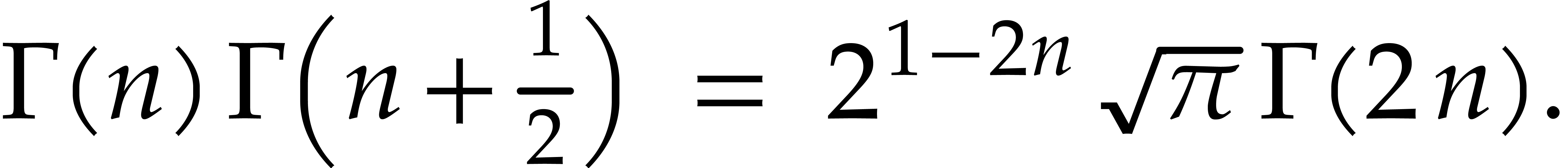 |
(10) |
In order to do this, we inductively construct a zero test for the  -ring
-ring
and then test whether the following expression is zero:
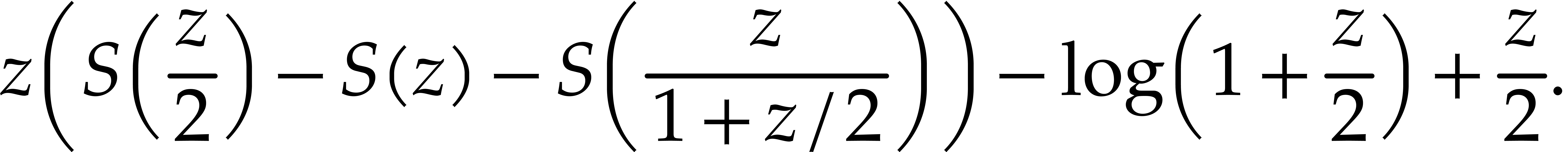
Our implementation allows to do this; the details can be found in the notebook https://github.com/pogudingleb/DifferenceZeroTest/blob/main/examples/LegendreDuplication.ipynb.
Note that, althought the identity (10) can be proved for
integer values of 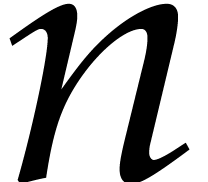 using the algorithms for
P-recursive sequences, we are not aware of an existing symbolic
computation algorithm that could be used to verify this identity
automatically.
using the algorithms for
P-recursive sequences, we are not aware of an existing symbolic
computation algorithm that could be used to verify this identity
automatically.
The example from the previous subsection required the incorporation of
logarithms in our base ring  .
Such logarithms are usually construed as solutions to differential
equations. In fact, it is possible to alternate the adjunction of
solutions to differential equations to our base ring
.
Such logarithms are usually construed as solutions to differential
equations. In fact, it is possible to alternate the adjunction of
solutions to differential equations to our base ring  with the adjunction solutions to difference equations, while preserving
our ability to do zero testing. Let us briefly explain how this works.
with the adjunction solutions to difference equations, while preserving
our ability to do zero testing. Let us briefly explain how this works.
Assume that 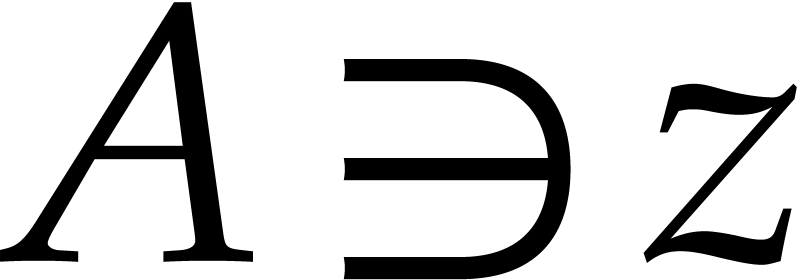 is an effective power series domain
that is closed under both
is an effective power series domain
that is closed under both  and differentiation
and differentiation
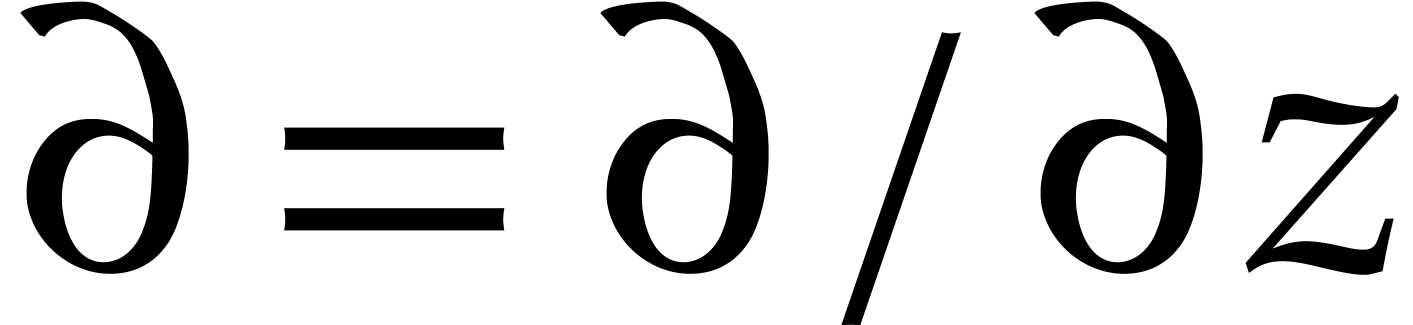 . Given a
. Given a  -algebraic power series
-algebraic power series  over
over  , we have seen that
, we have seen that  is an effective power series domain that is closed
under
is an effective power series domain that is closed
under  . Moreover, there is a
polynomial
. Moreover, there is a
polynomial 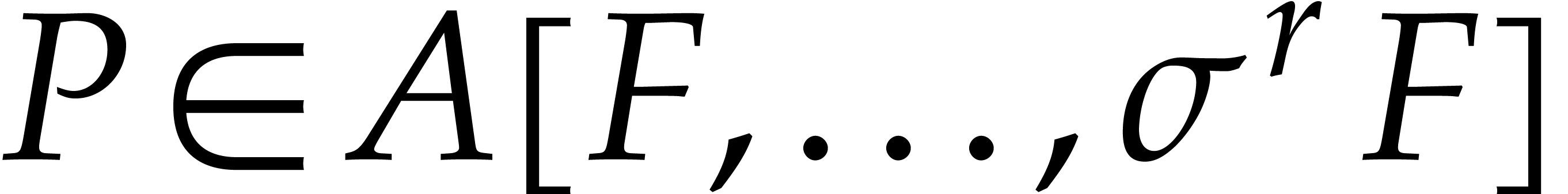 with
with  .
Differentiating this equation, we get
.
Differentiating this equation, we get
so 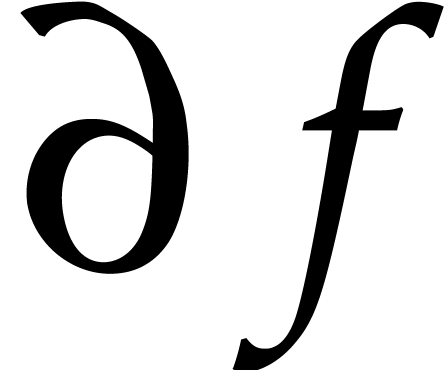 is
is  -algebraic
over
-algebraic
over 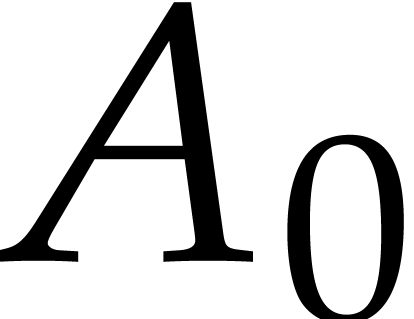 . Consequently,
. Consequently, 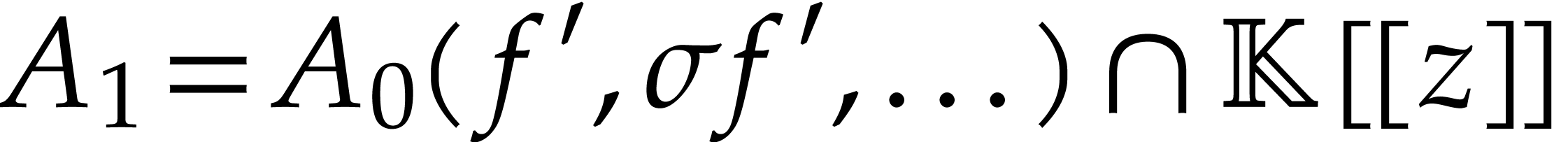 is an effective power series domain that is closed
under
is an effective power series domain that is closed
under  . By induction, we
obtain a sequence
. By induction, we
obtain a sequence 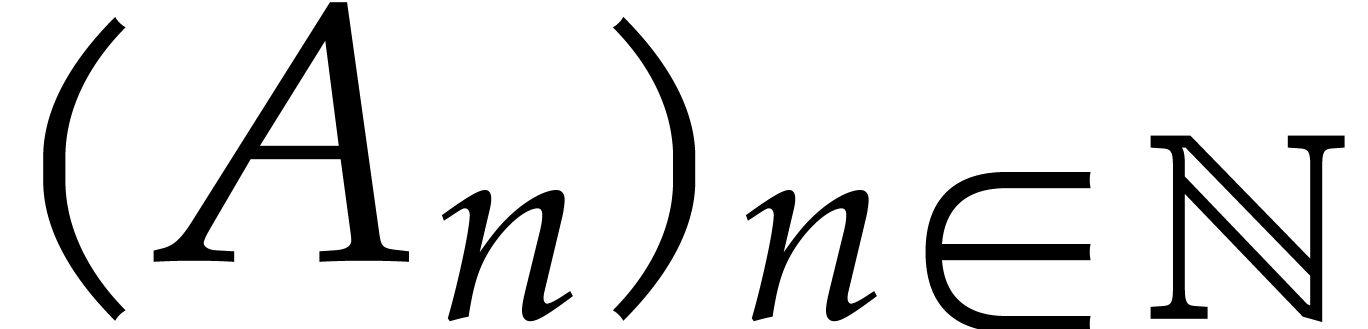 of effective power series
domains with
of effective power series
domains with 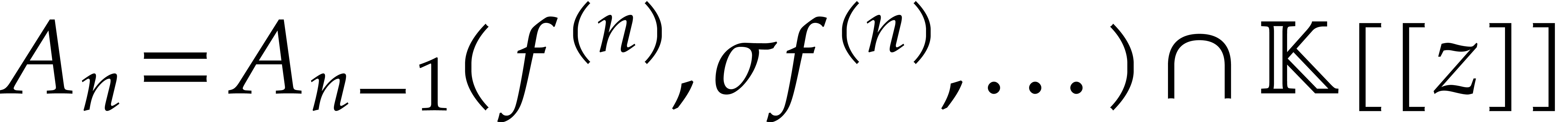 and such that each
and such that each 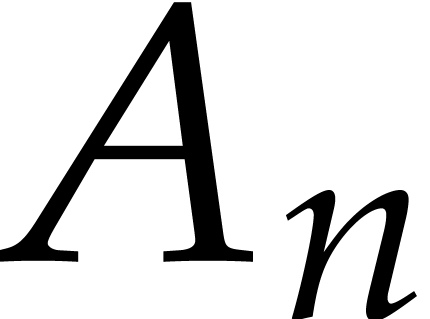 is closed under
is closed under  . We conclude
that
. We conclude
that 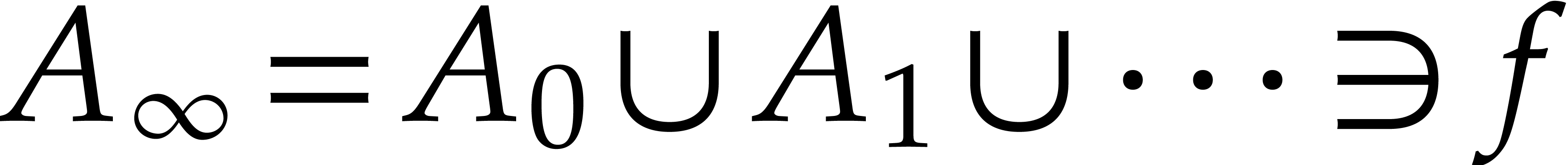 is an effective power series domain that is
closed under both
is an effective power series domain that is
closed under both  and
and  .
.
In a similar way, given a d-algebraic power series 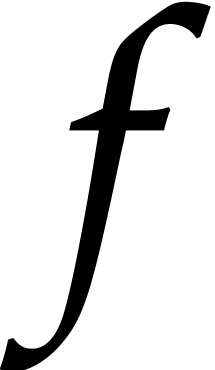 over
over  , and in view of the
algorithm from [4], we may construct a sequence
, and in view of the
algorithm from [4], we may construct a sequence 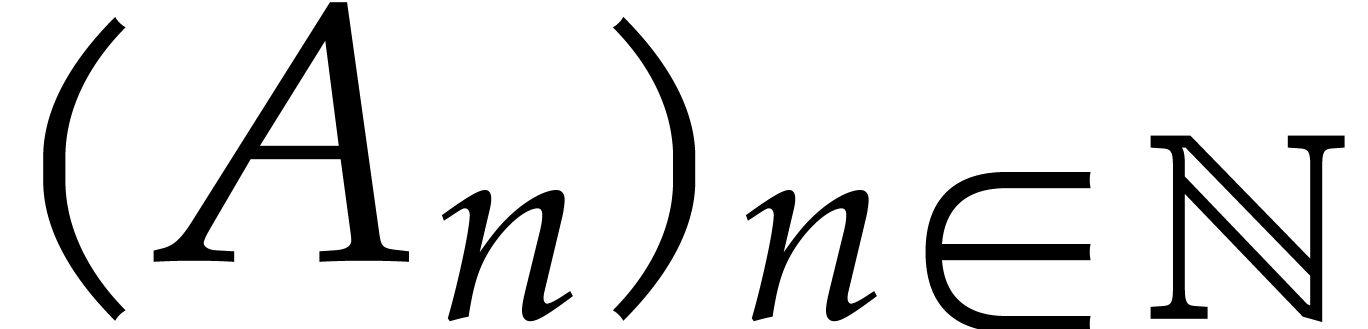 of effective power series domains that are closed under
of effective power series domains that are closed under
 , with
, with 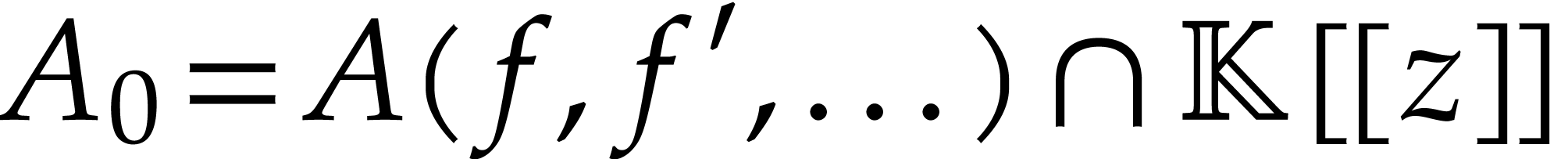 and
and 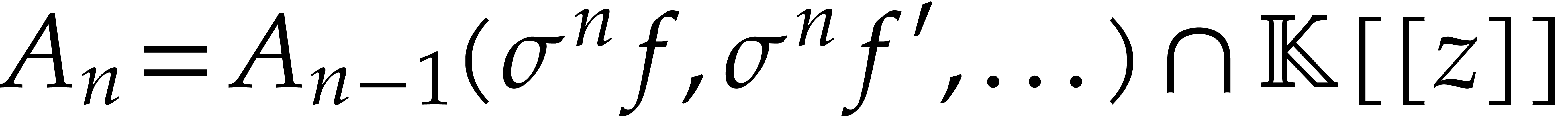 . Then
. Then 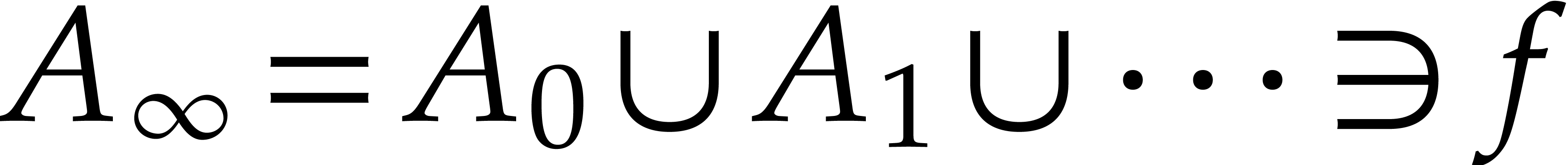 is an effective power series domain that is closed both under
is an effective power series domain that is closed both under  and
and  .
.
The Barnes G-function is a solution of the difference equation
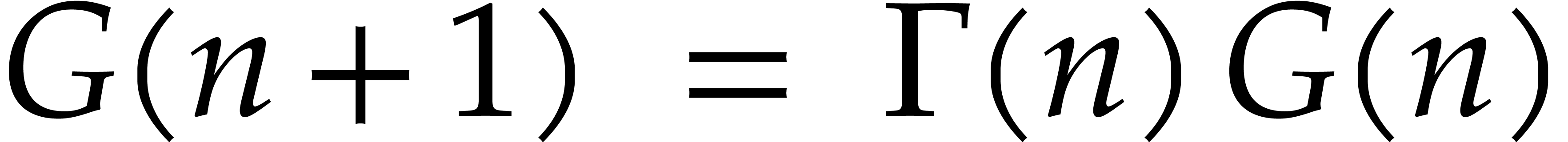
and the log-gamma integral is defined by
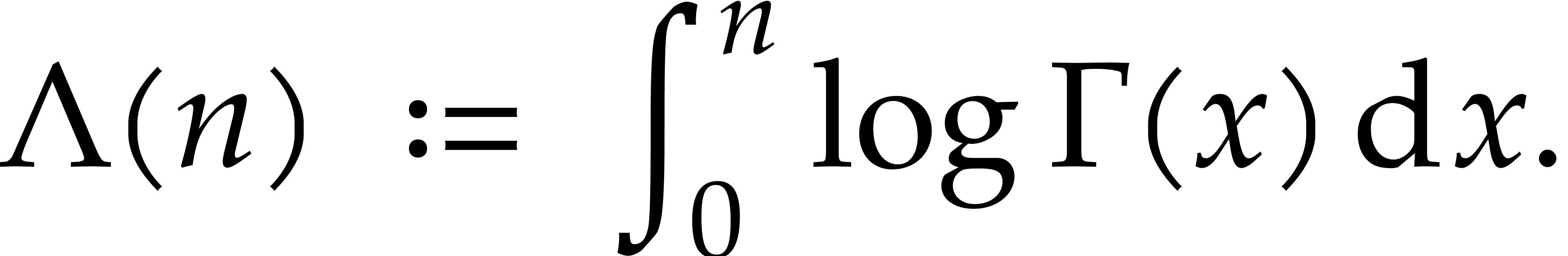
These functions are related via
In view of subsection 6.2, such relations can be proved
automatically using our algorithm in combination with the zero test from
[4]. Alternatively, we may derive a difference equation for
 :
:
After rewriting  and
and  in
terms of
in
terms of  , we may then
directly use our new algorithm. Our implementation allows to do this;
the details can be found in the notebook https://github.com/pogudingleb/DifferenceZeroTest/blob/main/examples/LoggammaIntegral.ipynb.
, we may then
directly use our new algorithm. Our implementation allows to do this;
the details can be found in the notebook https://github.com/pogudingleb/DifferenceZeroTest/blob/main/examples/LoggammaIntegral.ipynb.
The authors would like to thank the referees for helpful comments and suggestions. Gleb Pogudin was partially supported NSF grants DMS-1853482, DMS-1760448, DMS-1853650, CCF-1564132, and CCF-1563942 and by the Paris Ile-de-France region.
J. Della Dora, C. Dicrescenzo, and D. Duval. A new method for computing in algebraic number fields. In G. Goos and J. Hartmanis, editors, Eurocal'85 (2), volume 174 of Lect. Notes in Comp. Science, pages 321–326. Springer, 1985.
J. Denef and L. Lipshitz. Power series solutions of algebraic differential equations. Math. Ann., 267:213–238, 1984.
J. Denef and L. Lipshitz. Decision problems for differential equations. The Journ. of Symb. Logic, 54(3):941–950, 1989.
J. van der Hoeven. A new zero-test for formal power series. In Teo Mora, editor, Proc. ISSAC '02, pages 117–122. Lille, France, July 2002.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Computing with D-algebraic power series. AAECC, 30(1):17–49, 2019.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
Manuel Kauers. An algorithm for deciding zero-equivalence of nested polynomially recurrent sequences. ACM Transactions on Algorithms, 2007.
A. Péladan-Germa. Tests effectifs de nullité dans des extensions d'anneaux différentiels. PhD thesis, Gage, École Polytechnique, Palaiseau, France, 1997.
R. H. Risch. Algebraic properties of elementary functions in analysis. Amer. Journ. of Math., 4(101):743–759, 1975.
J. Shackell. A differential-equations approach to functional equivalence. In Proc. ISSAC '89, pages 7–10. Portland, Oregon, A.C.M., New York, 1989. ACM Press.
D. Zeilberger. A holonomic systems approach to special functions identities. Journal of Comp. and Appl. Math., 32:321–368, 1990.