Fast composition of numeric power
series |
|
| December 9, 2008 |
|
 . This work was
partially supported by the ANR Gecko project.
. This work was
partially supported by the ANR Gecko project.
Let
|
Let  be an effective ring of coefficients
(i.e. we have algorithms for performing the ring
operations). Let
be an effective ring of coefficients
(i.e. we have algorithms for performing the ring
operations). Let 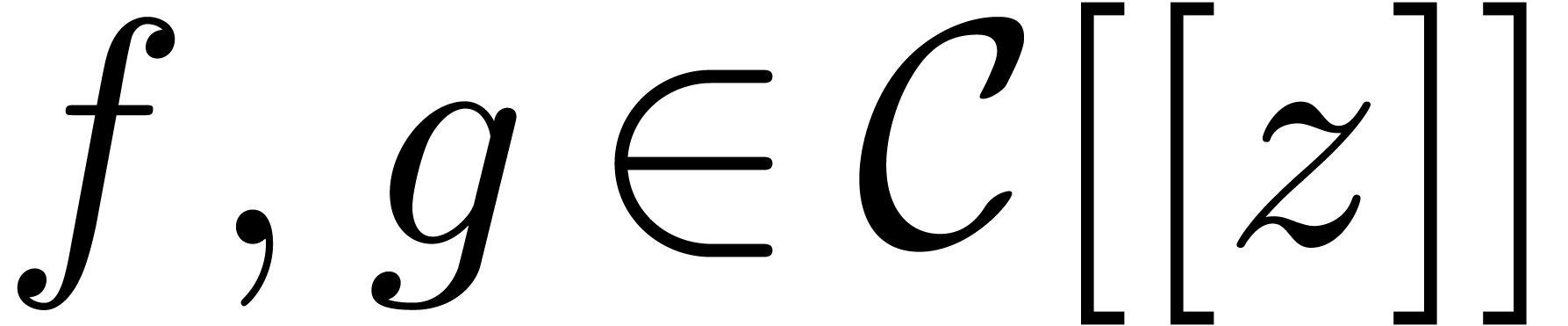 be two power series with
be two power series with 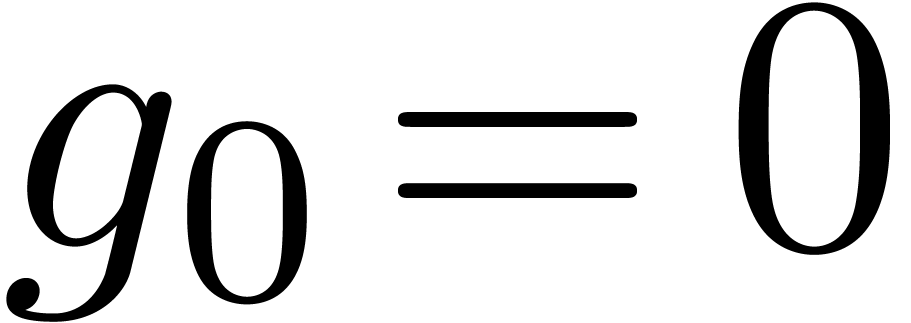 , so that the composition
, so that the composition 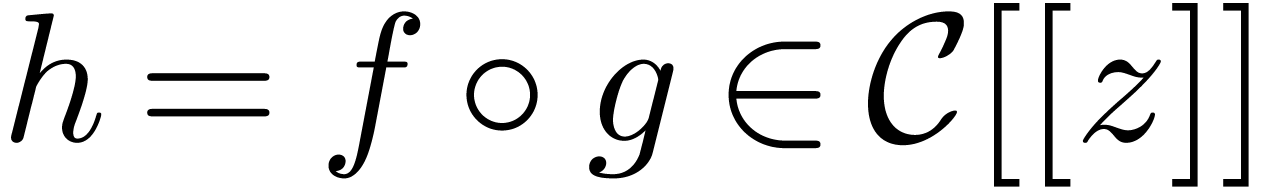 is well-defined. We are interested in algorithms for fast
composition: given
is well-defined. We are interested in algorithms for fast
composition: given 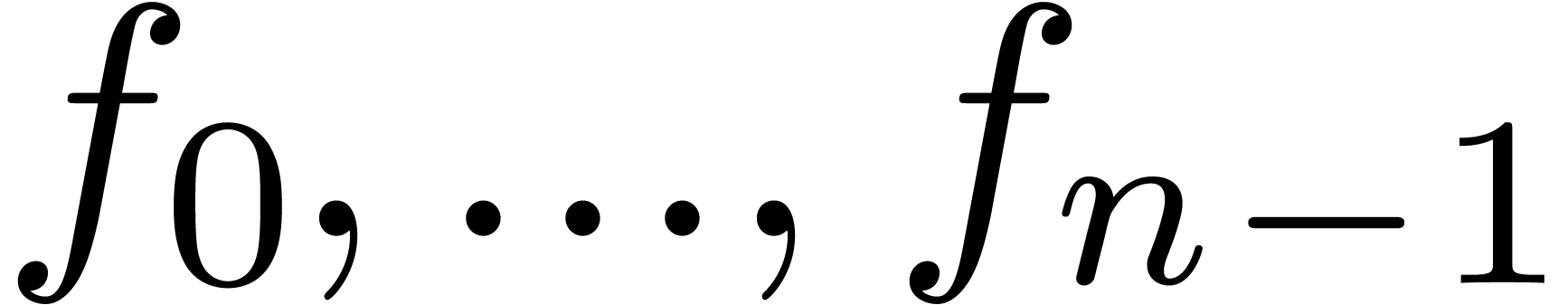 and
and  , how much arithmetic operations in
, how much arithmetic operations in  are needed in order to compute
are needed in order to compute 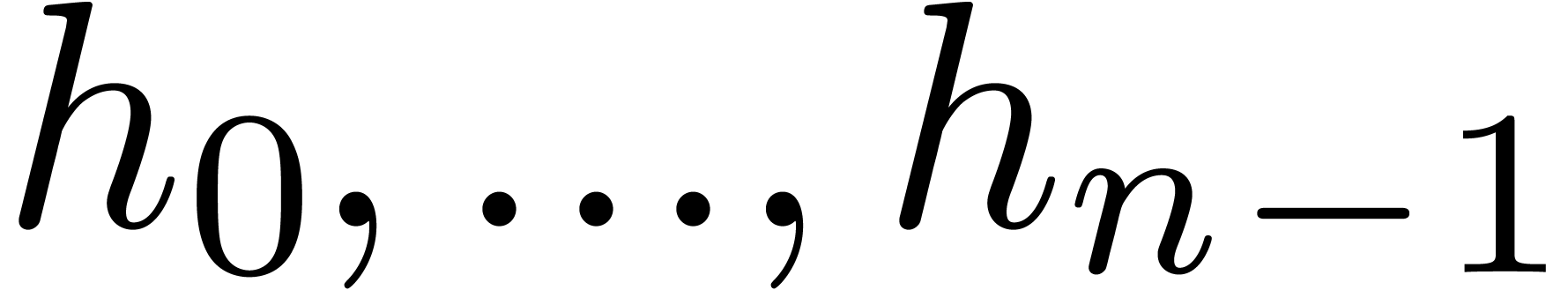 ?
?
A first efficient general purpose algorithm of time complexity 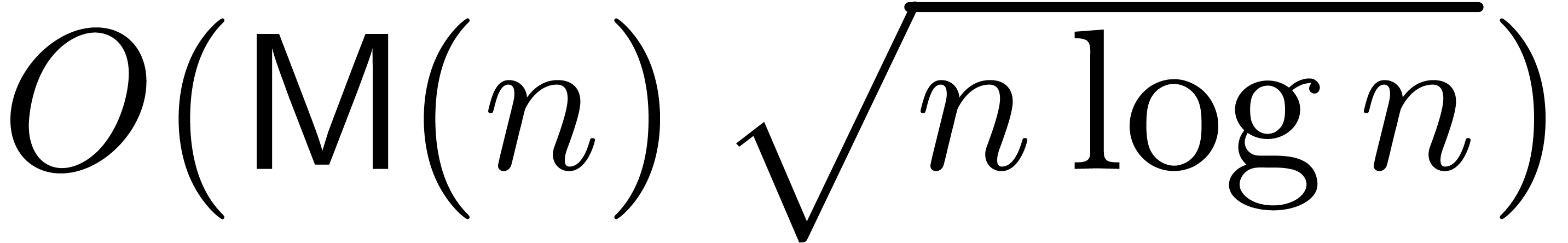 was given in [BK78, CT65, SS71]. Here
was given in [BK78, CT65, SS71]. Here 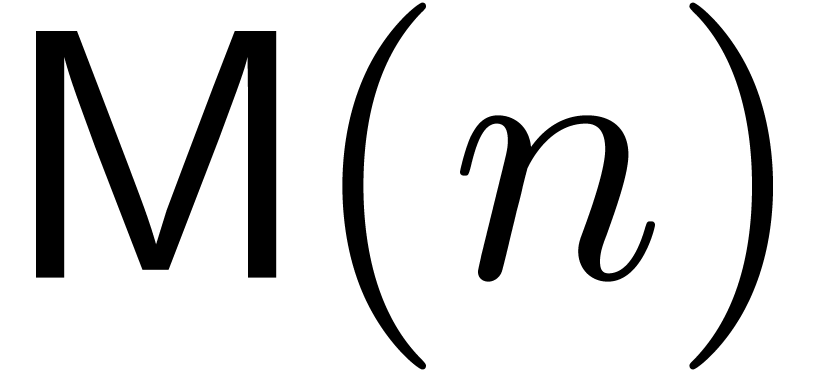 denotes the complexity for
the multiplication of two polynomials of degrees
denotes the complexity for
the multiplication of two polynomials of degrees 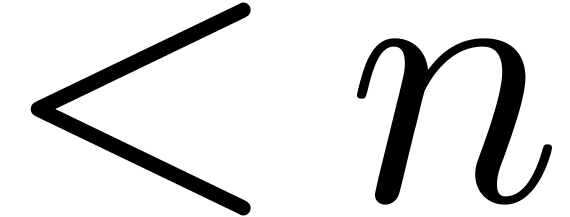 and we have
and we have 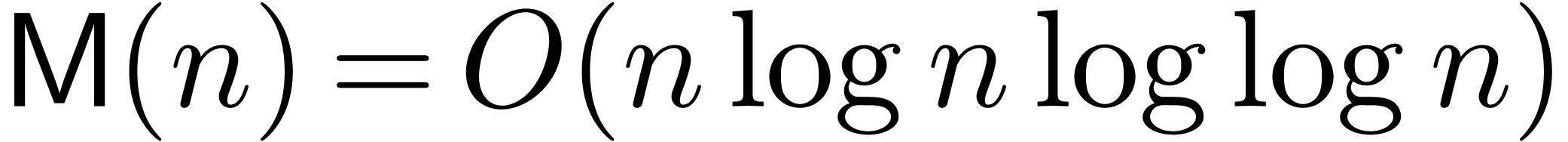 [CK91]. In the case
when
[CK91]. In the case
when  is polynomial [BK78] or
algebraic [vdH02], then this complexity further reduces to
is polynomial [BK78] or
algebraic [vdH02], then this complexity further reduces to
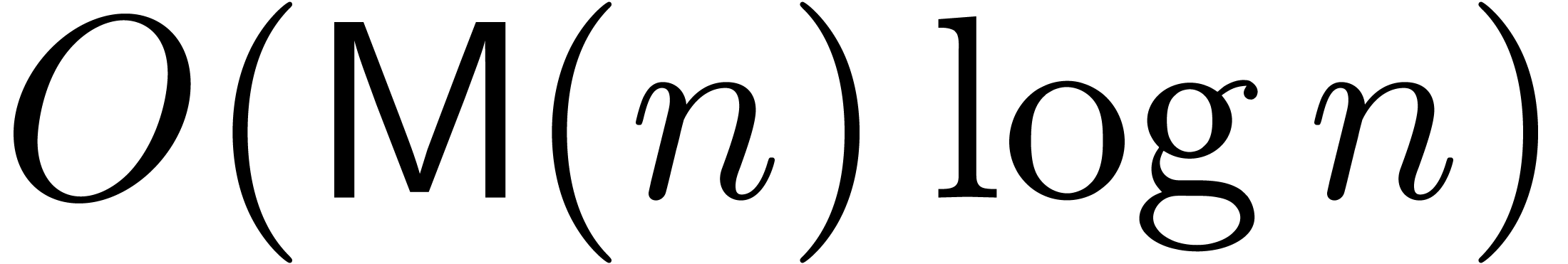 . For some very special
series
. For some very special
series  , there even exist
, there even exist
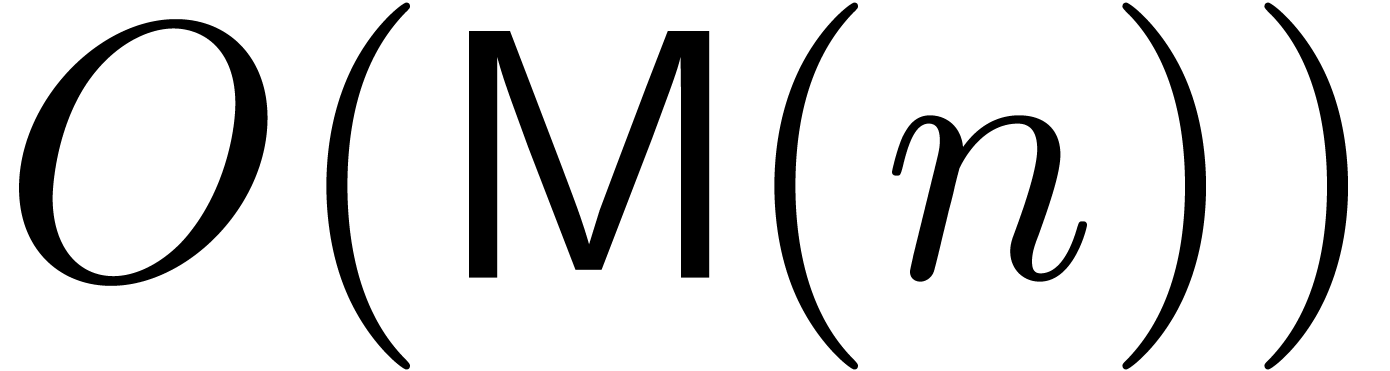 algorithms; see [BSS08] for an
overview. In positive characteristic
algorithms; see [BSS08] for an
overview. In positive characteristic  ,
right composition can also be performed in quasi-linear time
,
right composition can also be performed in quasi-linear time 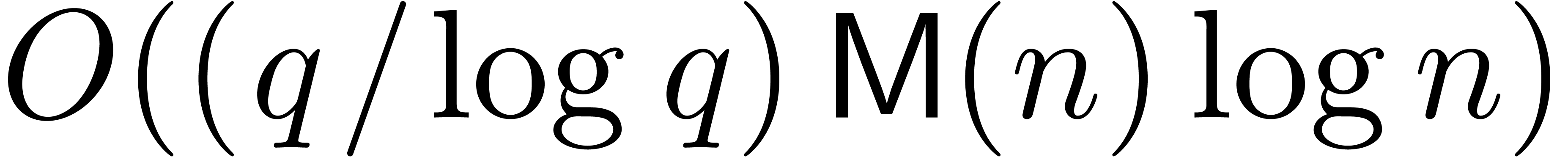 [Ber98].
[Ber98].
In this paper, we are interested in efficient algorithms when  is a ring of numbers, such as
is a ring of numbers, such as  ,
,  or a ring of floating
point numbers. In that case, we are interested in the bit complexity of
the composition, which means that we also have to take into account the
bit precision
or a ring of floating
point numbers. In that case, we are interested in the bit complexity of
the composition, which means that we also have to take into account the
bit precision  of the underlying integer
arithmetic. In particular, we will denote by
of the underlying integer
arithmetic. In particular, we will denote by 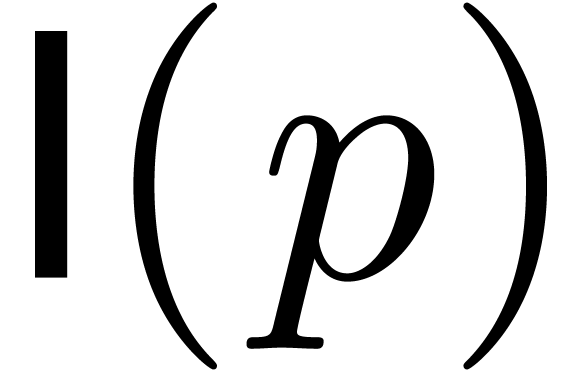 the
time needed for multiplying two
the
time needed for multiplying two 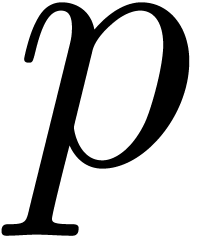 -bit
integers. We have
-bit
integers. We have 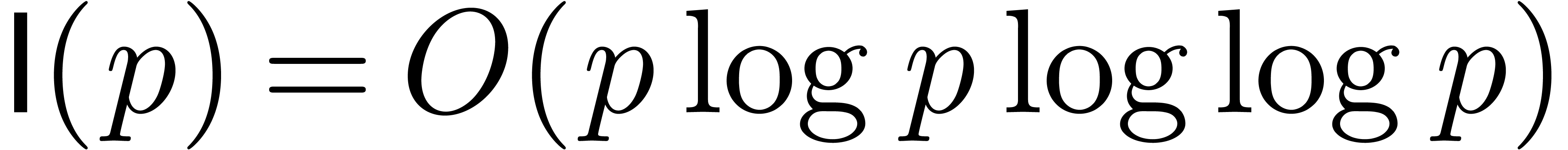 [SS71] and even
[SS71] and even
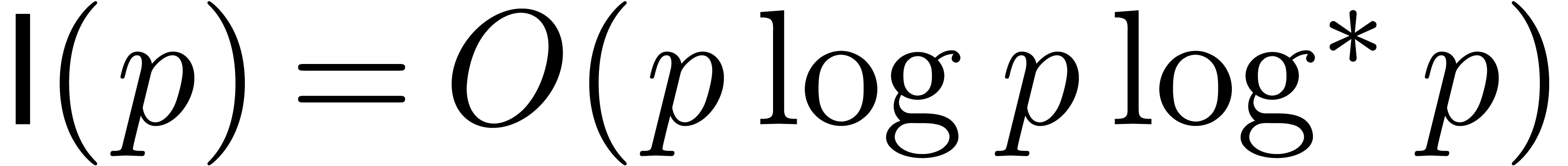 [Für07], where
[Für07], where 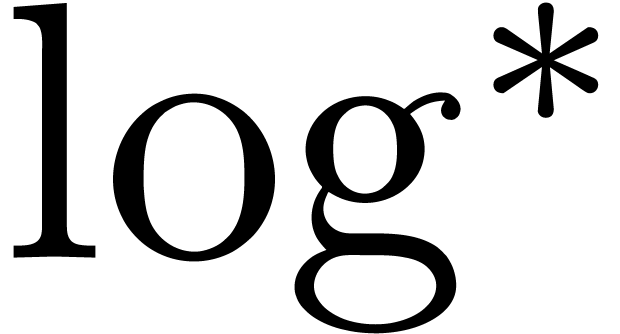 satisfies
satisfies 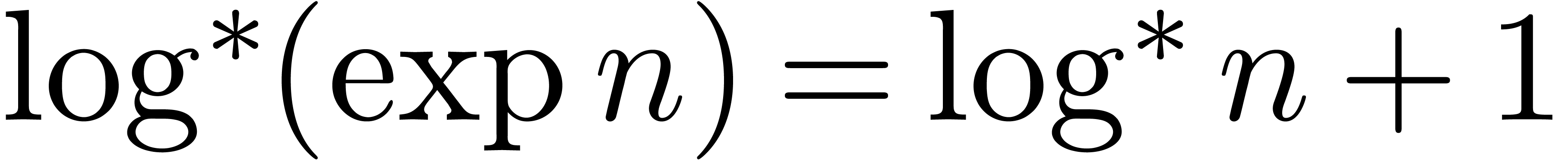 . If
all coefficients
. If
all coefficients 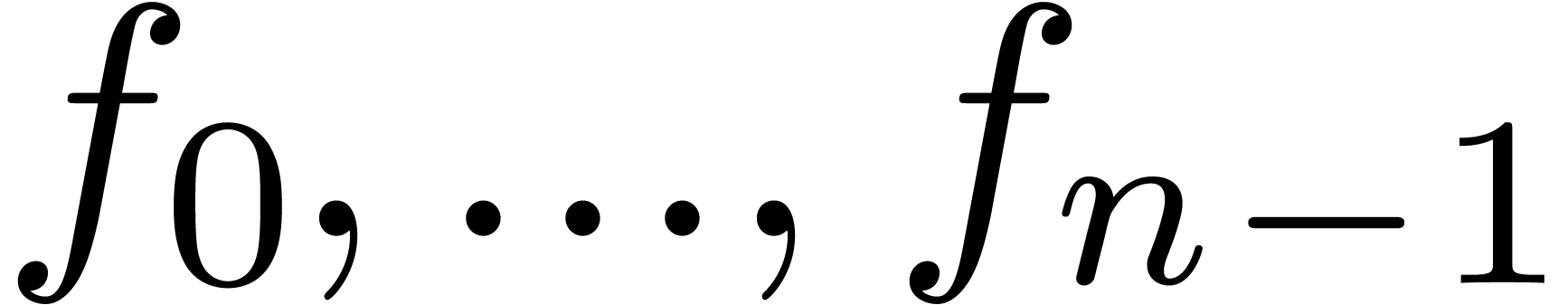 ,
,  and
and 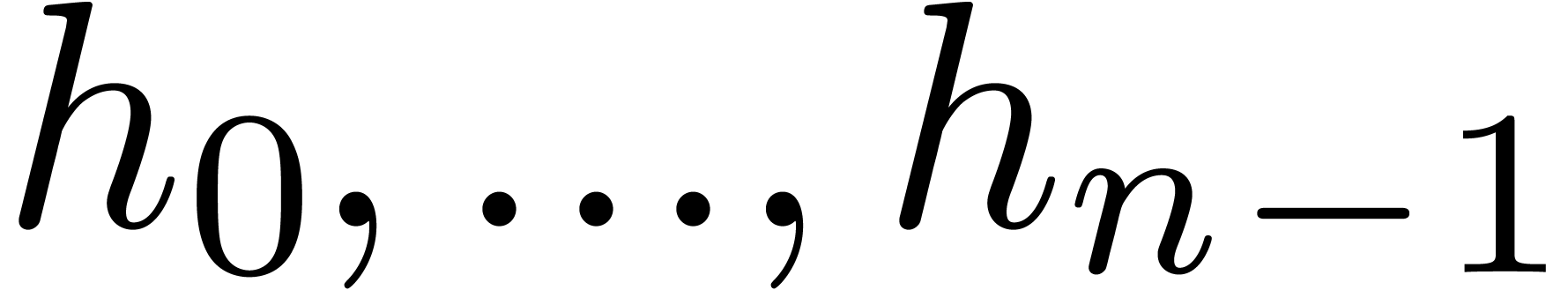 correspond to
correspond to  -bit numbers, then we will search for a
composition algorithm which runs in quasi-linear time
-bit numbers, then we will search for a
composition algorithm which runs in quasi-linear time 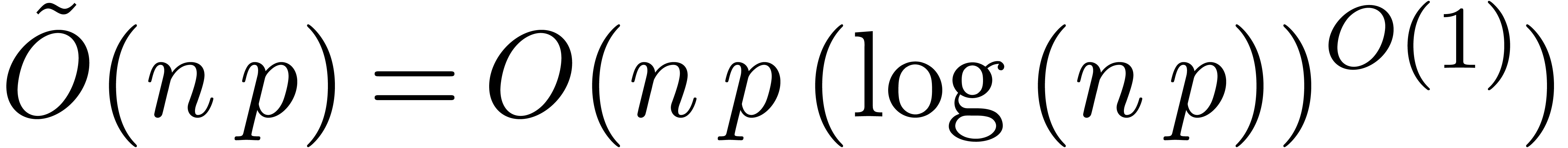 . Throughout the paper, we will assume that
. Throughout the paper, we will assume that
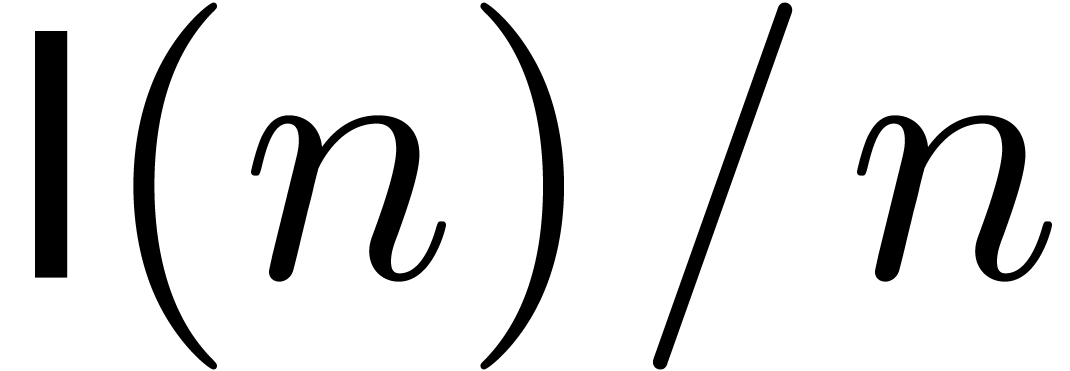 is increasing and
is increasing and  .
.
In section 2, we start by reviewing multiplication and
division of polynomials with numeric coefficients. Multiplication of two
polynomials of degrees 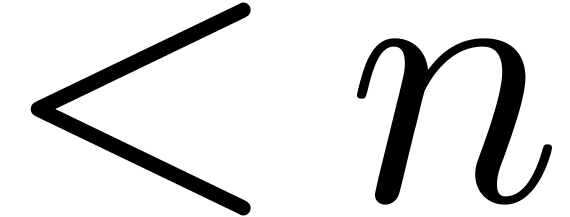 with
with 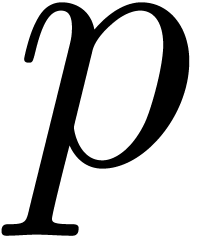 -bit coefficients can be done in time
-bit coefficients can be done in time 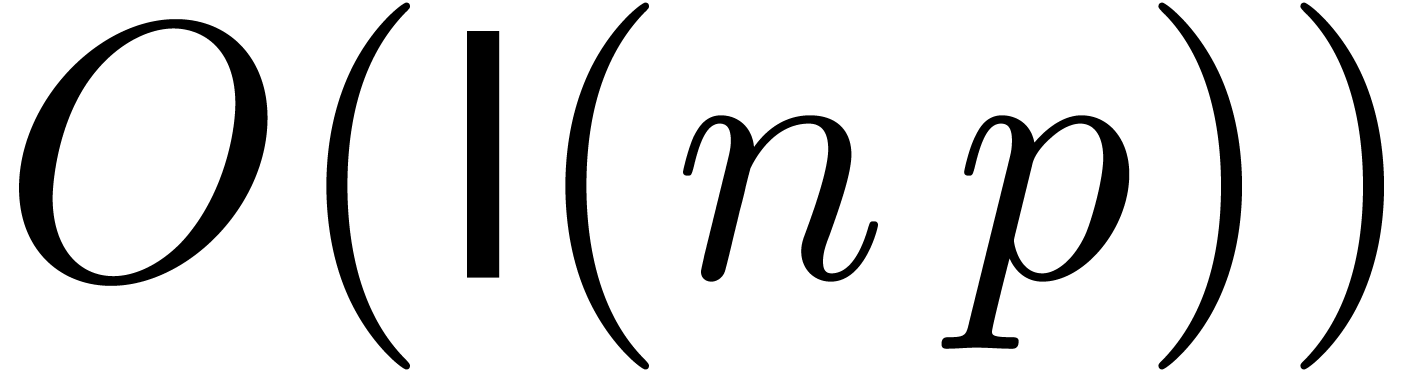 using Kronecker's substitution [Kro82].
Division essentially requires a higher complexity
using Kronecker's substitution [Kro82].
Division essentially requires a higher complexity 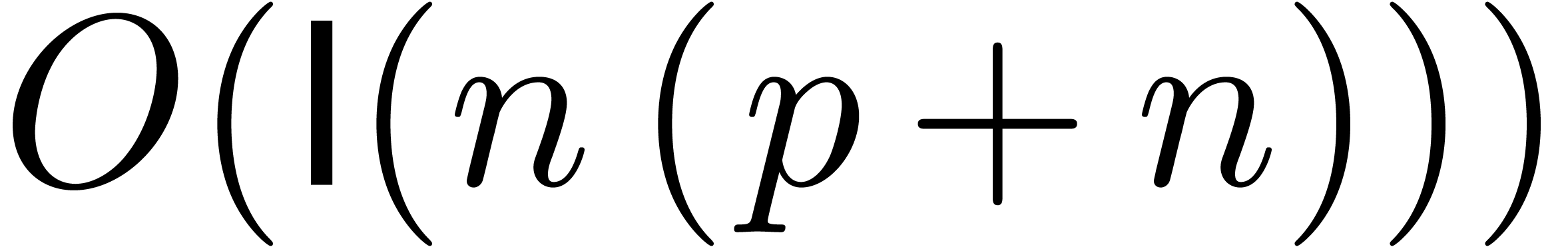 [Sch82], due to the fact that we may lose
[Sch82], due to the fact that we may lose 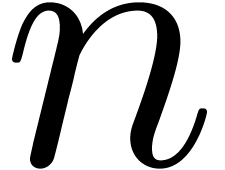 bits of precision when dividing by a polynomial of degree
bits of precision when dividing by a polynomial of degree 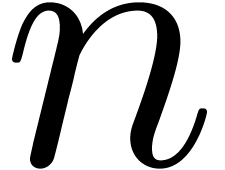 . Nevertheless, we will see that a best
possible complexity can be achieved in terms of the output precision.
. Nevertheless, we will see that a best
possible complexity can be achieved in terms of the output precision.
In section 3, we will study multi-point evaluation of a
polynomial 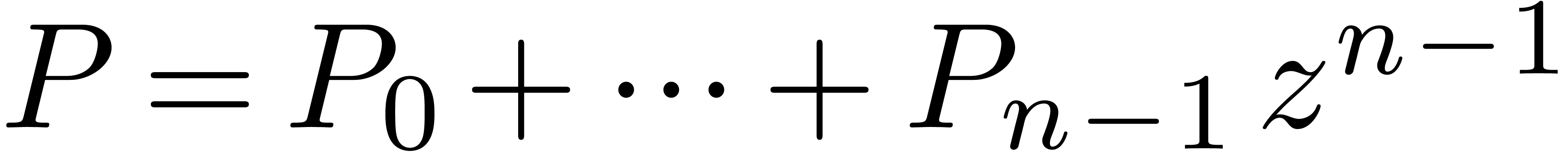 at
at 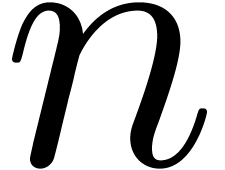 points
points
 in the case of numeric coefficients. Adapting
the classical binary splitting algorithm [AHU74] of time
complexity
in the case of numeric coefficients. Adapting
the classical binary splitting algorithm [AHU74] of time
complexity 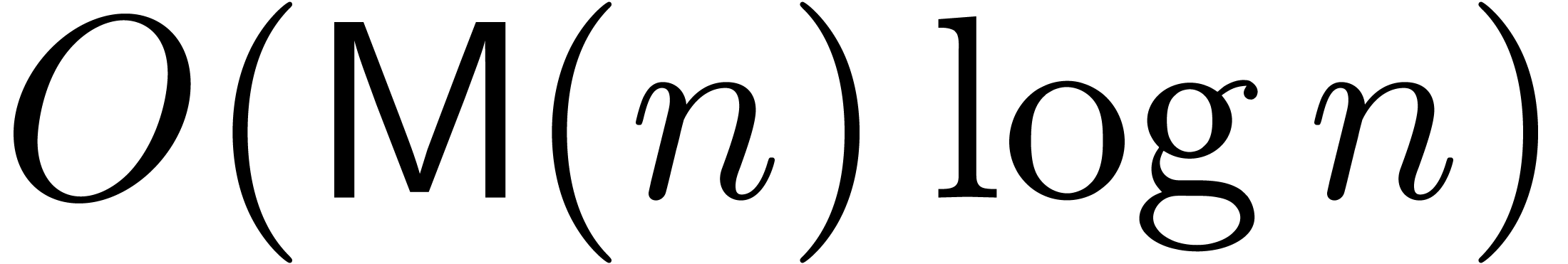 to the numeric context, we will prove
the complexity bound
to the numeric context, we will prove
the complexity bound 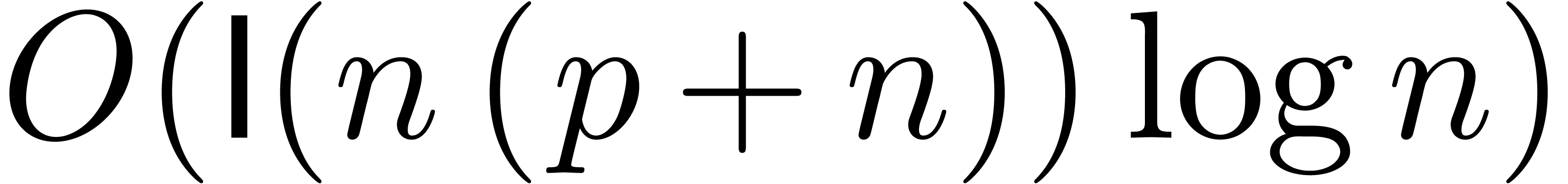 . In the
case when
. In the
case when 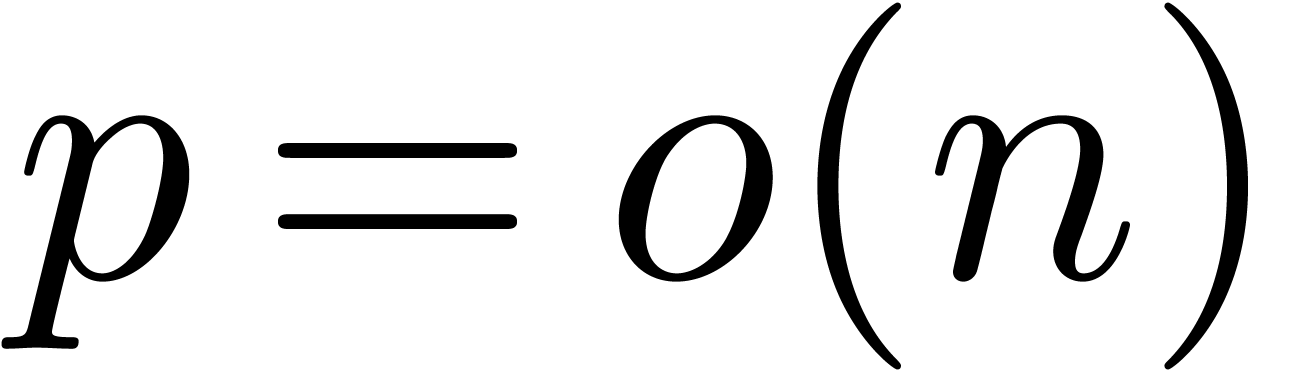 , this complexity
bound is again non-optimal in many cases. It would be nice if a bound of
the form
, this complexity
bound is again non-optimal in many cases. It would be nice if a bound of
the form 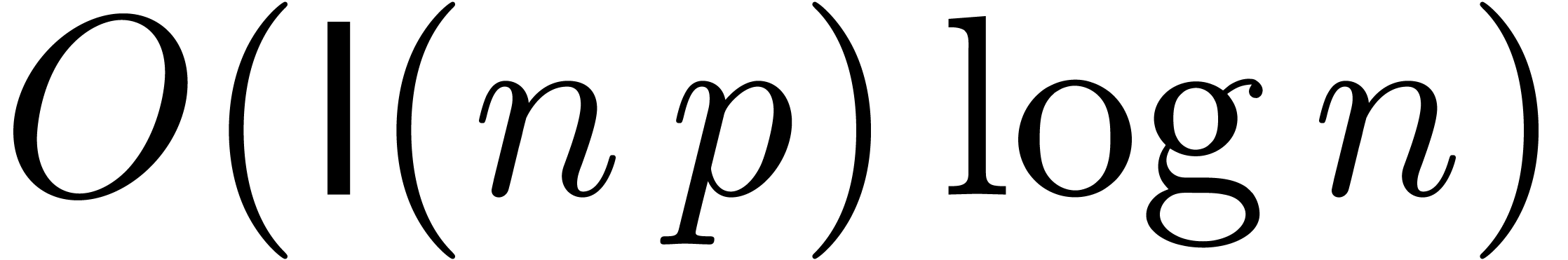 could be achieved and we will present
some ideas in this direction in section 3.2.
could be achieved and we will present
some ideas in this direction in section 3.2.
In section 4, we turn to the problem of numeric power
series composition. Under the assumptions 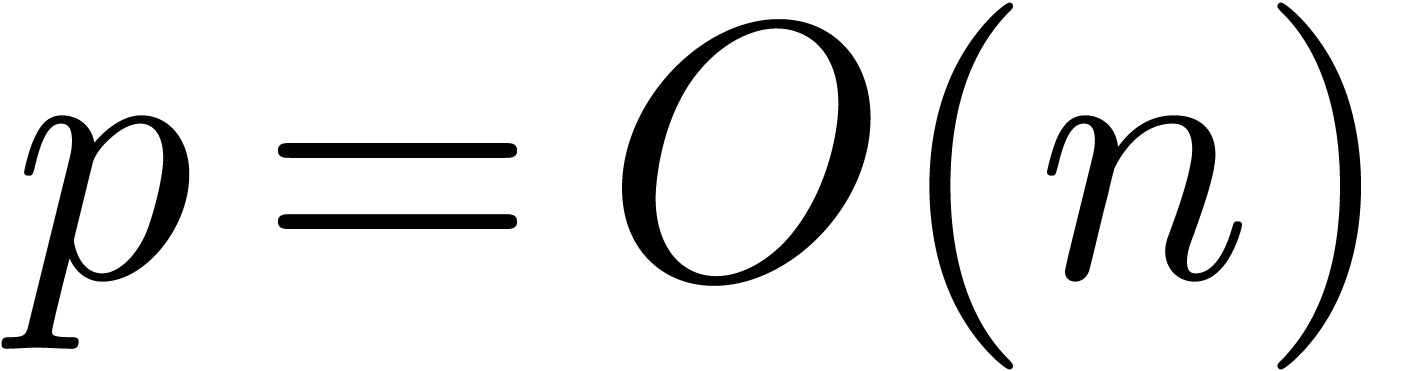 and
and
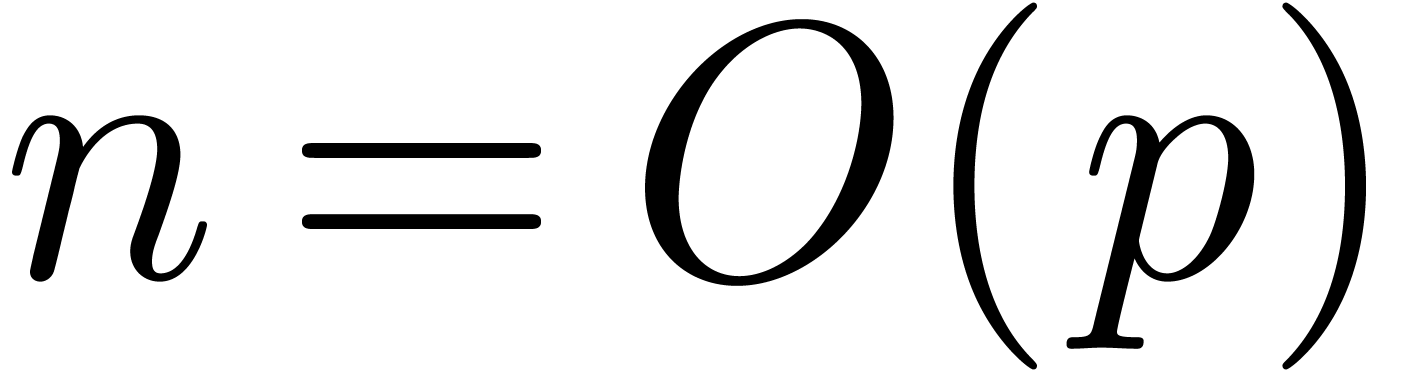 , we first show that the
computation of the first
, we first show that the
computation of the first  coefficients of a
convergent power series is essentially equivalent to its evaluation at
coefficients of a
convergent power series is essentially equivalent to its evaluation at
 equally spaced points on a given circle (this
fact was already used in [Sch82], although not stated as
explicitly). The composition problem can therefore be reduced to one
fast Fourier transform, one multi-point evaluation and one inverse
Fourier transform, leading to a complexity
equally spaced points on a given circle (this
fact was already used in [Sch82], although not stated as
explicitly). The composition problem can therefore be reduced to one
fast Fourier transform, one multi-point evaluation and one inverse
Fourier transform, leading to a complexity 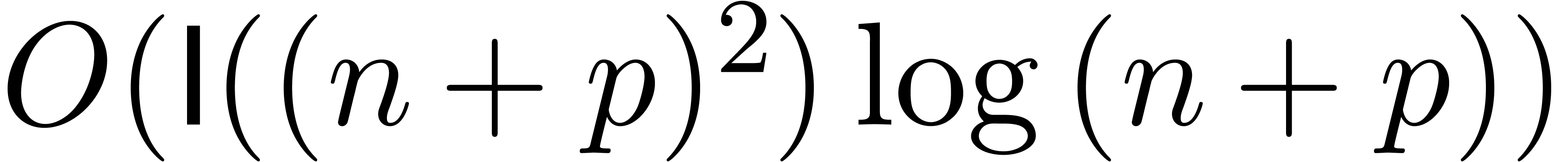 .
We first prove this result under certain normalization conditions for
floating point coefficients. We next extend the result to different
types of numeric coefficients (including integers and rationals) and
also consider non-convergent series. The good complexity of these
algorithms should not come as a full surprise: under the analogy
numbers
.
We first prove this result under certain normalization conditions for
floating point coefficients. We next extend the result to different
types of numeric coefficients (including integers and rationals) and
also consider non-convergent series. The good complexity of these
algorithms should not come as a full surprise: under the analogy
numbers series, it was already
known [BK77] how to compose multivariate power
series fast.
series, it was already
known [BK77] how to compose multivariate power
series fast.
In the last section, we conclude by giving relaxed versions [vdH02] of our composition algorithm. This allows for the resolution of functional equations for numeric power series, involving composition. Unfortunately, we did not yet achieve a quasi-linear bound, even though some progress has been made on the exponent. The special case of power series reversion may be reduced more directly to composition, using Newton's method [BK75].
Let  be a normed vector space. Given
be a normed vector space. Given 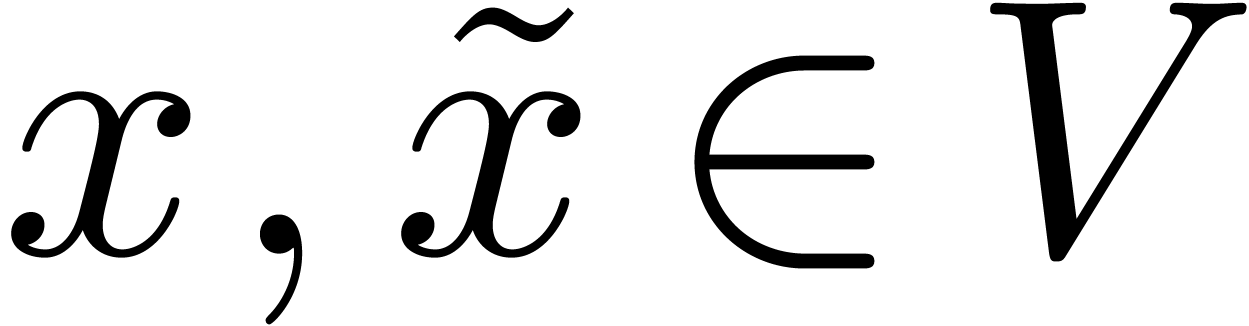 and
and  , we say
that
, we say
that 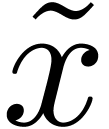 is an
is an  -approximation
of
-approximation
of  if
if 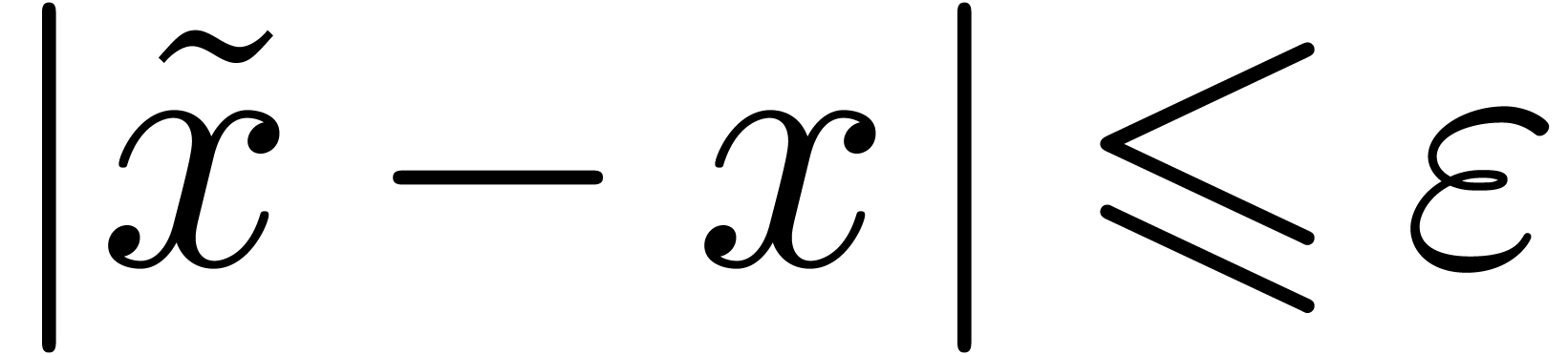 .
We will also say that
.
We will also say that 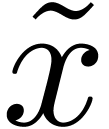 is an approximation of
is an approximation of
 with absolute error
with absolute error  or an absolute precision of
or an absolute precision of 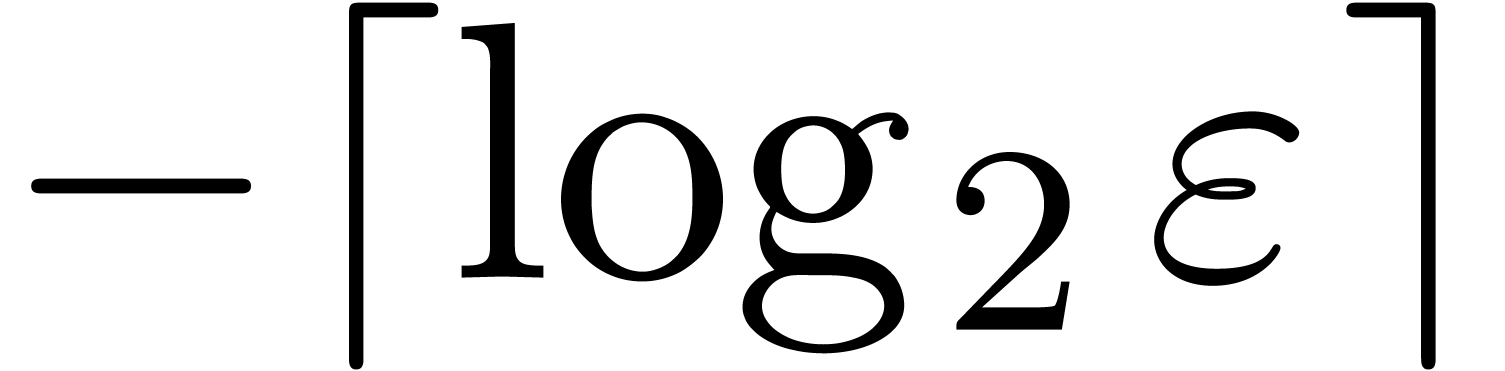 bits. For
polynomials
bits. For
polynomials  , we will use the
norm
, we will use the
norm 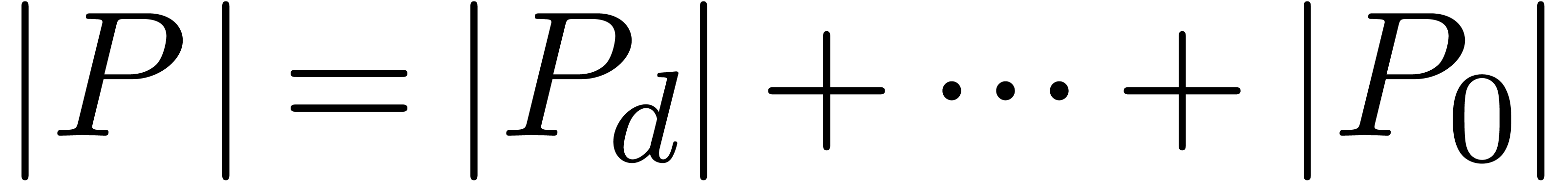 , and notice that
, and notice that 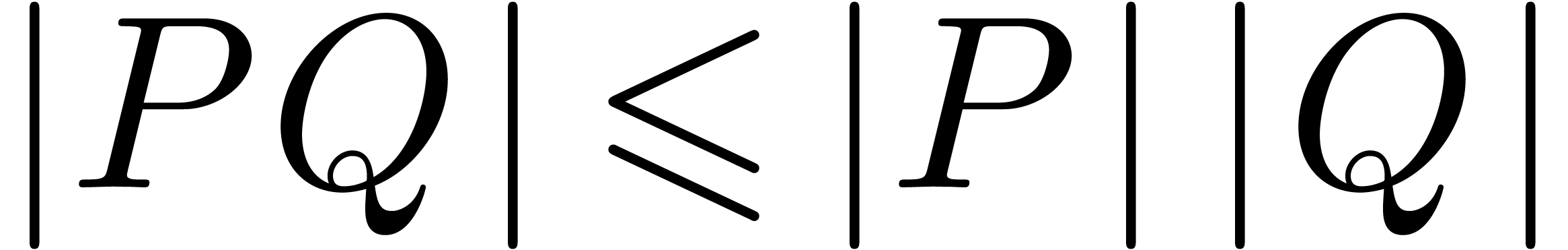 . For vectors
. For vectors 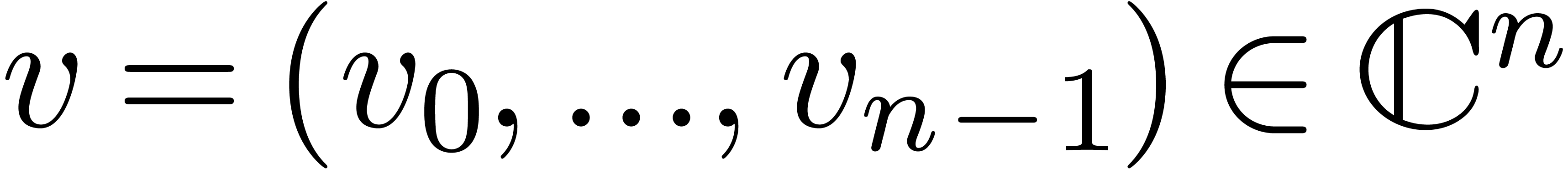 , we will use the norm
, we will use the norm 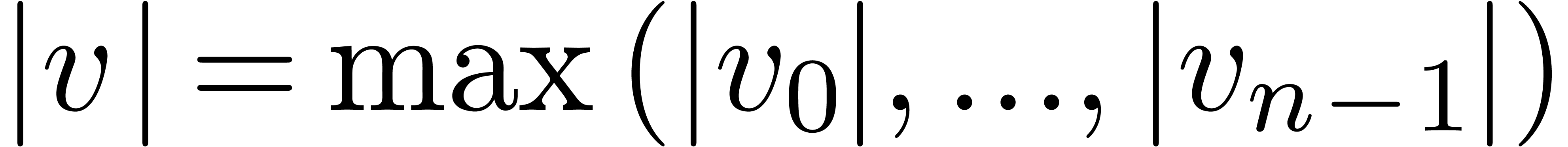 .
.
Given two polynomials 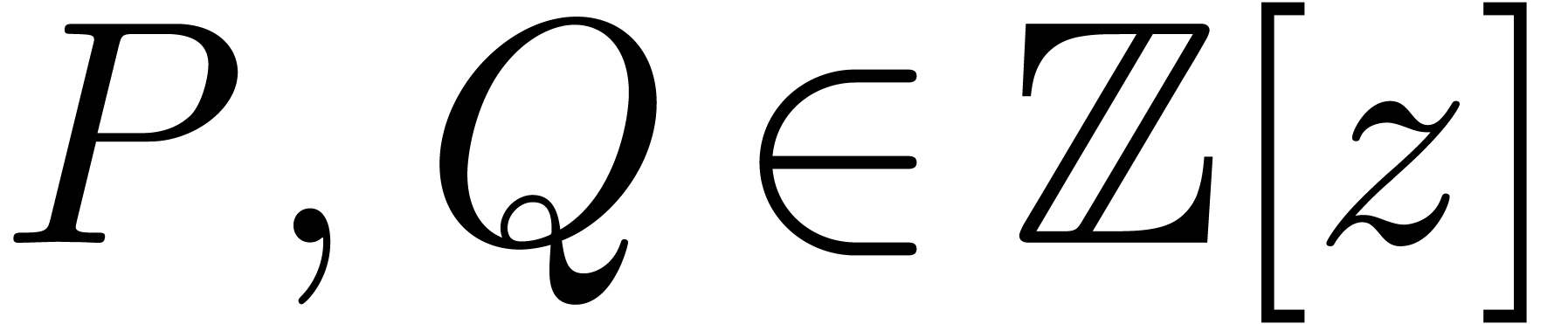 with
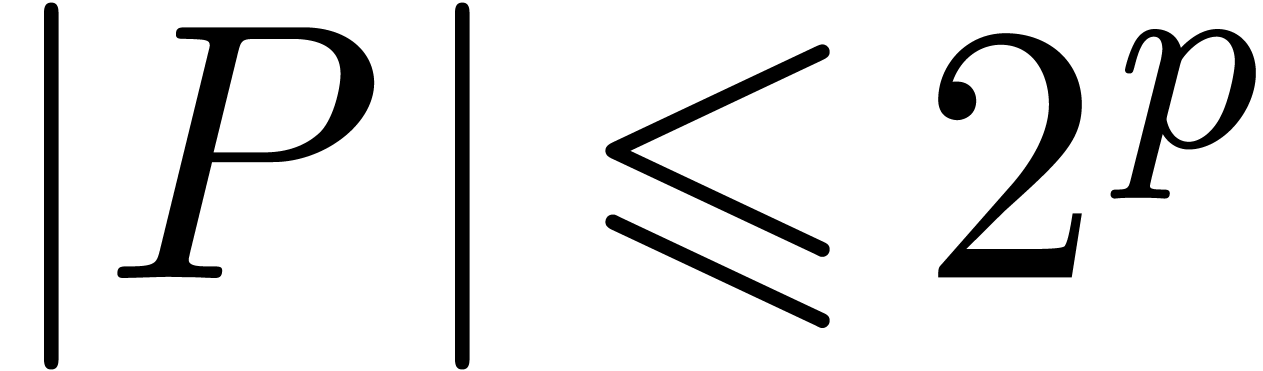
with 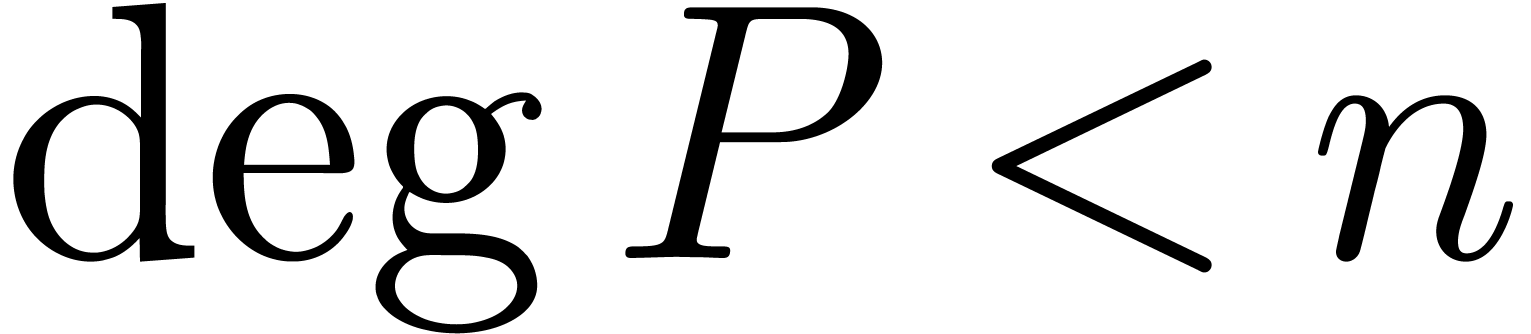 ,
,  ,
,
 and
and 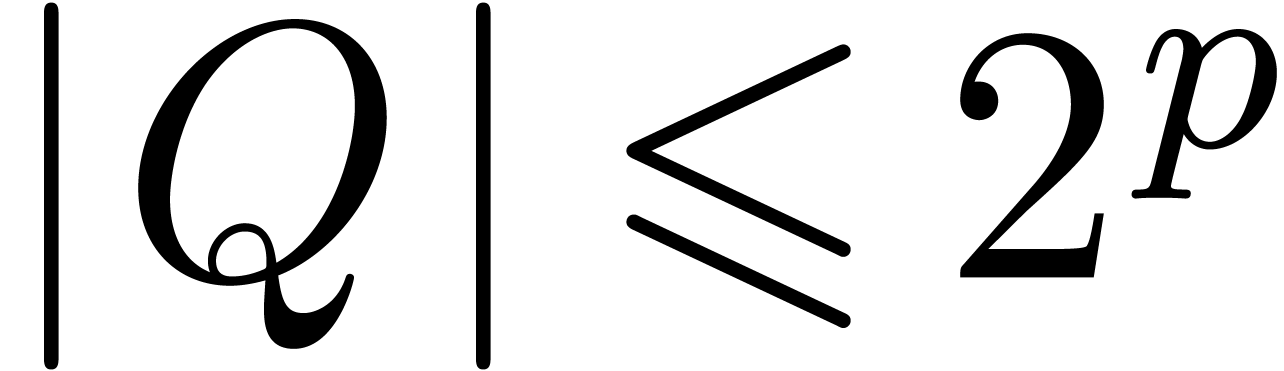 ,
take
,
take 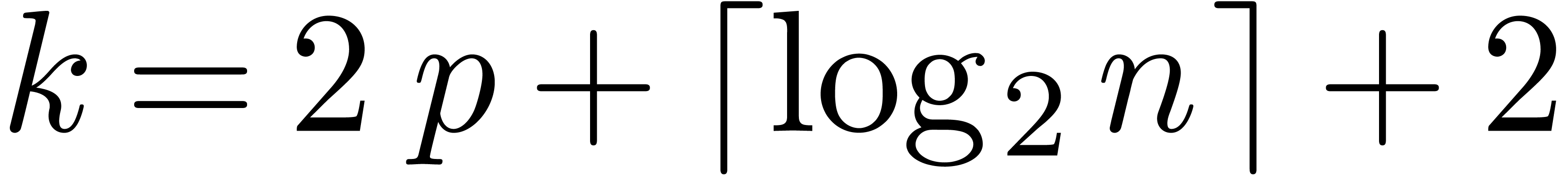 . Then the product
. Then the product 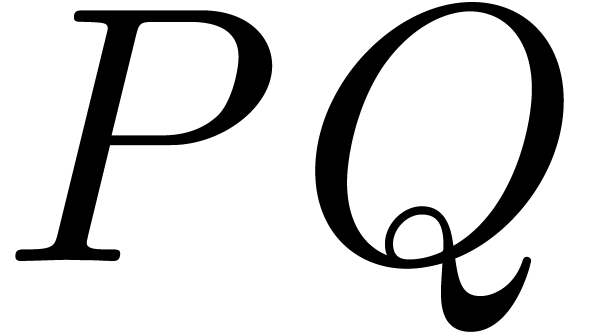 can be read off from the integer product
can be read off from the integer product 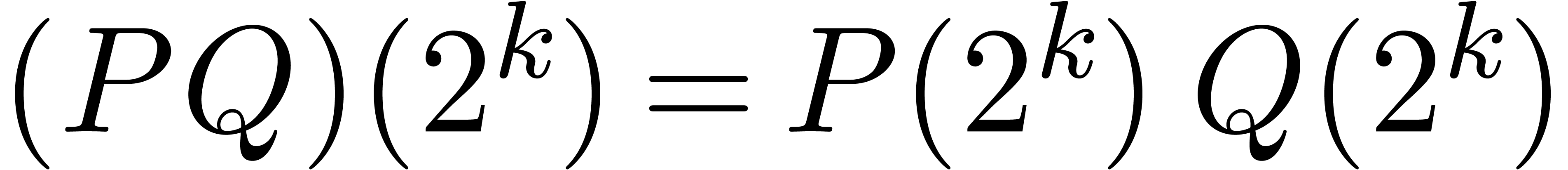 , since the coefficients of the result all fit
into
, since the coefficients of the result all fit
into 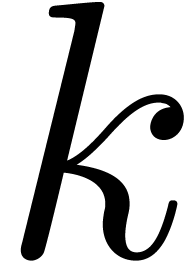 bits. This method is called Kronecker
multiplication [Kro82] and its cost is bounded by
bits. This method is called Kronecker
multiplication [Kro82] and its cost is bounded by 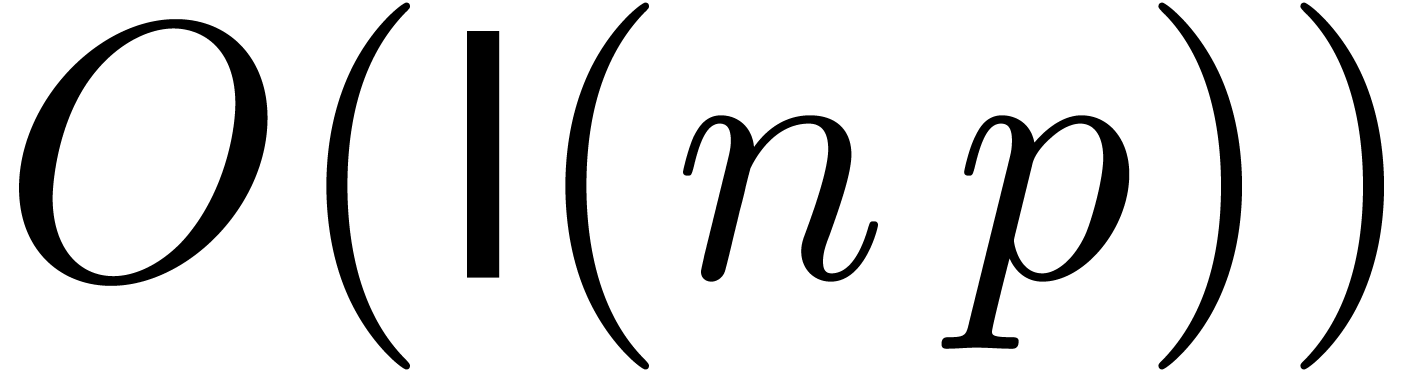 . Clearly, the method generalizes
to the case when
. Clearly, the method generalizes
to the case when 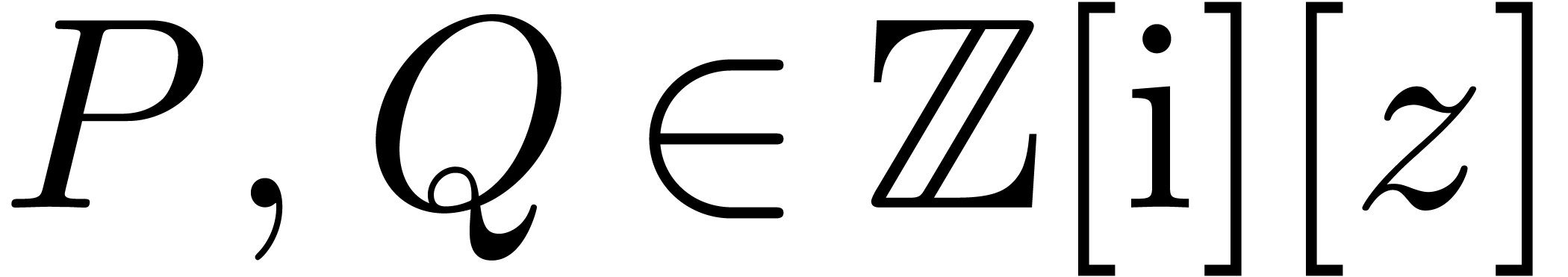 or
or  . A direct consequence for the computation with
floating point polynomials is the following:
. A direct consequence for the computation with
floating point polynomials is the following:
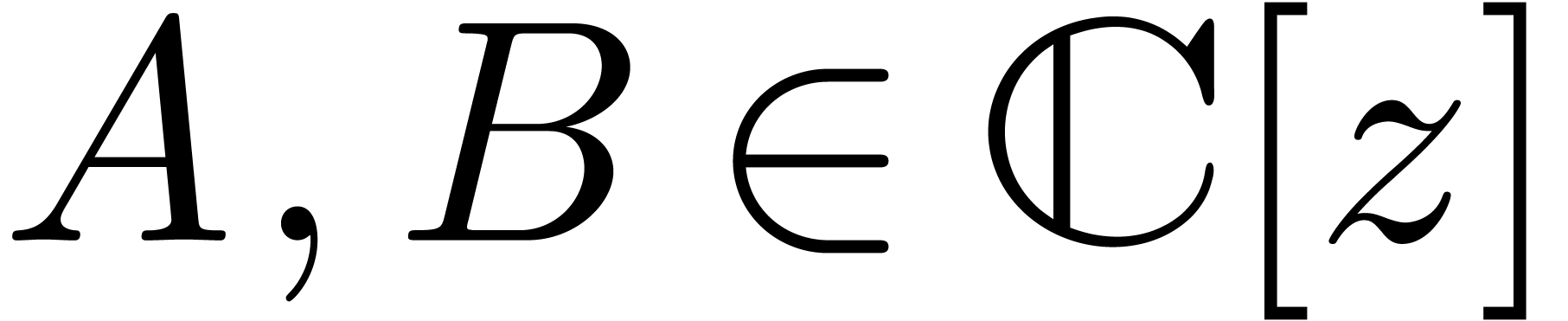 be two polynomials with
be two polynomials with  . Given
. Given 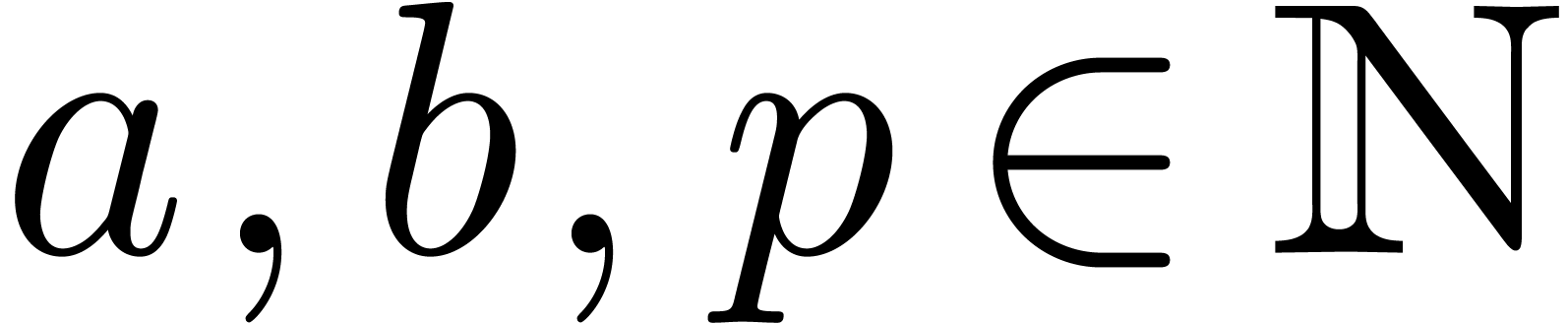 with
with 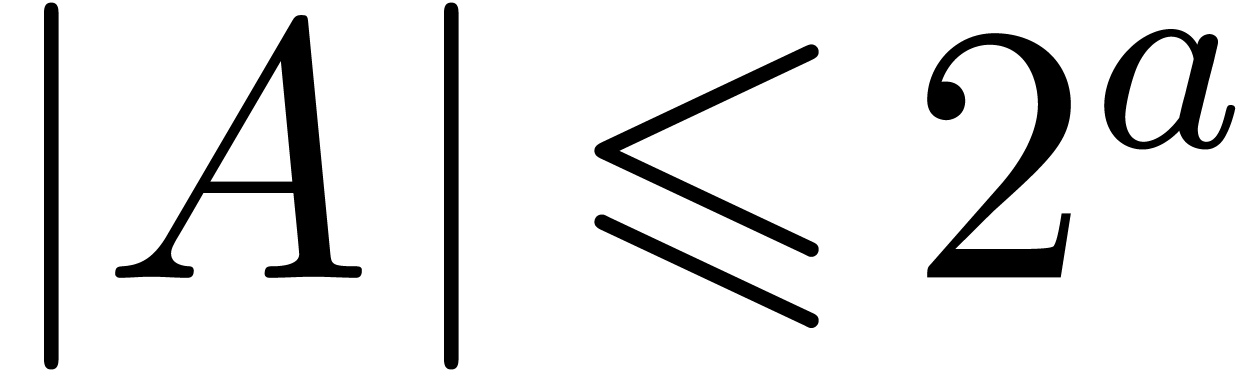 and
and 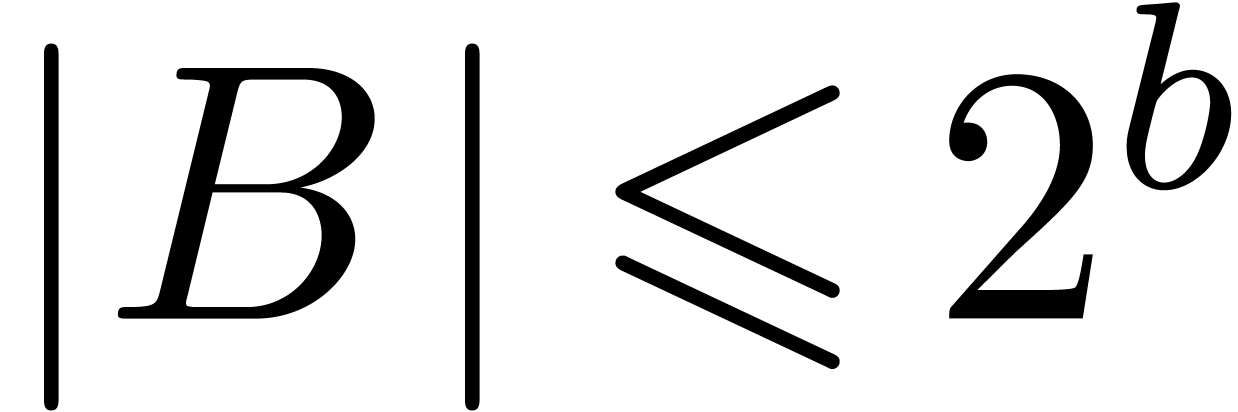 , we may
compute a
, we may
compute a  -approximation of
-approximation of
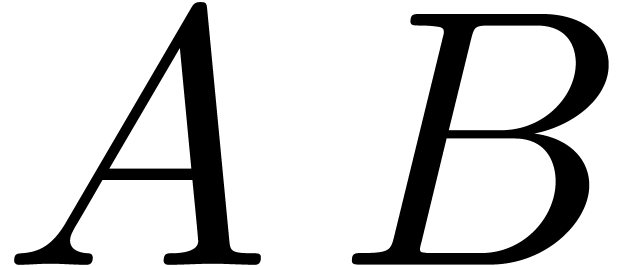 in time
in time 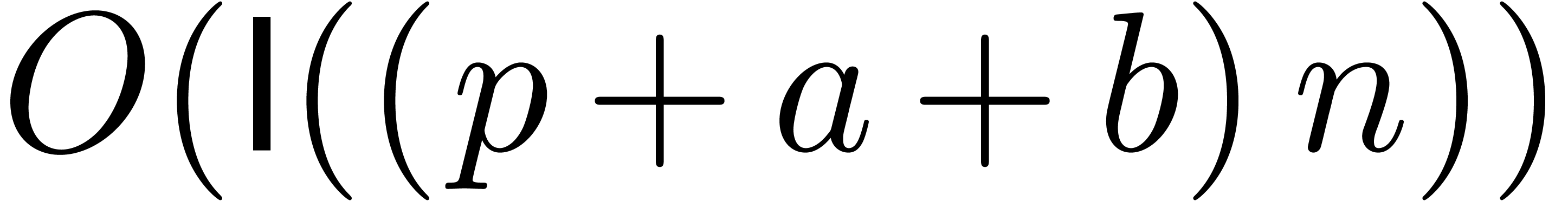 .
.
Proof. Let 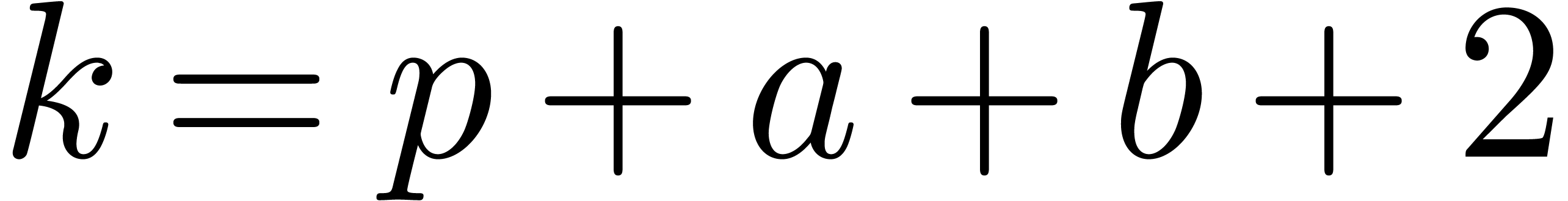 and consider
polynomials
and consider
polynomials 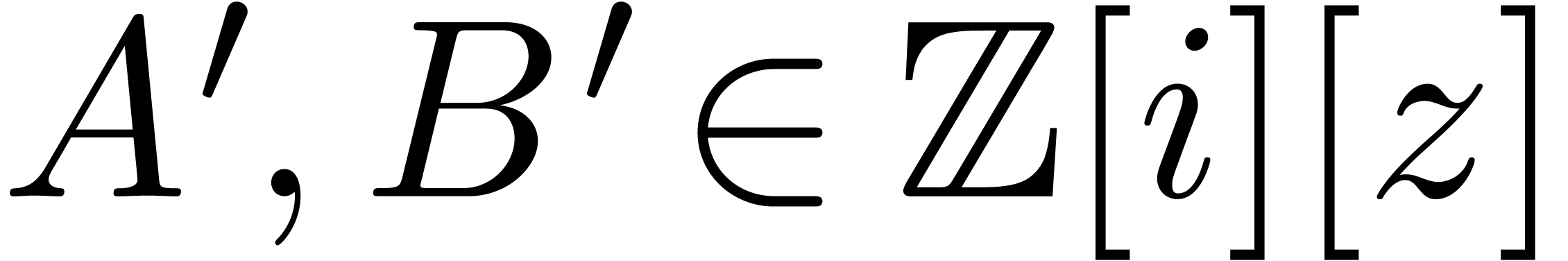 with
with
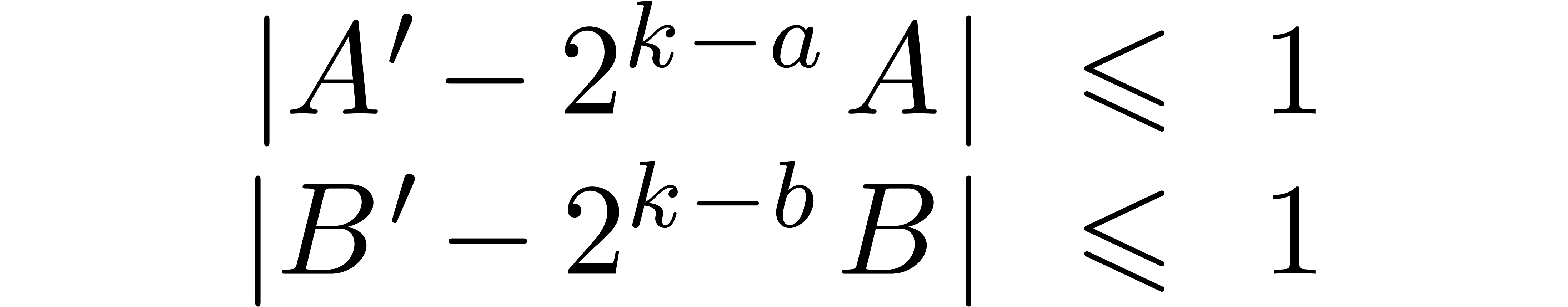
By assumption, the bit-sizes of the coefficients of 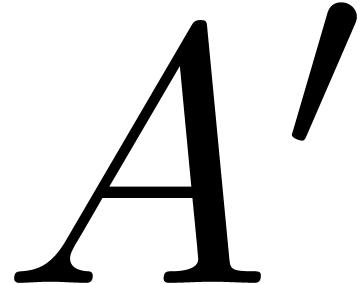 and
and 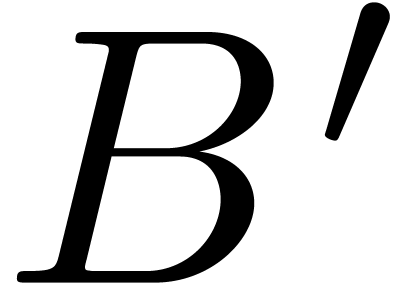 are bounded by
are bounded by  .
Therefore, we may compute the exact product
.
Therefore, we may compute the exact product 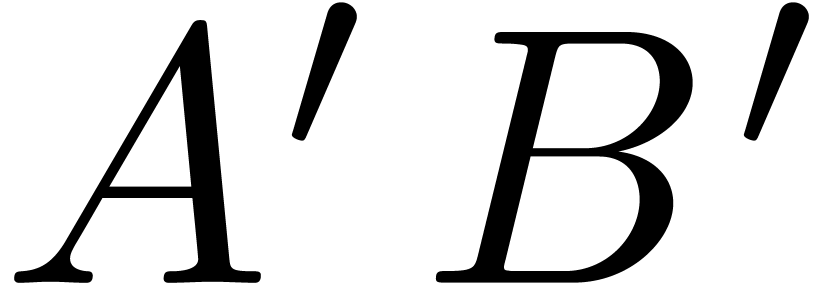 in
time
in
time 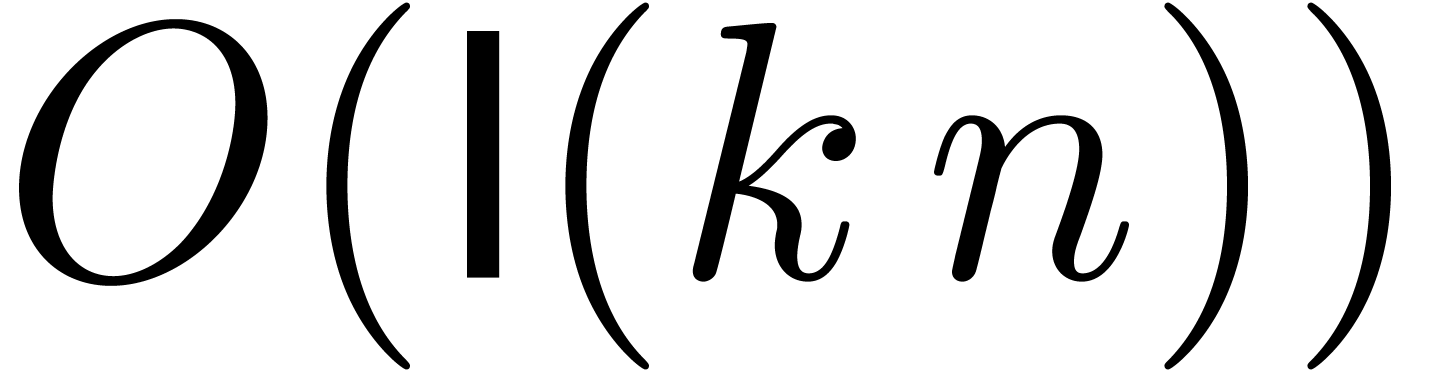 , using Kronecker
multiplication. We have
, using Kronecker
multiplication. We have
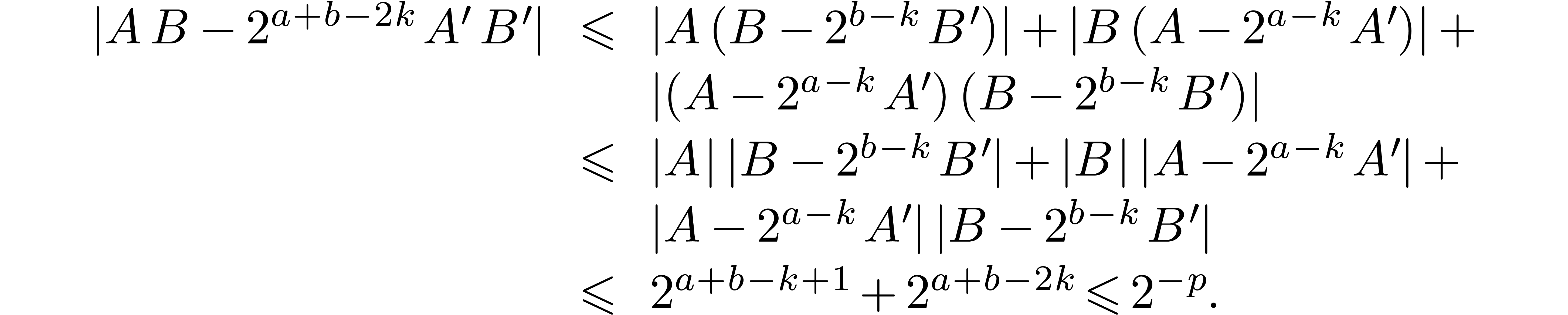
This proves that 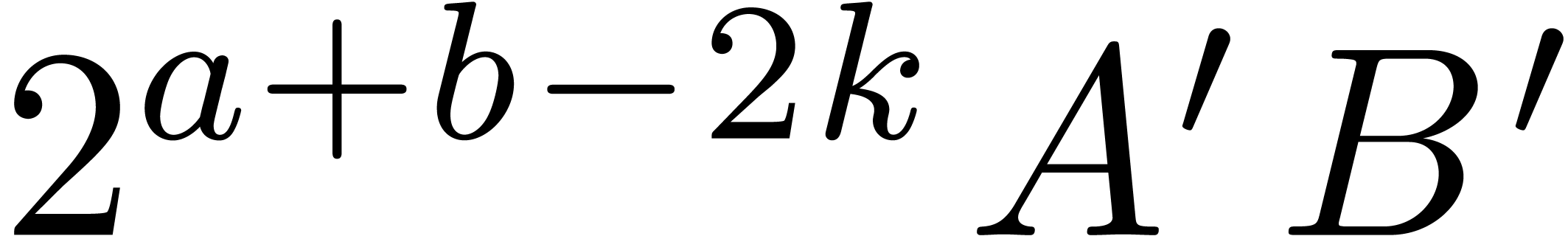 is a
is a  -approximation of
-approximation of  .
One may optionally truncate the mantissas of the coefficients of
.
One may optionally truncate the mantissas of the coefficients of 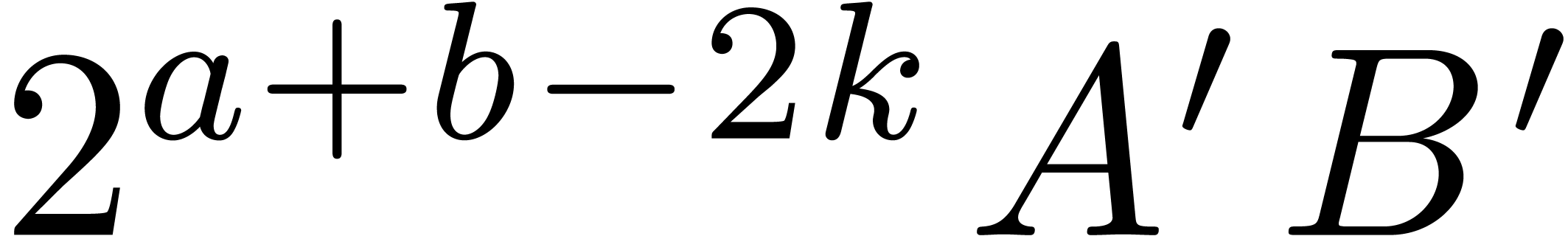 so as to fit into
so as to fit into  bits.
bits.
Remark
 be such that
be such that  for all
for all
 and
and

Let 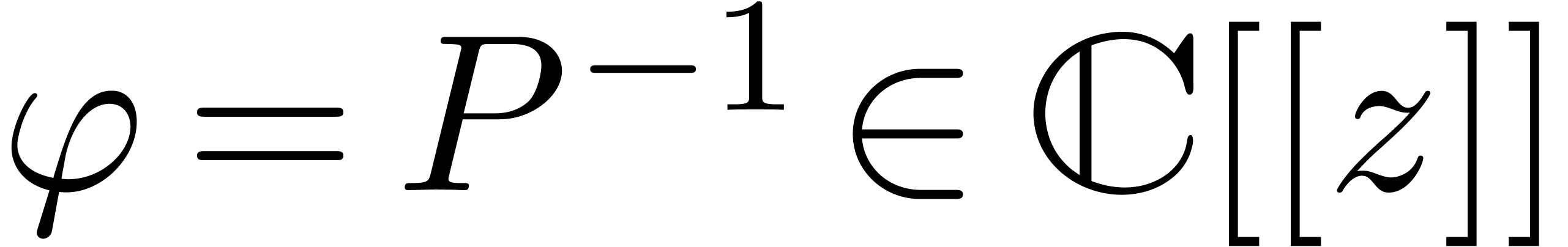 and
and  .
Let
.
Let 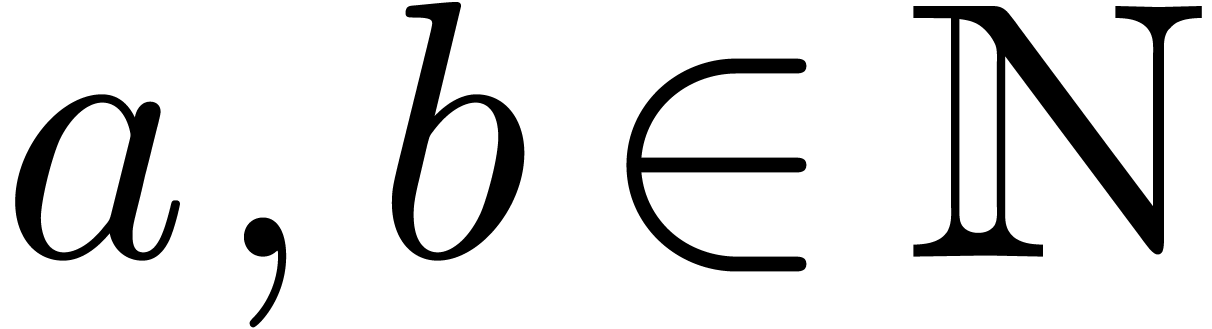 be such that
be such that 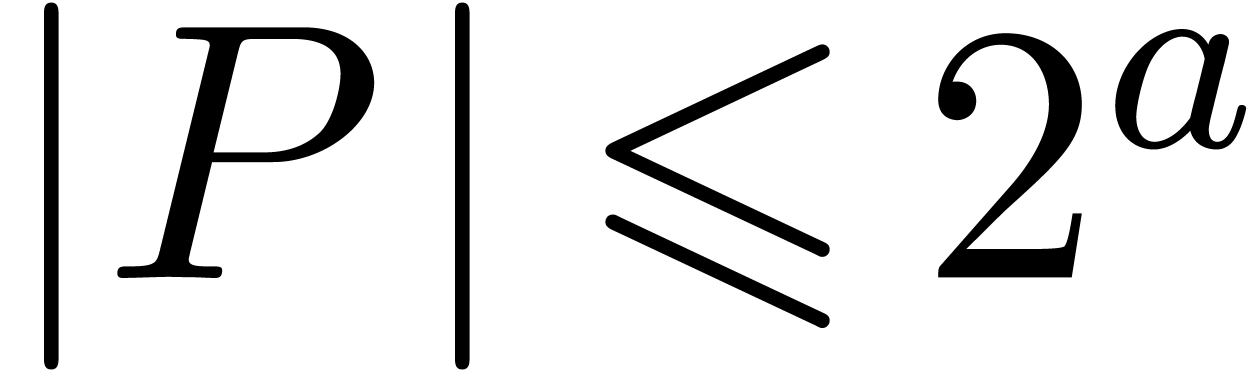 and
and
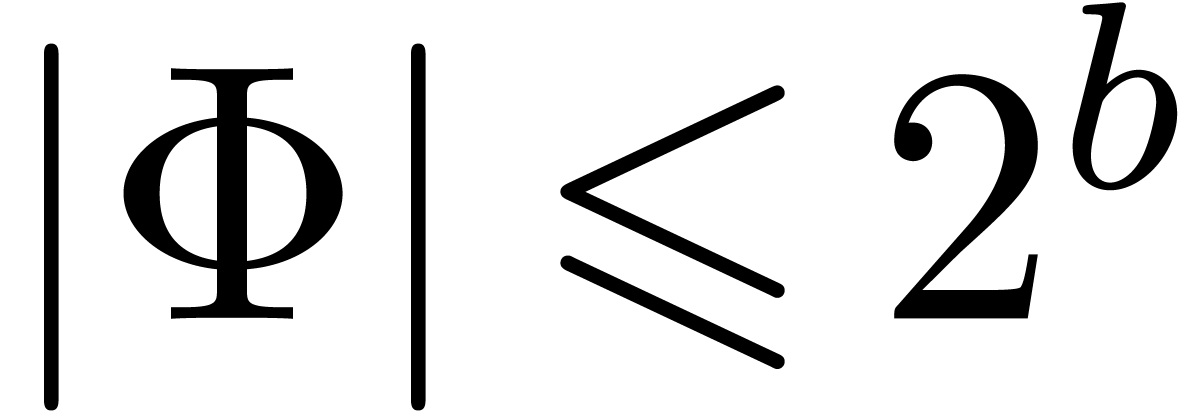 . Given
. Given 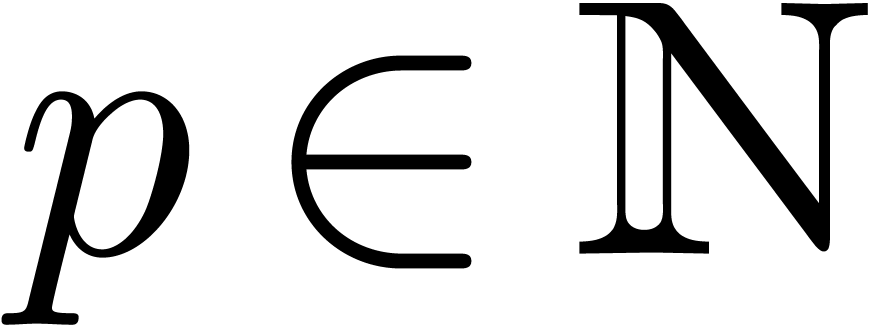 , we may compute a
, we may compute a  -approximation of
-approximation of  in time
in time
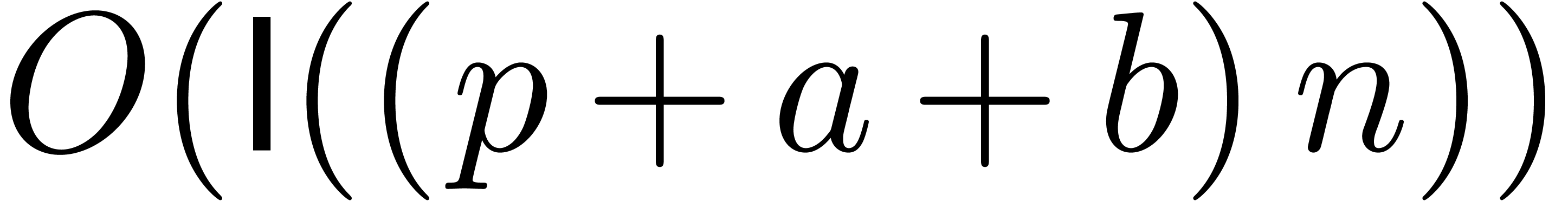 .
.
Proof. Assume that we are given an approximation
 of
of  .
Then we may compute a better approximation using the classical Newton
iteration
.
Then we may compute a better approximation using the classical Newton
iteration
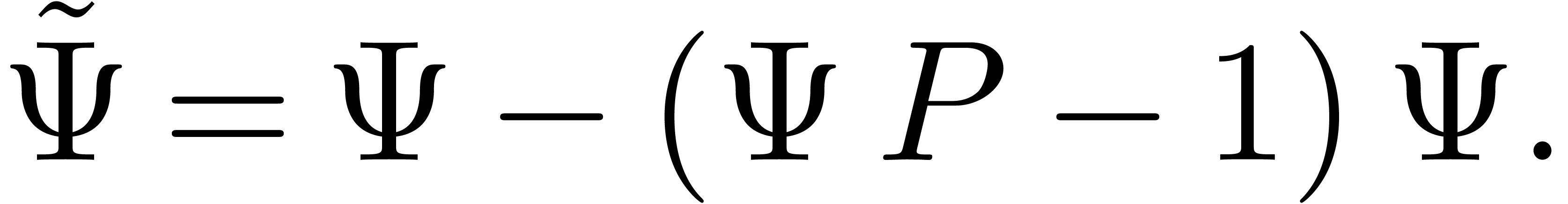 |
(1) |
If 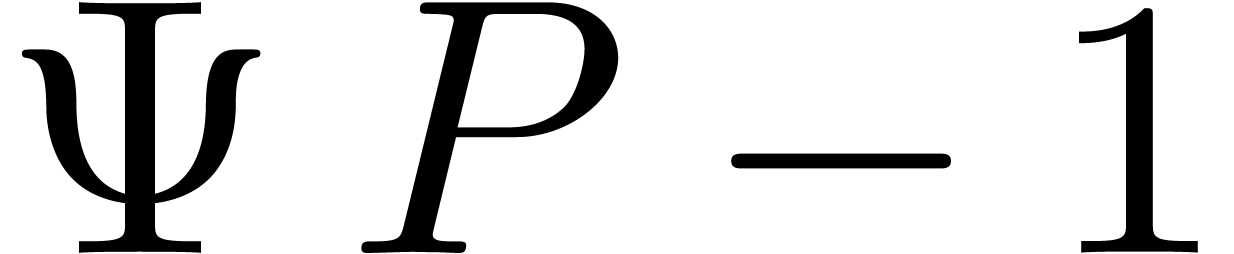 is “small”, then
is “small”, then
 |
(2) |
is about twice as “small”. We will apply the Newton
iteration for a polynomial  whose first
whose first 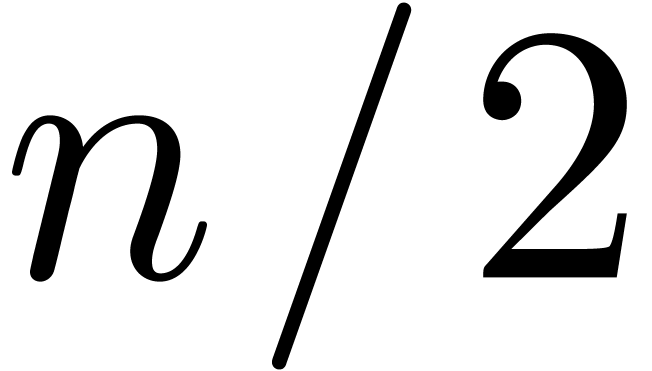 coefficients are good approximations of
coefficients are good approximations of  and the remaining coefficients less good approximations.
and the remaining coefficients less good approximations.
Given a polynomial 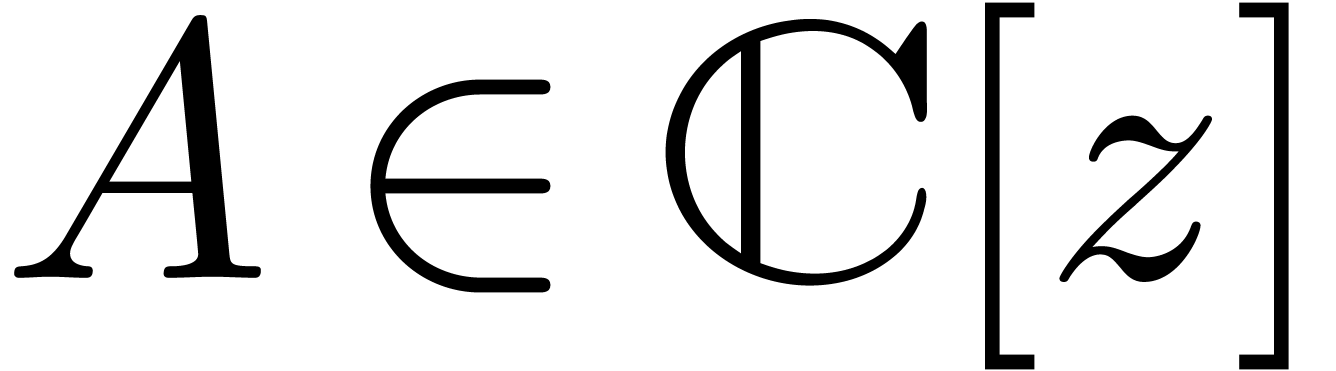 , we write
, we write
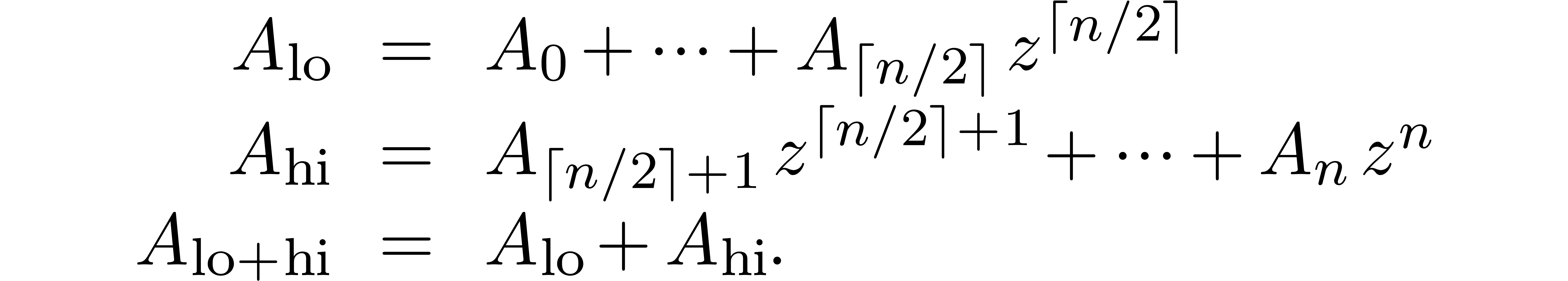
Assume that 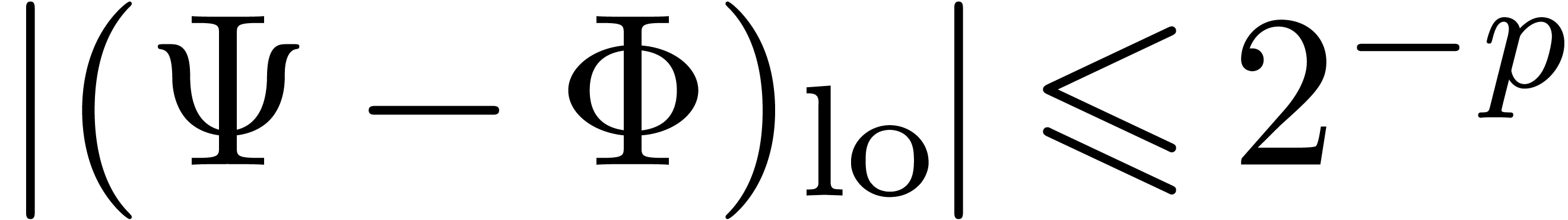 and
and 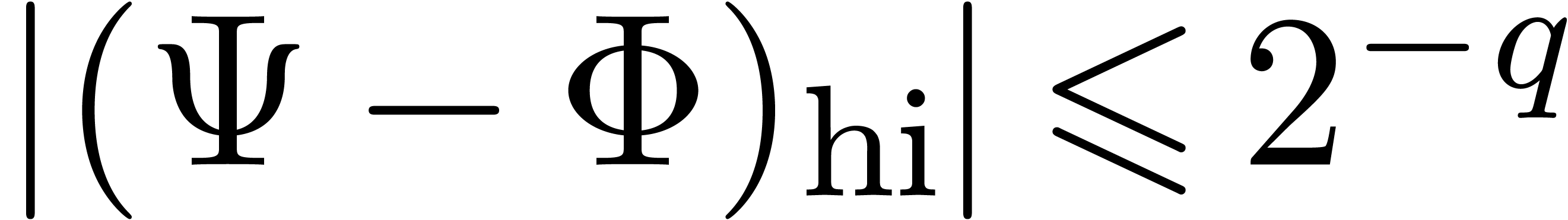 ,
with
,
with 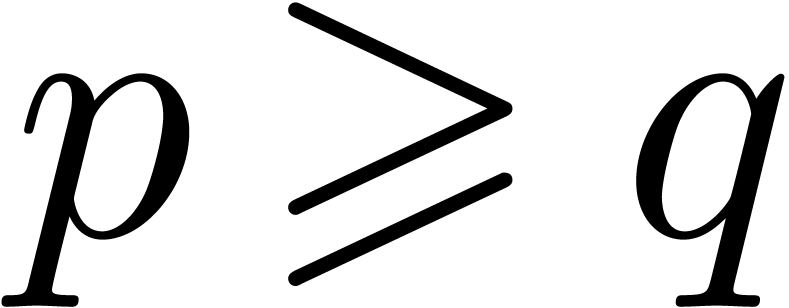 . Setting
. Setting 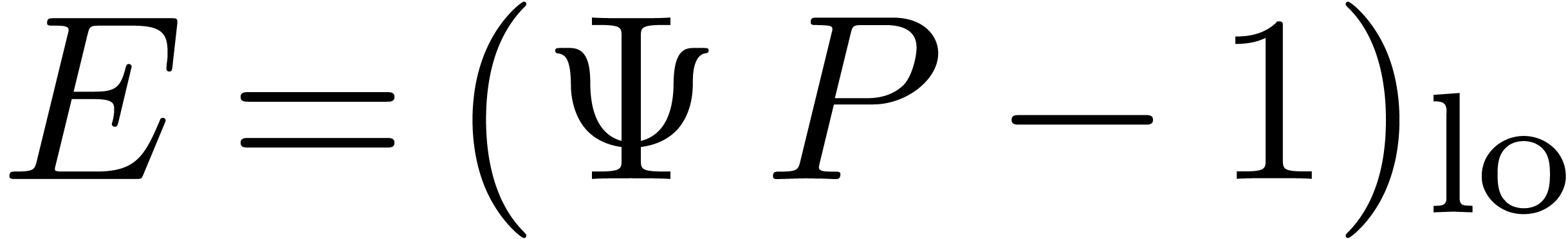 and
and 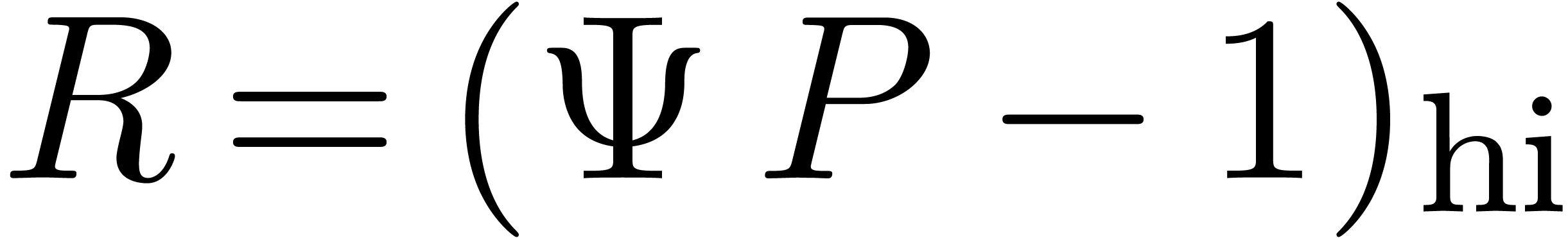 , we have
, we have
The relation (2) yields
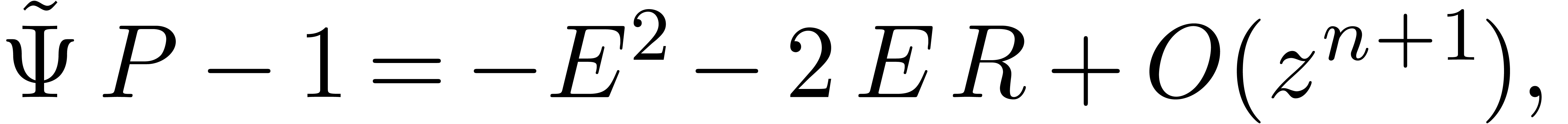
whence
When starting with 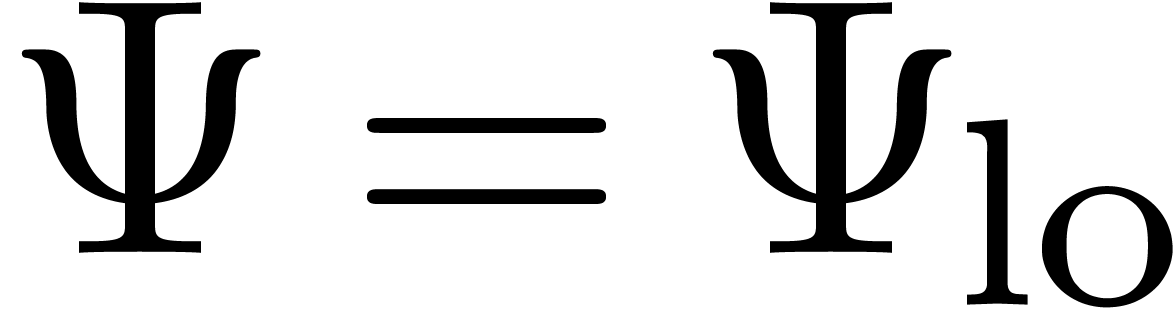 , we may
take
, we may
take 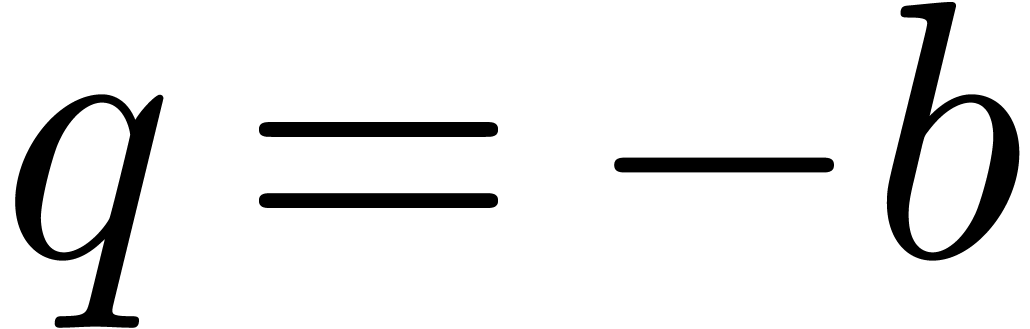 . If
. If 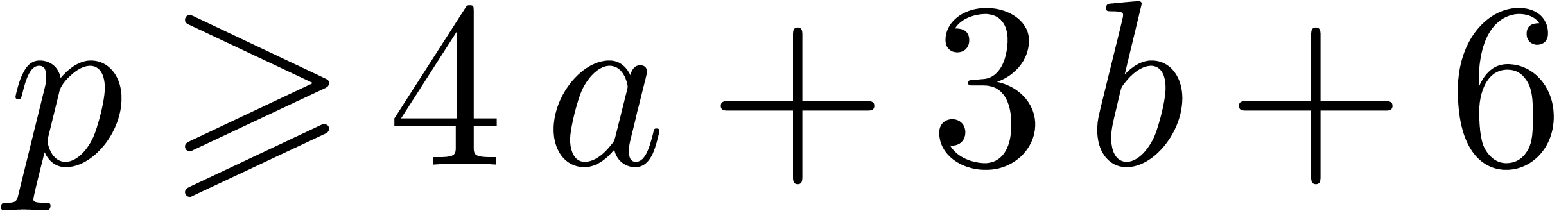 is sufficiently large, then one Newton iteration yields
is sufficiently large, then one Newton iteration yields  . Applying the Newton iteration once more for
. Applying the Newton iteration once more for
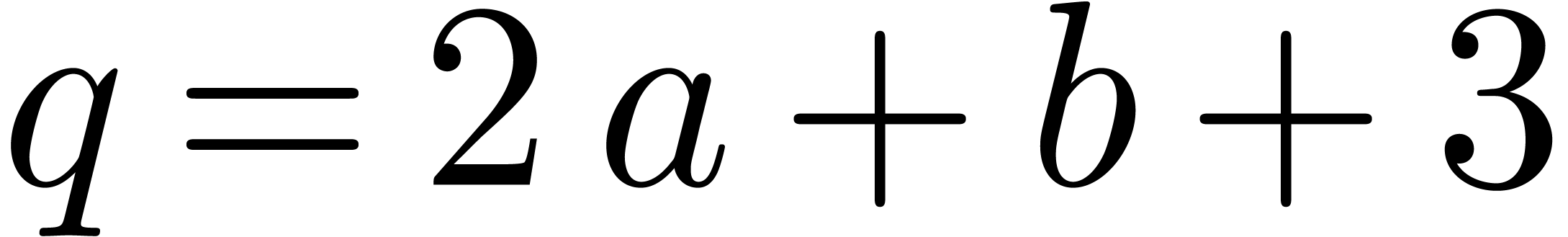 , we obtain
, we obtain 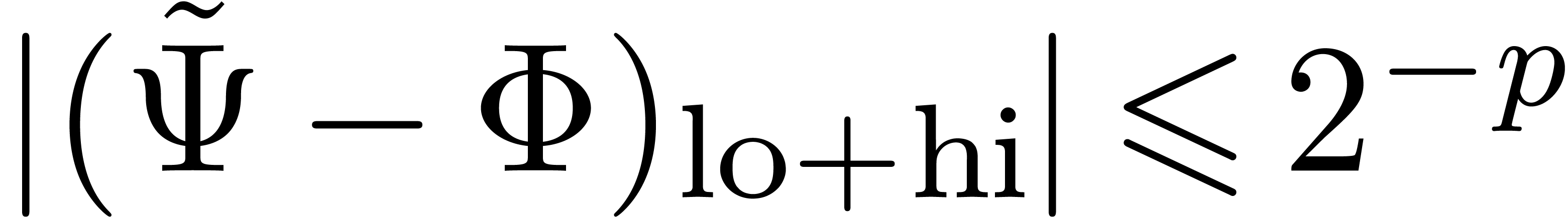 . In view of lemma 1 and the
assumption
. In view of lemma 1 and the
assumption 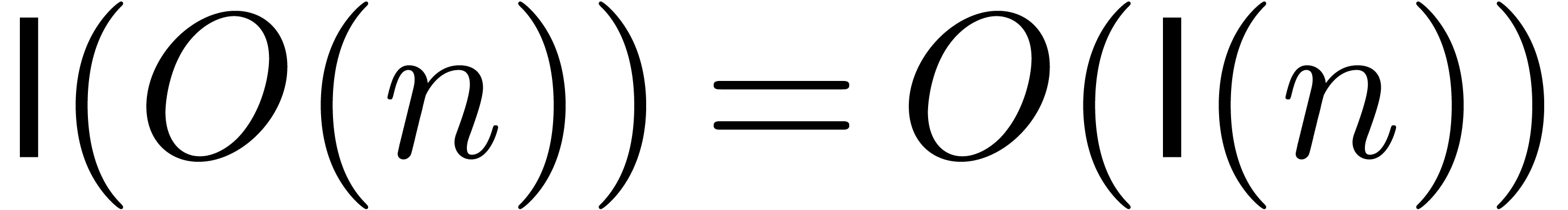 , the cost of two
such Newton iterations is bounded by
, the cost of two
such Newton iterations is bounded by 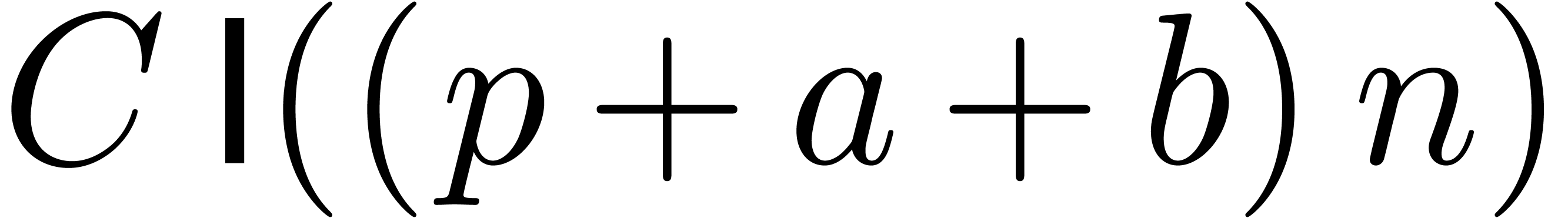 for a
suitable constant
for a
suitable constant  .
.
We are now in a position to prove the lemma. Since an increase of 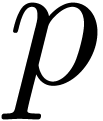 by
by 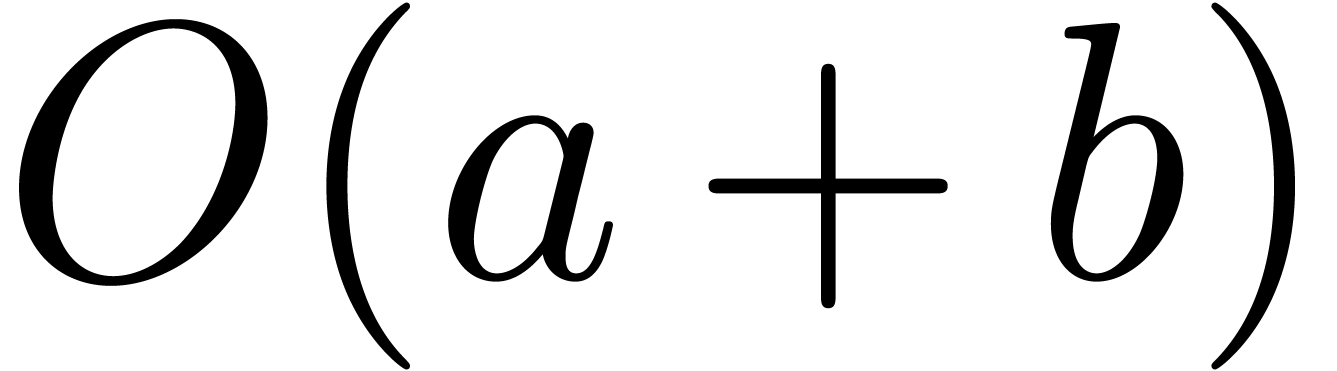 leaves the desired
complexity bound unaltered, we may assume without loss of generality
that
leaves the desired
complexity bound unaltered, we may assume without loss of generality
that 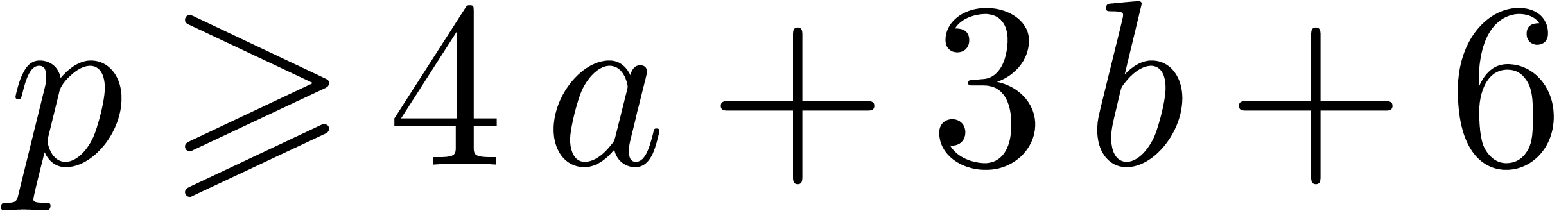 . Then the cost
. Then the cost 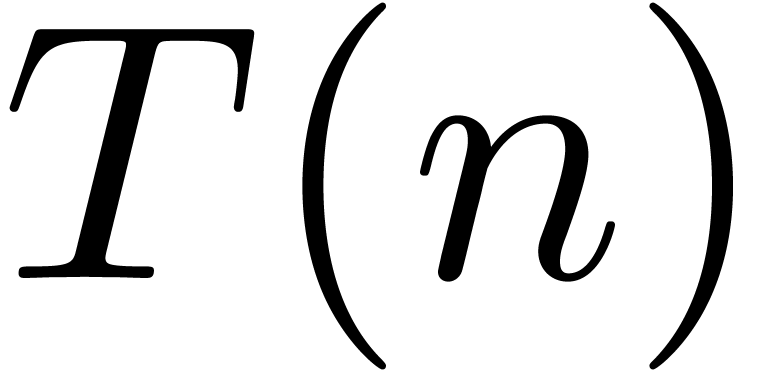 of the inversion at order
of the inversion at order 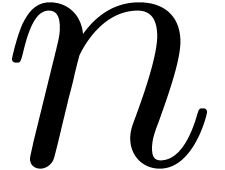 satisfies
satisfies 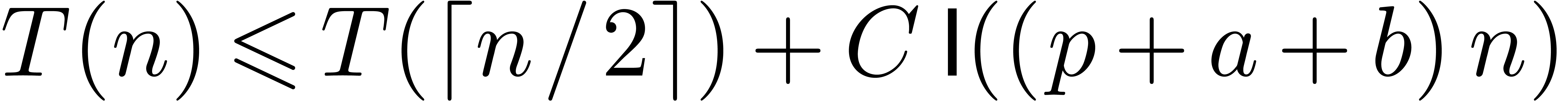 . We conclude that
. We conclude that
 .
.
Remark 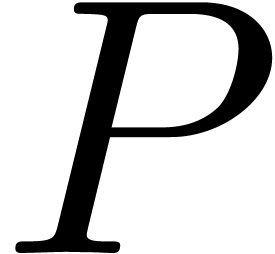 is given, then a constant
is given, then a constant  for
the bound
for
the bound 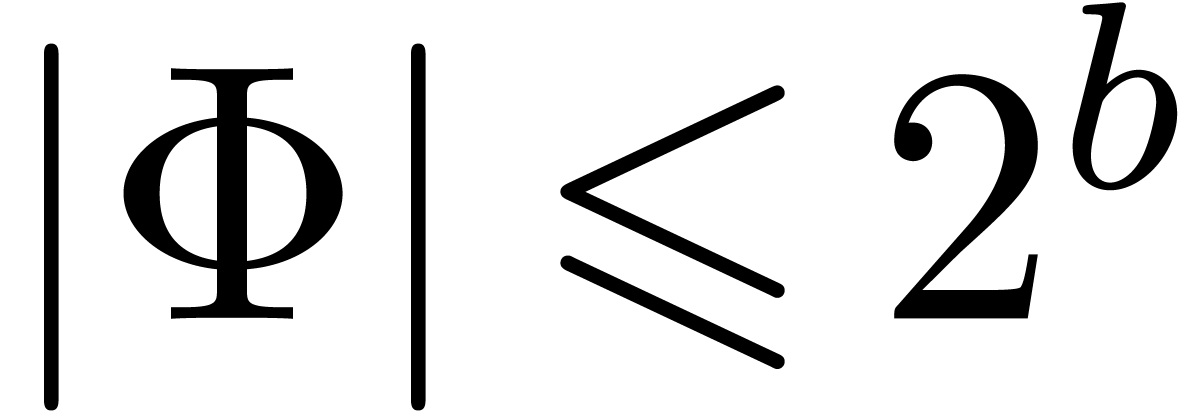 is not known a priori. Assume
that
is not known a priori. Assume
that 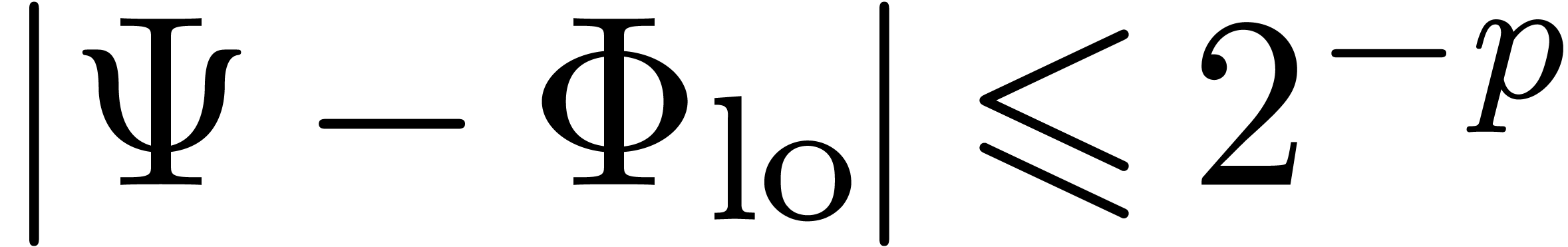 and write
and write 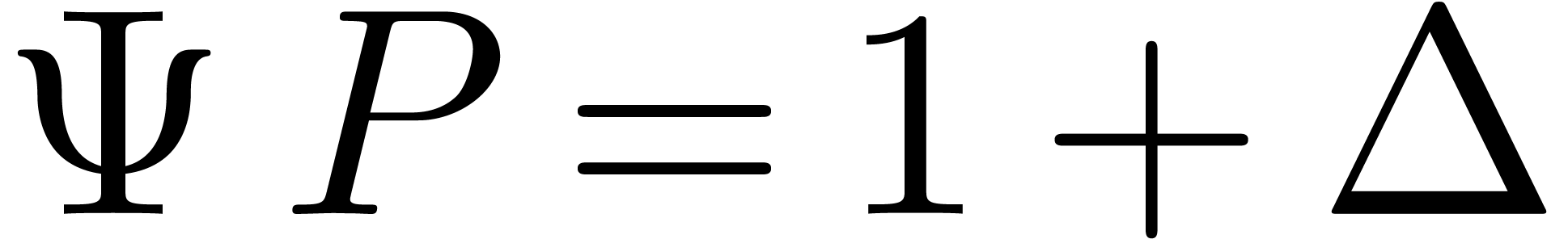 .
Then
.
Then  and
and
Assuming  , it follows that
, it follows that
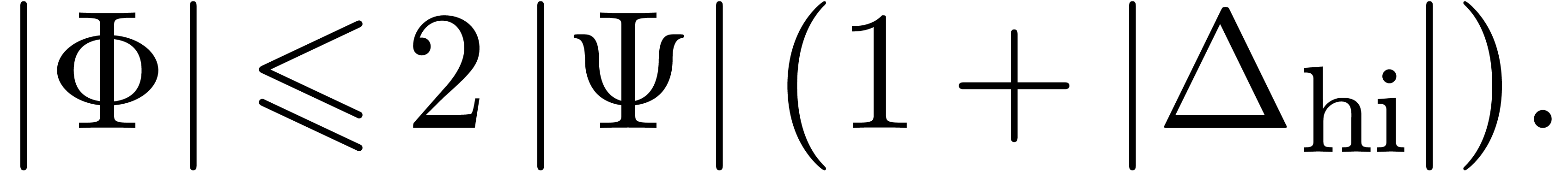
We may thus take 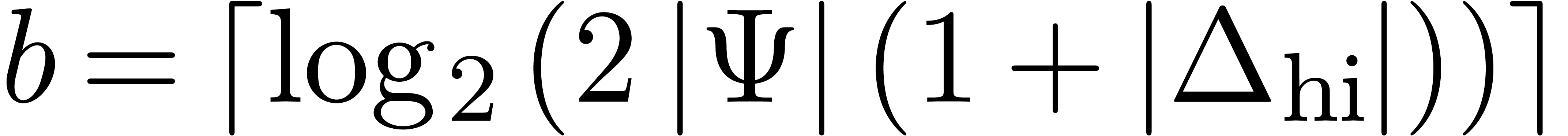 . Inversely,
we have
. Inversely,
we have
In other words, our choice of  is at most a
factor two worse than the optimal value.
is at most a
factor two worse than the optimal value.
Remark  is a variant of the method described in [Sch82,
Section 4]:
is a variant of the method described in [Sch82,
Section 4]:
Choose  sufficiently small and
sufficiently small and  sufficiently large, such that
sufficiently large, such that
 |
(3) |
Evaluate 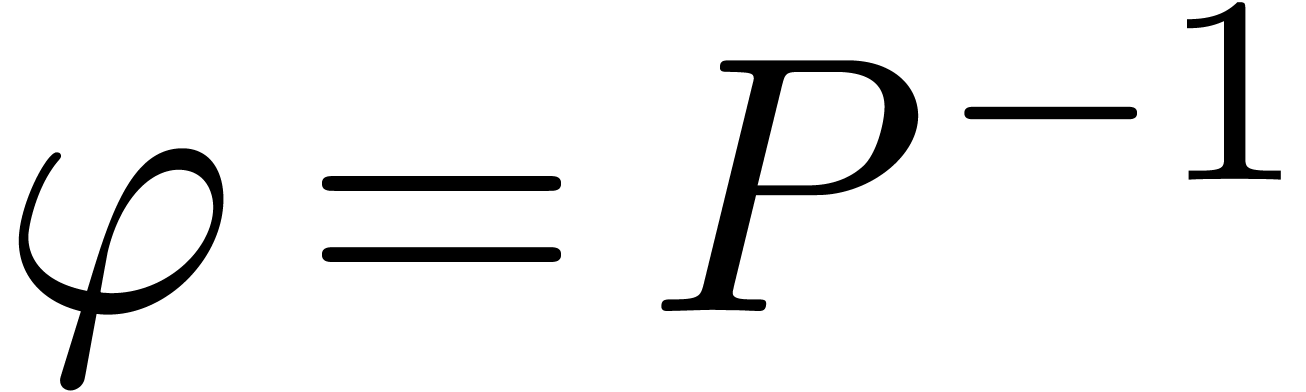 at
at 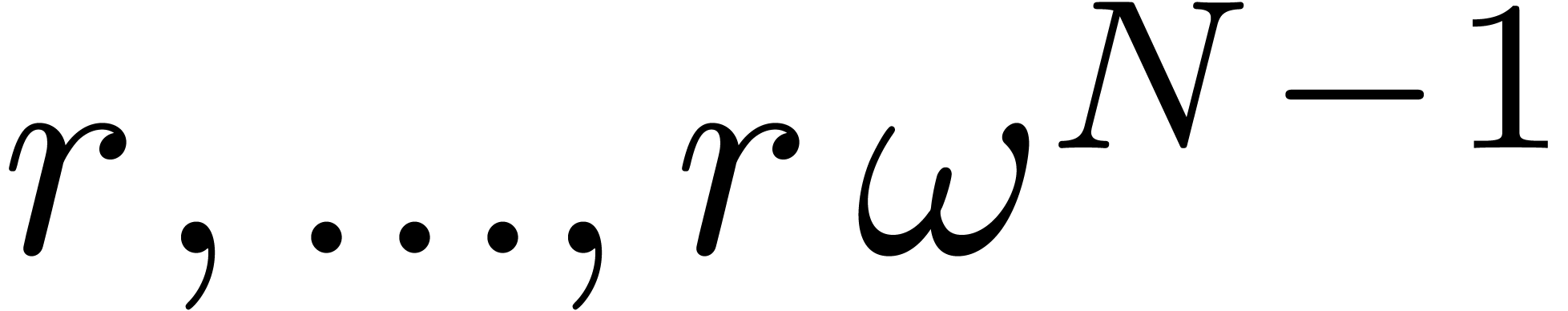 where
where
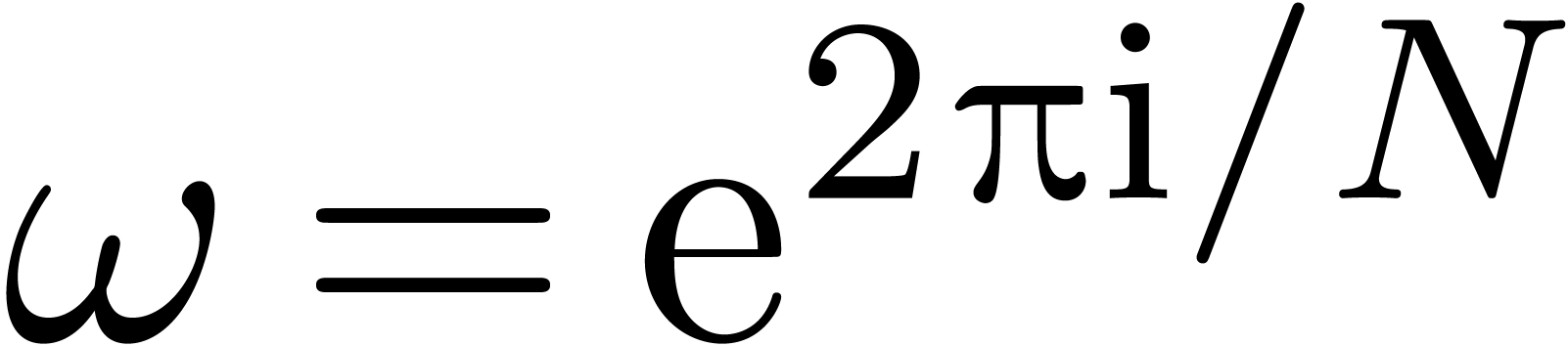 , using one direct FFT
for the polynomial
, using one direct FFT
for the polynomial 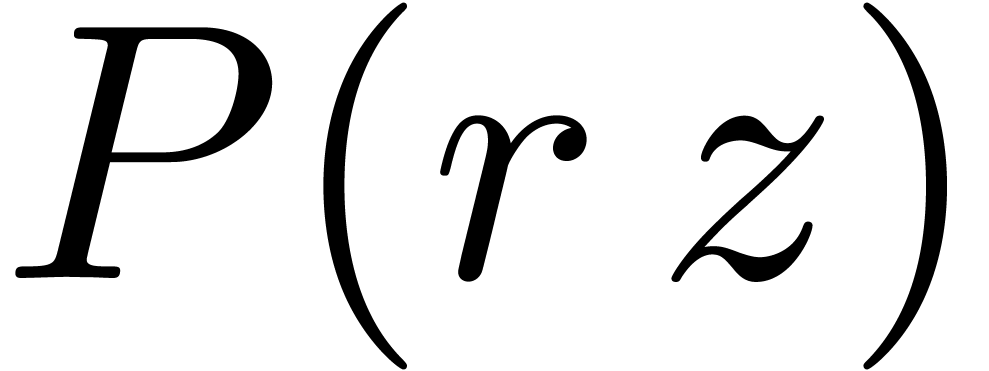 and
and 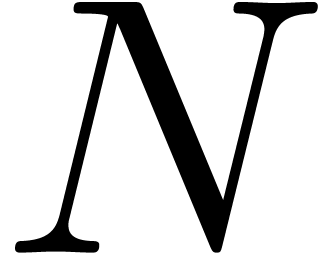 scalar inversions.
scalar inversions.
Let 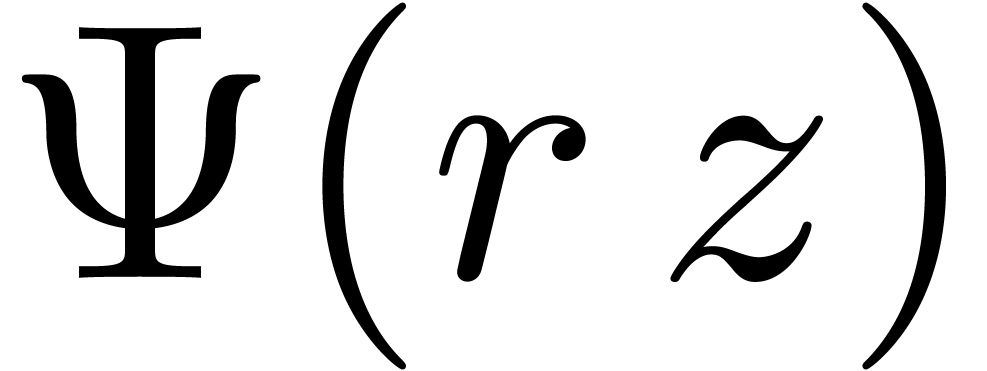 be the polynomial of degree
be the polynomial of degree 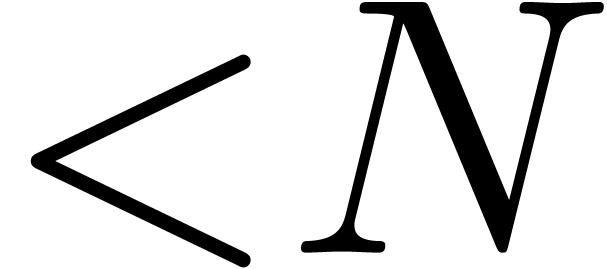 we recover when applying the inverse FFT on
we recover when applying the inverse FFT on 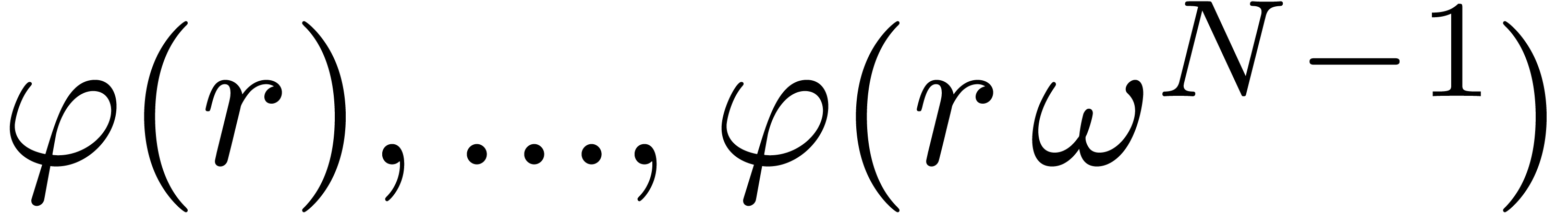 . Then (3) implies
. Then (3) implies
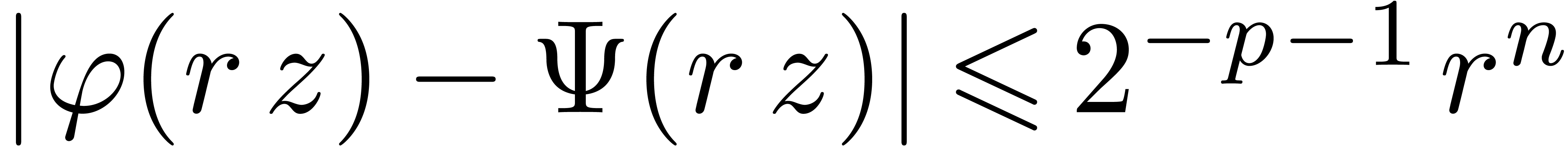 . Consequently,
. Consequently,  .
.
Because of (5) below, we may always take 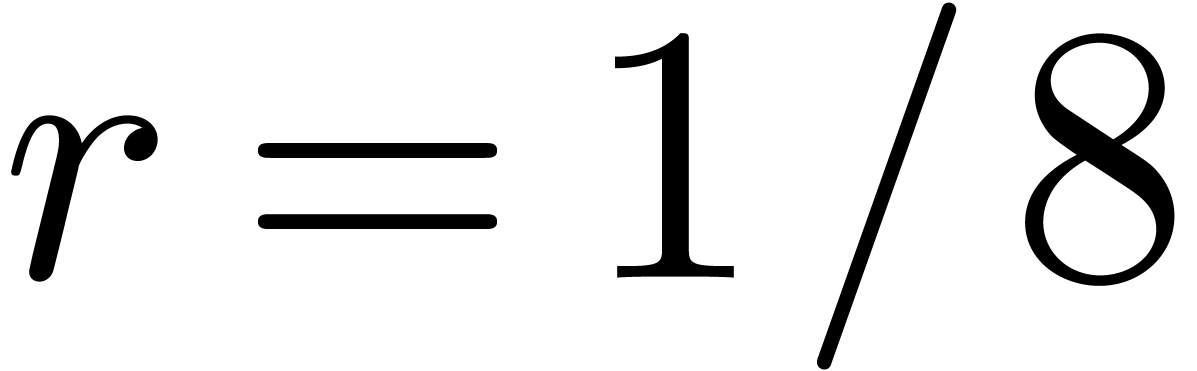 and
and 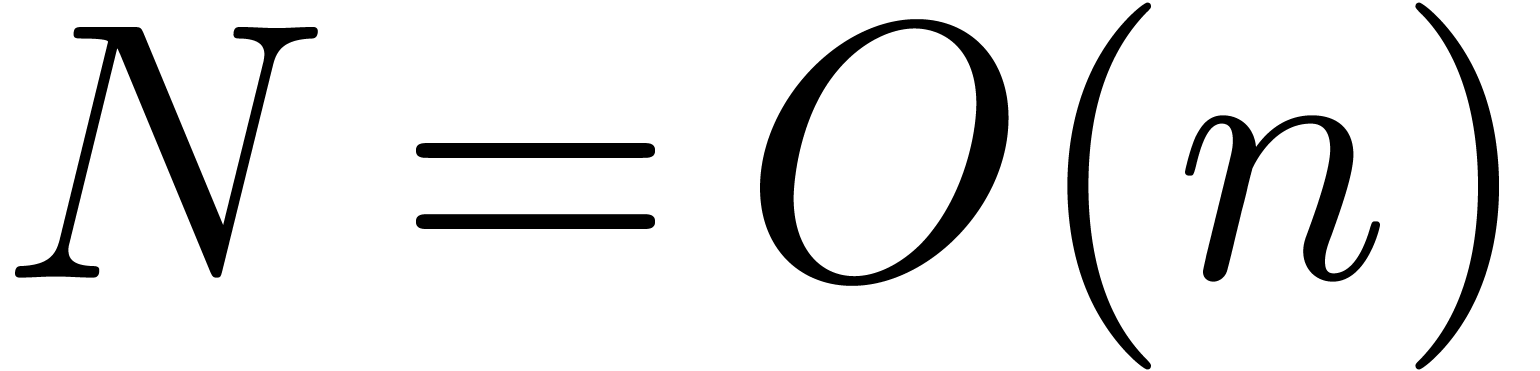 , which gives a
complexity bound of the form
, which gives a
complexity bound of the form 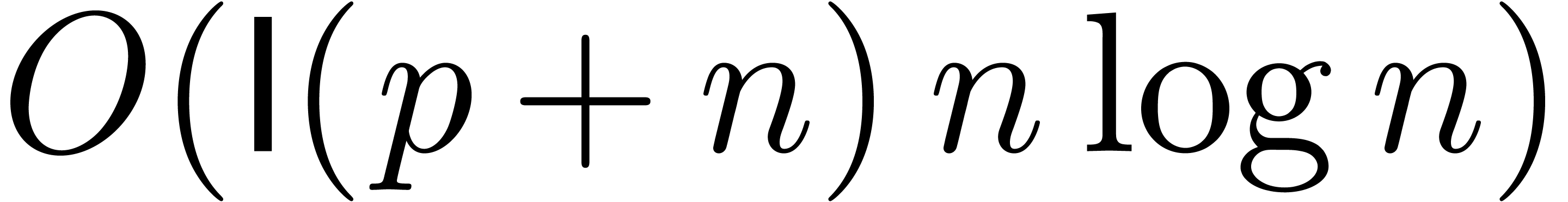 .
In fact the FFT of a numeric
.
In fact the FFT of a numeric 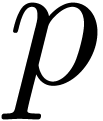 -bit
polynomial of degree
-bit
polynomial of degree 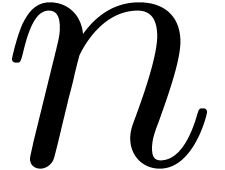 can be computed in time
can be computed in time
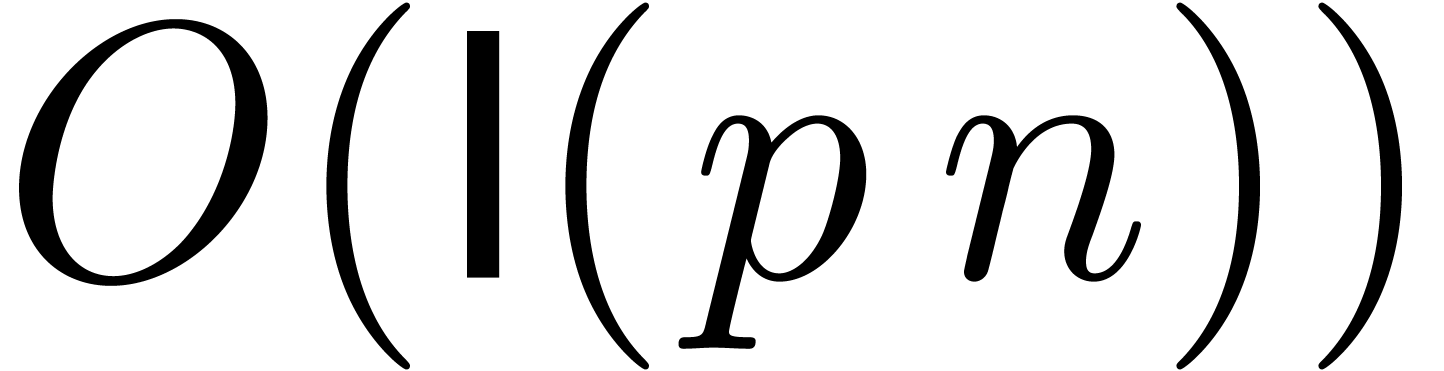 [Sch82, Section 3], which drops the
bound further down to
[Sch82, Section 3], which drops the
bound further down to 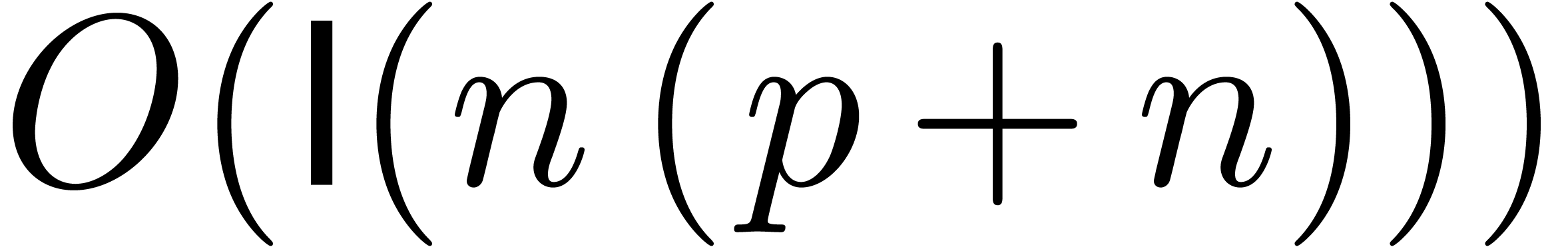 .
.
In practice, we may also start with  and double
and double
 until the computed approximation
until the computed approximation  of
of  satisfies the equation
satisfies the equation 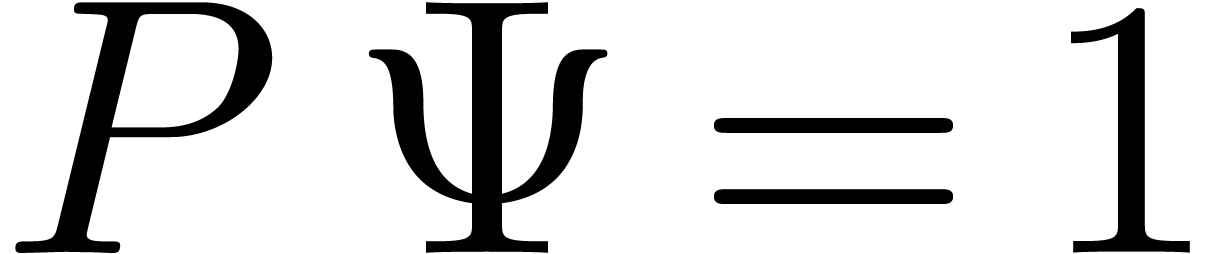 up to a sufficient precision. This leads to the same
complexity bound
up to a sufficient precision. This leads to the same
complexity bound 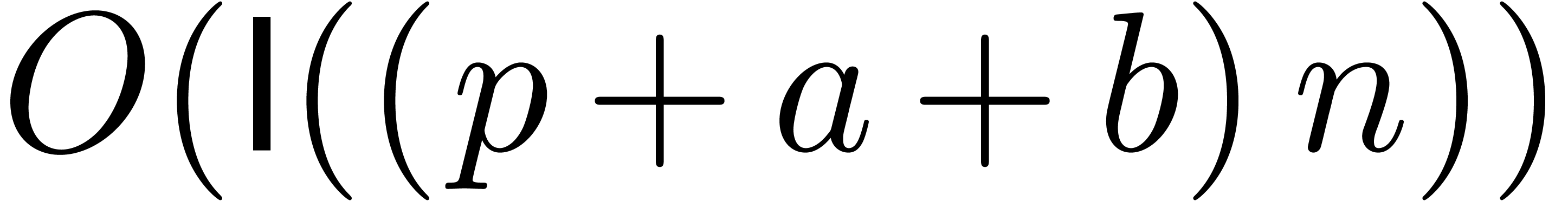 as in the lemma.
as in the lemma.
It is not clear which of the two methods is most efficient: Newton's
method performs a certain amount of recomputations, whereas the
alternative method requires us to work at a sufficiently large degree
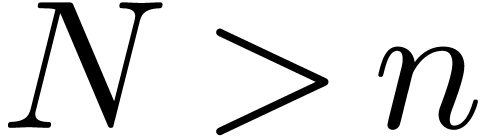 for which (3) holds.
for which (3) holds.
Given power series  and
and 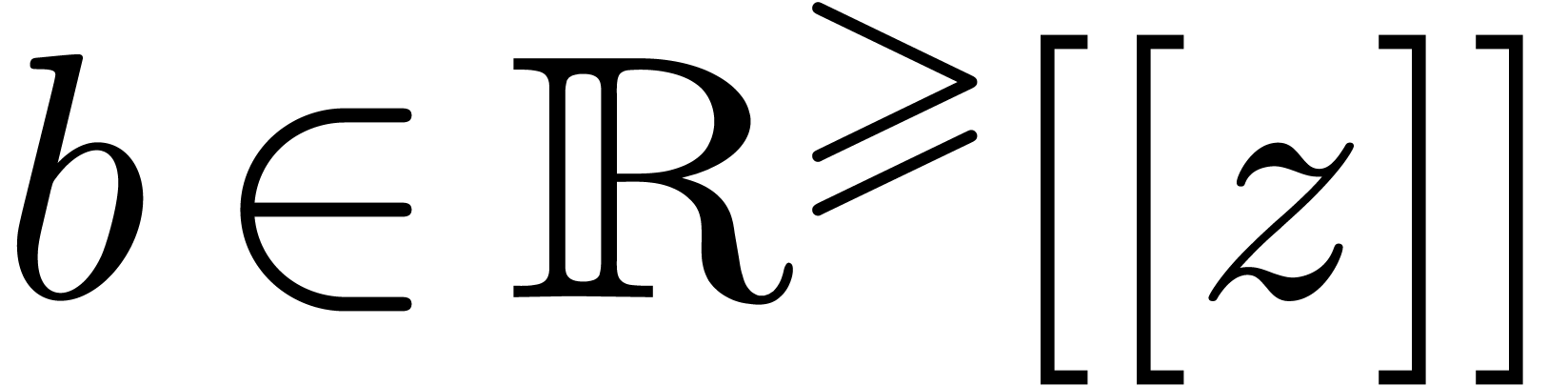 , where
, where 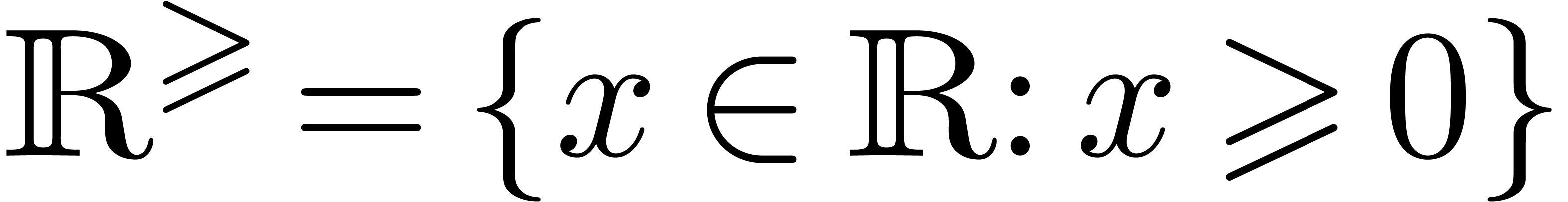 ,
we will say that
,
we will say that  majorates
majorates  and write
and write  if
if 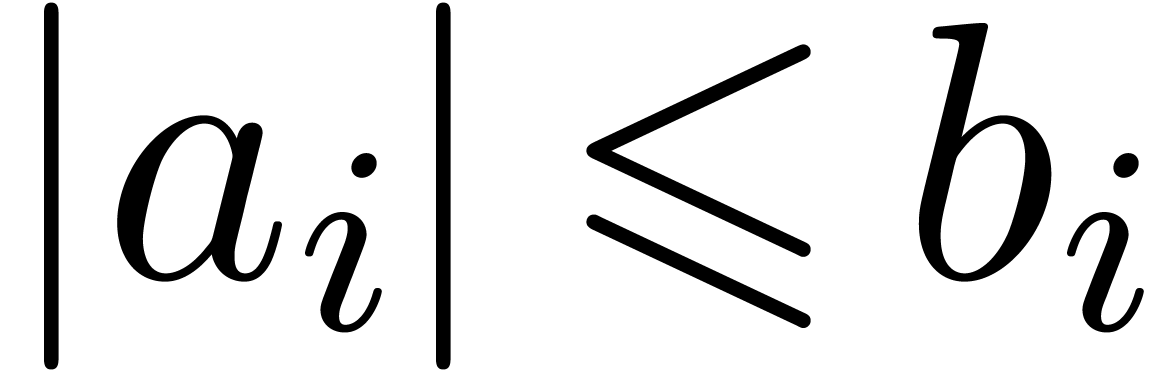 for all coefficients of
for all coefficients of  .
This notation applies in particular to polynomials.
.
This notation applies in particular to polynomials.
 and
and 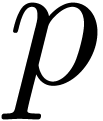 as in lemma 3, we may compute a
as in lemma 3, we may compute a  -approximation
of
-approximation
of  in time
in time 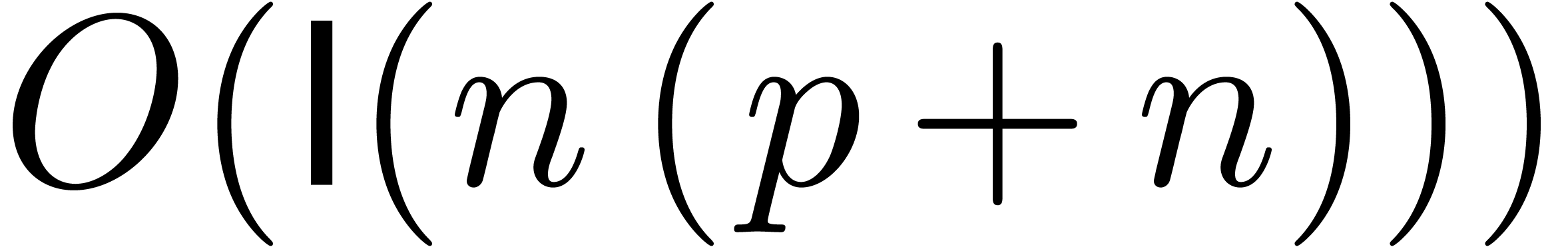 .
.
Proof. Then 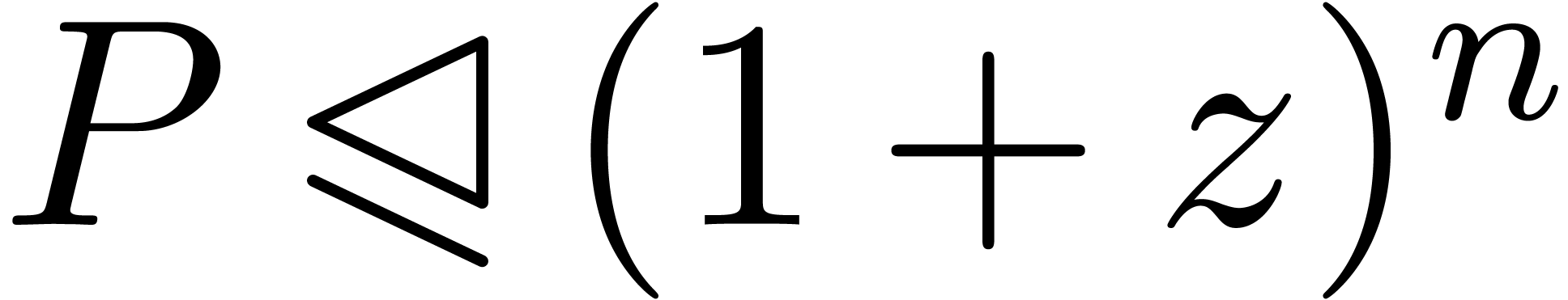 and
and 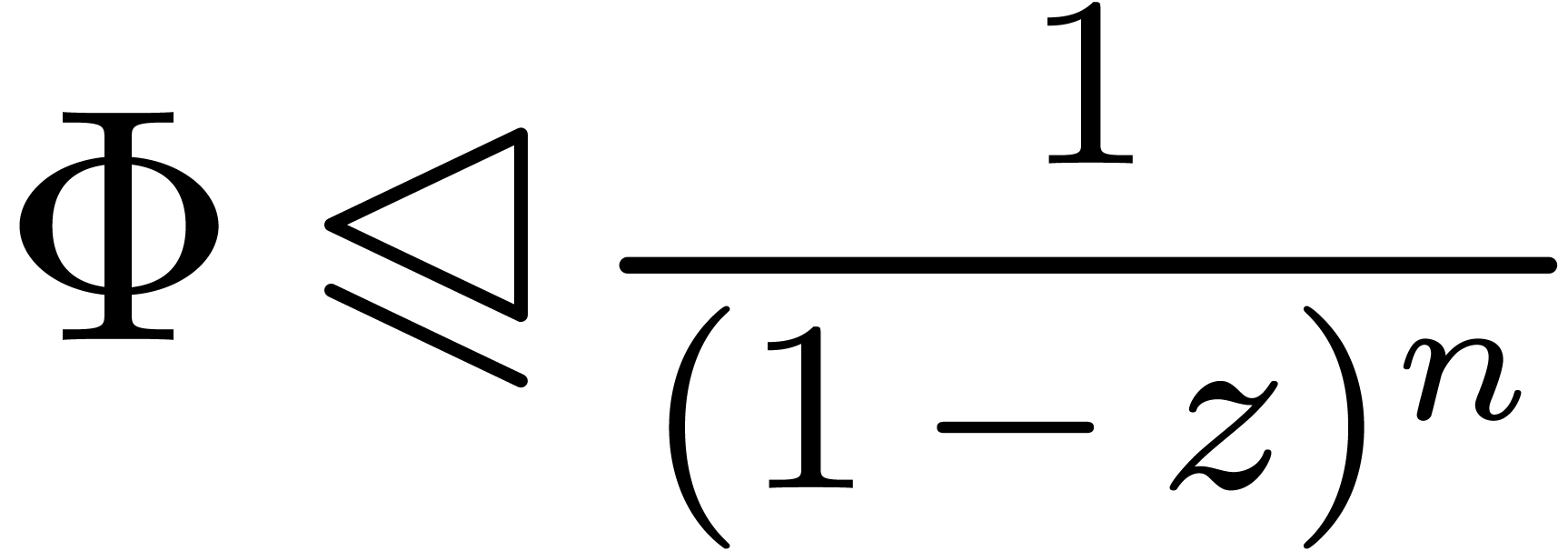 , whence
, whence
We conclude by applying lemma 3 for 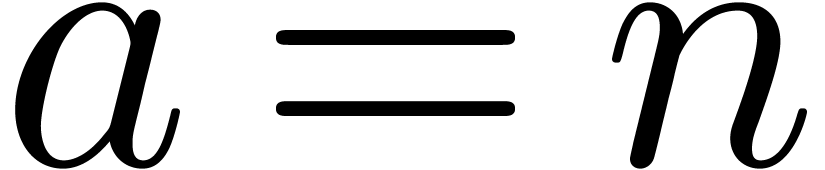 and
and 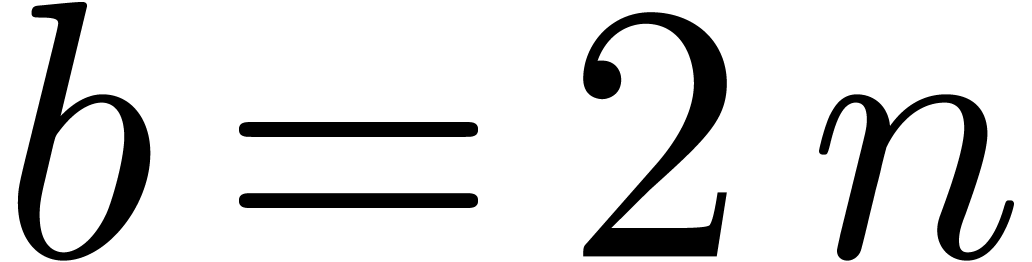 .
.
The following result was first proved in [Sch82, Section 4].
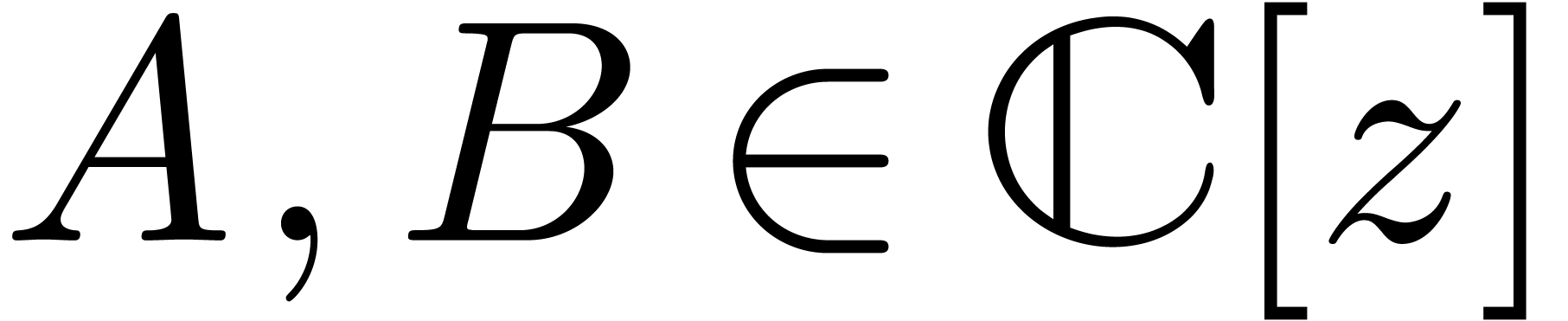 be polynomials with
be polynomials with 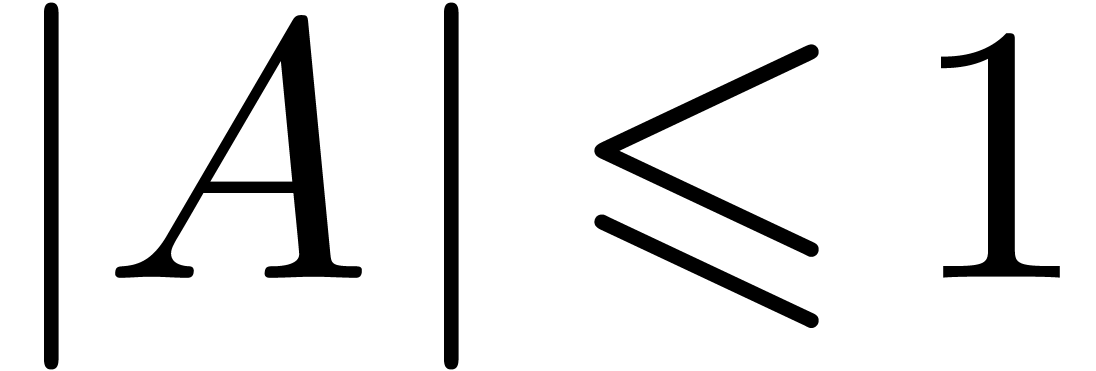 ,
, 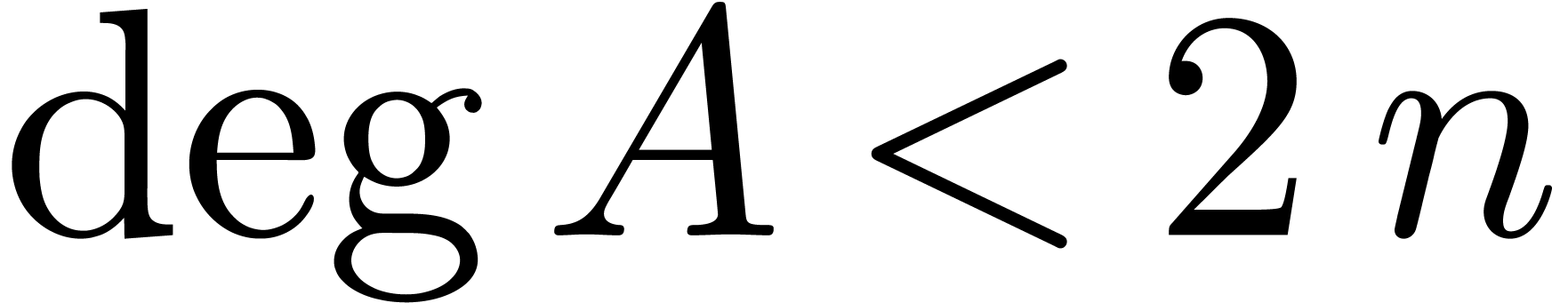 and
and
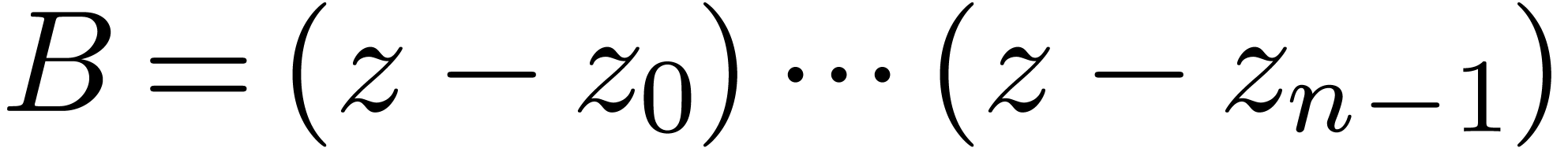
for 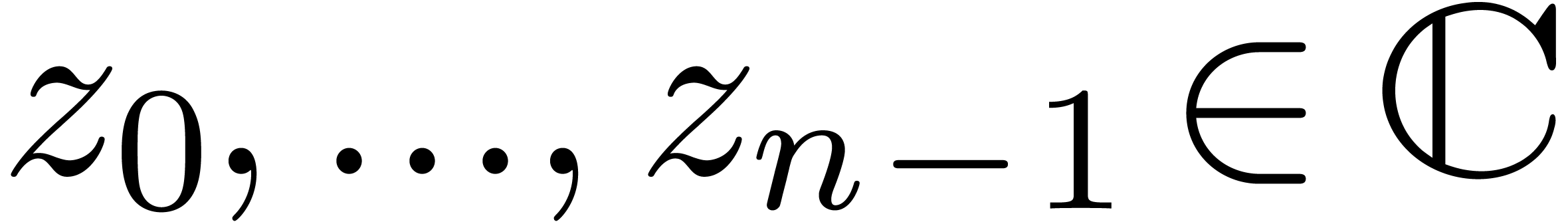 with
with 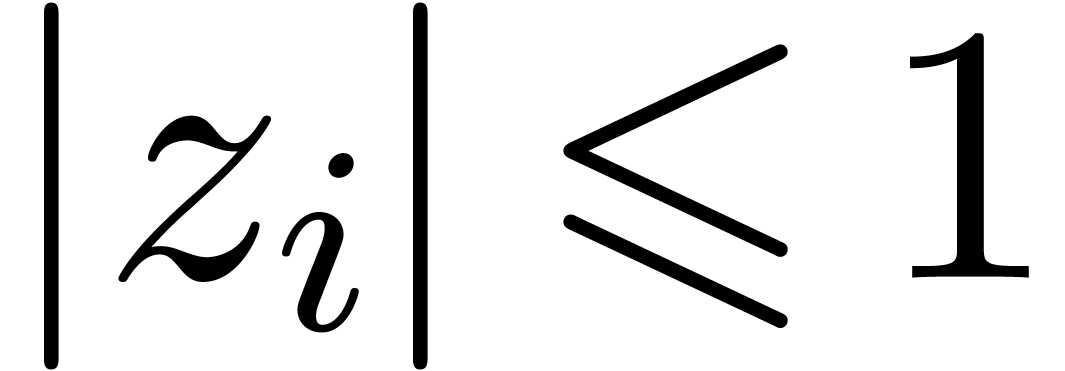 for all
for all
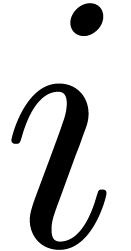 . Consider the Euclidean
division
. Consider the Euclidean
division
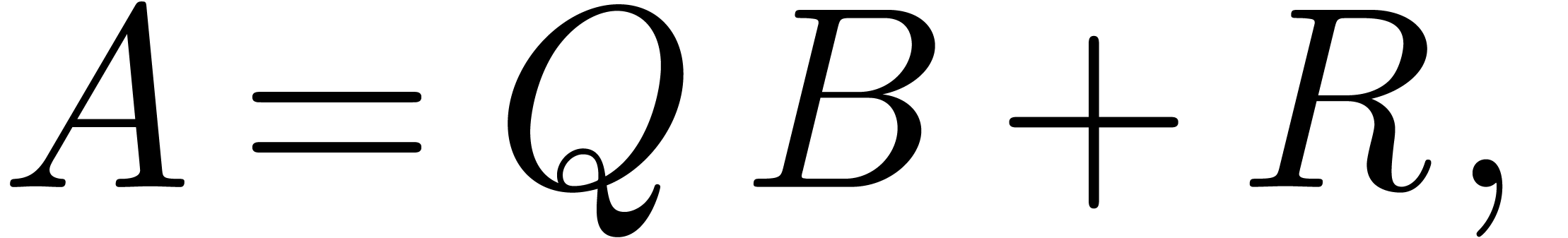
with 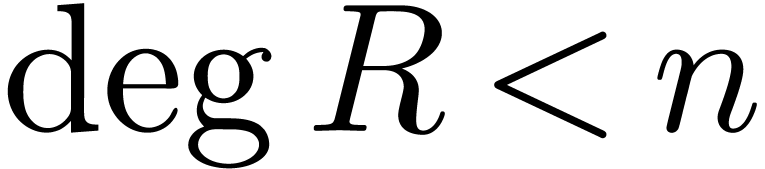 . Given
. Given 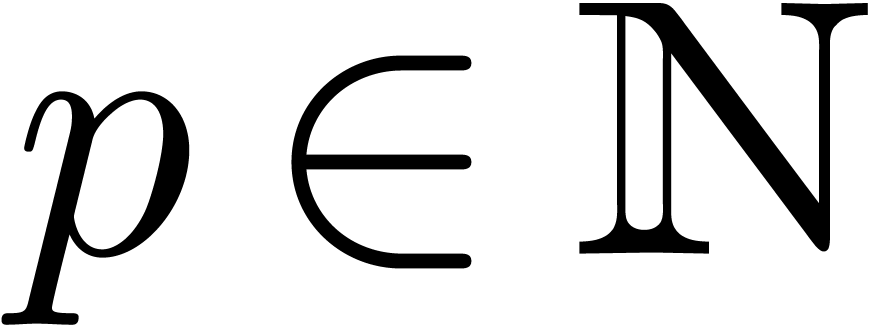 , we may compute a
, we may compute a  -approximations of
-approximations of  and
and 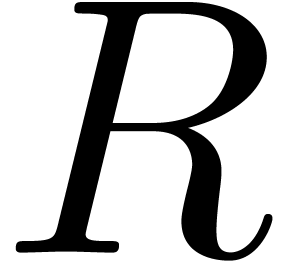 in time
in time 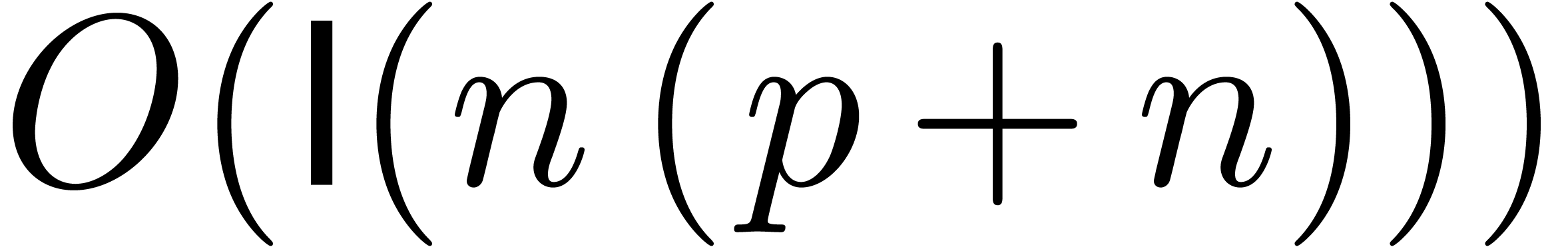 .
.
Proof. Setting 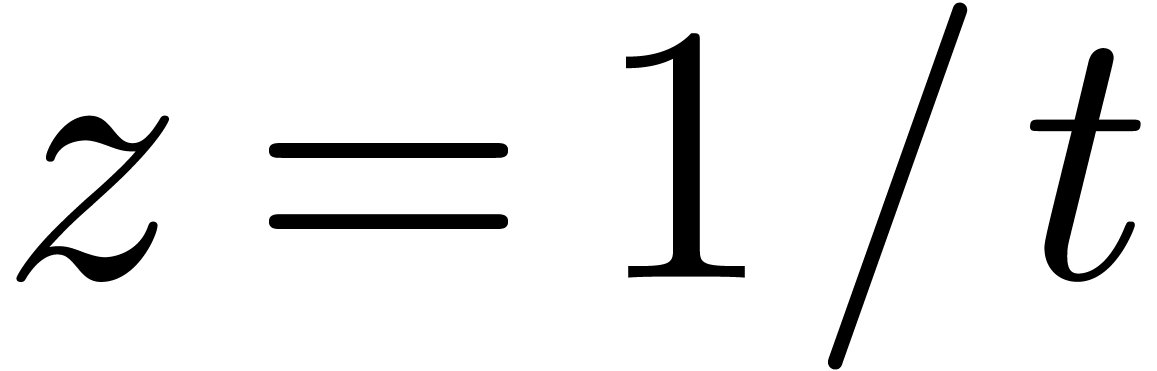 and
and  , we may write
, we may write
Setting  , we then have
, we then have
Our lemma now follows from lemmas 6 and 1.
Remark  ,
,  ,
, 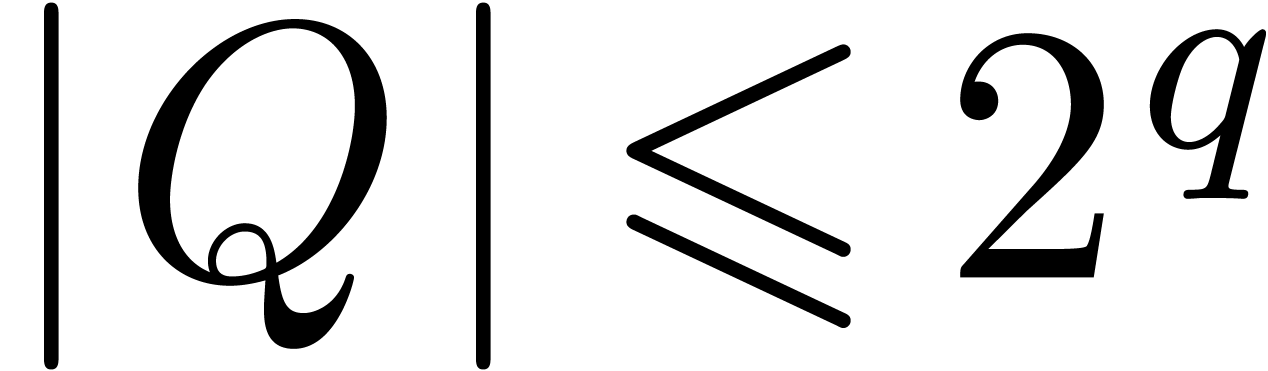 and
and 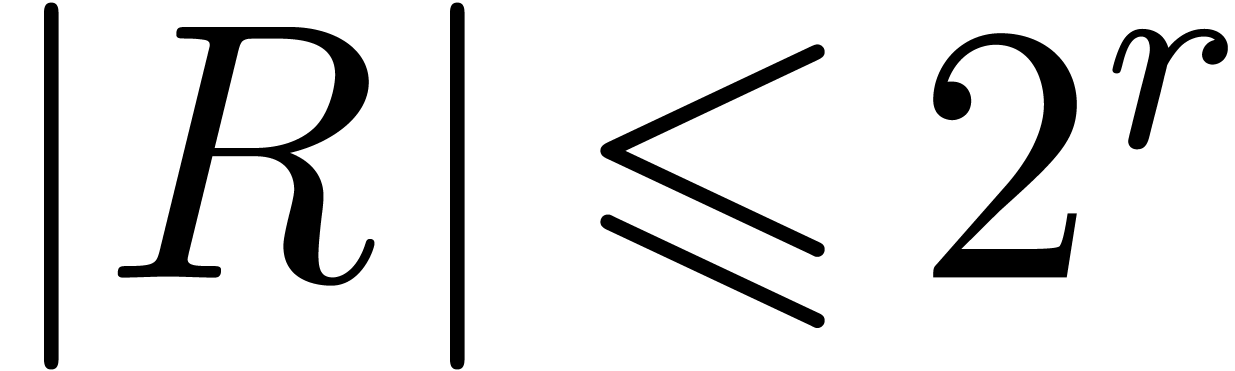 , it is again possible to prove the improved
estimate
, it is again possible to prove the improved
estimate 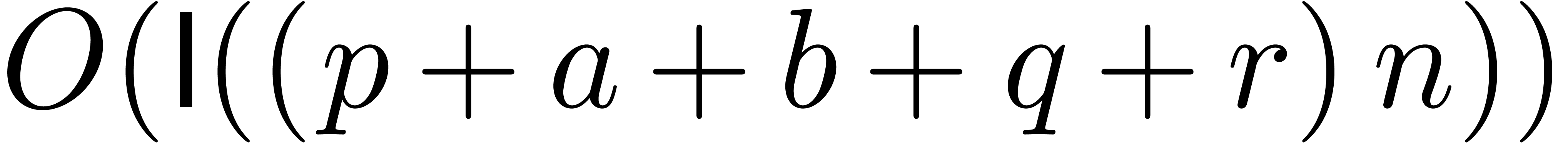 . However, the proof
relies on Schönhage's original method, using the same doubling
strategy as in remark 5. Indeed, when using Newton's method
for inverting
. However, the proof
relies on Schönhage's original method, using the same doubling
strategy as in remark 5. Indeed, when using Newton's method
for inverting 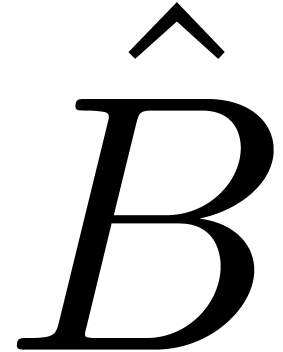 , nice bounds
, nice bounds
 and
and  do not necessarily
imply a nice bound for
do not necessarily
imply a nice bound for  ,
where
,
where  is the truncated inverse of
is the truncated inverse of 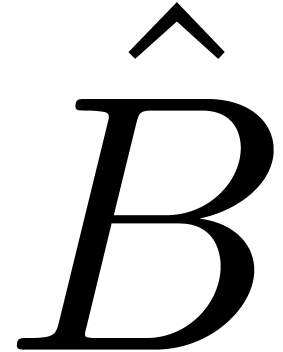 . Using a relaxed division algorithm [vdH02]
for
. Using a relaxed division algorithm [vdH02]
for 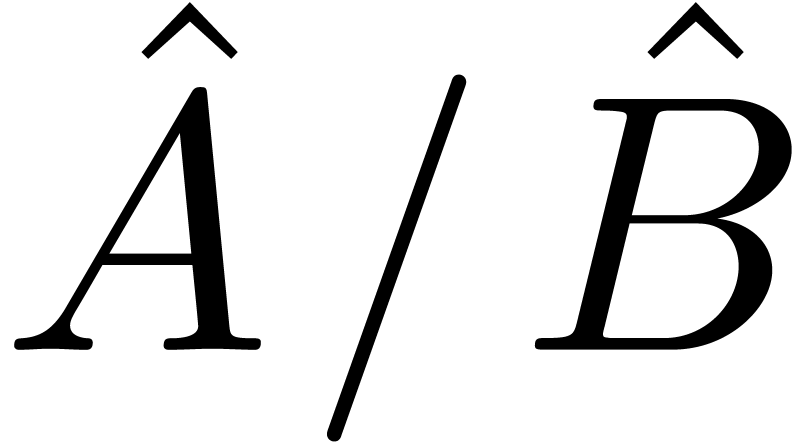 , one may still achieve
the improved bound, up to an additional
, one may still achieve
the improved bound, up to an additional 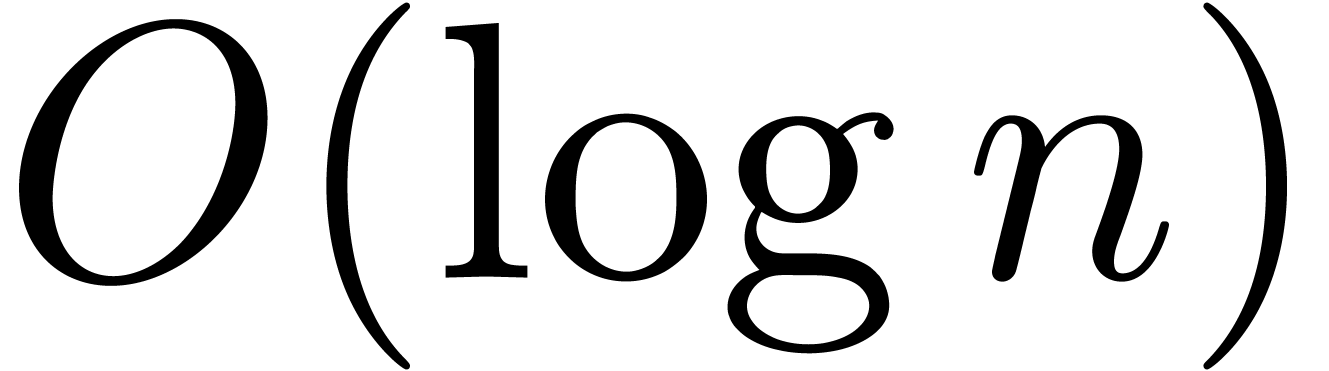 overhead.
overhead.
For applications where Euclidean division is used as a subalgorithm, it
is necessary to investigate the effect of small perturbations of the
inputs  and
and  on the
outputs
on the
outputs  and
and  .
.
Proof. With the notations of the proof of lemma
7, let  and
and  be the truncations of the power series
be the truncations of the power series 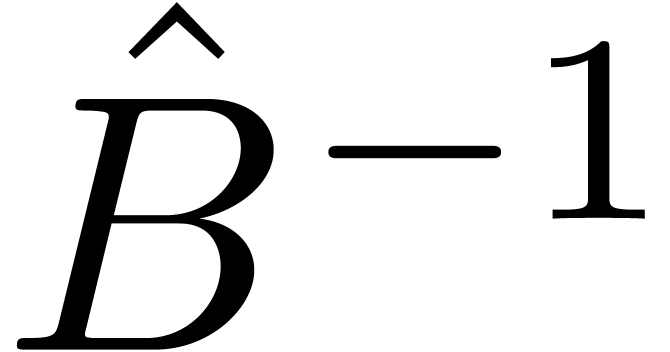 and
and 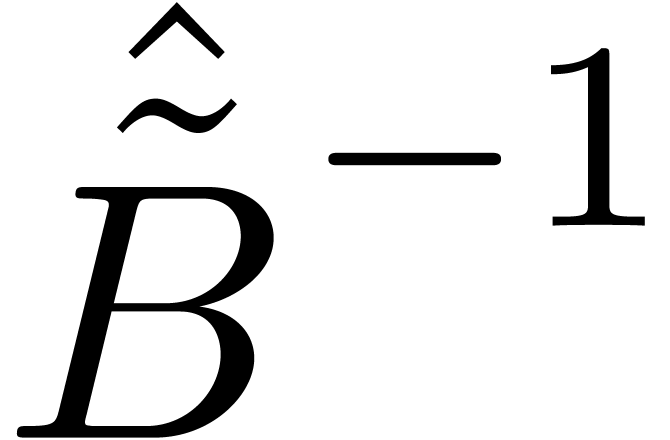 at order
at order  .
Let us first consider the case when
.
Let us first consider the case when 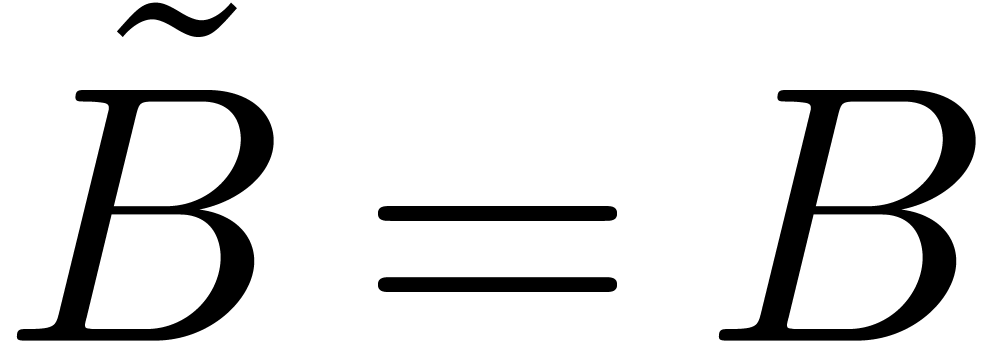 ,
so that
,
so that
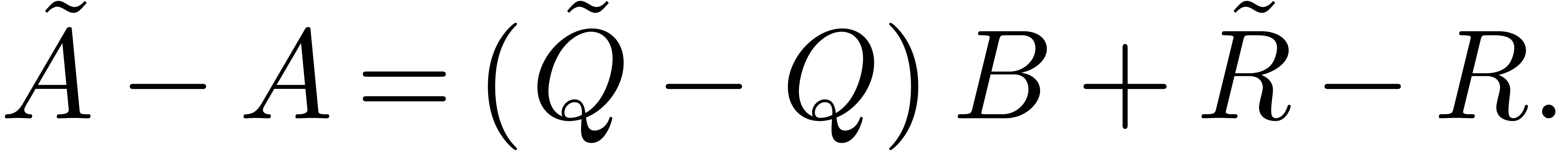
Then 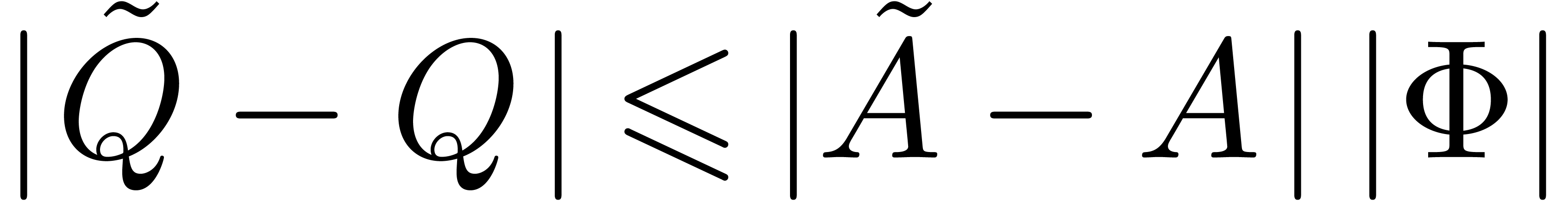 and
and
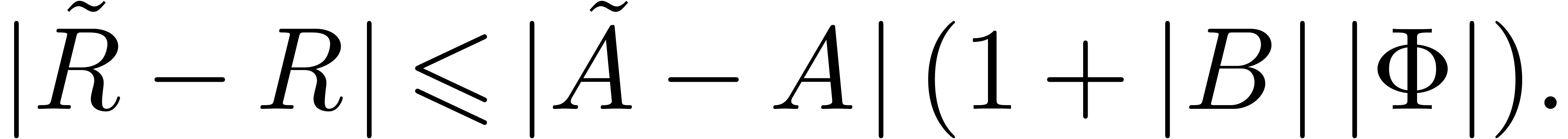
Let us next consider the case when 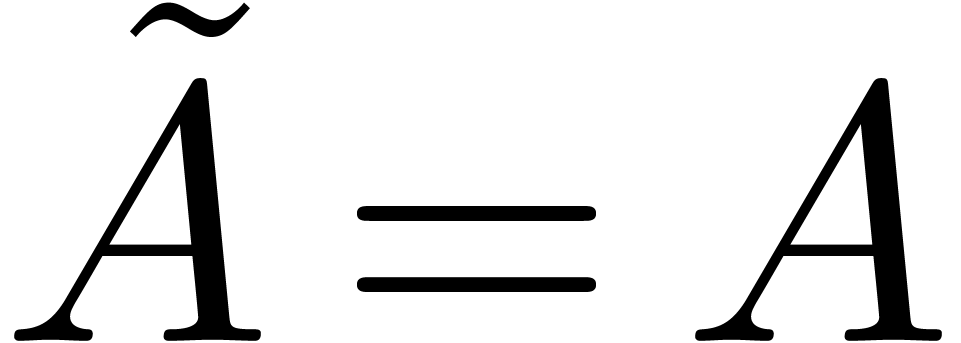 .
Then
.
Then
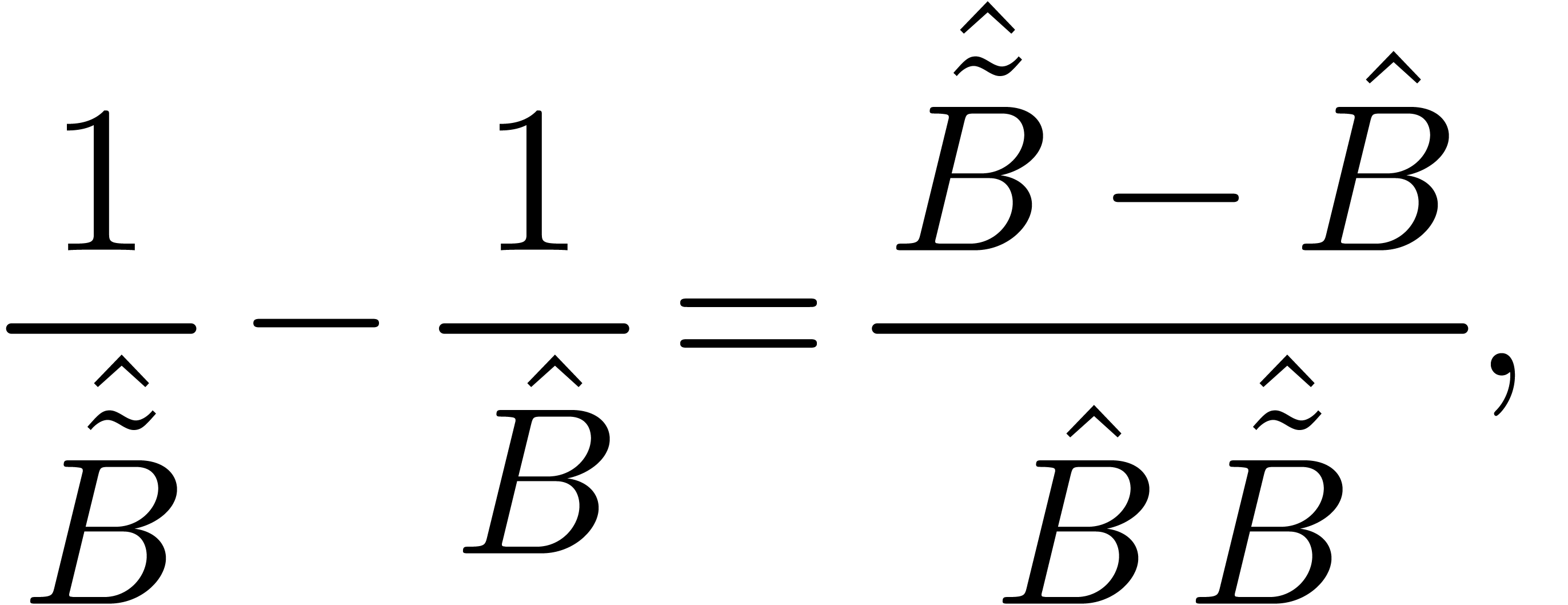
whence 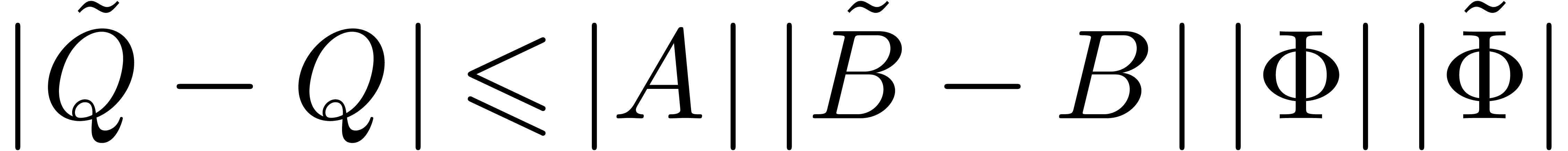 and
and
In general, the successive application of the second and the first case yield
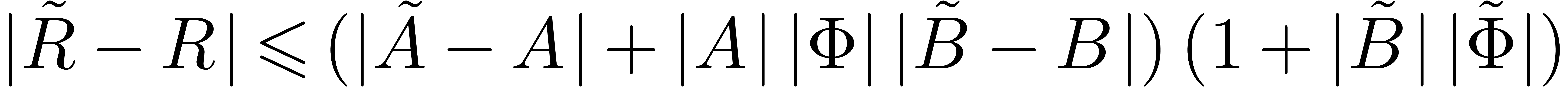
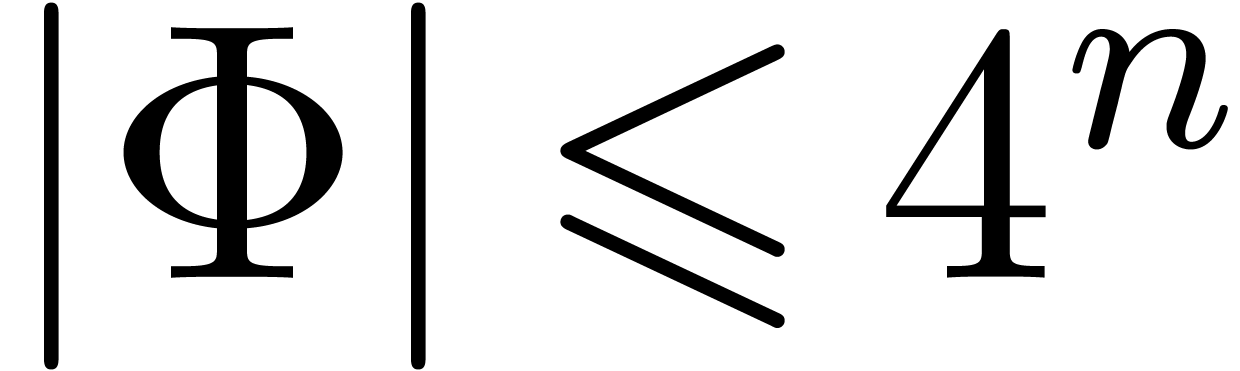
We have also seen in the proof of lemma 6 that 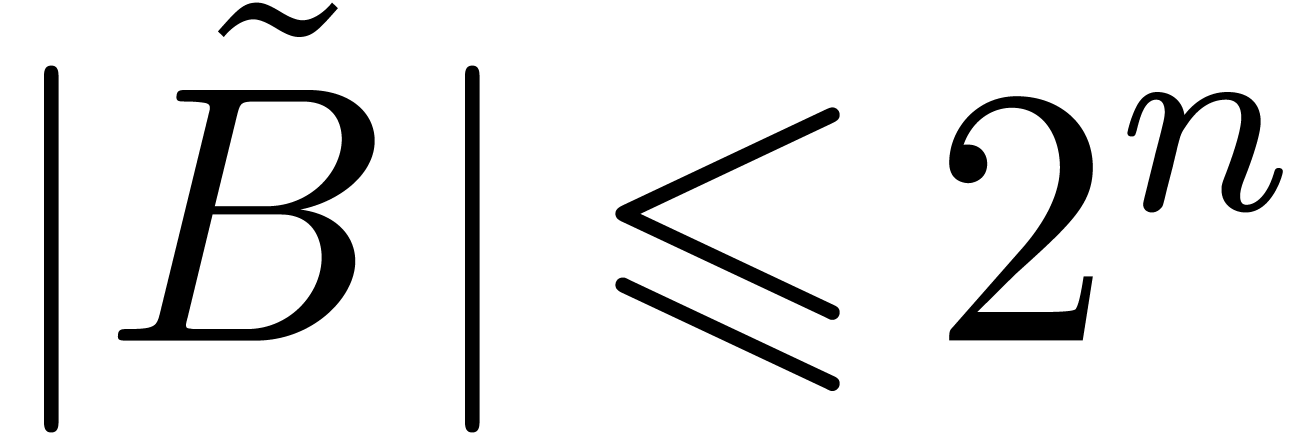 ,
,  and
and 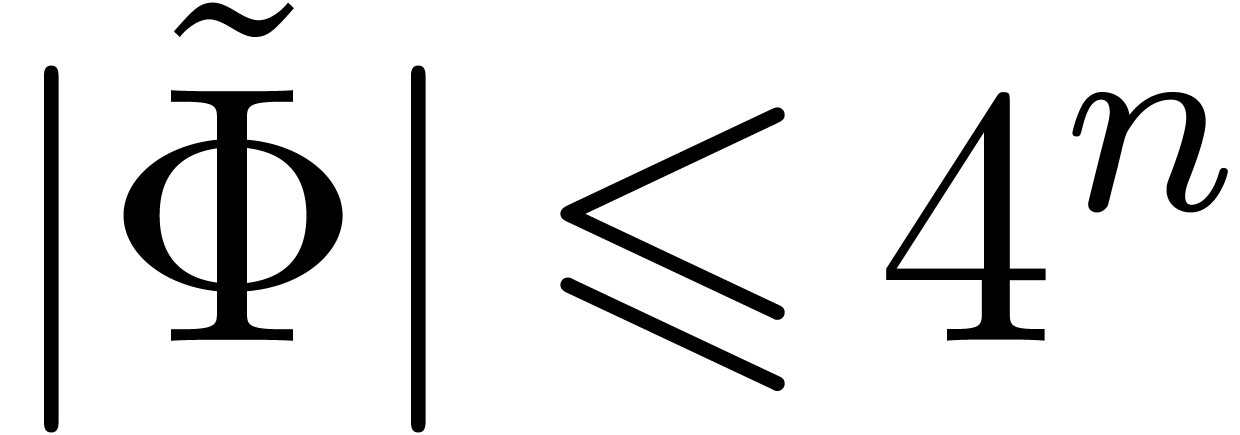 .
.
Proof. With the notations from the proof of lemma 7, we have
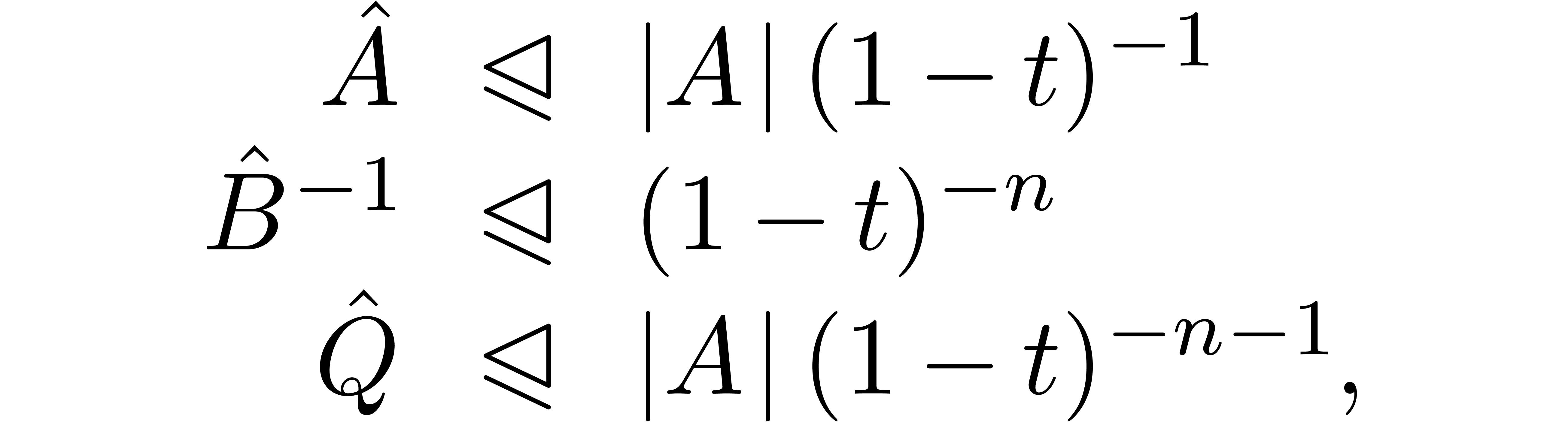
whence
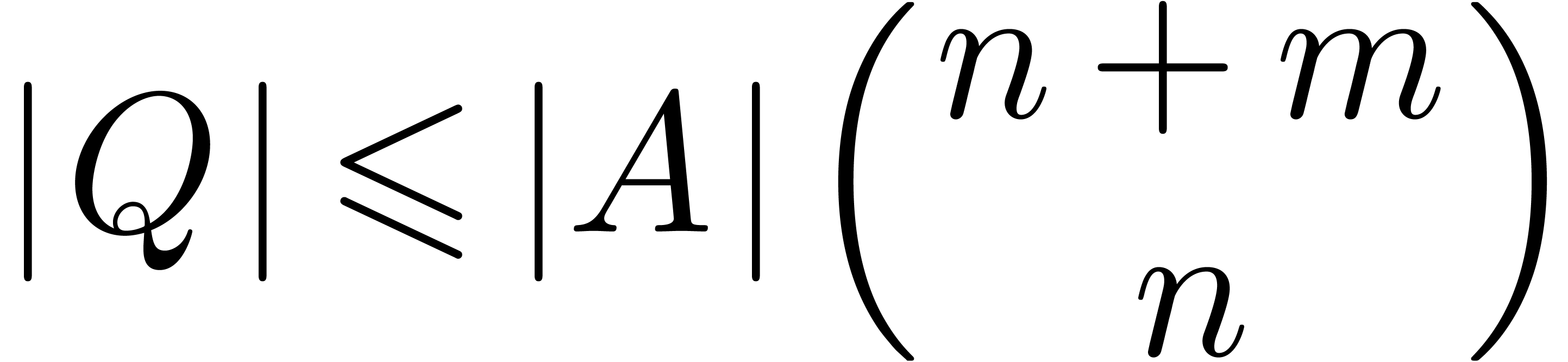
and

Consider a complex polynomial
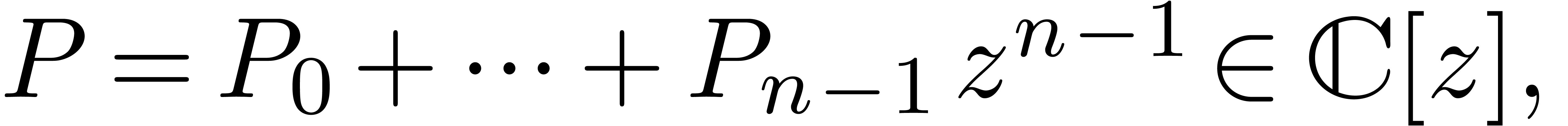
which has been normalized so that 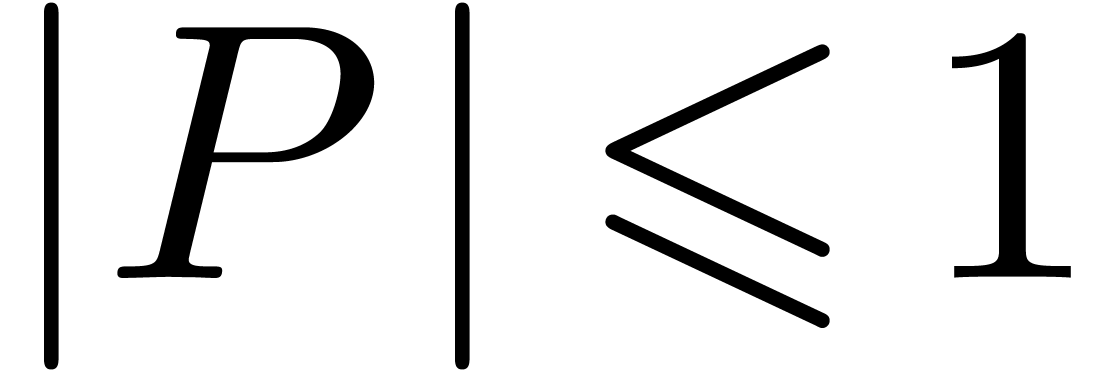 .
Let
.
Let
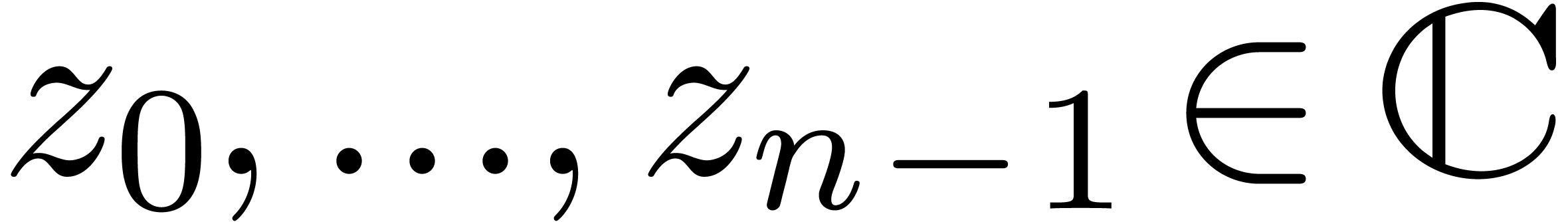
be pairwise distinct points with 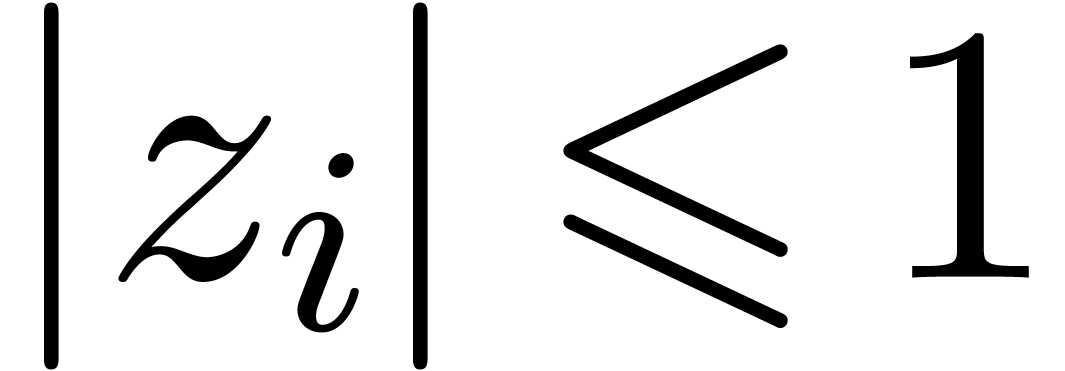 for all
for all 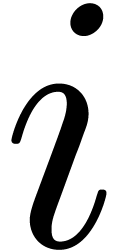 . The problem of multi-point
evaluation is to find an efficient algorithm for the simultaneous
evaluations of
. The problem of multi-point
evaluation is to find an efficient algorithm for the simultaneous
evaluations of  at
at  .
A
.
A  -approximation of
-approximation of 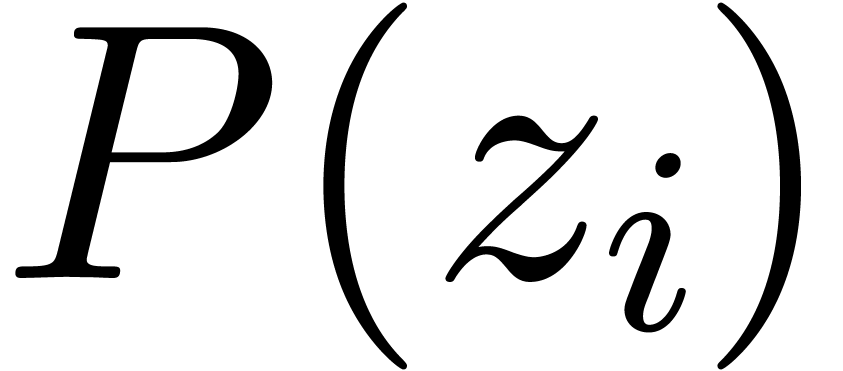 will also be called a
will also be called a  -evaluation
of
-evaluation
of  at
at 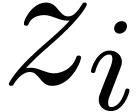 .
In order to simplify our exposition, we will assume that
.
In order to simplify our exposition, we will assume that 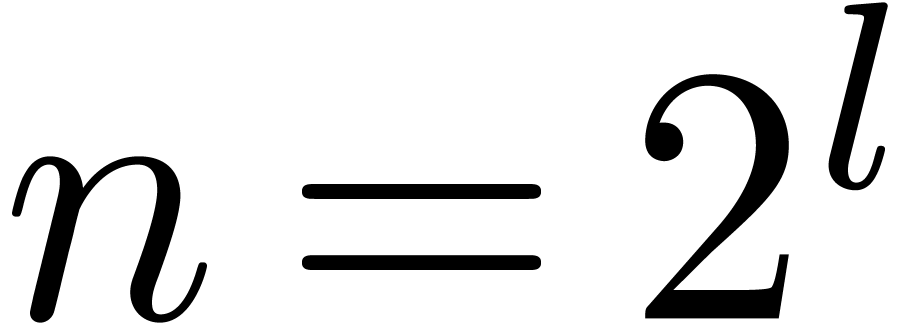 is a power of two; this assumption only affects the
complexity analysis by a constant factor.
is a power of two; this assumption only affects the
complexity analysis by a constant factor.
An efficient and classical algorithm for multi-point evaluation [AHU74] relies on binary splitting: let  ,
, 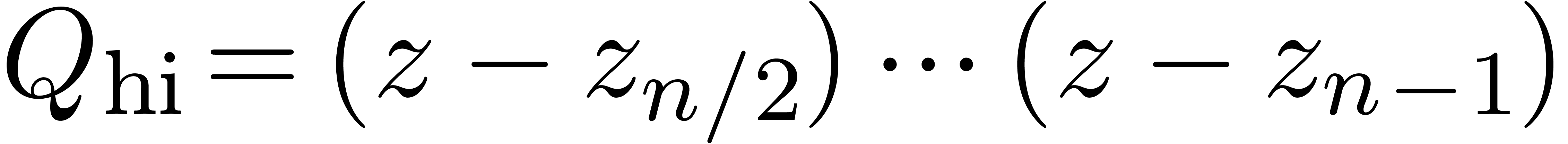 .
Denoting by
.
Denoting by  the remainder of the Euclidean
division of
the remainder of the Euclidean
division of  by
by  ,
we compute
,
we compute
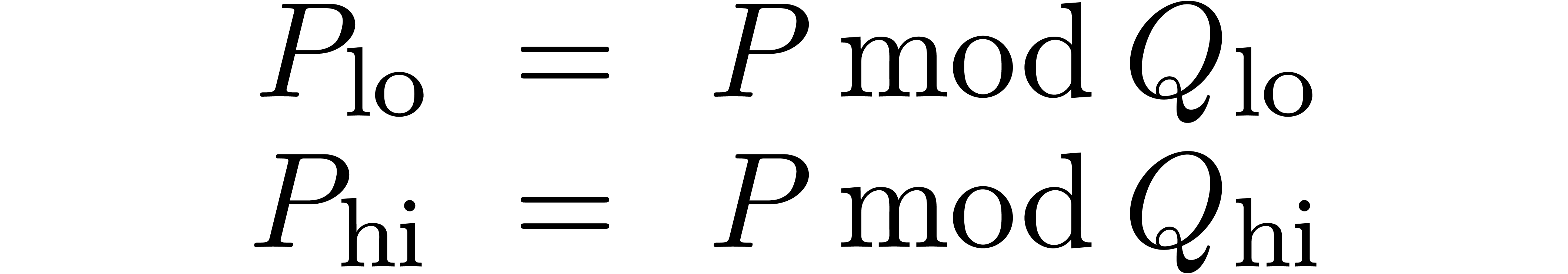
Then
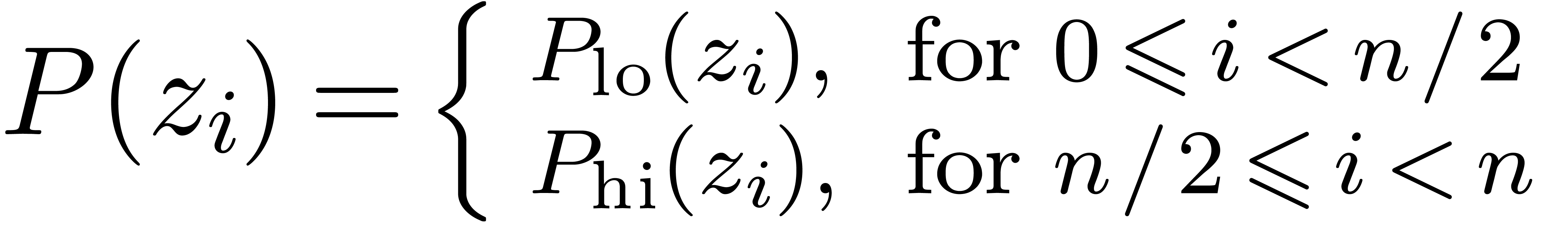
In other words, we have reduced the original problem to two problems of
the same type, but of size 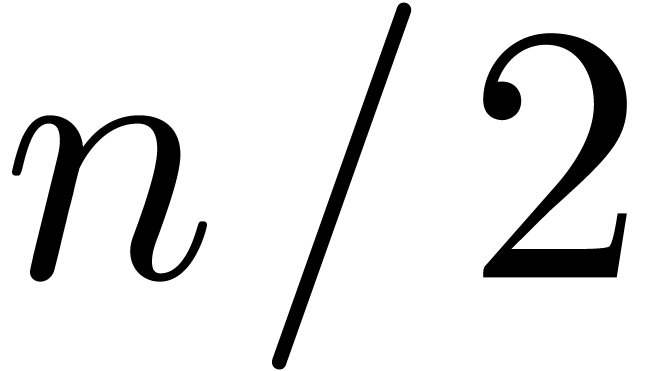 .
.
For the above algorithm to be fast, the partial products 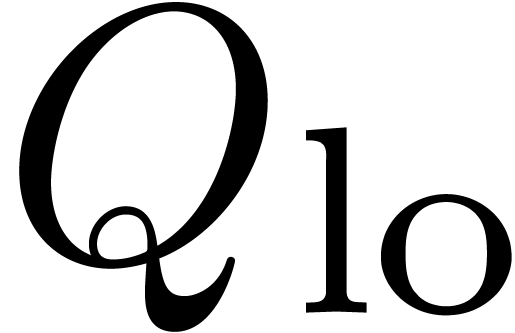 and
and 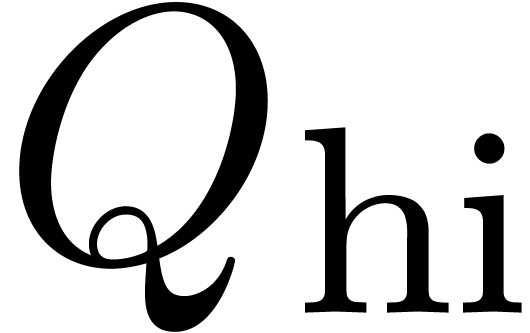 are also computed using binary
splitting, but in the opposite direction. In order to avoid
recomputations, the partial products are stored in a binary tree of
depth
are also computed using binary
splitting, but in the opposite direction. In order to avoid
recomputations, the partial products are stored in a binary tree of
depth 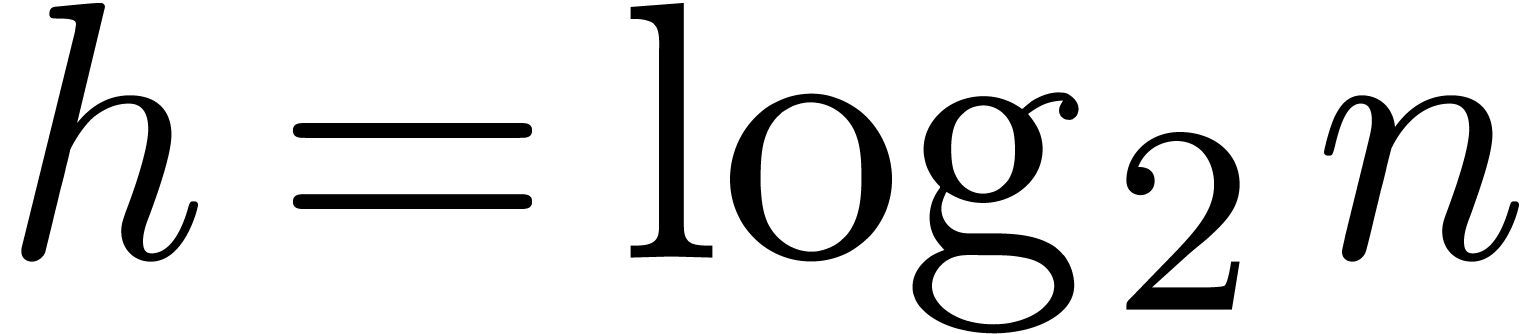 . At depth
. At depth 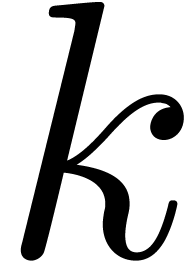 , we have
, we have 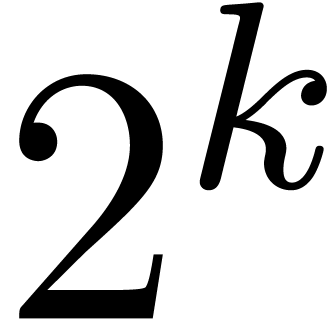 nodes,
labeled by polynomials
nodes,
labeled by polynomials  ,
where
,
where

For instance, for 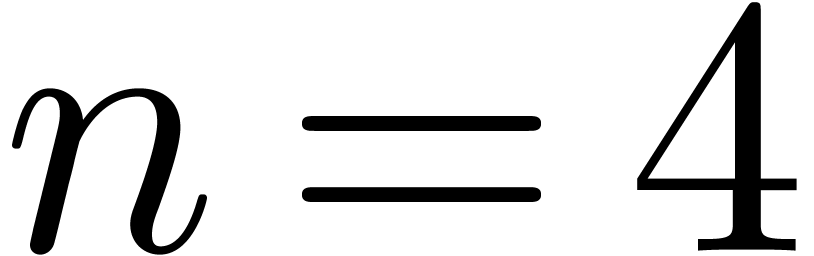 , the tree
is given by
, the tree
is given by
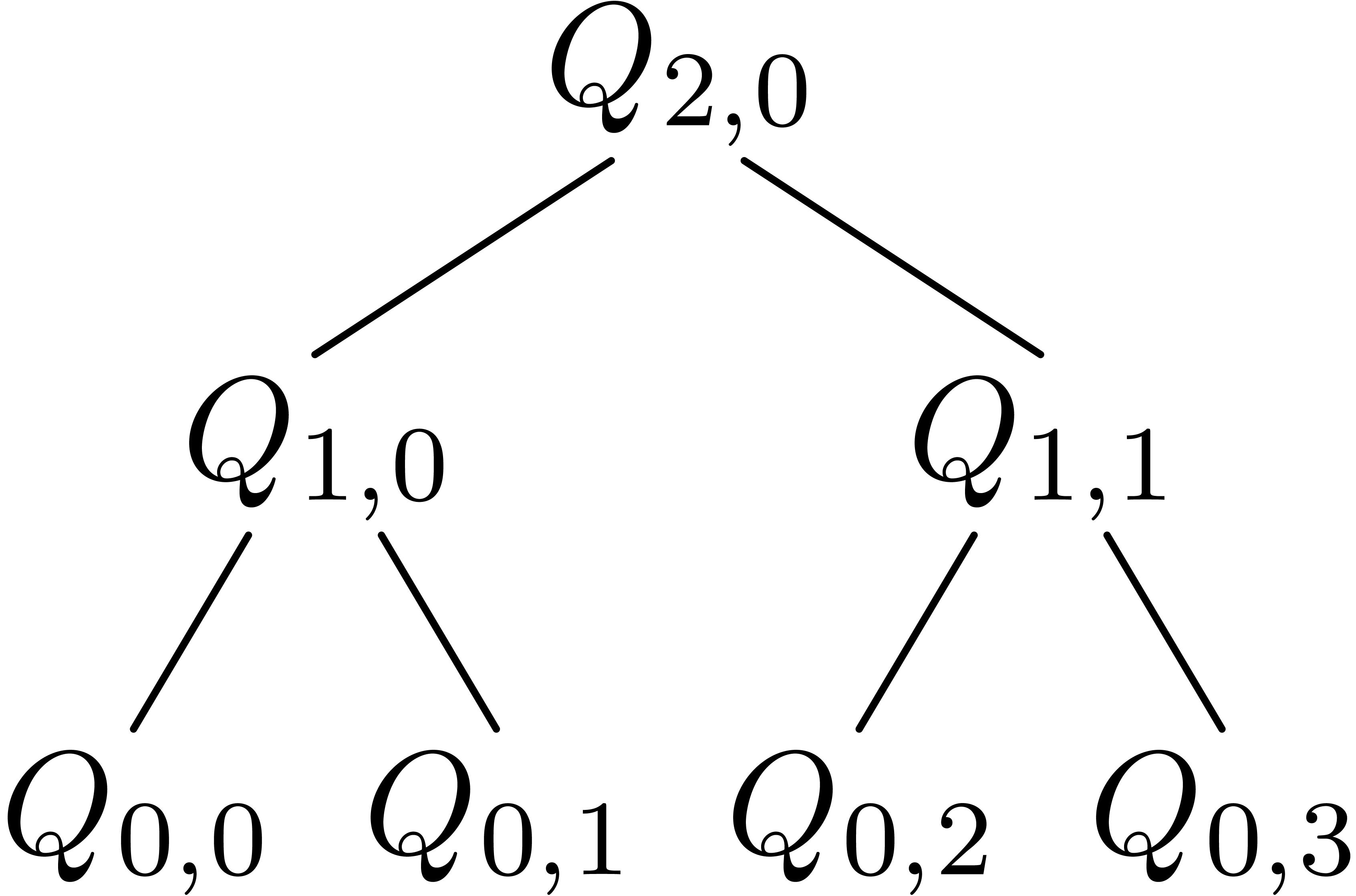
We have
For a given polynomial 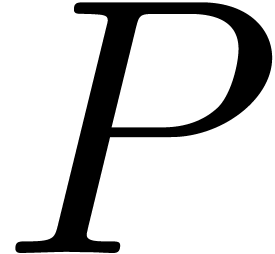 of degree
of degree 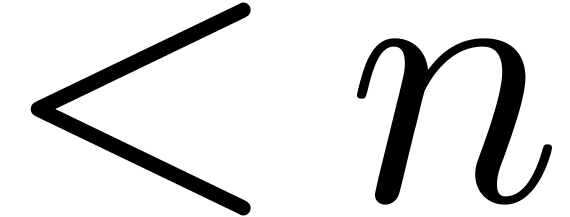 we may now compute
we may now compute
This second computation can be carried out in place. At the last stage, we obtain
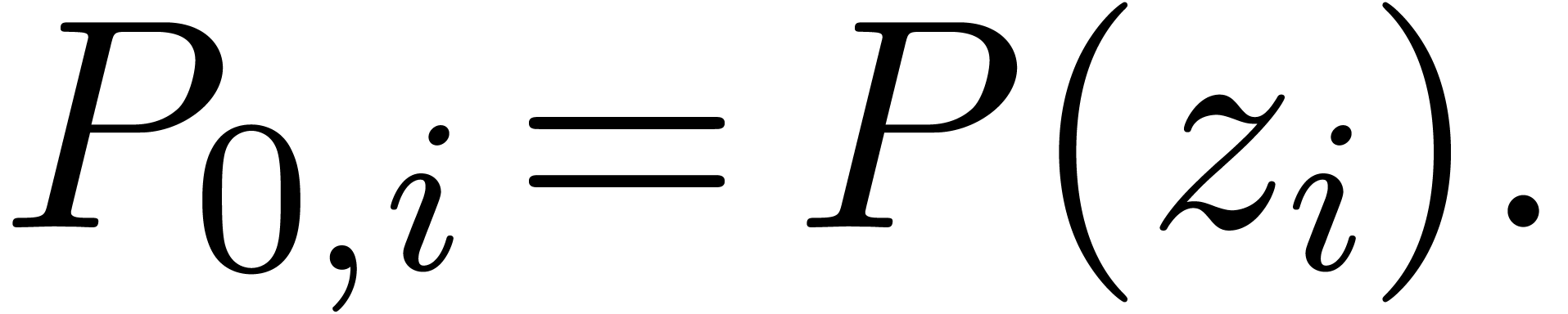
More generally,
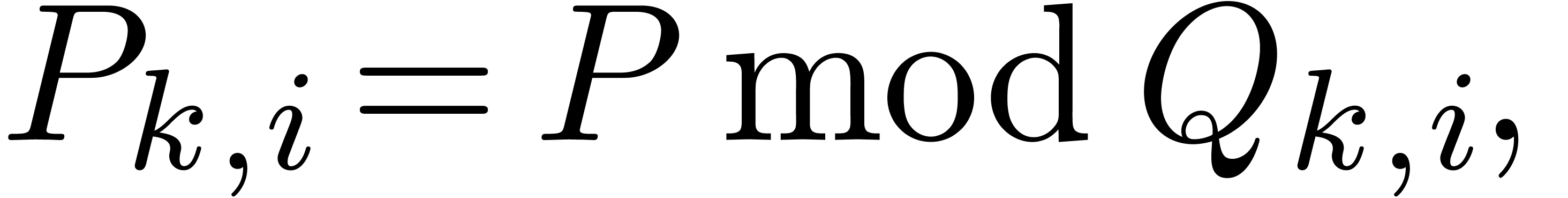 |
(8) |
for all  and
and  .
.
Proof. In the algorithm, let 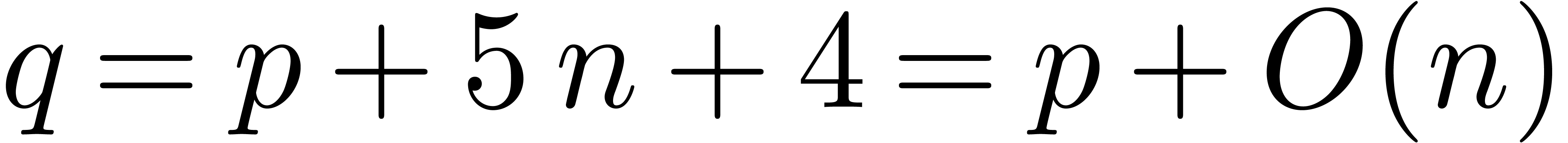 and assume that all multiplications (6) and all euclidean
divisions (7) are computed up to an absolute error
and assume that all multiplications (6) and all euclidean
divisions (7) are computed up to an absolute error 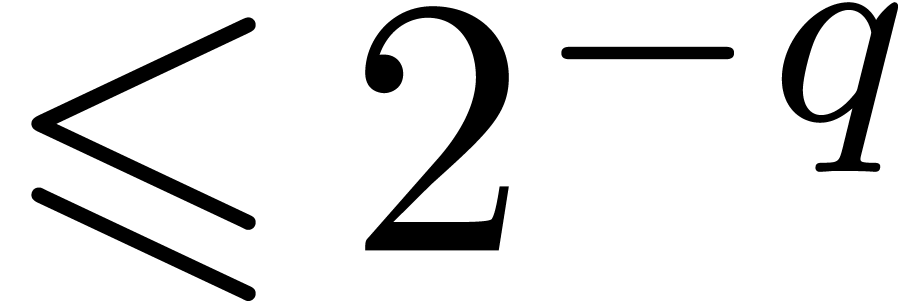 . Let
. Let 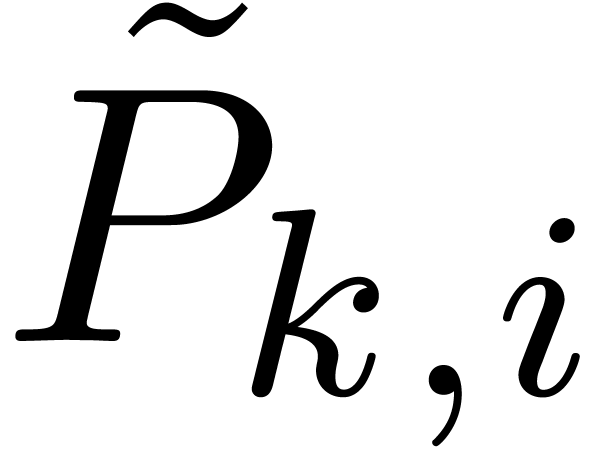 and
and
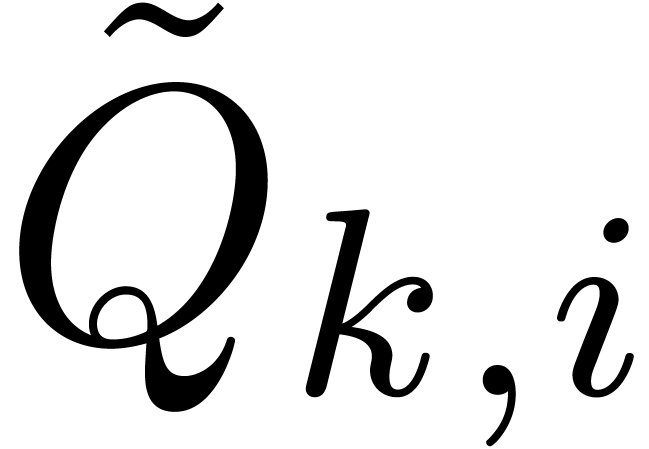 denote the results of these approximate
computations. We have
denote the results of these approximate
computations. We have
It follows by induction that
From (8) and lemma 10, we have
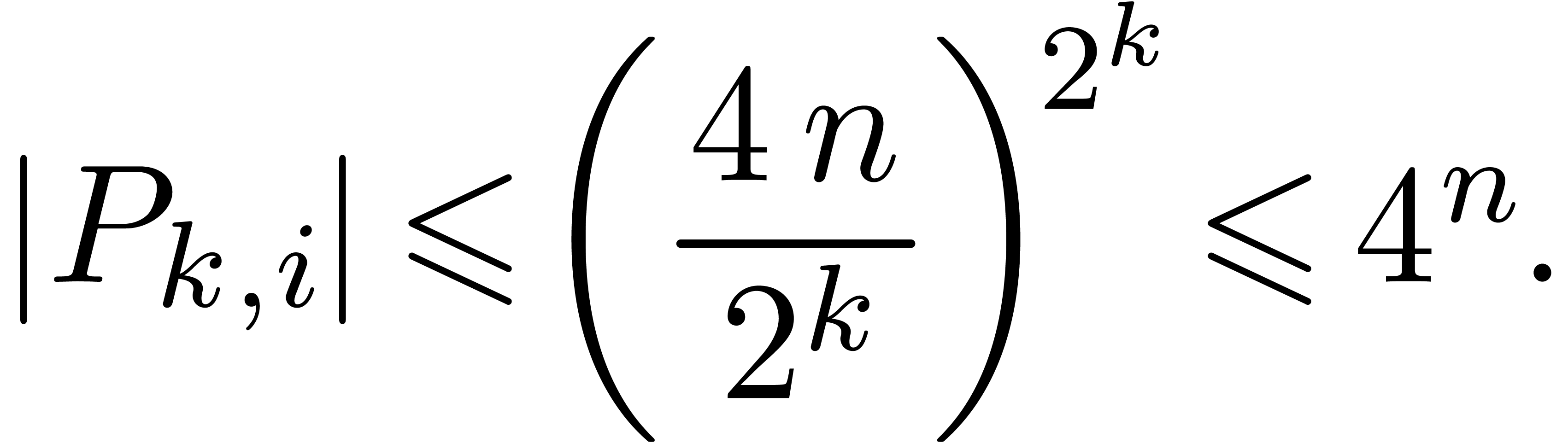 |
(11) |
In view of (7) and lemma 9, we also have
By induction over  , we obtain
, we obtain
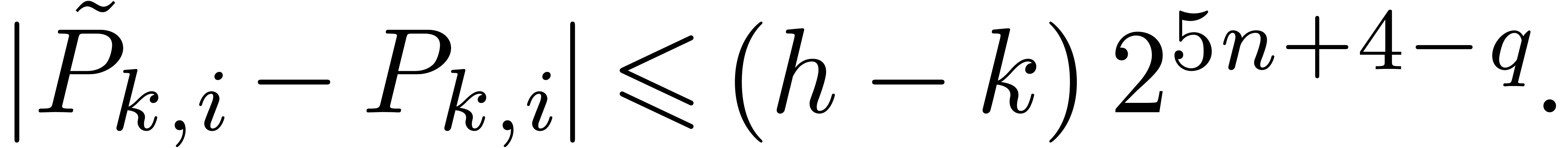
Using our choice of  , we
conclude that
, we
conclude that
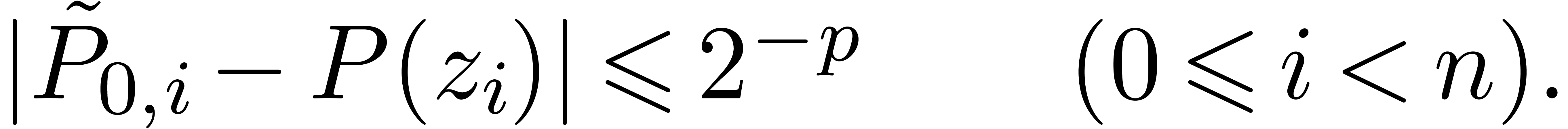
Let us now estimate the complexity of the algorithm. In view of (9) and lemma 1, we may compute 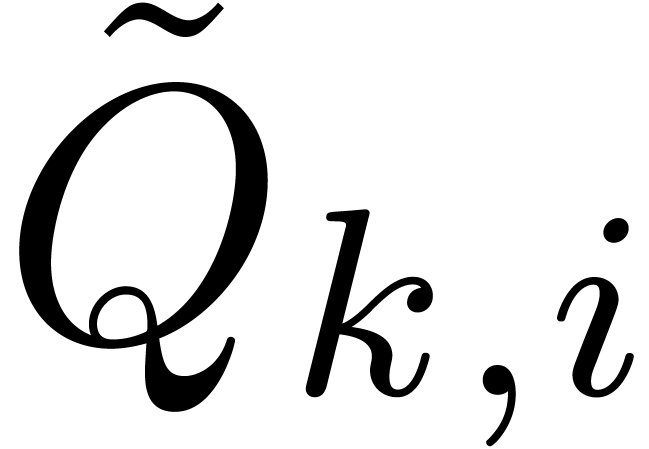 in time
in time 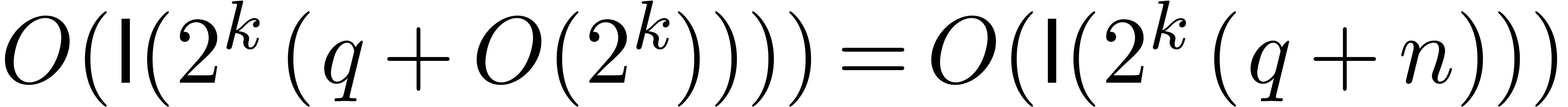 . In view of (11) and lemma 7, the computation of
. In view of (11) and lemma 7, the computation of 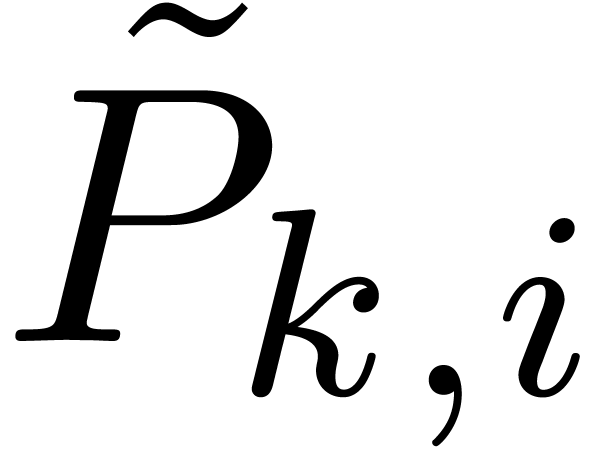 takes a time
takes a time 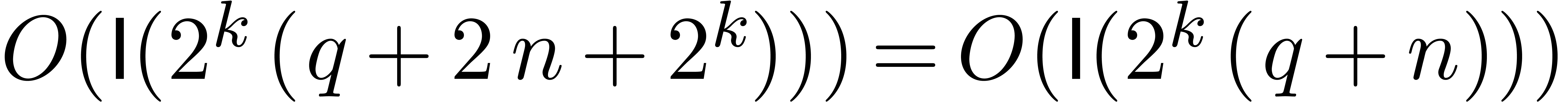 .
For fixed
.
For fixed 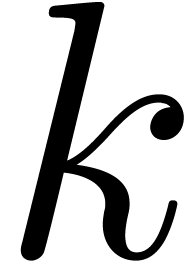 , the computation
of all
, the computation
of all 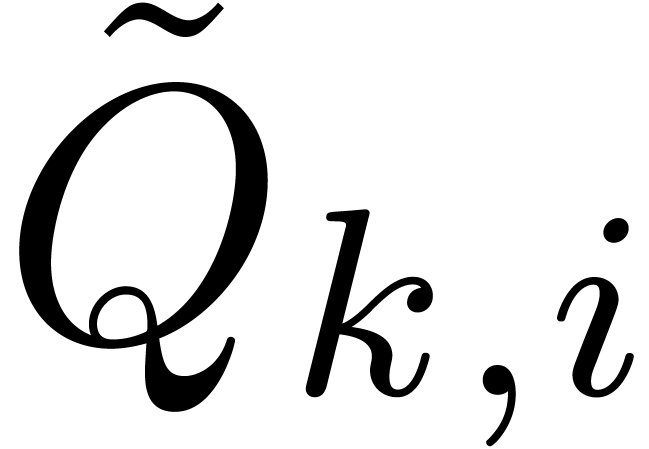 and
and 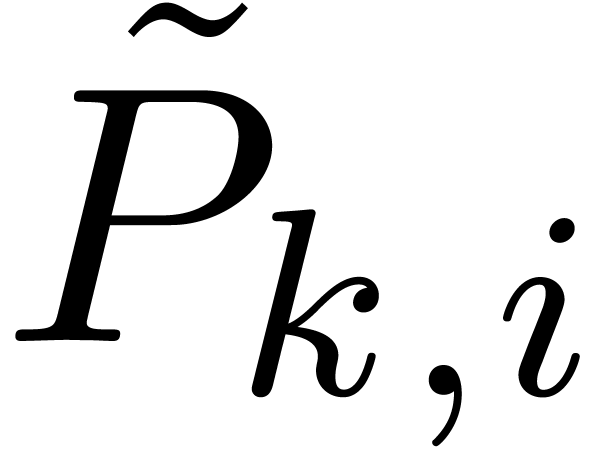 thus takes a
time
thus takes a
time 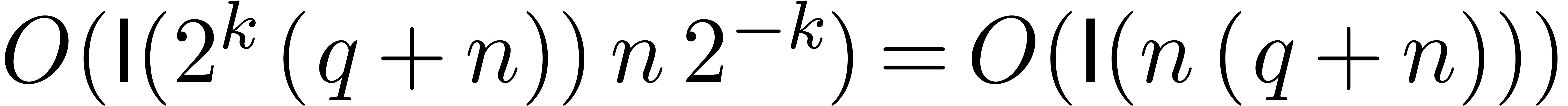 . Since there are
. Since there are 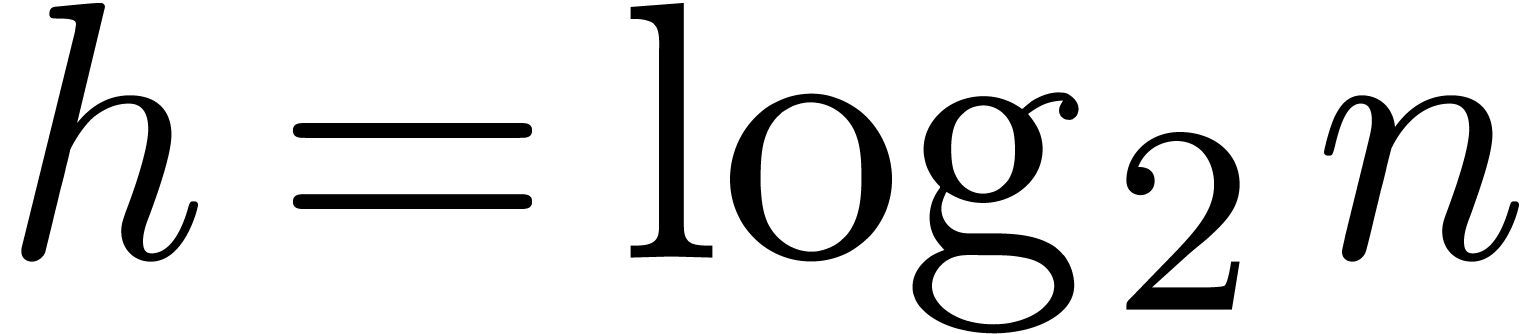 stages, the time complexity of the complete algorithm
is bounded by
stages, the time complexity of the complete algorithm
is bounded by 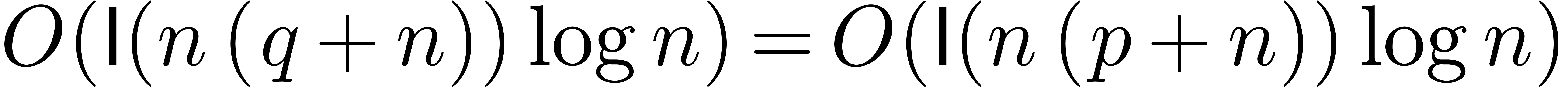 .
.
If 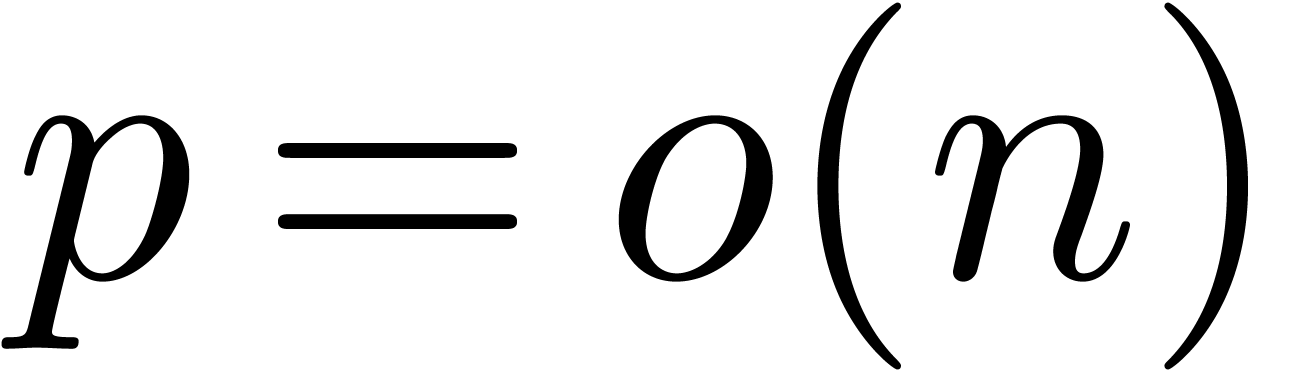 , then the bound from
lemma 11 reduces to
, then the bound from
lemma 11 reduces to 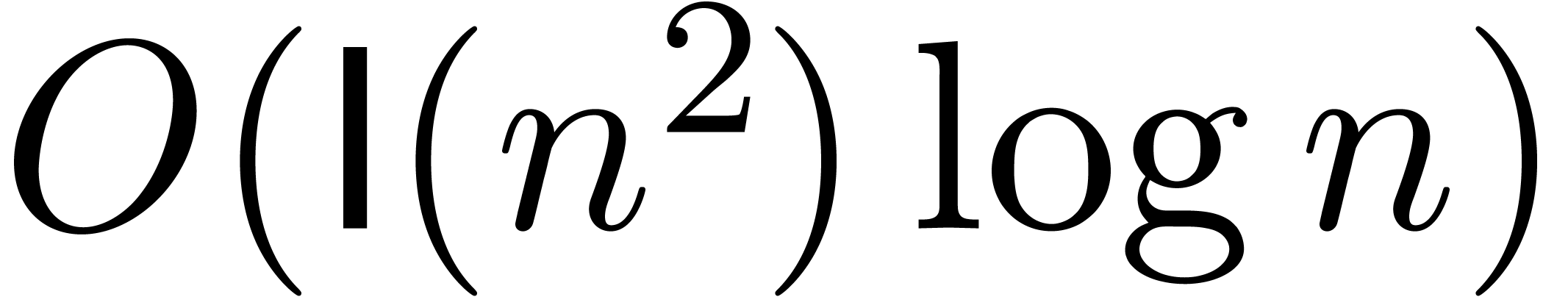 ,
which is not very satisfactory. Indeed, in the very special case when
,
which is not very satisfactory. Indeed, in the very special case when
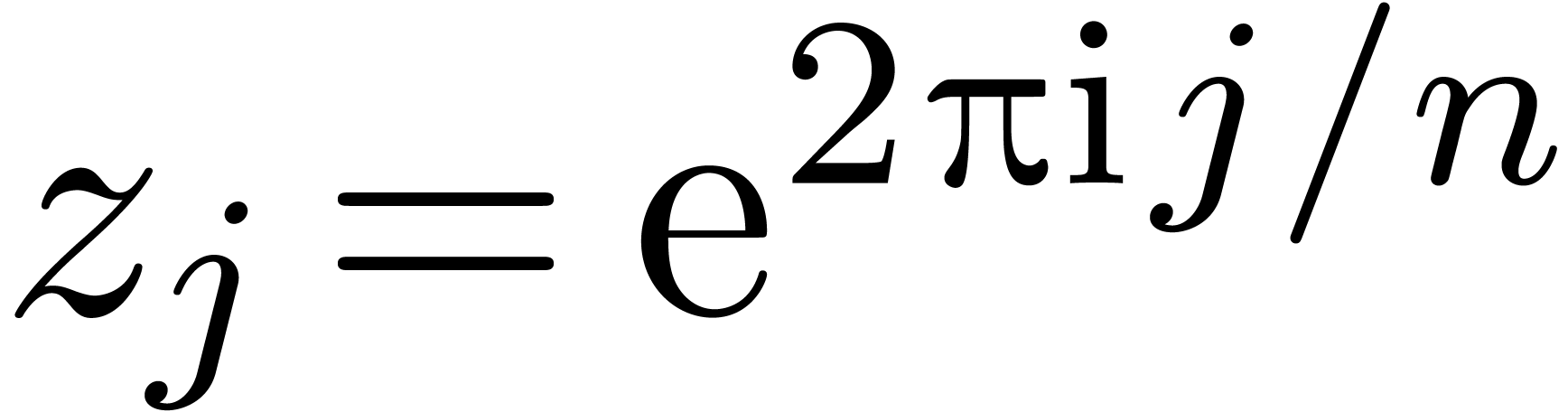 for
for 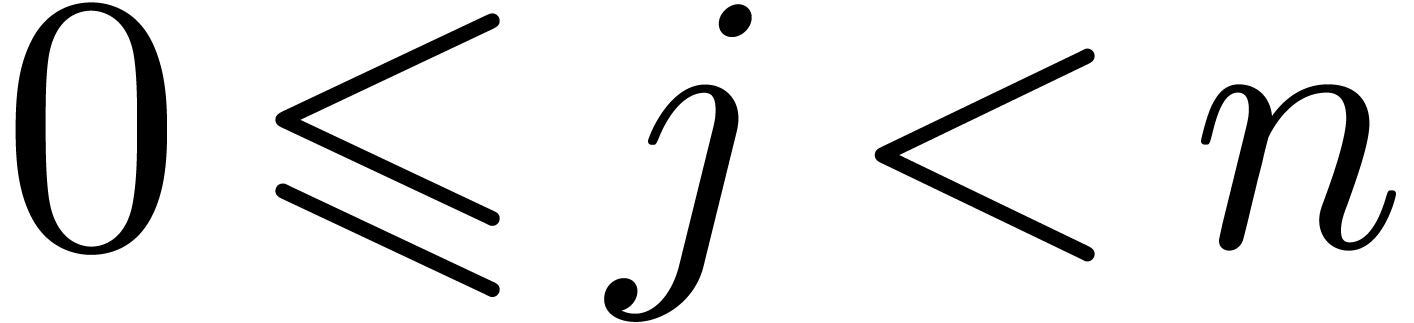 ,
we may achieve the complexity
,
we may achieve the complexity 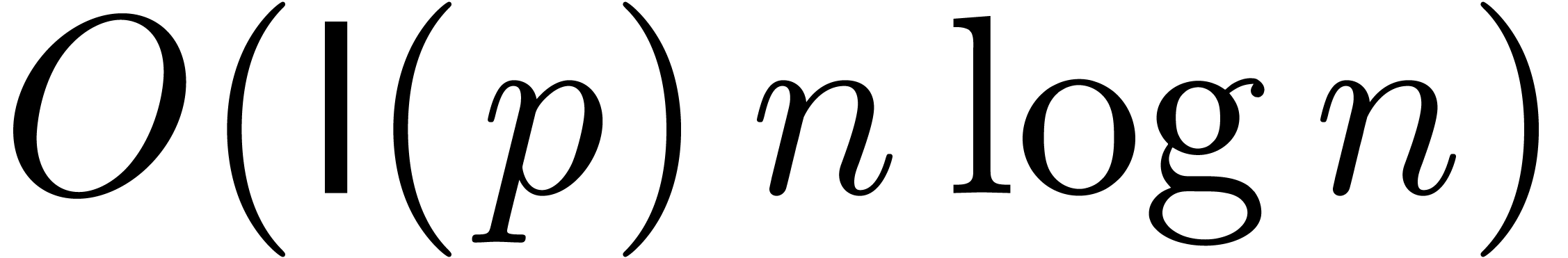 ,
by using the fast Fourier transform. In general, we may strive for a
bound of the form
,
by using the fast Fourier transform. In general, we may strive for a
bound of the form 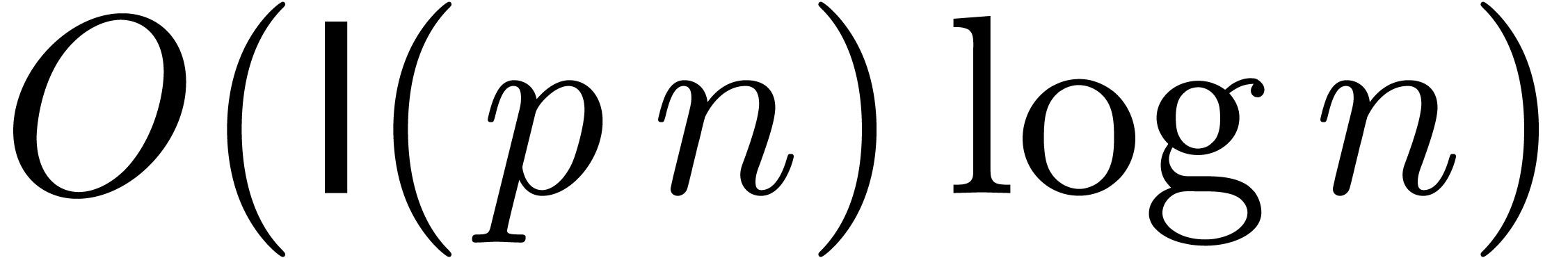 . We have
not yet been able to obtain this complexity, but we will now describe
some partial results in this direction. Throughout the section, we
assume that
. We have
not yet been able to obtain this complexity, but we will now describe
some partial results in this direction. Throughout the section, we
assume that 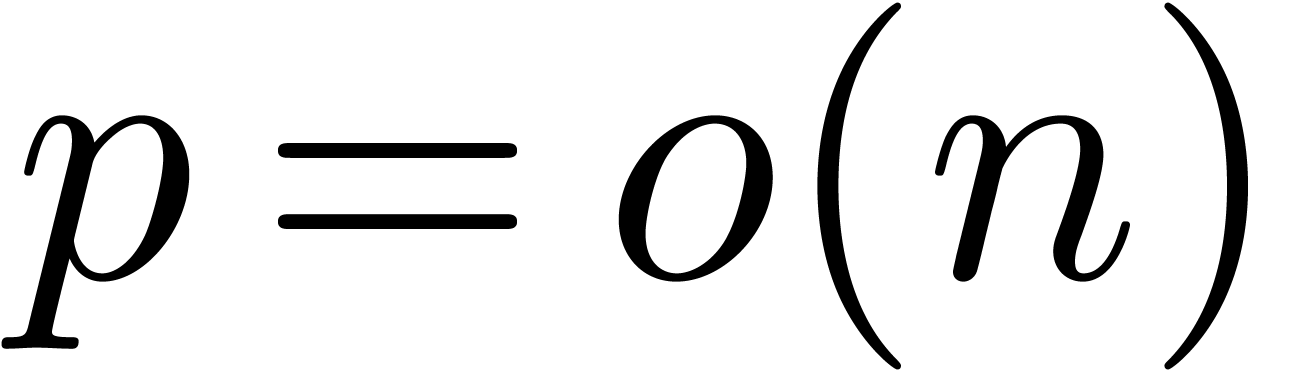 .
.
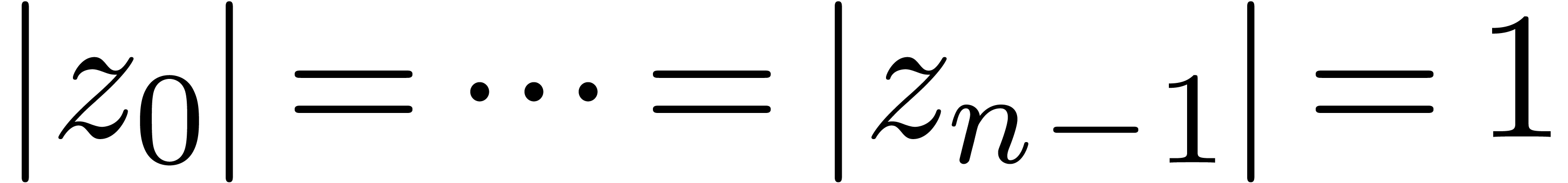 . Then we may
. Then we may
 -evaluate
-evaluate 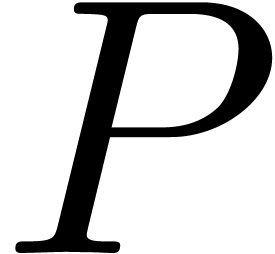 at
at  in time
in time 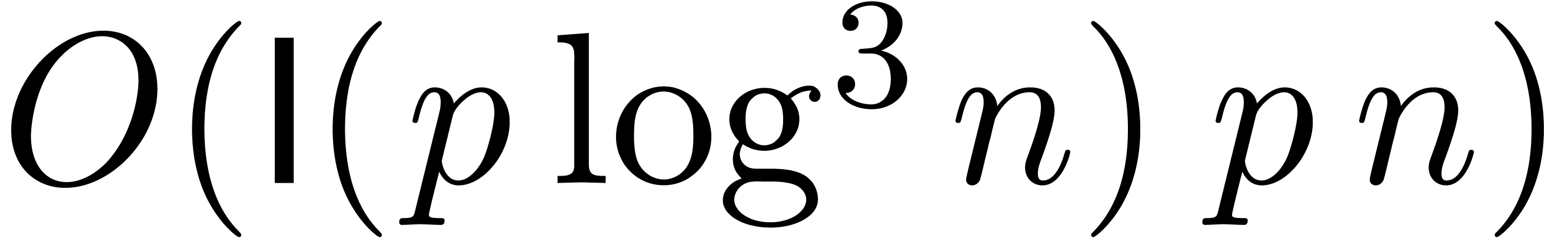 .
.
Proof. Let 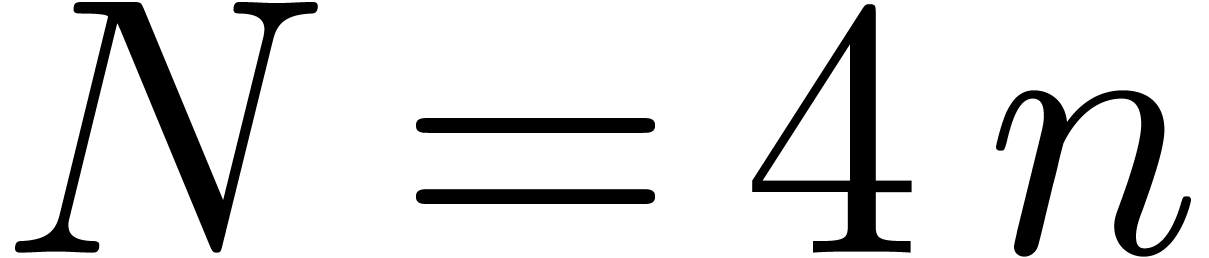 ,
,
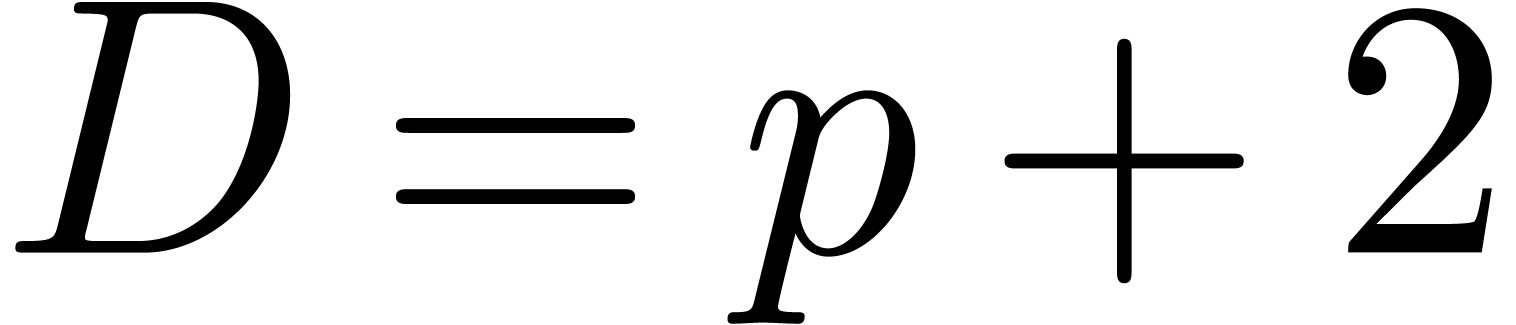 and
and 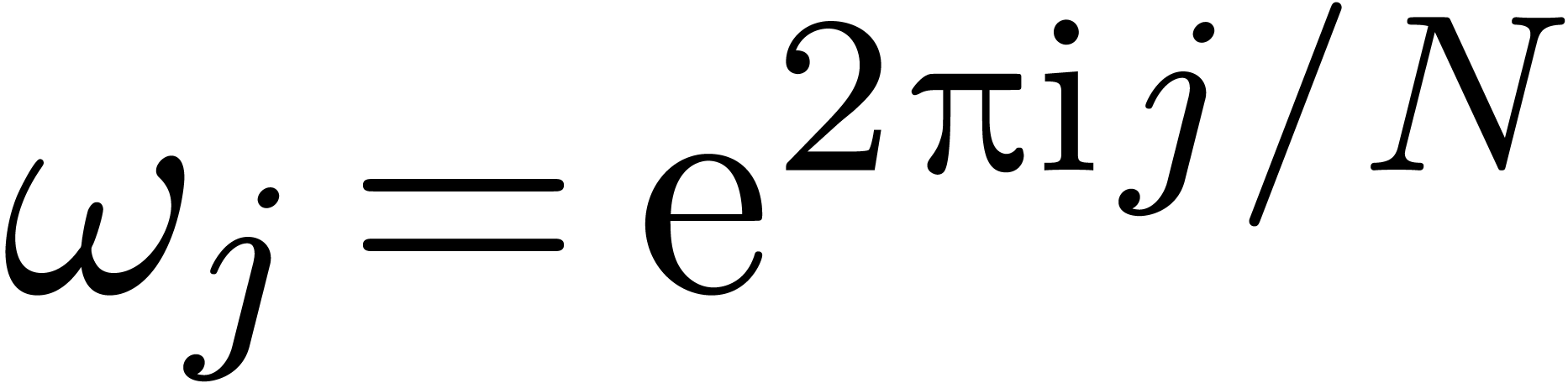 for all
for all 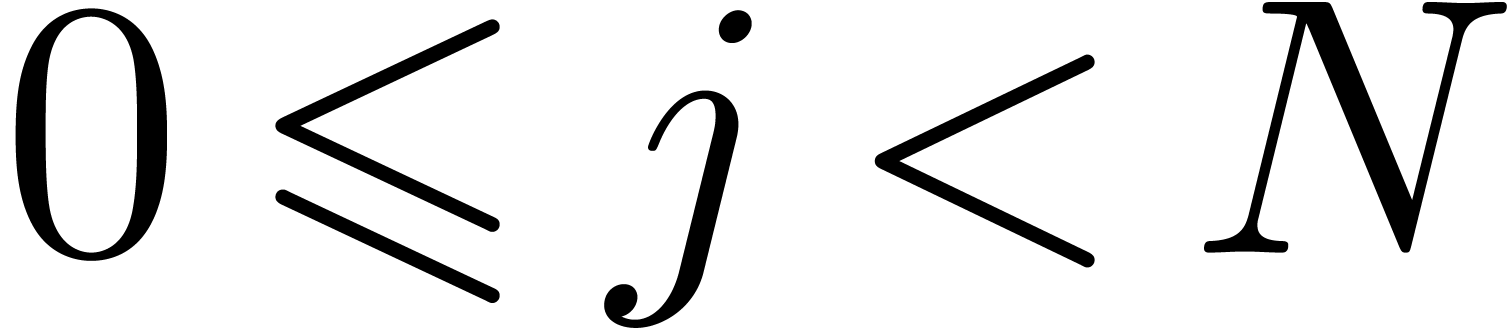 . Each of the points
. Each of the points  is
at the distance of at most
is
at the distance of at most 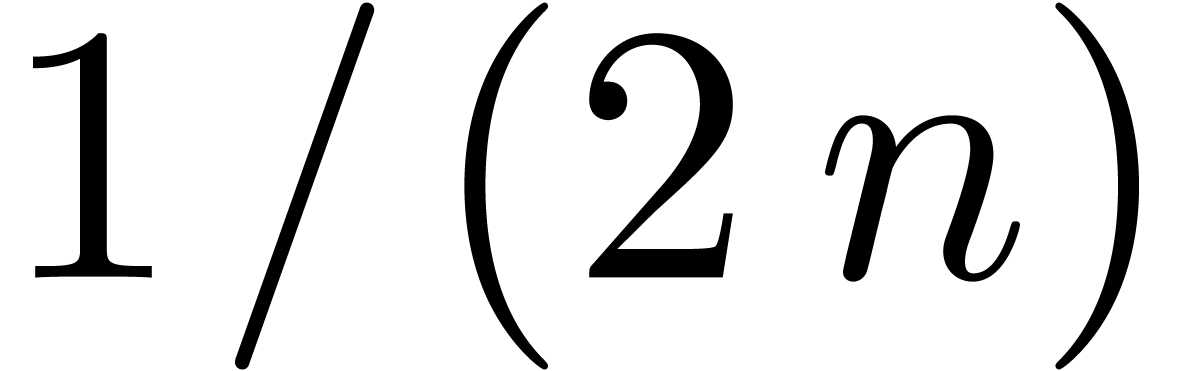 to one of the points
to one of the points
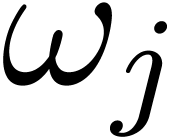 . We will compute
. We will compute 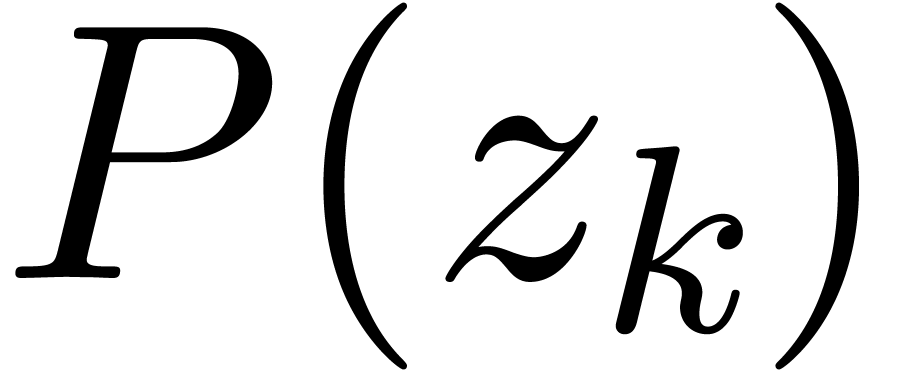 using a Taylor series expansion of
using a Taylor series expansion of 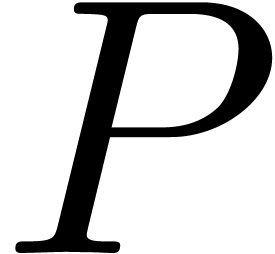 at
at 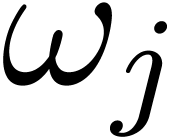 . We first observe that
. We first observe that
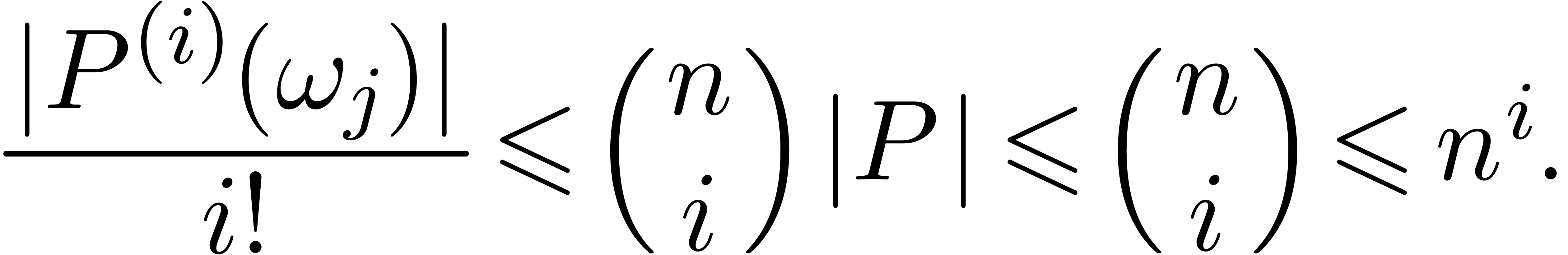 |
(12) |
Using  fast Fourier transforms of size
fast Fourier transforms of size  , we first compute
, we first compute 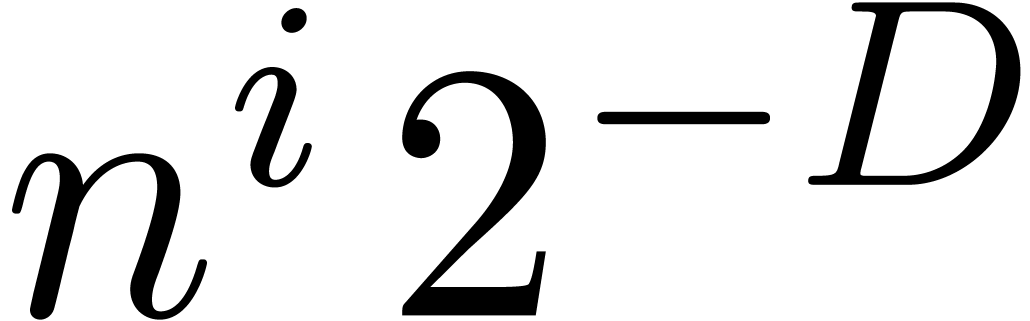 -approximations of
-approximations of 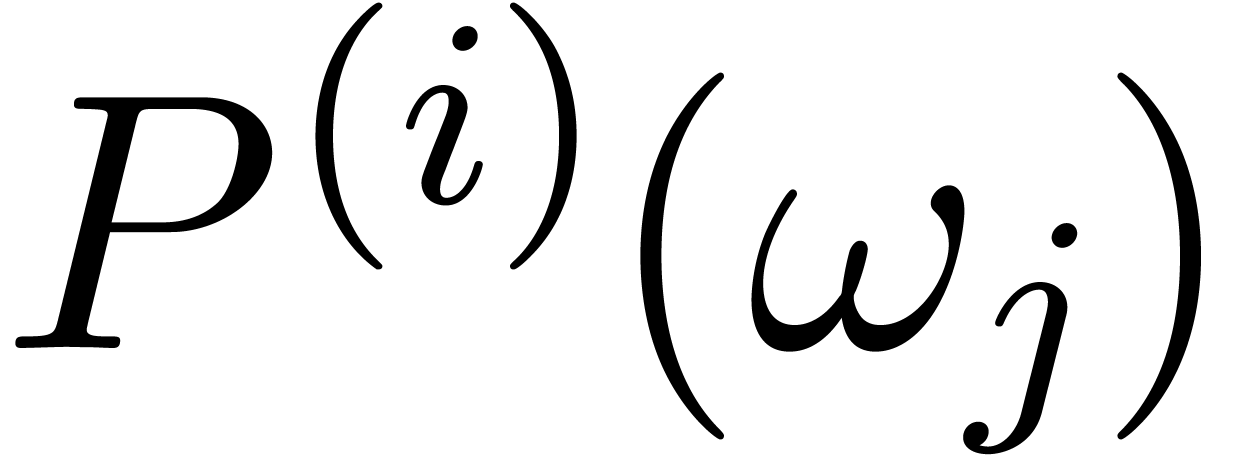 for
all
for
all 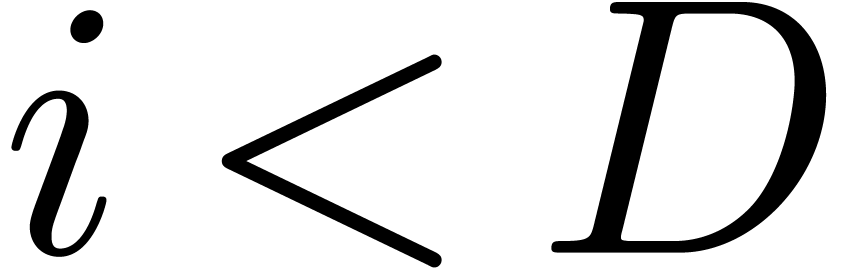 and
and 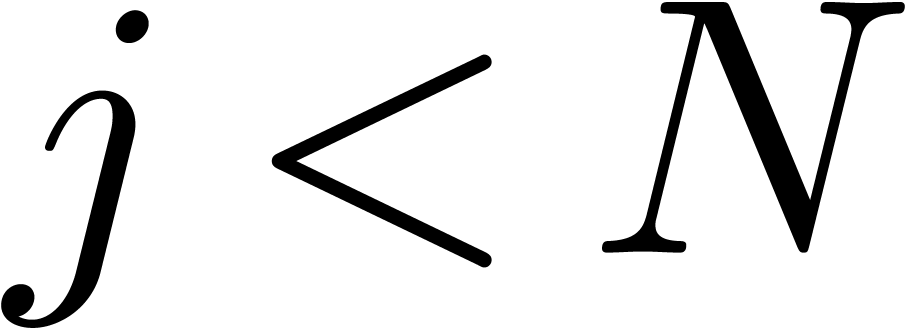 .
This can be done in time
.
This can be done in time
From (12) it follows that
The  -evaluation of
-evaluation of 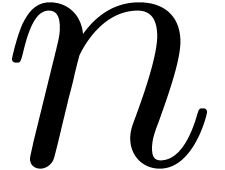 sums of the form
sums of the form 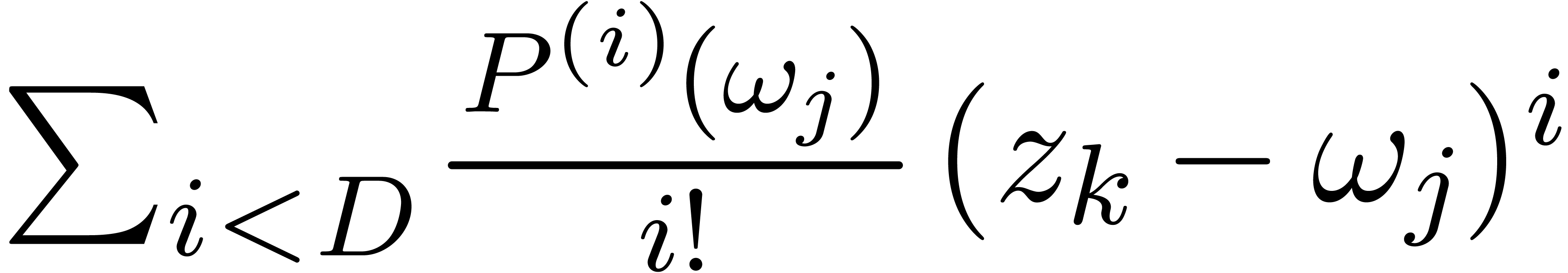 using Horner's
rule takes a time
using Horner's
rule takes a time 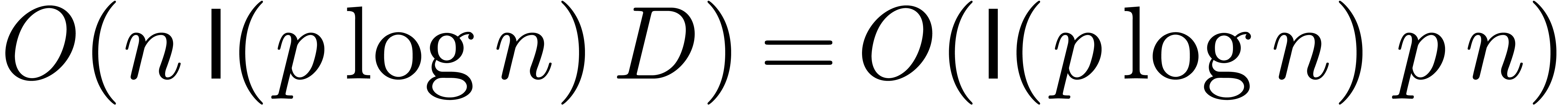 .
.
 -evaluate
-evaluate 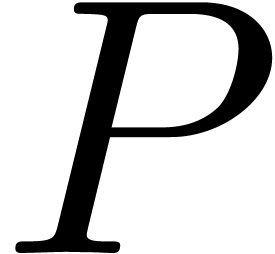 at
at  in time
in time 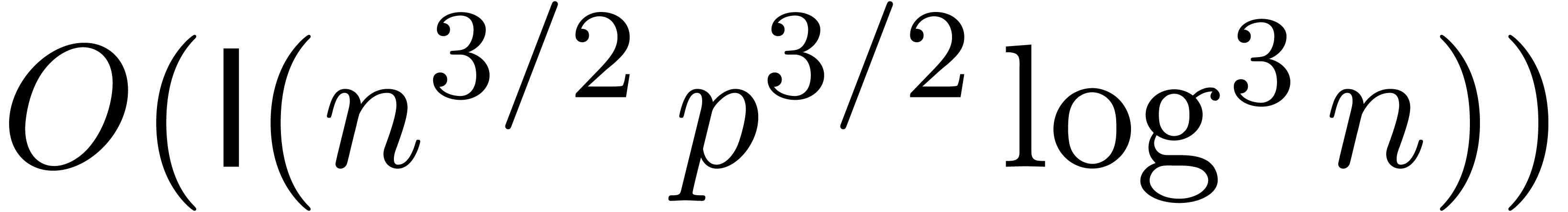 .
.
Proof. The proof of the above proposition adapts
to the case when 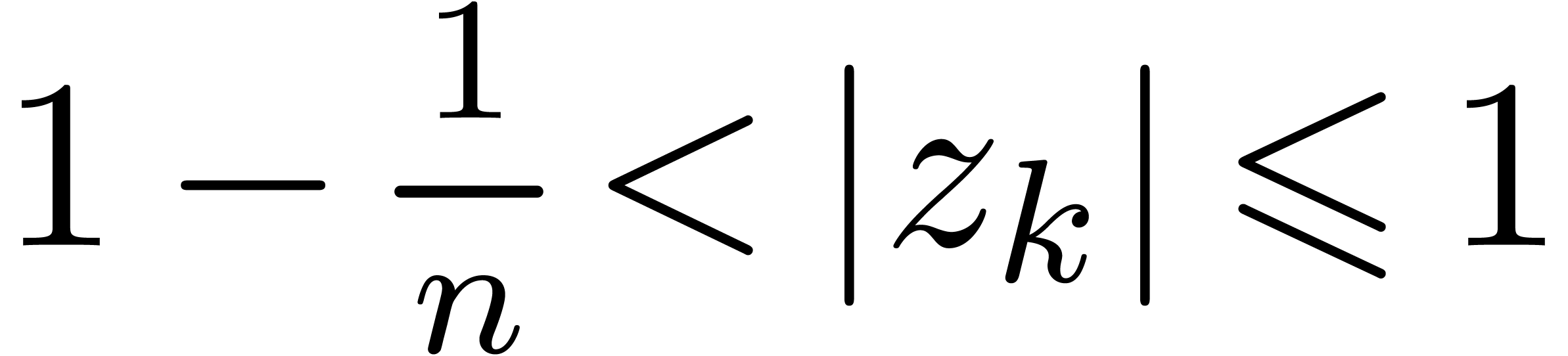 for all
for all  . Let us now subdivide the unit disk into
. Let us now subdivide the unit disk into  annuli
annuli 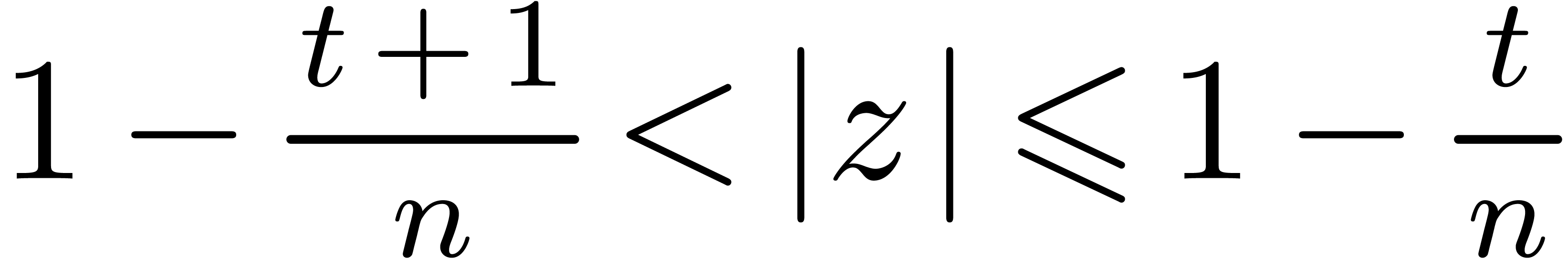 and the disk of radius
and the disk of radius
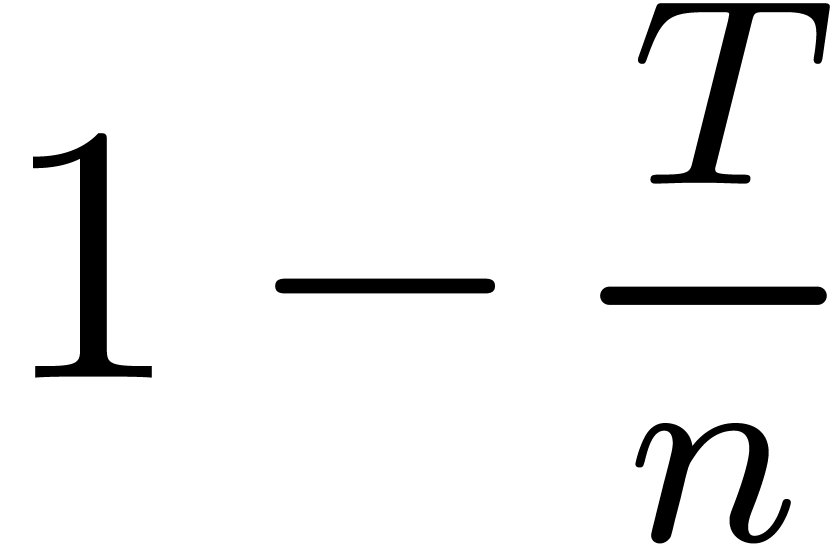 . For a fixed annulus, we may
evaluate
. For a fixed annulus, we may
evaluate  at each of the
at each of the 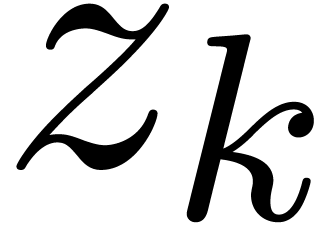 inside the annulus in time
inside the annulus in time 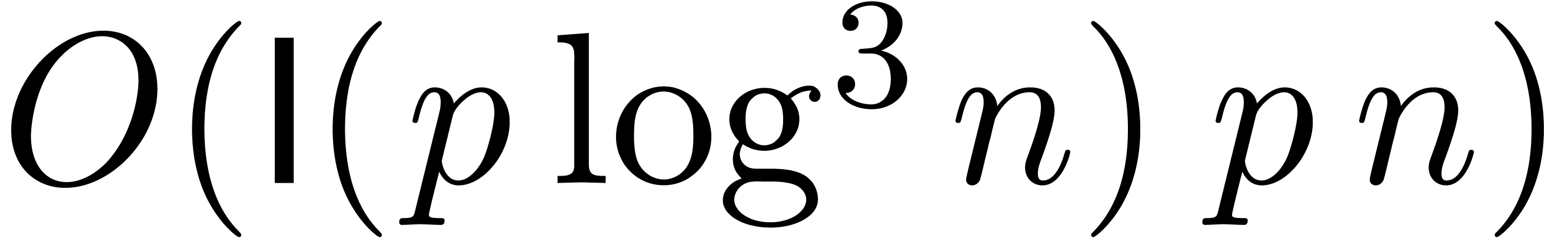 .
For
.
For 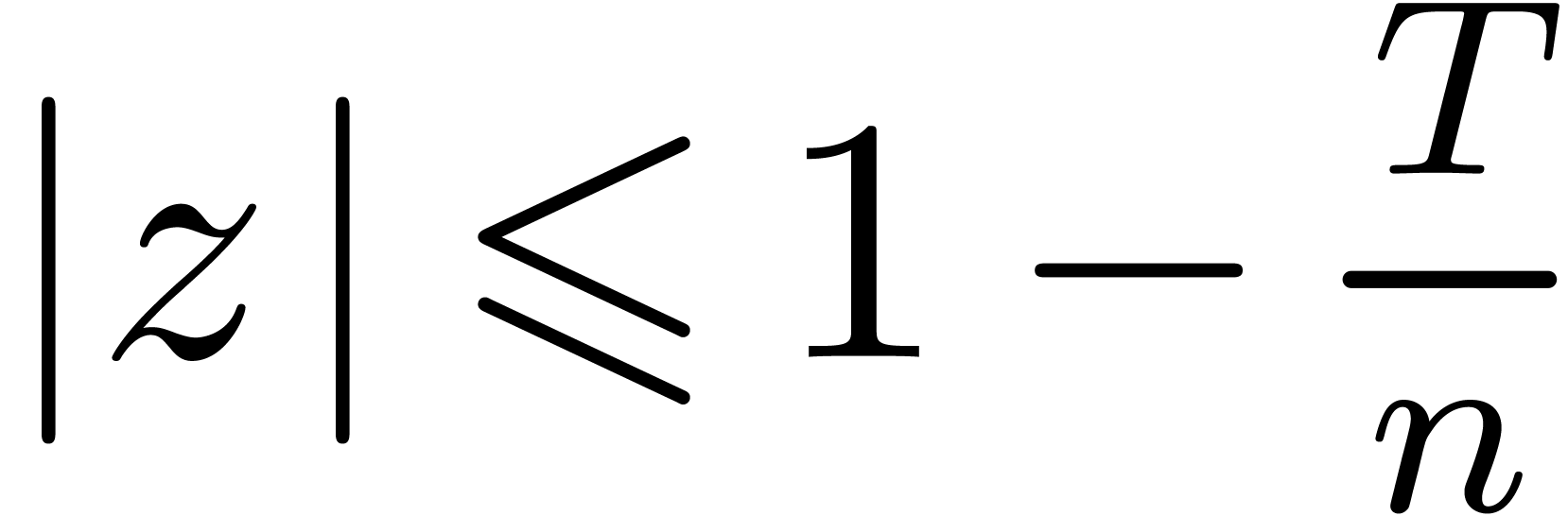 , we have
, we have
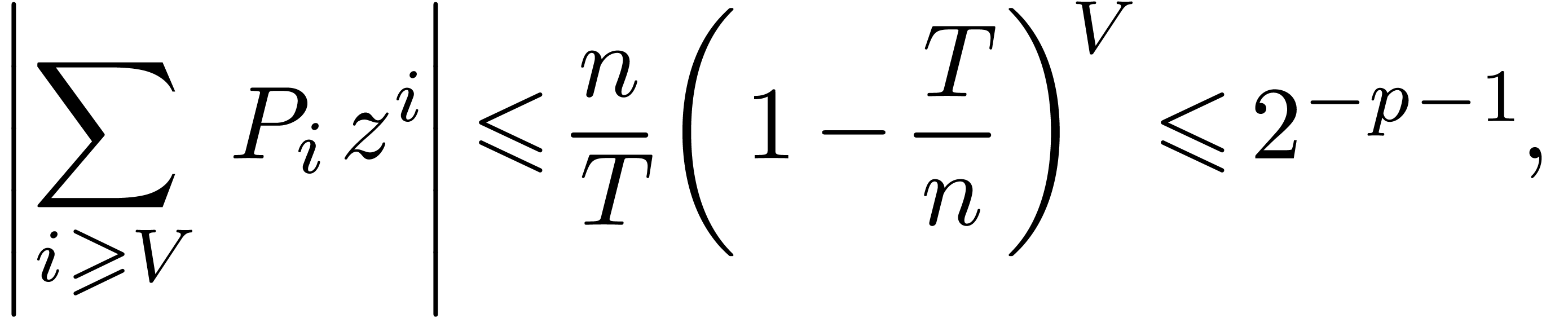
provided that 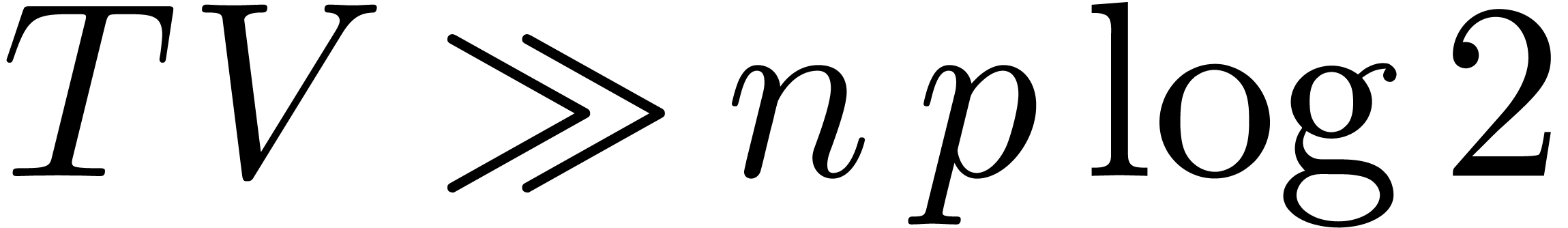 . Consequently,
taking
. Consequently,
taking 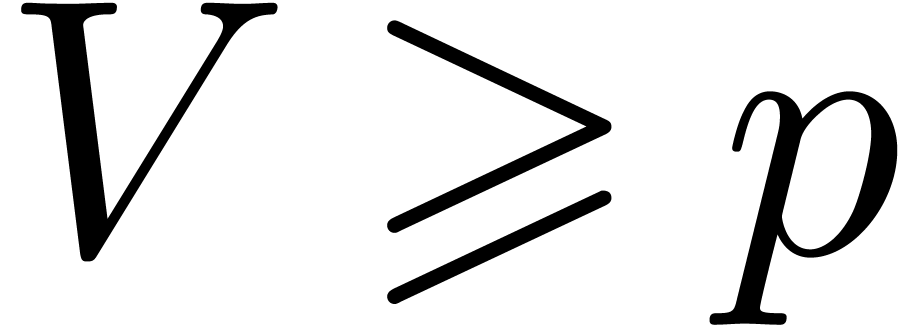 , we may evaluate
, we may evaluate 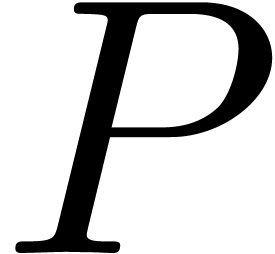 at the remaining points in time
at the remaining points in time 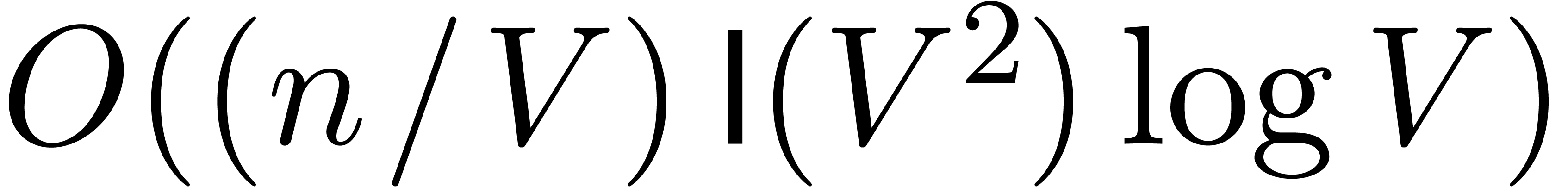 . Under the condition
. Under the condition 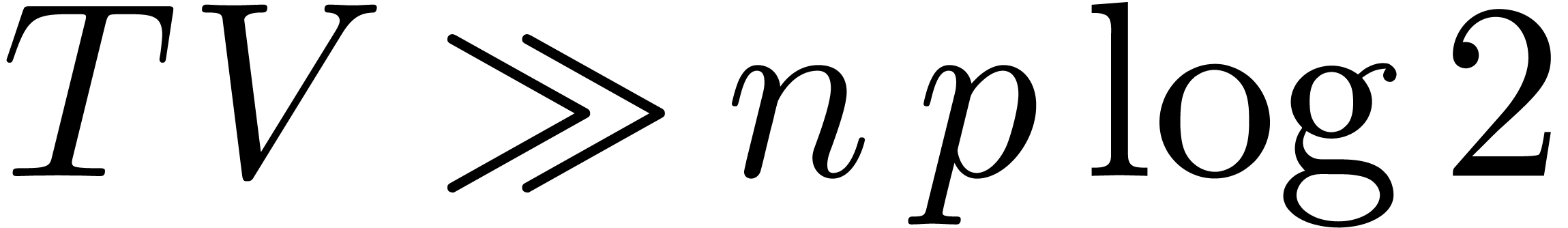 , and up to logarithmic terms, the sum
, and up to logarithmic terms, the sum
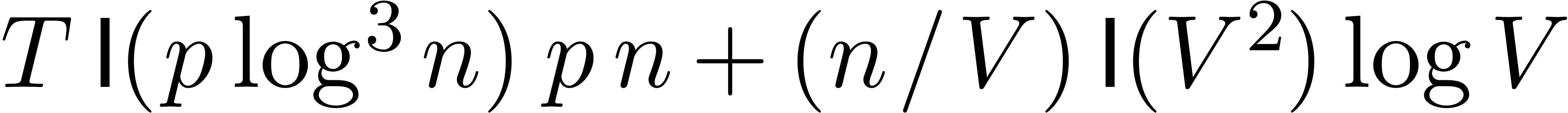
becomes minimal for 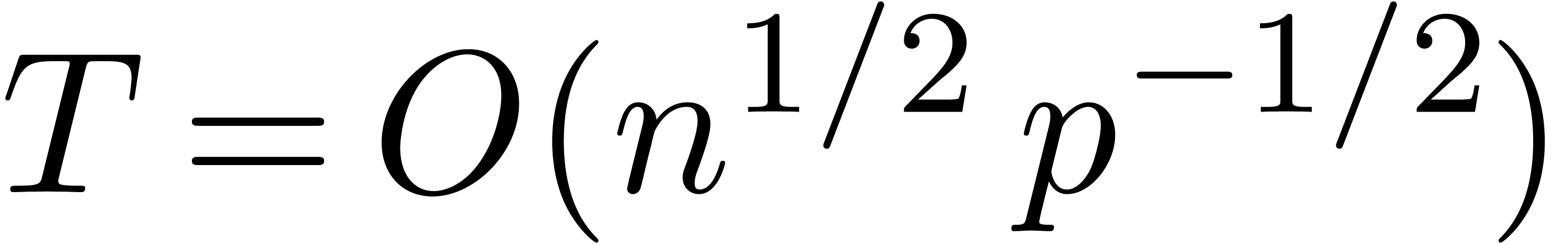 and
and 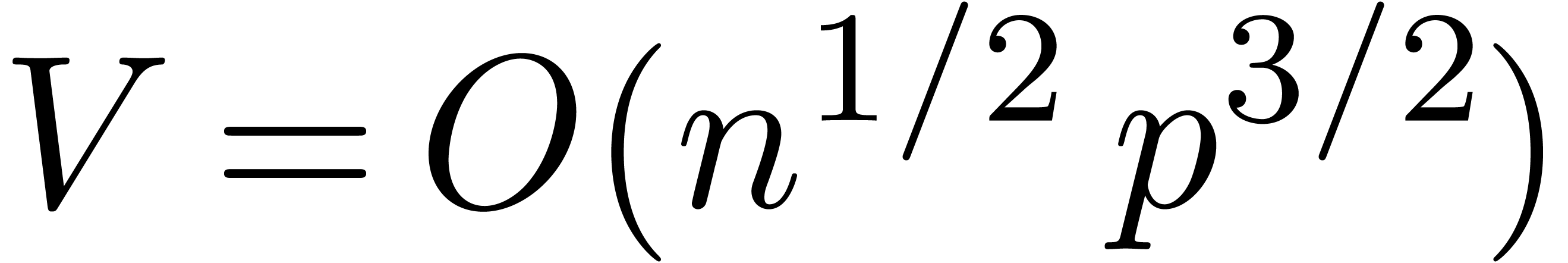 .
.
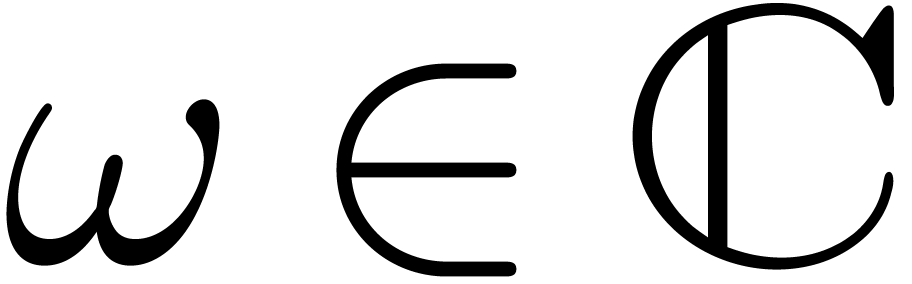 with
with 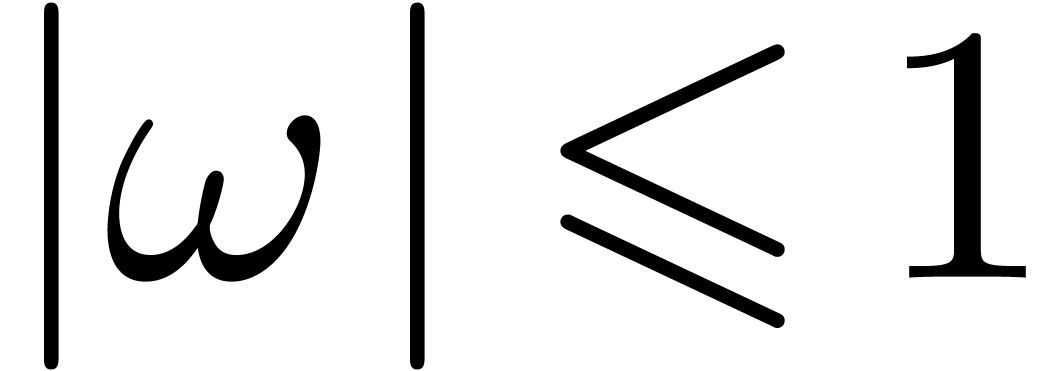 and
and  for all
for all  .
Then we may
.
Then we may  -evaluate
-evaluate  at
at  in time
in time 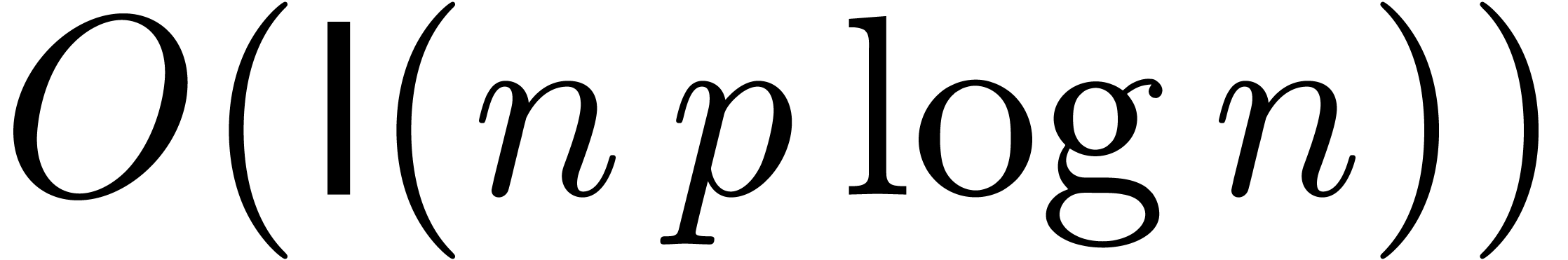 .
.
Proof. We will only provide a sketch of the
proof. As in the proof of proposition 12, we first compute
the Taylor series expansion of 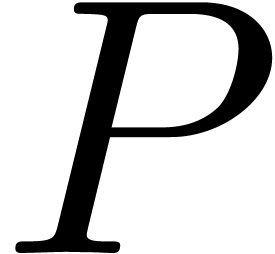 at
at  up to order
up to order 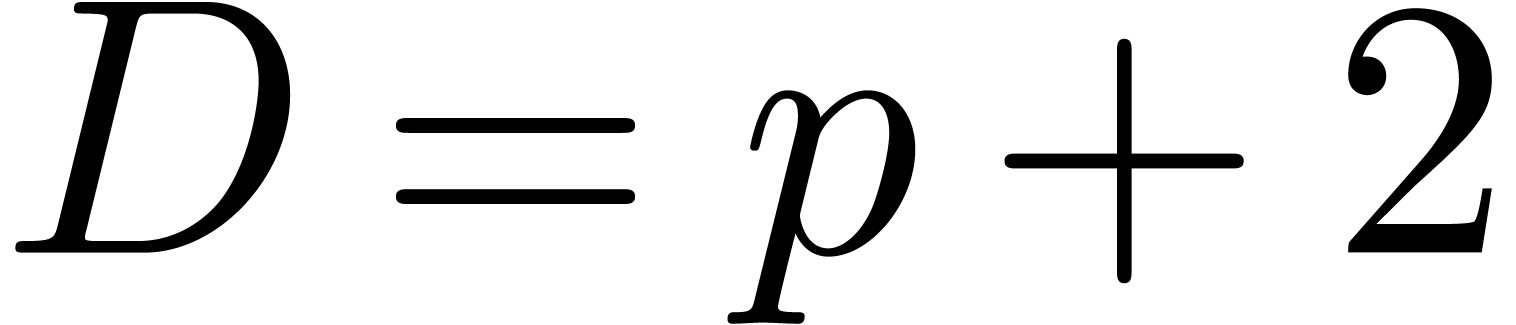 .
This task can be performed in time
.
This task can be performed in time 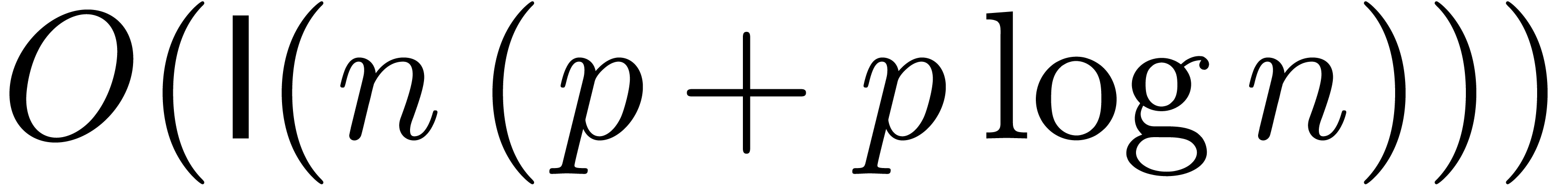 via a
division of
via a
division of  by
by 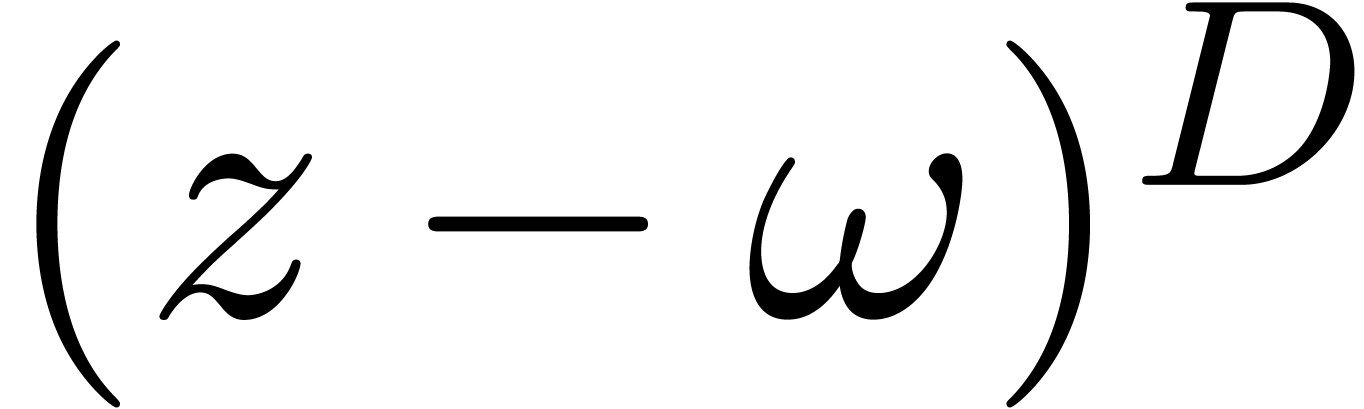 followed
by a Taylor shift. We next evaluate this expansion at
followed
by a Taylor shift. We next evaluate this expansion at 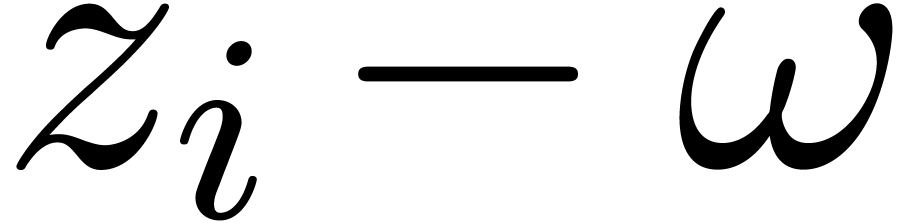 for all
for all 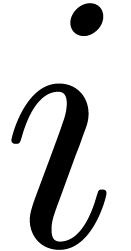 . According to
proposition 16, this can be done in time
. According to
proposition 16, this can be done in time 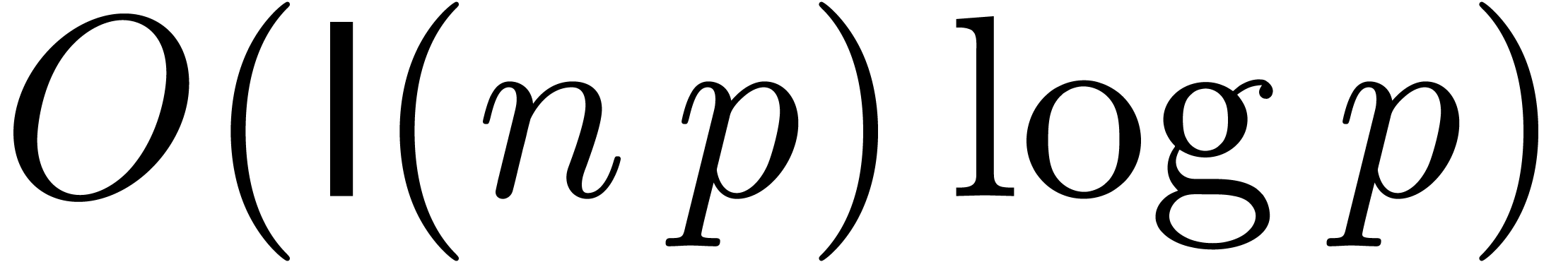 .
.
 be a fixed constant. With the
notations of proposition 11, assume that
be a fixed constant. With the
notations of proposition 11, assume that 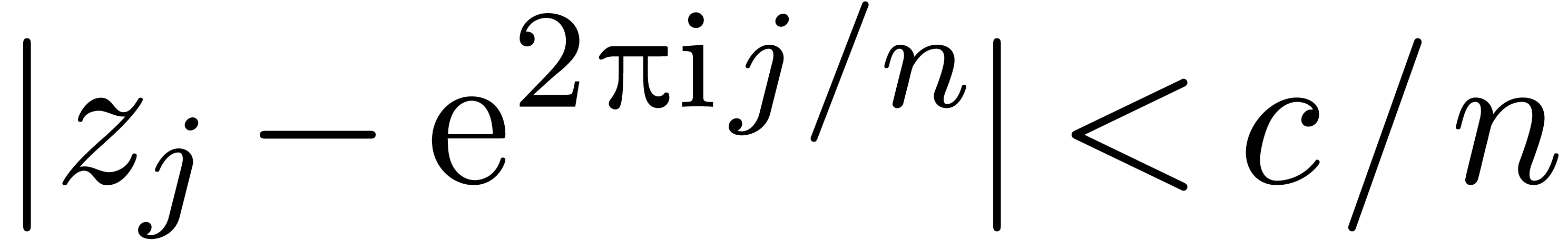 for all
for all  . Then we may
. Then we may  -evaluate
-evaluate 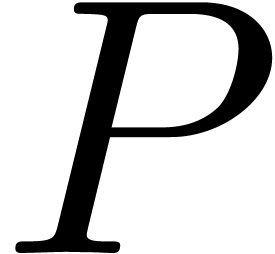 at
at  in time
in time 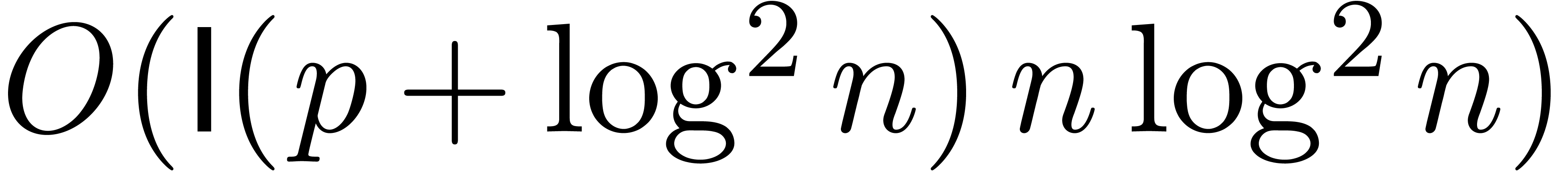 .
.
Proof. Again, we will only provide a sketch of
the proof. The main idea is to use the binary splitting algorithm from
the previous subsection. Let 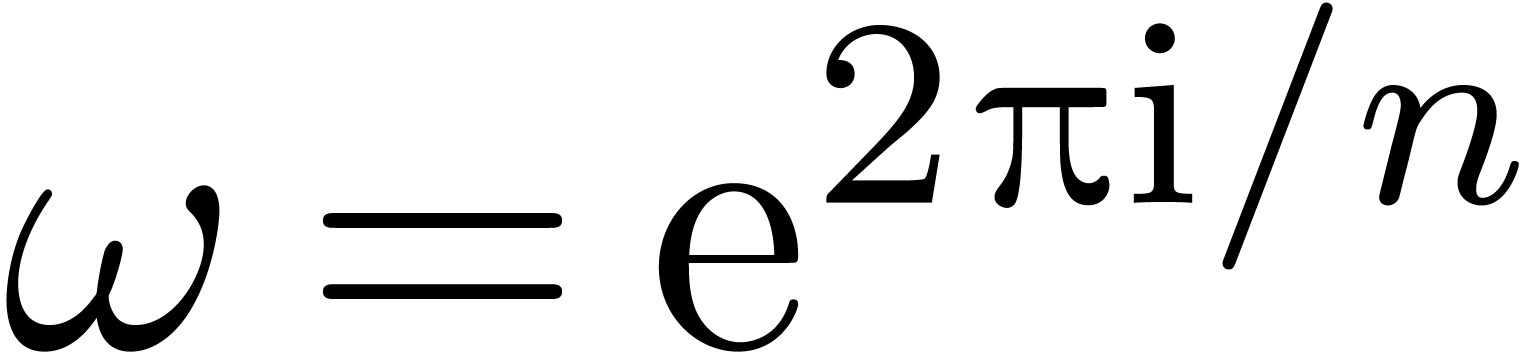 .
If
.
If 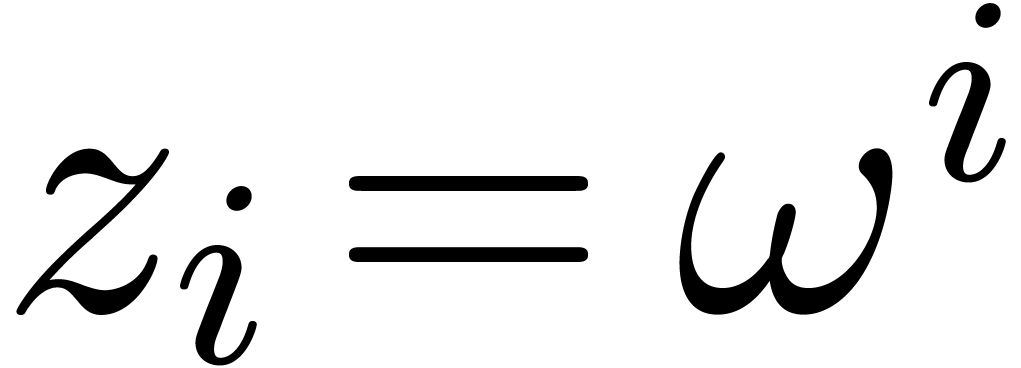 for all
for all  ,
then we obtain
,
then we obtain 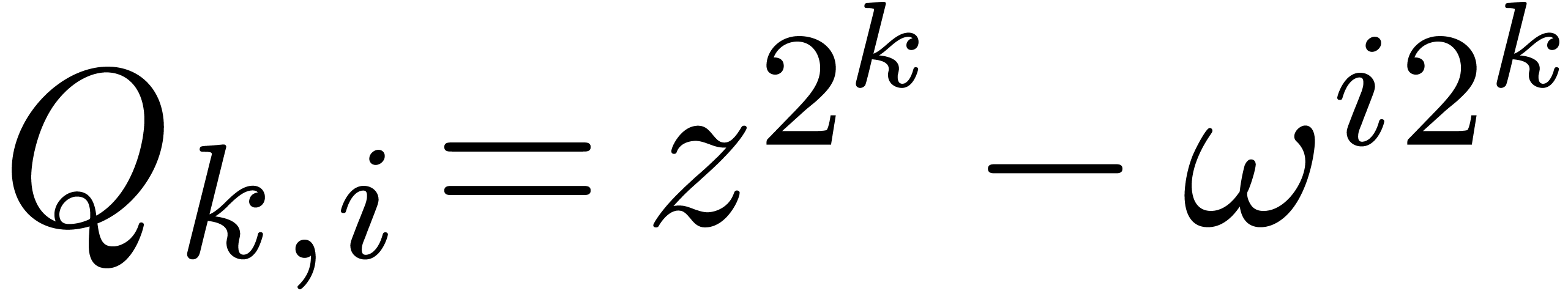 and the algorithm reduces to a
fast Fourier transform. If each
and the algorithm reduces to a
fast Fourier transform. If each 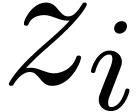 is a slight
perturbation of
is a slight
perturbation of 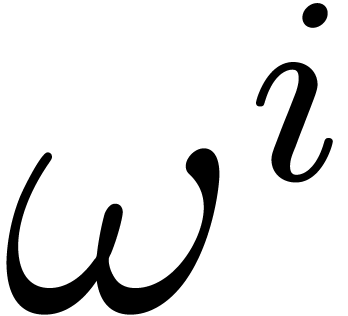 , then
, then  becomes a slight perturbation of
becomes a slight perturbation of  . In particular, the Taylor coefficients
. In particular, the Taylor coefficients  of
of 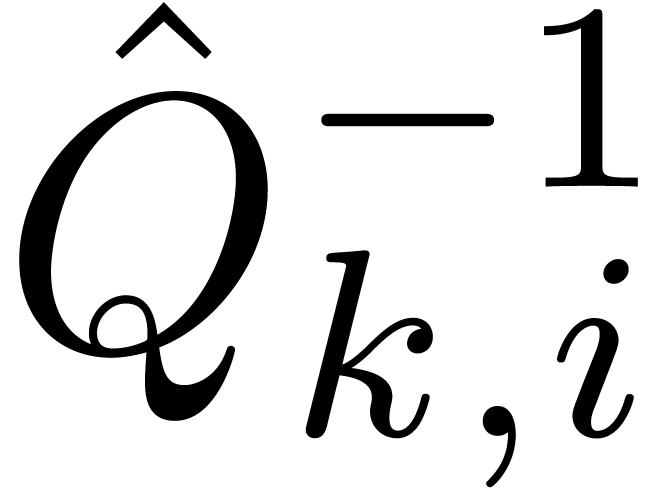 only have a polynomial
growth
only have a polynomial
growth 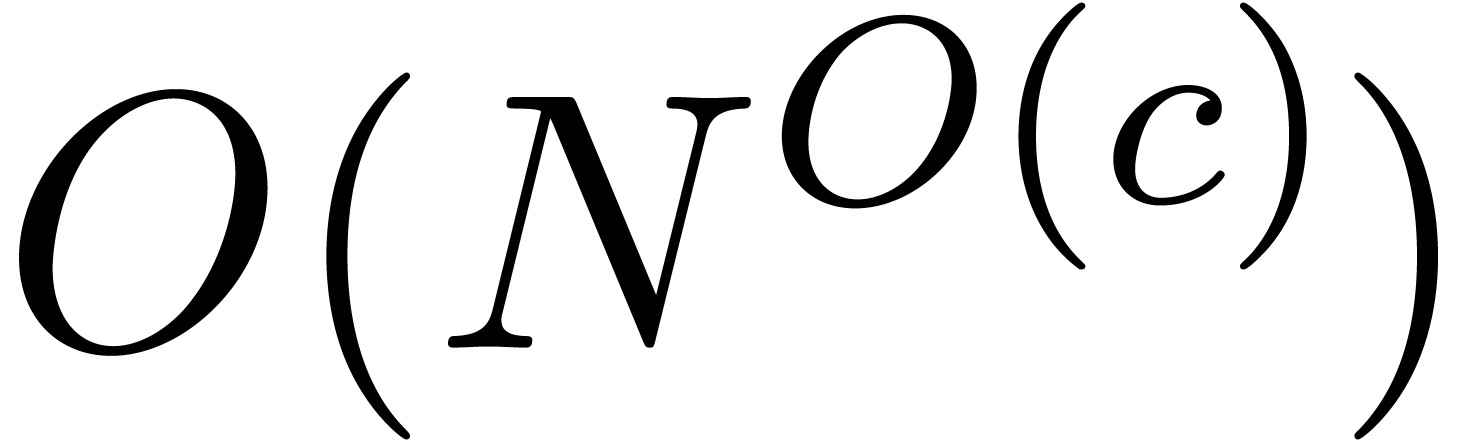 in
in 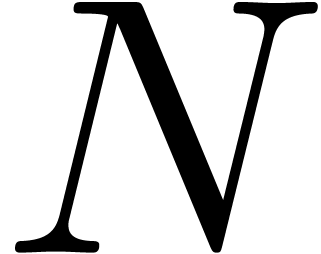 .
Consequently, the Euclidean division by
.
Consequently, the Euclidean division by 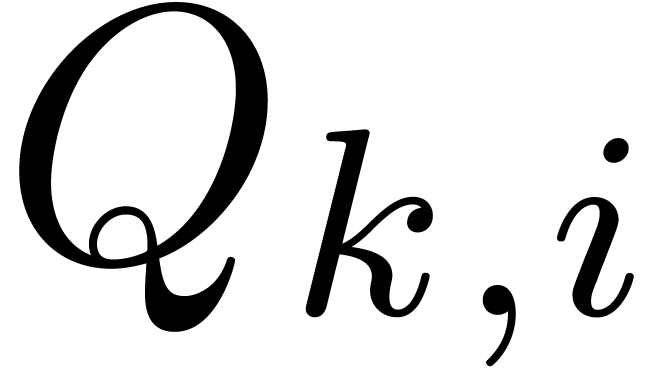 accounts
for a loss of at most
accounts
for a loss of at most 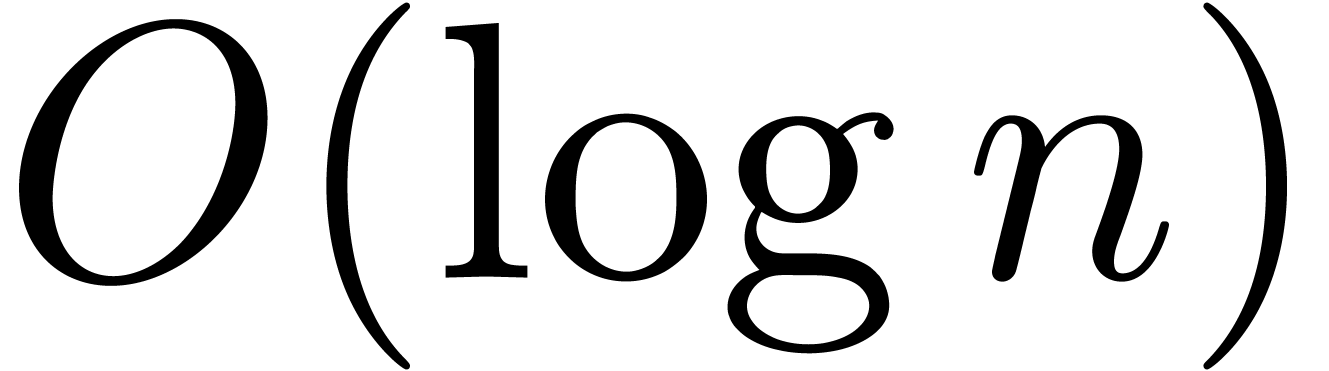 instead of
instead of 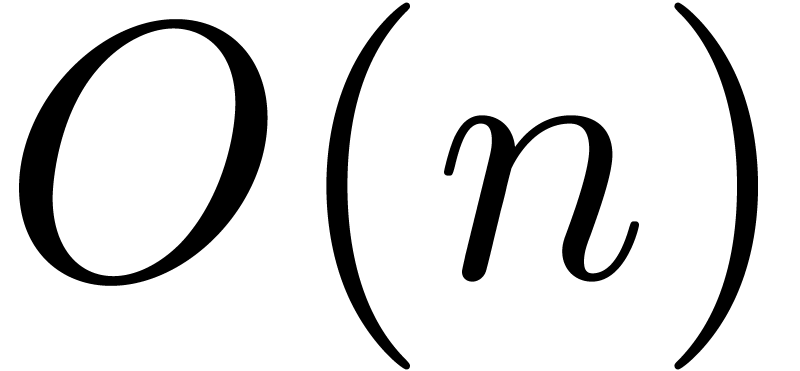 bits of precision. The binary splitting algorithm can
therefore be carried out using a fixed precision of
bits of precision. The binary splitting algorithm can
therefore be carried out using a fixed precision of 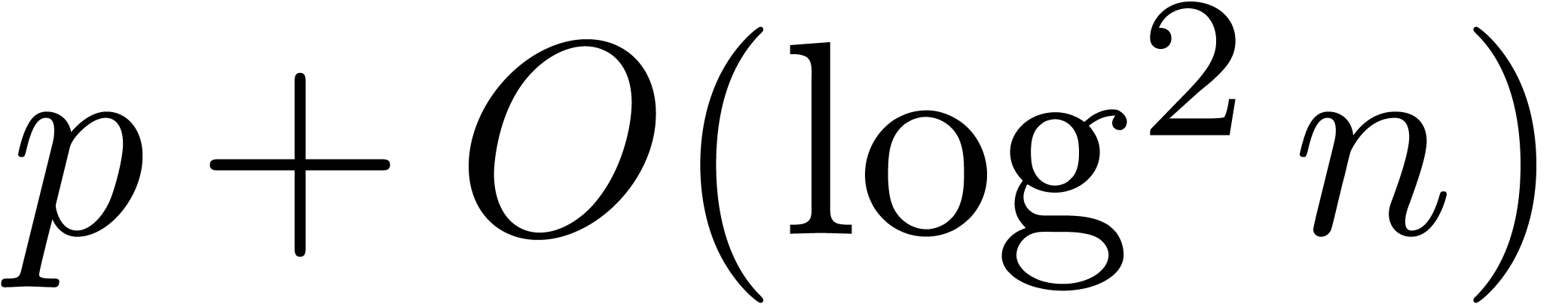 bits.
bits.
Sometimes, it is possible to decompose 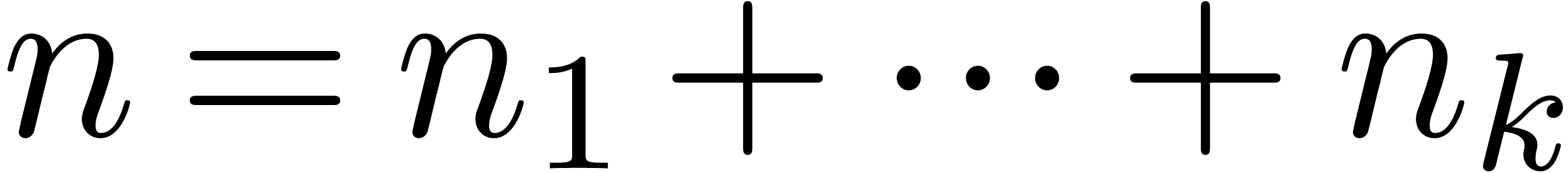 ,
such that a fast multi-point evaluation algorithm is available for each
set of points
,
such that a fast multi-point evaluation algorithm is available for each
set of points  . This leads to
the question of evaluating
. This leads to
the question of evaluating 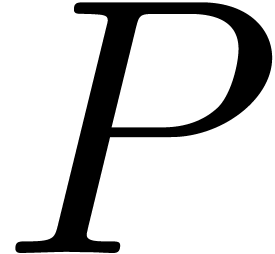 at
at 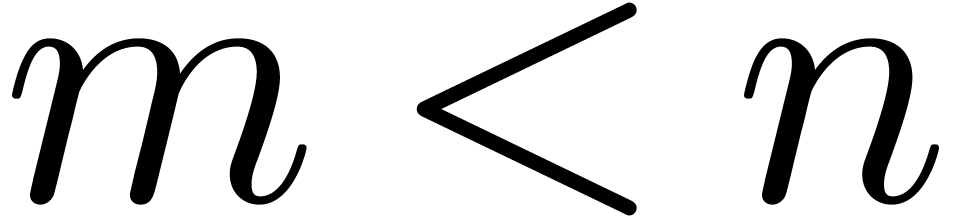 points.
points.
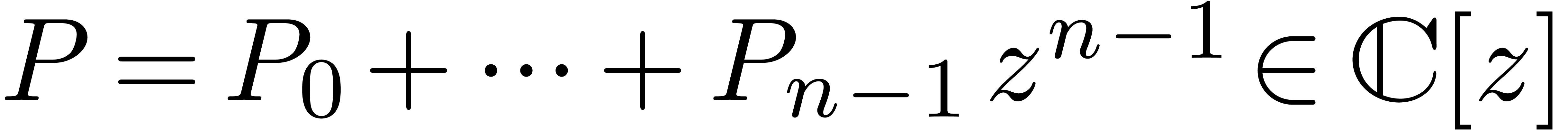 and
and 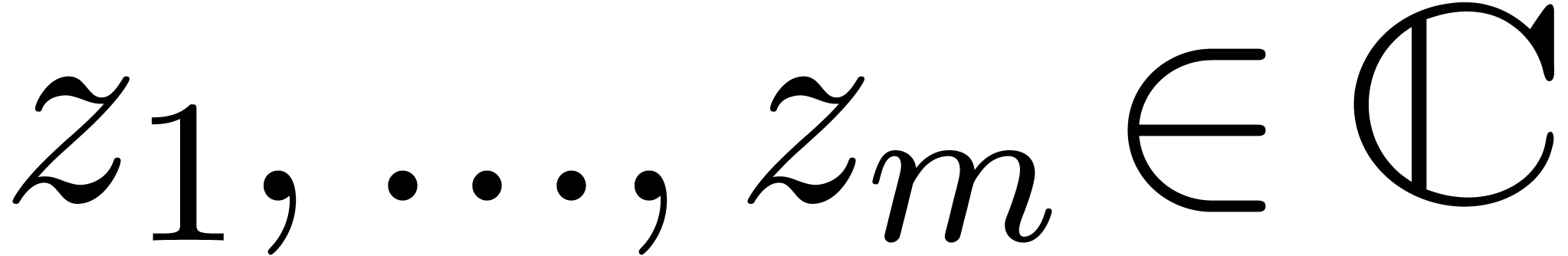 be such that
be such that 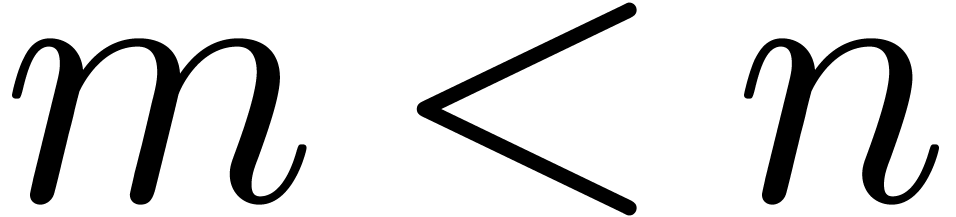 ,
,  and
and 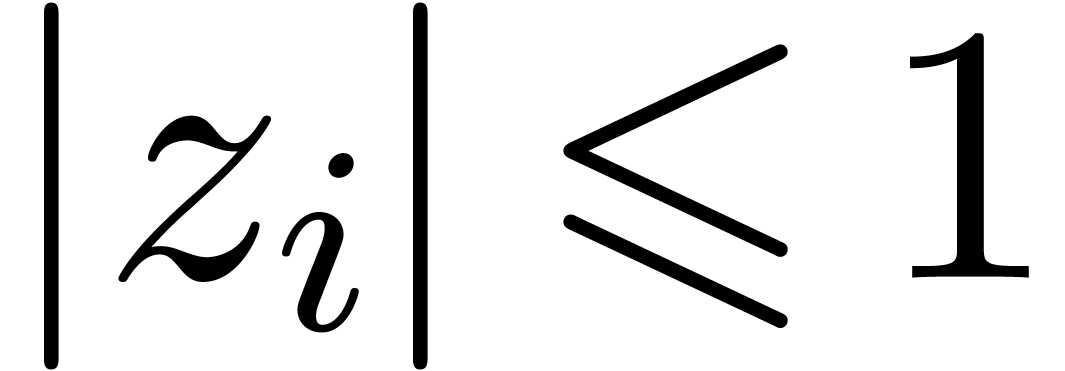 for all
for all  . Let
. Let 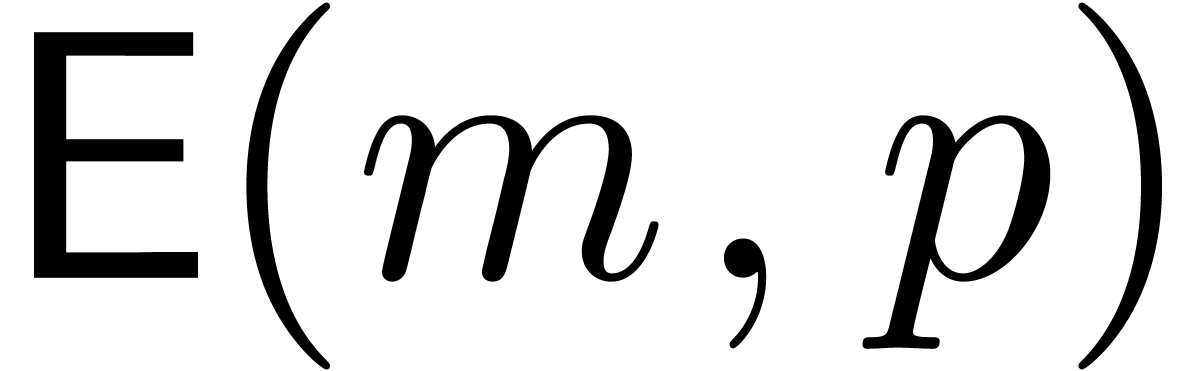 be the time
needed in order to compute
be the time
needed in order to compute  -evaluations
of polynomials
-evaluations
of polynomials 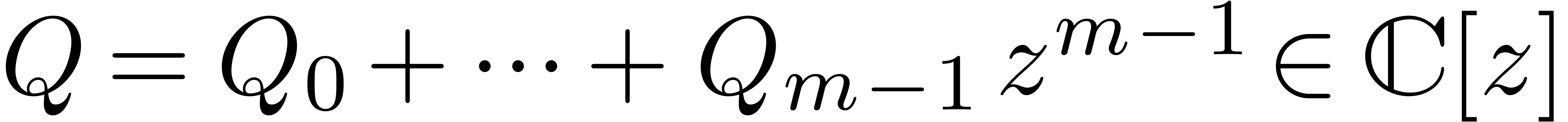 with
with 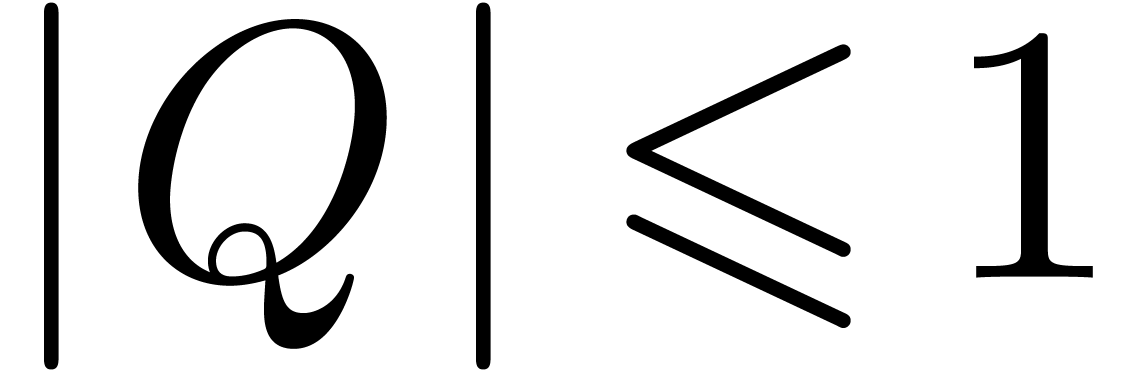 at
at
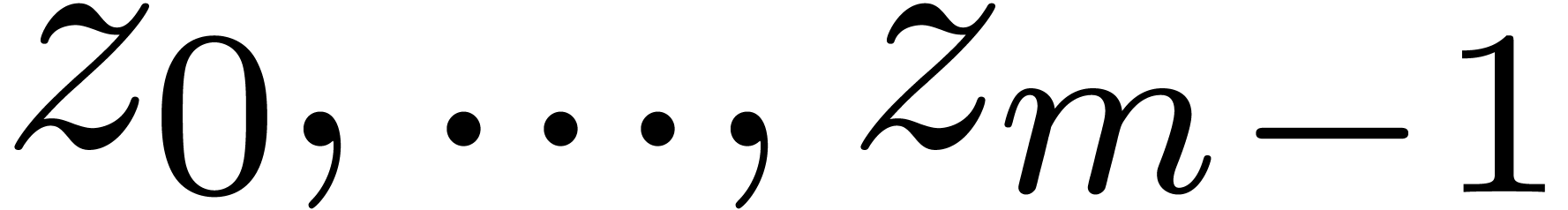 . Then
. Then  -evaluations of
-evaluations of 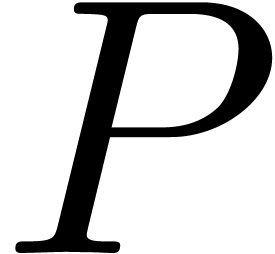 at
at
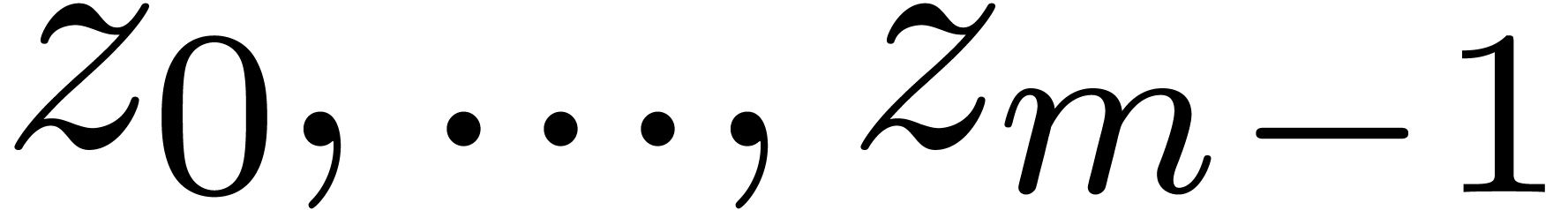 can be computed in time
can be computed in time 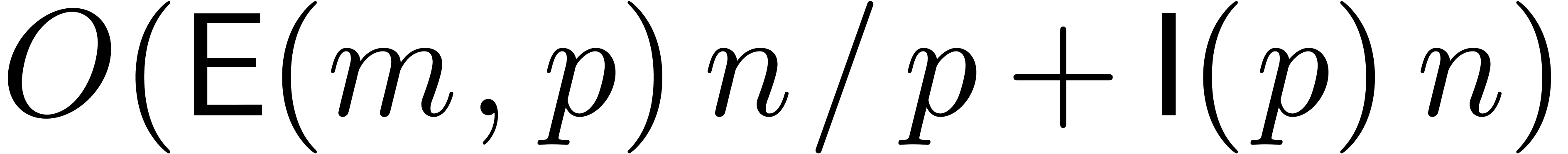 .
.
Proof. Without loss of generality, we may assume
that 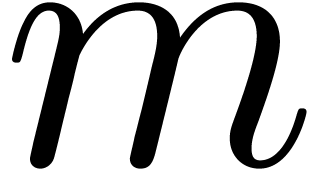 and
and 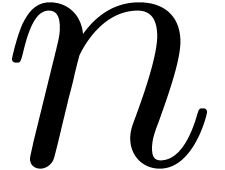 are powers of
two. We decompose
are powers of
two. We decompose  as follows:
as follows:
We may compute 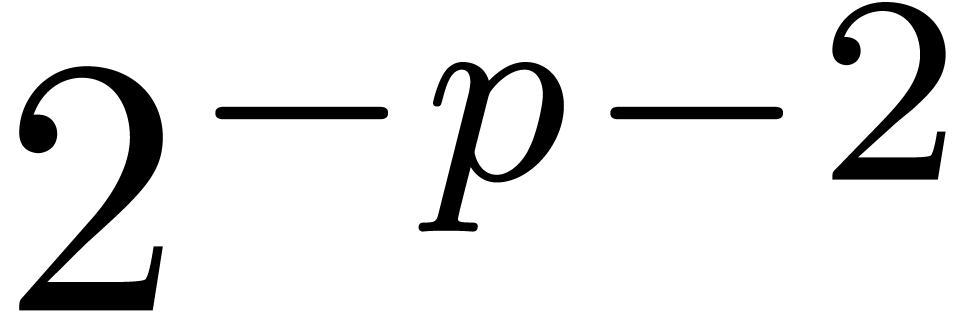 -evaluations
of the
-evaluations
of the 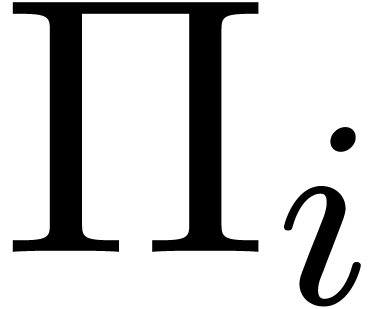 at
at 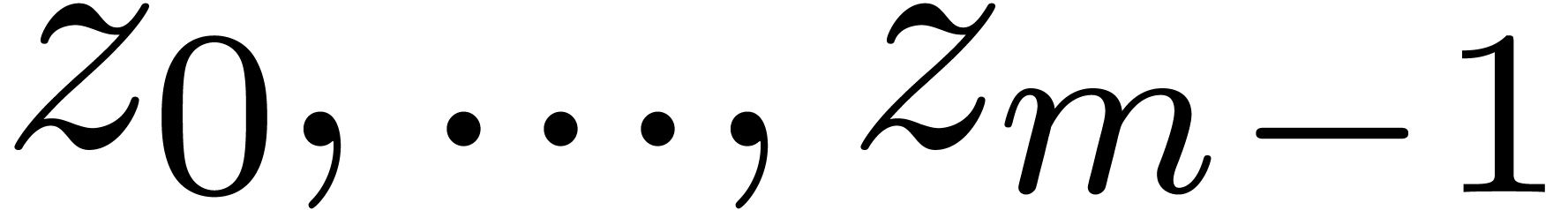 in time
in time 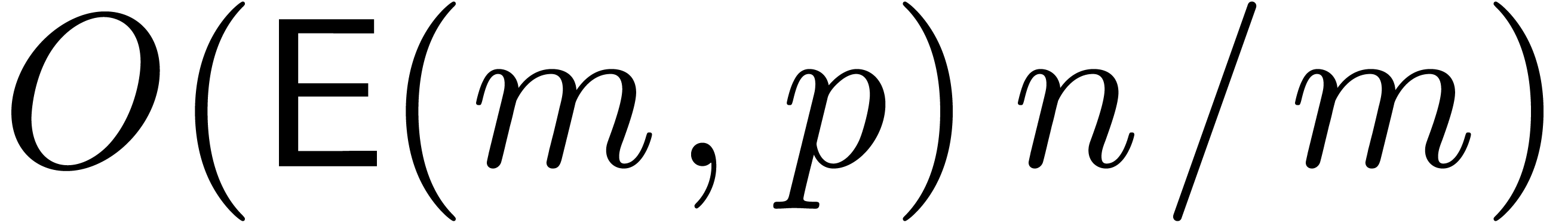 . We may also
. We may also 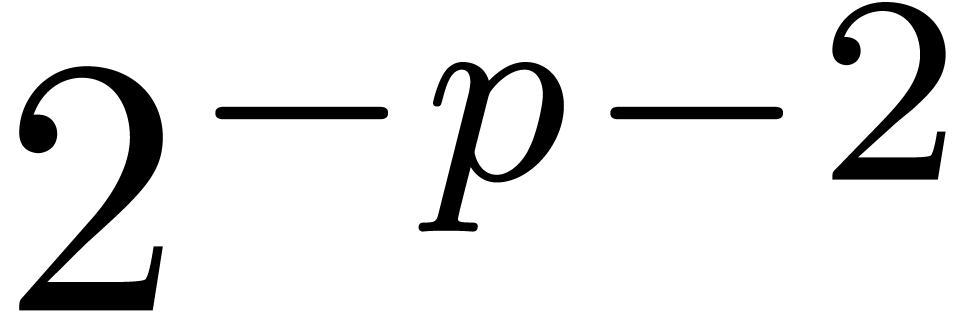 -approximate
-approximate 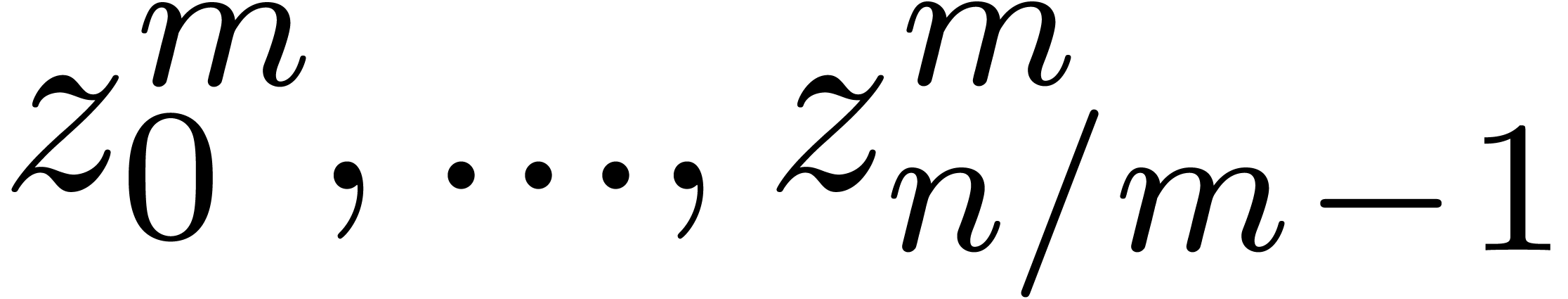 in time
in time
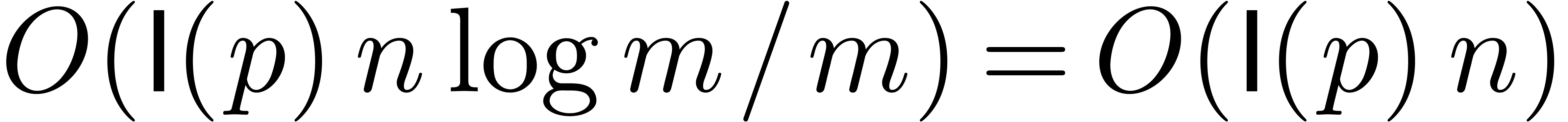 , using binary powering.
Using Horner's rule, we may finally
, using binary powering.
Using Horner's rule, we may finally  -evaluate
-evaluate
for  in time
in time 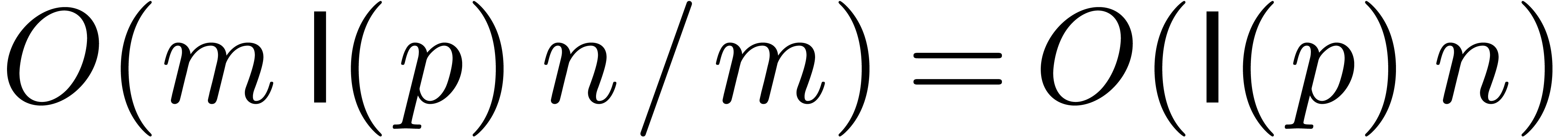 .
.
Let 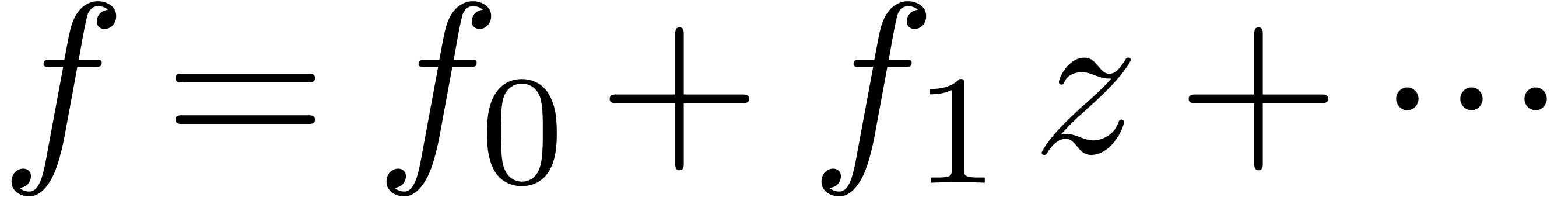 be a convergent power series with radius of
convergence
be a convergent power series with radius of
convergence 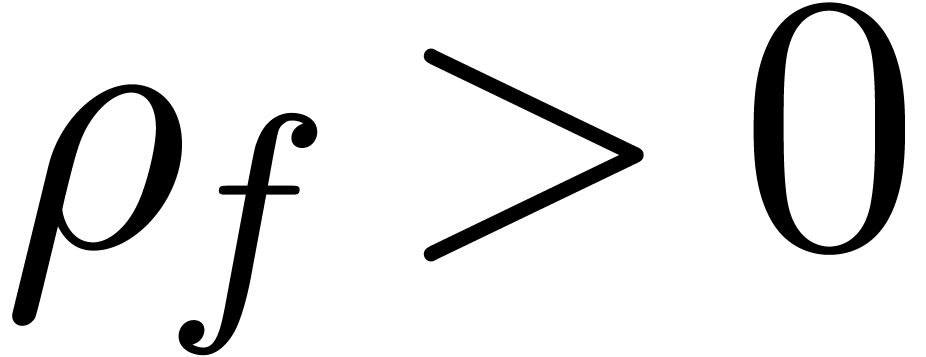 . Given
. Given 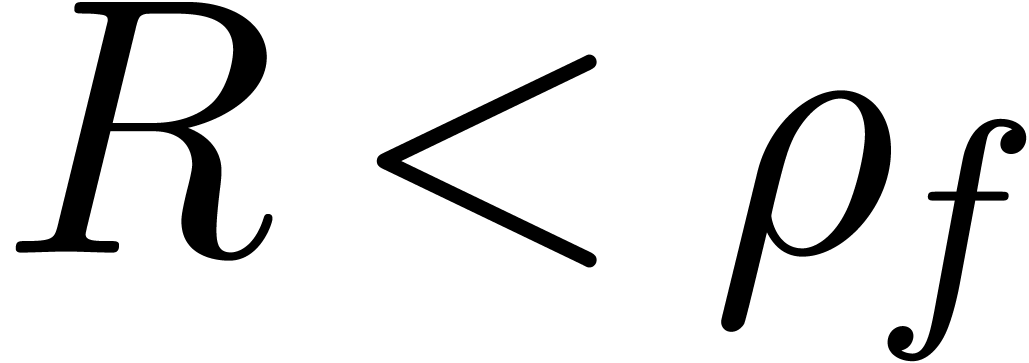 , we denote
, we denote
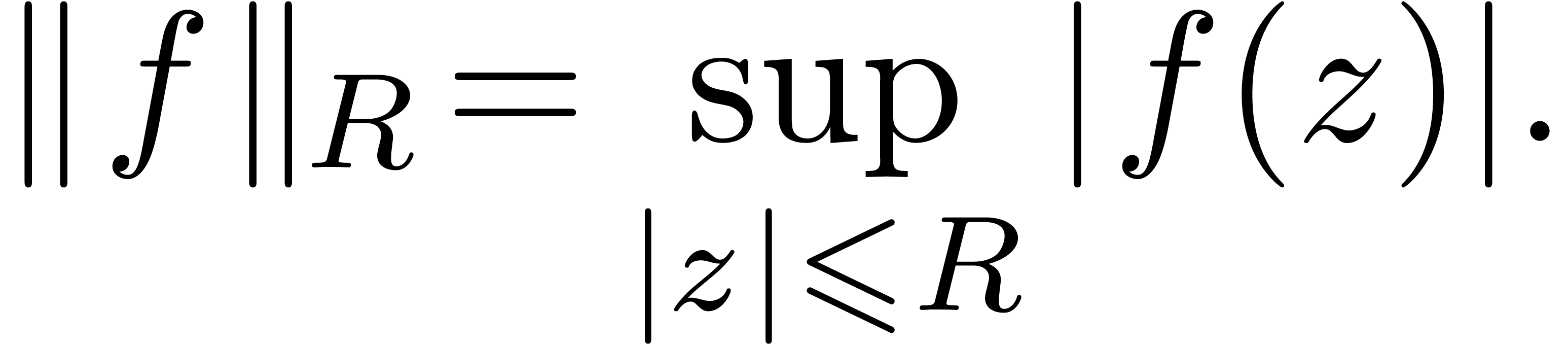
Using Cauchy's formula, we have
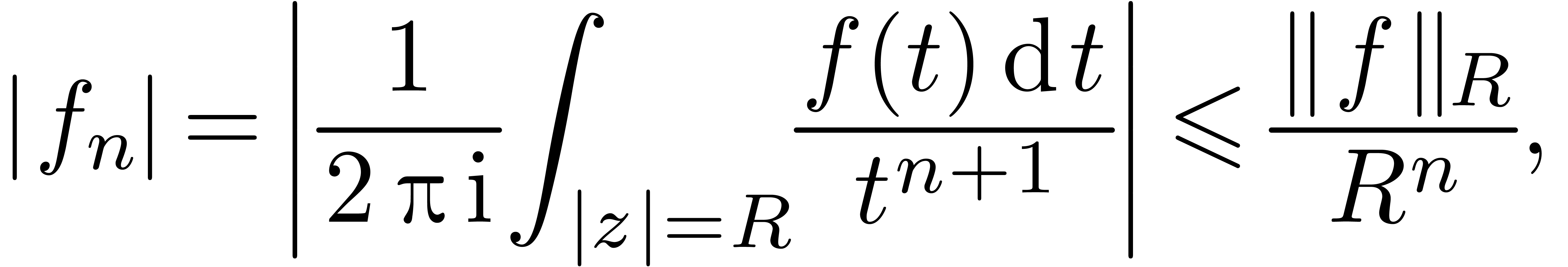 |
(13) |
For 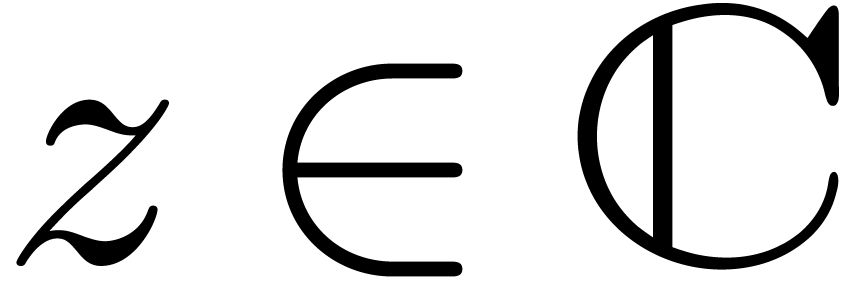 with
with 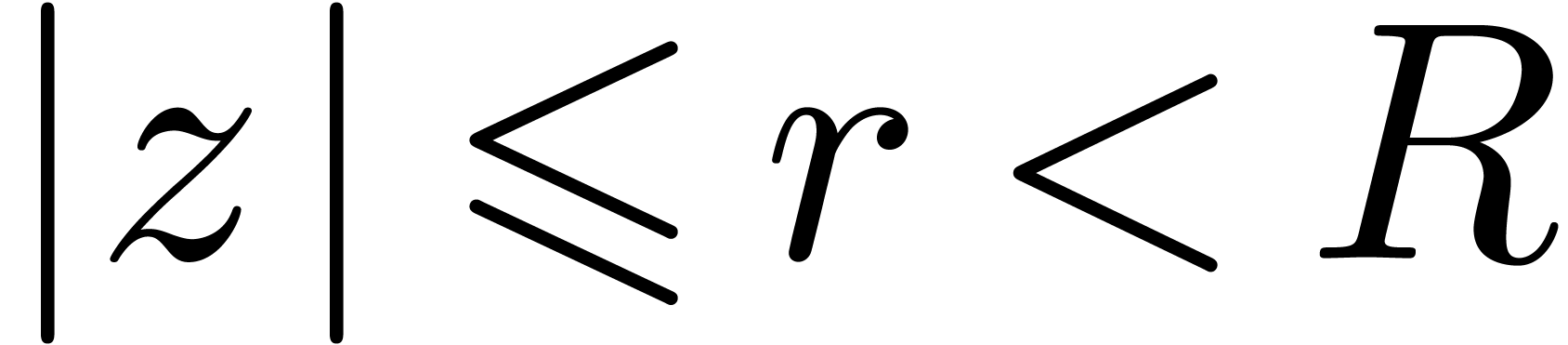 ,
it follows that
,
it follows that
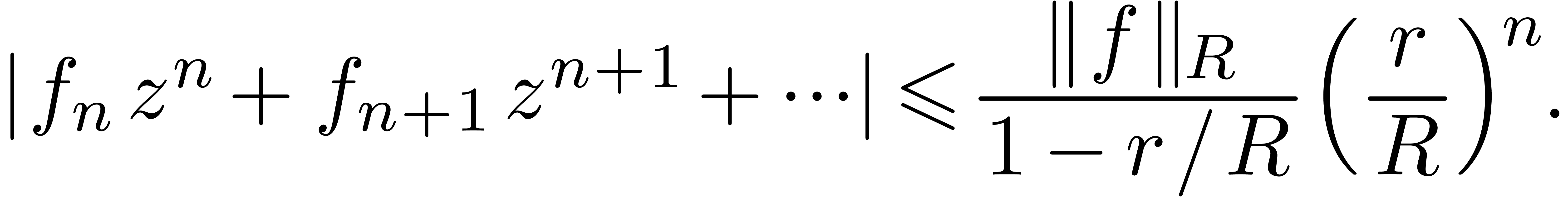 |
(14) |
Let  be the time needed to compute
be the time needed to compute  -approximations of
-approximations of 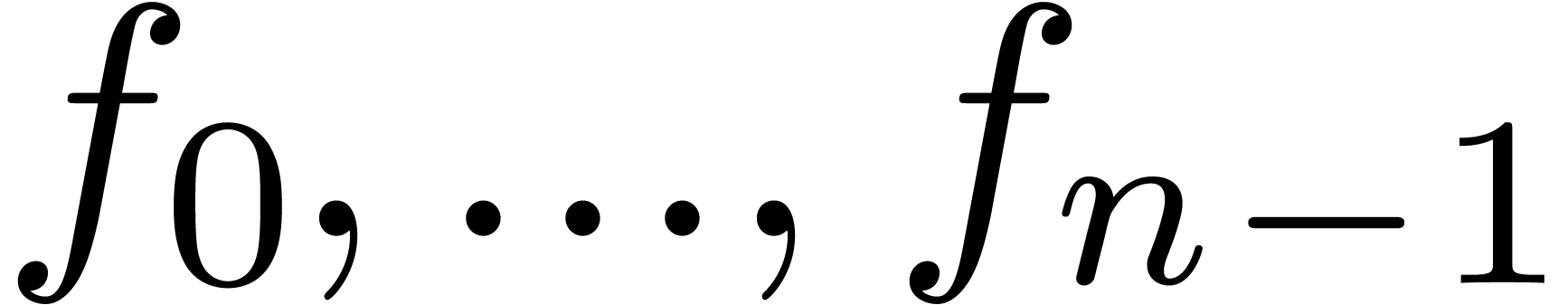 . Given
. Given 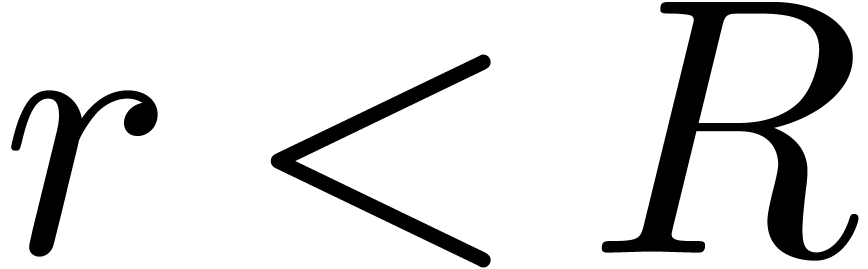 ,
let
,
let 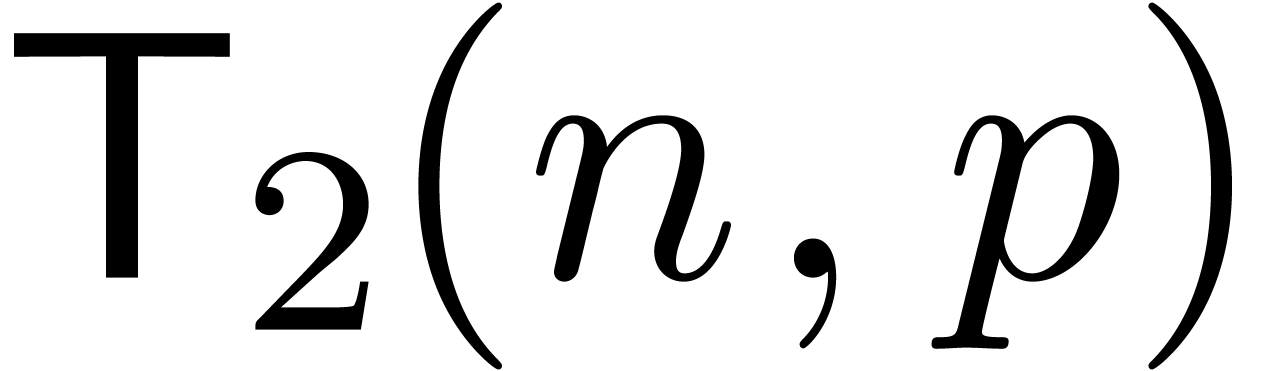 be the time needed to
be the time needed to  -evaluate
-evaluate  at
at 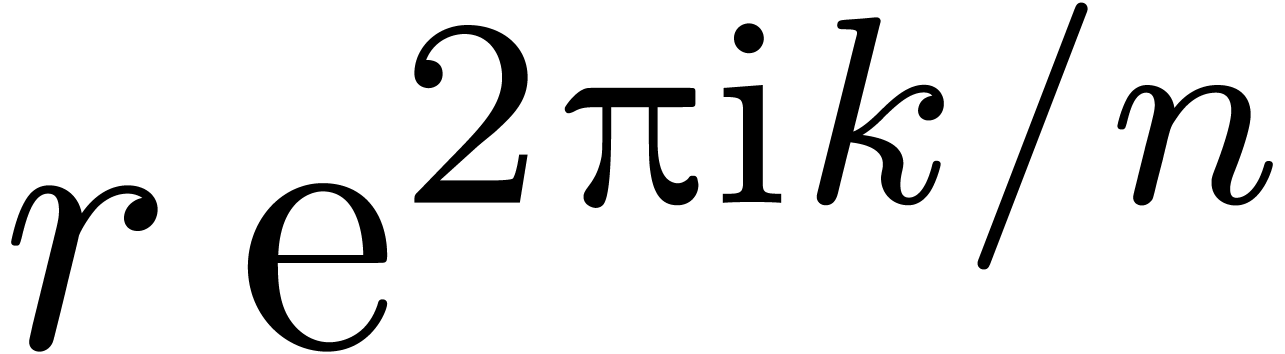 for
for  .
.
Proof. We first consider the case when 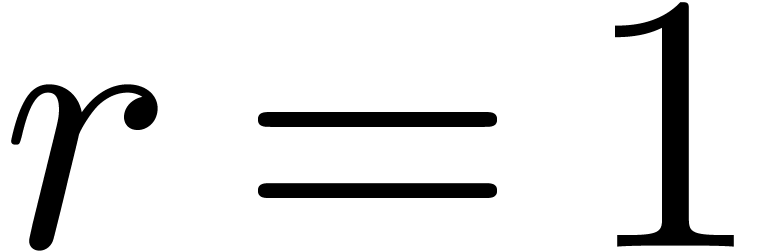 . Let
. Let 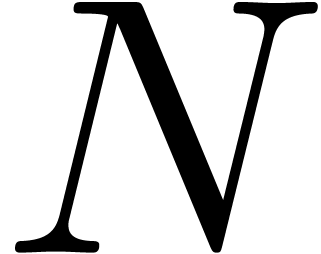 be
the smallest power of two with
be
the smallest power of two with
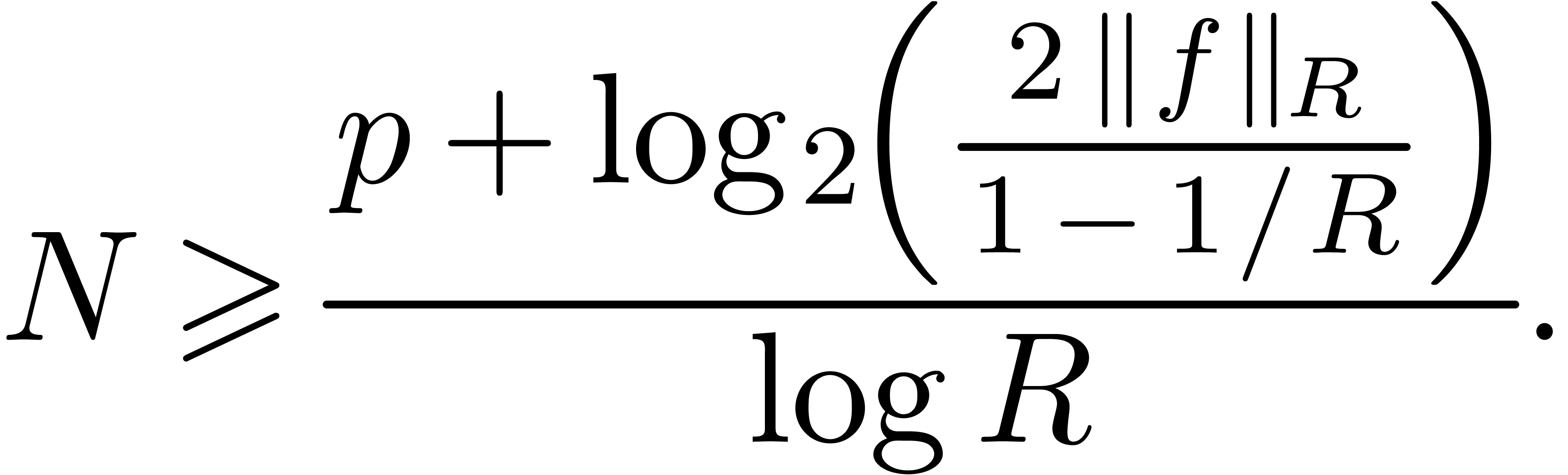 |
(15) |
For all 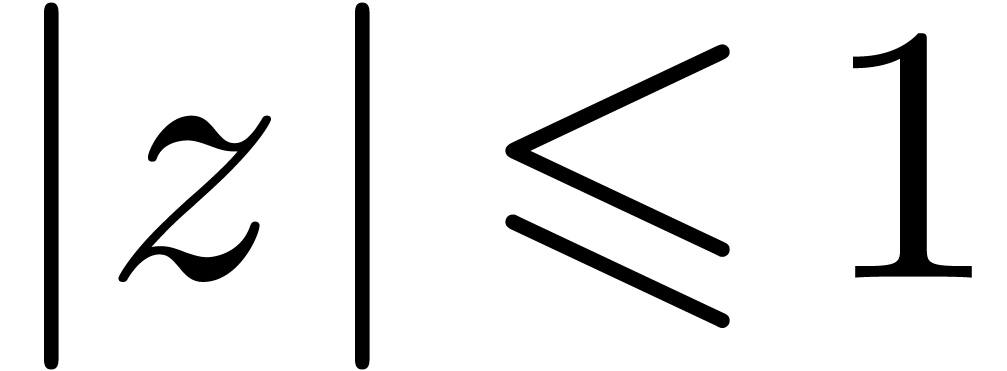 , the bound (14)
implies
, the bound (14)
implies
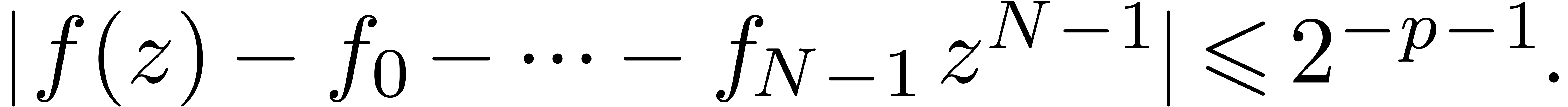 |
(16) |
The computation of 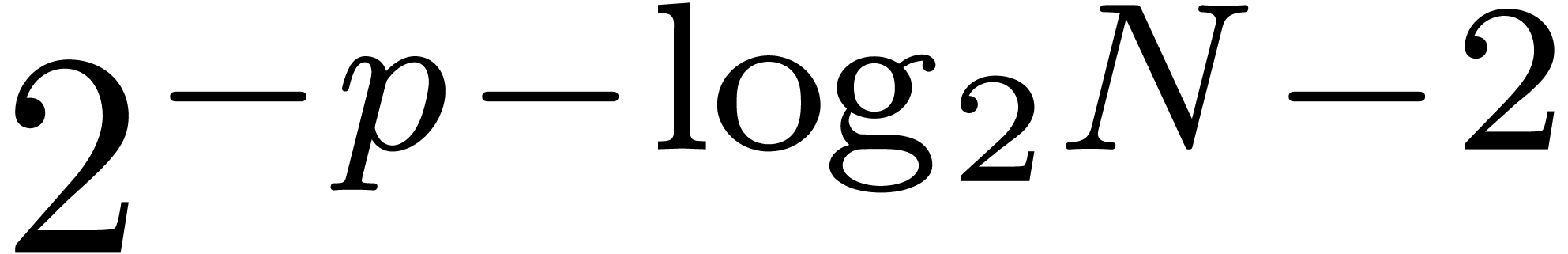 -approximations
of
-approximations
of 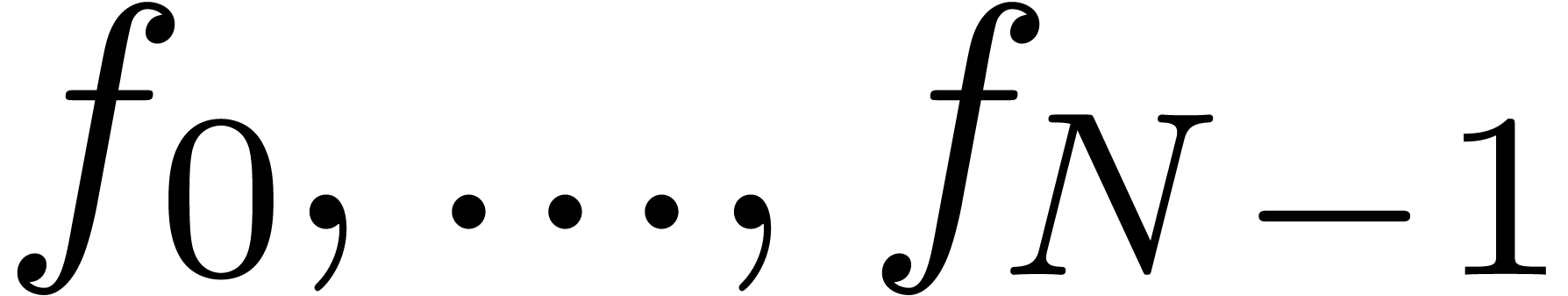 takes a time
takes a time 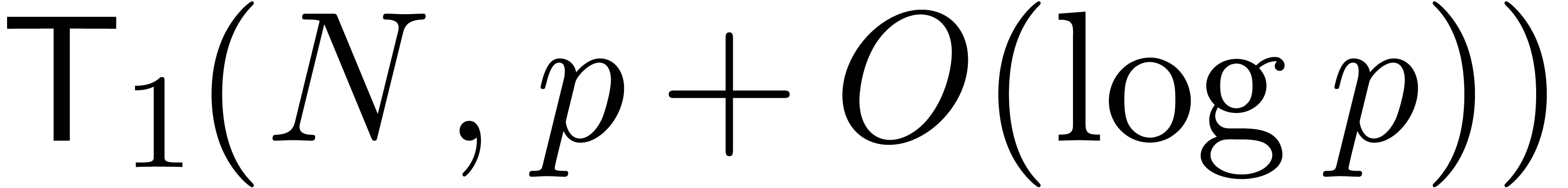 .
The
.
The 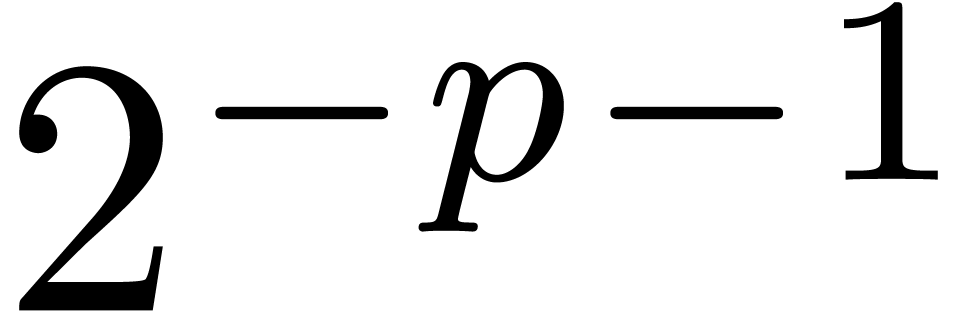 -evaluation of
-evaluation of 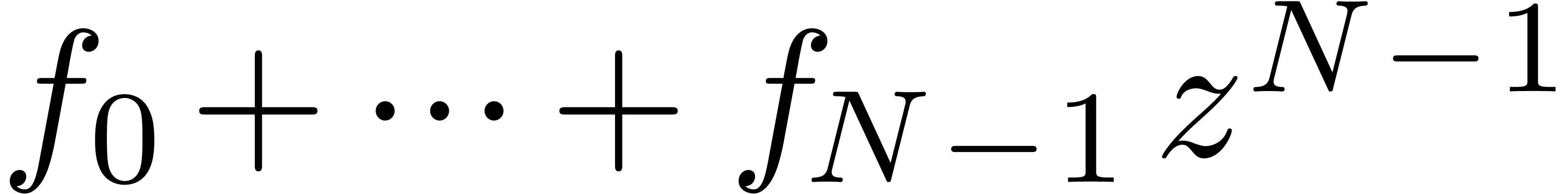 at
at 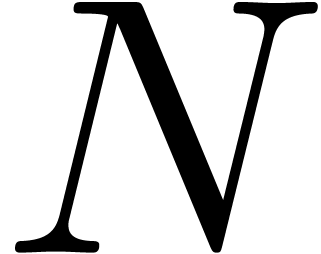 primitive roots of unity can be
done using
primitive roots of unity can be
done using 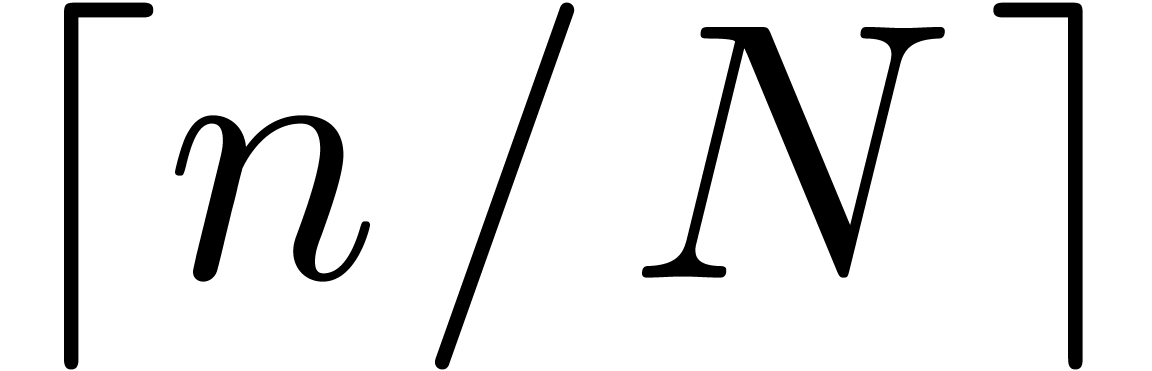 fast Fourier transforms of size
fast Fourier transforms of size 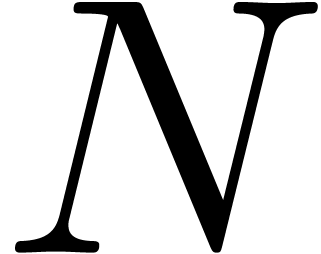 . This requires a time
. This requires a time 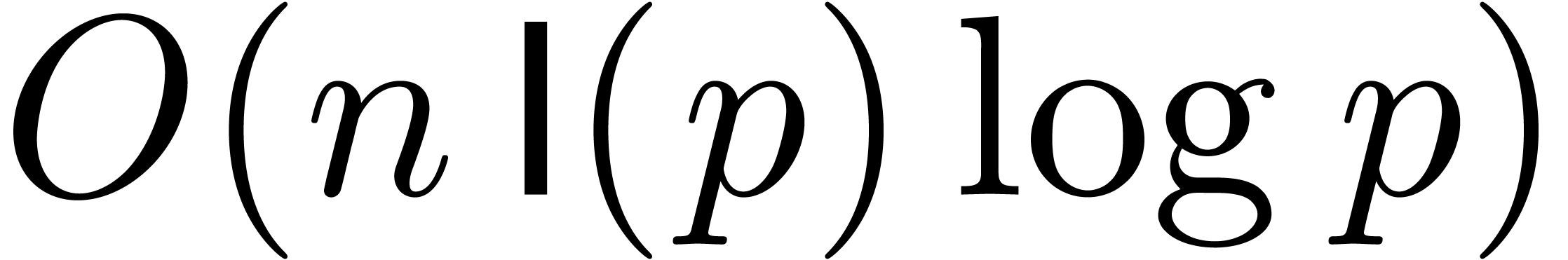 . If
. If 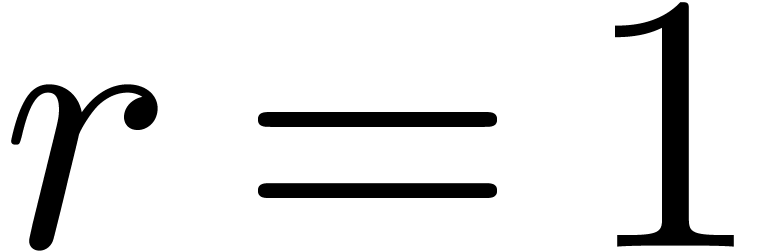 ,
we thus obtain the bound
,
we thus obtain the bound
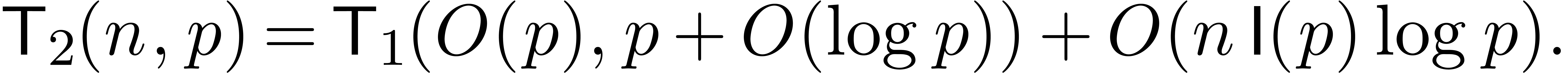
The general case is reduced to the case 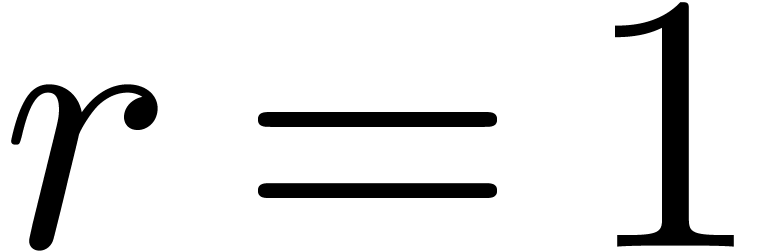 via a
change of variables
via a
change of variables 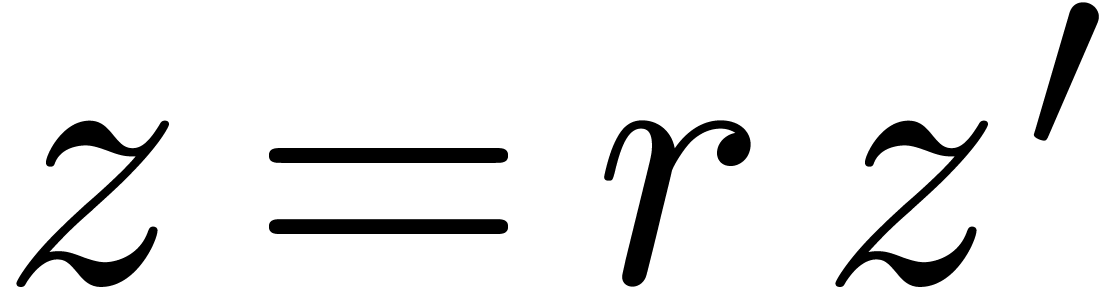 . This
requires computations to be carried out with an additional precision of
. This
requires computations to be carried out with an additional precision of
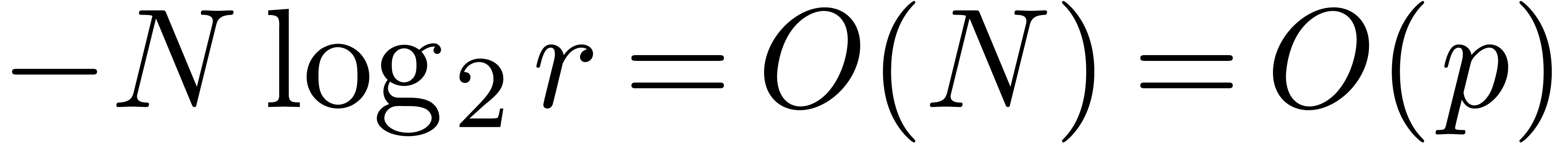 bits, leading to the complexity bound in
(a).
bits, leading to the complexity bound in
(a).
As to (b), we again start with the case when 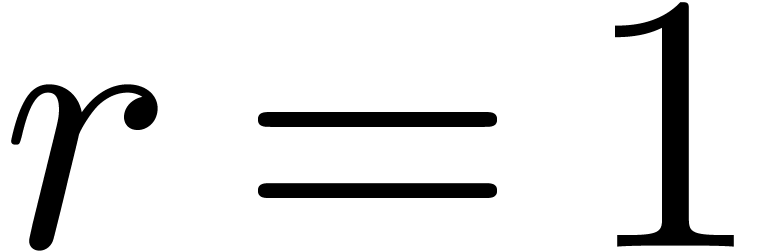 . Taking
. Taking 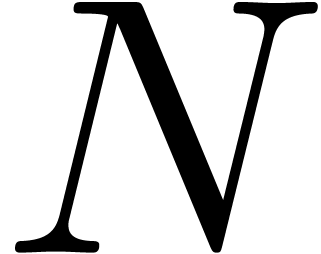 to be the
smallest power of two with (15), we again obtain (16)
for all
to be the
smallest power of two with (15), we again obtain (16)
for all  . If
. If 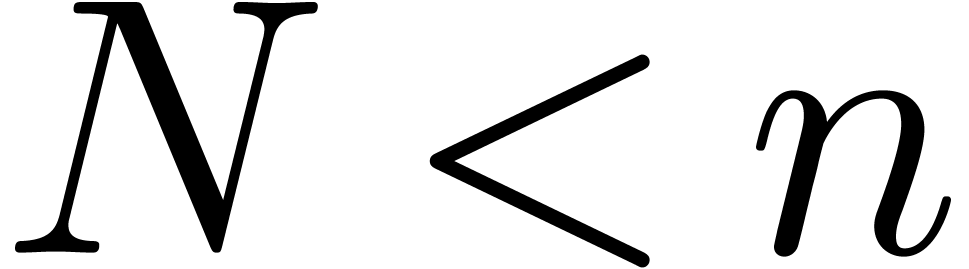 , then we also notice that
, then we also notice that 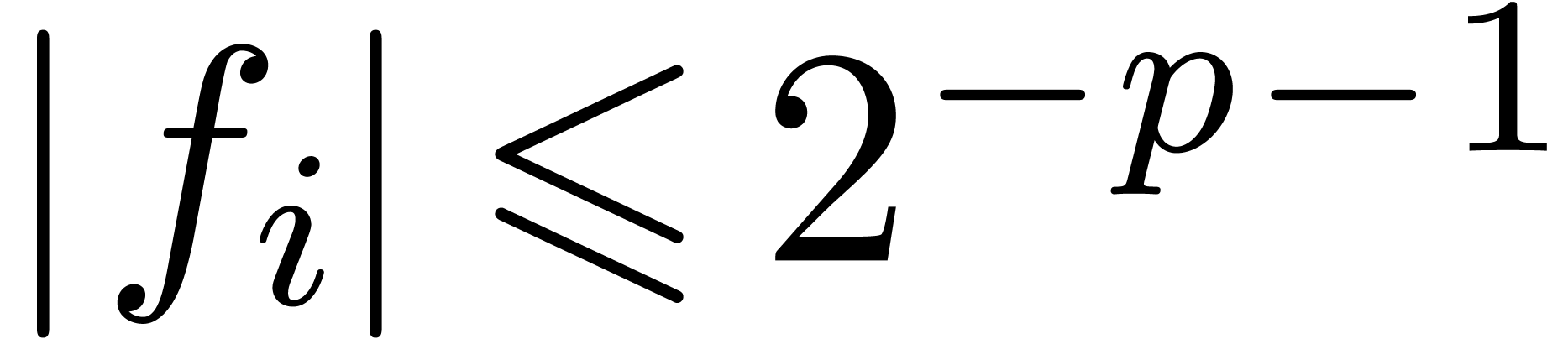 for all
for all 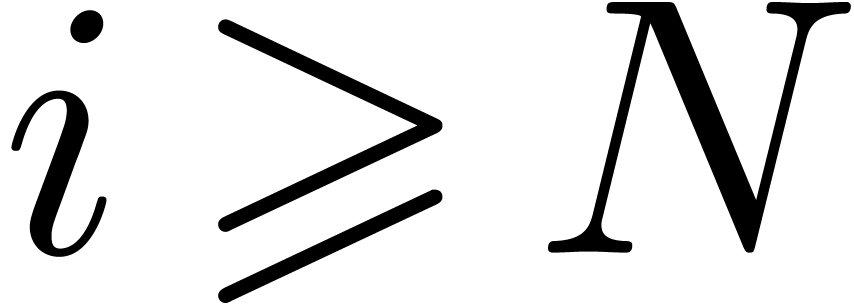 . We may
. We may  -evaluate
-evaluate 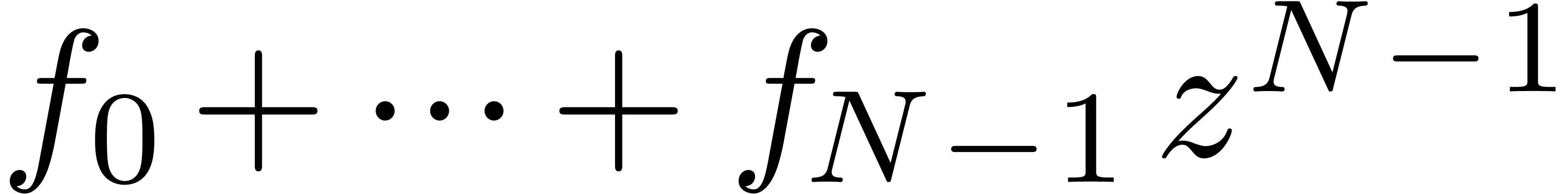 at the
primitive
at the
primitive  -th roots of unity
in time
-th roots of unity
in time 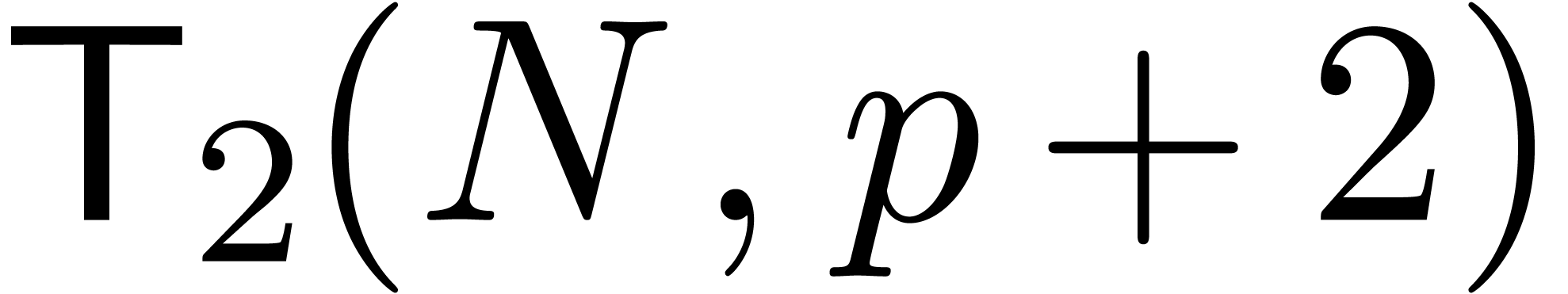 . We next retrieve
the coefficients of the polynomial
. We next retrieve
the coefficients of the polynomial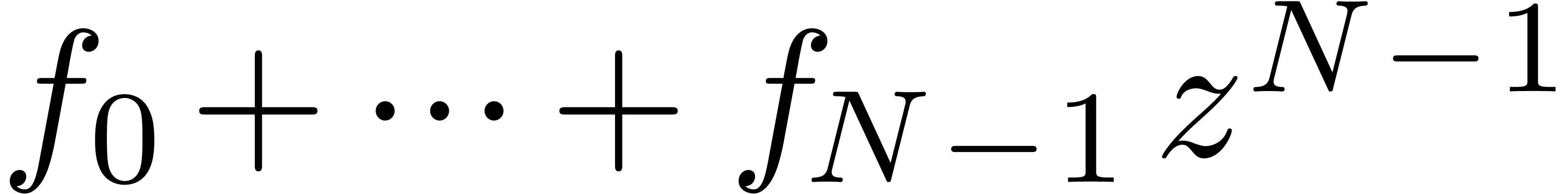 up to
precision
up to
precision 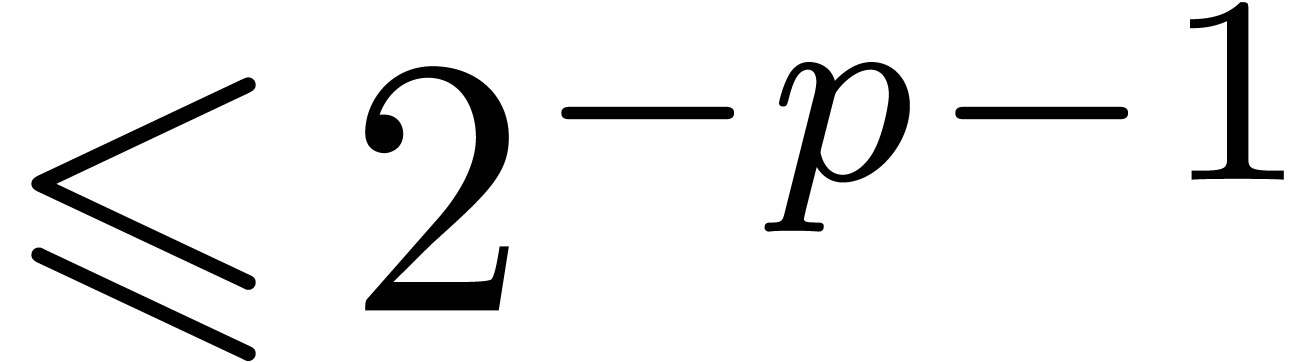 using one inverse fast Fourier
transform of size
using one inverse fast Fourier
transform of size 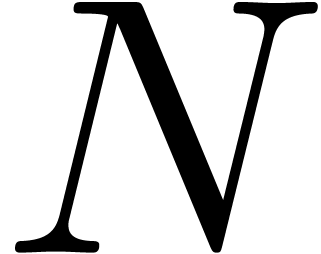 . In the
case when
. In the
case when 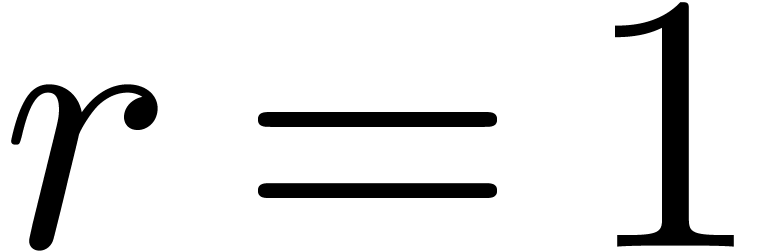 , we thus obtain
, we thus obtain
In general, replacing 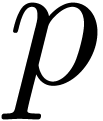 by
by 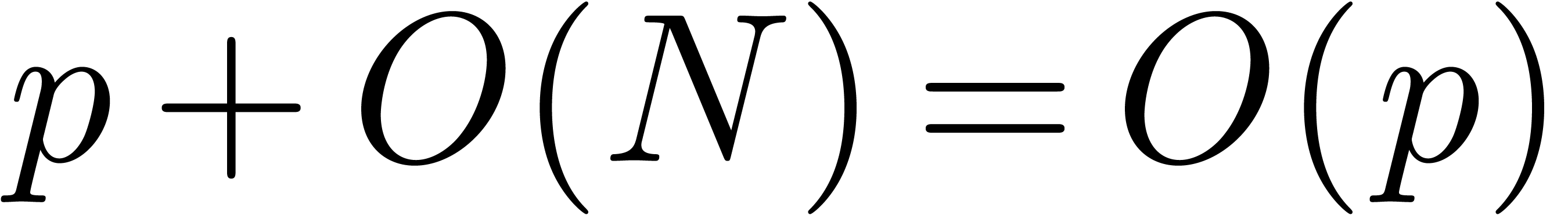 yields the bound in (b).
yields the bound in (b).
Let us now consider two convergent power series 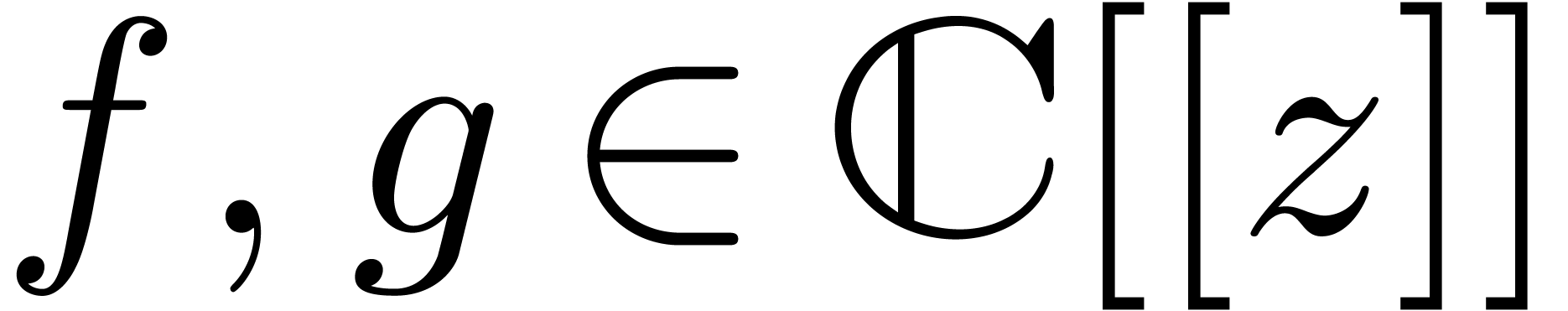 with
with 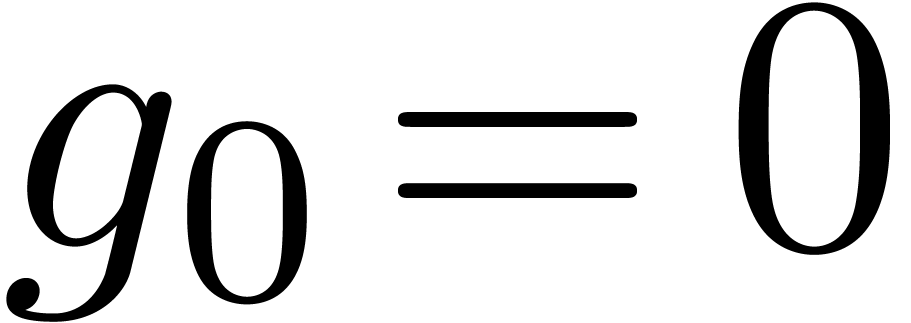 ,
, 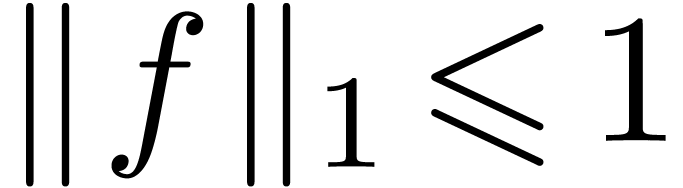 and
and 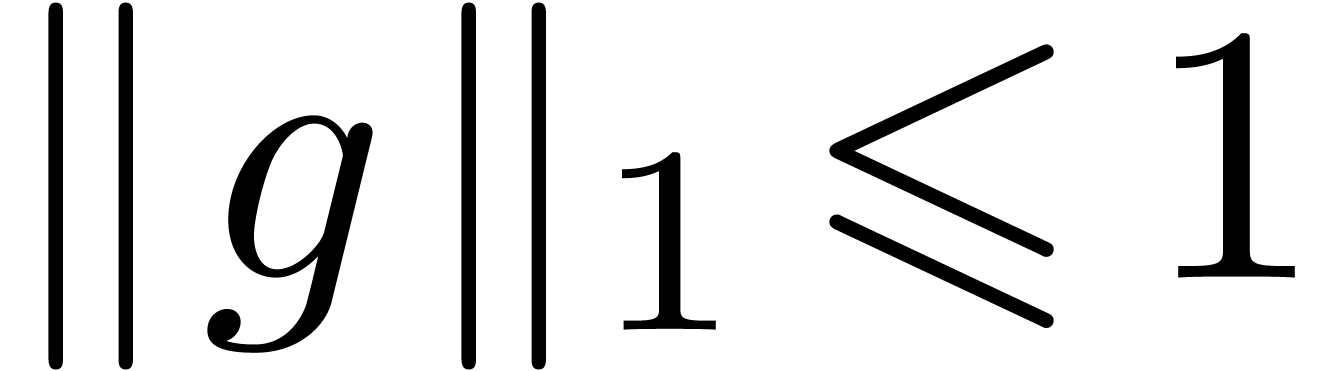 . Then
. Then 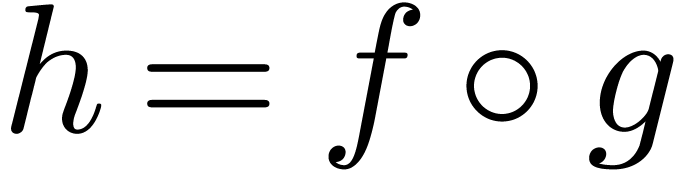 is well-defined and
is well-defined and 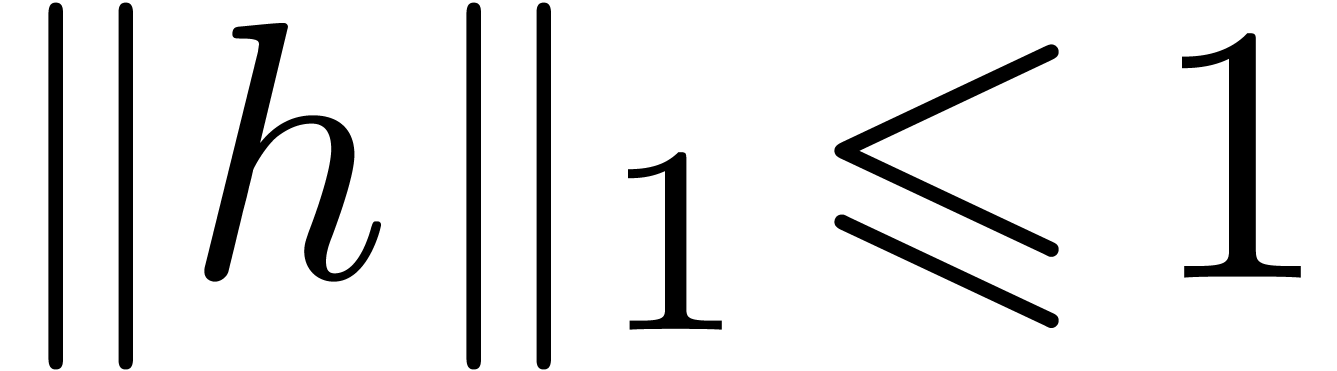 . In
fact, the series
. In
fact, the series 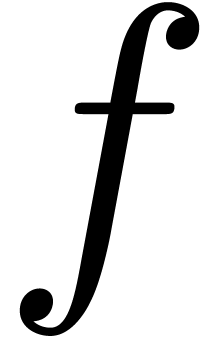 ,
,  and
and 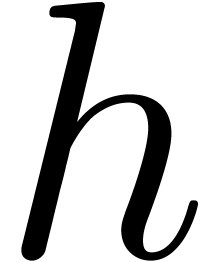 still converge on a compact
disc of radius
still converge on a compact
disc of radius 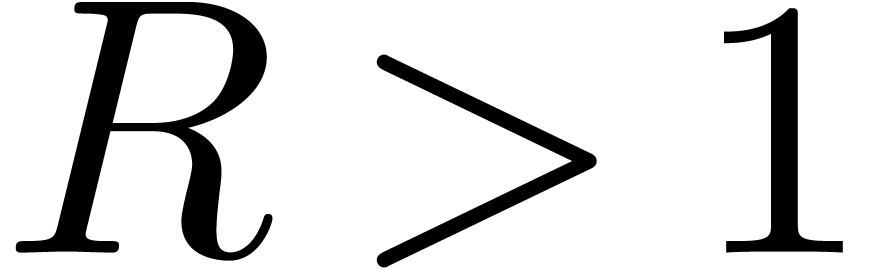 . Let
. Let 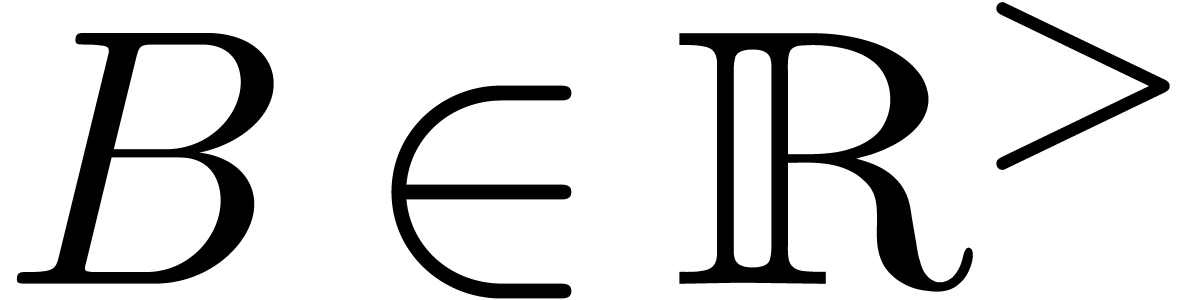 be such that
be such that 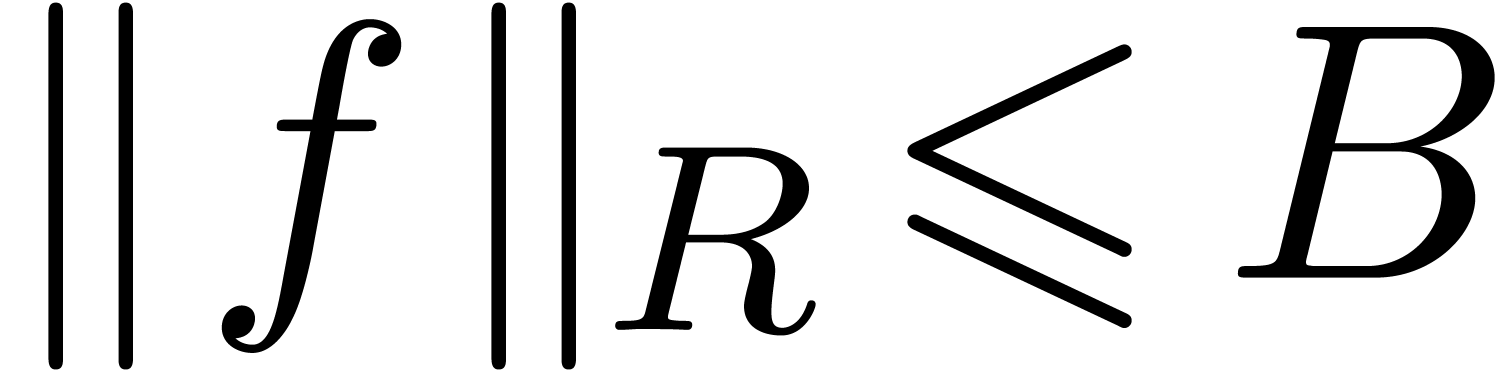 ,
,
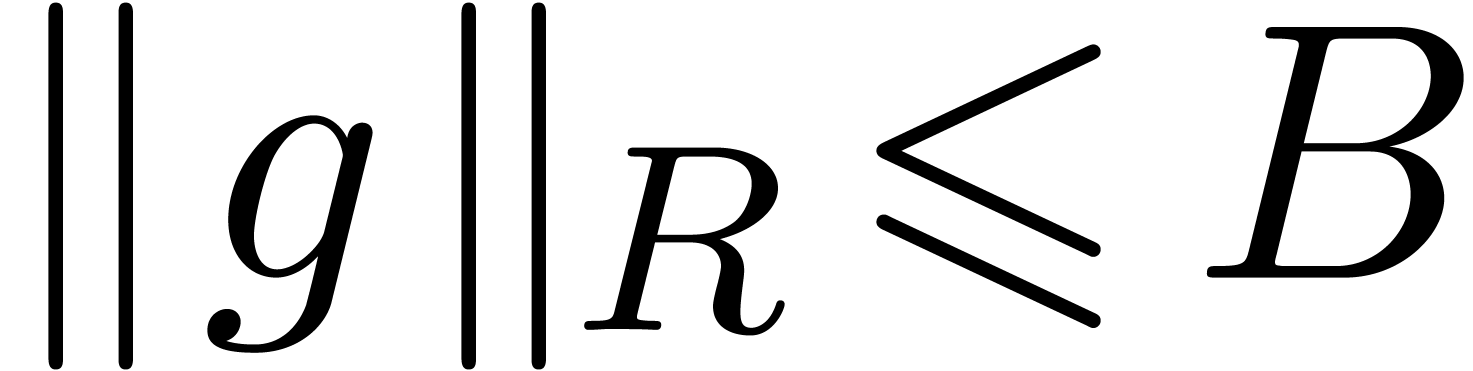 and
and 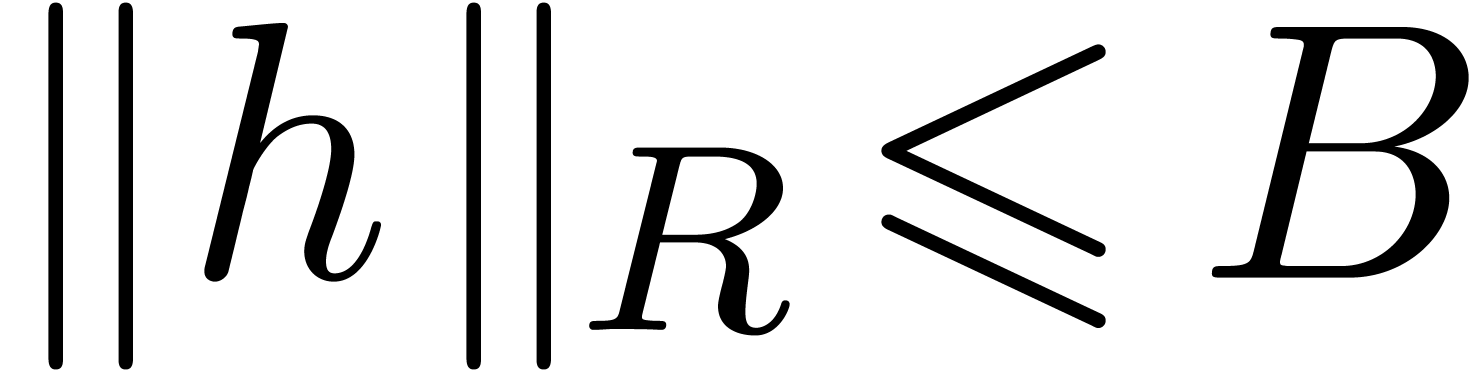 .
Then (14) becomes
.
Then (14) becomes
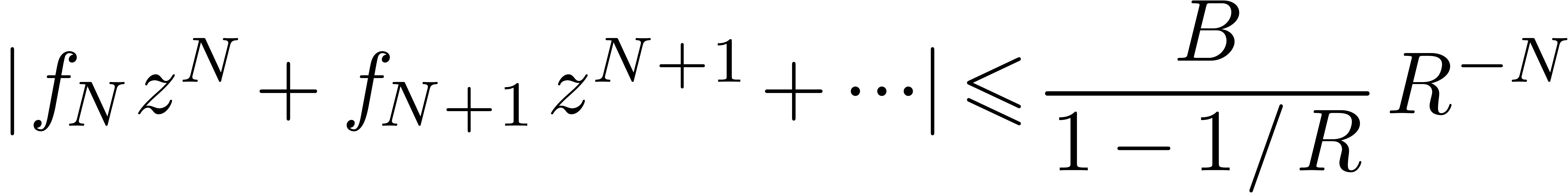 |
(17) |
and similarly for  and
and 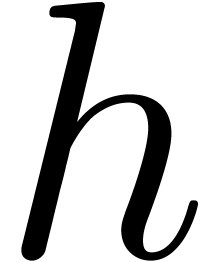 . In view of lemma 17, it is natural to
use an evaluation-interpolation scheme for the computation of
. In view of lemma 17, it is natural to
use an evaluation-interpolation scheme for the computation of  -approximations of
-approximations of 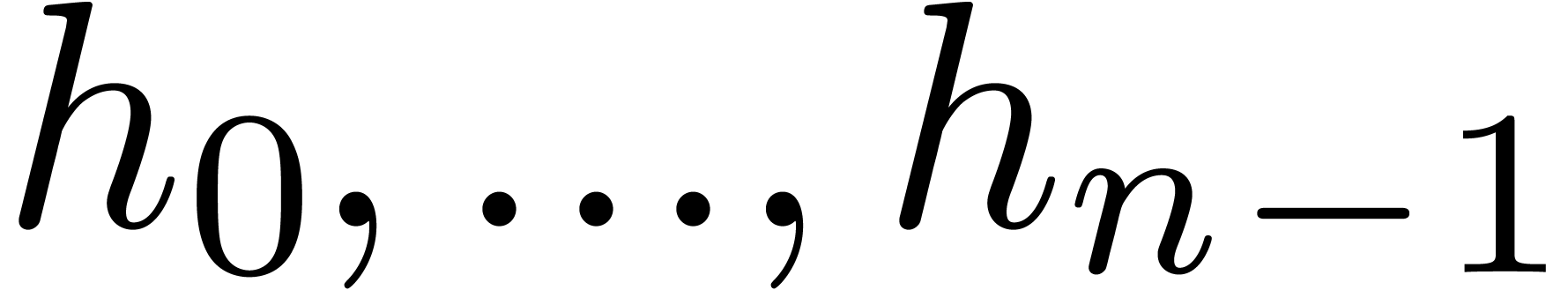 .
.
For a sufficiently large 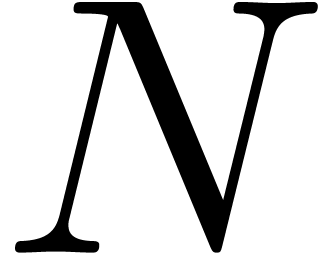 and
and 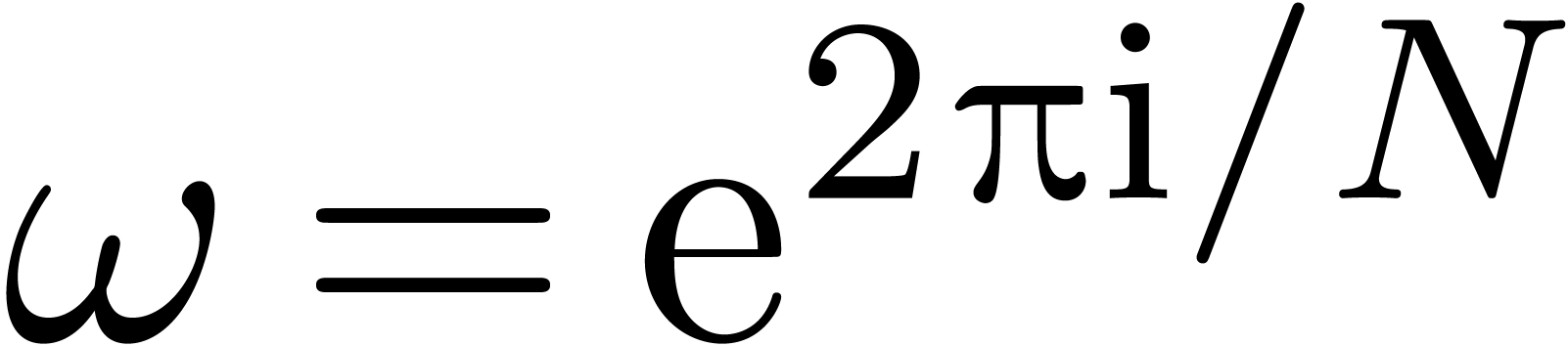 , we evaluate
, we evaluate  on the
on the
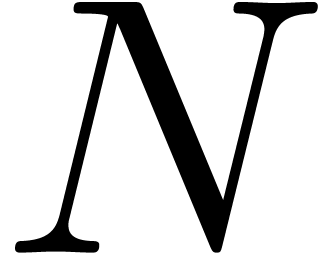 -th roots of unity
-th roots of unity 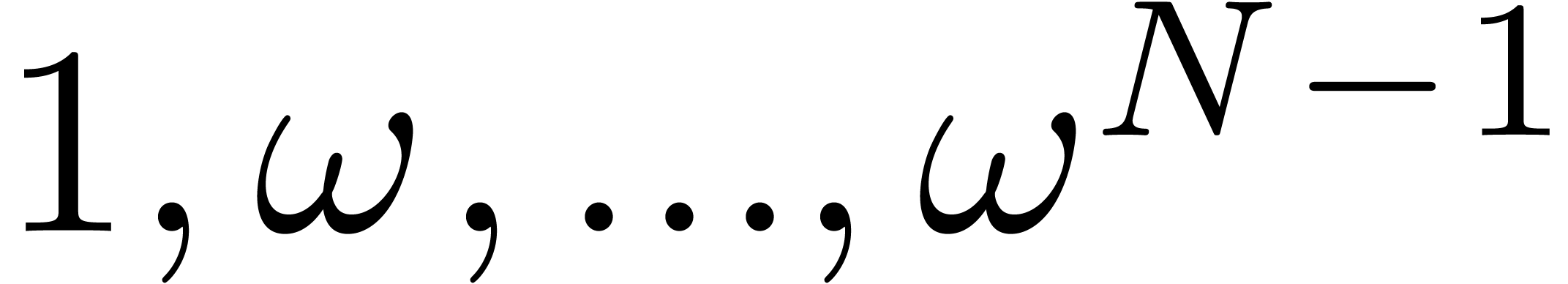 using one direct FFT on
using one direct FFT on 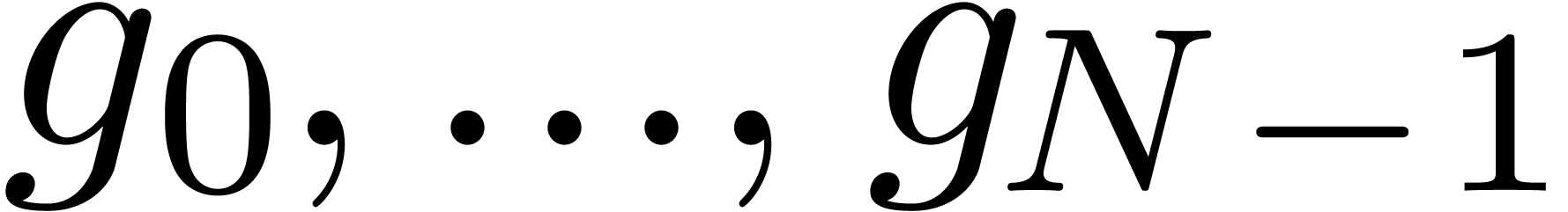 .
Using the fact that
.
Using the fact that 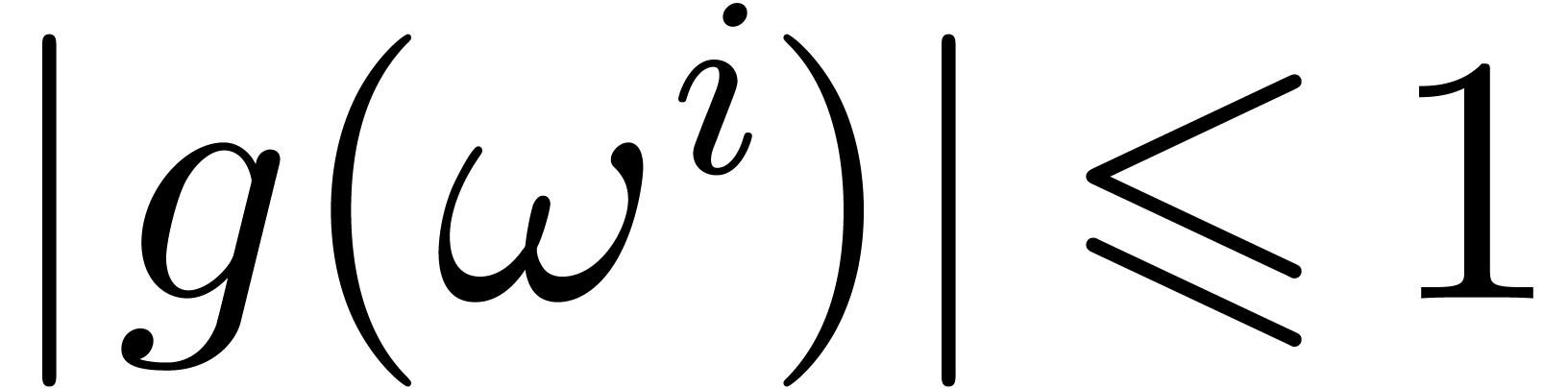 for all
for all 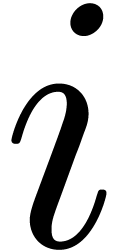 and the algorithm for multi-point evaluation from the previous section,
we next compute
and the algorithm for multi-point evaluation from the previous section,
we next compute 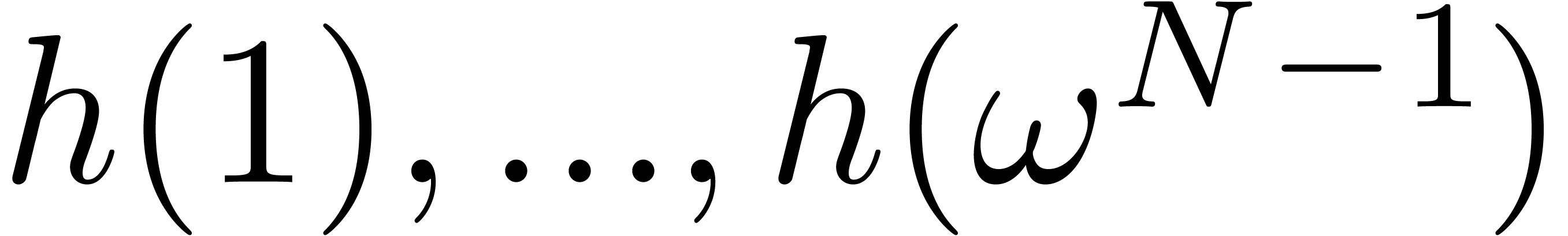 . Using one
inverse FFT, we finally recover the coefficients of the polynomial
. Using one
inverse FFT, we finally recover the coefficients of the polynomial 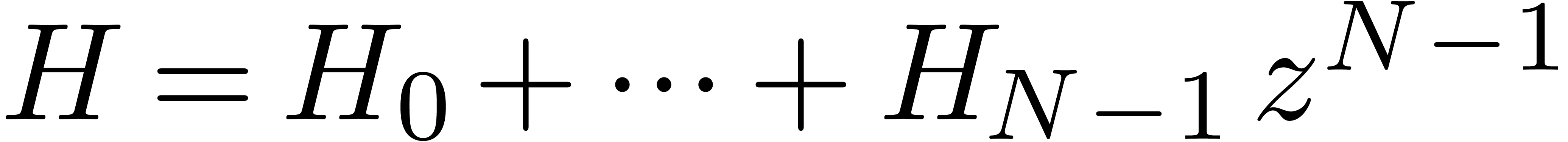 with
with 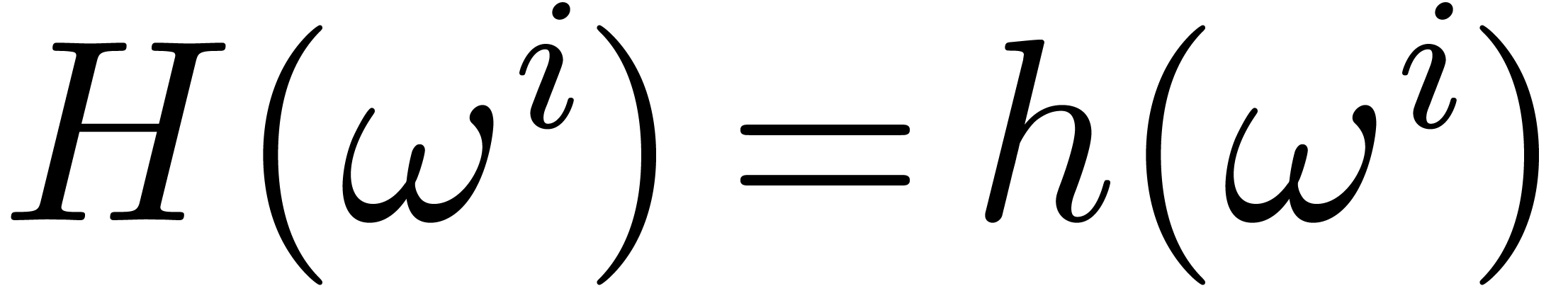 for all
for all 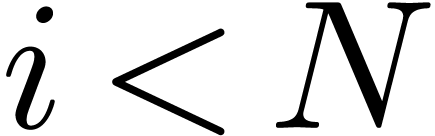 . Using the tail bound (17) for
. Using the tail bound (17) for
 ,
,  ,
,  and a sufficiently large
and a sufficiently large
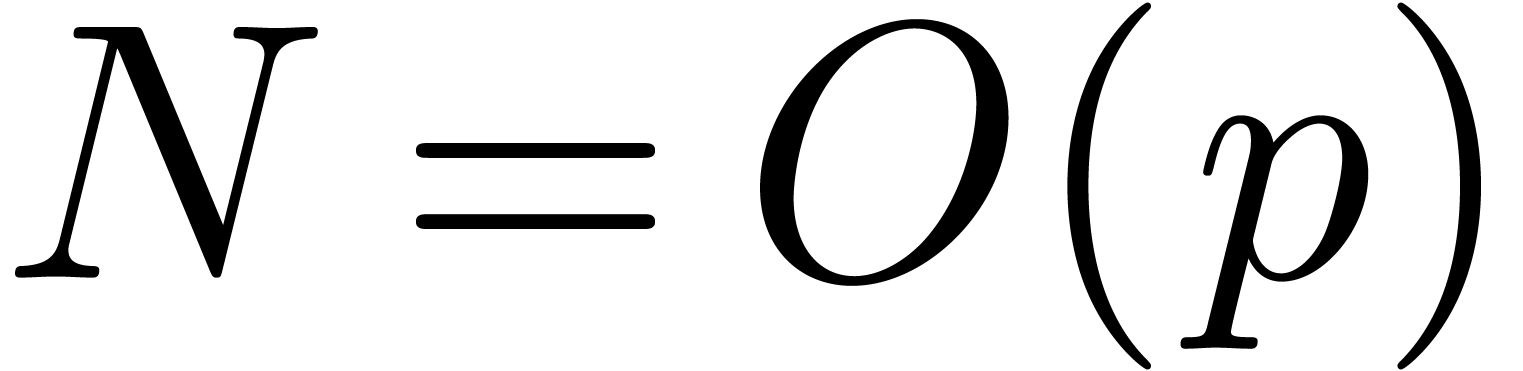 , the differences
, the differences 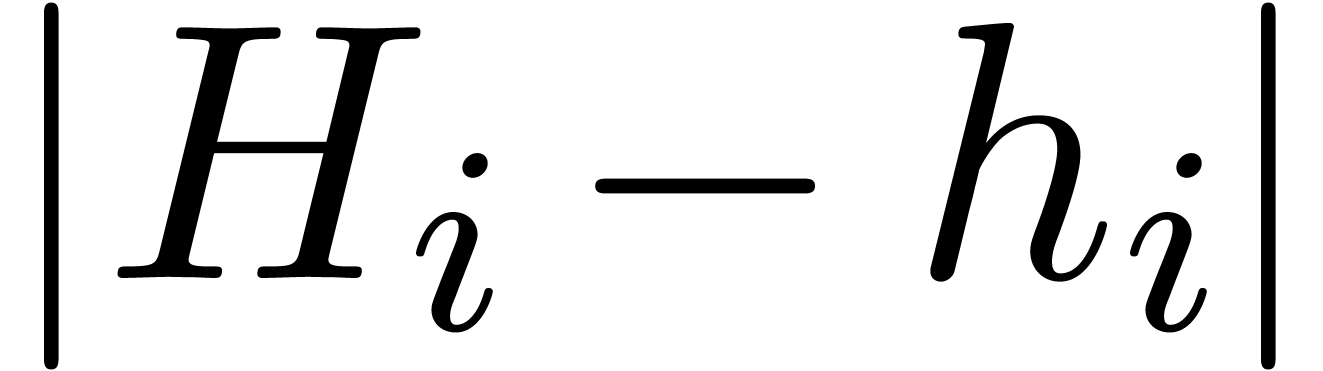 can be made as small as needed. More precisely, the
algorithm goes as follows:
can be made as small as needed. More precisely, the
algorithm goes as follows:
Algorithm compose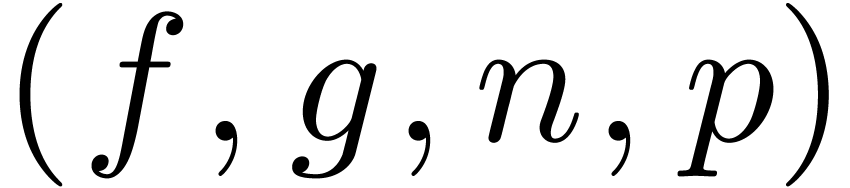
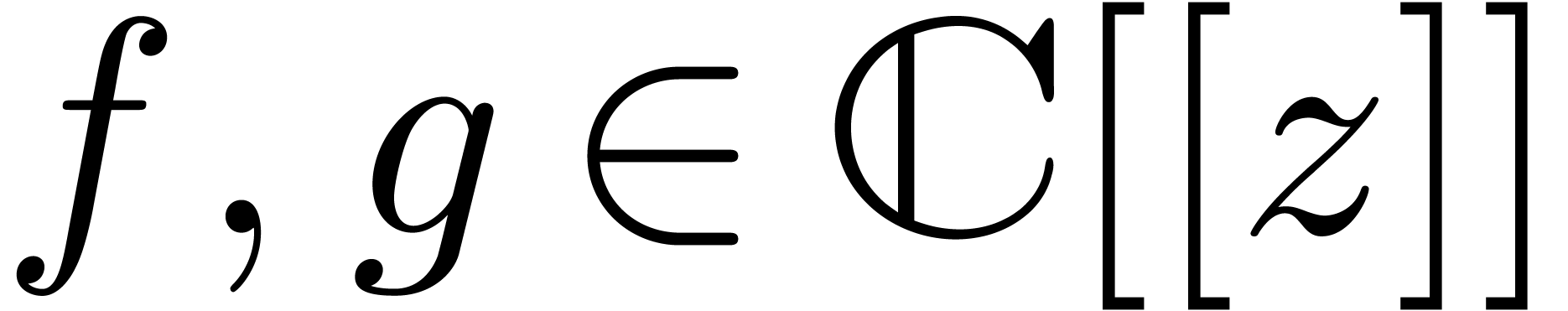 with
with 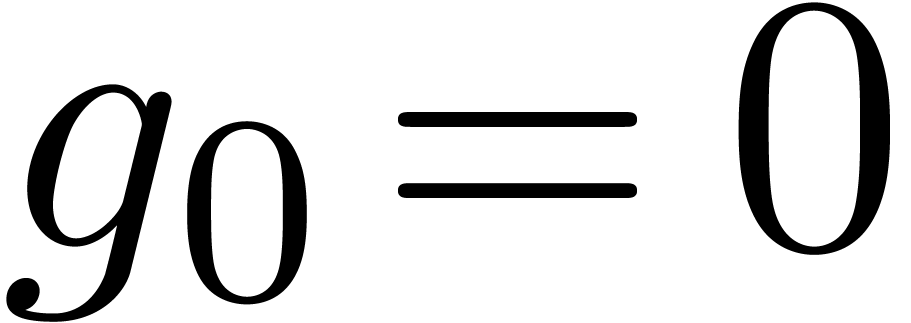 and
and 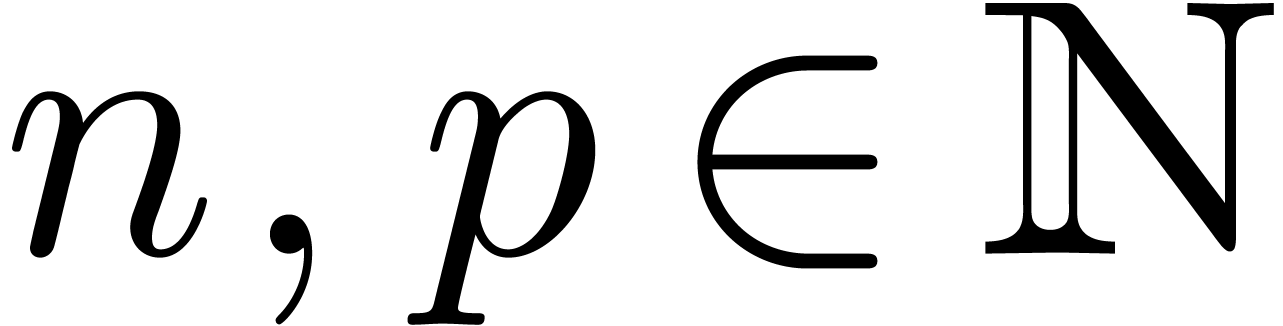 ,
,
such that we have bounds 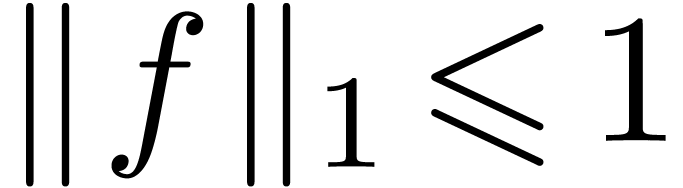 ,
,
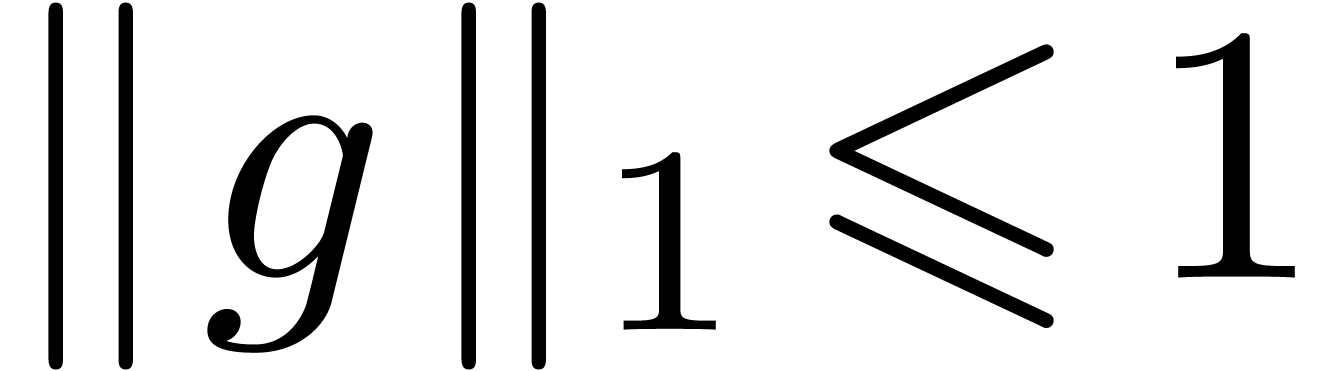 and
and
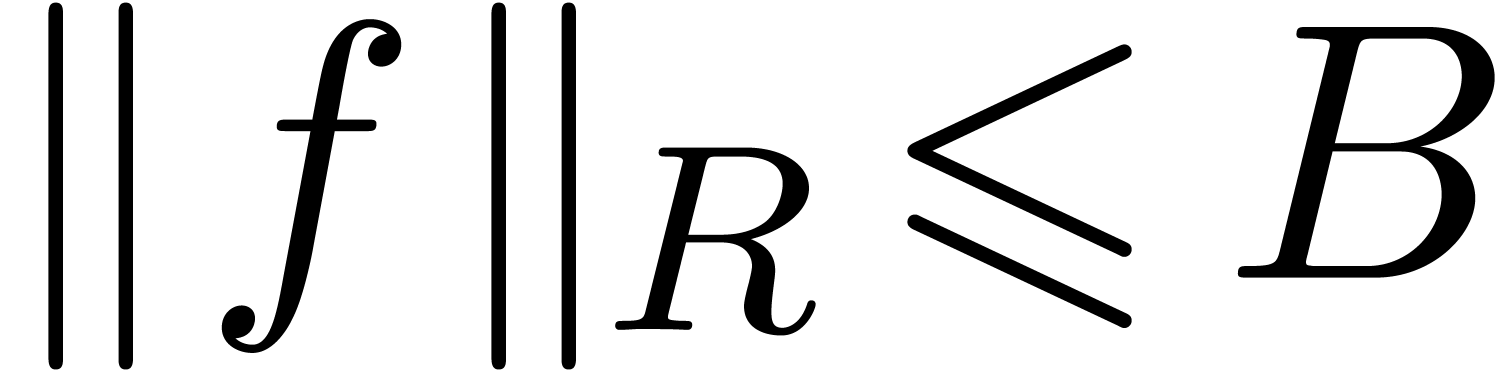 ,
, 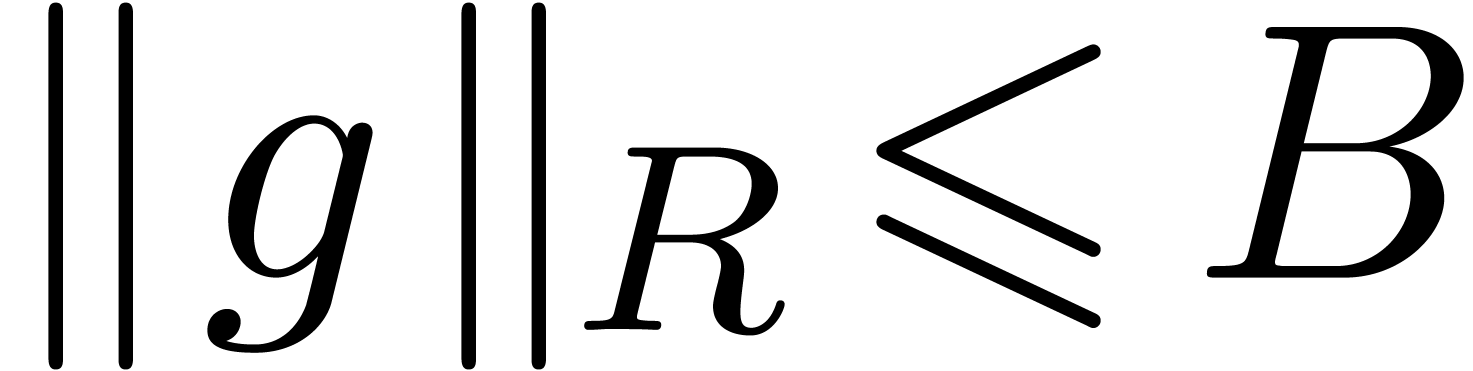 and
and 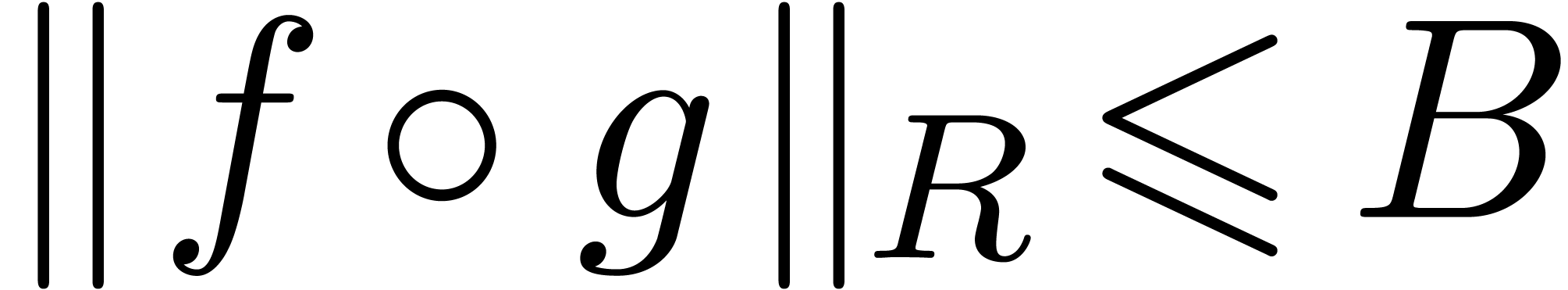 for certain
for certain 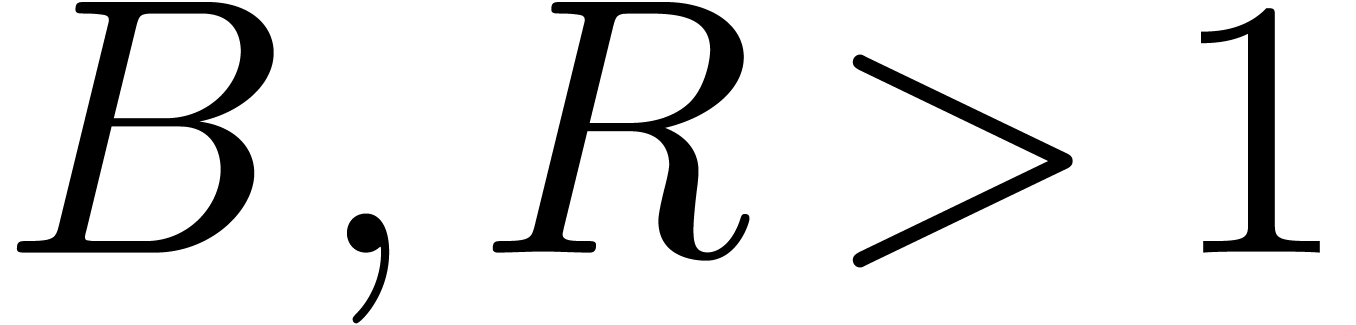
 -approximations
for
-approximations
for 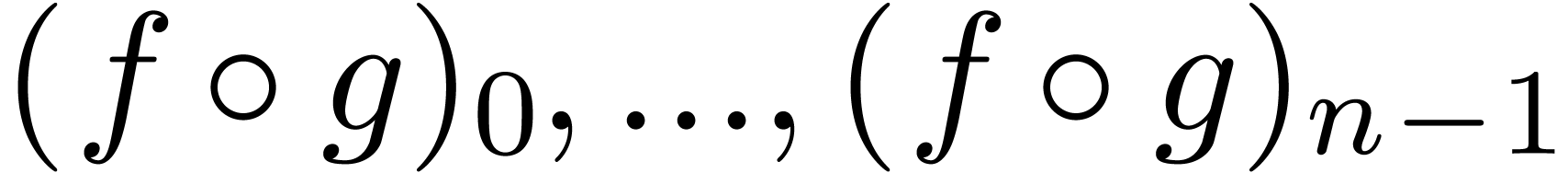
Step 1. [Determine auxiliary degree and precision]
Let  be smallest with
be smallest with  and
and 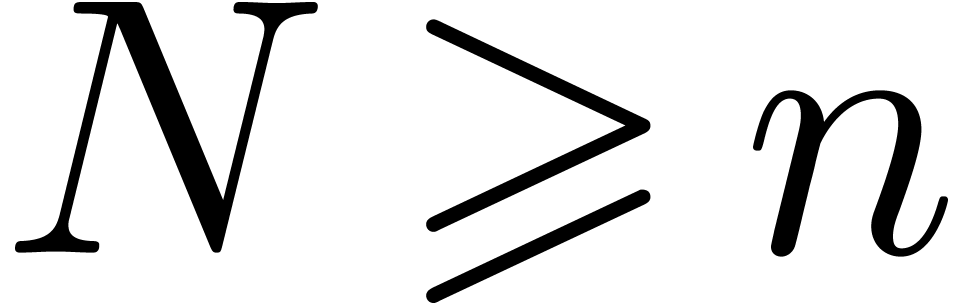
Let 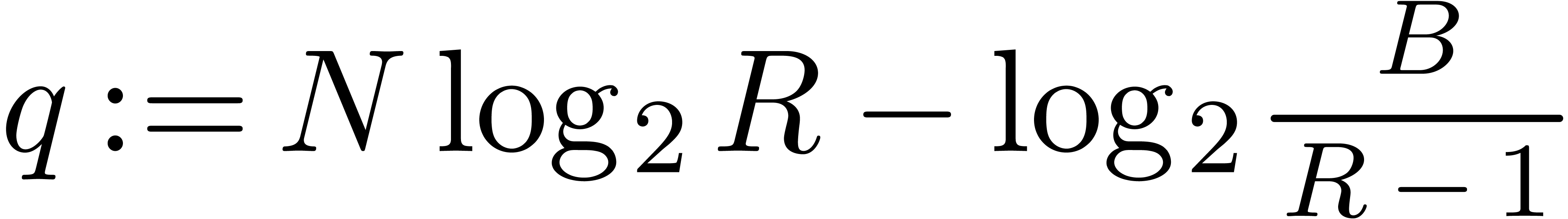 , so that
, so that 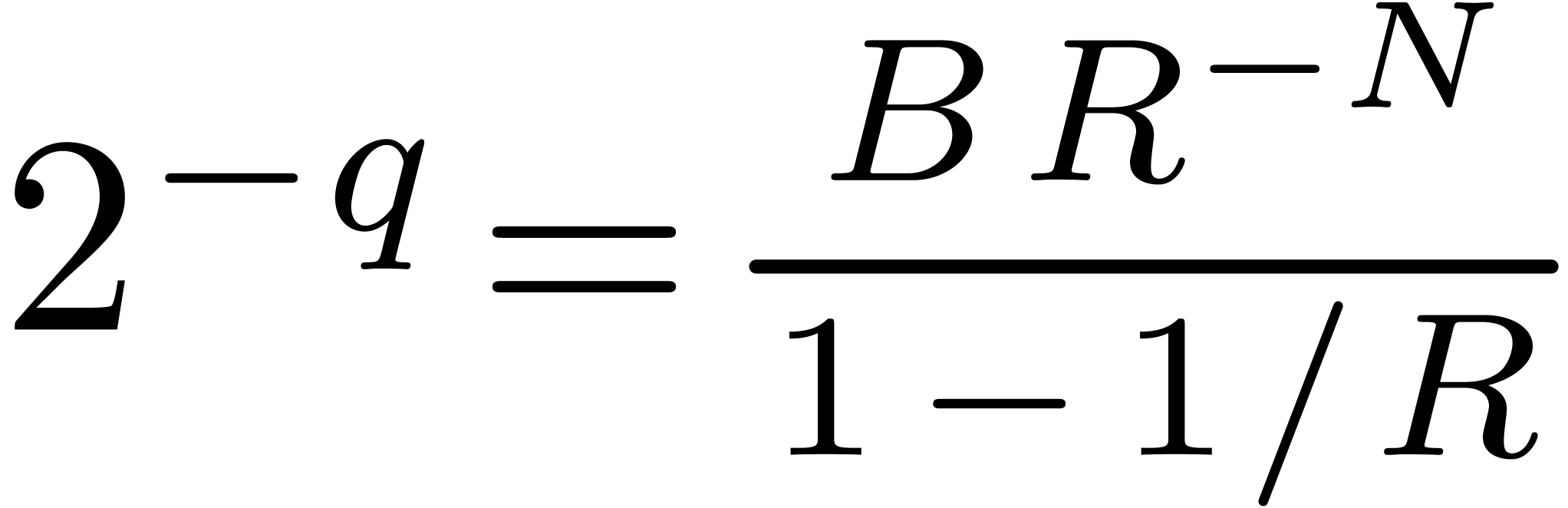
Step 2. [Evaluate  on roots of
unity
on roots of
unity 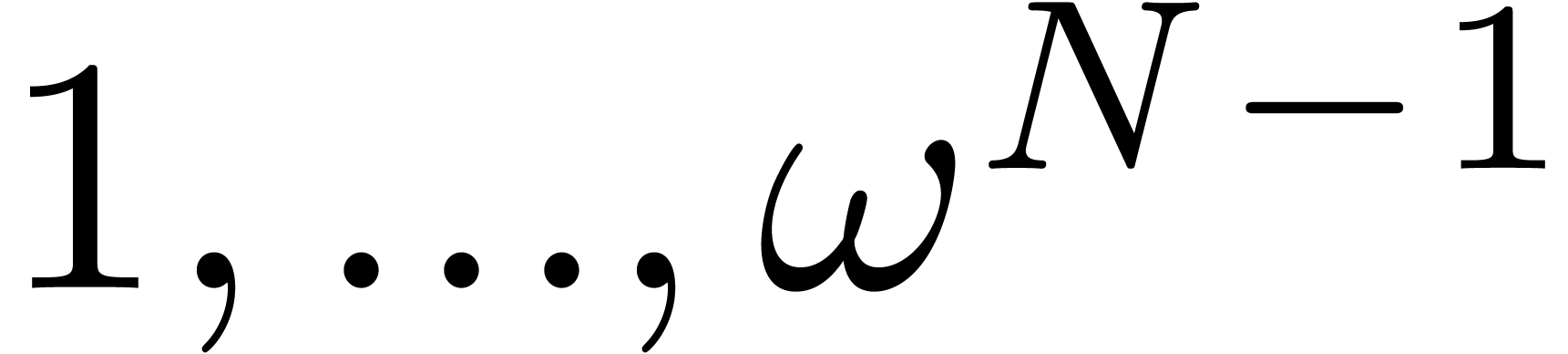 ]
]
Let 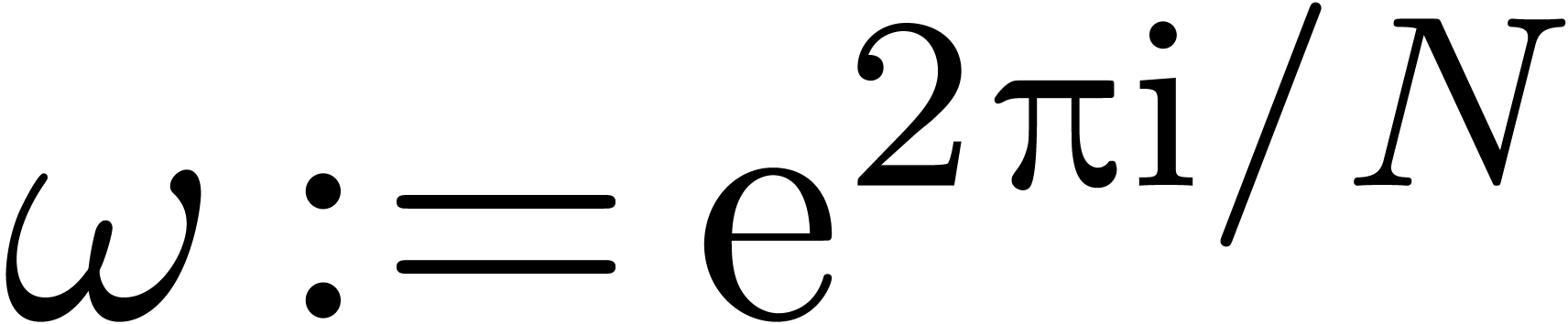
Compute a  -approximation
-approximation
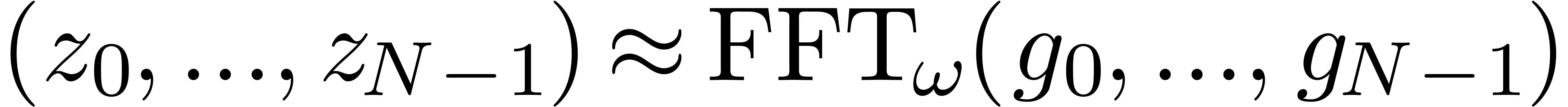 with
with 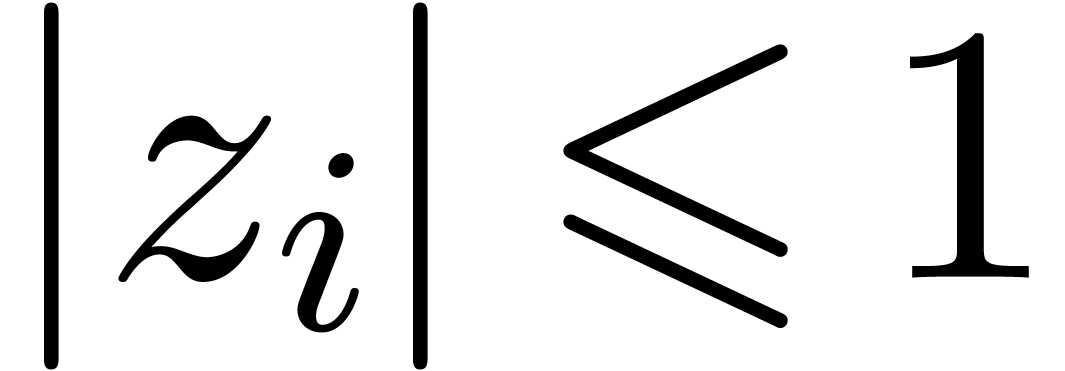
We will show that 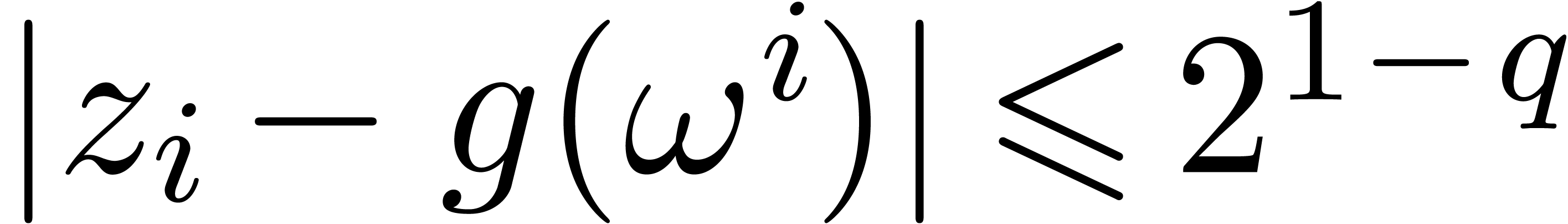 for all
for all 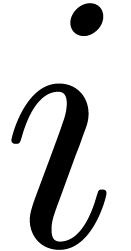
Step 3. [Evaluate 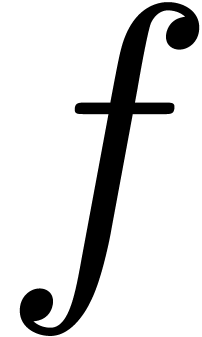 on
on 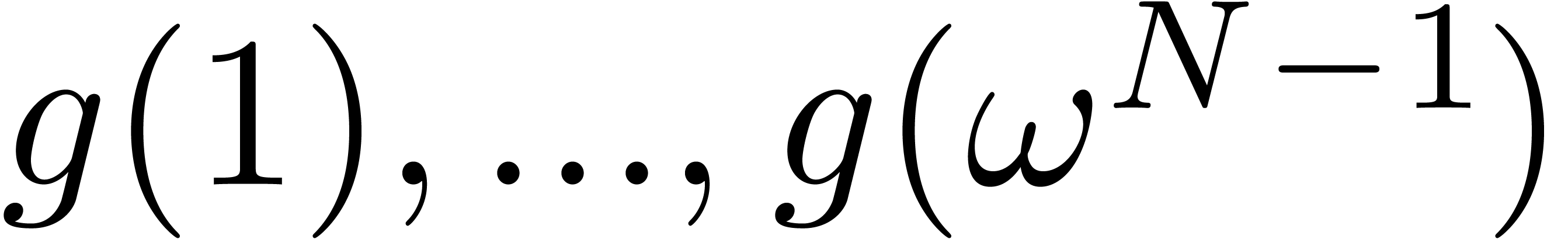 ]
]
Let 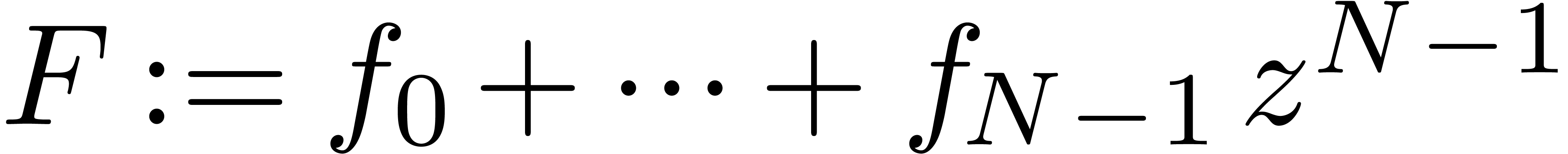
Compute a  -approximation
-approximation
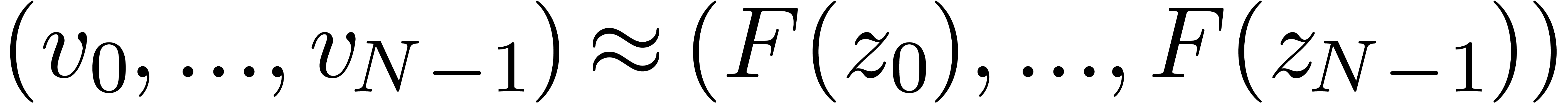
We will show that  for all
for all 
Step 4. [Interpolate]
Compute a  -approximation
-approximation
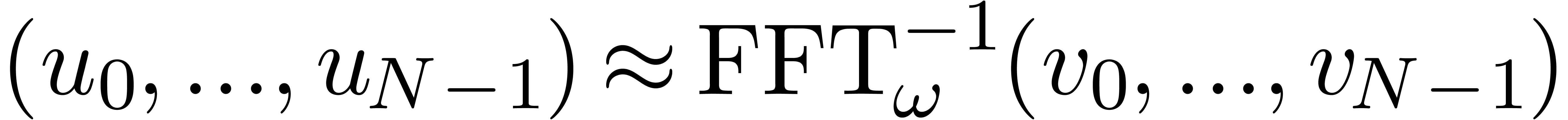
We will show that  for all
for all 
Return 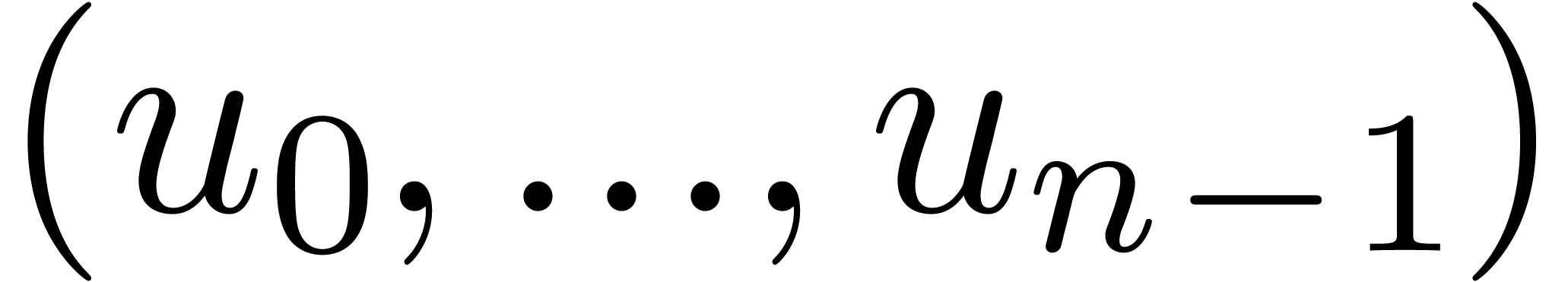
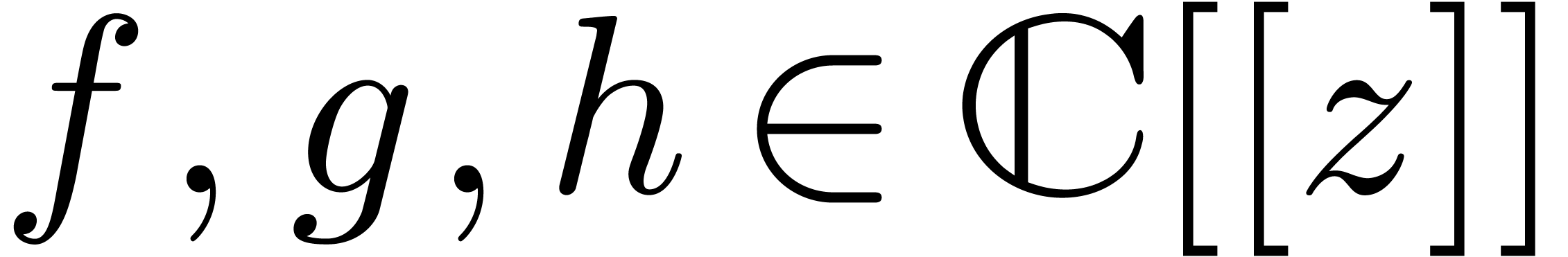 be power series with
be power series with 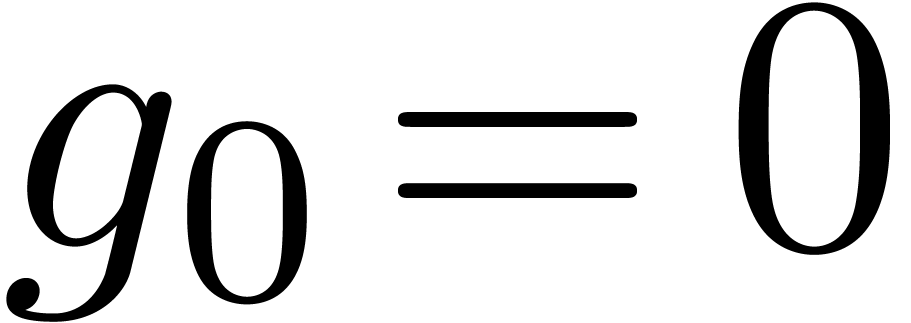 and
and 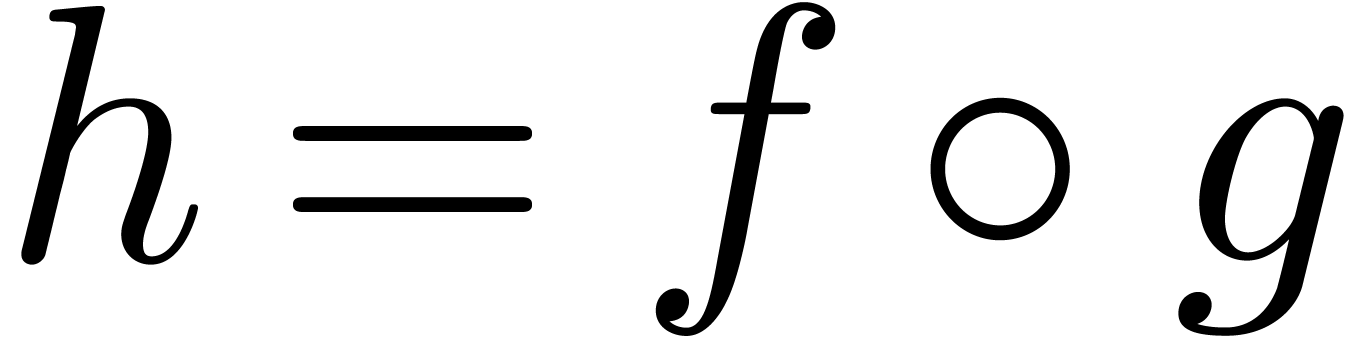 . Assume
that
. Assume
that 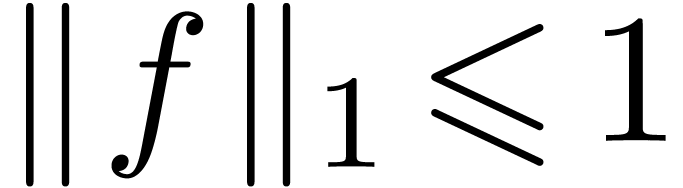 and
and 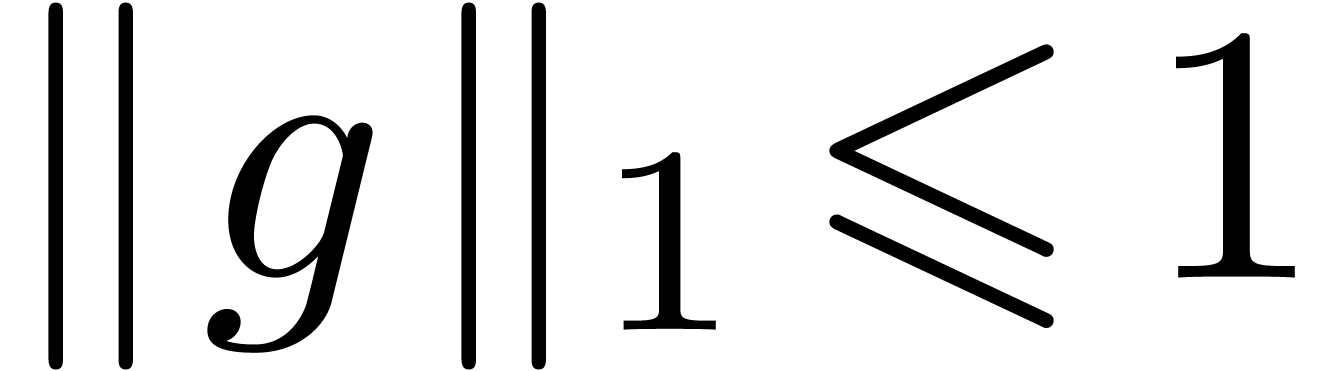 .
Given
.
Given 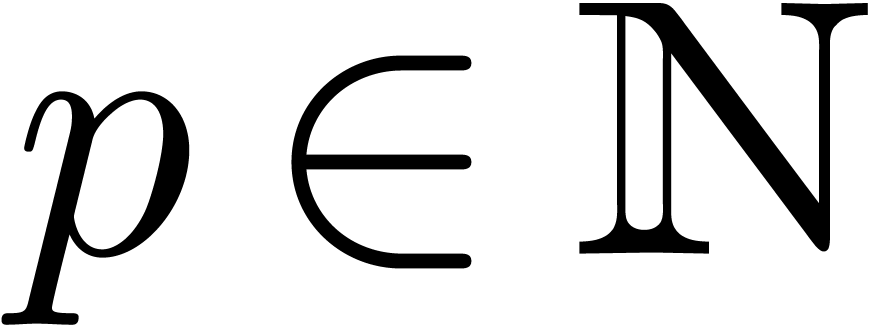 , we may compute
, we may compute
 -approximations for
-approximations for  (as a function of
(as a function of 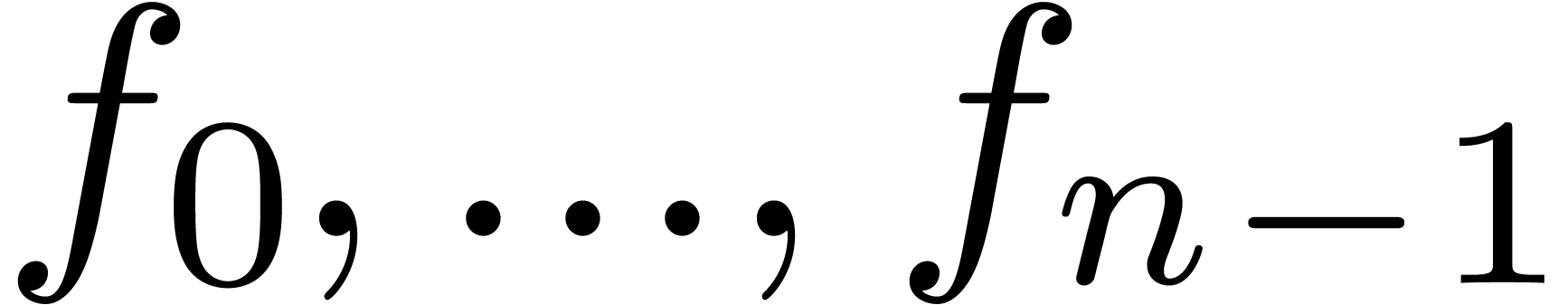 and
and  ) in time
) in time 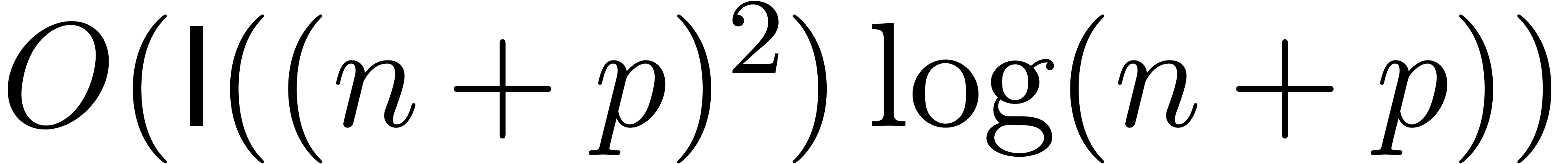 .
.
Proof. Let us first prove the correctness of the
algorithm. The choice of  and the tail bound (17) for
and the tail bound (17) for  imply
imply 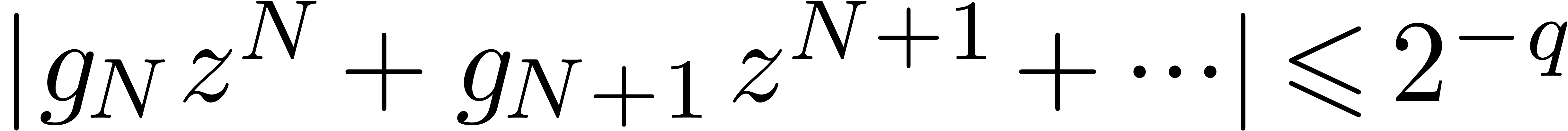 . This ensures that we indeed have
. This ensures that we indeed have 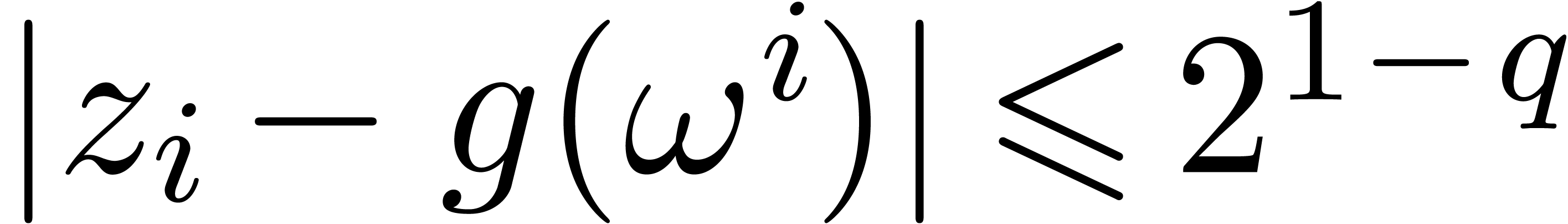 for all
for all 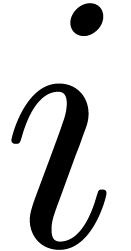 at the end of step 2. For
at the end of step 2. For 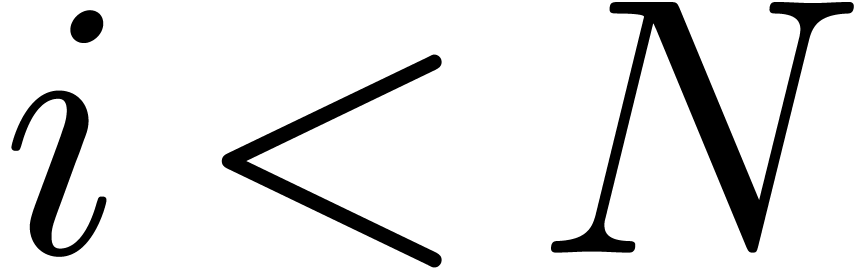 , we also have
, we also have
This proves the bound stated at the end of step 3. As to the last bound,
let 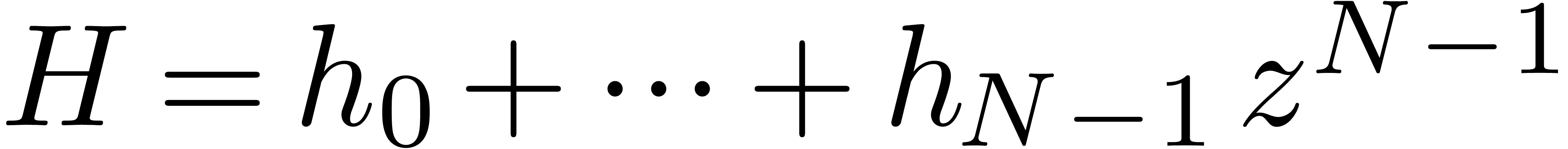 . Then
. Then 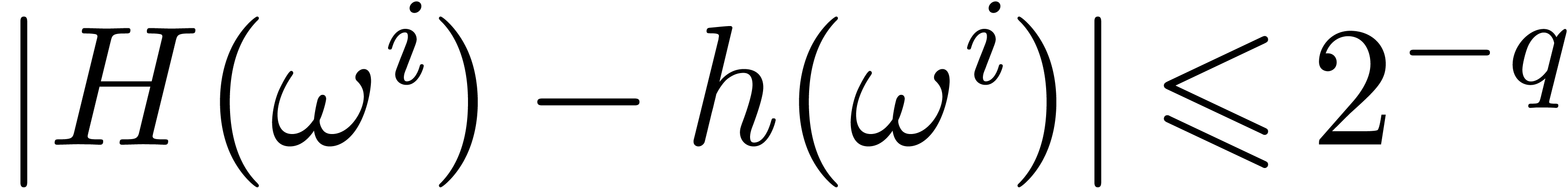 and
and 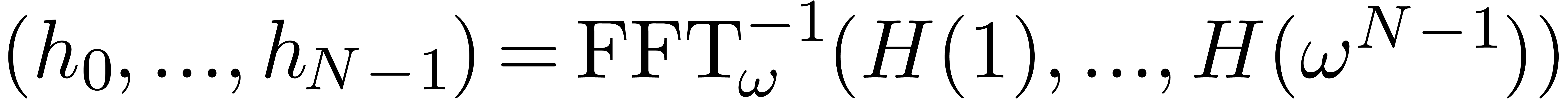 . Using the fact that
. Using the fact that
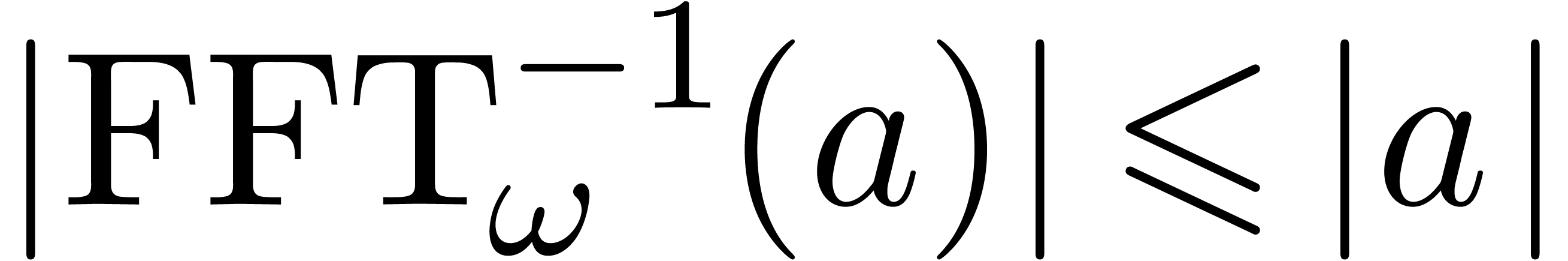 for all vectors
for all vectors  of
length
of
length  , we obtain
, we obtain
This proves the second bound. Our choice of  implies the correctness of the algorithm.
implies the correctness of the algorithm.
As to the complexity bound, the FFT transform in step 2 can be done in time
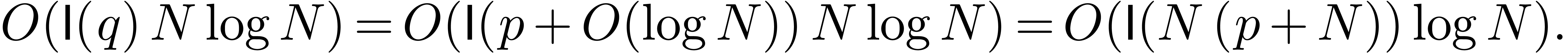
By lemma 11, the multi-point evaluation in step 3 can be performed in time
The inverse FFT transform in step 4 can be performed within the same time as a direct FFT transform. This leads to the overall complexity bound
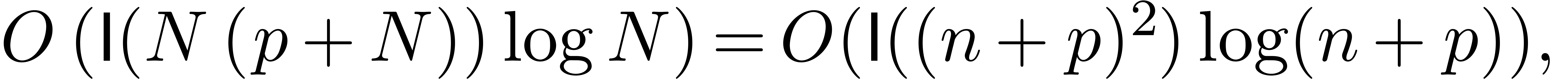
since 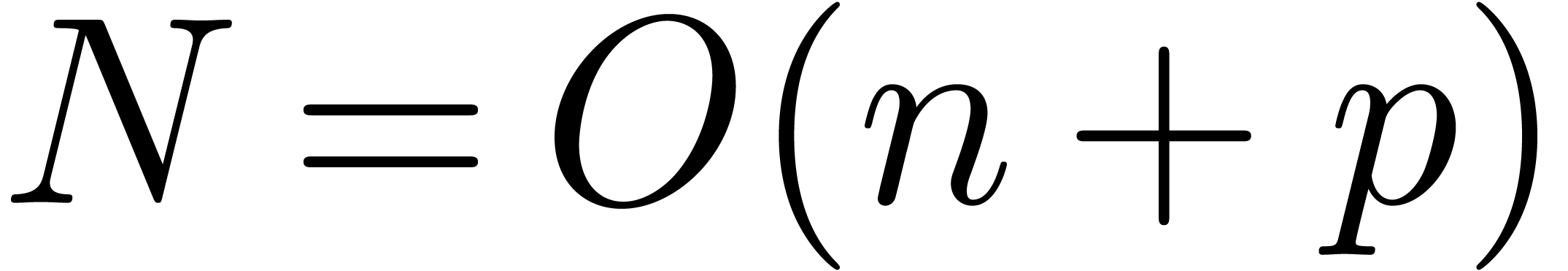 .
.
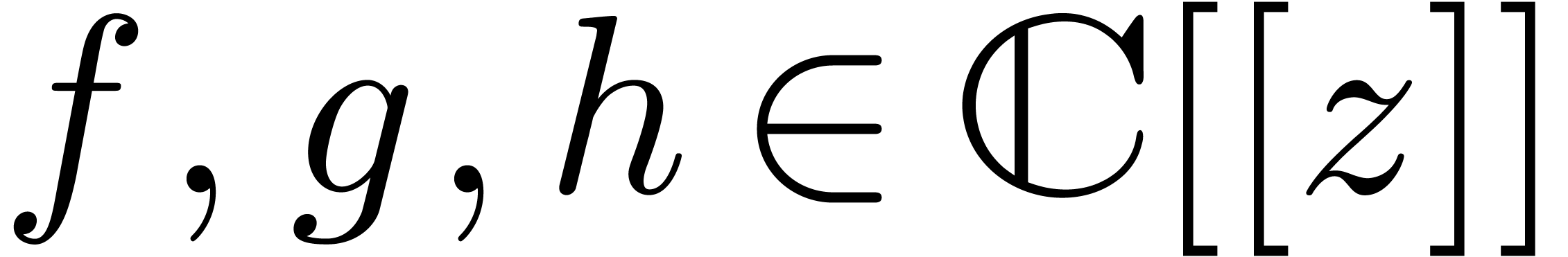 be convergent power series with
be convergent power series with
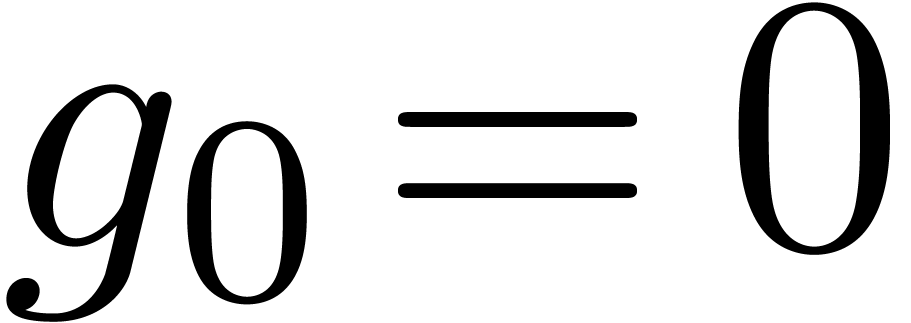 and
and 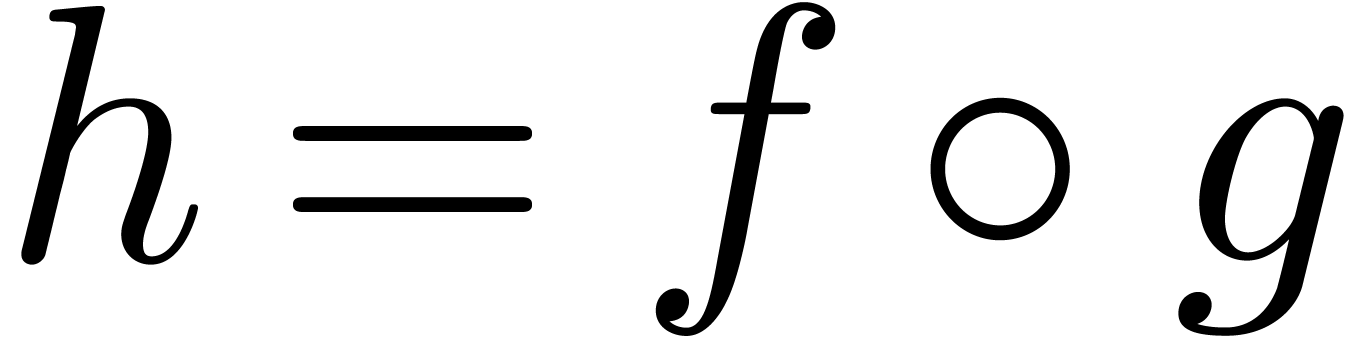 .
Given
.
Given 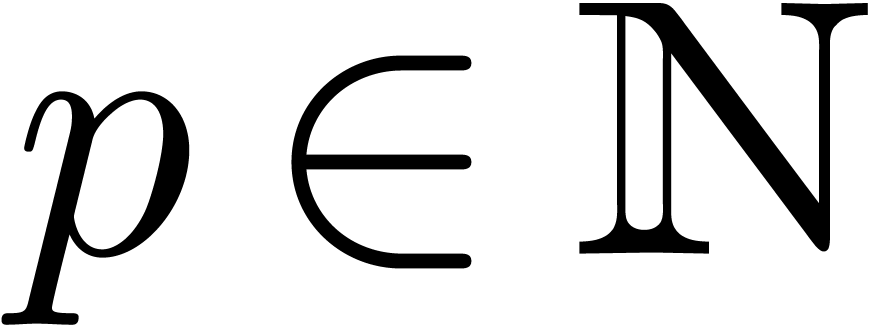 , we may compute
, we may compute
 -approximations for
-approximations for  (as a function of
(as a function of  and
and  ) in time
) in time
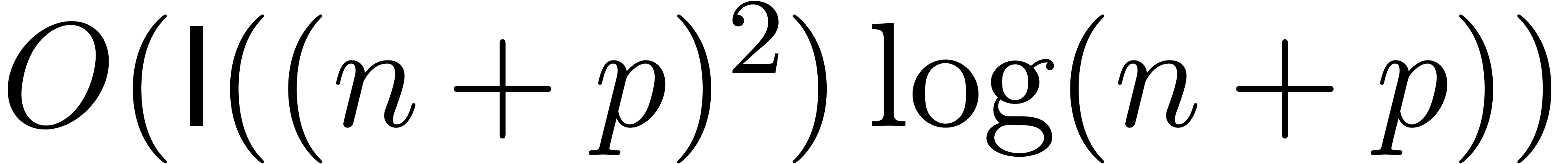 .
.
Proof. Let 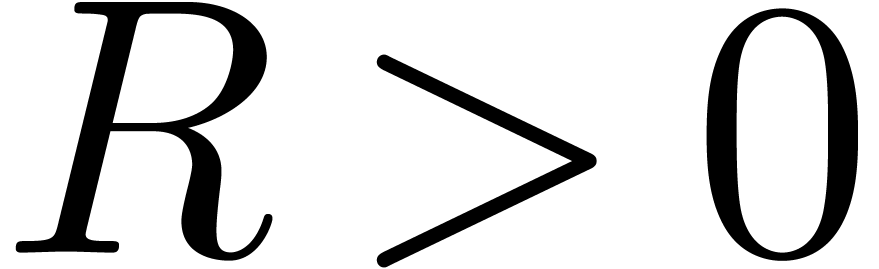 be
sufficiently small such that
be
sufficiently small such that 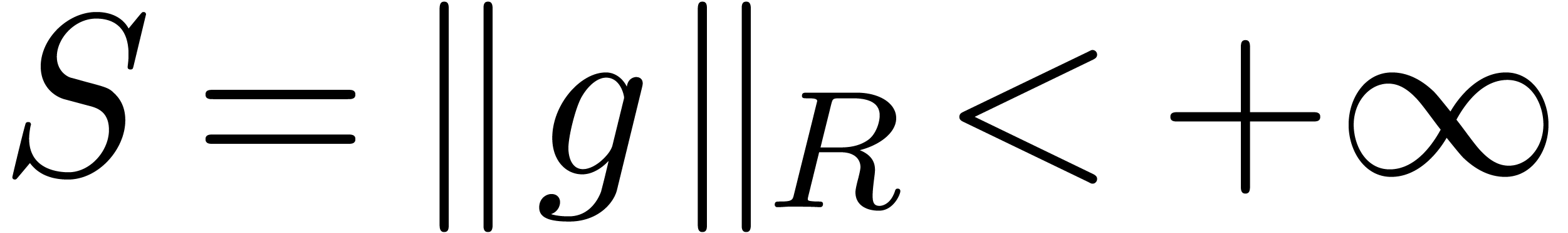 and
and 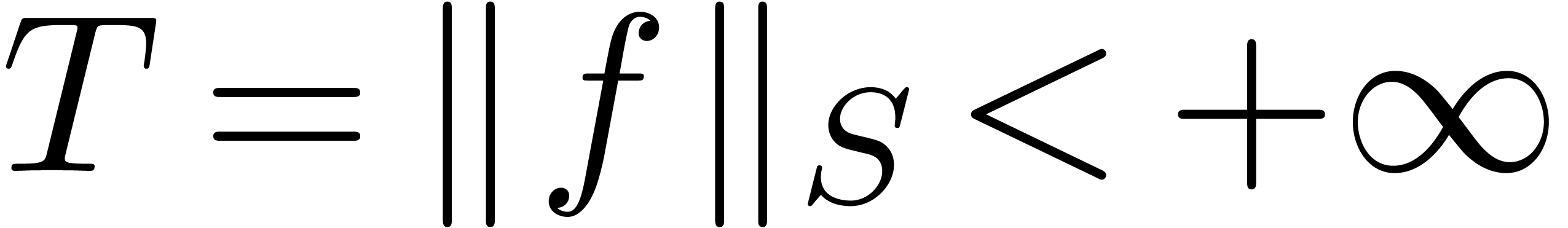 . Consider the series
. Consider the series 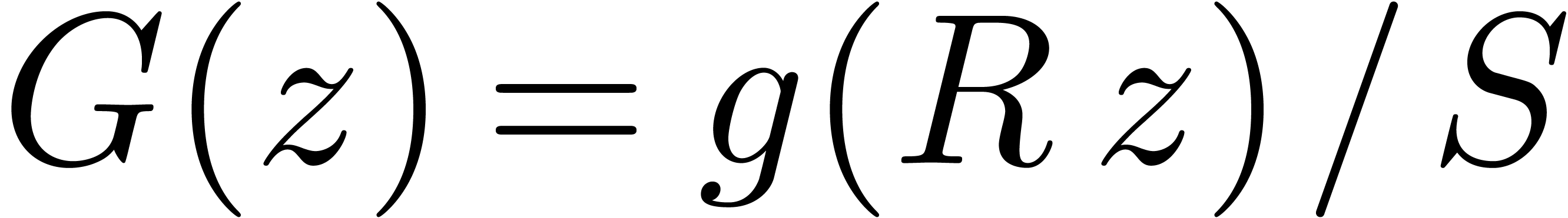 and
and 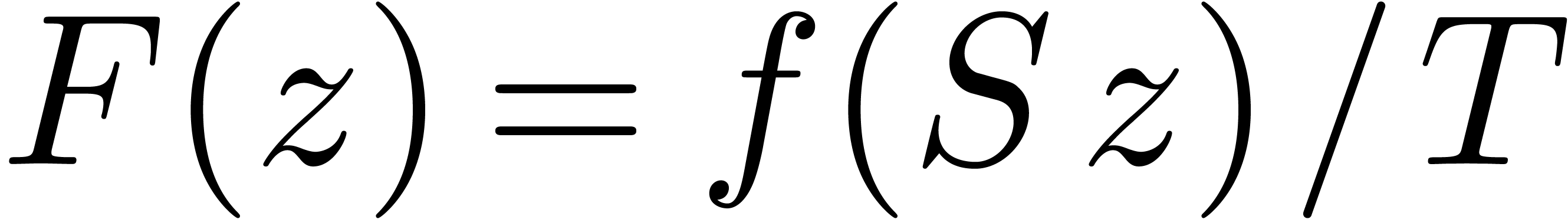 , so that
, so that
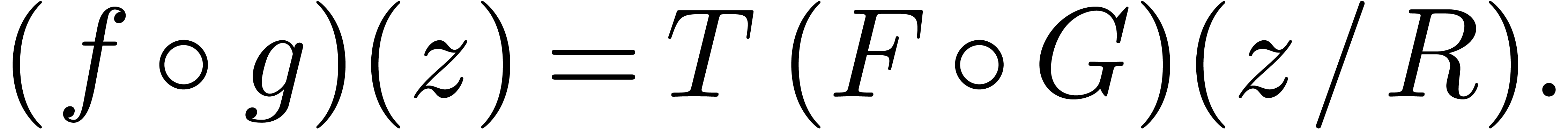
Let  . By the theorem, we may
compute
. By the theorem, we may
compute 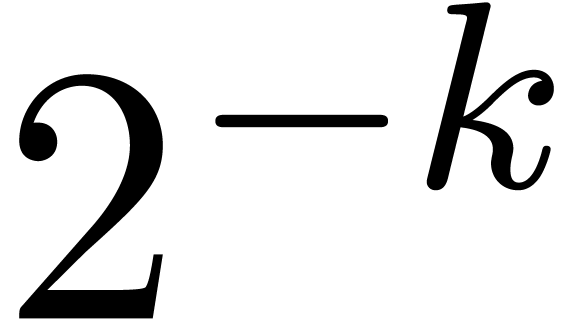 -approximations
-approximations 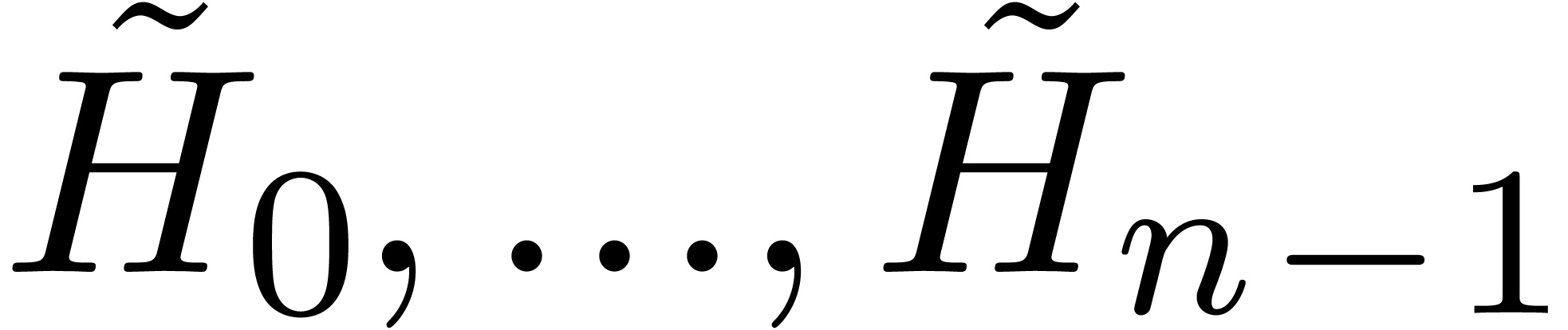 of
of 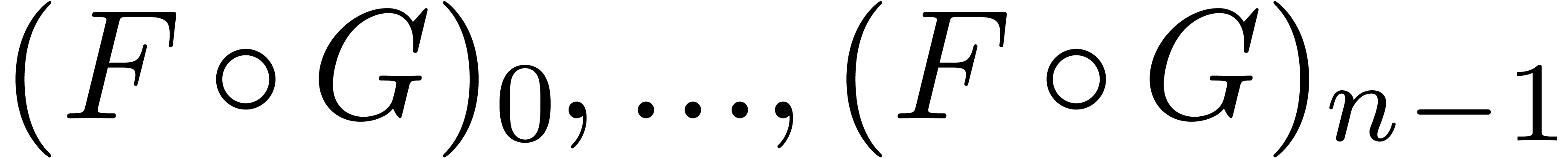 in time
in time 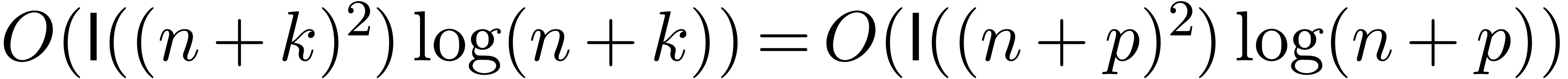 . Using
. Using 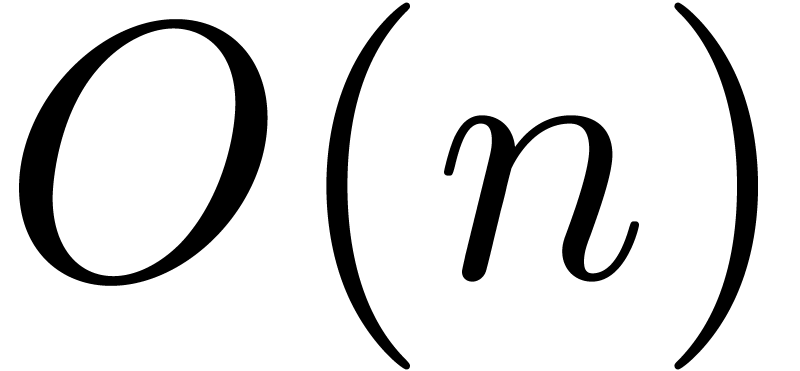 additional
additional
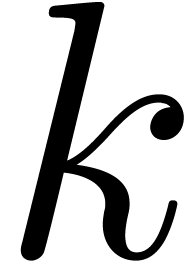 -bit multiplications, we may
compute
-bit multiplications, we may
compute
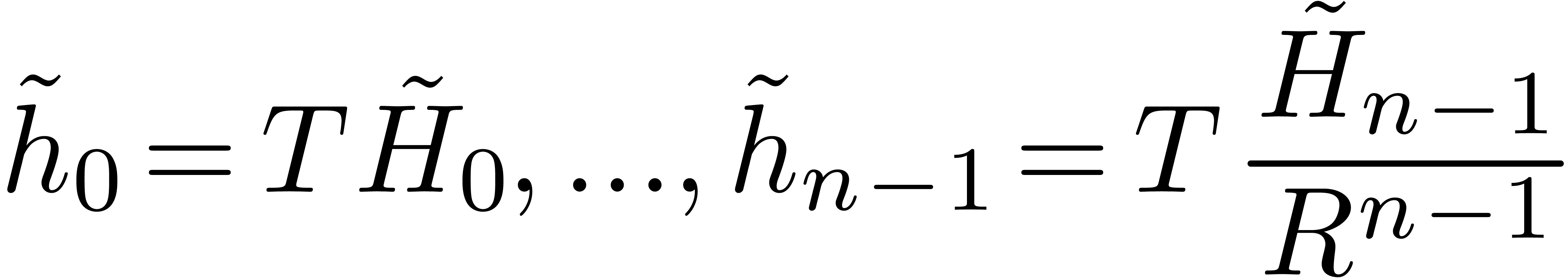
with 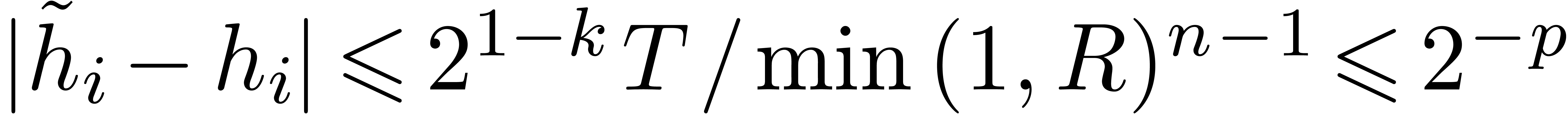 for all
for all 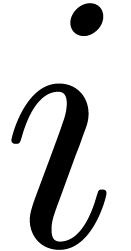 .
This can again be done in time
.
This can again be done in time 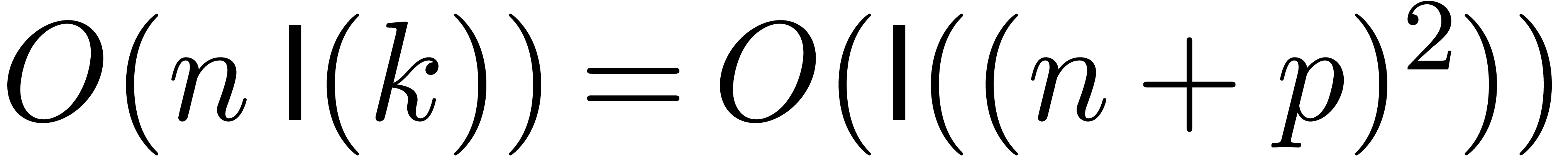 .
.
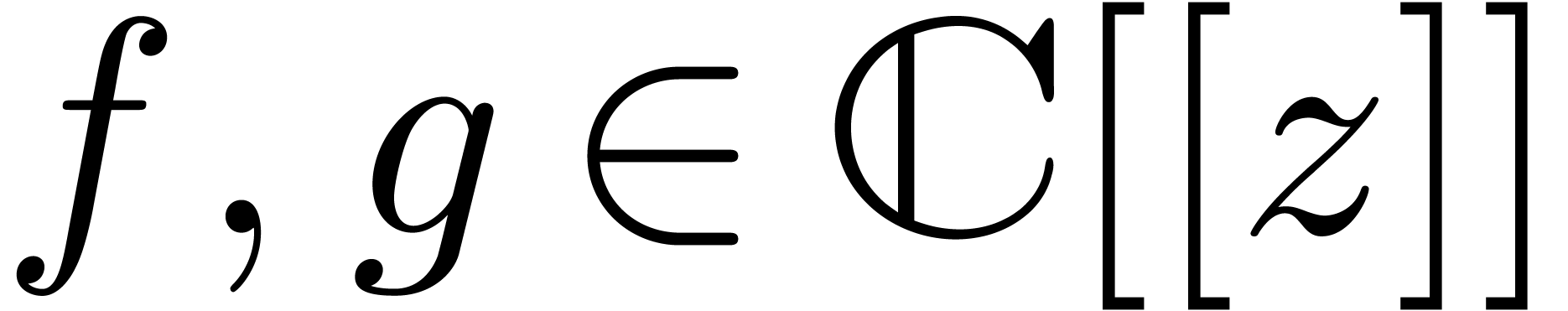 be convergent power series with
be convergent power series with
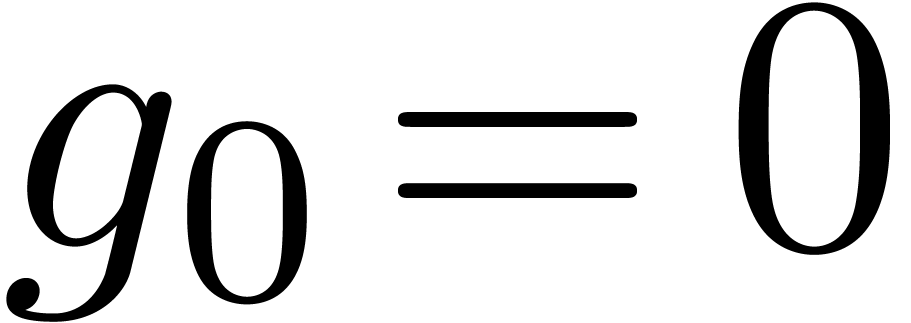 , such that
, such that 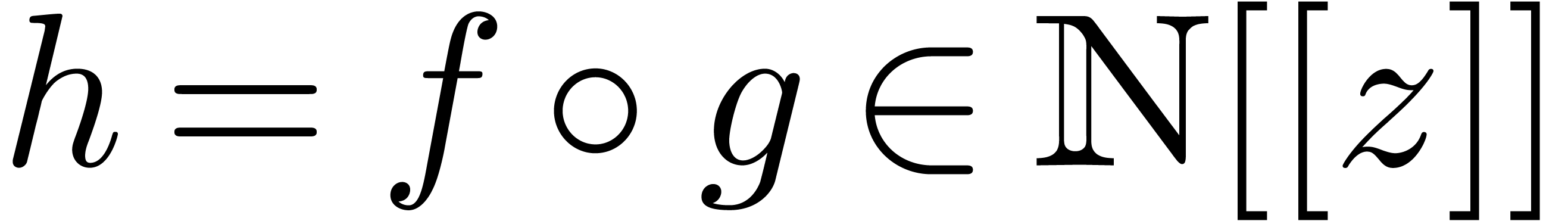 is an ordinary generating function. Then we may compute
is an ordinary generating function. Then we may compute
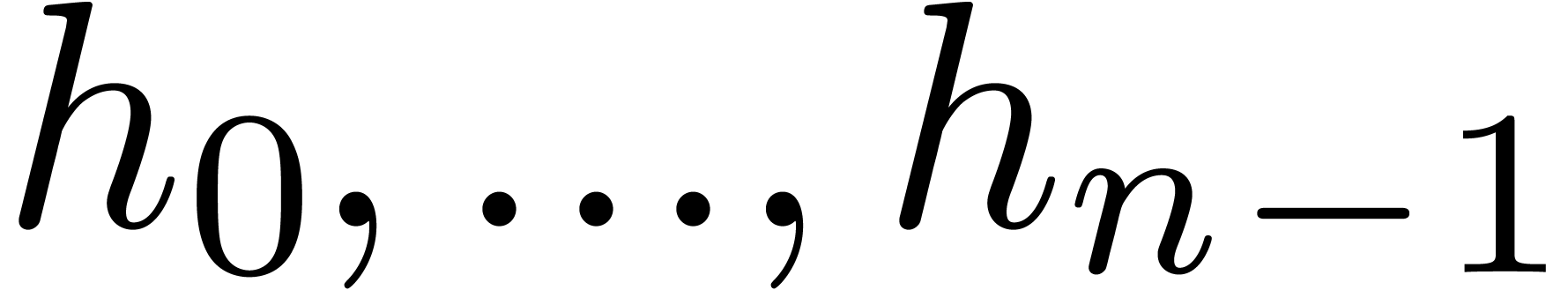 (as a function of
(as a function of 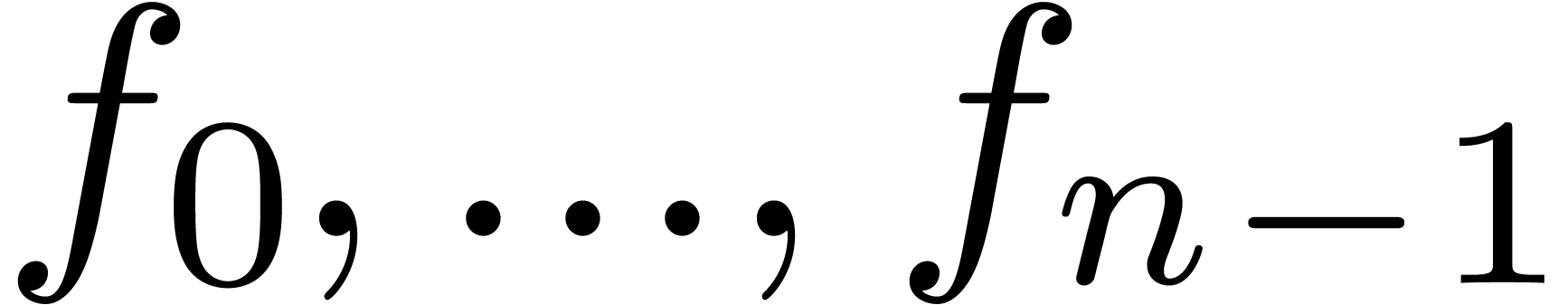 and
and
 ) in time
) in time 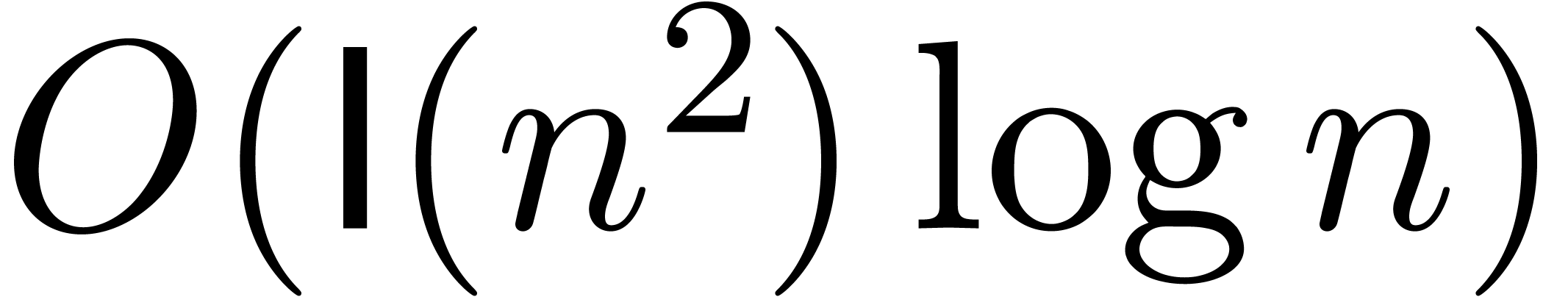 .
.
Proof. It suffices to take 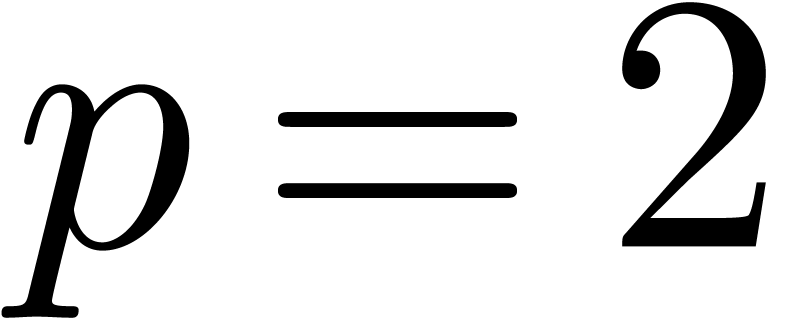 in corollary 19 and round the results.
in corollary 19 and round the results.
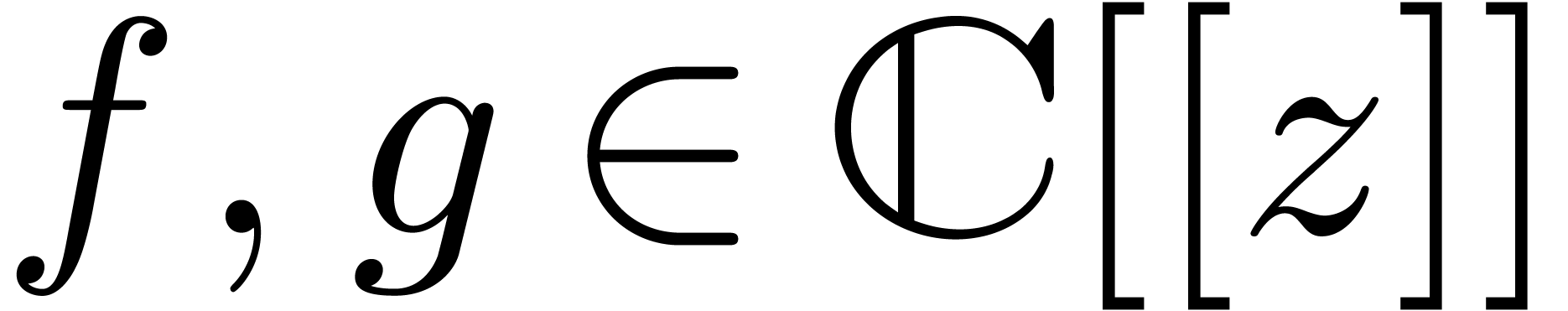 be convergent power series with
be convergent power series with
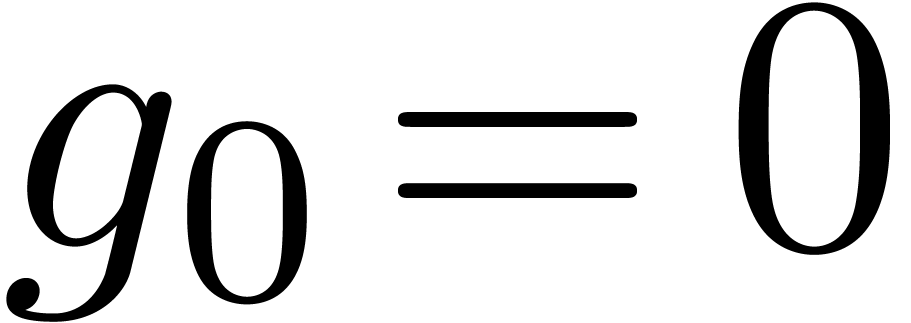 such that
such that 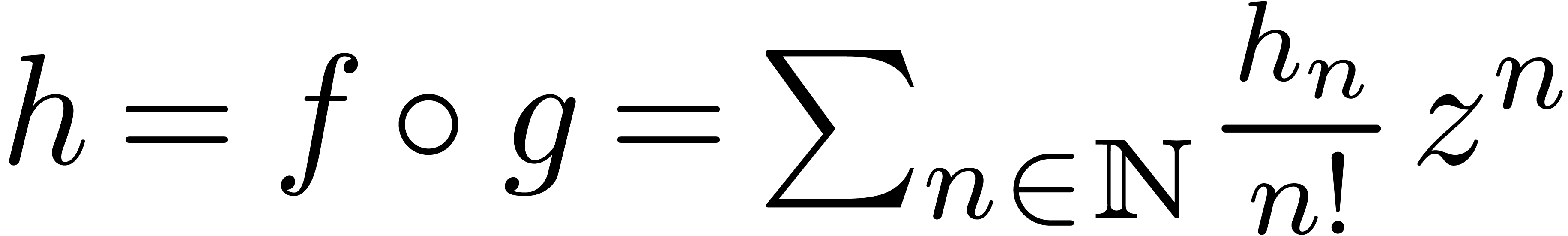 is an
exponential generating function. Then we may compute
is an
exponential generating function. Then we may compute 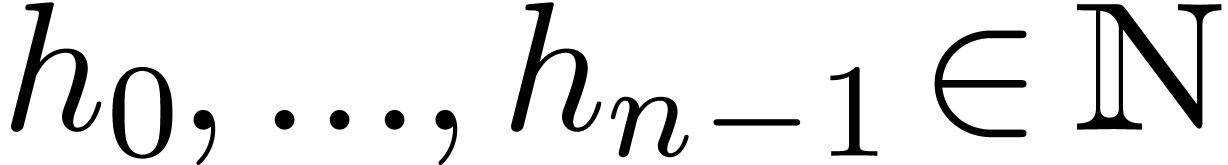 (as a function of
(as a function of 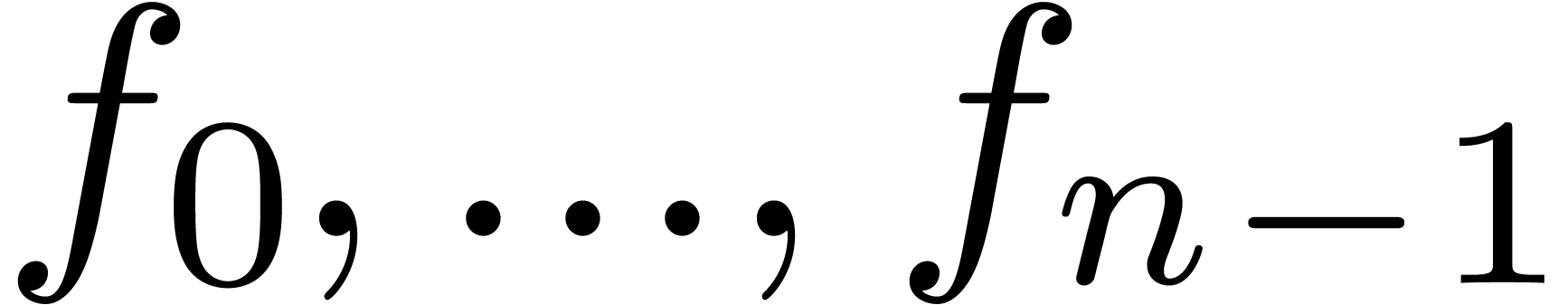 and
and  ) in time
) in time 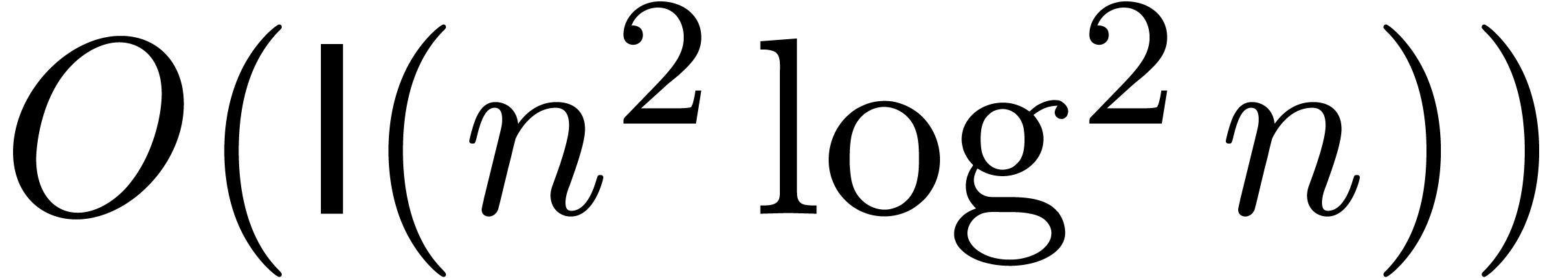 .
.
Proof. Applying corollary 19 for
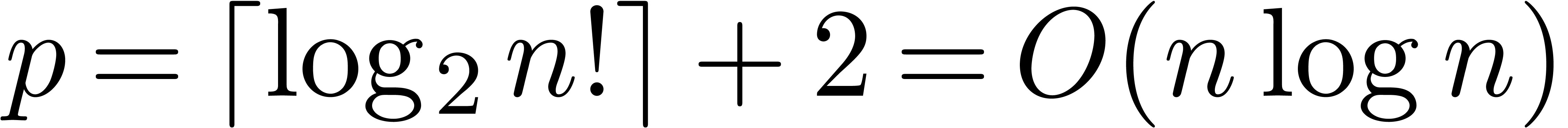 , we obtain
, we obtain 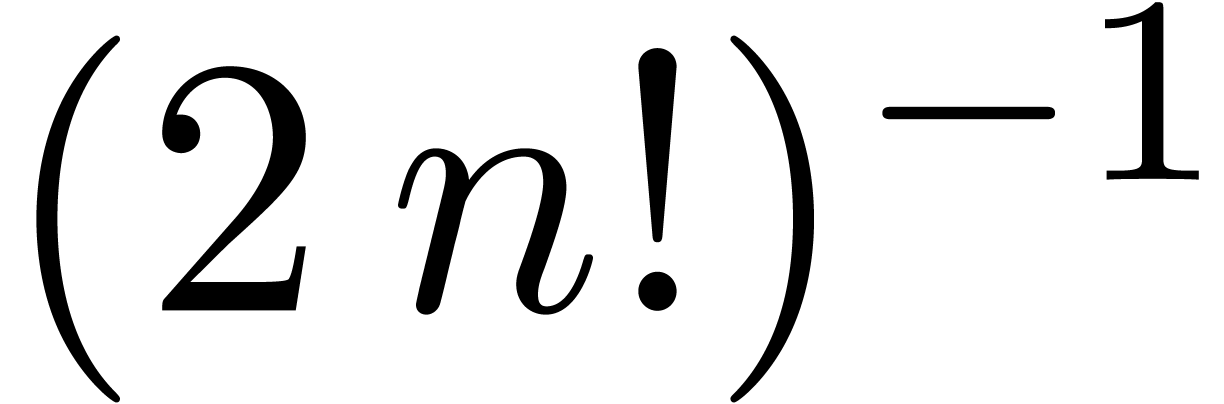 -approximations
-approximations 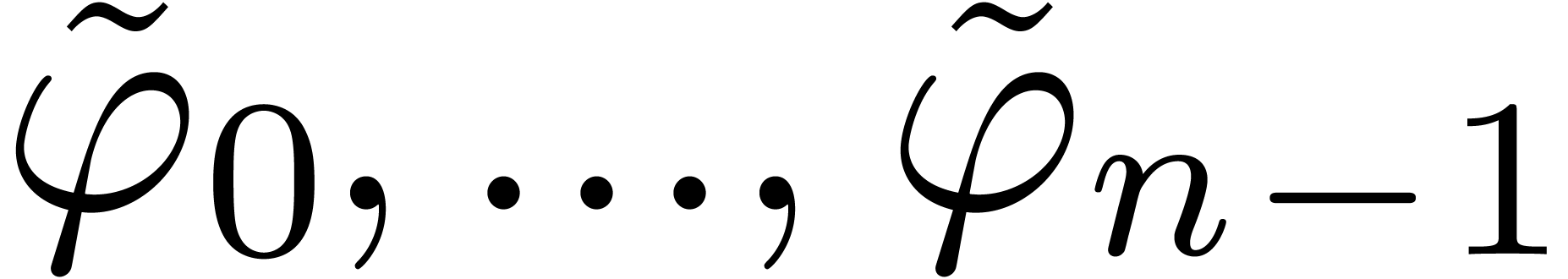 of
of 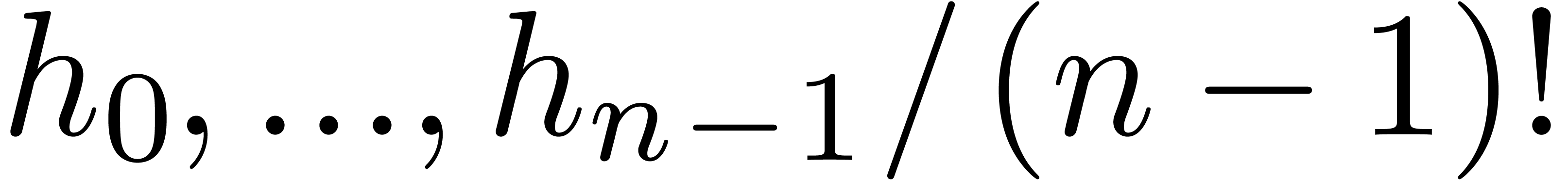 in time
in time 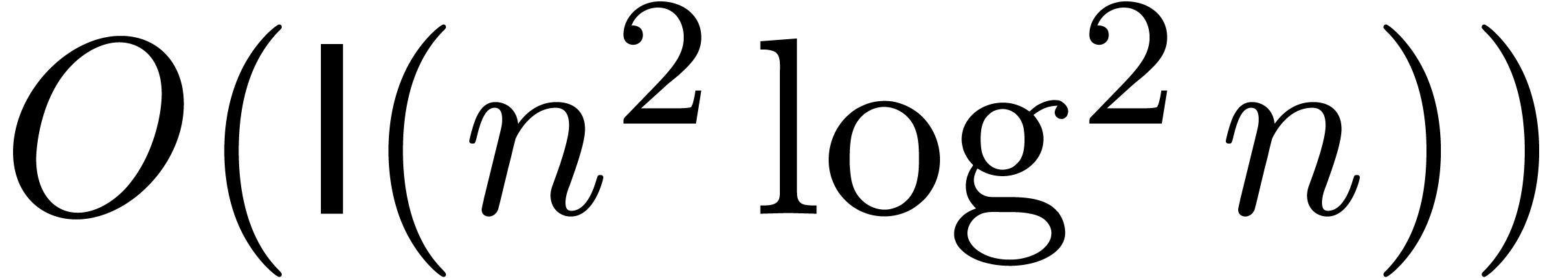 .
Using
.
Using 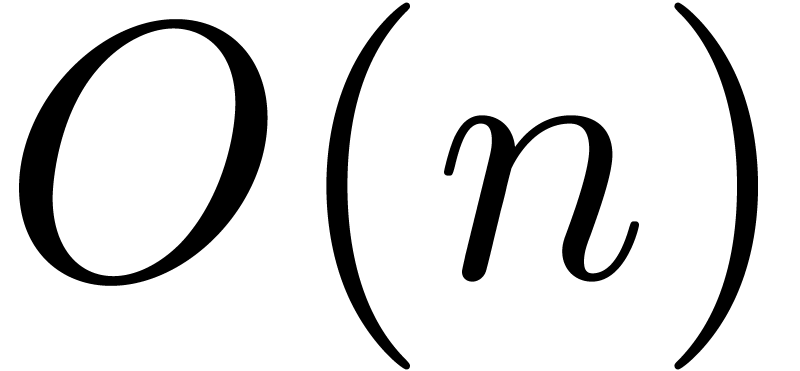 additional
additional 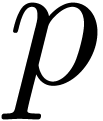 -bit
multiplications of total cost
-bit
multiplications of total cost 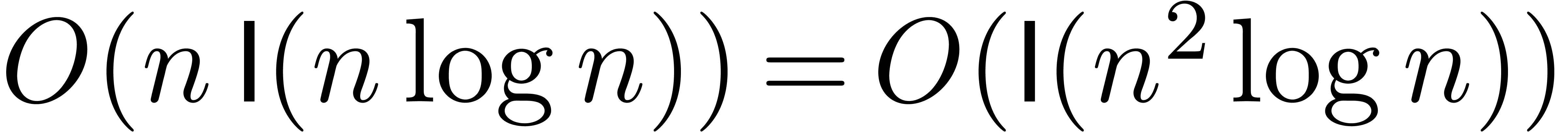 ,
we may compute
,
we may compute
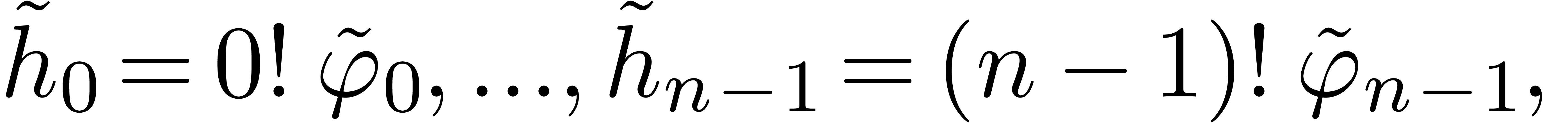
with 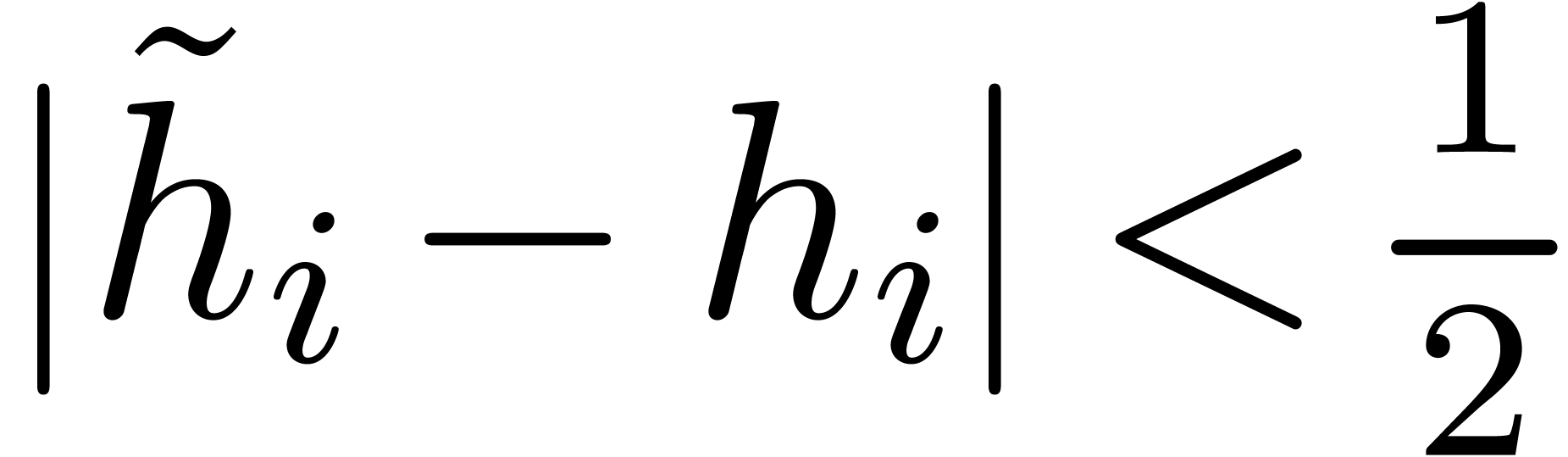 for all
for all 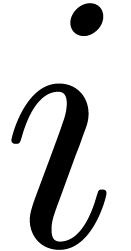 .
The
.
The 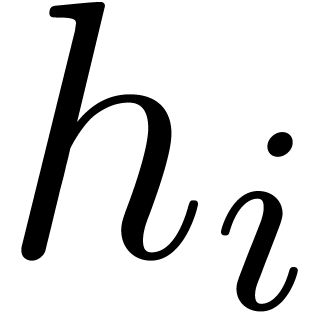 are obtained by rounding the
are obtained by rounding the 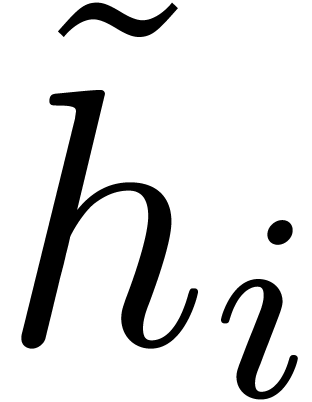 to the nearest integers.
to the nearest integers.
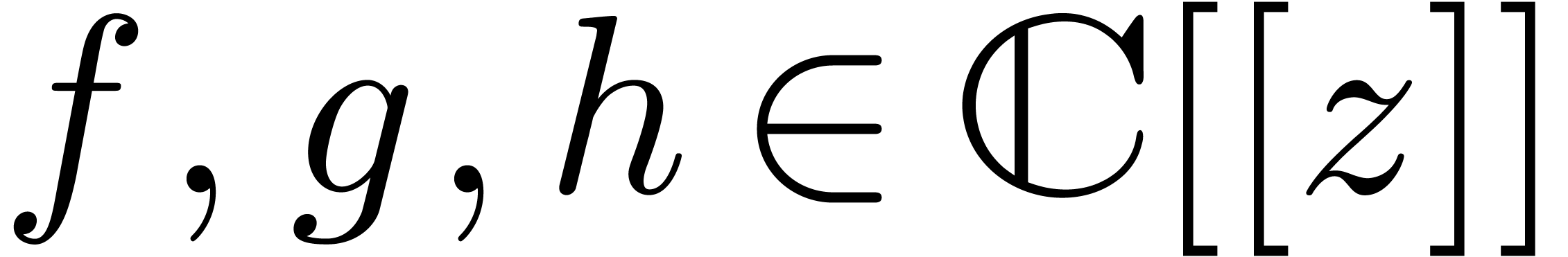 be power series with
be power series with 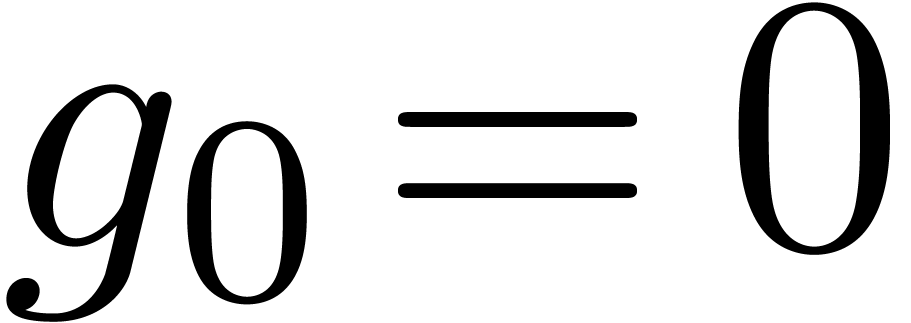 and
and 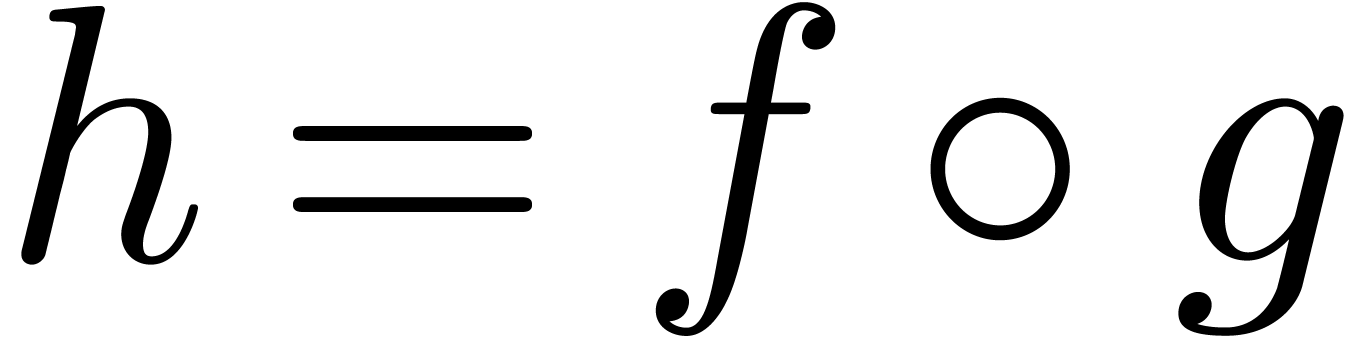 . Let
. Let
 and
and 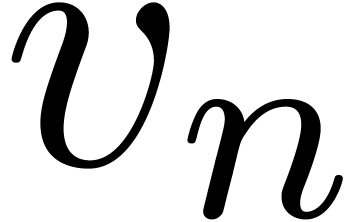 be positive
increasing functions with
be positive
increasing functions with 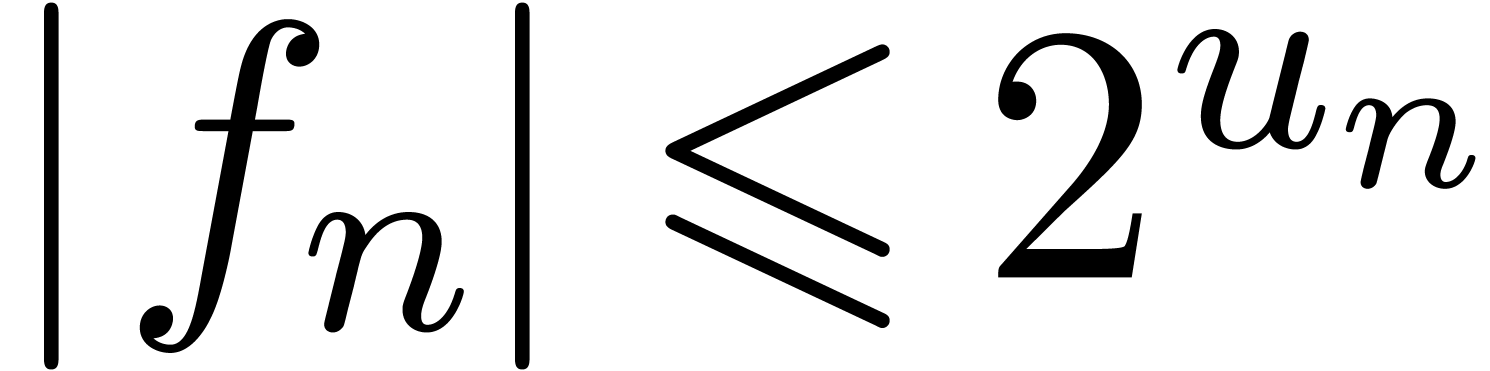 and
and 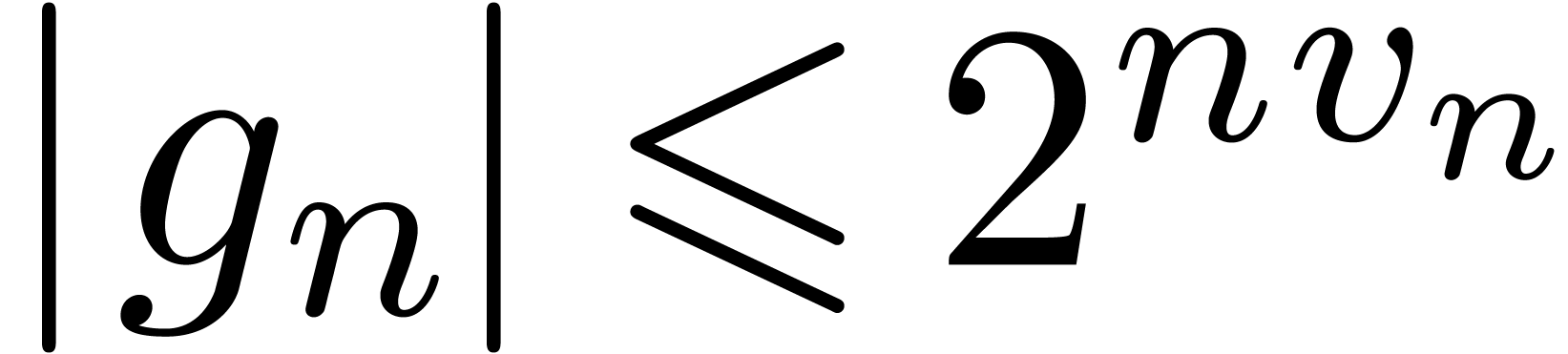 . Given
. Given  ,
we may compute
,
we may compute  -approximations
for
-approximations
for 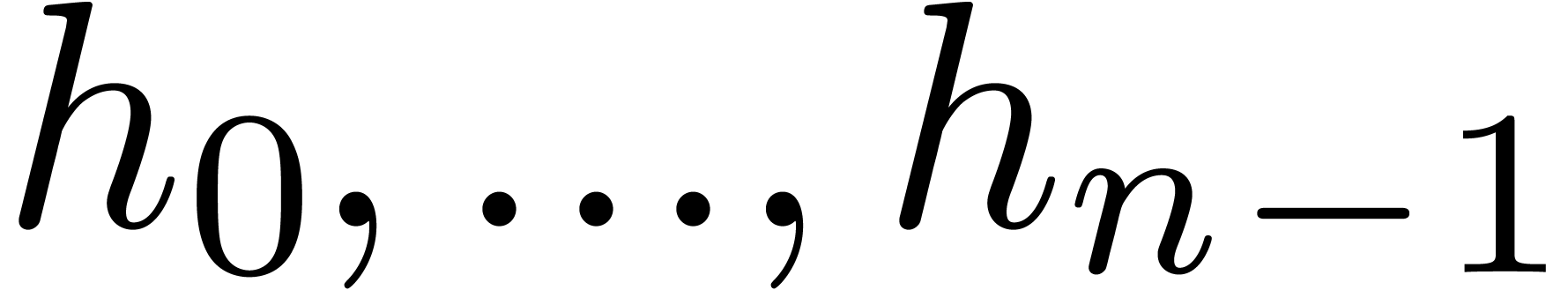 (as a function of
(as a function of 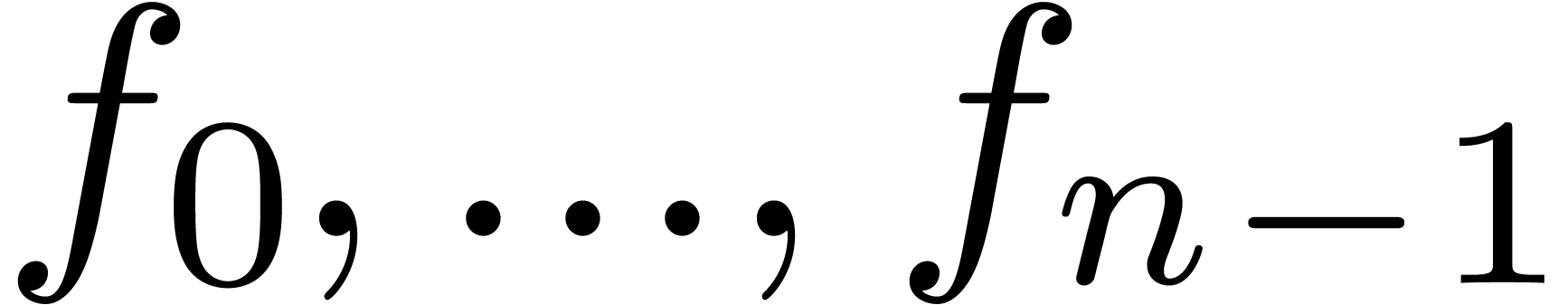 and
and  ) in time
) in time 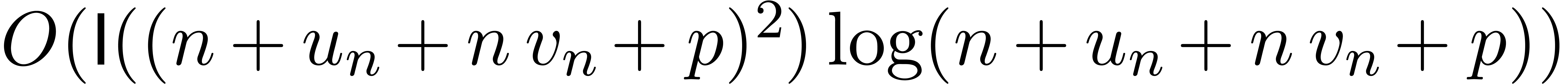 .
.
Proof. Without loss of generality, we may assume
that 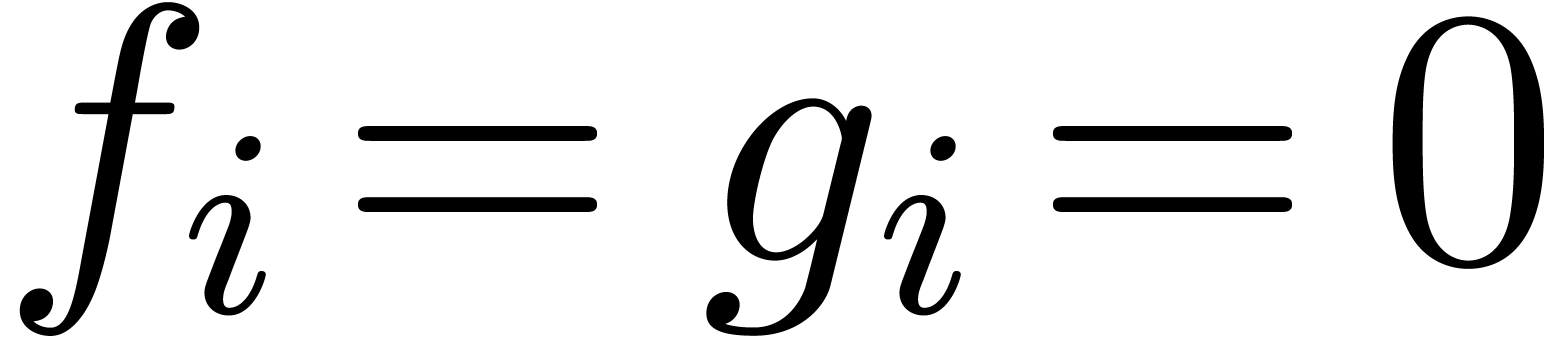 for
for 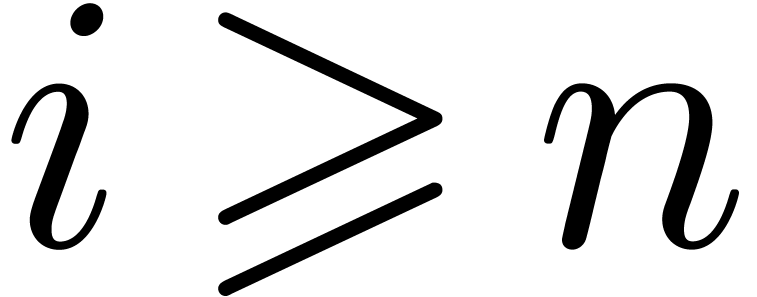 .
In the proof of corollary 19, we may therefore choose
.
In the proof of corollary 19, we may therefore choose 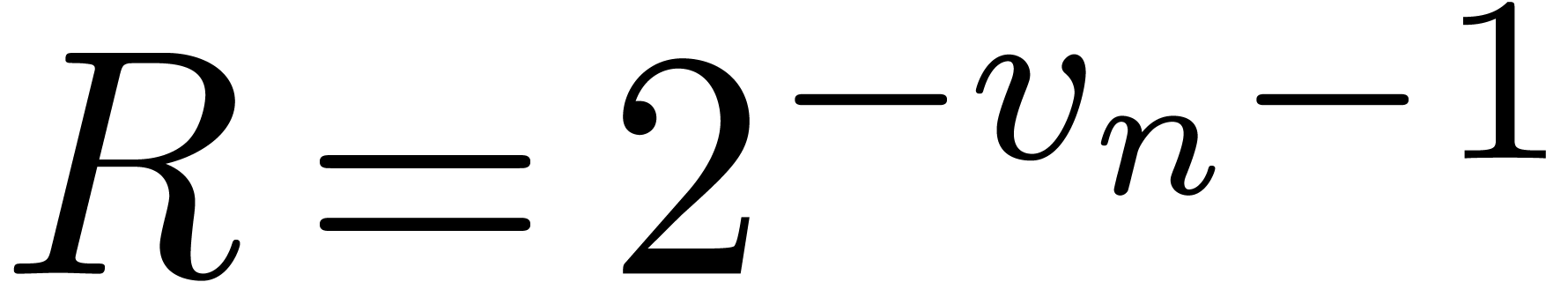 , which yields
, which yields 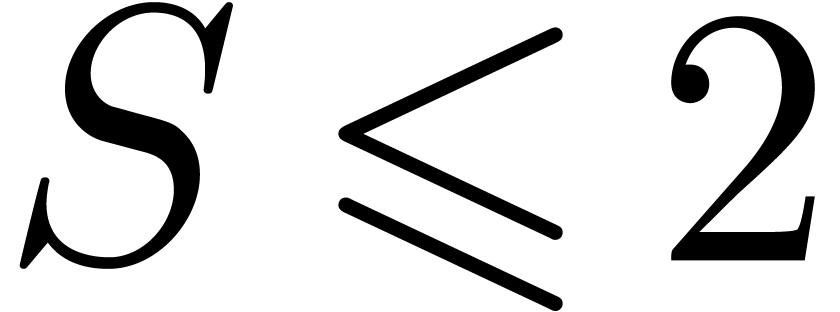 and
and 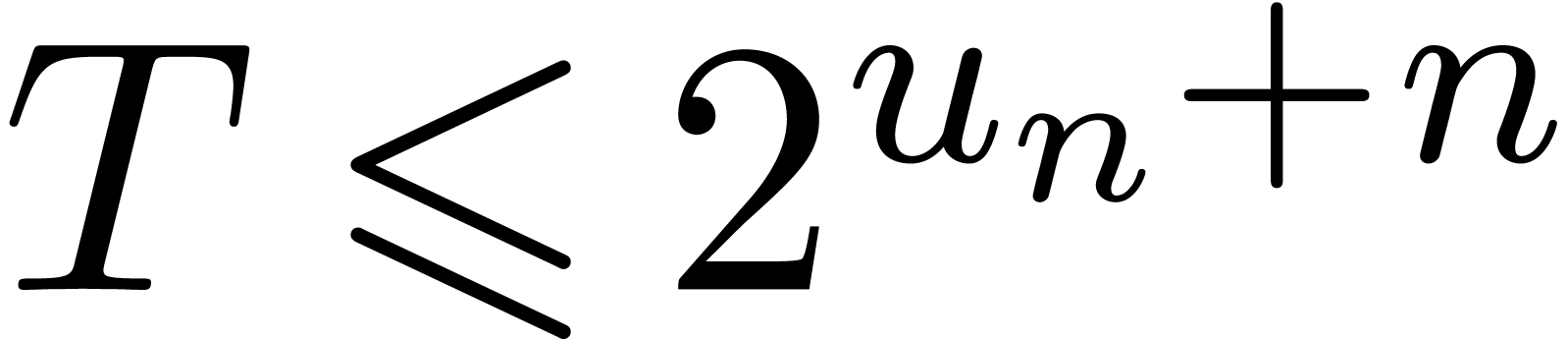 . It follows that
. It follows that  and we conclude in a similar way as in the proof of
corollary 19.
and we conclude in a similar way as in the proof of
corollary 19.
Let 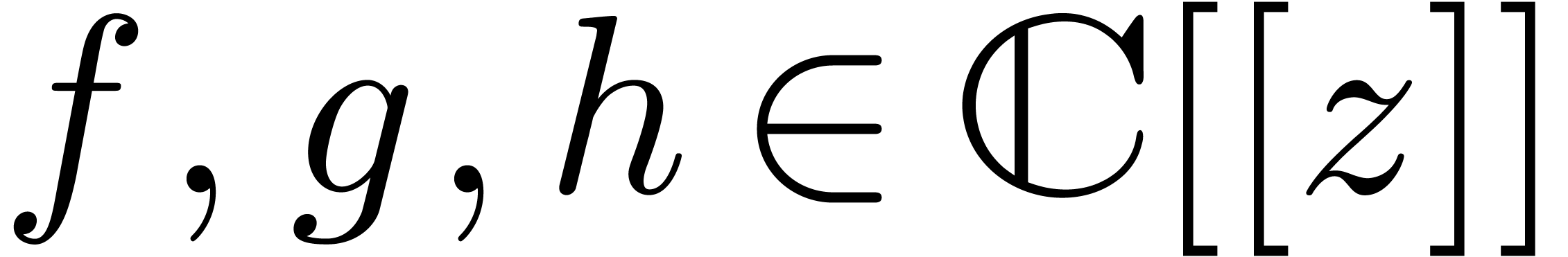 be such that
be such that 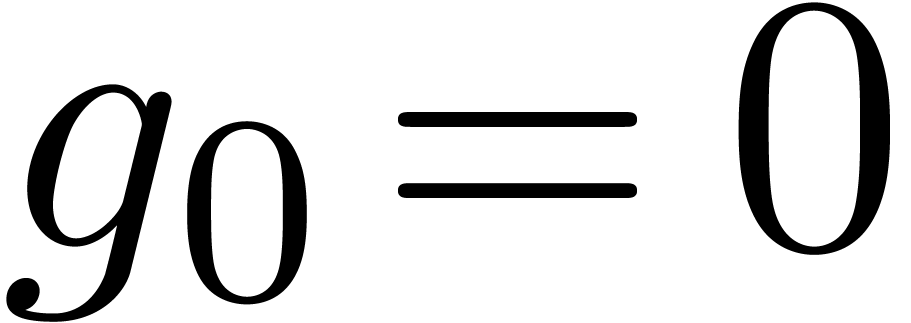 and
and
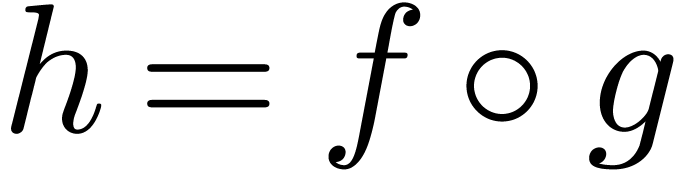 . Given an order
. Given an order 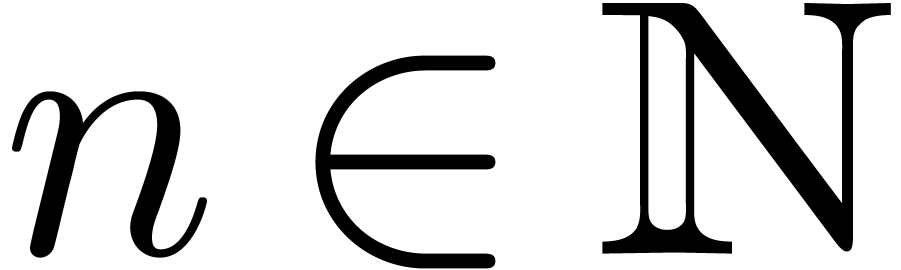 , we have shown in the previous section how to
compute
, we have shown in the previous section how to
compute 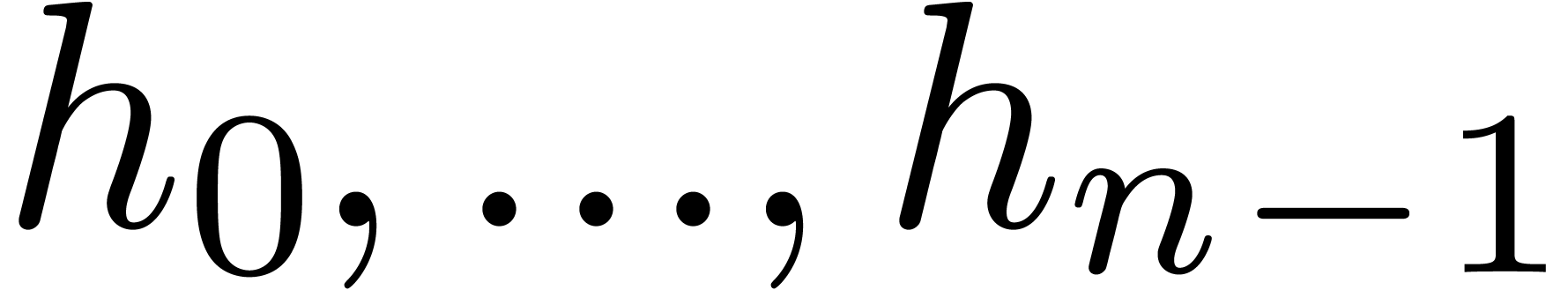 efficiently, as a function of
efficiently, as a function of 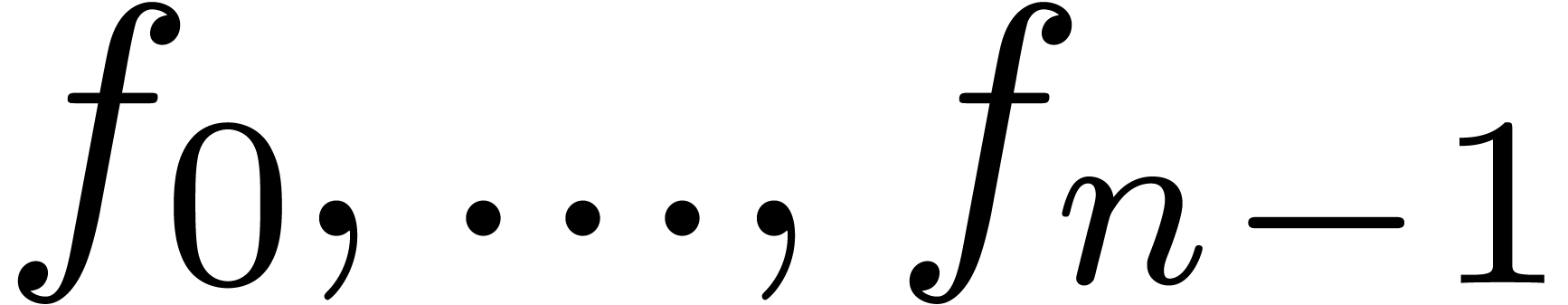 and
and  . Since
. Since
 only depends on
only depends on  and
and
 , we may consider the
relaxed composition problem in which
, we may consider the
relaxed composition problem in which 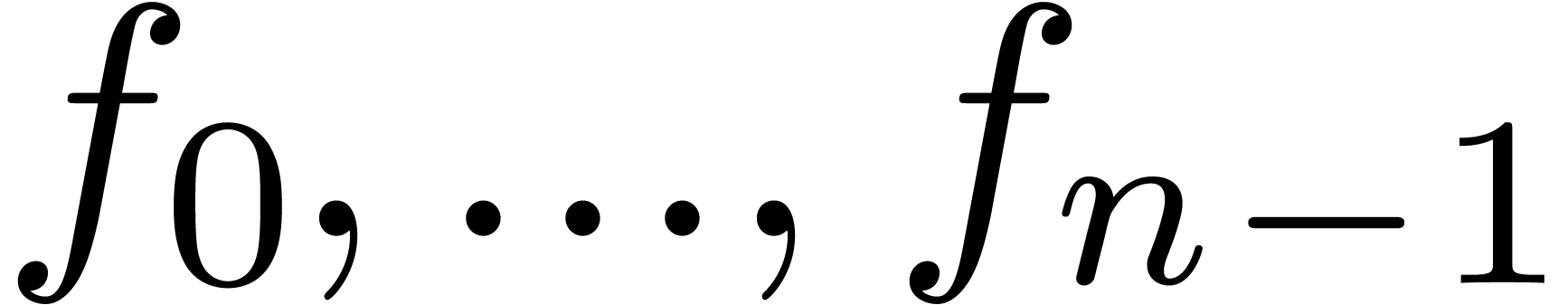 and
and  are given progressively, and where we
require each coefficient
are given progressively, and where we
require each coefficient 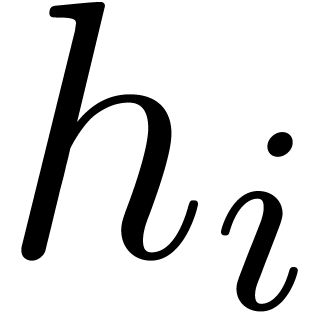 to be output as soon as
to be output as soon as
 and
and  are known.
Similarly, in the semi-relaxed composition problem, the
coefficients
are known.
Similarly, in the semi-relaxed composition problem, the
coefficients  are known beforehand, but
are known beforehand, but 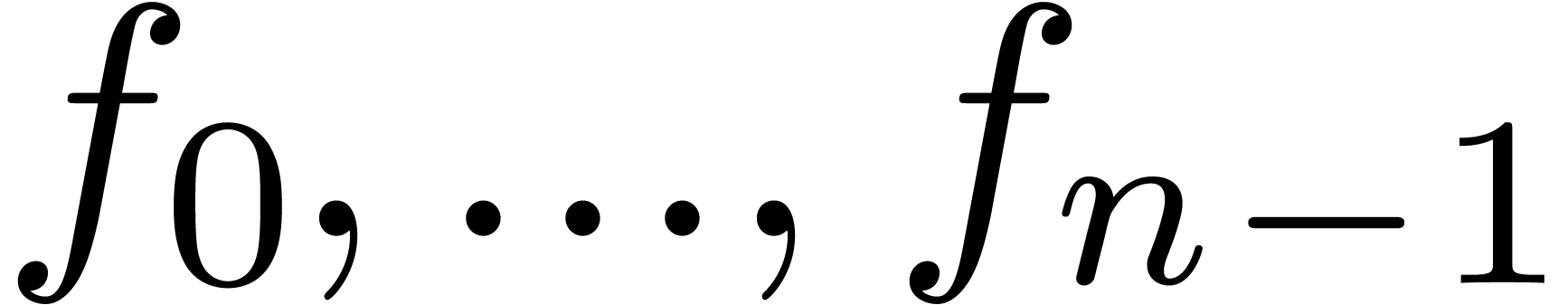 are given progressively. In that case, we require
are given progressively. In that case, we require 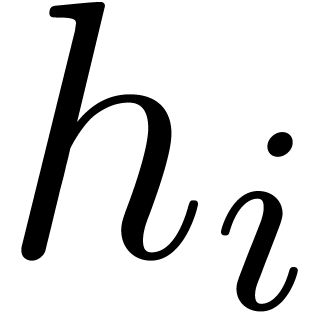 to be output as soon as
to be output as soon as  are
known. The relaxed and semi-relaxed settings are particularly useful for
the resolution of implicit equations involving functional composition.
We refer to [vdH02, vdH07] for more details
about relaxed computations with power series.
are
known. The relaxed and semi-relaxed settings are particularly useful for
the resolution of implicit equations involving functional composition.
We refer to [vdH02, vdH07] for more details
about relaxed computations with power series.
Let 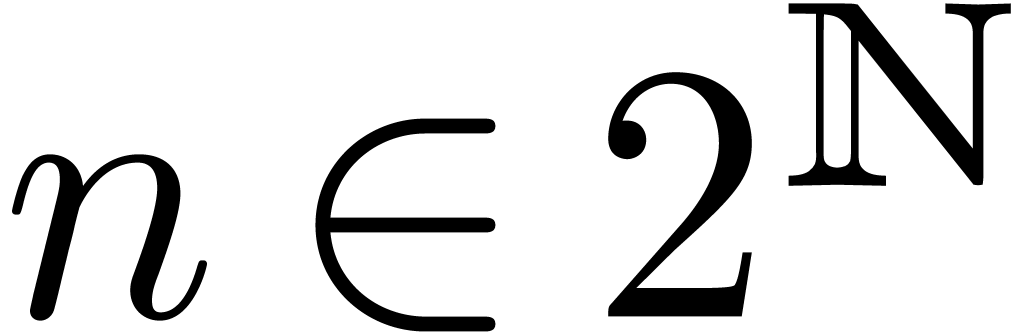 . In this section, we
consider the problem of computing the semi-relaxed composition
. In this section, we
consider the problem of computing the semi-relaxed composition 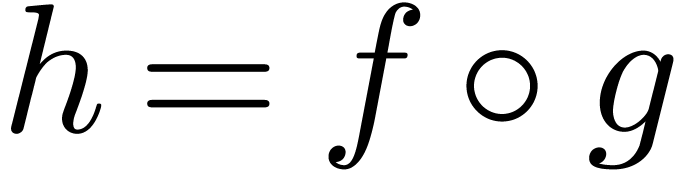 up to order
up to order 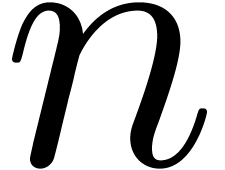 .
If
.
If 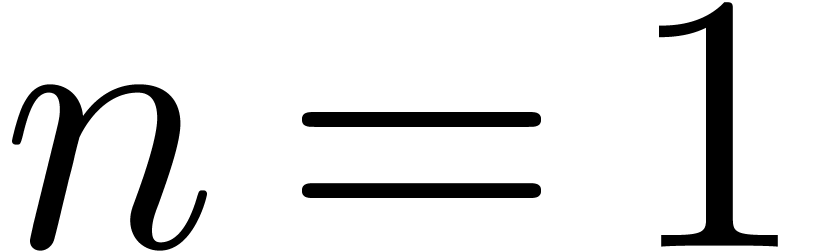 , then we simply have
, then we simply have
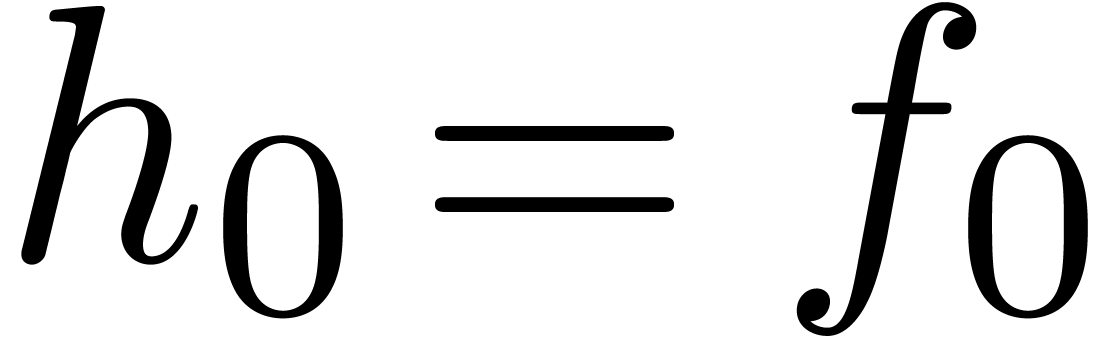 . For
. For 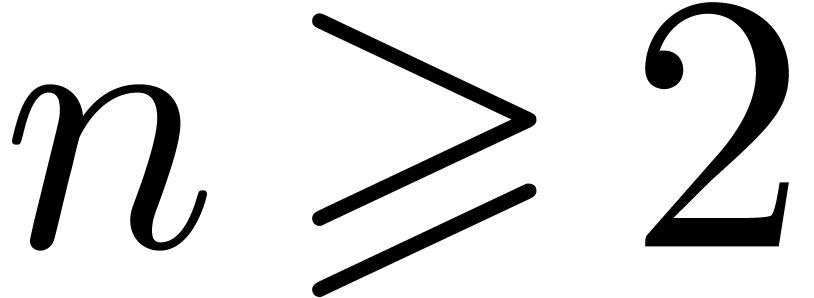 , we denote
, we denote
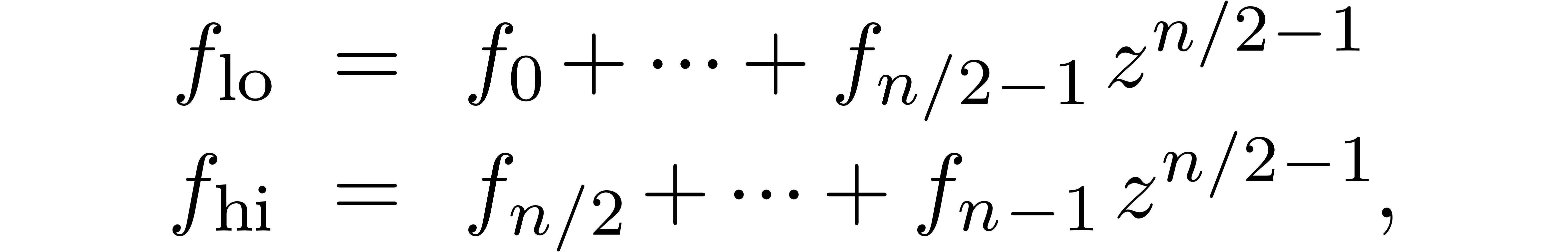
and similarly for  and
and 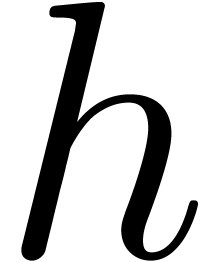 . Our algorithm relies on the identity
. Our algorithm relies on the identity
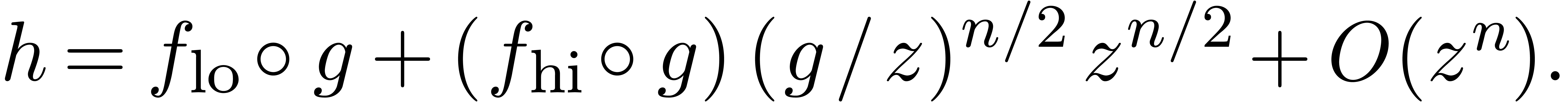 |
(18) |
The first part 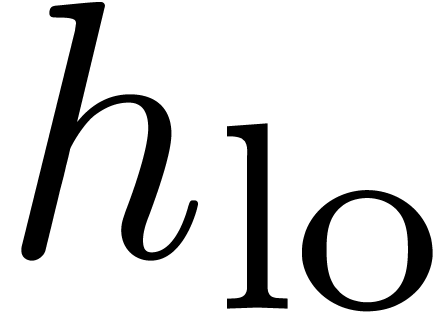 of
of 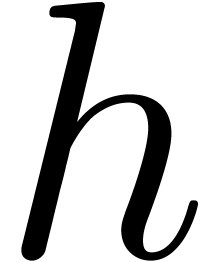 is
computed recursively, using one semi-relaxed composition at order
is
computed recursively, using one semi-relaxed composition at order 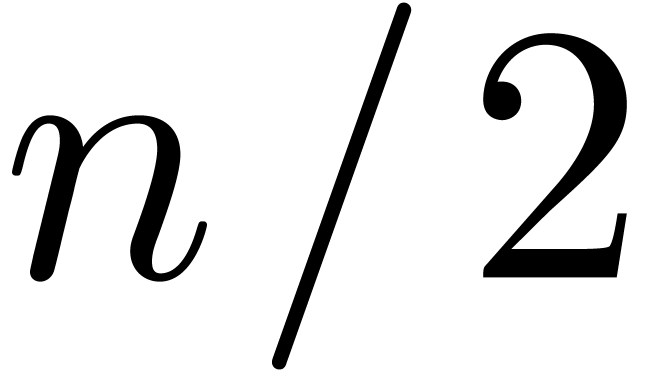 :
:
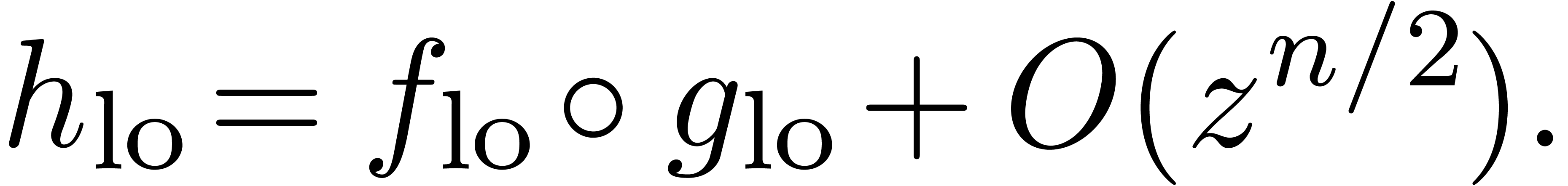
As soon as 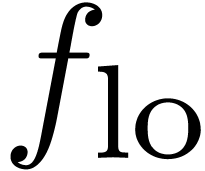 is completely known, we compute
is completely known, we compute 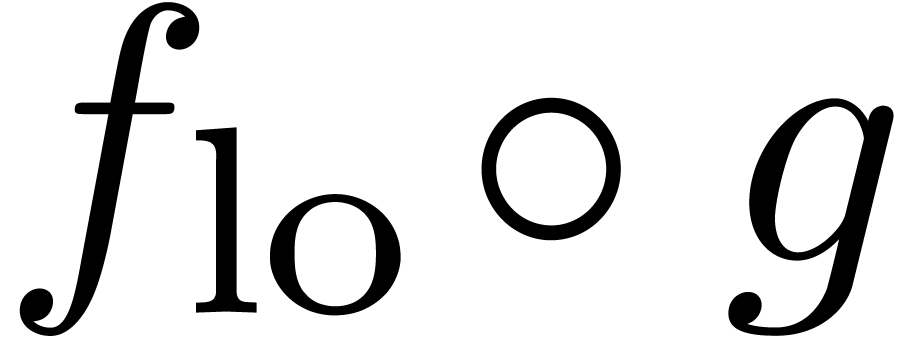 at order
at order 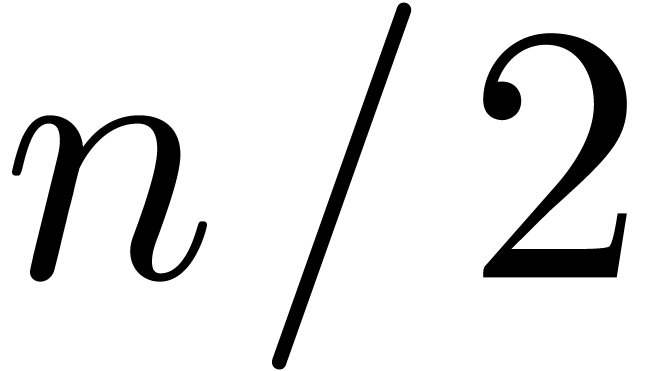 ,
using one of the algorithms for composition from the previous section.
We also compute
,
using one of the algorithms for composition from the previous section.
We also compute 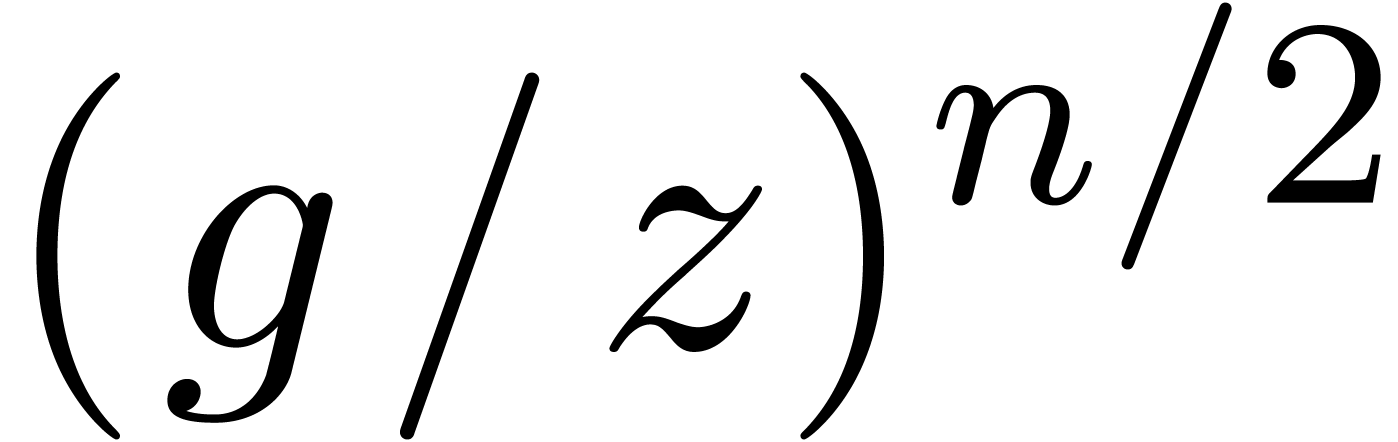 at order
at order 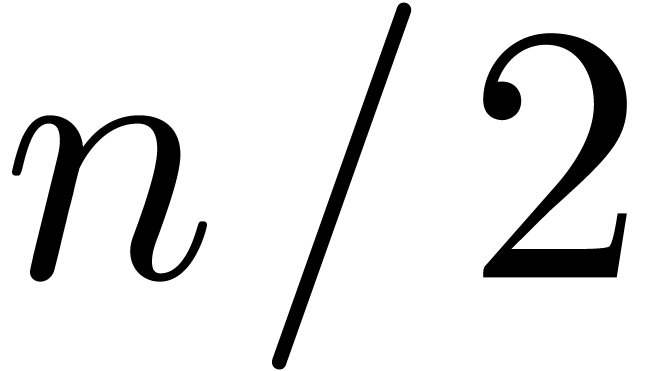 using binary powering. We are now allowed to recursively compute the
second part
using binary powering. We are now allowed to recursively compute the
second part  of
of  ,
using
,
using
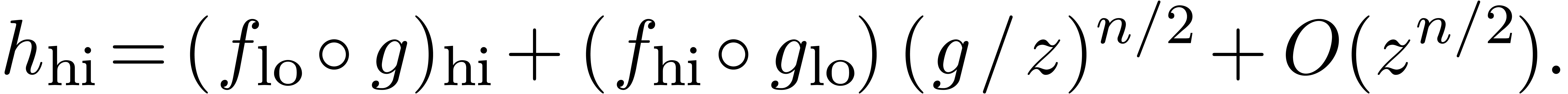
This involves one semi-relaxed composition  at
order
at
order 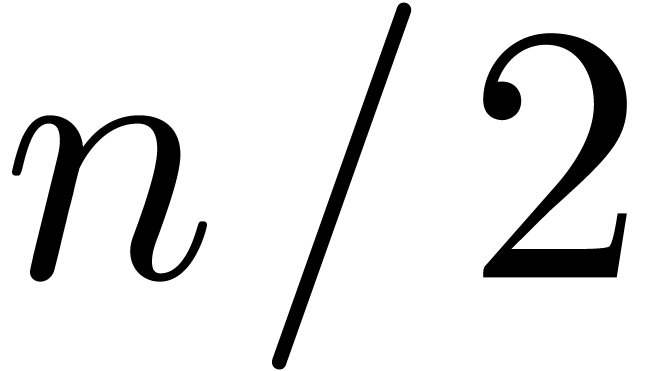 and one semi-relaxed multiplication
and one semi-relaxed multiplication 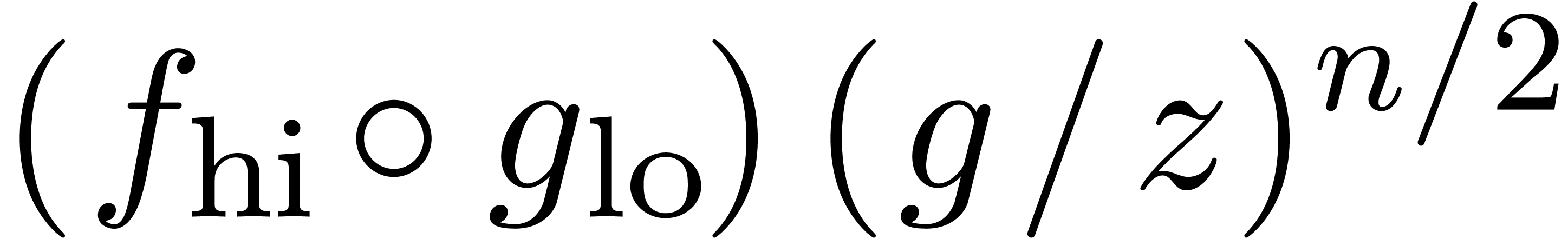 at order
at order 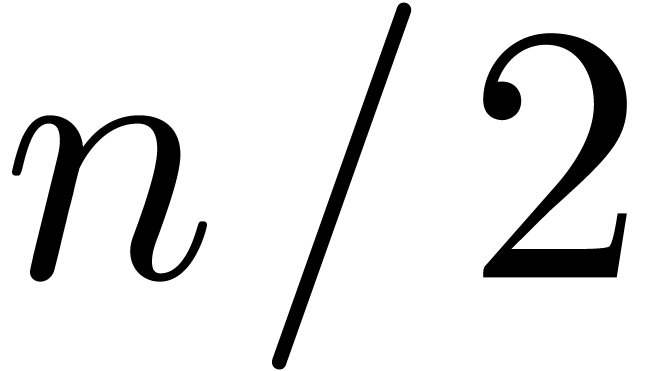 .
.
Assume now that  for all
for all 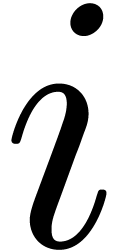 and
and 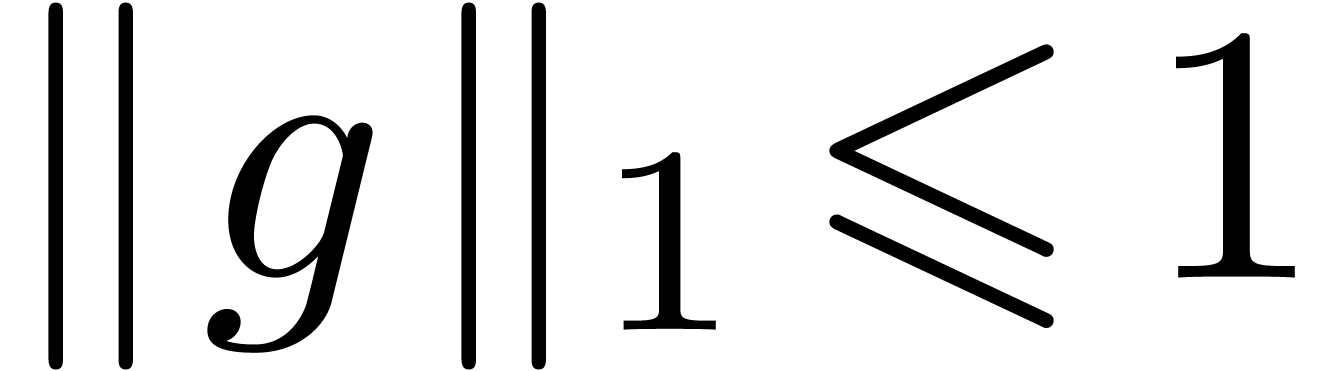 . Consider the problem of
computing
. Consider the problem of
computing  -approximations of
-approximations of
 . In our algorithm, it will
suffice to conduct the various computations with the following
precisions:
. In our algorithm, it will
suffice to conduct the various computations with the following
precisions:
We recursively compute  -approximations
of
-approximations
of 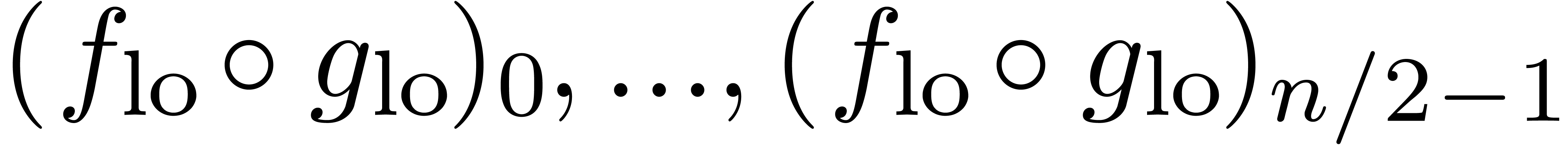 .
.
We compute 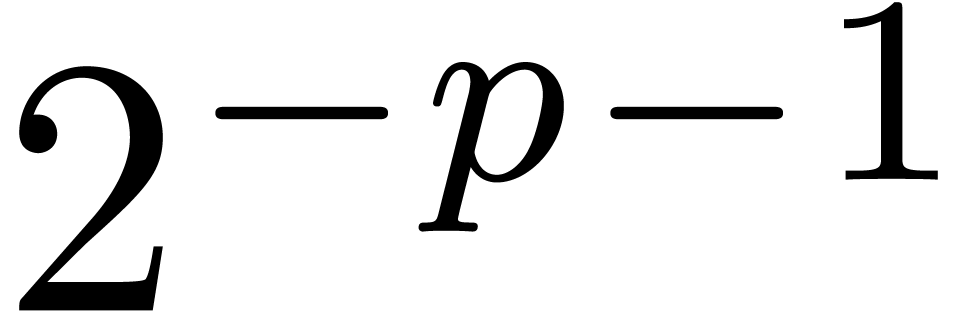 -approximations
of
-approximations
of  .
.
We recursively compute 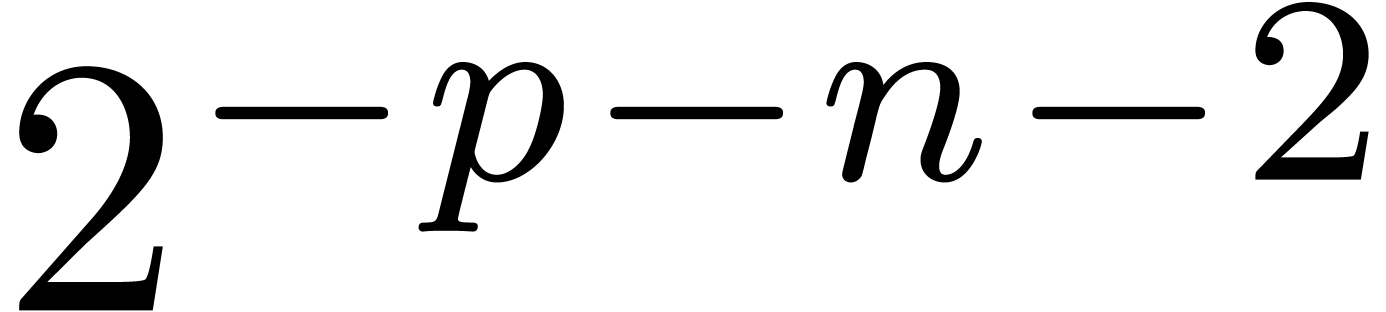 -approximations
of
-approximations
of 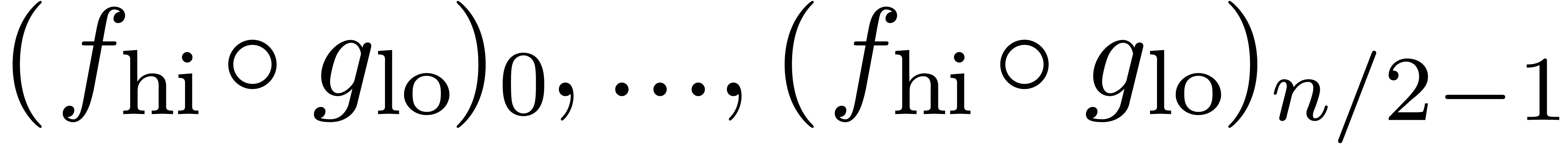 .
.
We compute 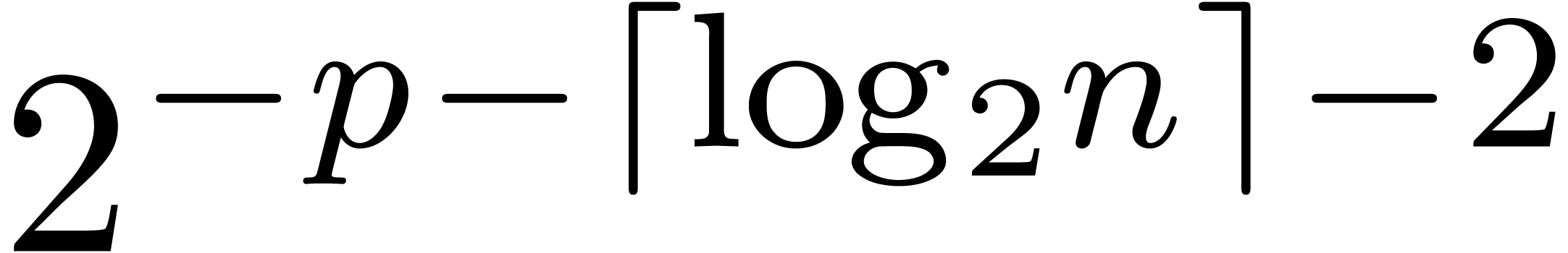 -approximations
of the coefficients of
-approximations
of the coefficients of 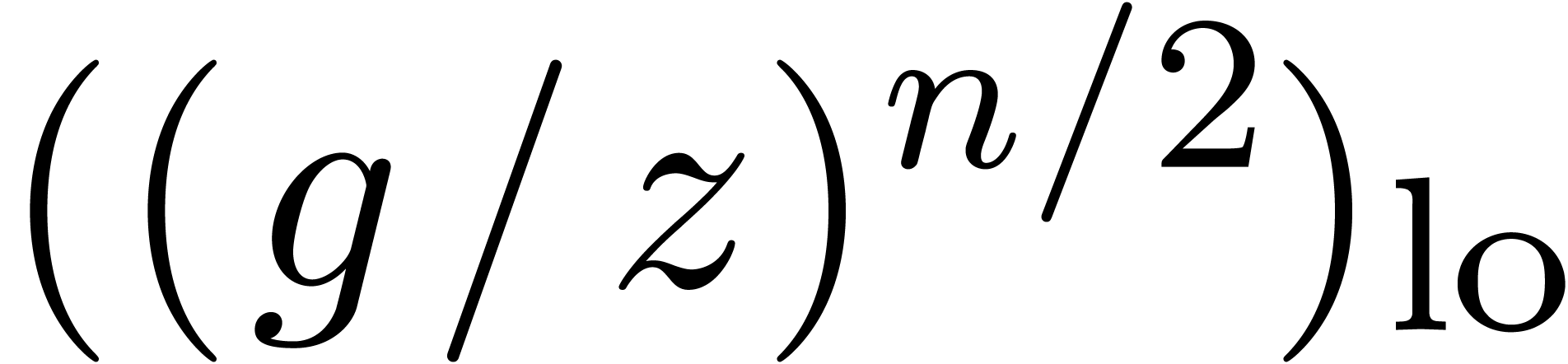 .
.
We compute 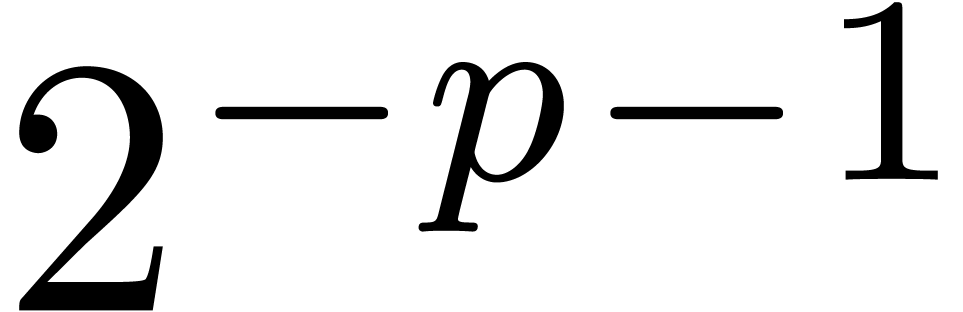 -approximations
of the coefficients of
-approximations
of the coefficients of 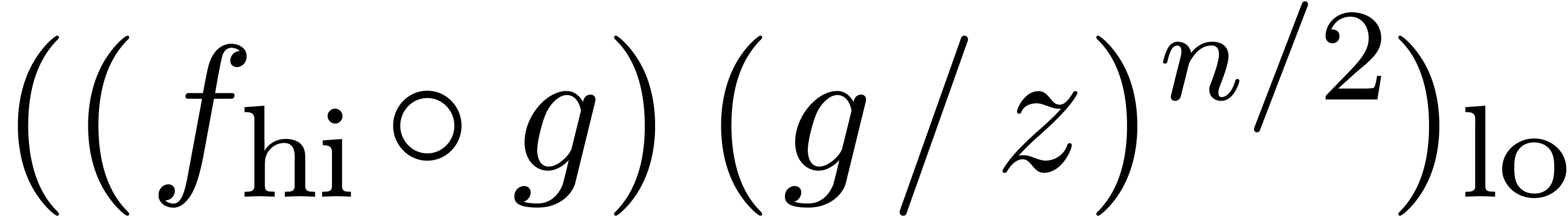 .
.
Let us show that this indeed enables us to obtain the desired  -approximations for
-approximations for 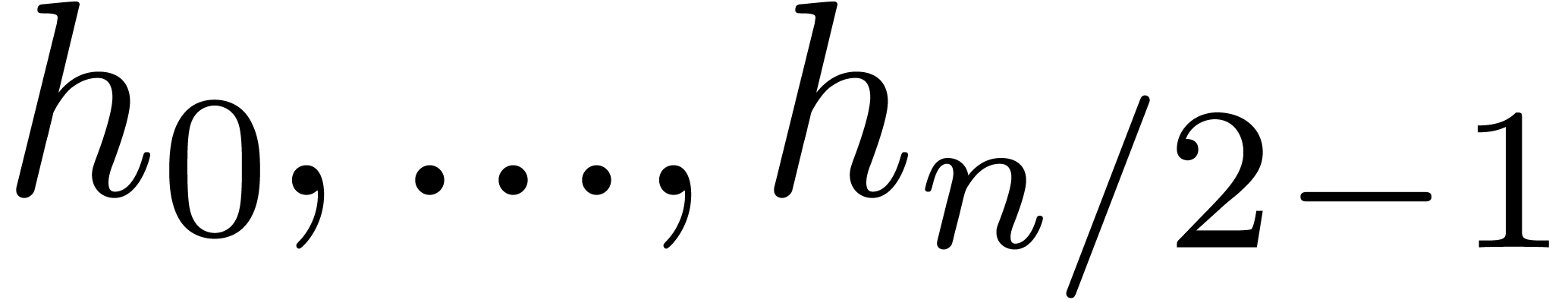 . This is clear for the coefficients of
. This is clear for the coefficients of 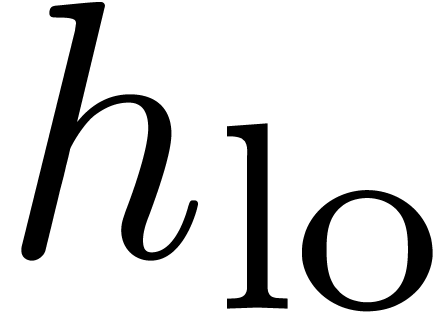 . As to the second half, we have
the bounds
. As to the second half, we have
the bounds
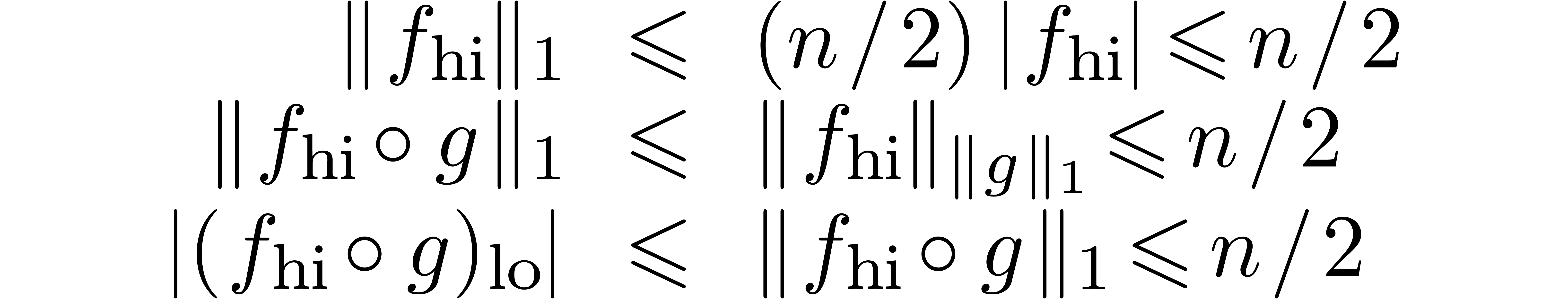
and
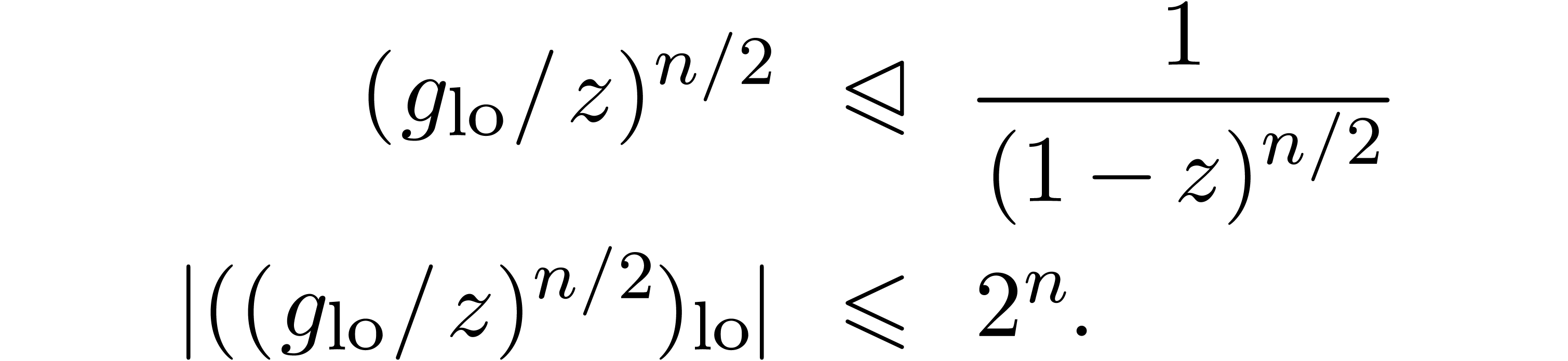
These bounds justify the extra number of bits needed in the computations
of 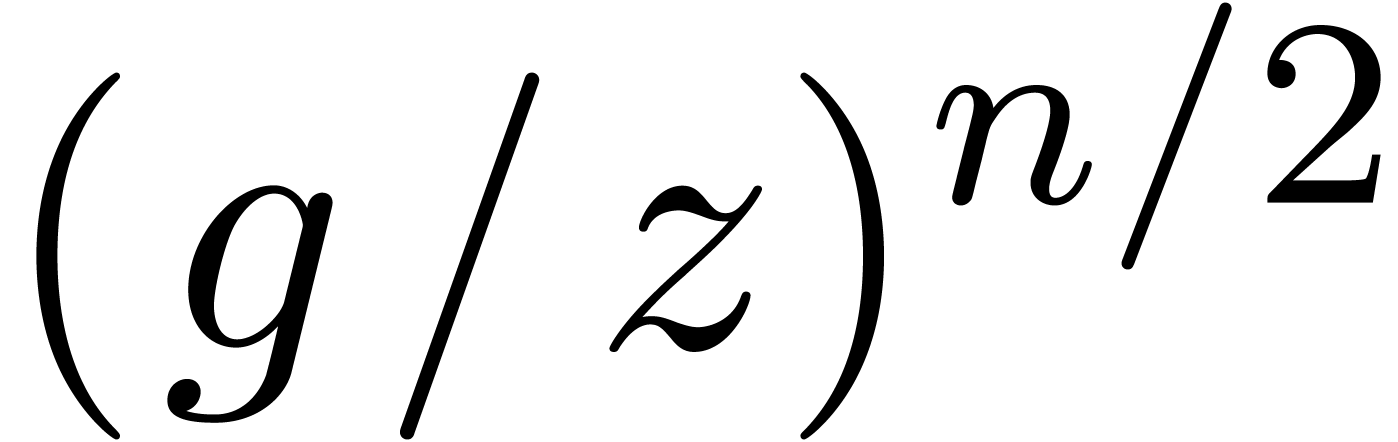 and
and 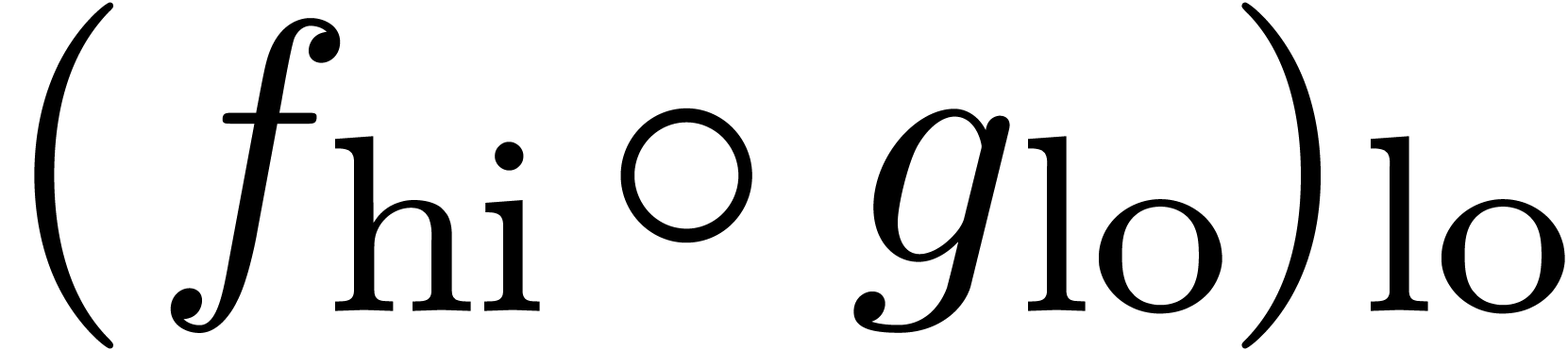 respectively.
respectively.
Let us finally analyze the complexity of the above algorithm. We will
denote by  the complexity of multiplying two
the complexity of multiplying two
 -bit integer polynomials of
degrees
-bit integer polynomials of
degrees 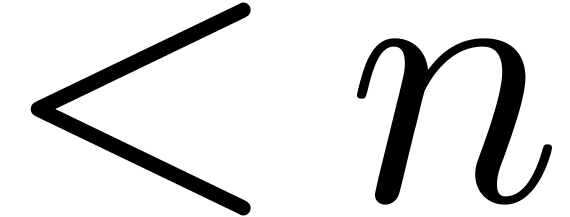 . Using Kronecker
multiplication, we have
. Using Kronecker
multiplication, we have 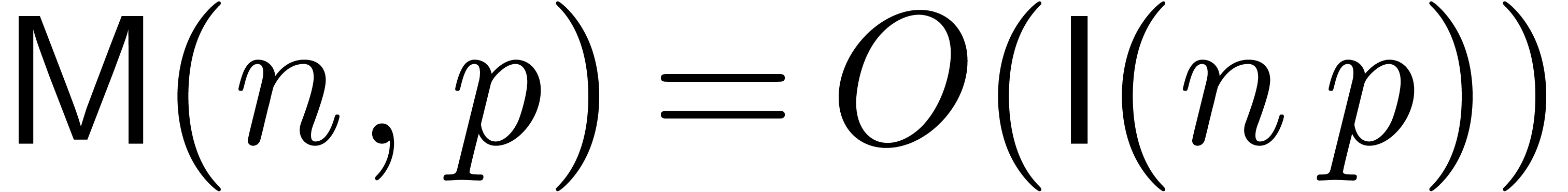 . We
denote by
. We
denote by 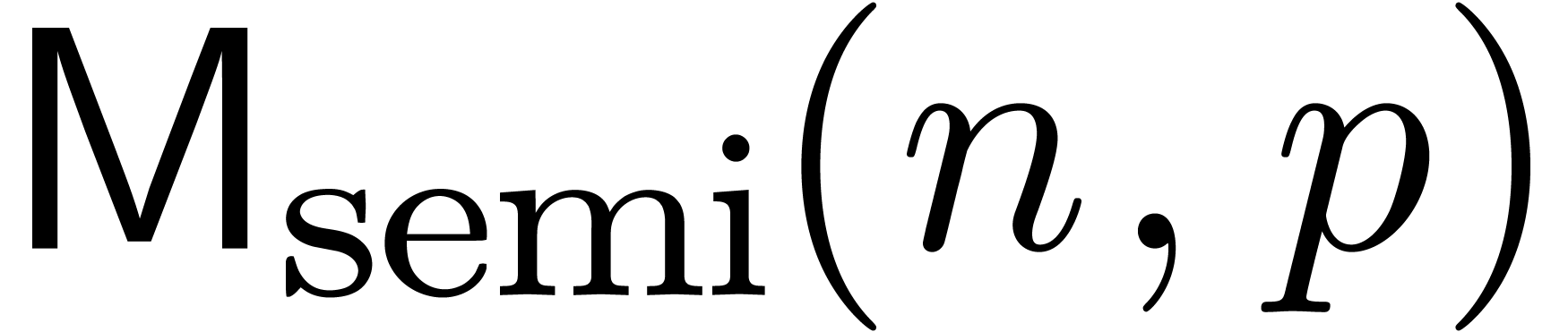 the cost of a semi-relaxed
multiplication of two
the cost of a semi-relaxed
multiplication of two 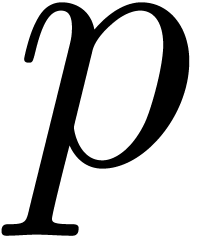 -bit
integer polynomials of degrees
-bit
integer polynomials of degrees 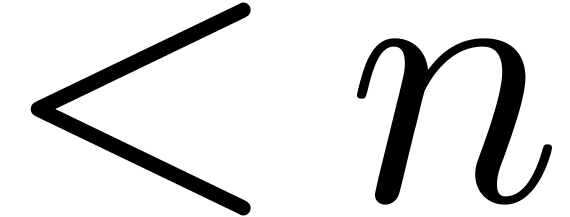 .
Using the fast relaxed multiplication algorithm from [vdH02],
we have
.
Using the fast relaxed multiplication algorithm from [vdH02],
we have 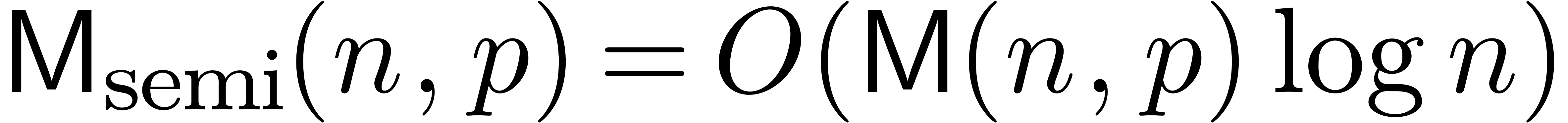 . We will denote by
. We will denote by
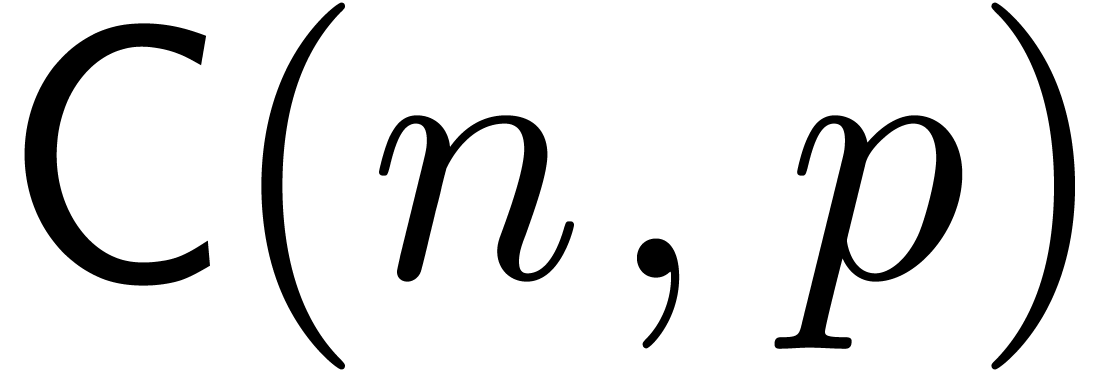 and
and 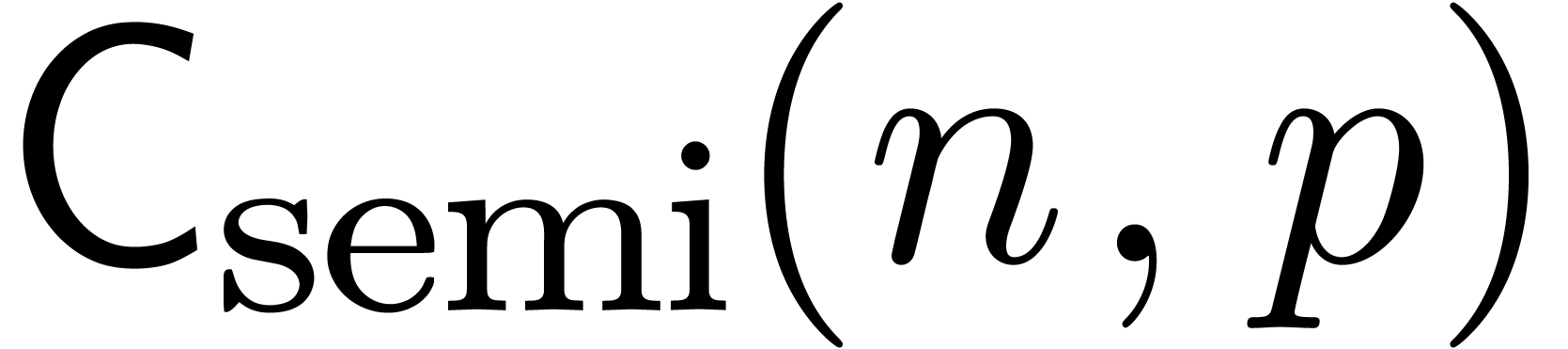 the cost of
classical and semi-relaxed composition for
the cost of
classical and semi-relaxed composition for 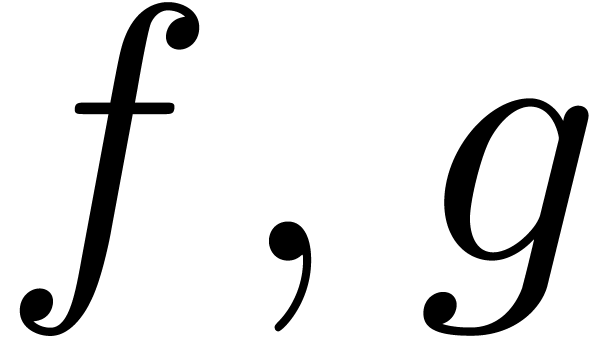 ,
,
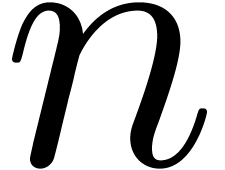 and
and 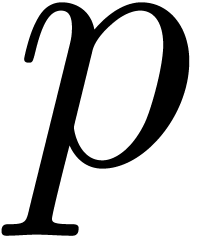 as described above.
By theorem 18, we have
as described above.
By theorem 18, we have 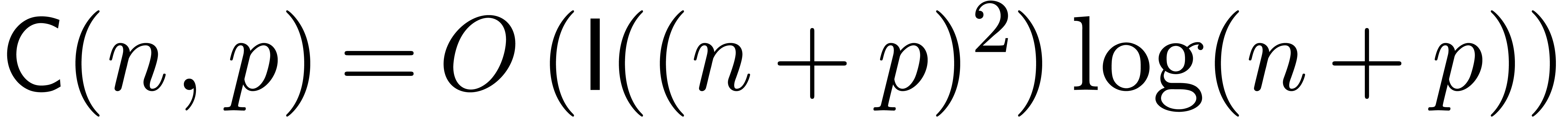 .
The complexity of the semi-relaxed composition satisfies the following
recursive bound:
.
The complexity of the semi-relaxed composition satisfies the following
recursive bound:
Using theorem 18, it follows by induction that
 |
(19) |
From [BK75, vdH02], we also have
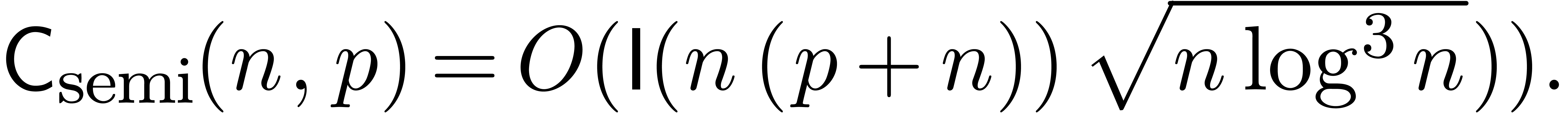 |
(20) |
Applying (19) for  and (20)
on
and (20)
on 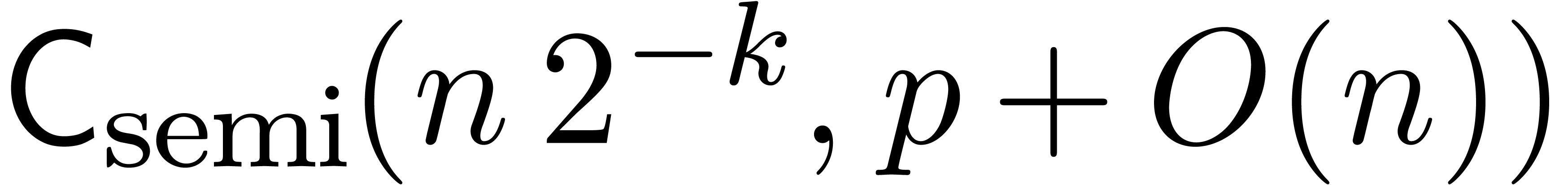 , we obtain
, we obtain
We have proved the following theorem:
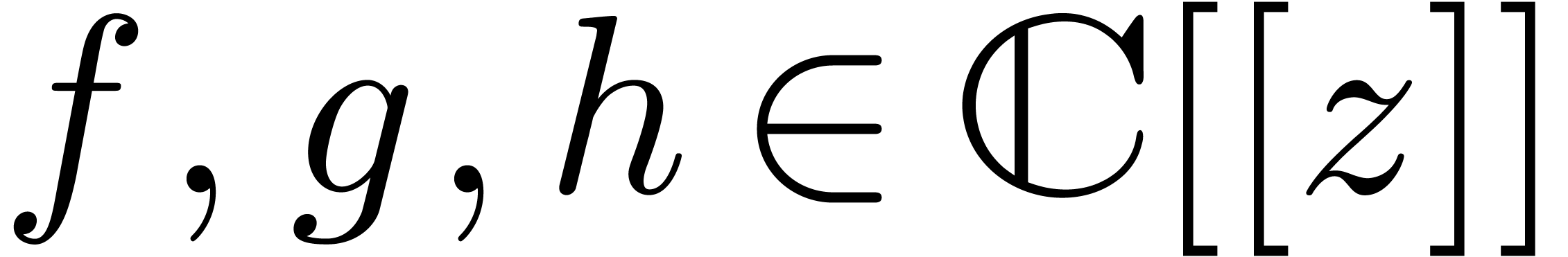 be power series with
be power series with  and
and 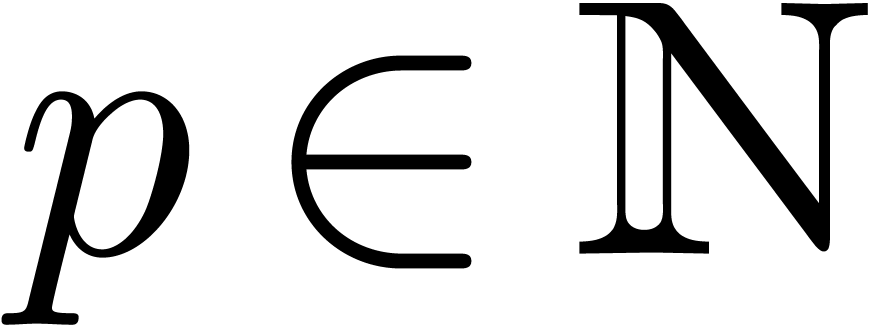 . Assume that
. Assume that 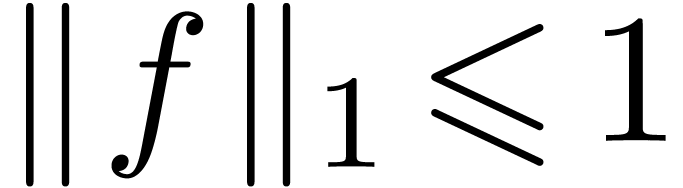 and
and 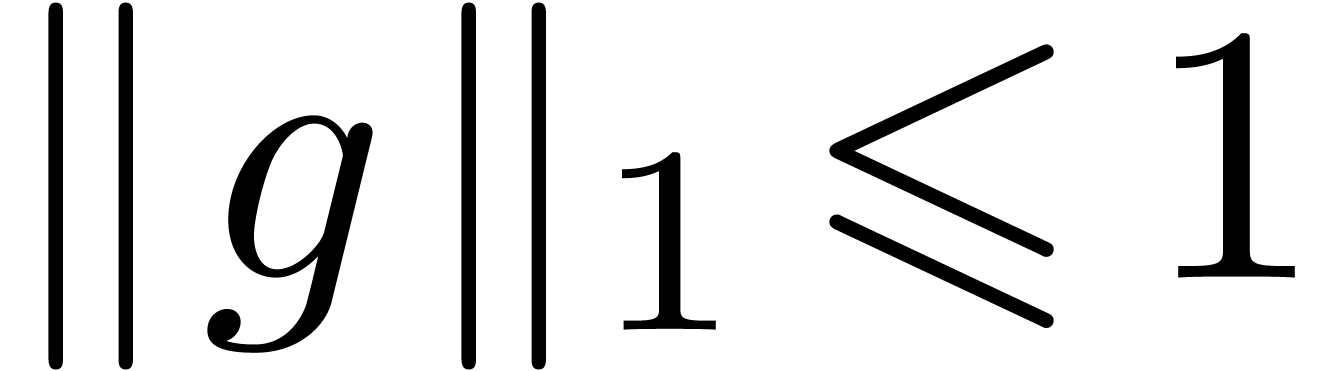 . The
computation of the semi-relaxed composition
. The
computation of the semi-relaxed composition 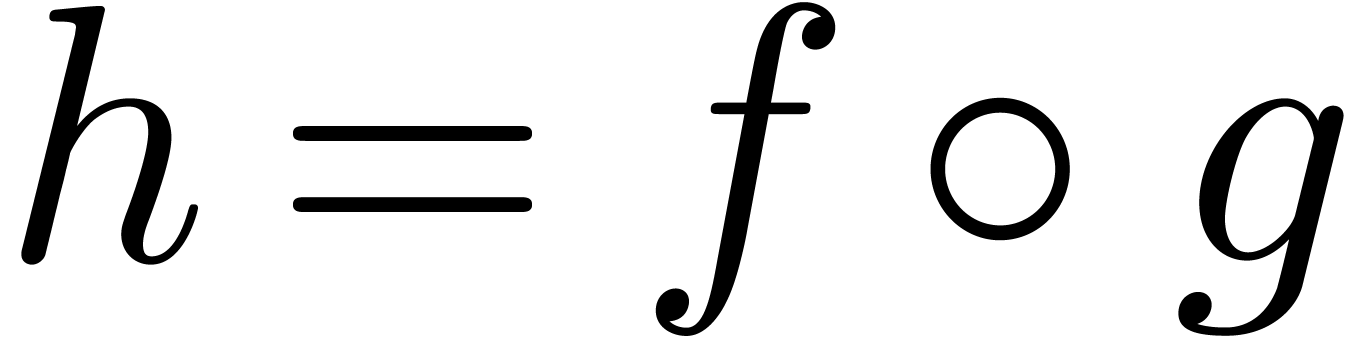 at
order
at
order 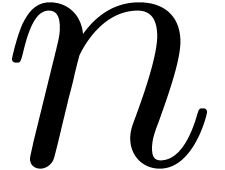 and up to an absolute error
and up to an absolute error 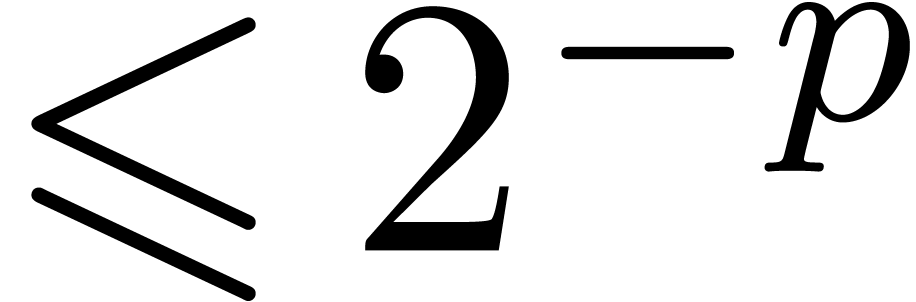 can be done in time
can be done in time 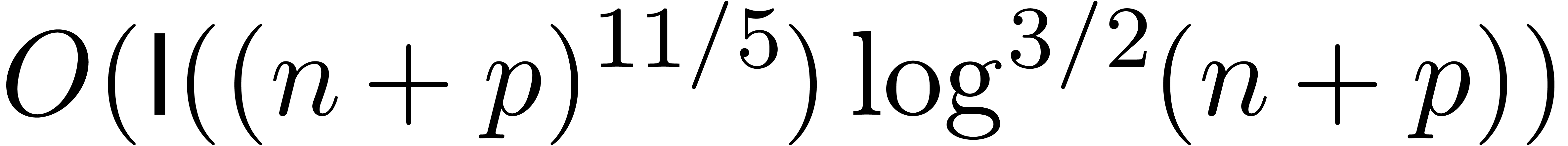 .
.
Let 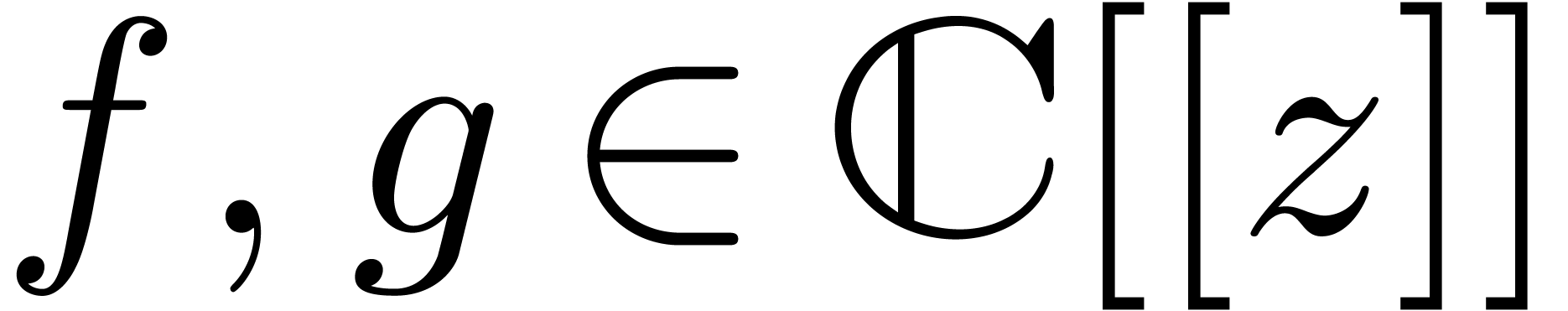 be as in the previous section and
be as in the previous section and 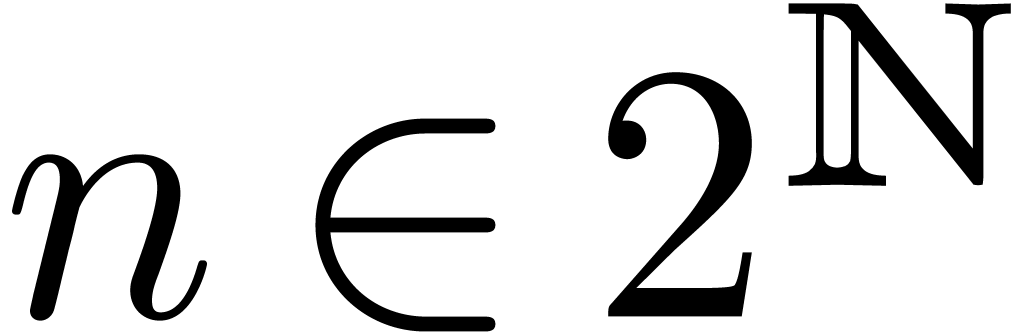 . Assume also that
. Assume also that 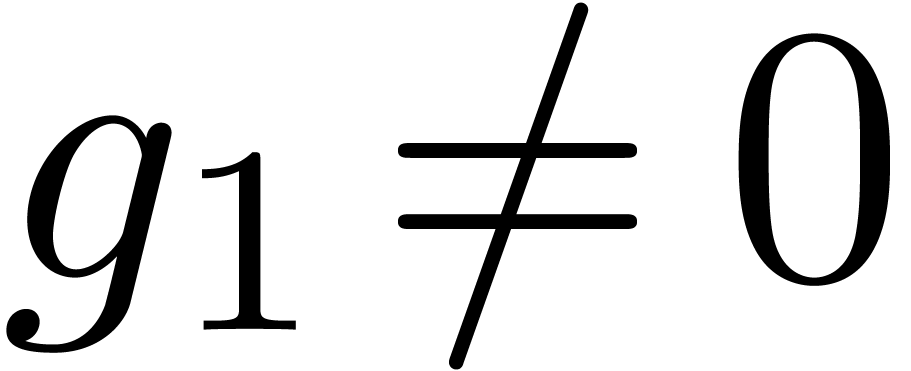 . In order to compute the relaxed composition
. In order to compute the relaxed composition
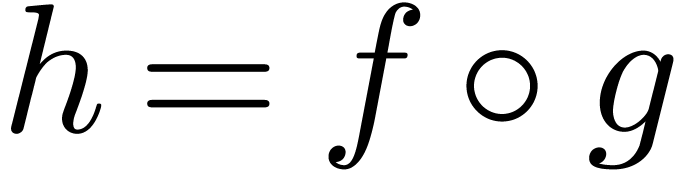 , we again use the formula
(18), in combination with
, we again use the formula
(18), in combination with
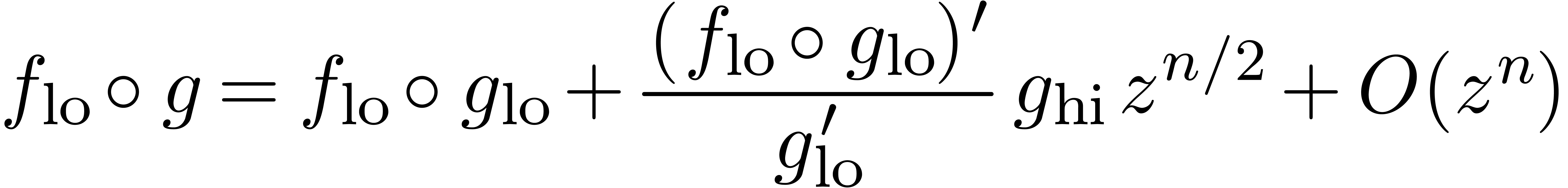
The first 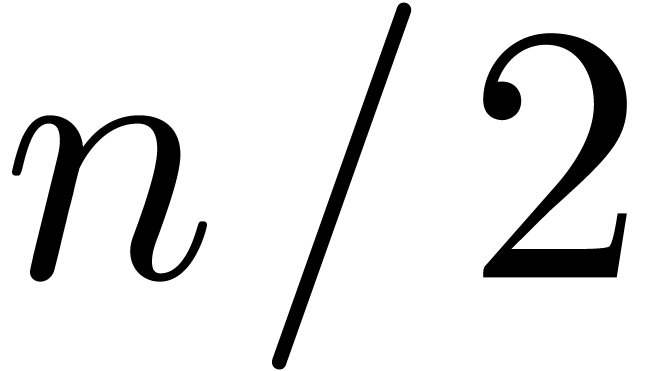 coefficients of
coefficients of  are still computed recursively, by performing a relaxed composition
are still computed recursively, by performing a relaxed composition 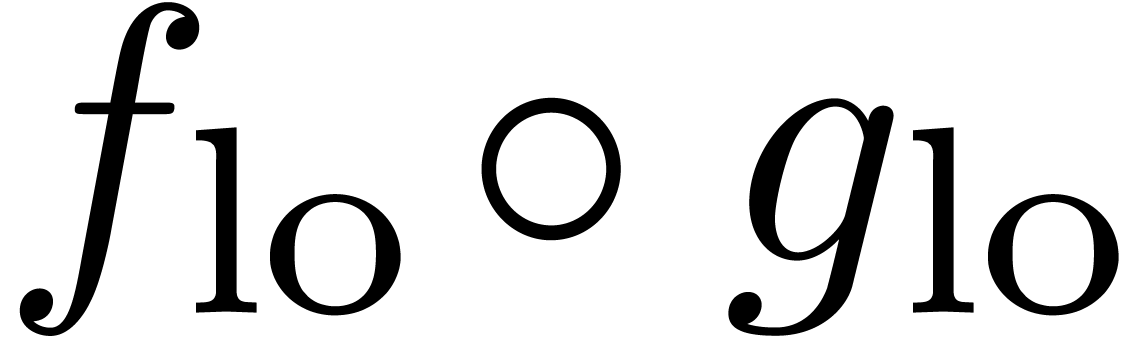 at order
at order 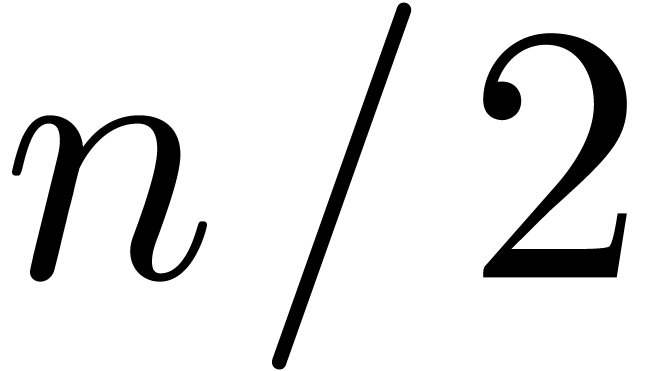 .
As soon as
.
As soon as 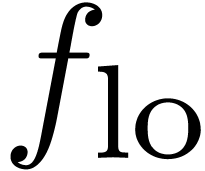 and
and 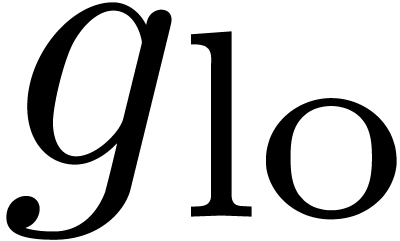 are
completely known, we may compute the composition
are
completely known, we may compute the composition 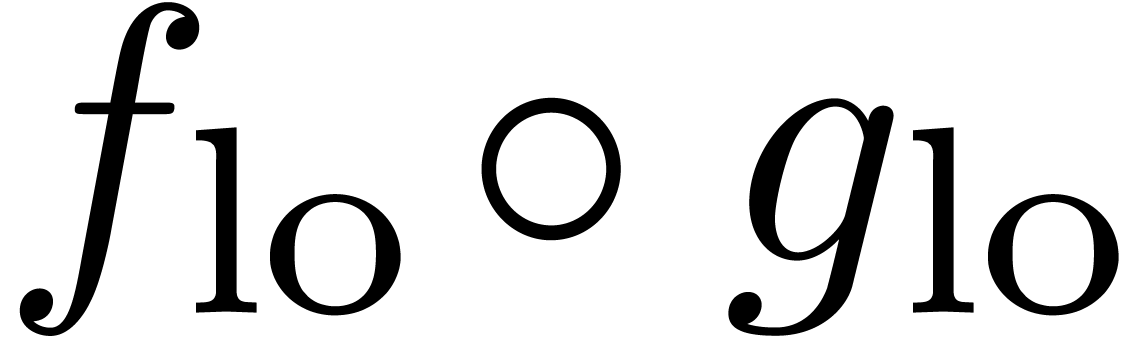 at order
at order  using the algorithm from section 4. Differentiation and division by
using the algorithm from section 4. Differentiation and division by 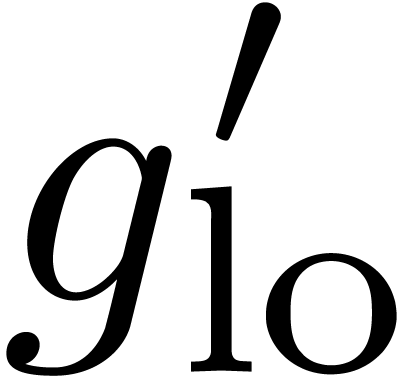 also yields
also yields 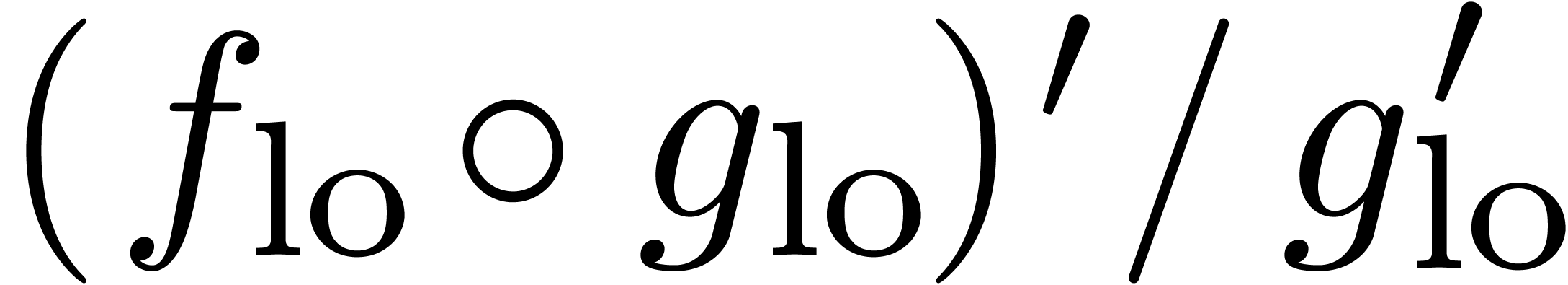 at order
at order 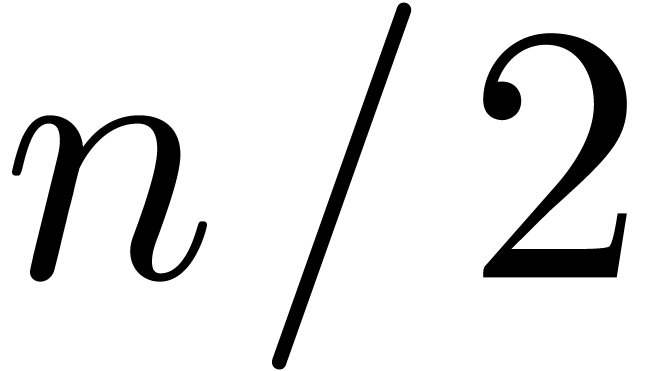 . The product
. The product 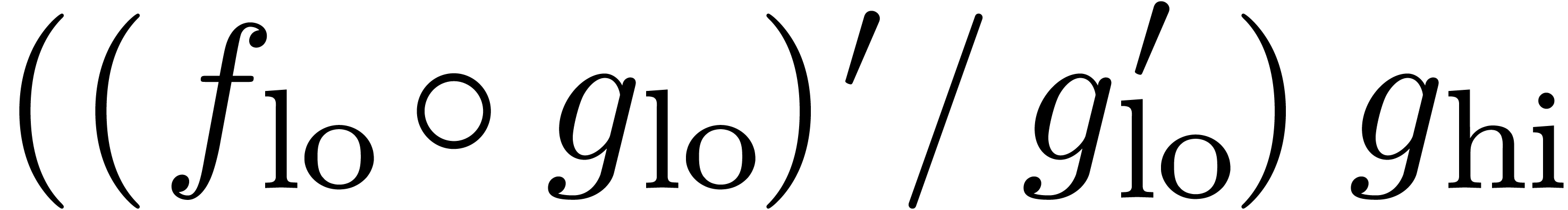 can therefore
be computed using one semi-relaxed multiplication.
can therefore
be computed using one semi-relaxed multiplication.
Let  . This time, the
intermediate computations should be conducted with the following
precisions:
. This time, the
intermediate computations should be conducted with the following
precisions:
We recursively compute  -approximations
of the coefficients of
-approximations
of the coefficients of 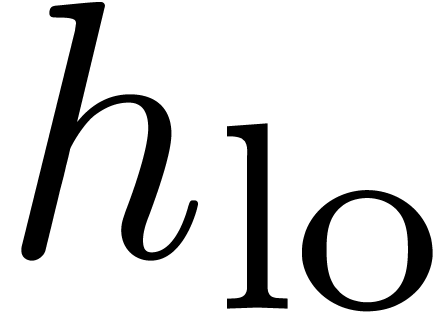 .
.
We compute 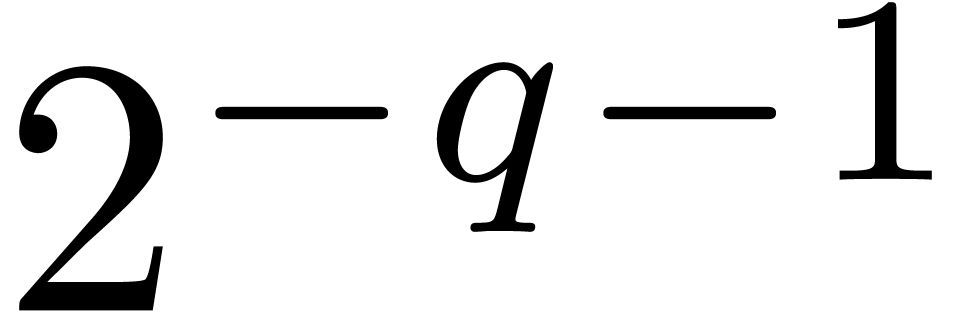 -approximations
of the coefficients of
-approximations
of the coefficients of 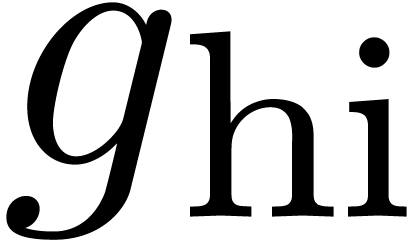 .
.
We compute 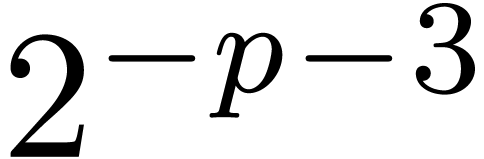 -approximations
of the coefficients of
-approximations
of the coefficients of 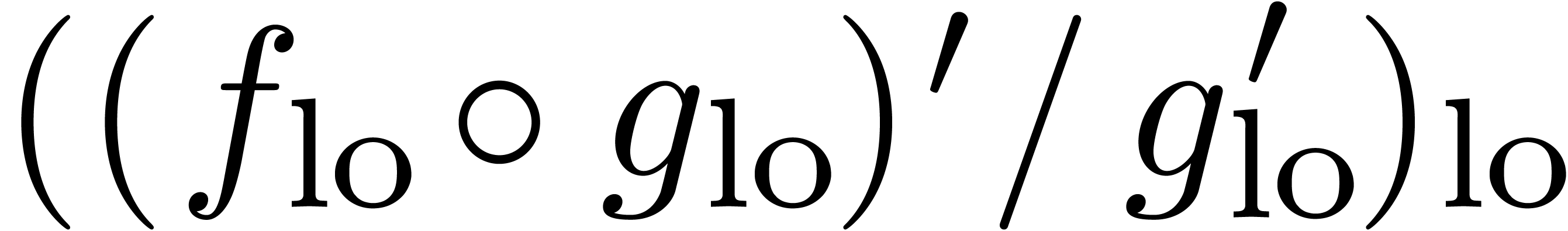 .
.
We compute 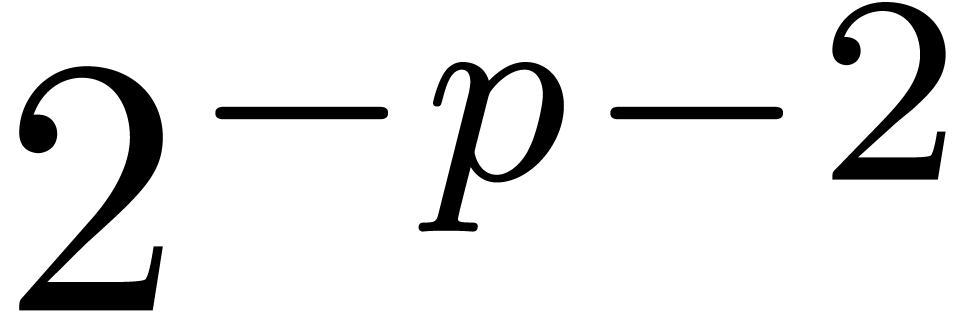 -approximations
of the coefficients of
-approximations
of the coefficients of 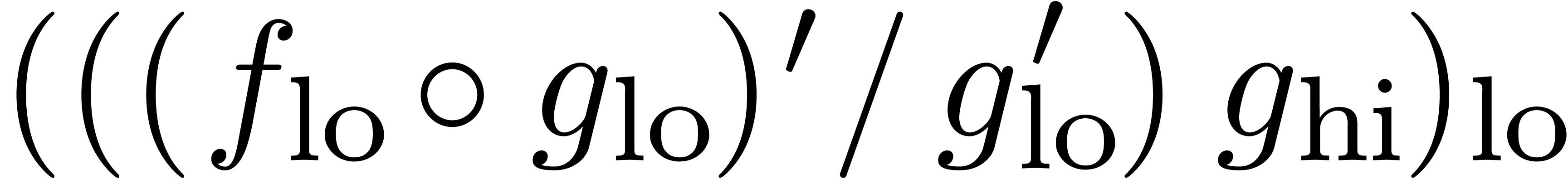 .
.
Indeed, we have
Denoting by 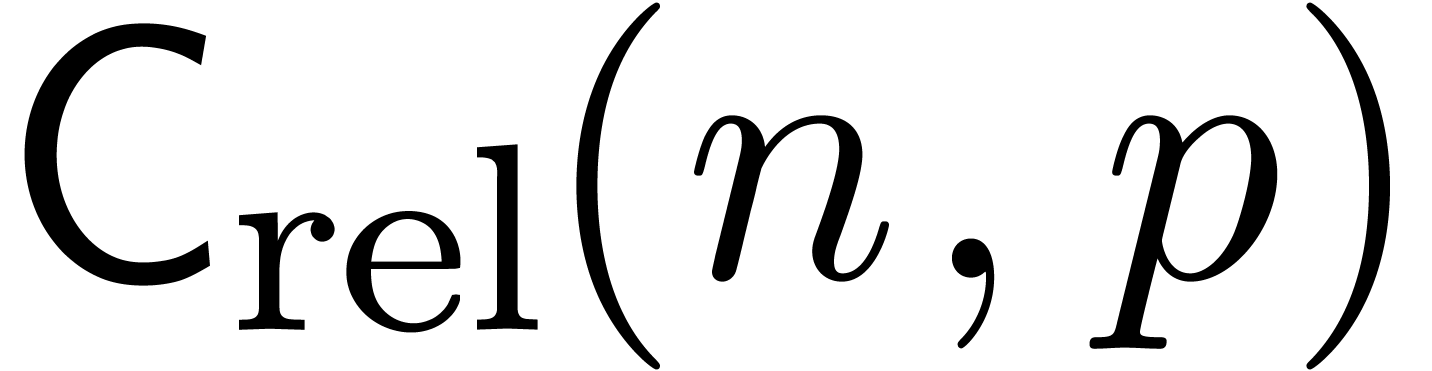 the complexity of relaxed
composition, we obtain
the complexity of relaxed
composition, we obtain
It follows that
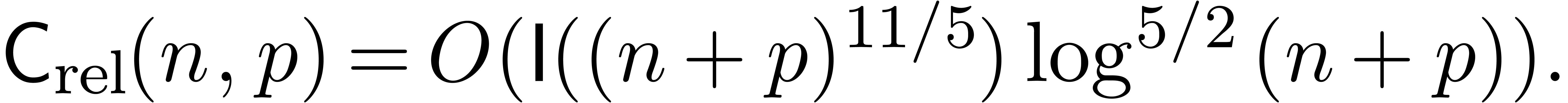
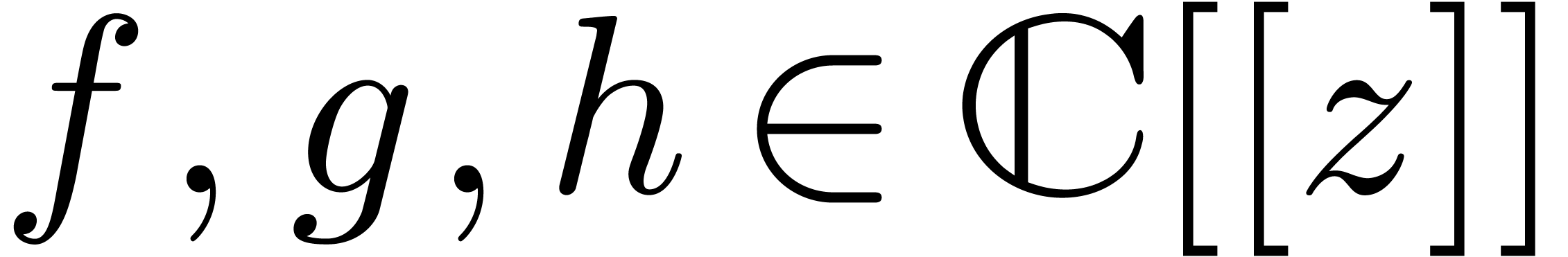 be power series with
be power series with 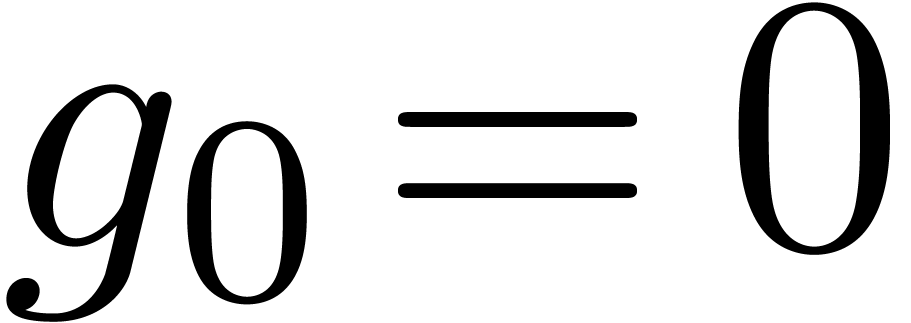 ,
, 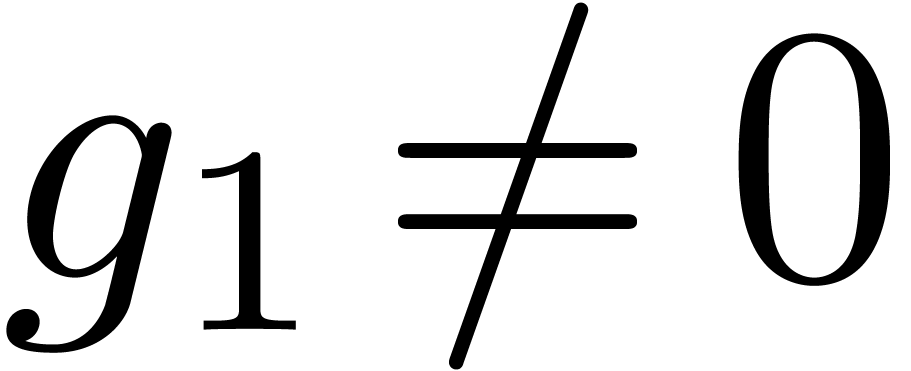 and
and  . Assume that
. Assume that 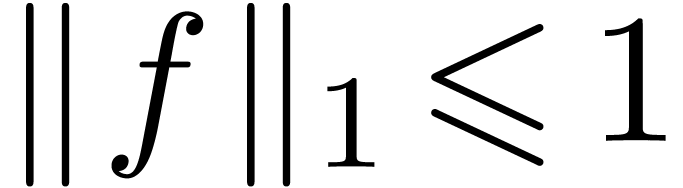 and
and
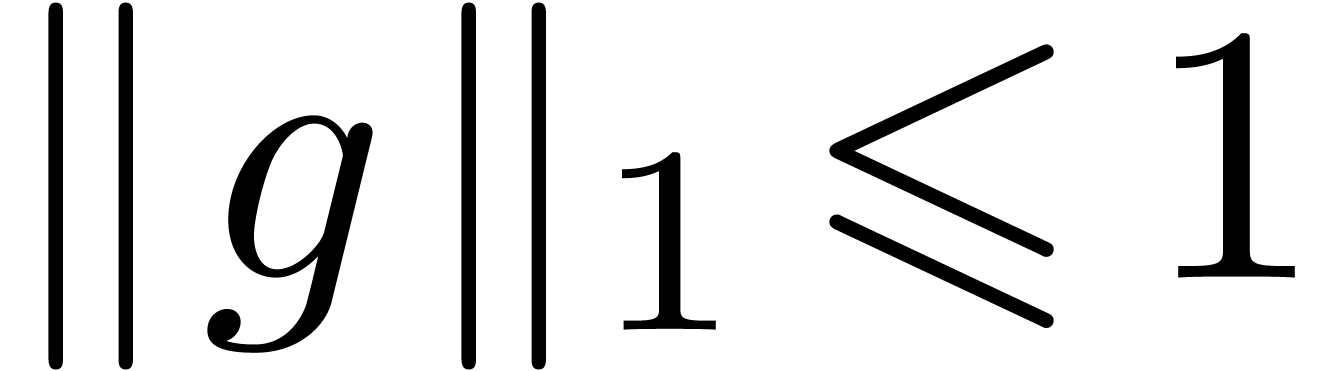 . The computation of the
relaxed composition
. The computation of the
relaxed composition 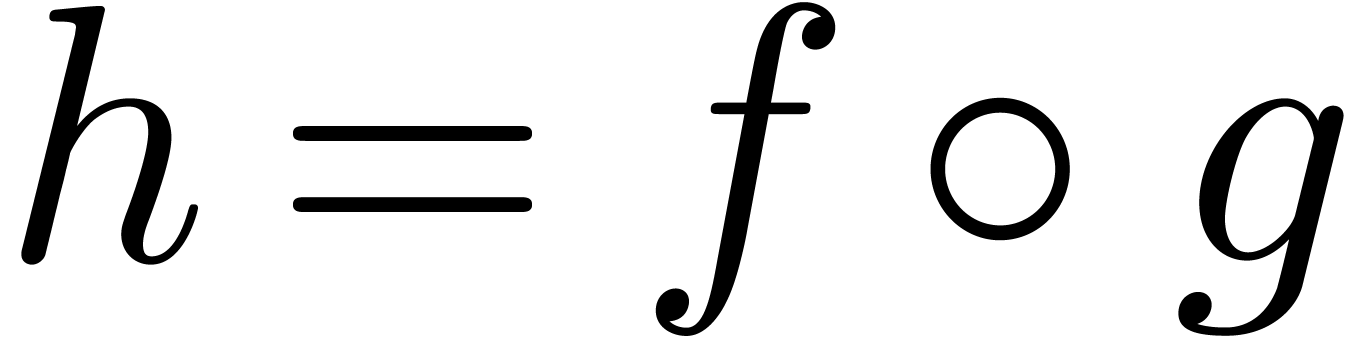 at order
at order 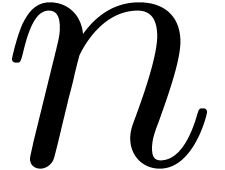 and up to an absolute error
and up to an absolute error 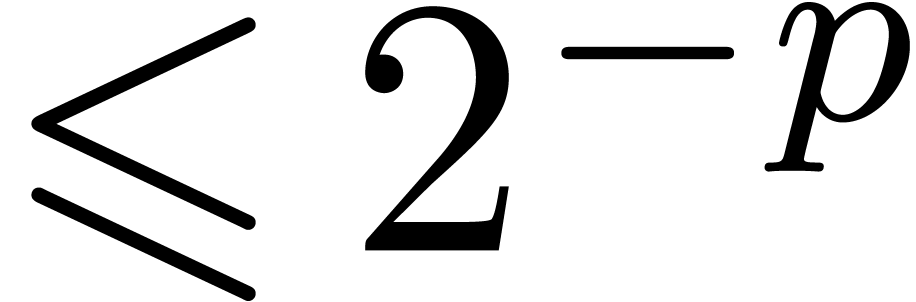 can be done in
time
can be done in
time 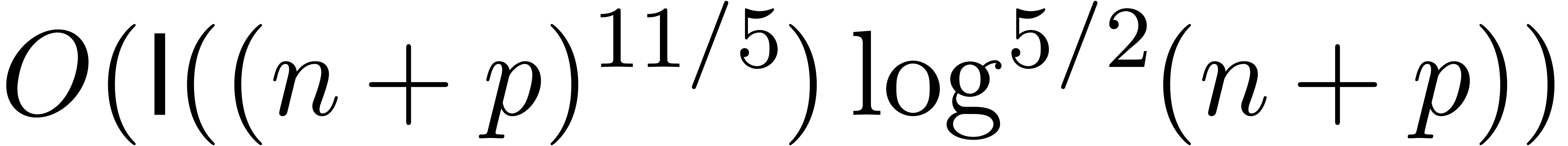 .
.
Remark
Theorem 24 improves on this bound in the frequent case when
 . Unfortunately, we have not
yet been able to prove a quasi-linear bound
. Unfortunately, we have not
yet been able to prove a quasi-linear bound 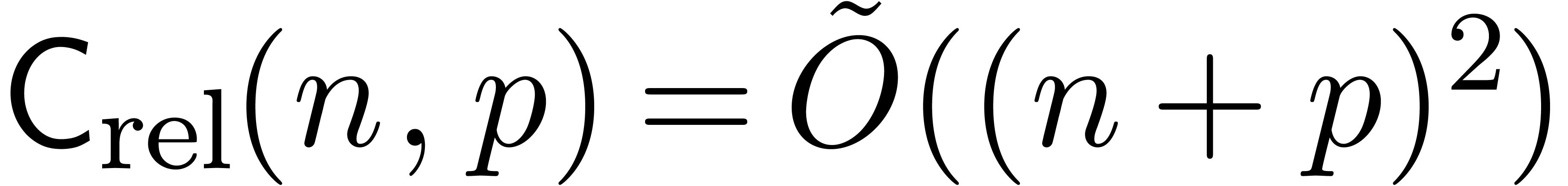 .
.
Remark
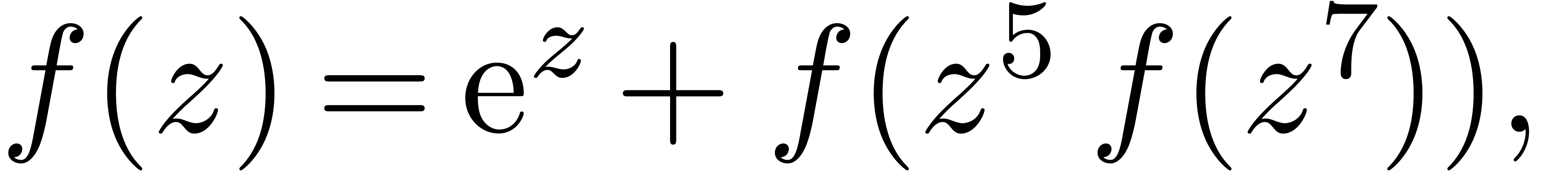
can be evaluated efficiently on small disks. Consequently, the Taylor
coefficients of  can be computed efficiently
using lemma 17.
can be computed efficiently
using lemma 17.
A. Aho, J. Hopcroft, and J. Ullman. The Design and Analysis of Computer Algorithms. Addison-Wesley, Reading, Massachusetts, 1974.
D.J. Bernstein. Composing power series over a finite ring in essentially linear time. JSC, 26(3):339–341, 1998.
R.P. Brent and H.T. Kung. 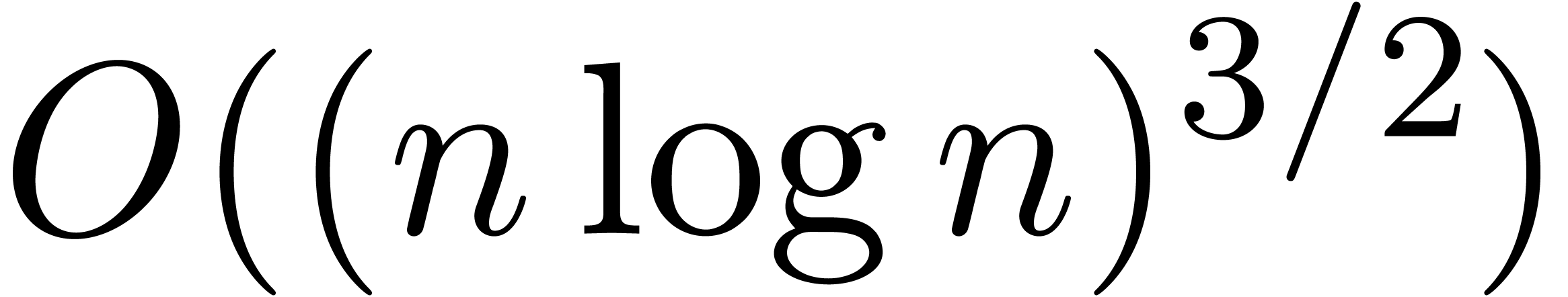 algorithms for composition and reversion of power series. In
J.F. Traub, editor, Analytic Computational Complexity,
Pittsburg, 1975. Proc. of a symposium on analytic computational
complexity held by Carnegie-Mellon University.
algorithms for composition and reversion of power series. In
J.F. Traub, editor, Analytic Computational Complexity,
Pittsburg, 1975. Proc. of a symposium on analytic computational
complexity held by Carnegie-Mellon University.
R.P. Brent and H.T. Kung. Fast algorithms for composition and reversion of multivariate power series. In Proc. Conf. Th. Comp. Sc., pages 149–158, Waterloo, Ontario, Canada, August 1977. University of Waterloo.
R.P. Brent and H.T. Kung. Fast algorithms for manipulating formal power series. Journal of the ACM, 25:581–595, 1978.
Alin Bostan, Bruno Salvy, and Éric Schost. Power series composition and change of basis. In J. Rafael Sendra and Laureano González-Vega, editors, ISSAC, pages 269–276, Linz/Hagenberg, Austria, July 2008. ACM.
D.G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
J.W. Cooley and J.W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
M. Fürer. Faster integer multiplication. In Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing (STOC 2007), pages 57–66, San Diego, California, 2007.
L. Kronecker. Grundzüge einer arithmetischen Theorie der algebraischen Grössen. Jour. für die reine und ang. Math., 92:1–122, 1882.
A. Schönhage. Asymptotically fast algorithms for the numerical multiplication and division of polynomials with complex coefficients. In J. Calmet, editor, EUROCAM '82: European Computer Algebra Conference, volume 144 of Lect. Notes Comp. Sci., pages 3–15, Marseille, France, April 1982. Springer.
A. Schönhage and V. Strassen. Schnelle Multiplikation grosser Zahlen. Computing, 7:281–292, 1971.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
Joris van der Hoeven. New algorithms for relaxed multiplication. JSC, 42(8):792–802, 2007.