Faster relaxed multiplication |
|
| April 13, 2012 |
|
 . This work has
been partly supported by the French ANR-09-JCJC-0098-01
. This work has
been partly supported by the French ANR-09-JCJC-0098-01
In previous work, we have introduced several fast algorithms for
relaxed power series multiplication (also known under the name
on-line multiplication) up till a given order
|
Let  be an effective (possibly non commutative)
ring. That is, we assume data structures for representing the elements
of
be an effective (possibly non commutative)
ring. That is, we assume data structures for representing the elements
of  and algorithms for performing the ring
operations
and algorithms for performing the ring
operations  ,
,  and
and  . The aim of algebraic
complexity theory is to study the cost of basic or more complex
algebraic operations over
. The aim of algebraic
complexity theory is to study the cost of basic or more complex
algebraic operations over  (such as the
multiplication of polynomials or matrices) in terms of the number of
operations in
(such as the
multiplication of polynomials or matrices) in terms of the number of
operations in  .
.
The algebraic complexity usually does not coincide with the bit
complexity, which also takes into account the potential growth of the
actual coefficients in  .
Nevertheless, understanding the algebraic complexity usually constitutes
a first useful step towards understanding the bit complexity. Of course,
in the special case when
.
Nevertheless, understanding the algebraic complexity usually constitutes
a first useful step towards understanding the bit complexity. Of course,
in the special case when  is a finite field, both
complexities coincide up to a constant factor.
is a finite field, both
complexities coincide up to a constant factor.
One of the most central operations is polynomial multiplication. We will
denote by 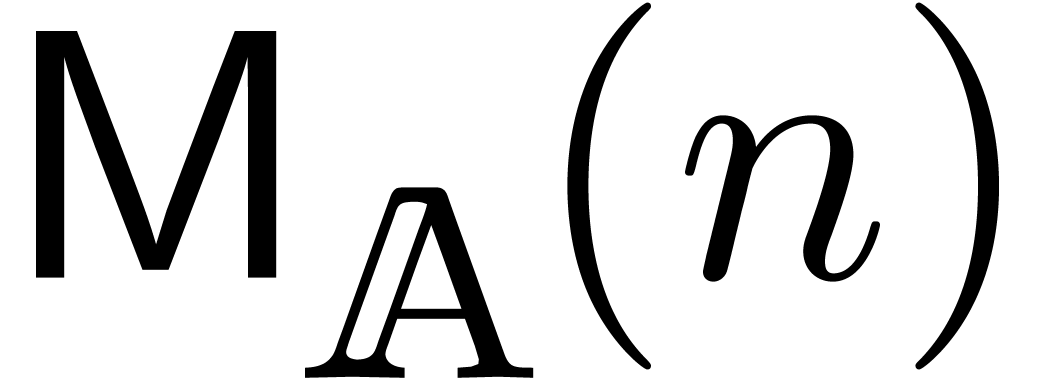 the number of operations required to
multiply two polynomials of degrees
the number of operations required to
multiply two polynomials of degrees 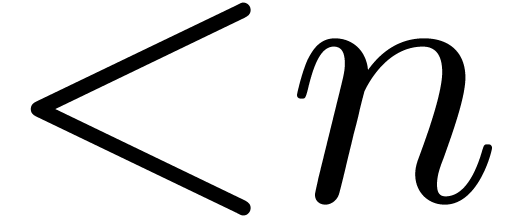 in
in 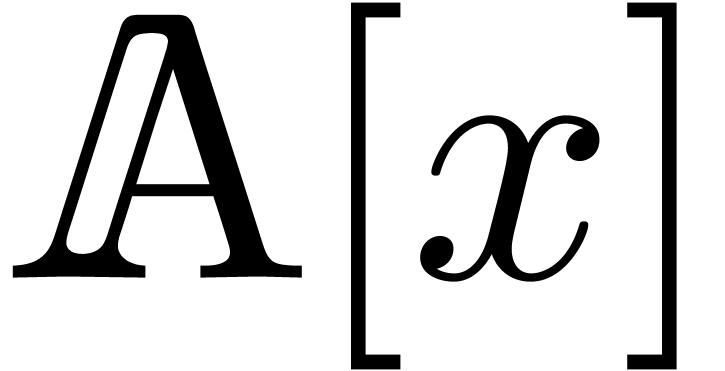 . If
. If  admits
primitive
admits
primitive 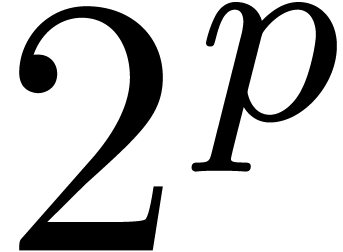 -th roots of unity
for all
-th roots of unity
for all  , then we have
, then we have 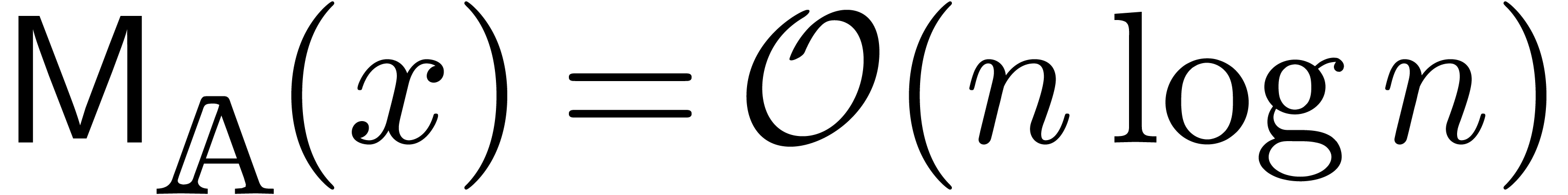 using FFT multiplication, which is based on the fast
Fourier transform [CT65]. In general, it has been shown [SS71, CK91] that
using FFT multiplication, which is based on the fast
Fourier transform [CT65]. In general, it has been shown [SS71, CK91] that 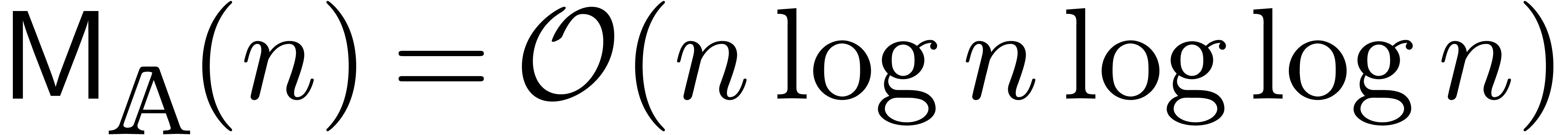 .
The complexities of most other operations (division, Taylor shift,
extended g.c.d., multipoint evaluation, interpolation,
etc.) can be expressed in terms of
.
The complexities of most other operations (division, Taylor shift,
extended g.c.d., multipoint evaluation, interpolation,
etc.) can be expressed in terms of 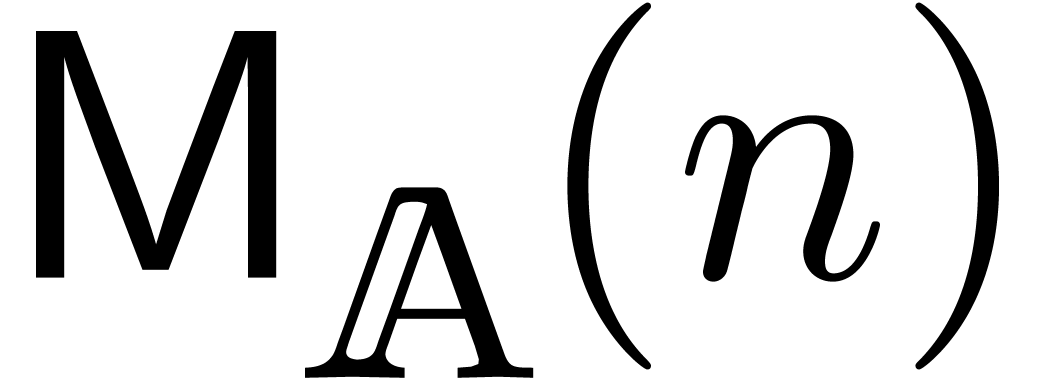 . Often, the cost of such other operations is simply
. Often, the cost of such other operations is simply
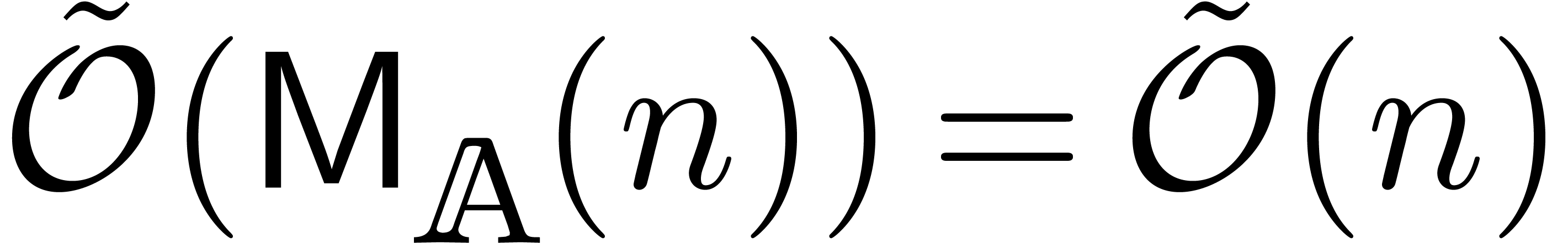 , where
, where 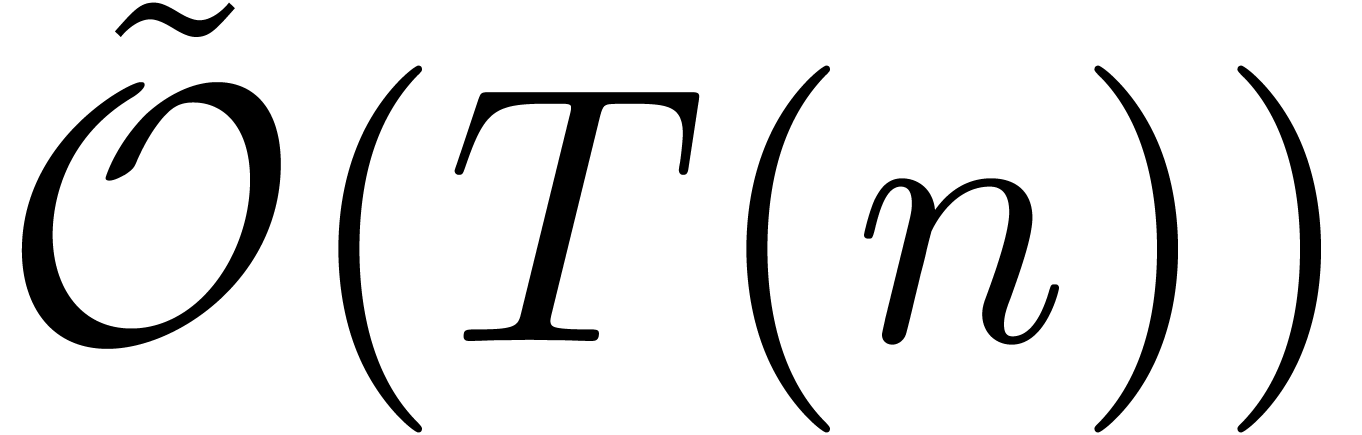 stands for
stands for 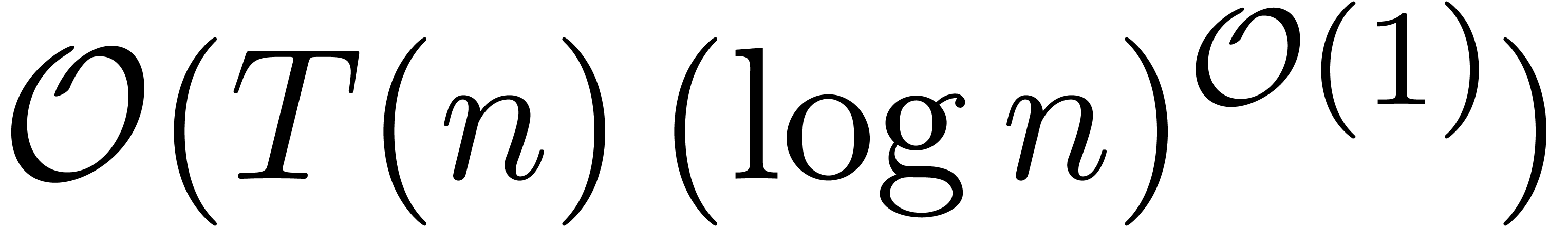 ; see [AHU74,
BP94, GG02] for some classical results along
these lines.
; see [AHU74,
BP94, GG02] for some classical results along
these lines.
The complexity of polynomial multiplication is fundamental for studying
the cost of operations on formal power series in 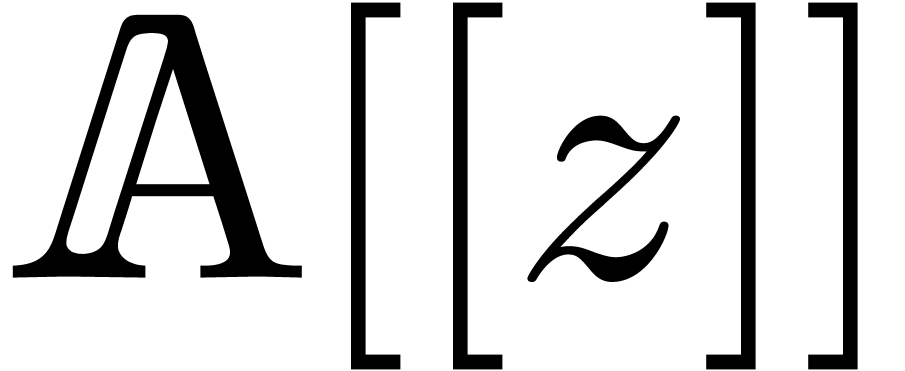 up to a given truncation order
up to a given truncation order 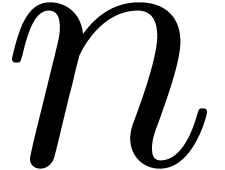 .
Clearly, it is possible to perform the multiplication up to order
.
Clearly, it is possible to perform the multiplication up to order 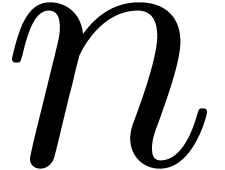 in time
in time  :
it suffices to multiply the truncated power series at order
:
it suffices to multiply the truncated power series at order 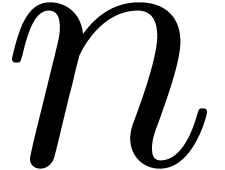 and truncate the result. Using Newton's method, and
assuming that
and truncate the result. Using Newton's method, and
assuming that  , it is also
possible to compute
, it is also
possible to compute 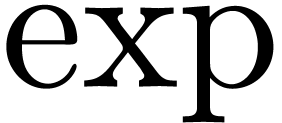 ,
,  , etc. up to order
, etc. up to order
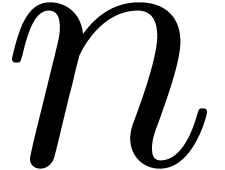 in time
in time  .
More generally, it has been shown in [BK78, Hoe02,
Sed01, Hoe10] that the power series solutions
of algebraic differential equations with coefficients in
.
More generally, it has been shown in [BK78, Hoe02,
Sed01, Hoe10] that the power series solutions
of algebraic differential equations with coefficients in 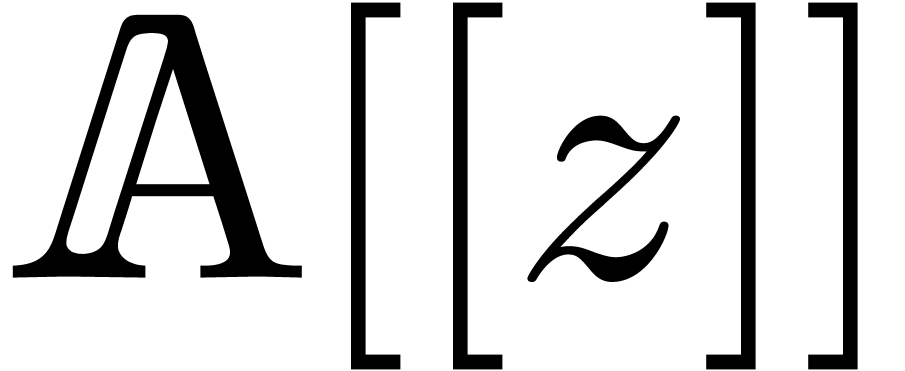 can be computed up to order
can be computed up to order 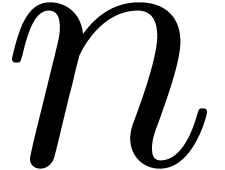 in
time
in
time  . However, in this case,
the “
. However, in this case,
the “ ” hides a
non trivial constant factor which depends on the size of the equation
that one wants to solve.
” hides a
non trivial constant factor which depends on the size of the equation
that one wants to solve.
The relaxed approach for computations with formal power series
makes it possible to solve equations in quasi-optimal time with respect
to the sparse size of the equations. The idea is to consider power
series  as streams of coefficients
as streams of coefficients 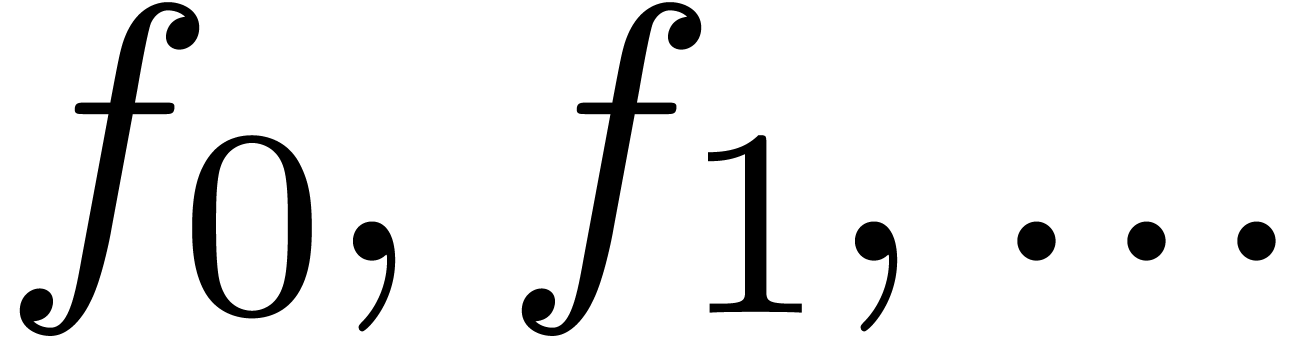 and to require that all operations are performed
“without delay” on these streams. For instance, when
multiplying
and to require that all operations are performed
“without delay” on these streams. For instance, when
multiplying 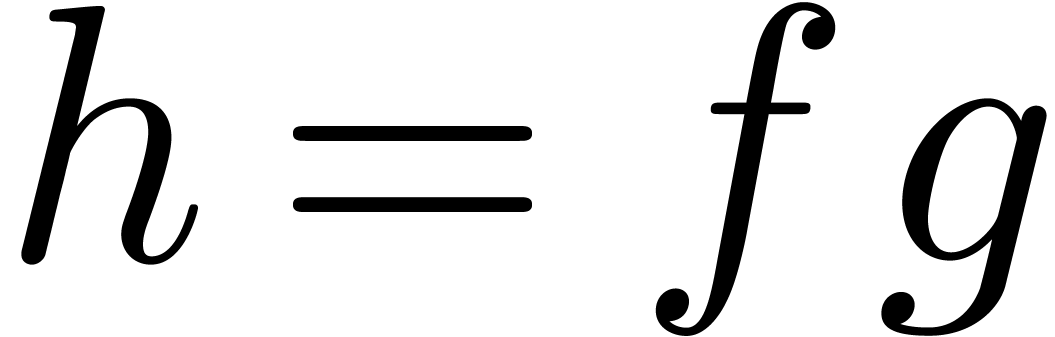 two power series
two power series 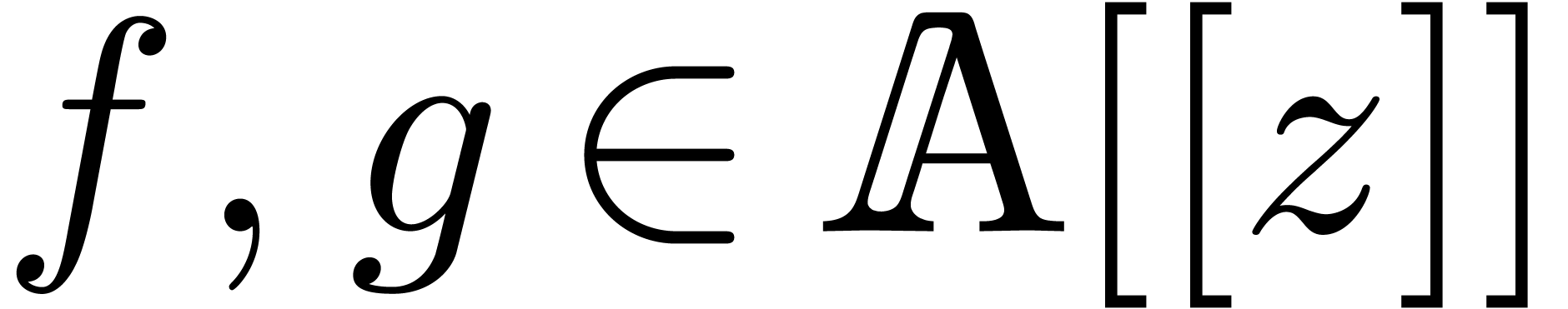 , we require that
, we require that 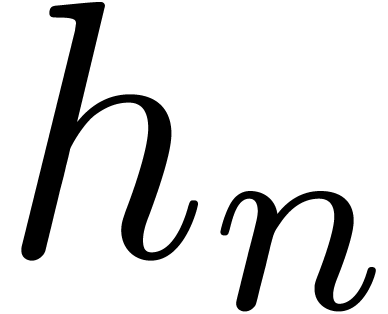 is
computed as soon as
is
computed as soon as  are known. Any
algorithm which has this property will be called a relaxed or
on-line algorithm for multiplication.
are known. Any
algorithm which has this property will be called a relaxed or
on-line algorithm for multiplication.
Given a relaxed algorithm for multiplication, it is possible to let the
later coefficients 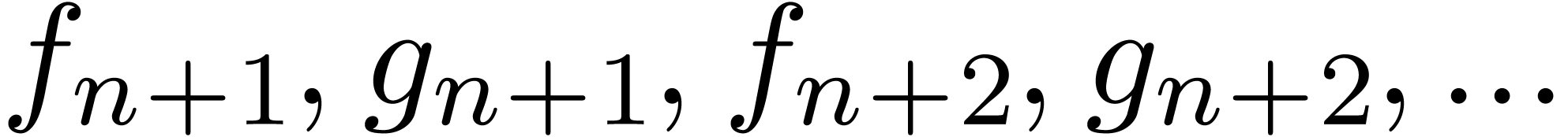 of the input depend
on the known coefficients
of the input depend
on the known coefficients  of the output. For
instance, given a power series
of the output. For
instance, given a power series 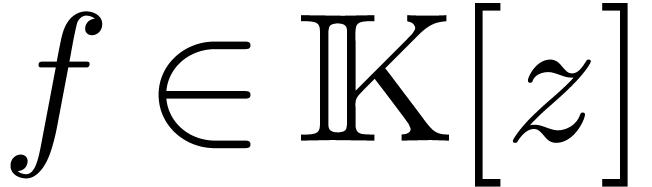 with
with 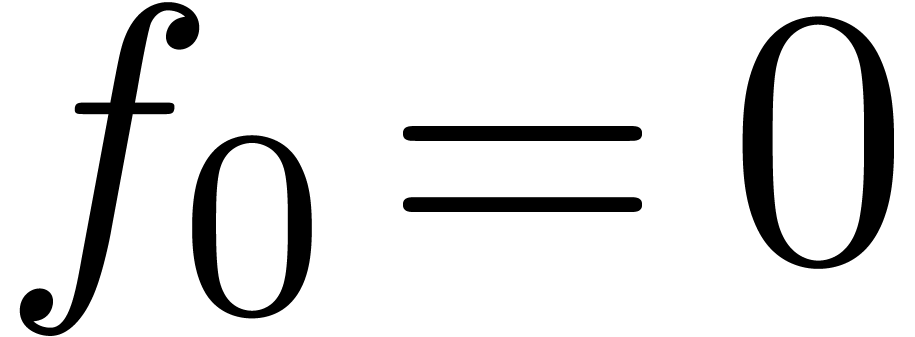 , we may compute
, we may compute 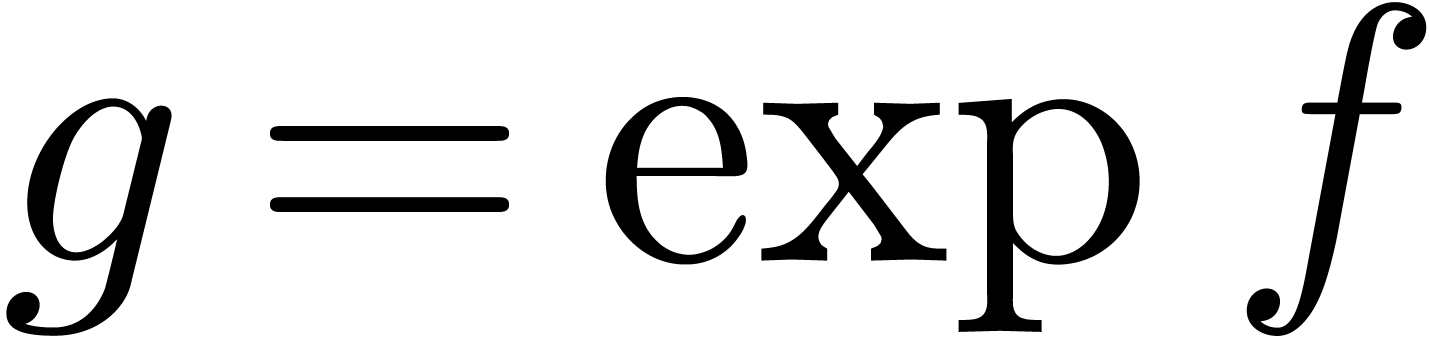 using
the formula
using
the formula
Indeed, extraction of the coefficient of  in
in  and
and 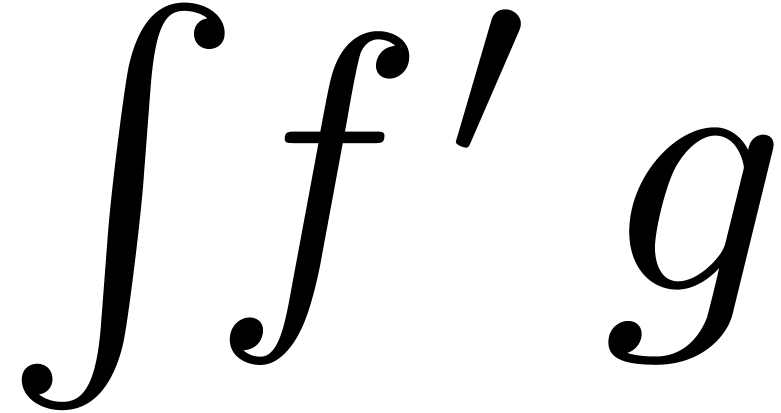 yields
yields
and  only depends on
only depends on  . More generally, we define an equation of the form
. More generally, we define an equation of the form
to be recursive, if 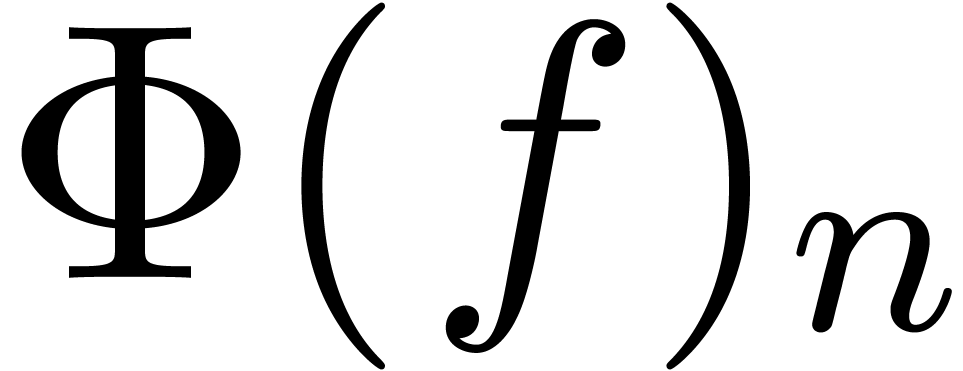 only depends on
only depends on
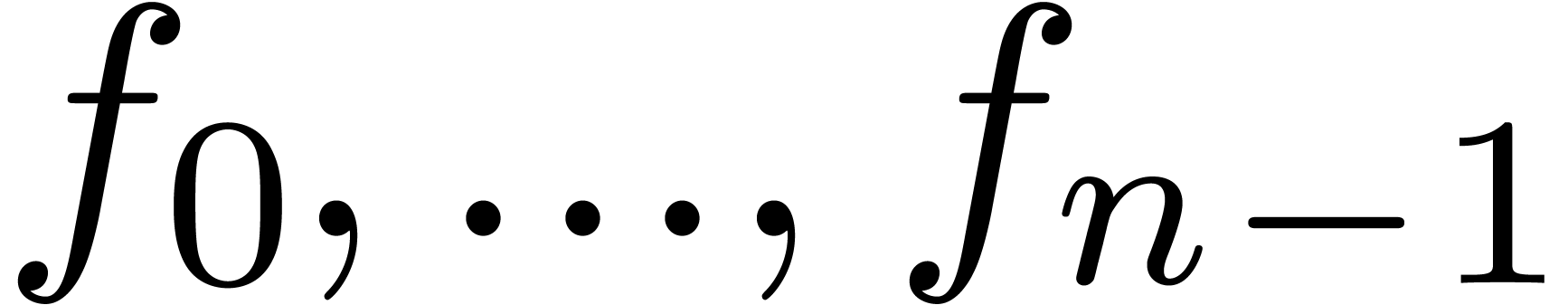 . Replacing
. Replacing  by
by  , we notice that the same
terminology applies to systems of
, we notice that the same
terminology applies to systems of 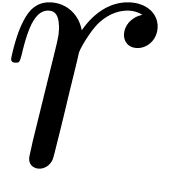 equations. In
the case of an implicit equation, special rewriting techniques can be
implied in order transform the input equation into a recursive equation
[Hoe11, Hoe09, BL11].
equations. In
the case of an implicit equation, special rewriting techniques can be
implied in order transform the input equation into a recursive equation
[Hoe11, Hoe09, BL11].
Let 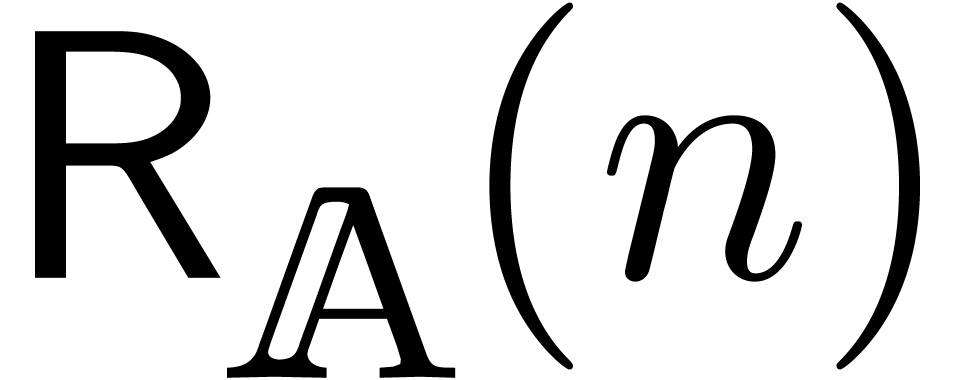 denote the cost of performing a relaxed
multiplication up to order
denote the cost of performing a relaxed
multiplication up to order 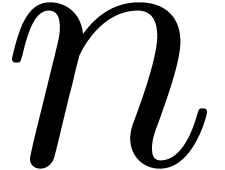 .
If
.
If  is an expression which involves
is an expression which involves  multiplications and
multiplications and 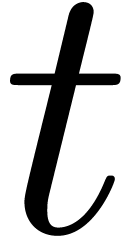 other
“linear time” operations (additions, integrations, etc.),
then it follows that (2) can be solved up to order
other
“linear time” operations (additions, integrations, etc.),
then it follows that (2) can be solved up to order 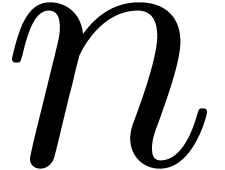 in time
in time 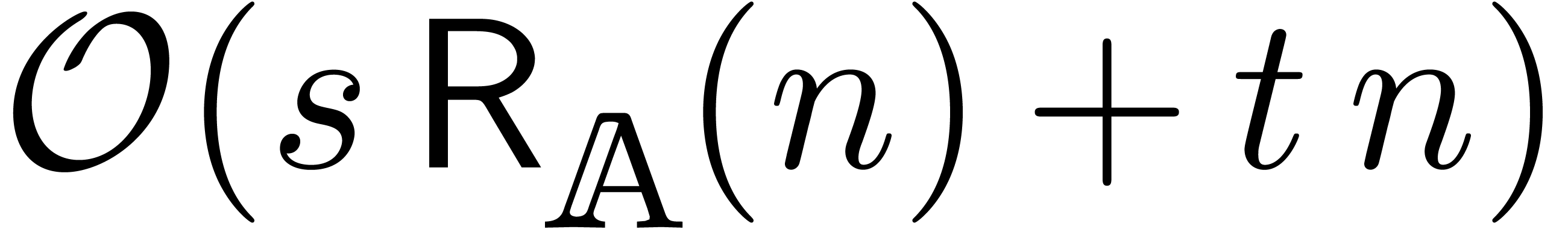 .
If we had
.
If we had  , then this would
yield an optimal algorithm for solving (2) in the sense
that the computation of the solution would essentially require the same
time as its verification.
, then this would
yield an optimal algorithm for solving (2) in the sense
that the computation of the solution would essentially require the same
time as its verification.
The naive 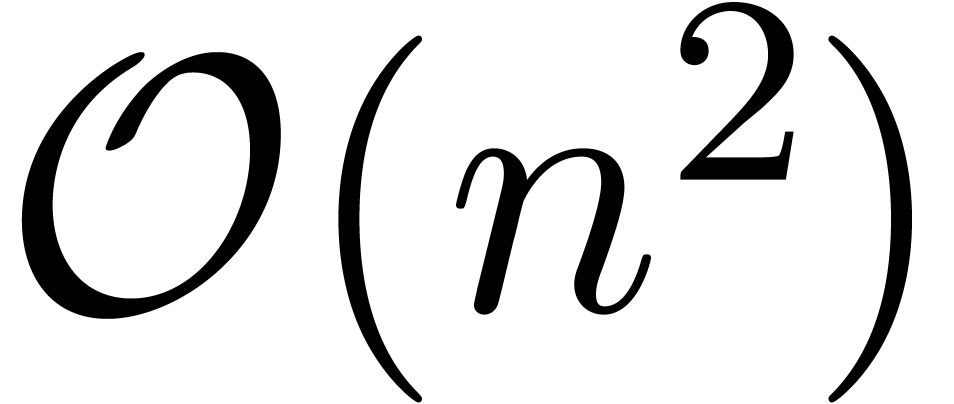 algorithm for computing
algorithm for computing 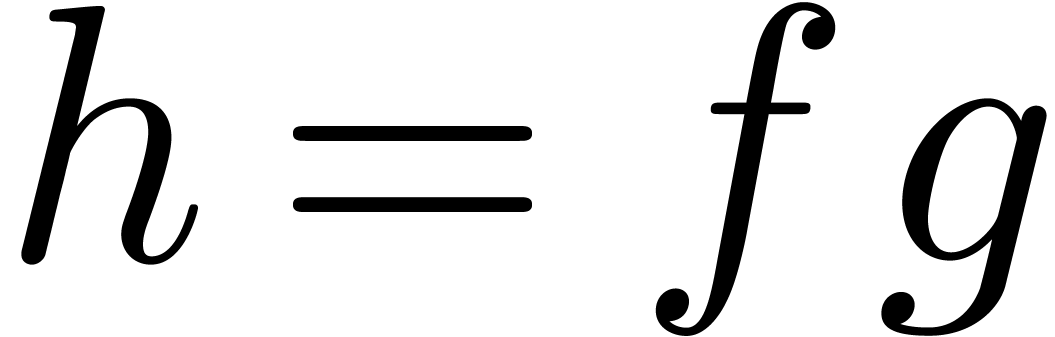 , based on the formula
, based on the formula
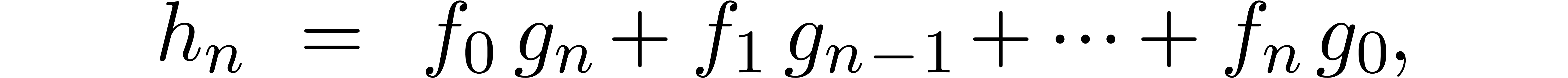
is clearly relaxed. Unfortunately, FFT multiplication is not
relaxed, since  are computed simultaneously as a
function of
are computed simultaneously as a
function of  , in this case.
, in this case.
In [Hoe97, Hoe02] it was remarked that
Karatsuba's 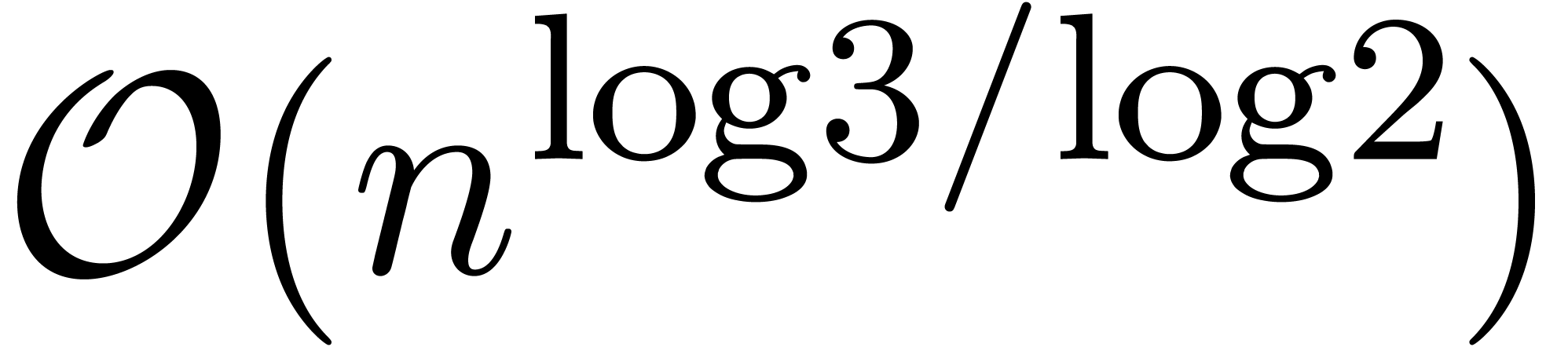 algorithm [KO63] for
multiplying polynomials can be rewritten in a relaxed manner. For small
algorithm [KO63] for
multiplying polynomials can be rewritten in a relaxed manner. For small
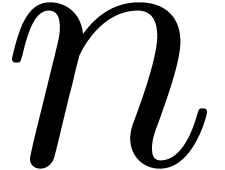 , Karatsuba multiplication
and relaxed multiplication thus require exactly the same number
of operations. In [Hoe97, Hoe02], an
additional fast relaxed algorithm was presented with time complexity
, Karatsuba multiplication
and relaxed multiplication thus require exactly the same number
of operations. In [Hoe97, Hoe02], an
additional fast relaxed algorithm was presented with time complexity
We were recently made aware of the fact that a similar algorithm was first published in [FS74]. However, this early paper was presented in a different context of on-line (relaxed) multiplication of integers (instead of power series), and without the application to the resolution of recursive equations (which is quite crucial from our perspective).
An interesting question remained: can the bound (3) be
lowered further, be it by a constant factor? In [Hoe03], it
was first noticed that an approximate factor of two can be gained if one
of the multiplicands is known beforehand. For instance, if we want to
compute 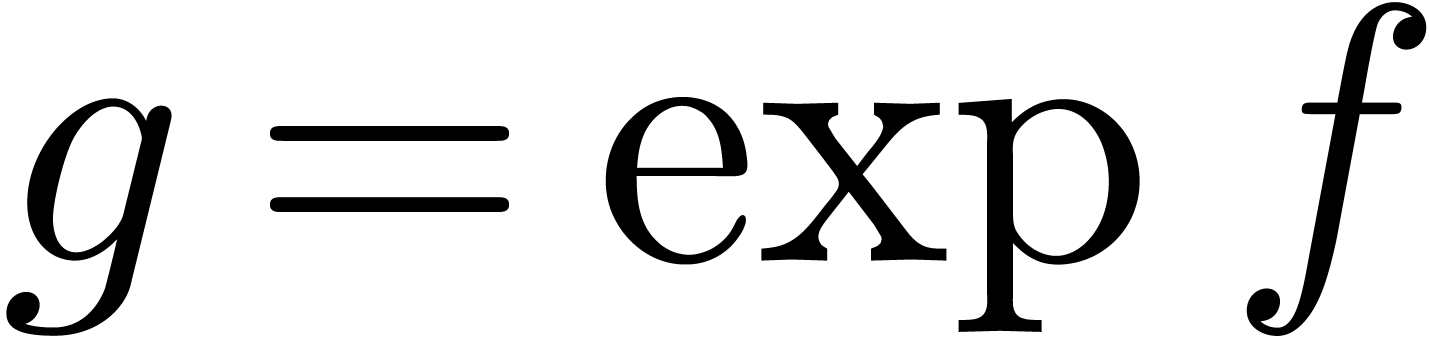 for a known series
for a known series 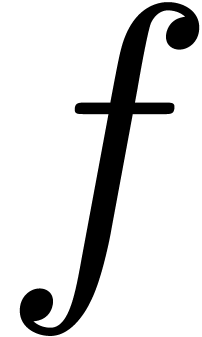 with
with 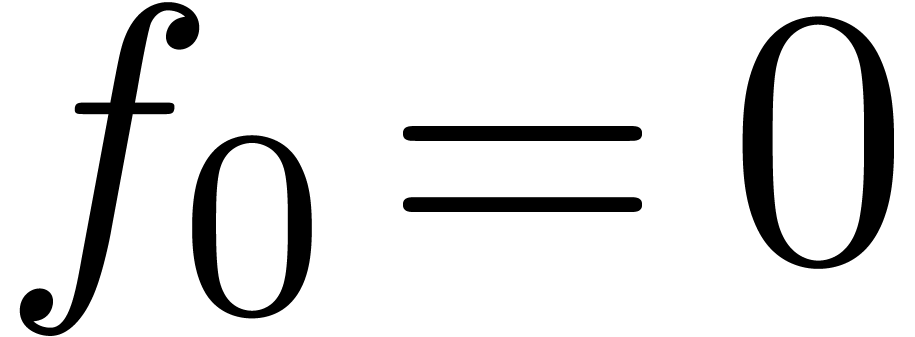 , then the coefficients
of
, then the coefficients
of 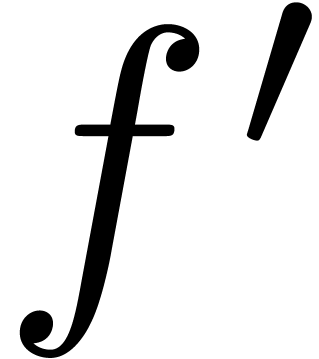 are already known in the product
are already known in the product 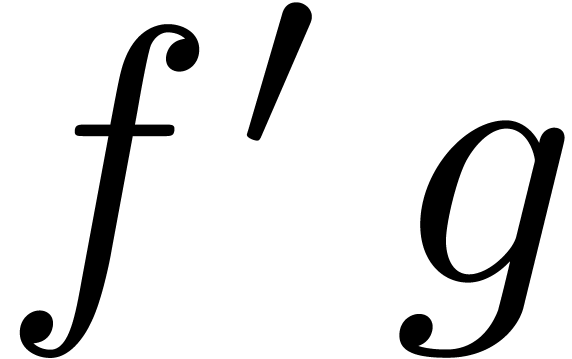 in (1), so only one of the inputs depends on
the output. An algorithm for the computation of
in (1), so only one of the inputs depends on
the output. An algorithm for the computation of 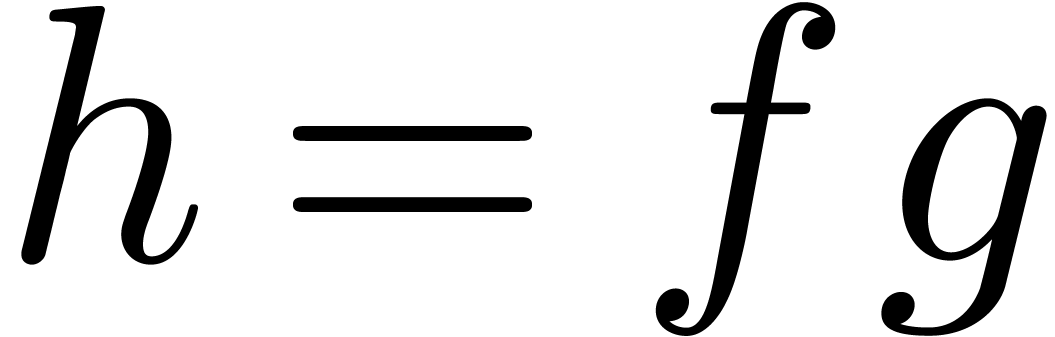 is said to be semi-relaxed, if
is said to be semi-relaxed, if  is
written to the output as soon as
is
written to the output as soon as  are known, but
all coefficients of
are known, but
all coefficients of  are known beforehand. We
will denote by
are known beforehand. We
will denote by 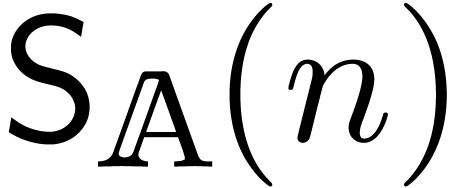 the complexity of semi-relaxed
multiplication. We recall from [Hoe07] (see also section 3) that relaxed multiplication reduces to semi-relaxed
multiplication
the complexity of semi-relaxed
multiplication. We recall from [Hoe07] (see also section 3) that relaxed multiplication reduces to semi-relaxed
multiplication

The first reduction of (3) by a non constant factor was
published in [Hoe07], and uses the technique of FFT
blocking (which has also been used for the multiplication of
multivariate polynomials and power series in [Hoe02,
Section 6.3], and for speeding up Newton iterations in [Ber00,
Hoe10]). Under the assumption that  admits primitive
admits primitive 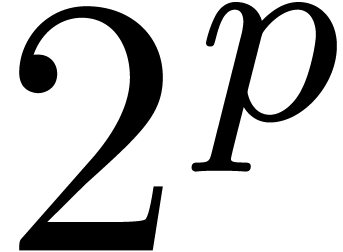 -th roots of
unity for all
-th roots of
unity for all  (or at least for all
(or at least for all  with
with 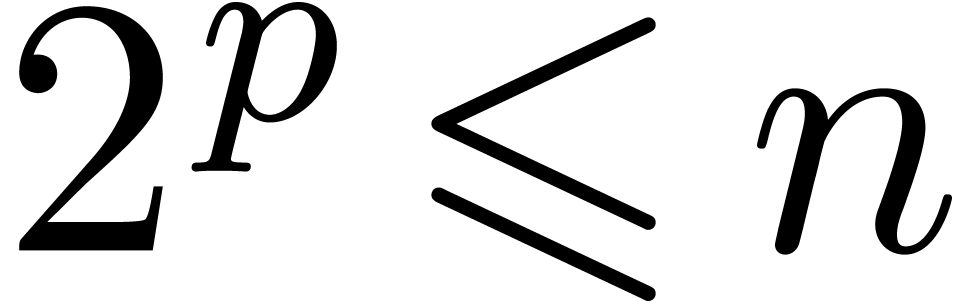 ), we
showed that
), we
showed that
Since this complexity will play a central role in the remainder of this paper, it will be convenient to abbreviate
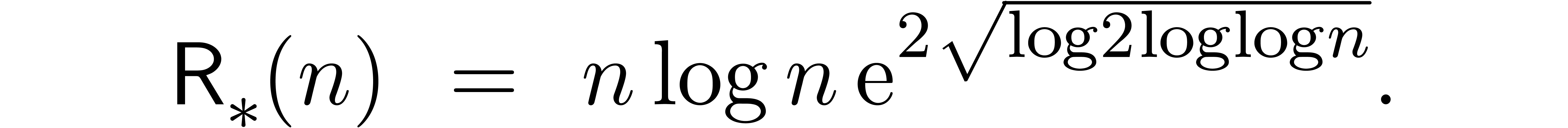
The function 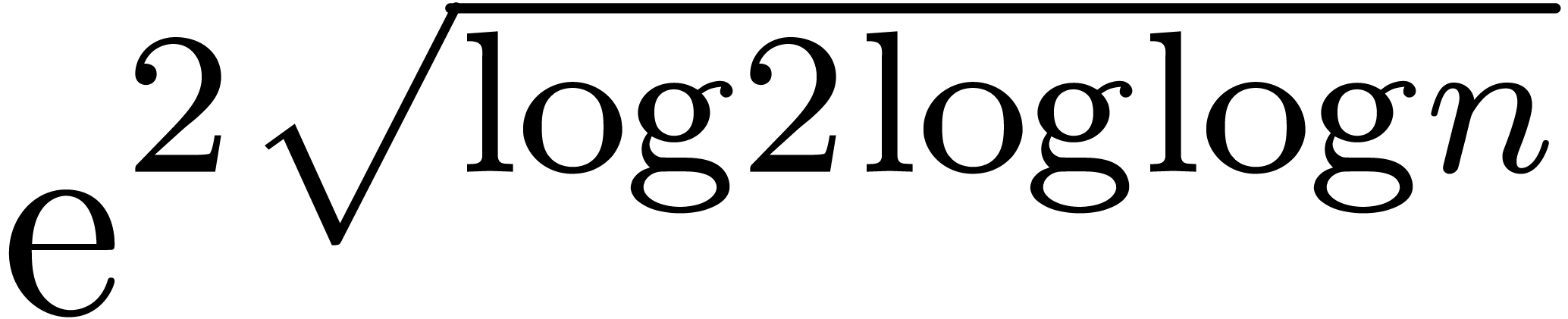 has slower growth than any strictly
positive power of
has slower growth than any strictly
positive power of 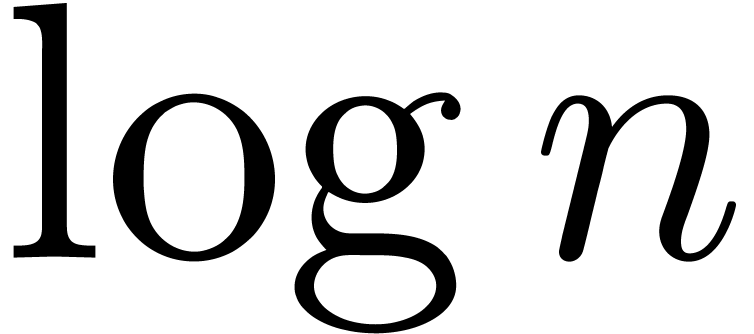 . It will
also be convenient to write
. It will
also be convenient to write 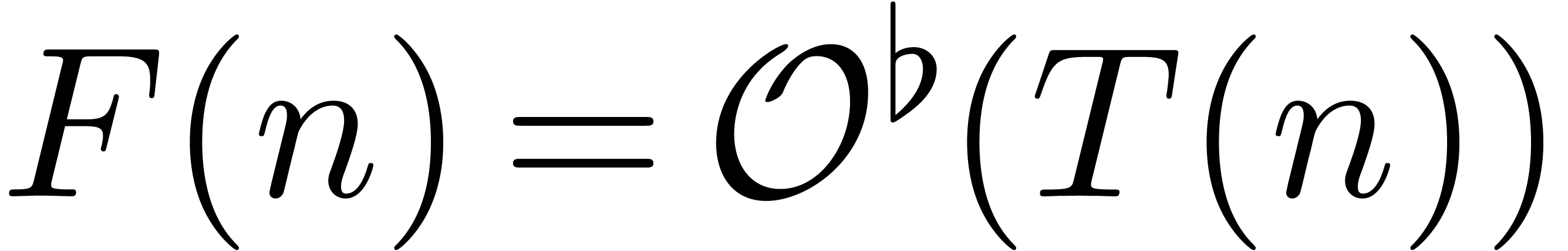 whenever
whenever 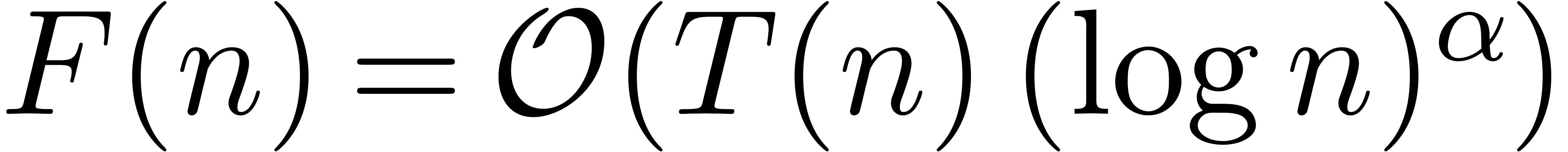 for all
for all  . In
particular, it follows that
. In
particular, it follows that

In section 3, we will recall the main ideas from [Hoe07] which lead to the complexity bound (4).
We recall that the characteristic of a ring  is
the integer
is
the integer 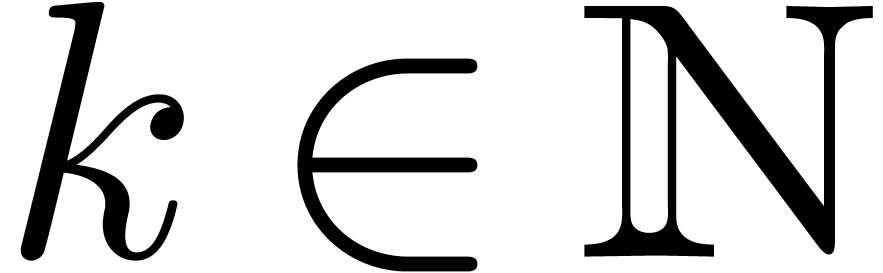 such that the canonical ring
homomorphism
such that the canonical ring
homomorphism 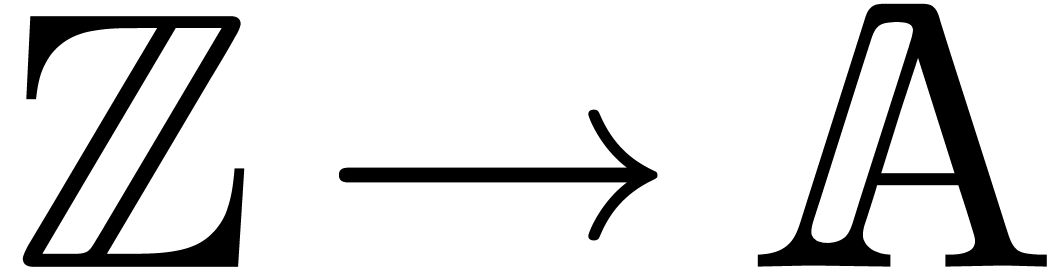 has kernel
has kernel 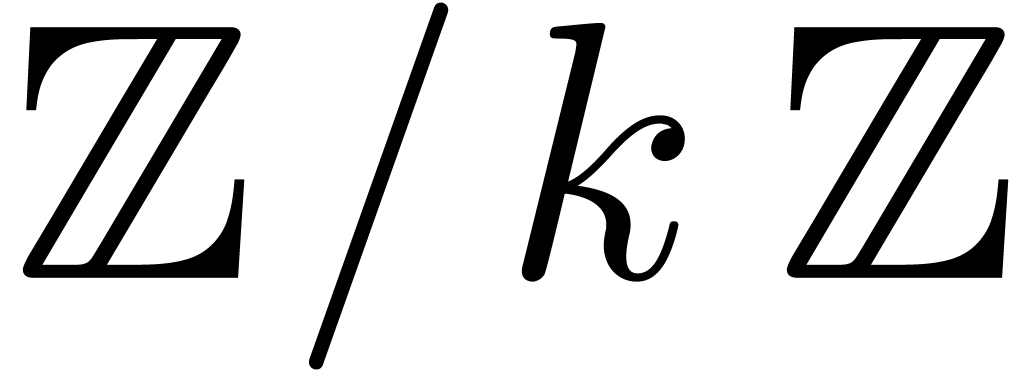 . If
. If  is torsion-free as a
is torsion-free as a
 -module, then we will say
that
-module, then we will say
that  admits an effective partial division by
integers if there exists an algorithm which takes
admits an effective partial division by
integers if there exists an algorithm which takes 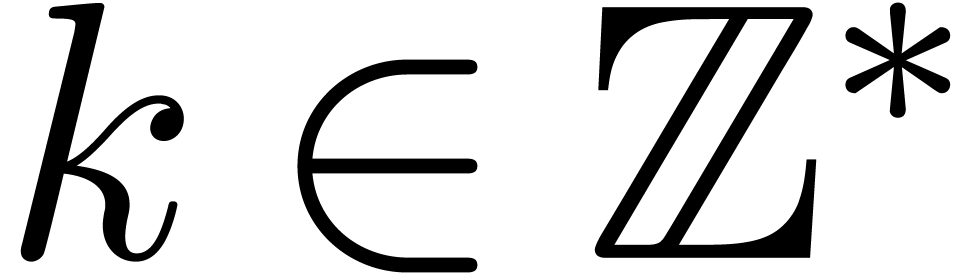 and
and 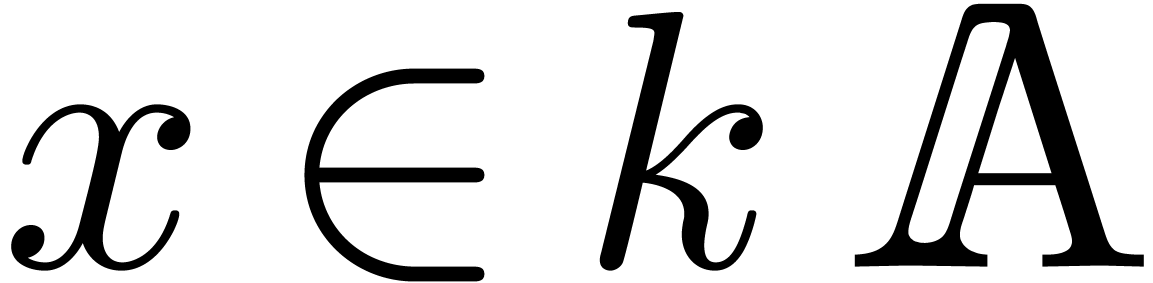 on input and which returns the unique
on input and which returns the unique 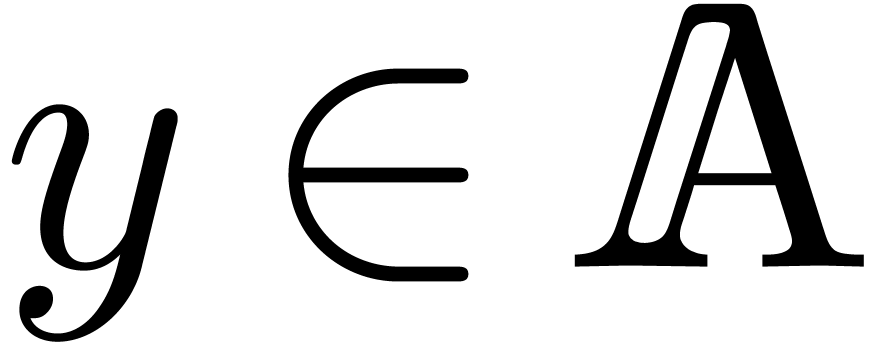 with
with 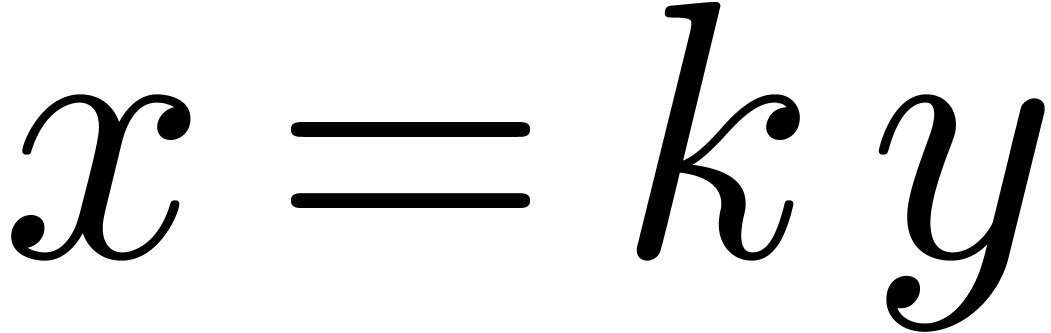 on output. The main
result of this paper is:
on output. The main
result of this paper is:
 is an effective ring of characteristic
zero, which is torsion-free as a
is an effective ring of characteristic
zero, which is torsion-free as a  -module,
and which admits an effective partial division by integers.
-module,
and which admits an effective partial division by integers.
 is an effective ring of positive
characteristic.
is an effective ring of positive
characteristic.
Then we have
We notice that the theorem holds in particular if  is an effective field. In Section 7, we will also consider
the relaxed multiplication of
is an effective field. In Section 7, we will also consider
the relaxed multiplication of  -adic
numbers, with
-adic
numbers, with 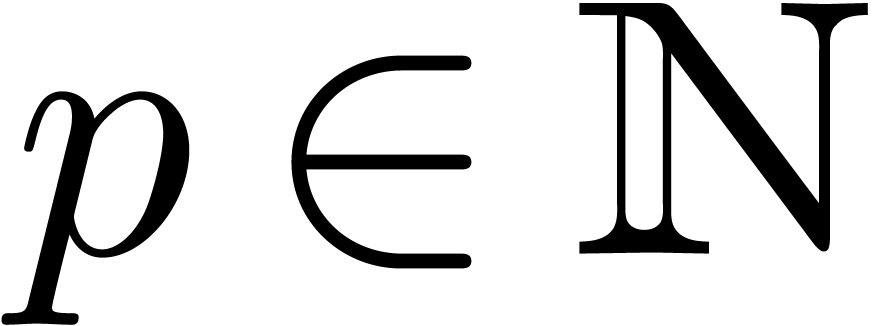 and
and  .
If we denote by
.
If we denote by 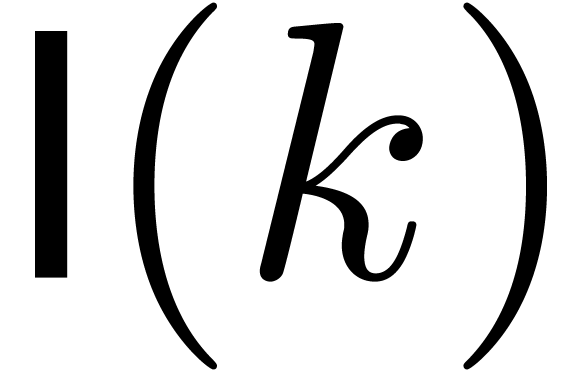 the bit complexity of
multiplying two
the bit complexity of
multiplying two 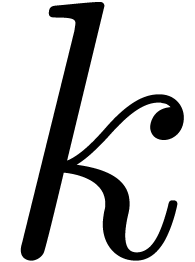 -bit
integers, then [FS74] essentially provided an algorithm of
bit complexity
-bit
integers, then [FS74] essentially provided an algorithm of
bit complexity 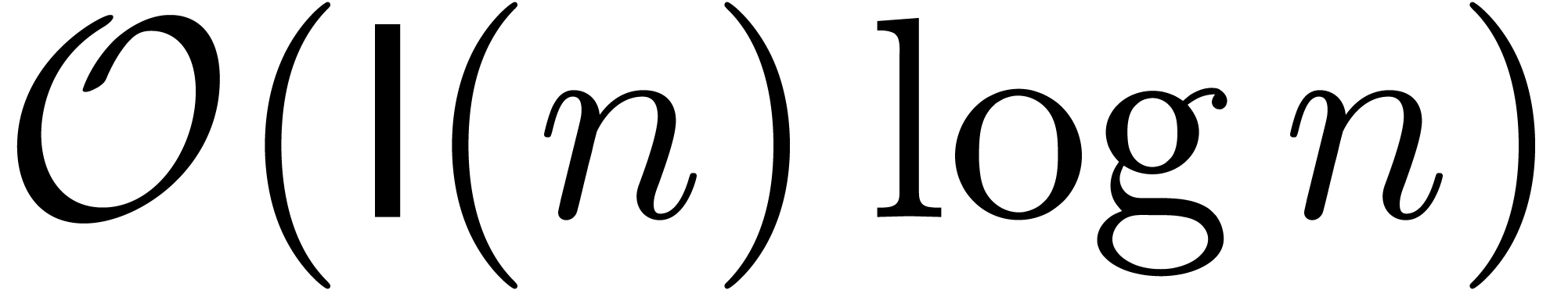 for the relaxed multiplication of
for the relaxed multiplication of
 -adic numbers at order
-adic numbers at order 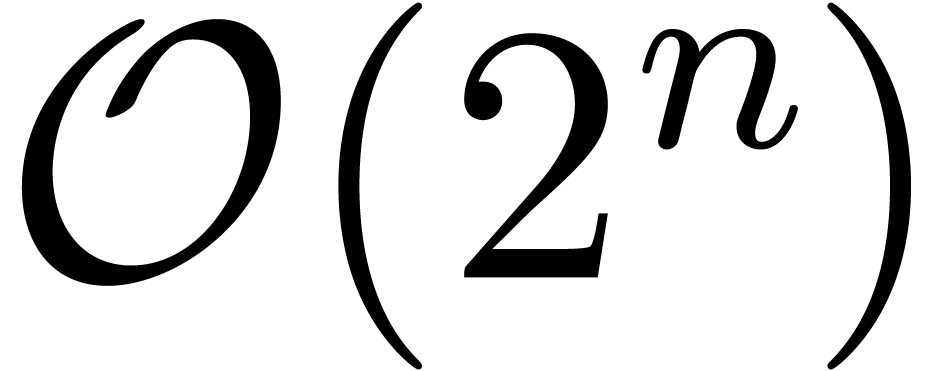 . Various algorithms and benchmarks
for more general
. Various algorithms and benchmarks
for more general  were presented in [BHL11].
It is also well known [Too63, Coo66, SS71,
Für07] that
were presented in [BHL11].
It is also well known [Too63, Coo66, SS71,
Für07] that 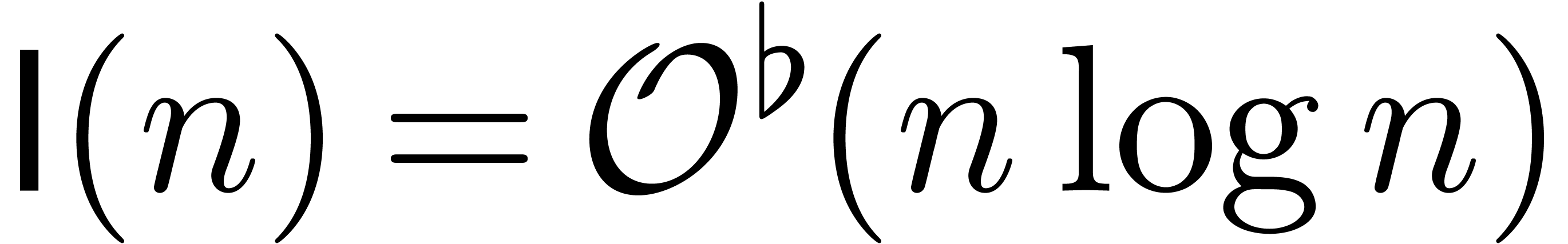 .
Let
.
Let 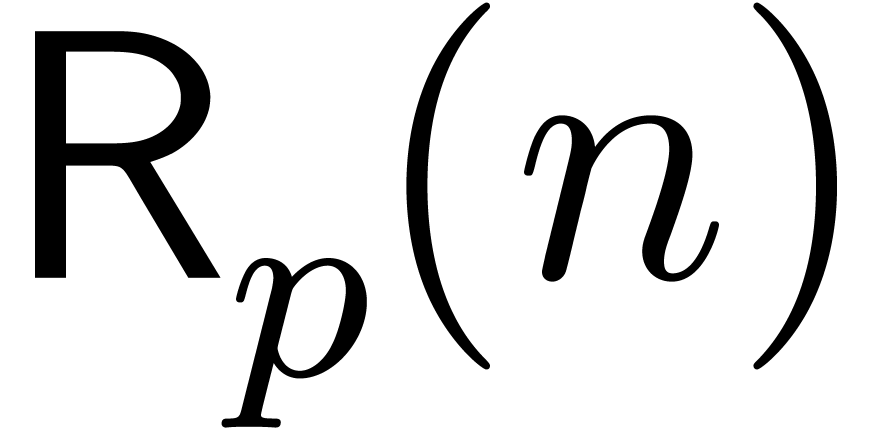 denote the bit complexity of the relaxed
multiplication of two
denote the bit complexity of the relaxed
multiplication of two  -adic
numbers modulo
-adic
numbers modulo 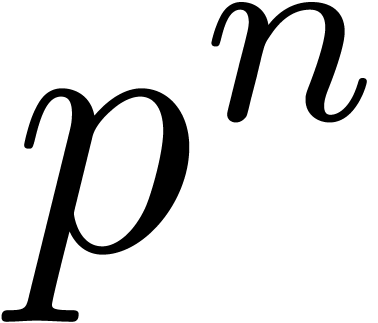 . In Section
7, we will prove the following new result:
. In Section
7, we will prove the following new result:
The main idea which allows for the present generalizations is quite
straightforward. In our original algorithm from [Hoe07],
the presence of sufficiently many primitive 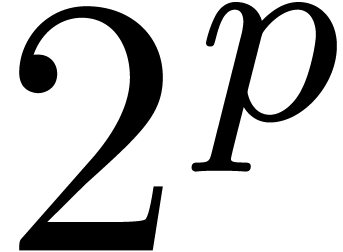 -th roots of unity in
-th roots of unity in  gives
rise to an quasi-optimal evaluation-interpolation strategy for the
multiplication of polynomials. More precisely, given two polynomials of
degrees
gives
rise to an quasi-optimal evaluation-interpolation strategy for the
multiplication of polynomials. More precisely, given two polynomials of
degrees 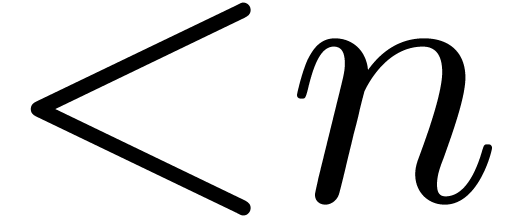 , their
FFT-multiplication only requires
, their
FFT-multiplication only requires 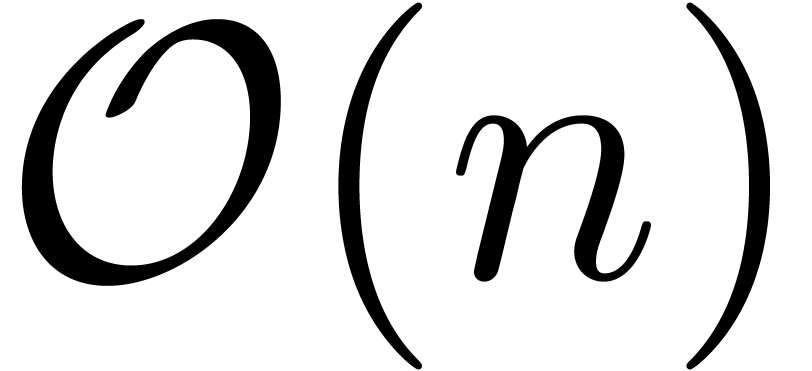 evaluation and
interpolation points, and both the evaluation and interpolation steps
can be performed fast, using only
evaluation and
interpolation points, and both the evaluation and interpolation steps
can be performed fast, using only  operations.
Now it has recently been shown [BS05] that quasi-optimal
evaluation-interpolation strategies still exist if we evaluate and
interpolate at points in geometric progressions instead of roots of
unity. This result is the key to our new complexity bounds, although
further technical details have to be dealt with in order to make things
work for various types of effective rings
operations.
Now it has recently been shown [BS05] that quasi-optimal
evaluation-interpolation strategies still exist if we evaluate and
interpolate at points in geometric progressions instead of roots of
unity. This result is the key to our new complexity bounds, although
further technical details have to be dealt with in order to make things
work for various types of effective rings  .
We also notice that the main novelty of [BS05] concerns the
interpolation step. Fast evaluation at geometric progressions was
possible before using the so called chirp transform [RSR69,
Blu70]. For effective rings of small characteristic
.
We also notice that the main novelty of [BS05] concerns the
interpolation step. Fast evaluation at geometric progressions was
possible before using the so called chirp transform [RSR69,
Blu70]. For effective rings of small characteristic  , this would actually have been
sufficient for the proving the bound (5).
, this would actually have been
sufficient for the proving the bound (5).
Our paper is structured as follows. Since the algorithms of [BS05]
were presented in the case when  is an effective
field, Section 2 starts with their generalization to more
general effective rings
is an effective
field, Section 2 starts with their generalization to more
general effective rings  .
These generalizations are purely formal and contain no essentially new
ideas. In Section 3, we give a short survey of the
algorithm from [Hoe07], but we recommentd the reader to
download the original paper from our webpage for full technical details.
In Section 4, we prove Theorem 1 in the case
when
.
These generalizations are purely formal and contain no essentially new
ideas. In Section 3, we give a short survey of the
algorithm from [Hoe07], but we recommentd the reader to
download the original paper from our webpage for full technical details.
In Section 4, we prove Theorem 1 in the case
when  has characteristic zero. In Section 5, we turn our attention to the case when
has characteristic zero. In Section 5, we turn our attention to the case when  has prime characteristic
has prime characteristic  . If
the characteristic is sufficiently large, then we may find sufficiently
large geometric progressions in
. If
the characteristic is sufficiently large, then we may find sufficiently
large geometric progressions in  in order to
generalize the results from Section 4. Otherwise, we have
to work over
in order to
generalize the results from Section 4. Otherwise, we have
to work over 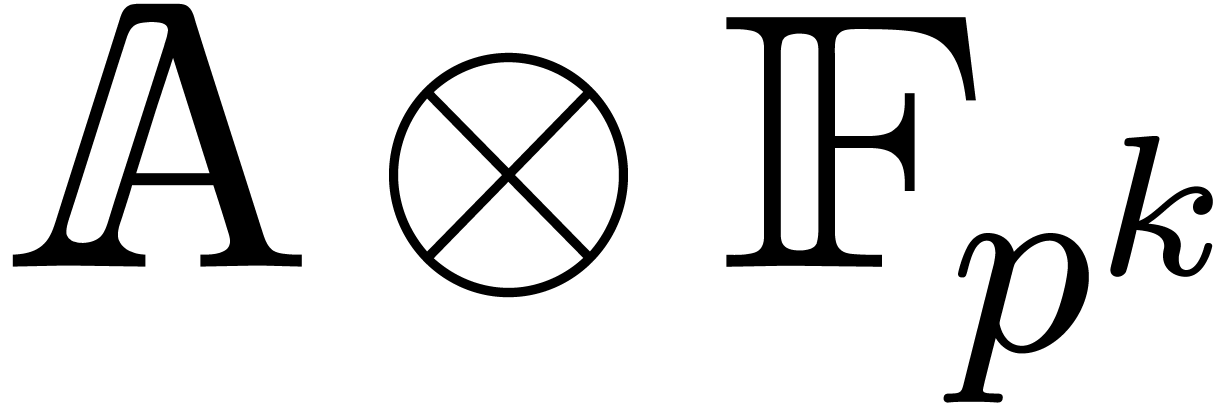 for some sufficiently large
for some sufficiently large 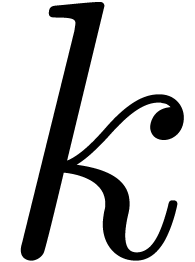 . In Section 6, we
complete the prove of Theorem 1; the case when
. In Section 6, we
complete the prove of Theorem 1; the case when  is a prime power is a refinement of the result from
Section 5. The remaining case is done via Chinese
remaindering. In Section 7, we will prove Theorem 2.
is a prime power is a refinement of the result from
Section 5. The remaining case is done via Chinese
remaindering. In Section 7, we will prove Theorem 2.
Let  be an effective integral domain and let
be an effective integral domain and let  be its quotient field. Assume that
be its quotient field. Assume that  has characteristic zero. Let
has characteristic zero. Let  be an effective
torsion-free
be an effective
torsion-free  -module and
-module and
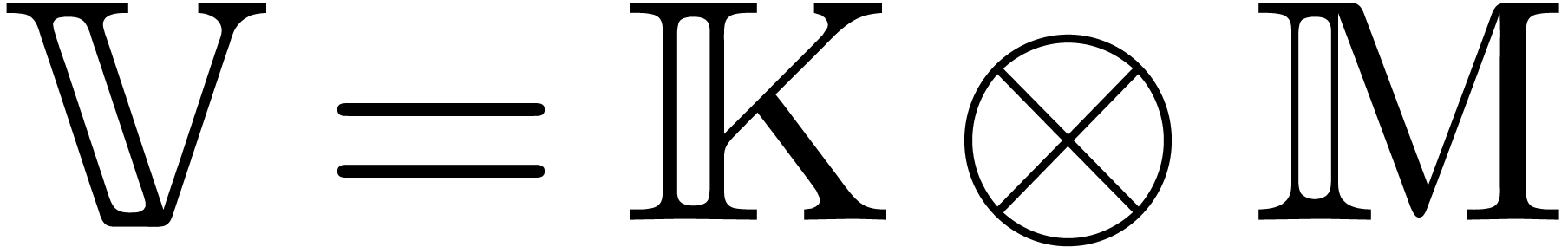 . Elements of
. Elements of  and
and  are fractions
are fractions 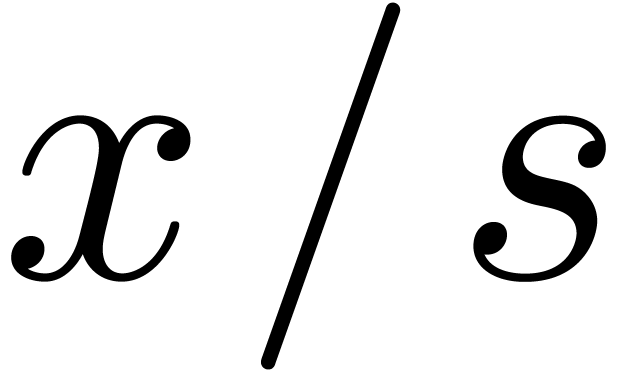 with
with 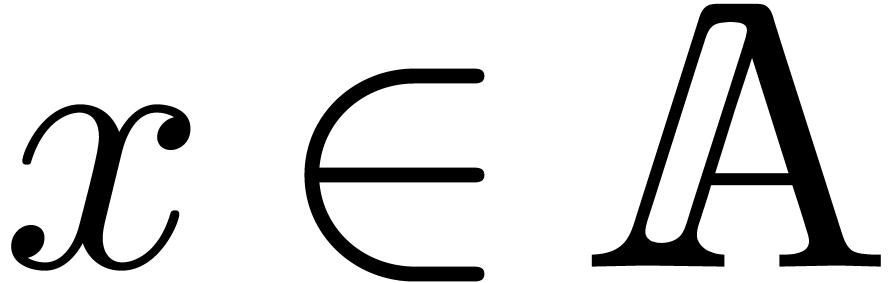 (resp.
(resp. 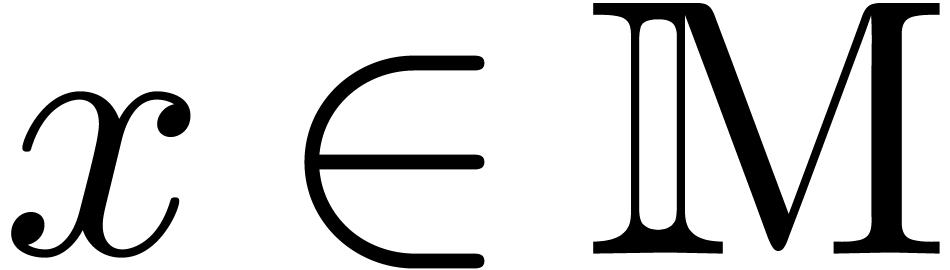 ) and
) and 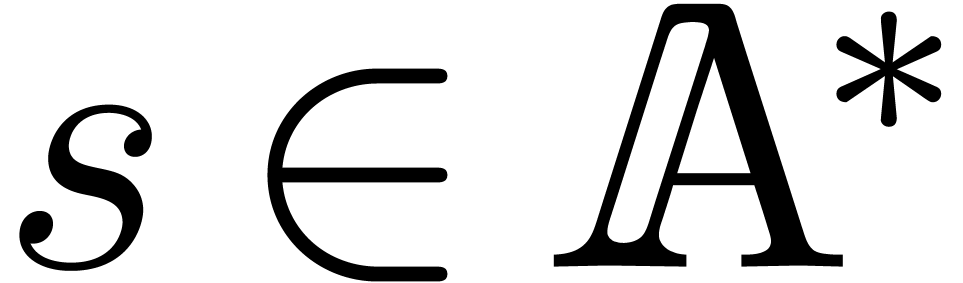 ,
and the operations
,
and the operations  on such fractions are as
usual:
on such fractions are as
usual:
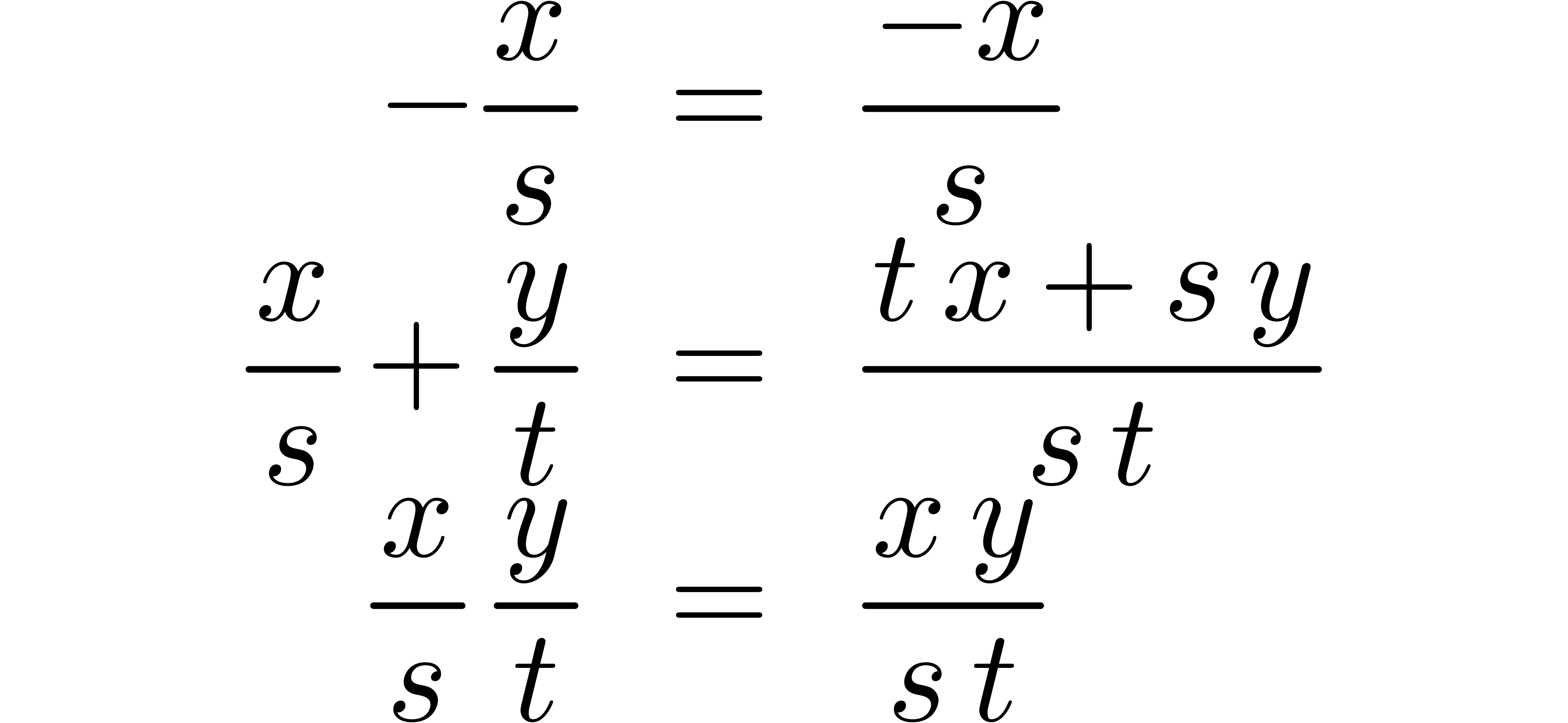
For 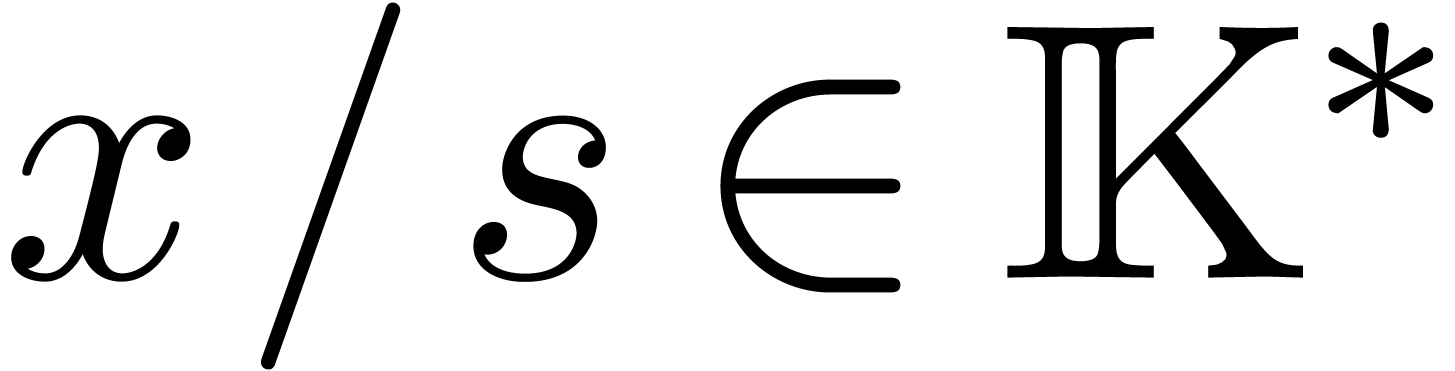 , we also have
, we also have 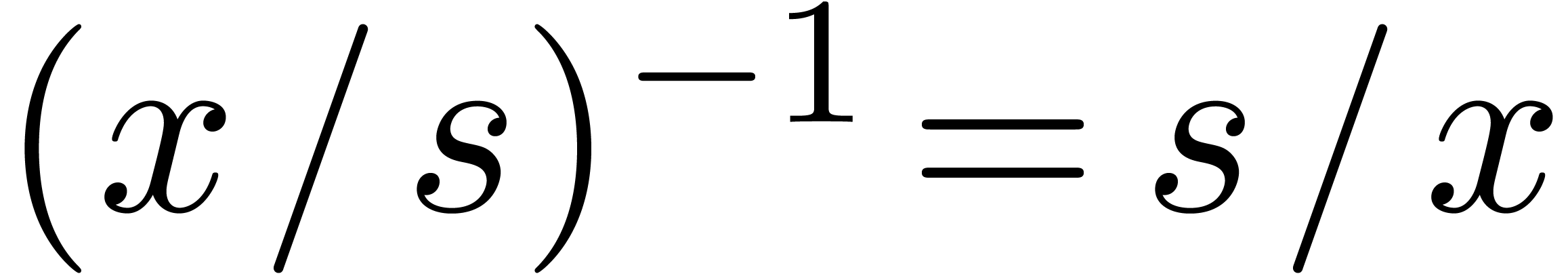 . It follows that
. It follows that  and
and  are effective fields and vector spaces.
Moreover, all field operations in
are effective fields and vector spaces.
Moreover, all field operations in  (and all
vector space operations in
(and all
vector space operations in  )
can be performed using only
)
can be performed using only 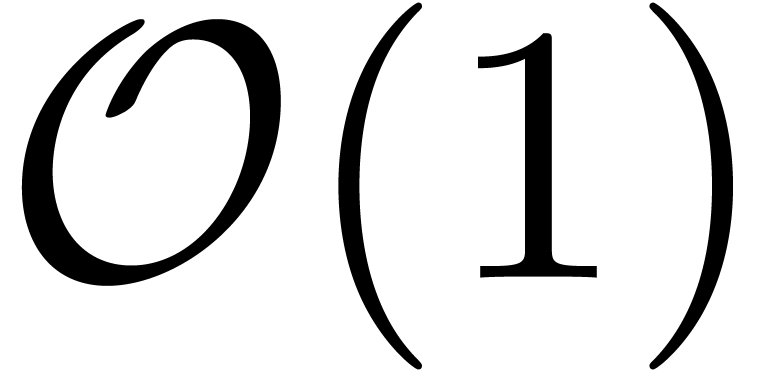 operations in
operations in  (resp.
(resp.  or
or  ).
).
We will say that  admits an effective partial
division, if for every
admits an effective partial
division, if for every 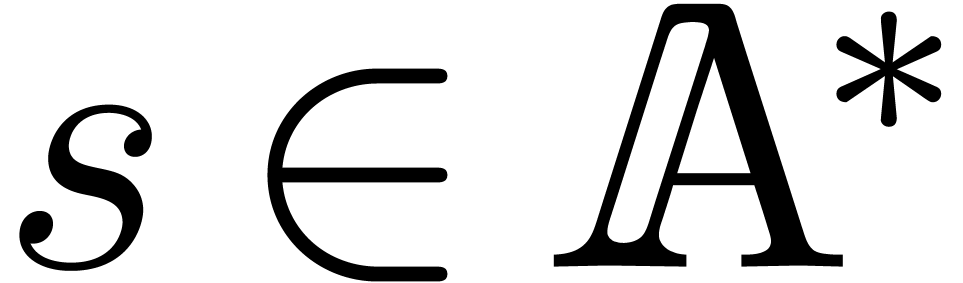 and
and  , we can compute the unique
, we can compute the unique 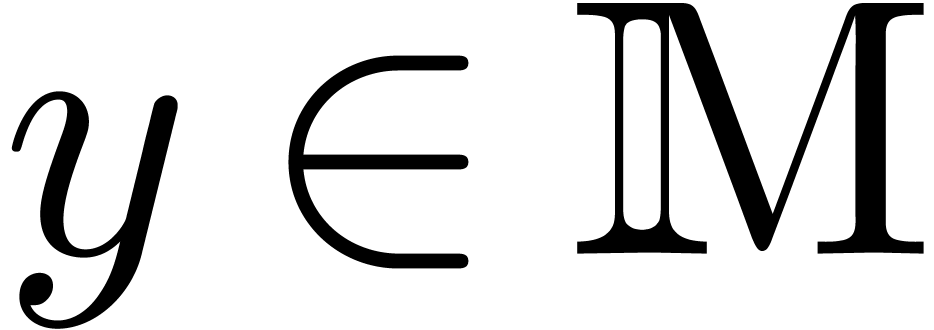 with
with 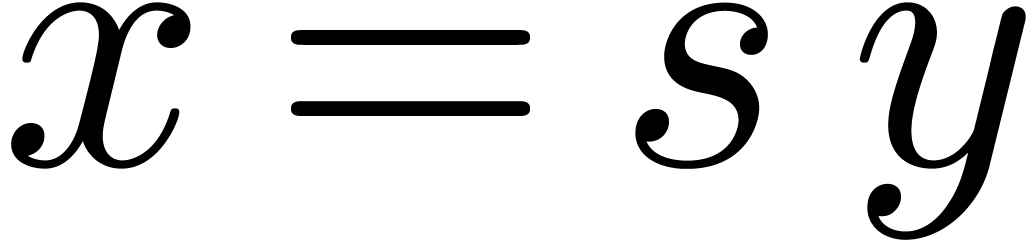 . From now on, we will
assume that this is the case, and we will count any division of the
above kind as one operation in
. From now on, we will
assume that this is the case, and we will count any division of the
above kind as one operation in  .
Given
.
Given 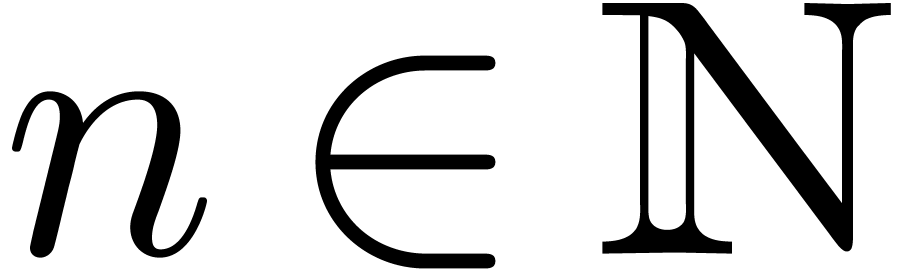 , we define
, we define
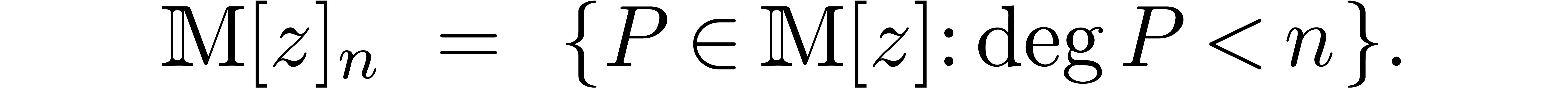
Given  and
and  ,
we will denote by
,
we will denote by 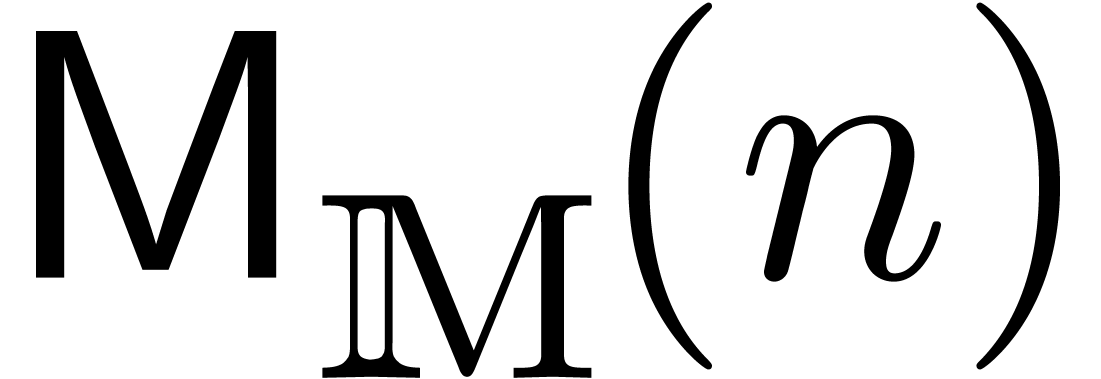 the number of operations in
the number of operations in
 and
and  which are needed in
order to compute the product
which are needed in
order to compute the product 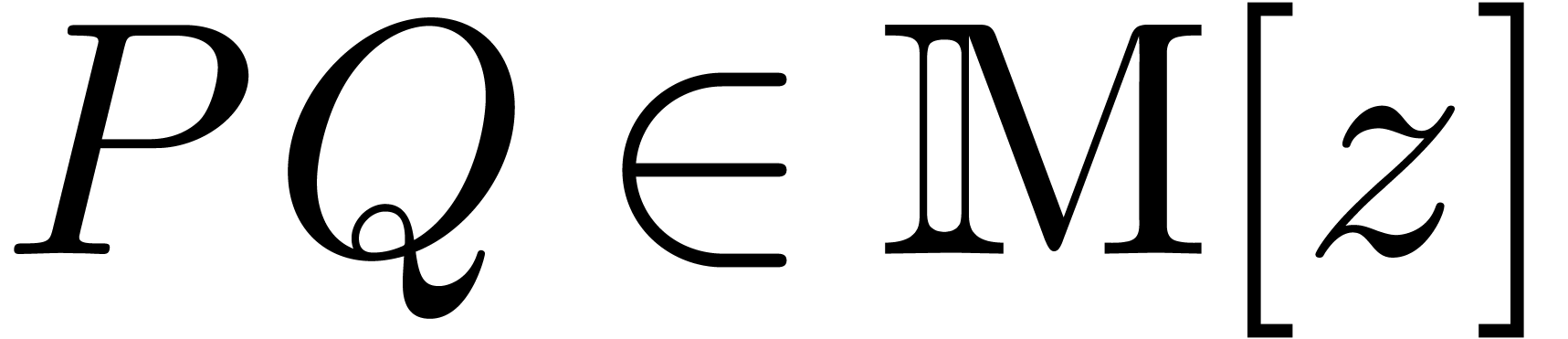 .
.
 be an effective and commutative integral
domain and
be an effective and commutative integral
domain and  an effective torsion-free
an effective torsion-free  -module with an effective partial
division. There exists a constant
-module with an effective partial
division. There exists a constant  ,
such that the following holds: for any
,
such that the following holds: for any  ,
,
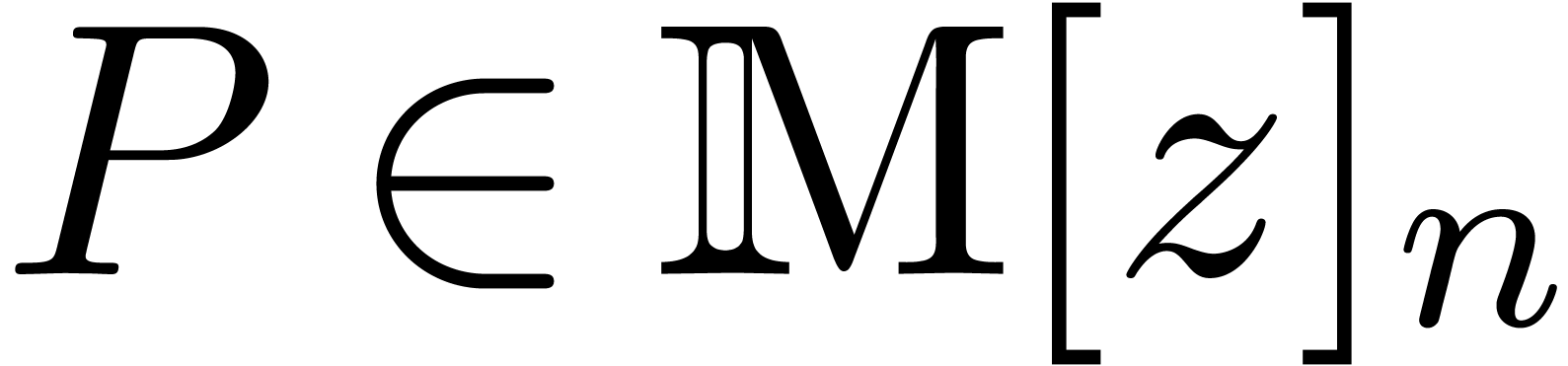 and
and 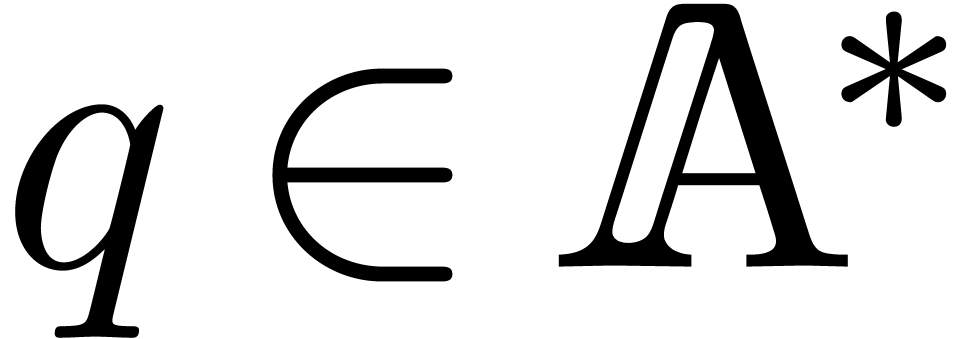 such that
such that  are pairwise distinct, we have:
are pairwise distinct, we have:
We may compute 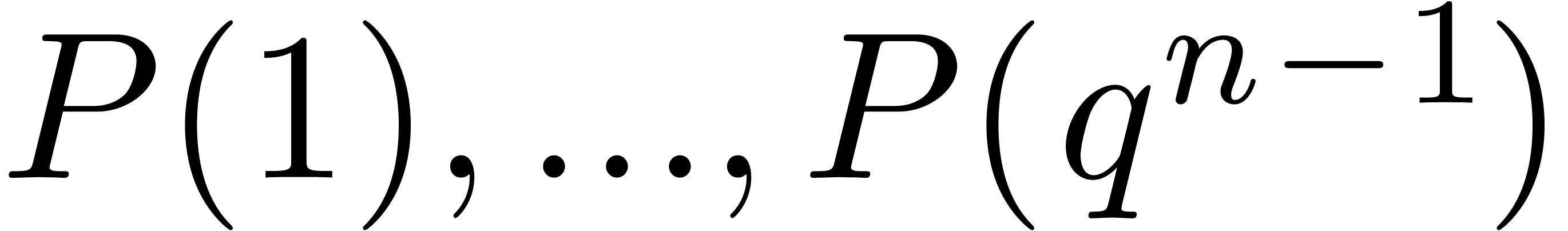 from
from  using
using 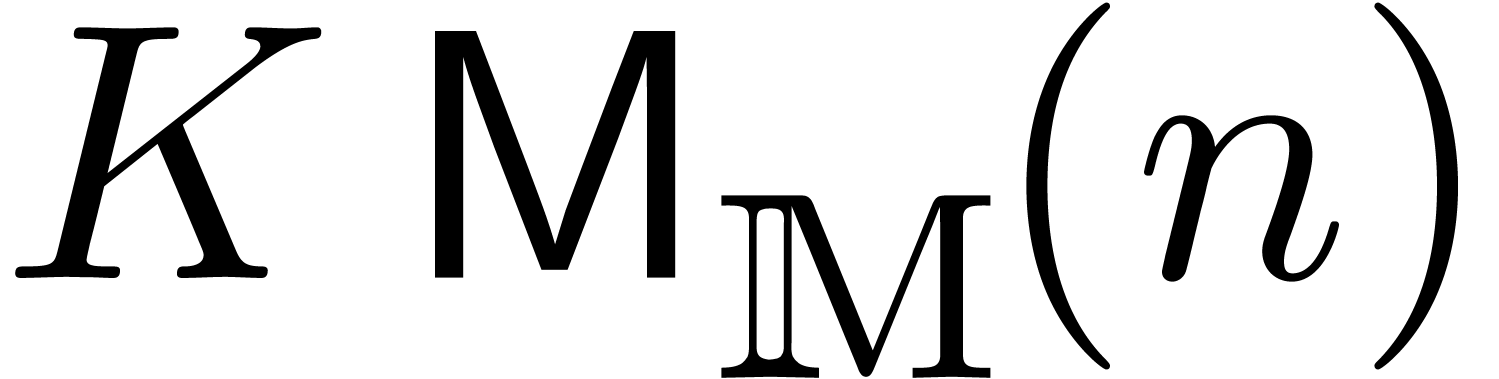 operations in
operations in  and
and  .
.
We may reconstruct 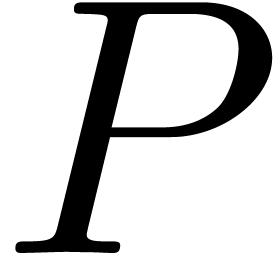 from
from  using
using 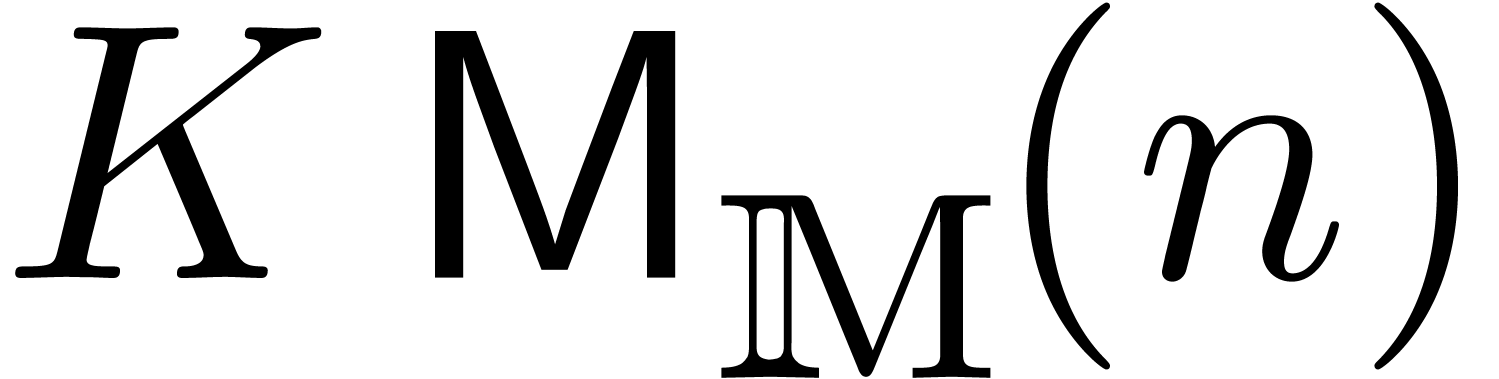 operations in
operations in  and
and  .
.
Proof. In the case when 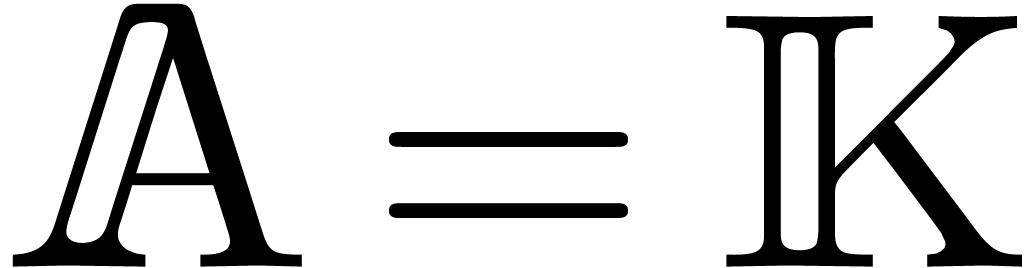 is a field of characteristic zero and
is a field of characteristic zero and  ,
this result was first proven in [BS05]. More precisely, the
conversions can be done using the algorithms
NewtonEvalGeom, NewtonInterpGeom,
NewtonToMonomialGeom and
MonomialToNewtonGeom in that paper. Examining these
algorithms, we observe that general elements in
,
this result was first proven in [BS05]. More precisely, the
conversions can be done using the algorithms
NewtonEvalGeom, NewtonInterpGeom,
NewtonToMonomialGeom and
MonomialToNewtonGeom in that paper. Examining these
algorithms, we observe that general elements in  are only multiplied with elements in
are only multiplied with elements in 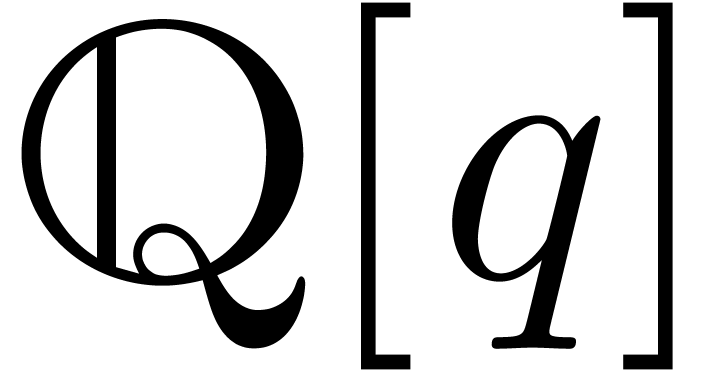 and divided
by elements of the set
and divided
by elements of the set 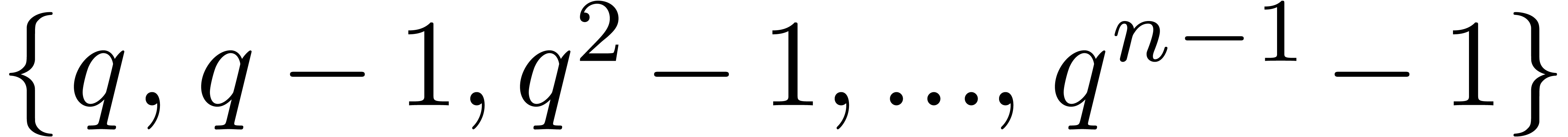 . In
particular, the algorithms can still be applied in the more general case
when
. In
particular, the algorithms can still be applied in the more general case
when 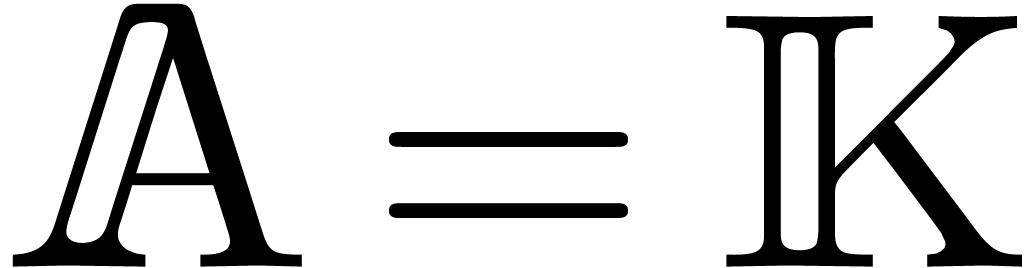 is a field of characteristic zero and
is a field of characteristic zero and 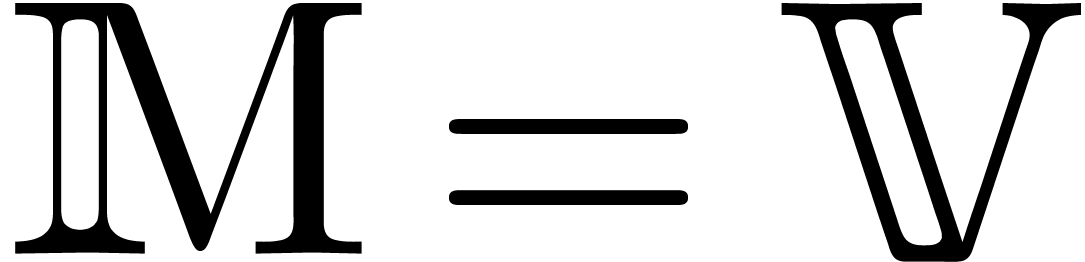 a vector space.
a vector space.
If  is only an effective commutative integral
domain of characteristic zero and
is only an effective commutative integral
domain of characteristic zero and  an effective
torsion-free
an effective
torsion-free  -module with an
effective partial division, then we define the effective field
-module with an
effective partial division, then we define the effective field  and the effective vector field
and the effective vector field  as
above, and we may still apply the generalized algorithms for multipoint
evaluation and interpolation in
as
above, and we may still apply the generalized algorithms for multipoint
evaluation and interpolation in  .
In particular, both multipoint evaluation and interpolation can still be
done using
.
In particular, both multipoint evaluation and interpolation can still be
done using 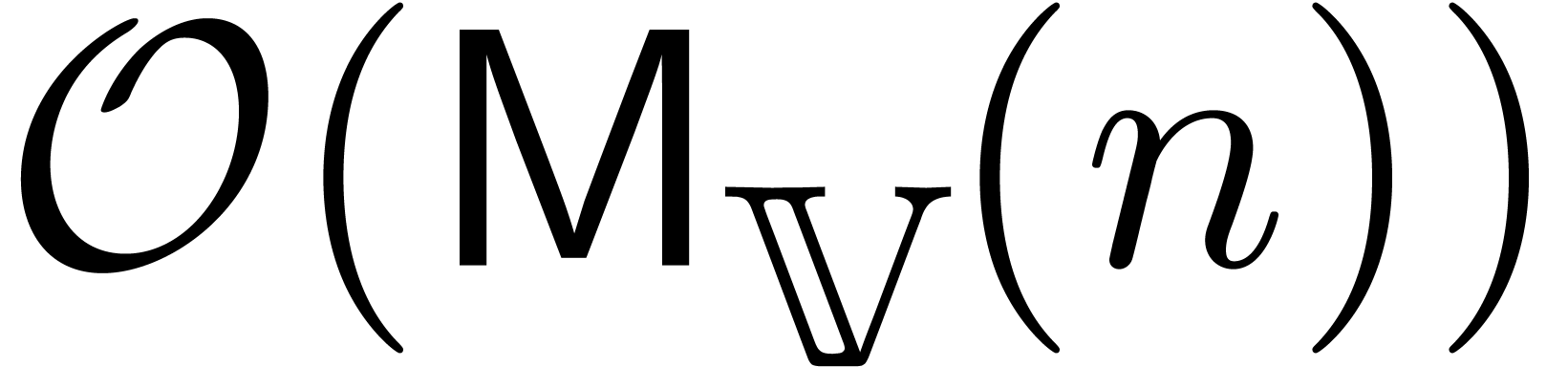 operations in
operations in  and
and  , whence
, whence 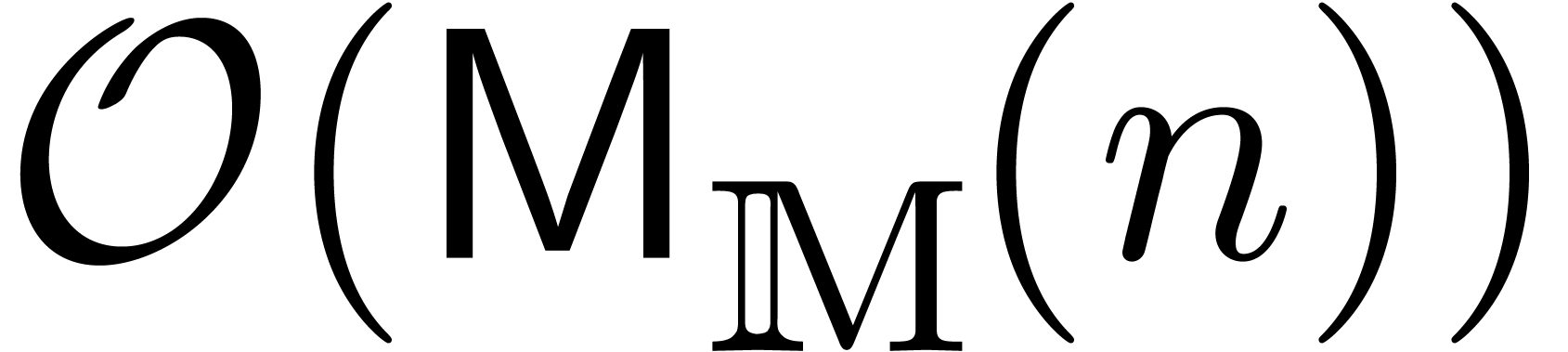 operations in
operations in  and
and  .
If we know that the end-results of these algorithms are really
in the subspace
.
If we know that the end-results of these algorithms are really
in the subspace 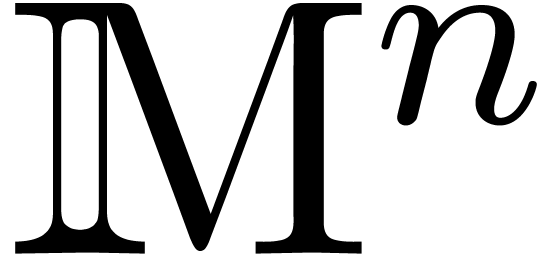 of
of  (or
in the subring
(or
in the subring 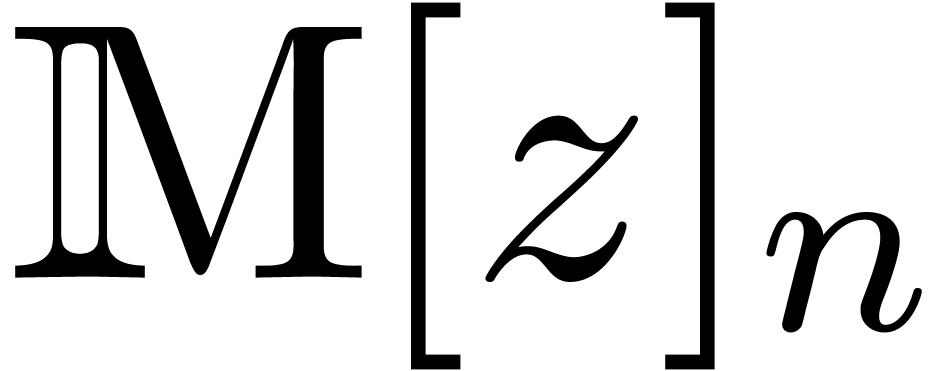 of
of 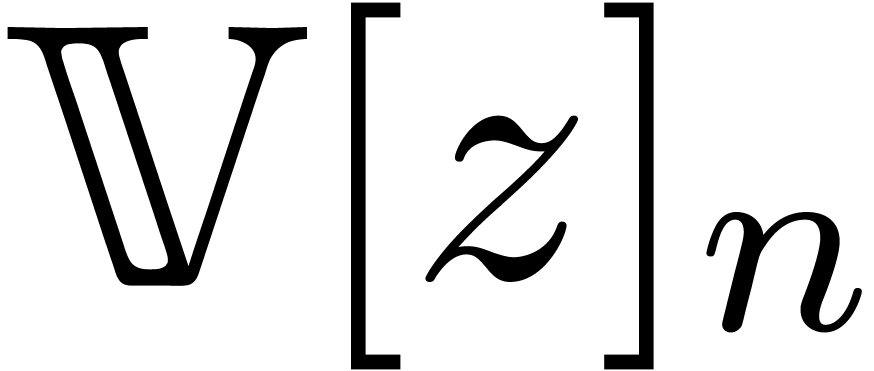 ),
then we use the partial division in
),
then we use the partial division in  to replace
their representations in
to replace
their representations in  (or
(or 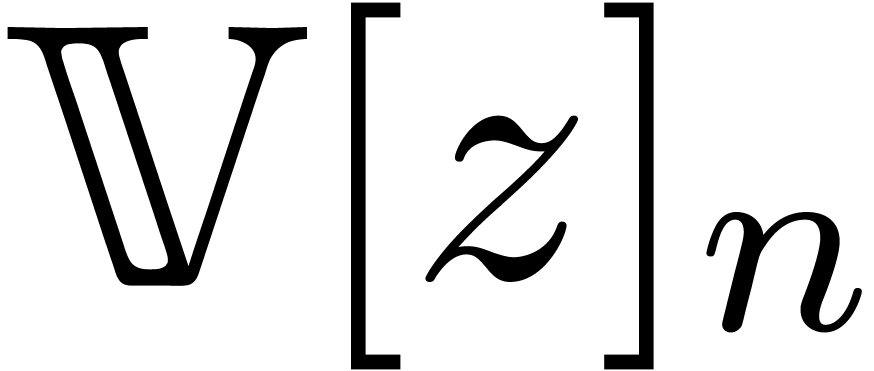 ) by representations in
) by representations in 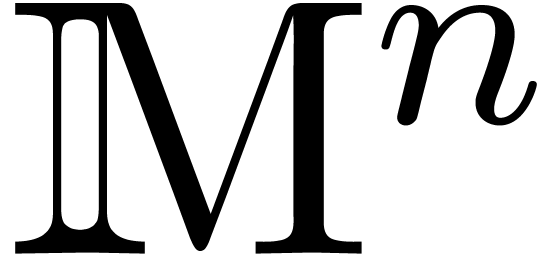 (or
(or 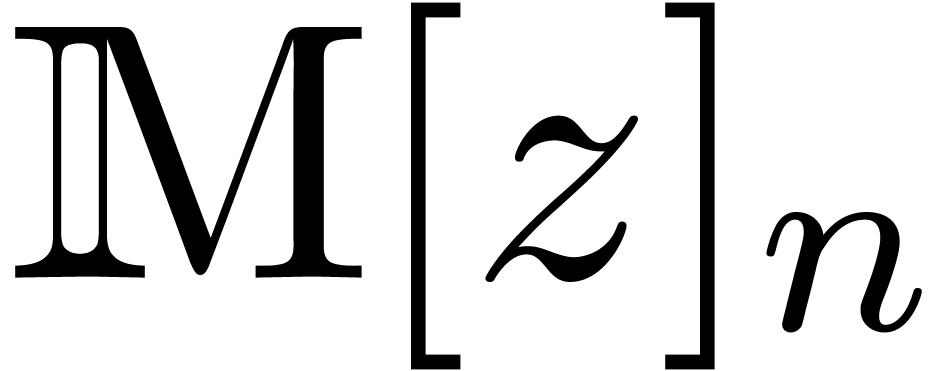 ).
).
 be an effective and commutative integral
domain and
be an effective and commutative integral
domain and  an effective
an effective  -module. There exists a constant
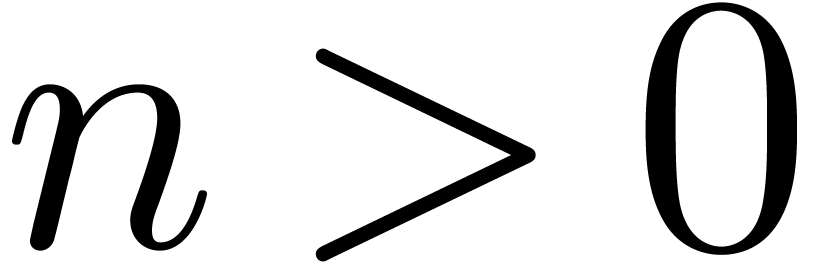
-module. There exists a constant 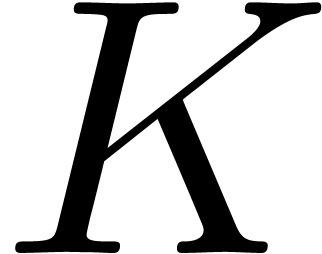 , such that the following holds: for any
, such that the following holds: for any
 ,
, 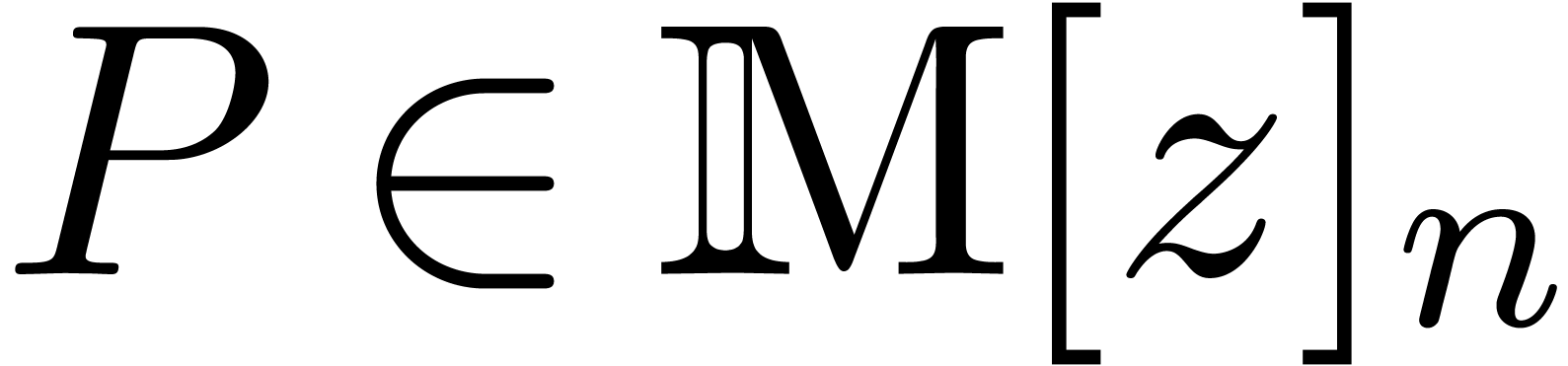 and
and 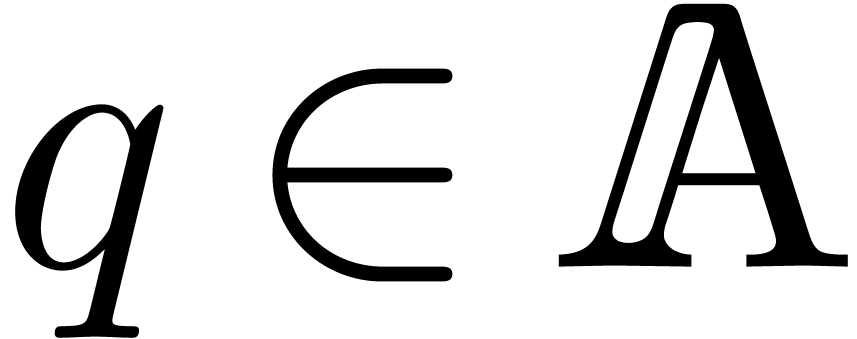 such that
such that  are
pairwise distinct and such that
are
pairwise distinct and such that  and
and 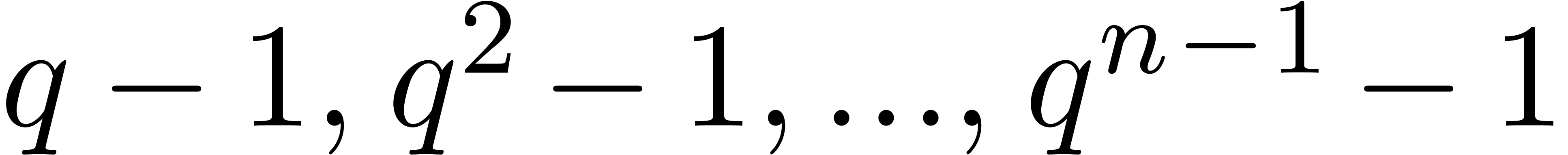 are all invertible in
are all invertible in  ,
we have:
,
we have:
We may compute 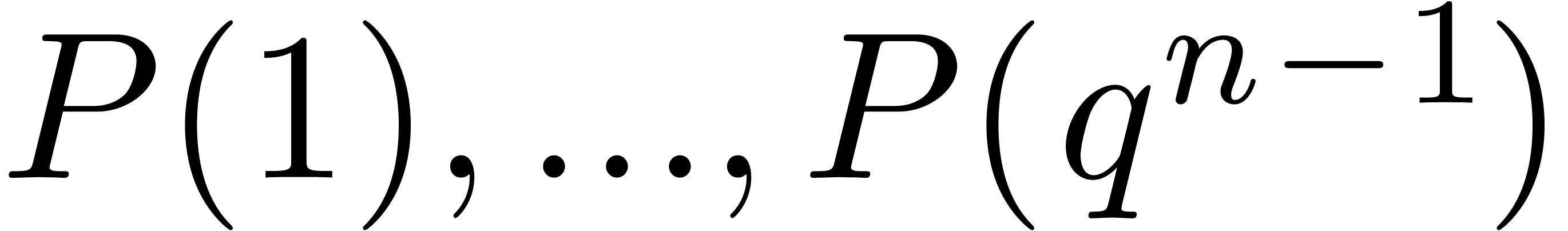 from
from  using
using 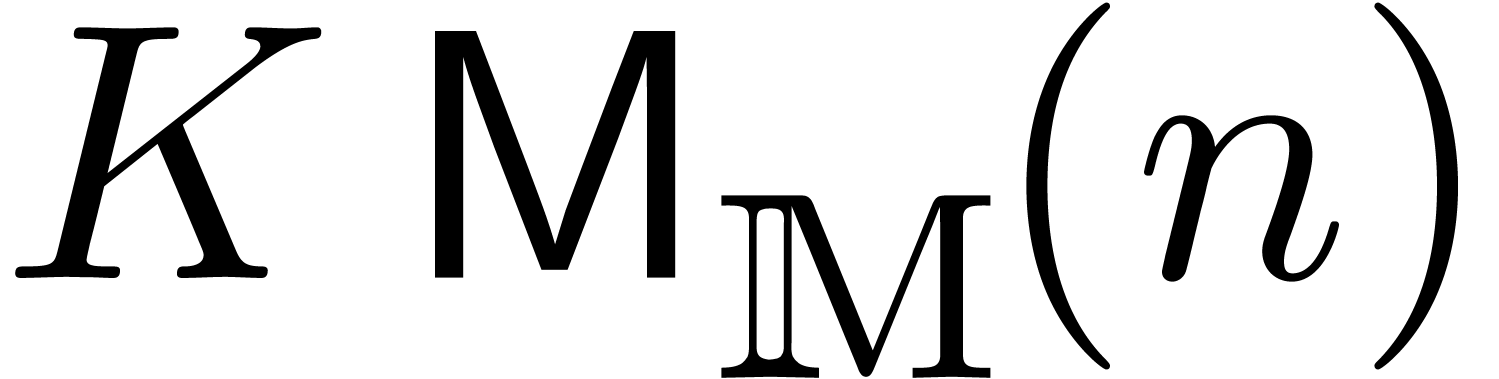 operations in
operations in  and
and  .
.
We may reconstruct 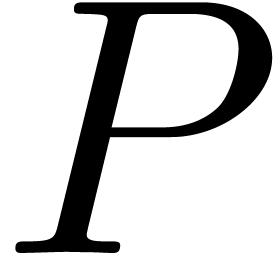 from
from 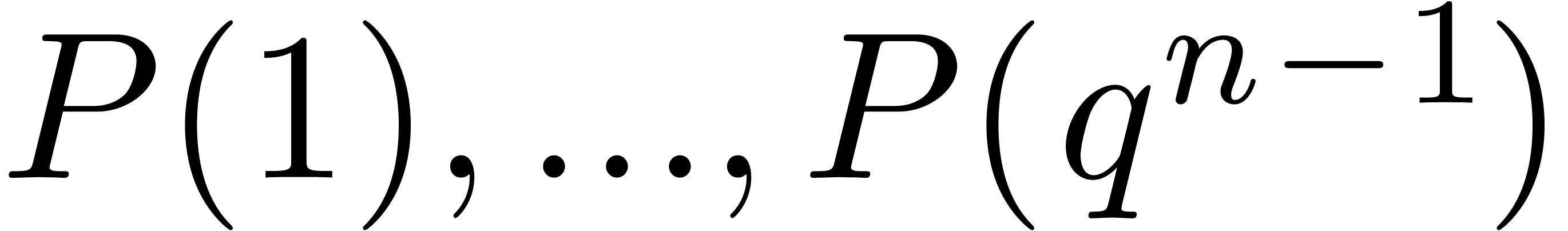 using
using 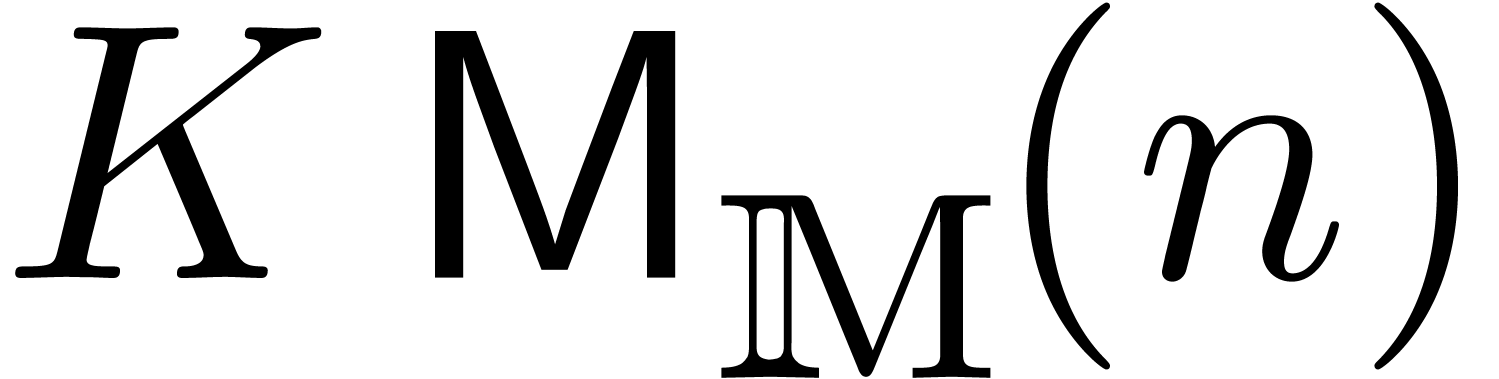 operations in
operations in  and
and  .
.
Proof. We again use straightforward
generalizations of the algorithms in [BS05], using the fact
that we only divide by elements in the set 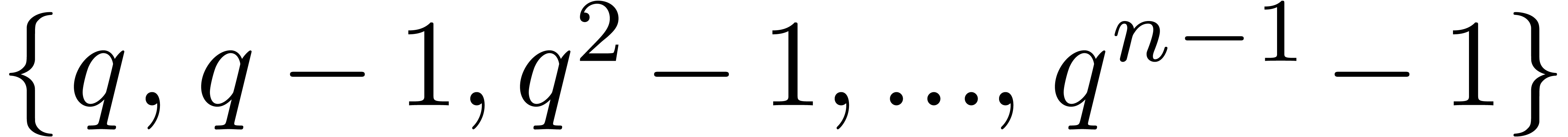 .
.
Let  be an effective (possibly non commutative)
ring and recall that
be an effective (possibly non commutative)
ring and recall that

Given a power series  and
and 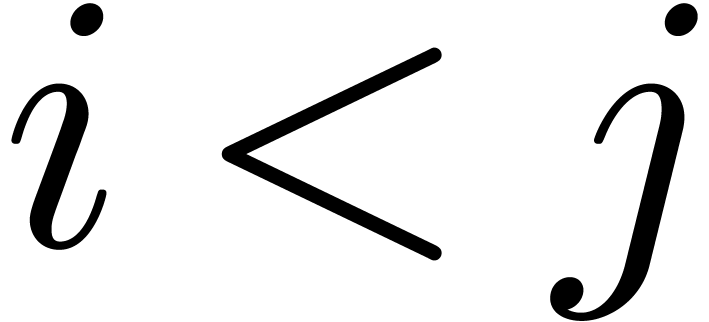 , we will also use the notations
, we will also use the notations
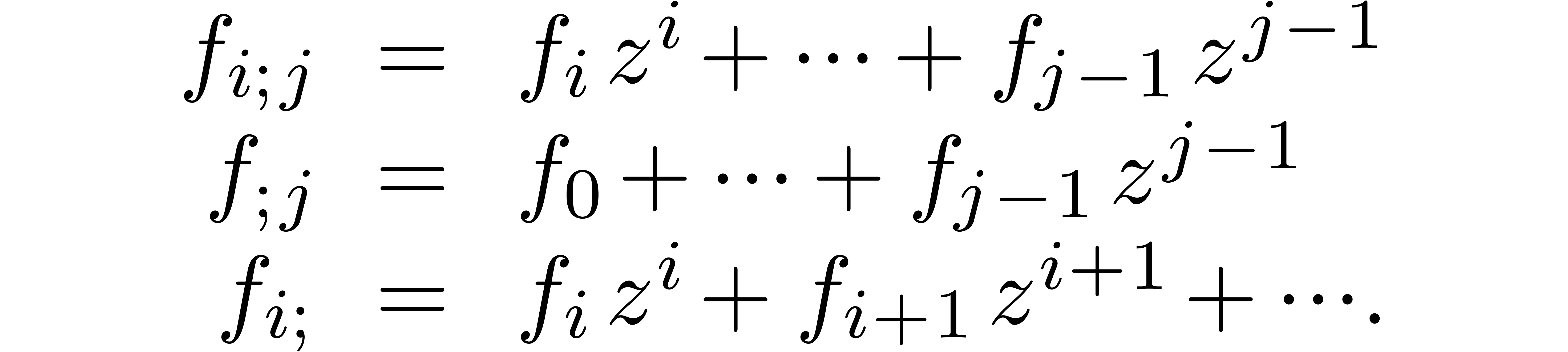
The fast relaxed algorithms from [Hoe07] are all based on two main changes of representation: “blocking” and the fast Fourier transform. Let us briefly recall these transformations and how to use them for the design of fast algorithms for relaxed multiplication.
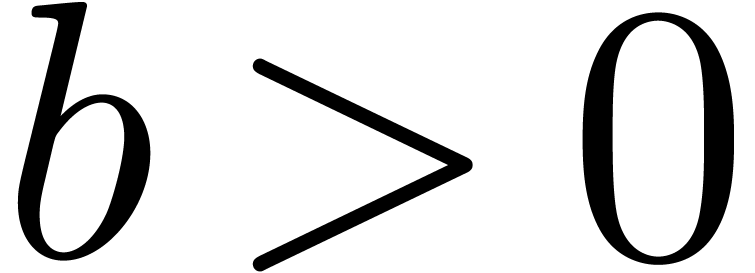 , the
first operation of blocking rewrites a power series
, the
first operation of blocking rewrites a power series  as a series in
as a series in 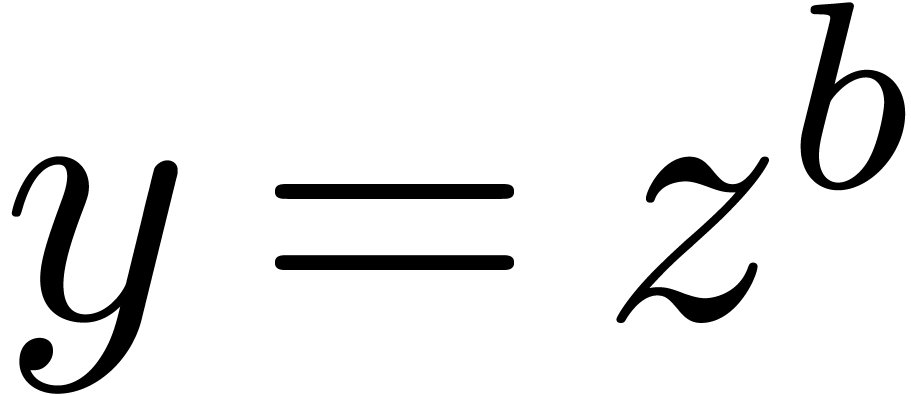 with coefficients
in
with coefficients
in 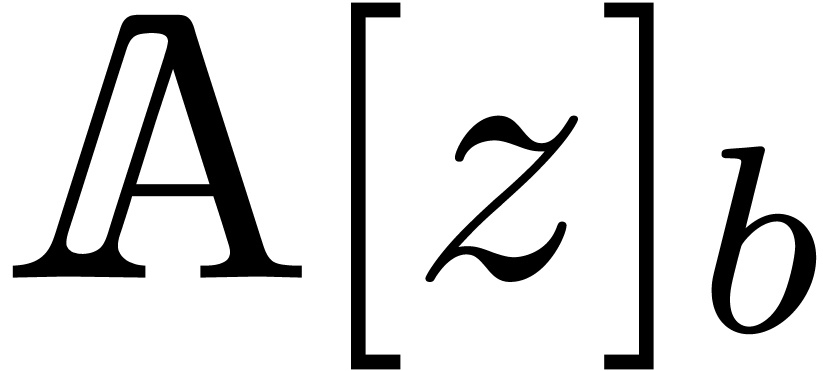
Given  , we may then compute
, we may then compute
 using
using
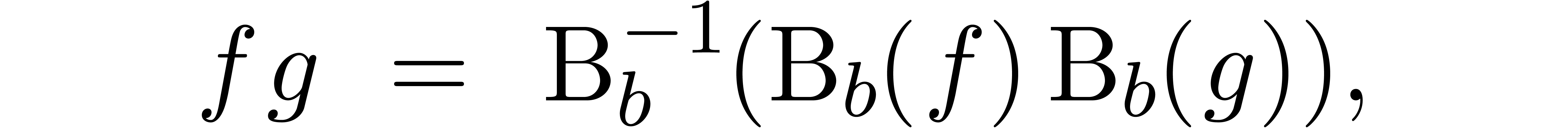
where 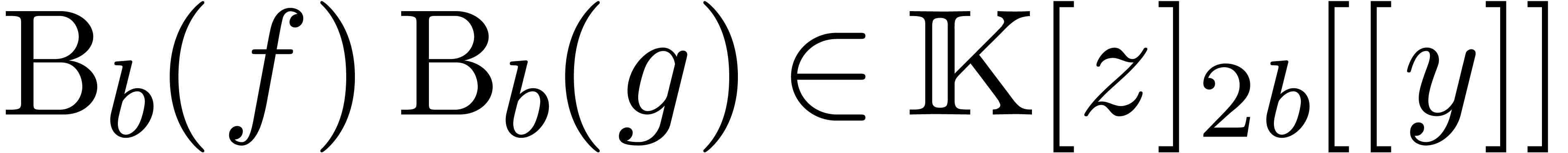 and
and
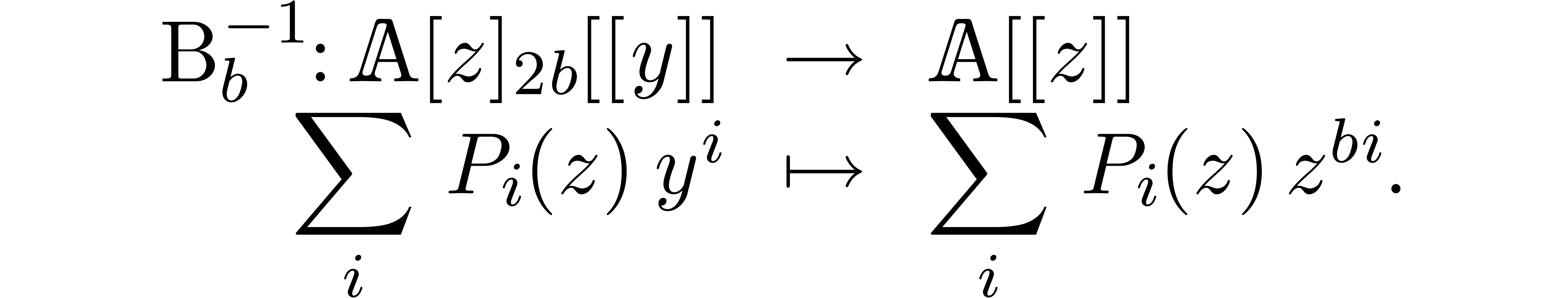
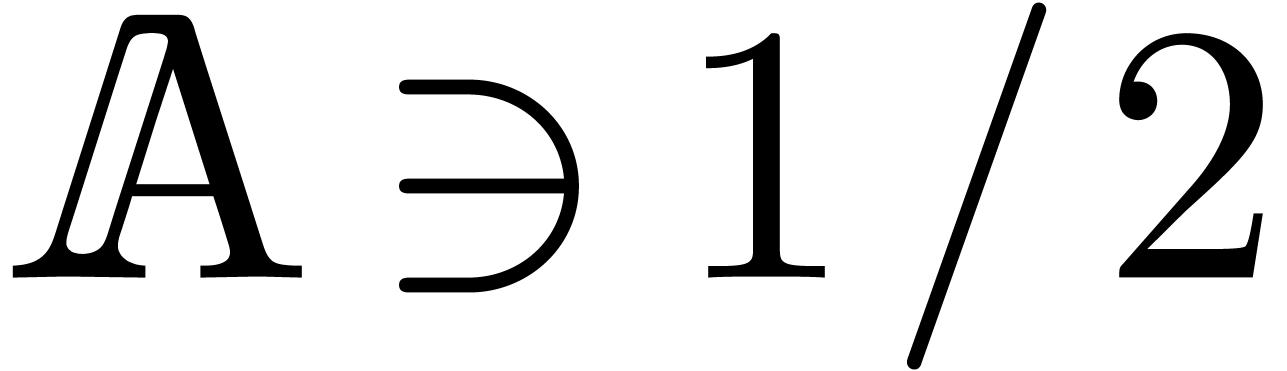 , that
, that
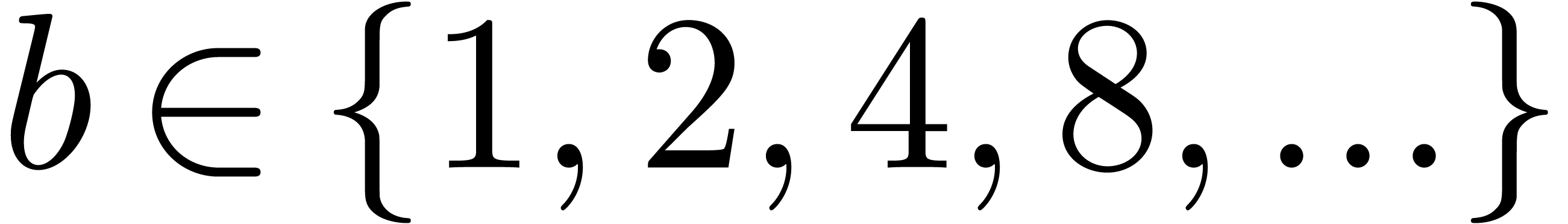 , and that
, and that  admits a primitive
admits a primitive  -th root
of unity
-th root
of unity  . Then the
discrete Fourier transform provides us with an isomorphism
. Then the
discrete Fourier transform provides us with an isomorphism
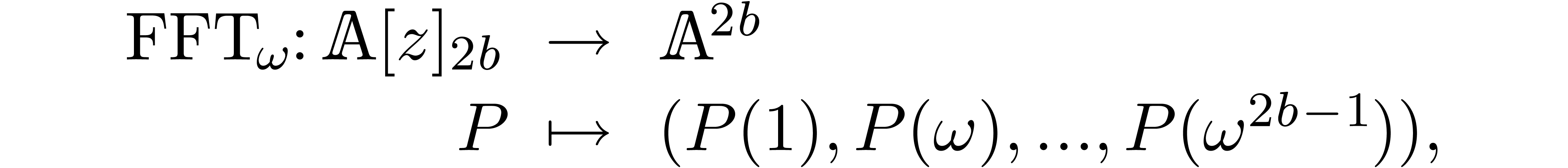
and it is classical [CT65] that both  and
and 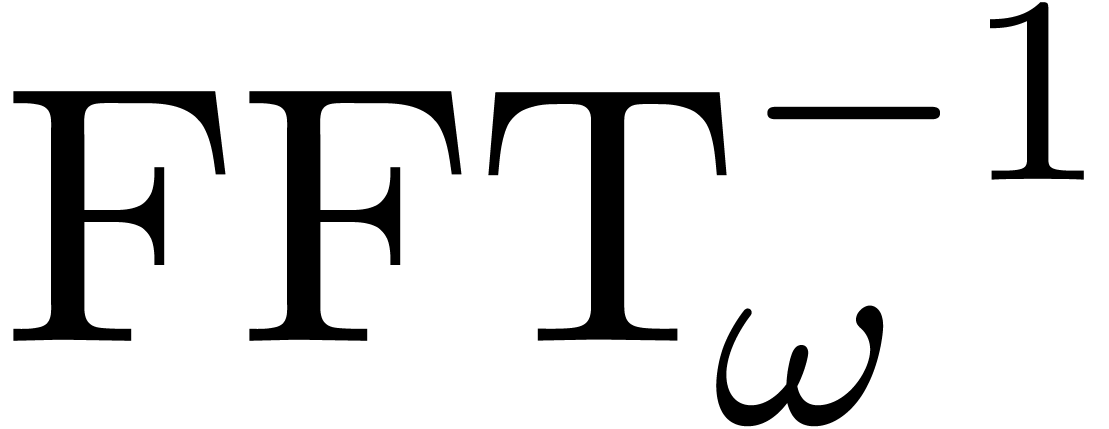 can be computed using
can be computed using 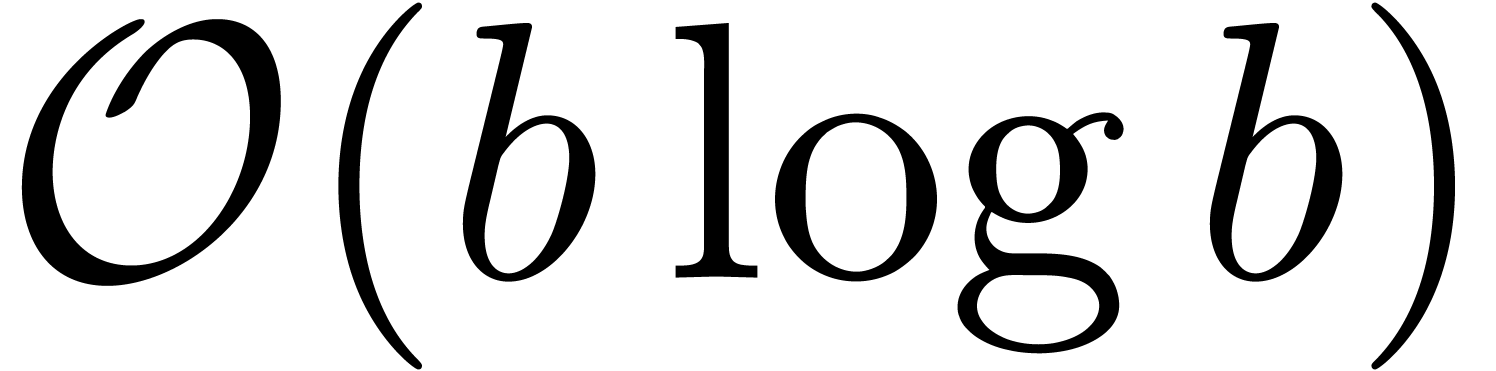 operations in
operations in  . The
operations
. The
operations  and
and 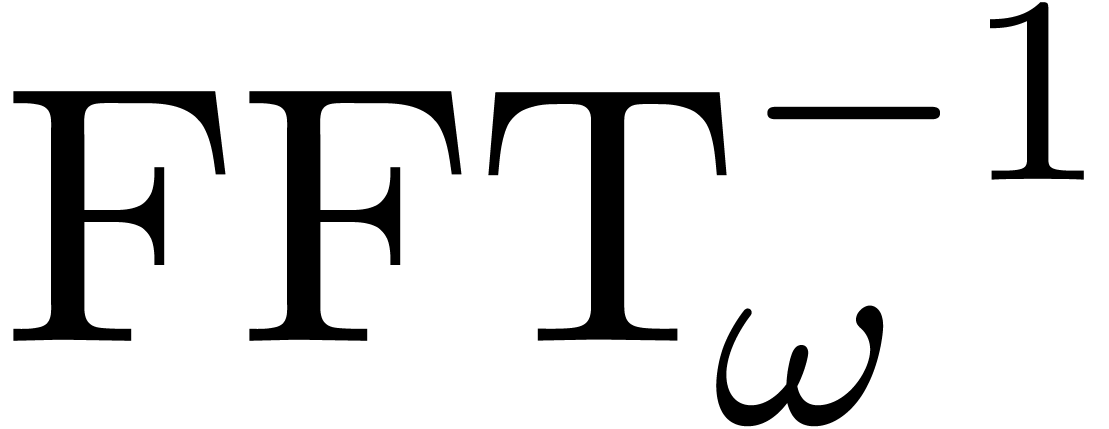 extend
naturally to
extend
naturally to 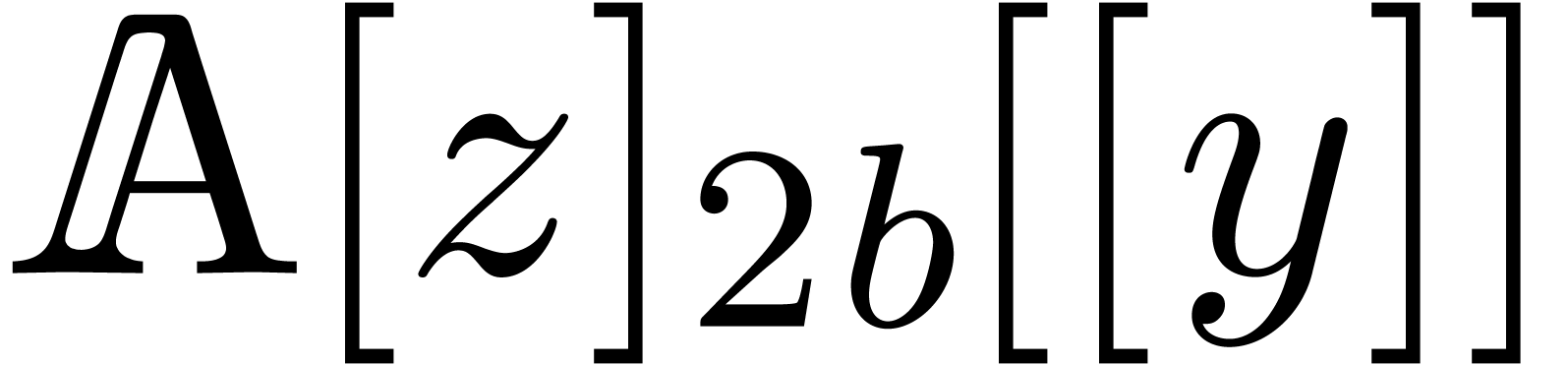 via
via
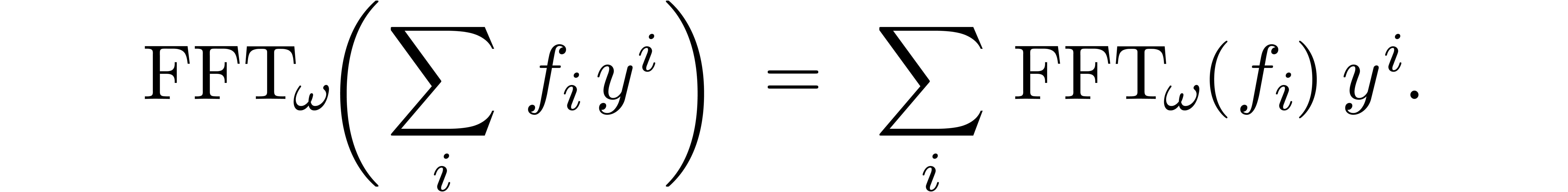
This allows us to compute  using the formula
using the formula
The first  coefficients of
coefficients of  can be computed using at most
can be computed using at most 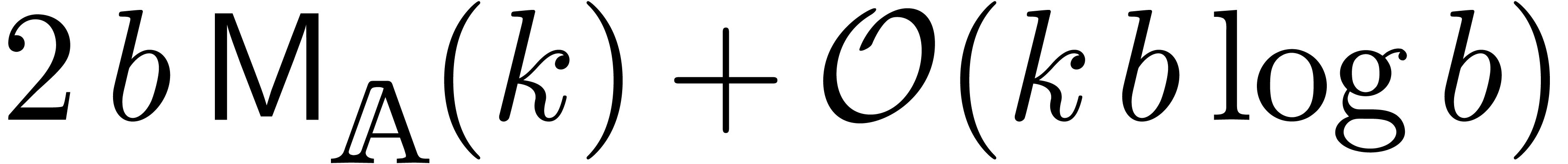 operations in
operations in
 .
.
 -th
coefficient of the right hand side may depend on the
-th
coefficient of the right hand side may depend on the  -th coefficients of
-th coefficients of 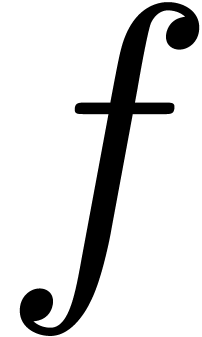 and
and  . In order to make (6) suitable for relaxed multiplication, we have to treat the
first
. In order to make (6) suitable for relaxed multiplication, we have to treat the
first 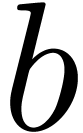 coefficients of
coefficients of 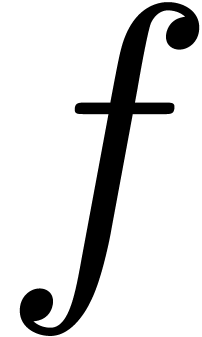 and
and  apart. Indeed, the formula
apart. Indeed, the formula
allows for the relaxed computation of 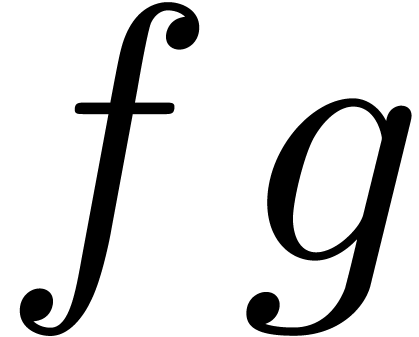 at order
at order
 using at most
using at most
operations in  . Similarly,
the formula
. Similarly,
the formula

allows for the semi-relaxed computation of 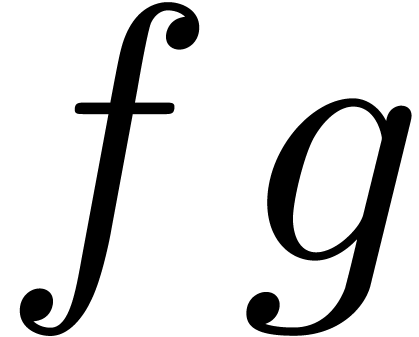 at
order
at
order 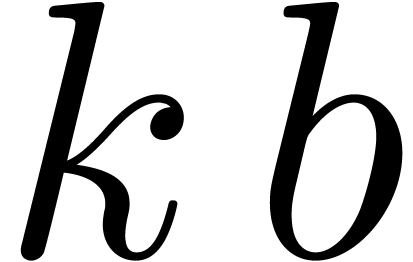 using at most
using at most
operations in  . For a given
expansion order
. For a given
expansion order 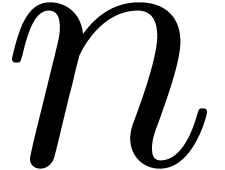 , one may
take
, one may
take  , and use the above
formula in a recursive manner. This yields [Hoe07, Theorem
11]
, and use the above
formula in a recursive manner. This yields [Hoe07, Theorem
11]
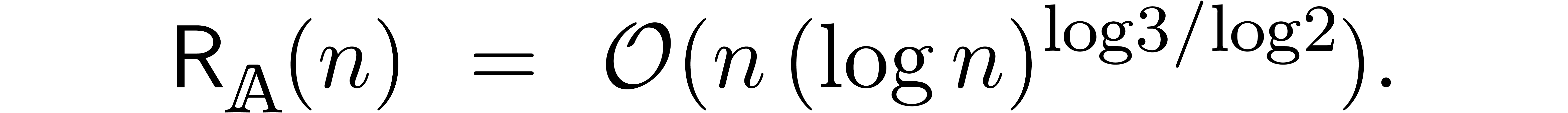
Remark 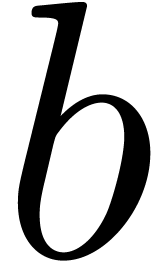 is chosen as a function of
is chosen as a function of 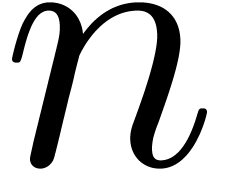 , the above method really describes a relaxed
algorithm for computing the product up to an order
, the above method really describes a relaxed
algorithm for computing the product up to an order 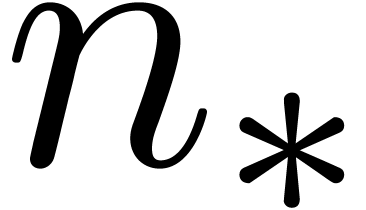 which is specified in advance. In fact, such an algorithm automatically
yields a genuine relaxed algorithm with the same complexity (up to a
constant factor), by doubling the order
which is specified in advance. In fact, such an algorithm automatically
yields a genuine relaxed algorithm with the same complexity (up to a
constant factor), by doubling the order 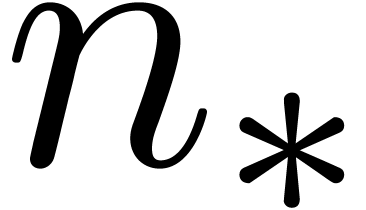 each
time when needed.
each
time when needed.
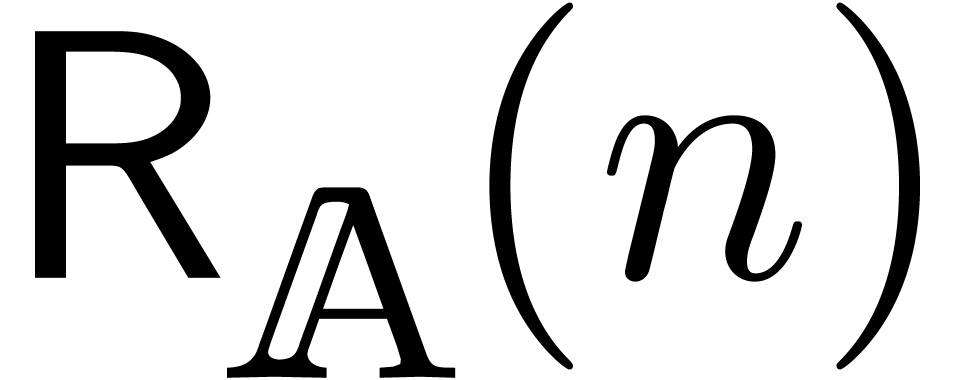 and
and 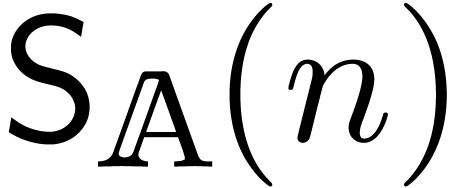 . In fact, there exists
a straightforward reduction of relaxed multiplication to semi-relaxed
multiplication. First of all, the relaxed multiplication of two power
series
. In fact, there exists
a straightforward reduction of relaxed multiplication to semi-relaxed
multiplication. First of all, the relaxed multiplication of two power
series 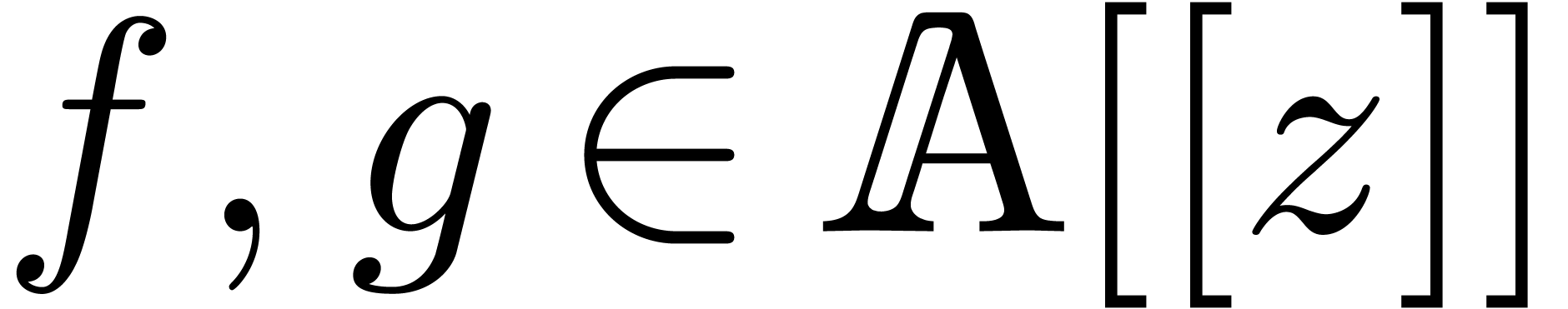 up to order
up to order 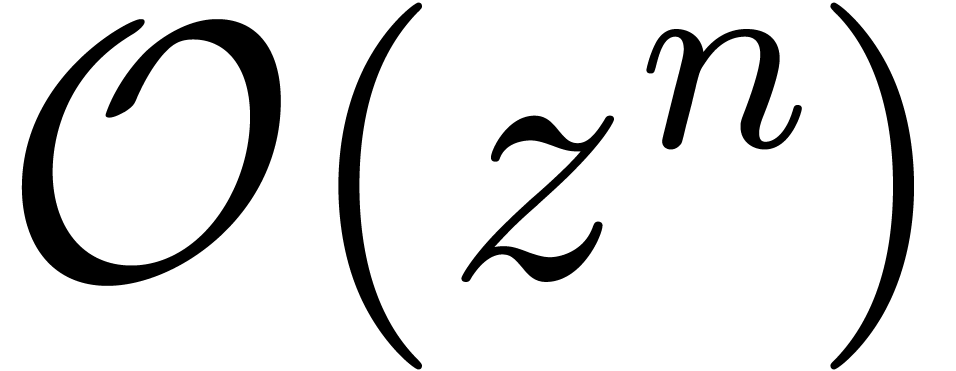 clearly reduces to the relaxed multiplication of the two polynomials
clearly reduces to the relaxed multiplication of the two polynomials
 and
and  up to order
up to order 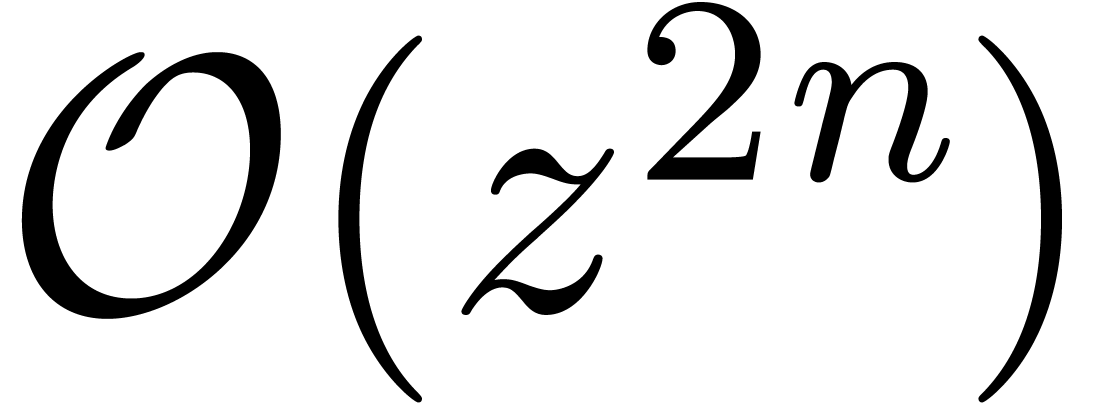 . Now the formula
. Now the formula
shows that a relaxed product of two polynomials 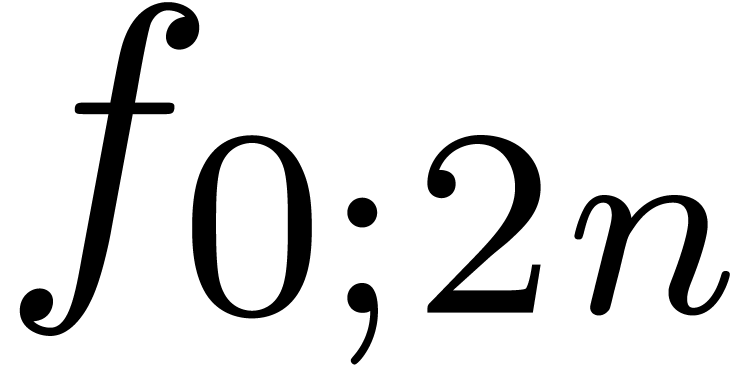 and
and 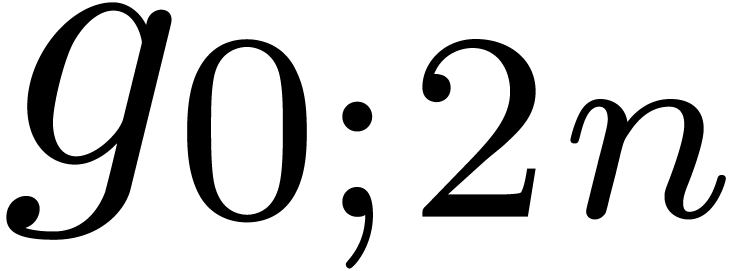 of degrees
of degrees 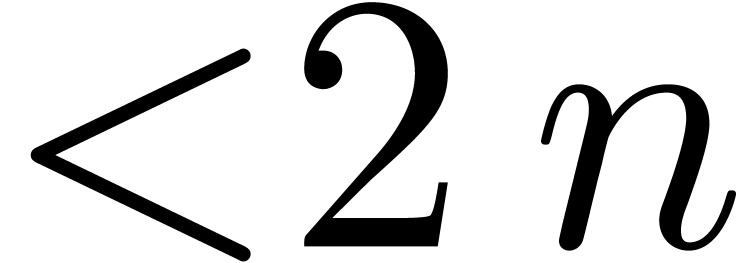 reduces
to a relaxed product
reduces
to a relaxed product 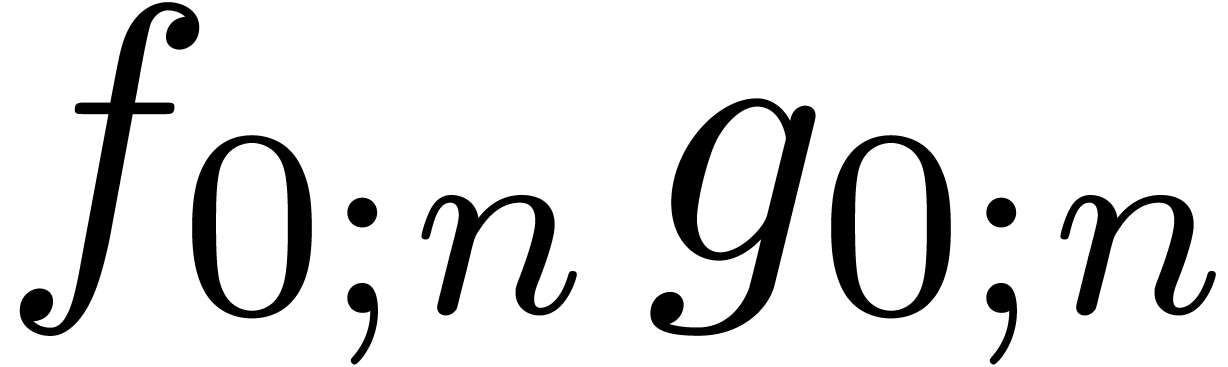 of half the size, two
semi-relaxed products
of half the size, two
semi-relaxed products 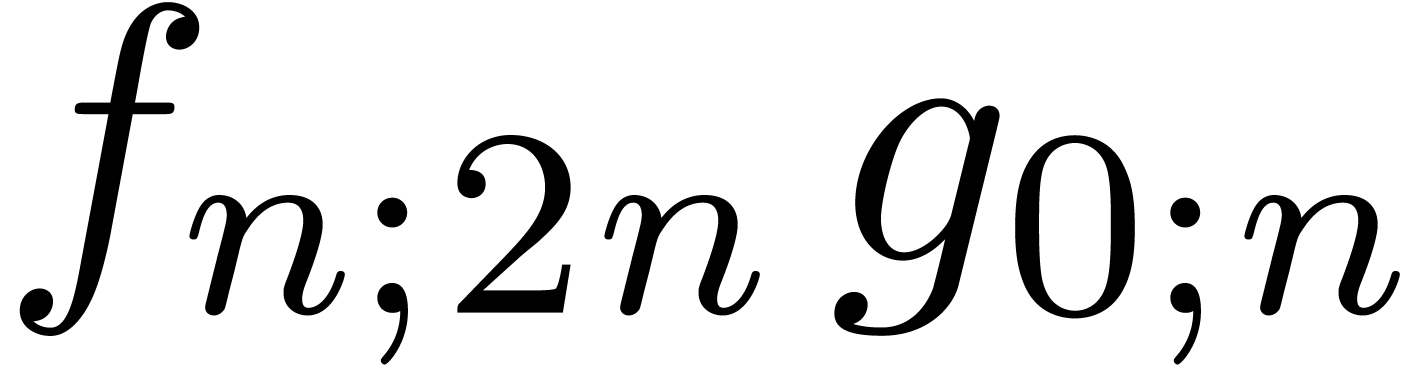 ,
, 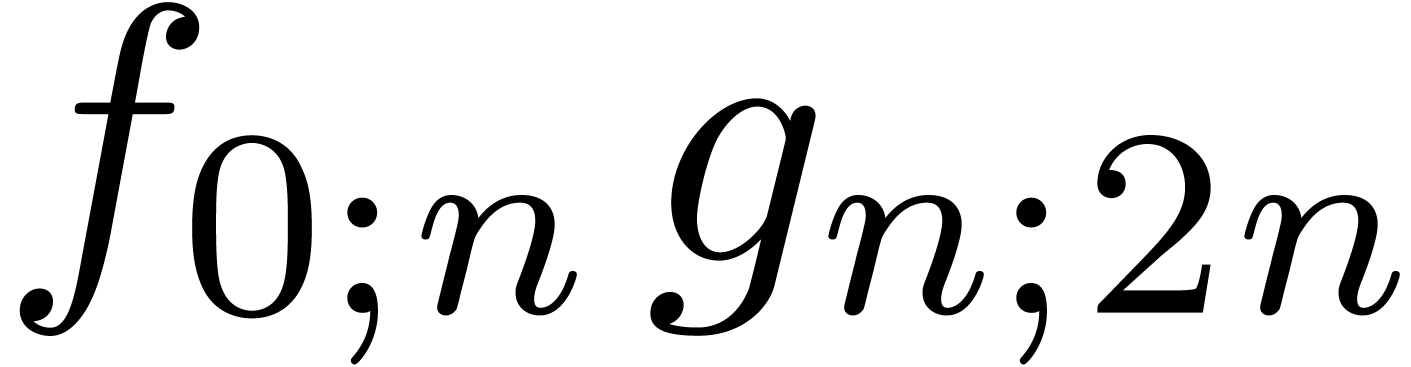 , and one non-relaxed product
, and one non-relaxed product 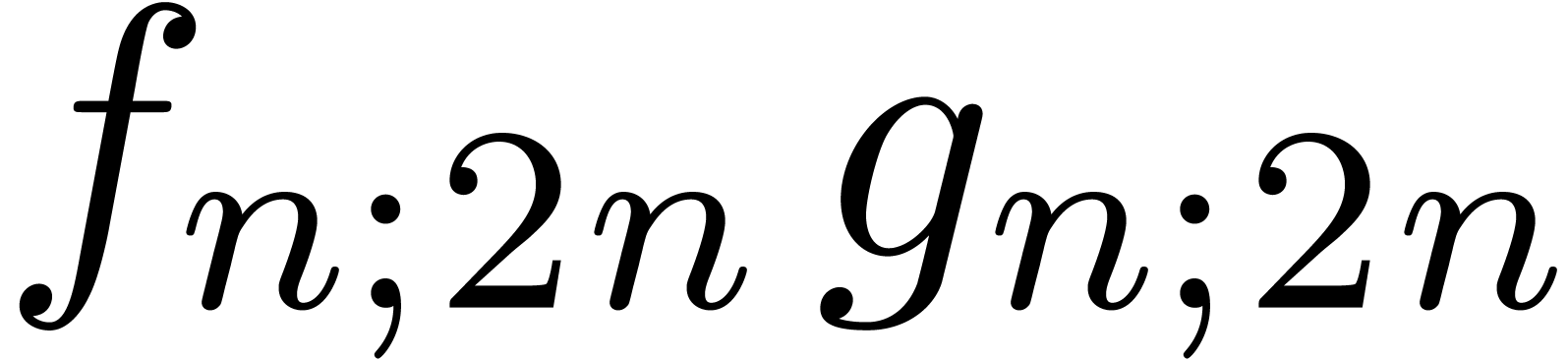 . Under the assumptions that
. Under the assumptions that 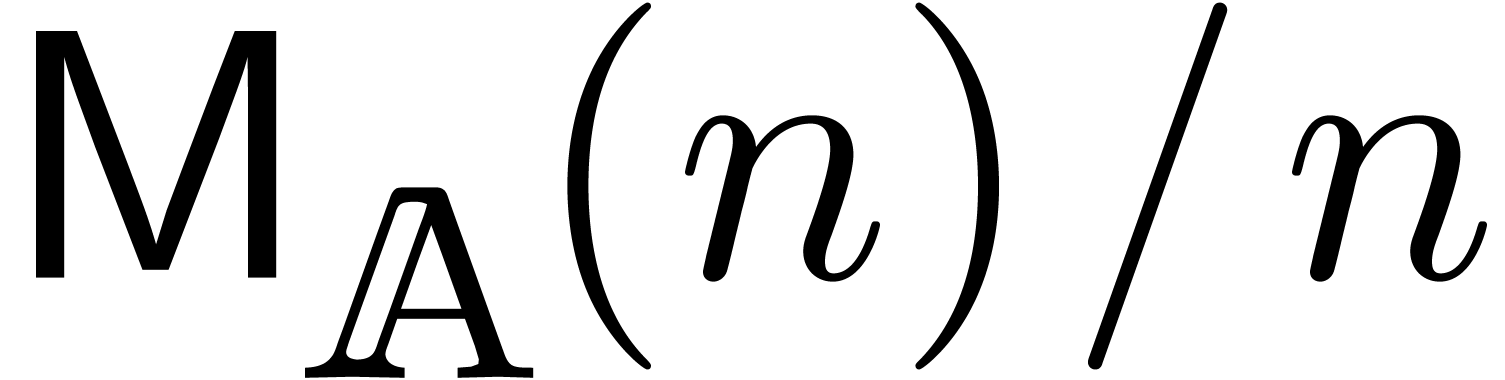 and
and 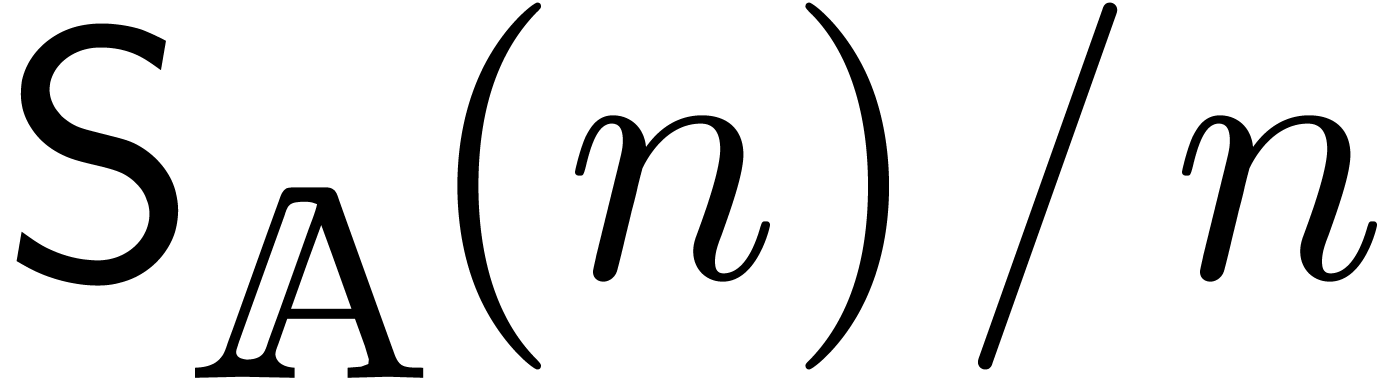 are increasing, a routine
calculation thus yields
are increasing, a routine
calculation thus yields

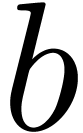 ,
we may write
,
we may write 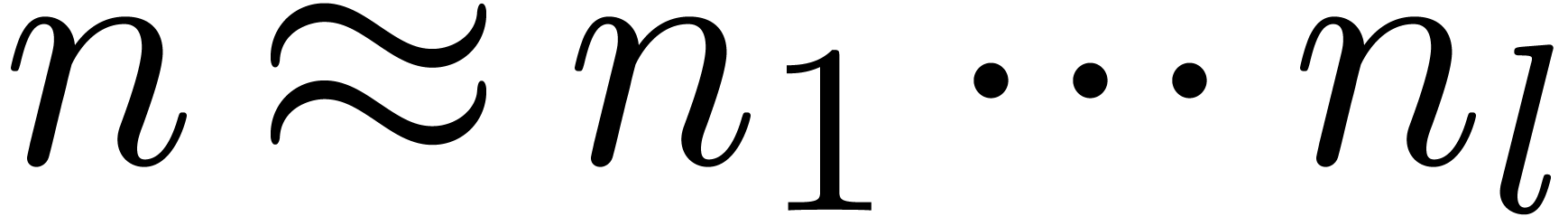 , take
, take 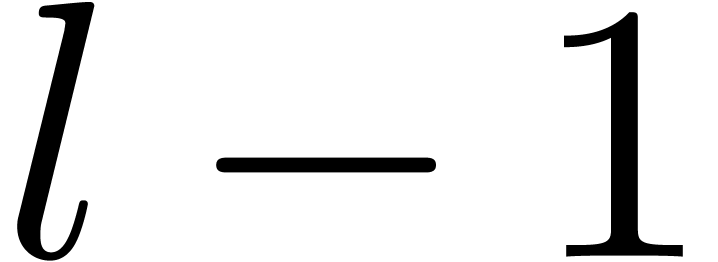 different block sizes
different block sizes  ,
and decompose
,
and decompose  in
in 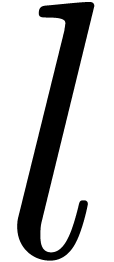 parts
parts
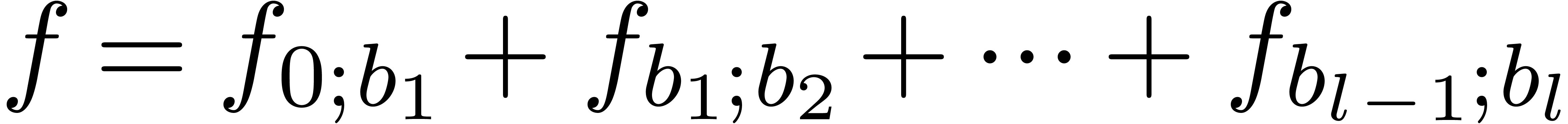 , where
, where 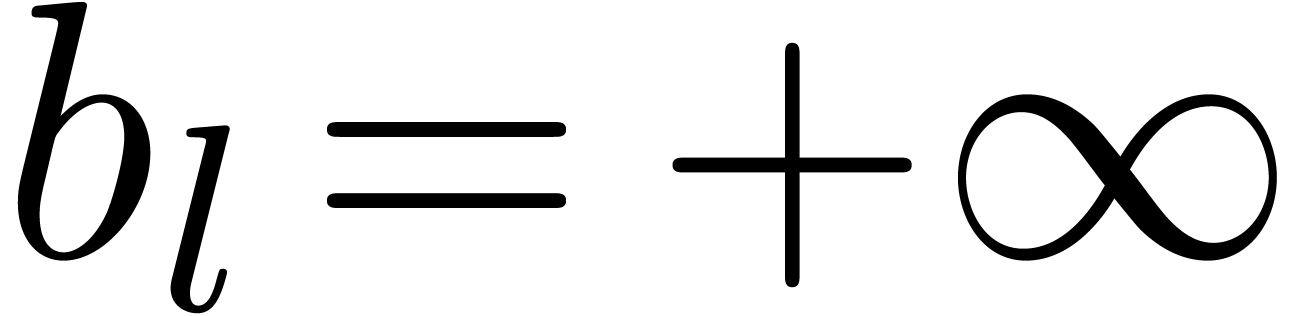 . For semi-relaxed multiplication, this
yields the formula
. For semi-relaxed multiplication, this
yields the formula
and the complexity bound
For  and
and 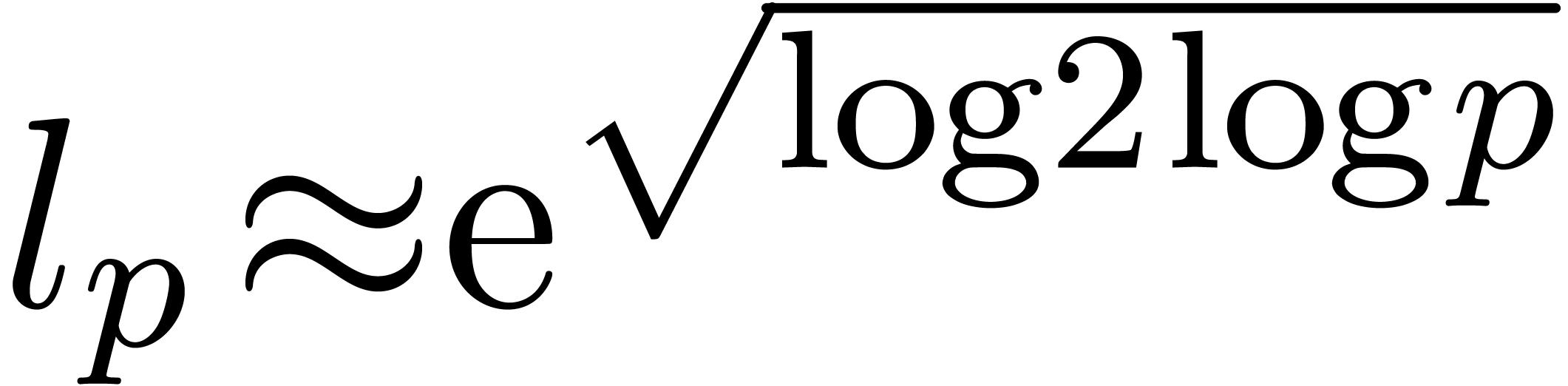 well chosen
block sizes (depending on the expansion order
well chosen
block sizes (depending on the expansion order 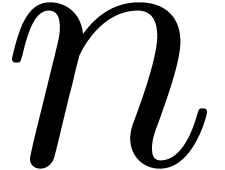 ), the recursive application of this technique
yields [Hoe07, Theorem 12]
), the recursive application of this technique
yields [Hoe07, Theorem 12]
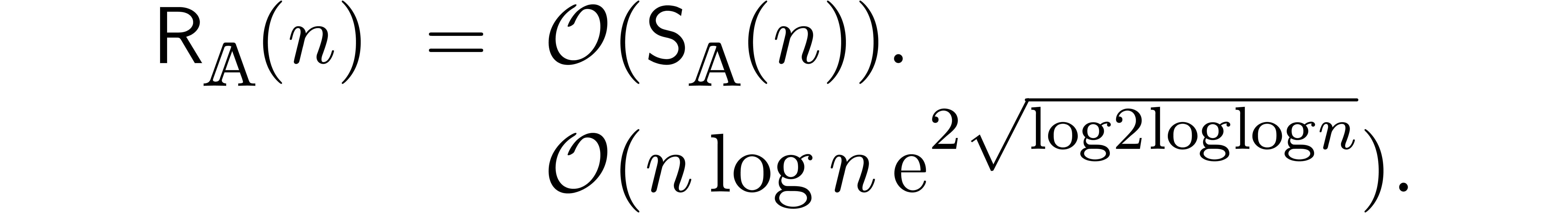
Let us now consider the less favourable case when  is an effective ring which does not necessarily contain primitive
is an effective ring which does not necessarily contain primitive 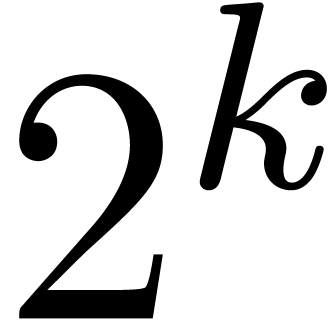 -th roots of unity for arbitrarily
high
-th roots of unity for arbitrarily
high 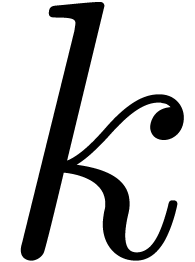 . In this section, we
will first consider the case when
. In this section, we
will first consider the case when  is
torsion-free as a
is
torsion-free as a  -module and
also admits a partial algorithm for division by integers.
-module and
also admits a partial algorithm for division by integers.
Given a block size  and
and 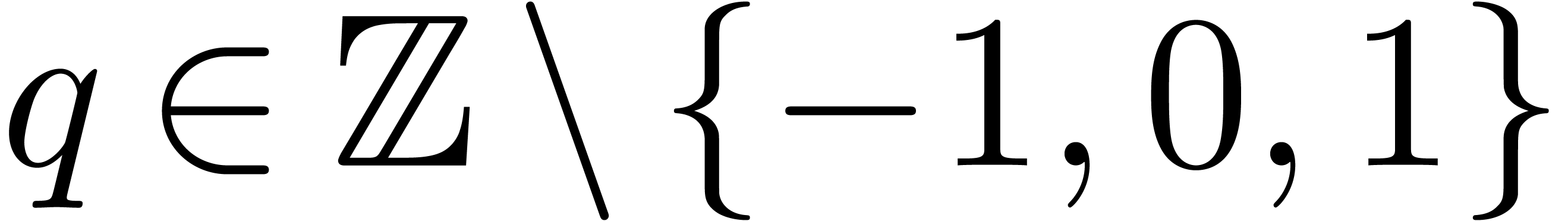 (say
(say 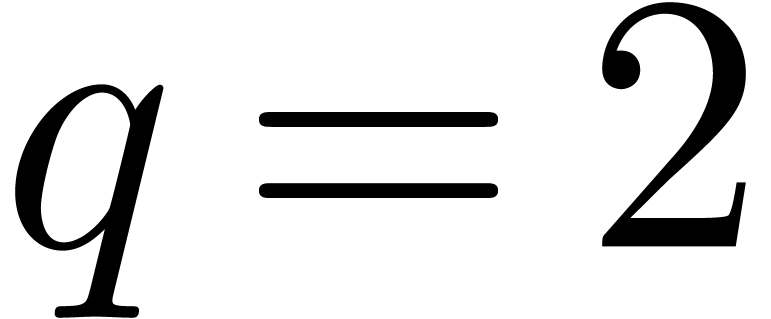 ), we will replace the
discrete Fourier transform
), we will replace the
discrete Fourier transform  at a
at a 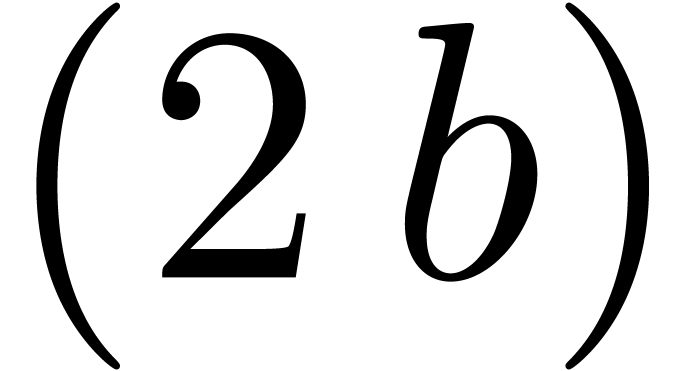 -th primitive root of unity by multipoint
evaluation at
-th primitive root of unity by multipoint
evaluation at 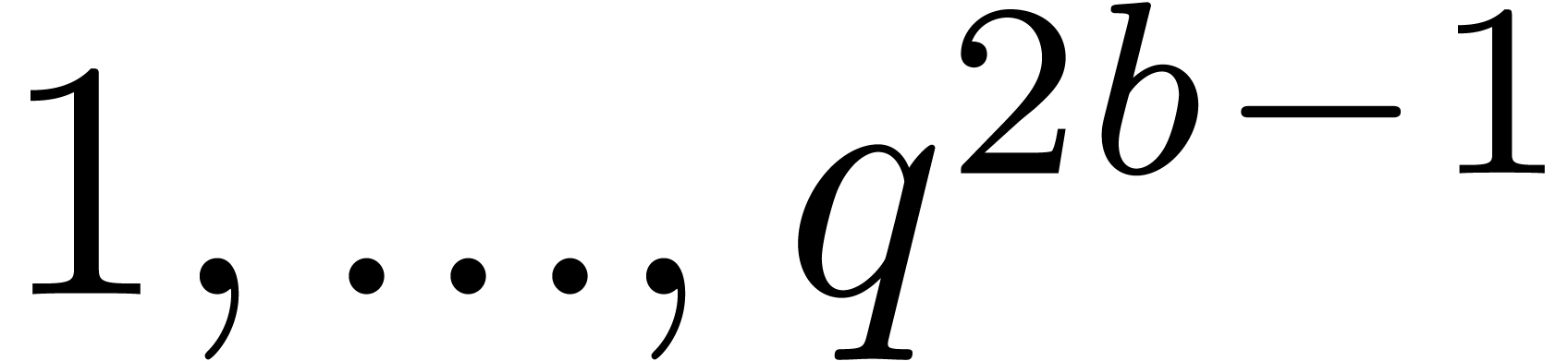 . More
precisely, we define
. More
precisely, we define
and the inverse transform 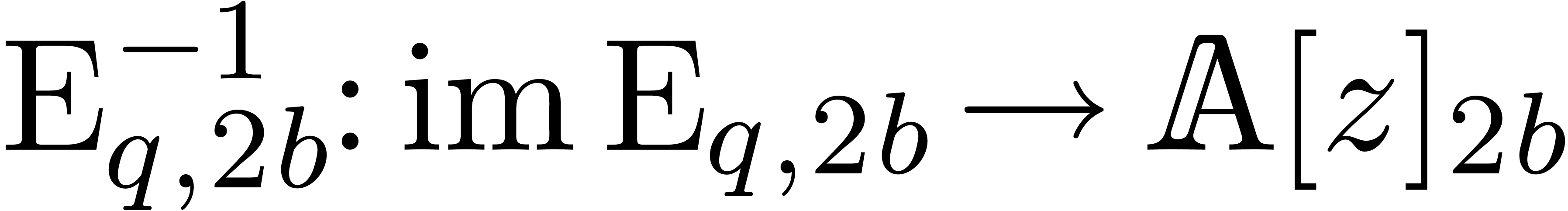 .
By Lemma 3, these transforms can both be computed using
.
By Lemma 3, these transforms can both be computed using
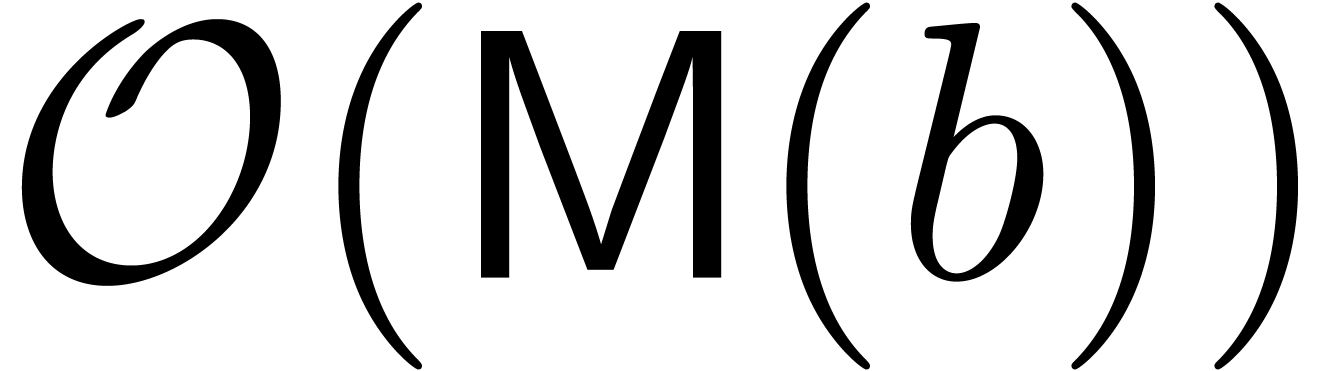 operations in
operations in  .
In a similar way as
.
In a similar way as  and
and  , we extend
, we extend 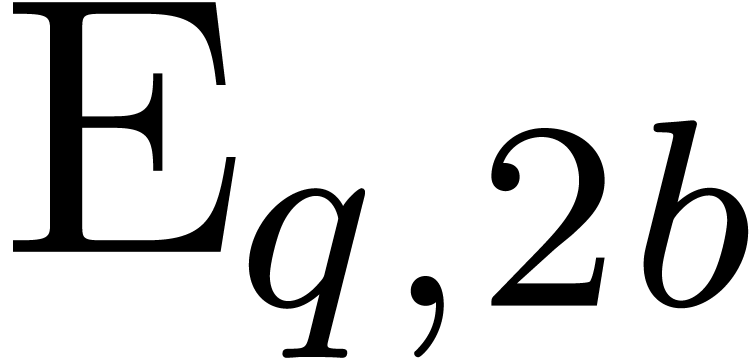 and
and 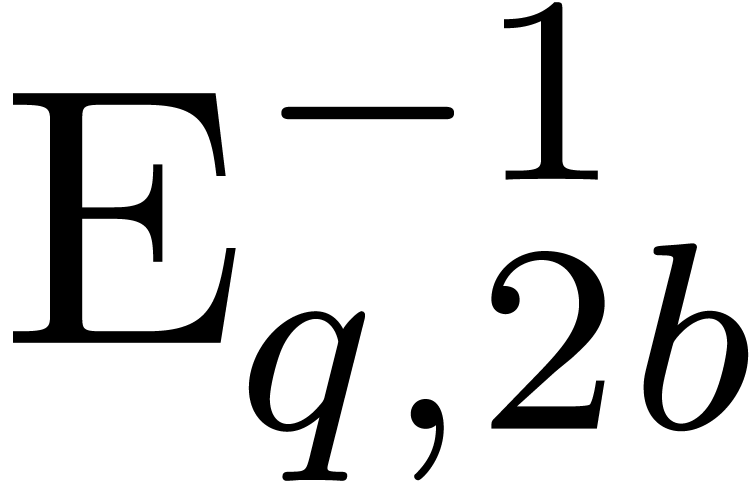 to power series in
to power series in  .
.
Proof. It suffices to prove the complexity bound
for semi-relaxed multiplication. We adapt the multiplication algorithm
with  different block sizes from the end of the
previous section, and replace (7) by
different block sizes from the end of the
previous section, and replace (7) by
This leads to the complexity bound
 |
We now follow the proof of [Hoe07, Theorem 12]. Denote
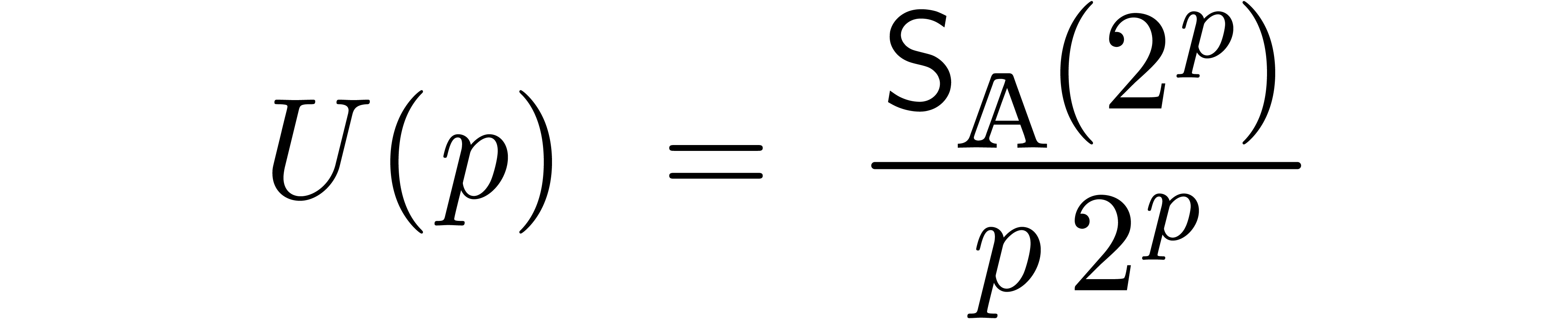
and take  . Using that
. Using that 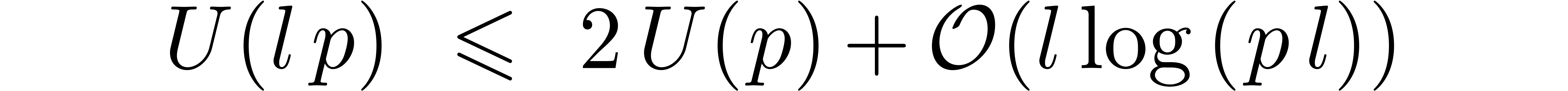 , this leads to
, this leads to
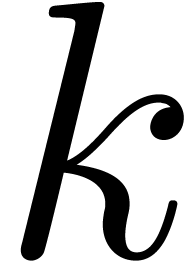
Applying this relation  times, we obtain
times, we obtain
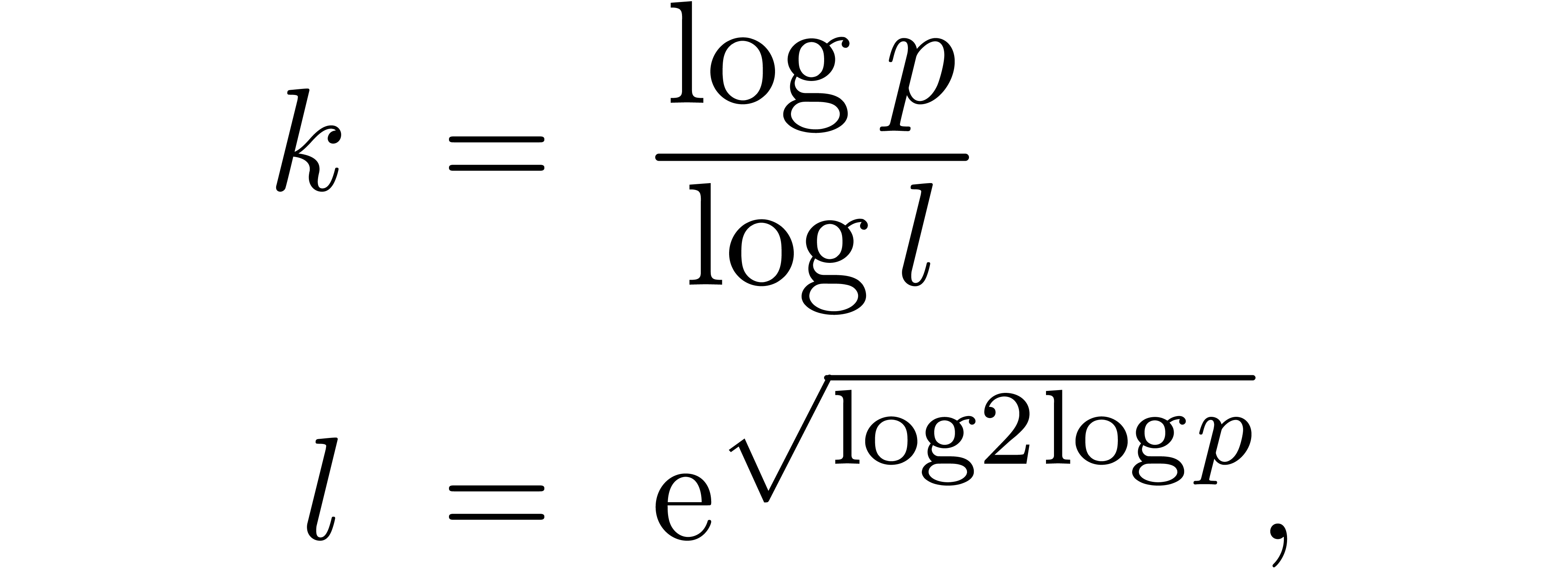
Taking
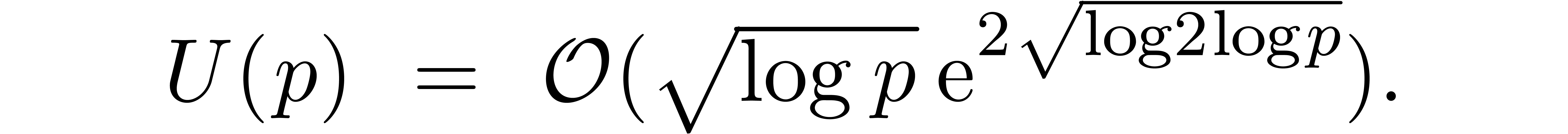
this yields

Re-expressing this bound in terms of 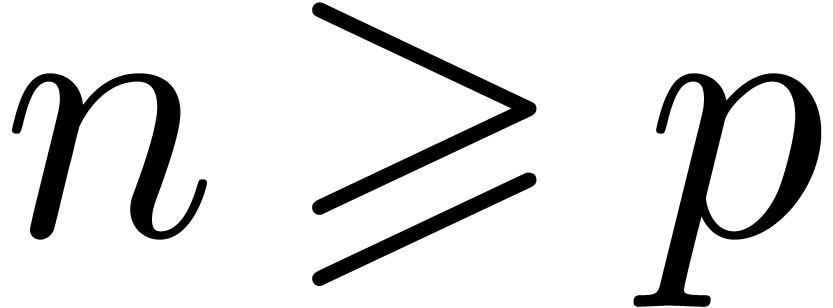 yields the
desired result.
yields the
desired result.
Let  now be an effective ring of prime
characteristic
now be an effective ring of prime
characteristic  . For
expansion orders
. For
expansion orders 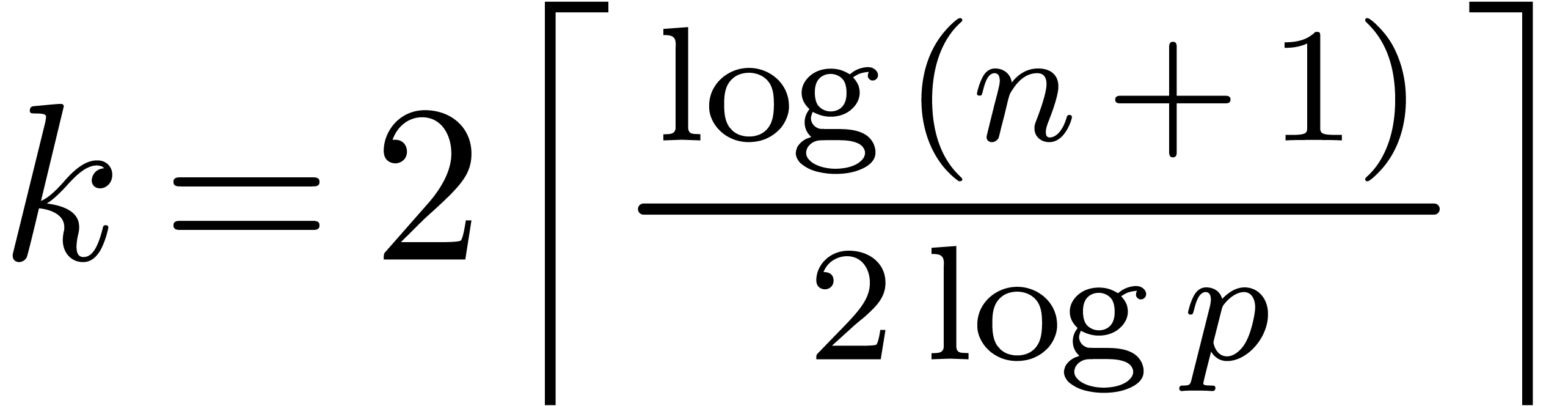 , the ring
, the ring
 does not necessarily contain
does not necessarily contain 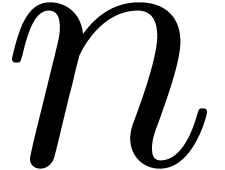 distinct points in geometric progression. Therefore, in order to apply
Lemma 4, we will first replace
distinct points in geometric progression. Therefore, in order to apply
Lemma 4, we will first replace  by a
suitable extension, in which we can find sufficiently large geometric
progressions.
by a
suitable extension, in which we can find sufficiently large geometric
progressions.
Given 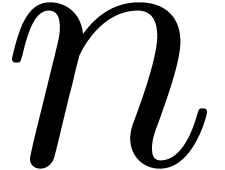 , let
, let 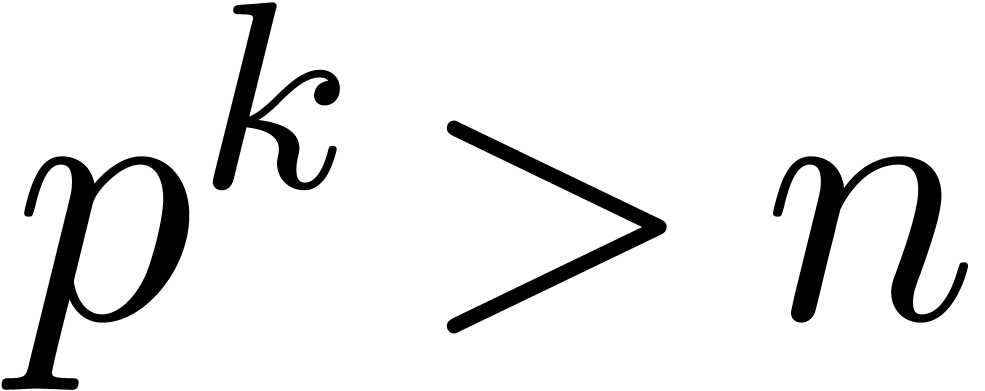 be even such that
be even such that 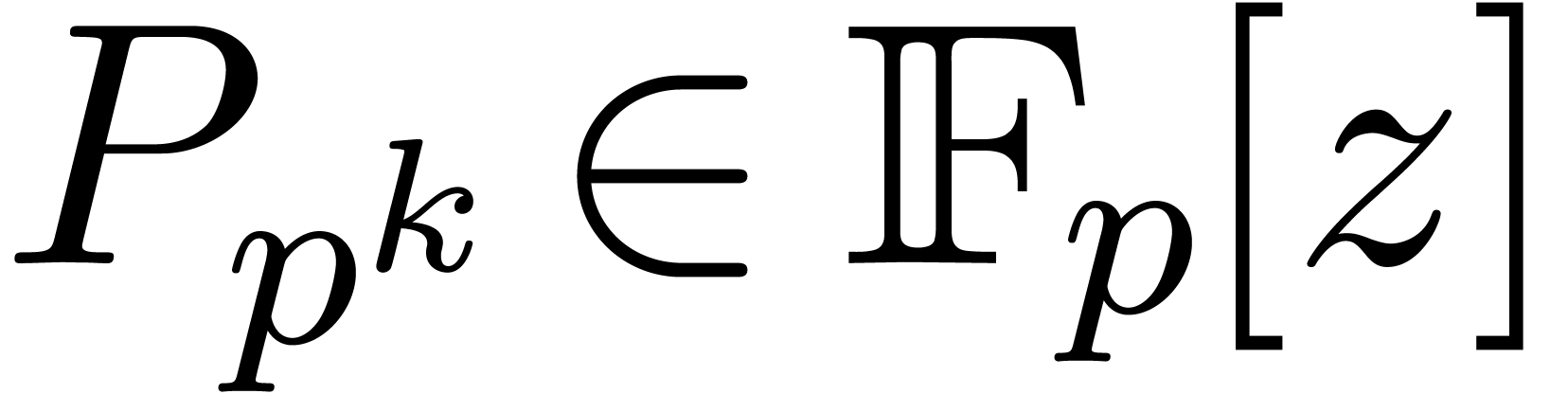 . Let
. Let 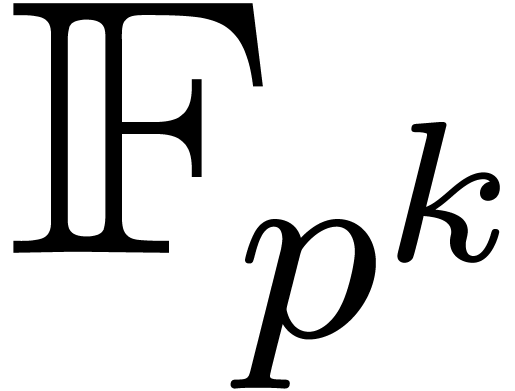 be such that the finite field
be such that the finite field 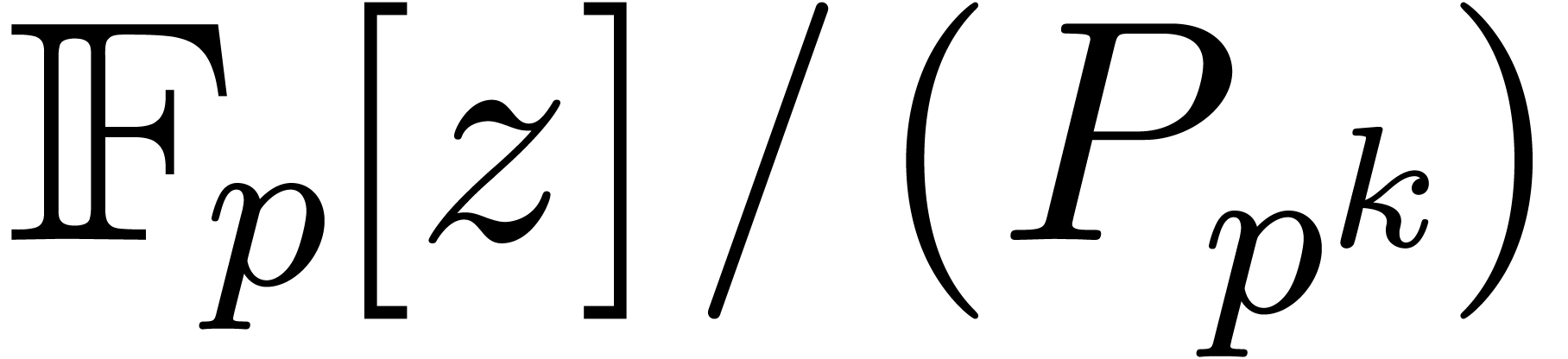 is isomorphic to
is isomorphic to  . Then the
ring
. Then the
ring

has dimension  over
over  as a
vector space, so we have a natural
as a
vector space, so we have a natural  -linear
bijection
-linear
bijection

The ring  is an effective ring and one addition
or subtraction in
is an effective ring and one addition
or subtraction in  corresponds to
corresponds to 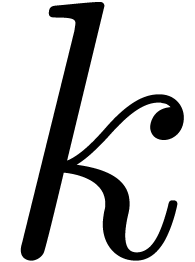 additions or subtractions in
additions or subtractions in  .
Similarly, one multiplication in
.
Similarly, one multiplication in  can be done
using
can be done
using 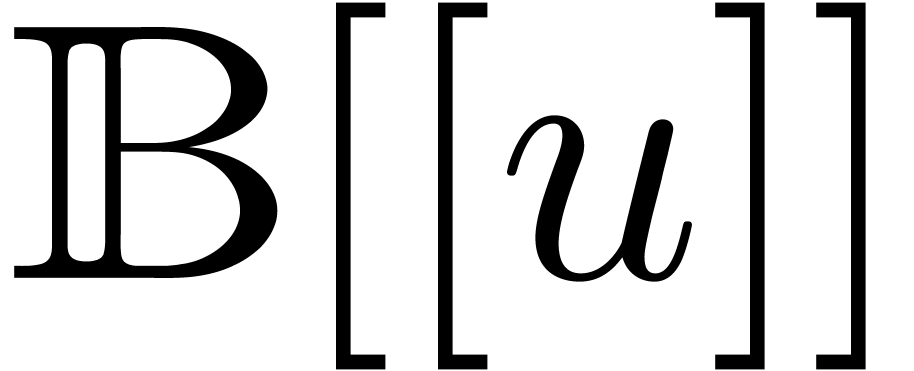 operations in
operations in  .
.
In order to multiply two series 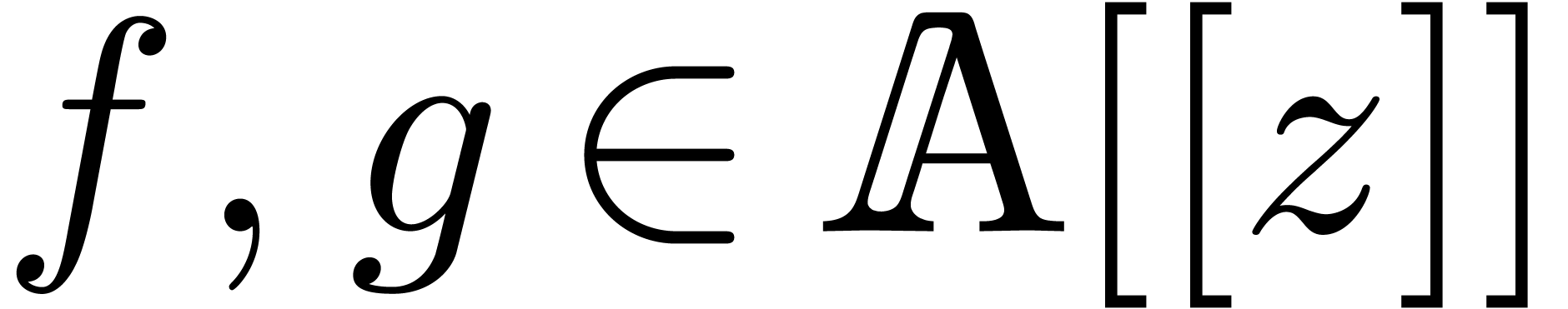 up to order
up to order
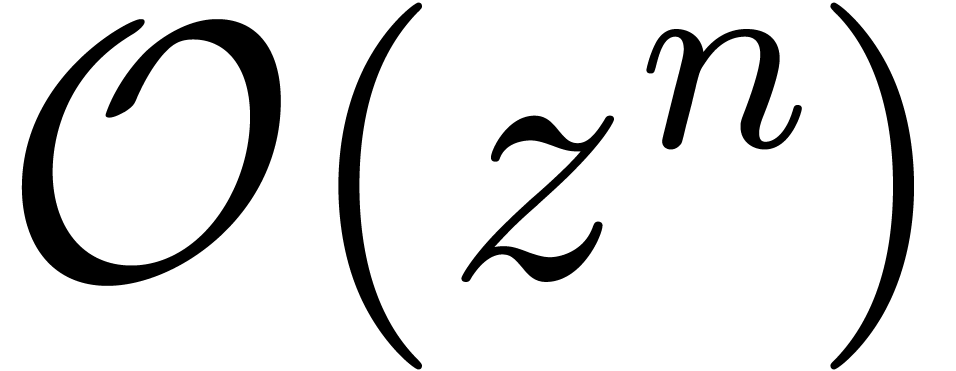 , the idea is now to rewrite
, the idea is now to rewrite
 and
and  as series in
as series in 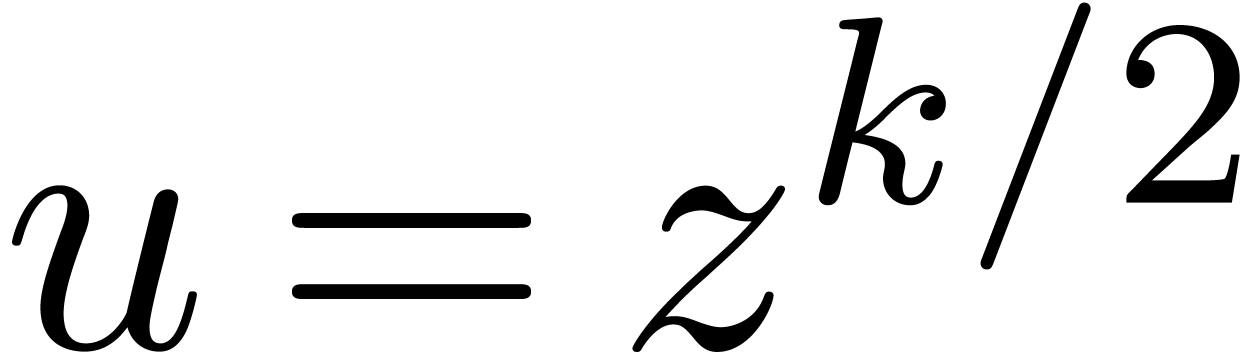 with
with 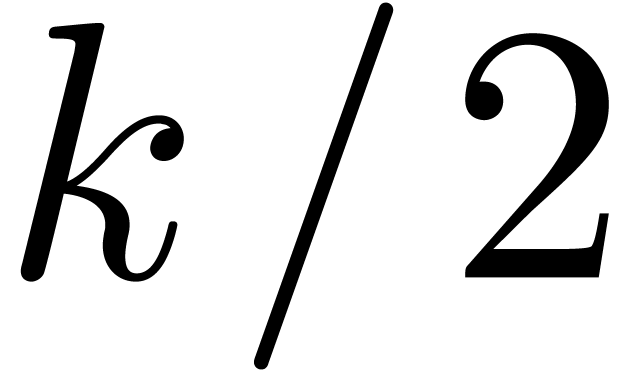 . If
we want to compute the relaxed product, then we also have to treat the
first
. If
we want to compute the relaxed product, then we also have to treat the
first  coefficients apart, as we did before for
the blocking strategy. More precisely, we will compute the semi-relaxed
product
coefficients apart, as we did before for
the blocking strategy. More precisely, we will compute the semi-relaxed
product 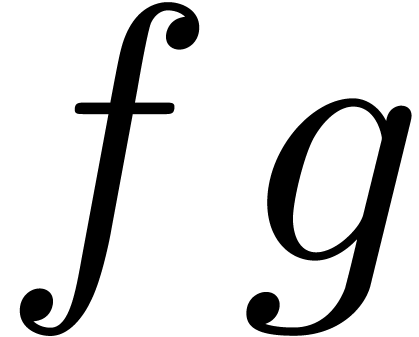 using the formula
using the formula
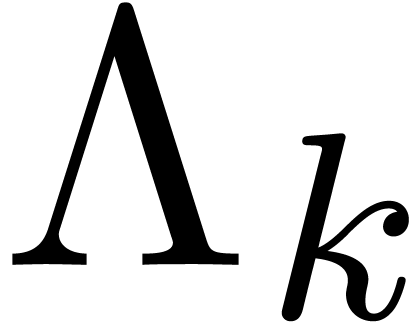
where we extended 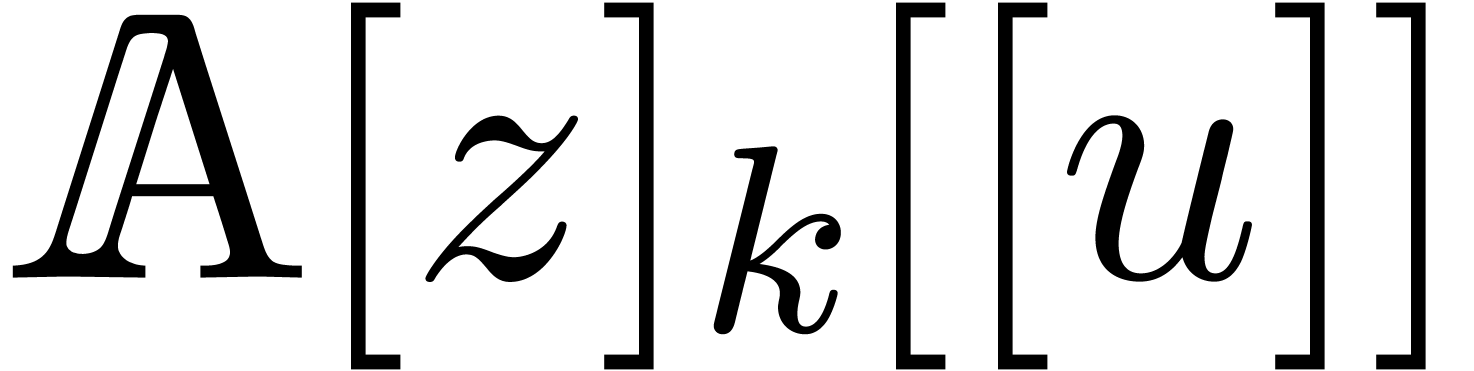 to
to 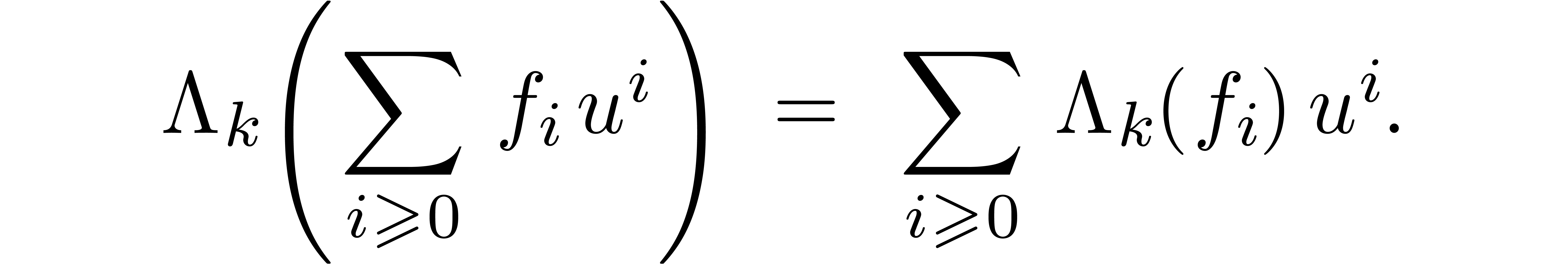 in
the natural way:
in
the natural way:
From the complexity point of view, we get
Since 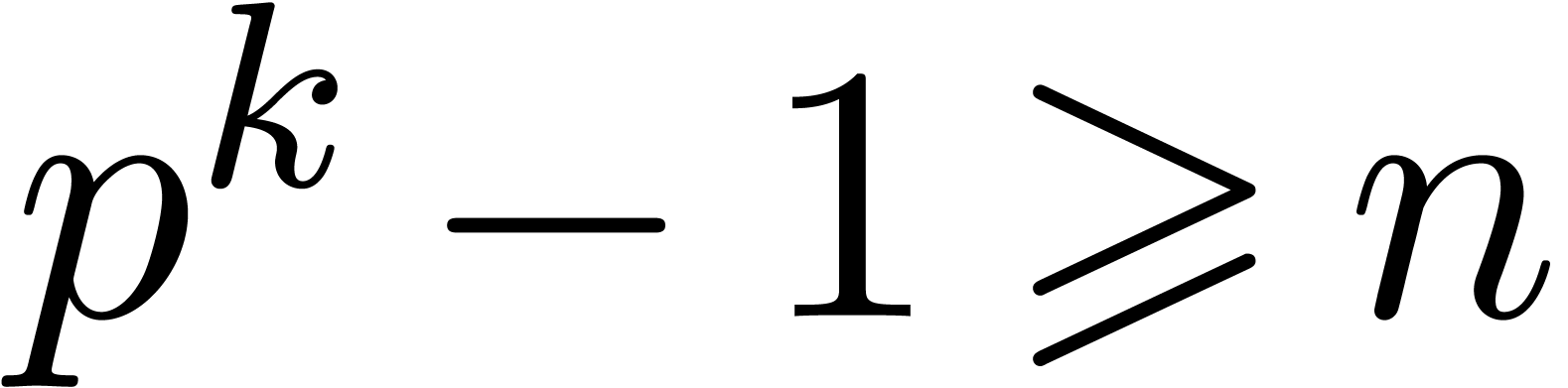 contains a copy of
contains a copy of 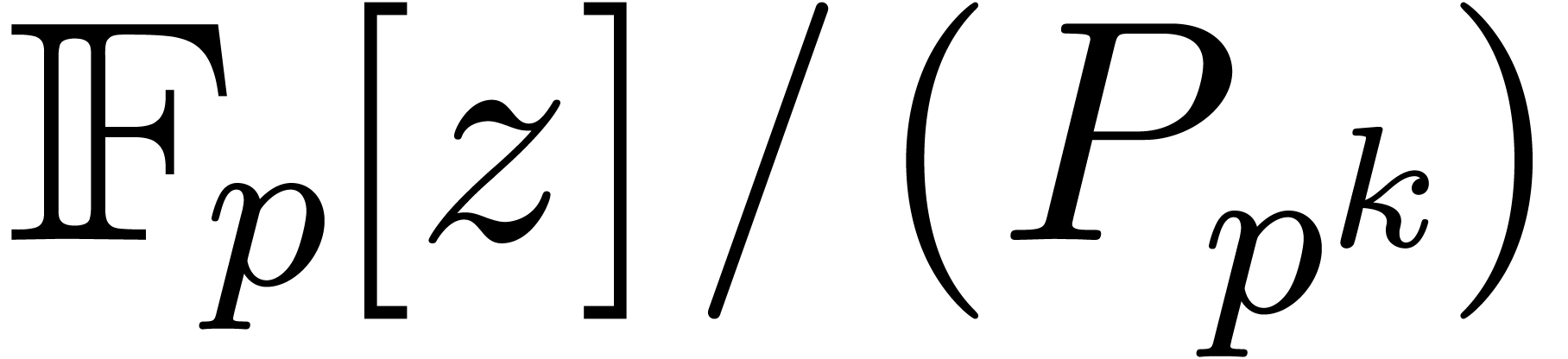 , it also contains at least
, it also contains at least 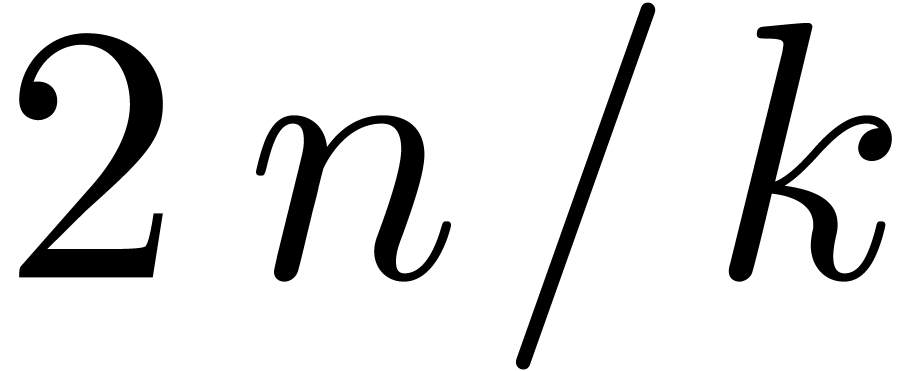 points in geometric progression. For the multiplication up till order
points in geometric progression. For the multiplication up till order
 of two series with coefficients in
of two series with coefficients in 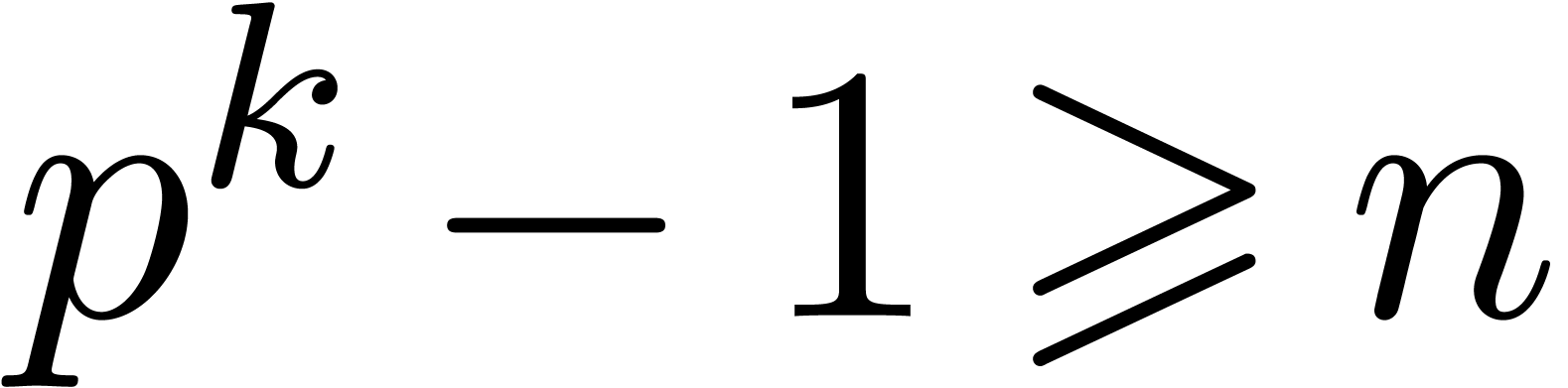 , we may thus use the blocking strategy
combined with multipoint evaluation and interpolation.
, we may thus use the blocking strategy
combined with multipoint evaluation and interpolation.
Proof. With the notations from above, we may
find a primitive 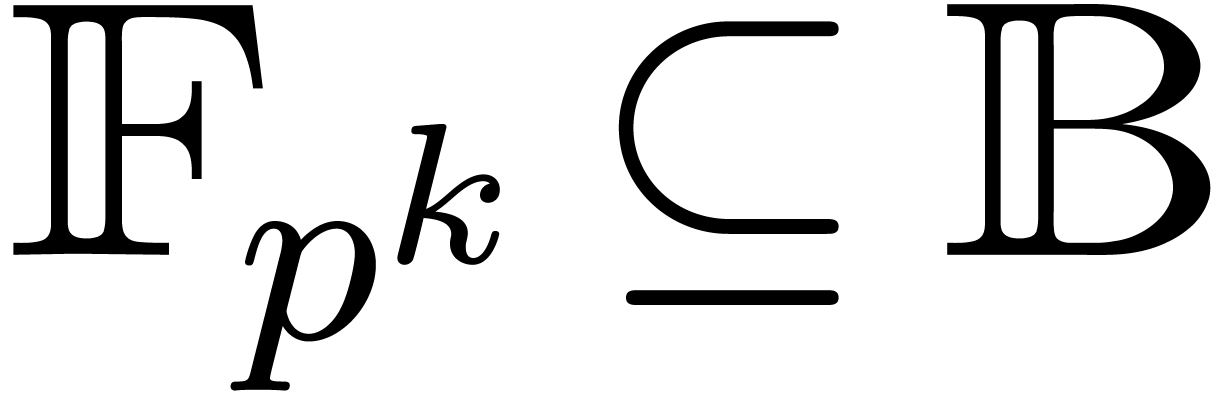 -th root of
unity
-th root of
unity  in
in 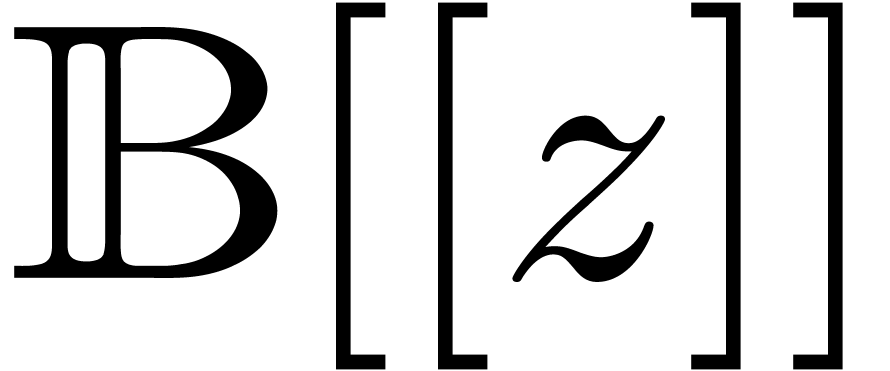 .
We may thus use formula (9) for the semi-relaxed
multiplication of two series in
.
We may thus use formula (9) for the semi-relaxed
multiplication of two series in 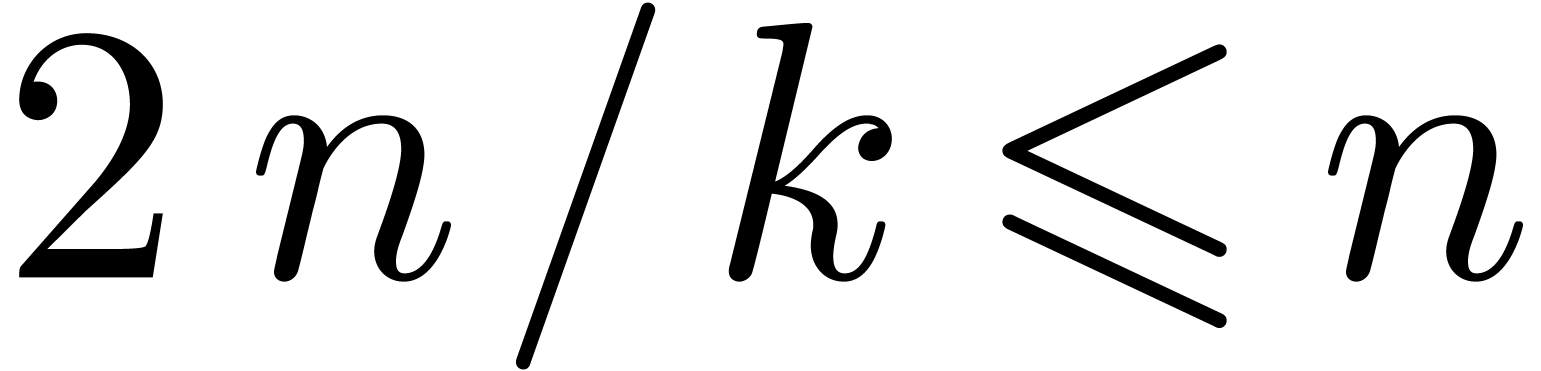 up till order
up till order
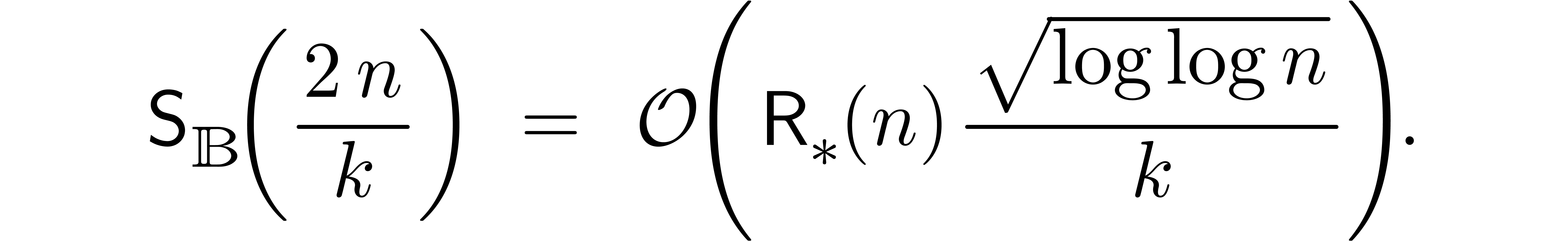 . In a similar way as in the
proof of Theorem 6, we thus get
. In a similar way as in the
proof of Theorem 6, we thus get
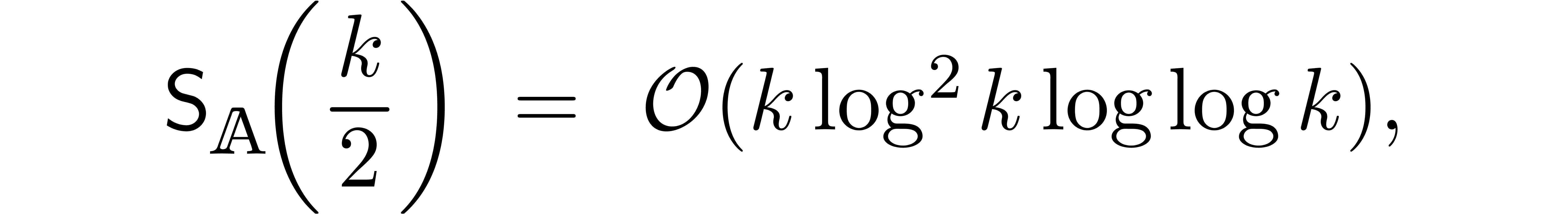
Using classical fast relaxed multiplication [Hoe97, Hoe02, FS74], we also have
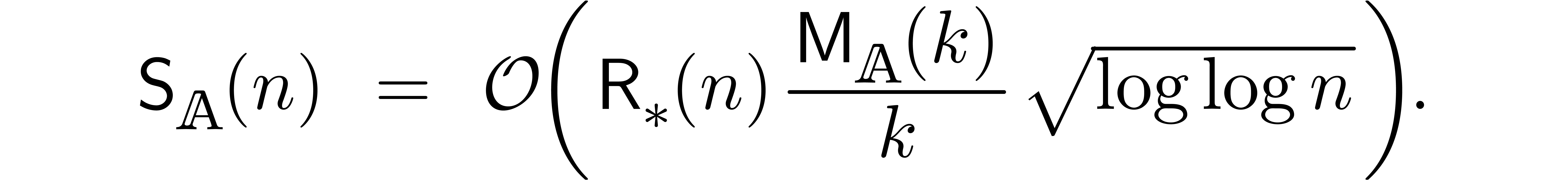
whence (11) simplifies to
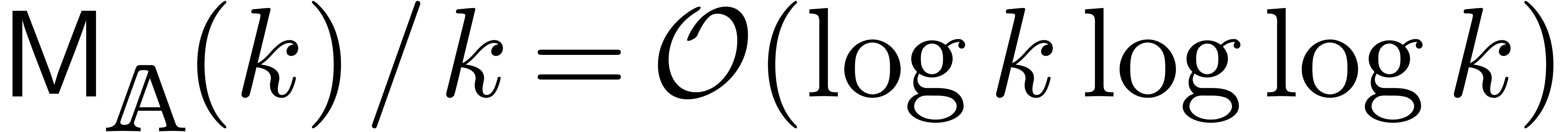
Since 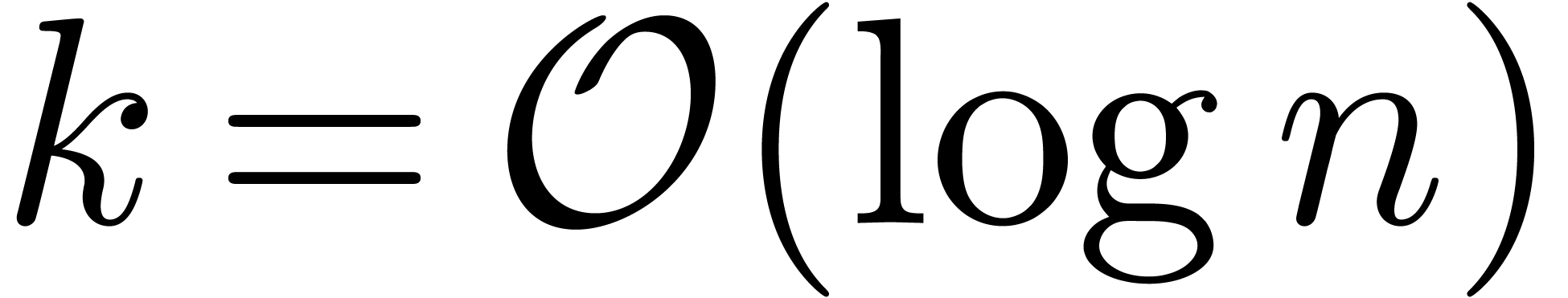 and
and 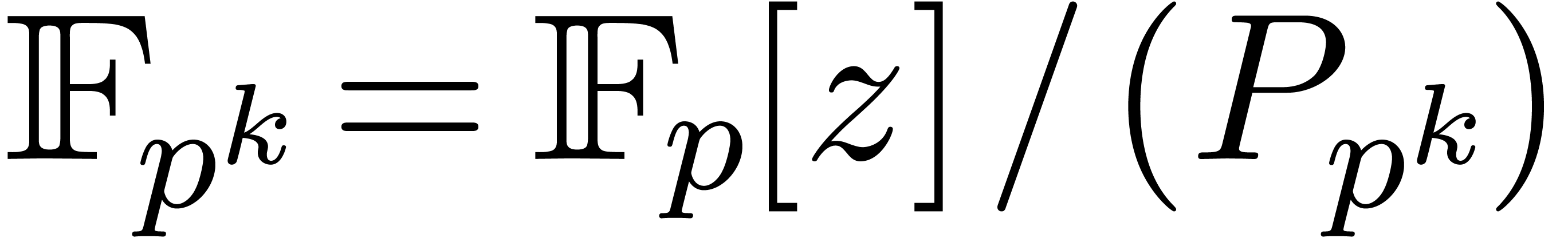 ,
the result follows.
,
the result follows.
Remark 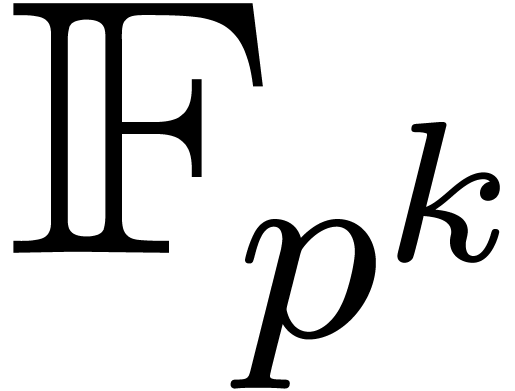 with
with 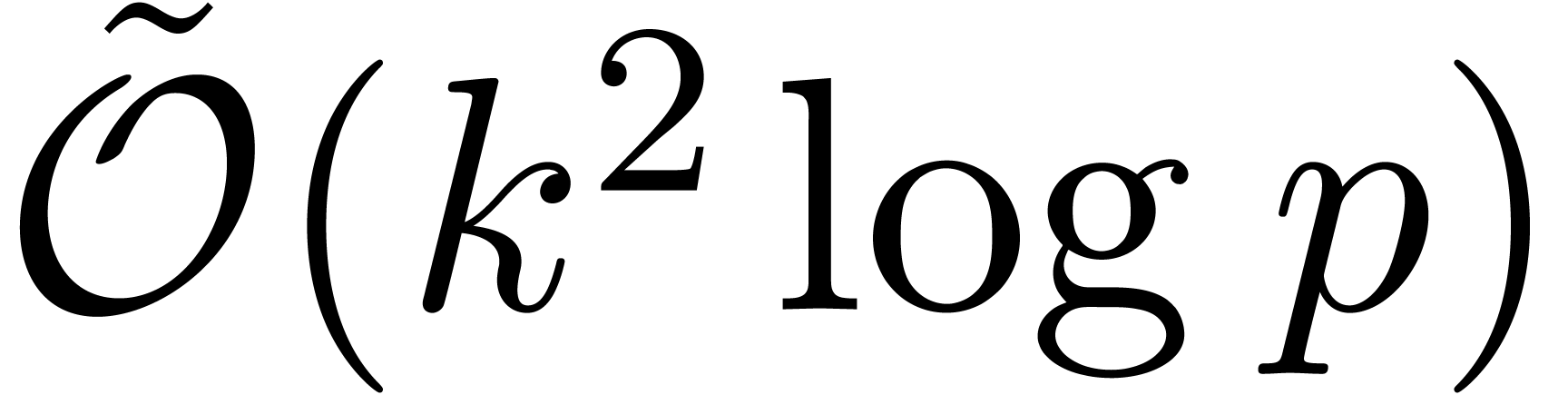 . Using a randomized algorithm, such a polynomial
can be computed in time
. Using a randomized algorithm, such a polynomial
can be computed in time 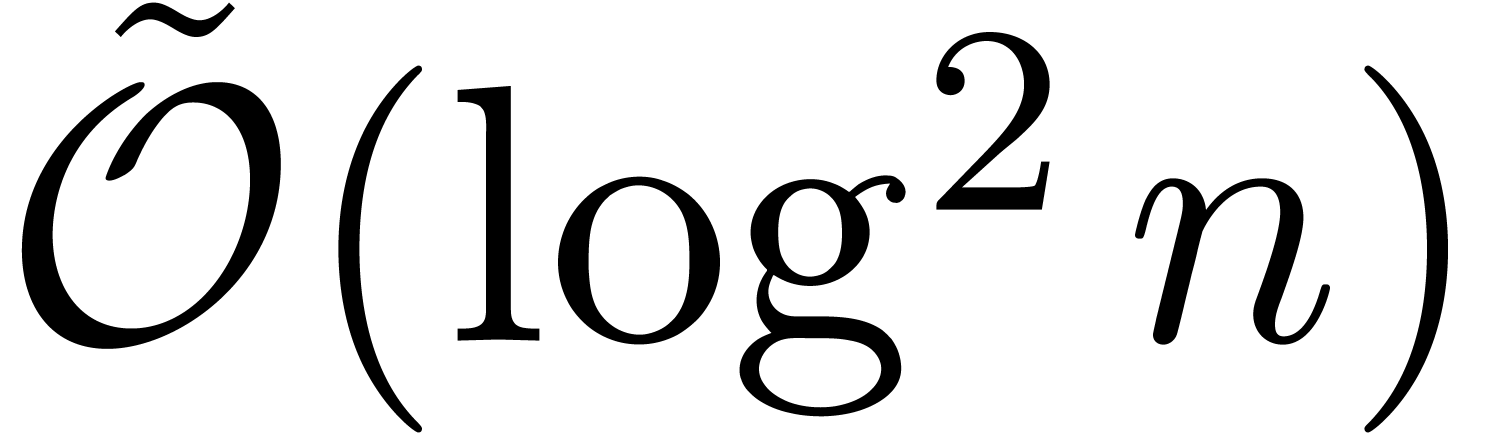 ; see
[GG02, Corollary 14.44]. If
; see
[GG02, Corollary 14.44]. If 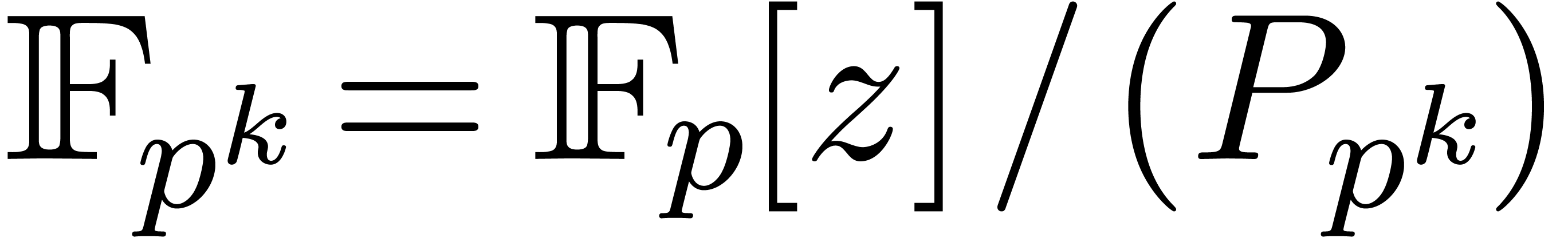 ,
then this is really a precomputation of negligible cost
,
then this is really a precomputation of negligible cost 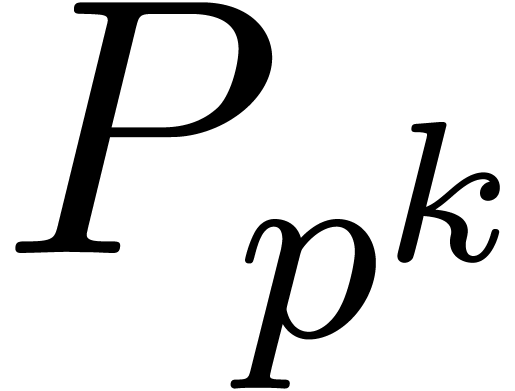 .
.
If we insist on computing  in a deterministic
way, then it is better to slightly change our algorithm, and
systematically choose
in a deterministic
way, then it is better to slightly change our algorithm, and
systematically choose  to be a prime number minus
one. Under this assumption, the cyclotomic polynomial
to be a prime number minus
one. Under this assumption, the cyclotomic polynomial 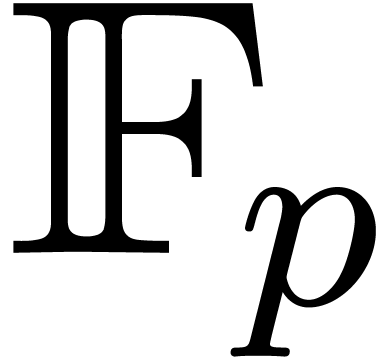 is irreducible over
is irreducible over 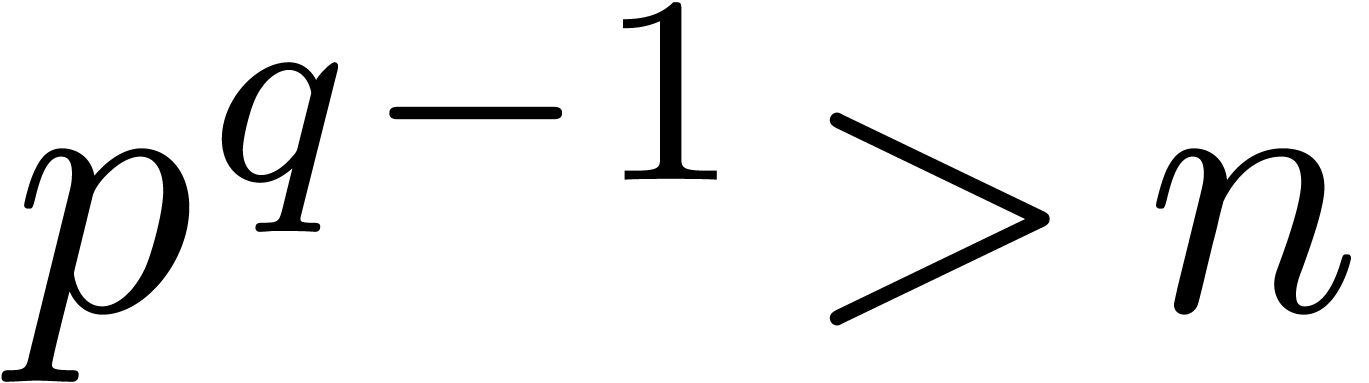 ; see [GG02, Lemma 14.50]. For a fixed
; see [GG02, Lemma 14.50]. For a fixed  ,
the first prime number
,
the first prime number  with
with 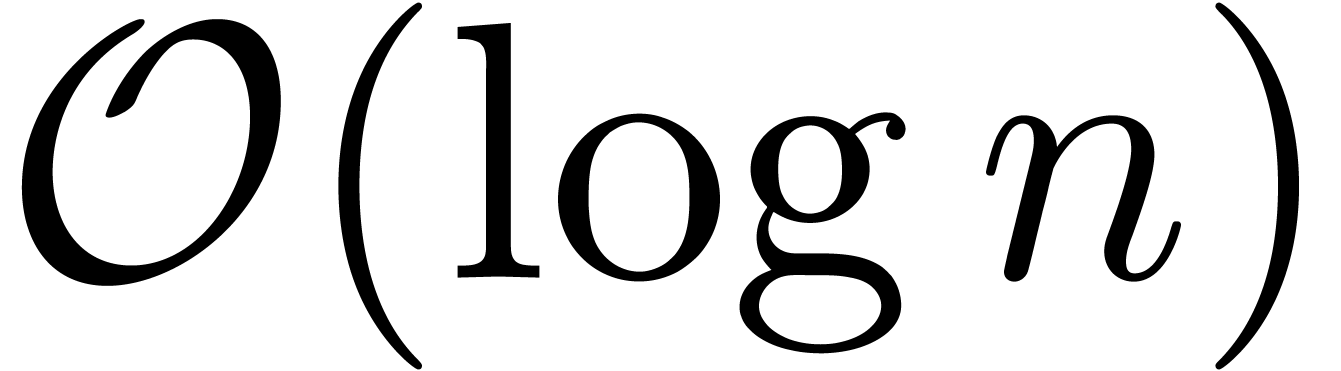 still has size
still has size 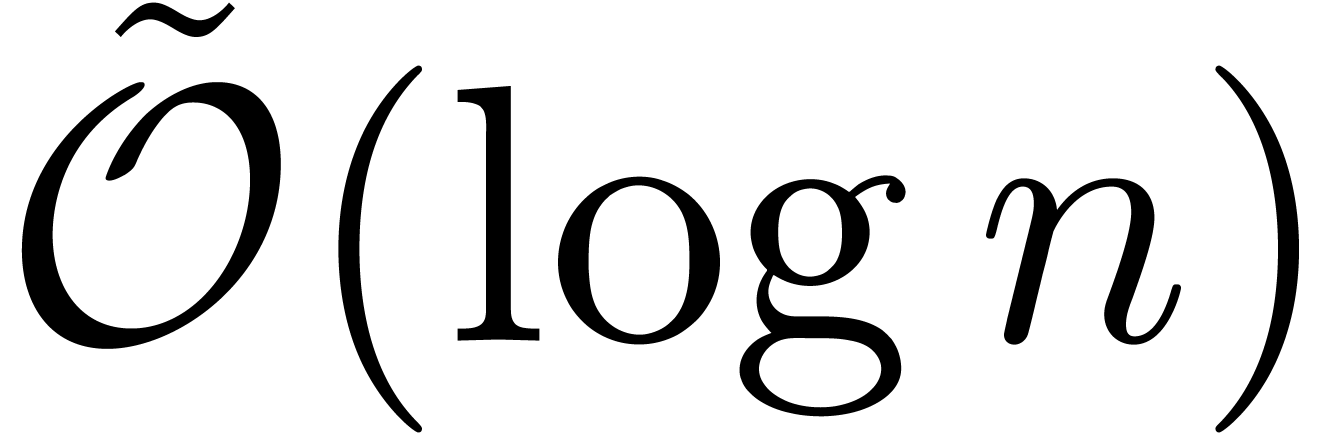 , by the prime
number theorem, and we may compute it in time
, by the prime
number theorem, and we may compute it in time 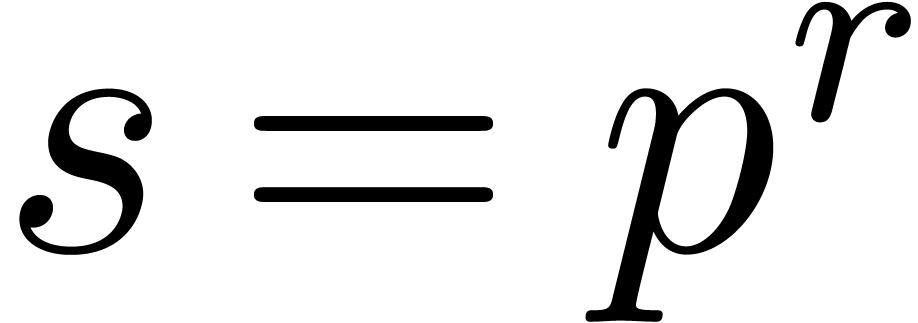 using the sieve of Eratosthenes. This again shows that a suitable
using the sieve of Eratosthenes. This again shows that a suitable  can be precomputed with negligible cost.
can be precomputed with negligible cost.
Let us now show that the technique from the previous section actually
extends to the case when  is an arbitrary
effective ring of positive characteristic. We first show that the
algorithm still applies when the characteristic of
is an arbitrary
effective ring of positive characteristic. We first show that the
algorithm still applies when the characteristic of  is a prime power. We then conclude by showing how to apply Chinese
remaindering in our setting.
is a prime power. We then conclude by showing how to apply Chinese
remaindering in our setting.
Proof. Taking 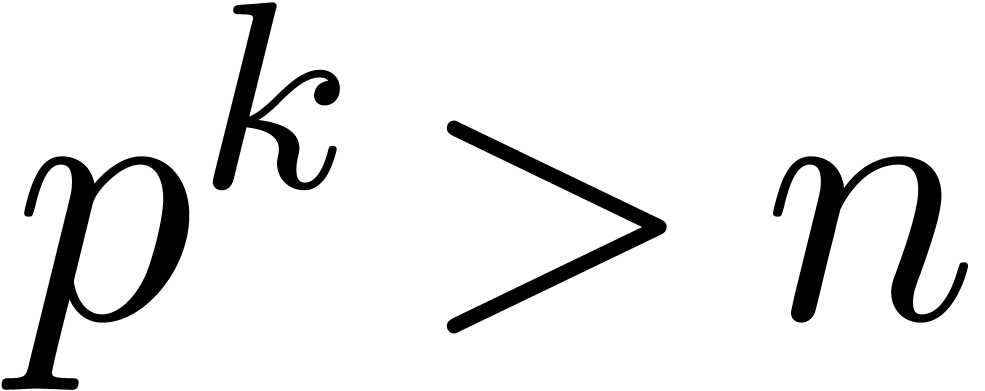 ,
let
,
let 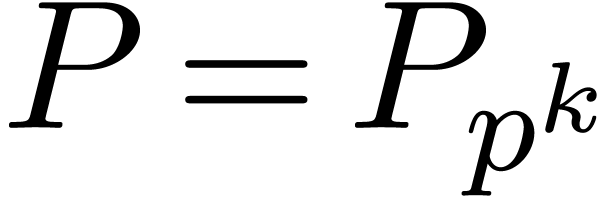 be as in the previous section and pick a
monic polynomial
be as in the previous section and pick a
monic polynomial 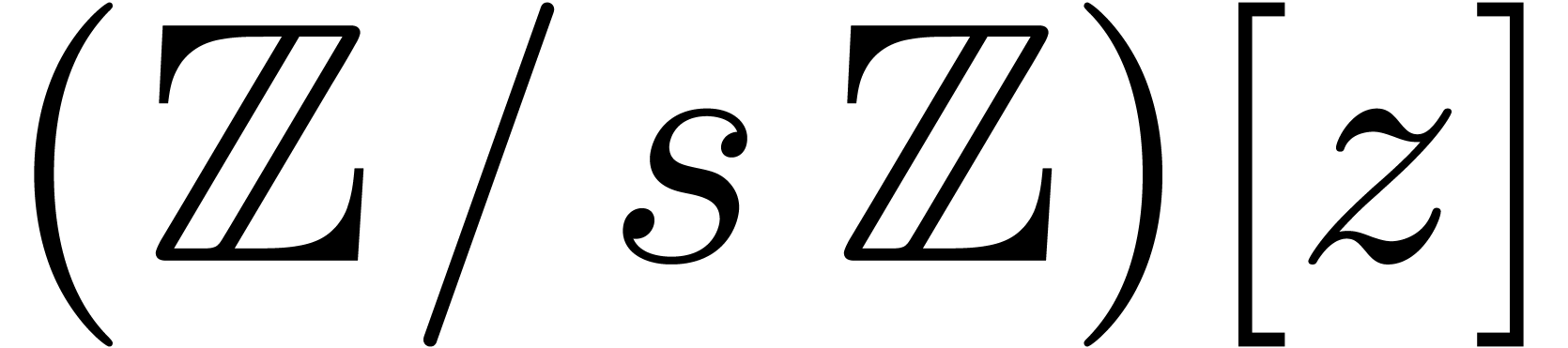 in
in 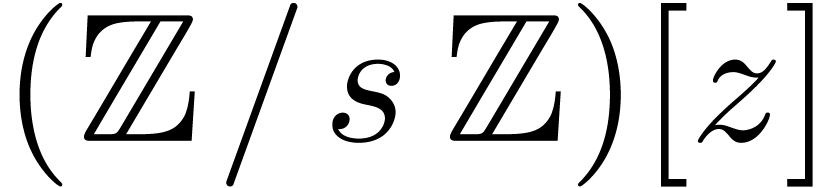 such
that the reduction
such
that the reduction 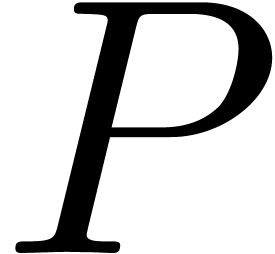 of
of 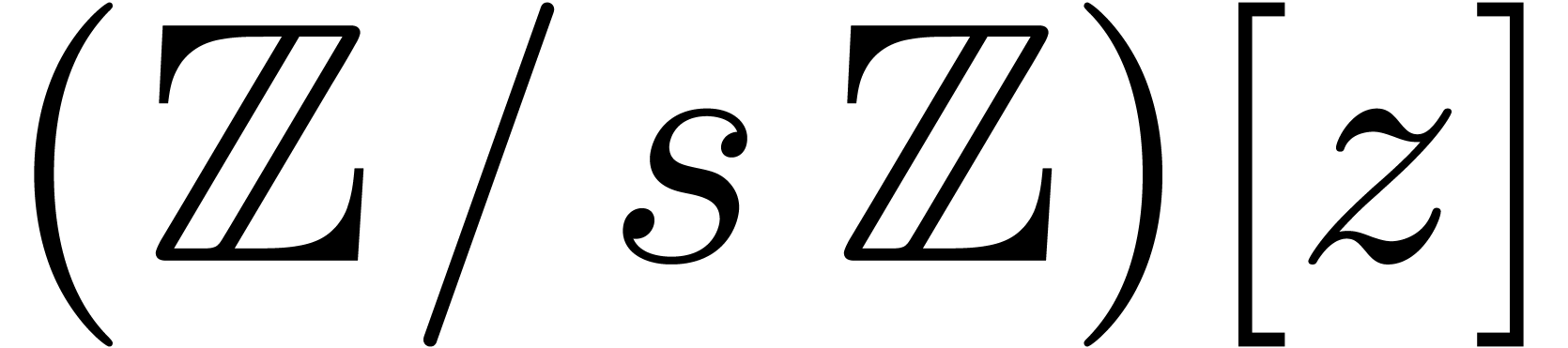 modulo
modulo 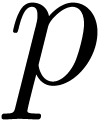 yields
yields  .
Then we get a natural commutative diagram
.
Then we get a natural commutative diagram

where  stands for reduction modulo
stands for reduction modulo 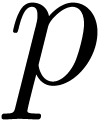 . In particular, we have an epimorphism
. In particular, we have an epimorphism
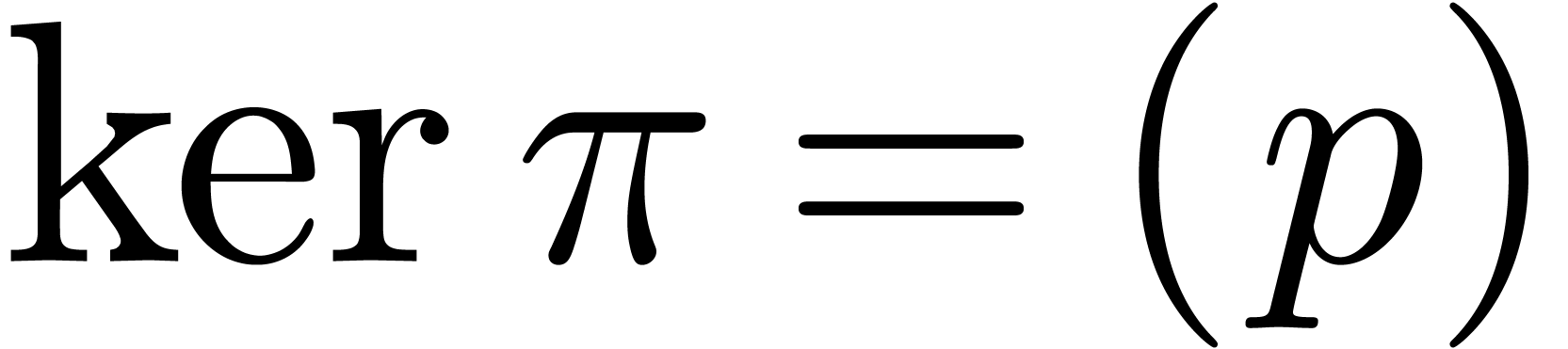
with 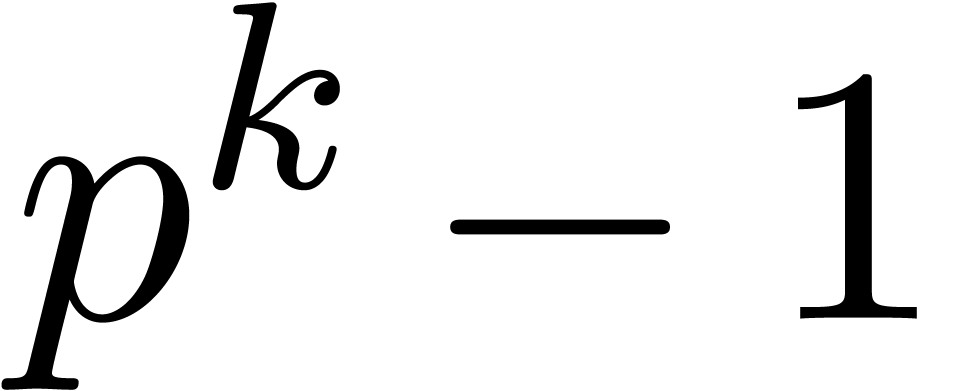 .
.
Now let  be an element in
be an element in 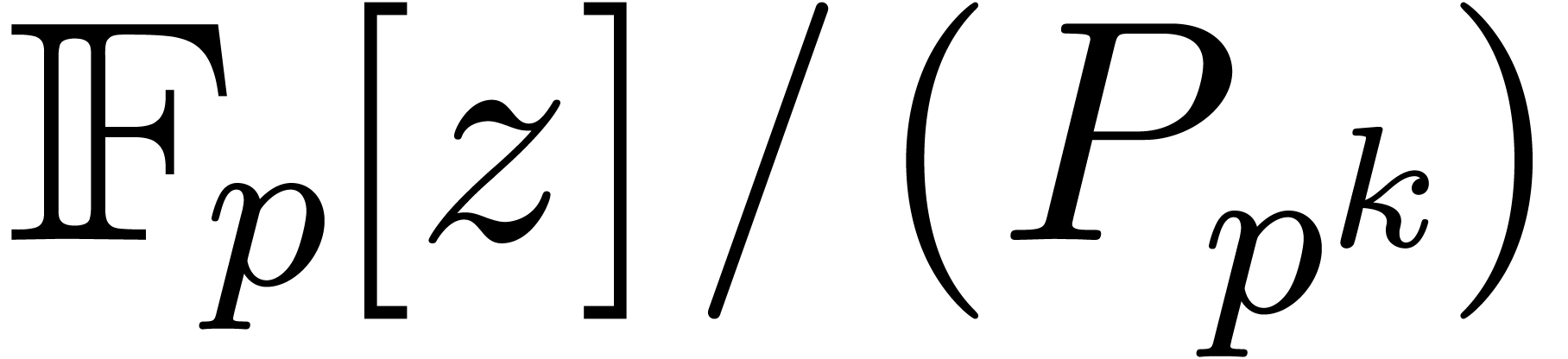 of order
of order 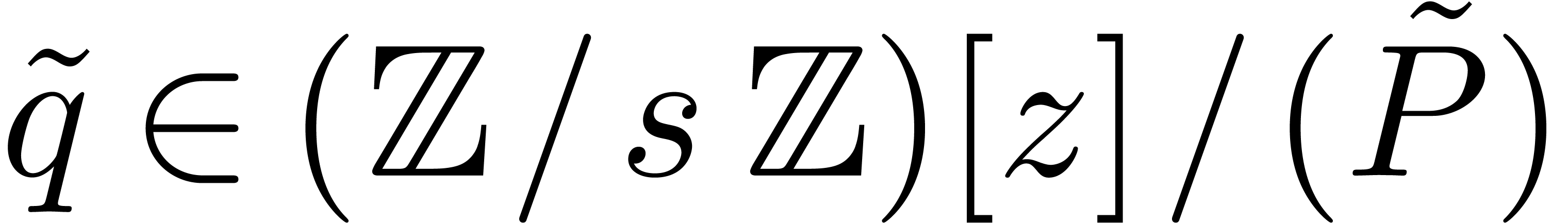 . Then any lift
. Then any lift 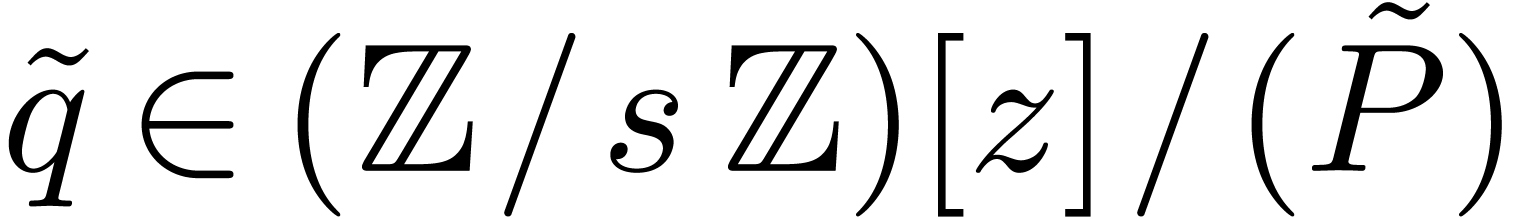 of
of  with
with 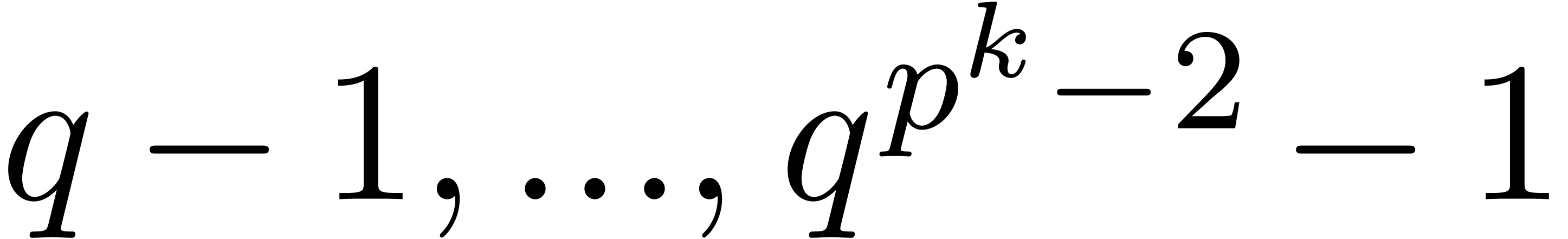 has order at least
has order at least 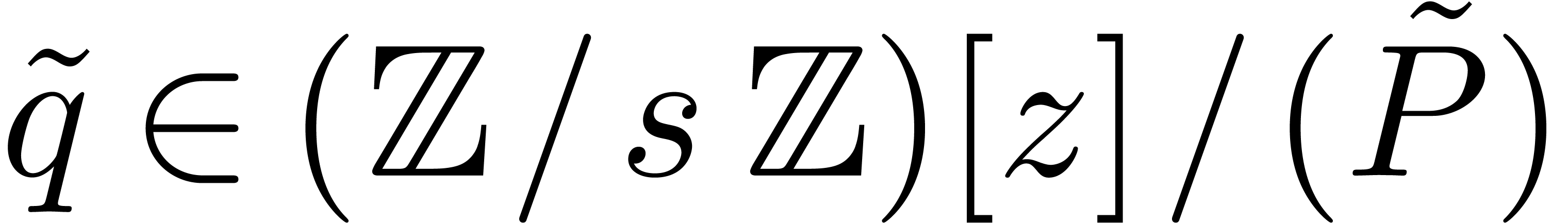 .
Moreover,
.
Moreover, 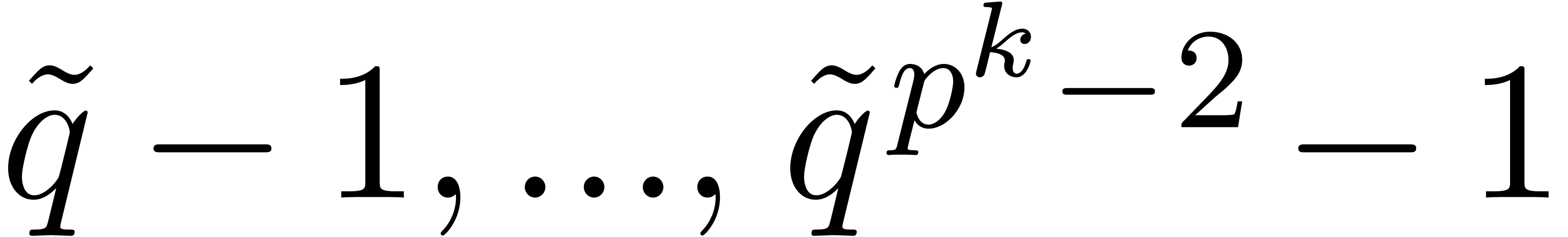 and
and  are all
invertible. Consequently,
are all
invertible. Consequently,  and
and 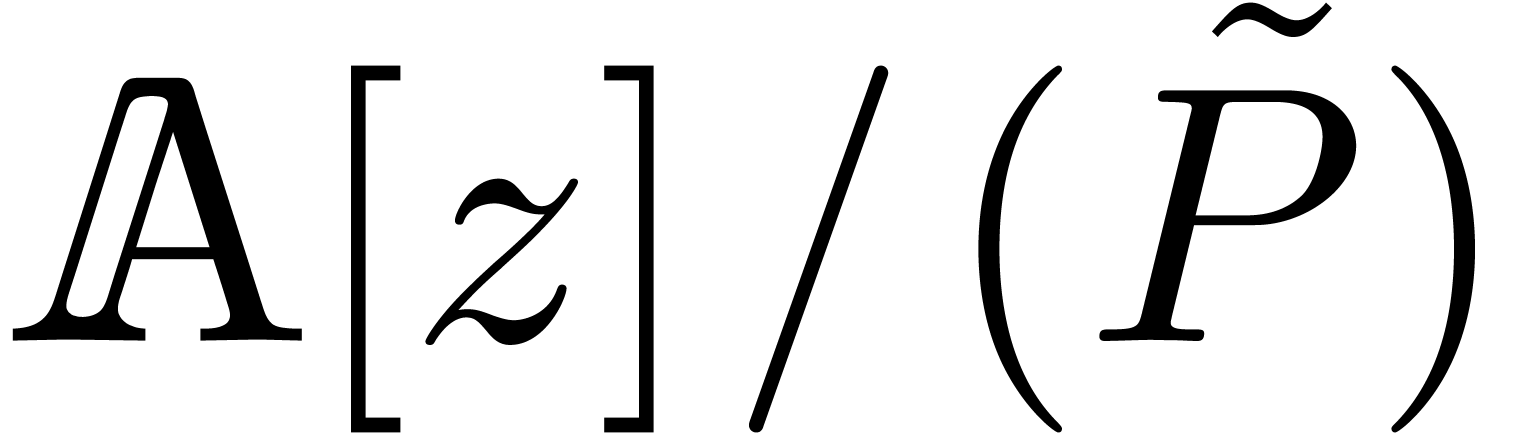 do not lie in
do not lie in 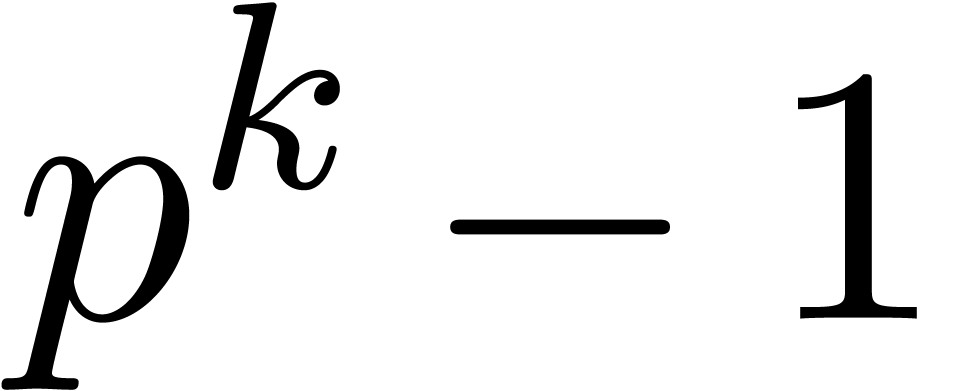 , whence they
are invertible as well. It follows that we may still apply multipoint
evaluation and interpolation in
, whence they
are invertible as well. It follows that we may still apply multipoint
evaluation and interpolation in  at the sequence
at the sequence
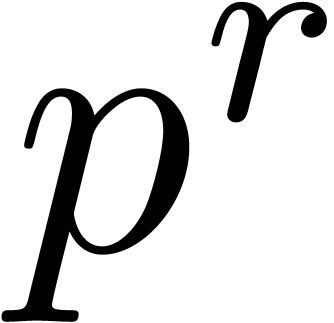 , whence Theorem 7
generalizes to the present case.
, whence Theorem 7
generalizes to the present case.
Remark 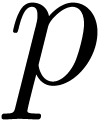 , we
notice that the complexity bound is uniform in the following sense:
there exists a constant
, we
notice that the complexity bound is uniform in the following sense:
there exists a constant 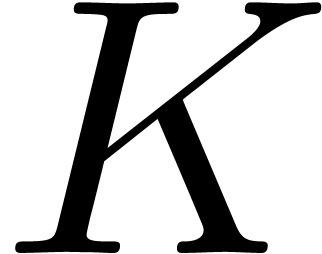 such that for all
effective rings of characteristic
such that for all
effective rings of characteristic 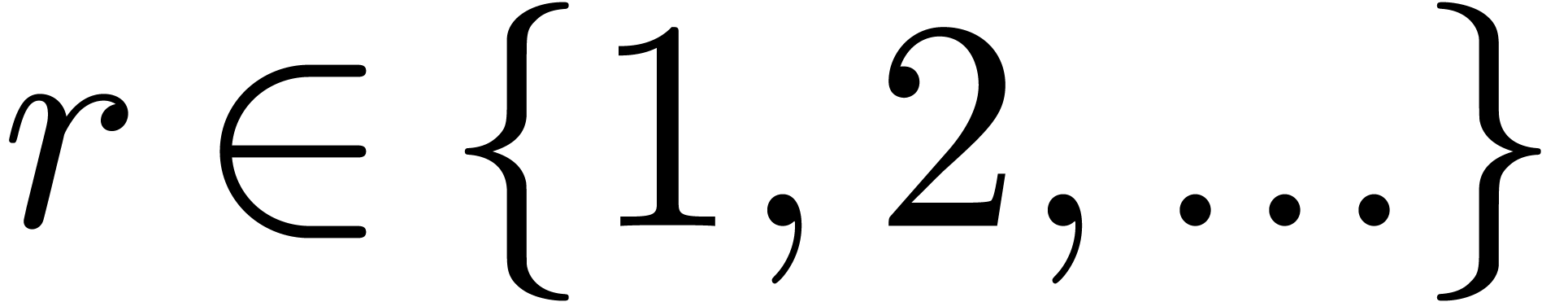 with
with  , we have
, we have 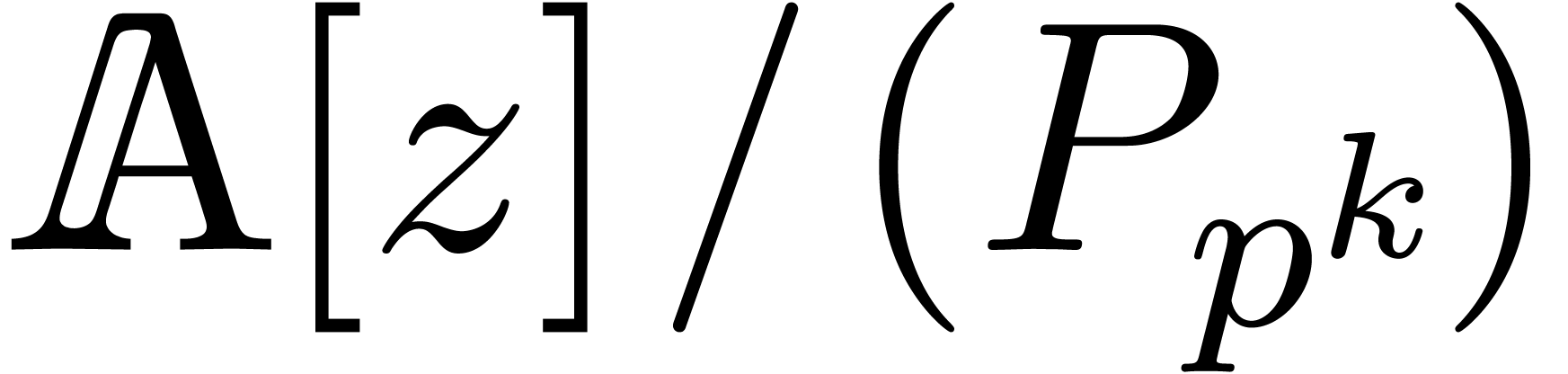 . Indeed, the choice of
. Indeed, the choice of  only
depends on
only
depends on 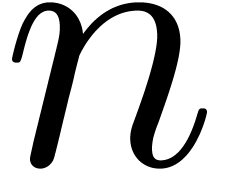 and
and 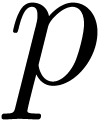 ,
and any operation in
,
and any operation in 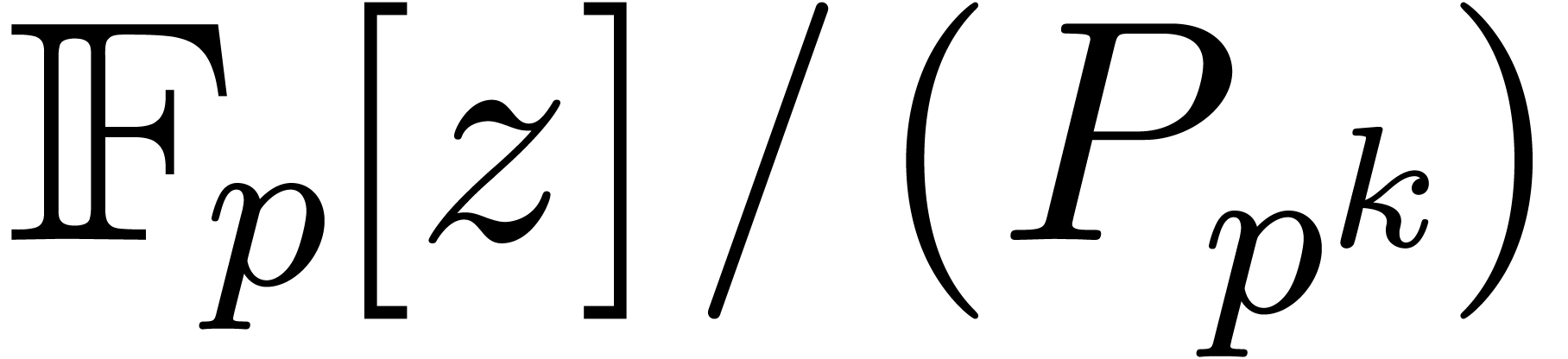 or
or 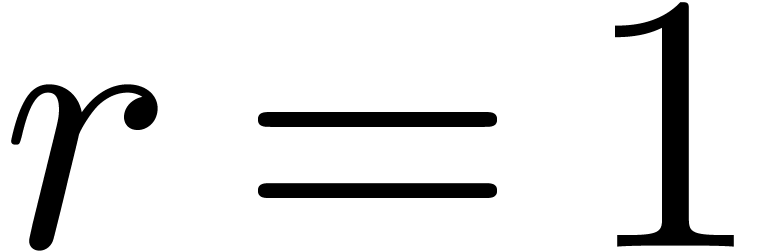 in the case
in the case 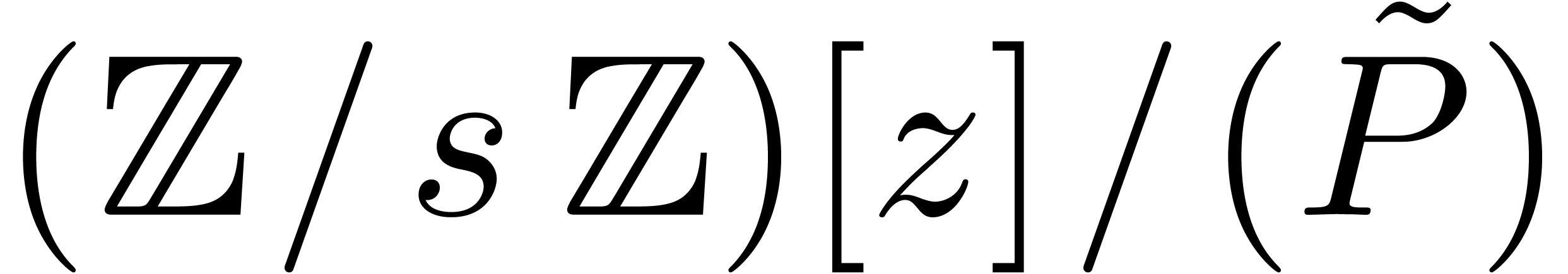 corresponds to exactly one lifted
operation in
corresponds to exactly one lifted
operation in  or
or  in the
general case.
in the
general case.
 be an effective ring of non zero
characteristic
be an effective ring of non zero
characteristic  . Then
. Then

Proof. We will prove the theorem by induction on
the number of prime divisors of  .
If
.
If  is a prime power, then we are done. So assume
that
is a prime power, then we are done. So assume
that 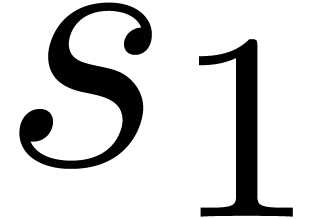 , where
, where  and
and 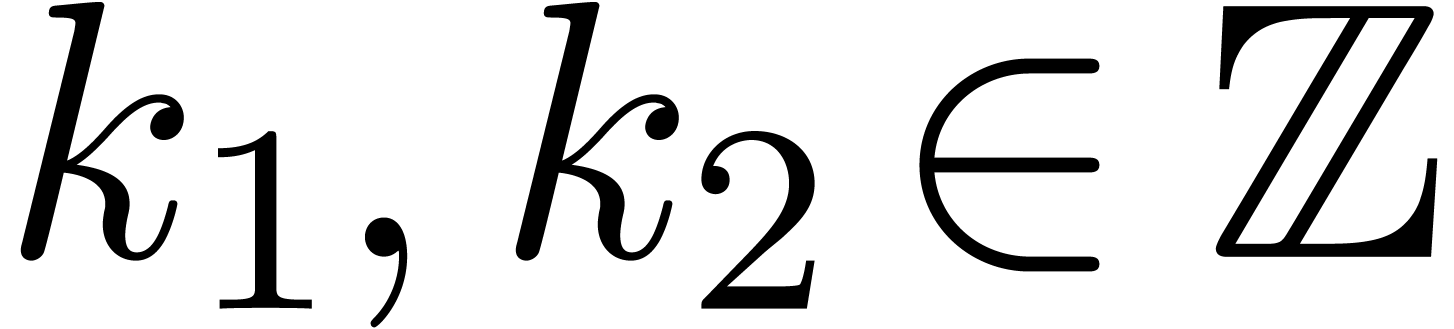 are relatively prime, and let
are relatively prime, and let 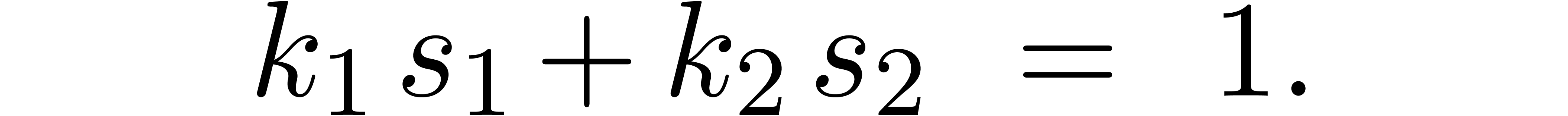 be such that
be such that
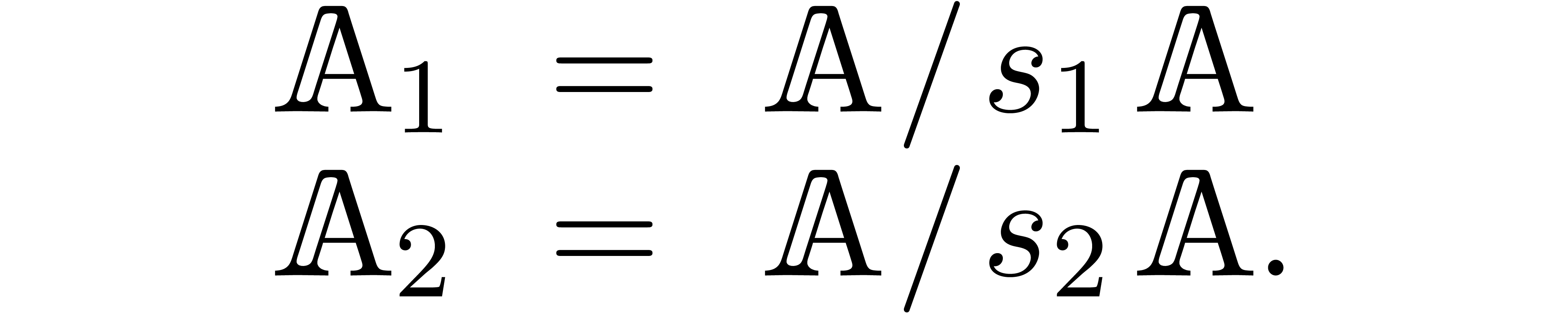
Then we may consider the rings

These rings are effective, when representing their elements by elements
of  and transporting the operations from
and transporting the operations from  . Of course, the representation of
an element
. Of course, the representation of
an element  of
of  (or
(or  ) is not unique, since we may
replace it by
) is not unique, since we may
replace it by 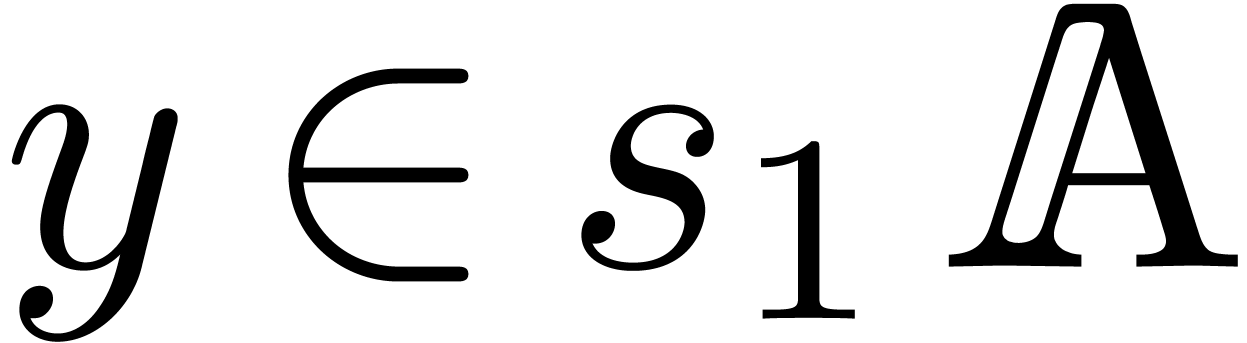 for any
for any 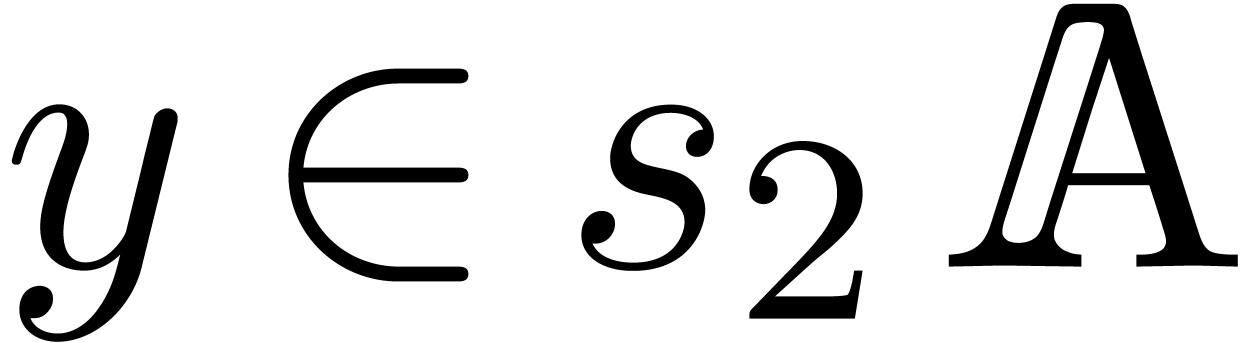 (or
(or 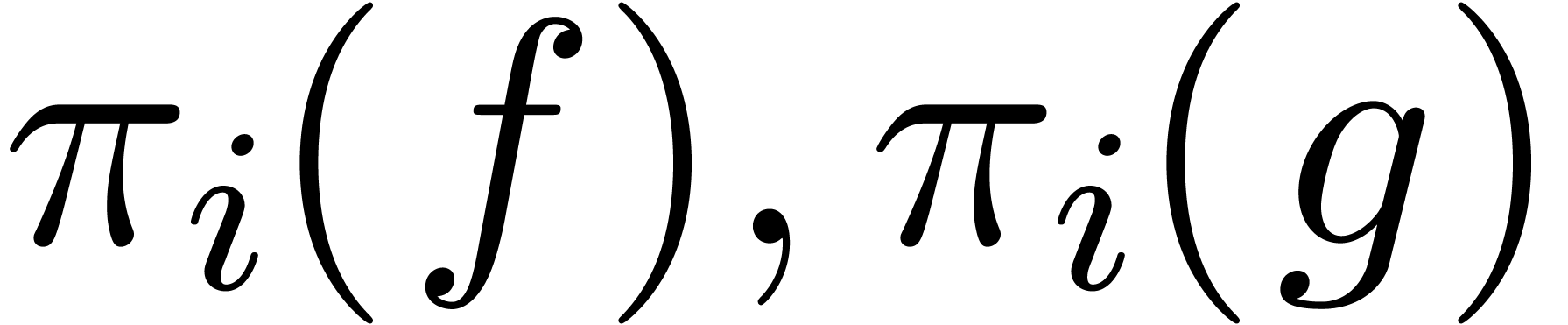 ). But this is not a
problem, since our definition of effective ring did not require unique
representability or the existence of an equality test.
). But this is not a
problem, since our definition of effective ring did not require unique
representability or the existence of an equality test.
Now let  and let
and let 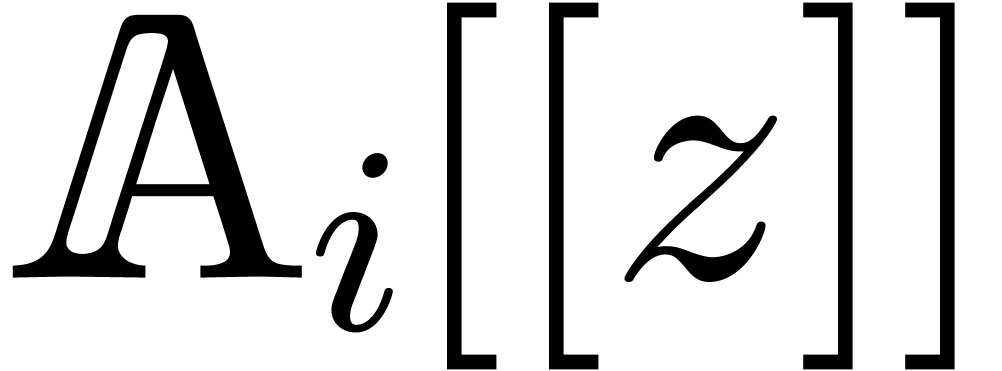 be their
projections in
be their
projections in 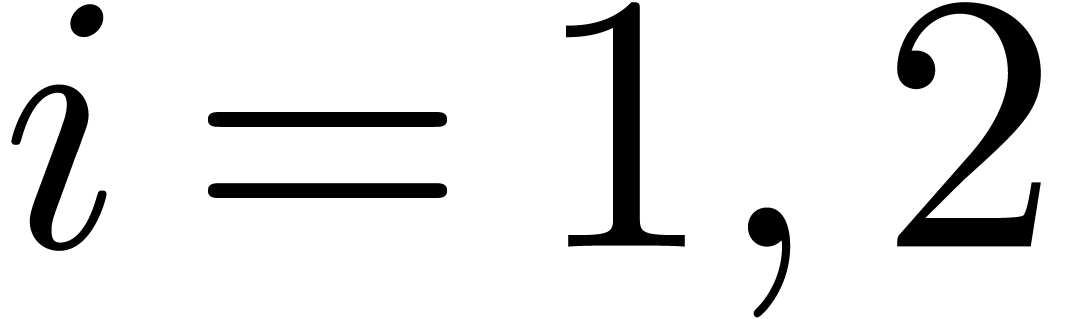 , for
, for 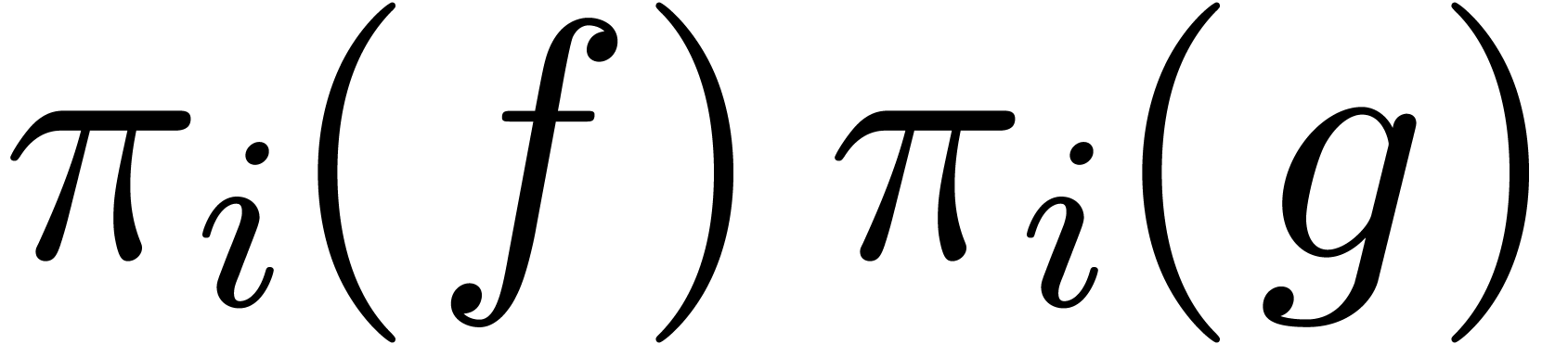 . Consider the relaxed products
. Consider the relaxed products
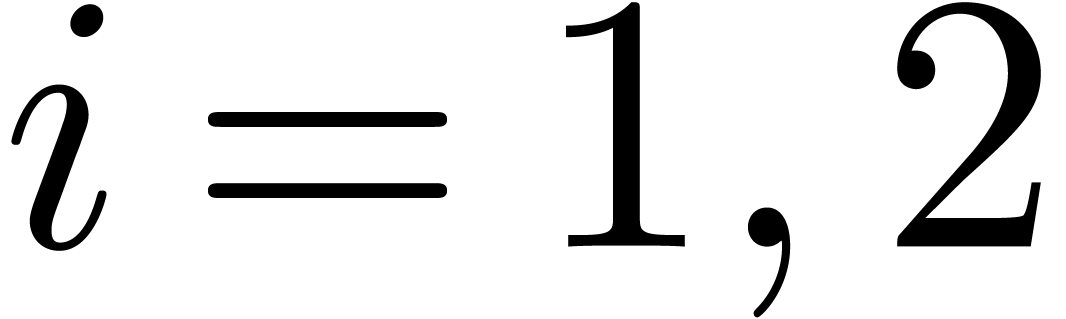 , for
, for 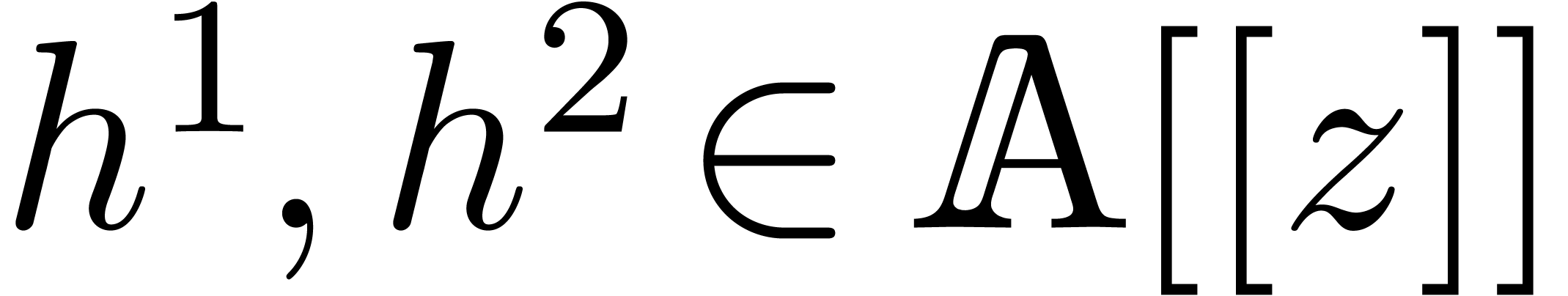 . These products are represented by relaxed series
. These products are represented by relaxed series
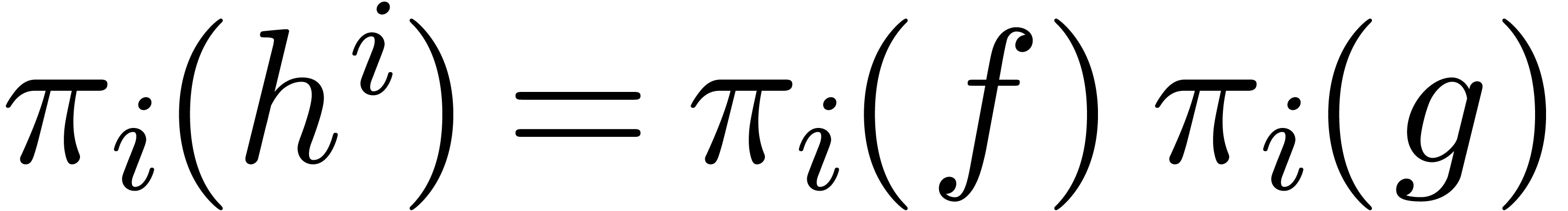 via
via 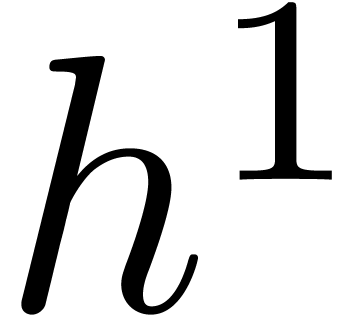 ,
for
,
for 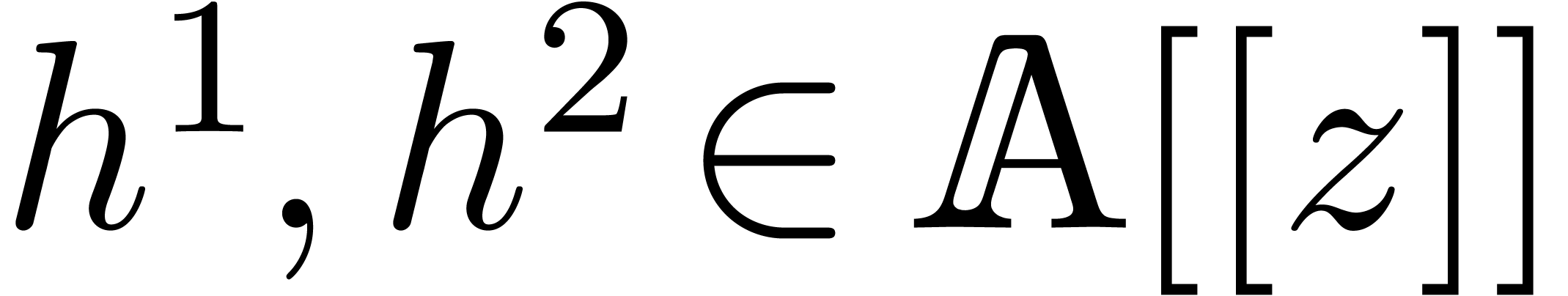 . By the induction
hypotheses, we may compute
. By the induction
hypotheses, we may compute 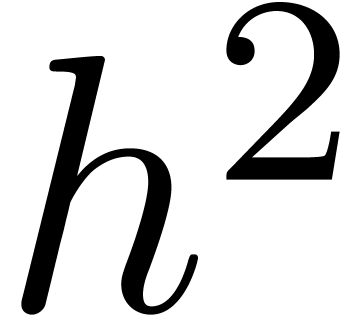 and
and 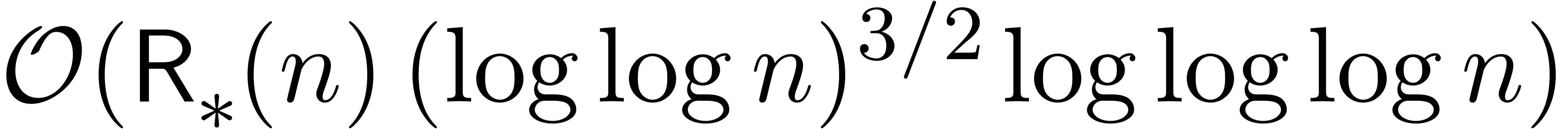 at order
at order 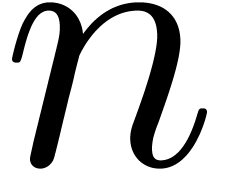 using
using
operations in  . The linear
combination
. The linear
combination 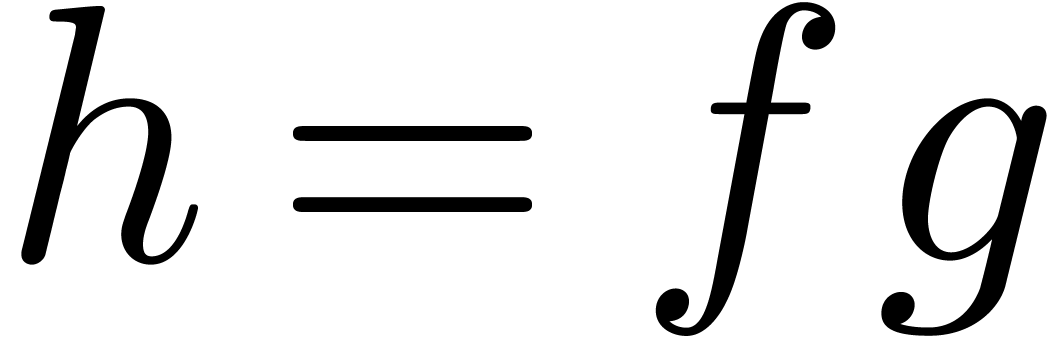 can still be expanded up till order
can still be expanded up till order
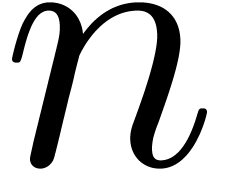 with the same complexity. We claim that
with the same complexity. We claim that 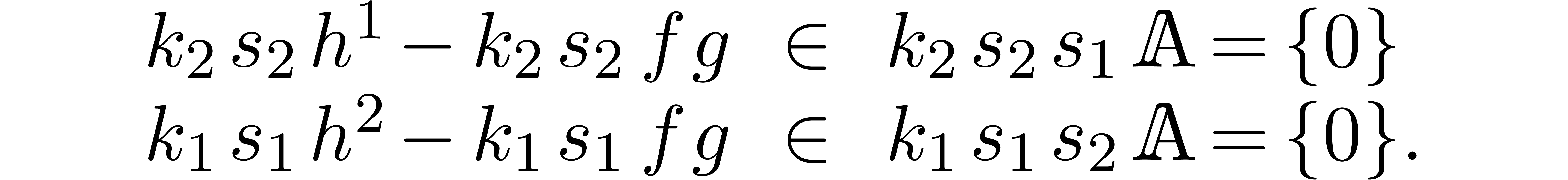 . Indeed,
. Indeed,

Summing both relations, our claim follows.
 -adic numbers
-adic numbers
Let  be an integer, not necessarily a prime
number, and denote
be an integer, not necessarily a prime
number, and denote 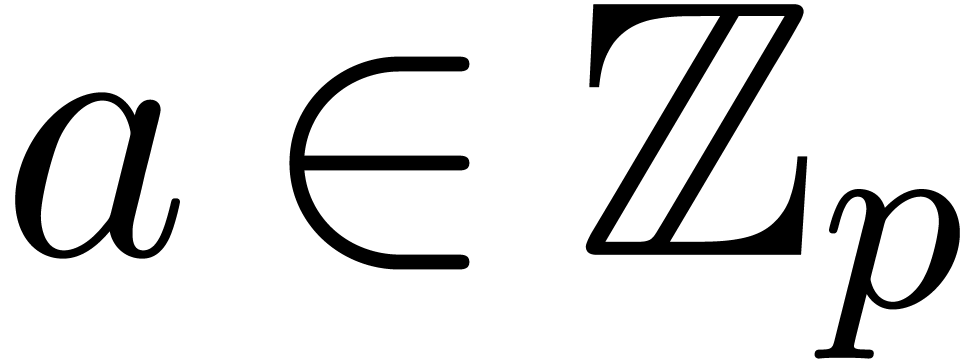 . We will
regard
. We will
regard  -adic numbers
-adic numbers 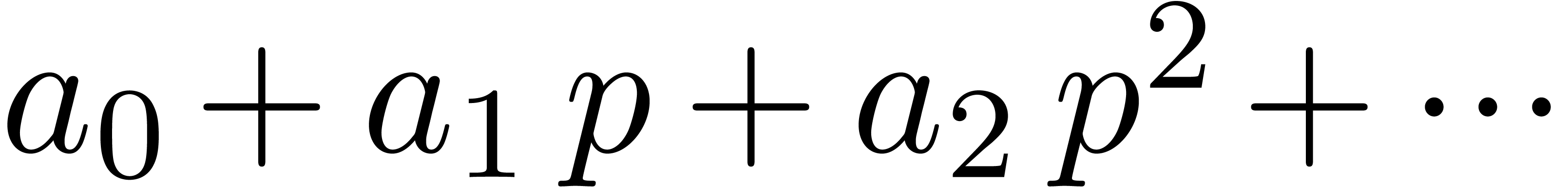 as series
as series 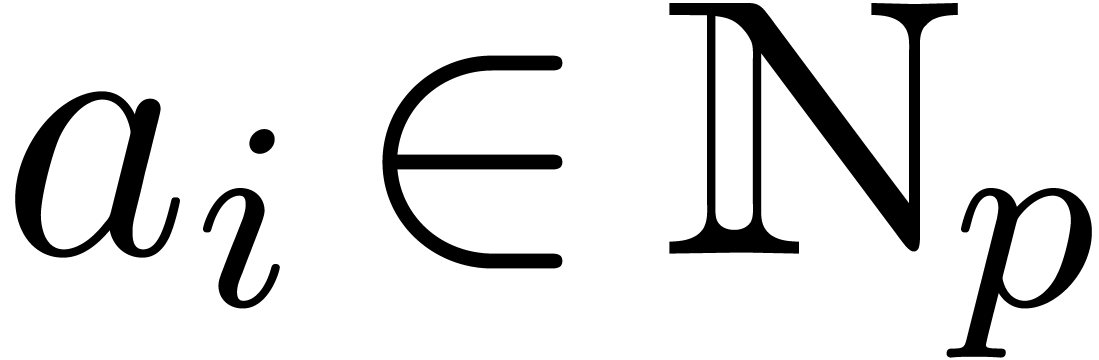 with
with 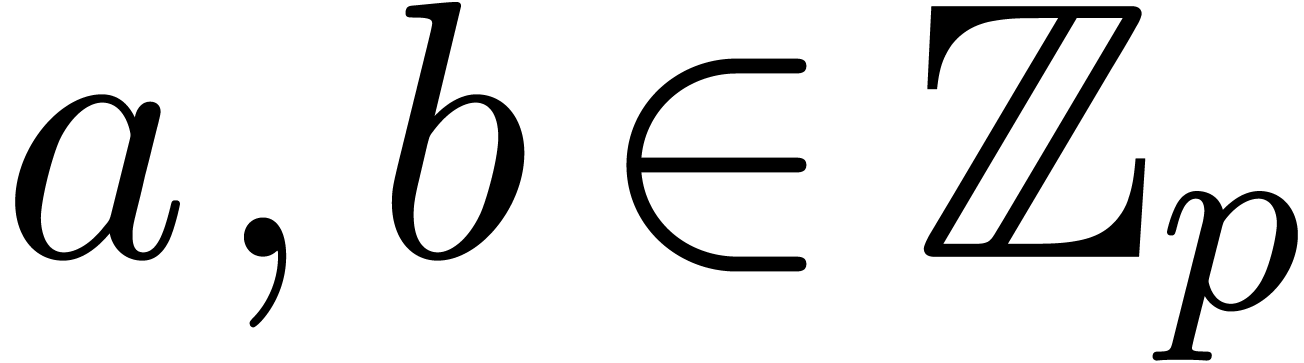 , and such that the basic ring operations
, and such that the basic ring operations  ,
,  and
and  require an additional carry treatment.
require an additional carry treatment.
In order to multiply two relaxed  -adic
numbers
-adic
numbers 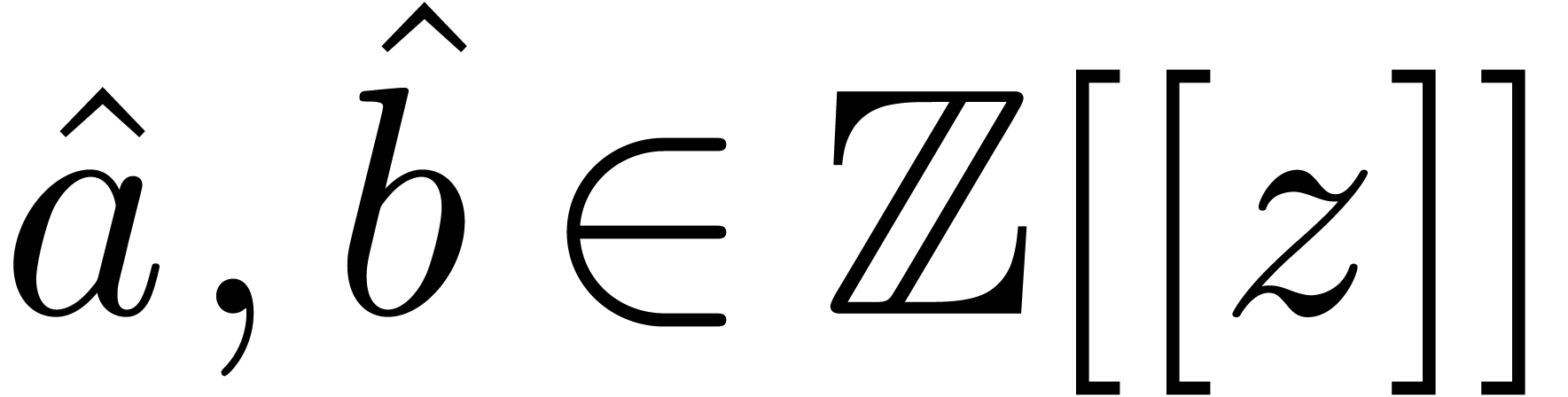 , we may rewrite them
as series
, we may rewrite them
as series 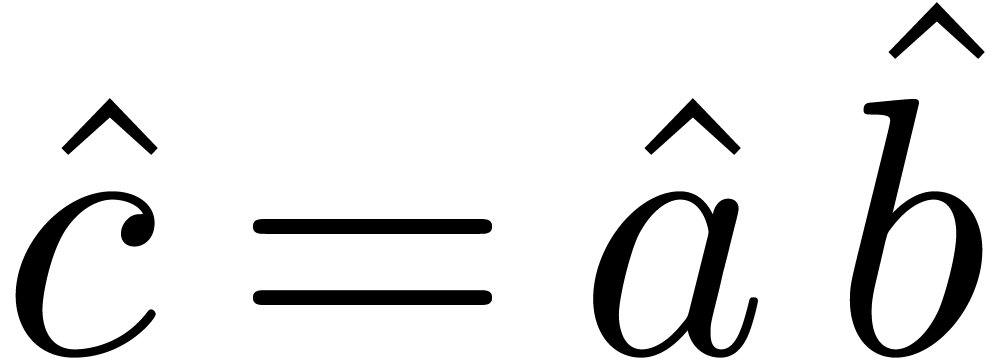 , multiply these
series
, multiply these
series 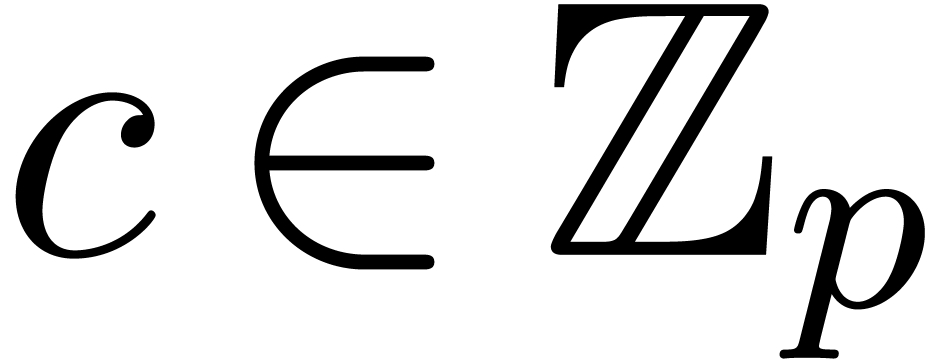 , and recover the
product
, and recover the
product 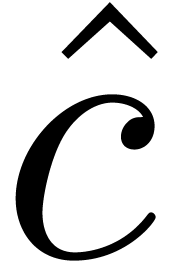 from the result. Of course, the
coefficients of
from the result. Of course, the
coefficients of  may exceed
may exceed  , so some relaxed carry handling is required in
order to recover
, so some relaxed carry handling is required in
order to recover 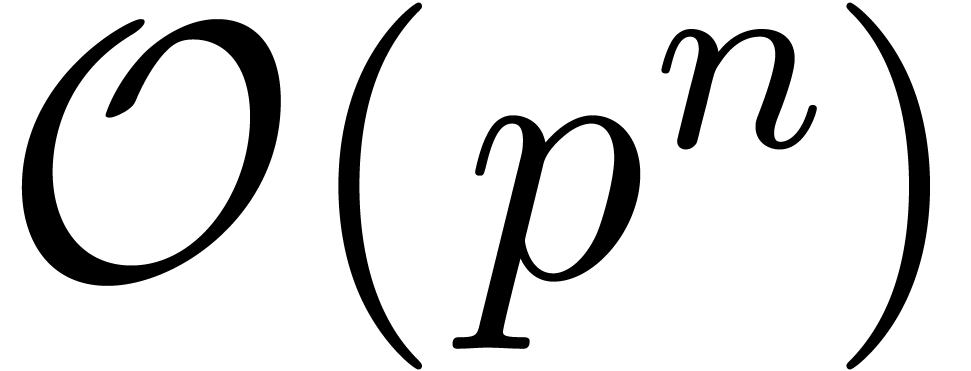 from
from  . We refer to [BHL11, Section 2.7] for
details. In particular, we prove there that
. We refer to [BHL11, Section 2.7] for
details. In particular, we prove there that 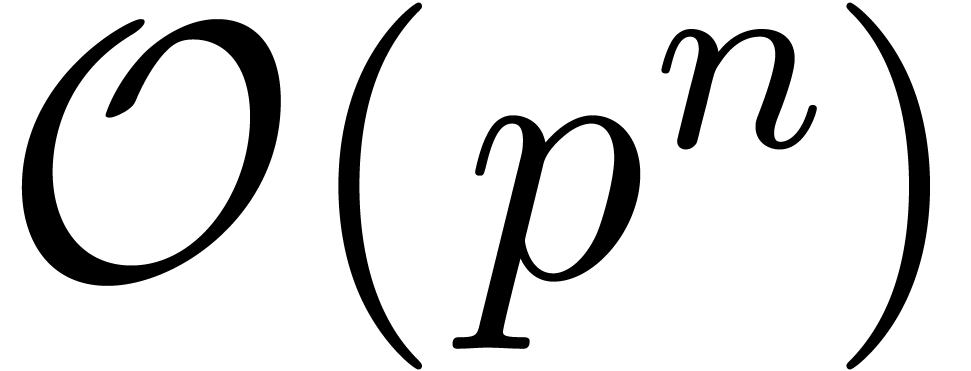 can
be computed up to order
can
be computed up to order 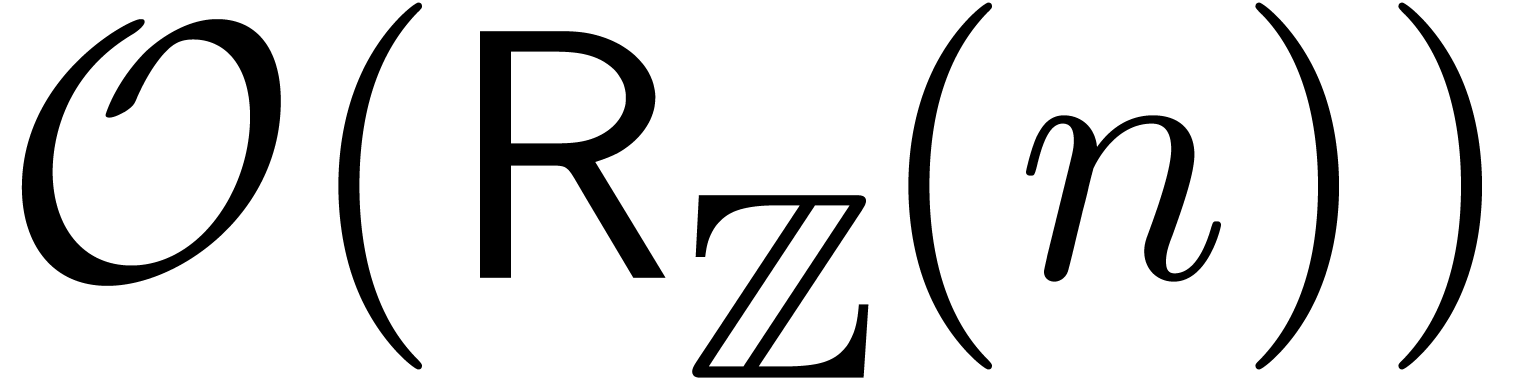 using
using 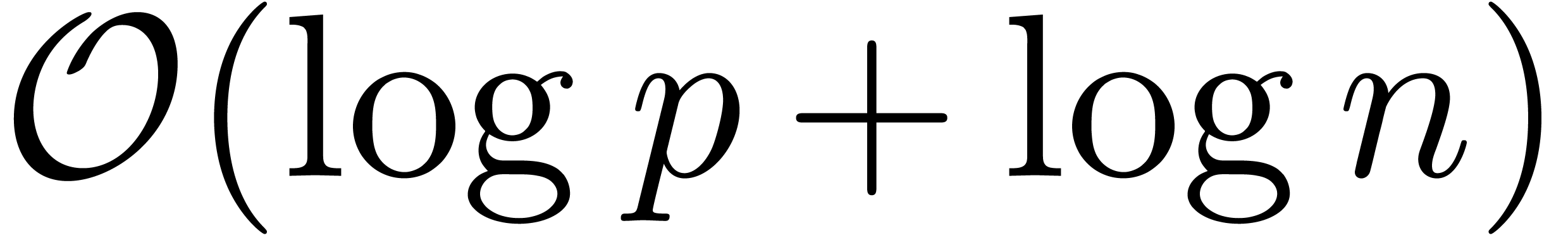 ring operations in
ring operations in  of bit size
of bit size 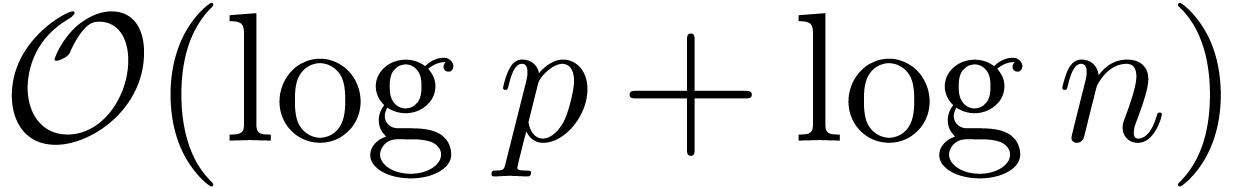 .
.
Given 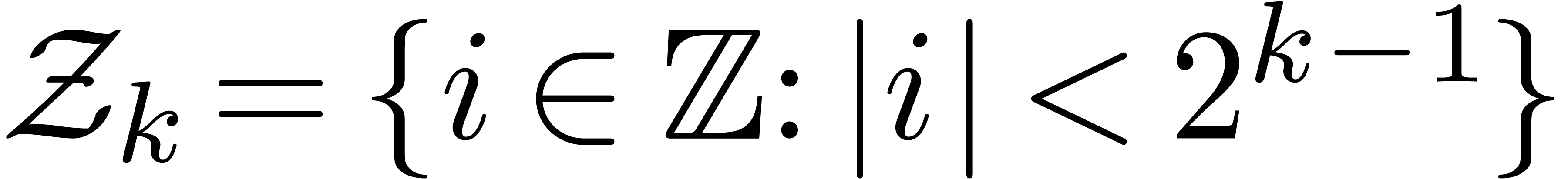 , let
, let 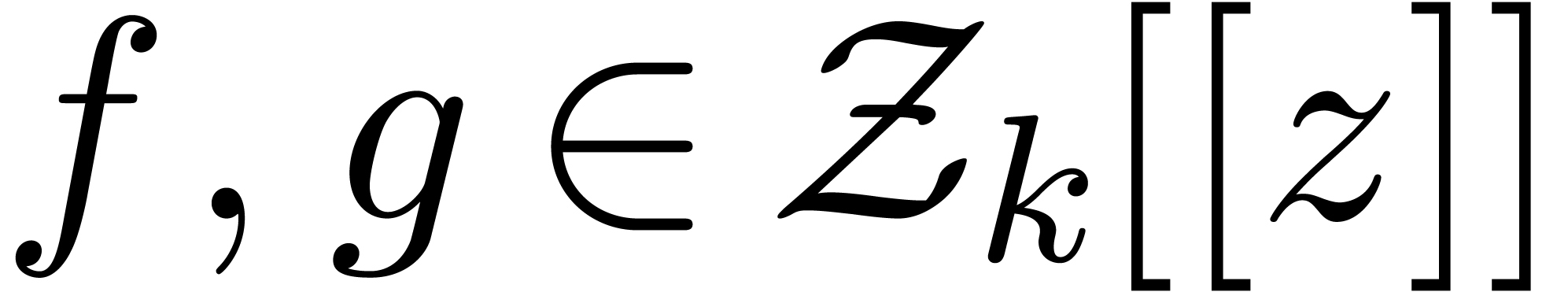 , and consider two power series
, and consider two power series 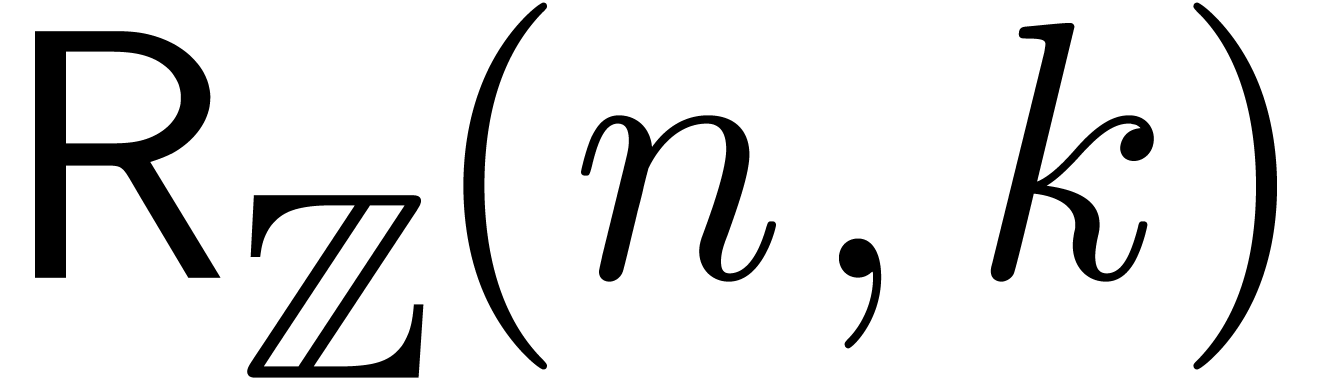 . We will denote by
. We will denote by 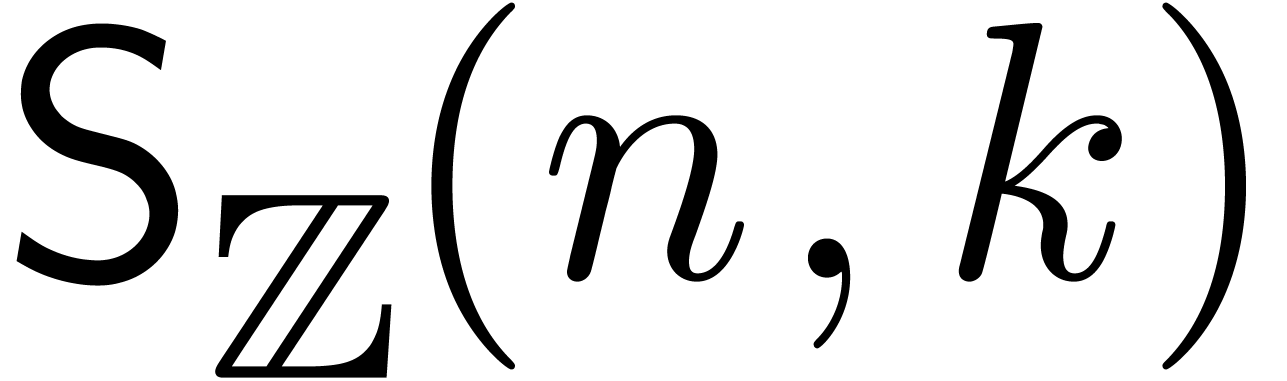 (resp.
(resp.  ) the bit
complexity of multiplying
) the bit
complexity of multiplying  and
and  up to order
up to order 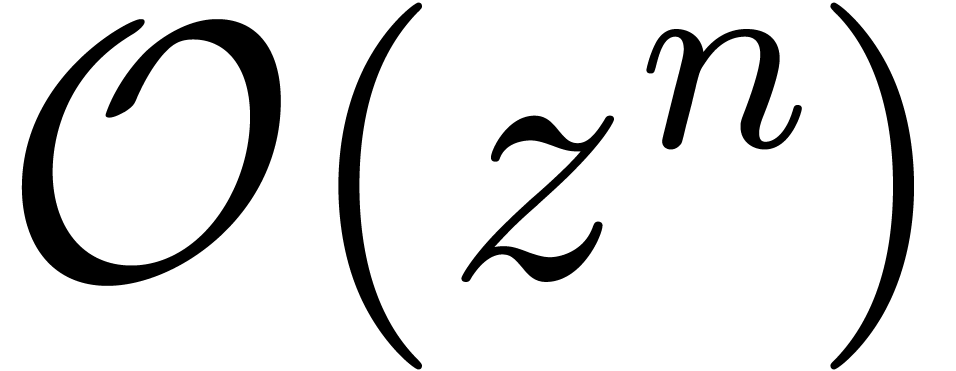 using a relaxed (resp.
semi-relaxed) algorithm.
using a relaxed (resp.
semi-relaxed) algorithm.
Proof. Let 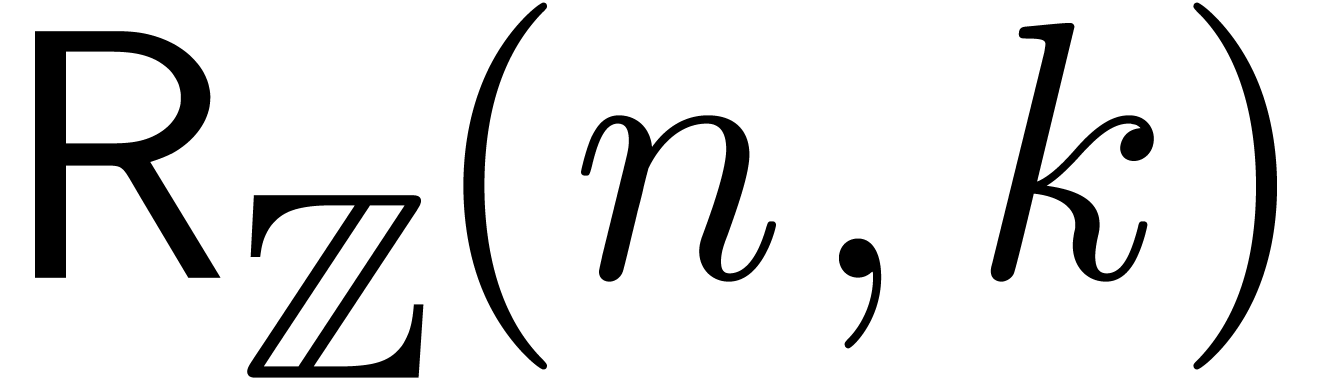 and let
and let 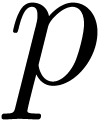 be a prime number (in practice, we recommend to take
be a prime number (in practice, we recommend to take
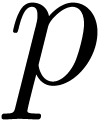 to be a prime number which fits inside one
machine word and such that
to be a prime number which fits inside one
machine word and such that 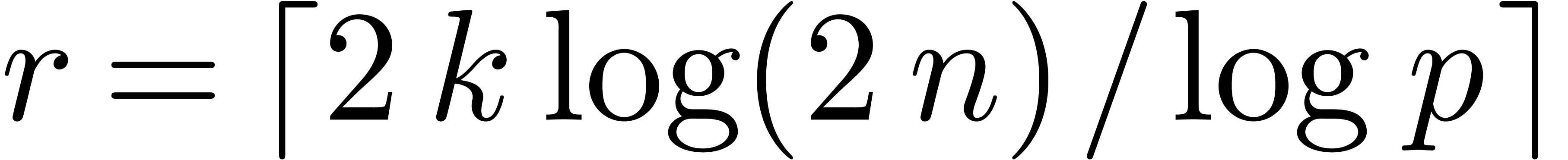 is divisible by a
high power of two). Let
is divisible by a
high power of two). Let 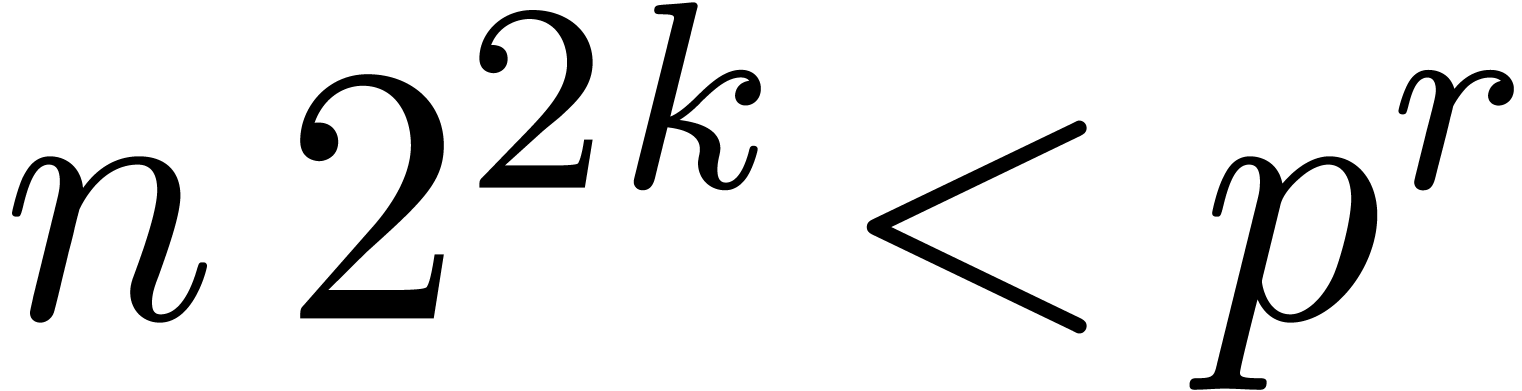 be sufficiently large
such that
be sufficiently large
such that 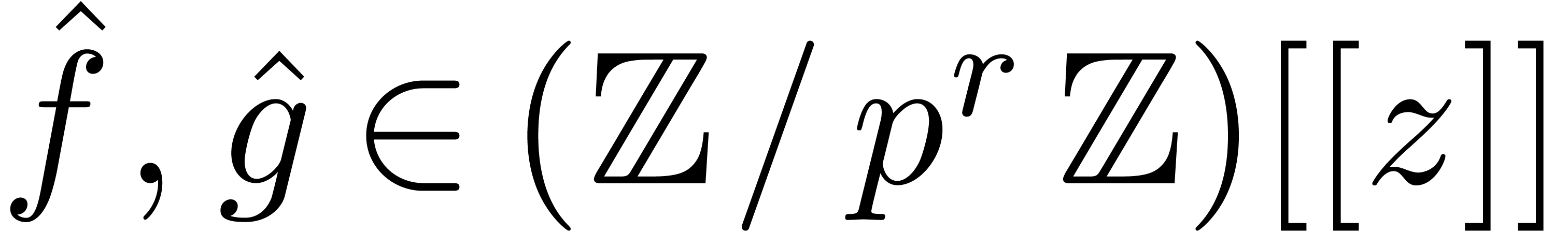 . Let
. Let  be the reductions of
be the reductions of  modulo
modulo 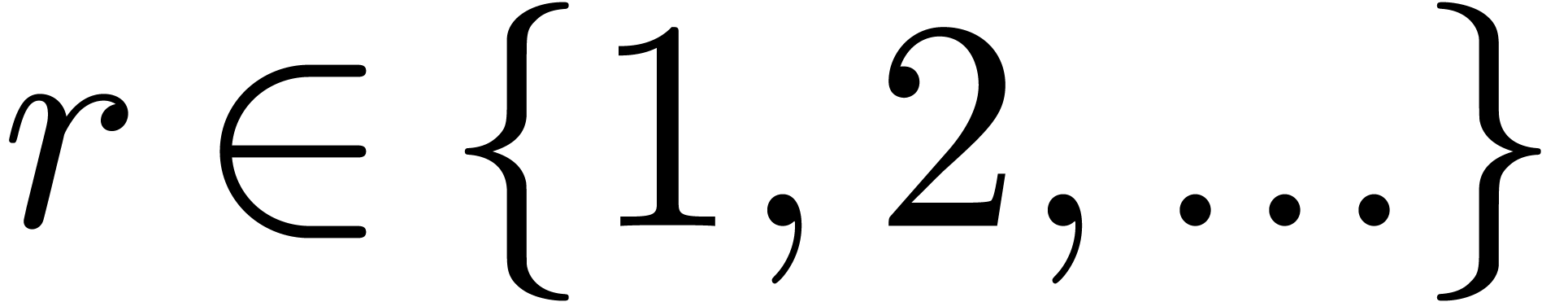 . Then
. Then  may
be reconstructed up to order
may
be reconstructed up to order  from the product
from the product
 . We thus get
. We thus get
By Theorem 9, we have
By Remark 10, this bound is uniform in 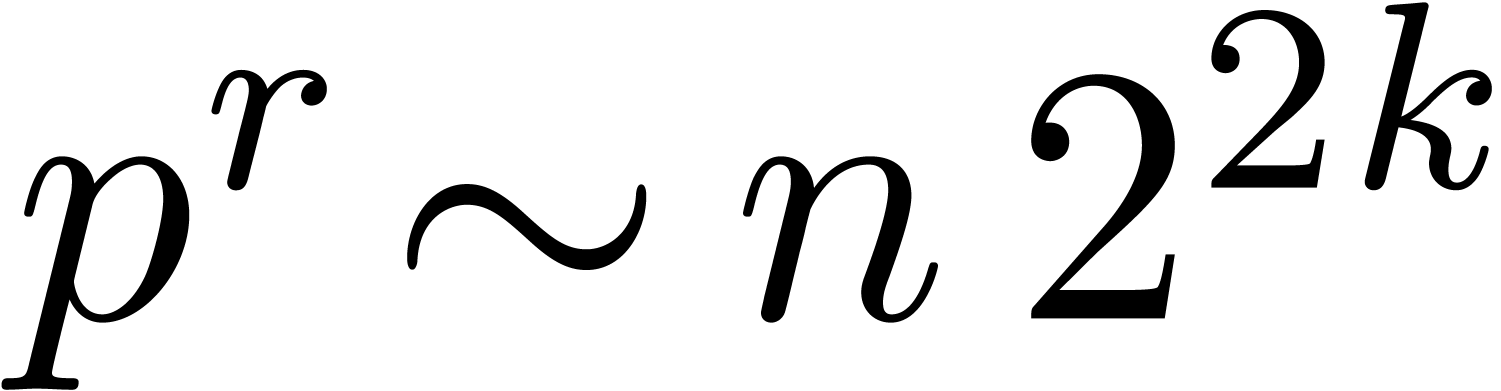 . Since
. Since 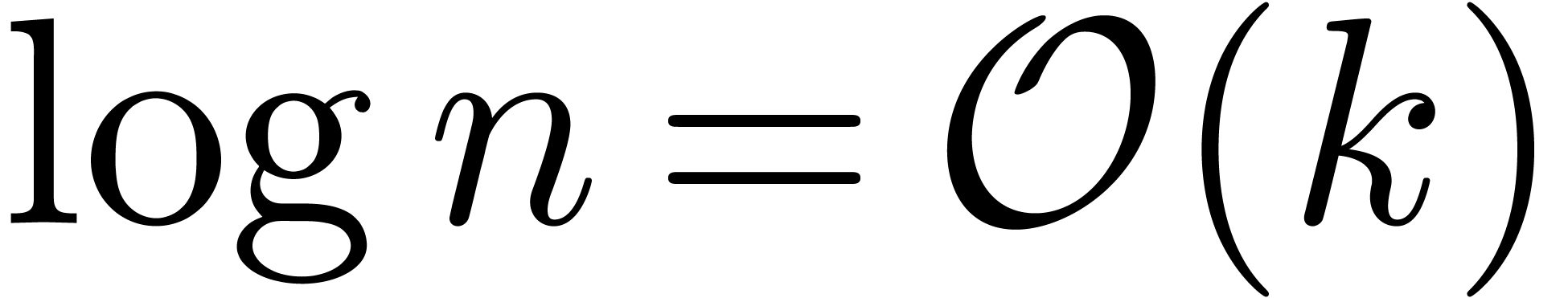 ,
the result follows.
,
the result follows.
For the above strategy to be efficient, it is important that 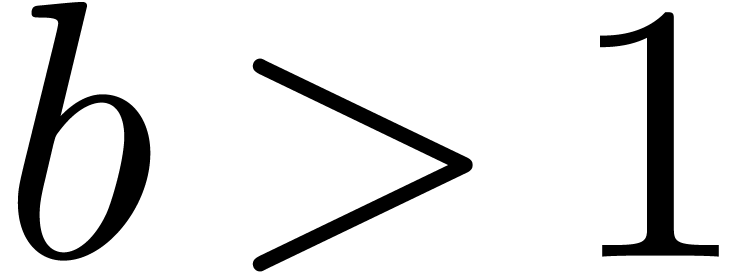 . This can be achieved by combining
it with the technique of
. This can be achieved by combining
it with the technique of  -adic
blocking. More precisely, given a
-adic
blocking. More precisely, given a  -adic
block size
-adic
block size  , then any
, then any  -adic number in
-adic number in 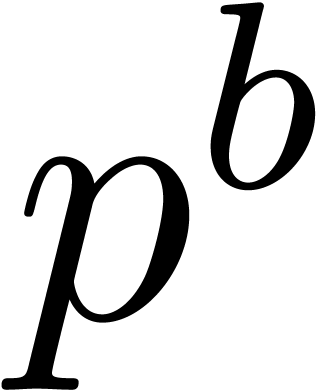 can naturally be considered as a
can naturally be considered as a 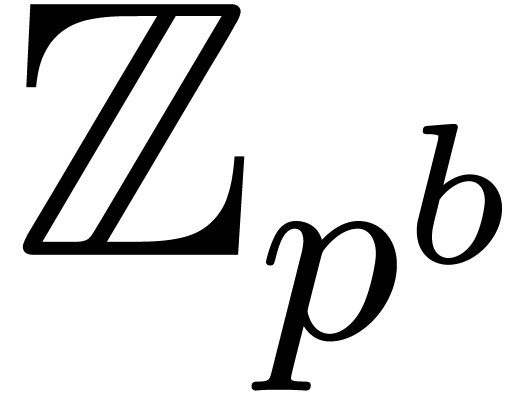 -adic
number in
-adic
number in 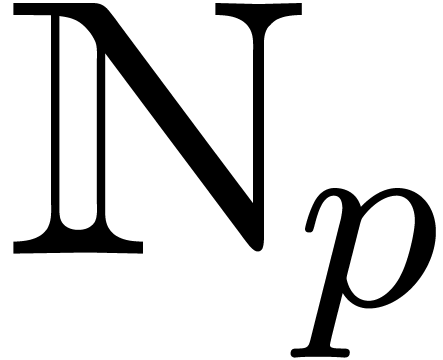 , and vice
versa. Assuming that numbers in
, and vice
versa. Assuming that numbers in 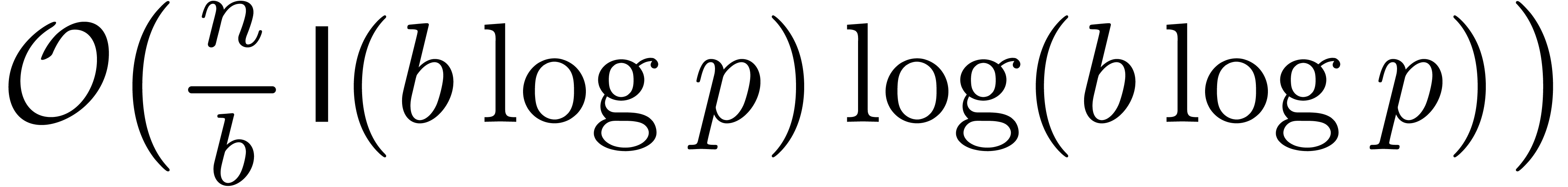 are written
in base
are written
in base 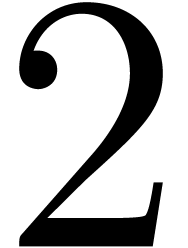 , the conversion is
trivial if
, the conversion is
trivial if  is a power of two. Otherwise, the
conversion involves base conversions and we refer to [BHL11,
Section 4] for more details. In particular, the conversions in both
directions up to order
is a power of two. Otherwise, the
conversion involves base conversions and we refer to [BHL11,
Section 4] for more details. In particular, the conversions in both
directions up to order 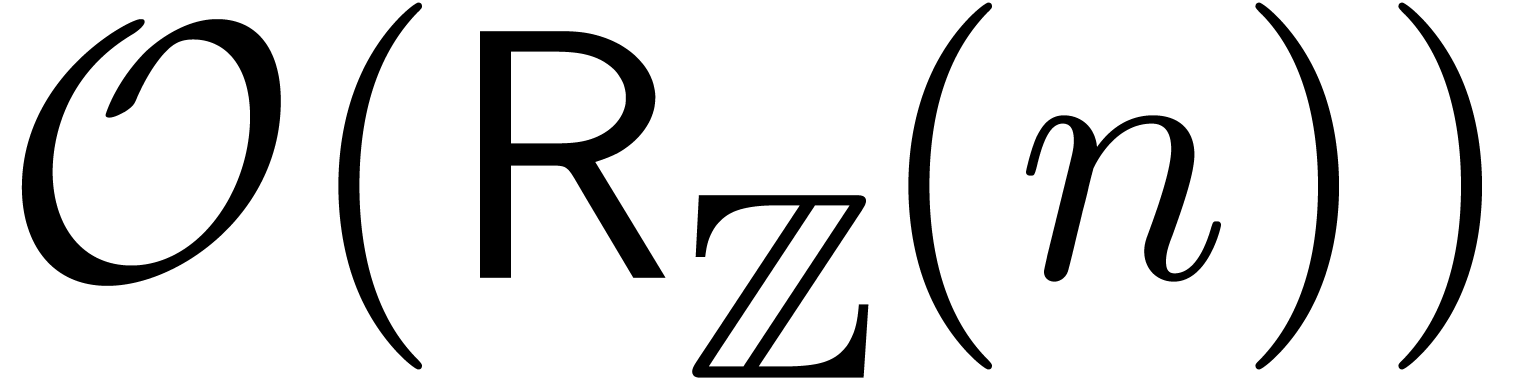 can be done in time
can be done in time 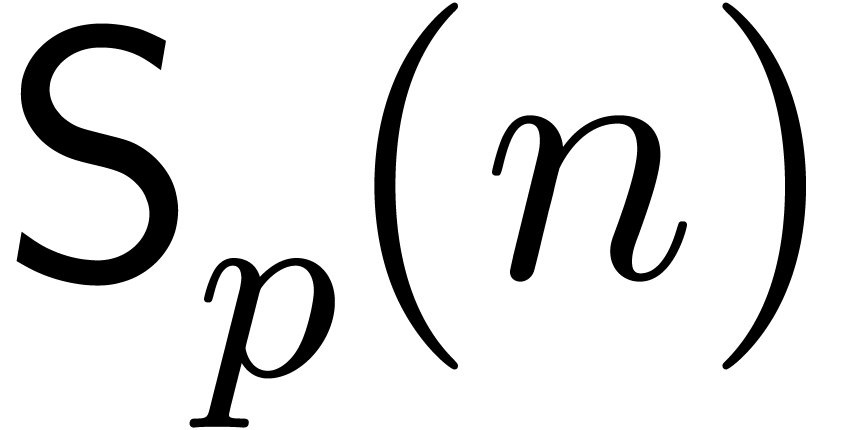 .
.
Let 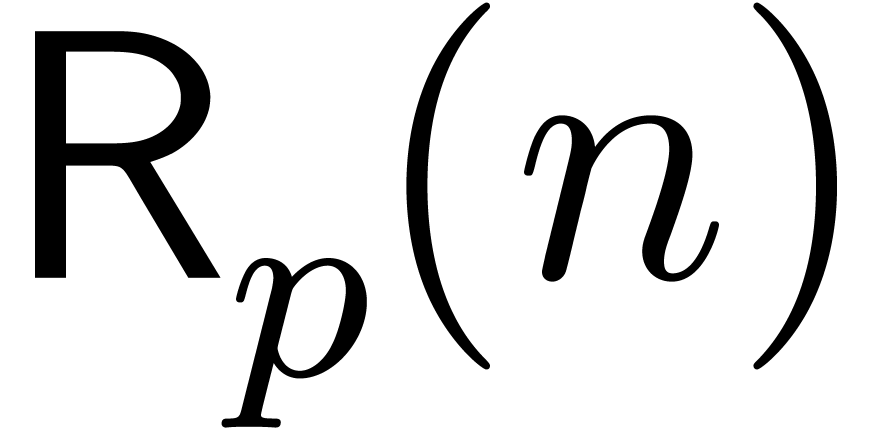 (resp.
(resp.  ) the complexity of relaxed (resp.
semi-relaxed) multiplication in
) the complexity of relaxed (resp.
semi-relaxed) multiplication in 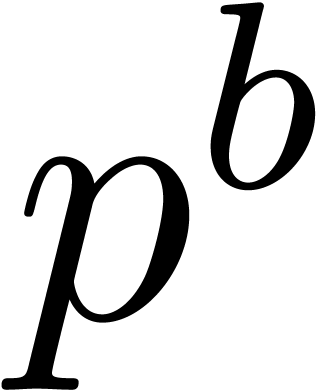 up till order
up till order
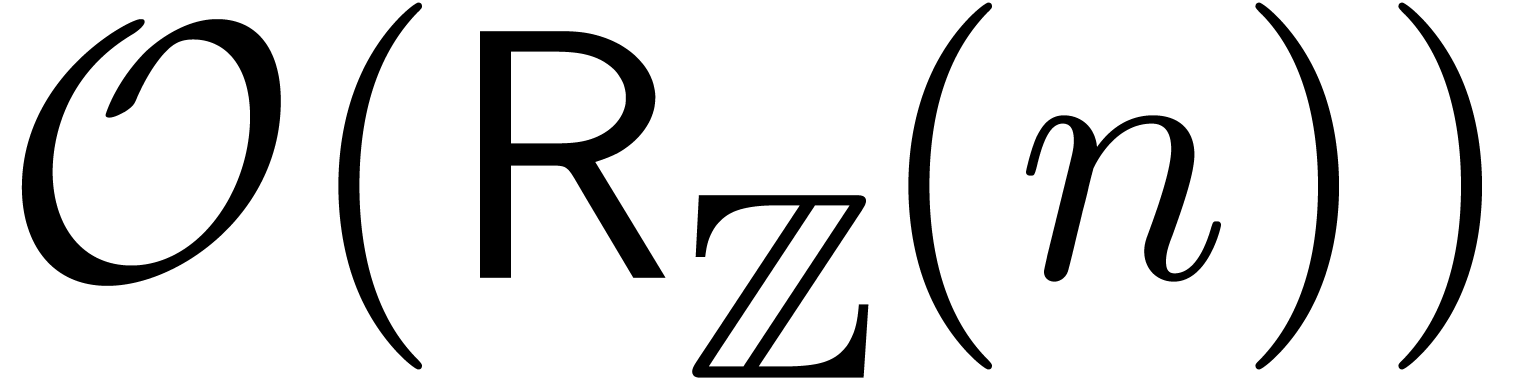 .
.
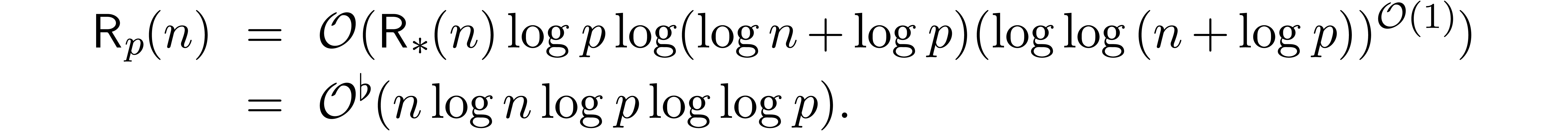
Proof. Let  ,
so that
,
so that
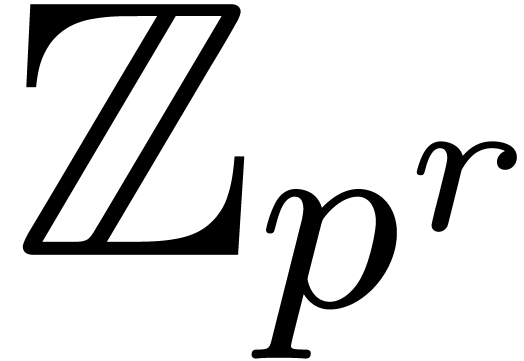
Using the strategy of 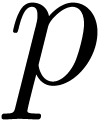 -adic
blocking, a semi-relaxed product in
-adic
blocking, a semi-relaxed product in  may then be
reduced to one semi-relaxed product in
may then be
reduced to one semi-relaxed product in 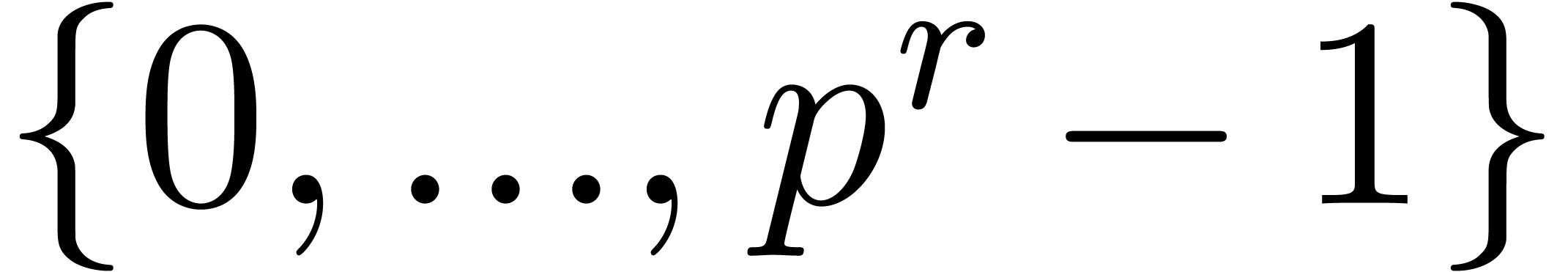 and one
relaxed multiplication with an integer in
and one
relaxed multiplication with an integer in  .
In other words,
.
In other words,
where  stands for the cost of semi-relaxed
multiplication of two
stands for the cost of semi-relaxed
multiplication of two 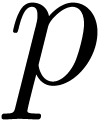 -adic
numbers in
-adic
numbers in 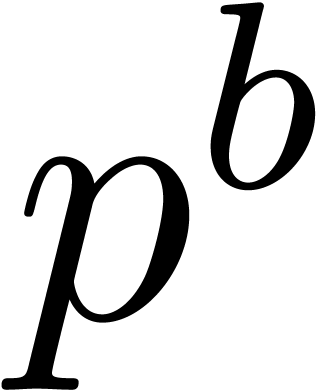 up till order
up till order  . By [BHL11, Proposition 4], we have
. By [BHL11, Proposition 4], we have
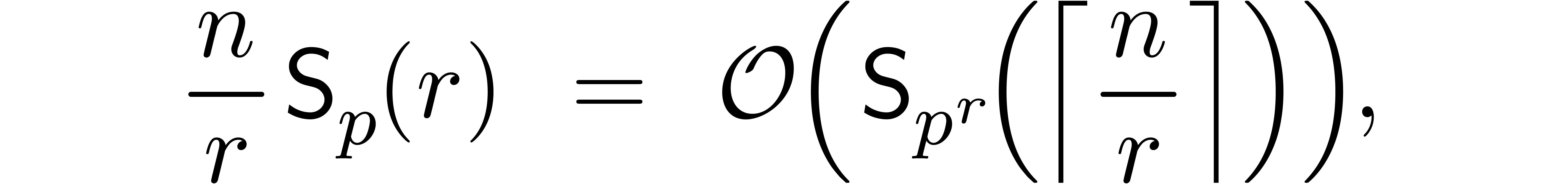
By Lemma 12, we also have
In particular,
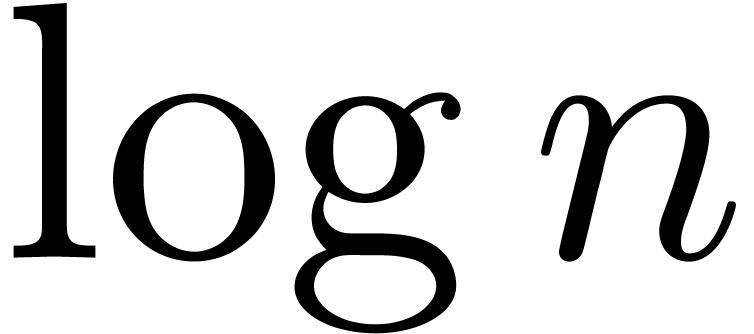
which completes the proof of the theorem.
Remark 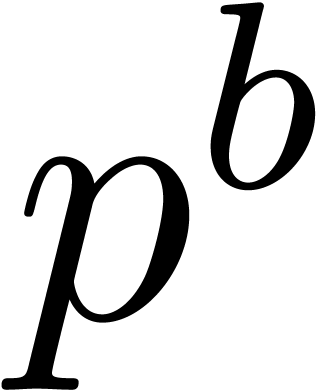 was
was
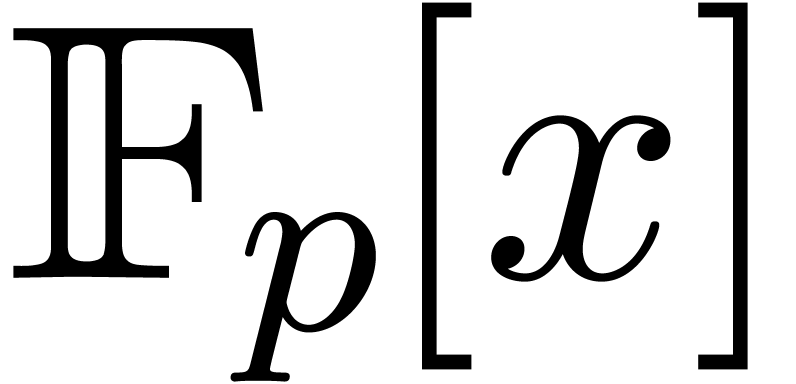
We thus improved the previous bound by a factor 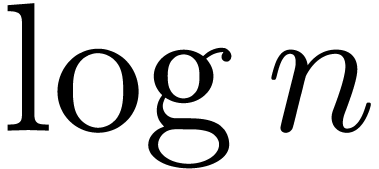 at least, up to sublogarithmic terms.
at least, up to sublogarithmic terms.
For the moment, we have not implemented any of the new algorithms in practice. Nevertheless, our old implementation of the algorithm from [Hoe07] allowed us to gain some insight on the practical usefulness of blockwise relaxed multiplication. Let us briefly discuss the potential impact of the new results for practical purposes.
In the case of integer coefficients, it is best to re-encode the
integers as polynomials in  for a prime number
which fits into a machine word and such that
for a prime number
which fits into a machine word and such that 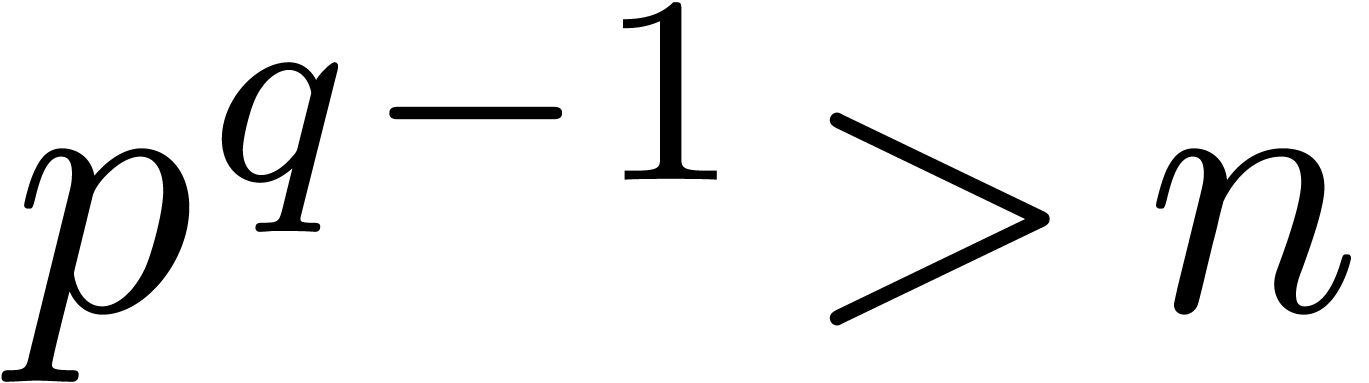 admits many
admits many 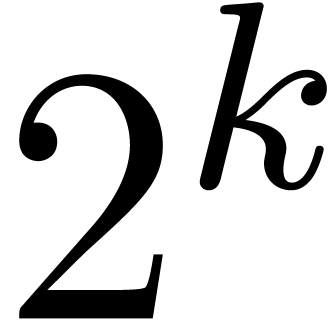 -th roots of
unity (it is also possible to take several primes
-th roots of
unity (it is also possible to take several primes  and use Chinese remaindering). After that, one may again use the old
algorithm from [Hoe07]. Also, integer coefficients usually
grow in size with
and use Chinese remaindering). After that, one may again use the old
algorithm from [Hoe07]. Also, integer coefficients usually
grow in size with 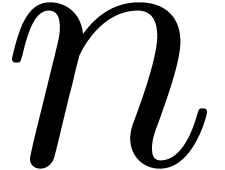 , so one
really should see the power series as a bivariate power series in
, so one
really should see the power series as a bivariate power series in 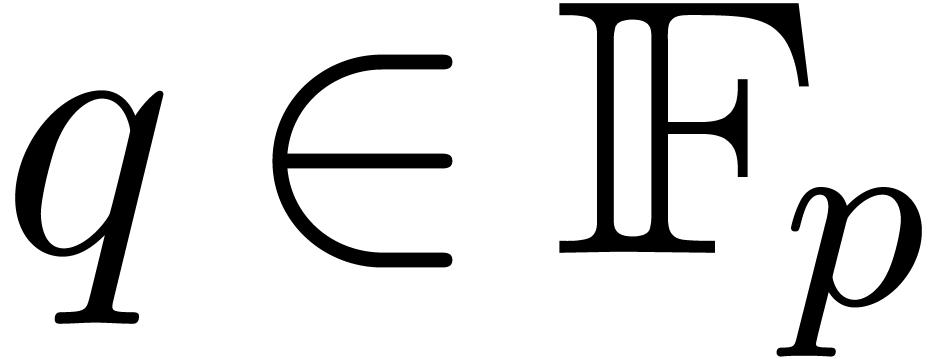 with a triangular support. One may then want to use
TFT-style multiplication [Hoe04, Hoe05] in
order to gain another constant factor.
with a triangular support. One may then want to use
TFT-style multiplication [Hoe04, Hoe05] in
order to gain another constant factor.
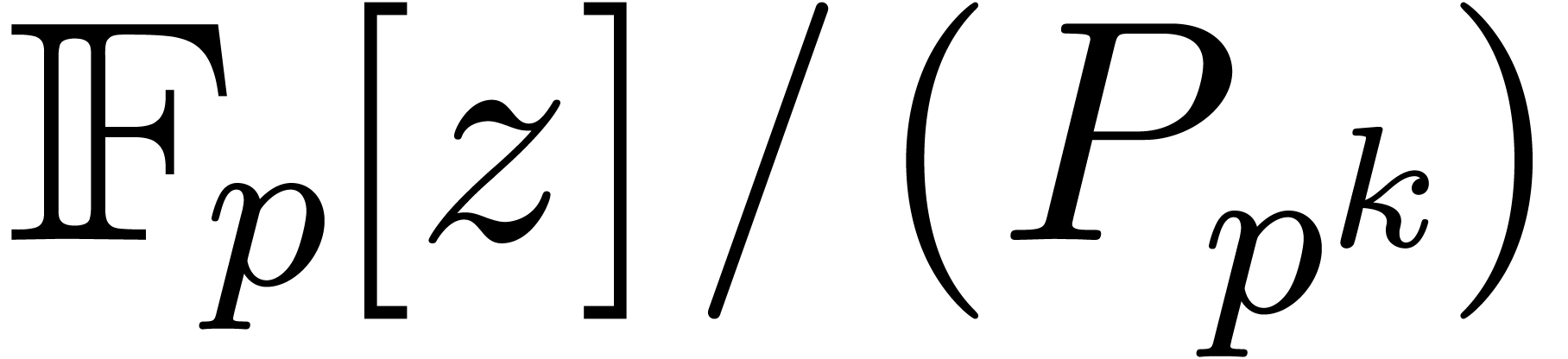 with
with  sufficiently large and
sufficiently large and 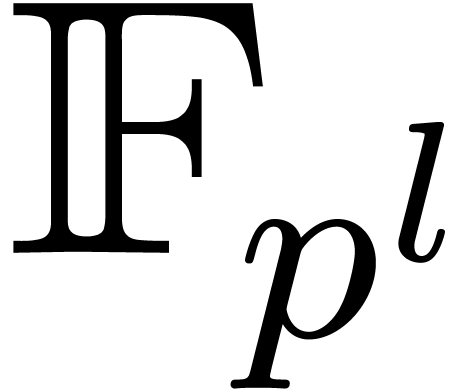 , it
is possible to choose
, it
is possible to choose 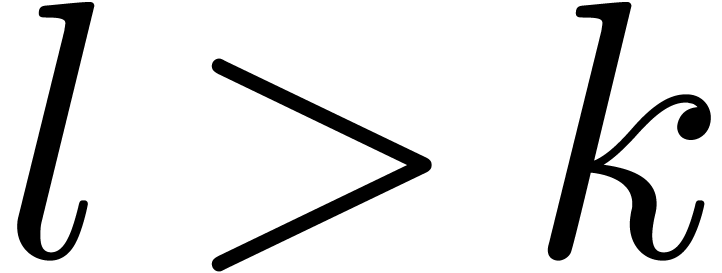 ,
thereby speeding up evaluation and interpolation. For small finite
fields of the form
,
thereby speeding up evaluation and interpolation. For small finite
fields of the form 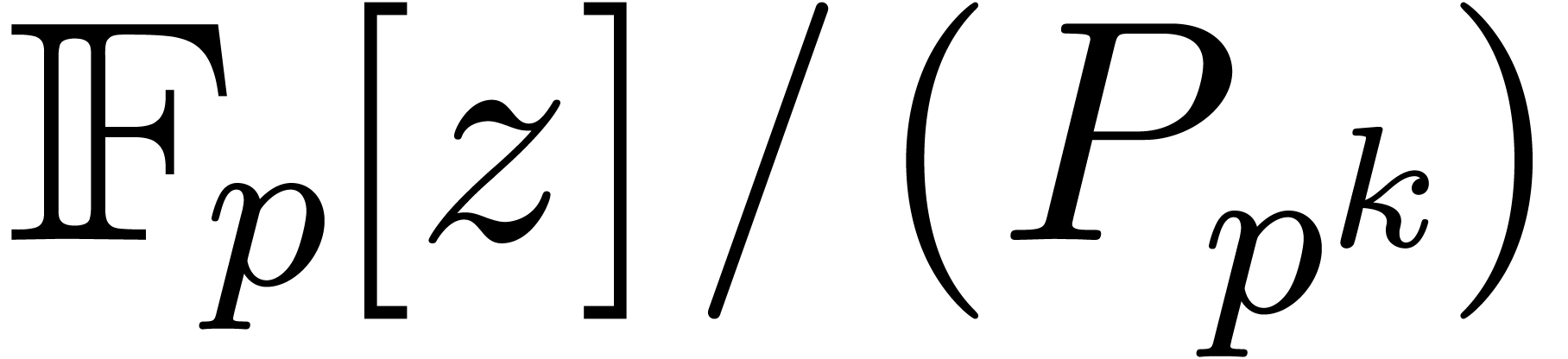 , it is
generally necessary to make the initial investment of working
in a larger ring with sufficiently large geometric progressions. Of
course, instead of the ring extensions considered in Section 5,
we may directly use field extensions of the form
, it is
generally necessary to make the initial investment of working
in a larger ring with sufficiently large geometric progressions. Of
course, instead of the ring extensions considered in Section 5,
we may directly use field extensions of the form 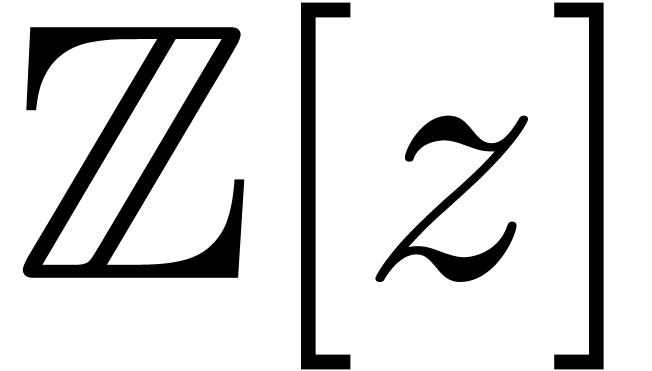 with
with 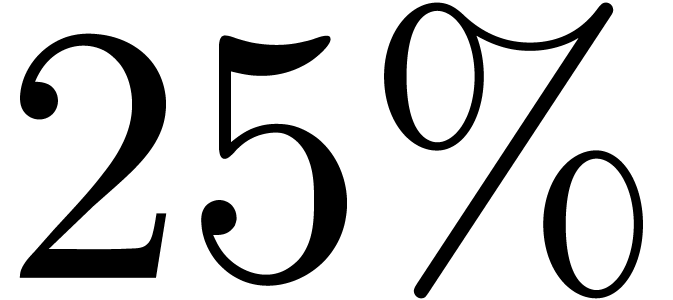 .
.
 with respect to the fully relaxed case,
using the technique from [Hoe03]. Unfortunately, the
middle product is not always easy to implement. For instance, if we
rely on Kronecker substitution for multiplications in
with respect to the fully relaxed case,
using the technique from [Hoe03]. Unfortunately, the
middle product is not always easy to implement. For instance, if we
rely on Kronecker substitution for multiplications in  , then we will need to implement an ad
hoc analogue for the middle product. Since we did not use a fast
algorithm for middle products for our benchmarks in [Hoe07,
Section 5], the timings for the semi-relaxed product in were only
about
, then we will need to implement an ad
hoc analogue for the middle product. Since we did not use a fast
algorithm for middle products for our benchmarks in [Hoe07,
Section 5], the timings for the semi-relaxed product in were only
about 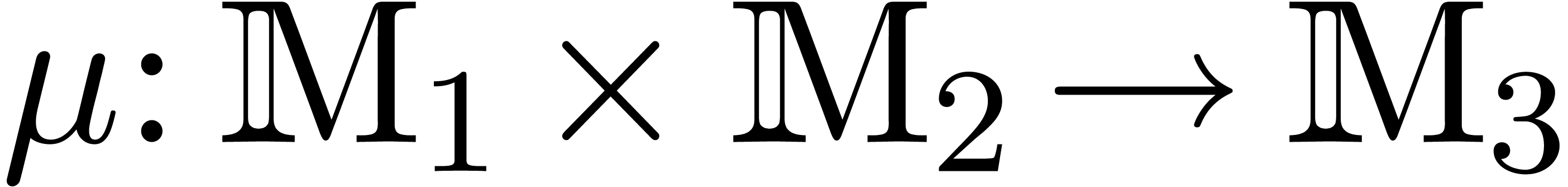 instead of
instead of 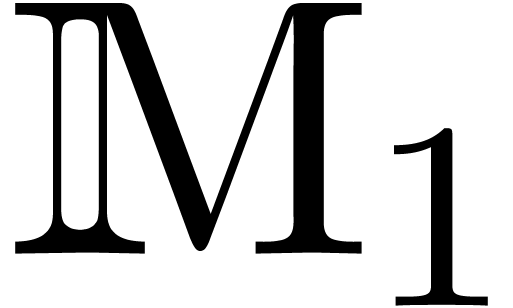 better than the timings for the fully relaxed product. Nevertheless,
modulo increased implementation efforts, we stress that a
better than the timings for the fully relaxed product. Nevertheless,
modulo increased implementation efforts, we stress that a 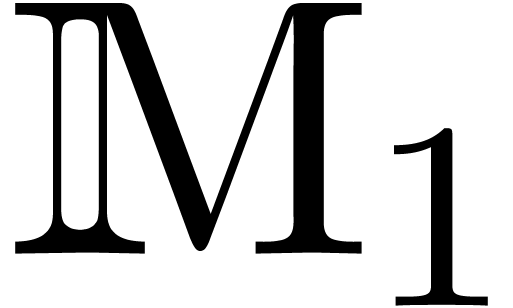 gain should be achievable.
gain should be achievable.
 is an effective ring. In
fact, a more general setting for relaxed multiplication is to consider
a bilinear mapping
is an effective ring. In
fact, a more general setting for relaxed multiplication is to consider
a bilinear mapping 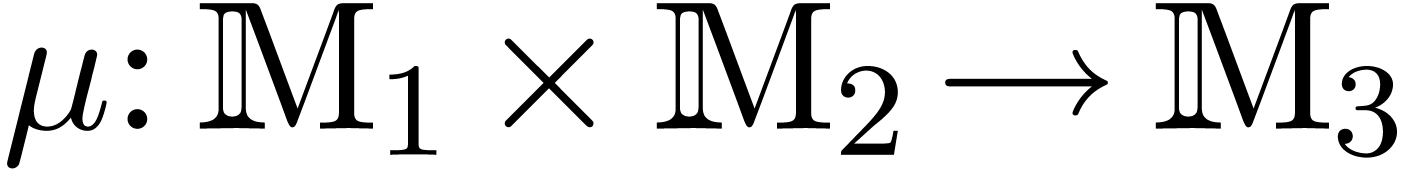 , where
, where
 ,
,  and
and  are effective
are effective  -modules, and extend it into a mapping
-modules, and extend it into a mapping 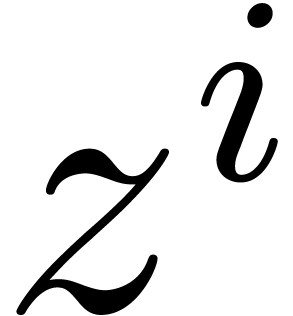 by
by 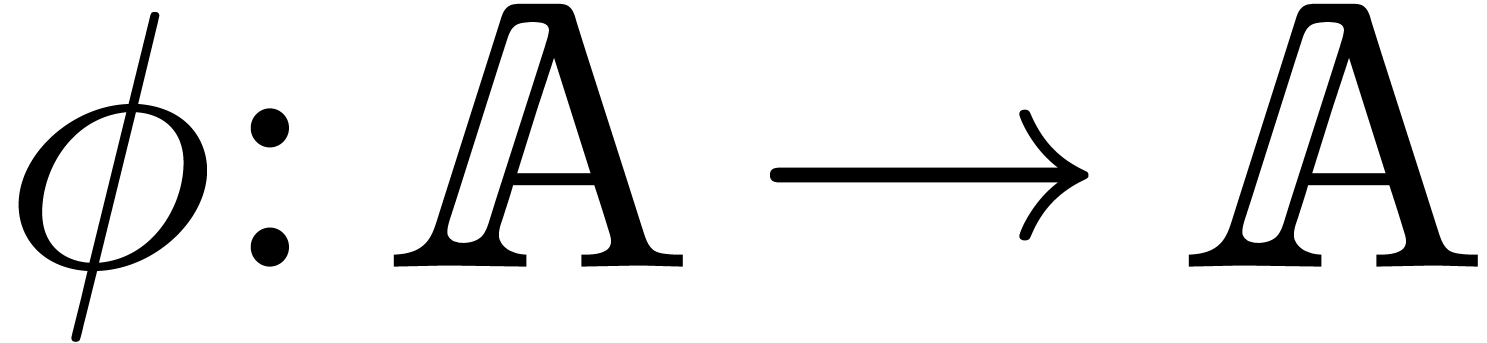 . Under
suitable hypothesis, the algorithms in this paper generalize to this
setting.
. Under
suitable hypothesis, the algorithms in this paper generalize to this
setting.
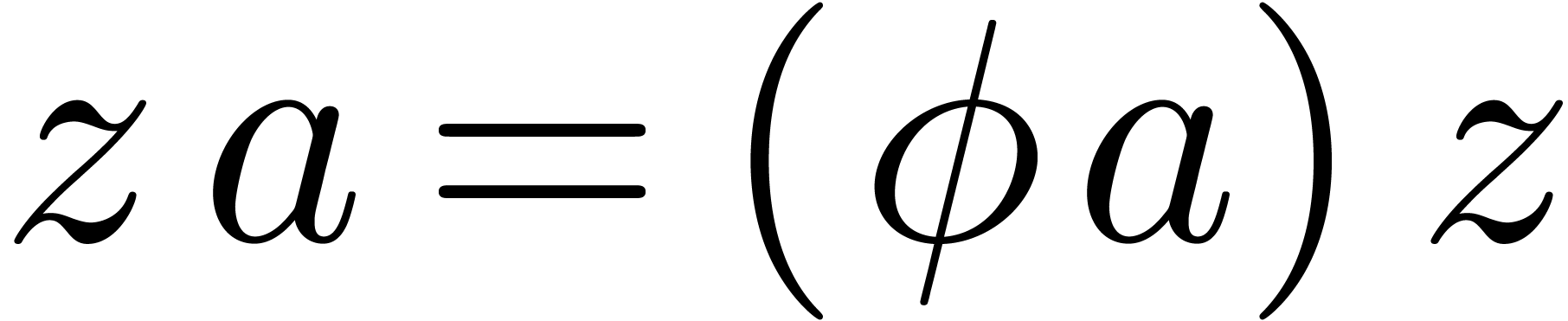 in a non trivial way. More
precisely, assume that we have an effective ring homomorphism
in a non trivial way. More
precisely, assume that we have an effective ring homomorphism  such that
such that 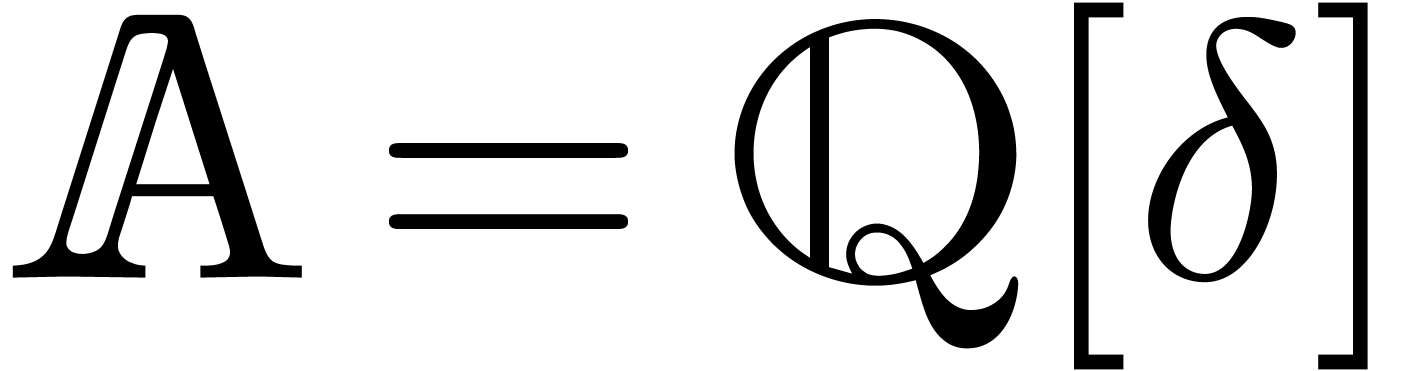 for all
for all 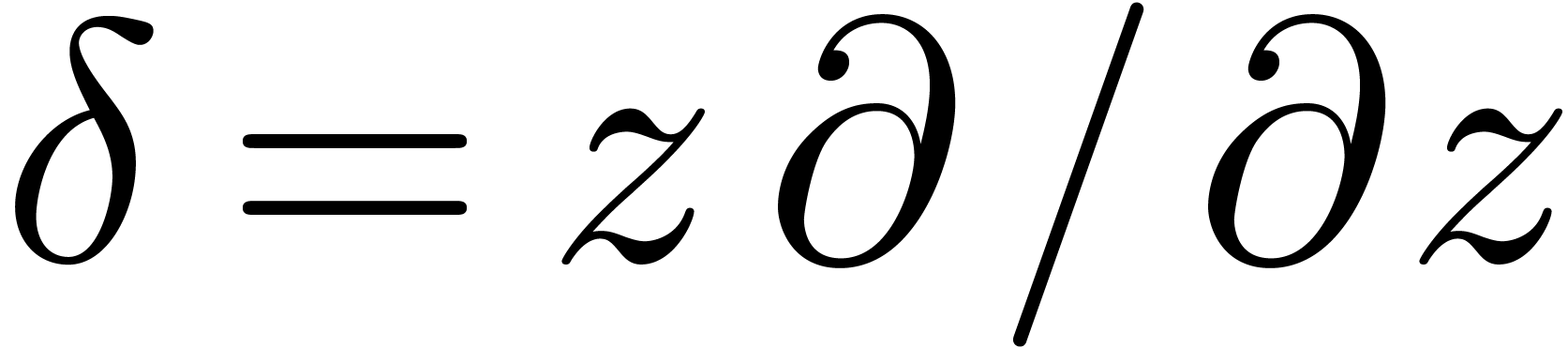 . For instance, one may take
. For instance, one may take 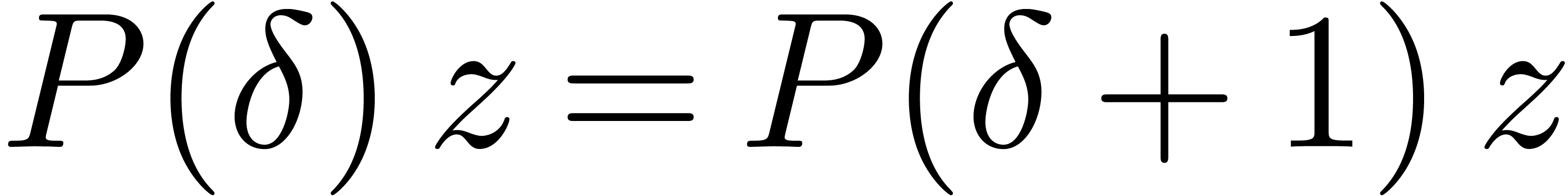 with
with  ,
so that
,
so that 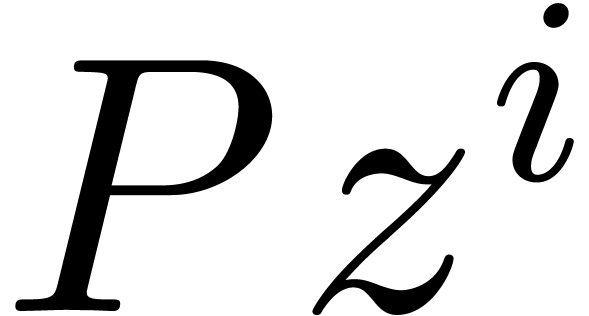 . Given a
commutation rule of this kind, we define a skew multiplication on
. Given a
commutation rule of this kind, we define a skew multiplication on 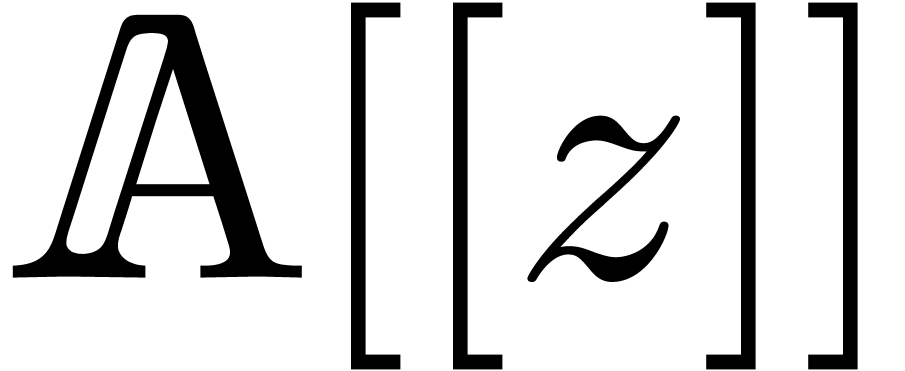 by
by
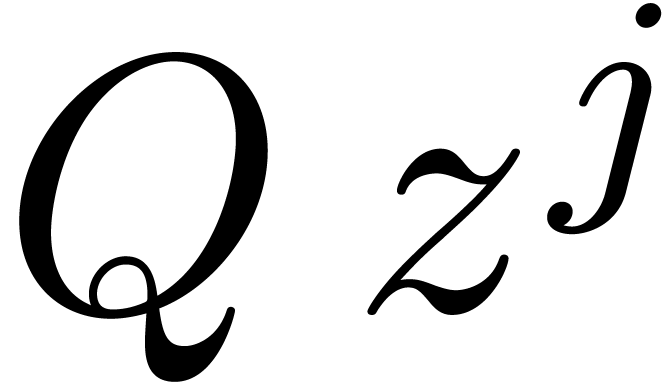
If 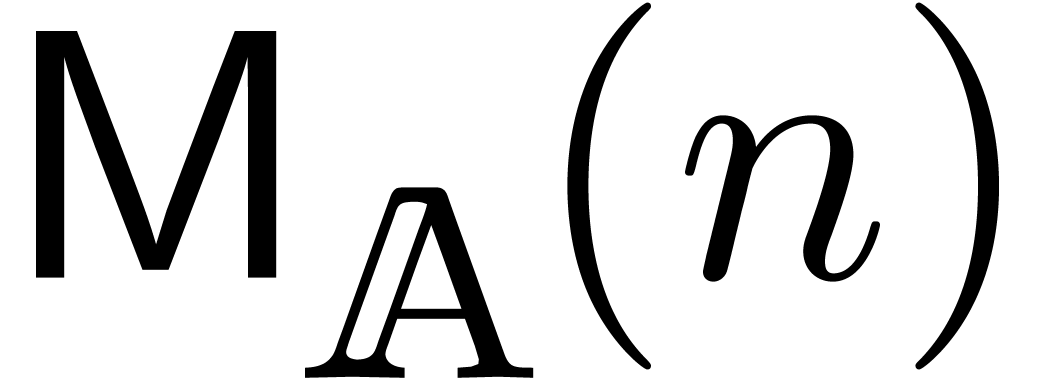 denotes the cost of multiplying two
polynomials
denotes the cost of multiplying two
polynomials 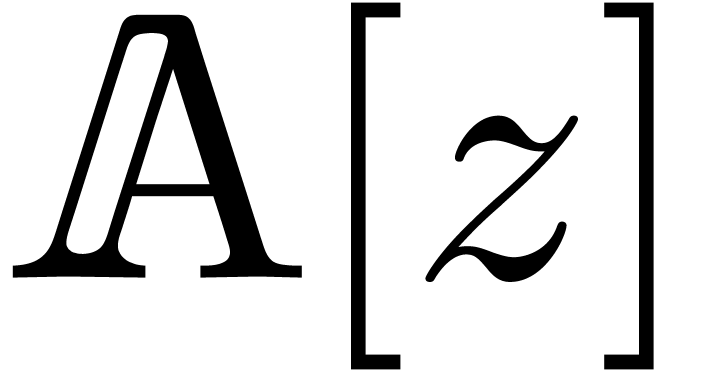 and
and 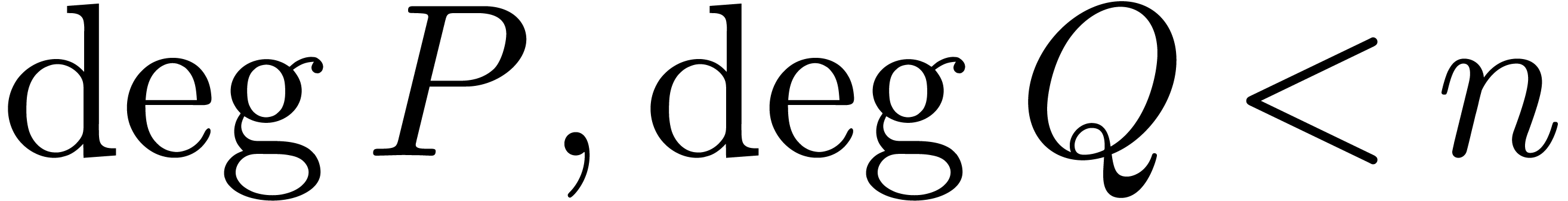 in
in 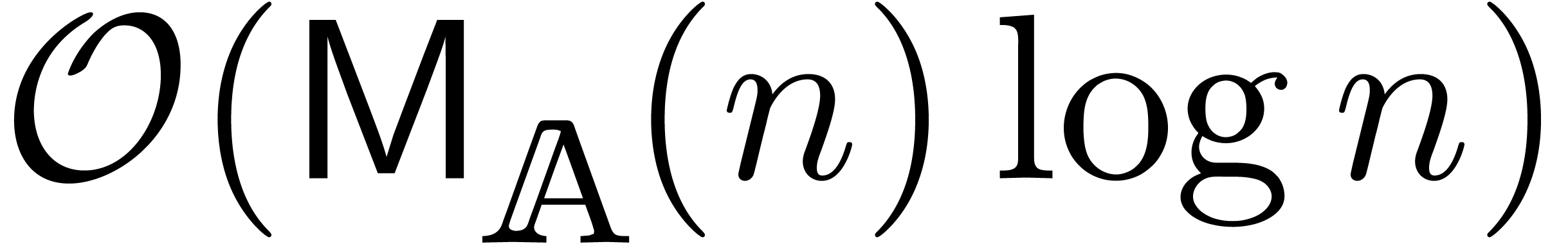 with
with  ,
then the classical fast relaxed multiplication algorithm from [Hoe02,
FS74] generalizes and still admits the time complexity
,
then the classical fast relaxed multiplication algorithm from [Hoe02,
FS74] generalizes and still admits the time complexity
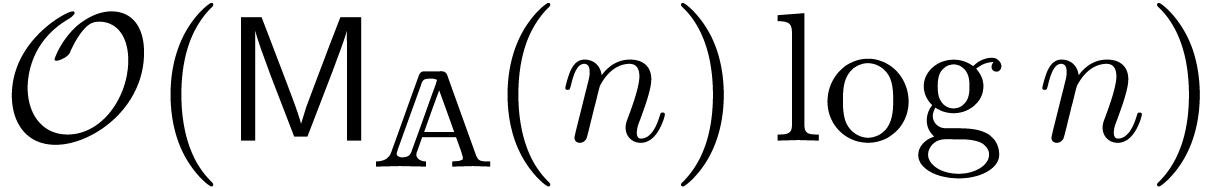 . However, the blockwise
algorithm from this paper does not generalize to this setting, at least
not in a straightforward way.
. However, the blockwise
algorithm from this paper does not generalize to this setting, at least
not in a straightforward way.
A. Aho, J. Hopcroft, and J. Ullman. The Design and Analysis of Computer Algorithms. Addison-Wesley, Reading, Massachusetts, 1974.
D. Bernstein. Removing redundancy in high precision Newton iteration. Available from http://cr.yp.to/fastnewton.html, 2000.
J. Berthomieu, J. van der Hoeven, and G. Lecerf.
Relaxed algorithms for  -adic
numbers. Journal de Théorie des Nombres de
Bordeaux, 23(3):541–577, 2011.
-adic
numbers. Journal de Théorie des Nombres de
Bordeaux, 23(3):541–577, 2011.
R.P. Brent and H.T. Kung. Fast algorithms for manipulating formal power series. Journal of the ACM, 25:581–595, 1978.
J. Berthomieu and R. Lebreton. Relaxed  -adic hensel lifting for algebraic
systems. Work in preparation, 2011.
-adic hensel lifting for algebraic
systems. Work in preparation, 2011.
L.I. Bluestein. A linear filtering approach to the computation of the discrete fourier transform. IEEE Trans. Electroacoustics, AU-18:451–455, 1970.
D. Bini and V.Y. Pan. Polynomial and matrix computations. Vol. 1. Birkhäuser Boston Inc., Boston, MA, 1994. Fundamental algorithms.
A. Bostan and É. Schost. Polynomial evaluation and interpolation on special sets of points. Journal of Complexity, 21(4):420–446, August 2005. Festschrift for the 70th Birthday of Arnold Schönhage.
D.G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
S.A. Cook. On the minimum computation time of functions. PhD thesis, Harvard University, 1966.
J.W. Cooley and J.W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
M.J. Fischer and L.J. Stockmeyer. Fast on-line integer multiplication. Proc. 5th ACM Symposium on Theory of Computing, 9:67–72, 1974.
M. Fürer. Faster integer multiplication. In Proceedings of the Thirty-Ninth ACM Symposium on Theory of Computing (STOC 2007), pages 57–66, San Diego, California, 2007.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, 2-nd edition, 2002.
J. van der Hoeven. Lazy multiplication of formal power series. In W. W. Küchlin, editor, Proc. ISSAC '97, pages 17–20, Maui, Hawaii, July 1997.
J. van der Hoeven. Relax, but don't be too lazy. JSC, 34:479–542, 2002.
J. van der Hoeven. Relaxed multiplication using the middle product. In Manuel Bronstein, editor, Proc. ISSAC '03, pages 143–147, Philadelphia, USA, August 2003.
J. van der Hoeven. The truncated Fourier transform and applications. In J. Gutierrez, editor, Proc. ISSAC 2004, pages 290–296, Univ. of Cantabria, Santander, Spain, July 4–7 2004.
J. van der Hoeven. Notes on the Truncated Fourier Transform. Technical Report 2005-5, Université Paris-Sud, Orsay, France, 2005.
J. van der Hoeven. New algorithms for relaxed multiplication. JSC, 42(8):792–802, 2007.
J. van der Hoeven. Relaxed resolution of implicit equations. Technical report, HAL, 2009. http://hal.archives-ouvertes.fr/hal-00441977/fr/.
J. van der Hoeven. Newton's method and FFT trading. JSC, 45(8):857–878, 2010.
J. van der Hoeven. From implicit to recursive equations. Technical report, HAL, 2011. http://hal.archives-ouvertes.fr/hal-00583125/fr/.
A. Karatsuba and J. Ofman. Multiplication of multidigit numbers on automata. Soviet Physics Doklady, 7:595–596, 1963.
L.R. Rabiner, R.W. Schafer, and C.M. Rader. The chirp z-transform algorithm and its application. Bell System Tech. J., 48:1249–1292, 1969.
Alexandre Sedoglavic. Méthodes seminumériques en algèbre différentielle ; applications à l'étude des propriétés structurelles de systèmes différentiels algébriques en automatique. PhD thesis, École polytechnique, 2001.
A. Schönhage and V. Strassen. Schnelle Multiplikation grosser Zahlen. Computing, 7:281–292, 1971.
A.L. Toom. The complexity of a scheme of functional elements realizing the multiplication of integers. Soviet Mathematics, 4(2):714–716, 1963.