| Univariate polynomial factorization over large finite fields   |
|
| November 23, 2020 |
|
 . This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
. This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
 . This article has
been written using GNU TeXmacs [15].
. This article has
been written using GNU TeXmacs [15].
The best known asymptotic bit complexity bound for factoring
univariate polynomials over finite fields grows with the input
degree to a power close to |
The usual primitive element representation of the finite field
 with
with 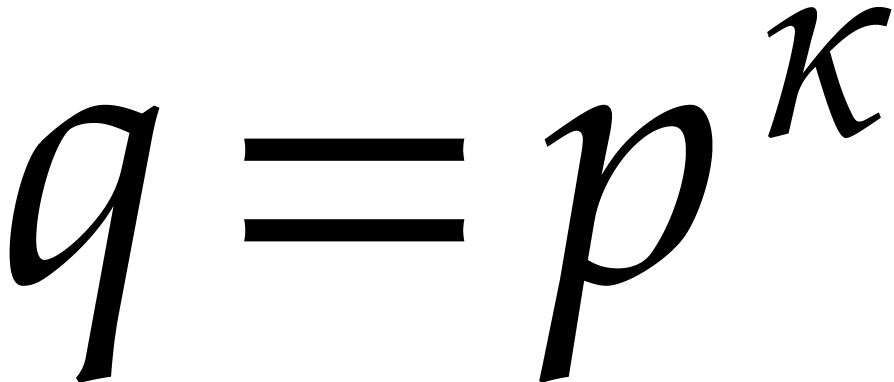 elements is
elements is 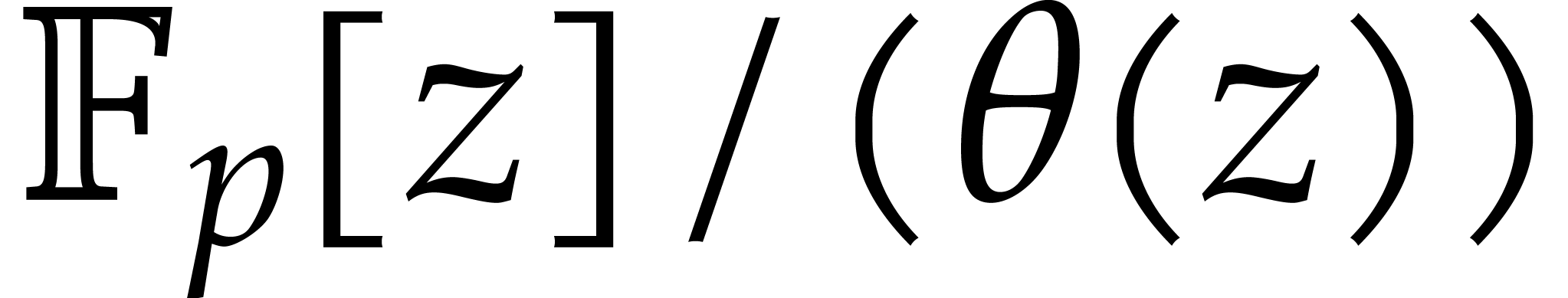 with
with 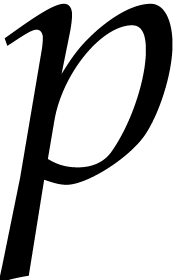 prime and
prime and  irreducible and monic of degree
irreducible and monic of degree 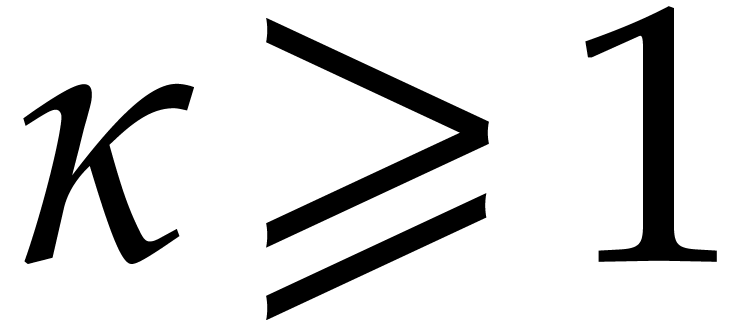 . For this representation, von zur Gathen, Kaltofen,
and Shoup proposed several efficient algorithms for the irreducible
factorization of a polynomial
. For this representation, von zur Gathen, Kaltofen,
and Shoup proposed several efficient algorithms for the irreducible
factorization of a polynomial  of degree
of degree  in
in 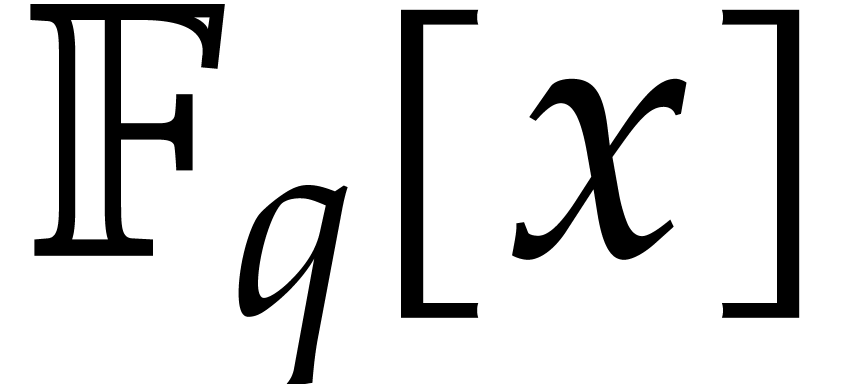 . One
of them is a variant of the Cantor–Zassenhaus method for which
large powers of polynomials modulo
. One
of them is a variant of the Cantor–Zassenhaus method for which
large powers of polynomials modulo  are computed
using modular composition [24, section 2]. Now Kedlaya and
Umans designed a theoretically efficient algorithm for modular
composition [25, 26]. Consequently, using a
probabilistic algorithm of Las Vegas type, the polynomial
are computed
using modular composition [24, section 2]. Now Kedlaya and
Umans designed a theoretically efficient algorithm for modular
composition [25, 26]. Consequently, using a
probabilistic algorithm of Las Vegas type, the polynomial  can be factored in expected time
can be factored in expected time
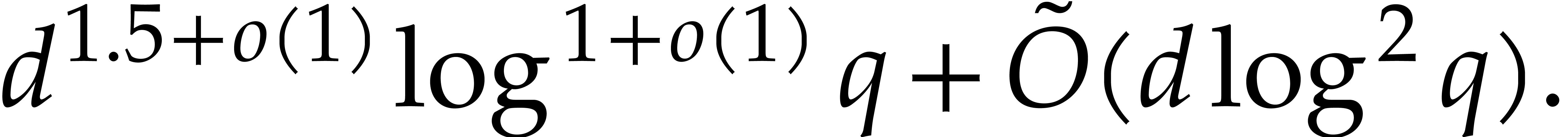 |
(1.1) |
It turns out that the second term of 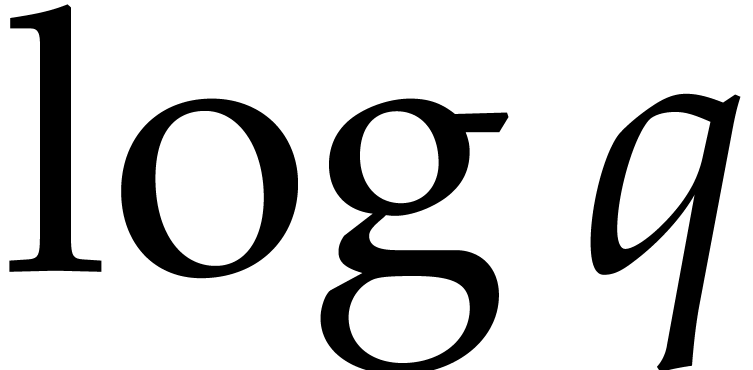 becomes large. The purpose of
the present paper is to prove the expected complexity bound
becomes large. The purpose of
the present paper is to prove the expected complexity bound
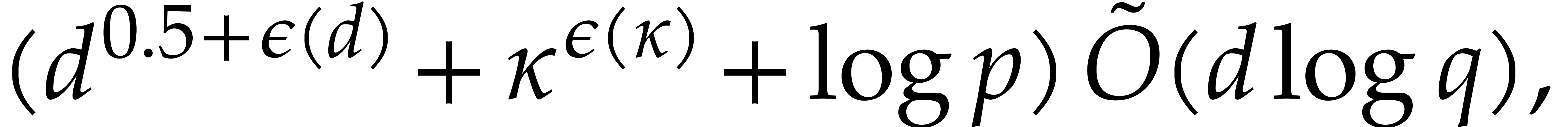
where 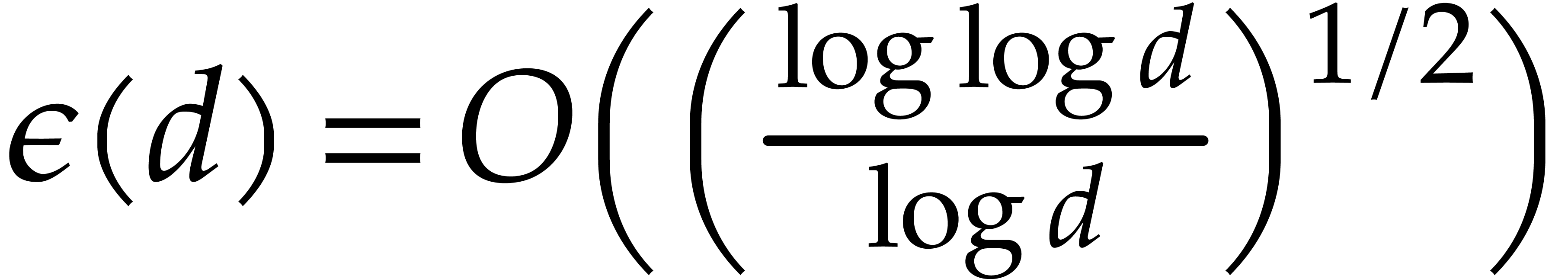 ; see Corollary 5.1. For this, we rely on ideas by Kaltofen and Shoup from [23]. In addition, we present improved complexity bounds for
the case when the extension degree
; see Corollary 5.1. For this, we rely on ideas by Kaltofen and Shoup from [23]. In addition, we present improved complexity bounds for
the case when the extension degree  is smooth.
These bounds rely on practically efficient algorithms for modular
composition that were designed for this case in [16].
is smooth.
These bounds rely on practically efficient algorithms for modular
composition that were designed for this case in [16].
Given a commutative ring  and
and  , let
, let  .
Given
.
Given 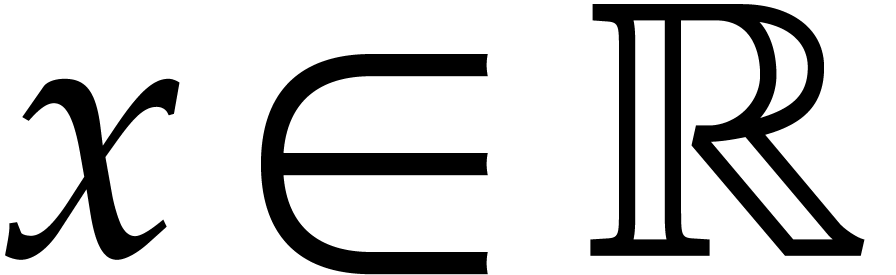 , we define
, we define 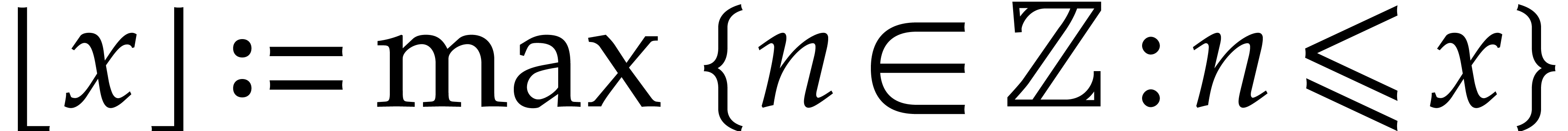 and
and 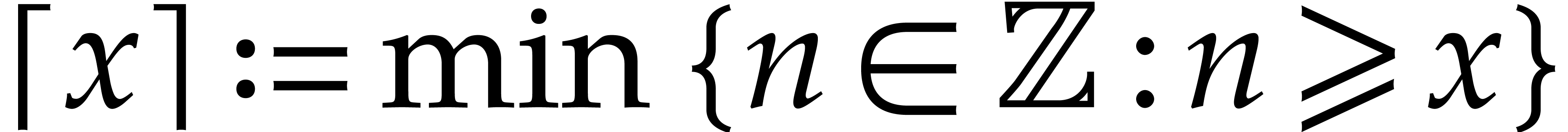 . For any
positive integer
. For any
positive integer  , we set
, we set
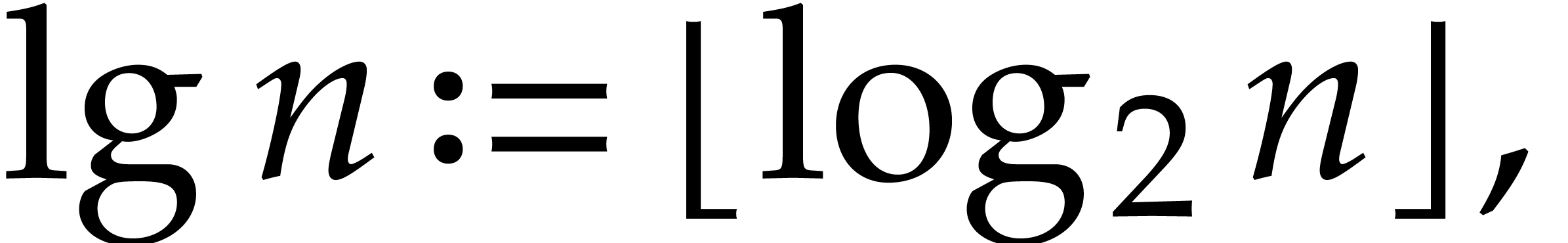
so that 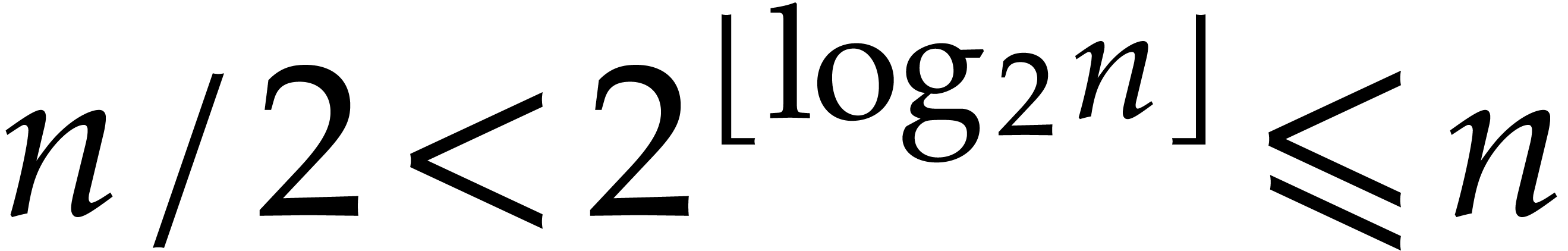 . We will freely use
the soft-Oh notation:
. We will freely use
the soft-Oh notation: 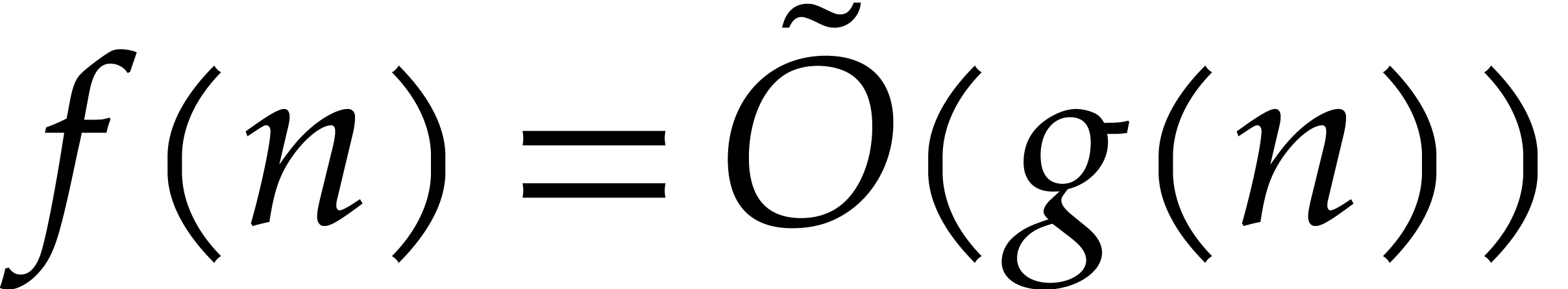 means that
means that 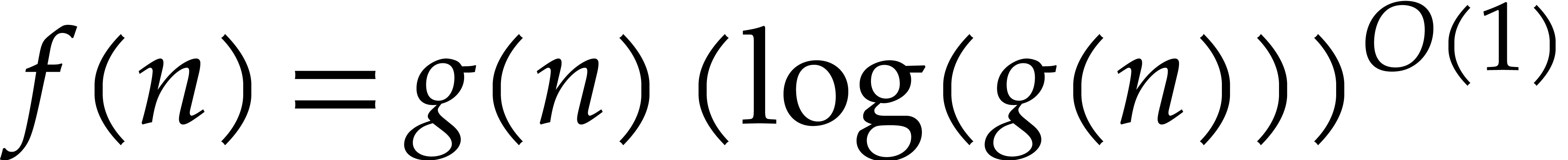 , as in [9].
, as in [9].
Until section 5.2, we assume the standard complexity model of a Turing machine with a sufficiently large number of tapes. For probabilistic algorithms, the Turing machine is assumed to provide an instruction for writing a “random bit” to one of the tapes. This instruction takes a constant time. All probabilistic algorithms in this paper are of Las Vegas type; this guarantees that all computed results are correct, but the execution time is a random variable.
Until section 5 we consider abstract finite fields
 , whose internal
representations are not necessarily prescribed, and we rely on the
following assumptions and notations:
, whose internal
representations are not necessarily prescribed, and we rely on the
following assumptions and notations:
Additions and subtractions in  take linear
time.
take linear
time.
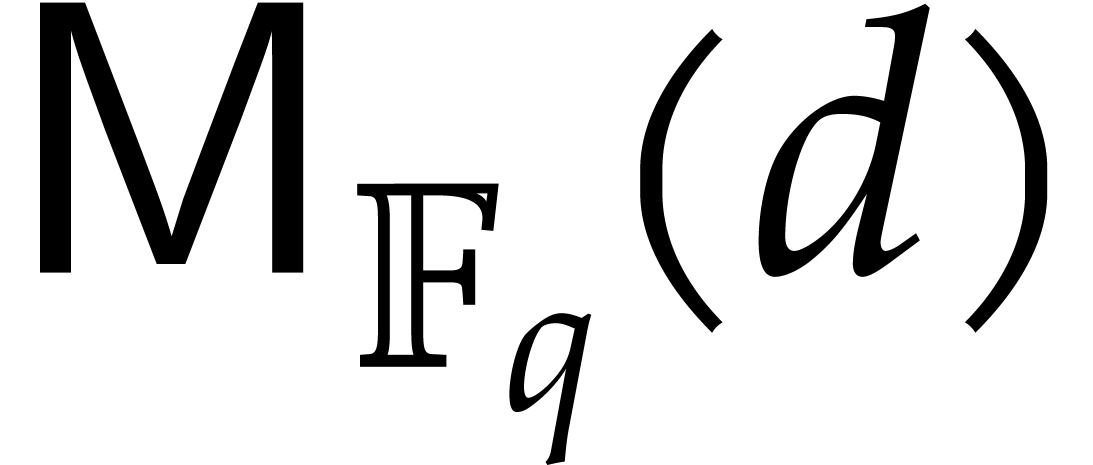 denotes an upper bound for the bit
complexity of polynomial products in degree
denotes an upper bound for the bit
complexity of polynomial products in degree 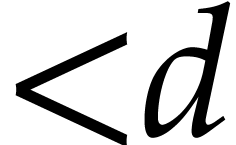 over
over  . It is convenient
to make the regularity assumptions that
. It is convenient
to make the regularity assumptions that 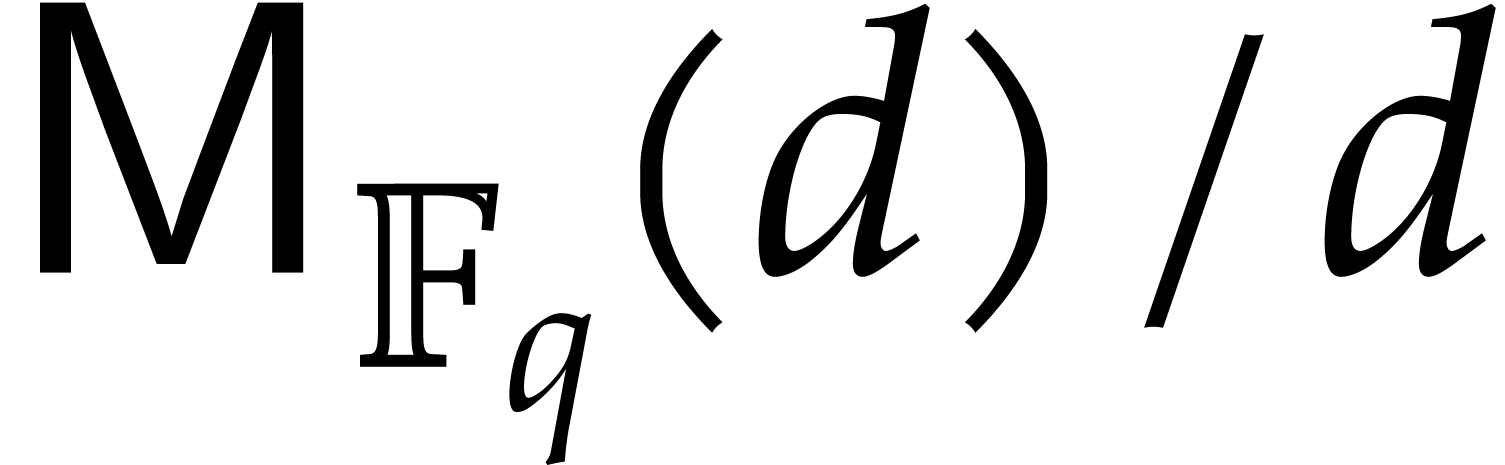 is
nondecreasing as a function of
is
nondecreasing as a function of  and that
and that 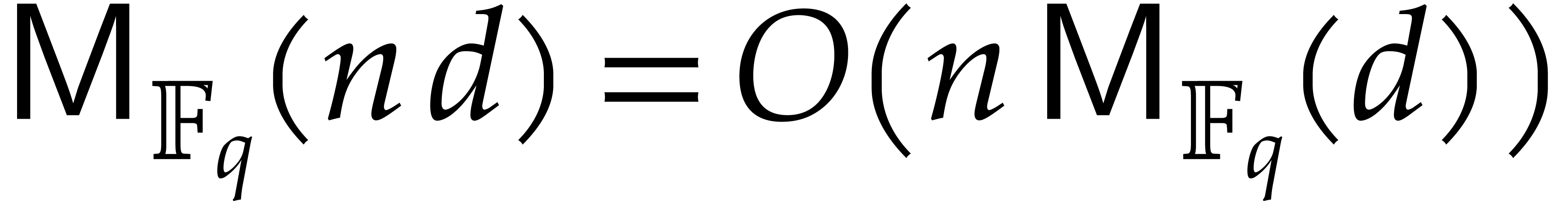 for
for  .
.
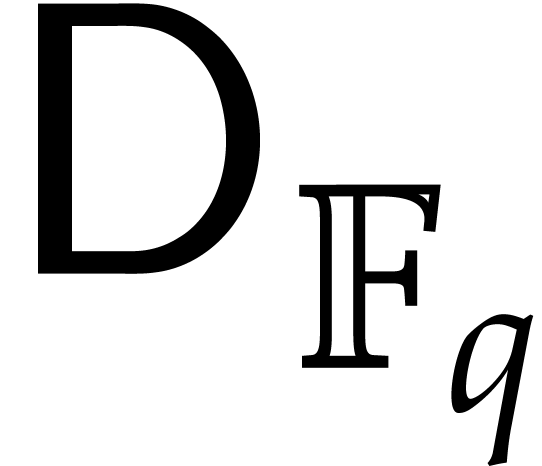 upper bounds the time needed to invert one
element in
upper bounds the time needed to invert one
element in  .
.
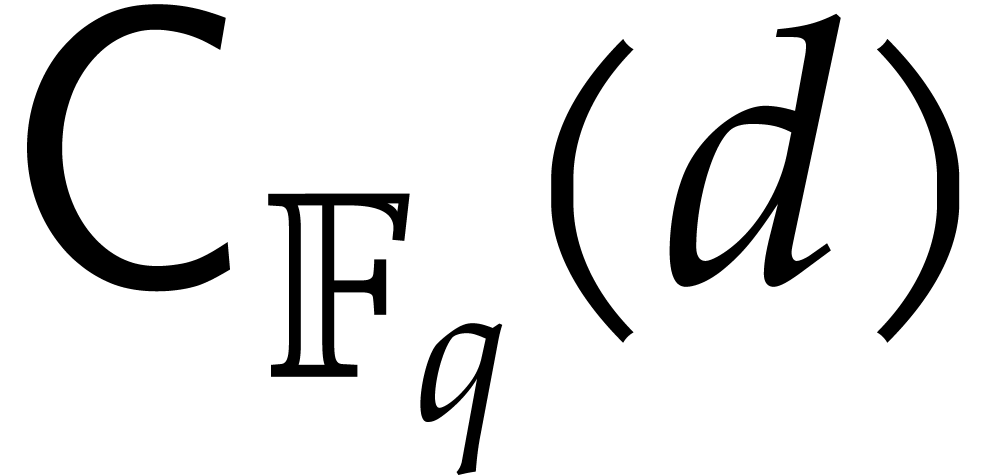 is an upper bound for the time to compute
is an upper bound for the time to compute
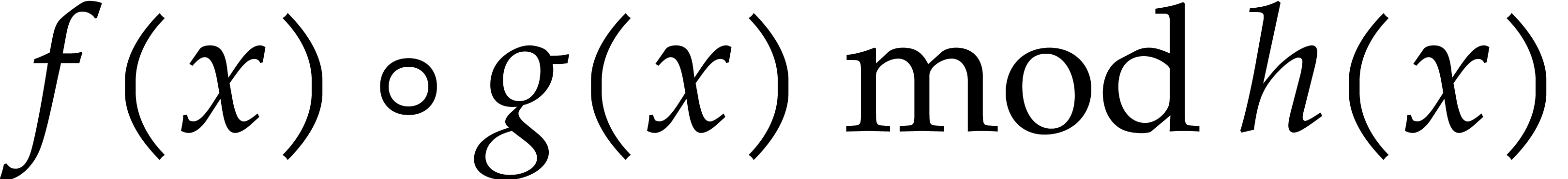 for
for  and monic
and monic 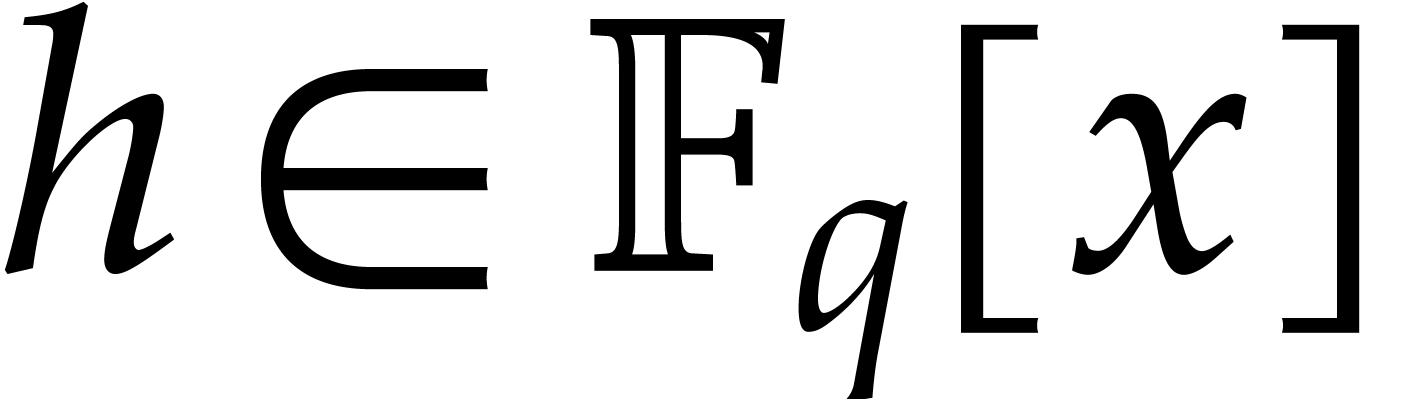 of degree
of degree  .
.
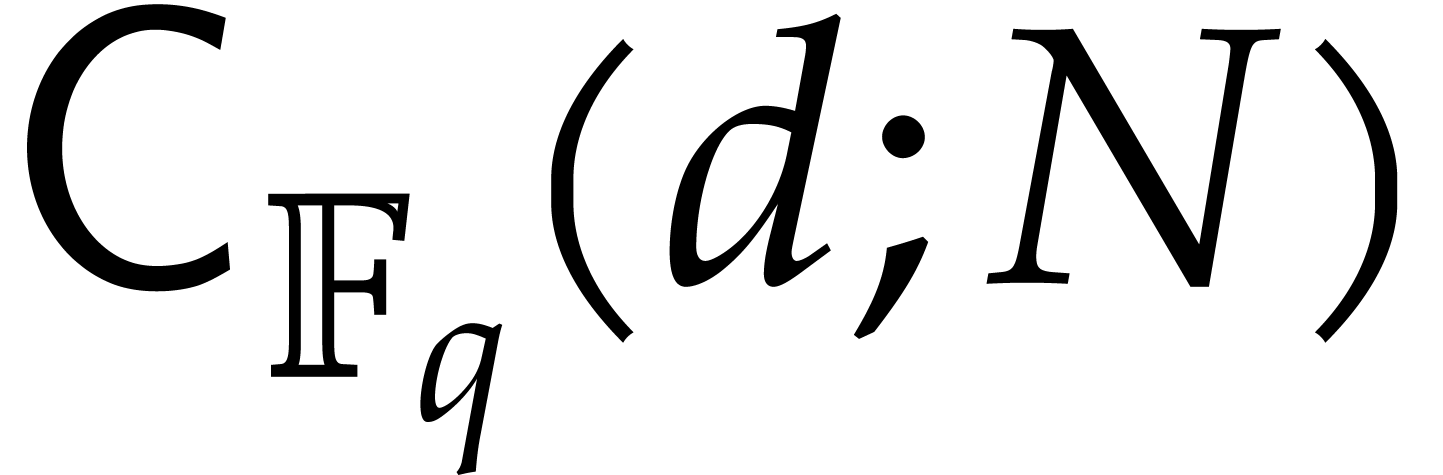 is an upper bound for the time to compute
is an upper bound for the time to compute
 modulo
modulo 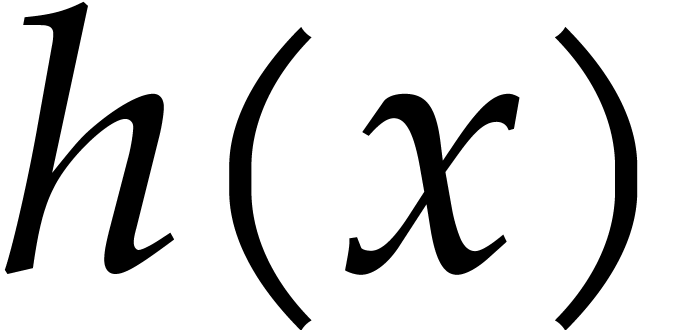 for
for 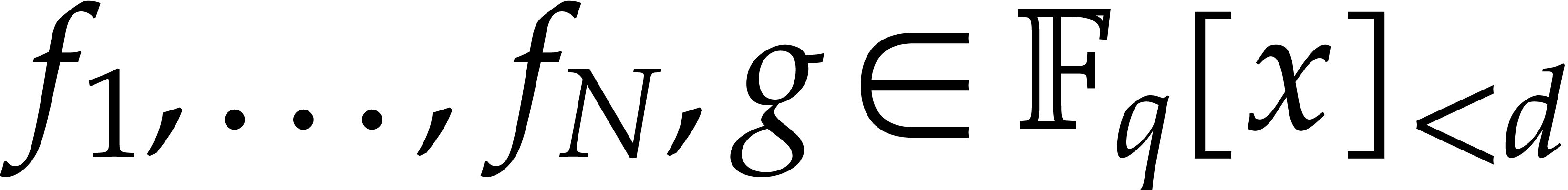 and monic
and monic 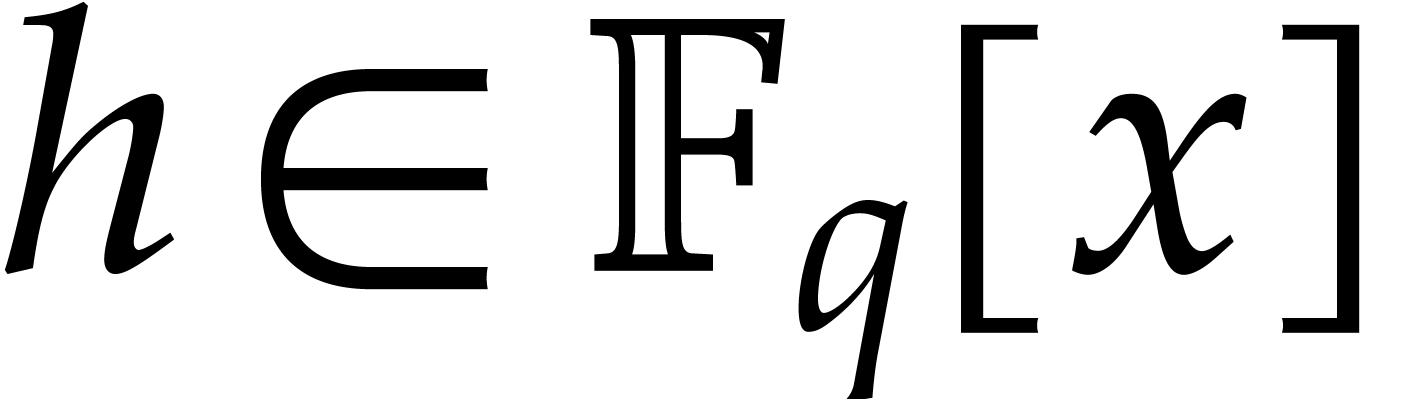 of degree
of degree  .
.
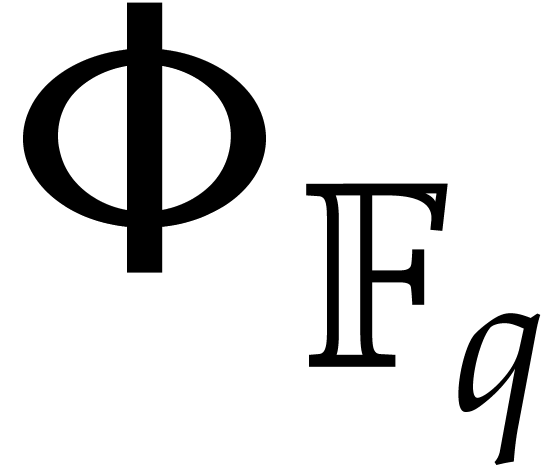 is an upper bound for the time to compute
is an upper bound for the time to compute
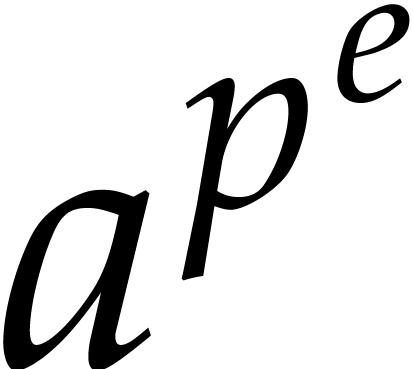 , given
, given 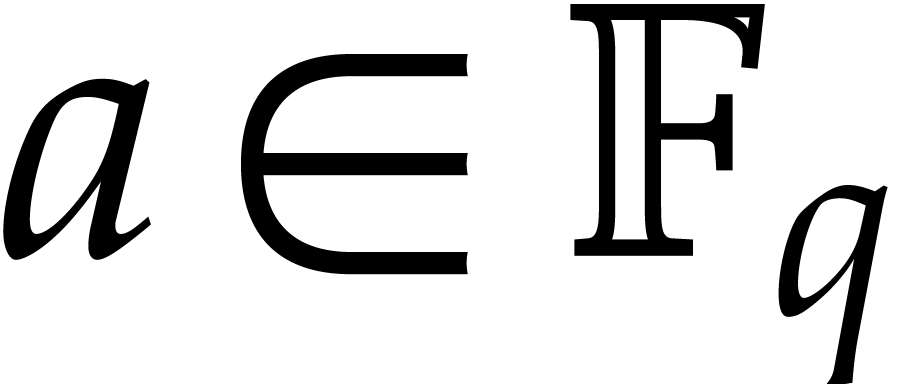 and
and 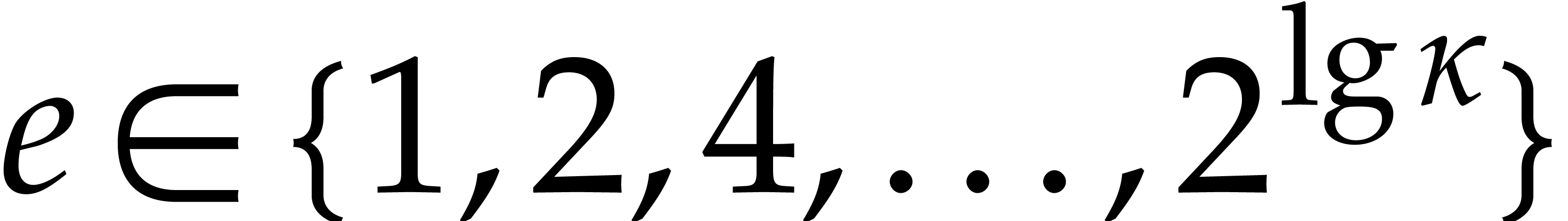 .
.
For general algorithms for finite fields, we recommend the textbooks [4, 9, 28, 35] and more specifically [9, chapter 14], as well as [8, 21] for historical references. In this paper we adopt the asymptotic complexity point of view, while allowing for randomized algorithms of Las Vegas type.
Early theoretical and practical complexity bounds for factorizing polynomials over finite fields go back to the sixties [2, 3]. In the eighties, Cantor and Zassenhaus [5] popularized distinct-degree and equal-degree factorizations. Improved complexity bounds and fast implementations were explored by Shoup [34]. He and von zur Gathen introduced the iterated Frobenius technique and the “baby-step giant-step” for the distinct degree factorization [11]. They reached softly quadratic time in the degree via fast multi-point evaluation. Together with Kaltofen, they also showed how to exploit modular composition [22, 24] and proved sub-quadratic complexity bounds.
In 2008, Kedlaya and Umans showed that the complexity exponent of
modular composition over finite fields is arbitrarily close to one [25, 26]. As a corollary, the complexity exponent
of polynomial factorization in the degree is arbitrarily close to 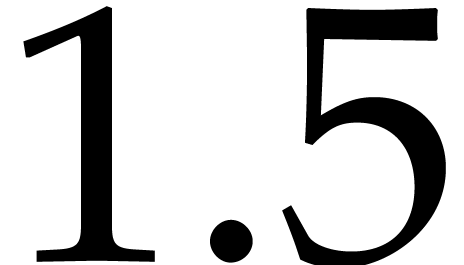 .
.
Von zur Gathen and Seroussi [10] showed that factoring
quadratic polynomials with arithmetic circuits or straight-line programs
over  requires
requires 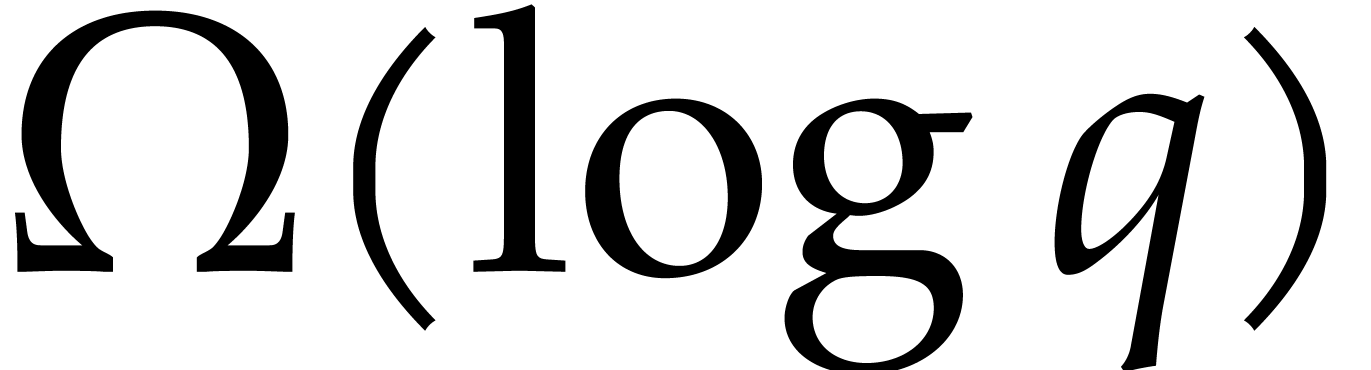 operations
in
operations
in  . However, this does not
provide a lower bound
. However, this does not
provide a lower bound 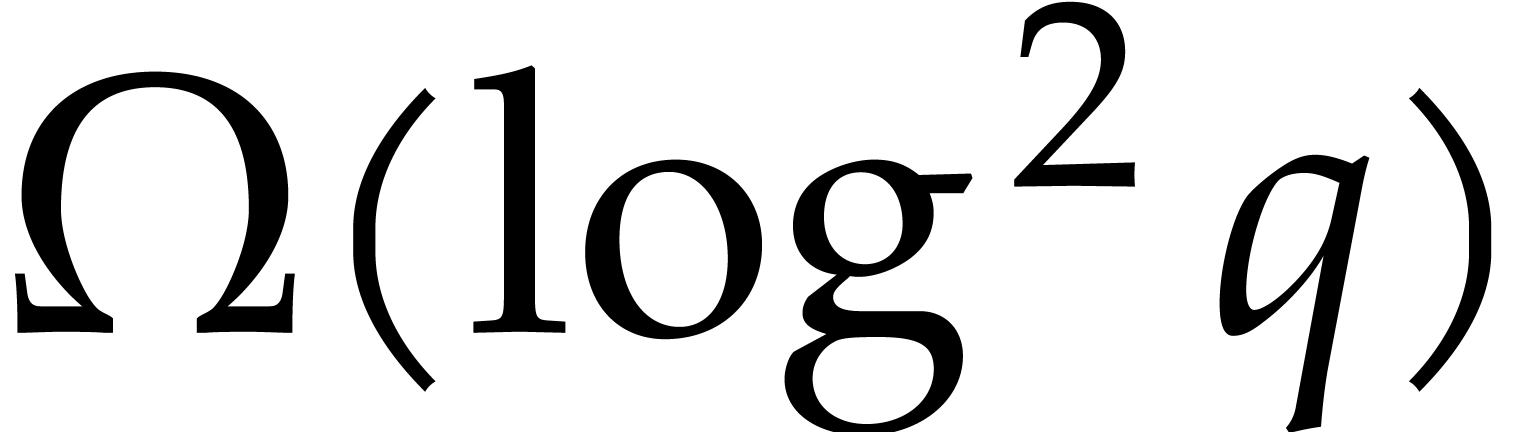 for boolean arithmetic
circuits. In fact, subquadratic upper bounds indeed exist for the
stronger model of arithmetic circuits over the prime subfield
for boolean arithmetic
circuits. In fact, subquadratic upper bounds indeed exist for the
stronger model of arithmetic circuits over the prime subfield  of
of  : the
combination of [23, Theorem 3] and fast modular composition
from [19] allows for degree
: the
combination of [23, Theorem 3] and fast modular composition
from [19] allows for degree  factorization in
factorization in 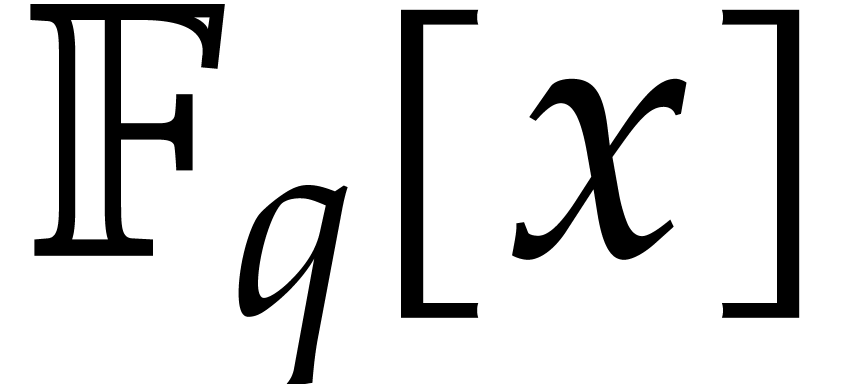 in expected time
in expected time
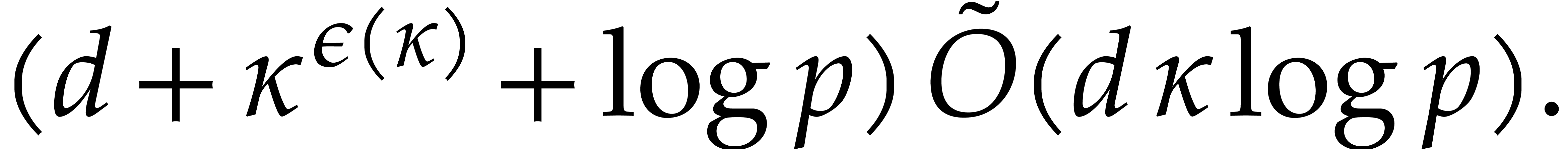
This bound is indeed subquadratic and even quasi-optimal in  . In this paper, we also achieve a subquadratic
dependence on
. In this paper, we also achieve a subquadratic
dependence on  .
.
In order to save modular compositions, Rabin introduced a randomization
process that uses random shifts of the variable [32]. This
turns out to be useful in practice, especially when the ground field
 is sufficiently large. We briefly revisit this
strategy, following Ben-Or [1] and [9,
Exercise 14.17].
is sufficiently large. We briefly revisit this
strategy, following Ben-Or [1] and [9,
Exercise 14.17].
Unfortunately, Kedlaya and Umans' fast algorithm for modular composition
has not yet given rise to fast practical implementations. In [16],
we have developed alternative algorithms for modular composition which
are of practical interest when the extension degree  of
of  over
over  is composite or
smooth. In section 6, we study the application of these
algorithms to polynomial factorization.
is composite or
smooth. In section 6, we study the application of these
algorithms to polynomial factorization.
The probabilistic arguments that are used to derive the above complexity
bounds become easier when ignoring all hidden constants in the
“ ”. Sharper
bounds can be obtained by refining the probability analyses; we refer to
[6, 7] for details.
”. Sharper
bounds can be obtained by refining the probability analyses; we refer to
[6, 7] for details.
In this paper we heavily rely on known techniques and results on
polynomial factorization (by von zur Gathen, Kaltofen, Shoup, among
others) and modular composition (by Kedlaya, Umans, among others).
Through a new combination of these results, our main aim is to sharpen
the complexity bounds for polynomial factorization and irreducibility
testing over finite fields. The improved bounds are most interesting
when factoring over a field  with a large and
smooth extension degree
with a large and
smooth extension degree  over its prime field
over its prime field
 .
.
Let us briefly mention a few technical novelties. Our finite field framework is designed to support a fine grained complexity analysis for specific modular composition algorithms, for sharing such compositions, and for computing factors up to a given degree. We explicitly show how complexities depend on the degrees of the irreducible factors to be computed.
Compared to the algorithm of Kaltofen and Shoup [23], our
Algorithm 4.2 for equal-degree factorization successively
computes pseudo-traces over  and then over
and then over  . The computation of Frobenius maps
is accelerated through improved caching. Our approach also combines a
bit better with Rabin's randomization; see section 4.5.
. The computation of Frobenius maps
is accelerated through improved caching. Our approach also combines a
bit better with Rabin's randomization; see section 4.5.
We further indicate opportunities to exploit shared arguments between
several modular compositions, by expressing our complexity bounds in
terms of 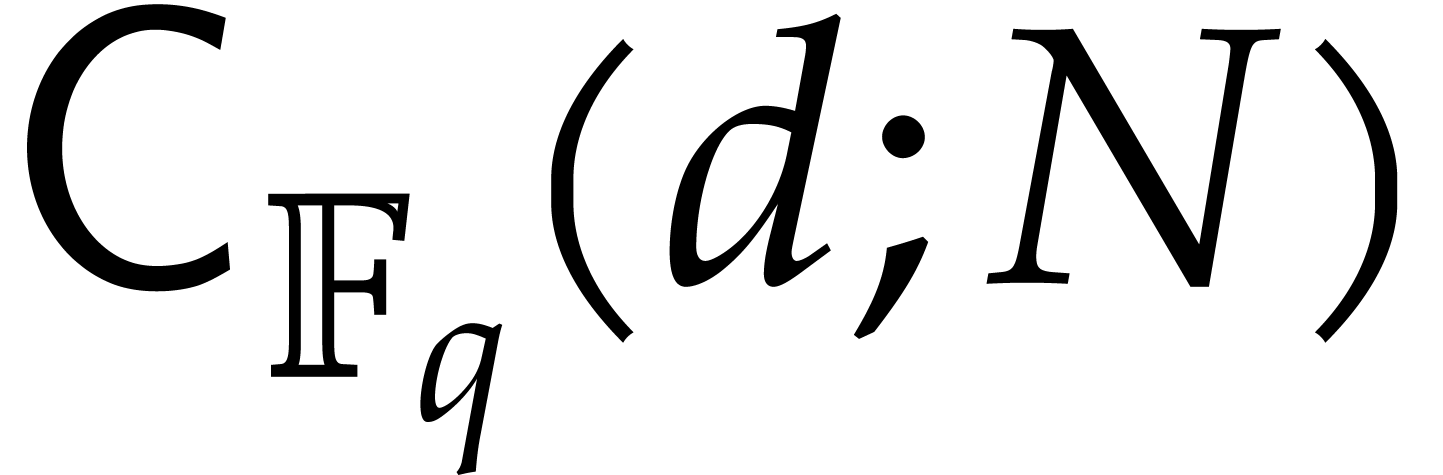 instead of
instead of 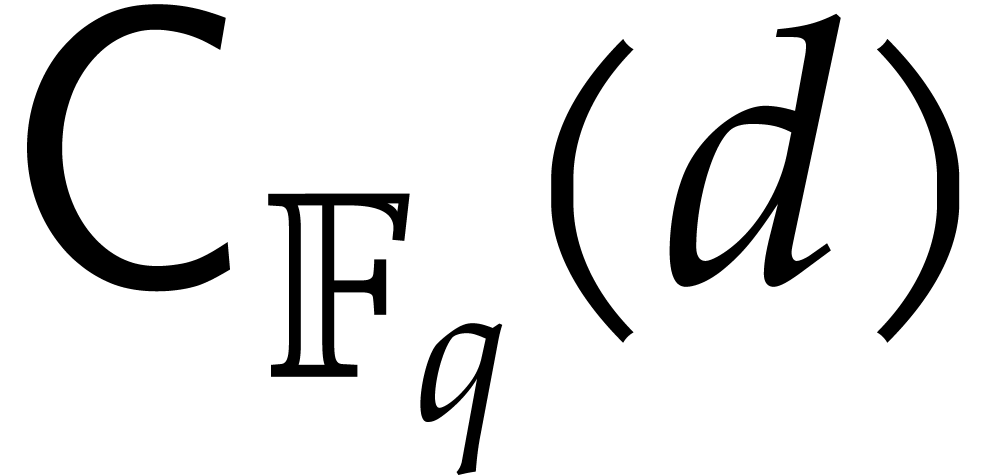 , when possible. We clearly have
, when possible. We clearly have 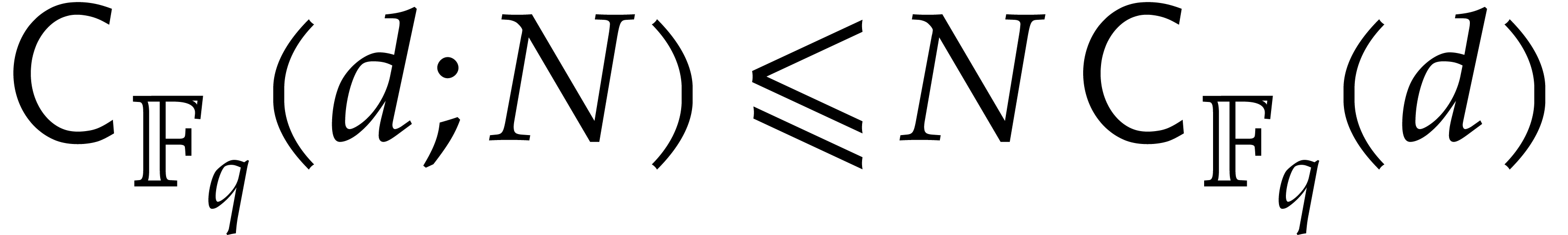 , but better bounds might be achievable through
precomputations based on the shared arguments. We refer to [18,
29] for partial evidence in this direction under suitable
genericity assumptions.
, but better bounds might be achievable through
precomputations based on the shared arguments. We refer to [18,
29] for partial evidence in this direction under suitable
genericity assumptions.
Our main complexity bounds are stated in section 4.4. The
remainder of the paper is devoted to corollaries of these bounds for
special cases. In section 5, we start with some theoretical
consequences that rely on the Kedlaya–Umans algorithm for modular
composition [26] and variants from [19]. We
both consider the case when  is presented as a
primitive extension of
is presented as a
primitive extension of  and the case when
and the case when 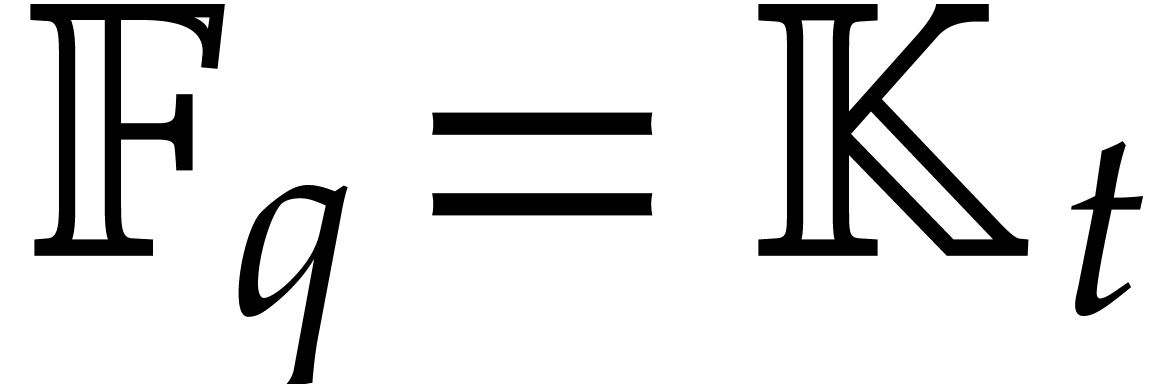 , where
, where  is
a “triangular tower”.
is
a “triangular tower”.
At the time being, it seems unlikely that Kedlaya and Umans' algorithm
can be implemented in a way that makes it efficient for practical
purposes; see [19, Conclusion]. In our final section, we
consider a more practical alternative approach to modular composition
[16], which requires the extension degree  to be composite, and which is most efficient when
to be composite, and which is most efficient when  is smooth. We present new complexity bounds for this case, which we
expect to be of practical interest when
is smooth. We present new complexity bounds for this case, which we
expect to be of practical interest when  becomes
large.
becomes
large.
The central ingredient to fast polynomial factorization is the efficient
evaluation of Frobenius maps. Besides the absolute Frobenius map 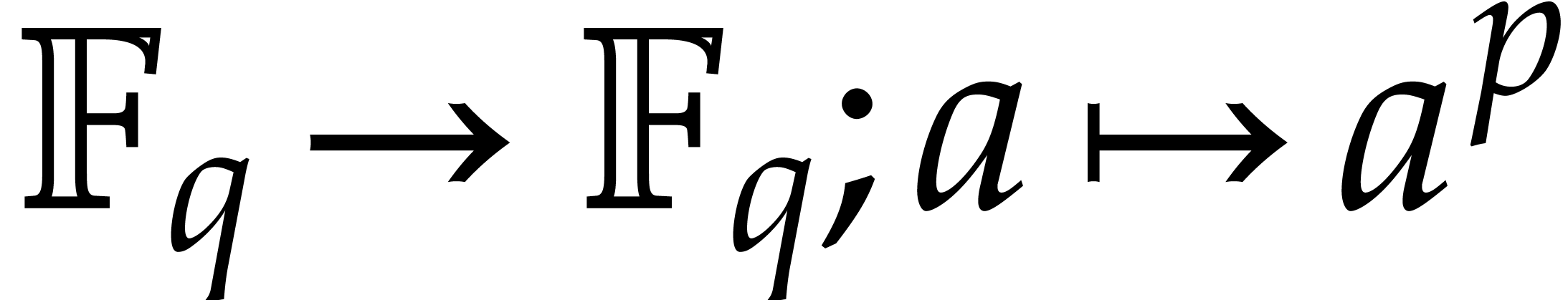 of
of  over its prime field
over its prime field  , we will consider pseudo-Frobenius
maps. Consider an extension
, we will consider pseudo-Frobenius
maps. Consider an extension 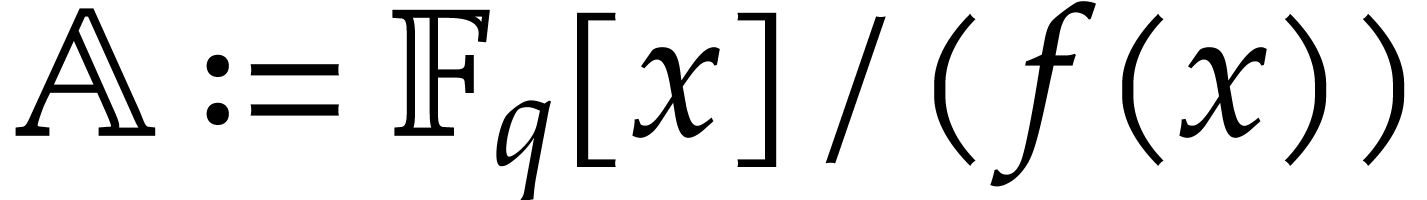 ,
where
,
where  is monic of degree
is monic of degree  and not necessarily irreducible. The
and not necessarily irreducible. The  -linear
map
-linear
map 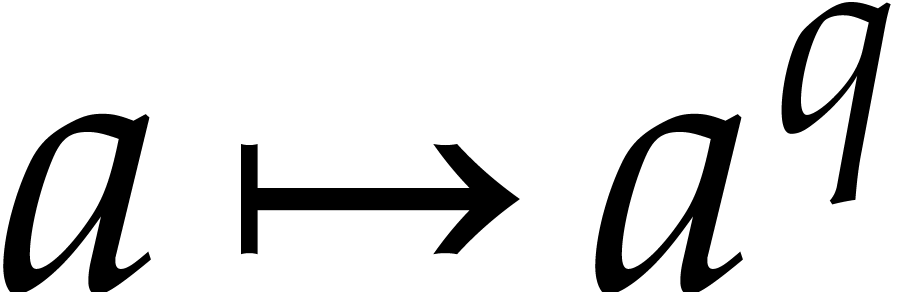 is called the pseudo-Frobenius map
of
is called the pseudo-Frobenius map
of  . The map
. The map 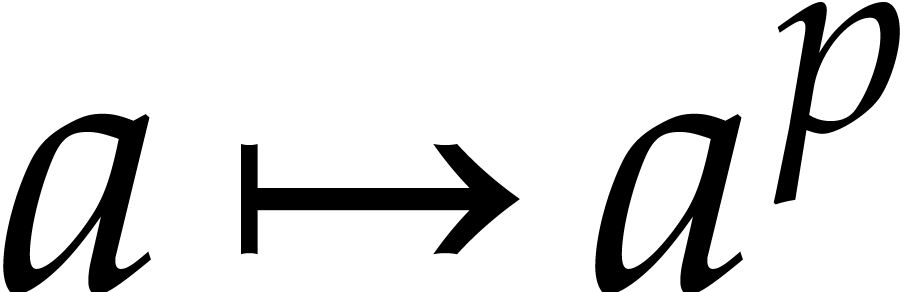 is called the absolute pseudo-Frobenius map of
is called the absolute pseudo-Frobenius map of  ; it is only
; it is only  -linear.
-linear.
Recall that 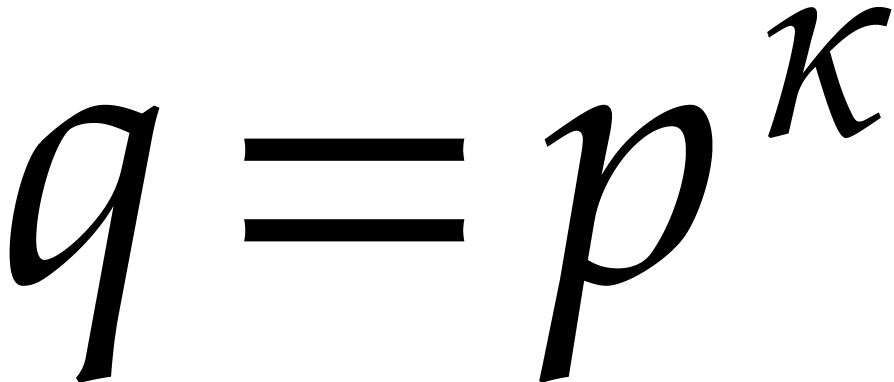 and consider a primitive
representation
and consider a primitive
representation 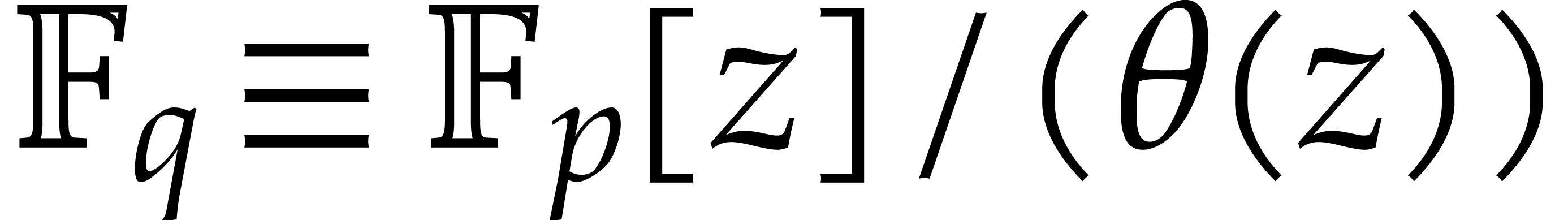 for
for  .
Let us show how to evaluate iterated Frobenius maps
.
Let us show how to evaluate iterated Frobenius maps 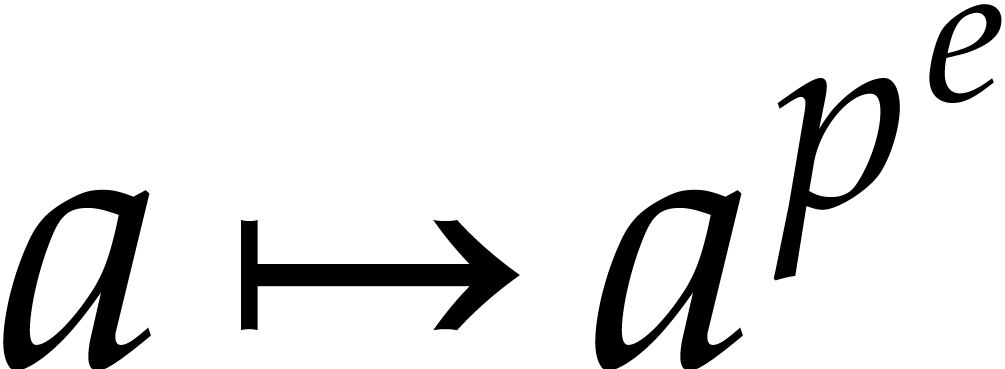 of
of  using modular composition. We introduce the
auxiliary sequence
using modular composition. We introduce the
auxiliary sequence
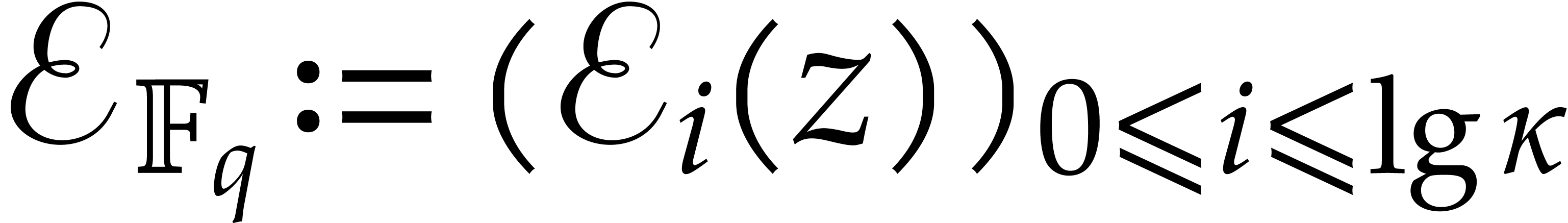
where
The sequence 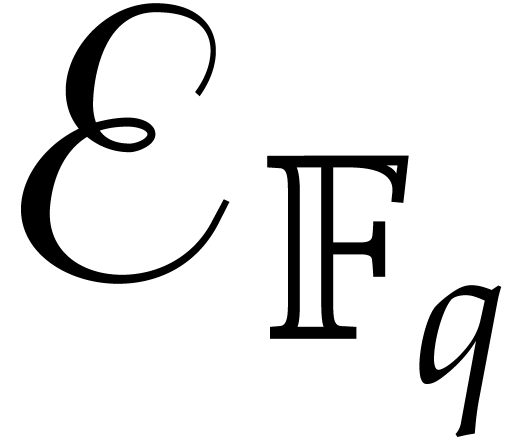 enables us to efficiently compute
enables us to efficiently compute
 -th powers and then general
-th powers and then general
 -th powers, as follows:
-th powers, as follows:
Proof. We verify that
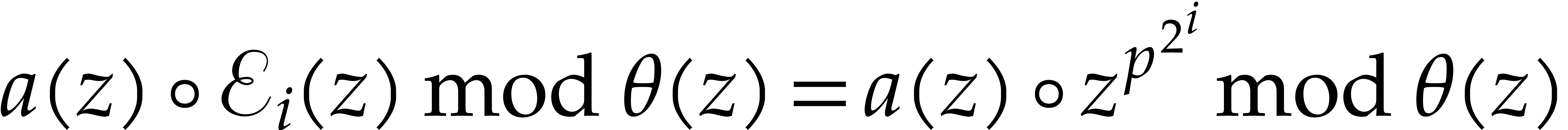
and that
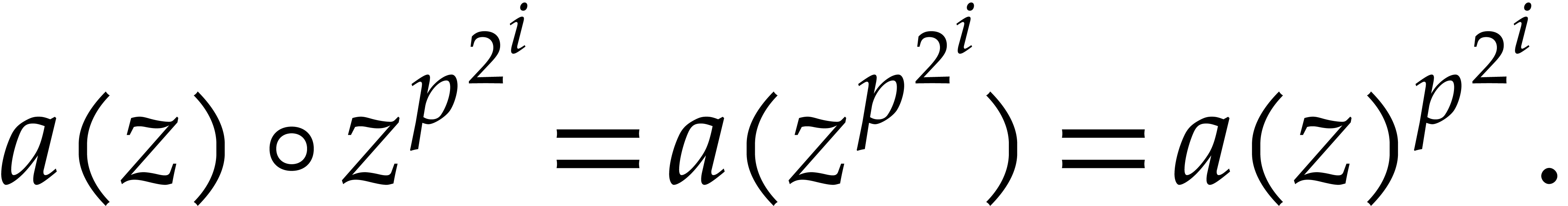
The cost analysis is straightforward from the definitions.
The cost function  corresponds to the time needed
to iterate the absolute Frobenius map
corresponds to the time needed
to iterate the absolute Frobenius map  a number
of times that is a power of two. For an arbitrary number of iterations
we may use the following general lemma.
a number
of times that is a power of two. For an arbitrary number of iterations
we may use the following general lemma.
 and
and  with binary expansion
with binary expansion 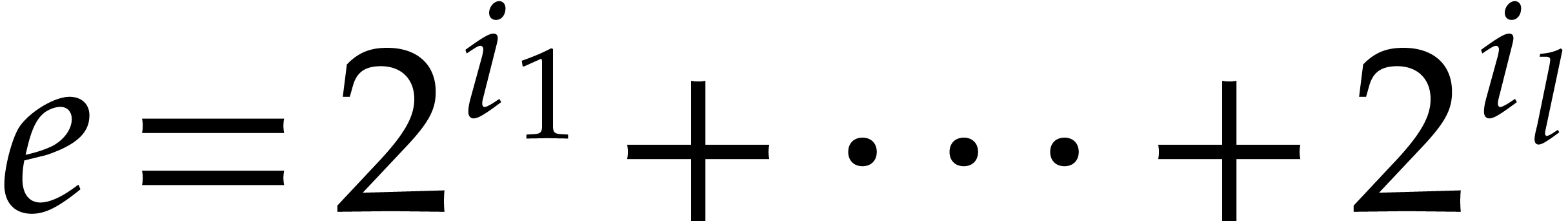 with
with  , we have
, we have
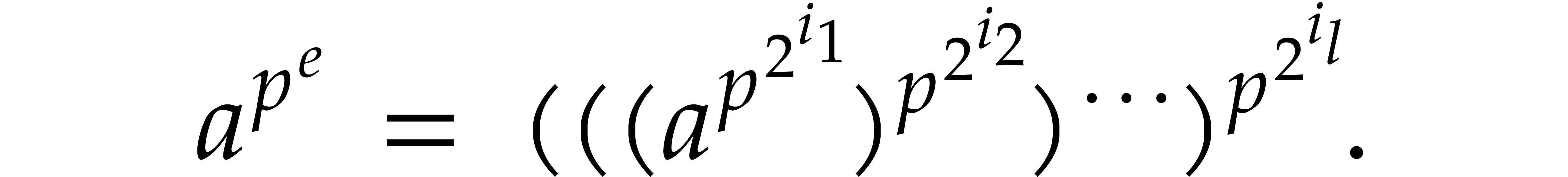
In particular, computing 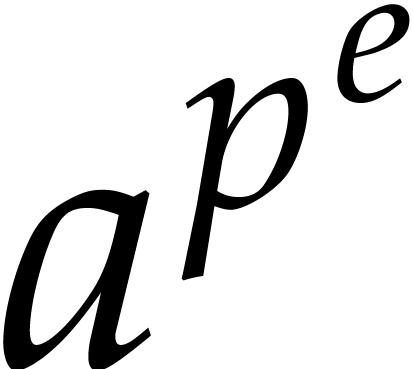 takes
takes 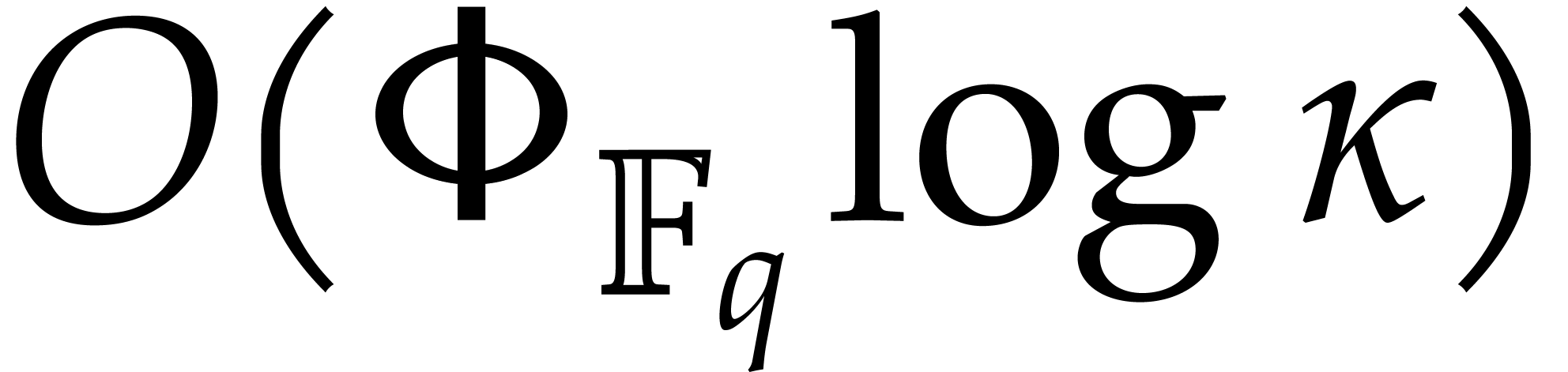 operations.
operations.
Proof. The proof is straightforward since 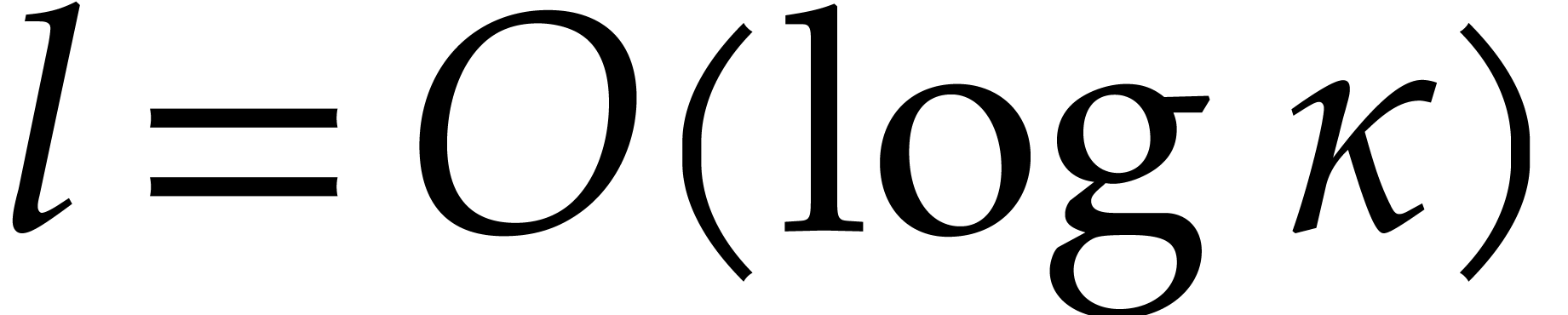 .
.
The computation of 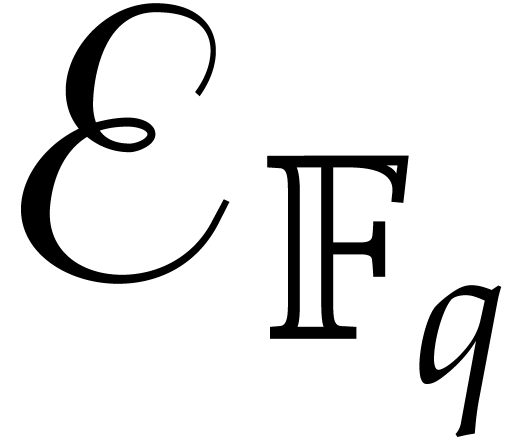 can be done efficiently with
the following algorithm.
can be done efficiently with
the following algorithm.
Algorithm
Compute 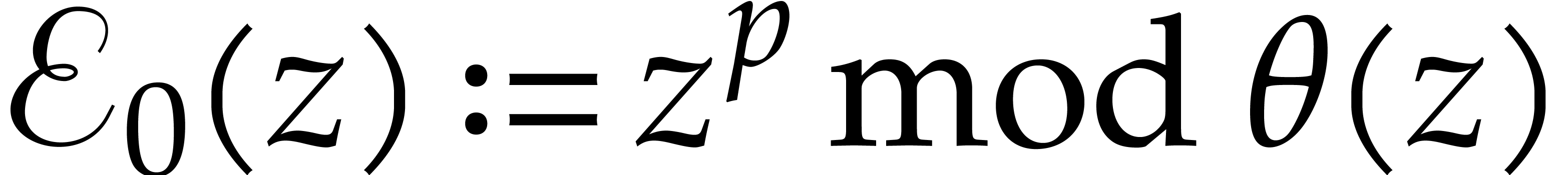 using binary powering.
using binary powering.
For  , compute
, compute 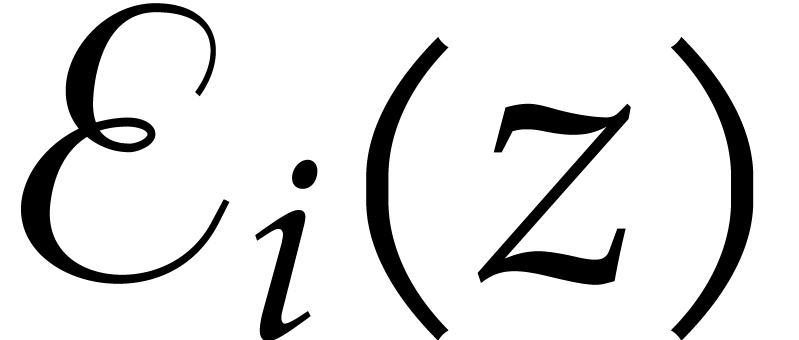 as
as 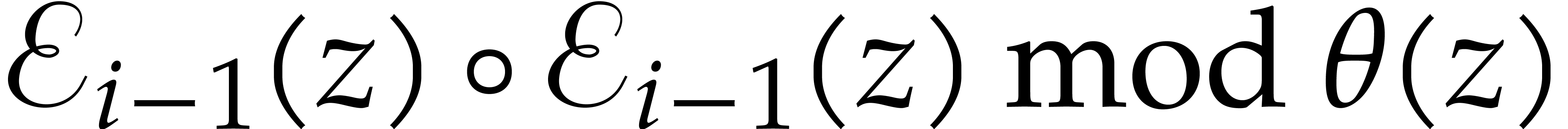 .
.
Return 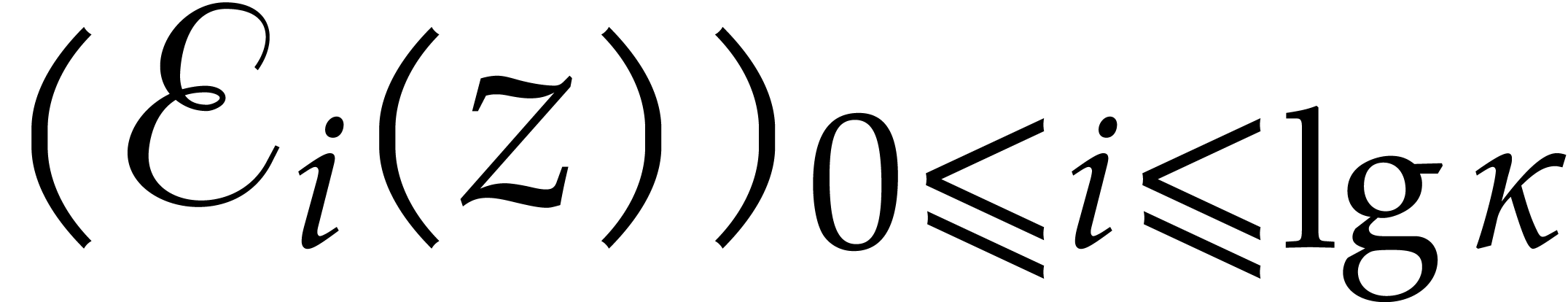 .
.
Proof. We prove the correctness by induction on
 . For
. For 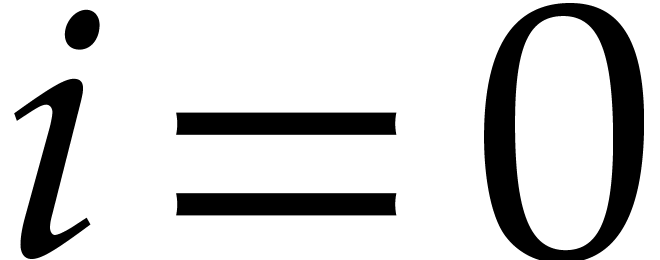 , we clearly have
, we clearly have 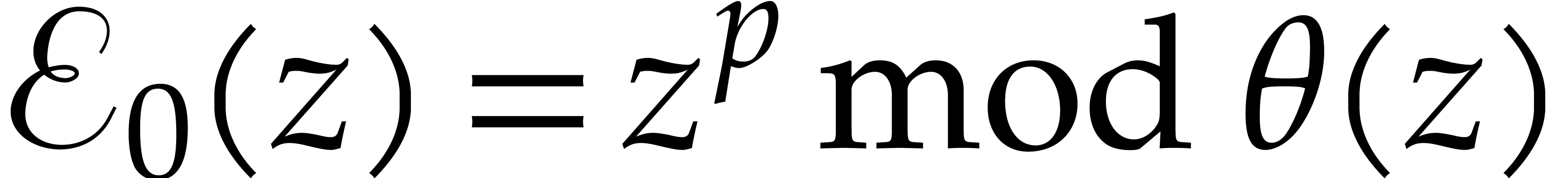 .
Assume therefore that
.
Assume therefore that 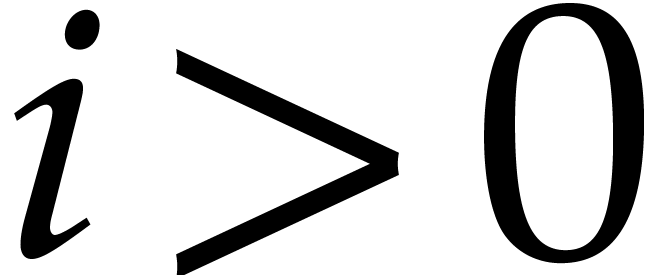 and let
and let 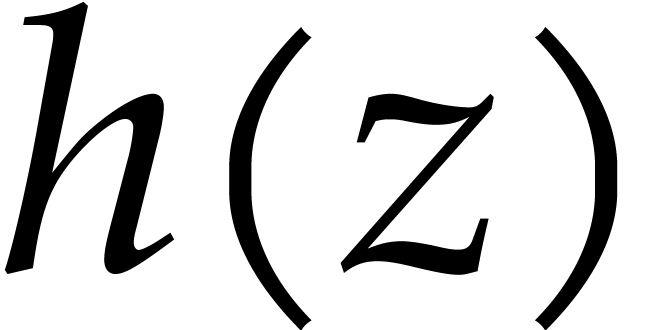 be such that
be such that
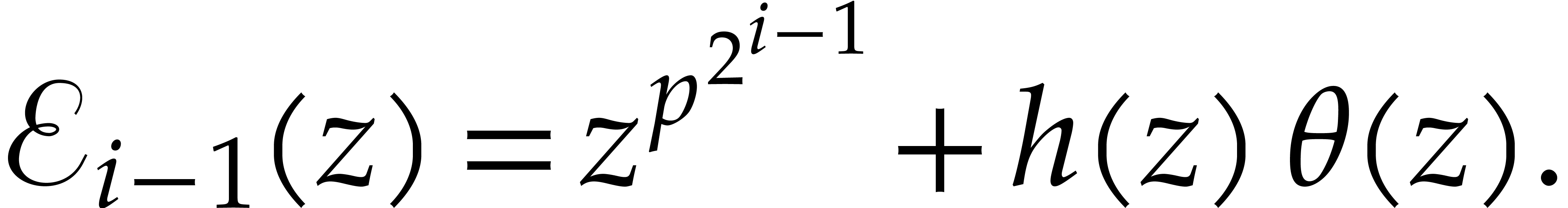
We verify that
This completes the correctness proof. The first step takes time 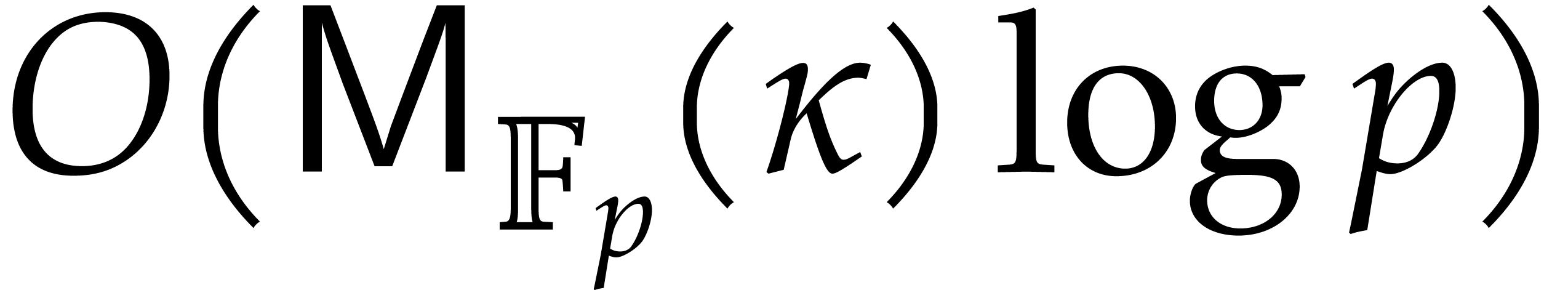 , whereas the loop requires
, whereas the loop requires 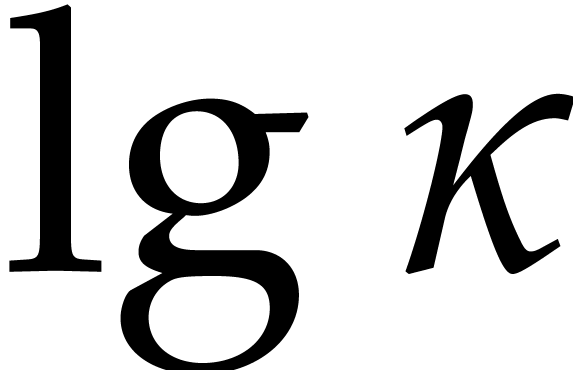 modular compositions, whence the complexity
bound.
modular compositions, whence the complexity
bound.
For the efficient application of the absolute pseudo-Frobenius map, we
introduce the auxiliary sequence 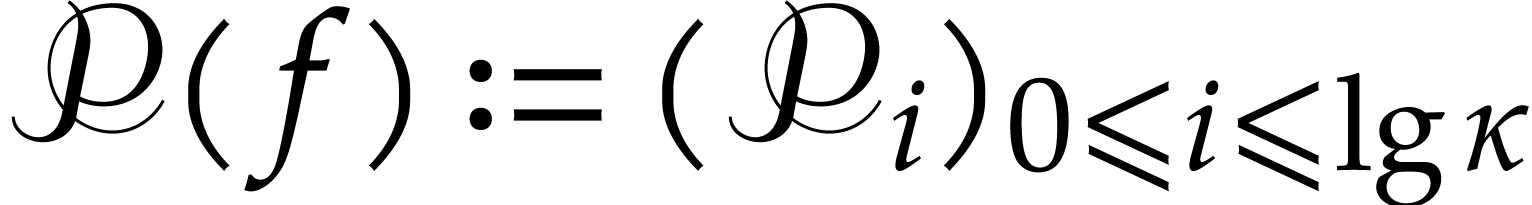 with
with
Proof. We verify that
The cost is straightforward from the definitions.
Once 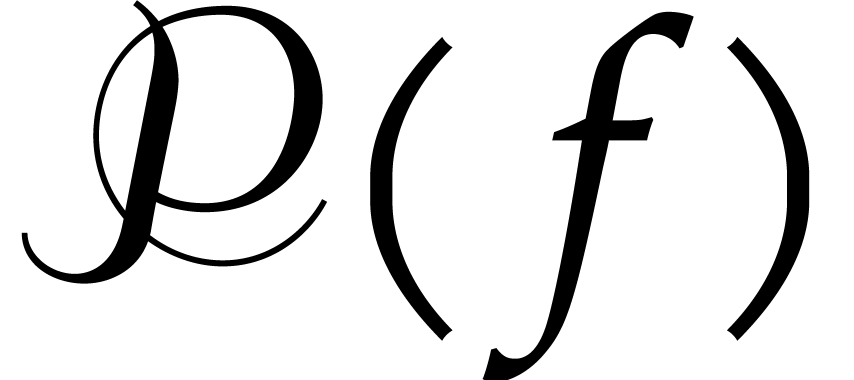 has been computed, the pseudo-Frobenius map
can be iterated an arbitrary number of times, using the following
variant of Lemma 2.2.
has been computed, the pseudo-Frobenius map
can be iterated an arbitrary number of times, using the following
variant of Lemma 2.2.
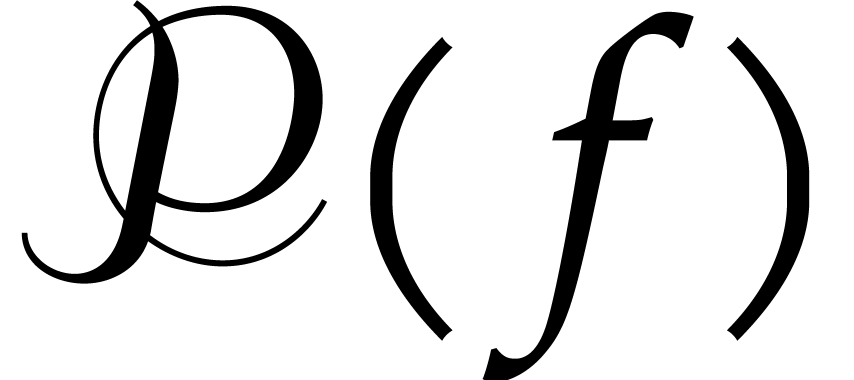 be given. For all
be given. For all  and
and 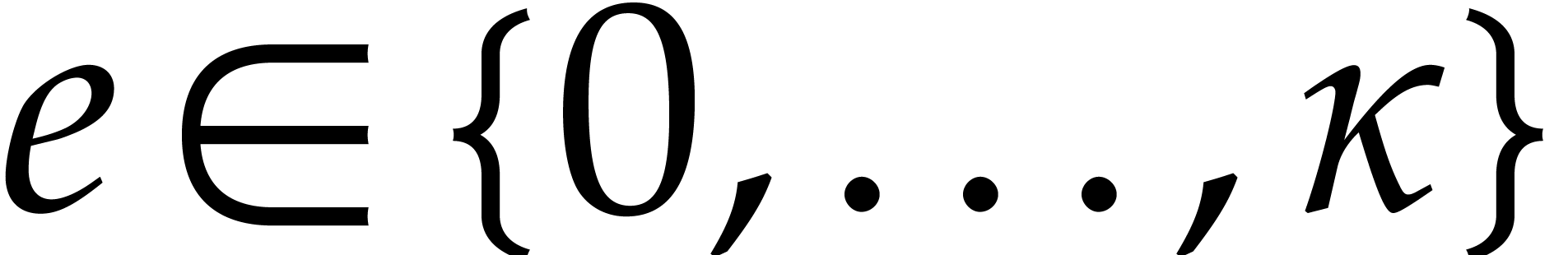 with binary expansion
with binary expansion 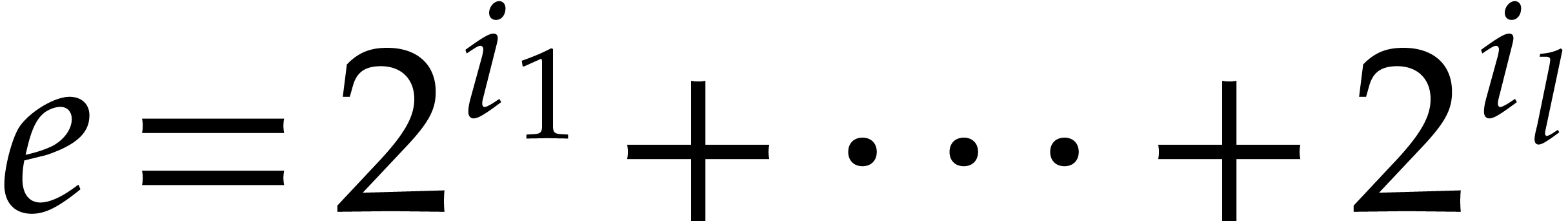 with
with  , we have
, we have
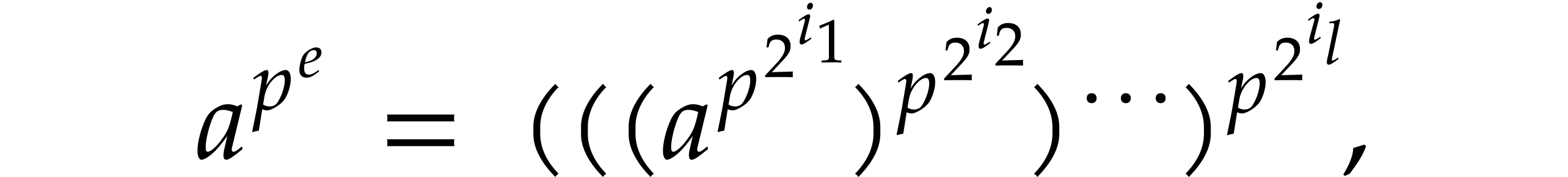
that can be computed in time
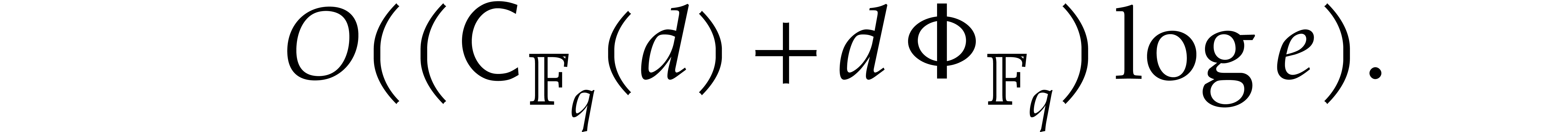
Proof. The proof is straightforward from Lemma
2.4.
The auxiliary sequence  can be computed
efficiently as follows.
can be computed
efficiently as follows.
Algorithm
Compute  using binary powering.
using binary powering.
For 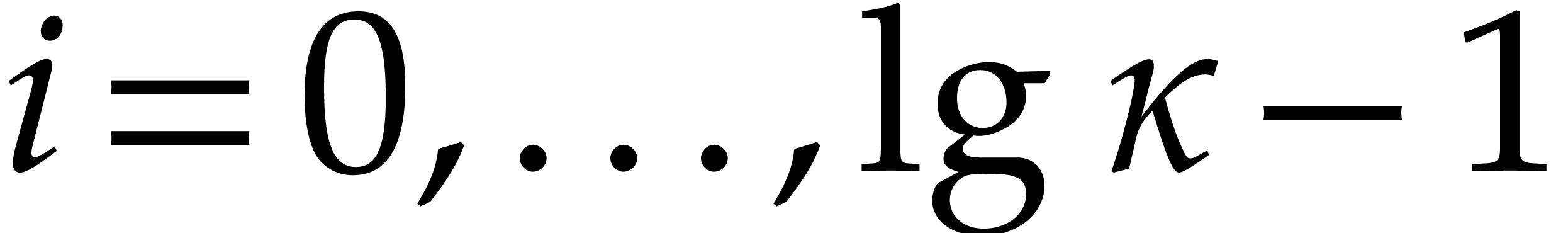 :
:
Write 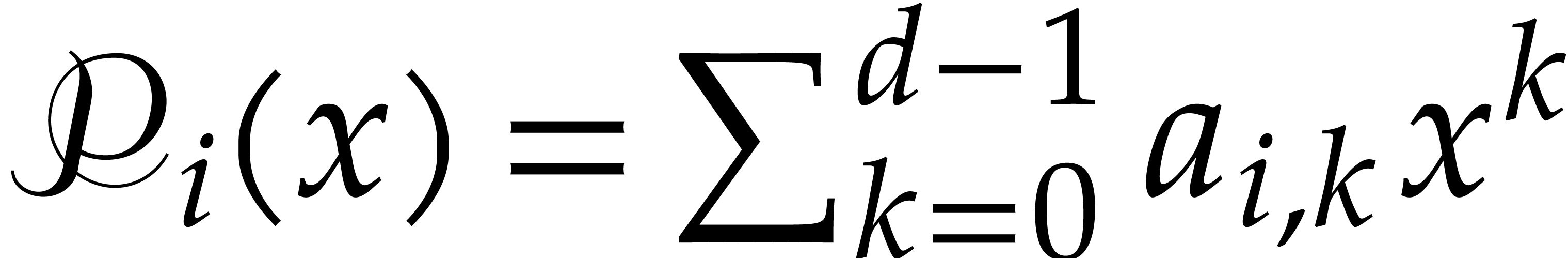 ,
,
Compute 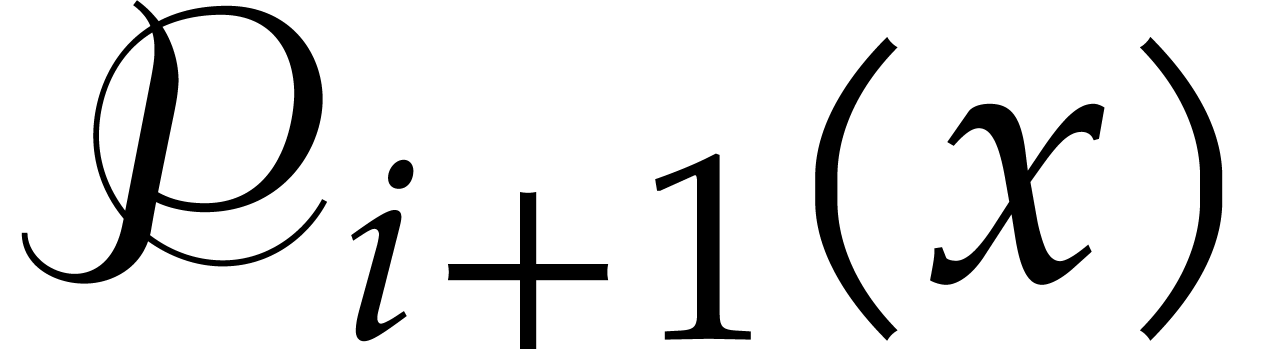 as
as 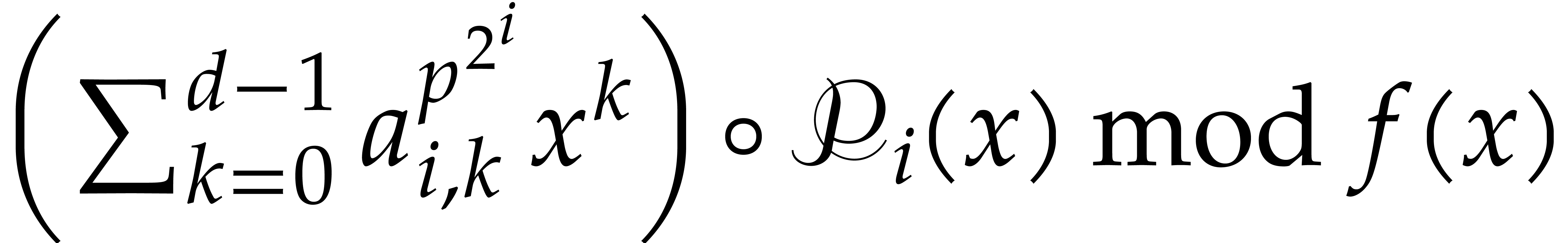 .
.
Return 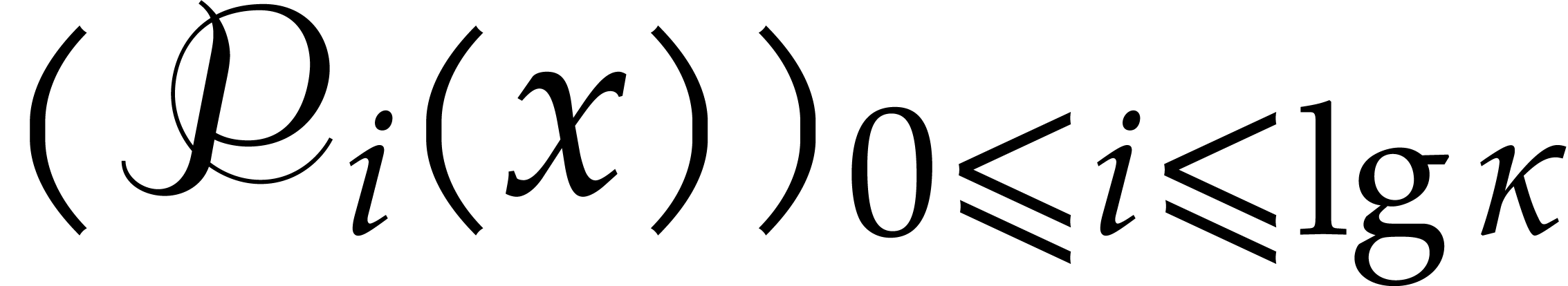 .
.
Proof. Let us prove the correctness by induction
on  . The result clearly holds
for
. The result clearly holds
for 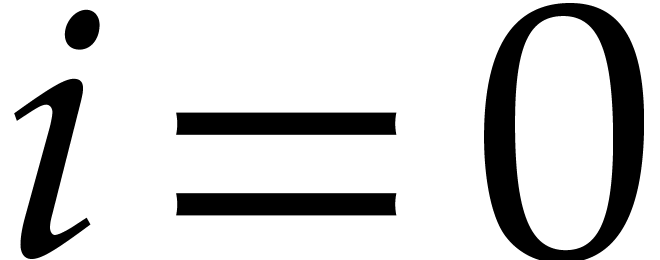 . Assume that it holds
for a given
. Assume that it holds
for a given  and let
and let 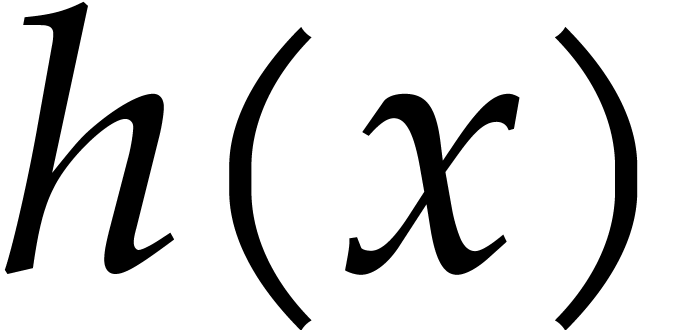 be
such that
be
such that 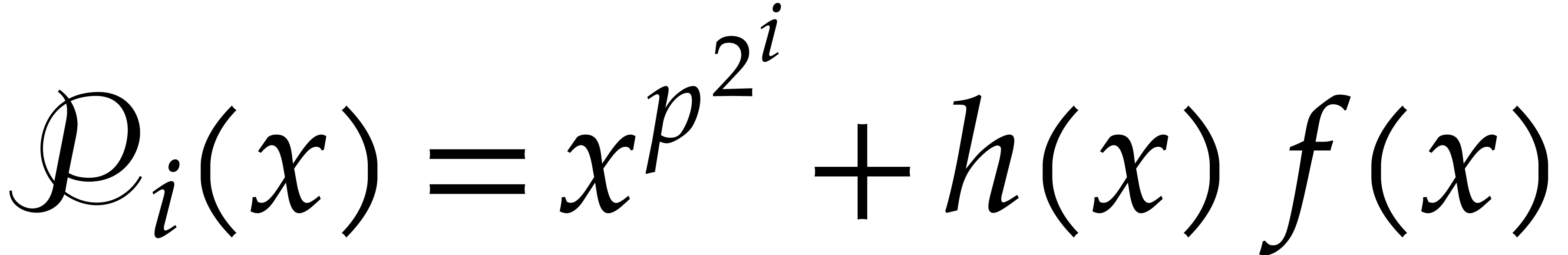 . Then
. Then
As to the complexity bound, the binary powering in step 1 takes 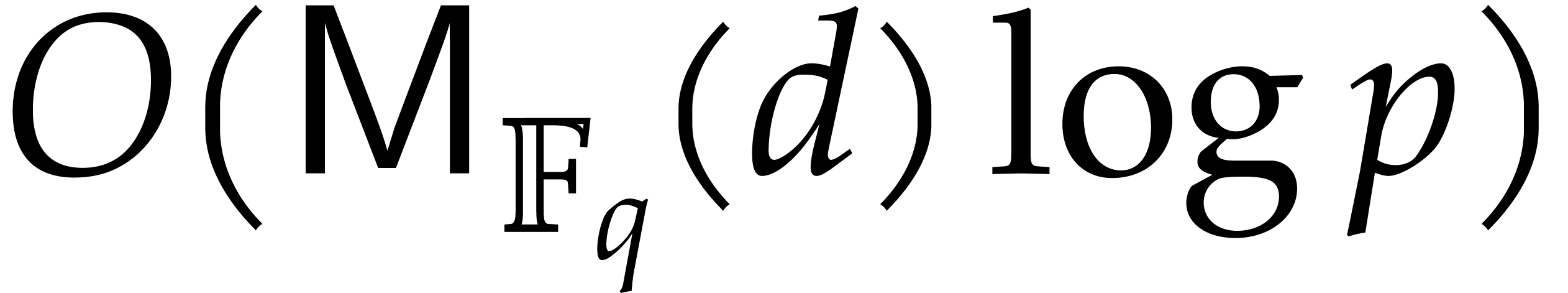 time. In step 2, we compute
time. In step 2, we compute 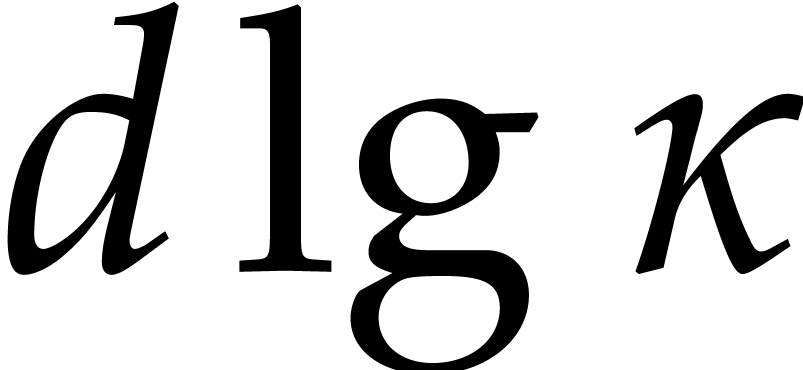 powers of the form
powers of the form 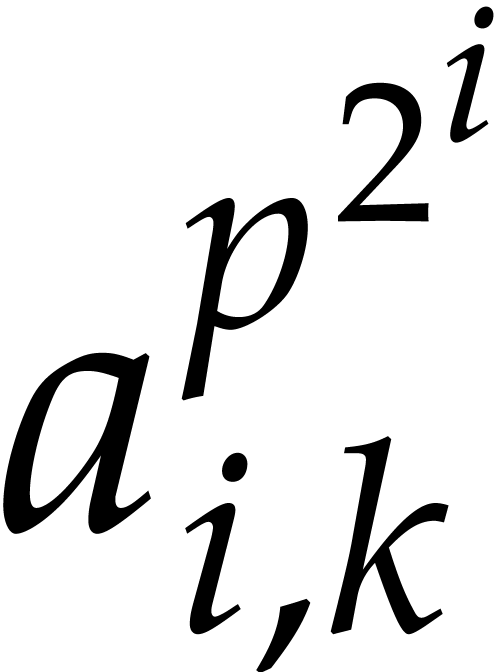 and we perform
and we perform 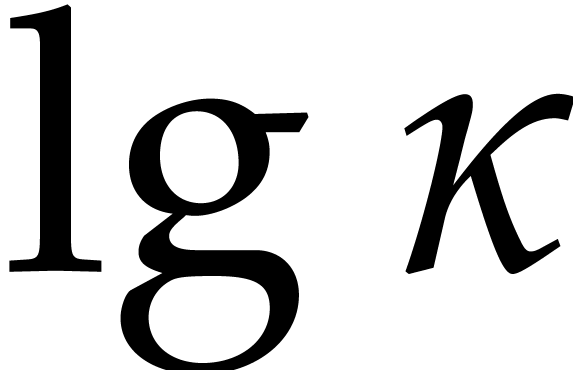 modular compositions of degree
modular compositions of degree 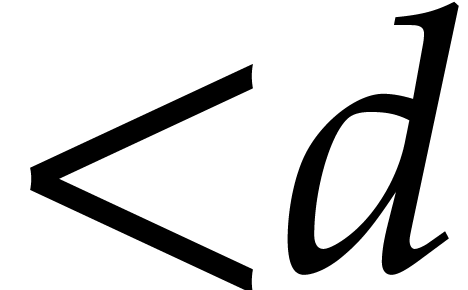 over
over  .
.
For the efficient application of the pseudo-Frobenius map, we introduce
another auxiliary sequence 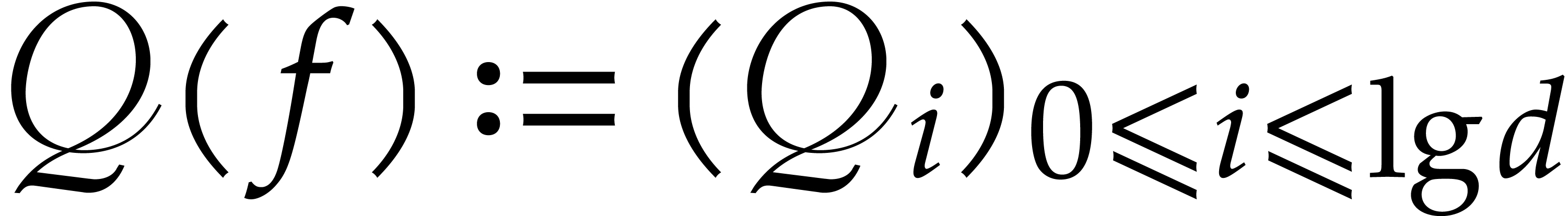 with
with
Proof. The proof is straightforward from the
definitions.
Once 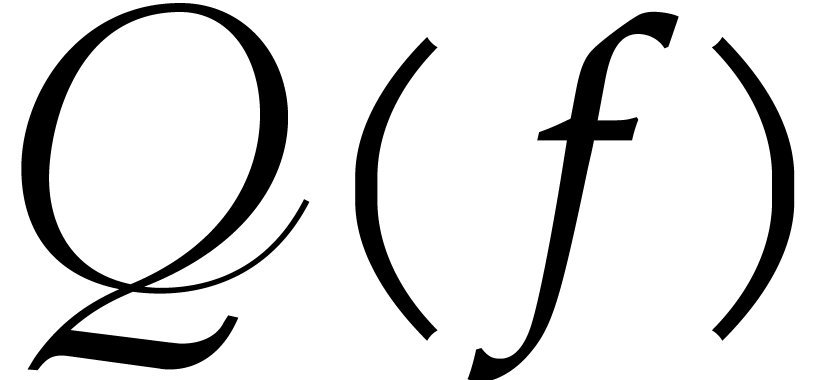 has been computed, the pseudo-Frobenius map
can be iterated an arbitrary number of times by adapting Lemma 2.2,
but this will not be needed in the sequel. The sequence
has been computed, the pseudo-Frobenius map
can be iterated an arbitrary number of times by adapting Lemma 2.2,
but this will not be needed in the sequel. The sequence 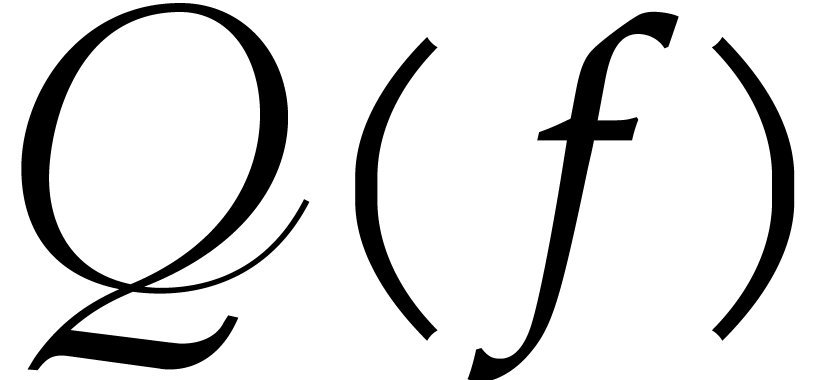 can be computed efficiently as follows.
can be computed efficiently as follows.
Algorithm
Compute 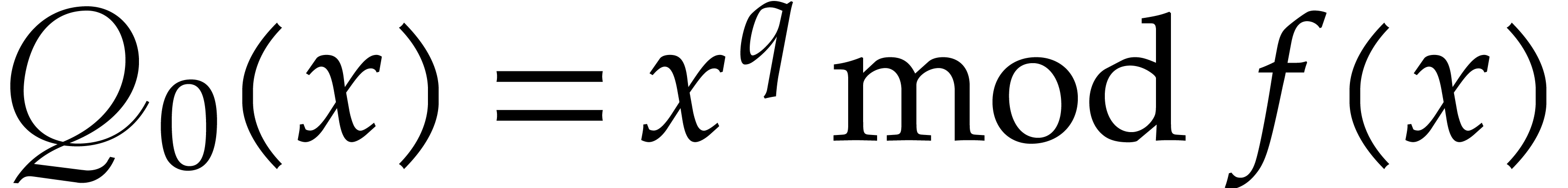 using Lemma 2.5.
using Lemma 2.5.
For  , compute
, compute  .
.
Return 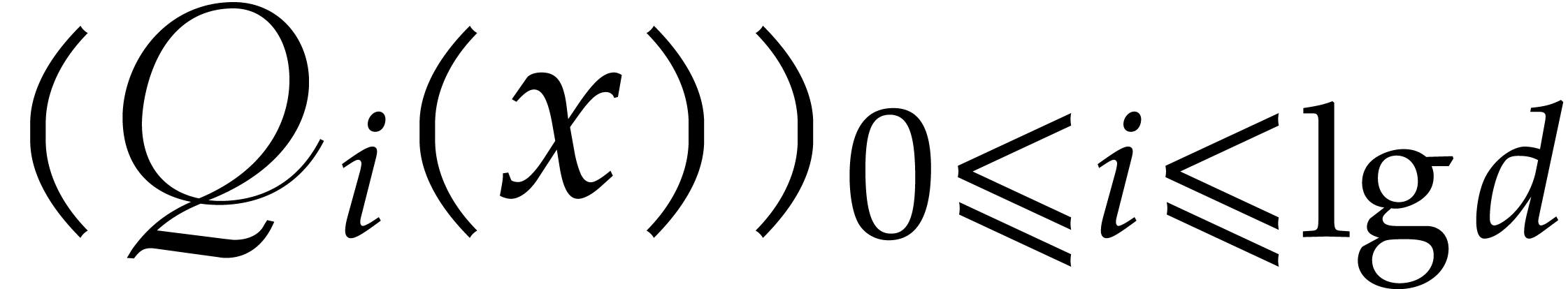 .
.
Proof. The correctness is proved in a similar
way as for Algorithm 2.1. Step 1 takes 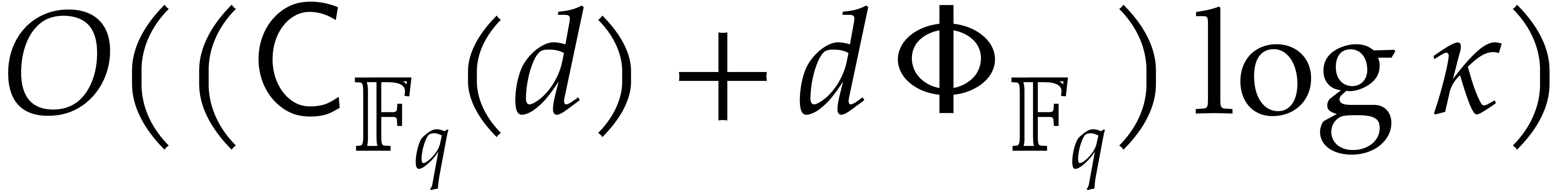 operations, by Lemma 2.5, whereas step 2 takes
operations, by Lemma 2.5, whereas step 2 takes 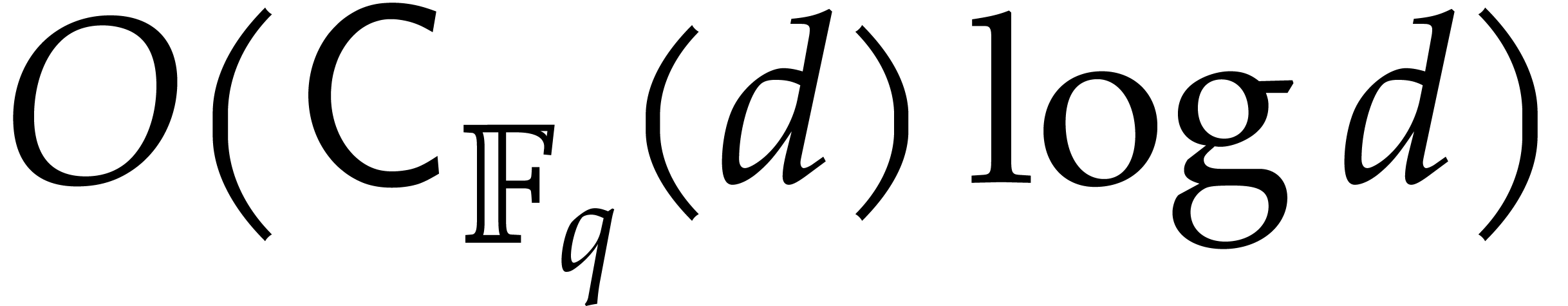 operations.
operations.
Let 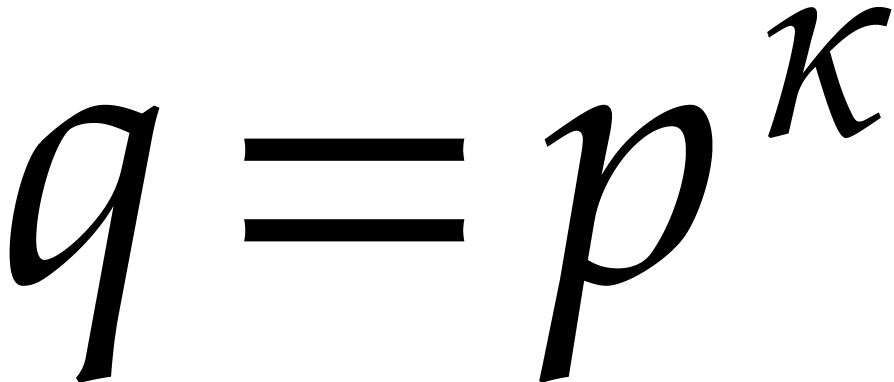 be still as above. Recall that the trace of
an element
be still as above. Recall that the trace of
an element 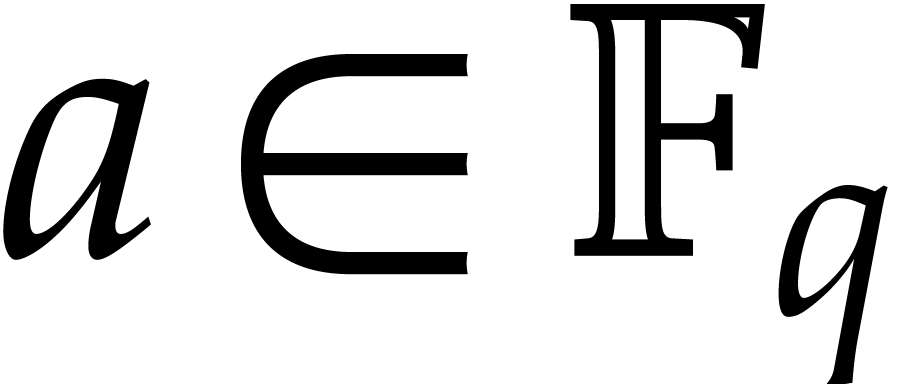 over
over  ,
written
,
written 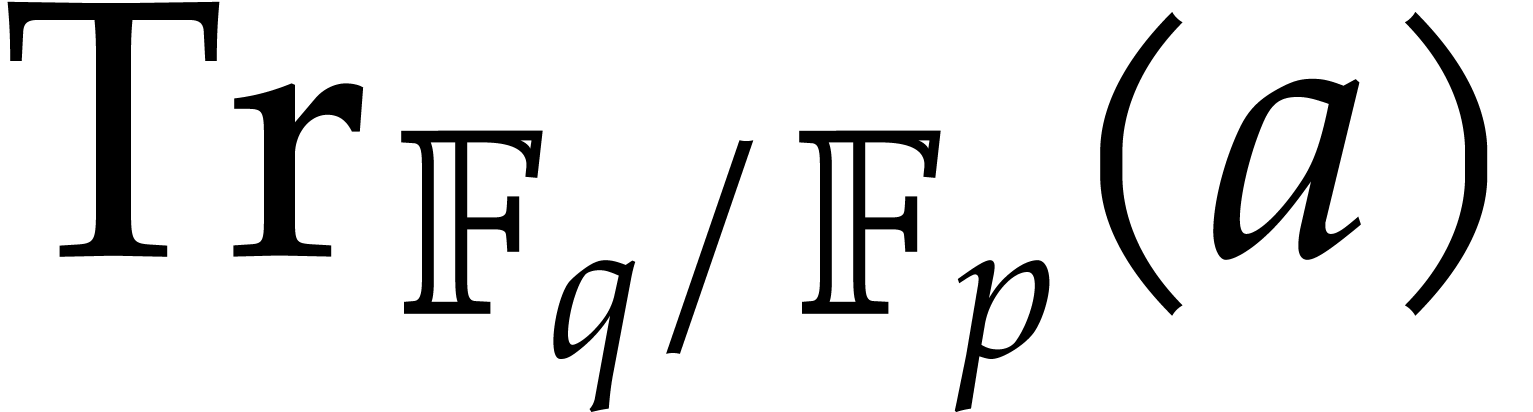 , is defined as
, is defined as
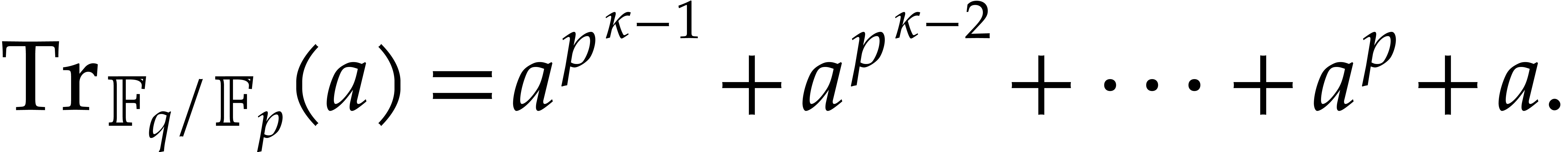
For a monic, not necessarily irreducible polynomial  of degree
of degree  , it is customary
to consider two similar kinds of maps over
, it is customary
to consider two similar kinds of maps over 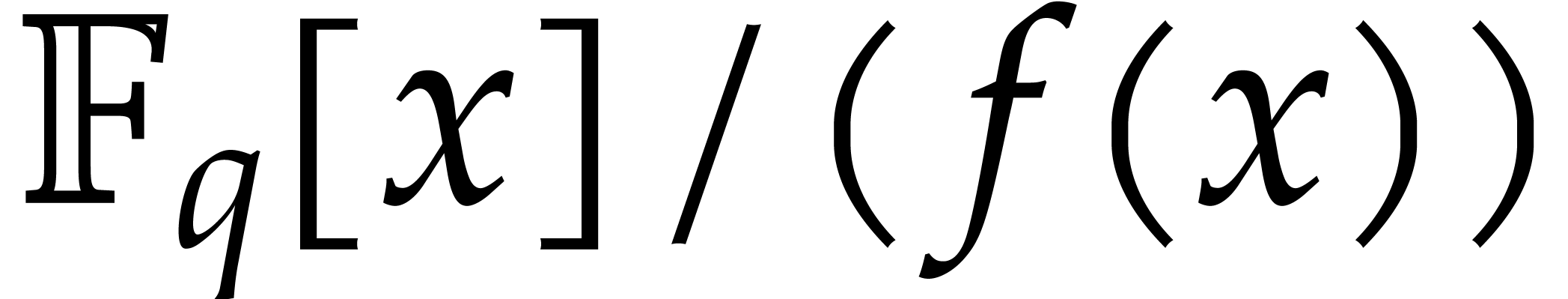 ,
which are called pseudo-traces: one over
,
which are called pseudo-traces: one over  and one over
and one over  . In this
section, we reformulate fast algorithms for pseudo-traces by Kaltofen
and Shoup [23], and make them rely on the data structures
from the previous section for the computation of Frobenius maps.
. In this
section, we reformulate fast algorithms for pseudo-traces by Kaltofen
and Shoup [23], and make them rely on the data structures
from the previous section for the computation of Frobenius maps.
Let 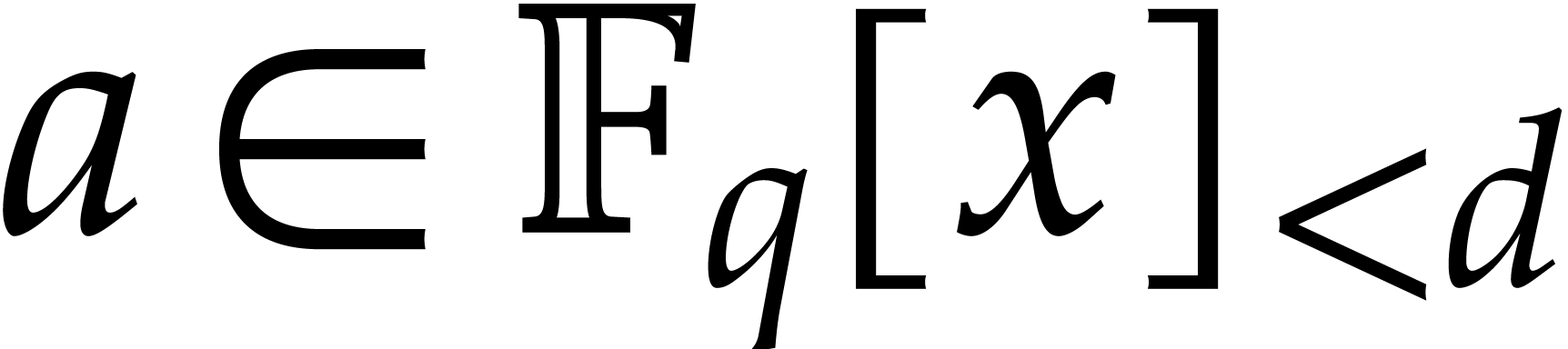 . We define the
pseudo-trace of
. We define the
pseudo-trace of 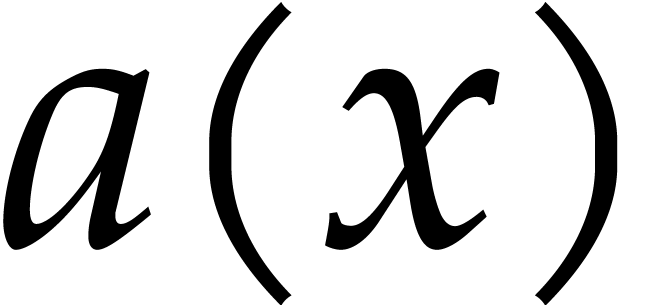 of order
of order  modulo
modulo 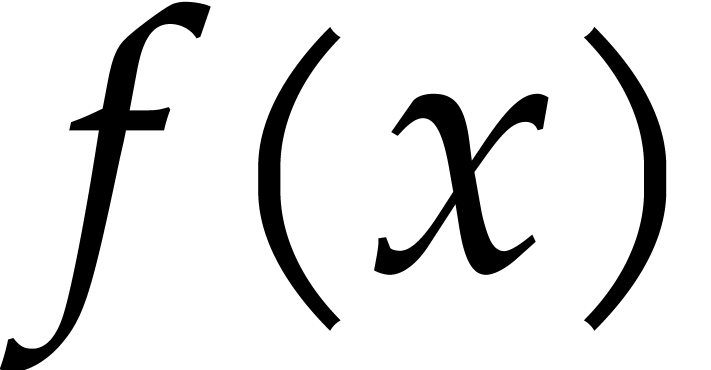 over
over  by
by
We may compute pseudo-traces using the following algorithm:
Algorithm
Let 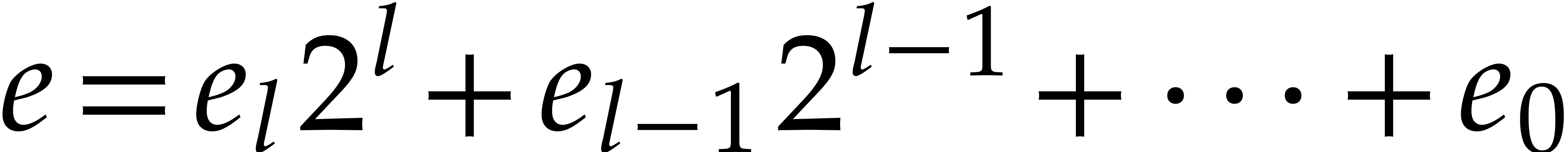 be the binary expansion of
be the binary expansion of 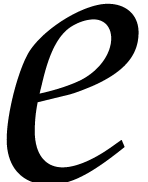 .
.
Let 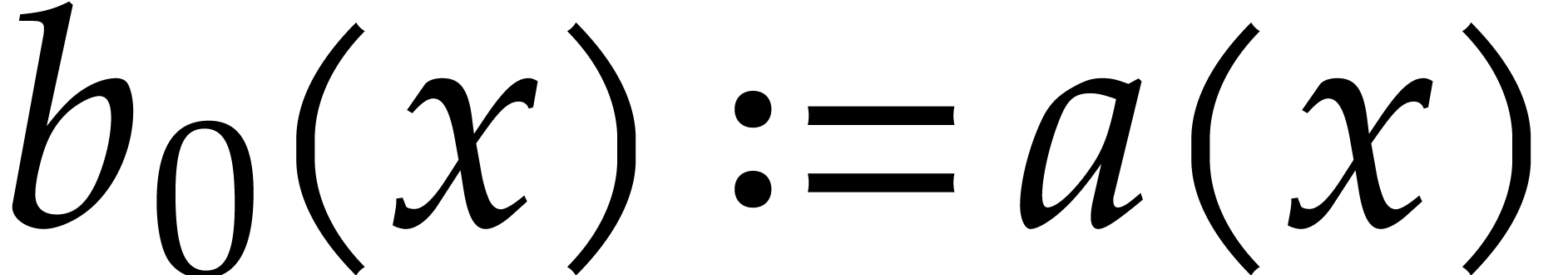 and
and
Let 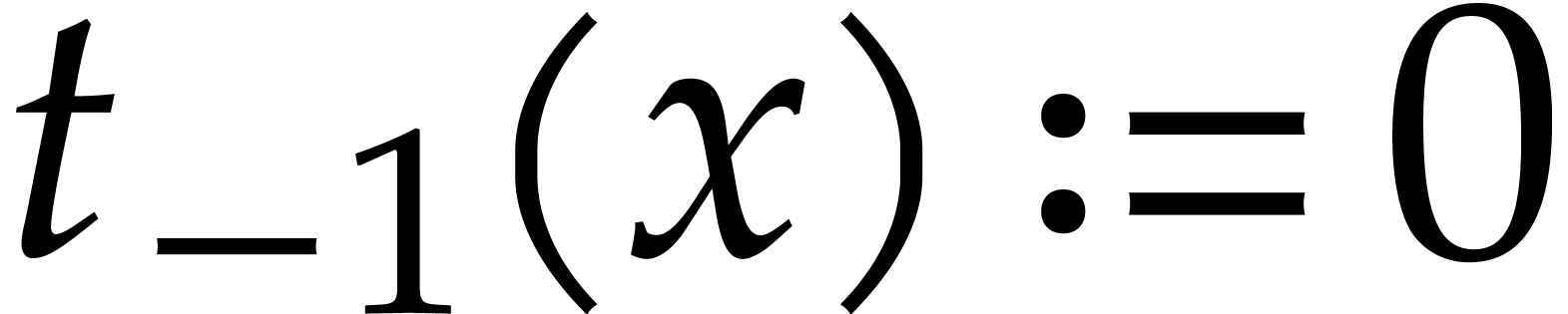 and
and
Return 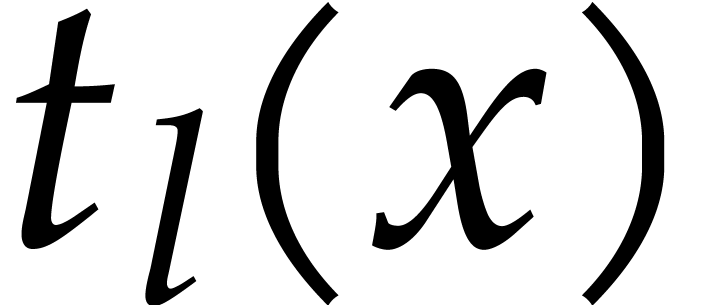 .
.
Proof. By induction on  , we verify that
, we verify that
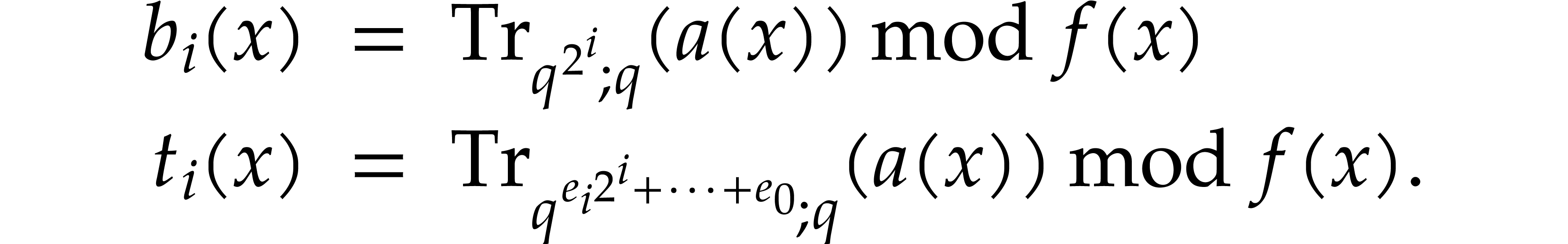
The cost follows from Lemma 2.7.
We define the absolute pseudo-trace of 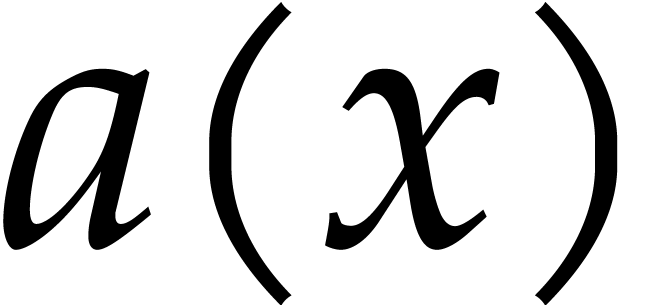 modulo
modulo 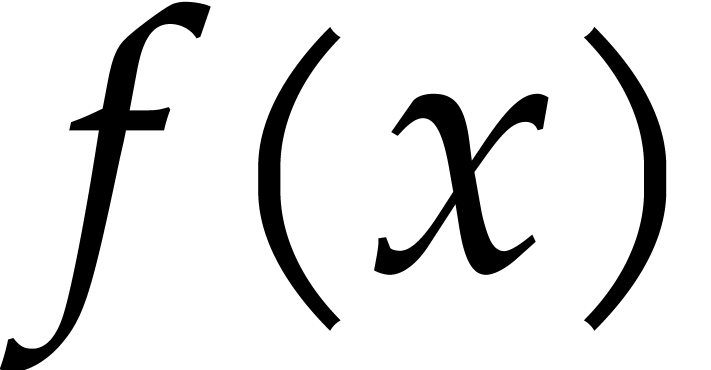 of order
of order 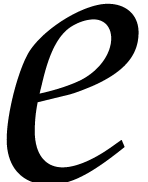 by
by
We may compute absolute pseudo-traces using the following variant of Algorithm 3.1:
Algorithm
Let 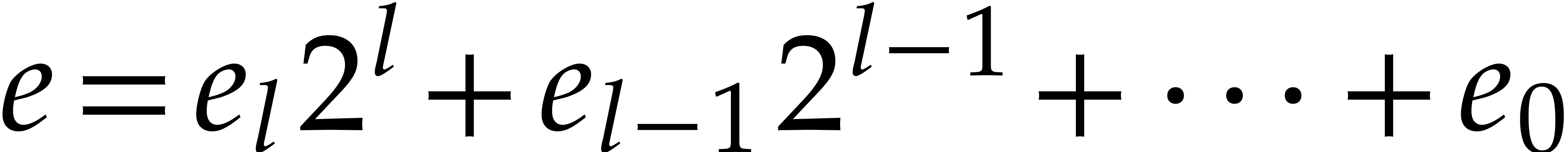 be the binary expansion of
be the binary expansion of 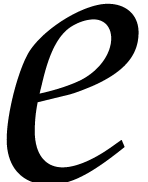 .
.
Let 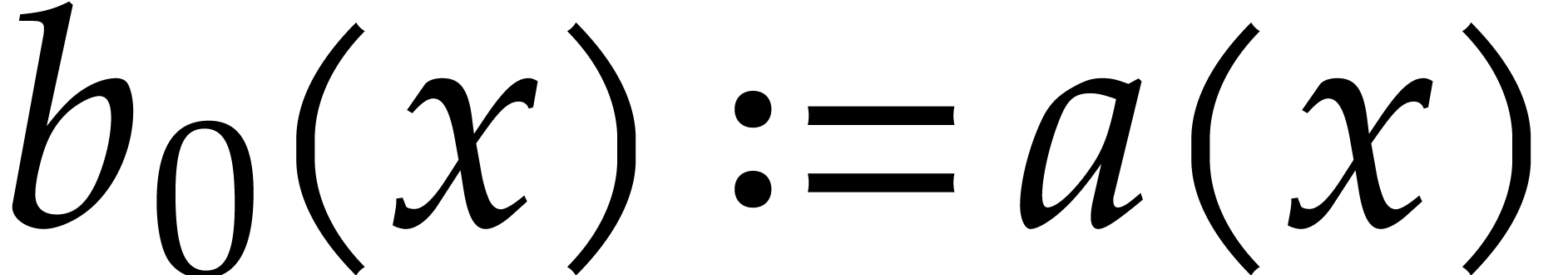 and
and
Let  and
and
Return 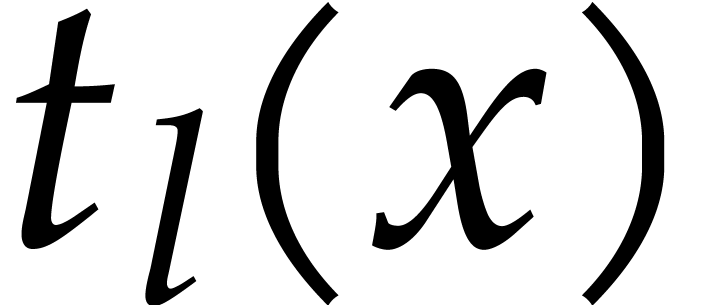 .
.
Proof. By induction on  , we have
, we have
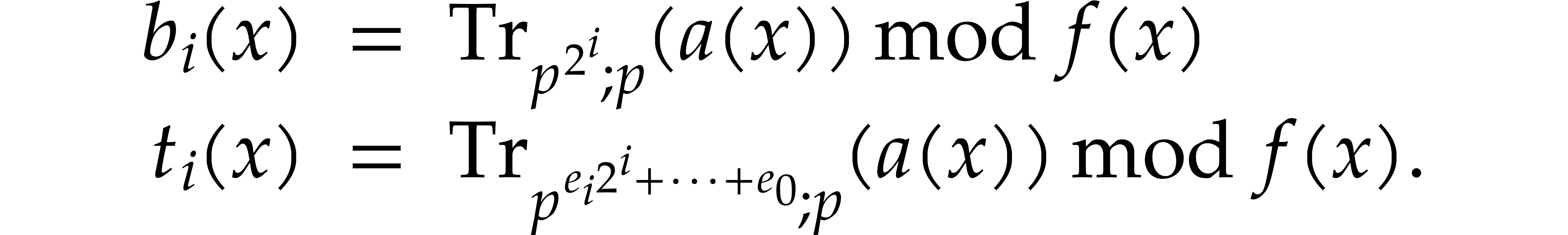
The cost then follows from Lemma 2.4.
We follow the Cantor–Zassenhaus strategy, which subdivides
irreducible factorization in 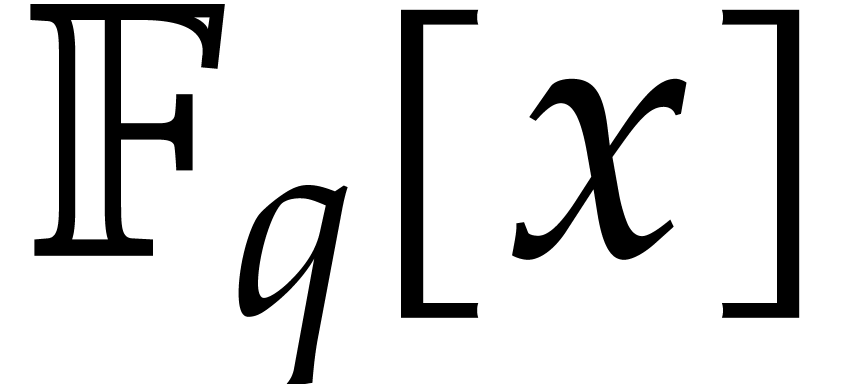 into three
consecutive steps:
into three
consecutive steps:
the square-free factorization decomposes into square-free factors along with their respective multiplicities,
the distinct-degree factorization separates irreducible factors according to their degree,
the equal-degree factorization completely factorizes a polynomial whose irreducible factors have the same degree.
For the distinct-degree factorization, we revisit the “baby-step
giant-step” algorithm due to von zur Gathen and Shoup [11,
section 6], later improved by Kaltofen and Shoup [24,
Algorithm D]. For the equal-degree factorization, we adapt another
algorithm due to von zur Gathen and Shoup [11, section 5],
while taking advantage of fast modular composition as in [23,
Theorem 1]. Throughout this section, we assume that  is the polynomial to be factored and that
is the polynomial to be factored and that  is
monic of degree
is
monic of degree  .
.
The square-free factorization combines the separable factorization and
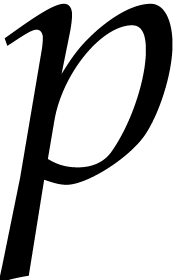 -th root extractions.
-th root extractions.
Proof. Let 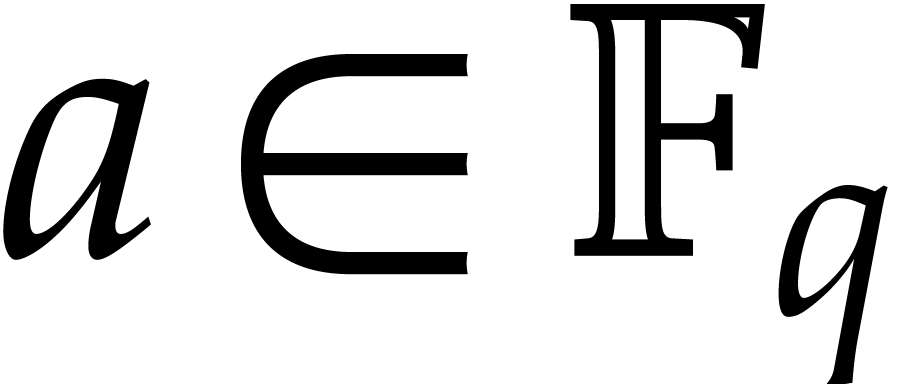 and let
and let 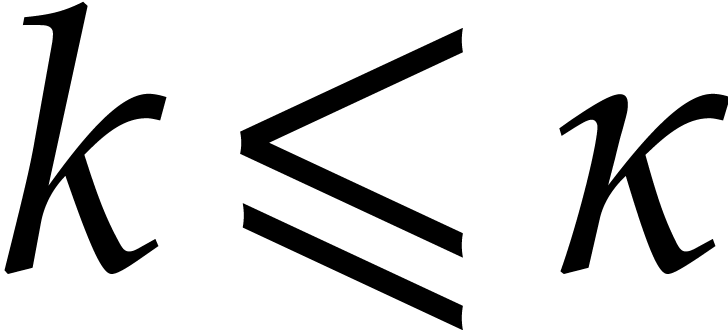 . The
. The 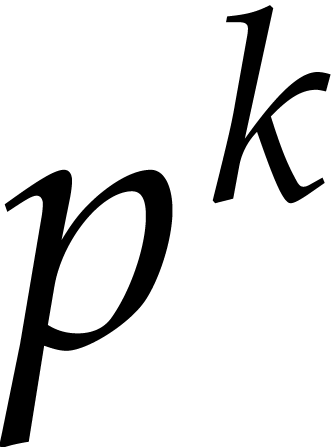 -th
root of
-th
root of  in
in  can be
computed as
can be
computed as 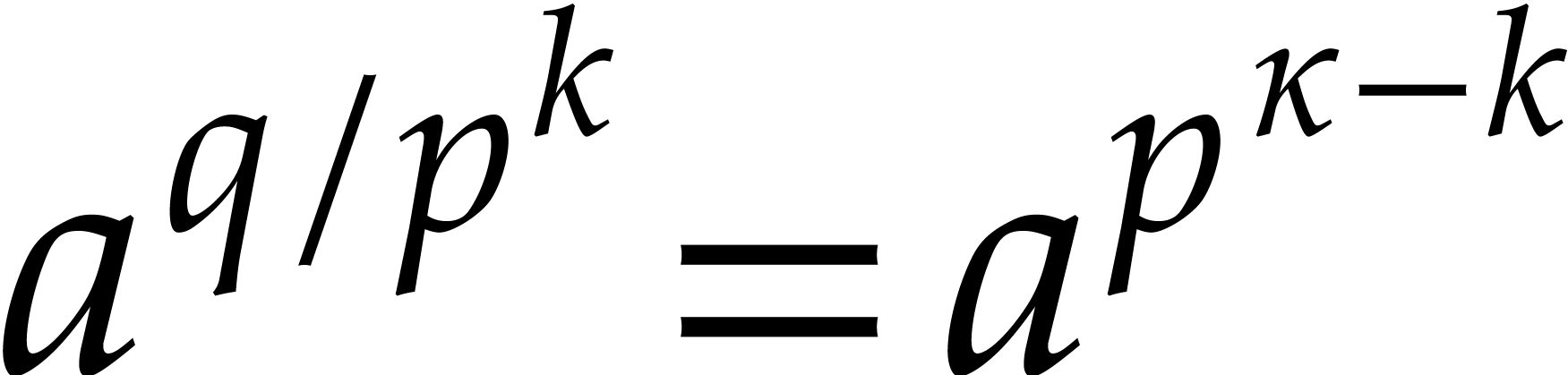 in time
in time 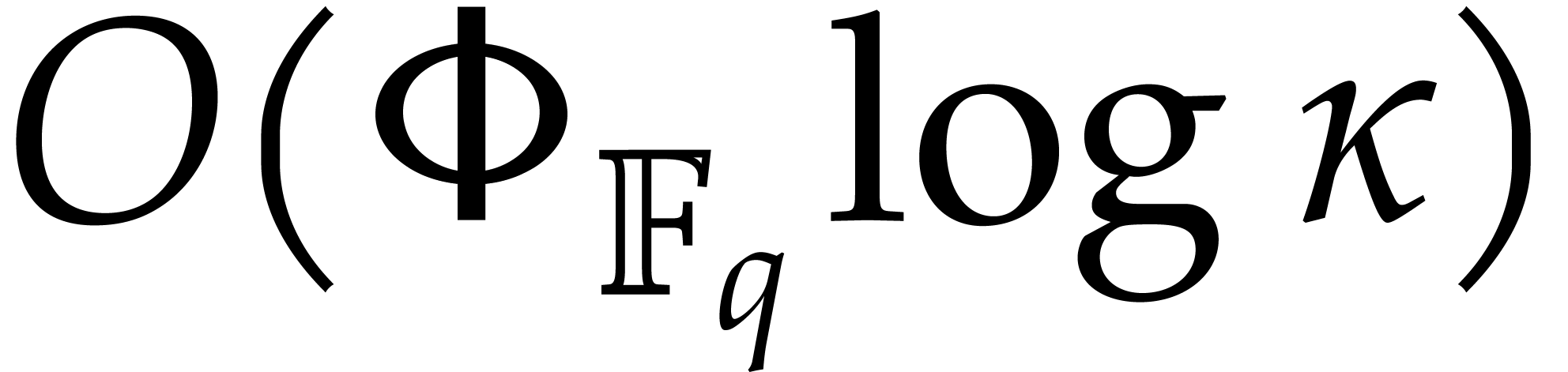 by
Lemma 2.2.
by
Lemma 2.2.
The separable factorization of  takes time
takes time 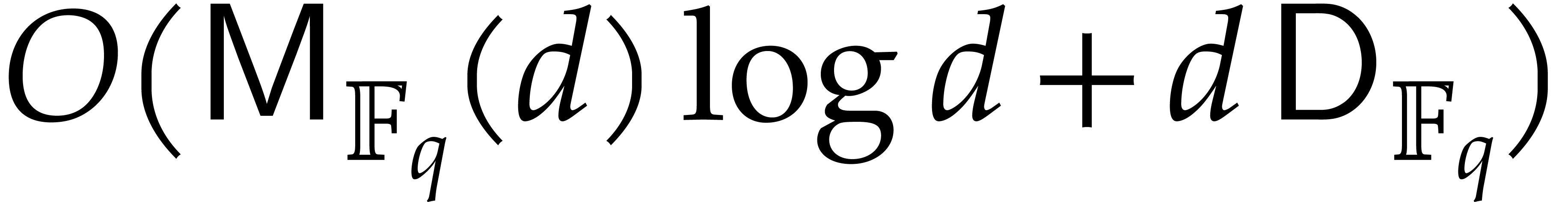 ; see [27]. This
yields
; see [27]. This
yields
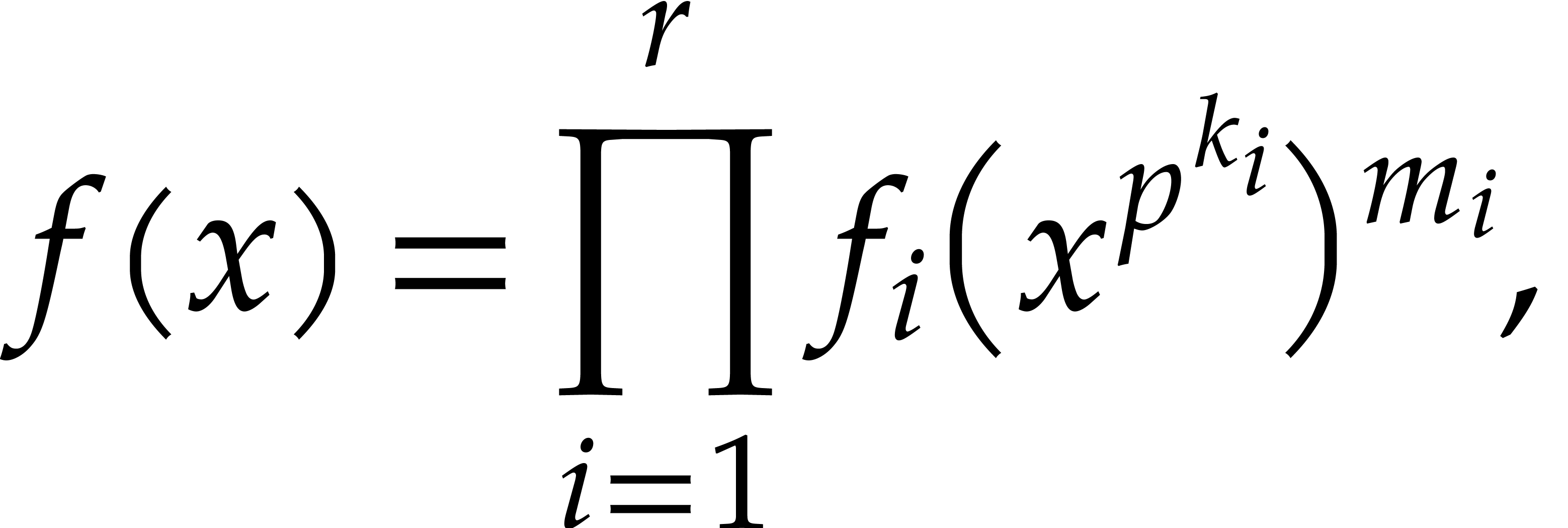
where the 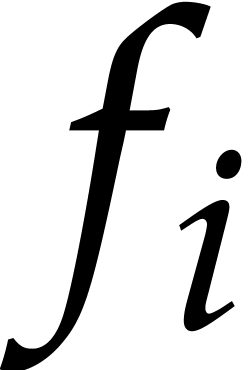 are monic and separable, the
are monic and separable, the 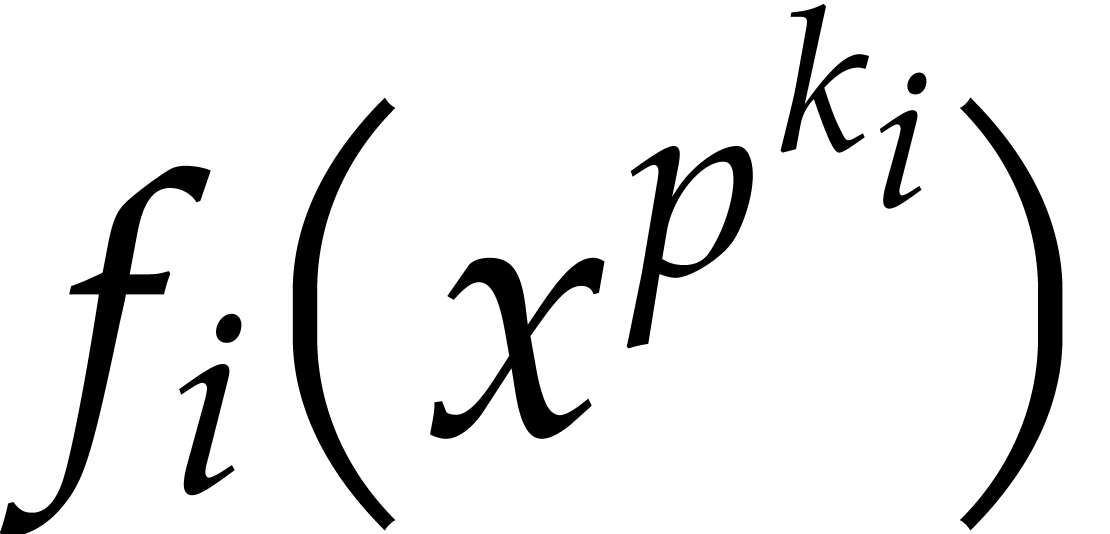 are pairwise coprime, and
are pairwise coprime, and 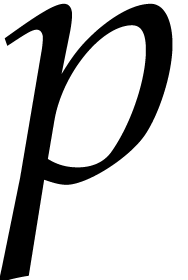 does not
divide the
does not
divide the 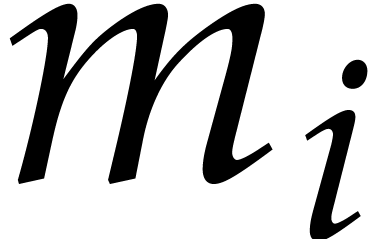 .
.
In order to deduce the square-free factorization of 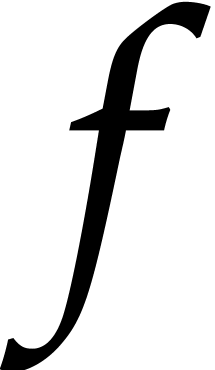 it remains to extract the
it remains to extract the 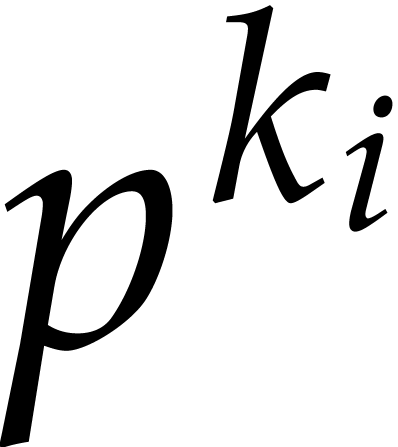 -th
roots of the coefficients of
-th
roots of the coefficients of 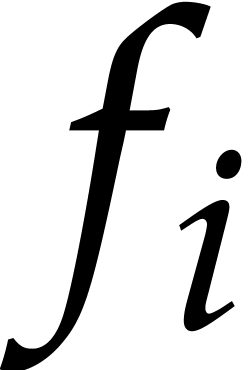 ,
for
,
for 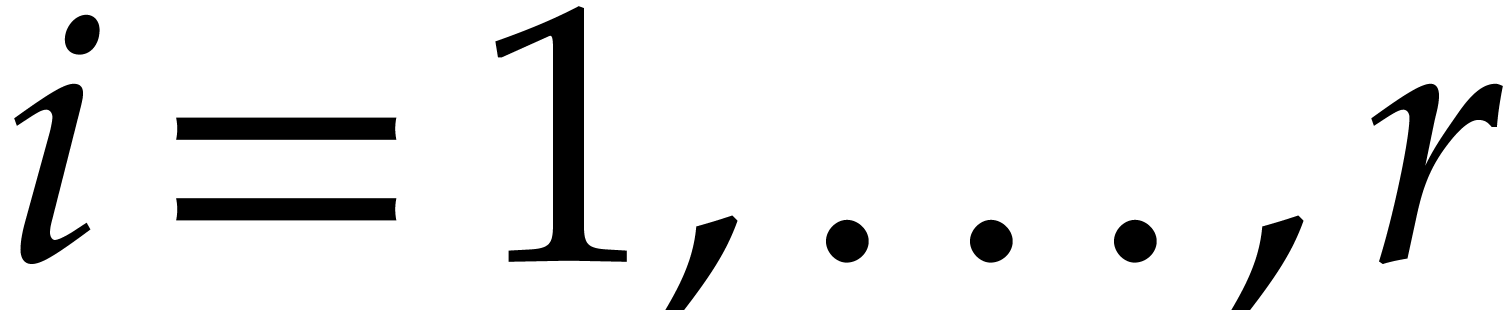 . The cost of these
extractions is bounded by
. The cost of these
extractions is bounded by
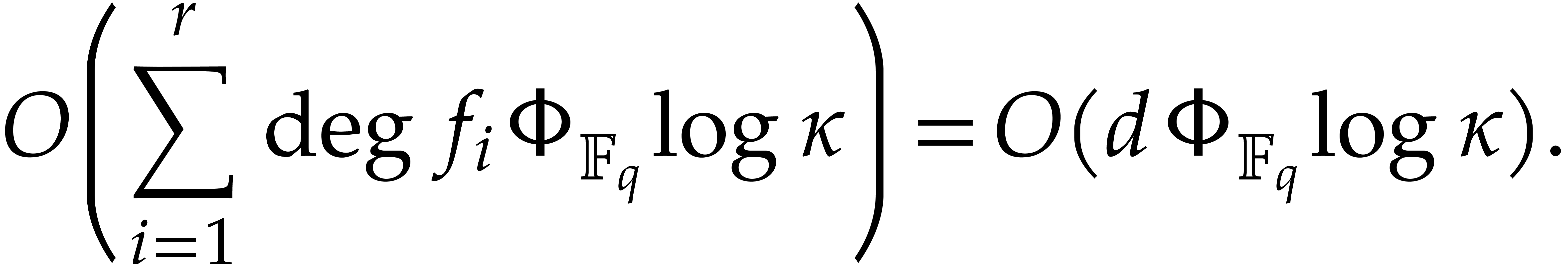

In this subsection  is assumed to be monic and
square-free. The distinct-degree factorization is a partial
factorization
is assumed to be monic and
square-free. The distinct-degree factorization is a partial
factorization  of
of  where
where
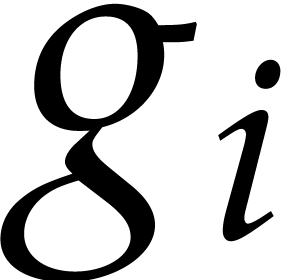 is the product of the monic irreducible factors
of
is the product of the monic irreducible factors
of  of degree
of degree  .
The following algorithm exploits the property that
.
The following algorithm exploits the property that 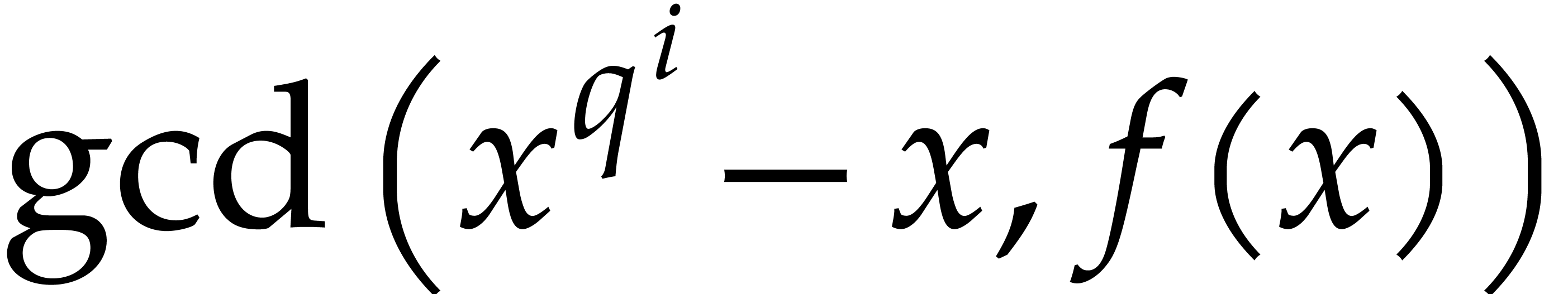 is the product of the irreducible factors of
is the product of the irreducible factors of  of
a degree that divides
of
a degree that divides  . The
“baby-step giant-step” paradigm is used in order to avoid
the naive computation of the
. The
“baby-step giant-step” paradigm is used in order to avoid
the naive computation of the  in sequence for
in sequence for
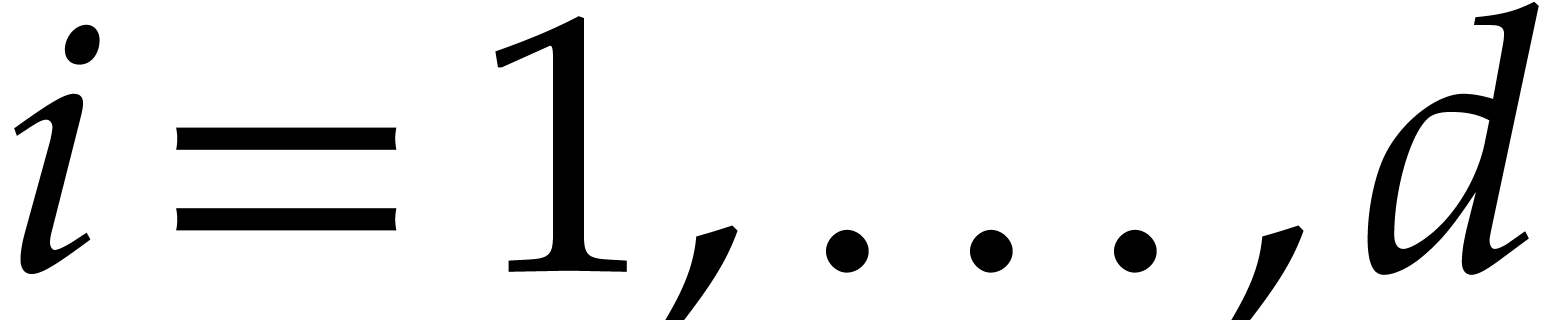 . As a useful feature, our
algorithm only computes the irreducible factors up to a given degree
. As a useful feature, our
algorithm only computes the irreducible factors up to a given degree
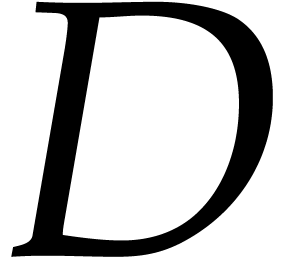 .
.
Algorithm
Let 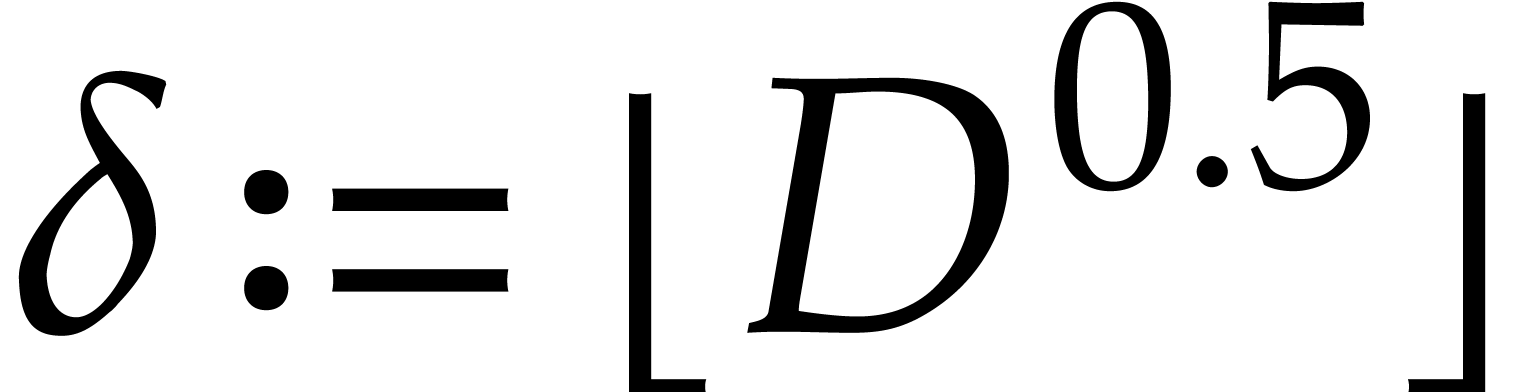 .
.
Compute  by using
by using 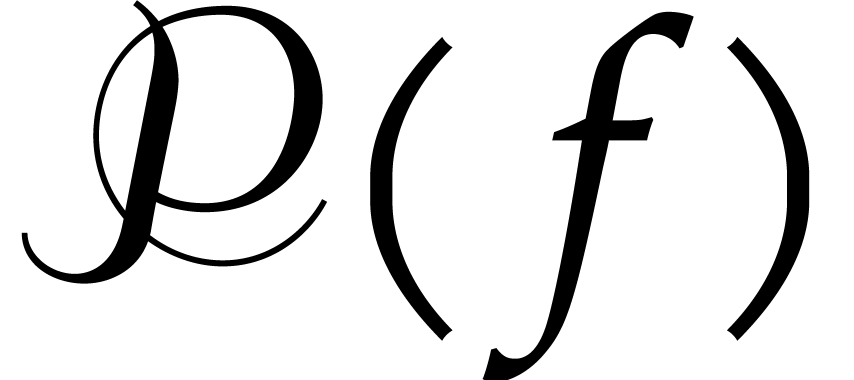 .
.
Compute  for
for 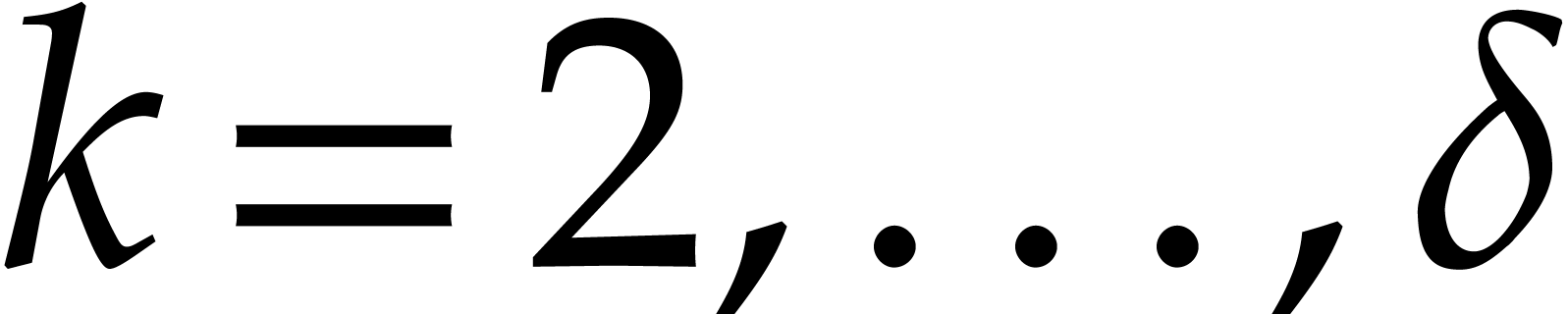 , via modular compositions.
, via modular compositions.
Compute  for
for 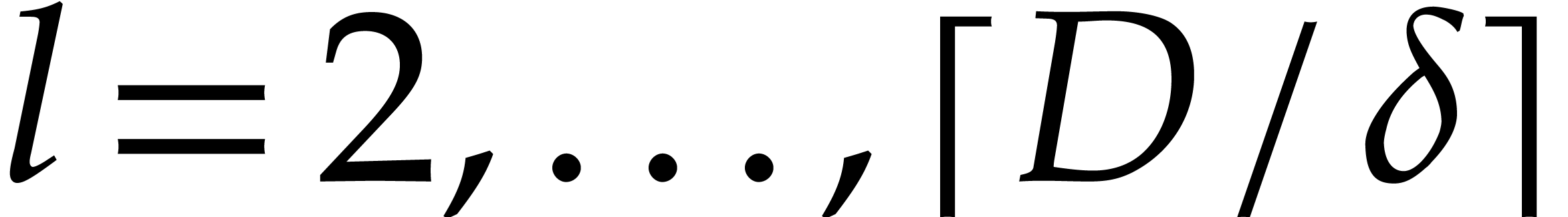 , via modular compositions.
, via modular compositions.
Compute 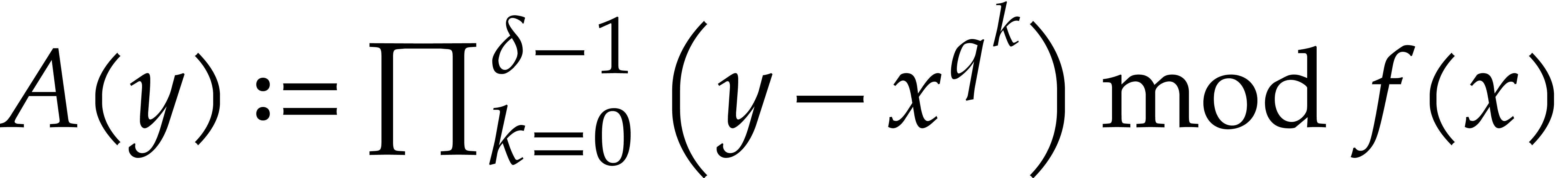 , where
, where 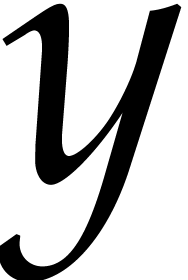 denotes a new variable.
denotes a new variable.
Compute 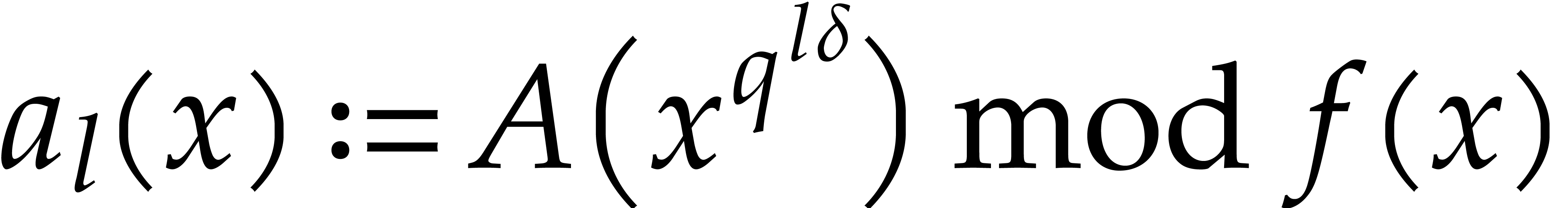 for
for 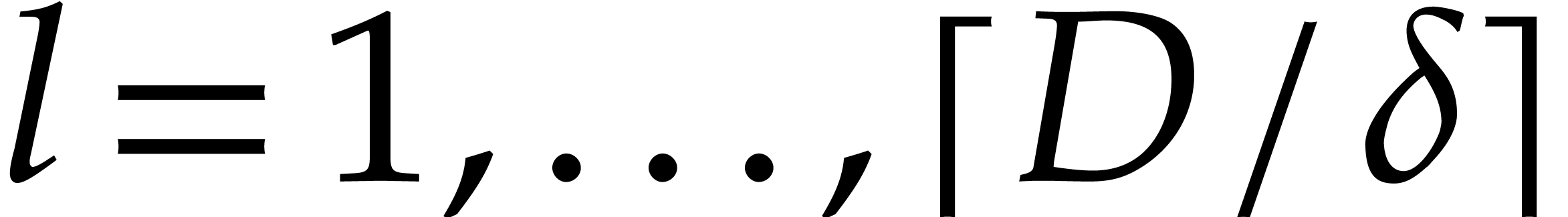 .
.
Set 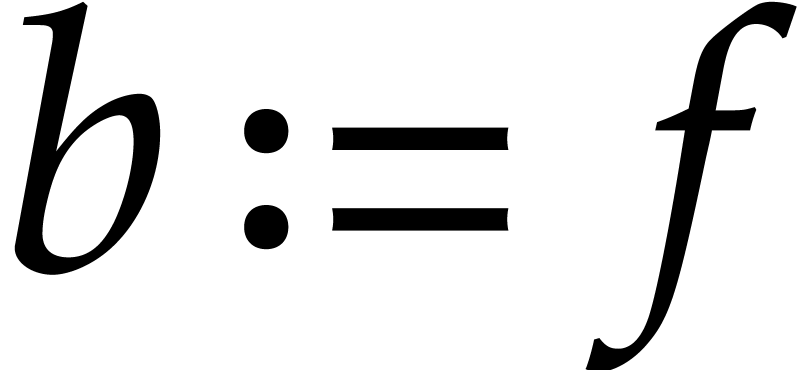 . For
. For 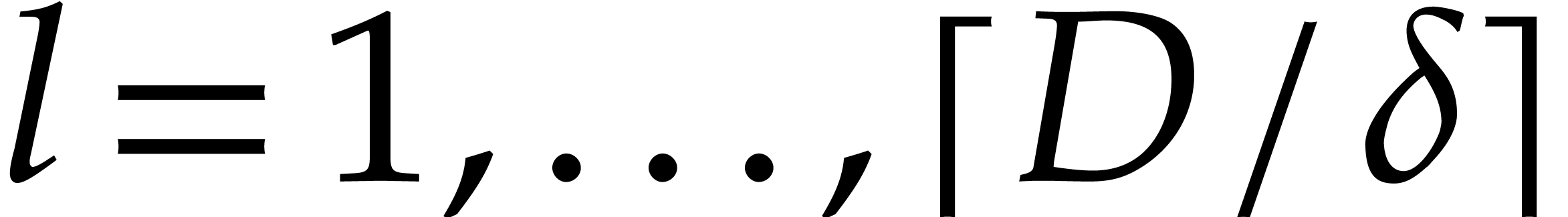 do:
do:
Compute 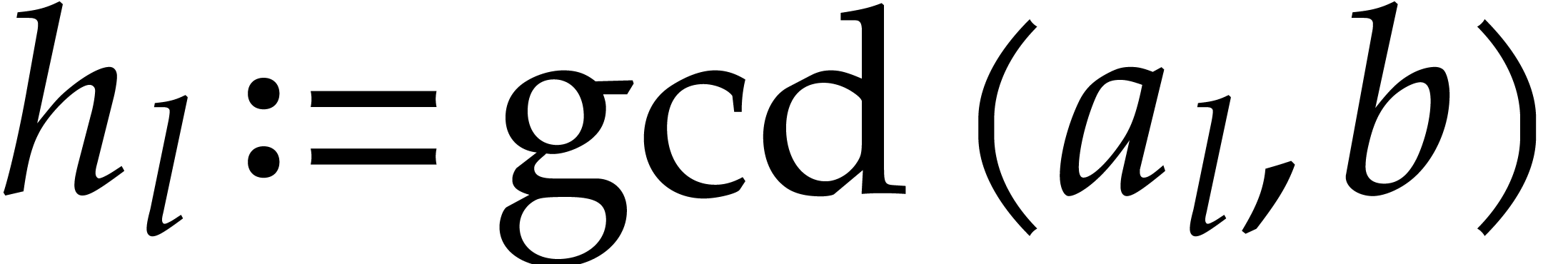 ,
,
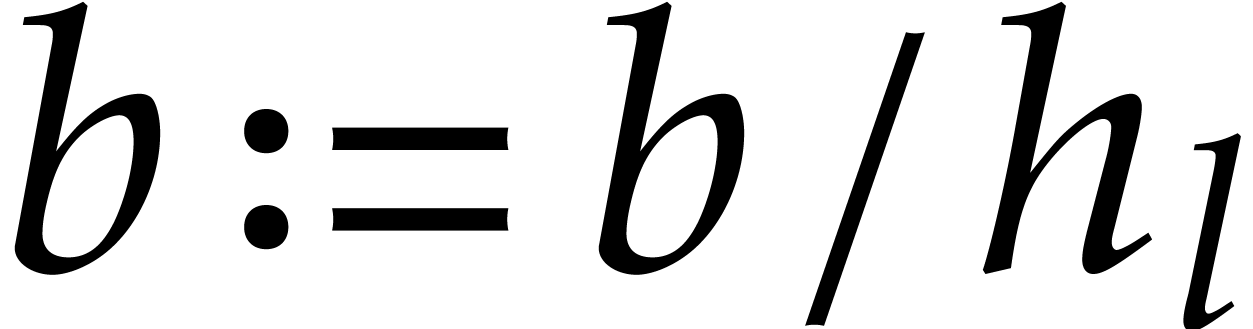 .
.
For  , compute
, compute  for
for  .
.
For 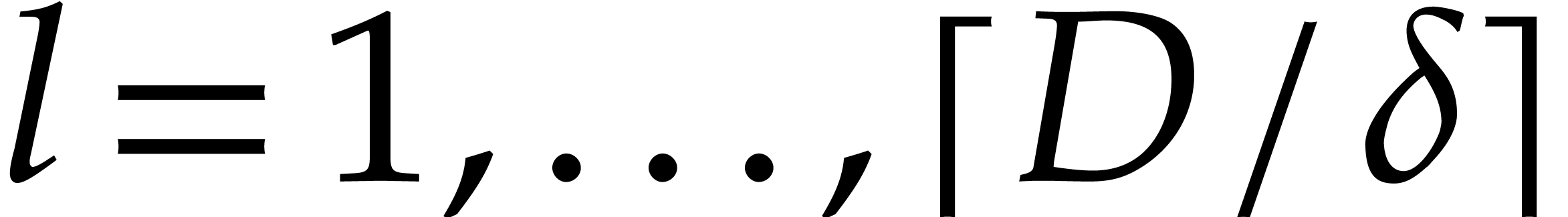 , compute
, compute  for
for  .
.
For 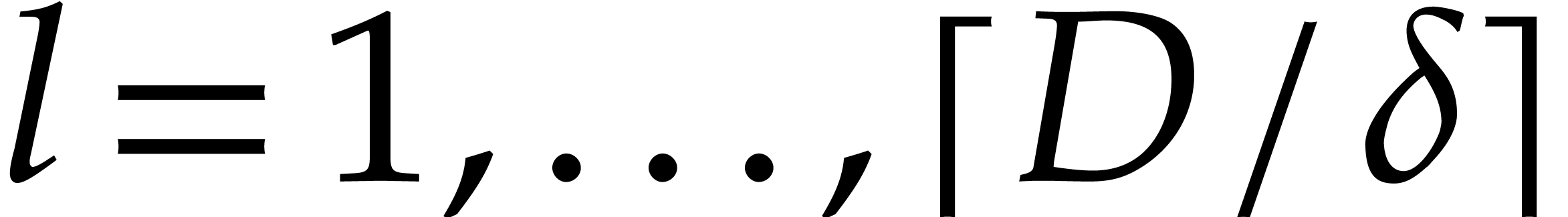 do:
do:
Set 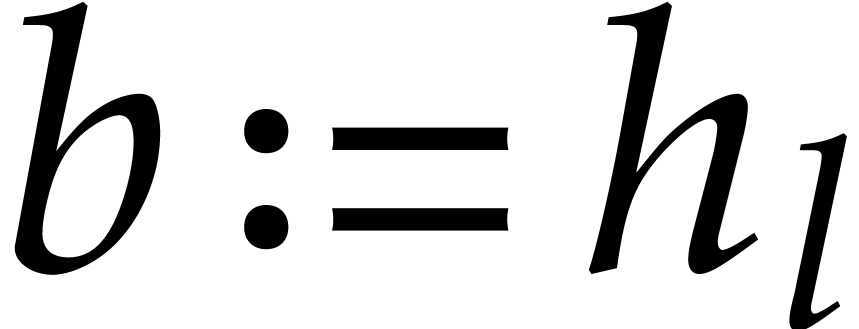 .
.
For 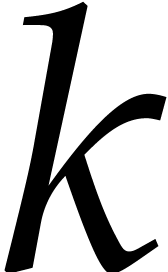 from
from  down to 0 do:
down to 0 do:
Compute 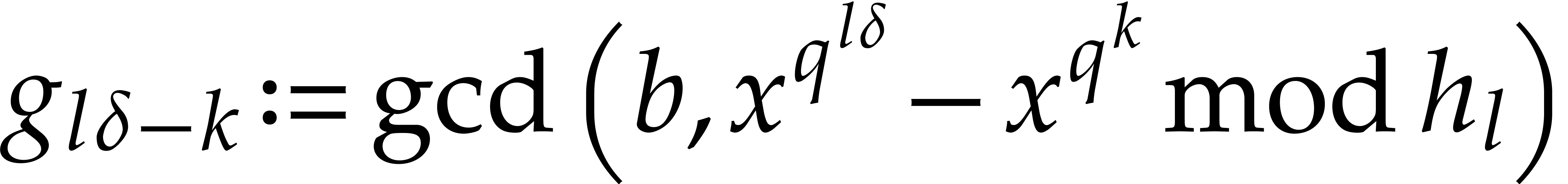 ,
,
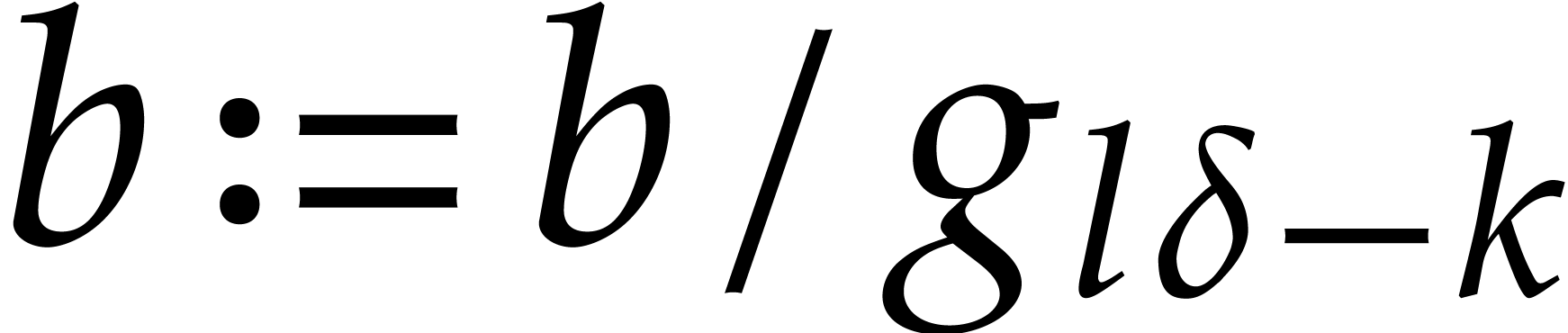 .
.
Return  .
.
Proof. First note that any positive integer 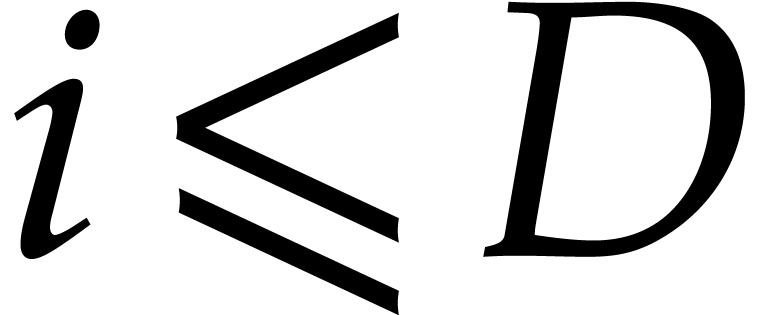 writes uniquely as
writes uniquely as 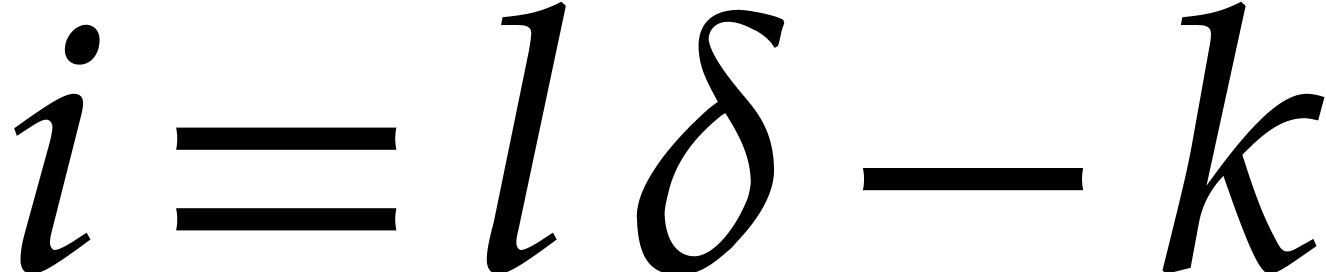 with
with 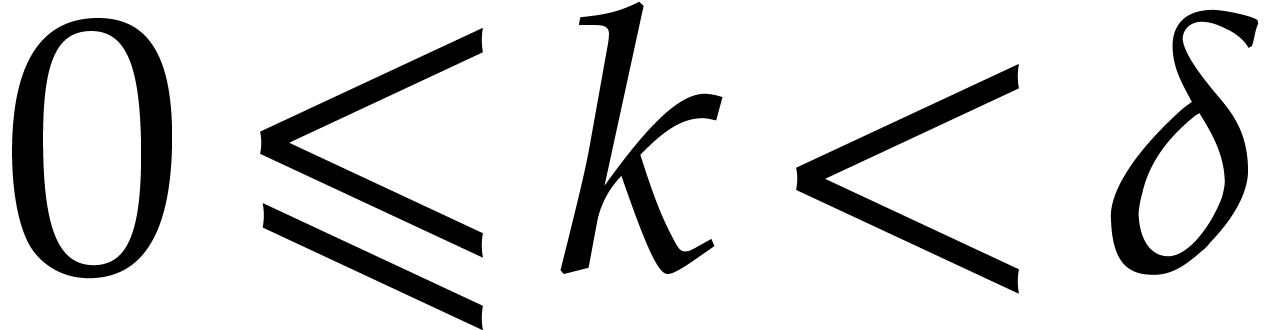 and
and 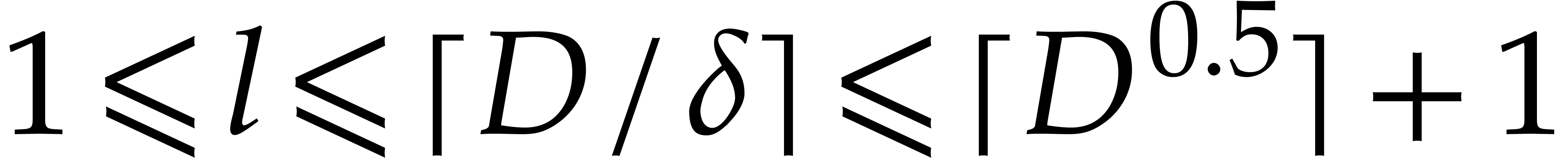 . Then
note that
. Then
note that
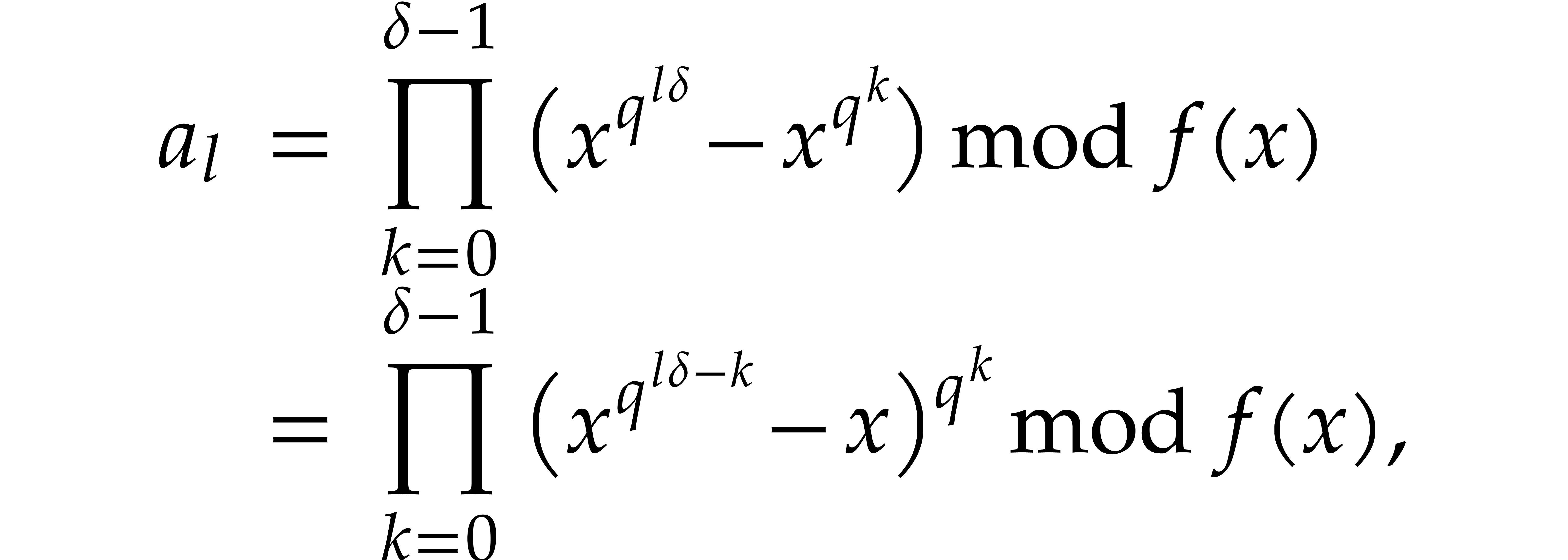
so 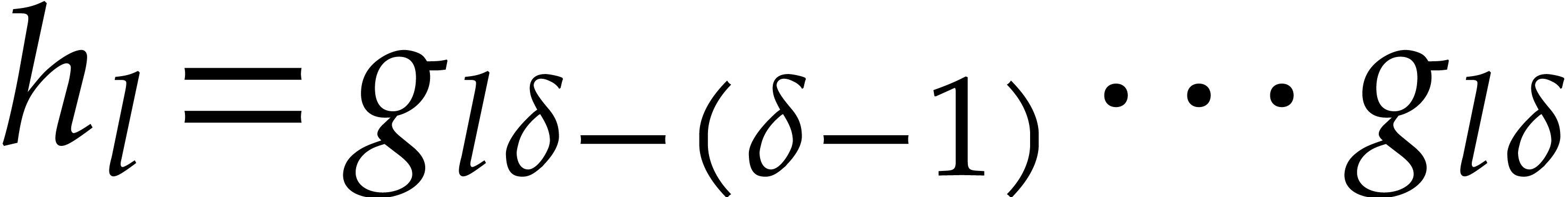 for
for 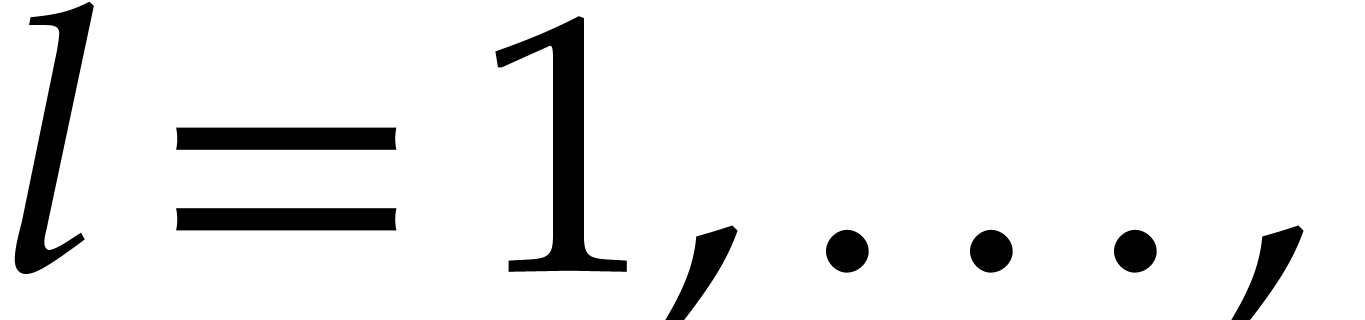
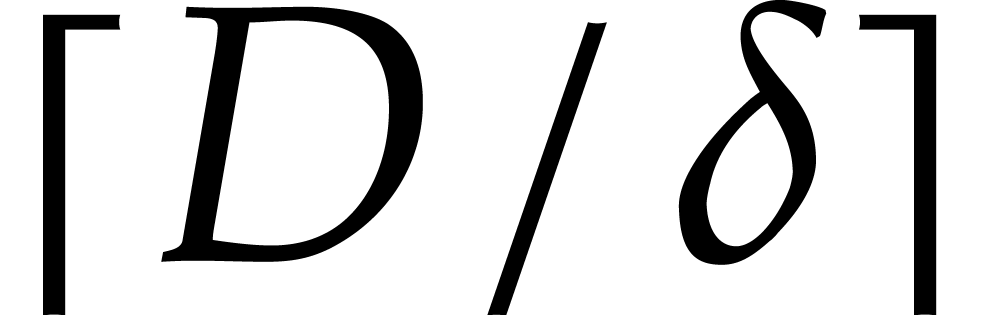 . This shows that
. This shows that  are
computed correctly.
are
computed correctly.
Lemma 2.5 allows us to perform step 2 in time
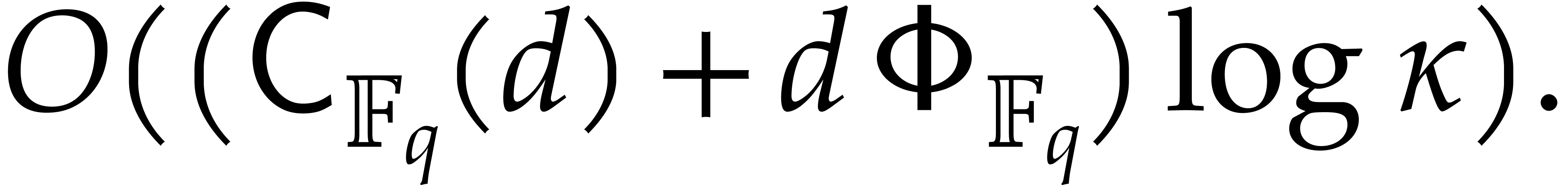
Step 3 requires  modular compositions of the form
modular compositions of the form
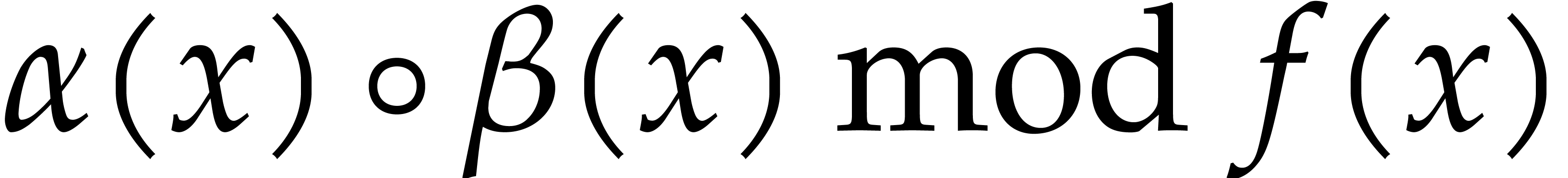 for which
for which 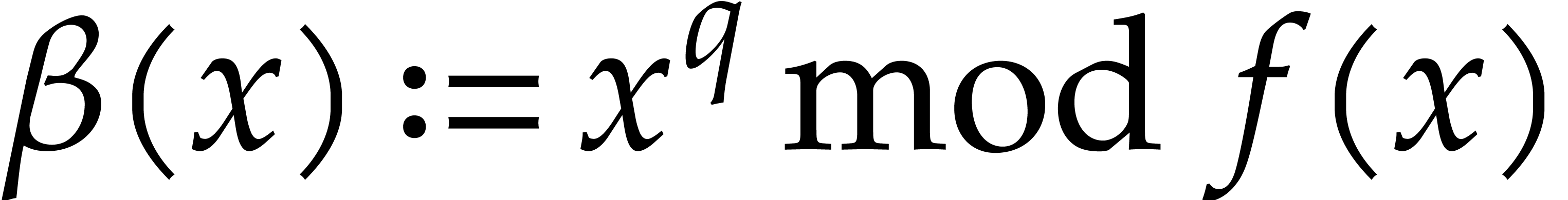 is fixed. The
same holds for step 4, this time with
is fixed. The
same holds for step 4, this time with 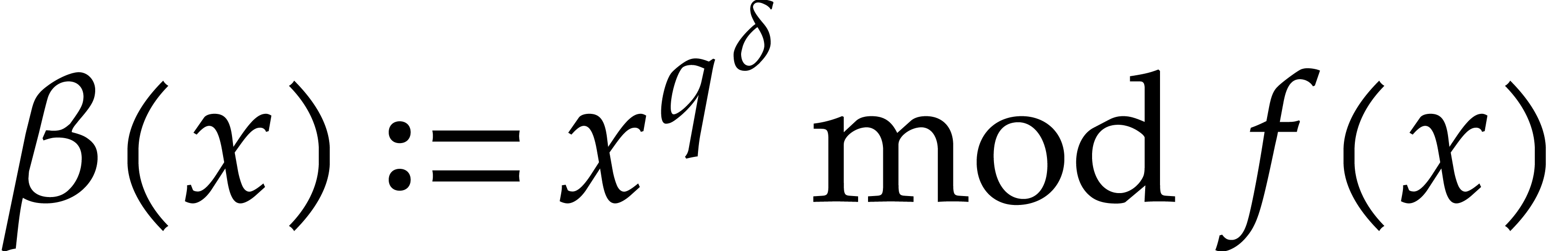 .
Consequently, steps 3 and 4 can be done in time
.
Consequently, steps 3 and 4 can be done in time
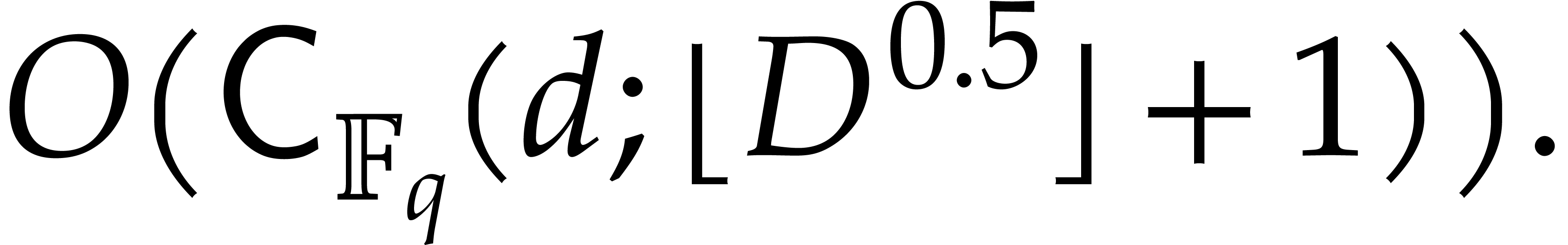
For steps 5 and 6, we use the classical “divide and conquer”
technique based on “subproduct trees”, and Kronecker
substitution for products in 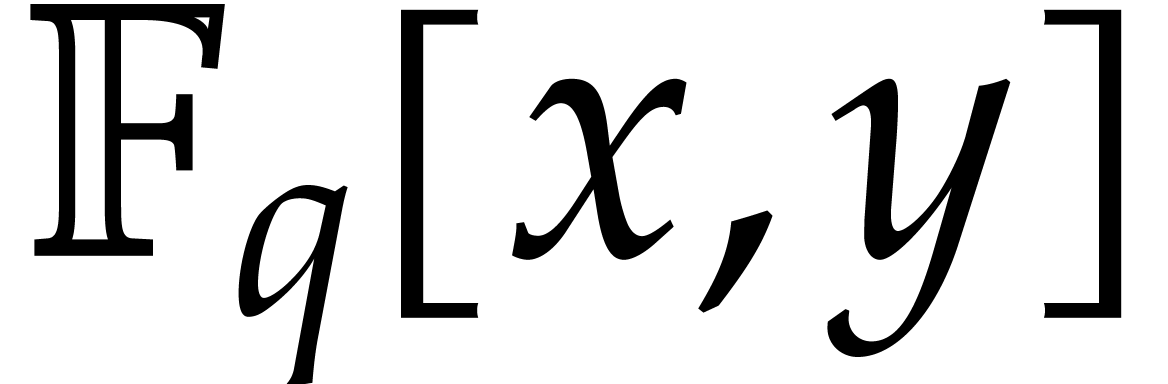 ;
see [9, chapter 10]. These steps then require
;
see [9, chapter 10]. These steps then require 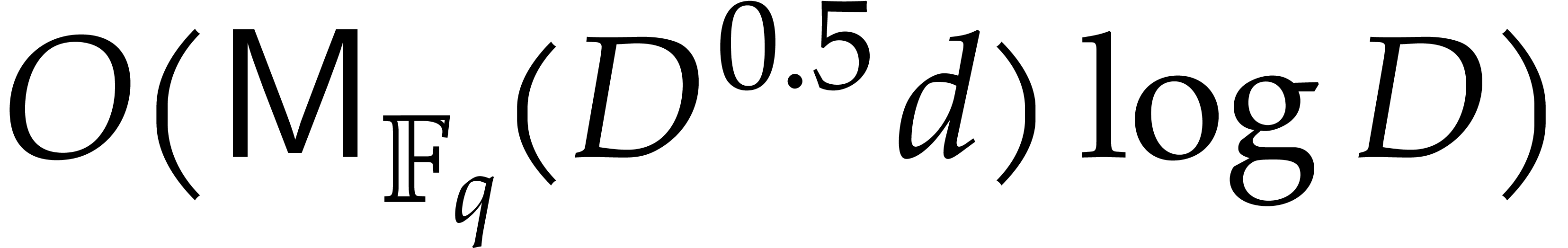 operations. Our assumption on
operations. Our assumption on 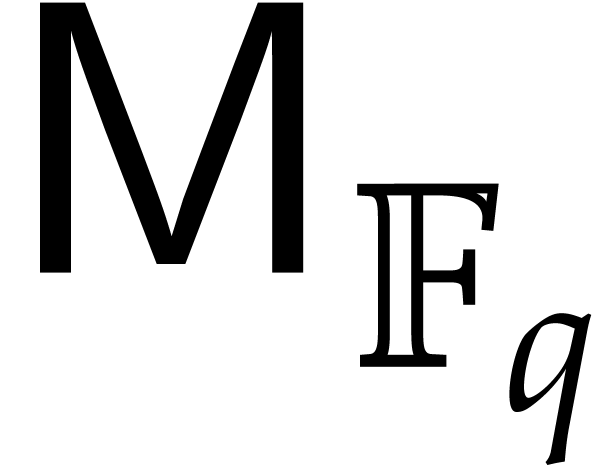 yields
yields 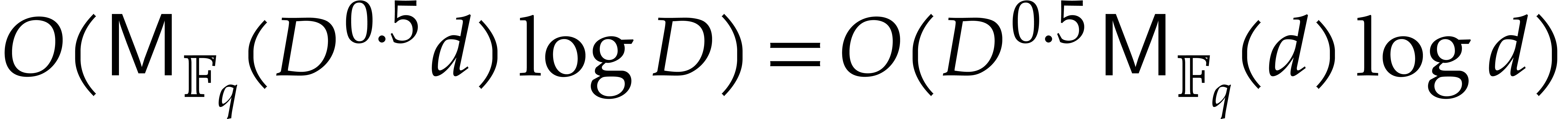 . Step 7 incurs
. Step 7 incurs
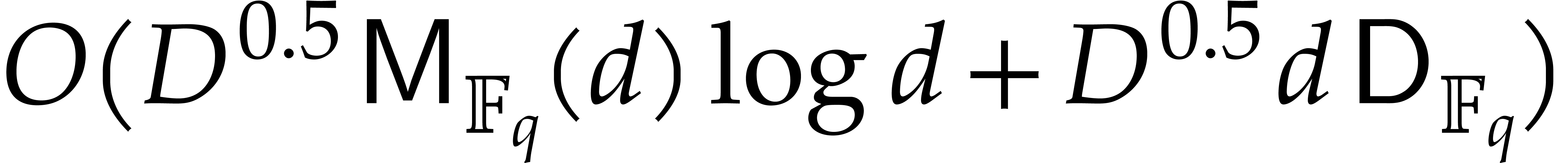
operations by means of the half-gcd algorithm.
By construction, the 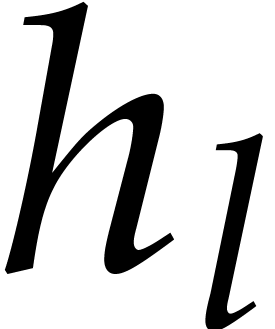 are pairwise coprime and
their product equals
are pairwise coprime and
their product equals 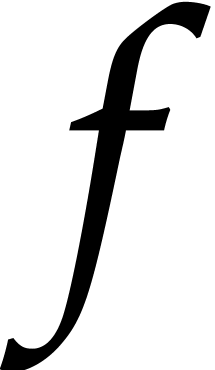 . Steps
8 and 9 take
. Steps
8 and 9 take 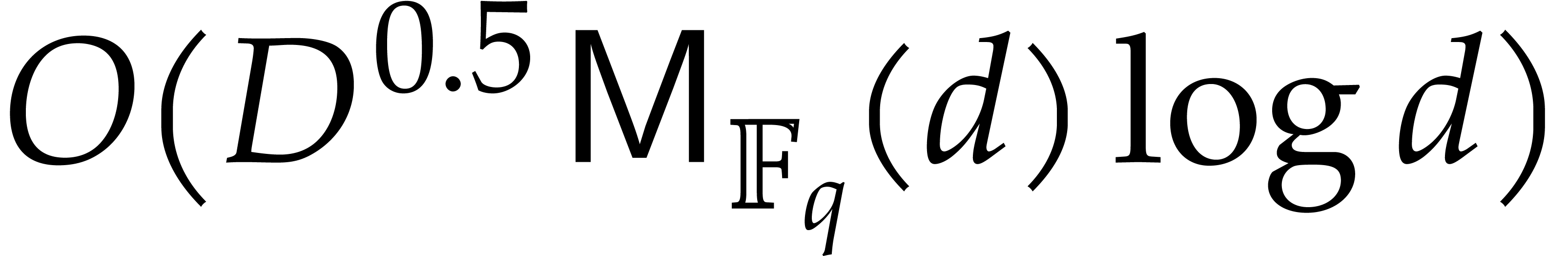 operations, by applying the fast
multi-remainder algorithm [9, chapter 10] to the results of
steps 3 and 4. Finally, the cost of step 10 is bounded by
operations, by applying the fast
multi-remainder algorithm [9, chapter 10] to the results of
steps 3 and 4. Finally, the cost of step 10 is bounded by

We now turn to the factorization of a polynomial  having all its factors of the same known degree
having all its factors of the same known degree  . This stage involves randomization of Las Vegas
type: the algorithm always returns a correct answer, but the running
time is a random variable.
. This stage involves randomization of Las Vegas
type: the algorithm always returns a correct answer, but the running
time is a random variable.
Algorithm
If 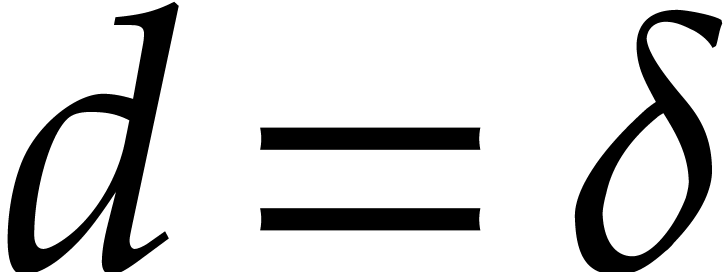 then return
then return 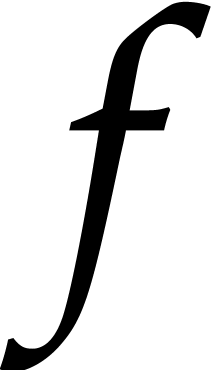 . Otherwise set
. Otherwise set 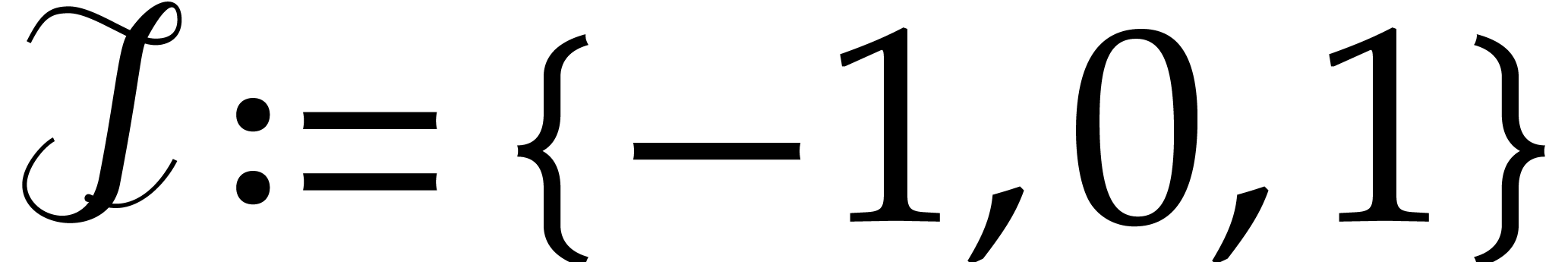 if
if
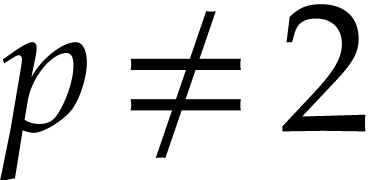 , or
, or 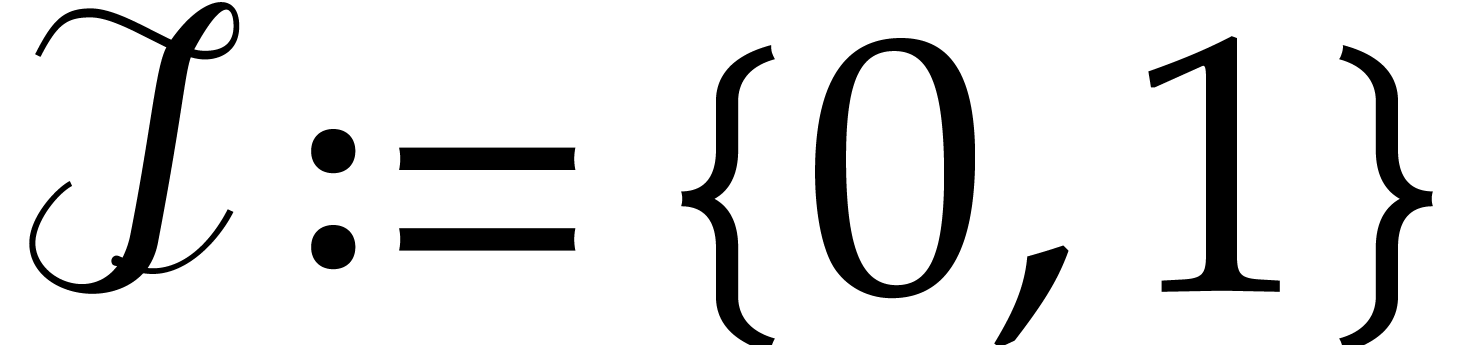 if
if 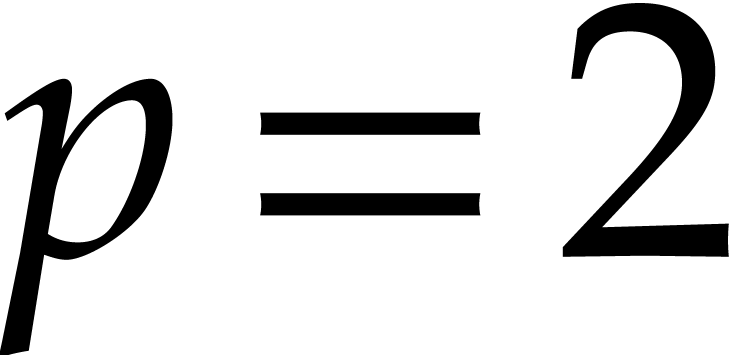 .
.
Take  at random in
at random in 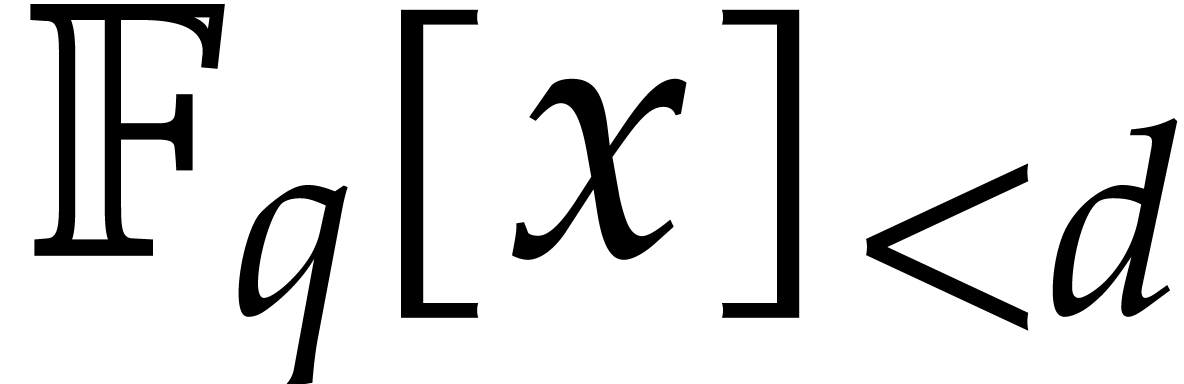 .
.
Compute 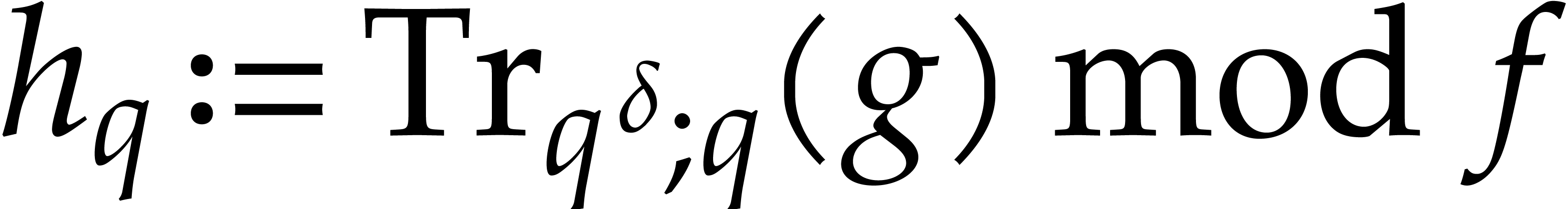 by Algorithm 3.1.
by Algorithm 3.1.
Compute 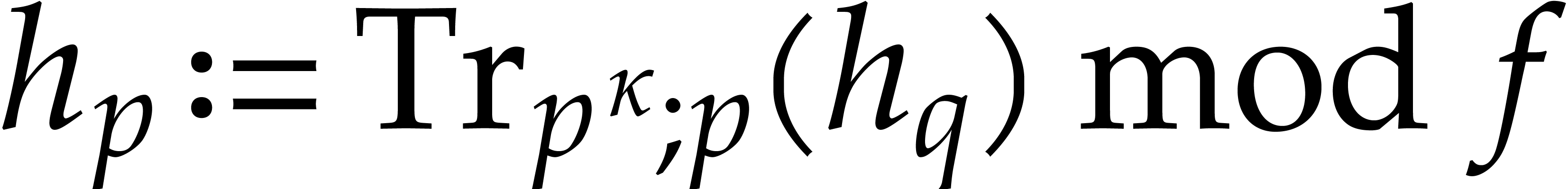 by Algorithm 3.2.
by Algorithm 3.2.
If 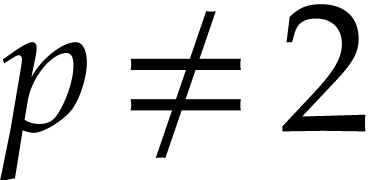 , then compute
, then compute
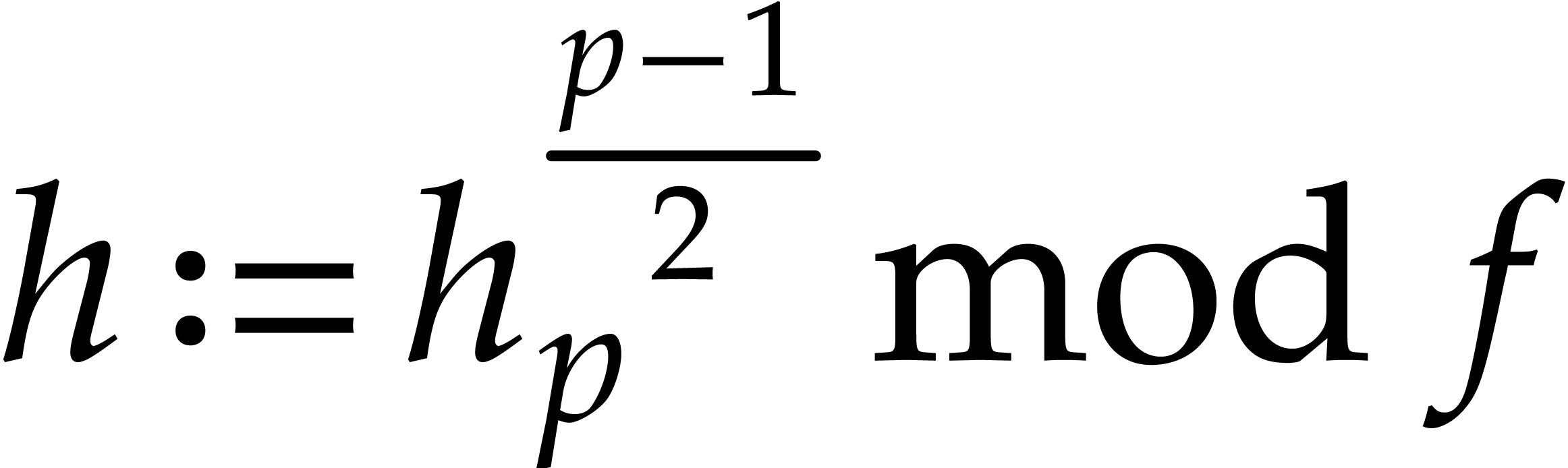 . Otherwise, set
. Otherwise, set
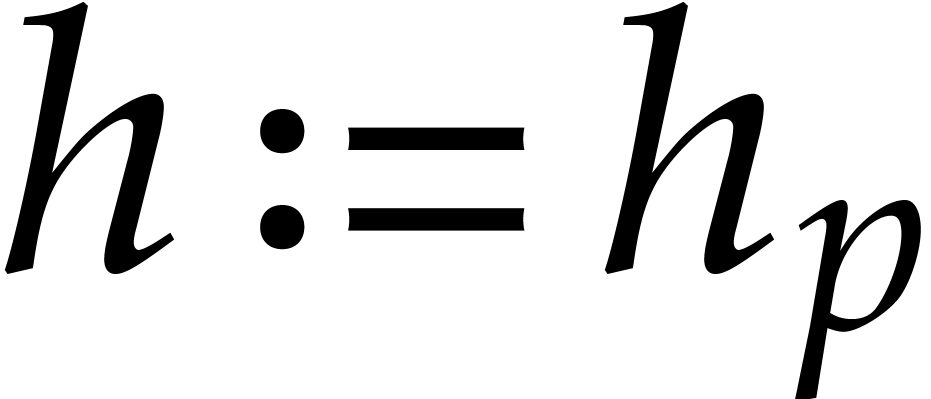 .
.
Compute 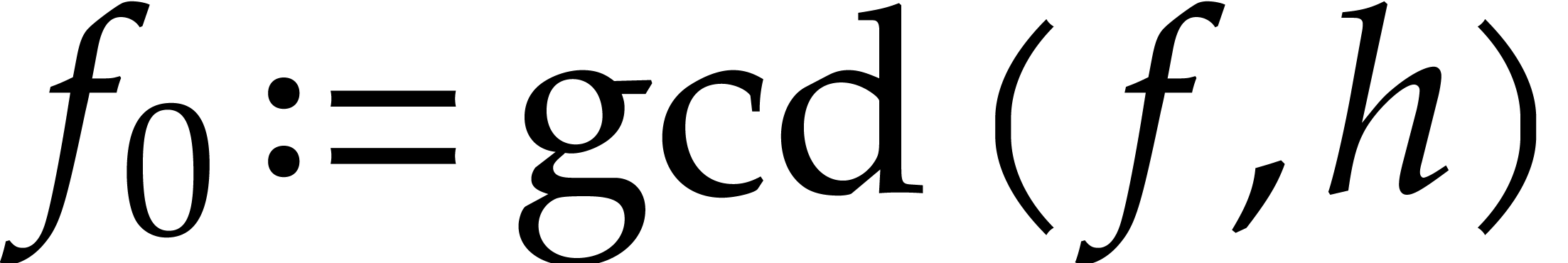 ,
, 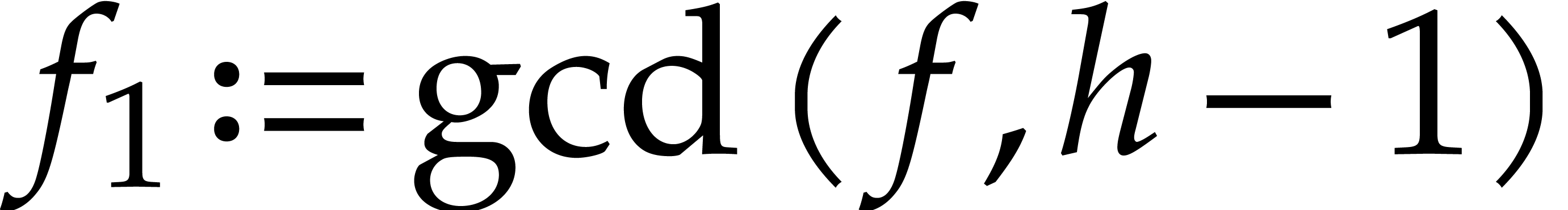 , and
, and 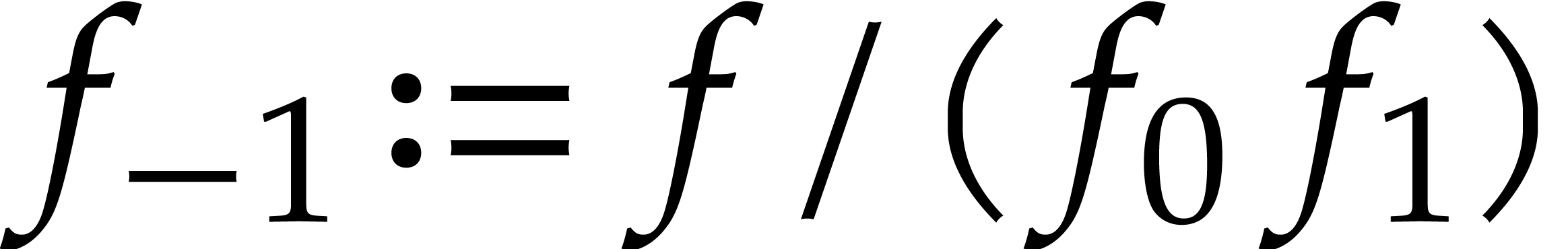 if
if 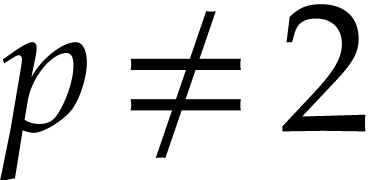 .
.
Compute 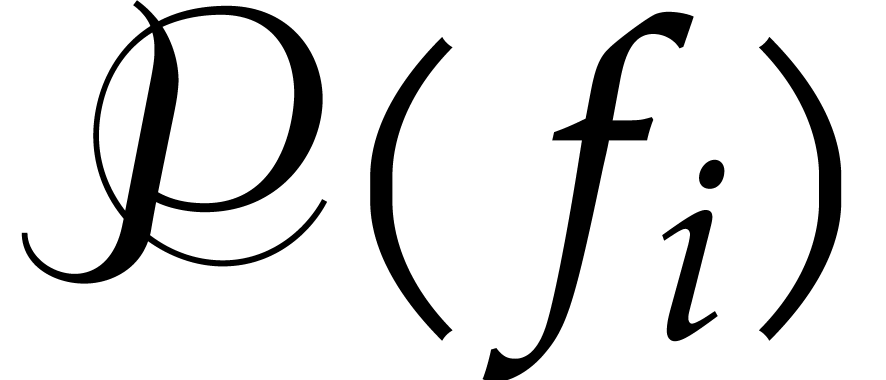 as
as 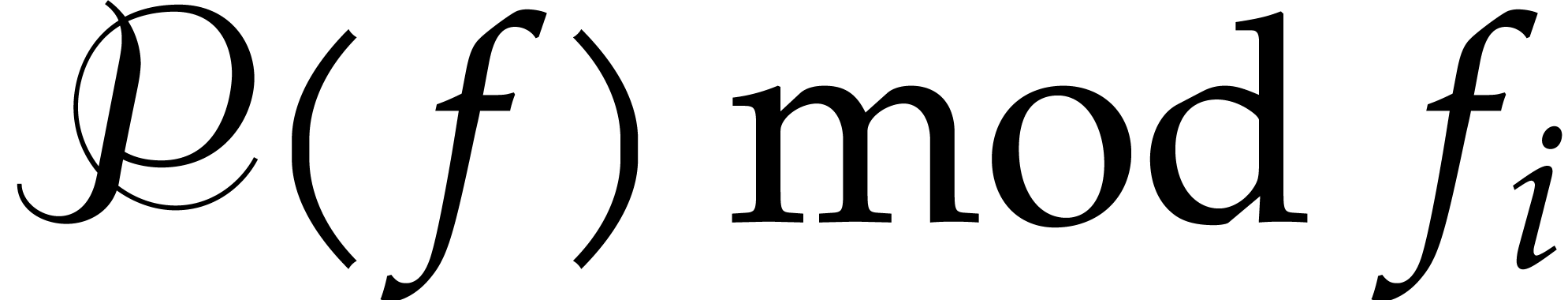 ,
,
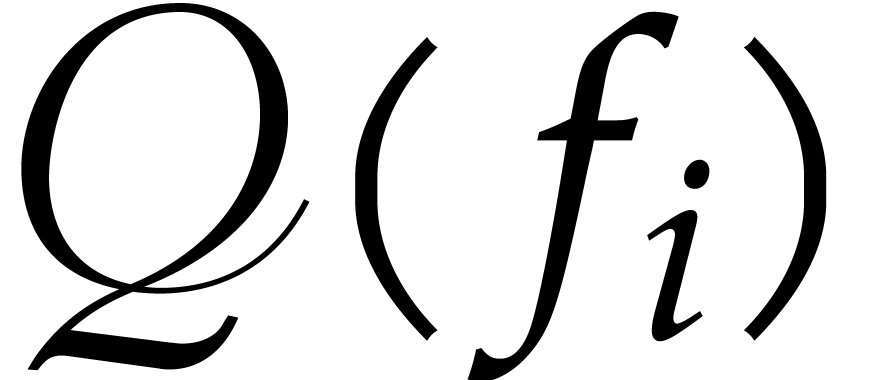 as the
as the  first
entries of
first
entries of 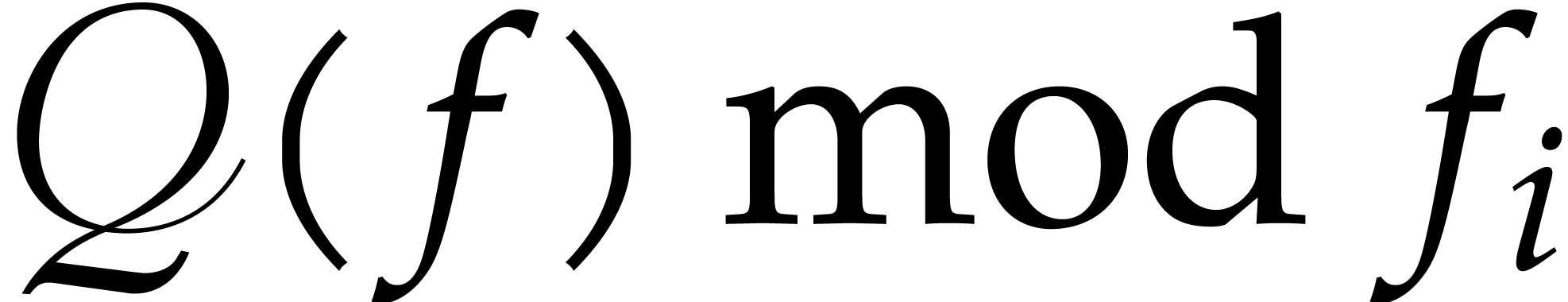 , for
, for
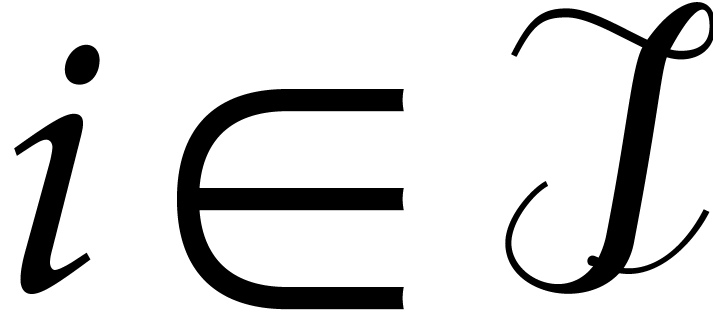 .
.
For 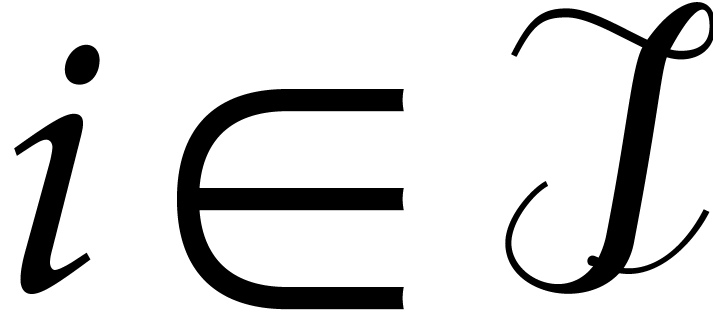 call recursively the algorithm with
input
call recursively the algorithm with
input 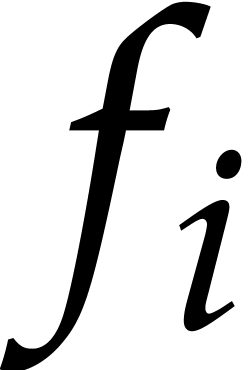 ,
, 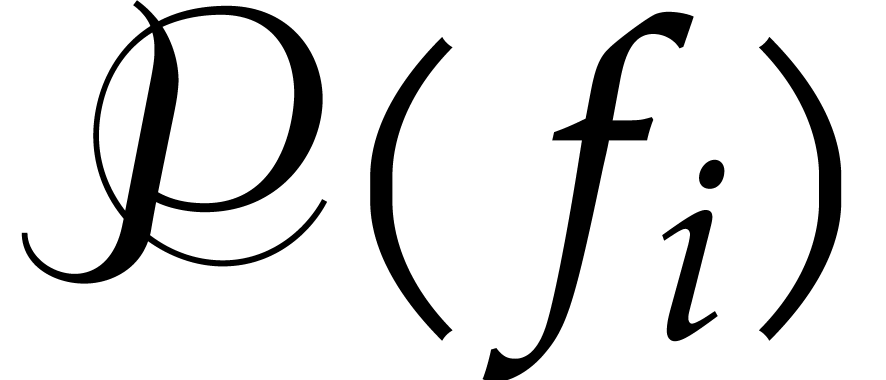 and
and 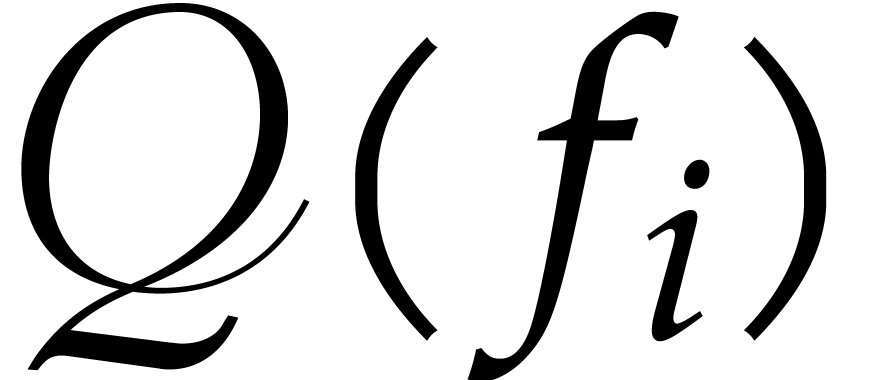 .
.
Return the union of the irreducible factors of  for
for 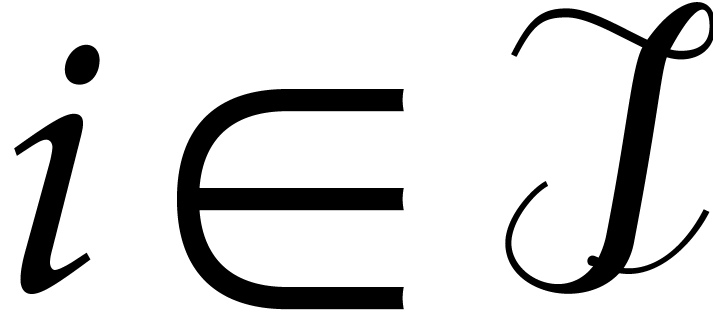 .
.
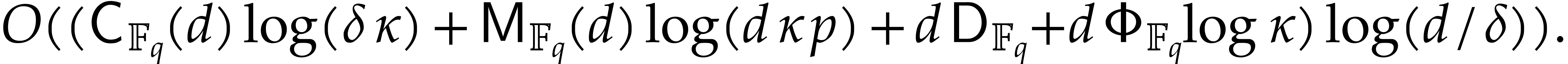 |
(4.1) |
Proof. The proof is well known. For
completeness, we repeat the main arguments. Let  with
with  be the irreducible factors of
be the irreducible factors of  . The Chinese remainder theorem yields an
isomorphism
. The Chinese remainder theorem yields an
isomorphism
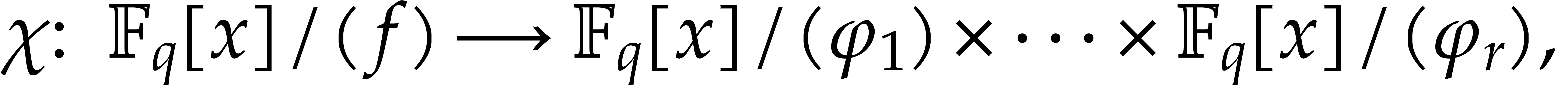
where each 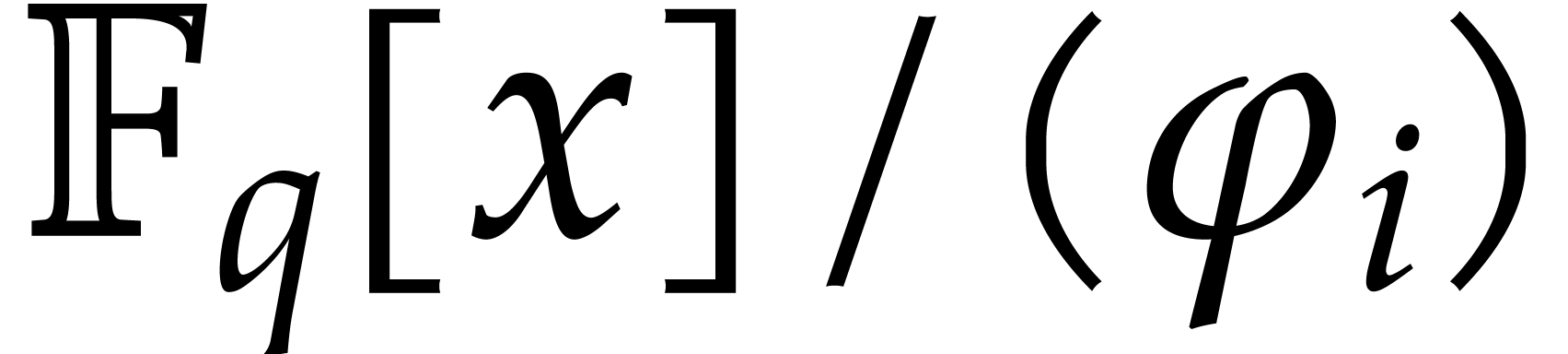 is isomorphic to
is isomorphic to  . For any
. For any  in
in 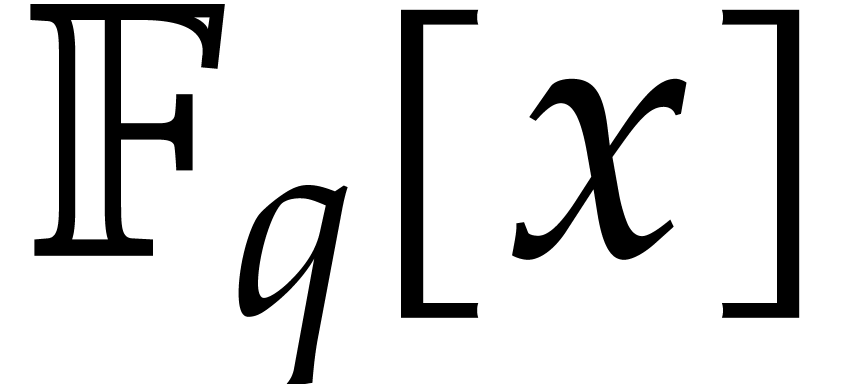 , let
, let

Now
and
where each 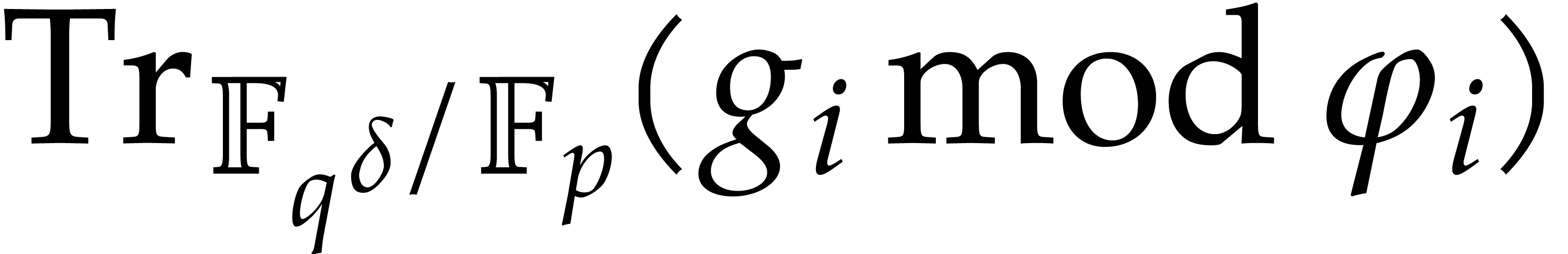 belongs to
belongs to  regarded as the prime subfield of
regarded as the prime subfield of 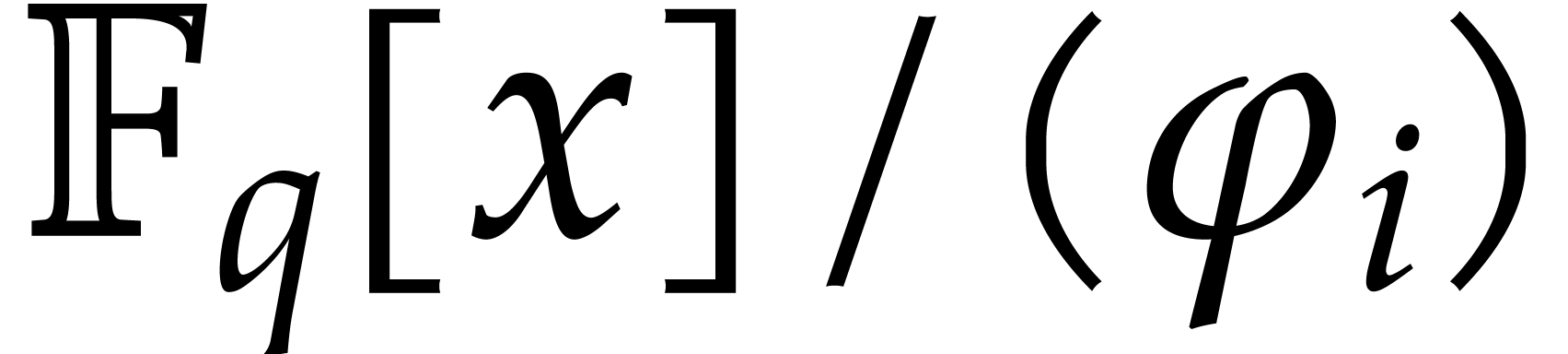 .
Hence
.
Hence  is a vector
is a vector  in
in
 , and
, and  is the product of the
is the product of the  with
with  , for
, for  .
.
Let 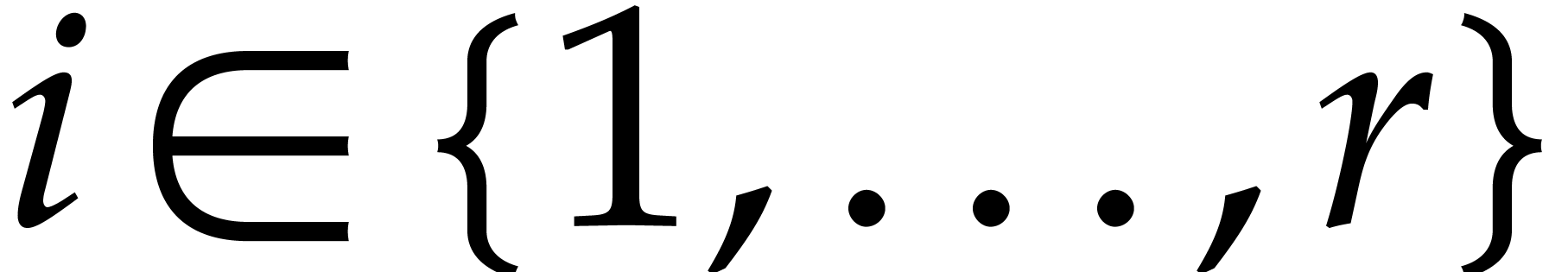 be a fixed index. If
be a fixed index. If 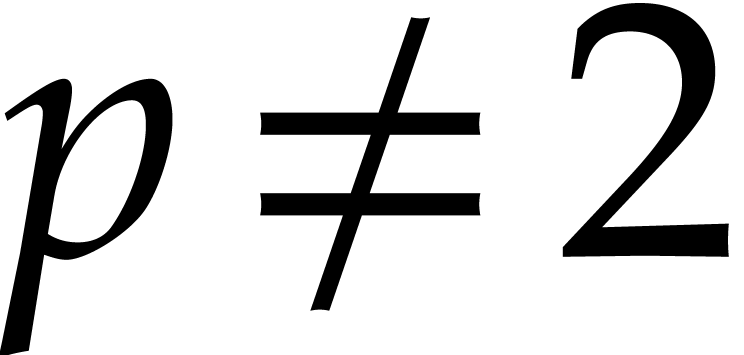 , then the probability that
, then the probability that 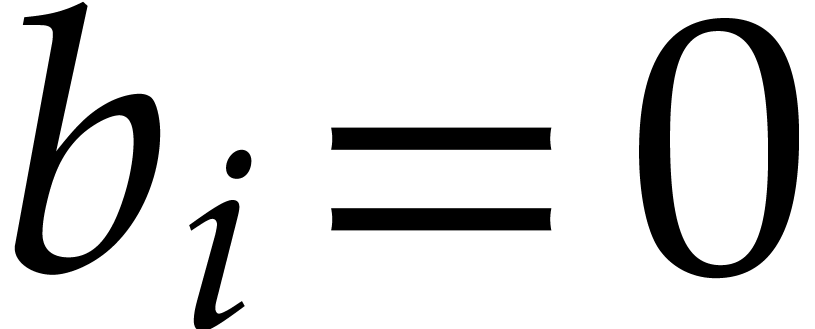 is
is 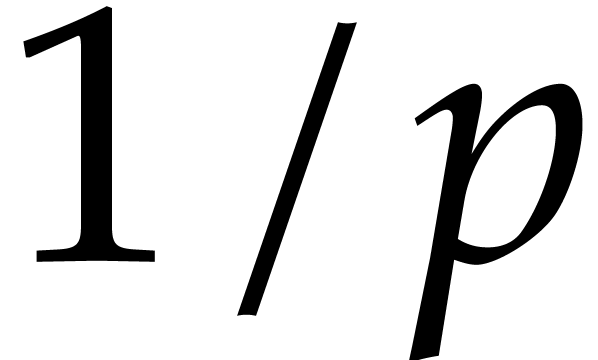 , the probability that
, the probability that
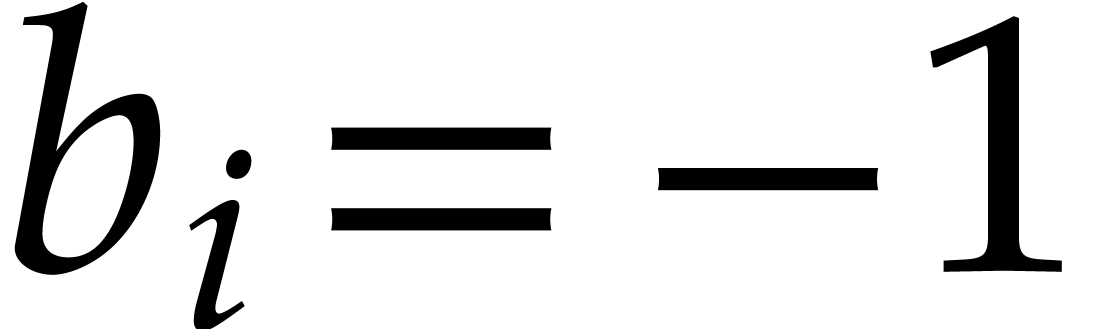 is
is 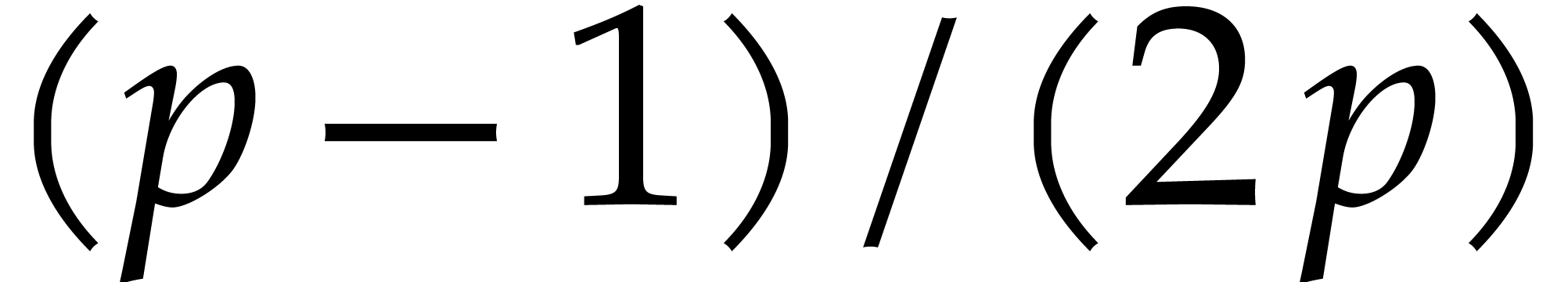 ,
and the probability that
,
and the probability that 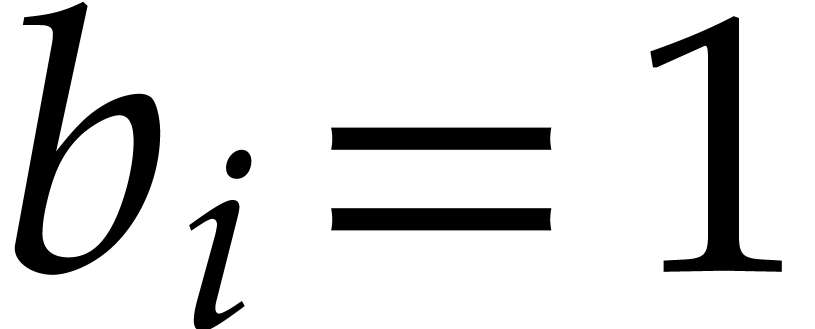 is
is 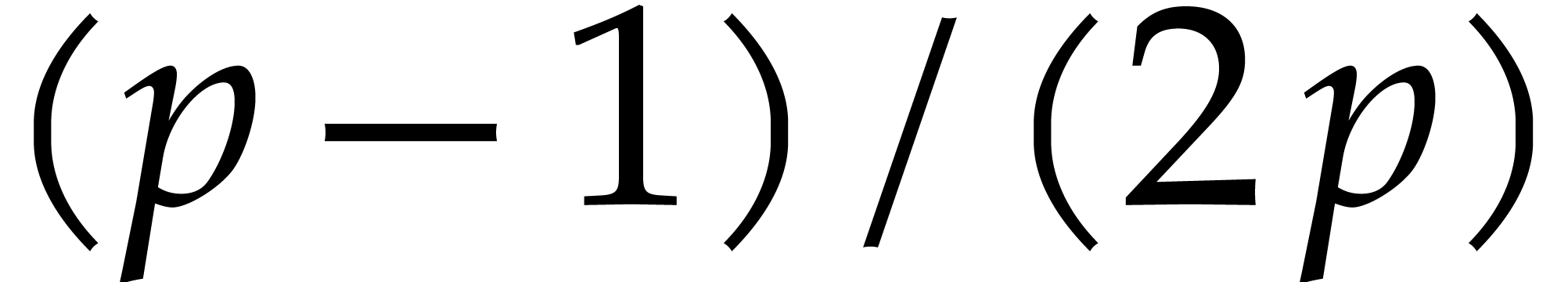 . If
. If 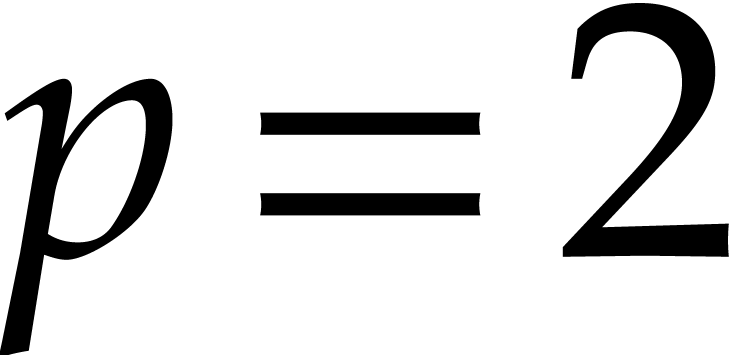 ,
then the probability that
,
then the probability that 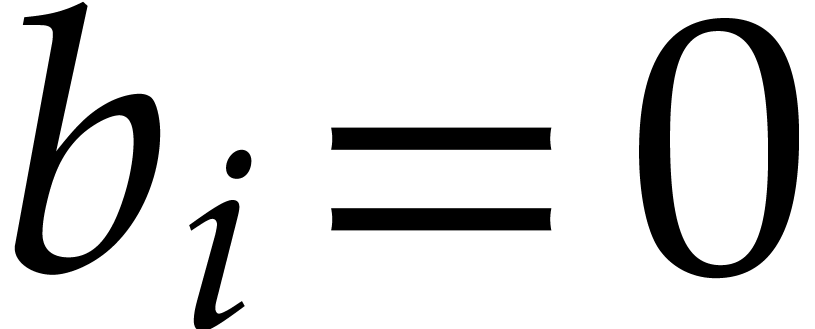 is
is 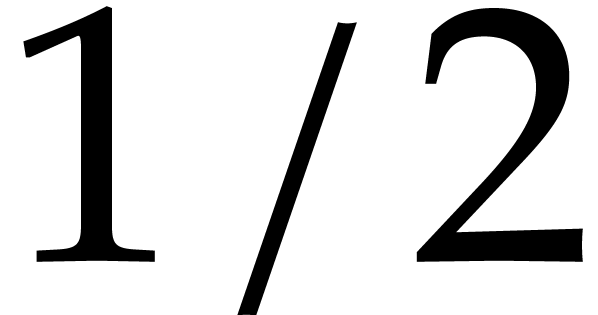 , the probability that
, the probability that 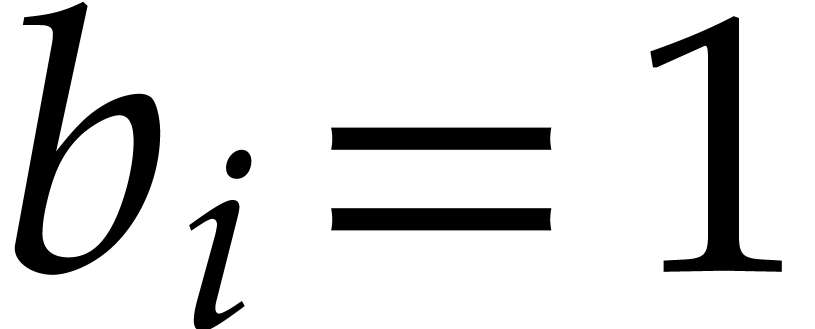 is
is 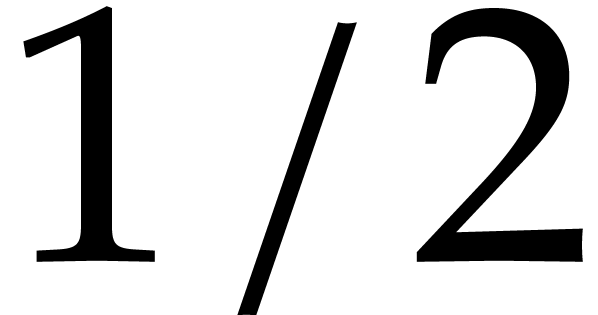 .
.
We now apply [11, Lemma 4.1(i)] with 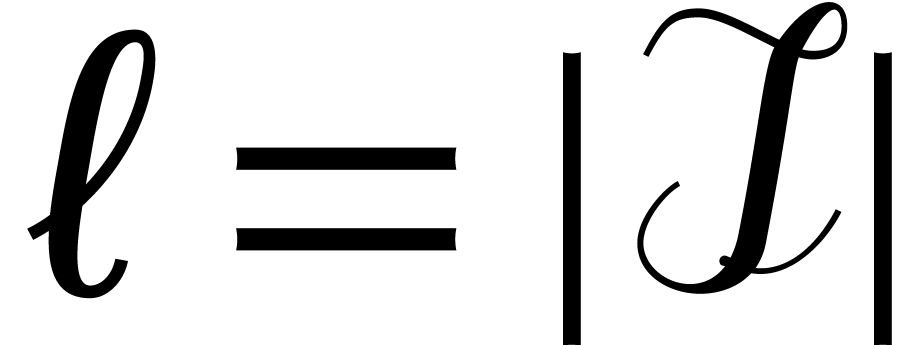 and
and 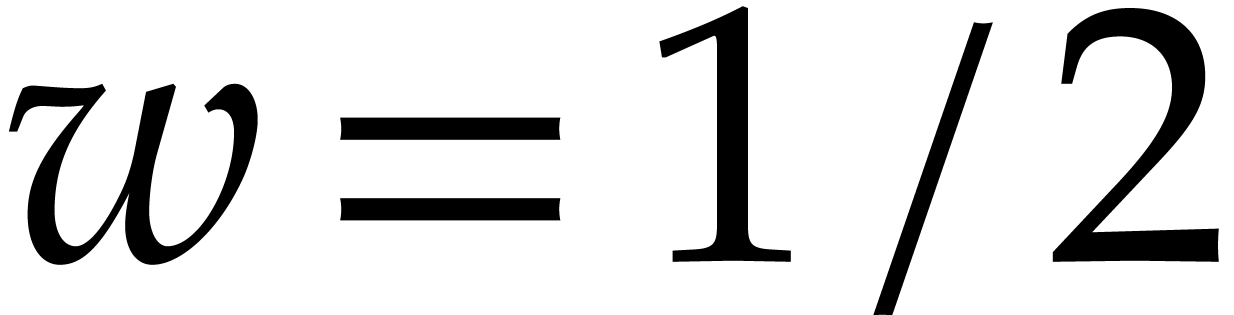 . This lemma concerns the
probability analysis of a game of balls and bins where the bins are
. This lemma concerns the
probability analysis of a game of balls and bins where the bins are  for
for 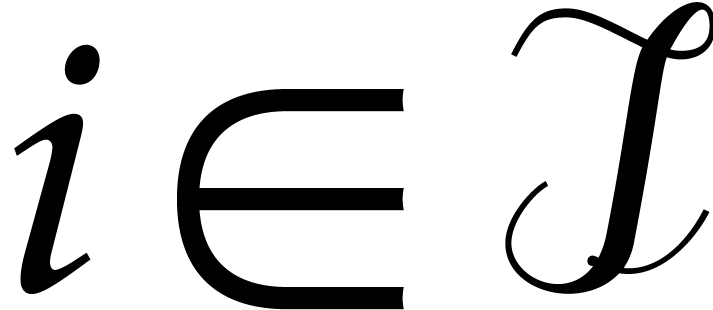 and the balls are the
irreducible factors
and the balls are the
irreducible factors  of
of  . The lemma implies that the expected depth of the
recursive calls is
. The lemma implies that the expected depth of the
recursive calls is 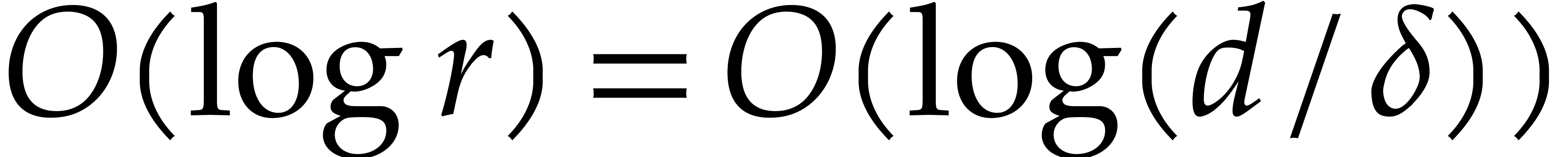 . Other
proofs may be found in [9, chapter 14, Exercise 14.16], [35, chapter 20, section 4], or [11, sections 3
and 4].
. Other
proofs may be found in [9, chapter 14, Exercise 14.16], [35, chapter 20, section 4], or [11, sections 3
and 4].
Step 3 takes 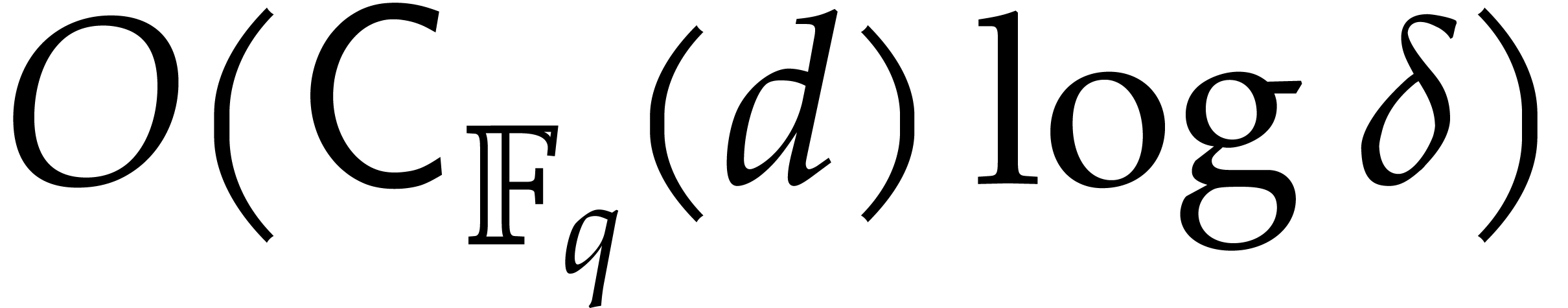 operations, by Lemma 3.1.
Step 4 takes
operations, by Lemma 3.1.
Step 4 takes 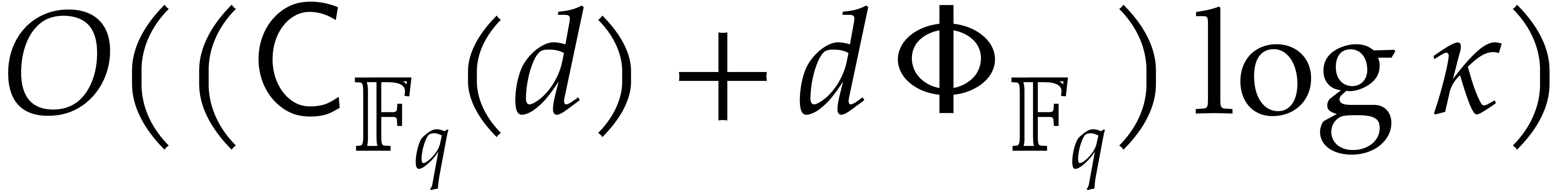 operations, by Lemma 3.2.
Step 5 requires
operations, by Lemma 3.2.
Step 5 requires 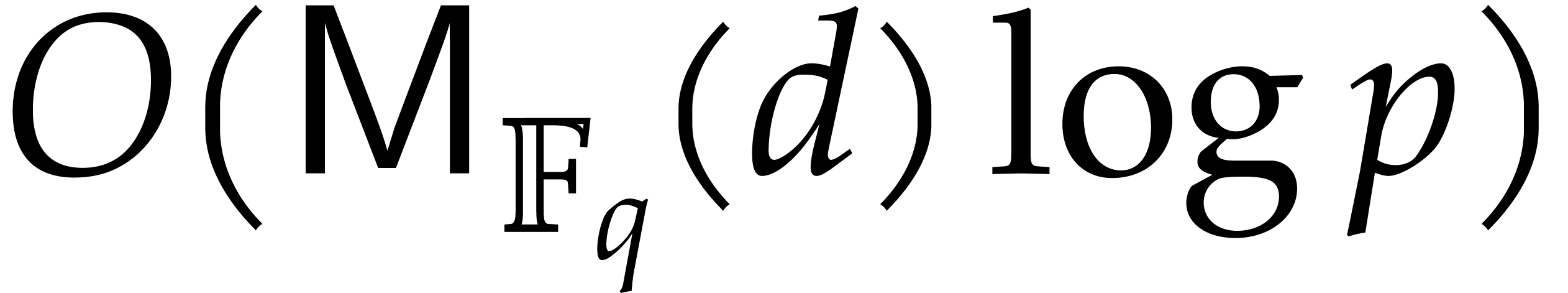 further operations. The rest
takes
further operations. The rest
takes 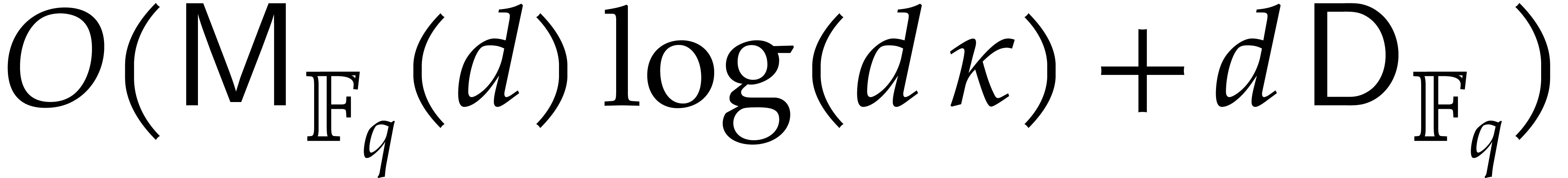 operations.
operations.
Cantor and Zassenhaus' original algorithm [5] uses the map
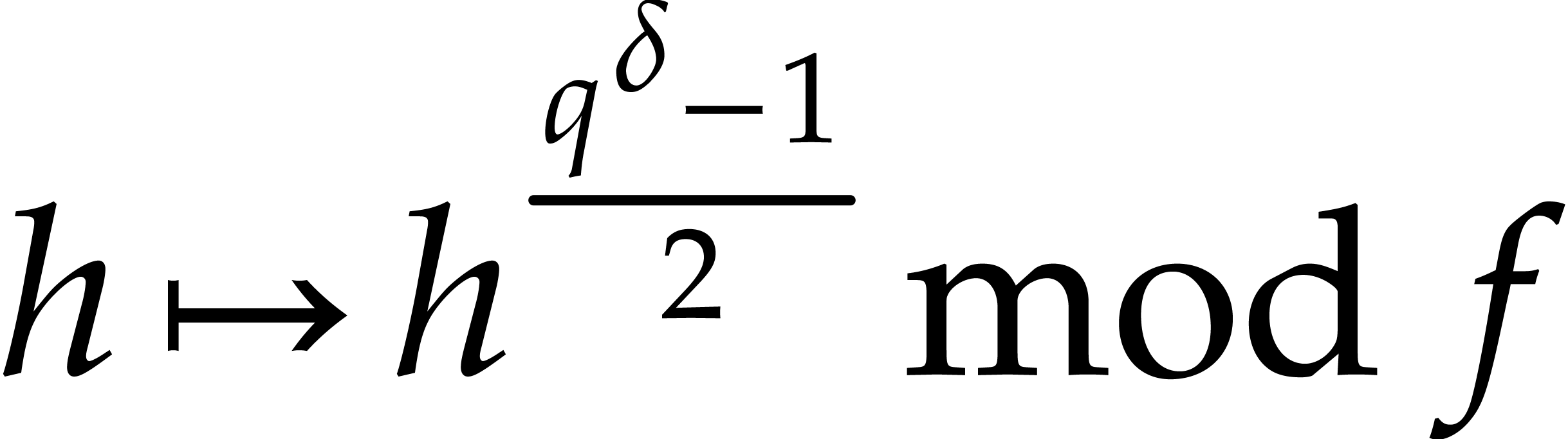 instead of pseudo-traces whenever
instead of pseudo-traces whenever 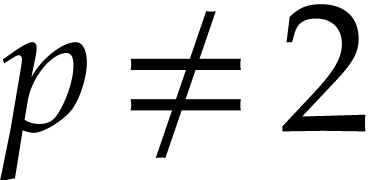 . For
. For 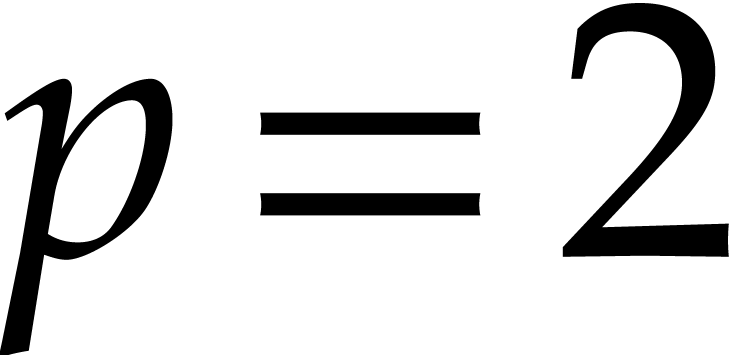 it uses a
slightly different map combined with an occasional quadratic extension
of
it uses a
slightly different map combined with an occasional quadratic extension
of  . The use of pseudo-traces
appeared in early works by McEliece [9, notes of chapter
14]. The modern presentation is due to [11]. Our
presentation has the advantage to distinguish the pseudo-traces over
. The use of pseudo-traces
appeared in early works by McEliece [9, notes of chapter
14]. The modern presentation is due to [11]. Our
presentation has the advantage to distinguish the pseudo-traces over
 from those over
from those over  ,
and to avoid recomputing
,
and to avoid recomputing 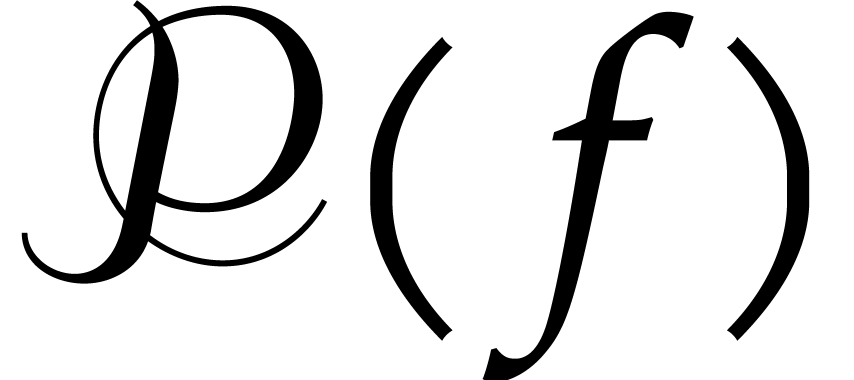 and
and 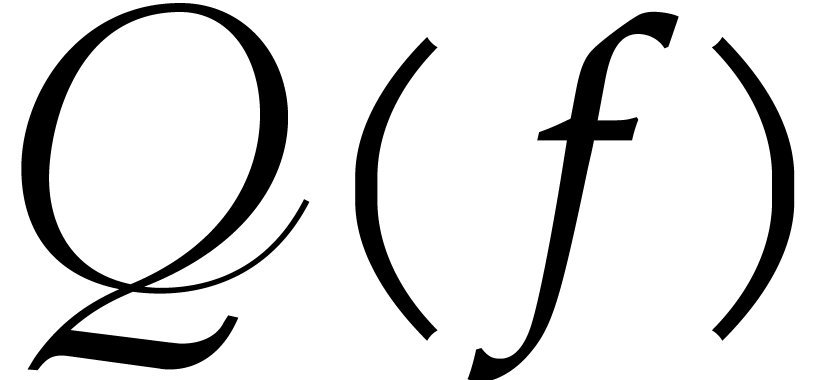 during recursive calls.
during recursive calls.
Remark 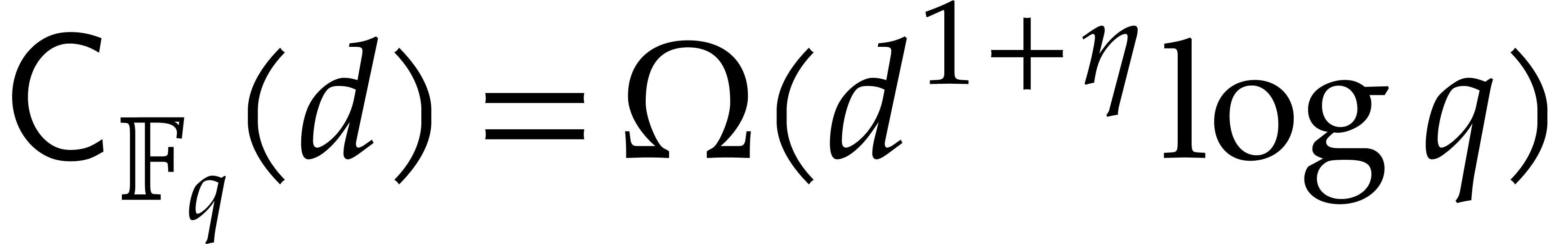 for some
for some  , then
, then
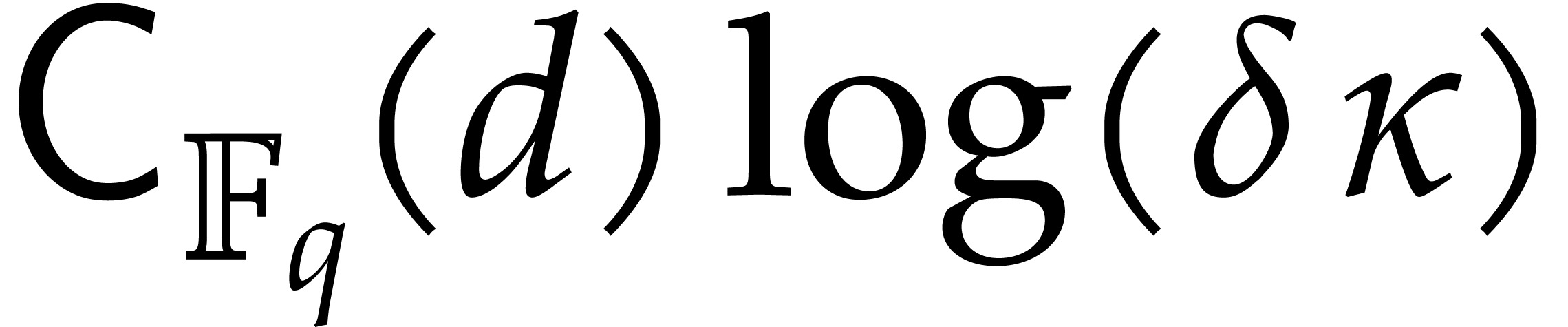 does not need to be multiplied by
does not need to be multiplied by 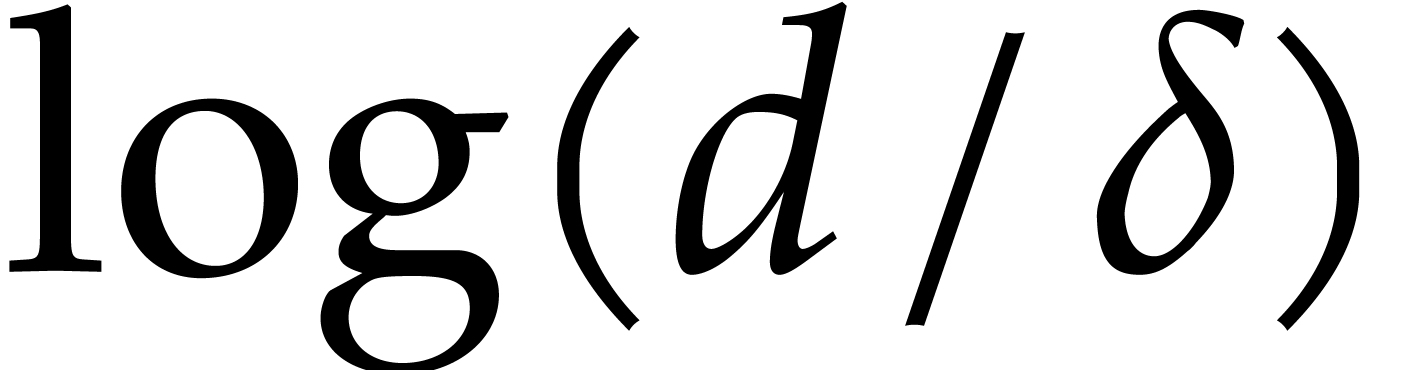 in
in
We are now ready to summarize the main complexity bounds for an abstract
field  , in terms of the cost
functions from section 1.1.
, in terms of the cost
functions from section 1.1.
 of a polynomial of degree
of a polynomial of degree  in
in
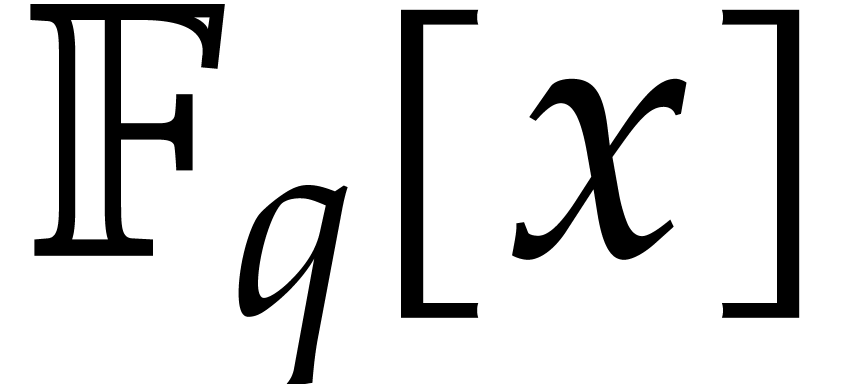 can be done in expected time
can be done in expected time
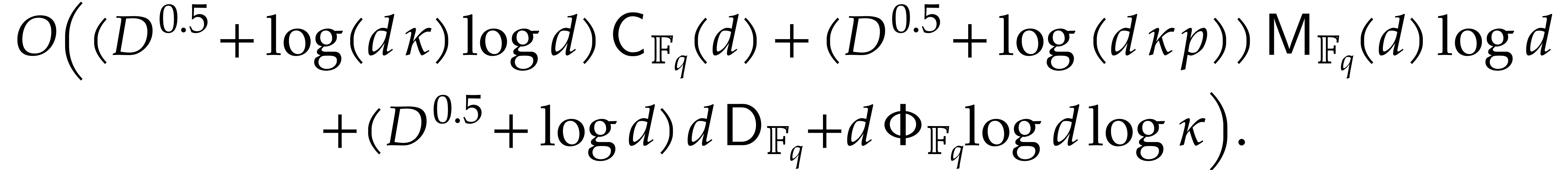
Proof. This bound follows by combining Lemmas 2.6 and 2.8, Propositions 4.1, 4.2, and 4.3.
Following [9, Corollary 14.35] from [33,
section 6], a polynomial  of degree
of degree 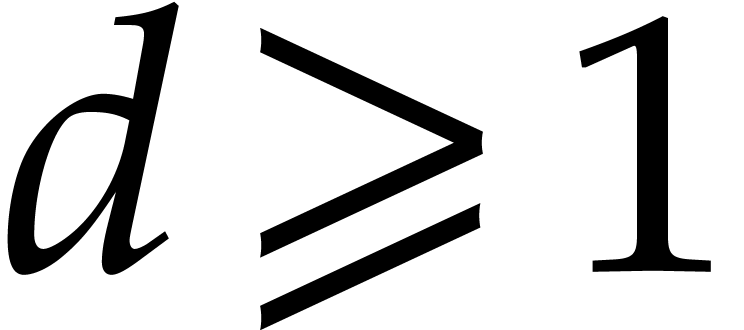 is irreducible if, and only if,
is irreducible if, and only if, 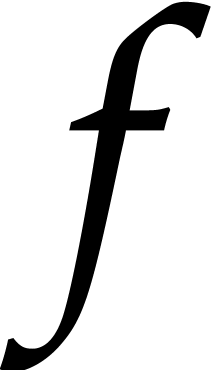 divides
divides 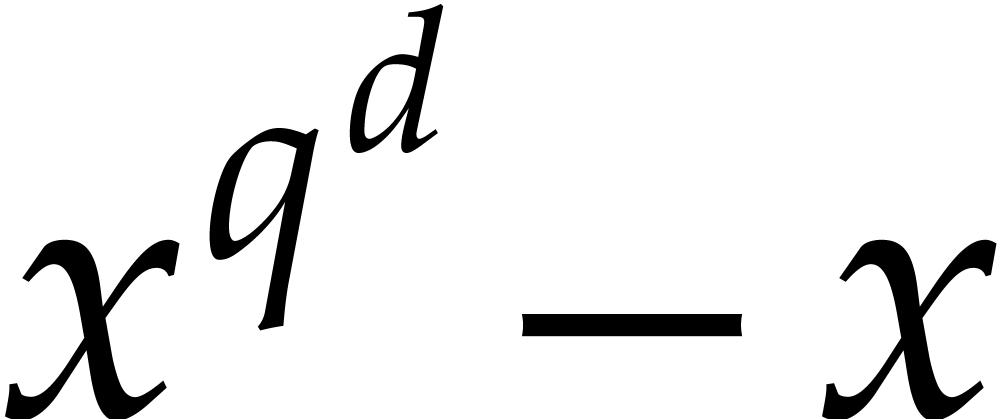 and
and 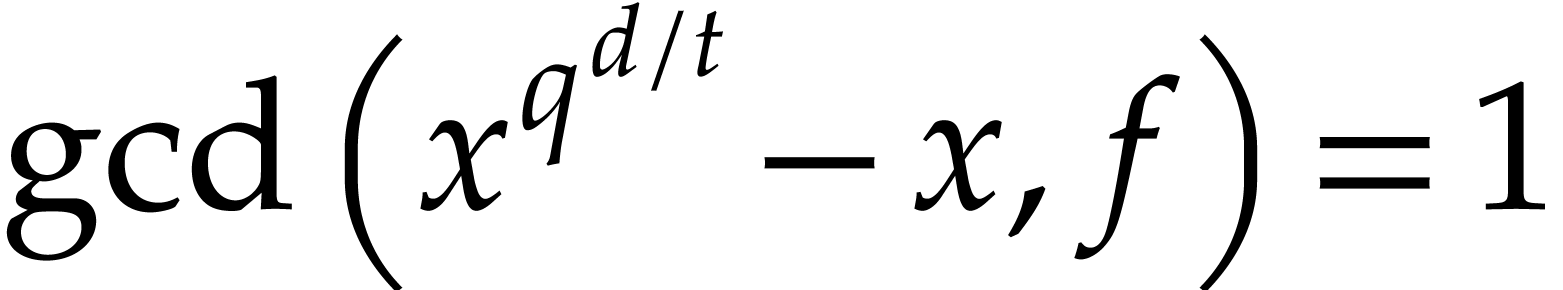 for all
prime divisors
for all
prime divisors 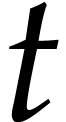 of
of  .
This technique was previously used in [32] over prime
fields.
.
This technique was previously used in [32] over prime
fields.
Proof. Computing the prime factorization 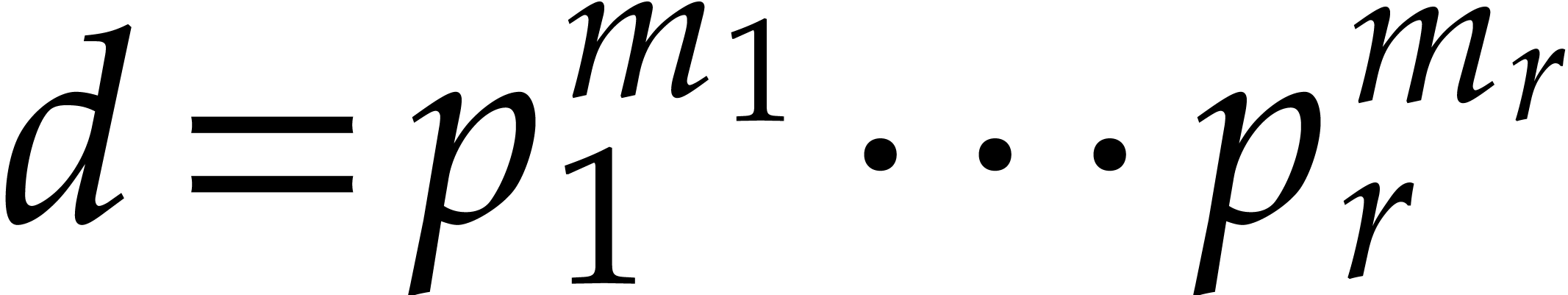 takes negligible time
takes negligible time  .
On the other hand, we can compute
.
On the other hand, we can compute 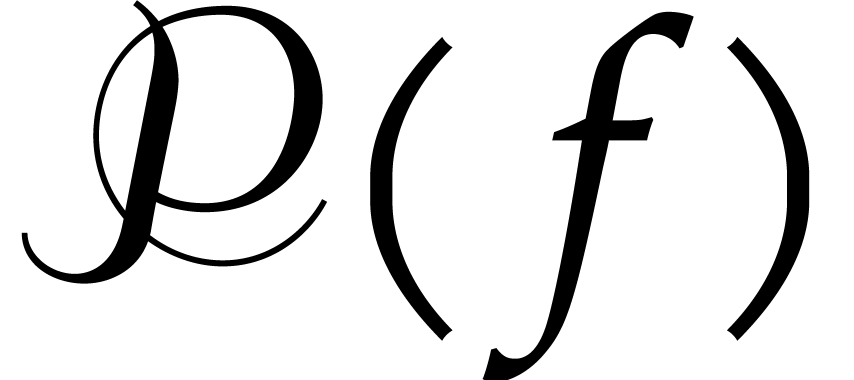 in time
in time
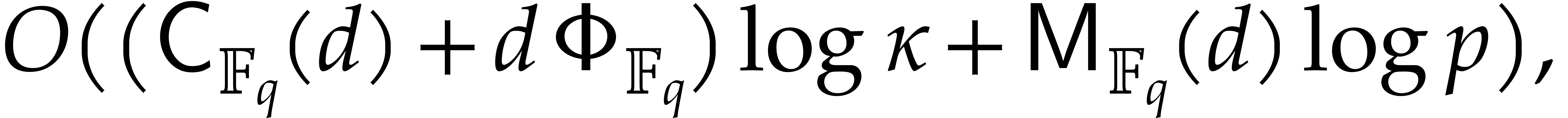
by Lemma 2.6. Then  can be obtained
in time
can be obtained
in time
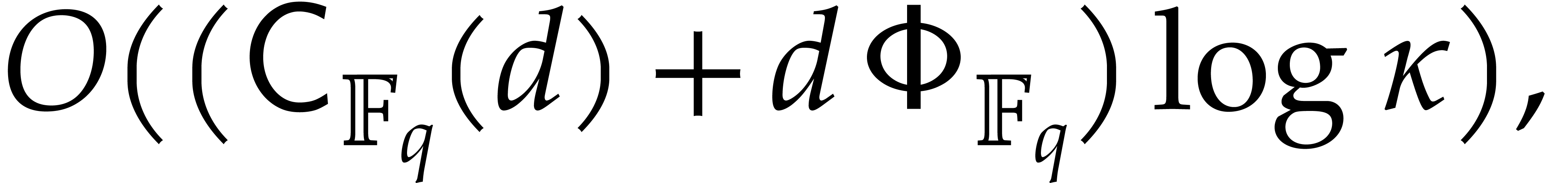
by Lemma 2.5.
The “divide and conquer” strategy of [33, Lemma
6.1] allows us to compute 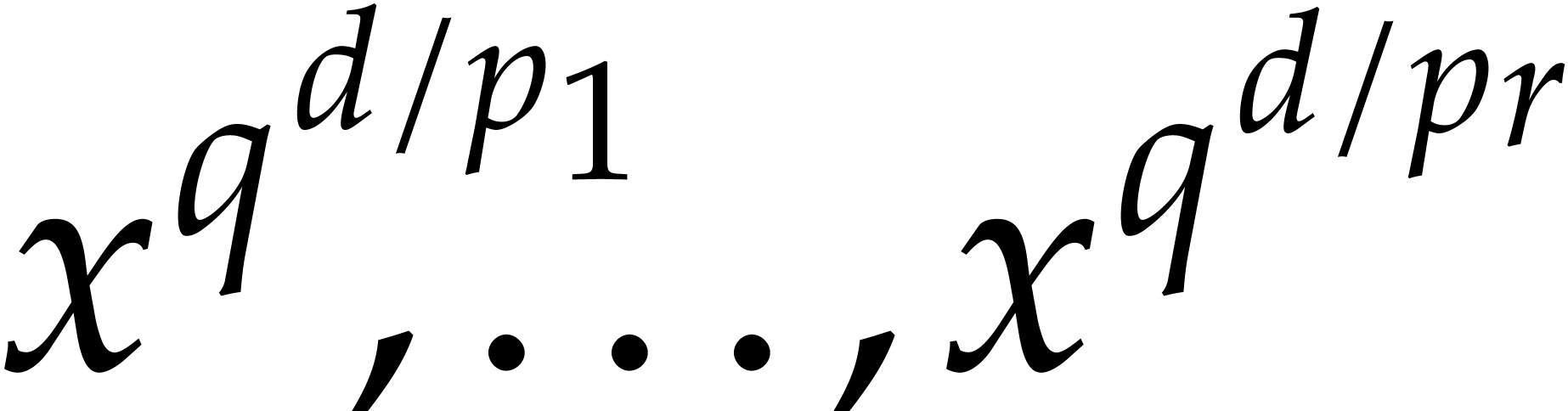 in time
in time 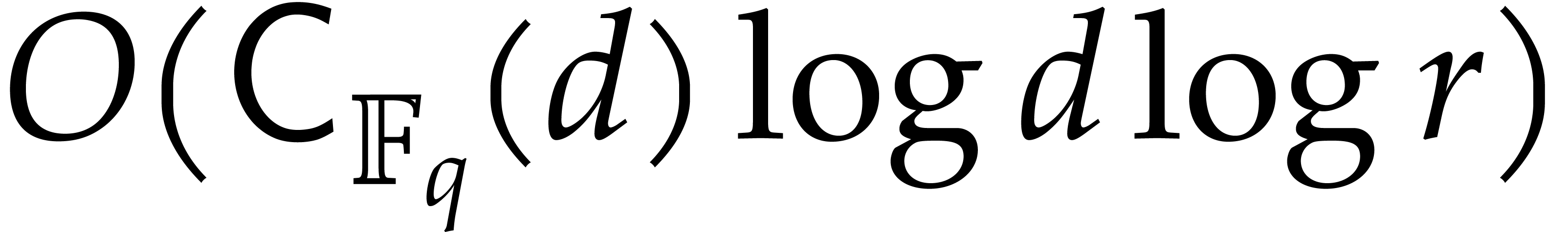 ; see the proof of [33, Theorem
6.2]. Finally each gcd takes
; see the proof of [33, Theorem
6.2]. Finally each gcd takes 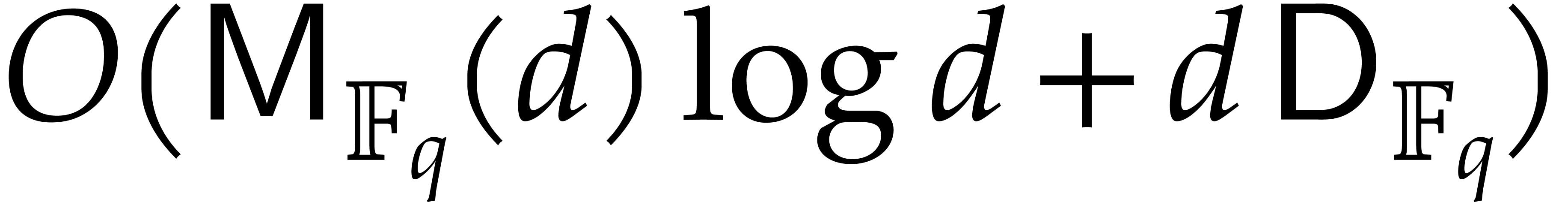 operations.
operations.
We finish this section with a digression on known optimizations for the
equal-degree factorization algorithm that will not be used in the rest
of the paper. These optimizations are based on a randomization strategy
due to Rabin [32] that saves pseudo-norm and pseudo-trace
computations. Here we focus on the case 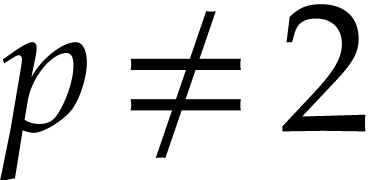 ;
in the case when
;
in the case when 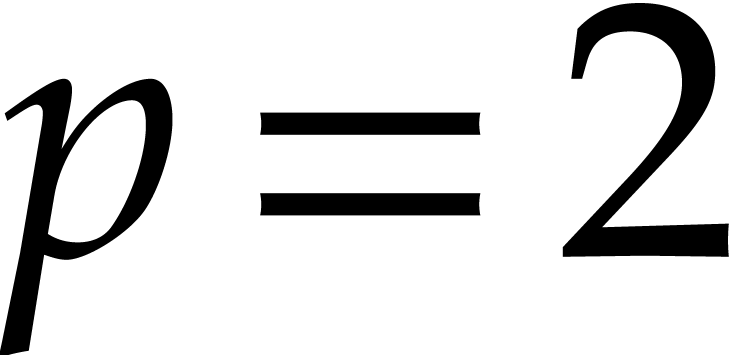 , similar
but slightly different formulas can be used [1, 32].
A concise presentation of Rabin's method is given in [9,
Exercise 14.17], but for pseudo-norms instead of pseudo-traces. For this
reason, we briefly repeat the main arguments. We follow the notation of
Algorithm 4.2.
, similar
but slightly different formulas can be used [1, 32].
A concise presentation of Rabin's method is given in [9,
Exercise 14.17], but for pseudo-norms instead of pseudo-traces. For this
reason, we briefly repeat the main arguments. We follow the notation of
Algorithm 4.2.
Assume that  is monic and square-free of degree
is monic and square-free of degree
 and a product of
and a product of 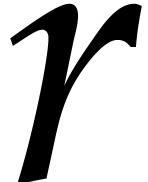 monic
irreducible factors
monic
irreducible factors  of degree
of degree 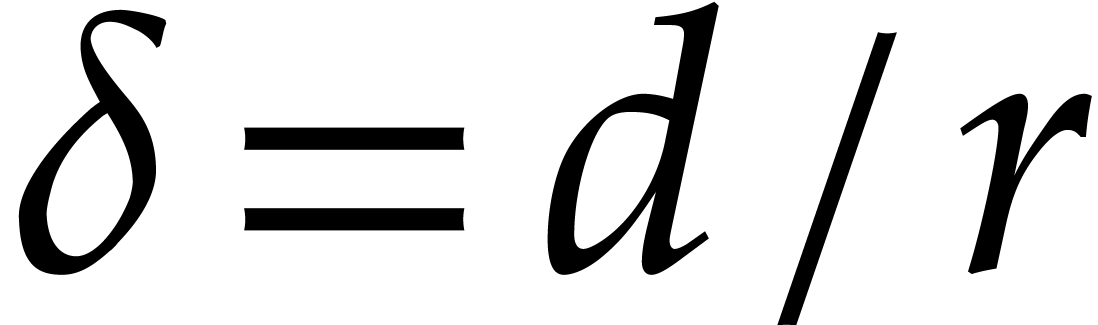 . Consider a polynomial
. Consider a polynomial 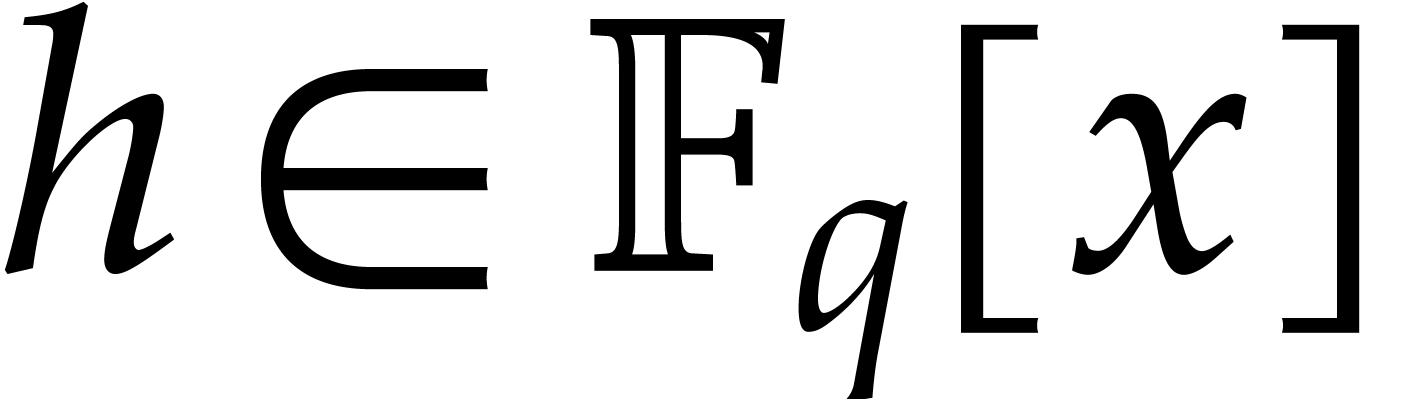 such that
such that 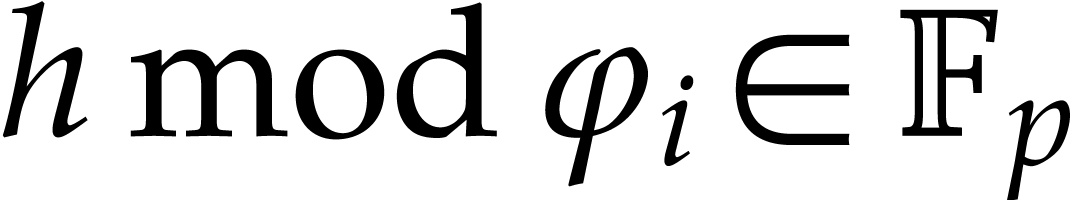 for
for 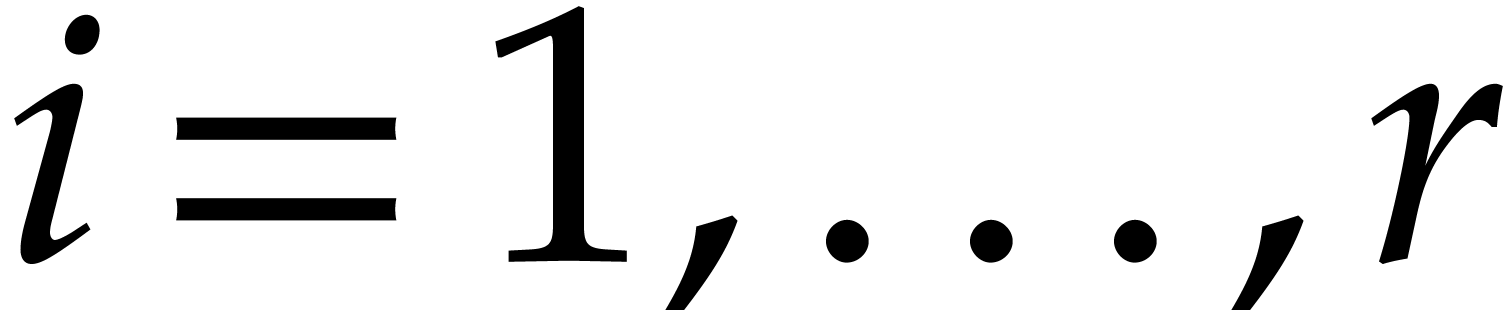 .
We say that
.
We say that  separates the irreducible
factors of
separates the irreducible
factors of  if
if 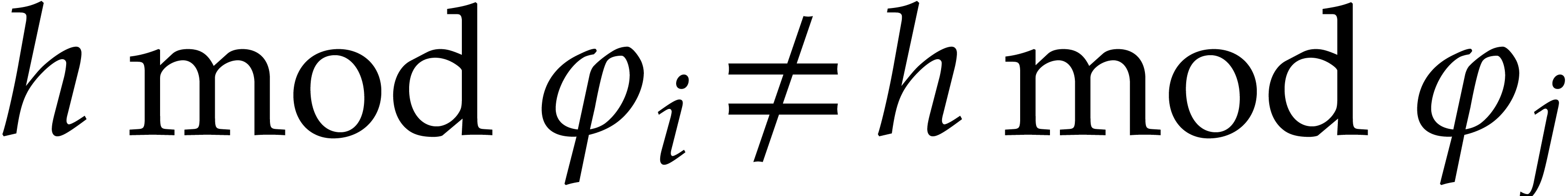 for all
for all
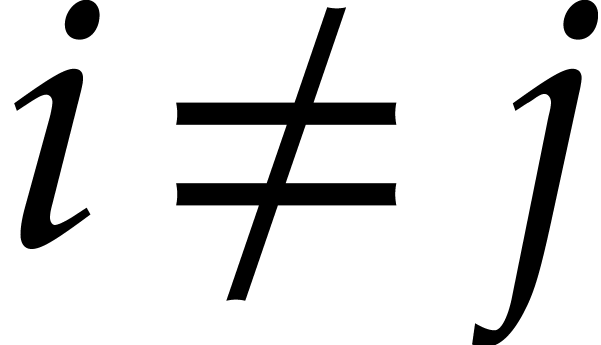 .
.
Algorithm
If 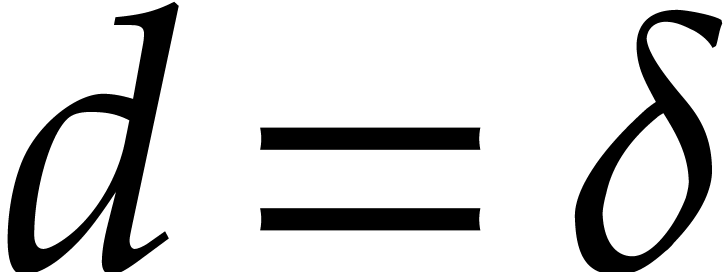 or
or  ,
then return
,
then return  .
.
Take  at random in
at random in  .
.
Compute 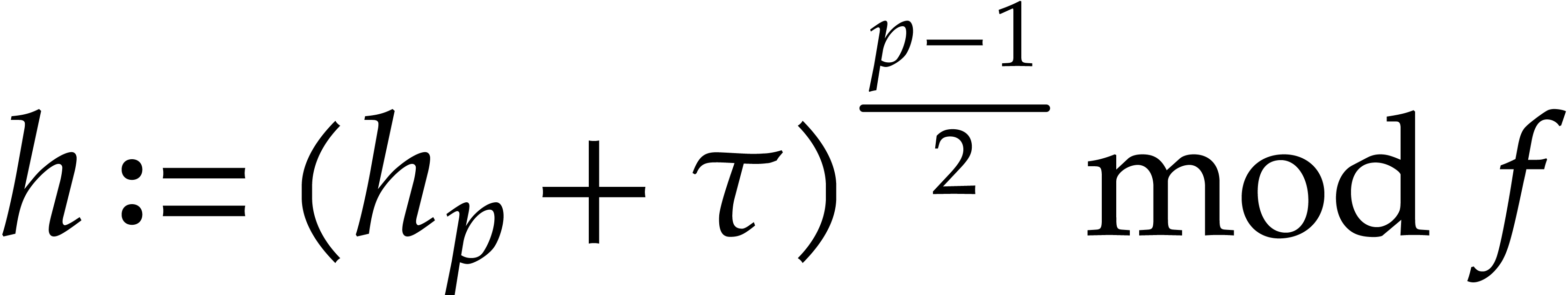 .
.
Compute 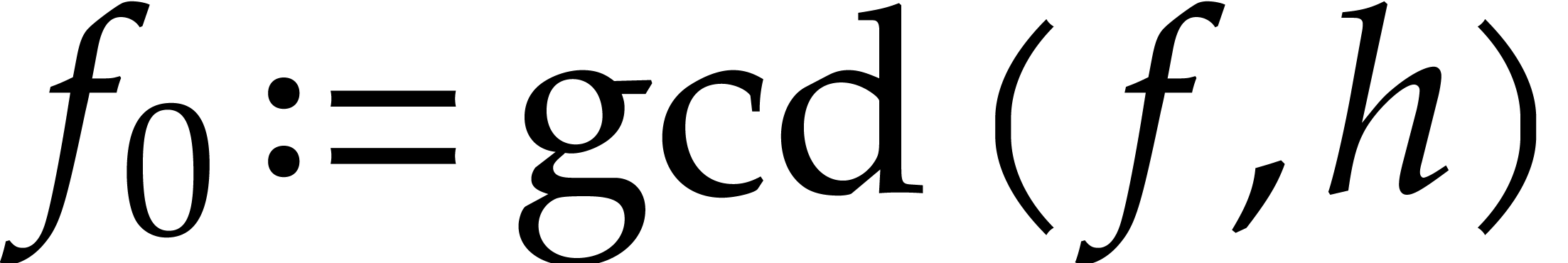 ,
, 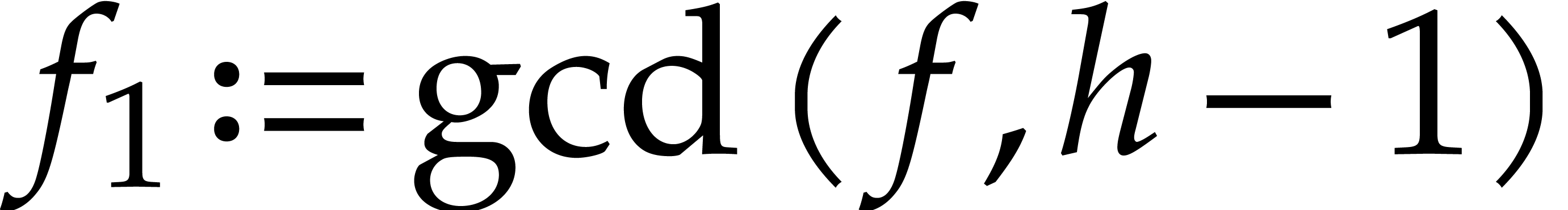 , and
, and 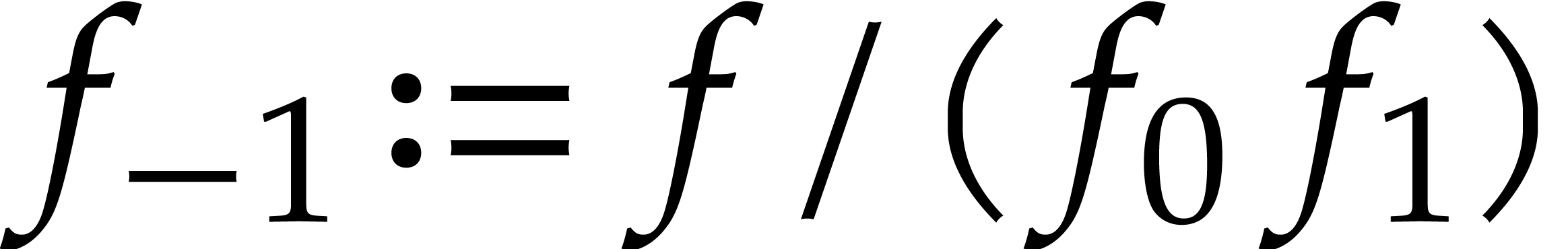 .
.
For 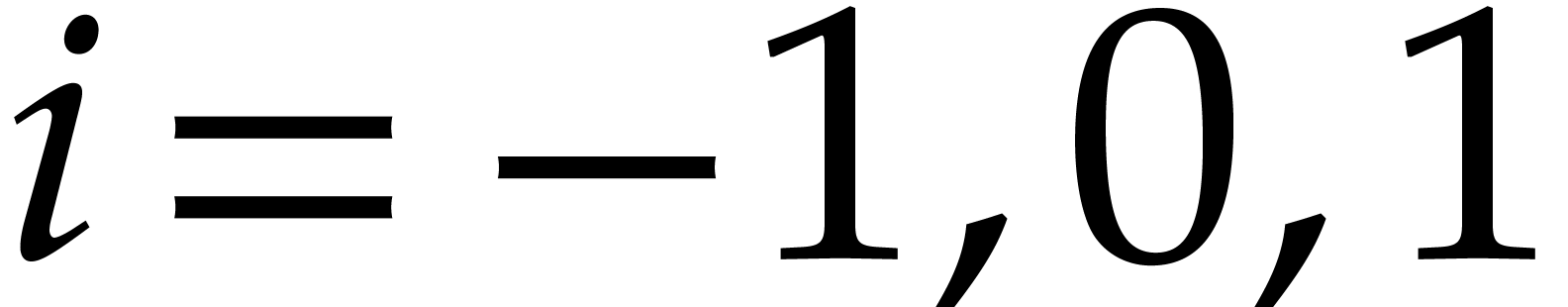 , call
recursively the algorithm with input
, call
recursively the algorithm with input 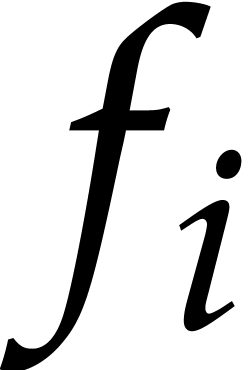 ,
, 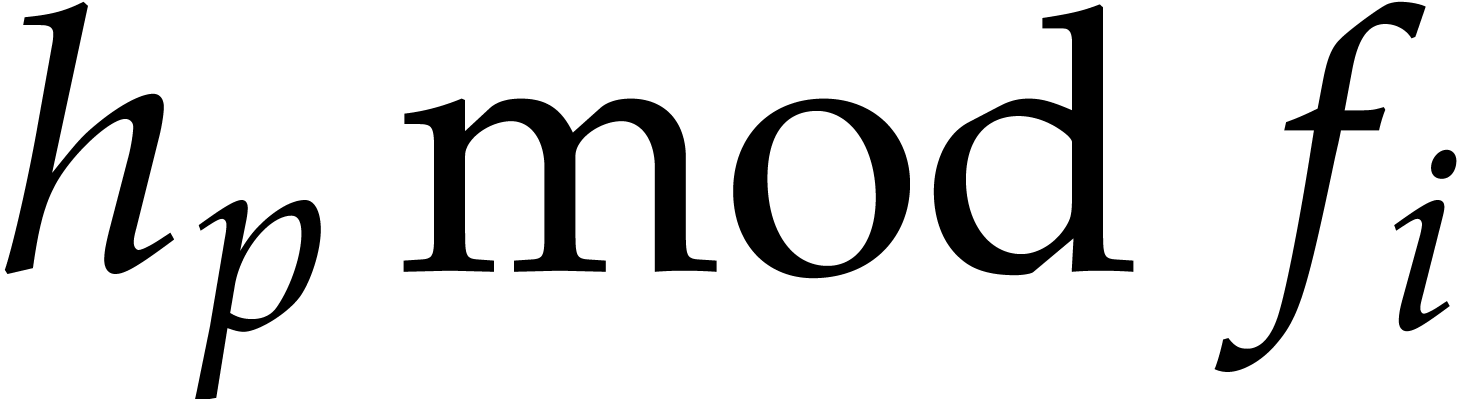 ,
and
,
and  .
.
Return the union of the factors of 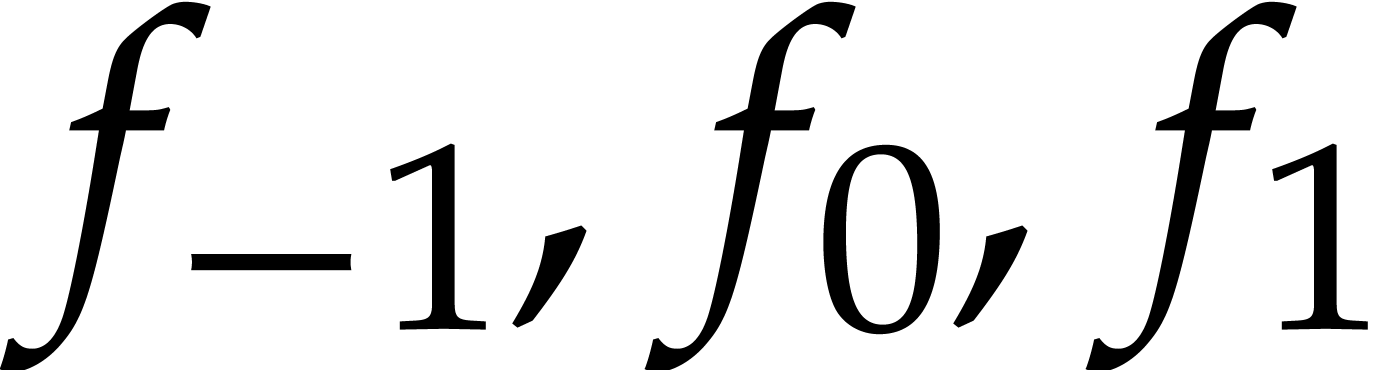 collected during step 5.
collected during step 5.
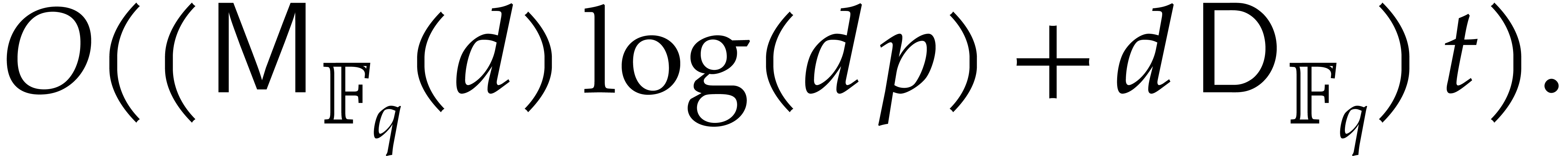
In addition the following assertions hold:
For  taken at random in
taken at random in 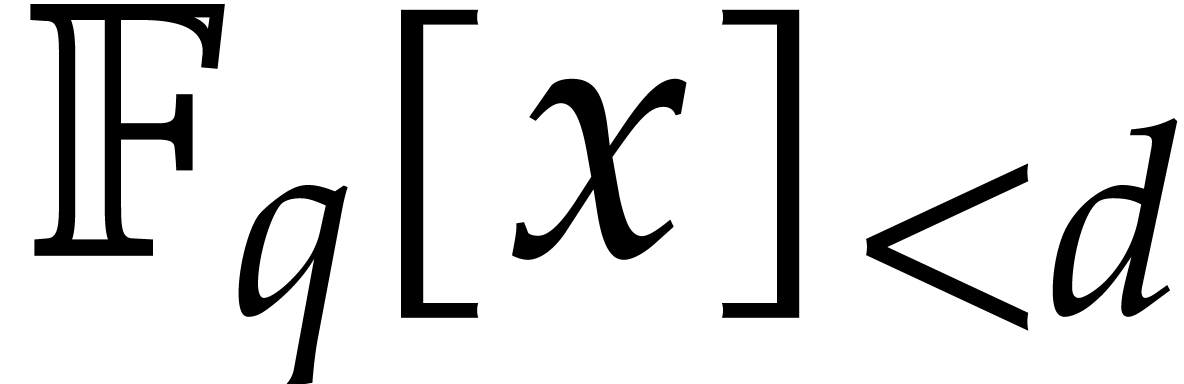 ,
,  does not separate the factors of
does not separate the factors of  with
probability
with
probability 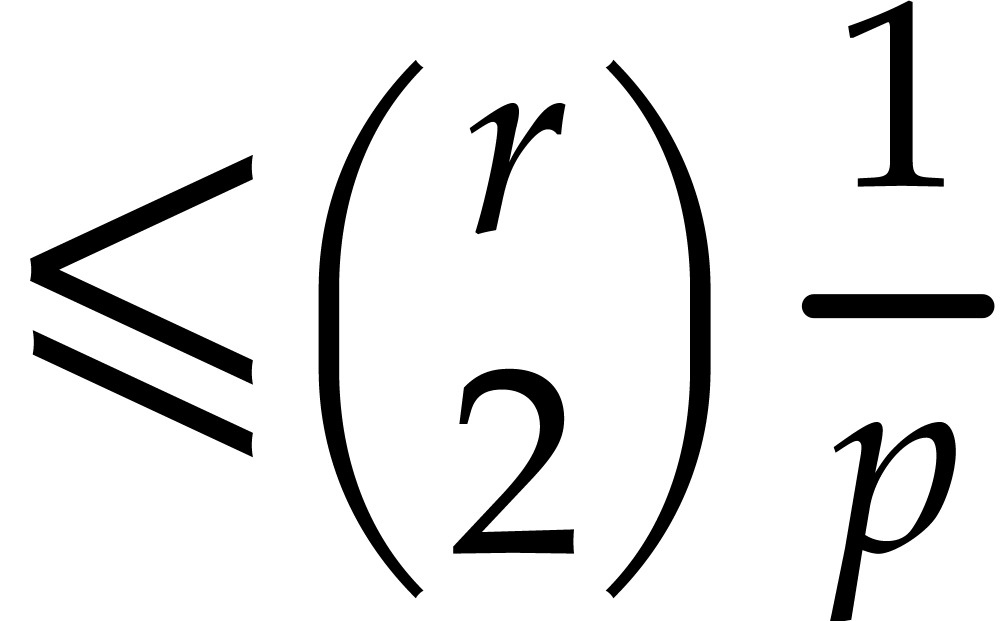 .
.
If 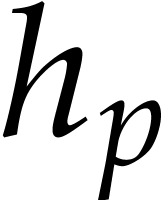 separates the irreducible factors of
separates the irreducible factors of
 , then Algorithm 4.3, called with
, then Algorithm 4.3, called with 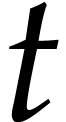 such that
such that
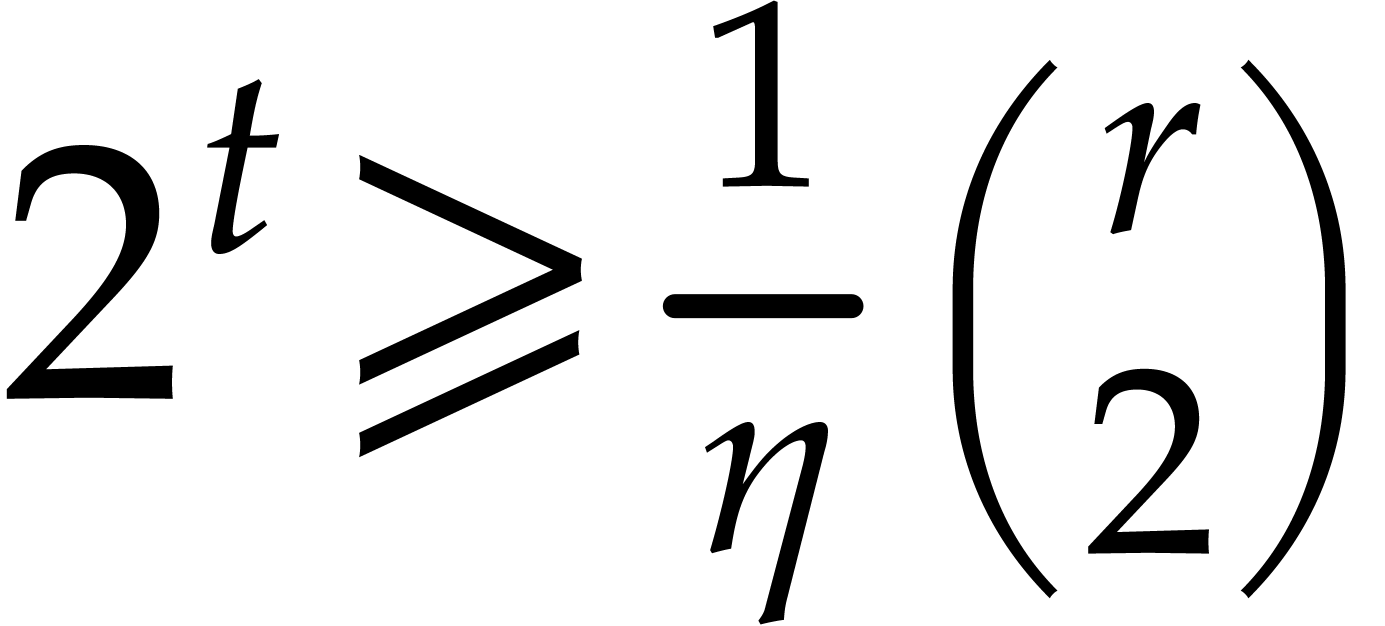 , returns all the
irreducible factors of
, returns all the
irreducible factors of 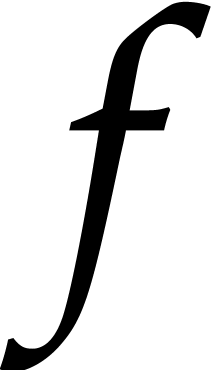 with probability
with probability
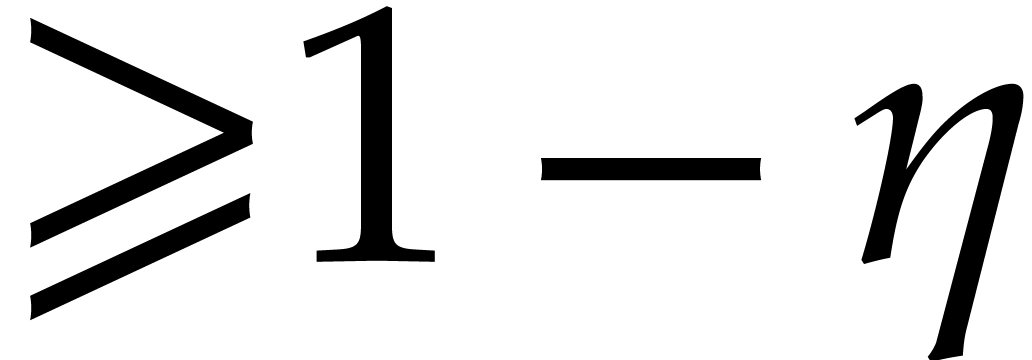 .
.
Proof. The proof of the complexity bound is
straightforward. A random  yields
yields 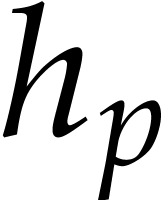 such that
such that 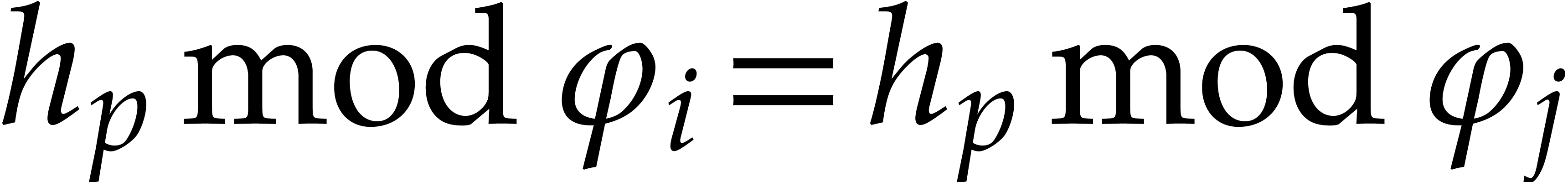 for
for 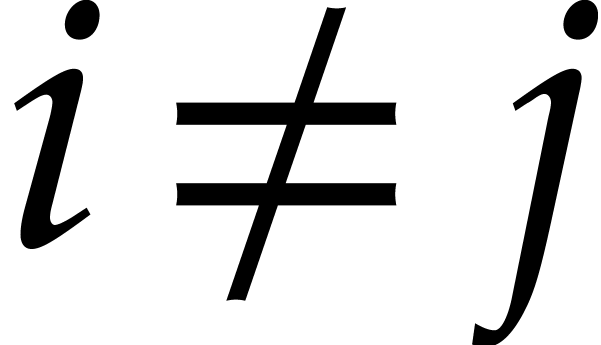 with probability
with probability 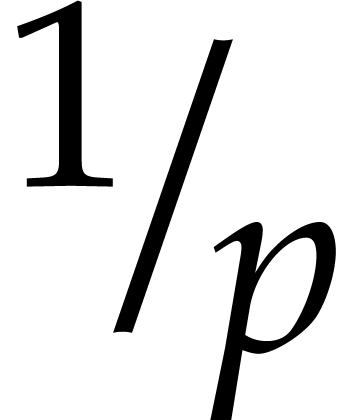 . Therefore
a random
. Therefore
a random  yields a polynomial
yields a polynomial 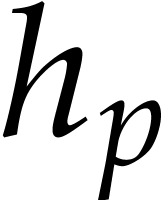 that does not separate the irreducible factors of
that does not separate the irreducible factors of 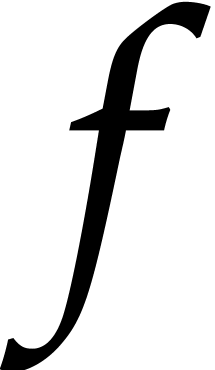 with probability at most
with probability at most 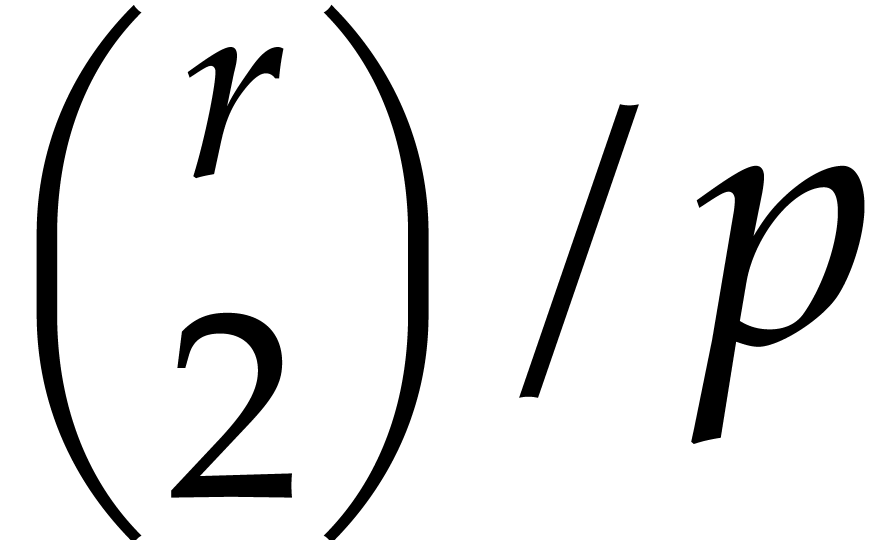 .
That proves assertion (i).
.
That proves assertion (i).
Now assume that 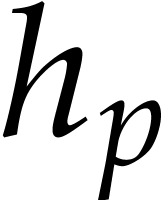 separates the irreducible
factors of
separates the irreducible
factors of  . Given
. Given  in
in  , we have
, we have
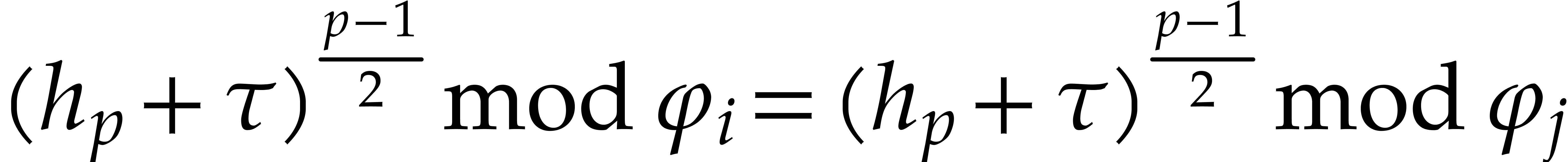 |
(4.2) |
for at most 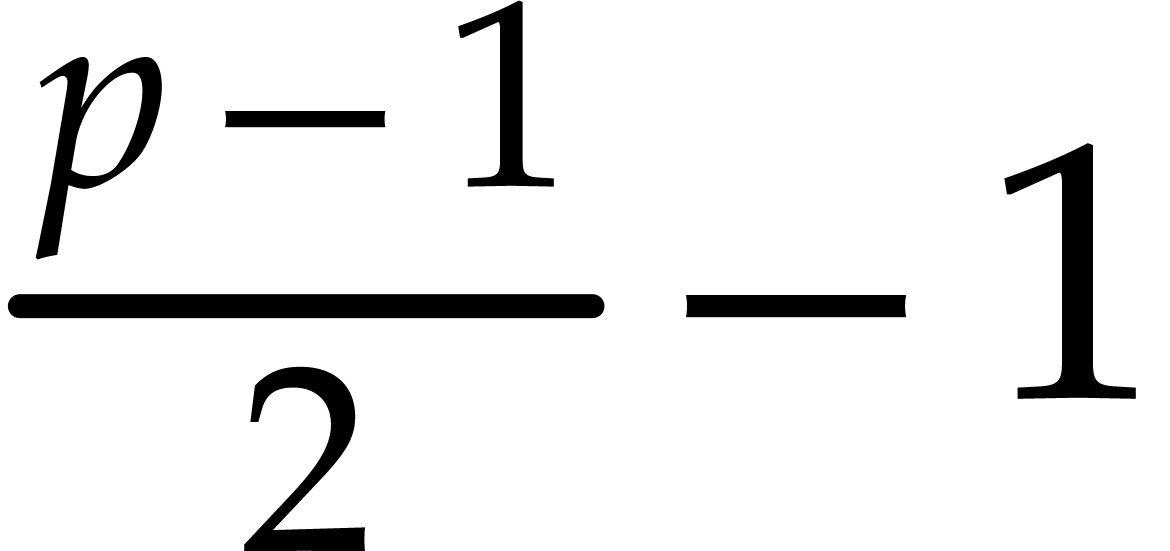 values of
values of  . With
. With  taken at random in
taken at random in
 , the probability that
, the probability that 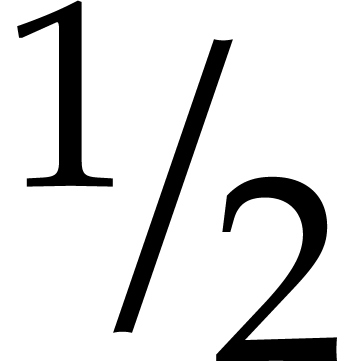 .
.
Let 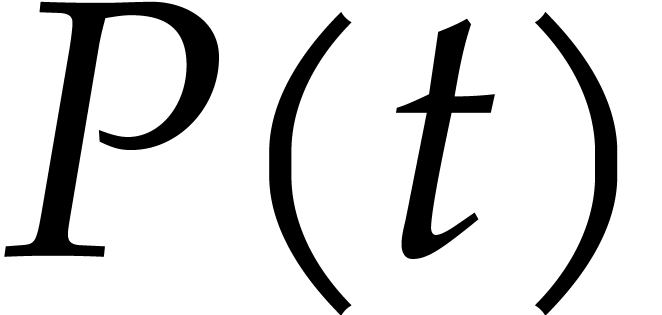 denote the probability that all the
irreducible factors are not found after the call of Algorithm 4.3
with input
denote the probability that all the
irreducible factors are not found after the call of Algorithm 4.3
with input  . There exist
. There exist 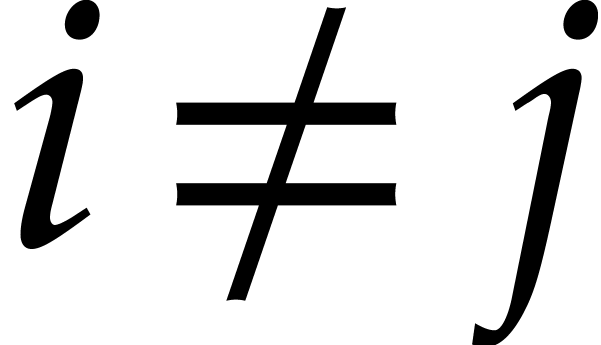 such that
such that  random values of
random values of  with probability at most
with probability at most 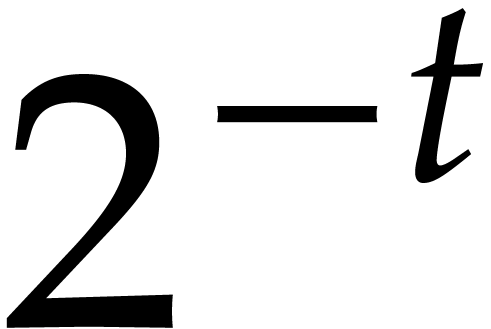 .
Considering the
.
Considering the 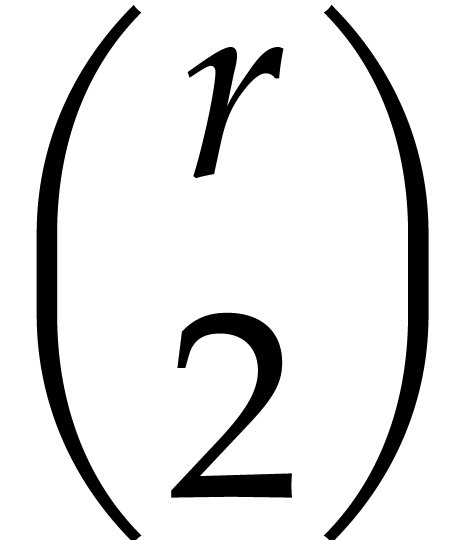 possible pairs
possible pairs 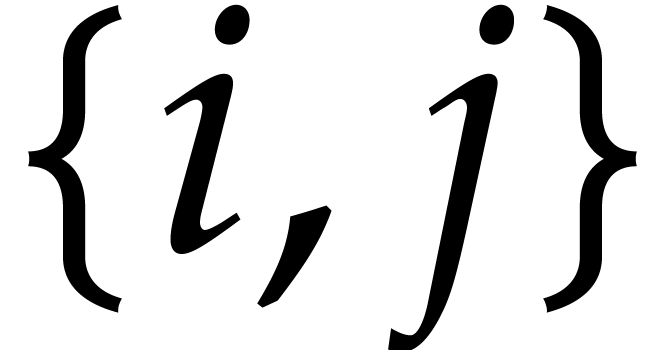 , we obtain
, we obtain 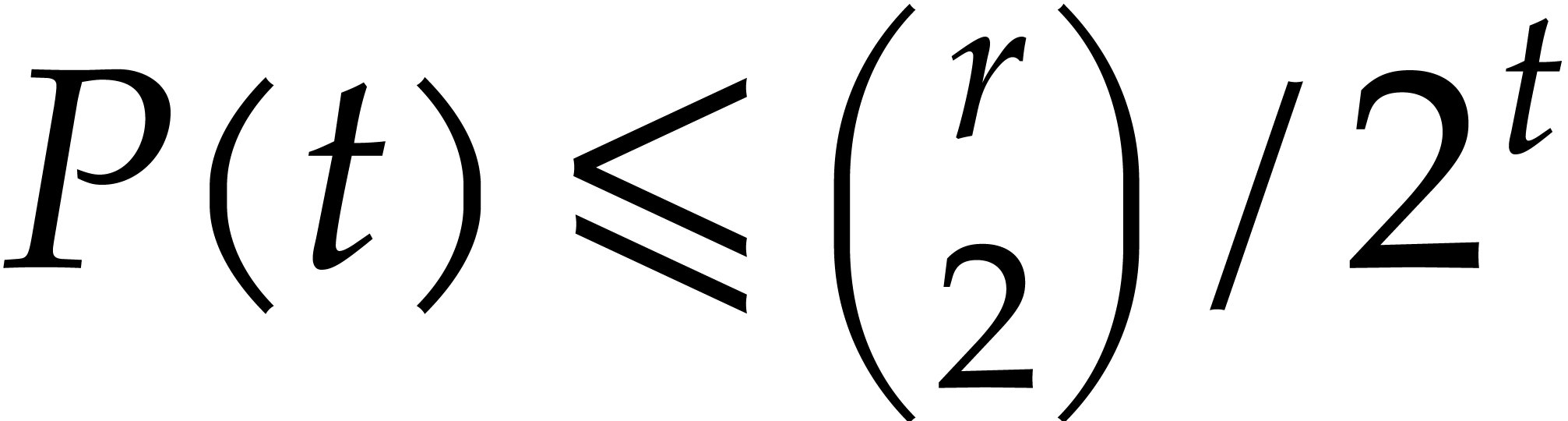 .
.
We may benefit from Rabin's strategy within Algorithm 4.2
as follows, whenever 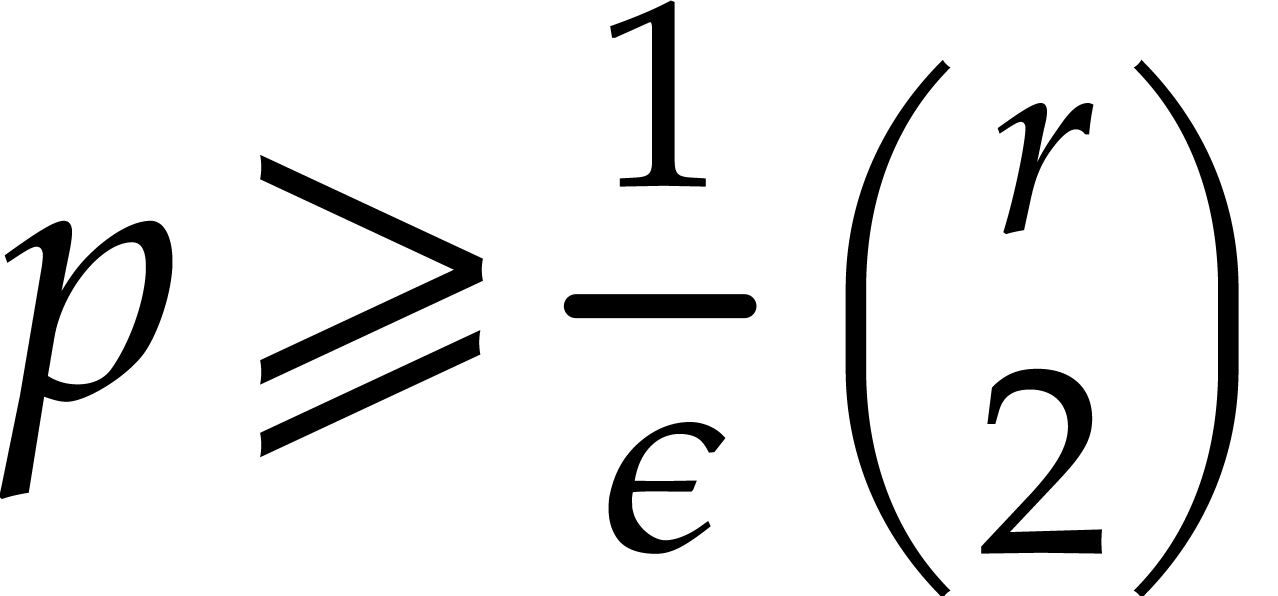 . A
polynomial
. A
polynomial 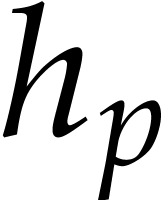 as in Proposition 4.4(i)
separates the factors of
as in Proposition 4.4(i)
separates the factors of  with probability
with probability 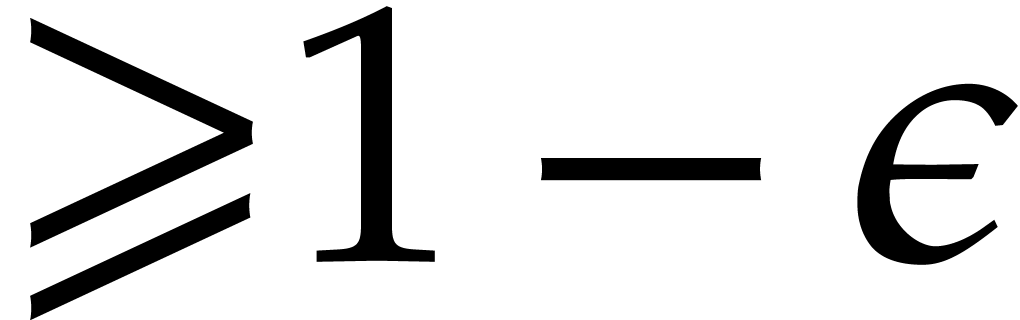 . We call Algorithm 4.3
with the first value of
. We call Algorithm 4.3
with the first value of 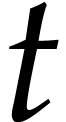 such that
such that 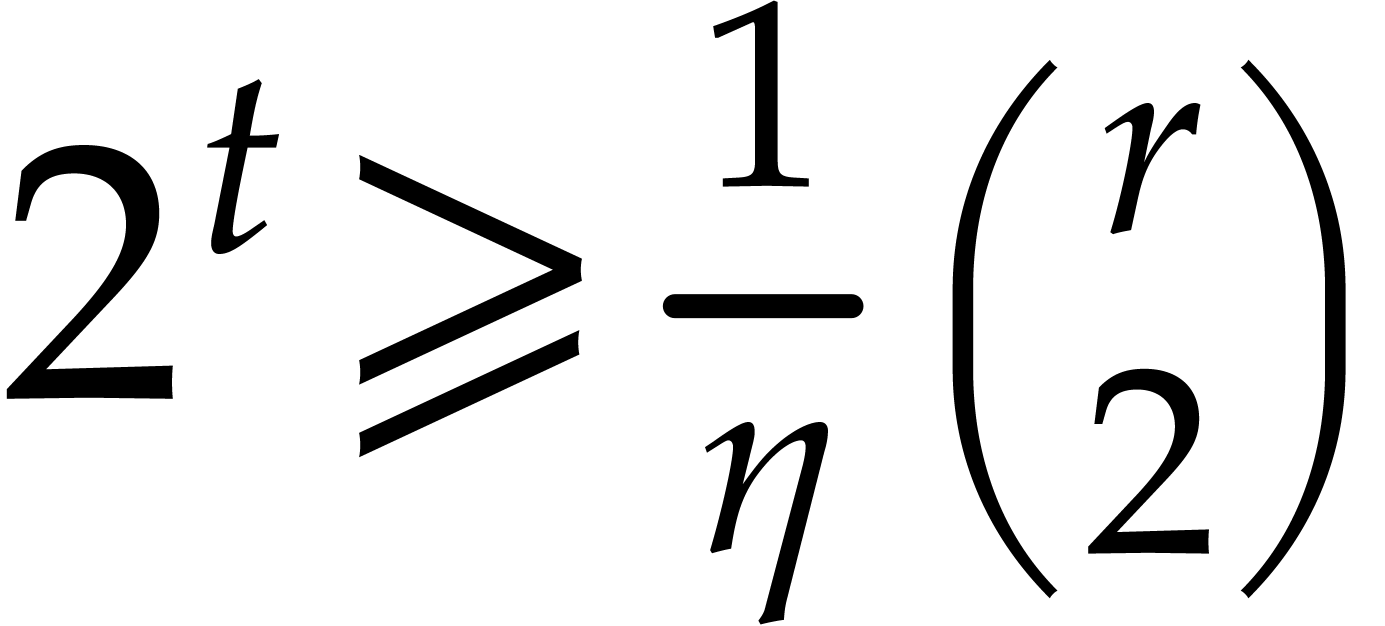 , so the irreducible factors of
, so the irreducible factors of  are found with probability
are found with probability 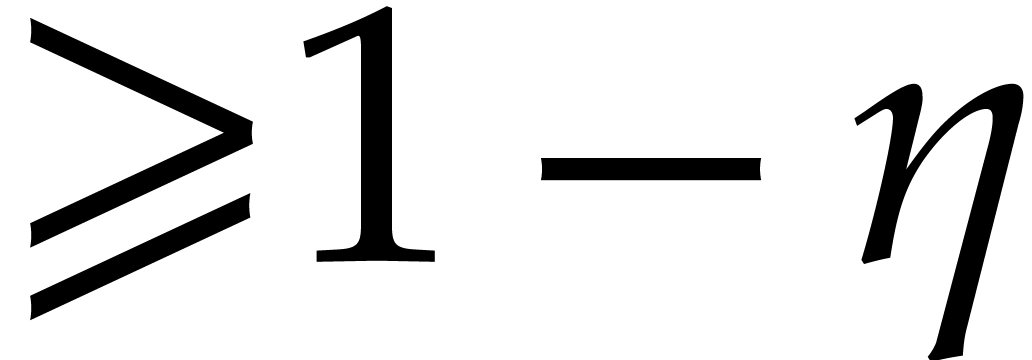 .
When
.
When 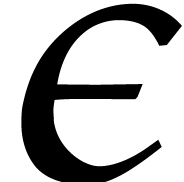 and
and 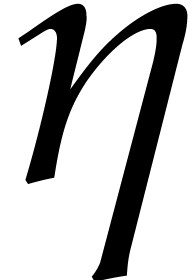 can be taken
sufficiently small, we derive a similar complexity bound as in
Proposition 4.3, but where the factor
can be taken
sufficiently small, we derive a similar complexity bound as in
Proposition 4.3, but where the factor 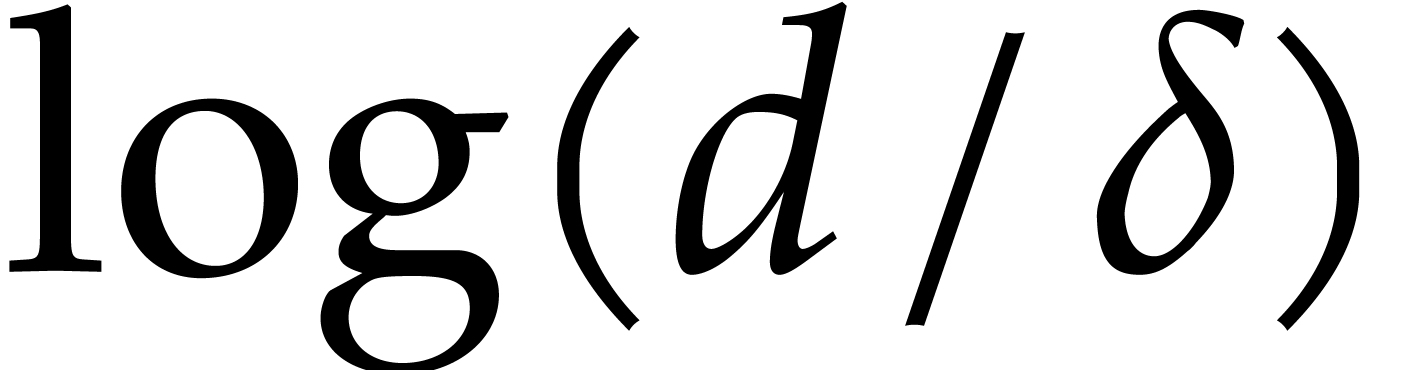 does not apply to the terms
does not apply to the terms 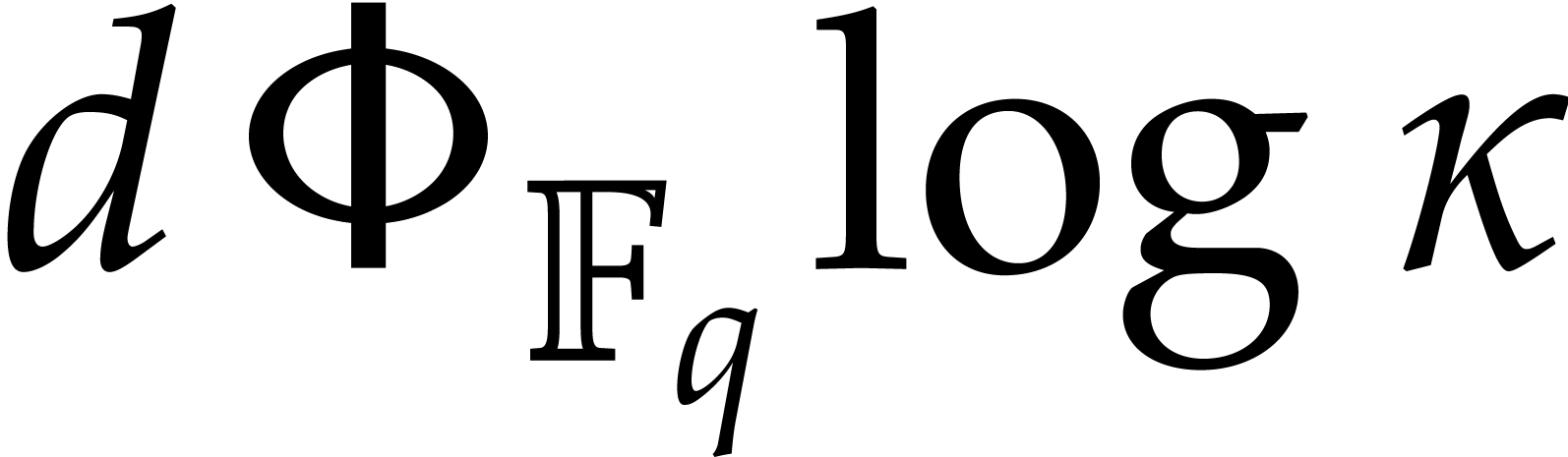 and
and 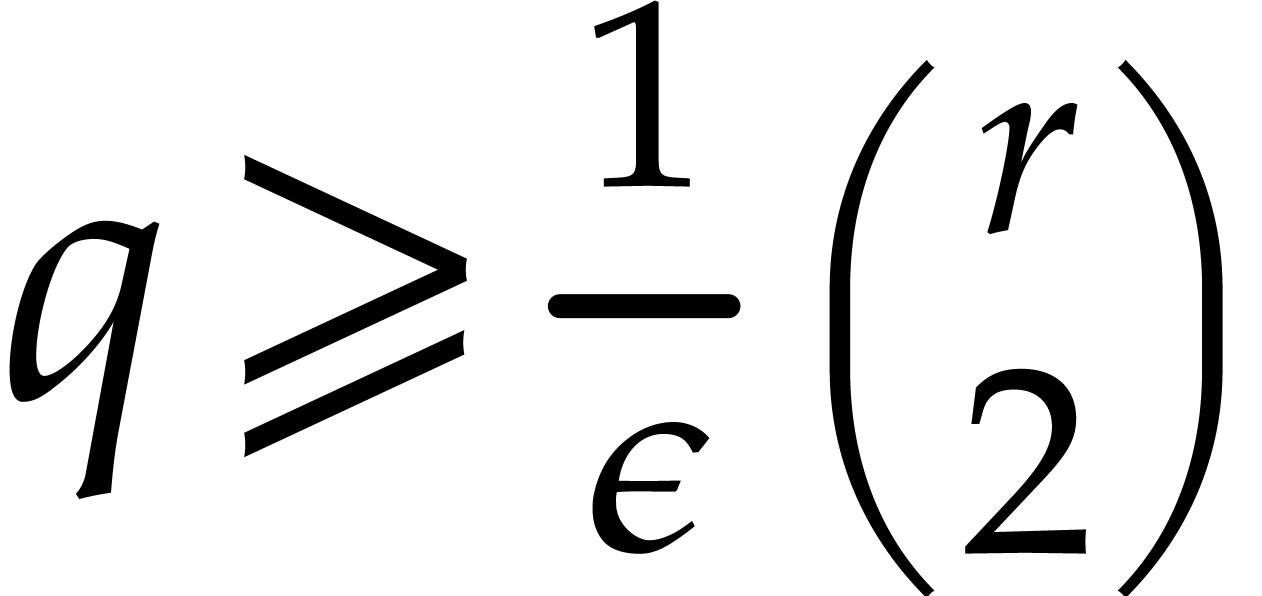 , which correspond to the costs of steps 3 and
4 of Algorithm 4.2.
, which correspond to the costs of steps 3 and
4 of Algorithm 4.2.
If 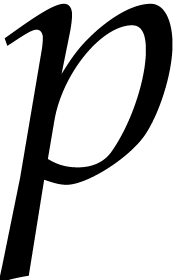 is too small to find a suitable value for
is too small to find a suitable value for
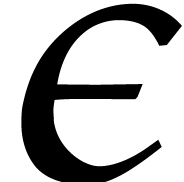 , then we may appeal to
Rabin's strategy a few rounds in order to benefit from more splittings
with a single pseudo-trace over
, then we may appeal to
Rabin's strategy a few rounds in order to benefit from more splittings
with a single pseudo-trace over  .
If
.
If 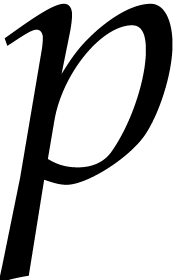 is actually too small for this approach, then
we may consider the case
is actually too small for this approach, then
we may consider the case  and apply Rabin's
strategy over
and apply Rabin's
strategy over  instead of
instead of  . More precisely, from
. More precisely, from  and a
random
and a
random 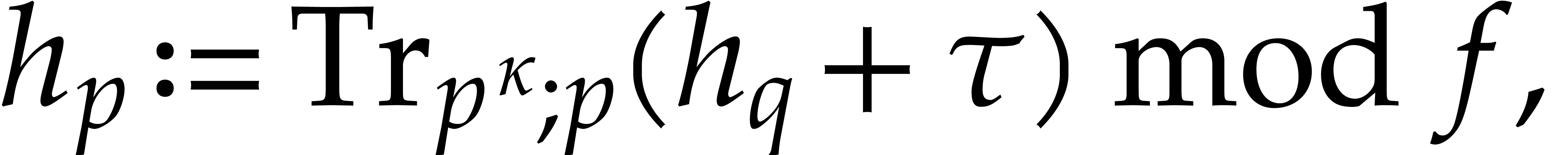 we compute
we compute
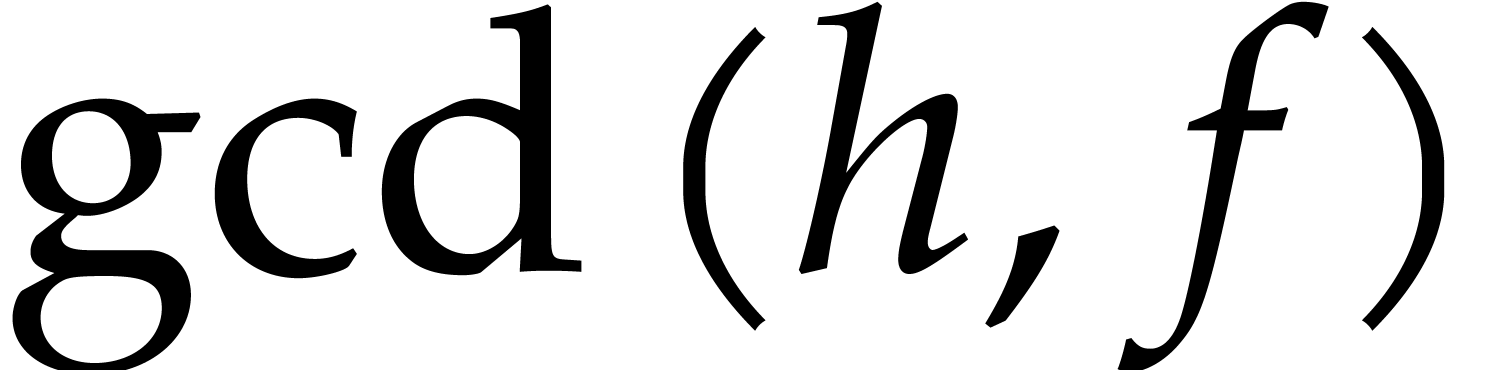
then 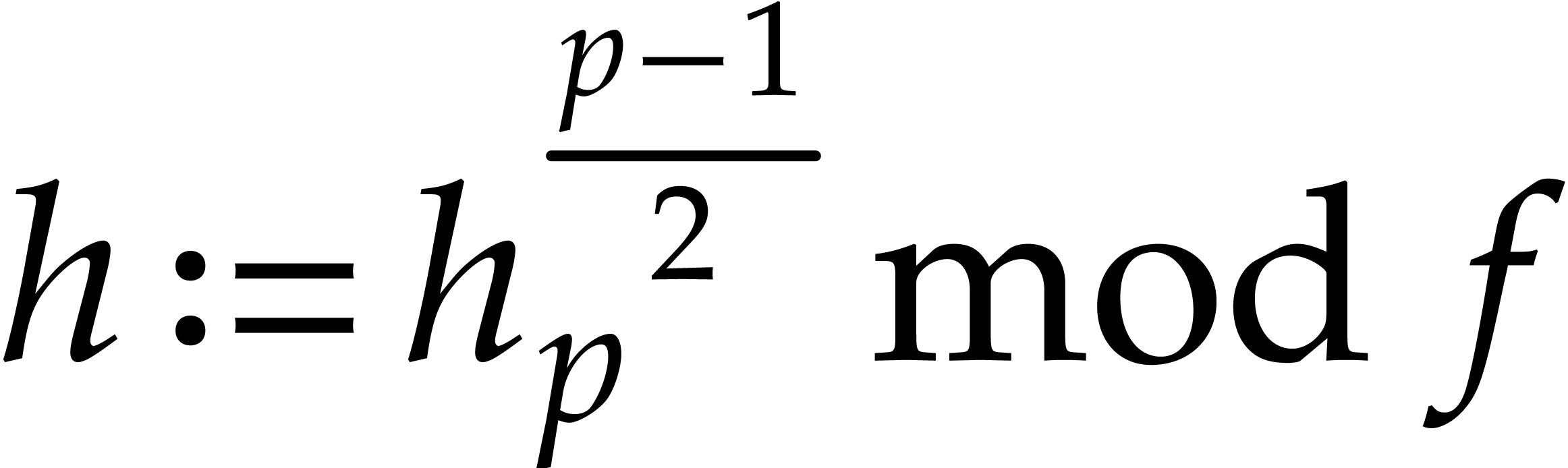 , and obtain the
splitting
, and obtain the
splitting 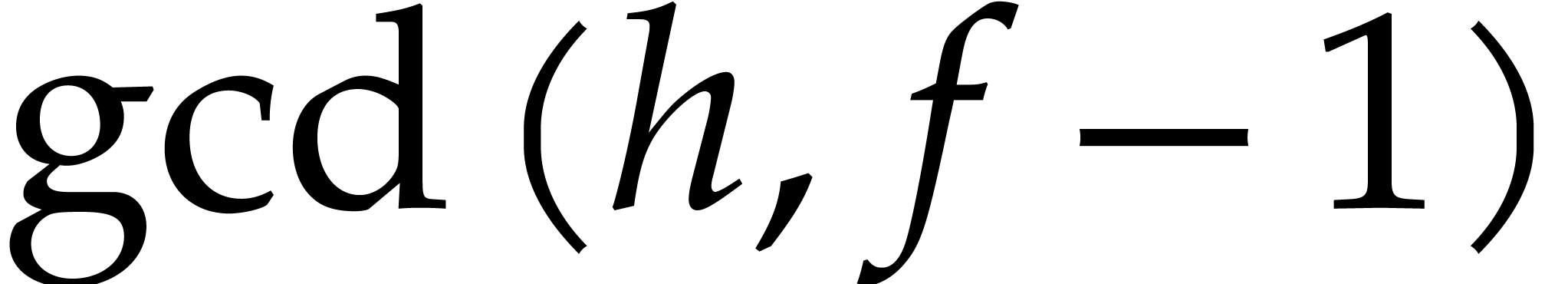 ,
, 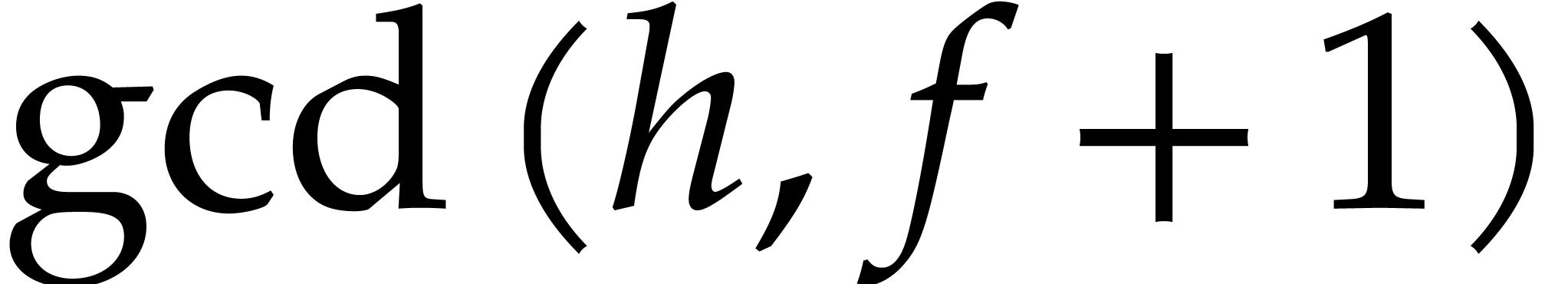 ,
,  on which to recurse.
This approach yields a complexity bound similar to the one from
Proposition 4.3, but where the factor
on which to recurse.
This approach yields a complexity bound similar to the one from
Proposition 4.3, but where the factor 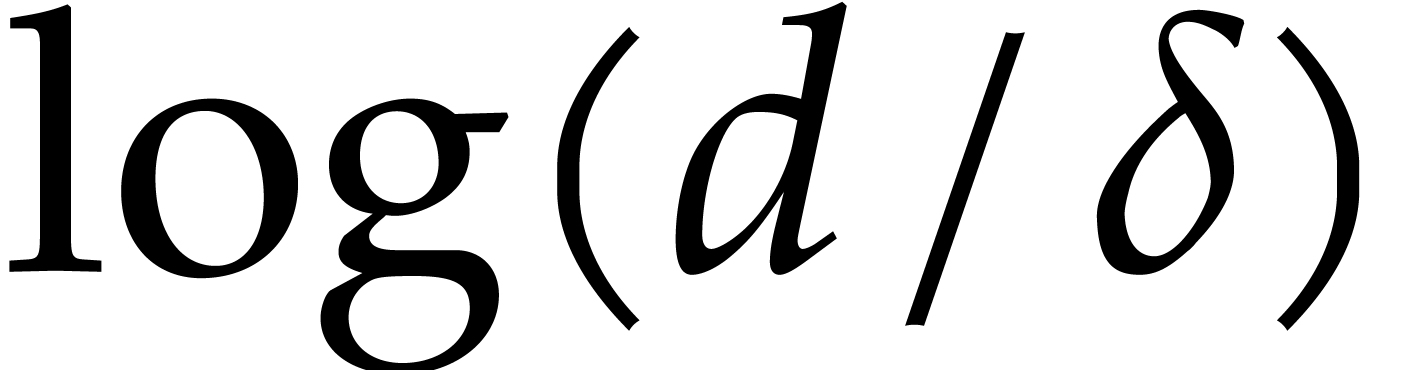 does not apply to the term
does not apply to the term 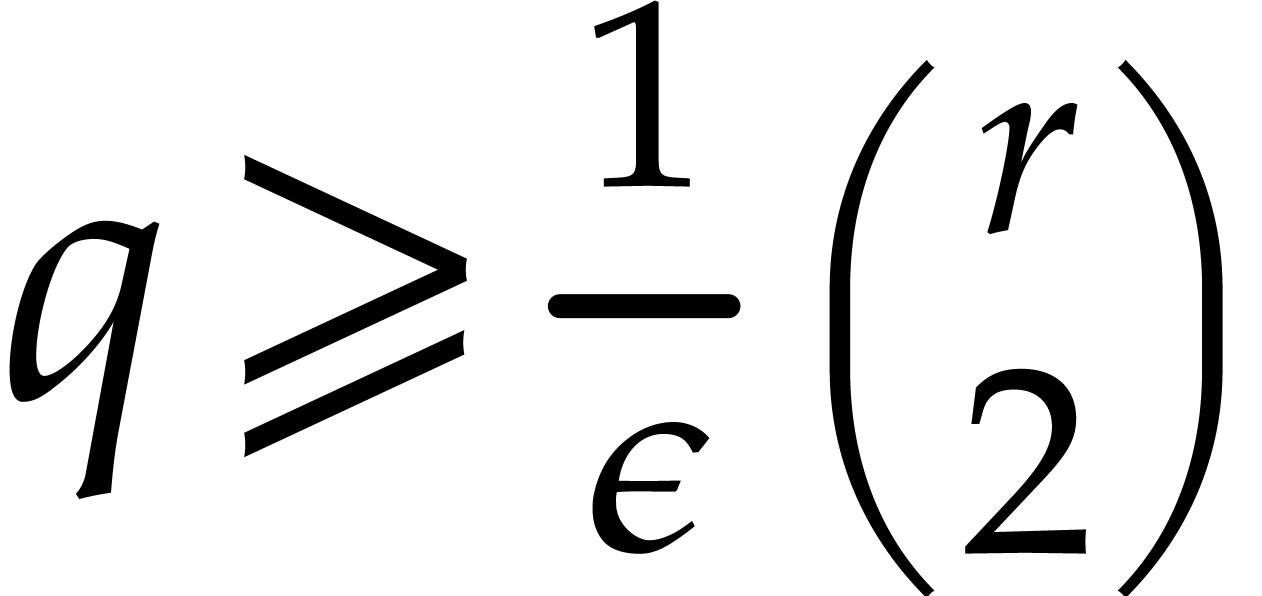 .
This latter term corresponds to the cost of step 3 of Algorithm 4.2.
.
This latter term corresponds to the cost of step 3 of Algorithm 4.2.
This section first draws corollaries from section 4.4,
which rely on Kedlaya and Umans' algorithm for modular composition. Note
however that it seems unlikely that this algorithm can be implemented in
a way that makes it efficient for practical purposes: see [19,
Conclusion]. We first consider the case when  is
a primitive extension over
is
a primitive extension over  and then the more
general case when
and then the more
general case when  is given via a
“triangular tower”.
is given via a
“triangular tower”.
Assume that 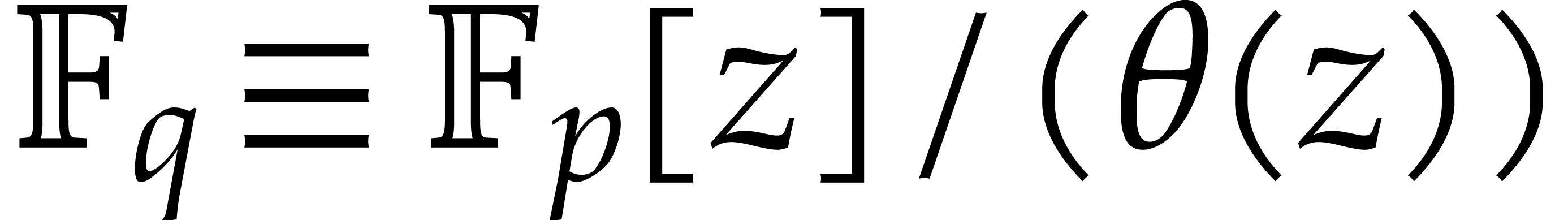 is a primitive extension of
is a primitive extension of  . Then we may take:
. Then we may take:
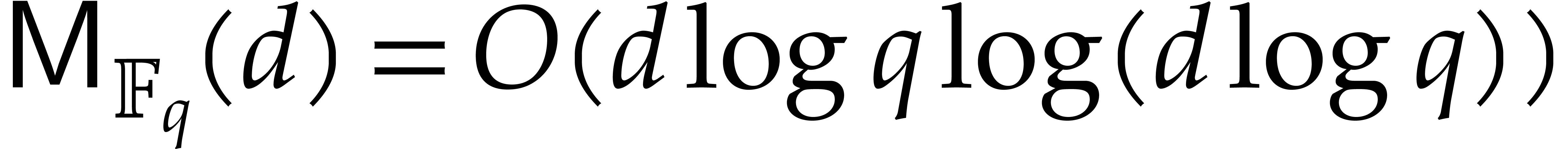 : see [13].
Under a plausible number theoretic conjecture, one even has
: see [13].
Under a plausible number theoretic conjecture, one even has 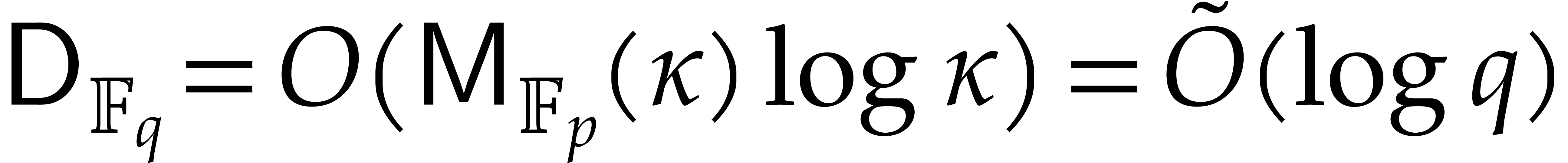 [14].
[14].
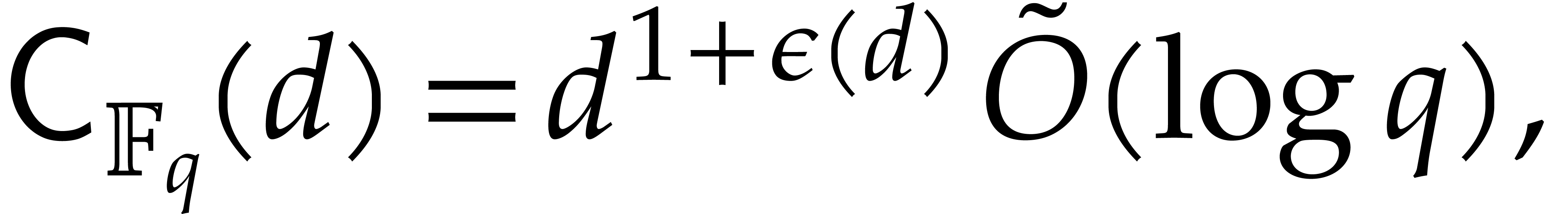 : see [9].
: see [9].
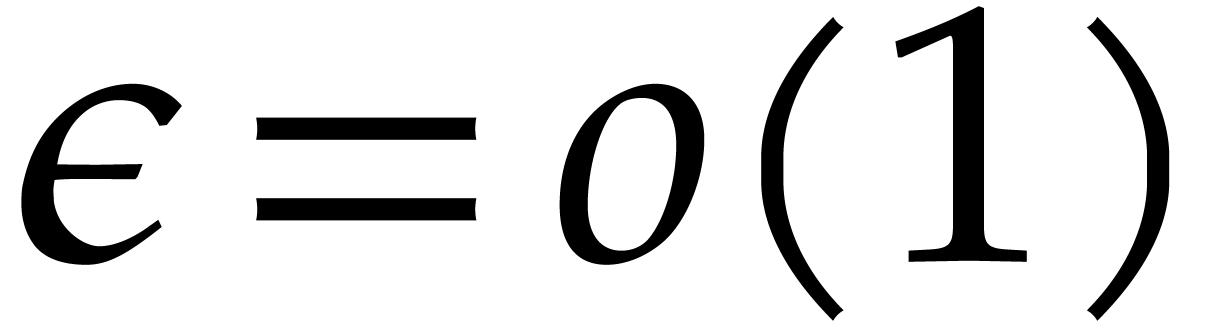 |
(5.1) |
where 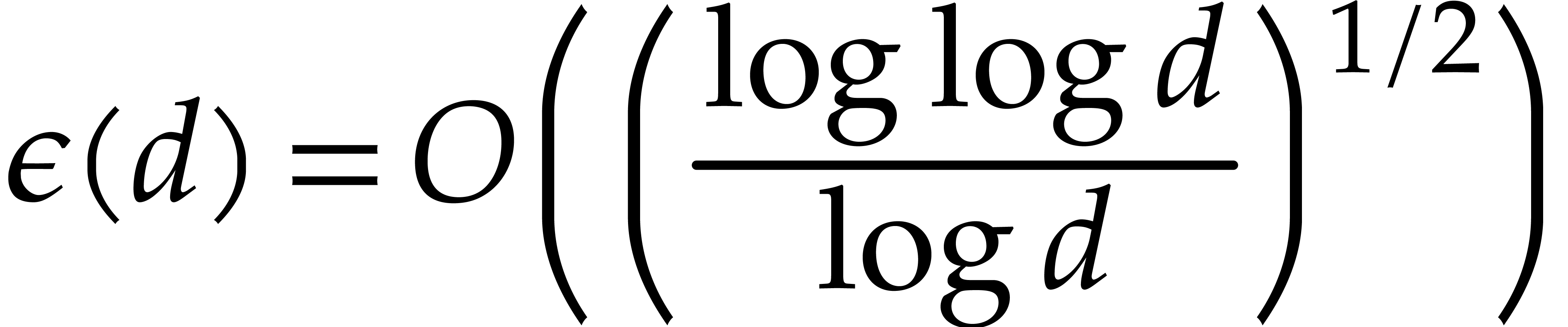 ; The refined bound
with
; The refined bound
with
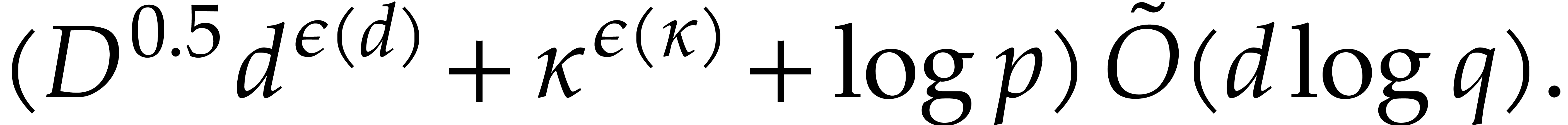
is proved in [19, section 6].
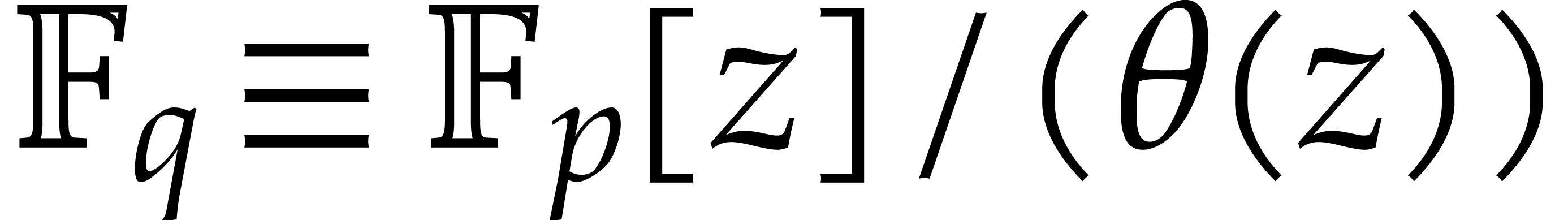 be as above. The
computation of the irreducible factors of degree
be as above. The
computation of the irreducible factors of degree 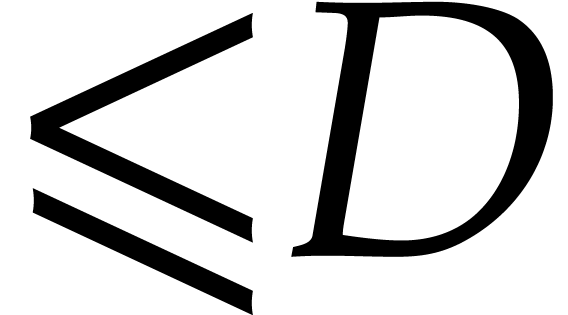 of a polynomial of degree
of a polynomial of degree  in
in 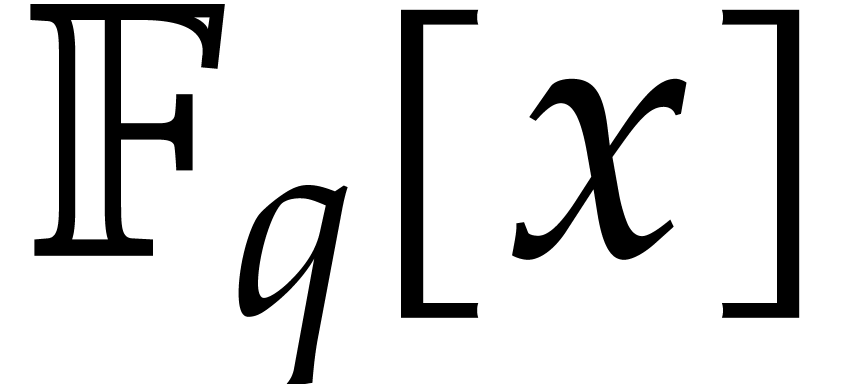 takes an expected time
takes an expected time
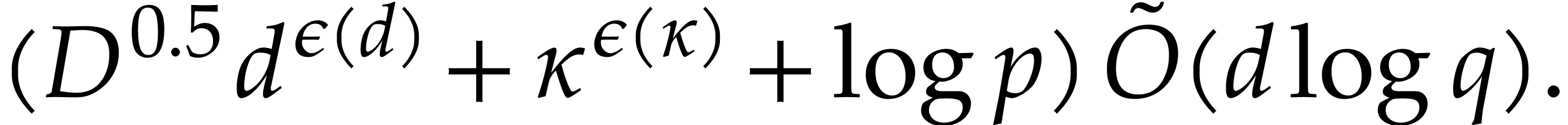
Proof. By means of
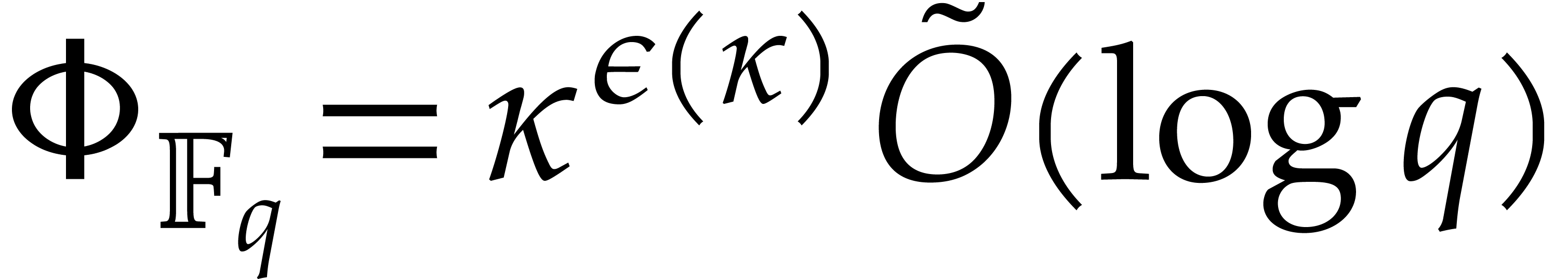
Then 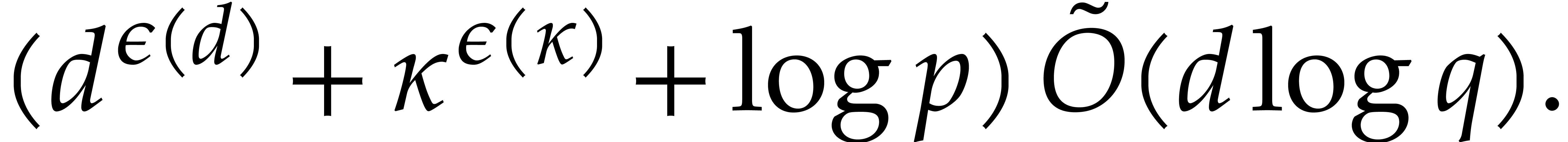 holds by Lemma 2.1. So the
bound follows from Theorem 4.1.
holds by Lemma 2.1. So the
bound follows from Theorem 4.1.
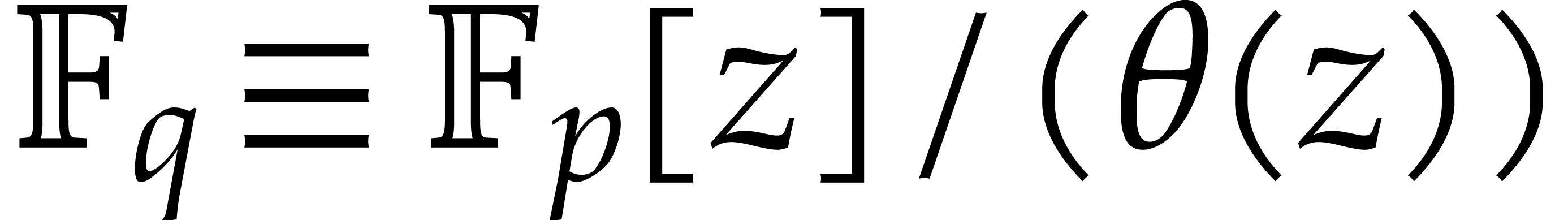 be as above. A polynomial of
degree
be as above. A polynomial of
degree  in
in 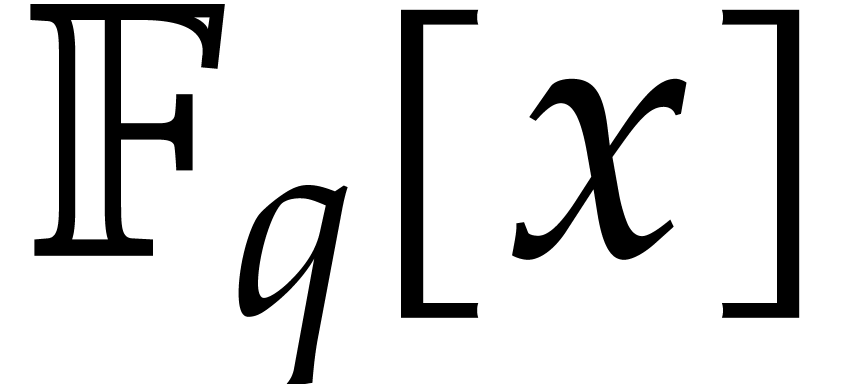 can be
tested to be irreducible in time
can be
tested to be irreducible in time
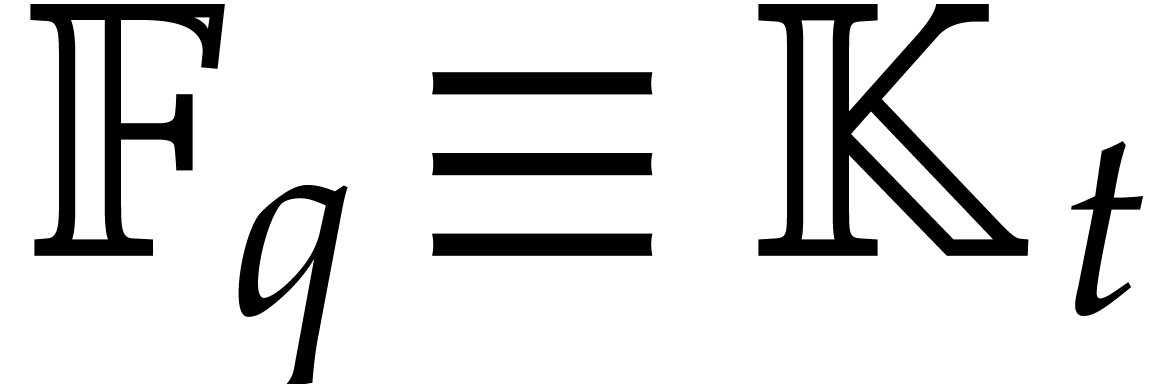
Proof. This follows from Theorem 4.2,
in a similar way as above.
Now we examine the case where 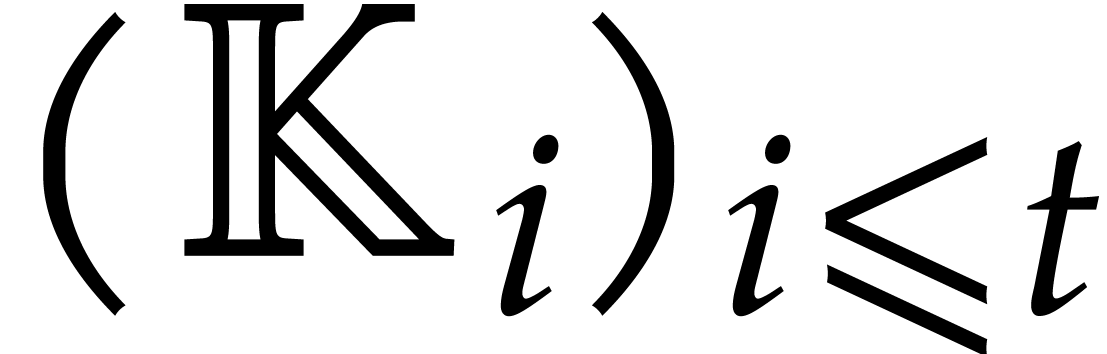 ,
where
,
where 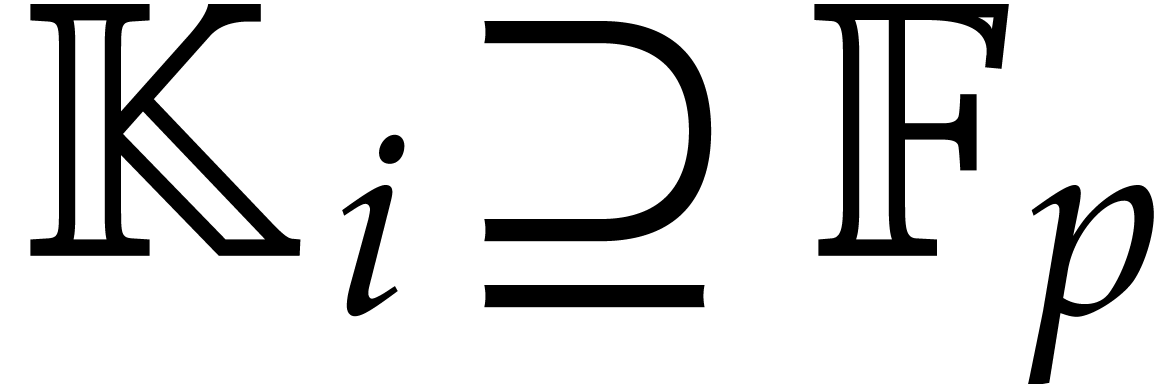 a triangular tower of height
a triangular tower of height 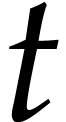 of field extensions
of field extensions 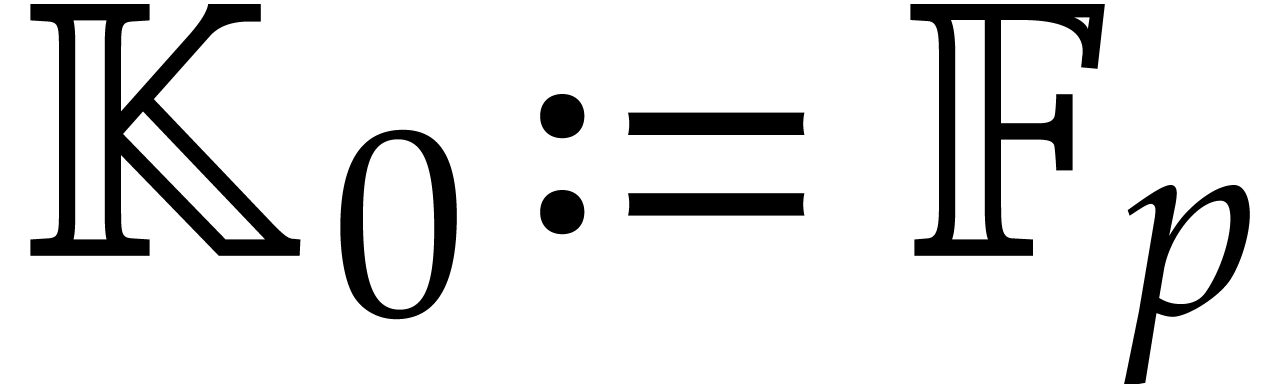 such that
such that
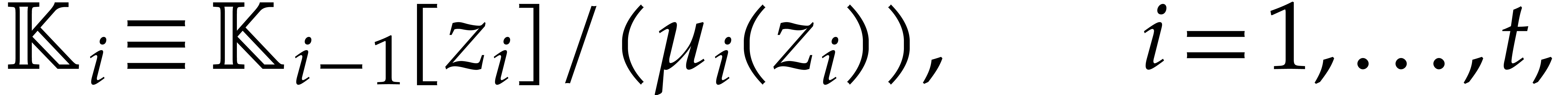 and
and
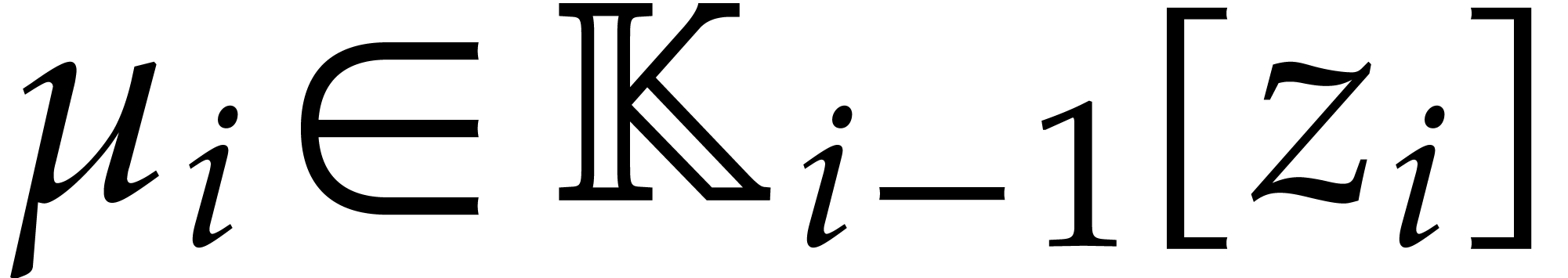
for irreducible polynomials 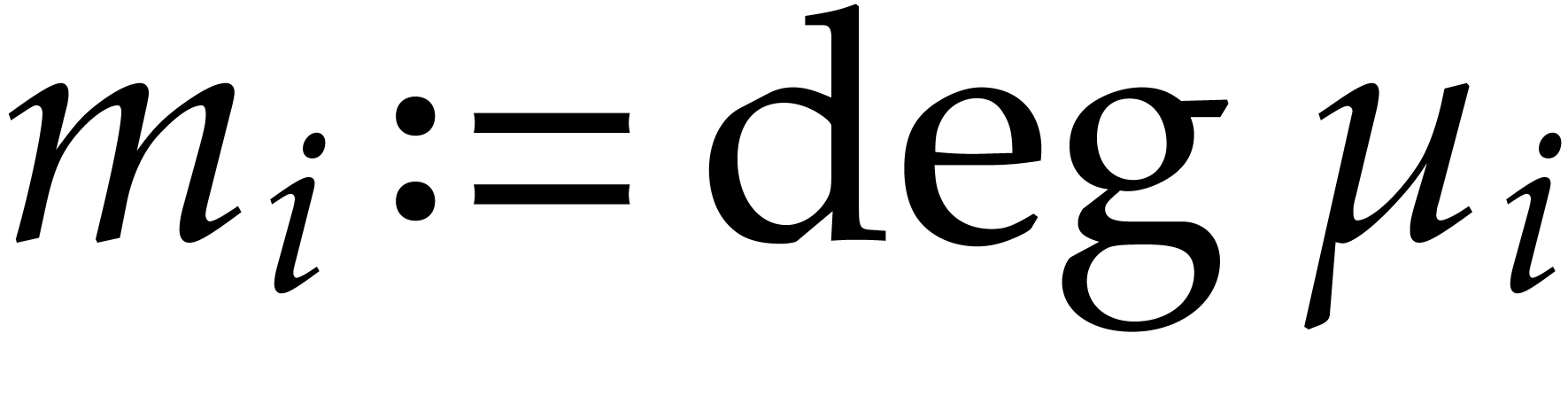 .
We write
.
We write  , so
, so 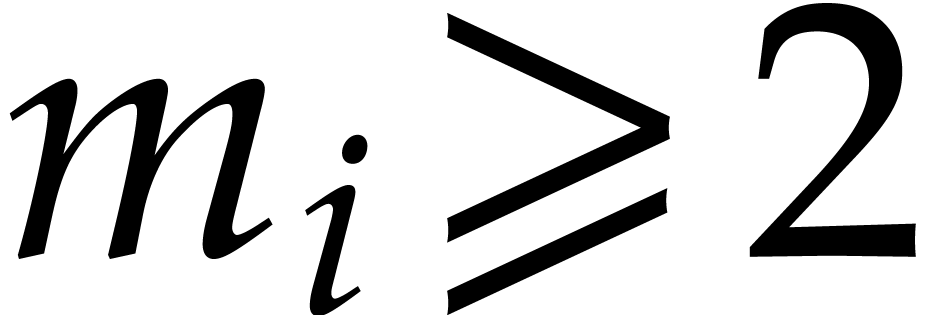 , and assume that
, and assume that 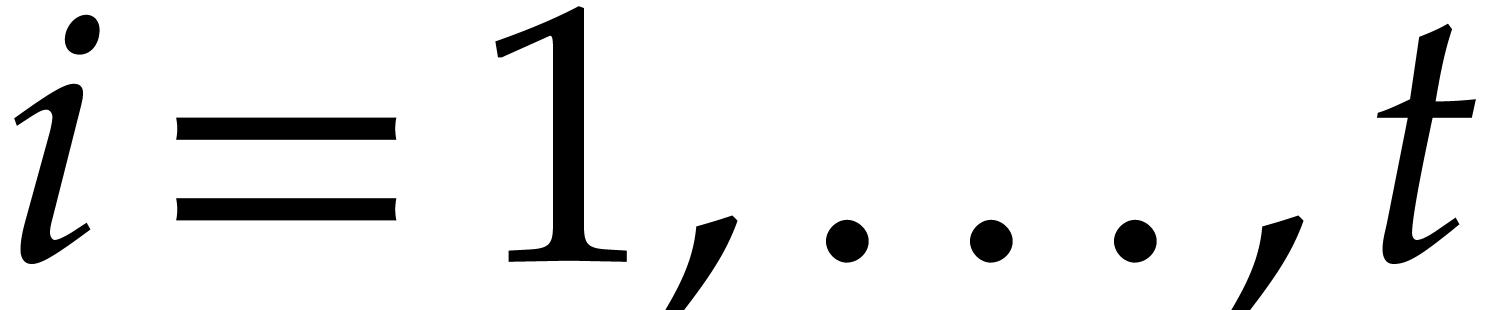 for
for
 .
.
Using [31, Theorem 1.2], we will describe how to compute an
isomorphic primitive representation of  ,
and how to compute the corresponding conversions. This will allow us to
apply the results from section 5.1. In this subsection, we
assume the boolean RAM model instead of the Turing model, in order to
use the results from [31].
,
and how to compute the corresponding conversions. This will allow us to
apply the results from section 5.1. In this subsection, we
assume the boolean RAM model instead of the Turing model, in order to
use the results from [31].
 . Let
. Let 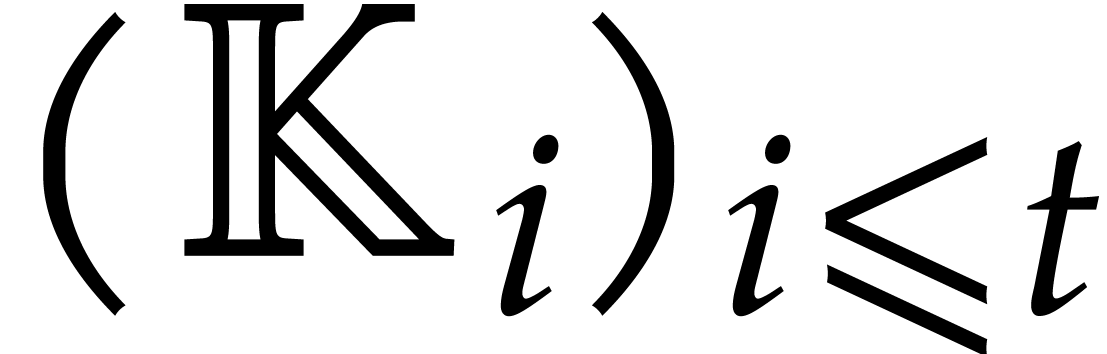 be given as above for a triangular tower
be given as above for a triangular tower 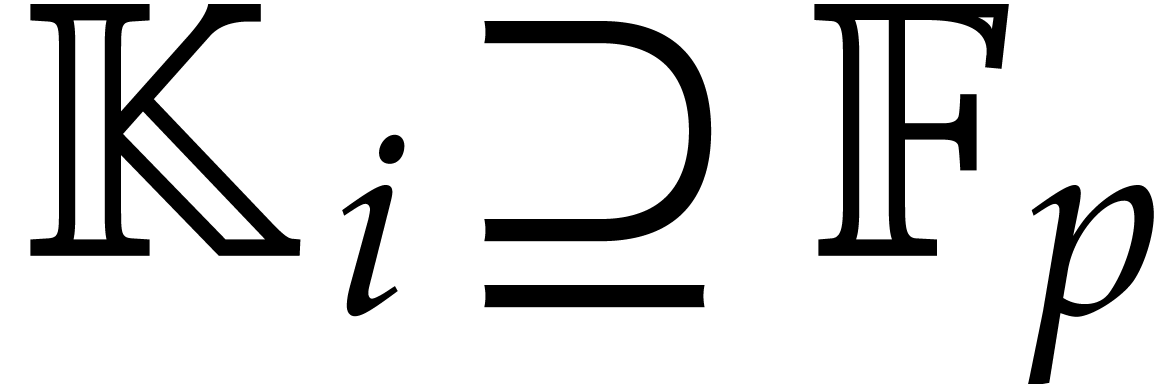 and assume that
and assume that 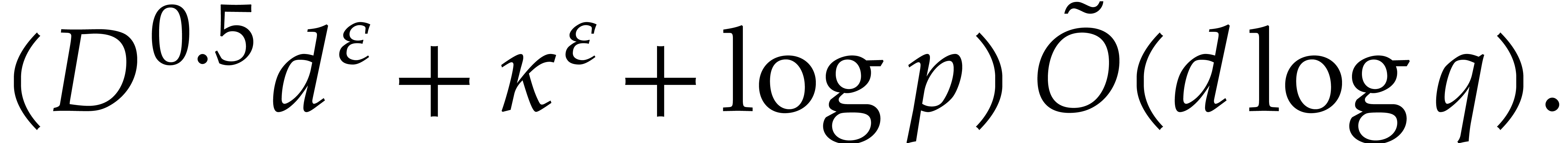 .
Then the computation of the irreducible factors of degree
.
Then the computation of the irreducible factors of degree 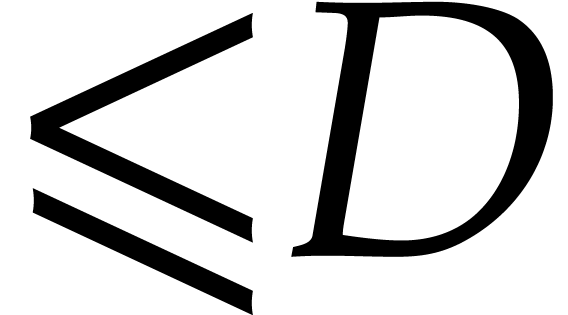 of a polynomial
of a polynomial 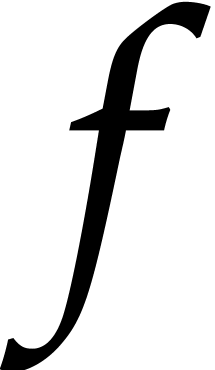 of degree
of degree  in
in 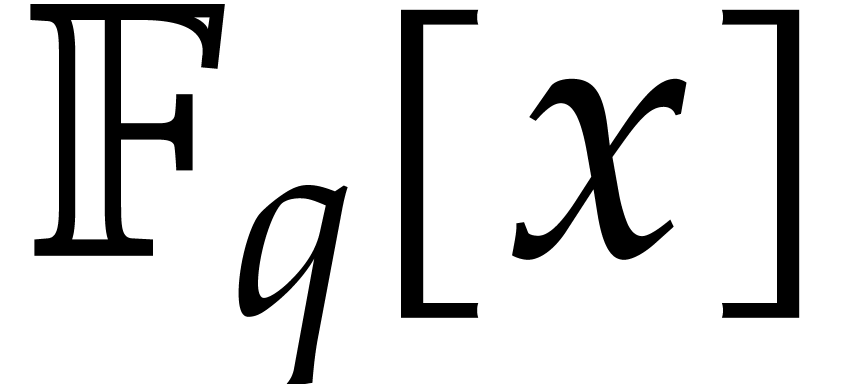 takes an expected
time
takes an expected
time

Proof. The number of monic irreducible
polynomials of degree 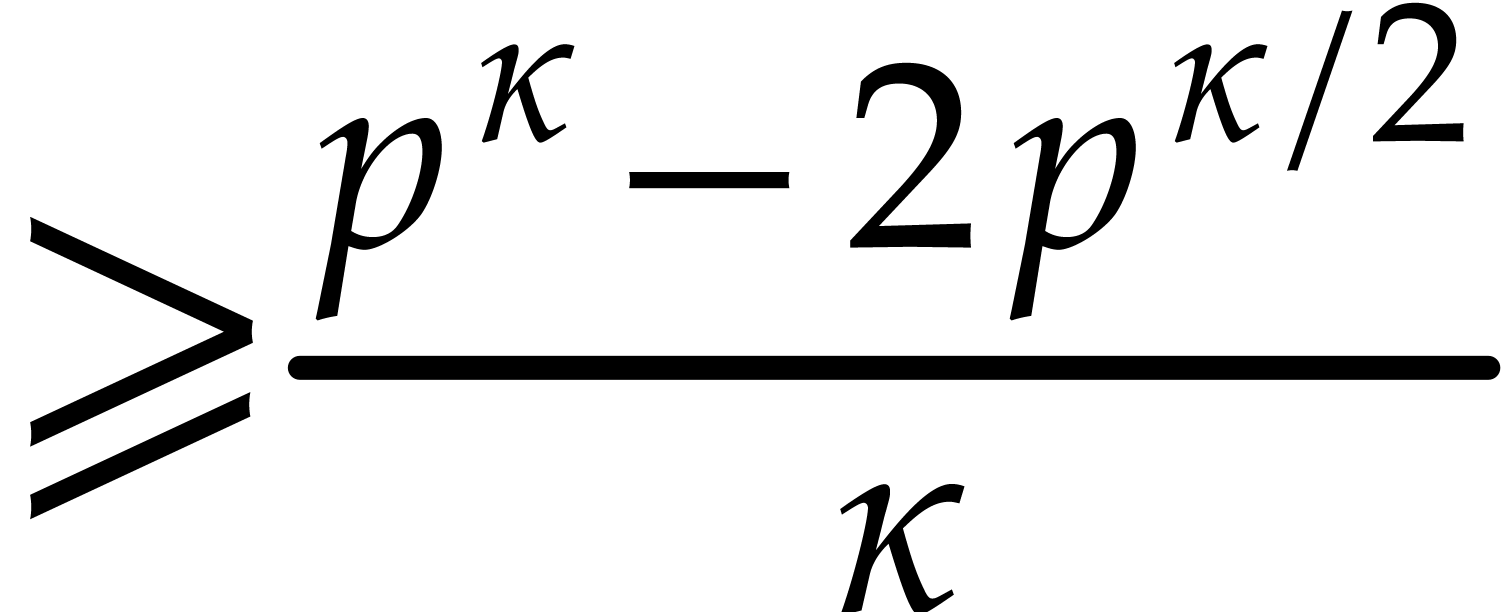 over
over  is
is  ; see for instance [9, Lemma 14.38]. Therefore the number of elements
; see for instance [9, Lemma 14.38]. Therefore the number of elements 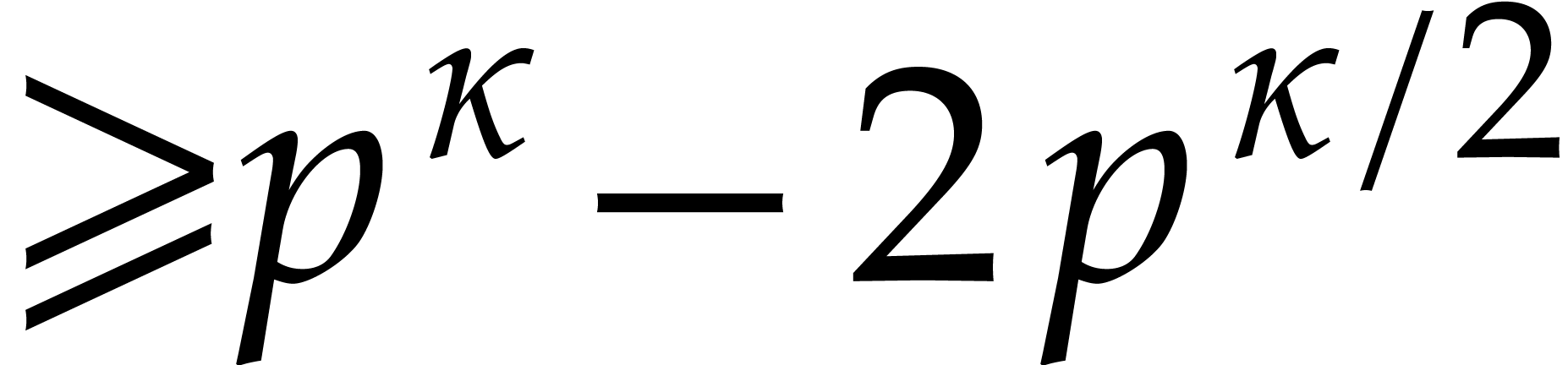 in
in  that generate
that generate  is
is 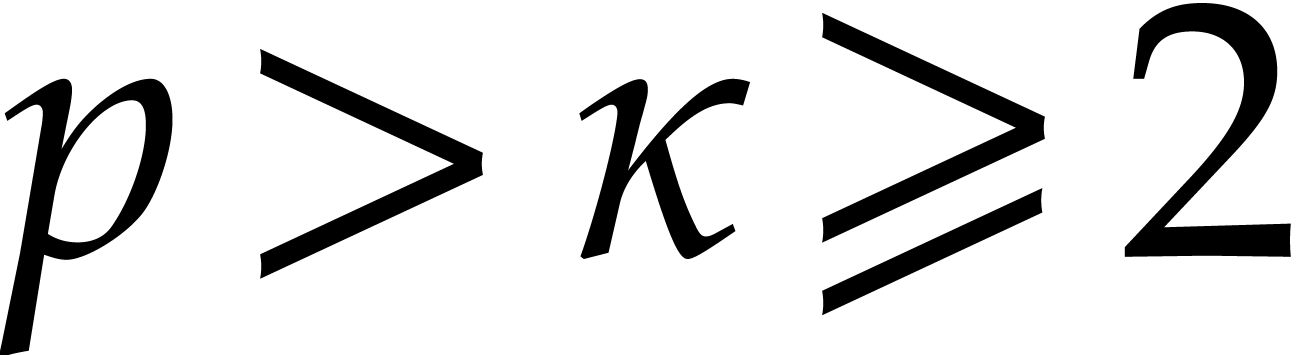 . The probability to pick
up a generator of
. The probability to pick
up a generator of  over
over  is uniformly lower bounded, since
is uniformly lower bounded, since 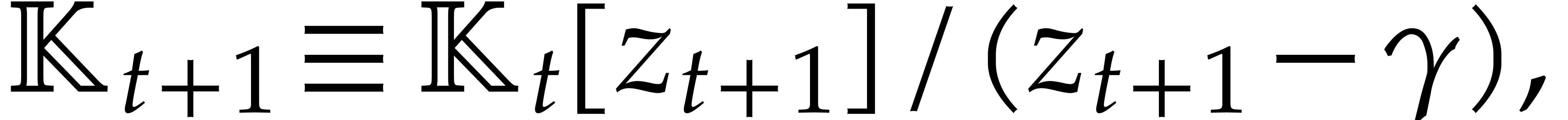 .
.
The assumption 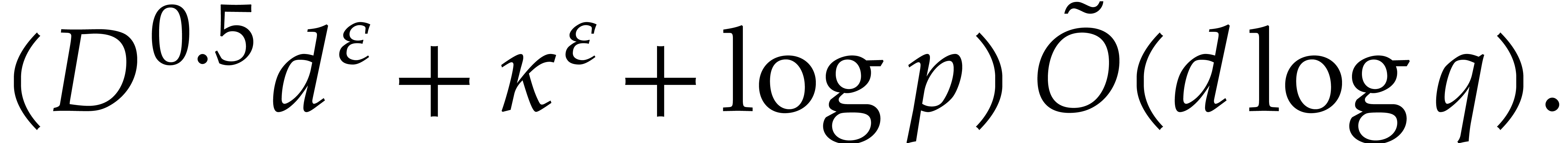 allows us to apply [31,
Theorem 1.2] to the following data:
allows us to apply [31,
Theorem 1.2] to the following data:
The tower 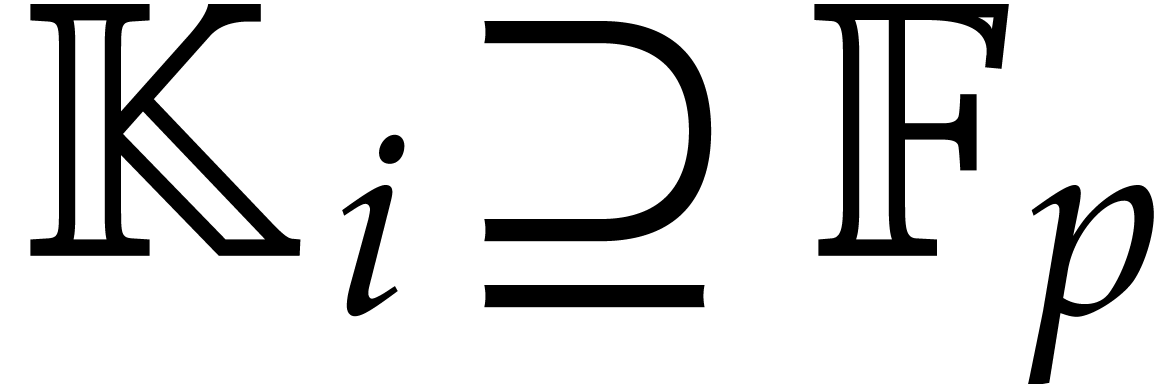 extended with
extended with
where 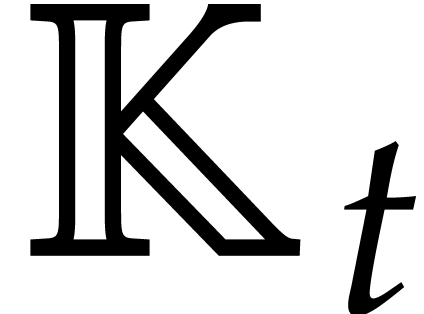 is an element picked up randomly in
is an element picked up randomly in
 ;
;
The “target order” 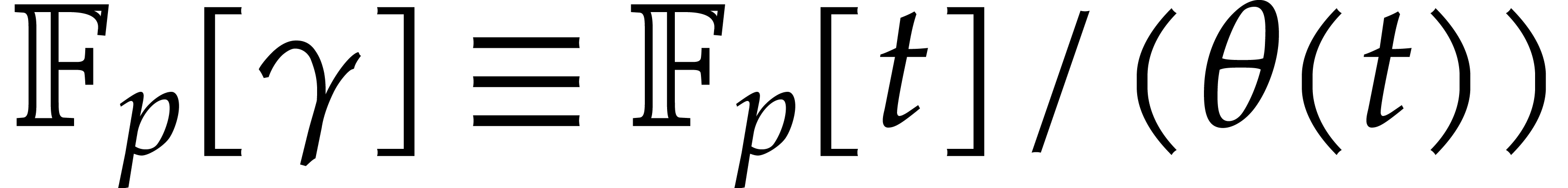 .
.
When 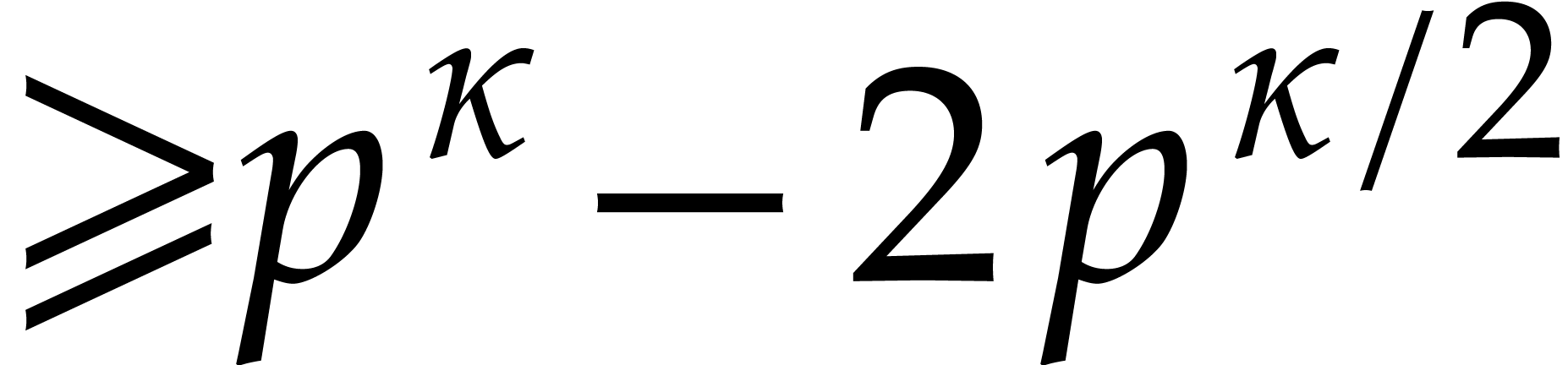 generates
generates  over
over  we obtain an isomorphic primitive element
presentation of
we obtain an isomorphic primitive element
presentation of  of the form
of the form 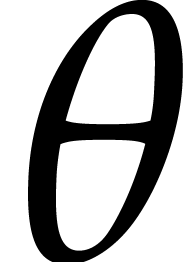 , where
, where 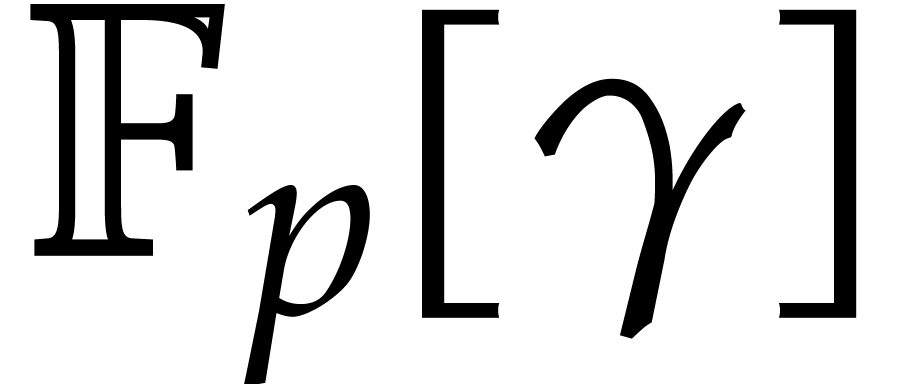 denotes the
defining polynomial of
denotes the
defining polynomial of 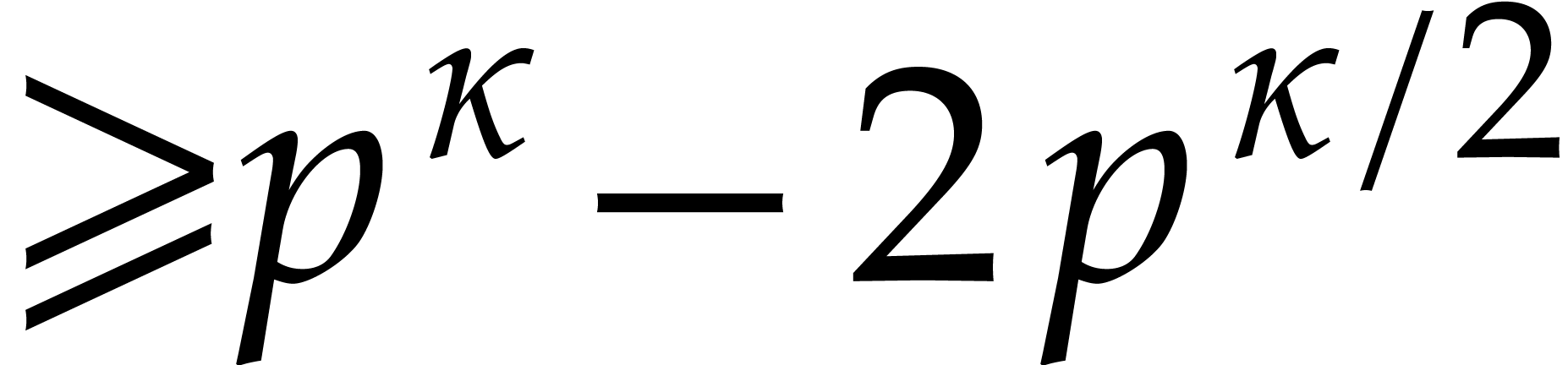 over
over  . If
. If 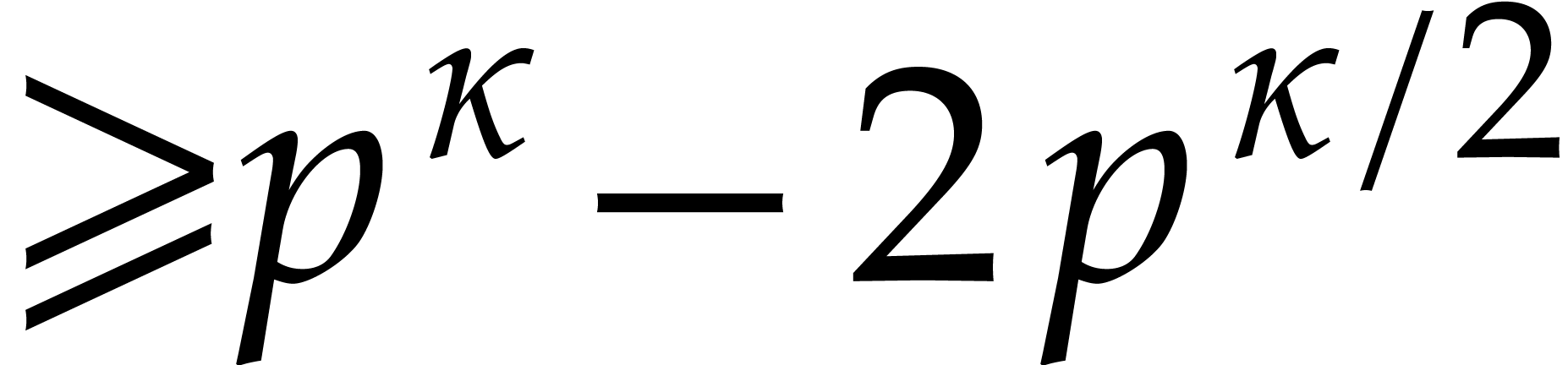 is not primitive
then the algorithm underlying [31, Theorem 1.2] is able to
detect it. In all cases, the time to construct
is not primitive
then the algorithm underlying [31, Theorem 1.2] is able to
detect it. In all cases, the time to construct 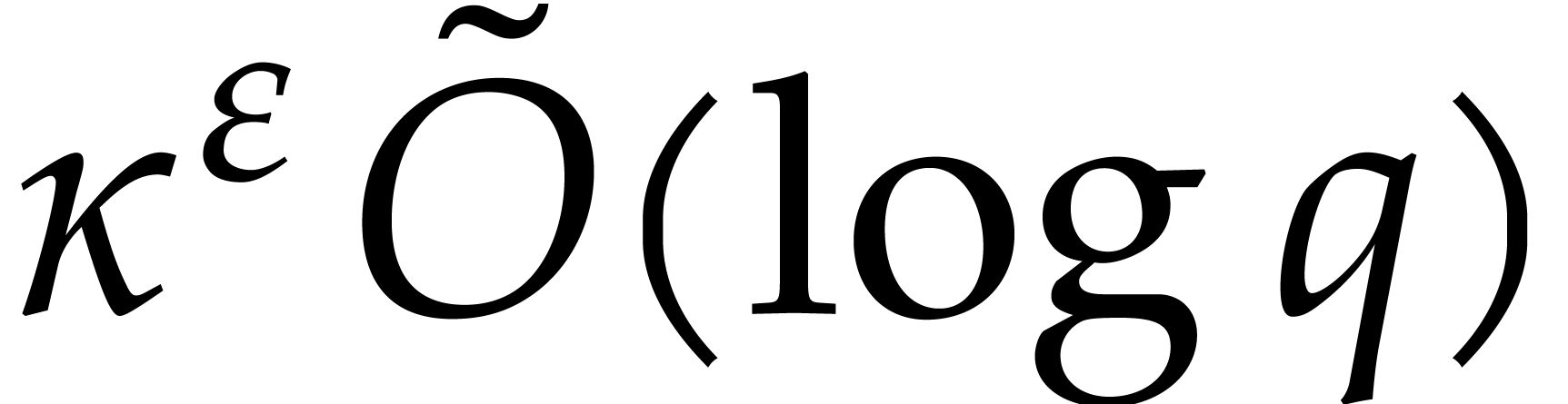 is
is 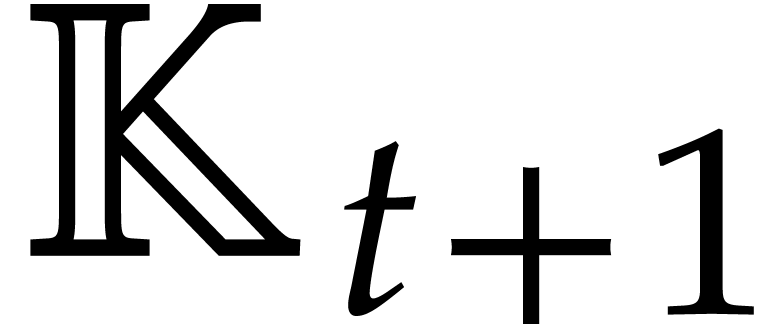 . If
. If 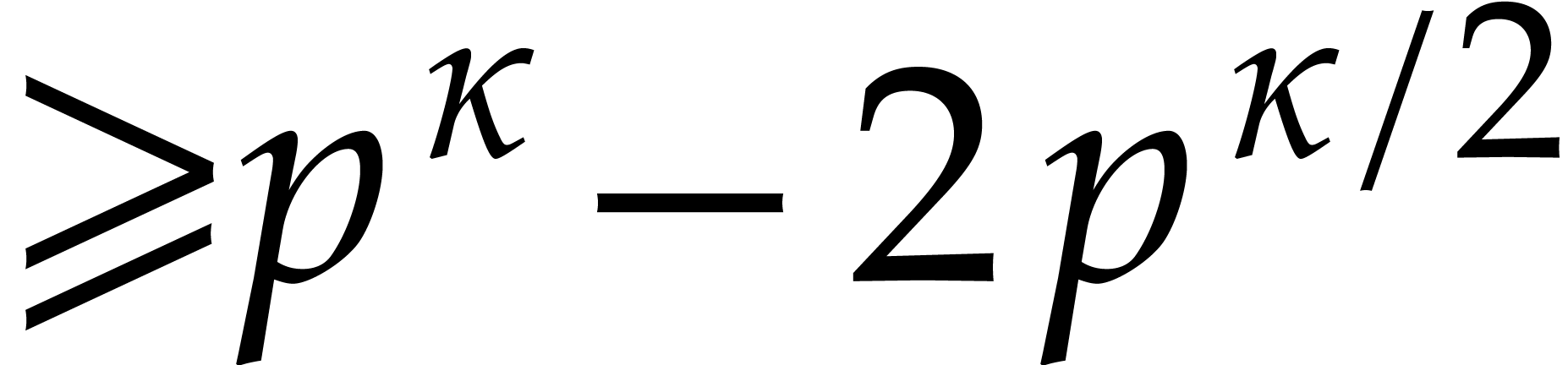 is primitive, then [31, Theorem 1.2] also ensures
conversions between
is primitive, then [31, Theorem 1.2] also ensures
conversions between  and
and 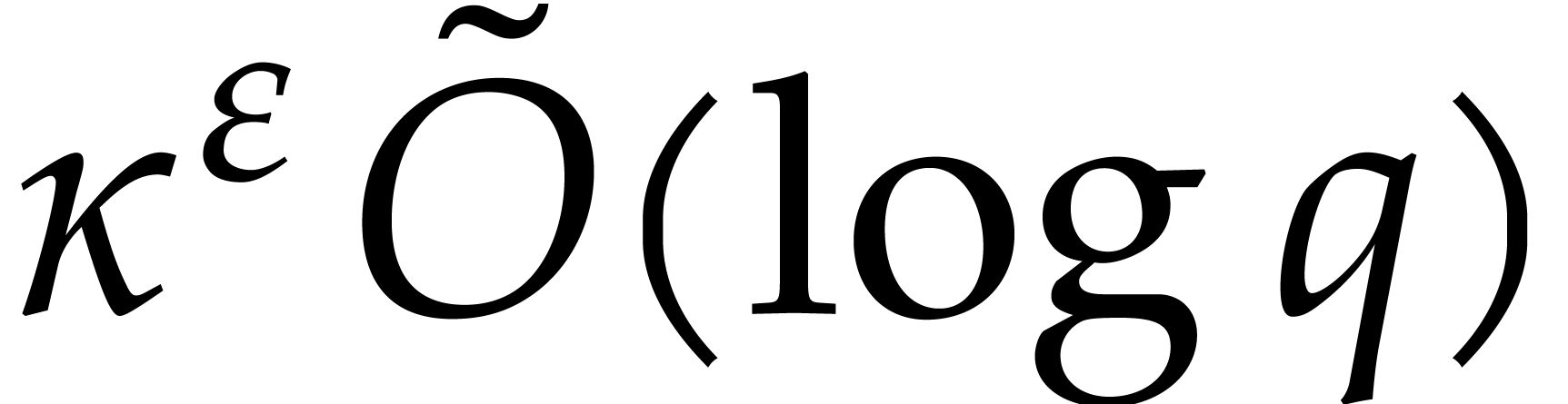 in time
in time 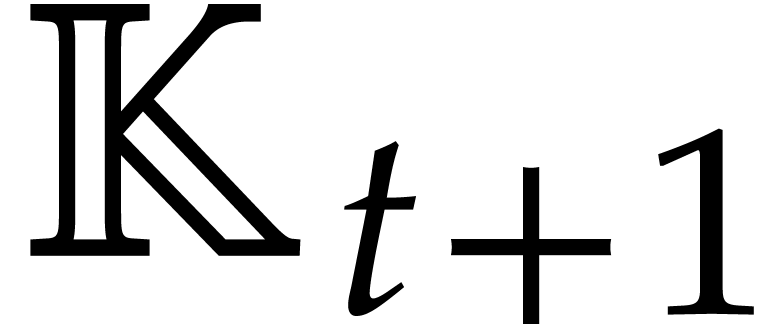 . Consequently the
result follows from Corollary 5.1.
. Consequently the
result follows from Corollary 5.1.
An alternative approach for modular composition over  was proposed in [16]. The approach is only efficient when
the extension degree
was proposed in [16]. The approach is only efficient when
the extension degree  over
over  is composite. If
is composite. If  is smooth and if mild technical
conditions are satisfied, then it is even quasi-optimal. It also does
not rely on the Kedlaya–Umans algorithm and we expect it to be
useful in practice for large composite
is smooth and if mild technical
conditions are satisfied, then it is even quasi-optimal. It also does
not rely on the Kedlaya–Umans algorithm and we expect it to be
useful in practice for large composite  .
.
The main approach from [16] can be applied in several ways.
As in [16], we will first consider the most general case
when  is presented via a triangular tower. In
that case, it is now possible to benefit from accelerated tower
arithmetic that was designed in [17]. We next examine
several types of “primitive towers” for which additional
speed-ups are possible.
is presented via a triangular tower. In
that case, it is now possible to benefit from accelerated tower
arithmetic that was designed in [17]. We next examine
several types of “primitive towers” for which additional
speed-ups are possible.
In order to apply the results from [16, 17], all complexity bounds in this section assume the boolean RAM model instead of the Turing model.
As in section 5.2, a triangular tower over  is a tower of algebraic extensions
is a tower of algebraic extensions
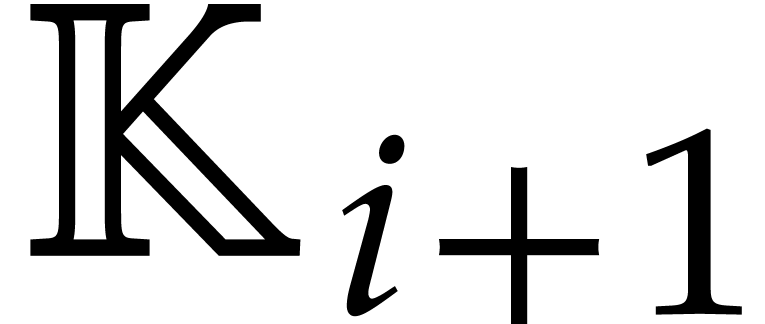
such that 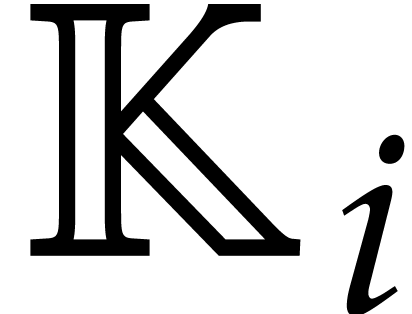 is presented as a primitive extension
over
is presented as a primitive extension
over 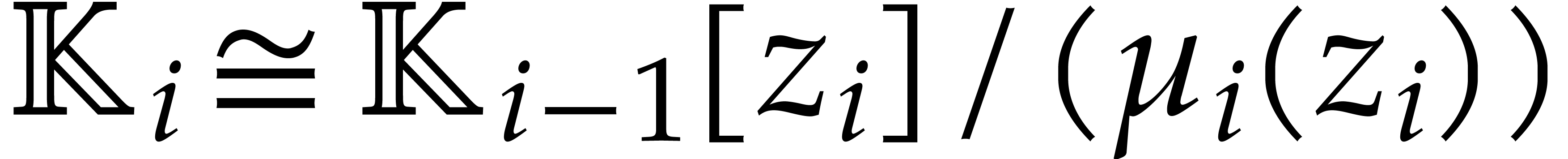 . In other words, for
. In other words, for
 , we have
, we have

for some monic irreducible polynomial 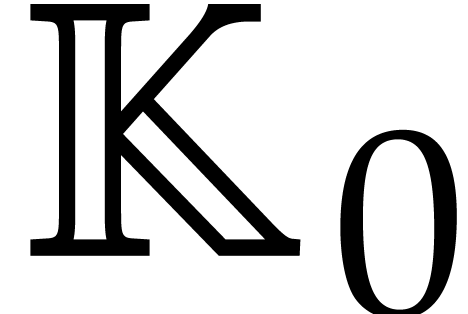 of degree
of degree
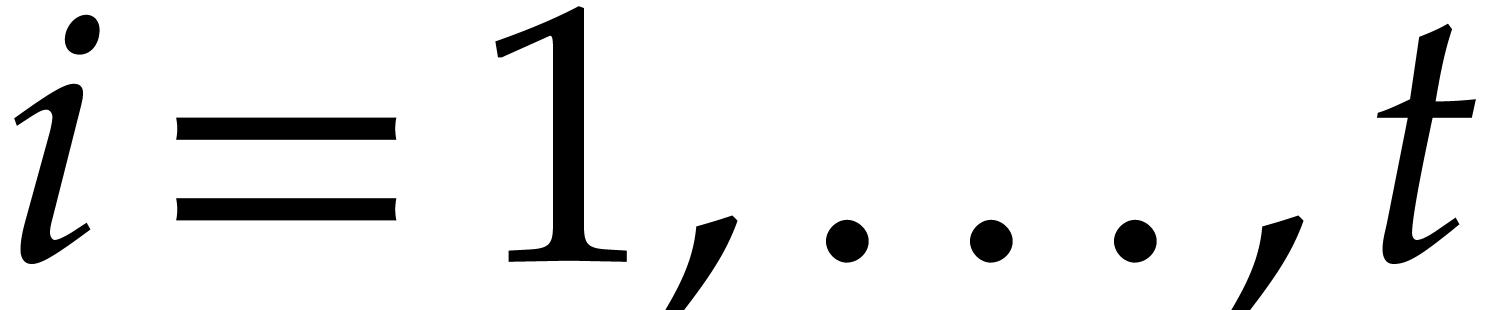 . Alternatively, each
. Alternatively, each 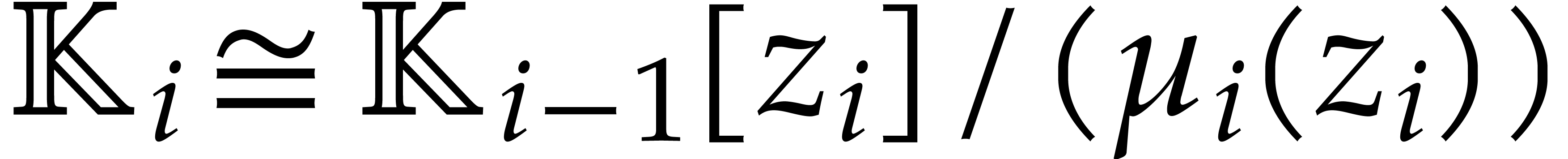 can be presented directly over
can be presented directly over 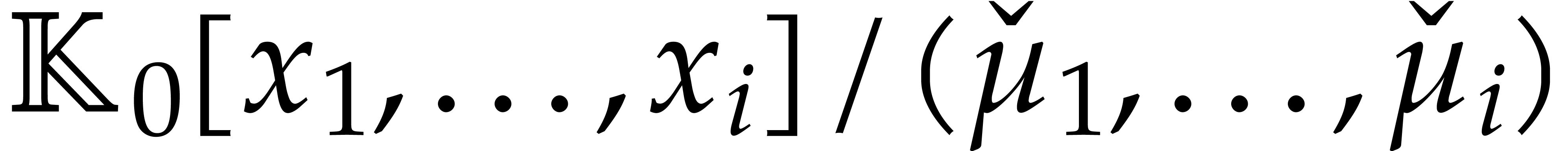 as a quotient
as a quotient 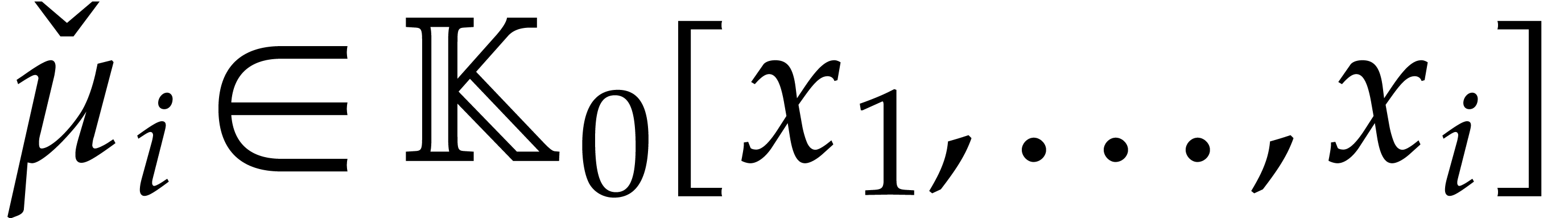 , where
, where 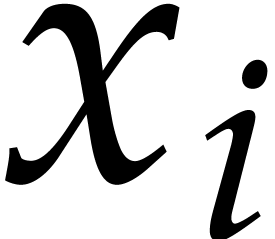 is monic of degree
is monic of degree 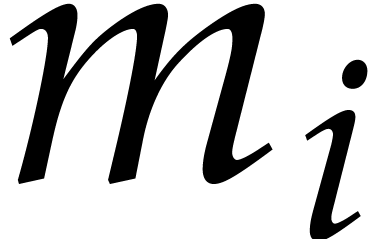 in
in  and of degree
and of degree  in
in  for each
for each 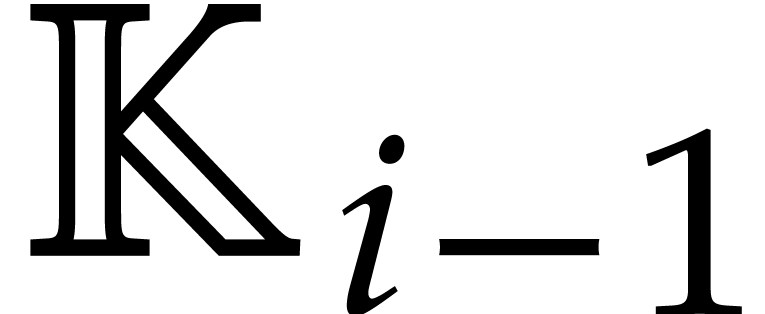 .
Triangular towers have the advantage that
.
Triangular towers have the advantage that 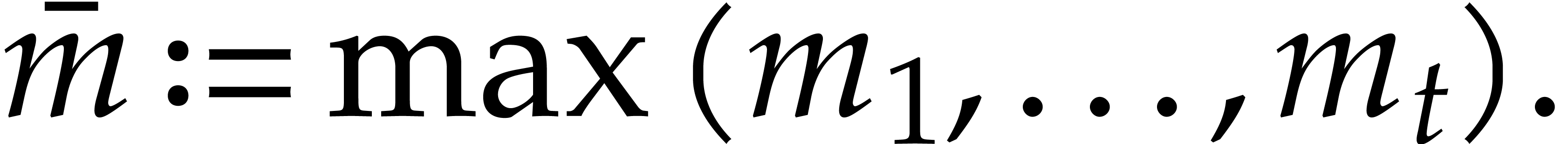 is
naturally embedded in
is
naturally embedded in 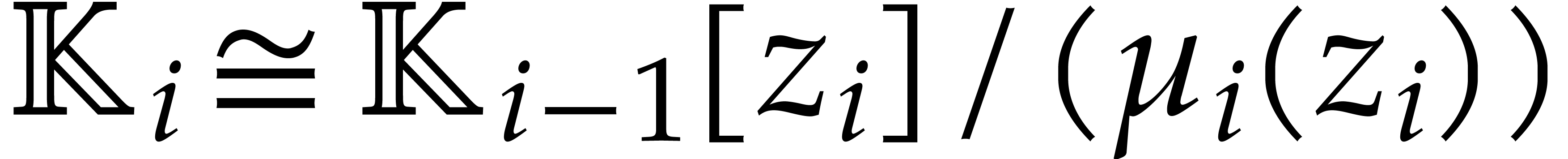 for each
for each  . We set
. We set
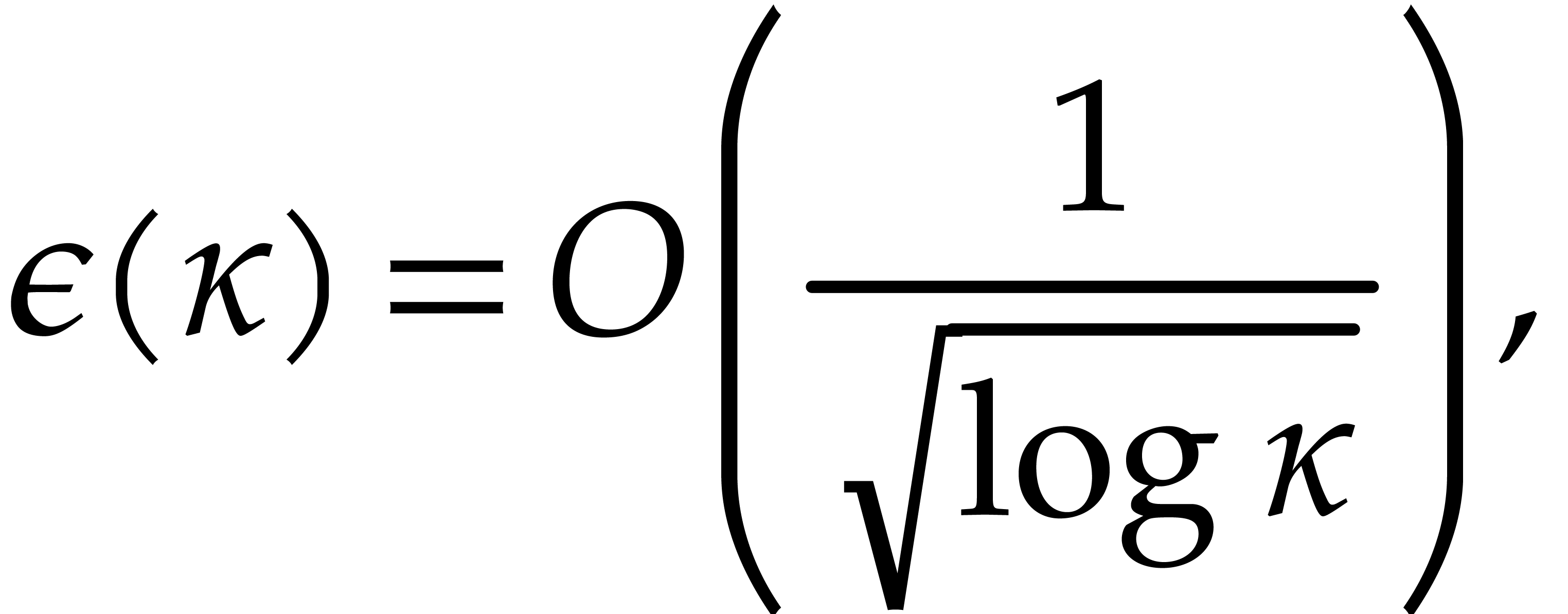
Proof. If 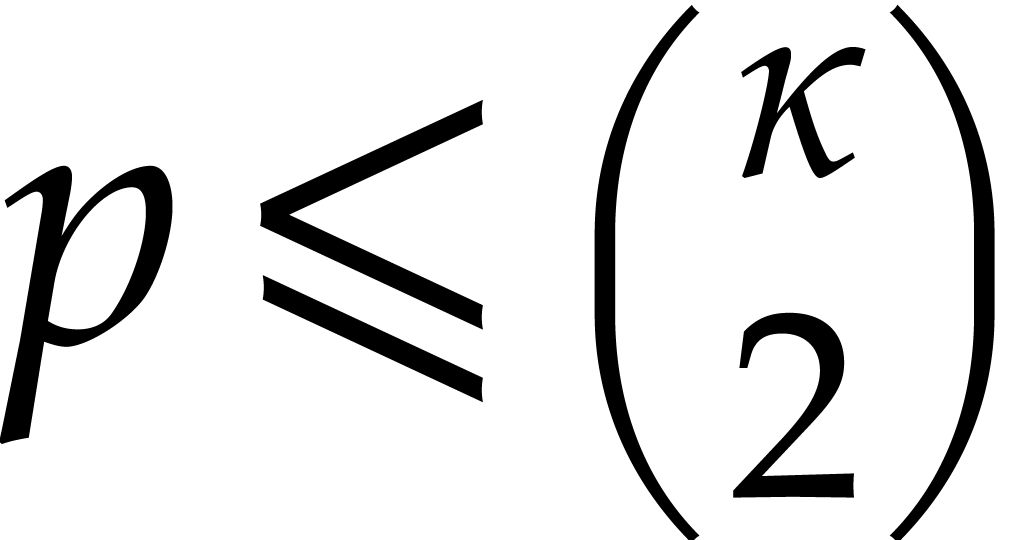 ,
then [17, Proposition 2.7 and Corollary 4.11] imply
,
then [17, Proposition 2.7 and Corollary 4.11] imply
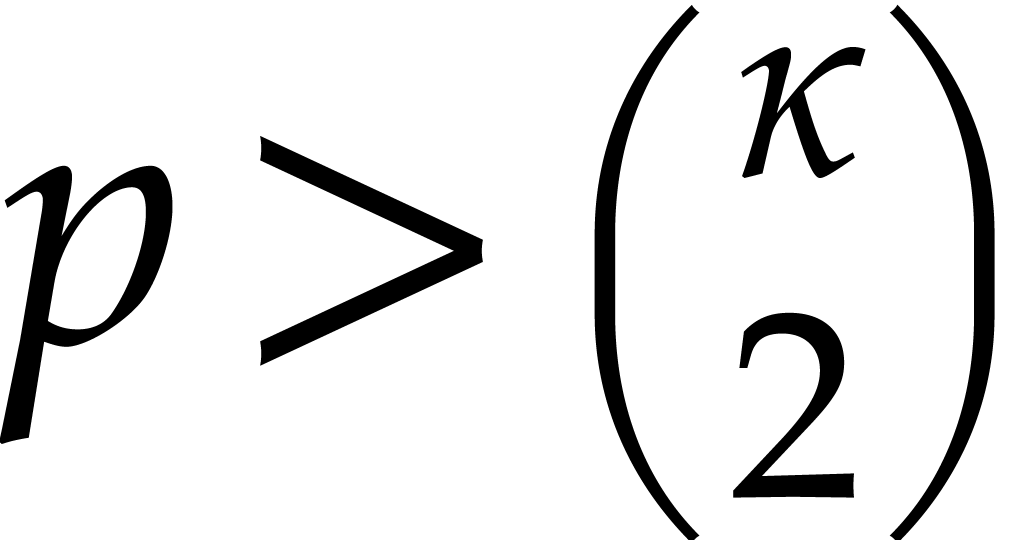
Now consider the case when 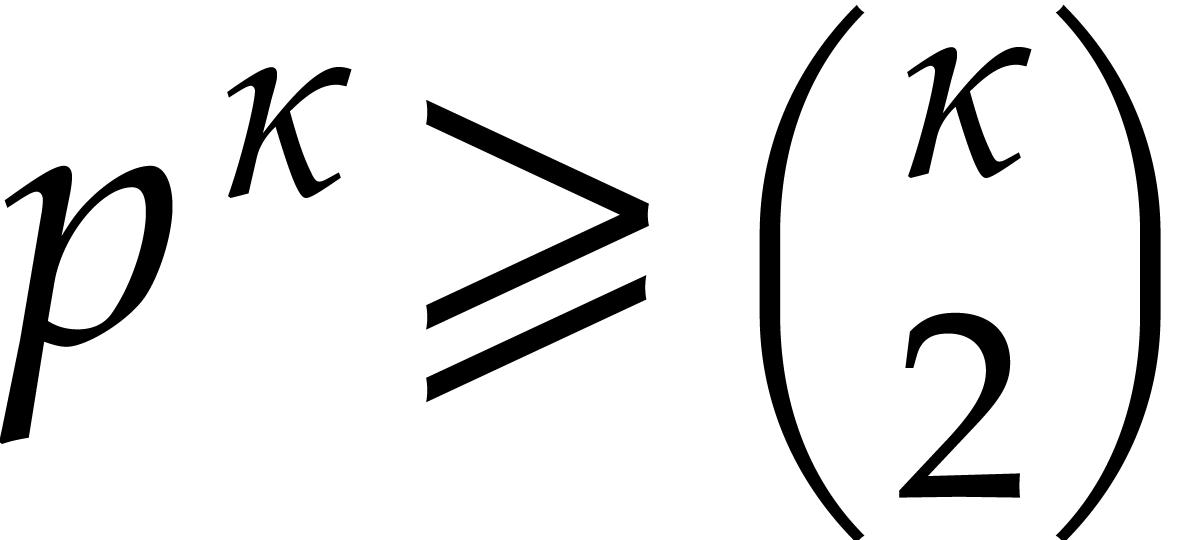 .
Since
.
Since  there exists a smallest integer
there exists a smallest integer 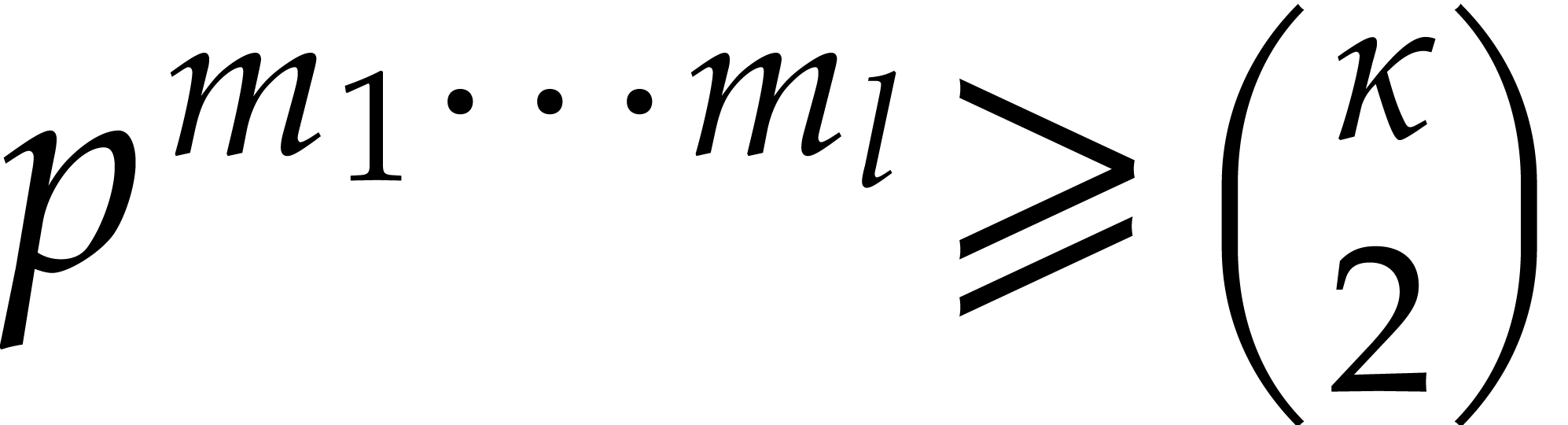 such that
such that 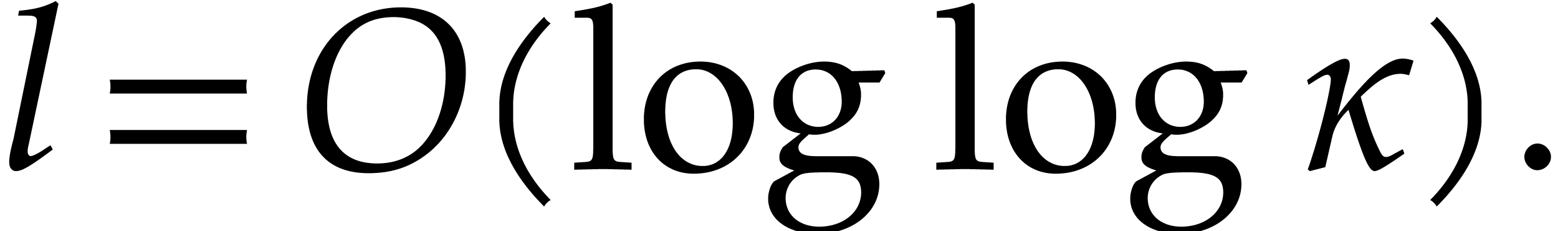 , and
, and
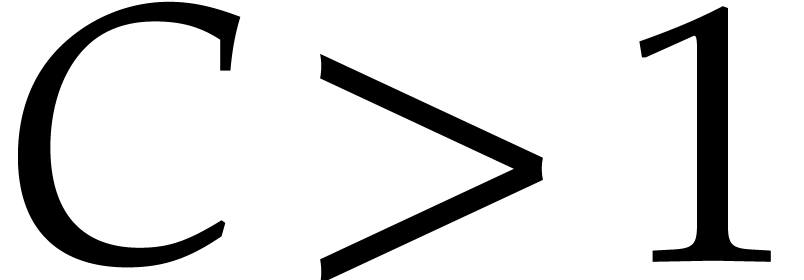
For any constant 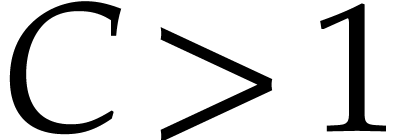 we note that
we note that 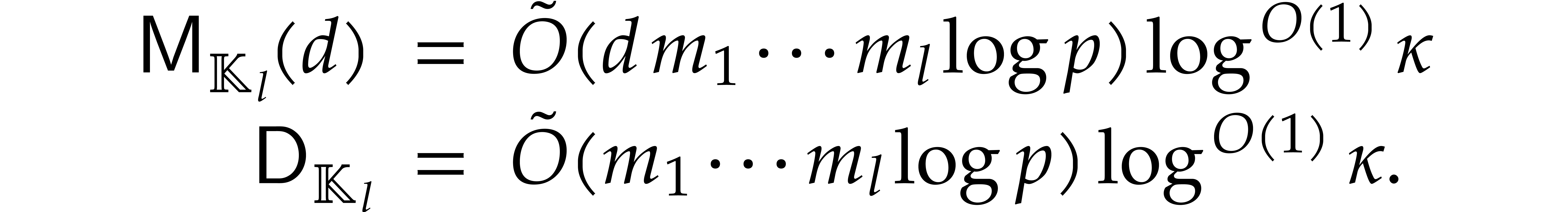 , so [17, Propositions 2.4 and
2.7] yield
, so [17, Propositions 2.4 and
2.7] yield

On the other hand, applying [17, Proposition 2.7 and Corollary 4.11] to the sub-tower
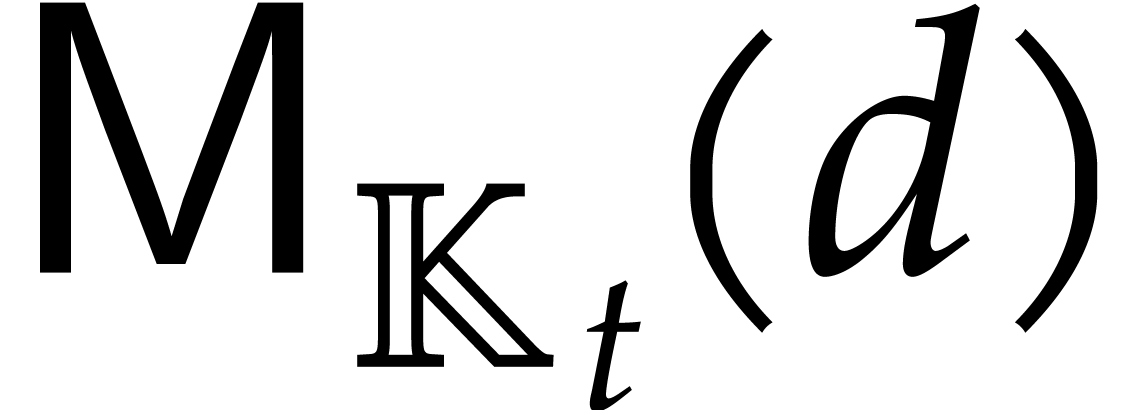
we obtain
 |
 |
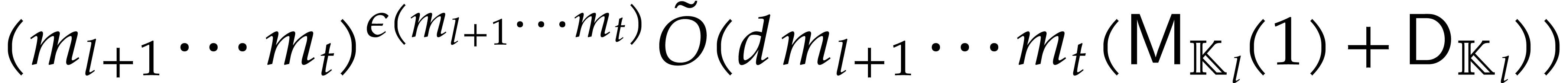 |
|
 |
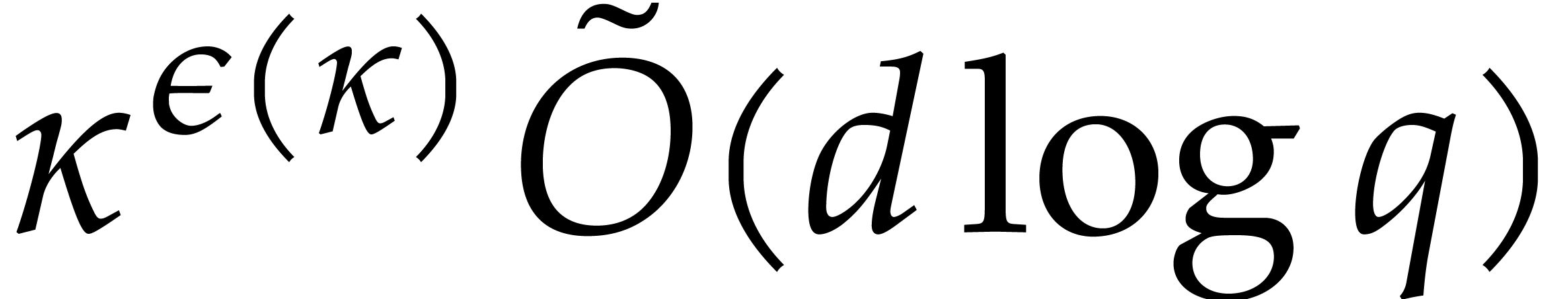 |
||
 |
 |
||
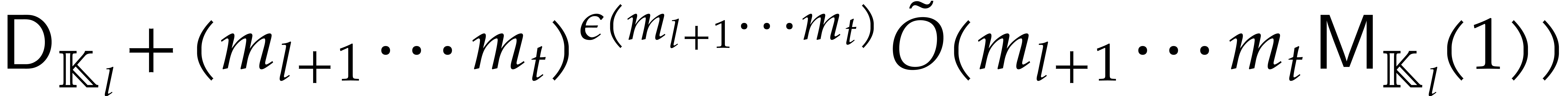 |
 |
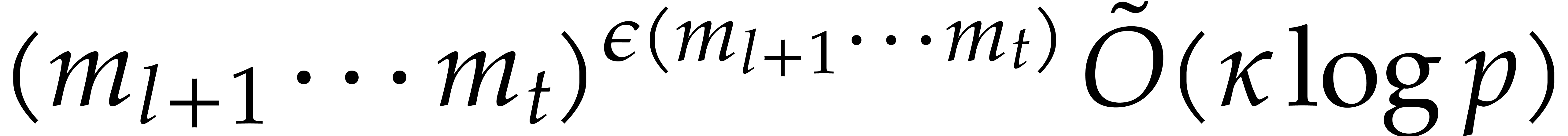 |
|
 |
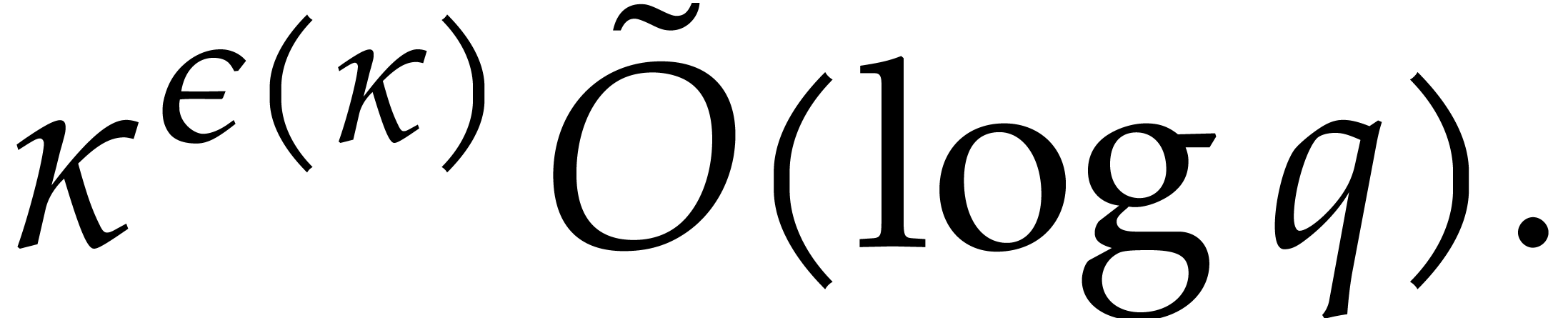 |
||
 |
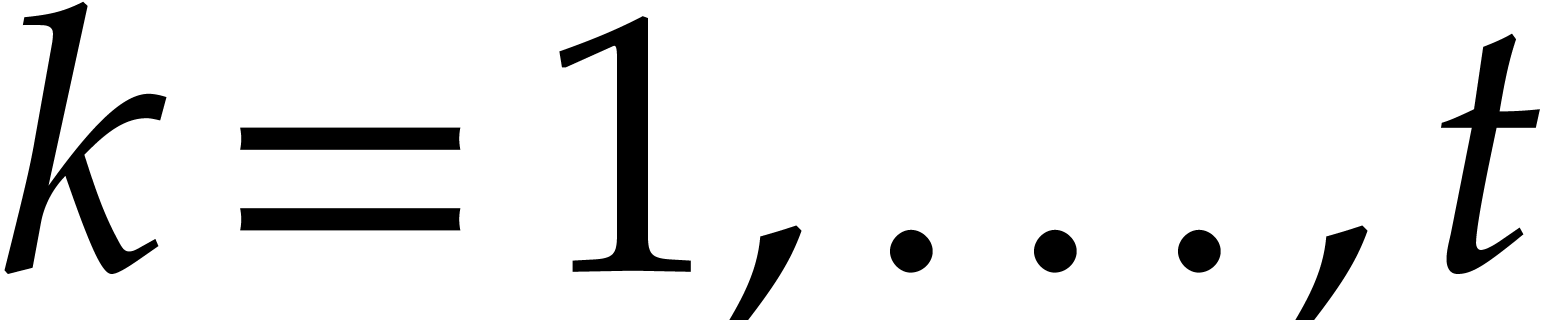 |
 |
In order to compute iterated Frobenius maps we extend the construction
from section 2.1. For this purpose we introduce the
following auxiliary sequences for 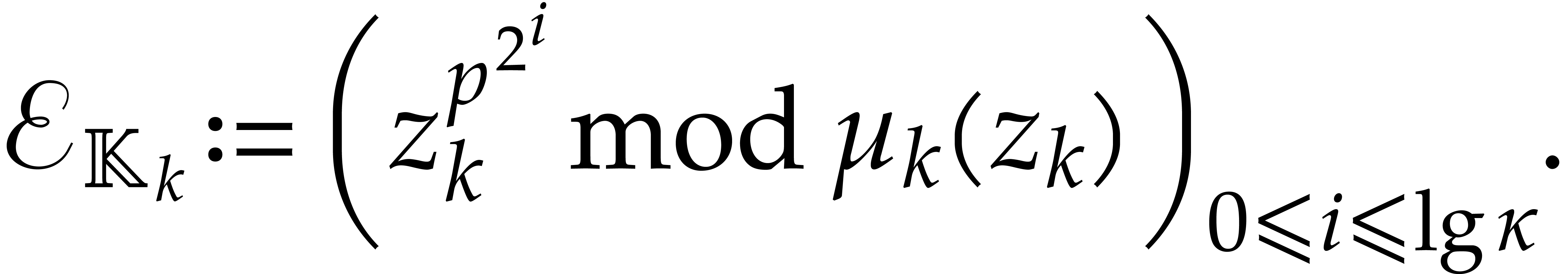 :
:
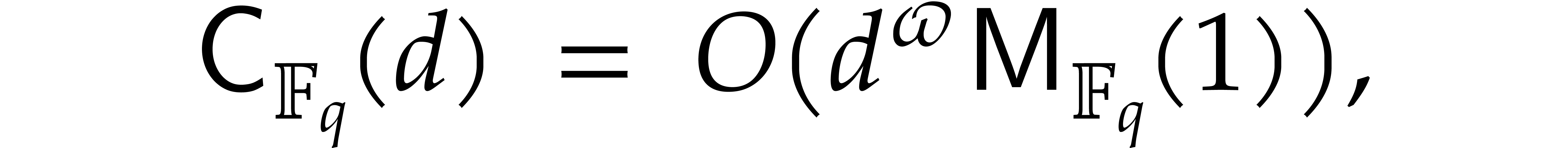
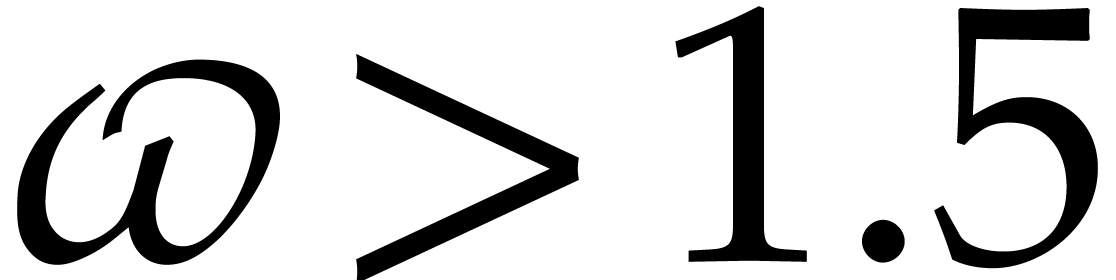
Since we wish to avoid relying on the Kedlaya–Umans algorithm, the best available algorithm for modular composition is based on the “baby-step giant-step” method [30]. It yields the following complexity bound:
where 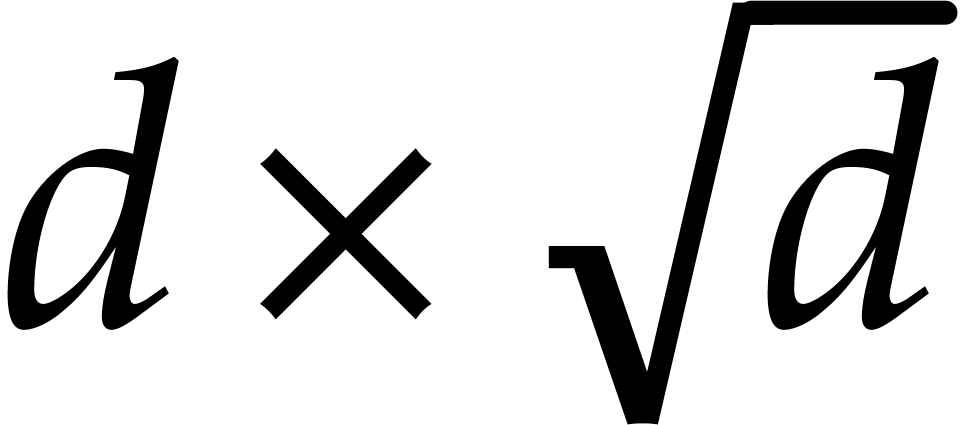 is a constant such that the product of a
is a constant such that the product of a
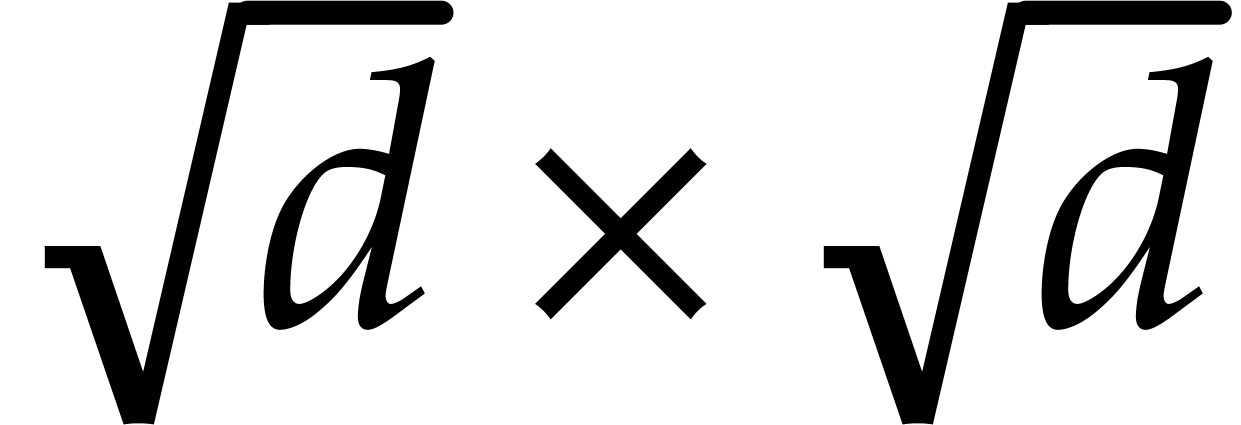 matrix by a
matrix by a 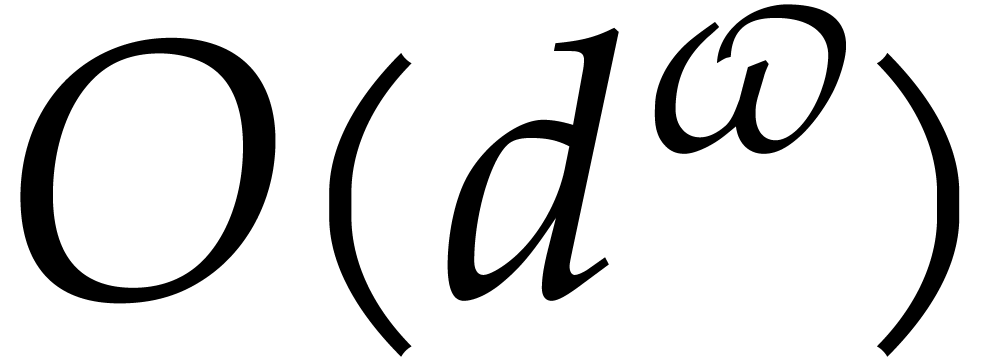 matrix takes
matrix takes
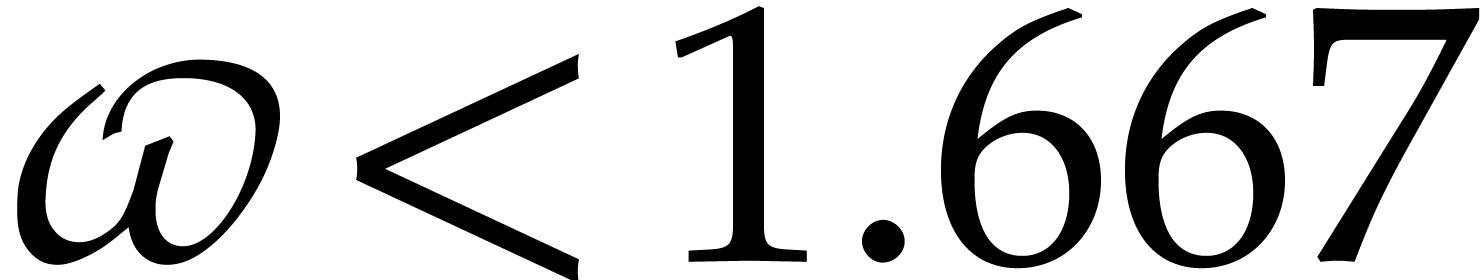 operations; the best known theoretical bound is
operations; the best known theoretical bound is
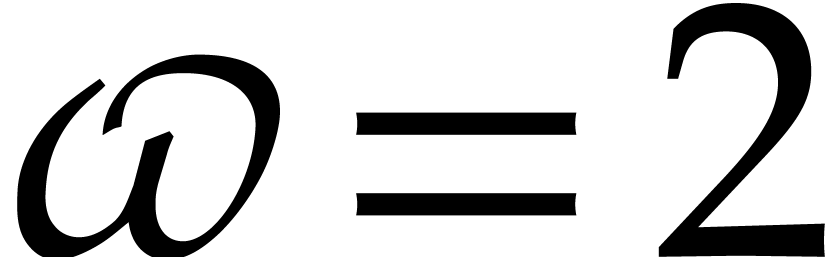 [20, Theorem 10.1]. In practice,
one usually assumes
[20, Theorem 10.1]. In practice,
one usually assumes  .
.
Proof. For  ,
let
,
let  be the time needed to compute
be the time needed to compute 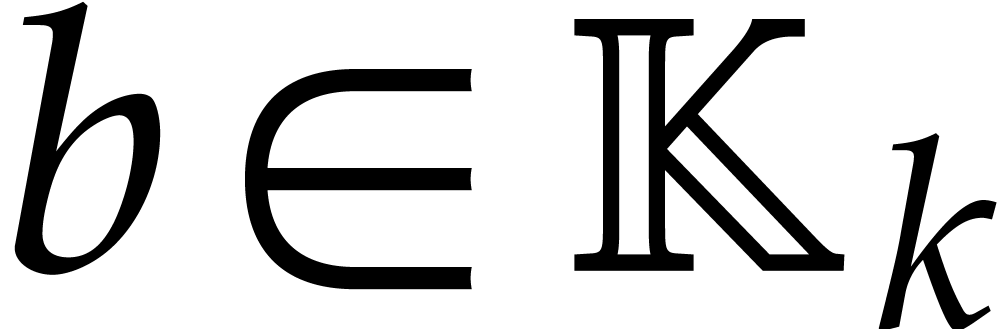 for any
for any 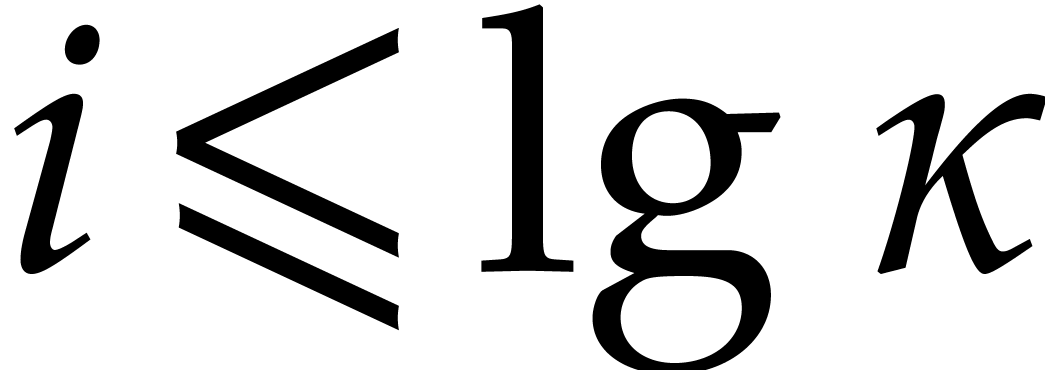 and
and 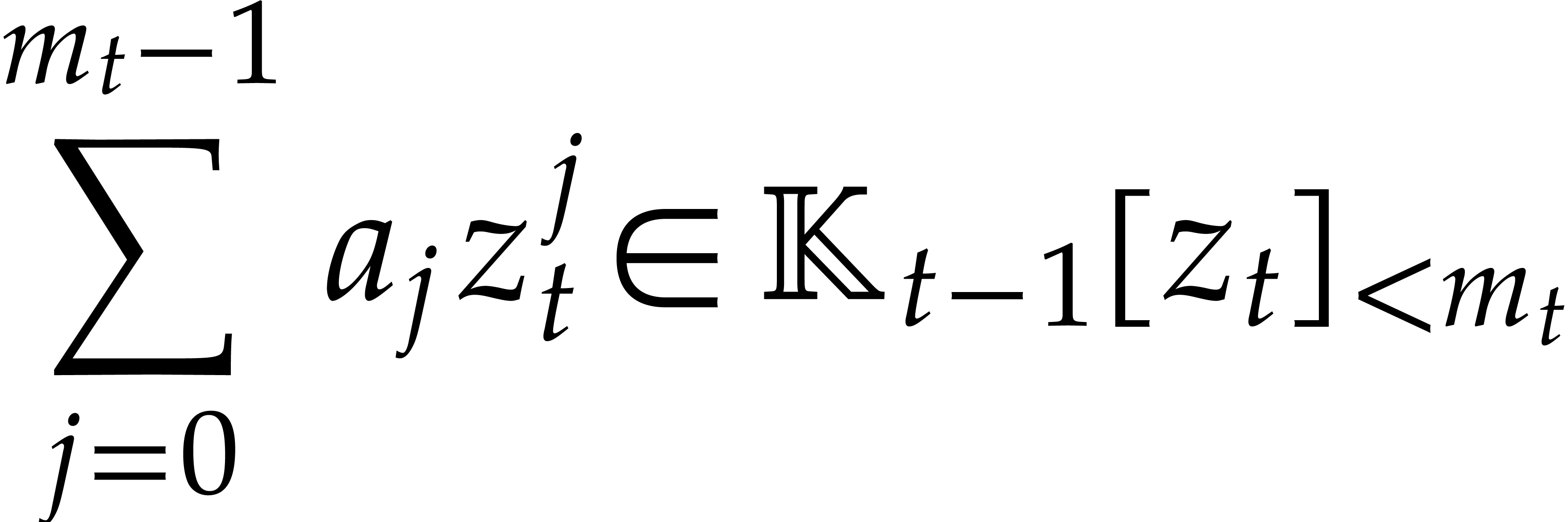 . Let
. Let
denote the canonical representative of 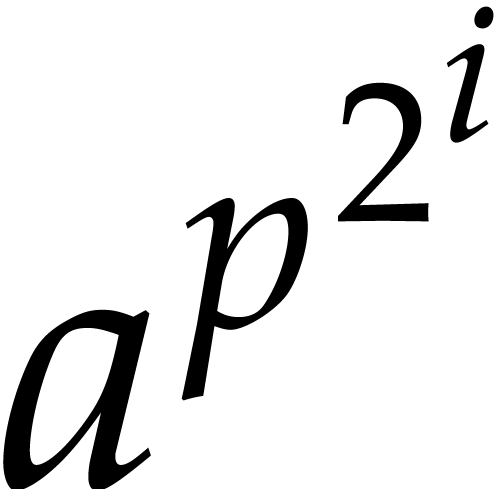 .
We have
.
We have
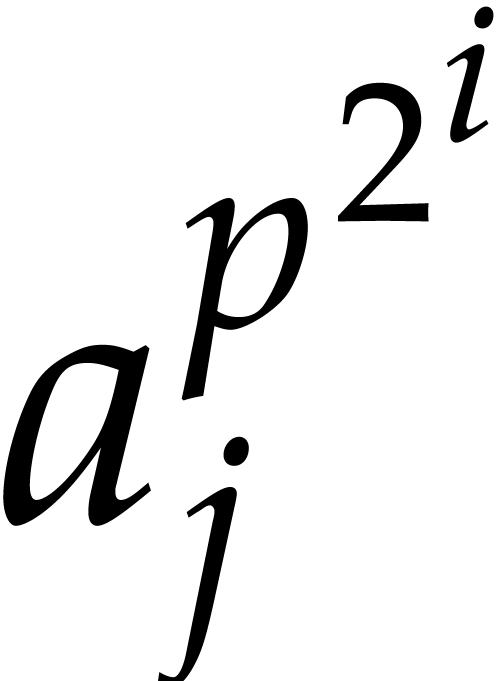
Now 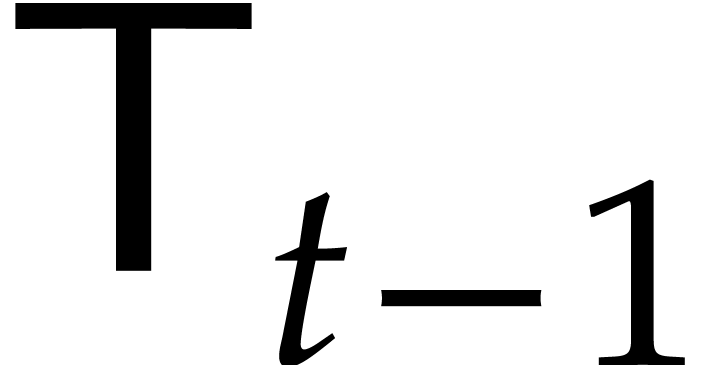 can be computed recursively in time
can be computed recursively in time 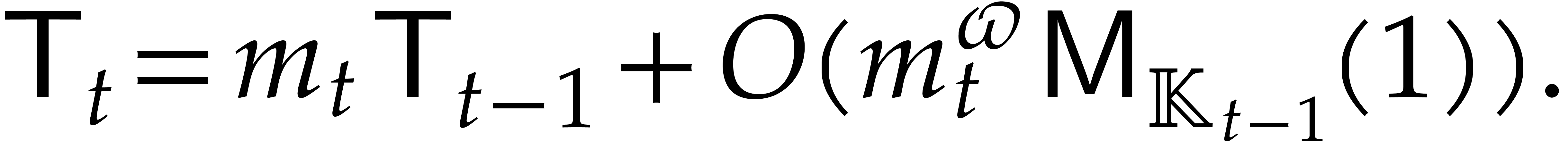 , so
, so
From Proposition 6.1 it follows that
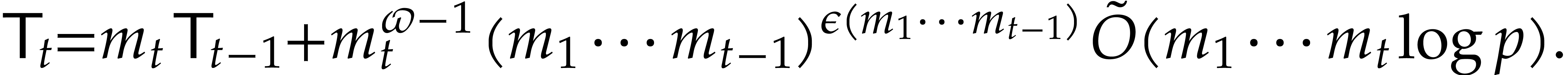
We conclude by unrolling this identity.
The auxiliary sequences 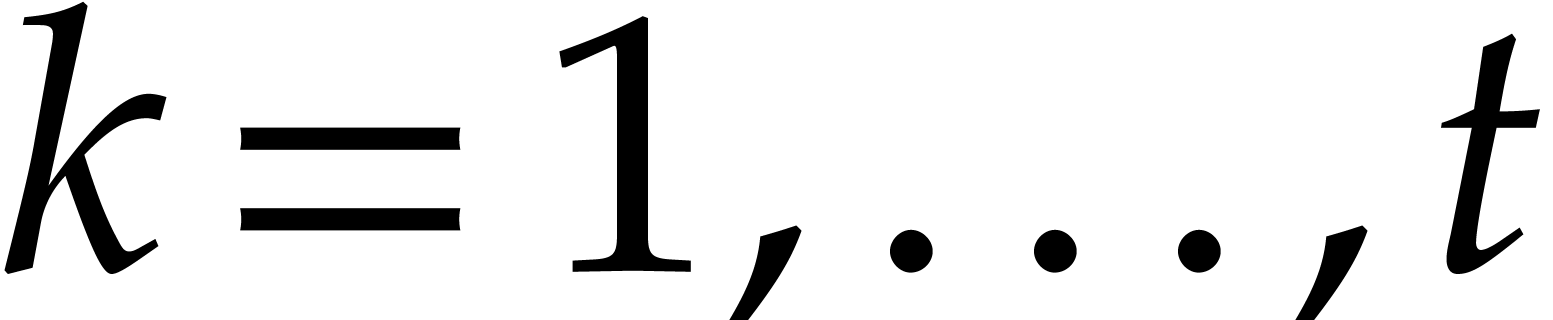 are computed by
induction using the following adaptation of Algorithm 2.2.
are computed by
induction using the following adaptation of Algorithm 2.2.
Algorithm
Compute 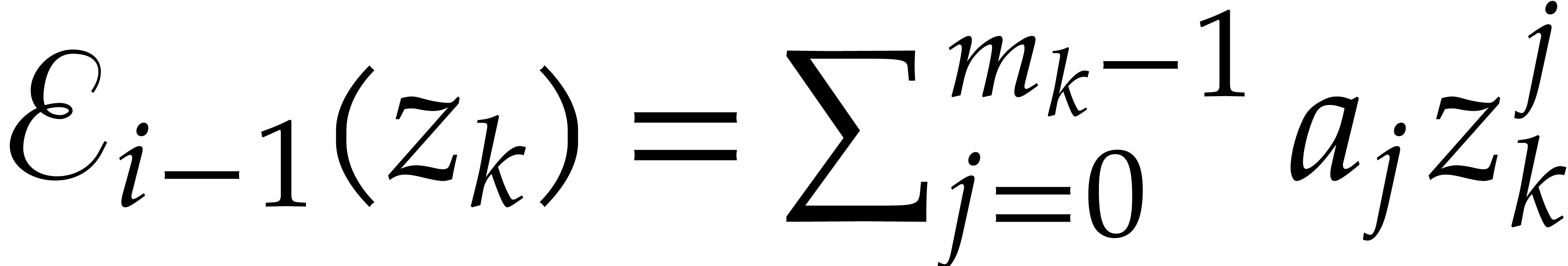 using binary powering.
using binary powering.
For  , write
, write 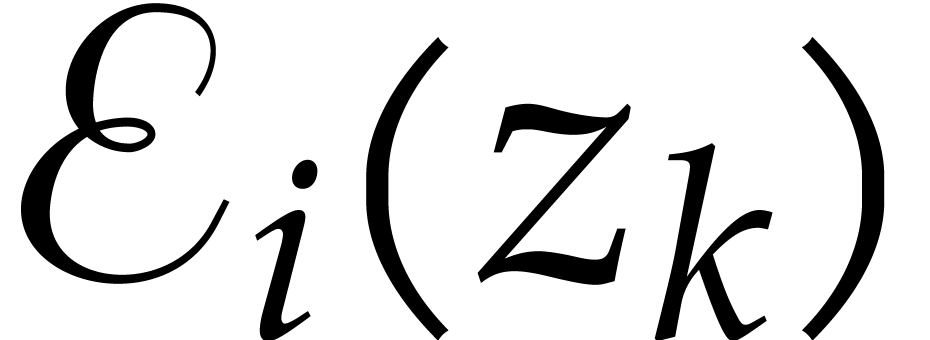 and compute
and compute 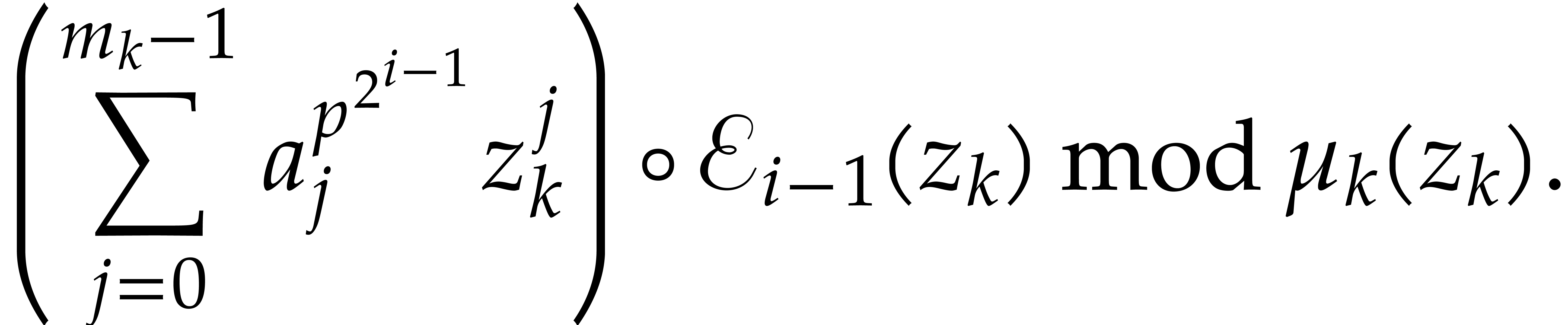 as
as
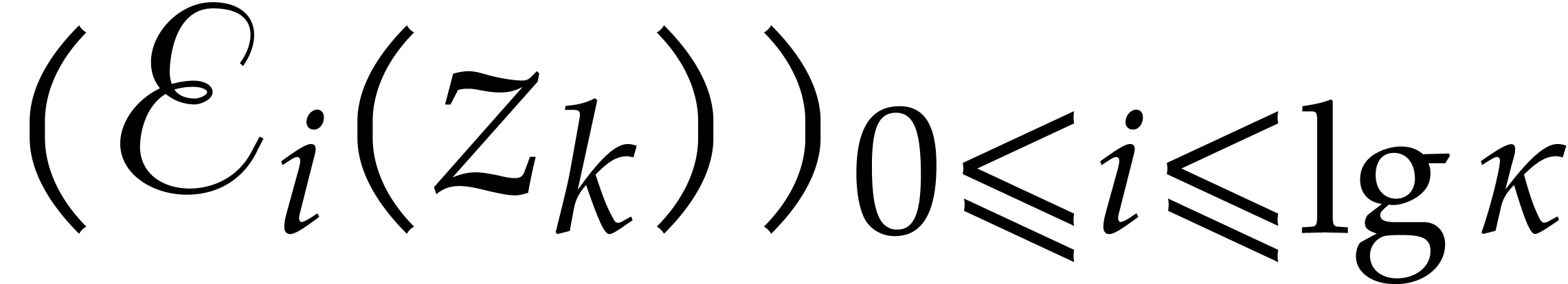
Return 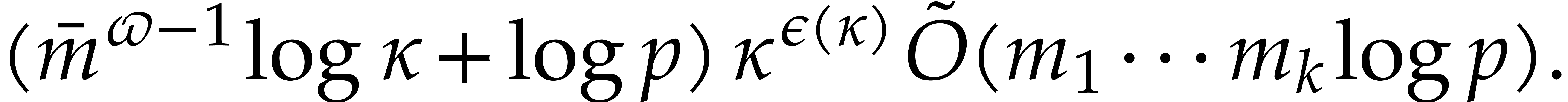 .
.
Proof. We prove the correctness by induction on
 . The case
. The case 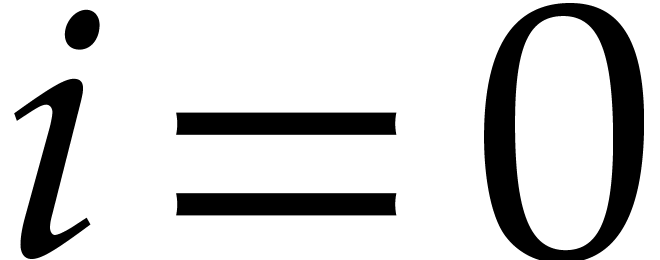 is clear. Assume that
is clear. Assume that  and let
and let 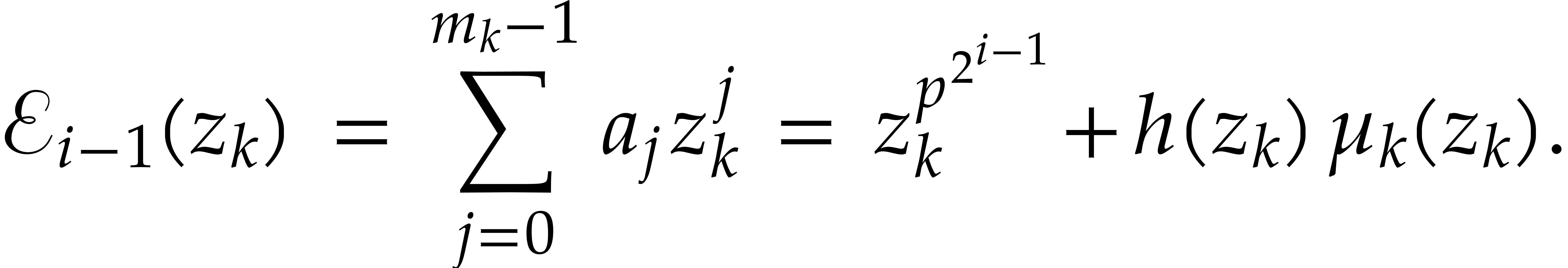 be such that
be such that
Then we have
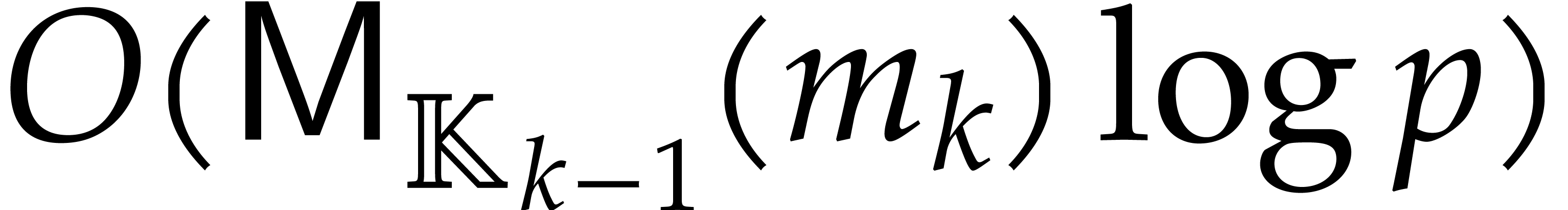
This completes the correctness proof. Concerning the complexity, the
first step takes time 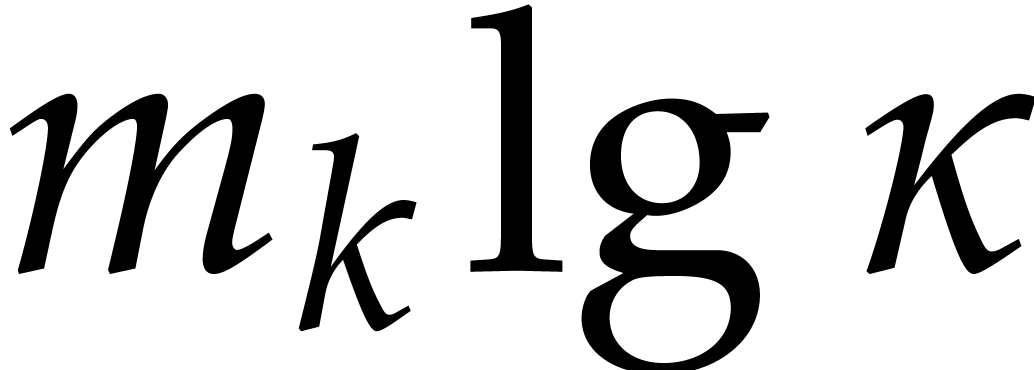 ,
whereas the loop requires
,
whereas the loop requires 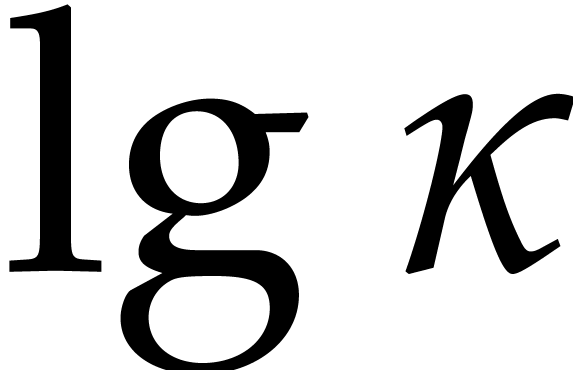 modular compositions
and
modular compositions
and 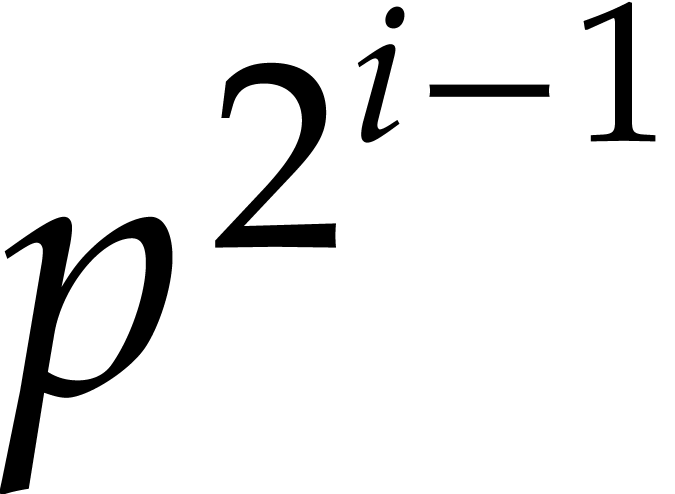 computations of
computations of 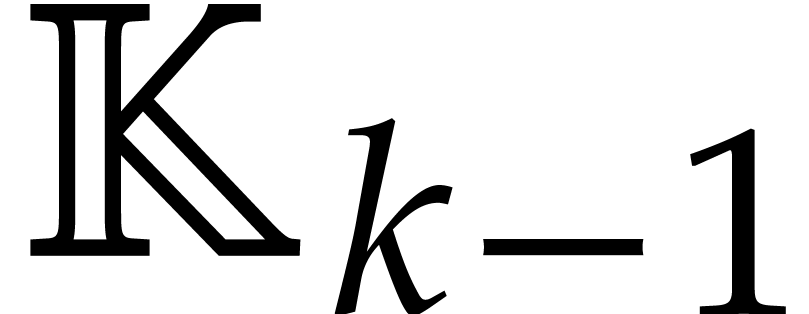 -th powers in
-th powers in  .
By Lemma 6.1, the total running time is therefore bounded
by
.
By Lemma 6.1, the total running time is therefore bounded
by
Using the bounds
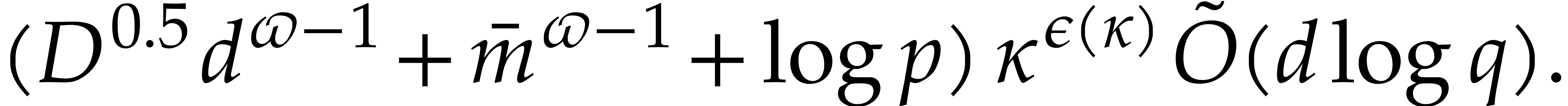
from Proposition 6.1, this yields the claimed cost.
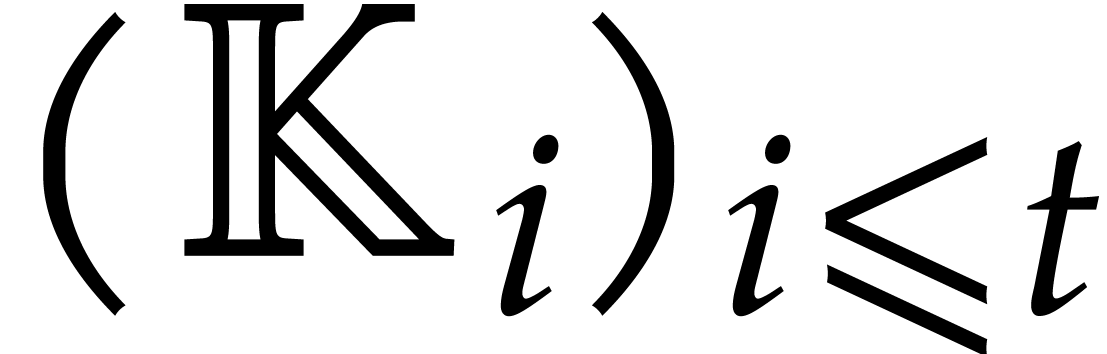 for a triangular
tower as above. The computation of the irreducible factors of degree
for a triangular
tower as above. The computation of the irreducible factors of degree
 of a polynomial of degree
of a polynomial of degree  in
in 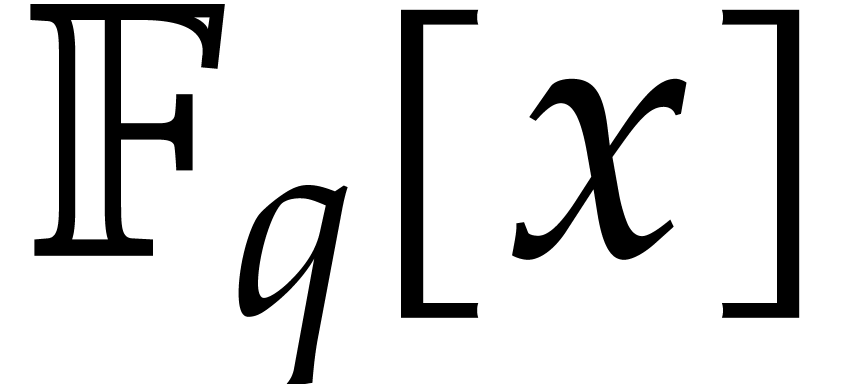 takes an expected time
takes an expected time
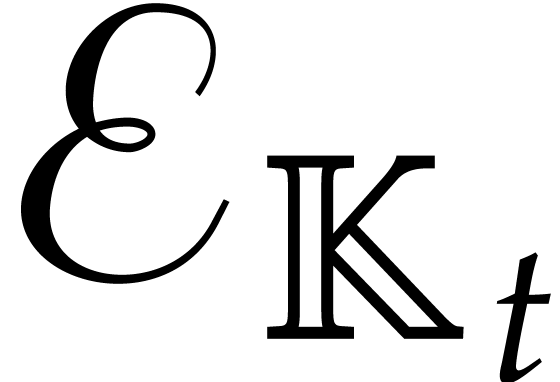
Proof. By Lemma 6.2, the auxiliary
sequences 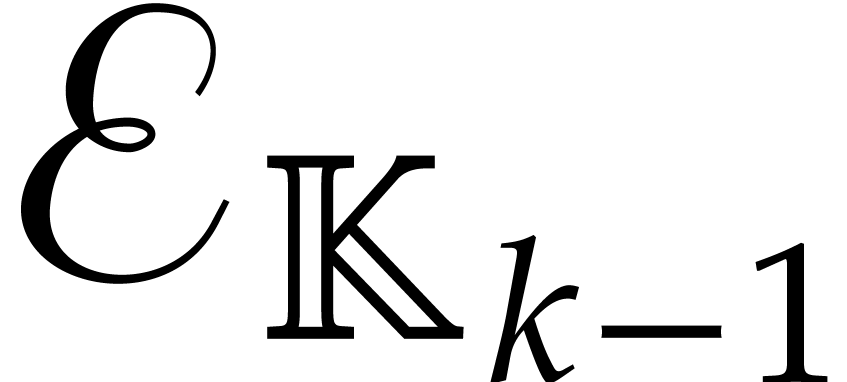 ,...,
,...,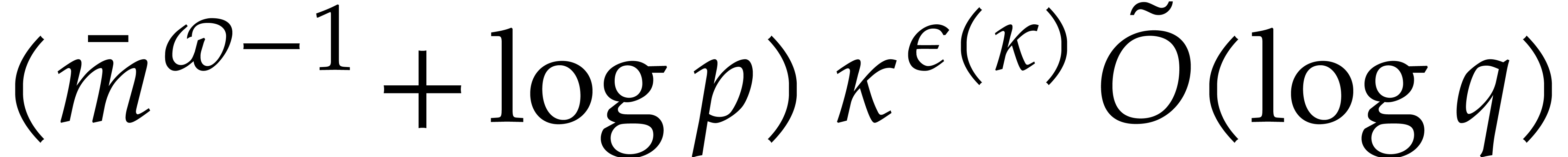 can be computed in time
can be computed in time 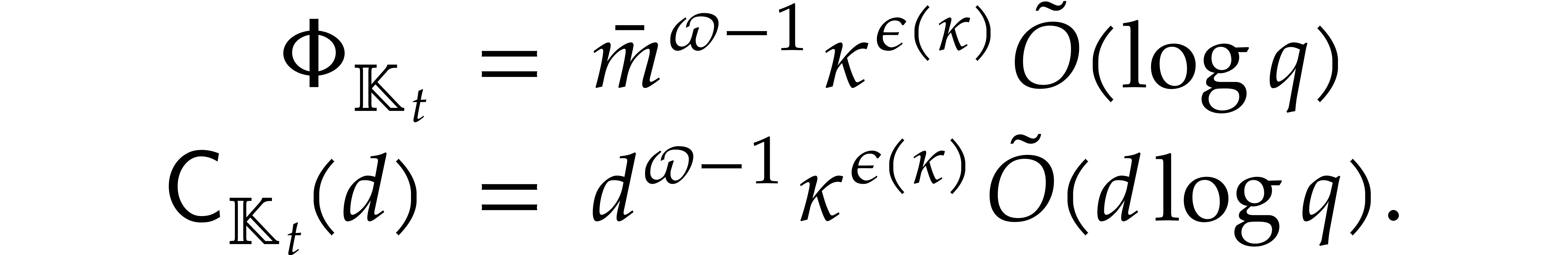 .
By Proposition 6.1 and Lemma 6.1, we may take
.
By Proposition 6.1 and Lemma 6.1, we may take
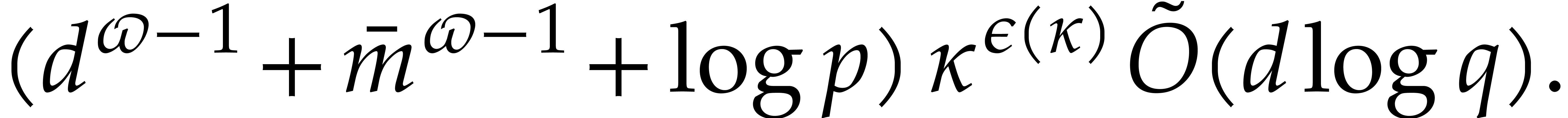
The bound now follows from Theorem 4.1.
 for a triangular
tower as above. A polynomial of degree
for a triangular
tower as above. A polynomial of degree  in
in 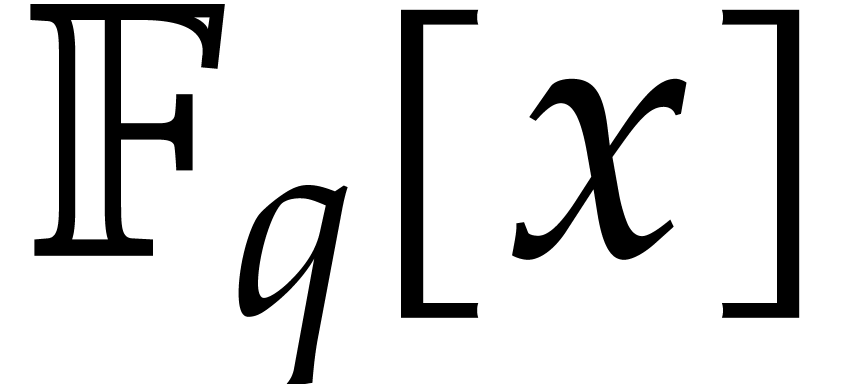 can be tested to be irreducible in time
can be tested to be irreducible in time
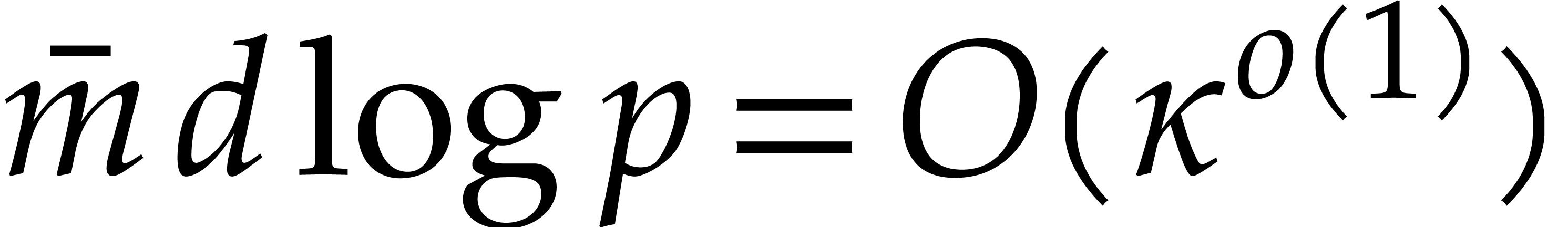
Proof. This follows from Theorem 4.2,
in a similar way as above.
If 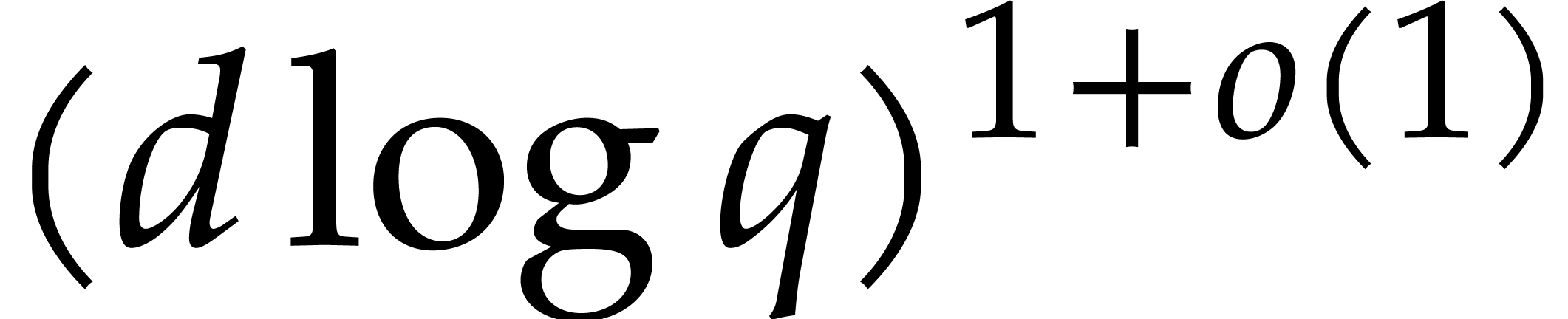 , then we note that the
bounds in Corollaries 6.1 and 6.2 further
simplify into
, then we note that the
bounds in Corollaries 6.1 and 6.2 further
simplify into  , which has an
optimal complexity exponent in terms of the input/output size.
, which has an
optimal complexity exponent in terms of the input/output size.
In the case when the extension degree  of
of  over
over  is composite, we
proposed various algorithms for modular composition [16]
that are more efficient than the traditional “baby-step
giant-step” method [30]. As before, these methods all
represent
is composite, we
proposed various algorithms for modular composition [16]
that are more efficient than the traditional “baby-step
giant-step” method [30]. As before, these methods all
represent  as the top field of a tower of finite
fields
as the top field of a tower of finite
fields
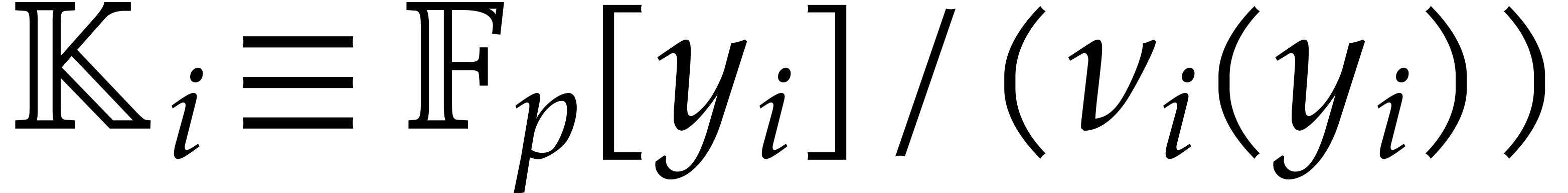 |
(6.1) |
Such towers can be built in several ways and each type of tower comes with its own specific complexity bounds for basic arithmetic operations and modular composition. In this section, we briefly recall the complexity bounds for the various types of towers and then combine them with the results of section 4.4.
The arithmetic operations in the fields 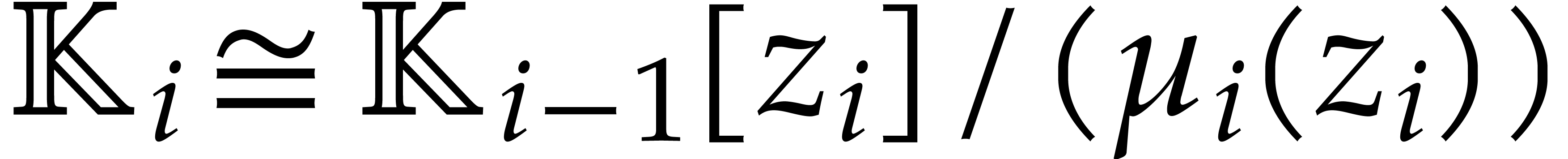 of the
tower (6.1) are most efficient if each
of the
tower (6.1) are most efficient if each 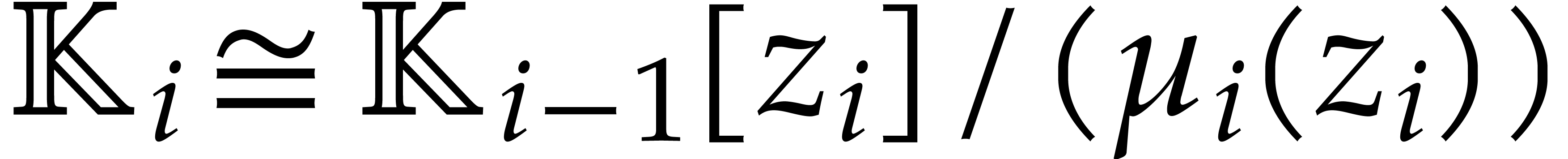 is presented directly as a primitive extension
is presented directly as a primitive extension 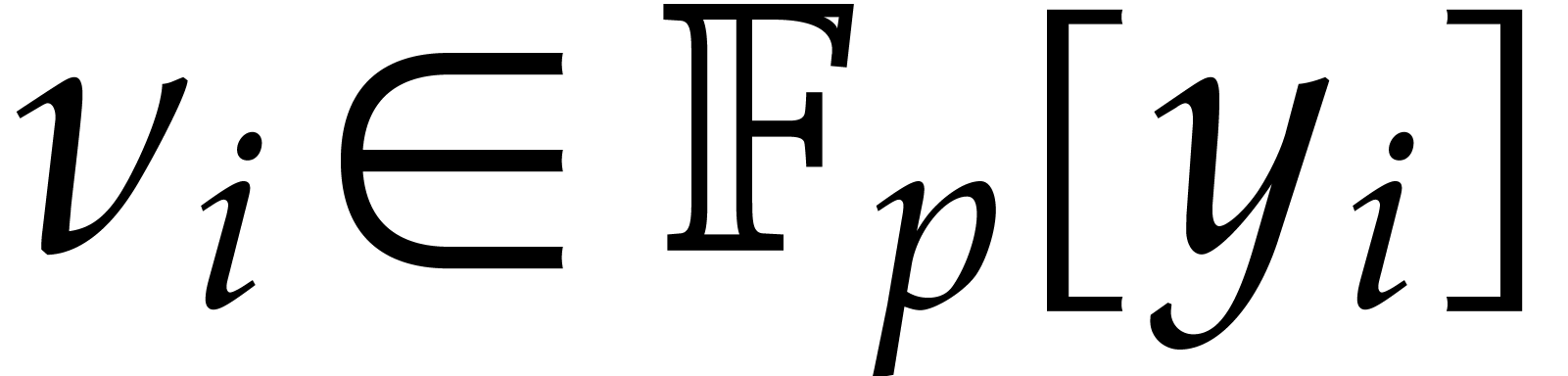 over
over  , where
, where  is a monic polynomial of degree
is a monic polynomial of degree 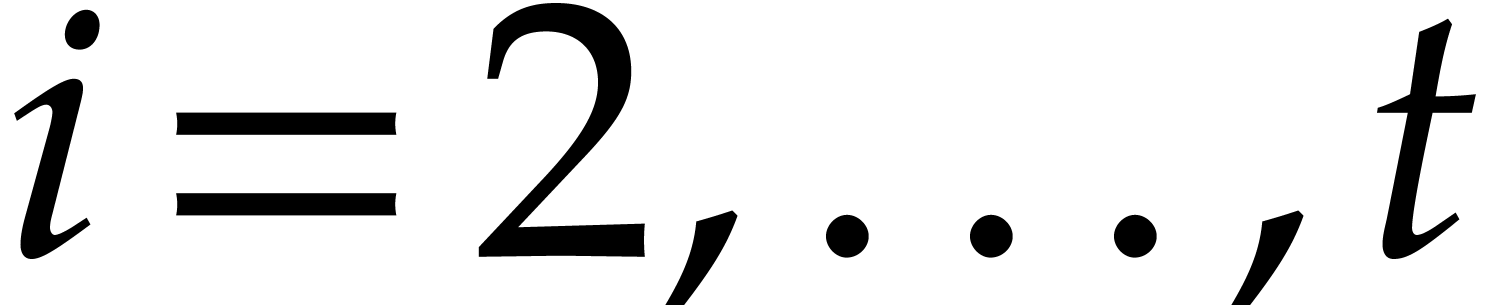 .
Towers of this type are called primitive towers. The primitive
representations will be part of the precomputation. In [16],
we studied the following types of primitive towers:
.
Towers of this type are called primitive towers. The primitive
representations will be part of the precomputation. In [16],
we studied the following types of primitive towers:
For 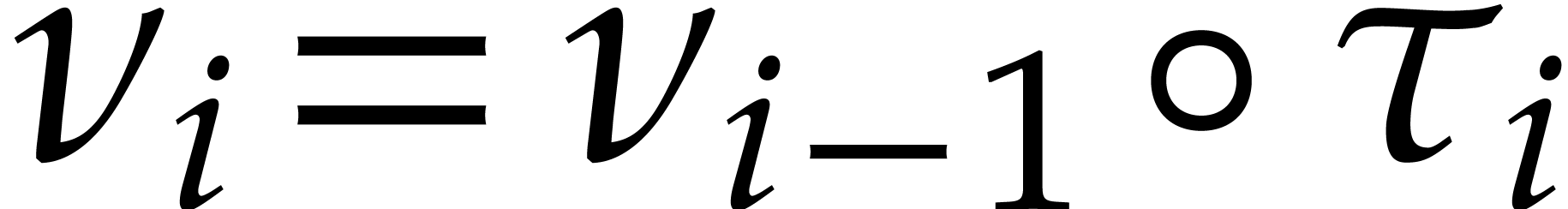 , we have
, we have 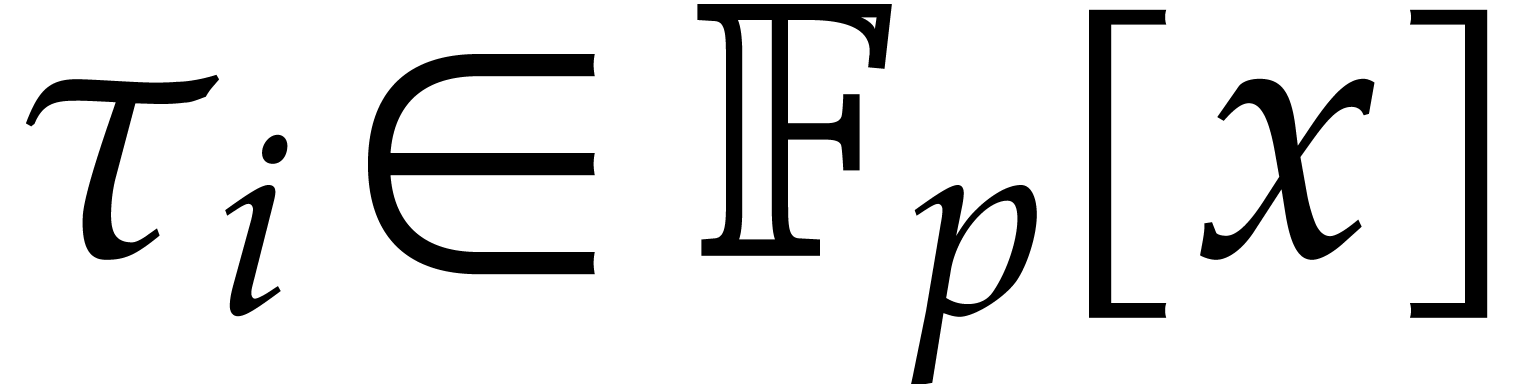 , where
, where 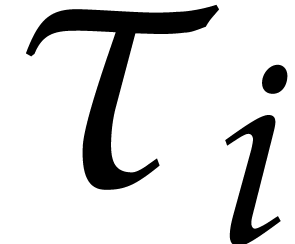 is a polynomial of
degree
is a polynomial of
degree 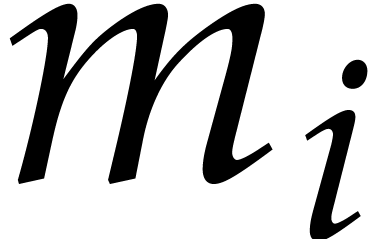 (more generally, for a suitable
generalization of composition,
(more generally, for a suitable
generalization of composition, 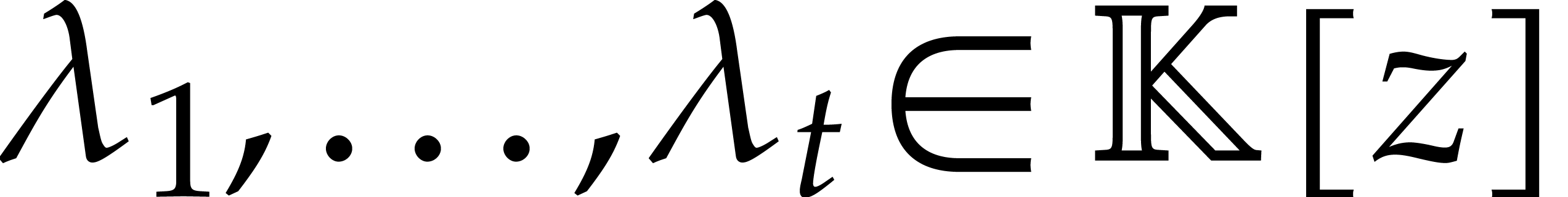 may even be
a rational function of degree
may even be
a rational function of degree 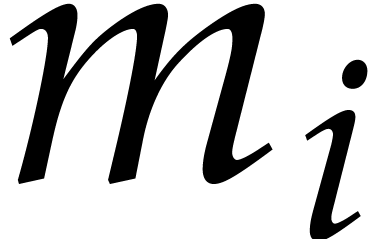 );
see [16, section 7.3] for details.
);
see [16, section 7.3] for details.
The 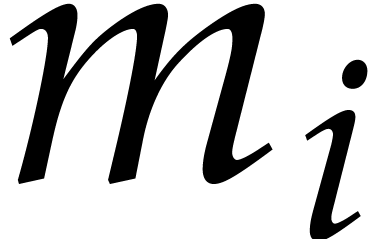 are pairwise coprime and there exist
monic irreducible polynomials
are pairwise coprime and there exist
monic irreducible polynomials  of degrees
of degrees
 such that
such that 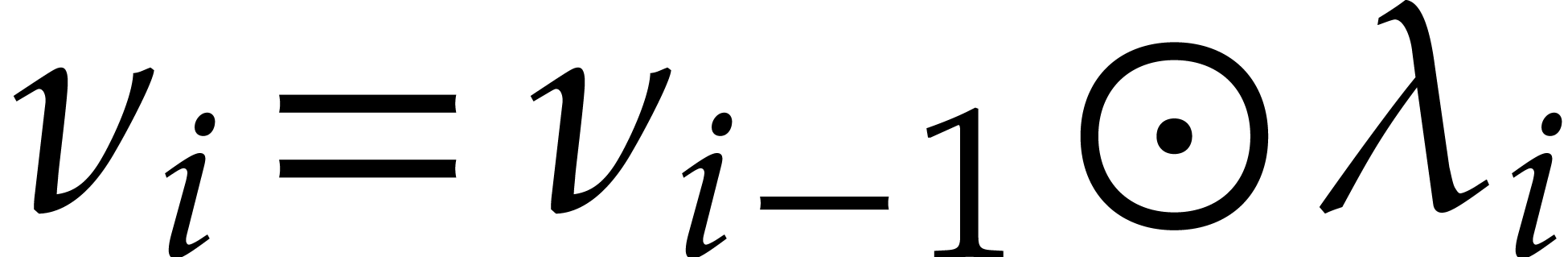 and
and  for
for 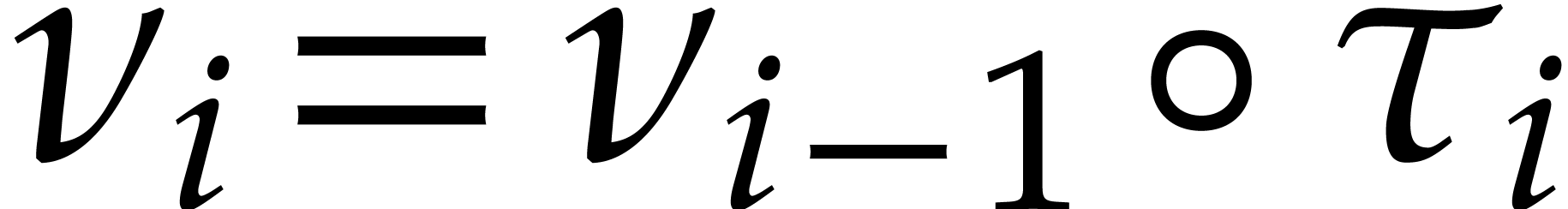 .
Here
.
Here 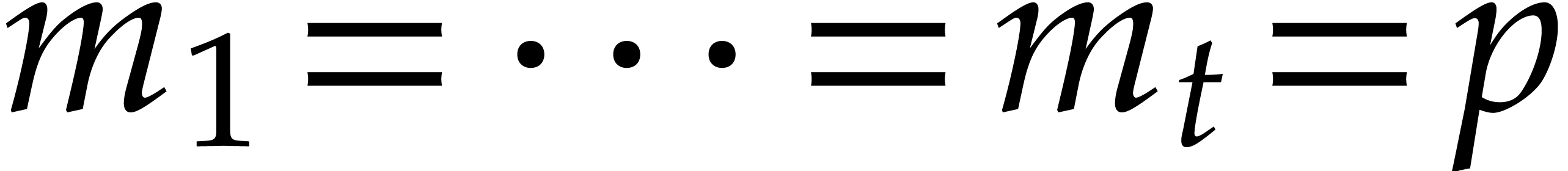 stands for the composed product of
irreducible polynomials; see [16, section 7.4].
stands for the composed product of
irreducible polynomials; see [16, section 7.4].
We have 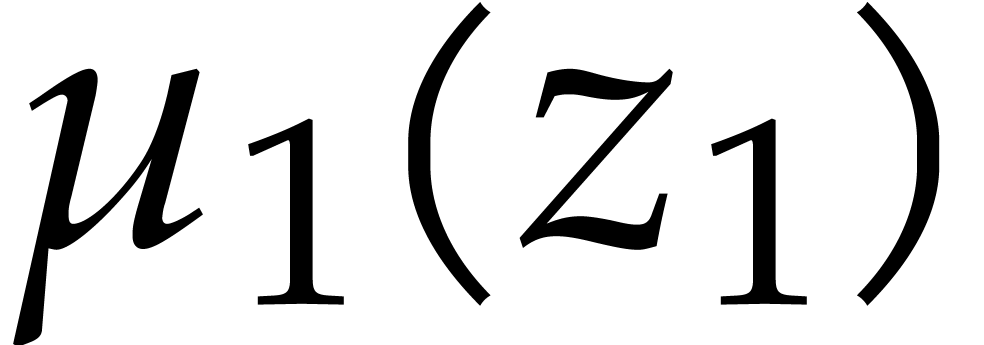 and the minimal polynomials of the
successive extensions are given by
and the minimal polynomials of the
successive extensions are given by
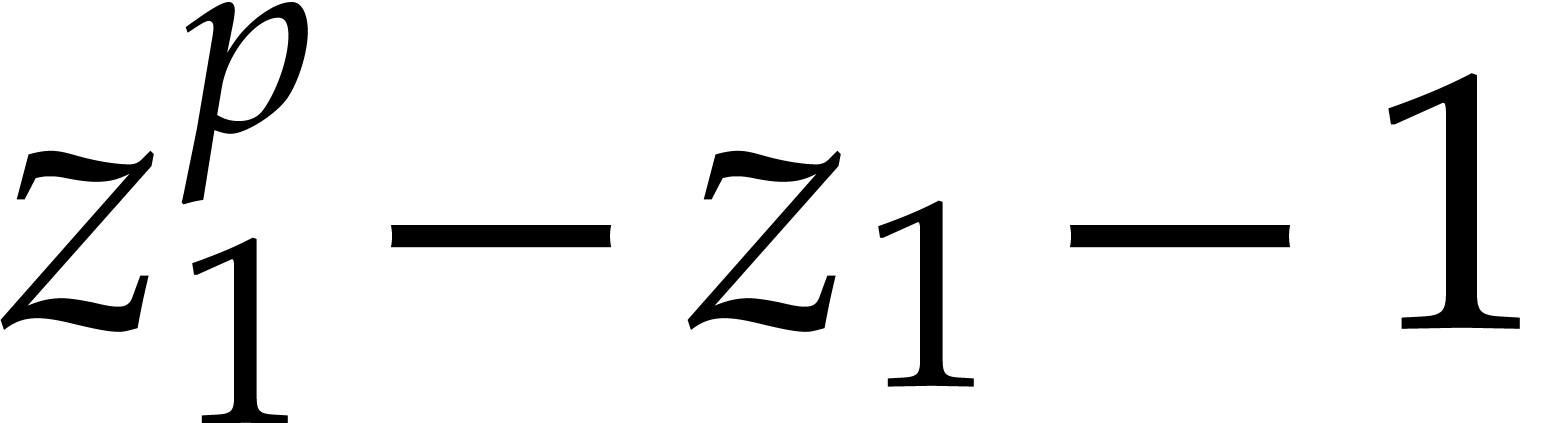 |
 |
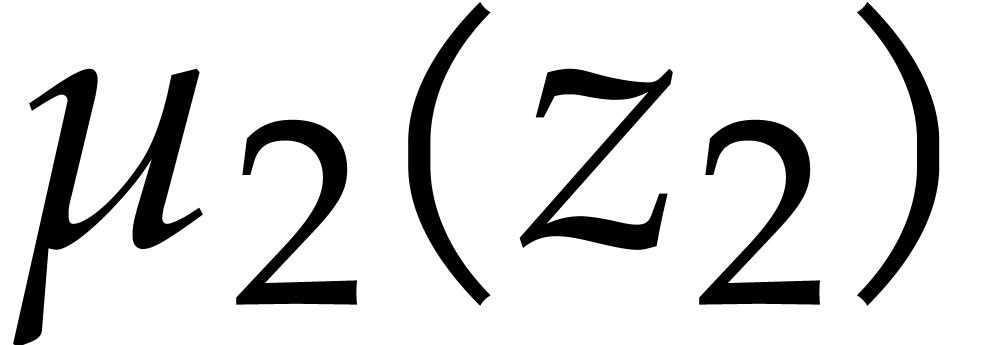 |
|
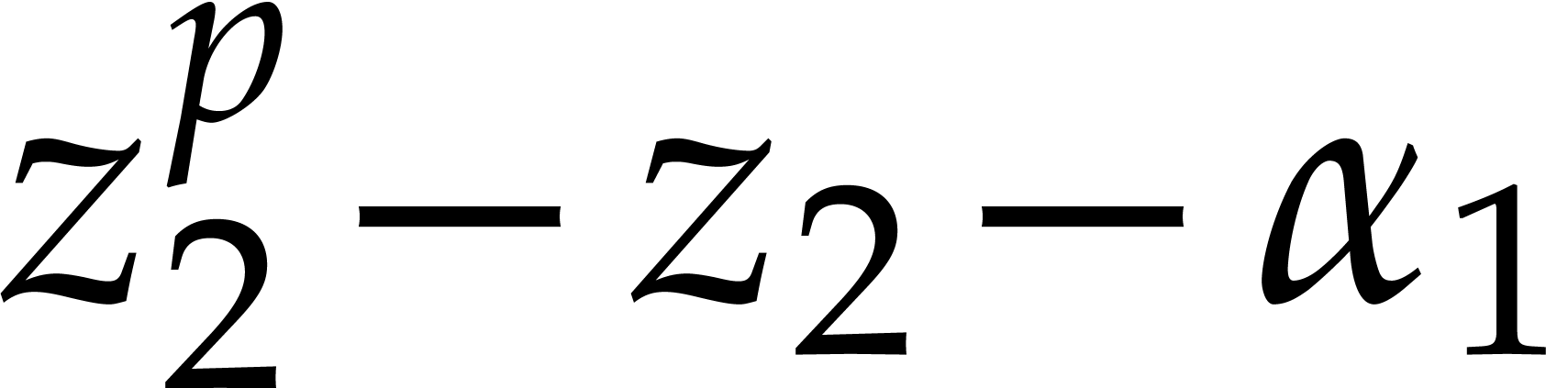 |
 |
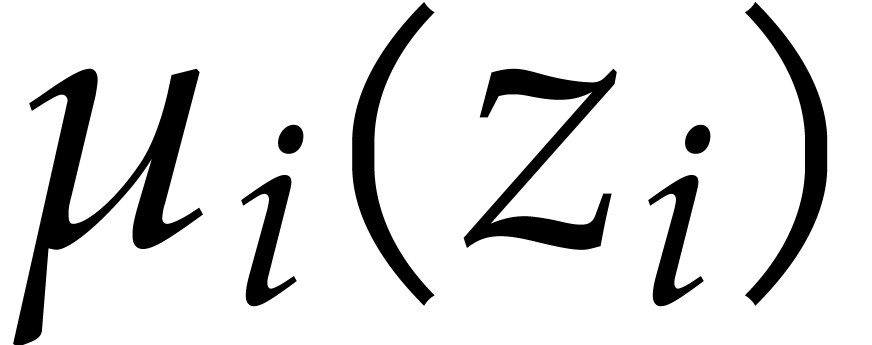 |
(i=2,p=2) |
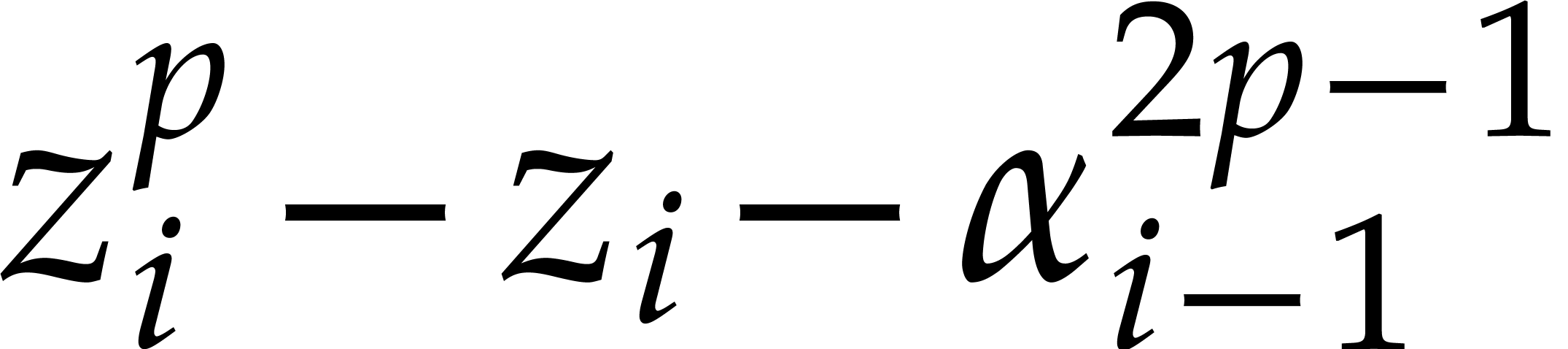 |
 |
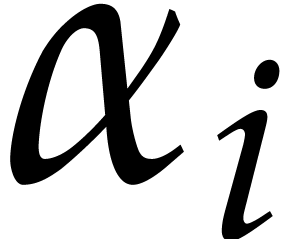 |
(all other cases), |
where 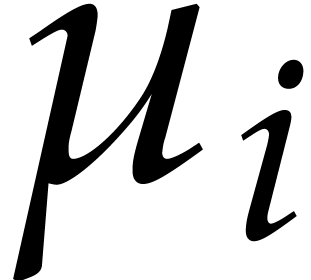 is a root of
is a root of  in
in 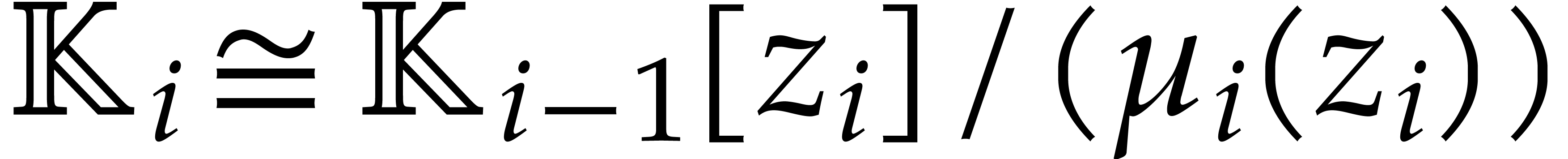 for
for  .
.
Composed towers and Artin–Schreier towers suffer from the inconvenience that they can only be used in specific cases. Nested towers are somewhat mysterious: many finite fields can be presented in this way, but we have no general proof of this empiric fact and no generally efficient way to compute such representations. From an asymptotic complexity point of view, nested towers are most efficient for the purposes of this paper, whenever they exist.
In [16], we have shown that one composition modulo 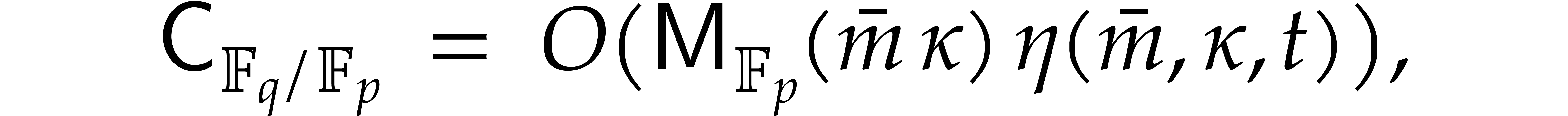 can be done in time
can be done in time
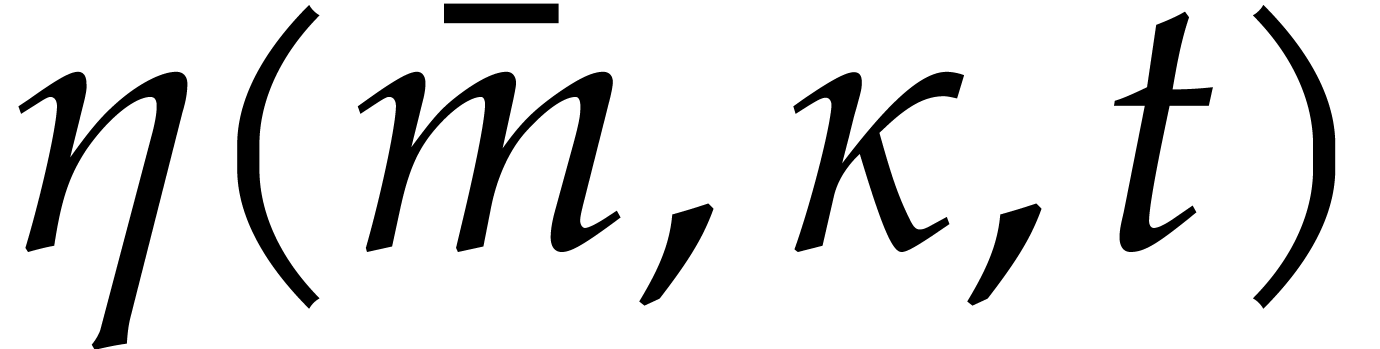
where the overhead 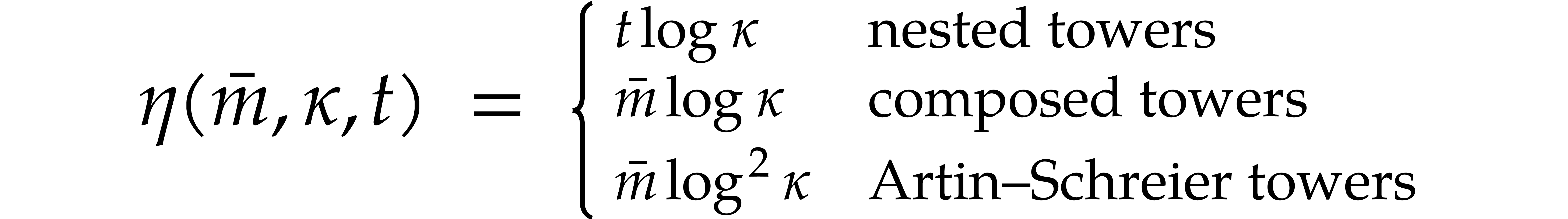 depends as follows on the
particular type of tower:
depends as follows on the
particular type of tower:
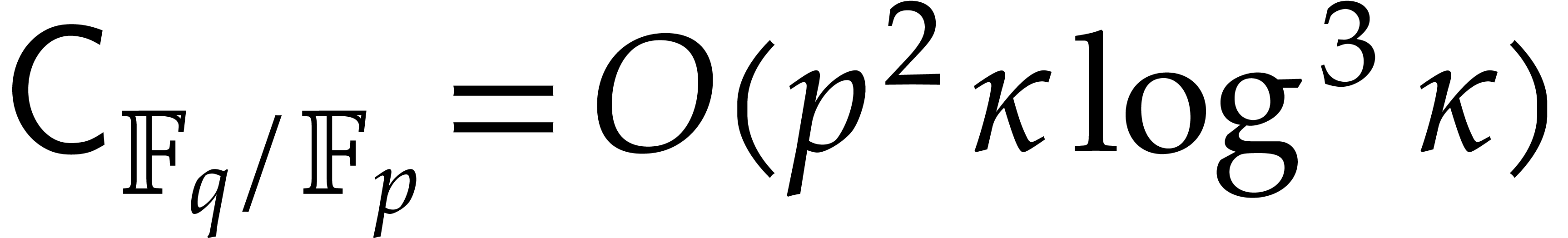
In the case of Artin–Schreier towers, we actually have 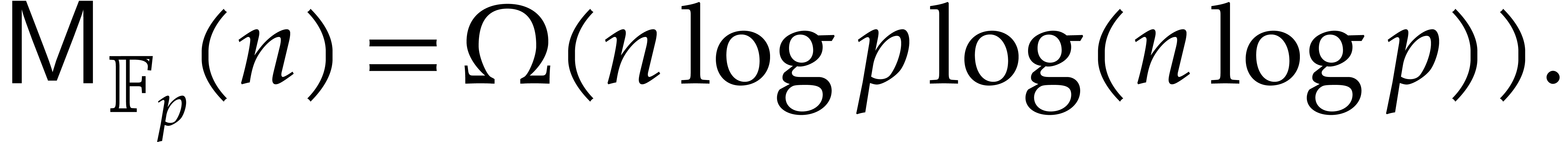 , which yields the announced value
for
, which yields the announced value
for 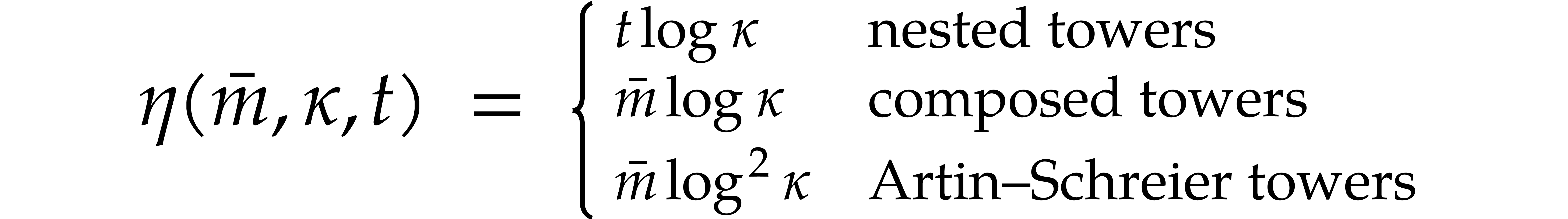 under the mild assumption that
under the mild assumption that
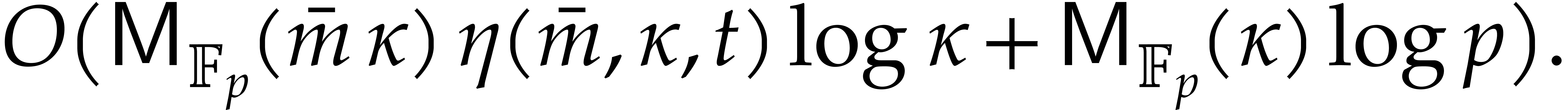
By Lemma 2.3, the sequence  can be
computed in time
can be
computed in time
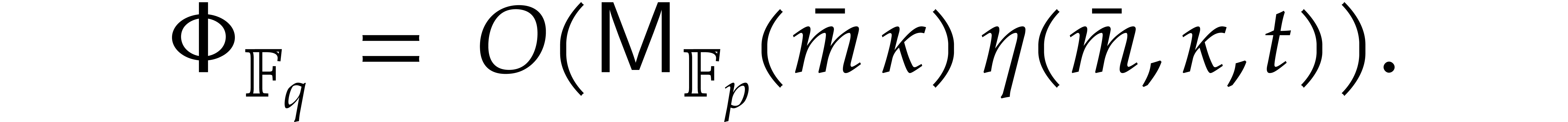
By Lemma 2.1, we may take
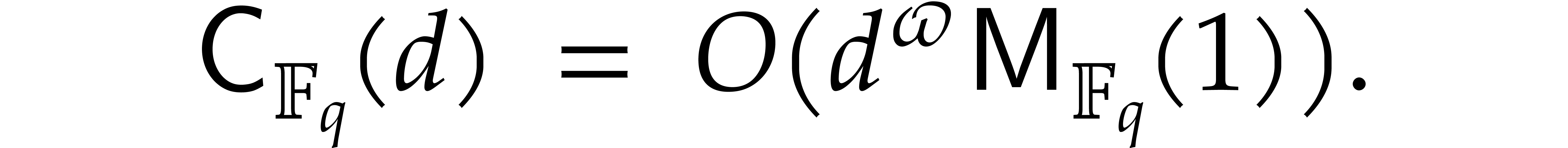
Since we wish to avoid relying on the Kedlaya–Umans algorithm, we again use
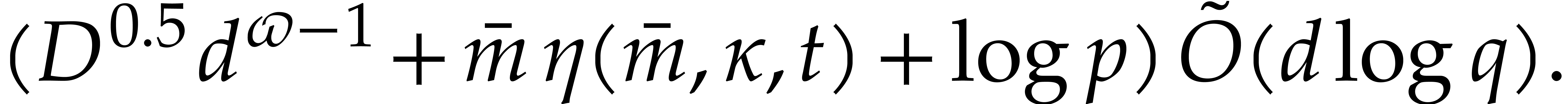
Plugging these bounds into Theorems 4.1 and 4.2, we obtain:
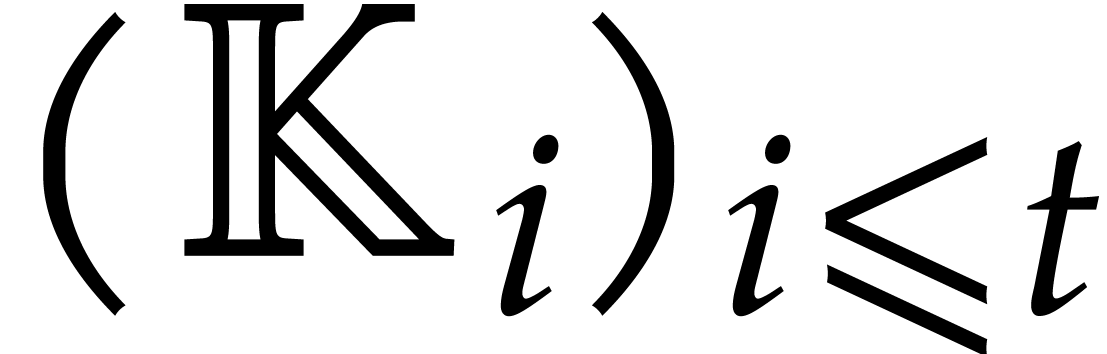 for a primitive
tower of one of the above types. Then the computation of the
irreducible factors of degree
for a primitive
tower of one of the above types. Then the computation of the
irreducible factors of degree 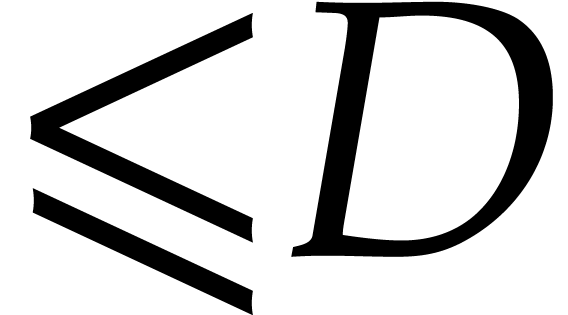 of a polynomial
of degree
of a polynomial
of degree  in
in 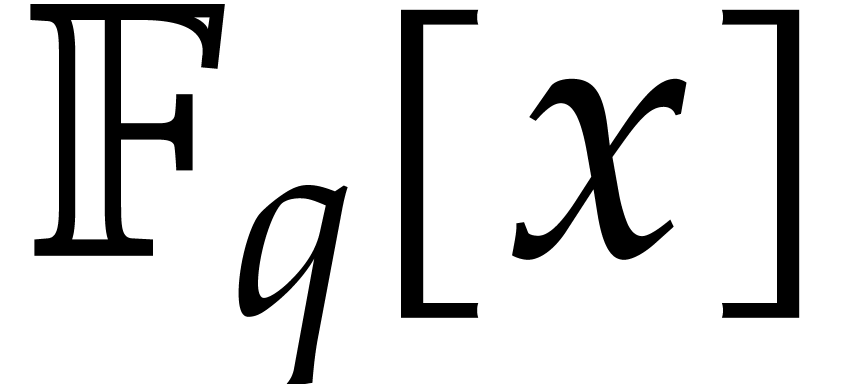 can be
done in expected time
can be
done in expected time
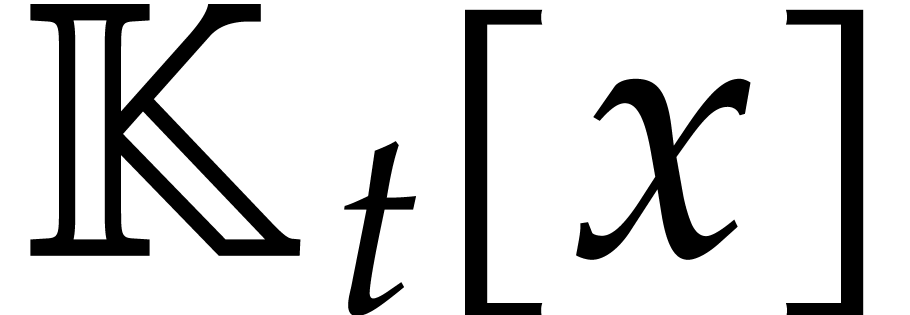
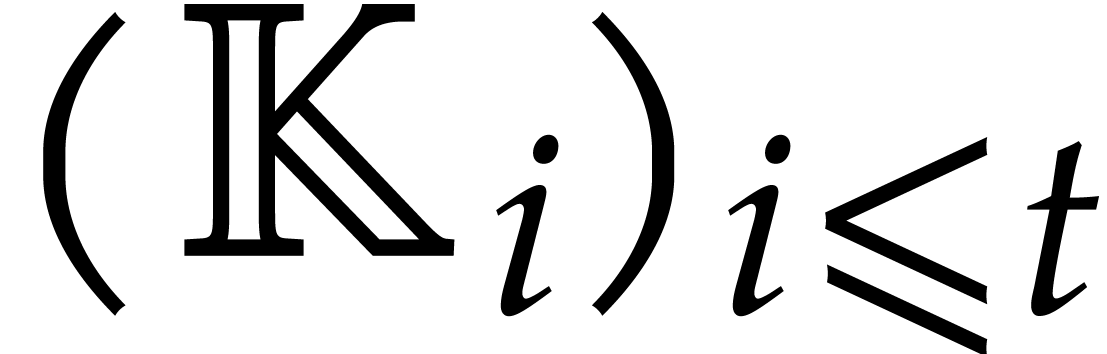 for a primitive tower of one of
the above types. Then a polynomial of degree
for a primitive tower of one of
the above types. Then a polynomial of degree  in
in 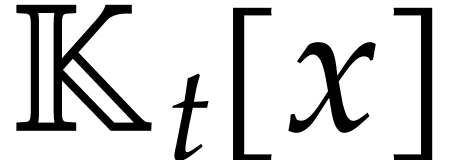 can be tested to be irreducible in time
can be tested to be irreducible in time
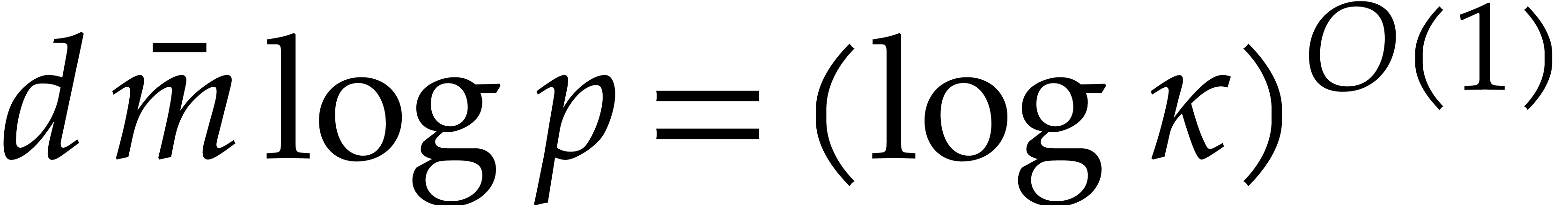
In the particular case when 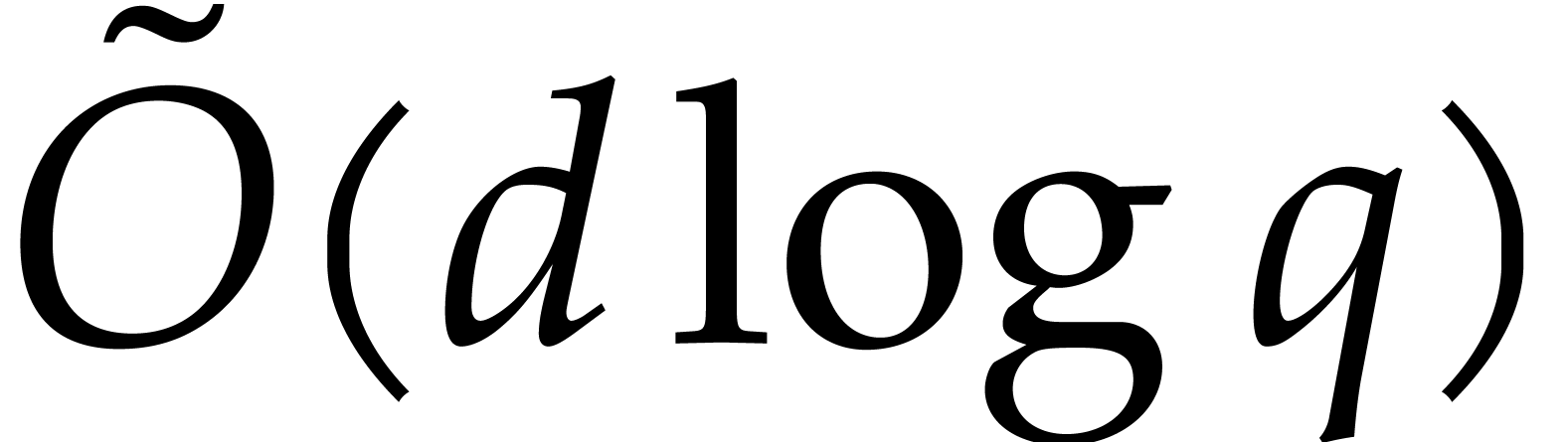 ,
we note that both bounds further simplify into
,
we note that both bounds further simplify into 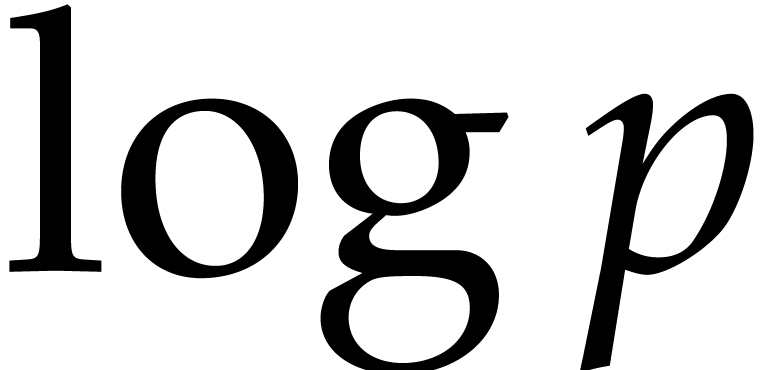 , which is quasi-optimal.
, which is quasi-optimal.
We have revisited probabilistic complexity bounds for factoring univariate polynomials over finite fields and for testing their irreducibility. We mainly used existing techniques, but we were able to sharpen the existing bounds by taking into account recent advances on modular composition. However, the following major problems remain open:
Do their exist practical algorithms for modular composition with a quasi-optimal complexity exponent?
The existing bit complexity bounds for factorization display a
quadratic dependency on the bit size 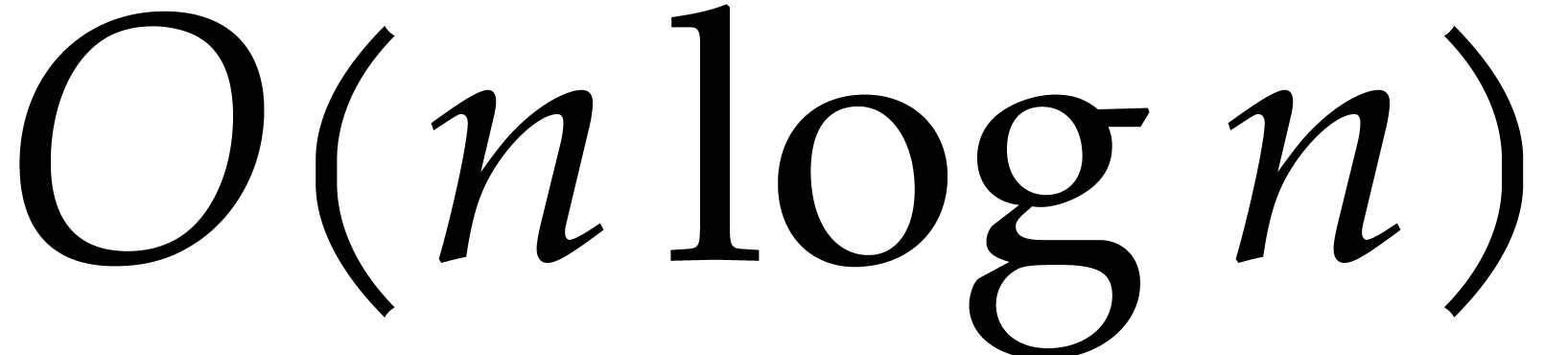 of the
prime field. Is this optimal?
of the
prime field. Is this optimal?
Is it possible to lower the complexity exponent 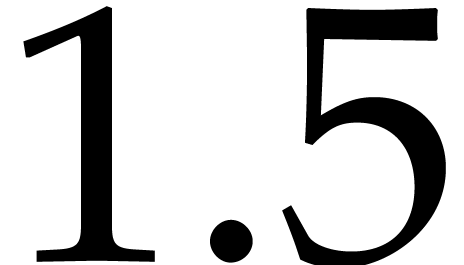 in
in  for irreducible factorization? This
problem is equivalent to several other ones, as explained in [12].
for irreducible factorization? This
problem is equivalent to several other ones, as explained in [12].
The improvements from this paper are most significant for finite fields of a large smooth extension degree over their prime field. Indeed, fast algorithms for modular composition were designed for this specific case in [16]. It would be interesting to know whether there are other special cases for which this is possible. Applications of such special cases would also be welcome.
M. Ben-Or. Probabilistic algorithms in finite fields. In 22nd Annual Symposium on Foundations of Computer Science (SFCS 1981), pages 394–398. Los Alamitos, CA, USA, 1981. IEEE Computer Society.
E. R. Berlekamp. Factoring polynomials over finite fields. Bell System Technical Journal, 46:1853–1859, 1967.
E. R. Berlekamp. Factoring polynomials over large finite fields. Math. Comput., 24:713–735, 1970.
A. Bostan, F. Chyzak, M. Giusti, R. Lebreton, G. Lecerf, B. Salvy, and É. Schost. Algorithmes Efficaces en Calcul Formel. Frédéric Chyzak (self-published), Palaiseau, 2017. Electronic version available from https://hal.archives-ouvertes.fr/AECF.
D. G. Cantor and H. Zassenhaus. A new algorithm for factoring polynomials over finite fields. Math. Comput., 36(154):587–592, 1981.
Ph. Flajolet, X. Gourdon, and D. Panario. The complete analysis of a polynomial factorization algorithm over finite fields. J. Algorithms, 40(1):37–81, 2001.
Ph. Flajolet and J.-M. Steyaert. A branching process arising in dynamic hashing, trie searching and polynomial factorization. In M. Nielsen and E. Schmidt, editors, Automata, Languages and Programming, volume 140 of Lect. Notes Comput. Sci., pages 239–251. Springer–Verlag, 1982.
J. von zur Gathen. Who was who in polynomial factorization. In ISSAC'06: International Symposium on Symbolic and Algebraic Computation, pages 1–2. New York, NY, USA, 2006. ACM.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, New York, 3rd edition, 2013.
J. von zur Gathen and G. Seroussi. Boolean circuits versus arithmetic circuits. Inf. Comput., 91(1):142–154, 1991.
J. von zur Gathen and V. Shoup. Computing Frobenius maps and factoring polynomials. Comput. complexity, 2(3):187–224, 1992.
Z. Guo, A. K. Narayanan, and Ch. Umans. Algebraic problems equivalent to beating exponent 3/2 for polynomial factorization over finite fields. https://arxiv.org/abs/1606.04592, 2016.
D. Harvey and J. van der Hoeven. Faster polynomial multiplication over finite fields using cyclotomic coefficient rings. J. Complexity, 54:101404, 2019.
D. Harvey and J. van der Hoeven. Polynomial
multiplication over finite fields in time 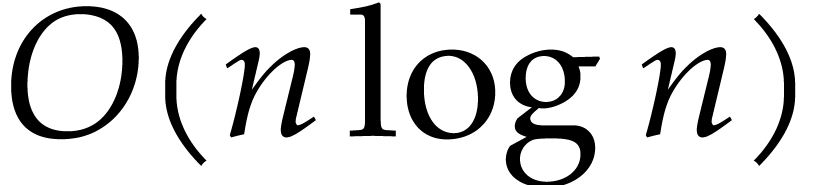 . Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070816.
. Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070816.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and G. Lecerf. Modular composition via factorization. J. Complexity, 48:36–68, 2018.
J. van der Hoeven and G. Lecerf. Accelerated tower arithmetic. J. Complexity, 55:101402, 2019.
J. van der Hoeven and G. Lecerf. Fast amortized multi-point evaluation. Technical Report, HAL, 2020. https://hal.archives-ouvertes.fr/hal-02508529.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. Complexity, 56:101405, 2020.
X. Huang and V. Y. Pan. Fast rectangular matrix multiplication and applications. J. Complexity, 14(2):257–299, 1998.
E. Kaltofen. Polynomial factorization: a success story. In ISSAC '03: Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, pages 3–4. New York, NY, USA, 2003. ACM.
E. Kaltofen and V. Shoup. Subquadratic-time factoring of polynomials over finite fields. In Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, STOC '95, pages 398–406. New York, NY, USA, 1995. ACM.
E. Kaltofen and V. Shoup. Fast polynomial factorization over high algebraic extensions of finite fields. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, ISSAC '97, pages 184–188. New York, NY, USA, 1997. ACM.
E. Kaltofen and V. Shoup. Subquadratic-time factoring of polynomials over finite fields. Math. Comput., 67(223):1179–1197, 1998.
K. S. Kedlaya and C. Umans. Fast modular composition in any characteristic. In Proceedings of the 49th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2008), pages 146–155. Los Alamitos, CA, USA, 2008. IEEE Computer Society.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
G. Lecerf. Fast separable factorization and applications. Appl. Algebra Engrg. Comm. Comput., 19(2):135–160, 2008.
G. L. Mullen and D. Panario. Handbook of Finite Fields. Chapman and Hall/CRC, 2013.
V. Neiger, J. Rosenkilde, and G. Solomatov. Generic bivariate multi-point evaluation, interpolation and modular composition with precomputation. In A. Mantzaflaris, editor, Proceedings of the 45th International Symposium on Symbolic and Algebraic Computation, ISSAC '20, pages 388–395. New York, NY, USA, 2020. ACM.
M. S. Paterson and L. J. Stockmeyer. On the number of nonscalar multiplications necessary to evaluate polynomials. SIAM J. Comput., 2(1):60–66, 1973.
A. Poteaux and É. Schost. Modular composition modulo triangular sets and applications. Comput. Complex., 22(3):463–516, 2013.
M. O. Rabin. Probabilistic algorithms in finite fields. SIAM J. Comput., 9(2):273–280, 1980.
V. Shoup. Fast construction of irreducible polynomials over finite fields. J. Symbolic Comput., 17(5):371–391, 1994.
V. Shoup. A new polynomial factorization algorithm and its implementation. J. Symbolic Comput., 20(4):363–397, 1995.
V. Shoup. A Computational Introduction to Number Theory and Algebra. Cambridge University Press, 2nd edition, 2008.