Sparse polynomial interpolation |
| Faster strategies over finite fields |
|
| Final version, May 2, 2024 |
|
 . Most of this work
was achieved in 2019 and presented in the preprint [32].
During that period, we note that Joris van der Hoeven was
working at the International Research Laboratory
#3069 of the CNRS.
. Most of this work
was achieved in 2019 and presented in the preprint [32].
During that period, we note that Joris van der Hoeven was
working at the International Research Laboratory
#3069 of the CNRS.
Consider a multivariate polynomial |
Consider a polynomial function 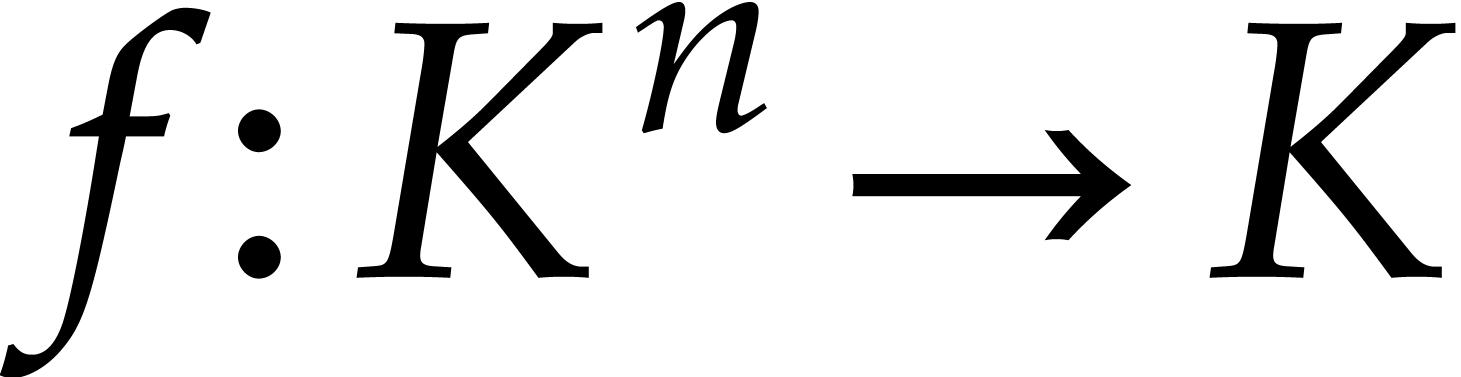 over a field
over a field  given through a black box capable of evaluating
given through a black box capable of evaluating  at points in
at points in 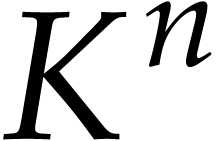 .
The problem of sparse interpolation is to recover the representation of
.
The problem of sparse interpolation is to recover the representation of
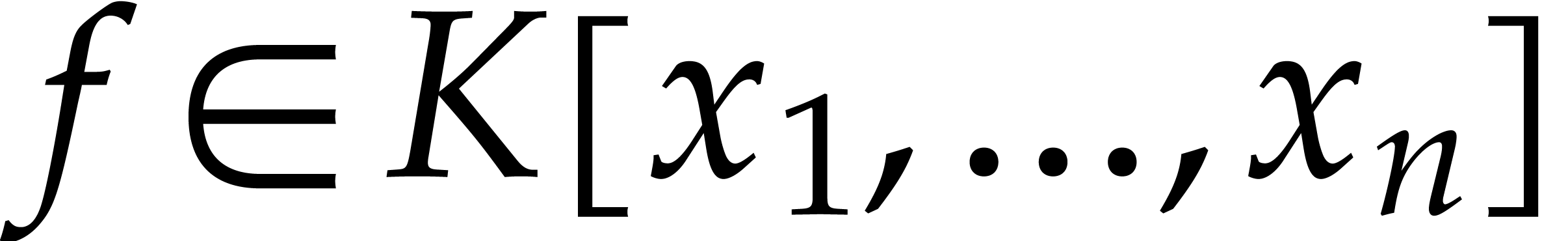 in its usual form, as a linear combination
in its usual form, as a linear combination
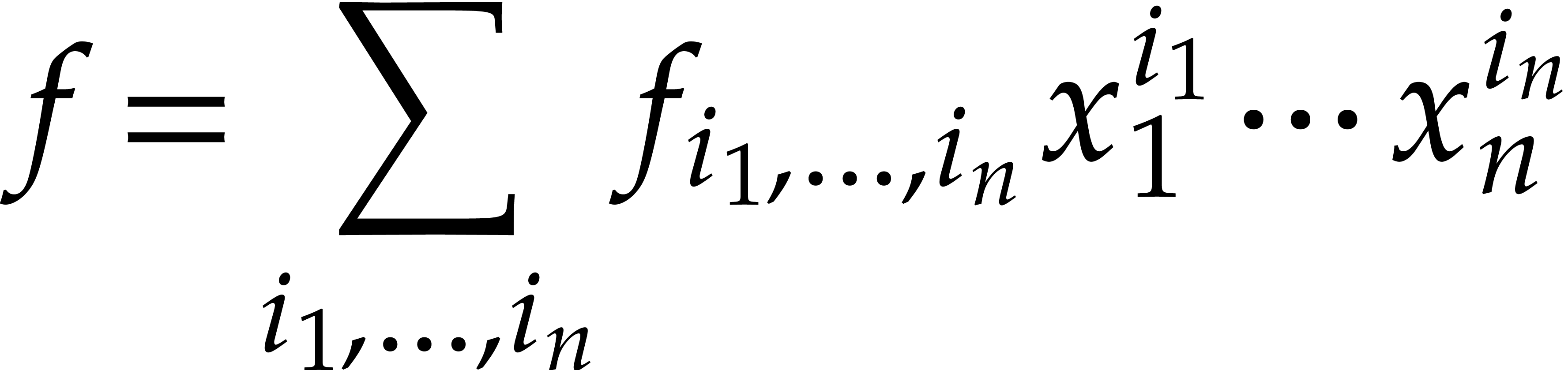 |
(1) |
of monomials. The aim of this paper is to analyze various approaches for
solving this problem, with our primary focus on the case when  is a finite field. We will survey and synthesize known
methods, but we will also present a few new algorithms, together with
improved complexity bounds for some important special cases.
is a finite field. We will survey and synthesize known
methods, but we will also present a few new algorithms, together with
improved complexity bounds for some important special cases.
Efficient algorithms for the task of sparse interpolation go back as far as to the eighteen's century and the work of Prony [50]. The first modern version of the algorithm is due to Ben Or and Tiwari [8]. This method was swiftly embraced in computer algebra [12, 34, 40, 42, 44, 45, 47]; for early implementations, we refer to [14, 16]. There has been a regain of interest for the problem during the last decade, both from a theoretical perspective [2–4, 17–19, 21, 35–38, 41] and from the practical point of view [30, 31, 33, 39, 43]. We also mention the survey paper [52] by Roche on the more general topic of computations with sparse polynomials and the recent PhD thesis [49] by Perret du Cray for the currently best known algorithm for univariate polynomials with integer coefficients; see [49, Théorème 3.18] or [21, Theorem 1.2].
Putting the most efficient algorithms into practice constitutes an important challenge for computer algebra systems. The ultimate implementation should be able to interpolate sparse polynomials almost as fast as dense ones of the same size. This motivates us to explore various methods under heuristic conditions that we expect to fairly reflect average behavior in practice. Sometimes we will prefer a relaxed and intuitive style of exposition to mathematically precise theorems with rigorous proofs.
Throughout this paper  stands for the total
degree of
stands for the total
degree of  and
and  for the
number of non-zero terms in (1). Whenever available, the
uppercase characters
for the
number of non-zero terms in (1). Whenever available, the
uppercase characters  and
and  represent upper bounds for
represent upper bounds for  and
and  . We also write
. We also write  for the
number of ring or field operations in
for the
number of ring or field operations in  that are
required in order to evaluate
that are
required in order to evaluate  at a point.
at a point.
The complexity analysis of sparse interpolation has to be carried out with a lot of care, due to the large variety of cases that can occur:
What kind of complexity/evaluation model do we use?
Do we count the number operations in  or
the number of bit operations?
or
the number of bit operations?
Are we interested in theoretic (asymptotic) or practical complexity?
Are divisions allowed for the evaluation of  and how do we count them?
and how do we count them?
Are we only allowed to evaluate  at
points in
at
points in  or also at points in
or also at points in  for certain extension rings or fields
for certain extension rings or fields  ?
?
What kind of coefficient field  do we use?
do we use?
A field from analysis such as  .
.
A discrete field such as  or a finite
field
or a finite
field  .
.
Fields with roots of unity  of large
smooth order in
of large
smooth order in  .
.
The univariate case (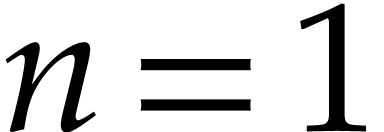 )
versus the multivariate case (
)
versus the multivariate case ( ).
).
Informally speaking, there are three levels of “sparsity”:
Weakly sparse: total degrees  of the
order
of the
order 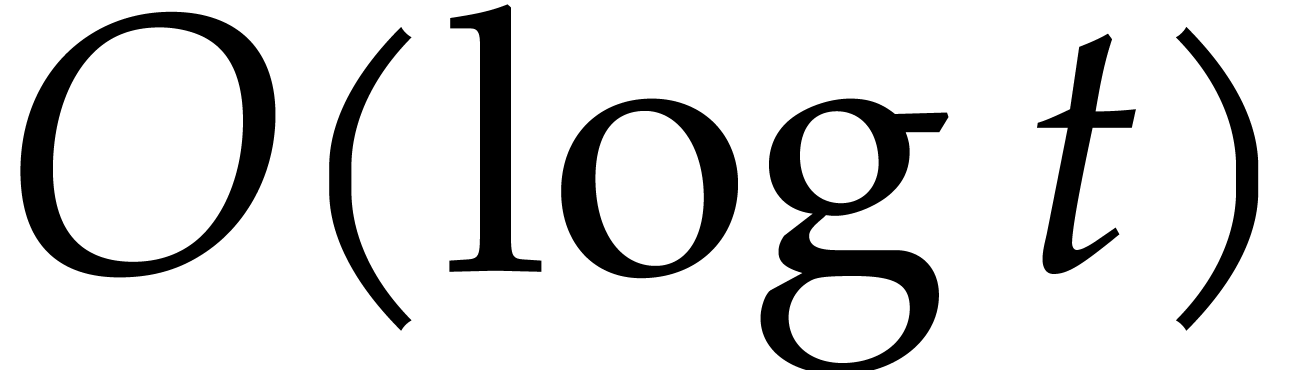 ;
;
Normally sparse: total degrees  of the
order
of the
order 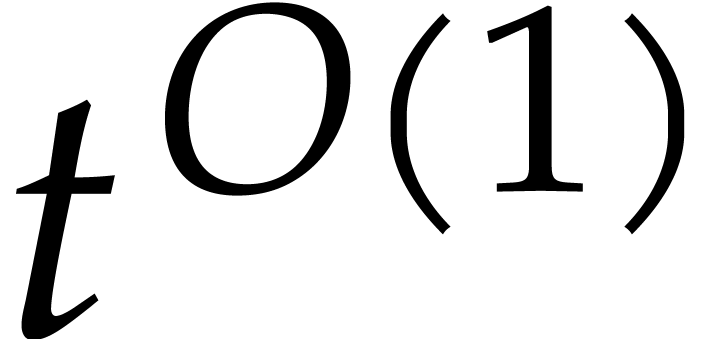 ;
;
Super sparse: total degrees of order  with
with 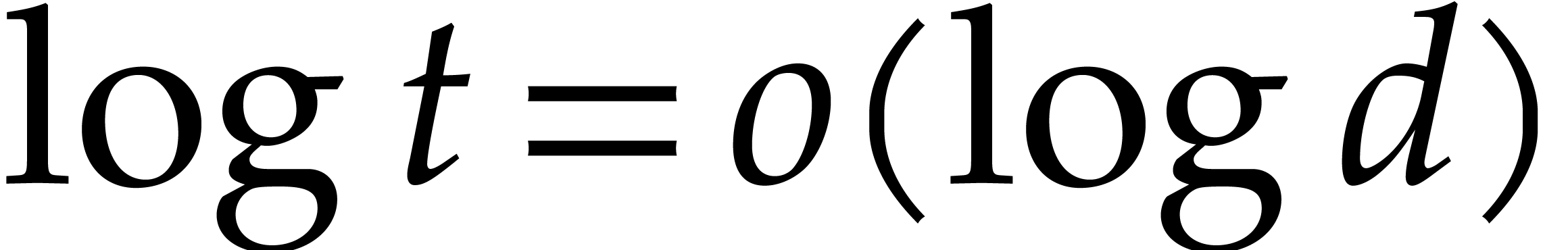 .
.
We also notice that almost all general algorithms for sparse
interpolation are probabilistic of Monte Carlo type. Indeed, without
further a priori knowledge about  ,
such as its support or its number of terms, the mere knowledge of a
finite number of evaluations of
,
such as its support or its number of terms, the mere knowledge of a
finite number of evaluations of  only allows us
to guess plausible expressions for
only allows us
to guess plausible expressions for  .
.
In this paper, we will be mostly interested in the practical bit
complexity of sparse interpolation over finite fields 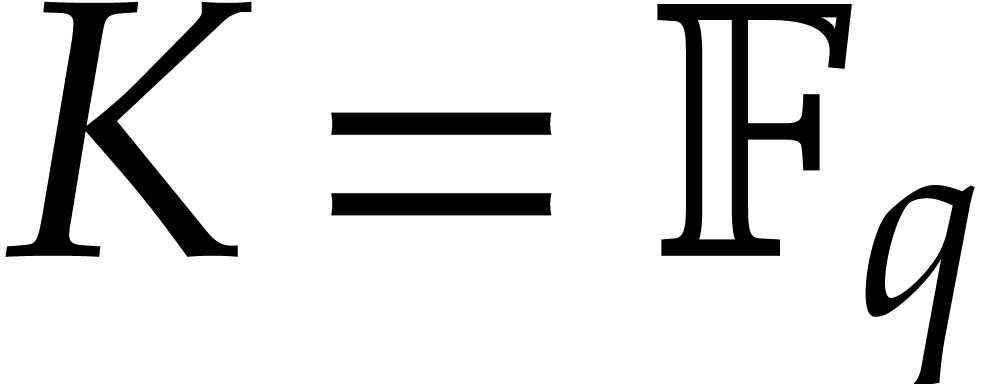 . Sparse interpolation over the rational
numbers can often be reduced to this case as well, in which case
. Sparse interpolation over the rational
numbers can often be reduced to this case as well, in which case 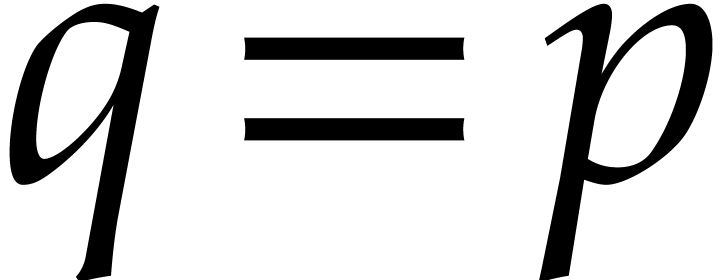 is a well chosen prime number that fits into 32 or 64
bits and such that
is a well chosen prime number that fits into 32 or 64
bits and such that 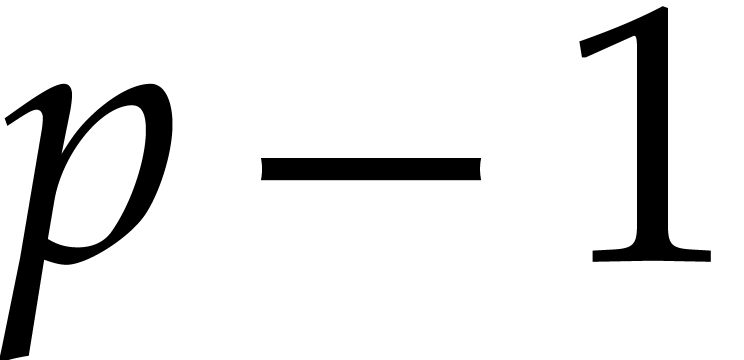 admits a large smooth
divisor; see section 6.5. We analyze the complexities of
specializations of existing algorithms to the finite field case and also
present a few new algorithms and tricks for this specific setting. Due
to the large number of cases that can occur, we will not prove detailed
complexity bounds for every single case, but rather outline how various
ideas may be used and combined to reduce the practical complexity.
admits a large smooth
divisor; see section 6.5. We analyze the complexities of
specializations of existing algorithms to the finite field case and also
present a few new algorithms and tricks for this specific setting. Due
to the large number of cases that can occur, we will not prove detailed
complexity bounds for every single case, but rather outline how various
ideas may be used and combined to reduce the practical complexity.
From our practical perspective, it is important to take into account logarithmic factors in complexity bounds, but it will be convenient to ignore sub-logarithmic factors. For this reason, we use the ad hoc notation
for any functions  .
.
We will also write  for the bit cost of
multiplying two polynomials of degree
for the bit cost of
multiplying two polynomials of degree  over
over  and abbreviate
and abbreviate  .
For instance, the naive multiplication algorithm yields
.
For instance, the naive multiplication algorithm yields 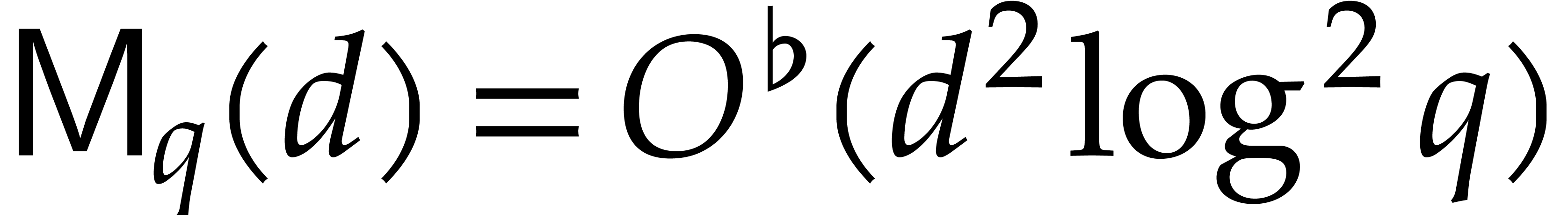 . For our complexity analyses we will give
priority to the asymptotic complexity point of view and use the well
known [25, 53] bound
. For our complexity analyses we will give
priority to the asymptotic complexity point of view and use the well
known [25, 53] bound 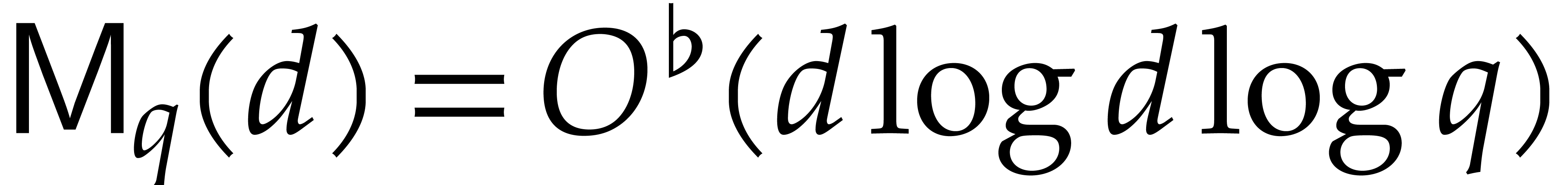 .
.
Many of the challenges concerning sparse interpolation already arise in
the univariate case when 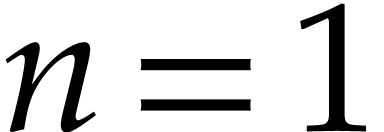 . As
we will see in section 7.1, the multivariate case can
actually be reduced to the univariate one using the technique called
“Kronecker segmentation”, even though other approaches may
be more efficient. For this reason, a large part of the paper is devoted
to methods for interpolating a univariate black box function
. As
we will see in section 7.1, the multivariate case can
actually be reduced to the univariate one using the technique called
“Kronecker segmentation”, even though other approaches may
be more efficient. For this reason, a large part of the paper is devoted
to methods for interpolating a univariate black box function 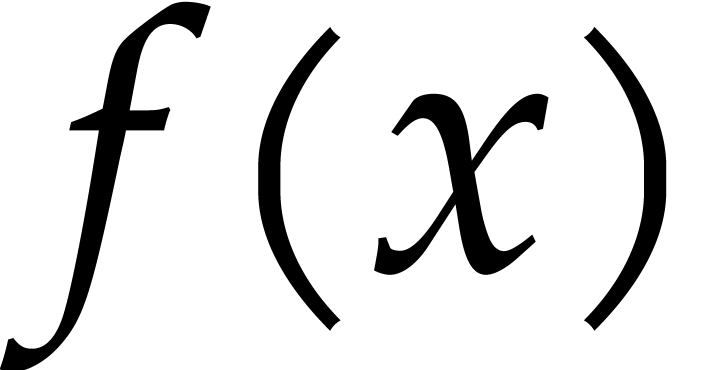 .
.
We distinguish three major types of algorithms:
Cyclic extension methods (section 4);
Geometric progression methods (section 5);
FFT based methods (section 6).
For the first two types of methods we mostly review existing algorithms,
although we do propose some new variants and optimizations. The third
FFT based method is new, as far as we are aware. For each of the three
methods, an important leitmotif is to evaluate 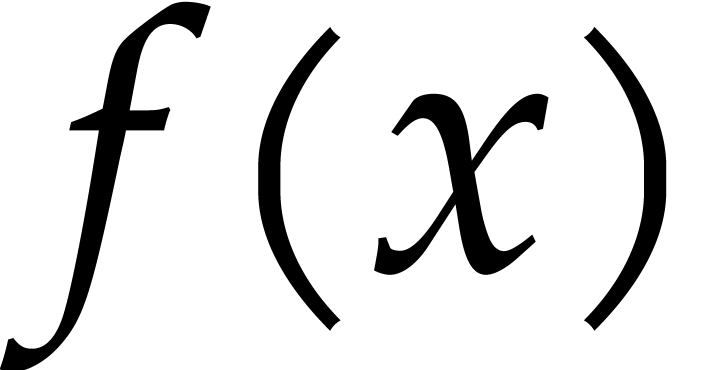 modulo
modulo 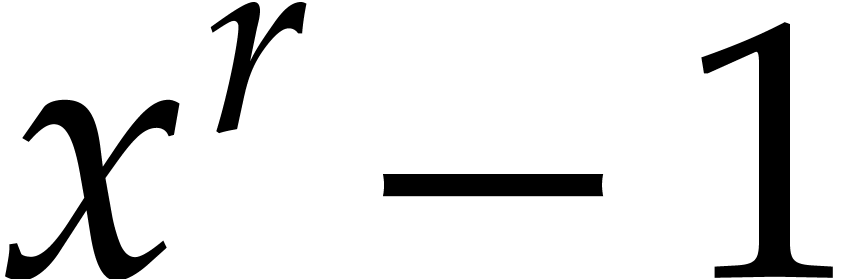 for one or more suitable orders
for one or more suitable orders  , after which we reconstruct
, after which we reconstruct 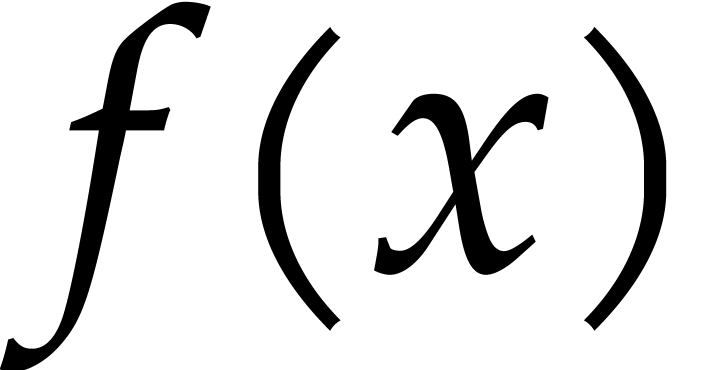 from these modular projections.
from these modular projections.
Cyclic extension methods directly evaluate  over
the cyclic extension ring
over
the cyclic extension ring 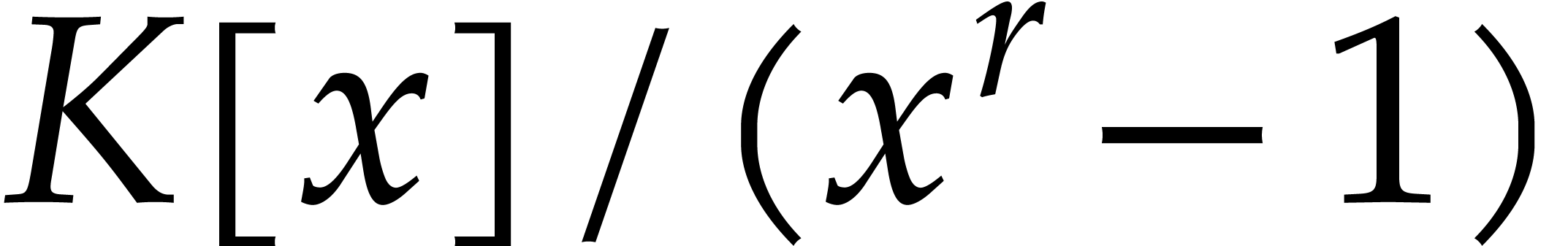 .
This has the advantage that
.
This has the advantage that  can be freely chosen
in a suitable range. However, the evaluation of
can be freely chosen
in a suitable range. However, the evaluation of  over such a large cyclic extension induces a non-trivial overhead in the
dependency of the complexity on
over such a large cyclic extension induces a non-trivial overhead in the
dependency of the complexity on  .
.
Geometric progression methods rather evaluate  at
a sequence
at
a sequence 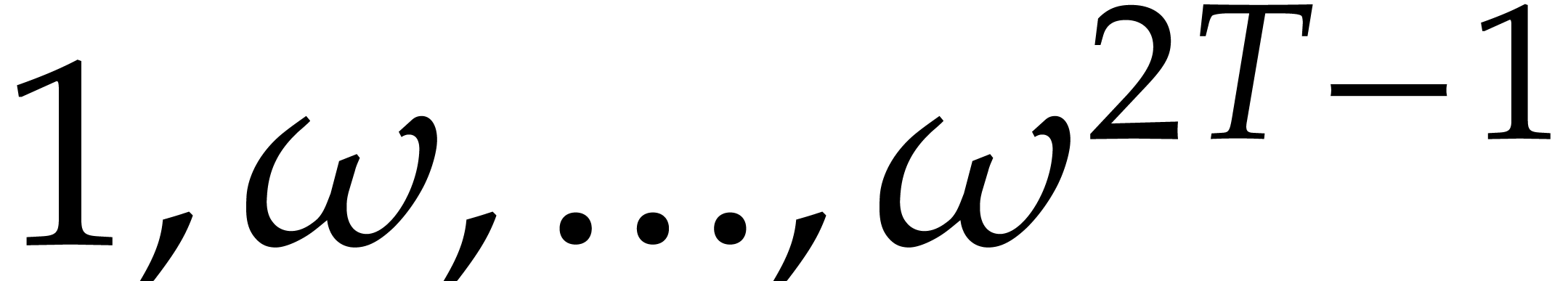 of pairwise distinct elements in
of pairwise distinct elements in  (or inside an extension of
(or inside an extension of  of
modest degree
of
modest degree  ). If
). If 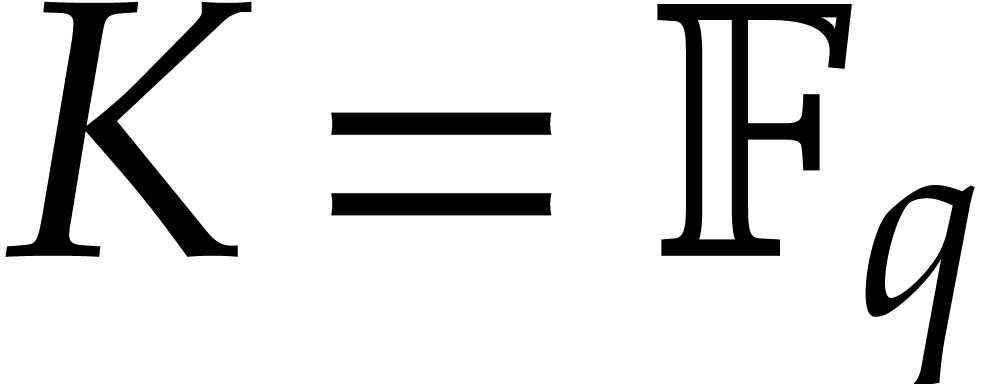 is a finite field, then
is a finite field, then 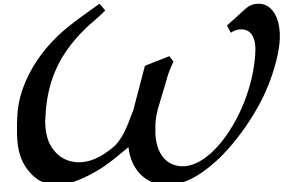 necessarily has an order
necessarily has an order  that divides
that divides 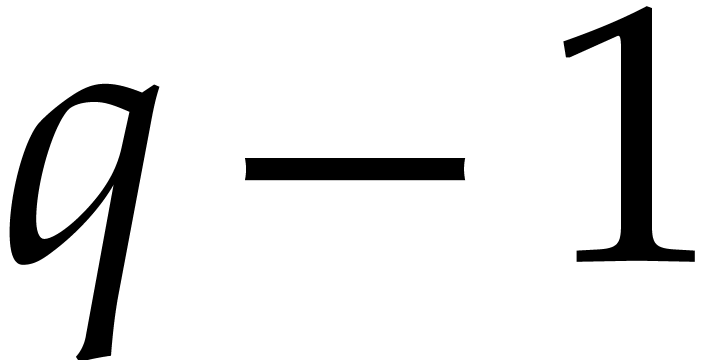 (or
(or 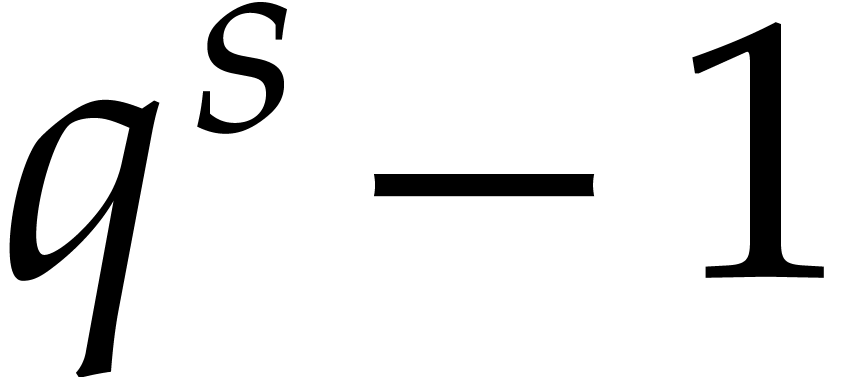 when working over an extension
of degree
when working over an extension
of degree  ). Although the
evaluations of
). Although the
evaluations of  become more efficient using this
approach, the recovery of
become more efficient using this
approach, the recovery of 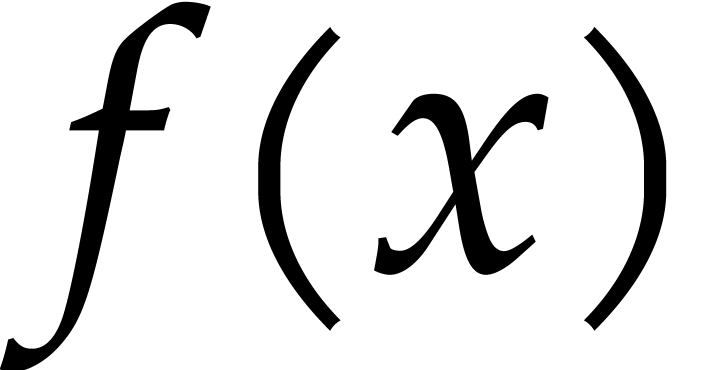 modulo
modulo 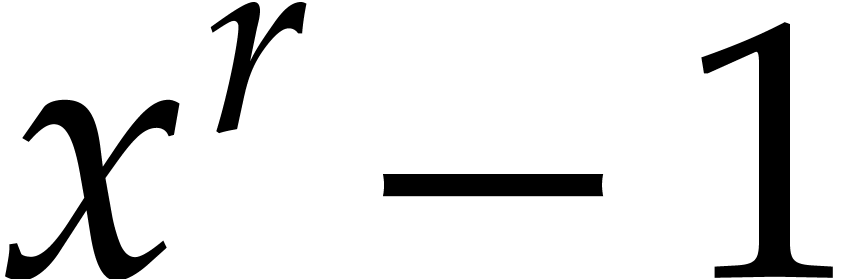 from
from 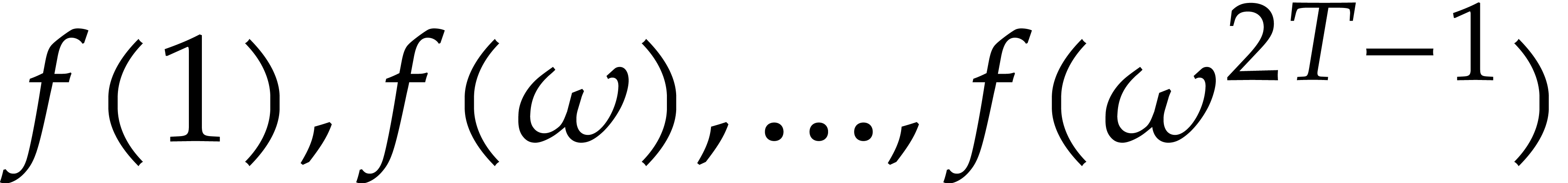 requires extra work. The cost
of this extra work highly depends on the kind of orders
requires extra work. The cost
of this extra work highly depends on the kind of orders  that can be taken as divisors of
that can be taken as divisors of 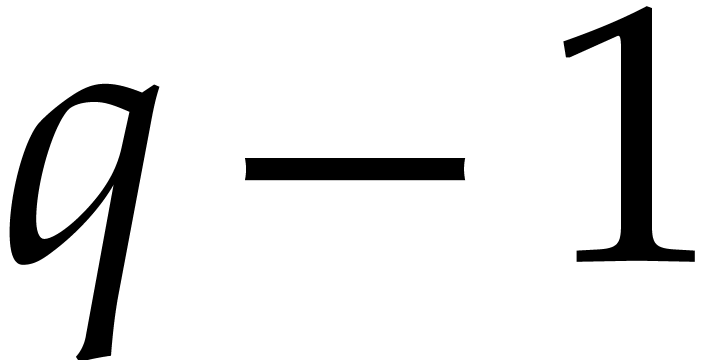 (or
(or 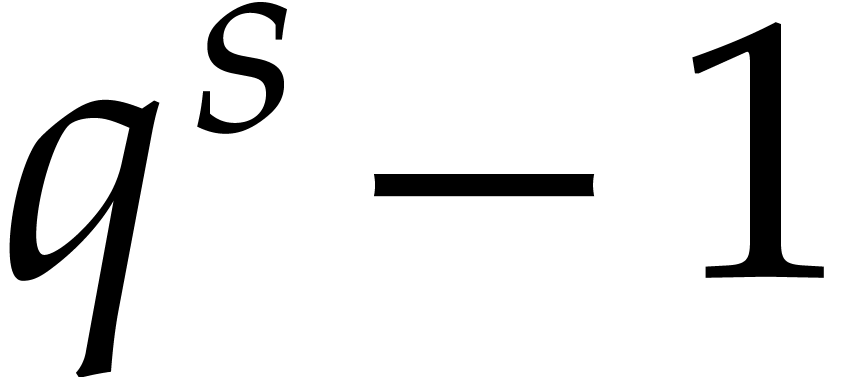 for small
for small  ).
Theoretically speaking, the existence of suitable orders
).
Theoretically speaking, the existence of suitable orders  is a delicate issue; in practice, they always tend to
exist as long as
is a delicate issue; in practice, they always tend to
exist as long as 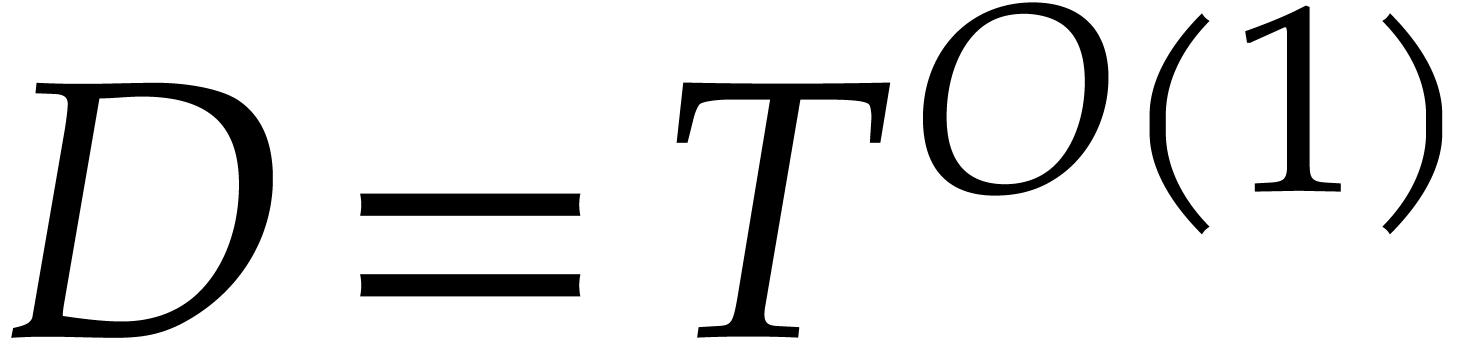 ; see
sections 2, 6.3 and 6.4 for some
empirical evidence.
; see
sections 2, 6.3 and 6.4 for some
empirical evidence.
Geometric progression methods allow us to take  much larger than
much larger than  , but they
involve a non-trivial cost for recovering
, but they
involve a non-trivial cost for recovering 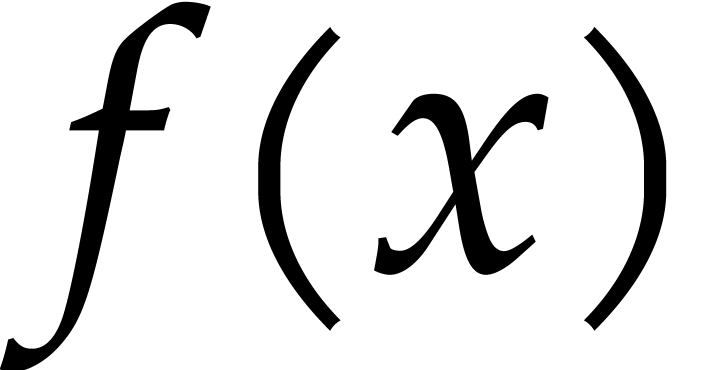 modulo
modulo
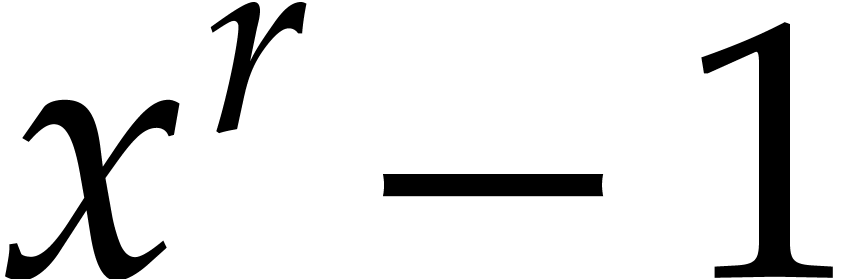 from
from  .
If
.
If  , then this cost may even
dominate the cost of the evaluations of
, then this cost may even
dominate the cost of the evaluations of  .
In such situations, an alternative approach is to evaluate
.
In such situations, an alternative approach is to evaluate  at
at  and to recover
and to recover 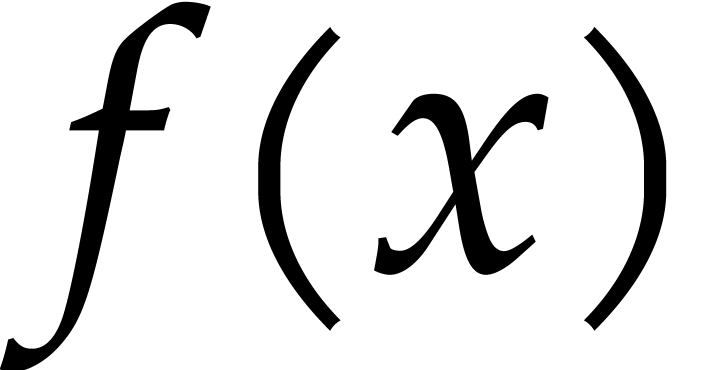 modulo
modulo 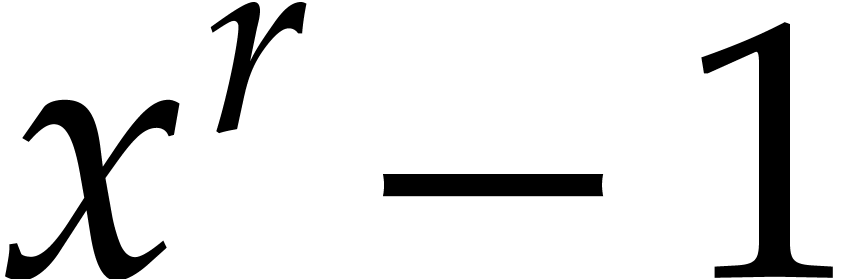 using one inverse DFT of length
using one inverse DFT of length  . However, this puts an even larger
strain on the choice of
. However, this puts an even larger
strain on the choice of  ,
since it is important that
,
since it is important that 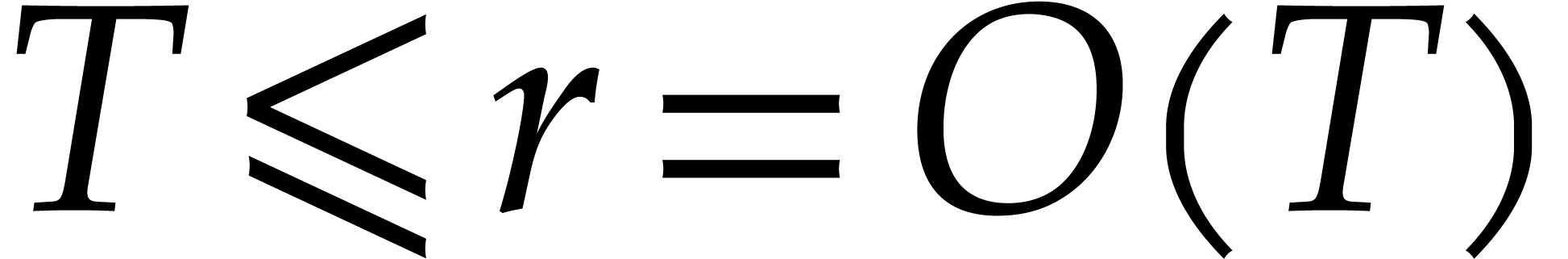 for this approach to
be efficient. Moreover, the recovery of
for this approach to
be efficient. Moreover, the recovery of 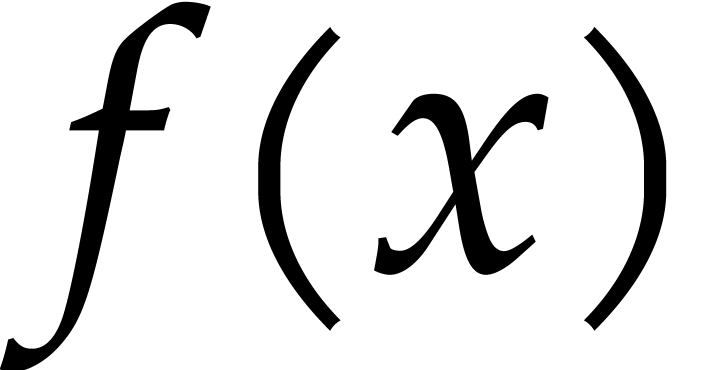 from its
reductions modulo
from its
reductions modulo 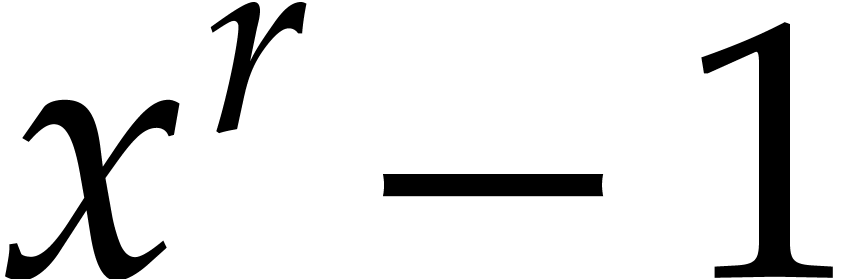 for several orders
for several orders  of this type is more delicate and based on a probabilistic
analysis. Yet, suitable orders
of this type is more delicate and based on a probabilistic
analysis. Yet, suitable orders  again tend to
exist in practice as long as
again tend to
exist in practice as long as 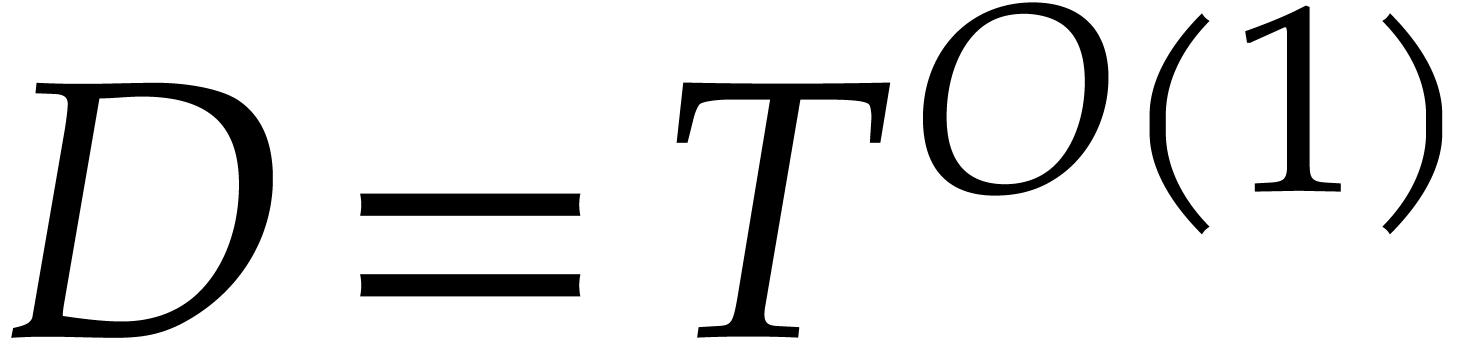 .
.
The expected complexities of the best versions of the three approaches are summarized in Table 1. These bounds rely on two types of heuristics:
For 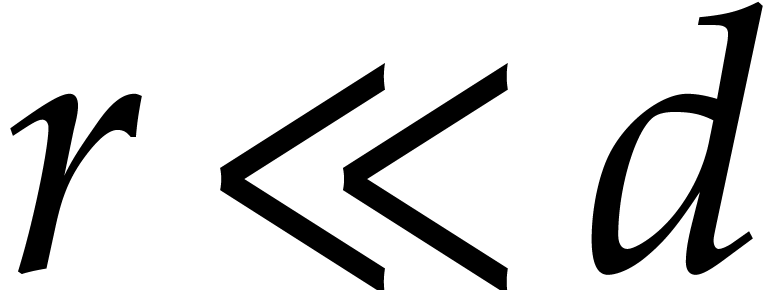 , the exponents of
, the exponents of
 are essentially randomly distributed
modulo
are essentially randomly distributed
modulo  .
.
For 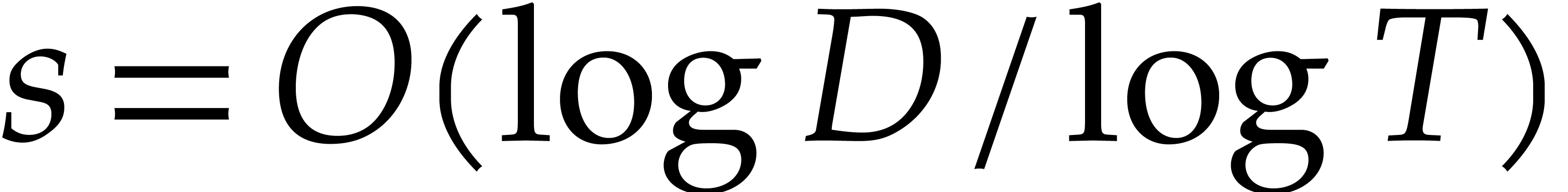 , the number
, the number 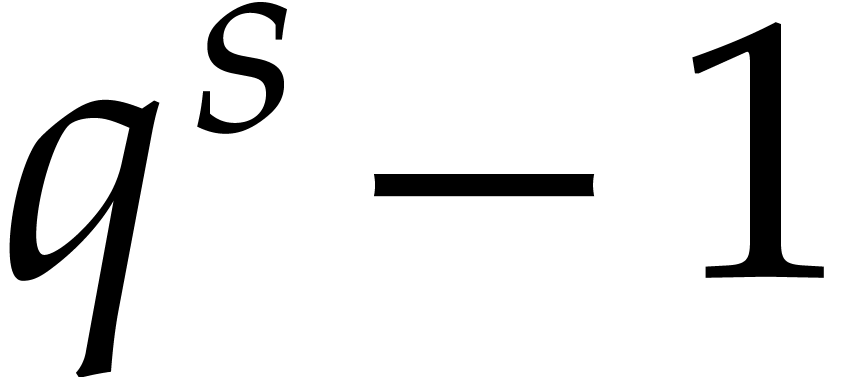 admits a “large smooth divisor”.
admits a “large smooth divisor”.
We will present a more precise version of H1 in section 4. The heuristic H2 will be made precise in sections 5.6 and 6.2 and numeric evidence is provided in sections 2, 6.3 and 6.4.
The last section
7
is dedicated to the interpolation of multivariate polynomials. We start
with the well known strategies based on Kronecker segmentation (section
7.1
) and prime factorization (section
7.2
). For sparse polynomials in many variables, but with a modest total
degree
 ,
we also recall the inductive approach by packets of coordinates in
section
7.3
. If
,
we also recall the inductive approach by packets of coordinates in
section
7.3
. If
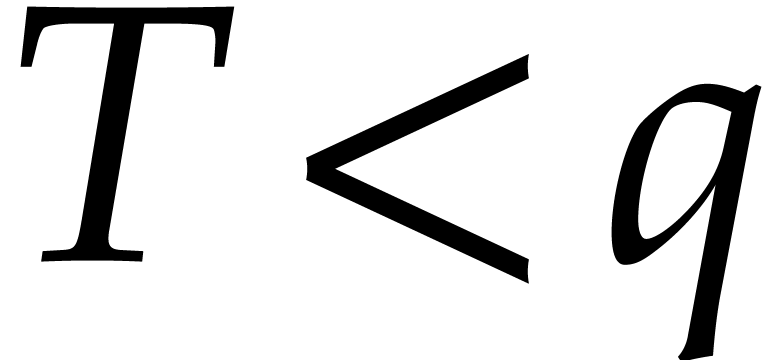 ,
then geometric progression and FFT based methods should be particularly
favorable in combination with this inductive approach, since one can
often avoid working over extensions of
,
then geometric progression and FFT based methods should be particularly
favorable in combination with this inductive approach, since one can
often avoid working over extensions of
 in this case. We conclude section
7
with a few algorithms for special situations.
in this case. We conclude section
7
with a few algorithms for special situations.
Acknowledgment. We wish to thank the anonymous referee for helpful corrections.
One remarkable feature of the finite field  with
with
 elements is that every
elements is that every 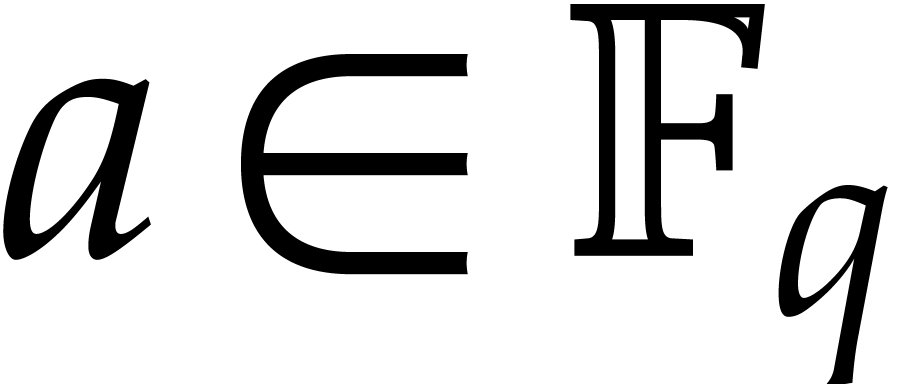 satisfies the equation
satisfies the equation 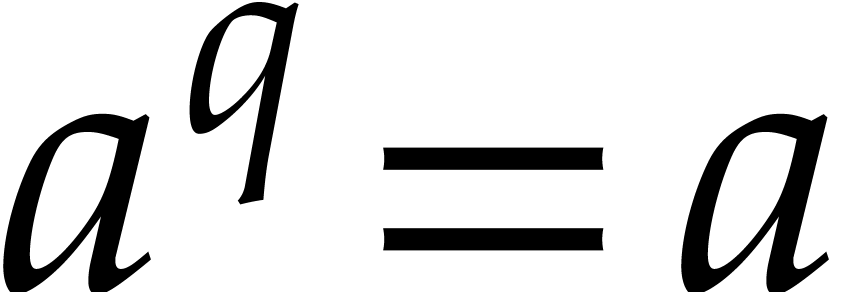 . In
particular, for any sparse polynomial
. In
particular, for any sparse polynomial  as in (1) and with coefficients in
as in (1) and with coefficients in  ,
the polynomial
,
the polynomial  takes the same values as
takes the same values as
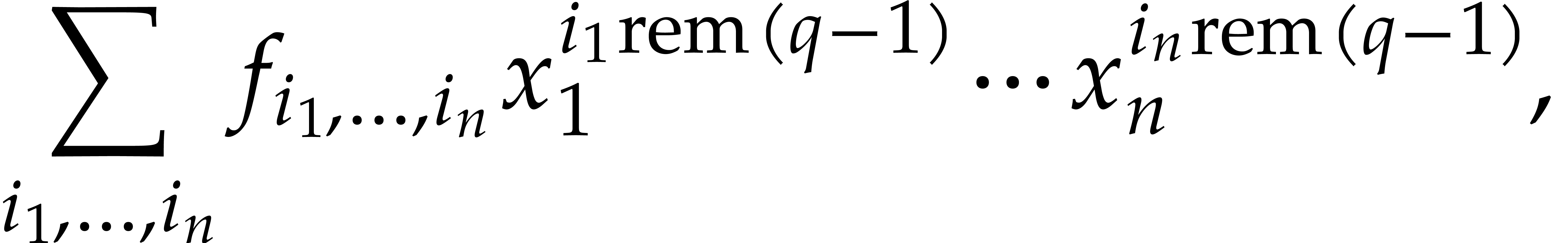
for 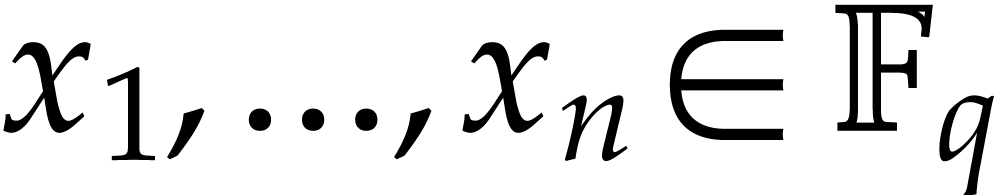 , where “
, where “ ” stands for the remainder of
a Euclidean division. In other words, the exponents of
” stands for the remainder of
a Euclidean division. In other words, the exponents of  are only determined modulo
are only determined modulo 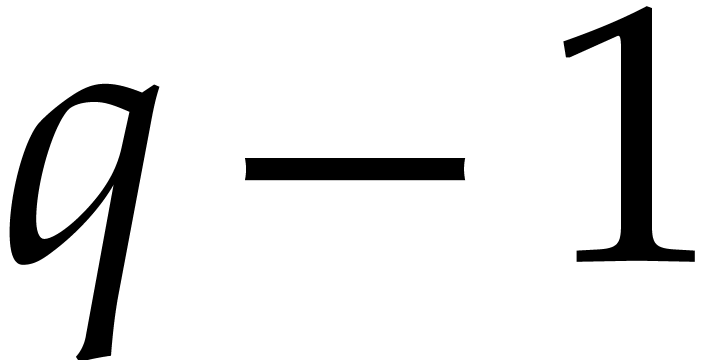 ,
so we may assume without loss of generality that they all lie in
,
so we may assume without loss of generality that they all lie in 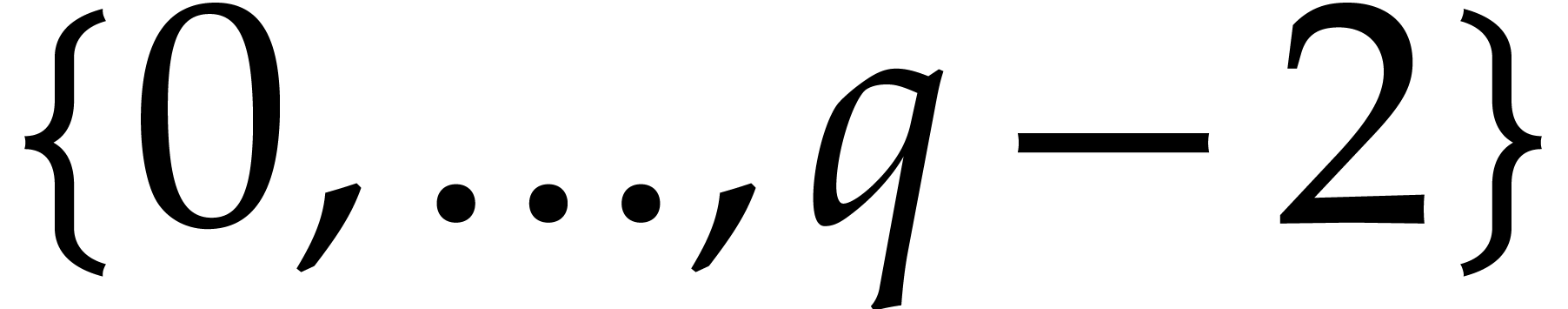 and that the total degree
and that the total degree  of
of
 satisfies
satisfies 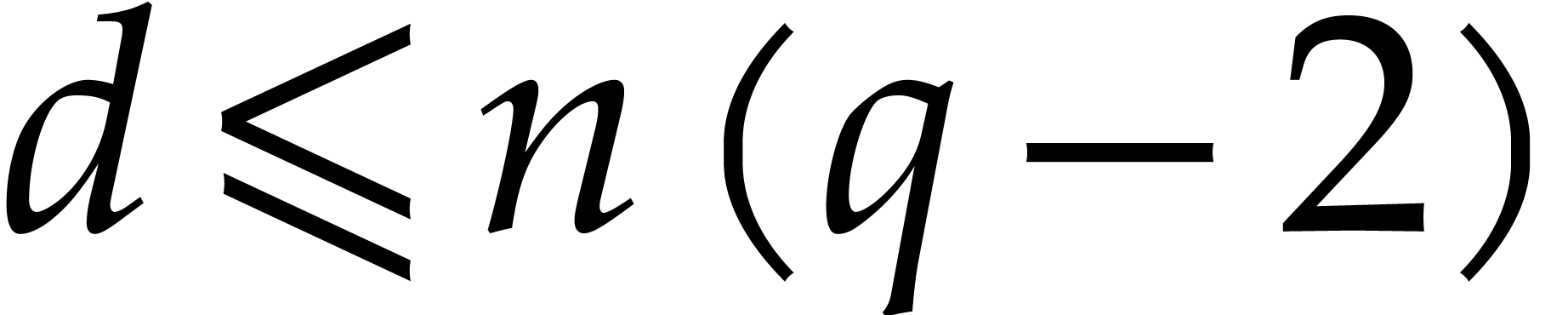 .
.
On the other hand, in the case where our black box function  can be evaluated not only over
can be evaluated not only over  , but also over field extensions
, but also over field extensions 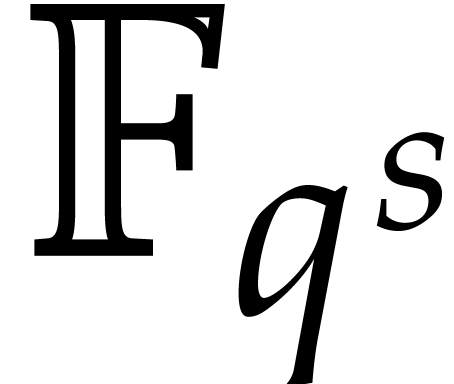 (this typically holds if
(this typically holds if  is given by an
expression or a directed acyclic graph (dag)), then the exponents in the
expression (1) can be general non-negative integers, but
the above remark shows that we will crucially need to evaluate over
extensions fields
is given by an
expression or a directed acyclic graph (dag)), then the exponents in the
expression (1) can be general non-negative integers, but
the above remark shows that we will crucially need to evaluate over
extensions fields 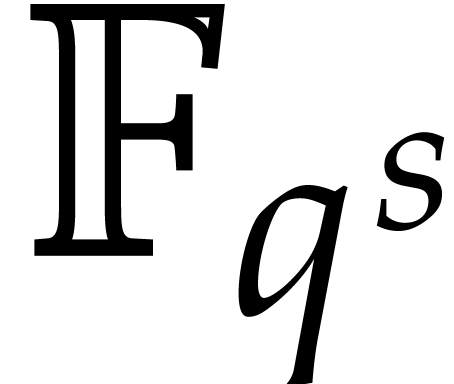 with
with  in order to recover exponents that exceed
in order to recover exponents that exceed  .
.
More generally, if we choose to evaluate  only at
points
only at
points 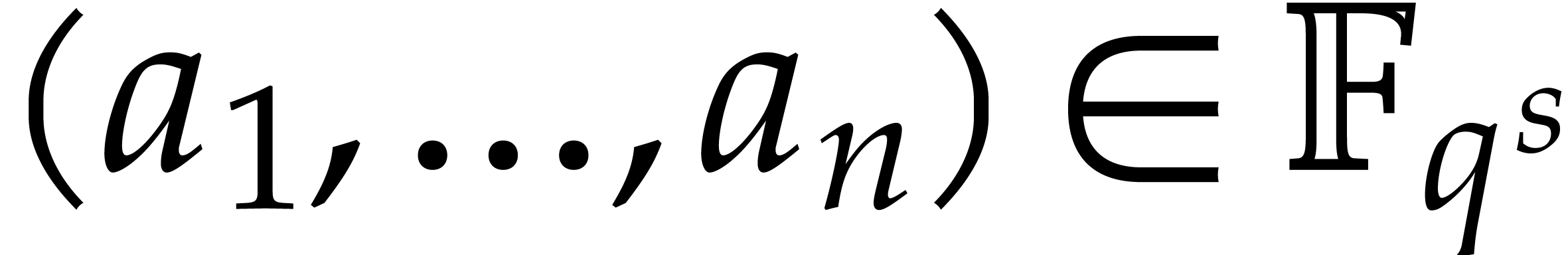 such that
such that  are
are
 -th roots of unity, then we
can only hope to determine the exponents modulo
-th roots of unity, then we
can only hope to determine the exponents modulo  in the expansion (1). In that case,
in the expansion (1). In that case,  must divide the order
must divide the order 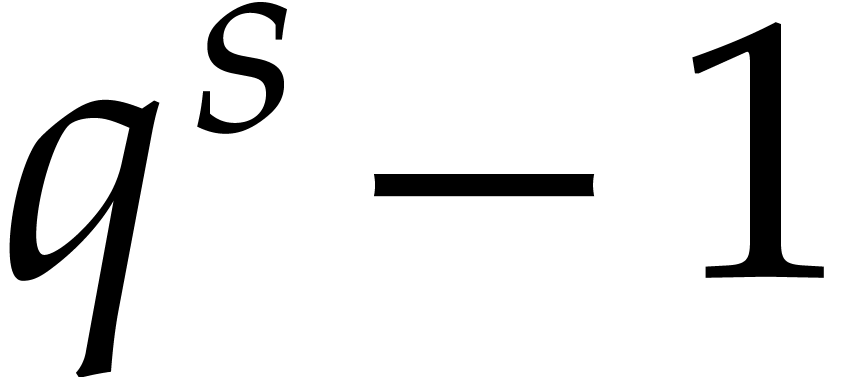 of the multiplicative
group of
of the multiplicative
group of 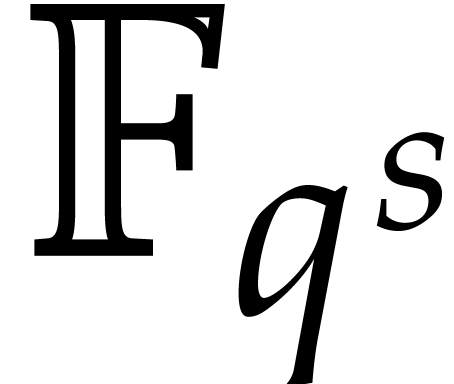 . In addition, as
recalled in sections 5.1 and 5.2 below,
several important tools such as polynomial root finding and discrete
logarithms admit faster implementations if we can take
. In addition, as
recalled in sections 5.1 and 5.2 below,
several important tools such as polynomial root finding and discrete
logarithms admit faster implementations if we can take  of the form
of the form 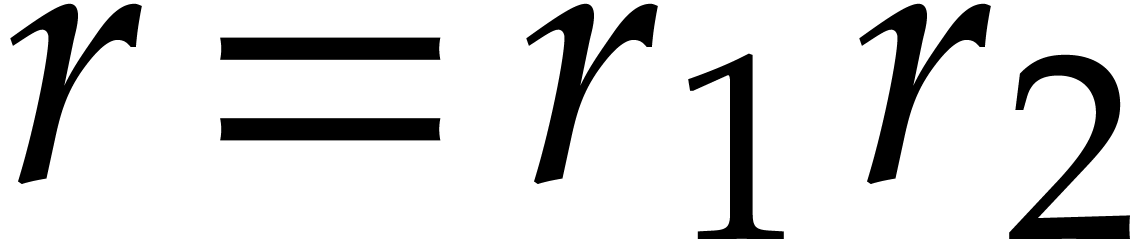 with
with  and
where
and
where  is smooth. Sometimes, primitive roots of
unity of such orders
is smooth. Sometimes, primitive roots of
unity of such orders  already exist in
already exist in  . If not, then we need to search
them in extension fields
. If not, then we need to search
them in extension fields 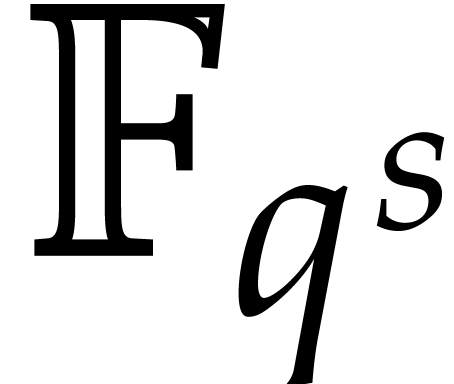 with
with  as small as possible.
as small as possible.
Let us briefly investigate the prime factorization of
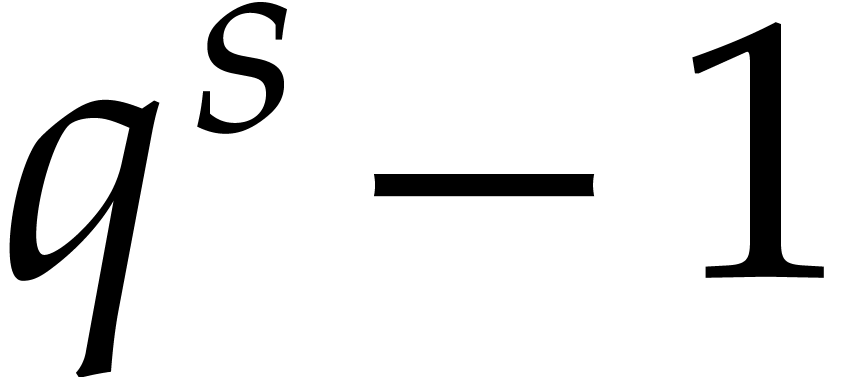 for various prime numbers
for various prime numbers
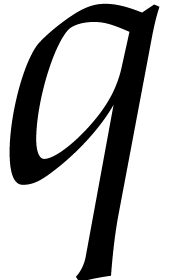 and small
and small
 .
As observed in [
26
, Theorems 4.1 and 4.6], the number
.
As observed in [
26
, Theorems 4.1 and 4.6], the number
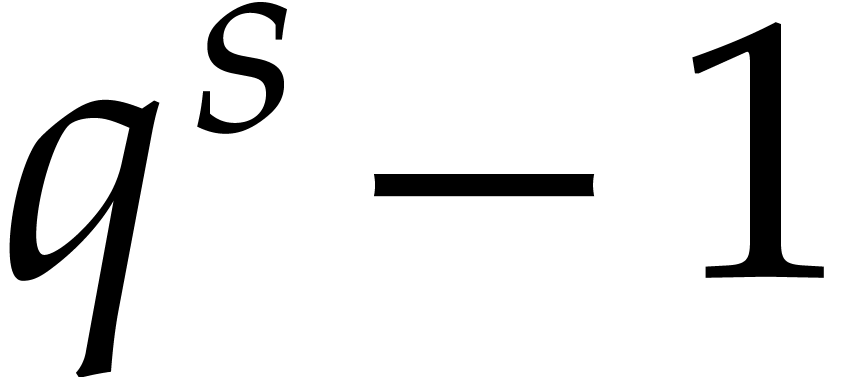 typically admits many small prime divisors when
typically admits many small prime divisors when
 is itself smooth. This phenomenon is illustrated in Table
2
for small values of
is itself smooth. This phenomenon is illustrated in Table
2
for small values of
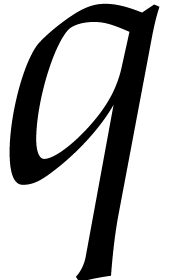 .
Given
.
Given
 ,
it seems easy in practice to find a small
,
it seems easy in practice to find a small
 and divisors
and divisors
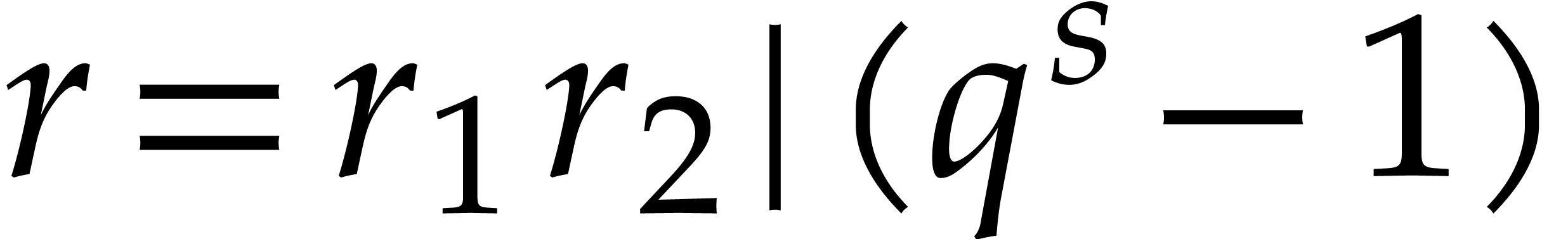 such that
such that
 and
and
 is smooth.
is smooth.
For larger  , we may need to
resort to larger extension degrees
, we may need to
resort to larger extension degrees  in order to
find appropriate orders
in order to
find appropriate orders  . A
natural question is whether
. A
natural question is whether 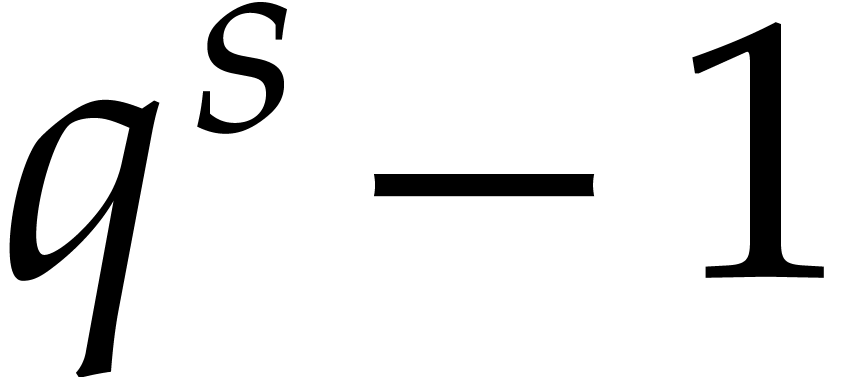 is guaranteed to
have a non-trivial smooth divisor for large
is guaranteed to
have a non-trivial smooth divisor for large  and
a fixed value of
and
a fixed value of  . This leads
us to introduce the following guaranteed lower bound:
. This leads
us to introduce the following guaranteed lower bound:
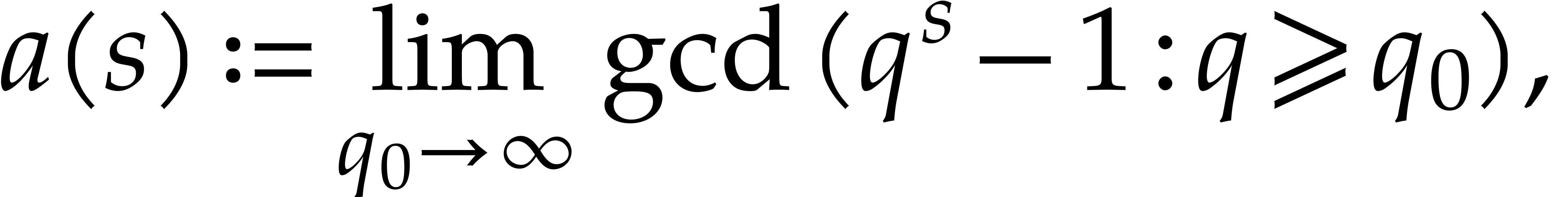 |
(2) |
where 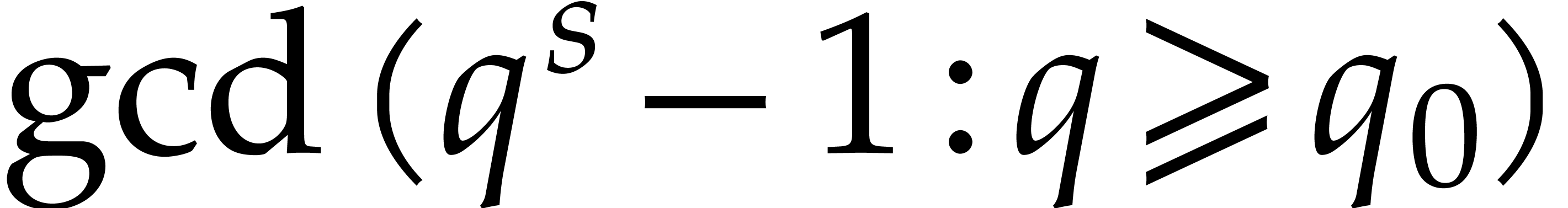 denotes the g.c.d. of the
integers
denotes the g.c.d. of the
integers 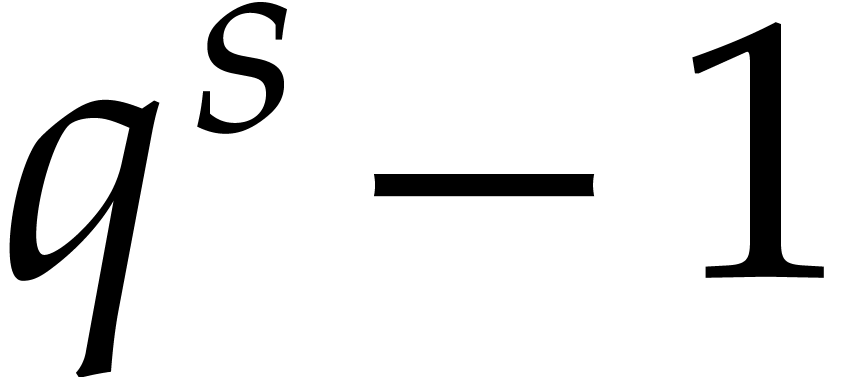 where
where  runs over
the prime numbers greater than or equal to
runs over
the prime numbers greater than or equal to 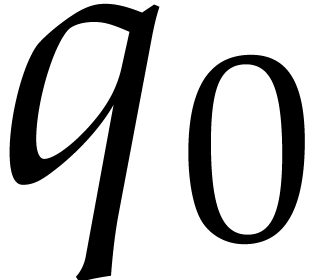 .
.
In Table
3
, we listed the prime factorizations of
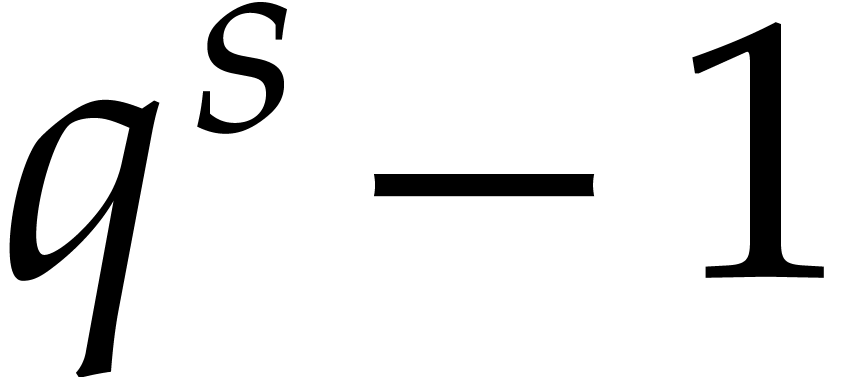 and
and
 for
for
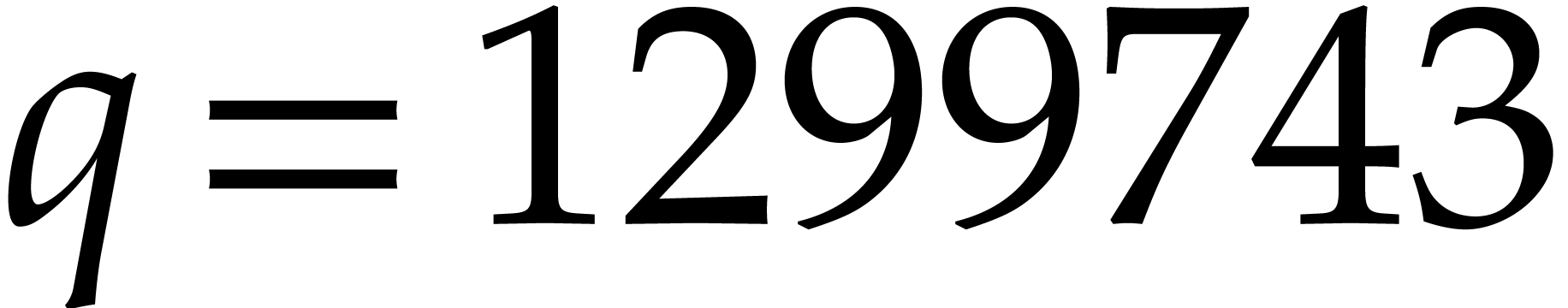 and various small smooth values of
and various small smooth values of
 .
Here
.
Here
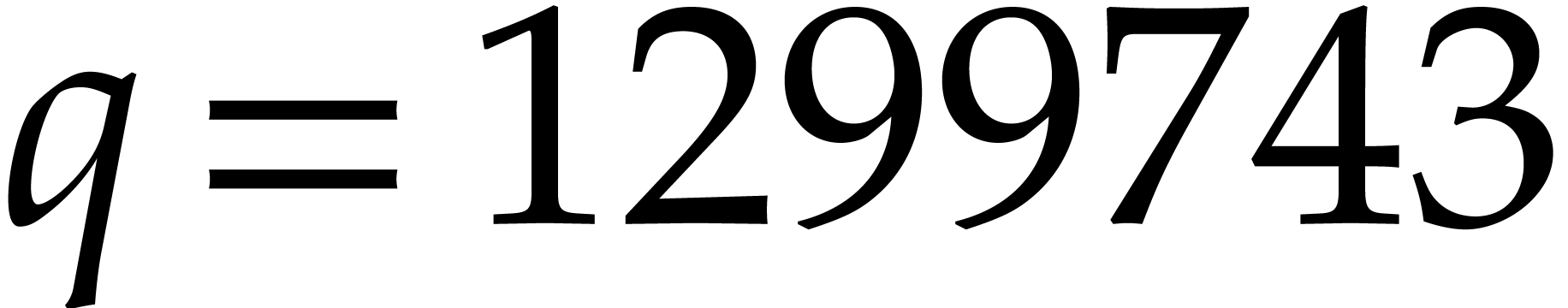 was chosen such that
was chosen such that
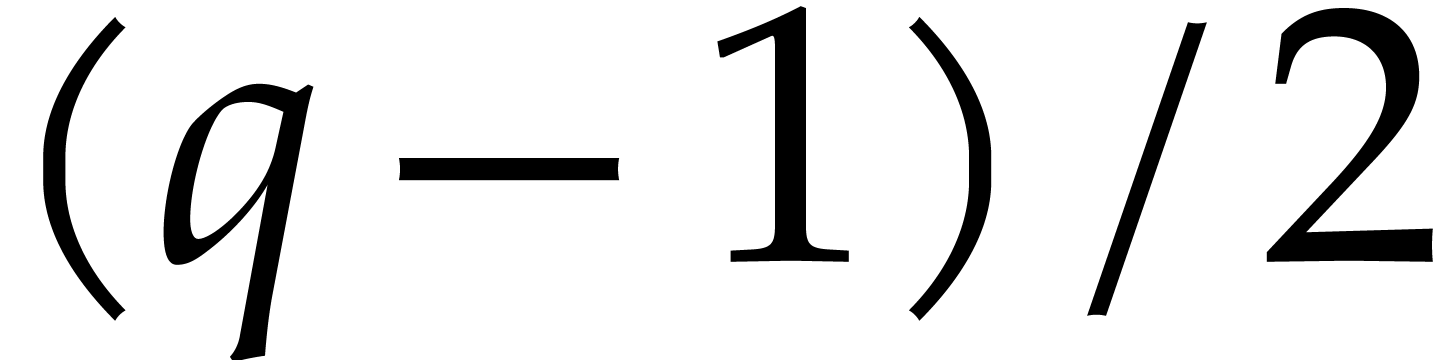 is also prime. For the practical applications in this paper, the table
suggests that it remains likely that suitable orders
is also prime. For the practical applications in this paper, the table
suggests that it remains likely that suitable orders
 can still be found whenever needed, and that
can still be found whenever needed, and that
 is usually quite pessimistic, even for large values of
is usually quite pessimistic, even for large values of
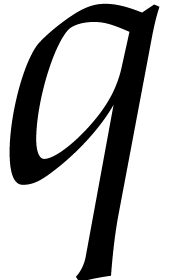 .
Let us finally mention that the sequence
.
Let us finally mention that the sequence
 coincides with Sloane's integer sequence
A079612
; see
https://oeis.org/A079612
.
coincides with Sloane's integer sequence
A079612
; see
https://oeis.org/A079612
.
As already mentioned in the introduction, most algorithms for sparse
interpolation are probabilistic of Monte Carlo type. We notice that it
is easy to check (with high probability) whether a candidate sparse
interpolation 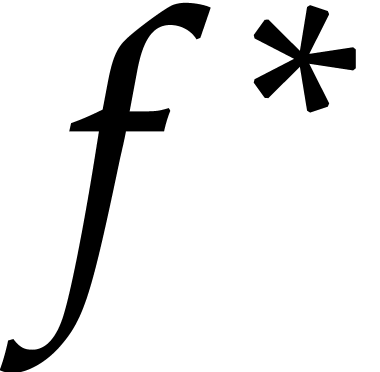 of
of  is
correct. Indeed, it suffices to evaluate
is
correct. Indeed, it suffices to evaluate 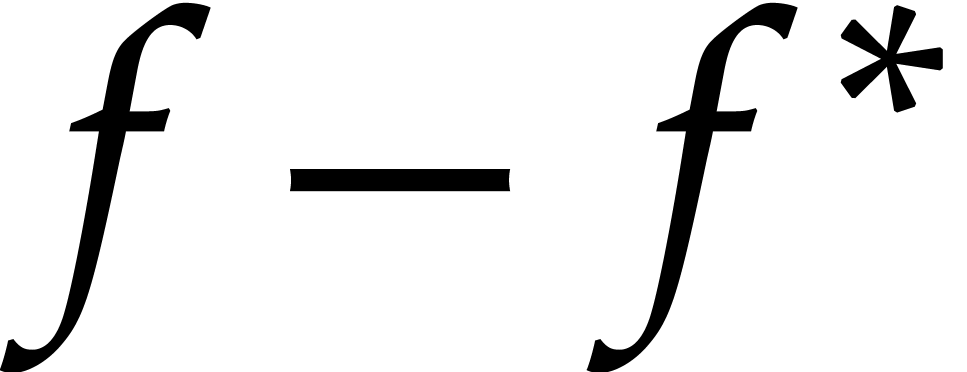 at
random sample points and check whether the result vanishes.
Deterministic algorithms exist but with higher complexities; see for
instance [27, 51].
at
random sample points and check whether the result vanishes.
Deterministic algorithms exist but with higher complexities; see for
instance [27, 51].
Many algorithms for sparse interpolation require extra information, such
as bounds 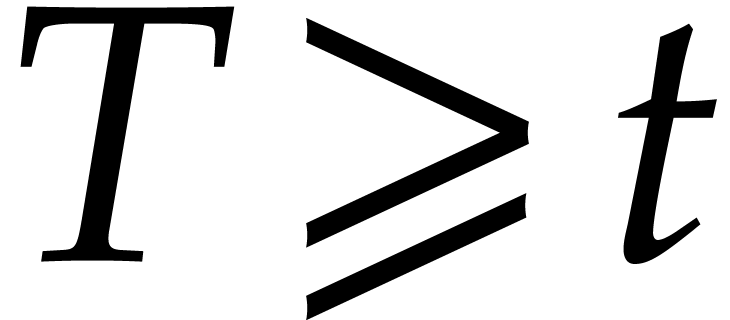 and
and 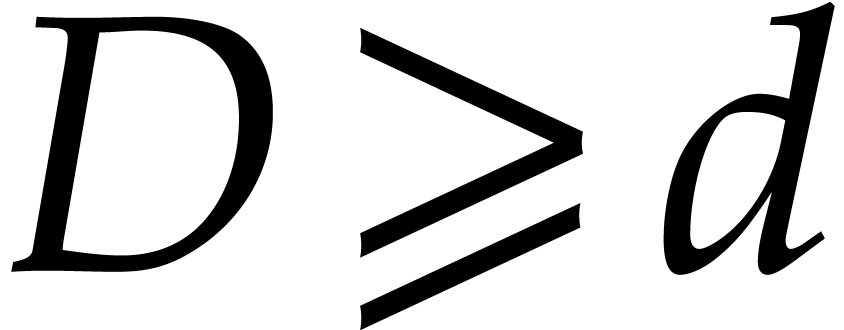 for the
number of terms and the total degree of
for the
number of terms and the total degree of  .
Furthermore, several algorithms are only able to guess some of the terms
of
.
Furthermore, several algorithms are only able to guess some of the terms
of  with high probability, but not all of them.
In this section, using ideas from [3], we show how to turn
such “partial” algorithms for sparse interpolation into
full-blown ones. Provided that the characteristic of
with high probability, but not all of them.
In this section, using ideas from [3], we show how to turn
such “partial” algorithms for sparse interpolation into
full-blown ones. Provided that the characteristic of  is zero or sufficiently large, we also show how to upgrade an
interpolation method modulo
is zero or sufficiently large, we also show how to upgrade an
interpolation method modulo  into a general
algorithm, following [37].
into a general
algorithm, following [37].
Assume that we have an algorithm for “approximate” (or
“partial”) sparse interpolation that takes a black box for
 as input, together with bounds
as input, together with bounds  and
and 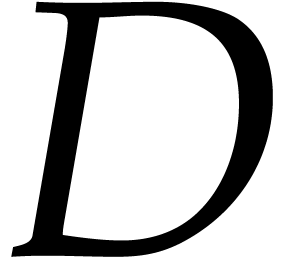 for
for  and
and  . The algorithm should always return a sparse
polynomial
. The algorithm should always return a sparse
polynomial 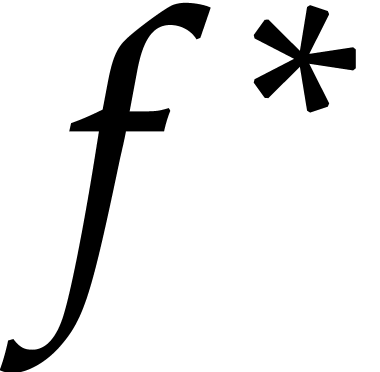 , of total degree
at most
, of total degree
at most  and with at most
and with at most  terms. Moreover, for some fixed constant
terms. Moreover, for some fixed constant  ,
if
,
if 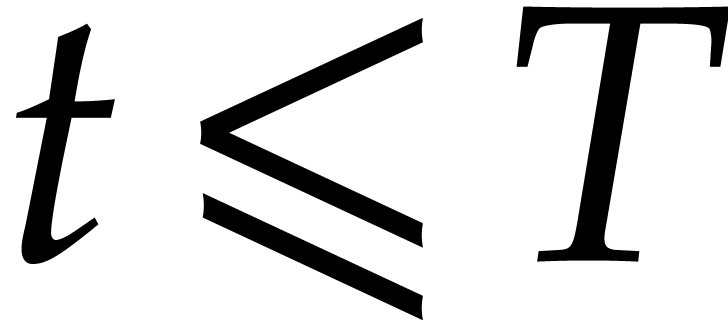 and
and 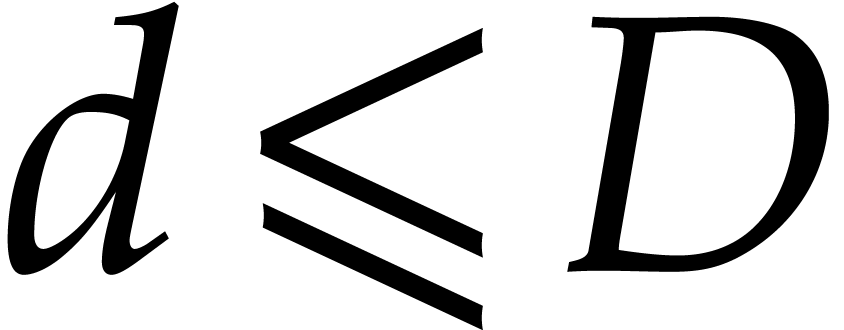 ,
then
,
then 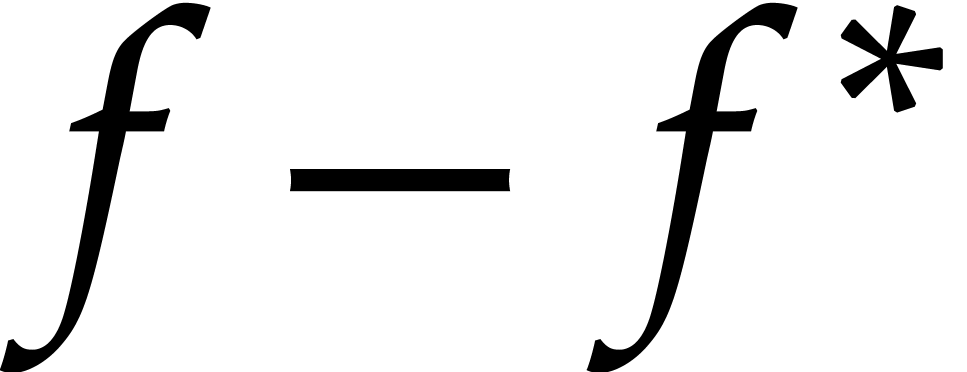 should contain at most
should contain at most  terms, with high probability. If
terms, with high probability. If  or
or  , then we allow
, then we allow  to be
essentially arbitrary under the above constraint that
to be
essentially arbitrary under the above constraint that  has at most
has at most  terms of degree
terms of degree  . Then we may use the following strategy for
“full” sparse interpolation:
. Then we may use the following strategy for
“full” sparse interpolation:
In step 6, the precise policy for increasing  and
and
 may depend on the application. We typically
double
may depend on the application. We typically
double  when
when  is suspected
to exceed
is suspected
to exceed  and we double
and we double  when
when  is suspected to exceed
is suspected to exceed 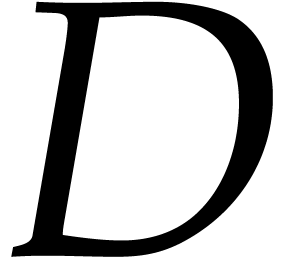 . In this way, the bounds
. In this way, the bounds  and
and 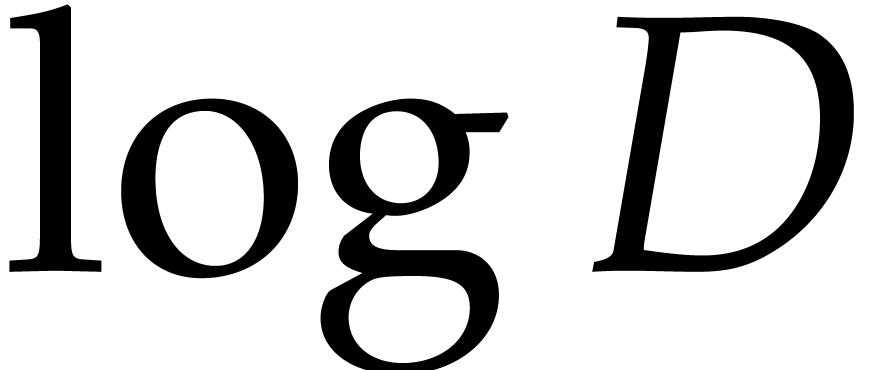 are at most twice as large as the actual
values
are at most twice as large as the actual
values  and
and 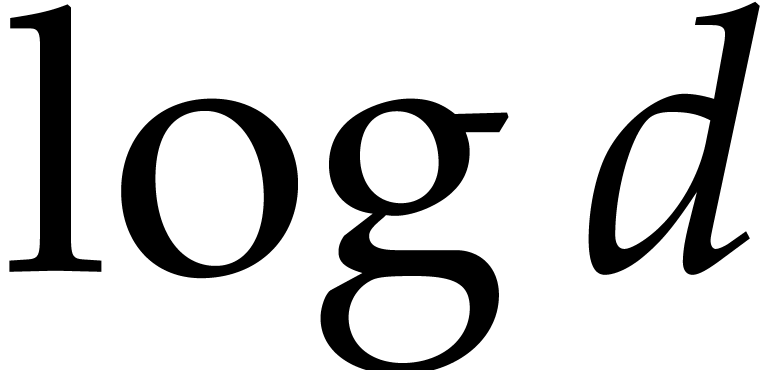 ,
and the running time is essentially a constant times the running time of
the approximate sparse interpolation with bounds
,
and the running time is essentially a constant times the running time of
the approximate sparse interpolation with bounds  and
and 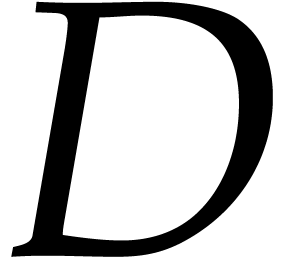 .
.
However, for this “meta complexity bound” to hold, it is
crucial in step 3 that the sparse approximation  can be evaluated efficiently at the sample points used during the sparse
interpolation (the naive evaluation of a polynomial with
can be evaluated efficiently at the sample points used during the sparse
interpolation (the naive evaluation of a polynomial with  terms at
terms at 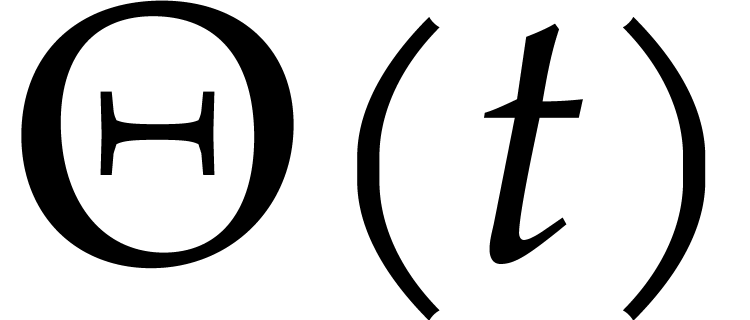 points would take time
points would take time
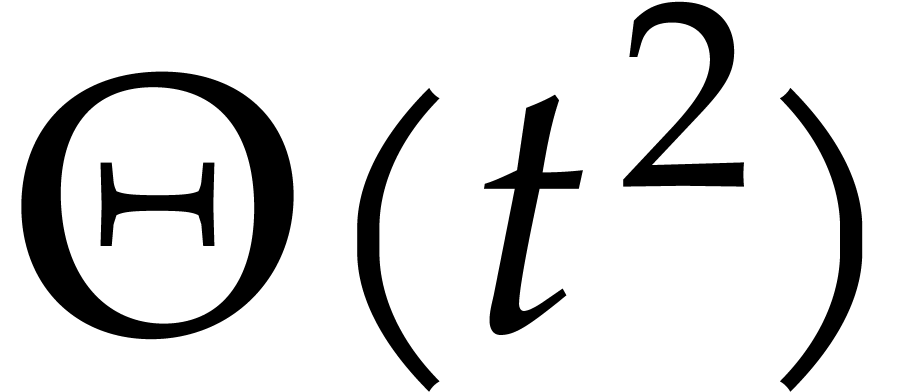 , which is too much).
Fortunately, this is the case for all sparse interpolation strategies
that will be considered in this paper.
, which is too much).
Fortunately, this is the case for all sparse interpolation strategies
that will be considered in this paper.
When do we suspect  or
or 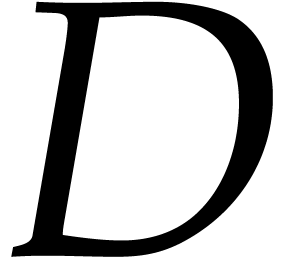 to
be too low in step 6? In the case of
to
be too low in step 6? In the case of  ,
a natural idea is to test whether the number of terms in
,
a natural idea is to test whether the number of terms in  or
or  exceeds a fixed constant
portion of
exceeds a fixed constant
portion of  . This strategy
assumes that
. This strategy
assumes that  be essentially random when
be essentially random when  is too small (if the number of terms of
is too small (if the number of terms of  is much smaller than
is much smaller than  whenever
whenever
 , then we might need more
than
, then we might need more
than 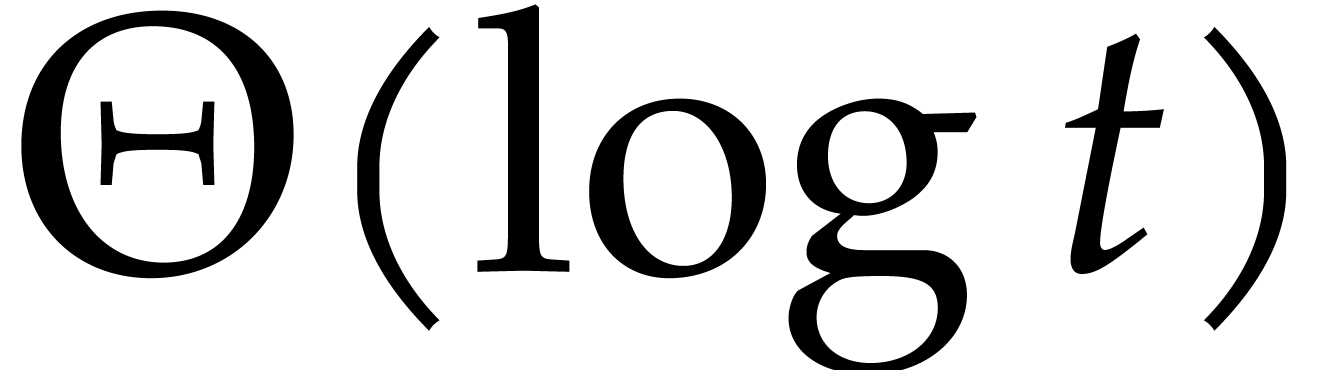 iterations before the algorithm converges).
iterations before the algorithm converges).
The handling of exponents and degree bounds is more involved. When
interpolating over a finite field, all non-zero evaluation points are
roots of unity, so the exponents can only be determined modulo a certain
integer  (or even modulo a submodule of
(or even modulo a submodule of 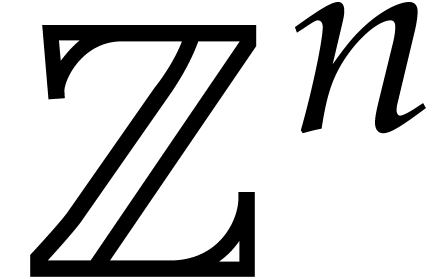 ). If the characteristic of
). If the characteristic of  is sufficiently large, then the exponents can be
computed directly: see the next subsection. Otherwise, we need to
recombine reductions with respect to several moduli: see section 4 below. This also provides a natural test in order to check
whether
is sufficiently large, then the exponents can be
computed directly: see the next subsection. Otherwise, we need to
recombine reductions with respect to several moduli: see section 4 below. This also provides a natural test in order to check
whether 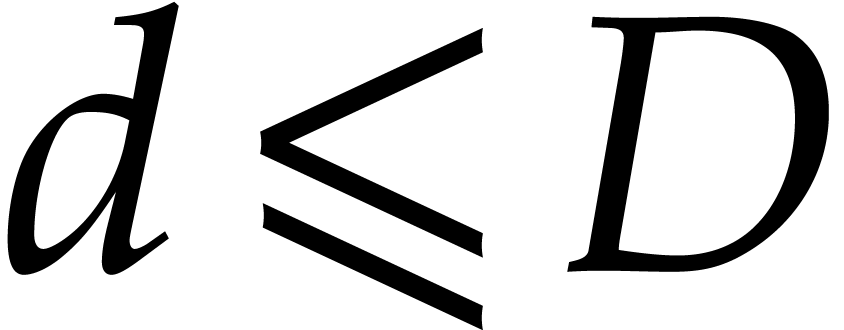 . Indeed, it suffices
to compute the sparse interpolation of
. Indeed, it suffices
to compute the sparse interpolation of  for one
or more extra moduli and check whether the results agree with our
candidate interpolation.
for one
or more extra moduli and check whether the results agree with our
candidate interpolation.
Assume that we have an algorithm that allows us to compute the sparse
interpolation of  modulo
modulo 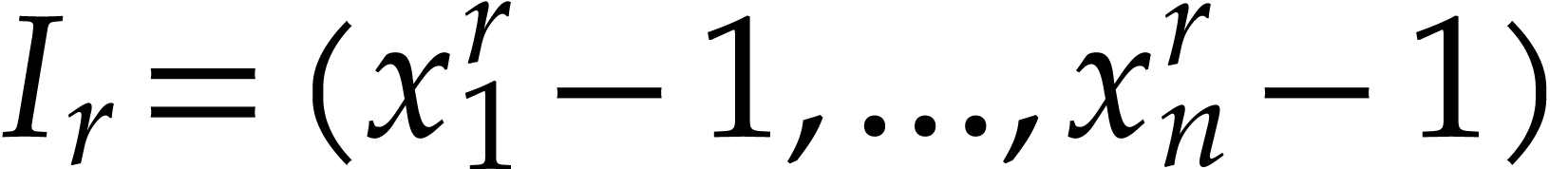 for given moduli
for given moduli  . Assume
also that we have access to the program that computes
. Assume
also that we have access to the program that computes  , typically in terms of a straight-line
program. If
, typically in terms of a straight-line
program. If 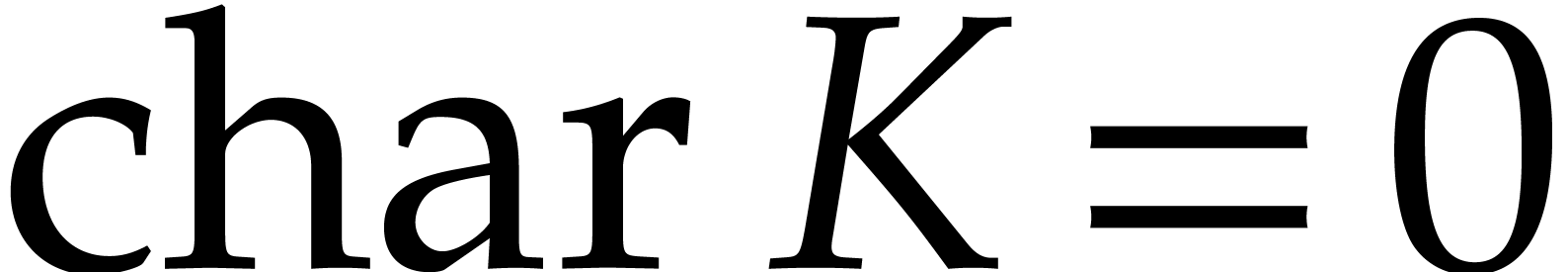 or
or 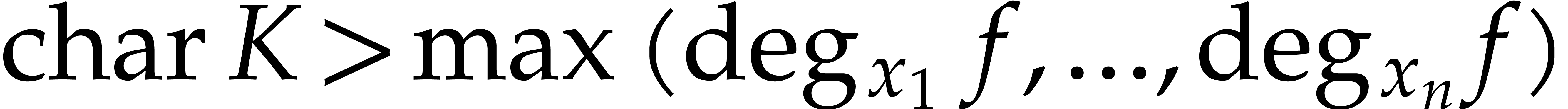 ,
then let us show how to derive an algorithm for the sparse evaluation of
,
then let us show how to derive an algorithm for the sparse evaluation of
 .
.
It is well known that the technique of “automatic
differentiation” (due to Baur and Strassen [7])
allows us to evaluate the gradient  using at most
using at most
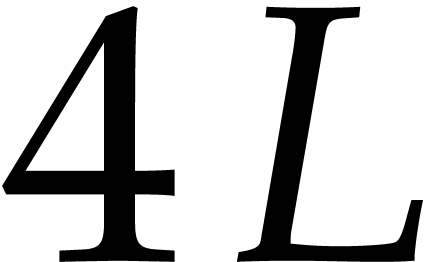 operations in
operations in  .
Using
.
Using 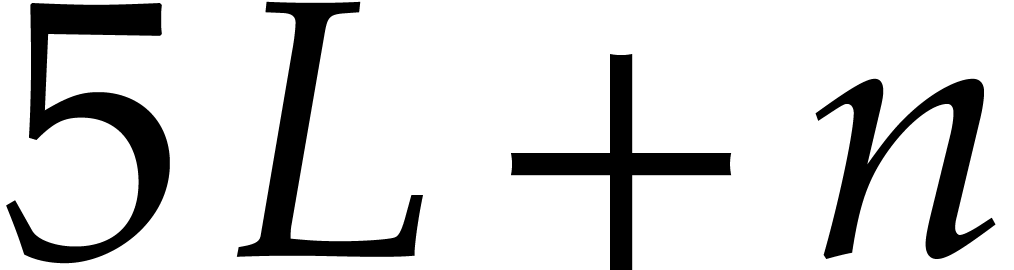 operations, this provides an algorithm for
the simultaneously evaluation of
operations, this provides an algorithm for
the simultaneously evaluation of 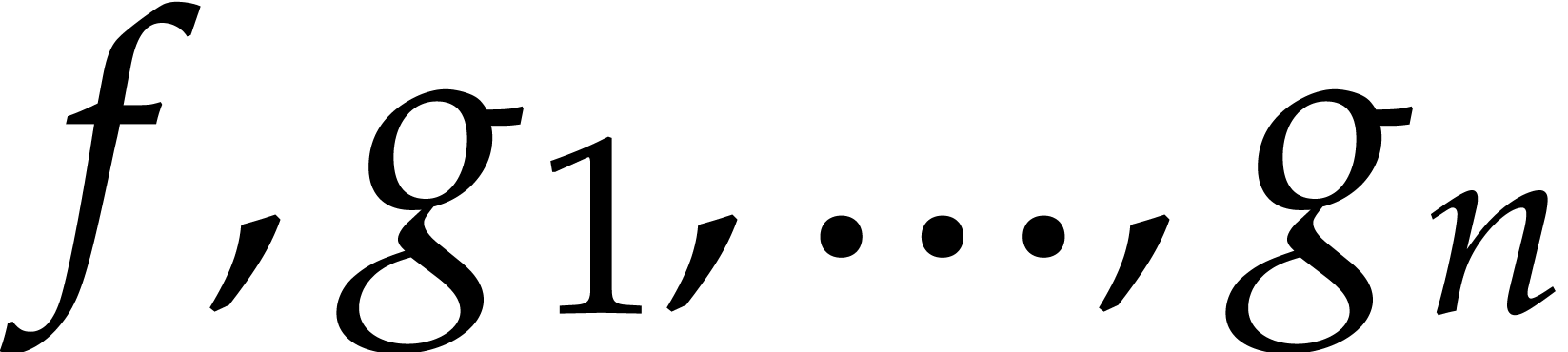 with
with 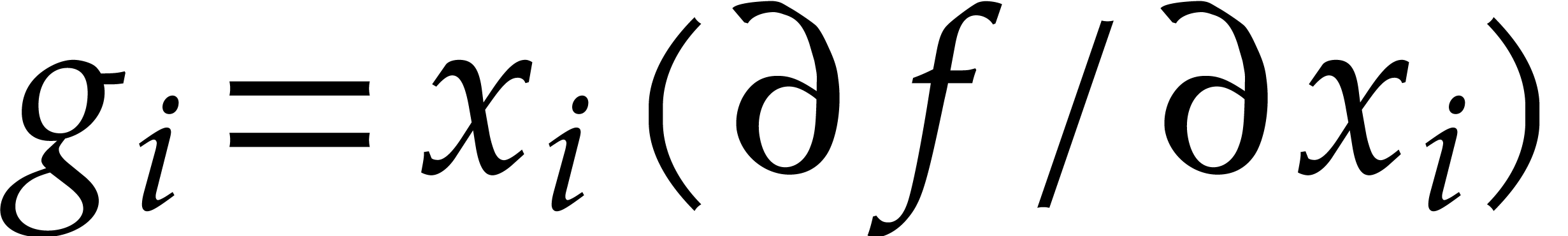 for
for 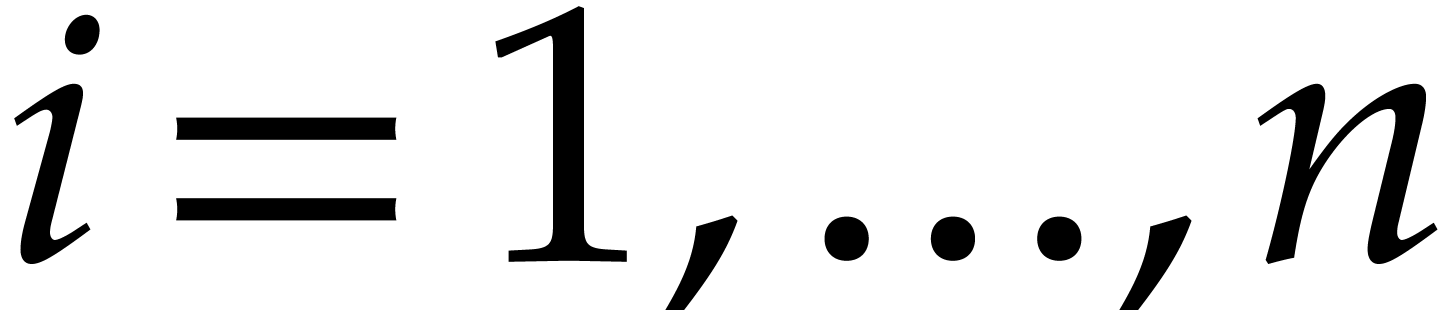 . With a
small overhead, this next allows us to jointly compute the sparse
interpolations of
. With a
small overhead, this next allows us to jointly compute the sparse
interpolations of 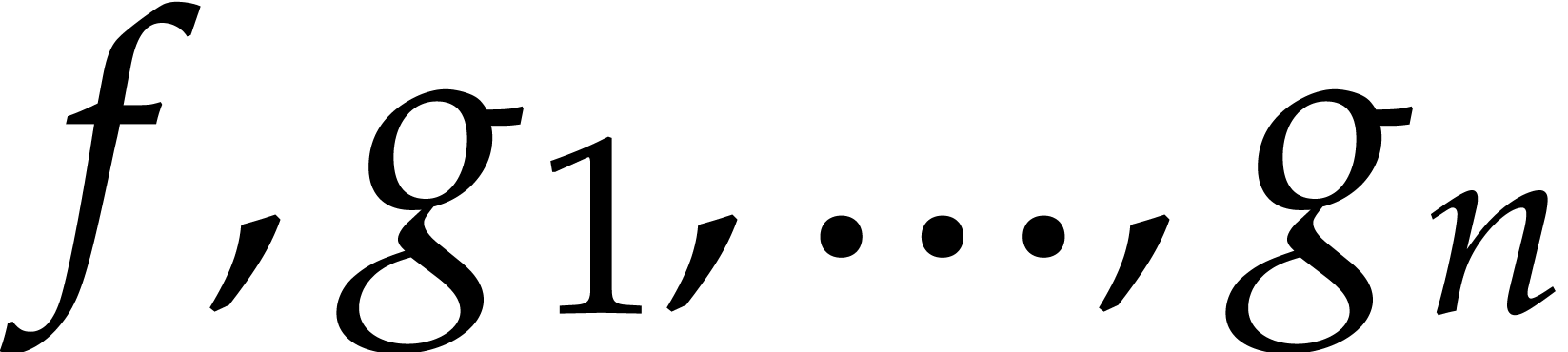 modulo
modulo  .
.
Now assume that 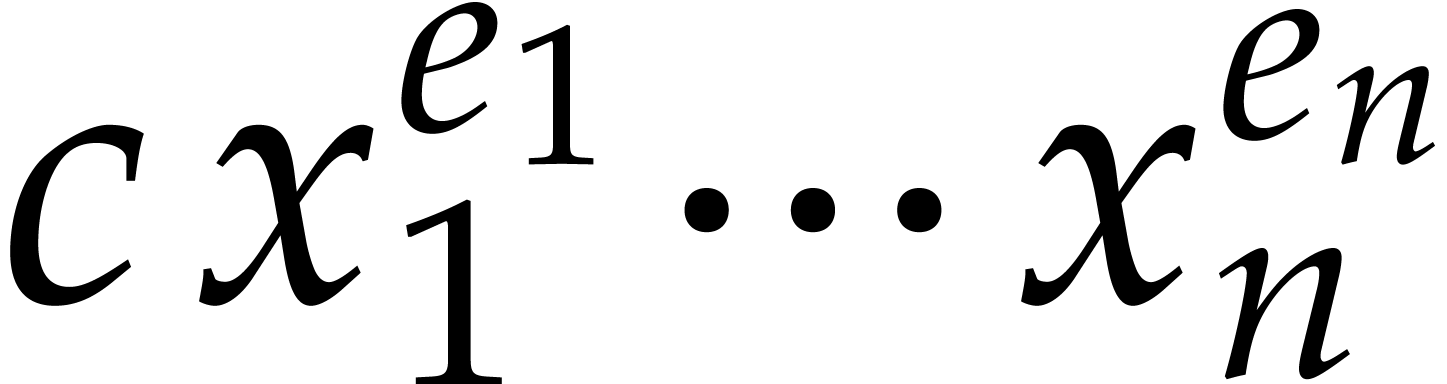 is a term of
is a term of  such that for any other term
such that for any other term 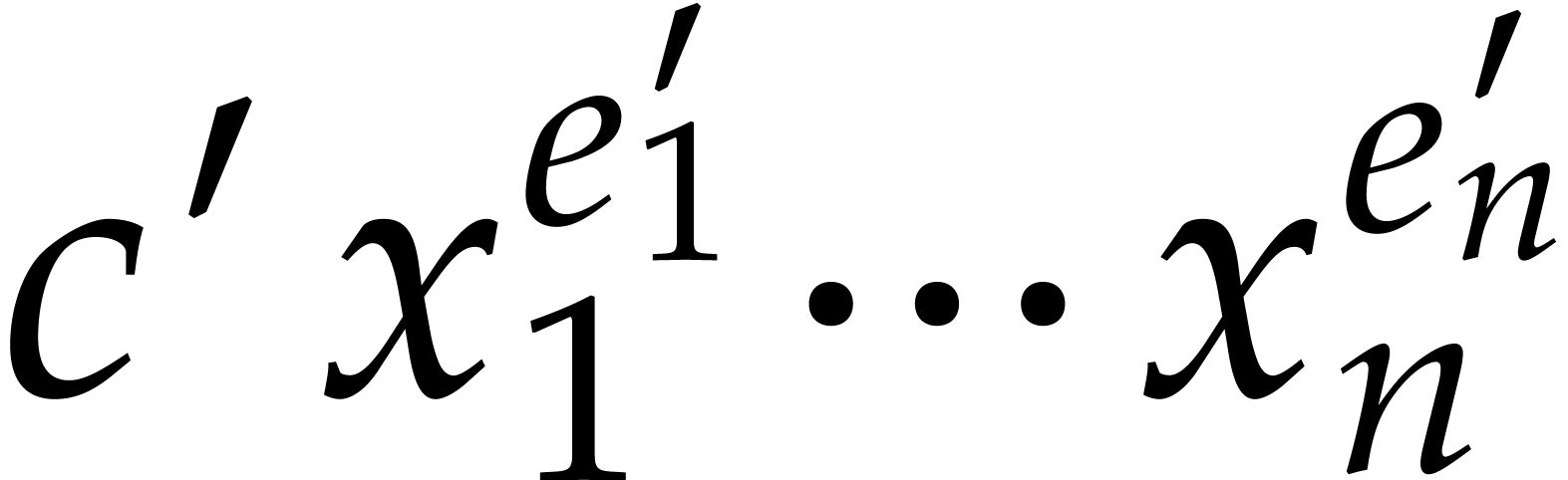 of
of  , we have
, we have 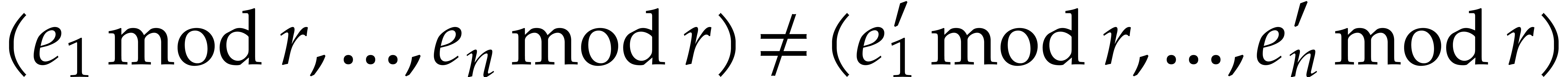 ;
we say that this term “does not collide” modulo
;
we say that this term “does not collide” modulo  . Then the sparse interpolation of
. Then the sparse interpolation of  modulo
modulo  contains the non-zero term
contains the non-zero term
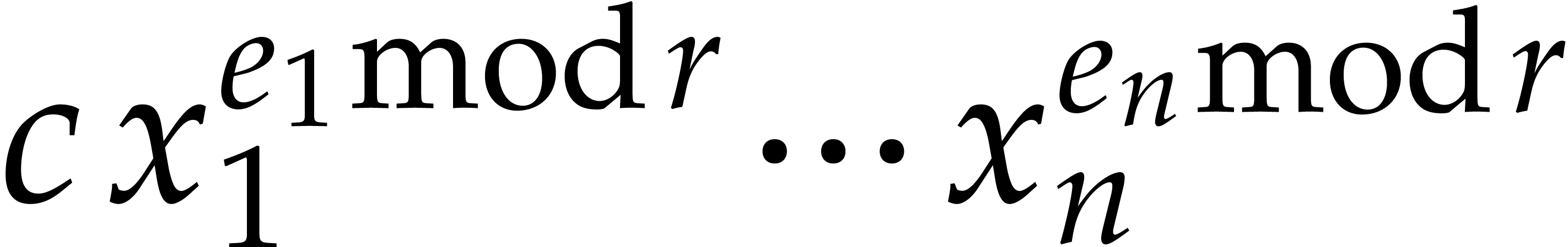 . Moreover, given
. Moreover, given 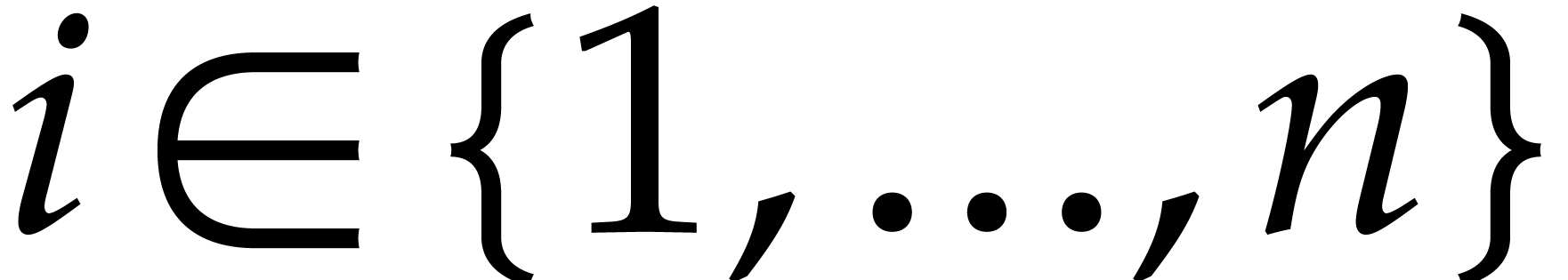 with
with 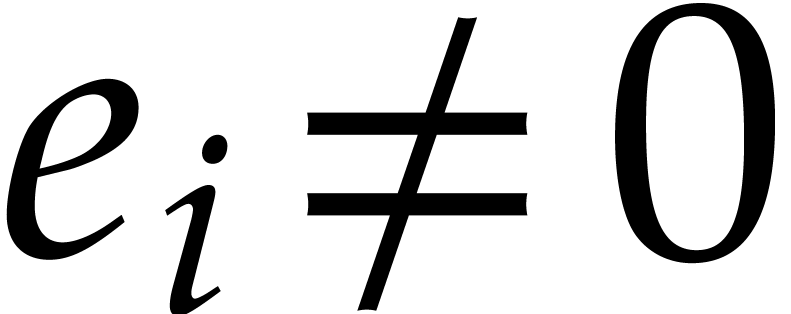 , the
sparse interpolation of
, the
sparse interpolation of  modulo
modulo  also contains the non-zero term
also contains the non-zero term 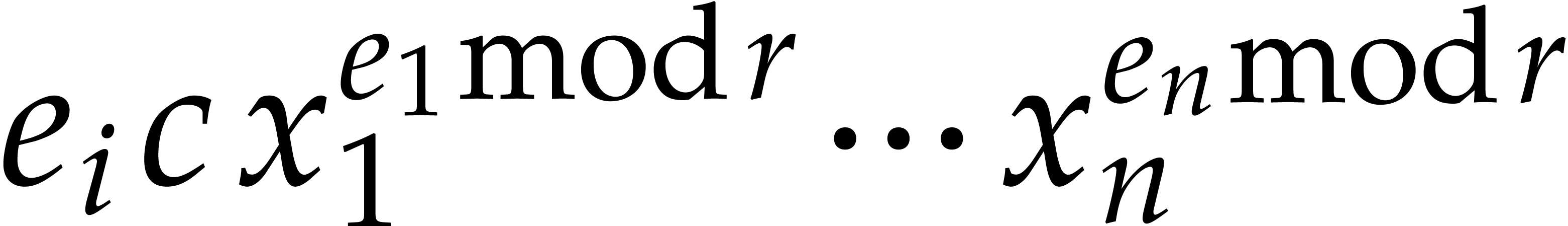 .
This allows us to retrieve
.
This allows us to retrieve  through one simple
division
through one simple
division 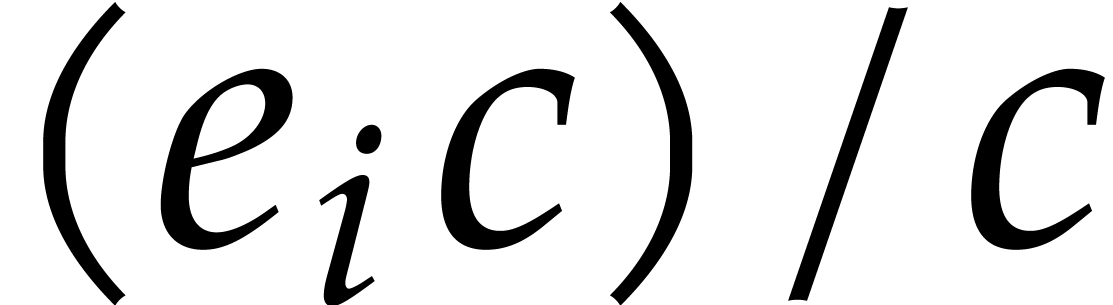 .
.
Furthermore, if the modulus  was picked at random
with
was picked at random
with 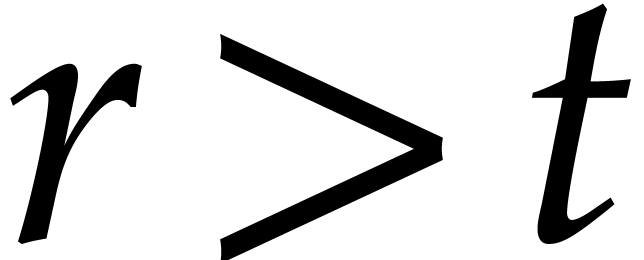 , then there is a high
probability that a fixed non-zero proportion of terms in
, then there is a high
probability that a fixed non-zero proportion of terms in  do not collide modulo
do not collide modulo  .
Combined with Algorithm 1, this yields an algorithm for
obtaining the sparse interpolation of
.
Combined with Algorithm 1, this yields an algorithm for
obtaining the sparse interpolation of  .
This strategy for sparse interpolation was first exploited by Huang [37].
.
This strategy for sparse interpolation was first exploited by Huang [37].
Remark. For simplicity, we consider sparse
interpolation of polynomials over fields  in this
paper. In fact, the algorithms also work for vectors of polynomials in
in this
paper. In fact, the algorithms also work for vectors of polynomials in
 , by considering them as
polynomials with coefficients in
, by considering them as
polynomials with coefficients in 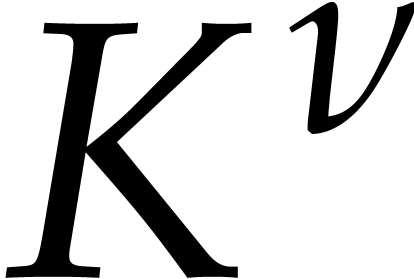 .
We implicitly used this fact above when saying that we
“jointly” compute the sparse interpolation of
.
We implicitly used this fact above when saying that we
“jointly” compute the sparse interpolation of 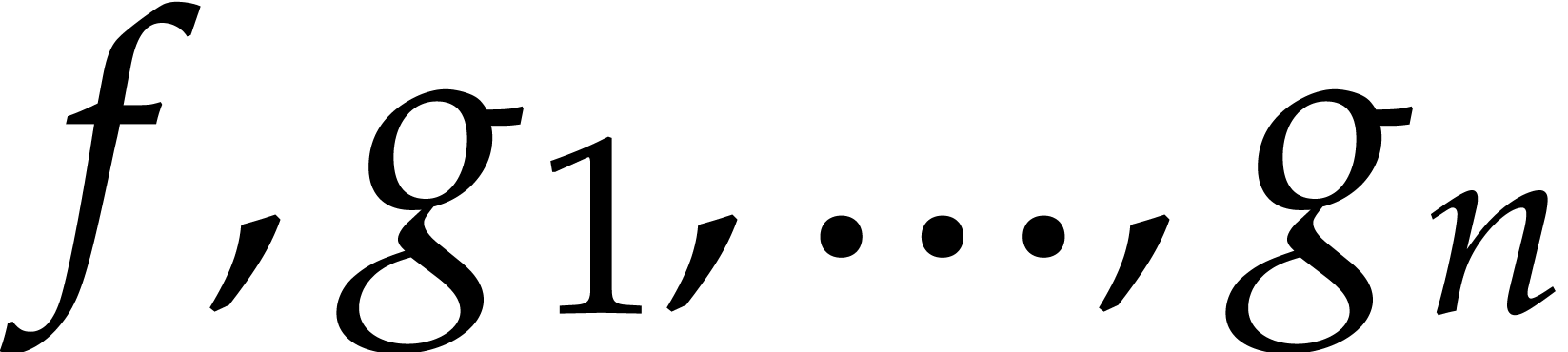 modulo
modulo 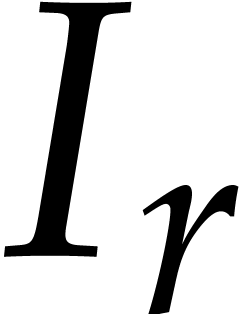 .
.
In summary, we have shown how to reduce the general problem of sparse interpolation to the case when
we have bounds for the number of terms and the total degree, and
we only require an approximate sparse interpolation (in the sense of section 3.1).
One general approach for sparse interpolation of univariate polynomials
over general base fields  was initiated by Garg
and Schost [17]. It assumes that the black box function
was initiated by Garg
and Schost [17]. It assumes that the black box function
 can be evaluated over any cyclic extension of
the form
can be evaluated over any cyclic extension of
the form 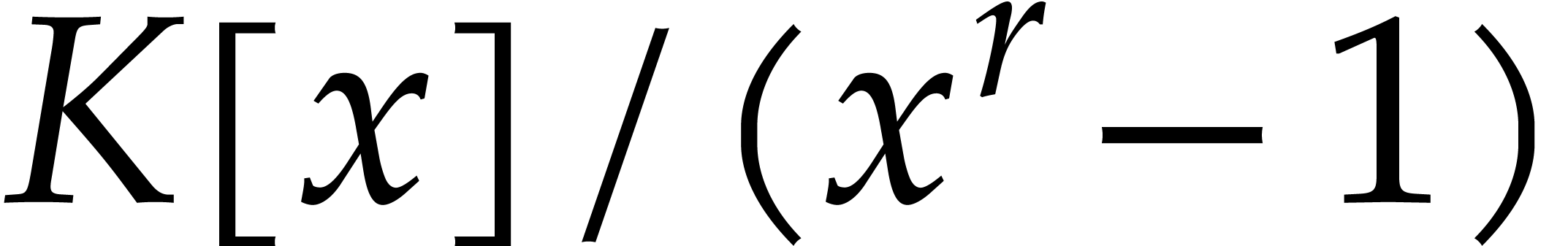 . The evaluation of
. The evaluation of
 |
(3) |
at  inside such an extension simply yields
inside such an extension simply yields
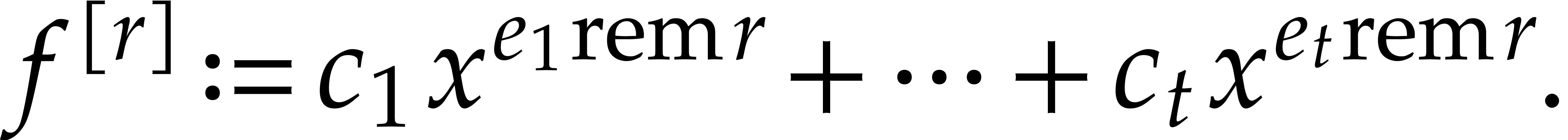
In absence of “collisions” 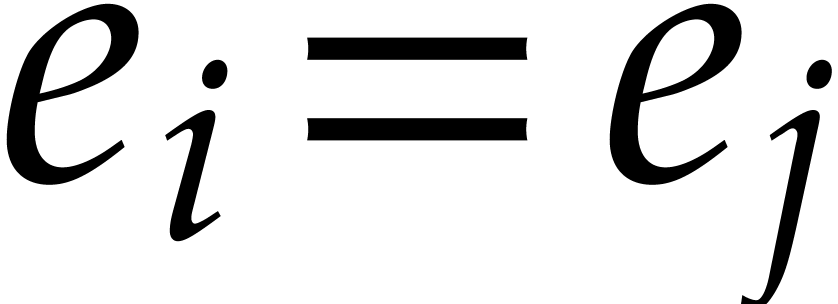 modulo
modulo
 for
for 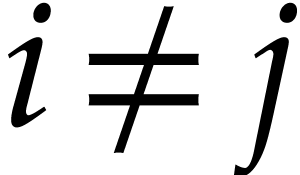 ,
this both yields the coefficients of
,
this both yields the coefficients of  and its
exponents modulo
and its
exponents modulo  . By
combining the evaluations for various moduli, it is possible to
reconstruct the actual exponents using Chinese remaindering.
. By
combining the evaluations for various moduli, it is possible to
reconstruct the actual exponents using Chinese remaindering.
Throughout this section, we assume that we are given bounds  and
and  for the degree
for the degree  and the number of terms
and the number of terms  of
of  . Garg and Schost's original
algorithm was deterministic under these assumptions. However, their
algorithm was not designed to be efficient in practice. In the past
decade, many variants have been proposed. Roughly speaking, they all
follow the same recipe that is summarized in Algorithm 2
below. The variants mainly differ in the precise way recombinations are
done in step 3.
. Garg and Schost's original
algorithm was deterministic under these assumptions. However, their
algorithm was not designed to be efficient in practice. In the past
decade, many variants have been proposed. Roughly speaking, they all
follow the same recipe that is summarized in Algorithm 2
below. The variants mainly differ in the precise way recombinations are
done in step 3.
For all matching strategies that have been considered so far, the cost
of steps 1 and 3 is dominated by the cost of step 2. If the evaluation
of  only involves ring operations, then the
running time of Algorithm 2 is therefore bounded by
only involves ring operations, then the
running time of Algorithm 2 is therefore bounded by  . The moduli
. The moduli 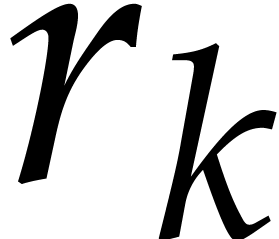 are usually all of the same order of magnitude
are usually all of the same order of magnitude 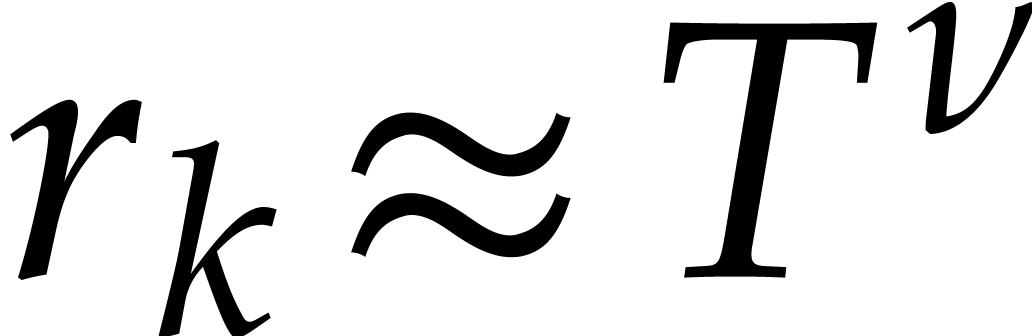 for some small
for some small  that depends on the matching
strategy. Then we may take
that depends on the matching
strategy. Then we may take 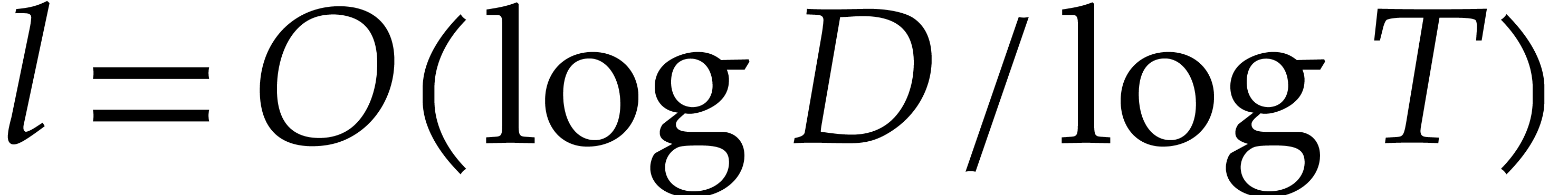 ,
so the cost simplifies to
,
so the cost simplifies to 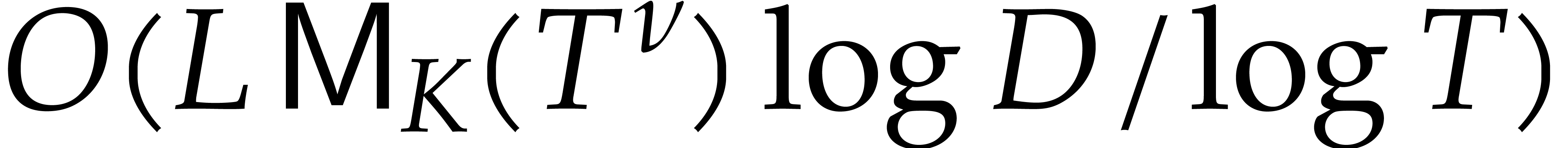 .
For finite fields
.
For finite fields 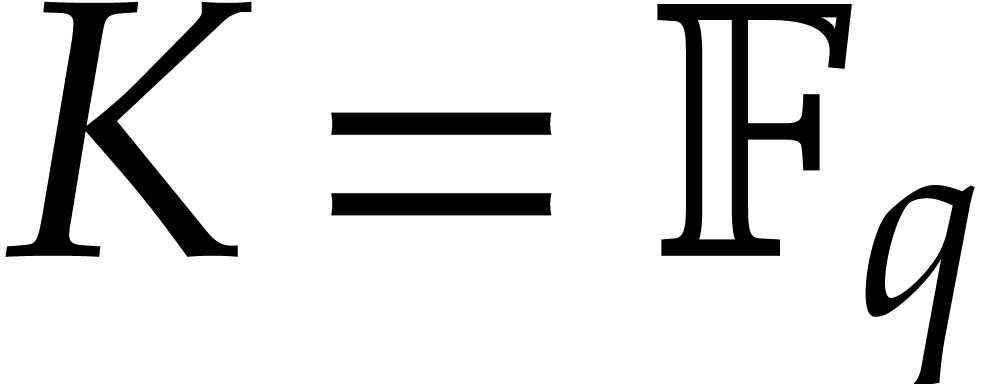 , this cost
becomes
, this cost
becomes 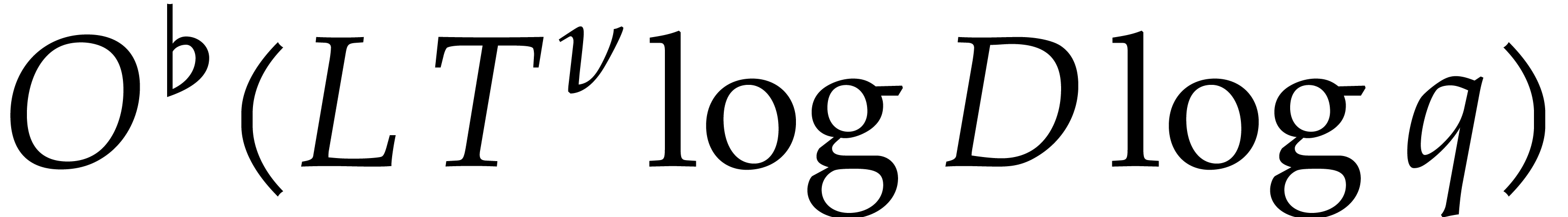 . For the design of
matching strategies, it is therefore important that we can take
. For the design of
matching strategies, it is therefore important that we can take  as small as possible.
as small as possible.
Remark. The above analysis can be refined by
maintaining separate counts  ,
,
 , and
, and  for the numbers of additions (or subtraction), multiplications, and
divisions that are necessary for one evaluation of
for the numbers of additions (or subtraction), multiplications, and
divisions that are necessary for one evaluation of  . Then the cost of Algorithm 2
over
. Then the cost of Algorithm 2
over  becomes
becomes  .
.
Remark. The complexity analysis may need to be
adjusted somewhat if  is so large that we run out
of suitable moduli
is so large that we run out
of suitable moduli  . If our
matching strategy requires prime numbers of the order of
. If our
matching strategy requires prime numbers of the order of  , then this happens when
, then this happens when  exceeds approximately the same order
exceeds approximately the same order  .
In that case, we need to replace
.
In that case, we need to replace  by an
appropriate power of
by an
appropriate power of  in our complexity bounds.
Alternatively, if the characteristic of
in our complexity bounds.
Alternatively, if the characteristic of  is
sufficiently large, then we may fall back on the strategy from section
3.2.
is
sufficiently large, then we may fall back on the strategy from section
3.2.
Garg and Schost's original algorithm from [17] uses prime
numbers 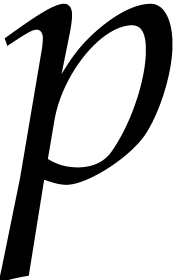 for the moduli
for the moduli  . Assuming that
. Assuming that  admits
admits  terms, the algorithm is based on the observation that
the projection of the polynomial
terms, the algorithm is based on the observation that
the projection of the polynomial  modulo
modulo 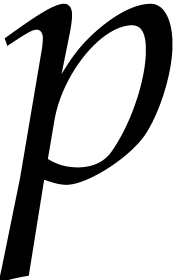 coincides with
coincides with  .
This allows for the recovery of
.
This allows for the recovery of 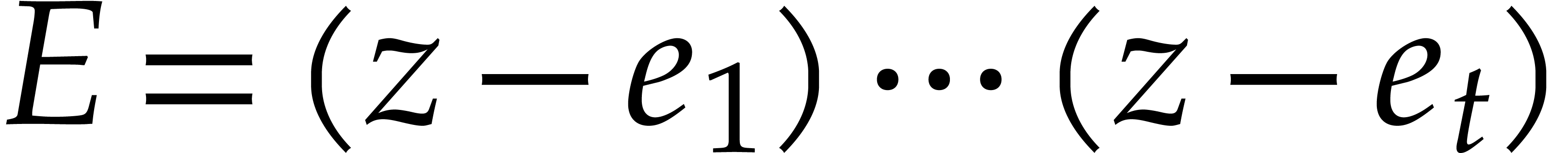 through Chinese
remaindering, by working with a sufficient number of primes. It then
suffices to determine the zeros
through Chinese
remaindering, by working with a sufficient number of primes. It then
suffices to determine the zeros  of
of  and to recover
and to recover  as the coefficient
of
as the coefficient
of  in
in 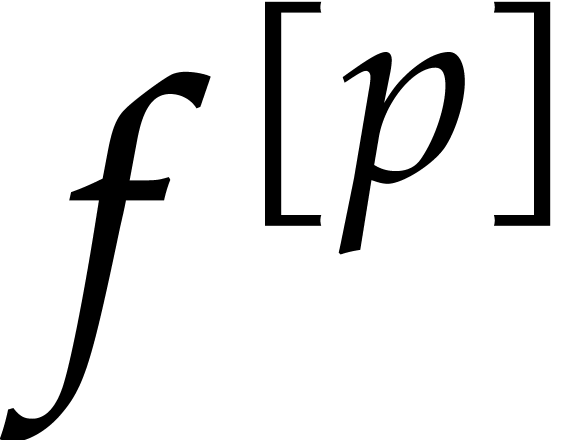 for
for  .
.
However, this strategy is very sensitive to collisions, and requires
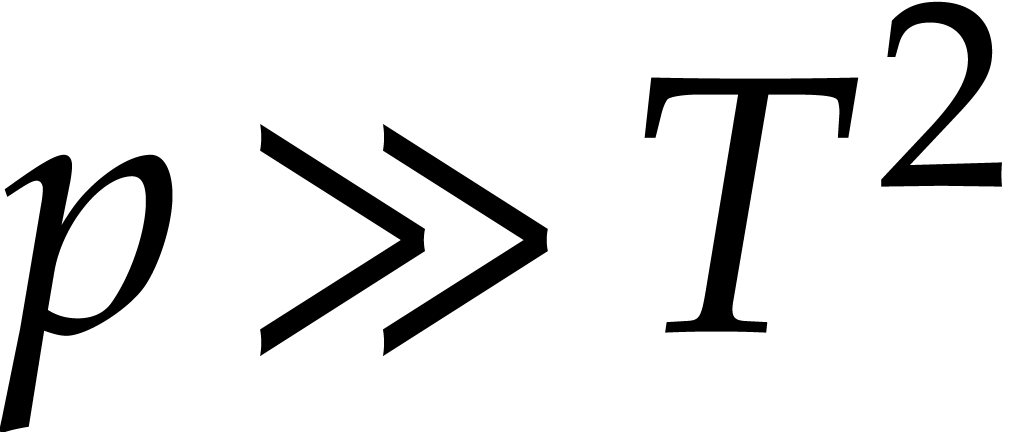 in order to ensure with high probability that
in order to ensure with high probability that
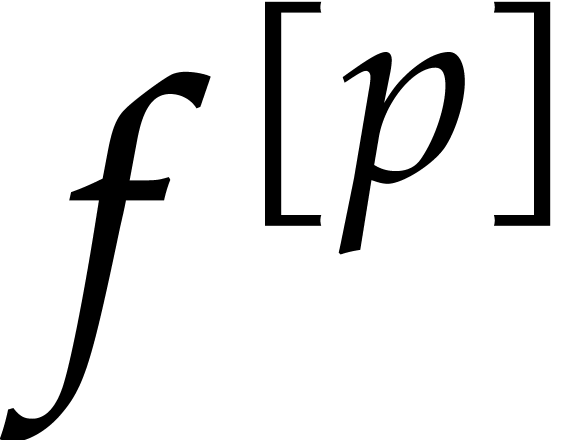 admits exactly
admits exactly  terms. In
other words, it forces us to take
terms. In
other words, it forces us to take  in the
complexity analysis. Garg and Schost's original algorithm is actually
deterministic and uses
in the
complexity analysis. Garg and Schost's original algorithm is actually
deterministic and uses 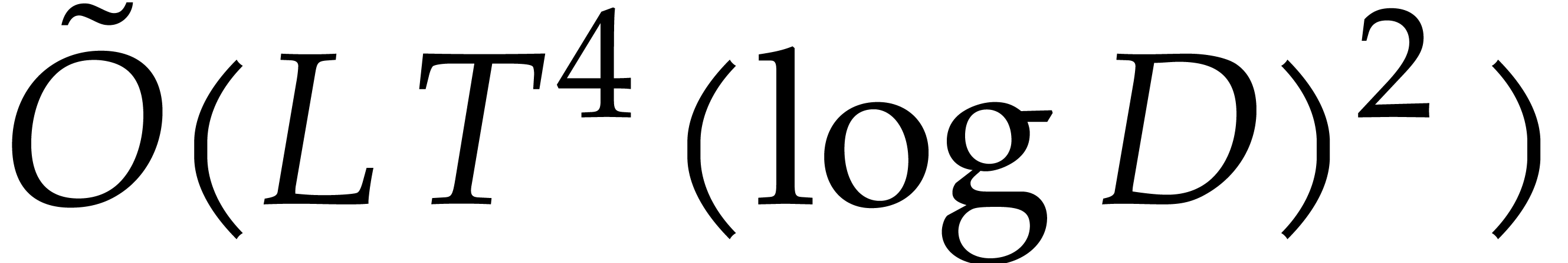 operations in
operations in  . The derandomization is achieved
by using
. The derandomization is achieved
by using 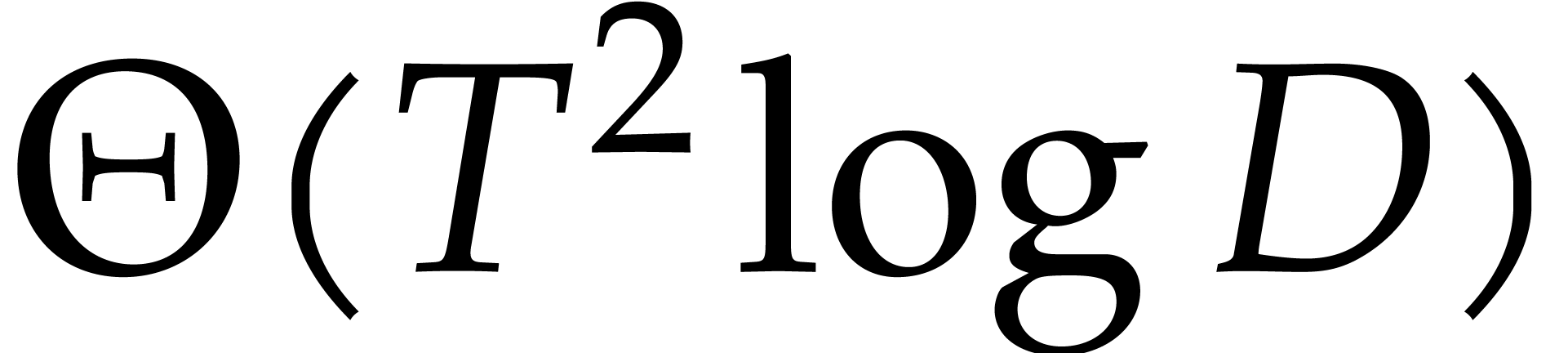 different primes
different primes 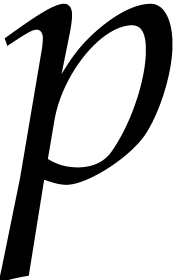 .
.
Another matching strategy for step 3 of Algorithm 2 has
been proposed by Arnold, Giesbrecht, and Roche [3]. The
idea is to pick 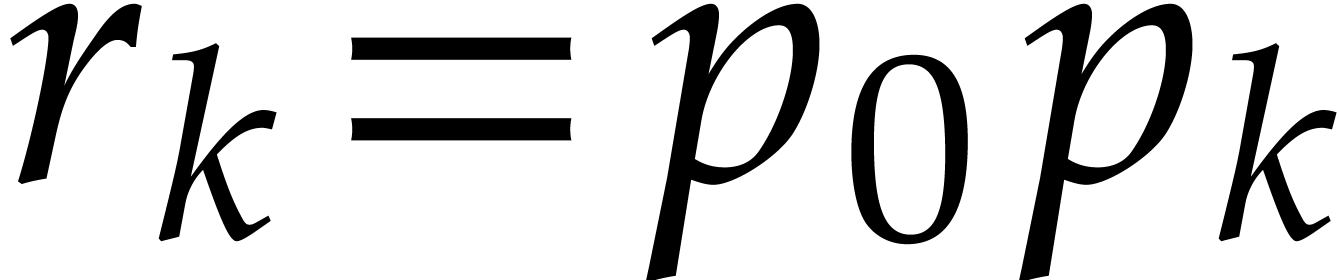 for
for 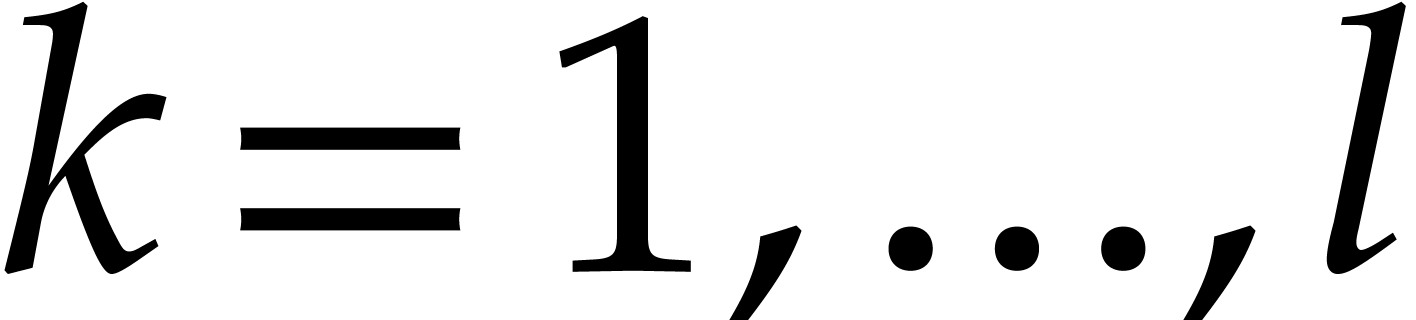 , where
, where  are primes with
are primes with 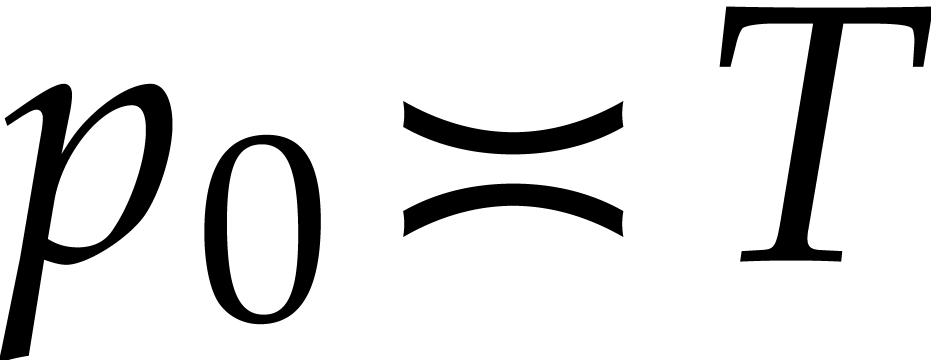 and
and 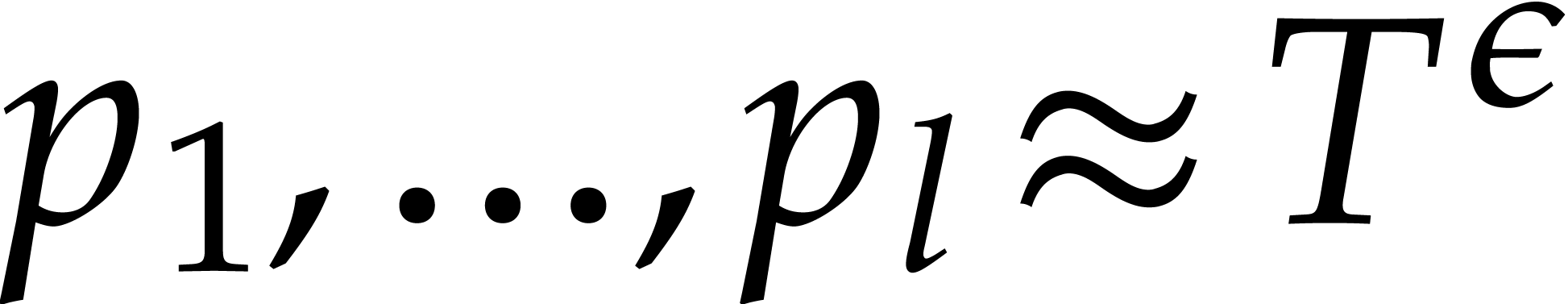 for some
for some 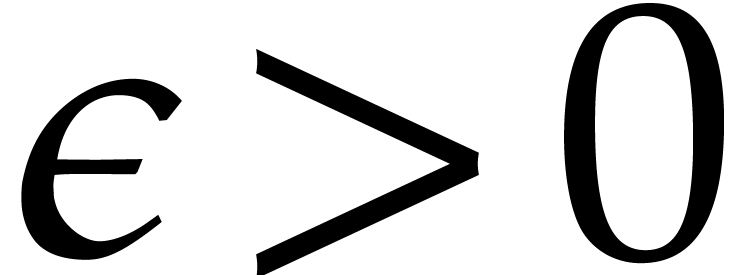 (so that
(so that  ). For
). For 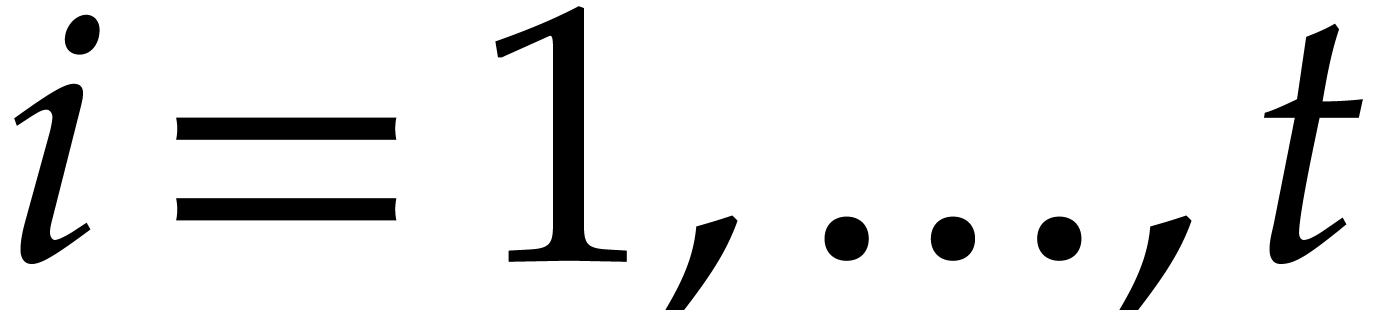 and
and 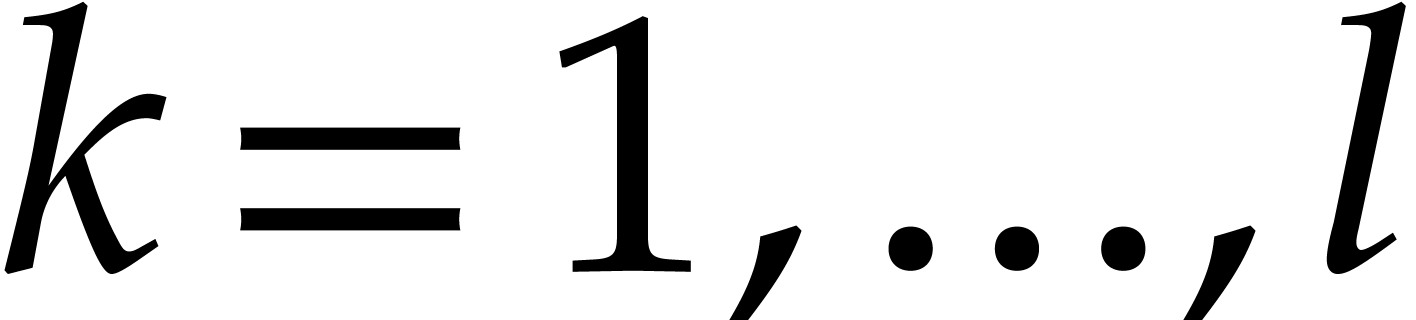 , there
then exists a fixed non-zero probability such that the term
, there
then exists a fixed non-zero probability such that the term 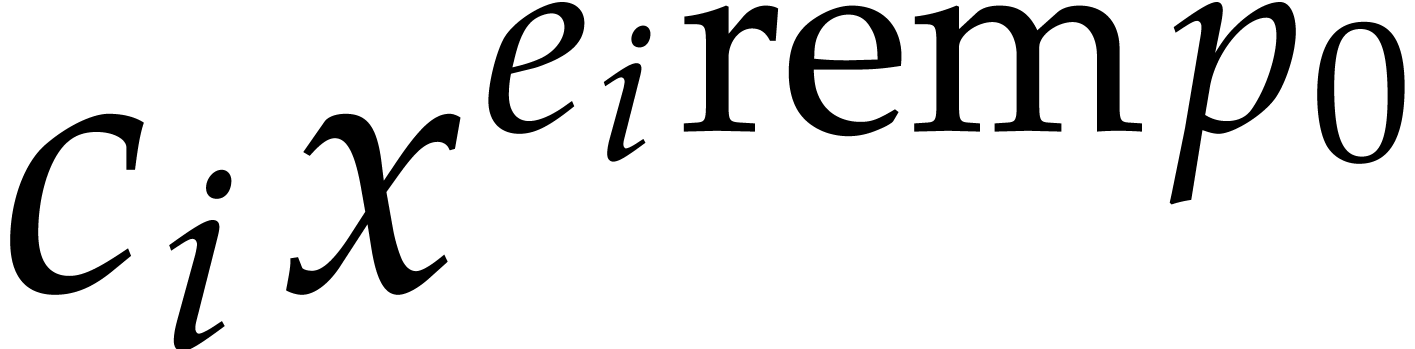 of
of 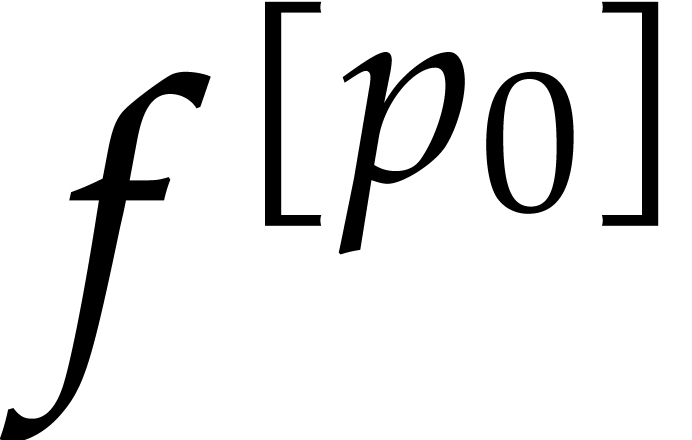 matches a term
matches a term 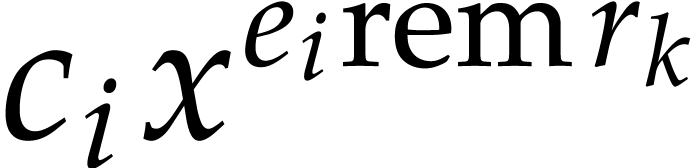 of
of 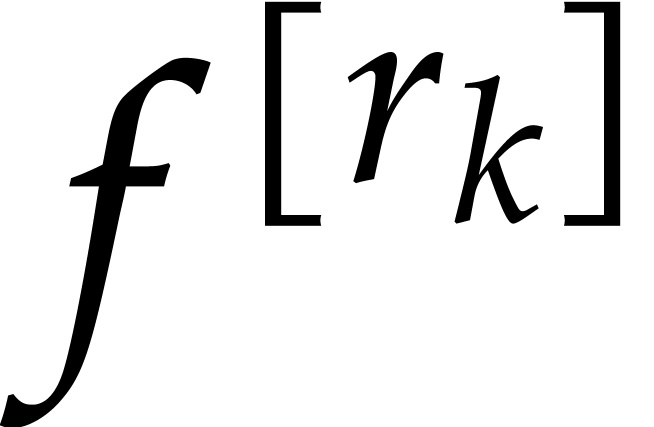 . Let
. Let  be the set of indices
be the set of indices  for which we have a match.
For some fixed constant
for which we have a match.
For some fixed constant  , we
then have
, we
then have 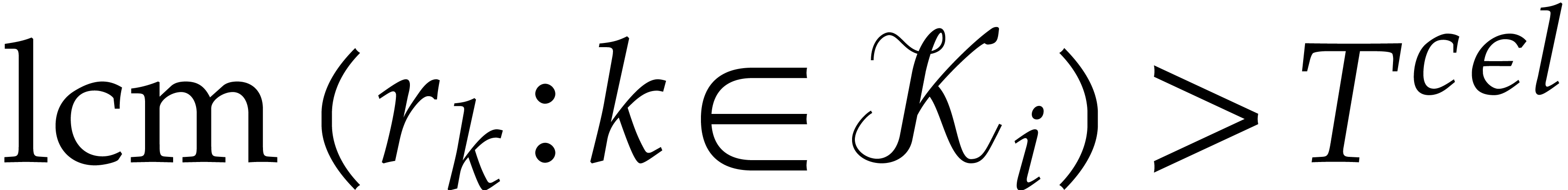 with high probability. By taking
with high probability. By taking 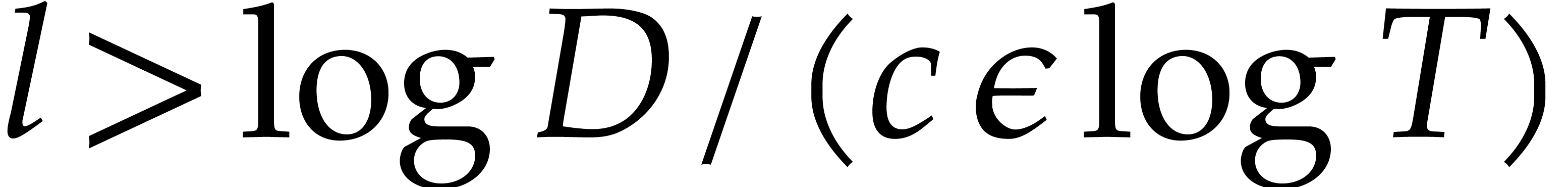 in step 1, this implies
in step 1, this implies 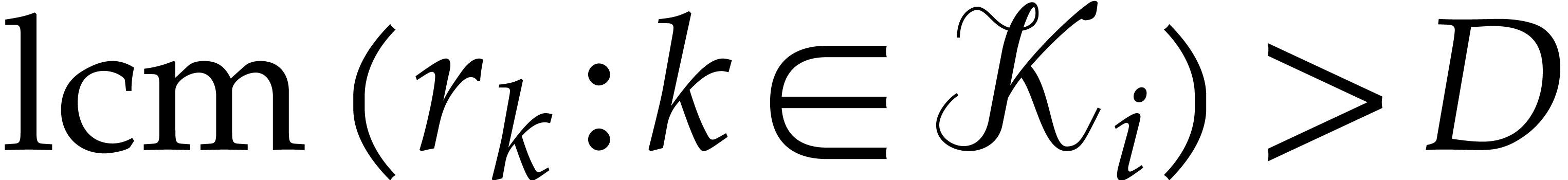 .
With high probability, this allows us to reconstruct those terms
.
With high probability, this allows us to reconstruct those terms 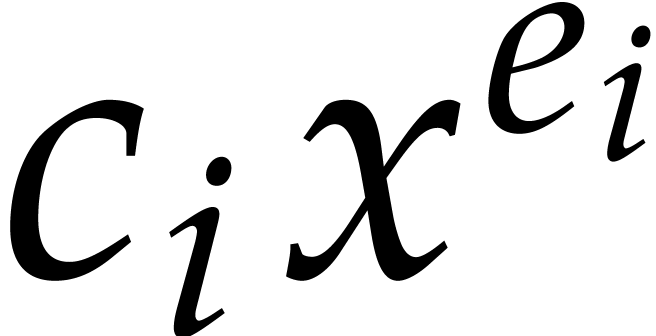 such that
such that 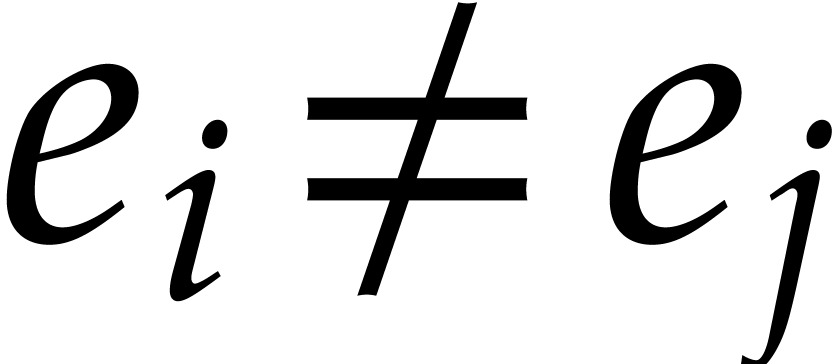 modulo
modulo  for all
for all 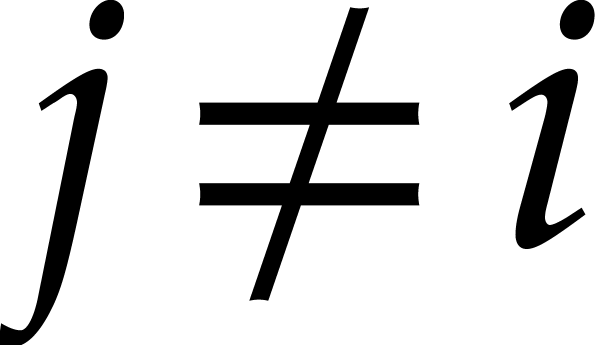 . The
sum of these terms gives the desired approximation
. The
sum of these terms gives the desired approximation  of
of  for which a fixed non-zero proportion of
terms are likely to be correct.
for which a fixed non-zero proportion of
terms are likely to be correct.
Giesbrecht and Roche proposed yet another matching strategy [18]
which is based on the concept of “diversification”. The
polynomial  is said to be diversified if
its coefficients
is said to be diversified if
its coefficients  are pairwise distinct. Assuming
that
are pairwise distinct. Assuming
that  is sufficiently large, it is shown in [18] that the polynomial
is sufficiently large, it is shown in [18] that the polynomial  is diversified
with high probability for a random choice of
is diversified
with high probability for a random choice of  . Without loss of generality, this allows us to
assume that
. Without loss of generality, this allows us to
assume that  is diversified.
is diversified.
In step 3 of Algorithm 2, we then match a term  of
of  with a term
with a term 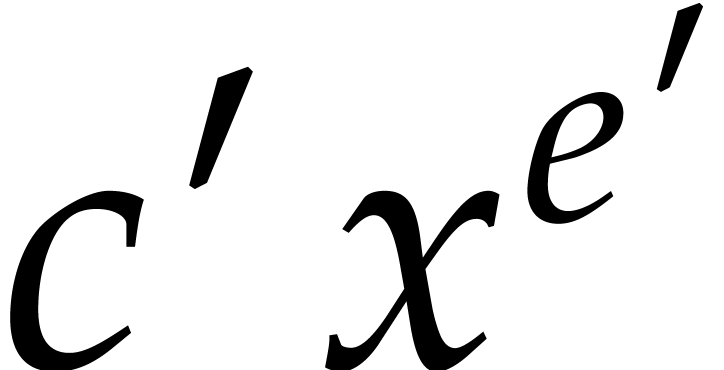 of
of 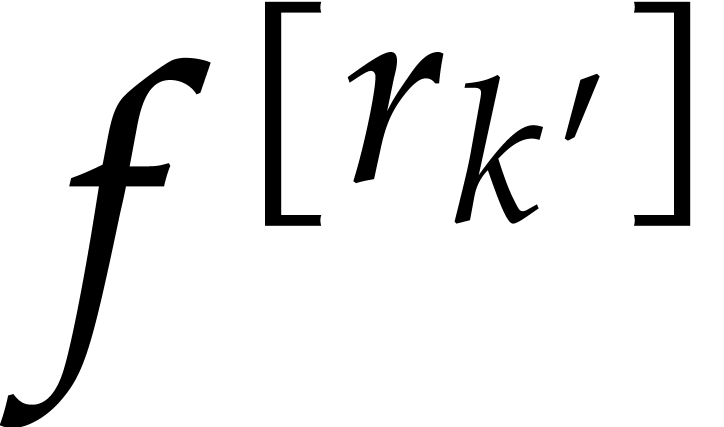 if and only if
if and only if  .
Giesbrecht and Roche's original algorithm uses
.
Giesbrecht and Roche's original algorithm uses  moduli
moduli  of size
of size 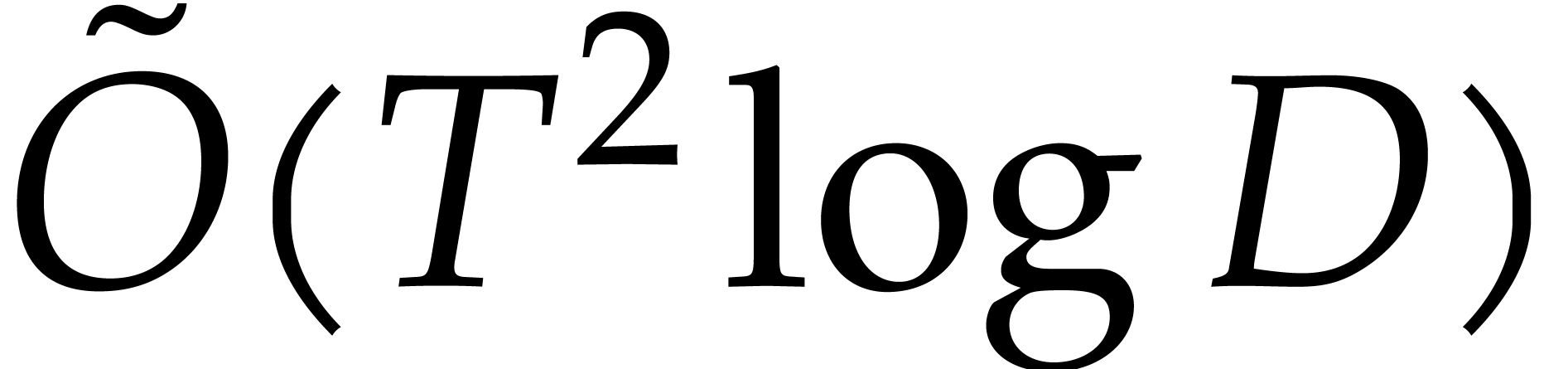 .
Consequently, their algorithm for sparse interpolation uses
.
Consequently, their algorithm for sparse interpolation uses 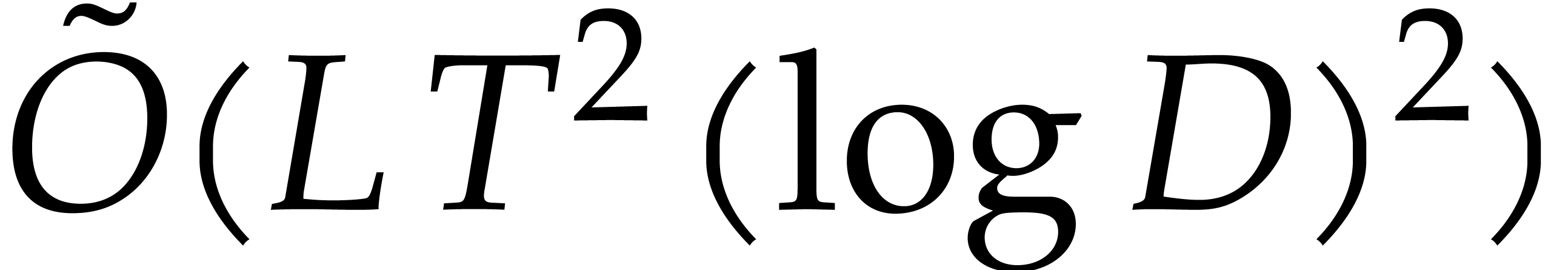 operations in
operations in  .
As we will see below, their probabilistic analysis is actually quite
pessimistic: in practice, it is possible to take
.
As we will see below, their probabilistic analysis is actually quite
pessimistic: in practice, it is possible to take 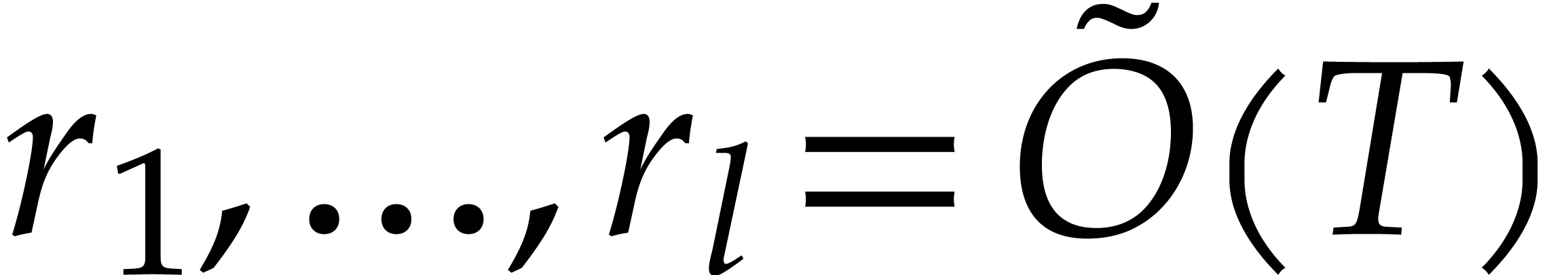 as long as
as long as 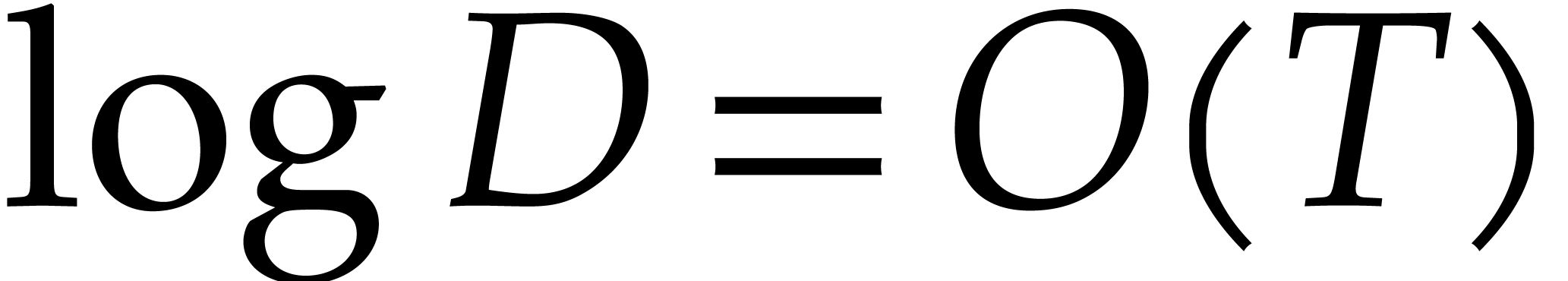 .
.
Let us now focus on the design and analysis of a probabilistic algorithm that exploits the idea of diversification even more than Giesbrecht and Roche's original method from [18].
Given a diversified polynomial  ,
together with bounds
,
together with bounds  and
and  for its degree
for its degree  and its number of terms
and its number of terms  , our aim is to compute
, our aim is to compute 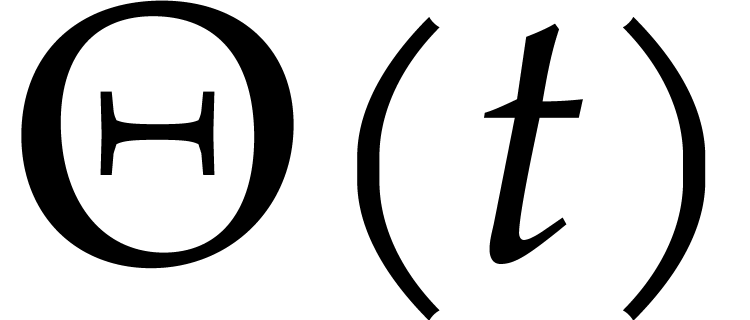 terms of
terms of  , with
high probability. Our algorithm uses the following parameters:
, with
high probability. Our algorithm uses the following parameters:
A constant  .
.
Orders  that are pairwise coprime, with
that are pairwise coprime, with  for
for  .
.
The minimal number 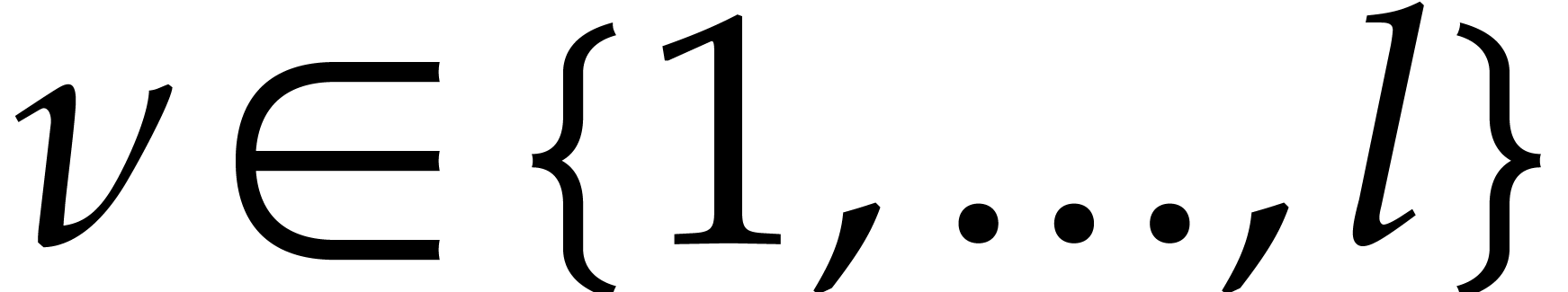 such that
such that 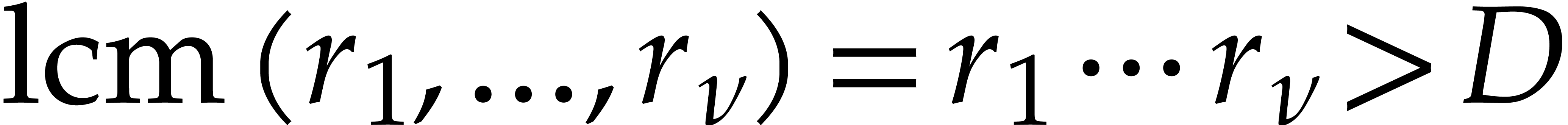 .
.
The precise choice of  and
and 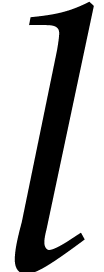 will be detailed below; the parameter
will be detailed below; the parameter  and the
ratio
and the
ratio 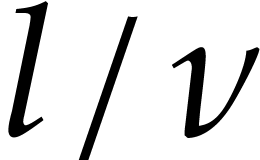 should be sufficiently small for the
algorithm to be efficient, but
should be sufficiently small for the
algorithm to be efficient, but  and
and  should also be sufficiently large for our algorithm to
succeed with high probability.
should also be sufficiently large for our algorithm to
succeed with high probability.
We now use Algorithm 3 below in order to compute an
approximate sparse interpolation of  .
It is a variant of Algorithm 2 with a matching strategy
that has been detailed in steps 2, 3, and 4. Each individual term
.
It is a variant of Algorithm 2 with a matching strategy
that has been detailed in steps 2, 3, and 4. Each individual term  of
of  is reconstructed from only
a subset of its reductions modulo
is reconstructed from only
a subset of its reductions modulo  .
.
How to ensure that a non-zero portion of the terms of  can be expected to be correct? In order to answer this question, we make
the following heuristic hypothesis:
can be expected to be correct? In order to answer this question, we make
the following heuristic hypothesis:
For 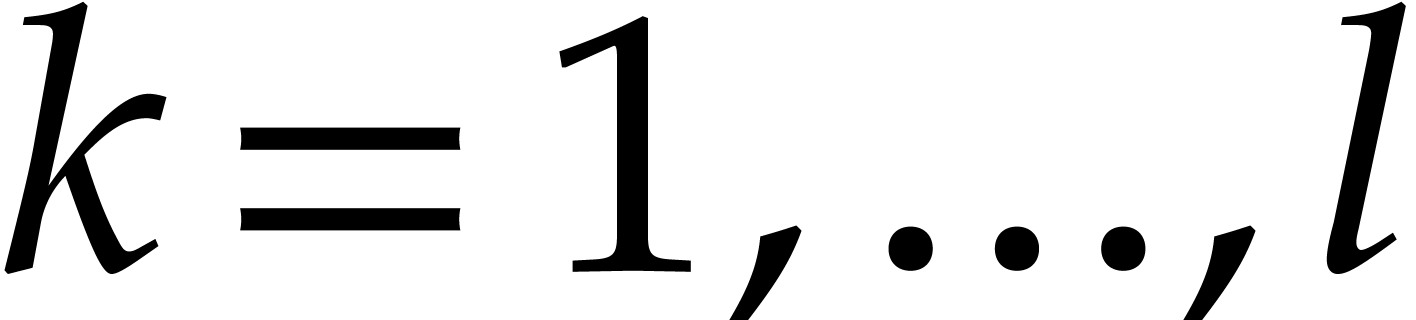 , the
modular reductions of exponents
, the
modular reductions of exponents  for
for 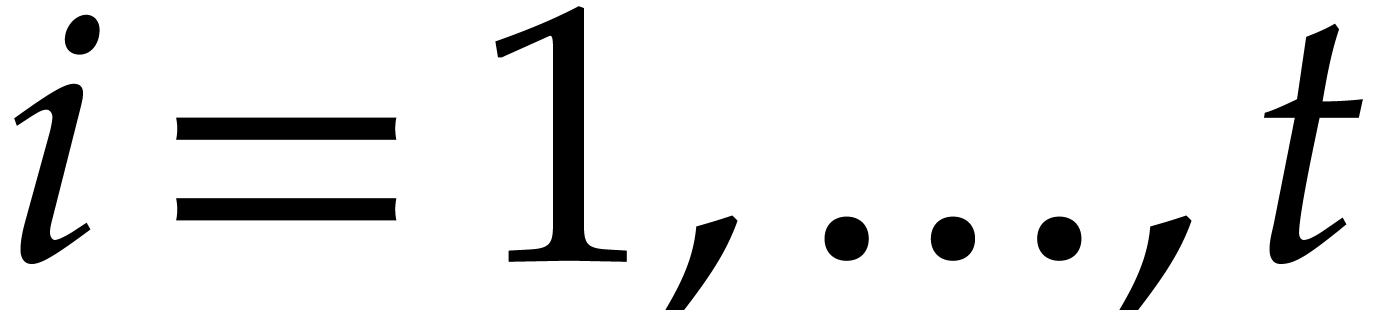 are uniformly distributed in
are uniformly distributed in 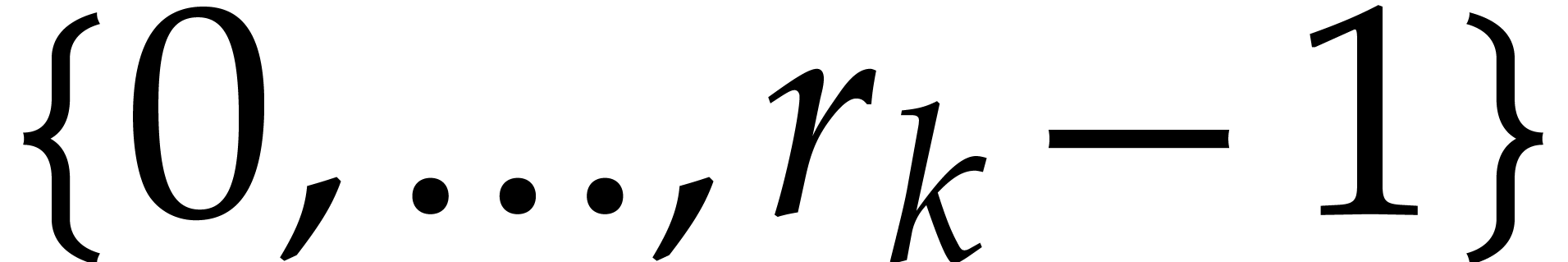 . The distribution associated to
. The distribution associated to 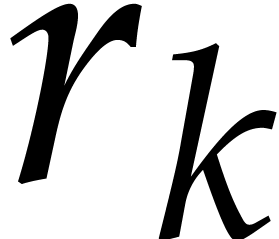 is independent of the one associated to
is independent of the one associated to 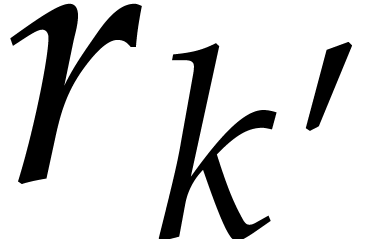 whenever
whenever  .
.
Such a heuristic is customary in computer science, typically when using hash tables.
According to Hred,
the probability that a fixed term  does not
collide with another term modulo
does not
collide with another term modulo  is
is
Setting 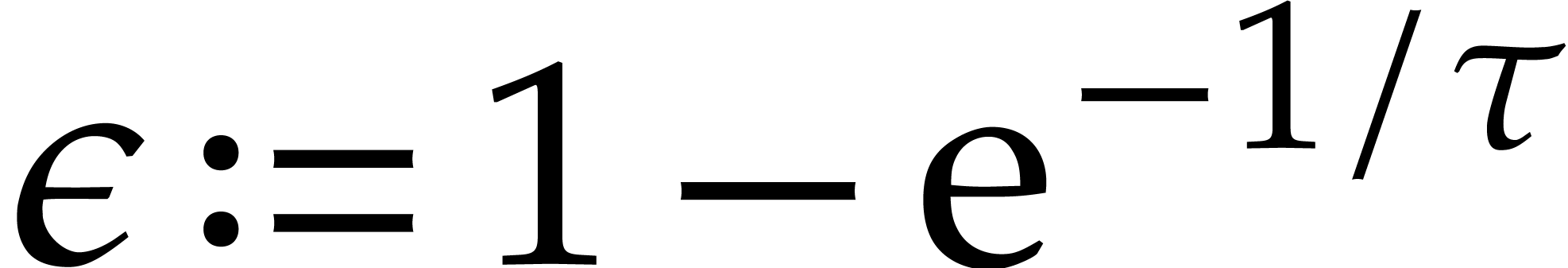 , this probability
tends to
, this probability
tends to  for large
for large  .
The probability that
.
The probability that 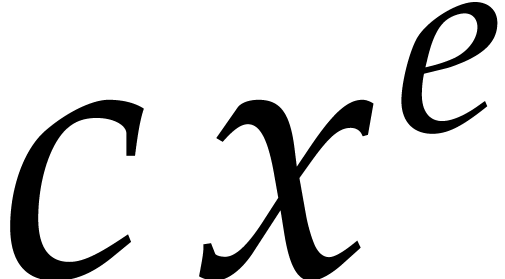 collides with another term
modulo
collides with another term
modulo 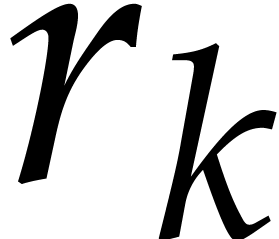 for exactly
for exactly  values of
values of 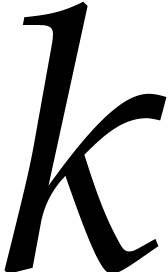 is therefore bounded by
is therefore bounded by
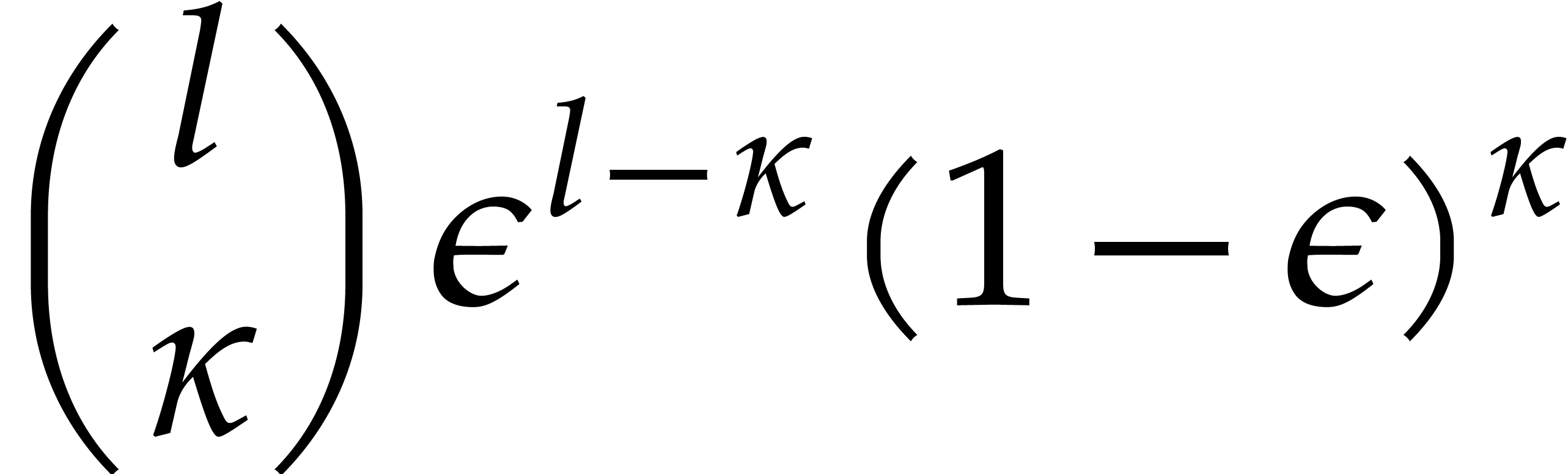
and this bound is sharp for large  .
Consequently, the probability that we cannot recover a term
.
Consequently, the probability that we cannot recover a term 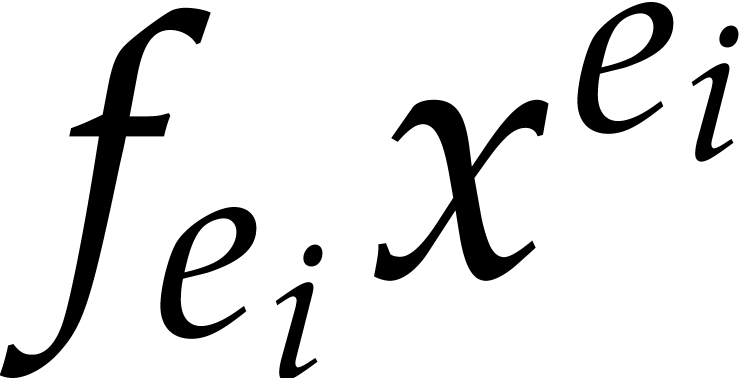 in step 4 from its reductions modulo
in step 4 from its reductions modulo 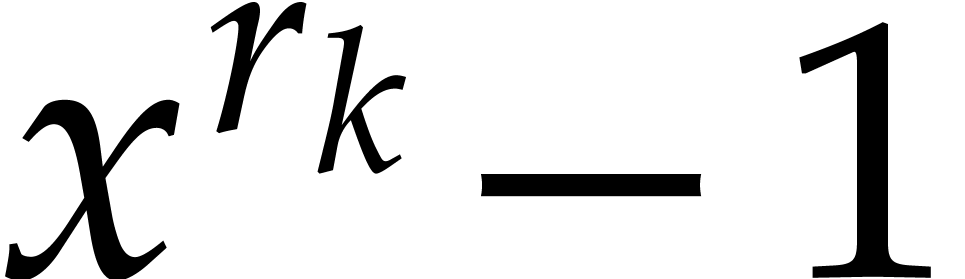 for
for 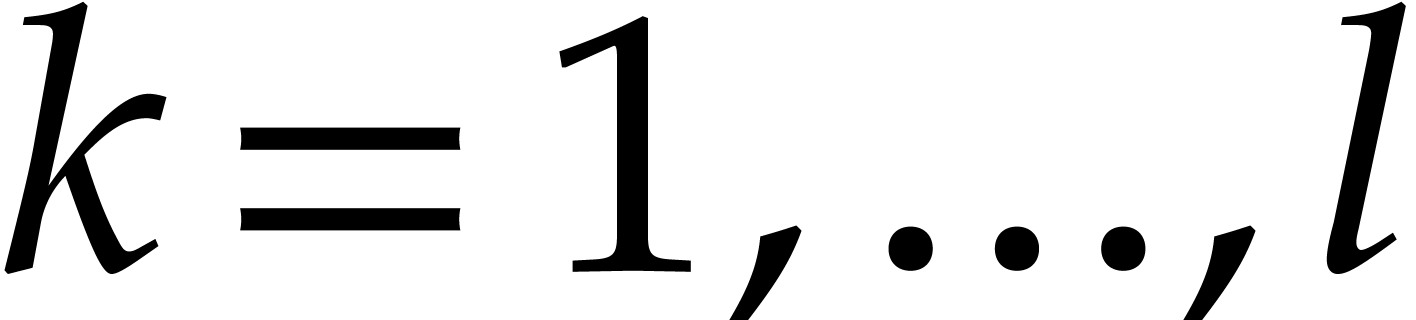 is at most
is at most
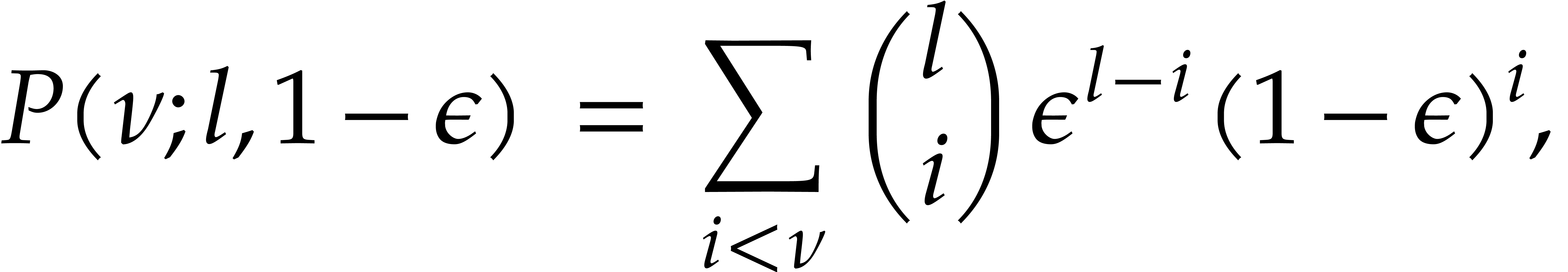 |
(4) |
and this bound is sharp for large  .
.
The probability (4) has been well studied; see [5] for a survey. Whenever
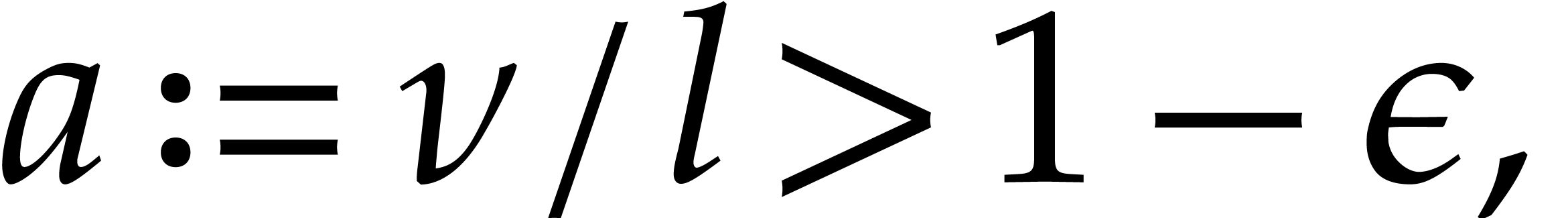
Chernoff's inequality [5, Theorem 1] gives us
Let  be a positive real parameter. In order to
ensure
be a positive real parameter. In order to
ensure 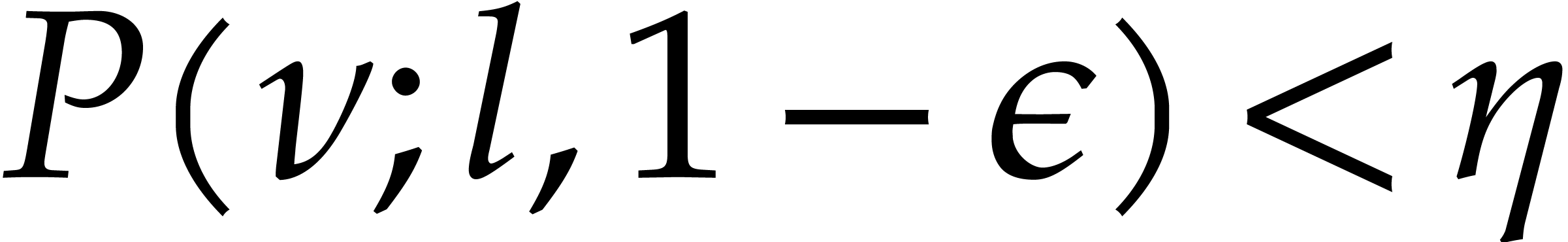 it suffices to have
it suffices to have
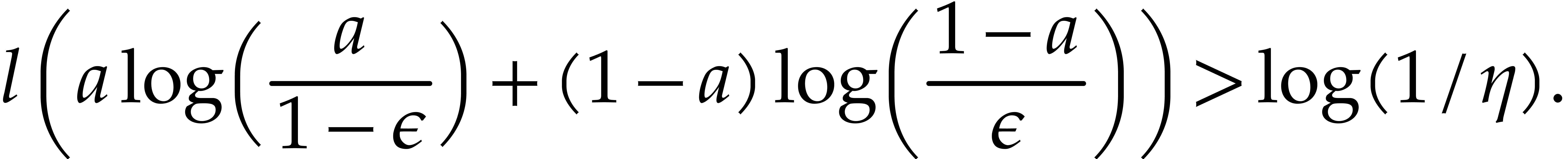
Now thanks to [48, Lemma 2(a)] we have
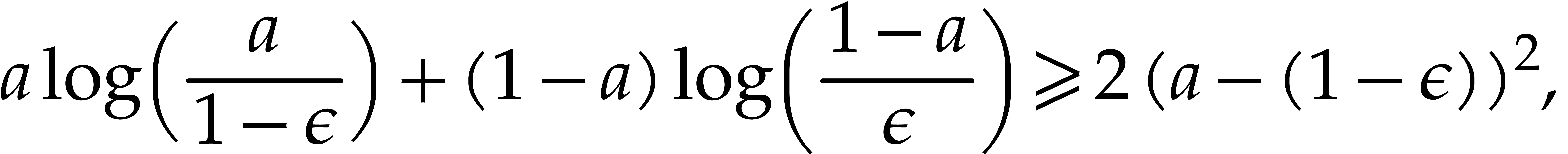
so it suffices to ensure that
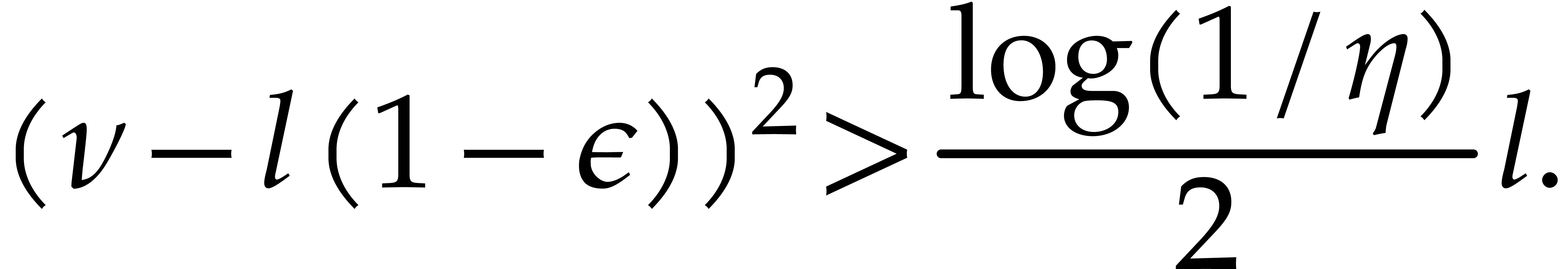 |
(5) |
Now let us take 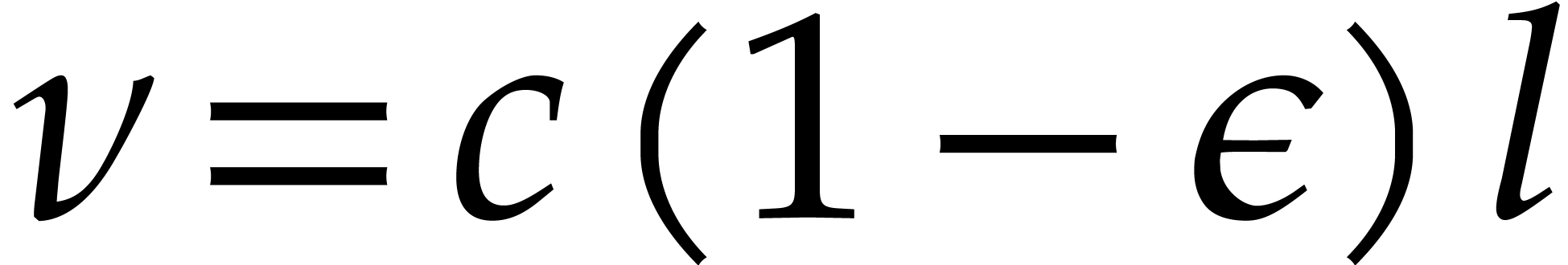 with
with  , after which
, after which
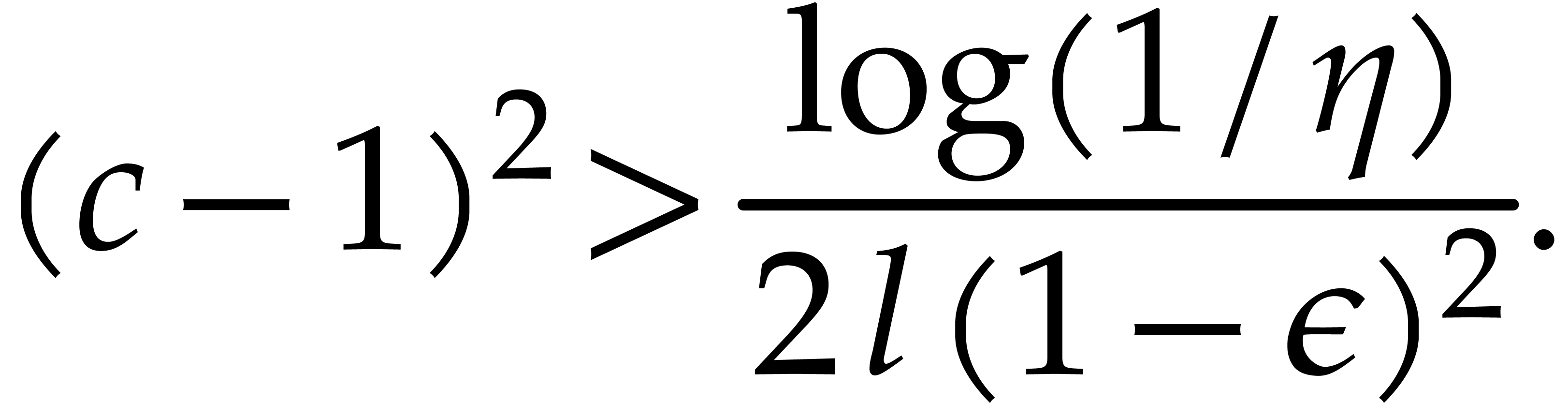 |
(6) |
For fixed 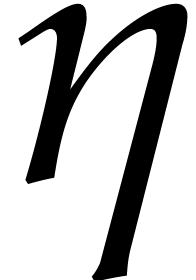 and large
and large 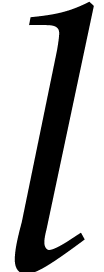 (i.e. for large
(i.e. for large 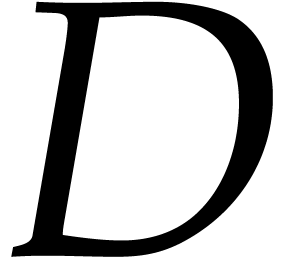 ),
it follows that we may take
),
it follows that we may take  arbitrarily close to
arbitrarily close to
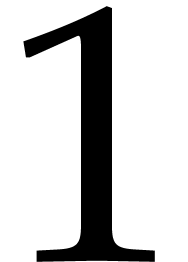 .
.
Summarizing, we may thus take 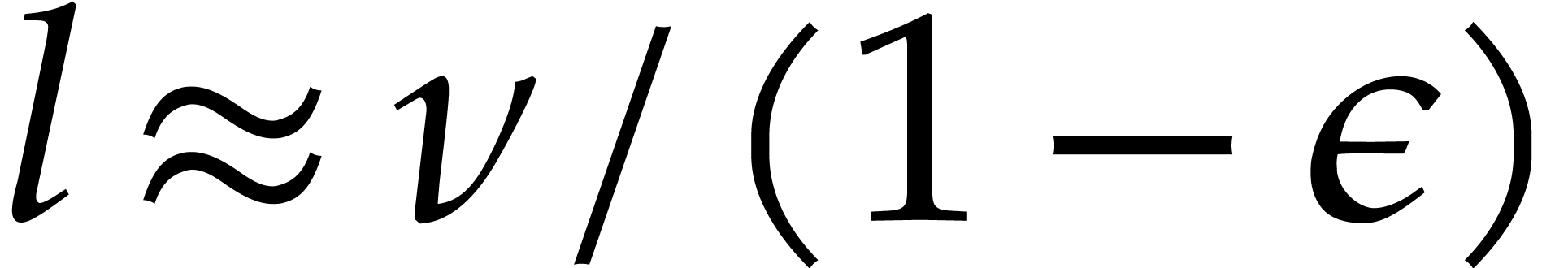 in order to
recover an average of at least
in order to
recover an average of at least 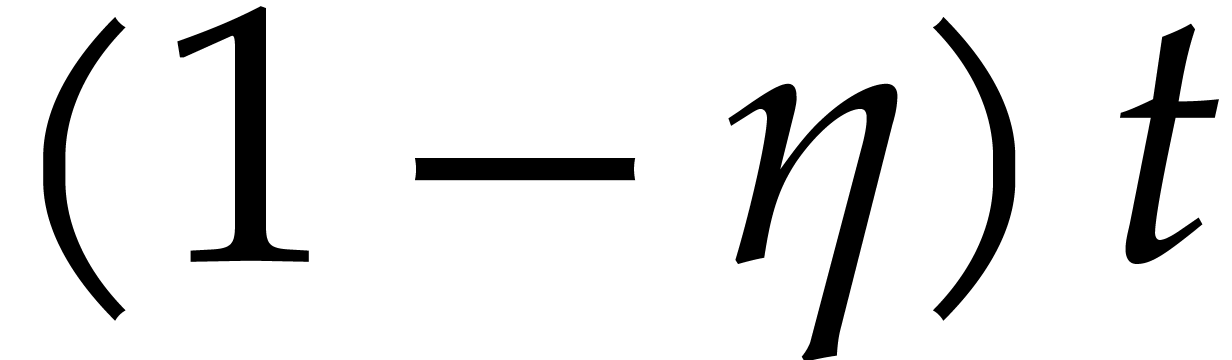 correct terms,
where
correct terms,
where 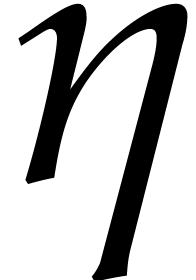 can be taken arbitrarily close to
can be taken arbitrarily close to 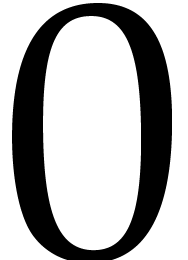 :
:
 ,
, 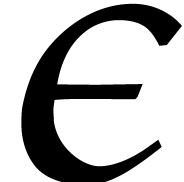 ,
, 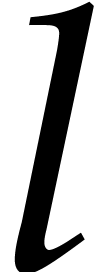 ,
,
 , and
, and 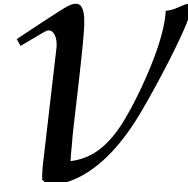 be parameters as above. Given
be parameters as above. Given  ,
assume that
,
assume that 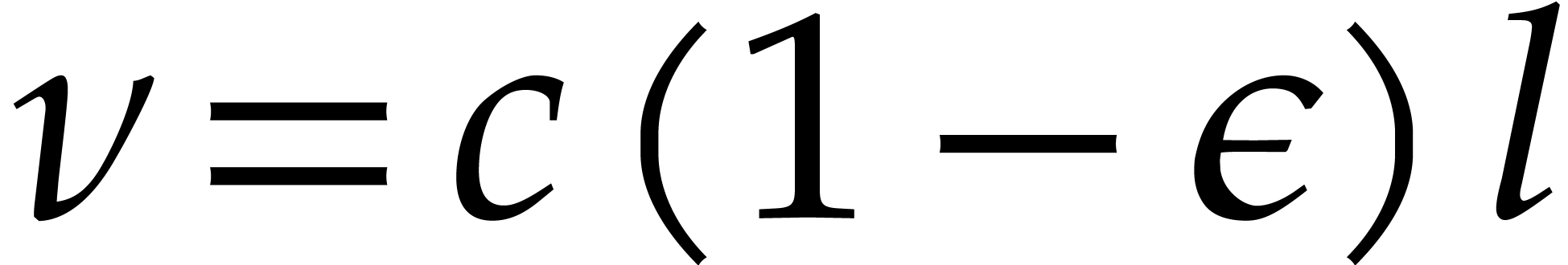 , where
, where  satisfies
satisfies 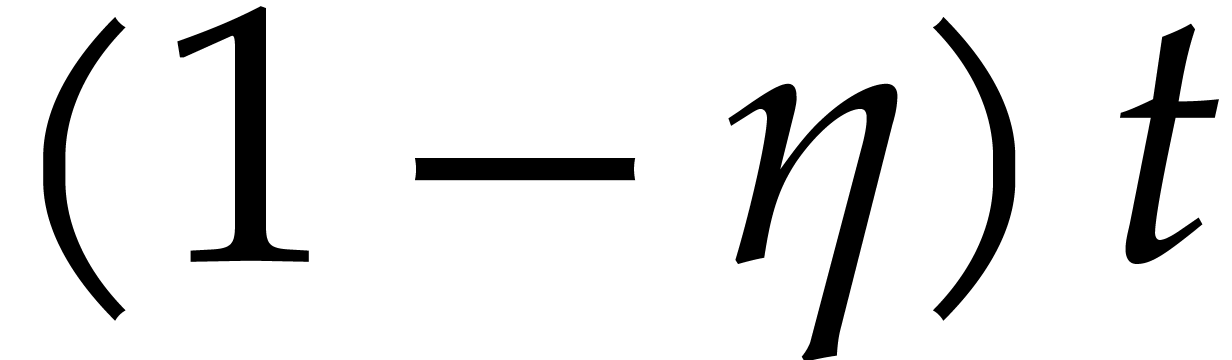 correct terms of
correct terms of  on average.
on average.
Let us now analyze the running time of Algorithm 3. Taking
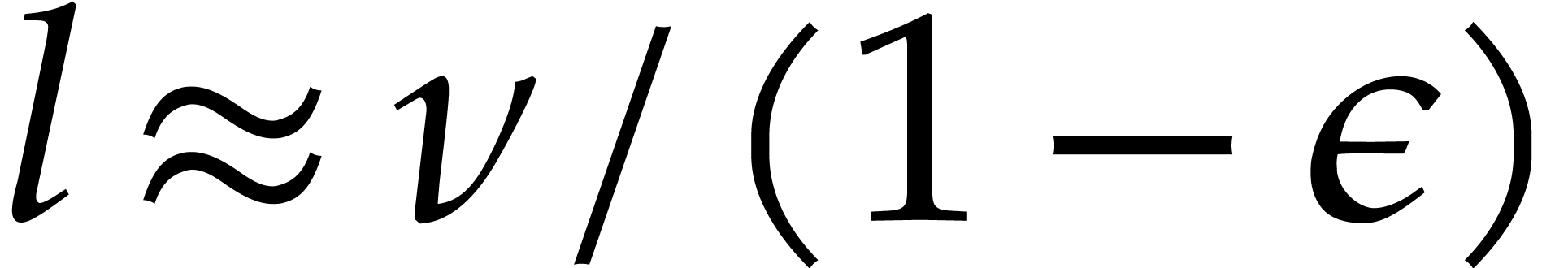 , and since
, and since 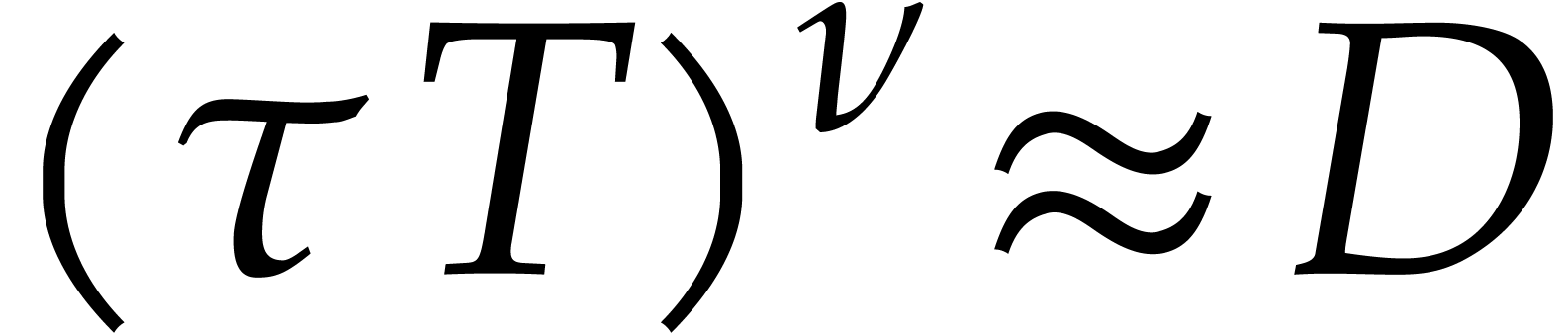 , the cost of step 1 is
, the cost of step 1 is
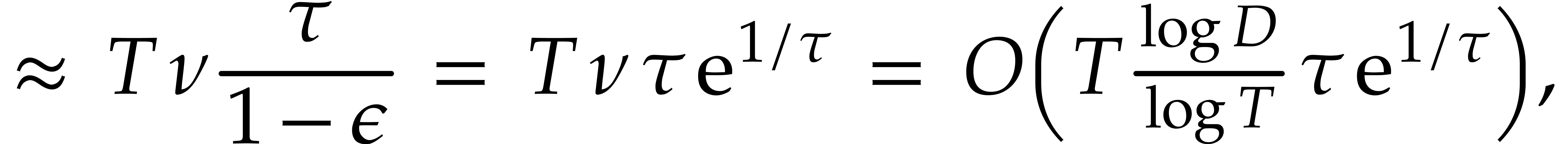
and 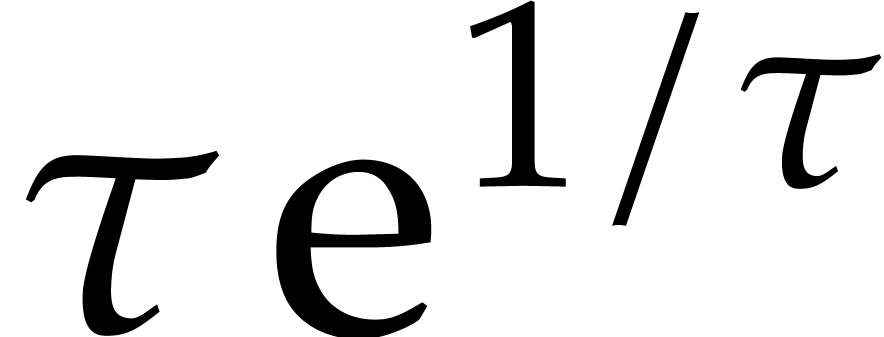 reaches its minimum value
reaches its minimum value  at
at 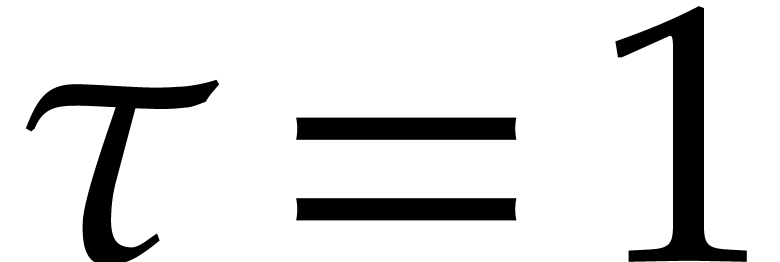 . This means that the
total complexity is best when
. This means that the
total complexity is best when  is close to
is close to 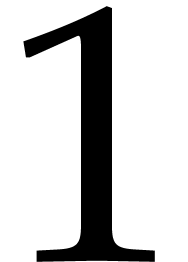 . In other words, this prompts us
to take
. In other words, this prompts us
to take 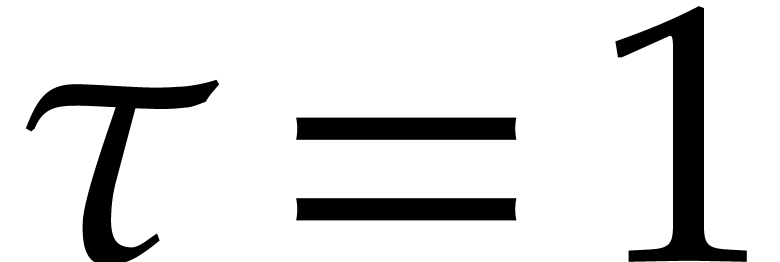 ,
, 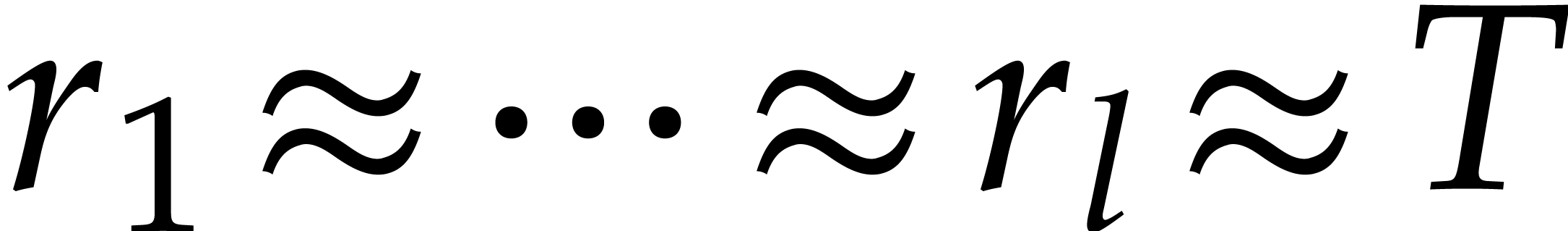 ,
, 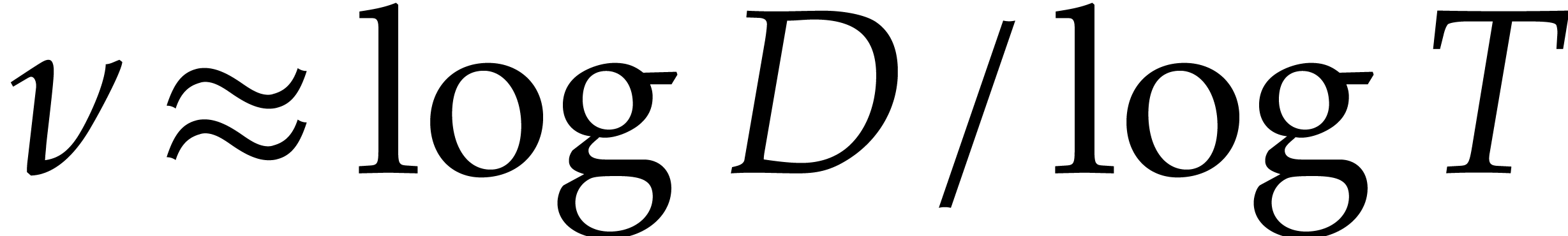 ,
and
,
and 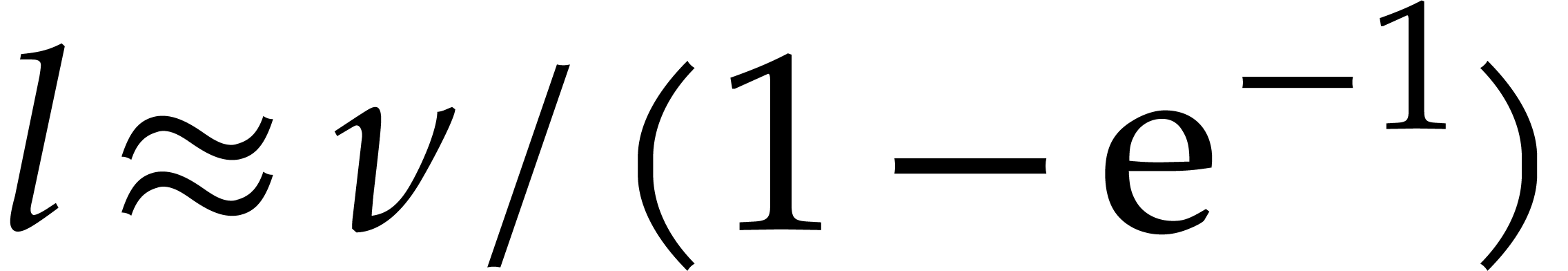 . For this choice of
parameters, we obtain the following heuristic complexity bound:
. For this choice of
parameters, we obtain the following heuristic complexity bound:
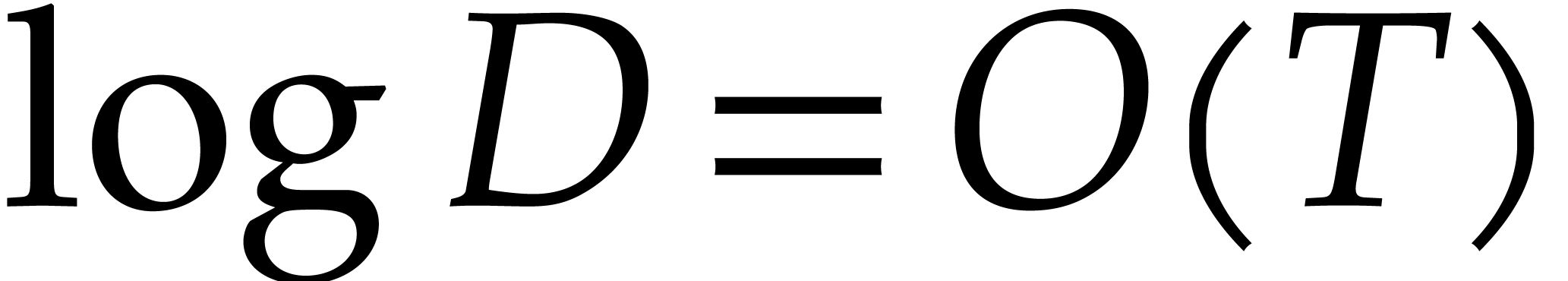 . Given
. Given 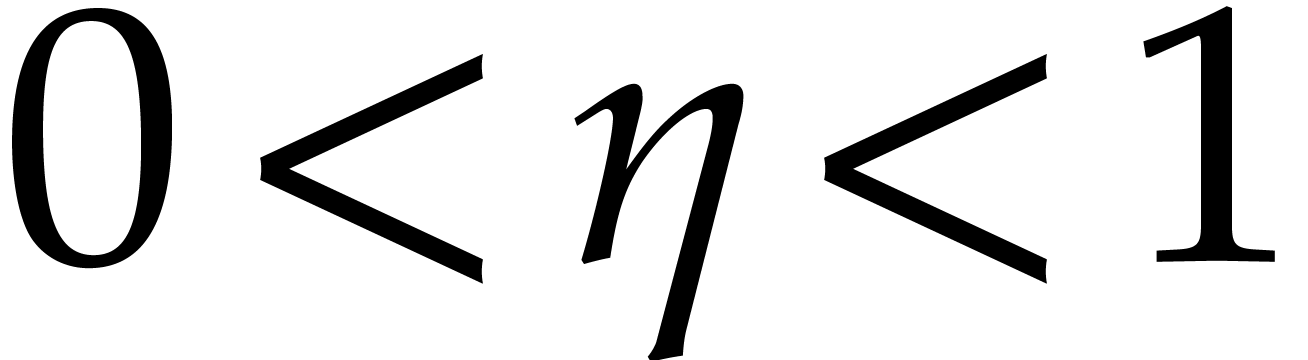 and a diversified polynomial
and a diversified polynomial 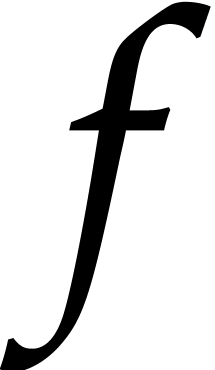 of
degree
of
degree 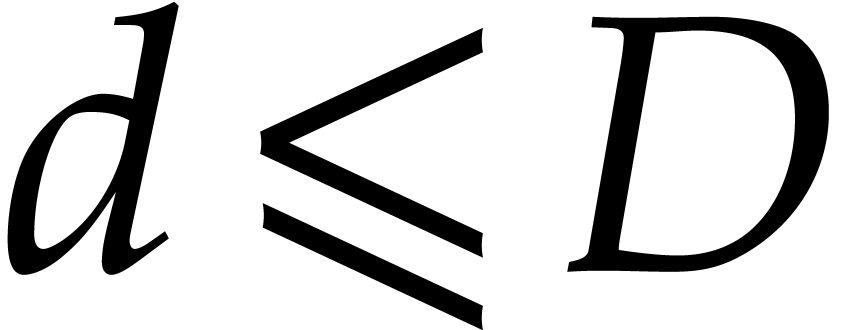 and with
and with 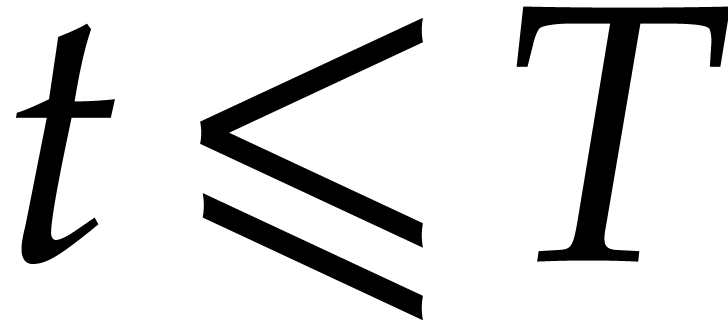 terms,
there exists a Monte Carlo probabilistic algorithm which computes at
least
terms,
there exists a Monte Carlo probabilistic algorithm which computes at
least 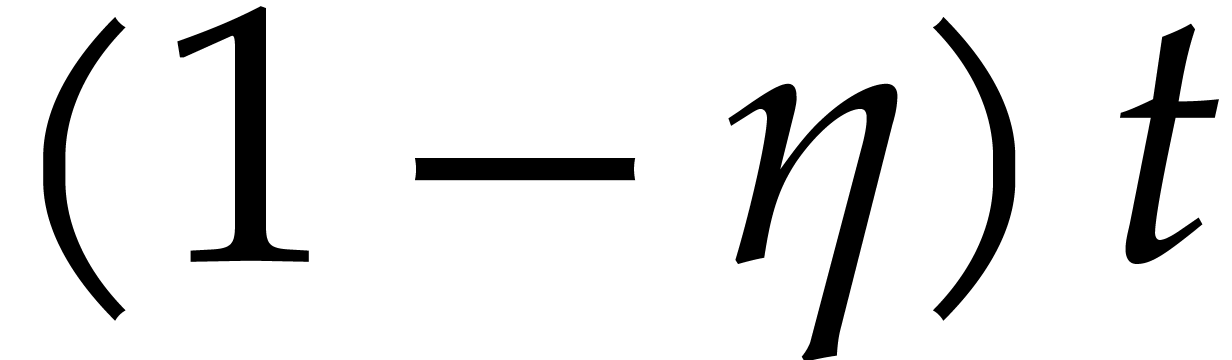 terms of
terms of 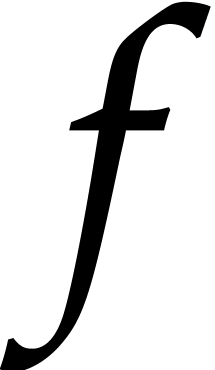 in
time
in
time
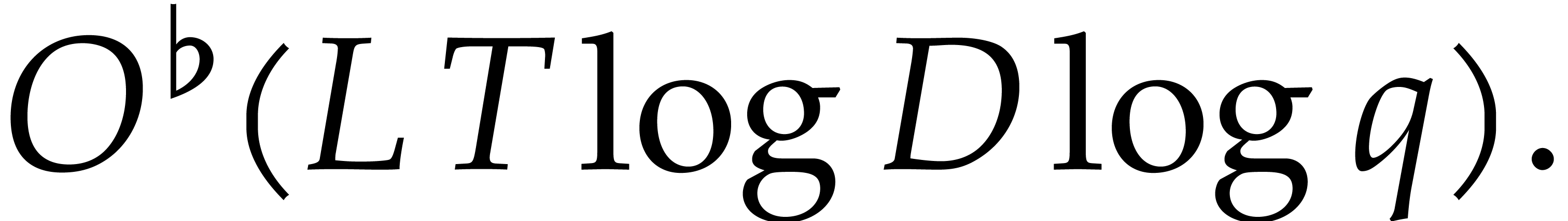
Proof. We take 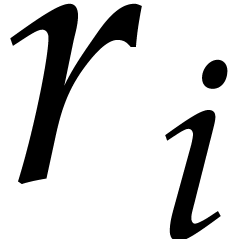 to be the
to be the
 -th smallest prime numbers
that is larger than
-th smallest prime numbers
that is larger than  , so that
, so that
 is the smallest number with
is the smallest number with 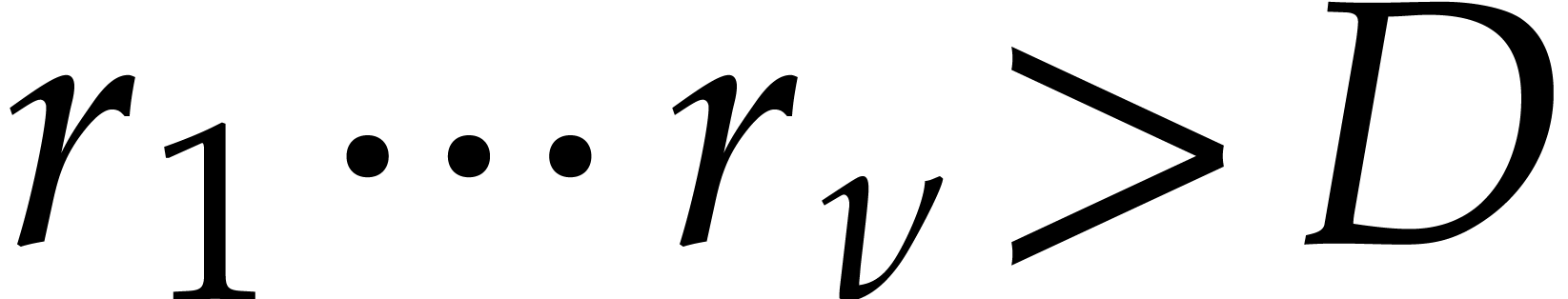 . We also take
. We also take 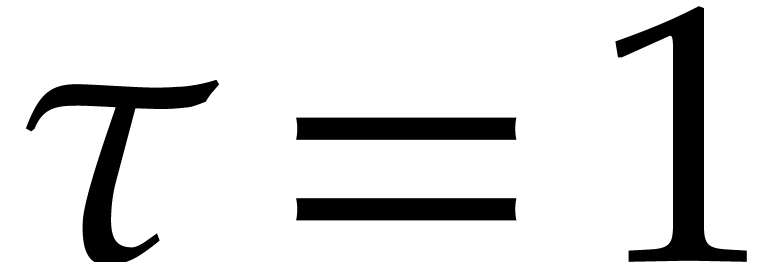 ,
,
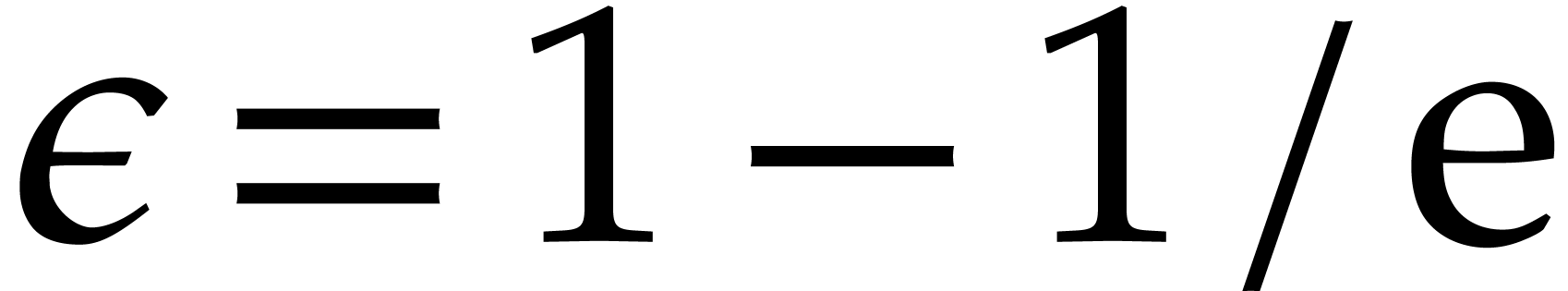 , and let
, and let 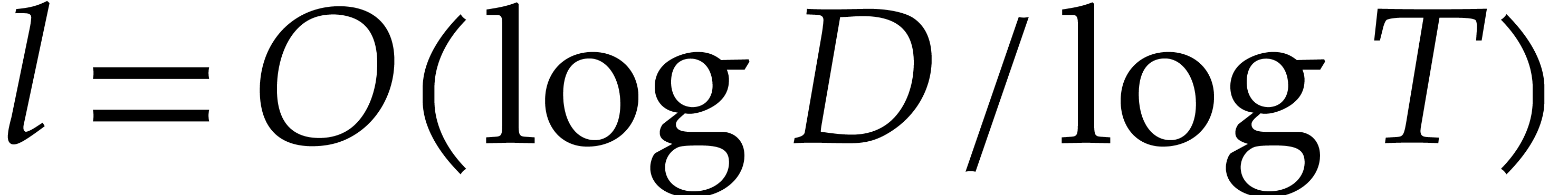 be smallest such that (6) is satisfied for
be smallest such that (6) is satisfied for 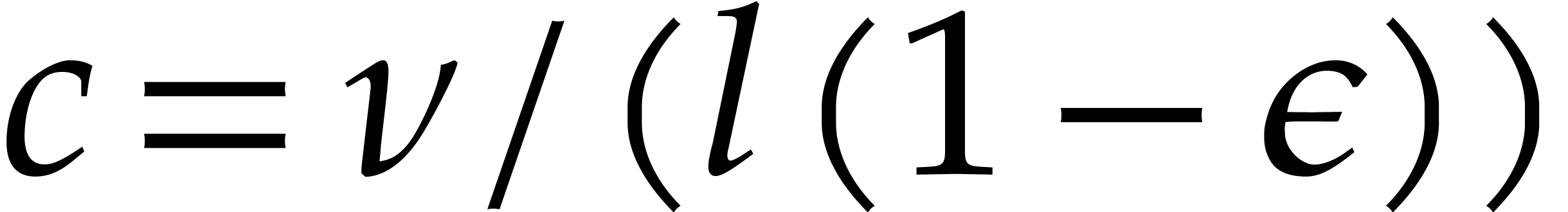 . Combining [6] and [1],
we may compute
. Combining [6] and [1],
we may compute  in time
in time 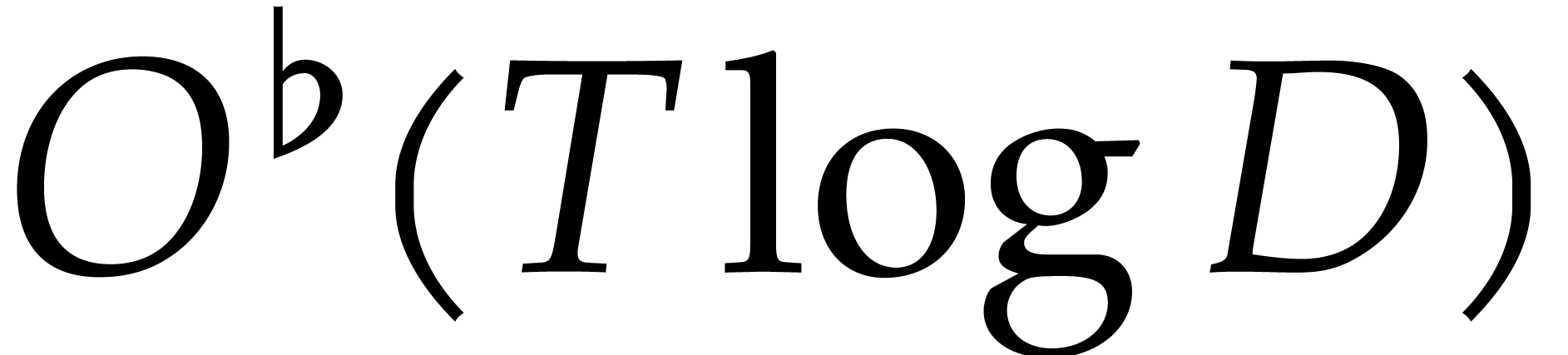 .
.
Now the running time of step 1 of Algorithm 3 is

With 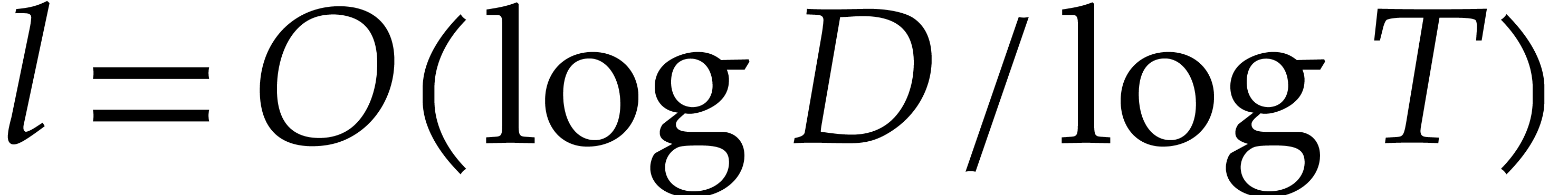 , this cost simplifies
to
, this cost simplifies
to
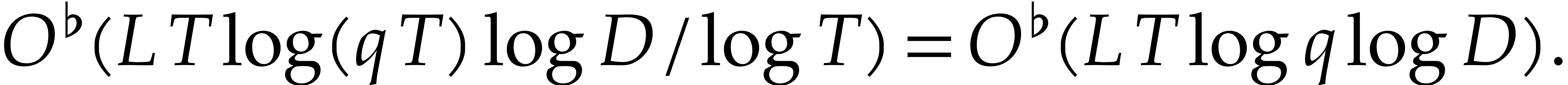
Step 3 may be obtained by sorting the coefficients of the 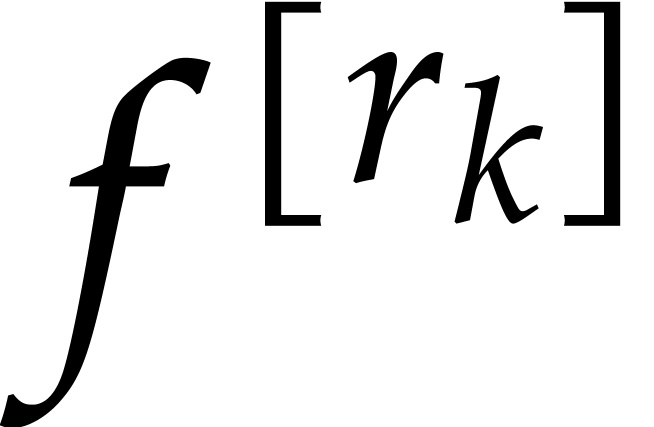 , in time
, in time
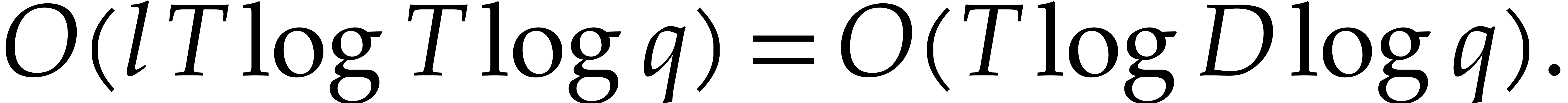
Using fast Chinese remaindering, step 4 takes time 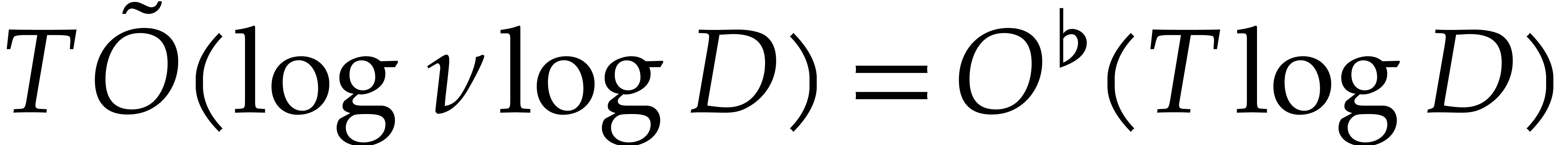 .
.
Remark. If  ,
then
,
then 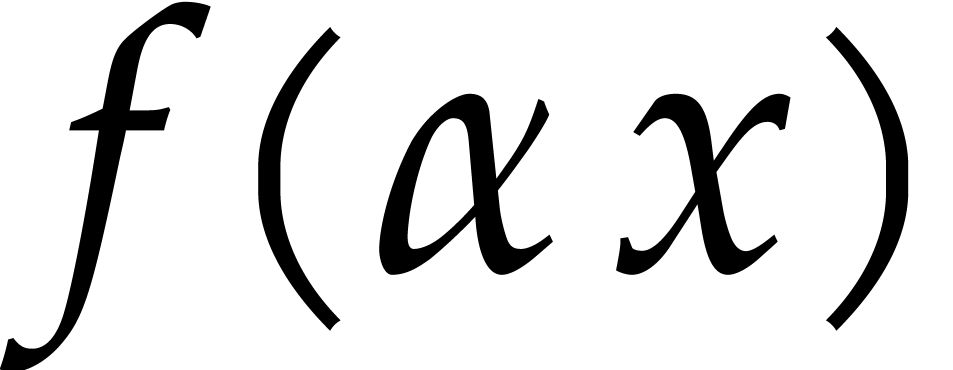 is diversified with high probability for a
random choice of
is diversified with high probability for a
random choice of 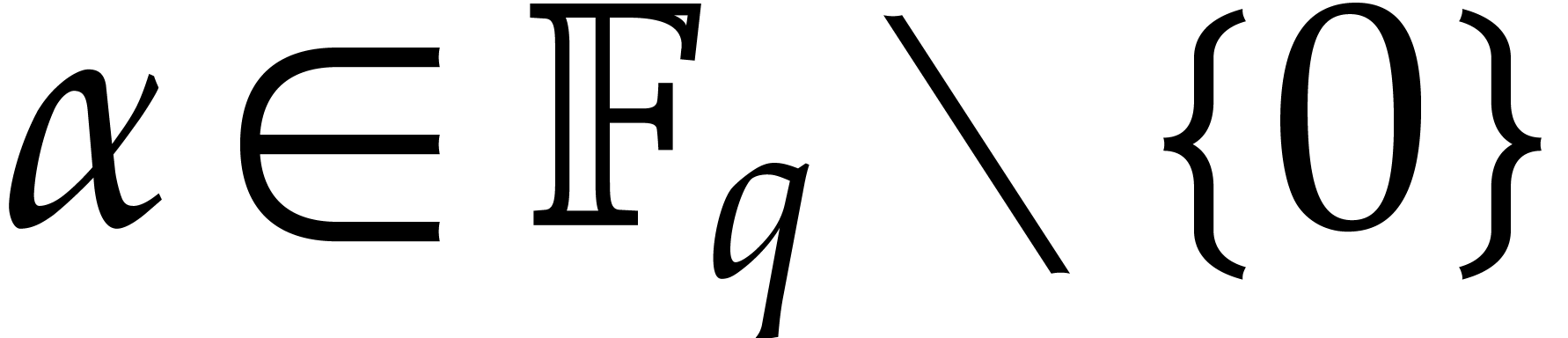 : see [18]. In the range where
: see [18]. In the range where  and
and 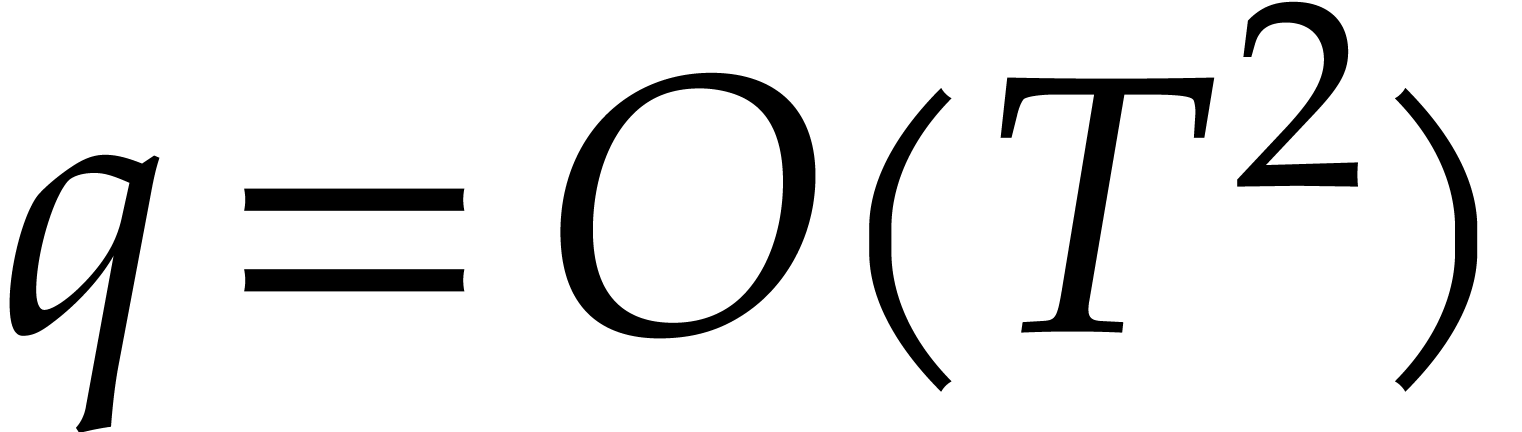 , it is possible to work with a
slightly weaker assumption: we say that
, it is possible to work with a
slightly weaker assumption: we say that 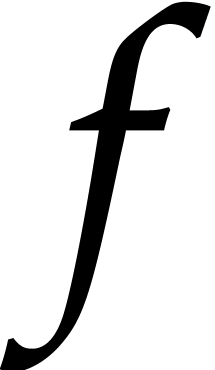 is
weakly diversified if
is
weakly diversified if  is of size
is of size 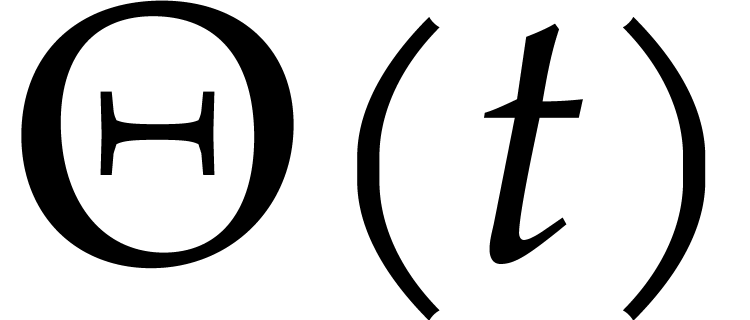 . If
. If  ,
then the polynomial
,
then the polynomial 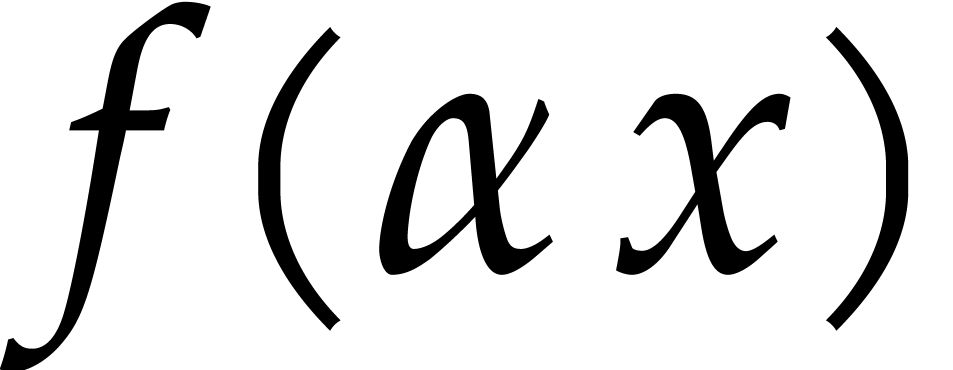 is still weakly diversified,
for a random choice of
is still weakly diversified,
for a random choice of 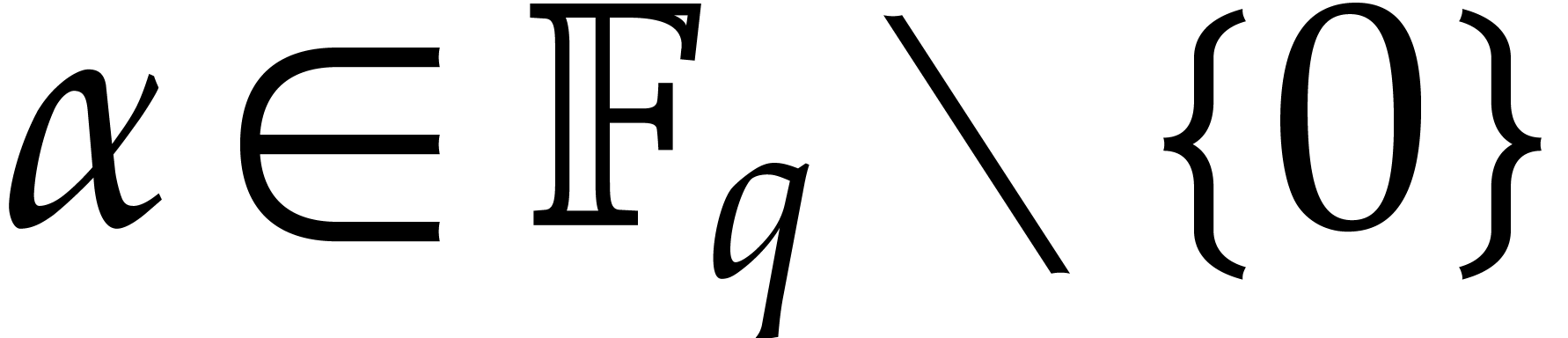 . If
. If
 is only weakly diversified and
is only weakly diversified and 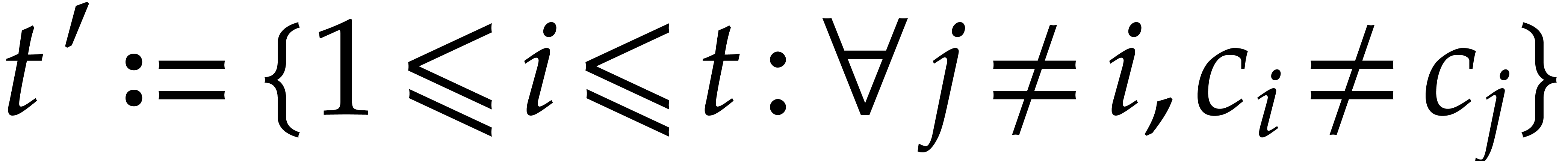 , then our analysis can be adapted to show that
Algorithm 3 returns about
, then our analysis can be adapted to show that
Algorithm 3 returns about 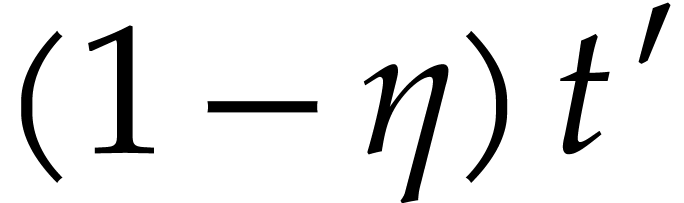 correct
terms of
correct
terms of  on average. Finally, in the range where
on average. Finally, in the range where
 , we need to work over a
field extension
, we need to work over a
field extension 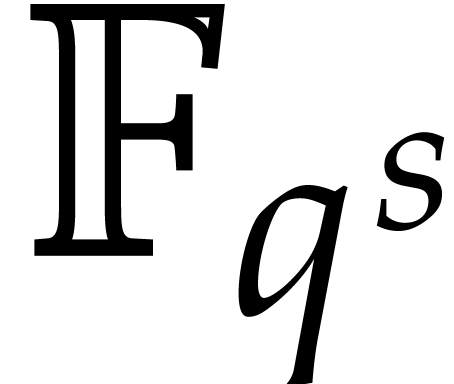 with
with 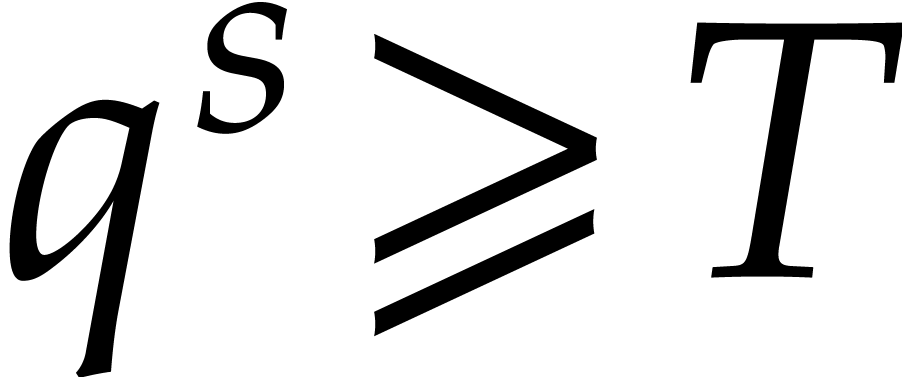 , which leads to an additional arithmetic overhead
of
, which leads to an additional arithmetic overhead
of 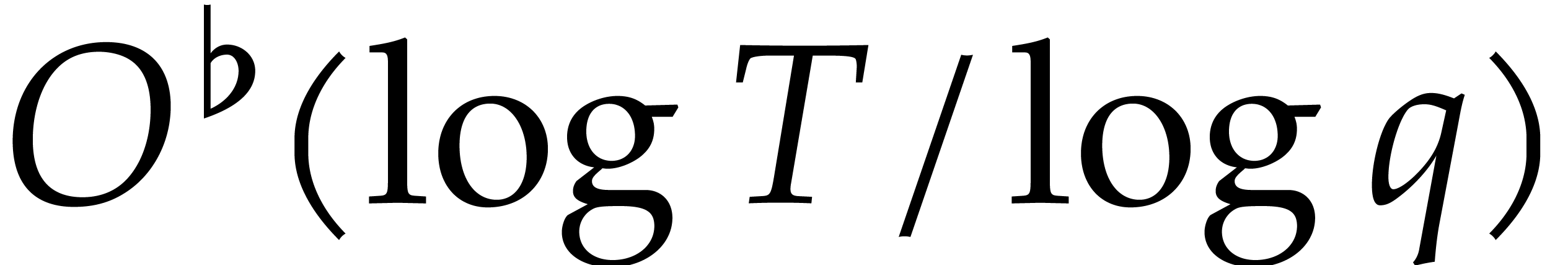 .
.
Remark. Let us show that with high probability,
the polynomial 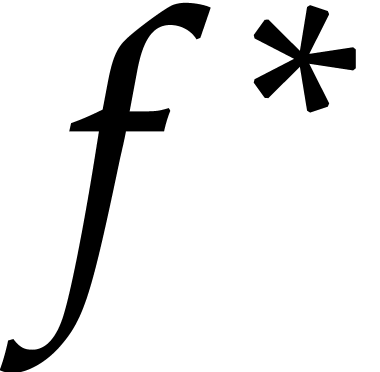 returned by Algorithm 3
only contains correct terms of
returned by Algorithm 3
only contains correct terms of 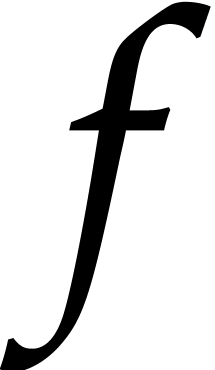 (although it does
not necessarily contain all terms). For this, we make the additional
hypothesis that the coefficients of
(although it does
not necessarily contain all terms). For this, we make the additional
hypothesis that the coefficients of 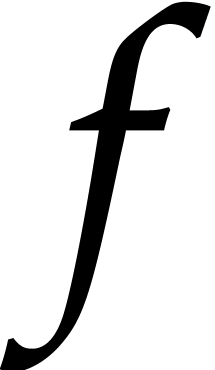 are
essentially random non-zero values in
are
essentially random non-zero values in  (which is
typically the case after a change of variables
(which is
typically the case after a change of variables  , where
, where 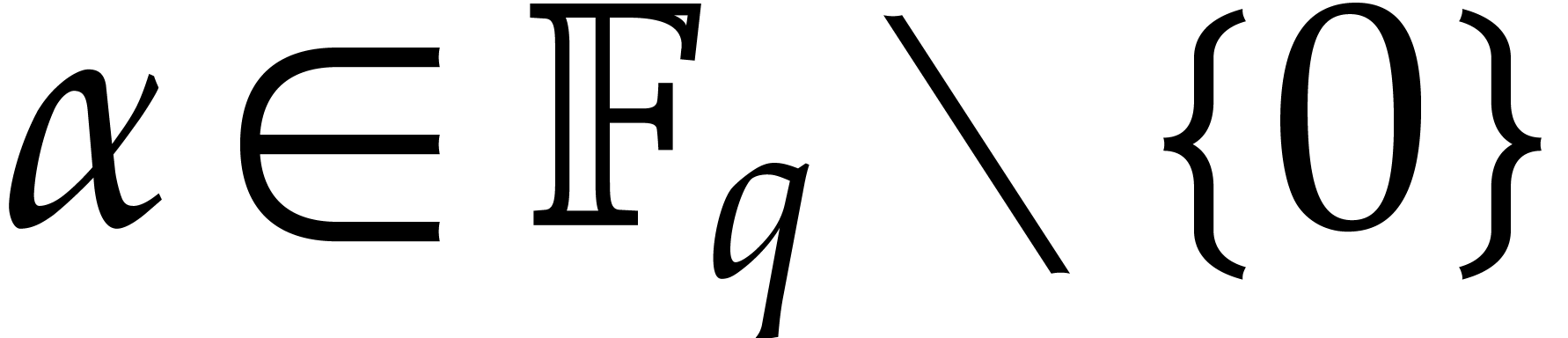 is random).
is random).
Now assume that some coefficient  in step 4 gives
rise to a term
in step 4 gives
rise to a term 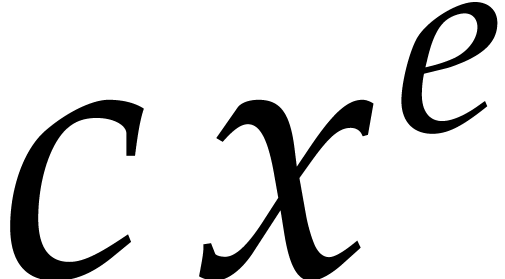 that is not in
that is not in 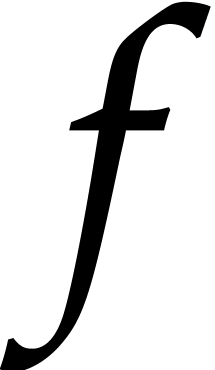 . Then for every
. Then for every 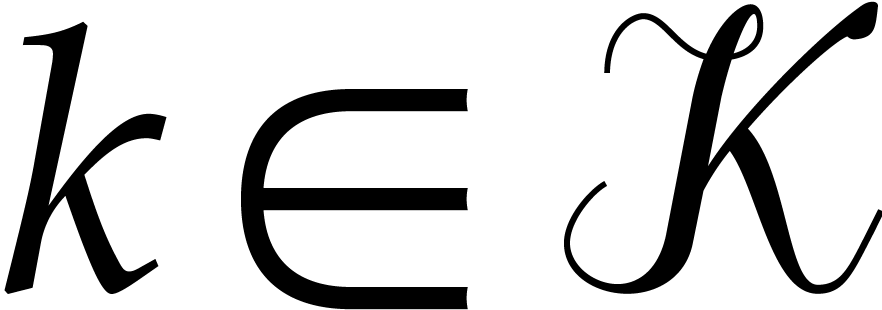 ,
there should be at least two terms in
,
there should be at least two terms in  that
collide modulo
that
collide modulo  and for which the sum of the
corresponding coefficients equals
and for which the sum of the
corresponding coefficients equals  .
The probability that this happens for a fixed
.
The probability that this happens for a fixed  is
bounded by
is
bounded by 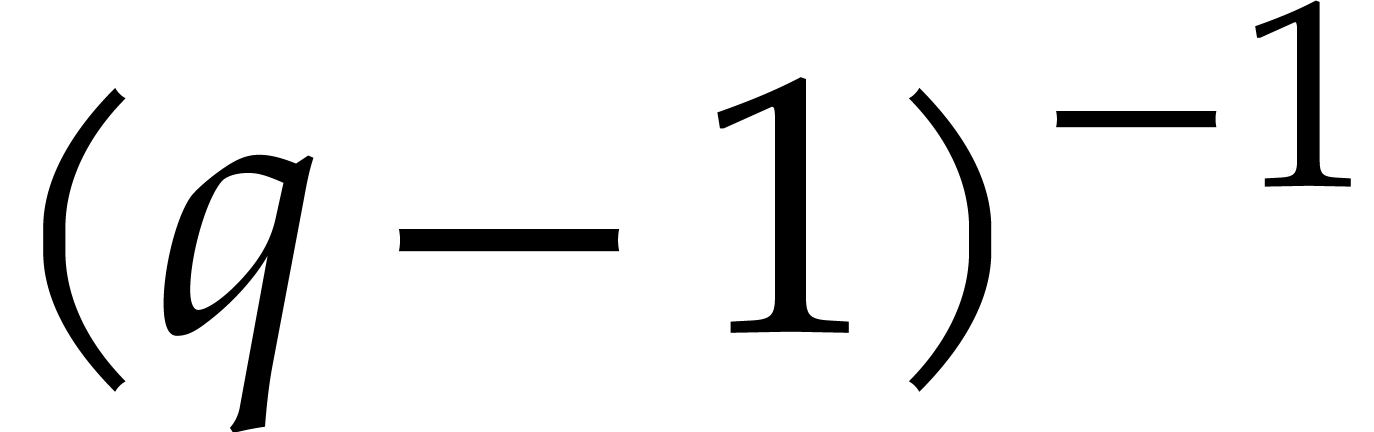 and the probability that this happens
for all
and the probability that this happens
for all  is bounded by
is bounded by  , where
, where  is minimal with
is minimal with
 .
.
For the algorithms in this section, we assumed that a bound  for
for  was given. It turns out that a
variant of our probabilistic analysis can also be used for the efficient
computation of a rough estimate for
was given. It turns out that a
variant of our probabilistic analysis can also be used for the efficient
computation of a rough estimate for  .
This yields an interesting alternative to the naive doubling strategy
described in section 3.1.
.
This yields an interesting alternative to the naive doubling strategy
described in section 3.1.
Let us still assume that Hred
holds. We will also assume that colliding terms rarely cancel out (which
holds with high probability if  is sufficiently
large). This time, we compute
is sufficiently
large). This time, we compute 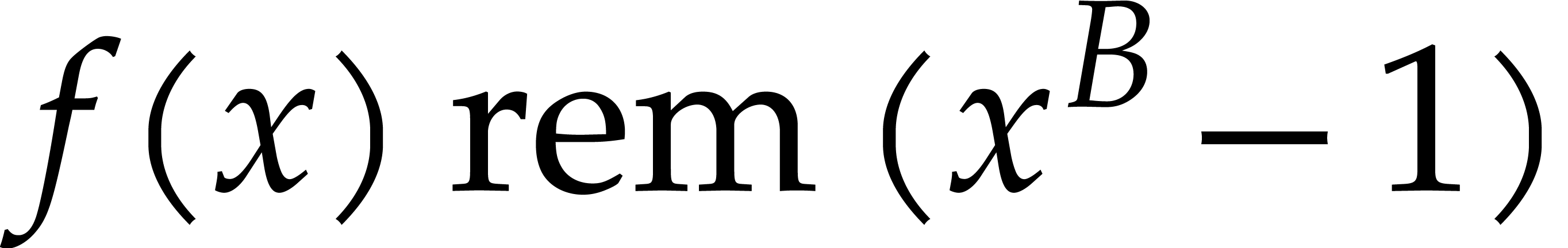 for
for  , where
, where 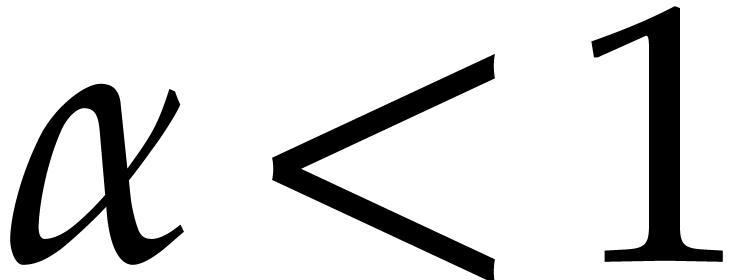 is to be
determined, and let
is to be
determined, and let 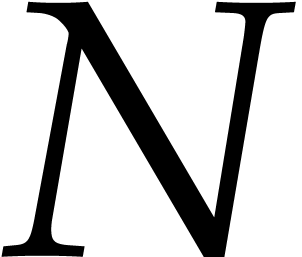 be the number of terms in
this remainder. When randomly distributing
be the number of terms in
this remainder. When randomly distributing  balls
over
balls
over 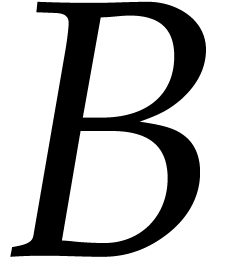 boxes, the probability that none of the
balls lands in a particular box is
boxes, the probability that none of the
balls lands in a particular box is 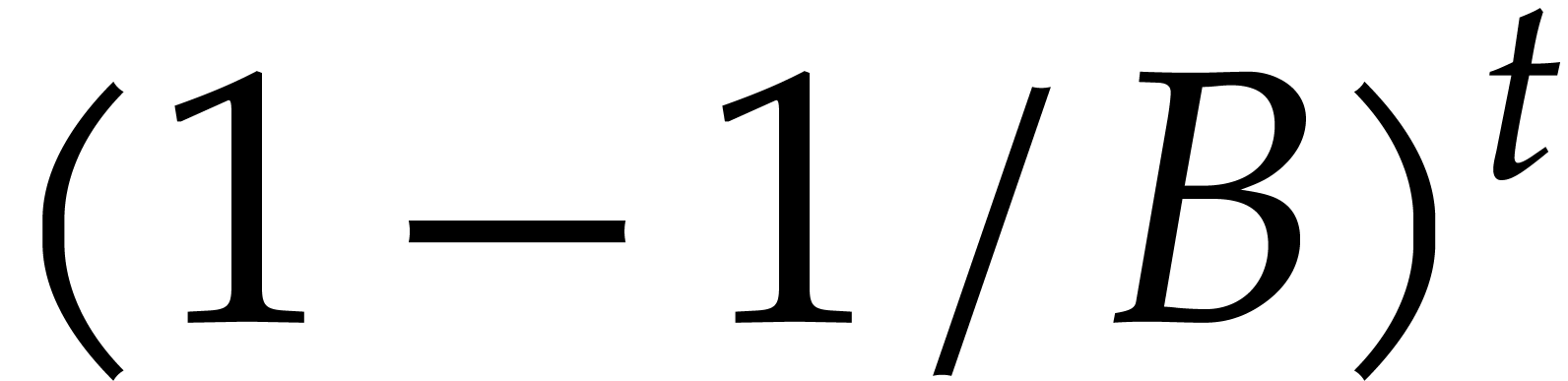 .
Consequently, the expected number of boxes with no ball is
.
Consequently, the expected number of boxes with no ball is 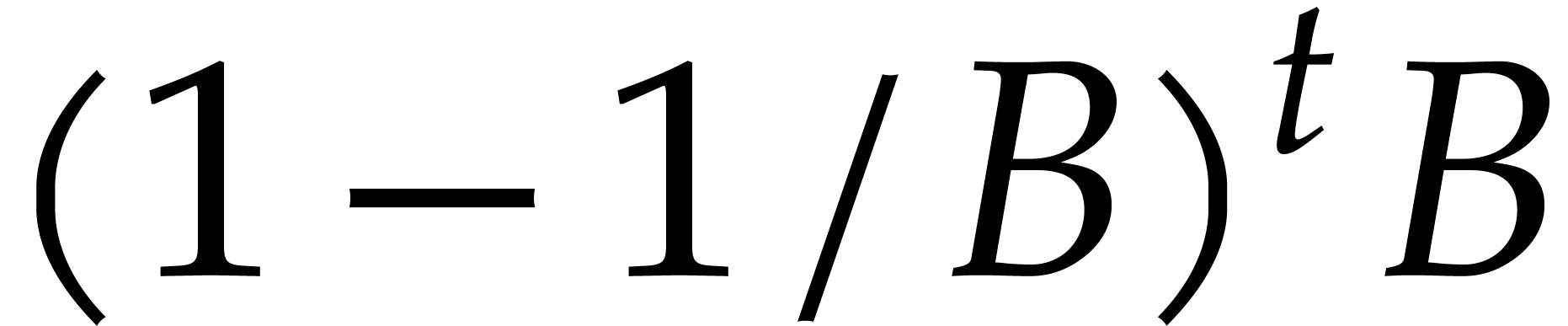 , whence
, whence
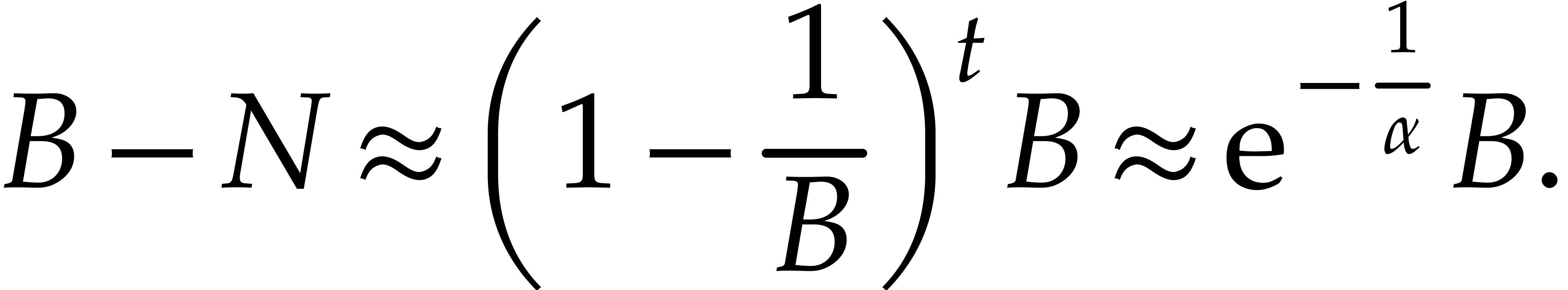
It follows that
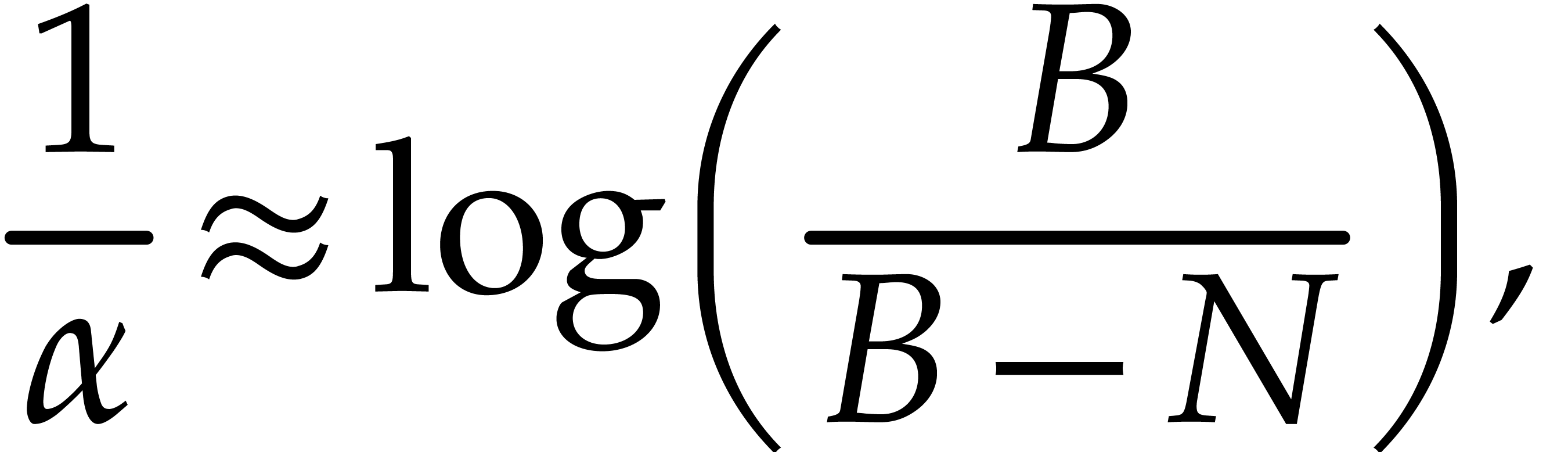
and thus
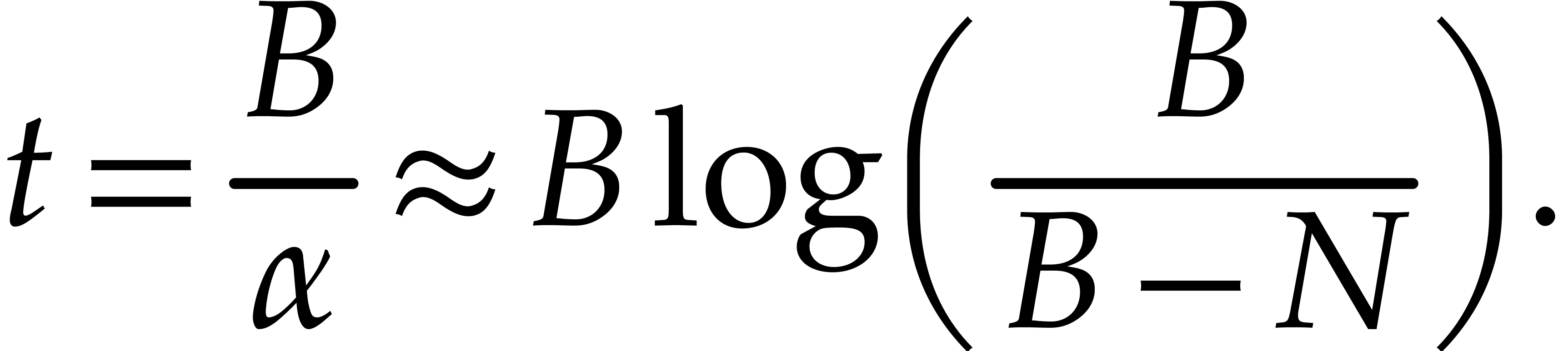 |
(7) |
By doubling 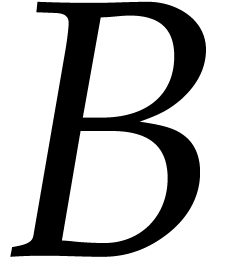 until
until 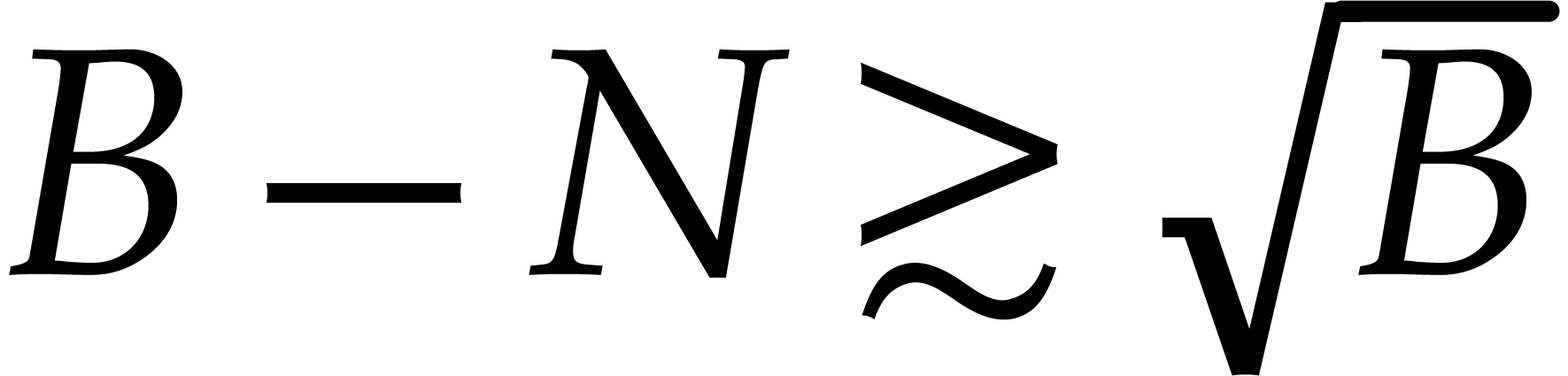 ,
we may then use the approximation (7) as a good candidate
for
,
we may then use the approximation (7) as a good candidate
for  . Notice that we have
. Notice that we have
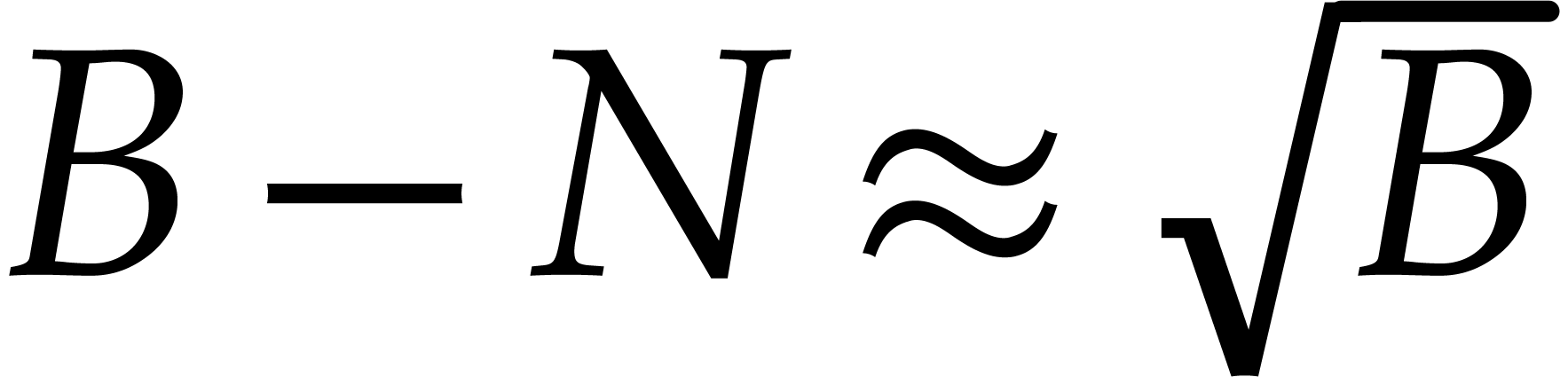 when
when 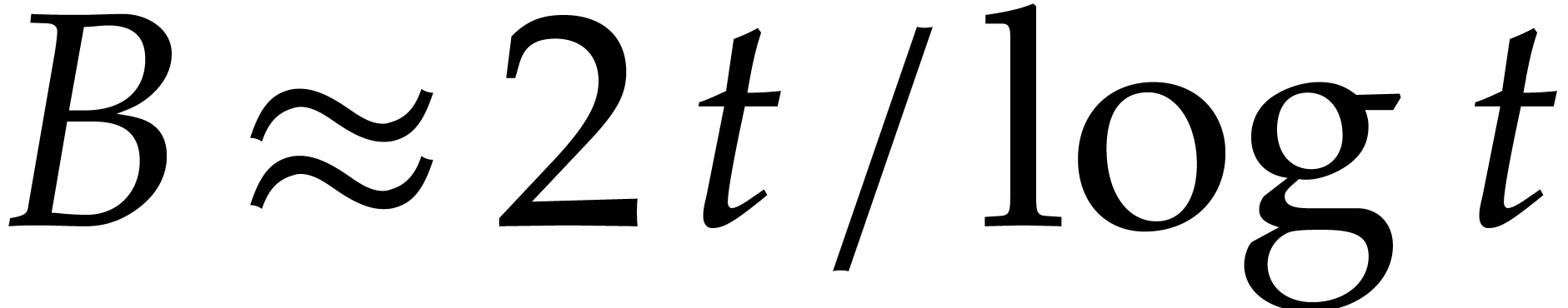 .
.
Cyclic extension methods for sparse interpolation are attractive due to
their generality and the possibility to derive deterministic complexity
bounds. However, even their most efficient probabilistic versions suffer
from the overhead of arithmetic operations in cyclic extension algebras
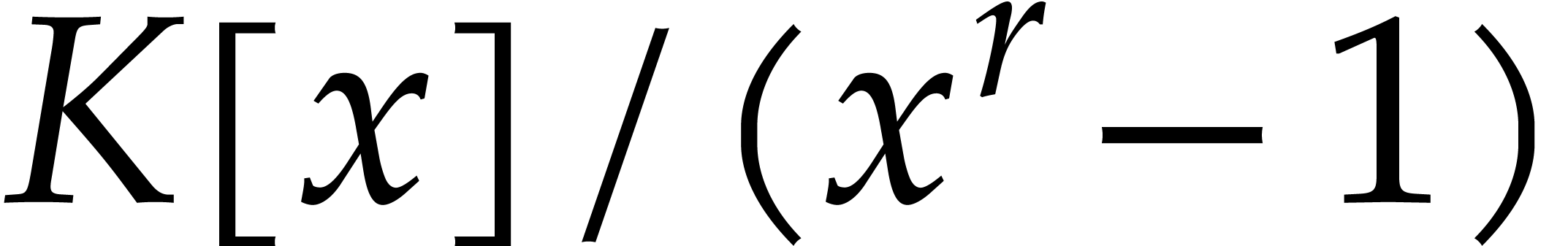 .
.
The matching strategy based on diversification leads to the best
practical complexity bounds, as shown in section 4.5.
Assuming Hred, 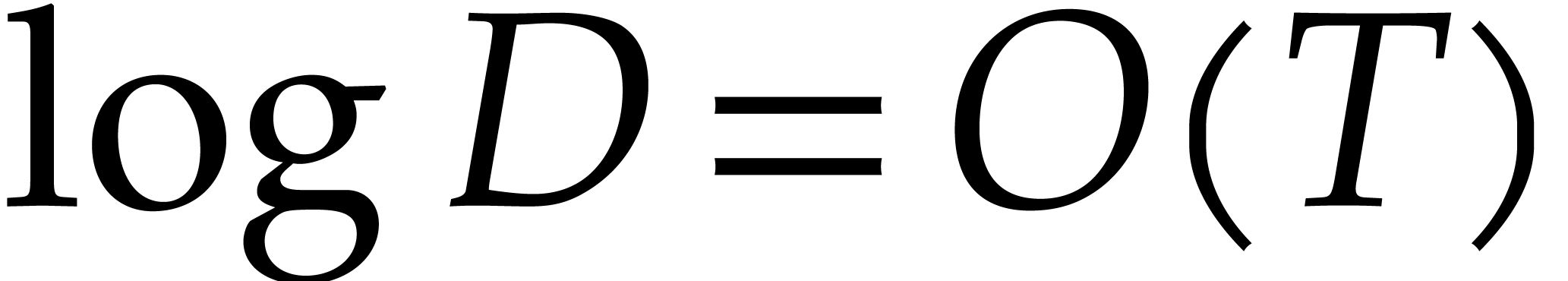 , and
, and  ,
we have given a Monte Carlo algorithm for sparse interpolation of
complexity
,
we have given a Monte Carlo algorithm for sparse interpolation of
complexity 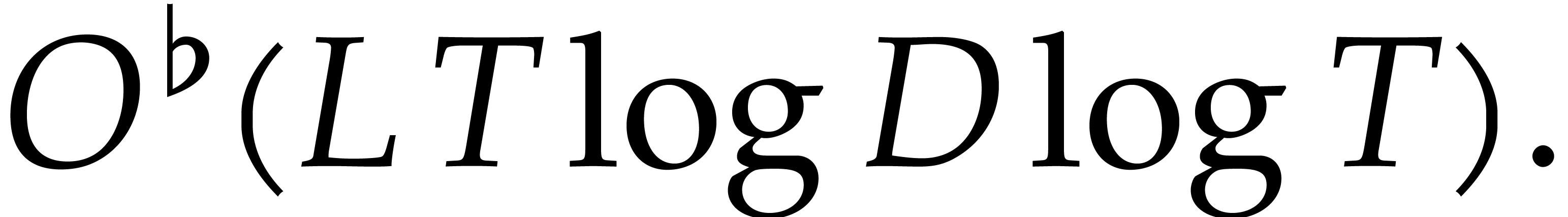 The case when
The case when 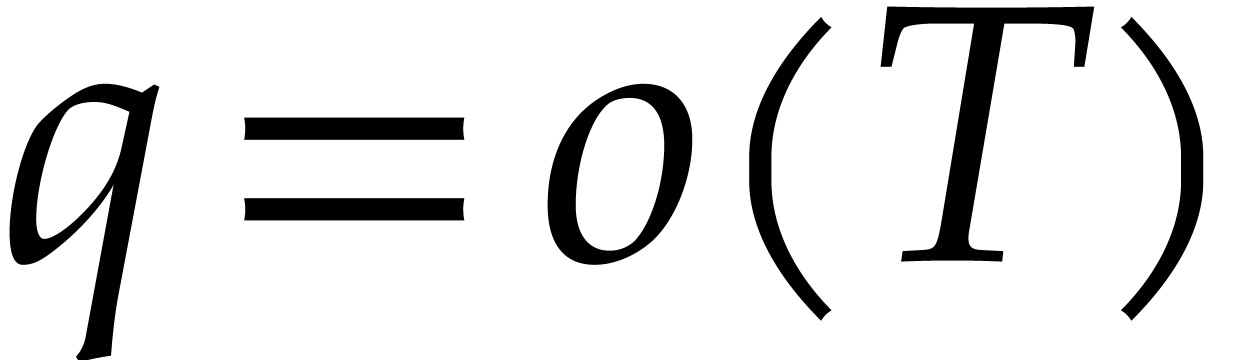 can be reduced to this case using a field extension of degree
can be reduced to this case using a field extension of degree 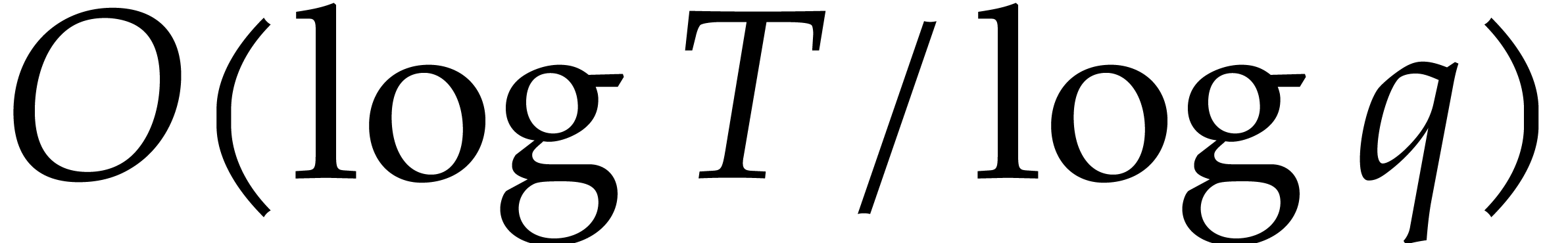 . Assuming only Hred and
. Assuming only Hred and 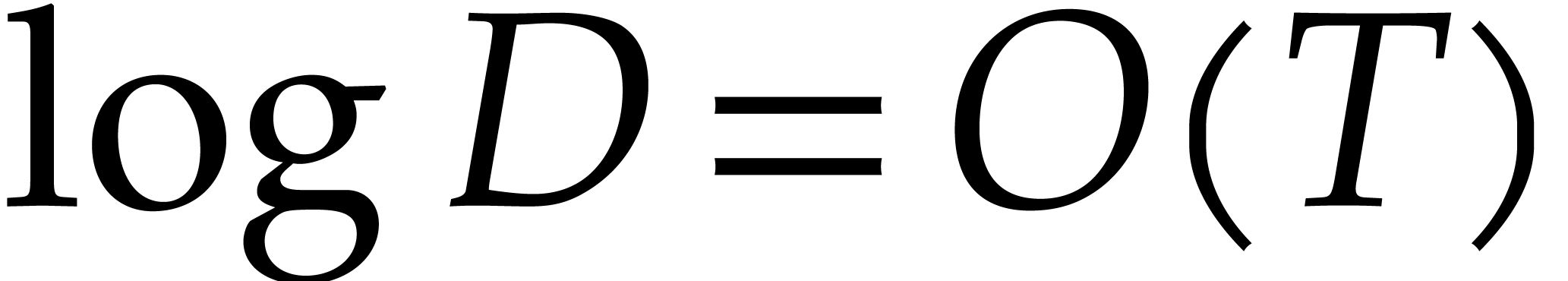 ,
we thus obtain a probabilistic algorithm that runs in time
,
we thus obtain a probabilistic algorithm that runs in time
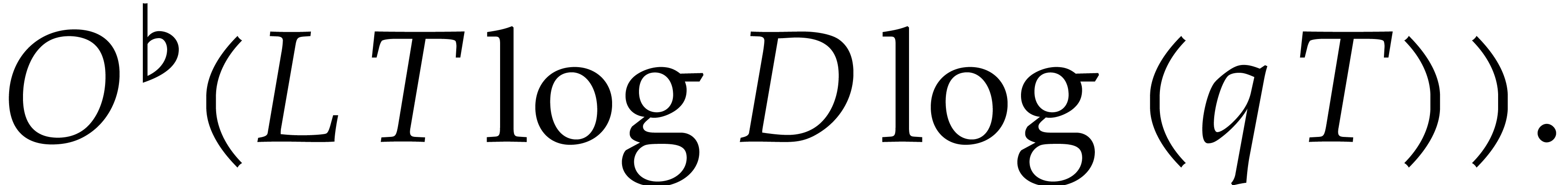 |
(8) |
Prony's method is one of the oldest and most celebrated algorithms for
sparse interpolation of univariate polynomials. It is based on the
evaluation of  at points in a geometric
progression. Since there are many variants, we keep our presentation as
general as possible. As in the previous section, assume that
at points in a geometric
progression. Since there are many variants, we keep our presentation as
general as possible. As in the previous section, assume that
 |
(9) |
and that we know bounds  and
and  for the degree and the number of terms of
for the degree and the number of terms of  .
.
Algorithm
Input: a black box polynomial
Output: the sparse interpolation |
||
|
It is well known that steps 3 and 6 can be performed in time 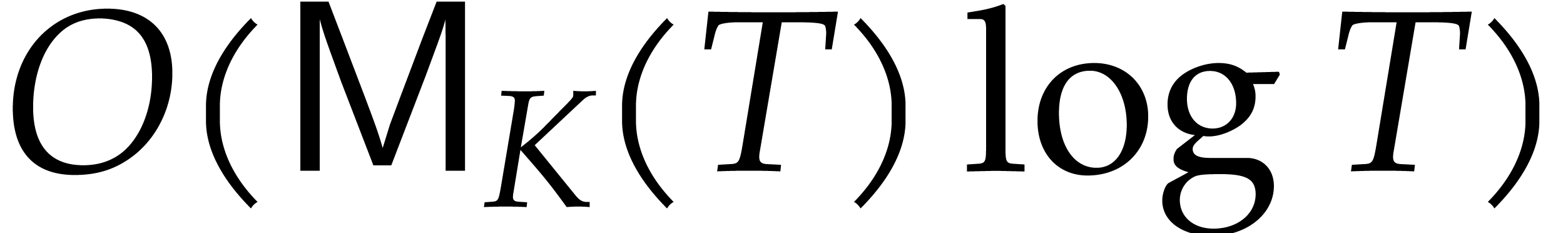 , through fast Padé
approximation [11, 46] in the case of step 3,
and using a transposed version of fast multipoint interpolation [10, 12] for step 6. If
, through fast Padé
approximation [11, 46] in the case of step 3,
and using a transposed version of fast multipoint interpolation [10, 12] for step 6. If 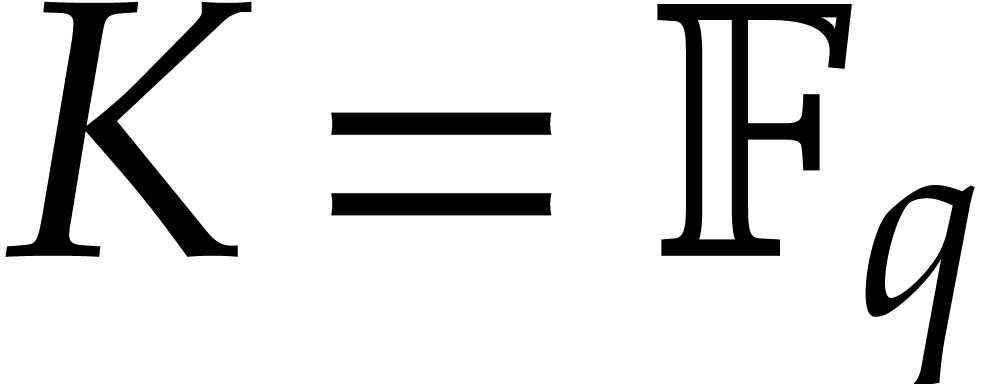 , then this bound becomes
, then this bound becomes 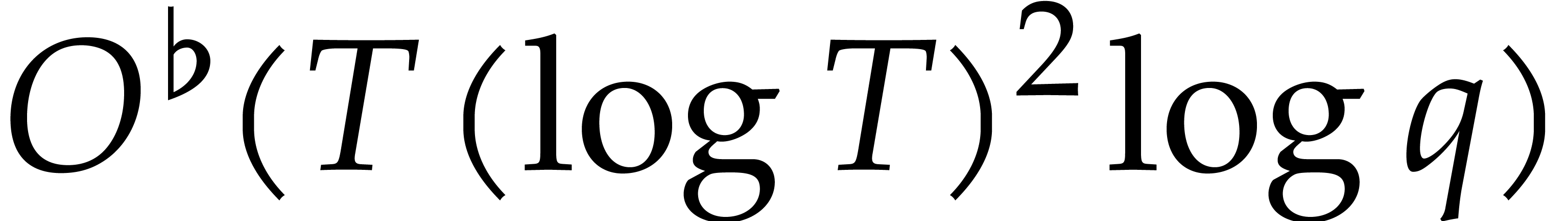 . The efficiency of steps 4 and 5 highly depends on
the coefficient field
. The efficiency of steps 4 and 5 highly depends on
the coefficient field  . In
the remainder of this section, we will discuss this issue in detail in
the case when
. In
the remainder of this section, we will discuss this issue in detail in
the case when 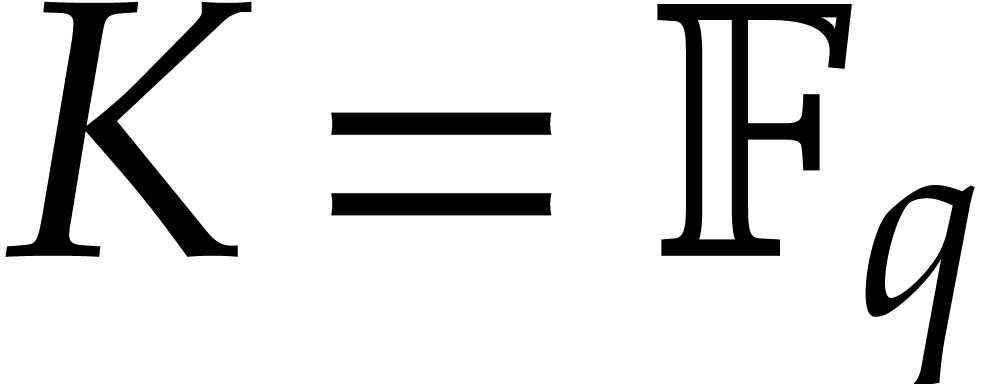 is a finite field.
is a finite field.
Finding the roots of a univariate polynomial over a finite field is a
well-known and highly studied problem in computer algebra. The most
efficient general purpose algorithm for this task is due to Cantor and
Zassenhaus [13]. It is probabilistic and computes the roots
of  in time
in time 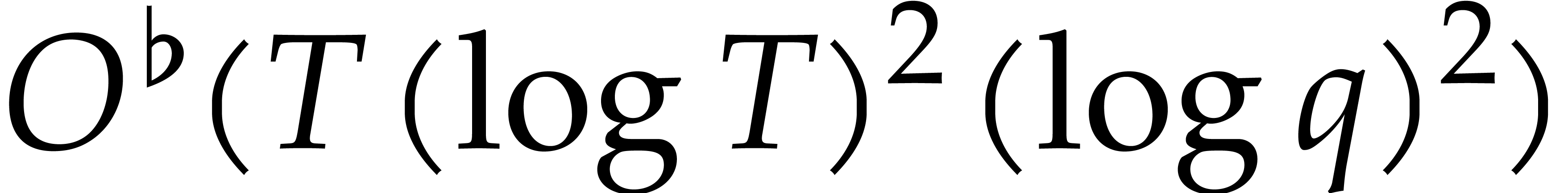 .
.
In [22, 23], several alternative methods were
designed for the case when 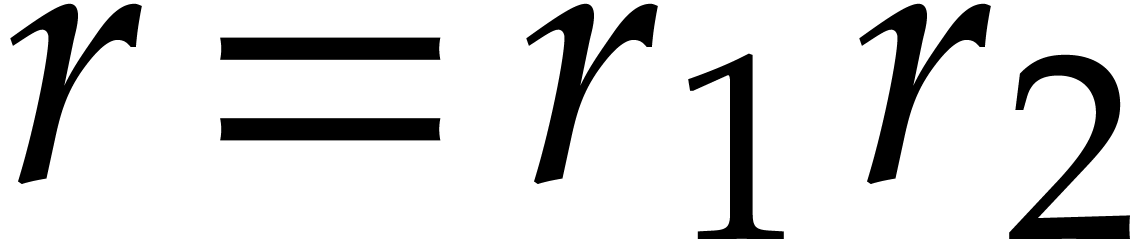 with
with  and
and 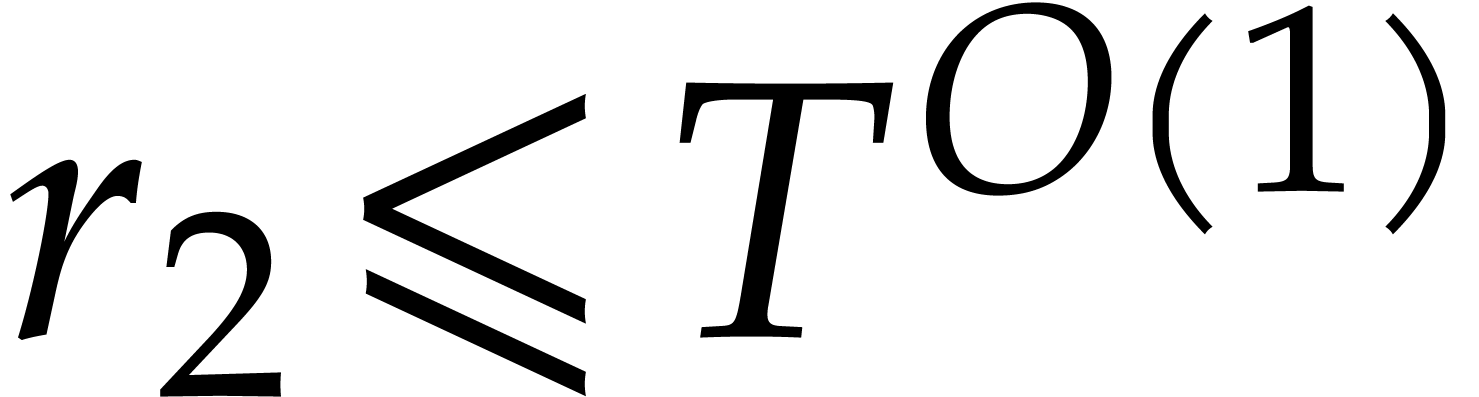 smooth (in the sense that
smooth (in the sense that 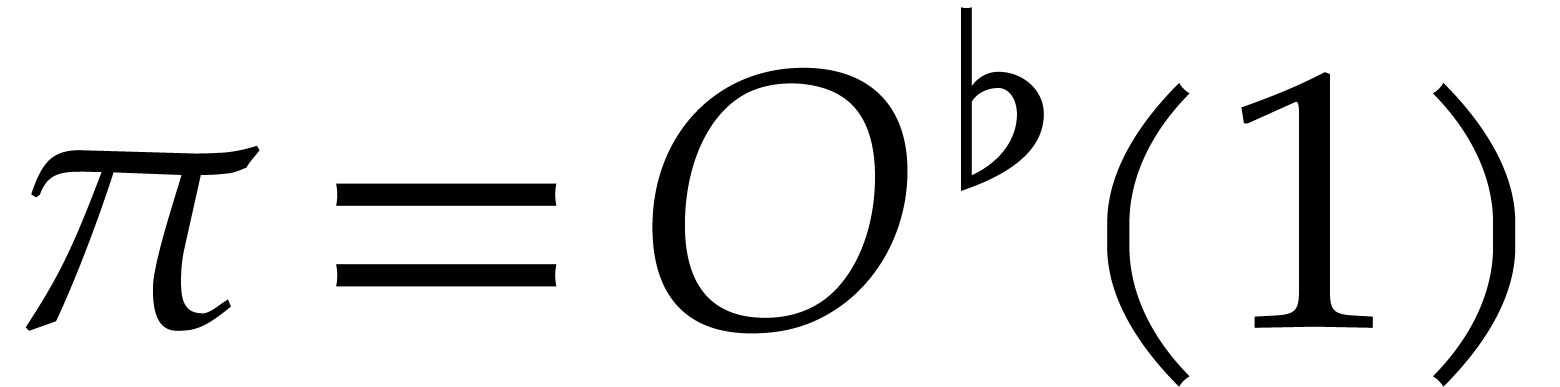 for each prime factor
for each prime factor  of
of 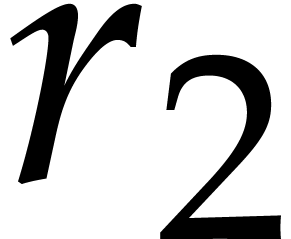 ). The idea is to proceed in three steps:
). The idea is to proceed in three steps:
We first compute the 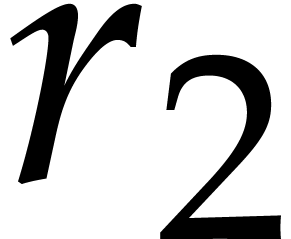 -th
Graeffe transform
-th
Graeffe transform  of
of  , whose roots are the
, whose roots are the  -th powers of the roots of
-th powers of the roots of  . This step can be done in time
. This step can be done in time  by [22, Proposition 5].
by [22, Proposition 5].
We next compute the roots of  through an
exhaustive evaluation at all
through an
exhaustive evaluation at all  -th
roots of unity. This step takes time
-th
roots of unity. This step takes time 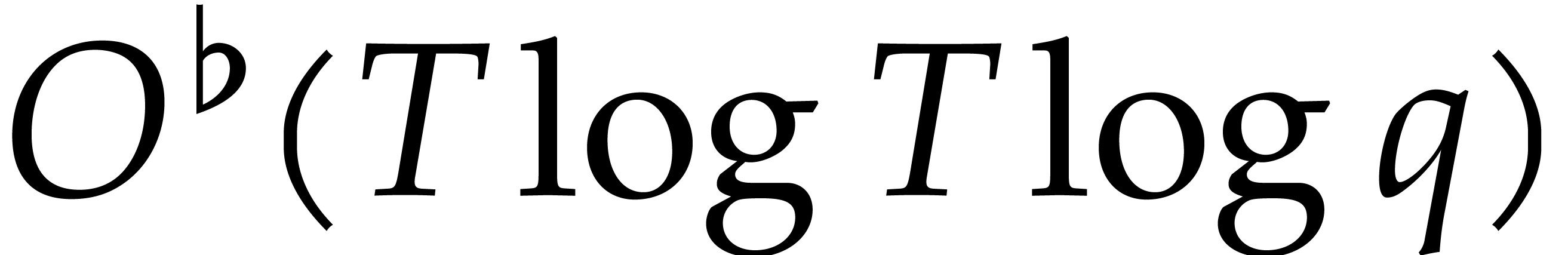 .
.
We finally lift these roots back up to the roots of  . This can be done in time
. This can be done in time 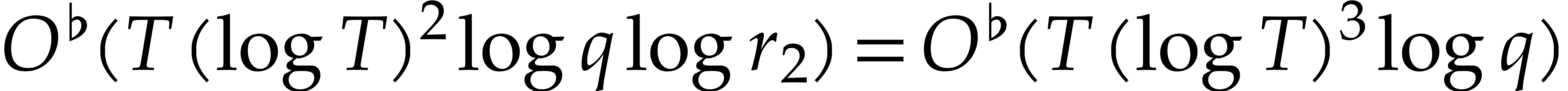 , using g.c.d. computations.
, using g.c.d. computations.
Altogether, this yields a sparse interpolation method of cost 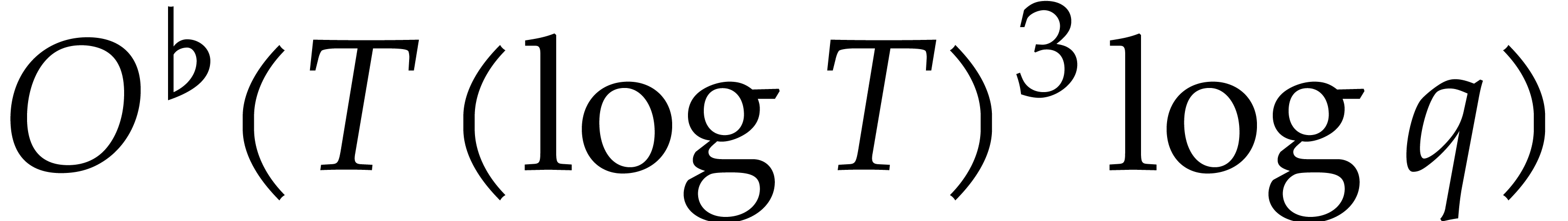 .
.
The back-lifting of single roots can be accelerated using so-called
“tangent Graeffe transforms”. The idea is to work over the
ring  instead of
instead of  .
Then
.
Then 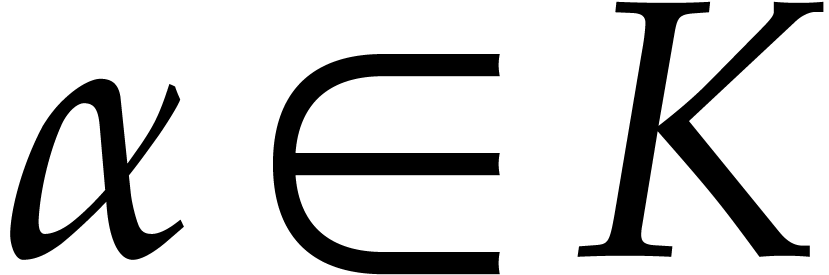 is a root of a polynomial
is a root of a polynomial  if and only if
if and only if  is a root of the polynomial
is a root of the polynomial 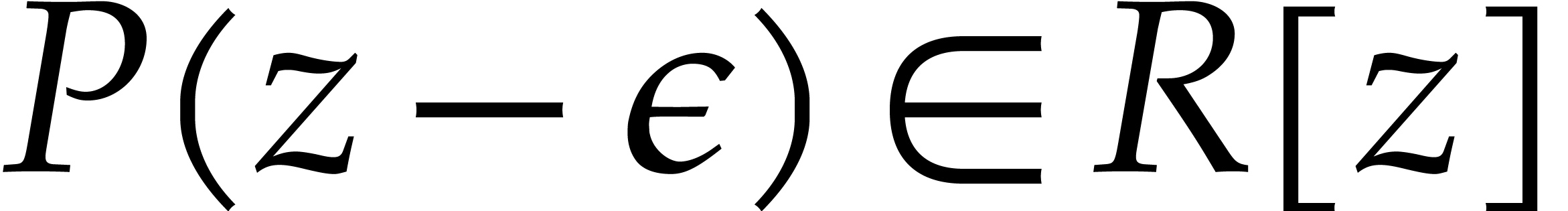 . Now if we know a single root
. Now if we know a single root 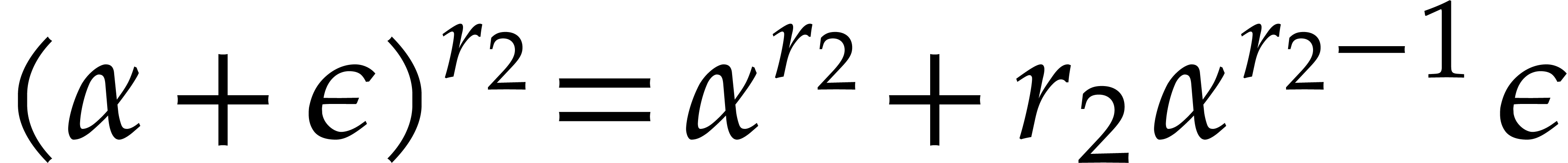 of
of 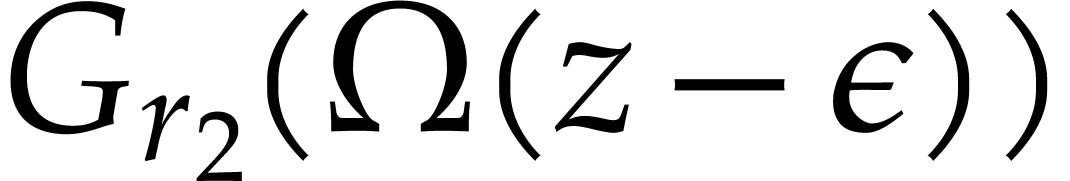 , then
we may retrieve
, then
we may retrieve  using one division of
using one division of 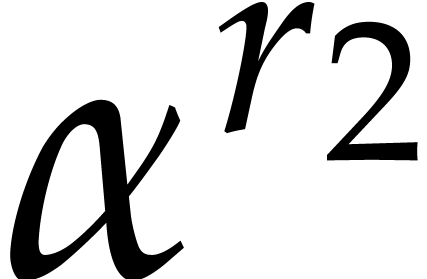 by
by 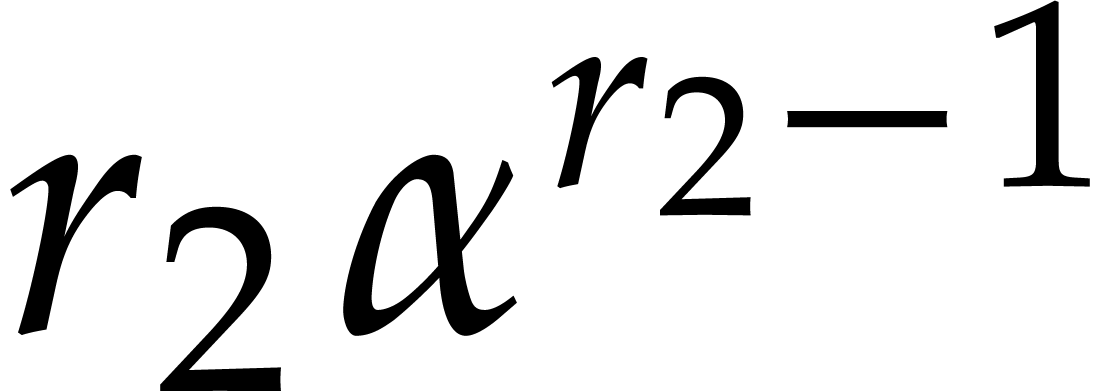 and one multiplication by
and one multiplication by  (note that
(note that  is invertible in
is invertible in
 since
since  divides
divides  ). In other words, the back-lifting
step can be done in time
). In other words, the back-lifting
step can be done in time 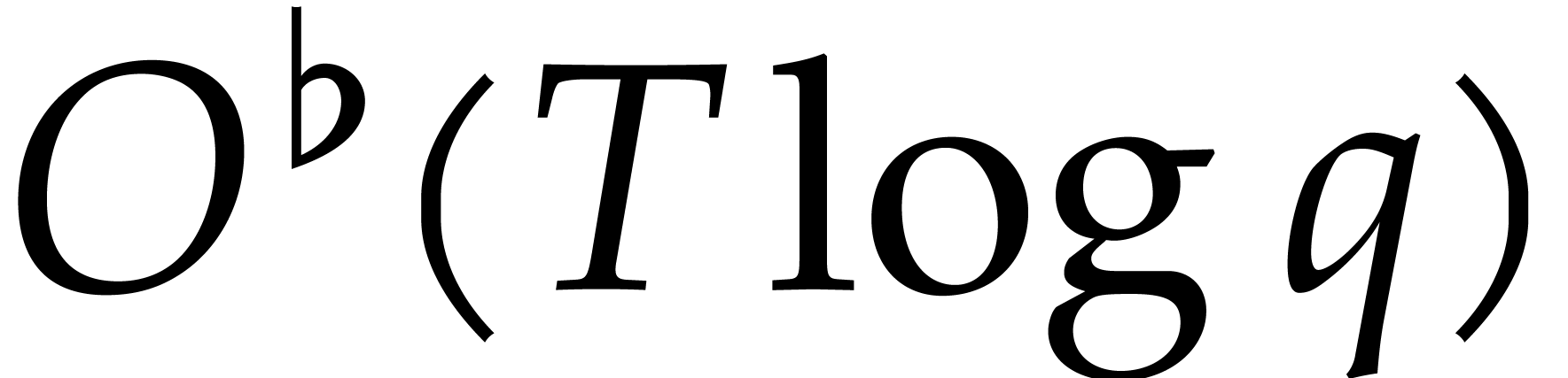 ,
using
,
using 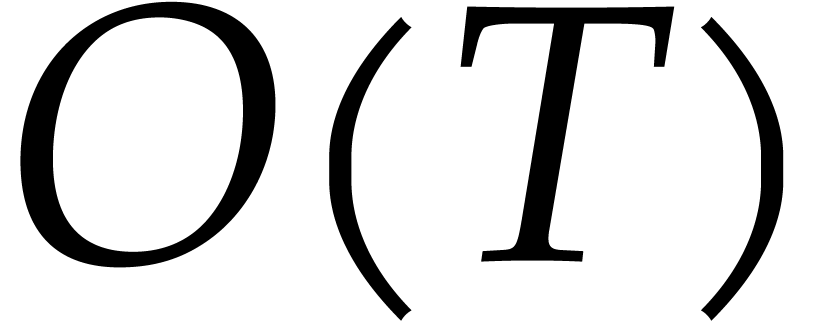 operations in
operations in  .
.
However, this method only works if  is a single
root of
is a single
root of  . When replacing
. When replacing 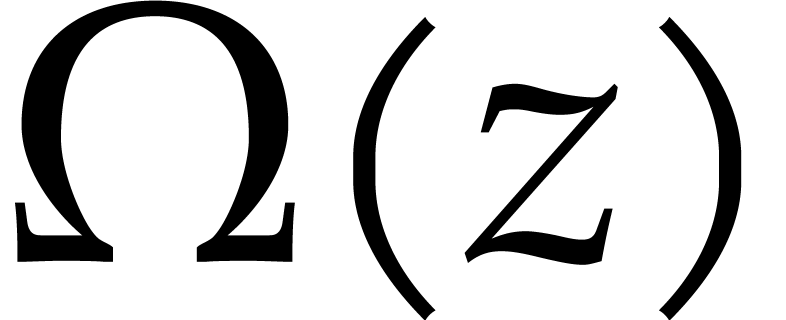 by
by 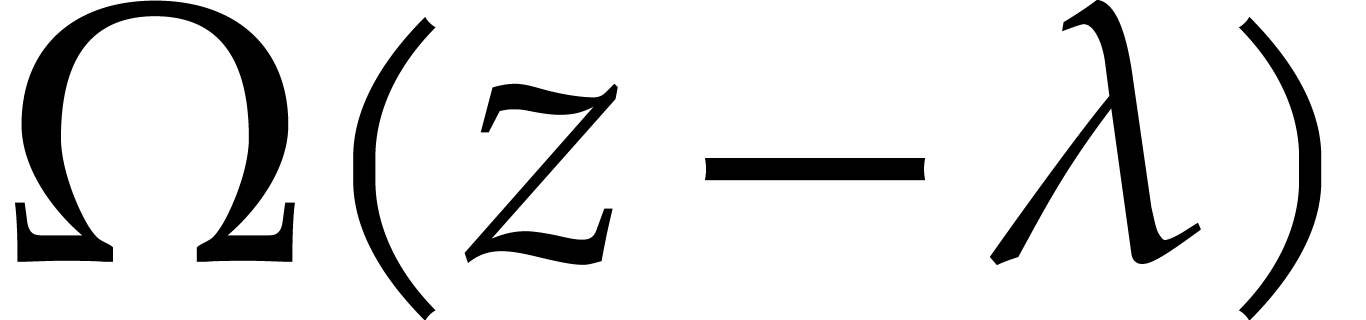 for a randomly chosen
for a randomly chosen
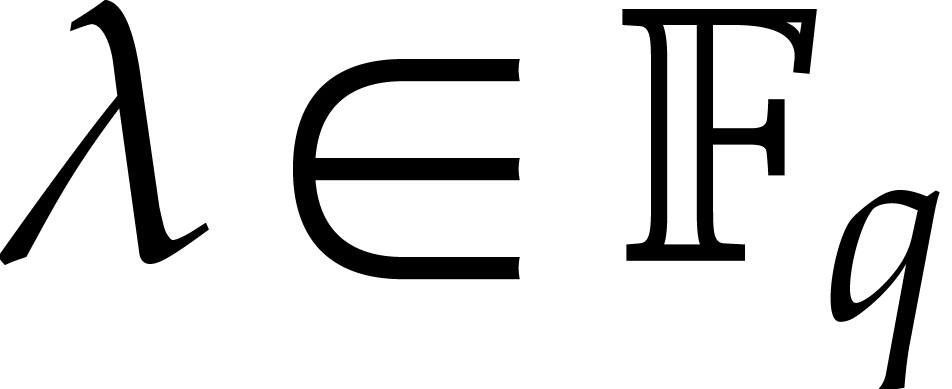 , the polynomial
, the polynomial  can be forced to admit a non-trivial proportion of single
roots with high probability. However, these roots are no longer powers
of
can be forced to admit a non-trivial proportion of single
roots with high probability. However, these roots are no longer powers
of 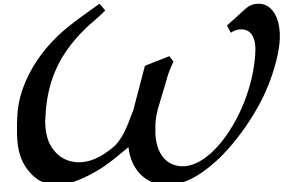 , unless we took
, unless we took  . Assuming that
. Assuming that 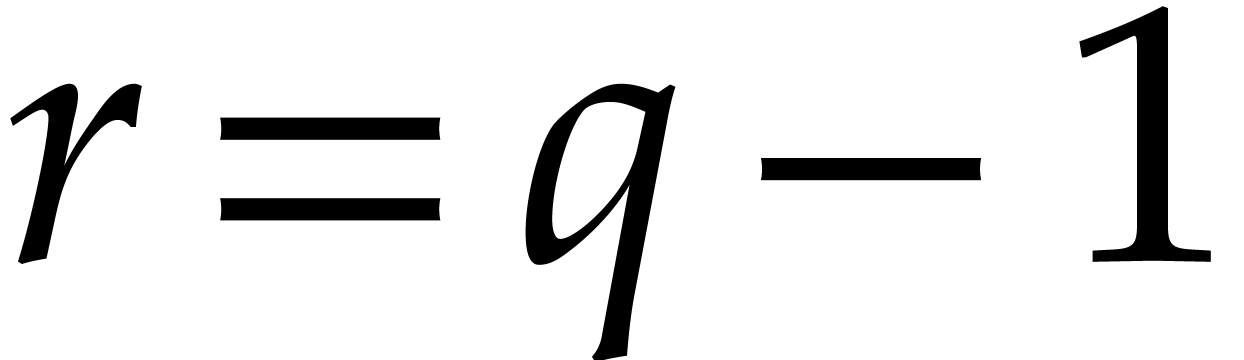 and using several shifts
and using several shifts 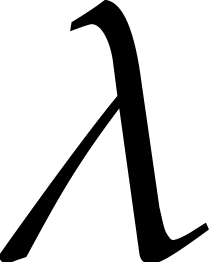 , it
can be shown [22, Proposition 12] that the tangent Graeffe
method yields a sparse interpolation method of complexity
, it
can be shown [22, Proposition 12] that the tangent Graeffe
method yields a sparse interpolation method of complexity 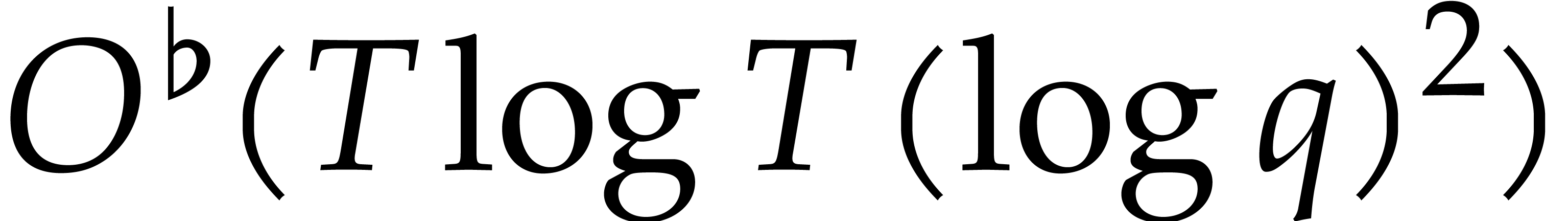 .
.
The discrete logarithm problem in abelian groups is a well-known problem
in computational number theory. If  is smooth,
then the Pohlig–Hellman algorithm provides an efficient solution;
it allows step 5 of Algorithm 4 to be performed in time
is smooth,
then the Pohlig–Hellman algorithm provides an efficient solution;
it allows step 5 of Algorithm 4 to be performed in time
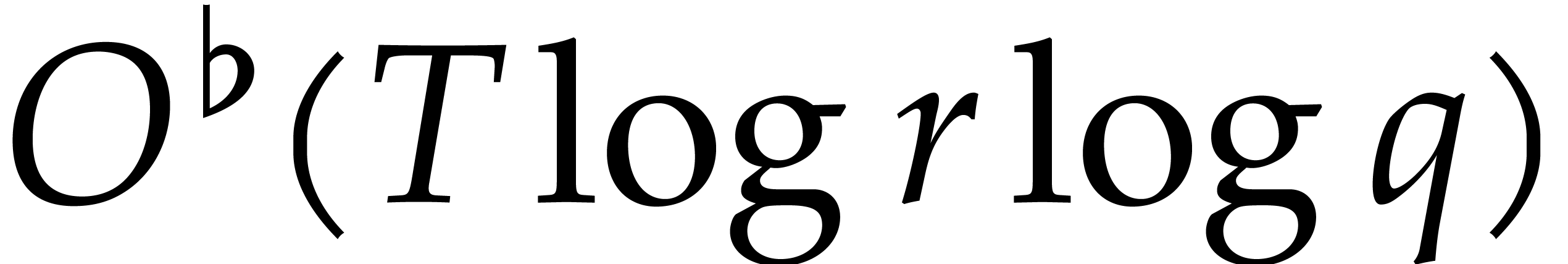 . Under the assumption that
we may take
. Under the assumption that
we may take 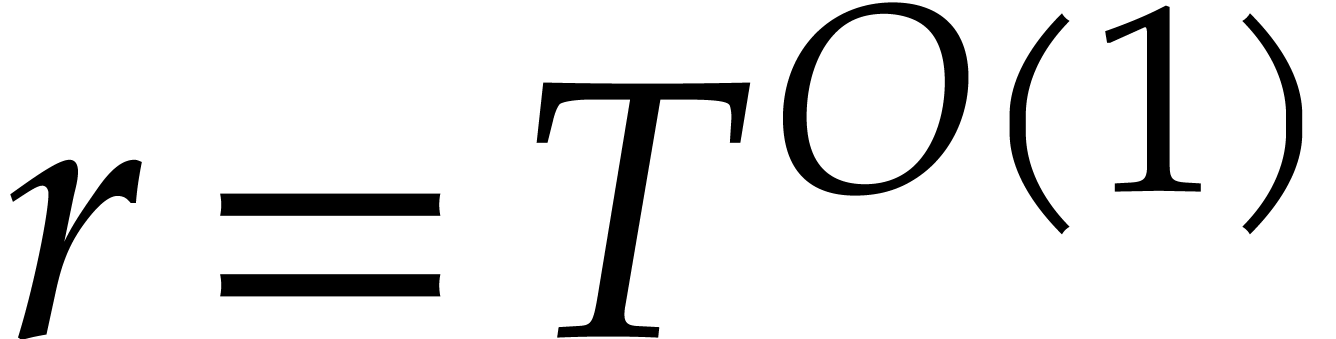 , this bound
reduces to
, this bound
reduces to 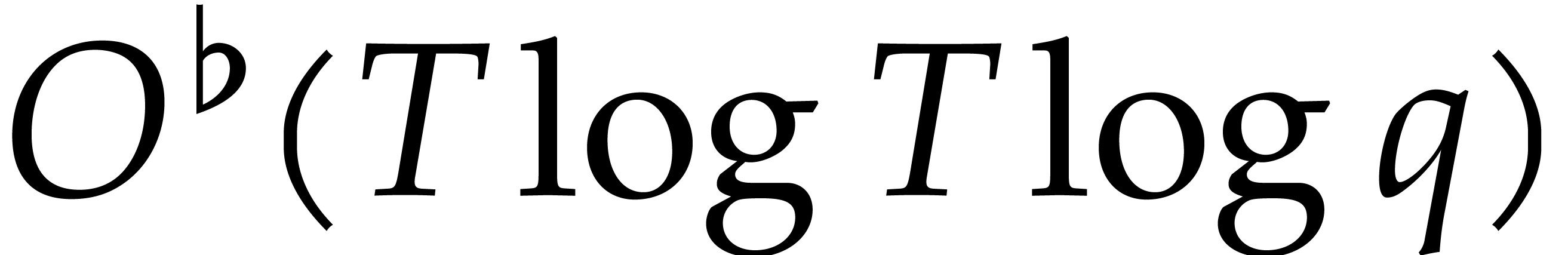 .
.
Again, the same bound still holds if 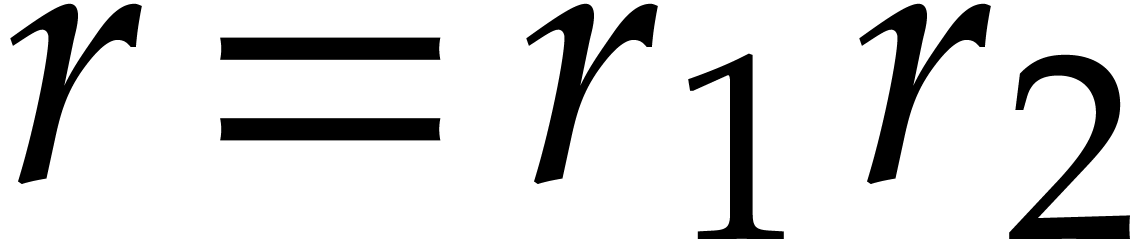 with
with  and
and 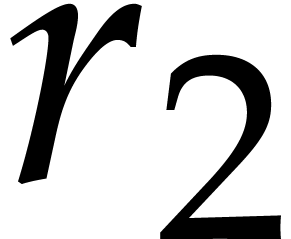 smooth. Indeed, in that
case, we may tabulate the powers
smooth. Indeed, in that
case, we may tabulate the powers 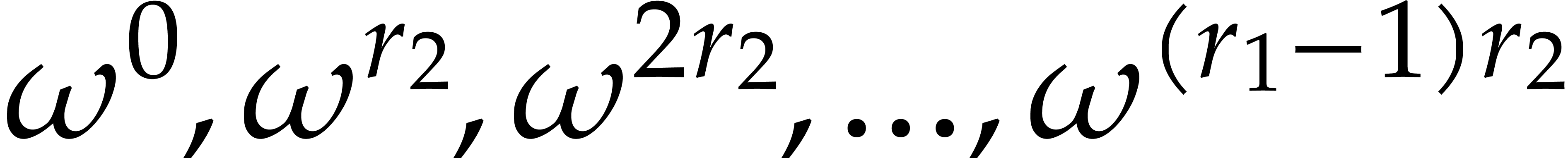 .
This allows us to efficiently determine the discrete logarithms of
.
This allows us to efficiently determine the discrete logarithms of  with respect to
with respect to 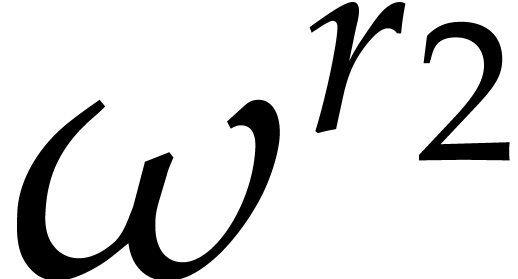 ,
which yields the exponents
,
which yields the exponents  modulo
modulo 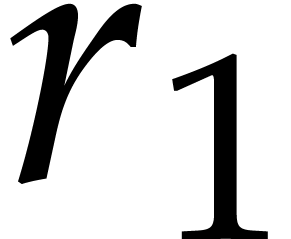 . We next use the Pohlig–Hellman
algorithm to compute
. We next use the Pohlig–Hellman
algorithm to compute  .
.
If 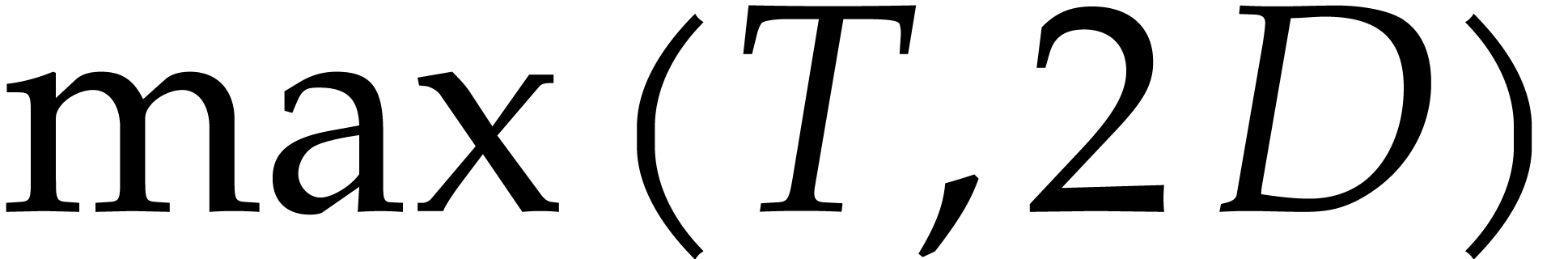 exceeds
exceeds  (or if
(or if  admits no suitable factors
admits no suitable factors  that allows us to apply the above methods), then we may need to work
over an extension field
that allows us to apply the above methods), then we may need to work
over an extension field  of
of  . Notice that this requires our black box
representation of
. Notice that this requires our black box
representation of  to accept inputs in such
extension fields.
to accept inputs in such
extension fields.
Since evaluations over  are at least
are at least  times more expensive, it is important to keep
times more expensive, it is important to keep  as small as possible. If
as small as possible. If 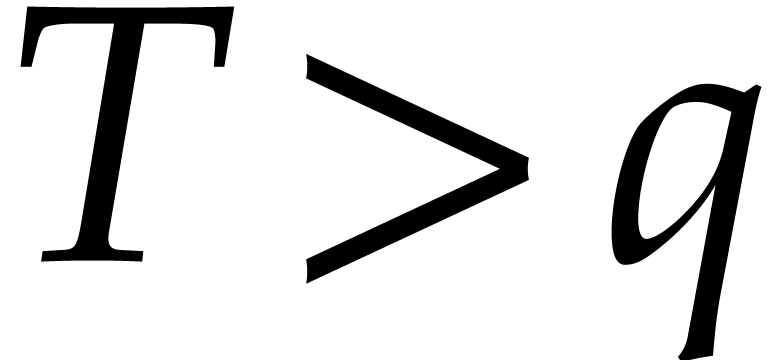 ,
then we must necessarily have
,
then we must necessarily have 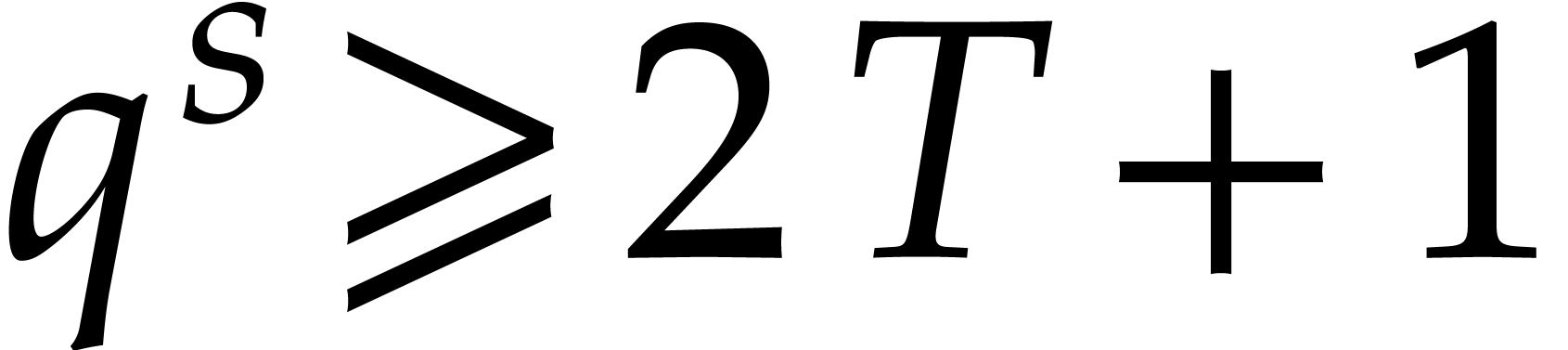 ,
whence
,
whence 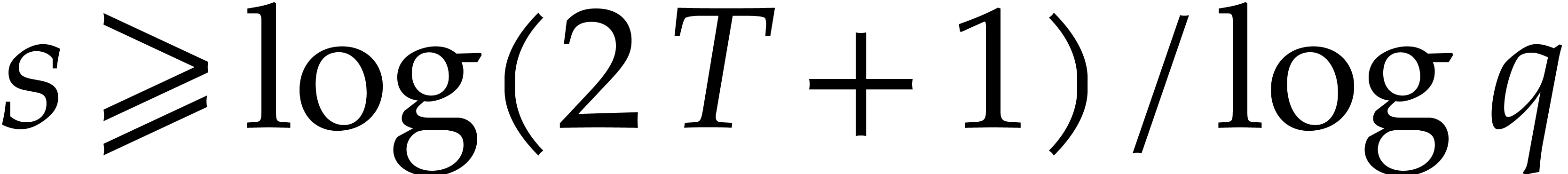 . In general, we want
to take
. In general, we want
to take 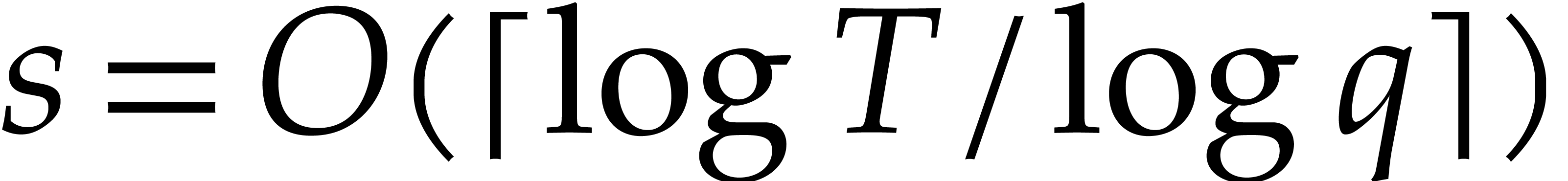 . Since we also need
. Since we also need
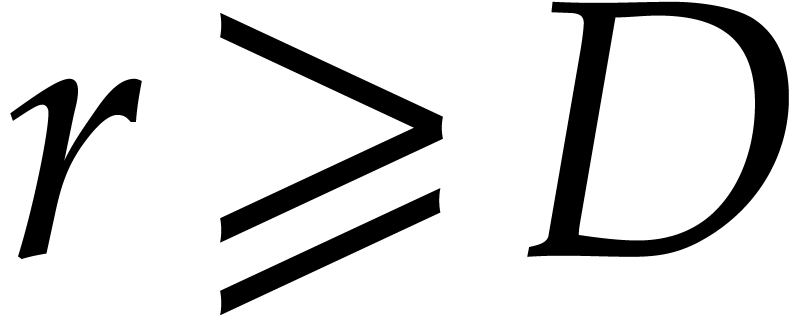 in step 1, this leads to the constraint
in step 1, this leads to the constraint 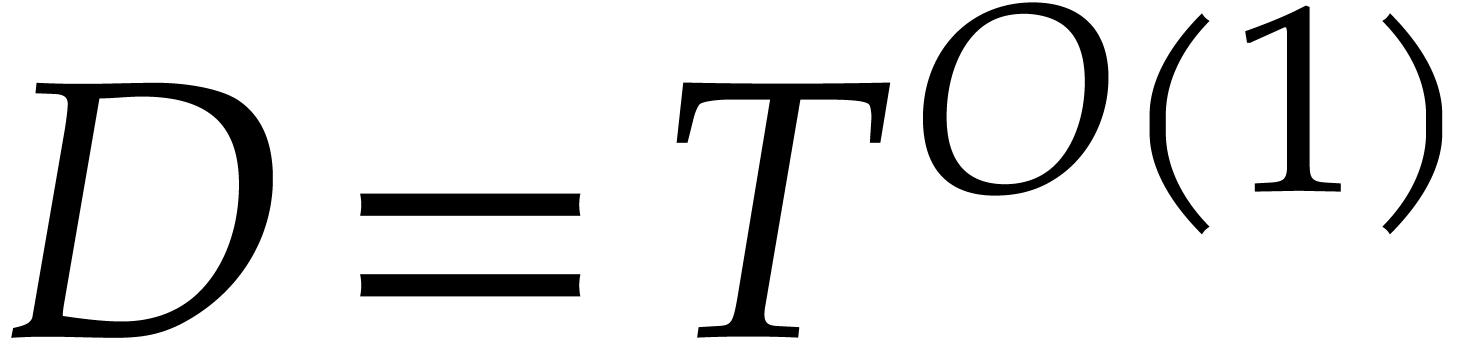 . Under this hypothesis and using
the observations from section 2, it is likely that a
suitable extension order
. Under this hypothesis and using
the observations from section 2, it is likely that a
suitable extension order  and divisor
and divisor 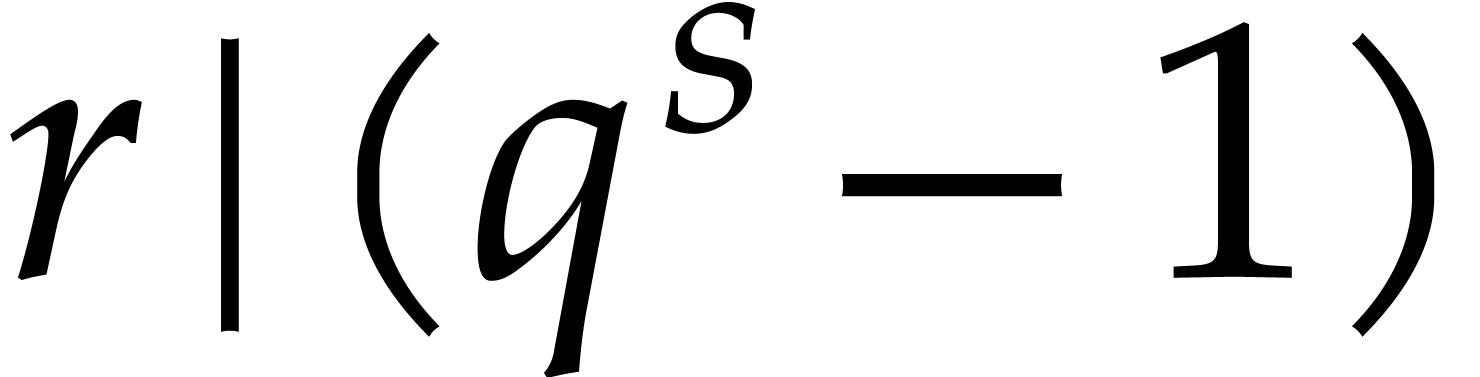 can indeed be found.
can indeed be found.
Still denoting by 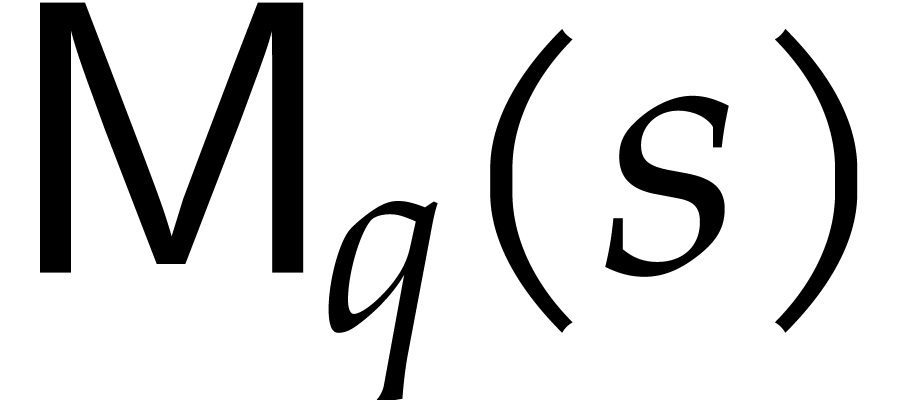 the cost of multiplication of
polynomials of degree
the cost of multiplication of
polynomials of degree  over
over  , the total cost of sparse interpolation then
becomes
, the total cost of sparse interpolation then
becomes
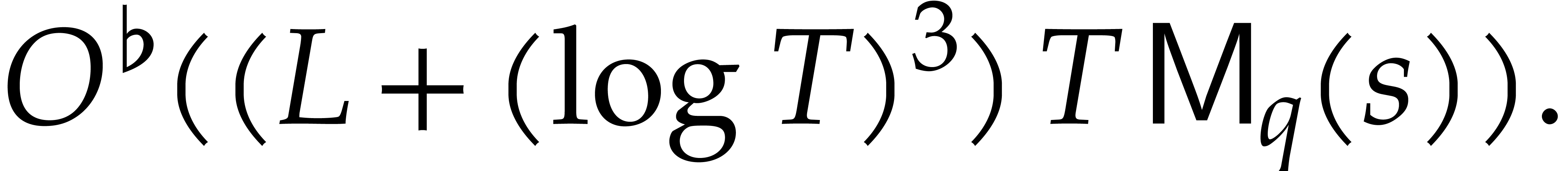 |
(11) |
An interesting question is whether we can reduce the number of
evaluation points when working over an extension field 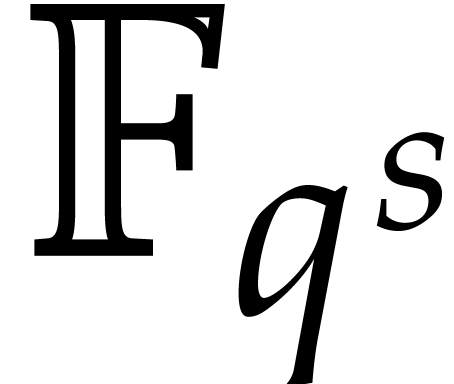 . Indeed, if
. Indeed, if  is the
Frobenius map of
is the
Frobenius map of 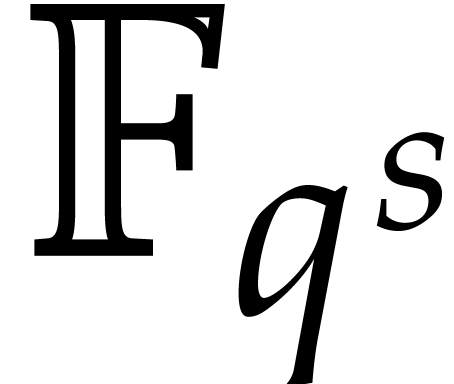 over
over  , then
, then 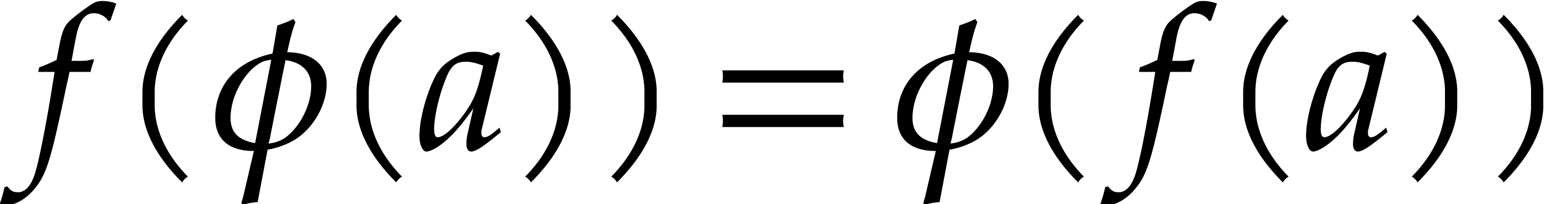 for all
for all 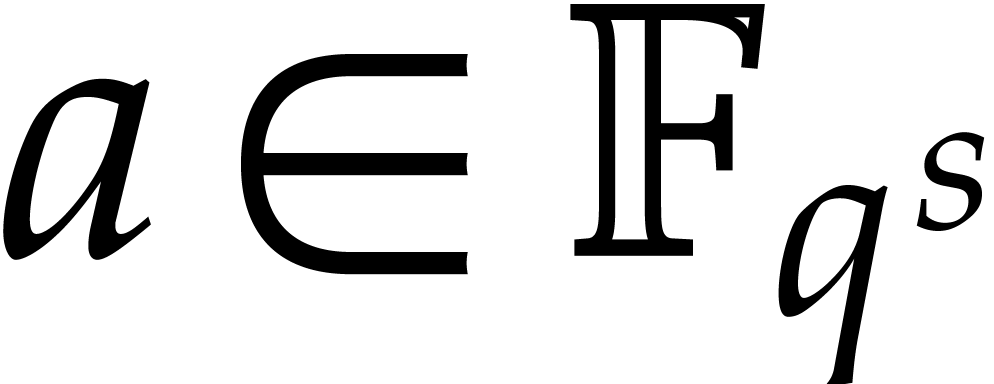 . If
. If 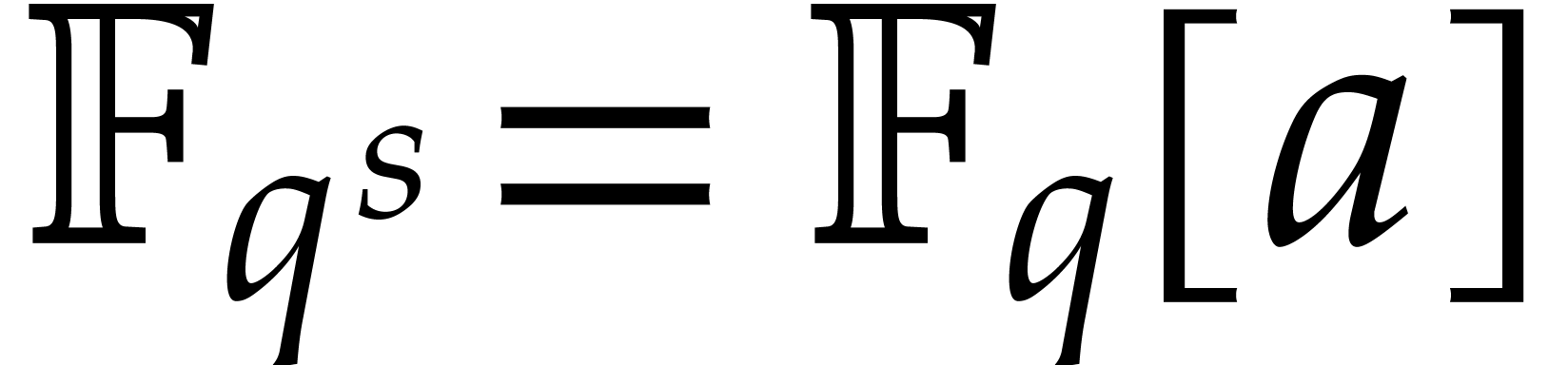 ,
then this allows us to obtain the evaluations at the
,
then this allows us to obtain the evaluations at the  distinct points
distinct points  using a single evaluation at
using a single evaluation at
 . In step 2 of Algorithm 4, we can therefore avoid the evaluations at
. In step 2 of Algorithm 4, we can therefore avoid the evaluations at 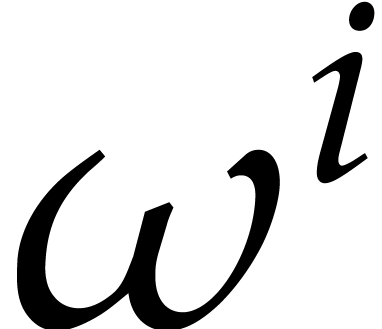 for
for 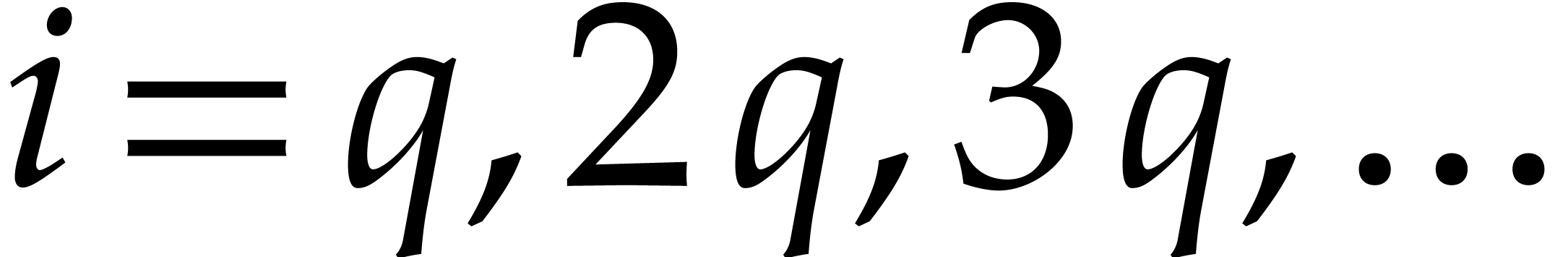 and gain a constant factor
and gain a constant factor 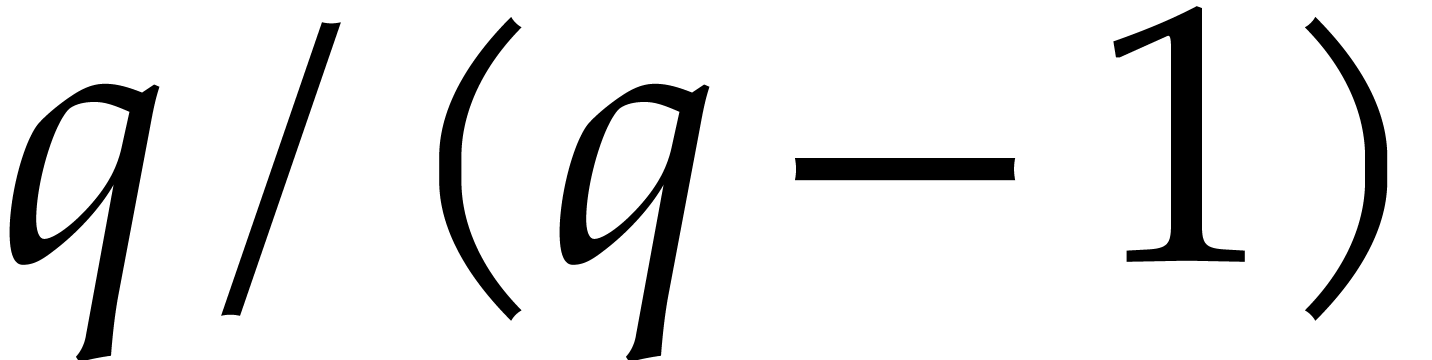 for large
for large  . Similarly, we may
compute all values
. Similarly, we may
compute all values 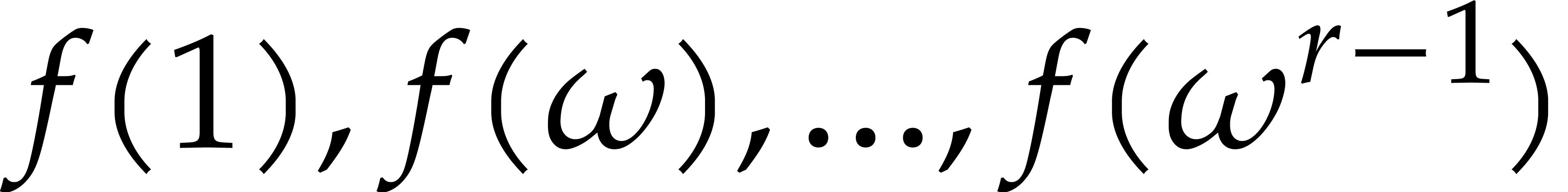 using approximately
using approximately 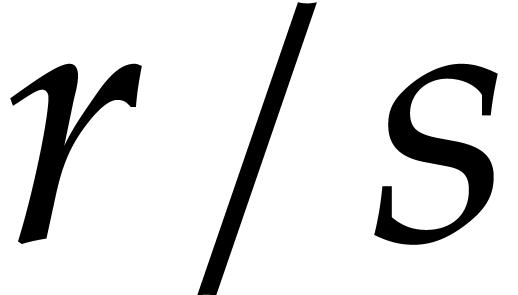 evaluations of
evaluations of  only; whenever
only; whenever 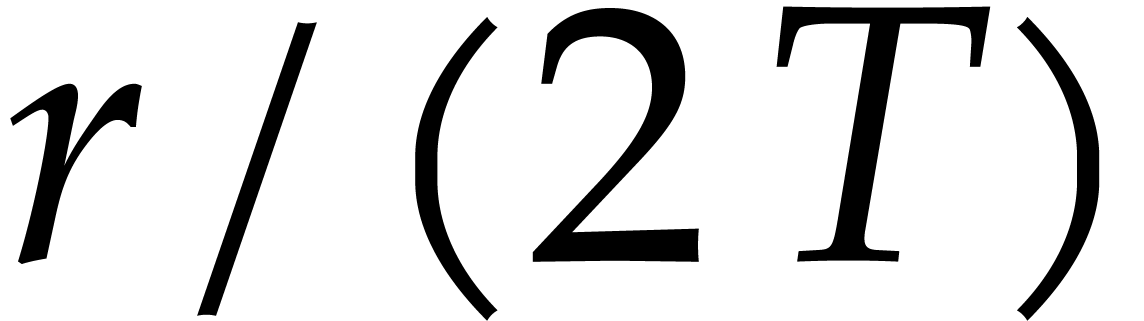 is small, this allows us to gain a factor
is small, this allows us to gain a factor 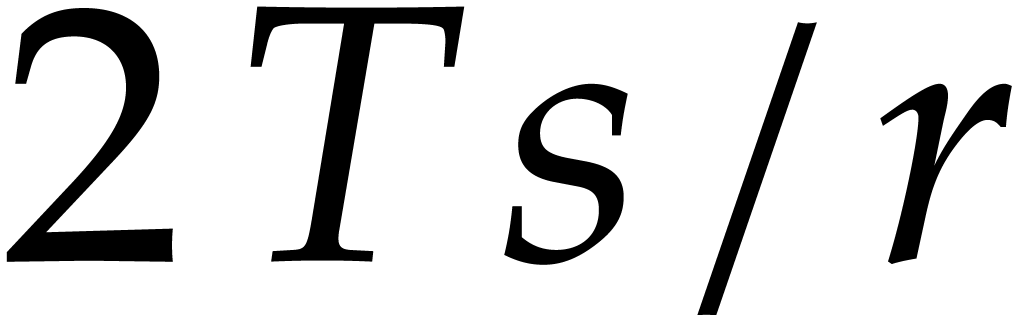 . It would be interesting to know
whether it is possible to do better and regain a factor
. It would be interesting to know
whether it is possible to do better and regain a factor 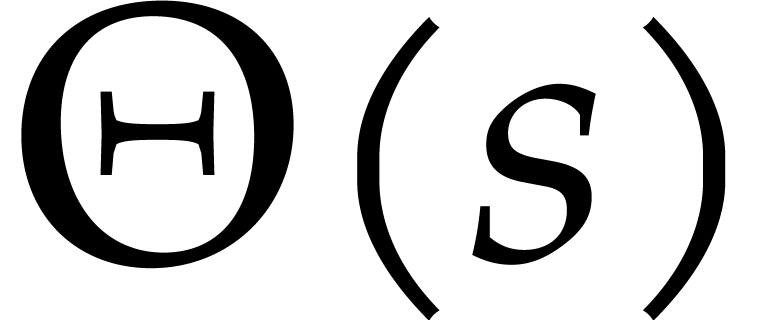 in general.
in general.
Besides working in an extension field, it may also be interesting to
perform part of the computations over a subfield of  . Indeed, the main aim of steps 4 and 5 of
Algorithm 4 is to find the exponents of
. Indeed, the main aim of steps 4 and 5 of
Algorithm 4 is to find the exponents of  . Now assume that
. Now assume that  admits a subfield
admits a subfield 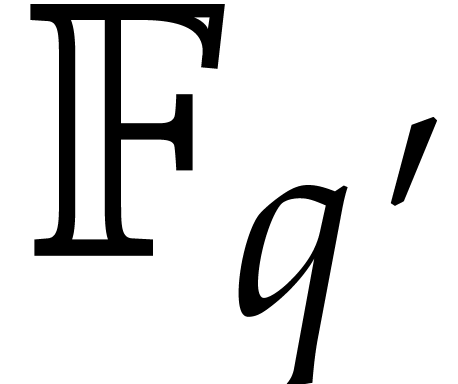 with
with 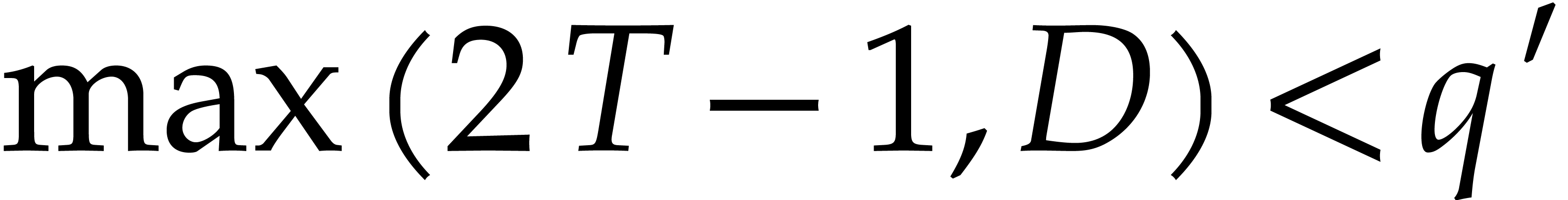 and let
and let 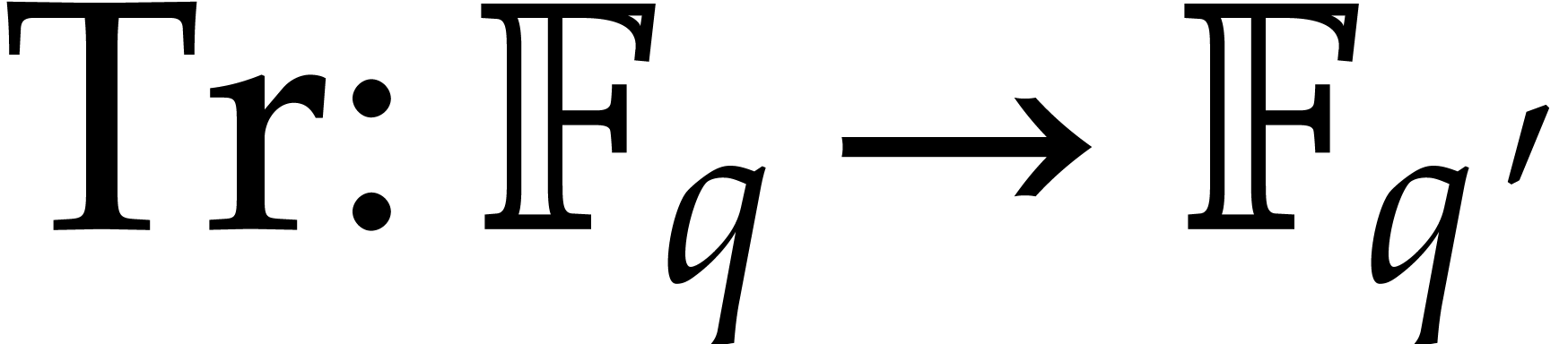 be the corresponding trace function.
Then
be the corresponding trace function.
Then  and
and  are likely to
admit approximately the same exponents. Taking
are likely to
admit approximately the same exponents. Taking 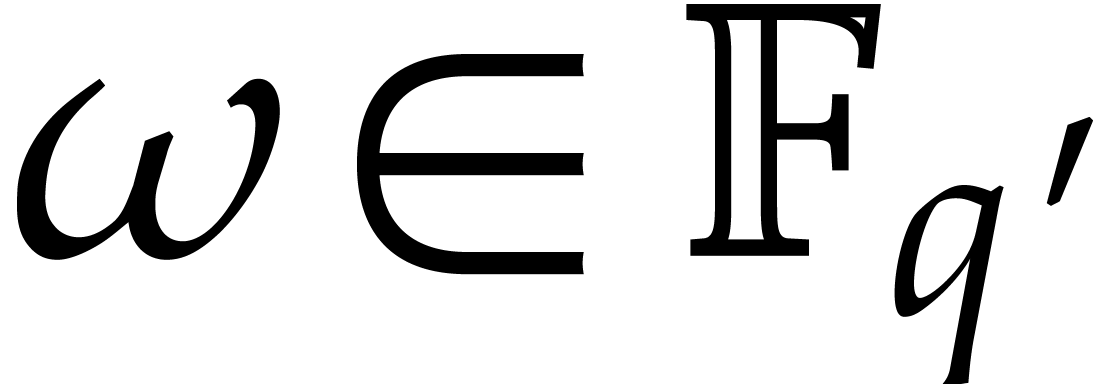 in step 1, we may thus replace
in step 1, we may thus replace  by their traces
after step 2, and determine the exponents of
by their traces
after step 2, and determine the exponents of 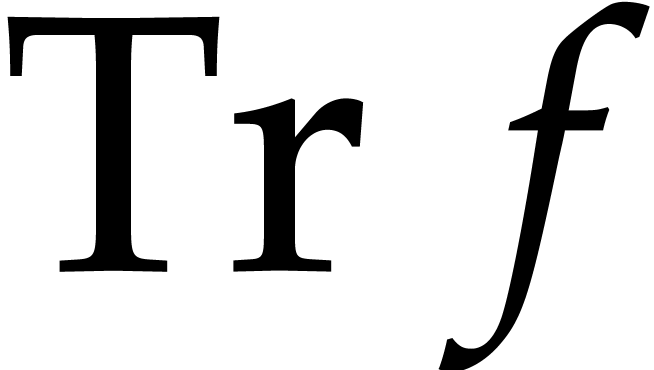 instead of
instead of  . Although this
does not allow us to speed up steps 2 and 6, we do gain a factor of at
least
. Although this
does not allow us to speed up steps 2 and 6, we do gain a factor of at
least 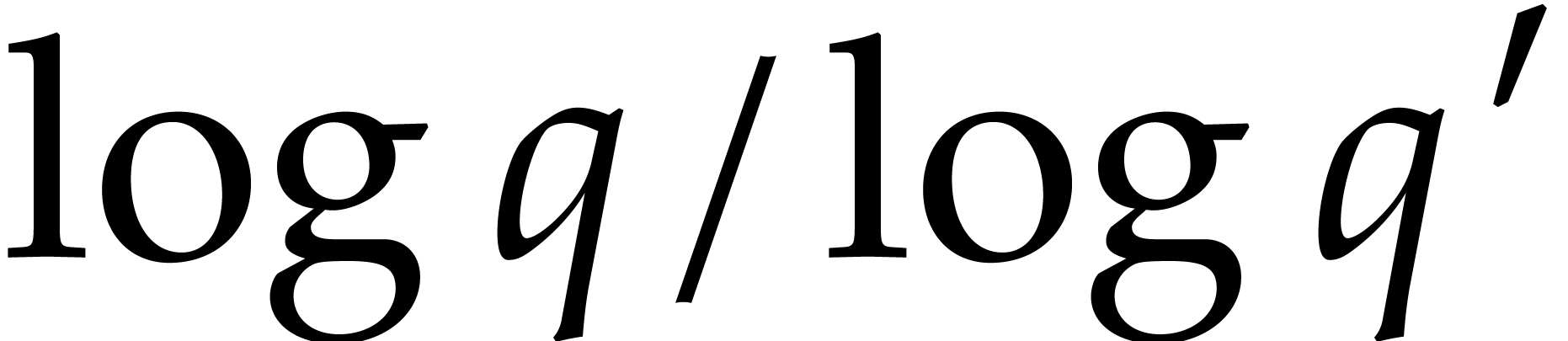 in steps 4 and 5.
in steps 4 and 5.

Once the order  has been fixed, Algorithm 4 essentially allows us to interpolate
has been fixed, Algorithm 4 essentially allows us to interpolate 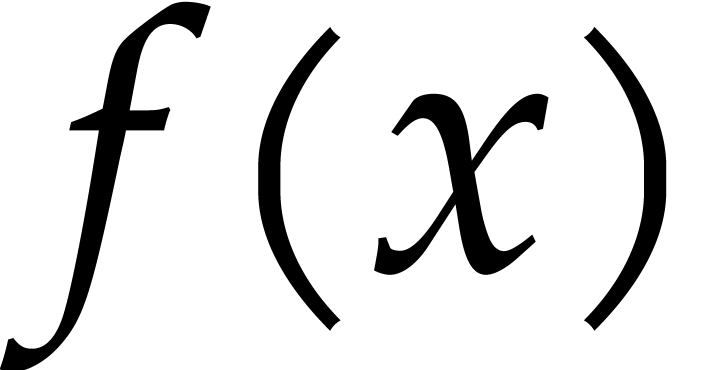 modulo
modulo 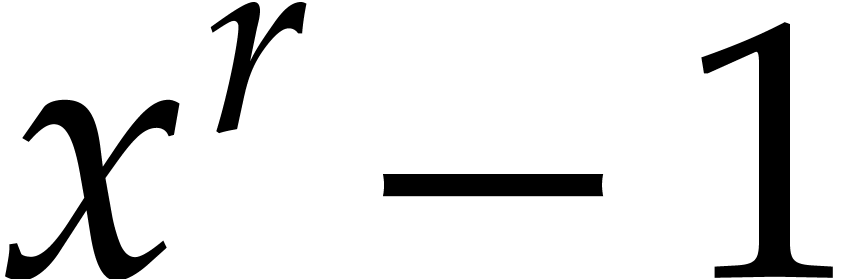 . With respect to the
cyclic extension approach, the main difference is that one expensive
evaluation of
. With respect to the
cyclic extension approach, the main difference is that one expensive
evaluation of  over the extension ring
over the extension ring 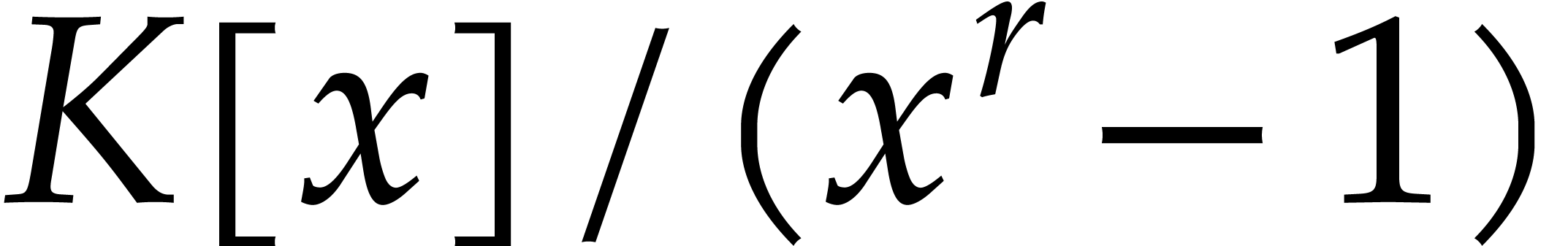 is replaced by
is replaced by  cheap evaluations
over
cheap evaluations
over  plus
plus 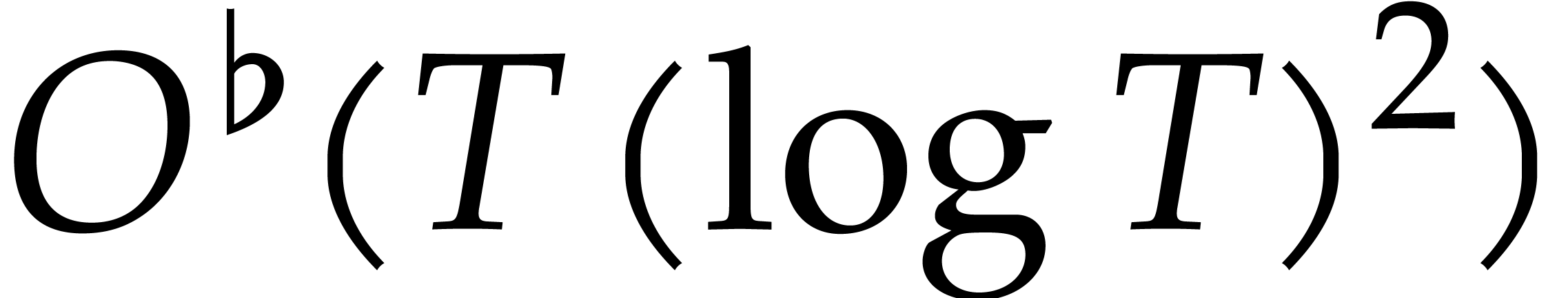 scalar
operations.
scalar
operations.
If 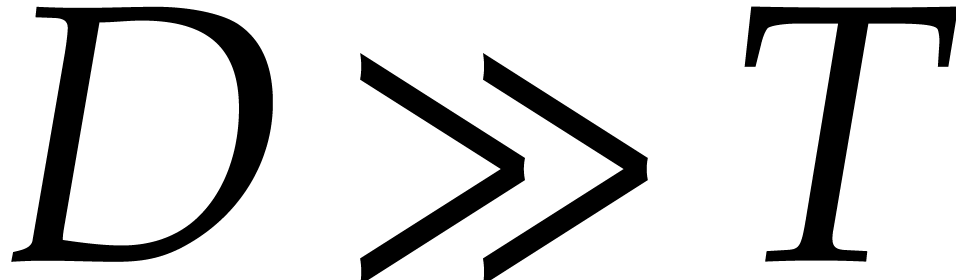 , then we may also
evaluate
, then we may also
evaluate 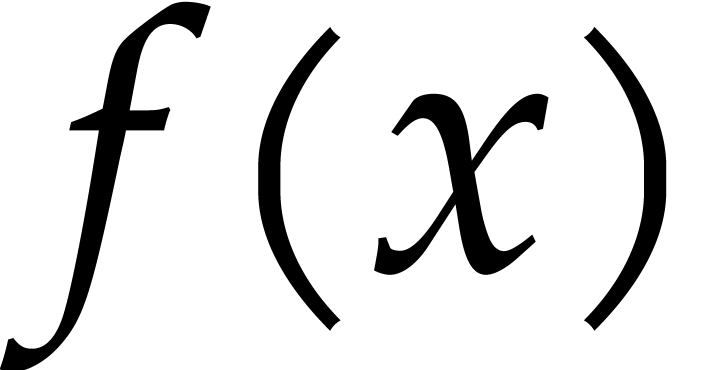 modulo
modulo 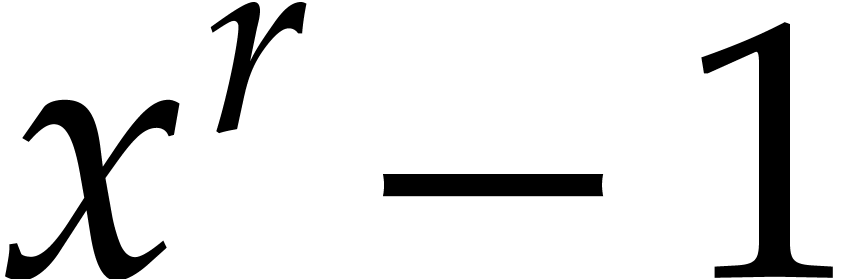 for
different moduli
for
different moduli 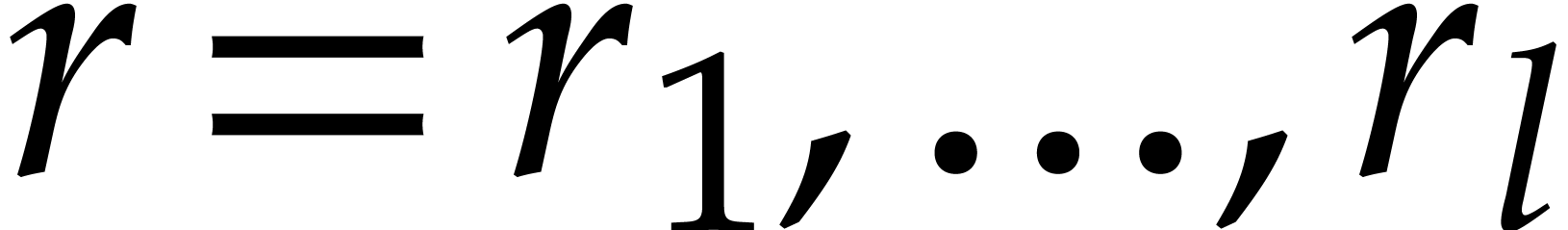 and recombine the results using
one of the matching strategies from section 4. However, in
the present context, we are not completely free to pick our moduli,
since we need corresponding primitive roots of unity
and recombine the results using
one of the matching strategies from section 4. However, in
the present context, we are not completely free to pick our moduli,
since we need corresponding primitive roots of unity  of orders
of orders  in small extensions
in small extensions  of
of  .
.
Let us focus more specifically on Algorithm 3, which
requires in particular that 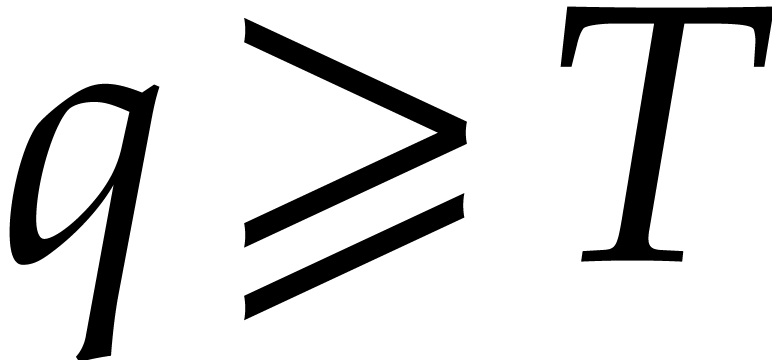 .
We need
.
We need 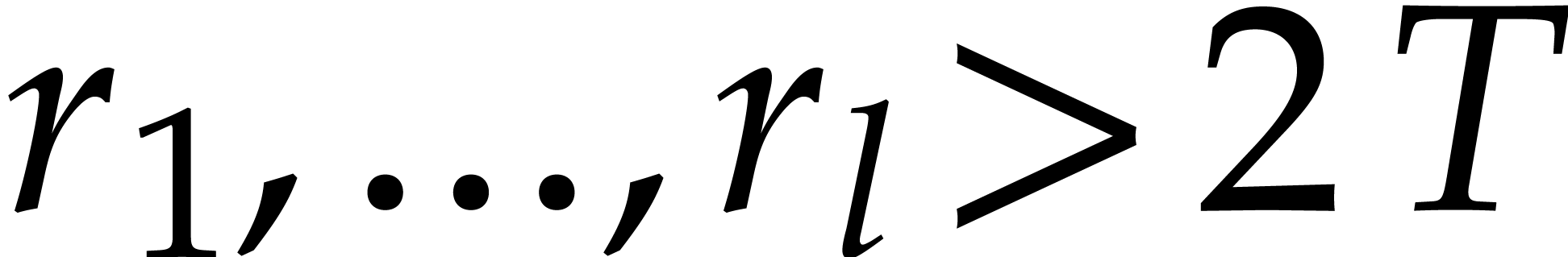 to be suitable for steps 4 and 5, so
to be suitable for steps 4 and 5, so
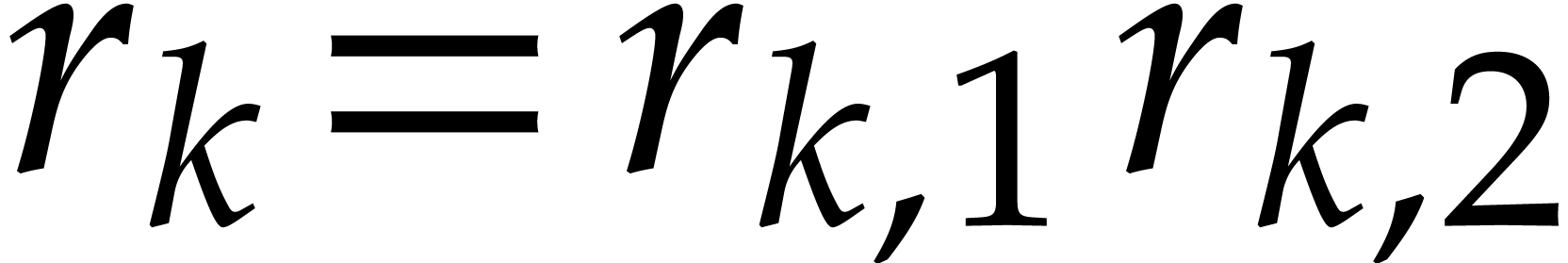 with
with 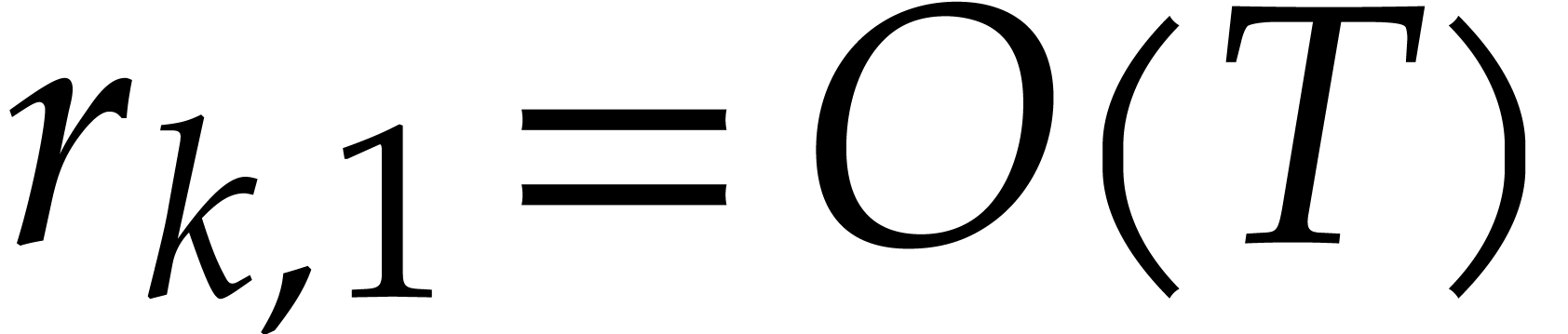 and
and 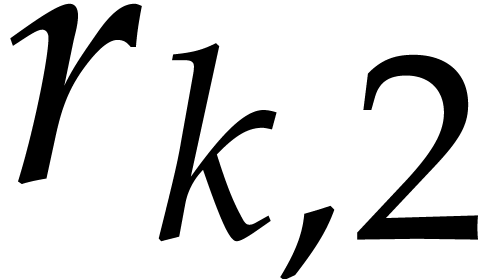 is smooth. On the other hand, we may relax the conditions
on
is smooth. On the other hand, we may relax the conditions
on  . In this case, the
complexity does not depend on
. In this case, the
complexity does not depend on  ,
so it is better to choose the
,
so it is better to choose the 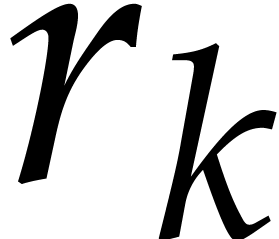 much larger than
much larger than
 , preferably of the order of
, preferably of the order of
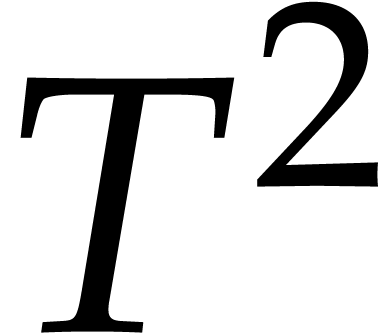 . It is also not necessary
that
. It is also not necessary
that  be pairwise coprime: it suffices that
be pairwise coprime: it suffices that  for any
for any  .
Ideally speaking, we should have
.
Ideally speaking, we should have 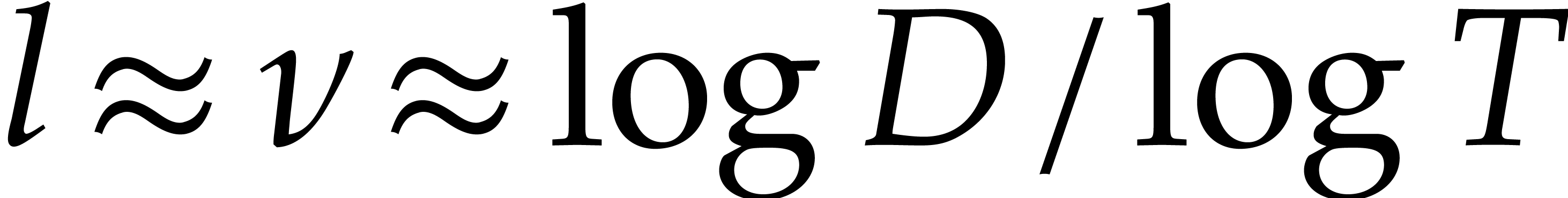 .
.
Although there is no a priori reason for suitable  of this kind to exist, we expect that this will often be
the case in practice, as long as
of this kind to exist, we expect that this will often be
the case in practice, as long as 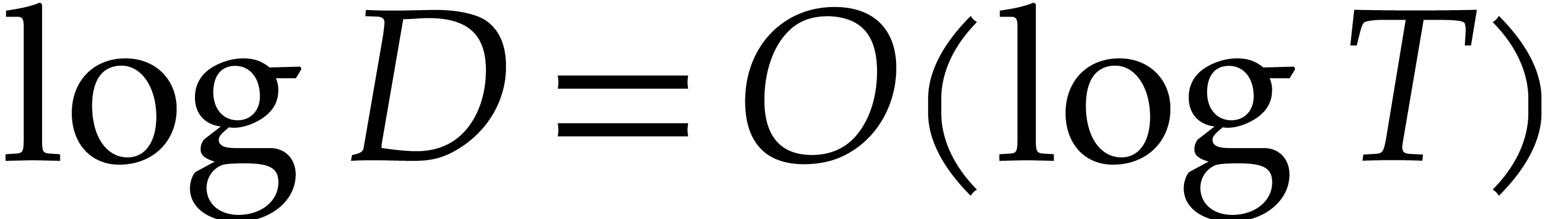 .
Evidence in this direction will be presented in sections 6.3
and 6.4 below, under even stronger constraints on the
orders
.
Evidence in this direction will be presented in sections 6.3
and 6.4 below, under even stronger constraints on the
orders  . Assuming that we are
indeed able to find suitable
. Assuming that we are
indeed able to find suitable  ,
the overall runtime complexity becomes
,
the overall runtime complexity becomes
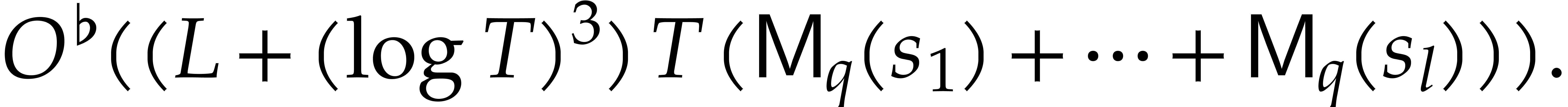
When using naive arithmetic with 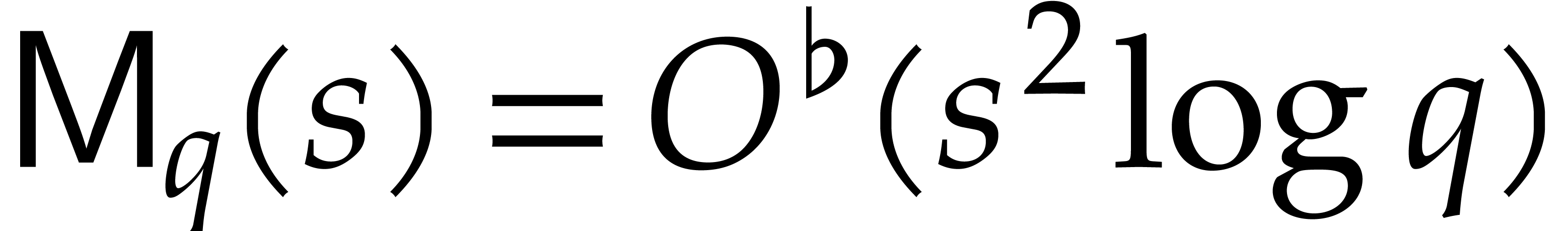 and assuming
that
and assuming
that 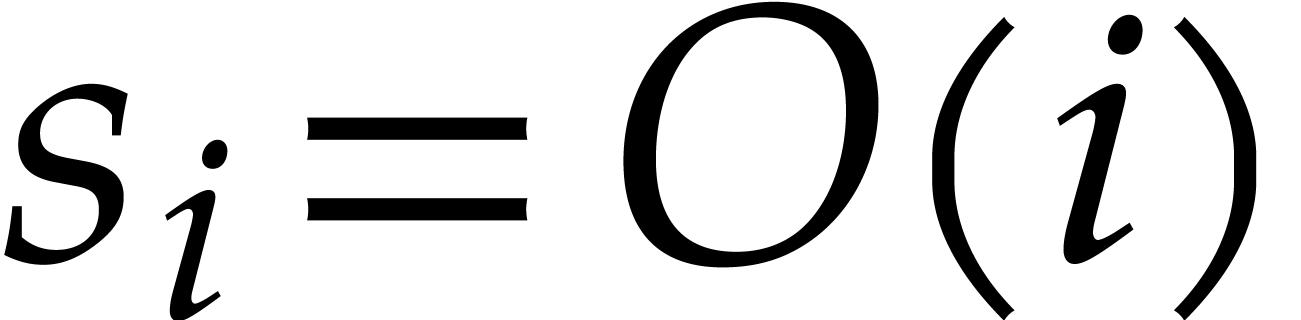 , this complexity bound
simplifies into
, this complexity bound
simplifies into
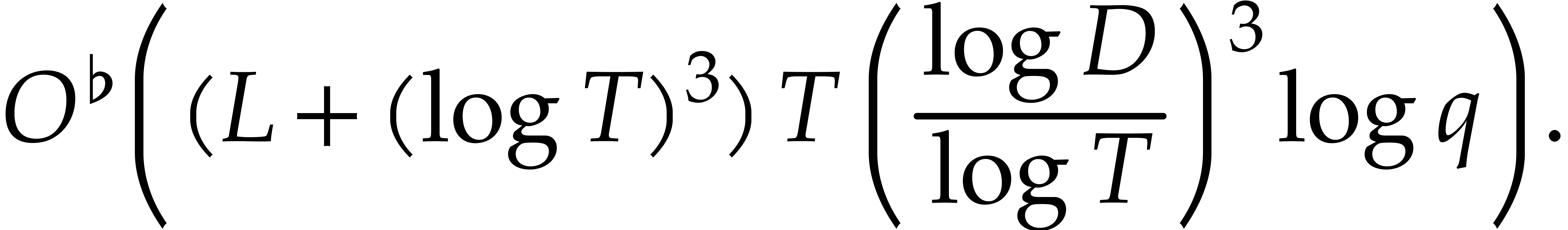
In summary, the efficiency of the geometric progression approach over a
finite field rests on our ability to find suitable divisors of 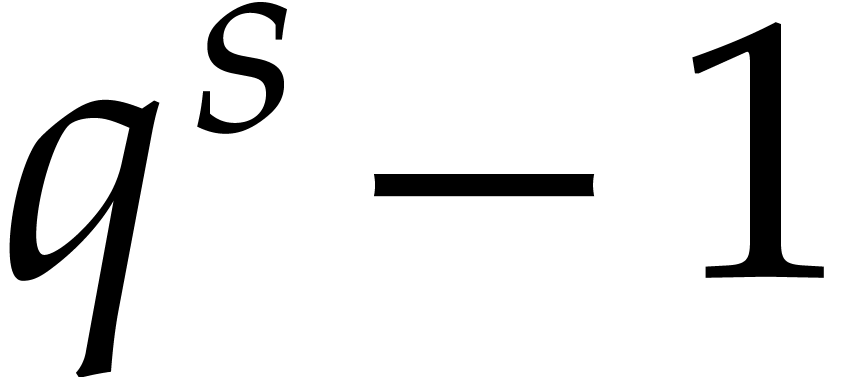 for small values of
for small values of  .
If
.
If 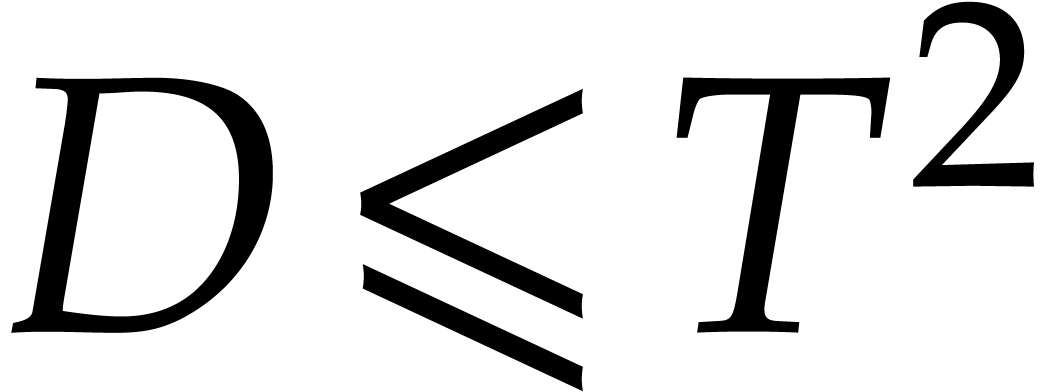 and
and 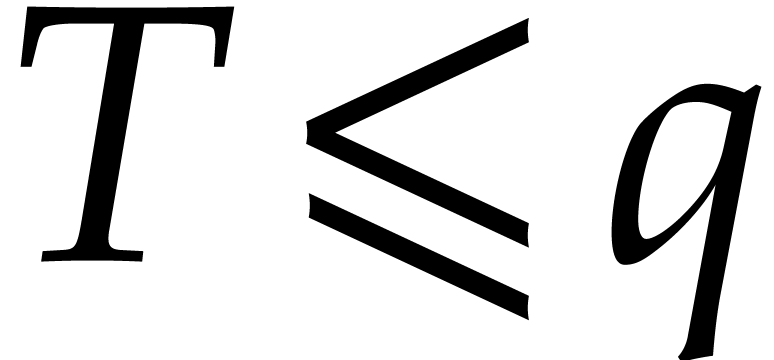 ,
then we essentially need an order
,
then we essentially need an order 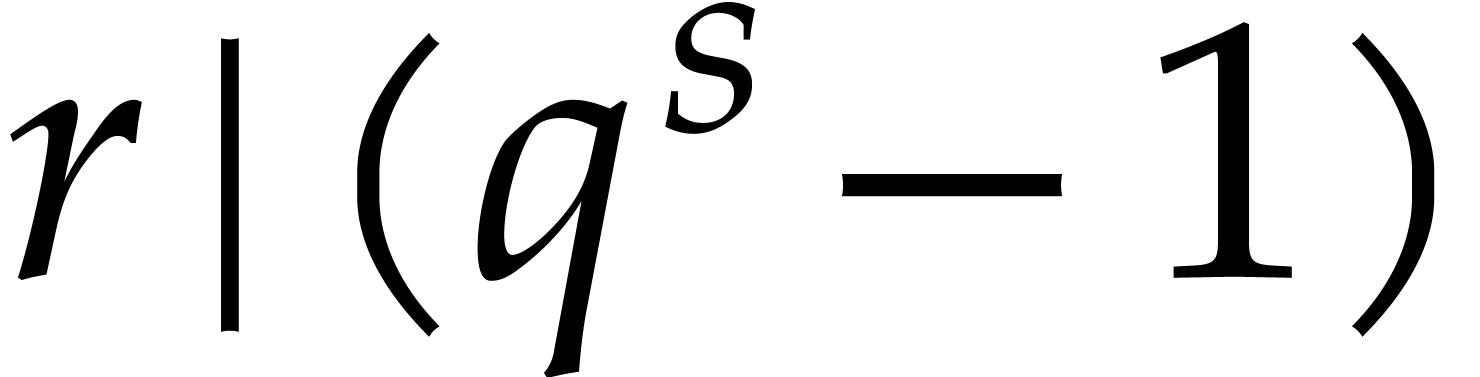 of the type
of the type
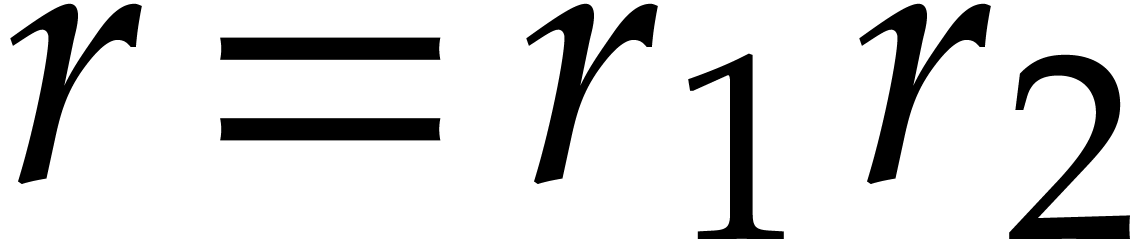 with
with  ,
,
 smooth, and
smooth, and  small. By
what has been said in section 2, it is very likely that
such
small. By
what has been said in section 2, it is very likely that
such  and
and  always exist.
If
always exist.
If  and
and 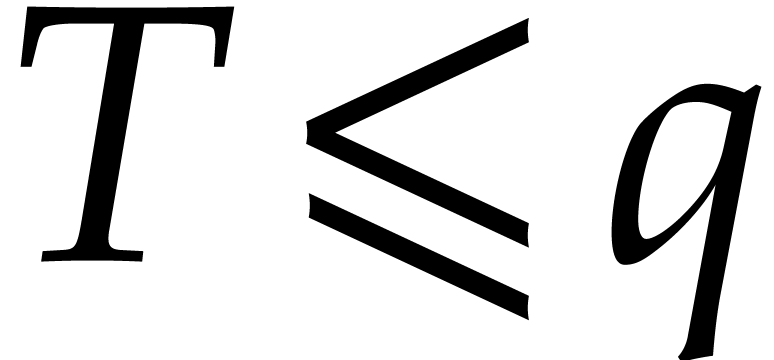 ,
then it remains likely that various divisors of this type can be
combined, as explained in section 5.6. If
,
then it remains likely that various divisors of this type can be
combined, as explained in section 5.6. If 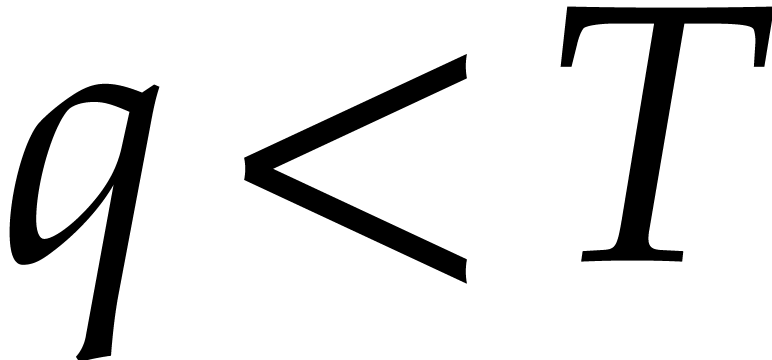 , then we first need to replace
, then we first need to replace  by a suitable extension.
by a suitable extension.
Assuming that 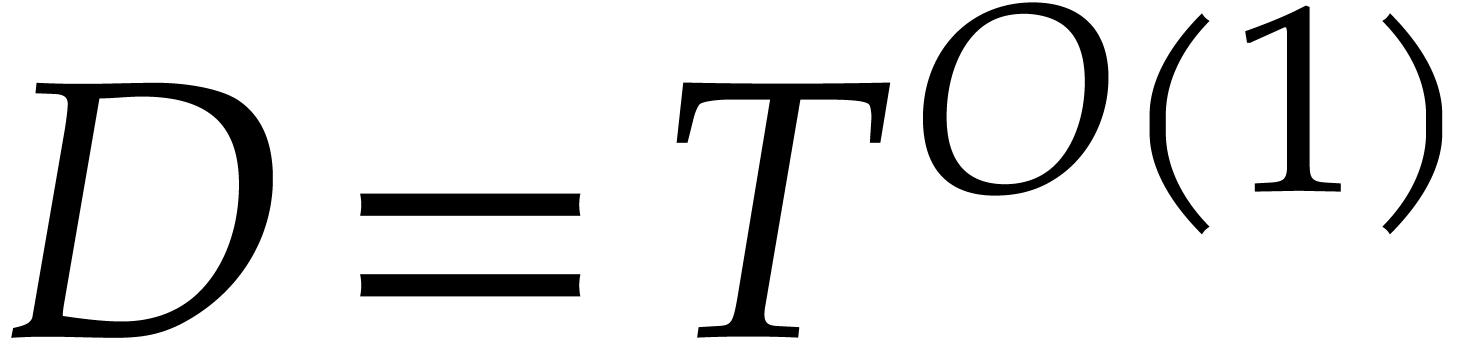 and that suitable orders as above
can indeed be found, the cost of the geometric progression approach is
bounded by
and that suitable orders as above
can indeed be found, the cost of the geometric progression approach is
bounded by
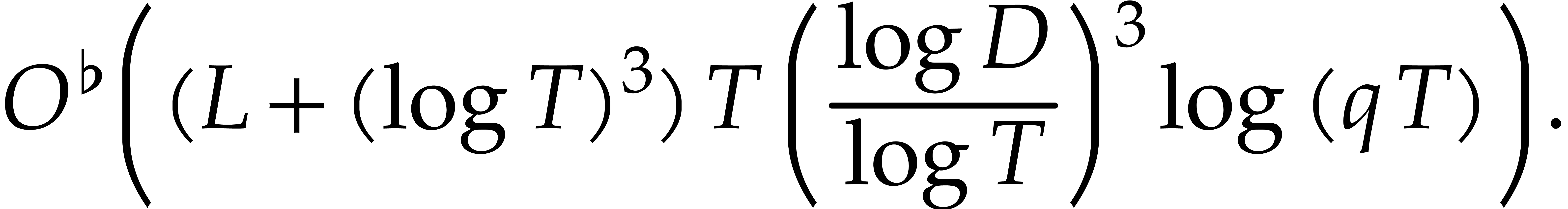 |
(12) |
In favorable cases when 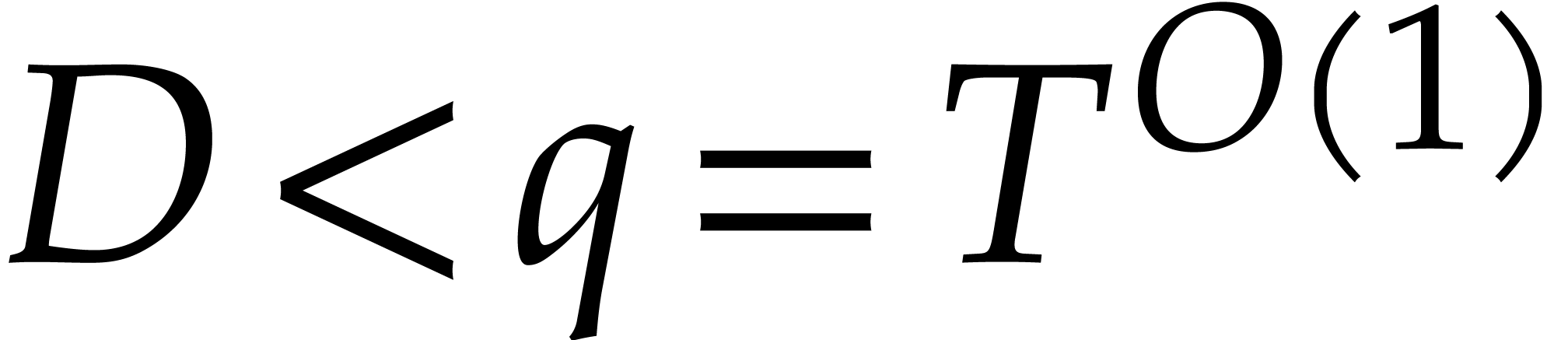 and
and 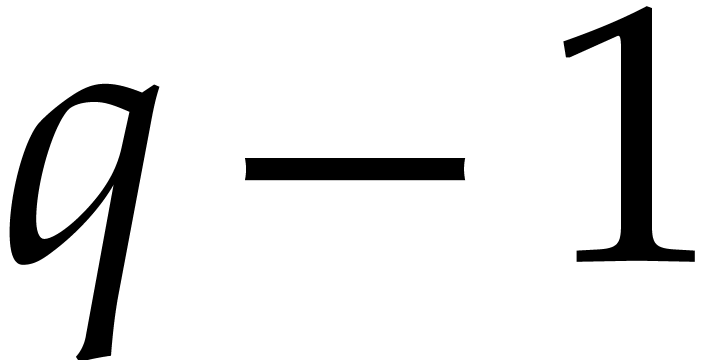 is smooth, we obtain the complexity bound
is smooth, we obtain the complexity bound
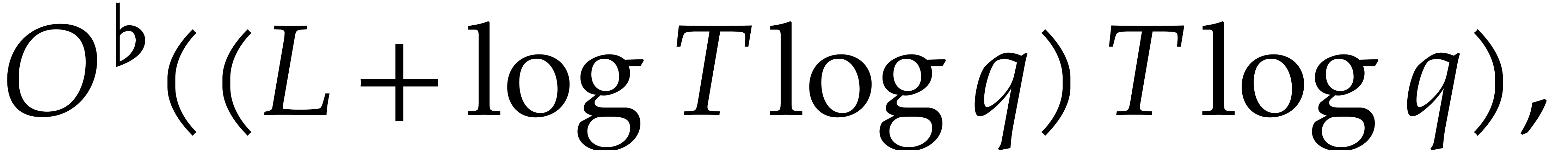 |
(13) |
instead of (12), by using the tangent Graeffe method.
In comparison with algorithms based on cyclic extensions, the main
advantage of the algorithms in this section is that we avoid expensive
evaluations over cyclic extension rings. On the other hand, the cost of
the root finding step may dominate the cost of the evaluations of  whenever
whenever 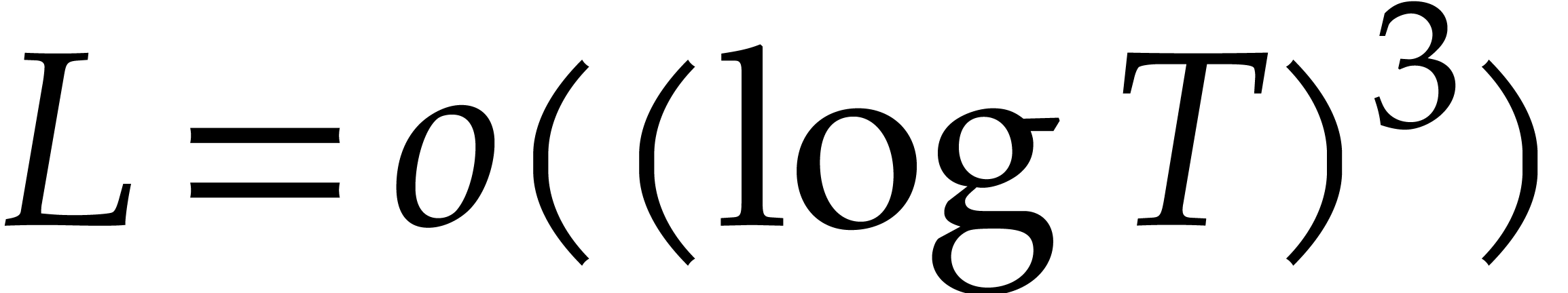 ;
in that case, cyclic extension methods may become competitive. Methods
based on geometric progressions are also less suited for the super
sparse case.
;
in that case, cyclic extension methods may become competitive. Methods
based on geometric progressions are also less suited for the super
sparse case.
Remark  or
or
 terms dominates the cost in (12).
Since we usually try to interpolate
terms dominates the cost in (12).
Since we usually try to interpolate  for
increasingly large bounds
for
increasingly large bounds  ,
it is better to test whether step 1 of Algorithm 4 requires
more running time than step 3 as we increase
,
it is better to test whether step 1 of Algorithm 4 requires
more running time than step 3 as we increase  . Whenever the cost of step 3 starts to dominate, we
may switch to a cyclic extension style approach (or an FFT based
approach, to be presented next).
. Whenever the cost of step 3 starts to dominate, we
may switch to a cyclic extension style approach (or an FFT based
approach, to be presented next).
Geometric progression style algorithms for sparse interpolation admit
the big advantage that they have a sharp complexity with respect to
 . However, if evaluations of
. However, if evaluations of
 are cheap, then the
are cheap, then the 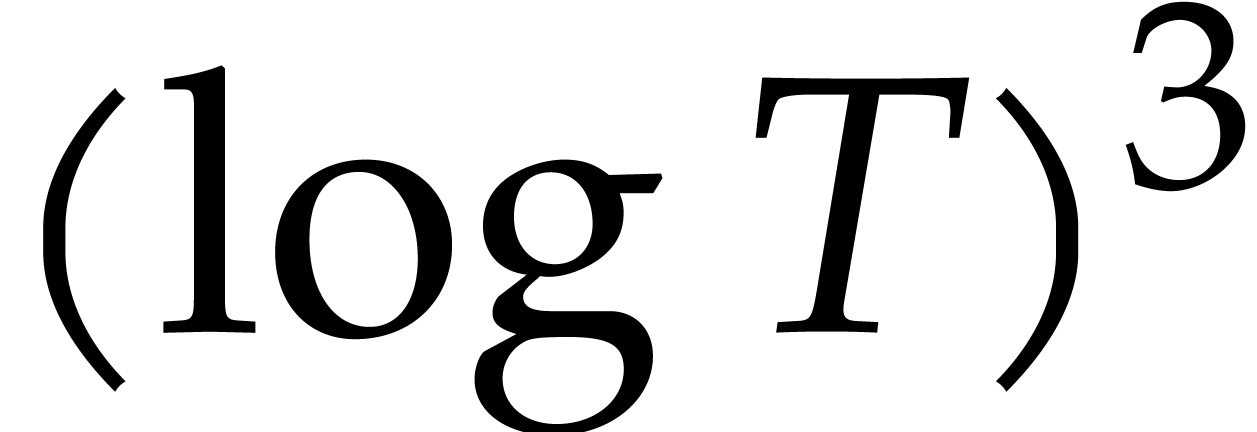 term
in (11) may dominate
term
in (11) may dominate  .
In this section, we will investigate a strategy to reduce the dependency
in
.
In this section, we will investigate a strategy to reduce the dependency
in 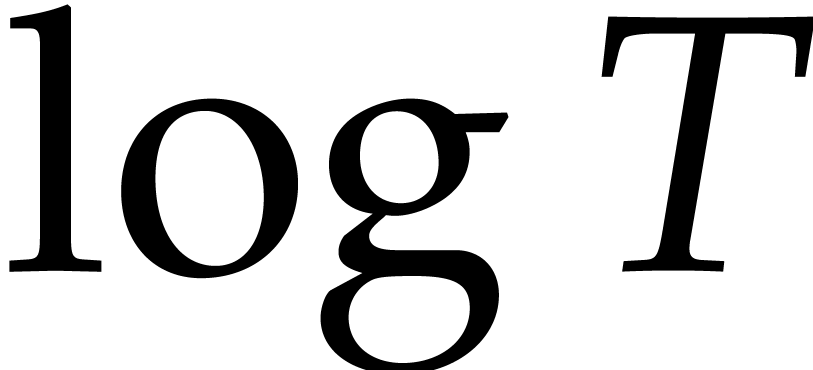 , at the price of
, at the price of 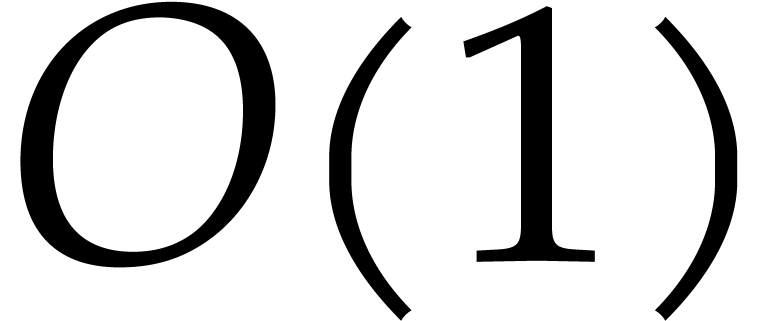 more evaluations. The idea is to more aggressively
exploit the observations from sections 5.6 and 5.4.
Alternatively, we can regard our proposal as a careful adaptation of the
cyclic extension approach that allows us to replace evaluations over
cyclic extensions by evaluations over
more evaluations. The idea is to more aggressively
exploit the observations from sections 5.6 and 5.4.
Alternatively, we can regard our proposal as a careful adaptation of the
cyclic extension approach that allows us to replace evaluations over
cyclic extensions by evaluations over  itself.
itself.
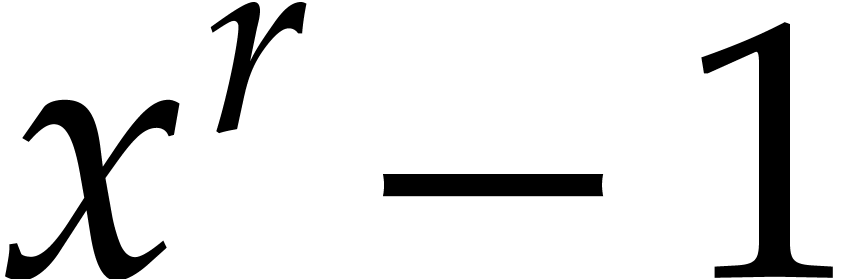
For a fixed parameter  that we control and a
modulus
that we control and a
modulus  close to
close to 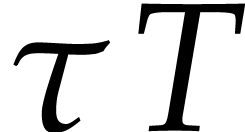 ,
let us first study how to evaluate
,
let us first study how to evaluate 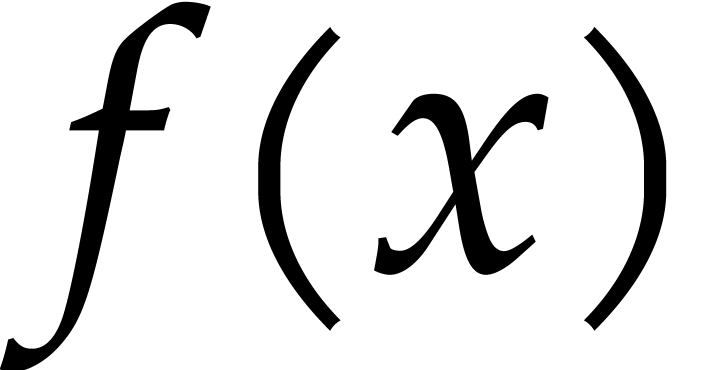 efficiently
modulo
efficiently
modulo 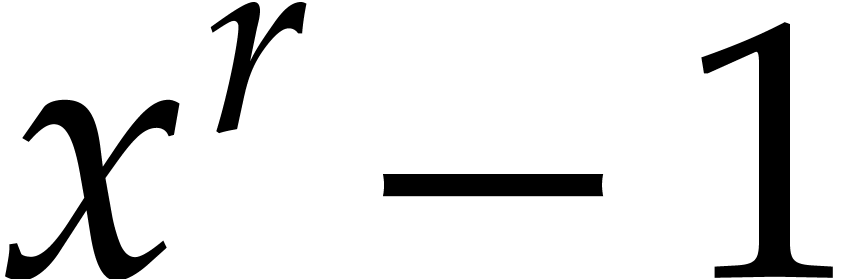 . Instead of
evaluating
. Instead of
evaluating  at only
at only  points
points  for a primitive
for a primitive  -th root of unity
-th root of unity  (as in
step 2 of Algorithm 4), we rather evaluate
(as in
step 2 of Algorithm 4), we rather evaluate  at all
at all  -th roots of unity
-th roots of unity
 . The advantage is that we
may then use FFT-based techniques as a replacement for the remaining
steps of Algorithm 4.
. The advantage is that we
may then use FFT-based techniques as a replacement for the remaining
steps of Algorithm 4.
Moreover, if  and
and  lives
in an extension
lives
in an extension  of
of  ,
then it suffices to evaluate
,
then it suffices to evaluate  at only
at only  points in order to determine all values
points in order to determine all values  using the Frobenius map. Recovering
using the Frobenius map. Recovering 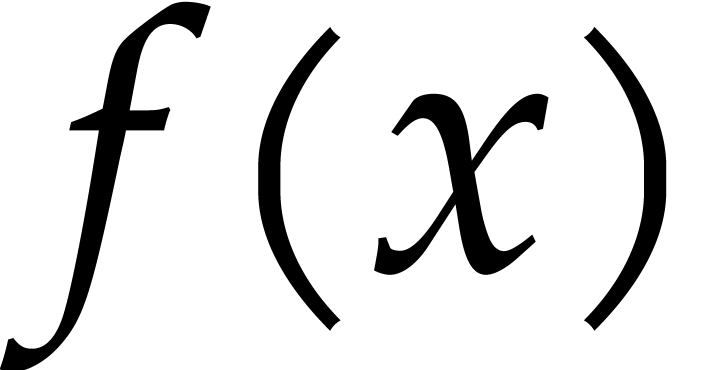 modulo
modulo  from these values can also be done efficiently using
the inverse Frobenius FFT [28].
from these values can also be done efficiently using
the inverse Frobenius FFT [28].
Assuming for simplicity that  and that the
computation of an inverse Frobenius DFT is
and that the
computation of an inverse Frobenius DFT is 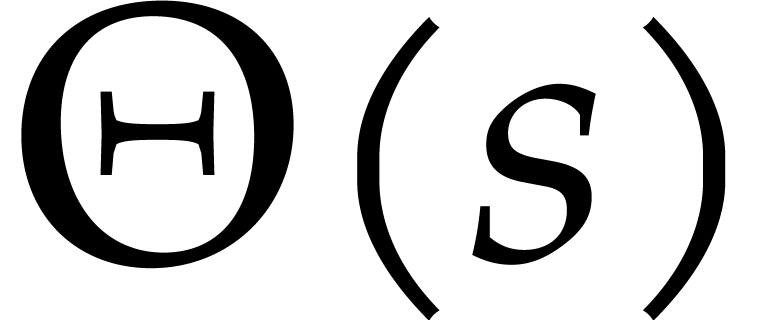 times
faster than the computation of a full DFT, we note that the cost of one
run of Algorithm 5 is bounded by
times
faster than the computation of a full DFT, we note that the cost of one
run of Algorithm 5 is bounded by
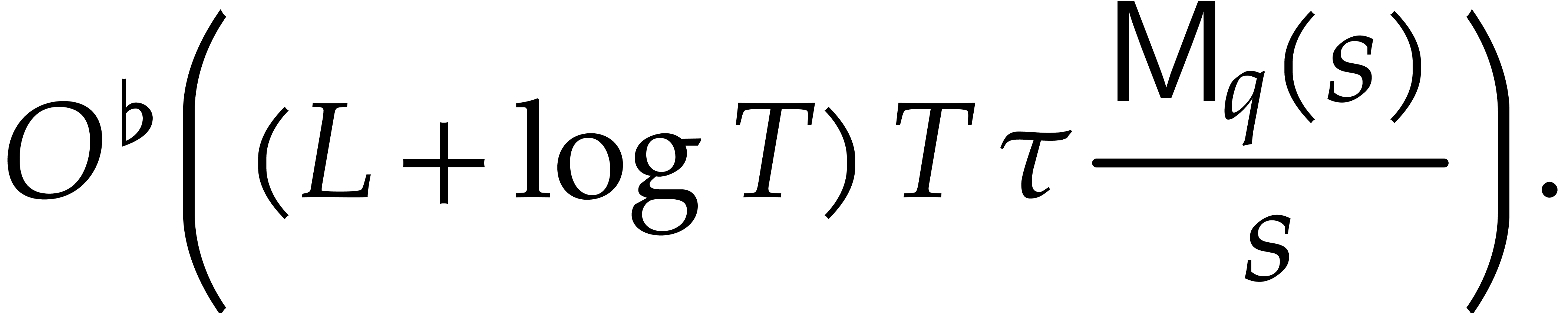 |
(14) |
If 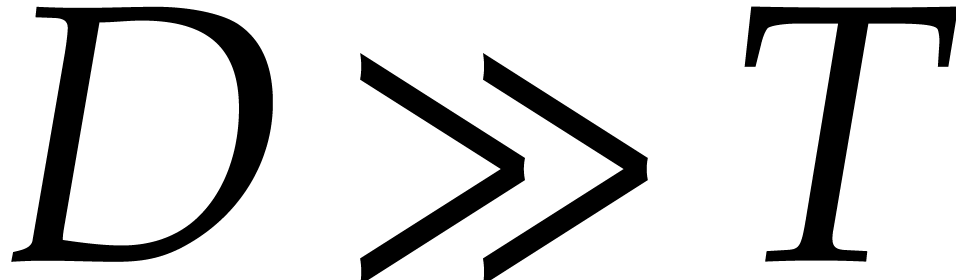 and
and 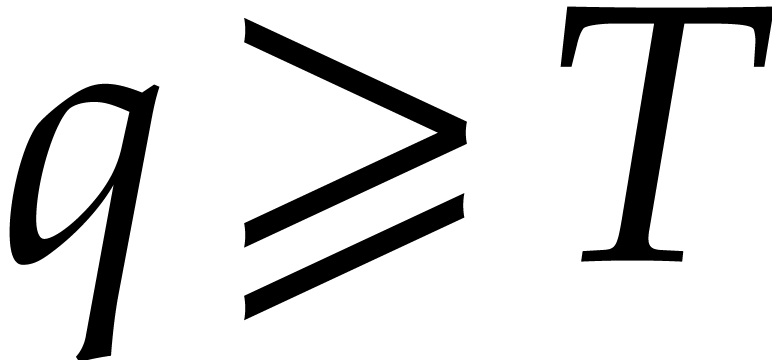 ,
then we wish to apply a similar strategy as in section 5.6
and recombine the values of
,
then we wish to apply a similar strategy as in section 5.6
and recombine the values of 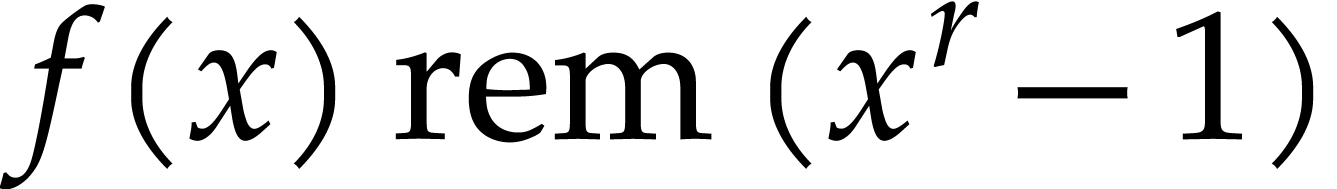 for various moduli
for various moduli
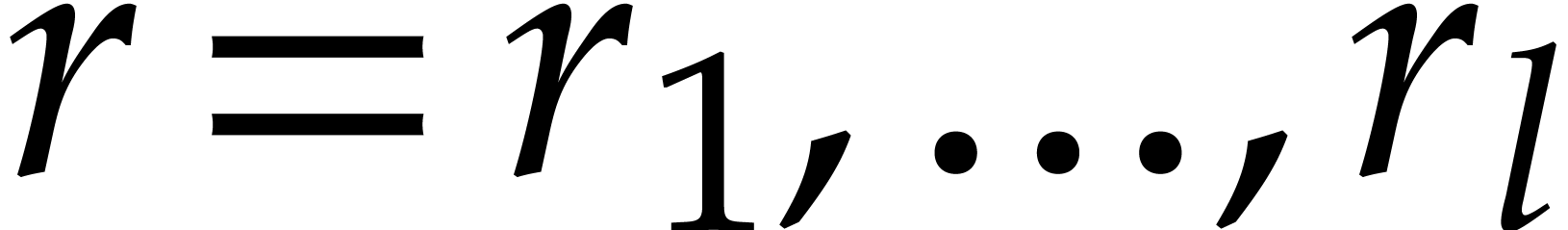 . This time, in order to
perform step 1 of Algorithm 3 using Algorithm 5,
we need the orders
. This time, in order to
perform step 1 of Algorithm 3 using Algorithm 5,
we need the orders  to be close to
to be close to  . With
. With  as in section 4.4, we thus assume
as in section 4.4, we thus assume  with
with 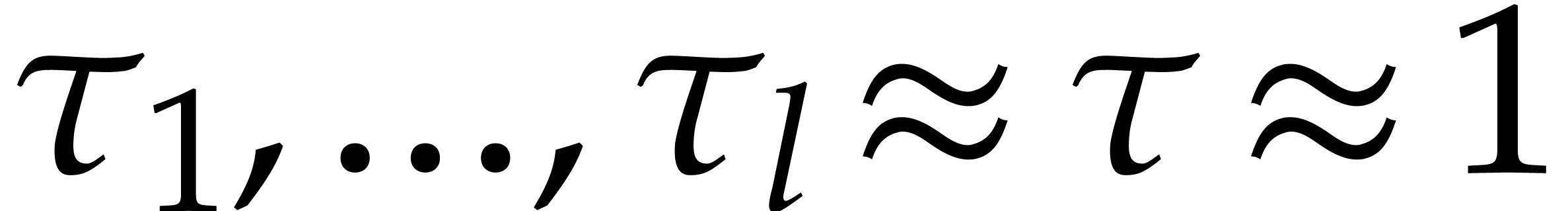 . As in section 5.6, we also
impose the condition that
. As in section 5.6, we also
impose the condition that  for any
for any  . Ideally speaking, we have
. Ideally speaking, we have  and
and  .
.
Under these conditions, thanks to
 |
(15) |
When using naive arithmetic with  and assuming
that
and assuming
that  , this bound simplifies
into
, this bound simplifies
into
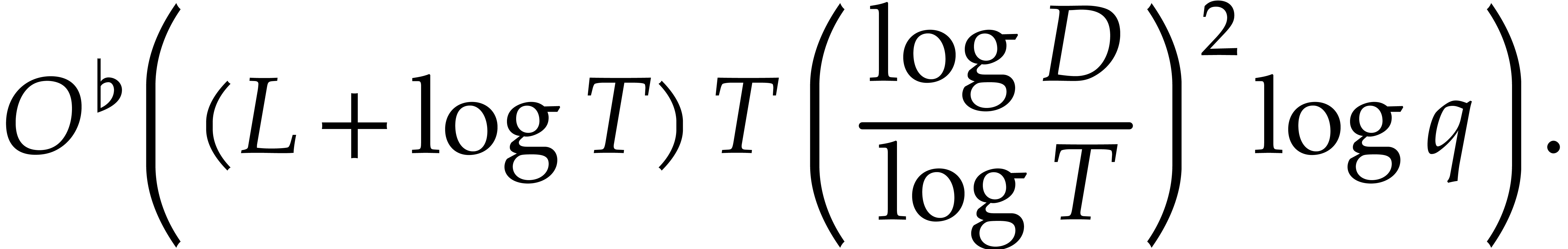
Due to our hypothesis that 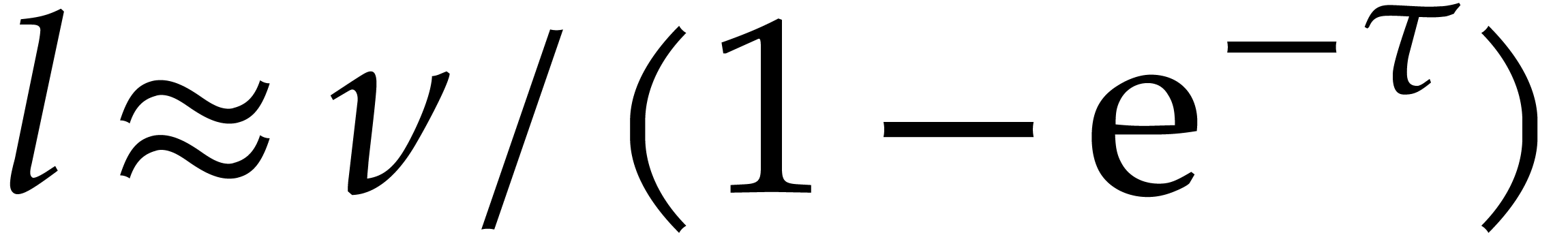 and the analysis from
section 4.4, we can still expect the algorithm to return
about half of the terms of
and the analysis from
section 4.4, we can still expect the algorithm to return
about half of the terms of  .
.
Remark 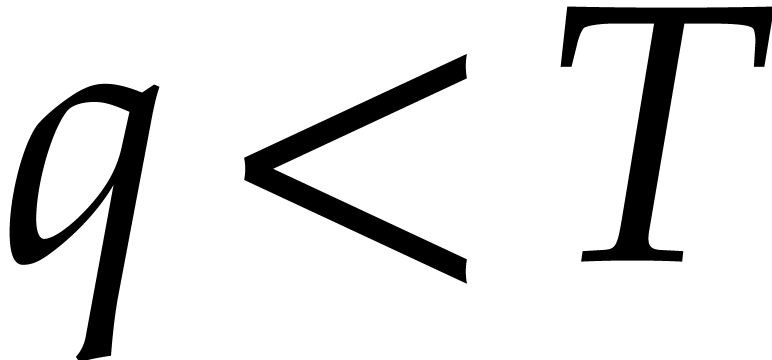 , then we need to replace
, then we need to replace  by an extension of degree at least
by an extension of degree at least 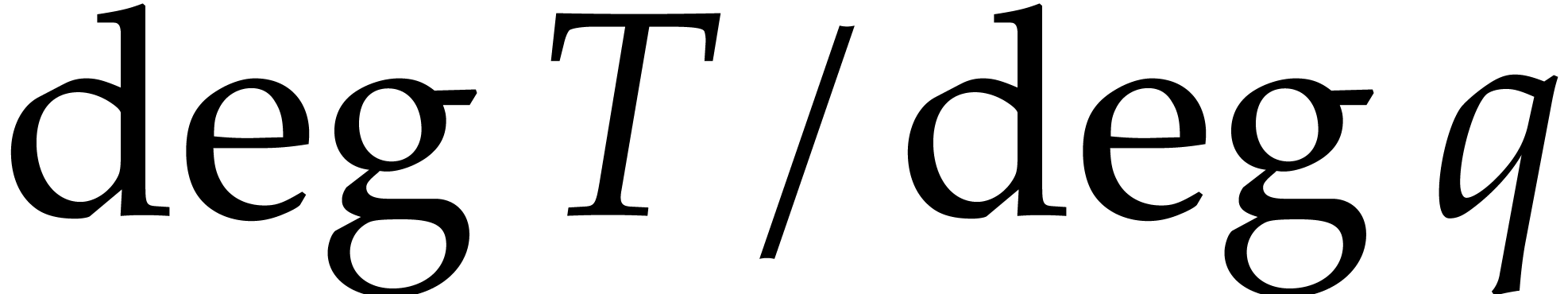 before being
able to diversify
before being
able to diversify 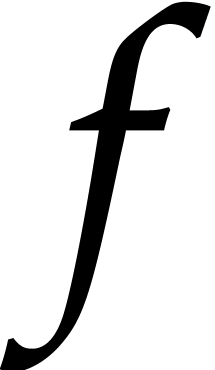 , without
being able to profit from the Frobenius map. This leads to an
incompressible overhead of
, without
being able to profit from the Frobenius map. This leads to an
incompressible overhead of 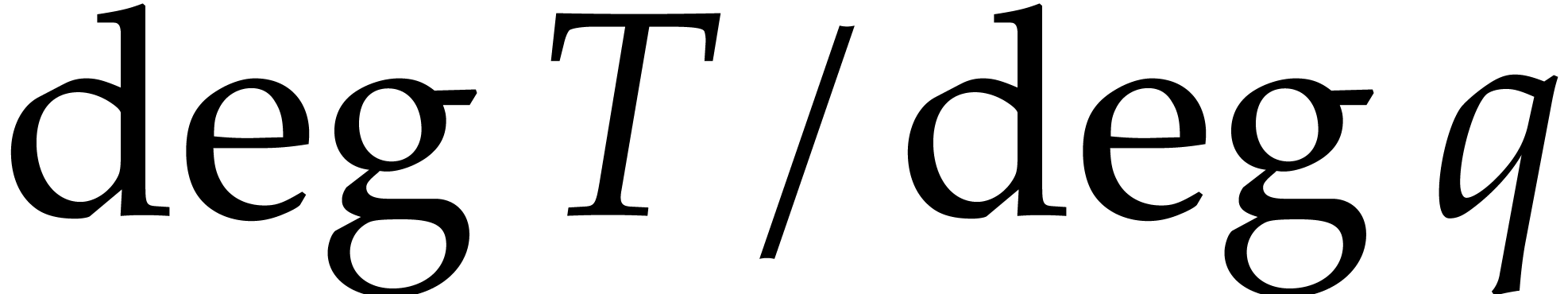 .
Nevertheless, in the special case when the exponents
.
Nevertheless, in the special case when the exponents  are already known, the matching step 4 of Algorithm 3 can
be simplified, and working over an extension can be avoided.
are already known, the matching step 4 of Algorithm 3 can
be simplified, and working over an extension can be avoided.

In order to apply Algorithm 3 as in the previous section,
we need primitive roots of unity of suitable orders  in algebraic extensions of
in algebraic extensions of  .
Although we have no general theory, it is instructive to study a few
practical examples in order to gain insight what we may reasonably hope
for. In this section, we consider the case when
.
Although we have no general theory, it is instructive to study a few
practical examples in order to gain insight what we may reasonably hope
for. In this section, we consider the case when 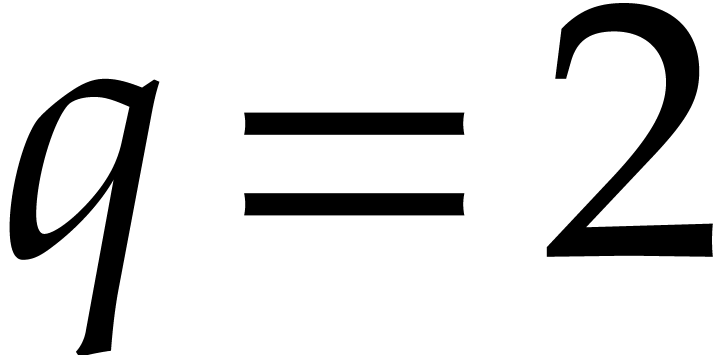 ,
, 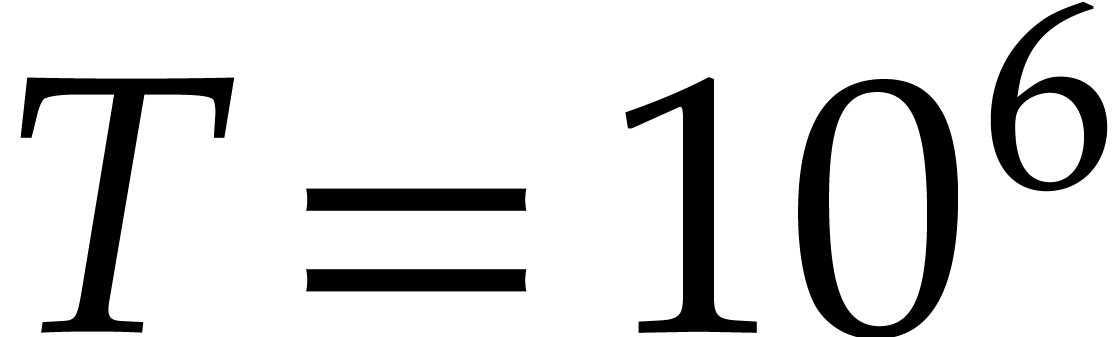 , and
, and
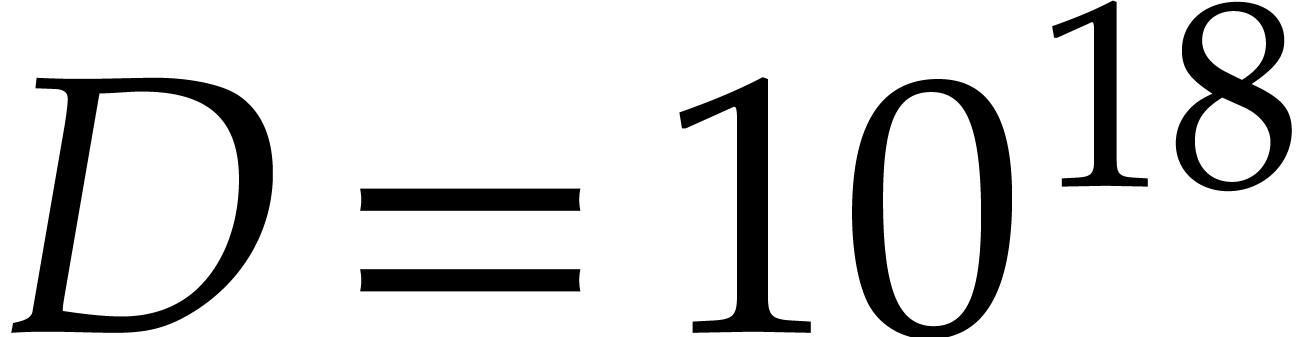 .
.
First of all, we need to replace  by a
sufficiently large extension
by a
sufficiently large extension 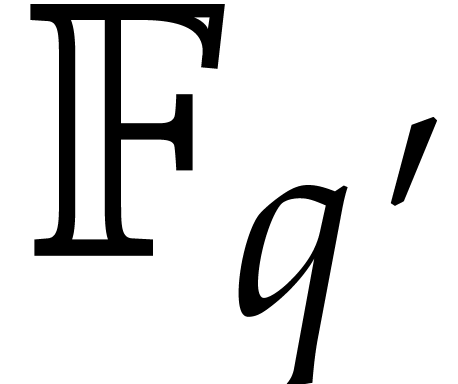 in order to
diversify
in order to
diversify  (at least in the weak sense from the
end of section 4.2.3). Since it is favorable to take
(at least in the weak sense from the
end of section 4.2.3). Since it is favorable to take
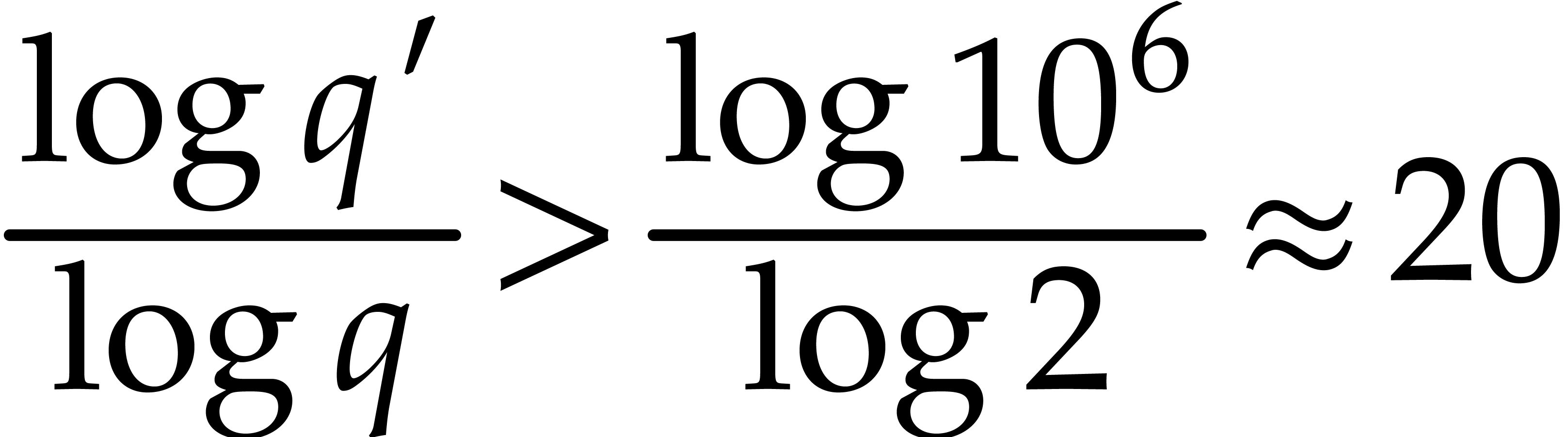
as smooth as possible, we opt for 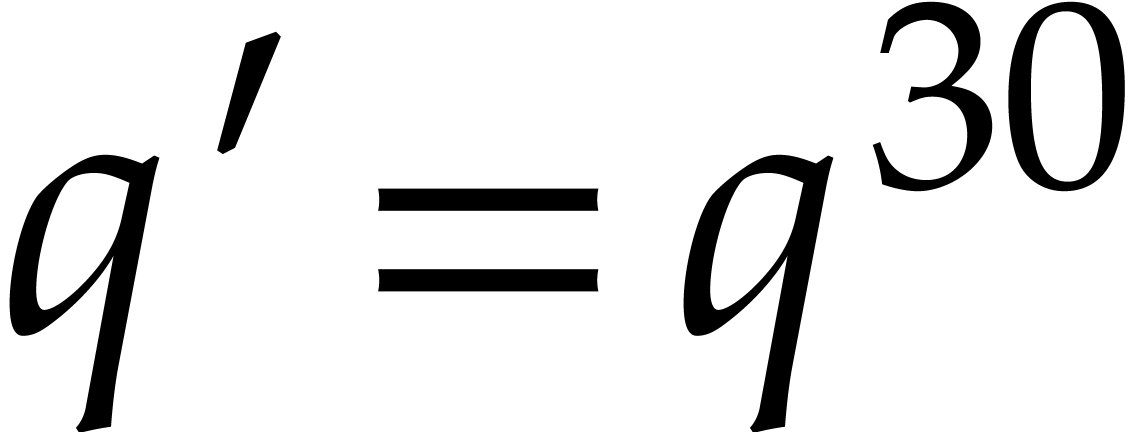 .
For
.
For 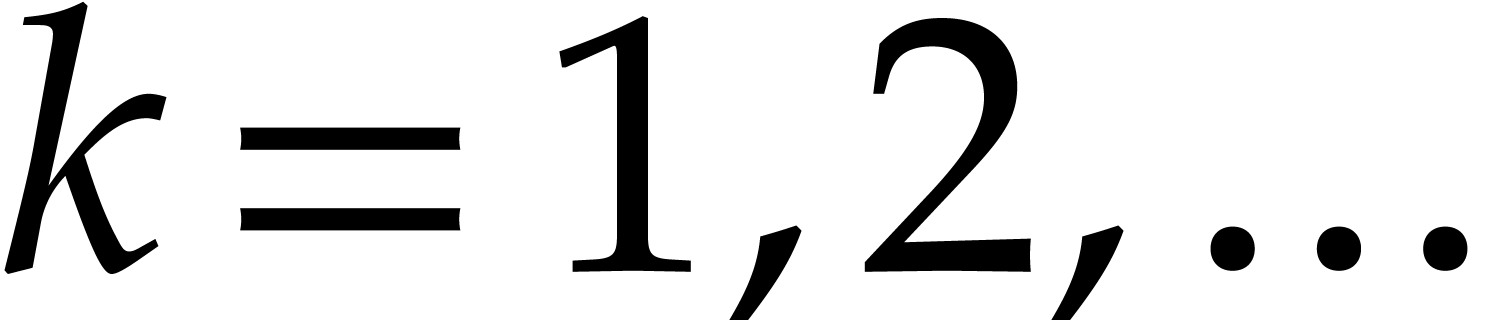 , we next take our orders
, we next take our orders
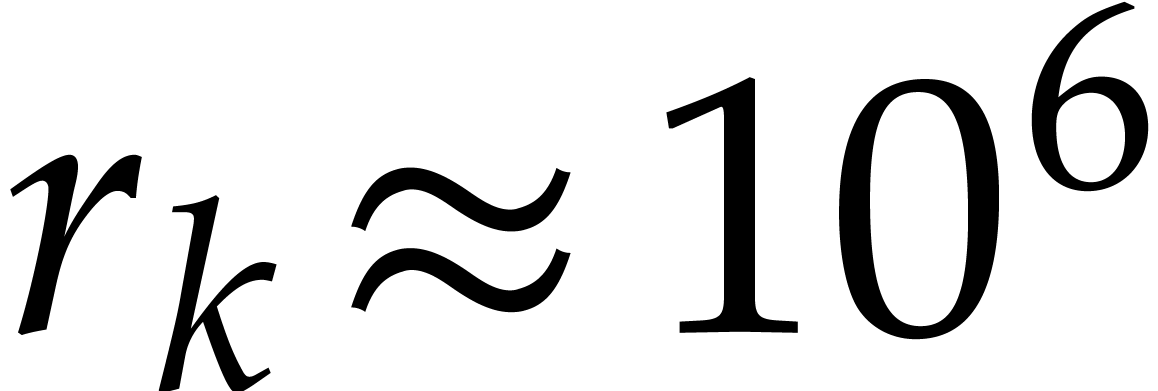 with
with 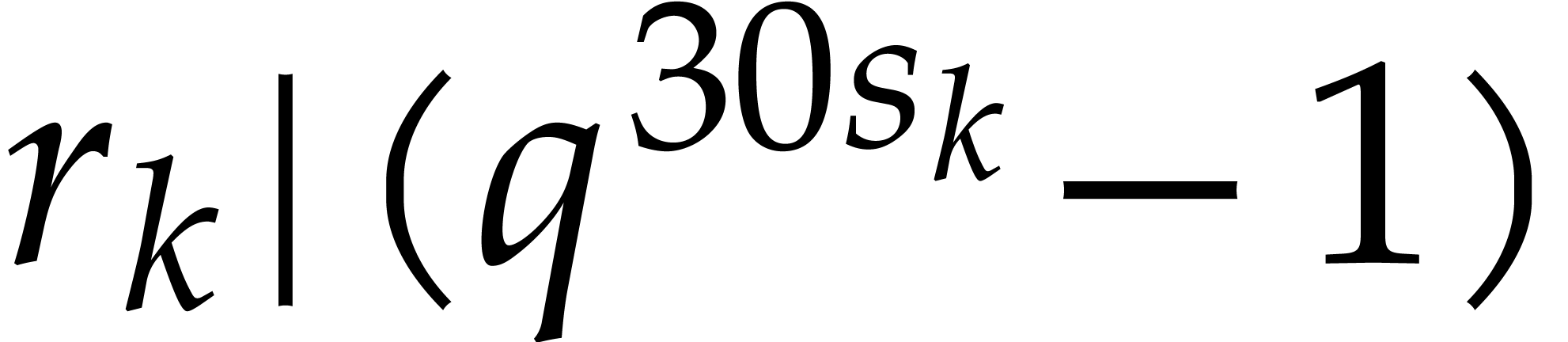 and
and 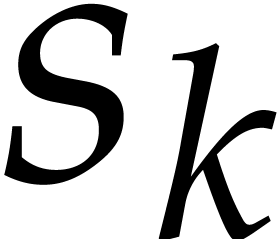 as small as possible, and such that
as small as possible, and such that
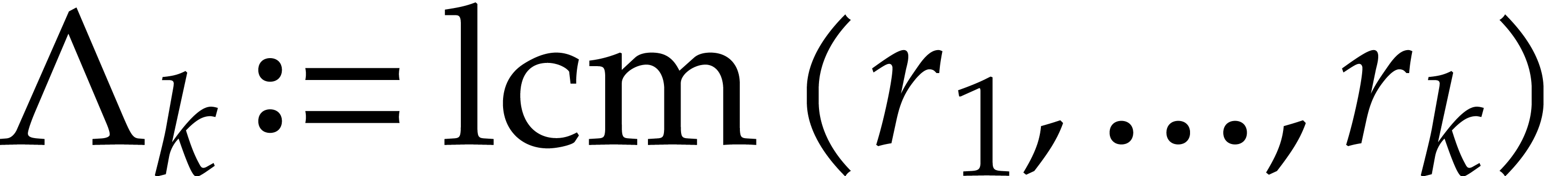
is as large as possible:

Taking 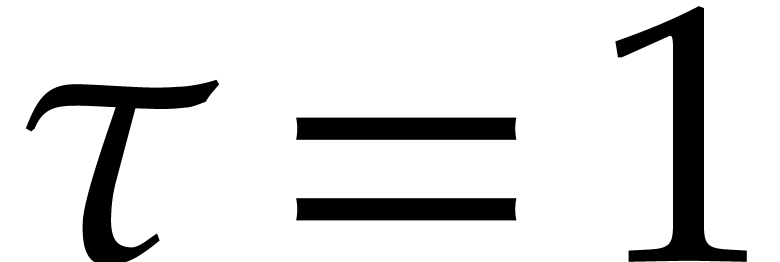 , we obtain
, we obtain 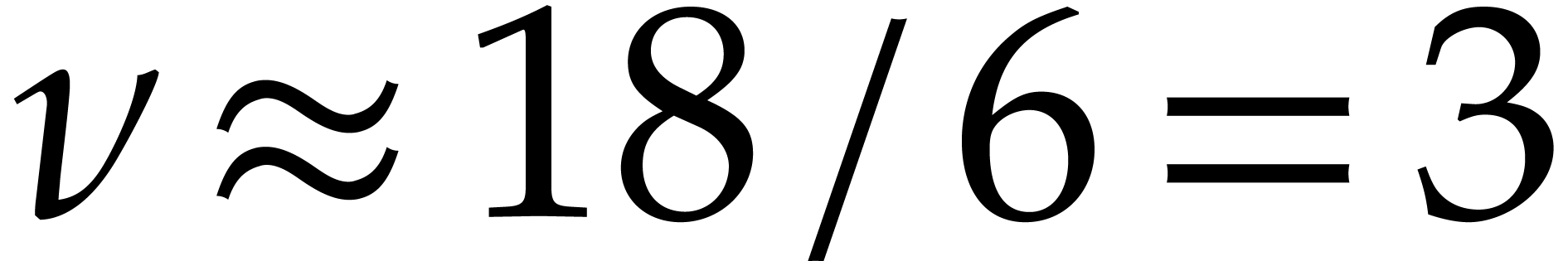 and
and 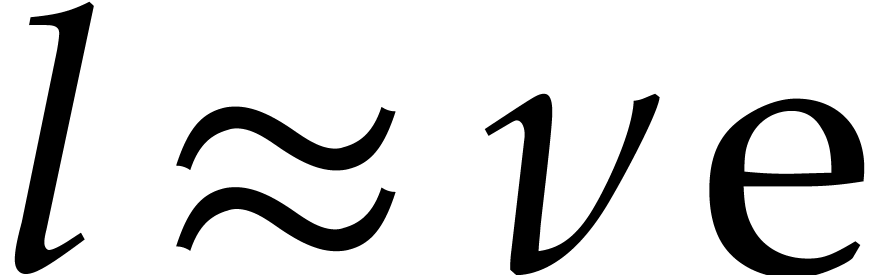 . To be on
the safe side, we take
. To be on
the safe side, we take 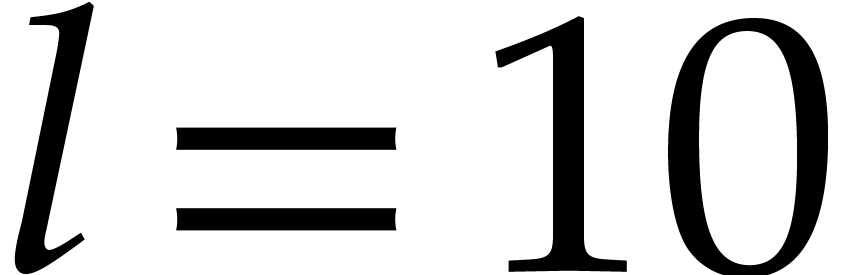 . The
minimum least common multiple of three (resp. four) orders
among
. The
minimum least common multiple of three (resp. four) orders
among  is
is
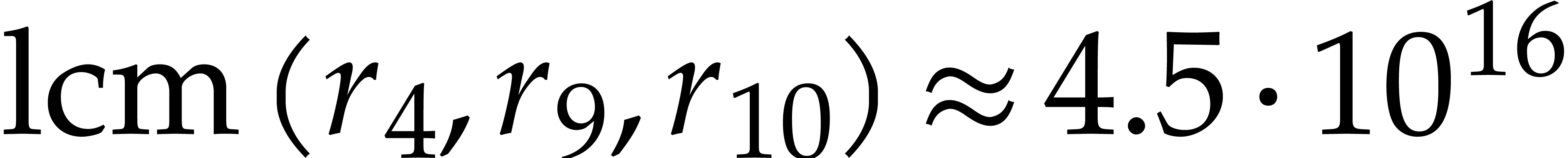
(resp. 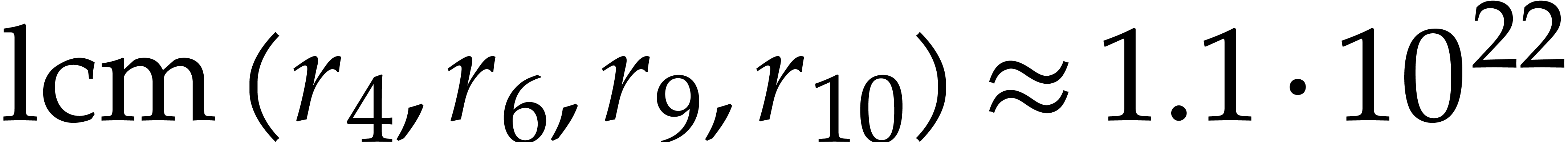 ), so we
have
), so we
have 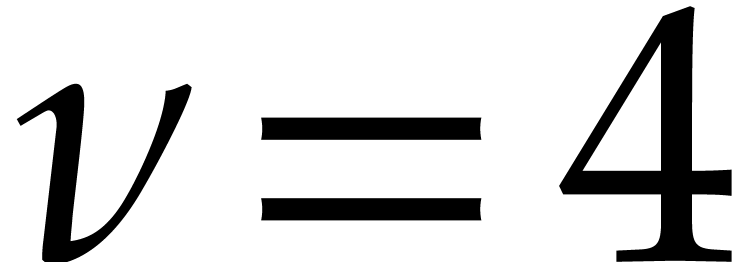 . Notice that some of
the
. Notice that some of
the  are quite a bit larger than
are quite a bit larger than  , with an average of
, with an average of 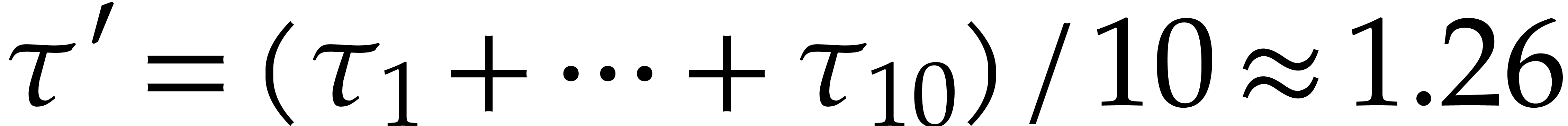 . For
. For 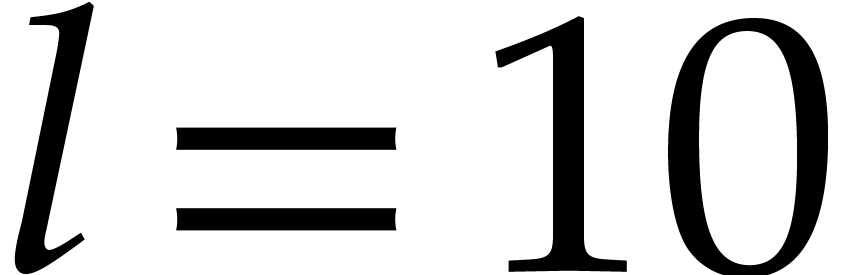 and
and 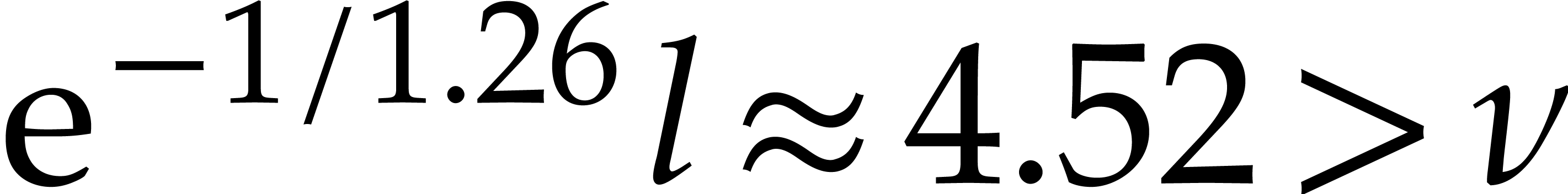 , we therefore consider it likely that the condition
, we therefore consider it likely that the condition 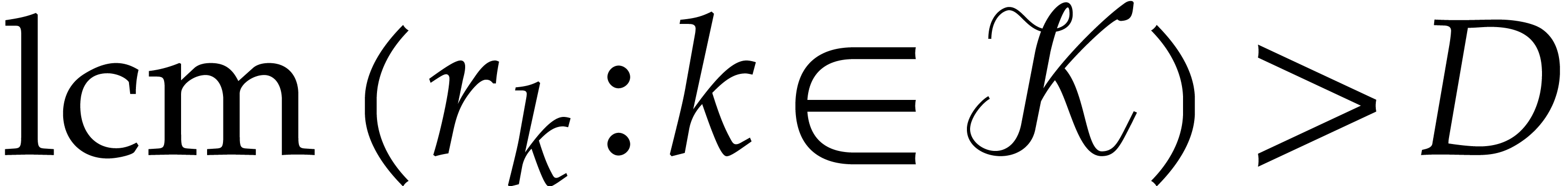 in step 4 of Algorithm 3 is satisfied with probability
in step 4 of Algorithm 3 is satisfied with probability 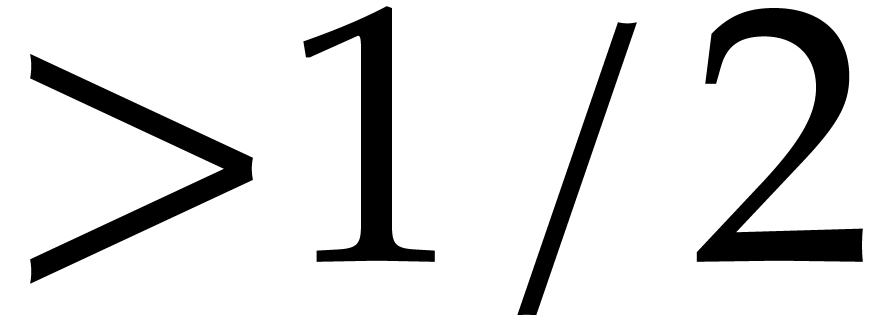 (a rigorous analysis would be welcome).
(a rigorous analysis would be welcome).
As our second example, consider the case when  (as in section 2),
(as in section 2),  ,
and
,
and 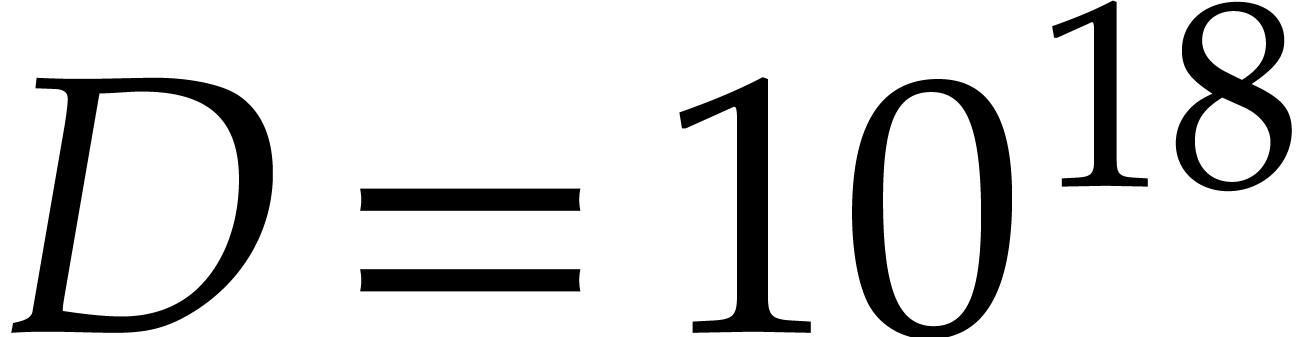 . This time
. This time  contains at least
contains at least  elements, so we
may directly work over
elements, so we
may directly work over  .
Proceeding as in the previous subsection, we may now take:
.
Proceeding as in the previous subsection, we may now take:

With 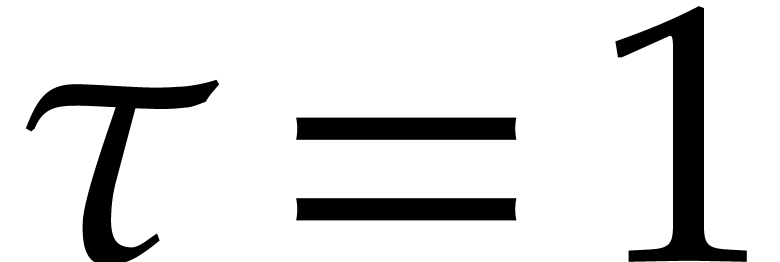 ,
, 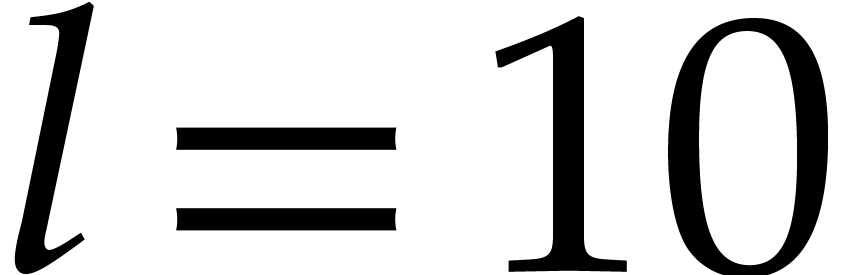 , and
, and 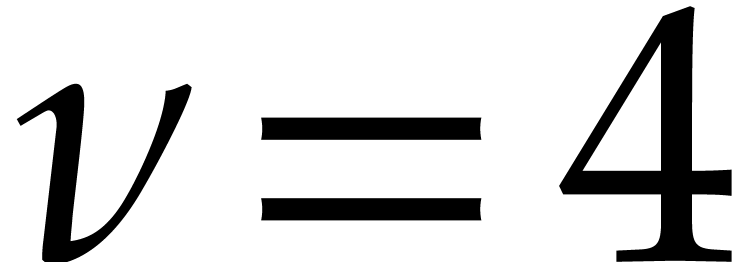 as before, the minimum
least common multiple of
as before, the minimum
least common multiple of  orders among
orders among  is
is 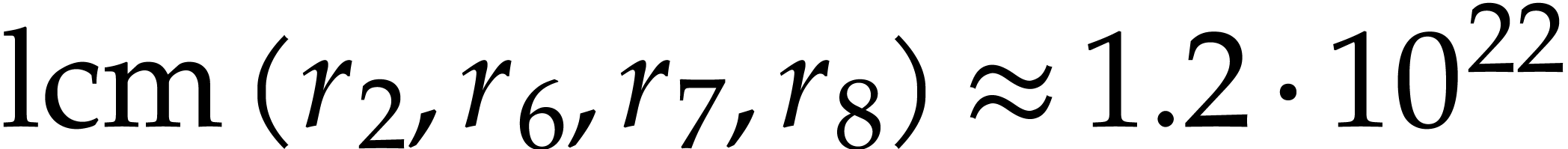 . Again, the
“effective” mean value
. Again, the
“effective” mean value 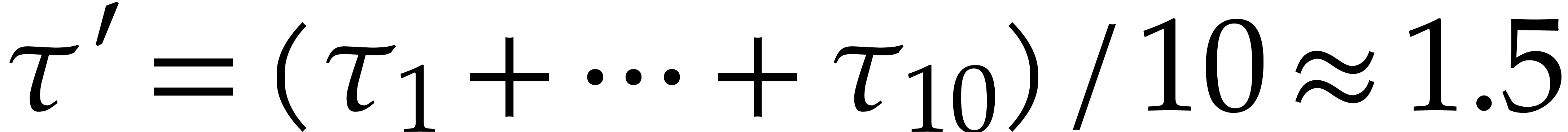 satisfies
satisfies
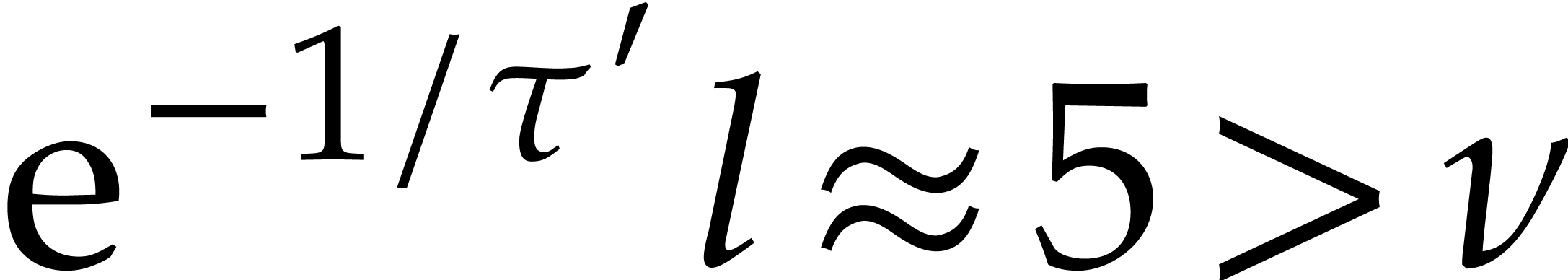 .
.
Notice that 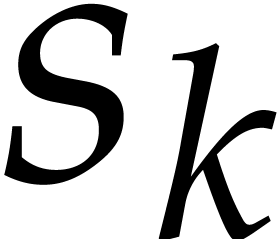 approximately grows like
approximately grows like  . On the first example from the
previous subsection, we rather have
. On the first example from the
previous subsection, we rather have  .
This suggests that the growth of
.
This suggests that the growth of 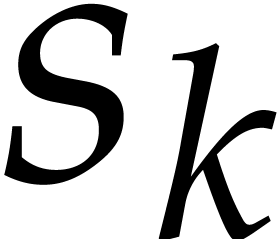 might often be
somewhat above
might often be
somewhat above 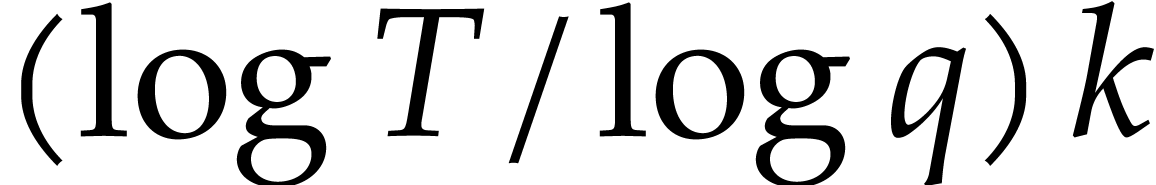 .
.
As an optimization, we also notice that it should be better to take  somewhat larger for small values of
somewhat larger for small values of  , so as to balance the terms
, so as to balance the terms 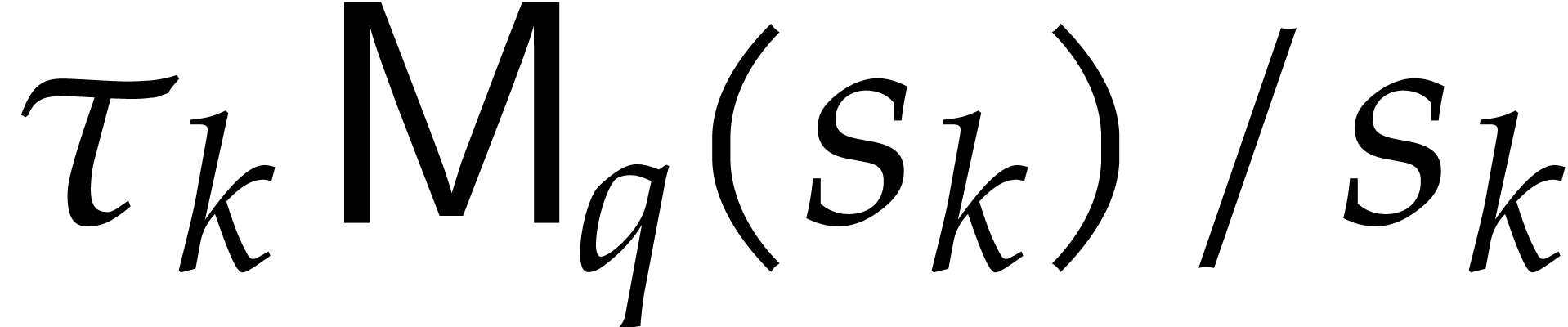 in the sum (15). For instance, the last number
in the sum (15). For instance, the last number  is quite a lot larger than
is quite a lot larger than  ;
it should be more efficient to resort to a larger extension degree
;
it should be more efficient to resort to a larger extension degree 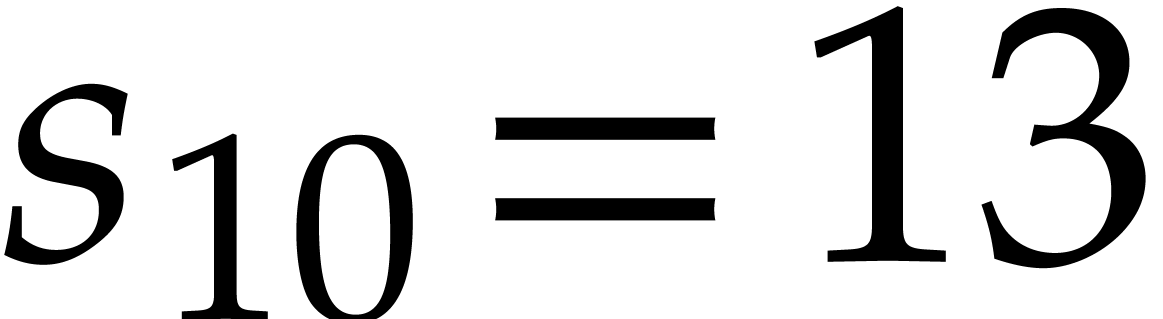 and take
and take 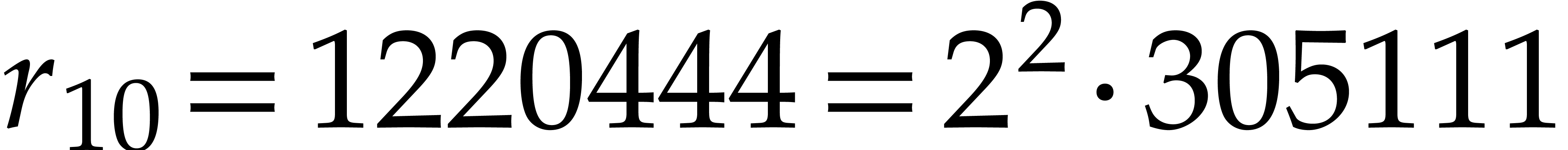 .
Another option would be to include
.
Another option would be to include 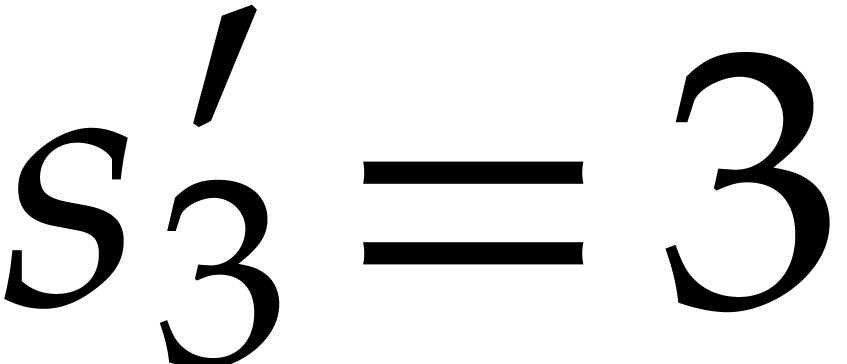 and
and 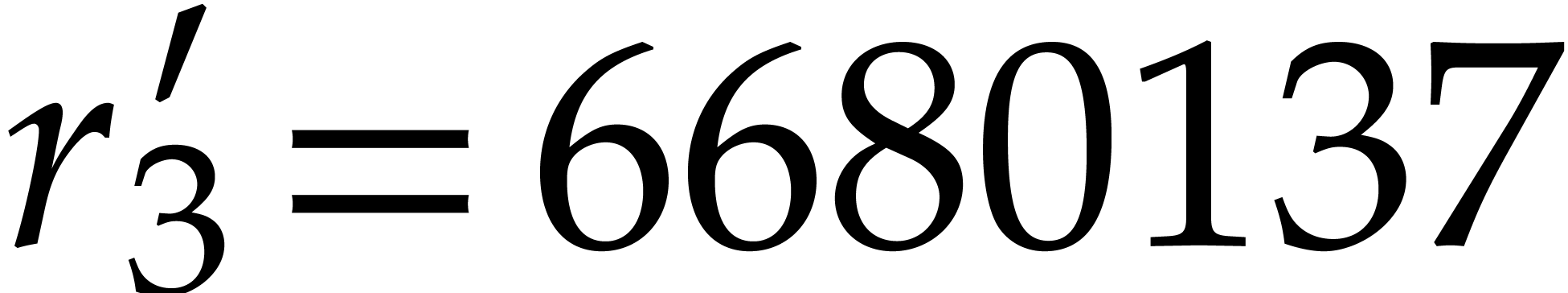 . In addition, by increasing
. In addition, by increasing  and
and 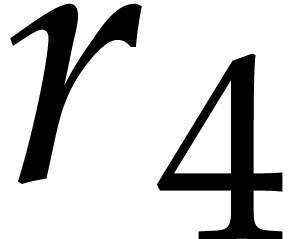 , it
might also be possible to take
, it
might also be possible to take 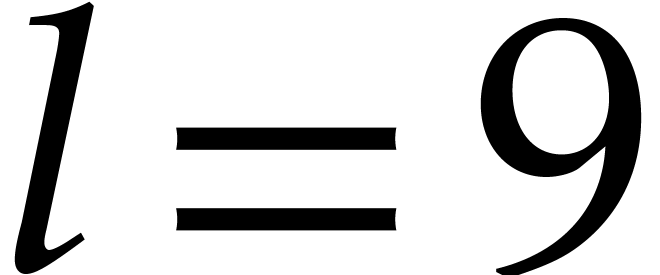 .
.
As mentioned in the introduction, one important application of sparse
interpolation over finite fields is sparse interpolation over the
rational numbers. In that case, we typically combine sparse
interpolation over different prime fields  for
which
for
which 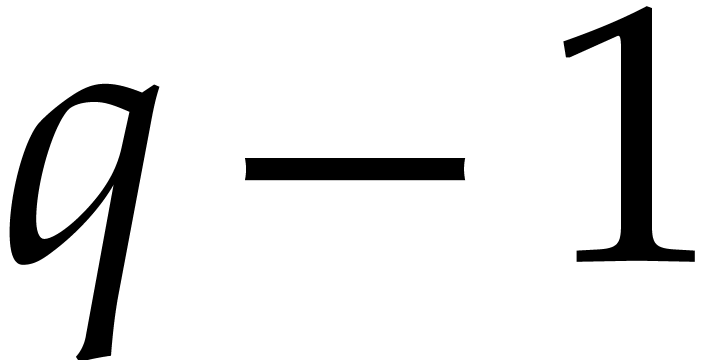 is divisible by a high power of two.
is divisible by a high power of two.
We usually proceed in two stages. We first determine the exponents  of
of  (typically using a few
primes
(typically using a few
primes 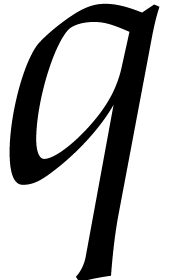 only). Once the exponents are known, the
computation of the coefficients modulo further primes
only). Once the exponents are known, the
computation of the coefficients modulo further primes  (typically many ones) becomes more efficient. We finally use the Chinese
remainder theorem and rational number reconstruction to determine the
actual coefficients.
(typically many ones) becomes more efficient. We finally use the Chinese
remainder theorem and rational number reconstruction to determine the
actual coefficients.
Let  denote the Euler totient function. For any
coprime positive integers
denote the Euler totient function. For any
coprime positive integers  and
and  we we write
we we write 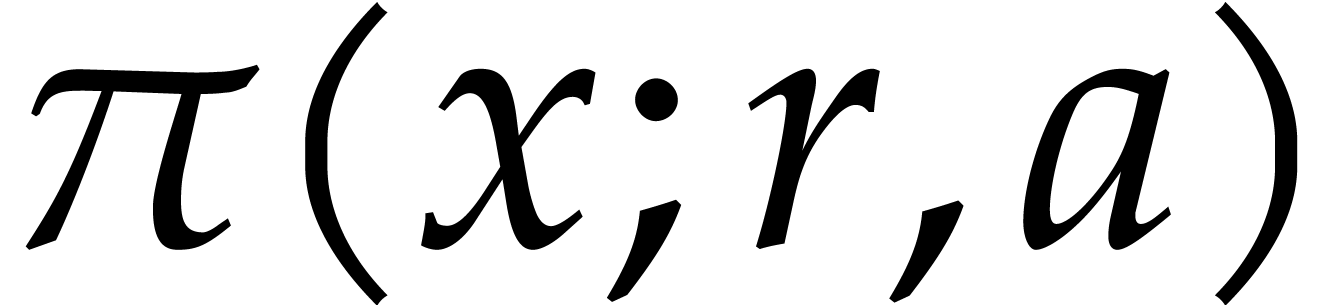 for the number of prime integers
for the number of prime integers
 such that
such that 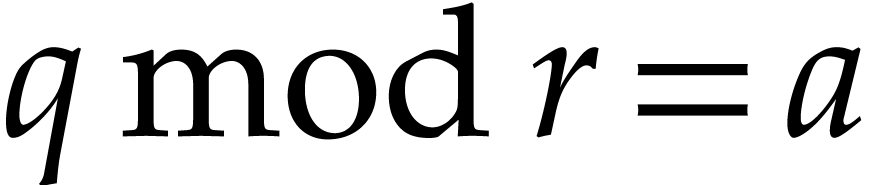 .
Roughly speaking we have
.
Roughly speaking we have
 |
(16) |
for sufficiently large values of  ;
recent advances in this research area can be found in [9].
Unfortunately, for practical purpose, the bounds presented in [9]
require
;
recent advances in this research area can be found in [9].
Unfortunately, for practical purpose, the bounds presented in [9]
require  to be exponentially larger than
to be exponentially larger than  . Assuming the Generalized Riemann
Hypothesis (GRH), known estimates of
. Assuming the Generalized Riemann
Hypothesis (GRH), known estimates of 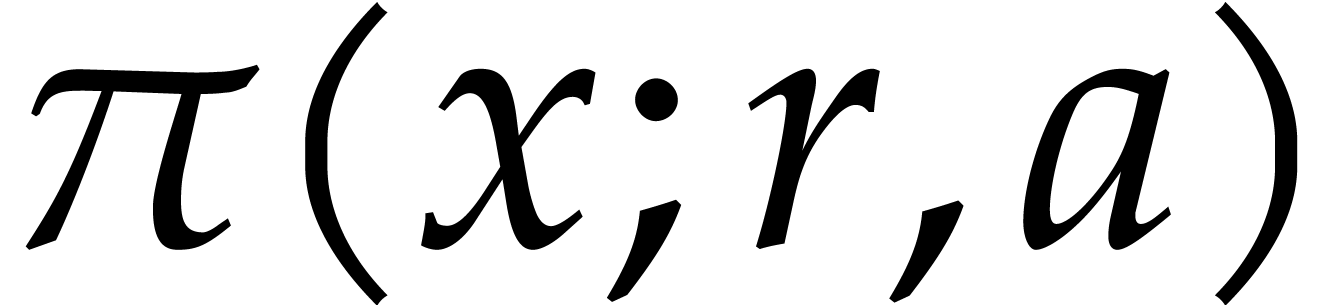 are more
favorable: in fact, the explicit bound proved in [15]
raises this requirement.
are more
favorable: in fact, the explicit bound proved in [15]
raises this requirement.
The techniques from this section may help to accelerate both stages. If
 is normally sparse, then we may directly apply
the algorithms from above to find the exponents. If
is normally sparse, then we may directly apply
the algorithms from above to find the exponents. If  is super sparse, then we will now present a multi-modular variant of the
strategy from section 3.2. Given a number
is super sparse, then we will now present a multi-modular variant of the
strategy from section 3.2. Given a number  , the aim is to determine with high probability
those exponents
, the aim is to determine with high probability
those exponents  such that
such that  for all
for all  and use this to reconstruct an
approximate sparse interpolation of
and use this to reconstruct an
approximate sparse interpolation of  .
We next apply Algorithm 1.
.
We next apply Algorithm 1.
So let  be fixed and consider successive prime
numbers
be fixed and consider successive prime
numbers 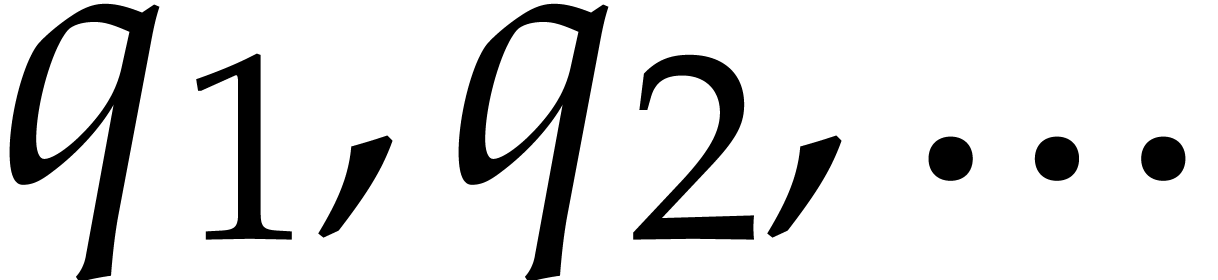 for which
for which 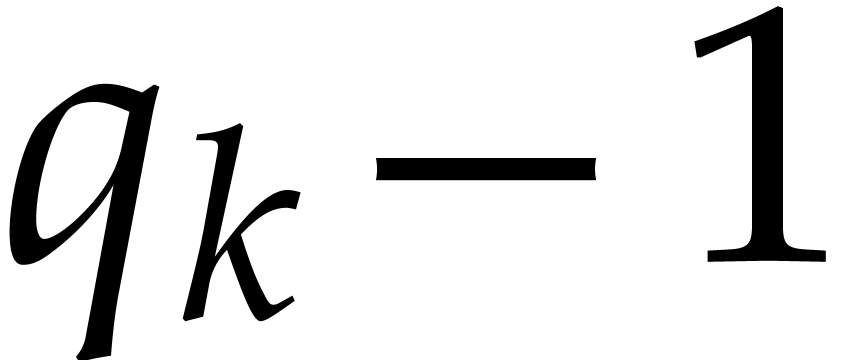 is
divisible by
is
divisible by  . Let
. Let  be minimal such that
be minimal such that 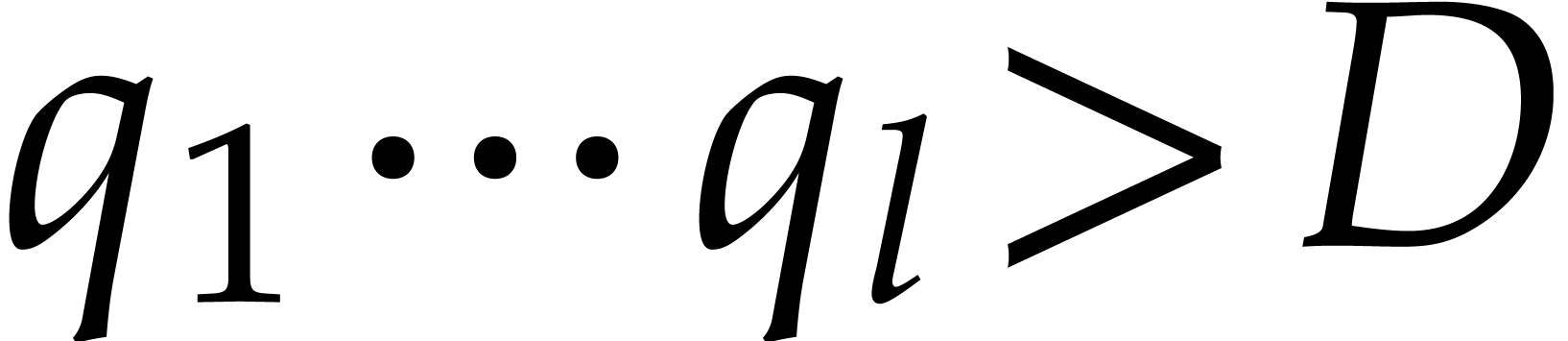 .
Under GRH, the estimate
.
Under GRH, the estimate 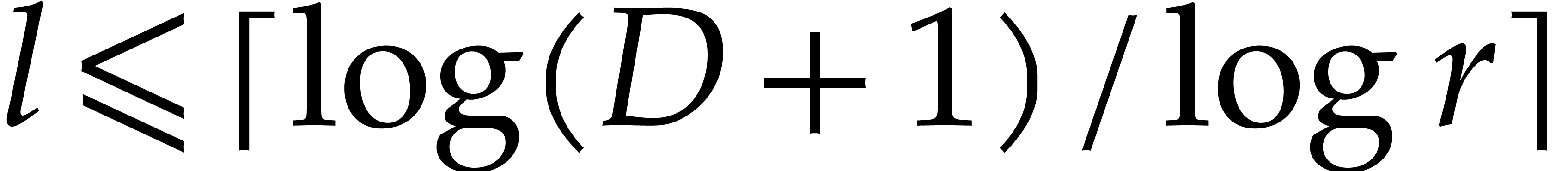 , since
, since 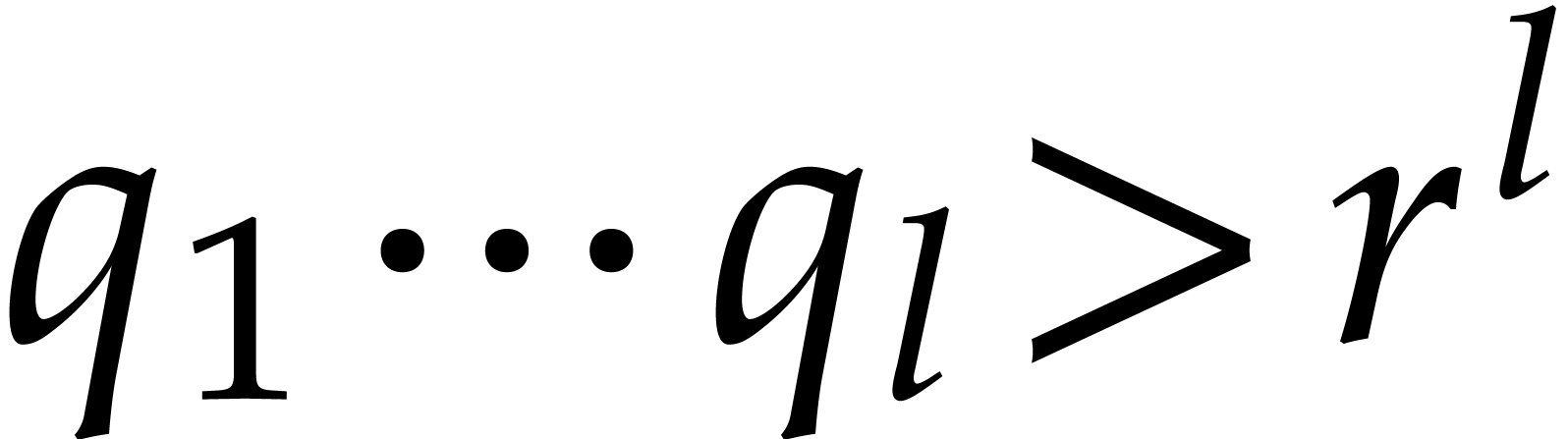 . Hence
. Hence 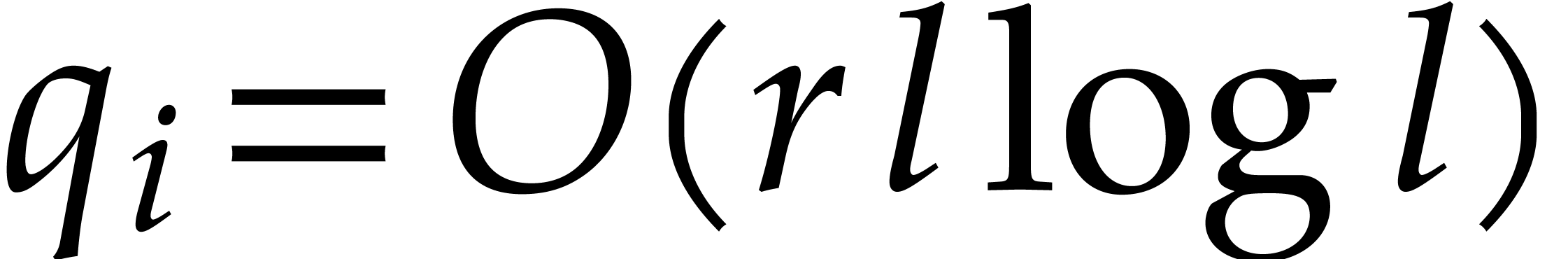 and
and 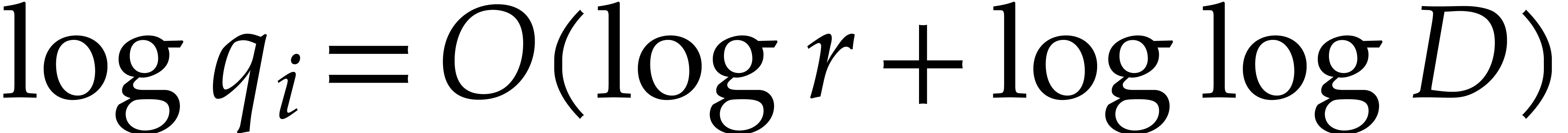 , for
, for 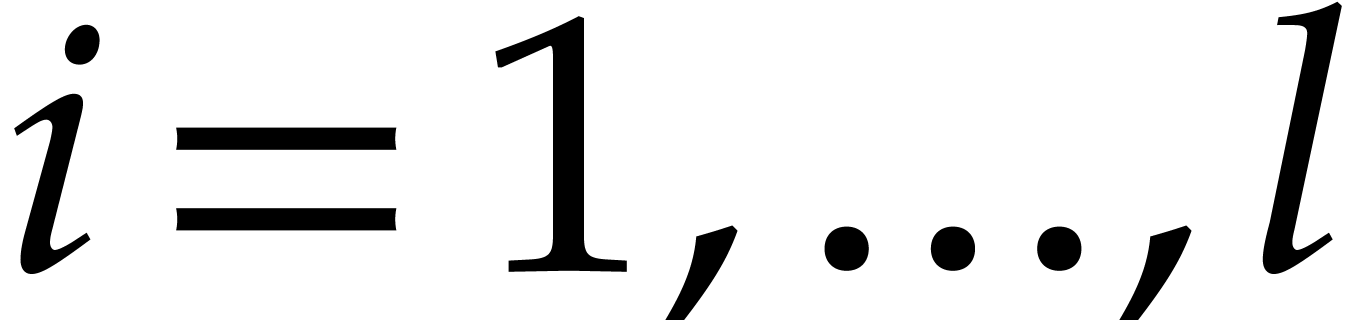 .
It follows that
.
It follows that 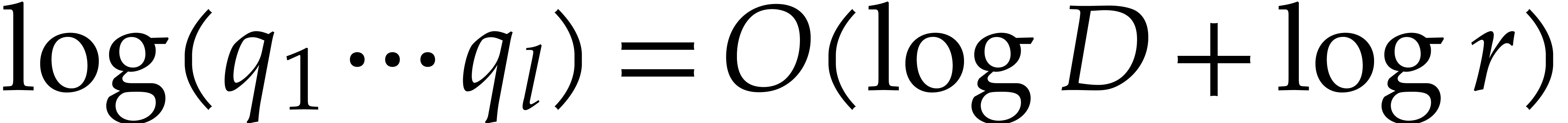 . Instead of
relying on GRH for bounding the
. Instead of
relying on GRH for bounding the 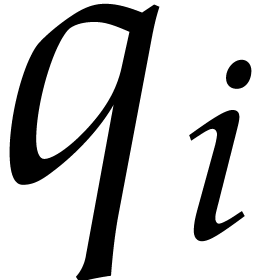 ,
we might have used the Bombieri–Vinogradov theorem, by adapting
[20, Corollary 3.4], that is based on the explicit bound
proved in [54, Corollary 1.5]. With high probability, this
yields a suitable
,
we might have used the Bombieri–Vinogradov theorem, by adapting
[20, Corollary 3.4], that is based on the explicit bound
proved in [54, Corollary 1.5]. With high probability, this
yields a suitable  at random among the primes in,
say, the range from
at random among the primes in,
say, the range from  to
to  .
.
We first compute 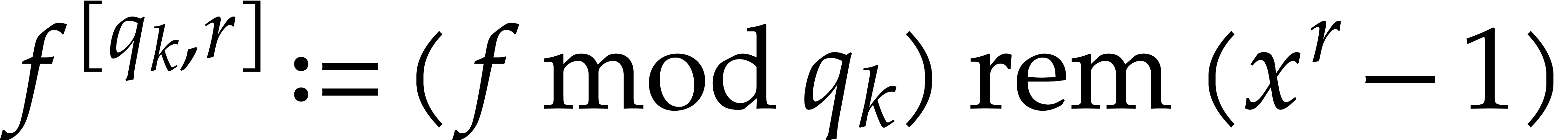 for
for 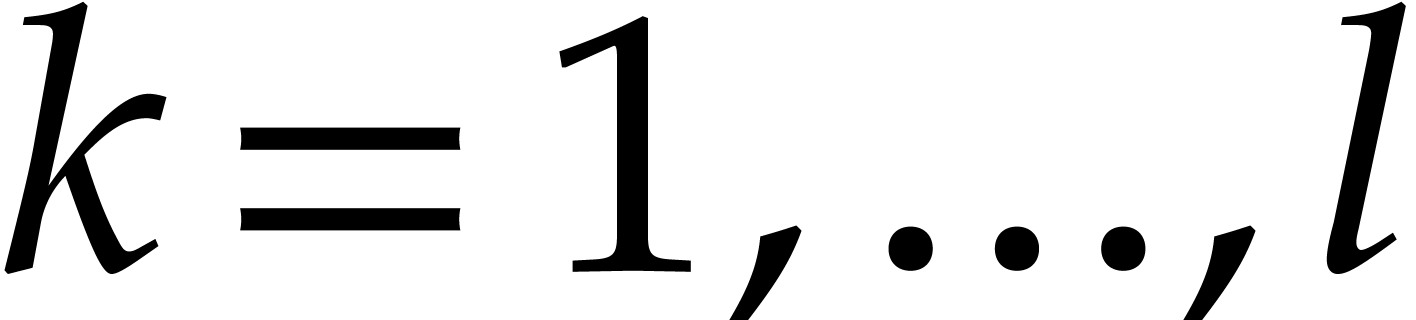 using Algorithm 5. We next reconstruct
using Algorithm 5. We next reconstruct 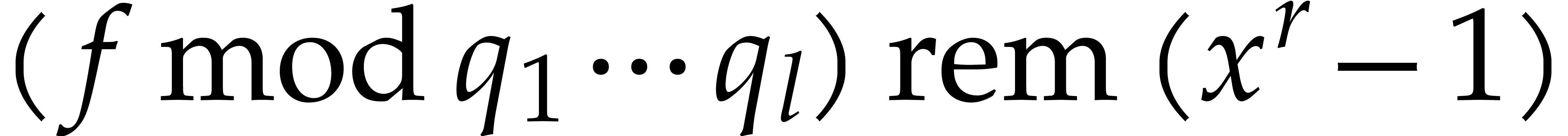 using Chinese remaindering. In a similar way, we compute
using Chinese remaindering. In a similar way, we compute  . For any coefficient
. For any coefficient 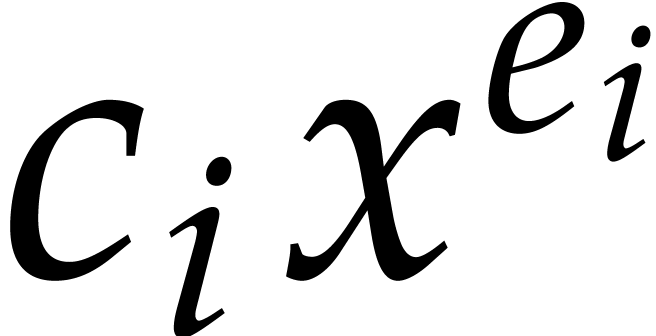 of
of  such that
such that 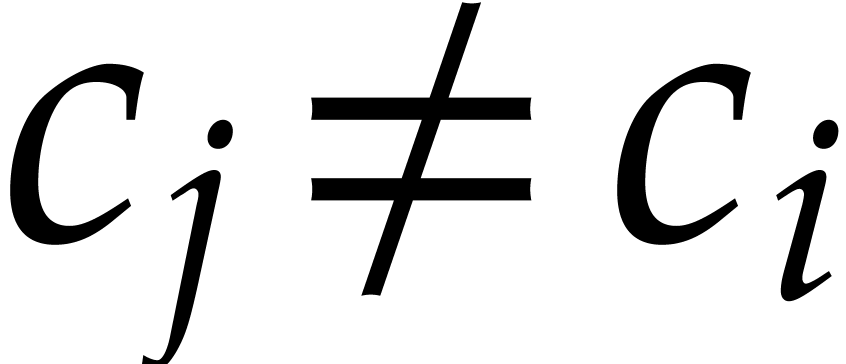 modulo
modulo  for all
for all 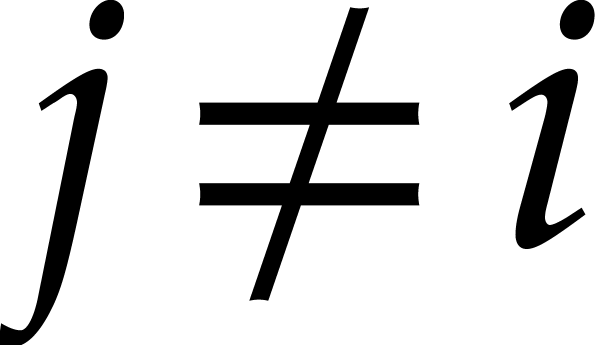 ,
we thus obtain both coefficients
,
we thus obtain both coefficients  and
and  modulo
modulo  .
Whenever
.
Whenever 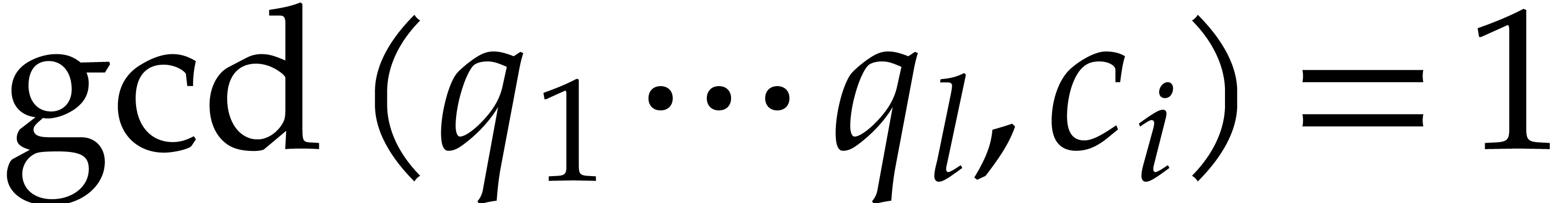 , this allows us to
retrieve
, this allows us to
retrieve  . By considering a
few more primes
. By considering a
few more primes  for sanity checking, we may thus
compute
for sanity checking, we may thus
compute  with high probability. The running time
of this algorithm is bounded by
with high probability. The running time
of this algorithm is bounded by 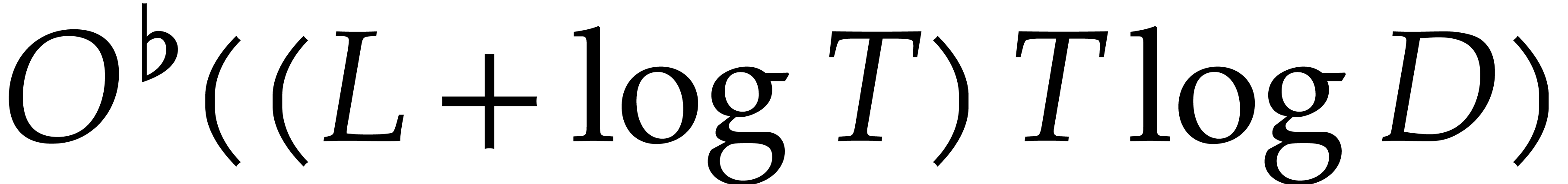 .
.
If the exponents  are known, then we may also use
the techniques from this section to further speed up the computation of
the coefficients
are known, then we may also use
the techniques from this section to further speed up the computation of
the coefficients  . For this,
let
. For this,
let  be an increasing sequence of pairwise
coprime numbers. Assume that the numerators and denominators of the
coefficients
be an increasing sequence of pairwise
coprime numbers. Assume that the numerators and denominators of the
coefficients  are bounded by
are bounded by  with
with 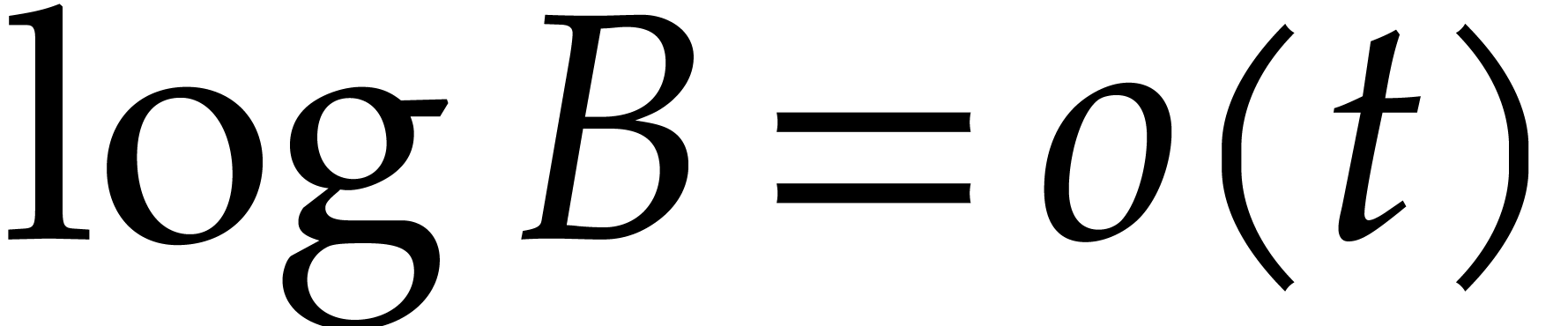 , and assume that
, and assume that 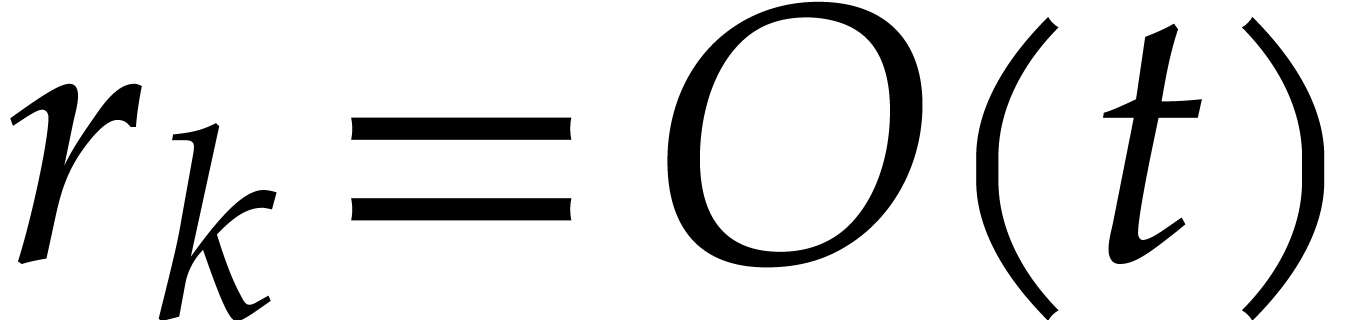 for the first
for the first 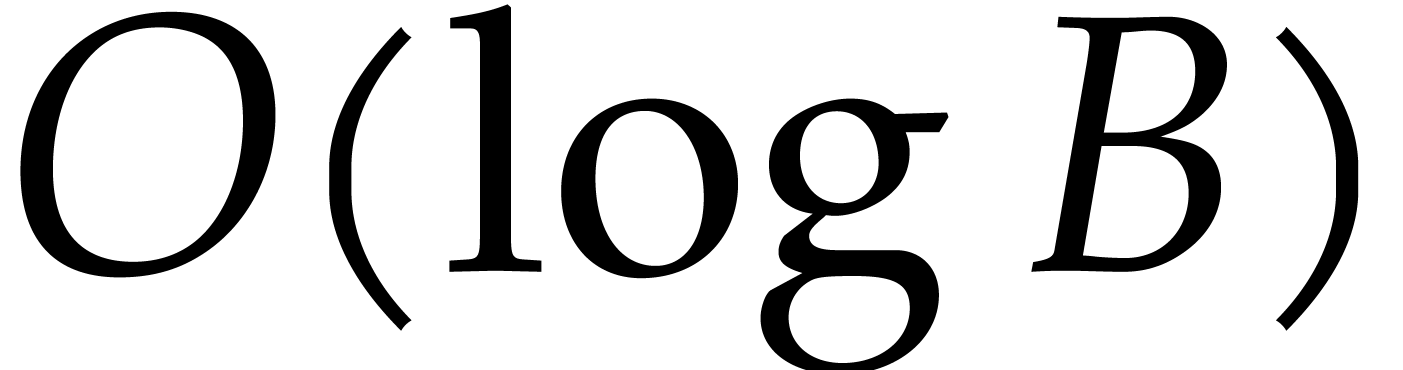 terms of the
sequence
terms of the
sequence  . For each
. For each  , let
, let 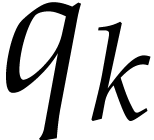 be
the smallest prime number such that
be
the smallest prime number such that 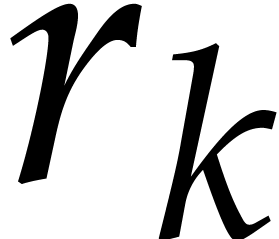 divides
divides
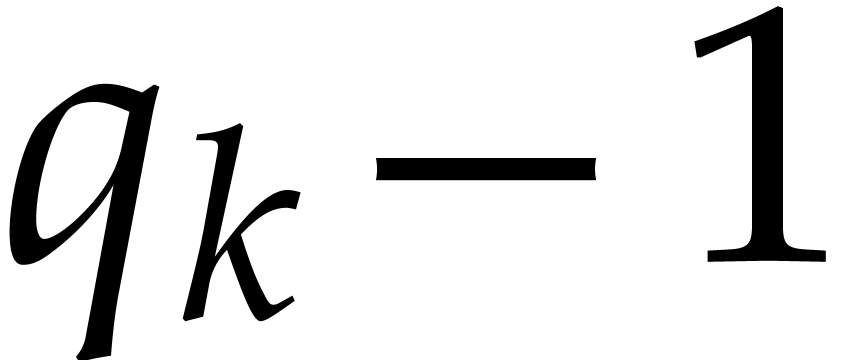 .
.
Starting with 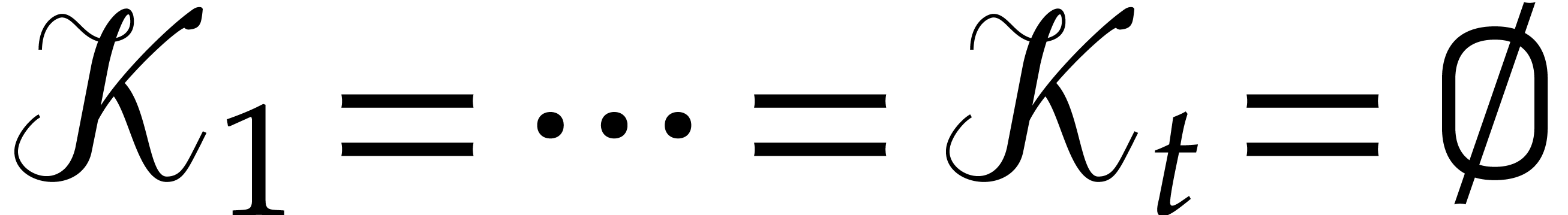 , we now repeat
the following loop for
, we now repeat
the following loop for 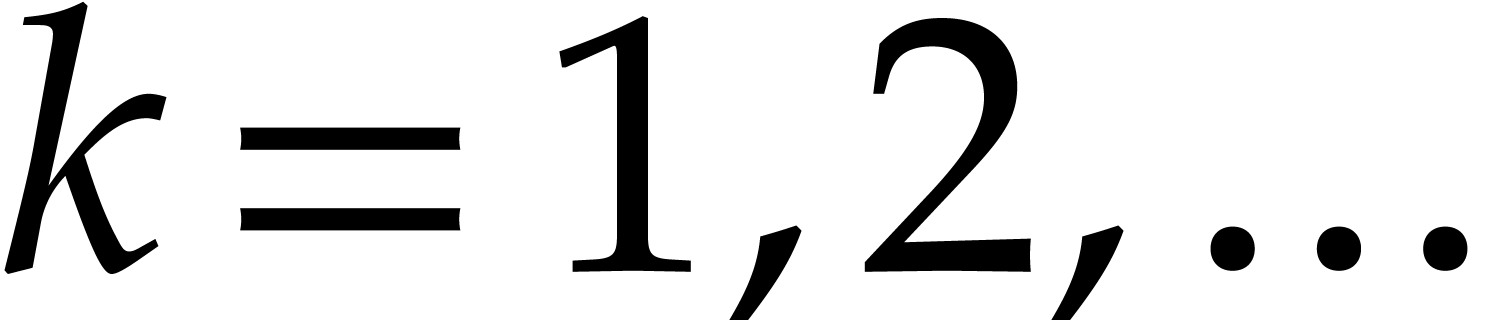 until
until 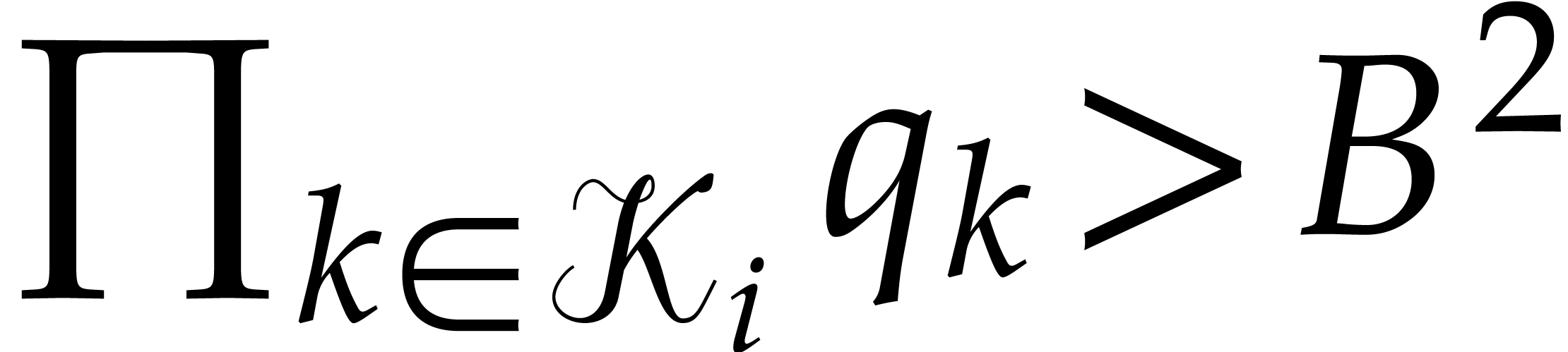 for all
for all 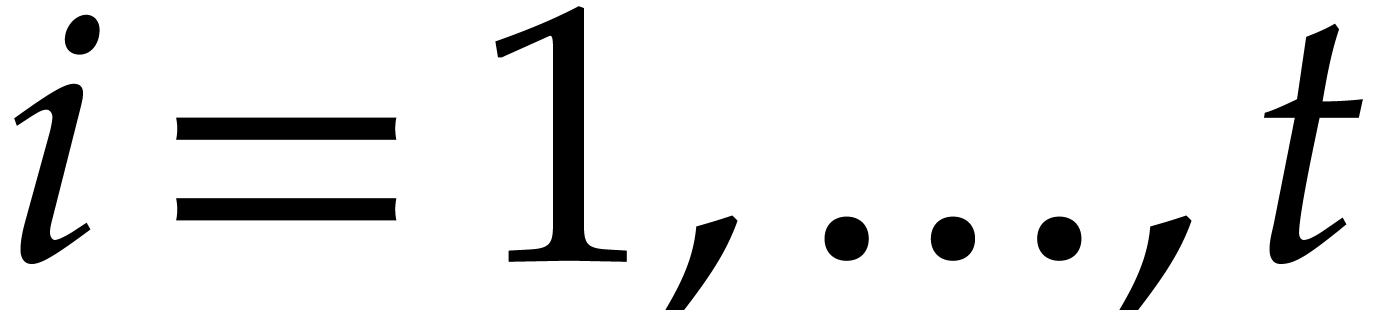 :
:
We compute 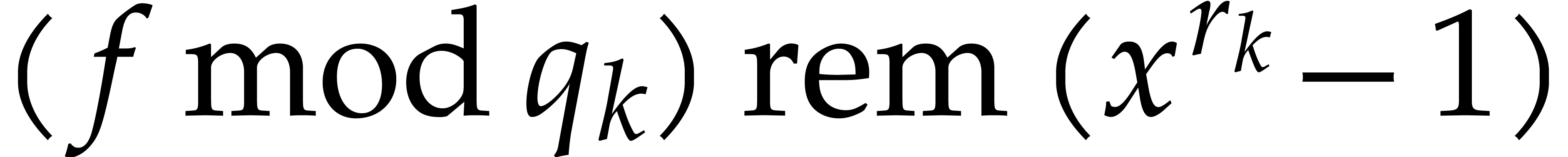 using Algorithm 5.
using Algorithm 5.
For 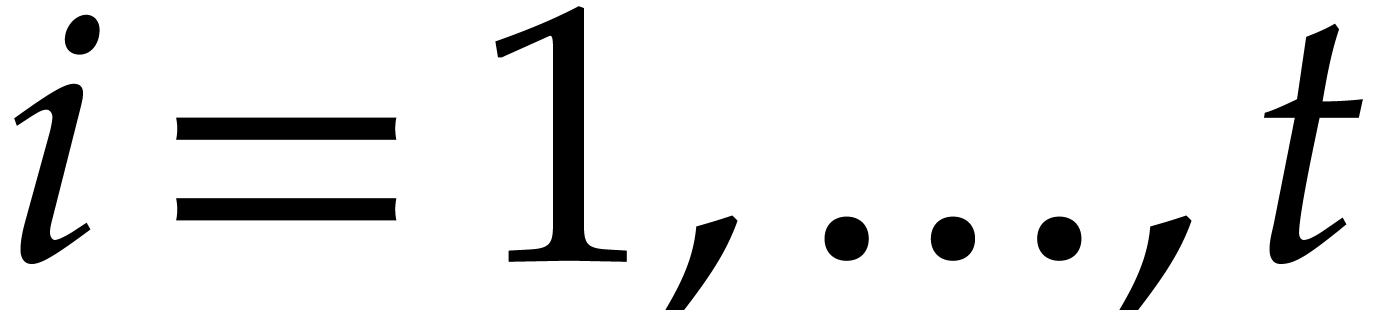 , if
, if 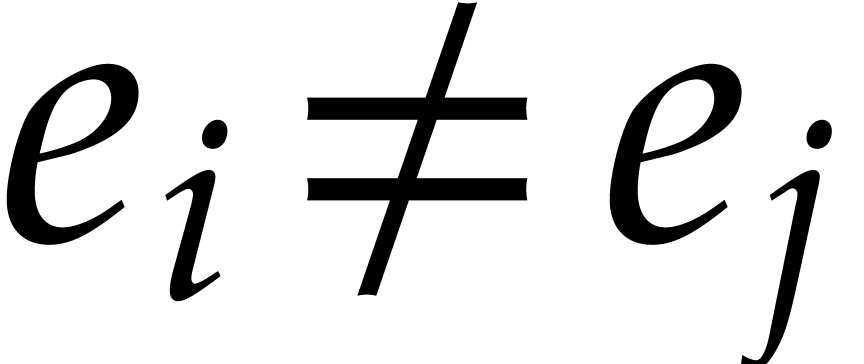 modulo
modulo  for all
for all 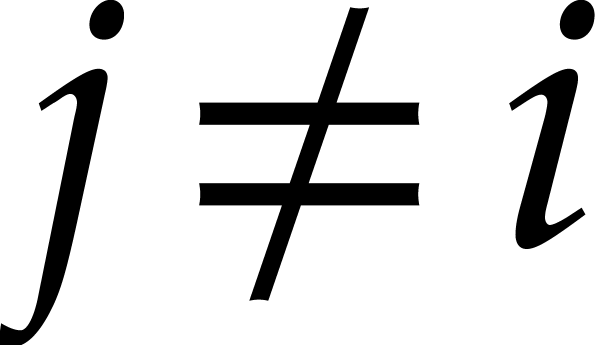 ,
then set
,
then set 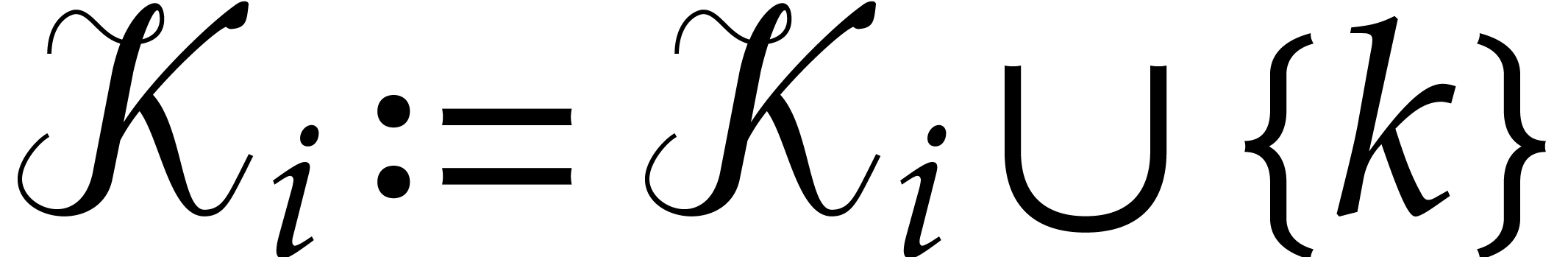 .
.
At the end of this loop, for 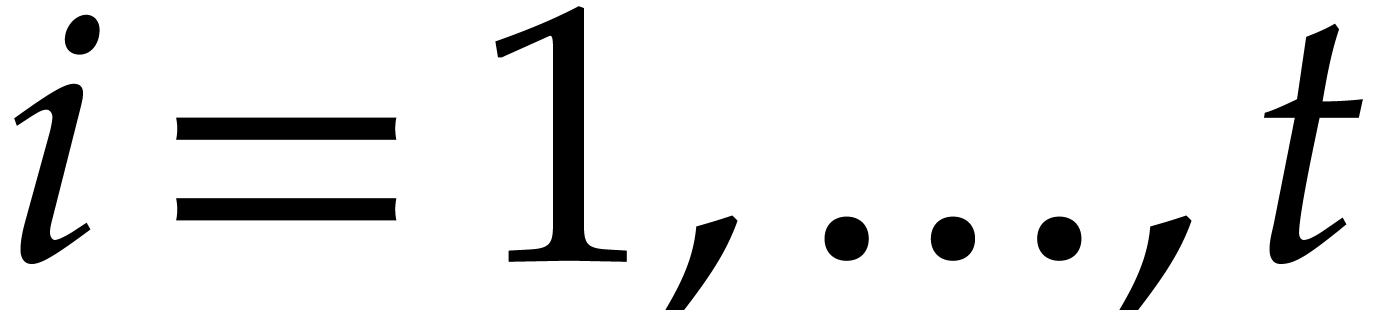 ,
we may recover the coefficient
,
we may recover the coefficient  from the
coefficients of
from the
coefficients of  in
in 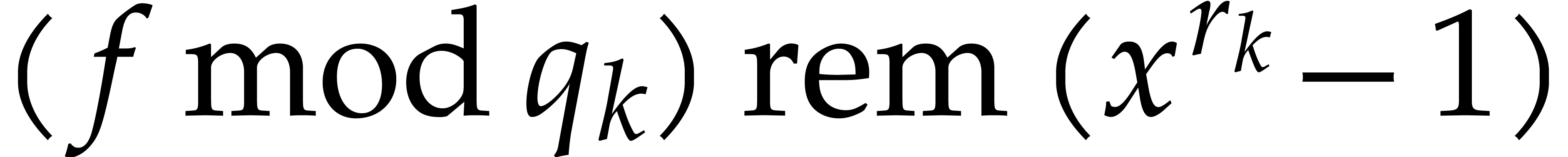 ,
where
,
where 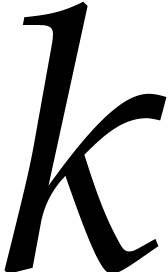 runs over
runs over  .
With high probability, this algorithm runs in time
.
With high probability, this algorithm runs in time 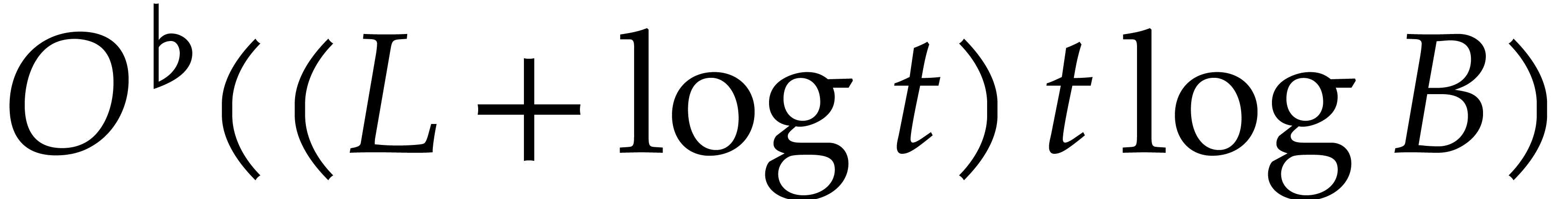 , modulo the heuristic Hred.
For comparison, the best known complexity bound for univariate
polynomials with integer coefficients is
, modulo the heuristic Hred.
For comparison, the best known complexity bound for univariate
polynomials with integer coefficients is 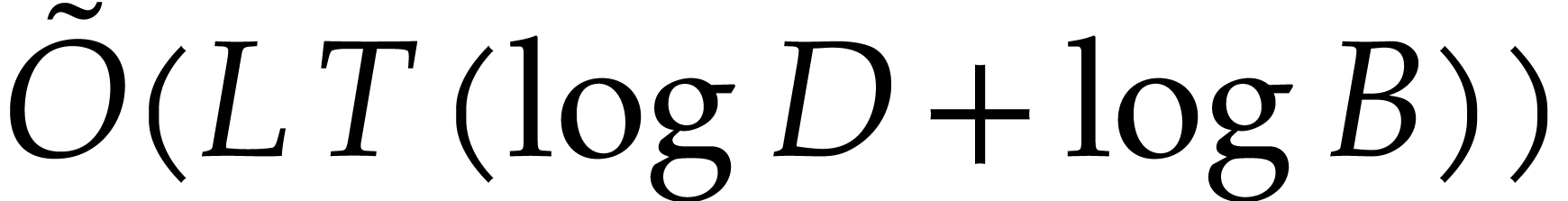 ,
unconditionally [21, Theorem 1.2].
,
unconditionally [21, Theorem 1.2].
The FFT based technique from this section is intended to be used in
combination with a probabilistic recombination method such as Algorithm
3 or the technique from the previous subsection. In the
most favorable case when we are always able to pick  close to
close to  , we have seen that
approximately
, we have seen that
approximately 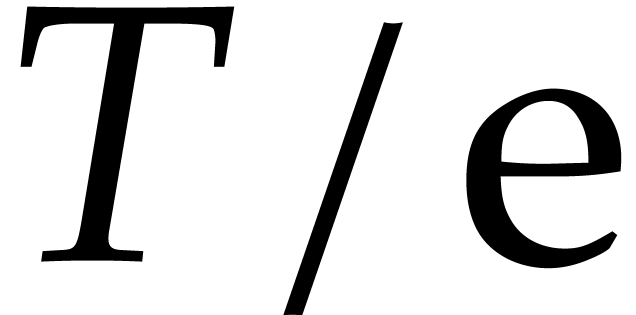 terms of
terms of  are expected not collide modulo
are expected not collide modulo 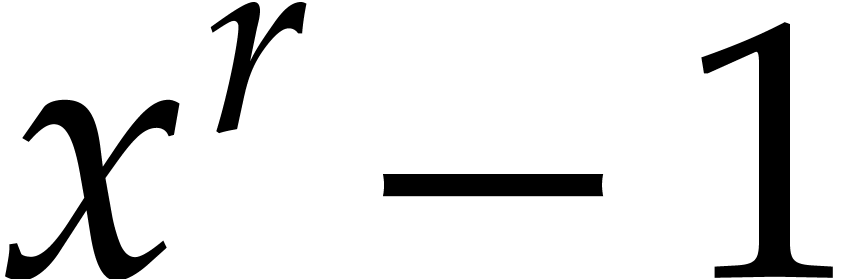 .
This means that we have evaluate
.
This means that we have evaluate  at least
at least 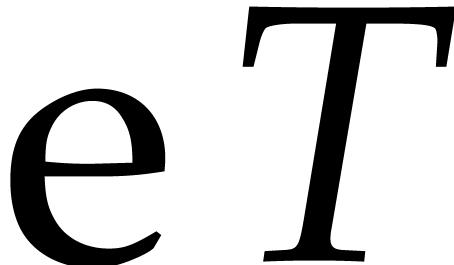 times in order to determine its sparse interpolation.
Recall that only
times in order to determine its sparse interpolation.
Recall that only 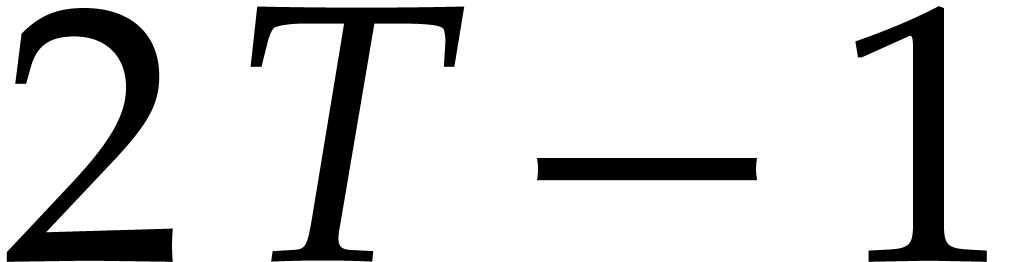 evaluations were required with
Algorithm 4. An interesting question is whether there exist
any compromises or improvements.
evaluations were required with
Algorithm 4. An interesting question is whether there exist
any compromises or improvements.
One idea is to exploit colliding terms better. For instance, assume that
we are computing  for various moduli
for various moduli 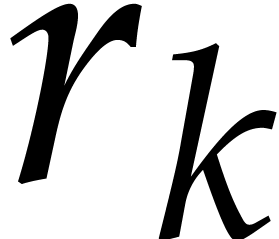 and that
and that 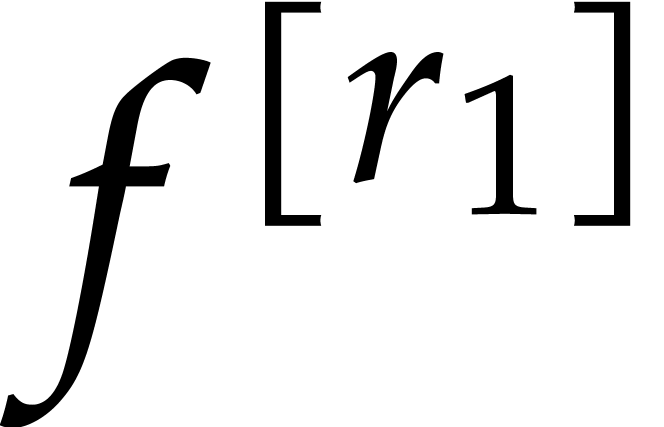 contains a term that
comes from the sum of exactly two terms
contains a term that
comes from the sum of exactly two terms 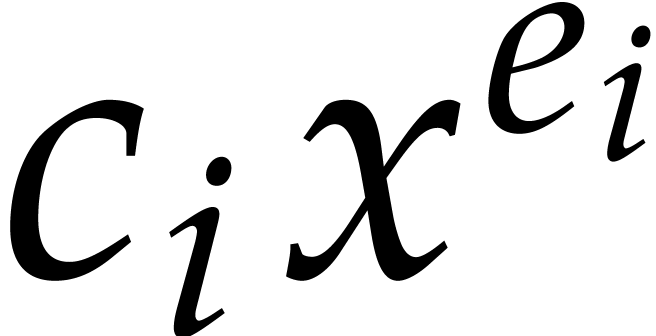 and
and 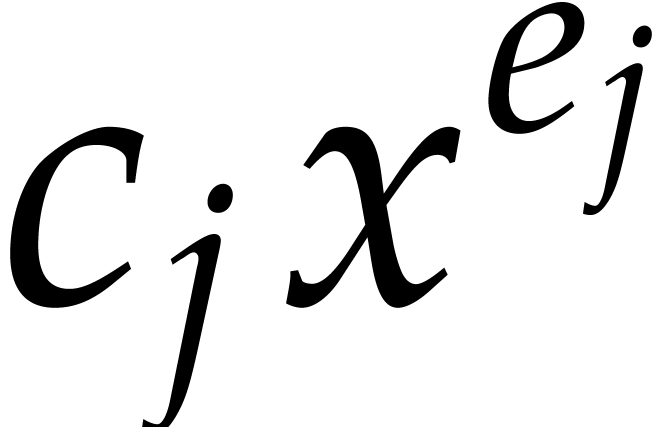 with
with 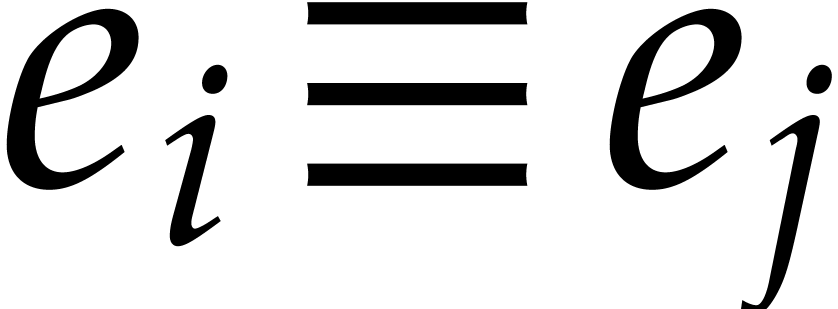 modulo
modulo 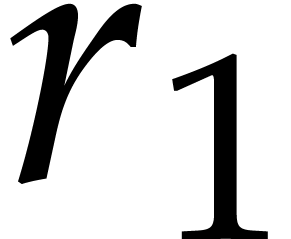 . Now suppose that we are able to determine
. Now suppose that we are able to determine
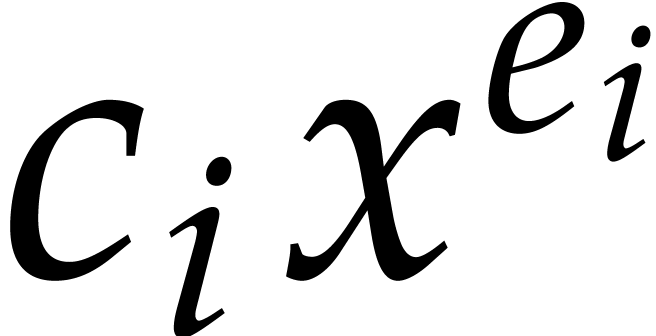 from the reductions
from the reductions 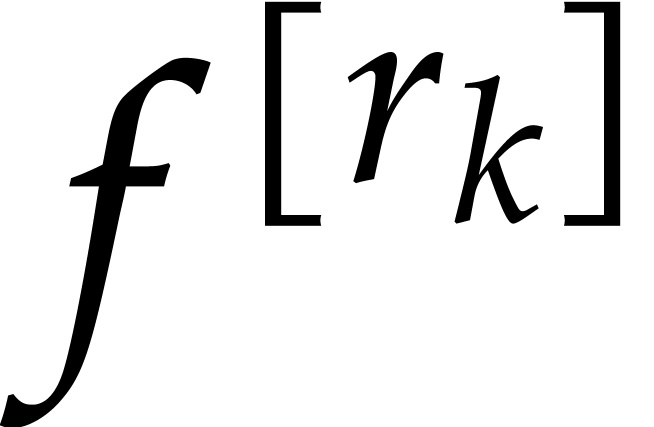 for
a few other moduli
for
a few other moduli 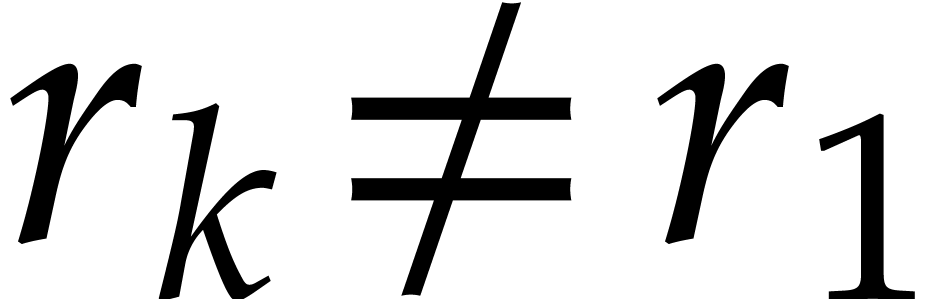 . Then we
might reuse
. Then we
might reuse 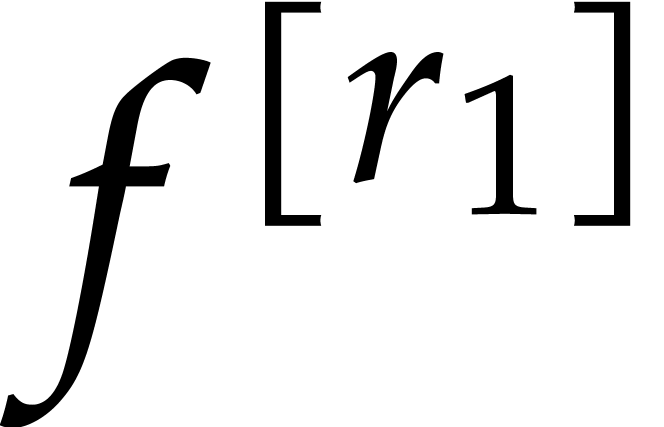 to compute the term
to compute the term 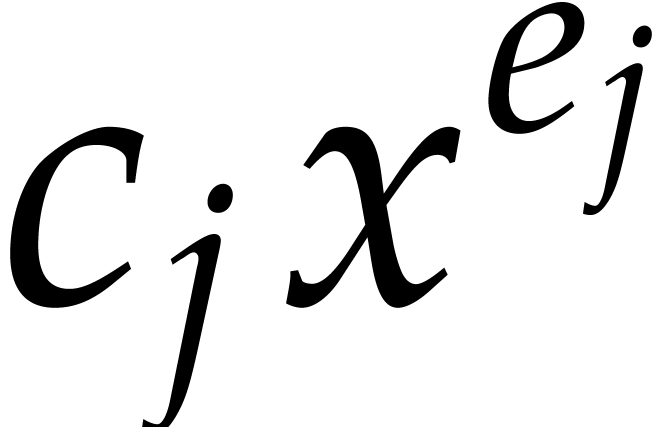 using a simple subtraction.
using a simple subtraction.
Another idea is to optimize the (non-tangent) Graeffe transform variant
of the geometric progression method. With the notations from section 5.1, we have seen how to achieve a complexity of 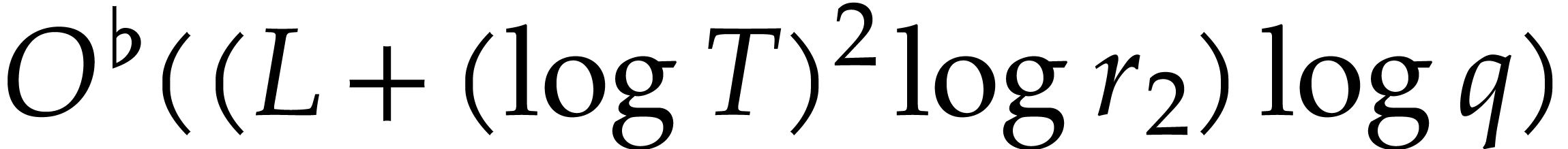 . When taking
. When taking 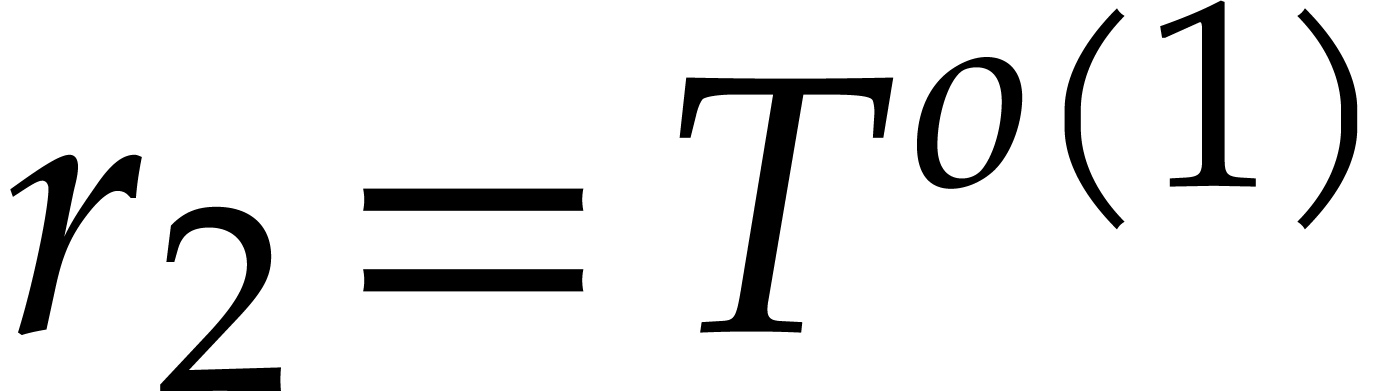 ,
this complexity bound reduces to
,
this complexity bound reduces to 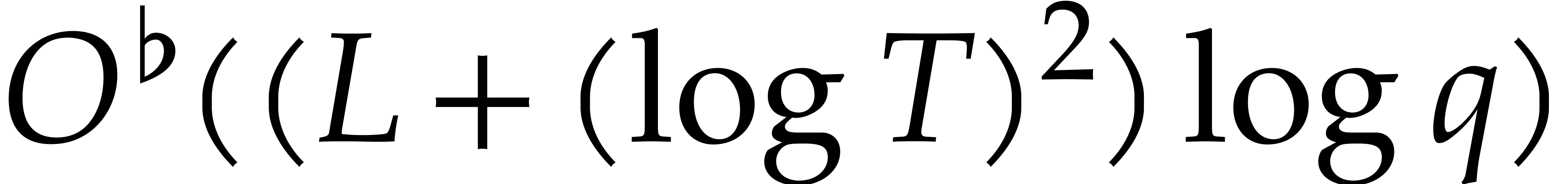 ,
whereas only about
,
whereas only about 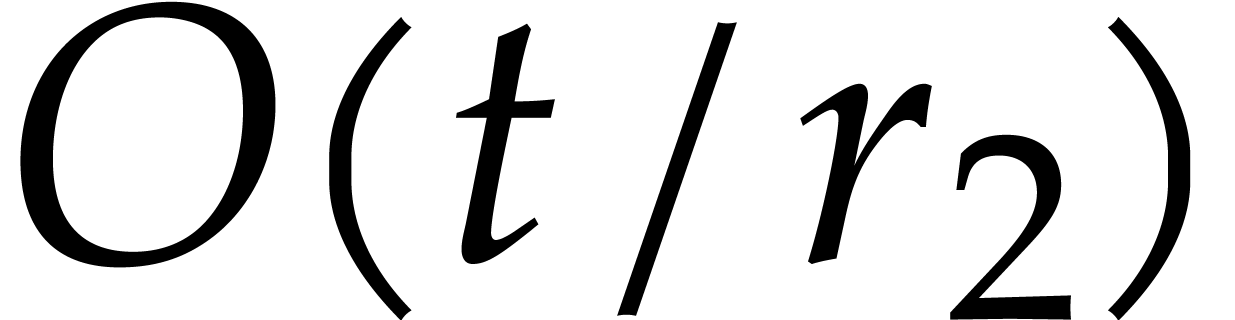 terms of
terms of  collide modulo
collide modulo 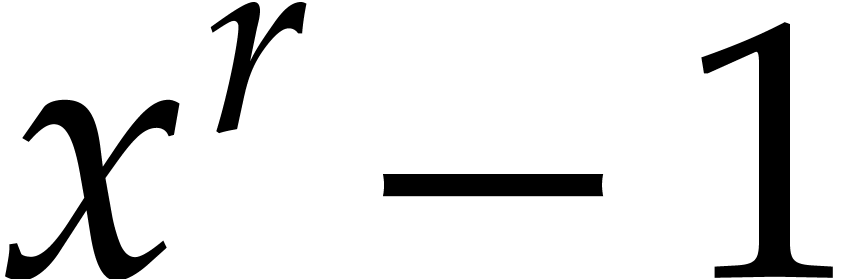 .
.
For functions  that can be evaluated
“fast” (more specifically, this means that the
that can be evaluated
“fast” (more specifically, this means that the 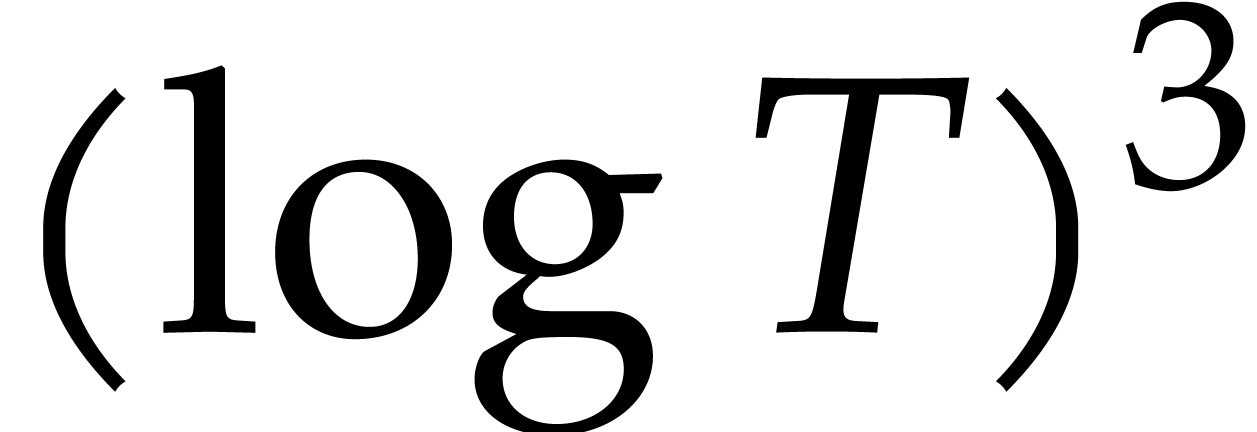 term dominates the
term dominates the  term in the
complexity bound (12) for geometric progression style
algorithms), it may be interesting to switch to the FFT-based approach
from this section. As a bonus, one may exploit the Frobenius map
whenever we need to work over an extension field of
term in the
complexity bound (12) for geometric progression style
algorithms), it may be interesting to switch to the FFT-based approach
from this section. As a bonus, one may exploit the Frobenius map
whenever we need to work over an extension field of  . Under the assumption that
. Under the assumption that 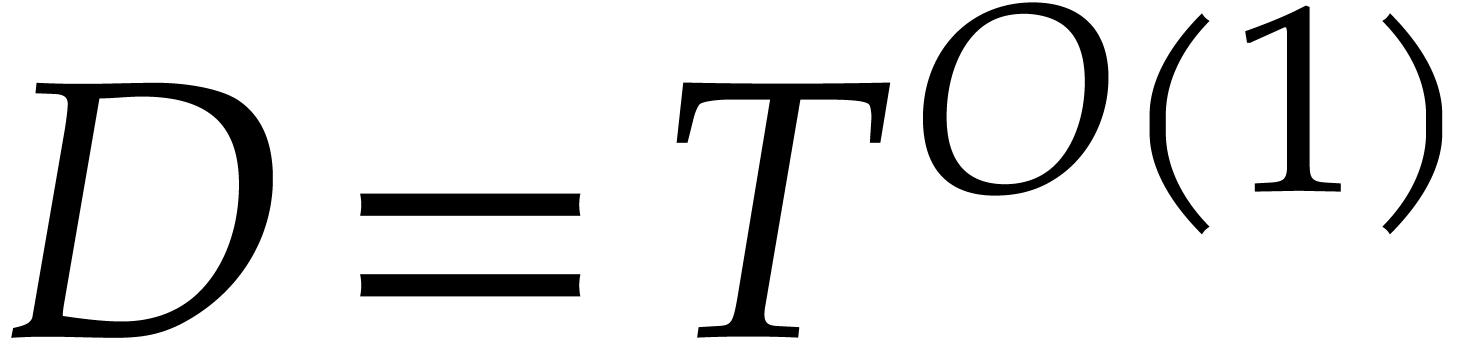 and that suitable orders
and that suitable orders  as in section 6.2
indeed exist, this leads to the complexity bound
as in section 6.2
indeed exist, this leads to the complexity bound
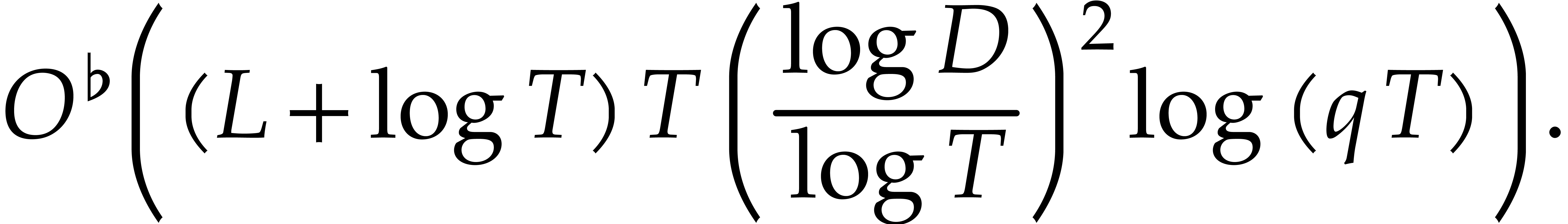 |
(17) |
We recall that this bound hides an increased constant factor with
respect to (12), so geometric progression based algorithms
should remain faster whenever 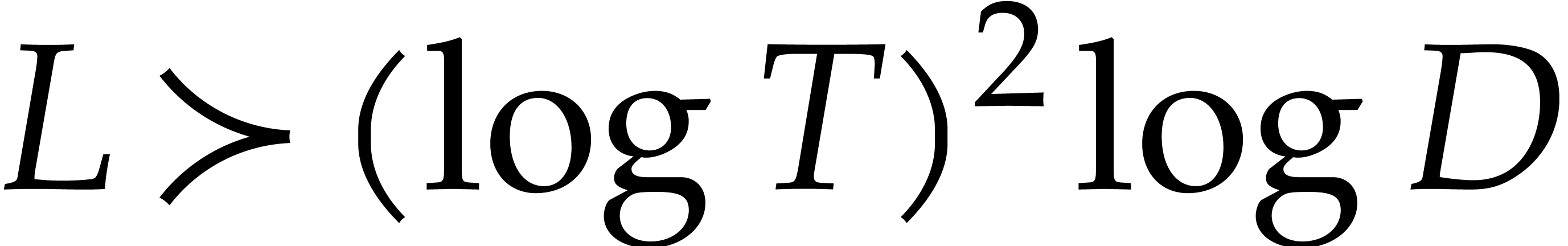 .
Under the assumption that
.
Under the assumption that 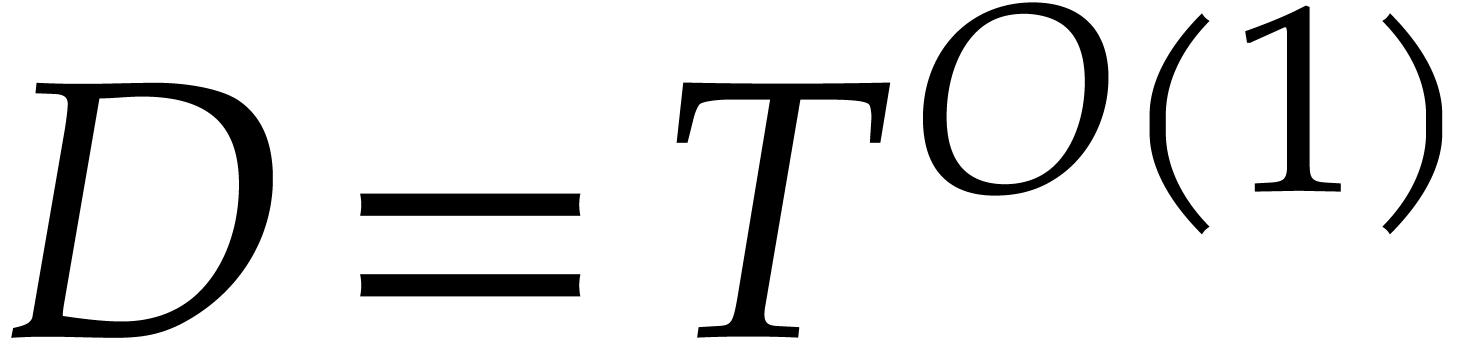 ,
we also notice that (17) is always better than (8).
However, cyclic extension methods should remain faster in the super
sparse case. One noticeable exception concerns sparse interpolation over
the rationals, in which case we may use the approach from section 6.5.
,
we also notice that (17) is always better than (8).
However, cyclic extension methods should remain faster in the super
sparse case. One noticeable exception concerns sparse interpolation over
the rationals, in which case we may use the approach from section 6.5.
In this section we focus on the case when  is a
multivariate polynomial in
is a
multivariate polynomial in 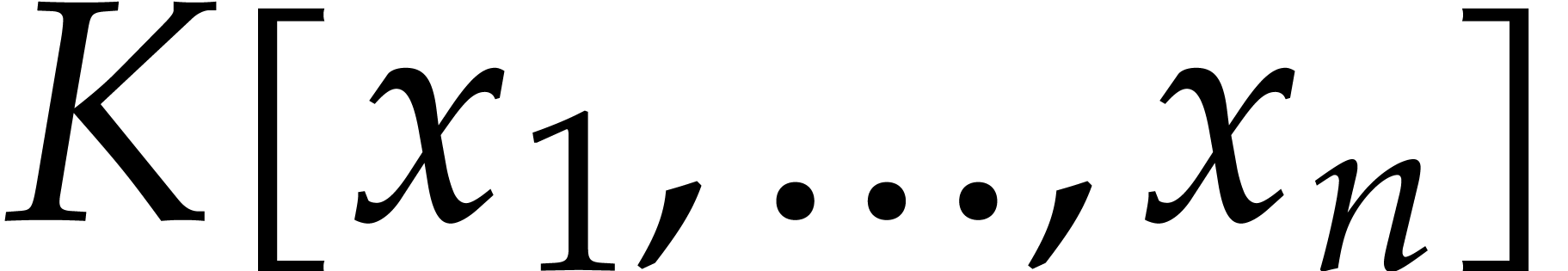 given as a black box
function. In sections 7.1 and 7.2, we first
survey the well-known technique of Kronecker segmentation and known
multivariate variants of Algorithm 4. In section 7.3,
we recall a technique that we introduced in [31] and in
section 7.4 we list a few generally useful ideas. In
sections 7.5, 7.6, and 7.7 we
propose a few new ideas for particular situations.
given as a black box
function. In sections 7.1 and 7.2, we first
survey the well-known technique of Kronecker segmentation and known
multivariate variants of Algorithm 4. In section 7.3,
we recall a technique that we introduced in [31] and in
section 7.4 we list a few generally useful ideas. In
sections 7.5, 7.6, and 7.7 we
propose a few new ideas for particular situations.
One first method for interpolating  is to reduce
to the univariate case using Kronecker segmentation. This reduction
assumes that we have strict bounds
is to reduce
to the univariate case using Kronecker segmentation. This reduction
assumes that we have strict bounds

for the partial degrees of  .
Then we may consider the univariate polynomial
.
Then we may consider the univariate polynomial
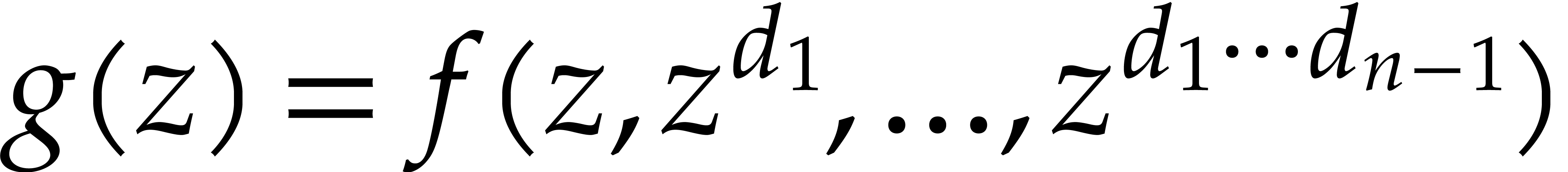
with 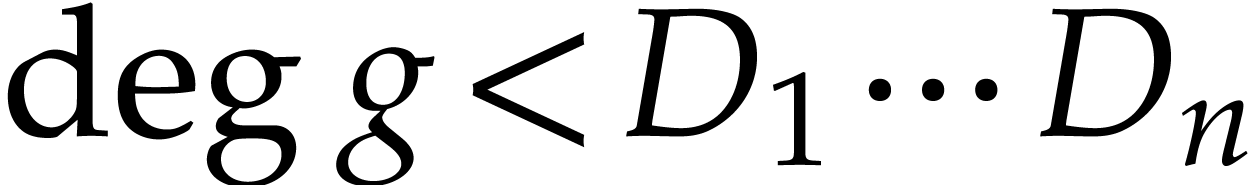 . We now compute the
univariate sparse interpolation of
. We now compute the
univariate sparse interpolation of  and retrieve
the sparse interpolation of
and retrieve
the sparse interpolation of  by mapping each term
by mapping each term
 of
of  to the term
to the term 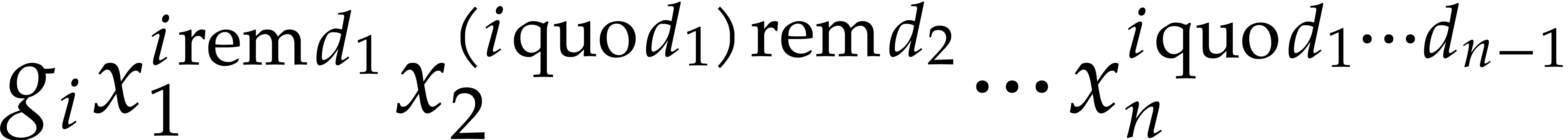 of
of  .
.
Another well known method for multivariate sparse interpolation is to
adapt Algorithm 4. Using the notation 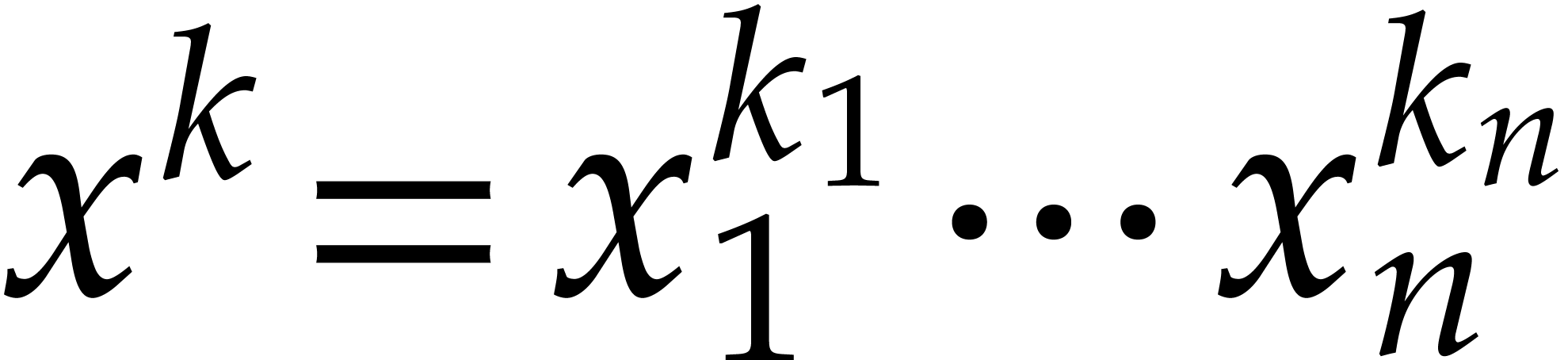 for
for  -tuples
-tuples 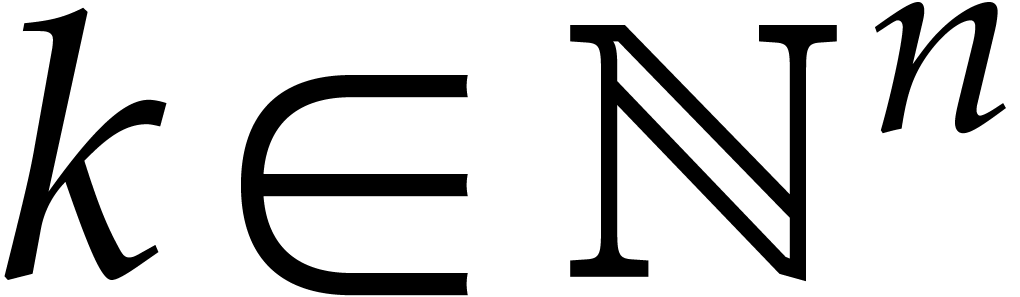 , we may still write
, we may still write
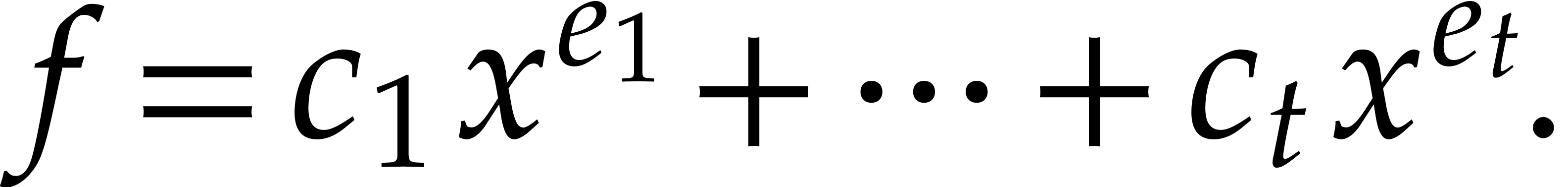
For a suitable vector  , we
again evaluate
, we
again evaluate  at
at 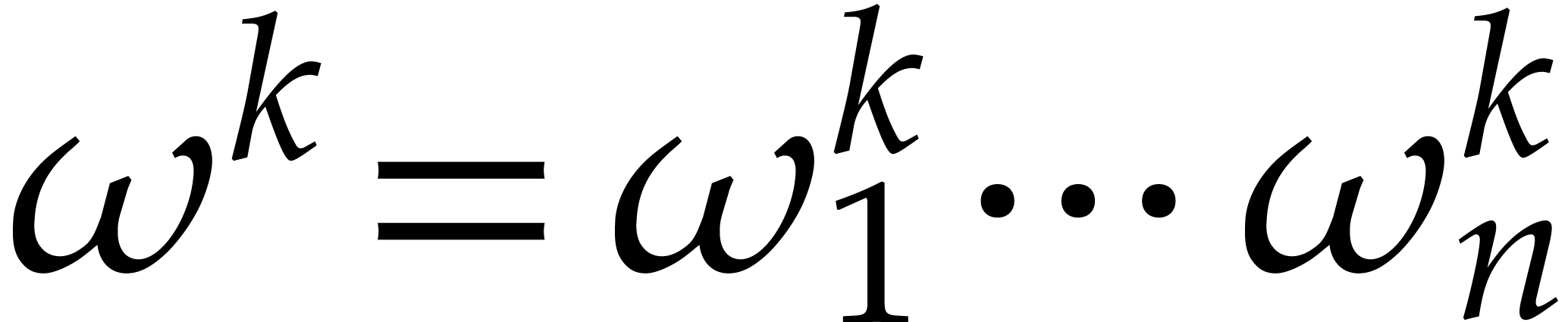 for
for
 , and determine the roots
, and determine the roots
 of
of  as in steps 3 and 4
of Algorithm 4 for the univariate case. The only subtlety
is that we need to chose
as in steps 3 and 4
of Algorithm 4 for the univariate case. The only subtlety
is that we need to chose  in a clever way, so
that we can recover the exponents
in a clever way, so
that we can recover the exponents  from
from  .
.
In the case when  has characteristic zero, Ben-Or
and Tiwari [8] proposed to pick
has characteristic zero, Ben-Or
and Tiwari [8] proposed to pick  , where
, where 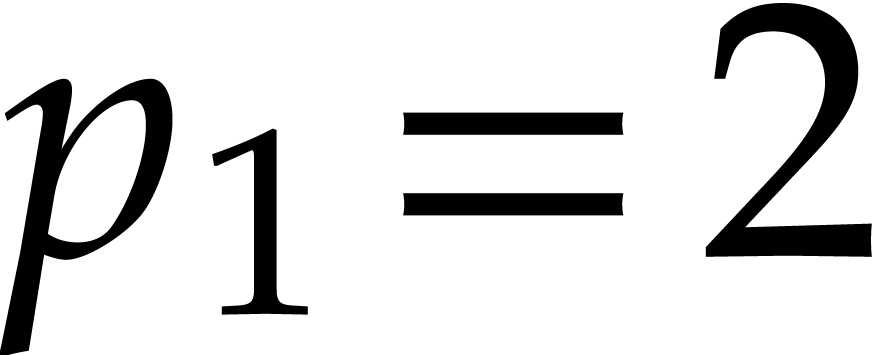 ,
,
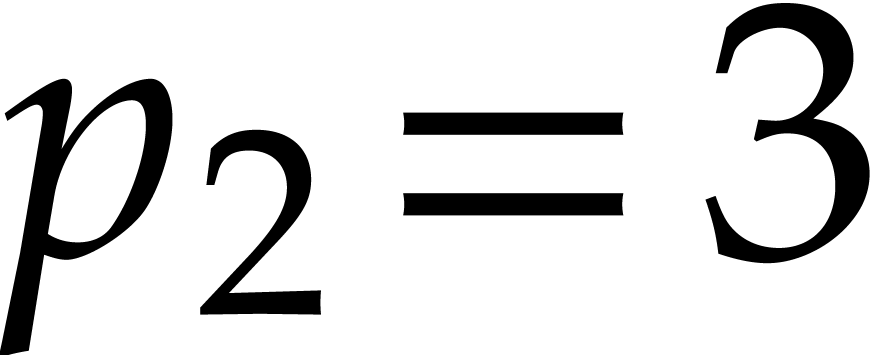 ,
, 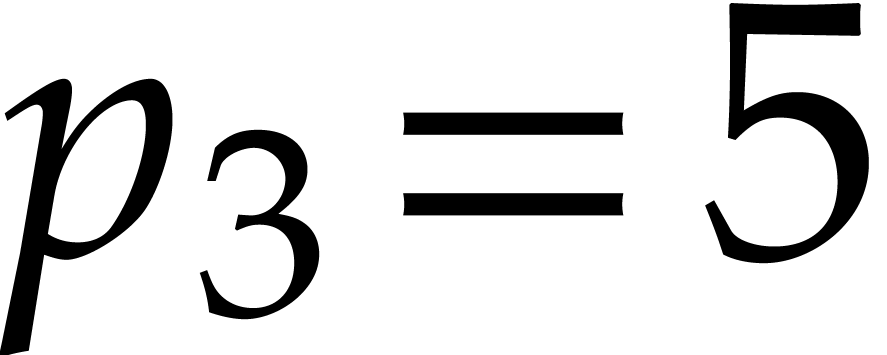 ,
,  is the sequence of prime
numbers; see also [24]. This allows to quickly recover each
is the sequence of prime
numbers; see also [24]. This allows to quickly recover each
 from
from 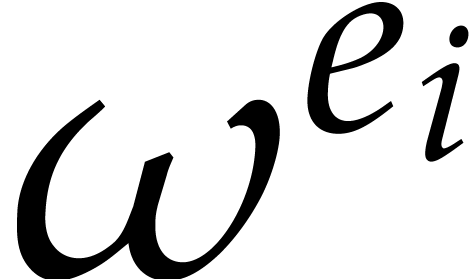 through smooth
prime factorization. The approach still works for finite fields
through smooth
prime factorization. The approach still works for finite fields  of characteristic
of characteristic 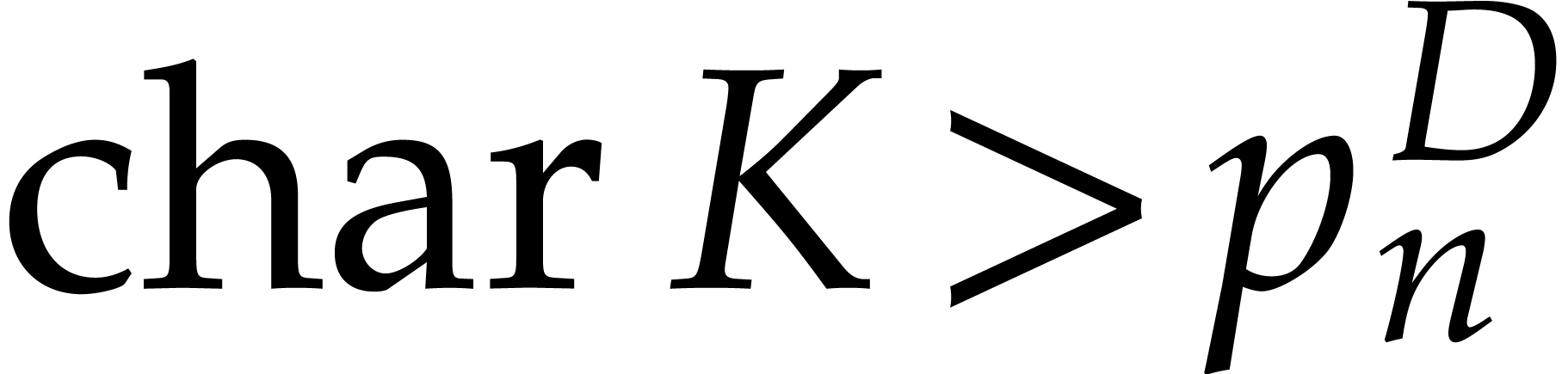 .
With respect to Kronecker segmentation, the approach is interesting if
the total degree
.
With respect to Kronecker segmentation, the approach is interesting if
the total degree  is much smaller than the sum
is much smaller than the sum
 of the partial degrees. Note that we really need
the weighted total degree
of the partial degrees. Note that we really need
the weighted total degree

to be bounded by 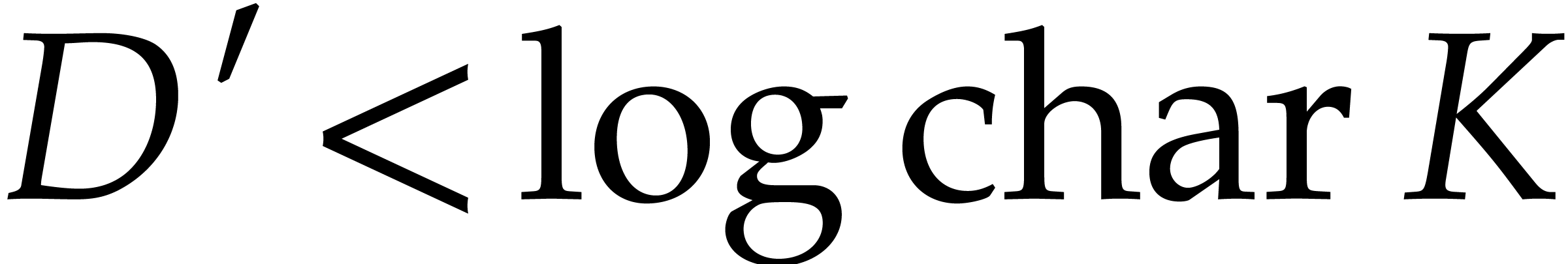 .
.
If  is a finite field, then we may still use a
variant of this idea, which partially goes back to [34].
Modulo going to a suitable field extension, we first ensure that
is a finite field, then we may still use a
variant of this idea, which partially goes back to [34].
Modulo going to a suitable field extension, we first ensure that  is of the form
is of the form 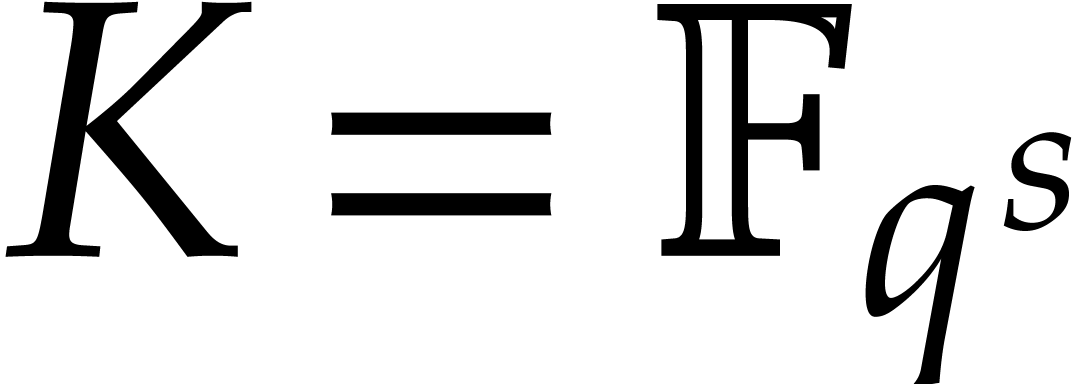 ,
where
,
where  and
and 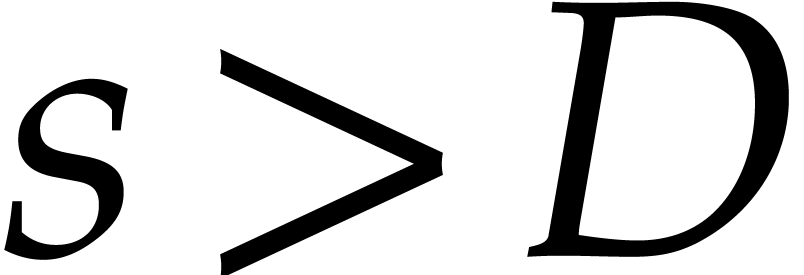 .
For some primitive element
.
For some primitive element 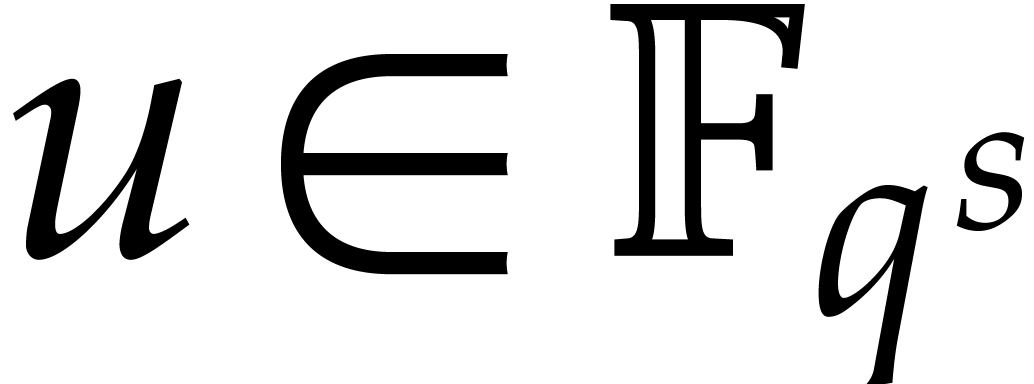 over
over  and
and 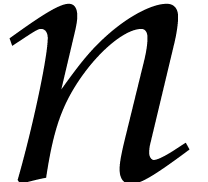 pairwise distinct points
pairwise distinct points 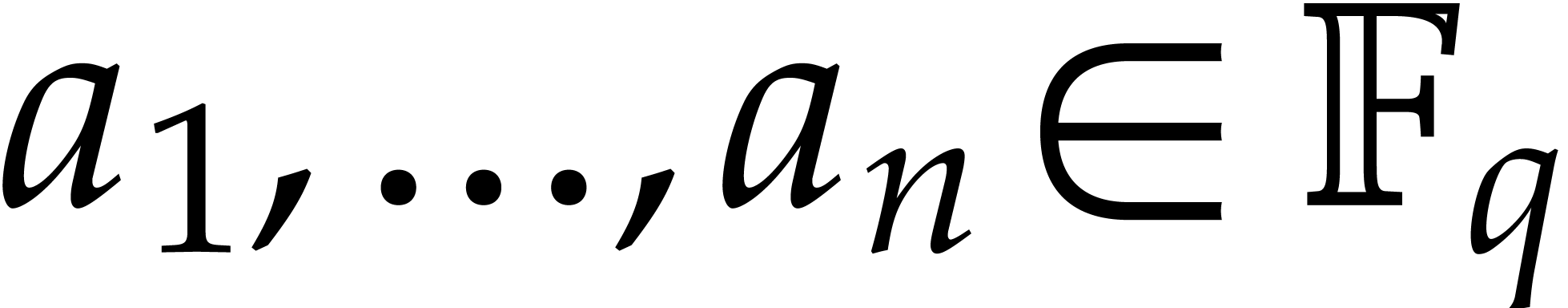 we then take
we then take 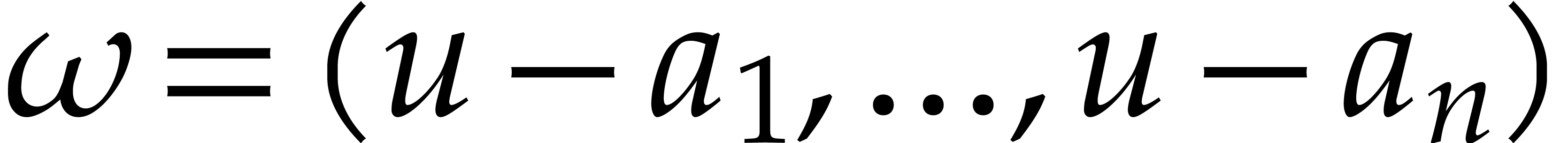 .
.
For sparse interpolations on GPUs, modular arithmetic is often most
efficient for prime numbers of at most  or
or  bits. This may be insufficient for the interpolation
of very large polynomials with
bits. This may be insufficient for the interpolation
of very large polynomials with  and thereby
forces us to use
and thereby
forces us to use 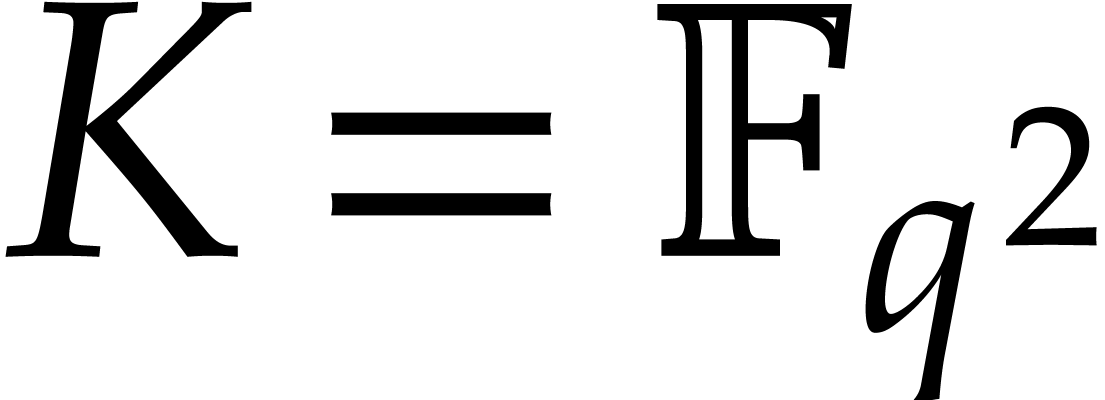 instead. In that case, we may
take
instead. In that case, we may
take 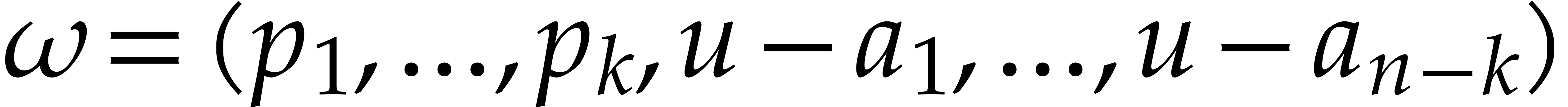 and
and 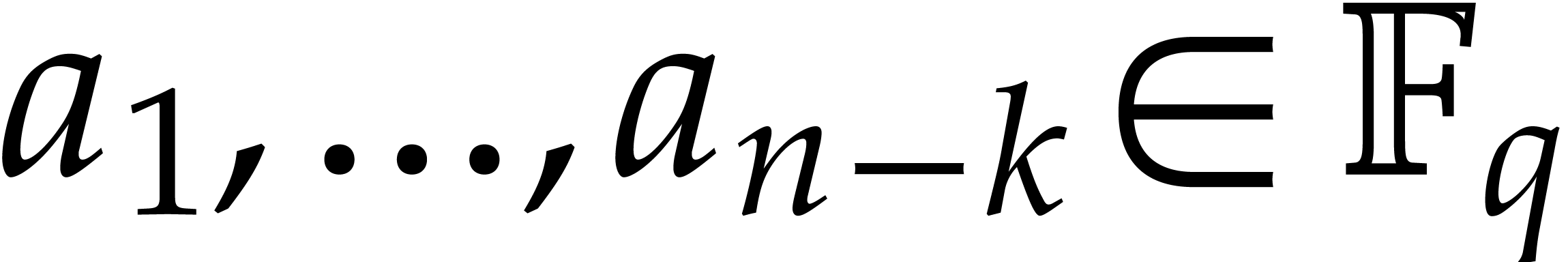 .
We next require the total degree of
.
We next require the total degree of  in
in  to be bounded by
to be bounded by  with
with 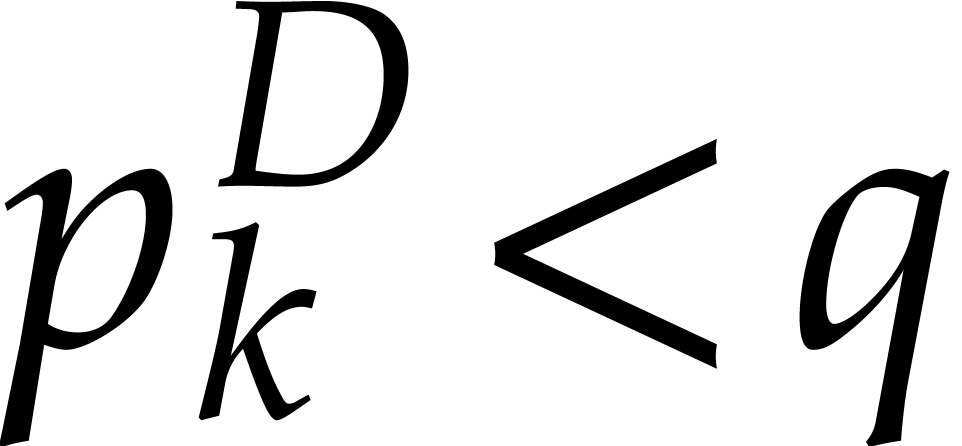 and we require
and we require  to be linear in
to be linear in
 .
.
If one of the above techniques applies, then the complexity analysis is
similar to the one for the univariate case. Indeed, after the evaluation
step 2 of Algorithm 4, the values 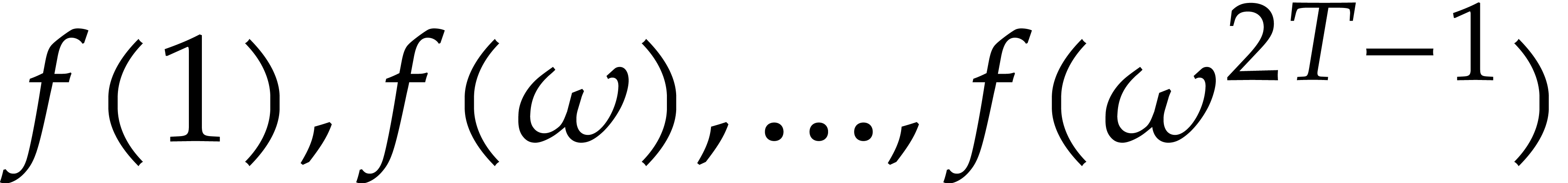 are in
are in  , so steps 3, 4, and 6
can be applied without changes, whereas the discrete logarithm
computations in step 5 are replaced by cheaper factorizations. Under the
assumption that we can find a suitable divisor
, so steps 3, 4, and 6
can be applied without changes, whereas the discrete logarithm
computations in step 5 are replaced by cheaper factorizations. Under the
assumption that we can find a suitable divisor 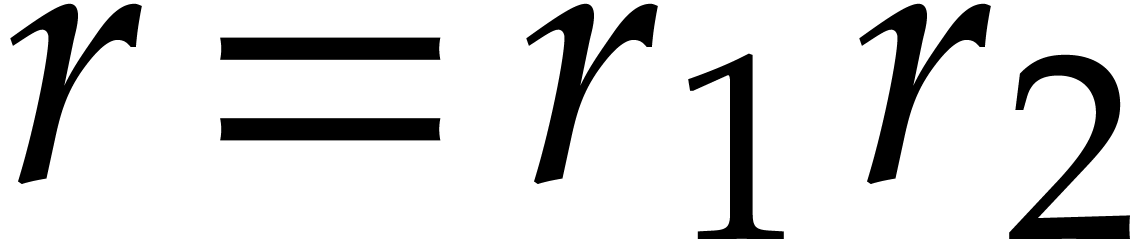 of
of  with
with  and
and  smooth, this leads to a complexity bound of the form
smooth, this leads to a complexity bound of the form
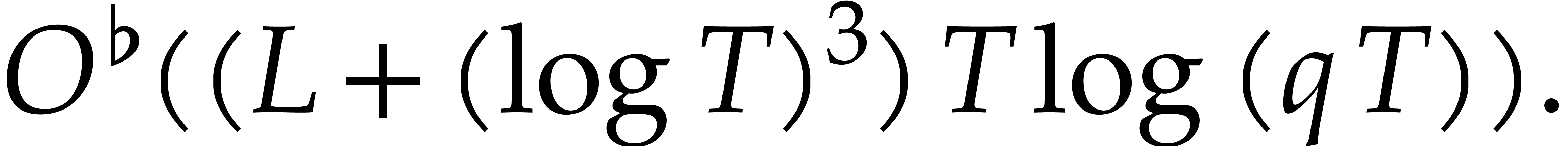 |
(18) |
For  and a random point
and a random point 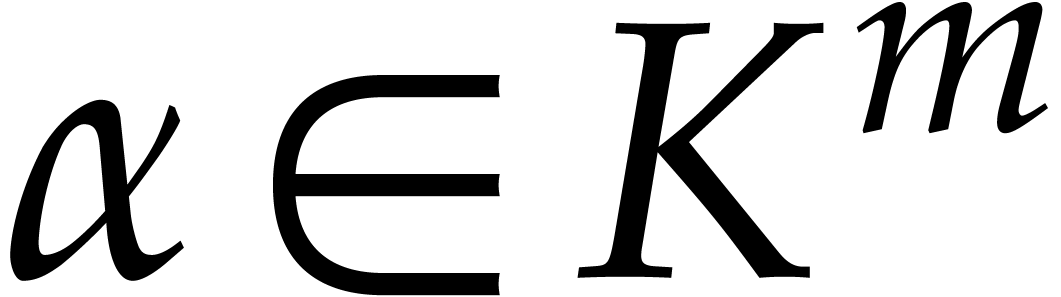 , consider the specialization
, consider the specialization
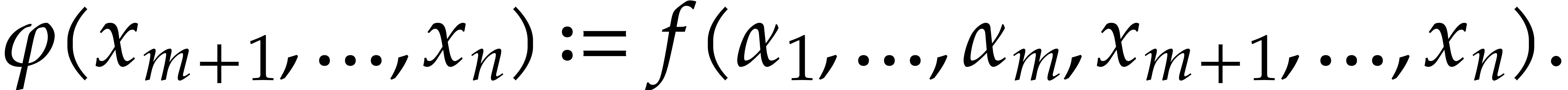
With high probability on  ,
the support of
,
the support of  coincides with the support of
coincides with the support of
 in
in  .
The knowledge of the support of
.
The knowledge of the support of  may sometimes
help with the computation of the support of
may sometimes
help with the computation of the support of  , which in turn facilitates its sparse
interpolation. Since
, which in turn facilitates its sparse
interpolation. Since  has less variables, we may
recursively use a similar strategy for determining the support of
has less variables, we may
recursively use a similar strategy for determining the support of  . This idea essentially goes back
to Zippel [55] in the case when
. This idea essentially goes back
to Zippel [55] in the case when  and
was applied successfully in [31] in combination with more
modern algorithms for sparse interpolation.
and
was applied successfully in [31] in combination with more
modern algorithms for sparse interpolation.
Let us show how to implement this strategy in the case when we know a
bound  for the total degree of
for the total degree of  with respect to
with respect to 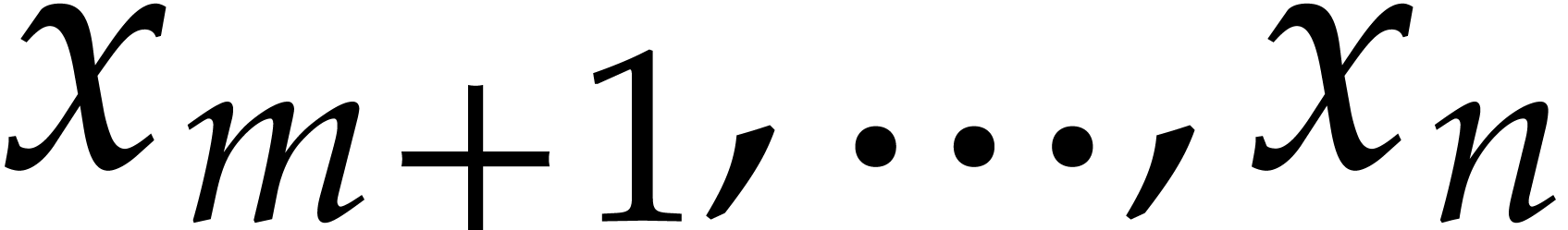 . We first
pick
. We first
pick 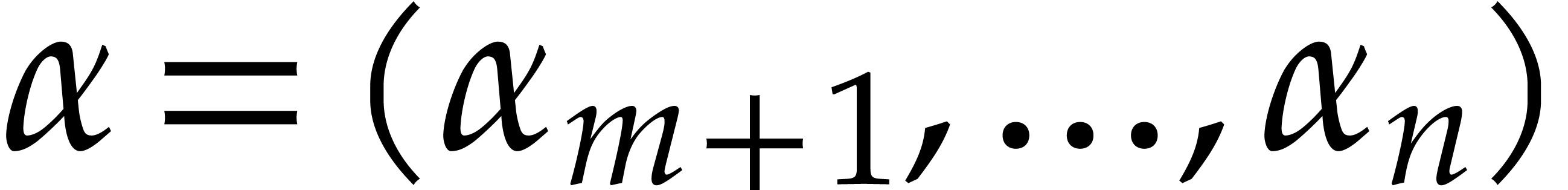 in a similar way as
in a similar way as  in subsection 7.2: if
in subsection 7.2: if 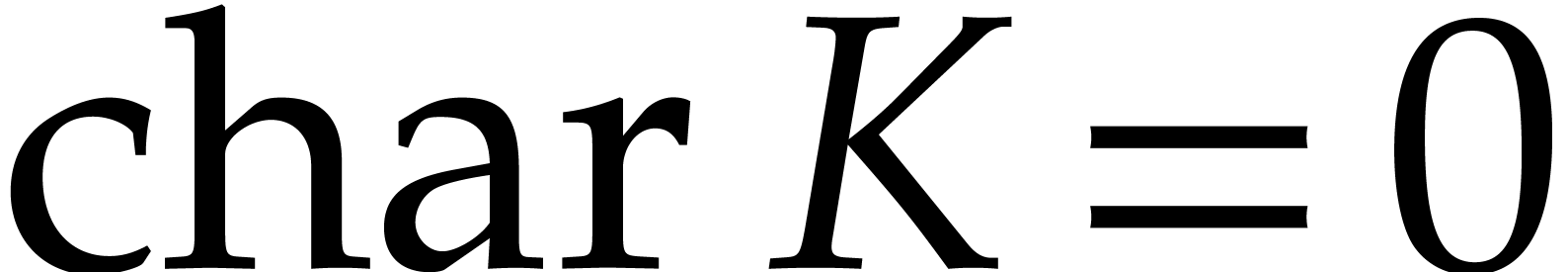 or
or 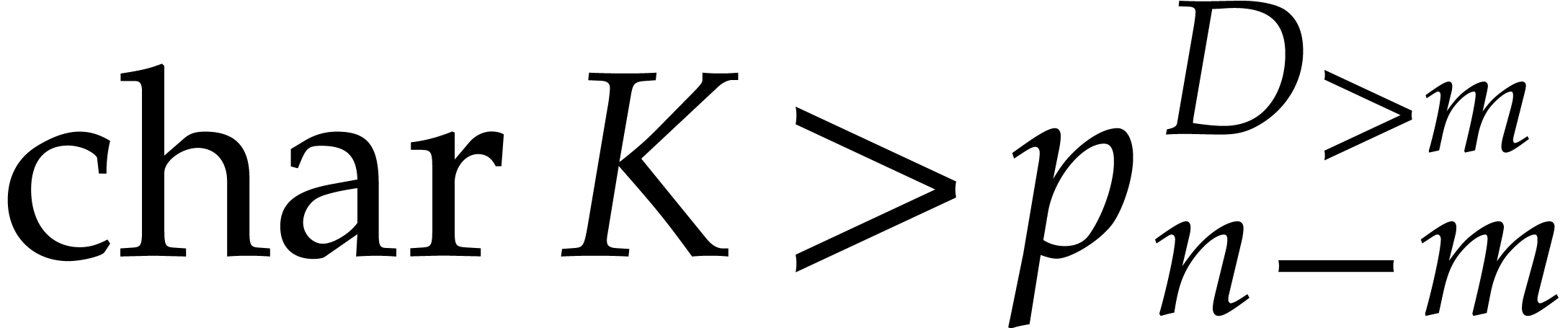 , then we take
, then we take  ; otherwise, we take
; otherwise, we take  with the notations from there. The auxiliary function
with the notations from there. The auxiliary function
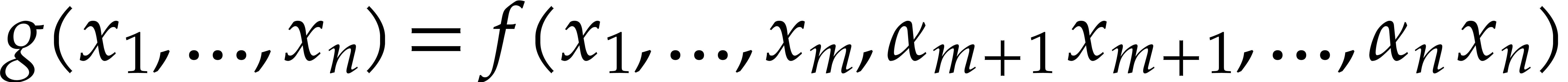
admits the property that the terms 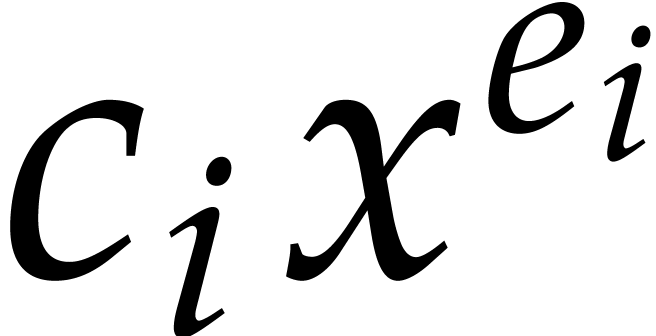 of
of  are in one to one correspondence with the terms
are in one to one correspondence with the terms 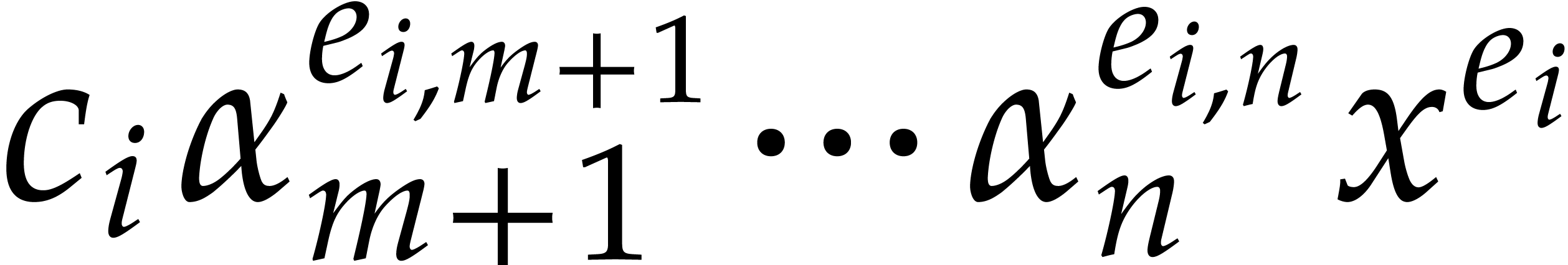 of
of  (where
(where 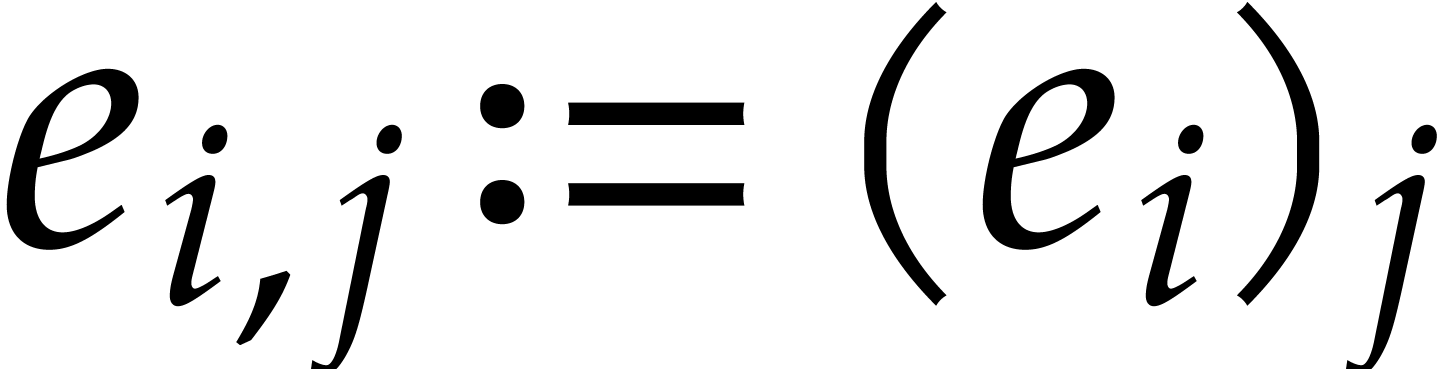 ). Moreover, knowing both
). Moreover, knowing both  and
and 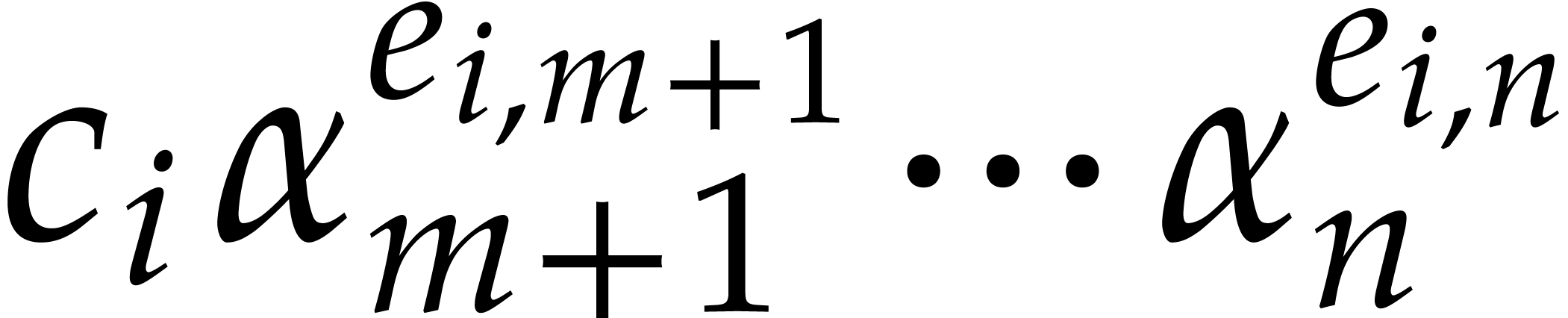 allows us to compute
allows us to compute 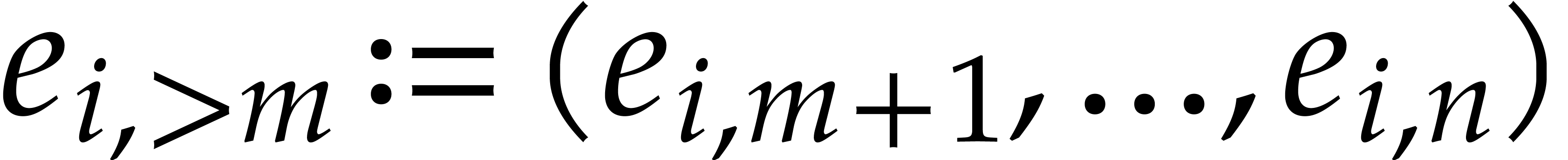 through factorization.
through factorization.
For a suitable element 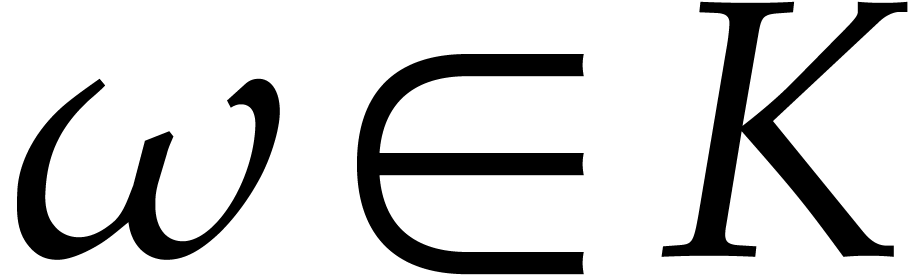 of order
of order  and suitable integers
and suitable integers 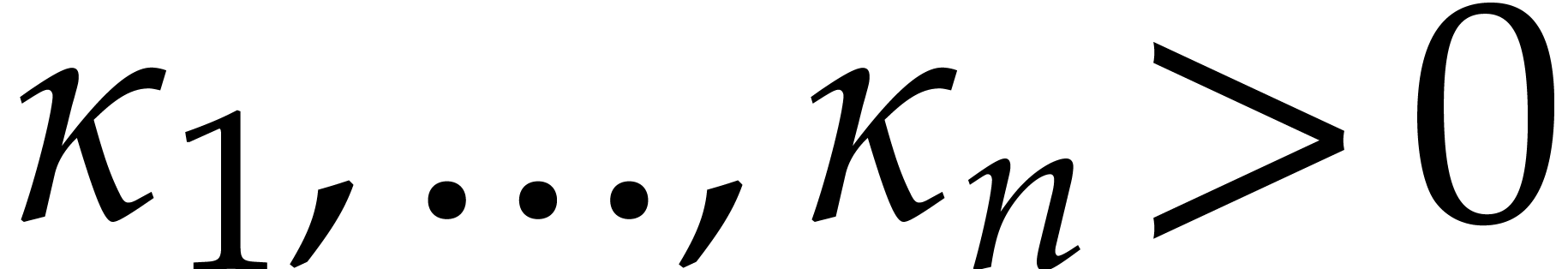 , the
next idea is to compute
, the
next idea is to compute
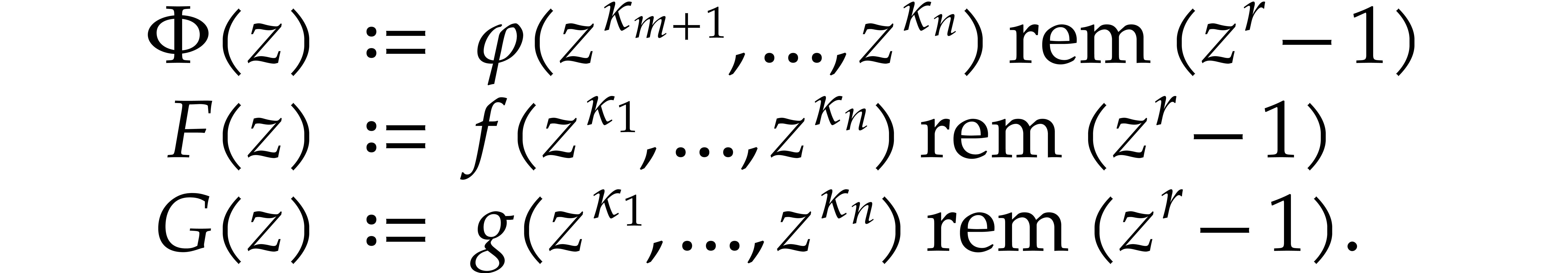
Mimicking Algorithm 4, we take 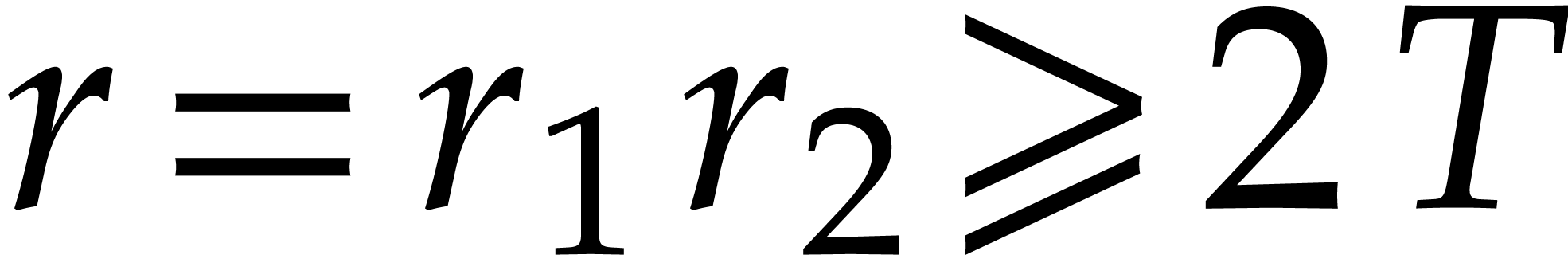 as
large as possible under the conditions that
as
large as possible under the conditions that  and
and
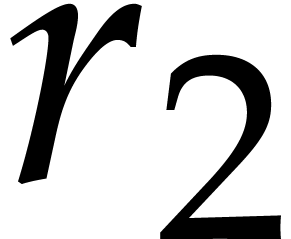 be smooth (ideally speaking,
be smooth (ideally speaking, 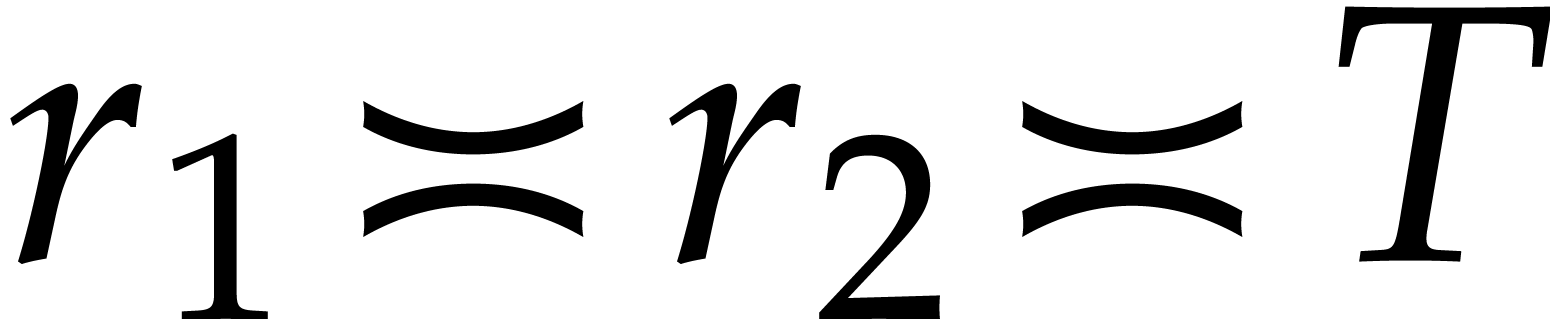 ). We compute the polynomial
). We compute the polynomial  , its roots, and the exponents
, its roots, and the exponents  modulo
modulo  as in Algorithm 4, which
allows us to recover
as in Algorithm 4, which
allows us to recover  . We
compute
. We
compute 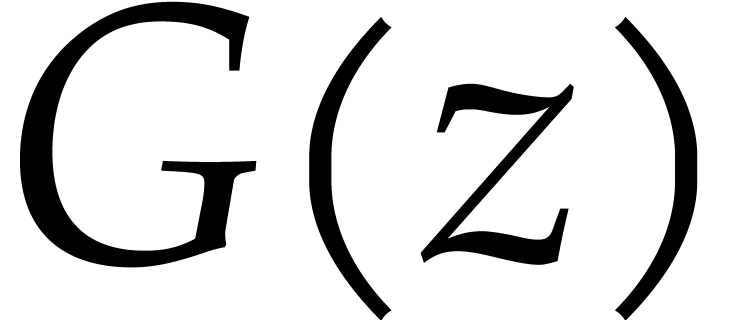 in a similar way (while exploiting the
fact that the polynomial
in a similar way (while exploiting the
fact that the polynomial  is the same in both
cases with high probability). Now consider some
is the same in both
cases with high probability). Now consider some 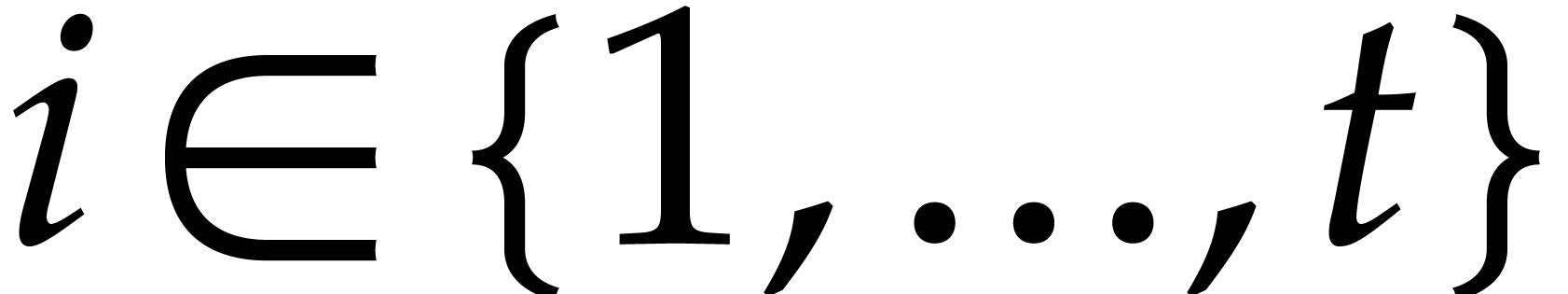 such that
such that 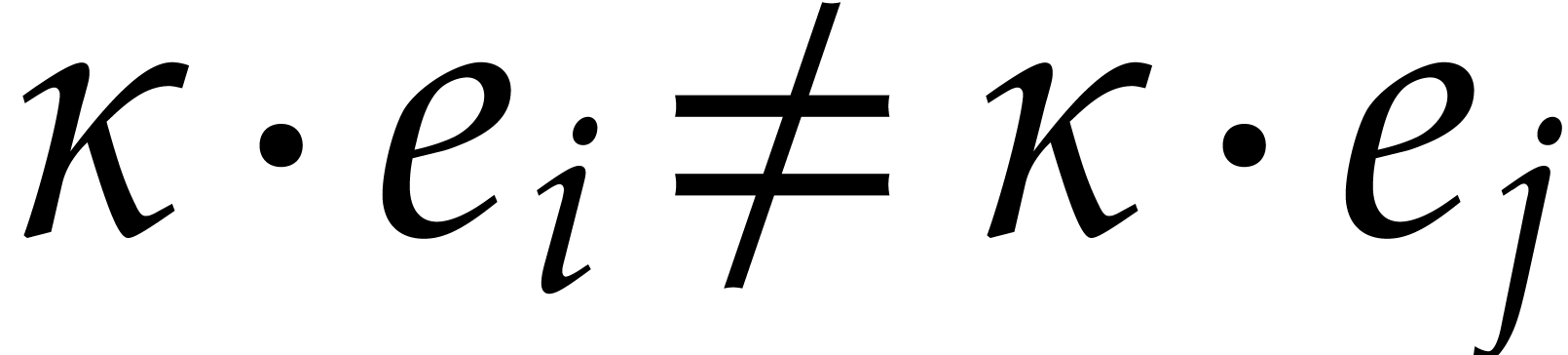 modulo
modulo  and
and
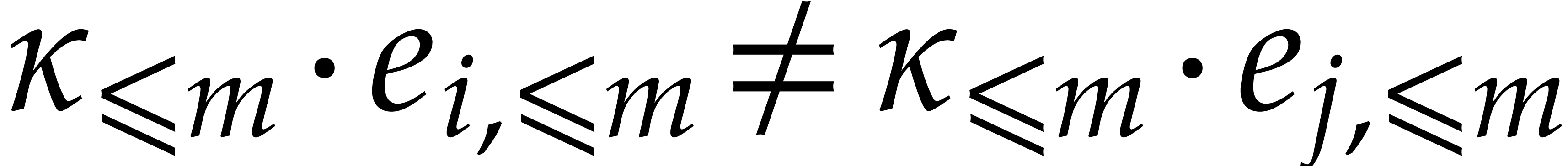 modulo
modulo  for all
for all  . Then we may recover
. Then we may recover  from the terms
from the terms 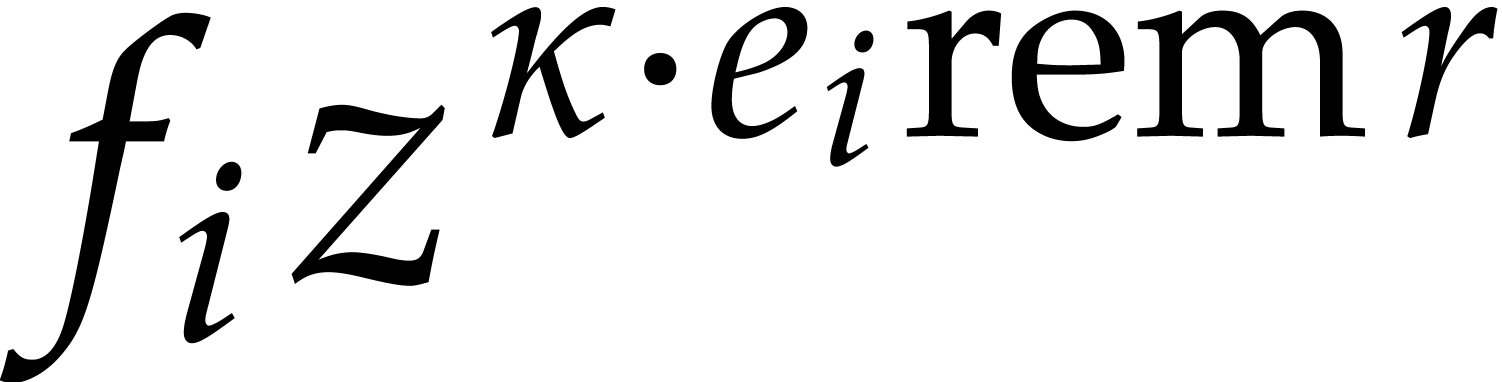 and
and 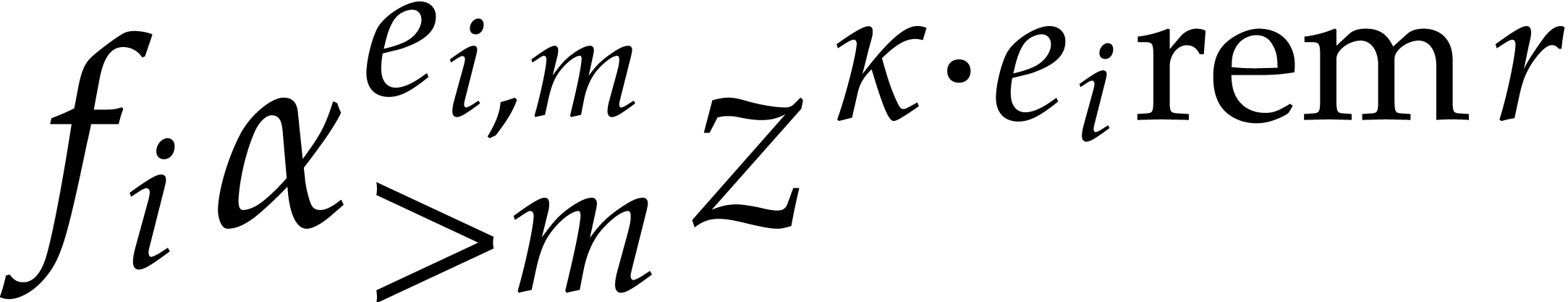 of
of  and
and 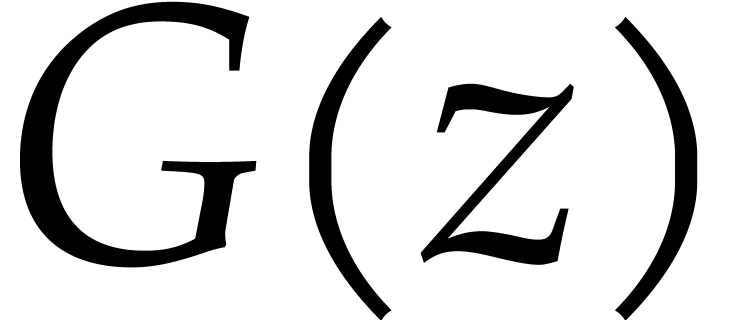 . Moreover,
. Moreover, 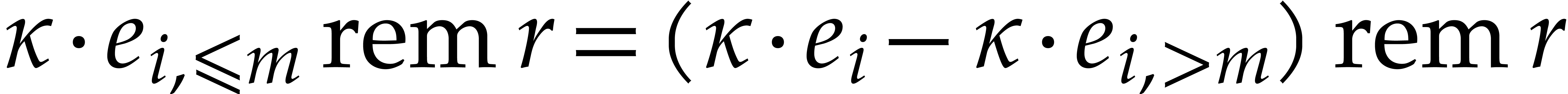 is an exponent
of
is an exponent
of  (with high probability). Since
(with high probability). Since  and
and  are both known, this allows us
to recover
are both known, this allows us
to recover 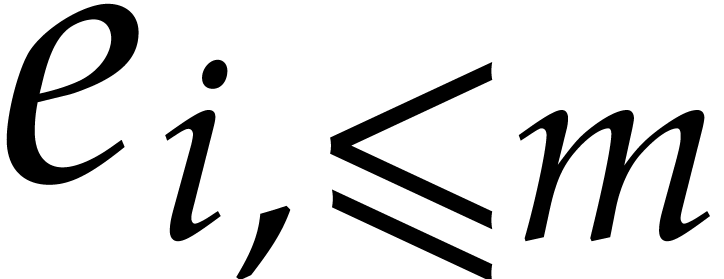 .
.
Instead of a geometric progression method, we may also opt for the
approach from section 6. In that case, we rather take an
order  close to
close to  ,
and we compute
,
and we compute  and
and 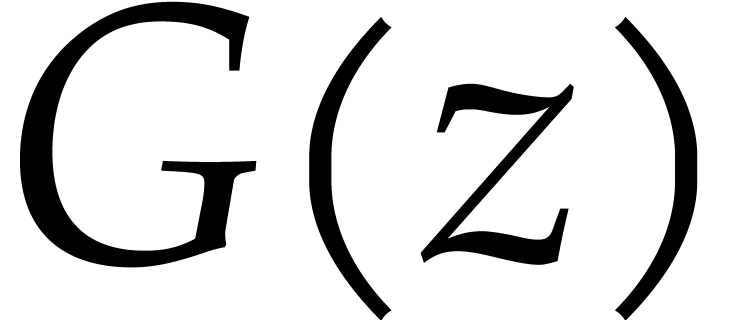 using
Algorithm 5. With high probability, this only leads to a
constant portion of the exponents of
using
Algorithm 5. With high probability, this only leads to a
constant portion of the exponents of  .
By varying the choices of
.
By varying the choices of  and
and  , we may increase this portion until we find
all exponents.
, we may increase this portion until we find
all exponents.
This way of interpolating multivariate polynomials by packets of
variables is particularly interesting if  admits
significantly less terms than
admits
significantly less terms than  (so that the
interpolation of
(so that the
interpolation of  only requires a small portion
of the total time) and
only requires a small portion
of the total time) and 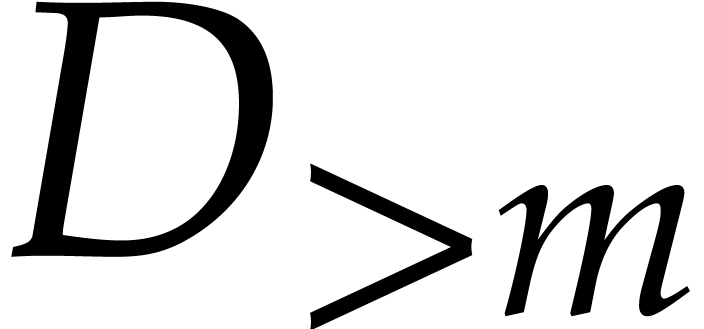 is small. In that case,
we can typically avoid expensive field extensions as considered in
sections 5.3, 6.3, and 6.4. If
is small. In that case,
we can typically avoid expensive field extensions as considered in
sections 5.3, 6.3, and 6.4. If
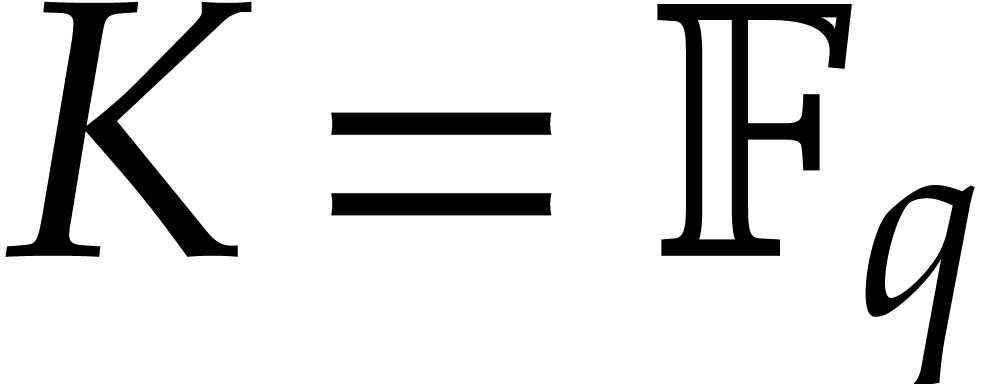 is a finite field with
is a finite field with 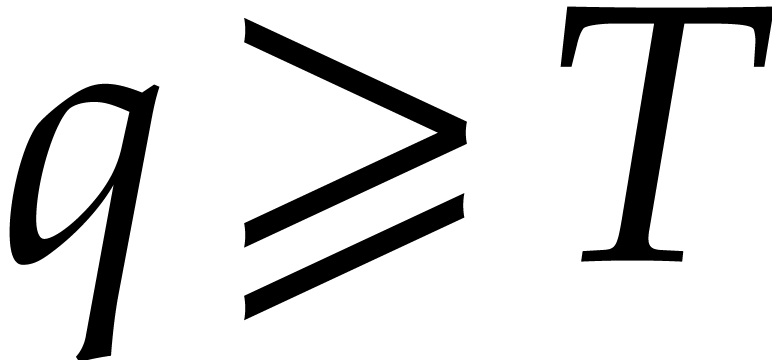 , this leads to a complexity of
, this leads to a complexity of 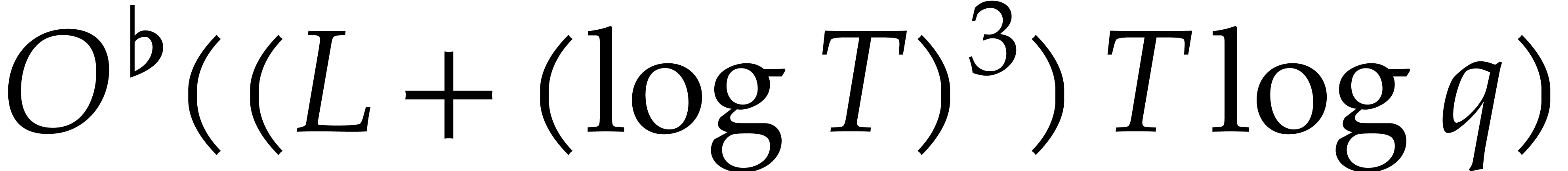 for the geometric progression method and
for the geometric progression method and 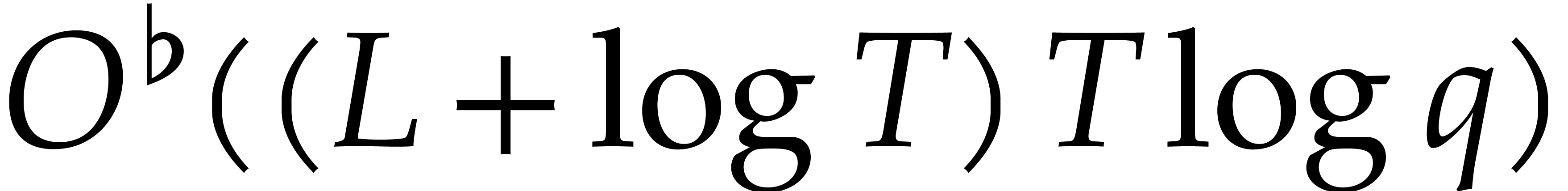 when
using FFTs (but with a larger constant factor for the dependency on
when
using FFTs (but with a larger constant factor for the dependency on
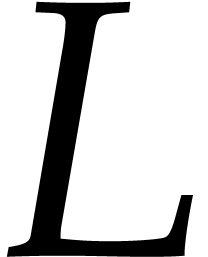 ).
).
Remark 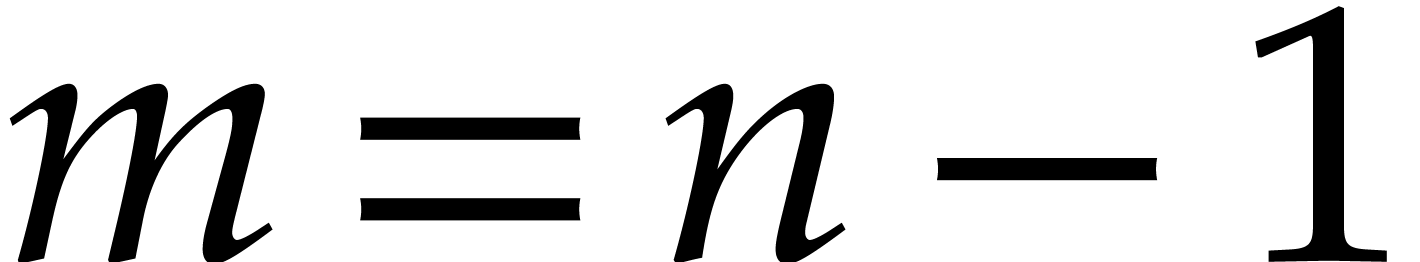 and the coefficients of
and the coefficients of  with respect to
with respect to  are dense
polynomials in
are dense
polynomials in 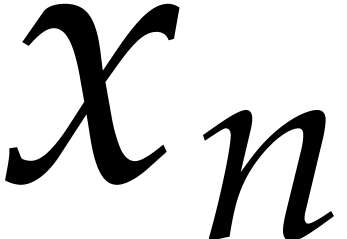 .
.
In the previous subsections, besides a bound on the total degree  , we have also used bounds on the
partial degrees
, we have also used bounds on the
partial degrees  and the total degree
and the total degree 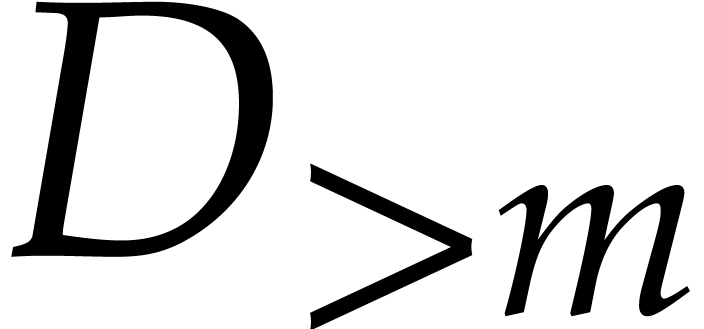 with respect to a packet of variables
with respect to a packet of variables 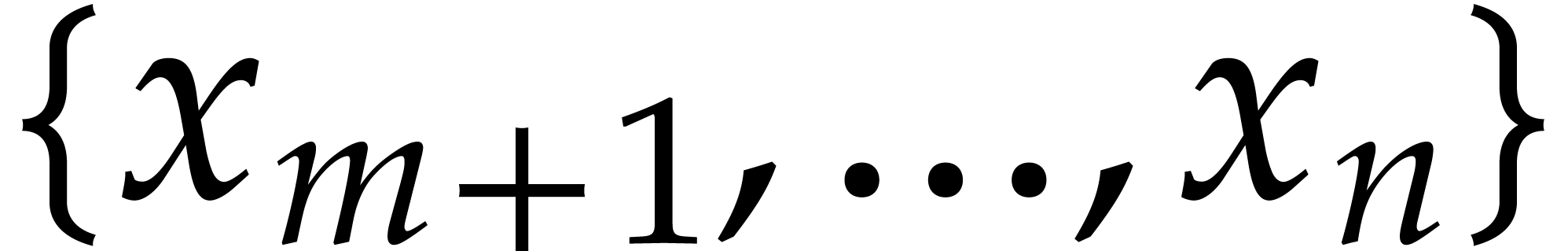 . More generally, for the sparse interpolation
of a large multivariate polynomial
. More generally, for the sparse interpolation
of a large multivariate polynomial  ,
it is a good idea to first gather some general information about
,
it is a good idea to first gather some general information about  . This can often be done quickly
and the information can be used to select a fast interpolation strategy
for the specific polynomial at hand. For instance, in the previous
subsection, it may help finding a packet of variables
. This can often be done quickly
and the information can be used to select a fast interpolation strategy
for the specific polynomial at hand. For instance, in the previous
subsection, it may help finding a packet of variables 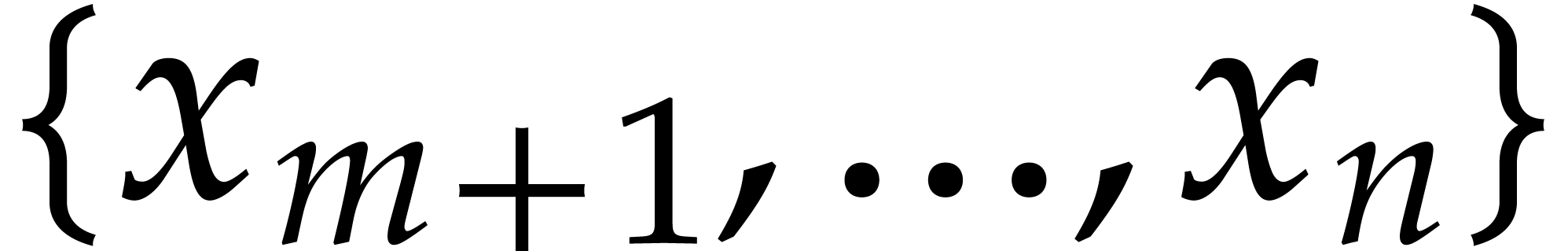 that leads to optimal performance.
that leads to optimal performance.
Let us now describe a few probabilistic methods to gain information
about  .
.
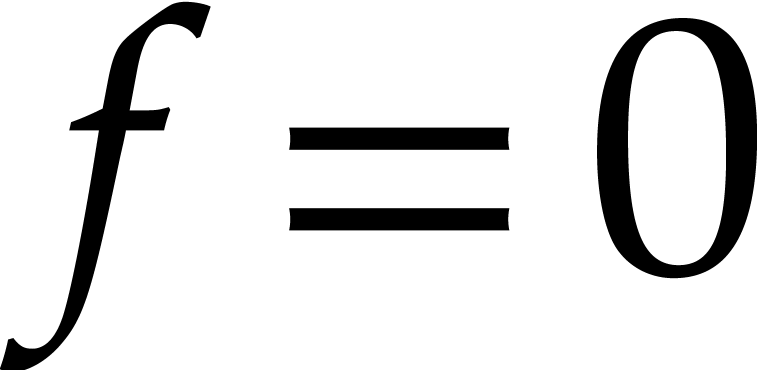 through one evaluation at
a random point
through one evaluation at
a random point  .
.
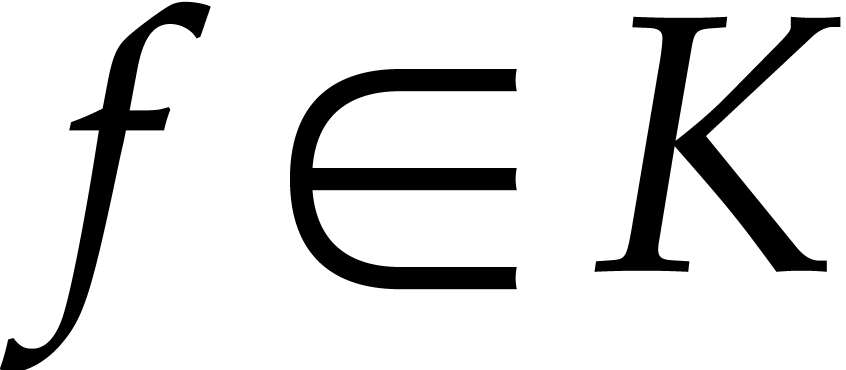 through one more
evaluation at a random point
through one more
evaluation at a random point 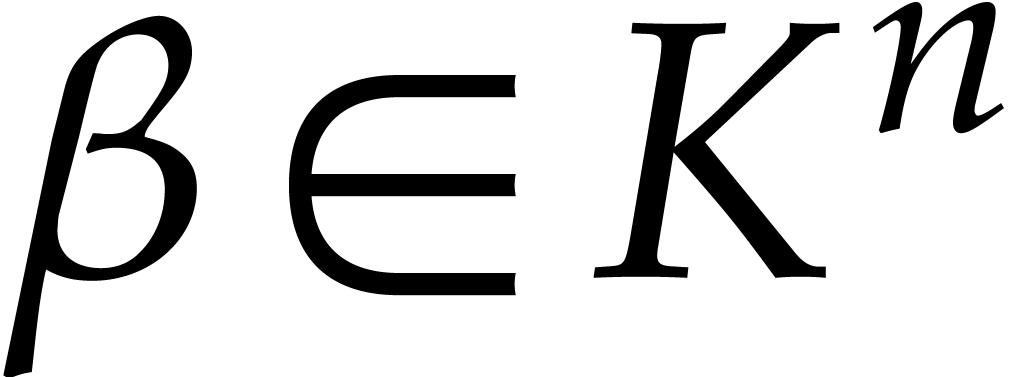 with
with  , by checking whether
, by checking whether  .
.
 is linear through a third
evaluation at the point
is linear through a third
evaluation at the point 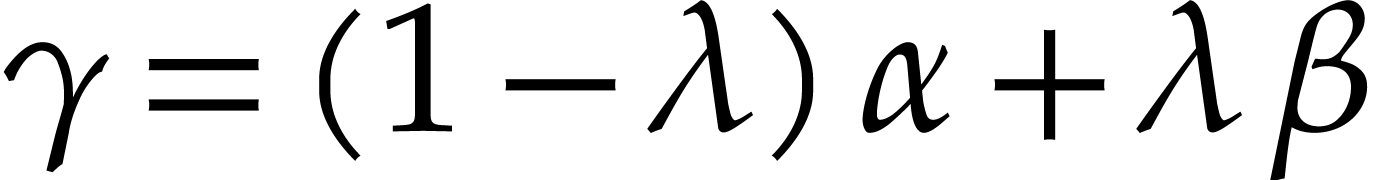 for a random
for a random 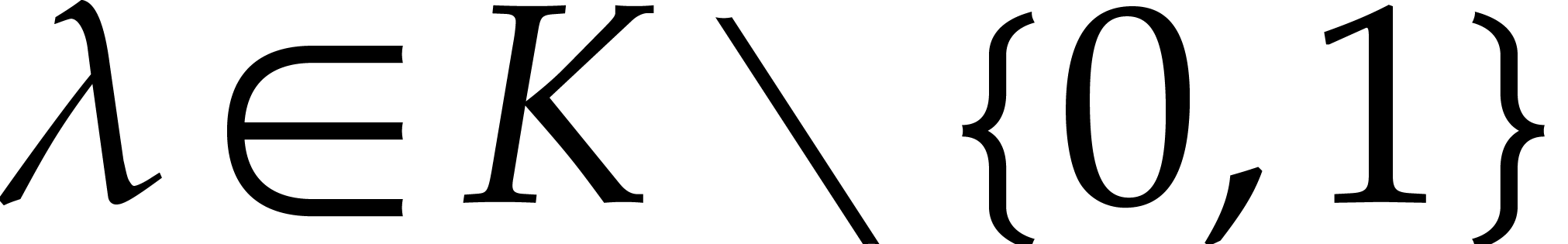 , by checking whether
, by checking whether 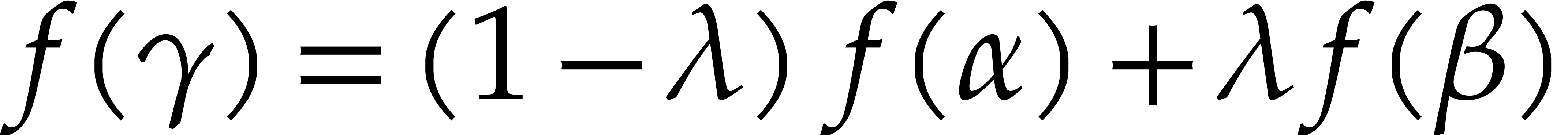 .
.
 of
of  is small, then we may determine this degree
is small, then we may determine this degree  using
using  evaluations of
evaluations of  : we first set
: we first set 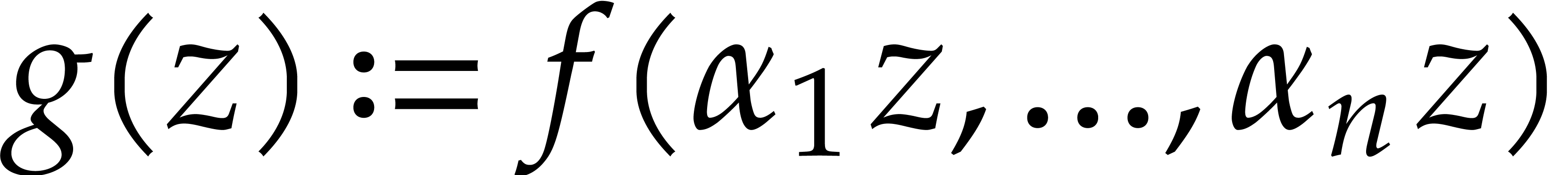 for random
for random 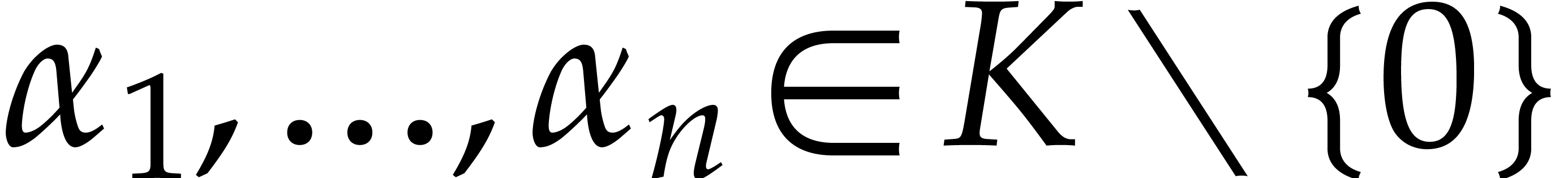 so that
so that  . For
. For  of order
of order 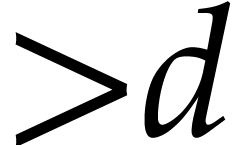 , we then compute
, we then compute 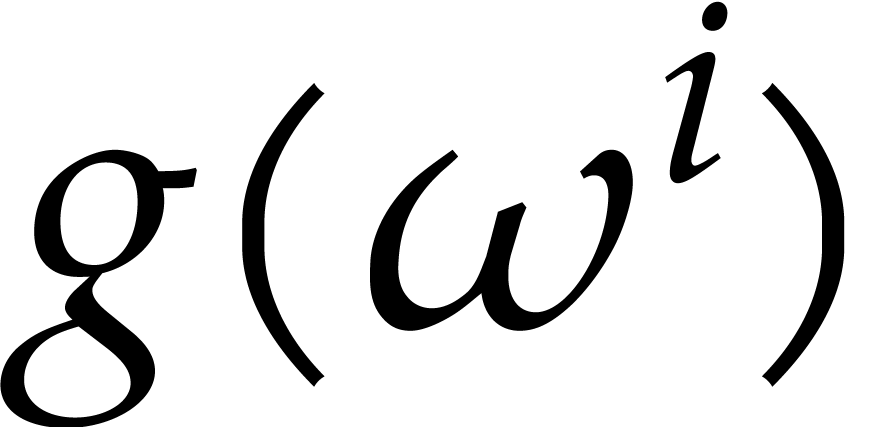 for
for  until
until 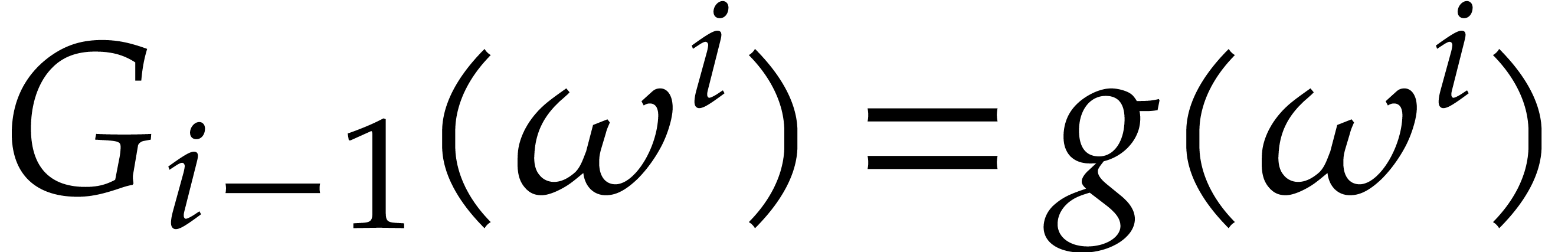 for the unique polynomial
for the unique polynomial  of degree
of degree  with
with 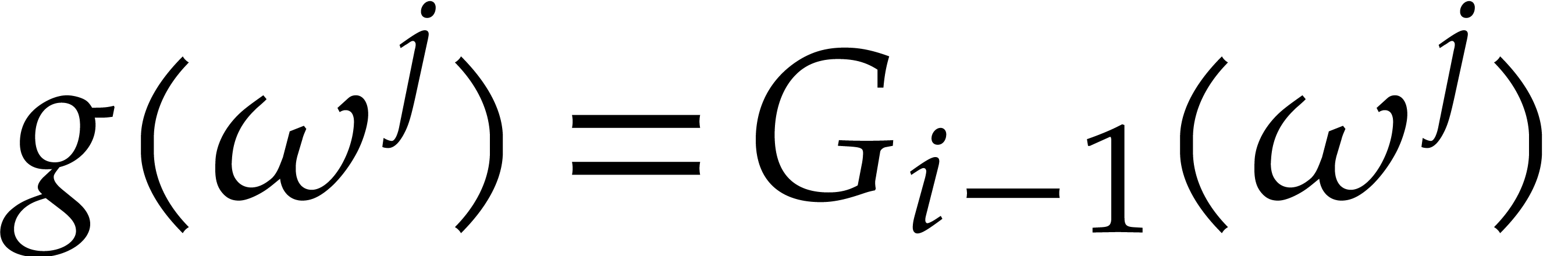 for
for  . At that point, we have
. At that point, we have  .
.
 with respect to all variables in a
subset
with respect to all variables in a
subset  of
of  .
Indeed, modulo renaming variables, we may assume
.
Indeed, modulo renaming variables, we may assume 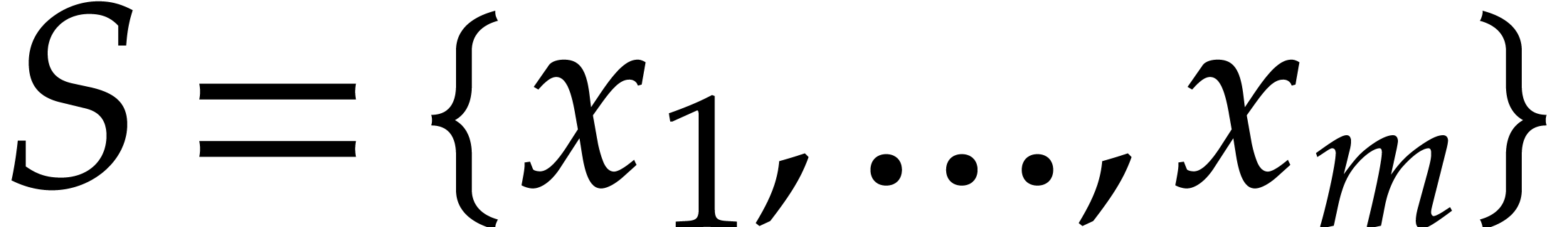 . We then take
. We then take 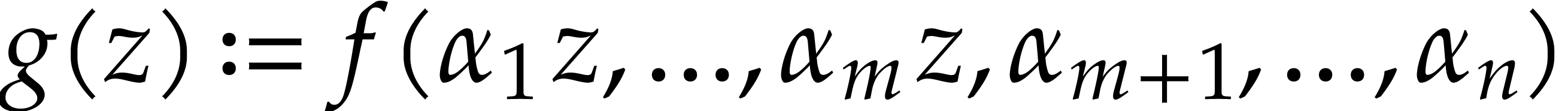 .
.
 of terms of
of terms of  as follows: for orders
as follows: for orders  that increase geometrically and random integers
that increase geometrically and random integers 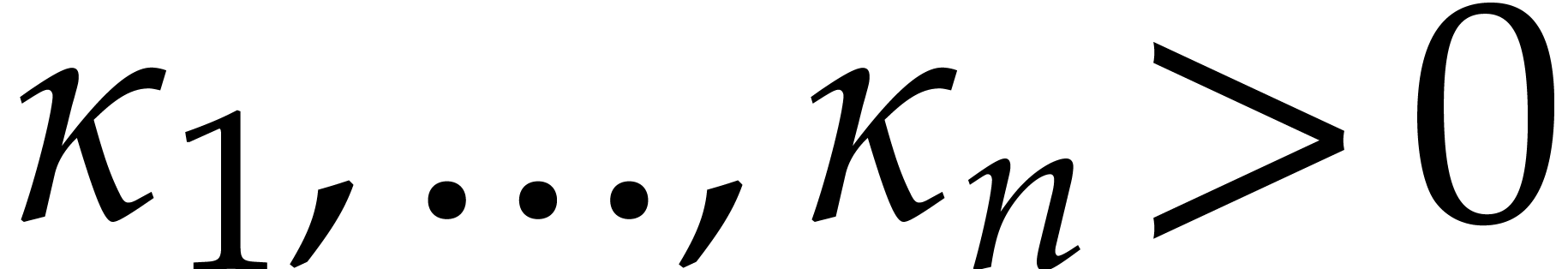 , we compute
, we compute 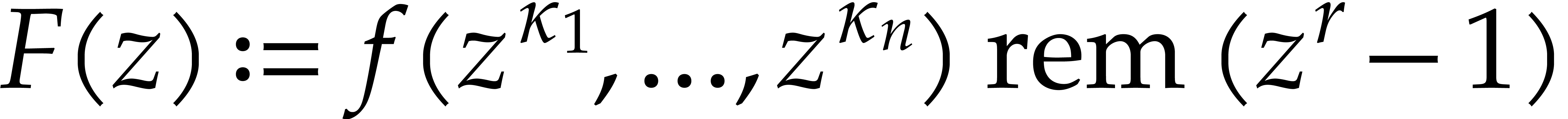 . As soon as
. As soon as  exceeds
exceeds
 , it becomes likely that
, it becomes likely that
 contains less than
contains less than  terms. This may be used to determine a rough estimate of
terms. This may be used to determine a rough estimate of  using
using  instead of
instead of 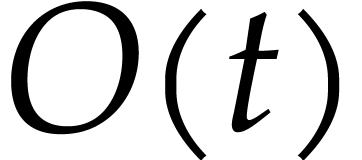 evaluations.
evaluations.
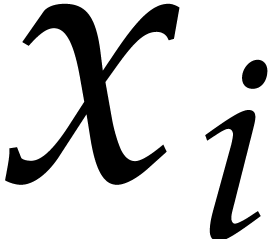 that occur in
that occur in  as follows. If
as follows. If  is constant, then we return
is constant, then we return 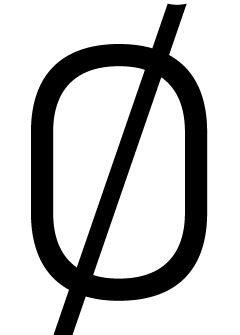 .
If
.
If  is not constant and
is not constant and 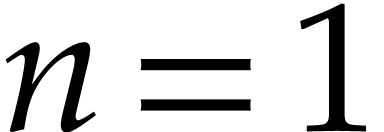 , then we return
, then we return 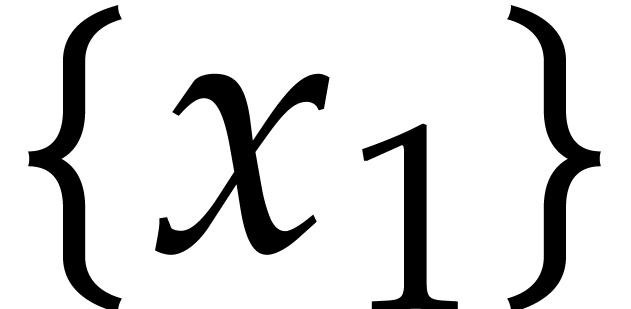 .
Otherwise, we pick a random
.
Otherwise, we pick a random 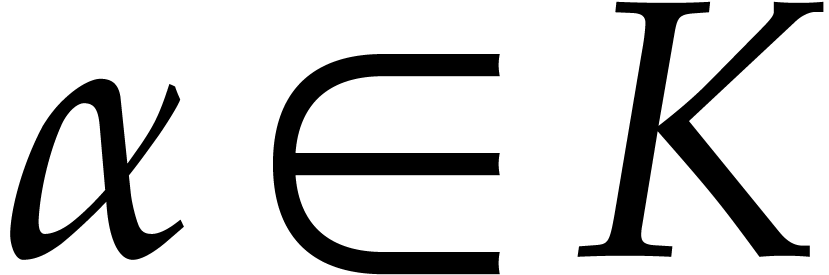 and consider
and consider 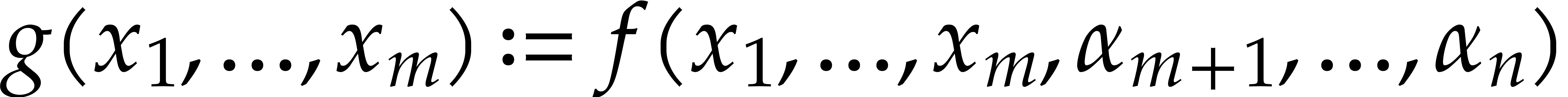 with
with 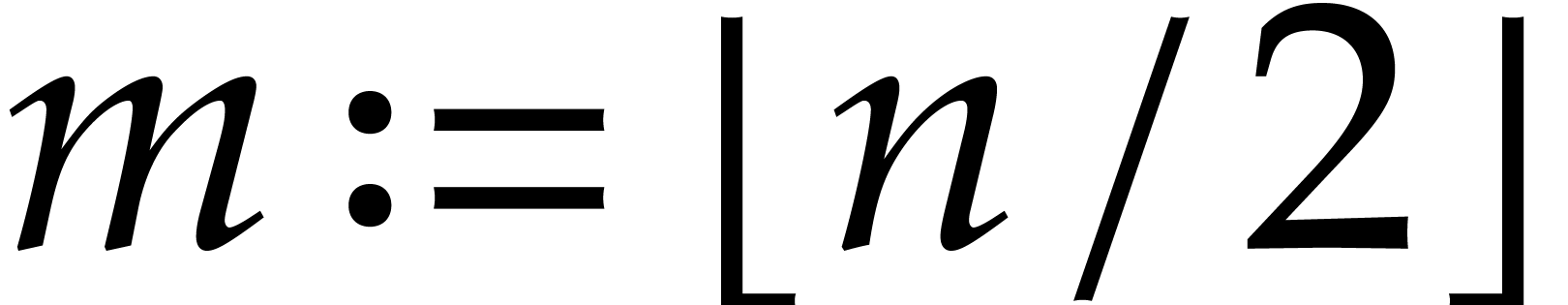 ,
as well as
,
as well as 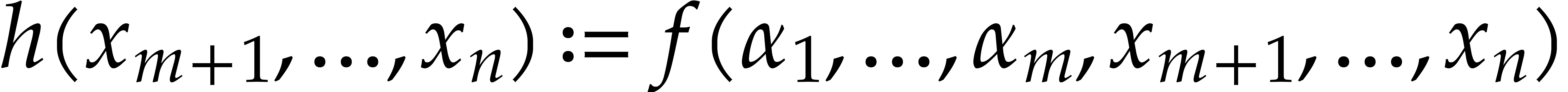 . We recursively
apply the method to
. We recursively
apply the method to  and
and  , and return the union of the output sets. This
method uses at most
, and return the union of the output sets. This
method uses at most  evaluations of
evaluations of  for an output set of size
for an output set of size  .
.
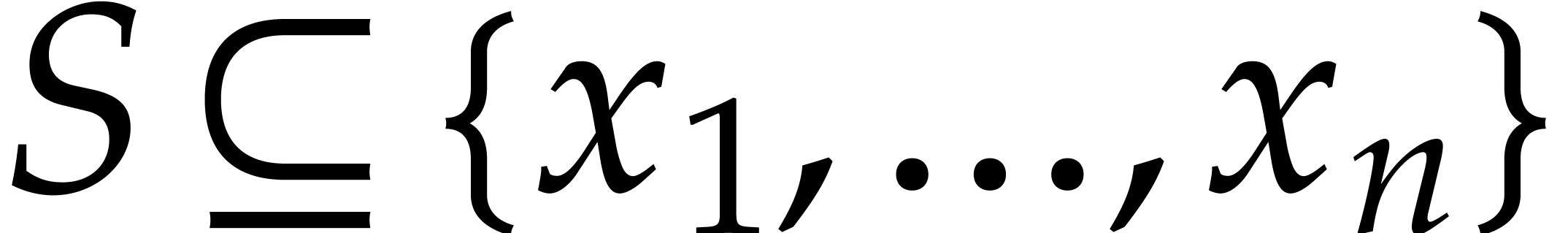 of
variables such that
of
variables such that  is linear with respect to
is linear with respect to
 . Is it possible to quickly
determine a maximal linear clique? Setting
. Is it possible to quickly
determine a maximal linear clique? Setting  we
must clearly have
we
must clearly have  and we may always put all
inactive variables inside
and we may always put all
inactive variables inside  .
Although we do not have a fast algorithm to compute a maximal linear
clique, the following randomized algorithm should be able to produce
reasonably large ones for practical purposes (especially if we run it
several times). Starting with
.
Although we do not have a fast algorithm to compute a maximal linear
clique, the following randomized algorithm should be able to produce
reasonably large ones for practical purposes (especially if we run it
several times). Starting with  ,
we iterate over all elements
,
we iterate over all elements  in a random
order, and add a new
in a random
order, and add a new 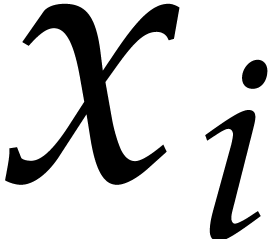 to
to  whenever
whenever  remains linear with respect to
remains linear with respect to  . Notice that this algorithm only
requires
. Notice that this algorithm only
requires  evaluations of
evaluations of  .
.
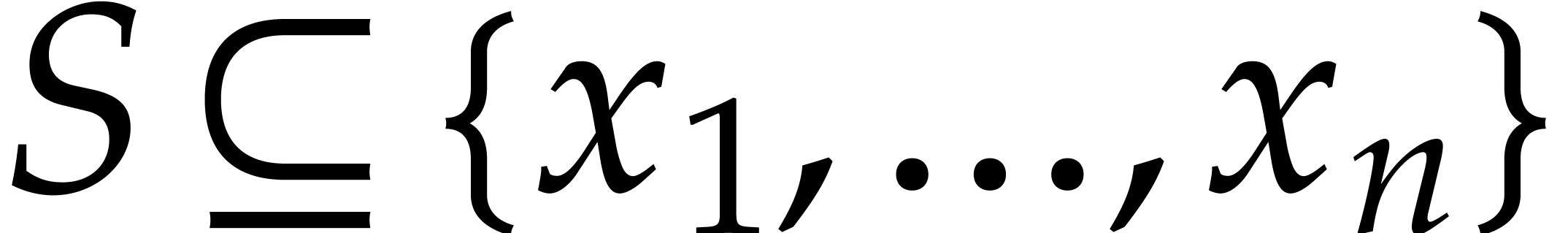 with respect
to which
with respect
to which  admits a small total degree. This is
the kind of packets that we need in section 7.3 (by
taking
admits a small total degree. This is
the kind of packets that we need in section 7.3 (by
taking  after a suitable permutation of
indices).
after a suitable permutation of
indices).
More precisely, for a finite field 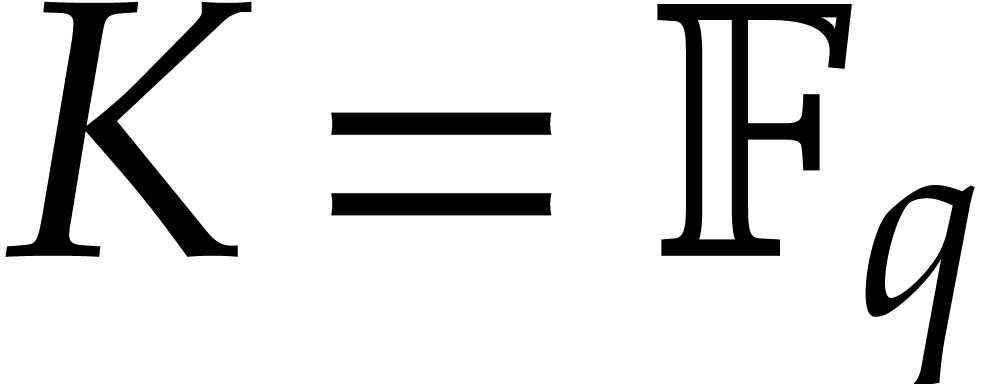 of size
of size  , assume that we wish to compute a
packet
, assume that we wish to compute a
packet  of size
of size  (as large
as possible) such that the total degree
(as large
as possible) such that the total degree 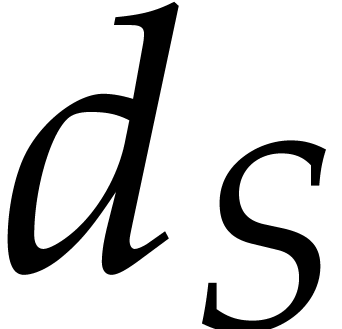 of
of  with respect to
with respect to 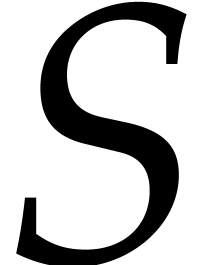 satisfies
satisfies
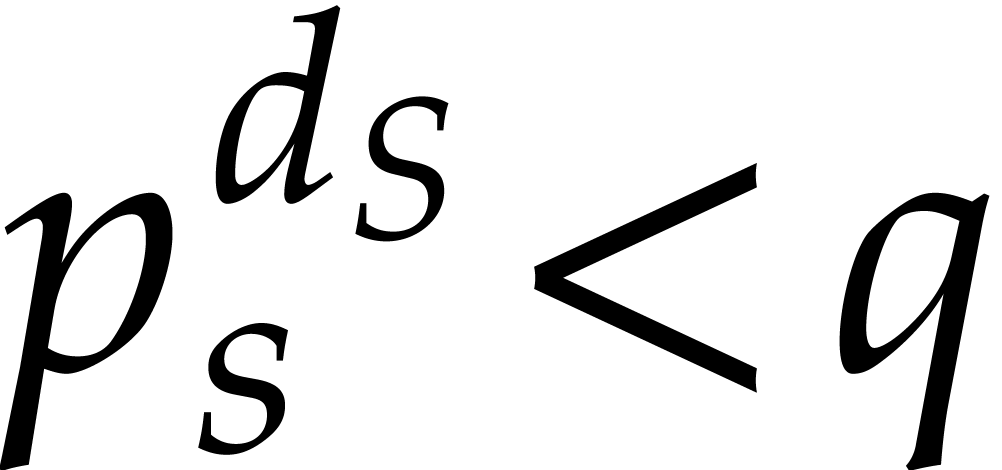 . During the algorithm, we
maintain a table that associates a degree
. During the algorithm, we
maintain a table that associates a degree 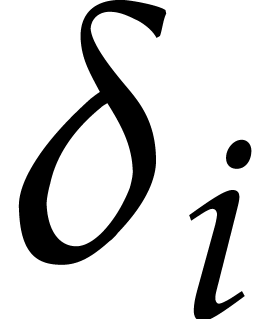 to
each variable
to
each variable 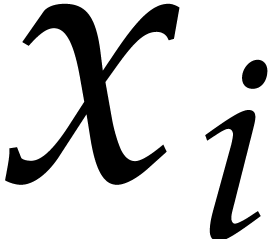 . The table is
initialized with
. The table is
initialized with 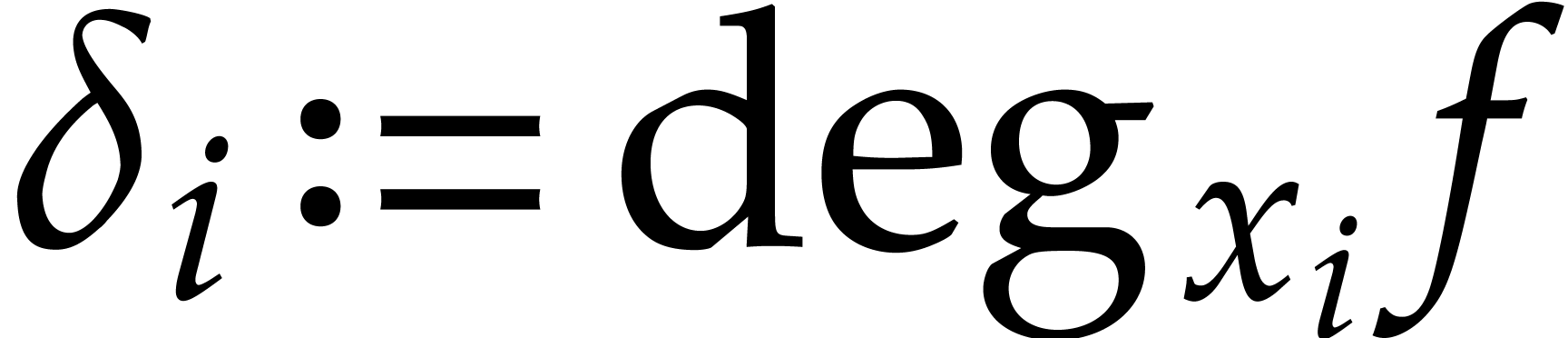 for each
for each  . Starting with
. Starting with  we now
repeat the following steps. We reorder indices such that
we now
repeat the following steps. We reorder indices such that  and
and  . For
. For  , we replace
, we replace 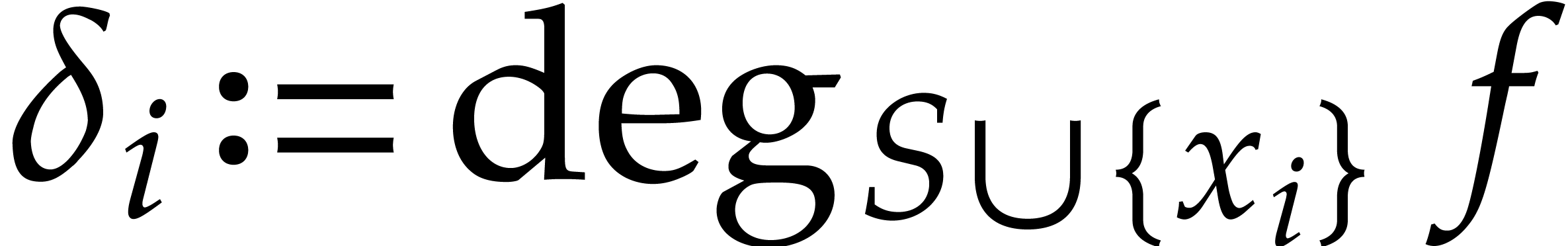 and stop as soon as
and stop as soon as  or
or  for some
for some  . We then determine
the index
. We then determine
the index 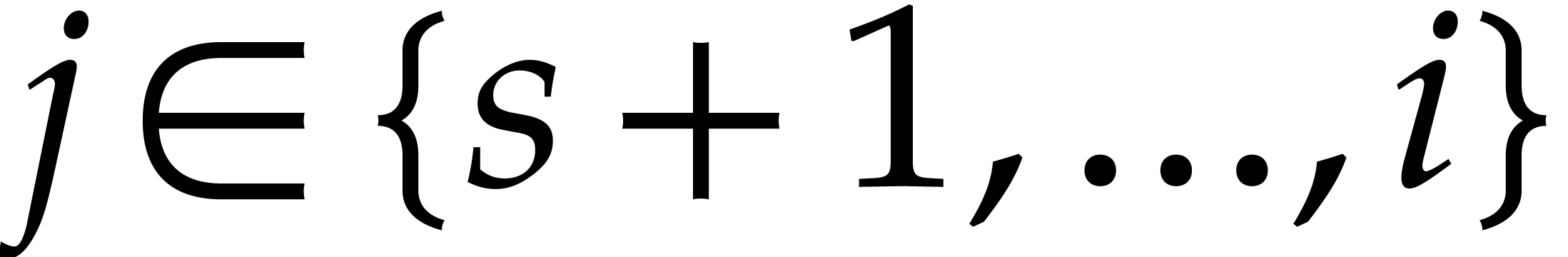 for which
for which 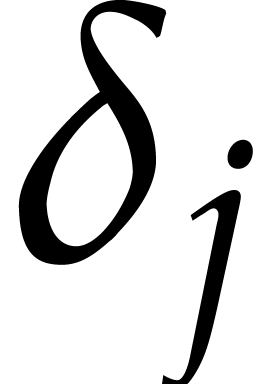 is
minimal. If
is
minimal. If 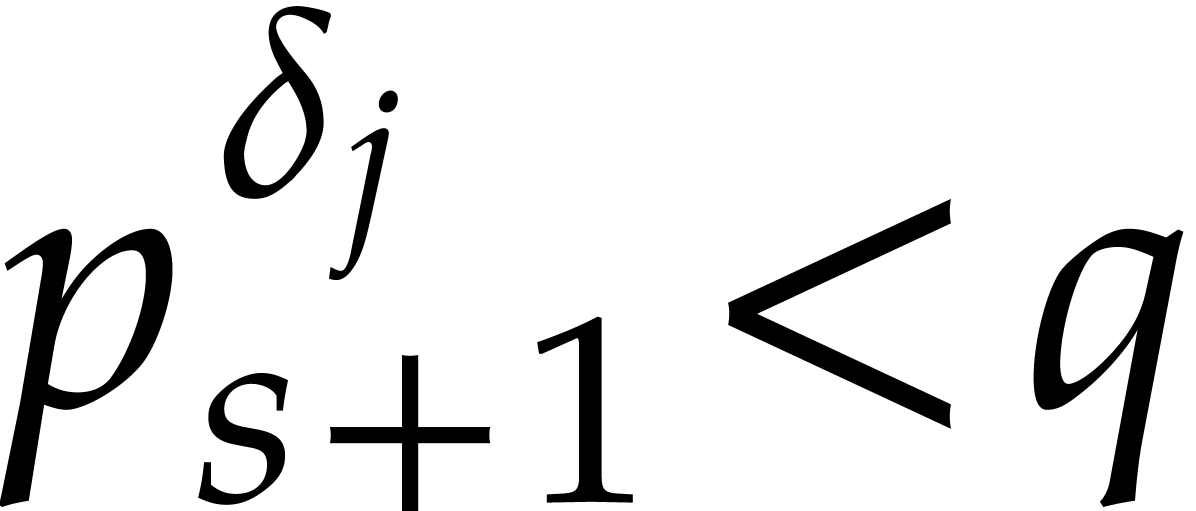 , then we add
, then we add
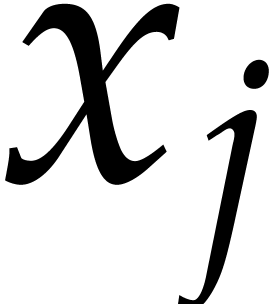 to
to  and continue;
otherwise, we abort the main loop and return
and continue;
otherwise, we abort the main loop and return  .
.
During the loop, we may also remove all variables  for which
for which  exceeds
exceeds 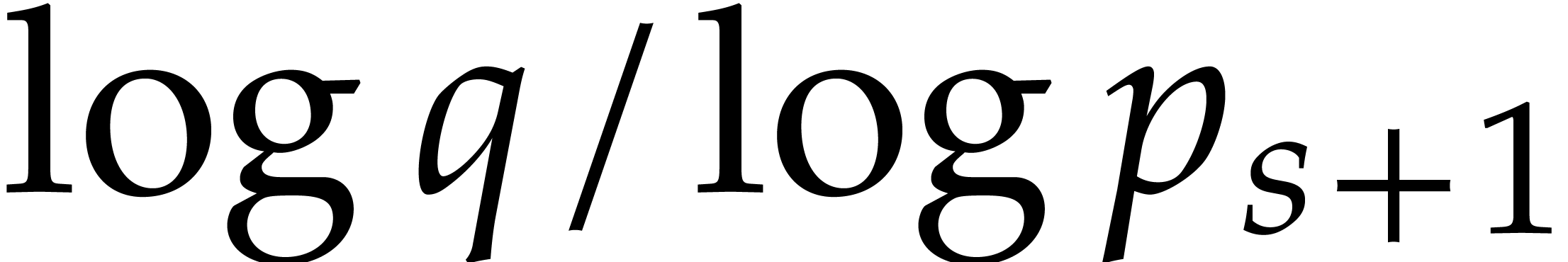 .
With this optimization, the number of evaluations of
.
With this optimization, the number of evaluations of  always remains bounded by
always remains bounded by 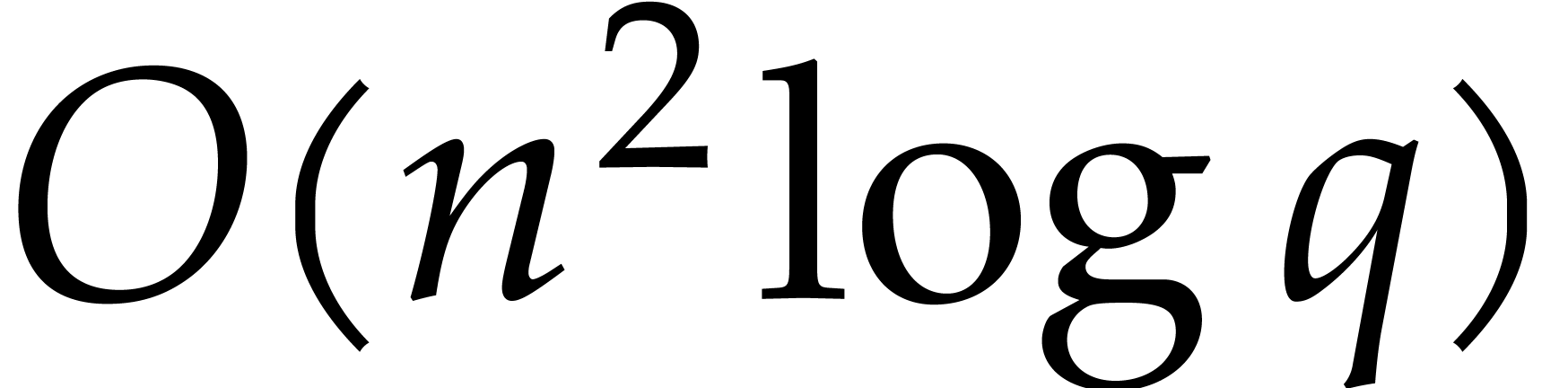 .
.
Let us now consider the interesting special case when there exists a
non-trivial linear clique  and assume that we
know the support of
and assume that we
know the support of  with respect to
with respect to  . Then the derivation strategy from section 3.2 yields an efficient interpolation method for
. Then the derivation strategy from section 3.2 yields an efficient interpolation method for  , even if
, even if  is small.
Indeed, in that case, we may write
is small.
Indeed, in that case, we may write
where 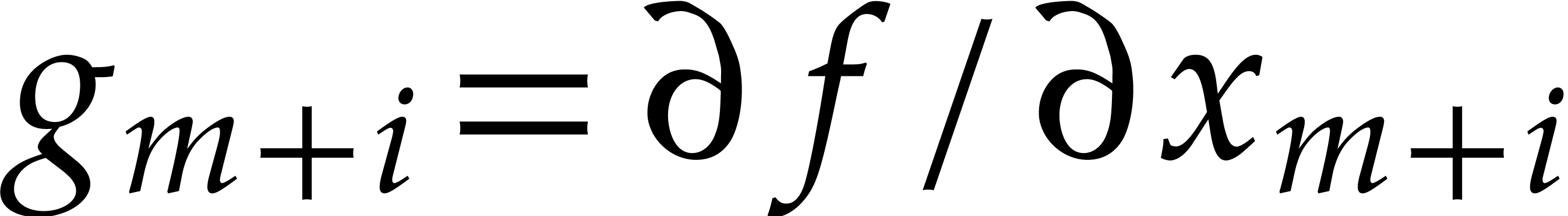 for
for  .
The idea is to jointly interpolate
.
The idea is to jointly interpolate  using the
fact that the vector
using the
fact that the vector  can be evaluated fast using
automatic differentiation. As usual, we may either rely on a geometric
progression style approach or on more direct FFTs.
can be evaluated fast using
automatic differentiation. As usual, we may either rely on a geometric
progression style approach or on more direct FFTs.
When using a geometric progression style approach, we assume that  and let
and let  denote a primitive
denote a primitive
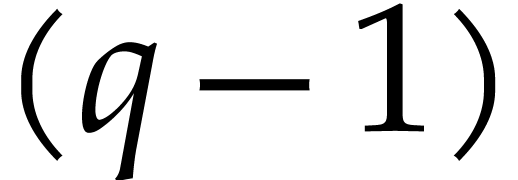 -th root of unity. We pick
random integers
-th root of unity. We pick
random integers 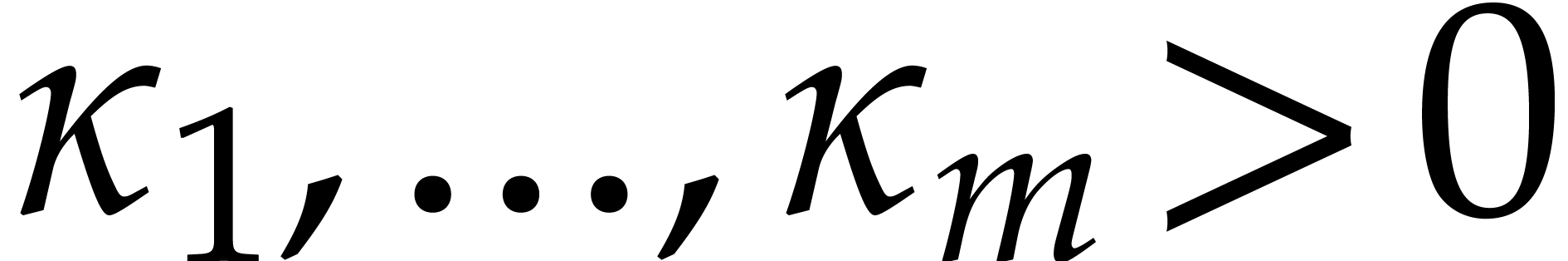 and set
and set 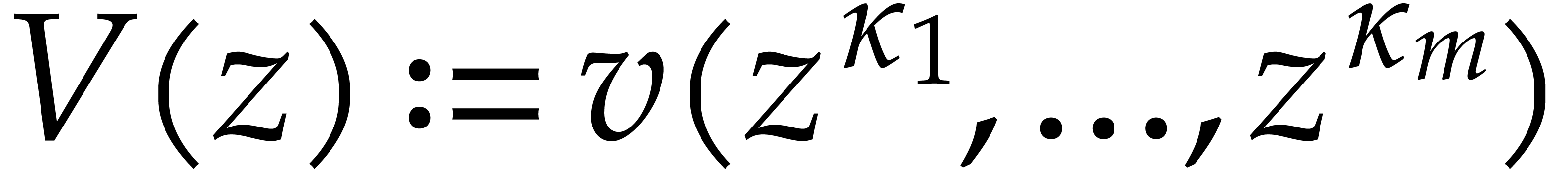 . With high probability, the known exponents
. With high probability, the known exponents  of
of  are pairwise distinct
modulo
are pairwise distinct
modulo 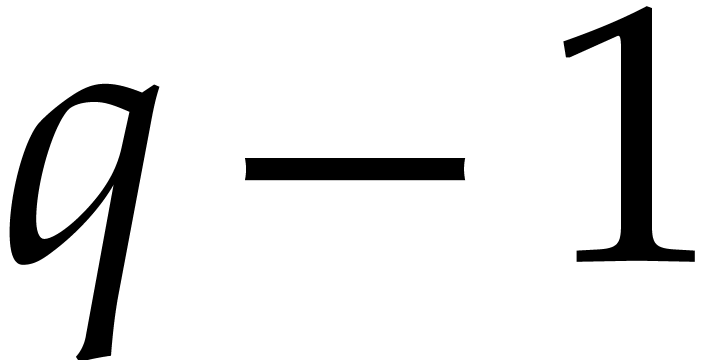 . We now compute
. We now compute 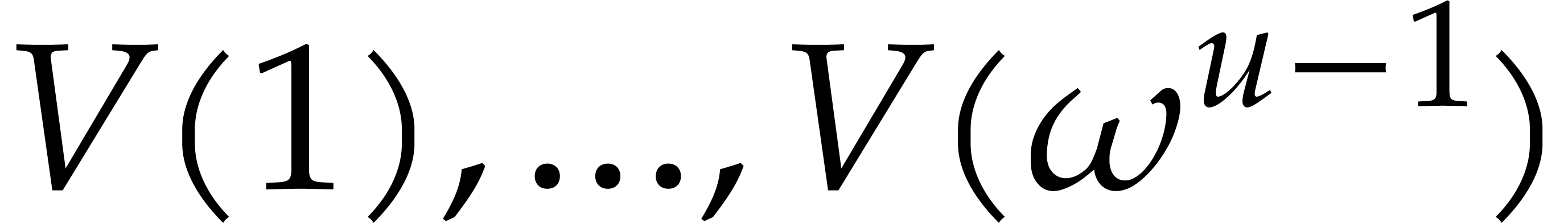 and interpolate the coefficients of
and interpolate the coefficients of  using transposed multipoint interpolation. This yields
using transposed multipoint interpolation. This yields  and
and  in time
in time
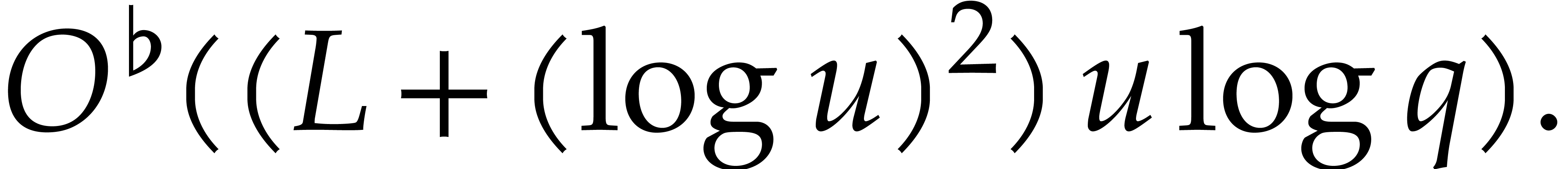 |
(19) |
When using FFTs, we rather take an  -th
primitive root of unity with
-th
primitive root of unity with 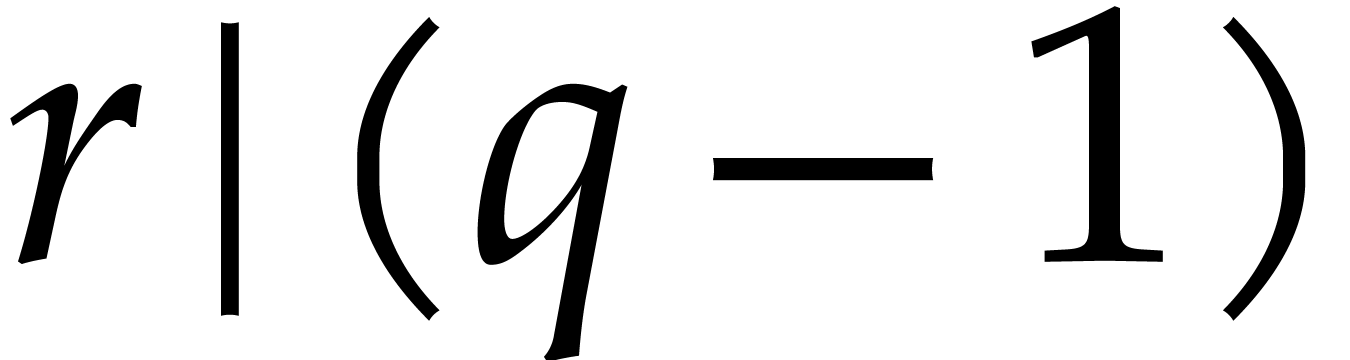 close to
close to  and only obtain a constant proportion of the coefficients
of
and only obtain a constant proportion of the coefficients
of  ; applying the same method
for different values of
; applying the same method
for different values of  ,
this leads to a runtime of
,
this leads to a runtime of 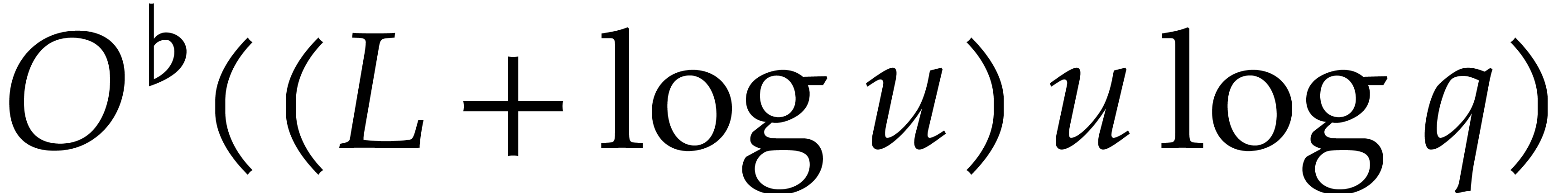 ,
with a higher constant factor with respect to
,
with a higher constant factor with respect to 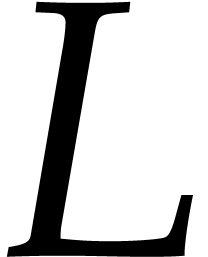 .
.
Example  of an
of an
 matrix with generic coefficients
matrix with generic coefficients  . Then the variables
. Then the variables  form a (maximal) linear clique. When specializing these variables by
random elements in
form a (maximal) linear clique. When specializing these variables by
random elements in  , we
obtain a new function
, we
obtain a new function  for which the variables
for which the variables
 form a (maximal) linear clique. And so on for
the successive rows of the matrix. Notice that the specialization of all
variables
form a (maximal) linear clique. And so on for
the successive rows of the matrix. Notice that the specialization of all
variables 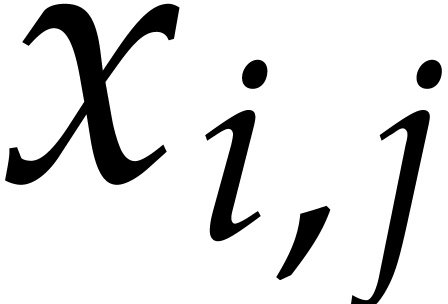 with
with 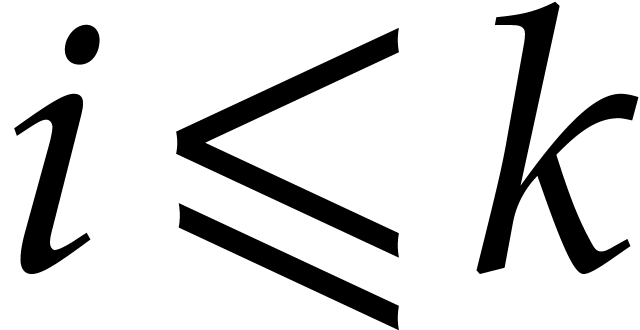 has a
support of size
has a
support of size  .
.
Using the geometric progression strategy of complexity (19)
in a recursive manner, it follows that we can compute the sparse
interpolation of  in time
in time
Notice that the traditional geometric progression method (of complexity (18)) takes time
Instead of evaluating 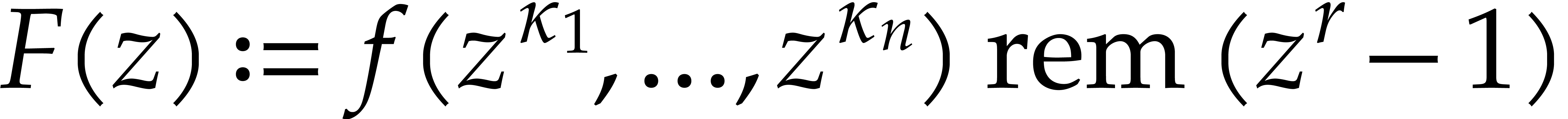 by using Algorithm 5 for random integers
by using Algorithm 5 for random integers  and a suitable
modulus
and a suitable
modulus 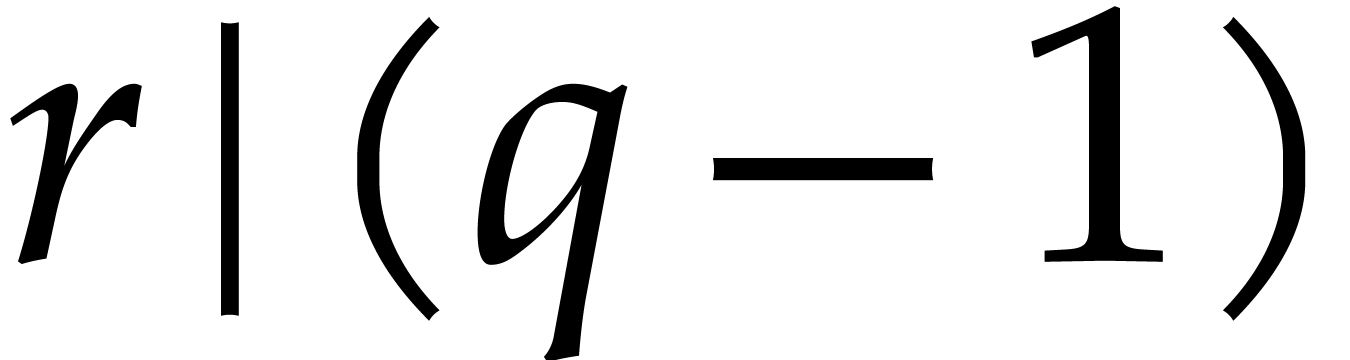 , the multivariate
setting also allows us to consider multivariate FFTs. To do so, we use
moduli
, the multivariate
setting also allows us to consider multivariate FFTs. To do so, we use
moduli 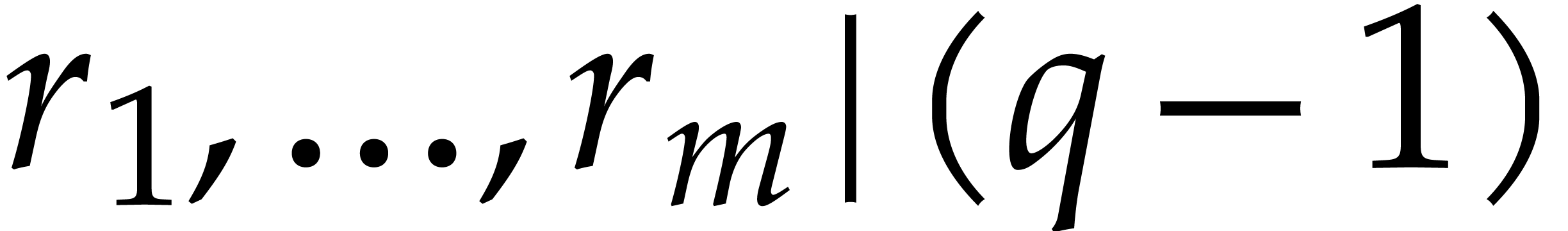 and an integer matrix
and an integer matrix  , and then take
, and then take
Moreover, the 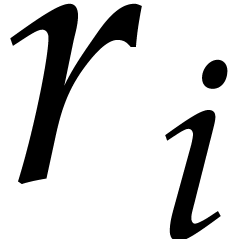 and
and 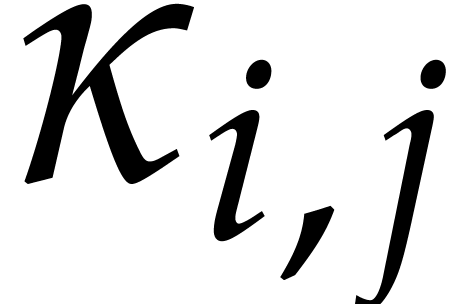 should
be chosen in such a way that
should
be chosen in such a way that  is close to
is close to  , the linear map
, the linear map
is surjective, and the exponents in the support of  are mapped to essentially random elements in
are mapped to essentially random elements in 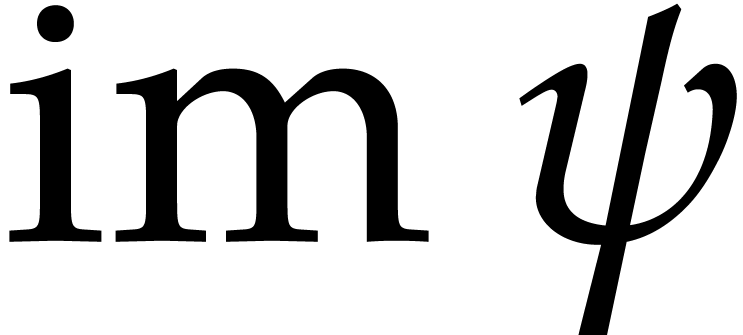 . This generalization admits the advantage that the
. This generalization admits the advantage that the
 do not need to be coprime, which may help to
avoid working over large extensions
do not need to be coprime, which may help to
avoid working over large extensions  if
if  . It would be interesting to
generalize the Frobenius FFT to this multivariate setting.
. It would be interesting to
generalize the Frobenius FFT to this multivariate setting.
Is it possible to speed up the interpolation if  admits symmetries? As a simple example, let us consider the trivariate
case with
admits symmetries? As a simple example, let us consider the trivariate
case with 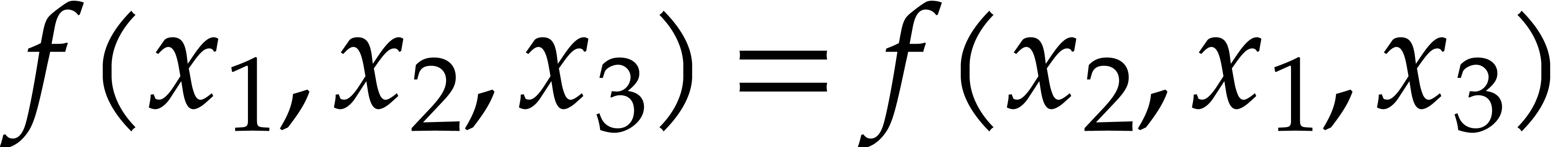 . It is easy to
detect such a symmetry by checking whether
. It is easy to
detect such a symmetry by checking whether 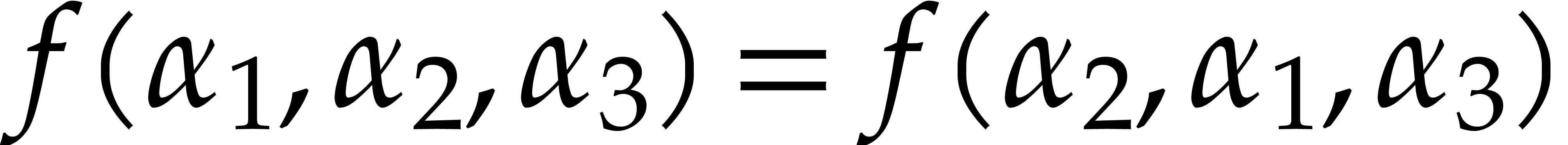 holds
for a random point
holds
for a random point 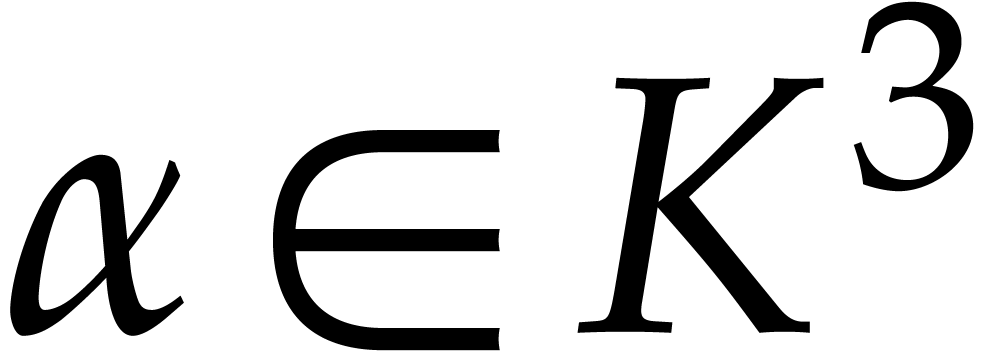 . When
using multivariate FFTs as in the previous subsection, the idea is to
pick parameters
. When
using multivariate FFTs as in the previous subsection, the idea is to
pick parameters  and
and 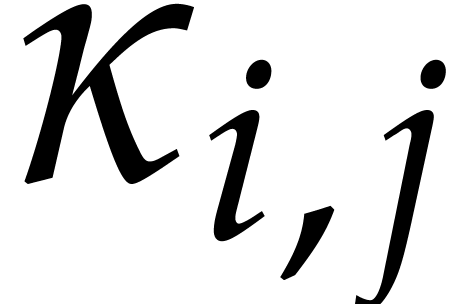 of
the form
of
the form
so that  is still symmetric with respect to
is still symmetric with respect to  and
and  . Now
let
. Now
let 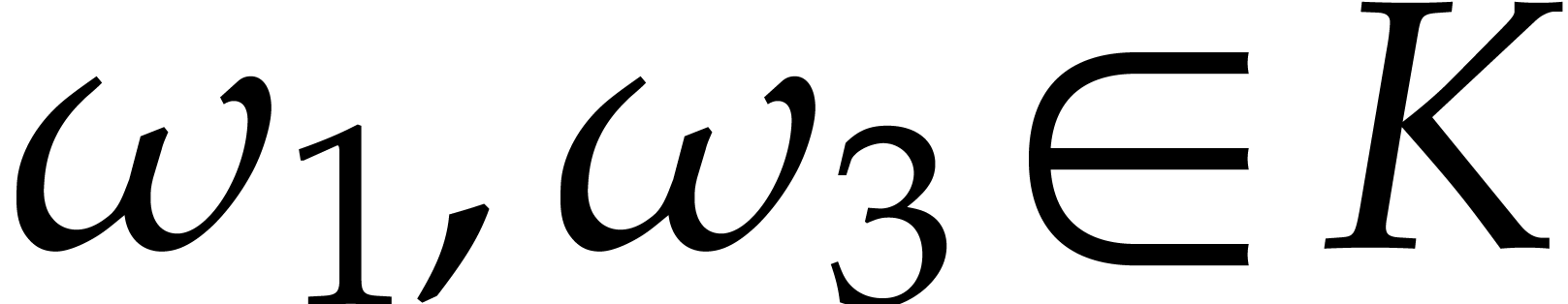 be primitive roots of unity of orders
be primitive roots of unity of orders  and
and  . In
order to evaluate of
. In
order to evaluate of  at all points
at all points 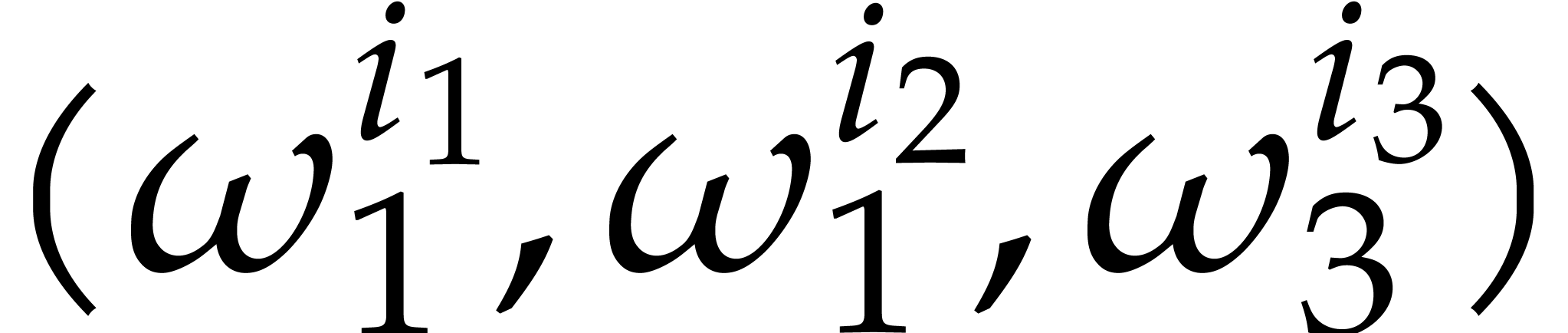 with
with 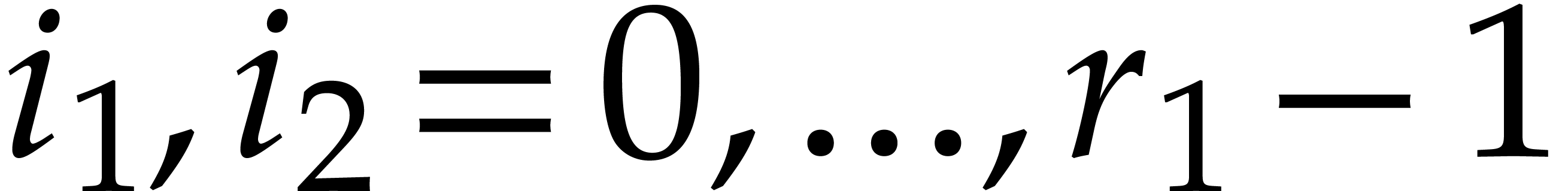 and
and  , it suffices to consider the points with
, it suffices to consider the points with  , thereby saving a factor of almost
two. We may recover the coefficients of
, thereby saving a factor of almost
two. We may recover the coefficients of  using an
inverse DFT. This can again be done almost twice as efficiently as for
non-symmetric polynomials, using a method from [29].
Overall, we save a factor of almost two when computing sparse
evaluations using the FFT method. This approach should generalize to
more general types of symmetries, as the ones considered in [29].
using an
inverse DFT. This can again be done almost twice as efficiently as for
non-symmetric polynomials, using a method from [29].
Overall, we save a factor of almost two when computing sparse
evaluations using the FFT method. This approach should generalize to
more general types of symmetries, as the ones considered in [29].
In order to interpolate a multivariate polynomial  , it is recommended to first gather useful
information about
, it is recommended to first gather useful
information about  , as
described in section 7.4. With this information at hand, we
may then opt for a most appropriate interpolation strategy:
, as
described in section 7.4. With this information at hand, we
may then opt for a most appropriate interpolation strategy:
If  admits special properties, then we may
wish to apply a dedicated algorithm, such as the linear clique
strategy from section 7.5 or the symmetric
interpolation strategy from section 7.7.
admits special properties, then we may
wish to apply a dedicated algorithm, such as the linear clique
strategy from section 7.5 or the symmetric
interpolation strategy from section 7.7.
Whenever 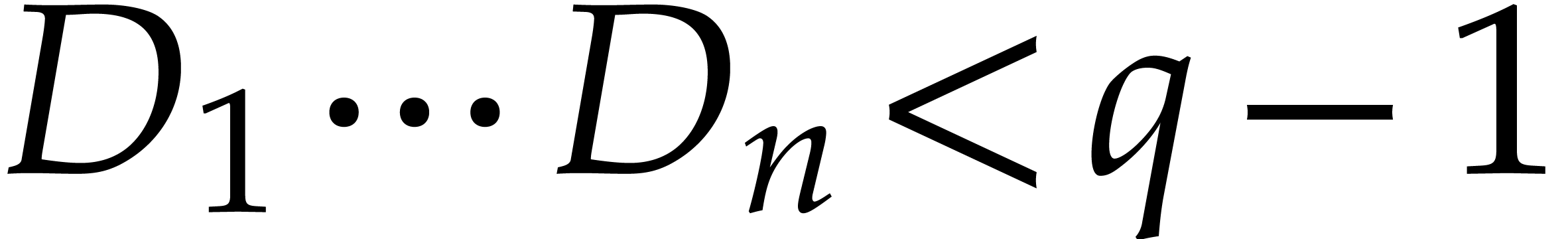 , Kronecker
segmentation can be combined with any of the univariate
interpolation methods in order to obtain an efficient algorithm for
the interpolation of
, Kronecker
segmentation can be combined with any of the univariate
interpolation methods in order to obtain an efficient algorithm for
the interpolation of  .
.
If 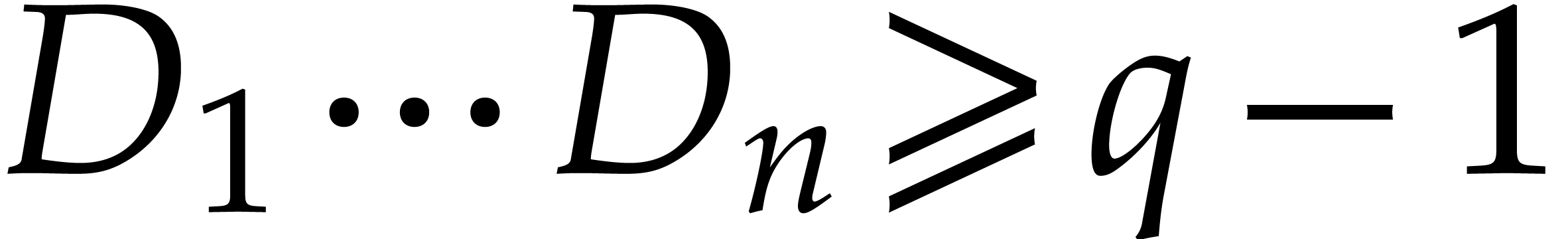 , but
, but  admits a reasonably small total degree, then we may use a variant of
the geometric progression style algorithm from section 7.2
in order to interpolate
admits a reasonably small total degree, then we may use a variant of
the geometric progression style algorithm from section 7.2
in order to interpolate  .
.
If  is normally sparse, but too large for one
of the above strategies to apply, then interpolation by packets is a
powerful tool. It typically allows us to reduce to the most
favorable cases from sections 5 and 6 when
we do not need any field extensions of
is normally sparse, but too large for one
of the above strategies to apply, then interpolation by packets is a
powerful tool. It typically allows us to reduce to the most
favorable cases from sections 5 and 6 when
we do not need any field extensions of  (except when
(except when 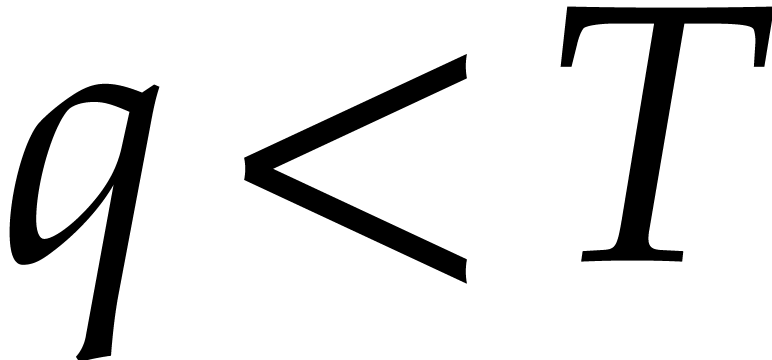 or when
or when 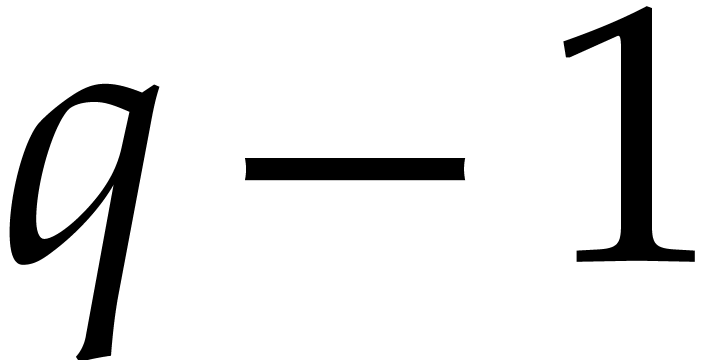 admits not enough small prime divisors). As in the univariate case,
we may then opt for a geometric progression style approach if
admits not enough small prime divisors). As in the univariate case,
we may then opt for a geometric progression style approach if 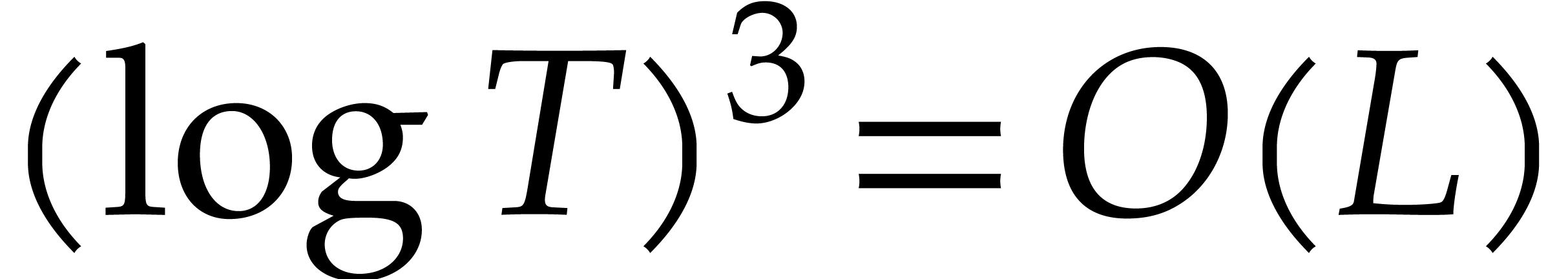 and for an FFT based approach if
and for an FFT based approach if 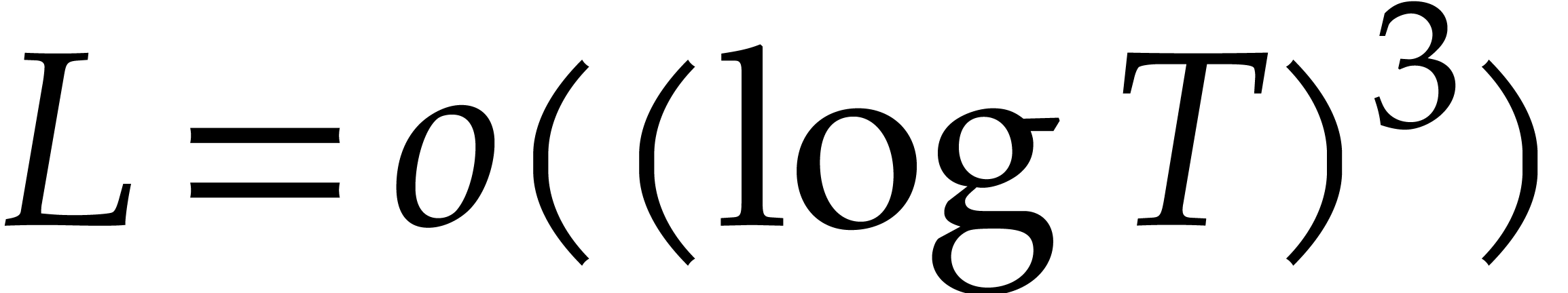 .
.
If  is super sparse, then we may use the
strategy from section 6.5 over the rationals and fall
back on a cyclic extension style algorithm when
is super sparse, then we may use the
strategy from section 6.5 over the rationals and fall
back on a cyclic extension style algorithm when  is a given finite field.
is a given finite field.
M. Agrawal, N. Kayal, and N. Saxena. PRIMES is in P. Ann. Math., 160(2):781–793, 2004.
A. Arnold, M. Giesbrecht, and D. S. Roche. Sparse interpolation over finite fields via low-order roots of unity. In ISSAC '14: Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, pages 27–34. ACM Press, 2014.
A. Arnold, M. Giesbrecht, and D. S. Roche. Faster sparse multivariate polynomial interpolation of straight-line programs. J. Symb. Comput., 75:4–24, 2016.
A. Arnold and D. S. Roche. Multivariate sparse interpolation using randomized Kronecker substitutions. In ISSAC '14: Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, pages 35–42. ACM Press, 2014.
R. Arratia and L. Gordon. Tutorial on large deviations for the binomial distribution. Bull. Math. Biol., 51(1):125–131, 1989.
R. C. Baker, G. Harman, and J. Pintz. The difference between consecutive primes, II. Proc. of the London Math. Soc., 83(3):532–562, 2001.
W. Baur and V. Strassen. The complexity of partial derivatives. Theor. Comput. Sci., 22:317–330, 1983.
M. Ben-Or and P. Tiwari. A deterministic algorithm for sparse multivariate polynomial interpolation. In STOC '88: Proceedings of the twentieth annual ACM symposium on Theory of computing, pages 301–309. ACM Press, 1988.
M. A. Bennett, G. Martin, K. O'Bryant, and A. Rechnitzer. Explicit bounds for primes in arithmetic progressions. Illinois J. Math., 62(1–4):427–532, 2018.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In ISSAC '03: Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, pages 37–44. ACM Press, 2003.
R. P. Brent, F. G. Gustavson, and D. Y. Y. Yun. Fast solution of Toeplitz systems of equations and computation of Padé approximants. J. Algorithms, 1(3):259–295, 1980.
J. Canny, E. Kaltofen, and Y. Lakshman. Solving systems of non-linear polynomial equations faster. In Proceedings of the ACM-SIGSAM 1989 International Symposium on Symbolic and Algebraic Computation, pages 121–128. ACM Press, 1989.
D. G. Cantor and H. Zassenhaus. A new algorithm for factoring polynomials over finite fields. Math. Comput., 36(154):587–592, 1981.
A. Díaz and E. Kaltofen. FOXFOX: a system for manipulating symbolic objects in black box representation. In ISSAC '98: Proceedings of the 1998 International Symposium on Symbolic and Algebraic Computation, pages 30–37. ACM Press, 1998.
A.-M. Ernvall-Hytönen and N. Palojärvi. Explicit bound for the number of primes in arithmetic progressions assuming the Generalized Riemann Hypothesis. Math. Comput., 91:1317–1365, 2022.
T. S. Freeman, G. M. Imirzian, E. Kaltofen, and Y. Lakshman. DAGWOOD: a system for manipulating polynomials given by straight-line programs. ACM Trans. Math. Software, 14:218–240, 1988.
S. Garg and É. Schost. Interpolation of polynomials given by straight-line programs. Theor. Comput. Sci., 410(27-29):2659–2662, 2009.
M. Giesbrecht and D. S. Roche. Diversification improves interpolation. In ISSAC '11: Proceedings of the 36th International Symposium on Symbolic and Algebraic Computation, pages 123–130. ACM Press, 2011.
P. Giorgi, B. Grenet, and A. Perret du Cray. Essentially optimal sparse polynomial multiplication. In Proceedings of the 45th International Symposium on Symbolic and Algebraic Computation, ISSAC '20, pages 202–209. New York, NY, USA, 2020. ACM Press.
P. Giorgi, B. Grenet, A. Perret du Cray, and D. S. Roche. Random primes in arithmetic progressions. Technical Report, arXiv, 2022. https://doi.org/10.48550/arXiv.2202.05955.
P. Giorgi, B. Grenet, A. Perret du Cray, and D. S. Roche. Sparse polynomial interpolation and division in soft-linear time. In Proceedings of the 2022 International Symposium on Symbolic and Algebraic Computation, ISSAC '22, pages 459–468. New York, NY, USA, 2022. ACM Press.
B. Grenet, J. van der Hoeven, and G. Lecerf. Randomized root finding over finite fields using tangent Graeffe transforms. In ISSAC '15: Proceedings of the 2015 ACM on International Symposium on Symbolic and Algebraic Computation, pages 197–204. New York, NY, USA, 2015. ACM Press.
B. Grenet, J. van der Hoeven, and G. Lecerf. Deterministic root finding over finite fields using Graeffe transforms. Appl. Algebra Engrg. Comm. Comput., 27(3):237–257, 2016.
D. Y. Grigoriev and M. Karpinski. The matching problem for bipartite graphs with polynomially bounded permanents is in NC. In Proceedings of the 28th IEEE Symposium on the Foundations of Computer Science, pages 166–172. IEEE Computer Society, 1987.
D. Harvey and J. van der Hoeven. Polynomial
multiplication over finite fields in time 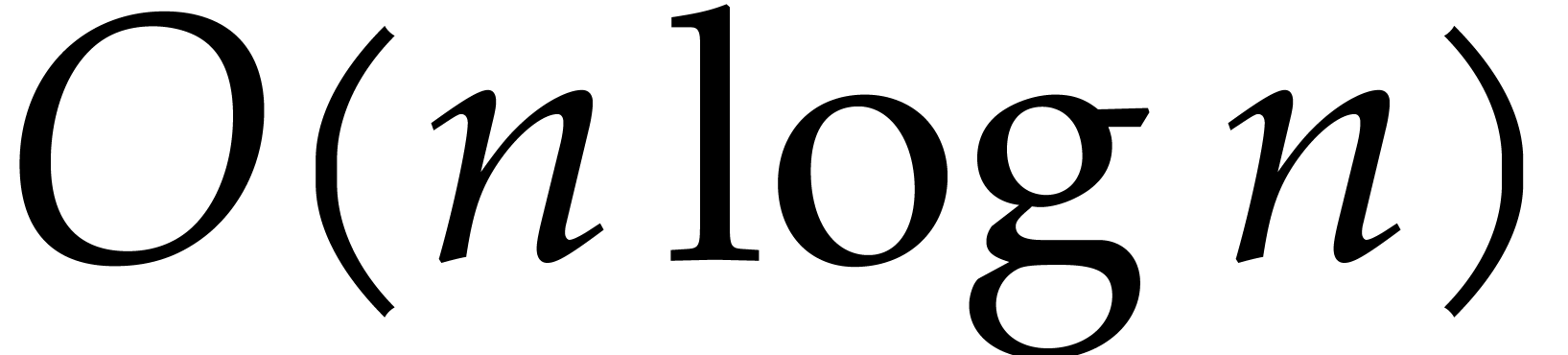 . J. ACM, 69(2):1–40, 2022.
Article 12.
. J. ACM, 69(2):1–40, 2022.
Article 12.
D. Harvey, J. van der Hoeven, and G. Lecerf. Faster polynomial multiplication over finite fields. J. ACM, 63(6), 2017. Article 52.
J. Heintz and C.-P. Schnorr. Testing polynomials which are easy to compute. In Logic and algorithmic (Zurich, 1980), volume 30 of Monograph. Enseign. Math., pages 237–254. Geneva, 1982. Univ. Genève.
J. van der Hoeven and R. Larrieu. The Frobenius FFT. In ISSAC '17: Proceedings of the 2017 ACM on International Symposium on Symbolic and Algebraic Computation, pages 437–444. New York, NY, USA, 2017. ACM Press.
J. van der Hoeven, R. Lebreton, and É. Schost. Structured FFT and TFT: symmetric and lattice polynomials. In ISSAC '13: Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, pages 355–362. New York, NY, USA, 2013. ACM Press.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial and series multiplication. J. Symb. Comput., 50:227–254, 2013.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation in practice. ACM Commun. Comput. Algebra, 48(3/4):187–191, 2015.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation. Exploring fast heuristic algorithms over finite fields. Technical Report, HAL, 2019. https://hal.science/hal-02382117v1.
J. Hu and M. B. Monagan. A fast parallel sparse polynomial GCD algorithm. In S. A. Abramov, E. V. Zima, and X.-S. Gao, editors, ISSAC '16: Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, pages 271–278. New York, NY, USA, 2016. ACM Press.
M. A. Huang and A. J. Rao. Interpolation of sparse multivariate polynomials over large finite fields with applications. In SODA '96: Proceedings of the seventh annual ACM-SIAM symposium on Discrete algorithms, pages 508–517. Philadelphia, PA, USA, 1996. Society for Industrial and Applied Mathematics.
M.-D. A. Huang and A. J. Rao . Interpolation of sparse multivariate polynomials over large finite fields with applications. J. Algorithms, 33(2):204–228, 1999.
Q. L. Huang and X. S. Gao. Sparse Polynomial Interpolation with Finitely Many Values for the Coefficients. In V. Gerdt, V. Koepf, W. Seiler, and E. Vorozhtsov, editors, Computer Algebra in Scientific Computing. 19th International Workshop, CASC 2017, Beijing, China, September 18-22, 2017, Proceedings., volume 10490 of Lect. Notes Comput. Sci. Springer, Cham, 2017.
Q.-L. Huang. Sparse polynomial interpolation over fields with large or zero characteristic. In ISSAC '19: Proceedings of the 2019 on International Symposium on Symbolic and Algebraic Computation, pages 219–226. New York, NY, USA, 2019. ACM Press.
Q. L. Huang and X. S. Gao. Faster interpolation algorithms for sparse multivariate polynomials given by straight-line programs. J. Symb. Comput., 101:367–386, 2020.
M. Javadi and M. Monagan. Parallel sparse polynomial interpolation over finite fields. In M. Moreno Maza and J.-L. Roch, editors, PASCO '10: Proceedings of the 4th International Workshop on Parallel and Symbolic Computation, pages 160–168. New York, NY, USA, 2010. ACM Press.
E. Kaltofen. Computing with polynomials given by straight-line programs I: greatest common divisors. In STOC '85: Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing, pages 131–142. ACM Press, 1985.
E. L. Kaltofen. Fifteen years after DSC and WLSS2 what parallel computations I do today: invited lecture at PASCO 2010. In PASCO '10: Proceedings of the 4th International Workshop on Parallel and Symbolic Computation, pages 10–17. ACM Press, 2010.
E. Kaltofen, Y. N. Lakshman, and J.-M. Wiley. Modular rational sparse multivariate polynomial interpolation. In ISSAC '90: Proceedings of the International Symposium on Symbolic and Algebraic Computation, pages 135–139. New York, NY, USA, 1990. ACM Press.
E. Kaltofen and W. Lee. Early termination in sparse interpolation algorithms. J. Symb. Comput., 36(3):365–400, 2003.
E. Kaltofen and B. M. Trager. Computing with polynomials given by black boxes for their evaluations: greatest common divisors, factorization, separation of numerators and denominators. J. Symb. Comput., 9(3):301–320, 1990.
E. Kaltofen and L. Yagati. Improved sparse multivariate polynomial interpolation algorithms. In ISSAC '88: Proceedings of the International Symposium on Symbolic and Algebraic Computation, pages 467–474. Springer Verlag, 1988.
R. Moenck. Fast computation of gcds. In Proc. of the 5th ACM Annual Symposium on Theory of Computing, pages 142–171. New York, 1973. ACM Press.
H. Murao and T. Fujise. Modular algorithm for sparse multivariate polynomial interpolation and its parallel implementation. J. Symb. Comput., 21:377–396, 1996.
M. Okamoto. Some inequalities relating to the partial sum of binomial probabilities. Ann. Inst. Stat. Math., 10(1):29–35, 1959.
A. Perret du Cray. Algorithmes pour les polynômes creux : interpolation, arithmétique, test d'identité. PhD thesis, Université de Montpellier (France), 2023.
R. Prony. Essai expérimental et analytique sur les lois de la dilatabilité des fluides élastiques et sur celles de la force expansive de la vapeur de l'eau et de la vapeur de l'alkool, à différentes températures. J. de l'École Polytechnique Floréal et Plairial, an III, 1(cahier 22):24–76, 1795.
J.-J. Risler and F. Ronga. Testing polynomials. J. Symb. Comput., 10(1):1–5, 1990.
D. S. Roche. What can (and can't) we do with sparse polynomials? In C. Arreche, editor, Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '18, pages 25–30. New York, NY, USA, 2018. ACM Press.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Inform., 7:395–398, 1977.
A. Sedunova. A partial Bombieri–Vinogradov theorem with explicit constants. Publications mathématiques de Besançon. Algèbre et théorie des nombres, pages 101–110, 2018.
R. Zippel. Probabilistic algorithms for sparse polynomials. In E. W. Ng, editor, Symbolic and Algebraic Computation. Eurosam '79, An International Symposium on Symbolic and Algebraic Manipulation, Marseille, France, June 1979, volume 72 of Lect. Notes Comput. Sci., pages 216–226. Springer-Verlag, 1979.