Fast modular composition using
spiroids  |
|
| Preliminary version of December 5, 2025 |
|
 . Grégoire
Lecerf has been supported by the French ANR-22-CE48-0016
NODE project. Joris van der Hoeven has been supported by an
ERC-2023-ADG grant for the ODELIX project (number 101142171).
. Grégoire
Lecerf has been supported by the French ANR-22-CE48-0016
NODE project. Joris van der Hoeven has been supported by an
ERC-2023-ADG grant for the ODELIX project (number 101142171).
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
 . This article has
been written using GNU TeXmacs [8].
. This article has
been written using GNU TeXmacs [8].
Given three univariate polynomials |
Let  be an effective commutative ring, so that we
have algorithms for the ring operations. Given a monic polynomial
be an effective commutative ring, so that we
have algorithms for the ring operations. Given a monic polynomial  of degree
of degree 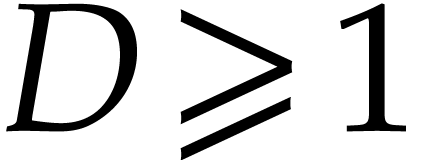 and polynomials
and polynomials
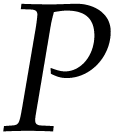 and
and 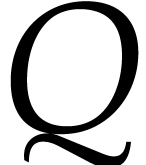 in
in 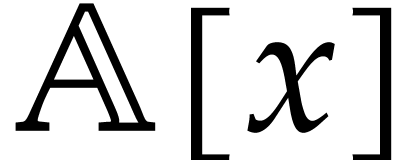 of degree
of degree 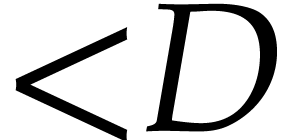 the computation of the remainder of
the computation of the remainder of
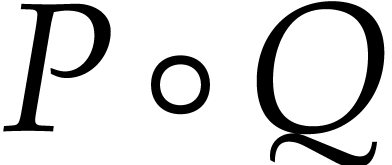 in the division by
in the division by  ,
written
,
written 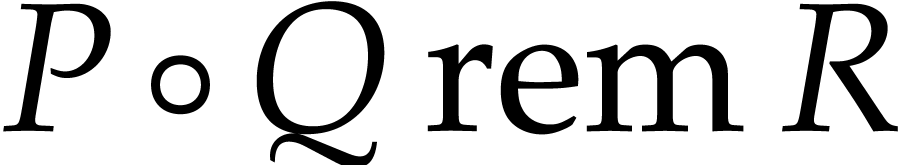 , is called the
problem of modular composition. Modular composition is a
central operation in computer algebra, especially for irreducible
polynomial factorization; see [12] for instance. It is
still unknown whether modular composition can be achieved in time nearly
linear in
, is called the
problem of modular composition. Modular composition is a
central operation in computer algebra, especially for irreducible
polynomial factorization; see [12] for instance. It is
still unknown whether modular composition can be achieved in time nearly
linear in 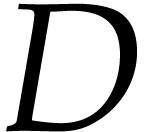 or not for any ground ring
or not for any ground ring  .
.
In this paper, we prove the following new complexity bound for when  is a finite ring
is a finite ring 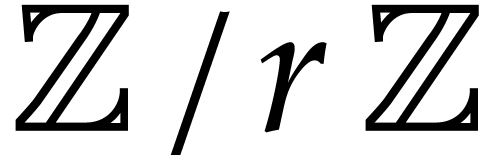 and where
and where
 is a common abbreviation for
is a common abbreviation for 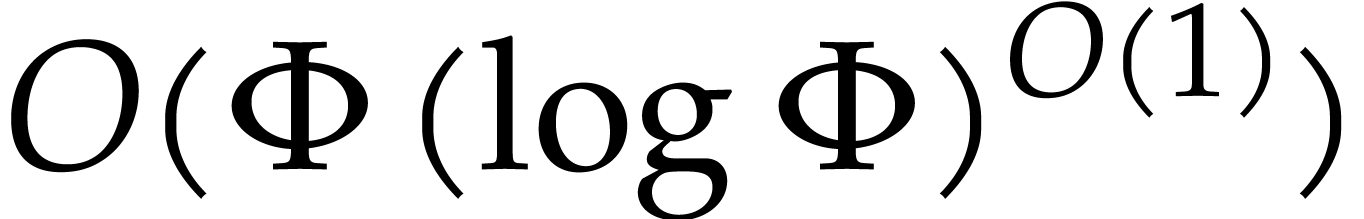 .
.
This result improves upon the best previously known bound
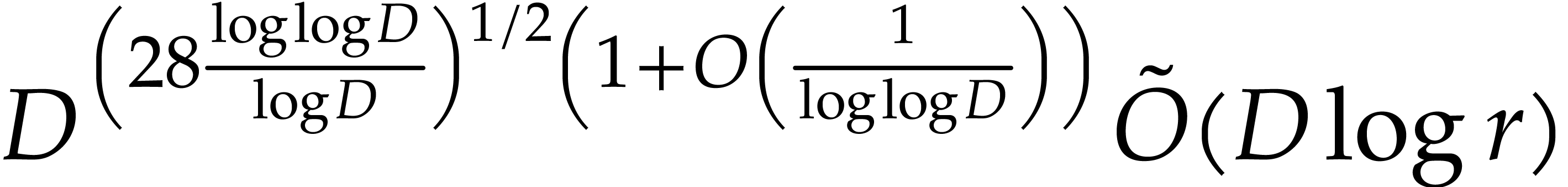
given in [11, Theorem 4], which is derived from an algorithm due to Kedlaya and Umans [14]. The novelty of our approach is a reduction of modular composition to the floating point evaluation of a multivariate polynomial at a special set of points, a so-called spiroid. We take advantage of fast Fourier transforms to perform these evaluations. In contrast, previously known methods, in the vein of [14], rely on number theoretic constructions.
Let 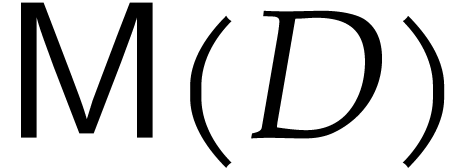 denote a cost function that bounds the
number of operations in
denote a cost function that bounds the
number of operations in  required to multiply two
polynomials of degree
required to multiply two
polynomials of degree 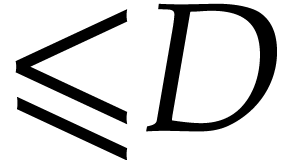 in
in  . Over any ring
. Over any ring  ,
modular composition can be performed with
,
modular composition can be performed with  operations in
operations in  by applying Horner's rule to
evaluate
by applying Horner's rule to
evaluate 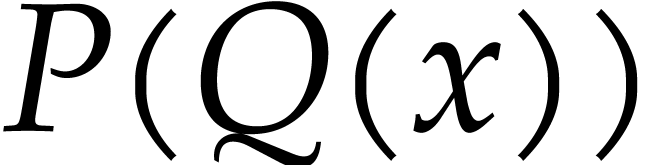 in
in 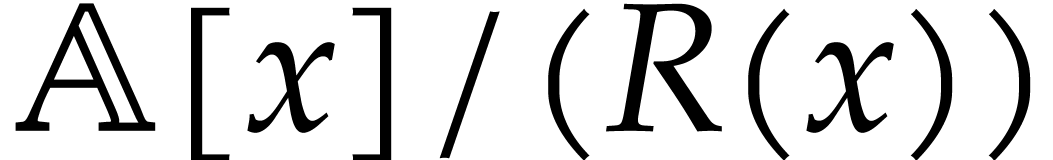 .
In 1978, Brent and Kung [3] gave a faster algorithm with
cost
.
In 1978, Brent and Kung [3] gave a faster algorithm with
cost 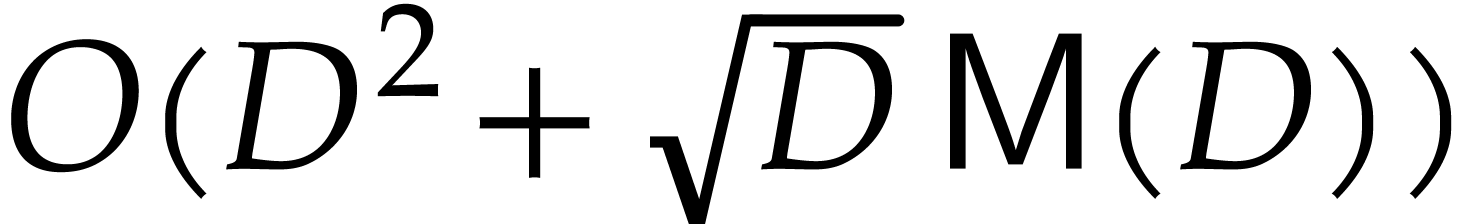 , that uses the
baby-step giant-step technique [17]. Their
algorithm even yielded a sub-quadratic cost
, that uses the
baby-step giant-step technique [17]. Their
algorithm even yielded a sub-quadratic cost 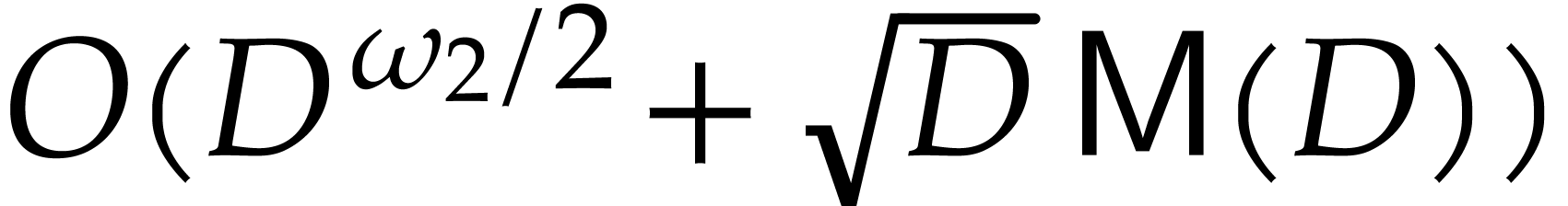 when
combined with fast linear algebra; see [13, p. 185]. Here,
the constant
when
combined with fast linear algebra; see [13, p. 185]. Here,
the constant 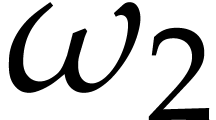 is a real value between 3 and 4
such that the product of a
is a real value between 3 and 4
such that the product of a 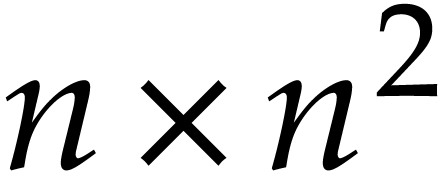 matrix by a
matrix by a 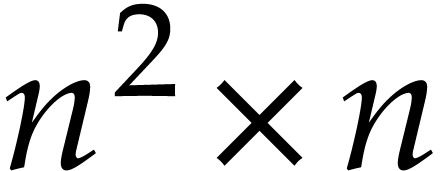 matrix takes
matrix takes 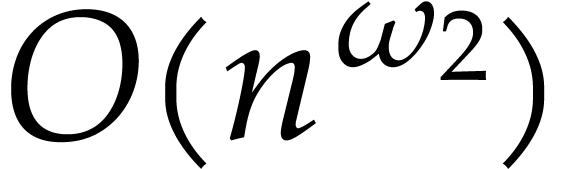 operations; one may
take
operations; one may
take 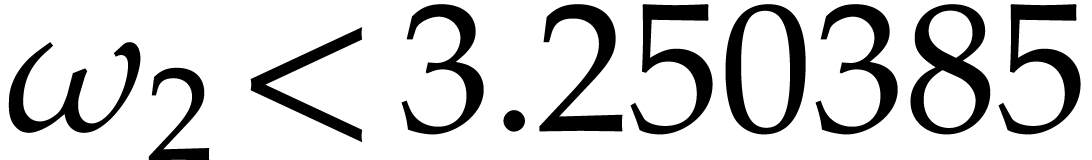 according to [19]. At present
time, the fastest known modular composition method over any ground field
according to [19]. At present
time, the fastest known modular composition method over any ground field
 is due to Neiger, Salvy, Schost, and Villard [16]: it is probabilistic of Las Vegas type and takes an
expected number of
is due to Neiger, Salvy, Schost, and Villard [16]: it is probabilistic of Las Vegas type and takes an
expected number of
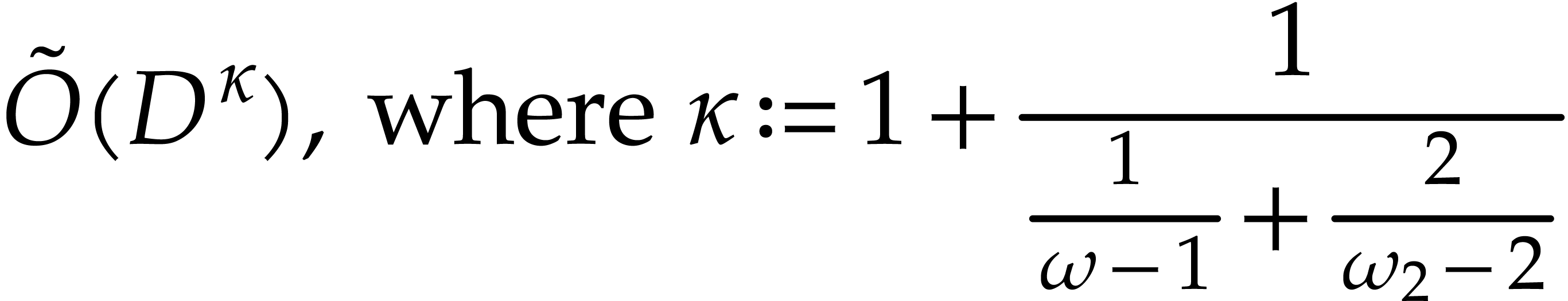
operations in  ; see [16,
Theorem 1.1]. Here, the constant
; see [16,
Theorem 1.1]. Here, the constant 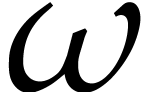 denotes any
real value between
denotes any
real value between 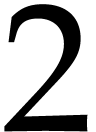 and
and 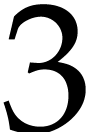 such that two
such that two  matrices over a commutative ring
can be multiplied with
matrices over a commutative ring
can be multiplied with 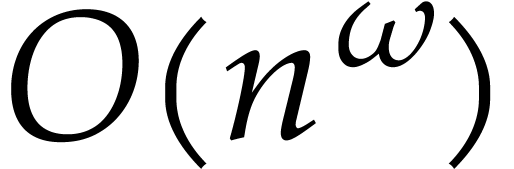 ring operations. The
current best known value is
ring operations. The
current best known value is 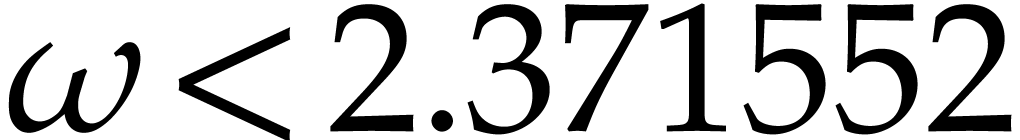 [19],
so we may take
[19],
so we may take 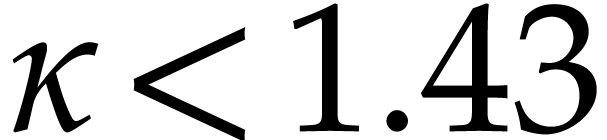 .
.
A major breakthrough for the modular composition problem is due to
Kedlaya and Umans [14] in the case where  is a finite field
is a finite field 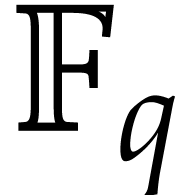 (and even more generally a
finite ring of the form
(and even more generally a
finite ring of the form 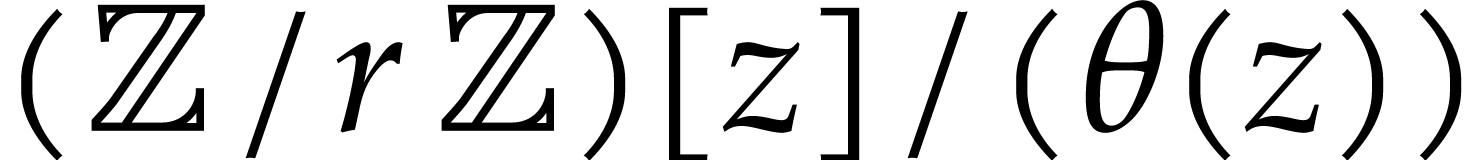 for any integer
for any integer 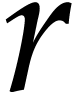 and
and 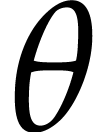 monic). For any fixed
real value
monic). For any fixed
real value  , they showed that
, they showed that
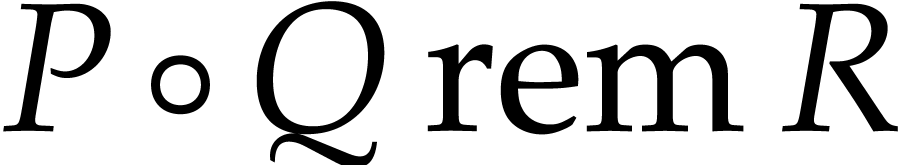 can be computed using
can be computed using 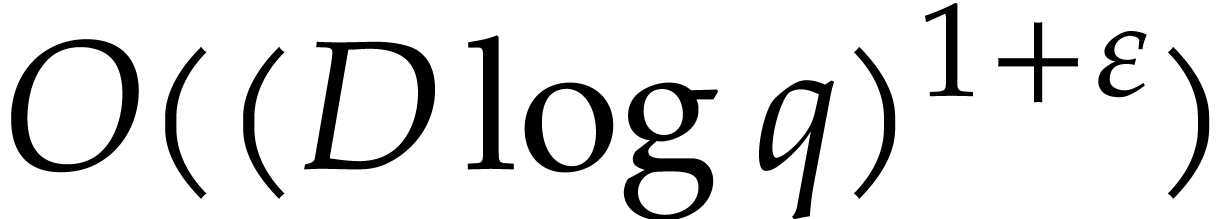 bit operations. The dependency in
bit operations. The dependency in  is analyzed in
[11]. Recent improvements of the Kedlaya–Umans
approach can be found in [1, 2], but the
dependency in
is analyzed in
[11]. Recent improvements of the Kedlaya–Umans
approach can be found in [1, 2], but the
dependency in  is not detailed.
is not detailed.
In [9, 10] it was shown how the knowledge of
factorizations of  can be exploited to speed up
modular composition. An important special case concerns the composition
of power series, which corresponds to taking
can be exploited to speed up
modular composition. An important special case concerns the composition
of power series, which corresponds to taking 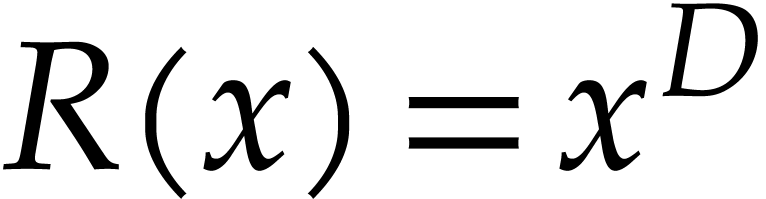 . Recently, Kinoshita and Li [15]
showed how to accomplish this task using
. Recently, Kinoshita and Li [15]
showed how to accomplish this task using 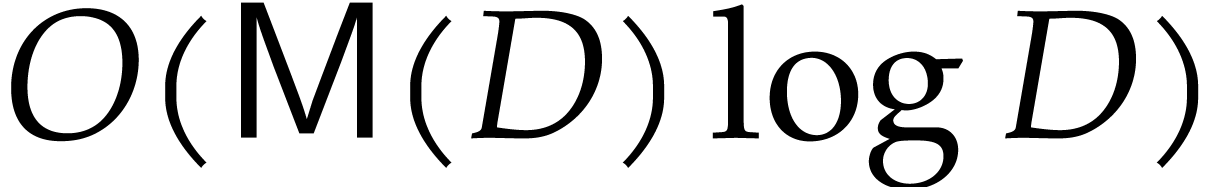 operations in
operations in  .
.
Our modular composition algorithm will be presented in section 5: Theorem 1 follows from the sharper complexity bound given in Theorem 24. As in [14], the problem will be reduced to the multi-point evaluation of a multivariate polynomial, using Kronecker segmentation. But, instead of relying on finite field arithmetic, we benefit from floating point arithmetic and reduce the multi-point evaluation to a deformation of the fast Fourier transform. The deformed evaluation point set is presented in section 3. Corresponding evaluation and interpolation algorithms are given in section 4. The next section gathers prerequisites.
For complexity analyses, we will consider bit complexity models such as
computation trees or RAM machines [4, 5]. The
function 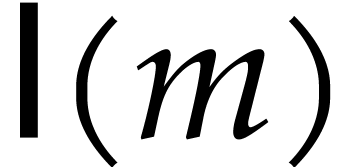 will bound the bit cost for multiplying
two integers of bit size
will bound the bit cost for multiplying
two integers of bit size 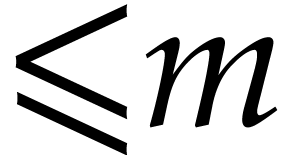 . We
will assume that
. We
will assume that 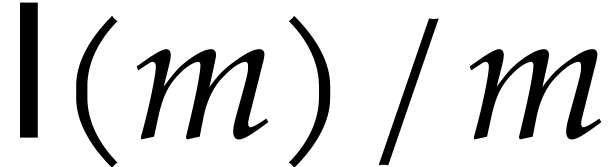 is nondecreasing. At the end,
we will make use of the fast product of [6], that yields
is nondecreasing. At the end,
we will make use of the fast product of [6], that yields
 .
.
Numbers will be represented in radix  ,
with a finite number of digits. We will represent fixed point numbers by
a signed mantissa and a fixed exponent. More precisely, given a
precision parameter
,
with a finite number of digits. We will represent fixed point numbers by
a signed mantissa and a fixed exponent. More precisely, given a
precision parameter  , we
denote by
, we
denote by  the set of complex numbers of the form
the set of complex numbers of the form
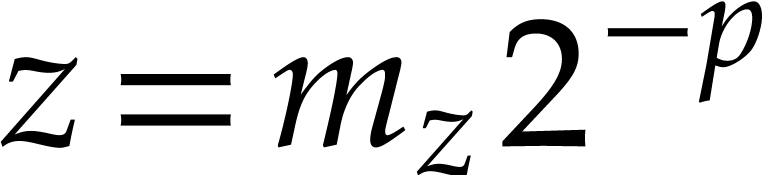 , where
, where 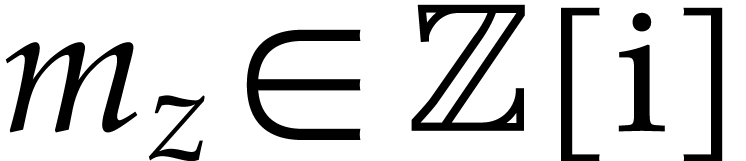 and
and 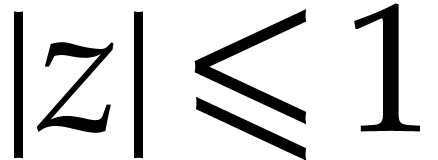 . We write
. We write 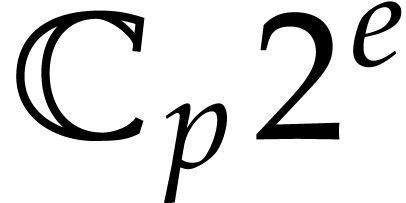 for the set of complex numbers of the form
for the set of complex numbers of the form 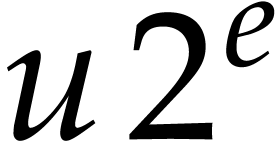 , where
, where  and
and  ; in particular, for
; in particular, for  we always have
we always have 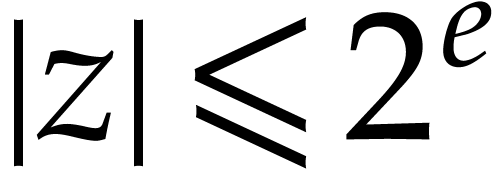 .
At every stage of our algorithms, the exponent
.
At every stage of our algorithms, the exponent 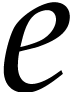 will be specified, so the exponents do not have to be stored or
manipulated explicitly.
will be specified, so the exponents do not have to be stored or
manipulated explicitly.
In the error analyses of our numerical algorithms, each  is really the approximation of some genuine complex number
is really the approximation of some genuine complex number 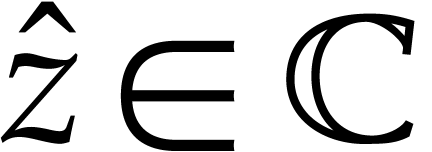 . So each such
. So each such  comes
with an implicit error bound
comes
with an implicit error bound 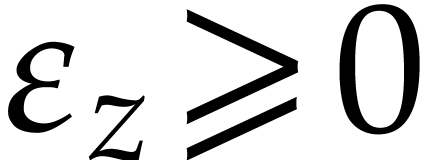 ;
this is a real number for which we can guarantee that
;
this is a real number for which we can guarantee that 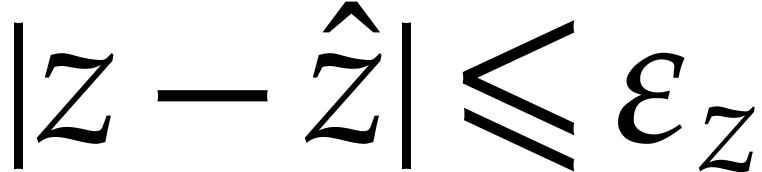 . A truncation of
. A truncation of  is an approximation
is an approximation  of
of  that is rounded towards zero in the sense that
that is rounded towards zero in the sense that  . Given
. Given  ,
the sum
,
the sum  can be computed exactly in time
can be computed exactly in time 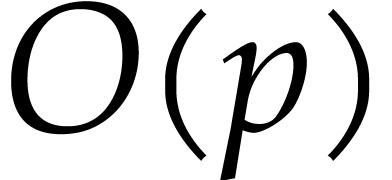 . The product
. The product 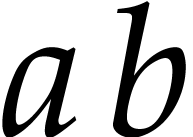 can be computed exactly in time
can be computed exactly in time 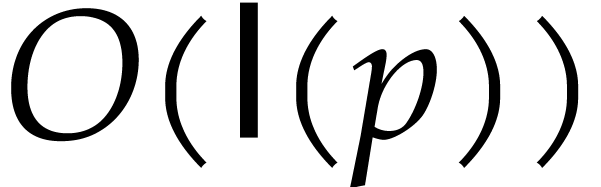 .
.
Proof. Rounding 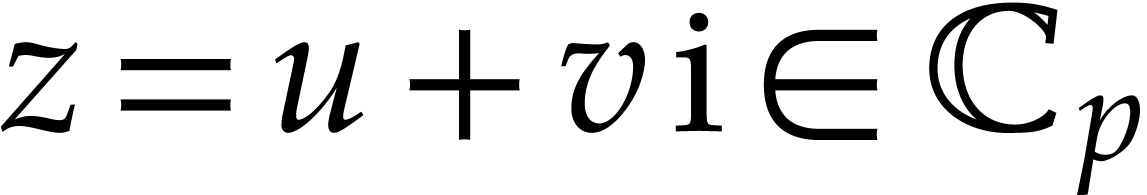 into
into
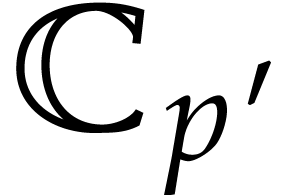 can be done as follows: let
can be done as follows: let 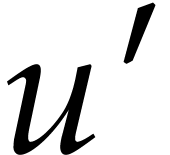 and
and 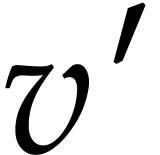 be the truncations to the nearest of
be the truncations to the nearest of 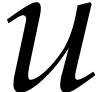 and
and  into
into 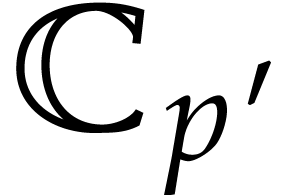 and let
and let 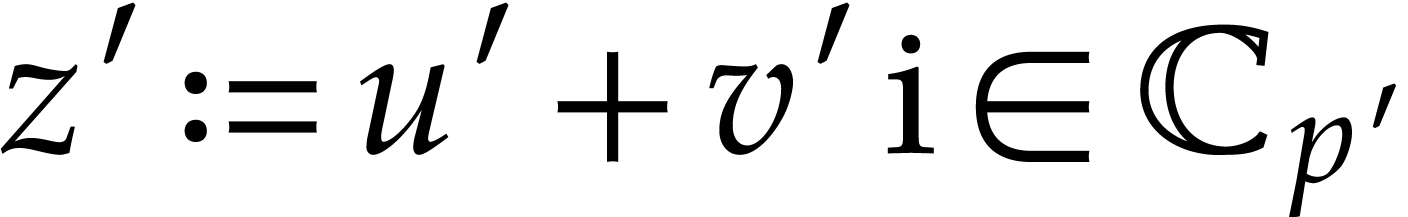 ; Then we have
; Then we have 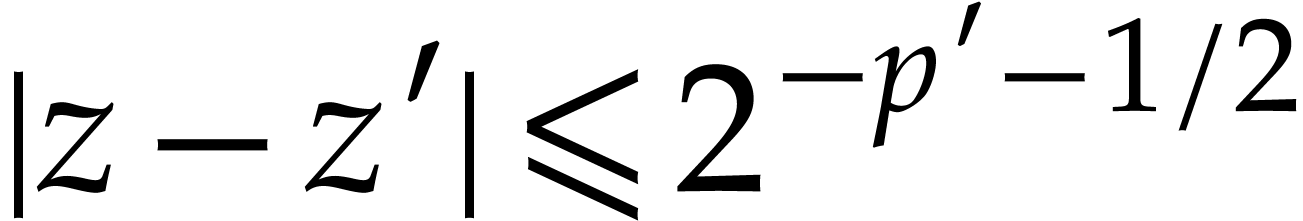 .
.
Proof. Rounding 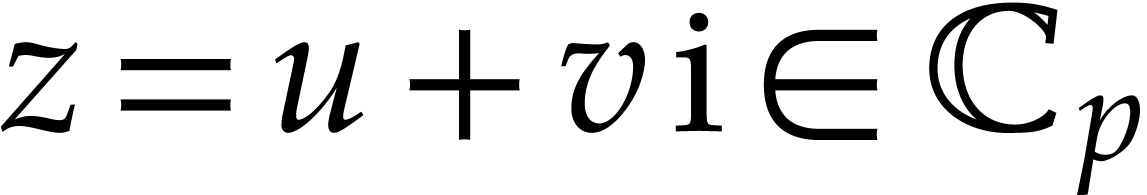 towards
zero into
towards
zero into 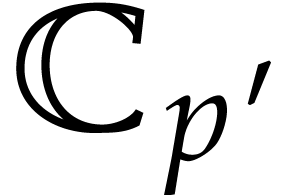 can be done as follows: let
can be done as follows: let 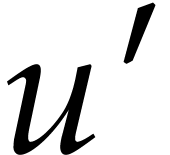 and
and 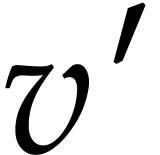 be the truncations of
be the truncations of 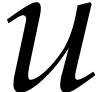 and
and  at precision
at precision 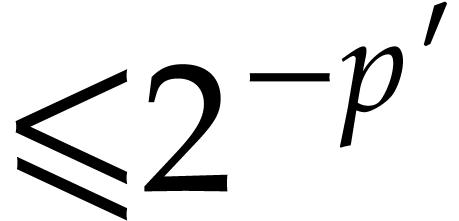 and let
and let 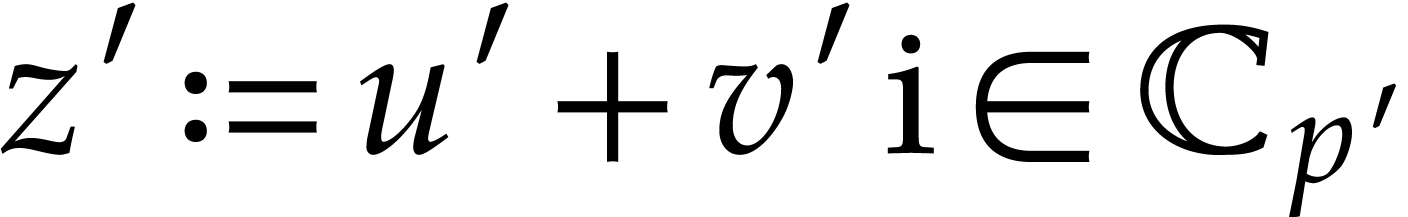 ; Then
we have
; Then
we have 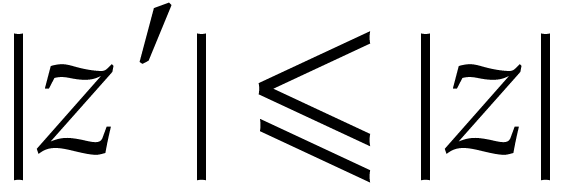 and
and 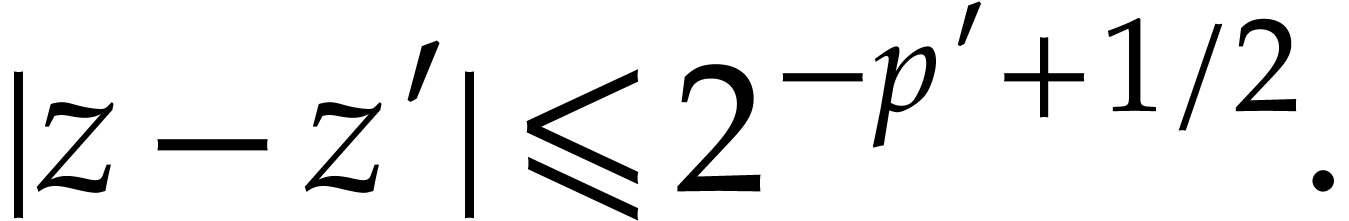

Let  be a power of
be a power of  and
let
and
let  be a vector of complex numbers. We write
be a vector of complex numbers. We write
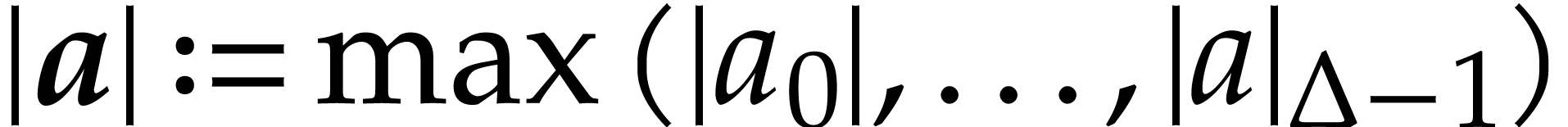 and
and 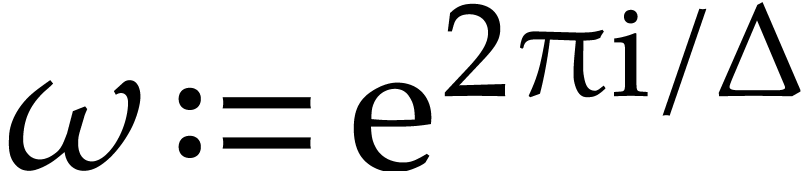 .
.
Proof. We use [7, Proposition 4] at
precision 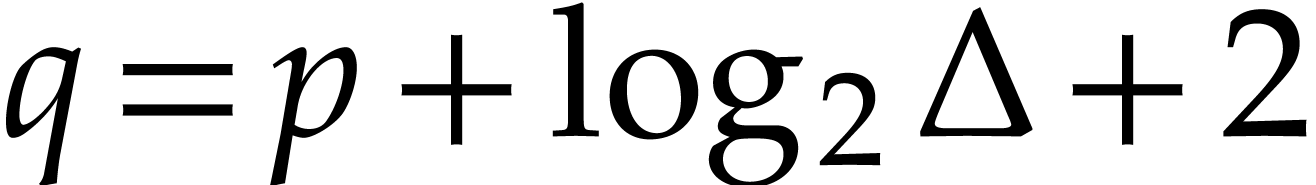 in order to obtain first
approximations of
in order to obtain first
approximations of 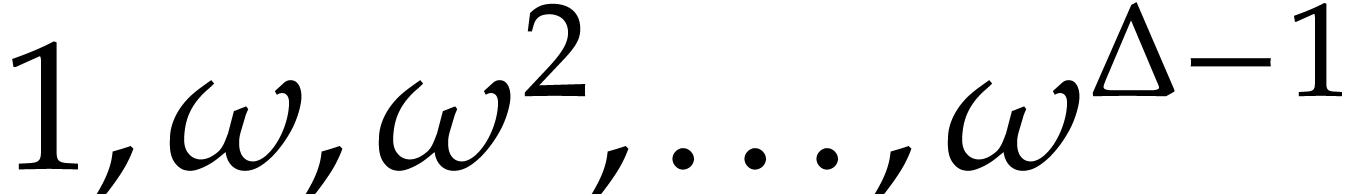 in
in  with error
with error 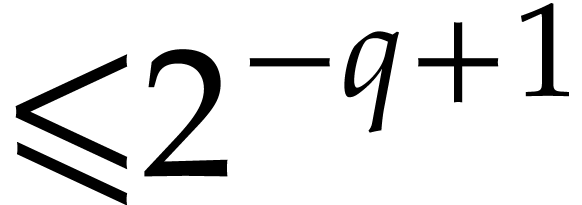 . We next truncate
these results in
. We next truncate
these results in  , which
yields an overall error
, which
yields an overall error 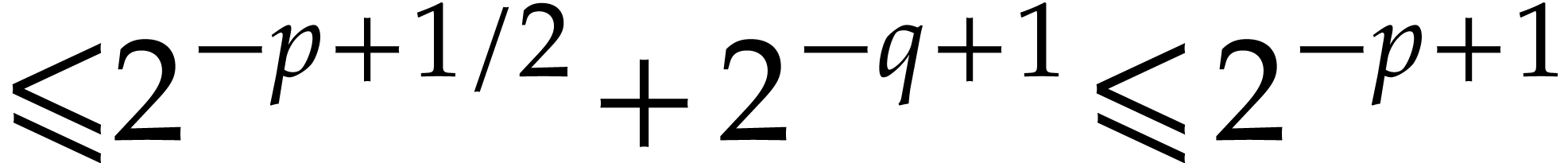 thanks to Lemma 3.
thanks to Lemma 3.
We define the fast Fourier transform of  to be
to be
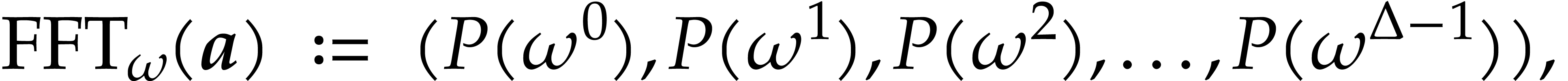
where 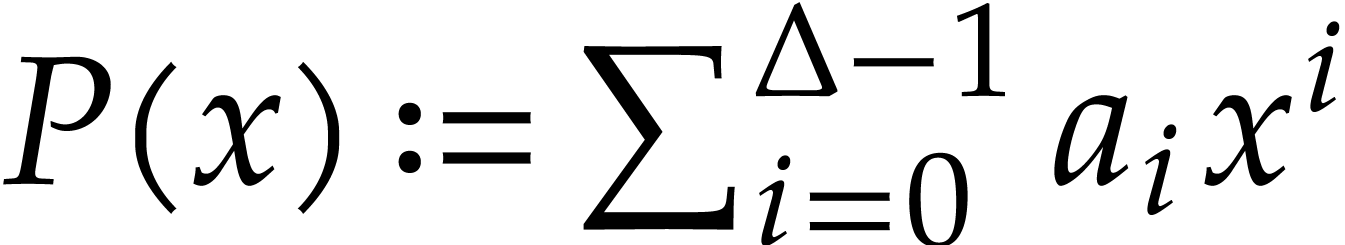 . In particular, we
have
. In particular, we
have 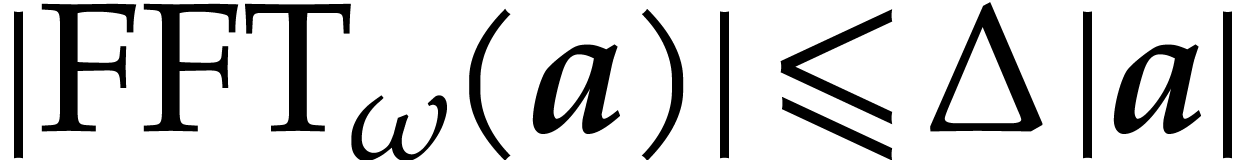 .
.
Proof. Thanks to [18, section 3] an
approximation of 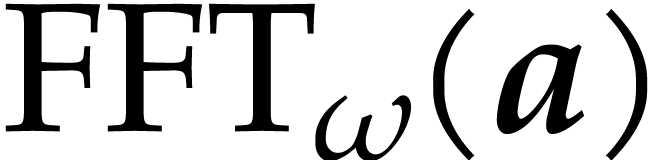 in
in 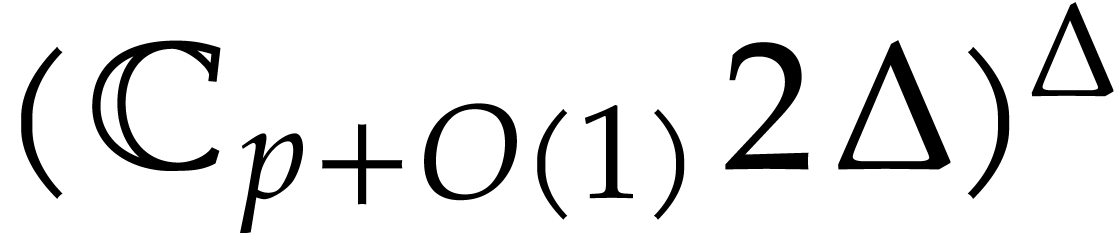 can
be computed with error
can
be computed with error 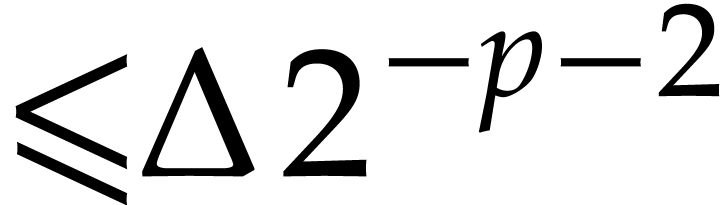 in time
in time  . Consider an entry
. Consider an entry 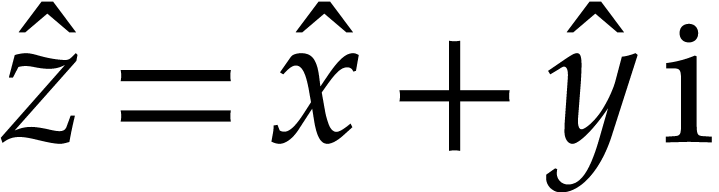 of
of
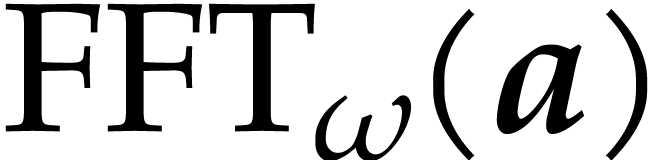 and let
and let 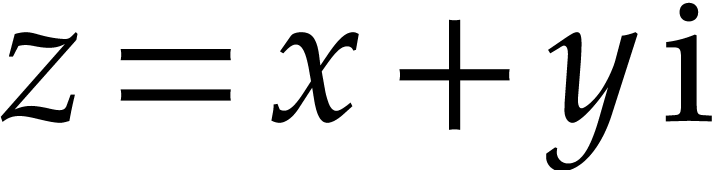 be the
corresponding approximation. Let
be the
corresponding approximation. Let 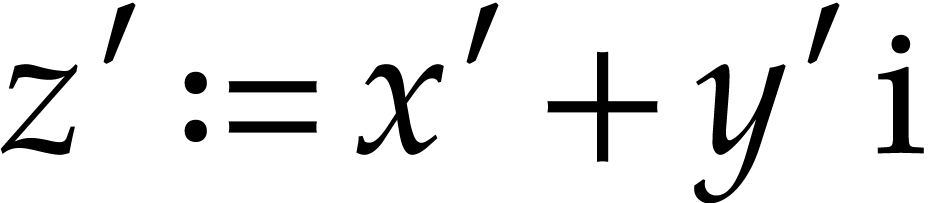 ,
where
,
where 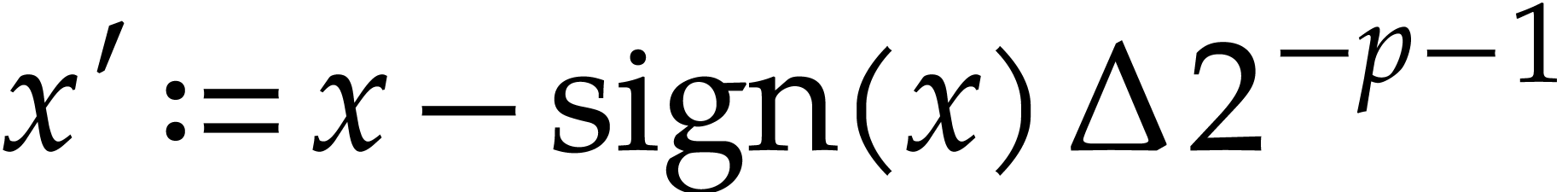 and
and 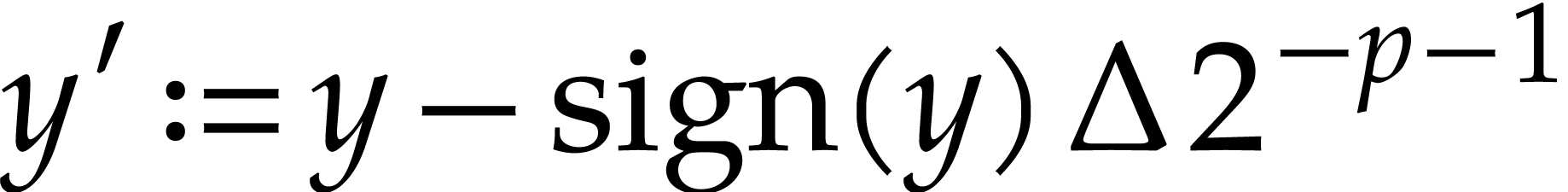 .
Then
.
Then 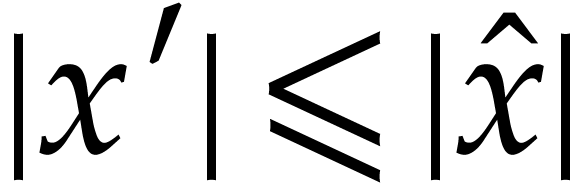 ,
, 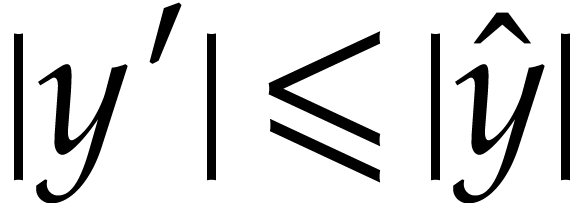 , and
, and 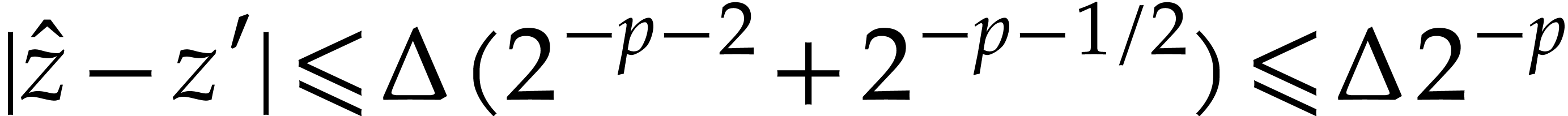 .
We may clearly compute
.
We may clearly compute  in time
in time 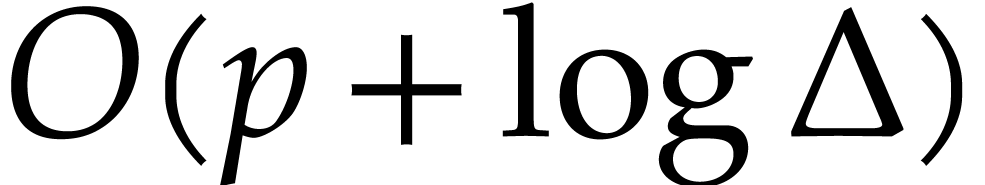 . Thanks to Lemma 3, and using
. Thanks to Lemma 3, and using
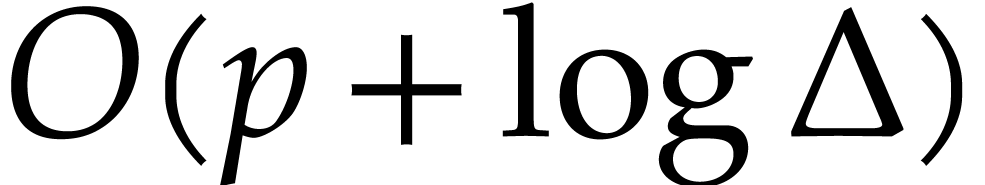 further operations, we may next compute a
truncation
further operations, we may next compute a
truncation 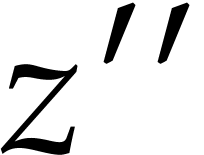 of
of  with error
with error
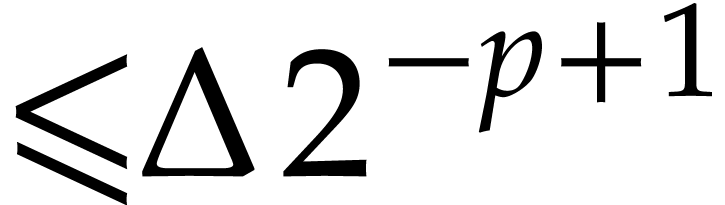 .
.
Proof. If  ,
then
,
then  . Otherwise,
. Otherwise,  and we have
and we have


Given integers  , we define
, we define
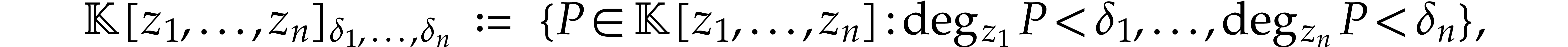
where 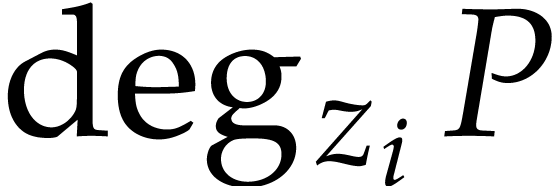 denotes the partial degree of
denotes the partial degree of 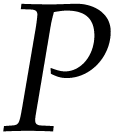 in
in  , for
, for 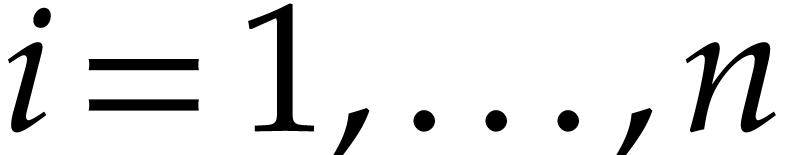 . In this paper, a dense
representation will be used for univariate and multivariate polynomials.
This means that a polynomial
. In this paper, a dense
representation will be used for univariate and multivariate polynomials.
This means that a polynomial  is stored as a
vector of size
is stored as a
vector of size 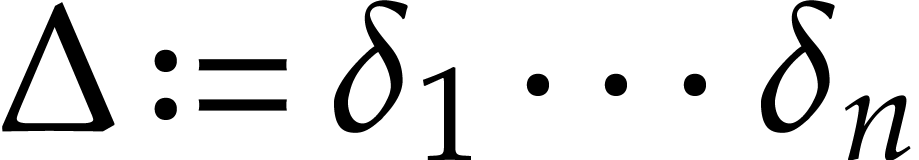 made of the coefficients of the
terms of
made of the coefficients of the
terms of  of partial degree
of partial degree 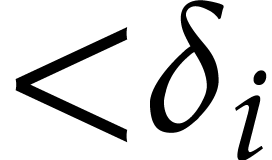 in
in  , for
, for 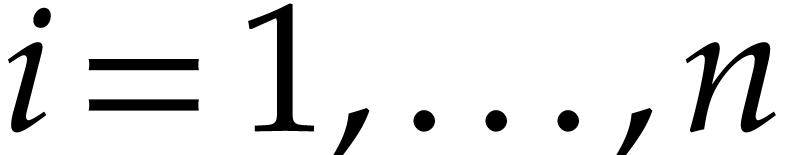 . Precisely, when
. Precisely, when 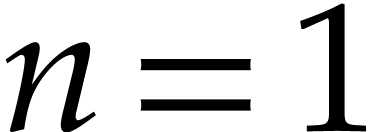 ,
a polynomial
,
a polynomial 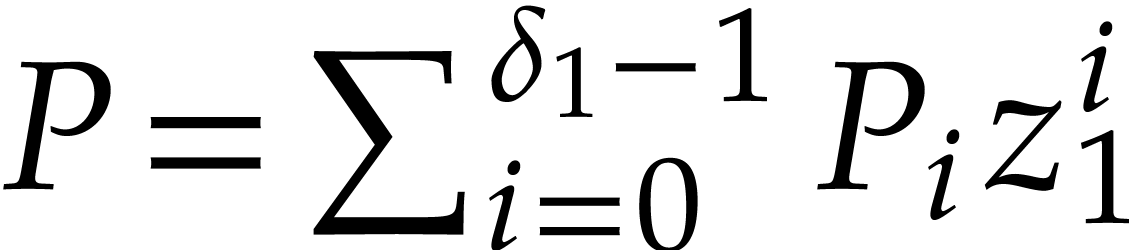 is stored as the vector
is stored as the vector 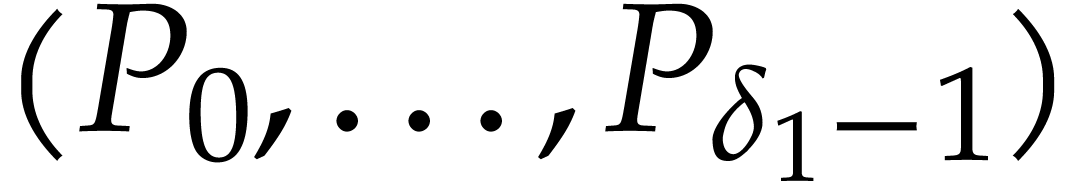 . When
. When  , a polynomial
, a polynomial 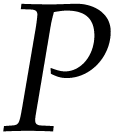 will be
regarded as a univariate polynomial in
will be
regarded as a univariate polynomial in 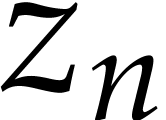 whose
coefficients are polynomials in
whose
coefficients are polynomials in 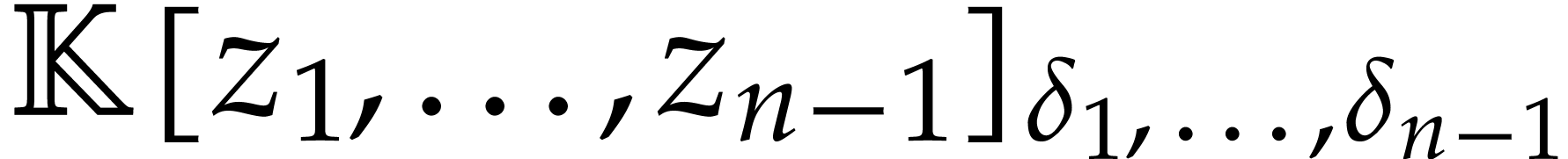 .
.
Given a polynomial 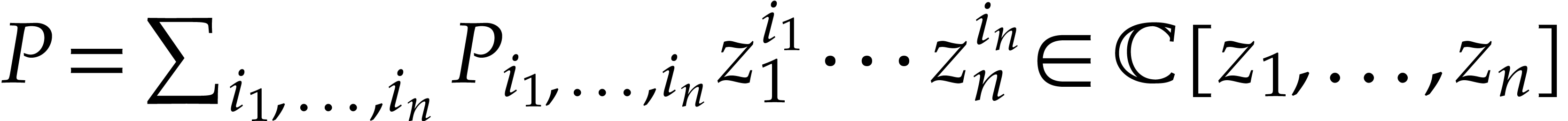 , we
define
, we
define
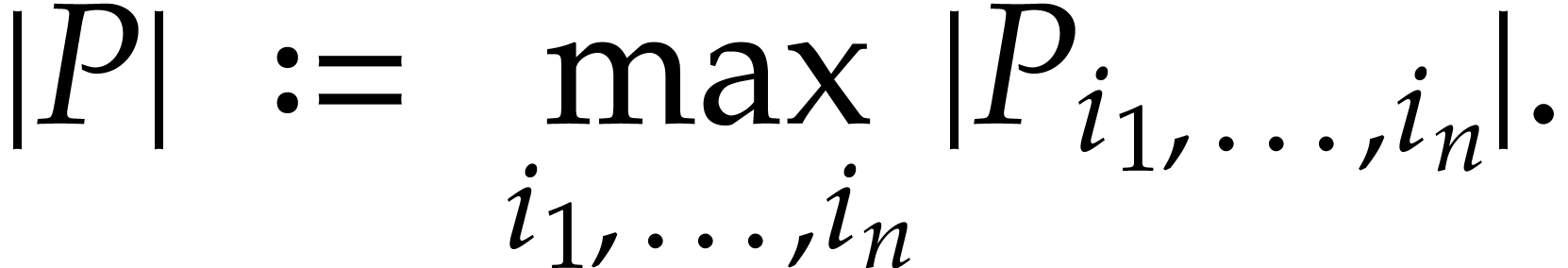
Given polynomials 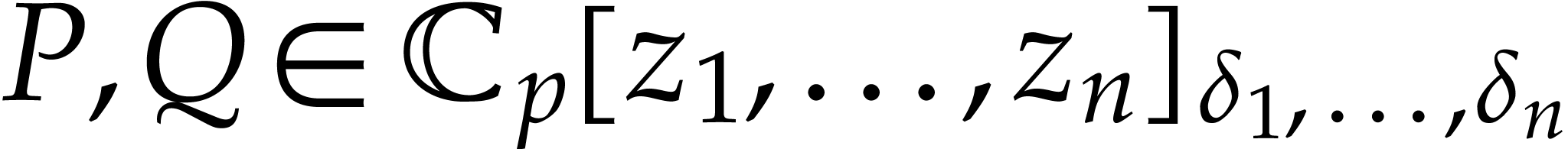 the sum
the sum  can be computed exactly in time
can be computed exactly in time 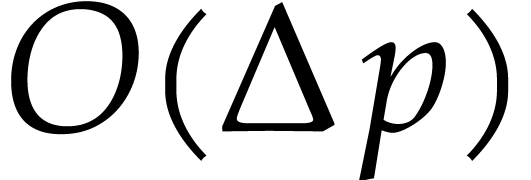 .
The product
.
The product  can be computed exactly in time
can be computed exactly in time 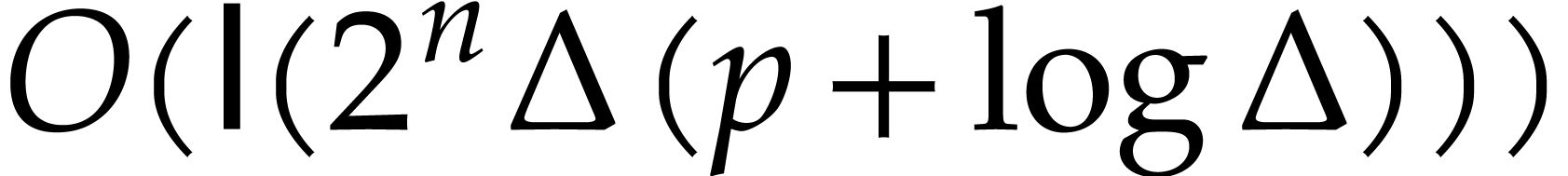 using Kronecker substitution; see [5,
Chapter 8]. In addition we have
using Kronecker substitution; see [5,
Chapter 8]. In addition we have 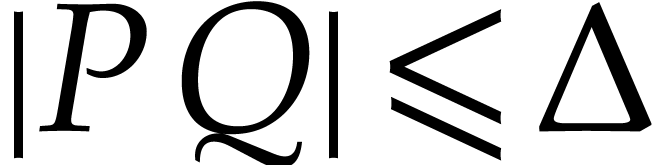 .
.
Given integers  , we let
, we let 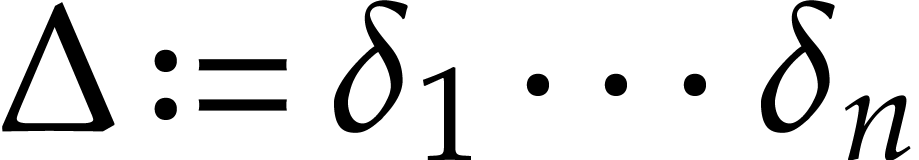 and consider a tuple of points
and consider a tuple of points

We define 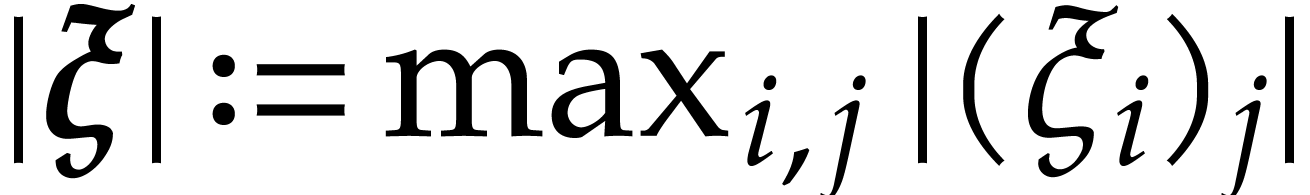 and call
and call

the vanishing ideal of  .
We also define the evaluation map
.
We also define the evaluation map
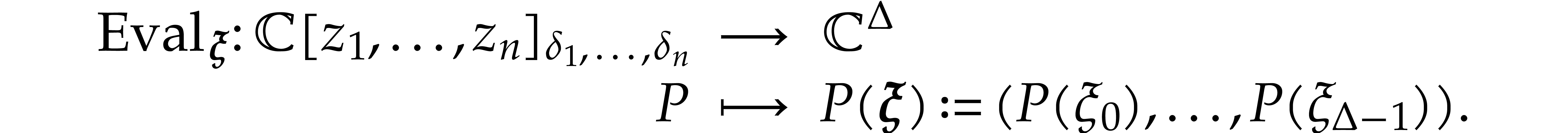
We refer to the computation of 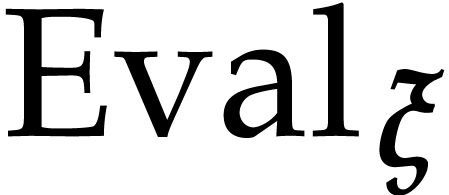 as the problem of
multi-point evaluation. The computation of
as the problem of
multi-point evaluation. The computation of 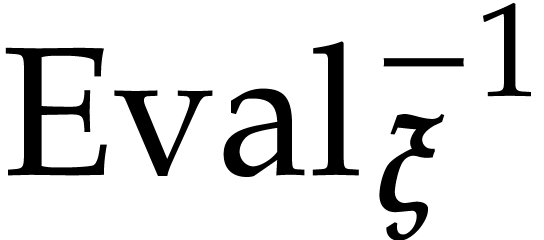 is called the interpolation problem.
is called the interpolation problem. 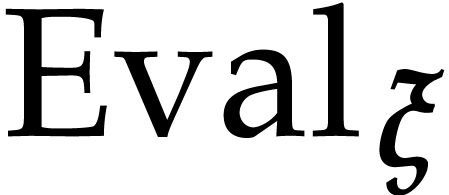 is
a bijection for a Zariski dense subset of tuples
is
a bijection for a Zariski dense subset of tuples 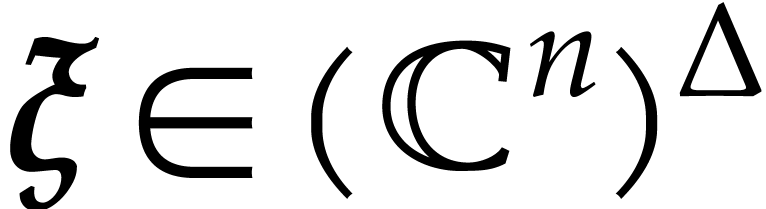 . Whenever this is the case, the points
. Whenever this is the case, the points  are pairwise distinct, so we have a natural bijection
are pairwise distinct, so we have a natural bijection
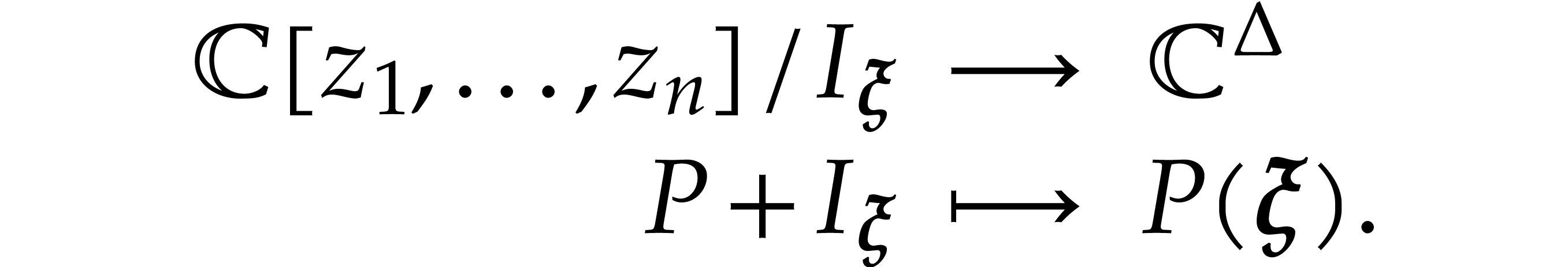
This allows us to use polynomials in 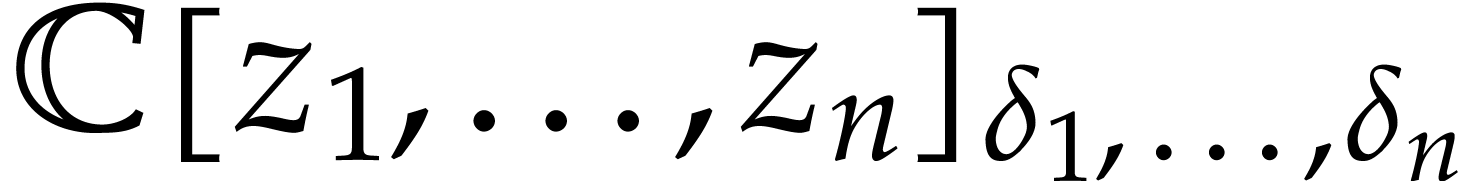 as
canonical representatives of residue classes in
as
canonical representatives of residue classes in 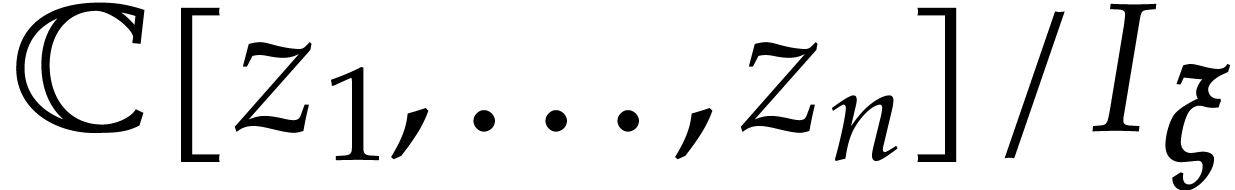 . In particular, given a polynomial
. In particular, given a polynomial  , we define
, we define  to be the
unique polynomial in
to be the
unique polynomial in 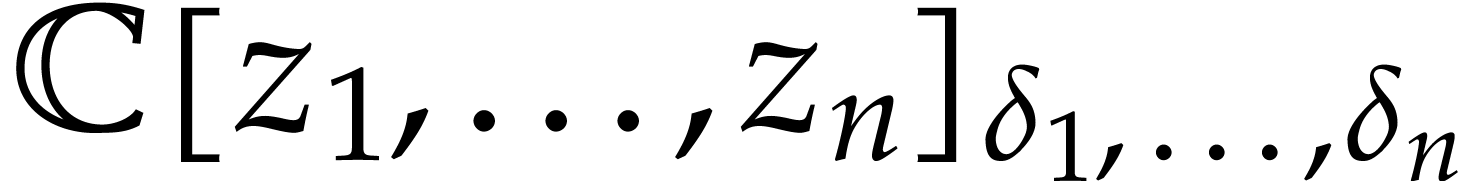 with
with  . For special tuples
. For special tuples 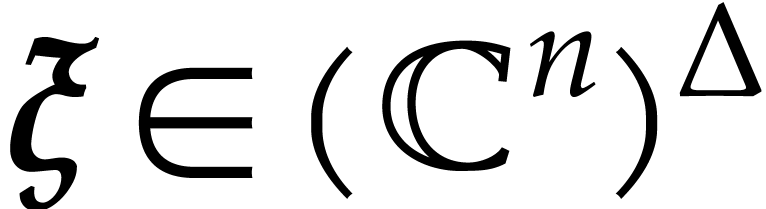 ,
called spiroids, we will show in this section that
,
called spiroids, we will show in this section that  can be computed efficiently.
can be computed efficiently.
Assume from now that 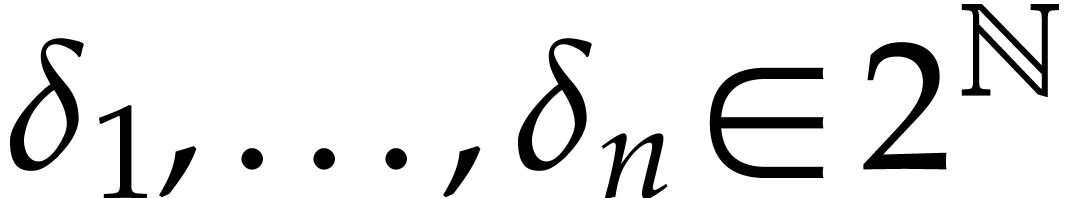 are powers of two and let
are powers of two and let
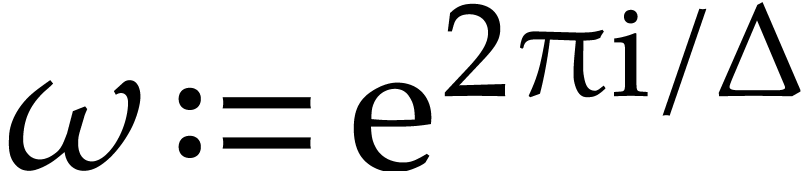 be the standard primitive
be the standard primitive  -th root of unity in
-th root of unity in  .
For each
.
For each  , we let
, we let
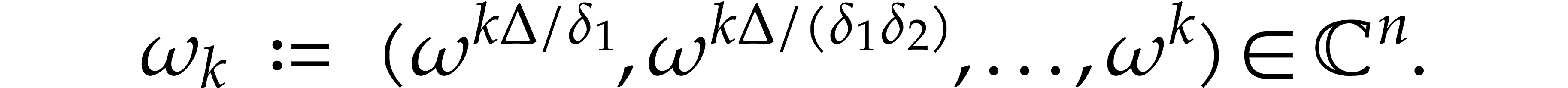
We call the tuple 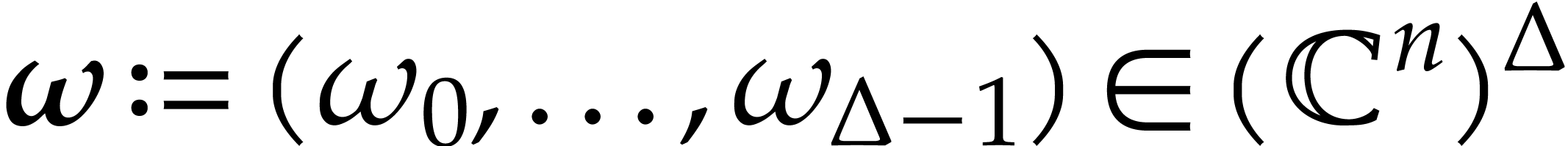 a regular spiroid.
The vanishing ideal
a regular spiroid.
The vanishing ideal 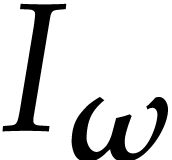 of this tuple of points is
generated by the polynomials
of this tuple of points is
generated by the polynomials
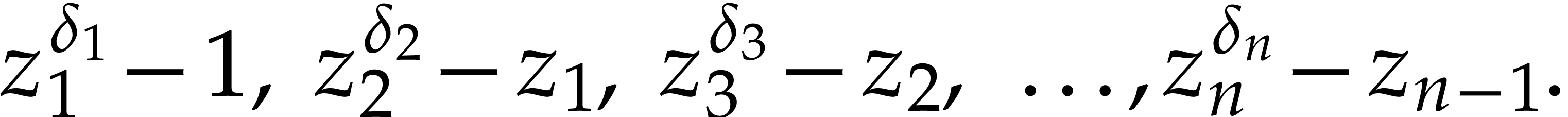 |
(1) |
A straightforward computation shows that these generators actually form
a Gröbner basis for the grevlex monomial ordering. For instance,
for  , the
, the  -polynomial of
-polynomial of 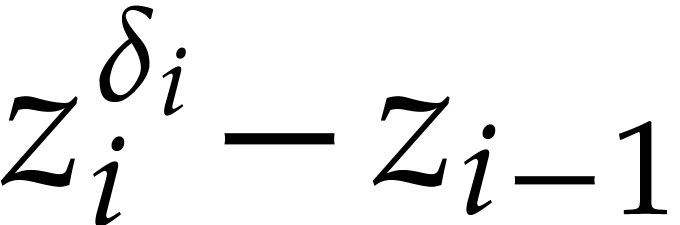 and
and 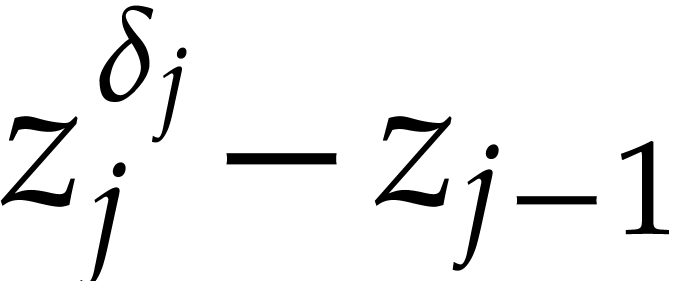 is
is
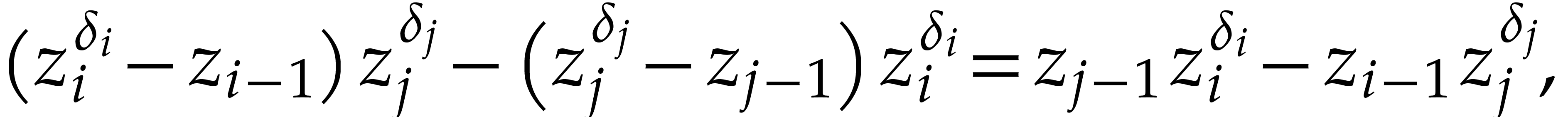
which reduces to 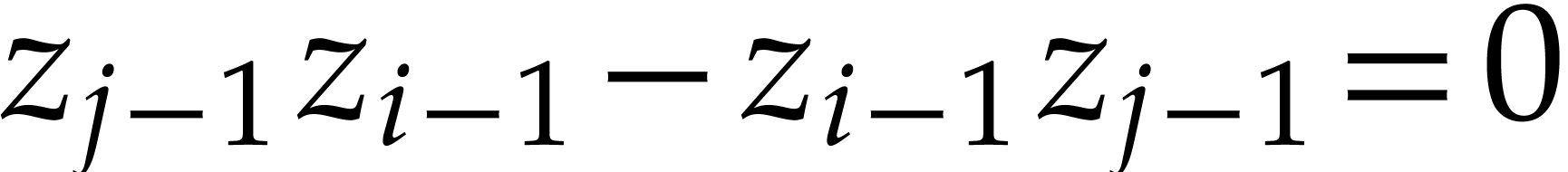 . In
particular, the monomials in
. In
particular, the monomials in 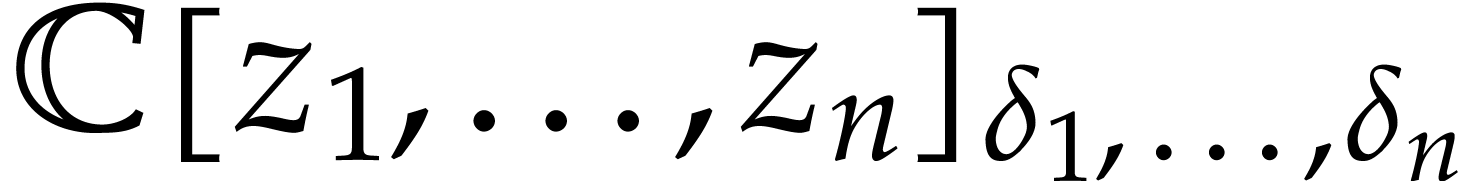 are reduced.
are reduced.
Let 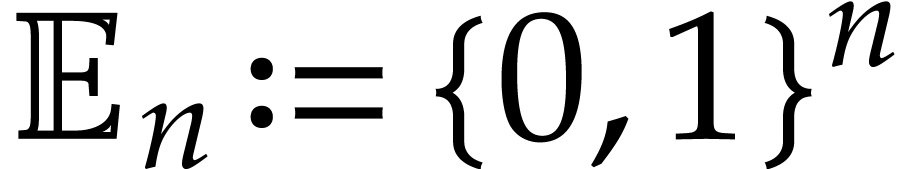 ,
, 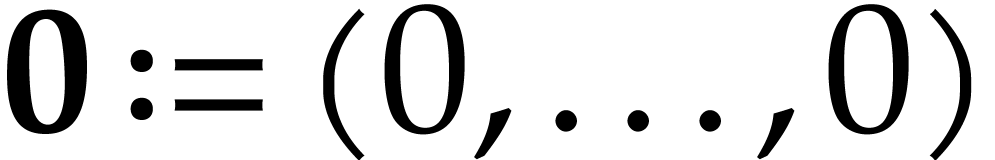 , and
, and 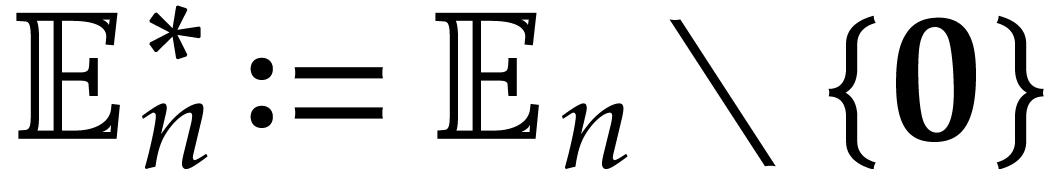 .
For
.
For  , we have
, we have
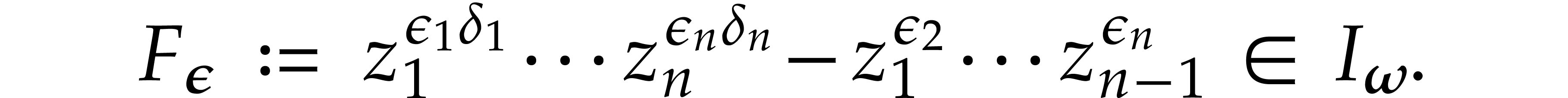
For convenience, we also set

Given 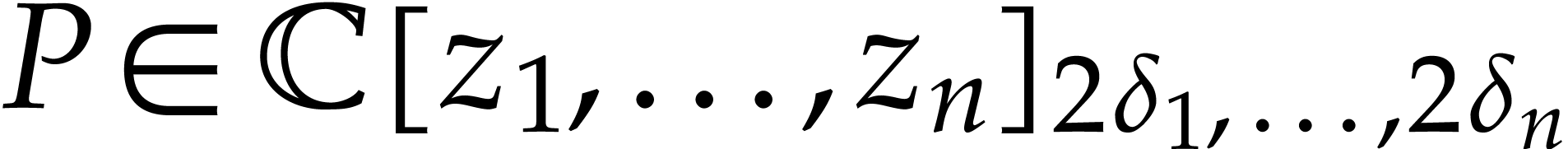 and a family
and a family
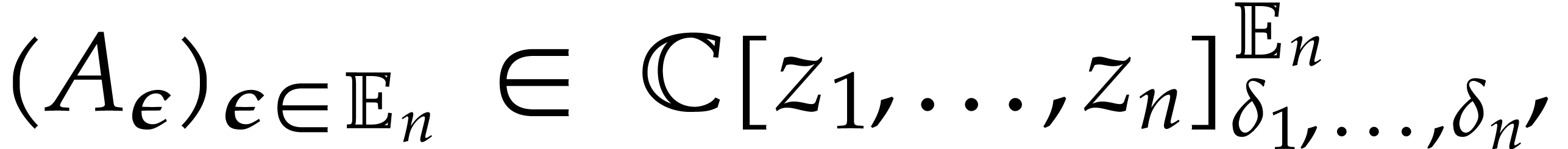
we say that 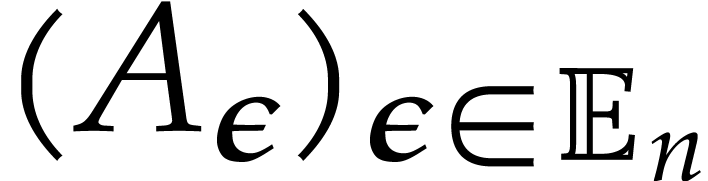 is an extended reduction of
is an extended reduction of
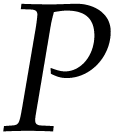 modulo
modulo 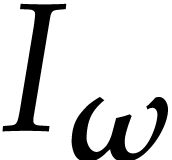 if
if

Since 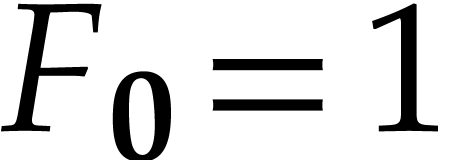 , we have
, we have 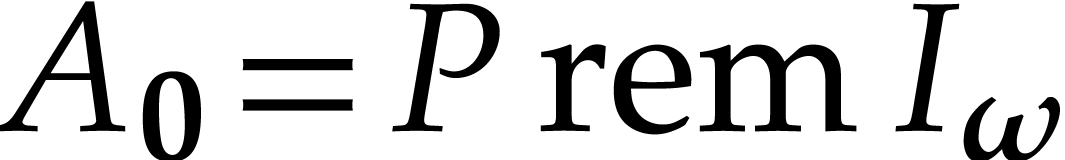 . We further define
. We further define
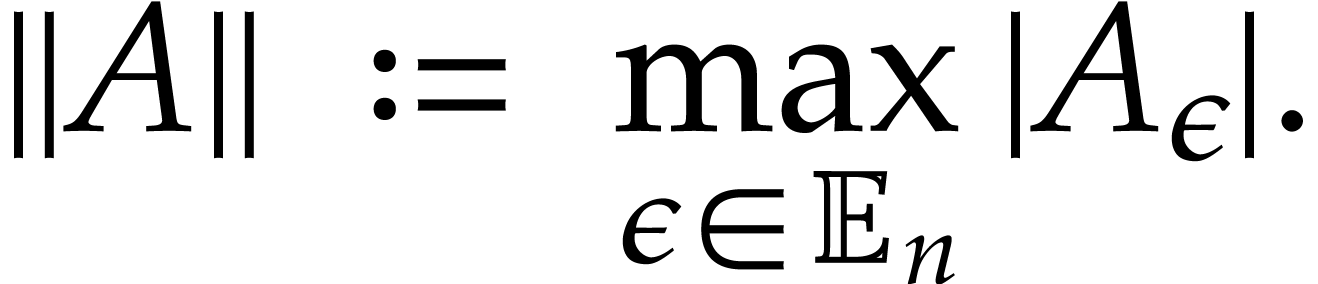
Given  we aim at computing an extended reduction
of
we aim at computing an extended reduction
of 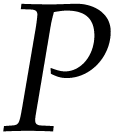 by
by 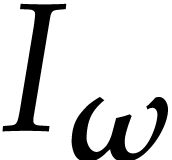 .
As a first step we begin with polynomials
.
As a first step we begin with polynomials 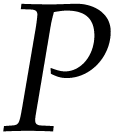 in
in
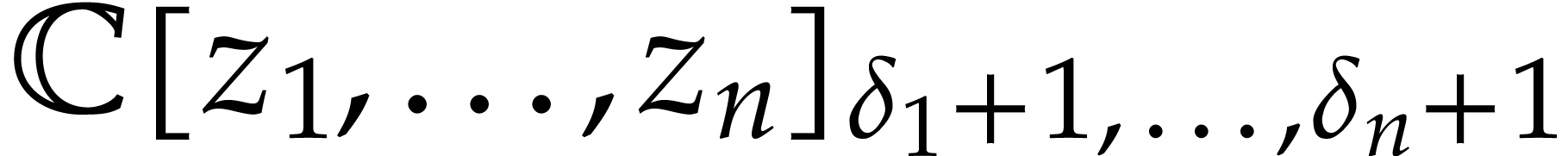 .
.
Proof. Since 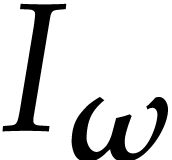 is
generated by binomial polynomials
is
generated by binomial polynomials 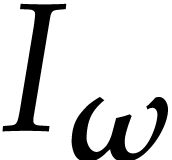 is a monomial.
The defining equations
is a monomial.
The defining equations 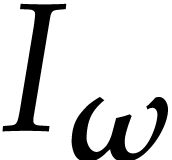 further imply that
further imply that  are
invertible in
are
invertible in  .
.
The support  of a polynomial
of a polynomial 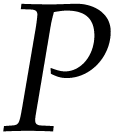 is the set of its monomials with a non-zero coefficient.
We say that the monomials of
is the set of its monomials with a non-zero coefficient.
We say that the monomials of  are pairwise
distinct modulo
are pairwise
distinct modulo 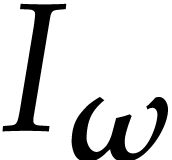 when any two distinct monomials
of
when any two distinct monomials
of  have distinct projections in
have distinct projections in  .
.
 be such that the monomials of its support are
pairwise distinct modulo
be such that the monomials of its support are
pairwise distinct modulo 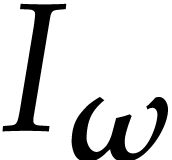 .
Let
.
Let  be defined recursively as follows:
be defined recursively as follows: 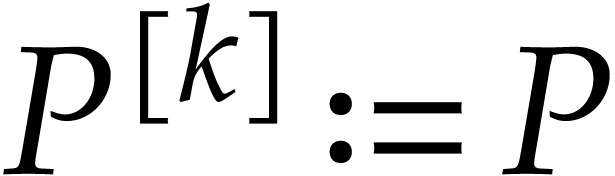 , and
, and
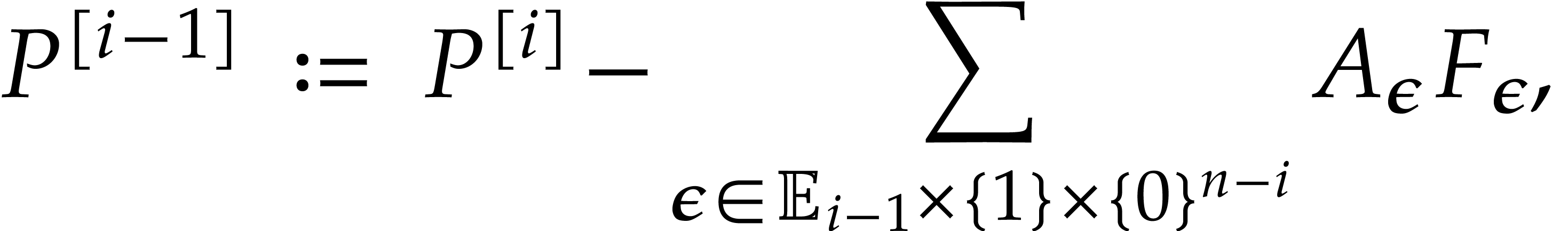 |
(2) |
where
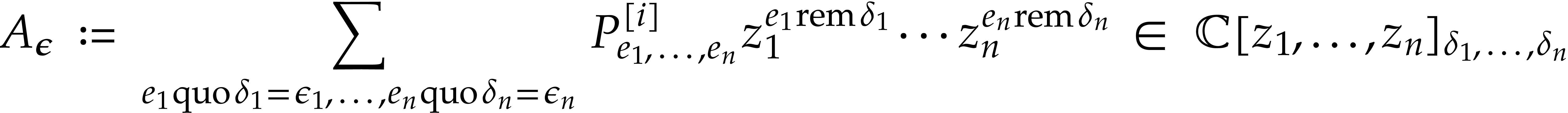
for 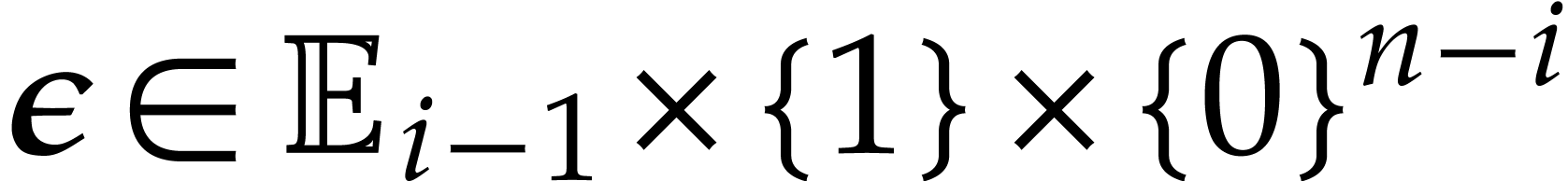 . For
. For  , the following properties hold:
, the following properties hold:
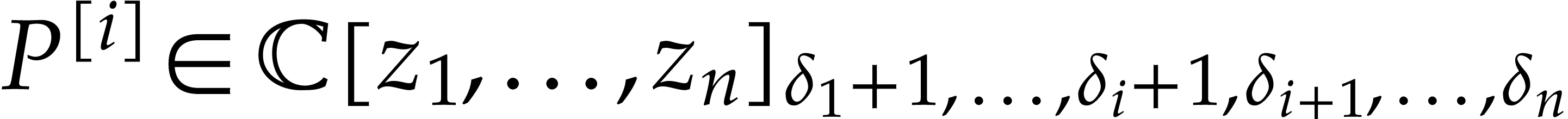 ,
,
the monomials of the support of  are
pairwise distinct modulo
are
pairwise distinct modulo 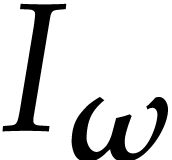 ,
,
the coefficients of 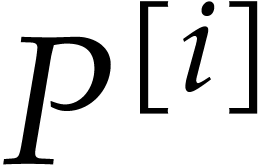 are coefficients of
are coefficients of
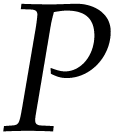 .
.
Letting 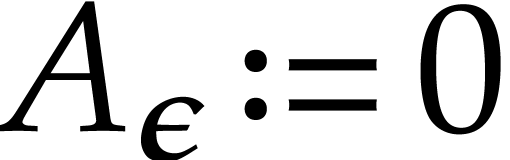 for
for 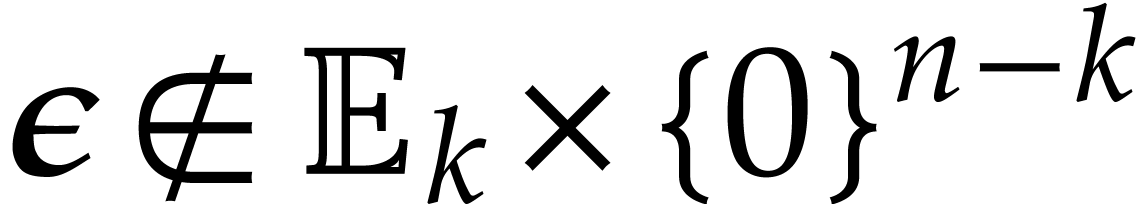 and
and
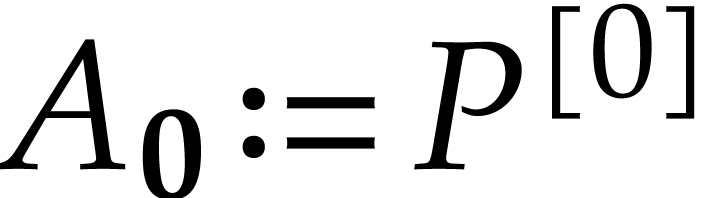 , the family
, the family 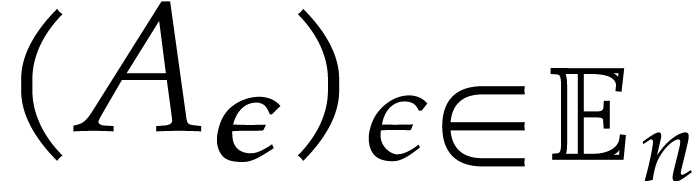 is an extended reduction of
is an extended reduction of 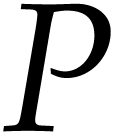 .
.
Proof. The proof is done by induction on  . The properties are clear for
. The properties are clear for
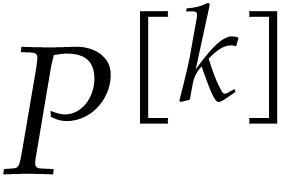 . Let us assume that they
hold for
. Let us assume that they
hold for 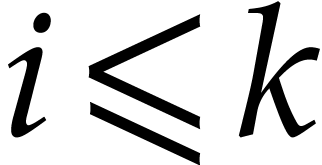 . We decompose
. We decompose 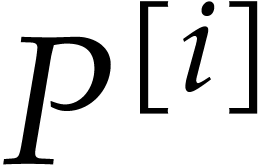 into
into 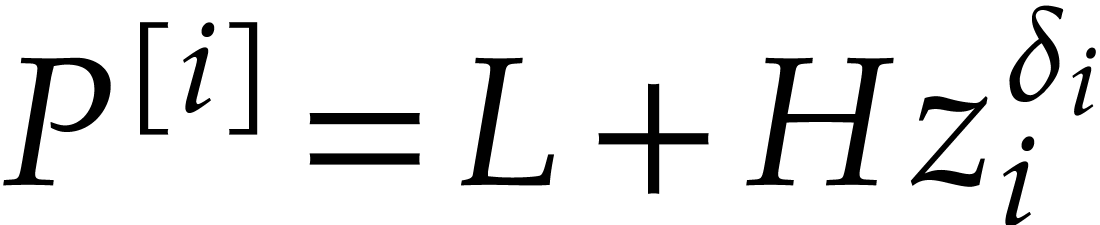 with
with
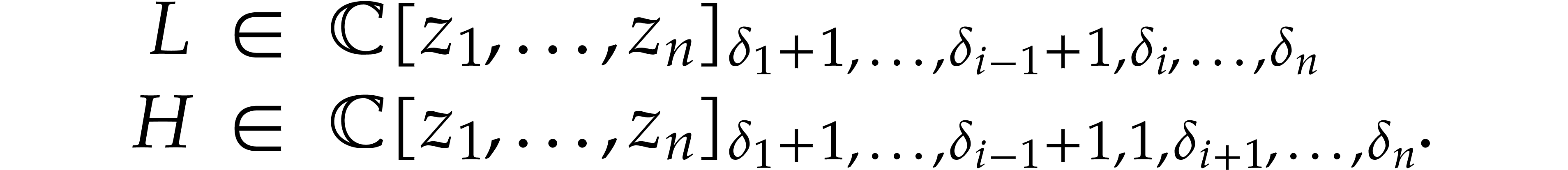
We verify that
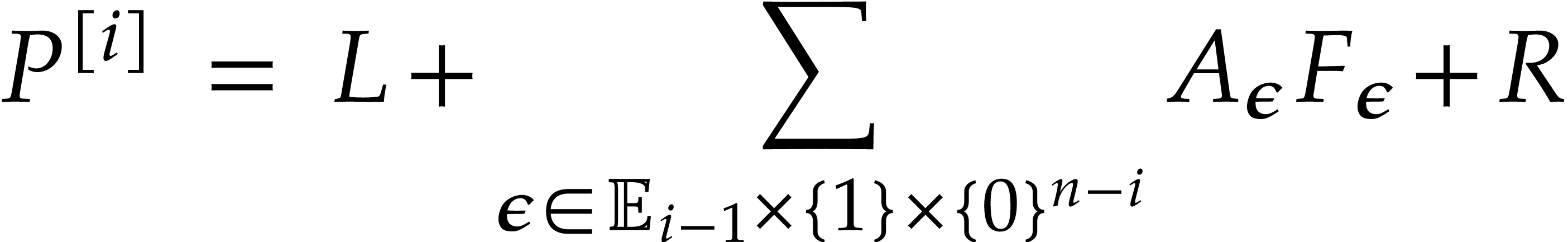
where

Since the monomials of the support of 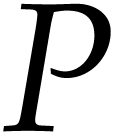 are
pairwise distinct modulo
are
pairwise distinct modulo 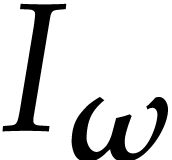 ,
the supports of
,
the supports of 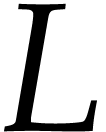 and
and  are
disjoint. In particular the monomials of the support of
are
disjoint. In particular the monomials of the support of 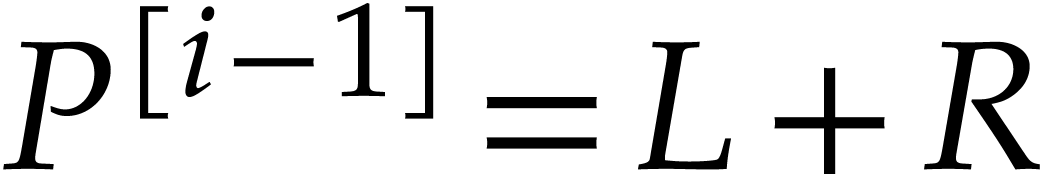 are pairwise distinct modulo
are pairwise distinct modulo 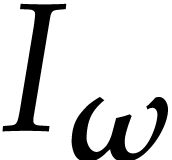 ,
and the non-zero coefficients of
,
and the non-zero coefficients of 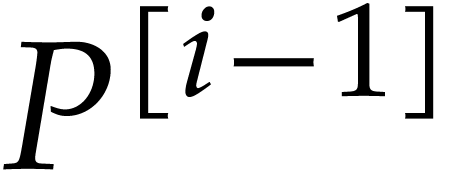 are
coefficients of
are
coefficients of 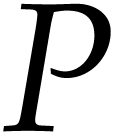 .
.
Finally unrolling
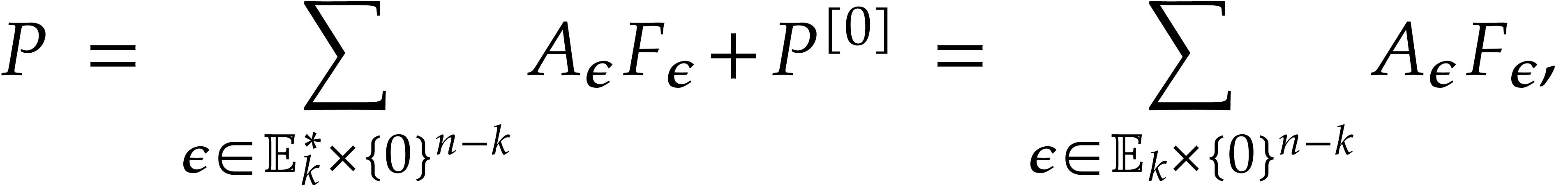
which constitutes the extended reduction of 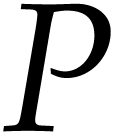 .
.
The reduction of a general  modulo
modulo 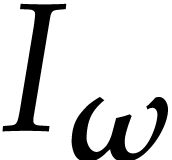 can be performed efficiently by the following algorithm.
can be performed efficiently by the following algorithm.
Algorithm
For all 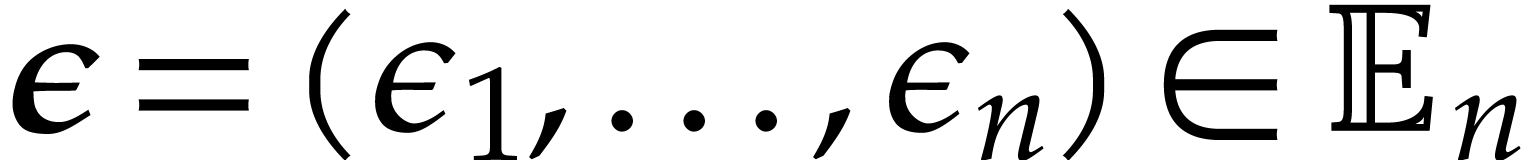 set
set
and compute
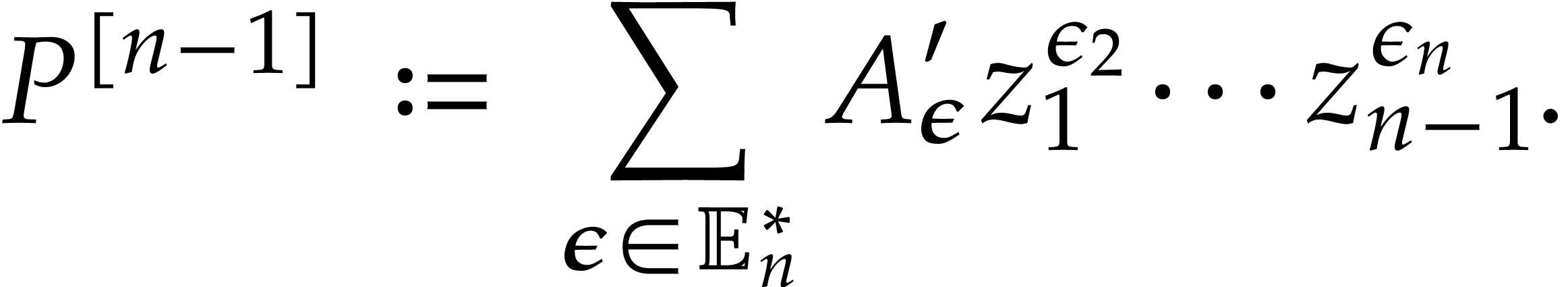
Let 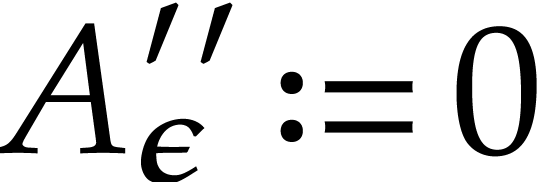 for
for 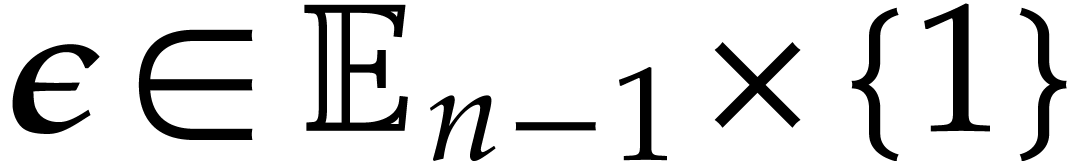 ,
and for
,
and for  from
from  down to
down to  do:
do:
For all 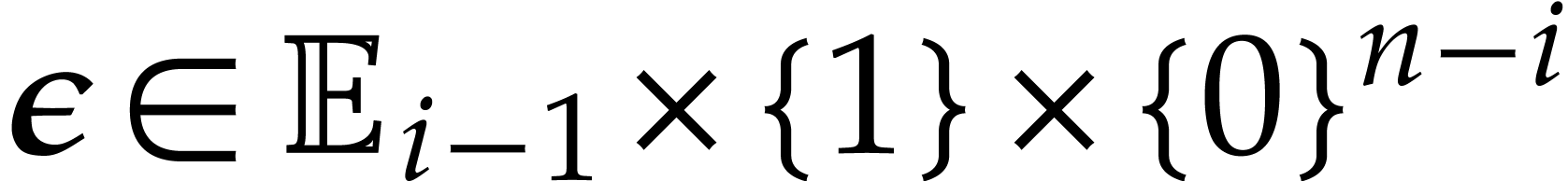 , set
, set
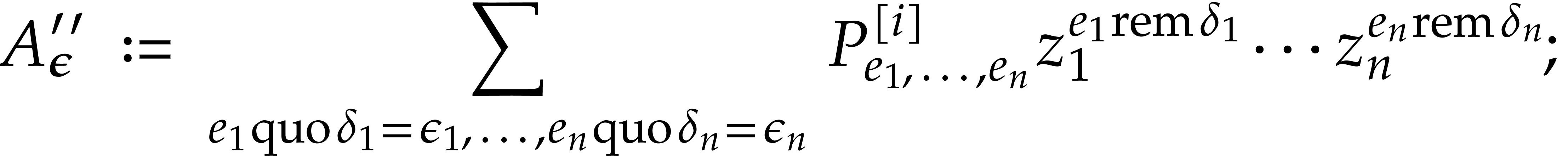
Compute 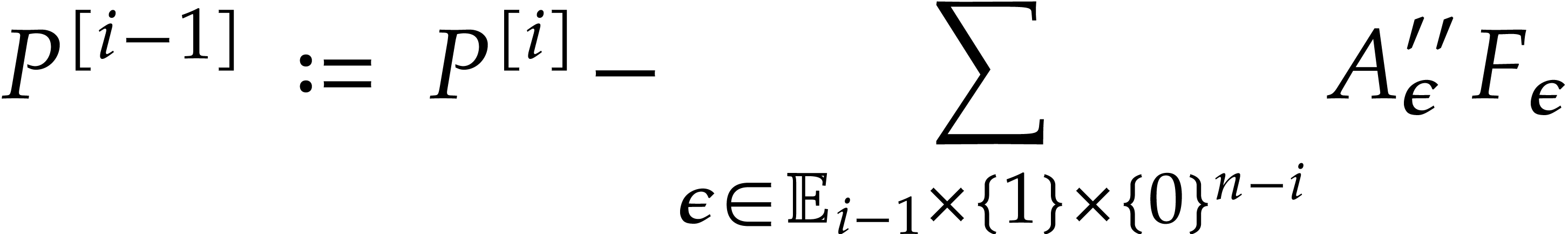 .
.
Let 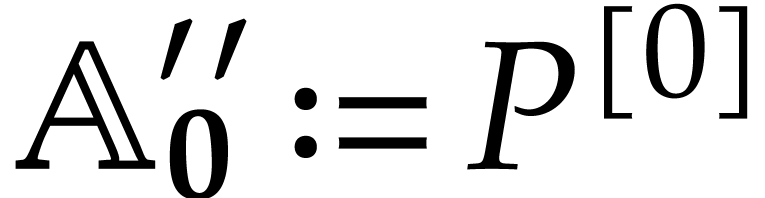 , compute
, compute 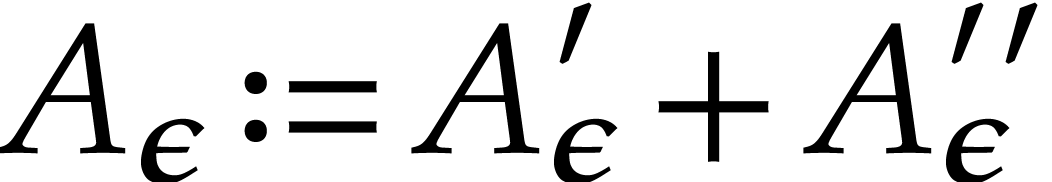 for
for 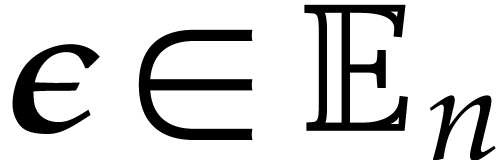 ,
and return
,
and return 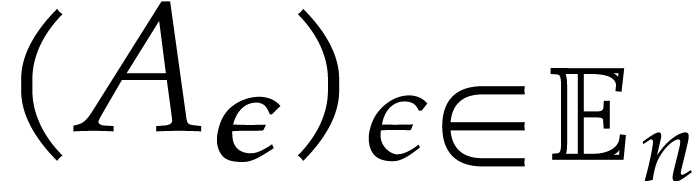 .
.
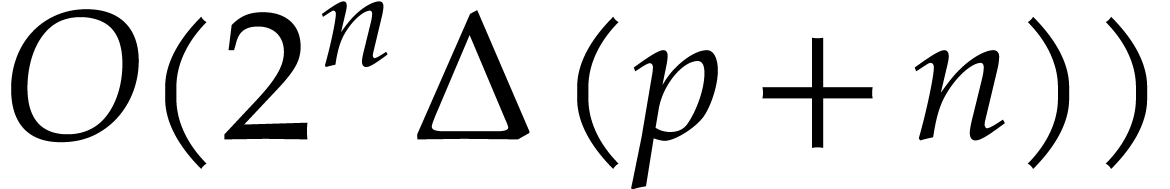 .
.
Proof. For all 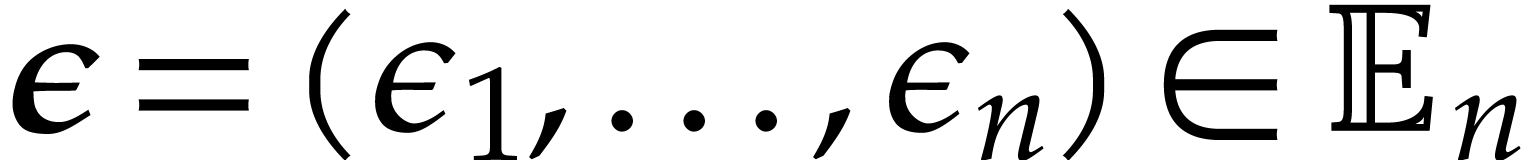 ,
we have
,
we have 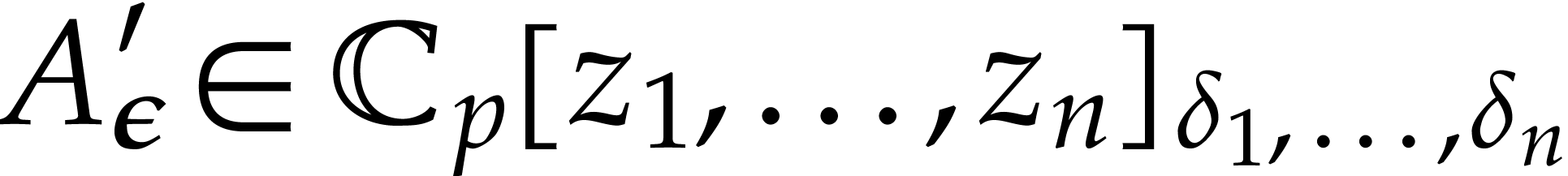 . Let us examine the
particular case where
. Let us examine the
particular case where 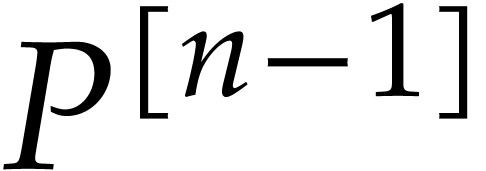 restricts to a single term
restricts to a single term
 for some
for some 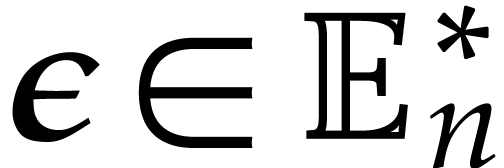 .
By Lemma 7, the monomials of the support of
.
By Lemma 7, the monomials of the support of 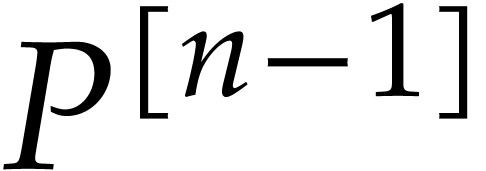 are pairwise distinct modulo
are pairwise distinct modulo 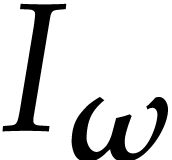 ,
so Lemma 8 implies the following properties, for
,
so Lemma 8 implies the following properties, for  :
:
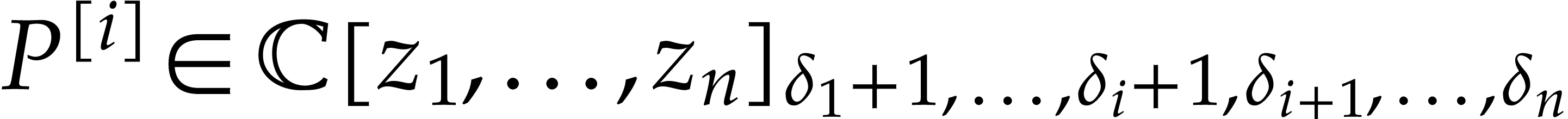 ,
,
the coefficients of 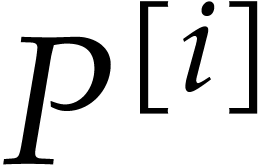 are coefficients of
are coefficients of
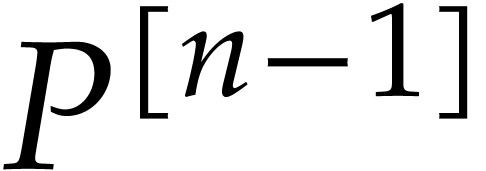 , hence of
, hence of 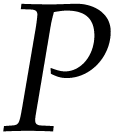 ,
,
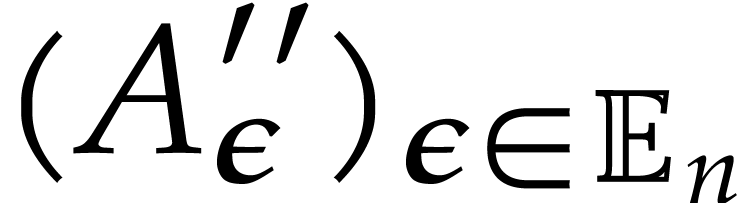 is an extended reduction of
is an extended reduction of 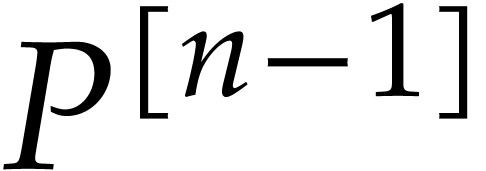 .
.
Since the operations in step 2 are linear with respect to the
coefficients of 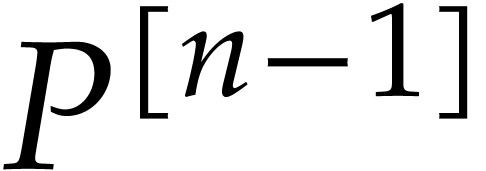 , the general
case where
, the general
case where 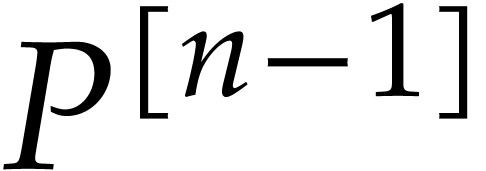 is a sum of
is a sum of  terms of the form
terms of the form  satisfies the following
properties:
satisfies the following
properties:
 ,
,
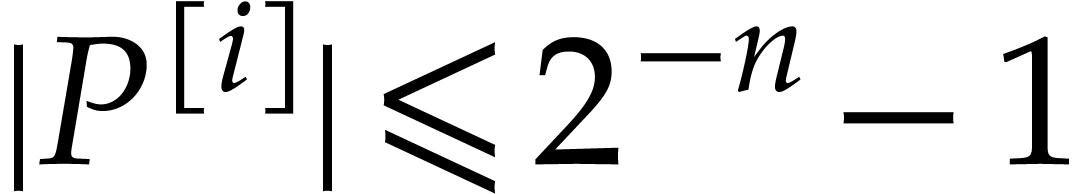 ,
,
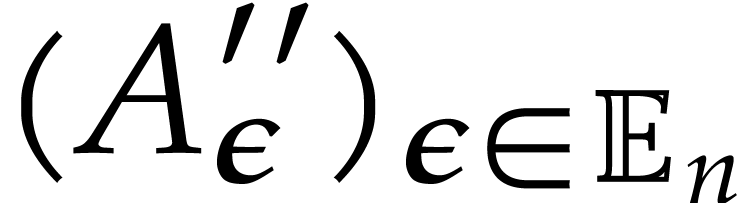 is an extended reduction of
is an extended reduction of 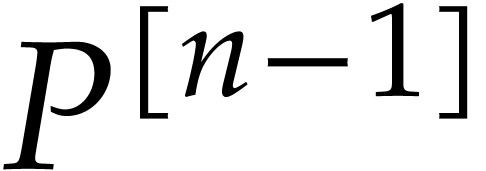 .
.
On the other hand step 1 yields

So the correctness proof is completed by noting that
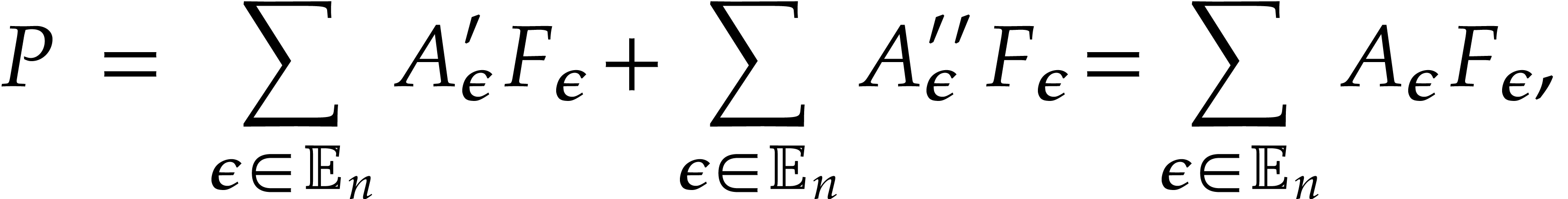
and 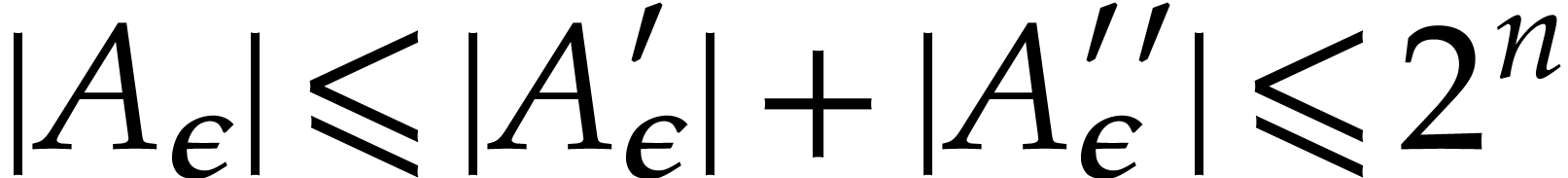 . As for the complexity
analysis, step 1 takes time
. As for the complexity
analysis, step 1 takes time 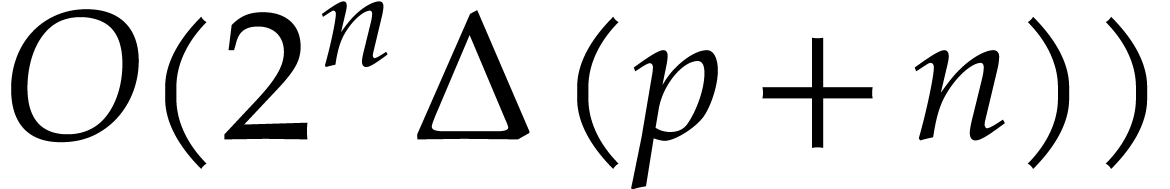 .
Step 2 runs in time
.
Step 2 runs in time
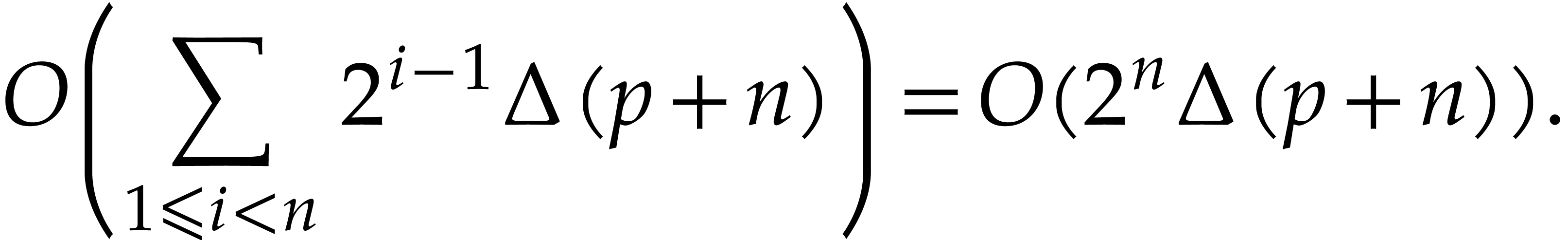
The cost of step 3 does not exceed 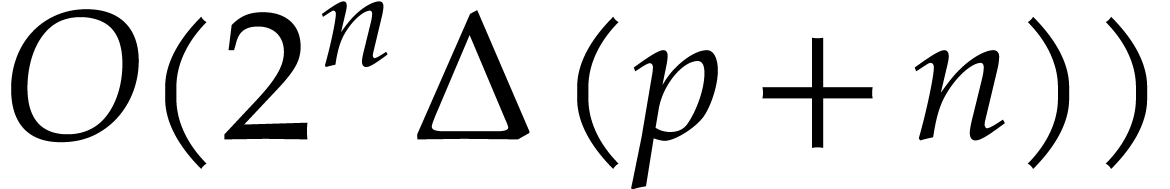 .
.
Example. Let 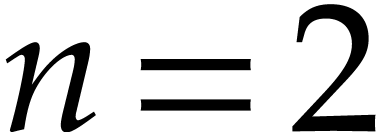 and
and 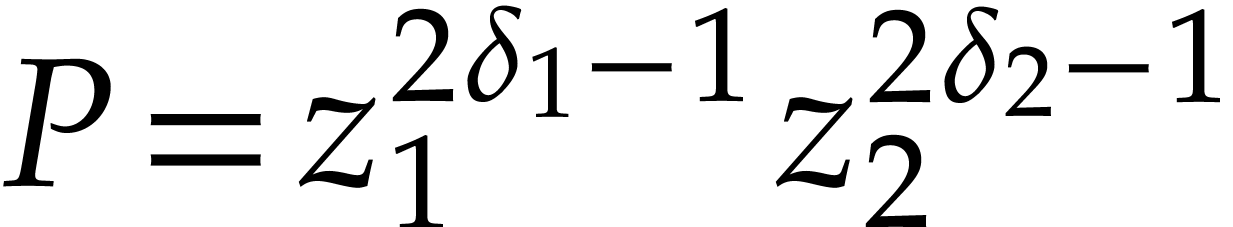 . With the notation as in Algorithm
1, the only non-zero
. With the notation as in Algorithm
1, the only non-zero  is
is 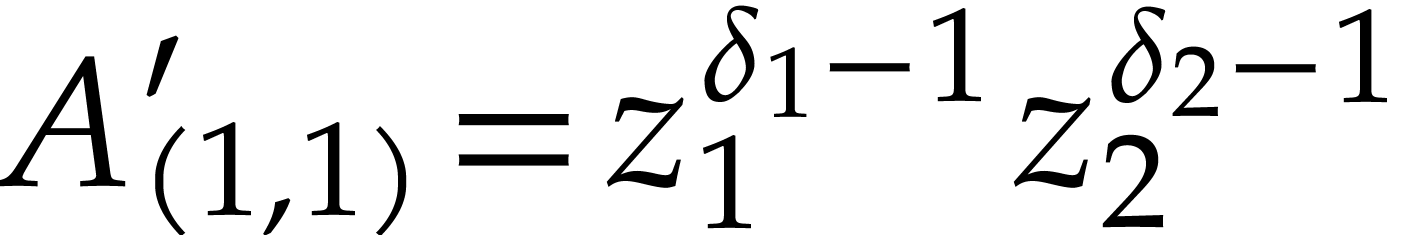 , and we have
, and we have 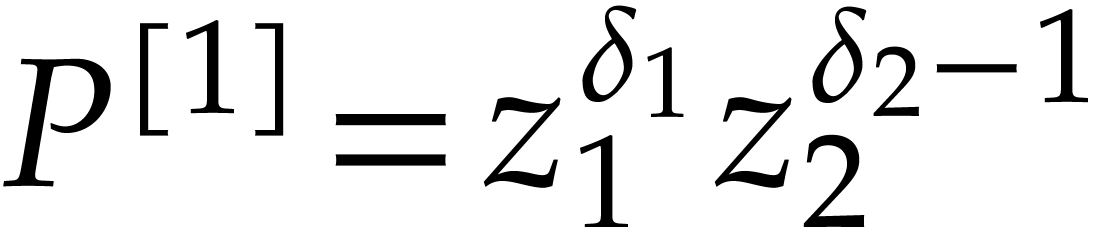 . It follows that all the
. It follows that all the 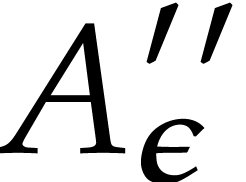 are all
are all 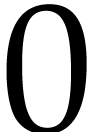 but
but 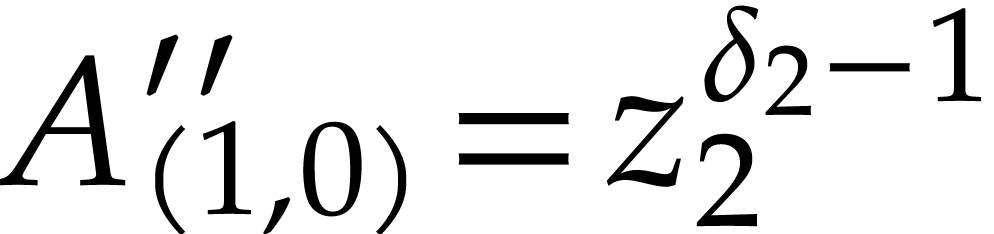 ,
so we have
,
so we have 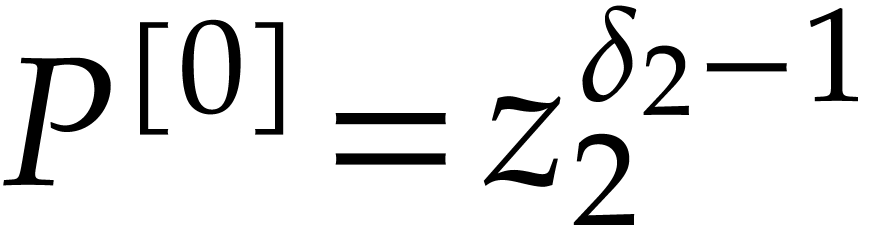 . The extended
reduction of
. The extended
reduction of 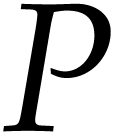 is
is

We now turn to the situation where 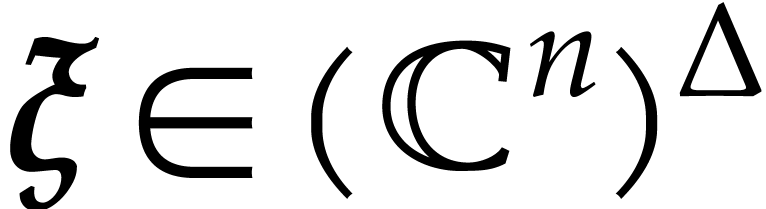 is a
sufficiently small perturbation of
is a
sufficiently small perturbation of 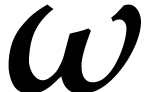 .
More precisely, we say that
.
More precisely, we say that  is a
spiroid when there exist polynomials
is a
spiroid when there exist polynomials

such that

for all 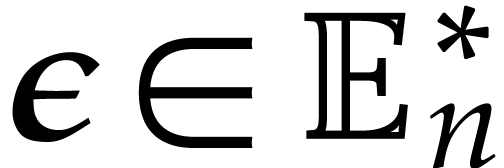 , and
, and
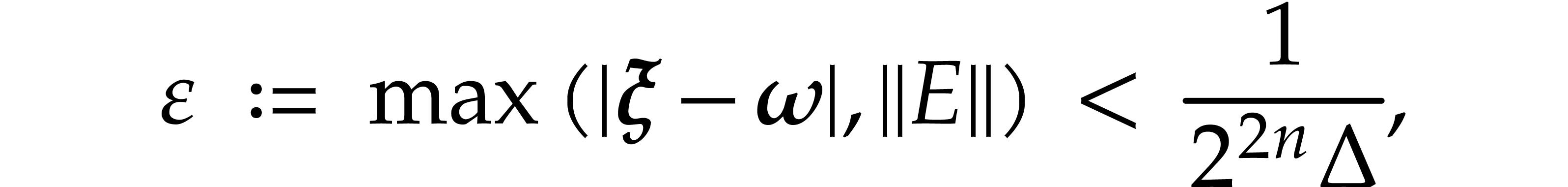
with the convention that 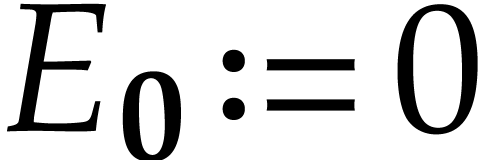 and
and 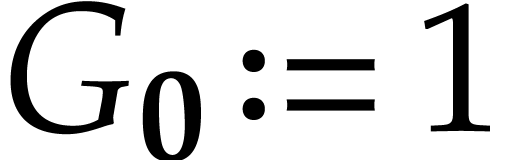 . We call
. We call 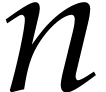 and
and  the dimension and the degrees of the
spiroid and let
the dimension and the degrees of the
spiroid and let
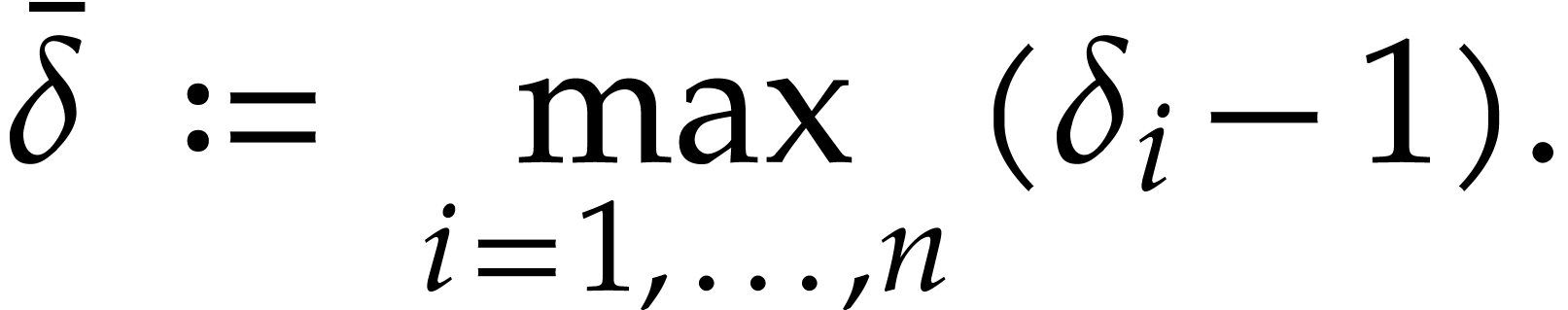
By Lemma 6 we have 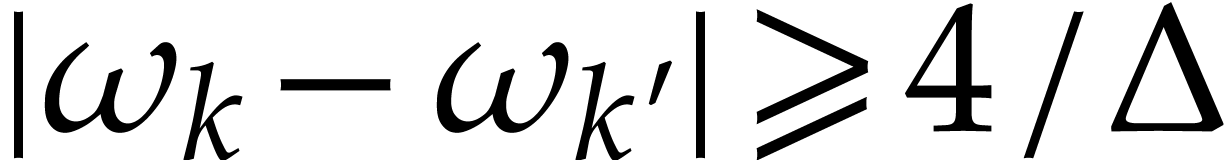 for all
for all  . Consequently,
. Consequently,
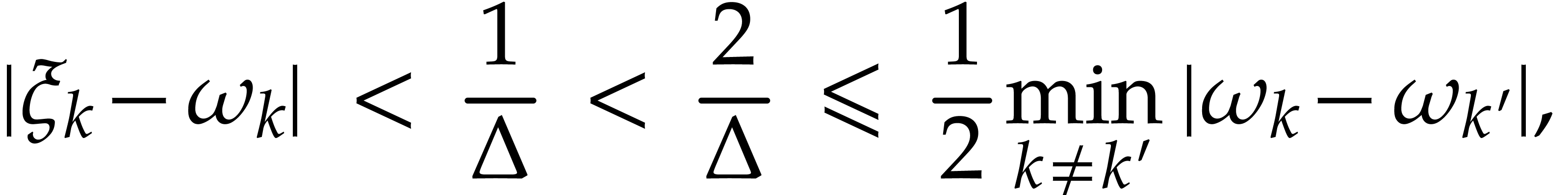
so the points 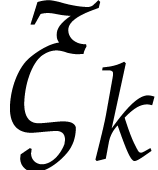 are pairwise distinct. We let
are pairwise distinct. We let
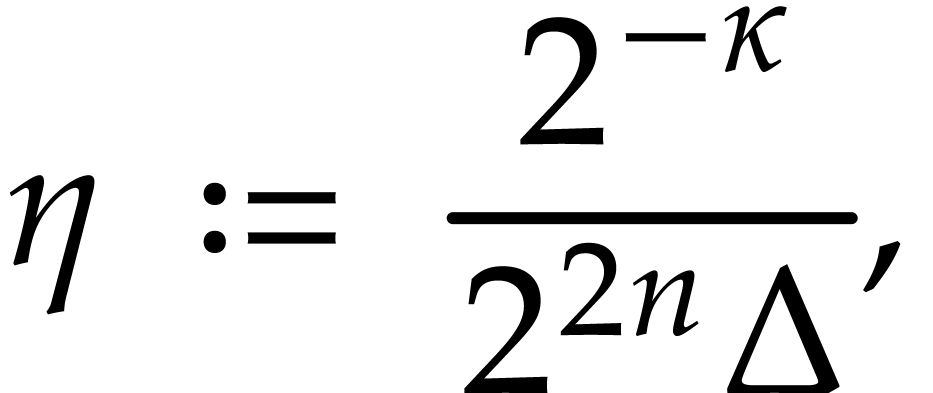
where 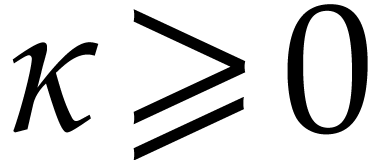 is a constant, that will be specified
later. We denote by
is a constant, that will be specified
later. We denote by  an approximation of
an approximation of 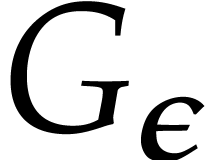 with error
with error 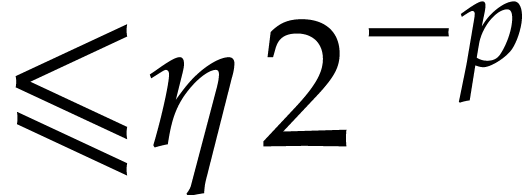 ,
where
,
where 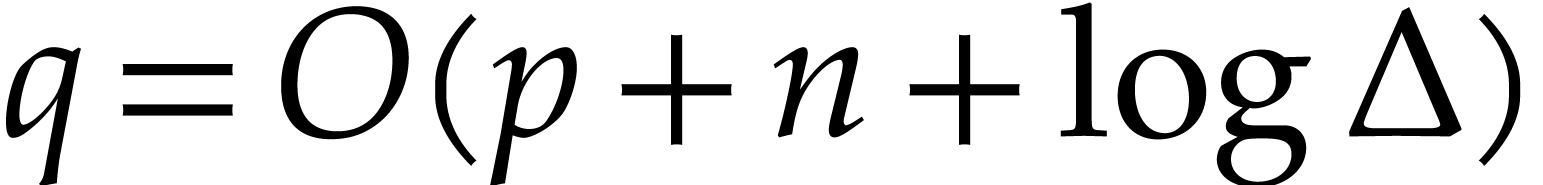 will also be defined later. For
convenience we always take
will also be defined later. For
convenience we always take 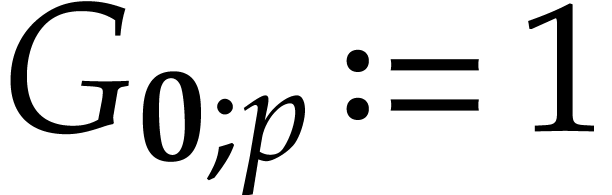 .
.
We are to show that  is a spiroid as soon as
is a spiroid as soon as 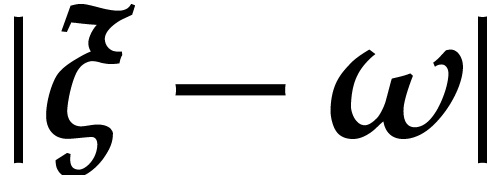 is sufficiently small.
is sufficiently small.
Proof. The polynomial  has degree
has degree
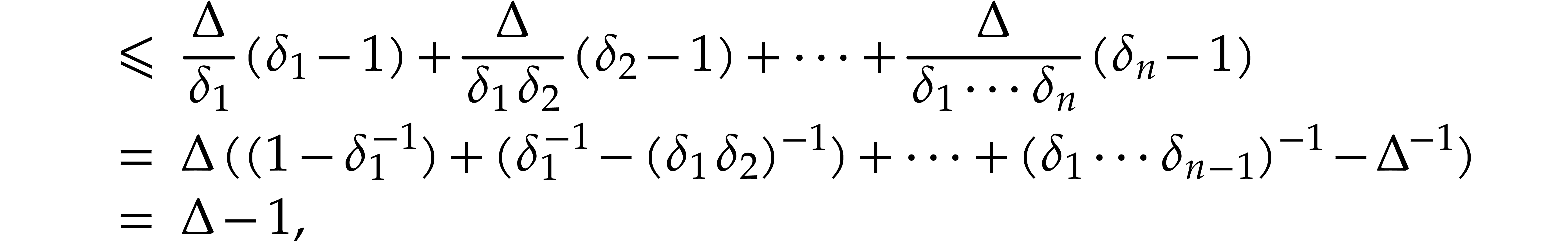
and satisfies 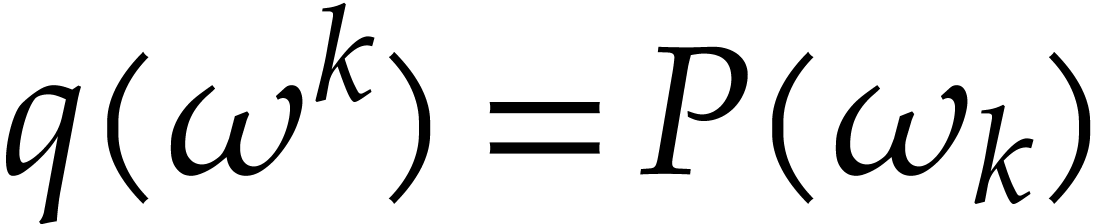 for
for  .
This means that
.
This means that 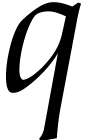 is the inverse Fourier transform
of
is the inverse Fourier transform
of  , that is
, that is 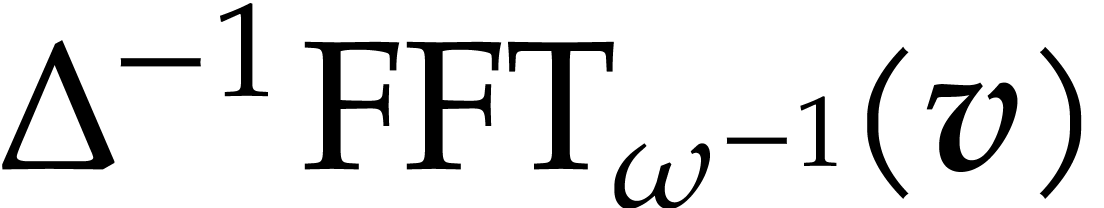 , following the notation of section 2.2.
We deduce that
, following the notation of section 2.2.
We deduce that 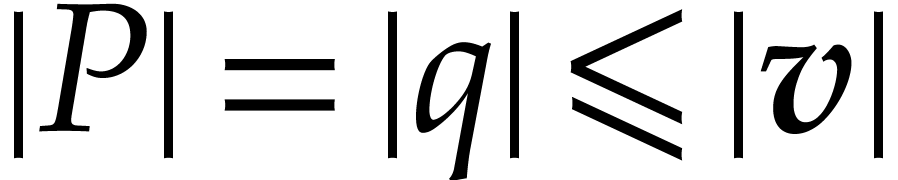 .
.
The two following technical lemmas will be needed several times in the paper.
Proof. We set 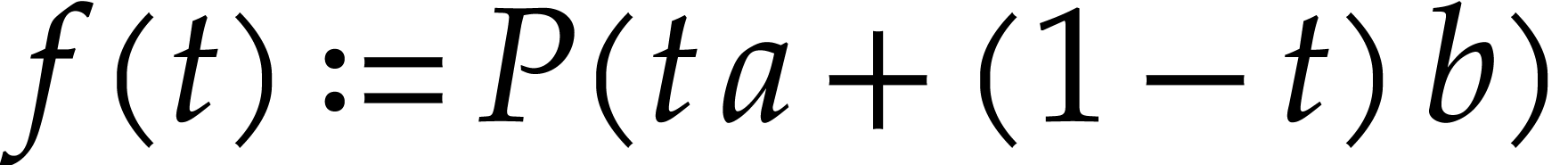 for
for  and use the classical inequality
and use the classical inequality
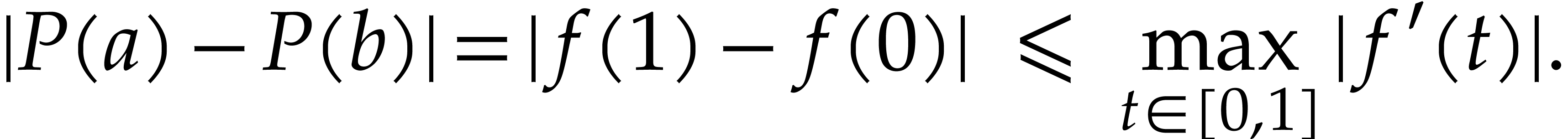
From 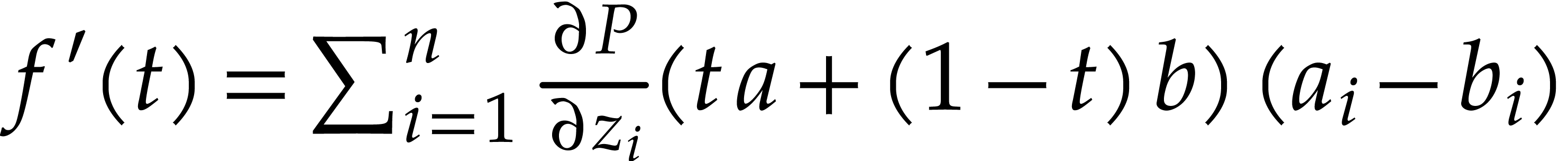 , we obtain
, we obtain
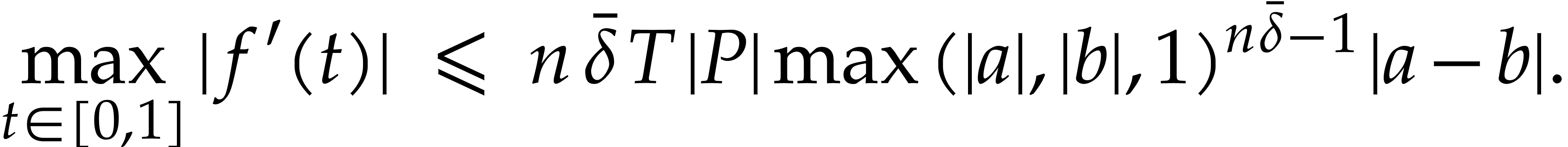

Proof. We verify that
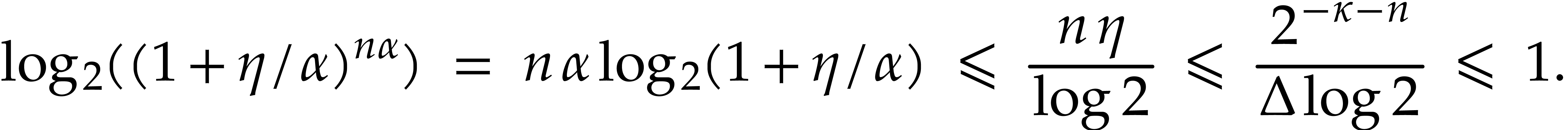

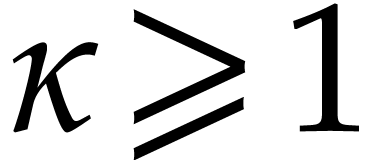 ,
,  , and let
, and let 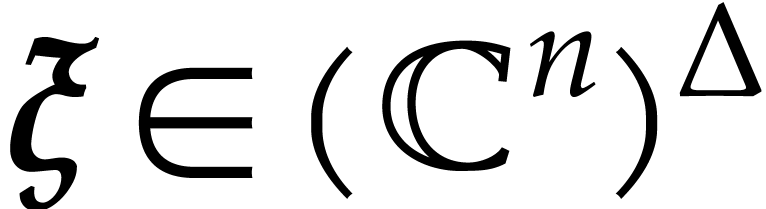 be such
that
be such
that 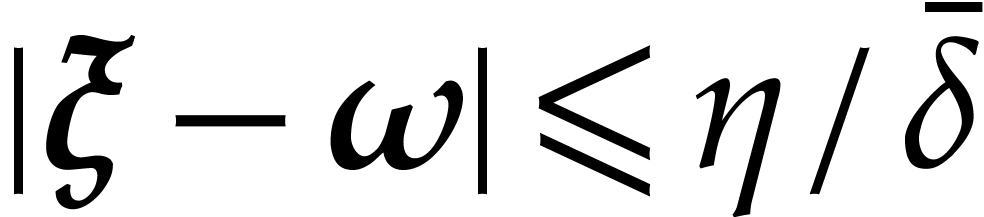 . Given
. Given  , there exists a unique
, there exists a unique  such that
such that 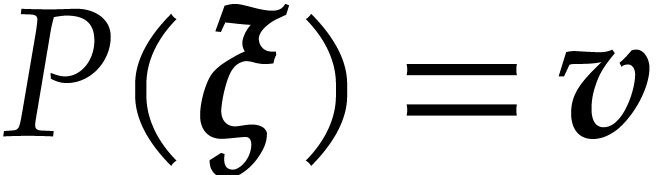 . Moreover,
. Moreover, 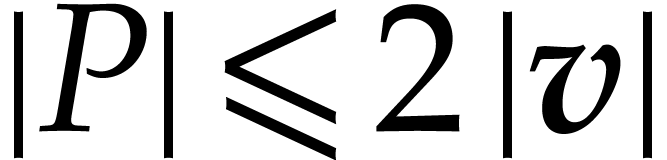 .
.
Proof. Let  and define
and define
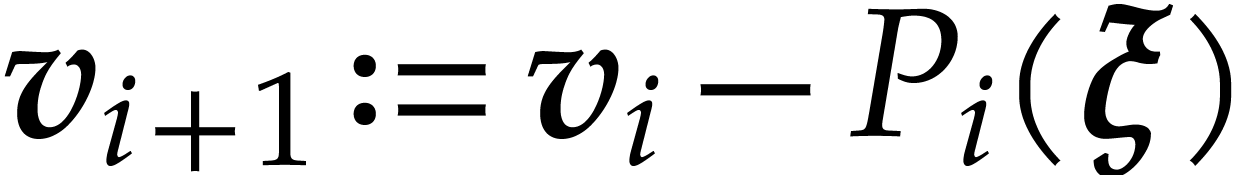 , where
, where 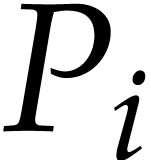 stands for the unique polynomial in
stands for the unique polynomial in 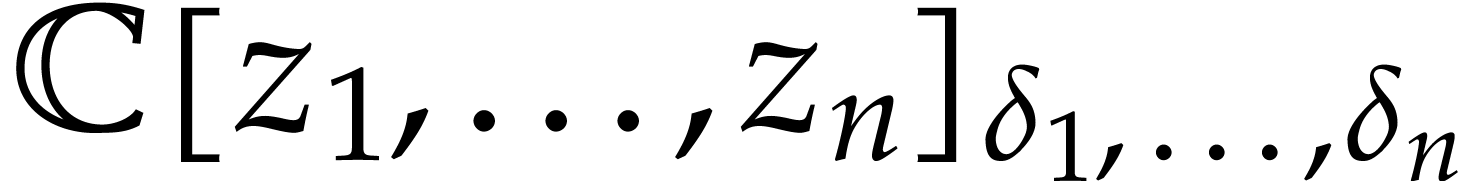 such that
such that
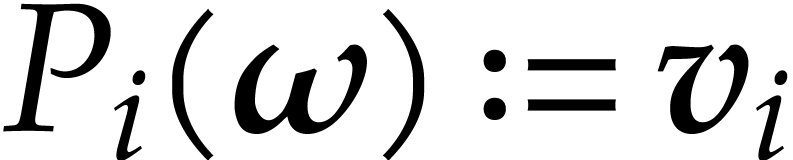 . From Lemma 10
we know that
. From Lemma 10
we know that 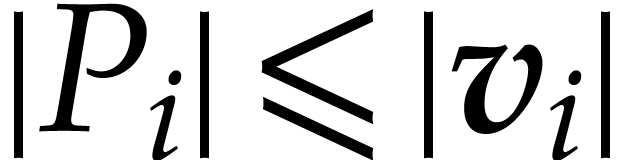 . Using Lemma 11, we deduce
. Using Lemma 11, we deduce
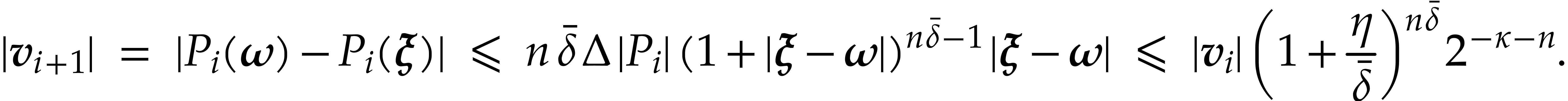
Using Lemma 12 and 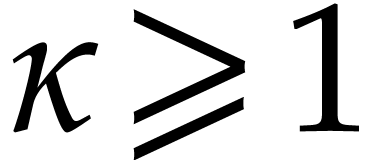 ,
we obtain
,
we obtain 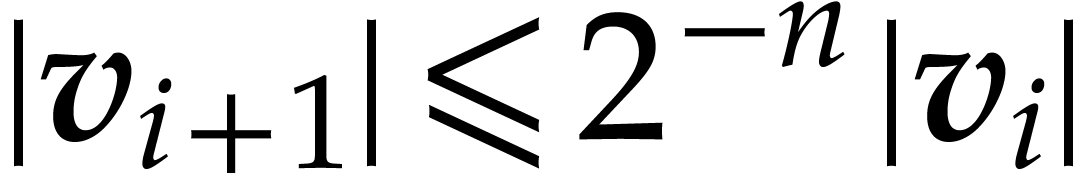 , hence
, hence 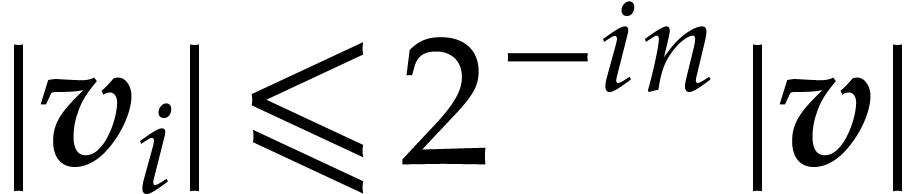 for
for 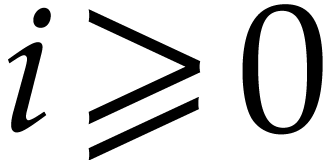 .
Consequently,
.
Consequently, 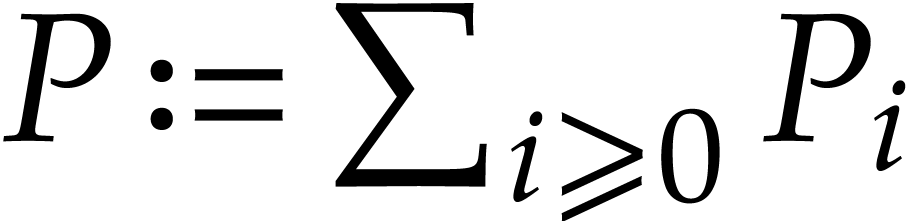 is well defined and we have
is well defined and we have

Finally, we verify that
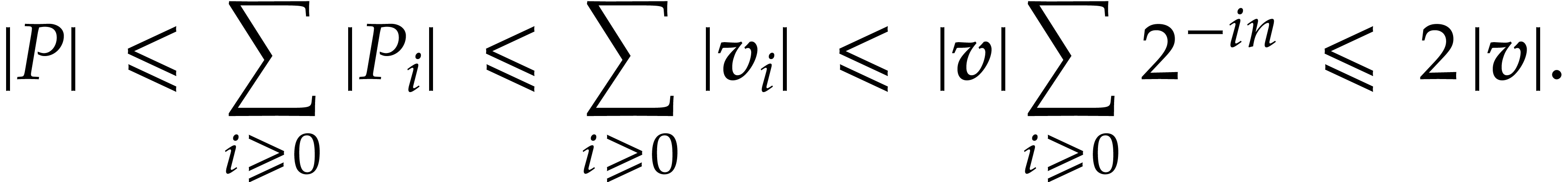

Proof. From Lemmas 11 and 12, and using
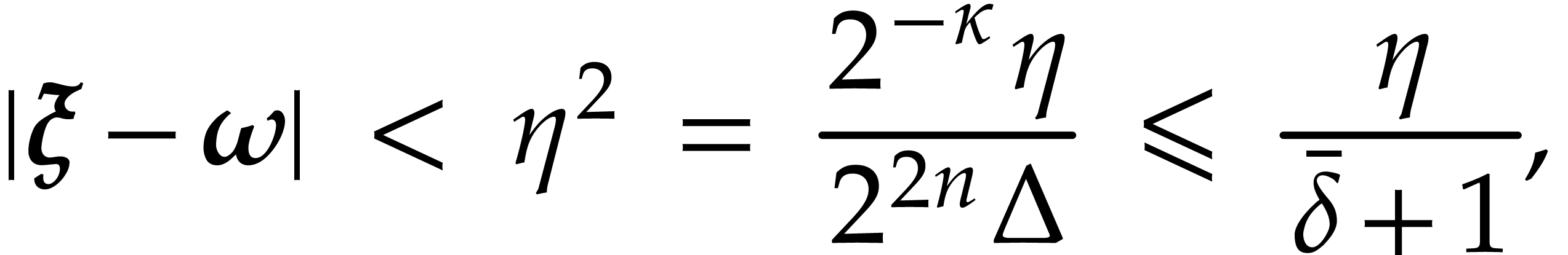
we obtain
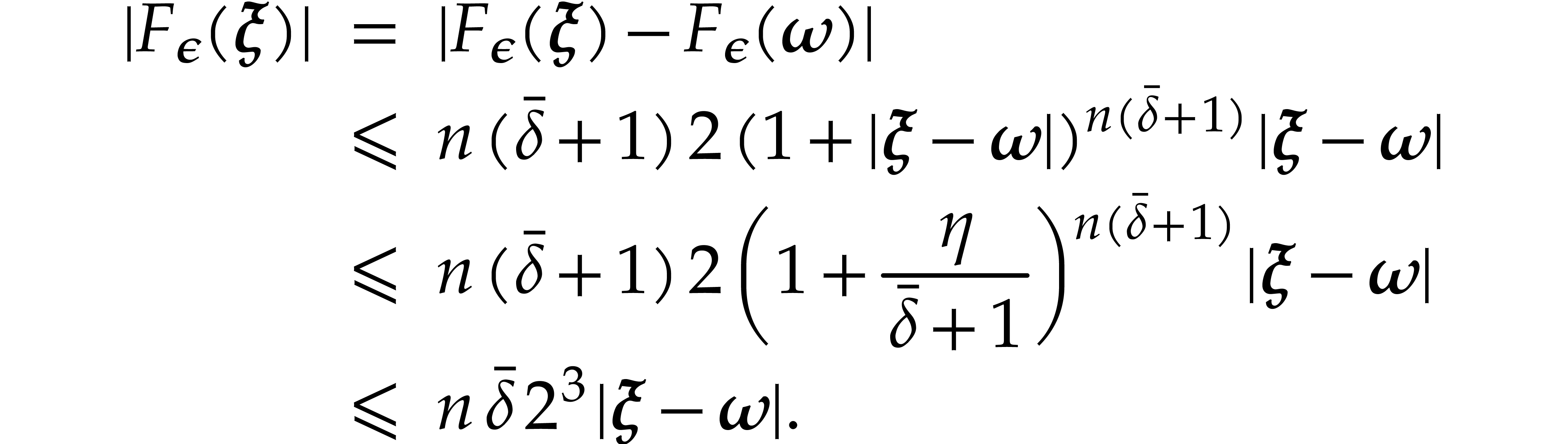
Thanks to Lemma 13, there exists  such that
such that 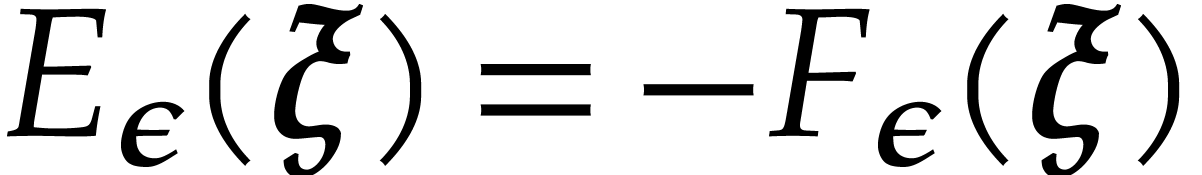 and
and

whence 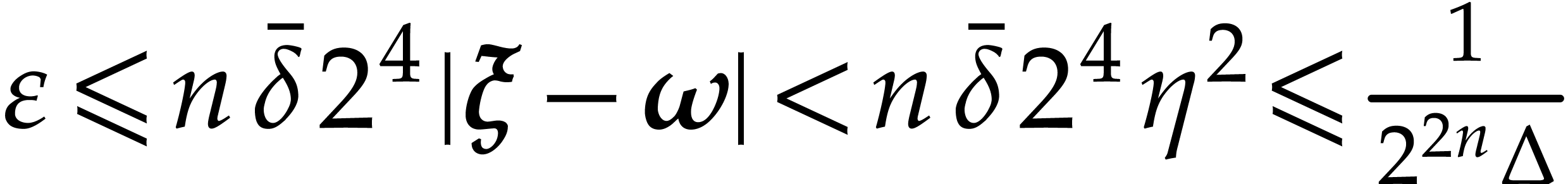 .
.
In the rest of this section, we fix 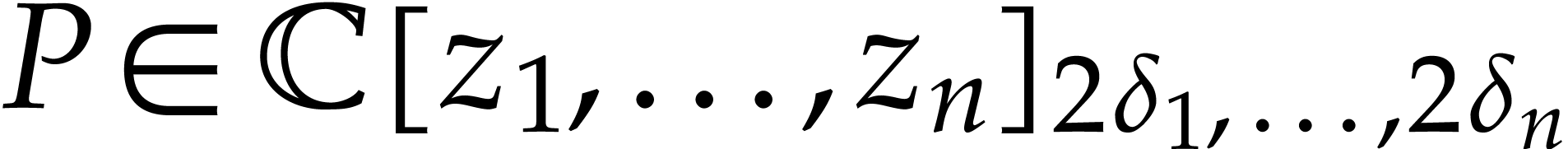 and assume
that
and assume
that 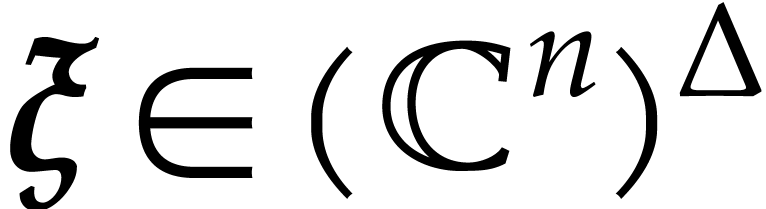 is a spiroid. A family
is a spiroid. A family
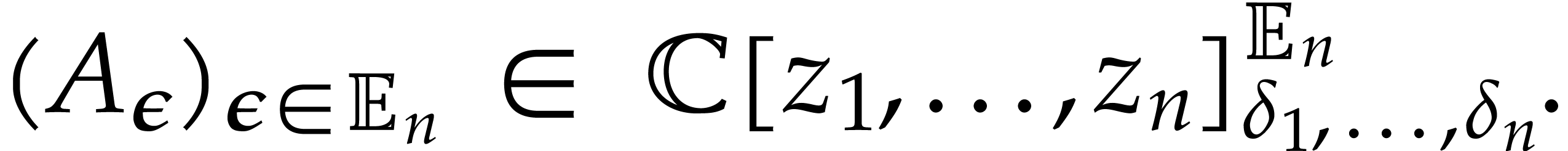
is called an extended reduction of 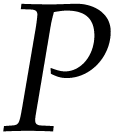 by
the spiroid
by
the spiroid  if
if
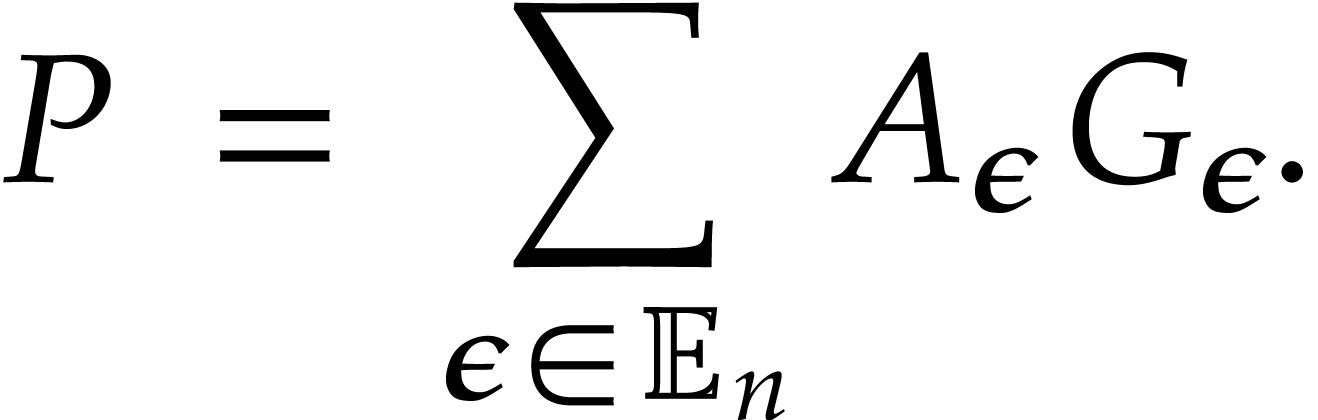
Since 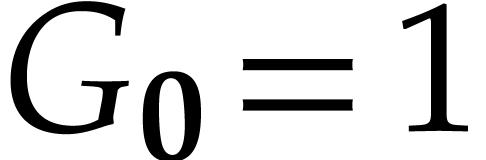 , we have
, we have 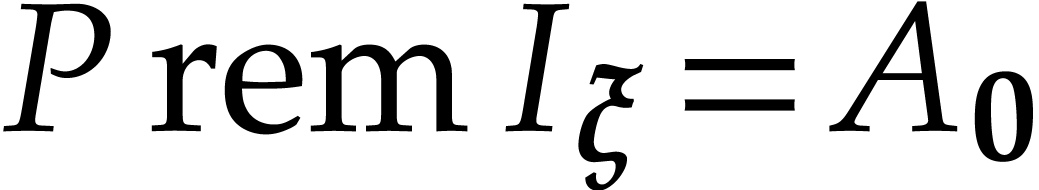 .
.
Proof. If 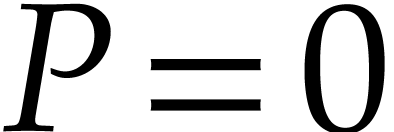 then we take
then we take
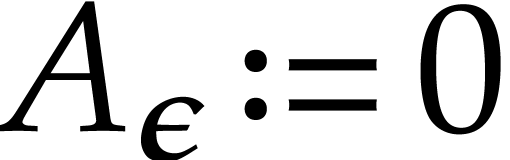 for all
for all 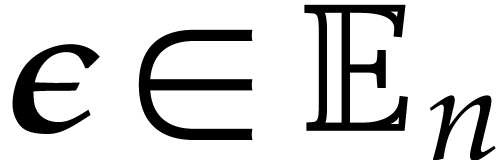 .
Otherwise, without loss of generality, we may assume that
.
Otherwise, without loss of generality, we may assume that 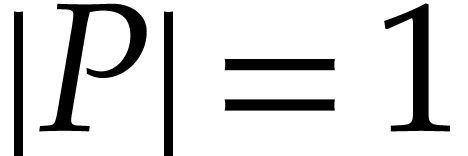 . For
. For 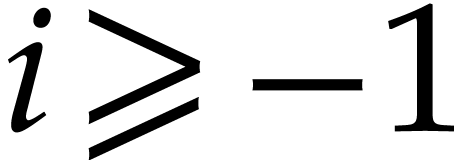 ,
we construct sequences
,
we construct sequences 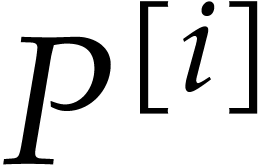 ,
, 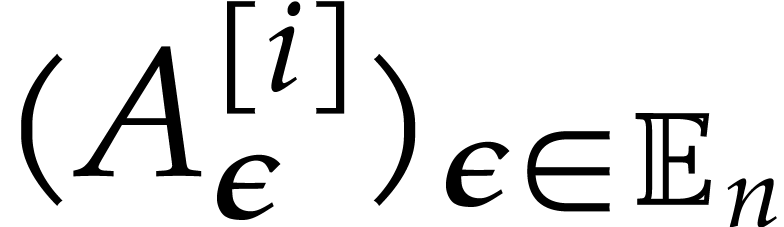 of polynomials as follows. For
of polynomials as follows. For  , we set
, we set  and
and 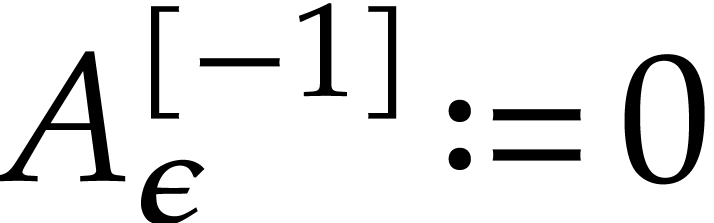 for
for 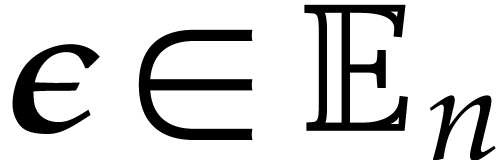 . By
induction, we assume that these sequences are defined up to some index
. By
induction, we assume that these sequences are defined up to some index
 for some
for some  .
We let
.
We let
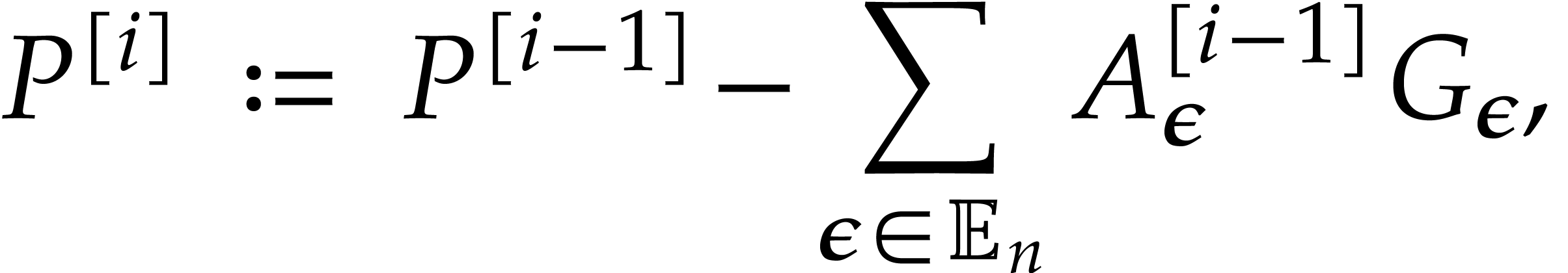
and apply Proposition 9 to 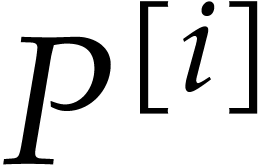 without
any rounding, and let
without
any rounding, and let 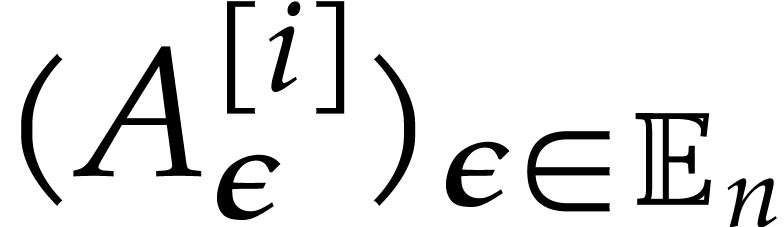 be the corresponding
extended reduction with
be the corresponding
extended reduction with 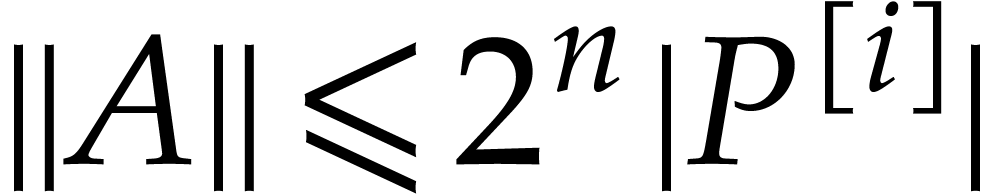 . We
have
. We
have
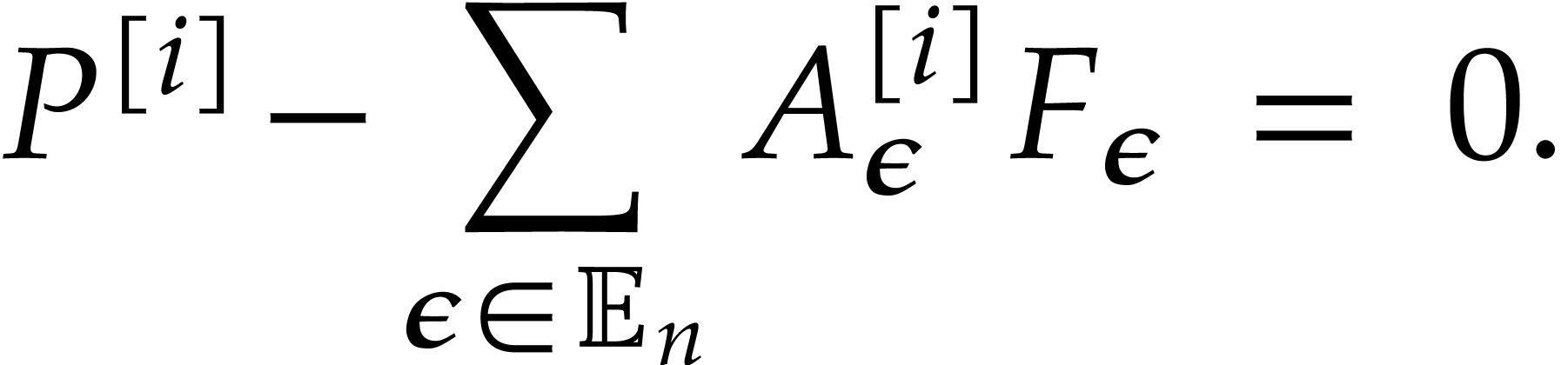
It follows that
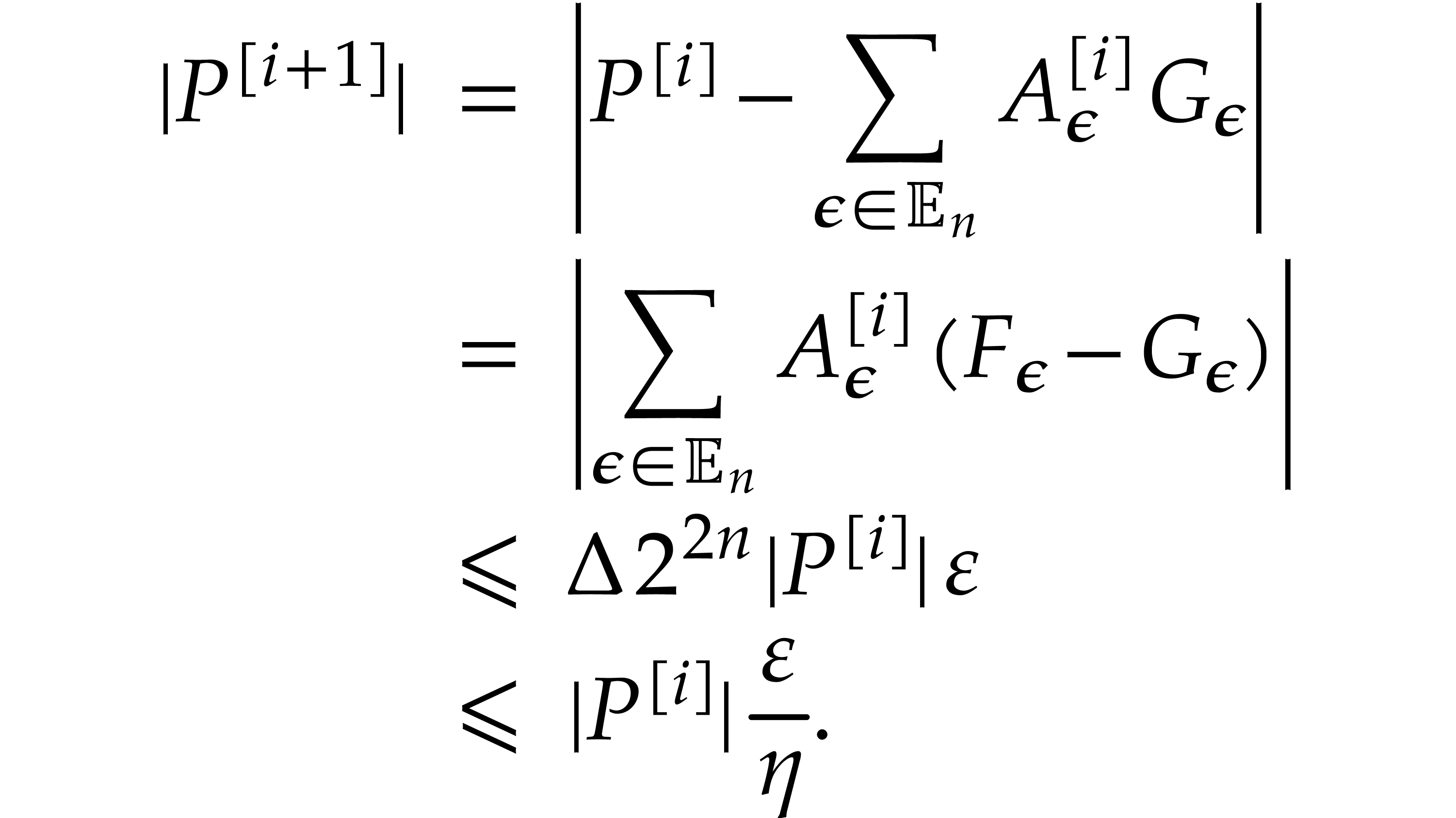
Hence,
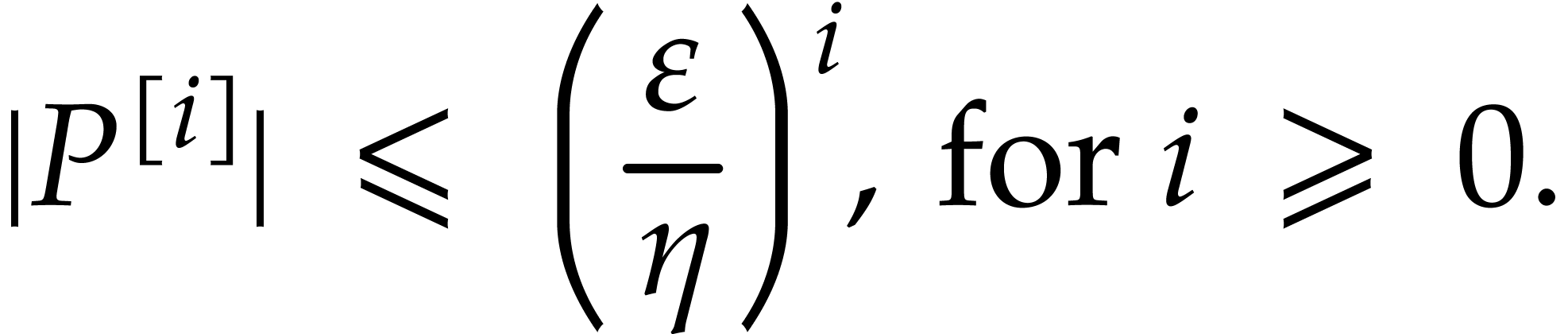
In particular 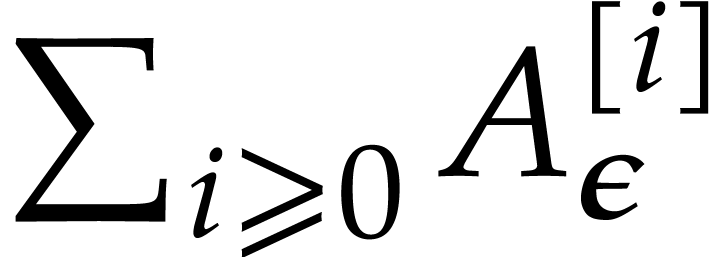 converges to a limit written
converges to a limit written 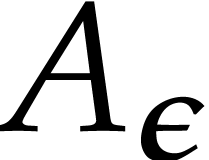 . For
. For 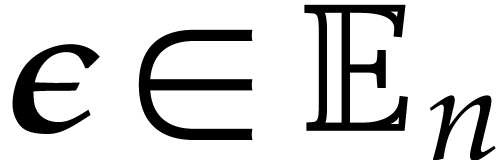 we
have
we
have
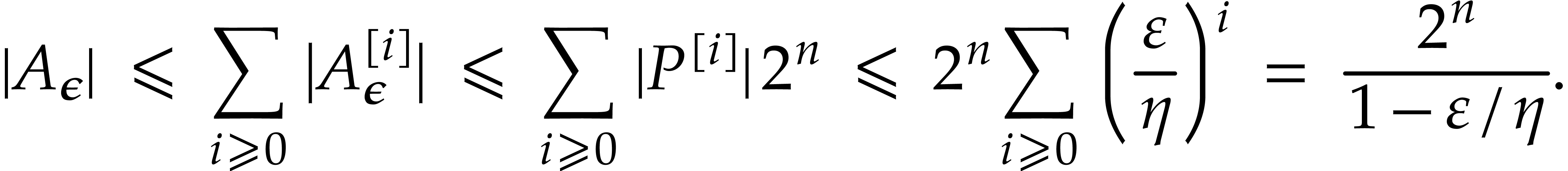

The proof of Proposition 15 can be turned into an algorithm
to compute approximations of extended reductions. For efficiency
reasons,  is required to be sufficiently small.
is required to be sufficiently small.
Proof. We adapt the proof of Proposition 15. For 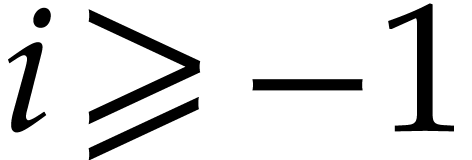 , we
construct sequences
, we
construct sequences  with
with 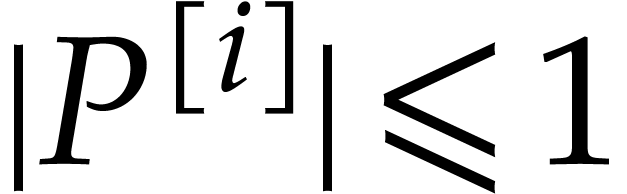 and
and  as follows.
as follows.
For  , we set
, we set  and
and 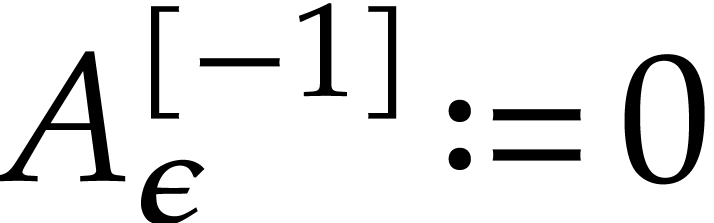 for
for 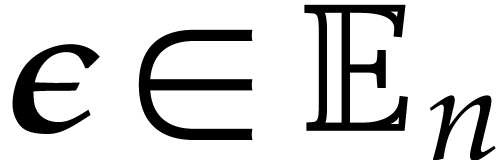 .
By induction, we assume that these sequences have been defined up to
.
By induction, we assume that these sequences have been defined up to
 for some
for some  .
We compute
.
We compute
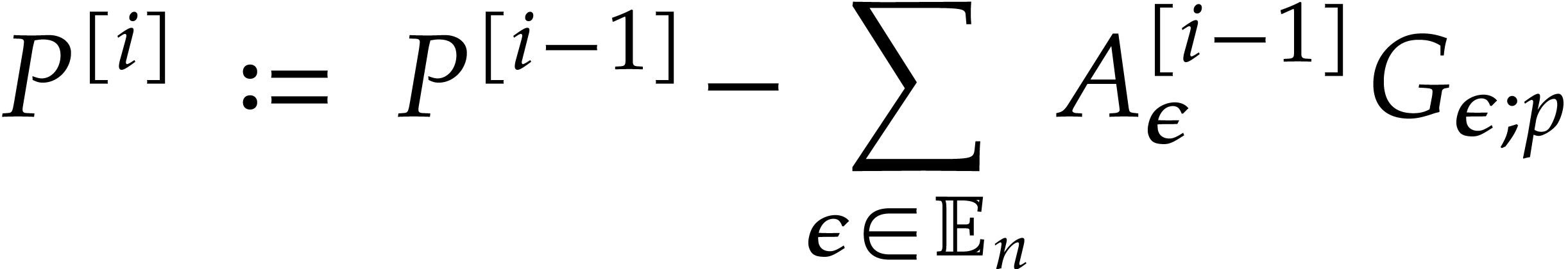
exactly. Note that 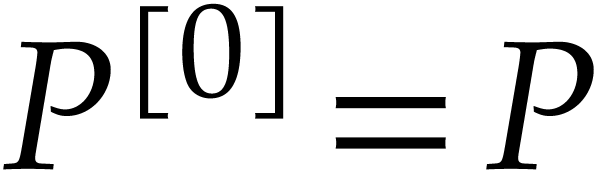 . We
further assume by induction that
. We
further assume by induction that 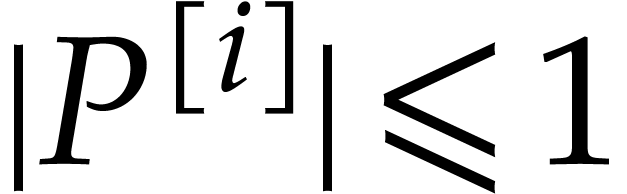 .
Applying Proposition 9 to
.
Applying Proposition 9 to 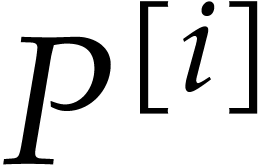 ,
let
,
let 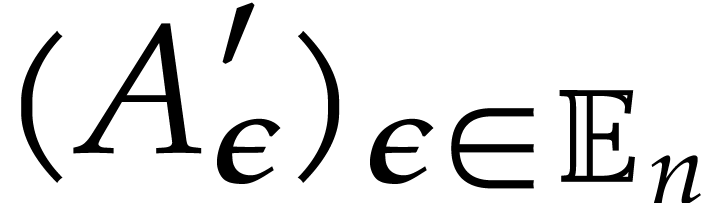 be the obtained extended reduction. Then
be the obtained extended reduction. Then
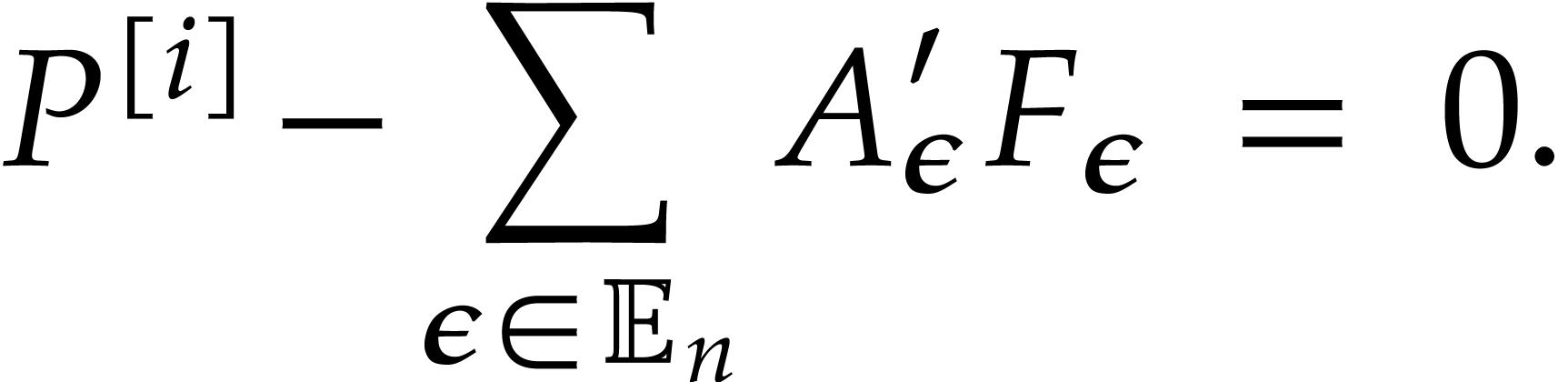
Using Lemma 3, we compute a truncation  of
of  in
in 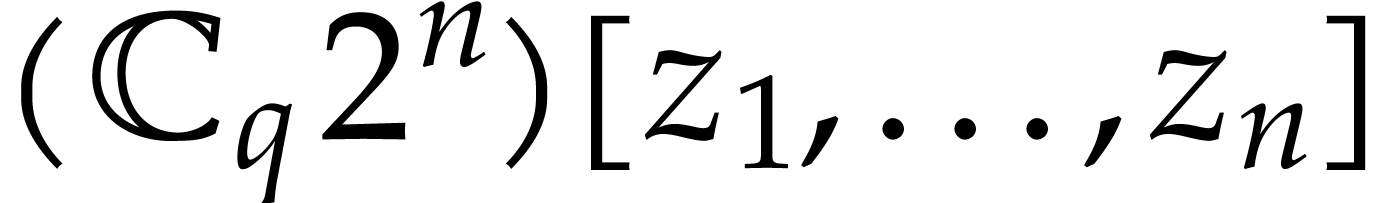 with error
with error 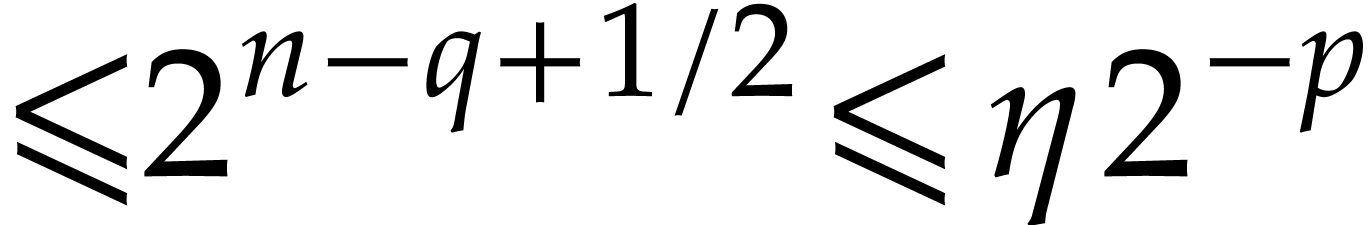 . We obtain
. We obtain
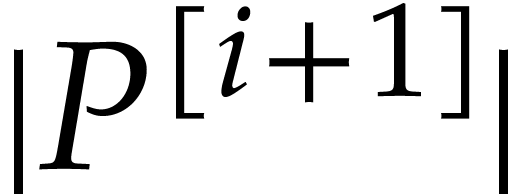 |
 |
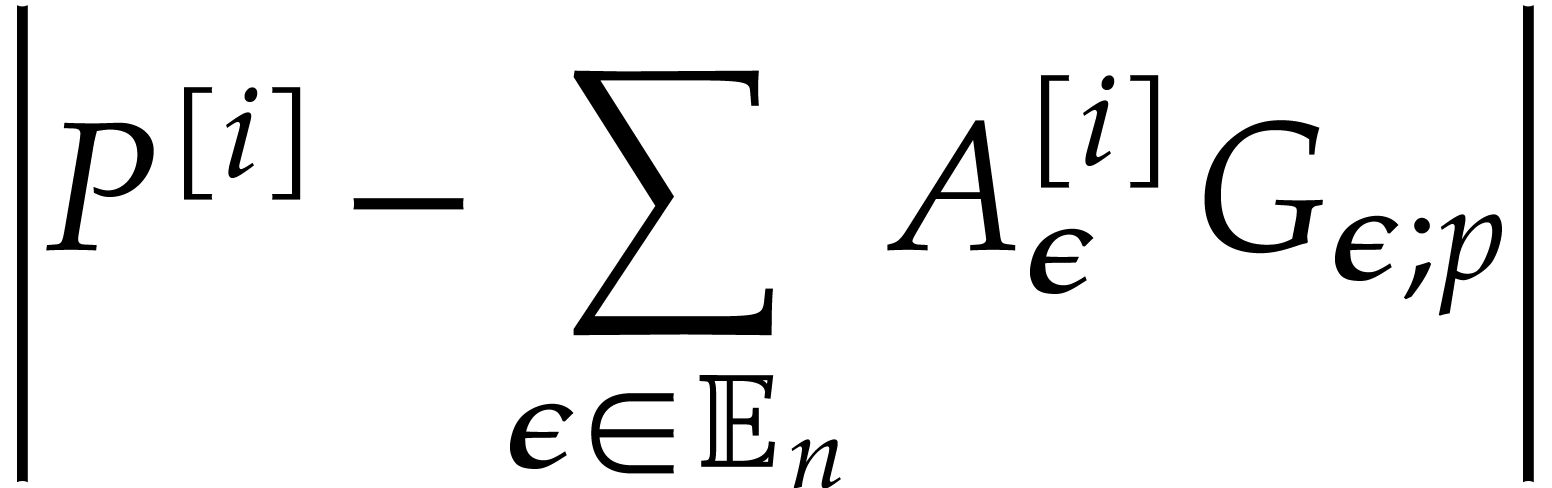 |
|
 |
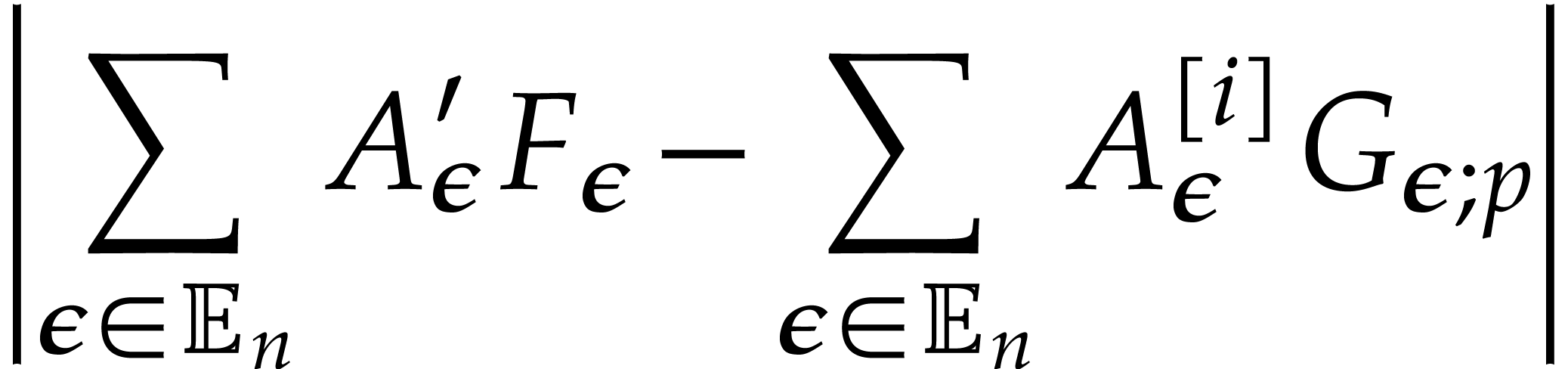 |
||
 |
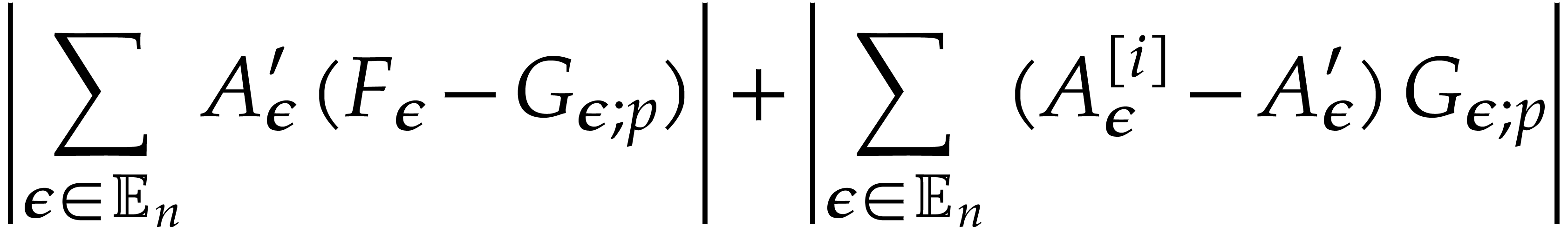 |
||
 |
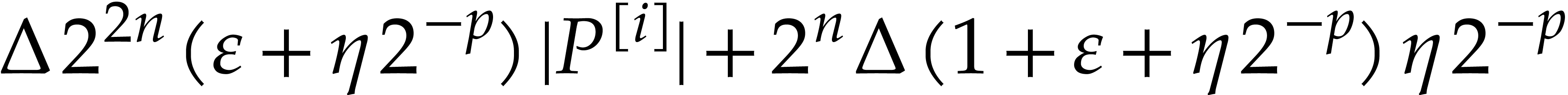 |
||
 |
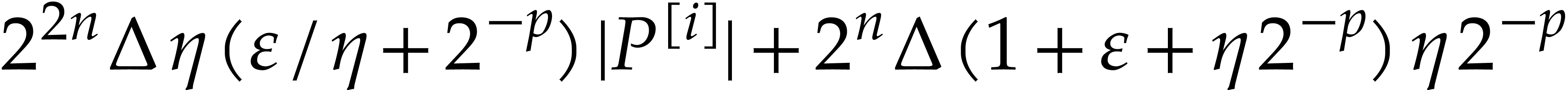 |
||
 |
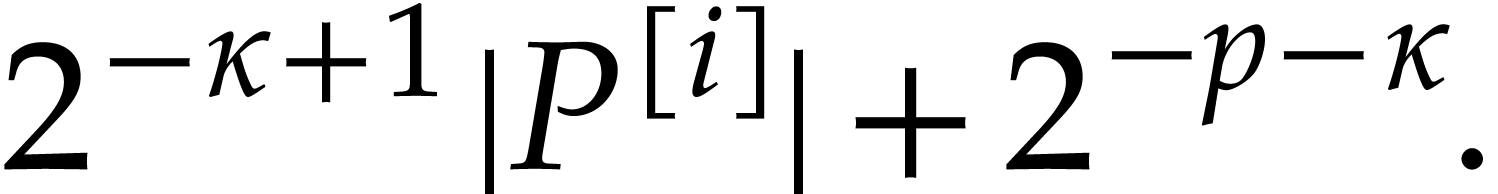 |
(since 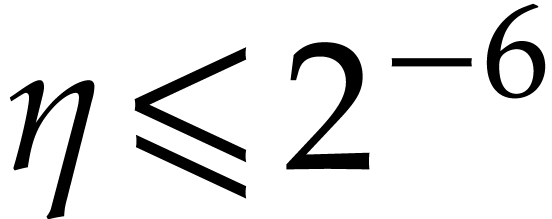 ) ) |
Iterating the latter inequality yields
In particular, 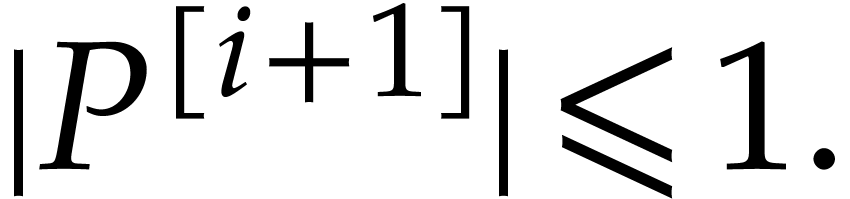 We are done with the construction
of the sequences
We are done with the construction
of the sequences 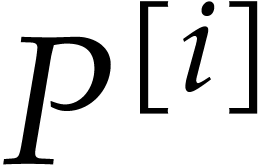 and
and 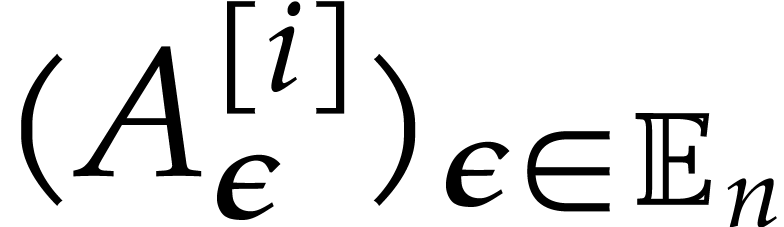 . Let
. Let  be the smallest
integer such that
be the smallest
integer such that
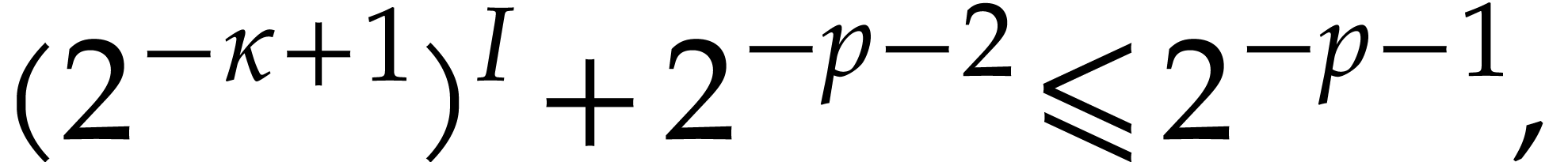 |
(4) |
that is
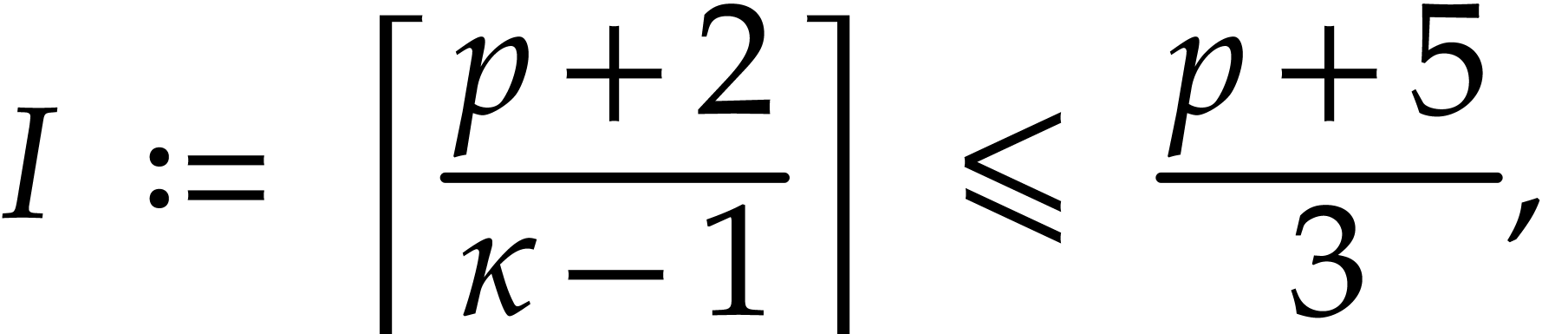
since 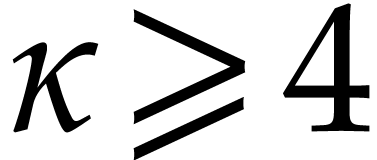 . Note that
. Note that
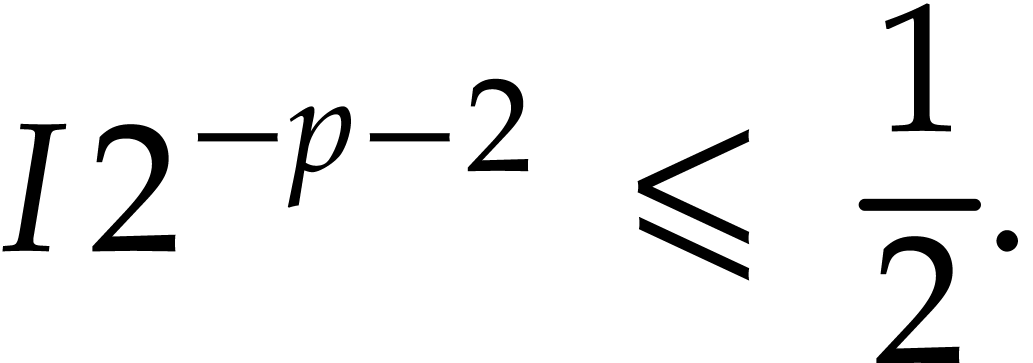 |
(5) |
We take 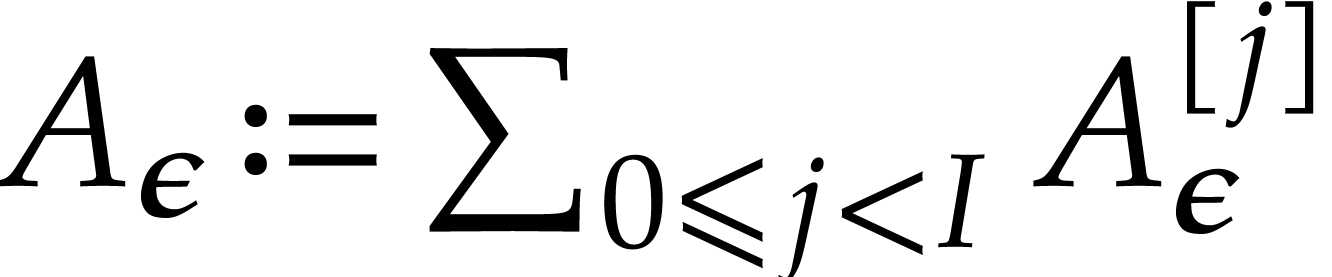 and verify that
and verify that
Finally, we obtain
As for the complexity, one product  takes time
takes time
 , and
, and 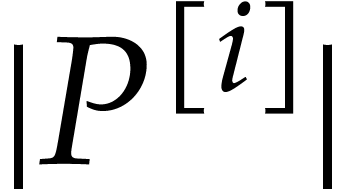 is computed with error
is computed with error 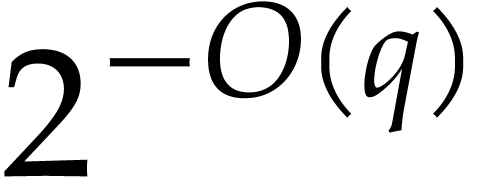 .
Consequently, the computation of
.
Consequently, the computation of 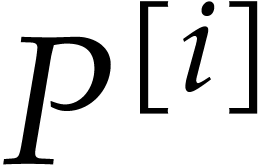 from
from 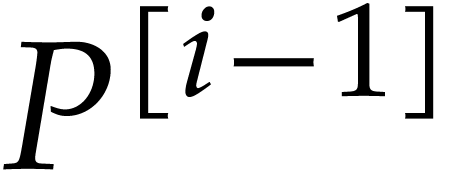 runs in time
runs in time
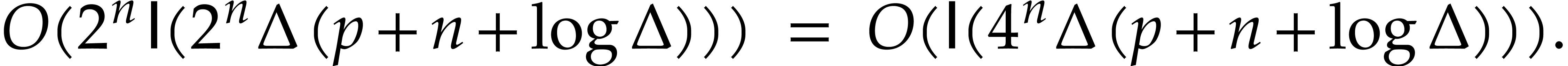
Each use of Proposition 9 contributes 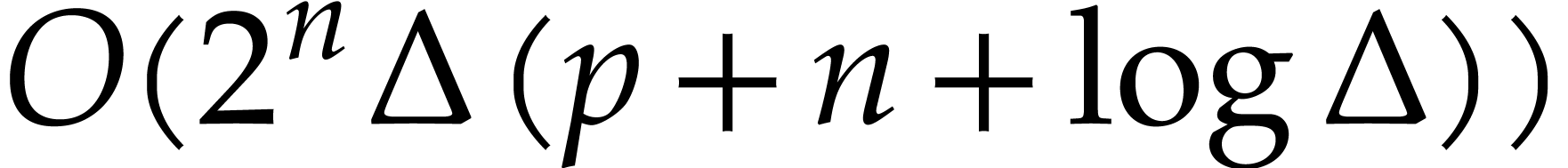 . Since
. Since  ,
the total cost for computing
,
the total cost for computing 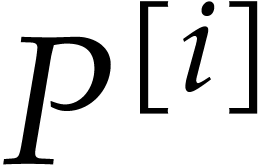 and
and 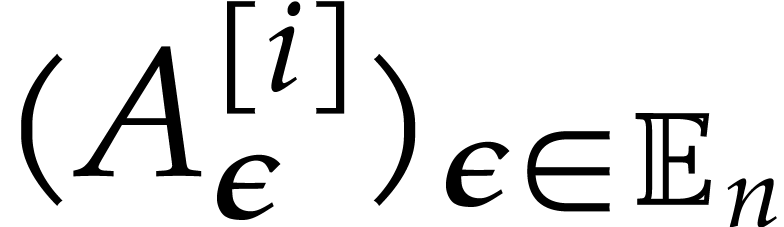 up to index
up to index  is
is 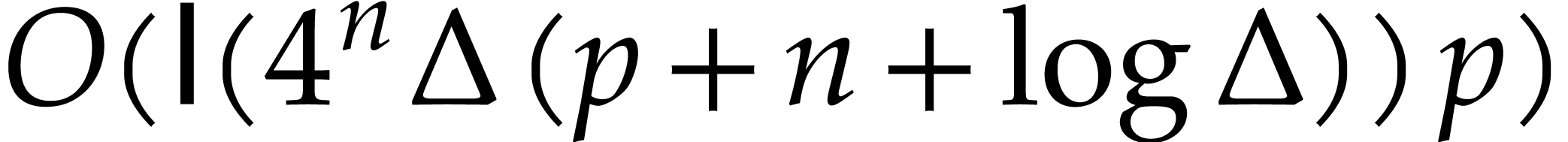 .
.
The numerical convergence of the method behind Lemma 16 is linear, which is sufficient for small precisions. For higher precisions, our next faster algorithm benefits from the “divide and conquer” paradigm. In order to upper bound the norms of the extended reductions, we introduce the auxiliary notation
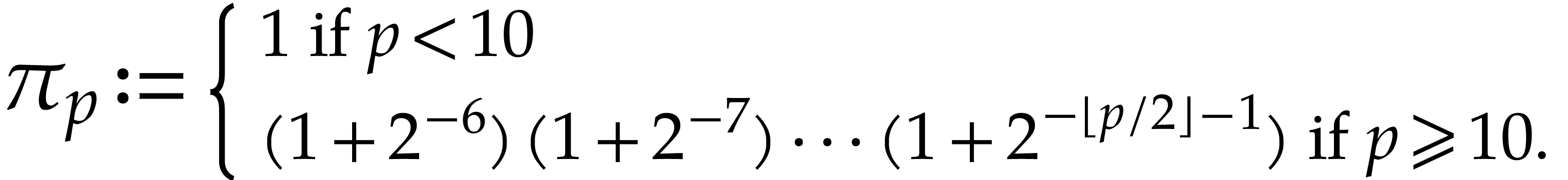
Note that 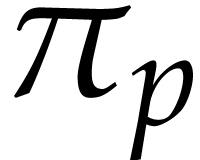 is nondecreasing in
is nondecreasing in 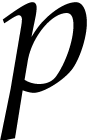 and that
and that  for all
for all  .
.
Algorithm
If 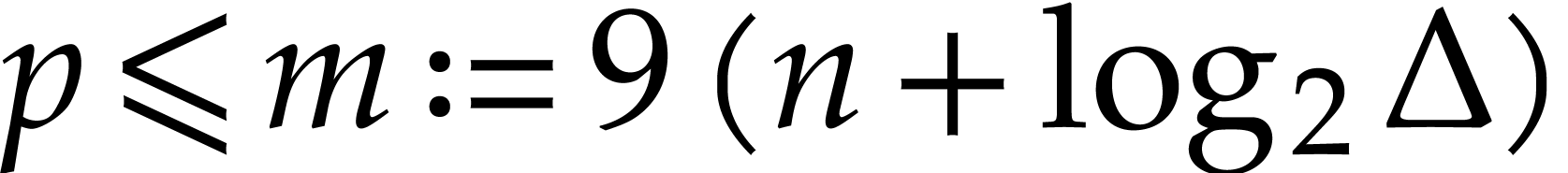 then return the extended reduction
from Lemma 16.
then return the extended reduction
from Lemma 16.
Compute a truncation 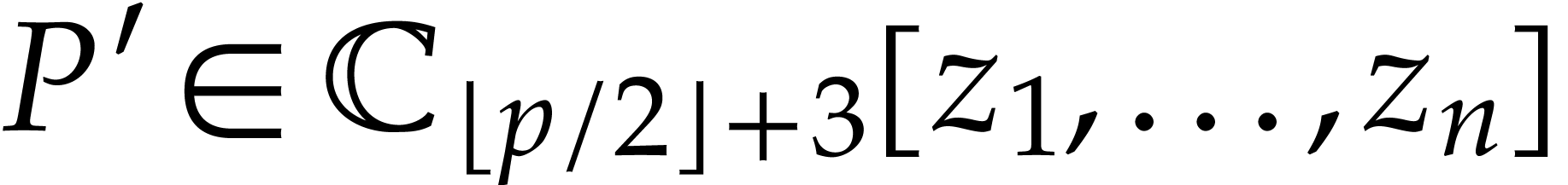 of
of 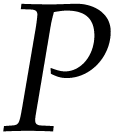 with error
with error  using Lemma 3.
Apply Algorithm 2 recursively to
using Lemma 3.
Apply Algorithm 2 recursively to 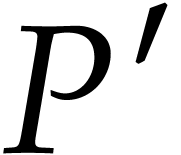 and let
and let 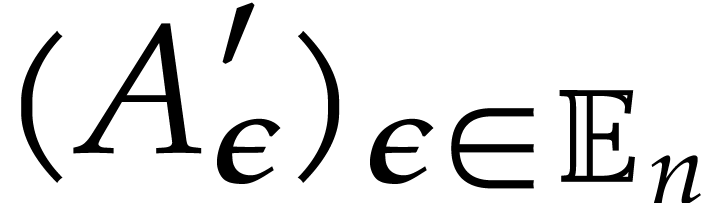 denote the result.
denote the result.
Compute a truncation 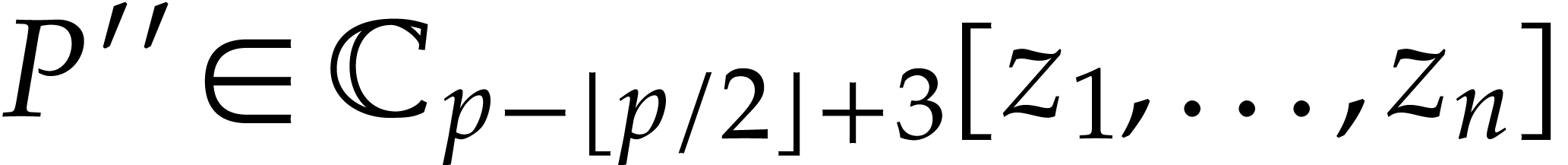 of
of
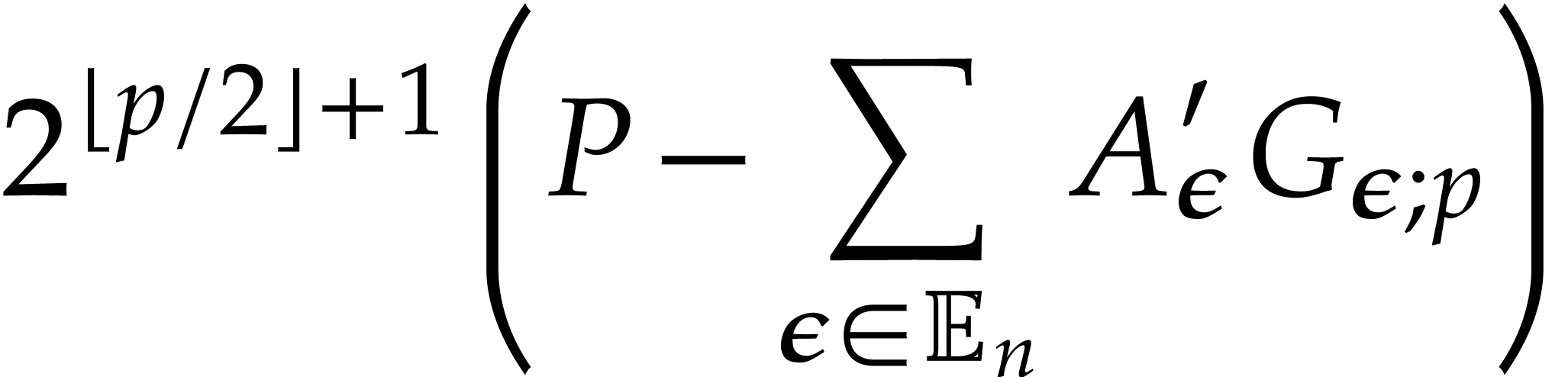
with error 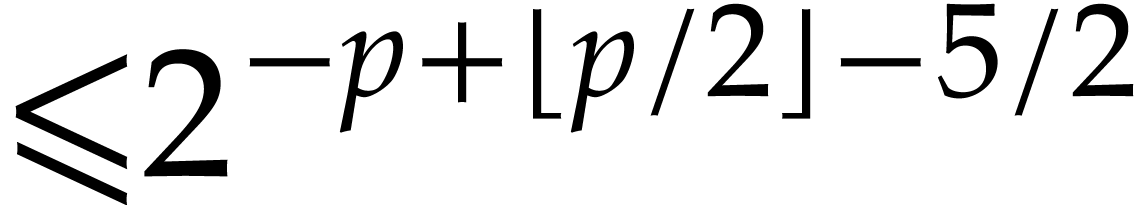 . Apply
Algorithm 2 recursively to
. Apply
Algorithm 2 recursively to 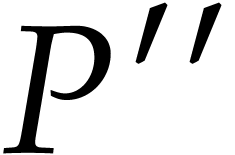 and let
and let 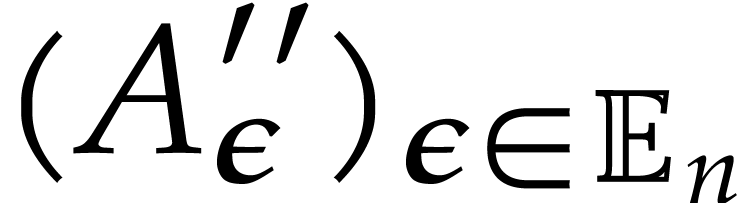 denote the result.
denote the result.
Return a truncation of 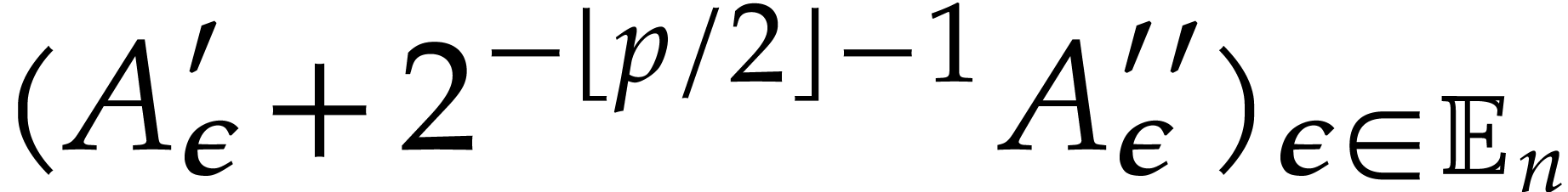 with error
with error 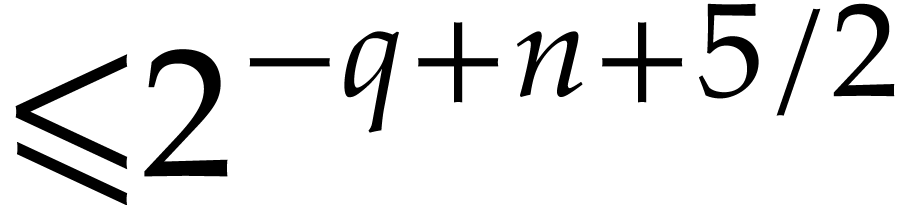 , by using Lemma 3.
, by using Lemma 3.
Proof. If 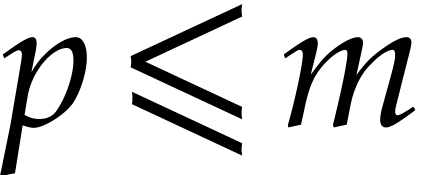 then the
output is correct in step 1 by Lemma 16. Otherwise
then the
output is correct in step 1 by Lemma 16. Otherwise 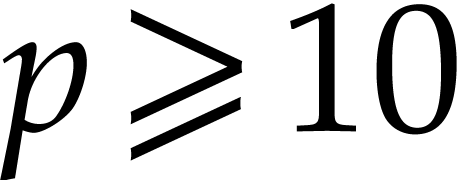 , so that
, so that 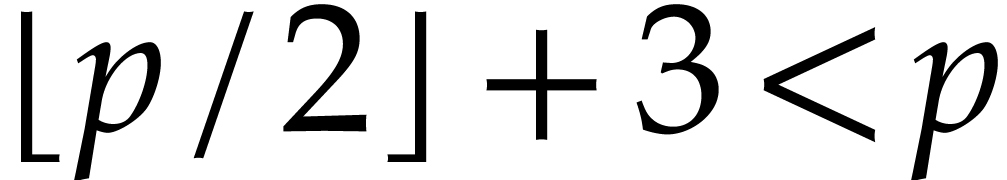 and
and  . Consequently, the
algorithm always terminates. In step 2, by induction, we have
. Consequently, the
algorithm always terminates. In step 2, by induction, we have
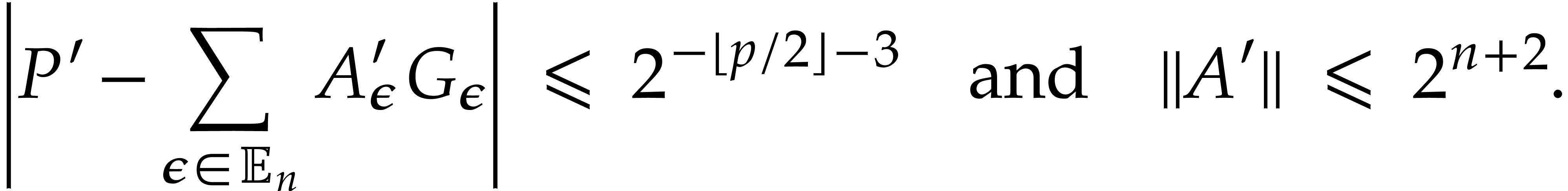
We verify that
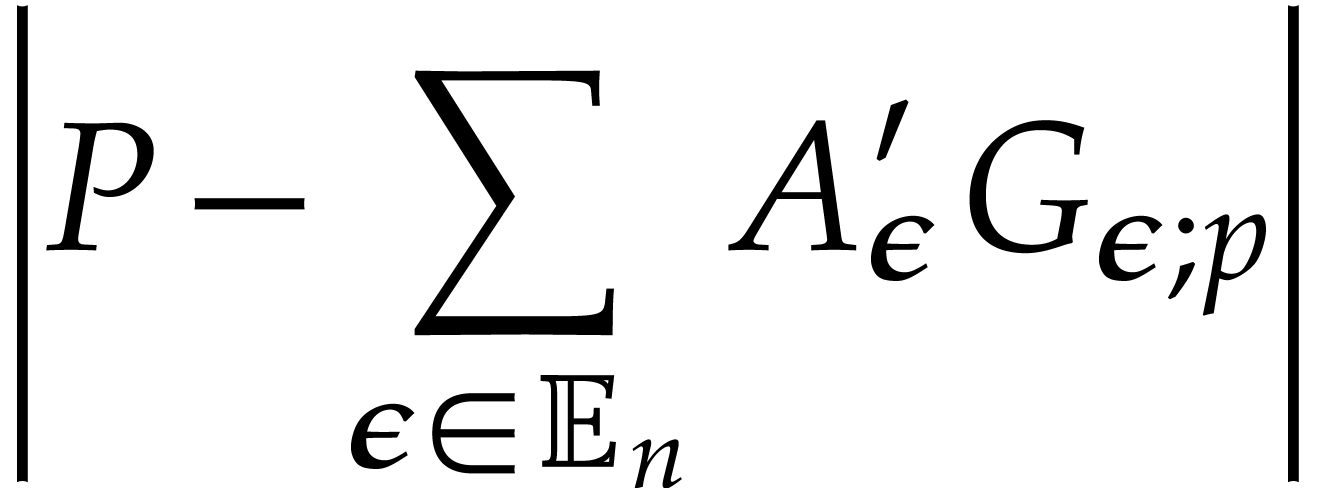 |
 |
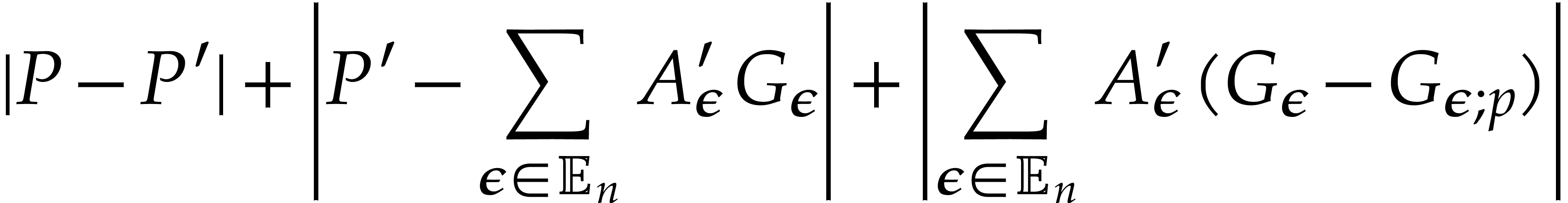 |
|
 |
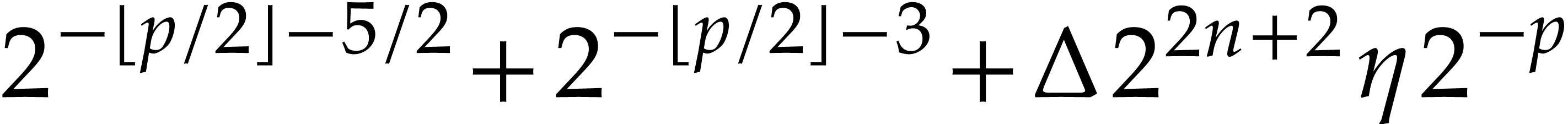 |
||
 |
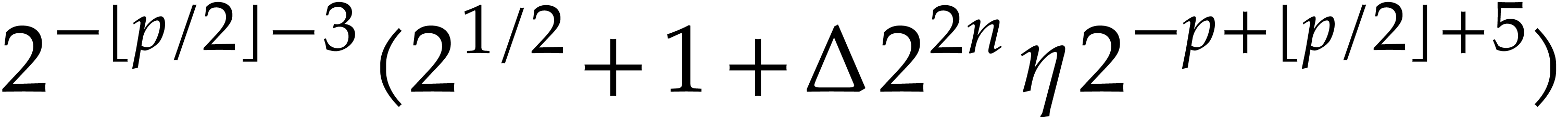 |
||
 |
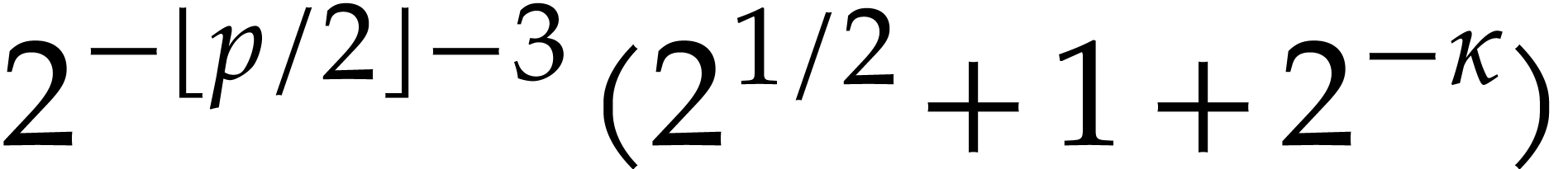 |
(since  ) ) |
|
 |
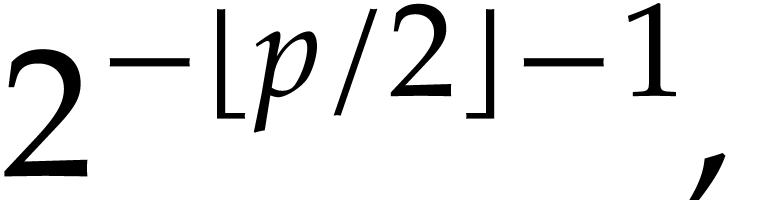 |
(since 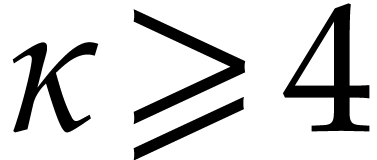 ) ) |
so the polynomial 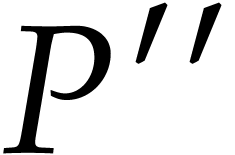 is well defined in step 3, and
we have
is well defined in step 3, and
we have
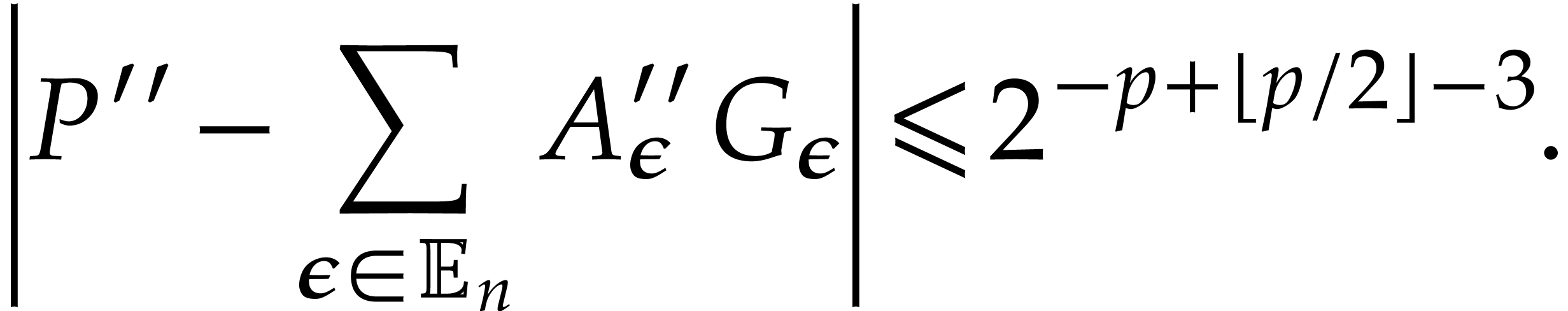
Let 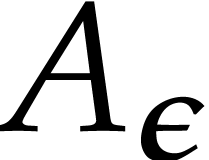 be a truncation of
be a truncation of  with error
with error 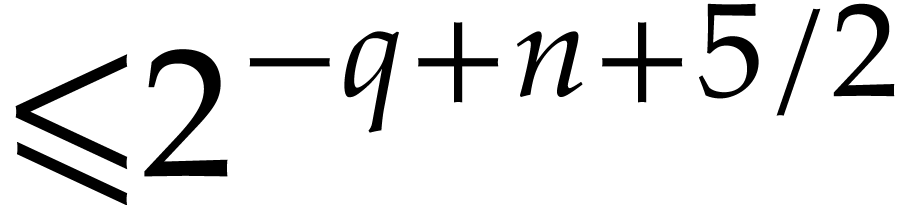 . On the one hand,
. On the one hand,
On the other hand, we obtain
 |
 |
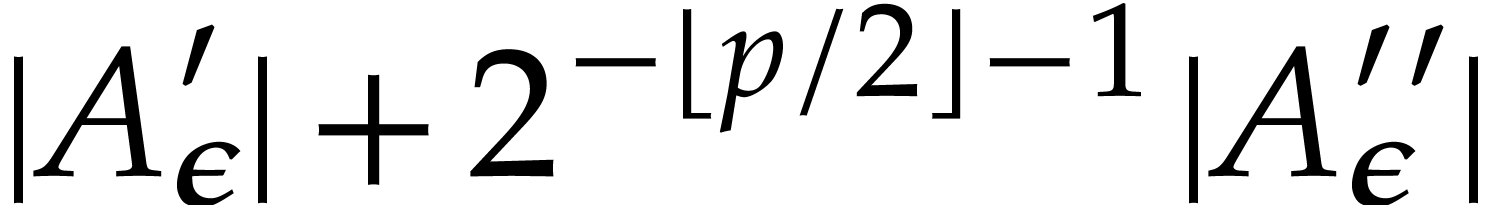 |
|
 |
 |
||
 |
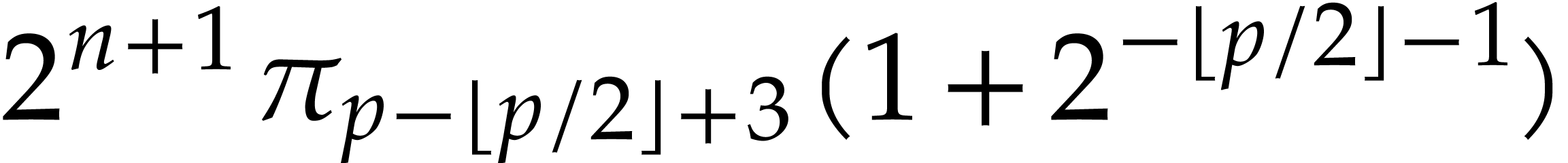 |
||
 |
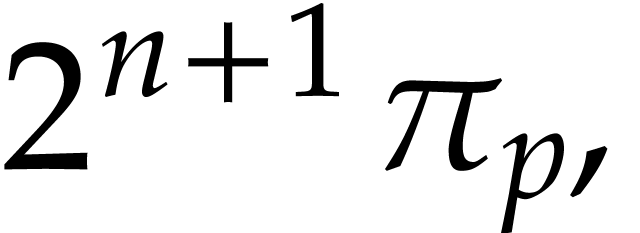 |
(since  ) ) |
which yields
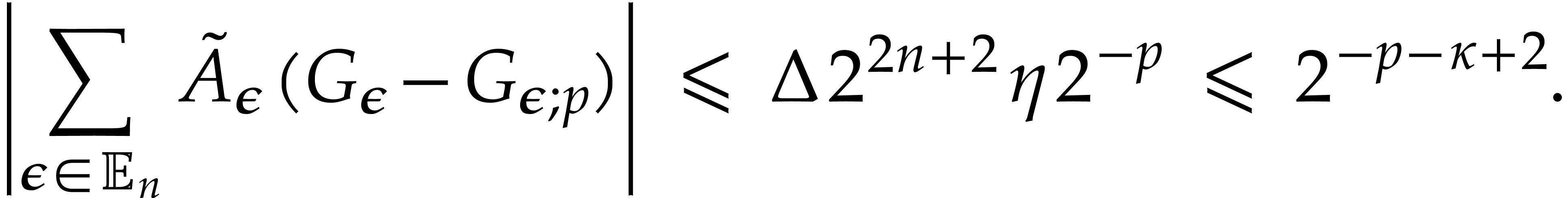 |
(8) |
Combining
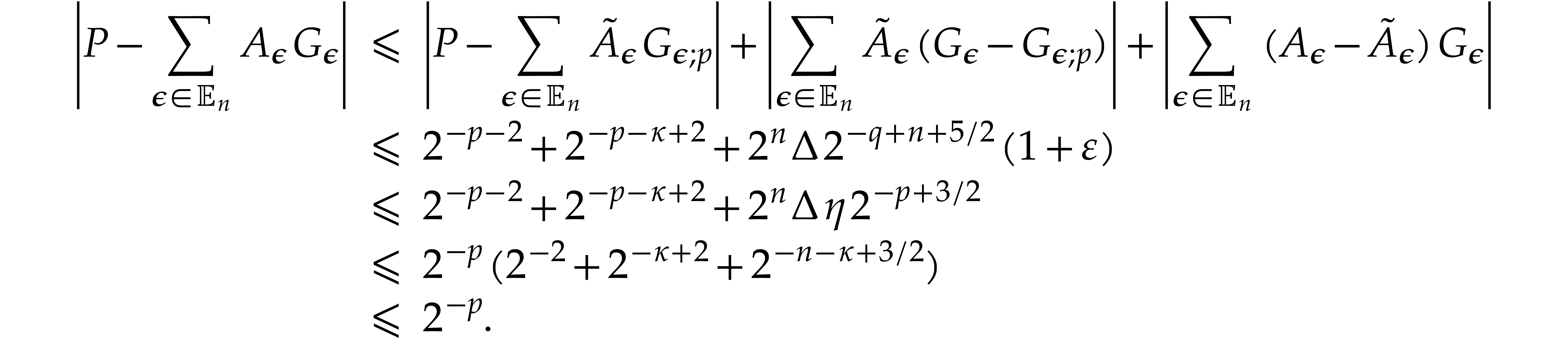
This concludes the proof of the correctness of the algorithm. Let us now analyze the complexity. By Lemma 16, step 1 contributes

Each product 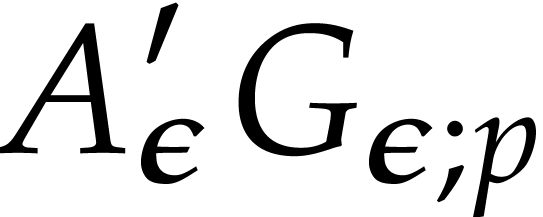 can be computed in time
can be computed in time
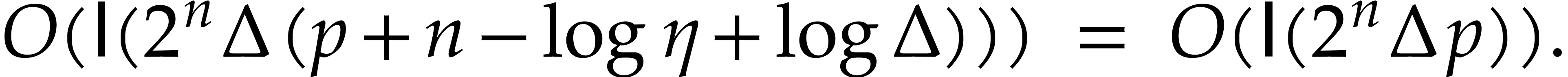
The total cost to obtain 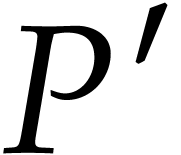 is therefore bounded by
is therefore bounded by
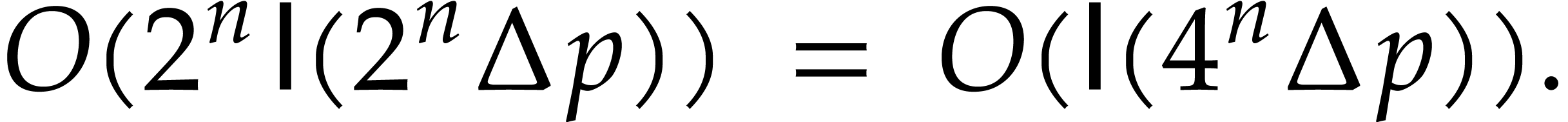
Let 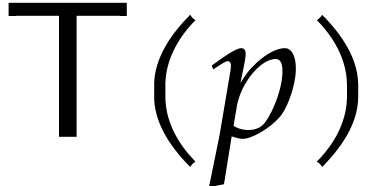 be the computation time as a function of
be the computation time as a function of
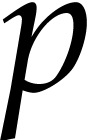 . So far, we have shown that
. So far, we have shown that
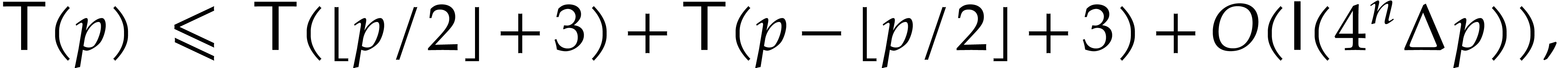
for 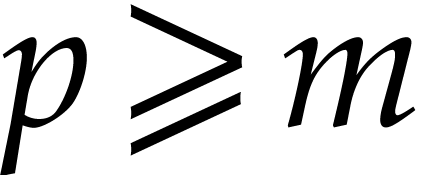 . Unrolling this
inequality leads to
. Unrolling this
inequality leads to
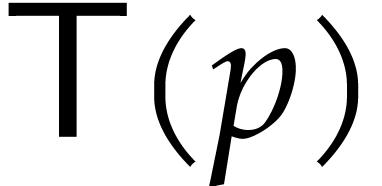 |
 |
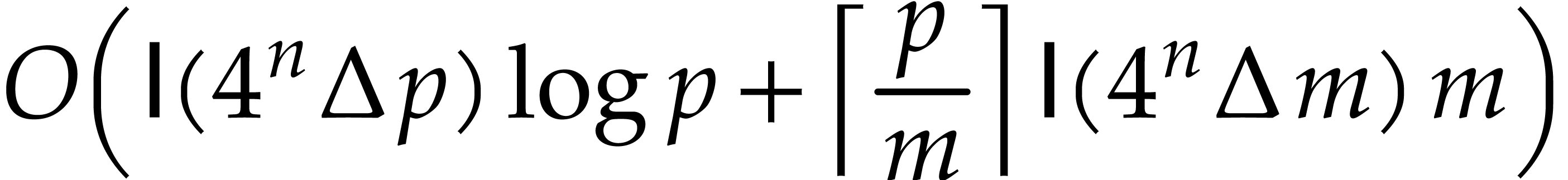 |
|
 |
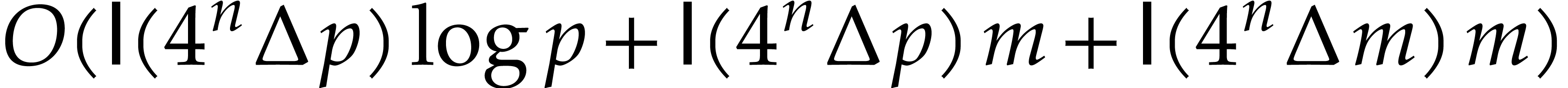 |
||
 |
 |
 |
The following corollary is the main result of this section.
Proof. Proposition 17 allows us to compute
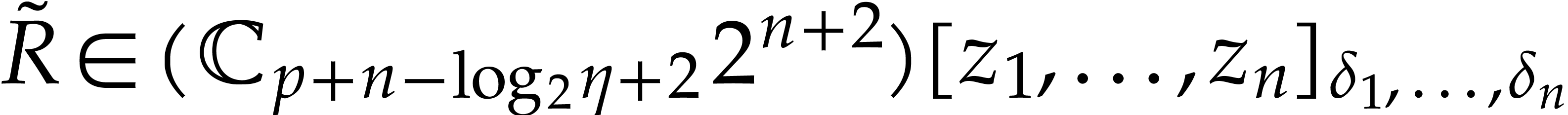
such that 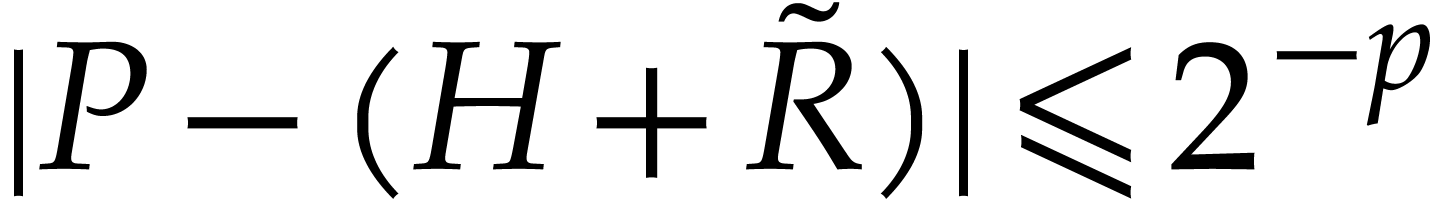 for some
for some 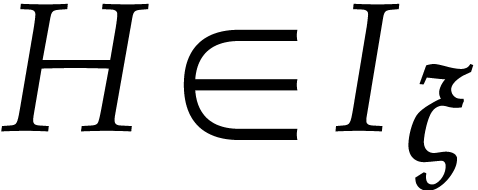 .
Using Proposition 15, we deduce that
.
Using Proposition 15, we deduce that
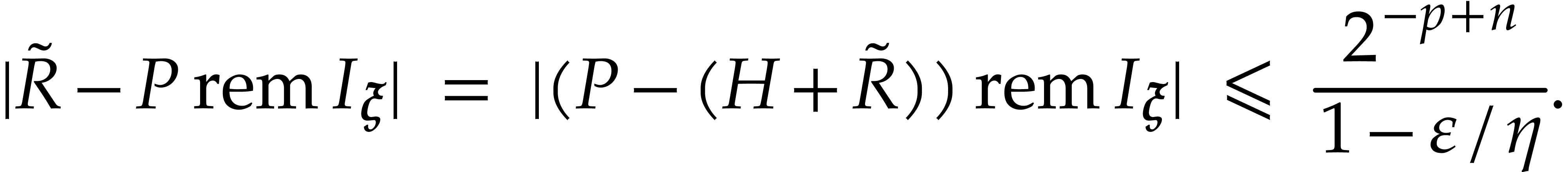
Using Lemma 2, we finally compute an approximation of 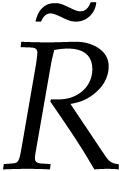 in
in 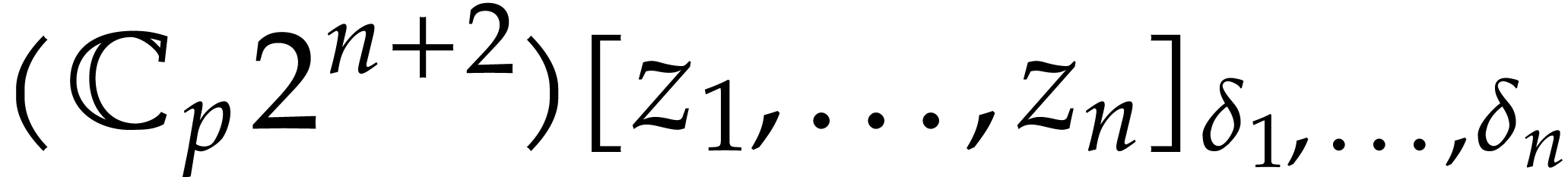 with error
with error 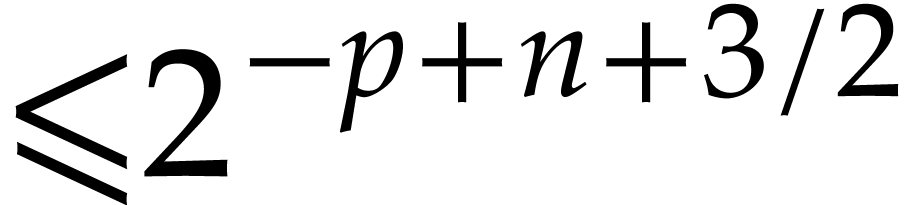 and verify that
and verify that
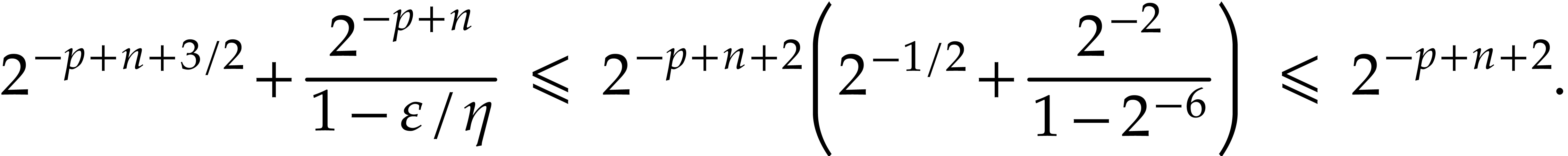

This section is devoted to multi-point evaluation and interpolation at a spiroid. Evaluation will follow the classical “divide and conquer” paradigm with respect to the number of evaluation points. Interpolation will reduce to evaluation.
Let 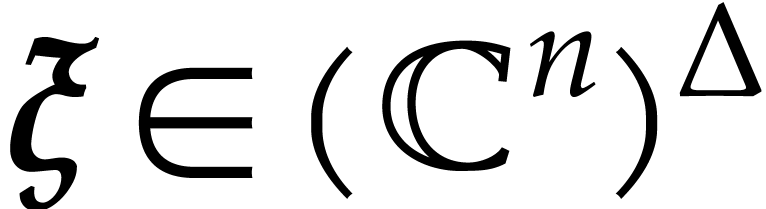 be as in the previous section. If
be as in the previous section. If  for some
for some 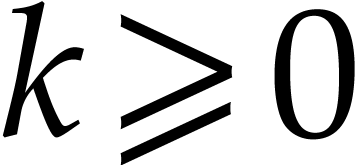 , then
, then
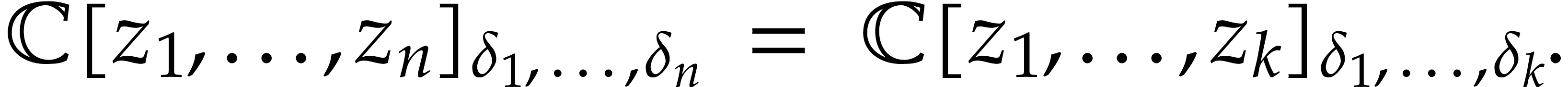
Without loss of generality, this allows us to replace  by
by  of dimension
of dimension 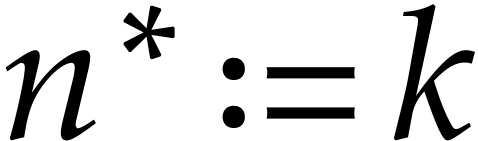 with
with
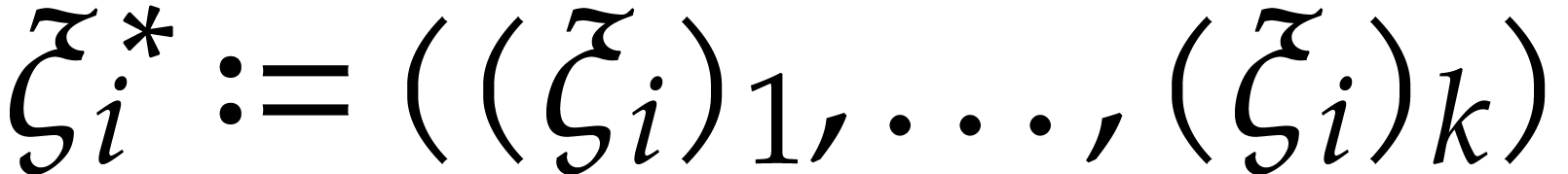 for each
for each  .
In what follows, we will only work with spiroids
.
In what follows, we will only work with spiroids  for which
for which 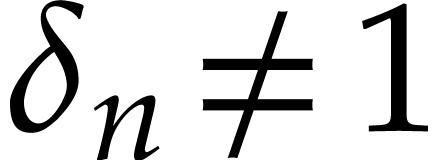 whenever
whenever  .
.
Our algorithm for multi-point evaluation of a polynomial  at
at  is based on a generalization of
the classical remainder tree technique used for the univariate case [5, Chapter 10]. If
is based on a generalization of
the classical remainder tree technique used for the univariate case [5, Chapter 10]. If 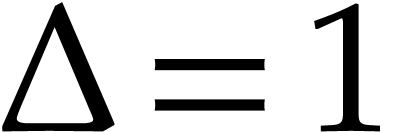 ,
then an evaluation tree for
,
then an evaluation tree for  consists of
a single leaf labeled by
consists of
a single leaf labeled by 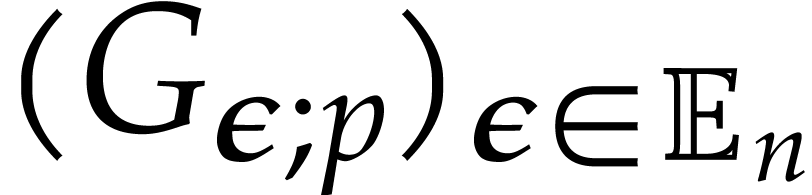 . If
. If
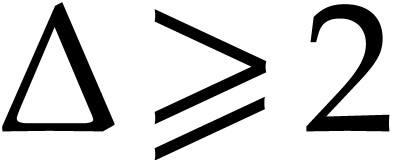 and
and 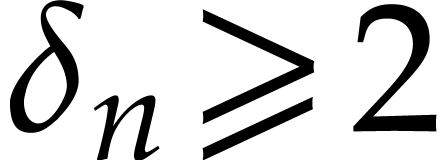 ,
then
,
then  induces two sequences of points
induces two sequences of points 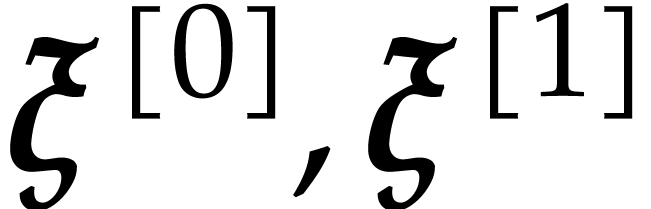 which are defined by
which are defined by
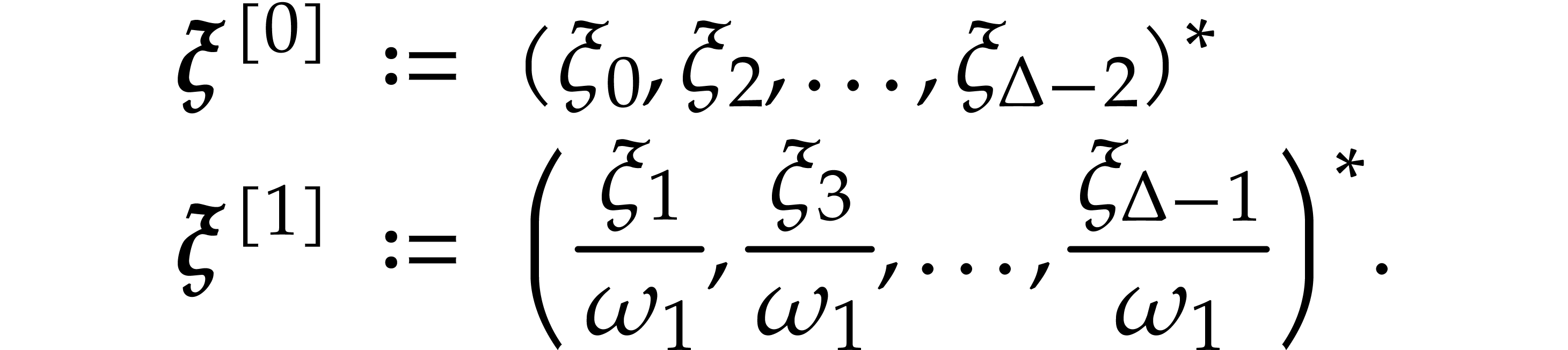
For 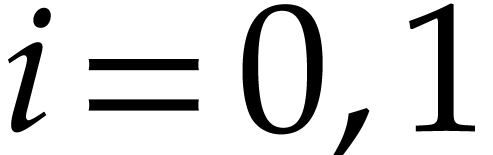 , we write
, we write 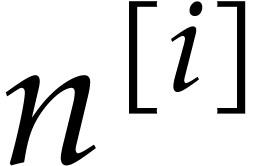 for the dimension of
for the dimension of 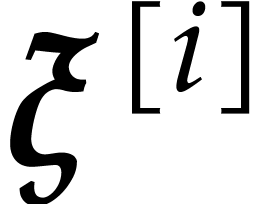 ,
,
 for its partial degrees, and
for its partial degrees, and 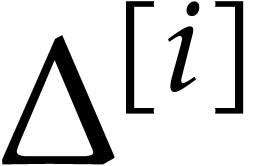 for its degree. The perturbations of the defining polynomials of
for its degree. The perturbations of the defining polynomials of 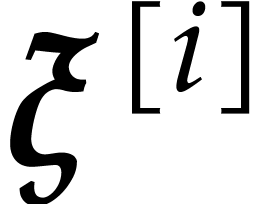 are written
are written 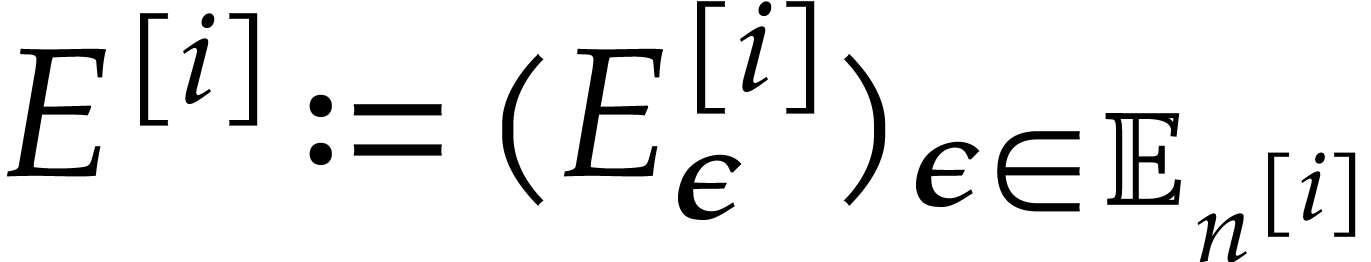 ,
so we have
,
so we have
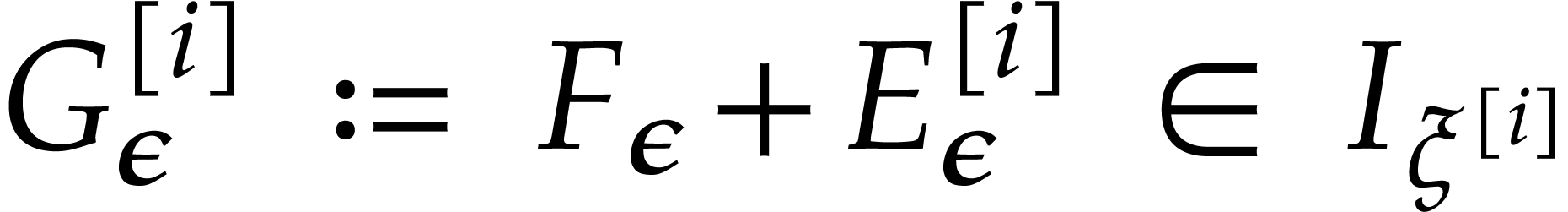
for all 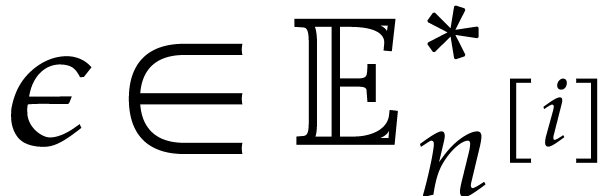 . We further define
. We further define

Note that 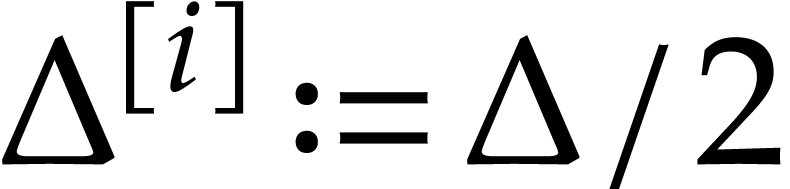 ,
, 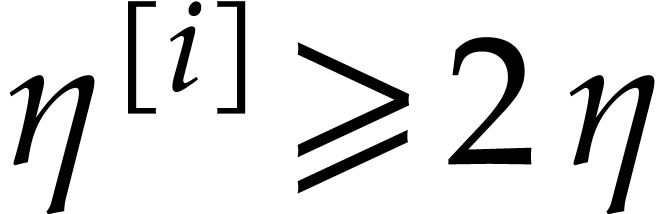 , and
, and 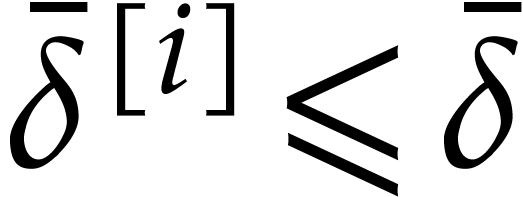 , for
, for 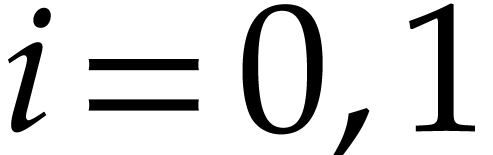 .
.
An evaluation tree for the spiroid  consists of a root that is labeled by the family
consists of a root that is labeled by the family 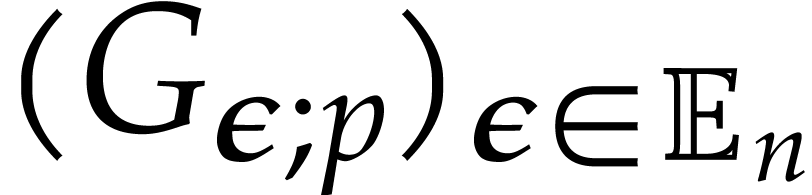 and two children which are recursively the evaluation trees for
and two children which are recursively the evaluation trees for 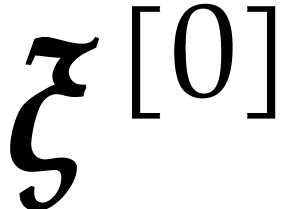 and
and  .
Since
.
Since 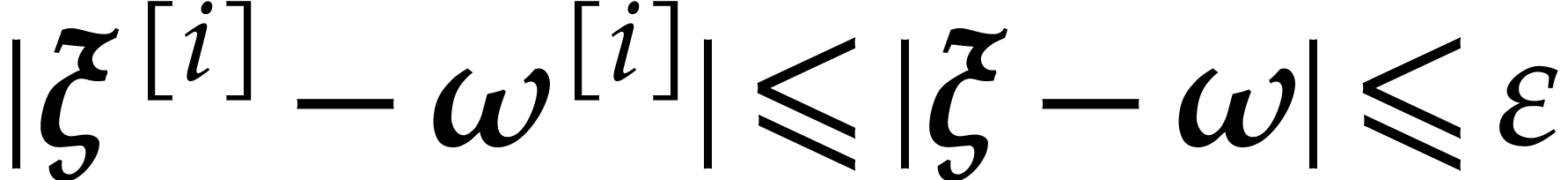 , if
, if 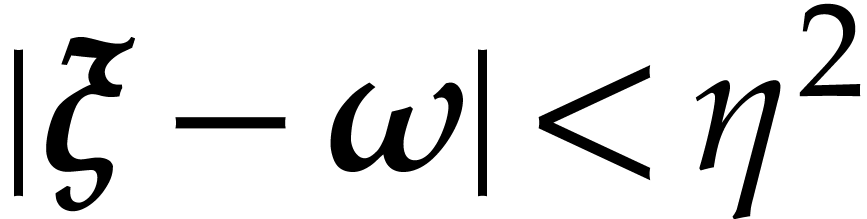 then
then 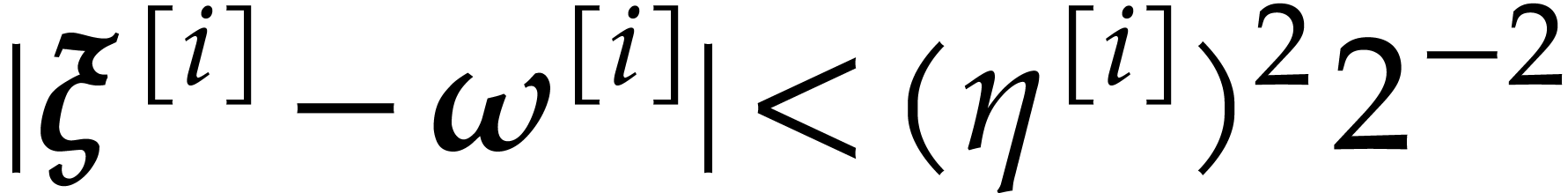 . So, Proposition 14 ensures that the
. So, Proposition 14 ensures that the 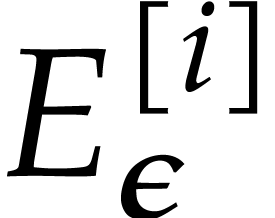 exists with
exists with 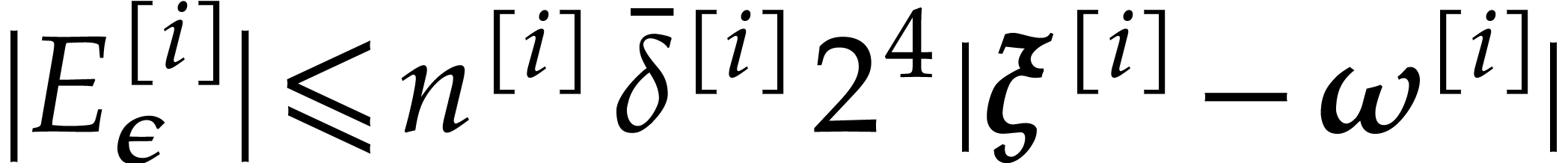 , whenever
, whenever 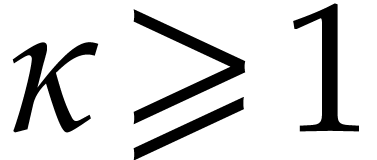 . This shows that evaluation trees exist whenever
. This shows that evaluation trees exist whenever
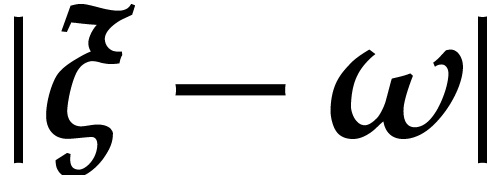 is sufficiently small. The construction of these
trees is postponed to the end of this section.
is sufficiently small. The construction of these
trees is postponed to the end of this section.
An evaluation tree for  is said to be known
with error
is said to be known
with error 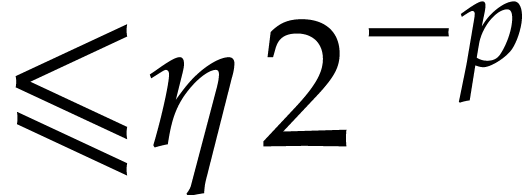 if
if 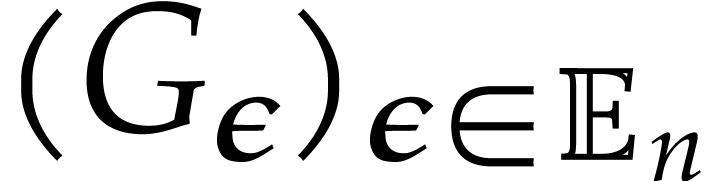 is given with error
is given with error 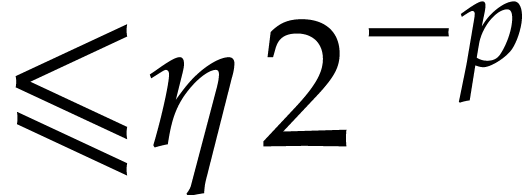 , and if
the evaluation tree for
, and if
the evaluation tree for 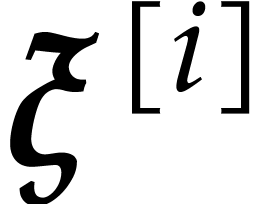 is known with error
is known with error 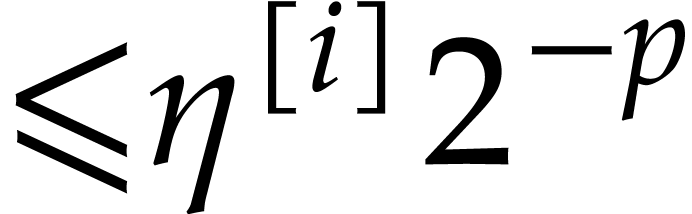 for
for 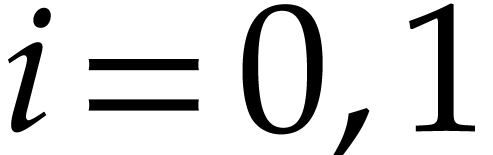 . We
will see in section 4.3 that for such an evaluation tree
with error
. We
will see in section 4.3 that for such an evaluation tree
with error 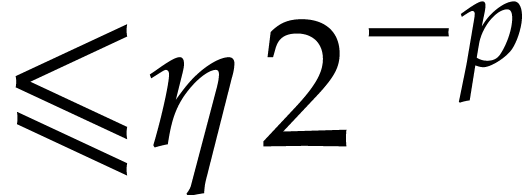 , the
, the 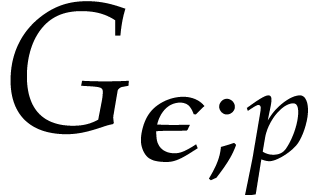 will be elements of
will be elements of 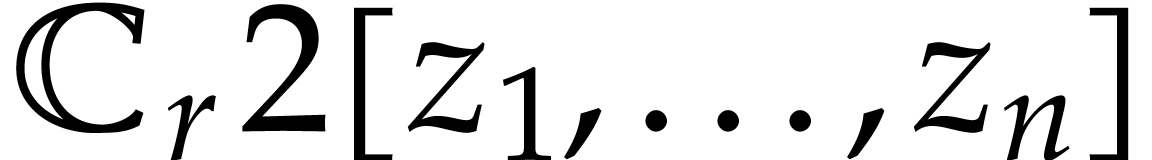 with
with 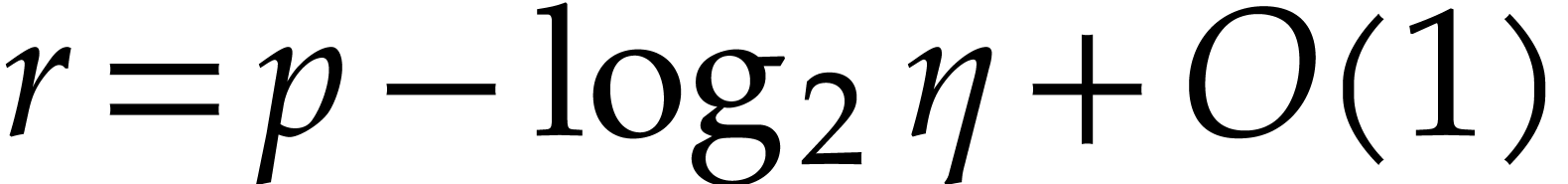 . Our next algorithm performs fast
evaluation at
. Our next algorithm performs fast
evaluation at  by taking advantage of evaluation
trees.
by taking advantage of evaluation
trees.
Algorithm
If 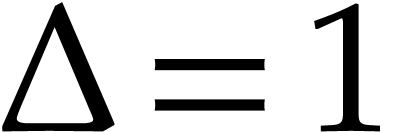 then return an approximation of
then return an approximation of 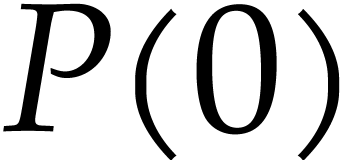 in
in 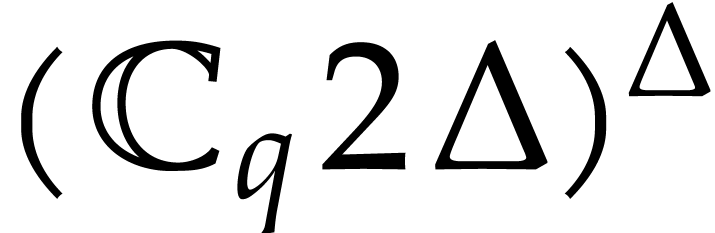 with error
with error 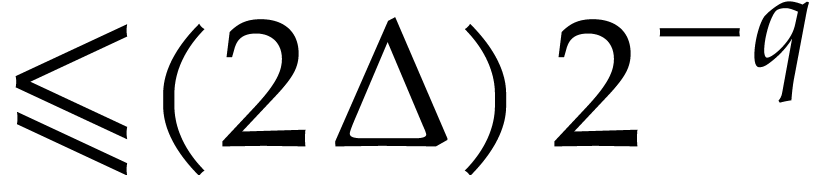 , by using Lemma 2.
, by using Lemma 2.
Compute a truncation  of
of 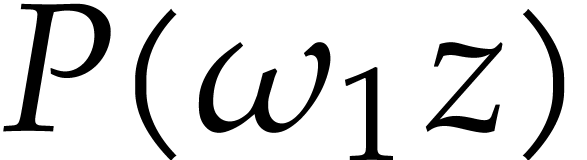 with error
with error  .
.
Compute truncations 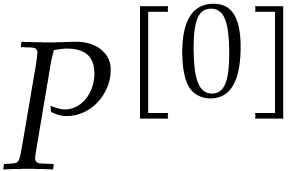 and
and 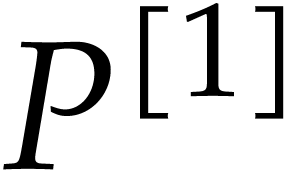 of
of  and
and  in
in 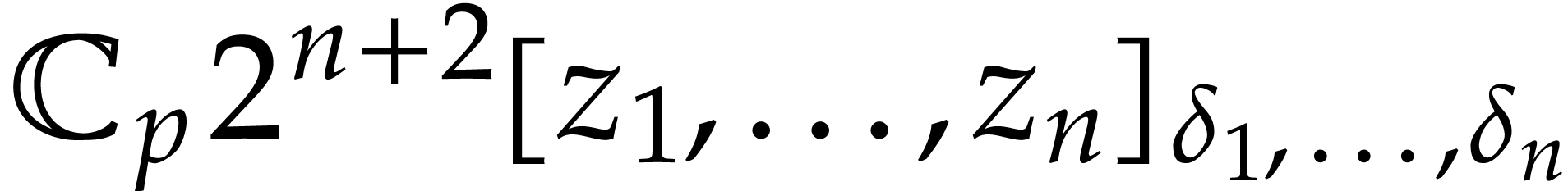 with error
with error 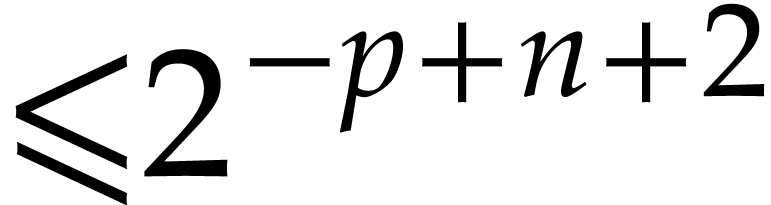 via
Corollary 18.
via
Corollary 18.
Apply Algorithm 3 recursively to 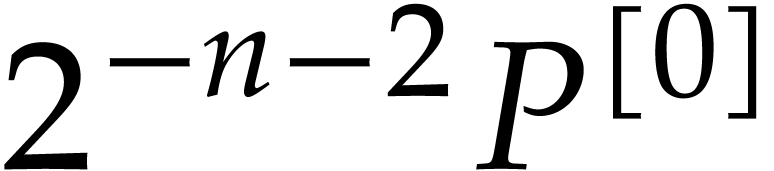 and the evaluation sub-trees for
and the evaluation sub-trees for 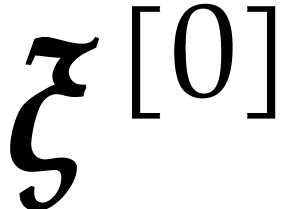 in
order to obtain approximations
in
order to obtain approximations  of
of 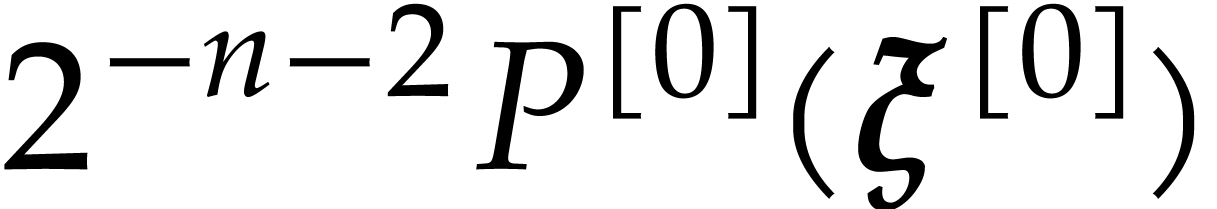 with error
with error 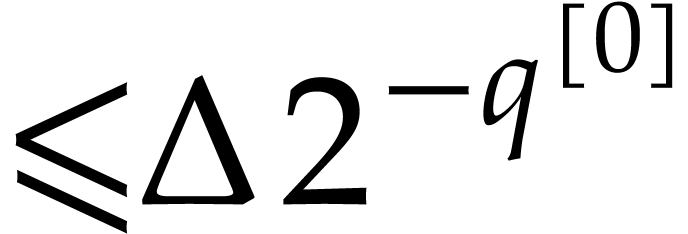 ,
where
,
where 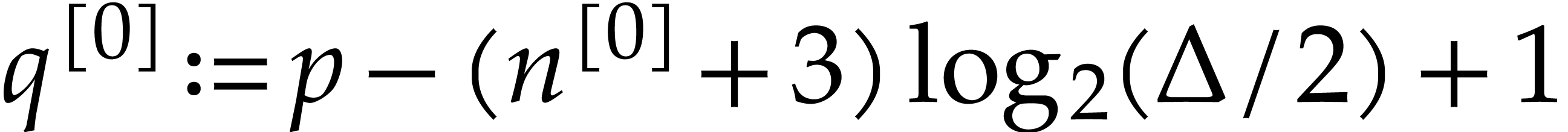 .
.
Apply Algorithm 3 recursively to 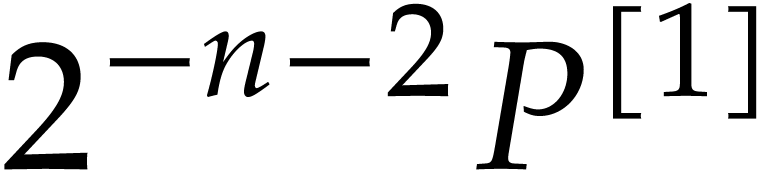 and the evaluation sub-trees for
and the evaluation sub-trees for  in
order to obtain an approximation
in
order to obtain an approximation 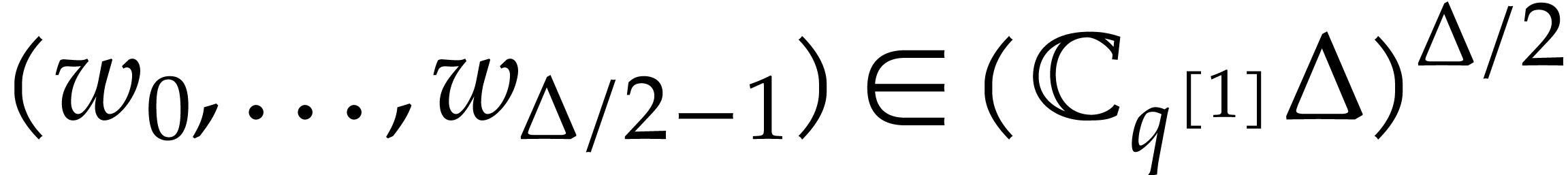 of
of 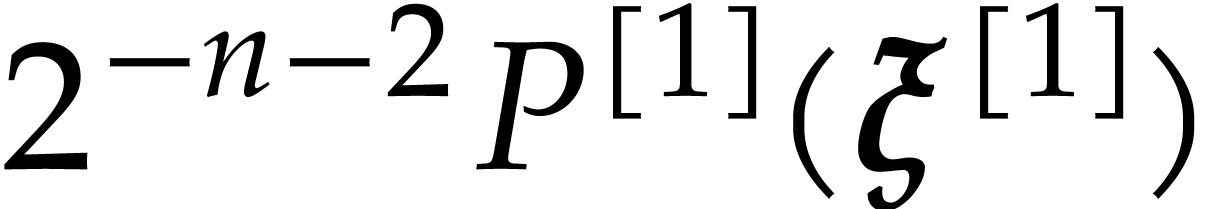 with error
with error 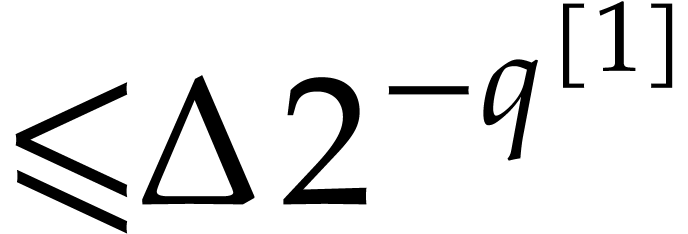 ,
where
,
where 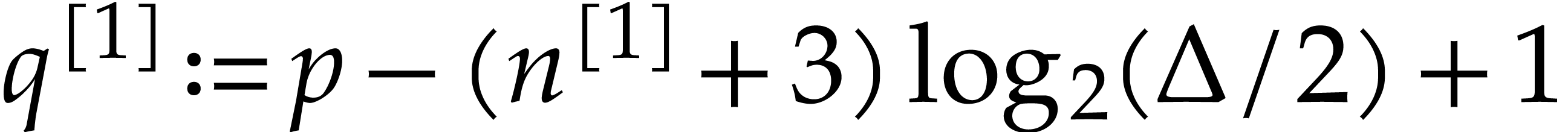 .
.
Return an approximation of 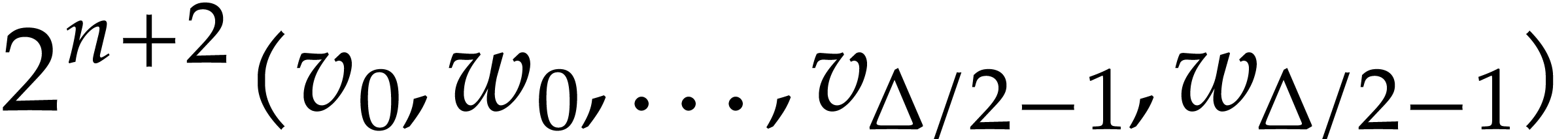 in
in 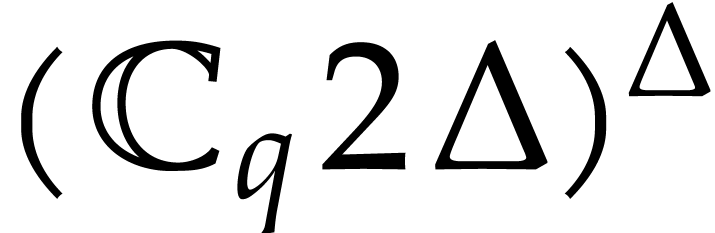 with error
with error 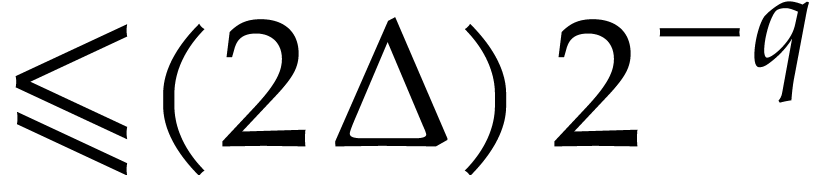 .
.
Proof. If 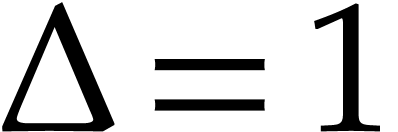 then the
algorithm behaves as expected. Let us now assume that
then the
algorithm behaves as expected. Let us now assume that  . The correctness mostly relies on the
identities
. The correctness mostly relies on the
identities
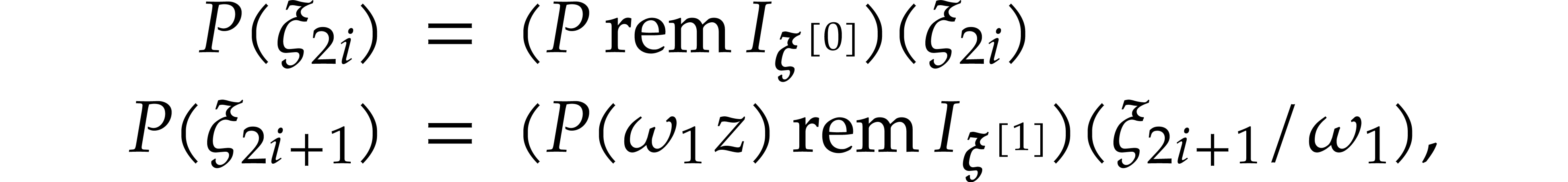
for  . Let us verify that
computations are done with sufficiently large precisions. By
construction, we have
. Let us verify that
computations are done with sufficiently large precisions. By
construction, we have 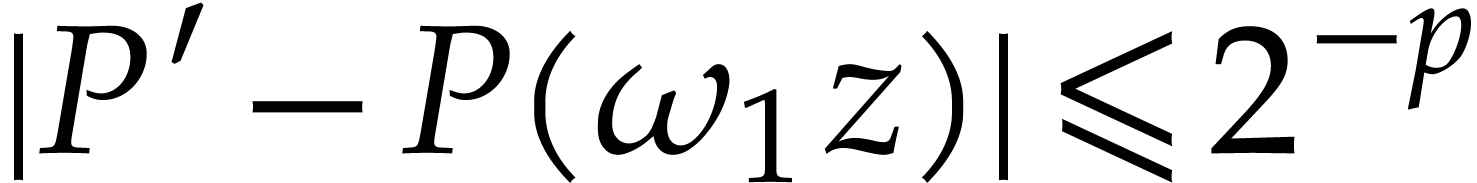 and
and 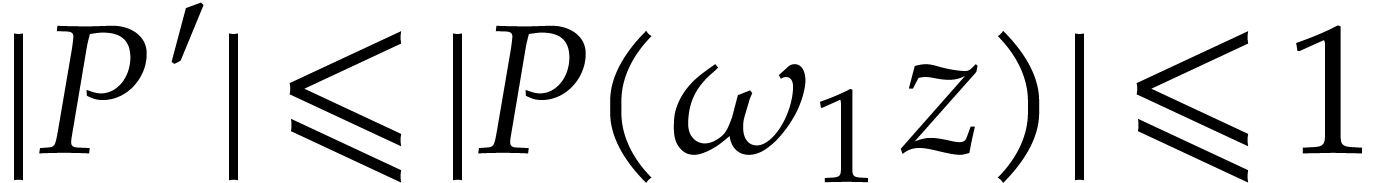 . Corollary 18 yields
. Corollary 18 yields 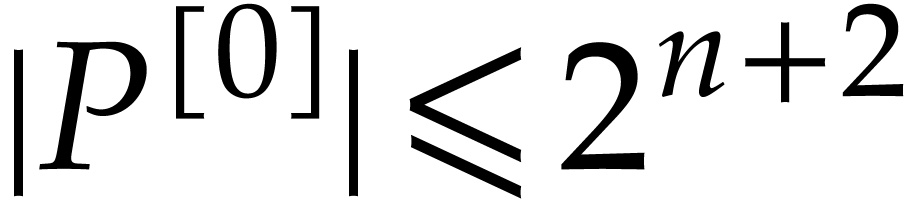 ,
, 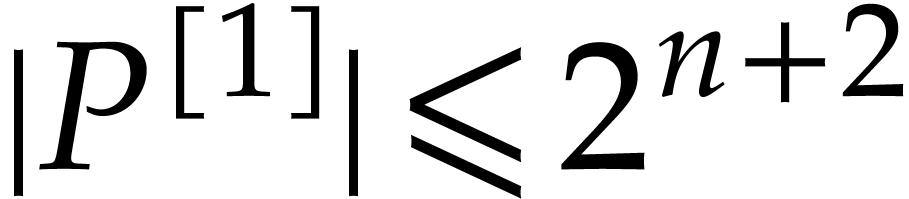 and
and
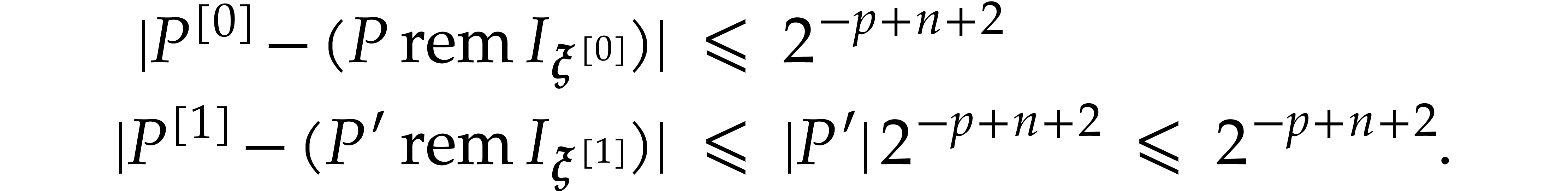
Since 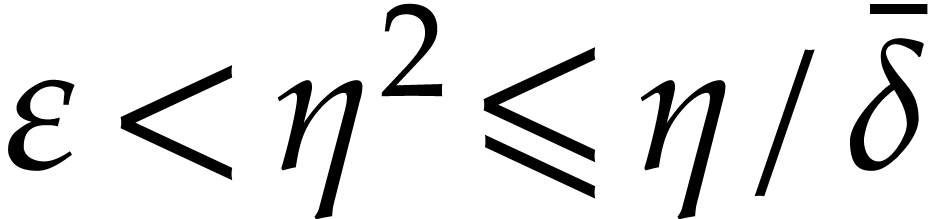 , Lemma 12
ensures that
, Lemma 12
ensures that
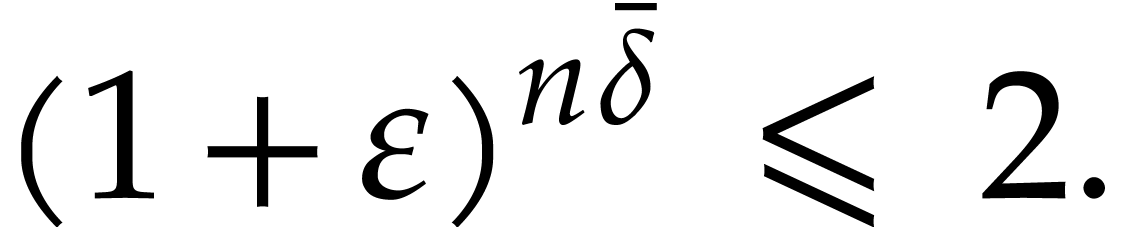 |
(9) |
In particular, it follows that 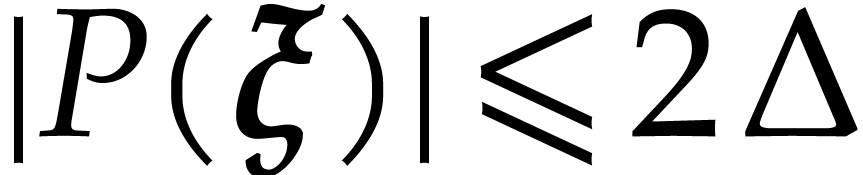 .
Assuming by induction that the claimed properties hold for the recursive
call in step 4, we obtain
.
Assuming by induction that the claimed properties hold for the recursive
call in step 4, we obtain
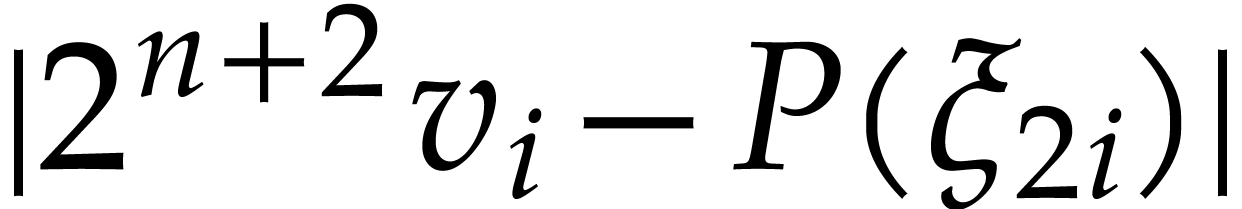 |
 |
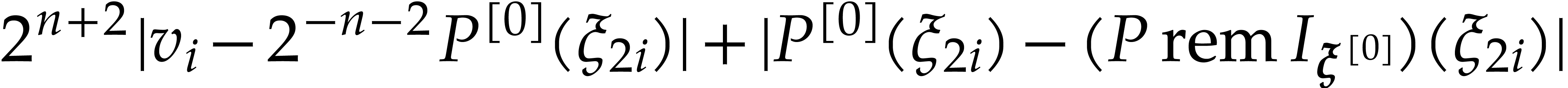 |
|
 |
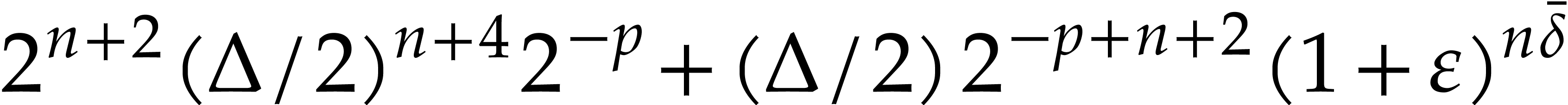 |
||
 |
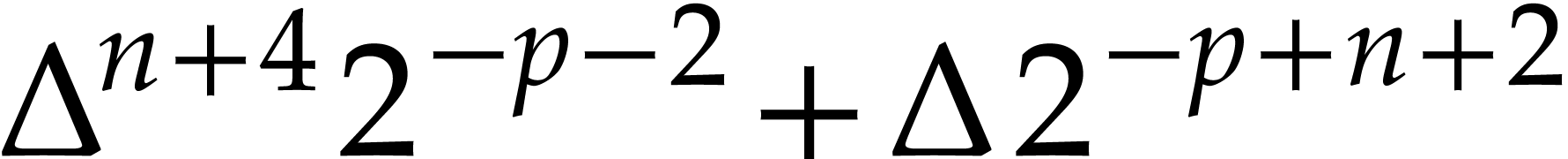 |
(using |
|
 |
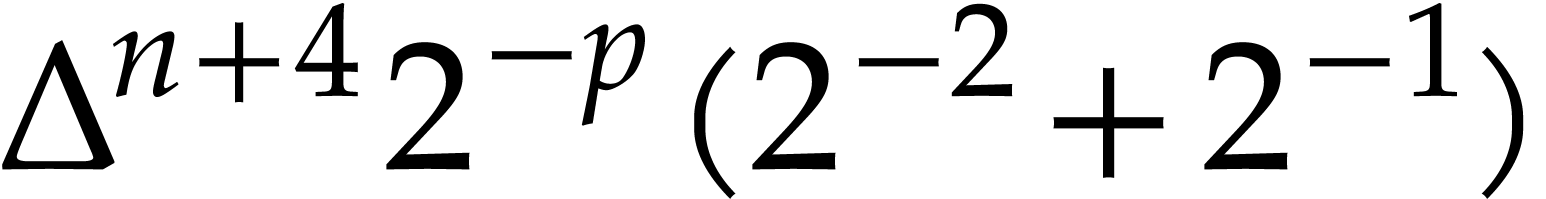 |
(since 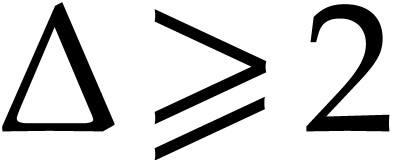 ) ) |
|
 |
 |
Similarly, for 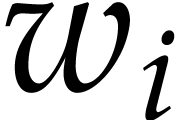 we obtain
we obtain
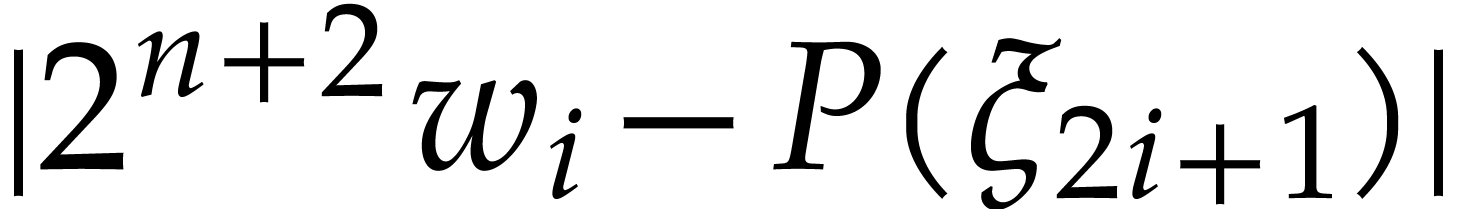 |
 |
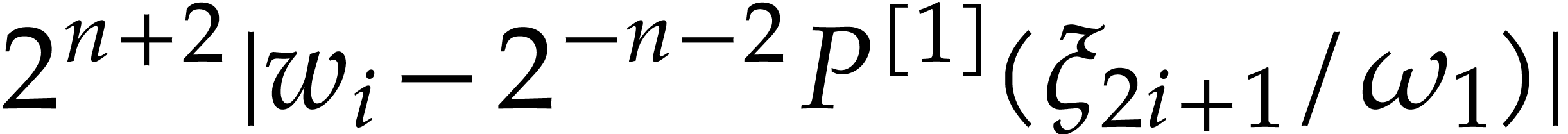 |
|
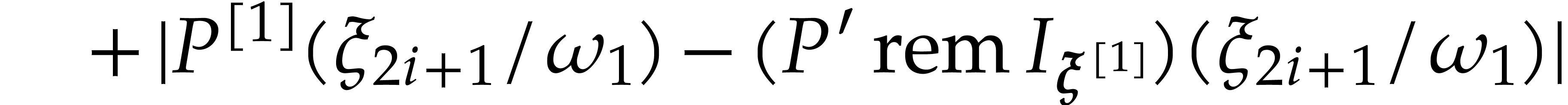 |
|||
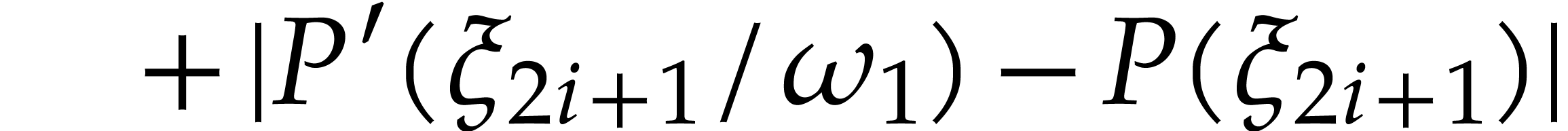 |
|||
 |
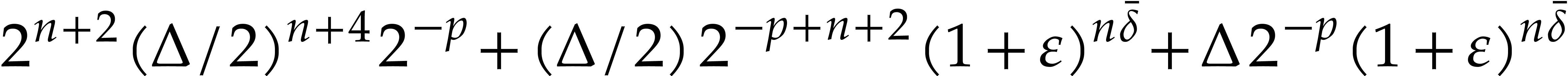 |
||
 |
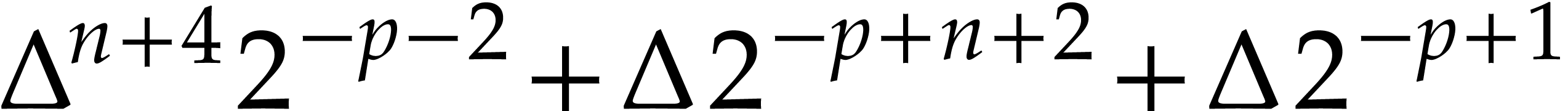 |
(using |
|
 |
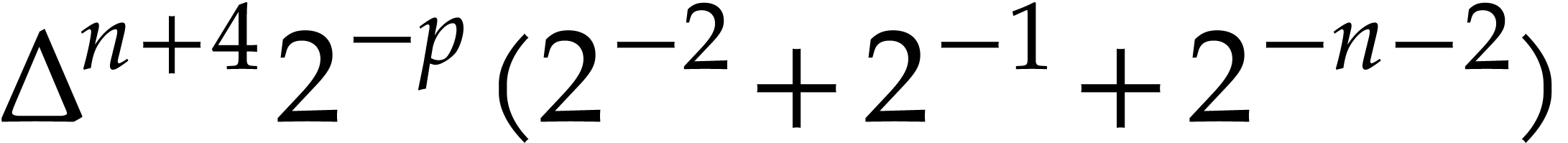 |
(since 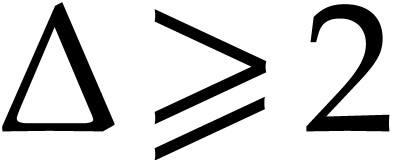 ) ) |
|
 |
 |
We are done with the correctness. As for the complexity analysis, the
computation of  and then of
and then of 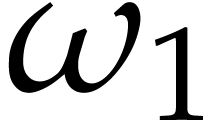 , with
, with 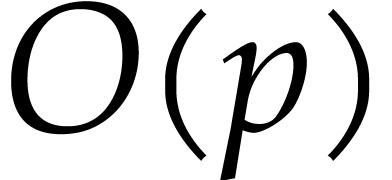 bits of
precision in step 2 can be done in time
bits of
precision in step 2 can be done in time 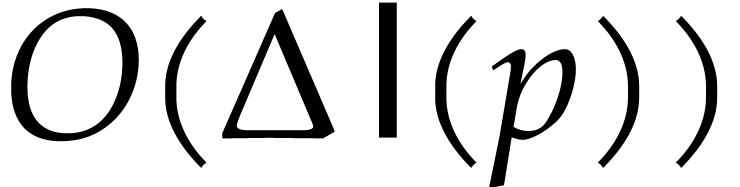 by Lemma
4, under the assumption
by Lemma
4, under the assumption  .
Therefore, step 2 runs in time
.
Therefore, step 2 runs in time 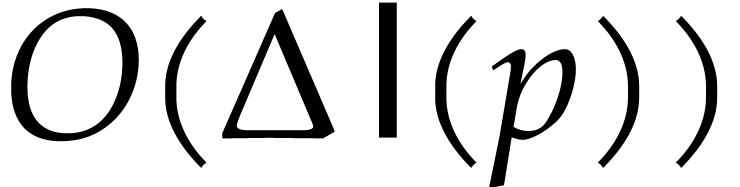 .
In view of Corollary 18, the complexity
.
In view of Corollary 18, the complexity  of Algorithm 3 satisfies
of Algorithm 3 satisfies

for some universal constant 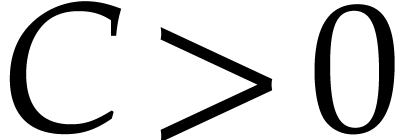 .
Unrolling this inequality, we obtain
.
Unrolling this inequality, we obtain
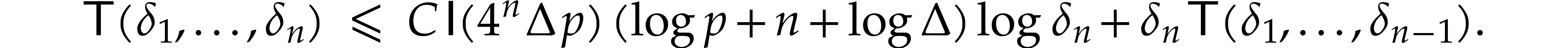
Unrolling this new inequality, while using the geometric increase of
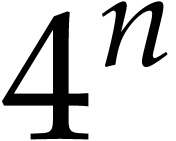 , we obtain the desired
complexity bound.
, we obtain the desired
complexity bound.
Our interpolation algorithms rely on the evaluation one. We begin with a method dedicated to small precisions.
Proof. Using Lemma 5, we compute
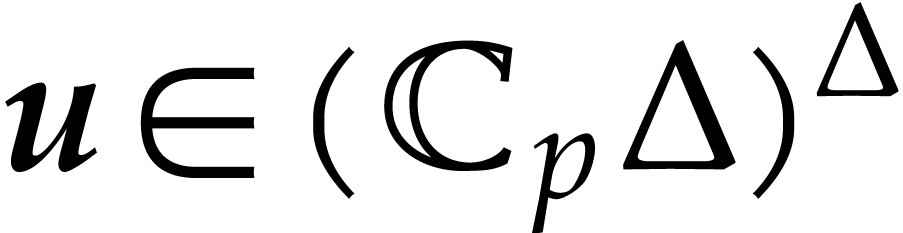 such that
such that
 |
(10) |
and 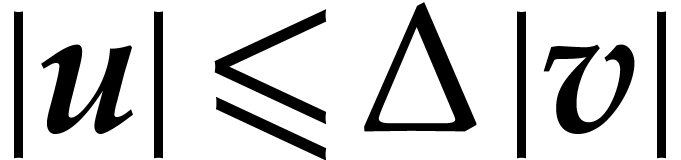 in time
in time 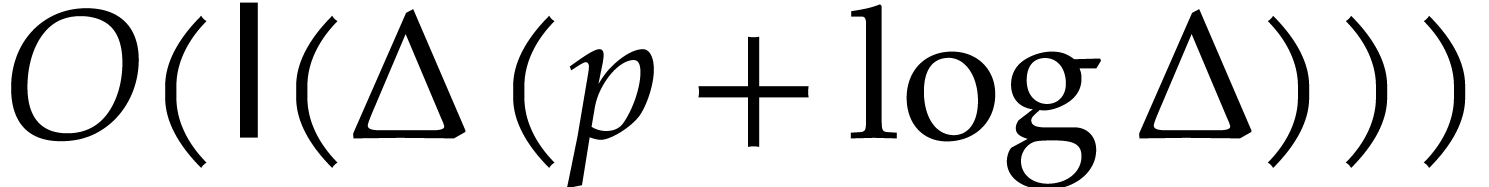 .
For
.
For 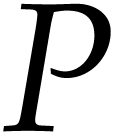 we take the unique polynomial of
we take the unique polynomial of 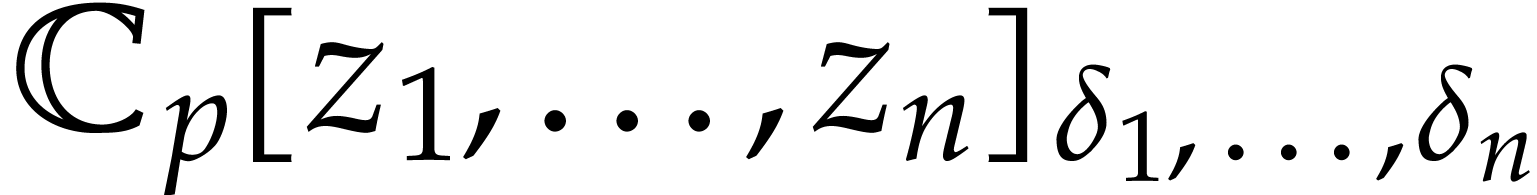 such that
such that
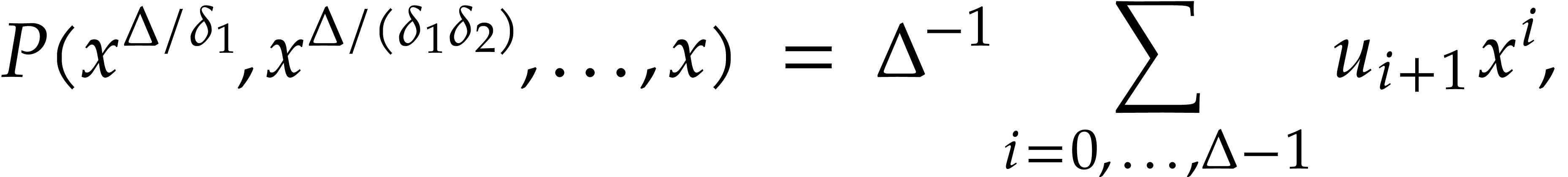
so we have 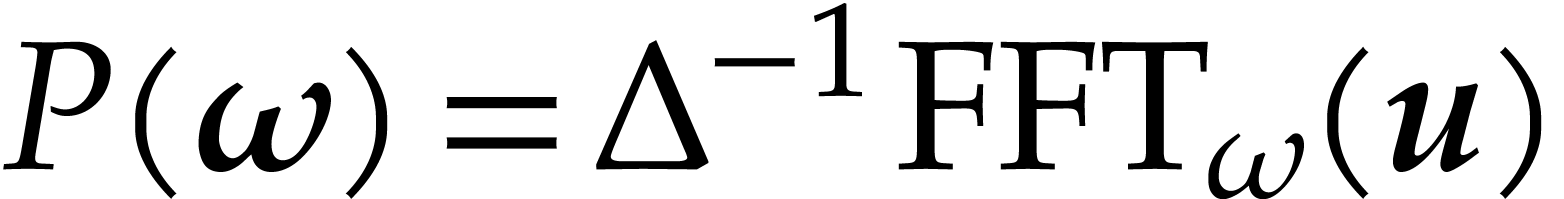 . Finally
. Finally
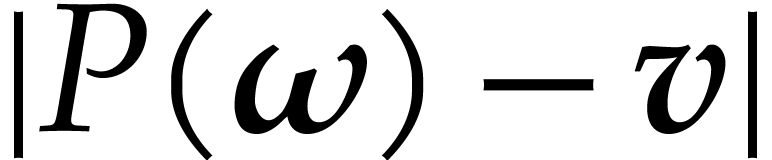 |
 |
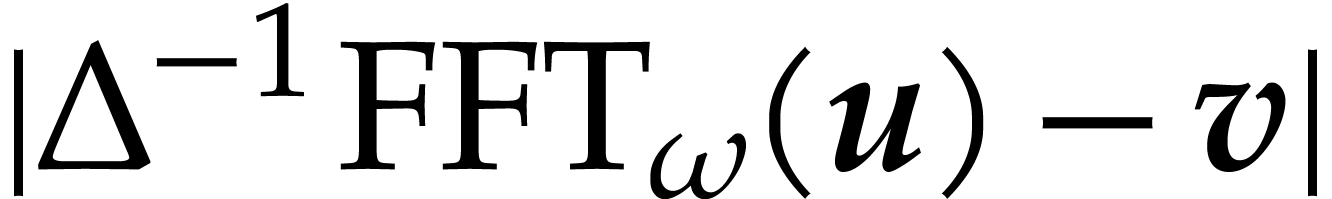 |
|
 |
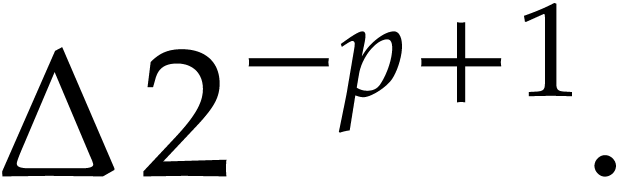 |
 |
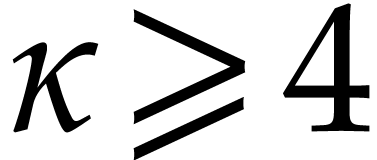 ,
, 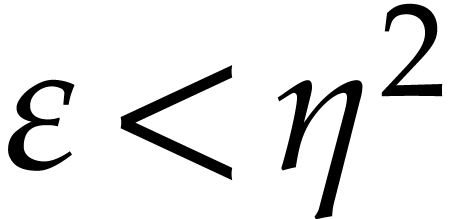 , and
, and 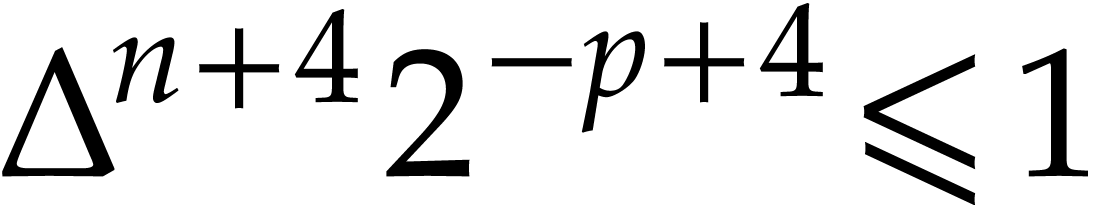 .
Given an evaluation tree for
.
Given an evaluation tree for 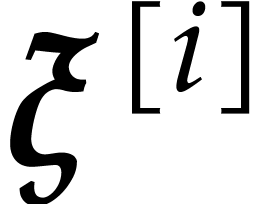 with error
with error 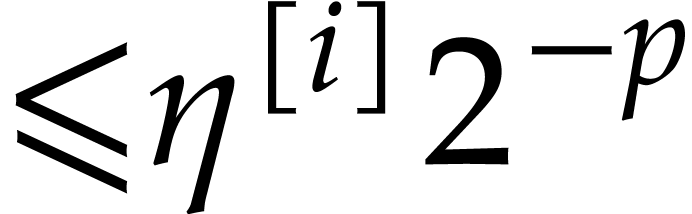 for
for 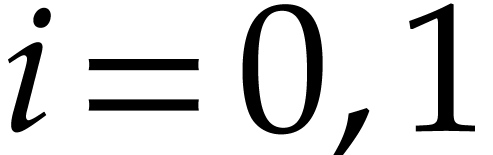 ,
and
,
and 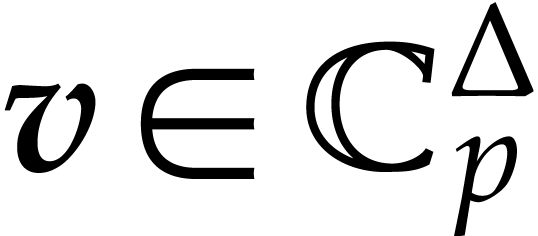 , we can compute
, we can compute 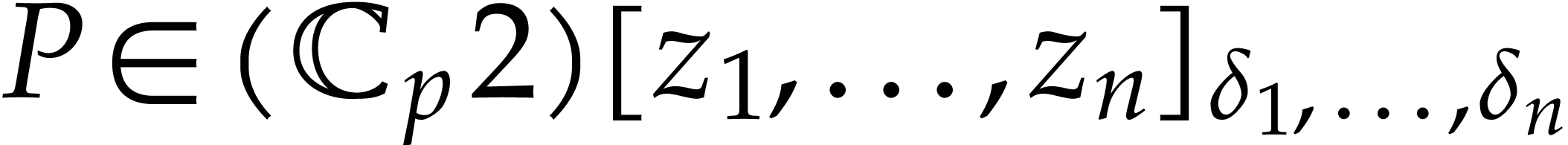 such that
such that

in time 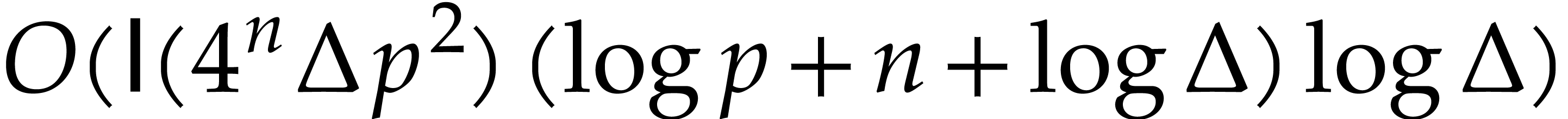 .
.
Proof. Let  .
By induction, we construct sequences
.
By induction, we construct sequences 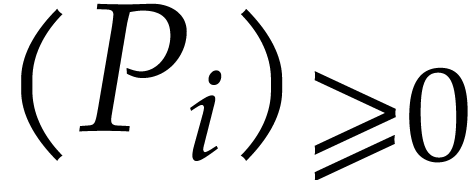 and
and 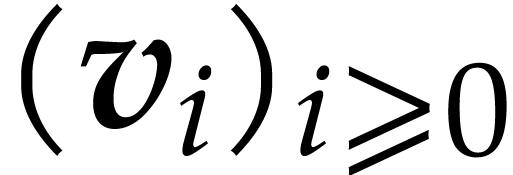 such that
such that 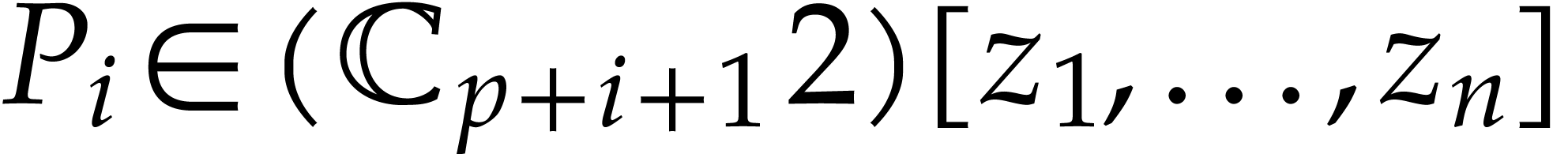 and
and  . We set
. We set 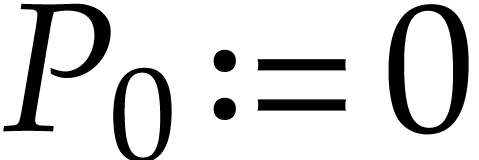 and
and 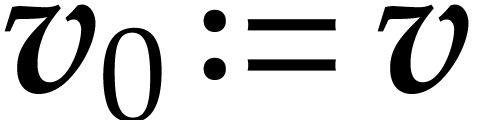 . For
. For 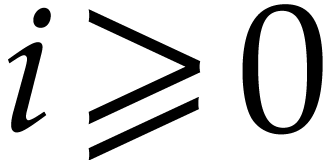 ,
we first compute
,
we first compute 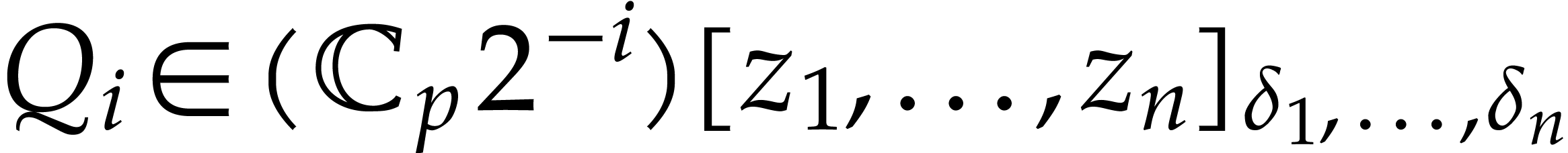 as the polynomial interpolated
from
as the polynomial interpolated
from 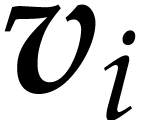 by inverse FFT as in Lemma 20,
so we have
by inverse FFT as in Lemma 20,
so we have 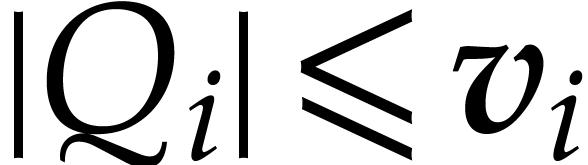 and
and 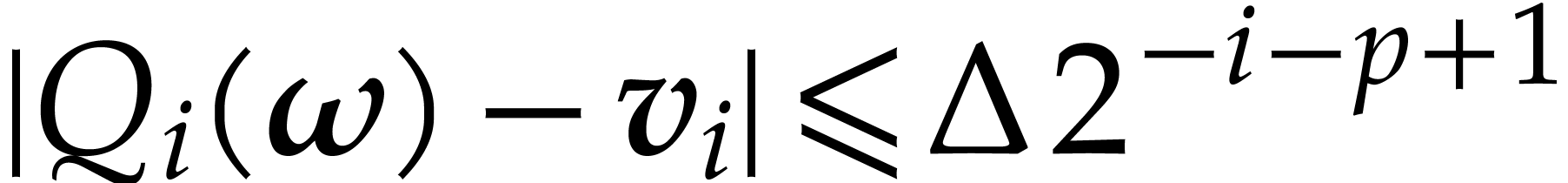 .
Using Algorithm 3, we then compute an approximation
.
Using Algorithm 3, we then compute an approximation 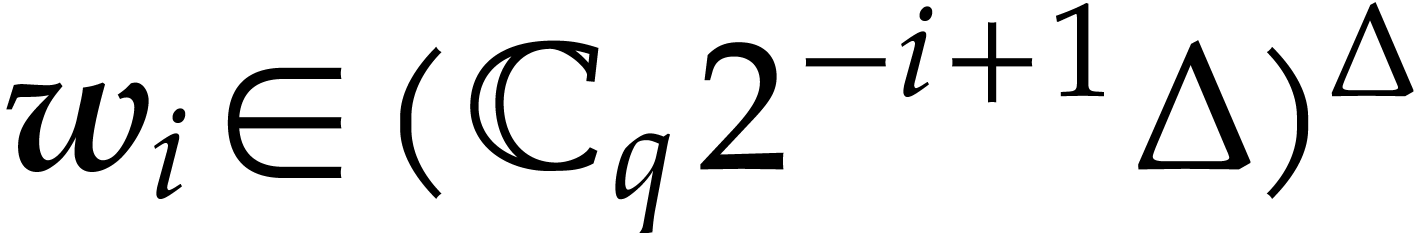 of
of 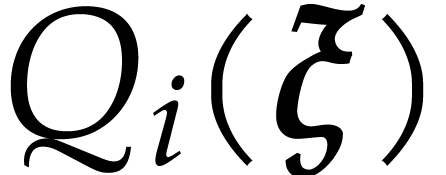 with error
with error
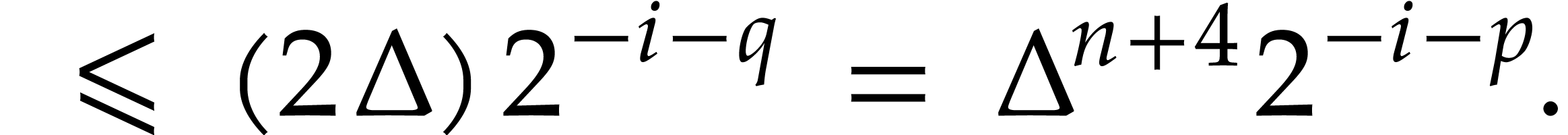
Using Lemma 3, we next compute a truncation  of
of  with error
with error 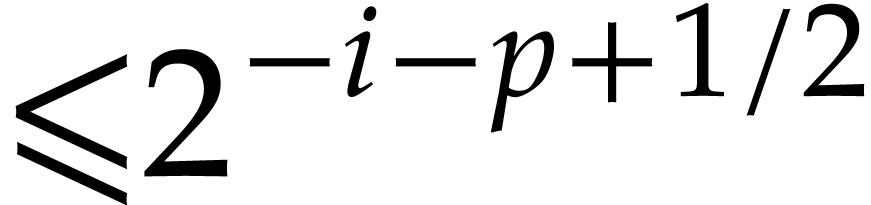 . Then
. Then
Using Lemmas 11 and 12, we obtain
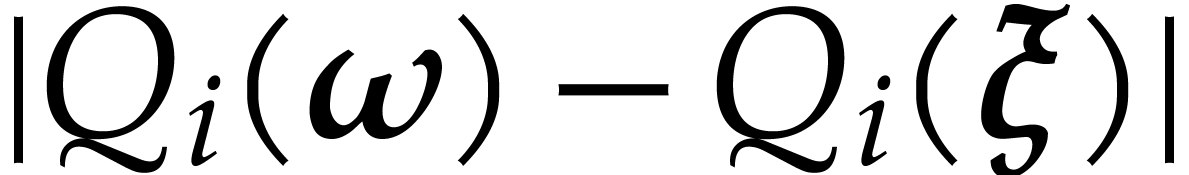 |
 |
 |
|
 |
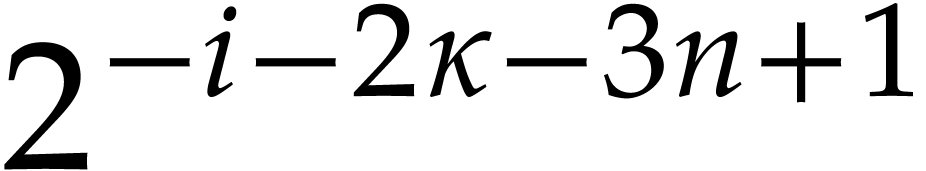 |
(using |
|
 |
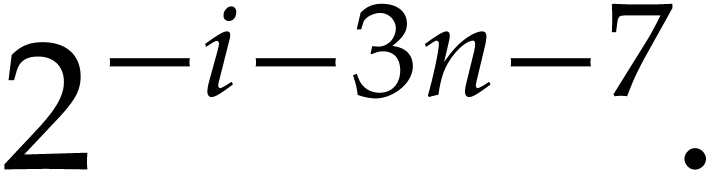 |
It follows that
so the sequence 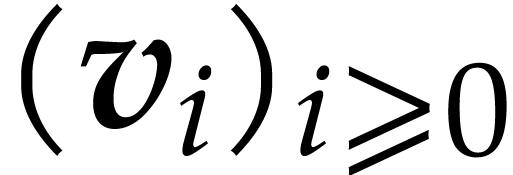 converges to
converges to 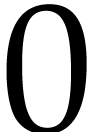 . We define
. We define  and verify
that
and verify
that
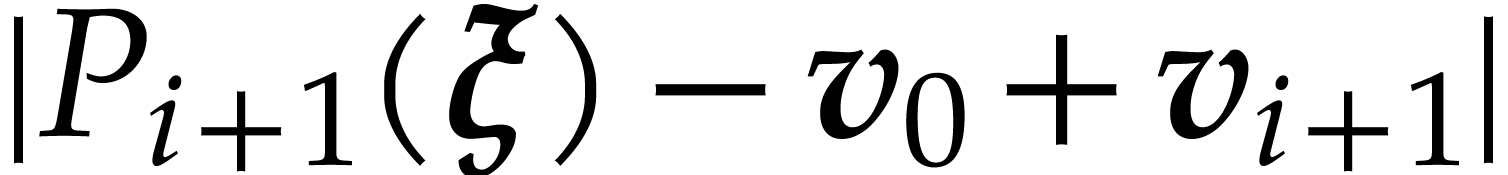 |
 |
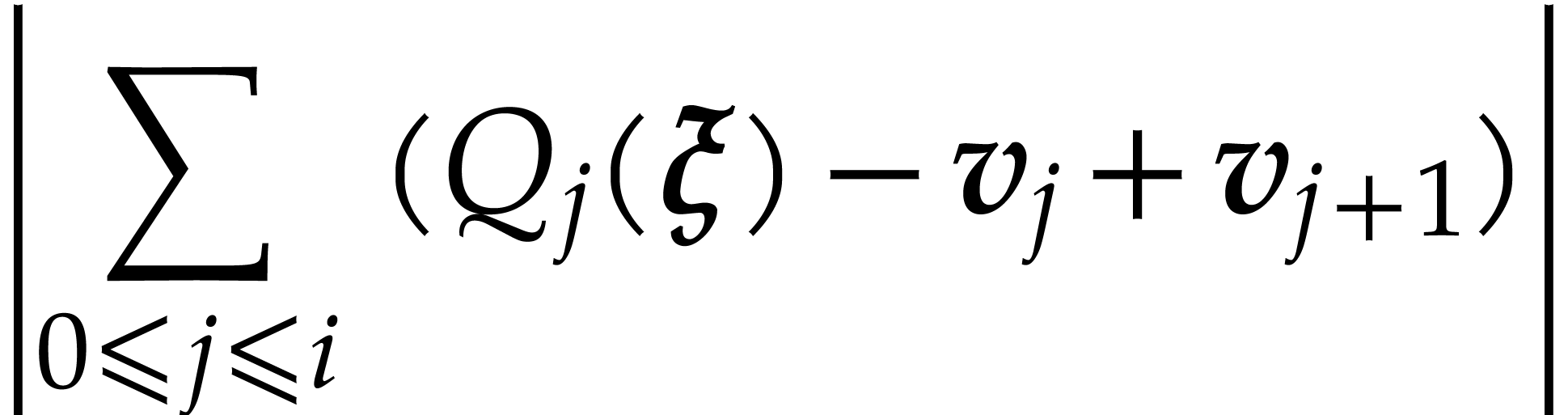 |
|
 |
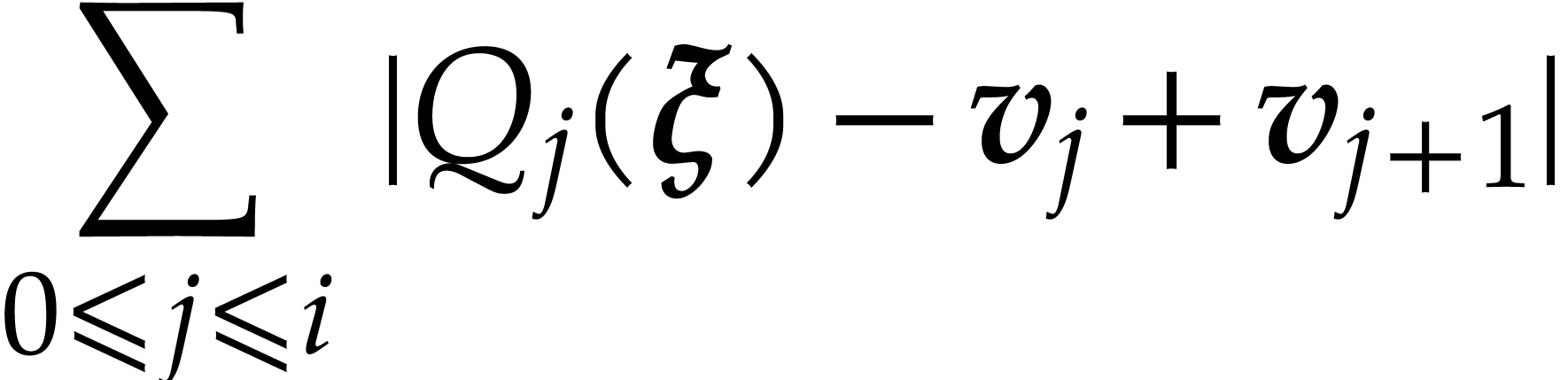 |
||
 |
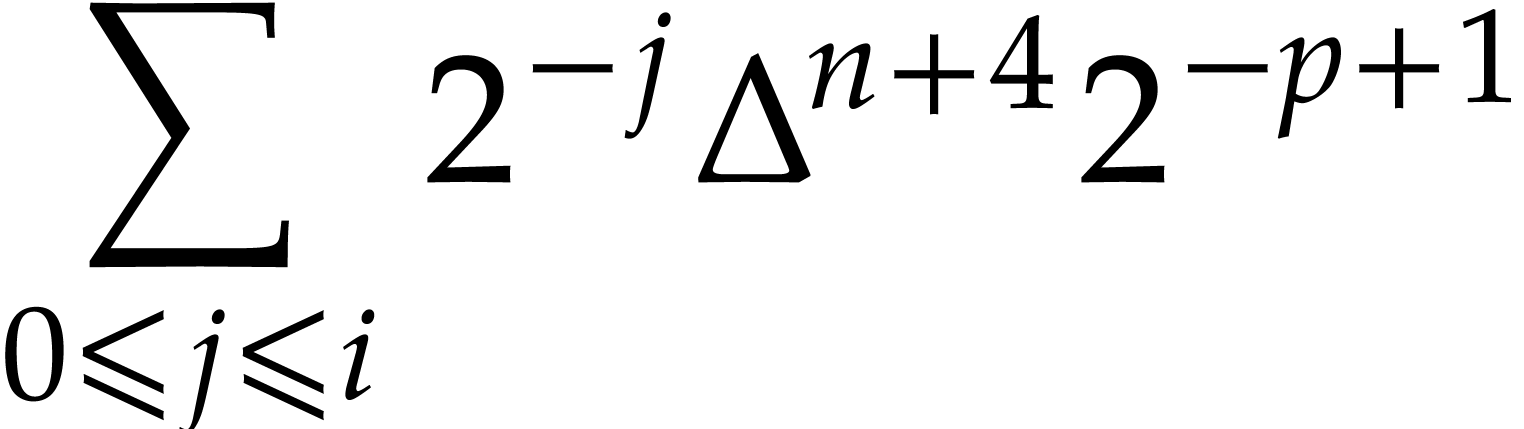 |
(using |
|
 |
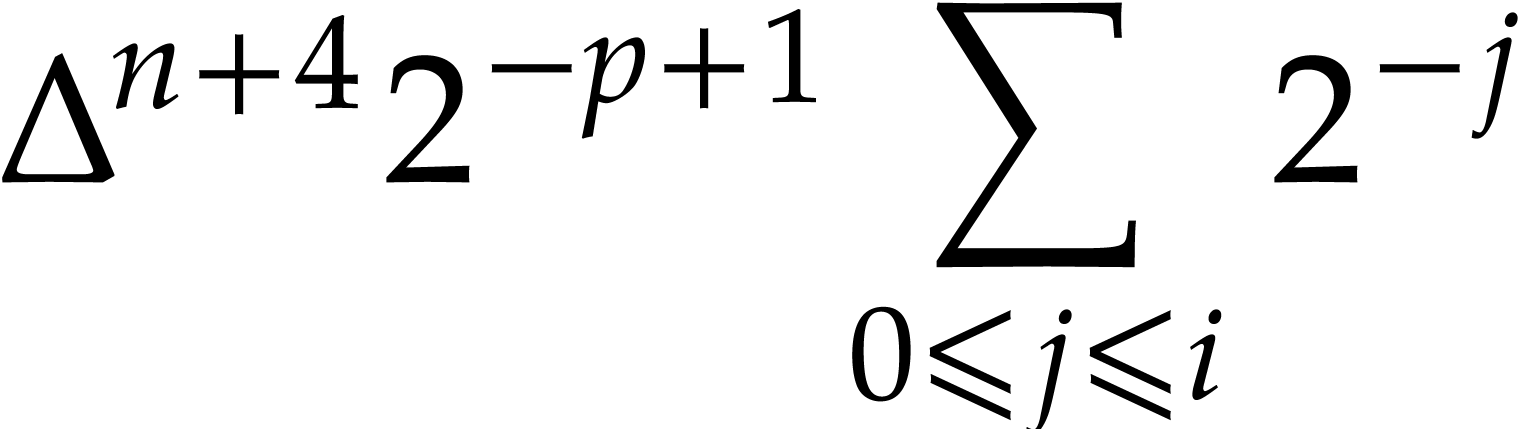 |
||
 |
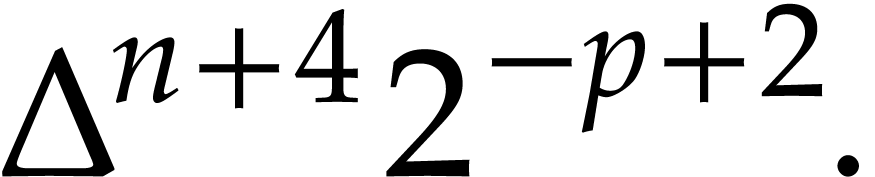 |
On the other hand, we have 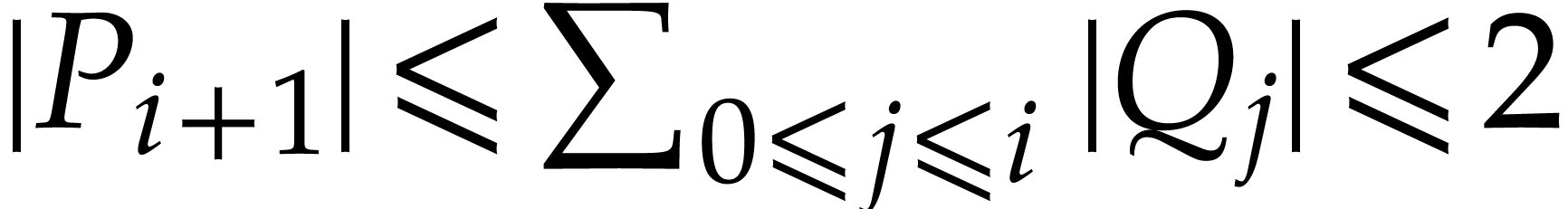 .
We take
.
We take  minimal such that
minimal such that
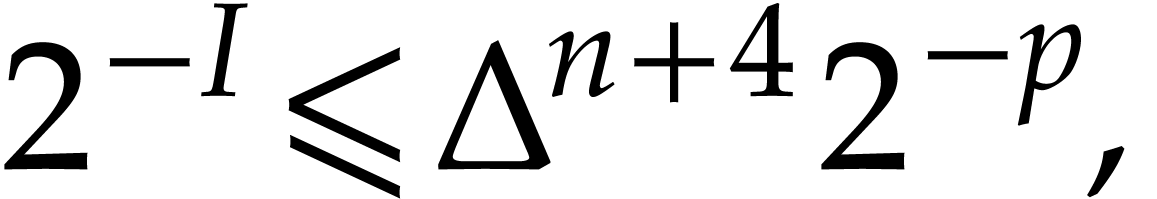
so we have  . Let
. Let 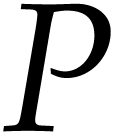 be a truncation of
be a truncation of 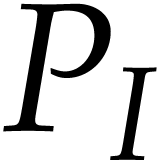 with error
with error
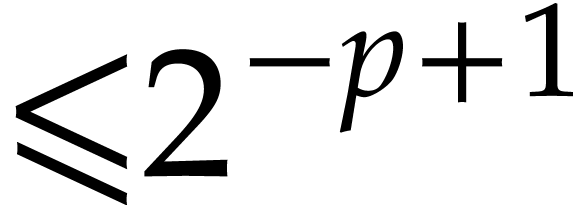 . Then
. Then
Finally, Lemma 20 asserts that each 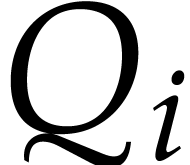 can be computed in time
can be computed in time 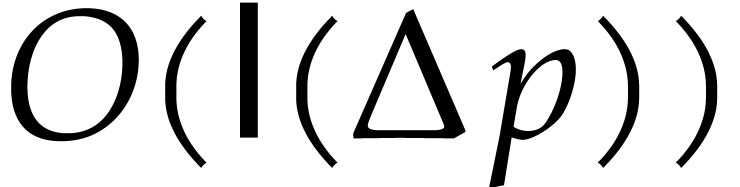 . By
Proposition 19, each
. By
Proposition 19, each 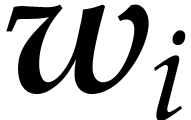 is obtained in
time
is obtained in
time  .
.
The next faster algorithm exploits the usual “divide and
conquer” paradigm for large precisions 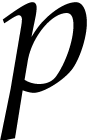 .
.
Algorithm
If  then compute
then compute 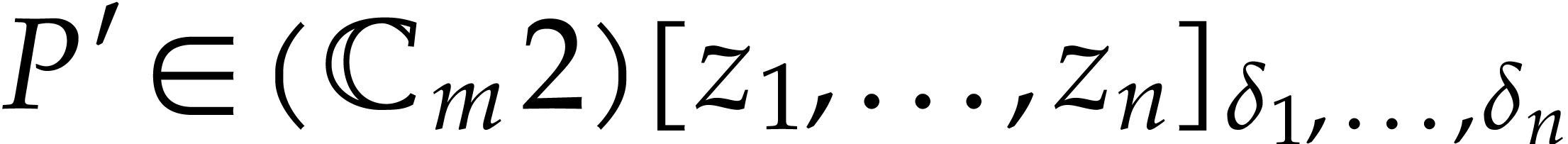 such that
such that  via Lemma 21.
Return an approximation
via Lemma 21.
Return an approximation 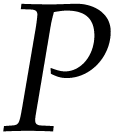 of
of 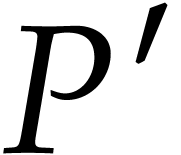 in
in  with error
with error 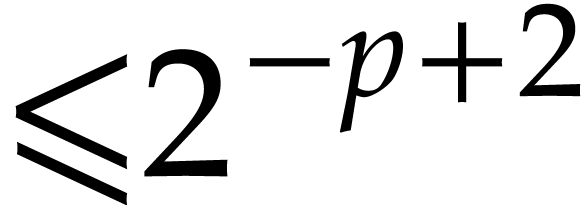 , by using Lemma 2.
, by using Lemma 2.
Let 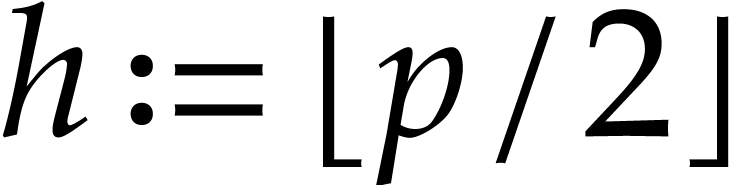 and
and 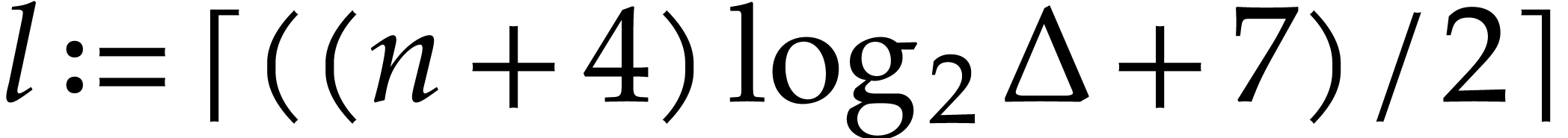 and let
and let
 be a truncation of
be a truncation of  in
in 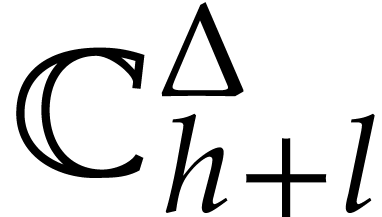 with error
with error 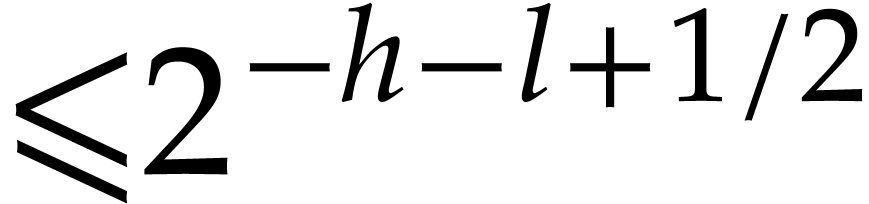 . Apply Algorithm 4 recursively
to
. Apply Algorithm 4 recursively
to 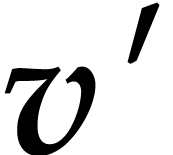 and let
and let 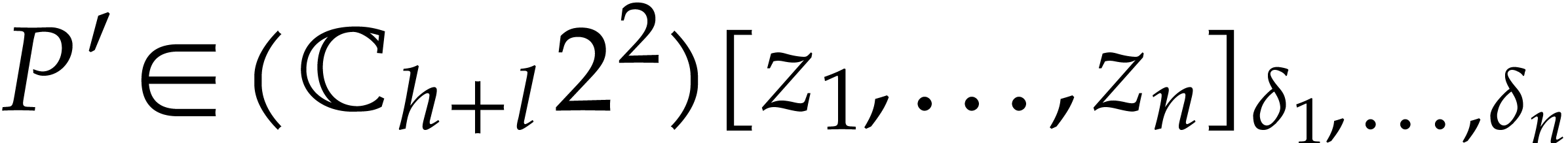 denote the output.
denote the output.
Compute an approximation 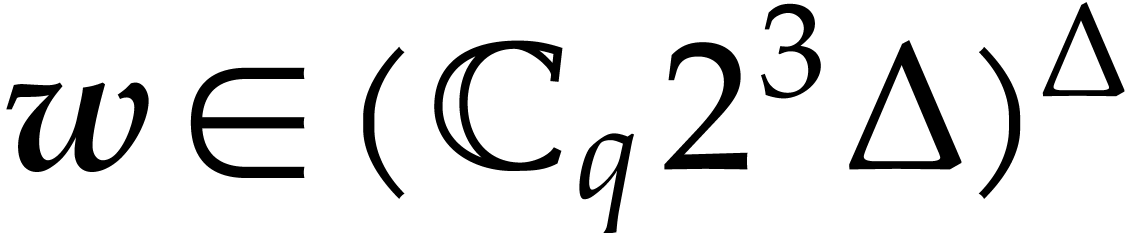 of
of 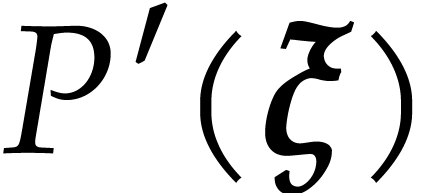 with error
with error  ,
by applying Algorithm 3 to
,
by applying Algorithm 3 to 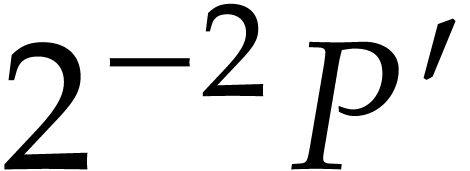 , where
, where 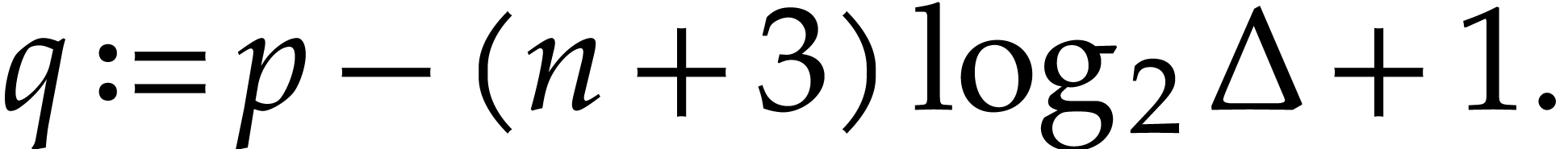
Let 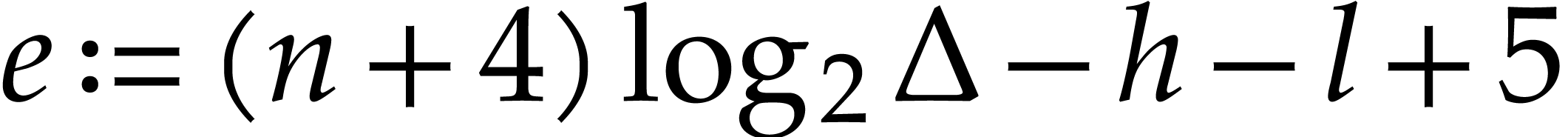 and compute a truncation
and compute a truncation 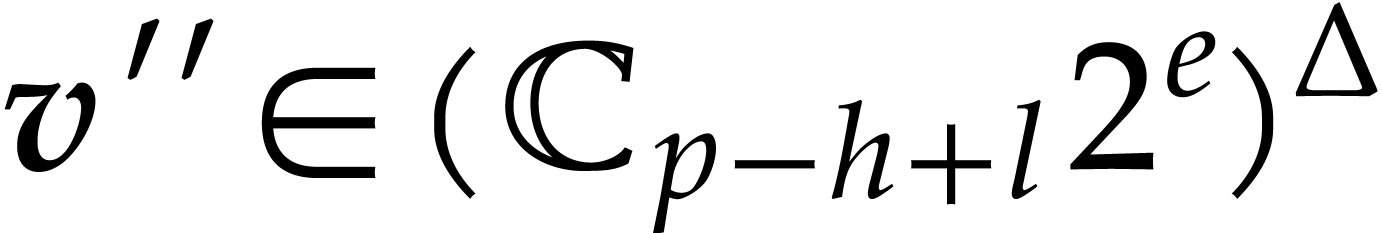 of
of  with error
with error 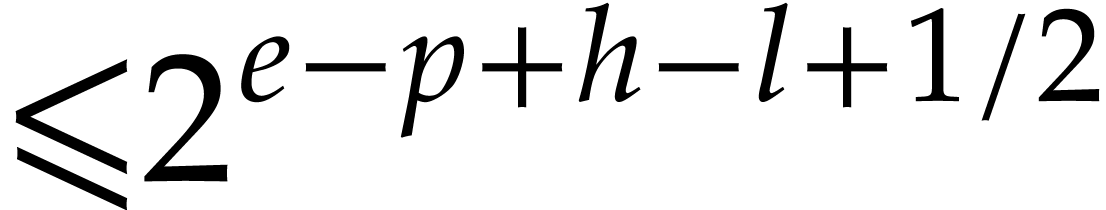 . Apply Algorithm 4
recursively to
. Apply Algorithm 4
recursively to 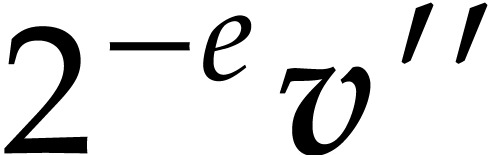 and let
and let 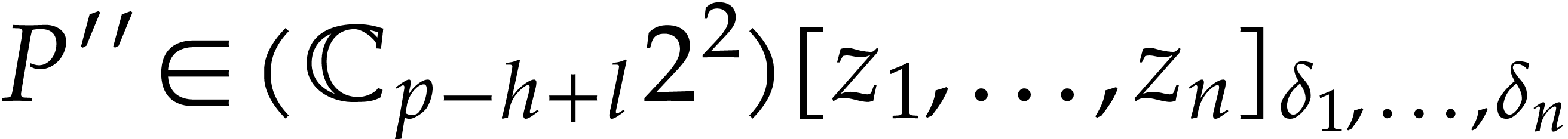 denote the output.
denote the output.
Return an approximation of 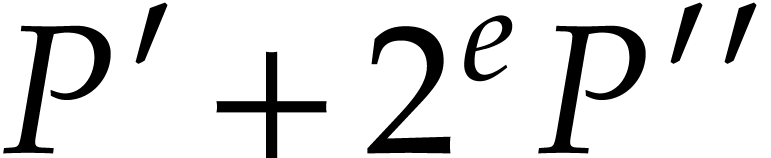 with error
with error
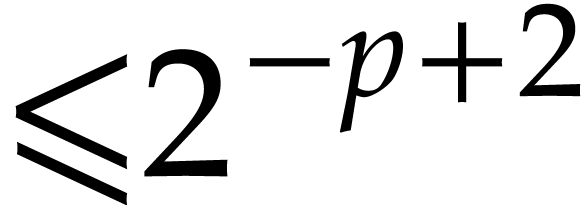 .
.
Proof. If 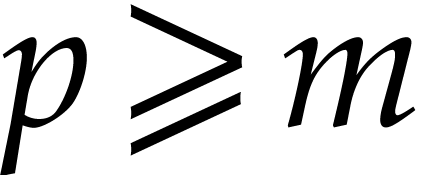 ,
then
,
then 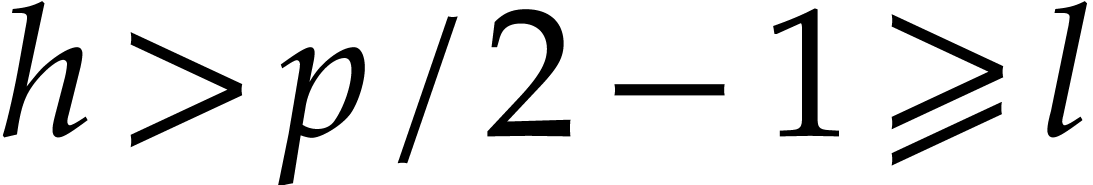 , whence
, whence 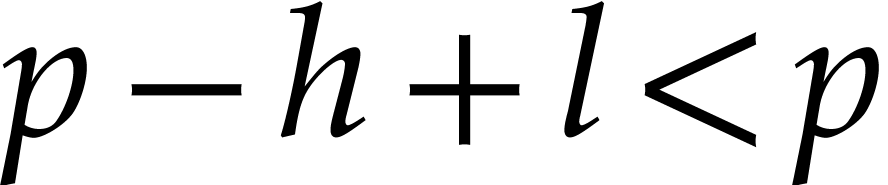 , which implies the termination of the
algorithm. In step 1 we obtain
, which implies the termination of the
algorithm. In step 1 we obtain
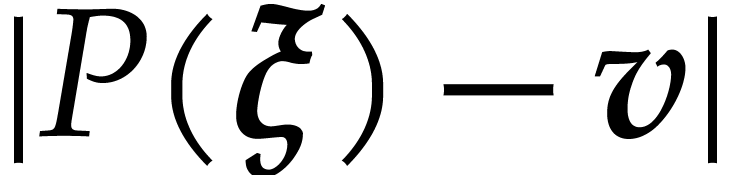 |
 |
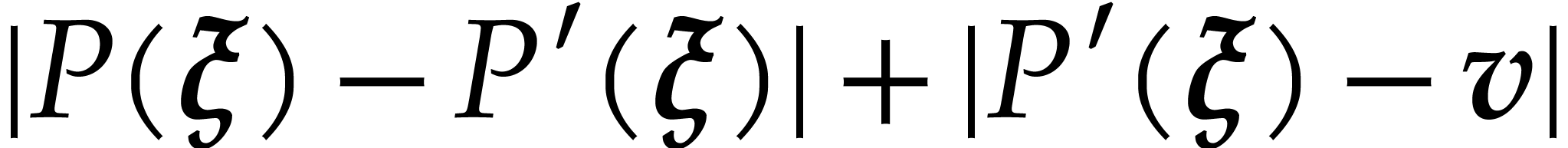 |
|
 |
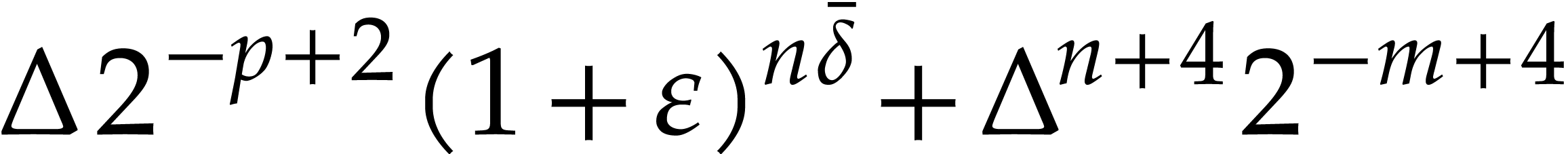 |
||
 |
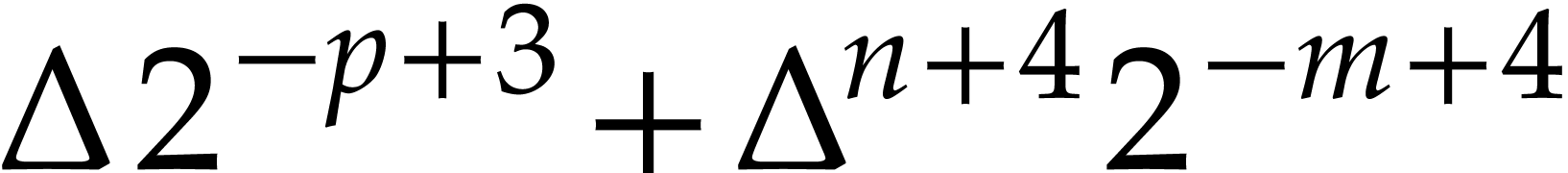 |
(using |
|
 |
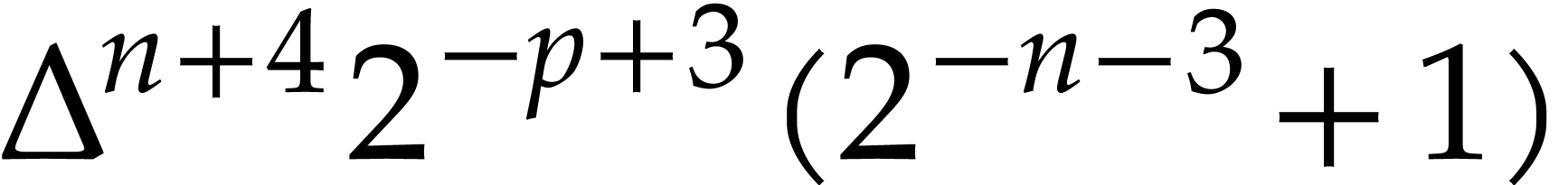 |
(since 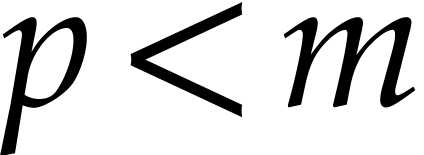 and and 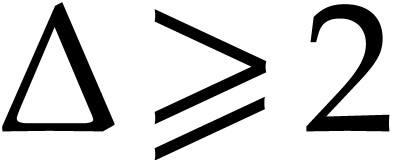 ) ) |
|
 |
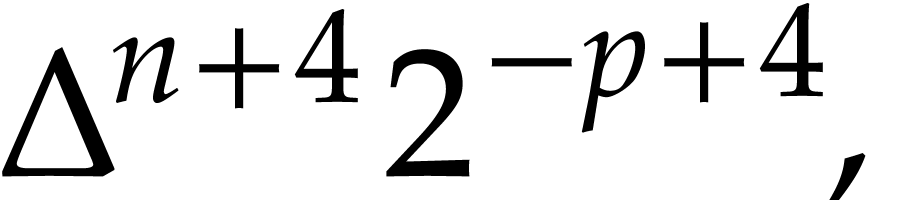 |
so the output is correct when the algorithm exits at step 1. After step 3 we have
In step 4, we note that
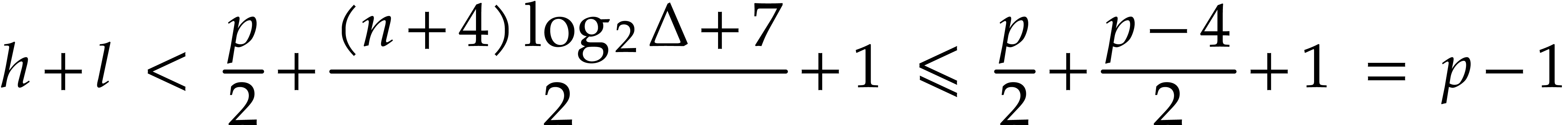 |
(16) |
and deduce
Therefore, the recursive call in step 4 is valid and gives
 |
(17) |
Combining
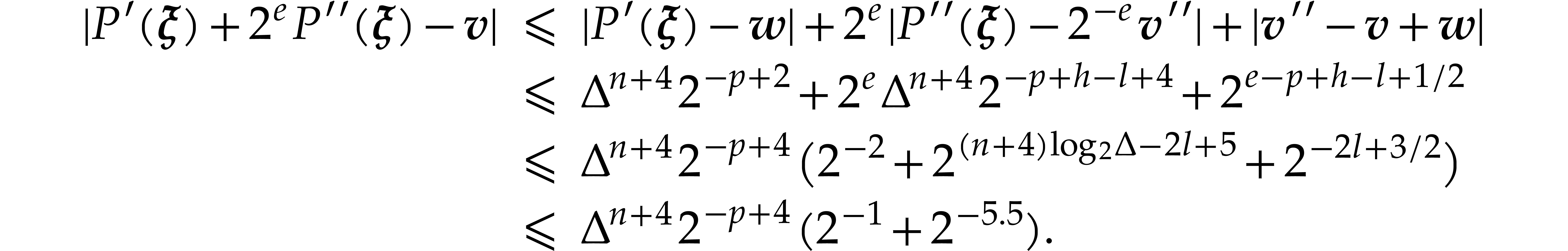
Consequently,
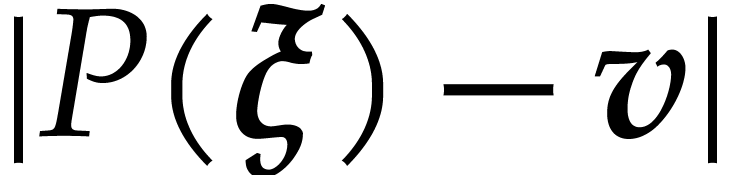 |
 |
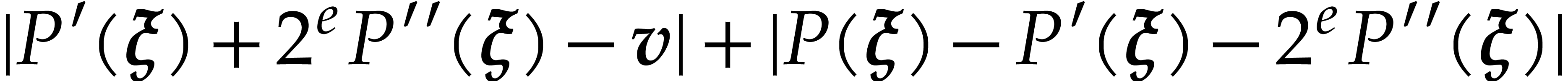 |
|
 |
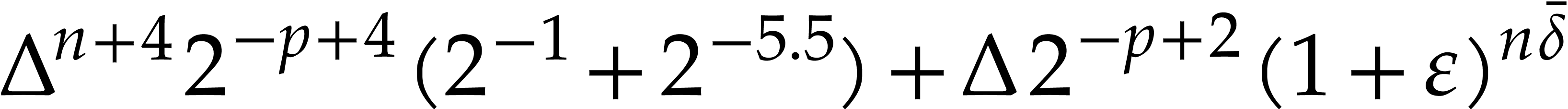 |
||
 |
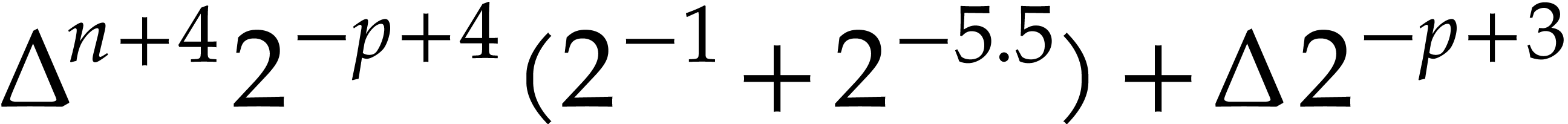 |
(using |
|
 |
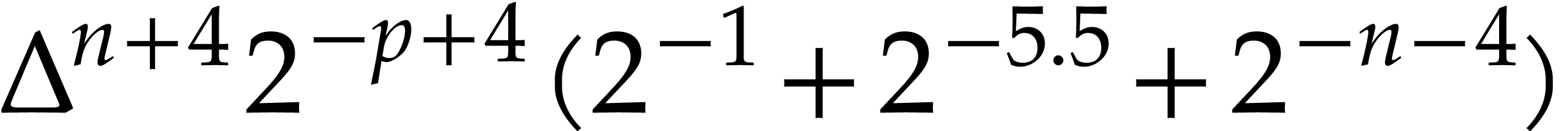 |
(since 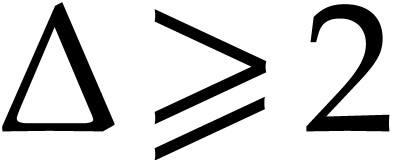 ) ) |
|
 |
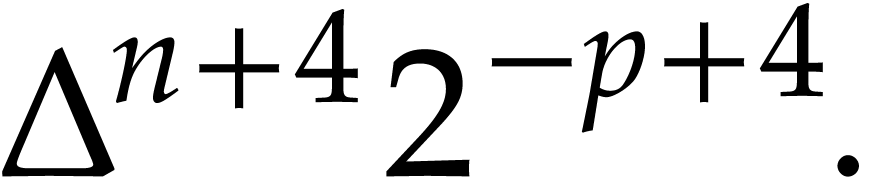 |
Step 1 takes time
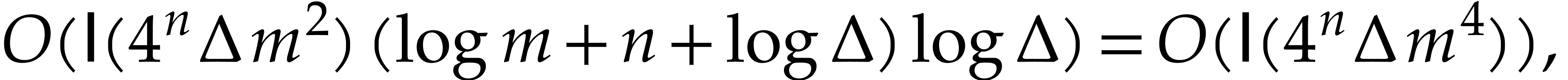
by Lemma 21. Steps 3 runs in time
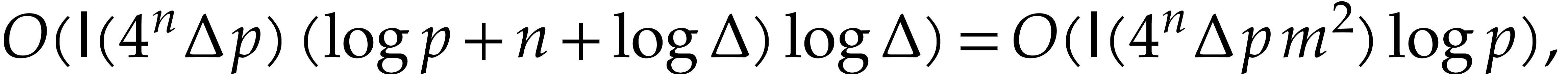
by Proposition 19. When 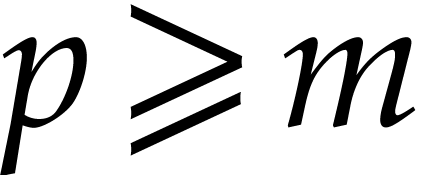 ,
the complexity
,
the complexity 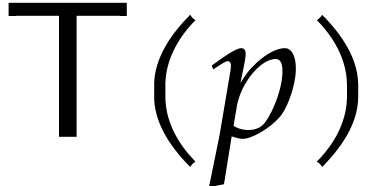 of our algorithm therefore
satisfies
of our algorithm therefore
satisfies
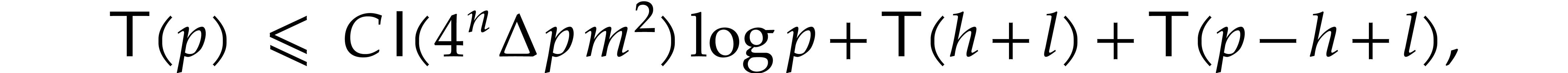
for some universal constant 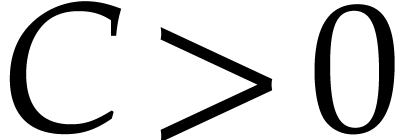 .
Unrolling this inequality, we obtain
.
Unrolling this inequality, we obtain
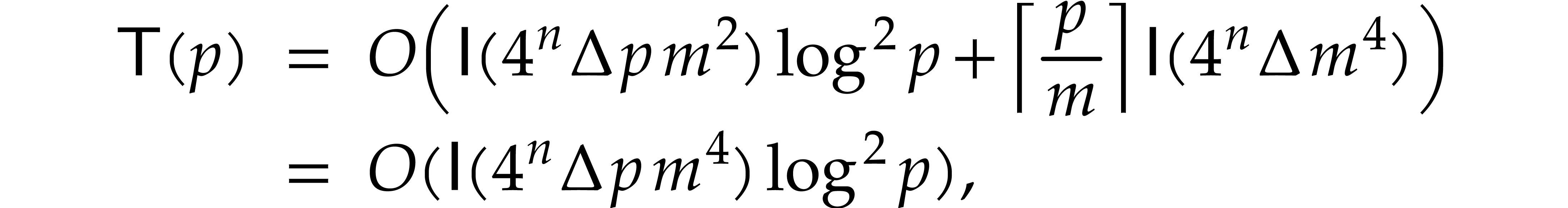
which concludes the proof.
The evaluation tree for  is obtained by
induction: we recursively compute evaluation trees for
is obtained by
induction: we recursively compute evaluation trees for 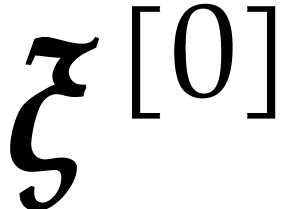 and
and  , and deduce the one for
, and deduce the one for
 as follows.
as follows.
Algorithm
If 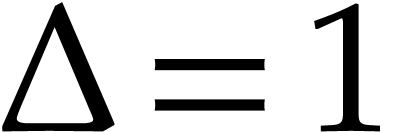 then return
then return  and an approximation
and an approximation 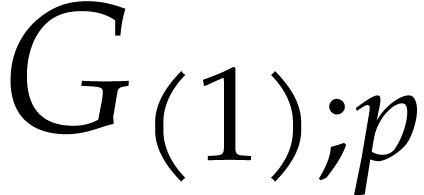 of
of  with error
with error 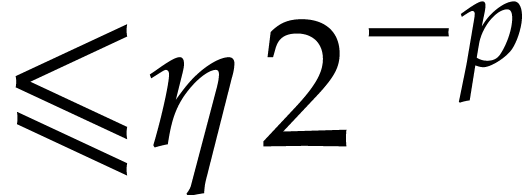 .
.
Let 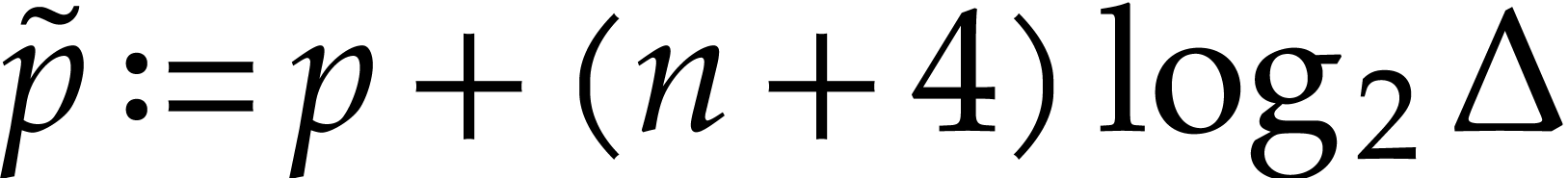 . For
. For 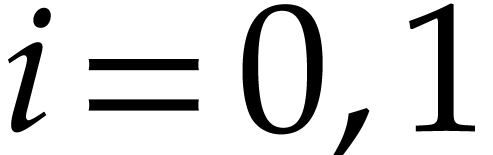 , let
, let 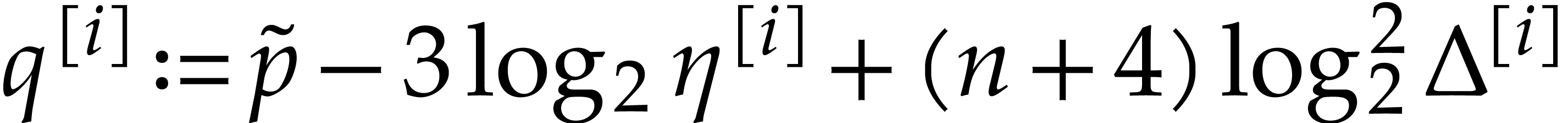 and compute
and compute 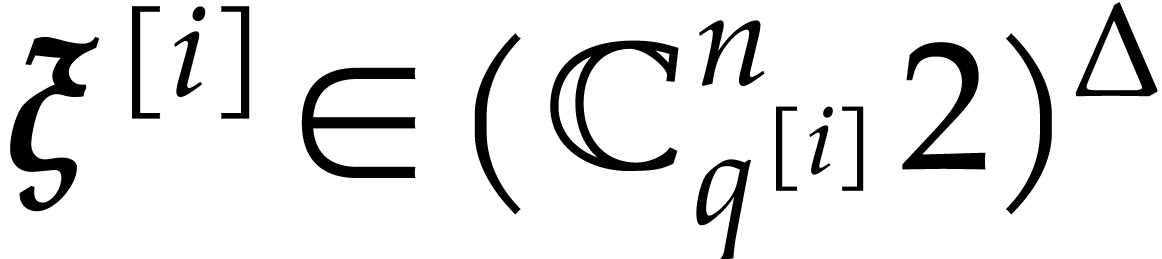 with error
with error 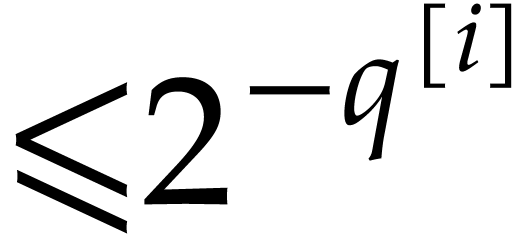 . Recursively compute the evaluation
trees
. Recursively compute the evaluation
trees 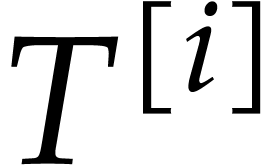 for
for 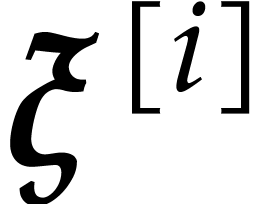 with
error
with
error  .
.
For each 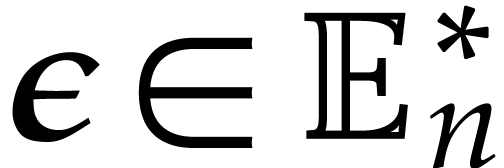 do:
do:
Compute an approximation  of
of 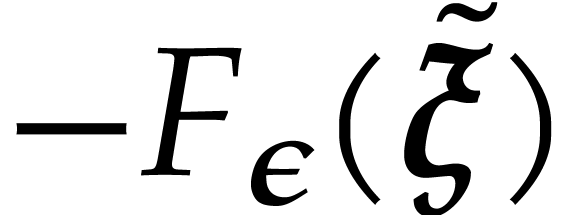 with error
with error 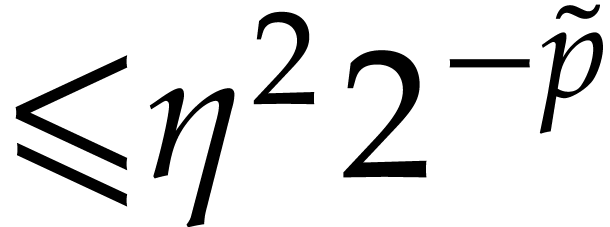 .
.
Apply Algorithm 4 to 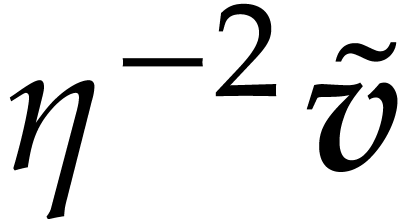 ,
, 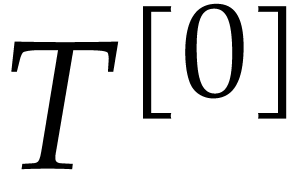 ,
,
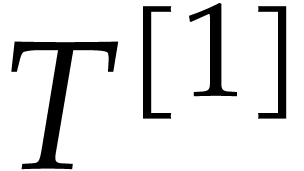 ; let
; let  be the returned polynomial, such that
be the returned polynomial, such that 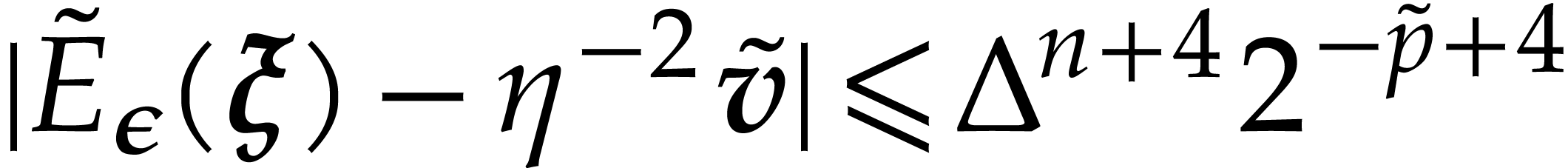 .
.
Compute an approximation 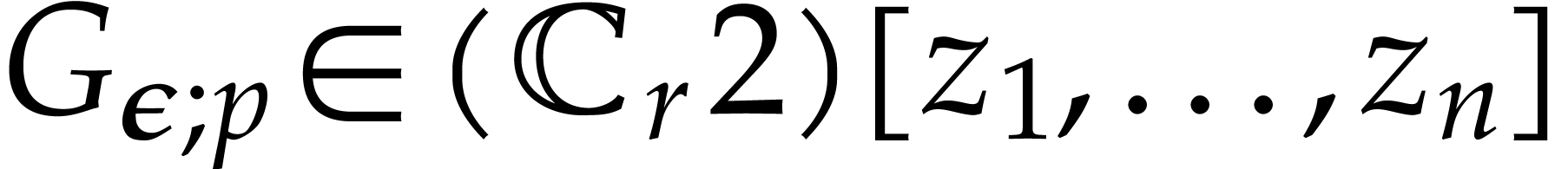 of
of 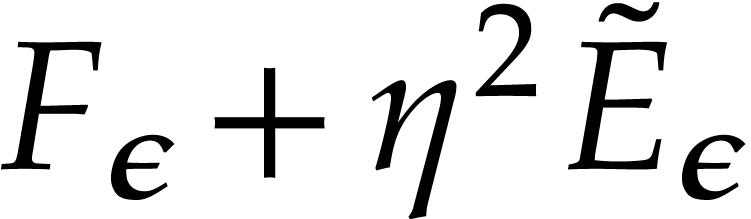 with error
with error 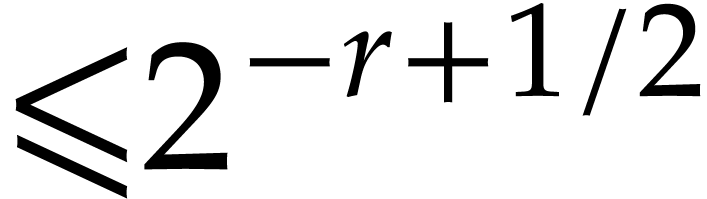 ,
where
,
where 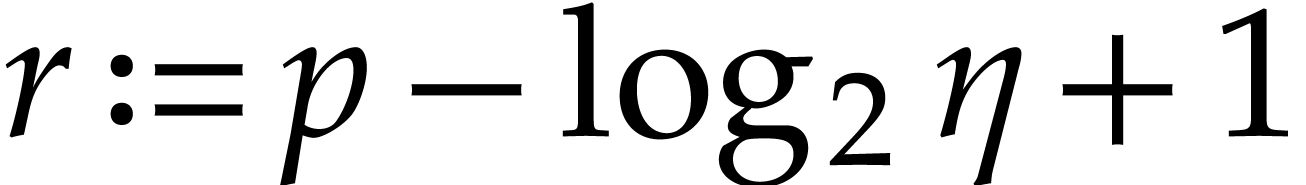 .
.
Set 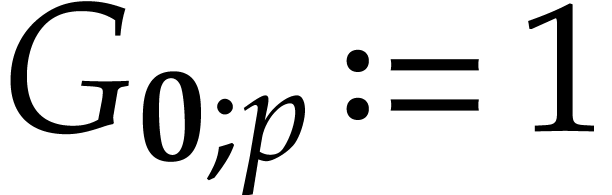 and return
and return 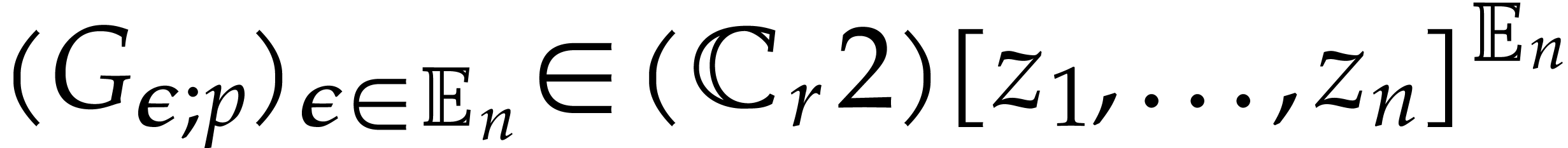 , and approximations of
, and approximations of 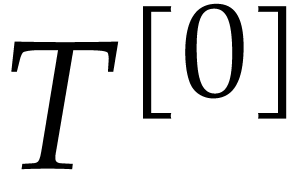 ,
, 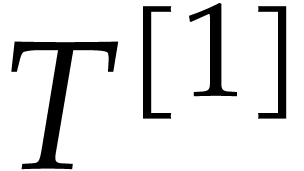 with errors
with errors
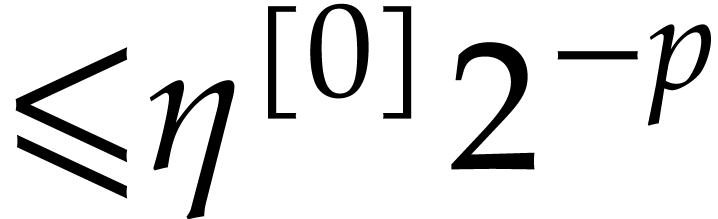 and
and 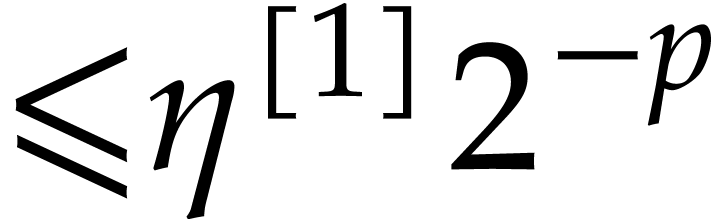 .
.
Proof. If the algorithm exits in step 1, then we
have 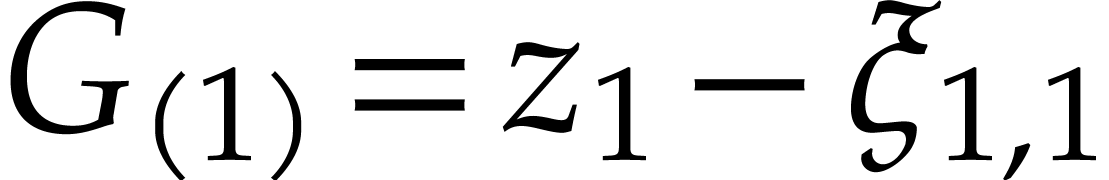 , so the output is
correct. Now, let us assume that
, so the output is
correct. Now, let us assume that  and note that
and note that
and
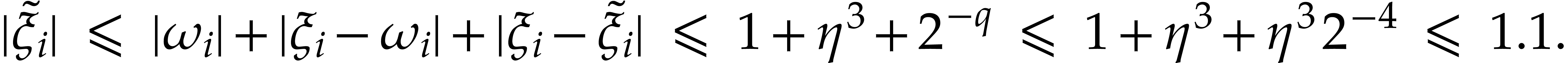 |
(19) |
For  , we compute
, we compute 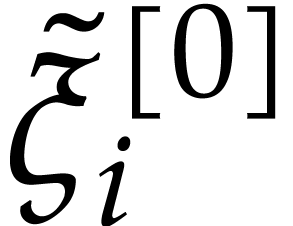 as the truncation of
as the truncation of 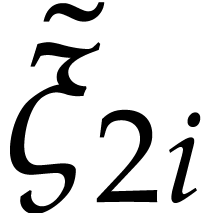 with error
with error
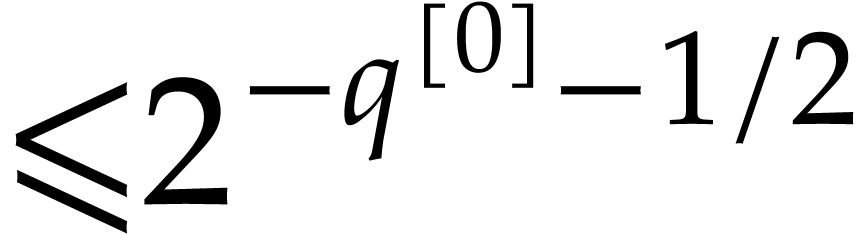 using Lemma 2. Hence,
using Lemma 2. Hence,
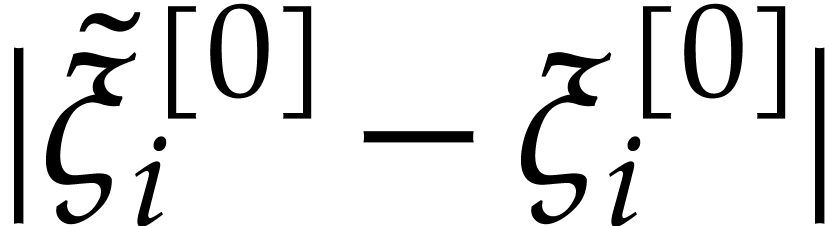 |
 |
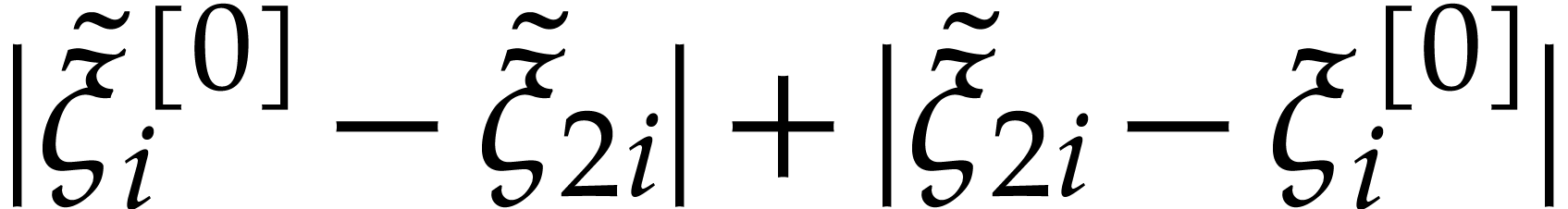 |
|
 |
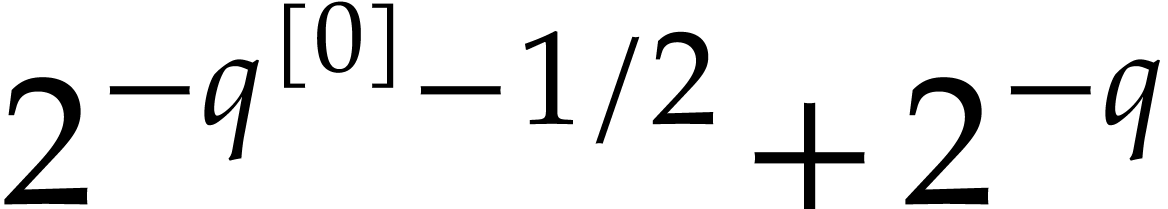 |
||
 |
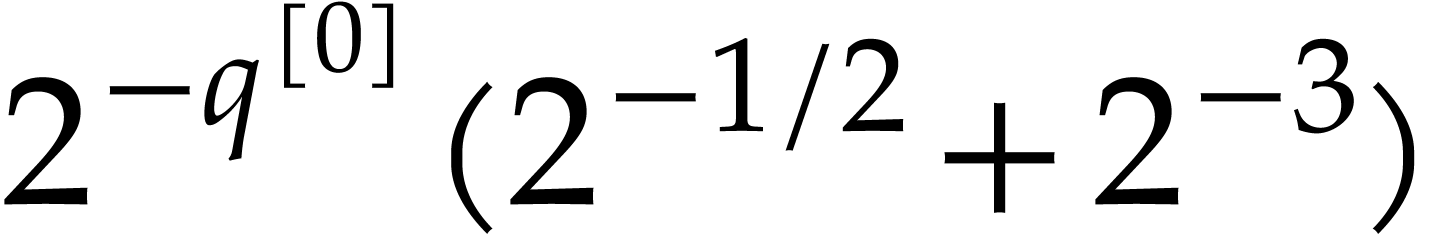 |
(using |
|
 |
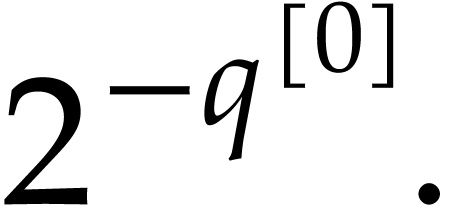 |
From Lemma 4, we may compute a truncation  of
of 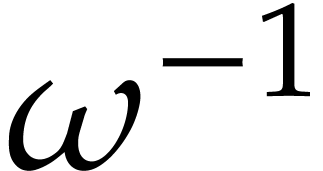 with error
with error  in time
in time
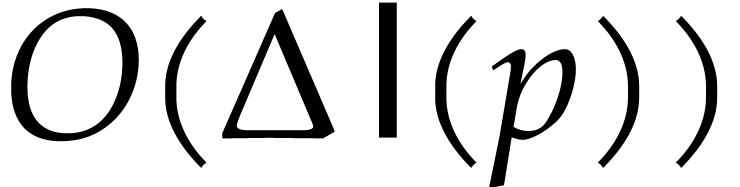 , provided that
, provided that  . We compute an approximation
. We compute an approximation 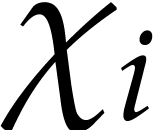 of
of  with error
with error 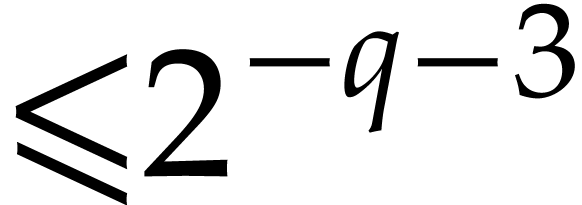 .
It follows that
.
It follows that
Using Lemma 2, we obtain 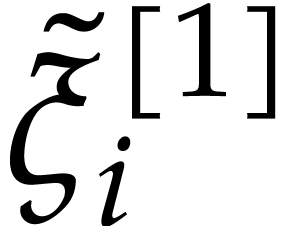 as the
truncation of
as the
truncation of 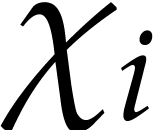 with error
with error 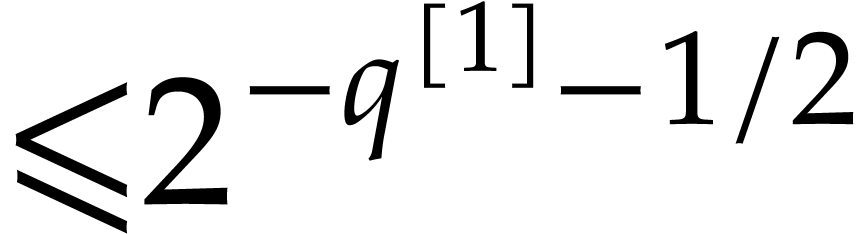 . Hence,
. Hence,
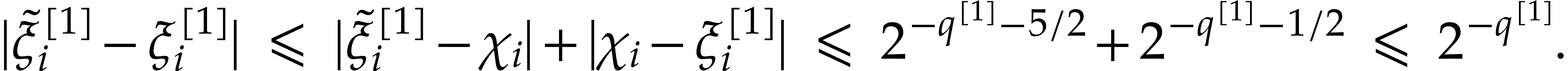
For step 3.a, we need to verify that
so the use of Algorithm 4 is valid in step 3.b. Thanks to
Proposition 22 and using that 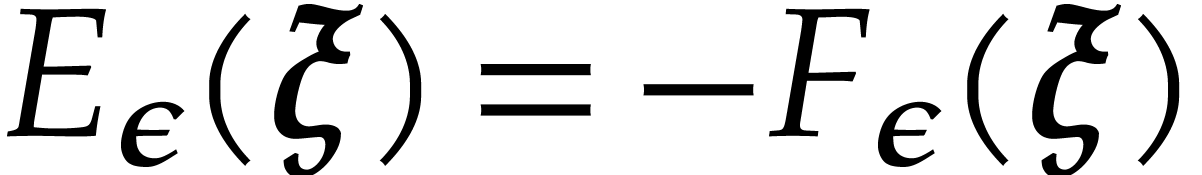 ,
we obtain
,
we obtain
Lemma 13 yields  .
It follows that
.
It follows that
This concludes the correctness proof. As for the complexity we note that
 whenever
whenever  .
In step 3,
.
In step 3, 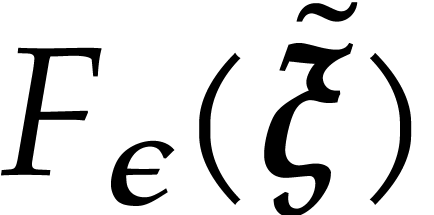 can be computed in time
can be computed in time 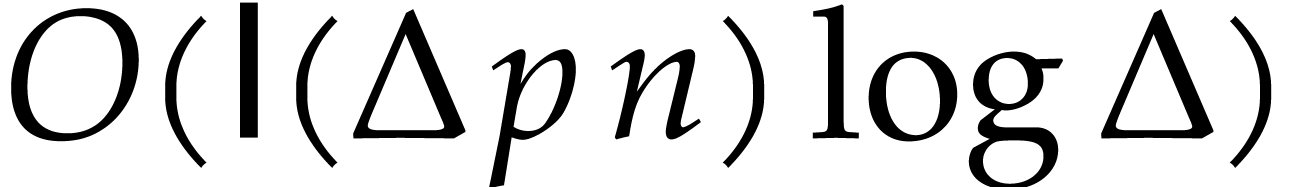 , using binary powering. In step 3.b, the
interpolation of
, using binary powering. In step 3.b, the
interpolation of 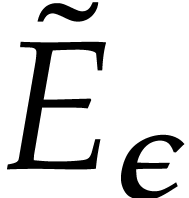 takes
takes
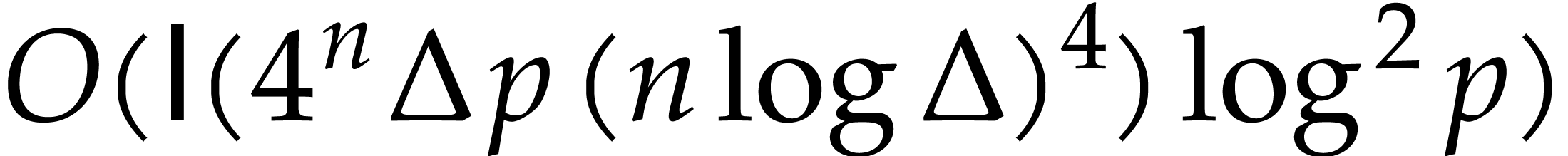
operations, by Proposition 22. Overall the complexity 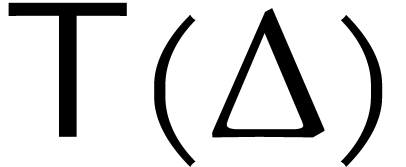 of our algorithm satisfies
of our algorithm satisfies
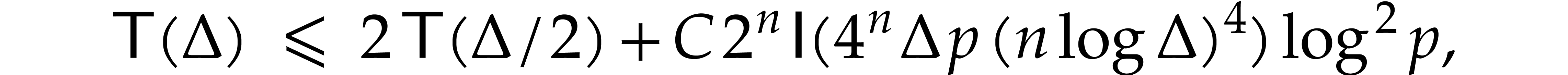
for some universal constant 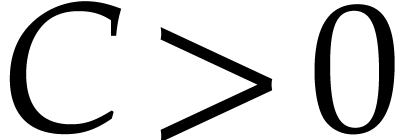 .
Unrolling this inequality yields the claimed complexity bound.
.
Unrolling this inequality yields the claimed complexity bound.
Consider 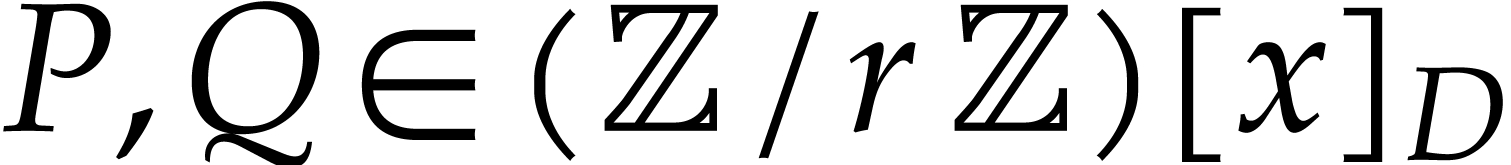 and
and 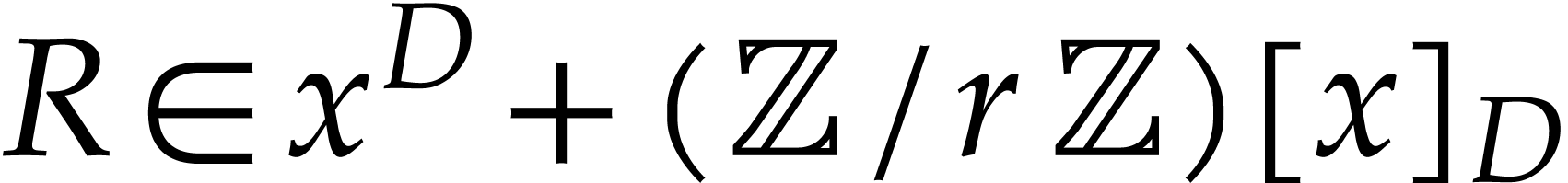 ,
where
,
where 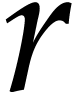 is a positive integer. Our goal is to
compute
is a positive integer. Our goal is to
compute 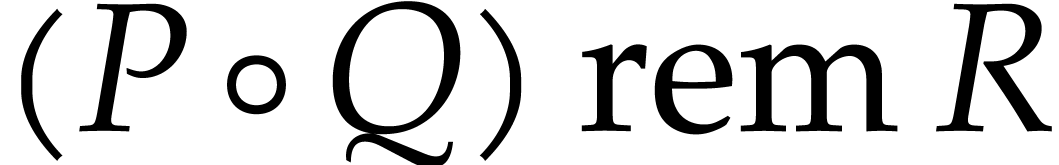 . We first follow
Kedlaya and Umans [14], by transforming the problem into a
multivariate one. For some
. We first follow
Kedlaya and Umans [14], by transforming the problem into a
multivariate one. For some 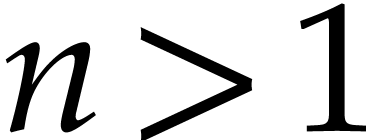 and powers of two
and powers of two
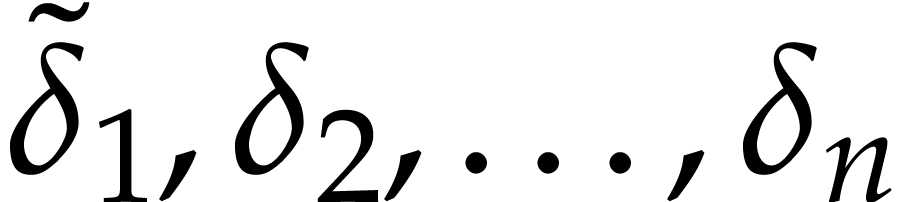 with
with  and
and 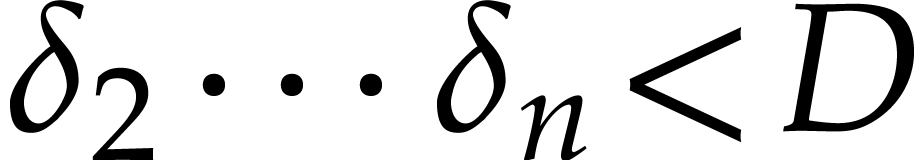 , there exists a unique lift
, there exists a unique lift

such that
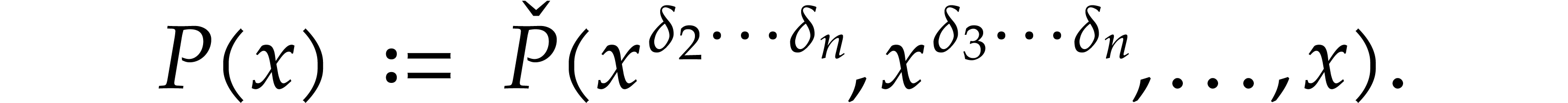
The first degree bound 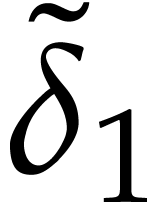 will be adjusted below to
a larger value
will be adjusted below to
a larger value  that will match the setting of
the previous section. We define
that will match the setting of
the previous section. We define

so we have
In order to compute the right-hand side of (20), we further
lift the problem into another one with integer coefficients: let 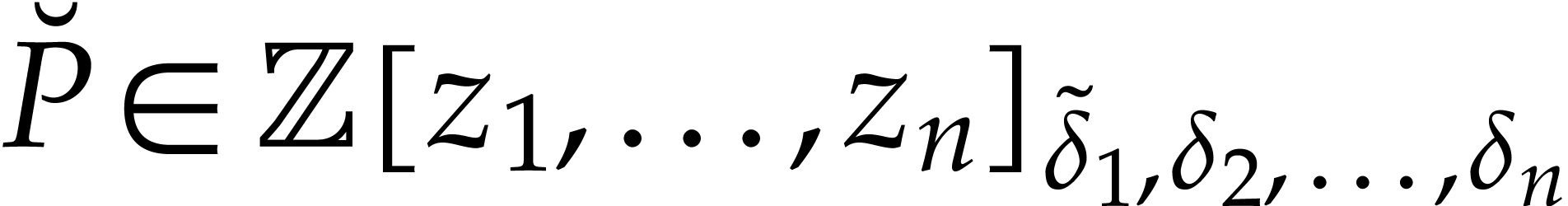 and
and 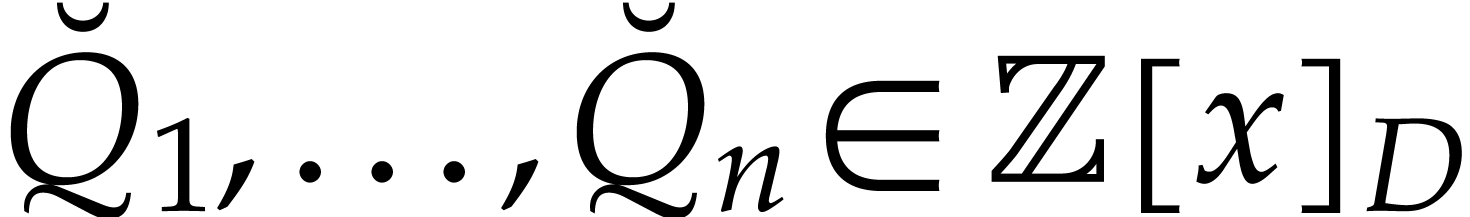 be the canonical lifts of
be the canonical lifts of
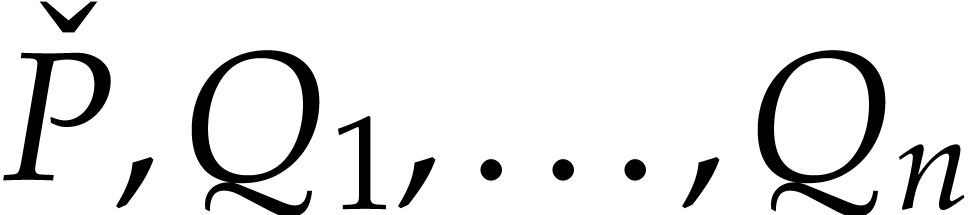 with coefficients in
with coefficients in  and
set
and
set
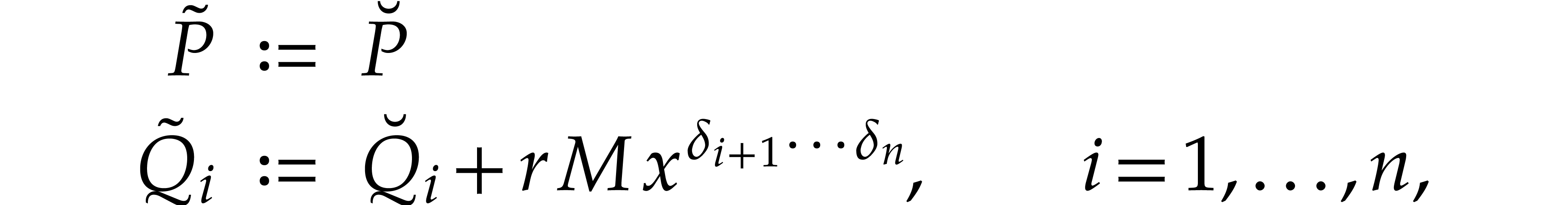
where 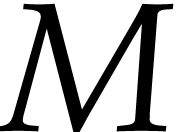 is a positive integer that will be
specified below. Note that
is a positive integer that will be
specified below. Note that 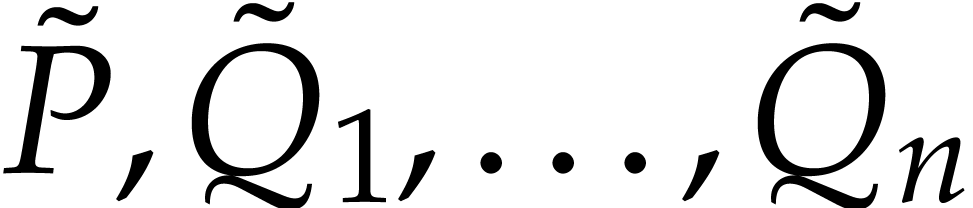 are still lifts of
are still lifts of
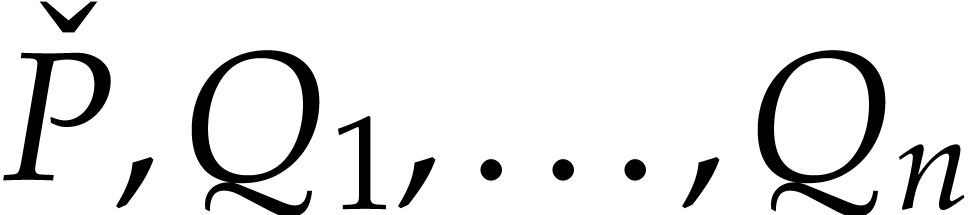 , so
, so
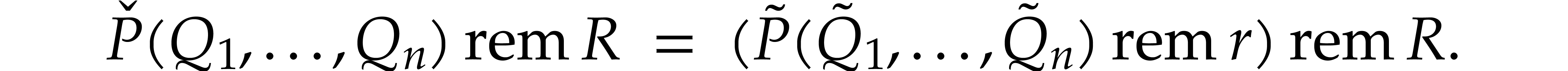
We finally rescale the polynomials, so that we can compute  using a spiroid:
using a spiroid:
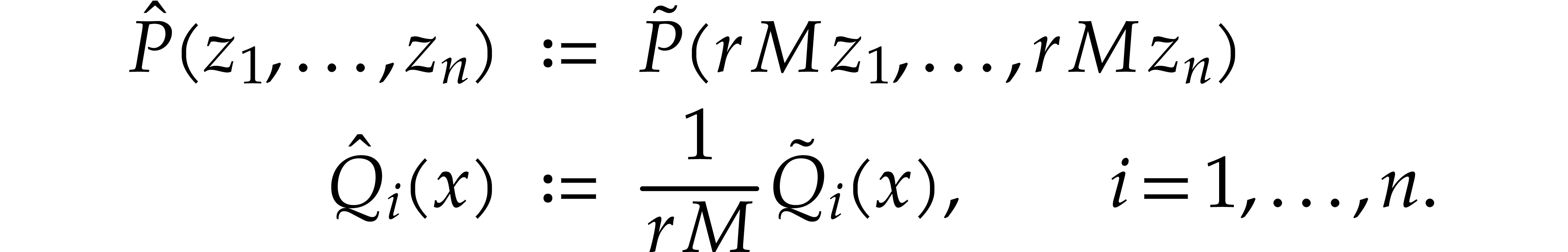
Note that
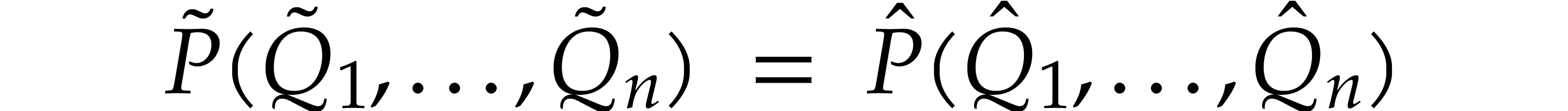
and
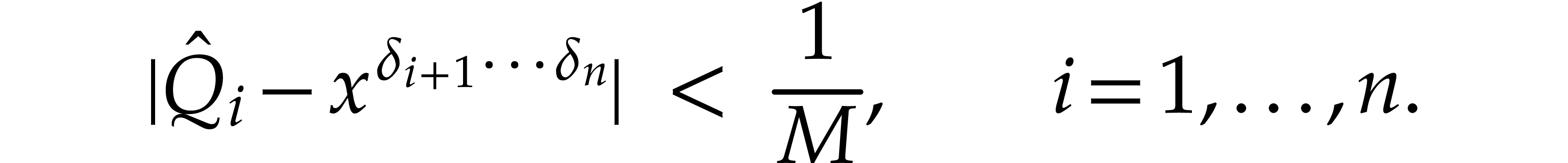
We will evaluate

numerically using fixed point arithmetic. Setting 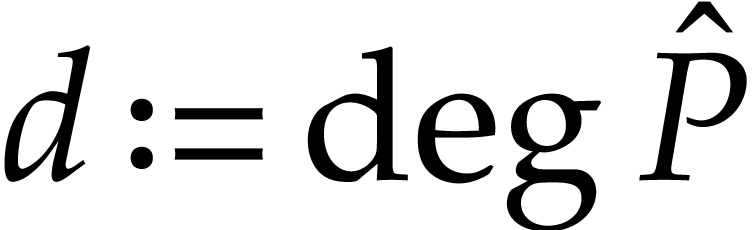 , we note that
, we note that
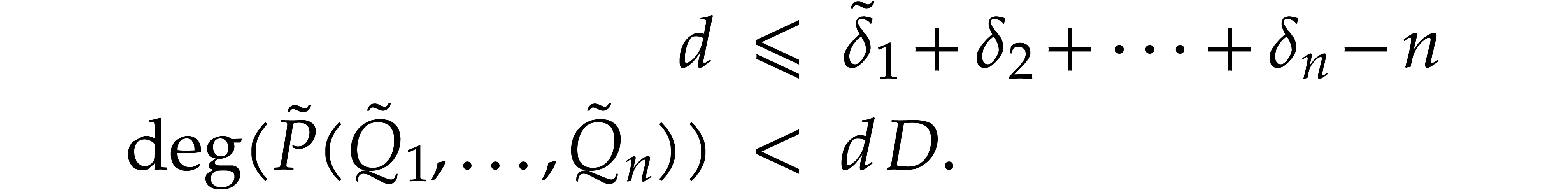
Let  be the smallest power of two satisfying
be the smallest power of two satisfying
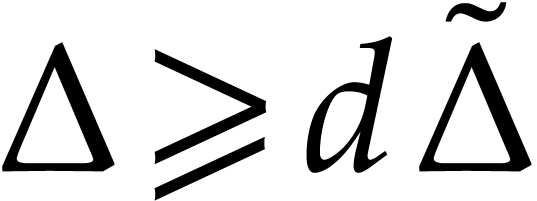 , let
, let 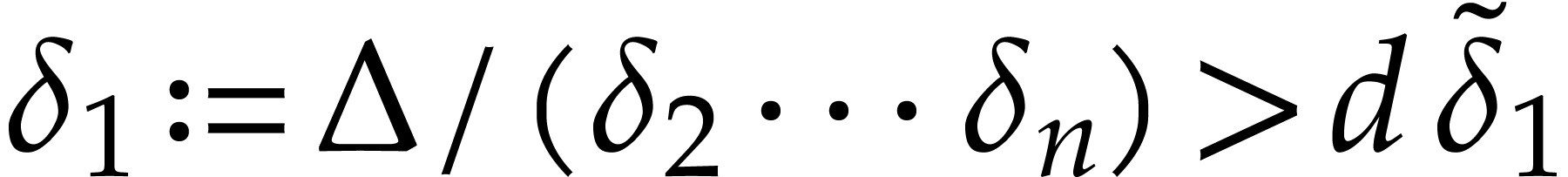 , and consider the standard primitive
, and consider the standard primitive  -th root of unity
-th root of unity 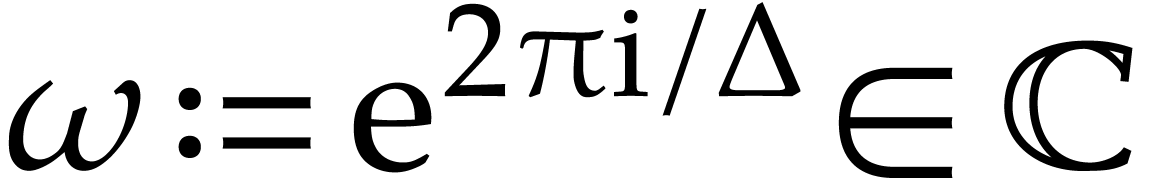 .
We wish to determine
.
We wish to determine  from its values at
from its values at  . For
. For  ,
we let
,
we let
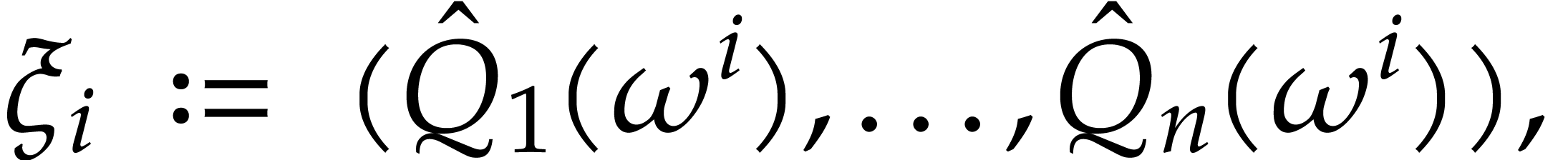
so we have
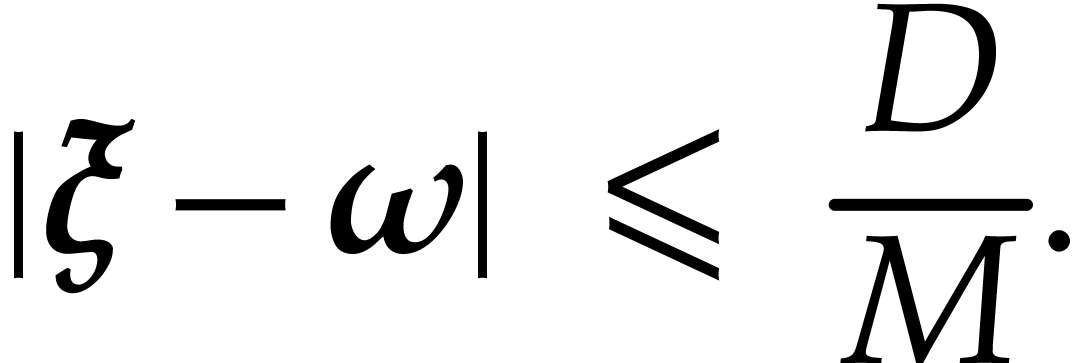 |
(21) |
and
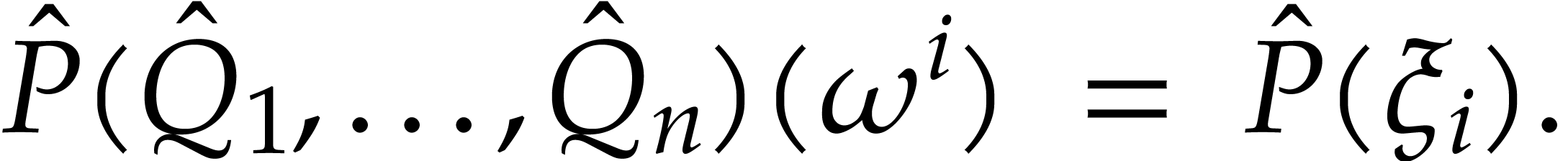
Choosing 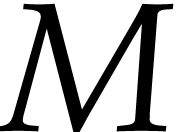 sufficiently large, we will be able to
apply Algorithm 3 in order to evaluate
sufficiently large, we will be able to
apply Algorithm 3 in order to evaluate 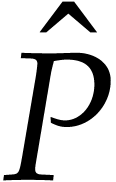 at the spiroid
at the spiroid  . We are now
ready to prove the main theorem of this paper, from which Theorem 1 follows.
. We are now
ready to prove the main theorem of this paper, from which Theorem 1 follows.
Proof. Using binary powering, the computation of
 takes time
takes time
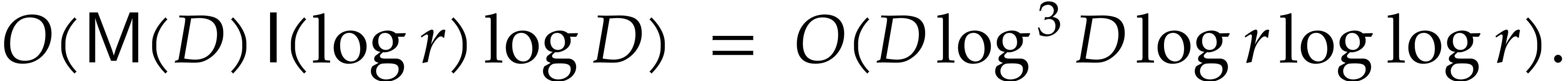
Now we take
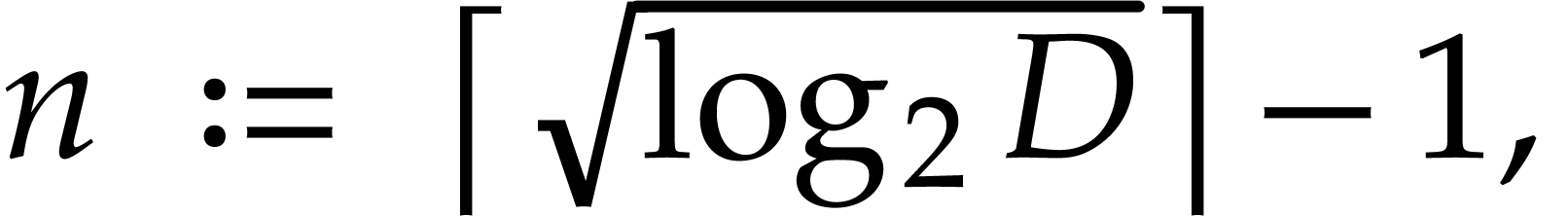
whence 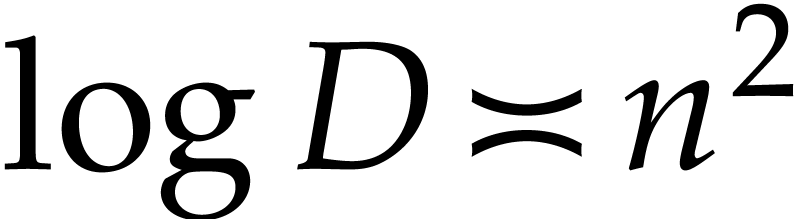 . More precisely, we
have
. More precisely, we
have
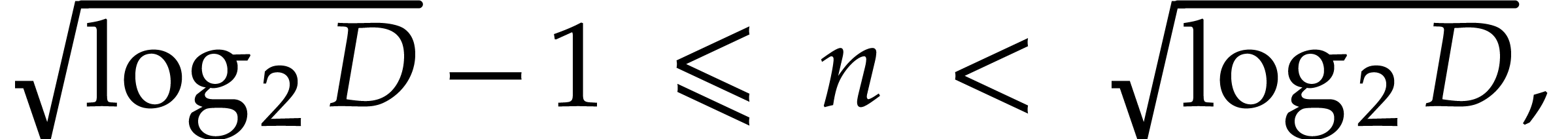
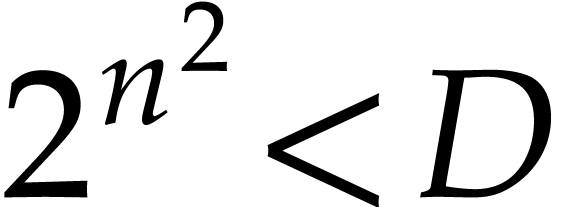 , and
, and  . We distinguish the following cases in order to
construct the sequence
. We distinguish the following cases in order to
construct the sequence 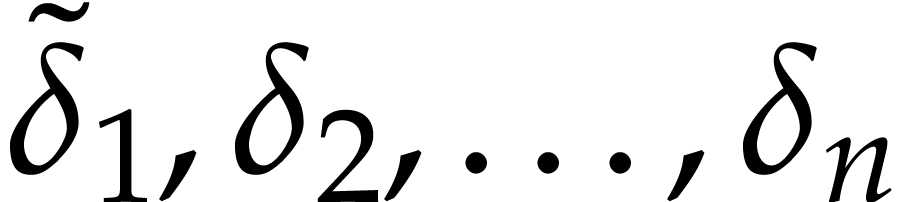 :
:
If 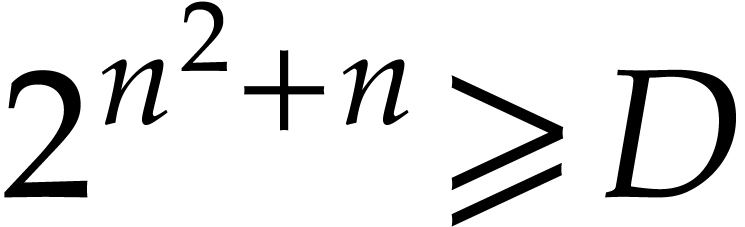 then we take
then we take 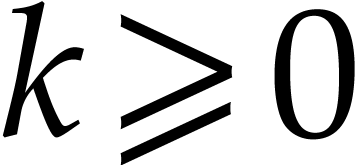 minimal such that
minimal such that 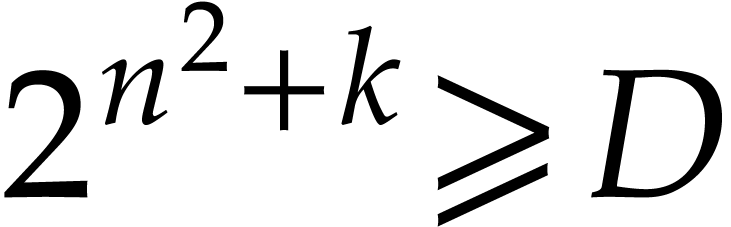 , and
then
, and
then 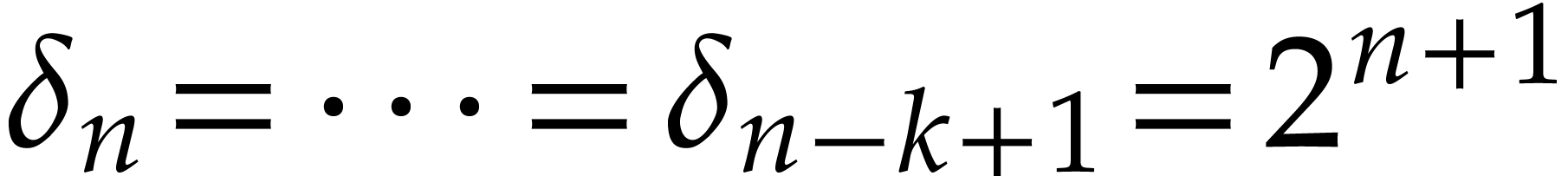 and
and  .
Note that
.
Note that 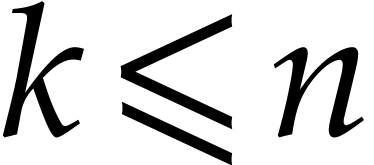 does exist.
does exist.
Otherwise, 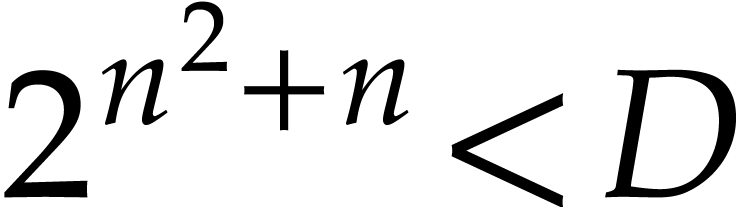 .
.
If 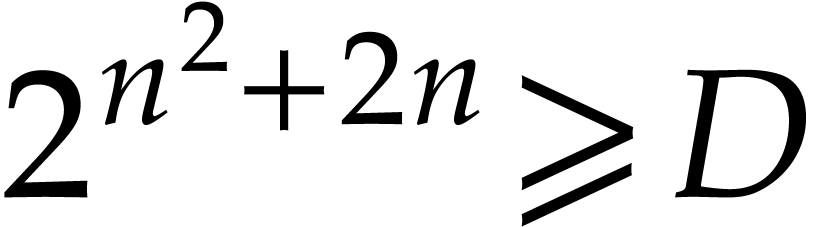 then we take
then we take 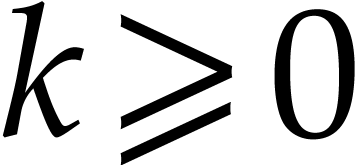 minimal such that
minimal such that 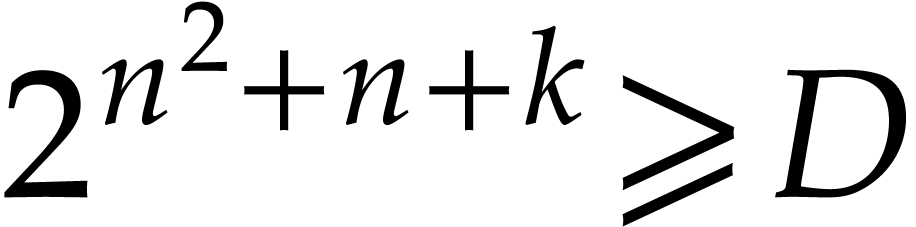 ,
and then
,
and then 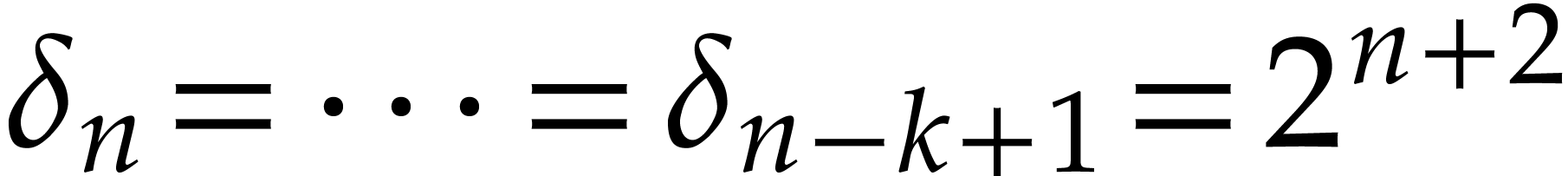 and
and  .
.
Otherwise we take 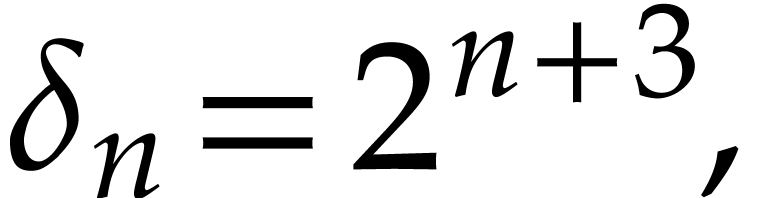
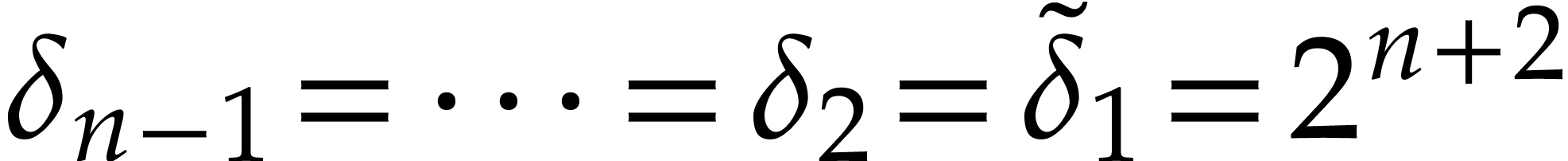 .
.
In this way we achieve 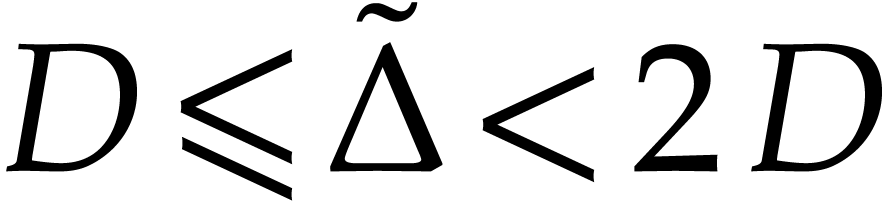 and
and
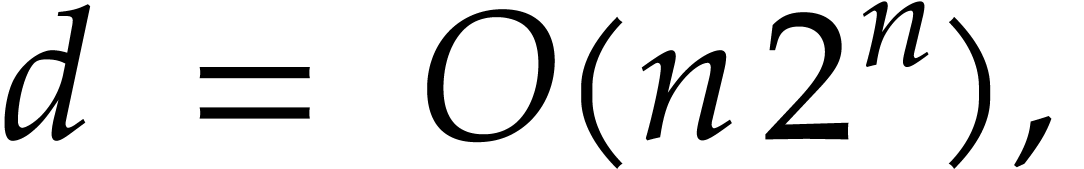 |
(22) |
whence
 |
(23) |
and
 |
(24) |
Recall that 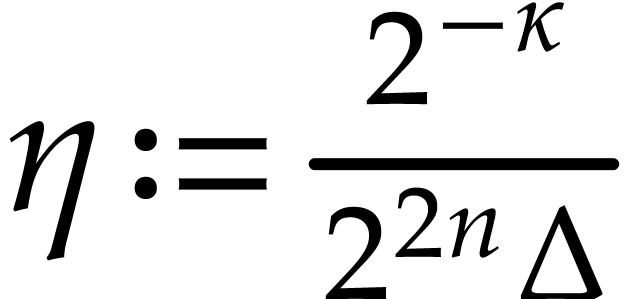 . Now we take
. Now we take
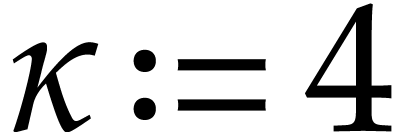 and
and 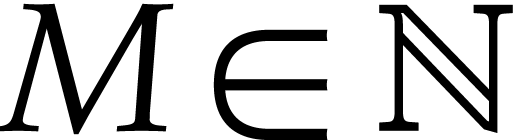 minimal such that
minimal such that
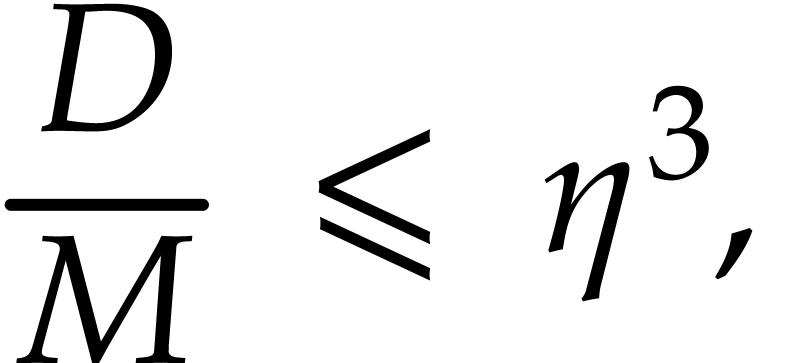
so, using
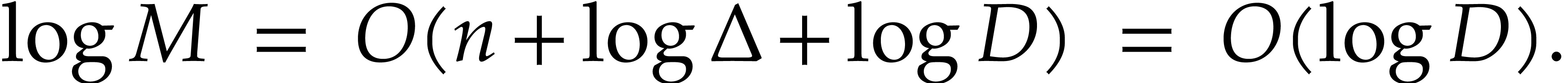 |
(25) |
With this choice for  , the
inequality
, the
inequality
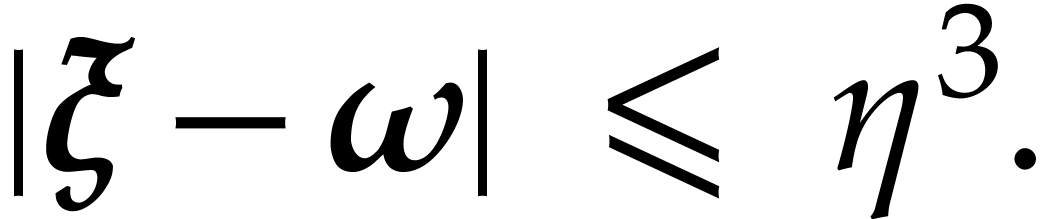
Let 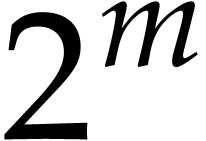 be the smallest power of two that satisfies
be the smallest power of two that satisfies
 , so we have
, so we have 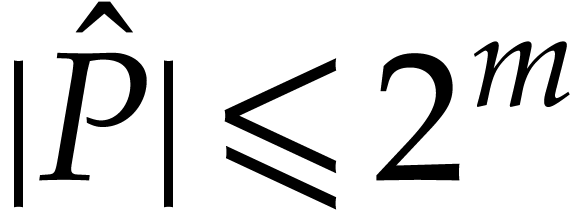 . We set
. We set
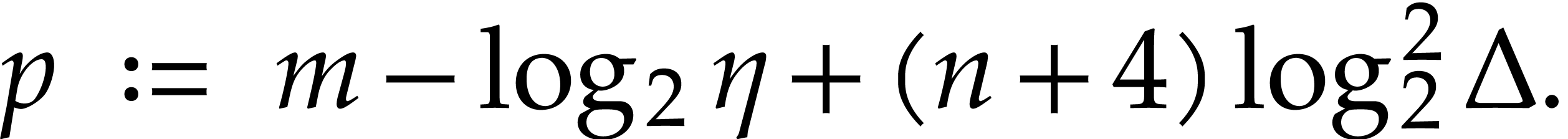
From
and that
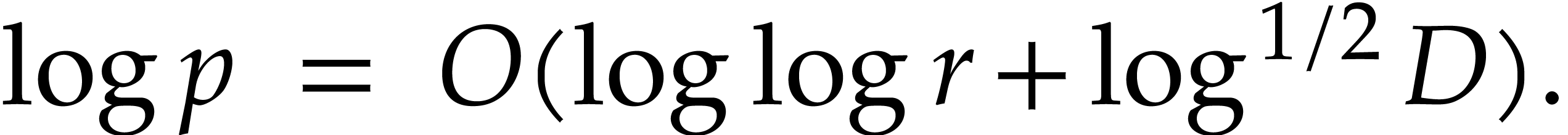 |
(27) |
Since 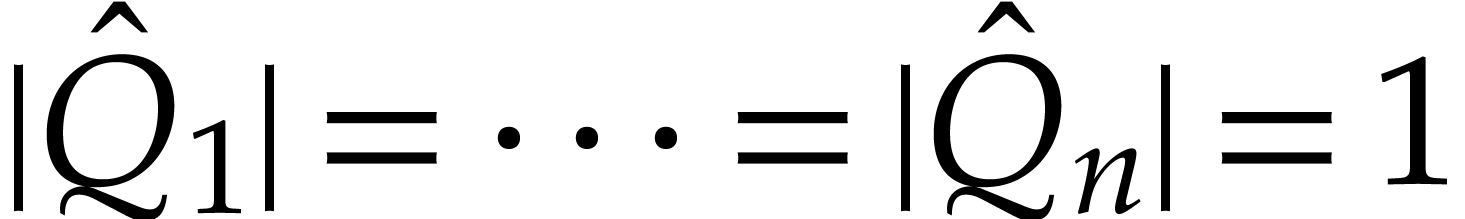 , using Lemma 5
with
, using Lemma 5
with 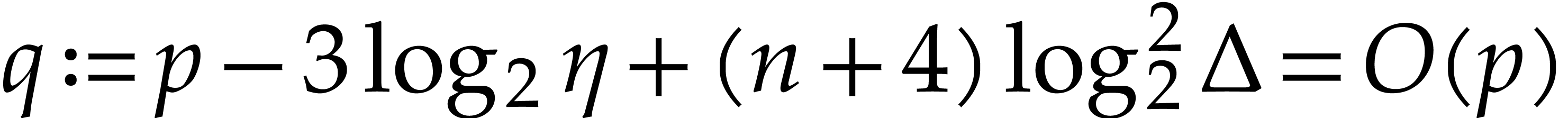 , we compute a
truncation
, we compute a
truncation  of
of  with error
with error
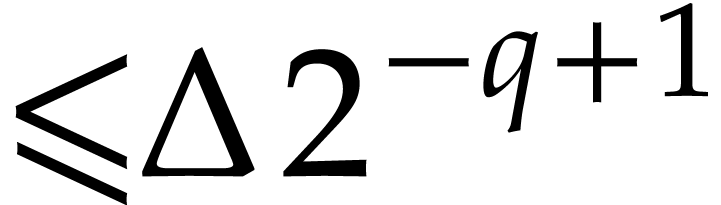 in time
in time
Since  , Proposition 23
allows us to compute an evaluation tree for
, Proposition 23
allows us to compute an evaluation tree for  with
error
with
error 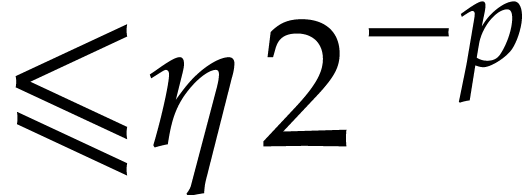 in time
in time
Following Proposition 19, this bound dominates the cost for
obtaining an approximation 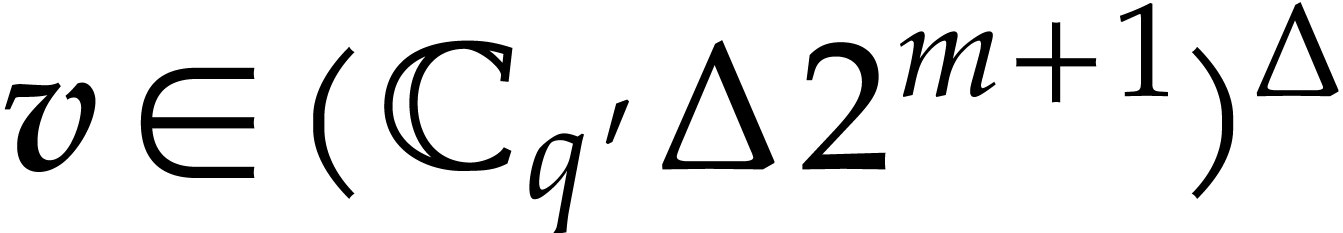 of
of 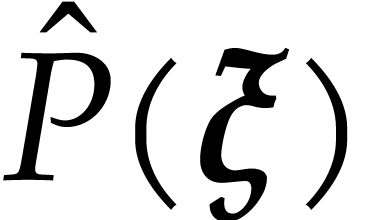 with error
with error 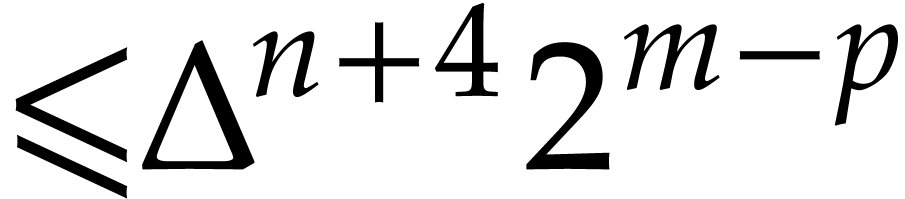 , where
, where  , so we have
, so we have
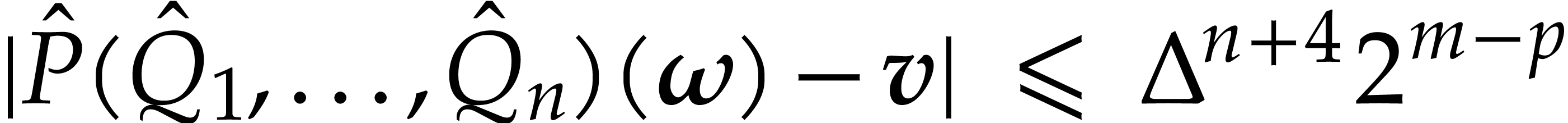
hence
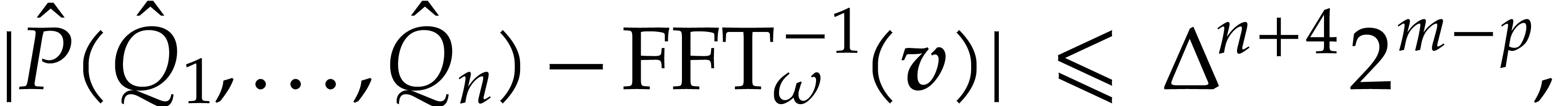 |
(30) |
thanks to Lemma 10. Via Lemma 5, we compute
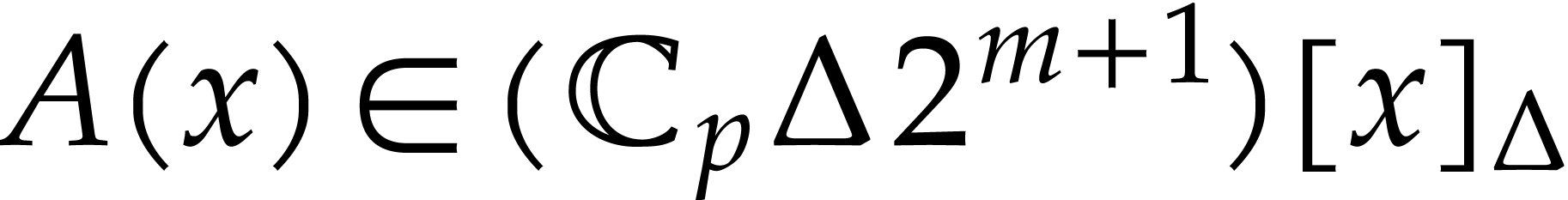 such that
such that
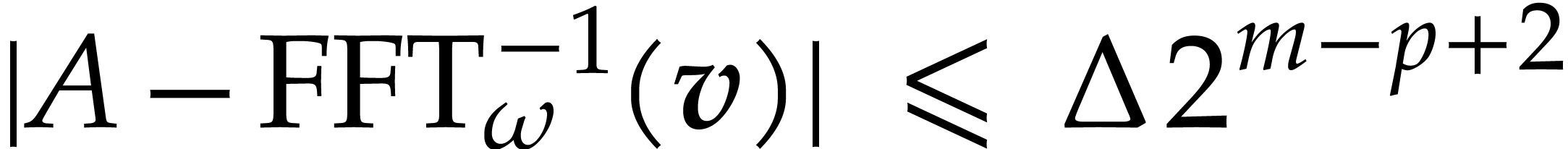 |
(31) |
in time 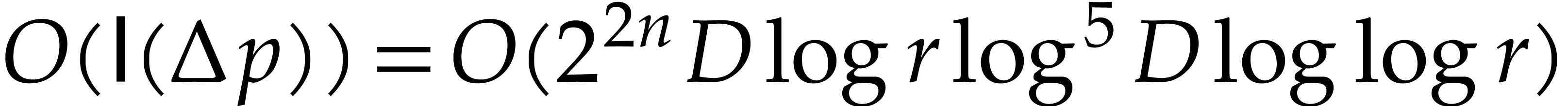 , using
, using
so rounding the coefficients of  to the nearest
integers yields
to the nearest
integers yields  . Since
. Since
we compute 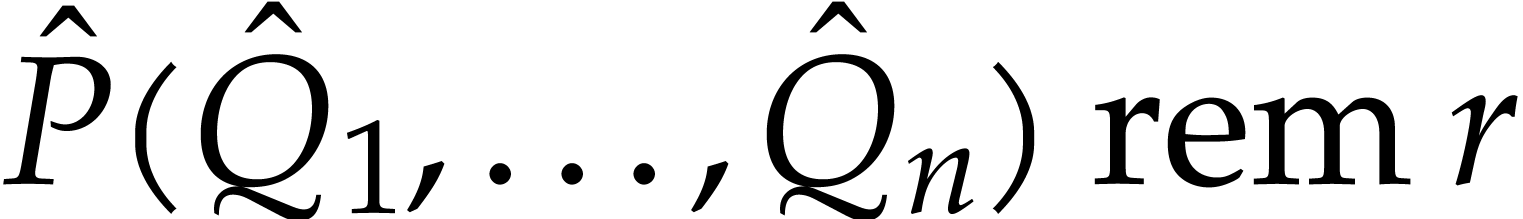 in time
in time
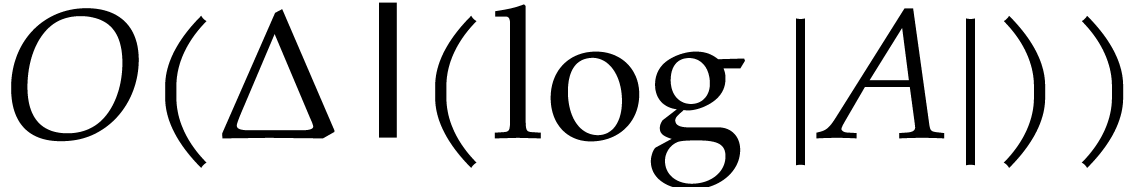 |
 |
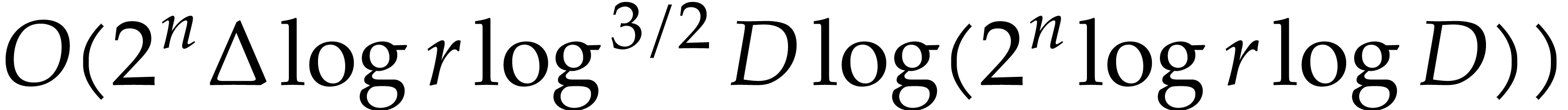 |
|
 |
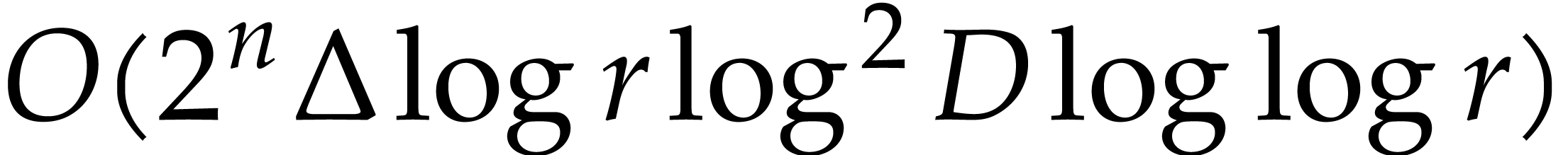 |
||
 |
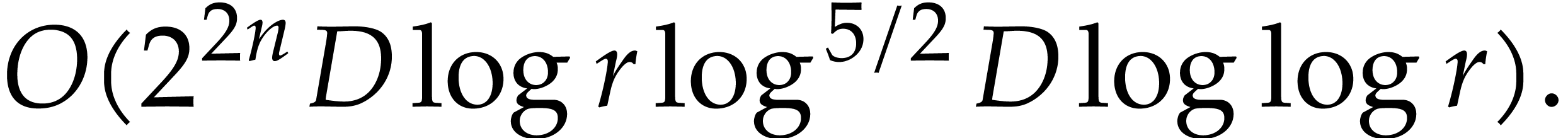 |
(using |
The final division of  by
by  over
over 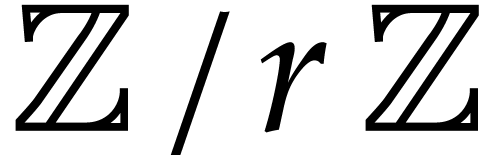 has cost
has cost
The total cost of the method is dominated by 
V. Bhargava, S. Ghosh, Z. Guo, M. Kumar, and C. Umans. Fast multivariate multipoint evaluation over all finite fields. In 2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS), pages 221–232. New York, NY, USA, 2022. IEEE.
V. Bhargava, S. Ghosh, M. Kumar, and C. K. Mohapatra. Fast, algebraic multivariate multipoint evaluation in small characteristic and applications. J. ACM, 70(6):1–46, 2023. Article No. 42.
R. P. Brent and H. T. Kung. Fast algorithms for manipulating formal power series. J. ACM, 25(4):581–595, 1978.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic Complexity Theory, volume 315 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, 1997.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, New York, 3rd edition, 2013.
D. Harvey and J. van der Hoeven. Integer
multiplication in time  .
Ann. Math., 193(2):563–617, 2021.
.
Ann. Math., 193(2):563–617, 2021.
D. Harvey, J. van der Hoeven, and G. Lecerf. Even faster integer multiplication. J. Complexity, 36:1–30, 2016.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and G. Lecerf. Composition modulo powers of polynomials. In Proceedings of the 2017 ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '17, pages 445–452. New York, NY, USA, 2017. ACM.
J. van der Hoeven and G. Lecerf. Modular composition via factorization. J. Complexity, 48:36–68, 2018.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. Complexity, 56:101405, 2020.
J. van der Hoeven and G. Lecerf. Univariate polynomial factorization over finite fields with large extension degree. Appl. Algebra Eng. Commun. Comput., 35:121–149, 2024.
E. Kaltofen and V. Shoup. Fast polynomial factorization over high algebraic extensions of finite fields. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, ISSAC '97, pages 184–188. New York, NY, USA, 1997. ACM.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
Y. Kinoshita and B. Li. Power series composition in near-linear time. In 2024 IEEE 65th Annual Symposium on Foundations of Computer Science (FOCS), pages 2180–2185. IEEE, 2024.
V. Neiger, B. Salvy, É. Schost, and G. Villard. Faster modular composition. J. ACM, 71(2):1–79, 2023. Article No. 11.
M. S. Paterson and L. J. Stockmeyer. On the number of nonscalar multiplications necessary to evaluate polynomials. SIAM J. Comput., 2(1):60–66, 1973.
A. Schönhage. Asymptotically fast algorithms for the numerical muitiplication and division of polynomials with complex coefficients. In J. Calmet, editor, Computer Algebra. EUROCAM '82, European Computer Algebra Conference, Marseilles, France, April 5-7, 1982, volume 144 of Lect. Notes Comput. Sci., pages 3–15. Berlin, Heidelberg, 1982. Springer-Verlag.
V. V. Williams, Y. Xu, Z. Xu, and R. Zhou. New bounds for matrix multiplication: from alpha to omega. In D. P. Woodruff, editor, Proceedings of the 2024 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 3792–3835. Philadelphia, PA 19104 USA, 2024. SIAM.