|
Laboratoire d'informatique, UMR 7161 CNRS
Campus de l'École polytechnique
1, rue Honoré d'Estienne d'Orves
Bâtiment Alan Turing, CS35003
91120 Palaiseau
|
|
|
Currently, only a limited number of fonts are available
for high quality mathematical typesetting, such as Knuth's computer
modern font, the Stix font, and several fonts
from the TeX Gyre family. An interesting
challenge is to develop tools which allow users to pick any existing
favorite font and to use it for writing mathematical texts. We will
present progress on this problem as part of recent developments in the
GNU TeXmacs scientific text editor.
1Introduction
For a long period, most documents with mathematical formulas were
typeset using Knuth's Computer Modern font [5]. Recently, a few alternative fonts were designed, such as
the Stix font [7] and the TeX Gyre fonts [3]. These handcrafted fonts all
admit a high quality, but they required an important development effort.
Now there exists thousands of fonts for non mathematical purposes. To
what extent is it possible to use such fonts for mathematical texts or
presentations, or on the web?
In this paper we describe recent developments inside the GNU TeXmacs
scientific text editor [1] which aim at a better support of
general purpose fonts, thereby making life a bit more colorful. The
focus is on fully automatic techniques for using existing fonts inside
structured documents with mathematical formulas. Further fine tuning for
specific characters in particular fonts is another interesting topic
which will not be discussed here.
There are obvious limitations of what we can do with a font if bold and
italic declinations or glyphs for various important characters are
missing. Nevertheless we will see that quite a lot is often possible
even though the resulting quality may be inferior to what can be
achieved via manual design. Since various special characters or
font effects are often only used at a reduced number of places inside
actual documents, the occasional loss of quality may remain within
acceptable bounds, even for professional purposes.
Our general strategy for turning existing fonts into full fledged
mathematical font families is to remedy each of the font's
insufficiencies. The most common problems are the following:
-
Lack of the most important font declinations as needed in scientific
documents: Bold, Italic, Small
Capitals, Sans Serif, Typewriter.
-
Lack of specific glyphs: non English languages, mathematical
symbols, and in particular big operators, extensible brackets and
wide accents.
-
Inconsistencies: sloppy design of some glyphs that are important for
mathematics (such as 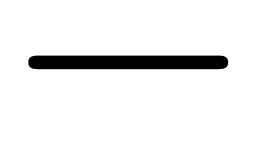 ,
,
 , etc.),
leading to inconsistencies.
, etc.),
leading to inconsistencies.
The main countermeasures are font substitution and font
emulation. The first technique (see Section 2)
consists of borrowing missing glyphs from other fonts. This can either
be done on the level of an entire font (e.g. for obtaining
bold or italic declinations) or for individual characters
(e.g. a missing 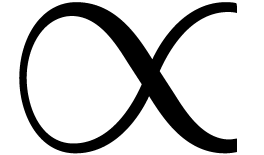 symbol, or lacking
Greek characters). Font emulation consists of combining and altering the
glyphs of symbols in a font in order to generate new ones. This can
again be done for entire fonts (Section 3) or individual
glyphs (Sections 4 and 5).
symbol, or lacking
Greek characters). Font emulation consists of combining and altering the
glyphs of symbols in a font in order to generate new ones. This can
again be done for entire fonts (Section 3) or individual
glyphs (Sections 4 and 5).
All techniques described in this paper have been implemented in TeXmacs,
version 1.99.5 and beyond. The software can freely be downloaded from
our website www.texmacs.org. The virtual character
definitions described in Section 4 below can be found in
the TeXmacs/fonts/virtual directory; interested users
may play with these definitions. Longer examples of what can be obtained
using the techniques described in this paper are available here:
In the TeX/LaTeX universe, there have also been several efforts towards
better support for modern OpenType fonts, most
notably XeTeX [4] and LuaTeX
[2]. The first system also contains features that are
similar to those described in Section 3. However, these
systems do not support full mathematical font emulation as presented in
this paper. XeTeX and LuaTeX
also tend to diverge from standard LaTeX through the introduction of
incompatibilities.
2Font analysis and font
substitution
In order to borrow missing characters from other fonts, it is important
to be able to determine fonts with a similar design, so that the alien
glyphs fit nicely into the main text:
The symbols

do not look very well inside
 .
.
Usually, rules for font substitution are specified manually for each
individual font. Although this often yields the most precise and
predictable results, it can be tedious to write such rules. For this
reason, we also implemented a more automatic mechanism in order to
determine good substitutes.
A prerequisite for our algorithm for automatic font substitutions is a
detailed analysis of the main characteristics of all supported fonts.
The results of this analysis are stored in a database. Using this
database, we may then compute the distance between two fonts. In the
case when a symbol  is missing in a font
is missing in a font 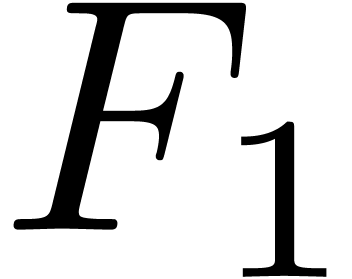 , it then suffices to find the
closest font
, it then suffices to find the
closest font 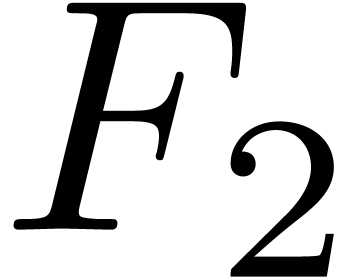 that supports this symbol
that supports this symbol  . Notice that the best substitution
font may depend on the fonts which are installed on your system.
. Notice that the best substitution
font may depend on the fonts which are installed on your system.
In our database we both use discrete font characteristics
(e.g. sans serif, small capitals, handwritten, ancient,
gothic, etc.) and continuous ones (e.g. italic
slant, height of an “x” symbol, etc.). Most
characteristics are determined automatically by analyzing the name of
the font (for some of the discrete characteristics) or individual glyphs
(for the continuous ones). Some “font categories” (such as
handwritten, gothic, etc.) can be specified manually.
One of the most important font characteristics is the height of the
“x” symbol (with respect to the design size). When the font
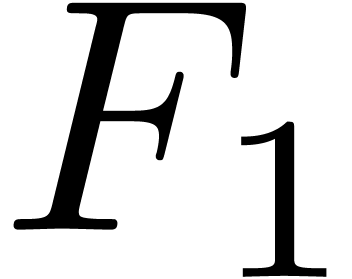 borrows a symbol from the font
borrows a symbol from the font 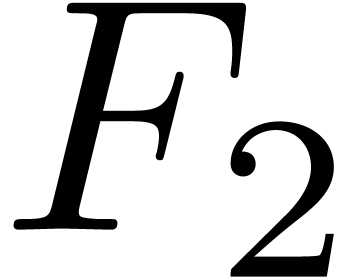 we first scale it by the quotient of these x-heights inside
we first scale it by the quotient of these x-heights inside 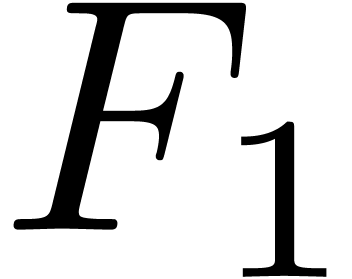 and
and  . In the
example (1) this was done correctly, contrary to (2).
. In the
example (1) this was done correctly, contrary to (2).
Other common font characteristics are also taken into account into our
database, such as the italic slant, the width of the “M”
symbol, the ascent and descent (above and above the “x”
symbol), etc. In addition, we carefully analyze the glyphs themselves in
order to determine the horizontal and vertical stroke widths for the
“o” and “O” symbols, the average aspect-ratios
of uppercase and lowercase letters, and the average area of glyphs that
is filled (how much ink will be used).
Our current implementation manages to find reasonably good font
substitutions. Notice that this may even be a problem on certain
occasions. For instance, in the example (3) below, the sans
serif font is such a good match that it can barely be distinguished from
the serif font, thereby defeating its purpose:
This sample text is a bit too good.
3Poor man's font emulation
Various font alterations such as Bold, Italic
and Small Capitals can be emulated in rather
obvious ways, although with significant loss of quality:
-
Emboldening can be achieved through the replacement of pixels by
small lines. In addition, it may be worth it to horizontally stretch
certain characters such as “m”. The appropriate
stretching factors are highly font and character dependent, but
using the factors corresponding to the computer modern font usually
leads to reasonable results.
-
Italic fonts can be approximated by slanted fonts, which may be
further narrowed for a better result. The most important drawback of
this method is that it often falls short of producing the correct
italic versions of certain characters (a/a/a,
f/f/f, g/g/g, etc.).
-
Small capitals can be emulated by rescaling capitals using a factor
that roughly turns an “X” into an “x”.
Instead of conserving the aspect-ratio, we found it more pleasing to
slightly widen characters as well. The transformed version of
“X” may also be taken slightly higher than
“x”.
With more work, the above “poor man's” strategies might be
further enhanced. For instance, the italic a might be better
approximated using a shortened version of d instead of a. In order to
improve bold font emulation, we might also replace pixels by small lines
of cleverly adjusted lengths.
More elaborate emulation strategies might greatly benefit from a toolkit
for “retro-engineering” the design of existing fonts. For
instance, given an outline, we might want to determine the curve(s)
followed by a “pen” and the size (or shape) of the pen at
each point of the curve. This would then make it easy to produce high
quality narrowed and widened versions of a font, as well as better
emboldened fonts, or variants in which the pen's size is uniform (as
needed for sans serif and typewriter fonts). Another interesting
question is whether it is possible to automatically detect serifs and to
add or remove them.
We have started to experiment with more elaborate emulation algorithms
for the generation of “blackboard bold” variants of glyphs.
The easiest strategy is to produce an outlined version of the possibly
emboldened input glyph. The standard AMS blackboard bold font uses this
method ( ,
,  ,
,  ,
,
 ,
,  ), but we consider the result suboptimal with
respect to adding a single stroke (
), but we consider the result suboptimal with
respect to adding a single stroke ( ,
,
 ,
,  ,
,  ,
,  ). We implemented an algorithm for
the detection of the part of contour to be “double stroked”.
We next embolden this part and hollow it out.
). We implemented an algorithm for
the detection of the part of contour to be “double stroked”.
We next embolden this part and hollow it out.
| Regular |
Bold |
Italic |
Small Caps |
Blackboard Bold |
Mathematics |
| Optima |
Bold* |
Italic |
Small Caps |
 , ,  , ,  , ,  , ,
 |
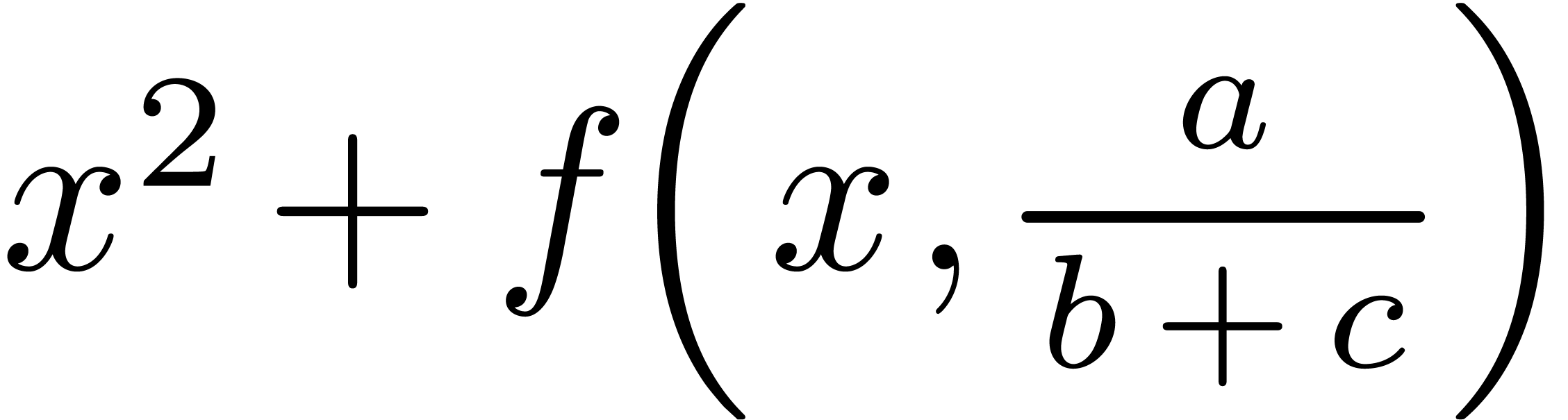 |
| Cochin |
Bold* |
Italic* |
Small Caps |
 , ,  , ,  , ,  , ,
 |
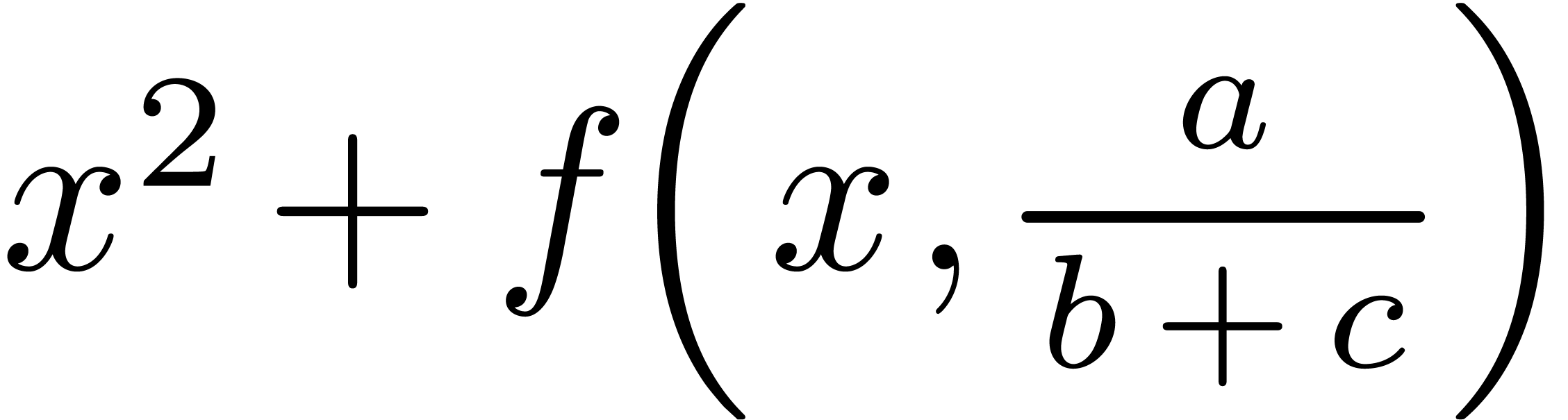 |
| Chartrand |
Bold |
Italic |
Small Caps |
 , ,  , ,  , ,  , ,
 |
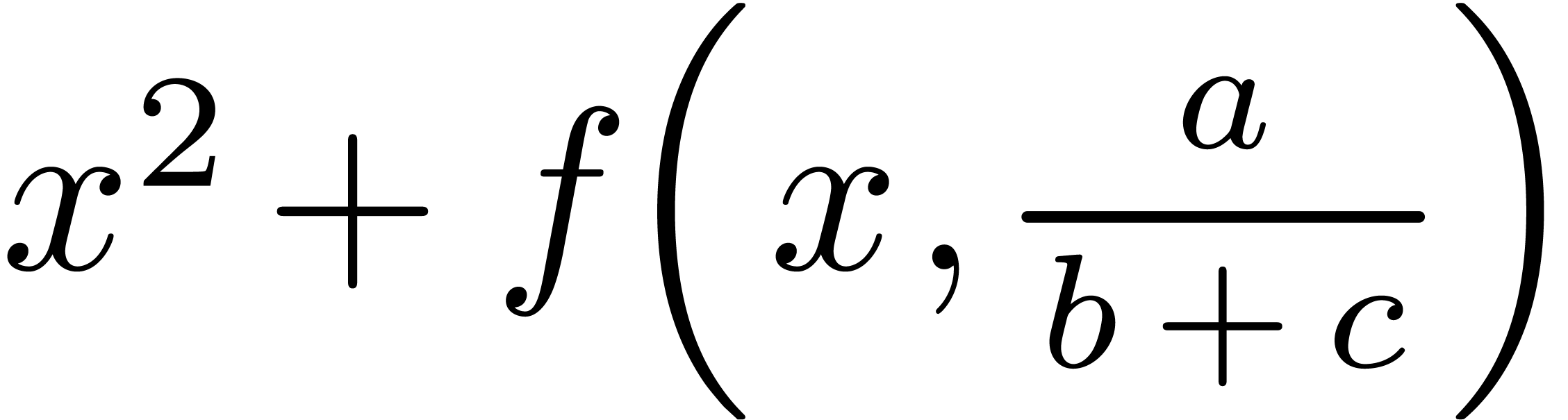 |
| Essays1743 |
Bold* |
Italic* |
Small Caps |
 , ,  , ,  , ,  , ,  * * |
 |
| Meyne Textur |
Bold |
Italic |
Small Caps |
 , ,  , ,  , ,  , ,
 |
 |
| Chalkduster |
Bold |
Italic |
Small Caps |
 , ,  , ,  , ,  , ,
 |
 |
| Comic Sans |
Bold |
Italic |
Small Caps |
 , ,  , ,  , ,  , ,
 |
 |
| Papyrus |
Bold |
Italic |
Small Caps |
 , ,  , ,  , ,  , ,
 |
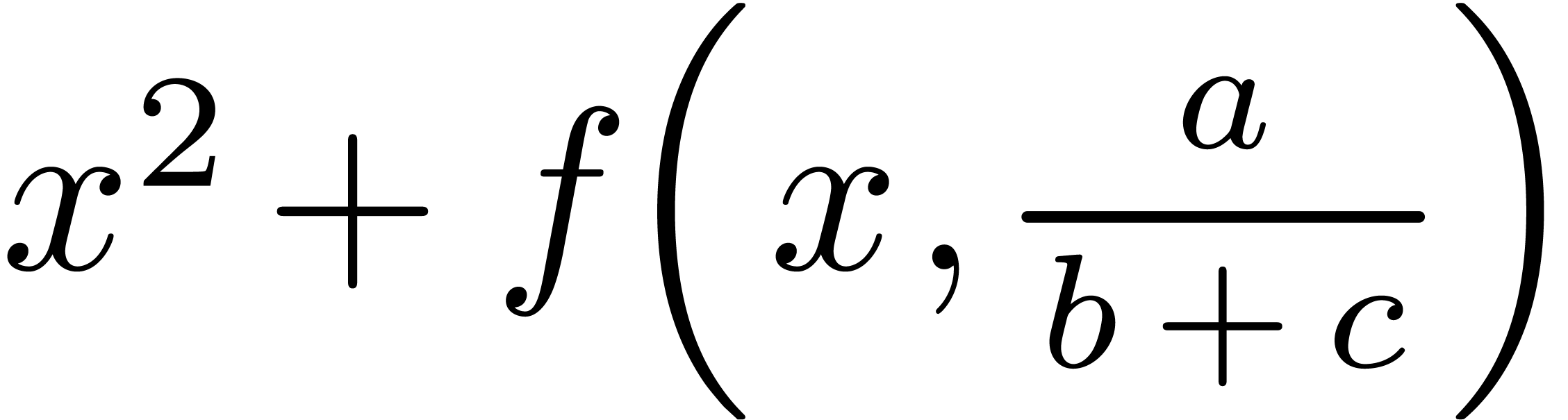 |
|
|
Figure 1. Emulation of bold, italic, small
capitals and blackboard bold.
* These declinations are already supported by the original font.
|
4Virtual characters
Missing glyphs can be generated automatically from existing ones using a
combination of the following main techniques, listed by increasing
complexity:
In a similar vein, we need various querying mechanisms: all glyphs come
with logical and physical bounding boxes, but we sometimes may want to
compute the exact width of some stroke or obtain other kinds of
information.
We developed a small language that can be used for defining new
“virtual” characters in terms of existing ones. The design
of every new virtual glyph can be regarded as a puzzle: finding a clever
way to combine existing glyphs into the desired one using the primitives
from the language. Of course, we are looking for robust solutions in the
sense that they should work for any reasonable font in which
the required basic glyphs are available.
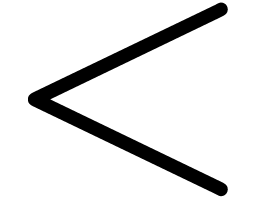
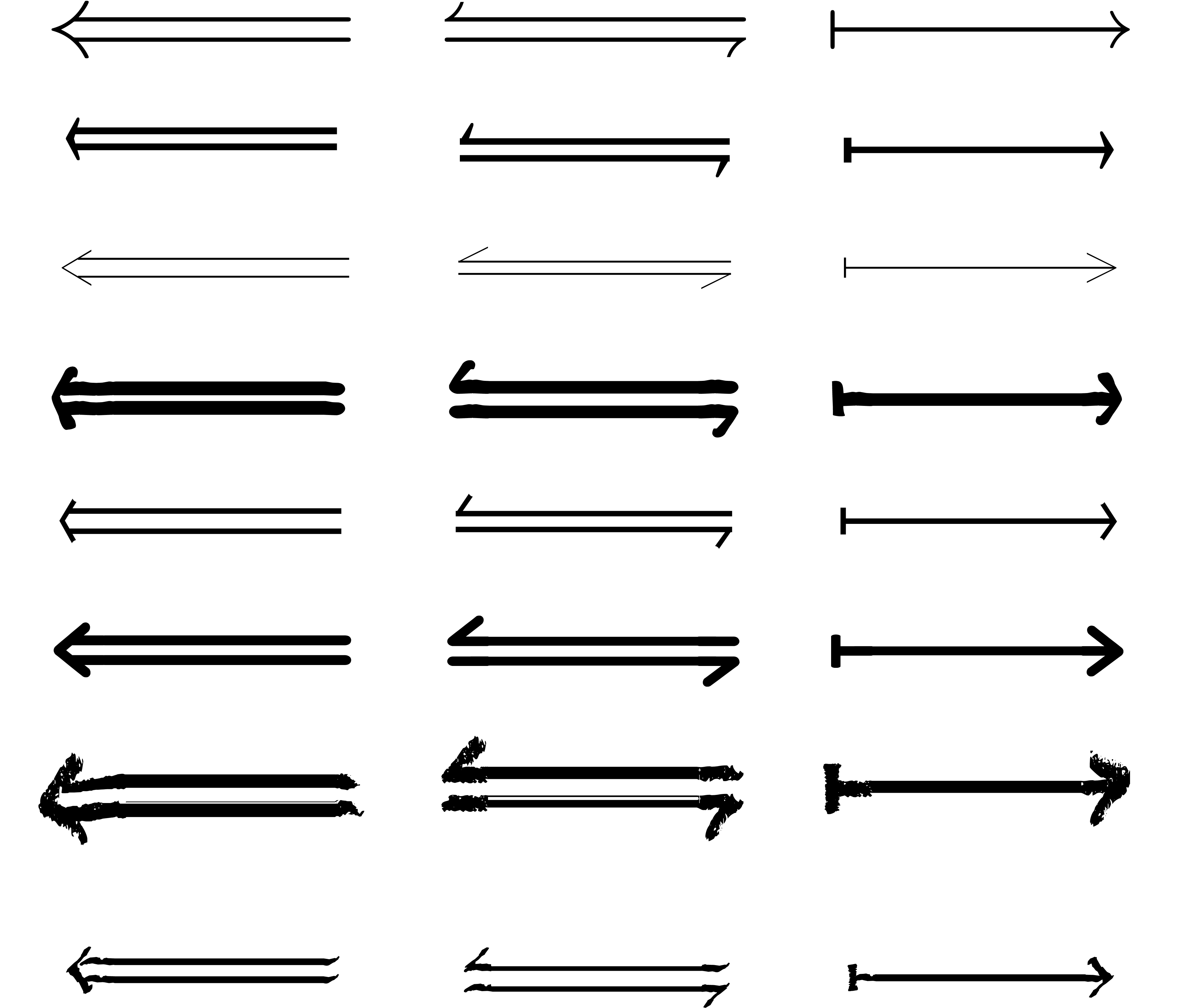
Let us consider a few examples. For the construction of arrows, it turns
out that the single guillemets ‹ and › are often
well suited for the heads (the rescaled symbols < and > are
acceptable fallbacks). The arrow bars are obtained from the minus sign
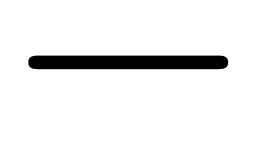 , but the determination of an
appropriate minus is non trivial. For instance, the width of the dash -
is usually too large, so we should avoid using this symbol. The
underscore is a better candidate; one may also cut the plus sign into
several pieces (avoiding the vertical stroke) and recombine them.
, but the determination of an
appropriate minus is non trivial. For instance, the width of the dash -
is usually too large, so we should avoid using this symbol. The
underscore is a better candidate; one may also cut the plus sign into
several pieces (avoiding the vertical stroke) and recombine them.
Assuming that we have an appropriate arrow bar and head, we may use the
following code for producing an actual arrow:
(rightarrow (right-fit arrowbar (align righthead arrowbar *
0.5)))
The align primitive is used to vertically align the
arrow head at the center of the arrow bar. The right-fit
primitive is less basic and corresponds to sliding the arrowhead from
the right to the left until the arrow bar goes past the head on its
right. More direct ways to produce arrows turn out to be less robust.
Left and left-right arrows can be defined using
(leftarrow (left-flip rightarrow))
(leftrightarrow (join (part leftarrow * 0.5) (part
rightarrow 0.5 *)))
These definitions potentially take advantage of an existing rightarrow
in the base font. The part primitive performs two
horizontal clippings between the middle and the extremities, whereas join is used for superposition.
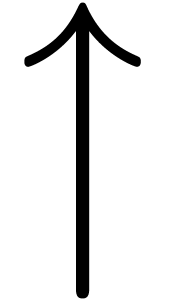
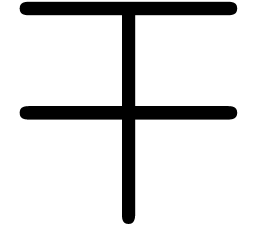
An interesting challenge is the emulation of Greek characters. This
seems intractable for the lowercase symbols, but is less hopeless for
the capitals. For instance, <Gamma*> can be obtained by flipping
the Roman L upside down and we already mentioned how to obtain a
reasonable <Phi*>. More interesting is the case of <Pi*>,
which can be obtained from H by moving the horizontal bar to the top.
However, extracting this bar is not so easy in some fonts: consider H.
For a robust method, we therefore cut the H into pieces: we first
extract <H1> <H2> <H4> and recombine them into
<H5>. We next take a tiny piece of the central bar, extend it to
the desired length, and move it to the top.
5Rubber characters
One specific problem with mathematical fonts is the need for rubber
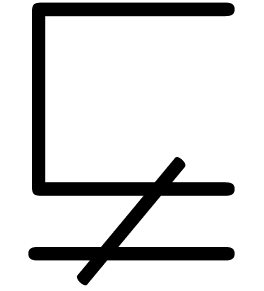
characters. There are essentially four types of them: big operators
(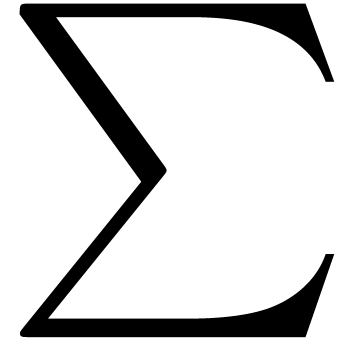 ,
,  ,
,  ),
large delimiters
),
large delimiters 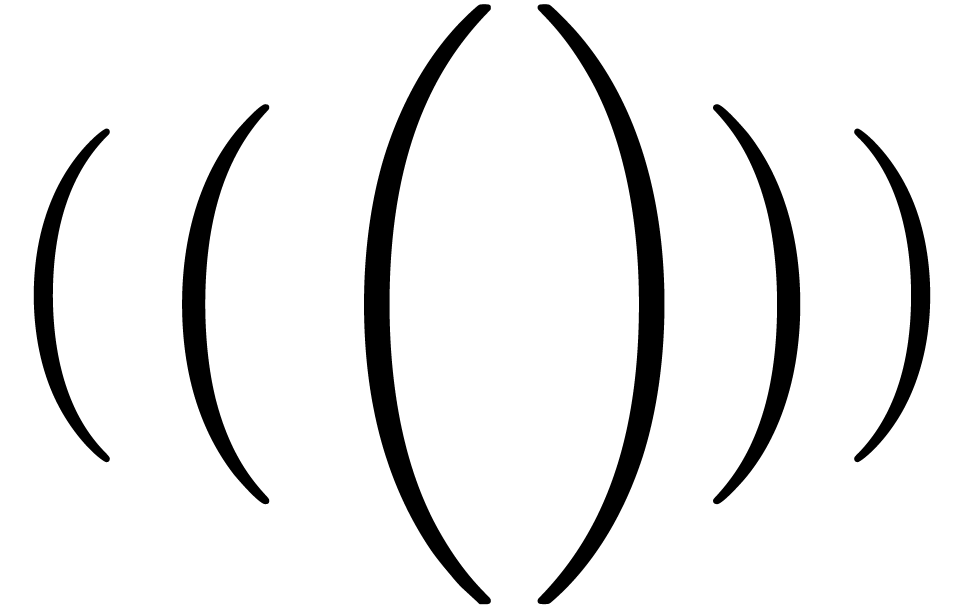
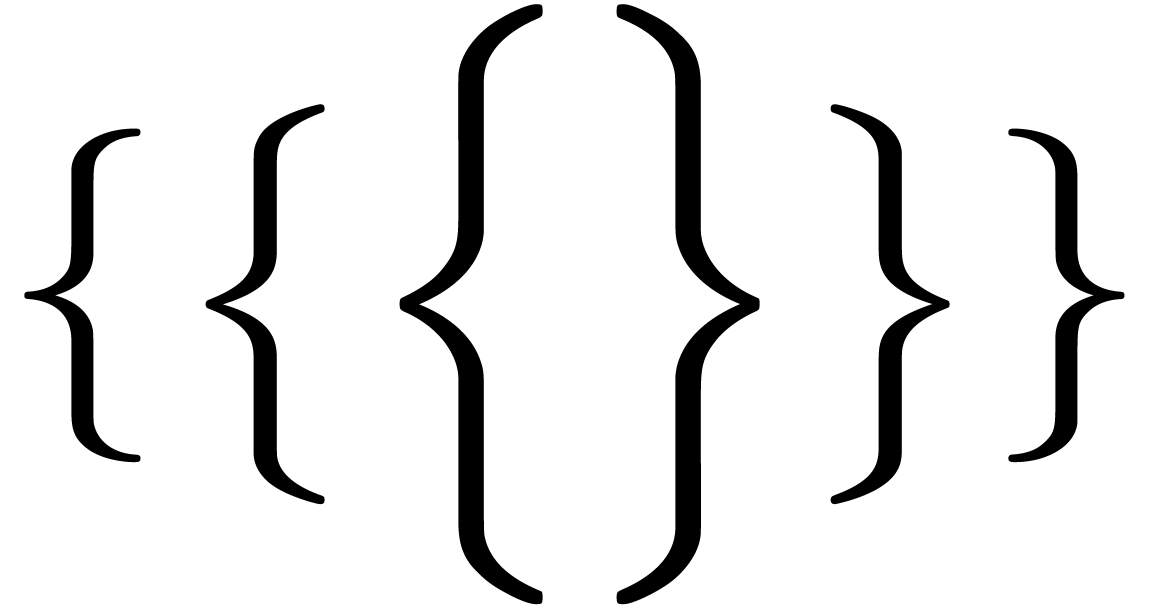 ,
wide accents (
,
wide accents (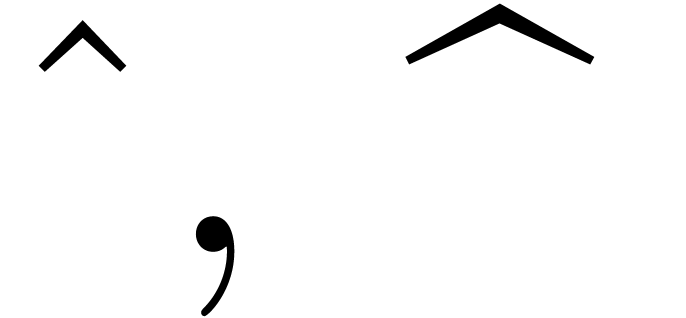 ,
, 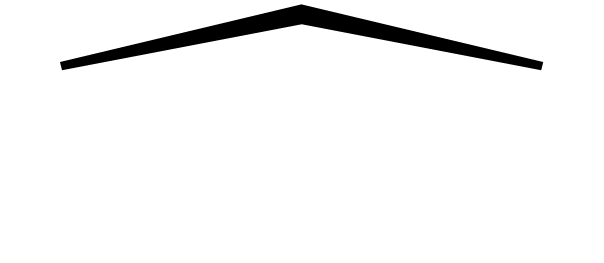 ), and long arrows (
), and long arrows (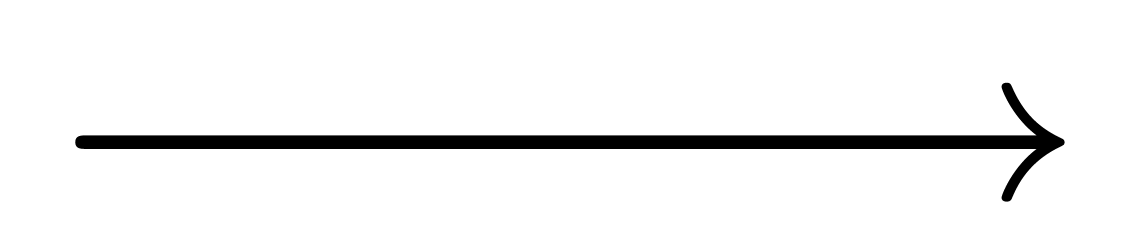 ,
, 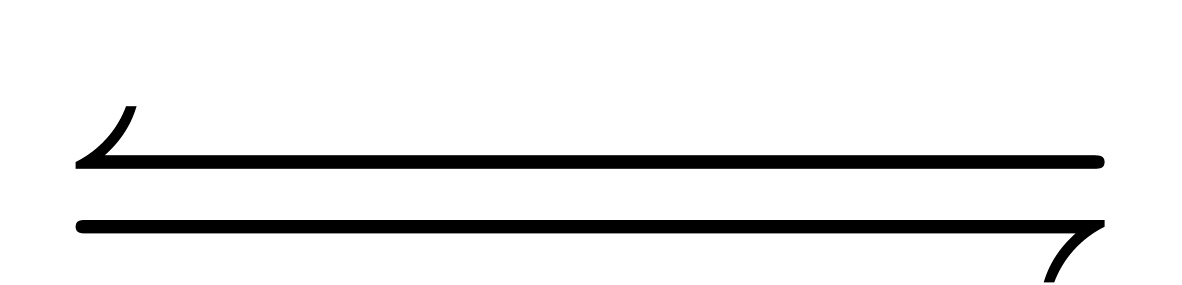 ).
).
We produce these rubber characters using essentially the same techniques
as in the previous section. Especially horizontal and vertical scaling
are very useful, as well as cutting symbols into several parts and
reassembling them appropriately.
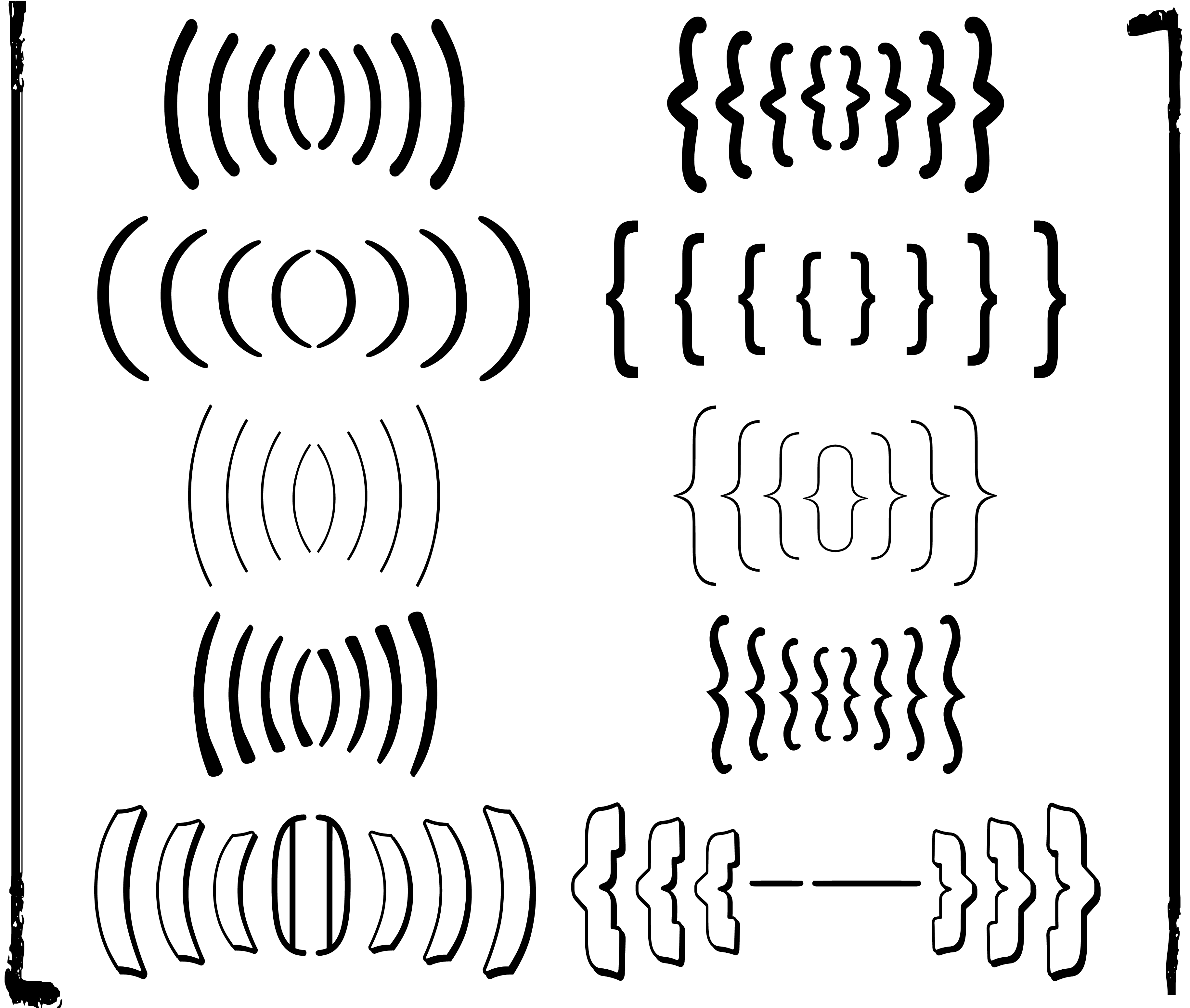
For instance, moderately large versions of the bracket ( are obtained
through magnification, typically with a higher stretch factor in the
vertical direction. For larger sizes, this method produces results that
are unacceptably thick. In that case, we rather cut the bracket into a
top, a bottom, and a tiny middle part. We next repeat the middle part as
many times as necessary in order to obtain a bracket of the desired
size.
The use of scaling is a very delicate matter. For instance, in the case
of square brackets [ (and their potential derivatives  and
and  ), the point where
horizontally magnified versions get too fat is usually reached much
earlier than for ordinary or curly brackets. In the case of wide
accents, we typically need very large horizontal stretch factors, which
yield unacceptable results. Magnified versions of
), the point where
horizontally magnified versions get too fat is usually reached much
earlier than for ordinary or curly brackets. In the case of wide
accents, we typically need very large horizontal stretch factors, which
yield unacceptable results. Magnified versions of 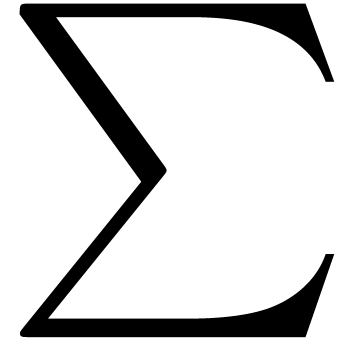 and
and  typically look allright, but this is much
less so for
typically look allright, but this is much
less so for  .
.
We are still in the process of fine tuning our implementation. For
better results, one major challenge is to develop magnification methods
with a finer control over the stroke widths. In particular, we need a
reliable magnification method that preserves all relevant widths.
|
|
Figure 3. Assorted rubber symbols from various
fonts.
|
6Conclusion and perspectives
After a moderate development investment, we are now able to use a lot of
existing fonts for mathematical typesetting. The quality of the obtained
results ranges from “better than nothing” to
“professional typesetting quality”. Our virtual font
implementation can be regarded as a genuine “metafont”.
Paradoxically, and in comparison, Knuth's Metafont
initiative [6] has essentially resulted in the creation of
a single mathematical font of extremely high quality.
One interesting question that occurred during our development of a
virtual mathematical metafont concerns the “essence of a
font”: which font features essentially contain all necessary
information to reproduce the entire font, and how? For instance, most
mathematical symbols can be reconstructed from a few basic glyphs: 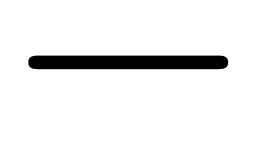 ,
, 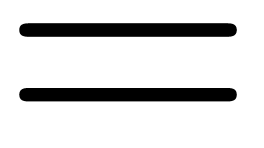 ,
,
 ,
,  ,
,  ,
, 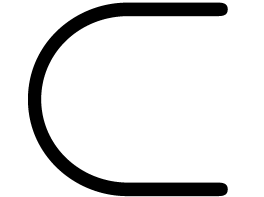 , › (or
, › (or 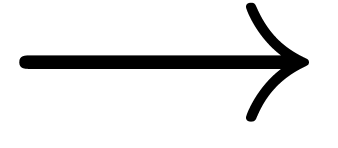 ),
),  ,
,
 ,
,  , (, [ and {. Similarly, the Greek capitals can
essentially be reconstructed from E, H, O, X and Z. So what is the real
“fingerprint” of a font?
, (, [ and {. Similarly, the Greek capitals can
essentially be reconstructed from E, H, O, X and Z. So what is the real
“fingerprint” of a font?
The development of more and better glyph emulation tools might be
valuable for font designers. On the one hand, such tools may be used to
automatically generate lots of glyphs. On the other hand, they allow
designers to compare their own handcrafted glyphs with automatically
generated alternatives. This may help to spot errors or increase
consciousness about the distinctive features of a personal design.
For the moment, we developed all our font substitution and emulation
tools inside TeXmacs. It might be worthwhile to conceive a separate
library with even more systematic tools for font analysis,
retro-engineering and glyph emulation. Such a library might come with
command line tools for generating mathematically enriched fonts,
emboldened or narrowed versions, etc. For the moment, several of our
algorithms are also limitated to operating on bitmaps. In the future, it
would be nice to systematically work with vector graphics only.
One final issue concerns the purpose of alternative fonts. For instance,
certain fonts such as Chalkboard, Chalkduster, Essays1743, Yiggivoo 3D
are mainly used in order to produce specific graphical effects: emulate
text on a chalkboard or on a blackboard, imitating a degraded
retro-font, or producing a 3D sensation. It can be questioned whether
these purposes are always best served through the use of a special font.
For instance, handwriting might be imitated better by dynamically
generating many different versions of the same letter. Better retro and
3D effects might be obtained by applying a suitable graphical filter to
an entire portion of text. This might even more be true in the presence
of fractions, square roots or geometric pictures.
Bibliography
-
[1]
-
Massimiliano Gubinelli, Joris van der Hoeven,
François Poulain, and Denis Raux. GNU TeXmacs: towards a
scientific office suite. In Mathematical Software - ICMS 2014
- 4th International Congress, Seoul, South Korea, August 5-9,
2014. Proceedings, pages 562–569. 2014.
-
[2]
-
T. Hoekwater, H. Henkel, and H. Hagen. Luatex. http://www.luatex.org/, 2007.
-
[3]
-
B. Jackowski, J. Nowacki, and J. Ludwichowski. The
TeX Gyre collection of fonts. http://www.gust.org.pl/projects/e-foundry/tex-gyre/.
-
[4]
-
J. Kew. Xetex. http://tug.org/xetex/,
2005.
-
[5]
-
Donald E. Knuth. Computer Modern Typefaces,
volume E of Computers and Typesetting. Addison-Wesley,
1986.
-
[6]
-
Donald E. Knuth. The METAFONTbook, volume C of
Computers and Typesetting. Addison-Wesley, 1986.
-
[7]
-
STI Pub companies. STIX fonts project. http://www.stixfonts.org/,
2010.
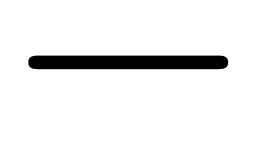 ,
,
 , etc.),
leading to inconsistencies.
, etc.),
leading to inconsistencies.
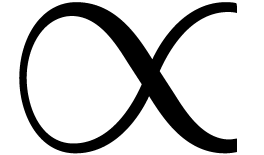 symbol, or lacking
Greek characters). Font emulation consists of combining and altering the
glyphs of symbols in a font in order to generate new ones. This can
again be done for entire fonts (Section
symbol, or lacking
Greek characters). Font emulation consists of combining and altering the
glyphs of symbols in a font in order to generate new ones. This can
again be done for entire fonts (Section  ,
,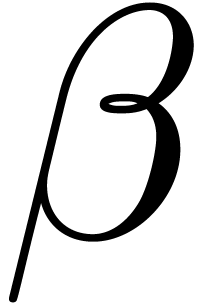 ,
,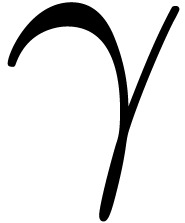 are acceptable
inside
are acceptable
inside  .
. do not look very well inside
do not look very well inside  .
. is missing in a font
is missing in a font 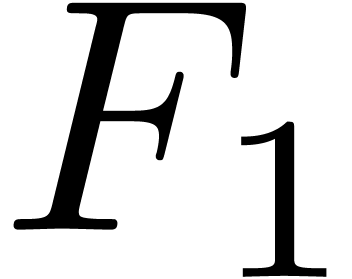 ,
,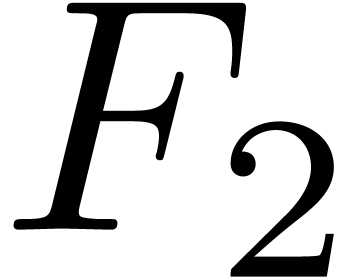 that supports this symbol
that supports this symbol  ,
, ,
, ,
, ,
, ),
), ,
, ,
, ,
, ,
, ).
).
 and
and 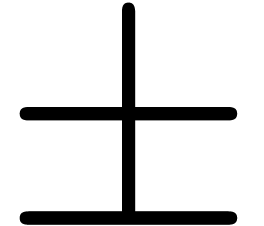 ,
,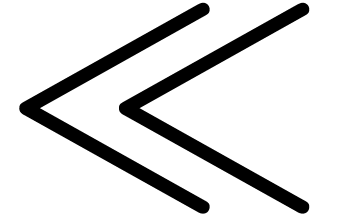 be obtained by
juxtaposing two
be obtained by
juxtaposing two 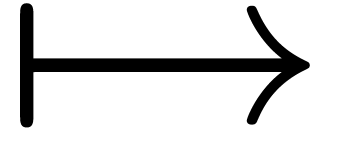 and
and  in their midsts and combining them yields
in their midsts and combining them yields 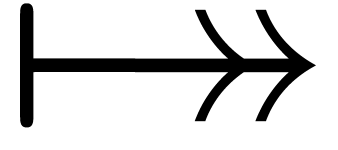 .
.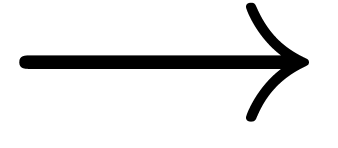 ,
, .
. .
. and
and  into
into  . Similarly, we implemented a “flood
fill” algorithm for transforming
. Similarly, we implemented a “flood
fill” algorithm for transforming  into
into
 .
.



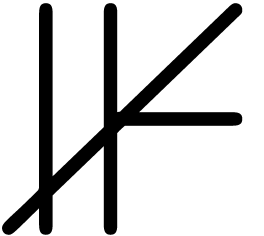
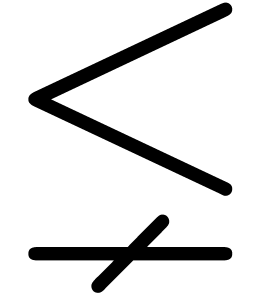

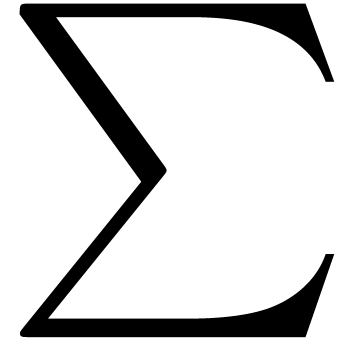 ,
, ,
, ),
),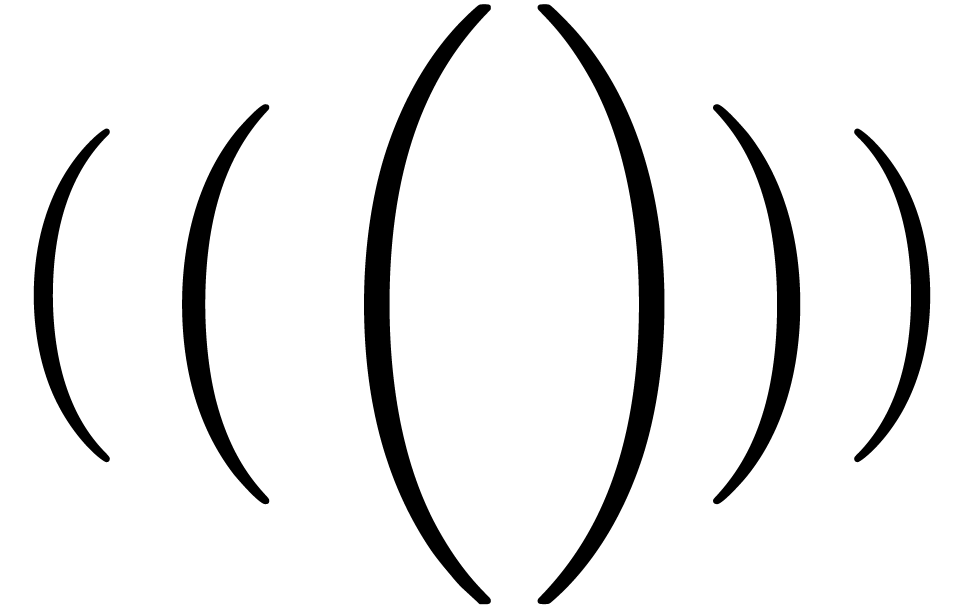
 ,
,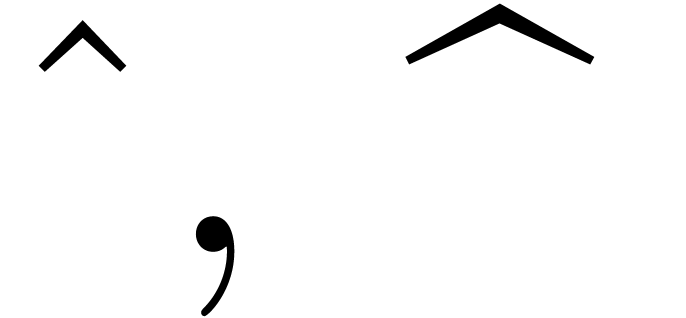 ,
, ),
),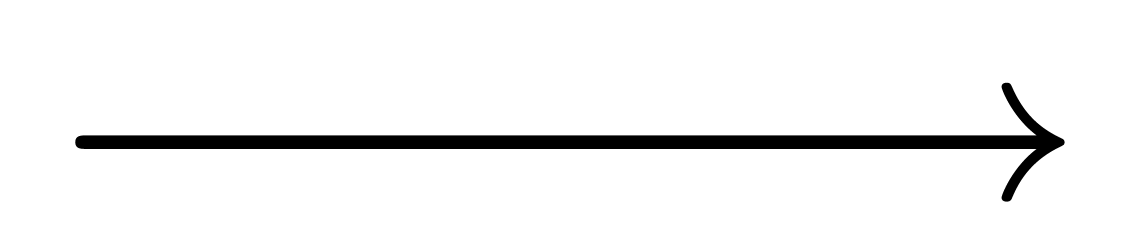 ,
, ).
). and
and 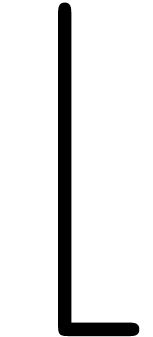 ),
),
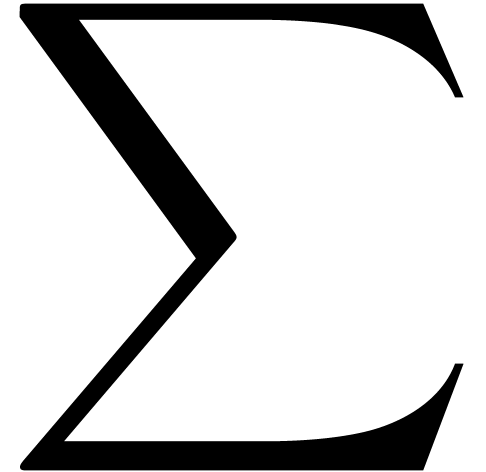

 ,
, ,
, ,
, ,
, ,
, ,
,