| A new zero-test for formal power
series |
|
Dépt. de Mathématiques
(Bât. 425)
Université Paris-Sud
91405 Orsay Cedex
France
Email: joris@texmacs.org
|
|
|
Abstract
In this paper, we present a new zero-test for expressions which are
constructed from formal power solutions to algebraic differential
equations using the ring operations and differentiation. We also provide
a survey of all existing methods that we know of and a detailed
comparison of these methods with our approach.
1Introduction
Zero-testing is an important issue on the analysis side of symbolic
computation. Standard mathematical notation provides a way of
representing many transcendental functions. However, trivial cases
apart, this notation gives rise to the following problems:
Often, one is interested in expressions which represent functions in a
ring. In that case, the third problem reduces to deciding when a given
expression represents the zero function.
As to the first two problems, one has to decide where and how we want
our functions to be defined. In this paper, we will be concerned with
expressions that represent formal power series (in fact, this approach
covers most elementary calculus on special functions, using analytic
continuation if necessary). The expressions will then be formed from the
constants and the indeterminates using the ring operations and power
series solutions to algebraic differential equations. The correctness
and non-ambiguity of expressions may be ensured by structural induction.
This may involve zero-testing for the series represented by
subexpressions.
Several classical approaches for zero-testing exist [9, 6, 10, 11, 7, 12]
and we provide a quick survey of them in section 2. Our new
zero-test, which is described in section 5, is based on a
similar approach as [10, 11, 12].
We believe the algorithm to be interesting for five main reasons:
-
We treat differential equations of arbitrary order.
-
Our method accommodates divergent power series solutions.
-
It reformulates previous work from [10, 11,
12] in the more standard setting of differential
algebra.
-
We believe it to be more efficient. With some more work, it might be
possible to give complexity bounds for the algorithm (or a modified
version of it) along the same lines as [12]. Such
bounds are also interesting in relation to “witness
conjectures” [17, 13, 16,
8].
-
On the longer run, the algorithm might generalize to the
multivariate setting of partial differential equations with initial
conditions on a subspace of dimension 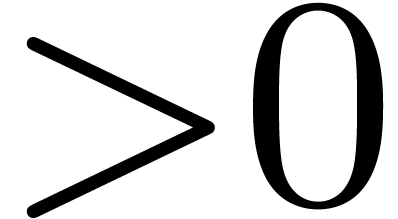 .
.
Throughout the paper, we will assume that the reader is familiar with
differential algebra and the notations used in this field; see section
3 and [2] for a nice introduction. The proof
of our algorithm also uses a result from the preprint [15],
which is too complicated to be presented here, although we do provide a
sketch of the proof in section 4.
We plan to provide some examples and more explanations in a forthcoming
journal paper. We are also writing a lecture note about the subject of
section 4. No implementations are available yet.
2A survey of the existing
approaches
A differentially algebraic power series is a power series 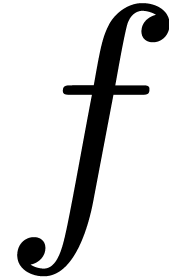 which satisfies a non-trivial algebraic differential
equation
which satisfies a non-trivial algebraic differential
equation 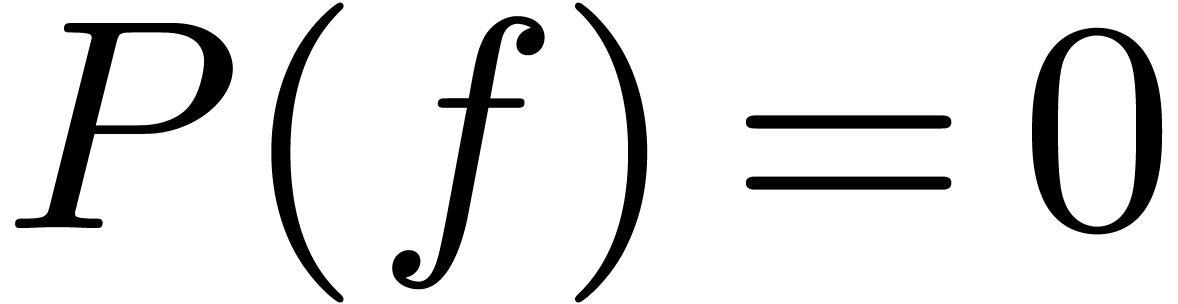 . Consider a power
series expression constructed from
. Consider a power
series expression constructed from  and the
constants in some field
and the
constants in some field  like
like  , using
, using  and left
composition of infinitesimal power series by differentially algebraic
power series
and left
composition of infinitesimal power series by differentially algebraic
power series  . Then it is a
classical problem to test whether such an expression represents zero.
There are many approaches for this problem.
. Then it is a
classical problem to test whether such an expression represents zero.
There are many approaches for this problem.
Structural approaches.
If the differentially algebraic power series are particularly simple,
then it is sometimes possible to characterize all possible relations
between the power series under consideration. This is clearly the case
if we restrict the differentially algebraic power series to be
algebraic.
A more interesting example is obtained when we also allow left
composition with 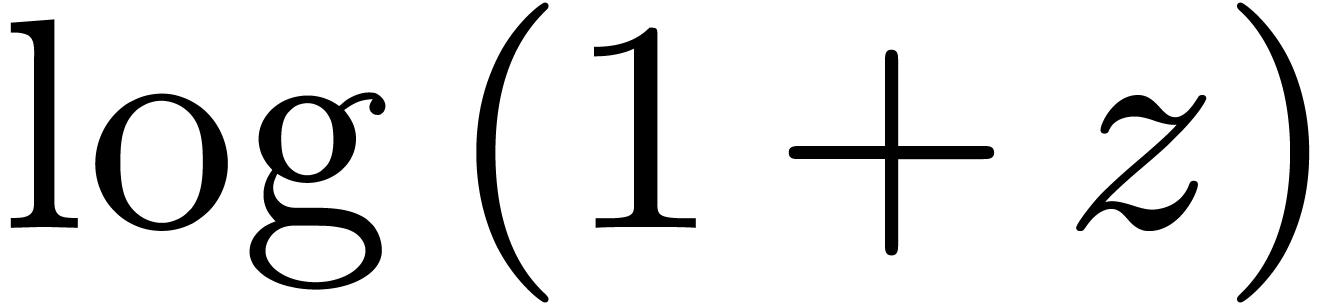 and
and 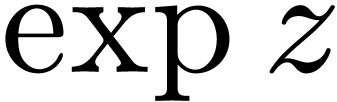 . In this case, the Ax theorem [1] and
the Risch structure theorem [9] may be used to design a
fast zero-test.
. In this case, the Ax theorem [1] and
the Risch structure theorem [9] may be used to design a
fast zero-test.
The structural approach may yield very efficient algorithms when it
works. However, it requires the characterization of all possible
relations in a given context, where we merely asked for a test whether a
particular one holds. Consequently, the approach usually only applies in
very specific situations.
Bounding the valuation.
An obvious way to test whether an expression represents the zero power
series is to obtain a bound for its valuation in terms of its size if
the expression does
not represent zero. Khovanskii has given
reasonably good uniform bounds (of the form
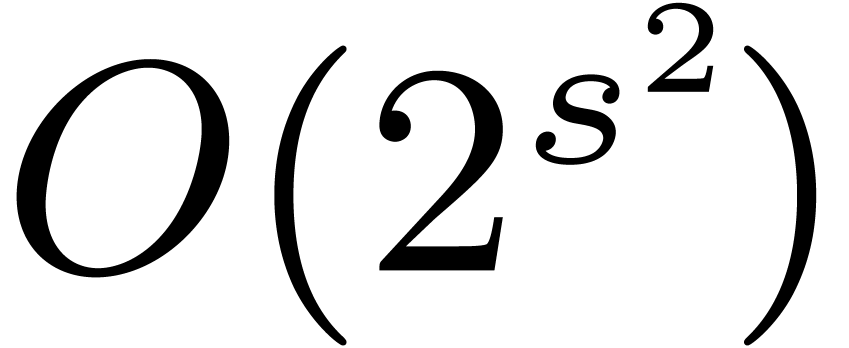 ,
, where

denotes the input
size) for the number of zeros for systems of real Pfaffian functions
[
6]. These bounds may be adapted to the power series
context.
This approach is interesting because it only requires fast power series
expansions [3, 14] for implementing a
zero-test. However, such a zero-test might be slow for expressions which
can be quickly rewritten to zero (like 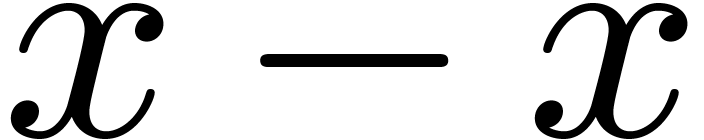 ,
where
,
where 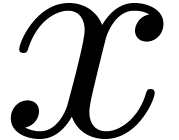 is a complicated expression). Also, if we
want the approach to be efficient, good bounds (such as the ones
predicted by witness conjectures [17, 13, 16, 8]) would be necessary. At the moment, we
only have Khovanskii-type bounds in the case of Pfaffian functions. A
new strategy for obtaining bounds, which might generalize to higher
order equations by adapting the algorithm in this paper, has been
proposed in [12]. However, the obtained bounds are still
doubly exponential.
is a complicated expression). Also, if we
want the approach to be efficient, good bounds (such as the ones
predicted by witness conjectures [17, 13, 16, 8]) would be necessary. At the moment, we
only have Khovanskii-type bounds in the case of Pfaffian functions. A
new strategy for obtaining bounds, which might generalize to higher
order equations by adapting the algorithm in this paper, has been
proposed in [12]. However, the obtained bounds are still
doubly exponential.
The logical approach.
From a theoretical point, it is also interesting to ask whether
zero-tests always exist. This question has been answered very
precisely and in a very general context by Denef and Lipschitz [
4,
5]. In the present setting of power series
expressions, their approach uses the well-known fact that the set of
differentially algebraic power series is closed under the ring
operations and composition. However, the equations one obtains for
sums, products,
etc. may be very complicated, so that
that approaches which essentially use this fact are deemed to be very
inefficient.
Groebner bases and saturation.
Another simple approach was proposed by Shackell in [
11]
(see the first algorithm). The idea is to keep all algebraic relations
which hold between a finite number of power series in a Groebner basis
 .
. If we want to test a new
relation, then we include it in

and look
whether we obtain a contradiction. If not, then we keep on adding the
derivatives of all relations in

into
 .
. Under certain hypotheses, this
process always ends up in a contradiction or a proof that the added
relations all hold. However, the approach does not seem to provide any
reasonable complexity bounds.
Varying the initial conditions.
Yet another interesting approach [
7] to the zero-test
problem is to change our point of view. The differentially algebraic
power series
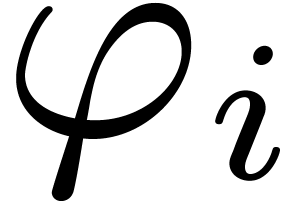
at the top of this section are
usually specified by a finite number of algebraic differential
equations and initial conditions. Now instead of asking whether a
given expression represents zero, we may ask for which initial
conditions for

the expression represents zero.
It turns out that the set of such initial conditions is a closed
algebraic set  . The
“difficult” cases in the zero-test correspond to the
situation in which the original initial conditions are in the closure of
an open subset
. The
“difficult” cases in the zero-test correspond to the
situation in which the original initial conditions are in the closure of
an open subset  of
of  where
the answer is “easier”. It would be interesting to
investigate whether this approach of varying the initial conditions may
yield a better power series analogue for Khovanskii's results. A present
disadvantage of the method is that it only applies in the convergent
case and that it is not yet clear how to obtain complexity bounds.
where
the answer is “easier”. It would be interesting to
investigate whether this approach of varying the initial conditions may
yield a better power series analogue for Khovanskii's results. A present
disadvantage of the method is that it only applies in the convergent
case and that it is not yet clear how to obtain complexity bounds.
The generalized solution approach.
The approach in this paper is similar to the algorithm in [
10].
A better understanding (and a complexity analysis) of this algorithm
were obtained in [
12]. In order to explain the underlying
idea behind the present algorithm, let us assume for simplicity that
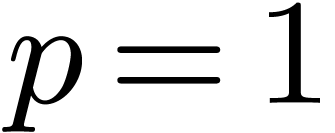
and that
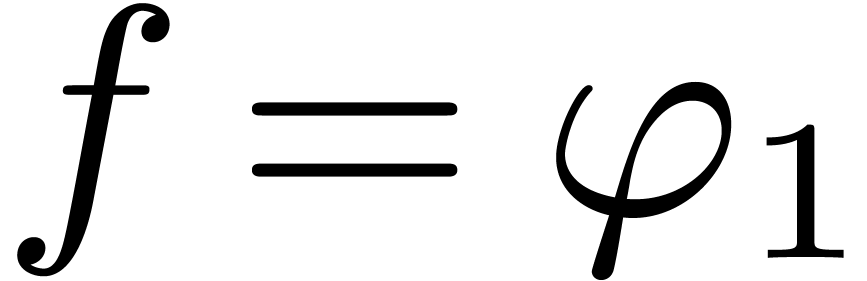
satisfies the
algebraic differential equation
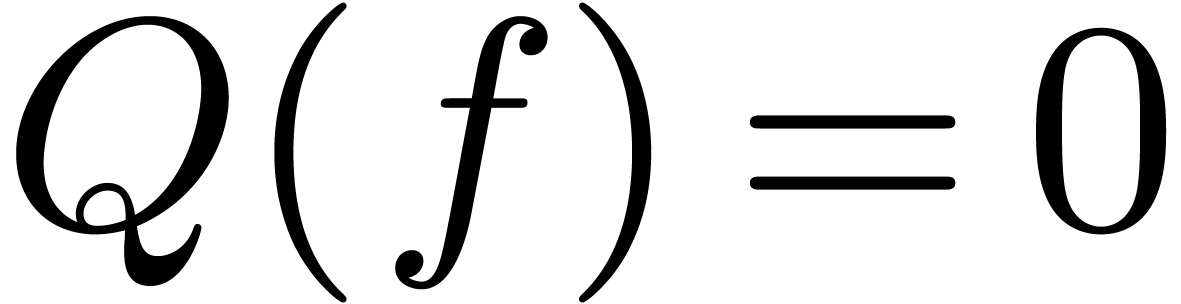 .
.
Now suppose that we want to test whether  for a
second algebraic differential polynomial
for a
second algebraic differential polynomial  .
Then we first use differential algebra to determine a third equation
.
Then we first use differential algebra to determine a third equation
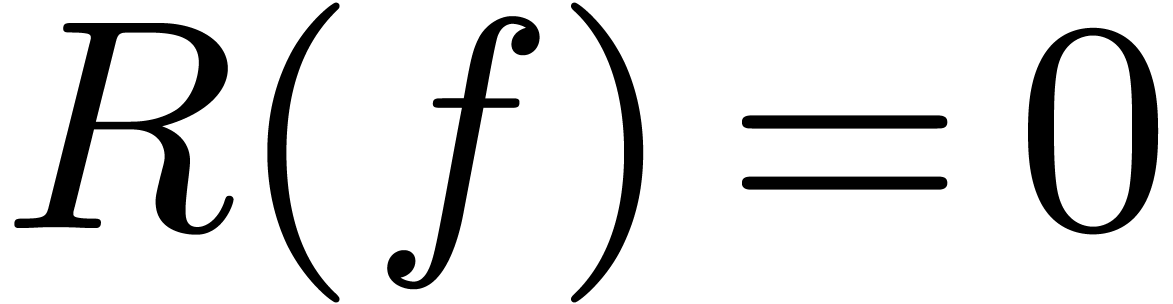 which is equivalent to
which is equivalent to 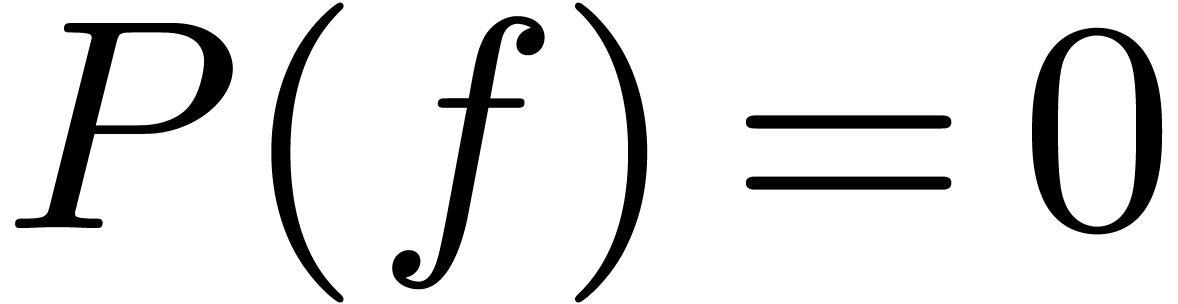 and
and 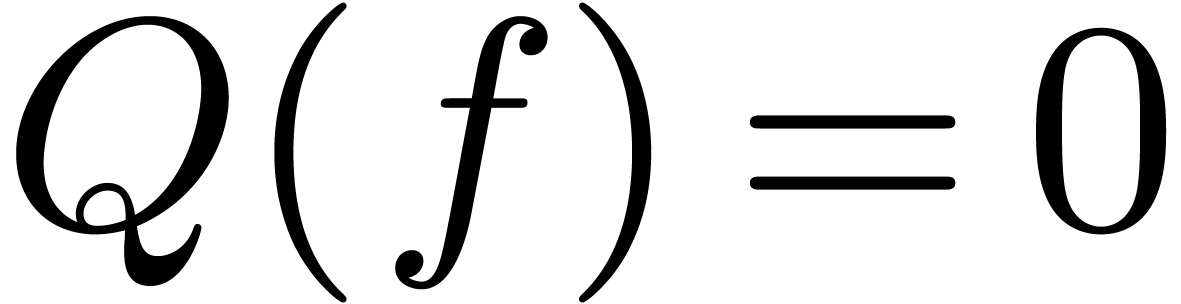 under certain non-degeneracy conditions. Now
we consider
under certain non-degeneracy conditions. Now
we consider 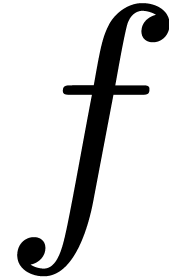 as an indeterminate and try to solve
as an indeterminate and try to solve
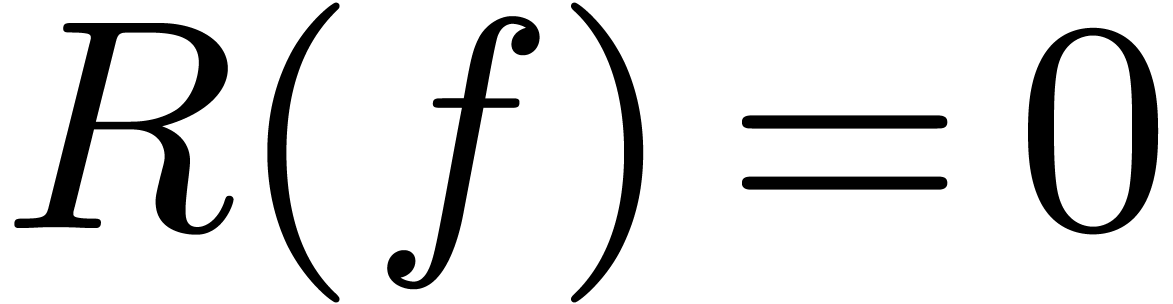 in a suitable differential overfield
in a suitable differential overfield  of
of 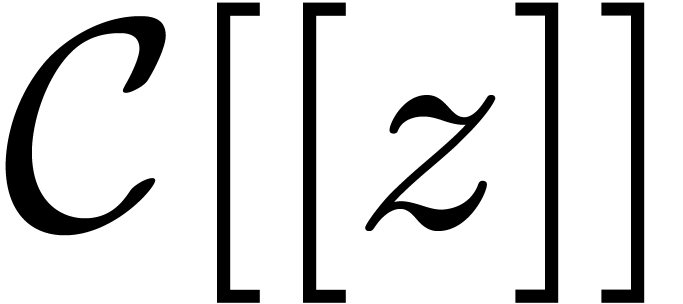 . This field
. This field
 consists of so called logarithmic transseries
and has the nice property that
consists of so called logarithmic transseries
and has the nice property that 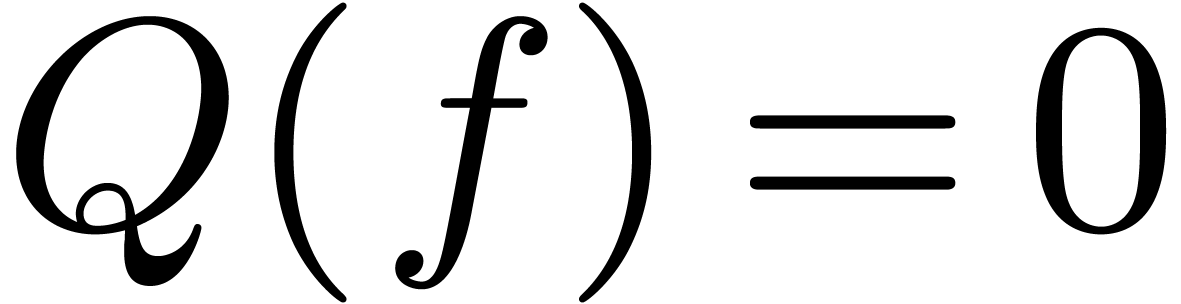 still has a
unique solution in
still has a
unique solution in  for the initial conditions of
for the initial conditions of
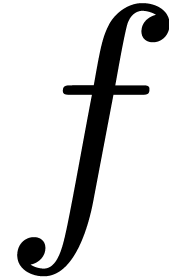 . Hence,
. Hence, 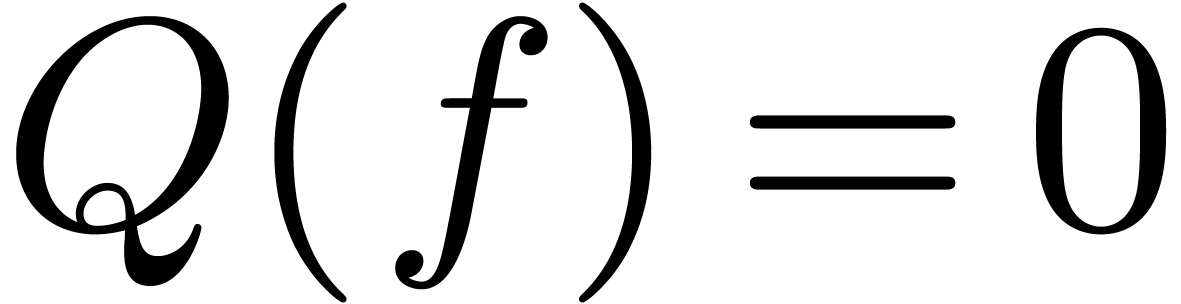 if and only if
if and only if 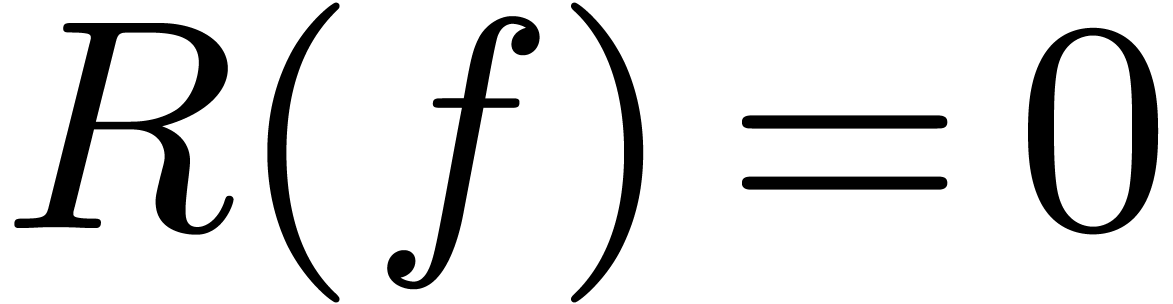 admits a solution
admits a solution 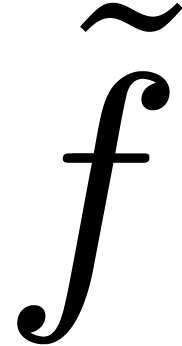 in
in  , in which
case we necessarily have
, in which
case we necessarily have 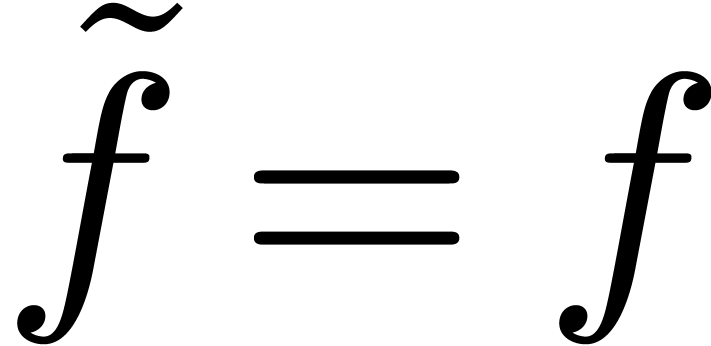 .
.
The approach has the advantages that it accommodates divergent
differentially algebraic power series  and that
the degeneracy of the initial conditions is not amplified during the
resolution process. We also have a good hope to obtain complexity bounds
along the same lines as in [12] and some hope to generalize
the approach to the multivariate setting. We finally expect the approach
to be one of the most efficient ones in practice, although no
implementations are available yet.
and that
the degeneracy of the initial conditions is not amplified during the
resolution process. We also have a good hope to obtain complexity bounds
along the same lines as in [12] and some hope to generalize
the approach to the multivariate setting. We finally expect the approach
to be one of the most efficient ones in practice, although no
implementations are available yet.
3The effective setup
Let  be an effective field of constants
of characteristic
be an effective field of constants
of characteristic  . This
means that all elements of
. This
means that all elements of  can be represented
effectively and that there are algorithms for performing the field
operations and testing equality (or, equivalently, for zero-testing).
can be represented
effectively and that there are algorithms for performing the field
operations and testing equality (or, equivalently, for zero-testing).
Let  be an effective differential ring
(i.e. the differentiation is effective too). We assume that
the elements of
be an effective differential ring
(i.e. the differentiation is effective too). We assume that
the elements of  are formal power series in
are formal power series in  , that
, that 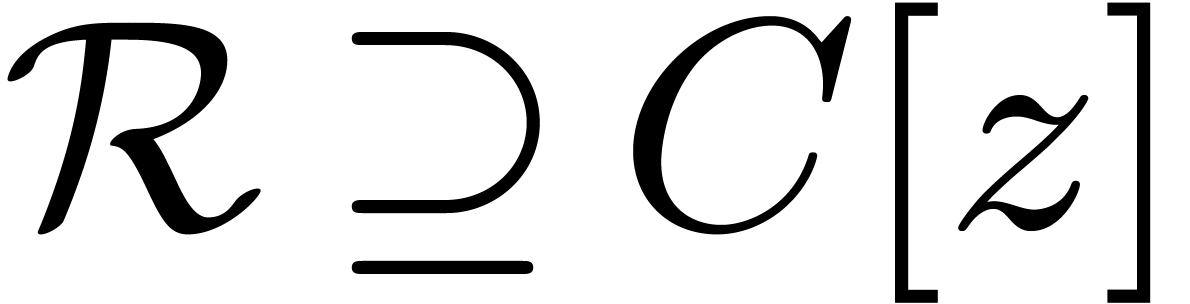 , and that the differentiation
, and that the differentiation  on
on  corresponds to the differentiation
corresponds to the differentiation 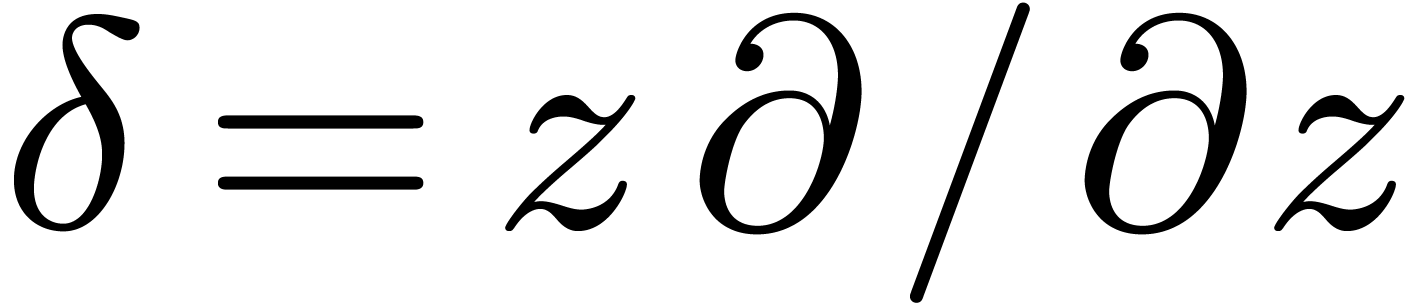 on
on  . Moreover,
we will assume that
. Moreover,
we will assume that  is an effective power
series domain, i.e. there exists an algorithm which
takes
is an effective power
series domain, i.e. there exists an algorithm which
takes 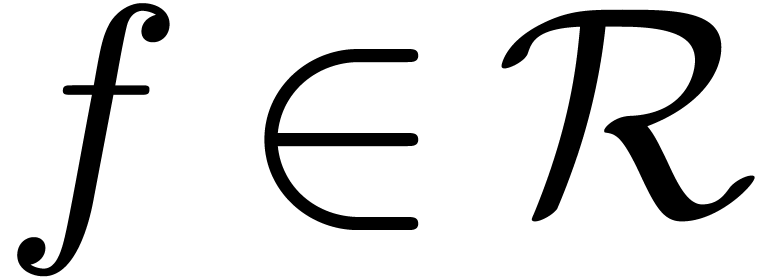 and
and  on input and
which computes the coefficient
on input and
which computes the coefficient  of
of  in
in  . Notice
that this implies the existence of an algorithm to compute the valuation
of
. Notice
that this implies the existence of an algorithm to compute the valuation
of 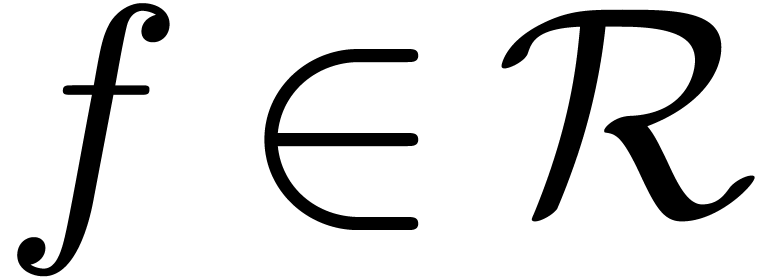 .
.
Now consider a non zero differential polynomial 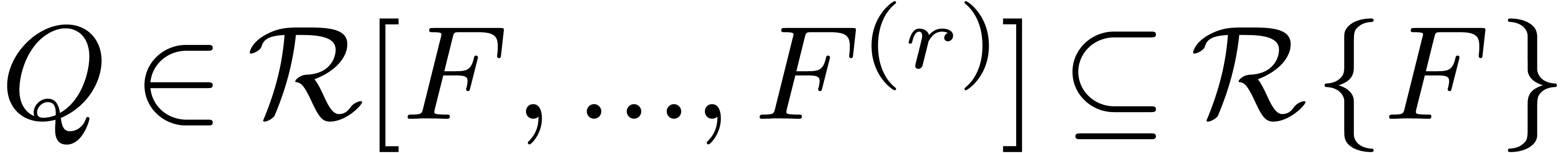 of order
of order 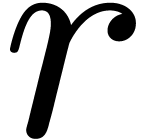 (recall that
(recall that 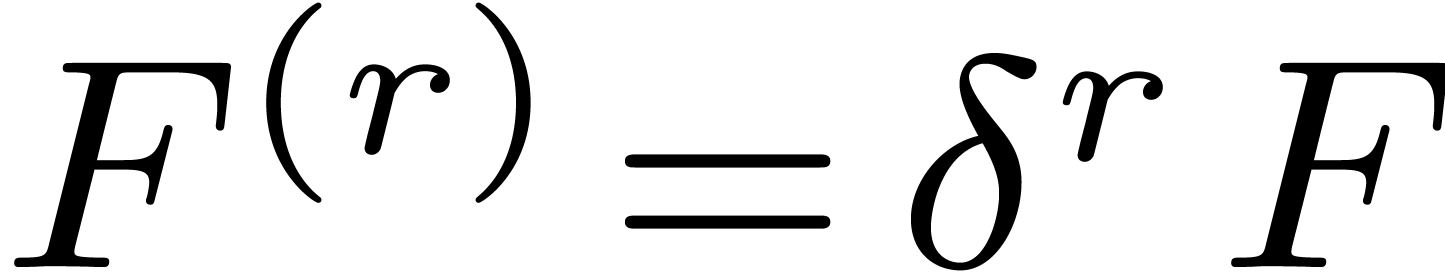 ) and a power series solution
) and a power series solution 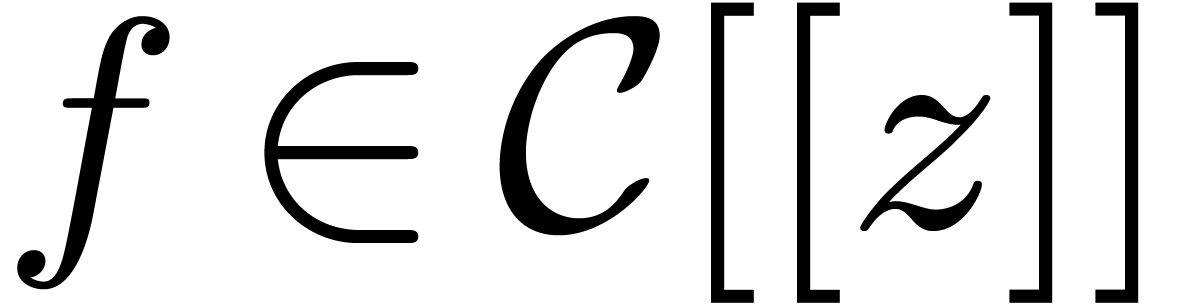 to
to 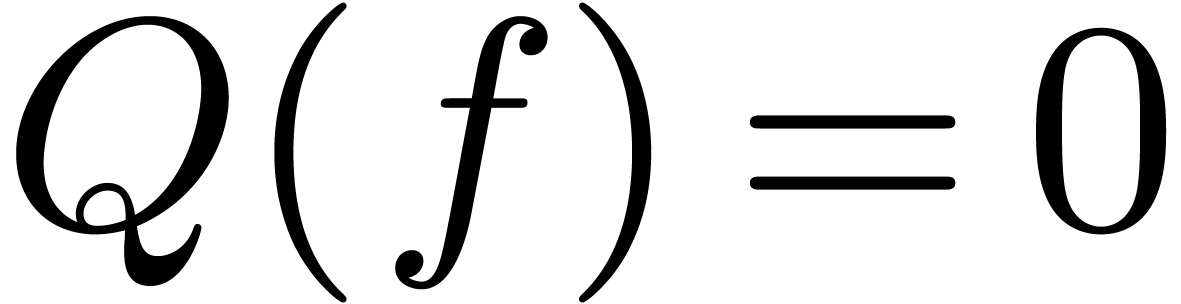 . We will assume that
. We will assume that  is not a multiple solution, i.e.
is not a multiple solution, i.e. 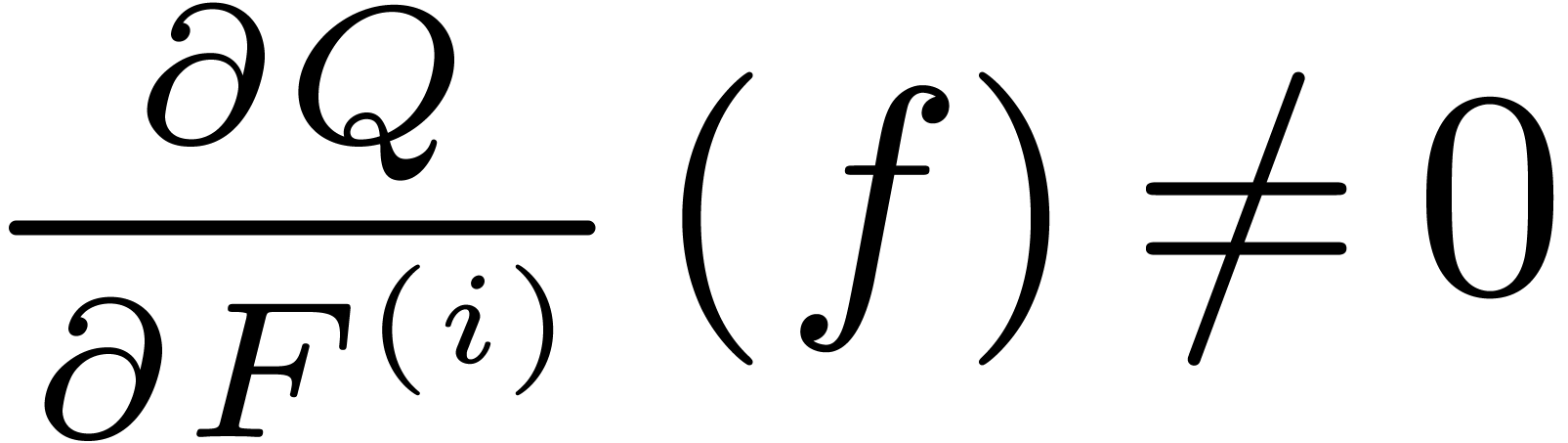 for some
for some 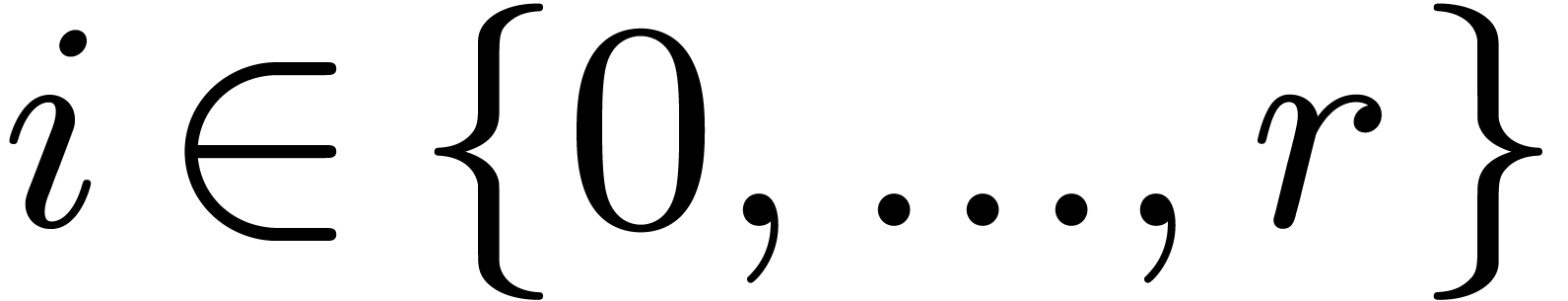 (if
(if  is a multiple solution, then we may always replace
is a multiple solution, then we may always replace  by a non-zero
by a non-zero  and continue doing this until
and continue doing this until  is no longer a multiple solution). Choose
is no longer a multiple solution). Choose 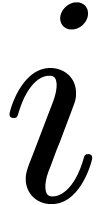 such that the valuation of
such that the valuation of 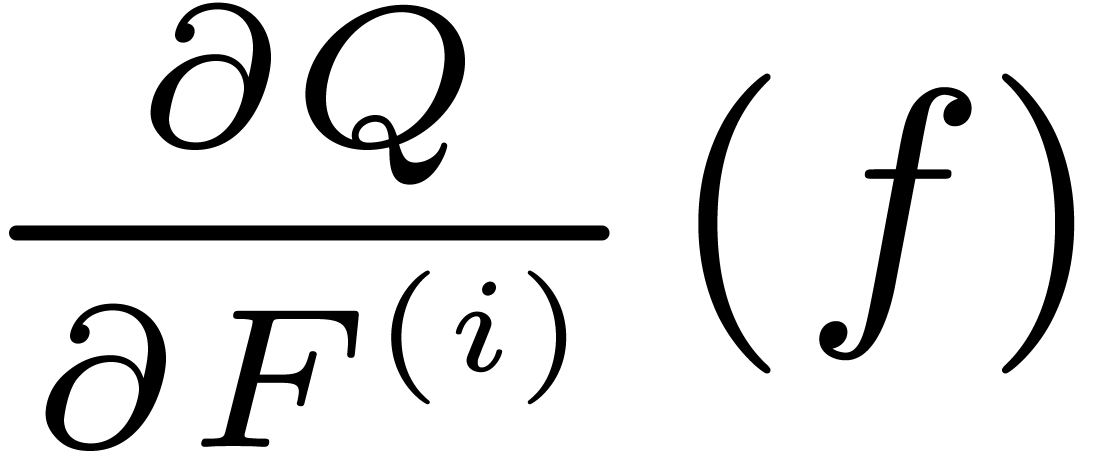 is
minimal, say
is
minimal, say 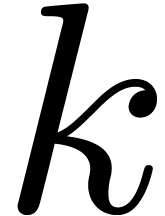 . Then modulo a
transformation of the form
. Then modulo a
transformation of the form
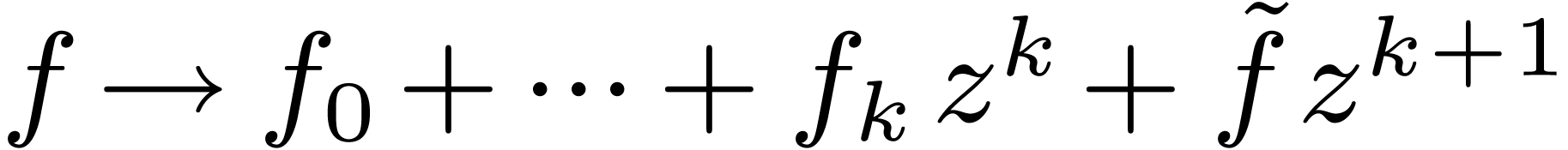
and division of the equation by a suitable power of  , we may also assume that
, we may also assume that
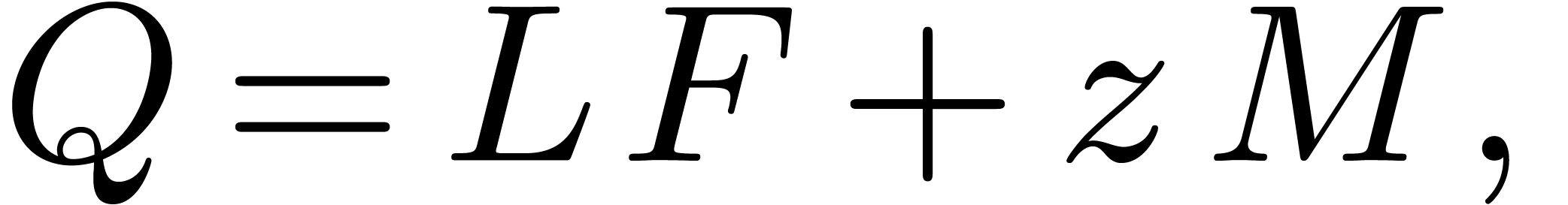 |
(1) |
where 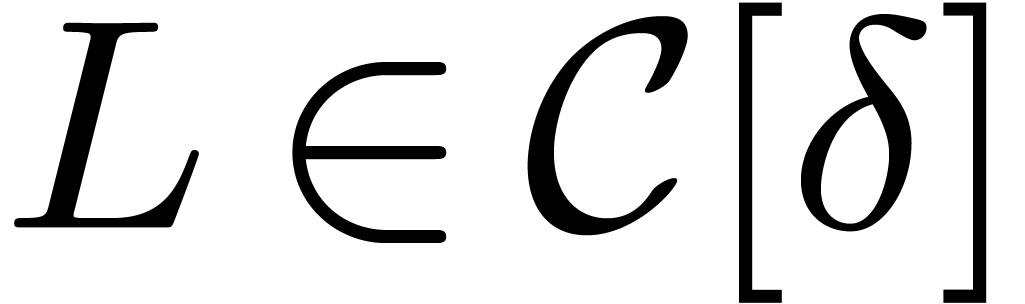 and
and 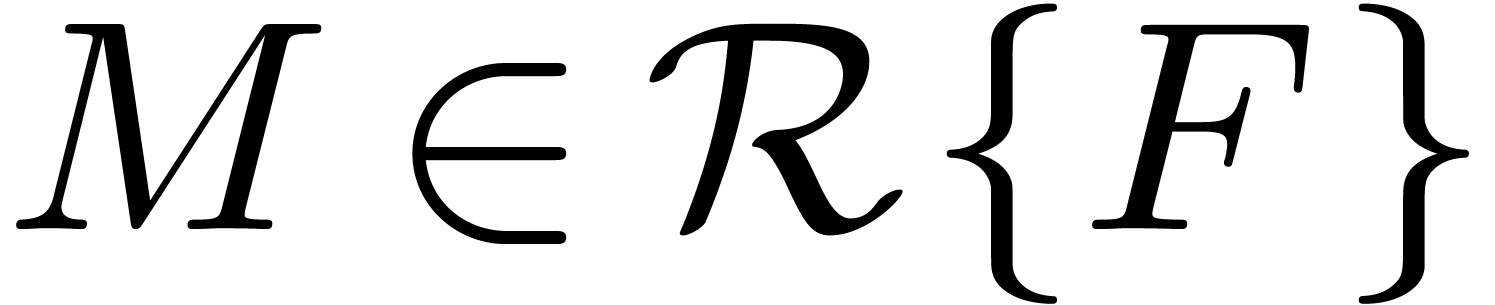 .
Let
.
Let 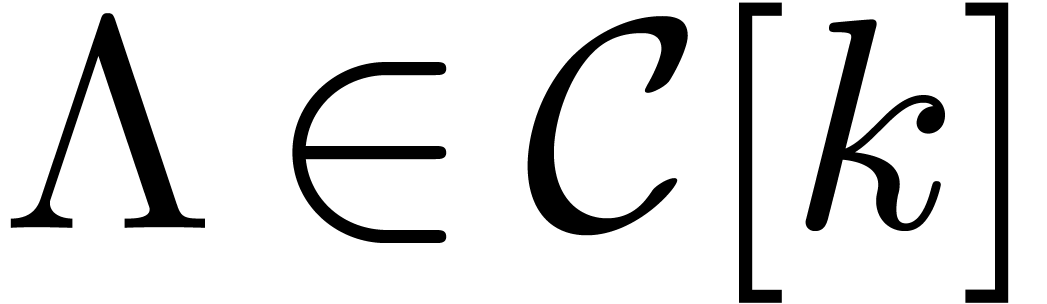 be the polynomial we get from
be the polynomial we get from  when reinterpreting
when reinterpreting  as an
indeterminate
as an
indeterminate  . Then (1) yields a recurrence relation for all but a finite number of
coefficients of
. Then (1) yields a recurrence relation for all but a finite number of
coefficients of  :
:
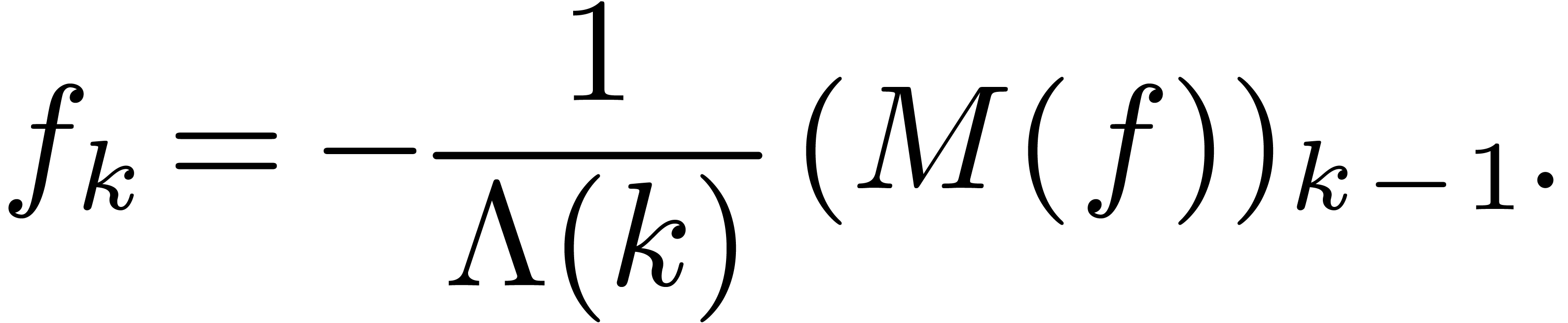 |
(2) |
Indeed, the only 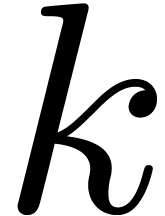 for which this relation does
not hold are roots of
for which this relation does
not hold are roots of  . There
are at most
. There
are at most 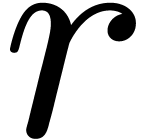 such
such 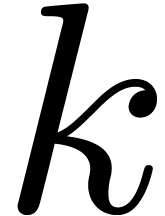 and
they correspond to the initial conditions for
and
they correspond to the initial conditions for 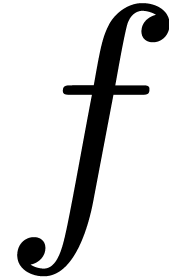 . Let
. Let  be the largest root of
be the largest root of
 in
in  (or
(or 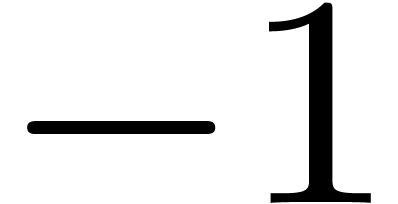 if such a root does not exist). Then we notice in particular that
if such a root does not exist). Then we notice in particular that 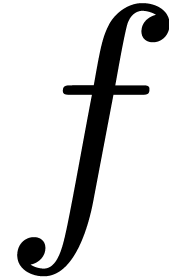 is the unique solution to
is the unique solution to 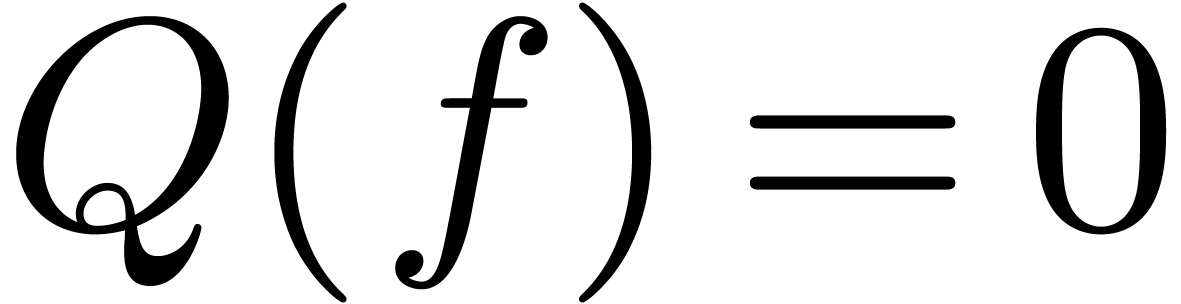 whose first
whose first  coefficients are
coefficients are  .
.
In what follows, we will show that the differential ring 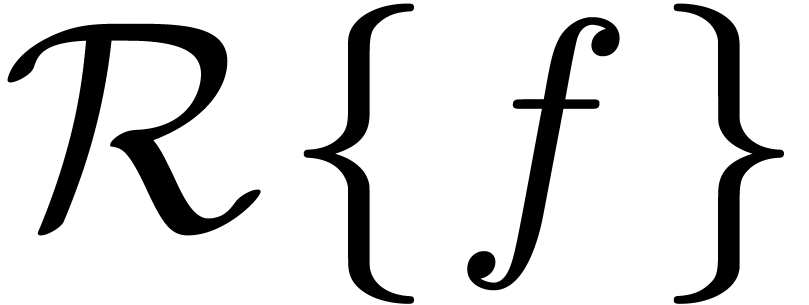 is again an effective power series domain. Now elements in
is again an effective power series domain. Now elements in
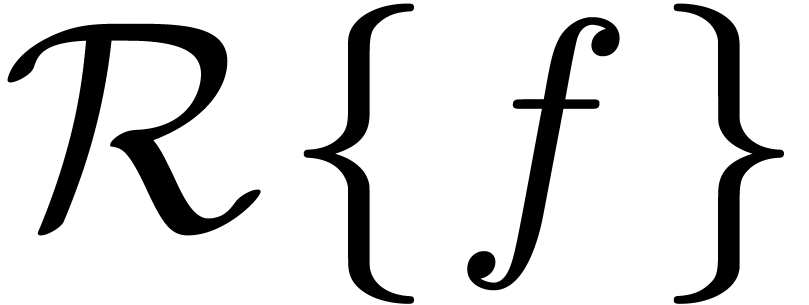 can naturally be represented as the images of
differential polynomials in
can naturally be represented as the images of
differential polynomials in 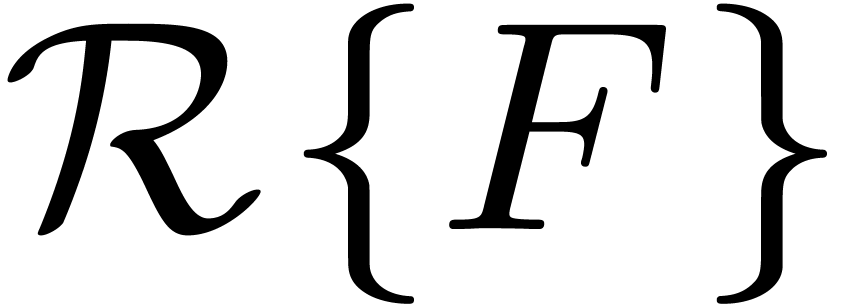 under the
substitution
under the
substitution 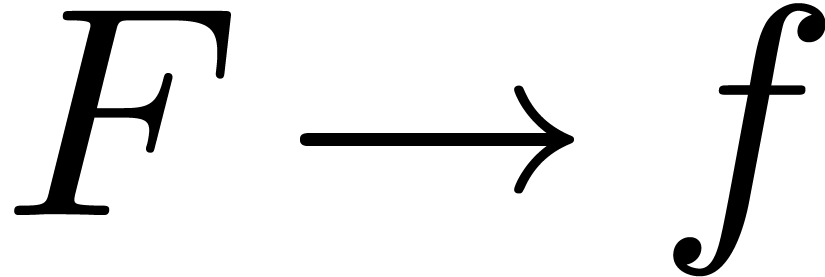 . It therefore
suffices to design an algorithm to test whether
. It therefore
suffices to design an algorithm to test whether 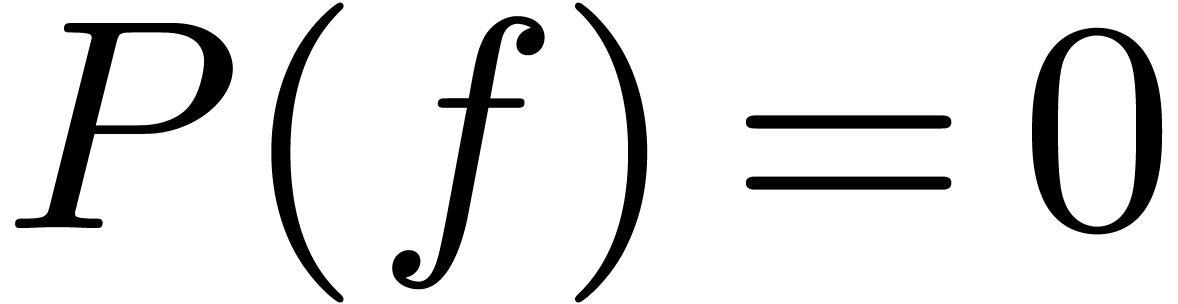 for a given differential polynomial
for a given differential polynomial 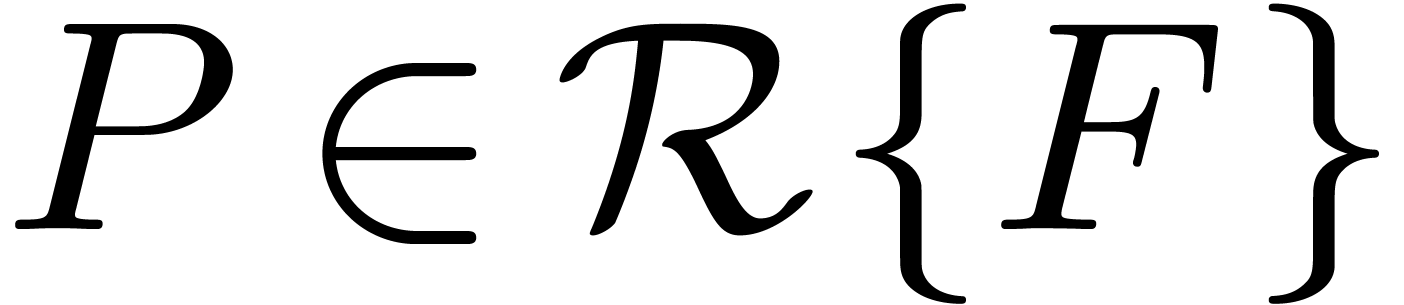 .
Our algorithm is based on Ritt reduction and the resolution of algebraic
equation in more general rings of formal power series. We will use
standard notations from differential algebra:
.
Our algorithm is based on Ritt reduction and the resolution of algebraic
equation in more general rings of formal power series. We will use
standard notations from differential algebra:
Remark 1. At a first glance, our
setting may seem less general than the one in the beginning of section
2. However, since we will prove that 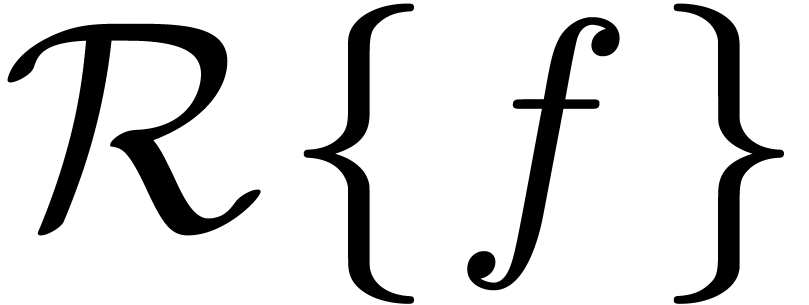 is again an effective power series domain, we may repeat the
construction after replacing
is again an effective power series domain, we may repeat the
construction after replacing 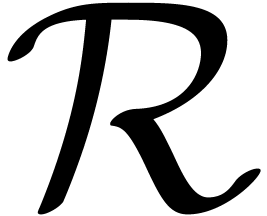 by
by 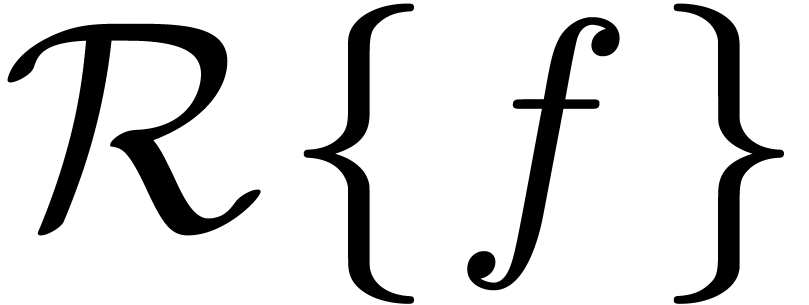 , and add as many other functions
, and add as many other functions  as we like. In fact, it suffices to add one
as we like. In fact, it suffices to add one 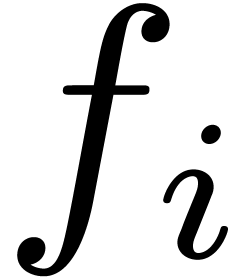 for each new subexpression of the form
for each new subexpression of the form 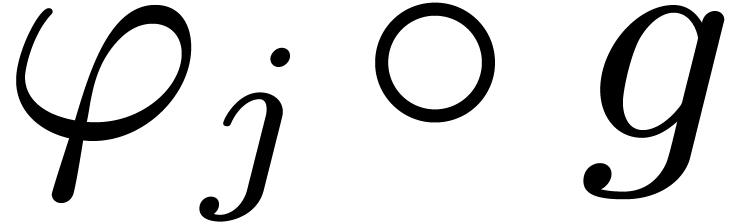 .
.
4Logarithmic transseries solutions
to algebraic differential equations
It is well known that any non-trivial algebraic equation with
coefficients in  has a solution in the field
has a solution in the field  of Puiseux series over the algebraic closure
of Puiseux series over the algebraic closure  of
of  . We
will sketch the proof of an analogous result in the case of algebraic
differential equations. For a full proof (of a more general result) we
refer to [15].
. We
will sketch the proof of an analogous result in the case of algebraic
differential equations. For a full proof (of a more general result) we
refer to [15].
4.1Logarithmic transseries
In order to solve equations of the form 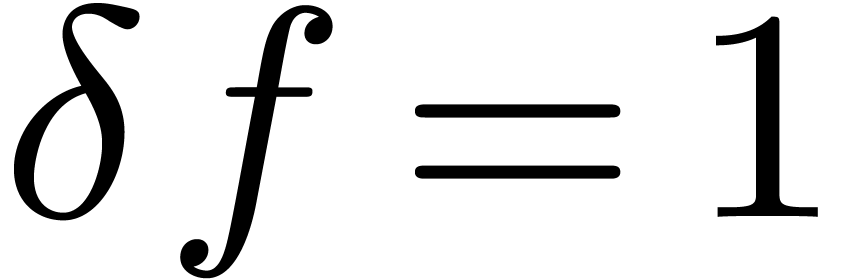 ,
it is clear that solutions to such equations might involve logarithms.
In fact, they may even involve iterated logarithms.
,
it is clear that solutions to such equations might involve logarithms.
In fact, they may even involve iterated logarithms.
Let  be the totally ordered group of
logarithmic monomials with powers in
be the totally ordered group of
logarithmic monomials with powers in  . More precisely, the elements of
. More precisely, the elements of  are monomials
are monomials
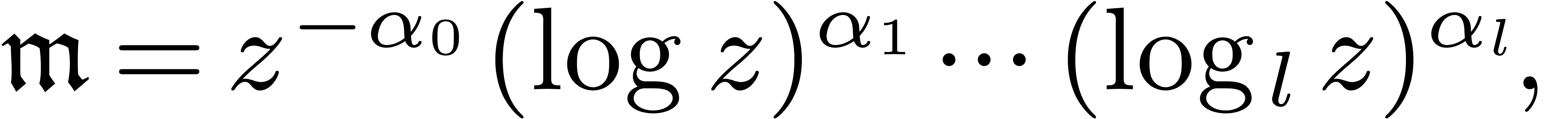 |
(3) |
where 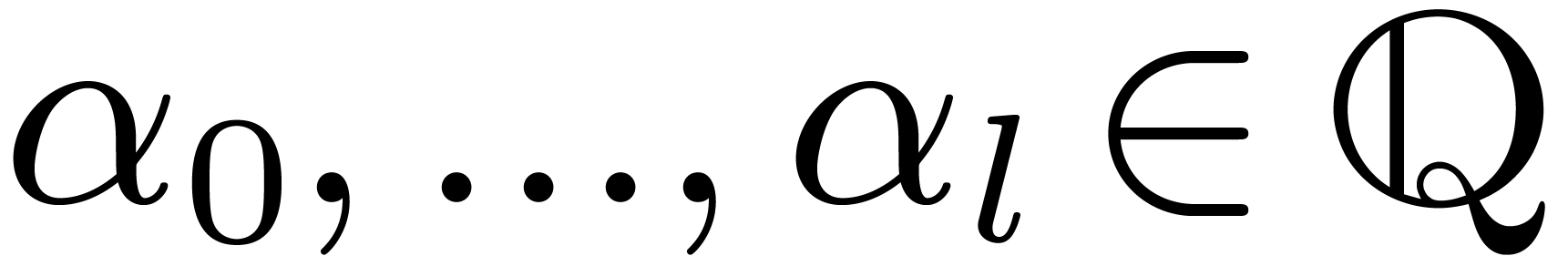 and
and 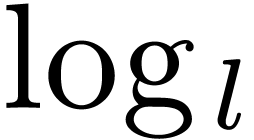 stands for the
stands for the
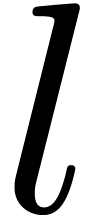 -th iterated logarithm. Given
such a monomial, we write
-th iterated logarithm. Given
such a monomial, we write  if and only if
if and only if 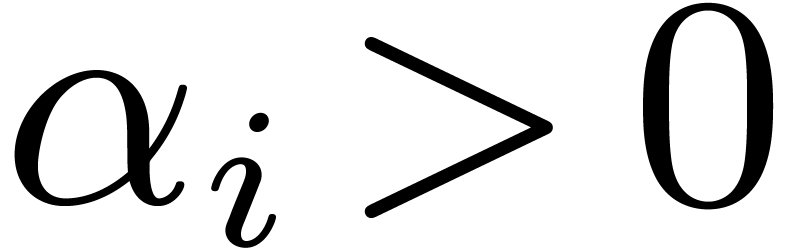 , where
, where  denotes the least
denotes the least  with
with 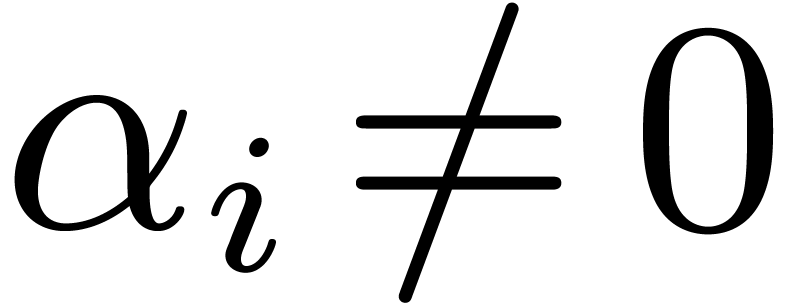 in (3). This defines a total ordering
in (3). This defines a total ordering  on
on  . The asymptotic relation
. The asymptotic relation
 corresponds to writing
corresponds to writing 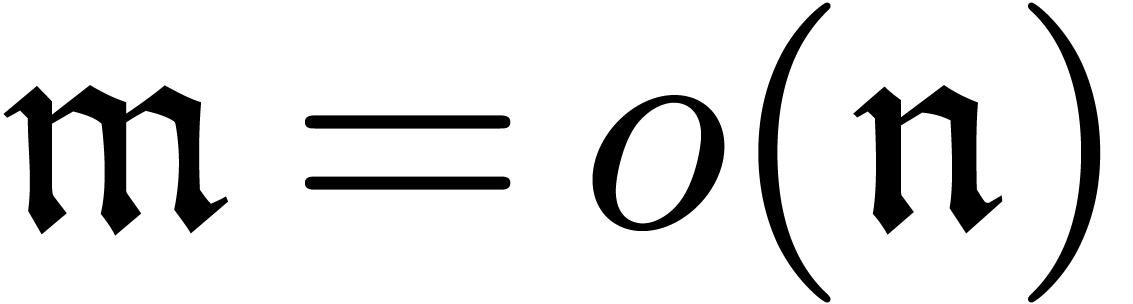 as
as 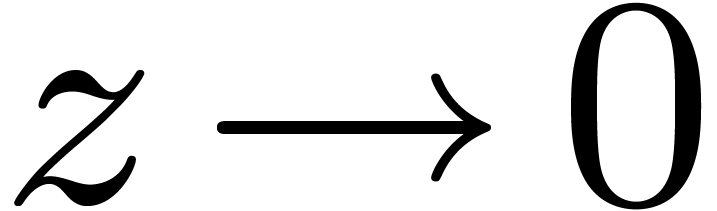 in analysis.
in analysis.
A subset 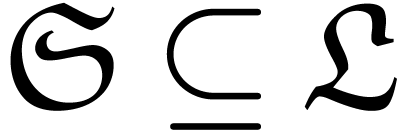 is said to be grid-based, if
there exist monomials
is said to be grid-based, if
there exist monomials  and
and  in
in  , such that
, such that 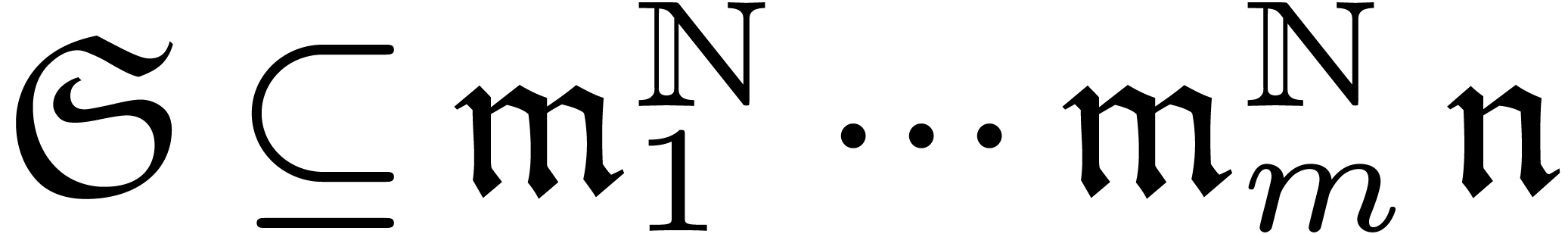 . A grid-based logarithmic transseries
is a mapping
. A grid-based logarithmic transseries
is a mapping  with grid-based support. We will
usually write such series using the infinite sum notation
with grid-based support. We will
usually write such series using the infinite sum notation  and we denote the set of all logarithmic transseries by
and we denote the set of all logarithmic transseries by
 . Since the support of each
non-zero
. Since the support of each
non-zero  is grid-based (whence well-ordered),
this support admits a
is grid-based (whence well-ordered),
this support admits a  -maximal
element
-maximal
element  which is called the dominant
monomial of
which is called the dominant
monomial of  .
.
It can be shown [13] that  is a
field for the operations
is a
field for the operations
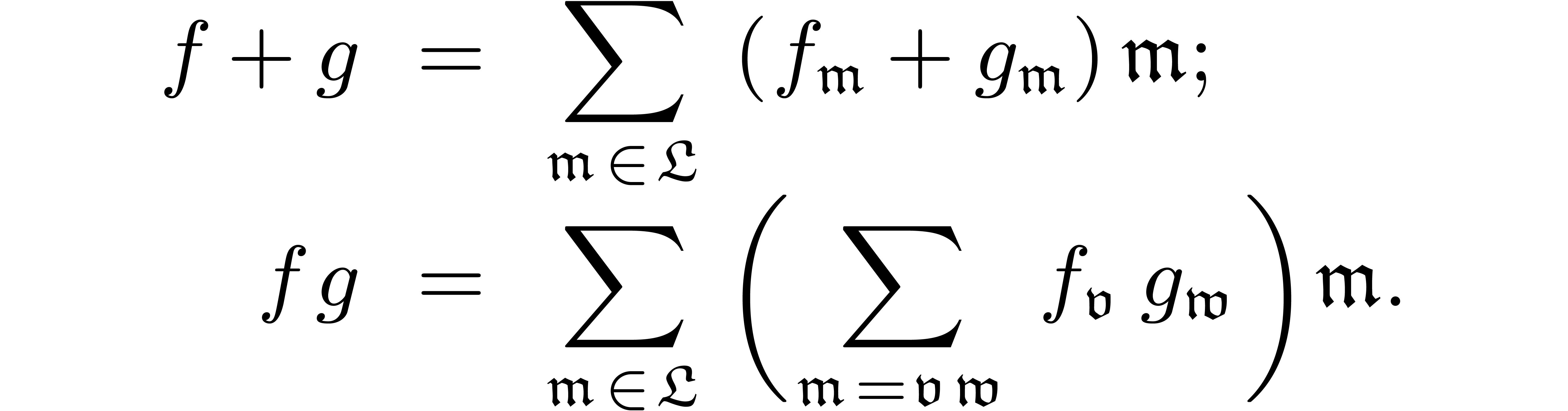
In the second formula, the grid-based support property ensures that  is a finite sum. There also exists a natural
derivation
is a finite sum. There also exists a natural
derivation  on
on  ,
which sends each monomial
,
which sends each monomial  of the form (3)
to
of the form (3)
to
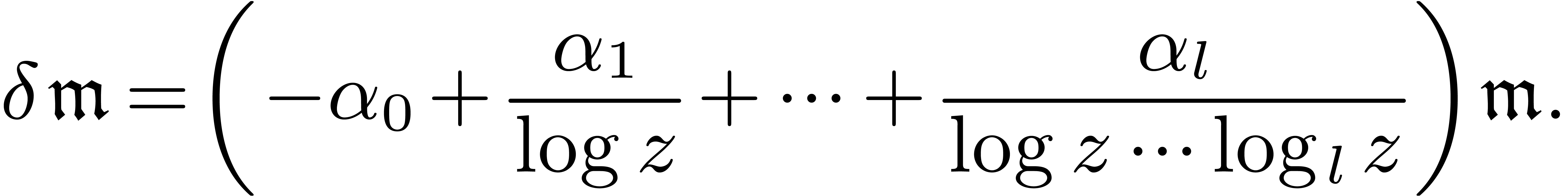 |
(4) |
This derivation extends to the whole of  by
(infinitary) “strong linearity” [13].
by
(infinitary) “strong linearity” [13].
Before proving that solutions to algebraic differential equations with
coefficients in  always exist, we first observe
that we have the following uniqueness result:
always exist, we first observe
that we have the following uniqueness result:
Lemma 2. Let 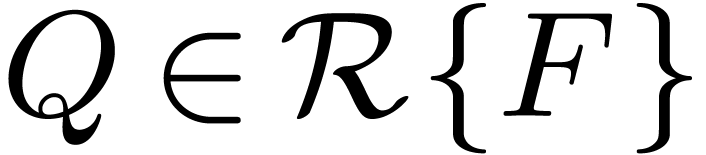 be a differential polynomial of the form (1), let
be a differential polynomial of the form (1), let 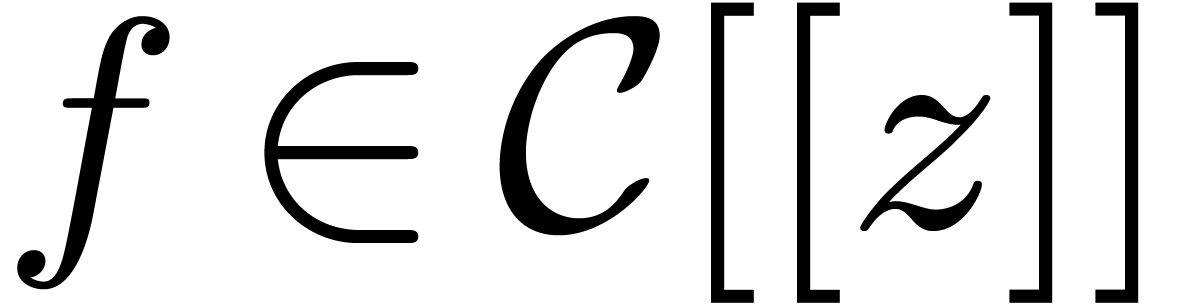 be a
solution to
be a
solution to 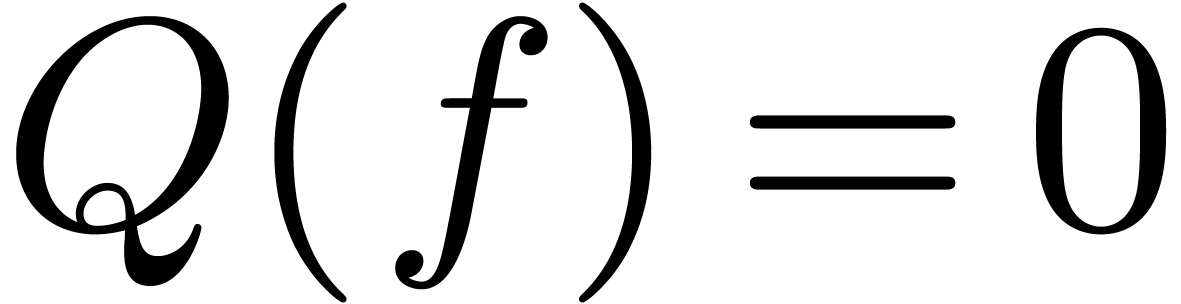 and let
and let  be
defined as in section 3. Then the equation
be
defined as in section 3. Then the equation 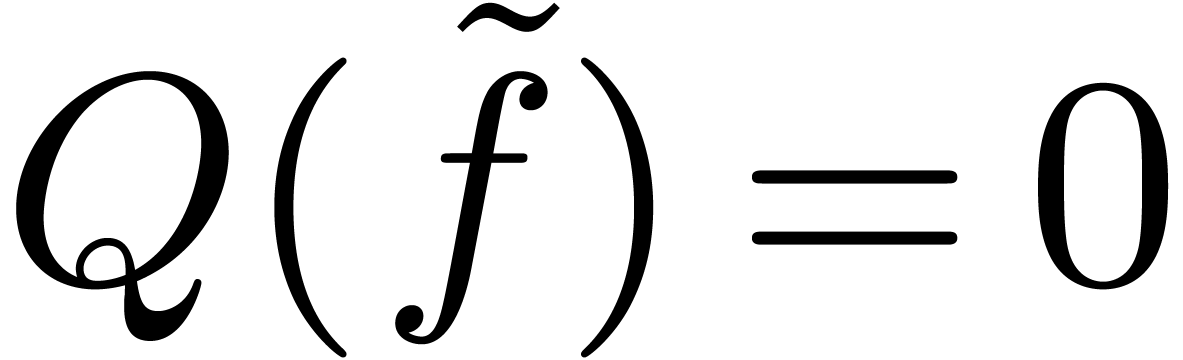 with side condition
with side condition 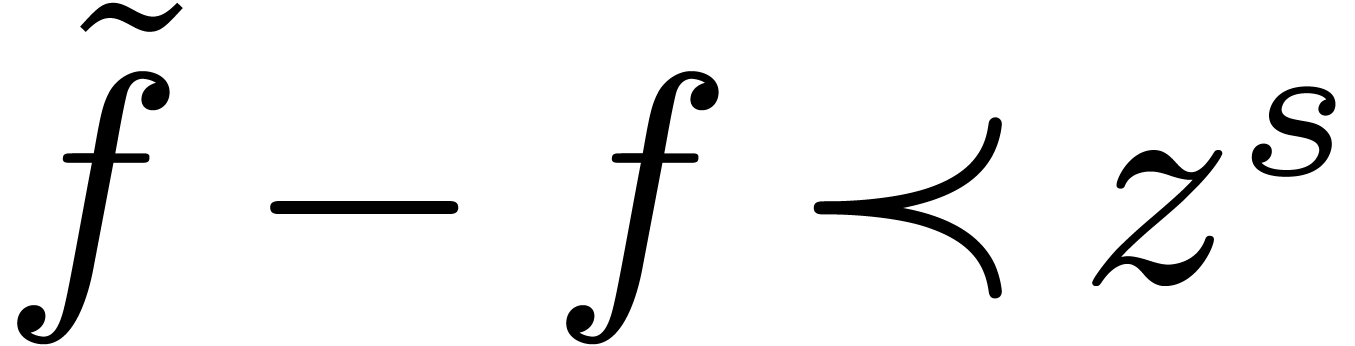 admits
admits 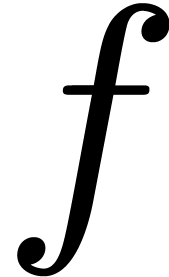 as its unique solution in
as its unique solution in  .
.
Proof. Each series 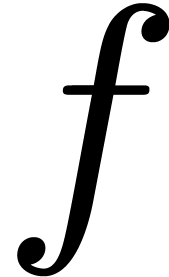 in
in  may be expanded as a Puiseux series in
may be expanded as a Puiseux series in 
 |
(5) |
where the coefficients 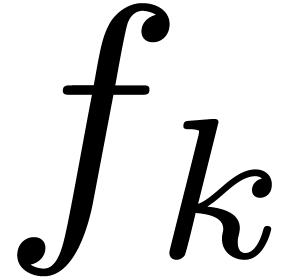 are series in
are series in  and
and  . Notice
that we may interpret
. Notice
that we may interpret  as the lexicographical
product of
as the lexicographical
product of  and
and  .
For the expansion (5), the recurrence relation (2)
still determines the coefficients of
.
For the expansion (5), the recurrence relation (2)
still determines the coefficients of  in a unique
way for all
in a unique
way for all  .
.
4.2Asymptotic differential equations
A classical way to solve algebraic equations over power series is to use
the Newton polygon method. We have generalized this method to algebraic
differential equations. In fact, it is more convenient to solve
asymptotic differential equations of the form
 |
(6) |
where 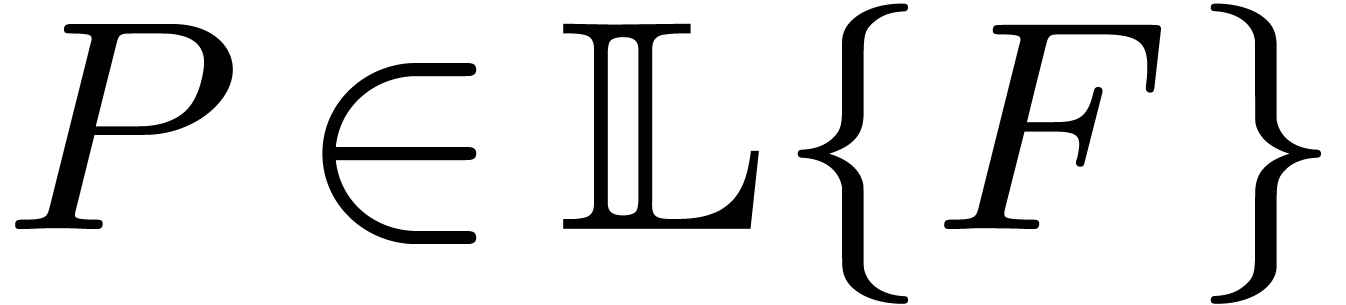 and
and 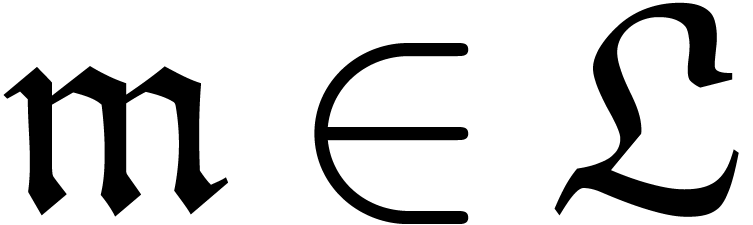 .
In the sequel, we will assume that
.
In the sequel, we will assume that  is
algebraically closed.
is
algebraically closed.
In order to solve (6), we start by determining all possible
dominant monomials  of non-zero solutions and
their corresponding coefficients. Actually, it is convenient to
characterize such potential dominant monomials first. It
suffices to characterize when
of non-zero solutions and
their corresponding coefficients. Actually, it is convenient to
characterize such potential dominant monomials first. It
suffices to characterize when 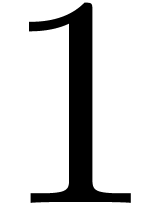 is a potential
dominant monomial: we will then say that
is a potential
dominant monomial: we will then say that  is a
potential dominant monomial, if
is a
potential dominant monomial, if 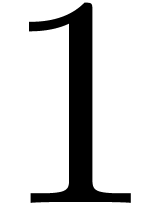 is a potential
dominant monomial for the equation
is a potential
dominant monomial for the equation

Here 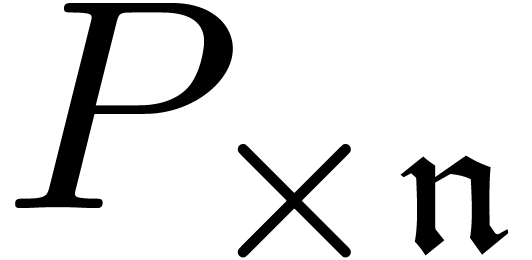 denotes the unique differential polynomial
in
denotes the unique differential polynomial
in  with
with  for all
for all  .
.
Write 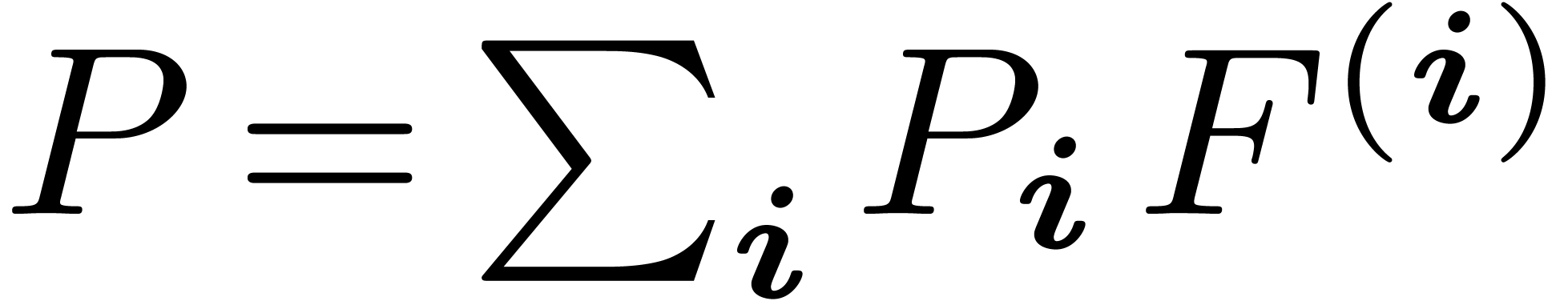 using multi-indices
using multi-indices 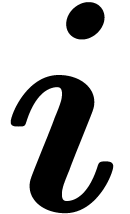 and let
and let  . Then the
dominant part of
. Then the
dominant part of  is defined to be the
scalar differential polynomial
is defined to be the
scalar differential polynomial
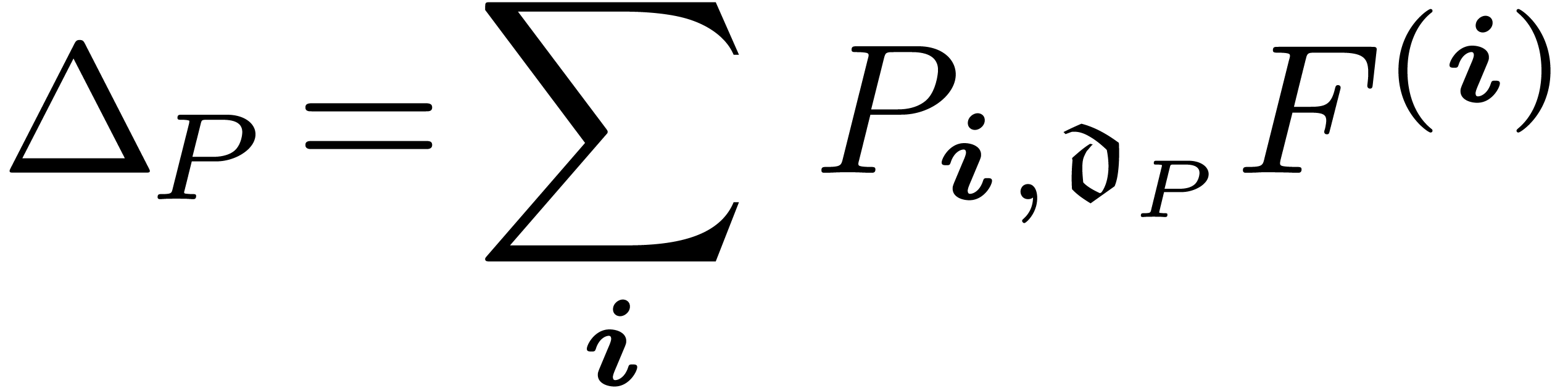
in 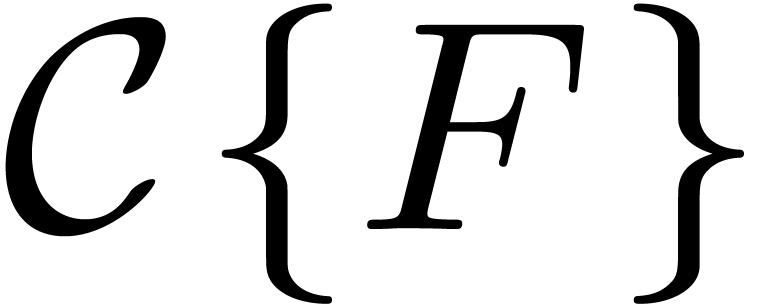 , where
, where 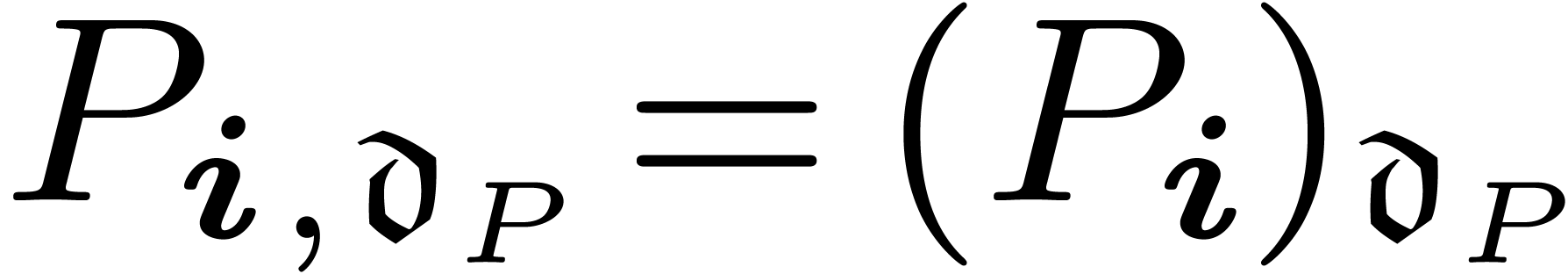 . We also define the dominant part
. We also define the dominant part  of
of  w.r.t.
w.r.t.  by
by
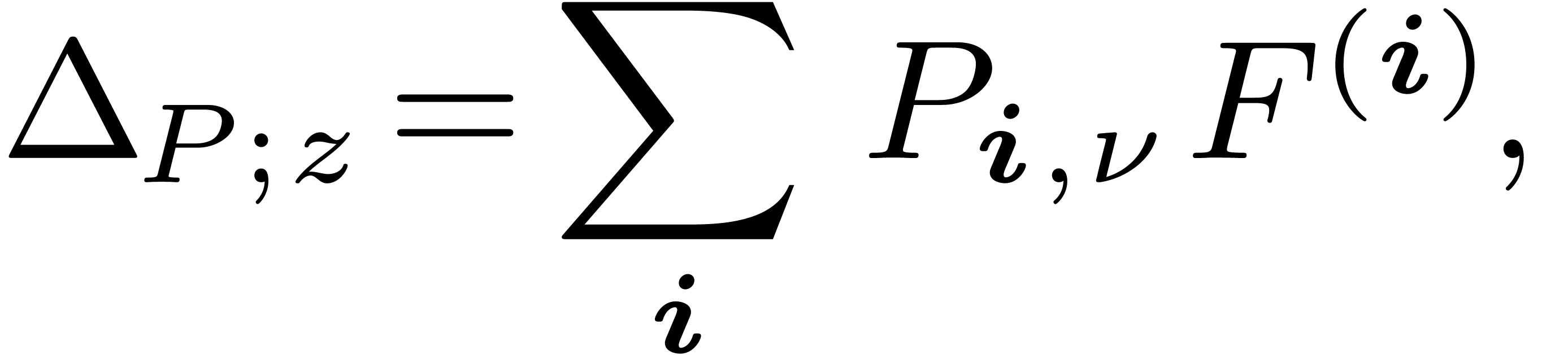
where  is the valuation of
is the valuation of  in
in  and
and  denotes the
coefficient of
denotes the
coefficient of  in
in  .
.
Assume first that 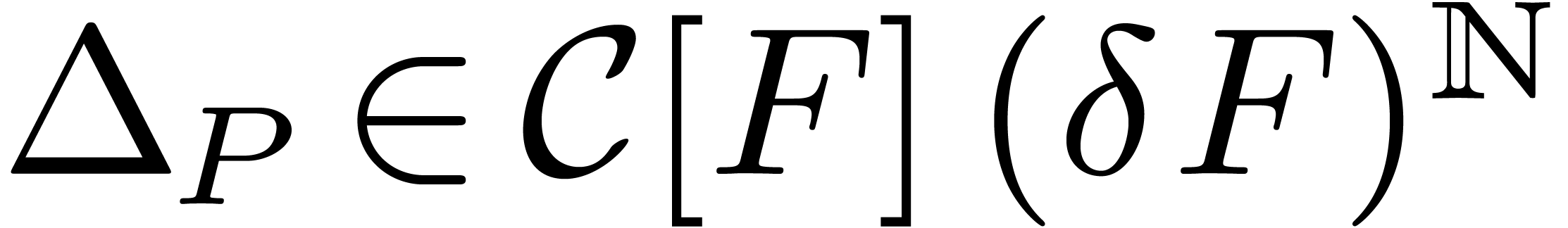 and
and 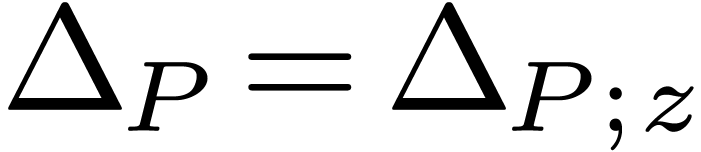 . Then we define the differential Newton
polynomial of
. Then we define the differential Newton
polynomial of  by
by 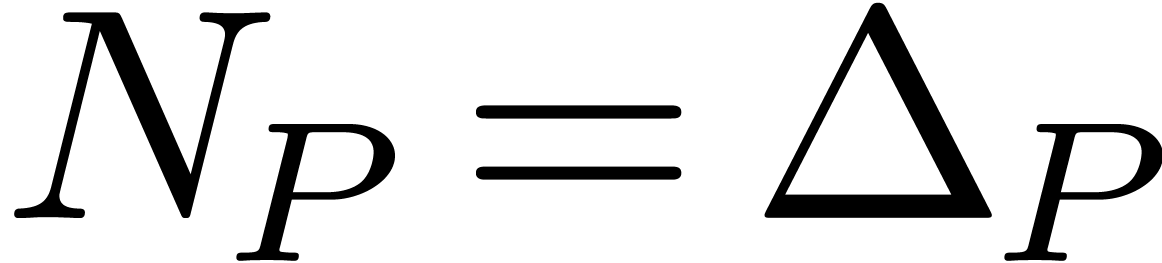 and we have
and we have
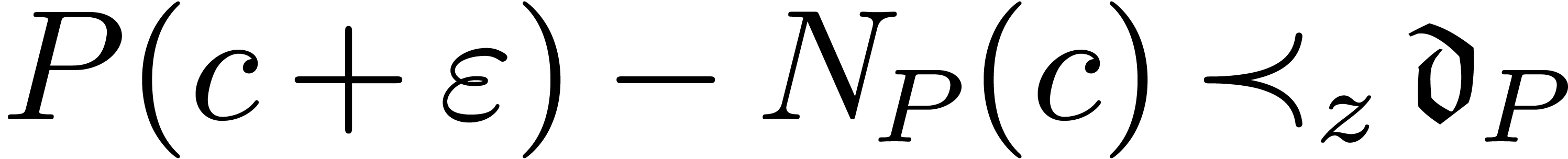
for all 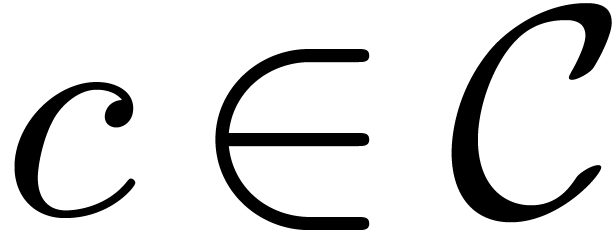 and
and  .
Here
.
Here  , if
, if 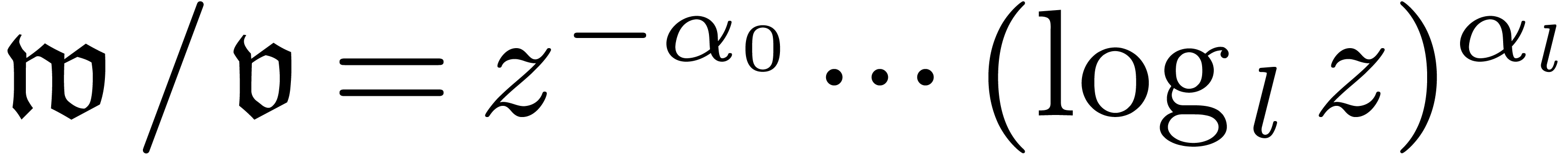 with
with 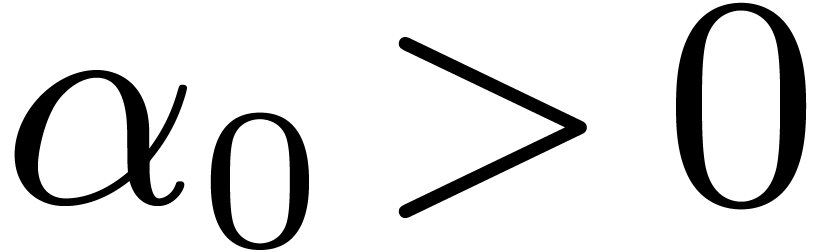 . We say that
. We say that  is a potential dominant monomial of a solution to
is a potential dominant monomial of a solution to 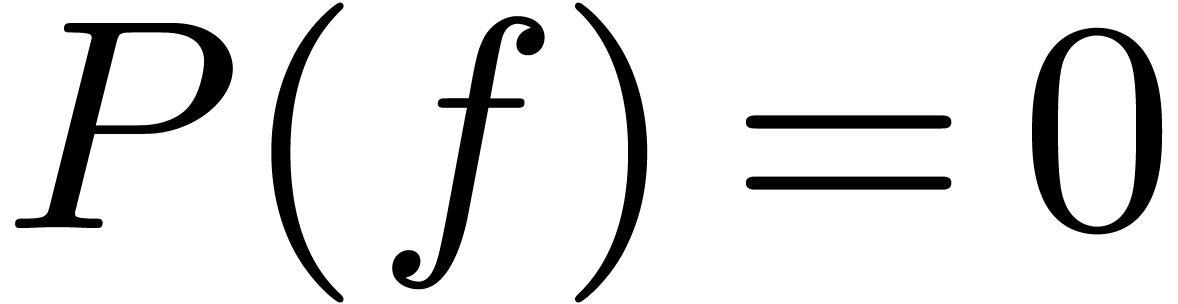 if and only if
if and only if  admits such a
non-zero constant root
admits such a
non-zero constant root 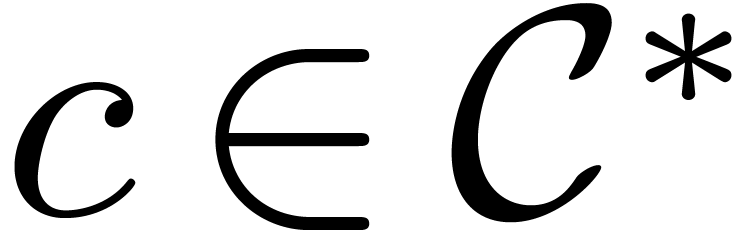 (and
(and  is a potential dominant term). Furthermore,
is a potential dominant term). Furthermore,  admits a non-zero root if and only if
admits a non-zero root if and only if 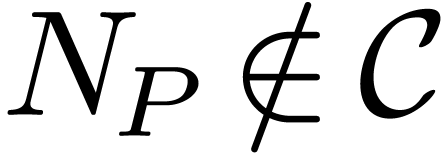 ,
because
,
because 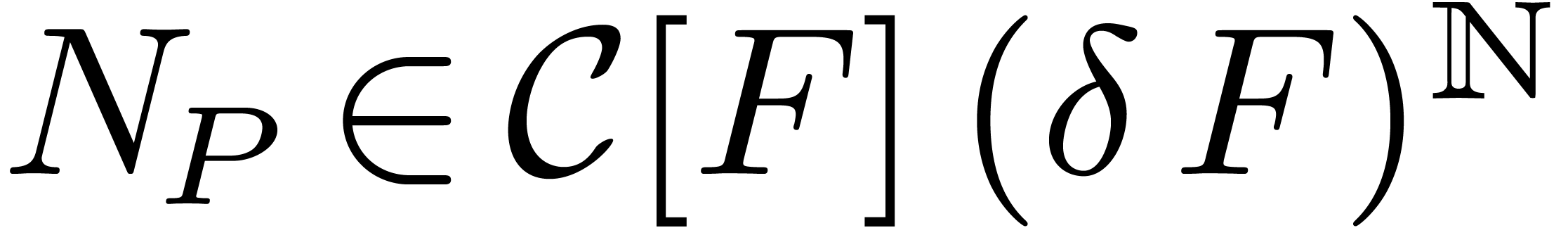 and
and  is
algebraically closed.
is
algebraically closed.
If 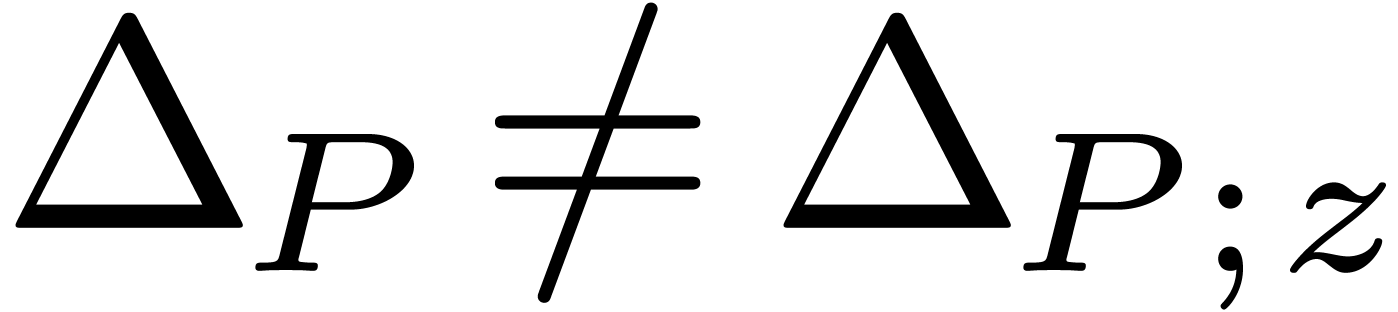 or
or 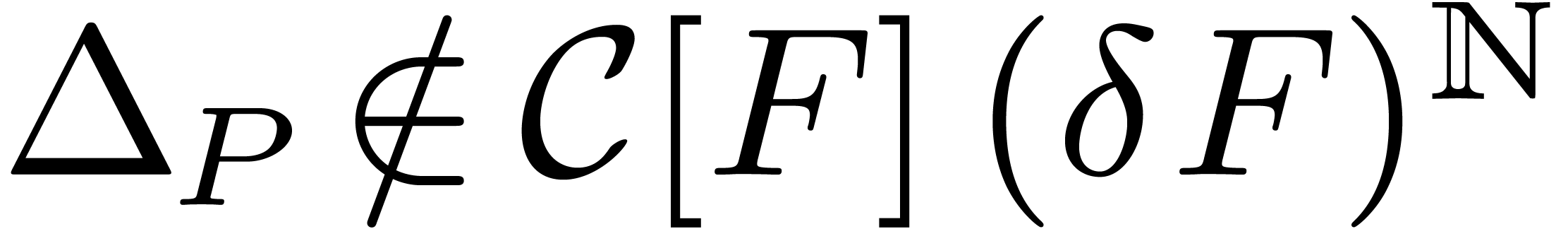 ,
then we use the technique of “upward shifting”. Given
,
then we use the technique of “upward shifting”. Given 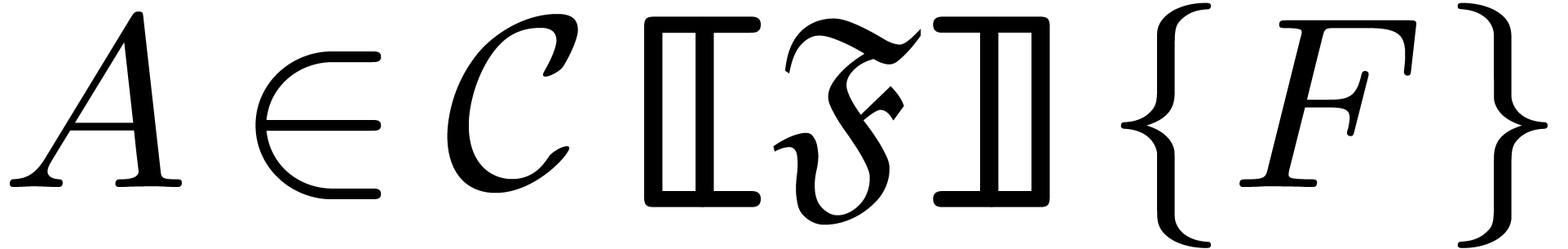 , we define
, we define  to be the unique differential polynomial in
to be the unique differential polynomial in 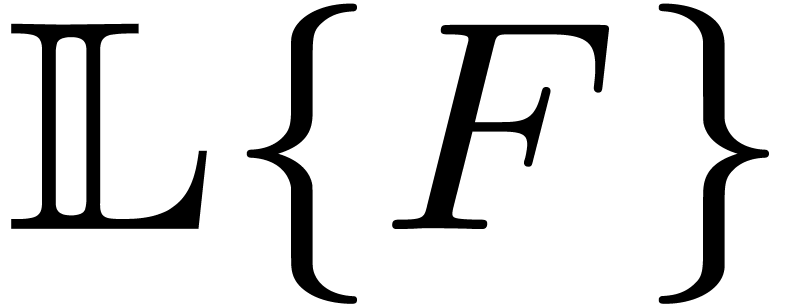 such
that
such
that
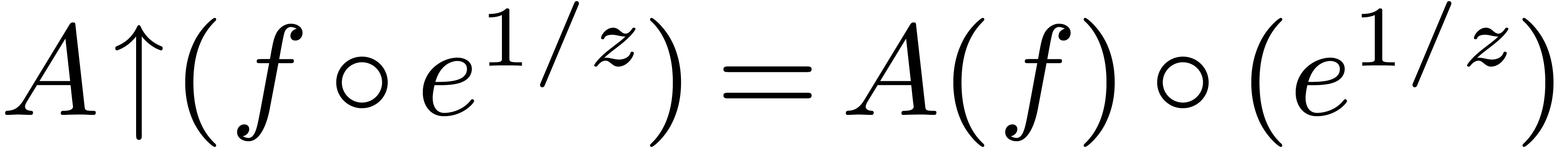
for all  . For instance,
. For instance, 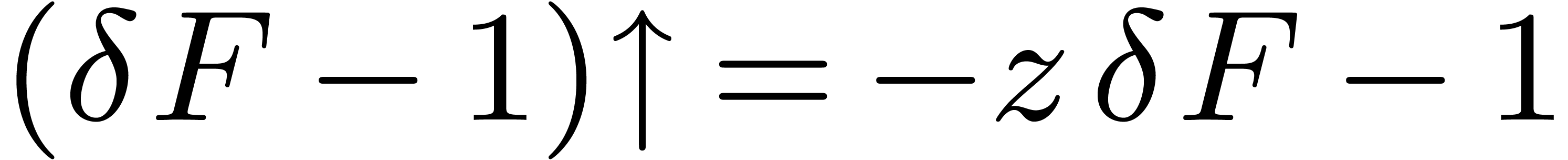 , and we notice that the
logarithmic solution
, and we notice that the
logarithmic solution 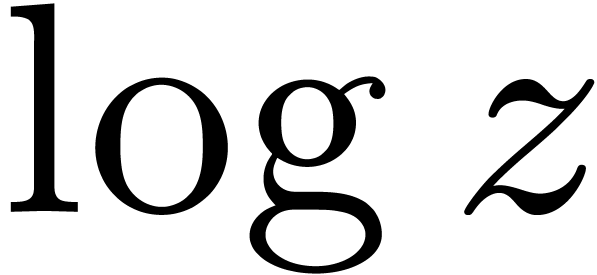 of
of 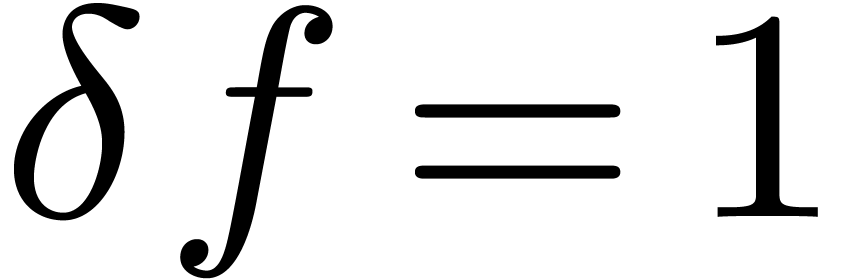 transforms to the non-logarithmic solution
transforms to the non-logarithmic solution 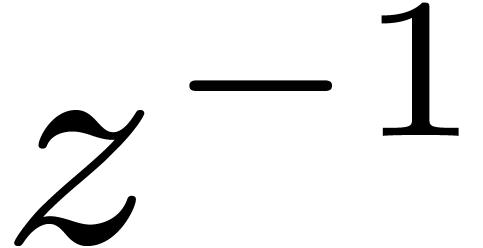 of
of
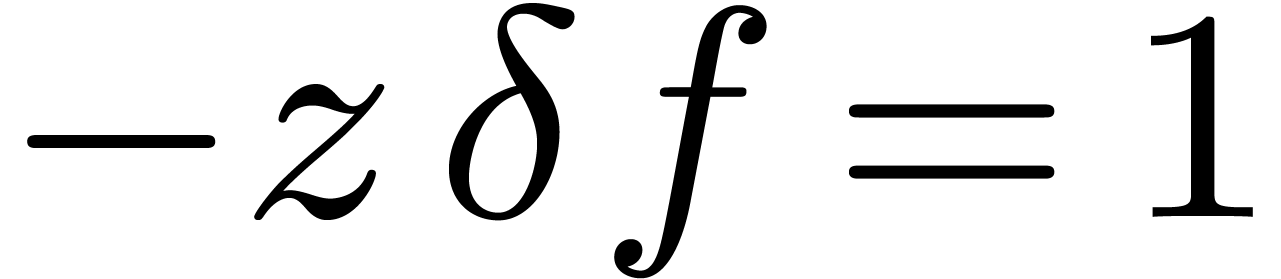 under upward shifting
under upward shifting 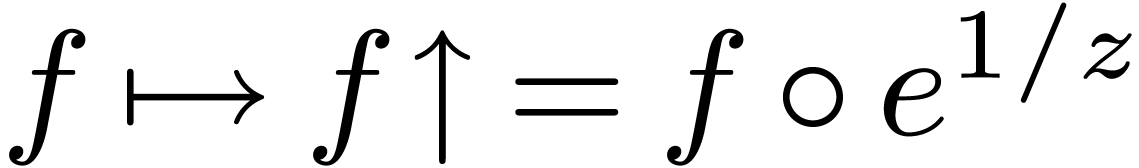 . Now we proved in [15] that after a
finite number of replacements
. Now we proved in [15] that after a
finite number of replacements  we obtain a
differential polynomial
we obtain a
differential polynomial 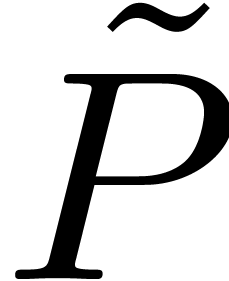 with
with 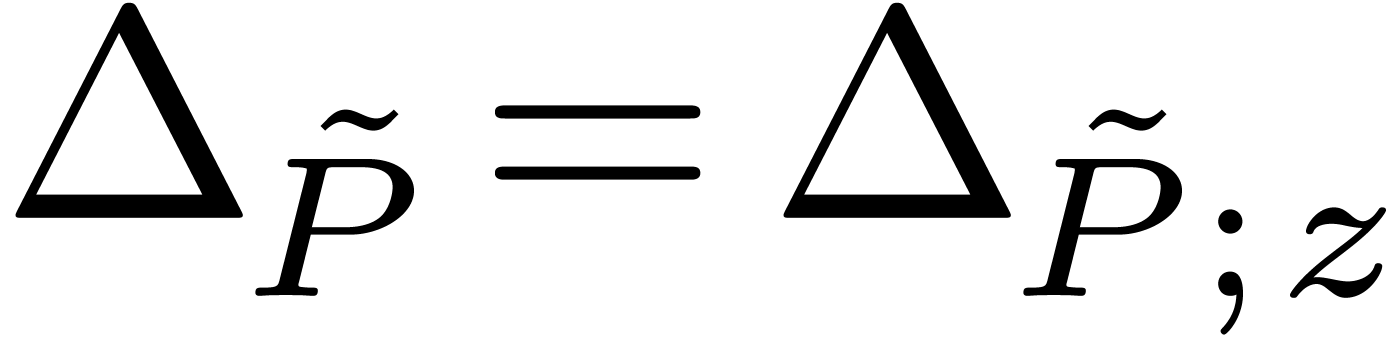 and
and 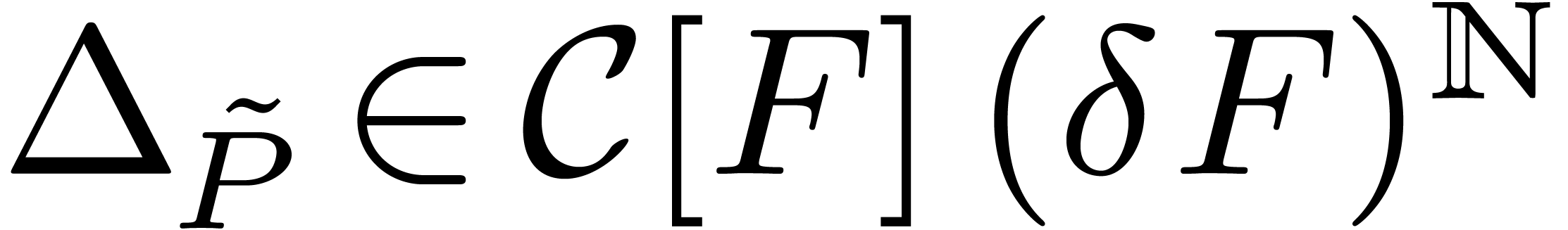 . We say that
. We say that  is a potential dominant monomial w.r.t. (6) if and only if
is a potential dominant monomial w.r.t. (6) if and only if  and
and  admits a non-zero root in
admits a non-zero root in  .
.
It is clear that if  is a solution to (6),
then
is a solution to (6),
then  must be a potential dominant monomial of a
solution. We say that a potential dominant monomial
must be a potential dominant monomial of a
solution. We say that a potential dominant monomial  is classical, if
is classical, if  is not homogeneous
(i.e.
is not homogeneous
(i.e.  ). These
classical potential dominant monomials are finite in number and they can
be determined from something which resembles the Newton polygon in the
algebraic case [13, 15], by using a succession
of multiplicative conjugations
). These
classical potential dominant monomials are finite in number and they can
be determined from something which resembles the Newton polygon in the
algebraic case [13, 15], by using a succession
of multiplicative conjugations  and upward
shiftings
and upward
shiftings  of the dominant parts
w.r.t.
of the dominant parts
w.r.t.  .
.
Once we have found a potential dominant term 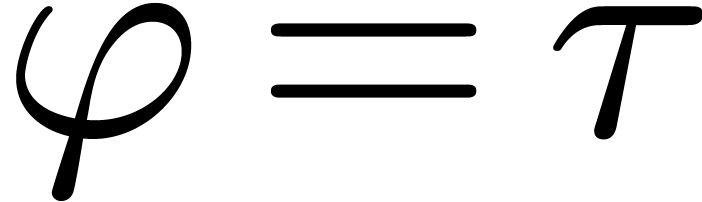 of
a solution to (6), we may consider the refinement
of
a solution to (6), we may consider the refinement
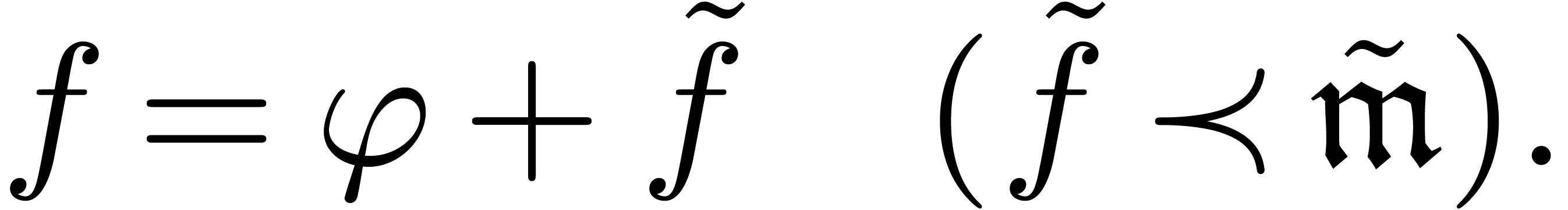 |
(7) |
In other words, a refinement is a change of variables together with the
imposition of a new asymptotic constraint. It transforms (6)
into a new asymptotic differential equation
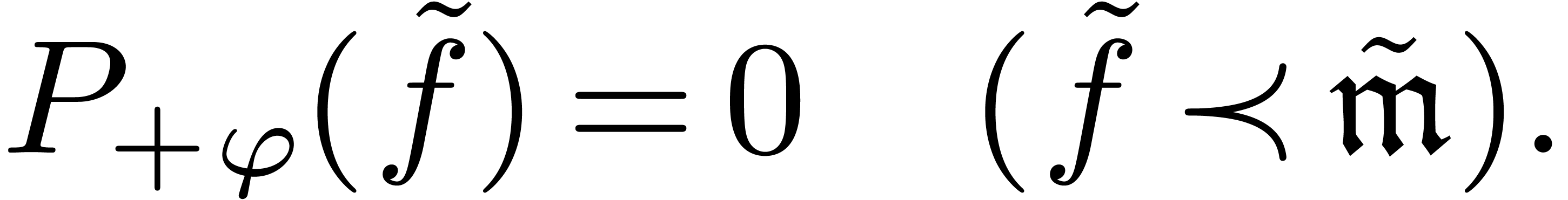 |
(8) |
Using the possibly transfinite process of determining potential
dominant terms and making refinements, one finds all solutions to (6). However, a more careful study is required to ensure that
one remains in the context of grid-based transseries and that (for
instance) no transseries like
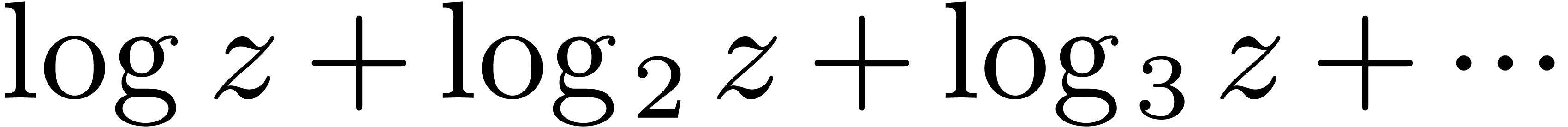 |
(9) |
may occur as solutions of (6).
In order to do this, it is convenient to associate an invariant to the
equation (6): the highest possible degree of the
differential Newton polynomial 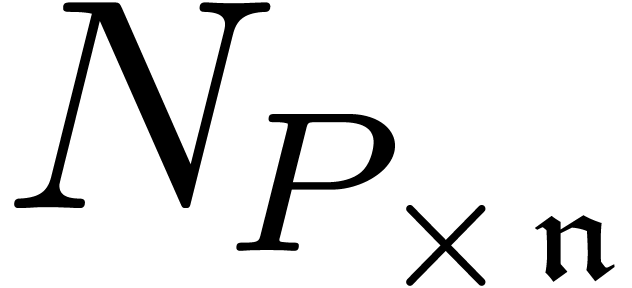 that we
can achieve for a monomial
that we
can achieve for a monomial  is called the
Newton degree of (6) and we denote it by
is called the
Newton degree of (6) and we denote it by  . In the algebraic case, the Newton
degree measures the number of solutions to the asymptotic equation (6), when counting with multiplicities. In the differential
case, it only gives a lower bound (see theorem 3 below).
Also, an equation of Newton degree
. In the algebraic case, the Newton
degree measures the number of solutions to the asymptotic equation (6), when counting with multiplicities. In the differential
case, it only gives a lower bound (see theorem 3 below).
Also, an equation of Newton degree 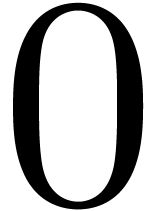 does not
admit any solutions.
does not
admit any solutions.
Now we have shown in [13, 15] that the Newton
degree decreases during refinements and that quasi-linear equations
(i.e. equations of Newton degree 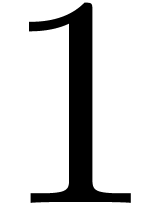 ) always admit solutions. Finally, in the case when
) always admit solutions. Finally, in the case when
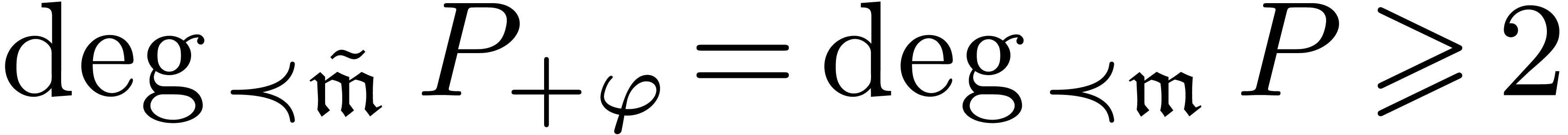 , it is possible to replace
, it is possible to replace
 by a solution to a quasi-linear equation of the
form
by a solution to a quasi-linear equation of the
form
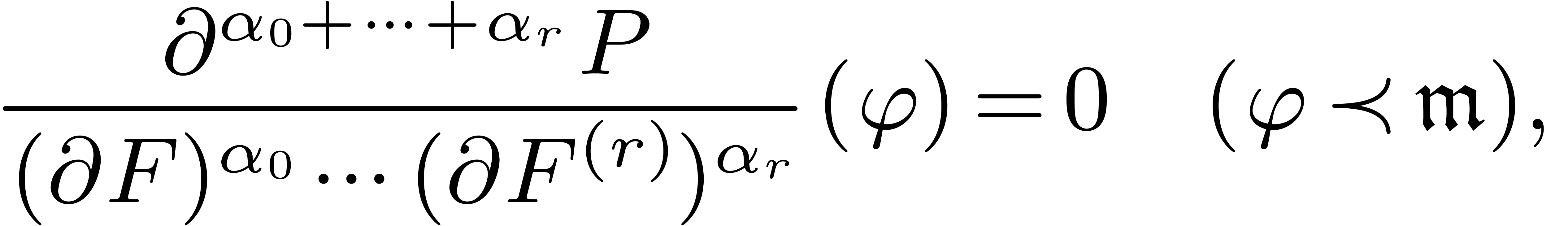 |
(10) |
and force the Newton degree to strictly decrease after a finite number
of steps. In other words, the transfinite resolution process has been
replaced by an essentially finite algorithm, which avoids solutions of
the form (9). In particular, these methods yield the
following theorem:
Theorem 3. Consider
an asymptotic algebraic differential equation (6)
of Newton degree 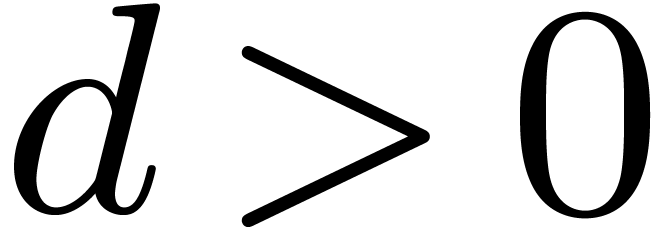 over
over  . Then (6) admits
at least
. Then (6) admits
at least 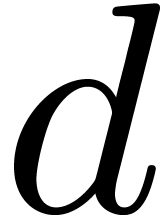 solutions in
solutions in  when counting with multiplicities.
when counting with multiplicities.
5The algorithm
In this sequel, we assume that  ,
,
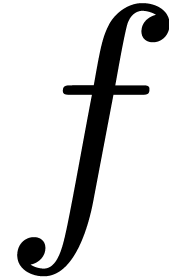 and
and  are as in section 3. We will give an algorithm to test whether
are as in section 3. We will give an algorithm to test whether 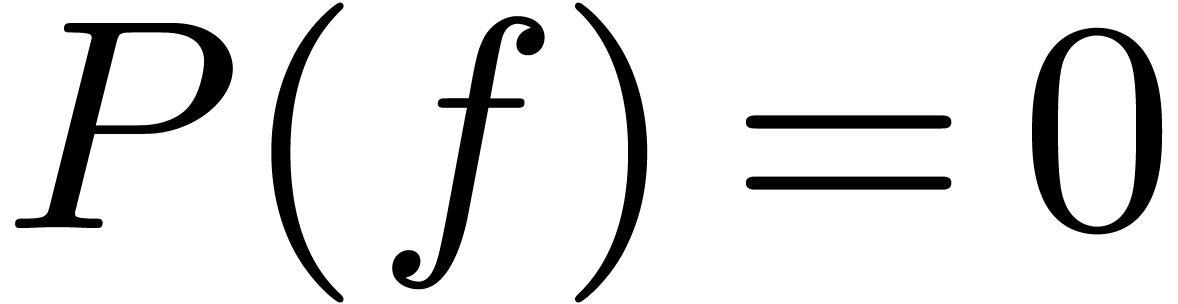 for given
for given 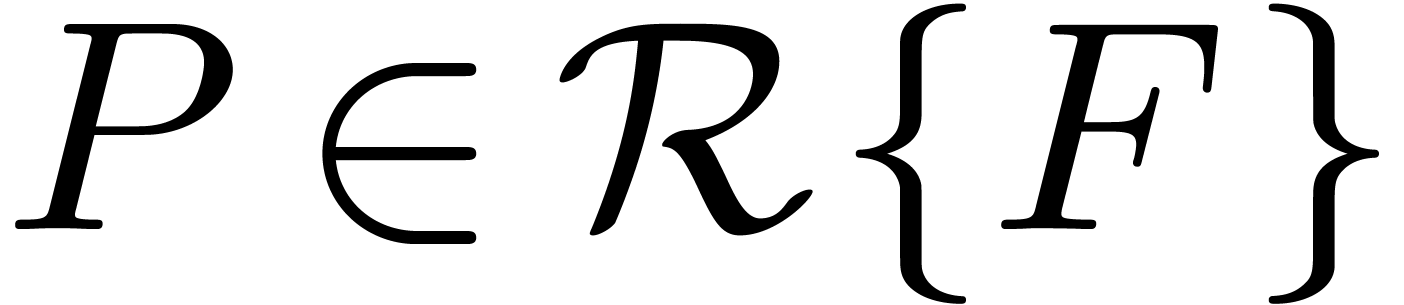 . We will write
. We will write
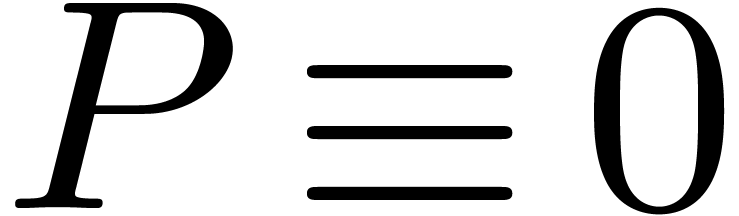 if and only
if and only 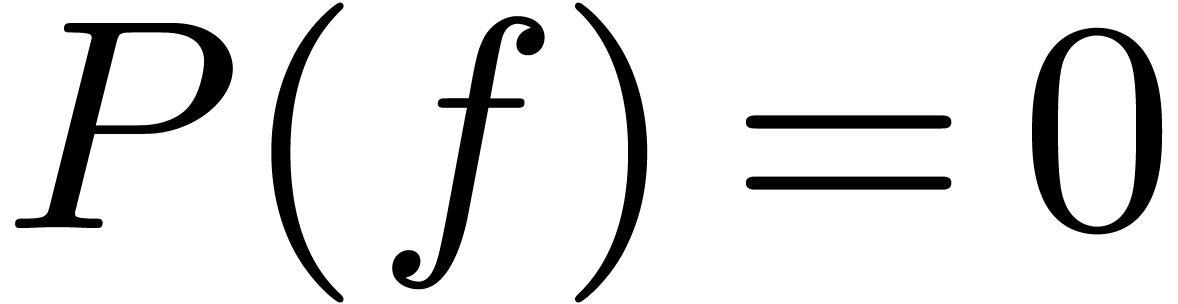 .
.
5.1Statement of the algorithm
Algorithm 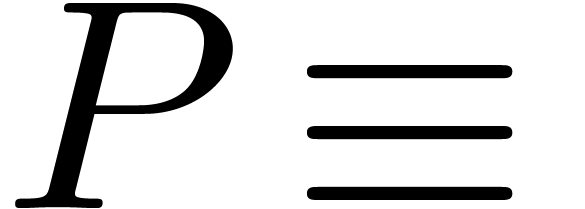 0
0
Input: a differential polynomial 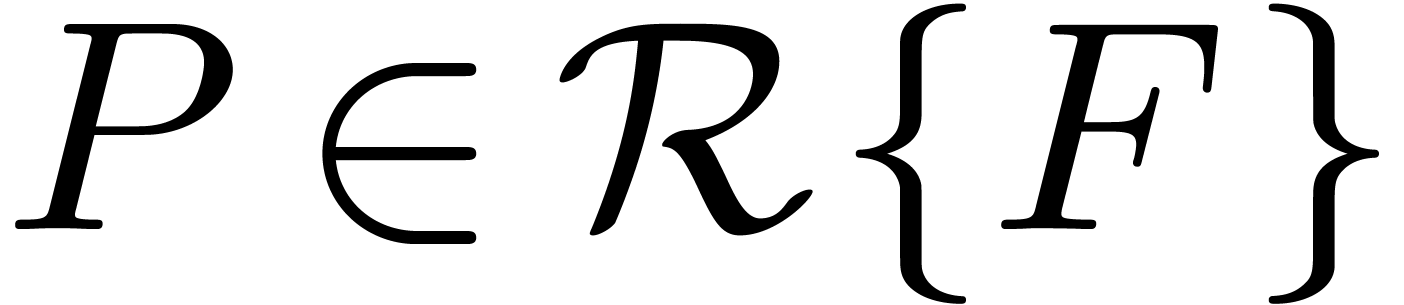
Output:  if and only if
if and only if
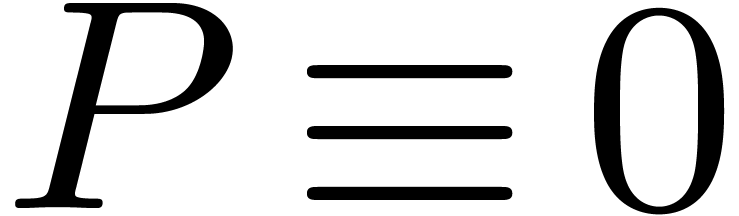
while 
if 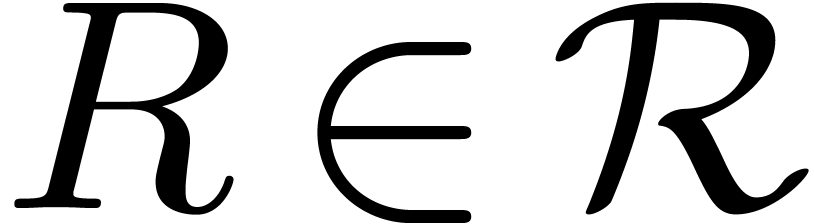 then
return
then
return 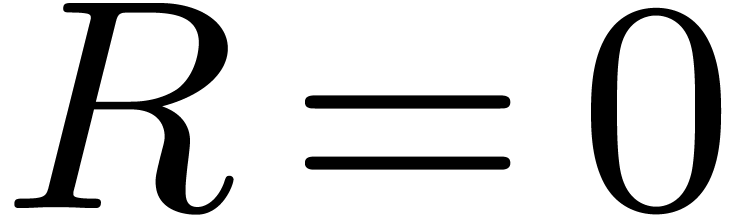
else if 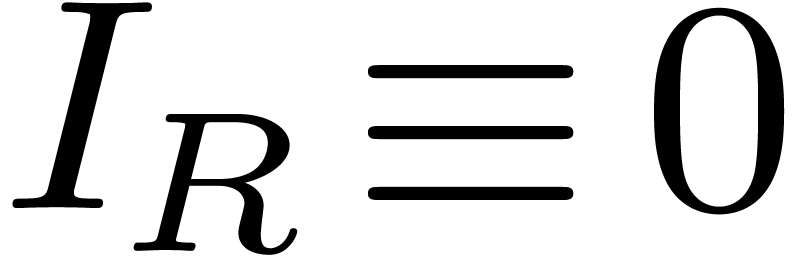 then
then
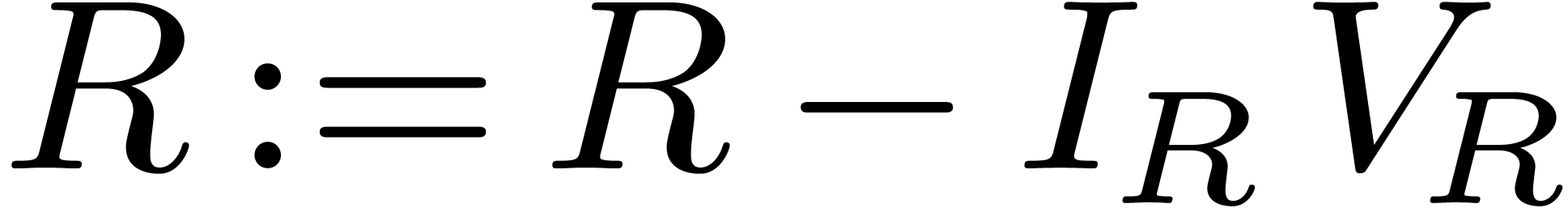
else if 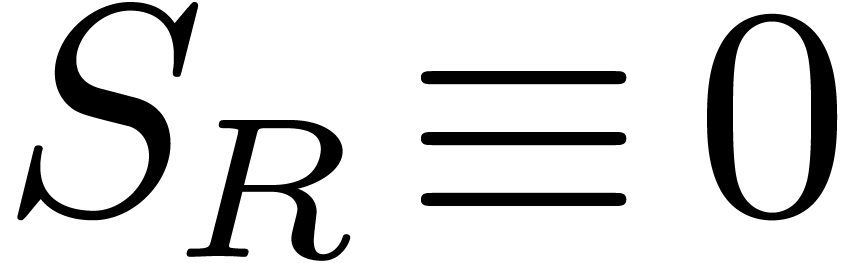 then
then
else if 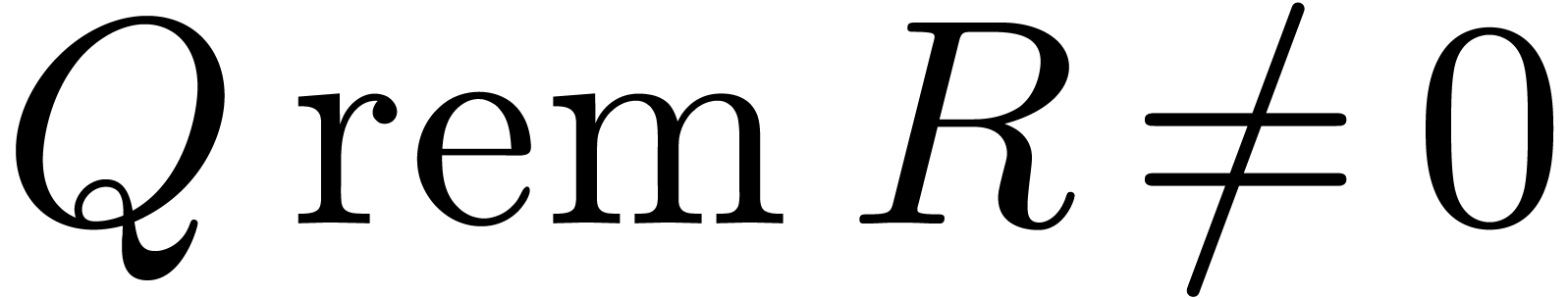 then
then
else 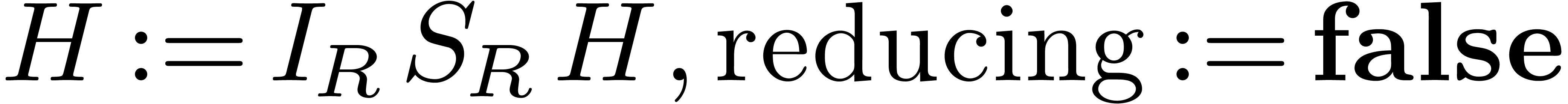
let  be minimal with
be minimal with 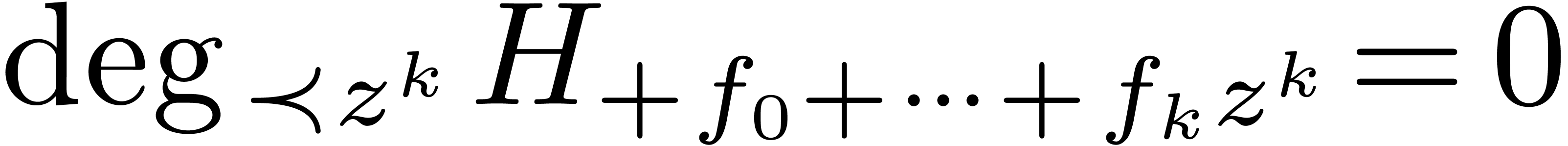
return 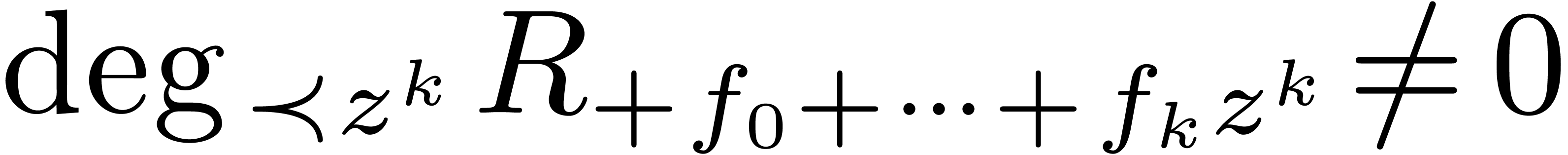
Remark 4. In the particular case
when an asymptotic differential equation (6) has power
series coefficients in  and
and 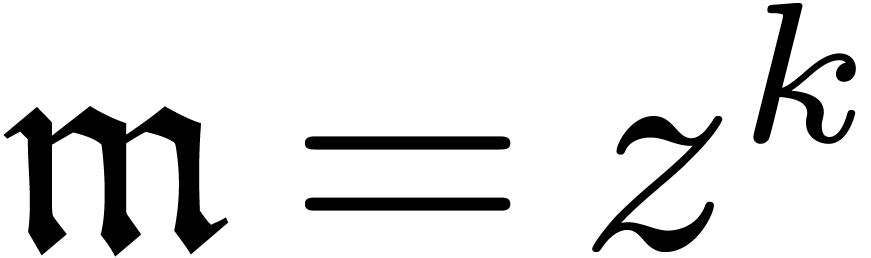 , its Newton degree
, its Newton degree 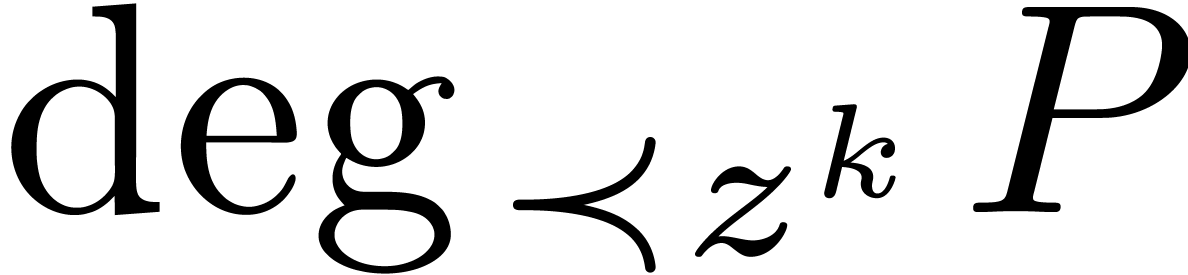 is
the minimal degree of a term
is
the minimal degree of a term 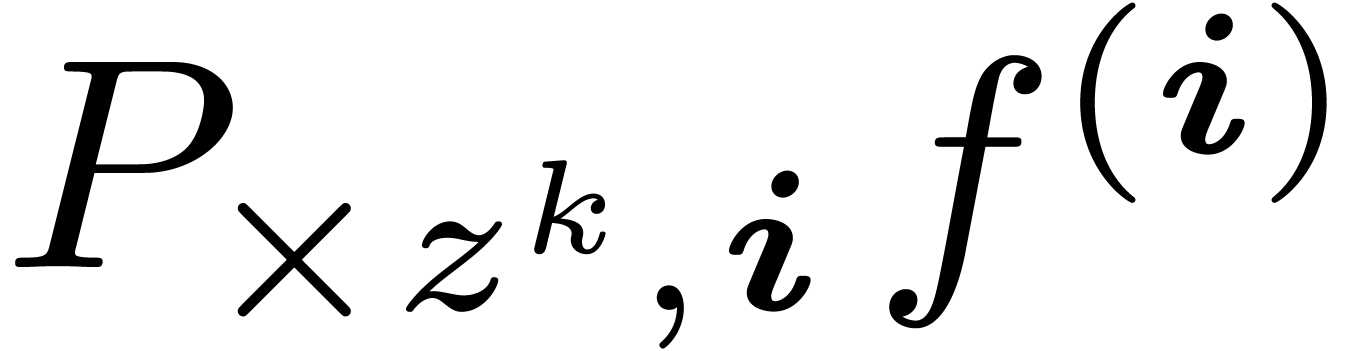 in
in 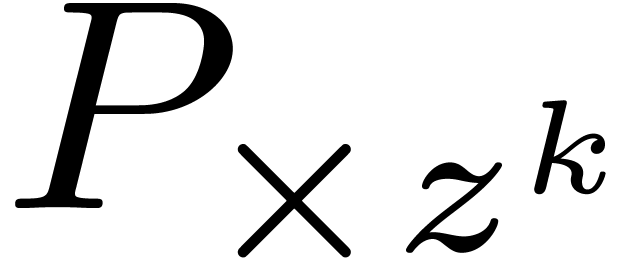 with
with  .
.
In particular, the minimal  in step 3 can be
found by expanding the power series coefficients
in step 3 can be
found by expanding the power series coefficients 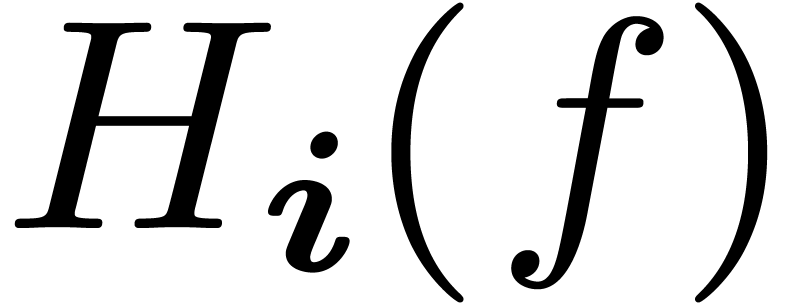 of
of  in
in  using any fast
expansion algorithm for solutions to differential equations [3,
14].
using any fast
expansion algorithm for solutions to differential equations [3,
14].
5.2Correctness and termination proof
Theorem 5. The above algorithm
for testing whether 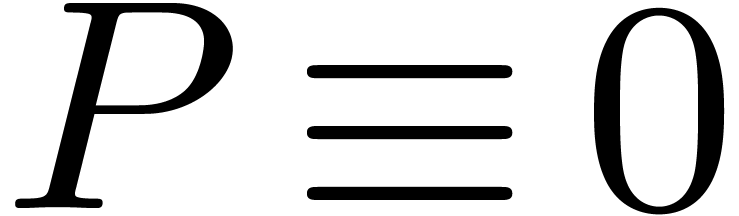 terminates and is
correct.
terminates and is
correct.
Proof. In the loop in step 2, we notice that the rank
of 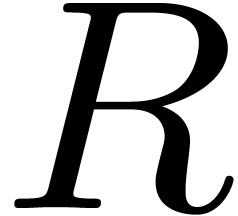 strictly decreases at each iteration. Also,
the rank of
strictly decreases at each iteration. Also,
the rank of  (or
(or 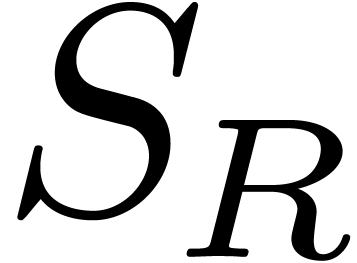 )
in each recursive call of the zero-test is strictly smaller than the
rank of
)
in each recursive call of the zero-test is strictly smaller than the
rank of 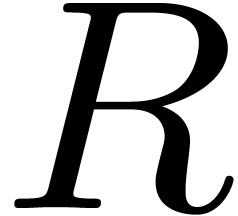 (and whence the rank of
(and whence the rank of 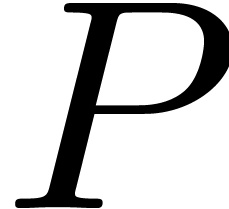 ). These two observations, and the fact that
the set of possible ranks is well-ordered, imply the termination of the
algorithm; the existence of a minimal
). These two observations, and the fact that
the set of possible ranks is well-ordered, imply the termination of the
algorithm; the existence of a minimal 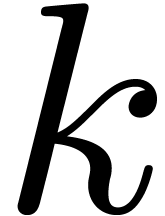 with
with 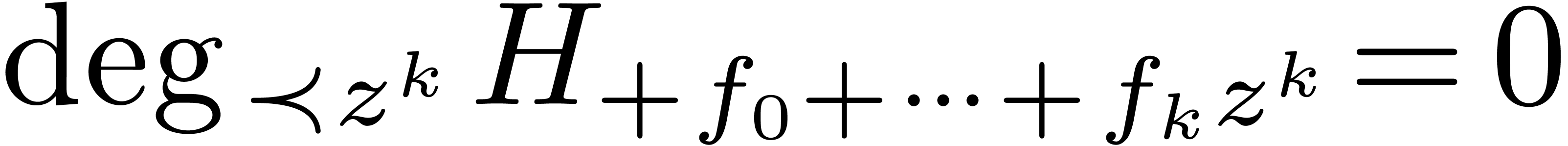 will be proved below.
will be proved below.
As to the correctness of the algorithm, we claim that at the start and
the end inside the loop in step 2, we maintain the properties that 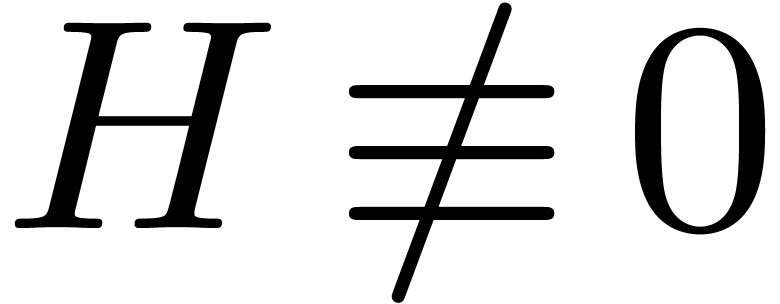 and the existence of a relation of the form
and the existence of a relation of the form
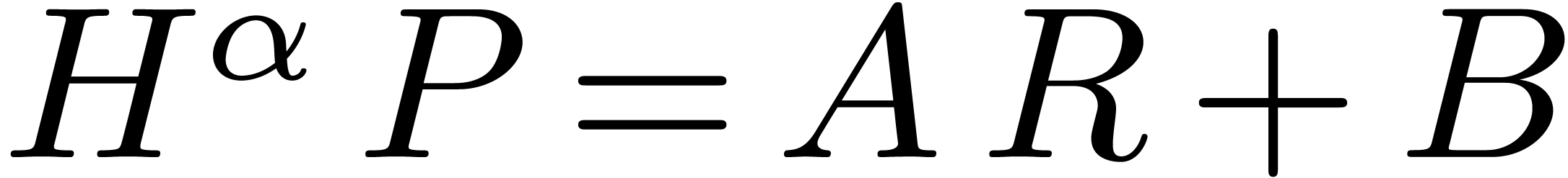 |
(11) |
for 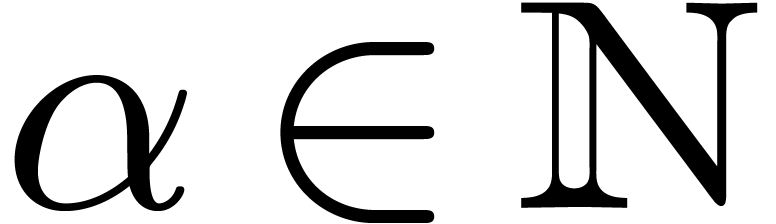 and differential polynomials
and differential polynomials  and
and  with
with 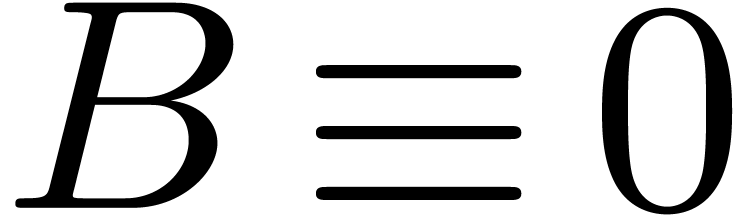 . Indeed, we have
. Indeed, we have  and
and 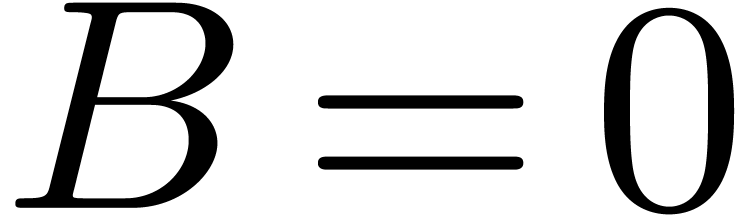 at the first entry. If
at the first entry. If 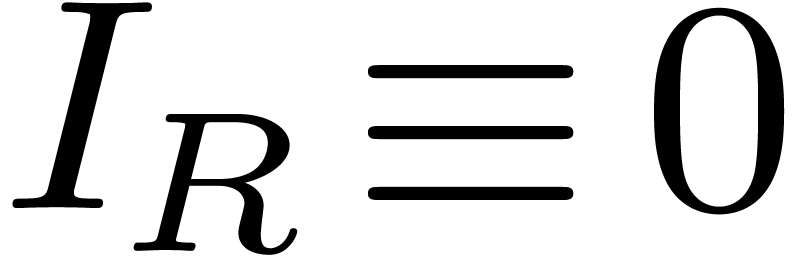 and
and
 , then we have
, then we have 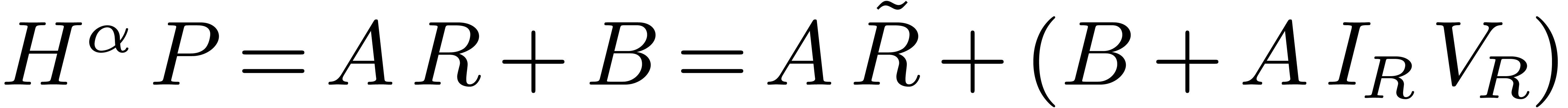 , with
, with 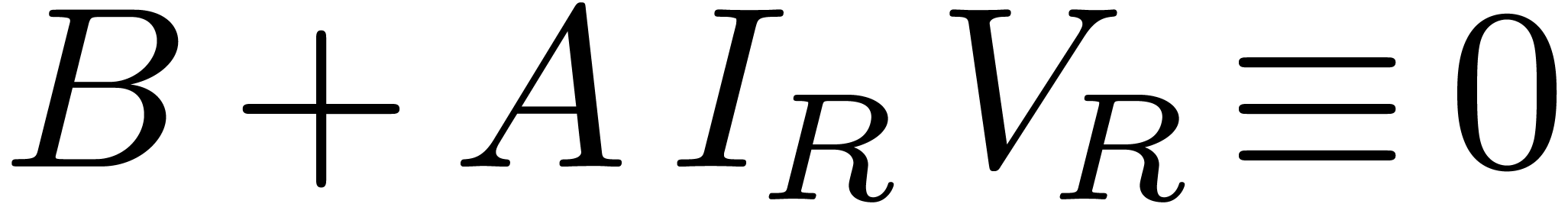 .
If
.
If 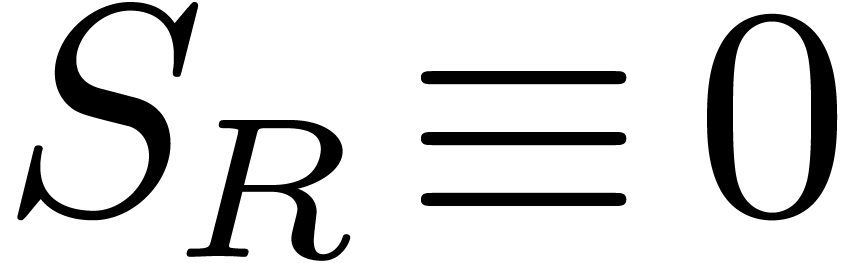 ,
, 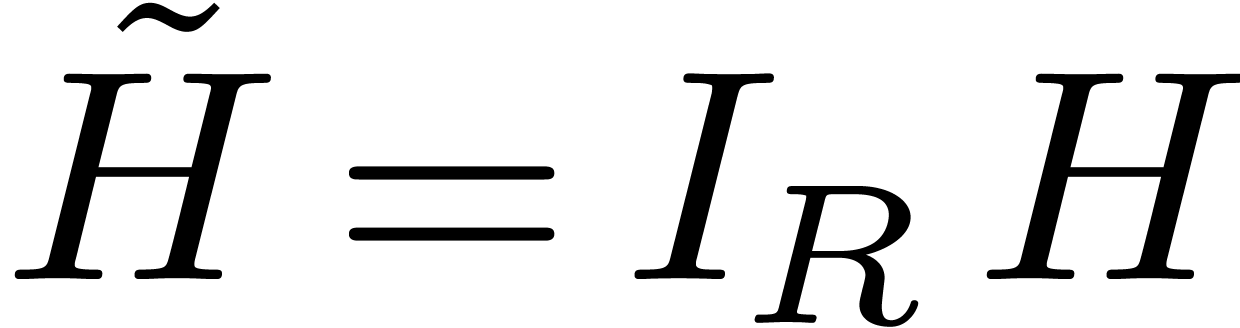 and
and 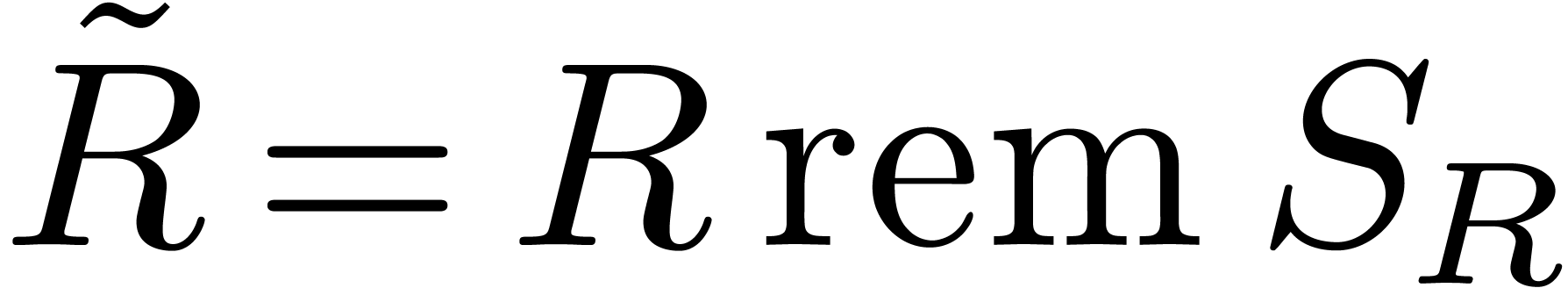 , then
, then 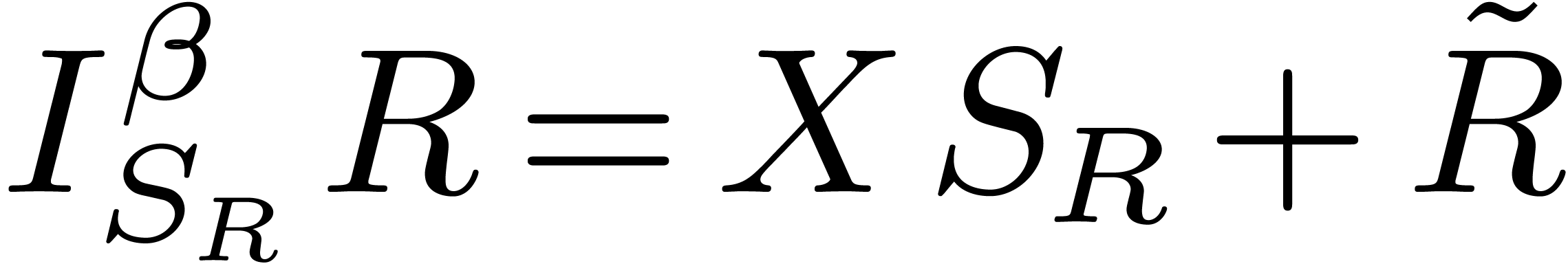 for some
for some  and differential polynomial
and differential polynomial  . Also,
. Also, 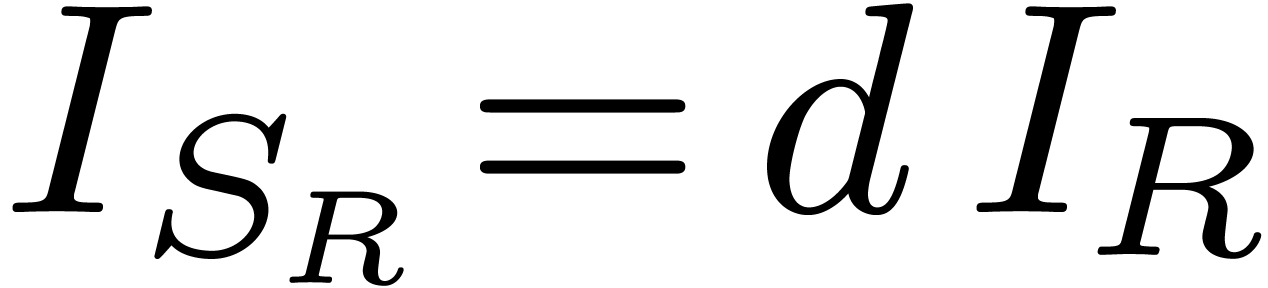 , where
, where 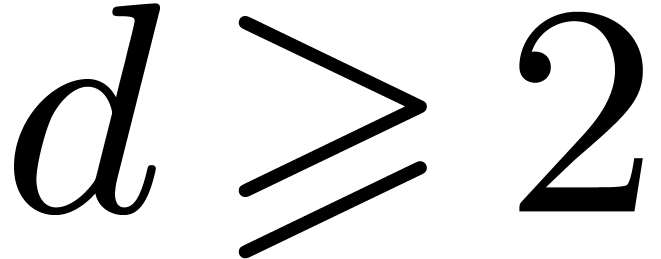 is the degree of
is the degree of
 in the highest
in the highest  occurring
in
occurring
in 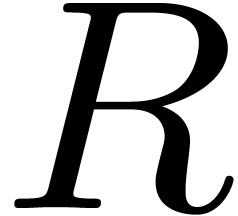 . Consequently, denoting
. Consequently, denoting
 , we have
, we have  . The case when
. The case when  is
treated in a similar way. This proves our claim; notice that (11)
implies
is
treated in a similar way. This proves our claim; notice that (11)
implies  . By definition, we
also have
. By definition, we
also have  if
if 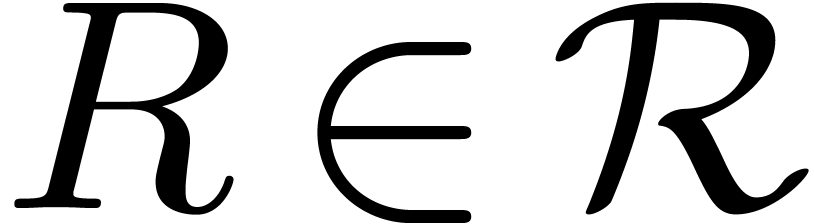 at the
first test in the loop.
at the
first test in the loop.
Let us now assume that the algorithm reaches step 3. Since 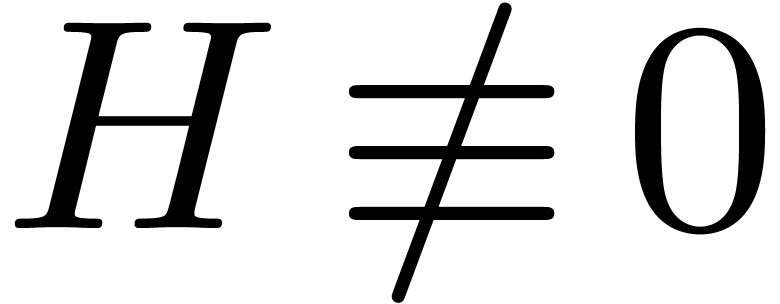 , we may write
, we may write 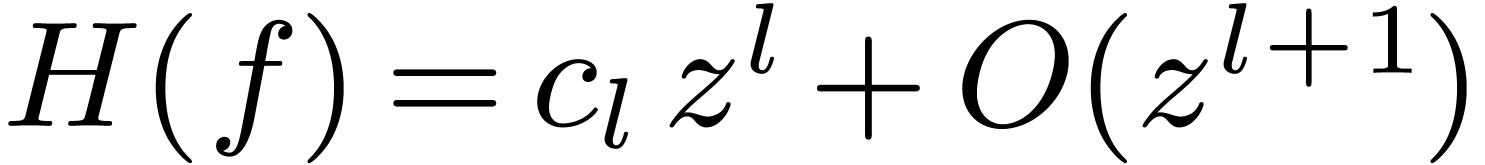 with
with
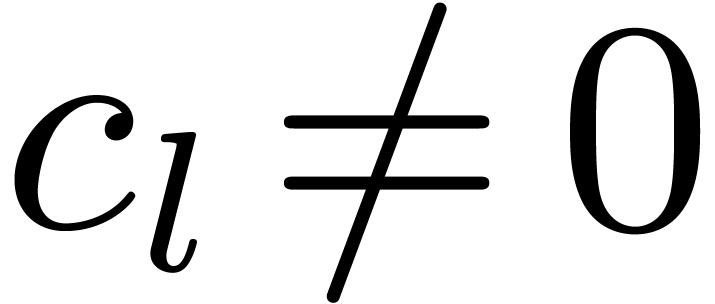 for some
for some  .
For this
.
For this 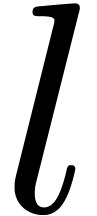 , we have
, we have  , which implies that there exists a
minimal number
, which implies that there exists a
minimal number  , such that
both
, such that
both 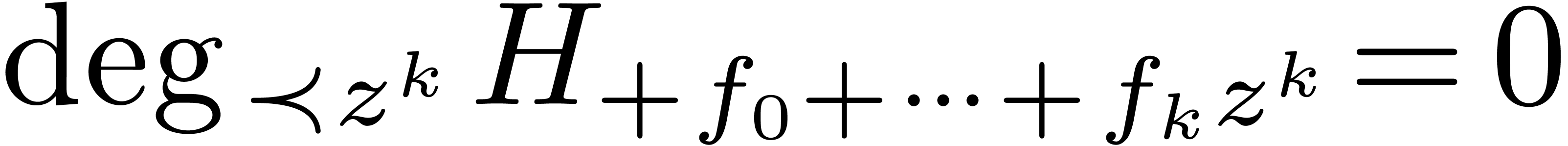 and
and 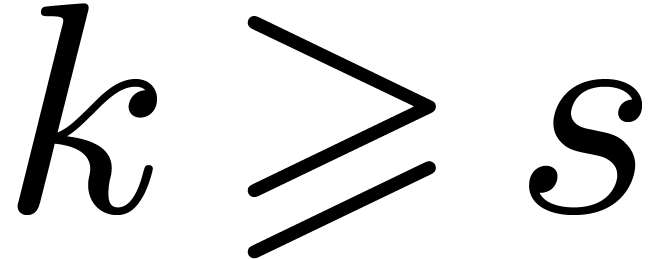 .
If
.
If 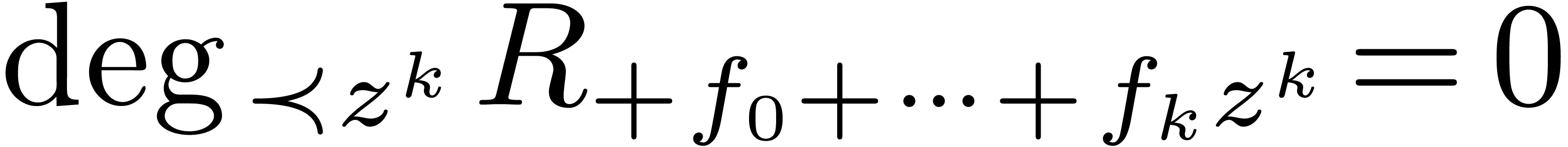 , then we have
, then we have 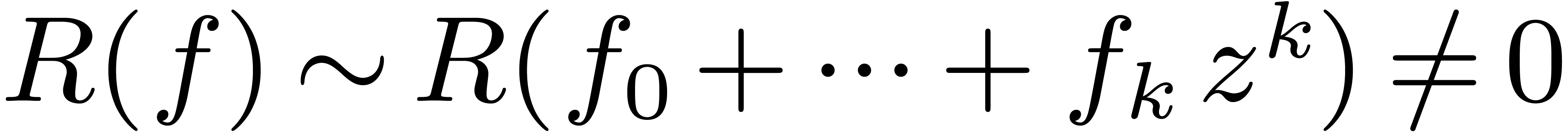 , whence
, whence 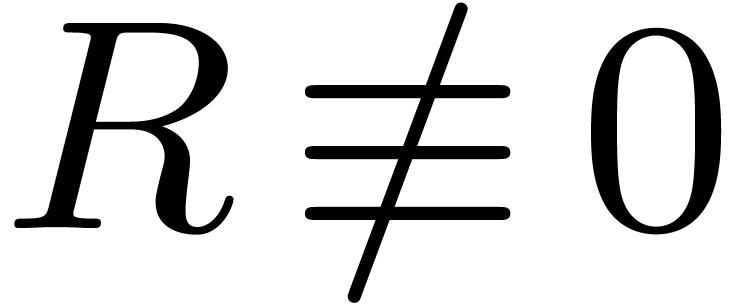 and
and  . Conversely, assume that
. Conversely, assume that
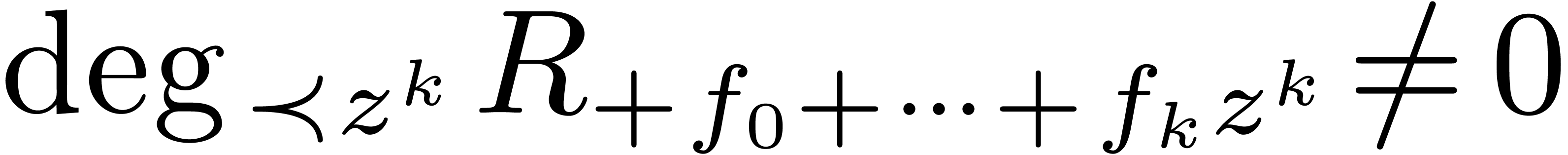 . Then theorem 3
implies the existence of a series
. Then theorem 3
implies the existence of a series 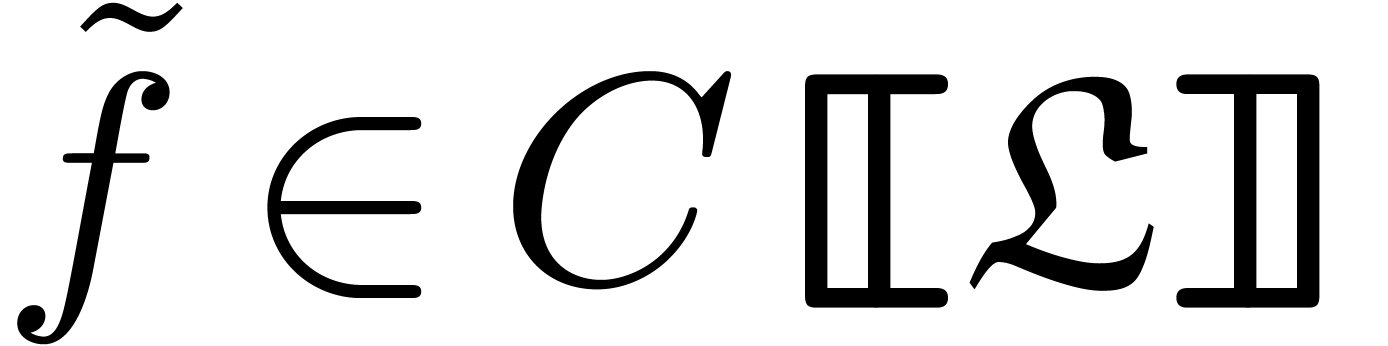 with
with 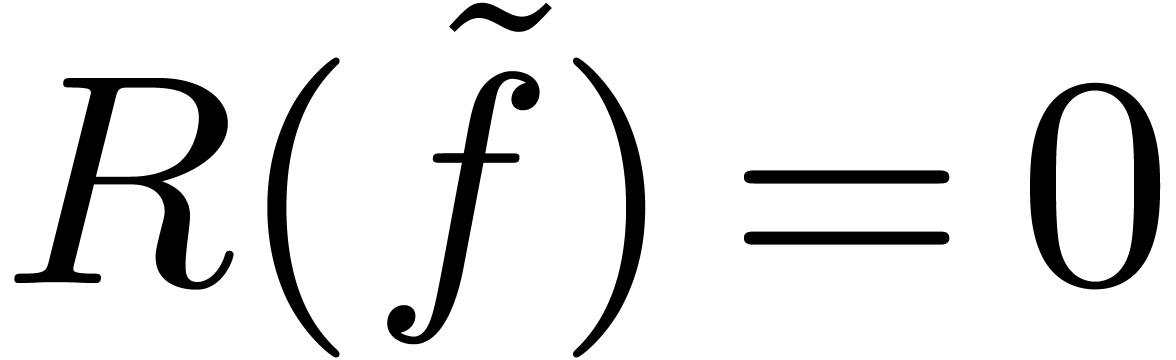 and
and 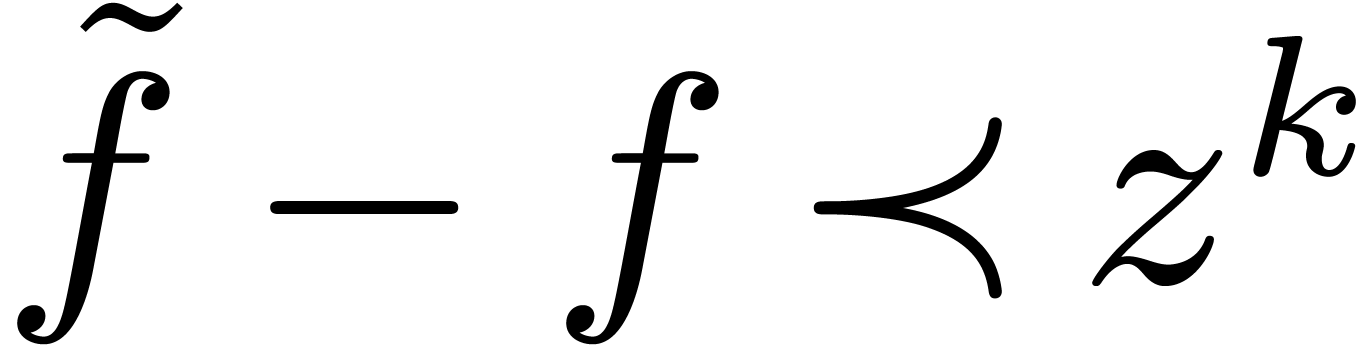 . Since
. Since
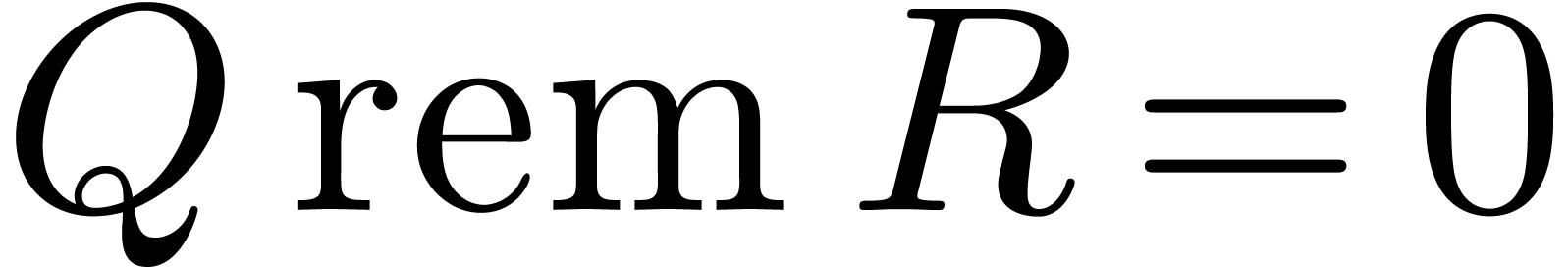 and
and 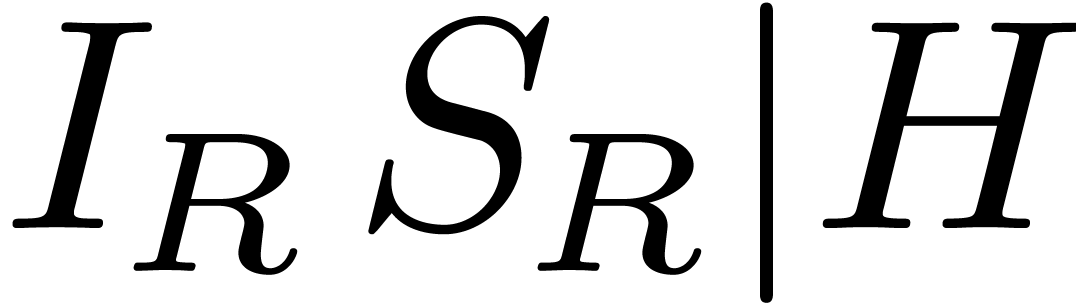 ,
we have a relation of the form
,
we have a relation of the form
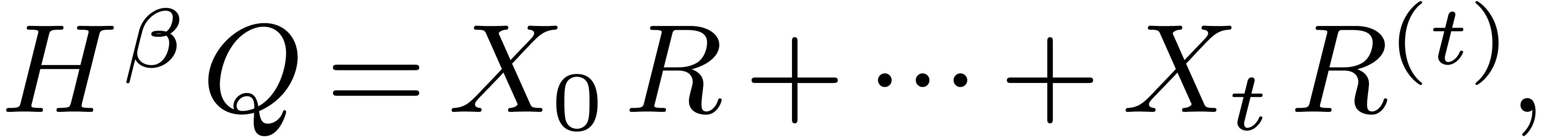 |
(12) |
where  and
and  are
differential polynomials. Now
are
differential polynomials. Now 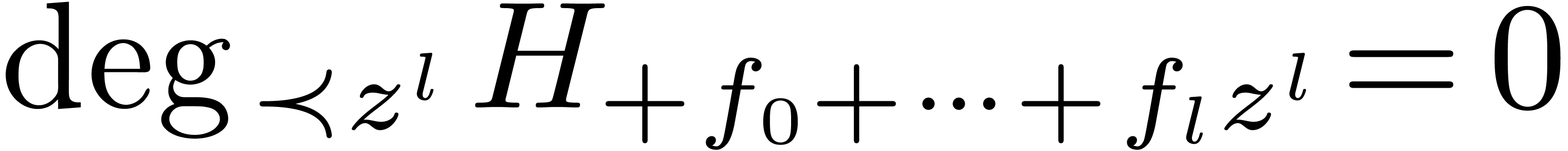 implies
implies 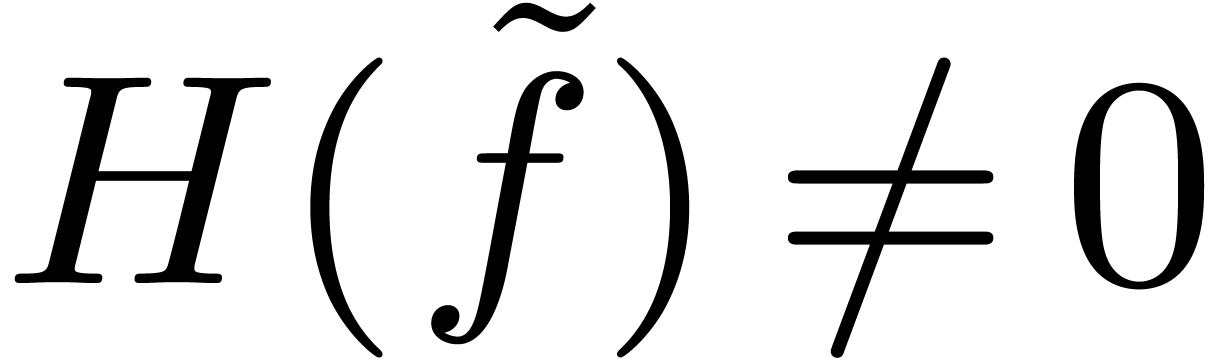 , so that
, so that 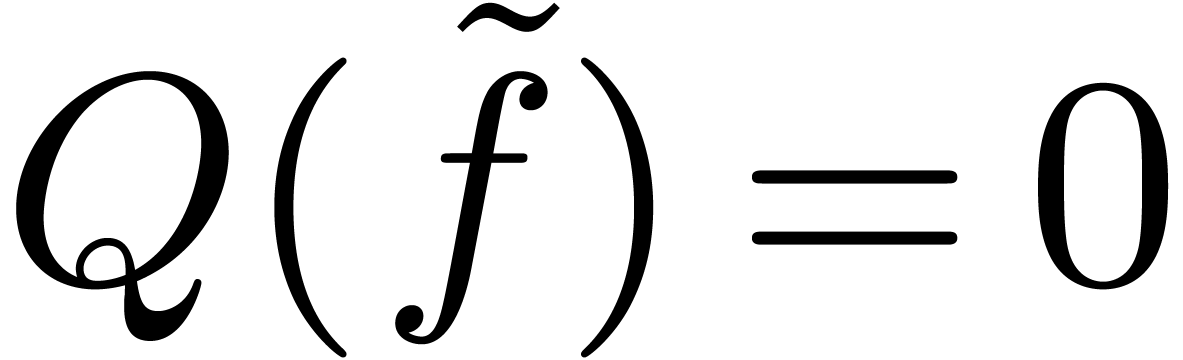 . But, by lemma 2, there exists a
unique solution in
. But, by lemma 2, there exists a
unique solution in  to the equation
to the equation 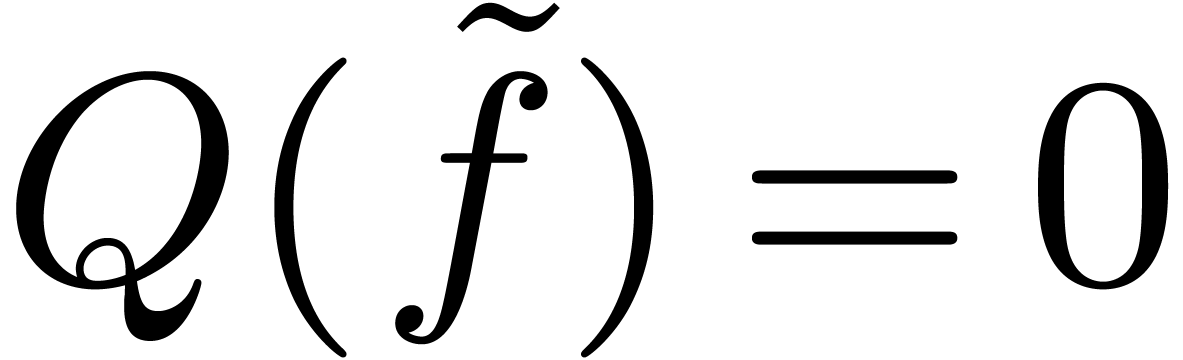 with the side condition
with the side condition  .
Hence
.
Hence 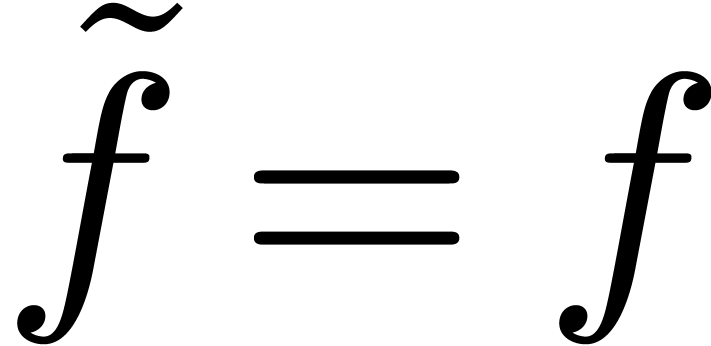 ,
, 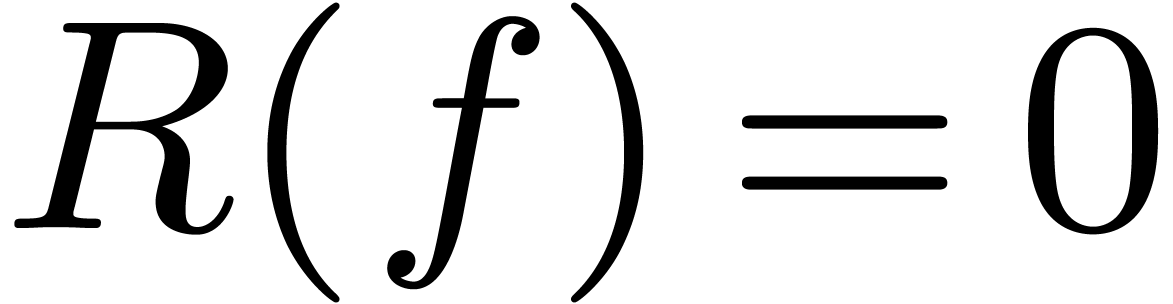 and
and 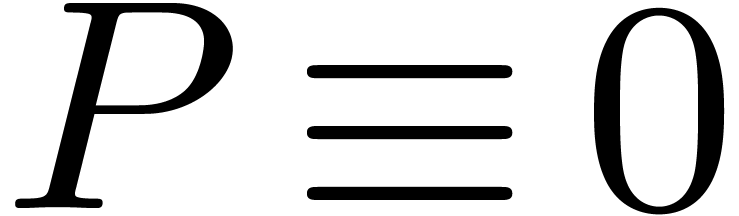 .
.
Bibliography
-
[1]
-
Ax, J. On Schanuel's
conjecture. Ann. of Math. 93 (1971), 252–268.
-
[2]
-
Boulier, F. Étude et
implantation de quelques algorithmes en algèbre
différentielle. PhD thesis, University of Lille I,
1994.
-
[3]
-
Brent, R., and Kung, H. Fast
algorithms for manipulating formal power series. Journal of
the ACM 25 (1978), 581–595.
-
[4]
-
Denef, J., and Lipshitz, L.
Power series solutions of algebraic differential equations.
Math. Ann. 267 (1984), 213–238.
-
[5]
-
Denef, J., and Lipshitz, L.
Decision problems for differential equations. The Journ. of
Symb. Logic 54, 3 (1989), 941–950.
-
[6]
-
Khovanskii, A. G.
Fewnomials. American Mathematical Society, Providence,
RI, 1991.
-
[7]
-
Péladan-Germa, A.
Testing identities of series defined by algebraic partial
differential equations. In Applied Algebra, Algebraic
Algorithms and Error-Correcting Codes (1995), G. Cohen, M.
Giusti, and T. Mora, Eds., Springer-Verlag, pp. 393–407.
Proceedings of the 11th International Symposium, AAECC-11,
Paris, France, July 1995.
-
[8]
-
Richardson, D. The uniformity
conjecture. In Lecture Notes in Computer Science (2001),
vol. 2064, Springer Verlag, pp. 253–272.
-
[9]
-
Risch, R. Algebraic properties
of elementary functions in analysis. Amer. Journ. of Math.
4, 101 (1975), 743–759.
-
[10]
-
Shackell, J. A
differential-equations approach to functional equivalence. In
ISSAC '89 Proceedings (Portland, Oregon, 1989), G.
Gonnet, Ed., A.C.M. Press, pp. 7–10.
-
[11]
-
Shackell, J. Zero-equivalence
in function fields defined by algebraic differential equations.
Trans. Amer. Math. Soc. 336/1 (1993), 151–172.
-
[12]
-
Shackell, J., and van der Hoeven,
J. Complexity bounds for zero-test algorithms. Tech.
Rep. 2001-63, Prépublications d'Orsay, 2001.
-
[13]
-
van der Hoeven, J. Automatic
asymptotics. PhD thesis, École polytechnique, France,
1997.
-
[14]
-
van der Hoeven, J. Relax, but
don't be too lazy. Tech. Rep. 78, Prépublications
d'Orsay, 1999. Submitted to JSC.
-
[15]
-
van der Hoeven, J. Complex
transseries solutions to algebraic differential equations. Tech.
Rep. 2001-34, Univ. d'Orsay, 2001.
-
[16]
-
van der Hoeven, J. Fast
evaluation of holonomic functions near and in singularities.
JSC 31 (2001), 717–743.
-
[17]
-
van der Hoeven, J.
Zero-testing, witness conjectures and differential diophantine
approximation. Tech. Rep. 2001-62, Prépublications
d'Orsay, 2001.
 ,
,  or
or  .
.
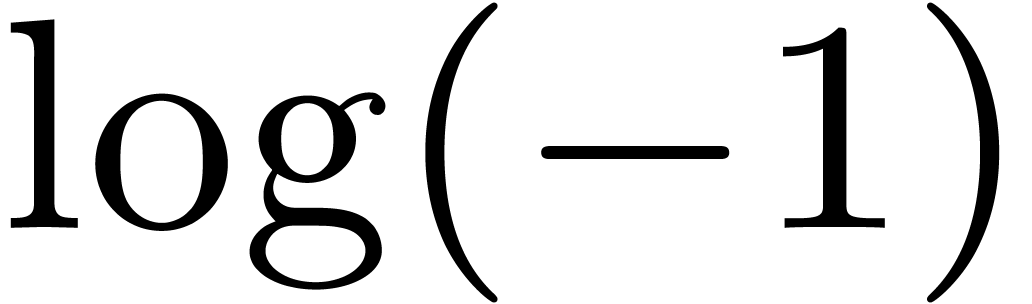 or
or 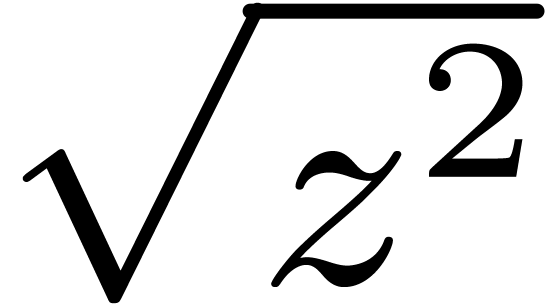 ?
?
 and
and  are different expressions, but they represent the same
function.
are different expressions, but they represent the same
function.
 .
. which satisfies a non-trivial algebraic differential
equation
which satisfies a non-trivial algebraic differential
equation 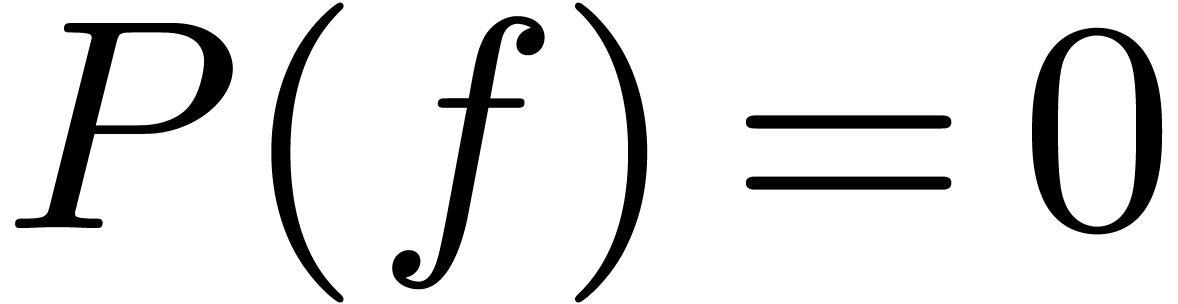 .
. and the
constants in some field
and the
constants in some field  like
like  ,
,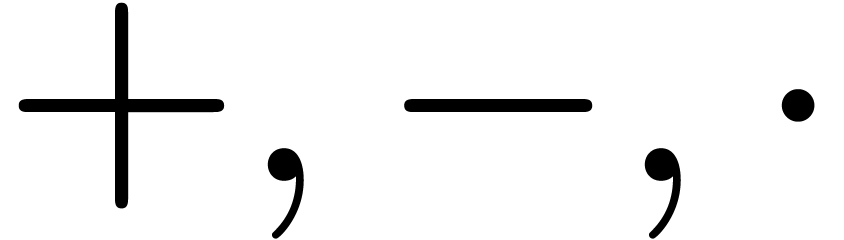 and left
composition of infinitesimal power series by differentially algebraic
power series
and left
composition of infinitesimal power series by differentially algebraic
power series  .
. and
and  .
.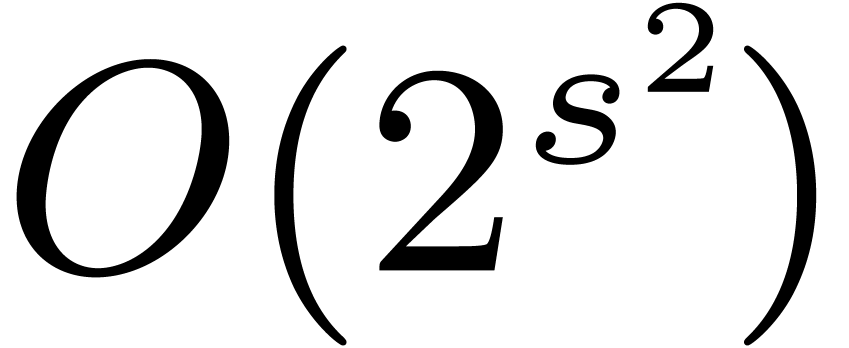 ,
, denotes the input
size) for the number of zeros for systems of real Pfaffian functions
[
denotes the input
size) for the number of zeros for systems of real Pfaffian functions
[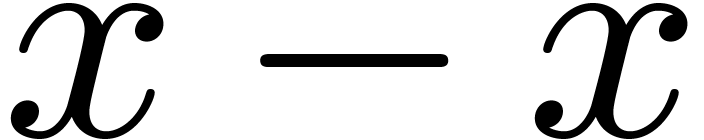 ,
, is a complicated expression). Also, if we
want the approach to be efficient, good bounds (such as the ones
predicted by witness conjectures [
is a complicated expression). Also, if we
want the approach to be efficient, good bounds (such as the ones
predicted by witness conjectures [ .
. at the top of this section are
usually specified by a finite number of algebraic differential
equations and initial conditions. Now instead of asking whether a
given expression represents zero, we may ask for which initial
conditions for
at the top of this section are
usually specified by a finite number of algebraic differential
equations and initial conditions. Now instead of asking whether a
given expression represents zero, we may ask for which initial
conditions for  .
. of
of 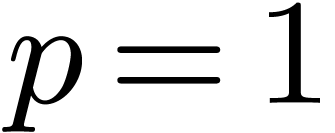 and that
and that 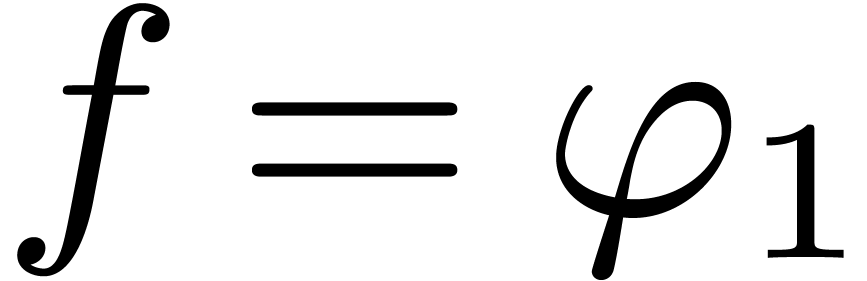 satisfies the
algebraic differential equation
satisfies the
algebraic differential equation 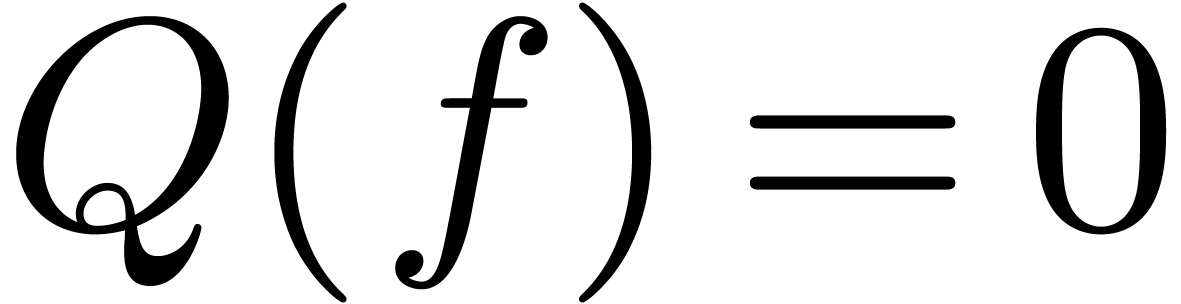 .
. .
.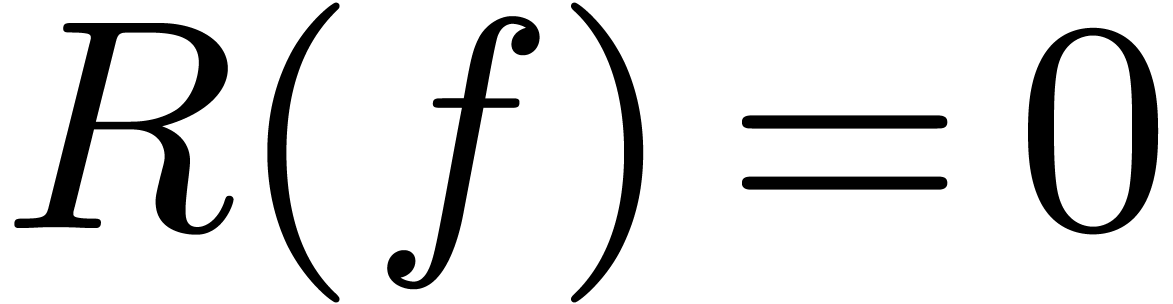 which is equivalent to
which is equivalent to  of
of  .
.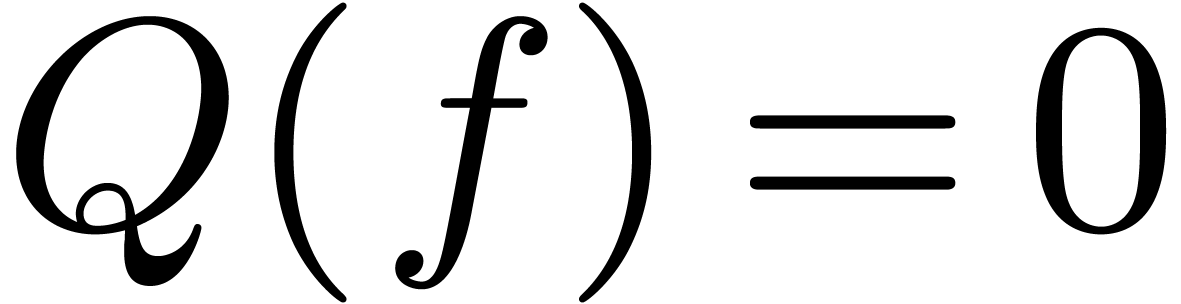 still has a
unique solution in
still has a
unique solution in  in
in 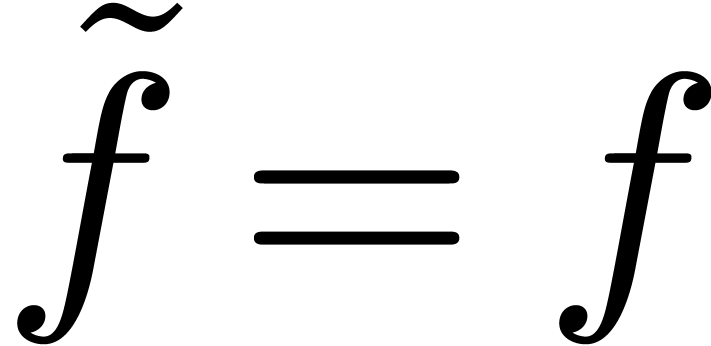 .
. .
. be an effective differential ring
(i.e. the differentiation is effective too). We assume that
the elements of
be an effective differential ring
(i.e. the differentiation is effective too). We assume that
the elements of 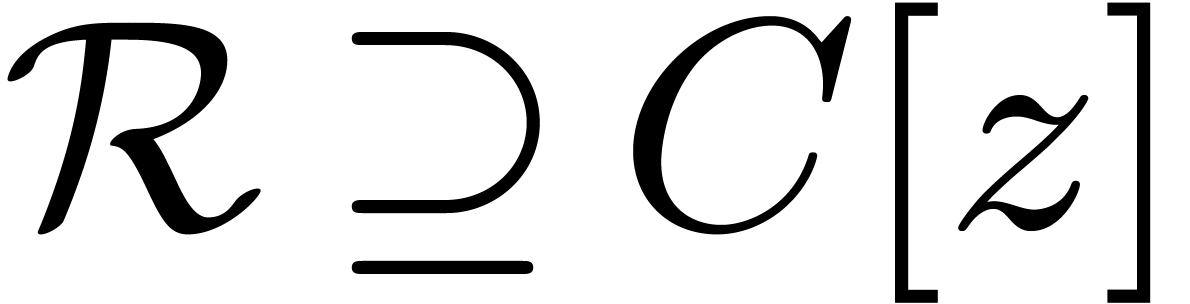 ,
, on
on 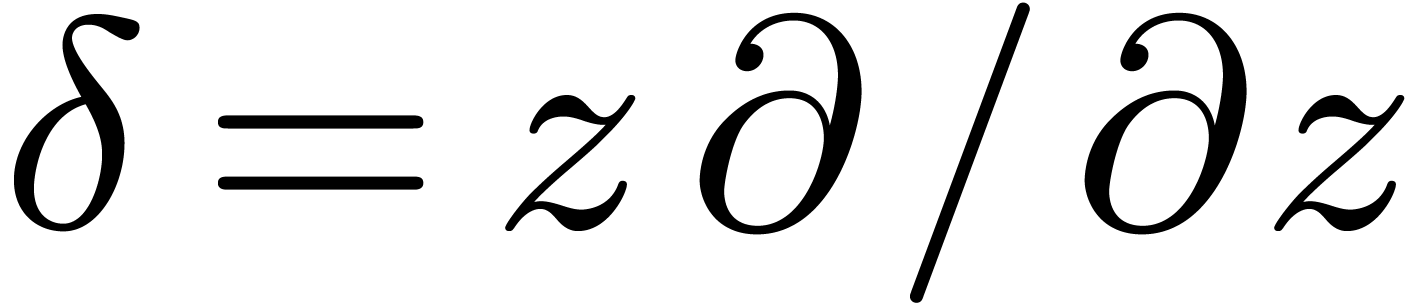 on
on 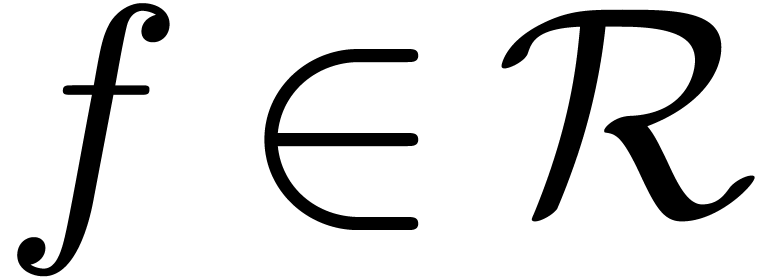 and
and 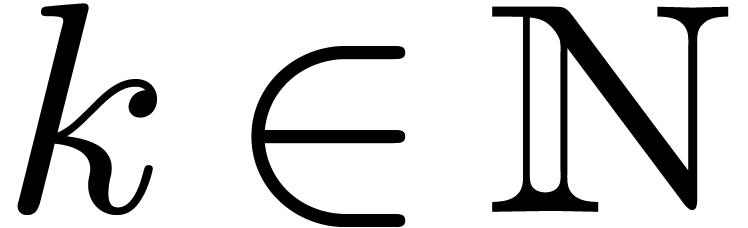 on input and
which computes the coefficient
on input and
which computes the coefficient 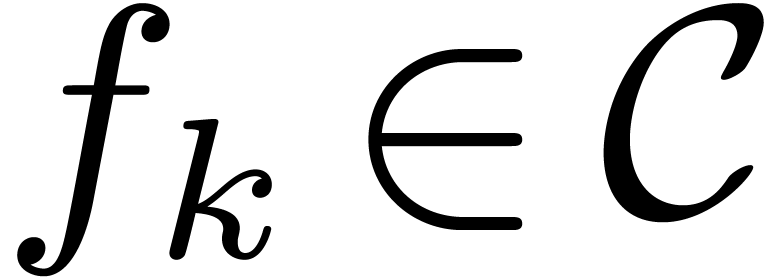 of
of 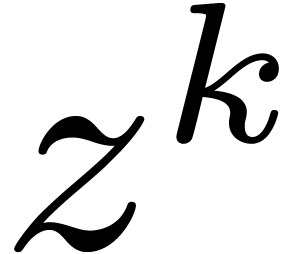 in
in 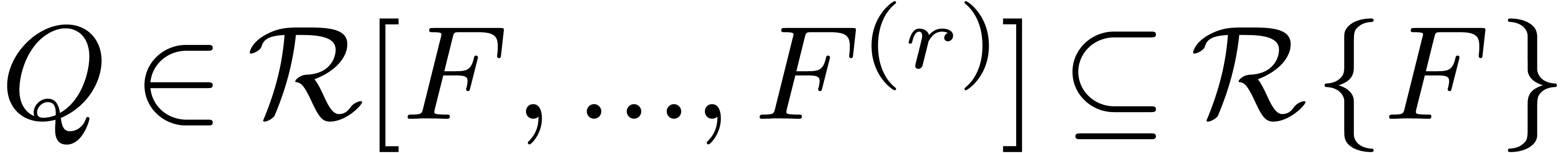 of order
of order 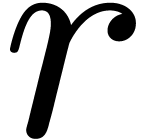 (recall that
(recall that 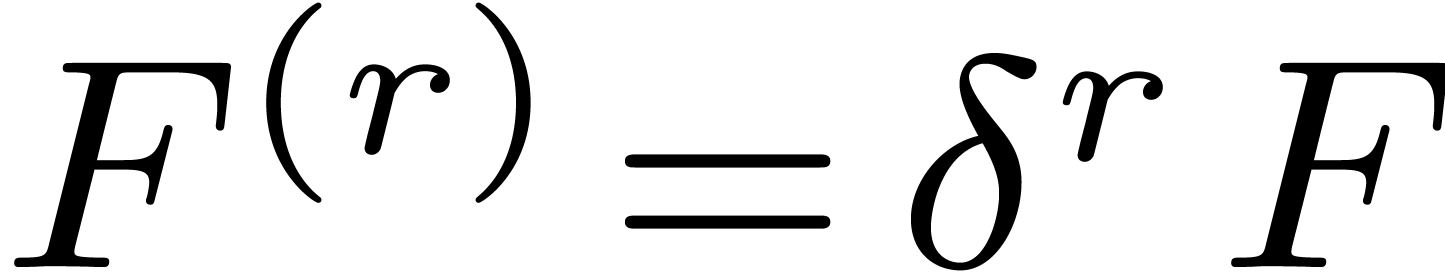 )
) to
to 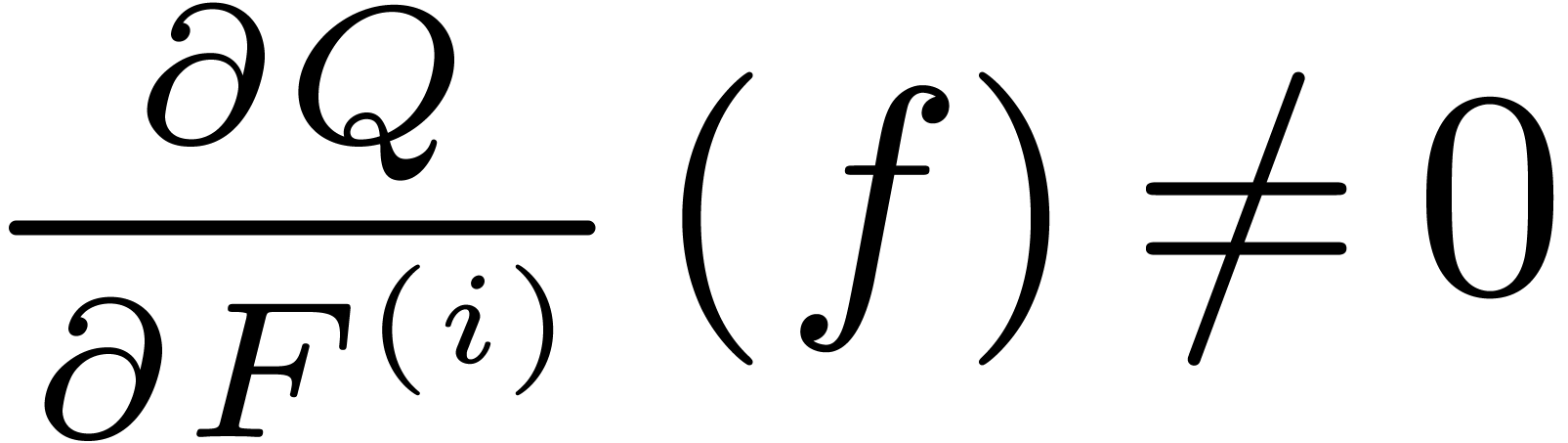 for some
for some 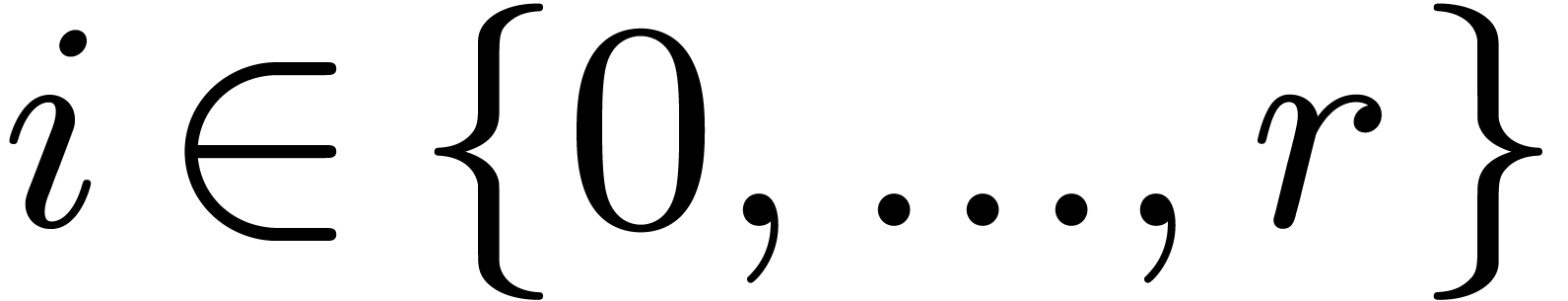 (if
(if  by a non-zero
by a non-zero 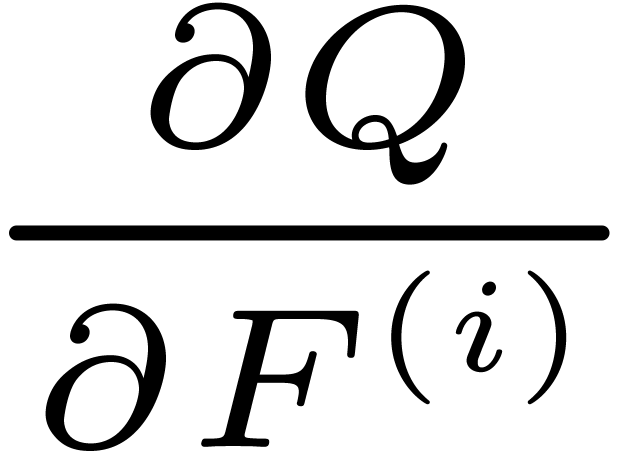 and continue doing this until
and continue doing this until  such that the valuation of
such that the valuation of  is
minimal, say
is
minimal, say  .
.
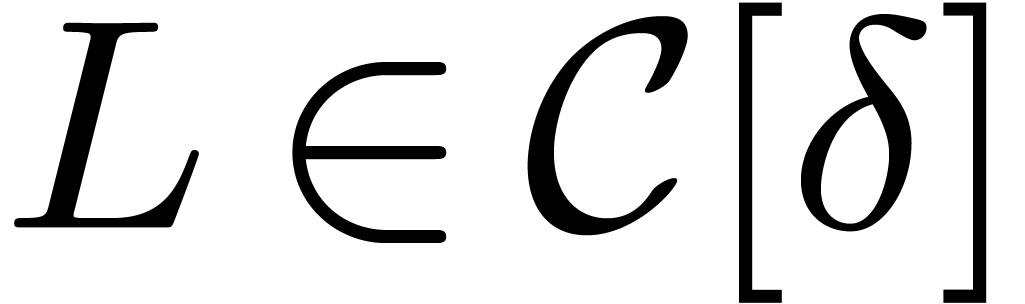 and
and 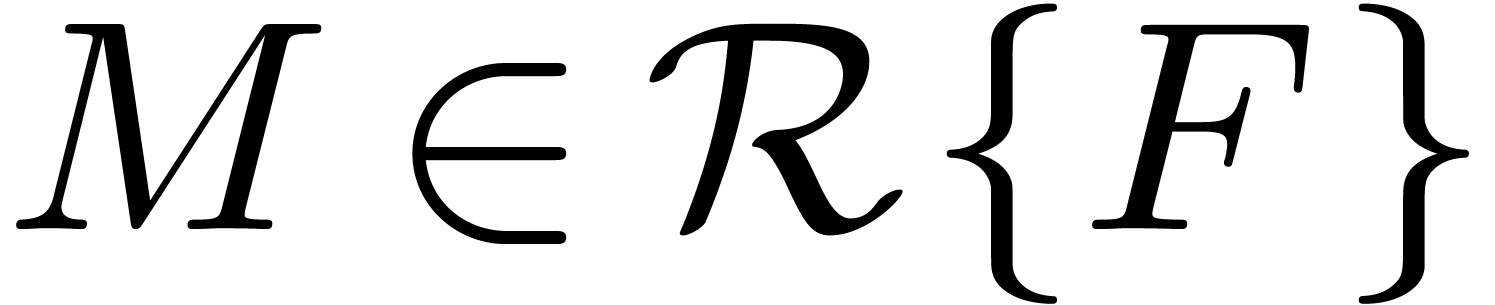 .
.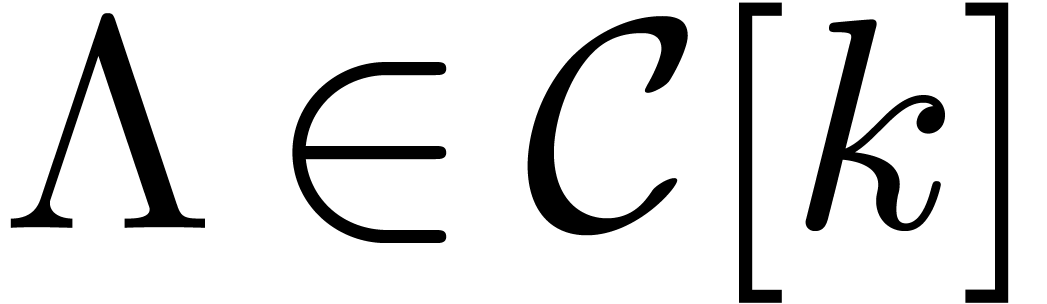 be the polynomial we get from
be the polynomial we get from 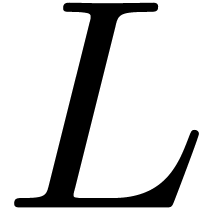 when reinterpreting
when reinterpreting 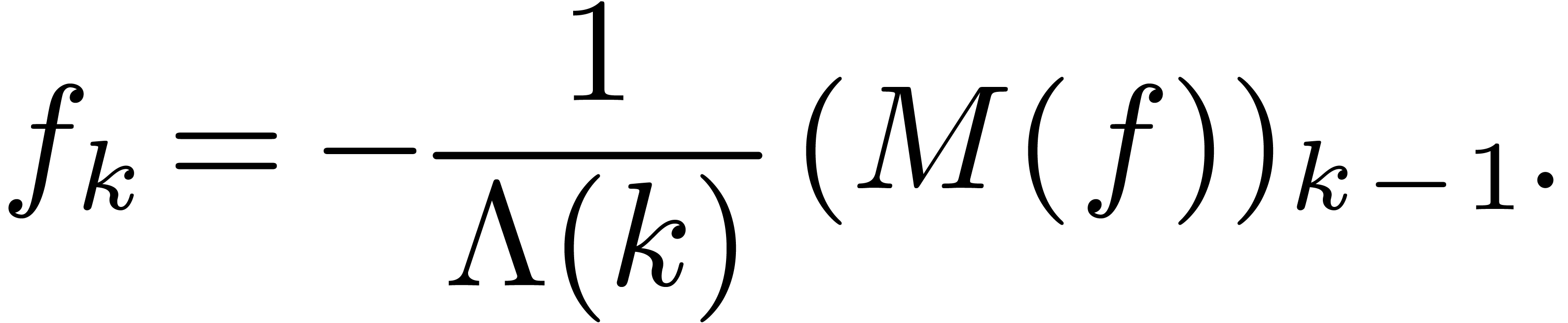
 .
. (or
(or 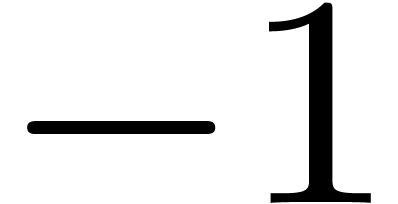 if such a root does not exist). Then we notice in particular that
if such a root does not exist). Then we notice in particular that  coefficients are
coefficients are  .
.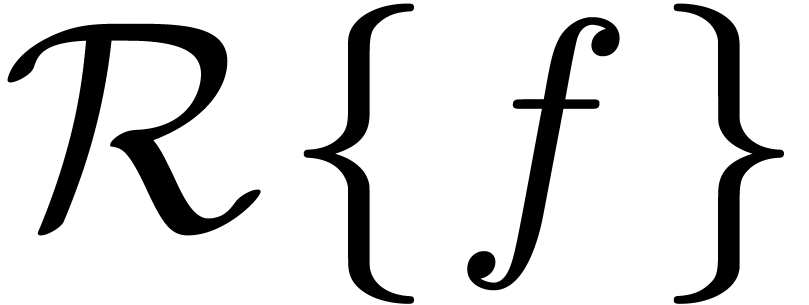 is again an effective power series domain. Now elements in
is again an effective power series domain. Now elements in
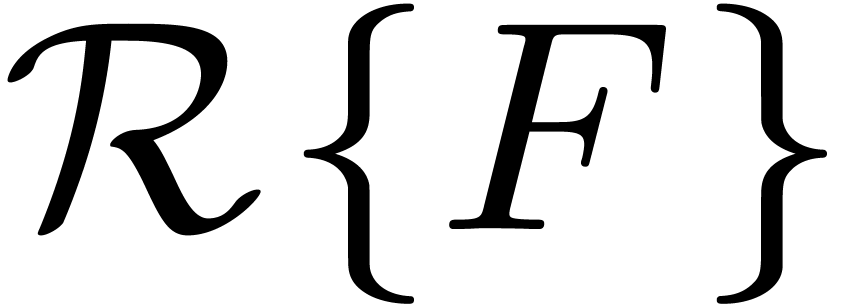 under the
substitution
under the
substitution  .
.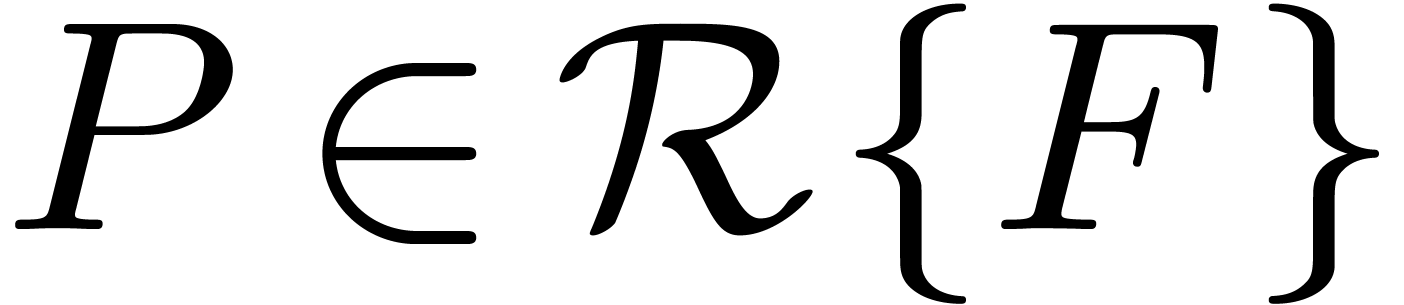 .
. denotes the initial and
denotes the initial and  denotes the separant of a differential
polynomial
denotes the separant of a differential
polynomial 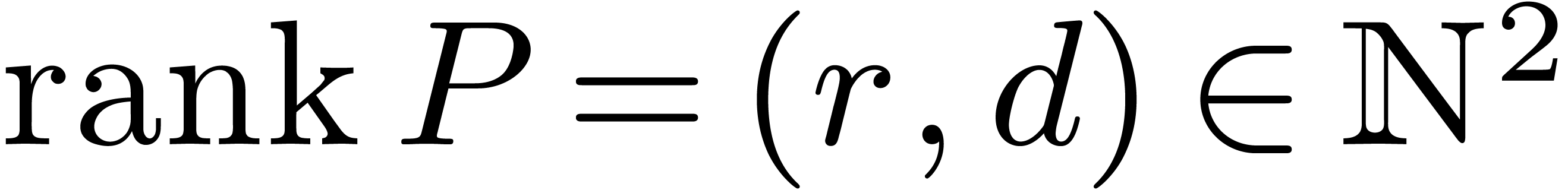 ,
,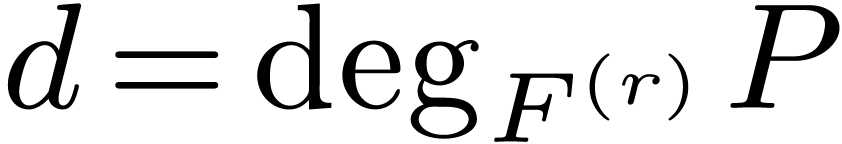 the degree of
the degree of 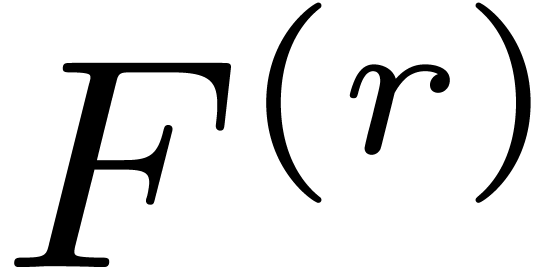 .
.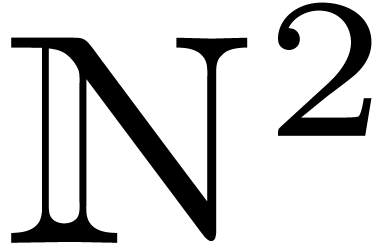 of
possible ranks is well-ordered w.r.t. the
lexicographical ordering. We will write
of
possible ranks is well-ordered w.r.t. the
lexicographical ordering. We will write  for
for
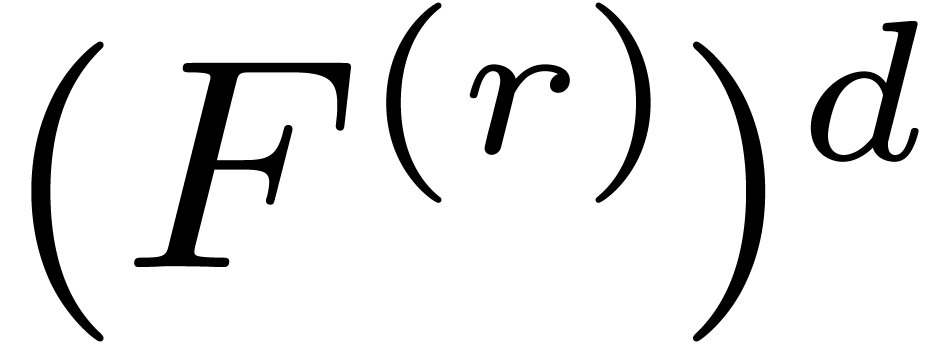 .
.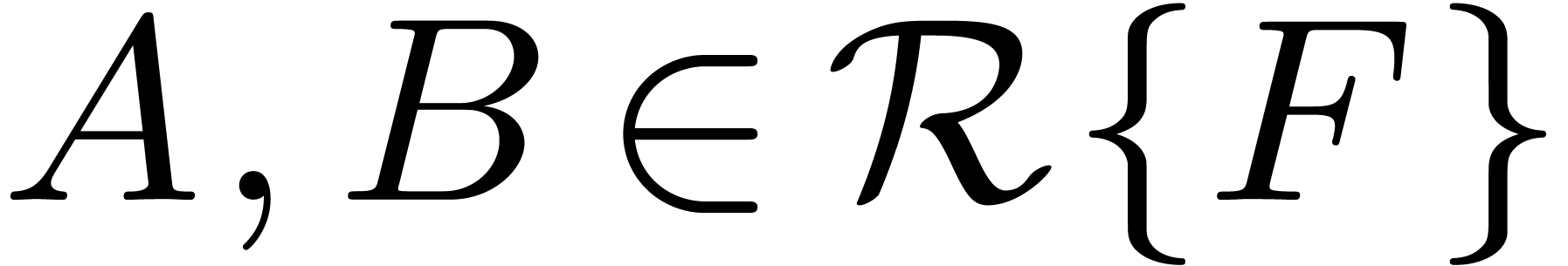 ,
, the Ritt reduction of
the Ritt reduction of  with respect to
with respect to  .
.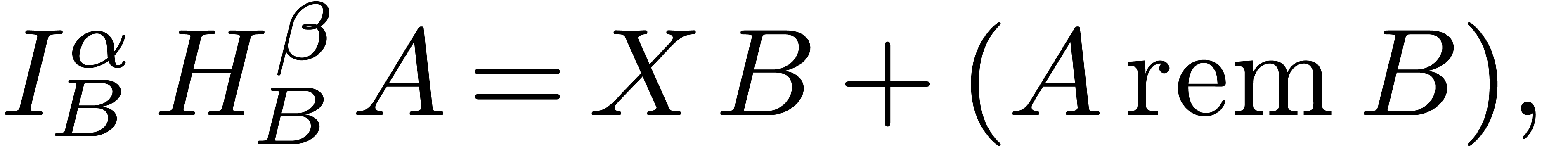
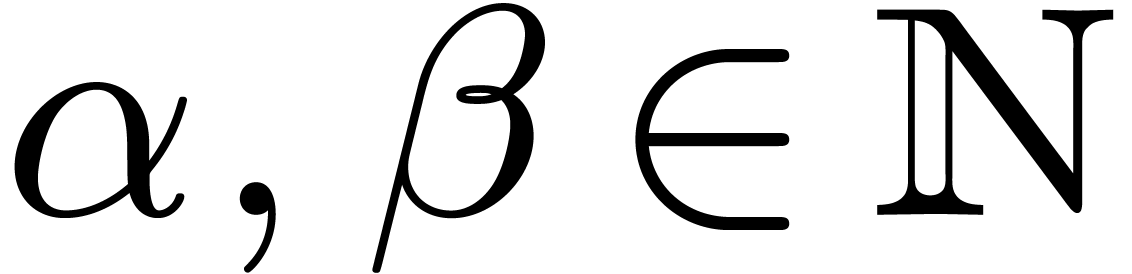 ,
,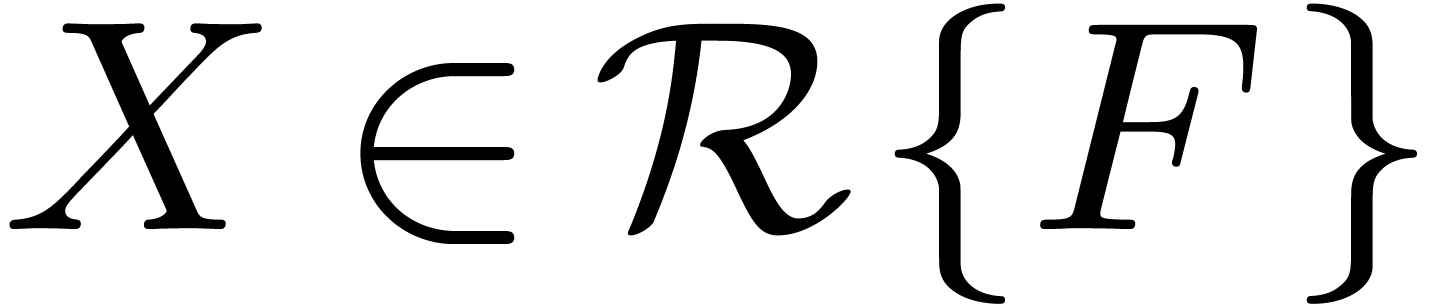 and
and  .
. by
by  as we like. In fact, it suffices to add one
as we like. In fact, it suffices to add one 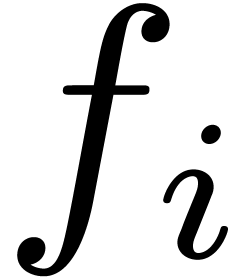 for each new subexpression of the form
for each new subexpression of the form  .
. of Puiseux series over the algebraic closure
of Puiseux series over the algebraic closure  of
of  ,
, be the totally ordered group of
logarithmic monomials with powers in
be the totally ordered group of
logarithmic monomials with powers in 
 and
and 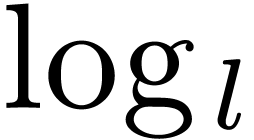 stands for the
stands for the
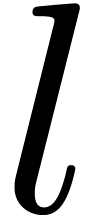 -th
-th if and only if
if and only if  ,
, in (
in ( on
on  corresponds to writing
corresponds to writing 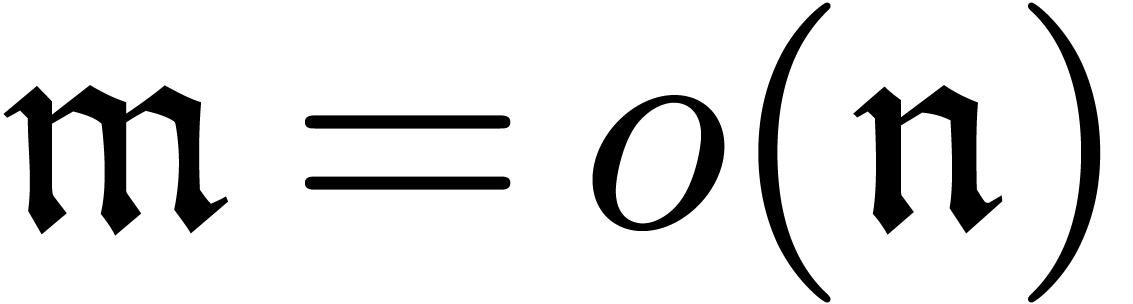 as
as  in analysis.
in analysis.
 is said to be grid-based, if
there exist monomials
is said to be grid-based, if
there exist monomials  and
and  in
in  .
. with grid-based support. We will
usually write such series using the infinite sum notation
with grid-based support. We will
usually write such series using the infinite sum notation  and we denote the set of all logarithmic transseries by
and we denote the set of all logarithmic transseries by
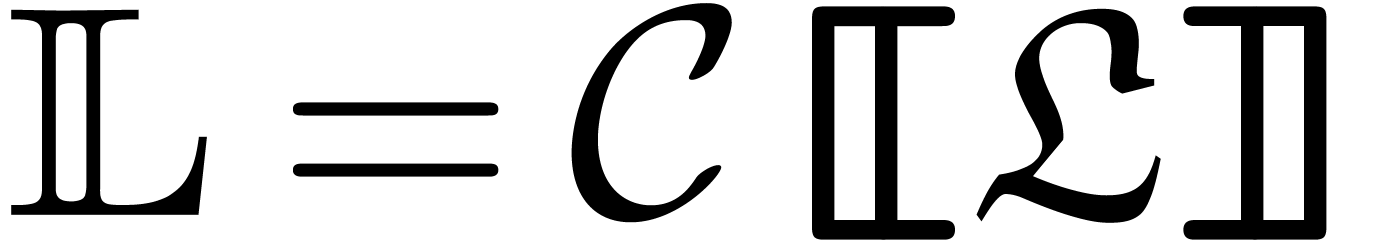 .
. is grid-based (whence well-ordered),
this support admits a
is grid-based (whence well-ordered),
this support admits a  -maximal
-maximal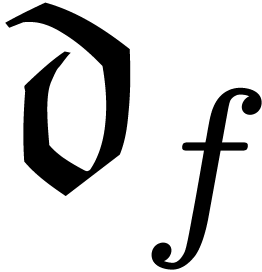 which is called the dominant
monomial of
which is called the dominant
monomial of  is a
field for the operations
is a
field for the operations
 is a finite sum. There also exists a natural
derivation
is a finite sum. There also exists a natural
derivation  ,
, of the form (
of the form (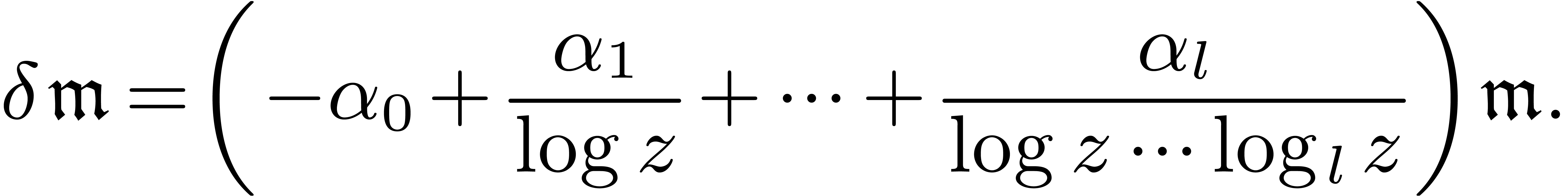
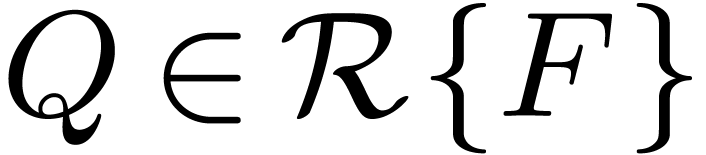 be a differential polynomial of the form
be a differential polynomial of the form  be
defined as in section
be
defined as in section 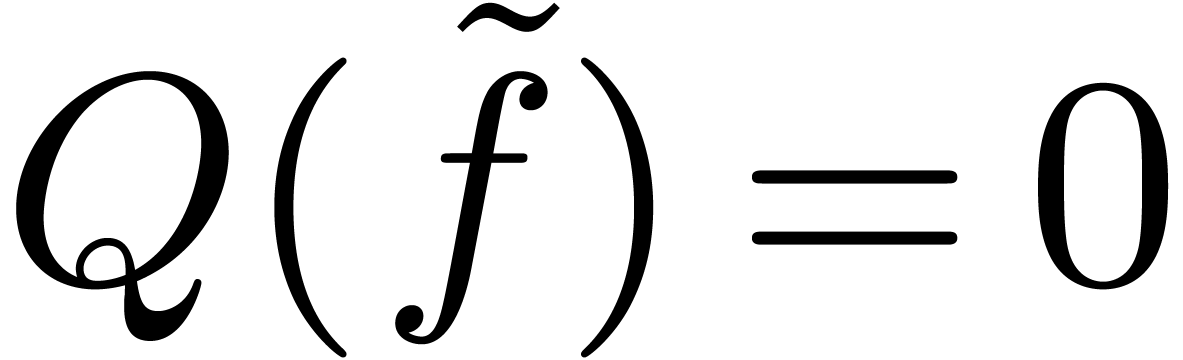 with side condition
with side condition 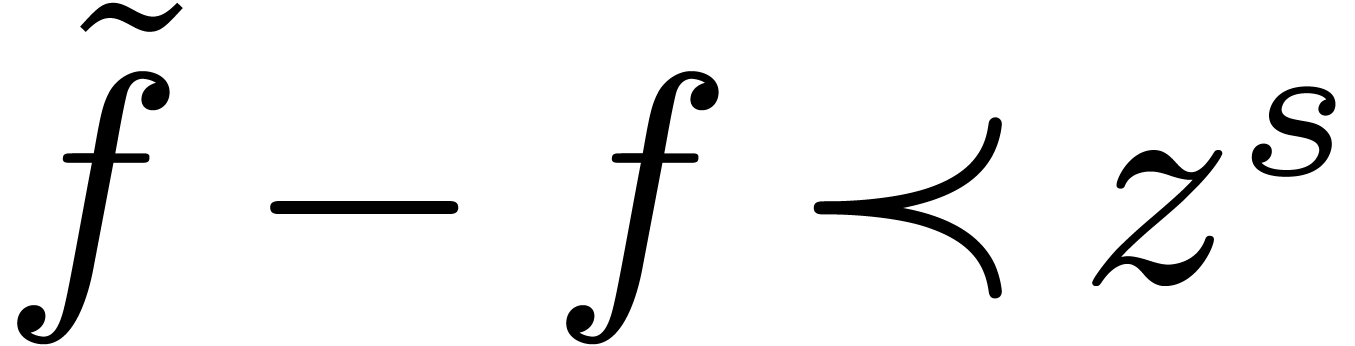 admits
admits 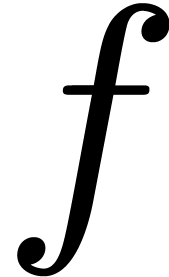 as its unique solution in
as its unique solution in  .
.
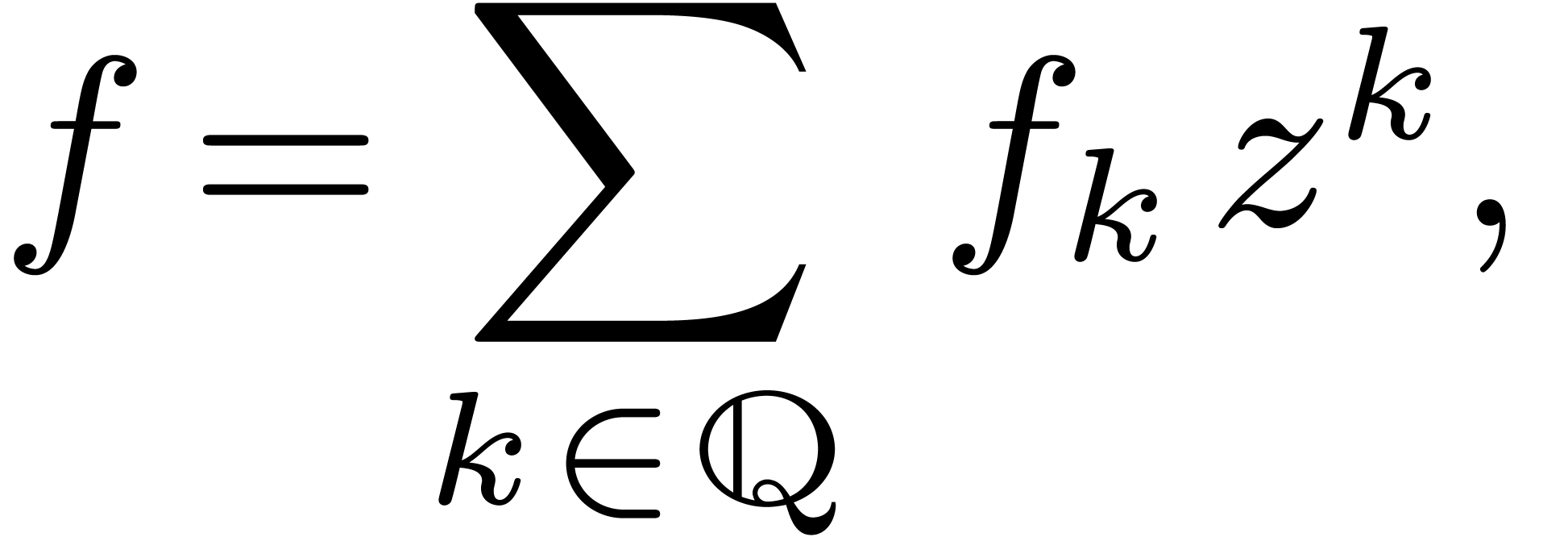
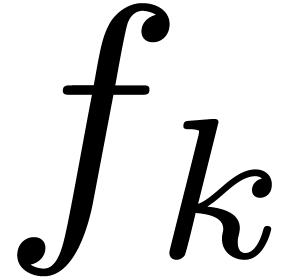 are series in
are series in  and
and 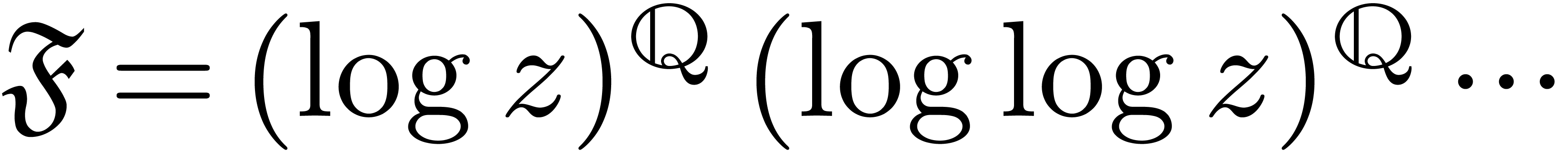 .
. as the lexicographical
product of
as the lexicographical
product of  and
and  .
. .
.

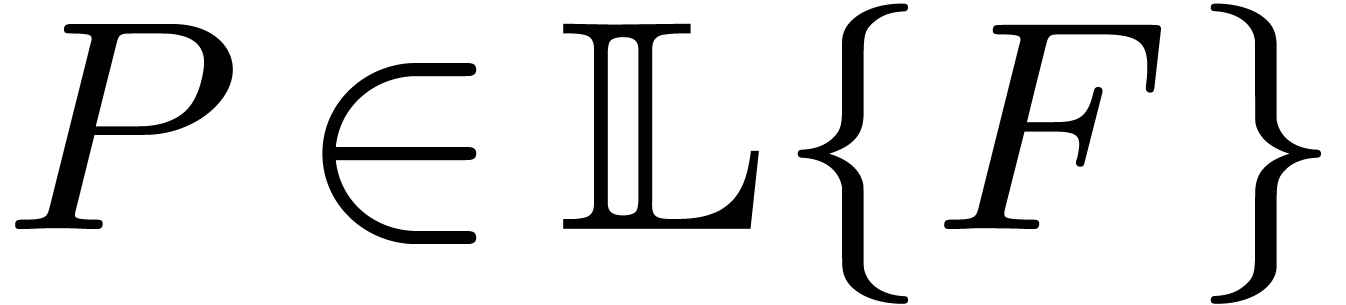 and
and  of non-zero solutions and
their corresponding coefficients. Actually, it is convenient to
characterize such potential dominant monomials first. It
suffices to characterize when
of non-zero solutions and
their corresponding coefficients. Actually, it is convenient to
characterize such potential dominant monomials first. It
suffices to characterize when 
 denotes the unique differential polynomial
in
denotes the unique differential polynomial
in  with
with  for all
for all  using multi-indices
using multi-indices 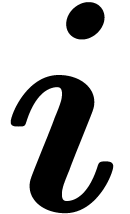 and let
and let 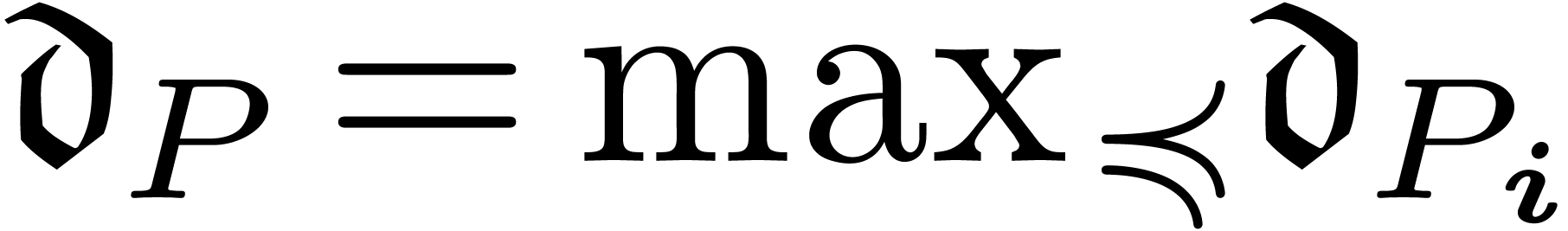 .
.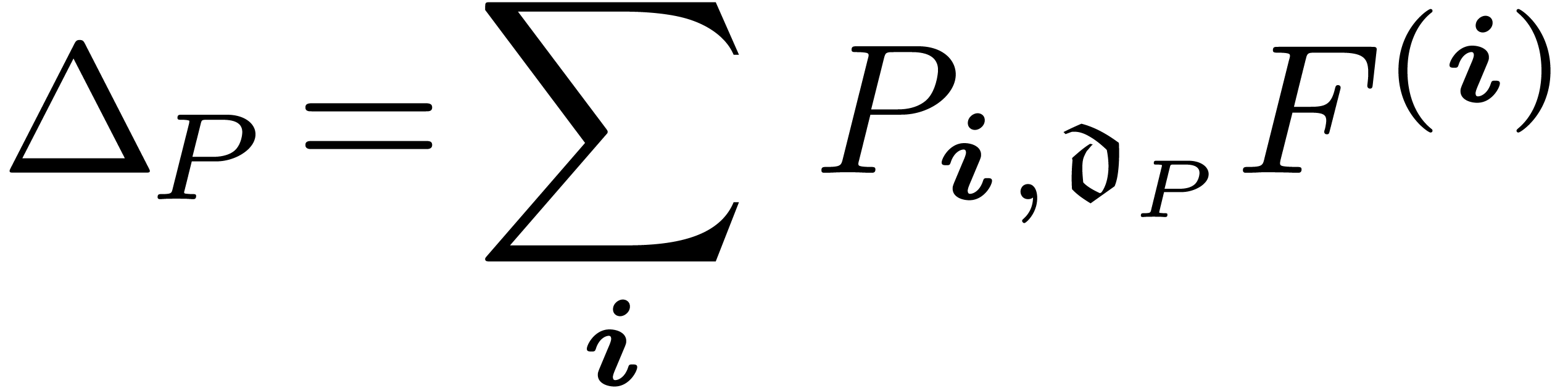
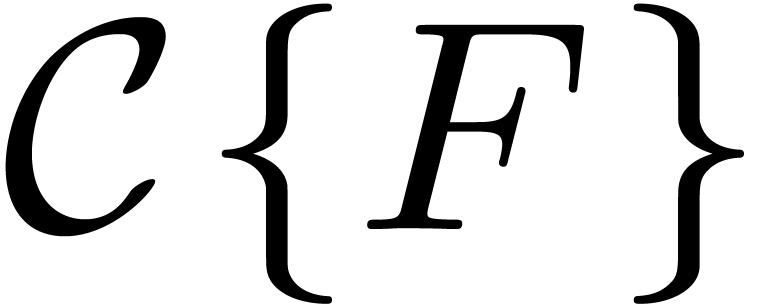 ,
,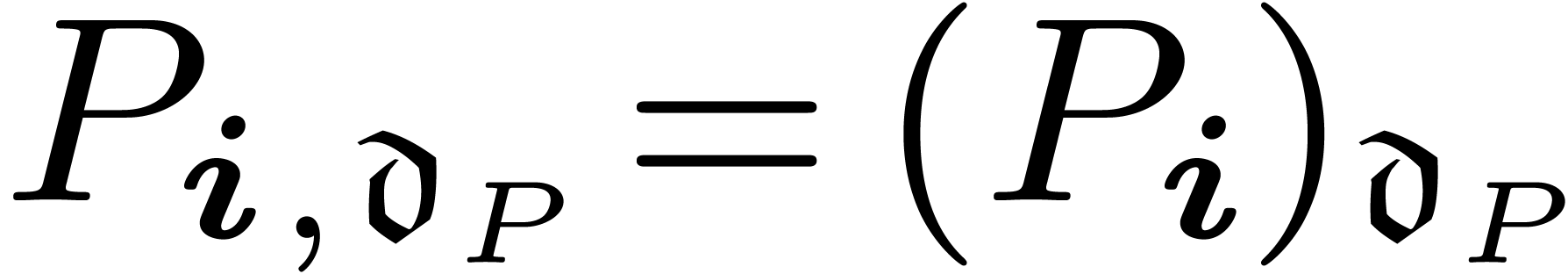 .
.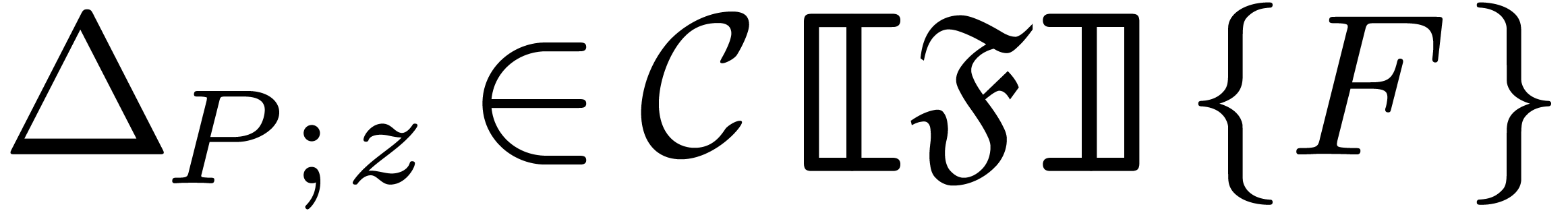 of
of 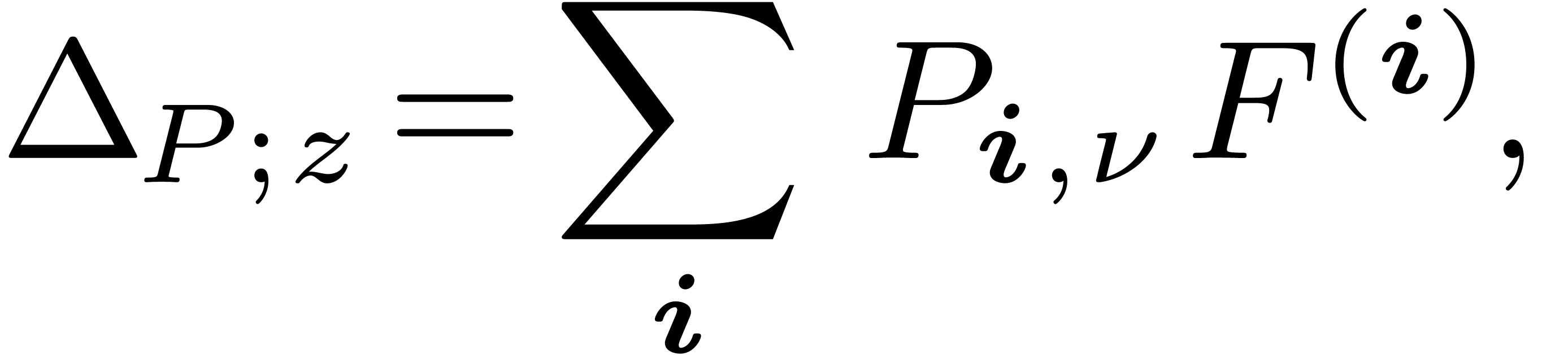
 is the valuation of
is the valuation of  denotes the
coefficient of
denotes the
coefficient of  in
in  .
. and
and  .
.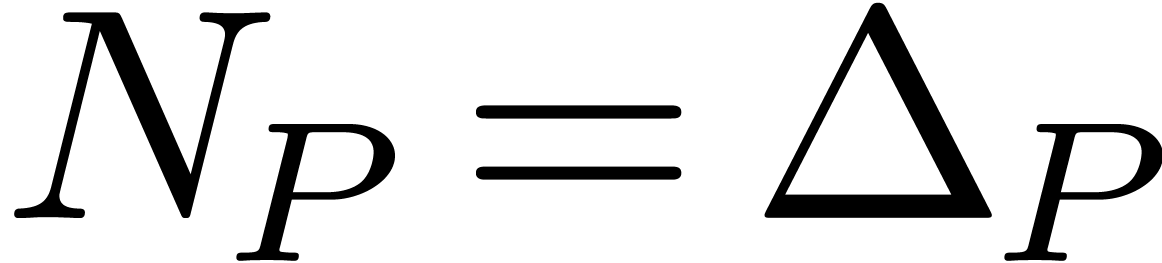 and we have
and we have
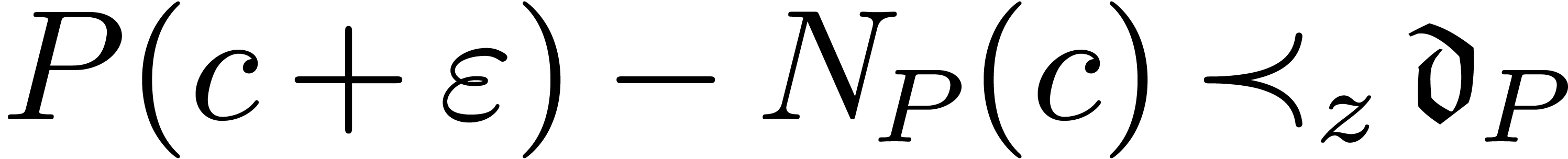
 and
and  .
. ,
,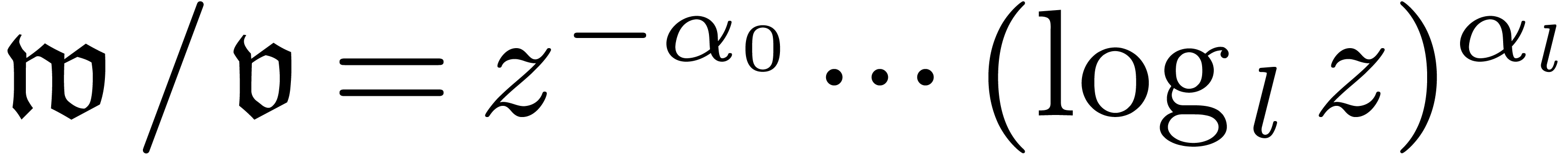 with
with 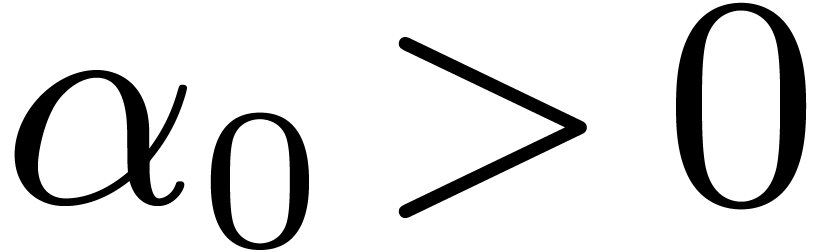 .
.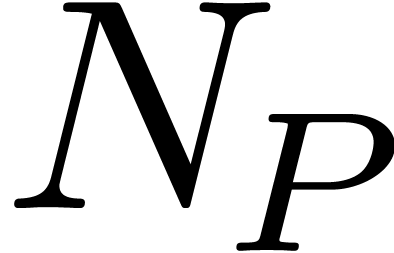 admits such a
non-zero constant root
admits such a
non-zero constant root 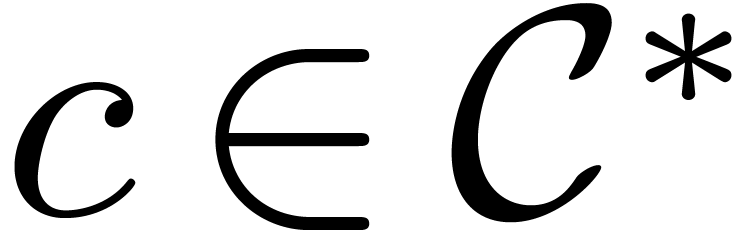 (and
(and  is a potential dominant term). Furthermore,
is a potential dominant term). Furthermore, 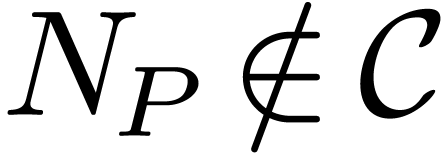 ,
,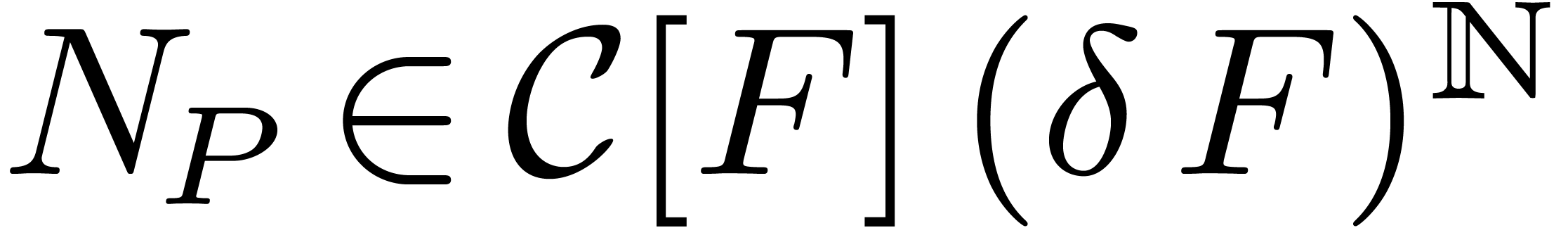 and
and 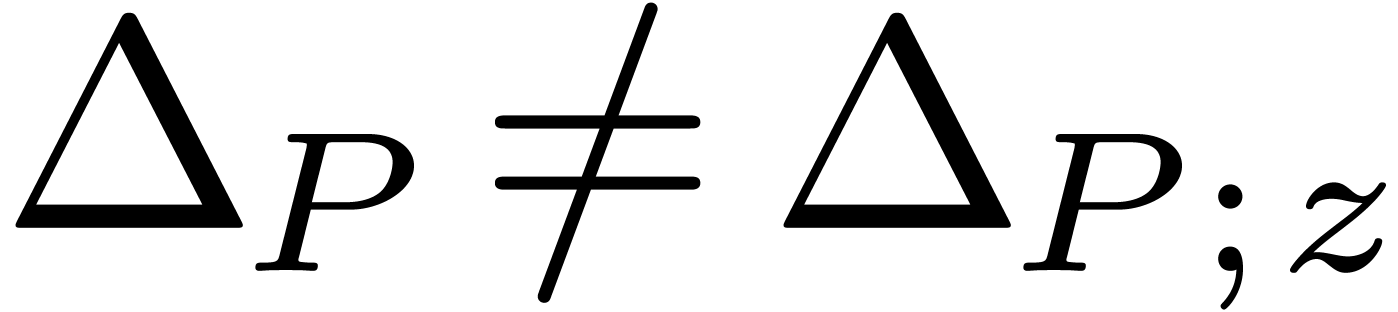 or
or 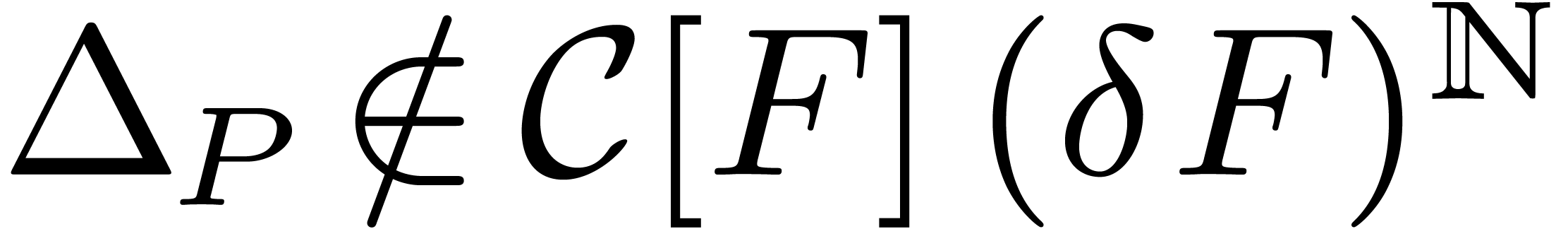 ,
,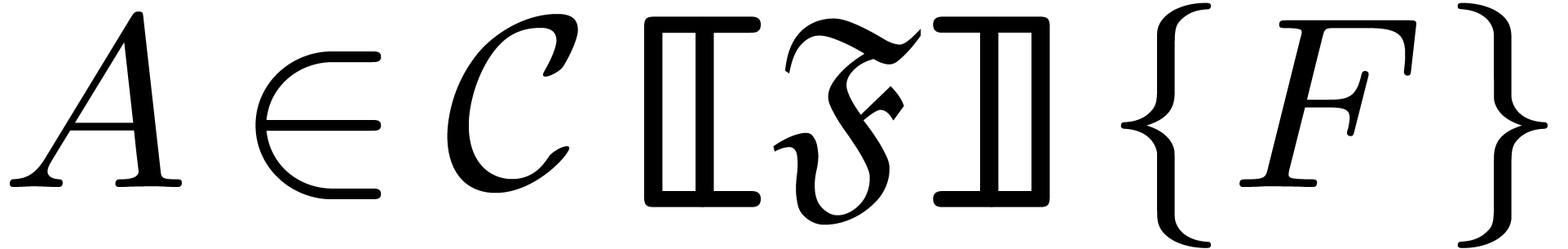 ,
, to be the unique differential polynomial in
to be the unique differential polynomial in 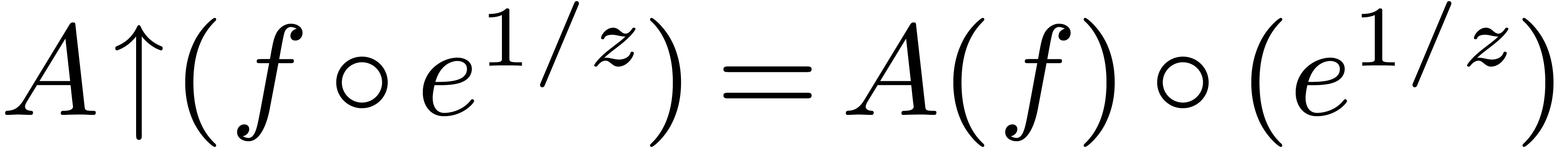
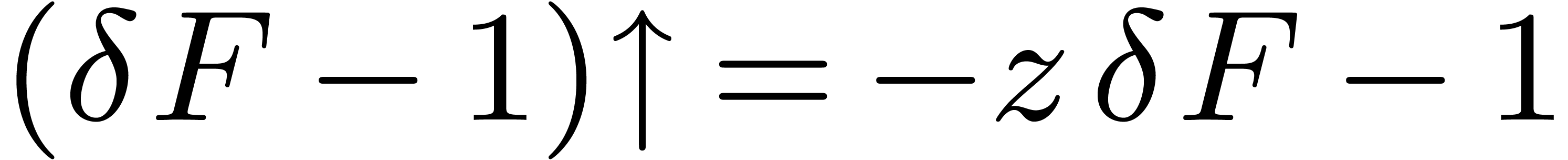 ,
,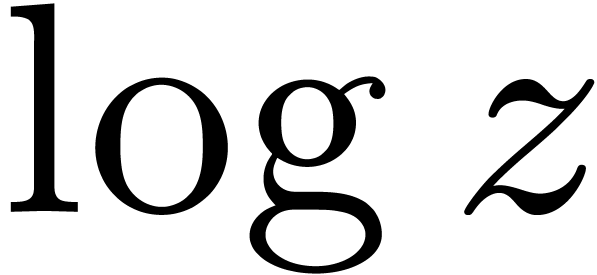 of
of 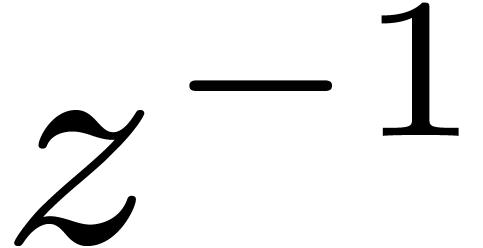 of
of
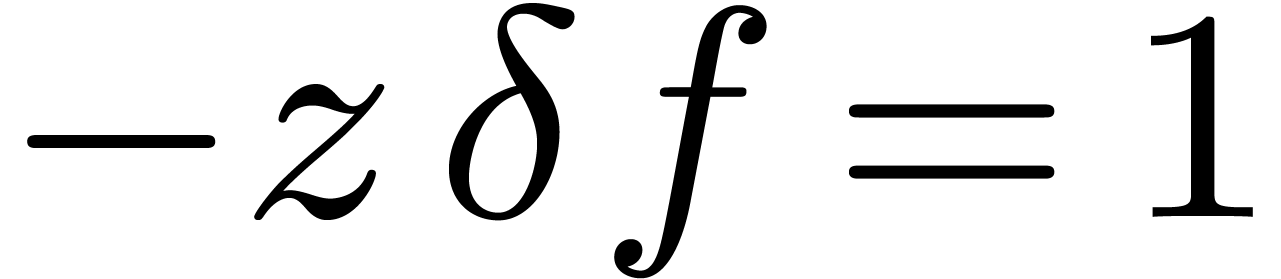 under upward shifting
under upward shifting 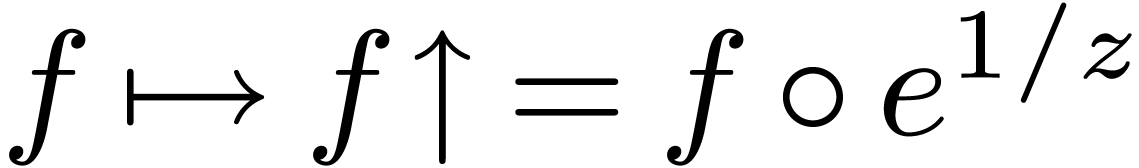 .
. we obtain a
differential polynomial
we obtain a
differential polynomial 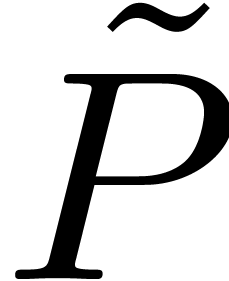 with
with 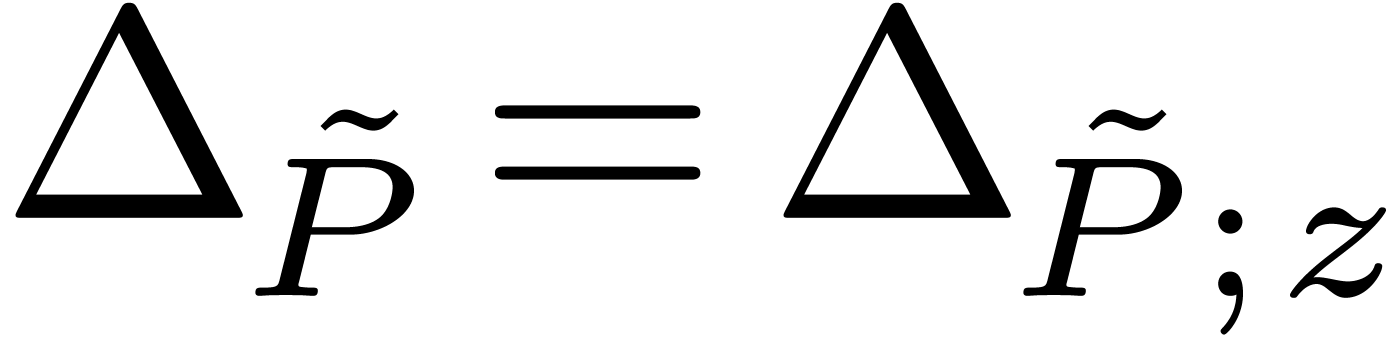 and
and  .
. and
and  admits a non-zero root in
admits a non-zero root in  .
. is not homogeneous
(i.e.
is not homogeneous
(i.e.  ).
). and upward
shiftings
and upward
shiftings 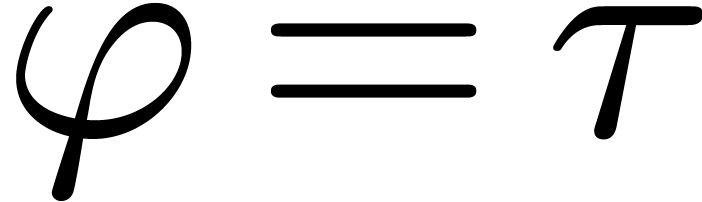 of
a solution to (
of
a solution to (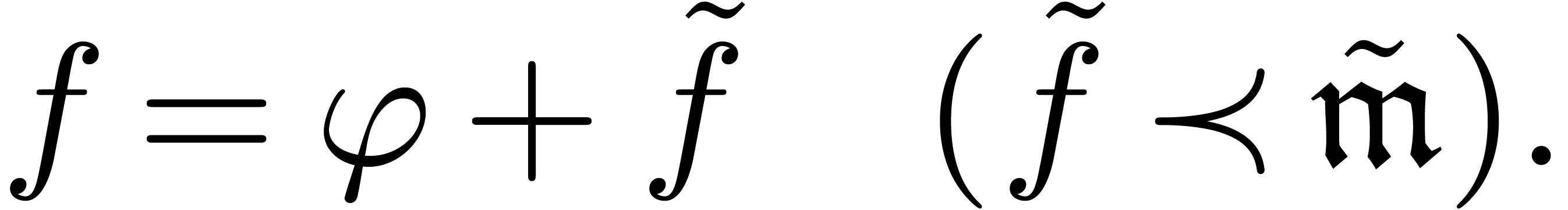
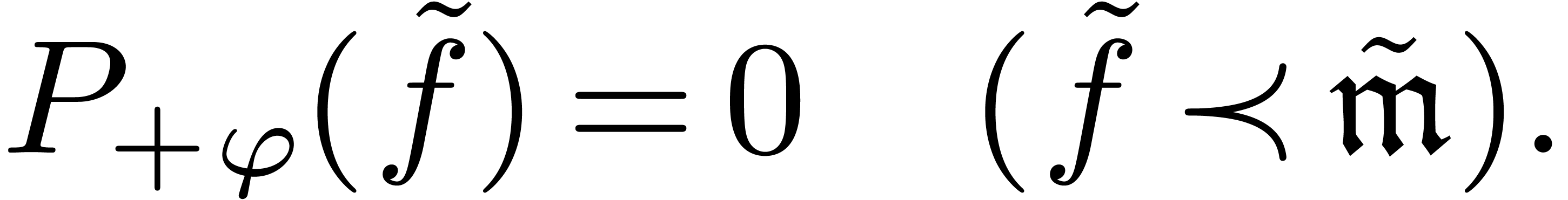
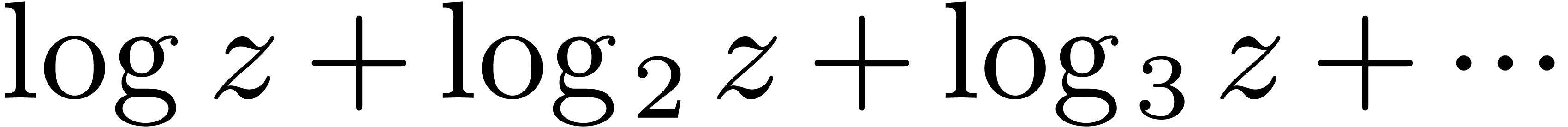
 .
.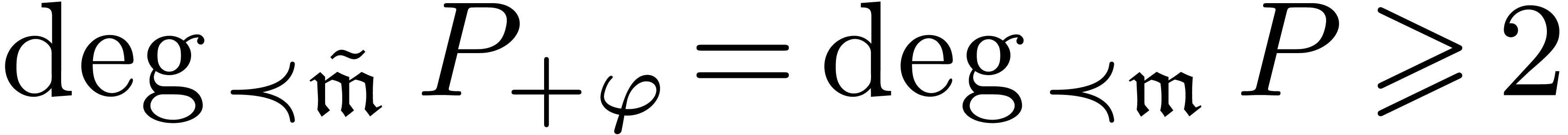 ,
, by a solution to a quasi-linear equation of the
form
by a solution to a quasi-linear equation of the
form
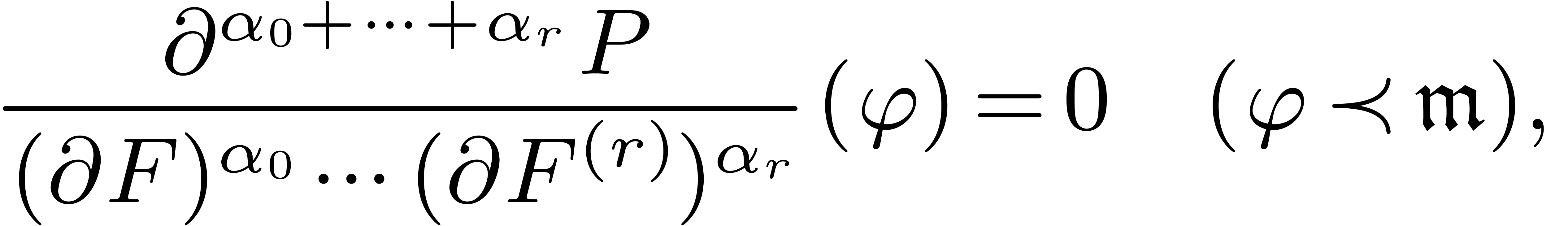
 over
over  solutions in
solutions in  if and only
if and only 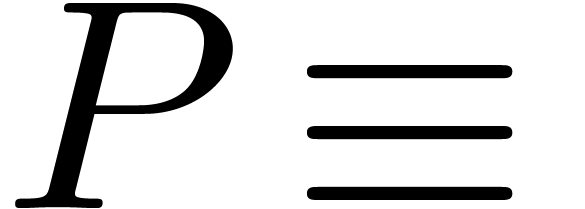 0
0 if and only if
if and only if
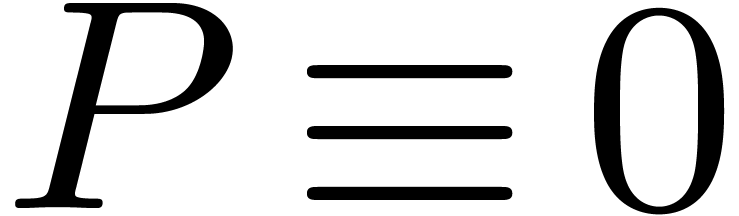
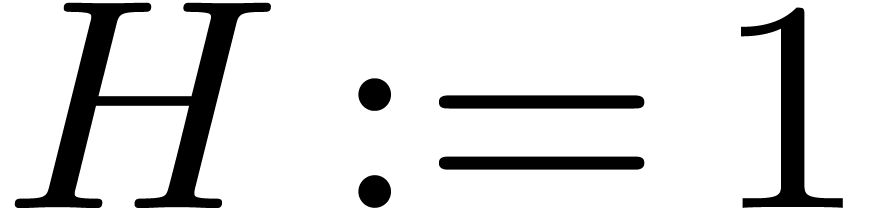
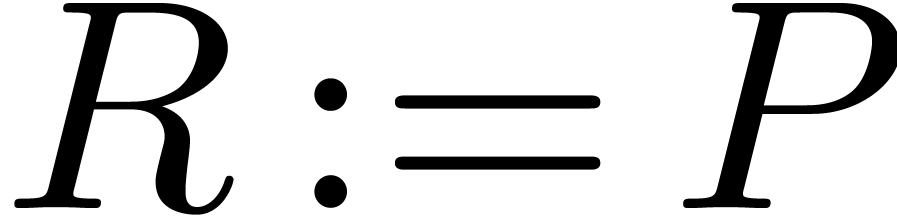
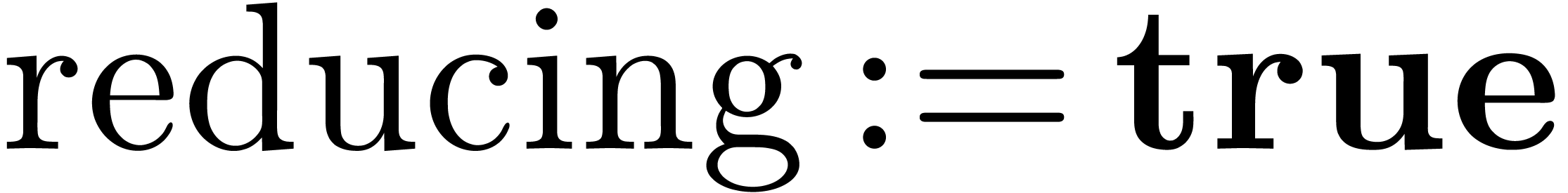
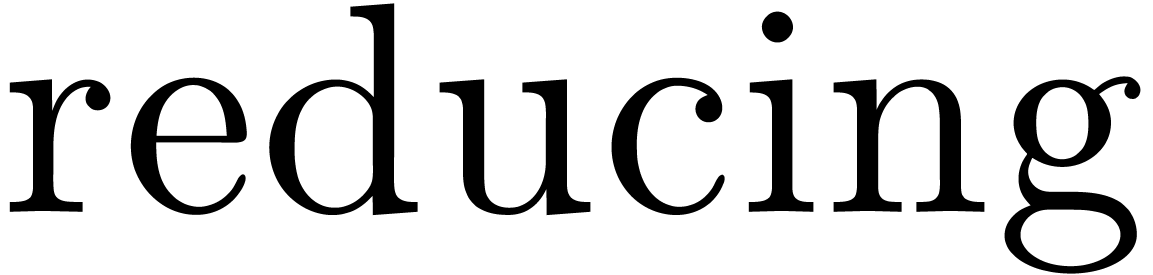
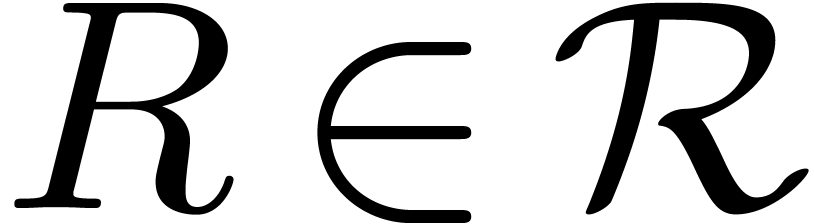 then
return
then
return 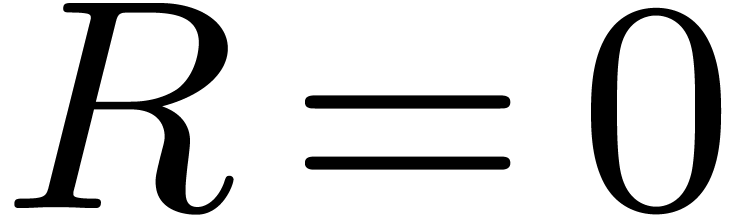
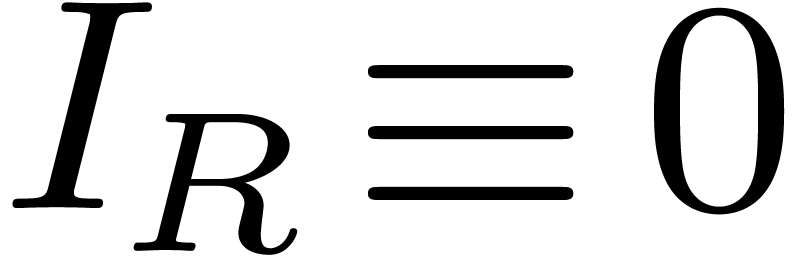 then
then
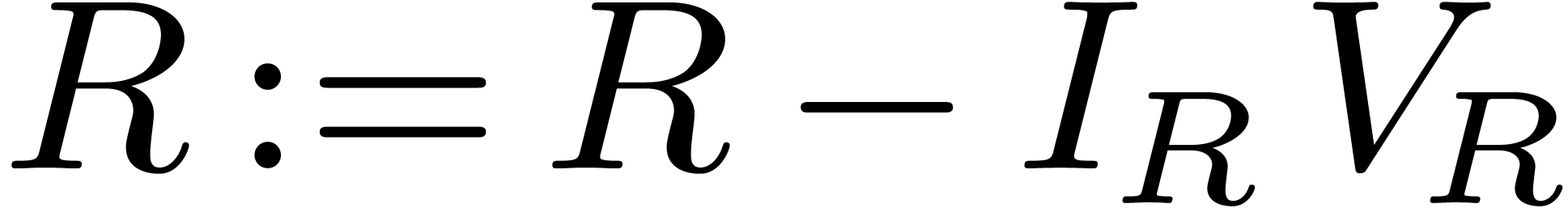
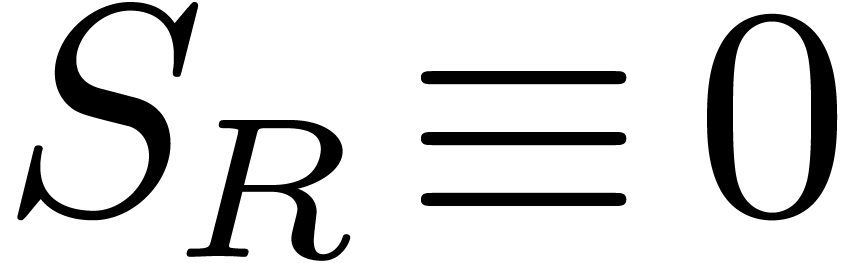 then
then
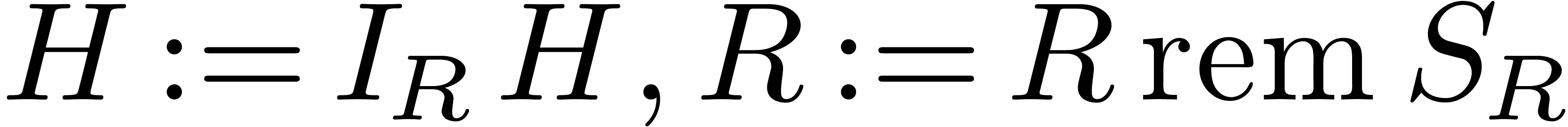
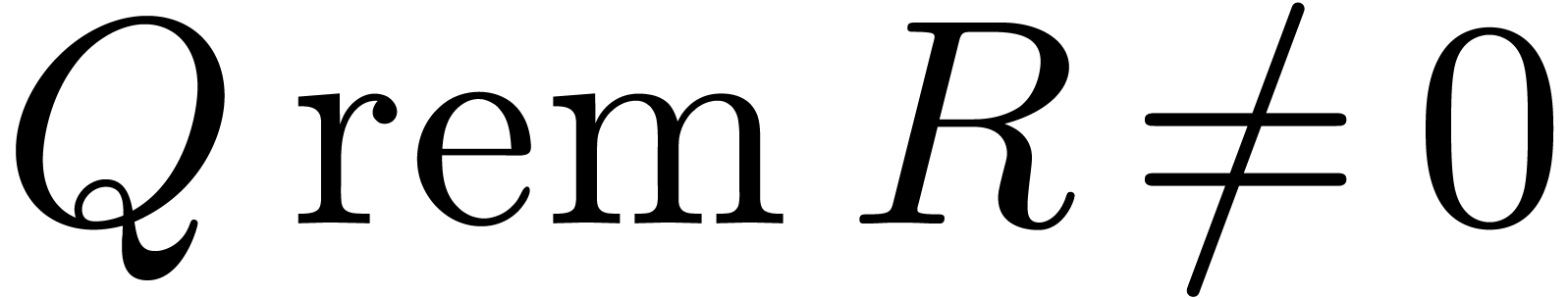 then
then
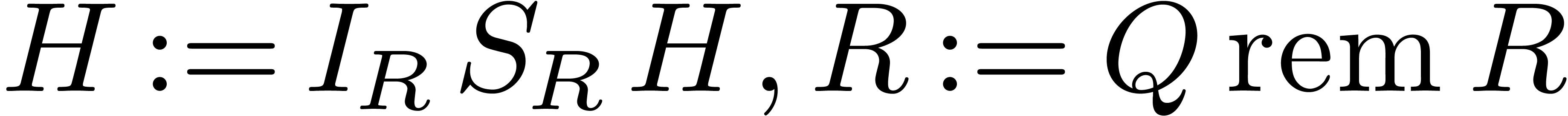
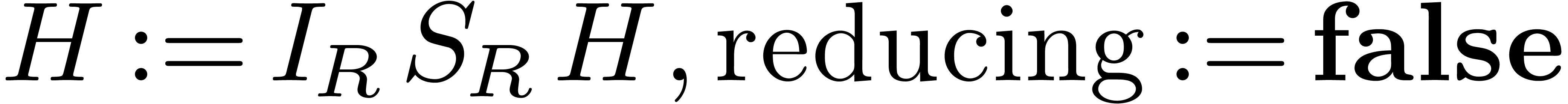
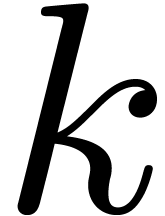 be minimal with
be minimal with 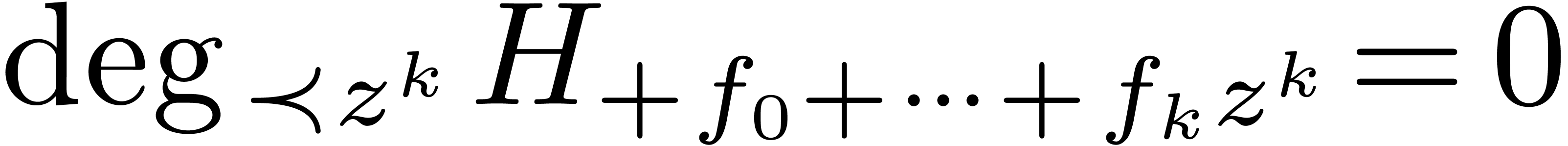
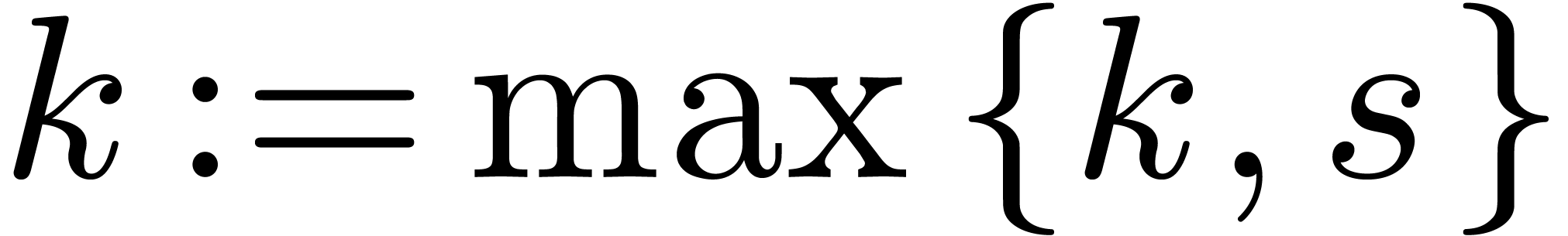
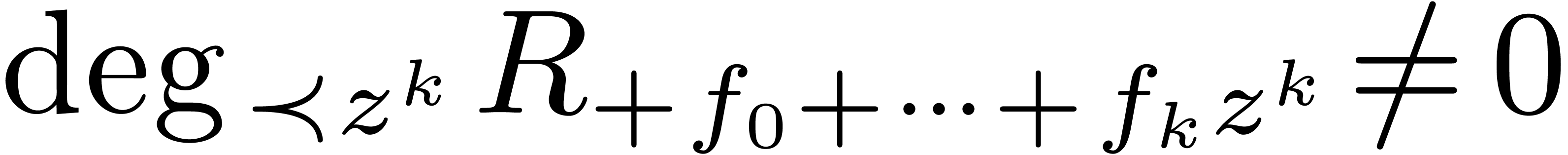
 ,
,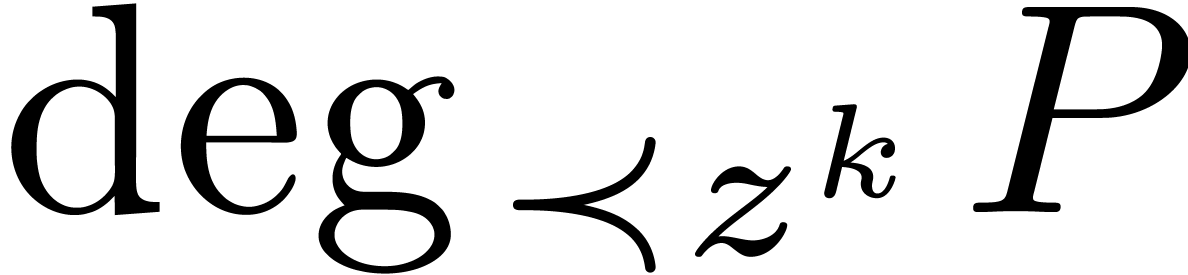 is
the minimal degree of a term
is
the minimal degree of a term 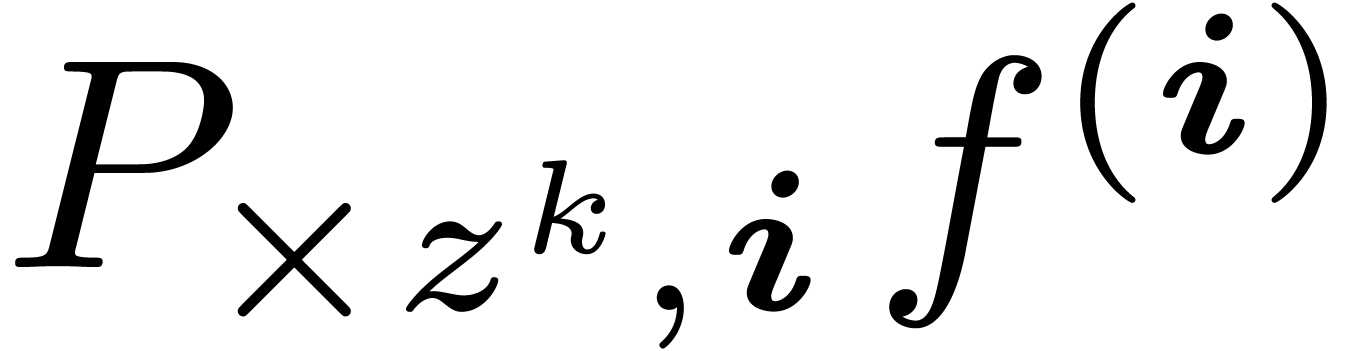 in
in 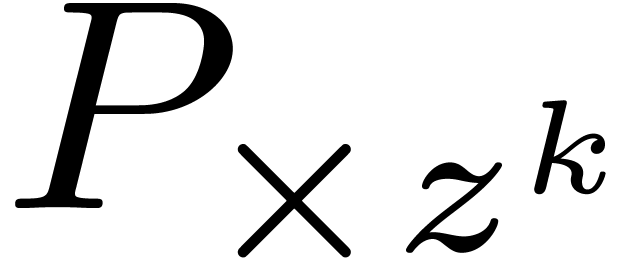 with
with 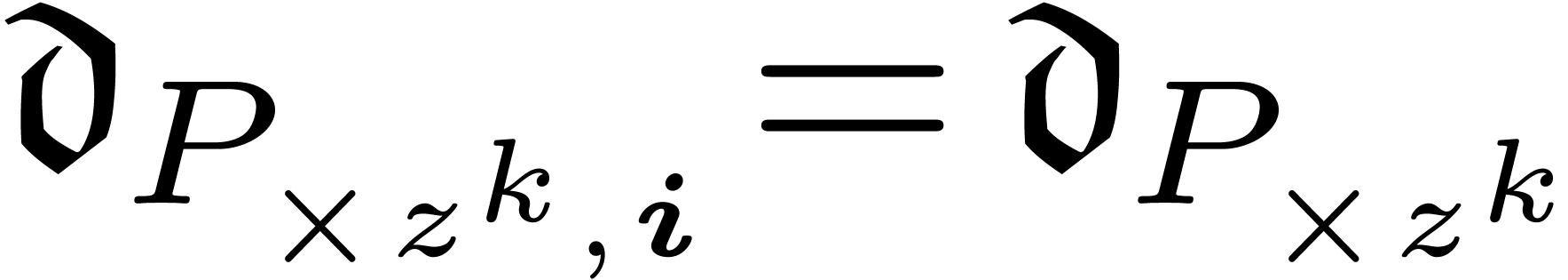 .
. of
of  in
in  strictly decreases at each iteration. Also,
the rank of
strictly decreases at each iteration. Also,
the rank of  (or
(or  )
)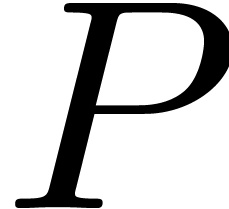 ).
).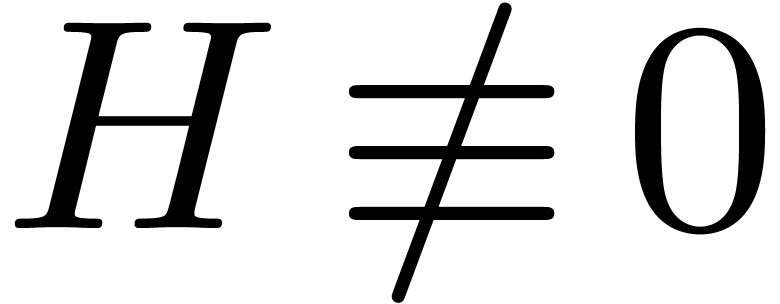 and the existence of a relation of the form
and the existence of a relation of the form
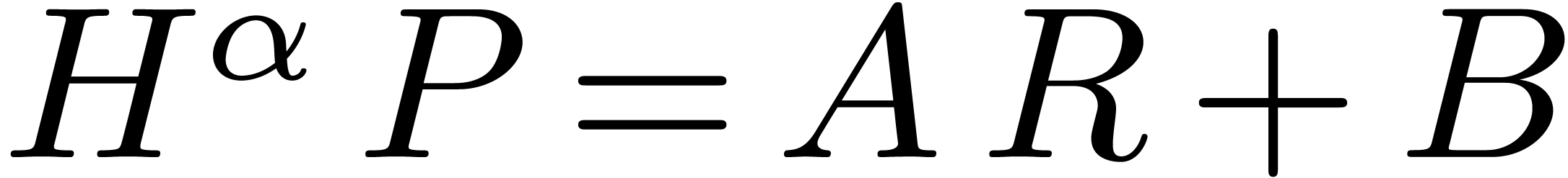
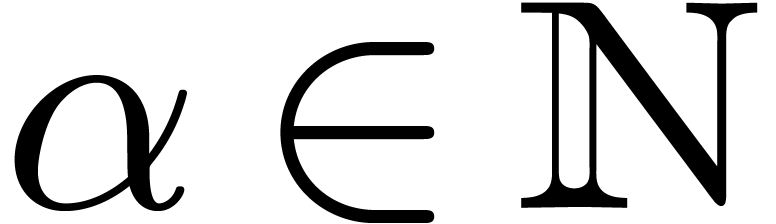 and differential polynomials
and differential polynomials  and
and  with
with 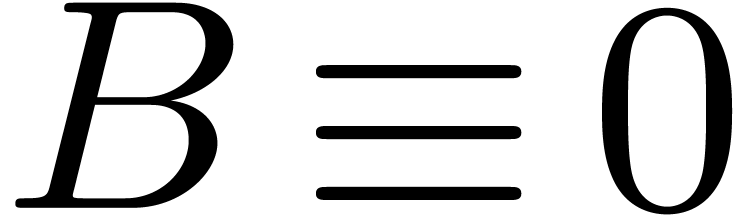 .
. and
and 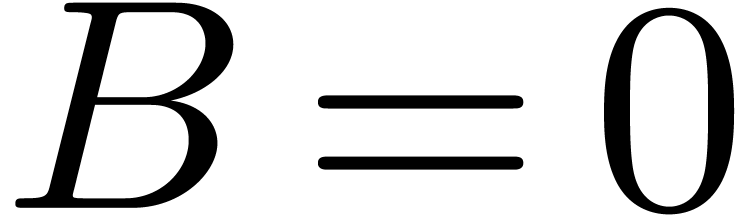 at the first entry. If
at the first entry. If  ,
, ,
,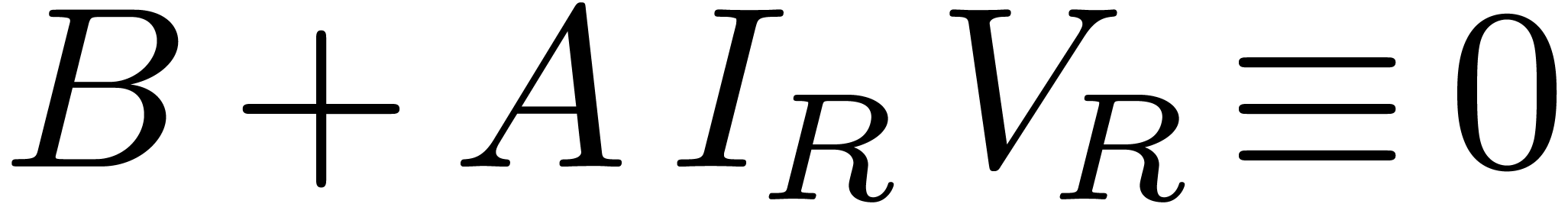 .
.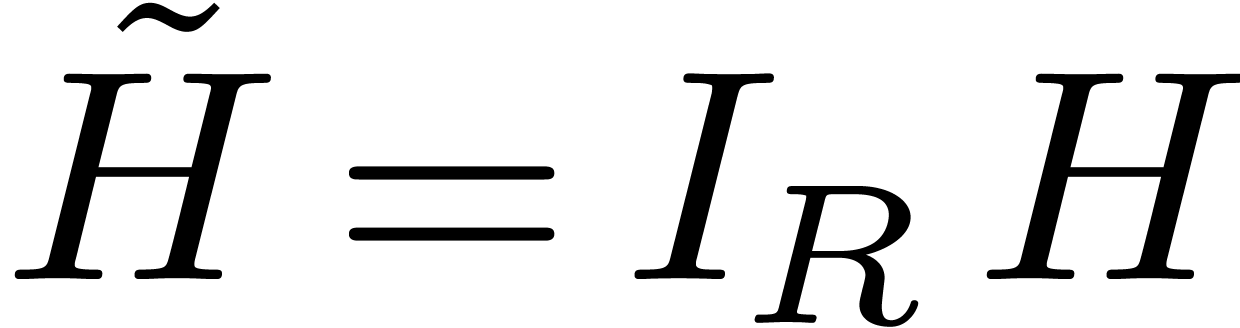 and
and 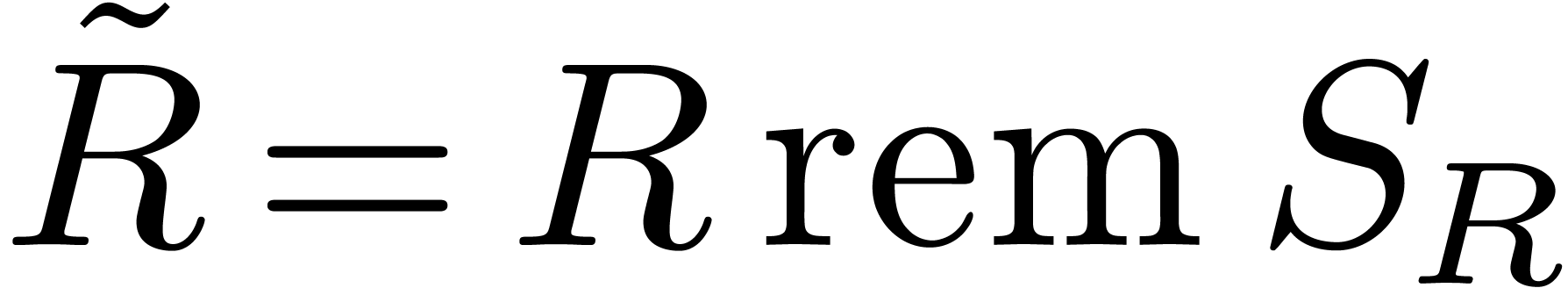 ,
,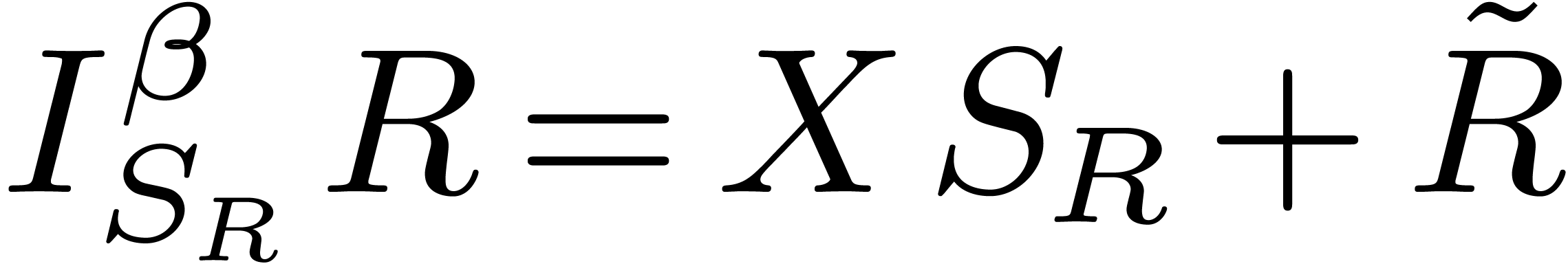 for some
for some  and differential polynomial
and differential polynomial 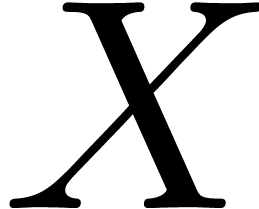 .
. ,
, is the degree of
is the degree of
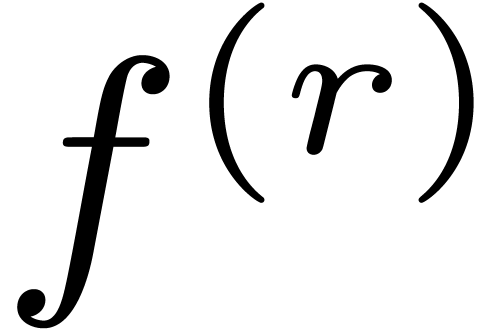 occurring
in
occurring
in 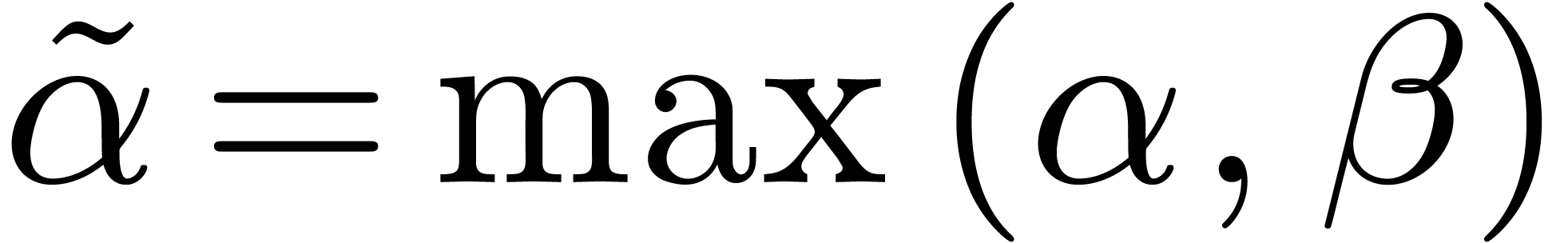 ,
, .
. .
. if
if  with
with
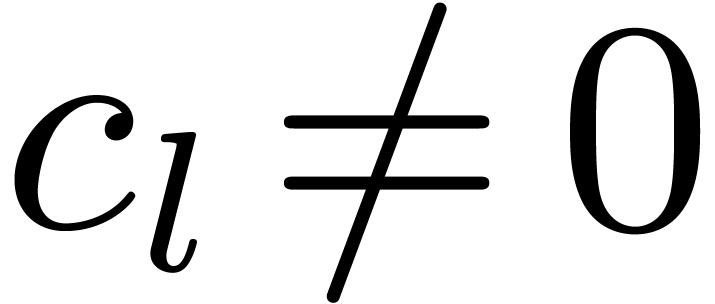 for some
for some 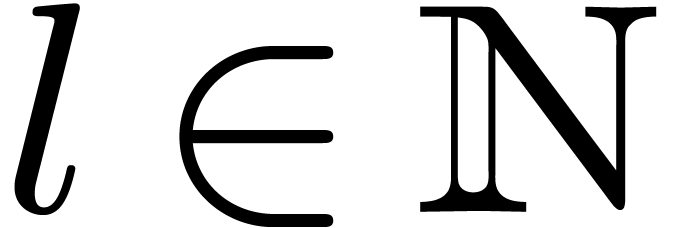 .
. ,
,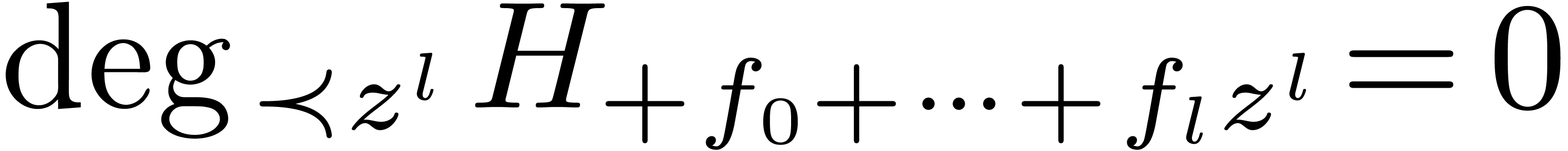 ,
, .
.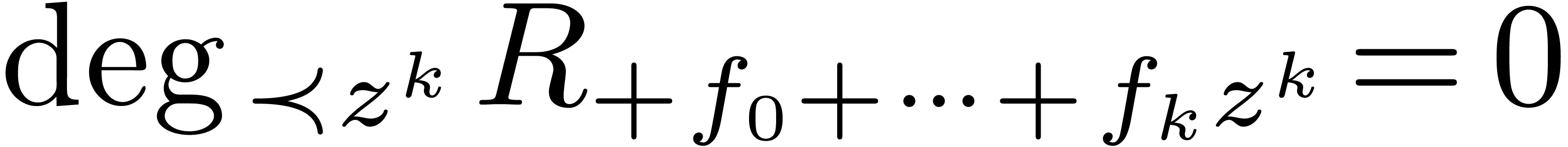 ,
,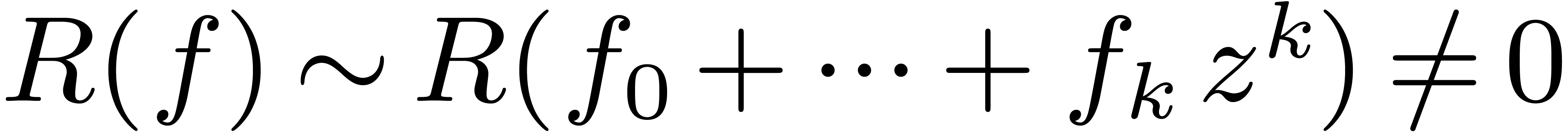 ,
,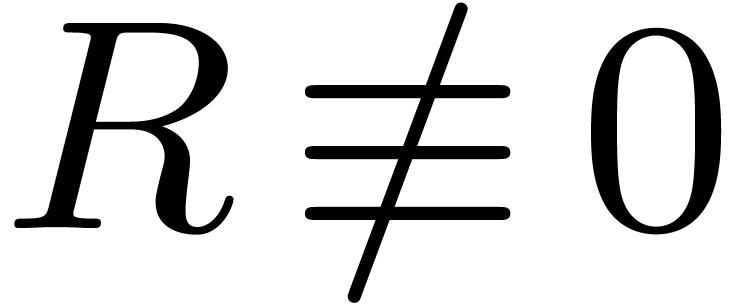 and
and  .
.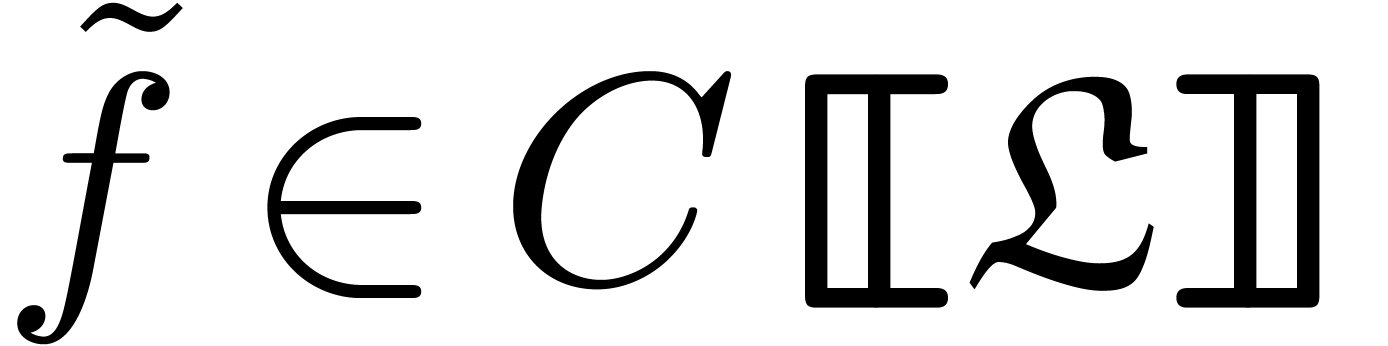 with
with 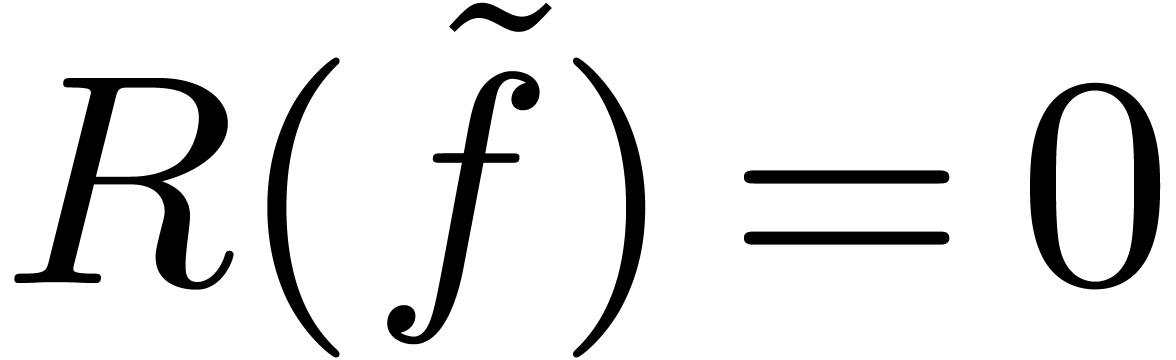 and
and 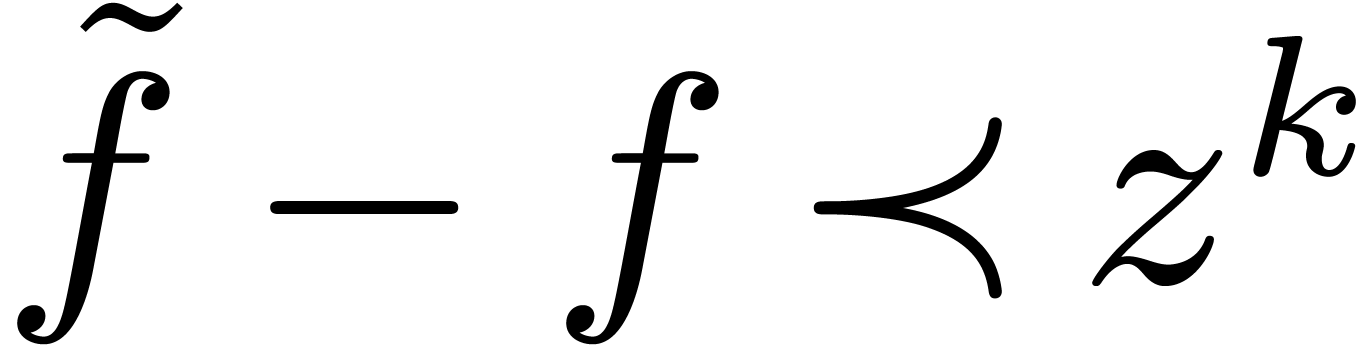 .
.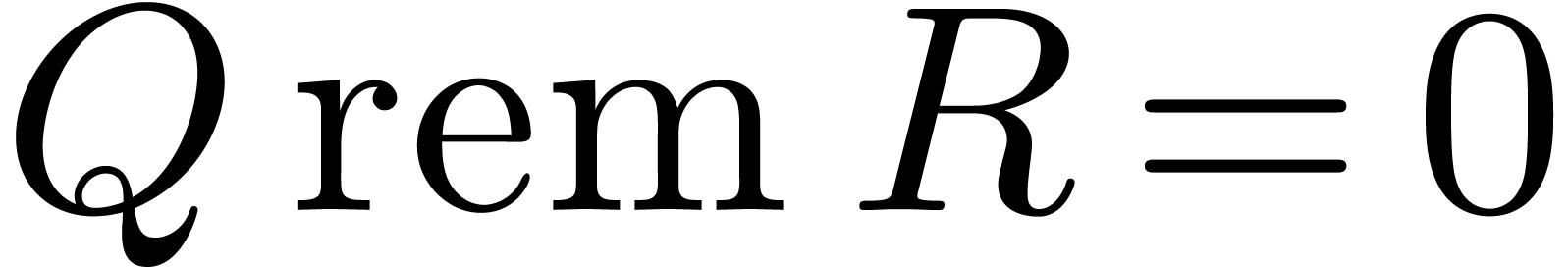 and
and 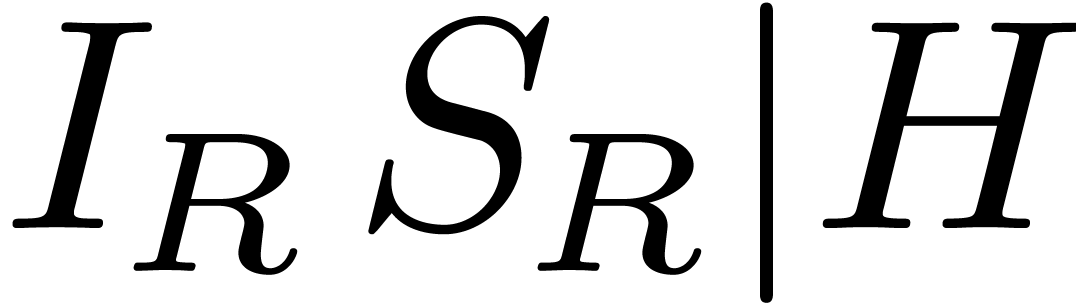 ,
,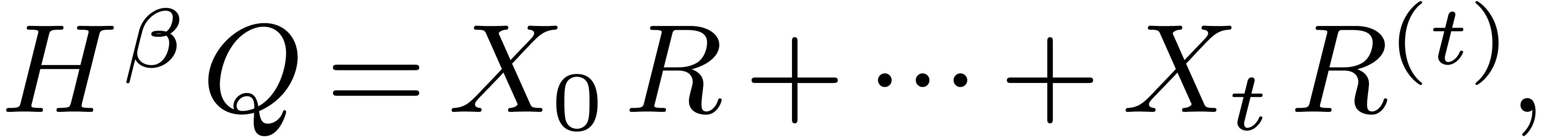
 and
and  are
differential polynomials. Now
are
differential polynomials. Now 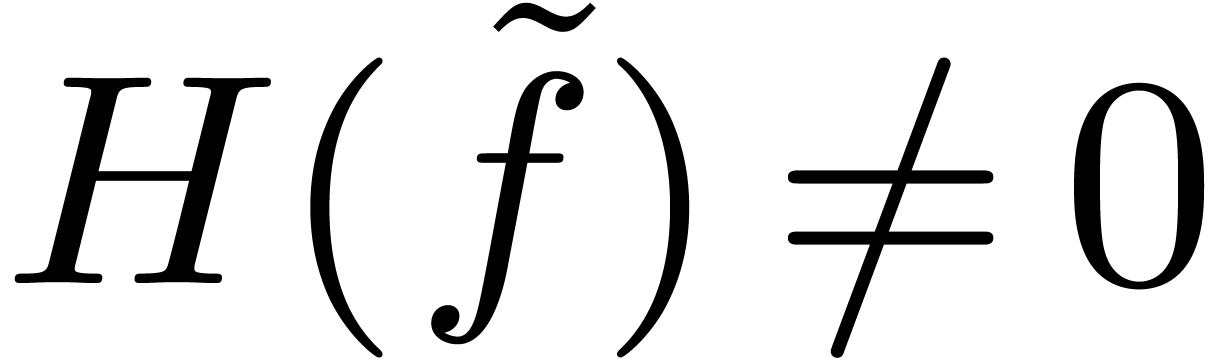 ,
,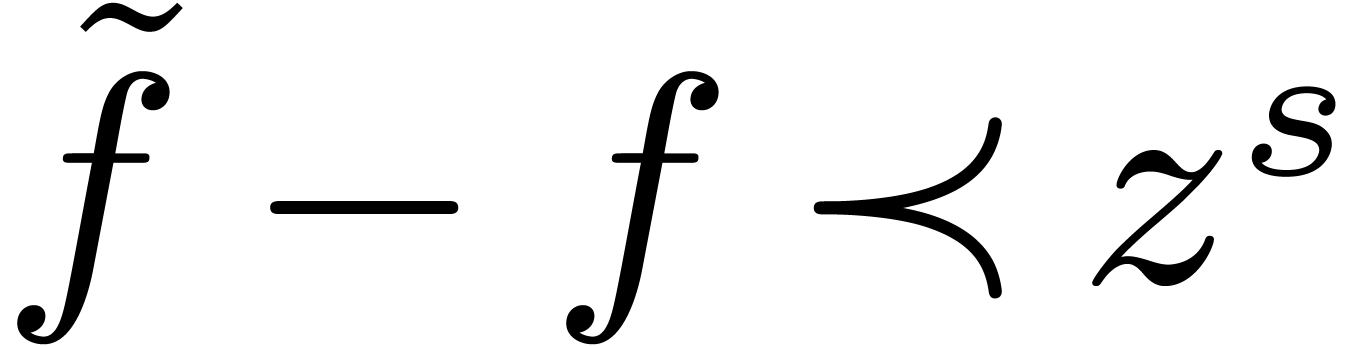 .
. and
and